\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"make_plot(log_likelihood_sgd, len_data=len(feature_matrix_train), batch_size=100,\\n\",\n \" smoothing_window=30, label='stochastic gradient, step_size=1e-1')\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Checkpoint**: The above plot should look smoother than the previous plot. Play around with `smoothing_window`. As you increase it, you should see a smoother plot.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Stochastic gradient ascent vs batch gradient ascent\\n\",\n \"\\n\",\n \"To compare convergence rates for stochastic gradient ascent with batch gradient ascent, we call `make_plot()` multiple times in the same cell.\\n\",\n \"\\n\",\n \"We are comparing:\\n\",\n \"* **stochastic gradient ascent**: `step_size = 0.1`, `batch_size=100`\\n\",\n \"* **batch gradient ascent**: `step_size = 0.5`, `batch_size=len(feature_matrix_train)`\\n\",\n \"\\n\",\n \"Write code to run stochastic gradient ascent for 200 passes using:\\n\",\n \"* `step_size=1e-1`\\n\",\n \"* `batch_size=100`\\n\",\n \"* `initial_coefficients` to all zeros.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 35,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.68251093\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.67845294\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.68207160\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.67411325\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.67804438\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.67712546\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.66377074\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.67321231\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.66923613\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.67479446\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.66501639\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.65591964\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.66240398\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.66440641\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.65782757\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.64571479\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.60976663\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.54566060\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.48245740\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.46629313\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.47223389\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.52216798\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.52336683\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.46963453\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.47883783\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.46988191\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.46365531\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.36466901\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.51096892\\n\",\n \"Iteration 5000: Average log likelihood (of data points in batch [23000:23100]) = -0.43544394\\n\",\n \"Iteration 6000: Average log likelihood (of data points in batch [27600:27700]) = -0.45656653\\n\",\n \"Iteration 7000: Average log likelihood (of data points in batch [32200:32300]) = -0.42656766\\n\",\n \"Iteration 8000: Average log likelihood (of data points in batch [36800:36900]) = -0.39989352\\n\",\n \"Iteration 9000: Average log likelihood (of data points in batch [41400:41500]) = -0.45267388\\n\",\n \"Iteration 10000: Average log likelihood (of data points in batch [46000:46100]) = -0.45394262\\n\",\n \"Iteration 20000: Average log likelihood (of data points in batch [44300:44400]) = -0.48958438\\n\",\n \"Iteration 30000: Average log likelihood (of data points in batch [42600:42700]) = -0.41913672\\n\",\n \"Iteration 40000: Average log likelihood (of data points in batch [40900:41000]) = -0.45899229\\n\",\n \"Iteration 50000: Average log likelihood (of data points in batch [39200:39300]) = -0.46859254\\n\",\n \"Iteration 60000: Average log likelihood (of data points in batch [37500:37600]) = -0.41599369\\n\",\n \"Iteration 70000: Average log likelihood (of data points in batch [35800:35900]) = -0.49905981\\n\",\n \"Iteration 80000: Average log likelihood (of data points in batch [34100:34200]) = -0.45494095\\n\",\n \"Iteration 90000: Average log likelihood (of data points in batch [32400:32500]) = -0.43220080\\n\",\n \"Iteration 95399: Average log likelihood (of data points in batch [47600:47700]) = -0.50265709\\n\"\n ]\n }\n ],\n \"source\": [\n \"step_size = 1e-1\\n\",\n \"batch_size = 100\\n\",\n \"num_passes = 200\\n\",\n \"num_iterations = num_passes * int(len(feature_matrix_train)/batch_size)\\n\",\n \"\\n\",\n \"## YOUR CODE HERE\\n\",\n \"coefficients_sgd, log_likelihood_sgd = logistic_regression_SG(feature_matrix_train, sentiment_train,\\n\",\n \" initial_coefficients=np.zeros(194),\\n\",\n \" step_size=step_size, batch_size=batch_size, max_iter=num_iterations)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We compare the convergence of stochastic gradient ascent and batch gradient ascent in the following cell. Note that we apply smoothing with `smoothing_window=30`.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 36,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAnIAAAFUCAYAAACgM9EjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX6wPHvCZAQeu8dkaJSFFQUFESxYC+sKOjaUNff\\nWrcorspiQ3Ft2F0VFSuKay+AgFhBpUgHISAt1ISEhIQk7++PM8P0mTuTmUwmeT/Pc5/M3HLuO5M7\\nM+8995xzjYiglFJKKaVST1qyA1BKKaWUUrHRRE4ppZRSKkVpIqeUUkoplaI0kVNKKaWUSlGayCml\\nlFJKpShN5JRSSimlUpQmckoppZRSKcpRImeMOcEYUy/EsnrGmBPiG5ZSSimllIrEaY3cbKBXiGXd\\nXcuVUkoppVQFcprImTDLMoDSOMSilFJKKaWiUDPUAmNMJ6CL16z+QS6vZgJXAhvjHllgPAa4HRgL\\ntAJWARNEZHqU5XQGlgG1gUNEZJ3f8kHAQ0A/IBd4E7hTRPaX+0UopZRSSsVRyEQOuBy4BxDXNBnf\\nmjlxPS8BbkhUgF7uA24FxgG/AhcD04wxI0TkiyjKeRbYg00GfRhjegNfAZ8DI4DOwCNAG2BUuaJX\\nSimllIozIyLBFxjTEeiETda+xiZry/1WKwJWi8juBMaIMaY58AfwgIhM8Jo/E2gmIn0dlnMJ8B/g\\nQeAxoJt3jZwx5gNsW8BeIlLqmjcGmAIcJSKL4vOKlFJKKaXKL2SNnIhsADYAGGOGAr+KSF5FBebn\\nNKAW8Ibf/KnAS8aYjq54QzLGNMImcbe5yvJfXhM4FXjEncS5vAu8CJwDaCKnlFJKqUrDUWcHEZmb\\nxCQObC1ZkYj87jd/GbbGMFSPWm+TgOUi8maI5V2x7eaWec8UkSLgd4f7UEoppZSqMOHayB1kjEkH\\n7sC2E+uA7anqTUTEUVkxagLkBJm/22t5SMaYwcBoINwlWHcZe0LsJ+w+lFJKKaUqmtPkaxK2jdzn\\nwHRs27iYGWOGATMcrDpHRE4q575qAc8Bj4rIqvKUpZRSSilVmThN5C4E7hGR++O03++AHg7WK3D9\\n3QM0CrLcXUsWrrPFLa5tJxtjGrrm1XX9bWCMqSci+Xhq4hqH2M/SYIUbY4L3FlFKKaWU8iIi4cbl\\njYnTRK4e8EO8duoak211FJssAzKMMV38xn07DDsMin9vWm89sUONbAmy7FdsB4Yjse3gilxlHmSM\\nycCOp/duqB2E6vmrqpfx48czfvz4ZIehKgE9FpSbHgvKzQ6HG39O7+zwMZDM+6l+gR2v7lK/+aOB\\npRF6rD4IDAWGeE0PYRPAS4CrAUTkgGs/I40x3u/LRUA68FE5X4NSqoJ8+SUceij07g0//ZTsaJRS\\nKnGc1shNBl4zxpQBnxHkUqb/HRLiSUR2GGMeBe4wxuTjGRB4CHCW97rGmFlABxHp5tp2NX61f667\\nOwDM94t7PLbmcZox5mnsgMAPA9NEZGG8X5dSKv7KyuDqq2HTJvv8ppvgxx+TG5NSKrxPPoEPP4Sh\\nQ+GSS5IdTWpxmsi5L6uOx97tIZga5Y4mvHFAHnAjnlt0XSQin/utl4bzmkYfIrLYGDMcW2P3CfYW\\nXVOAO2OMWVUjQ4YMSXYICti61ZPEQXJq5PRYUG56LET2669wlqtK5r//haZN4dRTkxtTKgl5Zwef\\nlYz5M/ZSZEgi8mqcYkopxhjRNnKqsps0CcaNg1atYPp0GDAg2RElzubN0K6d7zwRmDEDrr8e0tLg\\nxRfhxBOTE59SytegQfDdd57nLVvCtm3JiydRjDEJ6ezgKJFToWkiFz+lpfbHtnFjOOaYZEdTdezY\\nAS1aeJ4PGgTz5nmeHzgAd90FX38NZ59tE760mOq0K4dgiVxZGXTrBr+7hhQ/4ghYsqTiY1NKBWre\\nHHbu9J1XFX9WE5XIpfDXtapqRo6E00+HY4+FyZOTE4OIbacxeTLsTugdhCvOl1/6Pv/2W9/n06fD\\nQw/BggU2oZs9u3z7KyqCJ5+E//wH9u0rX1mxCPYDUFDgSeIAfvut/PvZtw9uvx2uuAJWrix/eUop\\nFYuQNXLGmJeBe0VkvetxOCIiV8U9uhSgNXLxsX49dOniOy8Zb+sTT8DNN9vH3brZH+jKWjs1Z45t\\nyJ+eDs8+C/37B19v6lQYM8Z3nvd7698jvksX36QnWmPG2H2CbefyxRexlxWLTZugfXvfefn5UK+e\\n77zyHl/XXw/PPWcft25t91tZjxWlKrNmzWDXLt957s/nH3/A3/5mT5zuvx/69Kn4+OKlwi+tGmPW\\nA+e6OgBkEb6NnIhIlzDLqyxN5OLj669h2DDfecl4W/2Tms8+s7WElY0IdO1qE2Cwl6JD9cwMlsjl\\n5sLEibb27NFHfZc1a2Yvx8bK/z3MzYUGDWIvL1rBErm8PKhf33deeY8v/9c5YwacfHL5yqwuli2D\\nK6+0P94TJ8KFFyY7Il979sCdd9r47rzTDmNTlYjYE8GiIhg+PPEnIMXFtoZ+2zZ7oty5s+/ycInc\\niBH2exjsd96aNYGfvVSRqEQuZK9VEens9bhTvHesqr5162DxYtsmq3nz8OtW1lx40aLEJXKlpbZ9\\nWu3a0W+7Y4cniYPoe2Y2bBh6WUlJ9PGEU1hYsYlcso6l/Pzk7Nff9u0wc6ZNPg4/PLptc3Jse8Im\\nCbyz9P79vnFddZXtsZjhfwfvJBo82CabAO++az+rVam29e674b777OMrr4SXXkrs/u64w3PC+P77\\nsHGj8/fTncSBvVKwbp1N6JRHFTo0VWWyaJH9ITn/fPu3PDU8yTRrVmLKXboUDjkEMjPhxhsTsw+3\\naBObnJz47r+sLPzyffviv09/8UzuROCjJAwPLmJrNXr1gksvtTWd/nJy7KWnSy+FI4/07dQSyRtv\\n2N6CLVrYNo6hlJXZz/eWYPfKcWDECN/ne/cGtttMNncS55ao74FkcSdxAC+/nPiTEO9a/82b7YlG\\nrOJ9ohlv+/bB6tW2trOiOE7kjDF1jDH/Z4yZZoyZ5fr7F2NMZiIDVM7t2mWrrW+4wY6lFclvv9lh\\nKLp1g//9Lz4xLF8OEyZAv36ehu7bttnhL8KprDVyZ5+dmHL/+U/IyrKPJ08O3fh+xw57ybTAddfh\\nefNsbUa0NS3JFC6R++ILaNPG1gB5/7g4VVoKK1YkPhH0NmkSnHNO4PzyXu7ZutUeC/5JQ0EBXHON\\nrcH429/s633zTdsu0t/TT3uGbThwwHbEcGr0aHsJrLTUtr08cCBwHRE491z7+T7kEPjqq+Bl7d5t\\nj2/35/qrr6BHD6hb1zajKK9vv7U1O8XF5S/LieHD7aX5xx+Pb7nvvmvfy/POc/adnSh5eYHziorg\\n3/+2NaZLg95pPHbujmTr1iV/mJHSUrjnHnsCdNNN5UvANm60FRfdu9tOe8FOthJCRCJO2AF4VwJl\\nwHrsAMHrXc9XAC2dlFMVJ/sWVg5nnCFivzpFjjkm8vrDh3vWb9JEpLi4fPvPzhbJzPSU6T316GHX\\n+e03kZkzRUpKfLf96qvAbbzNnCnyxBMiW7bY52VlIkVF9m80PvhAZNw4kYULgy/3j+HFF0OXtX+/\\nyIQJIldfLbJ0aXRx+O/nrLNEnn9eZNUqzzrLl4s0bepZ5+STRdq0Cf7+hjsMX3st9DbRlhXOV1+J\\ntG0bWNYff4TepkUL33V37XK+vwMHRAYPttu1aCGyeLGdv3FjYAx798bnNYqEfs/+97/Yy9y3z/e9\\neOcdO3/u3Oj+T0OGBK4ze7ZIp0722PnwQ+eva/v2wHV++MF3nRYtAteZMUOkfn27/Kqr7Ge0ffvw\\nr2PWLGfvU2mpSJ8+nu2GDnW2XbTCxRrsfYnFnj0itWp5yr3uOs+y1atF+vcXadbMfu9FUlYmMn26\\nyFNPieTkRF7f/zW5v1e9/fOfnuWNGtnvu1j57+/NN0VuvdXZse0/f8QI+xmPl5kzfcufMEFk5crY\\nyho71reshx/2Xe7KF4j35GwleA3IBo73m38csBWYkojgUmFKViK3b5/If/4j8vjjng+Y/wEf6QPt\\nv/5334Vfv7hY5MYbRbp2Fbn2WpHCQt/lN98c+kPZo4dNKNLSPB/GhQtFFiyw24ZL5N591zOveXOR\\nzZtFTjzRd91GjeyPdTjTp3vWT0+35UR6T8Ilcrff7lmvcWObWPrLyxM5/3z7w3bxxSIFBcH3457q\\n1hVZs8auc+aZoddz8qPuFq9EbssWmxSEep87dw5e1oYNdnlBgcidd9pEOi8v+Ptw3XUiS5aEfi3e\\n3n7bd9uTT7bzN2wILPdPfwqc5/QkoLTU93mo9+yDD5yVF8wTTwT/H/ToEf7/VFgoMmeOPZkYPdoe\\nh/7r9Orl+/nxfz2hXtf69YHrTJwY+VjxT+a//jry8eY0kXvggcBtDzlEZNMm3/W2bxc591yR7t1F\\nnnkmfJllZSJTpohcc43IF18Efy+cfid4Ky4W+egjkZ9+Cr786adDv5eXXuo7Pzs7/L4eesizbu/e\\nkY9t//0GS+T817n4YpH8fPs9t2NHdCfR/mU99pjz76BQy485xibyy5c7j2P1as/3q1vr1sHLHzcu\\ndDkFBfZEMtLrbNfOfzkikrxEbgdwZYhlVwE7EhFcKkzJSuRGjPD9gIkEHkRZWSK33CJy2WXBzzD8\\n1+/fP3yt3Icf+q7/5pvhy/Oewv0g/f3vIl9+GTjfrWZN3/mhaqWuuir8e1ajhu/6Z5wR+T158UX7\\nQzl9euB7EyyGfv1EFi3yrPPSS77L33gj8nt10UUiH38cfp1wX3z+Xn01+rIOHLCJvfvHfMkST5Jw\\nyCHBTxJCleUuw39+376ht7nppsg/XuecE/wY9q5JCDeFSmjc5s0TadXKJv1PPx35dQ4ZIvLee+F/\\n4NauFfnlF7vOb7+JfPutfXzFFcH/n5FeQ+/e0f9vt28XmT/f1iB617L4r/fKK4HxeycMoY47/+WH\\nHBI5JqeJXKjtL7nEd71//MN3+YYNIuvWBT8J+eAD33WXLw8f63PPOYv1lFM82zz/fODyJ58MLDvU\\niV6HDtG9L998E936W7bYY+Guu0SOPFLkttuCv/batW3tLtjvz+xskUceEZk6Nfxx71/O1VdHPiYK\\nC+3JfqT1nNbKep8EPPKInbdsWfiy8/N9yygr89S6dekSmET6b9++vf9yRCR5iVwhcFqIZacChYkI\\nLhWmWBO5pUvtB33YMM8lIX8//GBrHfwPpsLCwANGJHCed7LXvLlNKt55x/OBC3bgfvpp6JiDne27\\nFRWF/jA4mT76KHjZP/0UXTnXXSdy9NHBz8KDrR9pHf8E1F2TFKo8sLWF8+fbH0z/ZRkZ4bcFWyvX\\nsmX072EoxxwTfVlDh4Zf/sADzt5fsJcu9uyJPoaWLQNrWrydfXb5jjn/y/v+/C9TupPXSOW6fyT8\\nTZ3qezJhjP172WXBE7nS0vK9vlDTpEmex4MGhf4+mDAh8DU8/HDk4y6WmEIlcsuX2x9bJ2Xv3m2P\\nta1bw6/XtavvpbmMDN/lkWrCvZN6t5wce0nZfbwuXhz+fSoutiee/uucemr41zllSvD3Kdi6PXsG\\nv+oQbP2//KX8x1Ww4yXU/i6/PHJ5deo437e/F16wzVI6drRXRP7+98BtnHy+7rnHt7nHggWB61x/\\nvedyu/+yypbILQLeCLHsdWBhIoJLhSnWRG7AAM8/u2/fwOVTp3qW9+njW3uQnx/8QHZ60Ie6BAa2\\nmvndd0VGjbJnnt5nWcE+WG6zZzvff7Cpf//Aed6JaCxTpLMld/xFRbYGyEnCU6dO+EQ40pSeHvu2\\nkaZgli5NzL6OPNK+D998Y2uYwr2mE0+0NSax7Gf4cN/XU1Zma0i//z76S8/+U7Da56wskV9/tfvx\\nX/+GG+wlpVj/F+HWP+20wHmx1LbFMrmbVPjPv+02z3v+6qu2dv/UUyO/1lhicCdyBw7Yk9cPP/St\\nQbn3Xudle7crDTWdc07oeP0TO/9p8mRbc/bMM7bWcudOz3dqw4Y2ifNuDuKenntO5O67RVas8P3+\\n95+ys8Pv//PPbfxpabbZRLj3xX3i6Pbjj7Y5TqKOJW9PPSXSoIFIt26B6w0alLj97t0bePUl2OQk\\nmXRPLVvaY/Kii4IvP+204P+HDh3syf/SpfaYSXYiN9rVsWEmcCVwOnAF8CVQClySiOBSYYo1kfP/\\nh/u3r/Jf7l1Ttm9f4PJgPzzxmNwNuEtKgi8XsZcsgn1xJXtq1crWqP3zn/ZHO1T8/fpFV+5XXwX/\\nHzmZatWKfdtIk3fS/dtvIscem7j3tl8/3+Ts/vsTt6/0dPtj8N138S33uefspU636dPtvsCeyATb\\nJlxnE//jSsS2KU3U+xLPKVjbN7C1/1OmOHutob67nEzu2pwLLwy9TrxrKEVi+958/PHgibd7Gjq0\\nfN+H0R7n3jWswSb3b8u8eZ42yomaRGxFQyKTxVD7dZs2rWL37Z6uvDJwnjGeS9GHHSaS1ERORADG\\nAttcCZ172gpck4jAUmWKVyLn3yMo2IFy//32QxnsS8JpTUG0U926Np5nn01M+cmesrKi32by5ND/\\nIyfTCy8k5rV4N74dODCx71vHjsn/38VratfO9tqOZ5mzZ0dua5UKU7BOGP6T2+LFwTuVOJ28OyMF\\nm/x7F5Z3ys0Nfkk70nTnnZHXqUwnts8+azunVcS+ysqCX11J9OStMr33gROSiDwk5C26gjHGpAHd\\ngSbAbmCViEQY7rNqi/UWXf5jTu3YYW9TEmq5W0ZG8HFuNmyAjh2jDsORAwegVq3ElJ2KnnjCDuJb\\n2W4T07OnHZdt1iw7WrtSFUHE3r2jTp3E7qdTJ8/Yi5XdhRfCe+8lO4qK9913cPzxFb/fX36x47ct\\nWmTv7+wep67yqeB7rSpnYknkRAJvT9K0qf0QdO/uLje6OE45xd7rMRFeeAHGjk1M2amoTRto3Dhw\\n9PfK4LrrPDdyV0qp6qJXL3tHhcp954ckJ3LGmG7Av4CBQFtgM/A9cJ+IrI13YKkilkSurAxq1Aic\\nf/75drRyW24cglNKKaVUJZHERM4YMwT4DDsMyafYwYFbAiOAOtihSebGO7hUEEsiV1oKNWsGXzZ6\\ntL0FUOvWcQhOKaWUUpVEchO5X4D9wKkiku81vz7wFVBLRPrHO7hUEEsi9+OPMHBgggJSSimlVCWU\\n3ESuEPiTiHwUZNm5wFsikhnv4FJBtIlcVhZ07py4eJRSSilVGSUmkUuLvAoAm4D0EMvSse3llAP3\\n3JPsCJRSSilVVThN5B4C/m2MaeM90xjTFrgHeCDegVUlH3wADzxghwj57bdkR6OUUkqpqsLppdXX\\ngSFAc+BHPJ0djnU99u7oICJyedwjraQiXVqdMgWuuKLi4lFKKaVUZZTcNnLroyhTRKRL7CGllkiJ\\nnA4jopRSSqmkjyOngtNETimllFKRJbezg1JKKaWUqmQ0kVNKKaWUSlGayCXQZh2URSmllFIJpIlc\\nAp1zTrIjUEoppVRVpp0dyilUZ4e1a6FbtyQEpJRSSqlKSDs7pJSnnkp2BEoppZSq6rRGrpxC1cjp\\nsCNKKaWU8khyjZwxZqwxZqExpsAYU+o/xTuwVFVSAvfem+wolFJKKVUdOErkjDGXAZOBBUBt4BVg\\nKrAX+B2YkKgAvWIwxpg7jDHrjTGFxphFxpjzYyinsysZLTPGdPFbdo9rvv803Wn5r7wCd98dbVRK\\nKaWUUtGr6XC9m4EHgXuBq4FnRORXY0xjYA6wKzHh+bgPuBUYB/wKXAxMM8aMEJEvoijnWWAP0CrE\\ncgGOB8q85u12WvjYsVFEopRSSilVDk4TuW7AN9jkpgxIBxCRPcaY+4H7gYQ17zfGNAduAx4Qkcdc\\ns+caY7oBEwFHiZwx5hKgDzYpfSzMqvNFpCzMcqWUUkqppHPaRq4QqOlq1b8N8L4kmQ+0iXdgfk4D\\nagFv+M2fChxhjOkYqQBjTCPgP9iEMDfS6rEEqZRSSilVkZwmcr8Bh7oezwPGGWMGGmMGAOOBlQmI\\nzVsvoEhEfvebvwybdPVyUMYkYLmIvOlg3T+MMSXGmCxjzERjTO0o41VKKaWUSjinl1ZfALq6Ht8F\\nzAS+dT3PA86Nc1z+mgA5Qebv9loekjFmMDAa6BthP2uB24GF2LZyw4FbgH7AqVHEq5RSSimVcI4S\\nORF5x+vxWmPMYcBAoA7wvYjsjGanxphhwAwHq84RkZOiKTvIvmoBzwGPisiqcOuKiP+l21nGmM3A\\nY8aYoSIyuzyxKKWUUkrFk6NEzhhzAvCriOQDiMg+bK0cxpi6xpgTROSbKPb7HdDDwXoFrr97gEZB\\nlrtr4sL1Kr3Fte1kY0xD17y6rr8NjDH13K8rhLeAx4GjgaCJ3Pjx4wFYuRJgiGtSSimlVPU1xzUl\\nlqM7O7gG/B0oIvODLDsK28uzRgLic+9jDDAF6CYi67zm/xl4CegiIhtCbPsKcBmhOzAsEpEjw+y7\\nOZAN3CEiDwVZfvDODhkZUFzs5BUppZRSqnpJzJ0dnLaRC7fjDCDRd3b4AigBLsWOZec2GlgaKolz\\neRA7gLG304F/uMpbHWHfo7Ht5X6KFKQmcUoppZSqSCETOWNMJ3yHGelvjKnnt1omcCWwMe6ReRGR\\nHcaYR4E7jDH5eAYEHgKc5b2uMWYW0EFEurm2XY1fsmaM6ex6ON+vhu9n4FXX+gbb2eH/gM9FZE78\\nX5lSSimlVOzC1chdDtyDrY0S7C26vGvmxPW8BLghUQF6GYftIXsj9q4Mq4CLRORzv/XSiOIesn5W\\nu8pv7SpjHXZ4lUkxlqeUUkoplTAh28i5BtnthE3WvsYma8v9VisCVouI41tYVTXebeSMDiOslFJK\\nqaAS00bOaWeHE4FfIvTurJY0kVNKKaVUZElM5FRomsgppZRSKrLk9lrFGDMcuB7oDvjfskpEpGvg\\nVkoppZRSKlEcdQowxpwBfI69k0MP7L1VNwLtgTIgmsGAlVJKKaVUHDjt3XkX8DRwhuv5v0RkCHAY\\nUAOb5CmlVJXypz8lOwKVCg45JNkRqOrMaSLXA/gYW/smuC7JusZoG49N9Ko1HQxYqarl2Wfh7bdB\\nmxGrSPr3T3YEqjpzmsiVAaWuVv07gA5ey7YA1b593IcfJjsCpVQ8XXed5/HatcmLQ1V+jz6a7AhU\\ndeY0kVuFJ1n7GbjZGNPadR/S24CsBMSWUi6+ONkRKJU8//pXsiOIr7PO8n3etSvk5cHMmbAxofex\\nUYk0c2b8y8zPh8zM6LYpLHRe01u3bvD5AwbAH39Et9/KJtlNF0K9t6nGaSL3BnCo6/E92LZxm4Bt\\nwEnA3fEPLbWUlSU7AqU8atSouH117QrXXONs3TVrEhvLySfHp5wxYwLn1asHw4ZB+/bx2UeqaN0a\\nLroILr002ZGUz6232v/fd99Fv+2SJfDkk8GX1a0b/dBTtf3HfQgjPx8OHAicv2ABtGsHubnwwQeR\\ny1mzxp6MRJt0JlK8huzKyIhtu4p8L4YOTWDhIhL1BLQDrsbezqpXLGVUlcm+hSL2/Kp6T3/9q8jE\\niSKFhSLffhv99j/8ILJypUinTuWLo0aN5Lz+Pn1EDj00uf+DE04Q+fJLkdWrRR5+WGTWLJHFixO7\\nz65dRUREGjSIvG55PisXXhh++dVXi8ydG5/X9MMPEla4bf/+d5G//EVk2LDkHgvxmhYscPa6EzHd\\neafI5s3R/19btw6c98ADsb+OcNuJiOzdG7/ynK57772+x+QVV4Quo0kTz3r5+SI33yxy3nki8+aJ\\n3HefyNFHi1x7bWL/l5deGjhv1Kjyldmjh8jbb4tkZ4u0b5/44zHY1Ly5s/V27hRx5QvEPQ9JRKHV\\nadJEzk433CABoi3Dbf/+8sWSm+t5nJFRMYldy5Yia9aIlJYm73/w8suB/4NY/xfRTF262H3s2+fs\\nf3zSSbHt55FHwi+/5pr4JXI//xz6vYz0fs6YUTHve3mmM890vm5JSfJej9uuXdFtN2hQ4LwHHyz/\\nd1OoZXl5zstKT48uDrfly33nFxX5HpPhErGePcMfz+X9/z7+uLPX4T/vkktEateOfb/btnli//nn\\nij8+QWTLFpGzzgq/znPPuV8/IhL/PCTWm8urauDLL52vO3hwdGV36RJ6WUYG/Pe/0ZXnrUEDKCqC\\npUshOxv++tfYy3Liscdg2TI7BEGaw0/U4YfbOOPlxBNh1KjQy7t1i9++QqlTJ/xyd8++xx6LrfwW\\nLSKv07t3bGVHK1zj9mHDPI8T3Qbo3/+Obv3nn7efiY8+gpdfdrZNuGO6f3+YMqX8l8gitVVq3Bh6\\n9PA8b9Qo+n1EirFNm+jLdFq2tzffjG0fPXvCvn22XVxpKaSn+y7/299Cb/vss7Htc9So2C9bOmEM\\nDB8en7KOOso2cVqyJLrtvJuhTJgQuPzPf4ZmzfzazaYdgMzd0HADu2os5dLbv4euX0Kv96DvK3DM\\nkzD4fjj5dhjxF17JHcPzPz8fy8tyJlSGh6unqtMpEVlmKky4TjXineX//LPIVVeJ3H13/Mv2nxo2\\ntJcdvOeNH2/PIF5+2dZqhds+PV2kuDjg5C7ouuvX26r9zZsDl/mbPj221+Nvxgzf5R072tccavtx\\n4yLvY9Qoezli0iSRsrLIrxvspZDt2+0kYmvxIu2nQQORK6+MvJ53rUkw3bsn7vhx18iFe+1paSLz\\n53vWW7lS5NhjRUaODL3NXXd5HjdpYmsgwsVx9dW27AcfDF+W93TPPcHnb94c/v0sKxN59dXIx99N\\nNyXufQeRb74RqV/f+fqvvOKJ7cABkQ4dIm/jzf97YvlyO3/zZvs//fJLO0XzGu6809l7uWCByIkn\\nipx8ssiyZeHLDFYj99hjoY/Tnj1FVq2ylycvush32Zlnht6uVi0730ltNNgrF941aU62icajj9qm\\nDmedJfK3v4kMHy7y1FOB31Gh+O973jyR3btFBgwIHV+tWpH/H6edFrz80aNFzj479uN/xw5nrwNE\\nqFEk1NkhNF4rtPpV6DhHOPQj+cfrb8jhlz8nJ9w+Se746m7h1JuFs68SLhwpXHq6DHxxkPR5to90\\nfryz8PdRSN+pAAAgAElEQVRmwr8yhPFEPY2ePlpc+QLxnkLea9UYMx5wLzTAlUAmdjy5bKAVcCZQ\\nCLwkIlGeG1YNxhgpLpaAsyOn/vtfuPrqwPnuf0teXmDNTfv28e2t1LAh5OTAM8/YqXdvePppexYM\\ndoy8CRPg/vt9t7vpJrvsppuge/fAcv3PUpcuhcMO8zzv08dz9nTmmfDxx4FlvPIKXHlldK/H/5AW\\ngdNOg6++gvr14dNP7RnthAmwdSusXOm7fllZ+FqI8ePhnntCLw92dl6/PuzY4Xt226qVrR0JZ/Ro\\neP31yGf8IT7GB82aFb+OAP66dIHff7ePQ8X57bdw/PHBlzVsCHv3Bs4vLra1dxs22FrVHj3Cvw9X\\nXw0vvmgfP/WUpyY2MxM2b7adMvbs8azfooV9/+fPh9tvh9mz7fwLL4Rp00Lvx5t/PLVq+Y4pefPN\\n8MQTwbcdN87WqlxxhX2djz/uWXbHHfDgg5H3P3cufPIJTJrkLN5XXrE1DG47dsBbb9n35ssvYfJk\\n3/WvvRaee87zfO9euPFGWLjQdnD5v/8Lvp9u3YIP2VKjhv0cetdaFhXZ9+HFF2HsWM/8ceMCv3O8\\nhTsWjj/efr8884x9XqsWbN/uqcl76SXf793Zs2HIEM/z8ePtvjt1gv/9z/O95b/PVq3sd8j+/c4a\\nzvt/Tp3U5EX6bMeTfzzbtkHLlrBiBRx5pH2d/ty/H2PH2v9h48Z2G+/vVfd3v3/5Y8bYzhoffeQ7\\nf+1a+9kcPx5mzCyD9HzI2AsZufZv7VzaH5LLXfftJbcol71Fe8ndn8veYvv3g8886x3crlaQ4CvQ\\nOd3P4cNRHyIJuNdqyETOZyVj/gWcCpwqIgVe8+sCXwKfi0iYj1zVZYyRt96SsJe1wsnPh8svh/ff\\n953v/reUlkJNvzvibt1qe5LFi/uDGM6ePdCkie+84mL7BRnKhx/Cuefax2edFfhhzcqyl4YyM21S\\n1axZYBlvvGGTmWgEO6RLS+2XSatW9kvGbeFC+wXlv/2118ILLzgv31uwL+cZMwITqWCJXP/+8PPP\\nnufTptnEoryJXEkJ3HabLW/rVt9lTZrA7t3htw+na1fPj3aoOMPFd+GFgcd/qG2cJnIiNkFZssT+\\nWBx2WOCx9NFHvpdL5s61icoZZzjv9RspkbvpptC9Hf1fX2GhTdobNbK9RJ1cpp871yYh48f7zu/Q\\nIfgwKS+/bBPHYP74ww6jtHSpTWAmTLDvj9PmAt4GD7bJu7d//xtOOQUGDgy+TWkpXH+9fQ/694f3\\n3vP9rPqLlMi9/z785S+wfr1N1EeO9CwvKLBJ9rx5cMEFNjYn//Np03zL+fxze5JYVOSsJ2qqJXL7\\n93tOPpcts8fbDTf4rtOokecEafNme9LaoAH89BMsXVbG4GF5ZDTMYc/+PfQbmAO1cw4mZP2Os0nY\\n73/k+iRdh/d3JWZFe8ndvxdMBb4JCXJS55P4+vKvk5rI/QHcICIfBVl2LjBZRKpZp3zLGCODBwvz\\n5kW/7TPP2C+uX3+11/e9ef9bunaFdevs4w4dbA3Fpk32S3bRouBl16hhvxidcJLIQeCHPFIiB/aH\\n8cABaNrUWSz+pk4NPhSEW3a2TWrdw7/ccQc88IDz8kMlcllZcMkl8MMPgdtEm8i9+Wbw9mutW9sz\\nXm/z59s2Izk59sdozhybyJc3kfNWVmbHfduzx9YE7dljE57TTnNehjcnNXLh4lu9OniNbrBt3n3X\\nHg/B7qQydqxtAxZKURHccosdS+zss+Ghh8o/TIv/601Pt/txu/HGwFout1hOCLw1bGiP/7w8e1Lg\\n/rzffrv9HGzYYNtOetdCrl5dMe0lb7jBUxsGNskpLIzvPtw1QMEcf3xgIhkPxcX2szNzpr2KcPfd\\n9vPpJJE75xxbu+etsiVyL79sT2JLS2HiRPjHP6DwQCE5+3PI2W+TseOHuZKx2nugdg4ZjfYw+mrP\\n8pz9OewptH9zi3Ipkyo4NldZGhTXh6L69Oxan/oZ9amf7vnbIKMBFNUnraQ+h3SoT4OM+nRs2JGT\\nupyUkESuZuRVAGgGhLp4mA7E+DNdNcSSxHl/OI880v6IfvGFff7OO77r/v67HfuotBROOMHOa9cO\\nfvnFzsvLs7UIP/0Exx4Ln31mq7dzc2NrFBzK0KGey0/HHx85iYPyN+gP9yX21lv28thbb9nLUoce\\nar944qFTJ/j+e/t45Eh7Jl6jBrz6avRl+deougV7bQMGwKpV9sz2iCM8244ebZPaeEhL8012W7e2\\n08cfBw6E66127eCXVsrr0ENt8jFxYuR1R460tT0FBYH3t4z0o5iR4ZtcxMNbb/km6bE2ZI/GkUfa\\nGtSHH7avKSPDJriPPWaTtH/+037ujjjCzj//fPsdce21FZPEgU12XnrJk9S+/Xb89/HMM/YE2PsO\\nHImWnm7f91iESui91axpa8/jSUTYd2Afuwt3s6tgF7sLd7Nn/56DyZZPApaxhz5P5pBblMOjJXu4\\n+74cikqLfAv0G0+wCHhpYXxjTgRDGlLYAIoawv6GUFyf3t0b0KNLfRqkNziYhOXurM/H79WH4vpc\\nd0V9ju7tWXZoJ5u8caAOtsUZLK8ElYVOa+TmAU2AU0Rki9f8tsAMYIeInJiwKCsxY4x4mhI65/+2\\nl5baZK1FC9/eWU6VlNjErWFD38ThzDNtm7BwGjSw20aSnW3bhpWV2Us55enl5dSrr/q26QF7KXrg\\nQHtGXt7ecqFq5LyVlcGPP9paxWA1R/78Y1q+3PY489eypW23E27fbjt3QvPmofcZj7N2EZuIfPON\\nfd+L/L6/N2ywNYjHHOM7v7w1cmBrIv3LjbbG6vrr45+oRbJ/v619+uorOP10+2Pt3Q4yETVy0f6v\\nd++2iVzHjtFtV16//WYvj/bvH/4Eobw6dAhsM3zccbEN/BsrkdCXoOvWtd+dwXrmBmtz519L7/5/\\niwgFBwpsQlZoEzLv5Mx7vvfy3YW7KS5N8ZuBF9exCVhRAw7r2pA2TRvSIKMBDTNcf2v7Ph95jitZ\\nK2pwcLuy/XVp0cKwc6en2DVrAk8Iwwn2mYzm82iMSWqN3I3A18A6Y8yP2M4OLYFjgQLgkngHVt3U\\nqOGpbYtFzZrBL1/edZdvIvf88/bMPBYtW/o2fK4Iwe6YMWVKxcaQlmZ/GGIV6gf5lFNsuy23Y48N\\nXUazZrBrl611veceO6p7vBljR++/9FI7lIh343uwP5gdOgTftryOPhoGDfJcDotluIRY2nKVV+3a\\ntuYplIq8LBZKkyaB7VsrwhFH2CnRgr3Hffokfr/ejLG1s1ddZR//97+2bd7atbbTjX8Sd6D0ADsL\\ndkKLnVBnpx3KInM3NQ/dRYe6u9m4Yxdk7qbdobs5/BlPUhZQO5YC6qXXo1HtRjSq3YilCxrbBGt/\\nIyhqQN+eDfnTucETMvfjrFUNOOesmmzaZDu+/fcmByfwvwfOMsZe1bjgAjuMyzXXRJfEgf2O/vFH\\nz/M77ohu+0RxVCMHYIxpCtyKTd5aA1uBH4DHRGRXwiKs5GKpkbv88opLRkTsJZd337W1WA8+aNvc\\nbdniWeeoo3wb2Fcm/r3LIL4/jsXF9vKzu/3O0UfbZKk8/L9ksrODj4GWlWV/6PLz7SWb778PbCsZ\\nzOLF0Lev5/m//gX33luukANkZ9ve0e5bA3n3drzySvvc7ZFHbEcKCP4F+3//5+yy0v79tgNC69bO\\nxiX035fT/VSk778P3Vs30nE8fLjtJOOtomuaUoF/b1ewTRMq4ooB2JqyvOI8dhbsZOveHewq2Mnu\\noh3sLNjJjn072FHgelzgmZdb5OASSCVRK60WjTMb06h2IxrXbsxPcxvZRKywMexvRG3TiCcmepa7\\nk7bGmY1pmNGQWjU8bXD8P7P/+Y+9dVokRUX2O9ppU6FwNWc7d9q22+HGMg1lwQLbxGjfPtv8ZskS\\n27nDqUTVyDlO5FRw0SZy6em2wXFFX+bwNmOG7yCMP/wQvjYomfx7iUH8azneesv2LmzQwJ6xlfe9\\nuOsuuO8++/iCC+zlpVDWrrVDgwwc6HwwWxGbvL3wgq15eOON8L37YrVgAbz2GvTrZ3s6ur8cs7Lg\\npJNsjcORR9p2k+62kMG+QJ10iolFjRq+NbZTptiTpMpExHbO8K559V4WzooVtv3XN9/Y50OH2h6w\\nhx8e/zhT2b59tiPBrFn2+axZ9viMVWlZKbsKd7F93/aDiZdPIlYQmKRV9kuXtWvWpmlmU5pkNqFp\\nnaY0rt04IOkKlog1qt2IzJqZGK8Ptv9n3LvXaiTeTWUaN7aXxBNx4/p69exx4S1evxtZWfazefzx\\n0bcB10Sukoo2kauoXmORvPGGp+fVBRckO5rQiottkuLuVXvTTYGX/CobETsmV36+HX4lVGeHVJaf\\nb2s9Onf2HWH+tdd8k6n337eN7RPh/fftMB0i9ux65crEJIzlJWJPSPzv8qBfvfFTVmZrWerVC/55\\nKy4tZvu+7WTnZ5O9L9vncfa+bLLzXfP2ZbOzYGel7WmZXiOdpplNaVrHlZS5kjPvx+5l3vMya8Xv\\n7vDlSeTADku1bJltwpGoCo26dW2HKG+V4fOmiVwlFW0it3WrbdCqnFu0yA542ratbR+WiDM4FR/7\\n9tnLXO6ThGeeSewtfn76yZ4cnX227ehTWc2eHVhLpF+95bOveN/B5CtSgrZnfxSZRgUwGJrWaUrz\\nOs1pUKspGaVN6diyCS3rhU7GmtZpGlA7lpTYy5nIVYS//tUOCu7mHlg92TSRq6SiTeQqsu2GUqpy\\n0ETOGRFhb9FetuRtYWv+VrbmbT34d0v+Fp/necV5yQ73oMyamTSv25xmdZrRvI7fX//5dZvTuHZj\\naqSVcxDDJEmFRG7LFtsLftMme0Xnhx/s1YNkS3avVaWUUjFKRq/RykRE2F2421GCVlgS55GDY9C4\\ndmNa1G3hKDlrXrc5dWrVSXbIykubNrZT2JIl9q4u4YZuqgocJXLGmIbAfhFJvb7PlUxVbC+llAqv\\nd2/bSWHpUvs81D1KU1FJWQnb8rexae8mn2lz3uaDj7fkbUlqh4A0k0azOs1oWbclLeu1pGXdlrSo\\n28Lnuftv87rNSa8R482zq4GXX/a9/7V3D/bKpEkT3/vnVmURL60aY2oC+4HzRCTIbc2rt2gvrW7f\\nXvXPDpRSgXbssMOjNGliBxGujB0z/BWVFPkkZJv3uh7neRK2bfnbktI5oFZaLZuMeSViLeq0CEjM\\nWtZrSdPMpil7KbOy2bfPDgk1a5Yd6DnR7WCrkqS2kTPGbAauEZHP4h1Aqos2kcvJqdyNspVS1UOZ\\nlLE1bysbczeyIXcDG3I2sDF3Ixv3bjyYsO0o2FHhcdWuWZs29dvQul5rWtdvbf/Wa23nuZ/Xb02T\\nzCakmSSMAq1UjJLdRm4qcDWgiVyU/vQnz71TTzpJkzilVMXYX7LfJmmuBG1D7gafpG3T3k0cKDtQ\\nYfHUS6/nKEFrmNEw6T0zlUolThO5LOASY8wC4EPsXR18qqFE5OX4hlY1vPKKHVC1uNiOgaaUUvFQ\\ncKCArJws1u1Zx/o968nKyfJJ1rbv2x65kDhpXqc57Rq0o12DdrSt3/bg43YN2tG2QVva1m9L/Ywo\\nhsBXSjnm9NJqpAYQIiLVsgFCpEurOsSAUioWZVLG5r2bWZ+znnV71tmEzevxtvxtkQsppzSTRut6\\nrQ8mZO3qtwtI0trUb0PtmrUTHotSqS7Zl1YrwQgsSilVteTuzw1I0NzPs3KyEt7Ts0lmEzo27EiH\\nhh3o2LAjHRvZx+5ErVW9VtRM0672SlVmOiBwOWmNnFIqnL1Fe1m7ey1rdq1hzW7X5Hq8s2Bnwvab\\nZtJoW78tHRt19EnWOjTscDBhq5deL2H7V0r5SnaNnDuI3sAJQFPgeRHZZow5BMgWkYQOs21s69fb\\ngbFAK2AVMEFEpjvY9hXA/3baAjwhIrf6rTsIeAjoB+QCbwJ3isj+aGO+8MJot1BKpaL84vyQyVqi\\n2qqlmTQ6NOxAl8Zd6NyoM50bdT6YoHVs2JG2DdpqbZpS1YDTAYEzsD1XzwcMNgn6GNgGPAysxiZZ\\niXQfcCswDvgVuBiYZowZISJfONh+O3AWNn63rd4ruBLVr4DPgRHYS8qPAG2AUdEEO3o0PPZYNFso\\npSqzMinjj9w/WLlzJSt2rmDlzpWs3LmS1btWszV/a+QCYtA0symdG3emS+MudGnUxfO4cRfaN2hP\\nrRopMBidUiqhnHZ2eAS4CrgBmAFkA/1F5FdjzDXAX0SkX8KCNKY58AfwgIhM8Jo/E2gmIn0jbP8K\\nMExEOkRY7wOgF9BLREpd88YAU4CjRGRRkG0CLq3+3//ZgT+VUqmnqKSINbvXsGLHCp+kbdWuVRQc\\nKIjrvtJrpNO5UeeDtWruJK1zY1vD1rC2jlekVFWR7Euro4B/icibxhj/3qnrgU5xjSrQaUAt4A2/\\n+VOBl4wxHUVkQ3l24LqDxanAI+4kzuVd4EXgHCAgkQvmySfLE4lSqiLkFeWxbMcylu9YbpO2XStZ\\nsWMF63PWx/VOBTXTatKlcRe6Nelmp6aev+0btNc7DiilysVpItcUWBFiWRqQ6Bt09AKKROR3v/nL\\nsJdKewGRErkWxpgdQCNgHfASNmlzf2N3BWq7yjxIRIqMMb+79uGIjmWpVOVRVFLEql2rWLp9Kb9l\\n/8bSHfbvhtxynfv5qGFq0KlRJ0+S5pWwdWzUUduqKaUSxum3y3pgIPB1kGVHYzseJFITICfI/N1e\\ny8NZCPyMTdJqA+cBDwKHYDtPeJexJ8R+Iu1DKZVEpWWlrM9Z75OwLd2+lNW7VlNSVhKXfTSq3Yie\\nzXrSo1mPg3+7N+tO50adtb2aUiopnCZyrwHjjDFZwPuueWKMGQrcAoyPZqfGmGHYtnaRzBGRk6Ip\\nOxgR8b/Y+YUxZh9wozFmooisK+8+lFIVJ2d/Dou3LWbhtoUszl7M0u1LWbZ9GYUlhXEpv0PDDgEJ\\nW49mPWhRt4XePkopVak4TeQeBvoArwP/dc37Flu79baIRNu0/zugh4P13C2L92Avifpz15LtDrIs\\nkreAm4EB2Eut7pq4xiH2szR0UeO9Hg9xTUqp8hIRNudtZtG2RSzcupBF2fbv+pz15S47zaRxaNND\\nOaz5YfRq3utg0nZo00Opm143DtErpaqzOXPmMGfOnITvJ6oBgY0xg7EdD5oDu4AvRGRugmLz3q+7\\n52g379ozY8yfsW3dukTb2cEYMwD4CRglIu8YY2oBe4FJInK313oZ2Mu6E0Xk30HKCei1qoMAKxW9\\n0rJS1uxew8KtC1m4baFN3rYtjMugue0btOeIlkdwePPD7d8Wh9OjWQ+9tZRSqsIku9cqACIyD5gX\\n7yAc+AIoAS4F7vWaPxpYGmOP1dFAGTAfQEQOGGO+AEYaY8Z7dYK4CEgHPoo1eKWULxFhfc56Fmxe\\nwIItdvp166/kF+eXq9wmmU04osURHNHCJmtHtDyCw5ofpsN4KKWqrGjv7DAU2+mhLbAZ+F5E5iQg\\nLh8issMY8yhwhzEmH8+AwEOwg/x6xzgL6CAi3VzPOwCvYu/QsA7IxA5sfBnwnIh4X6MZD/yAHWj4\\naeyAwA8D00RkYcJeoFJV3Na8rTZhcyVuP2/5mV2Fu2Iur4apQY9mPejXuh99W/ald8veHNHyCFrW\\nbalt2JRS1YrTOzs0AaYBQ7G1WHuwbcmMMWY2MFJEYmmnFo1xQB5wI55bdF0kIp/7rZfmmtzyXPGO\\nA1pi418J/FVEnvXeUEQWG2OGY2/R9Qn2Fl1TgDvj/WKUqqryivKYv3k+P23+6WDytjlvc8zl1alV\\nh94te9OvVT/6tupLv1b9OLzF4WTWyoxj1EoplZqc3tlhKnA2cB22duqAq03ZSOAZ4CMRGZPQSCsp\\n/zZyxkBZ/MYSVapSExE25G7gu43f8f0f3/P9pu9Zkr0k5gF1m2Y25cjWR9KvVT9b29aqL92adNNB\\nc5VSKS9RbeScJnK5wDgReTrIsr8C94lItWyE4p/IpadDUVESA1IqgYpKili4baFN2lxTrPcZrZde\\nj6NaH8WANgMY0HYAA9oMoFOjTnppVClVJSW7s0MpsCbEslWu5QpoHGzwEqVS1O7C3czbMI/v/rA1\\nbj9v+Zmi0ujPVNJrpNO3VV+btLkSt+5Nu2tNm1JKlZPTRO5D4E/AV0GWXQz8L24Rpbj+/ZMdgVKx\\n21mwk282fMOcrDnM3TCX37J/Q4h+PJ3uTbszsP1Ajml7DAPaDOCIlkeQXiM9ARErpVT15jSR+xh4\\nzBjzKbbTQza248BI4DDgJmPMwTswiEiwW3lVC2lpkddRqrLIzs/mmw3fMHfDXOZkzWHZjmWRN/KT\\nWTOTo9sezXHtj+O49sdxbLtjaVanWQKiVUop5c9pIvee62974PQgy9237TLYBmPV9nqJJnKqMsvd\\nn8ucrDnMXDeTWetnsWLniqjLaN+g/cGk7bj2x9GnZR+9z6hSSiWJ00RuaEKjUEolxIHSA/y46Udm\\nrpvJjHUzmL95PqUSXZPW3i17c2LHExnUYRAD2w2kfcP2CYpWKaVUtBwlchVxGy6lVPmJCMt3LD+Y\\nuM3dMDequyUYDH1b9WVIpyGc2PFEBnccTJPMJpE3VEoplRRR3dlBKVX55BXlMWv9LD5d/Smfr/08\\nqsF300waR7Y+khM7nsiQTkMY1GEQjWo3SmC0Siml4kkTOaVSjIiwetdqPlvzGZ+t/Yy5WXM5UHbA\\n8fY9m/XklC6ncHKXkzmh4wl6H1KllEphmsjFmYPxlZWK2v6S/czNmsunaz7lszWf8fue3x1v26pe\\nK07ucjIndz6Zk7ucTNsGbRMYqVJKqYqkiVycnXBCsiNQVUXO/hw+Wf0J01dM58vfv6TgQIGj7erU\\nqsOQTkM4ufPJnNL1FA5rfpjeLUEppaooR7foUqH536IrPx/q1k1iQCqlbc3byoerPmT6iunMzppN\\nSVmJo+0OaXIII7qNYES3EZzQ8QQyamYkOFKllFLRSOq9VlVo/omcvp0qWr/v/p0PVn7A9BXT+XHT\\nj47upJBeI50TO57IiG4jOKPbGXRr2q0CIlVKKRWrCr/XqjHm5SjKERG5Kg7xKFUtrNq5ireXvs30\\nldNZkr3E0TZt67fljG5nMKLbCIZ1GUa99HoJjlIppVRlF66N3EngUzXQCGgIlAC7gKau7XOBPYkK\\nUKmqIisni3eWvsPby95m0bZFjrbp0awH5/U4j/N7ns9RrY/Stm5KKaV8hEzkRKST+7ExZhDwFnAt\\n8L6IlBpjagAXApOA0QmOU6mUtDVvK9OWT+PtpW/zw6YfHG3Tv01/zu9xPuf1PI8ezXokOEKllFKp\\nzFEbOWPMfGCKiDwTZNkNwOUicnQC4qv0tI2c8pdfnM/0FdN5bfFrfL3+64ht3tJMGid0PIHzepzH\\nuT3OpUPDDhUUqVJKqYpS4W3k/BwBrA2xbA1weHzCUSo1lUkZc7Lm8Nri13hv+XvsO7Av7PppJo2h\\nnYbyp8P+xLk9zqV53eYVFKlSSqmqxGkitw0YCXwVZNnFQHbcIlIqhazetZrXFr/G60teZ2Puxojr\\nH9f+OEYdPooLe11Iq3qtKiBCpZRSVZnTRO5x4DFjTGtgGjZxa4lN7k4Fbk5MeEpVPoUHCpm2fBov\\n/PIC3/3xXcT1+7Xqx6jDRzHysJF0bNSxAiJUSilVXThK5ETkCWNMPnAPcLrXoj+Aa0QkmqFKqqxb\\nb012BCqRlm5fygu/vMDrS14nZ39O2HXb1G/DmN5juKzPZfRq3quCIlRKKVXdOL5Fl4i85Bpbrh3Q\\nGtgKbBIdUfignj2THYGKt4IDBUxbNo3nf3k+Yq/TzJqZnNfzPC7vcznDOg+jRlqNCopSKaVUdRXV\\nvVZdSdsfrkn5SUtLdgQqXtbuXstT859iyqIp5Bblhl13cIfBXN7nci467CIaZDSooAiVUkqpKBI5\\nY8wR2EurJwKNsYMAzwbuFZHfEhNeatGxWlObiDBr/Sye+OkJPl39adhhQ5rVacaf+/yZq4+8mu7N\\nuldglEoppZSHo0TOGDMAmAsUAh9he7G2As4CRhhjThCRXxIWZYrQGrnUVHCggNcXv86T859k+Y7l\\nYdc9qfNJjD1yLOf2OFdvTK+UUirpnNbIPQgsBYaJSJ57pjGmPjDTtXx4/MNLLVojl1o27d3Ekz89\\nyX9//S979oe+y1yzOs24ou8VXHPkNXpzeqWUUpWK00TuWGCMdxIHICJ5xpiHgFfjHlkK0kQuNazY\\nsYKHv3+YqUumUlJWEnK9o1ofxU3H3MTIw0Zq7ZtSSqlKyWkiF6lnqvZcRS+tVnY/bfqJh757iP+t\\n/F/I9m81TA0u6HUBNx1zEwPbDdSb1CullKrUnCZyPwHjjDEz/S6t1gX+CfyYiOBSjf7mVz4iwox1\\nM5j47URmZ80OuV7TzKaMPWos1/e/nvYN21dghEoppVTsnCZy44A5wAZjzCfYMeRaAWcAdYAhiQgu\\n1WiNXOUhIny46kPu/eZeft36a8j1ujXpxt+O+xtjeo8hs1ZmBUaolFJKlZ/TOzvMN8YcC9yNvSVX\\nE2A3OvyID62RSz4R4bM1n3H3nLvDJnBHtT6K2wfdznk9ztOBe5VSSqWsaO7ssAS4MIGxpDytkUse\\nEWHmupncPeduftwU+kr/sM7DuH3Q7QzrPEzbvymllEp5Ud3Zwdhfvl7YGrldwAq9RZdHVlayI6ie\\n5mbN5a7ZdzFv47ygyw2G83qex+3H386AtgMqODqllFIqcRzXIRljrsa2jVuCbS/3G7DFGHNVYkIL\\n2L8xxtxhjFlvjCk0xiwyxpzvcNtXjDFlflOpMeZRv/XuCbJemTFmupP9bN0ayytTsfp5y8+c/NrJ\\nDHl1SMgk7sJeF/Lb9b/x/sj3NYlTSilV5Ti9s8OlwAvALGAqnjs7XAq8YIwpEJG3EhaldR9wK7bj\\nxakccJQAACAASURBVK/AxcA0Y8wIEfnCwfbbsXei8L6eFiz1EuB4oMxr3m4nAeqVuoqRlZPFuFnj\\neGtp6EPu7O5n8+8h/6Zvq74VGJlSSilVsZxeWv0H8IaIjPGb/6ox5nXsECQJS+SMMc2B24AHROQx\\n1+y5xphuwETASSJXLCILHO5yvoiURV7NP85ot1DR2FO4h/vn3c/k+ZMpLi0Ous5ph5zGhCETtPZN\\nKaVUteA0keuOTeaCmQr8Lz7hhHQaUAt4I8i+XzLGdBSRDXHcX0wpWV5e5HVU9ErKSnhmwTOMnzM+\\n5K20Tup8EvcOvZfj2h9XwdEppZRSyeM0kcsD2oVY1s61PJF6AUUi8rvf/GXYpKsXECmRa2GM2QE0\\nAtYBLwGPhKh5+8MY0wLYBLwNjBeR/ZGC1G4f8ff1+q+58fMbWbZjWdDlfVr2YdIpkzil6ykVHJlS\\nSimVfE4Tuc+BB4wxq0XkYKtyY8xAbNu1zxMRnJcmQE6Q+bu9loezEPgZm/jVBs4DHgQOAcZ6rbcW\\nuN21vgDDgVuAftjx88LS4UfiZ2PuRm776jbeW/5e0OXtGrTjvqH3Mbr3aB0HTimlVLUVTRu5Y4E5\\nxpjNeO7s0A6b/IS67BqUMWYYMMPBqnNE5KRoyg5GRJ70m/WFMWYfcKMxZqKIrHOt53/pdpbr9T5m\\njBkqIqHv8QS0aFHeSFVRSRGTvp/EA/MeoLCkMGB5/fT63DHoDm4+9ma9E4NSSqlqz+mdHbYZY/oC\\nVwKDsTVgWcBcYIqIFES53++AHg7Wc5e7B3tJ1J+7Js5Rr1I/bwE3AwOwl1rDrfc4cDT2ThZBjAdg\\nzhyYM2cIQ4YMiSEcNW/DPMZ+MpaVO1cGXf7nvn/mwWEP0qpeqwqOTCmllIrOnDlzmDNnTsL3Y1Jh\\nPF9jzBhgCtDNXXvmmv9nbFu3LtF2djDGDAB+AkaJyDth1msOZAN3iMhDQZaLvQoL//wnTJwYTRQK\\nYHfhbv4x4x+8tPCloMv7t+nP5NMnc2y7Yys4MqWUUio+jDGISNzHt4jqzg5J9AVQgh237l6v+aOB\\npTH2WB2NHStuvoP1BJv0hTVoUAxRVGMiwltL3+KWL29h+77tAcub12nOg8Me5Ip+V5BmtAGiUkop\\n5c/pgMDpwB3AKKADkOG3iohIwpJCEdnhugvDHcaYfDwDAg/BDvLrHessoIOIdHM97wC8CryJvYSa\\nCZwPXAY8JyLrvbb92bXuamxv2OHA/wGfi8icSHGecUa5Xma1si1/G9d+ci0frfoo6PKr+13NQ6c8\\nRJPMSP1YlFJKqerLafI1CbgB2zt1OlCUsIhCG4cd5uRGbEeLVcBFIuLfYzYN31uP5WHb2I0DWmJr\\n4VYCfxWRZ/22Xe0qv7WrjHXYBnCTnASovVYjc9fC/fXzv7K7MLBpY89mPXn+zOcZ3HFwEqJTSiml\\nUoujNnKunpvPiMj9iQ8ptXi3kUuB5oZJlZ2fzfWfXs8HKz8IWJZRI4M7B9/JP47/Bxk1/St8lVJK\\nqdSW7DZy9YAf4r1zVX18sOIDrvn4GnYV7gpYNrDdQF455xW6N+uehMiUUkqp1OX0YuDHwAmJDERV\\nTQUHCrjuk+s4/93zA5K4jBoZTDplEvOumKdJnFJKKRWDkDVyxpguXk8nA68ZY8qAzwgybpv3sCDV\\nUdu2yY6g8lm8bTGj3h/Fip0rApYd3fZoppwzhZ7NeyYhMqWUUqpqCNlGzpW0eS90X9cNuoGIVMv7\\nJLnbyHXsCFlZyY6mchARJs+fzN9n/J3i0mKfZTXTajJhyAT+fvzfqZmWKqPfKKWUUuWTjDZyV8R7\\nZ1WZ9li1cvbncNkHl/Hx6o8DlnVr0o03L3iT/m36JyEypZRSquoJmciJyKsVGUiqM3HPsVPPom2L\\nuODdC1i3J/Aq+xV9r+DJ05+kXnq9JESmlFJKVU16bStOqnuN3KuLXuW6T69jf8l+n/kNMxry3JnP\\ncfHhFycpMqWUUqrqCtfZ4WXgXhFZ73ocjojIVfENLbVU1xq5opIibvriJp7/5fmAZQPaDODdi96l\\nU6NOFR+YUkopVQ2Eq5EbCjzhenwSITo5uFT7oXBrVMOuHlvytnDeO+cxf3Pg7Wqv7389j536mA7u\\nq5RSSiVQuDZynb0ed6qQaFJYdbu0+uvWXzn7rbPZnLfZZ35mzUyeP/N5xvQZk6TIlFJKqepD28jF\\nSXWqkZu+YjpjPhhDwYECn/ldG3fl/ZHv06dVnyRFppRSSlUv4drIdYimIBHZWP5wUld1qJETESZ+\\nO5FxX48LWHb6Iafz5gVv0qh2oyREppRSSlVP4Wrksoiu7Vs1qpMKVNVr5IpKihj7yVheW/xawLKb\\nj7mZR4Y/Qo20Kv4mKKWUUpVMuETuSrQTg2NVuUYuryiP8945j1nrZ/nMr5lWk6fPeJqxR41NUmRK\\nKaVU9Raus8OUCowj5VXVRG77vu2c8cYZ/LL1F5/5jWs35v2R7zO089AkRaaUUkqpqDo7GGPSgF5A\\nU+BnEdmXkKhSUFW8tLp+z3pOnXoqa3av8ZnfrUk3Pr3kU7o17ZakyJRSSikF4LgeyRhzA7ANWAJ8\\nDXR3zf+fMebGxISXOqpajdyS7CUc9/JxAUncgDYD+O7K7zSJU0oppSoBR+mHMeYa7ODA/wNGAt73\\nMZgHXBD/0FJLVaqR+27jd5zwyglsy9/mM3941+F8ffnXNK/bPEmRKaWUUsqb03qkW4H/iMhY4AO/\\nZStx1c5VZ1WlRm7ehnmcOvVUcotyfeaPOnwUH4/6WG96r5RSSlUiTtOPzsCXIZbtA6r94GFVoUZu\\nbtZcTn/jdPYd8G36eOPRNzL1/Kmk10hPUmRKKaWUCsZpIrcT6BRiWXdgc4hl1Uaq18jNXj+bM948\\nIyCJmzBkAo+f9jhpJsVfoFJKKVUFOf11/gS42xjTxWueGGOaAbdg285Va6mcyH29/mtGvDki4JZb\\nDw57kLtOvAtjTIgtlVJKKZVMTtOPfwFFwFJgJnag4CeBFUApMCEh0aWQVL20OmvdLEa8OYLCkkKf\\n+Q+d/BC3D7o9SVEppZRSygkj4uzmDcaY+sDNwKlAC2AX8AXwmIjsTViElZwxRkCoXRsKCyOvX5n8\\nuOlHhr02LKAmbtIpk/jbcX9LUlRKKaVU1WOMQUTifonLcSIXthBjaopISRziSTnuRA4gDm9lhVm2\\nfRmDXxnMnv17fOb/Z/h/uHXgrUmKSimllKqaEpXIOR1H7h9hltUE3o1bRCrhsnKyGD51eEAS9+jw\\nRzWJU0oppVKI0zZy9xpjxvjPNMbUAN4Gqv0NN889N9kROJOdn80pr5/ClrwtPvPvOfEebhl4S5Ki\\nUkoppVQsnCZy1wEvGmNOc89w3Xf1LeAU4PQExJZSatVKdgSR5e7P5fQ3Tmft7rU+828YcAP3nHhP\\nkqJSSimlVKxqOllJRF4xxrQGphljhgELgDeB04DTROTHBMaYEir78CNFJUWc8/Y5LNy20Gf+qMNH\\n8eTpT+oQI0oppVQKcpTIAYjIA65k7lPge+Ak4HQR+T5RwaWSypwHifx/e/cdHkXVPXD8ezZACKEG\\npHcBlV5UwBpAEFBBEVBABSuCAuorFlApij99X+zlFSsqKCrYXhBEUEKRIoTehAABAekqveX8/pjJ\\nsrskmw1sEjY5n+eZh8ydOzNnZ5ZwuDP3XuW+ifeRkJzgV962RltG3zjaBvs1xhhjIlTIiZyrP87Q\\nI+2B61R1dvhDikzncovci3Ne5JOln/iVNa/YnPFdxtu0W8YYY0wESzeRE5EtpI6rcfo+HmCMz+M4\\nVdUq4Q8vcpyrLXLfrP6GJ6c/6VdWq2QtJnafSGyB2ByKyhhjjDHhEKxFbjppJ3ImDedii9zi7Yu5\\n7Zvb/MpKFCzBxG4TiYuJy6GojDHGGBMu6SZyqtorG+PIkDjNf08A9wFlgbXAcFX9OsT9C7r7dwcq\\nA38BC4BOvoMZi8gVwItAI+BvnE4dg1X1SLDjn2uJ3Pb927nh8xv8Zm3I58nH+K7jqVmyZg5GZowx\\nxphwyew7cjnpOeARYBCQCNyK04v2OlWdEmxHd9DiKUAV4HmcOWLPwxk6JQo44darD0wFJgPXAdWA\\nkUB5oFvwc5zpxwq/w8cP03FcR7bu3+pX/lb7t2hZrWUORWWMMcaYcAv2jtwdwCRV3eP+HJSqfpJR\\nnTMlIucB/wKeV9VX3OIEEakJvICTpAXzKNAQqK2qviPhfhNQbxiwBeiqqieBX0TkODBaRF5U1SXp\\nneBcapF78IcH+W3bb35lDzV9iPua3JdDERljjDEmKwRrkRsNNAP2uD8Ho0CWJXI449XlB8YGlI8B\\nPhCRKqqaHGT/PsCXAUmcH7fV7lpgpJvEpfoSeA/oCJzzidzoJaP5cMmHfmXtarRjZJuRORSRMcYY\\nY7JKsESuGrDd5+ecVBs4qqpJAeUrAXG3p5nIiUgloBKwUUTeBW4BCgBzgH+p6lK36vlAQfeYXqp6\\nVESS3HOk61x4tLpi5wr6TurrV3ZByQsY13kcUZ6oHIrKGGOMMVklWGeH5LR+ziFxOJ0TAu312Z6e\\n8u6fT+B0buiKk7ANx3l0Wl9V//A5xr7TD8HeDM6R4y1yB44doPOXnTl84rC3LCZfDF91+Yqi0UVz\\nMDJjjDHGZJUcST9EpJWIpISw/ByG06V+xoPA9ar6o6p+h9OZoRDwQBjOkaMtcqpK74m9WbtnrV/5\\n29e9Tb0y9XIoKmOMMcZktWCdHTYS+jhyqqrnZ+K8c4ALQ6iXOnbGPqB4GttTW8n2prEt1Z7Uc6rq\\n0dRCVf1DRNbgdIJIPQdAiXTOsyL9Uwxl4UIYOhTi4+OJj48PEk74vbvoXT5b/plf2V0N76JXw17Z\\nGocxxhhjHDNmzGDGjBlZfp5g78glkEUDArtjsv2eiV1WAtEiUl1VN/iU18GJcVWQfTcAh4NsT5UE\\nHHWP6SUi0UB1nE4P6RhKs2ZOIpfdErcn0n9Kf7+yeqXr8Ub7N7I/GGOMMcYApzfsDBs2LEvOEykD\\nAk/BGeutB/CsT/ltwIpg7/Cp6gkRmQRcKSIxqnoYQEQq47QKfufWOy4iU4CuIjJUVVPcQ3TB6Rzx\\nfbAAc+LR6sFjB+k2oRvHTh7zlhUuUJivunxFofyFsj8gY4wxxmSriBgQWFV3icjLwJMicoBTAwLH\\nAzf41hWR6UBlVfWdvmAIMB/4QUReAmKAZ3Aeyb7pU28oMBdnoOG3cHrr/hv4SlUXB4sxJzo7PDr1\\nUX7f49+w+f4N73NBqQuyPxhjjDHGZLuISORcg4D9QH9OTdHVRVUnB9TzENCJQ1VXi0hLnKm3xgHH\\ngZ+Bgaq6y6feUhFp49abiDNF12hgcEbBZXciN+n3Sbyz6B2/svsa38ctdW/J3kCMMcYYk2NENUte\\ng8szRERBeeQReOml7DnnroO7qPvfuuw8uNNbVjOuJot7Lya2QGz2BGGMMcaYkIkIqhr2F7HOkfkI\\nIl92tsg9OPlBvyQuSqIY02mMJXHGGGNMHmOJXJhkV2eH8avG8+VK/w60T1/1NJdWuDR7AjDGGGPM\\nOcMSuTDJjha53Yd2nzYFV5NyTRh8VYav8BljjDEmFwqps4OIXBVkcwpOp4A1qno8LFFFoOxI5PpP\\n7s+uQ96+GeT35Oejjh+RzxNJfVaMMcYYEy6hZgAzyHhw4EMi8rqq5snmoax+tDp53WQ+X/G5X9nT\\nVz1tU3AZY4wxeVioiVxH4A1gKTAe2AGUwZmAvj7wNHAp8JiI7FPVkVkQ6zktK1vkDh47SN8f/B+p\\nNizbkCeueCLrTmqMMcaYc16oidyNwBRVvT+g/FMRGQW0UNU7RSQFuBvIc4lcVrbIDU8Yzqa/NnnX\\nPeLh/RveJ39U/qw7qTHGGGPOeaG2I90ETEhn23icFjtwptKqdrZBRaKsapFbtmMZL831H6Cu/6X9\\naVK+Sdac0BhjjDERI9T0Iwo4P51tNdzt4Ew6f/Rsg4pEWZHIqSp9J/XlpJ70llUsWpHhLYaH/2TG\\nGGOMiTihph8/AM+LyM0iEgUgIlEi0hkYAUxy69UBksIf5rkvKx6tjl0+ljlb5viVvdnuTYpEFwn/\\nyYwxxhgTcUJ9R64f8A3wFXBCRPYBJdz957jbwRmG5PlwBxkJwt0i98/Rfxj400C/sutrXU/HCzum\\ns4cxxhhj8pqQEjlV3Q1c6U4o3wxn0vrtwDxV/cmn3sdZEmUECHci92zCs/x54E/veoGoArx67avh\\nPYkxxhhjIlqmRpJV1anA1CyKJaKF89Hq73t+59X5/knbwMsGcn5ceq8pGmOMMSYvylQiJyLXA1cD\\nccBe4BdV/SErAos04WyRe3za45xIOeFdr1S0Ek9e8WT4TmCMMcaYXCHUKbqKABOBK4ETwB6gJPCI\\niMwCrlfVA1kWZQQIV4vczOSZfLvmW7+yf7f+N7EFYsNzAmOMMcbkGqG2Iz0PNAZuB2JUtRwQA9zh\\nlufJDg6+wtEil6Ip/Gvqv/zKmlZoyi11bjn7gxtjjDEm1wk1/bgZeEpVx6o6g5qp6klVHYszPdfN\\nWRVgpAhHIjduxTgWblvoV/ZSm5eQrJ7I1RhjjDERKdT0oySwKp1tq9ztedrZ5lpHTxxl8M+D/cpu\\nvuhmLq98+dkd2BhjjDG5VqiJ3Ebg+nS2tXe352ln2yL3fuL7fvOp5vfk54VrXji7gxpjjDEmVwu1\\n1+oo4CURKQyMxRlDrixwK3AP8EjWhBc5ziaRO3jsIM/OfNavrHeT3tSIq3GWURljjDEmNwt1QOBX\\nROQ8nIStl1sswDHgBVV9LWvCixxn82j1zQVvsuPgDu96TL4YBl81OMgexhhjjDGZGEdOVQeJyH9w\\nZnZIHUdunqruy6rgIsmZtsj9feRvXpzzol/ZgKYDKFu4bBiiMsYYY0xultmZHfYBk7Moloh2pi1y\\nr8x7hX1HTuXCxaKLMfDygUH2MMYYY4xxpJvIichVmTmQqs48+3Ai15m0yP195G9em+//VPrRyx4l\\nLiYuTFEZY4wxJjcL1iI3A9AQjiFuvahwBBSpziSRe3PBm/x15C/velxMHAOaDghjVMYYY4zJzYIl\\nci2yLYpcILOPVg8cO8Ar817xK3uo6UMUiS4SxqiMMcYYk5ulm8ipakJ2BhLpMtsi99/f/suew3u8\\n60Wji9Kvab8wR2WMMcaY3CwME0sZyFyL3OHjhxk5d6RfWf9L+1O8YPEwR2WMMcaY3MwSuTDJTIvc\\nx0s/ZufBnd71wgUK81Czh7IgKmOMMcbkZpbIhUmoidzJlJO8NPclv7L7m9xPyUJ5frpaY4wxxmSS\\nJXJhEuqj1e/Wfsf6veu96/k9+a01zhhjjDFnxBK5MAmlRU5V+c+v//Er616vOxWKVsiiqIwxxhiT\\nm2VqZgcR8QC1gZLAQlU9mCVRRaBQErk5W+Yw7495fmWPXvZoFkVkjIlkVatWJTk5OafDMMZkQpUq\\nVdi0aVO2njPkRE5EHgCG4CRxAJcAiSLyLfCzqr6eBfH5nl+AJ4D7gLLAWmC4qn4d4v4F3f27A5WB\\nv4AFQCdVPeHWGYLzGQN9q6qdgh8/4xhG/urfU7VdjXbULV03hOiNMXlNcnIyqqGMyW6MOVfImc7X\\neRZCSuRE5F7gNeBDYCrwpc/mWcDNQJYmcsBzwCPAICARuBX4SkSuU9UpwXYUkXzAFKAK8DywGjgP\\naI0zI8UJn+oKXA6k+JTtzSi4jFrkNu7byPdrv/crG3iZzalqjDHGmDMXaovcI8BLqvq4iAROxbUG\\nyNKMRETOA/4FPK+qqdMhJIhITeAFnCQtmEeBhkBtVd3mU/5NOvUXqGpKOtvSiTH49rd/exv1mfGs\\nYdmGxFeNz8wpjDHGGGP8hNrZoRrwYzrbDgJZPZJtWyA/MDagfAxQT0SqZLB/H+DLgCQumEy3jQZr\\nkTt0/BAfLP7Ar6zfpf1ypAnWGGOMMblHqIncbqBqOtsuALaGJZr01QaOqmpSQPlKnKSrdno7ikgl\\noBKwUUTeFZG/ReSwiEwTkQbp7LZFRE6IyCYRecF9vy6oYInc2GVj2Xdkn3e9ZExJutXtltEhjTHG\\nGGOCCjWRmwg8IyLVfcpUREoBDwPfhj0yf3E4nRMC7fXZnp7y7p9P4LQsdsV5v+484BcRqehTd71b\\n7w7gWuALnM/3XUYBpte4pqq8seANv7J7Gt9DTP6YjA5pjDHGGBNUqIncU8BRYAUwDadDwOs4nQZO\\nAsMzc1IRaSUiKSEsP2fmuOlI/YwHgetV9UdV/Q64DigEPJBaUVXHqup/VHWaqk5X1cdx3v+7RkRa\\nBD1JOldy1uZZLN+5/FQ98dDn4j5n83mMMcb4aNGiBf3798/28yYkJBAVFcXevRn2h8vVqlWrxssv\\nv5zTYeRZISVyqrobuBj4P5x31ZJwOkq8CTRX1b8zed45wIUhLHe49feR9nt4qS1xwf4W7Uk9p6oe\\n9flMf+B01GiYQayf4zy+vTT9KkP5/POhDB06lBkzZvhtGbVolN96xws6UqV4Rq/0GWNM7vPxxx9T\\npEiRnA7jjKSVrFx++eVs376duLhgD4XC51y9fgsXLqRv3745dv6HHnqISy65hJiYGKpXr57xDiH6\\n5ptvaNu2LaVLl8bj8TBz5sxM7T9jxgyGDh3qXbJKyOPIqep+4Fl3OSuqegT4PRO7rASiRaS6qm7w\\nKa+D0zq4Ksi+G4DDmY8yM4Zy223Qrp1/6Z5Dexi/arxfWd9Lcu7LbowxOUlVc1Unr3z58lG6dOls\\nO9+5ev1KlszZucJVlV69erFs2TJ++umnsB334MGDXH755dx+++3ccccdGe8QID4+nvj4eO/6sGHD\\nwhabr0iZomsKzlhvPQLKbwNWqGq6w5+7g/1OAq4QEe+LaSJSGafVb0EG574NJ1mcH6xSWo9WP132\\nKcdOHvOuVy9RnZbVWmZwOmOMyZhI1i5naubMmTRv3pwiRYpQvHhxmjVrxqpVq0hISOCuu+7i4MGD\\neDweoqKiGD7ceSvnr7/+omfPnsTFxVGoUCFat27NqlX+/z+fN28erVq1onDhwhQvXpxrrrmGP//8\\n07s9JSWFwYMHc95551GmTBkGDvQfFWvs2LFceumlFC1alDJlytC1a1e2bTs1kMGJEyfo378/FSpU\\noGDBglSpUoVBgwYBzqPb5ORkBg4c6I0dnBYXj8fj92g1oziz4vodP36cxx9/nEqVKhEbG0vTpk2Z\\nOnWq95gJCQl4PB4mTZpEo0aNiImJ4eKLLyYxMTGkmP755x9uv/12ypQpQ0xMDDVq1OD1108NHevb\\nWjls2DBvfB6Px7ukxgrw0UcfUadOHWJiYrjwwgt59dVXQ74+aXnttdd44IEHqFWrVrp1fv31V+Lj\\n44mNjaVixYr07duX/fv3Bz3ubbfdxtNPP03btm3P7cG5VTXDBfg5yDINmIAzUG+ZUI53JgvOY91D\\nOJ0Prgb+i5PctQuoNx1YF1B2EfAP8AtwPdAFWA5sA87zqbcQ6IfT0aEt8DJwDJgYJC4F1R9/VD8p\\nKSl60ZsXKUPxLv836//UGGNC4fx6DrY9a5czceLECS1RooQ+9thjunHjRl27dq1+/vnnumbNGj1+\\n/Li+9tprWrhwYd25c6fu2LFDDx48qKqqHTp00Isuukhnz56tK1as0A4dOmilSpX0yJEjqqq6ZMkS\\njYmJ0fvvv1+XLl2qa9eu1ffff1+3bNmiqqrx8fFavHhxHTJkiK5bt06/+uorzZcvn44bN84b20cf\\nfaSTJ0/WjRs36m+//aYtW7bUq666yrt95MiRWrlyZZ09e7Zu2bJF586dq6NHj1ZV1b1792qlSpV0\\n2LBhumPHDt2xY4eqqs6YMUM9Ho/u2bMnpDiz6vp1795dmzdvrrNnz9aNGzfqW2+9pdHR0bps2TJv\\nnCKiF110kf7000+6cuVK7dKli5YvX14PHz6cYVwPPvigNmrUSBcuXKibN2/WhIQEHT9+vHd71apV\\n9aWXXlJV1YMHD3qv0Y4dO/TTTz/VAgUK6M8//6yqqu+++66WL19ev/76a920aZNOnDhRy5Urp2+9\\n9Zb3eO3atdPChQunuxQpUiTNOEeOHKnVqlU7rXzZsmVauHBhfeWVVzQpKUkXLFigl112mXbp0iWk\\n+7J7924VEU1ISMiwbrC/t+628OdHIVVyEqCtOLMdJAG/un+muOWJOI8vd+EMupsViZy4yeJG91xL\\ngJvSiTUpjfKL3STvAM47dxOA6gF1PgPWuXUO4XTuGATkDxKXgupPP/nfsNnJs/2SuHzD8+n2/dvT\\nv/vGGOMjEhO5vXv3qsfj0ZkzZ6a5ffTo0af9I7xu3ToVEZ09e7a37O+//9ZixYrpBx98oKpOonLZ\\nZZele974+PjTtrdu3VrvvffedPdZvXq1iohu3bpVVVX79++v11xzTbr1fZOVVIGJXI8ePYLGmZEz\\nuX5JSUnq8XhOSxZvvPFGfeCBB7xxioh+/vnn3u0HDhzQ4sWLe69xMB06dNC777473e1pXRtV1TVr\\n1miJEiX09ddf95ZVrlxZx4wZ41fv1Vdf1dq1a3vXt23bpklJSUGXtKSXyN1xxx16zz33+JUtXrxY\\nRUR37dqV7udKda4ncqG+I/cy8Cpwsap622JFpAnOdF3DgEU403eNAG4K8bghcy/C8+4SrF6avUtV\\ndSHQKoN9u59pfIGPVt9NfNdvvcMFHShbuOyZHt4YY855JUqUoGfPnrRp04ZWrVrRqlUrOnfuTKVK\\nldLdZ/Xq1URFRdGsWTNvWdGiRalXr5738eqSJUvo1CnodNfUr1/fb718+fLs3LnTu56YmMjw4cNZ\\nsmQJe/fuRdV532zz5s2UL1+eXr160bp1a2rVqkWbNm1o37497dq1y9Q7aYsXL84wzmDO5PolJiai\\nqtSuXTu1cQGAY8eO0bLlqVd5RMTvGsfGxvpd42D69OlD586dWbhwIa1bt+aGG27gqquuCrrPYlWk\\nfwAAIABJREFUX3/9RceOHbn11lvp168fALt372bLli307t2b+++/31v3xIkTfte5XLlyGcaUGYsW\\nLSIpKYlx48Z5y1QVj8dDUlISU6dOpXfv3oBznSZPnszll18e1hiyUqiJ3HPAUN8kDkBVF4nIMOA5\\nVa0nIv8BRqZ5hFzO9+/630f+5suVX/ptv7fxvdkckTEmN/P5N/uc8uGHH/Lwww8zZcoUvv/+ewYP\\nHsx3331H69atM32szCRR+fPnP23flBRnpsVDhw7Rtm1b2rRpw5gxYyhdujS7du3iyiuv5Ngx5z3m\\nRo0akZyczI8//sj06dPp2bMnDRo0YNq0aZmO+2xk9vqlpKTg8XhYuHAh+fL5/5MeExOe8Urbtm3L\\n5s2bmTx5MtOnT+e6666jS5cufPjhh2nWP3nyJF26dKFSpUq88capcVRT78eoUaNo3rx5uudr3749\\ns2bNSne7iPDPP/+EHH9KSgr33HMPjzzyiF+yC1ChQgXq1q3rl+RWqFAh5GOfC0JN5GrhPDZNyy6g\\nhvtzEhB7tkFFIt8WufGrxnPkxBHveuVilWldPfO/xIwxJhLVq1ePevXqMXDgQNq3b8/HH39M69at\\nKVCgACdPnvSre9FFF5GSksLcuXO54oorAOfl+uXLl3P33XcDTpL1888/8+yzZzZowpo1a9izZw8j\\nRoygShVn+KcVK1aclijGxsbSqVMnOnXqRM+ePWnWrBnr16+nRo0aacYe6GzjTJWZ69eoUSNUle3b\\nt3P11Vene0xVZd68eVStWhVwemSuWLGCXr16hRRTXFwcPXr0oEePHrRt25bu3bszatSo0xJogAED\\nBrB582YWLFjg7RgCULp0acqXL8/69evp0SOw7+IpH3zwAYcPh2+wicaNG7Ny5UqqVauW5vbo6Oiw\\nDluS3UJN5DYB95L25PT3udsBSnFq3LY8xff3wSfLPvHbdkf9O4jyRGGMMbnZpk2bGDVqFB06dKBC\\nhQokJSWxbNkyHnjAGXe9atWqHDlyhGnTptGoUSMKFSpEjRo16NChA71792bUqFEUK1aMwYMHU6xY\\nMbp1c6YyHDhwIM2bN6d379488MADFCxYkFmzZnHttddSsWLFYCEBULlyZaKjo3njjTd44IEHWLVq\\nFc8884xfnVdeeYVy5crRsGFD8uXLx9ixYylWrJj3+FWrVmXWrFn06NGD6Oho75Abvi08ZxvnmVy/\\nmjVr0r17d3r16sXIkSNp3Lgxe/fuZcaMGZx//vnceOON3uM/99xzlCpVinLlyjF8+HCio6O91ziY\\nIUOG0LhxY+rUqcPx48eZMGEC559/fppJ3EcffcRHH33ElClTOHLkCEeOOI0ahQsXJjY2lmHDhtG/\\nf3+KFStG+/btOX78OImJiWzdupUnnngCyPyj1aSkJA4cOMDWrVs5duwYS5cuBaBOnTrky5ePxx9/\\nnObNm9OnTx969+5NkSJFWL16NRMnTuSdd95J97j79u1j8+bN7NvnTLG5bt06ihUrRtmyZSlTpkym\\nYsxSobxIB3TDmcFhGTAEZxL6Ie56CnCrW+9t4OuseJnvXF1wOzvMmuW8zLhh7wa/Tg4MRdfuXnv6\\nW4/GGBMEZ9rjIAft2LFDO3XqpBUrVtSCBQtqlSpV9IknntATJ0546/Tt21dLlSqlHo9Hhw0bpqqq\\n+/bt0169emlcXJwWKlRI27Rpo6tWrfI79pw5c/Tqq6/WQoUKaYkSJbR169b6559/qqpqixYttF+/\\nfn71e/XqpTfccIN3/csvv9QaNWpoTEyMNm3aVKdOnaoej8f7Avt7772njRs31qJFi2qxYsU0Pj5e\\n582b591/3rx52rBhQy1YsKB6PB5VPb2zQ0ZxfvTRRyoimpycHNbrd+LECR02bJief/75Gh0dreXK\\nldOOHTtqYmKiX5z/+9//tH79+lqwYEFt0qSJLlq0KMN7qqo6YsQIrVu3rsbGxmrJkiX1uuuu0zVr\\n1ni3V6tWTV9++WXvdfd4PKctqbGqqo4bN06bNGmiMTExGhcXp1deeaV+8cUXIcWSlvj4+DTP6Xud\\nFy1apO3atdNixYpp4cKFtX79+jpkyJCgxx09erSKSNDPEijY31uyqLODaIgvWohIa5xODU1wZnc4\\njjNcxxBVnebWKQicVNXj4UgyI4GIKChz5sBll8GzCc/yzIxT/9NrVrEZc++em4MRGmMikYic9j6P\\niWxDhgzh66+/ZunSpXjSm9cxCyQkJNCyZUt27dqVbbNQ5FXB/t6628I+onNmZnb4CfhJRDw4j1B3\\nq2pKQJ0jae6cyw0bBpUqOa2bgY9VezbomUNRGWOMOZdMmTKFt99+O1uTuFT2n4LcK9PfJlVNUdWd\\ngUlcXvbMM04iN++Peazfu95bXiCqAF3rdM3ByIwxxpwr5s+fz5VXXpkj5w7WA7h9+/YUKVLktKVo\\n0aK88MIL2RilORMht8iJSAGgHXABUDBgs6rqWc/BGuk+Xfap3/oNtW4gLsaasY0xxuScq6++OmiP\\n22C9RO1R7LkvpERORMoDs4GqOPOOpqb2vm21eTqRO5FygvGrxvuV3V7/9hyKxhhjjAlNuAfgNdkr\\n1Eer/8EZL64yThLXFKiOM4vDevfnPO2Xjb+w69CpofaKRRejXc12ORiRMcYYY3K7UB+tXgk8ijPJ\\nPECKqm4CnhGRKOB1oGP4w4scX6z8wm/9potuokBUgRyKxhhjjDF5QagtciWB7W4Hh4NACZ9tPwPx\\nYY4rohw7eYyvV3/tV3ZLnVtyKBpjjDHG5BWhJnJ/AKXdn5OANj7bLgXy5LAjqaZtmMa+I/u86yVj\\nStKqWqscjMgYY4wxeUGoj1Z/Aa4CJgCjgLdEpCHOoMDXumV5VuBj1U4XdSJ/1OlTlxhjjDHGhFOo\\nLXJPAW8BqOp/gQFAIaAc8G/gX1kSXYT4ds23fuv2WNUYk1e1aNGC/v37Z/t5k5OT8Xg8JCYmZvu5\\nc9rHH39M0aJFczoMk0NCTeSOA8mpK6r6hqpeoaqNVXVQXp3RIdU/R//x/lw6tjRXV706B6MxxpjI\\nlpCQgMfjYe/evZnaL9igt+FSrVo1Xn755Sw/T2bceuutbNiwIcfOP2zYMDwej99Svnz5sz7u0aNH\\nufPOO2nQoAEFChSgZcuWYYg298nw0aqI5AP2ADcB/8vyiCLczRfdTD5PyOMsG2OMCaCqZzTXbF6d\\nhio6Opro6OgcjeHCCy8kISHBew+ioqLO+pgnT54kJiaGfv368cMPP/DXX3+d9TFzowxb5FT1BLAD\\nSH9YaON104U35XQIxpg8QIZJli5n48SJEzz00EPExcURFxfHY4895rd97NixXHrppRQtWpQyZcrQ\\ntWtXtm1zRrdKTk72trycd955REVFcdddd3n3femll6hVqxYFCxakcuXKDB482O/YmzZtok2bNsTG\\nxlKnTh2mTZuW6dj79+9PhQoVKFiwIFWqVGHQoEGA89g4OTmZgQMH4vF4/JKVX3/9lfj4eGJjY6lY\\nsSJ9+/Zl//793u0tWrSgT58+Qa9LMF9//TUNGjSgUKFClCxZkhYtWrBrlzN26ejRoylSpIi3bmps\\ngX+m2rZtG7feeqs3juuvv57169efds7MyJcvH+eddx6lS5emdOnSlCxZ0m/78ePHefzxx6lUqRKx\\nsbE0bdqUqVOnBj1moUKFePvtt7nnnnuoUKHCWcWXm4X6aHUMcE9WBpIbFIsuZo9VjTF53pgxY1BV\\n5s2bx7vvvsu7777Lq6++6t1+/Phxhg8fzrJly5g0aRJ79uyhe/fuAFSqVIkJEyYAsHr1arZv385r\\nr70GwJNPPsmIESMYPHgwq1ev5uuvv6Zy5cp+537qqad46KGHWLZsGZdccgndunXj0KFDIcf+2muv\\n8d133/Hll1+yfv16vvjiCy644ALASaYqVqzIkCFD+PPPP9m+fTsAy5cv59prr+XGG29k+fLlfPPN\\nNyxdutQvAQX47LPPgl6X9OzYsYNu3bpx5513smbNGmbNmsXtt5+aOUhE/B4rp8b2559/smXLFpo0\\naUJ8fDwAhw8fpkWLFsTGxjJr1izmzZtH+fLlueaaazhyxHlLavbs2WnOvRpsDtYNGzZQoUIFqlev\\nTrdu3di4caPf9l69ejFr1izGjRvHypUr6dmzJx06dGD58uUh3hmTHgmlKVpE+gCDgD+B74Dt+E/P\\nhap+mBUBnutERBnq/Ny9XnfGdhqbo/EYY3KHjB4tnm2rWUZ0yJk9pmzRogXbt29nzZo13rIRI0Yw\\natQoNm/enOY+a9asoXbt2vzxxx+UL1+ehIQEWrZsya5du7xzfR48eJBSpUrx+uuvc++99552jOTk\\nZKpVq8a7777LPfc47Q7btm2jYsWKzJ49m8suuyyk+AcMGMCqVav46aef0txerVo1+vXrxyOPPOIt\\n69mzJwUKFOC9997zli1ZsoTGjRuzc+dOSpUqdUbXJdXixYu5+OKL2bRpE5UqVTpt+8cff0y/fv34\\n559/TtvWt29fpk2bxoIFCyhevDgffvghL774ImvXrvXWOXnyJGXKlOGdd96hc+fOHD16lK1btwaN\\nKS4ujuLFiwPw448/sn//fi688EJ27tzJs88+y5o1a1i1ahUlSpRgw4YN1KxZk+TkZCpWrOg9xk03\\n3USFChV48803g54LoF+/fqxcuZKff/45w7o5KdjfW3db2P/ihvoy11vunxWAJmlsVyBPJnK+Ol6Q\\npye3MMYYAJo1a+a33rx5c5555hkOHDhA4cKFSUxMZPjw4SxZsoS9e/d634nbvHlzui/Jr1q1imPH\\njmX4wnu9evW8P6cea+fOnSHH3qtXL1q3bk2tWrVo06YN7du3p127dkE7UixatIikpCTGjRvnLUv9\\nTElJSZQqVQrI+Lqkp0GDBrRq1Yo6derQpk0brrnmGjp37uw9bnreeustxo0bx7x587xJV2JiIhs2\\nbPB7FAtOS11SUhLgvHNXvXroM29ee+21fuvNmjWjWrVqfPzxxzz00EMkJiaiqtSuXdsvyTl27Bit\\nWjljrtatW5fkZKdP5VVXXcWkSZNCPn9eF2oiVy1Lo8gFCkQVoG2NtjkdhjEmjzjTFrOcdujQIdq2\\nbUubNm0YM2YMpUuXZteuXVx55ZUcO3bsrI+fP//pY3impKSEvH+jRo1ITk7mxx9/ZPr06fTs2ZMG\\nDRoEfdcuJSWFe+65h0ceeeS01phwvNvl8XiYOnUq8+fPZ+rUqXzwwQc8+eSTzJw50y9x9TV9+nQG\\nDhzI999/T61atfxibdSoEV988cVpsaa2fs6ePZt27dKfK1xEGDRoEE888USa2wsVKkSdOnVYt26d\\n95wej4eFCxeSL59/2hETEwPA5MmTOX78uF+ZCU1IiZyqJmdcK29rVa0VRaNtHB9jjJk/f77f+ty5\\ncylfvry3NW7Pnj2MGDGCKlWqALBixQq/Fq8CBZx5qk+ePNXH7qKLLqJAgQJMnz6d888/P0vjj42N\\npVOnTnTq1ImePXvSrFkz1q9fT40aNShQoIBfXACNGzdm5cqVVKsWvM0j2HUJRdOmTWnatClPP/00\\nderU4YsvvkgzkVu3bh1du3Zl5MiRXHPNNafFOm7cOEqWLJnu2HOXXHIJS5cuDRpLatKXliNHjrBm\\nzRpv62mjRo1QVbZv387VV6f9Hnlaj4xNaELt7ACAiNQXkQdFZIiIlHXLaohIkYz2ze1uvPDGnA7B\\nGGPOCdu2bePhhx/m999/Z/z48YwcOdL7TlnlypWJjo7mjTfeYOPGjUyaNIlnnnnGb/8qVaogIkya\\nNIndu3dz8OBBChcuzIABA3jyyScZPXo0GzZs4LfffuOdd94Ja+yvvPIK48aNY82aNaxfv56xY8dS\\nrFgx77tdVatWZdasWWzbto09e/YA8Pjjj7NgwQL69OnDkiVLSEpKYuLEidx///0hX5dg5s+fz4gR\\nI1i4cCFbtmzhu+++448//qBOnTqn1T1y5AgdOnSgdevW3HzzzezYscO7APTo0YMyZcrQsWNHZs6c\\nyaZNm5g5cyaPPvroaY9Wgy2pj2oBBg4c6D3W/Pnz6dy5M4cOHaJnz54A1KxZk+7du9OrVy8mTJjA\\nxo0bWbRoES+99BLffvvtaZ/B1+rVq1myZAm7d+/mwIEDLF26NMMkM89R1QwXIBr4CmcIkhT3z8bu\\ntq+BF0I5Tm5cAGUouu2fbWqMMeHi/HqOPC1atNA+ffpov379tHjx4hoXF6cDBw7UlJQUb50vv/xS\\na9SooTExMdq0aVOdOnWqejweTUhI8NZ57rnntHz58hoVFaV33nmnqqqmpKToiy++qOeff75GR0dr\\n5cqV9amnnlJV1U2bNqnH49FFixb5xePxeHTChAne9SpVqniPl5b33ntPGzdurEWLFtVixYppfHy8\\nzps3z7t93rx52rBhQy1YsKB6PB5v+aJFi7Rdu3ZarFgxLVy4sNavX1+HDBni3R4fH5/hdUnP6tWr\\ntV27dlq2bFktWLCg1qxZU0eOHOndPnr0aC1SpIjfdfBdRMQv1p07d+pdd92lZcqU0YIFC2r16tX1\\n7rvv1j179mQYS1puvfVWrVChgkZHR2vFihW1c+fOunr1ar86J06c0GHDhnnvXbly5bRjx46amJgY\\n9NhVq1YN+lnONcH+3rrbwp6HhNprdSRwN/AA8BPOuHIXq2qiiNwL9FXVRuFNMSODiGiz95sx9+65\\nOR2KMSYXOZMBcU1whw8fpmTJkowePZquXbtm67lbtGhBvXr1eP3117P1vCZ7ncu9VrsBT6nqZyIS\\nOFzzRqBqWKOKMP0u7ZfTIRhjjMnAL7/8QrNmzbI9iTMmK4X6jlxJYHWQY+Ts3CA5rHu97jkdgjHG\\nmAy0b98+x8YhCzZ8SeoAvEWLFk1z8F1jggm1RW4j0BxI62/ApcDaNMqNMcYYA0ETyFB6iRqTnlAT\\nuU+AQSKyCZjglqmItAAehtS5DYwxxhiTGZkdgNcYX6F2dogCxgJdgaM4j1IPAwWBcaraIyuDPJeJ\\niNoLycaYcLPODsZEnpzo7BBSIucTxJXAtUBpYA8wRVUTwh1UJLFEzhiTFSyRMybynPOJnDmdJXLG\\nmKxgiZwxkeecHX5ERBYDHwOfq+qOcAcRYgwCPAHcB5TF6WAxXFW/zmC/KjidNdJzq6p+6VP/CuBF\\noBHwN/AZMFhVj5zdJzDGmNClzm5gjIkcqdPOZadQ35H7AWgNKDAdJ6n7NjuTGxEZATwCDAISgVtx\\nkrrrVHVKkP0KAA3T2DQCuBwop6p/u3XrA/OAycCbQDVgJPCjqnZL5/jWImeMMcaYoHL80aqIlAa6\\nA7cBjYH9OD1YP1XVX8IdWMC5zwO2AM+r6nCf8mlAKVVNK1ELdrwY4E9gsqre6lP+DVAbqK2qJ92y\\n24HRQBNVXZLGsSyRM8YYY0xQWZXIhTogMKq6U1VfVdWLgTrAW0BLYJqIJIc7sABtgfw4PWd9jQHq\\nuY9PM+NmoDBOyyIAIpIPpyPHF6lJnOtL4DjQMbNBm7xlxowZOR2COUfYd8Gksu+CyWohJ3K+VHU1\\nMBwYDGwDKoYzqDTUBo6qalJA+UpA3O2Z0RPYCfzoU3Y+znAqK30rqupRIOkMzmHyGPuFbVLZd8Gk\\nsu+CyWqZTuREpKWIfATswBko+A8gqycbjQP+SqN8r8/2kIhIeaAFMEZVUwLOAbAvnfOEfA5jjDHG\\nmOwQaq/VujjvxnXHaX3bBLyG837cusyeVERaAT+FUHWGqrbM7PEzcAdOK97HGVU0xhhjjDmXhdpr\\nNQVnKI6vgE9UdfZZnVSkIFA5hKqHVPUPEXkB6K+qhQKOcwkwH6fn6uQQz70SOKKqTQLKLwRWAd1U\\n9Ys09lmhqrekcTzr6WCMMcaYDOXYOHI4U3P9z31f7Ky5w5b8noldVgLRIlJdVTf4lNfBGRJlVSgH\\ncRO/i4ABaWxOwpl+rE7APtFAdZxOD6fJiptijDHGGBOKkN6RU9Xx6SVxInK1iHwY3rBOMwU4AQTO\\n6XobTktZqL1me+L0QP08cIOqHnfP01VEfK9LF6AA8H1mgzbGGGOMyUqhtsj5EZEaOO+a3Q5UAQ4B\\nd4UxLj+quktEXgaeFJEDnBoQOB64ISC26UBlVa0ZUJ4fuAX4QVV3p3OqocBc4CsReQtnQOB/A1+p\\n6uLwfSJjjDHGmLMXcq9VESkmIveJyByc6bEG4/Tw7AOUz6L4fA0CngP647ScNQe6pPFunIe0P9d1\\nOD1P0+3koKpLgTY4U4BNdM83GujlW09EKorIeBH5S0T+FpEJIlLpTD6UiQxuy3NKGsvegHrFReR9\\nEdklIgdE5Ce3s5CJUCJSQUTeEJFfReSge99Pe8c31HsvItEi8h8R2SYih9zjXpk9n8acjVC+CyJS\\nJZ3fFSdFpGhAXfsuRCAR6Swi34jIZve+rRGR50WkcEC9bPmdELSzg/uIsS3OI8kbcMZZ2wZ8DTwA\\ntFDVmaGeLDdwZ4VYBhzGSWbBme4rBqivqodzKjaTdUTkauBnnKF2FvpsOqGqiT71ZuN05HkUZ8ic\\nQTjvXTZQ1W3ZF7EJF/fejwMWAVE4/9mrpqqbA+qFdO9FZCzQzq23EXjQXW+mqsuy/AOZMxbKd0FO\\nze89AvhfwCF+850KyL4LkUlE5uIMvfaN+2dDYBiwWlUv86mXPb8TVDXNBXgJ2A6cBA7izKrQBqe1\\nqziQAlyV3v65dcHpKHEc5y9vallVt+yhnI7Pliy771e7fxdaBqnT0a1zlU9ZUWAP8GpOfwZbwvI9\\nuNu9x5XP5N4DDdzfnXf4lEUBa3Dmr87xz2jLWX8Xqrj3+K4M9rfvQoQuQMk0ym53vw/x7nq2/U4I\\n9mj1YaA08IP7Re2hqlPVGUQ3Lw+5cQMwT1U3phao6iZgDjaNV26XUQ/lG4Bt6tNKrar/4Pyv3L4b\\nuVuo974DcAyfXvDqTAk4DrjWfZfX5A32XYhQqronjeLfcP6NqOCuZ9vvhGCJ3AfAfpx3y9aKyJsi\\ncmlGB8wD6gAr0ihfiU3jlReMFZETIrJbRMYGvBsZ7LtRWUQKpbHN5A6h3vvawEZ1hmAKrFcAqJF1\\nIZps9n8ictx9l/q7NN6Nsu9C7hKP/3Bo2fY7Id1ETlXvxXnpvwfOO0G9gbkishp4nLzbKhdH+tN4\\nlcjmWEz2+RsYCdyDM8XbcOAa4FcRKeXWCfbdAPt+5Gah3vuM6tlUgJHvKPAOzr+Z8cC/gHrAHBGp\\n5VPPvgu5hIhUwHlH7ic9NcJFtv1OCNprVVWPqOrnqtoW54W9J3Ge+T6B04T4gojcJs5MDcbkWqq6\\nRFUfU9VJqjpLVV/H6QhUlqyfa9gYEyFU9U9V7auq36rqHFX9ALjK3Tw42L4m8ohILPAdzuPRLBuG\\nLZiQhx9R1e2q+m9VrQtcCrwF1AQ+wekUkVfsI+2WlfSyapNLuf/z+h3n7wME/26kbje5U6j3PqN6\\ne9PYZiKcqv4BzObU7wqw70LEcxuxJuJ0eLxW/UcmyLbfCSEncr5UdaGq9sMZP+5mYMaZHCdCrSRg\\nGi9XbUKcKszkWsG+G5tV9VA2x2OyT6j3fiVQLY2nGHVw/ke/PutCNOcY+y5EMBHJB0wAGgPtVDXw\\n3/9s+51wRolcKlU9rqrfqOpNZ3OcCPM90ExEqqYWuD9fjtO8avIIEbkYuACY5xZ9D1TwHcjRHQD0\\nBuy7kduFeu//h/MCcxefelE481n/qM5UgSaXcQcNvoJTvyvAvgsRS0QE+AznHciOqvpbGtWy7XdC\\n0AGBzencniZLcAYEftotHg7E4gzyZ60uuZCIfAokAYuBf3D+F/YEcABooqp73b/cs4GKwGM4A0A+\\nCdTF+W5szYnYzdkTkZvdH6/BeYm9L7AL2KWqMzNz70Xkc5wxOR/DGfyzL9AeaK7O7DLmHBbCd2Ek\\nzrhg83Aei12I87uiCM4Ar+t8jmXfhQgkIv/FuffPAZMCNv+hqluz9XdCTg+sF4mLe2O+cm/M3zjN\\nq5VzOi5bsvSeP4GTwO/D6ZWWDPwXKBNQrzjwPrAbJ8mbCtTN6fhtOev7n4LT0Stw+Tmz9x6IxukB\\nvQ1nnuq5wJU5/RltCc93AbgTmI8z8OtR9z5/CtS070LuWNxkK63vwEngGZ962fI7wVrkjDHGGGMi\\n1Fm9I2eMMcYYY3KOJXLGGGOMMRHKEjljjDHGmAhliZwxxhhjTISyRM4YY4wxJkJZImeMMcYYE6Es\\nkTPGGGOMiVCWyBljABCR20Uk2Wd9pYjcH+ZzNBOReSJyQEROikj9cB7fZD8R2SQiH57Bfh1F5OGs\\niMmYvMQSOWNMqsbAQgARicWZR3ZRmM/xIRAFXAc0B34P8/FN9jvTUeVvBCyRM+YsWSJnjEnVhFOJ\\nW2Oc6WbCNt+jiHiAWsAkVU1Q1QWqeiRcxzdnT0QK5HQMxpjMsUTOGJOaZDXkVCJ3CbBKVY+FuH8R\\nEXlTRLaKyBERWSMiD/ls7wmcAAR4RkRSRGRDkOMNdevUFZGfReSgiGwTkWEB9aJF5GURWS4i+0Vk\\nu4h8LyIXBNQrIyIf+8S3za1Xyt0eJSLPish6ETksIrtEZKaIXBZwnPtEZIlPnfdFpERAnQEiskpE\\nDonIXhH5TUQ6hnANbws49iciUtZn+0QROa2FVETKishxERngU1ZVRMaKyE738y4WkRvTucZ1RGSK\\niOwHvsggxgEistGNcYGIXJFGnVIi8o6IrHXv22Y3lvI+dT4CegIV3Bi834dQ76kxxpEvpwMwxuQc\\nEdkIVHFXFfhBRCR1XURS3PJqqro5nWMI8ANOIvg0sALn0enLIlJKVZ8CJgKXA3NwJpF+H2dC8fSk\\nPq77Budx7PPAtcDTInJSVYe726OBIsAInAmnSwB9gbkicqGq7nTrjQEqAf8C/gDKAK2AQu72J4AB\\nwCCcVsiiwMVAnM/nfAF4BHgVeBSo4J63johcpqoqIj1wJr8eCswGYoD6vsdJ5xreB7y8Zs2FAAAG\\nlklEQVQDfO7GUh74P+BSEWmsqodwJl7/zP1ca3x27+Fer8/cY1UEFgB/up9pN3ALMEFEOqrqxIBr\\n/C3wAfACzoTw6cV4N/AKzv34Eqjhxls4oGoczr0dBOwEyuFc99lu7MeA4cB5ONf4BpwEP/X7EOo9\\nNcYAqKotttiSRxfgQpxE4yVgOVDPXf8b6O/+XB/IF+QY1+MkALcHlL8HHAbi3PUot94zIcQ1BOfR\\n7sCA8nfd2Iqms58HJ3n6BxjgU74feDDI+f4HjA+yvQpOi+LggPLm7mfq4K6/ASzM5D3w4CRd0wLK\\nL3eP/aC7XhD4CxgRUG8xMNFn/QNgB1A8oN5UIDGNa5zudfGpK8BmnMfivuVd3Rg/zODzVXTrdfQp\\n/wjYHOL1Oe2e2mKLLc5ij1aNycNUdY2qLsNprZqhqsuBQzitLF+p6jJ3ORHkMFfiJASfB5SPAQrg\\nJDtn6quA9XFubHVTC0Skq9sTdh9OsnUQSO2skeo3YKCI9BeRupzuN6C9iDwnIpeLSP6A7a1xkpnP\\n3MewUSIS5e63H7jK5zgNReR1EWklIjEhfMYLgNK4LWqpVHUOkAxc7a4fAcbjtMClfvZ6QAPgE59d\\nr8VpId3vE2s+nESugYgEtqB9G0KMFd0l8H5MwLnmfkSkj/uYeL+7fTNOC2BIj0dDvKfGGOwdOWPy\\nLBHx+PwjfznOo6sonKRkK7DTXc9IHLA3jWTvT5zkJ+hjxQzsSGNdcB5rIiI34CR3K4FuwKU4j+t2\\n47RgpeoKfA8MBJa678o97bN9BE4L1Q3ATGCPiHwoIqmxl3bPmwQc91mO4SSWJQFU9ROgjxvHFGCv\\niEwQkSqkL/Uc29PY9if+1+9ToLKIXO2u347TUvWdT53SwB1pxPlvd3vJgHOkdd5A5dw//e6Hqp4E\\n9viWiUg/4C2cxPEmnPctm+JcP997kqZM3FNjDPaOnDF52XTc1h6c1pJPcVrRUteP47wn10JVZwY5\\nzl4gTkTyBSRzZX22n6kywKaAdXASTXDe/VqnqnenVnATU7/kUVV3A/2AfiJSE+dF+2EislNVR7kJ\\nyX+A/4hIaZzHxa/gPNLrhpOsKE7L3F9pxOlNZlT1PeA9ESkGtAFexklM0muZTL0+ZdPYVhZ3SBj3\\n2Akishm4TURmurF9paq+7xvuwUlGX8BJngJtC1gPZfiQ1GSvjG+hm+gHJoa34DwmfsynXtUQzuG7\\nf4b31BjjsBY5Y/Ku+3BaOkYC692fLwZ2AYPdny8h47HkEnDef+sSUH4bzgvsc88ixq4B691wHmUu\\nd9cLcfqjvTvceNKkquvU6YCxD59HtD7bd6rqh8A0n+0/4bzjVUVVE9NYktM4zt+q+hVOx4C0Huem\\nWovT0nWrb6E4PWarAL8E1B8DdAba47RMfhqwfQrOe42r0on1eJBY0vMHsIXT70dnTm8QKITznwBf\\nd3F6wngUJ1EOlOl7akxeZi1yxuRRqroOQESewXmJfbE7xEMpnJfXQ+0dOBmnh+Y7bmvWSpxeq3cB\\nz6vqmbbICXCvz7tobd1jDlHV/W6dKUBHEXkZp2fsJcCDOEka7ucripOUjQXW4CQZNwLFgR/dOt/i\\n9FZNdPdt7J7vvwCqukFE/g28KSIX4iSvR4DKwDXAe25r2SicRHMuTo/NC3Aef/6Y3odU1RT3Hrwj\\nIqmtohWB53CSvI8CdvkUp0foO0ByGq2lzwDzgVki8iZOi2YJnGSymqrek14sQWJUcYZ+eU+cWRzG\\nATWBx3E6n/iaAjwmIk/i9J5tiZPwBVqFc3/vx2l1PKKqKwjhnhpjfOR0bwtbbLEl5xYgP847Vq3d\\n9QHAb2dwnMLA6ziPPI/gJEz9A+pE4XSKeDqE46X2qKwN/Izzsvs2YGhAPcEZyuIP4ABO61UDYAPw\\ngVunAE5Cttz9rH/hJDq3+BznYeBXnNbIg8BqnKFUogLO18Ott9891kr3c5d3t9/hxvsnTo/dJJwW\\nz8IhfObuOD1QD7txjAbKpFN3gXt9nk1ne3mcHr5b3PuxFSeZ7B5wjU8Ankzc537ARpwOMQuAy3yv\\ntVunIM47cjtwkrzvcFoW/e49TsvbWJxHwSeBDaHeU1tsseXUIqpnOruKMcZkDREZgtOylF9V0x3b\\nzBhj8jp7R84YY4wxJkJZImeMOVfZ4wJjjMmAPVo1xhhjjIlQ1iJnjDHGGBOhLJEzxhhjjIlQlsgZ\\nY4wxxkQoS+SMMcYYYyKUJXLGGGOMMRHKEjljjDHGmAj1/yEd2PcZ9aYFAAAAAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"make_plot(log_likelihood_sgd, len_data=len(feature_matrix_train), batch_size=100,\\n\",\n \" smoothing_window=30, label='stochastic, step_size=1e-1')\\n\",\n \"make_plot(log_likelihood_batch, len_data=len(feature_matrix_train), batch_size=len(feature_matrix_train),\\n\",\n \" smoothing_window=1, label='batch, step_size=5e-1')\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Quiz Question**: In the figure above, how many passes does batch gradient ascent need to achieve a similar log likelihood as stochastic gradient ascent? \\n\",\n \"\\n\",\n \"1. It's always better\\n\",\n \"2. 10 passes\\n\",\n \"3. 20 passes\\n\",\n \"4. 150 passes or more\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Explore the effects of step sizes on stochastic gradient ascent\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"In previous sections, we chose step sizes for you. In practice, it helps to know how to choose good step sizes yourself.\\n\",\n \"\\n\",\n \"To start, we explore a wide range of step sizes that are equally spaced in the log space. Run stochastic gradient ascent with `step_size` set to 1e-4, 1e-3, 1e-2, 1e-1, 1e0, 1e1, and 1e2. Use the following set of parameters:\\n\",\n \"* `initial_coefficients=np.zeros(194)`\\n\",\n \"* `batch_size=100`\\n\",\n \"* `max_iter` initialized so as to run 10 passes over the data.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 37,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69313622\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69313170\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69313585\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69312487\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69313157\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69313113\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.69311121\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69312692\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69312115\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69312811\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.69311286\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.69310301\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.69310725\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69311567\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.69310836\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.69308342\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.69298918\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.69277472\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.69228764\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.69222554\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.69186710\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.69230650\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.69174220\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.69139955\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.69123818\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.69088883\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.68976850\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.68569701\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.68597545\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.68736824\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69303759\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69299241\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69303389\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69292442\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69299113\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69298668\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.69278828\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69294460\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69288708\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69295651\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.69280480\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.69270635\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.69274924\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69283249\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.69275924\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.69251197\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.69158805\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.68946852\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.68492418\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.68415366\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.68114554\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.68489867\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.68027821\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.67693088\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.67561867\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.67367588\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.66156206\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.62798175\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.64157978\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.64571292\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69205420\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69160695\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69201686\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69095428\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69159348\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69154386\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.68964000\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69112685\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69056997\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69124730\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.68980179\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.68882576\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.68929536\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69003572\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.68929307\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.68702353\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.67916061\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.66049079\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.63235099\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.62183600\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.61150928\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.62979300\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.61553432\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.59156014\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.58842264\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.59076267\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.54480104\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.45761063\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.54362587\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.56306510\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.68251093\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.67845294\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.68207160\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.67411325\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.67804438\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.67712546\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.66377074\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.67321231\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.66923613\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.67479446\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.66501639\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.65591964\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.66240398\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.66440641\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.65782757\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.64571479\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.60976663\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.54566060\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.48245740\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.46629313\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.47223389\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.52216798\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.52336683\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.46963453\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.47883783\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.46988191\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.46365531\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.36466901\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.51096892\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.54670667\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.61201447\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.58843678\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.59771677\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.58770466\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.56939710\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.57554451\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.54068090\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.55212916\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.55311029\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.57672007\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.55455807\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.49771894\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.54708765\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.54286814\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.52361054\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.49731367\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.50102061\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.42406927\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.35064478\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.38344116\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.40170047\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.45117863\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.46493371\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.45343350\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.43128394\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.43169967\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.43029376\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.32703099\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.49162447\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.52452720\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.51319004\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -2.20035379\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -3.34199720\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -3.06285156\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -2.80822162\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -2.99629286\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -2.71489944\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -3.61713200\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -1.19526584\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.75357081\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.71310829\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.59361318\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -1.53764659\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -2.69588686\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -1.89731473\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.81254441\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -1.19013437\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.48968363\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.72860037\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.58719556\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.31220572\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -1.89468446\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.96096585\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.66616640\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.46114004\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.47236476\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.45227508\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.29378688\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -2.47834692\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -2.48776279\\n\",\n \"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -2.44471310\\n\",\n \"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -36.66862050\\n\",\n \"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -25.49870239\\n\",\n \"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -40.14565040\\n\",\n \"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -27.03748522\\n\",\n \"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -32.62294582\\n\",\n \"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -25.88017915\\n\",\n \"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -37.30720216\\n\",\n \"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -10.87360529\\n\",\n \"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -6.60878996\\n\",\n \"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -7.15375088\\n\",\n \"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -6.04741293\\n\",\n \"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -18.17389834\\n\",\n \"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -27.14619228\\n\",\n \"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -20.50685042\\n\",\n \"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -7.74332305\\n\",\n \"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -10.64501703\\n\",\n \"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -4.03599975\\n\",\n \"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -14.21901031\\n\",\n \"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -6.19993978\\n\",\n \"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -6.36502333\\n\",\n \"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -11.39823729\\n\",\n \"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -8.46797053\\n\",\n \"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -5.24553417\\n\",\n \"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -4.68839629\\n\",\n \"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -4.40273027\\n\",\n \"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -16.44320616\\n\",\n \"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -1.24273340\\n\",\n \"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -25.08431933\\n\",\n \"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -4.18699295\\n\"\n ]\n }\n ],\n \"source\": [\n \"batch_size = 100\\n\",\n \"num_passes = 10\\n\",\n \"num_iterations = num_passes * int(len(feature_matrix_train)/batch_size)\\n\",\n \"\\n\",\n \"coefficients_sgd = {}\\n\",\n \"log_likelihood_sgd = {}\\n\",\n \"for step_size in np.logspace(-4, 2, num=7):\\n\",\n \" coefficients_sgd[step_size], log_likelihood_sgd[step_size] = logistic_regression_SG(feature_matrix_train, sentiment_train,\\n\",\n \" initial_coefficients=np.zeros(194),\\n\",\n \" step_size=step_size, batch_size=batch_size, max_iter=num_iterations)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### Plotting the log likelihood as a function of passes for each step size\\n\",\n \"\\n\",\n \"Now, we will plot the change in log likelihood using the `make_plot` for each of the following values of `step_size`:\\n\",\n \"\\n\",\n \"* `step_size = 1e-4`\\n\",\n \"* `step_size = 1e-3`\\n\",\n \"* `step_size = 1e-2`\\n\",\n \"* `step_size = 1e-1`\\n\",\n \"* `step_size = 1e0`\\n\",\n \"* `step_size = 1e1`\\n\",\n \"* `step_size = 1e2`\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"For consistency, we again apply `smoothing_window=30`.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 38,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAnIAAAFSCAYAAAB2ajI+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4VMX6xz+zNb2RUAOEjlRBwIIgWBDl2rjqVW7B+9OL\\nHfXqtWADO+oVFTtWxK4I2PDaQIoISJcOAQKBkF43W+f3xyYhu3t2s5vdTcH5PE+e7JkzZ8572pzv\\neWfmHSGlRKFQKBQKhULR+tA1twEKhUKhUCgUisahhJxCoVAoFApFK0UJOYVCoVAoFIpWihJyCoVC\\noVAoFK0UJeQUCoVCoVAoWilKyCkUCoVCoVC0UpSQUygUCoVCoWilBCXkhBCjhRAJftYlCCFGR9Ys\\nhUKhUCgUCkVDBOuR+wno52ddn5r1CoVCoVAoFIomJFghJwKsMwPOCNiiUCgUCoVCoQgBg78VQogs\\noHu9pGEazauxwP8BByJumUKhUCgUCoUiIH6FHDAZeBCQNX+z8fTMyZplB3BjtAxUKBQKhUKhUGgj\\npJTaK4ToCmThFms/4hZrW72yWYGdUsqiKNoYMkKITOBZ4Gzc9n8P3CqlzGlWwxQKhUKhUCgiiF8h\\n55FJiDOAdVLK8uibFB5CiFhgE2AB7q1JfhR3M/AgKaWluWxTKBQKhUKhiCSBmlbrkFIujbYhEWQK\\nbk9ibyllNoAQYjOwC7gWt6dOoVAoFAqFotUTrEfOBNwDXAl0wT1StT5SShmUKIw2QojvAbOUcpRX\\n+hLcdo5tFsMUCoVCoVAoIkyw4usp3H3kvgHm4+4b11LpDyzQSP8duLSJbVEoFAqFQqGIGsEKuUuB\\nB6WUj0bTmAiRBhRrpBcBqU1si0KhUCgUCkXUCDYgcALwSzQNUSgUCoVCoVCERrAeuS+A0bjDkLR0\\nitH2vPnz1CGEaLijoEKhUCgUCkWEkVIGmj2rQYIVcrOBuUIIF/A17mZKb0P2hmNIBPkddz85b/rh\\nGwevjmAGfShaDtOnT2f69OnNbYYiBNQ1a32oa9a6UNer9SFEWBoOCF7I1TarTsc924MW+rCtiQyL\\ngKeEEFlSyn1QN93YSODO5jNLoVAoFAqFIrIEK+T+D/eUXK2BObhH2C4UQtxfk/YQsB94rdmsUigU\\nCoVCoYgwwQYEfjvKdkQMKWWVEOJMYBYwl2NTdN0mpaxqVuMUEWPMmDHNbYIiRNQ1a32oa9a6UNfr\\nj0lQAYGPd4QQMtTzIKXEUezAWeHElmfDlmfDftQOOjAkGxB6gamdCXMXM/p4PZY9Fqqzq7HsteAo\\nciAMou7PkGLAkGxw/29jwJhuxNTehM6ko2p7FRWbKnCWOtHF6HBWOTF1MJEwKAF9gp6qnVVYdliw\\n5dsQeoHO5B6I7LK5cJQ4sOfbiekeQ0xWDMY0I8IgqN5fjXS4j9dR4sBV7aqzWRerw5BsAAGOYge2\\nfBvSLpFOiT5Wjz7B/WfqaELaJC6bC1eVC0Oqgbg+cegT9FhzrVhzrNjybLgsLpwVTpzlTpxVTqyH\\nrBjTjRjTjcQPiCeudxzOKie2XHfesjVlmDuZiesbh/2onaodVdiL7NgO29DF6Eg6OYmkU5KIOyEO\\naZfuc59ro3p/NdZcK9XZ1e6y+8cT3z/efR5jdUiHdJ/7Qge2IzaEWZBwYgK2Izaq91VTvroca44V\\nQ6oBfaIec2cz0iaxHrRibOs+bzFdYnDZXOCCmO4xHn0bpEMiDAJ7gd19zmwSfaIeY5oRY1sjxjQj\\n9mI7zlIn1fuqMWeasR2x4ShxENMthphuMQijwHbEhvWAO0xjXJ844k6Iw2VzYT1gpXxNOZVbKzGk\\nGjB3MmNsYwQd2HJtmNqbSB6VjD5Bj2WXhbJVZUinxFZkx1rqQB61kzA4AWEUSJvE1MEEuLeN7R2L\\nMd2IPkGPs9JJ5eZKpEOii9FhTDPiqnZhL7Rjr3AQ2ymGpJFJJJ+ajM6sw2V3UbW1isIvCynfVEH5\\nnipcLknGyFQSBsRjSDXgLHdStucAZfurMJa2wRirJyYrhqKfS4jvE4eprRFThglDGwM6kw7pcp/3\\npJOT0CfqwQUI0MfpEQaBPlGPMAqcFU4cpe7raS+wgxNMHUwY0gy4qlyUriyleF05lmI7xo4mkrvG\\nojMIKvZYSMyKwZRuIrZHLMY2RuxFdqq2VlG1vQpTB5P7Pi62U1low251IW0u2vSMJ75PHOZMM/YC\\nO1Xbq7AdsmFsa8RZ6URn1mFIMaAz6zB3MWNMNeKyu7AdtmHPt+N0unDowWTWQ4ULfaKetPFpoMP9\\njDkkLqsLoRfo4/Q4Sh04yhzYj9qRDom9yI7T6qJgdyUV+VZMFkjsEkPaSUnEdI0BAVVbq6jYUEHC\\n4AScVU4OzDxA0qlJZEzMwFnpdD+PlU4cNc+kvcqJsZ2RmDQTmARVZXaodiF1Al28DuECp0NSnW2h\\n4rcK5BE7AsicmknKKUm4LC5KtldQlm8lrmssbbrFYUxy12GOIoe7fjULdGYdlb9XYjtkw5BqQJgE\\n5g5mDGkGrAesuOwuzB3N2IvsVOyvJjbViDSAKc2IIcWAJaea3NUlWPdUY9FJ4tqZ6XZGG4xp7mdB\\nOt31saPEQfX+anddmmig7EAVhzeVI6VEVjgxJxoxHHFgitOjzzLhsLgwJRtIPy2F+H7xWA9ZKd9n\\n4eCaEqzbqtDF6JCJemIyjLTLisdpd18jW7GdpM6xmDPNpI1Pw15op3x9BUezKykqsUKZE5MDOo9M\\no+25bRAmgaPIQeXvlRR8VYgzWUfl+gooctL55k7E9Y3DdsjG0U1lFC0vQVfqwtzBRNrwJHRSENMt\\nxl1flzsoP2zFhgtjsoGEFBNJfeOJ7RWL9aCV4u+Kyfu1BGecjoQuMSR3ikEXp8dSasdaaKe63EF1\\noY20nvHoTDr0TrA6XCQl1Lwb9lWDURDXMxZzJzOWvRbiT4gHHTjLnO663OLEmmvDbnFi7GAioVMM\\nulgdQi+wHrbisrjcdSJgzbeRNMD9rqqt64ROIJ2Syp1VFO2qxOgUxKYbMXc0Y8m1cnB5ETanC1O6\\niYye8cQa9cQPiCe2ZyxCL9x11NZK9Anu+sCYbsRR7KBqj4V9G0so316Fo9qJSDOQ0T2edj0SMCXo\\nKS+1U1lgw+lwkd4+lsQ+cRiSDFTtq6ZkfxWxsXqkxUV1iQNR4cIhJIldYhECLDstJAxJAEAXpwMB\\nlt0W7BYXcb1ikRYX+hgduhgdSLDrQWcUmIw6pF1ibGPEWeGkYF8l+VsrwCWJTzeT0jWWXrd2DXuw\\ng18hJ4R4E3hYSpld8zsQUkp5dTiGNCf1hZyUEsseCyU/lVC1rYrq7Gr3y/WQFSQIk8Ceb8dlcyGt\\nSgQr/gCkFEP3vfB7f7DG+M8nXDBoEySXwqpTwFYzAcz1L8Hln7h/rxsCtz8TfZu9MdjBYcDtoFco\\njmN67oLOObB2GJQnNZ8d6fkQVwUHujafDa2AsYyN6qjVscBzNb/PJHAfuVavaBwVDvLm5ZH7Ui6V\\nmyubZqcDNsNNL7hfkgsvgo/+AgUZjSvrxPVw1dsweBMsOx02DobF46EyIaIm/6HothfSC2DDiWA3\\nhb69cIEMNlRjPVKLQOeCwvTQtw2WkcvhkfuPLd85E9aM8M039Dd45D6IrYbCNPjXHChO0y7zsWlw\\nyq/u39lZcMNLkHnwmIgDGLoezl0M346P2KE0yGUfw9/fBZcOHr1X+zhbHBJO/hV67YJfToU9PSNb\\nfJf98J+noGMufDUB3vtrYJHelIxc7q4XF14EH18OrgDj6GKr3AK9Mc9nqCSVQtujsLd7YJsag84J\\nieVQmhJeOWN+gvsfBl3NK/mv8yC3k/t3x0Mw+mfIawdLxjSubgrFjmmPgdEBiy6AWf+O3r5aI0ab\\n+4O3sE1E1JNqWsXtkfs56WecZc7QN+54CO55HMoT3UKsLAmyu9Hgl/+wNfCUxiDayz+C/Laeae0P\\nuyv1HX1g+wm+27Q/DB9M8k3f3gemPh9+JXfZx3DDy+7fS0fDjAejUwmYrO6y93eFTy/1FbV//hQu\\n+MJd4T31H/j1ZE87jDbIyHc/HI19KV38OdzyvGfa5gFw+39DO49Xvg9XfAjVMW6Bs/HE4LY7dzHc\\n8TQYau7F56bCogsj++KIscA35/umf3Q5vHL9sWWdE96fBO2OHkub91d44xrfbf/2Llzt5bh/cDpM\\nnO/+uKjP1hPgxpdCNFrSKG/aaSvg0fuOLZcluq+LJc4zX4wF2h+Bv81z/5/zL99r1n0P3PgidDkA\\nWwa4RaHD6LvPnrugXZ47T2NezOZqePVa6HrgWNrrV8N7fwu9LE0kvHQDnLDdd9V//+2uw8qS3B+D\\nUufO3zkHDnfQPt5gSSqFCV+5hddXE6Aq3nN9fAW8fRWkFx5Le/Of8O4/ICsbsvZBbke3uF09Aoau\\ng9tmgdkGCy+EZ28l5HtEuNzXM6ez+xkbuMn9/HXJgS8nwH9vd5d54np48k63MAGYdSt8+Sf/z2X7\\nw+7j9PdhLlww8y4YvhaOtIOYakgphX1d4d5H4Uh77bINdvd5OJgJ1bG+69/5h9v2+pz/FcRa4DOv\\nGSonfub7UTZ4A4xcAZZYt9jL7u67j4yj7vtha79jNgz9ze2Q+OEsd5mvXw096kUku+IDyGvvWc7w\\n1XDOd25h3JBgD4Y2BXDeN2CyQXEqLBvlPv/tjsCFi9zewTn/8r3vwkXvcJ8zm8ndElF7DyaVunWB\\n97vy/96Av8+rWxw7Nvw4ckrI4RZyS8xLPJtKk0qhzw7YdgJUxblvhG7ZsPQM2DwQ7CacacXoP5vo\\nU17hpjPY9f6DtD0qaFPo1h157eBAF3ddWJQG54+7hfbtN/lsa/vtZKzTn8BsBZMdik/7ndRHb6pb\\nv/ud6Zh+OIPkUnDqQQqIf/0KYlLz/B7f1p+nEL+xJ/ZNQ7Eb9OR2dG8bU+22yxILCRWQkS+JTzlE\\nx7HvYXS6KFsxHkv/bPqdM9ujvLyll1I270YcJ68la+IsYtNy2f/+XcQuGI/ZCgXpkJ/h1jCV8e7/\\nZUnQsfsyBg9+l/ZJuyg90oviNeNwLroE4dRh+POHdJngOah41YNfY+y0n5OmXI8WFfOmUPztlRzu\\nAFWDdjFi4t3ExRXhcJjY8f2NGOdfSI89IKTbGeMwQN6k74k/9Xsq9/XHMn8SsvMhTG0Oc0jXgT6X\\nPka71B1+z+OSh78jPc+AJdZ9PG4kicYi2nReT8rw77ELI7s2X8yoiXfUbWevTGb7Ax/R/oCZjAL4\\nvZ/7XogZ/AvGuFIc60eQcjgWYYmh/+MXYoir8Nhv9SeTyPvyXxzu6KR02G46DlqMszSNwz//BZtw\\ni8vUYuixB+K7b8I88UP27R/NvooBJPdYx2mnzgJg85IbyP3lMk4d8xhJp37nc3zSJfjtubnsN2QS\\nVwUdT/uEwaN8BVfhlYtpc8R8bLl3Pm1evdzvedPi+09e5mBlX4athb19bPQ8+T36nPgRepO7f6Dc\\nPJDCZx6mQiaTdPanJF00D2d+B8pmPYjhYHukcN+3VXFQmuKkIl5PWpHbYWIzuZ+Lw0OOcMqtV/rs\\ne+s3Uzm89hKq4qDTIeiYsIOMabehj7F45Nu89Hp+OXwxSQn7uOJP12oexyuff0NccQxWs/s57z90\\nLgNHvAWArSSdXS8+y2HZiZIUsBskBpy0La/iRMNahMGBecBv2G3xlCz6BzZLCgYHpJy+iKQps3z2\\n9eOzC3BUJVPeoRCbwUJJbAoxlhiGxywjxVFFwZ4R2Esz6Jbt/pYU0u1wkwIckz4icehSCku6k5CW\\nQ4d2vnWPN9bqRL545yPOmzSZ+MR8yuypzF39JAm7O9N7hxmz1X3+y3vngr4Sw4EuxFWYSSlx6waH\\nAcxWSCqTWMeuoMPN93uUv+PaH7GZBHqnW5vEfT1W047Cny+izeiFDdq765UnSem0FXO/9RRtO42c\\nXy9DCoEt1oHttF+xWuKw7zuBtkdicBigpO9Bzj5nGinJOdgL2lH86FOkP3YduthjY+IqKtJZ/OEz\\nnPfnu4lPzfXYX/FvZ5J6h/uY8tPhaFsoOWUTI/9+yzHb507F/PElANji7BR1sNJu6r0k9mj4/Occ\\nHsqOH26i/apuJAz7idiTl9DuhJ/r1lsrU9jy4kt0WteB9nm4nQoaYn/3t9fSbui3JGbs80h3Okz8\\n8sYczLlpiKxs2vReRbeR73vkKZvxFElLhrGrJ1hO2cCgq2/zWL96wcOk6orodeGx+3X5J7M4/TLP\\nfEfm3oH+iwlUx9S8b3qup8MdtyNqPId7Vv+F/Yuvw2aC8iQb1vhy9HYDPaqLOKnwAPoHpwNgWXwx\\nsc9cD3YTq0+10+nUT+l0gf9gFAX7TyS96waPNGtVMkc/vgnLyrNxppSRetlrxHbZQXK73e7zvnk8\\n63+8DYvJAOjq6taSFPe722QDR4yNlPTd9Jv4KLFtPO+L/H3DyMhaW7dc/vpUjv5yMebJr5E5+kMf\\nG5tUyAkh4nCHITkD9ywJRcBPwFtSSkugbVs6Qgh517k/Mf5b97Iz8xC8fg16czUA28uG0Tdprcc2\\n+TKdDFHgt8wv+BMH6EIXDrBSnka26MbpLOdnRqPHyQdoeNBqOIvvSZcFPML99BK7fNbfwItsox8g\\nmch8buaFkI/ZIfUYxDEP5Pa8QfQNonKvZcPBUzgxc5VH2sq8MawpGImu0MDwbks4IWUzpcUZ7Fs9\\nBAMOTrv005DttJXGYUr2P9j4qx+u4vwz30YrpuL3/7uSLXH9sBvcPQhGu5Zy8mmLQ7ahFsemNAoW\\nDMaYWIX5rIPokyzEZvnExtYk+5uTyTnSh6TKCnoPXU3caQcbbUd92rydQIfPBTu6dCX77BgyL1ob\\nMH/5mwOIn7QNXYx/77NhYxxtfxTk3ua/i8GaD/9OWUwSscl5nDY29Osa92M8/Z5yYu/oYOMbDr/5\\nyr7pRdJ5ns/AprcuIDatlF4X/eyZ+dme5Jd0whXjwtw/n5QLNDxONfR8yIhjayoHO6TjmOU3TjiJ\\n26BcwwleS8d5euIWphJrs1HRRZA9u9QnT/y1vehUWIT+hCK2TZd+I26a7+zFodj2pM9Yprk+5tdY\\nkg7bOHqx/2vX/tVY8rb1xGR3kuoqIv+uIpxZNv8H0Ajafi0o3JFF9dgyjCcWeqwzlELSl/FUppiQ\\nWVXY+lv9llOxuDtla7uRVlZGcuZhrFMj80zU0ulVE7auDvLHuzzS0xYbMdnsHLnQM7/LqkdnDq1V\\npmJeX0r3Z5KZn0/Hzrs4dLtXXeWCva+dRXrWAZLG+9blkSD9mVQ2VQ3l6GVWTuyzPOLlZ17TFl2i\\njQOzShpdRsx6M/L1HlSbTCRVVVF96wHsJ1R75Gk7PYXOq63oHBbK2sCOD/yX53r8BHT3bGu0PbWY\\ntpiwDfB9PhLWQtcHwaE34jDEUpUcT/WFhRRfEtlnCZpQyAkh2gNLgN6447EdAdoDXYEdwBgppX+X\\nUAtHCCGHP/0Fdz+awFcToP2kZzgn9ouo7U/aBcLo/7yXvjaYxPG70XXx/yJt858OWIZYqZoUnJBo\\nKgzl0Olz2P+P5rbETeJ2OHEqOJLhl08azh9NRp0HO2+BvCh0D9NVg6uFdHEKBpcdjn4J7S9pfjt0\\nYbQWAhzeCGu/gYEXQZaG6Mv5CER7yDwjvP0cj7zwClj0cPmfoGuH5rYmdNZlw2fLIdkEd/5FO8+a\\nHTC8T/RtOVoKbZMjX+6RSthTBiPDvD6ProNDh+GG4TCgrXae+QchKx6Gak2yWY/Sakhugvru2t8g\\nzwoLTovePppSyM0FzgUmSilX1Es/DfgM+FZKeVU4hjQnQgg57MXn2dBrIC6jkx84u7lNUkSQg7+D\\n1QE9Bje3JS2TcjskhilmWtJ+FMGTVw2PbIPZQ5pn/98chsw4GBgFAdJUTFwJ86P4olcc30RCyAXb\\nY/084J76Ig5ASrkSuA+YEI4RLYEBu7YzfMcW3jk6pcn3XZjbcJ5g+c83cOtiyG68F/y4I7N/6CJu\\nX6mJVza1xe5qOG9r5tcDbXn9l4ZPzorsjkGVl1+h0QEb2JnXhi83DAzJtpbIf96/rLlNiBgVlhhm\\nzPkPW957hXPvns3NL/yH+cvObFIbzuugLeIqLdr3US2fLz2XdTsGRMmq0GipIs7l8tUGazedwoo1\\n2n0RFU3HNdesY8KEEsaOi0yEjGA9chbgEimlTwcjIcS5wAIpZeAnrwUjhJDffvAl1fYCkjpfFdK2\\nkhiKxRqMYj2JrtDbEyUx2IyfYLZfEDCfy3AHOsfTAfPoYlcidCcghEAgkK48pP1ZnPZQRwj6kpy8\\nE5vtAywWf1PtRgaDYQQuVyEu1x6NtTrM5kuxWj+Oqg2JiXOIjZ2MTmfE4dhNQUGvqO7PG6PxJNLT\\nV1FU9Ces1m811g/Dbg/cFy5YUlJmk5BwEyUld1JR8ZRmnvj4a0hNfY3S0nsoL58ZsLyMjO+R0kZB\\nwQTqj6tPTp5BbOzFHDniXzTGxl5KRsbH5OQkEMlJWDIzD6HTJZGbeyIOh9Z9FRyxsWfTocN3FBXd\\nS0nJY2HbFRs7HoslcJ/N1NQHKC5+KOx9ee73bNq3fw+9PgOdzvdl73SWsmdPmGEwNMjImElc3Gj2\\n7z81YL6uXddgMvXi8OF/UlHxeV26TpdEjx67MBiOtcvl5l5NaWlDYU5Dx2w+Aat1F3Cs/6YQJvr1\\ns7Jv3zgqK30HC4VCx44voNe3IS7uNKqrN2A298fhyMNq/R0p7eTm3uh329jYoXTu/A57947D4Tis\\nmadz57lUVa2isNCz7u/deyM6XRz79l1MdfXvPtuZTD3p1m0BVVUrycnRdmro9Wm0bfsfDh++J4Qj\\nDo/MzGc5ePBWv+vbtp1KYuI5JCefR0nJ5+zd+xfckcTddO36OklJY8nO/gcVFSv8ltMY2rW7HYMh\\njfLyJZSVue8Lo7Ejdruvh0ani6dfv1XExR37CImPF03WtLoB+F1K+VeNde8CA6SUzeScD5/agMC7\\ndk3l0KHZPusNhjTi4nrTtet9OBzlbNt2bCRcVtYMsrIewOWysWpVV2y2I0HvNz5+IN27P0GbNuez\\nbt2plJWt0swzbNgGhNCRl/ce27ZphyAYOPAb2rQJ3PnK5bJy4MAT7Ns3A+/gNQkJQxgyZCV6fQxV\\nVbtZt+5kHI4i9PpkTj31AAaDe5hmQcEitmy5KOhj1GLIkBUUF3/Pvn3HRKFen4DZnEm/fh8Dkg0b\\nxuJwHOv/l5R0GkOGLEcIgdNpITt7GgcPPutRbvfuM+nU6WYKCxexdesVQdmSlnYeAwd+ic12BL0+\\nEYMh0SfPrl03c+iQ9oCSpKRT6Nr1Qc1z73I5+Pln/22Jp512hEOHXmb//hke6cOHbyU+/gRcLgcF\\nBQs4dGg2paXujv19+75N+/aTAcjNfY2dO31HU5544jJSUk5HSokQgkOHXmHXLu2Rv6ecso+YGHfA\\nzurq/axe3R+Xy/2V2L79VWRlTa9bX1y8hI0btb/mMzNvo0ePpxFCV5P3Rw4dehG7vYA2bSbQufPt\\nSClZtiwOKe0+22dkXEa/fh8hhMBiyebXXz3DHpx88m5ycmaRm/uiV/pe9PpEVq7UDvMwYMBC0tPd\\nvdqllOzYcTVHjrylmTcr6yGysu5nz567ycnxFKw6XQwnn7wbs7kT1dUHWbt2EA5HsWY5nTrdTGbm\\nbT7HUEv37k+QkXE5sbHdADSPNzFxOEOHrsLlsrJsWZxPGSec8AEGQxIuVzU2Wx67dt2guS+Atm2v\\npEuXu4iPH4AQwYV4qKjYxM6dN2C3HyUj4zKysh4gO/t+cnI8xX5sbE/6959PQsJAKiq2cPjwqx7P\\nyuDBP5Ca6unl27373xw86Dsq133cIzjppF/rlu32EnJynsJmyyUz83YSEjy9cDZbAdu3T6ao6FvA\\n/0CFIUOWExPTg19+OdbRKyPjMnr1eokNG0ZTVXWs43xKyhgGDfqOoqKv2bHjGuz2fLp0uYfu3d3i\\nPS/vfbZt83kVetCv30ds3ardae6kk9aSmHhSwO3t9mLKy3/DbM6kqOgrjMYMMjIuQ68/5i+R0sXS\\npb7X02TqwGmn5WK3l7B27YlYrfsBPI6hFoslm6NHP8Rs7kjbtn9Fp3MPDKus3MqaNf01bUtP/zP9\\n+n3I1q1/oaBgPgC9e88hNrY7GzeeVS+nnn79PmDrVv8j2jt3vpOcnCf9rh8xYidxce4P6QMHnmbv\\n3v9o5hs92l5nO0BV1S4KChaQkDCI1NRz6uolm63Ab10xalQVen0sOTnPsmfPbZp54uL6MmzYJnQ6\\nY1396g+b7Sjr15+OxbKL5OQzGDz4f+h0viGshGg6Ifc33POW/gi8DxzGPdjhCuBs4O9Syvf9l9Cy\\nqRVya9cOoaLi2FBlnS6eUaPK6m6CWsrLfyM39zXi4nrTqdNUdDW9pcvKVrNt29+wWHxHJ5lMnejT\\n53UcjmKcznLatr3SQzRYrYf45ZdMn+369fuEtm2Pxf9Zs2YwlZWeo0u7d59Jly4aMekCUF29n4qK\\nzaSkjMFg8A0a7HRaqK7eS1xcX5/Kv6joO7Kz78NgSKVXr+eJi+vNwYMvsHv3zR75UlLGkpp6DtnZ\\n0+rSYmN7M2LEdoQQlJQspbo6h/T0i9Dr4wBd3YPhcJRTXv4b4EJKBykpY+vOcy0HDsxk7967AYiJ\\nyWL48N9ryoE9e+70eenU0qvXi3TseH3Ah9Cb3Nw5HDnyNmVlKzEa25GSMobevV/GaAzcK9dqPcwv\\nv/g2S7Zt+1f69XPHEnK57BQWfondnk96+sWYTH56AmsgpaSiYh12eyEpKWM0Kwqr9YjHC6wWg6EN\\nI0fme5wHqzWXkpKlJCYOq6tAa3E6K1m1Kgu7/dho7cTEEaSlnUvnzndq3kfeFBf/wMaNnn1QBw78\\nijZtfOPaWSx7qKz8ndTUs9Dr3bGfysrWsm7dcOCYYAUoLV3Jhg1nIKUDgyGFIUNWEh/vO/KgqmoH\\na9YMQkrP0WcmUweGDduEyZSOlE5KS1ficJRSXb2PysottG9/FcnJp9QrZzeFhV+wZ49noNMhQ1aQ\\nnOxua3PEB9sdAAAgAElEQVQ4ylm+3DOy/hlnOH3qE4Ciov/x+++X43JV06PHk2RmTq1b53I5yM6+\\nh/z8T4mJ6cEJJ8zDbPaMySWlJC/vXbZvn+yR3rv3HNq1+xt6ffg9w6V08ttvw6io2IBOF8+gQV+T\\nkjI65HKs1lxWrermcw1Axxln2IIWm772SazWHITQs2nTeVRWbkYIM0OGLCcpaVhdPru9CIMhpe46\\nOJ2VlJauJC6uLzExnYPaz7Ztf+fo0fc0148aVYlOF8vGjWdTUvKjx7r6wiQS7N59OwcPHpspJSHh\\nRIYNW1/PVhdFRYvR6WJISRkbUp23bdvfycub55M+erStri6224vQ6+PR6Y6FI3I4yiktXU5CwiDM\\n5k7s2/eQx0c7QGbm7fTs6W5hcrnsrF7dh+rqbI88I0bsIC6ut0fahg1nUlLyk0fakCHLSU4eGfRx\\n2e1FHDr0Imlp43E4irHZ8khPvxCDIbnGHis//6z9vGh9mARCSondfhSTqZ3fPE0m5Gp2NgV4CKj/\\nlskDHpBSzgnHiOamVsgtW5aE01lel96//3wyMho3rE5KJ0VF32EyZZCYeFKD6h2guvogq1Z5ViRj\\nxnhen4qKLezefQslJT8SG9uHIUOWBrxJmhK7vZCysjWkpp7t8XWUk/MsBw8+g04XQ58+c0hJidzw\\nveLiH7FaD9KmzQUeoqqiYgtr1/r2yTIa2zJixPYGBVgkWbt2KBUV6z3STj+9TNP7Fy02b76AwsIv\\nPdLatLmIgQMXhFROUdF37N17FzpdDL16vUhiYuiOeJfLxr59MzCZ2tGx43Wa4rMxWCx7KC1dQXLy\\naGJjs/zmKyz8ikOHXiQurh8dOlyNxbKblJSxQQlRLY4e/ZjKys20aXMhSUnDPdZVVe1g//5HEMJM\\nt24zMJs7+S3H5XIgpa3uY6Qx7Nv3CPv23Y/BkMKAAV/UCd2Wxs6d15Ob+0rdsk4Xy+jRkWtOl1JS\\nVbWD2NhuHiIjkixfnorD4dkZedQoS51ollKyc+cUDh9+HYMhjZ49n6nzpkcKl8vG77//mcLCL0lJ\\nGUP//vMjWrd5twKNHFkUcvk2Wz6bNo2nomIdZnMmQ4f+itns+XFbWbmdnTv/hcNRQlbWw2RkXKxZ\\nlpRODh58jiNH3qo5p882qg5qCKezmtzcl2q8we5Wtp49n/P4wIoUTSrkanaoA/pwLI7cDillq+8O\\nLoSQdnspy5d79ro94wxXSF8wkaC09Bdycp7EaGxL1673BfWFqNCmsnI7W7ZchMWysy5t0KD/kZZ2\\nTpPaUVq6kvXr3V+MOl0MJ574s88LP9qUlCxj48YzkfJYn5/apgSFoqmR0kVOztOUlPxMhw7/R0aG\\nb2D1ls6RI/PYvv3vdct9+rxFhw5X+eRzOCrQ6+Oj+i5xuaxRE6yRwmo9gsnUrsnfqS2dJhdyxytC\\nCFlRsZU1a/rVpcXEdOOUU/YG2ErRWnA6LQhh9PASNjVW62HKylaSmDicmJguzWJDefk68vM/JS6u\\nH23bXtGs50OhOB44cmQeRUWLSUs7l3bt/qZEiiJkmrpptRfuUCOnAp2AQ8BK4BEp5e5wjGhuhBCy\\nuHgJGzaMqUtLSjqNoUMjO7pFoVAoFAqFopZICLmgPsmFEGOArwEL8BXuvnHtgAuAvwghxkspl4Zj\\nSHNjs+V7LBuNfiY7VigUCoVCoWghBNu28l9gPXCulLJuRm8hRCLwv5r1w/xs2yqw2z2FnMmkhJxC\\noVAoFIqWTbAzO/QDZtYXcQBSynJgJqAdcKYV4S3klEdOoVAoFApFSydYIXcQ8BcjwIS7v1yrxjvO\\njRJyCoVCoVAoWjrBCrmZwAwhhEfwFyFEJ+BBIPz5aloYBkPkp6hRKBQKhUKhiCTB9pE7A0gC9goh\\nVnFssMMpNb/H1AyIAJBSyshGPWwCkpJGUlZ2bJRqYmKr7vKnUCgUCoXiD0CwU3RlN5jpGFJKqT3J\\nYJSpCZEyFTgT6AKUA2uA+6WUmwJsJ8vLN7Fhwxk4HMV07HgdvXu/3DRGKxQKhUKh+EOiAgJ7IYS4\\nEbgOeBv4DUgG7gJOBEZKKdf72U5KKXG5HNjtBT7zGCoUCoVCoVBEGiXkvBBCpEkpi7zSkoB9wCIp\\n5VV+tpPH03lQKBQKhULR8omEkAt2sEOrwFvE1aSVATtxz0ahUCgUCoVCcdxwXAk5LYQQqcAAYGtz\\n26JQKBQKhUIRSY57IQe8UPP/uWa1QqFQKBQKhSLCtGghJ4Q4SwjhCuLvRz/b3wNcAdwopdzbtNYr\\nFAqFQqFQRJdg48g1FyuAvkHkq/JOEEJcBzwKTJNSvtNQAdOnT6/7PWbMGMaMGRO0kQqFQqFQKBQN\\nsWTJEpYsWRLRMo+rUau1CCH+jjsEydNSyruCyK9GrSoUCoVCoWhSmnTUqhBiihBivRCiSgjh9P4L\\nx4hIIoS4BHgTeC0YEadQKBQKhULRWgmqaVUI8Q9gNvAOMBi3UDICFwL5wHvRMjAUhBCjgfeBDcBc\\nIcTJ9VZbpZQbmscyhUKhUCgUisgTbB+5W4HHgYeBa4CXpJTrakJ7LAEKo2NeyIwFTMBQYLnXuv1A\\ns0wdplAoFAqFQhENgp1rtRy4CPgJsAOnSylX1ay7HHhUStkrmoZGE9VHTqFQKBQKRVPTlH3kLICh\\nRu0cwdOzVQF0DMcIhUKhUCgUCkXoBNu0uhnoDfwPWAZME0JkAw5gOrA9KtYpFAqFQqFQKPwSrJB7\\nDehR8/t+4HuO9UErBy6OsF0KhUKhUCgUigZoVBw5IUQ8cCoQB6yUUhZE2rCmRPWRUygUCoVC0dRE\\noo9csIMdRgPrpJQVGuvigZOklD+HY0hzooScQqFQKBSKpqYpBzv8BPTzs65vzXqFQqFQKBQKRRMS\\nrJALpBbNQIuZ2UGhUCgUCoXij4LfwQ5CiCw8w4wME0IkeGWLBf4POBBxyxQKhUKhUCgUAQk0anUy\\n8CAga/5m4+mZkzXLDuDGaBmoUCgUCoVCodDG72AHIURXIAu3WPsRt1jb6pXNCuyUUhZF0caoowY7\\nKBQKhUKhaGqactTqGcBvWqNWjweUkFMoFAqFQtHUNJmQO95RQk6hUCgUCkVTEwkhF+zMDgghxgHX\\nA32AGK/VUkrZw3crhUKhUCgUCkW0CCr8iBDifOAb3DM59MU9t+oBoDPgAlptMGCFQqFQKBSK1kqw\\nceTuB14Ezq9Zvk9KOQboD+hxizyFQqFQKBQKRRMSrJDrC3yB2/smqWmSlVLuBKbjFnoKhUKhUCgU\\niiYkWCHnApw1IwLygS711uUCqn+cQqFQKBQKRRMTrJDbwTGxtha4VQjRQQiRAdwO7IuCbQqFQqFQ\\nKBSKAAQ7avU9oHfN7weB74GDNctOYFKE7VIoFAqFQqFQNECj4sgJITKB8bhHsX4vpfSe8aFVoeLI\\nKRQKhUKhaGpUQOAIoYScQqFQKBSKpiYSQi7YPnKtEiHEFUIIlxDiQHPbolAoFAqFQhFp/HrkhBC1\\noUaCQkqpj5RRkUAIkYw7cHHtiNsuAfIqj5xCoVAoFIomJdpTdD3EMSEngP8DYnHHk8sD2gN/AizA\\nG+EYESWeAjYAR4CzmtkWhUKhUCgUiojjV8hJKafX/hZC3AfsB86VUlbVS48HvgUcUbQxZIQQI3GP\\npB2EClasUCgUCoXiOCXYPnLXAk/VF3EAUspK4Gngukgb1liEEAbgVeBJKeXe5rZHoVAoFAqFIloE\\nK+TSAZOfdSagTWTMiQh347bpieY2RKFQKBQKhSKaBCvk1gIzhBAd6ycKITrhnmt1TYTtqi3/rJpR\\npw39/ViTvycwDbhRSmmLhk0KhUKhUCgULYVgZ3aYCvwI7BVCrMI92KEdcApQRfRmdlgB9A0iX22T\\n7/PAD8DqmlGrArd3TtQsW6WU1VoFTJ8+ve73mDFjGDNmTOOtVigUCoVCofBiyZIlLFmyJKJlBh0Q\\nWAjRBvg3bvHWATgM/ALMklIWRtSqRiKEyAa64BZw3kjgOSnlvzW2U+FHFAqFQqFQNClqZgcvhBAj\\ngBiv5HuAocClwCGtARBKyCkUCoVCoWhqlJALAiHEW8BZKiCwQqFQKBSKloSaoit4lEpTKBQKhUJx\\n3HHce+SCQXnkFAqFQqFQNDXKI6dQKBQKhULxByYoISeESBZCmKNtjEKhUCgUwWK1WnE4WtQMkQpF\\nk9OgkKuZ8qoQGBd9cxQKhUKhaJjZs2eTkJBA27Zt+d///tfc5igUzUZQfeSEEIeAf0kpv46+SU2P\\n6iOnUCj+SNjtdl566SWKi4u58cYbycjIaG6TQqKyspKEhIS65WHDhrFmTVQmGFIookpT9pGbB1wT\\nzo4UCsUfk7Vr13LZZZdxyy23UFxc3NzmKIDbb7+dW2+9lRkzZnDmmWfS2j5kN23a5LG8du3aZrJE\\noWh+gp2iax8wSQixBliIe1YHjydfSvlmZE1TKBStjWXLllFUVMSECRMwGAzYbDbGjRtXJ+CsViuv\\nvPJKM1upmD17dt3vLVu2sHnzZgYNGtSMFoWGzaam0lYoaglWyL1Y878TcJLGegkoIdcISkpKqKys\\npFOnTmGVU1FRwbvvvktaWhqXX345QoTlqVUoQua///0vd9xxBwAXXHABixYtYsWKFR5euFdffVUJ\\nuRZIUVFRc5sQElpCzuVyodOpQAyKPx7BCrluUbXiD8oPP/zAxIkTKSsr48Ybb+SFF15oVDlSSs49\\n91xWrlwJuJsdHn300UiaqlA0SK2IA/jiiy84cOAA1dXVzWiRIlha24dfWVmZT5rFYiE+Pr4ZrFEo\\nmpegPl+klPsb+ou2occjV199dV2F9OKLL3LgwIFGlbNu3bo6EQfw2GOPRcQ+LaSUra4/jaJ5OHz4\\ncIu4VxwOBytXriQnJ6e5TWkRaHmz7HZ7M1jSeLT6WlZVVTWDJQpF8xOSH1oIMUgIcZMQ4kEhRPua\\ntJ5CiMTomHf8YrVa2b/fU/9+//33jSrr999/j4RJDbJ27Vq6deuG2WzmqaeeapJ9KpqXnJwcJk2a\\nxMUXX+zTwbw+WoItJiYGl8sVVN5o4XK5OPPMMxk5ciR9+vThxx9/bLJ9t1QqKip80iorK5vBkuDI\\nz8/noosuonv37nX1jtZHrxJyij8qwQYENgshPgHWA88DDwAda1Y/CdwbHfOOX5YuXeqTptfrG1WW\\nVjNDNJg2bRr79+/Hbrczbdo0jh492iT7VTQfU6ZM4YMPPmDhwoVcdtllfkWYPyGgFay1KTuq//zz\\nzyxbtgxwN71NnTq1yfbdUtm9e7dPWksWcs8++yyLFi0iOzubO++8k127dlFSUuKTrzV5FS0WC3/+\\n858xmUyMHz+e0tLS5jZJ0YoJ1iP3KHA28HegHVC/Q8U3wLkRtqvVUFVVxTfffMOuXbtC2k7ri1Lr\\nSzkYmkrIfffdd3W/HQ4Hy5cvb5L9KpqPxYsX1/3euXMne/fu1cyndQ/a7XZNIWe1WiNnYAN8++23\\nHstN5b1uyTz33HM+aS1ZyHl3FXn66ac1RVtrmuFh4cKFzJ8/H7vdzrfffsuHH37Y3CYpWjHBCrkr\\ngfuklO8D3sObsoGsSBrVWrDb7QwfPpzzzz+fAQMGhNRso1VxNrYi0hKATdF81Zq+gBWho3UPlZeX\\na+b1J+S07pGm9MipUYy+rFq1yietJQs5b5xOZ6sXclOmTPFYvu6665rJEk9cLhcvv/wyl1xyCW+8\\n8UaL6OOqaJhga7k2wLYAZfwh52H9+OOP2bp1K+B+OXk/nIEoLCz0SWusMNLqh3TLLbc0qixF85OX\\nl8e6detwOp3NaoeW58xfE1BL9ci15nhjNpuNkpKSiL9MzznnHJ+01iTkjEZjqxdyWnV2NLFarVxx\\nxRUYDAbOPPNMv+FmFi9ezA033MCCBQu45ppr+Pnnn5vUTkXjCFbIZQOn+lk3AtgRGXNaF96DE/bs\\n2RP0ttu2+erixgo5rdABs2fPjmjnXy1R0dSV0R+BFStW0KtXL0466STOOeecZj3HWi93rQ8Q0BZM\\nNptN855WQq5hdu7cSe/evUlNTWXSpEkRFXPt27f3SWttQk5LtCkh559vv/2Wjz76CKfTyU8//cQb\\nb7zhk8dqtTJhwgSPtGnTpjWViYowCFbIzQXuFkL8FTDWpEkhxFjgNv6gwYDDib306aef+qRpVURS\\nSl5//XUmT57MV199FdI+nnjiiUbb543Wy1c1rWqTnZ3Na6+9FnCUpz8eeOCBuubLn376iZ9++inS\\n5gWN1odAQUGBZl6te9efR64pRYPFYgkpf3l5OVu2bGn2+He1A4sAPvzww4jOI6r13LY2IdfaPXKh\\n3pfhcs8993gs33nnnT55nn/+eZ801ae0dRCskHsS+Ap4F6gN4LMc+B5YLKWc7W/D45lIB9HU6rvy\\n2Wef8a9//Yu5c+fypz/9iRUrVgRtx8MPPxyxyu14iD3VFOTk5DB48GCuvfbaRk3k7d3P8rPPPouk\\neSERikfOn5DTukea8is/FIGyf/9+BgwYwMCBAxk+fHizjiT0vu61I28jQUNCrrq6mh07doTlzdyz\\nZw+HDh1q9PaBMBgMrVrINcdHgtFobDCPlrhrLee0tSCl5PHHH2fIkCHceuutETu/wQYEdkoprwDO\\nAJ4BXscdhuRMKeVfI2JJKyTSHam//vprH4+Hd/PtTTfdFFKZjQ0y7I2/pjOFJw8//HCdR81ut3Pr\\nrbc2s0X+cTqdzJ07l1dffVXTQ6DlkQtVyGmlf/nll42wtnGEco/OnDmz7nnZsmWLZvNTc2E2R64b\\nciAhl5+fz0knnUTfvn0ZMGBAo6buuvfee+nZsydZWVm88847YdvrTbQ9ctu3b+f555/nt99+i0h5\\n3tQfCd5UNDa0VXN7po83VqxYwbRp09iwYQPPPfcczzzzTETKDUmJSCmXSSnvlVJOkVLeI6X0DYb2\\nByIcj5xWPxWAWbNmeSzXD/kBsGHDBp9tAnWKj1RoEtW0Ghxff/21x3L9GTcaQzTP8dSpU5k8eTLX\\nXXcdEydO9FkfrkfOXx+5pkRr//76m7388ssey7fffntUbGoIrf5Tkfxo1DontSPfP/nkk7oBXLt2\\n7eLJJ58MqezS0tK6cCEOh4OrrroqPGM1MBgMUesjl52dzdChQ7nllls4+eSTWb16ddhleqMVQzTa\\nNPZd1dwDro43vK/9XXfdFZFyQ53ZYawQYpoQ4sWa/2MiYkUrRatyDbZTsr9Kx3sQhL8XZ30CPWz+\\nwkWESkvwyO3du5f77ruPd955p8UOtIi0XdEcGPDSSy/V/V68eDF5eXke67WEnL8v9FA8ck2Jlr2h\\nXKPmsD+U894YtITcl19+icvl4r///a9H+syZM0Mq23u2mmgQzabVGTNm1HmnnU5nVDzq/vqdrVix\\notk/fBThs379evr27UtqaiqvvPKKx7pIdpGojyGYTEKINOATYCzgwt1PLtW9SvwEXC6lDN0H38pJ\\nSkrySauoqCAxseEZy/yJIO8HOZi+DYGE3Pz58xk1alSDZTSElqBoSiFXXV3NiBEj6oRtSUlJiwyx\\nEulQEdESrFqe3by8PNq1a1e3rNW06u9FE0ofuaZESwA5nc6gm5qqqqo0n/NoohUXMpKd4/1dk5kz\\nZxITExNW2U3xgWU0GjVjdkZCyHkHkP7ll1/CLrM+2dnZPq0stZx++umMGjWKpUuXRrz/tYoHFz5H\\njhzBbDaTmpoaMN8DDzzAjh3uQB633XYbV155JcnJyUD04loGW+rzwHDgb0CslDIDiAX+UZPuGyq8\\nGRFCdBRCvCmEOCyEqBZC7BVCPBrp/YQz+svfF3akhdyzzz4blD0N0dxNq4sWLfLwTrbUvmeRfpFp\\nled0OsN+ab311ls+ad7CPJSg1f4C//rL35i+V43Bn5Dzxt91i8ZoTofDwdy5c3n88cc5fPiwz3ot\\nIRfJUEL+ntt33nkn7KY0re1DEREul4tDhw7VCVetbbVmpoDW0TH/wQcfDLh+2bJl/PDDD01kjSJY\\n7rvvPjp06EBmZiYLFy4MmLd+H+Dq6mqPj4NoDaAKVshdANwjpXxfSmkHkFLapZTvAfcBF0bFukYg\\nhOgKrAZ6AjcD5wAPAhF/yrVeEsFU/C6XK2hvlsHQsNO0KfoxaAm5powHFq0RcFJKjh496rcJ7ssv\\nv+SLL74IWqBF+svX+35asWIFHTt2JCYmpm4C8cbQuXNnnzTve7Ihj5zT6eSjjz7itdde4+qrr9bM\\n6080RNrT4Q8tT5bW87Jv3z7N7aMxEftjjz3G5MmTmTZtGqeffrqPPVr3erSbVgF27NgR9oeIlp3B\\n1nU2m41x48aRmZnJgAED2Lt3r2Z5WuIXIiPkjhw5EnYZUkq+/vpr5syZ49O15d13321w++YMOaTw\\npbCwkEcfdfuBqqqqQgr8D57vSX/hm8IlWCHnBPxNJrqjZn1L4VXgIDBGSvlpzQCNd6WUgT+FGoFW\\nJbNkyZJGbVeL9+i0YPq4BRJyHTp0aHD7YGjuptVgmquD4eOPP+biiy/miSeewOFwcMUVV9CuXTu6\\nd+/u03flpptu4oILLuDCCy/kxhtvDKr8SHvkFi1axHvvvVe3fPfdd3P06FGcTid33nmnpmdr06ZN\\njB49mlNOOcXvfLhaLwvvF7zWR0n9PDfccANXXHEF1157raZgCtRHLlxP18aNG/n3v//NO++8E1A8\\nB+ORc7lc9OjRIyp2emOxWDy8Mnv37vW577Q8MpH0fgcqK1zhqnUfBCtC58+fX3fse/fu5Yknngip\\nj29L8chNnz6dCRMmMGXKFAYPHhzyx10wrTCK0HC5XFgslkZ9aG/evNlj+ejRoyFtv2DBgrrf0bpH\\ngxVyC4G/+Fl3BbDAz7omRQjRHRgHPC+ljHpnDa1K67bbbmvUdrXU76PicDgoKSlpsLxAQm7gwIEN\\nbq+FlJIZM2bQq1cv/vrXv2revI0VclJKCgsLQ7qp4+LifNJC9UT+/vvv/OUvf2HhwoXcc8893HLL\\nLXz88ceA+yv/8ssv97Cx/ijGV155JajjjUYfoRtuuKGuAvIWZlpC7ZprrmHZsmX8+uuvjBo1SvNF\\n6j26FoJrWq0vAl577bWAdgfyyIUjGAoLCznllFOYNWsWV111lWYzcS3BeOSuv/56v9tHUsg5HA6P\\nPoi1eIvxdevW+eSJ5EdTICGn1awbClrbB+u5924ynTNnTkij7luKkHvooYfqfmdnZ/Prr7+GtL3J\\nZIq0SZocT/3mcnJy2LJli+YxFRUVMWrUKOLi4hg3bpzmM52Xl8fdd9/NY4895lNnhHue5s+fX/c7\\nWt2RghVyXwBnCyG+EkJcJYQ4r+b/18BZwCIhxJm1f1GxNDhGAhKwCiH+V9M/rkgI8U7NgI2IovUy\\nCuYLMpCQq++R++abb4KyI5CgaWzFvHr1aqZPn87u3bt5//33efHFF33yNKZp1W63YzAYSE9Pp2fP\\nnkHHuSsuLvZJC2ZEb33uu+8+j+X6ozYBtm7dWvcy0Dq27OzsBvcRDSFXVlbmV9BrVTLeQYgnT54c\\n1H68xcILL7zgkyeUl2WgPnLhCLnnn3/eQ5xqNevWEoxHLpAg1Wpubuw1/vHHHzXrB297+vfv75On\\nqTxy4XaX0BKhwXrktO7lpvTIRUIIatXtoY7kvffee/nHP/4Rti0NEcmZf5qTTz75hB49ejBw4EDN\\nZs+33367LgzU999/z/vvv++TZ9y4ccycOZN777036NaXxhCtVqxghdynQGfgPNzTcX1V8398Tfpn\\nwHe4Z3rQHpLTNHQEBPAG7ibf8cCdwAQg4lEY/b2MNm7cGHC7QEKufp84fwEpvftxRCP8iLfo0Yp9\\n1JhKv3fv3nUvwv379/P66683uM17772nGQi5Xbt2mi8OfwQz3UztQ+4digPcwVIbIpyvt0Db+uu7\\n4y0qtF5GtV7HhvB+wWt5YWvzBHOc1dXVfl+O4YzCrB0R1hAul0vzQyYUT26t/Xa7nUsvvZT4+Hj0\\nej1vv/120GXUcumll2qme58LrX6xTeWRCzdcy8MPP+yTFmw9obWfphRy/j56Q7lftK5Tenp6yLa8\\n++67zJkzJ+Tt/KF1boOZYUWrJaSlMXny5Lp7+vXXX/cRzt7xIP/97397LO/atctjOsW33nqLtWvX\\n1i1rXVPv81lQUMDu3bs168Xhw4fX/W5uj9zYBv7OrPmr/R0RhBBnCSFcQfzVjkWvPZ6fpJQ3SymX\\nSClfB24AThJCnBsp28B/s8upp57K3r17/W4X6CVW/waJj4/XzOPdMTsaHrlgKtAFCxZw9OhRdu3a\\nFVQlevPNN/vYrlXxe/PPf/7T77r6zRgNEYwXaPLkyXz44Yce7vBagjnGcDxygcr3N8rTu+IIp1N8\\nMGKhtiIK5uX29NNPs3PnTs114Xjkgg3NUFxcHPRgB3/UHu9PP/3kMW3WP//5T83p8gLh75nyvmZa\\n9jWVRy7U/FLKBkX9xRdfjJSS559/nq5duzJu3DhNT7zWsxPK/RyukPNXZwf74QCRvXahdqoPhL97\\nvvac+1vf2NA7ZWVlPPnkk7z00ktRj27g/YxrhVaqj7c9Ws33f/vb3+rua63WoPr35f33309GRga9\\nevXSDC+SmZnpd9+RItgpupaG8hdB+1YAfYP4q/VD17a1ec5rBf/D7ak70d+Opk+fXvcXzIAF8P8y\\nslgsAefIDFQ51a+M/H0Neb9wG+uRKykp4amnnuLNN99s1MjX0tJS2rVrR+/evRk9enTA49qzZ49m\\nU11DNBSLrHYo+K5duxg4cCBms5n7779fM2+wxzhp0iS6dOmiaUtDhCPkApVvt9uZO3euT7r3vRCM\\np8tfc3akhZzdbteM9wXheeS0hJx3IG3w/5w1xiOn1RwTqVkLvM+Fv1kyIkWkhNz06dOJjY2lf//+\\nmue/lq1btzJv3jxuueUWDhw4wHfffacZPkjruoTi9Q9XyGl54SG086VlQzjN1eH2z7LZbFx//fU+\\nHRbxfcsAACAASURBVPZr2b59O+D/GBtbn51//vncdddd3Hjjjdx8882NKqOxNPR8W61Wj2uiJb52\\n7NhRJ+C06qr6aY888kjA/dWvryIVoN+b6ESnixBSymop5c4g/g7WbNJw25kf6gu5MWPGBLVNoI7Q\\ngTq4BnqJ1b8J/eULRcj588hJKTnzzDO58847ufrqq7nnnnt81ofCL7/8ElC8BtvfzxvvuWb9MXPm\\nTLZs2YLNZuORRx7R/LoO1pMjpdQMjBrMiyKcUDCBXhgrV67U7Ovm/TERzGAbf3OI1t9/Q/Hiwg15\\nE44w0bqOWsGhgxVyCQkJfvdVex60msd2794d0M76BHohtkaP3P79+5kxYwZWq5Vt27bVdcXwN+LS\\nu8/X559/7pNH654IZQqjcIWcv36oBw8e1EzXQuvahWOX9znZuXMns2fP9mgKDMTChQt9ZheoT+0A\\nE3/3RGOe8wMHDnh4q1999dWQywiHYM73qaee2uBAptpzH85IbDh2DqMZrqtFC7lGsAo4Ang3oZ6H\\nexDEGp8twiCQIBsyZEijtqv/4PgLHuj9cAe6cWv7KX322WcIITjvvPM4fPgw69evZ/369XX5vGOS\\nNeZL0Huuyvr4i4fXsWPHgGWef/75Qe3bW5xo9S8JJVp6KLMa1CfUL9j8/HwuueQS+vTpEzB48733\\n3quZ7l0Z1Q9VUp/695U/EVU/3V+lU/sFH+6gjnCEidZ11IqWH6yQC/Syqn22wg0JEeh4vesDLXu0\\nPt4ef/xxTj/9dB566KGAdYDL5eL555/n4osv5u23346IkPOeamj+/Plhz+ShtW0gT583/s7B0qVL\\nOe+887j66qsDDpDy91wE04+3lkgLufrP4a+//kr//v2ZOnUqI0aMaLAJsaCgwGMkvha19YW/Y69v\\n+zPPPEO7du0YOXKk37iLtfuNJFVVVcyePZs5c+YEdX95n2+tWVzWr1/P7NmzAf91Xe1zqVWP1G4T\\nij3BDJZrLMeVkJNSOoG7gQlCiJeFEOcIIW4AXsTdb067naeRhBIPrj6BhFz9m9Bf53rvm8fflC+1\\nfP3113UdrRcvXsy5556r2bz2+eefh1URBzpmf1MipaWFP5hYS3SGO/G4VgXYWI/cJ5984jf/rFmz\\nWLBgATt37mT69OlB21dLsH3N6nsb/PW9rF+ZB/KYFRQUhO2Ri7SQA9/n0V9TWWOEXLhTJoUywCCQ\\nR85ut7N582Y+/vhjpk2bxooVK3jwwQfp1q2b3/po0aJF3HLLLSxcuJB//vOfDQ7GCsZ2rX2FG4Mu\\n3OZjrefzt99+Y8yYMSxevJg333wzYAd/f893/ThgjbEhUh656dOne4yqDzSIKT8/n0GDBjVYfm2o\\nk4am3jtw4AB33HEHR48eZeXKlTz22GN+y/SOBhAuEydOZOrUqUyZMiVgqKBavJ8ffx9hta1Q/oRc\\n7f2sda/XeuODuedr7dHqaxcpjishByClnIu7z9xIYBFwLzCXKMw+EUjIBfJYBOuR8yfkvCu8rKws\\nv+UBXHTRRR7Lmzdv1uzgOXHiRC644AKgcR65QPM0+vPIRSJyvpaLXOtlGO48dw1VyIsXL9a87tdc\\nc43fbR5//PGwbKp/7IHuufqViL8g0cF45MDd8T9cIRfOy82fqPJ+XvxV+qEIuUg1JUfCI2e32xk7\\ndiyDBg1i0qRJHusPHjzo88HgdDp55plnuOSSS8KwHB599FEGDx7MlClT6rpqaF2/rVu3hrWfcJuP\\nvbdft24dw4YN80gLFGrG3zUeN25c0DZ4z9UKkfPILV7sGXjBn/cd3K0j/mbAqE9tR3x/M07UnpN5\\n8+Z5vBMCjajV6rrR2L5+hYWFHufUX7eQ+nhfx4ZmR/L3Hg8k5Gqb/IOJM1lcXExRURHjx49vMG9j\\nOe6EHICU8j0p5SApZayUspOU8lYpZdCKoby8nCuuuIIOHTpw8803az6IUsqoC7lgm1Yb85LJzc3V\\nTP/222/Zt29fox68QIEs/T1MgUbVBmuDVl8lrSaUaHpVJkyYwHnnnae5LpSgpqFSvyIJdtCLv3vz\\njjvuqPsdyDuSmJjYIj1y8+bN81j2N2K2MR65cPtfheKR03rubTYbS5cuDThS1rsf2qxZs3xCLzSG\\nl19+mU2bNjFnzpy64Mta9/Tf/5+9M4/Lotr/+OcACjyKihKguCEq5ZbinokoogahVlqmFpj7jnVR\\nU1Iwy31LsUsmhmVhy81cyCVN1Eq9iHu3LBX1KvDTVHAB2b6/P2DmPsss59lYbN6v1/OCZ+bMmTPz\\nzMz5zPd8z/f72mtW7cfWFjn969mS7QUCAgLE///v//4PkyZNwocffih5H0mFSbLm2lHqY5QsPF9/\\n/TVX/V26dAFgGm5KQD/8jjHC85mI8OWXX+L999+X7Vcsvd+ljlGtLuPzrWYskHtpFdwHpH4DYVib\\nR8gdO3YM7733nl37gcdSyFnLZ599hq1btyIrKwvr1q2TTJlTVFSkKNaU1ilZO/QvQt7JDpY8AJXE\\n5LVr18yuD1AWSnIBLpVuBN6bX2qYeMeOHVzbmoNSAnipTAn62MvRVf8hpSRI9PfPc16V2ltSUlKh\\nPnJy1/ucOXO4Hqz6+1Z7WVAKEG0O5ljk5DqvrVu3mrXP6Ohos8rzIExakvoNrM2HbK1Fzvj+5MlZ\\neu7cOTz33HMIDQ3FuXPnJMsIx5qfnw8vLy98+OGHmDRpEkaOHKnaBrllvCxZskR2ndK1qzQ6ok9B\\nQQFu3Lghe08JzxSpF3FBzKxduxavvPIK5s6dKwpDYyy9f6Qmrem7ifDMdFZ7Vsm1TRh6VRLTvOJs\\n5cqVXOUsRdbmyBhLNKMeIiL58OpVjEmTJhl8nzJlCv74wzDVrNqsFaWLR6nDtWTWqiU3iZKQu3Xr\\nlkUWObljVrrYhUj5UsOevAJV6i2wa9euJsusncov9UD+5Zdf8Mwzz6hum5OTA09PT6v2LwWvRY5X\\nyAm/hdI1lZ+fb7VFbsuWLSYWNF6Urt0dO3Zg2LBhitvrHz/v2721SevNschJlS0oKICPj49VbbAF\\nSkLOXNcF4/u+IjIzvP766waTvqQQjtU4ZuUXX3xhEJZG7vlnzXFt2LBBdjhYqY9xdXXlqv+3335T\\nTONIRLLP523btqFDhw6YN2+euExOzD969IgrX7YQb/Czzz5Dly5dJLe5c+cOnnjiCQDS16H+84FH\\naMk965RmrQKl2Y/MzS5kL5QGj/ugdKanQB0AtQEUoTReW72y7XMA2M+LrxIg9RBXe7Drd3R37tzB\\n1atX0aZNGzg6OnILObl9GD/ojS9mFxcX1fYpDWnOnDnTrNAKAlJZBrZs2aI484yIkJeXhxo1aiAv\\nLw8LFizAlStX8Oabb6JZs2Zc+5USclIWMmuFnPF5JyKMHTuWa9vc3FwTISeXucMc9C1yvCEu1FI0\\nubq6KopoWwg5oPShb4k4URJywjqlc6F/bGr3SUVY5KSGVgsLC+3yImAJhYWFklZ7d3d3s3xeCwsL\\nDSZIlZeQKy4uhqOjI/Ly8lRFHFB6vWRkZKj6s8o95/TbVbt2bVmXGTmISHK0wxYWOeN0flIUFRVJ\\nRiQQns88x6P0PLl37x7++usvNGnSBKdOnRJjDKalpcHf39+kvP7Lq9QMWf376b333lNtm9q9LfeM\\n6Nq1K1e4p/JA9hWKiJoSkS8R+QJ4DcB9AMMAuBJRfQCuAF4FcA+AqY35MUKq0+K1yJ0+fRotW7ZE\\n+/bt0aNHD9UhWZ6hVf30IYDpTcKTVkUpMKElIg4wfbCMGzcOkZGRisMDwP9uzPnz52Px4sX44osv\\nEBwczG22VsqioY+1w4HGHcWtW7e40n4Bpr/ll19+aZC6xVJ4LXK8Qk4op2aRs0VOWakguzzwzPpW\\nuj/1wwCo3cfCuSovi9wff/whmXbu0aNHdsnjawn+/v6SKcrkso/IYXxOymsCjdD58z5fCgoKFGdp\\nCvuWCzml3y5LR08++OADyeVyWBsuR5/r169b7G4jIHfcJ06cgJ+fH3x9fTF48GADf0RAOquG8LKQ\\nl5cnGbh93rx5mDlzJgD1vqykpET13lZav2rVKsVtywteW/hKAIuI6MuyEB8gomIi2gpgCQD5AFiP\\nAdYIuXXr1okPjmPHjiE5OdnqodWkpCSD78Y3CY9Z3R4Rpo3N74JjtBoTJ07EzZs3DWLZ5ebmys6k\\nMkbOqd3S9GRyGHcU5gheY7H9yiuvWG0hBAx/e1sMrfIKOVtY5Hj82aRQ6oCFdinVrZ8hQ+7aEVCy\\nyAnDOzzwWuTkBMOdO3fsnuqIF7l4WOZm6zA+HltY5H7//Xd8++23is83YTjMHCGnlvd0165dqiE8\\neESDFC+88IJkwGtAfijT2old+hjnJhUoKCjgfrmQe57Mnz9fnG2+fft2rrqE60xpNvayZctw5swZ\\n1efU559/brFFrjKhPC/3f7QFINdr/QGgjW2aUzmResDwCjnjYJIffvihGOJDbV9K+3j06JE4LGEs\\nEuRitulja5HDu18p/vWvf0lGVed9C5R7mBmfF1sNrRYVFWHz5s1m+XjZa7IDr5AbN24cnn76afj7\\n+6sOmwLKQyEVLeTkwvIA//uNlYb49OPoqVmLlSx85vymvBY5KUsXUPriZa/0PhXF008/bbWlR5/1\\n69dzxTBr3bq1WfUqWY55BNPs2bMxe/Zss/apz969e2XX6efxtBdycfTGjRvHnQ/2qaeesll7QkJC\\nuMo9/fTTqmXUZlrbShA7OzvbNbMDr5DLAvAySnOWGjMMgHTkzccES5I5y3V0P//8s2K2Av0HvtI+\\n/vrrLzRo0ADFxcUG+2KMyebS1MceQk7fImfuMJBUTk7eoRo5h1NjAS43NZ4Xob4JEyZwxTPSx143\\nsb7gUhJXOTk5eOaZZ3Djxg2rLXJ5eXk2EXKWhptQsvzwCDn9iTD/93//p7gvJYucrYQcryXLnFmh\\ntrD22ptr165ViXZqaFiLLS2kUvAOra4G8AZjbBdjLJIx9lzZ3xQAESgden1skbLIqYWbsHTWqtA5\\nEJFiRyEIMePOkNc3wh5v9/oPZWuHSQAo5m7VR+486bfh0KFDVrdHqM9cEQfYNum5PvrHrraP27dv\\n48svv1Sd7KBWl5qPnFKGD30sfbgpveAIokjJ2qd/znx9fRX3pWaRMxYiZ8+elZzEYs6sVTnMEXLH\\njx/nLquhoVG14bLIEdEaxth9APNRmrdU4BqAsURkTqiSKodxp3bv3j3VdEpKHZ2SZUjYl5o/jNBh\\nGb/Nq804FLCHRU5foNpCyFmLfnuMQ8pYgjU+SvayyJ09exaFhYWoVq0a12967do1u1vkeIcRLMm0\\ncf78eUULliDglIScvnBSu1eEcyUXfLWwsFAMhL1ixQqDILRXrlwRnbF5LHJqQ808OSyFGZm8L0Ea\\nGhpVH+4nKRFtBNCk7NOt7G/Tx13EAf972N+9excbN26UDARpjCDkpGaQJiQkqO6L1wHTeAiJZ8Yq\\nYH8hp+9QXlHoi0ne2aVq9Vk6pGhP/4iFCxcC4PtNi4qKrBZy9+/fVzwPShk+9Ll9+zYGDRoEX19f\\nLF++nGsb43RzxvAIOf3jV/tdBAd64ziSAvqi0DiTQJMmTUSLHc85/+677xTbwuNTKIhC3ueAhoZG\\n1cesV2Iq5RoRHS/7+1g6OEgN+aSkpMDd3R1jxoyRnF1j3HkJHZ2508B5hrYAZYscD/YYWhWE07Fj\\nx7iSG9sbW1sFi4qKLBZk+r+nrcNICIFKeTp6xphJTk597t27hytXrsjOTBTKyAm5NWvWcA+tJiUl\\nYfv27cjIyEB0dLQYKV6OBw8e4OLFi6plANN0Xfro/xbG91n//v0NvhcVFSm+uKldD8LMZp7hbLW4\\ngjxCXXixU8svqU+dOnW4y2poaFQ+uIUcY6wtY+xrxthNxlhR2d8vGWPyYaGrKFL6NCwsTHEb4w5B\\n6KzNeaDq16PWQQhCzFjI8b6J2yOUgdC5y01XtyX6Mw/lsLWQKywstImDvjlBU82Bp6PX6XSKk0gG\\nDhwIX19fvPvuu7Jlrl69KilGU1NTMW3aNEkhx/NCI1gW5eD5PR88eIA7d+7giy++kC2jZJEzvq4u\\nXLhgErdRH32fVimEc610vwnHJRX8VB+e31cQsuaERrFnMm+NyoGvr6/d00Rp8CO8MPIGvVeDS8gx\\nxjoDOAagN4CdAJaV/e0D4ChjrKNNWlOFqVevnsH3a9euYcSIEWan8BCEgtyUb4HVq0tD9xmLAl6L\\nnD0QhBxvgF5rMD7fUthiZqU+N27csNgipx9ehUfI9enTx6z6CwsLuaysPEJfzdB+5MgRzJ0712BZ\\nt27dEBgYCEB6sgOPle6bb75RdOjnefn45JNPVOMX6otxNSHHm0NX7loTBLzShAZByKm9nPAIOWF/\\n5ryoxcbGWhw6SMOQpKQkrlRU5U1aWppN/IQtJSoqCp07d4arq6tZ4iU2NhY+Pj7Q6XTo3bs3fv31\\nV5u0JzU1FZ06dYKrqyuaN2+u6O70xRdfwMHBAQMHDrTJvgEgOTkZRKQ6wsALr0VuEYBzKPWJG0VE\\nbxPRKAC+ZcuVc5f8DRgxYoTB9++++86iyPVCxzB58mTFckK4DkuHVu2B0CFZ4sRuLh4eHqplbG2R\\ny83Ntdgipy+yeIZABw8ebFb9Dx8+lEyjY4ytxO2+ffsMvutbnqXEoqOjo2R0emOk4k2VlJRg4cKF\\n3FamLVu2KK7XFznGvyePpVcfNVcI4f5UegHQj0+oBM/sVuElgfeFo0+fPvD398fRo0e5ymsoI5dO\\nq6KpV68ed9oue0BEiIyMxOuvv869zZIlS7Bq1SrEx8cjLS0Nnp6eCAkJsTj+pEBGRgbCwsLw7LPP\\n4tSpU5g9ezamTp2Kb7/91qTspUuXMHPmTPEl1VaYO1KnBm+P2w2lmR0MXvnLvi8B0N2mraqCNGjQ\\nwCb1qKXwEhAsNjt37jRYXpFOzoJIKI8HGU+nbmshl5eXx9VBRkVFIS4uzmCZvnhQexB17drVbN/K\\nhw8f4qefflItZ68wKPoWHSkx5OTkxPXwunfvnkFQXCJCWFgY3nnnHe62SKW40scci5wawvZyFjBz\\nLHK2uF559qePkD+0U6dOVu/b1jBmv4+1HDp0CN27d4ebmxvq1KmDbt26IT4+Hm+88QYePHgABwcH\\nODo6iv6rhYWFmDVrFho1aoQaNWqga9euBoF+U1NT4eDggF27dqFDhw5wdXVFp06dVK9lgdzcXLz2\\n2mvw8vISrUz6L076Q6txcXFi+xwcHMSP0FagNCtP69at4erqiieffFIcAbKUNWvWYPLkyWjZsqVZ\\n27z99tsYPHgwWrVqhaSkJNy7d8/AQJKbm4tx48bBy8sLtWrVQu/evVV9TT/88EP4+Phg9erV8Pf3\\nx5gxYxAREWEy4aqoqAjDhw/H+++/rxqmyFxsmUIN4BdyapMaHstJD+ZQu3Ztm9XFMywimO+N/R7u\\n3r1rM1FpLoKQKw+LnLe3t2oZewg5HiHUoUMHk7df/baoDa1Wq1bN7Dc2Xr87e6Wb0W+vlBhydHTk\\nHr7Tt0afPHkSu3fvtr6BepjjI6eGsL1ch8sjrHgtcjwIIUp4XjhCQkLQpUsX8fvatWvF/728vHDz\\n5k2bDWU9ThQXF2Pw4MEIDAzE2bNncfz4cURFRSEwMBCrV6+GTqdDdnY2MjMzxZnMkZGROHz4MJKT\\nk3H+/HlERERg4MCBOHv2rEHd0dHRWLZsGU6cOIFmzZohPDyc656dO3cuzp8/j5SUFFy4cAGJiYnw\\n8fGRLBsdHY2srCxkZmYiKysLmzdvRrVq1dCzZ08AwIYNGxATE4OFCxfit99+w4oVK7B06VKDrBmh\\noaFwc3OT/dSqVcvS0wugNA1cVlaWQRYHFxcXBAYG4ueffzZoR1ZWFlJSUnDq1CkEBgYiODgY2dny\\nOQqOHj2Kfv36GSzr378/0tLSDEYs5syZg2bNmqlmf7AEWws53t7iGIA5jLEf9K1yjLEaAGYB+Nvb\\n5XlDLvDAYzqWK3Py5El89913CA8PL/fcjOU5tMozhCzclGpvaLzwWuRKSkpMhJg5FjlLhBzvcENF\\nCjneY9IXpampqdY3zghbW+ROnjwp69NoT4tcTEwMDhw4YNCx7dq1Cy+88ALX72w8iWPy5Mnw8PDA\\nH3/8gcjISHh4eFTKYcKKJjc3Fzk5OXj++efRtGlTABAtTenp6WCMGYwYXLp0CcnJybhy5YqYUmvS\\npEnYt28fEhISsG7dOrHsvHnz0LdvXwClVrGGDRvi888/xxtvvKHYpqtXryIgIAAdO5a6qzdq1Ei2\\nrE6nE0dufv/9d0ybNg3Lly9H7969AZROOlq6dKmYy7RJkyaYNWsW4uPjRT+7jRs3mp1b1xyysrLA\\nGIOXl5fBci8vLzEO64EDB3DmzBncvHlT9MGNi4vD9u3b8emnn5qEA9Kv2zjNl5eXF4qKinDr1i14\\neXlh7969+Prrr3H69Gk7HJ3t+0je3mIOgIMArjDGdgLIBOANIBSADkCQTVtVBbHlD8MzQULO8blG\\njRro378/Tp8+jT///NOmDppqCMJJTewEBQXh4MGDVu2Lx3le6BhtFeU+Ly+Pq4MkIpM3Lv1OWi0t\\nlJqQa9iwIf773/8aLKtMFrmaNWtKrrfEoZ43lIk52NJHLi0tDSdPnpRdz+MjV1JSgpKSErOF3MCB\\nA01m+jZv3lx1fwJvv/22wXfGGIYNG2awrDxeyqoa7u7uiIiIQL9+/RAcHIzg4GAMGTJEVjylp6eD\\niNCqVSuDiUQFBQUGLwCMMXTr1k38XqNGDbRt25bLKjpx4kQMGTIEaWlpCAkJQXh4uKpf1927dzFo\\n0CAMGzYMU6dOBVBq0b127RrGjx+PCRMmiGWLiooMRH39+vVV22Rv0tPT8eDBAxN/6UePHokT7oSR\\nK8YYRo4cyZWL99atWxg1ahSSk5Mr5cQVKXgzOxxnjHUDMA9AfwB1AdwG8COAd4norNL2VYlz586Z\\nvc1PP/0kxouyBTxCTq7jFjqip556yqaJinkQhJz+DE0prDW7A3wWUKFj5HHwf/fdd038sHQ6ncF5\\nzsvLk01qro+UkBPEQ0ZGhklnacyFCxdkhdyAAQPwwQcfmPiaHDlyBO3atcOZM2cU67ZUyEVERCAp\\nKUl2vS0tcvrY0tItYEuLnNxbvwCvz1pRUZHZQs7Z2Rnjx483mHEnHA/P76zfUcthjZBbsWIF3nrr\\nLYu3r8xRShMTEzFjxgzs3r0b27dvR0xMjGykgZKSEjg4OCAtLc3kHrDV5LQBAwbg6tWr+P7777F/\\n/36EhYVh6NChSEyUjtdfXFyMoUOHolGjRgZD6oJ/dkJCArp3l3d9Dw0NxeHDh2XXM8aQm5tr4dGU\\nus4QEbKzs0UrJgBkZ2eLbjUlJSXw9vbGkSNHTGbaC32MvkVNWObt7W0y9JqdnQ0nJyd4eHjgyJEj\\nyMrKQnBwsFivcF6qV6+O8+fPo0WLFhYfmz3gfrIS0RkAQ+zYlkpBTEyM2dt0797dpiE3eFLxyL1x\\nS1lDygulvJT6WOtP+M4773BNCBHaoxaWw8/PD0OHDjURcrVr1zYQcg8fPsRHH32kul9PT09kZWUZ\\nLEtISEBmZibc3d1Vt8/IyJAVPbt27ZLsXLds2cIllCwVcmq/mZqQs9QiZ+0MNSls6SOnhjlCztwZ\\nxY6OjiZWIOF4eIa9eGYxWiPkbH0uKxtt27ZF27ZtER0djdDQUCQlJSEsLMzkd+zQoQOICJmZmejV\\nq5dsfUSEo0ePisO1Dx48wLlz5xAZGcnVnrp162LEiBEYMWIEBgwYgOHDhyMhIUHSH2v69Om4evUq\\njh8/bnBfenp6okGDBvjzzz9NIjHoY++hVV9fX3h7e2Pfvn3icHF+fj4OHz6MFStWAAACAgKQnZ0N\\nxpjsZASpUCfdu3c3Ed179+5Fp06d4OjoiM6dO5v4Ls6dOxd3797F+vXrrZ740KRJE6u2l8KsV2RW\\naltthVKL3F8A/vO4ZXdQS5NjTIMGDcAYs2kcpoyMDNUy+fn5kj5w9hiK4oXXomCNRe7jjz/GqFGj\\nVIPHAqVvqf/9739VhZyzs7Nkp1a7dm1kZmaK33keXI0bN0a/fv0kA9JKZQSRQ0qQu7q6ynasrVu3\\nNsmMcPToUYOhGsBUUDg6OnIJCLXo/7a2yBUWFsLJyQlRUVGyZTp16oStW7fCz8+Pu16hbqC04zQe\\nWrX1rG/hmlmzZo1iOUsscsXFxSb3uyDkeGIK8vwe1rwYVuRLpT3JyMhAQkICBg4cCB8fH1y8eBFn\\nzpzB5MmT0bRpU+Tn5+OHH35Ahw4doNPp0KJFCwwfPhyRkZFYvnw5AgICcPv2bRw8eBB+fn4GoYYW\\nLlwIDw8P1K9fHwsWLICzszNeffVV1TbNnz8fAQEBaN26NQoLC/HNN9/Az89PUsRt2rQJmzZtwu7d\\nu5Gfny8+E2rWrIkaNWogLi4O06ZNQ+3atREaGorCwkKkp6fj+vXrmD17NgDzh1YvXryI+/fv4/r1\\n6ygoKBAtZa1bt4aTkxNu3LiB4OBgLF68WEzDFxUVhUWLFsHf3x8tWrTAwoUL4ebmJp6Pvn37okeP\\nHhg0aBCWLFmCJ598EpmZmdizZw9CQkLQo0cPybZMmDAB8fHxmDFjBsaPH48jR45g8+bNSE5OBlD6\\nDGjVqpXBNnXq1EFxcbFNRrl4hnfNxZzMDmNQ6ht3BqX+cmcB3GCMjbZ5q6yAMVaXMbaGMXaRMfaQ\\nMXaJMbaWMaYeeMwCBNO4LX1JpGbcGHekjx49khxetbdPy4YNGzBr1ixMmjRJ9McRuHDhgmoML8By\\nITdu3DiMHj0aDg4O3ENuq1atUu3U9J1l9TG2QqlZVSIiIpCSkoLq1atbPStJ6kGp/7Iwb948g3Xe\\n3t4moqROnToGwyaA6THwWk3UfEXUfOTMmbUKlGZS+c9//qO6T0siowvnqaioyGBIxtHR0eYvKoBy\\nugAAIABJREFUQg8fPuTyVyssLDRbyNWtW9cqIcczkYExhjZt2pjVLoHHVcjpdDpcuHABL7/8Mvz9\\n/TFq1Ci89tprmDlzJrp3744JEybg1VdfhaenJ5YtWwagNFD1qFGjMGvWLDz11FMIDw/H4cOHDawz\\njDEsXrwYb731Fjp16oSLFy9i165dXMOvzs7OiImJQfv27dGzZ088ePDA4MWRMSb+3ocOHUJ+fj6C\\ngoLQoEED8SNYukaPHo3ExER89tlnaN++PQIDA7FhwwarshCMGTMGAQEBWLNmDTIzMxEQEICAgABx\\n4kJhYSEuXLiAnJwccZuZM2dixowZmDJlCrp06YLs7Gzs3bvX4JmVkpKCPn36YNy4cXjyyScxbNgw\\nXLhwQTFyQ9OmTZGSkoLDhw+jQ4cOWLRoEdauXWt27E5LEWYH2xQiUv0AGAGgBMA+ABEo9ZOLALAX\\nQDGAV3nqKY8PgJ8AZAMYByAQwAQANwH8rLANCaA0lAr3p3Xr1kRE9OWXX5q9rdwnKirKZNknn3xi\\n8N3d3Z2uX79uUq5Tp06kzxtvvGGzdgGgdevWiXXfvXvXojoWLVpk0XYTJkwQ971ixQru7SIiIlTL\\n3Llzx2RZYGAgVa9e3WCZq6ur5PaTJk0yOO9bt2616jxnZ2ebLKtdu7ZY//r16w3WjRs3jpo0aWKw\\n7PLly5SQkGCwLDw83OD7E088wdWeTZs2qZ5jgX/+858m69u1a0ffffedWeegcePGiuufffZZrnu2\\nQ4cOBt9btWpFRET37t0zWK7T6ejgwYNW/W7GnzFjxlBKSopquX/9619m101EJr/vmDFjiIjo2Wef\\n5dqeh7Nnz1p07D/88IPN2vC4c/DgQXJwcKC//vqropuiYQf0r/mCggKTdWSl7uE138wEsIWIQogo\\niYj2lP3tB+BzlIYgqXAYYy1QGpx4LhF9RESHiOifAGIAdC1bLwtZMEosDMnZ0hJm/Dbt7u6OIUMM\\n3RPz8/Ml/YemTZtm8H3OnDk2Dfapbxm0dEaPpT5y+hYEc5zgf/nlF9UyUkOrjDGTt2G54SjjctZY\\n5Hr37i2ZuUL/bdX43N+7d8/E8lOtWjWTdkgNrT733HOqbZKLSaVfj4CtJjtcvXpVcb1Qn5qlwPjt\\nXC6fcfXq1W0ecT0vL88kC4YUL774oskyJUvM/PnzAZi6UqhlmrCENm3aWDTz+3G1yNkLS/ofjaqH\\nrWPIAfxDq/4APpNZ91nZ+sqA0LvnGC0XviseryXpi4SHrS195Ixn+7zyyiuSD+xVq1aZbPvyyy8b\\nfPfz88O///1vrqj/POibny0Vr7aY0m2OkLtw4YJF9aWmppp0pnJDVrYUcu+//77quTUenr53756J\\nz6TUEK+UkONJpm0cz8kYfbEsJeQuXrxo83yewn7UUpMZuyXcuXMH//rXv0yGp52dnVWFnCCgeCko\\nKDCYdSfQuHFj1W2V/PWEWXPGz4XU1FQ8evTI4pzAclgiyjQhZx5KQ91yAXhr1aqFxYsXl2MrNazB\\n1i+KYr2c5e4BMH0aldKwbH2FQ0TnGWOpAN5hjF0C8BuA1gDeAZBCRL8rbW9JAF1bWOSeeOIJ3Lx5\\nU/xuHCNOsBToO6aXlJRIdmByPj5qvj9NmjTBlStXFMskJCTYZCaapQ94fbFk67AUcr8fb3gAY5Fi\\nzQ1rPEFBCmMxLJUHllfI8Qjrtm3bKq7X92eT+n1zc3Nt/hCrV68eAIiz2uRo0aIFHBwcxJnOf/31\\nF1566SWTcjxCrl+/fti5cyd3kOmvvvoKX331lcGyadOmmaTWk6JBgwayoYiE69/49xUCw/LGFeTF\\nkhcTTcjx06tXL0VDgtIs0bp169qrWRo2Rj+Tii3hVR/fA3ifMWbgpccY6w5gYdn6ykIYgD8A/Bul\\nAvMogIvgCJ1iyXCELYSc8QwZY6uPIMKsccRWEz5CQEgpXnrpJRARxo0bZ/H+9bH0Aa8vOOwRX0wK\\nXiFn/BC2pONzcnIymBYvzBATECKtA9JDq8YvItWqVTM5T8ZCzsHBgUvIMcYUA4zqx7Xz95c20Nva\\nIidYrNTui4KCAq60dc7Ozqq/d/Xq1SVFoDl4e3tzXR+enp6K7QCkz+mvv/7KNfPdHCy5nisy7/Pj\\nRv369dGsWTPJj9qMco3Kg72iSpjjI5cD4CBj7Cpj7Bhj7AqAIwByy9bbHMZYMGOshONzQG+zjwF0\\nxf8mO4wH0BnAN2r7s0TICRkKrBFygmVBwFjICQ9taywaasKHJzioFEOHDjV7G0sf8PYScnJWxi5d\\nunALOWMrqjkd308//YQ9e/bg7Nmz4tR7ABg5cqTYturVqxsM6/EKOR6LnJqw7ty5MwAohvkQUvcA\\n8sOGthZygguC2sPR19dXNUg1UHqO1SzOzs7OVsdBdHNz47qXlfajJOTsgSX3G0+cOg2NvxNyIVGs\\nhTezQxZjrD2ANwD0RGkcuQwAqQA+ISLb2vH/x08AnuQo9xAAGGNhAIYB6ENEB8vWHWGMXQawlzEW\\nTkQ7pCqIjY3lmrJvjNCBW/pAbdWqlclDUs4iZ02kbLUHsZK4Ugq+++STPD+PIZb6j+lbQqTq6Nat\\nG44eNT/t79atWyWXz549m8t/DDAV2eaIbm9vb0mH/datW+PMmTM4cuQInn32WYMyxkIuJyfHxCro\\n5ORkcp7++OMPg++FhYWqLyFCCBOlY+KJdG7roVXBD0yt3saNG8PV1VU2rZ2As7Oz6kuGs7Oz1W/V\\nNWvW5DoXSpYWc4Vcjx49rPKTtUSUVWRMSw2NysiUKVNw8OBBq1NUGmNOZoeHANaVfcoFIsoHoO6p\\n/j/aoHSKr7EDizDl6ikAskIuIyODu+MWEPwTLLXITZkyBceOHTNYJmeRU0NIeiyFUh1OTk6KjrZK\\nlkpLzPqWCLnx48eLEc8B6Q7MUqEQGhoKoHRSiSDqGjRogPDwcIOE1koYJ7U25xj1j8sYYfjEGGMh\\nd/v2bZP9M8ZU26E2MxQAunbtCkBZNPCce1tbj4QXDLV4aE5OTnB3dzfwQ5WCR6RVr17d6sjubm5u\\nXBZCpSwg5go5a/3VLBFy9pidp6FRVXFxcYGXlxe8vLwQFBQkLo+Li7O67sctI7KQF8k43obgPX5d\\naWNLJjsIkectFXJ16tQxEVl37twx+M47FKl0QSh1UML+J06cKLleKTyFJULOEsFlLLClOm/eWcfJ\\nycmoWbMm3N3dsWPHDrGuDz74ABEREQgPD8e2bdvg5OSk2tbatWtj3rx5JhG/zenELLl2jIcA5Xz0\\nbDkErSQaeI7X1hY5noC2wn55hkOrVaumKuTq1aun+MLEQ82aNVUnFgG2tchZO0nJEusaYwyTJ08W\\nv2tDrRp/ZywZveKFqwdhjFVnjM1njP1Wli2h2OhjXkhy+/EvlGaf+JQxNoExFsQYmwggCcAVAN8q\\nbWyJj5zgD2SpkGvUqJFJZ2sc4V14m1YTTUo53JQ6dGHde++9h3HjxhnMgvL19VXM9WfJjClz39Sl\\n4rlJxVzijYz/yiuvIDc3F7dv38bzzz8vLvf09MQnn3yC7du3i35hSuKjfv36uHv3rqSAttc0cwEH\\nBwdFK4vcrEZz0Y9faE+L3Jw5c8xrmBlUq1aNS8gxxlQt125ubmCMYfz48Ra3h1dUKbVZ+F15nzvW\\nTjyQ28+4cePQr18/2e1iY2Px2muvoWfPniazdzU0/k5YmueaB171sQylITz+ALAawAKjz7t2aZ2Z\\nENE9lE50+B5ANIAUAP8A8B2AZ9R8+SyxyAkdmKXDRs8884zq267w4FdLIcIj1qQQOgV3d3ckJCTg\\nr7/+wp9//ont27fj5MmTih1PeQyt6nQ6E+uLlN8ej5Br3749APOsOXIoWRjKY1hJKdWZsH/eduze\\nvdtkWd26dbFkyRLxu9K5MF5nfD/odDrZ7du0aaMaQsQanJycDIYy5NBPYySF/jHFx8dL5tPlgVfI\\nKVmYzY1faQ9/NScnJyQkJGDPnj2y59fDwwObN2/GoUOH8PzzzyuKPg374evra7bbkIZtqQxCbgiA\\n+UQUTkRziCjO+GO3FpoJEV0norFE5EdEurK/E4goU21bNYuclEO38LC11ALDkzdUsLyovVVbKuSk\\n1vn5+SE8PFzVklEeQk6qE5IScjxDq+b+TuaIF314j9Eac7uQp1Bp/7xDq/369cOsWbPQuHFjhISE\\n4JtvvsF//vMfA/88c4ZWN2/ebPB92bJlstsnJyerWpakYiYKbg1qODs7Y8qUKarl1MS9fhsdHR0x\\nbNgwrv0bwyvkwsLCZNcJLxG8Qs54Zrwt0N+38W+RlJQkuU1iYqLN21GZSEpKsknAc1uTlpZmMLO8\\nvImKikLnzp3h6upqVs7W2NhY+Pj4QKfToXfv3vj1119t0p7U1FR06tQJrq6uaN68ORISEgzWf/31\\n1+jcuTPc3d1Rs2ZNdOjQweSZZi6WGIp44RVyNQGo5zmq4hif6K5du6JDhw4ASjvE+Ph4k22EhzuP\\nM/Gzzz5r8L1v375i3UoID361UBhK4kGpo7TGj6pdu3Zmb1OtWjWzBKCUYJI6Vh6LnLkiUkmsKQlH\\nXsG4YMECs9rDi+BMz3u8QsLuK1euYO/evXjxxRdN4piZM7Q6ZMgQDB48GIwxBAcHY/jw4ZLb+/v7\\no3Xr1qrtGzVqFM6fPy9+HzdunMn9JEeTJk1Qu3ZtjB07lqu8HDzDmDzCikfI9ejRQ3EmsLkWuenT\\npxu039wMFVLo7zs0NBRvvvkmWrRogUmTJuHVV1+V3MbHx0e0ij+OEBG3tb88qVevXoX6KBIRIiMj\\n8frrr3Nvs2TJEqxatQrx8fFIS0uDp6cnQkJCJFNTmkNGRgbCwsLw7LPP4tSpU5g9ezamTp2Kb7/9\\nn+eVh4cH3nnnHRw7dgxnz57FqFGjMHr0aMmRC17sKeR4E9F/BiDW2sSulfWDsuTNBw4cMEhu26tX\\nL8rPz6c9e/bQhQsXiIgoKCjIoMyNGzeIiOjixYuqCaIPHz5M7u7u4vdt27YREdF7772nuF1aWhoR\\nEb3zzjuK5fLz80kJue1atmypuJ0ahw4dMiuZ9q1bt+irr74iR0dHrvJ16tQx2WdeXh7VqlVLLDNs\\n2DDy9/dXrat3795mHdvw4cNl62rSpInsdjdu3OA6tqNHj5p7ukWU6vXx8SEi9evymWee4d7f3Llz\\nZes5e/as5DYlJSXi/5cuXTLZbtmyZUREtG3bNq7k6oWFhfTw4UOzzoXQhmvXrnFdG3Lra9Wqpbrf\\nOnXqqP7md+7cUS0zbtw4IiL66KOPJNffvXuXiIiOHTvGdZ0REW3dupV69uxJ48aNo5ycHO7fXe5Y\\nq1evbnYdREQ9evQw+V0l9xcLu32sJTU1lbp160Y1a9ak2rVrU9euXWndunXEGCMHBwfxb1xcHBER\\nFRQU0MyZM6lhw4ak0+moS5cutGfPHrG+gwcPEmOMdu7cSe3btycXFxfq2LEjnThxgqs9OTk5NHLk\\nSPL09CQXFxfy8/OjNWvWiOubNm1KK1asICKi2NhYg3YKH6GtRESJiYnUqlUrcnFxIX9/f1q1apXV\\n54yIaPny5eTr68tVtn79+rRo0SLxe15eHrm5udFHH30kLsvJyaGxY8eSp6cnubm5UVBQkNhfyjFz\\n5kyTPm/MmDGqz8KAgACaM2cOV9uNAUDu7u6y68hKDSP7iskYayZ8AKwF8CpjbB5jrJP+Or0yVR6p\\nFEfOzs7o16+f+HYcExMjDjfOnTsX9evXB8CXP7Rhw4Y4deoUVq5ciR9//FEM/so7tCqVSF0fS/2y\\nrJ3Z2LNnT/VCejg5OWHIkCE4f/68SfYCKaTif7m4uOCLL75Ap06dEBYWhsWLF3NZ5KTyXqq1VQ4l\\nixzvb2FNSI4VK1bIrrt+/TpXOxYtWsS9P0uGmfWtE1LHaomFlDdIs3Eb1CwSapYUnt+KxzLPY5ET\\njnHMmDGKdfBYCYWZoy+//DIOHTqEhIQERf9KXiyZHAbYfyKQvSkuLsbgwYMRGBiIs2fP4vjx44iK\\nikJgYCBWr14NnU6H7OxsZGZm4h//+AcAIDIyEocPH0ZycjLOnz+PiIgIDBw4EGfPnjWoOzo6GsuW\\nLcOJEyfQrFkzhIeHc/lWzZ07F+fPn0dKSgouXLiAxMRE+Pj4SJaNjo5GVlYWMjMzkZWVhc2bN6Na\\ntWric3zDhg2IiYnBwoUL8dtvv2HFihVYunQp1q9fL9Yhl/tVPwesNVy+fBlZWVkICQkRl7m4uCAw\\nMBA///yzQTuysrKQkpKCU6dOITAwEMHBwcjOzpat++jRoya+mv3790daWprsM33//v24cOECevXq\\nZfExWXq/8KB0R/2J0rcmAQYgFsB8mfLlE2LcjkglHTcmODgYN27cQH5+vsGMTZ4HuE6ng6enJ2bM\\nmGGwXM0RWahbyV/NycnJ4pmz5ZXuSkDovP39/REcHGyS9Fk/LyYgP2QaGhoqxoADIJuLUB+esA/6\\nKHXeSsKRt7OyZrjDOOSJPrzD9movB/pYG35E6joXtrNXmqFRo0Yp7l8fQciNGzcOH330kcl6nvuL\\n53fnOVeCPyxjDA0bNsR///tfyf3wiMvly5erlilPqrqQy83NRU5ODp5//nkxBqSQoi49PR2MMTzx\\nxBNi+UuXLiE5ORlXrlwRXyQnTZqEffv2ISEhwSBW5bx588R7d9OmTWjYsCE+//xzkziVxgg5doVJ\\nQ40aNZItq9PpxOvr999/x7Rp07B8+XIxrM7ChQuxdOlSMSVgkyZNMGvWLMTHx4t+dkq5X21BVlYW\\nGGPw8vIyWO7l5SX6Bh84cABnzpzBzZs3xXs7Li4O27dvx6effiqKaKm69QWiUG9RURFu3bol7jM3\\nNxc+Pj549OgRnJycEB8fb9VkHSESgj1QuqNGKax7LDFWzHIPXP0bQYCnQ5azJKh1toK1T6kjsmaW\\nZHkH7tTfnxCdX5/atWubxNLjYeDAgfjnP/+pWKZ///5m1WmpRY7XamRNwmulXJx9+vQBoP6CYc5v\\nb234ESmHe0E89ezZU1KwWMP06dMRGxsrfud9YVmxYgXc3d0NZuwCfKLJVv5R+ve60rlVa9O7775r\\nN98oS536yyutmL1wd3dHREQE+vXrh+DgYAQHB2PIkCGy4ik9PR1EhFatWhmETSooKBDvU6D02unW\\nrZv4vUaNGmjbti2Xg//EiRMxZMgQpKWlISQkBOHh4Yq5kYFSP9pBgwZh2LBhYq7tW7du4dq1axg/\\nfrxB2saioiKDa1sYiapI0tPT8eDBA5OX0UePHuHSpUsA/neNMsYwcuRIA6uiGm5ubjh9+jTu37+P\\n/fv3Y8aMGWjatKnFcSTXrFlj0XY8yD4hiEh62tFjDI9FTg6eB7ilQk4YRlF6IFtjVStvi5x+xyT1\\nVlerVi2LhFxUVBQ2b96Mhw/lo8wo5QuVwlIhxxPuISgoiCuZuxxKHalgEdDpdCYWTn1sJeR4LGpS\\n5zInJwdAqbXrwIEDWLp0KT7++GPuNsnh6emJ1atXGyzjPdaaNWti8eLFFgk5NYT4c5GRkfjkk09k\\ny+nfk0rtVmsT74QQHjZu3IjRo0eL3/fs2WNRPbwWOZpP6oUqiMTERMyYMQO7d+/G9u3bERMTg23b\\ntkmWLSkpgYODA9LS0kyO3Vw3ATkGDBiAq1ev4vvvv8f+/fsRFhaGoUOHys4SLi4uxtChQ9GoUSMx\\nBZ/QVgBISEhA9+7dZfcXGhqKw4cPy65njFmVUtLb2xtEhOzsbAN3mOzsbHh7e4tt9fb2xpEjR0zi\\nigpDu6dPnzZZ5u3tbTL0mp2dDScnJwNRyBgTZ9i2a9cOv/76K95//32LhZwlEwN5edwyO1gFr0XO\\nUuQeYGqdvvCwtlbIyZmay9sipy96/f39TdZbGoXe398faWlpkqEqBMx9cFoq5AAYdHpS7NghmS2O\\nGyVrmxComjHGFTiYB6VzYWkief1UVS1atMCGDRtMyqjFT5RCSriqDY2aE35EqY6lS5fKrn/nnXcA\\nlPraKqF/Tyrd92pCzlJ3CyneeOMN/Pjjj5g+fTouXbqk2NErUdUtcgJt27ZFdHQ0fvzxR/Tq1QtJ\\nSUmoXr26yXOhQ4cOICJkZmaKKfeEj75li4gMckU/ePAA586dQ6tWrbjaU7duXYwYMQKJiYnYuHEj\\nNm/eLDtTcvr06bh69Sq+/vprg9/D09MTDRo0wJ9//mnSVv2wIRs3bsTp06dlP6dOneJqsxy+vr7w\\n9vbGvn37xGX5+fk4fPiwmHg+ICAA2dnZouDS/wiCTGpZ9+7dDeoFgL1796JTp06K12ZJSYnkCFJl\\nQPbJzBhLBPAuEV0u+18JIiLlXqsKYI1FDii1CBlbAQTklgOlY/Y8WCvk5s+fDyJSdJIvb9q2bYu+\\nffvihx9+AAB8/PHHkmFeeHnqqafw1FNPyaYbM3eYSUm8GOfENaZ58+ay6y5fvmx1/ksli5wQNkco\\nJ/d2bAuLnH7no8aAAQMMpvDzDHUb+8nwIGeBtAZeUaT0xi5cf2qWYf37WSl+pFqbbC2agoKCuIIr\\nK1HVfeQyMjKQkJCAgQMHwsfHBxcvXsSZM2cwefJkNG3aFPn5+fjhhx/QoUMH6HQ6tGjRAsOHD0dk\\nZCSWL1+OgIAA3L59GwcPHoSfn5/Bi8rChQvh4eGB+vXrY8GCBXB2dpYN5aLP/PnzERAQgNatW6Ow\\nsBDffPMN/Pz8JO/vTZs2YdOmTdi9ezfy8/PFyRQ1a9ZEjRo1EBcXh2nTpqF27doIDQ1FYWEh0tPT\\ncf36dXFymrlDqxcvXsT9+/dx/fp1FBQUiJay1q1bw8nJCTdu3BD9pYVJgFFRUVi0aBH8/f3RokUL\\nLFy4EG5ubuL56Nu3L3r06IFBgwZhyZIlePLJJ5GZmYk9e/YgJCREFHzGTJgwAfHx8ZgxYwbGjx+P\\nI0eOYPPmzUhOThbLvP/+++jatSuaNWuGR48eYdeuXfjss8+4c2+XO3LTWQFcBvB02f8ZZd/lPpes\\nnT5bkR+UTYP/8MMPJUMA8FJUVEQrV65UDJ8gxcaNG2XDBjDGxHK//PKLbLmmTZtyt9N426CgILOO\\nk6dO4ePm5mbwvW7duibbFhQU0M6dO+nf//43ERF17drVrPNnTntSU1PNqic6Olo1rIMcctfC66+/\\nbvbxSFFcXCzbruLiYrGcUlgWIYwFD1LhbyZOnGhWm1NSUsjZ2ZkAUN++fQ3CkwgY72Py5Mmq9Rpv\\nIxWyRqqc/mfAgAGKZaXusVmzZhmUSUxMpDNnzsjuIzc3l6st69evF8v17t1b9rr7888/Fev55Zdf\\nVM9deTNkyBCL7+vKQHZ2Nr344ovUsGFDcnFxoSZNmtDs2bOpqKiIiIgmTZpEHh4eBuFHioqKKC4u\\njvz8/MjZ2Znq169PgwYNovT0dCIqDT/i4OBAO3bsoHbt2pkdfuS9996jNm3aUI0aNahevXoUFhZG\\nv/32m7je19eXVq5cSUREkZGR5ODgYPLRDz+SnJxMHTt2JFdXV6pbty717NmTtm7davE5CwoKktzn\\nlStXiIgoIyODHBwcKCkpyWC7uLg4atCgAbm6ulJQUBCdP3/eYP39+/cpKiqKGjVqRM7OztS4cWN6\\n9dVX6dKlS4rtOXToEHXs2JFcXFyoWbNmBiFNiIjefvttatmyJel0OqpXrx716NHDquNXutbL1lmn\\nYayt4HH4CCf5gw8+MHgITpkyRfbky1FUVGTyMPXy8lLcJjMzU/ZBHB0dLZY7efKkbDlzYsEZbxsY\\nGGj2carVKXzS09PJw8ND/D5jxgzVuuwp5I4dO2ZWPW+//bZsXUuWLFHcNj4+XnI7c18QlJCq39nZ\\n2aBMQECA7DE8ePCAe1+DBw822X7v3r1mtzkjI4N+/vlnA7GpdEz/+Mc/VOts1qyZwTZ9+vThqlv/\\nM2jQIMWyfn5+JvVdv36d2rRpQ0Bp3MkHDx7QhQsXZPeRl5cnbqsUP3LXrl1iuQkTJsjeD5cvX1Y8\\nJnOv9/Jg2LBhVVrI2QNByP31118V3RQNO2BvIaf5yOkhFUfOXKSGMpRi2gDKISD0neGVfOmsmbBg\\nj2EoAOLwwo8//oioqCisXbtW0X9IwHi2lTkpXdSwpY+cWpRyud+k9N61H8ZDcUo+h+YMrb7yyitW\\nbS/QpEkTdO/eXXZY0HgoKSIiQrVO4yEP45A2PKj5rUn9bg0aNMCJEyeQnZ2N/fv3Q6fTcc8unzVr\\nFtasWSP6M+rz3HPPif8bh57Qd41QGzqtjP5olbFNlQF7Pxc0Hl+UAgI3NudTno22F/ae7CCHUpBT\\nfZ8ue81atYeQc3JyQnBwMIDSpOirVq3ClClTuPxj3nrrLQPxoTR5wVxs6SMnzJ6SQ+43UfOtM4f3\\n33/fZJnxtaQk5MzxV5LyZ1OaIWwp0dHR4gvM9OnT0aZNG9VtBgwYgE8++QSvv/66mCeRlxo1aiAq\\nKkqMwSWH3H1SvXp1eHp6igJFyfdRX8Q4Ojpi2rRpuHLlCvLy8rBo0SLMmTNHjKEl0KlTJ6xYsQIB\\nAQGYMGGCQViI8vaRswVV3UfOXihNtpELwFurVi2LXlo0Hi+U7qgMlJq/eal8TwwzsXaygzVUq1ZN\\nMhSH/tt9VRJySg7aanh5eeHkyZP47rvv0KVLF9V4SFLExsYaxBATMFfIyXWEPBkp5DrZoUOHmtUG\\nJaRiyfEKuWrVqpkV98zd3d28xllIhw4dRHHDG6uMMYaIiAgu653xdlKZQ6TgvU8sCW7s4uIie00x\\nxvDmm2/izTffNFnn5uamGF5GE3JVg169einOglcKwGtNLEqNxwOlO+oNmCfkqjzGyXgtDaQ5evRo\\nbNy40axt5Kx/vELOGuuhPYSctXW2aNFCNlwKD5MmTcLKlStNZmvaamh14cKFFrUrODjYonAackj9\\n7sbHKCeqLRH/r732Gj799FMApSJCP6CpLXFycrI44Kw5mDOcxXtN2zLkhxq1atXC0KG3+xNLAAAg\\nAElEQVRDsXXr1gpvCy+VUVxWdipDAF6NyotSQOBPyrEdlQIhOKmApWmDunbtahchpyRCKptFjtfK\\nYS+eeOIJ7N+/32SIzRZDq2fOnOHqjKREwr59+2wW/R+Qbp+xj5ZcWy0R/4sXL0ZeXh4yMzMxb948\\nu2UNKC+ksk3Yi4SEBLvUu2XLFrz++usICwszWVcZRZNmkdPQsC1mva4xxhwYY20YY70YY5ZFba3E\\nGAs5S4OcjhgxwqCD4Ik9I9ep6icfttdkB1sEOXz55ZcNvo8YMcLqOq1FqhOzhZCzxvppSxEHlL+Q\\na9CgAb766iscOXLEqryDlQX9lEhqmCNAWrRoYfD9hRdewLhx47i3NwdHR0eEhoYiICBAcl1lozK2\\nSUOjKsMt5BhjkwFkATgD4AAA/7Ll2xhj0+zTvPLFVkJOp9Ph+PHjiImJwaeffiomGlZCrlPVH15S\\nEgEVbZFbsWKFaDF0cHCwW6dlDlLHZa41QKo877nWTy1jL6TaZyxW5TrO8k7NVhlR8ksyntxhjm+j\\n8T1vi7RjaqSnp5ssq4yiSbPIaWjYFi4hxxgbC2ANgG0AXgagrygOA3jJ9k0rf4yHA62JvN+sWTO8\\n++67GDlyJJcVRq4MrwXJHOuKcWL56Oho7m3laNiwIU6fPo3ly5fjyJEjFk1QsDVFRUVW12GNkAsM\\nDDRIQSaXbcIaytsi97ih9BKzePFi0b/Qw8PDLJ/NqKgobN++HYsXL0Z2dnaFOaRXRh85TchpaNgW\\n3jvqTQAriGgWY8y4V/gNgPVKoBJgHErB0pyfliAn5Iwfel9//TWGDBliUs4c60pERAR27tyJ77//\\nHgMGDMBLL9lGh7do0QJvvfWWTeqyBe3atYNOpxN/1/DwcLPrsEbIOTo6Yt++fVi7di3q1auHqKgo\\ns/evhlRbjNusWeTkUbLItW/fHqdPn8bJkycRGBgoOUNYifDwcIuuOVtSGS1ytkoUr6GhUQqvkPMF\\nsEdm3QMAls0KqGQYz1qtjELuxRdfxNSpU7F27VqD5eZ0yi4uLtixYweIyOY+W5UJV1dXbN68GTEx\\nMfD09MTy5cvNrsMaIQcAjRo14gqCbClS1+iuXbsMvstZZWxhsazqqLkVNG/eXDFnbmWnMgo5a3MM\\na5iPr68vpk6dKhnCRqPqw2t3vwWgqcw6fwDXbdKaCsbYImdNLDRz4RVyjDEsWrTIpJwl1pXHWcQJ\\nvPTSS/jPf/6D1NRUtGzZ0uzteXzQKhKpa9RYnMh15pcuXbJLmyozAwcONPhubty5qoalfr72pDzC\\nylQUSUlJlfL40tLSuHy17UVUVBQ6d+4MV1dXszL1xMbGwsfHBzqdDr1798avv/5qk/akpqaiU6dO\\ncHV1RfPmzU1mlH/88ccIDAxE3bp14e7ujj59+uCnn36yyb7tAa+Q2wlgHmNM/xcgxpgHgBko9Z2z\\nK4yxNxlj2xljNxhjJYyxeQplxzLG/sMYy2eM/cYYG8+zj6pgkZNbpg2T2QepECJKs4fLm6eeekq1\\nTGW0ylQUixcvFjNydOnSRTLt2ONEeT7DeHmcLXKVdZSjXr16FfoCSkSIjIxUTWuoz5IlS7Bq1SrE\\nx8cjLS0Nnp6eCAkJMemnzSUjIwNhYWF49tlncerUKcyePRtTp07Ft99+K5ZJTU3FsGHD8OOPP+L4\\n8ePw9/dH//79cfHiRav2bTd4ErIC8ADwO4CHAH4EUIzSSQ43AZwHUNvapK8cbfgVwC8A4sv2P0+m\\n3Niy9QsA9Cr7WwxgvELdRESk0+kMEk7n5uaq5cK1GU8++aRk0utr166ZlC0sLDQpx5OMXsN8NmzY\\nIJuwvLJg3L5u3boZrJ81a5ZsUvW/I3fu3KFz585RQUFBRTfFpnTv3t3gt23VqlVFN0mSbdu2Vfnr\\nLzU1lbp160Y1a9ak2rVrU9euXWndunXEGCMHBwfxb1xcHBERFRQU0MyZM6lhw4ak0+moS5cutGfP\\nHrG+gwcPEmOMdu7cSe3btycXFxfq2LEjnThxgqs9OTk5NHLkSPL09CQXFxfy8/OjNWvWiOubNm1K\\nK1asICKi2NhYg3YKH6GtRESJiYnUqlUrcnFxIX9/f1q1apUtThstX76cfH19ucrWr1+fFi1aJH7P\\ny8sjNzc3+uijj8RlOTk5NHbsWPL09CQ3NzcKCgqitLQ0xXpnzpxJLVu2NFg2ZswYeuaZZxS38/b2\\npnXr1nG13Rila71snVX6iMsiR0S3AHQCsAhANQAXUepftw5AdyLKUdjcJhBRKyLqDmAaDGfNipRN\\nxFgIIImI5hFRKhHNA/AJgHclJmoYYOz4XJ6zq+SGQKTaIGVh0WYg2of8/PyKboIqU6ZMMfj+0Ucf\\nGXzXLHKG1KlTB61bt37s7pmVK1eKx+Tk5IQDBw5UcIuk4bbIMWa/jxUUFxdj8ODBCAwMxNmzZ3H8\\n+HFERUUhMDAQq1evhk6nQ3Z2NjIzM8WZzpGRkTh8+DCSk5Nx/vx5REREYODAgTh79qxB3dHR0Vi2\\nbBlOnDiBZs2aITw8nOsZNHfuXJw/fx4pKSm4cOECEhMT4ePjI1k2OjoaWVlZyMzMRFZWFjZv3oxq\\n1aqhZ8+eAIANGzYgJiYGCxcuxG+//YYVK1Zg6dKlWL9+vViHXO5X/Ryw1nD58mVkZWUhJCREXObi\\n4oLAwED8/PPPBu3IyspCSkoKTp06hcDAQAQHByM7O1u27qNHj5rEwOzfvz/S0tJkJz89evQI+fn5\\n5Zam0Fy4lQoR3QPwbtnHAMaYExFVBs/p7ii1Hm4xWv4pgEgAzwJIldvY2LeoPKfuP/HEE5LLpYSc\\nlOle66ztQ1WYELB27VqEhoYiJSUFo0ePRtu2bQ3Wy10bUgFkNaou3bp1w4kTJ5CWloaQkBB4eXlV\\ndJMkqYw+ZOaQm5uLnJwcPP/882jatCkAiP636enpYIwZPM8vXbqE5ORkXLlyRYwtOWnSJOzbtw8J\\nCQkGAePnzZuHvn37AgA2bdqEhg0b4vPPP8cbb7yh2KarV68iICAAHTt2BFA6yUoOnU4n+tb+/vvv\\nmDZtGpYvX47evXsDKE0/uHTpUrzwwgsAgCZNmmDWrFmIj48X/eyUcr/agqysLDDGTK5hLy8v3Lhx\\nAwBw4MABnDlzBjdv3hTdXeLi4rB9+3Z8+umnsuGCjAWiUG9RURFu3boled/ExMTAzc3NxMe2ssAl\\n5BhjM4lIcuodY8wJwJcAXrRlwyykddnfc0bLz6PUitcKlVTIyT3ceK2CmpCzD4MGDcKbb74p+soJ\\nD7fKxnPPPYfnnntOcp2cz86775q8k2lUcdq2bWsi5CsbVd1Hzt3dHREREejXrx+Cg4MRHByMIUOG\\nyIqn9PR0EBFatWpl4HNbUFBgkKuYMWaQaaRGjRpo27Ytl4P/xIkTMWTIEFHEh4eHq8byvHv3LgYN\\nGoRhw4Zh6tSpAIBbt27h2rVrGD9+PCZMmCCWLSoqMniOVIbcr+np6Xjw4AE8PDwMlj969EicyCX0\\nq4wxjBw50sCqyMuaNWuwYcMG7N+/v9Jeu7wWuXcZY5lE9Kn+wrKhymQAvW3eMssQom7eMVp+22i9\\nJBUp5OT2xTv8UxkdbB8HfH19sW7dOsybNw9eXl6YP39+RTfJbAoKCiSXt2nTppxboqFR9S1yAJCY\\nmIgZM2Zg9+7d2L59O2JiYrBtm/Scv5KSEjg4OCAtLc3kxdxWMfUGDBiAq1ev4vvvv8f+/fsRFhaG\\noUOHIjExUbJ8cXExhg4dikaNGhmEshL6wISEBHTv3l12f6GhoTh8+LDsesYYcnNzLTwawNvbG0SE\\n7Oxsgww52dnZ4mSlkpISeHt748iRIyaT0oSh3dOnT5ss8/b2Nhl6zc7OhpOTk4koXL16NebPn4/d\\nu3eL1s7KCK+QmwBgA2PsJhHtBkrzrgL4AkAIgP5KGxvDGAsGsI+j6EEi6qNezHrofxMfRMpTyMnN\\nxOG1yFWmmZSPG5MmTRKzMlRFwWwcVkfgcehQNaoe3FYNiRnjlQnB+hkdHY3Q0FAkJSUhLCzMxM+q\\nQ4cOICJkZmaiV69esvUREY4ePSoO1z548ADnzp1DZGQkV3vq1q2LESNGYMSIERgwYACGDx+OhIQE\\nSWPA9OnTcfXqVRw/ftxgNMfT0xMNGjTAn3/+qZgv295Dq76+vvD29sa+fftEAZWfn4/Dhw9jxYoV\\nAEpdQ7Kzs8EYg6+vr2Q9UqFOunfvbiK69+7di06dOhmci5UrVyIuLg4pKSmKorYywKUSiGgTY6w+\\ngK/KRNi/AXwOYACAAUR01Mz9/gTgSY5y0j2QPIIlzh2AvuQWLHG3IUNsbKzJsvLstO/duye5nFfI\\nVabYZo8jVVHACcgJucrquKvxeFPVXyAyMjKQkJCAgQMHwsfHBxcvXsSZM2cwefJkNG3aFPn5+fjh\\nhx/QoUMH6HQ6tGjRAsOHD0dkZCSWL1+OgIAA3L59GwcPHoSfnx8GDx4s1r1w4UJ4eHigfv36WLBg\\nAZydnfHqq6+qtmn+/PkICAhA69atUVhYiG+++QZ+fn6SIm7Tpk3YtGkTdu/ejfz8fHEyRc2aNVGj\\nRg3ExcVh2rRpqF27NkJDQ1FYWIj09HRcv34ds2fPBmD+0OrFixdx//59XL9+HQUFBaKlrHXr1nBy\\ncsKNGzcQHByMxYsXY9CgQQBKY88tWrQI/v7+aNGiBRYuXAg3NzfxfPTt2xc9evTAoEGDsGTJEjz5\\n5JPIzMzEnj17EBISgh49eki2ZcKECYiPj8eMGTMwfvx4HDlyBJs3b0ZycrJYZtmyZYiJicGWLVvQ\\nvHlz0YLn6upq9USOgwcP4uDBg1bVYYI5U1wBrEVpyJHvANwD8Ky102bN/QBwBFACifAjAHqWretj\\ntLxX2fJeMnWahPRwcHCQnS5sD9566y3J8BAlJSWS5Y3LxcfHl2t7NaoOI0aM0EKPaFQqqvI1mJ2d\\nTS+++CI1bNiQXFxcqEmTJjR79mwqKioiIqJJkyaRh4eHQfiRoqIiiouLIz8/P3J2dqb69evToEGD\\nKD09nYhKw484ODjQjh07qF27dmaHH3nvvfeoTZs2VKNGDapXrx6FhYXRb7/9Jq739fWllStXEhFR\\nZGQkOTg4mHz0w48kJydTx44dydXVlerWrUs9e/akrVu3WnzOgoKCJPd55coVIiLKyMggBwcHSkpK\\nMtguLi6OGjRoQK6urhQUFETnz583WH///n2KioqiRo0akbOzMzVu3JheffVVunTpkmJ7Dh06RB07\\ndiQXFxdq1qyZQUgTotJwLVLtHTVqlEXHr3StwwbhRxiZYb5mpWaJZAChAMKI6JCZutFqyvzyCgHE\\nEtECo3VOAG4A2EFEo/WWfwxgEID6JDG7ljFGBQUFBkF1nZycUFhYaKejMOXatWto3LixyXK538fY\\nQrRx40bVmU0af09eeOEFSf8dc+59DQ1bIjy/tGuwlNTUVPTp0wc3b95E3bqKrtwaVRDGmGJfTkRW\\nDfnIjtsxxq6h9K1JahsHAJ/piQkioibWNEQNxlhHlKYJEwaxWzHGhGzvu4gon4iKGGPvAIhnjN0A\\n8AOAYJSGHpkiJeIEKnKiA1A6XTwqKgqrV6+2aHttaFVDDqmhVX9//wpoiYaGhhyaqNWwFCUHrP2Q\\nFnIVxRQAQn4PAjC07AMAvgCuAgARJTDGSgC8BeAfZcsnE5FhMjUjKlrIAaX+Arw888wzYmBER0dH\\ng2nsGhr6SAk5LaWbRkXyzjvvaOFvjFDyw5WbJcoYw5w5c0TfNY2/J2YNrT6uMMbo/v37BrOpdDqd\\n1TndzOXChQsGlpIBAwbg+++/lyx7+PBhDB06FPfv38fSpUsrNCGyRuVmyJAh+OabbwyWzZ8/X3KC\\nj4ZGeUBEcHBw0KxQnGRmZsrOEq1bty7q1KlTzi3SMAd7D61qQg6lQi43N9dgNkrNmjVlZ5Lak8mT\\nJ2P9+vVo3LgxduzYgXbt2smWJSIUFhZq1hUNRc6cOYOnn37aYNmdO3e0h79GhaLUuWloPE5UmJBj\\njL2OUt+zv8r+V4SINlvTkIqEMUZ379416Nhq1aqFnBy7p5CV5OHDh3ByctIEmobN2LJlCxYsWABX\\nV1fs2bOn0qZv0vj7oAk5jb8LFSnkSgB0I6LjZf8rQURUZXNEMcbo9u3bBrOF6tSpgzt3jBNEaGho\\naGjYAk3IafxdqLBZqyidQJCp9/9jTWWY7KChoaGhoaGhYQ6yQo6Irkj9/7iiCTkNDQ0NDQ2Nqoam\\nVsrQhJyGhoaGhoZGVUMpIPBl8MeRIyLys02TKgZNyGloaGhoPI74+vpi6tSpePPNNyu6KRp2QEmt\\npJrxKfdUXbZGE3IaGhoaGtaQlJQENze3im6GCWlpaRUaazQqKgqdO3eGq6srmjVrxr1dbGwsfHx8\\noNPp0Lt3b/z66682aU9qaio6deoEV1dXNG/eHAkJhvkCfv31VwwdOhR+fn5wcHDAggULZGqqHCj5\\nyEWWYzsqHE3IaWhoaGhYAxEpZmioKOrVq1eh+yciREZG4syZM9i3bx/XNkuWLMGqVauQlJSEli1b\\nIi4uDiEhIbhw4QJq1KhhcVsyMjIQFhaGMWPGYMuWLTh8+DAmTZoET09PvPDCCwBKQ4D5+vripZde\\nQkxMjMX7KjeI6G//AUAZGRmE0qFkAkCNGzcmDQ0NDQ37UNr9VE1SU1OpW7duVLNmTapduzZ17dqV\\n1q1bR4wxcnBwEP/GxcUREVFBQQHNnDmTGjZsSDqdjrp06UJ79uwR6zt48CAxxmjnzp3Uvn17cnFx\\noY4dO9KJEye42pOTk0MjR44kT09PcnFxIT8/P1qzZo24vmnTprRixQoiIoqNjTVop/AR2kpElJiY\\nSK1atSIXFxfy9/enVatW2eK00fLly8nX15erbP369WnRokXi97y8PHJzc6OPPvpIXJaTk0Njx44l\\nT09PcnNzo6CgIEpLS1Osd+bMmdSyZUuDZWPGjKFnnnlGsnybNm0Mzo0lKF3rZeus0jBK4Uf+VmgW\\nOQ0NDY3KAzt40G51U1CQxdsWFxdj8ODBGDt2LL744gsUFBQgPT0drVu3xurVqzF37lxcunQJRCSm\\nfYyMjMTly5eRnJwMHx8fpKSkYODAgfj3v/+Ntm3binVHR0fjgw8+QIMGDRAbG4vw8HBcvHgRLi4u\\nim2aO3cuzp8/j5SUFHh6euLy5cu4efOmZNno6GhMnDhR/L53716MHj0aPXv2BABs2LABsbGxWLdu\\nHQICAnDu3DmMHTsW1atXF4dn5XK/CjDGkJuby3dCJbh8+TKysrIQEhIiLnNxcUFgYCB+/vlnjB07\\nVmxH3bp1kZKSAnd3dyQlJSE4OBi///67bNDzo0ePol+/fgbL+vfvj82bN6O4uBiOjlUvJK4m5MrQ\\nhJyGhoaGhhq5ubnIycnB888/j6ZNmwIAWrZsCQBIT08HYwxPPPGEWP7SpUtITk7GlStX0LBhQwDA\\npEmTsG/fPiQkJGDdunVi2Xnz5qFv374AgE2bNqFhw4b4/PPP8cYbbyi26erVqwgICEDHjh0BAI0a\\nNZItq9PpoNPpAAC///47pk2bhuXLl6N3794AgIULF2Lp0qXiMGOTJk0wa9YsxMfHi0Ju48aNsrlf\\nbUFWVhYYYyZizMvLCzdu3AAAHDhwAGfOnMHNmzfh7OwMAIiLi8P27dvx6aef4h//+Ids3foCUai3\\nqKgIt27dqpJZbzQhV4Ym5DQ0NDQ01HB3d0dERAT69euH4OBgBAcHY8iQIbLiKT09HUSEVq1aGUT3\\nLygoQJ8+fcTvjDF069ZN/F6jRg20bduWy8F/4sSJGDJkCNLS0hASEoLw8HAEBgYqbnP37l0MGjQI\\nw4YNw9SpUwEAt27dwrVr1zB+/HhMmDBBLFtUVGTg+1e/fn3VNtmb9PR0PHjwAB4eHgbLHz16hEuX\\nLgGAOPGEMYaRI0di/fr15d7O8kATcmVoQk5DQ0NDg4fExETMmDEDu3fvxvbt2xETE4Nt27ZJli0p\\nKYGDgwPS0tLg5GTY5bq6utqkPQMGDMDVq1fx/fffY//+/QgLC8PQoUORmJgoWb64uBhDhw5Fo0aN\\nsHbtWoO2AkBCQgK6d+8uuz97D616e3uDiJCdnS1aMQEgOzsb3t7eYlu9vb1x5MgRk/RXtWrVAgCc\\nPn3aZJm3tzeys7MNymdnZ8PJyclEFFYVNCFXhibkNDQ0NCoP1vixlQdt27ZF27ZtER0djdDQUCQl\\nJSEsLAzFxcUG5Tp06AAiQmZmJnr16iVbHxHh6NGj4nDtgwcPcO7cOURGRnK1p27duhgxYgRGjBiB\\nAQMGYPjw4UhISEC1atVMyk6fPh3/397dx2VV348ff71B40bRiYaImBIzC9RvYjeaPxVFzGGKlS5F\\nK6q5ypY3leVWU3E2tXnTjbZR33TWVnZjOWumUQ3T0q8SS8tmW3iDqTBdS9NFKL5/f5zDNe6uiwsE\\ngXo/H4/zgHPO55zzvq4L5c3nNj8/n23btpXrExYREUFUVBSff/4548eP9/qs+m5ajYmJITIykqys\\nLE9zcVFREZs2bWLRokUAJCQkUFhYiIgQE1P1KqJVTXXSt2/fSkn3W2+9xWWXXdYk+8eBn4mciPiq\\noz0DHAN2q+qpOomqAVgiZ4wxpjr79u0jMzOTkSNH0rFjR/Ly8ti5cyd33XUXXbp0oaioiLfffpte\\nvXoRGhpK165dSUtLIz09nYULF5KQkMCXX35JdnY2sbGxjBo1ynPvuXPn0q5dOzp06MCcOXMICgpi\\n3Lhx1cY0a9YsEhISiI+P59SpU6xevZrY2Ngqk7gVK1awYsUK1q9fT1FREUVFRQC0bNmSFi1akJGR\\nweTJk2ndujUpKSmcOnWK3NxcDh48yIwZM4CaN63m5eVx4sQJDh48SHFxsaemLD4+nmbNmnHo0CGS\\nkpKYP38+qampgDP33Lx58+jWrRtdu3Zl7ty5hIWFed6PIUOG0K9fP1JTU1mwYAEXX3wxhw8fZsOG\\nDSQnJ9OvX78qY7njjjtYtmwZ06ZN4/bbb2fz5s08++yzrFq1ylPm1KlTfPrpp6gqRUVFFBQUsGPH\\nDlq2bElsbCNc+8Cfoa04yVpJNdvXwMNnO4y2ITZAd+7cWW76ke7du/sYTGyMMeZs0ESnHyksLNTr\\nrrtOo6OjNTg4WDt37qwzZszQ06dPq6rqpEmTtF27duWmHzl9+rRmZGRobGysBgUFaYcOHTQ1NVVz\\nc3NV1Zl+JCAgQF9//XXt2bNnjacfefjhh7V79+7aokULbdu2rQ4fPlx3797tOR8TE6OLFy9WVdX0\\n9HQNCAiotJWdYmPVqlXau3dvDQkJ0fDwcO3fv7+++OKLtX7PEhMTq3zm/v37VVV13759GhAQoCtX\\nrix3XUZGhkZFRWlISIgmJibqrl27yp0/ceKETp06VTt16qRBQUF6wQUX6Lhx43TPnj0+43nvvfe0\\nd+/eGhwcrBdeeGG5KU1K4ymdoqXsNmjQoFq9fl8/69TB9COiWv0qXCIyAngC2AG8AhQC7YEfAz2B\\nXwJXALcDP1fVhXWRZJ4rIqIfffQRl156qedYz549y7WvG2OMqTsiUqlv0/fVxo0bGTx4MEeOHCE8\\nPLyhwzF1zNfPunvurGaR9reP3ChgvareUeH4cyKSCQxS1VtE5AxwG9CkEjmwplVjjDENx5JaU1v+\\nZivXAqu9nHsFSHW/Xw9U3euwkbNEzhhjTEPxtbRXSkoKYWFhlbZWrVoxf/78cxilaYz8rZELBGKB\\nqhZJ+6F7HuBbd2tyLJEzxhjTEAYOHFhptGtZvkaJWlOs8TeRWwf8WkSOAGtUtUREAnFq6h4G/uyW\\niwfy6j5MEJF7gETgMiASmK2qcyqUiQSmAcnAhUAxsBPIUFXvk95giZwxxpjGqTFMwGsaL3+zlbuB\\nXcDLwDciUgh8A7zkHr/bLXcM+HVdB+n6CXA+8BrOyNKq9AbGuGVGAze7cWaLSIqvm1siZ4wxxpim\\nxq8aOVU9CvQXkaFAH5wascPAVlXNKlNuZb1E6dw7DsCtCbzTS7FNQFdV9dRRi8hbOMnm/Tg1i1Wy\\nRM4YY4wxTU2NVnZQ1beAt+oplrOmqpXWBHGbgT/Cqa3zyhI5Y4wxxjQ1NUrkROQaYCAQDnwJ/EVV\\nvdZyNQYi0hzoC3zkq5wlcsYYY4xpavxdoisMeAPoD5wG/gW0Be4RkU3ANap6ot6iPDsZQEfA5zon\\nlsgZY4wxpqnxN1v5NZAA3AiEqGoHIAS4yT1eowEOIpIkImf82N6tyX2reE4a8AAwR1U/8FXWEjlj\\njDHfRTExMSxevLihwzD1xN9s5XrgIVX9Y+lAAlUtUdU/4izPdX0Nn/s+cLEf2001vK+Hu6zYCuDp\\nitOUVOX3v/99uX1L5IwxxtTEypUrCQsLa+gwKsnJyWHSpEkN9vypU6dy+eWXExISwoUXXuj3dbNn\\nz6Zjx46EhoYyaNAgPv3003qM0rF69Wri4+MJDg6me/furFmzplKZJ598kgsvvJCQkBAuu+wyNm/e\\n7Pf9s7OzmT17tmerC/5mK20Bb+/gp+55v6lqkar+3Y/ti5rct5SIJOFMjbK6imXFqjRhwoRy+5bI\\nGWOMqQlV9blCQ0Np27YtwcHBDfZ8VSU9PZ2bbvK/bmbBggUsWbKEZcuWkZOTQ0REBMnJyZw8ebLW\\ncWzcuJGYGO+LT23ZsoWxY8dy4403smPHDtLS0hgzZgzbt2/3lHnxxReZOnUqDz30EB999BFXXXUV\\nP/rRj/jiC//SlcTExDpP5FDVajdgN/CYl3NLgL/5c5+62HBWkTgDzPRyvi/wNbAWCPTznrpu3TrF\\nmZ9OAR02bJgaY4ypH86vn6Zp48aN2qdPH23ZsqW2bt1ar7zySl26dKmKiAYEBHi+ZmRkqKpqcXGx\\n3n///RodHa2hoaF6xRVX6IYNGzz3y87OVhHRN954Qy+99FINDg7W3r1764cfftz2bDEAACAASURB\\nVOhXPMeOHdMJEyZoRESEBgcHa2xsrD722GOe8126dNFFixapqurs2bPLxVm6lcaqqrp8+XKNi4vT\\n4OBg7datmy5ZsqQu3jZduHChxsTE+FW2Q4cOOm/ePM/+N998o2FhYfrUU095jh07dkwnTpyoERER\\nGhYWpomJiZqTk+P1ntnZ2T6ff8MNN+jQoUPLHRsyZIimpaV59q+88kq9/fbby5Xp2rWr/uIXv/B6\\nX18/6+65s8qL/B21mgksEpGWwB9x5pCLBMbiTNR7z1nmk9USkd5AF/67HFiciJQ26f5ZVYtEpBvO\\nKhNHgEXAZWX/OlLV//N2f+sjZ4wxjUe2ZNfbvRM1sdbXlpSUMGrUKCZOnMgLL7xAcXExubm5xMfH\\n8+ijj/Lggw+yZ88eVJWWLVsCkJ6ezt69e1m1ahUdO3Zk3bp1jBw5ku3bt9OjRw/PvadPn87jjz9O\\nVFQUs2fPZsSIEeTl5VVbm/bggw+ya9cu1q1bR0REBHv37uXIkSNVlp0+fTp33vnfqVjfeustbrvt\\nNvr37w/A008/zezZs1m6dCkJCQl88sknTJw4kfPOO8/TPJuSksKmTd4XSxIRjh+vNBuY3/bu3UtB\\nQQHJycmeY8HBwQwYMIAPPviAiRMneuIIDw9n3bp1tGnThpUrV5KUlMRnn31G+/bta/zcLVu2MHny\\n5HLHrr76apYtWwbAqVOn+PDDD5k+fXq5MkOHDuWDD3x2w69X/k4IvEREzsdJ2NLdw4KzBNZ8VX2s\\nfsIr52f8t8+c4qzgMMbdjwHycSYrbu1uVQ2UCKziGGCJnDHGmOodP36cY8eOcc0119ClSxcALrro\\nIgByc3MREc4//3xP+T179rBq1Sr2799PdHQ0AJMmTSIrK4vMzEyWLl3qKTtz5kyGDBkCwIoVK4iO\\njub555/n1ltv9RlTfn4+CQkJ9O7tTJfaqVMnr2VDQ0MJDQ0F4LPPPmPy5MksXLiQQYMGATB37lwe\\neeQRrr32WgA6d+7MAw88wLJlyzyJnK+1X+tCQUEBIlIpGWvfvj2HDh0C4N1332Xnzp0cOXKEoKAg\\nADIyMli7di3PPfcc9913X6X7OhVgvp9b1TMLCgoAOHr0KCUlJVWWeeedd2r2IuuQ3/PIqeovROQ3\\nOMlS6TxyW1X13/UVXIXn3wLcUk2ZlUCtVpeomMg1xn4OxhhjGlabNm24+eabGTp0KElJSSQlJTF6\\n9GivyVNubi6qSlxcXLlEori4mMGDB3v2RYQ+ffp49lu0aEGPHj386uB/5513Mnr0aHJyckhOTmbE\\niBEMGDDA5zVfffUVqampjB07lrvvdlbZPHr0KAcOHOD222/njjv+27389OnT5X4nNoa1X3Nzczl5\\n8iTt2rUrd/zbb78lL89Z8v3AgQPExcUhIqgqJSUlFBcXewakiAgTJkzgySefPOfx16Waruzwb+DN\\neoqlQVmNnDHGGH8sX76cadOmsX79etauXctDDz1U5ehGcH63BAQEkJOTQ7Nm5X/lhoSE1Ek8w4YN\\nIz8/nzfffJN33nmH4cOHM2bMGJYvX15l+ZKSEsaMGUOnTp144oknysUKkJmZSd++fb0+r76bViMj\\nI1FVCgsLPbWYAIWFhURGRnpijYyMZPPmzZVq2lq1agVAVFQUO3bs8BzfunUrM2bMYOPGjZ5rSsuW\\nPrewsLDcvco+s127dgQGBvos0xC8JnIi4judr0BV3zv7cBqOJXLGGNN4nE0/tnOhR48e9OjRg+nT\\np5OSksLKlSsZPnw4JSUl5cr16tULVeXw4cMMHDjQ6/1Ula1bt3qaa0+ePMknn3xCenq6X/GEh4cz\\nfvx4xo8fz7Bhw0hLSyMzM5PmzZtXKjtlyhTy8/PZtm0bgYH/7XEUERFBVFQUn3/+OePHj/f6rPpu\\nWo2JiSEyMpKsrCxPc3FRURGbNm1i0aJFACQkJFBYWIiIeB2JGhgYWG66kwMHDtCsWTOv5fv27UtW\\nVhb33nuv51hWVhZXXXUVAM2bN6d3795kZWVx/fXXlyszZsyYSvc7V3zVyGXj9EWrjrjlvPY/awos\\nkTPGGFOdffv2kZmZyciRI+nYsSN5eXns3LmTu+66iy5dulBUVMTbb79Nr169CA0NpWvXrqSlpZGe\\nns7ChQtJSEjgyy+/JDs7m9jYWEaNGuW599y5c2nXrh0dOnRgzpw5BAUFMW6cz0WJAJg1axYJCQnE\\nx8dz6tQpVq9eTWxsbJVJ3IoVK1ixYgXr16+nqKiIoqIiAFq2bEmLFi3IyMhg8uTJtG7dmpSUFE6d\\nOkVubi4HDx5kxowZQM2bVvPy8jhx4gQHDx6kuLjYU0sWHx9Ps2bNOHToEElJScyfP5/U1FTAmXtu\\n3rx5dOvWja5duzJ37lzCwsI878eQIUPo168fqampLFiwgIsvvpjDhw+zYcMGkpOT6devX41iBCfB\\nHThwIAsWLGDUqFG8+uqrZGdn8/7773vK3HPPPdx0001cfvnl9OvXj9/+9rccPnyY22+/vcbPqzPe\\nhrPirKnq93a2w2cbcgN01apV5aYfGTNmjNfhwsYYY84OTXT6kcLCQr3uuus0Ojpag4ODtXPnzjpj\\nxgw9ffq0qqpOmjRJ27VrV276kdOnT2tGRobGxsZqUFCQdujQQVNTUzU3N1dVnWkxAgIC9PXXX9ee\\nPXvWePqRhx9+WLt3764tWrTQtm3b6vDhw3X37t2e8zExMbp48WJVVU1PT9eAgIBKW9npR1atWqW9\\ne/fWkJAQDQ8P1/79++uLL75Y6/csMTGxymfu379fVVX37dunAQEBunLlynLXZWRkaFRUlIaEhGhi\\nYqLu2rWr3PkTJ07o1KlTtVOnThoUFKQXXHCBjhs3Tvfs2VNlHNVNP6Kqunr1ar3kkks0KChI4+Li\\ndM2aNZXK/Pa3v9WYmBgNDg7Wyy67TDdv3uzznr5+1qmD6UdEqxnF8X0gIvr888+TlpbmOXbDDTew\\natWqBozKGGO+u0o7oBtnotrBgwdz5MgRwsPDGzocU8d8/ay7585qdKW1H7qsadUYY0xDsaTW1JZl\\nK66K/4gskTPGGHOu+JryKiUlhbCwsEpbq1atmD9//jmM0jRGNZp+5LvMauSMMcY0hIEDB1Ya7VqW\\nr1Gi1hRrLJFzWSJnjDGmMWoME/CaxsuyFZclcsYYY4xpamqUrYhIgIh0F5GBItKivoJqCJbIGWOM\\nMaap8TtbEZG7gAJgB86C9N3c42tEZHL9hHfuWCJnjDHGmKbGr2xFRCYCjwFrgBtwVnMotQm4vqrr\\nmhJL5IwxxhjT1PibrdwDLFLVnwKvVTi3G7d2rimzRM4YY4wxTY2/2UoMsMHLuZPAD+omnIZjiZwx\\nxpjvopiYGBYvXtzQYZh64m+2chTo4uVcN+BgnUTTgCyRM8YYczZWrlxJWFhYQ4dRSU5ODpMmTWqw\\n50+dOpXLL7+ckJAQLrzwQr+vmz17Nh07diQ0NJRBgwbx6aef1mOUjtWrVxMfH09wcDDdu3dnzZo1\\n5c5v2rSJ1NRUoqOjCQgI4Nlnn633mKrjb7byBjBTRMp+Aioi7YBpOH3nmjRL5IwxxpwNVfW5QkND\\nadu2LcHBwQ32fFUlPT2dm266ye9rFixYwJIlS1i2bBk5OTlERESQnJzMyZMnax3Hxo0biYmJ8Xp+\\ny5YtjB07lhtvvJEdO3aQlpbGmDFj2L59u6fMiRMn6NGjB48//jihoaG1jqVOqWq1G9AO+Az4D/AX\\noARnkMMRYBfQ2p/7NNYN0EWLFing2aZNm6bGGGPqh/Prp2nauHGj9unTR1u2bKmtW7fWK6+8Upcu\\nXaoiogEBAZ6vGRkZqqpaXFys999/v0ZHR2toaKheccUVumHDBs/9srOzVUT0jTfe0EsvvVSDg4O1\\nd+/e+uGHH/oVz7Fjx3TChAkaERGhwcHBGhsbq4899pjnfJcuXXTRokWqqjp79uxycZZupbGqqi5f\\nvlzj4uI0ODhYu3XrpkuWLKmLt00XLlyoMTExfpXt0KGDzps3z7P/zTffaFhYmD711FOeY8eOHdOJ\\nEydqRESEhoWFaWJioubk5Hi9Z3Z2ts/n33DDDTp06NByx4YMGaJpaWlVlm/ZsqWuXLmy2tfi62fd\\nPXdWOYxfKzuo6lERuQyYClwN5OGsCrEUWKKqx+sqsWwoViNnjDGNR3Z2/dVsJSbWfoH6kpISRo0a\\nxcSJE3nhhRcoLi4mNzeX+Ph4Hn30UR588EH27NmDqtKyZUsA0tPT2bt3L6tWraJjx46sW7eOkSNH\\nsn37dnr06OG59/Tp03n88ceJiopi9uzZjBgxgry8vGpr0x588EF27drFunXriIiIYO/evRw5cqTK\\nstOnT+fOO+/07L/11lvcdttt9O/fH4Cnn36a2bNns3TpUhISEvjkk0+YOHEi5513nqd5NiUlhU2b\\nNnmNR0Q4frz2acHevXspKCggOTnZcyw4OJgBAwbwwQcfMHHiRE8c4eHhrFu3jjZt2rBy5UqSkpL4\\n7LPPaN++fY2fu2XLFiZPLj+b2tVXX82yZctq/VrOBb+X6FLVr4Ffudt3jiVyxhhjqnP8+HGOHTvG\\nNddcQ5cuXQC46KKLAMjNzUVEOP/88z3l9+zZw6pVq9i/fz/R0dEATJo0iaysLDIzM1m6dKmn7MyZ\\nMxkyZAgAK1asIDo6mueff55bb73VZ0z5+fkkJCTQu3dvADp16uS1bGhoqKdJ8LPPPmPy5MksXLiQ\\nQYMGATB37lweeeQRrr32WgA6d+7MAw88wLJlyzyJnK+1X+tCQUEBIlIpGWvfvj2HDh0C4N1332Xn\\nzp0cOXKEoKAgADIyMli7di3PPfcc9913X6X7OhVgvp9b1TMLCgrO5uXUO1tr1WWJnDHGmOq0adOG\\nm2++maFDh5KUlERSUhKjR4/2mjzl5uaiqsTFxZVLJIqLixk8eLBnX0To06ePZ79Fixb06NHDrw7+\\nd955J6NHjyYnJ4fk5GRGjBjBgAEDfF7z1VdfkZqaytixY7n77rsBOHr0KAcOHOD222/njjvu8JQ9\\nffp0ub5/jWHt19zcXE6ePEm7du3KHf/222/Jy8sD4MCBA8TFxSEiqColJSUUFxd7BqSICBMmTODJ\\nJ5885/HXJb8SORF518fpM8Ax4EPgGVUtrIvAqojhHiARuAyIBGar6pxqrrkK2IzT7625qp7xVtYS\\nOWOMMf5Yvnw506ZNY/369axdu5aHHnqo0ujGUmfOnCEgIICcnByaNSv/KzckJKRO4hk2bBj5+fm8\\n+eabvPPOOwwfPpwxY8awfPnyKsuXlJQwZswYOnXqxBNPPFEuVoDMzEz69u3r9Xn13bQaGRmJqlJY\\nWOipxQQoLCwkMjLSE2tkZCSbN2+uVNPWqlUrAKKiotixY4fn+NatW5kxYwYbN270XFNatvS5hYXl\\nU5iyz2ys/K2RE+AioAOwFygE2uPML3fY3U8BponIQFWtjzHCP8FJGF8D7qimLCLSDPidG1+1n4Il\\ncsYY03icTT+2c6FHjx706NGD6dOnk5KSwsqVKxk+fDglJSXlyvXq1QtV5fDhwwwcONDr/VSVrVu3\\nepprT548ySeffEJ6erpf8YSHhzN+/HjGjx/PsGHDSEtLIzMzk+bNm1cqO2XKFPLz89m2bRuBgYGe\\n4xEREURFRfH5558zfvx4r8+q76bVmJgYIiMjycrK8jQXFxUVsWnTJhYtWgRAQkIChYWFiIjXkaiB\\ngYHlpjs5cOAAzZo181q+b9++ZGVlce+993qOZWVlcdVVV9XVS6sX/iZyi4FHgctUNbf0oIj0Bl4C\\nMnBq5N4CHgaureM4UdU495mBwJ3VFAe43/26Avh5dYUtkTPGGFOdffv2kZmZyciRI+nYsSN5eXns\\n3LmTu+66iy5dulBUVMTbb79Nr169CA0NpWvXrqSlpZGens7ChQtJSEjgyy+/JDs7m9jYWEaNGuW5\\n99y5c2nXrh0dOnRgzpw5BAUFMW7cuGpjmjVrFgkJCcTHx3Pq1ClWr15NbGxslUncihUrWLFiBevX\\nr6eoqIiioiIAWrZsSYsWLcjIyGDy5Mm0bt2alJQUTp06RW5uLgcPHmTGjBlAzZtW8/LyOHHiBAcP\\nHqS4uNhTSxYfH0+zZs04dOgQSUlJzJ8/n9TUVMCZe27evHl069aNrl27MnfuXMLCwjzvx5AhQ+jX\\nrx+pqaksWLCAiy++mMOHD7NhwwaSk5Pp169fjWIEJ8EdOHAgCxYsYNSoUbz66qtkZ2fz/vvve8qc\\nPHmSzz//HFXlzJkz5Ofns2PHDsLDw332TaxX/gxtBXYAN3o5dxPwsfv9LcC/znYobTWxBOI05870\\nUSYWZ8WJfsAsnOlSAnyU11mzZpWbfmTWrFlehwsbY4w5OzTR6UcKCwv1uuuu0+joaA0ODtbOnTvr\\njBkz9PTp06qqOmnSJG3Xrl256UdOnz6tGRkZGhsbq0FBQdqhQwdNTU3V3NxcVXWmxQgICNDXX39d\\ne/bsWePpRx5++GHt3r27tmjRQtu2bavDhw/X3bt3e87HxMTo4sWLVVU1PT1dAwICKm1lpx9ZtWqV\\n9u7dW0NCQjQ8PFz79++vL774Yq3fs8TExCqfuX//flVV3bdvnwYEBFSayiMjI0OjoqI0JCREExMT\\nddeuXeXOnzhxQqdOnaqdOnXSoKAgveCCC3TcuHG6Z8+eKuOobvoRVdXVq1frJZdcokFBQRoXF6dr\\n1qypdI/S6VvKbrfccovXe/r6WacOph8RrWYUB4CIfANcq6rrqzj3I+BVVQ0RkQHAW6pabzMPujVy\\np/DRR05EsoADqnqriMwCZuKjj5yI6C9/+Ut+9av/DsjNyMhg5syZdf8CjDHGeDqgG2ei2sGDB3Pk\\nyBHCw8MbOhxTx3z9rLvnzmquHX/bD/cBE72c+6l7HpyJg/91NgGdLRGZAPQCptfkOmtaNcYY01As\\nqTW15W+2MgcYJSI7RWSWiNzpft0JpOL0kQMYAvxfdTcTkSQROePH5mu0bFX3bQMsAn6uqjVKKC2R\\nM8YY01B8Le2VkpJCWFhYpa1Vq1bMnz//HEZpGiN/V3Z4QUSO4iRsvwCa4zRv5gBDVfVtt+g9OP3R\\nqvM+cLEf5f7jT3xlPAwcAl4RkdbusdLx3T8QkSJVrfKe7733Xrl9S+SMMcacCwMHDqw02rUsX6NE\\nrSm2acnOziY7O7tO71mTlR2ygCwRCcBpQj1asc+Zqhb5ea8i4O81CdRPlwA9qbp59yiwBriuqguv\\nuuqqciNTLJEzxhjTGDSGCXhN3UhMTCQxMdGzn5GR4b2wn2q8soObvP3zrJ9cP6YAP6hw7BackbVJ\\n+IjbmlaNMcYY09T4nciJyHnAj4BuQMVRqaqq9boGqztnXRec6UcA4kTkevf7P6tqkarurOK6Qe63\\n73kbtQqWyBljjDGm6fF3ia4onKWuuuDMs1baK7PsMJt6TeSAn+HUrJU+d4y7gbPCRL6Pa6sdDmSJ\\nnDHGGGOaGn+zld8AR4ALcJK4K4ELcQYXfO5+X69U9RZVDfSyeU3iVDVDVZv5qo0DS+SMMcYY0/T4\\n27TaH7gPZ0QowBlV3QfMdCfofRxnGpImyxI5Y4wxxjQ1/mYrbYHDbq3WSaBNmXPvAol1HNc5Z4mc\\nMcYYY5oaf7OVL4AI9/s8YGiZc1cAfk070phZImeMMea7KCYmhsWLFzd0GKae+Jut/AUY4H6fCdwn\\nIm+JyJ9xBjm8Uh/BnUuWyBljjDkbK1euJCwsrKHDqCQnJ4dJkyY12POnTp3K5ZdfTkhICBde6H+X\\n+tmzZ9OxY0dCQ0MZNGgQn376aT1G6Vi9ejXx8fEEBwfTvXt31qxZU+78vHnzuOKKK2jdujURERGM\\nHDmSXbt21XtcvvibrTwELANQ1d/izNcWCnQAHgHurZfoziFL5IwxxpwNVfW51FZDadu2LcHBFWcN\\nO3dUlfT0dG666abqC7sWLFjAkiVLWLZsGTk5OURERJCcnMzJkydrHcfGjRuJiYnxen7Lli2MHTuW\\nG2+8kR07dpCWlsaYMWPYvn27p8x7773Hz372M7Zs2cJf/vIXmjVrxpAhQ/jqq69qHddZU9VqN6A1\\nEORP2aa4AXrLLbcozjQlCugzzzyjxhhj6ofz68f3+fraztbGjRu1T58+2rJlS23durVeeeWVunTp\\nUhURDQgI8HzNyMhQVdXi4mK9//77NTo6WkNDQ/WKK67QDRs2eO6XnZ2tIqJvvPGGXnrppRocHKy9\\ne/fWDz/80K94jh07phMmTNCIiAgNDg7W2NhYfeyxxzznu3TpoosWLVJV1dmzZ5eLs3QrjVVVdfny\\n5RoXF6fBwcHarVs3XbJkyVm/Z6qqCxcu1JiYGL/KdujQQefNm+fZ/+abbzQsLEyfeuopz7Fjx47p\\nxIkTNSIiQsPCwjQxMVFzcnK83jM7O9vn82+44QYdOnRouWNDhgzRtLQ0r9ecOHFCAwMD9Y033vBa\\nxtfPnHvurHKYaqudRKQZzpJXQ6sr25RZjZwxxpjqlJSUMGrUKAYMGMDHH3/Mtm3bmDp1KgMGDODR\\nRx8lNDSUwsJCDh8+zH333QdAeno6mzZtYtWqVezatYubb76ZkSNH8vHHH5e79/Tp0/nNb37Dhx9+\\nyIUXXsiIESMoKqq+C/qDDz7Irl27WLduHX//+99Zvnw5HTt2rLLs9OnTKSgo4PDhwxQUFPDss8/S\\nvHlz+vfvD8DTTz/NQw89xNy5c9m9ezeLFi3ikUce4cknn/TcIyUlhbCwMK9bq1atavv2ArB3714K\\nCgpITk72HAsODmbAgAF88MEH5eIoKChg3bp1fPTRRwwYMICkpCQKCwtr9dwtW7YwdGj5VOfqq68u\\n98yKjh8/zpkzZ2jTpo3XMvWt2ulHVPW0iBQC3lf0/Q6wRM4YY0x1jh8/zrFjx7jmmmvo0qULABdd\\ndBEAubm5iAjnn3++p/yePXtYtWoV+/fvJzo6GoBJkyaRlZVFZmYmS5cu9ZSdOXMmQ4YMAWDFihVE\\nR0fz/PPPc+utt/qMKT8/n4SEBHr37g1Ap06dvJYNDQ0lNDQUgM8++4zJkyezcOFCBg1yFkGaO3cu\\njzzyCNdeey0AnTt35oEHHmDZsmWefnbPPPMM33zzjX9vWC0UFBQgIrRv377c8fbt23PokDML2rvv\\nvsvOnTs5cuQIQUFBgLNu6dq1a3nuuec8SXRZTgWY7+dW9cyCggKv10yZMoWEhAT69u3r12urD/7O\\nI/cH4CfAunqMpUFZImeMMaY6bdq04eabb2bo0KEkJSWRlJTE6NGjvSZPubm5qCpxcXHlEoni4mIG\\nDx7s2RcR+vTp49lv0aIFPXr08KuD/5133sno0aPJyckhOTmZESNGMGDAAJ/XfPXVV6SmpjJ27Fju\\nvvtuAI4ePcqBAwe4/fbbueOOOzxlT58+Xa7vX4cOHaqNqb7l5uZy8uRJ2rVrV+74t99+S15eHgAH\\nDhwgLi4OEUFVKSkpobi42DMgRUSYMGFCudrGmrjnnnv44IMPeP/99xu0b6S/idw+IE1EtgN/Ag5T\\nYdkrVV1et6GdW5bIGWNM41Fd7UlDWr58OdOmTWP9+vWsXbuWhx56qNLoxlJnzpwhICCAnJwcmjUr\\n/ys3JCSkTuIZNmwY+fn5vPnmm7zzzjsMHz6cMWPGsHx51b+WS0pKGDNmDJ06deKJJ54oFytAZmam\\nzxqmlJQUNm3a5PW8iHD8+PFavhqIjIxEVSksLPTUYgIUFhYSGRnpiTUyMpLNmzdX+lkpbdqNiopi\\nx44dnuNbt25lxowZbNy40XNN2WbgyMjISs2yZZ9Z1rRp03jppZfIzs6mc+fOtX6tdcHfRG6Z+7Uj\\n0LuK8wpYImeMMeZ7oUePHvTo0YPp06eTkpLCypUrGT58OCUl5Xsh9erVC1Xl8OHDDBw40Ov9VJWt\\nW7d6mmtPnjzJJ598Qnp6ul/xhIeHM378eMaPH8+wYcNIS0sjMzOT5s2bVyo7ZcoU8vPz2bZtG4GB\\ngZ7jERERREVF8fnnnzN+/Hivz6rvptWYmBgiIyPJysryNBcXFRWxadMmFi1aBEBCQgKFhYWIiNeR\\nqIGBgeWmOzlw4ADNmjXzWr5v375kZWVx773/nYgjKyuLq666qly5KVOm8PLLL5OdnU3Xrl3P6rXW\\nBX8TOe/jdb8jKiZyjXEIuTHGmIa1b98+MjMzGTlyJB07diQvL4+dO3dy11130aVLF4qKinj77bfp\\n1asXoaGhdO3albS0NNLT01m4cCEJCQl8+eWXZGdnExsby6hRozz3njt3Lu3ataNDhw7MmTOHoKAg\\nxo0bV21Ms2bNIiEhgfj4eE6dOsXq1auJjY2tMolbsWIFK1asYP369RQVFXkGU7Rs2ZIWLVqQkZHB\\n5MmTad26NSkpKZw6dYrc3FwOHjzIjBkzgJo3rebl5XHixAkOHjxIcXGxp5YsPj6eZs2acejQIZKS\\nkpg/fz6pqc5qn1OnTmXevHl069aNrl27MnfuXMLCwjzvx5AhQ+jXrx+pqaksWLCAiy++mMOHD7Nh\\nwwaSk5Pp169fjWIEJ0EbOHAgCxYsYNSoUbz66qtkZ2fz/vvve8rcdddd/OEPf+BPf/oTrVu39tTg\\nlb5/DeJsh71+FzZAr7/++nLD01966SWvw4WNMcacHepgGpCGUFhYqNddd51GR0drcHCwdu7cWWfM\\nmKGnT59WVdVJkyZpu3btyk0/cvr0ac3IyNDY2FgNCgrSDh06aGpqqubm5qqqMy1GQECAvv7669qz\\nZ88aTz/y8MMPa/fu3bVFixbatm1bHT58uO7evdtzPiYmRhcvXqyqqunp6RoQEFBpKzv9yKpVq7R3\\n794aEhKi4eHh2r9/f33xxRdr/Z4lJiZW+cz9+/erquq+ffs0ICBAV65cWe66jIwMjYqK0pCQEE1M\\nTNRdu3aVO3/ixAmdOnWqdurUSYOCgvSCCy7QcePG6Z49e6qMo7rpR1RVWvSsBAAAEzJJREFUV69e\\nrZdccokGBQVpXFycrlmzptz50qlbfL1/Ffn6WacOph8RrUE/BBHpibPCQ1sgU1ULROSHQKGqfl3H\\nOeY5IyJ67bXX8tprr3mOvfLKK1x//fUNGJUxxnx3lXZAN85EtYMHD+bIkSOEh4c3dDimjvn6WXfP\\nnVUToF9NqyIShDNy9TpAcGqtXgcKcFZ2+Dsw42wCaWjWR84YY0xDsaTW1Ja/2crDwBDgRqA9TjJX\\n6k3g6jqO65yr+I/IEjljjDHniq9+2d4m4G3VqhXz588/h1GaxsjfwQ7jgIdU9XkRCaxwbi/QpU6j\\nagBWI2eMMaYhDBw4sNJo17J8jRK1pljjbyLXFvibl3MBQFDdhNNwbNSqMcaYxqgxTMBrGi9/q532\\nAt5mB7wC+Kxuwmk469aVX7Ti6NGjDRSJMcYYY4x//E3kngVmiMh4oHRiGhWRQcA0mvhkwFU5depU\\nQ4dgjDHGGOOTv4ncI8CfgeeAf7vHNgNvA+tV9QlvFzZVlsgZY4wxprHzq4+cqpYAY0VkGc4I1Qjg\\nXzhJ3MZ6jM9DRO4BEoHLgEhgtqrO8VL2B8Bs4FqcUbZHgCxVvdXf51kiZ4wx9adz587WF9l8L9T3\\nWqz+DnYAQFU3Ad5Xyq1fPwGOAa8Bd3gr5CZx7wMlwC+A/UAUUKP1OiyRM8aY+rNv376GDsGY7wR/\\nJwT+K7ASeEFVC+s3pKqpapwbSyBwp4+i84FQoLuqnixz/KWaPM8SOWOMMcY0dv72kTsM/AY4ICJv\\nishYEQmux7hqRURCcSYtfrpCEletYcOGldsfM2ZMHUZm6lp2dnZDh2BqyD6zpsc+s6bFPq/vJ78S\\nOVVNAToC9wPnA88DhSKy3B252lj0BoKBIyLysoj8R0S+FpHXRKSLrwsXLFjgaceePn06P/zhD+s9\\nWFN79h9W02OfWdNjn1nTYp/X95PffeRU9Z/Ao8CjInIJTs1XGnCziHyhqvXbm88/UTjLhy0E1gEj\\ncBLP+cBfRKRic6tHz549ycvLo6SkhPPOO++cBWyMMcYYU1u1WodKVf8GzAEeBA4B0TW5XkSSROSM\\nH9u7NQyt9PV8rqrjVPUdVV0F/BjoDEzwdXFgYKAlccYYY4xpMqTiYvHVXiAyGKc27jqgJbANeE5V\\nn6zBPYKBC/wo+h9V/aLCtYHAKaqYfkREhgLrgUWqOr3Cua9wBmtUGighIjV7E4wxxhhj6oCqntU8\\nPP6OWu2OU5uVhlP7tg94DCeB+0dNH6qqRcDfa3qdH3bV5qKzfRONMcYYYxqCv33kduLM4fYy8Kyq\\nbq6/kGpPVQ+KSA6QXPa4iPQFWuHUHhpjjDHGfCf4m8j9GHhdVb+tz2B8EZHeQBcg0D0UJyLXu9//\\n2a3lA5gBrBeRV4D/xVmFYi7wKc5oW2OMMcaY7wR/px95xVsSJyIDRWR53YZVpZ/hTOr7AqDAGHf/\\nJZxkrTTWd3FGq3YCXgUWAe8Ag8q+BhGJFpFXROQrETkmIqtFpNM5eB2mFkRktDuNTL47rcxuEfm1\\niLRs6NiMf0RkvTuIqcql9UzjISIpIrLRnb7pmIhsE5HEho7LVCYi/URkg4gUishxEflQRG5p6LiM\\nQ0Q6isgTIvKBiJx0/w+sNEZARH4gIv8rIkdE5ISIZLnd2qpVq1GrIvJDEZkjInuBv+DU2NUrVb1F\\nVQO9bPkVym5Q1StVNVRVz3evPVIm/hA37otwBm5MALoC77rnTONzL3Aap8Z1GPAkzgofbzVkUMY/\\nIjIO6InzR5hpxETkdmANsB0YBYzG6VYT2pBxmcpEpAeQhdO69hOc9cW3Ac+4n6NpeD/E+Tf0JfAe\\n3v8PfAMYCtyFM5i0Oc60aVHVPcDvUasi0hq4AbgZ6OMe3gFk4owGPe7XjRoBEZmCM9fcRaq61z3W\\nBfgHMF1VH2246ExVRKStqv6rwrEbgd8DSaqa3RBxmeqJSBucrg1TcWrU56rqzIaNylRFRDoDfwMe\\nUNUnGjoe45uI/Bq4B2ijqt+UOf4BoKpaozXGTf0SkduAp4CYshVQIpKK04I4SFXfc4+1AvbiDCqd\\n6uu+PmvkRCTArWJ/EWeZrt/hzMe2zC0yVVUzm1IS5xoBbC1N4gBUdR/wPpDaUEEZ7yomca7tOBNA\\ndzzH4ZiaWQDsVNUXGzoQU63bgBKcP9BN49ccKC6bxLmOUcsWN9MgRgCHSpM4ADeveh0/chKvH7SI\\nLAIOuje6BngNp0nrAmAmzi/Qpioe+KSK47uAuHMci6m9RJxq6r81cBzGCxH5fzhdF+5q6FiMX/oB\\nu4FxIvK5iJwSkX+IyKSGDsxU6feAiMjjItJBRFqLyERgMLC4YUMzNeArJ7nAXUfeK1+jVqfh/JJc\\nB6SXrRH5DkygGw78u4rjXwJtznEsphZEpCOQAWSpam5Dx2MqE5HmOLX4v1HVzxs6HuOXKHd7BPg5\\nsAdnYNlSEQm05tbGRVV3ueudv4YzIBCgGLhDVV9uuMhMDYXjNKNW9KX7tQ3wH28X+6p6fQb4GhgO\\nfCYiS0XkitpGaUxdEZEWwJ9w/sO6tYHDMd49AAQDv27oQIzfAnBW7Pmpqi5X1WxVvQtnxZyfN2xo\\npiIR+SGwGvgY53d1Es4fT5nuACPzPeA1kVPViUAkMB7IAW4HtojI33D+g27KtXL/puqaN281daaR\\ncJd3ewNnTsGrVfVQw0ZkquJO5fML4JdAsNvk8wP3dJC7b314Gp/Slpe3Kxx/C2gvIu3PcTzGt3k4\\nf9COVNU3VfUvbsf4l3BWXzJNg6+cpPS8Vz7/I1XVIlV9QVVL+8b9HKcj7AycPnLzRWSC+8u1KdmF\\n0yZdURzO6DrTCIlIM5y/PhOAH6mqfVaN14VAEPAHnP+E/o3TTKDAdPd7v+ZIMudUrZY5NA2mO85A\\notMVjm8D2opIRBXXmMbHV06Sr6pem1WhBqNaVPWwqj6iqt2BK3BGrnYFnsUZ0dqUrAX6uFOOAJ7p\\nR/rhNNmZRkZEBGdljkQgVVW3N2xEphp/BQa5W2KZTYDn3O+t31zj85r79eoKx38EfKGqhec4HuNb\\nAdDT/SO3rD5AEf/tY2Uat7VARxHpX3rAnX5kBH7kJH7PI1flxU5n5muAm1T12lrf6BxzR4B8BHyD\\n0/QDMAdoAfxPddmvOfdE5Lc4zftzgT9XOP2Fqh4891GZmhKRM9g8co2aiLyDM3nzQziDHX6M0xc1\\nXVWfa8jYTHnuMpUv4UwK/CTO77RUnMnSF6vq9AYMz7jKLCc6BOf32CTgCHBEVd9zKyo2A9HA/cBX\\nOC2g3XFyEp+/384qkWvKRCQaWAIk49QSvA1Mq7hKhGkc3FVEKi1r4spQVVv2qQkQkRKcRG5WQ8di\\nquYuezcPZzb6NjjTkcyzeQAbJxG5GqffejzO4KI8nHkAn9Lv6y/4Rsb9A7aqz2Kjqg52y/wAZ6GC\\nUTif4wfAPapa1bQk5e9vn7MxxhhjTNNko8aMMcYYY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SMMcYY\\nY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SM+R4SkRtFZH+Z/V0ickcdP6OPiGwVkRMi\\nUiIiPevy/ubcE5F9IrK8Ftelisi0+ojJmO87S+SM+X5KAHIARKQF0A34sI6fsRwIBIYDfYG/1/H9\\nzblX2xnkRwGWyBlTDyyRM+b7qTf/TdwSgBJgR13dXEQCgIuAP6vqRlXdpqpFdXV/c/ZE5LyGjsEY\\nc/YskTPme8ZNsi7lv4nc5cCnqlrs5/VhIrJURA6KSJGI7BaRqWXO3wycxlnDeKaInBGRPT7uN9st\\n011E3hWRkyJySEQyKpQLEpHFIvKxiHwtIodFZK2IdKtQrr2IrCwT3yG3XDv3fKCI/EpEPheRb0Tk\\niIi8JyJXVbjPT0XkozJl/ldE2lQoM0VEPhWR/4jIlyKyXURS/XgPJ1S497MiElnm/BsiUqmGVEQi\\nReSUiEwpc6yLiPxRRP7pvt6/isgoL+9xvIisF5GvAZ9rp7qvba8b4zYR+X9VlGknIr8Tkc/czy3f\\njSWqTJkVwM1ARzcGz8+Dv5+pMca7Zg0dgDHm3BCRvUBnd1eBdSIipftlFnaOUdV8L/cQYB1OIvhL\\n4BOcptPFItJOVR8C3gD6Ae8D/+tu3/oIrbS57jWc5thfA1cDvxSRElWd454PAsKAh4FDOAu6TwK2\\niMjFqvpPt9wfgE7AvcAXQHsgCQh1z88ApgC/wKmFbAVcBoSXeZ3zgXuAR4H7gI7uc+NF5CpVVREZ\\nj7PI9WxgMxAC9Cx7Hy/v4U+B3wEvuLFE4SxSf4WIJKjqf4DngOfd17W7zOXj3ffrefde0cA2oMB9\\nTUeBG4DVIpKqqm9UeI/XAM8A84EzPmK8DViC83m8BPzQjbdlhaLhOJ/tL4B/Ah1w3vfNbuzFwBzg\\nfJz3eAROgl/68+DvZ2qM8UZVbbPNtu/BBlyMk2gsAj4Gerj7x4DJ7vc9gWY+7nENTgJwY4XjTwPf\\nAOHufqBbbqYfcc3CadqdXuH4U25srbxcF4CTPB0HppQ5/jXwMx/Pex14xcf5zjg1ig9WON7XfU0j\\n3f0ngJwafgYBOEnX2xWO93Pv/TN3Pxj4Cni4Qrm/Am+U2X8GKAR+UKHcW0BuFe+x1/elTFkB8nGa\\nxcse/7Eb4/JqXl+0Wy61zPEVQL6f70+lz9Q222zzvlnTqjHfE6q6W1V34tRWZavqx8B/cGpZXlbV\\nne522sdt+uMkBC9UOP4H4DycZKe2Xq6wv8qNrXvpARH5sTsS9t84ydZJoHSwRqntwHQRmSwi3als\\nO5AiInNFpJ+INK9wPhknmXnebYYNFJFA97qvgQFl7nOpiDwuIkkiEuLHa+wGRODWqJVS1feB/cBA\\nd78IeAWnBq70tfcA/gd4tsylV+PUkH5dJtZmOInc/4hIxRq0NX7EGO1uFT+P1TjveTkicqfbTPy1\\nez4fpwbQr+ZRPz9TY4wXlsgZ8z0gIgFlfsn3w2m6CsRJSg4C/3T3qxMOfFlFsleAk/z4bFasRmEV\\n+4LTrImIjMBJ7nYB44ArcJrrjuLUYJX6MbAWmA7scPvK/bLM+YdxaqhGAO8B/xKR5SJSGnuE+9w8\\n4FSZrRgnsWwLoKrPAne6cawHvhSR1SLSGe9Kn3G4inMFlH//ngMuEJGB7v6NODVVfypTJgK4qYo4\\nH3HPt63wjKqeW1EH92u5z0NVS4B/lT0mIncDy3ASx2tx+lteifP+lf1MqlSDz9QY44X1kTPm++Ed\\n3NoenNqS53Bq0Ur3T+H0kxukqu/5uM+XQLiINKuQzEWWOV9b7YF9FfbBSTTB6fv1D1W9rbSAm5iW\\nSx5V9ShwN3C3iHTF6WifISL/VNVMNyH5DfAbEYnAaS5egtOkNw4nWVGcmrmvqojTk8yo6tPA0yLS\\nGhgKLMZJTLzVTJa+P5FVnIvEnRLGvfdGEckHJojIe25sL6tq2f6G/8JJRufjJE8VHaqw78/0IaXJ\\nXvuyB91Ev2JieANOM/H9Zcp18eMZZa+v9jM1xnhnNXLGfD/8FKemYyHwufv9ZcAR4EH3+8upfi65\\njTj938ZUOD4BpwP7lrOI8ccV9sfhNGV+7O6HUrlp7yY3niqp6j/UGYDxb8o00ZY5/09VXQ68XeZ8\\nFk4fr86qmlvFtr+K+xxT1ZdxBgZU1Zxb6jOcmq6xZQ+KM2K2M/CXCuX/AIwGUnBqJp+rcH49Tr/G\\nT73EespHLN58ARyg8ucxmsp//Ifi/BFQ1q1UThi/xUmUK6rxZ2qMKc9q5Iz5HlDVfwCIyEycTux/\\ndad4aIfTed3f0YFv4ozQ/J1bm7ULZ9TqrcCvVbW2NXICTCzTF22Ye89Zqvq1W2Y9kCoii3FGxl4O\\n/AwnScN9fa1wkrI/ArtxkoxRwA+ADW6ZNTijVXPdaxPc5/0WQFX3iMgjwFIRuRgneS0CLgCGAE+7\\ntWWZOInmFpwRm91wmj83eHuRqnrG/Qx+JyKltaLRwFycJG9FhUuewxkR+jtgfxW1pTOB/wM2ichS\\nnBrNNjjJZIyq/sRbLD5iVHGmfnlanFUcVgFdgQdwBp+UtR64X0R+jjN6djBOwlfRpzif7x04tY5F\\nqvoJfnymxphqNPRoC9tss+3cbEBznD5Wye7+FGB7Le7TEngcp8mzCCdhmlyhTCDOoIhf+nG/0hGV\\nccC7OJ3dDwGzK5QTnKksvgBO4NRe/Q+wB3jGLXMeTkL2sftav8JJdG4oc59pwAc4tZEngb/hTKUS\\nWOF5491yX7v32uW+7ij3/E1uvAU4I3bzcGo8W/rxmtNwRqB+48bxe6C9l7Lb3PfnV17OR+GM8D3g\\nfh4HcZLJtArv8WkgoAaf893AXpwBMduAq8q+126ZYJw+coU4Sd6fcGoWy332ODVvf8RpCi4B9vj7\\nmdpmm22+N1Gt7Yorxhhz9kRkFk7NUnNV9Tq3mTHGmMqsj5wxxhhjTBNliZwxpjGwpgFjjKkFa1o1\\nxhhjjGmirEbOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOM\\nMaaJ+v+Dy6GJ+uoh9QAAAABJRU5ErkJggg==\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"for step_size in np.logspace(-4, 2, num=7):\\n\",\n \" make_plot(log_likelihood_sgd[step_size], len_data=len(train_data), batch_size=100,\\n\",\n \" smoothing_window=30, label='step_size=%.1e'%step_size)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Now, let us remove the step size `step_size = 1e2` and plot the rest of the curves.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 39,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAnIAAAFSCAYAAAB2ajI+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdclEf+x99DRxABQRAVe8Uu9gKmmZ5cLr1eyqXXM5d6\\nicb0fql3SS69/pJLMV66SbD33qKgiKCA9A7L7s7vj2HZ9uyywIKazDsvXnHnabO7zz7zmW8bIaVE\\no9FoNBqNRnPsEXCkO6DRaDQajUajaRtayGk0Go1Go9Eco2ghp9FoNBqNRnOMooWcRqPRaDQazTGK\\nFnIajUaj0Wg0xyhayGk0Go1Go9Eco2ghp9FoNBqNRnOM4pOQE0LMEkJEetgWKYSY5d9uaTQajUaj\\n0WhawleL3K/ACA/bhjZt12g0Go1Go9F0Ir4KOeFlWyhg8UNfNBqNRqPRaDStIMjTBiFEP2CAQ1Oq\\ngXs1HLgKOOD3nmk0Go1Go9FovOJRyAFXAPMA2fT3Es6WOdn02gzc1FEd1Gg0Go1Go9EYI6SUxhuE\\n6Av0Q4m1X1BibafLbg3AHillaQf20dYfAdwDXAskAruBBVLKL1o4riswFzgZGIxyJ+8EnpJSLuzQ\\nTms0Go1Go9F0IB6FnNNOQqQBG6WUVR3fJY99eBT4G3AfsBG4ECXqTpNSfu/luBTgZ+AdIAMVz3cR\\n8BfgJinlvzqy3xqNRqPRaDQdhU9C7kgjhIgHcoHHpJQLHNoXA3FSyrFejg0HpJSy3qV9MTBIStmv\\nY3qt0Wg0Go1G07H4WkcuRAgxTwjxmxCiVghhcfkzd3A/TwaCgQ9d2j8ARjW5gQ2RUta5irgm1gNJ\\n/uuiRqPRaDQaTefiLdnBkadRMXLfAV+gYuM6kxFAg5Ryr0v7DlQM3wggp5XnTAN+80PfNBqNRqPR\\naI4Ivgq5c4F5UspHO7IzXogFyg3aSx22+4wQ4lpgEnBJO/ul0Wg0Go1Gc8TwtSBwJLDKXxcVQhwv\\nhLD68PeLv67pcO104AXgXSnlJ/4+v0aj0Wg0Gk1n4atFbhEwC1WGxB+sAIb5sF9t0//LgGiD7TZL\\nnE/lT4QQE4GFwGLgry3se/RngWg0Go1GozmmkVJ6Wz2rRXwVci8B7wkhrMC3GAgnKeU+Xy/alHyw\\nx9f9UbFwoUKIAS7XSUEVJnatb+eGEGIU8D2qdMm5UsoWlxU7FjJ6NYr58+czf/78I90NjY/o7+vY\\nQn9fxw76uzq2UCVy24evQs7mVp2PWu3BiMB298Yz36NWkLgEeNih/VJgu5TSa6KDEGIw8COQBZwh\\npezsZA2NRqPRaDQav+OrkLsKZfk6Ikgpi4QQzwH3CiGqsRcETgfOcNxXCPEzkCylHNz0Oh74CVW+\\nZD6Q4qKAN0opGzv6PWg0Go1Go9H4G5+EnJTynQ7uhy/cB1QBt2Jfous8KeV3LvsF4JzEMQLo0/Tv\\n/xmctz9wwL9d1XQ26enpR7oLmlagv69jC/19HTvo7+qPxzGxssORQAgh9Wej0Wg0Go2moxBCdFyy\\ngxDiLeBhKWV207+9IaWUV7enIxqNRqPRaDSa1uHNtTobVW8N4Di8x8hp05VGo9FoNBpNJ6Ndqx7Q\\nrlWNRqPRaDQdiT9cq76u7KDRaDQajUajOcrwtfwIQoguqDIkaagVFUqBX4G3pZR1HdM9jUaj0Wg0\\nGo0nfHKtCiESgQxgCJADFKBKgPRFlQFJl1IWdlw3Ox/tWtVoNBqNRtORdKZr9SkgBpgppewvpZwq\\npewPzECtgfpkezqh0Wg0Go1Go2k9vlrkioC7pZRuZUiEEFcDT0gp4zugf0cMbZHTaDQajUbTkXSm\\nRS4SOORhW17Tdo1Go9FoNBpNJ+KrkNsNXOZh26XAb/7pjkaj0Wg0Go3GV3zNWn0GeE8IkQB8BOSj\\nkh0uBE7As8jTaDQajUaj0XQQPhcEFkJcCywAejg0FwIPSinf6IC+HVF0jJxGo9FoNJqOxB8xcq1a\\n2UEIEQAMxV5HbreU0tqeDhytaCGn0Wg0Go2mI+l0IfdHQgs5jUaj0Wg0HUmnLtElhBgshHhXCLFH\\nCFHT9P93hBCD2tMBjUaj0Wg0Gk3b8LWOXDrwLVAHfIOKjUsATgO6ACdLKZd0XDc7H22R02g0Go1G\\n05F0mmtVCLEBqAfmSCmrHdq7Aj8CwVLK1PZ05GhDCzmNRqPRaDQdSWe6VkcATzqKOAApZRVqea6U\\n9nRCo9FoNBqNRtN6fBVyeUCIh20hwEH/dEej0Wg0Go1G4yu+CrkngYeEEEmOjUKIXsA84DF/d0yj\\n0Wg0Go1G4x1fV3ZIA6KAfUKI1diTHaY0/Tu9KSECQEopr/B3RzUajUaj0Wg0zvia7JDdinNKKeWA\\ntnfp6EAnO2g0Go1Go+lIdEHgDkQLOY1Go9FoNB1JpxYE1mg0Go1Go9EcXWghp9FoNBqNRnOMooWc\\nRqPRaDQazTHKMSPkhOJeIUS2EKJOCLFZCHFOG87TXwhRK4SwCiGO+aQMjUaj0Wg0f1yOGSEHPAI8\\nCLwInAysAj4TQpzcyvP8CygDdCaDRqPRaDSaY5pjImtVCBEP5AKPSSkXOLQvBuKklGN9PM/FwLPA\\n48DzwGAp5T4P++qsVY1Go9FoNB3GHylr9WQgGPjQpf0DYJQQom9LJxBCRKNE3Fygwu891Gg0TjQc\\nbKBidQXSoidEvxey52eTITLIEBnsvHjnke6ORqOhFUJOCHGtEGJTU3yZxfWvIzsJjAAapJR7Xdp3\\nAKJpe0s8DeyUUn7k785pOhcpJbVZtZgrzEe6KxoPlP1axur+q9k0dRNLQpYgrVrMHes05DeQ81BO\\n8+vDHx9m29nbjmCPOhZplVRtrsJS39HDmzNWk5Wtp24lQ2Rw6LVDnXptzbGJT0JOCHE58BKwDggD\\n3kZZwyqBvcACz0f7hVig3KC91GG7R4QQM4FLgRv93C9NO5BWJcisjVbfj5GS9WPXs3bwWpZHLyfv\\nxTzP+1ok5cvKqc+tb12/pGTj1I3Nlof6PHW8udJM+bLyVvW3IzFXmsl/O5/qrdW+7V9tpvjrYhry\\nGzq4Z7DluC3IxibxZoWcR+0CwFyt+p3/dn6n9AWgYmUF68auI0NkUPx1cauOtZqtFH1ZxP5H9rPt\\nrG3kvZx3VNwD+W/nN9+jhZ8UtutcVnPL72f31bvd2koWlmCu6twJlZSSoq+K2HH+DirXV7b6WEtt\\ny8LM2mhlSeASNozbwLLwZWSIDEq+KcFq6vjvfWnoUkq/U0Pbnuv3UPJ9SauOl1JSs6vGp+/0aKRy\\nXSUZIoNlXZdR9mtZq46VVknWnVnNv4uyjNYdf6zi6xJdG4GvgYeBRiBVSrlRCBEDZABvSClf9vmi\\nQhwP/OTDrhlSyuOEEK8BZ0gpk1zOMxDIBC6TUrq6XW37BAObga+klPc3tV0BvMUfLEaufGk5m9M2\\nA5DyRQrxf4pv87lsn40QbXPtm6vNbJm9har1VQAMfHYgff7Wp8XjCj8uZNfFu5zaph2eRkh8iFOb\\npc7Csi7Lml/3uKQHIz7wxXALmbdmcvClg05tvW7txcEX7W3xF8ST8kmKT+frCOqy61gzYE3z66Fv\\nDaXnlT2bBUZAsPMczVJjYVmk/fPoOrkrfe7oQ9w5cWCFgFDfoyyKFxZz6PVDRI6JpN+CfgQEOR/7\\n21W/UfB2gVNb5IRIUtenUptVy9rBa522Jd+TTH1OPeUZ5cT/OZ5BLwxCBLQrZMQJq8nK0tClTm2j\\nfxxN7Ile53/N5D6by947nZ0B4YPCmZw5ufn8xV8XY6mwEH9ePEFRvi5h3XYaChpY1XOVU9uYxWOI\\nOT7Gp+NNRSYOvnLQycIWf148KZ/a72lro5WKFRUEdQsiYkQES8OWGp2KYe8OI/HyRGV1FW1/JvhK\\n5u2ZHHzB/lsc+dVI4s6K87i/lJLSb0vZdrrdehh7ciyjvh2FEAJroxVTvomQniHNv5vCTwrZddEu\\nt3OF9Axhau5URKDn9ygtksOfHKZ8aTm9bupF5OhIw/2sZisVSysI7BpI1MQoAKq3VrN+zHrnHQWk\\nW9M9Xs/pnA1WViatxFyqxPWETRPoOrZr83bTYROZt2RSv6+eXrf2IvGyRJ/O21lUrKxg0/RNTm1T\\nD04lNCnUp+OLvihix593OLVNzppM+MBwn/tgNVspeLuA2l21JF6VSORI4++vLVSsriDnoRyCugcx\\n8KmBhCaFdt4SXUKIKuAs4FeUkJshpVzdtO184FEp5WCfLypEGJDsw661Uso8IcQTwK1Syi4u55kI\\nrAFOk1J+5+FadwG3AROAuqbmS1AWxglAlpTSzaQhhJDz5s1rfp2enk56eroPXW4dUkqK/lvEzvPt\\n8Saxp8Uy8suRboNxq85rkZiKTIQmqh9Aw8EGVvV2fvBPL5lOcGywU1vF6gpKvysldk4s3aZ1Mzz3\\n/of2s3/+fgD6zutL8l3JBHYJ9LlfawavoT7b3Uo25N9DSLouyeAoRX1uPauTV7u1j/5+NLFznAfl\\nradubZ7V2og+LpqxP3vPi5FWyZLAJV73sdHzup4MfnEwASHG35OUkvw38yn9ppTYU2KJPy+e4Jhg\\nw31Lfyxl65ytgPPnYG20gsBJLDWWN7IiZoXbOYa9P4ys27NAwuCXBpNwcQL1OfWs7uf+mTkSFBvE\\niI9GuH2GAMWLitl+5nYAev+tN0k3JLF22FpoMmp0P7M7oxaOat7fXGlmebflhtdJl+msTVlL7c5a\\nr/0Z/sFwEi5J8LpPa8j6WxZ5z3u23IYNCCN1SypBkXYBJqXEXGEmKCrI4/0wafckugzpwoaJG5on\\nJI5MK5hGSILLBKPGQtbtWeS/mU/yfcn0OK8HkWNaP1BkiAzD9mlF0wiJC3Frr8uuo2ZrDd3SumE6\\naGLdyHUezz2zdiYbJ22kZnuNT33pNqMbQ14bwroU+zlnNc5yE/ig7ufir4qpz6kn8bJEt8+neT+z\\nFWuNlaBu9u+koUC5dg/9293dmC7TPfYv+4Fsch7J8bjdkdQtqUSOjmRVn1U05Blbi/s/3p/se+3L\\nj8+snUlguP35t+3sbZQsdLaipVnTnASulJKd5++k6L9FAAz65yB639ab/Q/vZ/+D+92uOfiVwfS6\\nsRcA5gozWXOziBgeQdJNSQQEBzQLy0OvHWLP9Xucjp1RMaN5crH7+t3kv5bfvG3I60M4/PFhRKAg\\n6fok4v/s2+S+ZkcNOy/aSfjgcIa9Nczpe2oNpiIT5RnlVCyvoNeNvdh93W4qlriHsM+qn9XiZLNm\\nZ43TPeh0fMMsyn8tp+R/JZiKTMT/OZ64P8UZ3qN7795L7lO5za+HvD6EpL96Hpd8pW5/HWv6r2Fz\\n038Afe7qwyNPPdJpQu4wcKmU8kchRB5wly3WTAhxKvCZlDKiPR1p4fqXAe/gYkETQvwFeBMYIKU0\\n/KUKId4GLkfF0hmxWUo53uC4DrfISSlZEuBZNMyomuE0uNhoLGlky4lbqN7krD/TzGmIQMGBJw+w\\n7x67oTE6PZryDHfPdPJ9yQx4dACmQhMH/+U8OweIGB3BsLeHETk2EoRylxmdByB8SDiTdk3yaEkx\\nssQYYZvd22g42EDNrhrCB4SzZuAaw2PCBoQxZe+U5tfexMukzEl0GWSfD2yYvIGqtWoQ7juvL/Hn\\nxLvPiL3Q4+IejPjQ2NJXvLCY7Wdvd2sfu3Qs0TOjm1/nPpfL3rnOFp+JOyZS8HYBuc/YHyiT904m\\nfEA4++7bx4HHD7TYtxlVM1je1VhUecM2mFWur2TjxI0t7j9532TC+6sZ7+7rdpP/er7hfl1SulC7\\nw7uIszHwuYH0uaNlC60jUkrKl5RjrbMSe1Js8+DmSfS4MjZjLFHTo8i8MZP8N4zfgyMBXQIY/NJg\\nQ5ejI7aBtOzXMrYct8Vte0sWJVdKF5ey9cSthtuGvTOMxCsSqcuuo/FwI/lv5Xv8PvxFcI9gGg83\\nurUbiaucR3PI/oddBEVNj2L8cvX4NVeasdZZqc+tZ/sZ2zEVmegztw8DnxwIGAskG65iykZLz1gj\\nZjXOYmmwsfXRE7b3WrunlrVD3Z9zrs+oPTfv4dArzoJ0VuMsdl64k+LPjV3/08umExAc4GRZt9Hv\\noX70e7Afa4atoW53ndv2lM9T3CxVLZF4ZSKDXx7cPEmXUiKEYO9de8l9Otdp39HfjyZqahR7rttD\\nxYoKQpNDGfX1KGp/q1UW3RR3eZA1N4u85zxPsBzpdXMvBr/k3Va0+YTNlP9sPD4Z0eOiHgx7bxhr\\nh6w1NCw4EntqLF3Hd8VSbaHHRT0oXlhM4XuFzWK/53U9iT8nntrfajEdNpH3fB7WWiuxp8Yy6n9q\\nouvpPpzN7E4Tcj8DX0opXxZCfAyMAv4KmIFXgEAp5YT2dKSF68cDecAjUsqHHdoXA/FSyjFejh0C\\nuNqPTwHuQlnm9kgp3Uar9gq5rDuzyHvWfpP2urkXve/oTfgAu4k3e362m3hyZfCrg0m6PslpNudp\\nYEq8MpGk65LYOKXlwdfGgKcGsO8uQ++yE0nXJxnOhD0RNT2KUV+PIjg2uNUP07YIkL7z+tJ/fn+q\\nt1WzfrR3IWZ76BqJjvhz45tnyb4SOS6SXjf3ovtp3anZUUPRF0VuD2lXJv02iS5Du1C3t441g4wF\\nqiuBXQOZkjOFFbHu1jgjet3Wy8kF1RpG/ziarScZiwVXet/em0HPDwJgZdJKTPmmNl3TEzFzYhj5\\nxcjmAcVcZSYwItBt0rDlpC2U/WSPiZlRNYPqDdVsTt/s03XCB4WTcFkC++ft91vfbQz/YDi7LnV3\\n1dloKbSgcm0lu6/dTc2Wlq1kve/o7dUC2VmM/mE0sSfZrbyengND3x5KSEIIO8/fiaXaOH5t5KKR\\nbD/DfVLkiM3DUPZzGTmP5lD+q++DuiPRs6NbfeyIT0fQ47weXicN0wqnERwfzO6rdlPwToHH/TyR\\nfH8yRZ8WUZfpLtQAUremsvPCnS1avFtD+KBwxq0YR8G7BS2OE4l/SfT4vgY8MYAeF/dQ7uugAKxm\\na5vFshGeJs1HCxPWT2BD6gbDbZ0p5C4ABkopHxNCDAIWA7anThVwtpQyoz0d8aEPj6NcpPcDG4EL\\nUWLyDEe3apPoTPbm6u3oGLnV/VdTv9+zwp9ZN5OA4ACWBPkubmwDv1FszNHMjIoZFLxTQNZtWR1+\\nrTRzmk+f6ZT9UzAVmFoleDuC0ORQGg50TrB/R5Mu0zEVmliZuLJDzp94VSLdT+3OjnPtVoVR346i\\n+yndAeWiWdmjY67dWcyomoFsUFbFsP5hdB2nYpsa8htYlXTs/OaNCE0Opfdtvd0sz/4k+Z5kEq5I\\nYN1wz27jjiIkMYSYE2MofN9z0smQ14YQFB3Ezgs6pmxLj0t6cPjDwx1ybn/SdXJXYk6I4cCjLXsV\\nHLFN1gEq11Qe8ee3v+g0Ied2kBARwFSgC7BSStm6NLA2IJRJ6l6UeEsEdgMPSSm/dNnvV5SQG+jl\\nXB0m5Ixi0Vzp93A/9j+wv9XnnlE1g10X7aLkf63LYvqjED4onLos49lqW+mW1s0wZkPjzLiV46ha\\nX0XWrS0I9vjD8K8boCwG7ngeqrt6378FJmdNJvOWTLd4yN8LqVtSW+XqbwutFQDl3WDFdDjt2w7s\\n1FFERhqkt847a0jCFQkUvtu+7OI/Ov0e6tchFvMjSWda5GYBGz0kBUQAE6SUrbOTHuW0Rci111qW\\n8kUKO87xHMcQOTaS6s2+lZo4Fug6qSvJ9yaz40+ti91oDQFhAVjr256Gn2ZNI++5PLesRY0zcWfH\\nqbIe3j5qYYVfjm9+aTFFEjhnUcd3zoG7n4An72n78WsnwqTON/h4pCgO4tsxjT73MyhpCs/74dko\\nQv5nL+dhDoRH/gF/fw4imnI5nrgbfjgZ/vxfuPmVdnT8CHHXkzB+I1z4f74fM+d7eHABTO9kg++i\\n0+GM/3XuNX8vtPd30Zn4Q8j5mhb5K56L7g5r2v6HxlJraZeIG/bOMOL/FE+aJY34C4wzh9or4gY+\\nP5A0a1qL+41cNJLYk72XZki6oe1ZPAHhAYz6bhQT1kwg/ux4ZlTNaNXx3c/sTrpMp2uqd2tOz2t7\\nMqtuFiM+9a3siBGfFxXRZ24fUrelMmHTBNIsaaRZWv4MO4s5P8DjPgqTb06F4u6etweEe34cBCcZ\\nZxfaKP7KXcR9eh6cudChoa9zPGhgSDUbTlBP26I4uPBj+OvrXi/TbtZOhks+sL/e00KufXCiet/V\\nEXDSD/DYfZ73PeEn2HtoKNOLpzPo7aFez/vs33ztsXeuegtOaaNl7JH77SIOYM7cSs74Gh67F655\\nA05cDEvS4ZL34IEFcN6nSsQBHPCl5kAHk9OGPqybBP89FzJVSCcbx8FpXsRSSSyYQuEfj7T+Wle+\\n1fpjHHnub/DDSZ63LzzT+/ElBo/wL/6k7r2zvoLZv8CrN7S9f/66hz3x8k1tP/b8z+D4xW0/fvVk\\ndfz3c9p2fHULqZ9nLlS/p9m/tO38rvhqkbMCU6SUbuk4QohpqHpv3p/0xxi+WOTMFWZMhSZ2XrDT\\no8ga9c0ocp/O9ZjtacM1kNO1DlpbGPyvwfS6vpdbe/a8bHIWuCdZDH51MFFTo5rrDm2cvpHKle4F\\nNyPHRZK6MZXGkkbyXsgj52HfUvsBEi5LYPh7w93aD/7rIJk3Zrq1p3yZ4maxm7J/CmF9wzj46kEy\\nb3I/xoYt+Ll2d60qmdFKbn8etjRVK9k7eTLdg4N5r6CAQeHhzImNJfP6PS1mBE6pms4+YWJAWBgB\\nZRZWxnue1o/JnsTBn4spvqbl5BMAUzDM+dH++r7kZDKfPcCNrxrvP/sXCLQoPZXbBwq6jCX3uyJ6\\nXdGT6MQwArsGsuuyXW5utpO/g4YwCDbBe3GDuKgiiyF74LXrvffvqjche4CD9WbEDnjlZqd9ruEN\\nKooGURoL1qakw2c+68KEV/0XsG3DZk1y5ZzP4RaDKpgn/AQWg6oKU1bB4y6CzvZeHfFktTp9EdRE\\nKgFx57O+99/Gc3co12apgyg/+0u47UXj/TOHCz79k6QoHv55h2r71/Xw6fl4zuVvgWAT/GgwyN39\\nBIzZAhd/7P34jeNg/Cbv+3jjvE+hOB5+ne3b/qsnw/2P2u8xACTN79/TeU78EcwOFYOG7Fa/oV3D\\n4U9fwq0vGR+3bAY8NA8WnQHhXhIin74TbnkJwlxCZec+AxsnQFQFLDzb/bg7n4YNqTBzKSyY574d\\nlCXRFAIXfQx9clVfdg3H7TsPr4XrXoOe+eq+GrUNJmyAGIMhqzrC2Up49X/gUoMKrutS1fU89c2V\\n4xdDQiGc+bUS2iVxEFoP35/i2/E2VkyDfzxqf51QAJ9cZH99zRtw+Xswy2BoPX4xjNgJXatg0zio\\nb8pLnLEMHn7Qed+fj1P3zPaRUBHtfi5QE8Zr3nRvv/xdyHWchMzuQNeqEKIfYHs0LQZuBn5z2S0c\\nuAoYI6Uc1J6OHG20JOR2X7vbpxIFNoHmqcAk2MuGuFK9vZr1ozzHxyTfm0xIUghZtxjHJU3cPtEw\\n7dvaYHUr7hn35zhG/nek276V6yop+abEKbt23PJxdJuuasw5FvbtOrEro38YTV1WHRsnuQeixp0d\\nR8oXKR4LhrpmfI3NGEt0mvuvZEl5OembN3scTMA5Y66l2nC730wg5YNazL8q/9FFH0FJd2hsYWrS\\nOGsWQQHKitVwsIHM2zIp+6GMLildSL4nmaA53Zi8dROZdfa4vRkBkTyc5iz6E+/sxfDT7Nml894K\\nJv19Vc4hIDqQb9f15KTheQS4FNBf8AD8epxzm6fPZPcQuP417+8HlPfz/qWRnL8plOW3hHNjkIfs\\nR+l+bVdm/4KqgWeBa/4D06s2k3znHU773MY/2Ypx0vnoLfDC7S332ZVbXoSXbnVvP+1/UOthpuw6\\nkN//CKyc7uUiUg06KTvg5+OVpc+IS9+Hqx0sM8cvtouJAAv8fIKXaxhw1ldQaVDeMdgEN72iBuE1\\nk+H1a2mzSPOVftnw9lX212//Bd67Qv37yrfg8vc9H3vO58pdOdalGss1b0DaEsjpC0vSIKYMPr3A\\nvr2yK1z9phJxAAP2wpvXuJ//jWvgo4vx+TMYuc34npntzdfk5TdgE+uP3QtTPZRxvOVF2D7K/Tdb\\n0wXO/a9dSMxaAg/Nh7owePR+WOHiwPAkQr32vQUCLHDPE3DcLxBoVZbBTy6E/f3d903ZDi/fYn/9\\n6H2w+ARAwKBMeONa79dyEzYODMyC//zV936f8zmUGVgiAyz2311ivnpvKTsgyAI/ngjP32H/vP2G\\nwf3xj4fdv7+OFnLzgHmqO/Zm524iUCVIbpJSvtGejhxteBNyB/99kMwbPFuCbMysm0lgmH0KmPdS\\nnmEwuLe0am/p7Oky3bBqvS/nBch7OY+sW7KI+1Mcwz8cbliHyYal1kLlqkq6jOhCaE/nKttSShqL\\nGgmOD24WaTlP5DgVzRz04iB639Lba38ACt4r4OBLBxn0wiDDgsTrKyuZuNEuEv/xlOD475y/p57X\\n9WTov4fyaE4O/8hWfcgQQ5DpzoUyAfb1tw+0p8bG8u8hQ0he7b2AriNLx45lZrTxlOyEzZv5udx9\\nWpuYD19+GE3QITN9Hu5HYoR72vxscwSnhMVwl1kJKddBPycZrv+38cOn/z5462rntjMXQlWUz2/L\\nJ7xZQ576O3x3qnPbBNbzDH93aruXx1jNVI/nCTTD6f+Di78J4HD/QP51ViMX/J/xjPq7k+Hpv4MM\\ncJ+Jv3oDfHa+5/4e9zM80OQ+WzNJPeg7WgiBuxgC+OkE5dZ0xduA19kkhYRwyKTKzCQUQH2Yu2Wi\\n5yFlCarqCq86uMmeuwMWNbkFh/4Go7cqV+2aKRgSYIFJayG+SIk7VyF71ldw+wv21xd+DIVtWLDA\\nVXRd+xpkDoFz4+PJrK1lS4176ZfhO53fG8D7l9p/f11q4JvT3a+18Ey7dRRg7Ca4+0kIMcELt8HS\\nVkRvGFnF3rvM/b5qC8Kqfk/tJf6wXZB/ewrsSFGegR9Pgr0tmIDiiox/u0/crSYtZ34NQipLXk1T\\nbe0xERFdIwgVAAAgAElEQVQkhoTwQ9kRXqJLwkk/wpVvq7CMbaMN9ulgIdcX6Id6nP0C3AS45k03\\noOqw/e5SxoyEnLXRyvpx630qauoq4mwUfV7kVELBtUCtK1azlbXD1lK/19k+P37deKJSm5Z12VZN\\n5i2ZTtmV/Rb0o98D/VrsZ0dSvqyc0u9LiT051qkAro0ik4kfy8oYHxnJ8IiW60ln1tYyZK2zizTA\\nAj9mJBL4SAFhA8MY/e1ougzpwrclJZy2zXlB75V9R2EeuxNLpb1Wlav77Jy4OL4obluU7JcpKcyJ\\njWVdVRVpm1uuXVYxYwbdlreuXl6PQkgsgN1DlbvTE8EmOGORcld8cxoc6Nuqy/jE6Ytg7nPu7VYB\\nxxvEfkxhFY/j7JN8hPv5mVaapZoIsMCyz3vwWf5h3rja/hB3pGsl1ES4uNQ80DsX4oph62jf9vcX\\njtYrm0sNqRINpq9UWaI3vgr57S8u78a7w4ZRZbFwc6bxxPQviYm8U+BcG+zg1KncmpnJ5238nRxJ\\niqZN4+StW9lQ7R4KE1MK9z0GqRtg3ny7mCqaNo0DDQ1M2GBcB+za1+CiT9S/H7nfPuFaPm4cMzZt\\n4pH7nRMldozwkCgiIcBqv/dmdOvG8grvGfPjIyPZWF3NQw/aJzdFccqdahQWYEPgbKE5FnB0Vdos\\nnp6omzkTIQRhS4/OHMzcKVP4tKiI46KjGRcV1WlZq2nABqOs1d8rRkLOU8yYK6lbU4kc5fkus5qt\\nNOQ2ENIzxFDsuSKlZPvZ2yn5WpUdSflviuFSKjW7aij6vIjQpFASLkto1xJfHcm9+/bxxAH3GkJ5\\nU6fSKzSUCrOZ83fs4Mem2dTs6GjOjY/nJg+DDcCOiRMZ0SQGw5YsocHDfZ1tTqHy2Xy2htZz+6W1\\nTsHemtbhyTX48k3w+bnu7TNZygKcg2a+4ixeoA3+0zZySY8efDBiBFm1tSyrqOCFvDxDS4snNqem\\nMna9/8uBBJtACud4LICQBhVs74nl48bxTkEB/8lv/eoNf0lM5O1hw5pfW6Qku66OfJOJiV27EhYY\\niJSSlw4e5OviYk6KjWVunz4ECsHf9+7lmdxct3NOjYpiVWXrFrJvCwv69WNi166c4jJZ88b/jRjB\\n+T168GNpKXO22otdfzpiBOfvNK7tlhwaSs5UZTH+qLCQS3ap8JibkpJ45ZDnot/DunRh/YQJdFu2\\njNAauPgjFVO38Czl8rVV3bksIYH3C41LkljS0rhr716ezTMOb9iWmkq91erkoXBkbu/e3JOczPRN\\nm9hTV8dD/fpxT3IyIQH2cSGjrIzZW9xXG/HG3N69ebh/f8IDAzlxyxYWd5DV6+cxYzi+lX0DJeLC\\nAtW4+kJeHrdnOXvBLk1I4AODz3zFuHHcsGcPxY2NPDZgACfFxJC0yv/1G/dMmsTgLnbjTaettfpH\\nxFXI5b+V3+JSPGOXjiViVATB0cbrabYX2xIpR5ofSks5uelBeHZcHFclJnJKbGxzvJgR++rqGLim\\n5RUMPhw+vPlh2RoEcHjaNOJXtlwjYNW4cUzd5FukdUqXLuyo9X/g/bFG96AgSsxmt3bX+J7Fx8Oj\\n/7C/Ns2aRUjTrPg4fuYBnNP/9tOXK3kHgDt69+Z5D4OWv7CmOa95Wd7YSMwK31bKsA0Q6yormeQy\\neH48fDgDw8PJKC/nx7IyMsrLMXt5tlrS0ui2fDnVFuOVDHyhcsYMugYps8vde/fylIGw8sQDffvy\\nUL9+bX6evFdQwBW/uYZMw4+jR5MeHd38nbeHgWFhpHbtyv8VOa+0sm78eFKjlDdCZGR4PD5nyhSS\\nw4zN1msrK9lUXc1Z3buTEBJCwBLjGNrqmTOJCDSebD954AD37DNOTKqaMYPIoCB6rlxJgcl4pZPn\\nBg7kjj59uGLXLt5zERbbUlMZGRlJo9Vq+Fk2zJrVLMg8fQbmtDQCffh+rVLyRVER/ysp4dz4eDZV\\nV9MzJIT99fU86jLhfnrAAO5Mdvbvn7FtG/8rca5t2jc0lJ6hoaz2QdSnR0fz0qBBjGqaIP1z0CBu\\n663CcGZu2tSiVdKR8hkz6BbkbIrcVl3NJ4cPkxASwsU9ehAbHMzC4mLO2WH3jH07ahSndO+Obcx3\\n/F1Um808nZtLfHAwIyMi+E9+Ptf07EladHTzfo7j27MDB/K3Pn14/dAhrtvjHM5zVvfufDVqlFNb\\npwo5IcRJwA3AUMD11yG9FeA9FnEUcpZ6C8vCjTNI4/4cx4hPRhguvnu0IaVkW00NFikZ19W4dIdV\\nSvbX19MvLIwAh5vZbLXypx073H6wjvw0ejRToqKIdPghSSnZU1fHsLWtzxo9GpDp6XxQUMBlBoNW\\na4gNCqLUQAi1F9OsWRSaTHxy+DBToqL496FDfHjYuLhr0bRpXPHbb3xbahwJ8Vj//tyXnW24Taan\\nU2QysbKykulRUbxZUOA8iEkIbrQniERSxWdRbxNn3c+28Mu4qmgcc/iee3jS7dyFIwoZHRHR7F73\\nx+dtxA1JSbw6ZIhbe43FQuQy599379BQcqd6jt0D9fDeUl3N8TExRLkMHlJKTFIaunayJ0+mX3g4\\nBxsa6N3KGX/W5Mn0CQ11sqqAsqY9kpPDsvJyLk1I4MTY2OZz39yrF9f27MmwLl0I9jLZag1SSjfx\\nMzUqipXj1bqpBQ0NXLBzJ5urq6k0EKtXJibydoHxck4vDRrEBT16EB8SgkVKnjpwoPm+/M/QoVzd\\ns2fzvvOys1mQ4541v2HCBMZ7eMYZXjMvj1uz3OOXZXq61+OMRNTW1FRGRSqPzI6aGkaucy88OCYi\\ngs0TJza/PmvbNr5uerZe3KMHH45wLplU2/QZdjEQlZ8dPuxmUUziIFtGdiM6Op2gIC8+SB9pyYiQ\\nV1/PopIS1ldVMTs6mksTnYMUM2trmbBhA1Uu98Kg8HB2TZzo1Qjgq9Xv+9GjmRPrvWyWKx1pHDES\\n4dsnTiTFJYyo04ScEOJUYBEqe/VE4HvUqg7TgRxgmZTyyvZ05GjDUchVbapiw3j3+IjpxdMJ7t4x\\n1jd/U9LYSJyL5cH1IVVtNjNi3TpyG5xz4R/t35/7PQzw3pjfrx/z9+9v9XFHCxMiI1mfmgpAsclE\\noBAIYMS6deR7mGUbYbOc5Dc0eDXVb0lNZW1lJX91mcWFBQRQbzWutOv6HXoaOFz3/VtWVrP1Ky44\\nmE9HjGB2TAwbqqpIdYkFOjR1Kj1DlX9PSklt7S7KRQ96r/W8tuENvMr5fNb0KpBfE76juDyD8xoe\\nc9ovPHwwkye7J6EAlDU2EuujtcyRZwcOZO5e9wLOjlYMVz4vKuK8HTuQwOndu7Nw5EiniUx7KDKZ\\nWJCTQ2xQEPf17UuoQx8O1NfT1yW55rmBA/mbQf/rZ81yOvZIU2OxcOrWrSytqODfQ4ZwXZJxEF+V\\n2UyUSyyoJS2NMrPZ7ZnkajFtiVqLhQgXEf5lSgpnxxvX4vTGOdu386VD3N/OiRNbjN3dXVvrNEm9\\nLzmZRwfY69BIKQldupRGl3HW0ZoKSoj/WlaGSUpOiInxeJ96YurGjc3WrxS287L4O8h6wsL6M3Hi\\nDgID/Z2S2T7qLBaKGhvpExrq0/ddbDIZelt+mzSJIeHhSLD/Xmtq4L33IDkZTj4ZPFhUO4vdtbUc\\nbGhgVteuBA0fDrYJw6+/Qnp6pwq5VcA64A6gEUiVUm5sWpD+B+BuKeWn7enI0YajkMt9Ppe9f3N+\\nsPZ/vD997+mACHI/YZWSosZG4oKDeSA7m8cNYtJAPTgrLRb+feiQRzfB0cihqVN9il9YN348N2dm\\nsqaqqtXXaGlQabBaeePQIR7JyaGwsdFt+7AuXdg5caLTOVZWVDDdwK3rGNfx6sGDzfGASSEhZE6e\\nzM6aGrdYmJ9Gj+YEgxno7M2byXDJlv08JYVzfBzczFYrtVargZXJypYtx1NenkFQUHcuNz9FNgMM\\nz/GLOAkh7Z9Jz55/JSJiNFlZtzjtFxk5jtRUz2smSikpNJnYXF3NsC5d6BsWRuLKlRw2+Lz/3qcP\\nTw20OwZWVVQwremzLpo2jbgQ7/VkcurryW9oYELXrn6zXPnCV0VF3LNvH92CgnhtyBDGdu2K2Wpl\\n+qZNrG26b0unTycm+NiYNHqiwWql0Wp1stgDFJpMFJlMjIxsu+VoQ1UVu2trmRMbS/c2fk71Fgtz\\n9+7lh9JS3hk2jBkestFdKWhoYHVlJTO6dTO8x74sKnJy492TnMzjA4x/N+2hzmJhW00NIfsvo7z0\\n6+b2wYNfpVevdlT+bSP19QfIzX2aoKBokpPvITCw5YQ2b5isVpZVVDA+MtLzb2HLFhg71rktMxMG\\nNaXGPvEE3Huv+nd2NvTr164+eaSgAHbvhilTIDQUpAQPzxQBnSbkyoDzURY5MzDVVhy4ad3SO6WU\\no7yc4pjDUchtPX0rpd84u6NaKu1xJNlYVeUxw+r3wPx+/ZjXrx/76+ro7yXuzlbnzcgi4Ig5LY34\\nFSsoa3J9vjtsGJcntqF+AWow+OjwYfqEhnJ8TIyhVeflvDxuaZqVjejShR2TJvl07rz6ei7cuZPM\\nujquTEzk8QEDDIWmlJLLdu1qdrGOiYhg3YQJ7RYnJSXfsW2bvaZIccRpnFdzp9t+Z3Tvzt9KnPPs\\nu3c/nejo2ezdO9epvUuXEUya1Lol2qxS8mhODg86WHvPi4/n05SUVp1Ho+ksbGEtEhjji2A9fBjK\\nymDwYI8CwBMZGc7PhKioKYwf7zDpLS2FgwdhxIgOs1ZJKVm7dhh1dcranpj4F4YNe9u3g7Oy1PsG\\nCA6G4mKI8qF20g8/KAucEfffD48+6t6+bx/07w+1tbB/PwgBy5fDp5/C4sVw1VVw5ZXQrRsMGwbl\\n5Uqk7dwJc+ZAQwNERIDjd/rcczDX4TlXUKA+7wkTDLvWmUKuBDhPSvmLEKIAuFlK+d+mbScCC6WU\\nnmtoHIPYhJy10cqK2BVYqu2+/ZayUjuDWosFk9XKgYYGNlVXc3ZcHN2CgjyaoI8m3ho6lLCAAPbW\\n1XFejx4M7dKFt/LzuXq3czKJzRXmOKO9tVcv/jloULOAuX/fPh5zsTZOj4pi6bhxTiLKU0BweEAA\\ntbNmAUqEhQYEdEpCyZ7aWkobG5kcFdXq6/kS12GVkp/KythbV8e58fH0aMEa5Qt79tzEoUPOy0bM\\nNlidr2LGDDYud54xx8TMITo6nezse53aw8MHMXlyyzUZPVFtNmMBtwBnj/tXb+XgwVcJDx9I7953\\nEBDg23GaPyBSwm+/QffuSkiUlYFDfJ5Hqqqchcfrr8NfDaraWq3KvRYaCjOaqsRaLEpY2BJX5syB\\n//s/JSQcj3v/fbj5ZqiuhjPPhBdeaLYuuQq5iLARTJyyQwm4jAz485/tG99+W4mf7t1h2TI43r4W\\nMqmp8PHHdmuWI/PmwYIF9tfffeckoqqrt7J+vXOh7/TRJeDoQaithd691ecKEBYGH30E55zjfr0v\\nv4SzDZa4sLFggerTkSIuTln+Kiuhb+s8dZ0p5FYCb0sp3xBC/A+IBs5DWefeB5KllG1f0PIoxCbk\\nKlZVsGma3RUWHB/MtMJpRzR79ImcHO41iFnbPnEi52zfzh6HlQQ6Cpmezr66Ot4pKOBhg2BjTxRP\\nn+7V9VFhNhMiBOGtmCkuLC7mgexsrk9K4pqePQ3jS4wC2sGeXfZHp7JyDbt2XUp8/Hn07/8wQrh/\\n/ps3z6a8PMOpLT1dct3u3byen08gsHjMGNJjYtwGk9jYU4mKmsT+/fOd2kNDk5k61ff7pz1YLDWs\\nWtUbs1m5nfv1W0C/fg90yrU1fmTZMmiafAFQ4iIQjCguhu3bYfVqZYk6/nhlSfFEYyMYTX4CA8Fk\\n8mwlO3DAeCBviocCICcHZs60izUbZ5wBF18MF13kdjighE94uOqDUcxsZSVUVZGxx3lZxoh9MPFq\\n9919prhYxZ3deissXOh5v4QE9b6Skqi4aDSb6p2X3Ei3FRD/5hslUFv73N2xQ313NvLyYMgQ6ITx\\nriPxh5Dz1Wb7IWBL95oHpAB5QAFwHPCgh+OOeYo+dU59jz4u+oiKuNcPHTIUcQAj161rUcR9PNx9\\nnVNXxkdGYk1L464+fQy3m5oeogPCw3mgb18uS0ggITiYKxISqJ05E2taGi/bTONNZE2ejExPbzF+\\npVtQUKtEHMBZcXFsnTiRG3v18hgkHBEYiExP5yWH2eXa8eO1iANqa/ewceMU6uqyOHDgcXbuvNhw\\nv8ZG4wKwrw0dikxPx5yeTnpMjOE+QgRitboniEjpe9JIeykoeLdZxAHs3/+7fWz5TH19Hps3z2bF\\nikQOHHDPKHajuBhuvFG5oN73sgZX+zqlRM2ECbBmjXJLgbKQLVniLOJAWZNcsVrhuutUP4WA+HiY\\nPVvFR511lnKFzZ6tLGDr1sFTTymxYsOT+9NiUULq3nvVeW+7zbnfnqwxs5tUzIYNynJmVCpm0SLP\\nIg6gSxd1TQ+JTzzwAPRyX1u73SszxMWp9+VNxAEUFsJ//wsvvghXG6ybZuO001ov4gBSUtT7N5uV\\nBa5Pn2NexPmLNtWRE0L0Bk5GZa4ullIaV1M8hrFZ5NaNWUfNVvsPfPjHw0m4MKFDriml5PasLJZW\\nVHBFQgK39e7tJBpvz8zkhYMHvZzBTjAm7uZJprKKDUxgfcxTfDV6CkIIr2UP/ta7N88MHNh83dz6\\neqKCgnx2XTnSaLWyraaG0RERXtPLNUeWDRsmU1XlXB4mPd39ubByZU9MpoIW9wN39058/LmEhfUj\\nN/cZp/agoFhmzPBc0saf7NlzA4cO/dupzVP/jwkOH1ausfHj4YQT1CDnK9XV8PLLZIa/ycEx9rIb\\nkydlEh42wN3ilJ+vrEFGQl1KZWWyBY4//7yy3tjOYTIZW7ccsViUkNm2DR40ENhz5yrBdt997ttA\\nuf9soRkhIep8beG772DVKme3oS/YBJ43/vlPuL3ji19nuEQ7dNkPkzq5pkTFcNjkHIVht8h1Fq+/\\nDte2sNDrkeDqq+E//4G//AUiIxGvvNJui1ybzBFSyjzgP+258LGAtdFK7S7nYrC2hdj9hWtl7Qiq\\nGcIeHqruzx1799IrJITtEycSu2JFq5ZUmckyjueXpn8v55oeuxBC1cXqFRrKgSlTnNYUXT5uHNO7\\nua9t2sdDQU1fCA4IaFUtJ82RwVXEecJiafvsV4hQrNYGt/bOtMg1Nh7hdRf9hacMuJtugpdechd0\\nUiqhUVioLFM//KDiqoCDLoP+wb8PZpDLANwikyYpq5aNO+5Qf6689x5ceim88YayltlYsgTSWlhc\\n9NlnvW/PylJB5n//u/f9WuKUU9p2nC9ehE4QcUcLfvFZvfqqsv62lgMHlLUOIDGx+V5vJi9Pudk9\\nJUZ0JCedpEQcwFtvqd/xK0brtbUObSbxQu3uWmSjXT6FJIUQHOu/EgCuIi6KCv7DNTzHXL7kHHqR\\nx0GTiZhWijiA+3Cu17Vnj/MPok9YGDI9nYNTp1I7c6ahiNP8cbFa2168WEp3a0hAQJiha9WoraOw\\nWAwqxF91lYotaon8fLj7brurzluB64MHVTyUzaXn6kb74Qc1G//uO2M3mZTw/ffKOoX6PGtrdmN+\\n8kEV9O7Juv3KK2qbrY+2v4AAlf3Xu7cKrHcd2BywtGXe5qFuoRuXX6764ijioGUR5yvtFXFHG//3\\nf345jZNrNToarr9e3ZOeVsXwx+fY2gErOxtspYPCwmDjRrjhBvj559adx2KxizhQLvoDB5SVeNEi\\nlWXaq5eK0du3T/2m771X/dasVmWNXbhQxSNKqdqys9Vv5sor1W97/XqoqFAu3vJy40nGgQPqHK48\\n4rCyjR+9VB5dq0IIK634OqSUR7bqnp8RQsiCDwvYdYl9uajYk2MZ/d1oL0f5jlVKAl0qo5/Hp9zI\\nv5zajLICbXyRkkKv0FAmG6y19yvuduyxYzOIjvbTQ1Pzu8HVDQoQETGSiROd17FcvjzGKcYMjF2T\\npaU/snXrHKe2pKTrsVobKChwL0GQlmbt+LhTKdm4qD+VUc6JFc3unm7doKhICR4pYeVKNZvv3x+6\\ndjV+KP/4oypJ8N137uLElaIiFWs0cKAaQBy58kr417/gtdecY65Qg/DW93pS1iuf4HIYfSd0da8V\\n3GZc3XCJ38Gwp/x3/rYiA2Drk1CWCnFLYfhjEOhu0O0czGY1eE+Z0rrjamq8J1RERytLopRK8Dvy\\nww/KegPKJWtk4dy0SbmUXbwert9pePgQJk9WbmeT6TCHD39KRMRwYmKOV/f16tX2TNuZM+3xax9/\\nrJIvbPTpowRWdbXq94wZSnSZzTBunLJyNVE5FDY6RzGQdnIIosFg4lZV5TkmEZTL3GFNYDfuvFMJ\\nNtfYyc7EZFJhDpWV6rtyDEWqrlYTv4kT3b4r8M/KDt4k4QKHv4eBg0Ap8C7wFPBe0+uDTfv87qjZ\\n5ryYdsSo9hU0dOQ0g8Wez+Rrt7a5POPWBmqR+D/FxzMpKopfx4yhi4O6P8lDwLnKOmz/Goia3z81\\nNUarNvj2rMnNfdqtTUqLoWsVQC7+XgVTp6QowWPDZFLWHk/B3b5SWgoBAYj9XrJjKypUbNW996qZ\\n8owZapAMDDQWcaAG2uTklkUcqIE6IsJdxIEaAMLC3EQcQMUIKOuVD0BjNOy7vuVLtQfrUZL7s/d6\\nJeIAimdB/mkGO/lS5qFHD+VuzstTgklKZUXxtRxPTo66ByZPVlYsWy2wHj28H1dZqZITPCUIfP65\\nKrvRvbsS+NXVqs7Zgw+qumM2EQfKJSulEky7dqmSKFarKnwbGenD76NpqUlLHevWjSIr6xa2bDmB\\nQ4deU3087jiVADJ7trMAuegi+2cmpbIyxcWpWMgTTlD3LKhjtm1Tmb5ff63qr61Z7d6L2hp1nrIy\\nWLFCJUY0NnoXcQBDh6rjPvjAuf3UU9XxTz99ZEUcqPvpuuuUNdM1njwyUn3GHRhm5FHISSnnSykf\\nklI+hCozkgP0lVJeJaW8t2lJrn7Agabtvzuqt1Y7vY4Y3XYht6W6mv8VF5PftPzV9wbrXdbiXorv\\ndL4hAecA810TJzLCYaaXHhNDzaxZyPR0ZHo6P4wZ43qaJiS5uc+1+T38kbFaTeTlvUBOzuOYzb4v\\n4vxHJMDiHn4gP/kIuW+3wd4gzzxVDRI7d6oB0hZLFRqq4q8CA1Wxzh07lLtl4EAVTG/zJtTXqxIU\\n+fnOLsV33oFDh4yzGpuwuj4Bn3iibW/aFzwJQi8Uu4xPNnHTUUhfIkc2b1aWGSP89Pnlnef82mlB\\nkLffVt/3/v3KGmPEqaeq+6OwUNVbc8zm7NZNudhsAsWTEEpKUkLdRu/eyjJnO6+U7vFN116r2m2D\\n9plnuguVESPca6VFRKhEjoceUmU8jAgMVJapoUOd4yCFsL+PTPeajFKq91dSsojGRvs6zPv23eu2\\nb7sIClKWseOPR+IeXiFlk0yIjoZp01Q9u9Yk0V1yibOw/OabtmW//g7x1Ul7HfC0lNLpSSSlrAGe\\nATp4nnhkcMxWBVpdBFhKyXsFBYiMDMauX88Z27eTtGoV5+9wr2T/7ahRzEqcYXieEaik4NXjxyPT\\n0xnWwvp/3igpaSGFXGPInj3Xk5V1O9nZ97Ft2xmddl0pLdTV7cdiqWl5Z2/YlrQqKvLZwiWlVOn9\\nixc3xXMZRFo4DnRNRC7a5dYm62uwbjFebcTNCnTFFfDhh85t/fvDyJHw738rq9ZLL9njwcLDlaXA\\nda3PK690GsCtBiLF2vZcnk5BeJsin3SSsjYarMvaItdcoyw8LshTTlQiyXHAlNJ+30gJY8YoV9oL\\nLzgfvHevijmyiYqPPlIWpqY1fZ0IDlb3lGPh3L177dcz4sUX1bn+8hd73TjHmCMbH36oBnlfEUK9\\nZ1cMntONjSXk579DZWXTijI33qjE3XPPKdfia6+5n2fDBjUhAZg/vzn20e8IYVi8t75e3R9VVc6/\\nP7O545J/jOJkpXRfVk/jH3yVs3GAJ1t0COB5ynsME9Q9CFOhCdkoEUGCLsN8X7yi3mKh96pVlBg8\\nLD8rKnJrO6V7d3YUGM/YPxjSm6SkdJ+vrfE/jrFdFRXLaGg4SGioe80mf2K1NrJ16ymUl/9MSEgv\\nxoxZTESEQ6xIRYWyOiUkwIUXGp9k507lsnTljTdUwO/+/QTRFTPua9FaP/uQwAsuszd8BbjmxOTm\\n2mtbCQHffIPM2+92LhlgLKTARyuQH7AaPMEsYRDUekNZy1x+ufpMXN1BrcSwBtjmzUpM2YiJMRY/\\neXlKNJx4os+Wi+K6n5AxMe5O9Lg4951vvVX9GSGEc000KeGzz1SF/quvtq8gUNEK6/Ytt7i3Na1j\\naSrPISg0hoBwH5ZyMiI2Vn1fn36qsmifeMJtWSiLpZ7168fR0JALCFJSviA+/mzlbvWw/BKgitZ6\\nWUqwM2hsLEOIzsttbLa+tdD2R8VqbaC+PpfwcP+suevrN7seeEgI4TTlFUL0AuYDPqYtHVtM3DyR\\nmTUzmbh9IilfphAQ6tvHlVlbS/iyZYYizohH+/cHPGTV4d/MvoCA39VKakeMxkZ313i72bVLDXRN\\nNbAqKpZSXq6ytkymg+zbd5faT0qVuh4dreJnLrrI2aXYtataL7CmxljEgVoyKDkZZs3CWu8u4gDM\\nN1xm2O5Is3ywWcdOP91QMMlAkB60RGfFZRla5PKy4PTTWz44IEDFMUmpiuJmZtpjhEC5Gi0WZcGU\\nEt59VxXMdbUs2qisVPvPn+/cfuGFdsvXmjWYEtw/HDnax4Sr3r1VOY1Wup8c19P1K+edp6x0jstA\\n+YgQoYbtUkp27bqclZv7sXrTCKqqPLh8fbsIXHCBKnthsLbn4cMfNok4AMlvv13R9mu5YLWa2bfv\\nXtatG8vevff4PZv70KHX8FNREJ/QFjnP1NfnsXbtCNauHcyGDV4mAK3A11/4rcAvwD4hxGqgEEgA\\npmwUiJ4AACAASURBVAC1gHEp+N8BAcEBRKREEJHiuztziLfSBAbc1xS0azYbl0EICPCfycLoB9a2\\n80jM5lICAyMJCDB+yP6esVrrfdsxLw/ef5+y0F0U9NlJ18Bh9Er/JyLWwcJRXOyetQbk/3eck627\\npGSRb0Vfq6tV9pmPeLKUNSRAqKNeNZjHyAAQLp5aIyFHAFjCja/TaRa5bmGA8/dmsdSosgRWK7z5\\npirJ8Mwz3tfU7N5d/RlVlXetu3jxxSoo37aW5uzZKtvVJq7mzfO8RuSkSRyudZ8MWq31BAZ6+DBb\\ngadnQWnp9+0+t7/xlNVcXb2FwkK1woSa7NzNmDE/tft61dVbKSr6nKioqXTvruqNNbtTm7BYfChb\\n4yMlJYs4cEDFF9bUbCE8fABJSa0vZuvpO62u3kx4uMGaqR2EsUVOCzmAwsL3qa9XSU/V1Zv9ck6f\\nTExSyk3AIOBZwAKMavr/M8BgKaV/evM74MrffmvV/pc7BLZWVhovdm8LVvUHUja0+3xSWtm+/U+s\\nWBHH2rXDqa3d46feHUWYzWpQf/995IRxbpstdWXKalJdrWod5ec7Z1zW1cGoUdCnD/XP3ceWMe9T\\nGL+BrNgPyb88XrmZNm+GwYMNRRxA6E+bDNv9iQwAPBQOKnfJmTEqMGRkZTO0yA0ZSGO8cXSG5ZTj\\n1BJJVqtyQS1YoOKvFi+GL77w/gZcWbBAffbr1qkli2w8+STWOHcri8XS5FcNCFBWyg8/9G1h9NYw\\nfbo99uuXX3y2kJlMhYbt/kq28TYZacuKPx2LsZCrqXGONysrW9zuK9XX57FhQyo5OQvYtu0USkq+\\na9rif9dkVdVmdu26gh07nJMf9uzxIRPaAE+WPCECDcWwP8cWZ7wkO/zBKSx8z+/n9NnmLqUsAe73\\new9+R7yQl8c7BQVu7f8aPJjre/XCbLXyen4+NzVlFv21Z09eG6KWsPX2g/L3TMZqbWjXjD4v75/N\\nSRP19dlkZz9ISson/uqezxQXLyQ391nCwwcycOCzBAe3ctWNxkaVZfbOOyo9/PvvVRD2li0qtb8J\\nw9iqc+aAse52I+98nMTSnjshafb5LR4X2AnLCHqyxgGYHKvYPPMMMtA9Q1AGAS5jh6GQGzUCS2U1\\nNLqLE/Mz8yC6KT1z0iR7YHjzwdL99ZIlqo7W6NGqvpdrAlBqqvpzWGrJusy5SDaA1drOJJIOxGKp\\nNmwvL/+VhAQva3L6fH7PN5jFUklQ0JEpEm5cjNpYyBmJA7O5mqCg1iWmOZKT87DTMzcr61a6d8+k\\n9VVuvWOx1LNly2y32oztwdNYERAQavhZlZX9QmzsCX67vr0f7kLOatUWOYDa2tYZe3zhmFnZQSju\\nFUJkCyHqhBCbhRDntHxk8/FhQoj5Qog9Qoh6IUSBEOJrIYRfInQey8nh9iy1ZuEQdvMCt6q/pBqu\\nb8qcCwoI4MZevZrLhLw+dGjzLMmbWPP3TMZqbZ9C2Lt3rtProiL/VCBvDY2NpezYcS4VFcsoKHiH\\nnBz3QdordXWq9s8776jXv/yiMr727HEScYdOg7Xvuh9ubkXicF1bDTy+TpYTE1veZ84cJYAWLVI1\\noGyX8CLkZBB2S9ncuVhD3U1yRhY5i4GnXUozVqtxVkFjYyvXWhVCrZxwxx0q3srHLG4jC1R7soFL\\nS38gP/8dzGZjwdV+jMWLindqP96eAzt2tDzR6CgKC90TRDwF6hvdU1K2r3Jweblzofa6uqym8/r3\\nOVxc/KVfRRx4E3LhduuzA/n5/rmX3Puhkx06k2NGyAGPAA8CLwInA6uAz4QQLS6Y1iTWvgeuAJ4G\\nTgBuAPLw6FjynX6rVnF/dnbz67t4itFsYzTbmFb5D5/O4S241f8WOR/ju1pBp7li6urg5JM5/Ofu\\nTg+GvDyHZVKkVIU4HRMAzjlHuTKtVlWyoYtB0seBA6pGk+1SCcp61mCgkyytEHKuMWRecSg0KgzC\\nXWocVp9prmmVn+9cE8u1juCAAUrAgQrs/+mn5v1libsF2Yb1pqYCl6ryOEbuEuvhfOVeHjJEVS7P\\nyqLEoIqOlGbDgQTaIOTagJTScIBva1D5gQPPsHXryezefSUbN070W+ypI54GPrPZP4k23oRcWdmP\\n7Vpbtz3s3m20wruxqDWb3RN12isYPK3/6+/ncGNjsV/PB56tXlKaDV3yYWH9/N4Hdb2Wkx1MpsNs\\n2XIiy5d3JyvrzqPQnX/scEwIOSFEPDAXeFxK+byUcomU8gbgV8CXCpR3AmOB6VLKN6SUy6WUX0op\\nb5TtnL59X1JCToP9FIGYGYi9ent19WafHvLeFg8/2ixyRjgWmvQLVVXwxhvI3FyktKgf+SefKAH2\\nww/GGZCOa0uefbbzti+/VLWvAgO9Foh1xLUoqSOtsciZo32I5r/wQvWeCwuVWH3/fUTz+lF2Nn8Q\\nh/nHhaqgqVHJAyGUYG1sVNbF5ctVJfhg4z54Wm0BnB+8nu5hKc3KIrZ7N6xdi7mvcTFTi6UKIyEI\\nYDZ3vJDzfM+3TYDt22dfj7K29jdKS39s03m84el3HxPjH1dYSxM6TzF67aWycj3btp3N7t3XumV/\\newoxEcJDfKXFoGxOO114xmsCmw2/j5KSb9t1Lc+0zb7gSWxarQ2G1j8/OaQM+tGyRS4v70XKyhZj\\nNpeSl/csVVUdV/yipmYXhYWfdNg9faQ5JoQcygIXDLjm8n8AjBJCtLRWyw3Ap1LKQ/7slMlq5RSX\\n4o7BuP+QfLGAeRtQjR5MZnMlNTW/tWlx8/Za5MLDBxv0p5UuAinh8GFVpuHRR+H881WAupTNNZxM\\nd13LxkXJLFkSxM6HArBeZo8LCugEK73FS6UWJyF3++3OS+rYePVVkBKRlu75ROefr8pQfPyxvQJ8\\nWBhceiniFPd1iRqtxRSOONTyEkNBQSqRYvp0jyIOWhJyJod/e5rpO7d7sjJ4K9diZFXxNyZTvmG7\\nJ7FUUbGCjAxBRobgwAHnZfKysua67V9X515Rv7146pu376w1tDSh64j4Qau1kW3bTqWkZCH5/8/e\\nd4fHUdzvv3P9dKfeqyWrWHKv2KaalhhCDYROCiWEAKETICF0CHwJNSRAElOCgQRIIECABIIJGDAY\\n29i4F7lItixZvZ6u7O+PvdVtmZmdvVsJwy/v8/ixbnd2dnZ3yjufuucP2Lr1Gt15+tzkdNJ3ToOD\\nxmDIqUrOaO8lHN5LrXf9+u+noJ5nS6Dc7uRCs7IEArHYEIaHjdJ32rw9NNSE7u5PLBPi7u5P0NX1\\nISRJovZR/fvbufNOze/du3XJWZPArl0PYsWKg7Ft2y9H2t/R8S989tkUrF9/Jj77bApCIbYWYrQx\\nONhoXigJCNFxQkgmgKFUpVcpYCKAkCRJ+lG7FrLMfSLkFGIGEELKAZQDaCSEPAHgdMhBjJcCuFqS\\npC+SaVB7OIy8pUsNxz16y28o4QL4Ihy+alU7off1rcHq1QsxPLwb6elzMWPG+5ZCgKSqMqG1laU2\\nAyCnUHI65cTglHySI3jxRc3PTVcAvRPlv9sWAEVvAbnxCABUtWMlENjObbolDJ4wEwjT41JFr7oI\\neFxs4qHuegXUCCzpxNDQdqH7ioAnCVZ/Zxap0E/OrPoGB9mezSzbOTsRCjVTj9NVQDGsXJnQD2/b\\ndi1ycr6FYHAqwuEONDUZ09zRvlUk0oM9e/4Eh8OD4uILLIfpYb9ze2KMmc0DfX1rEAgw4hAmia6u\\n9xAOJ7y7W1qeRH39opHfPMmvJMXQ1vYiotEBpKfPjP822uemqsFwOgMG9XUk0sXYULejr28VMjMP\\nSumeerhc9HzZZmCRr1hsCL29xqDE+tzbHR3vYPXqo0d+V1bejnHjfsEM/6KgsfFm7NghOxaVll6O\\nQKDBUMaMYKfqQdvZ+R62br0SANDTsxQDAxswadKL2LPnj1Ak7+FwG/bufRYVFYzUbklgYGALNm36\\nMcLhdlRV3YG8PHbmn87Od227rxqmErm4fVk7AIrIYcyQA4Am8ulQnWdBCWJ8PYAqAKcBOANAPoD3\\nCCFlVhsTicWwYBU94sreeXMMx8QkcrxQANoBsGvXvRgeloWLvb3L0NHxtmn9VtvDA20hia75VE5G\\nHYvJKsK2NjlmlpJCyePhkzgK9h2m/b1VnQiOMt9vuM5S9TIuuUQmVa+8kjh2zjlANIpuBokDgIiF\\nGFKEJKsmoS9IdsYVFFetihE5LqFnIOX0Yyncg/Zc+/YZ09h9+eXJAID+/nWMOxiJ+dq1p2Hr1quw\\nefOl2LDhfPHGctoG2Of9ZyaRW7/+TCxZQrB79x9suR9AV4WqwZb8DmPLlquwbt0Z2LjxPCxfPh2f\\nfz7TUh2ioG26Y7EQs95QiC7tTQXJklG2apXe/wcG1mnil27cqO2n27ffhK6u90zvq5A4AGhufoga\\nE9XsmVyuLNP78NDYeJPm9759L6Ox8Rdoa3vRcNxObNt2Lbq63kN//2qsX38ud4PECjGWKkyJnCS/\\n/b1I1piEAkLIkYSQmMC//9hwO+UZ+wEcJ0nS25IkvQrgOwDSAFxitcIXWlvxZb92YLgIQduBB1JJ\\nzurVCw157vTgTar6AaD36uroeFPz22xnk5KNXE8PYt1G9Vns8p/IqYKcTjkqekGBHIctSdDkVQ7V\\nqyXXGFlbbwMgKRvHU07ROgB8xrC/UPJFnnhiovyf/yzb2XHACt5MR3IWDCzphNNpX1gIvkrfXCKn\\nl84m07fsUhXywDZg1z5XLDZsiOkFYCSA5/AwXbLX3a2Vzg8ONqKzM7HBam1lZHjgQJQ8JwvRDd2m\\nTRchFNqDoaFd2LXr/pSkCmYG7bx+1tz8EPWcsQ5r7ycS6UFj403YsuVKhEK7qf2RR+RoNp6x2DAa\\nG2/Gl1+ego4OeoBi3prAe4bW1r/iiy+Oxtat1yEa1X5DluSZZxumtu8MhXYazisBl/Vt2Lz5cnR3\\nf0Sdp2gOOeoNCG2NStVer6fHqCFrbv6d4ZjbTY/bmSz27UsIAaLRbnR2su1l1ake7YTom3sWwAUA\\n7LLsXAqg3rSUnDUCADoB0Oi6IonjuXEpo2ypWjUsSVITIWQDZCcIKm5Rpc9ZsGABFixYgPZwGDc0\\nGvXc/50+HXkeD7q7jQOpv/9LrF79Hcyf3wSHg/7KrUjk9Bga2qX5beZcYTqBb90KPPGEnKQ6LU32\\nRnQ6gX/Kn1+i5KOO2px8nJYFIFsRkLW2gsT+DRhzsyMWHoTTKTdm9ervoKPjn/B4ijBnzjq4FVK3\\nbp3s8JBC4FdWOjUa7JbI2aVaA/geoyI2cnv3LkZ6eiJgcjJEzs7nYYFFFvVjZf3671PL5eXJErlQ\\niJIAHsZdfnf3h4Yy0ejQSN8UAcvcwj4iJ/qtJOzZ8wSamh4aSbQ+adLLyM8Xjv6kviv/TjaQV6vS\\nrE2bLkZr63MA5LhqdEP9YWYbaCSpqemhESnVvn2v4MADd8Pj0ToC8QLDhkI7sWbNCair+70mp/Pg\\n4FasW3cGAAmdne/A4ylCeflVI+dbWp4SbqOC/v4vAJzKPK8n7mvWHI/29tcBAM3ND2P2bKN2iuYh\\nq36vdPOc5G1lWRtr2jzd15eUNZUwuruXwuXKRkvLMwgGp6Ok5CeadX/VKvmfnRAlctsBnEUI+QzA\\nqwD2QCc0kSRpEeU6KiRJGgJgJR3AWgBeQsh4SZK2qY5PireDpe8AgG0AkhJBqYkcAEQliWoX9++p\\nUzE/U5aSbN9+m+E8IBvL9vYuY9pS8MiV2YSrXwhZht0j9T35GHDFQq0R/O7dwDPPADfcoC08NAS8\\nrVXdUnNWJpOlq6YGuOgiORhvb68cVf8PfwDmzUPPP24G1h6jKU5+dhXw2G8QCjWjZ+cn1Cplru7D\\n9u23oqNDJp7Dwy1YujQHCxZIsqRt8uQkGquFNYmcUQoRi0WYpD4BOiG30+tYr3bQ3sdcItfe/g/U\\n1CScAZKTyI0FkTOXyElSlBkT0emUs0LwnDYkKTYS70whPGpEo92WiNxoh8Gw8q327PmT5pnWrTsL\\nhx1m3UTDTFswOLiNetxKW62qnhUSBwD9/asZdYaY9dKcCEbyIstXo6npQYwff/fIEZFQG+3tr2HH\\njgrU1f125NjOnfdAPZ9s3Xq1hsixJMa8qAJm70s914VCzSMkTgHd+WeL4ZjWVMNeIrdr12/MC8VB\\nkzraiVgshFWrjoAyf0ciXaislMOQZWcfhenT31GHKsXTlDilViFK5B6N/18KgJblVQIgTOSSwFsA\\nIgDOBnC76vg5AL6UJInq6ADIqmFCyBsADiGE+CVJGgQAQkgFZKmg0SCGgVu3bzccu6a8HEflJEz0\\neGJV3oLFI3JDQ8zHo9ZLW0Q05d/9J3CdidcjAxJAzY2phAOJOQDJAzj1j1NcDFx6KXDjjezKDztM\\nlgQCWL2Ekk7G60Bn53tYs+Y4poG8InnZtesBw7lIpBcuVzr7/jqkpU3EwAB9j2Bl0qEb1IdgNvxY\\n5CkZOzQWeI4T6j6p9y5UEAxq05cl40jDIibR6AC6u5ciLW0CfL4KAEBT0yNoaroffv8E1Nc/Ca9X\\nTKrK8tNSfxsRe0FeDLdIpAdud1a87UabpEik2yCV4YFt72QPkbPyrYaHtUQgWb832gKu3tQ0NT2Y\\nVL3ae4hL5PSqSRa6ut7jjEfzucD4/sTauHv3oxoiNzTEJyE5OcdQpcE8sDKIKFAHY161aoHhfFeX\\nUdXe2WlUJ2slcsb+Y21zrIXetMEMH+/6GFMLp8LtdMPjTKyF4XAHCHEDDj8isQh6Q73oG+7DYGQQ\\nHqcHy3cvx+q9q9E/3I+oFEEpvsB8XXSD5uaHNb+3b78Ju51H4KLXL8Kt1V8iJ7mllwtRIldl/63F\\nIUlSGyHkfgA3EEL6AKyA7LCwAIDGRYQQ8i6ACkmS1DEybgawDMA/CSG/AeCHHFy4A8BvIYCucBi3\\n79ASqrnp6bizSvtqXK4sZigOnoqNR+TUXl406CfH6FaegBLYcD1QZM0/InEvRo+JHXkYBr57KNZM\\neBKDUhMKM09D/bTnQTi2ZpIkoavrP4jFhpCTcwwzevvIPWJD2LLlcq6XozJB0ETq4XCrJSLHCw9g\\nZtcVi4XR0/MRfL4q6oIsp0njezKzVOSpSOT27HkKu3bdB7+/BnV1jyEQmIzu7v9Sy6oNpFmSO32f\\ntku1Go0OYfnyGRgc3ASHI4Dp0/8Dj6cIW7b8DIBMQHftuhc1NUbCTkN//1rGvdWLi7l5Ay9Egprc\\n0Iic2YKpB1uKmJoEc3i4FQ6Hz6LTkz3BWmmbEPWmxo64ZpIURjQ6CEmKmI73MCVlHA07d/4awSDd\\nuUKMEGs3plbsQiUpOjLOzOaMZGAWZkb9TWiSNlG09e+BP7MPQU+Q2ofX7v0ML/7nJjT1NmFd2zpM\\nK5wGB3Hg46aPcfHsi3Fy/ckoDMobofVt63HO38/Bij2yvc2/DgHcFkyRD1x0oOZ30AWcVwmcXAr0\\nhIG7NwCfmMTdPrsCOFWQGR206CA4CZBjdOa1BUKjhifxGkPcCKAXwM8AFAHYCOB7kiS9qSvngM66\\nXJKk9YSQIwDcA+AFAGEA/wFwrSRJfJYUx4WbjJrgZxsa4NERlczMw0bykOrBNyxnTwampGHTOmDN\\n00BzM3DTTYhNiwHGCAkaDJYAftGoetnZcvT+vDzEplQDMO74pLNOx87e5RhskW2I9nb/FaV9VyEj\\nYy6z2sbGm0ZiCRUWfh8NDbKMmZXyKBYLGZJk08oAgN9fZwh5QVtcY7EQBgY2wOerNOSW5KmwFK9h\\nGiQpipUrD0Rv73I4HGnU3bfIRM4icslK5Pr7141EzR8YWIudOyu50gQRb1J9W5IJJUIjLK2ti0e+\\nXyzWj507fw2/v05TpqnpQSEiJ0kSmppY5axJ5HhQPwdtcbSqEmURNpq0QxSNjbdgx45b4XCkWQwt\\nYk9yddp7UYdnysw8MOWUf+3tr+PLL09GNNqL8ePvRkUF253dSoBYXow2NXp7V3LrGQwPYm3Lp8L3\\nnfuIC591Ag7iwN+PPAAZuvPkVpkklmWU4YjsJvyoUrhqAMALa57CrX95CgDw3mHG8y19bSP3oJ0X\\nxc/evATvtsq+hcU+4Dnd0jAQasUdn98x8vvT5sQ7uviNi3HxGxcz67ZC4tRwALh5InCoyv8hwy2T\\nOjMid4FF8Va1/Rx8BJa2P4SQqQAOBZAL4HFJkloIITUA9kqSNKpRPSXZqOCu+D9eOWM4fPn4cgBH\\nJnPvL/v68FKblu/9uLgYNZQ0T7xdN1+SxLORi08gkgTcf79BuS31dwMX/DDRBgF7ta7pHCL3wx8C\\nixbJoUPi9+/oeBMeT4msGvrEGH9ZksJoadFq15ubf88lcuqAkHv3PoPKyl/B769m7hBFJAiKVMTt\\nzsGgjhvryXIk0osVK+ZjYGAtPJ5SzJjxX/j941Xl+QtvT89nyMgwhpvZu/d59PYuj9fBVwHzn4Xl\\nwZcckVu1SjsLd3X9B4HAVGZ5EcKo/1bhMF+tTwNtgdy48QLN7337/o6ysist1w3wF2tRiVwsFjbt\\nD+pvSt800IlAONyODRt+hN7eFSguPh+VlbeAEGKbClV9nx07bo23ZcAQSZ8QNyf8hz1BC2jBn/v6\\n1iA7ewHWt63Hrrb1SFXzpI7zt23bz7G4sQdOVwZ6Qj3IT8vH2ra1aOppQlVWFU6oKIOoee+mfV+i\\nlOKE1TGwB29ufhPHPncsAOCX9cCROg36luZn8cedWfj7hr9jW+c2fKsQuEHE3Q/ASaXAZ51AhisG\\nx+AnhlW7Ph3Y0As09TTBkUT4OZ8JCbKHwgMuQv9bQYZJVCXlmohOOJwMh7ugCvhjIzA1S0viFNRa\\nUdwIwE2A40uMx6/nyyWEIRoQ2AvZc/W7kGXEEoDXALQAuBey48L19jRp/8N9u3YZjt1c4sGKFfPR\\n17cKxcU/Rk3NgyCEcDMc8CQcXLXOQPcIqQIgJyZTX6sbADEBe+qN1wLF2ycCVVVyqI5x44BDD5Uz\\nAqjvLUn44otvobtbTiSdlkaffWgLgFVbjWXLajBp0t+Qnj6bel6E/Chl6CEEtG3cvftxDAzIKrfh\\n4Wbs2nUf6upkd/WhoSaEQnxB9LZtN2D69HcMx9XG0yyI2BixFk8zVTsL+qwL/f38gK9qkub311Kz\\nF+jJXjJ5QPXfhU0gk9t28zZXWhs5vmrVitMRbayzJDrNzY+ivV3Ohbtjx23IyzsZ6enTbffm7e7+\\nOIWrjarVk144CT2hHnSHulGeUY6ZxTOxt28vdvftxqoW2S1ve9f2kfK//87vMc31paGeR945HDfH\\nrUG+Vwb8tDqFZlLw3Io78SXD/OqzrcC97L2MBh5G9/ty7wpc9vaxI7/1JA4ANvWE8JvVskF+wClO\\n4gCgNihf86fZsgpQjx+MA26Iv1YnP24vFa74c7FGl10pUNVto71L1vsFgKmZwENxB4FndgBPbpf/\\nDrqAS5LoL2dXAO+1AnN5EWhtxHHF8j89Dqq7CsvM1GcCEJXI3Qk50fy5AP4NOa6cgjcB/BTfUCLX\\nNDSExa1aQ9VHamow2PoIenpkz8nm5odRVPR9pKfPYnoNAQzVSiwGvPEGYp89AhzBuK4zsQAPUXYP\\n+gTuw0Kd0wmspdsNqdHXt2KExAFyXkka6FHP2dIZlvfa5s2XYPp0ls2WeGBl2rs25vrTqtt27/49\\n6up+B0mKYfXqhab3ohn5AmLqmlQkcjTXftY9mpoeQSTSiZISulqC50UYjfZDkiQQQpi2OXrpYDKB\\nTLVhTmJYvfoYajmz6PIsRDnBm80MsBPlwoiY2LjFYiFEY1FsbN+I5u4t0AsYFIncYHgQWzq2IOAJ\\noGuoCz3bb9aUe+2z07GRnIFYzys4khEysOHRBmzYpx2LOf4cVGdXw+fy4YOdHxiuWVgI/JxDIPYM\\nhlFkIYzQqxsTJiQr9qzQ/Kbh4jcuxu2TgIPztMerVF3Ln1yknqQhSnxiEuBlEA3Wcc31qr9PKxe7\\np4L+CHBCCZhG8vNU2bySIXJuwr82FG98ZopxyNX1uyjvTH0oLy0PDXkNkCBh9e4PR0gcAHx/HPBK\\nM9ATAR6bCaqUVAQvH3c5mts/BML0eH7/PvffqMutQzgaxidNn4AQgu9N/B7cTvlFLKE45LFwWZ0P\\nkLTrV37+6fjNpN/g/jEkcmcC+KUkSc8Ro8V+I4DKlFuyn+LBpiZEVFuSOr8fF5eW4oP379WUa2p6\\nGPX1i0zUODH1DznTwWOPAeEwYmeDSeRiqq+0+h7jeX0C9/DEEgAJvSndASOKjo63kZPzbWZ7AV4k\\ney1oxImXkoilZhoe3sOUVlmRyNFjQYWpZfXo7f18RFKXDJIhct3dn6Cp6X54PMWoqrotbq/HcnYQ\\nk9Rs3vwz7NkjewErEh89+CozKW6/5GeSaL3kKRkip34XHR1vMZ0vTOuRYugb7kNrfyvKMsrgc8ms\\nZJij7r3zv7fjy3f/hVA0hHG+flzByNr8afPHOPbtUoNdjxrHLf42lu3rQSgawv9NBWbr1FwnPn8s\\ntoaK0NKXCFdRmQY8qdPOb+vYhNvW3obvloJJ5PQkDgA6BjvQMciWiDpM1p1VXcDCIn6ZVKEncQDw\\nX5Wg+OwK++/Jk/TQVHw0OAjgY5BMXv0j16v+PpTyDnhY22MuOSr1A82D5t+YhqDHB2AIxcE8AMZg\\n78rqd+mEfADJaQMA4KZDr8ekJmDdvnXY1/EeZJP3BLJ86ZBuNm66mpoeGXFyUvD6d+9FdXY51q8/\\n01BeFAEXQVl6PjoYQ+bIqiNGHPCqc1ITExPJOH/y7KytQpTI5YIafhWA3EeTiSK236MrHMbjexIx\\n2QrRgluyOhEOGWWkhDjj3kscOfT77wHDTmDvXuDRRwGVF2yMYxiiDvcRokjkYj4HpIE+2UPU60V0\\nyzVAUyKujtudT1X5rl69EDNmfIzMzHnMe3d0vMVumLqNFCKXljaBU57n+MEickNwOAJcL6uEUDDp\\nIwAAIABJREFUatVcIkcjJ42Nt6C5+RFm/SIQUYlp7akGsHr10SMqwHB4HyZOXGwaELin51OsWCEz\\ni2BwBmbN+kzjRaq2WWQ7ifAtYKLR/jiRo3+T4UjviNROkiQMha15ZgLA5vZ1mCtgTP3y+r/hgKD2\\n2MRHJyIUDaGlrwUDYaNKtiS9BJWe3biTETrQSYBlzXIOSikTAIPIRaJD+JZJ5JCuoTaE4ryYZnfk\\nItCQuMPzgV9QvNiUGYQnXXHA+OVmZgE/rAQ6h4FHtgD7dN3QbI3/vBPIcmslPHaCZYs1oOrmIqTI\\nKtKc8ru/cLwL8/PS8GpTD15uBpzEicqsIgBsLYoarLYF3E6YJT6SneLkLxYhGQDEQ218p5hvvwgA\\nH595H8rLr8bmzVcIZ8BQMK1gEqSblyMc7sDSpcaPX5czHtLNW/HRR8UYTkHbXxQowN1HyXaunZ3v\\n4osvjtKcZ2kH9CQOAOoLZnBDfYmgr28NnE62OE+SwpCtymjnUtc3BwJTUq5DgSiRawQwH7Knpx4H\\nQPYg/cbhsd270ReVB2gJmvEHXIS0Pf34rFXvNwQAxNTuSVr8Z+B1Y7oTgE/kRiRyN9+MjML/orNf\\nn/suBsnrAonn4NTb8rjd+VT7JgDYvPmnmD2bnlO0s/M9IXsvgKXKZJMEfrgVeraB7u734XCYhewQ\\nl8jRCJdiDJ4KRAzD1X2lu/sDjR1Xa+tzaGh4lllPz1AHFq1chKruC0cW576+lXj+k/MRTTsSLocL\\nA8P9qBaQjn2w4300cF5p9UPlaA3F8NwBYeRS+mjnQAsctyVWuKtrgeMoRr08KAu8mXRka8c2A5Fb\\nv4+1v5Sxu3c3JhawzztM7HYUuIhMknhQt5+mItR71l1YRSdryhrh5rwPlwMYVg0vN5G97xSD8XAM\\nuEMntDPz7BuMyrZWop6JB5YfiD29e9DYJWe6uWDKd9A2sA+vbl0Gl8OFBZULsLVjKxq7GjG9aDom\\ne+jh7BU12w0H3wDgbmqZVPDiqU9DkmJxj+0eXFoD/Ol7HyEzcz727n0O69efnVL9xYFcSDcnpPA0\\nldshlUdBOlGO+fTll9/Fvn1/t3QPM49nJQRKsqYNTU0PobWV7i2s1OnxFFODH4vfJ/EMdK2Cdr6L\\nxSLYtOknlHKymQUhqel6u7reRW4uO8F9LDbM1CrZYb/K86a2ClEi9wyAGwkh2wEouWgkQsjhAK4E\\ncIttLdqP8FBzYqf2AzyNNMiSILrNTQyxPr6ht8SZmGOZfrASUEgeAsRJkXvdWQBFIBWLhUaSqRuJ\\nHFuW39fHdpXfvv1X7AbrQM8nyCNybNLLSoMkX8cPiZFQrZpL5AhxpRwl//I3L0fnUCeiUhRepxeV\\n/mEc6jE3+P/NR7/Gyu770T7QjjxswDU12vPBu3y4Z/IwJlNUa91D7bjx4/Pxgk6QWhJ6Gof/Sw7h\\nMikD+O0M47V6dA51ABwiF4sNYTjKJlkZbtkQuz8+Bydjo6OorMy81sKUTXCaExgw4c0BzixnZoBN\\nK8eCcr2DOJDudkKOcsSuo5ghDPA6XZiYXwefcyNYkp7y9CJ8f8bFKE0vRWlGKYIDryDS8fjI+SML\\ngZyK+7Gnbw+2dm5FbU4tSmIfQs6OSMerZ76JmG8W1n7GYb4qLD0vUdfy5TPQ1/cGkAPcN+9qTbYP\\nQF6U//tf+ge+5bBf4ukqOc77Rx89mRJZoCES6TFIdbZs+RlmzfrMliwZaltSFtTzXX+/0eEjVSTm\\nNuvexf39a7BlyxWcuuV35PWWc9cLM5jZo+o3/l1d76Gl5U/UupqaHmLG9bOCjg52QFW5jXT3VTuC\\nsvt8DPF/EhAlcvcCmAbgzwD+GD/2IQAfgBckSUpNF7WfQpHGAcBRMHonqtHS8hSyr1jMd/lgLRRL\\nl0LKWwzsNib4lSGNBIVkSatkCVdQ9XcCLlcSPumw5nXa12c0GE1WIrdx43nC99XjyZWPY2foFXwv\\nw2h/8H9L78aa/j9gKDIEAoJrSgeRlkL80b4I8PCniSje+V5gEd3h1oD3G9/Bh/FPeUqp8fxzBwwz\\njYvdDuCmifRzLiK75x8oqB4z02Qp0hIeyTmuGPhLnHunQuTMjMZpbXA7YLp2pXEM6GuyK3HvUT/F\\n7t7d2LfvJQD0TURlZikQ5avgHll4P4oLT0NxejE++bjUQEgOH3cw6sbNwLeqv4XZBeOwYRXdXfLY\\n2mPw8+/+A9u2/QI7d9KjLa08/5/YseN2RCLvozLvZqxa9bihzJXzteFaduz4NRob2UTO6UxDbiAf\\nlZW3YPv2W7jPqkYo1IK+voS0ranpN6iuvlcT4JtHANRmEB5Pie1ETo6VqN0FKOGBkpFg6RGL9SMS\\n6R7J6uF2FxhSYikS+L17X2BqR1KBYjpjx/PoodRpJeYevR5+ii69BmLrVmPqLwWyzW9yzk/ae7Il\\na+wUeVFD6B6ryMqiRklLGqIBgaMAziCEPApgIYB8yMno35Ik6X3uxV9j7Jw3D4/t3o2HmpoghV3Q\\n77D1WH89/7xUlA+cdjgQiQAlJcABBwBnnw04HJA2shMoA7KY1+n0G0JIjNStUtXpJXL6QLfU+qUY\\nhiJD2DewDy19LQhFkkvBo8a6tnW4/MlD4ulMoghFQohKUXQPdSPX2YXfp76hMmBjy3+obt4AsHLP\\ncryjml+vsKgCPOJ94D8qtVPQJZMPxavroFx6eAAa1F5bNKLB8xALumSJGw0NGcCabqBLQNDQFzE3\\njlbUezw130+qUyNyTgI8dcIfMTk7A73bT6OWicGHE6pnA8PazcXvj30Eab5yTEjrQtuOKyBJIdTV\\nPYFA9olo6WuBz+VDx5570dlCT+BybO1C1NVdCwBoaZmBDRt+QC0XcPswZEIYyzOKUZghs3Ja+JGz\\np5yOsrJLMTjYiM8/ZzN+ZQPEW2Q2bbpoZDFZtYpm8UKrl68OcjhkEWFJycWmRE4d7V/JaaxGNNoH\\nlyvRSbW5R/XtSnRWkSDUamRmHoxgcKYhLZK2LayE6v2Ws22woJ1/jZvUWGwYra1/Tck4n4cEkbMn\\n3p8a4XAbJElCJEIXIohCTdjpGhntxt/sWdrb/5FSe8xAU/9KkoQ1a06g9nkrKC29JKXr9bAkj5Ak\\n6QMARr/2byiy3W7cMG4criwowKefOBBLdQPwy18AZZdrDkmShOFICMMmOf+W7lyC/gjgGdgFmoDh\\n3g/vQHc0gEgsglmOZShX2TM9tfpFHM2R0HzrMRcOzo1idTewvFOW6mztTy2KNwB0h7rw4U554XUA\\nmJMjpz9pGwDybA64qODIArabvp5kWDVXlQDsCwF5KrOJdBcQio/32iD1MirUwiWrBt48srRw/MHw\\ntAyim+FSr0aay4tJ+eOBKNvO7Jlvn4/66nuw+lO+q13rNa0YCA+gt+mauGTLGs6afAoGBzdixXb6\\neQeGkDZslBCfXH88fL5x+PjjcYhG5cVs8+ZLcPDBZ6I2V87SN7g3BpbfqpUUXV5vhSbhdkbGvJEQ\\nRHKZYUgSEIlIVIKgEKm9exdz4+3FYlGEQkA4zCZeIhKBlhbZ3k75193N35w1Nfnh8wHhcAHy83vQ\\n1sbYLUB+bx999A4IOQrDw8Y02x9+2I1YLAOxmBwC0+lcwqyruTmM7duBgQEgGOwAJ6ufAXv3Hou2\\ntn3wcGyMt2xpoZ5/882XkJb2f5bux8JLL4UxMAAMDwP19SFDnfv2DaOn5zxb7kXDli3LsWgRMG1a\\nBGVl9td/441LcNBBYQQtzHF6vPJKBJ9/Dni9QG3tMObP15eQcMIJEiSJIBoFzjtPQp5FD187cdpp\\nw2hrA6JROUpYNAqUlKzEddelRuIA4Ac/8OHzz+U67YClbkUIOZwQciMh5NH4/wvsacb+ibaHf4uu\\nY46FOz8PpD91CdW9/70PNQ9MRNl9lcj7dSECd6bDdbsLvjt9+PMXT3OvPf65Y3H1a8fCGaO7f/9p\\nxWP4zce/wUPLHkL7wB7Nuc1de6jXKLixPopD84FLa4Cn5gB/nA1cNJ57iRDUneu2ScCvpwC/mwmc\\nVDI63mkAP6ZQMtIiNerDZyKqi748f/haHDHwGI4eWITCCCc2hQ4Ths7Eod2PYWHHazgxj6JbTRLR\\n96/HuLeXY07TH03LxiIS2rbyk84Pt/8J119hHg7k24fk46TDx2HZsuTUL/Pn9+PMM63bnRx5ZBi1\\ntdAQrGi0BzNmtGP8eDne9Wuvsd38//znKDIygIwM4Oqr2WO8uTmM5matmPOdd7QmCxdeKC/gweAQ\\naNuE668fhtMJrFjBt0T5979j8PmAxx9PzaC6uFgW/FdWDuHuu69AZyc3KQ6OOCId1dVAfT0weXI6\\n9u7lBzwbHj4ap5++AZ9/bmRJZ58dwpFHAqed1oIPPzyVW88rr4Rx9NHAiScCoZC1PvC73+XgpZf4\\nxpUez1PU488/vxsOh5jHqhmuuWYYF14I/OpXu+FwGPtRW1sIDoc1aaMVpKevxX33ARs32q9aBYCh\\noRcxYGaMaoItW8J47jngySeBZcvoY+2NN2J4/XXgzTeB/n6bIhEnibVrQ1i2DFi+HFixAvjiC8Dn\\nY5smWEFbmxutrUB7akLOEQgtp4SQnHgy+ncB3AbgtPj/7xJC3iGEjFF85LFF7uWXIeutN+HsH4DD\\nhvHRMtiErT3r0dy/A+2hVgxE+hCLq1HMVFxeJ3ArJzWi2iNtepb23PYk5o8zLAatpEF5pBIfcJBq\\nZ3V5LTsm02jCueJC4C8vA689BryyCI5ha2LBDXc+h1CbluF+sehHWP7Yqcjc1oVZ5cuE69r2r2/j\\nvw9chLSmbUgP2LOYAMAHHzjxt78Ba9aYkwBCIujs1KozYhSx81lnfde0rpUrgcbGNlRXiwnsIxGt\\nMqClZQAdHdaJXFNTGNu20QbnOjQ2Aq2tPZg16xXm9bFYBL29QG8vkJm5k1nO5QrD7dYuPv396boy\\n8jv3+egD7sILb0BMIN8RIXHHJrc9mR2OOeZJnHoqPyTF3r3laGvTinIiEXOvwPPOuwmDg0YxzeLF\\ntaitXYEf/ehmHHbYy5QrE0g8pwSPRyQBfQJNTbWIRpMzdK2qss/pwOWSSf7ixfR4Y3Z9Sz4kOBz2\\nq1btqtvrHVT9TR/r6nsQ8tUSOdo3C4WMaTmTQTicaiI6LUTlIg8DmAPgHAB+SZLyAfgBfD9+3Frg\\nmq8JPitKuPORJIhcv+4aJwHm5chBLwt1Xs1mRK46IBvTs6CEcMigzGkdw3Jak7EG6agBnlyC0iXG\\n7uH9+7Nj3h5X2xRg/XeBzy8CVv0IRLIuFgyHtR/B7Q7h/vsPxyWXXGWpHqdT7hw//am168ygTH7K\\nwsJvQ2ykHQpCIfMw6d3dWj19NCq/x4MPZhMmPfr6tLsNn2+ASYB4cLnCmgVCwR13nAhAwrx5b3Cv\\nVy8cc+awPdhkIqed2AcGtEROIXp+P/s53O4hwzvXw+eTF7l5817nlhPFj3/8c9My9977JGIx7e4q\\nGjUncgcd9CoyM+l2u+ef/wscf/wTpnUo38/pjMDpFM/suW3bZKxcebgQ4aThqKPEQiuJQCHxXi9d\\nPa+cH01UV39h2reShdMZTZnIBQKJjDRZWXTNkrKJ0f/9VYD2zVgE1CpExpYViG5ljgdwgyRJIz1f\\nki1UF8elcXfY2qr9BG9V5WFuizwpJxM25h+7gTNVkcqPKgCq45vX08qAs5bFwzZEXXDEAIA9CD2d\\ntQDY3k4XZI/DFS//FLMmrQEO0pKk4b88jye3zULZz36OIw6zFr8oFUyo3ILyWCFIR63hnMc59rst\\n4yRnvQ3Dw1oiV1W1FtXV1jMfK5Oi02nvDlohcE6nWFgFPTkZHvbD7+dPVkNDaQgGO0cWXaczBocj\\nghkz9PEN2RgYSEdWVoIA+Hz9SU2SLlcY3/ueMcVNMNiD/PwmLjkD5MX8wQd/h/7+TOTlsVWwwaAx\\nLZqeyCUkcuznyM9vMl1sJ0/+CG63hJycVm45MxQUyPZpgYAxUb0av/rVBvT1TUBNjeyH5XYDTifg\\ndJovNm53GJMn03O4zp0rFky8qmo3Dj8cyMgwT8GnoKnpILzxxj9x/PEENTX2LorJ4Pjjw+jhxPhN\\nT0/dNMcM117bjIKC0SFyCxb0wu9Pba465JBuPPMMEAoBeXl0yeuLL0bjNpVAWpp4fxgNPPZYCG43\\n4HDI7SGkFz09xuDEyeCVV9wIBOR6C8Si/XAhSuSiYLMIdrCjrzn+Nb4BTqkTr43LxCXBVlRAfDD+\\nY9mR8IbTgIpEaqRqlQYiww18v/UOvPvv6+CAG1nnnwEU0wMyAkDtzl9BTnVLx7TKHZgXvQ6nzTjO\\ncG568YEYH6iAE1MAjB2RA4BFi2biiy+MMVmOOMIebzErWLiwHTU1GJkofD5rO7577wXKyrRE7gc/\\n4NsfsnDWWVEce6x5Oau47rowwmEgLU1s5zFhgrZcRkYuZId0NoqKfJAkL9RxDz/5ZC/6+58XbmdF\\nRToiqjXn+ef7EYkMoFssjewInnrqJoRCb1LPffDBMDo7WzFksh68/noWpk/vx+rVISHVp4Irrwyi\\nSRWt5I47Qli8GOjrG8DnDF+TDRuAlSsjpvfZs+ctrLG+P9CgpUWObbZkCb/c22974KcIYpcvd6Nv\\nDIbptGmDOO88YHh4CB99JHbN0UdfgnPOkZ0xdu50Ydu2UWygAG67bRiZmWC+a7/fWt9KBqee6kRz\\nc5SZcioVVFT0oKcnqhmzVuH1voFz40vYpk1h7KbsmxYu7IXXK2vC3n9/L2xIoJA0Jk0aRo7KaGzj\\nxqu4ZN0KCgo8SLfR4U9Ut/QqgNMZ584AIK5T+Rph6bNv4pcfd2PZCzsxodBa8L5LvzcXV5xFjxM1\\nUuYna7FxvRvr1wPHHMPnwrfeat6Dli6NoL7eqEp68UUXliwBzj577MmTyzWIWbNuNhw/88zkc/Yl\\ni+rqO3HXXTHcdRdw++2Ax2Ntlrj2WqC8XGvbcNBBfGkHC4ccEsHF9Dz2KWHq1FU49VRg4kQxiVww\\nqCVy6QKzS1qaFy6XltAWFNAzlrAQCGgdBfLz96K727pLPovEAUBZWVhYitDScpnlaO1utz7D/DAI\\nSUTZp8HhCAnF+ko1/ZAMMebgcNDtdVKNnC8KJVwSz2tYD3Wbx6qdaqSna8PHmAUWNgtkbgdisYFR\\niSMHyA5EdtQdjUdnoKVQBIC1axP2uGlpdSnfLxXow4/s2WPuQCYKJXi/bfUJlnsNwFGEkDcIIT8k\\nhBwT//+fAI4E8A9CyBHKP1tb+DWFw+HTBMSkob9/DTZvvgzd3R+bxsyJRMxFFZEIPciC2y0naNUH\\nqfwqMTDw1WR16+lJqIGSmVz1KVtEvgsNVuM9eTxiQe927LgDAwObhSPWG2NsmbeLEK8hd29j4w1C\\n91Pg8WgTl+7e/ail60VgZWFraVlkmcgRoiVAiTy/bCIXiw0JfftIJLkNghqifUz/HInjY0XkhjT/\\ni0Ddtq+CyDmd2tAsqaZsSkujJN21CDnbgNg3dzisGe1HIj22xKjr718NgP2+eno+xvDwXgwMbByV\\nDBhWsHlzYqfd3s7eMCYDu/usKJF7CUA5gGMALALwRvz/hfHjLwP4N4B34v9/A2FNeiMTOb5rZn//\\nl2hu/i1WrjzQNC6UCGFgLVoK+x8e3n+IXGvr4q/kvgMDsoVAX5+1SSIQkLOuG4kcK0IZH1u3XsnN\\nfKFGXt4plgb+9u23MnIZGqFPh5aXZ+6hyso/aAUeT5Hmtzoem12IRgcQCHBcvVVwOq0HyNK/ByUo\\nrBmRE1lsh4a2W26PHhs2/ACRiLkkny2RSyHtiQWwJHJpaZNQVETP8qIlcmPTTgV+f61hPIqONz0q\\nKn6BOXPW44AD1mHevO1wuQRTslAQiw0KbVwI8TK/OQvDw7ttIXJKZiLeRnN4uBWfflqfVP0Ohw/F\\nxRdSz9XVPYHq6vuo52gIhZrQ1SV74a9ZY68dDGvzlCxEidzhJv+OiP9T/v7GQXTRVeBw+GAlTB8v\\nvygAgwSEBlrql+LiC0b+zss7Qbg9IigtvdTW+sYCw8NyqI/Gxl9auq66+jcAjDspOf1PcgiFxMKO\\nOBweS6L41tbFSeeQTEubINAevUqRDb3kQoFeIjca2Lv3GTQ3a2O2VVbeRi2bmXmw5fr1k3Fz828h\\nSTETIidmZ9vV9a7l9ujR2voCmpvpGS3UIIROzO1W/7DAksg5HD7U1/8JeXknG65Rj8OxaqcCtzvX\\nQIQS481aXKWSkh8jEJBJi883DnPmrMakSfxwLSyISqAlKSS0nqj7RTi8z5ZE8YoGgKValc/RnYXM\\ntBIlJT/FjBkfGTaJCrKzj4LXay2u1tat16acmowGu/usaIqub2waLlFYtQ8QUa1agUj+wdbWFwzH\\n1IOxoOAs7Nhx9wiZSRXBoEBW9v0MjY2/RHn5NWhvf1X4GqcziJycbwEw7v6TVa0C4uplQjyWJHKE\\nuJOWEIgROXGJnMPhp6ZIUtT9PGRnH43OzuQF/Hv2/MFwjE0grUeLpr2HnTvvZS4kgDX1oR1obPyF\\naRnWopKKdMgKFJtCGpED6MnFtTZyYyuRczj8VImcJEmw6ven70Nebwny882l4jREo3222ciVlV2J\\nrq730de3wpb6FCgSYh4pZKVN83gKMTxM9yx3OjNRVyebZ3R00L2lXa5sy32lt3cZ9u2zPxWY3X12\\nlOLrf/NgpibVw6pEzgjt/QYHN5leQVu81XlW3e5szJ69CnV1j6XQrgSs2lnsL+jqMs9UoMb48feO\\n/K0fgF1dYnku6RA1RndbGvjB4Mykbc4IcSE9fY5Je7zwePgZIdT10eswl+rl5Hxb6B5WwLqv1Ryf\\ncl1G9Uhj4w0CqlUjAoEplu9vF1hzm99vQ3oXASgSGL0kRvlWNDXUV20jR5PIJUOiWP3RbAzSEA53\\n2rJRyM4+CpWVt5hKzZN578rGl6cxYJkDOJ1sRyz1PEN/pwQuV4bldRwQs38sLbUalsRe6vU/IicI\\nq3ZBIjZyZterISL5oS2aJSUXaX57PHkoKbkIBx+cvCRJgdNpHjx2f4SIdFONoqJEInU7d1Kik65V\\nidzQUCqxGByor3+GX8LhQ0WFMaQMvSyt3U6h53G5sk3LWAXLFi6Z5OkslSSPyLFsYV2uLOrxrxKi\\nZN0qCgu/rzsiIRYLGWx43W5ZIkgjzF8lkevqes9wTznPrnVzBlYfSmaeCYdb4w4PqaGm5mG4XBkm\\nG3WxMaxHNNqDSKSHKTUDgHCYHtGANx9oiZxxXXK7C+IaMutrsshzjh9/F3w+sY2P318Lj8dcI2EF\\n/yNygrCqqkpVIqcnSSILDc0L0+eroJQEXK6MlKUArEloLDF5sriKVIHVnbPTmZjQ7Fw0du82j3oP\\nyAuZlfuyJkIREOJEIFCPyspbOe3xCW9s3G7jrp4Ql9BCpZYm2wWWrateheT313BNB7Kzj2IajPMI\\n+s6dv2acSTERcJLIyzuFeU5E/W0VBQVnob7+KcPxzs73MDi4VXNMsWeiSeTUG4SxVq3K99R7LIeT\\nInKscZSMEGDv3j8LaW7Ky/mZPpS5hucQIY9h63NhOLwPTU1m6eLojnBeL3tjYSaRU0xGzPpKMDjd\\ncKyv7wvuNQDgdAYwZ86Xpu8WAKZNS93+VY//ETlBjLWNnL4z0oicXrqgL0PrlLx7sODz0fMHjrWR\\nsR55eafEHTisTXqpOCiILhpebzlKSy/F3LnbUF//DLKyFhjKdHTw00cl7mnN2SEVKAsLb5J2OAJC\\n7yEtrQEZGfMMxwlxChI5+6VUweA0oXKyZx9b4lxYeC5zEeZJ5Nj3G3syUlT0Q9TWsp0hfD7rCZfN\\n5pyJExeDECNp7etbgWhUqyXwemXjdlpfVBOpr0a1SpPIWVet0t5F/A4mVzpRUvJTgTsY6/F48jFj\\nBjvysvJsvM2a6BjWY2hoJ7Zv/xW3THe30fQlK+twroRQ3RaapkgRaJgR5LKyKwzHIhF+hOWKil+M\\n3Hf8+LtQVXUnMjLmU8suWCAlNa7M8D8iJwiruy15ENhH5Gj2VMXFWrWpnsiZDTTRhbKk5MfU41/F\\nBKqGsmO06kpvhchlZx+t+S06eTU0PIfa2kfg91ehqOhcBIMzLbVRe083V61QVPRD0zqKis5DTc0j\\nmDSJn9kjYZfE/rZud67pewgEpmL69Pc00kwFoosAy+M1FTgcflRXG1N6Gct5TBYyDzOEQDIx4FIx\\nw0gGDkca6uufhNfLdswIBmdZrpf3zWjSWQUuV5bBNkqpy0y1OvYbSqfh20tSmOuJaRU8IUBBwdmY\\nO3cTysqu5NbhcATgducYjjudGcjMnI8ZM5ZSpa7Ku+VpXAhxJvXekw2MXFf3BHfOMJPIKQ5IZvNO\\nTs5CwzHWeK6peQQNDc+hqup2VTscGDfuRsycaSTKo6nB+h+RE4R1IpeqjRzf/mzixL+O7FgV6Duc\\nWacVVZ3QFjSvt/wrkSKokZhwrBG5UEgsrRYhLoMtmOgzG2OMJR+DyeHwwOstZZ7XR5mnIT//FJSV\\nXQqPh5/YT+l3vElatl3i9+3x4++Bx1NI3UXLahnzsWElzIkoCHFpbB7Z9/aaSCXdTKInEtrBWN/Y\\nOg7RFho9nE7r759nkF5ZmZDElJVdpTkXifQYvJtdLpnI7W+qVaczwPBatY/Iud3scZqdfQT8/vFw\\nu/O4dXg8hVTyoJgsZGYeSJXIKgSaT5yStZFLjsilpdWYtkeBy2Ukrwkix593HA4fCgrO0Byjed0X\\nFp6DsrJLUVh4JkeqqoUSZ3I0wHwzhJBFFuqRJEk634b27LdIjsjZKZHTn/eYql/NBprZRAAA2dnf\\nok6kEyYs+sqJnBK+w+HwImqBJ5m51KenH4CysssRCExBMKi1IxQnch7db+P3dLvzhezZCPFwnV2K\\niy/C5s38mH6BgJIujt8nExI59nNmZh6KgYENJvXIfS8ViVxamrWgoA5HGjMGVeLeLrjf328GAAAg\\nAElEQVTdOZgx40OsXMmOHSdL3NiTvqzuto/IjRv3C25InNLSywwx8ZJBRsZ8zJjxYdJzk9dbjlBo\\nF/O84qBAg99frSqnXWyj0e6kJXJjrRnIyVnI8Fq1j8hVVt6Ktra/Us8p0nkzG1I5XIfRsUt9Hc2e\\n0+WSTXb4pCc51WoyTkUKRCVyNCcdUYmcvMnUB303Ermqqru49ch1eUeVvKnBG81KgF/l38kAfgjg\\nHMgZHs6J/z45fn5UQWTcQAhpJIQMEkJWEUKEAu4QQhyEkCsJIWsIIX2EkN2EkL8RQoSt/ZOxkUtN\\ntcoXw8oLiRmRM5PImRO5urrfUSdStzvPNnVQsvGqFFsklmrV5cqF319jOD4wsJ5bb2/v5ygsPMtA\\n4gBxIqefDGiERnRSczg8GB5mSxEdDpeJa74XPl9Z/G9+n0xIOemLY17eSUhPn2767RMG00bJcjjc\\nbvoea2t/a1l1I2IqoNzXTIorO5iw2yifp9dhNRVeXt5JyMiYQ7WjVCAS308E8sYs+XnJzJPV56tk\\nnlOPCb0KlieRo5FDrY3c2G4ox4+/iyGRsy/PaSBQj+rqB+D31xrOKe/DTBIkS8SN64j63fM2iLx+\\nMtYSOfmeYhI5WhxHRa0vMm/p1xO97WZh4feF7NzsjCNrBuadJEmqlCSpSpKkKgDnAugDcAYAvyRJ\\nxQD8AM4E0AuZ1I027gDwKwAPQ04N9jGAFwkhRqU2/dr/A/A3AMcB+BmA8QD+QwgRSmLJs3+g2ZKk\\nqlrt71/HPS9L5PSerVZVq+YEyuXKpS5YTmdaUmmNaLBq46ZAmehZ7XA6A5g9ezWmTNHmyTO3YWKL\\n95JVrWZmHmIoI2oUT4ibGt1eC3YKuexs9T6LNzl7RhYH1iStRJ0X2dkCrBhMkun1mZmHcc/TIBKu\\nJEHk+IsQIV4TiRxbtWo1Fd7EibLkZfr09zj3MyOeYmrQ0Q4ZxEt0rh7nemlSJNJtIBUK4aDZ1mlV\\nq2MnkfN4SuD3V1MkctZVq3l5J3HPl5dfgblzjV6o6uwESsYZGuS5m0bkEptK/mae1/+T9Vptt3yN\\n+p7sc4m2KBJFNRKmKWZEzmUYa/p+6fNVmbR0pDbBcqlDlDLeD+BuSZL+KsWNfSRJikqS9BcA9wB4\\ncLQaCACEkHwAV8fb8IAkSe9LknQxgPcAsPz51fgBgBckSbpZkqQlkiS9BOB0ALkAviPSBt4gVQiF\\nGqlK5MwXSppEzhqRExmIDgc9L5/DkQa/nz1pW0GyuTuVAcdS8xHihtPpR27uQt2z8vWwPIPtZFWr\\nPGmLSF35+adRbT8U8KR74XAiHyxvl6j+DrS+kZZWP3K9aN9i2fqYXZ+MIbXbbU7kEh55/Prl78dX\\nrbIlcuIpferqHtO0heUhzvu+2dlH49BDRTcFqRlc9/Z+yj3Pi6Wlfl96IkdTrfIkcurNmxVCUVJy\\nsXkhDhSvZ2McOevODuPH3yNUTu1wFQhM0Ug9jTH5EpBjwRm/t7oP5OWdBKcz8S0qK7WG+ywk67Wa\\nrLODfE8xiRwAVFTcMPJ3MDhjxEzDfN5yGOZufb8cDdvdVCHKNKYA2MI4txnAZHuaw8RCAG4A+gAz\\nzwKYQggx5nDRwgNAL0NWfpu+Azn2FDsKP23hT9VGrrDwLO55mo2cnmyaESS9RybrPqxdHSEEU6cm\\nn0JJgZm0IVnVq3rQWnGIqK1lZ0UQJ3Lab0MIMc3nyXJZJ8QDr7cIs2evSiokhzYnLl8il/jb+JzV\\n1Q+ozoupVnNzjzOc8/v5hsvq663A7xdPL2ZWv+zswH5GnlerFTsgfcBuNsFk7+6t9O1kN00i7QCA\\nYHCqhhho751op37ODIc7DapVpYzXW2ZsherbWCEUNFUlC7RNiOK0ZIwjZ00iN2nSS1zppRr19U+j\\nqOiHKCg4E5MmvahRqfI2JMPDrdQc3uprnE4/Zs78GKWll6G6+gFUVCTioPEl0k4b+pIYGhqejd+T\\n/az6PlBVdScaGp5DdfUDmD79PZWmwVxLZhxP2o2/OJHb/yRyLQBOY5w7A4D9WWW1mAggJEnSVt3x\\ntZDf1kST638H4BxCyAmEkHRCyPj4sZ0A6BalKpjZPoyGRC4ri2926HCkmXq28uymAMDvrzRNfC8P\\nWJpqNQBAnrhThZlq1czTUr2L1NabnGdbQQGrq4vXQ1PzdXd/yL1mwoQ/Ii3N2JWV9+PzlaOuTps/\\nVMTzWE0g+eTEq/rbOGlmZSXUw6KqVZcrHQ0N2v1XQcFZwkTQCpzOINUmMpn6ZYkbX5WTrEmAgszM\\nQyn1su7JVp2PG2eeT1VBqouvWewypzOAiRONOZ8BrX2dXiLX07PUoFFwudJH/i8ru3rkeE2NVgFk\\nRV1s7ZsZF2KFyBnjyFlL0WVFquP1FqO+/klMnPicwVaSb8fppuYm1ROVQKABtbUPo7z8Ct1z8dYv\\np2kKL7uQn386AHFnB/k3QWHhmSgvv0LT10Tmb7M+sj9K5ERXtwcBPEAIKQbwImTiVgiZ3H0bgDGK\\nnr3IAUBzBetQnWdCkqSbCSHDkG3klN65EcDhkiR1sq9UrufvtFixeFKxkeMl3gZkI3KzDiUSh0uO\\ndVaDLVt4n9A4oSmTgULoUoHZc8jvl+agILdr3LgbsX37TcazGgmT+LfgDWQaaachGWmsw+HHwIDR\\nNlJNOvLzT0Za2sR4OQfq6syzQ2hVpjzVKj/IqtZTUFw1KkuXJeza9QByc49Defk1pmnEkiFyDocH\\neXnfxa5d9wqV5Z/3IhZjkyeWpNoK6B69xueePv0D8DQCmZl0SS4NqRK5QGAi5CmU3Z7c3IVwu/MQ\\nDu/THFenJTKTLOu9hmtq7kNR0bkgxItAQOvNbCXeoLVF2GiCobSJJpFbufLAUWoHG7xxmJ9/Glpa\\nnqJcIza2zCRyqdi7iUIOzK3YtYqrVlMpZ5c9qmhYEjsgtNpIkvQQgAshq1gXAXgj/v8kABdKkmTJ\\nL54QciQhJCbwL5WM5Or7XQzgFwBuA7AAwKmQnTT+TQjhMybwHR0AumceISRp1Wpl5S2mjgROZ5pp\\nh1J2tGbweNgxygC6RFLppGZSQRGY1WFmxM56z1oCY49nW0bGQaZlWAFnS0sv517H+p56Qjpr1qeY\\nOPFFzJq1HPn5J8WP0xdopzOoe3+iqlUakVOrqq1J1AoLz8bs2ctRVXULXK6gsETPCgjxcDcWasNu\\nMYmcWfiR1CRy9G9hPJaZeRBTLa82fBeBVfKplxBnZR0h9Nw1NQ/rfmulaDzvVoDuJBMMTjOQOECe\\nH8y0DwmIb+jC4X3Iz/+e5pgSg1Dff0KhncL1ytfbo5bkjROnM90Qrw8Ql0ry+78LPT3msQhThXo8\\nW5HIscuJxK/kf5uvs0QOkiT9KR5brgxAMYA9AJokSWJvW9lYCkAkSJQSFKoTAG0Lp0jimDk0CCHZ\\nkJ017pEk6TbV8fcAbAdwLWRHCgNuueUWAEA0OoDcXGA6JftMQ8NiTi62ZInczRgYYJkkxmt2+E0Z\\nv+jkxlJNFBaeC4CvWrbDxdqMyPl8dBNI9fM7nekUZw/7QxQEg3xz0IkTX0B+Pl01O27cL9HczM4z\\nyJog9BOv0xlAQcGpmmP19X/C+vVG5/HKyls1gV1FnR1oUF+bKhETlejl55+KtraXuGUT13io9lQK\\n6uv/rLq/uY0cL2eqLHFPzVuSnvqHJgUiAAhyc49De/vrunYmpHrp6XPQ2/sZ955WJXLV1fdh7dpT\\nEYsNoLj4AgQC9fFxZXw3anvIvLwTkZt7ItrbX0d29lEoKvqR7pnsC83gcLhQVXUntm69ylS9acWO\\nbdy4m1BcfD66uv6LcHgvAoHJyM39Tvye2jHZ2WnNVtg+MsB+j05nEJmZB6KpSbuxFO+3fGcHORuH\\n9ZiJatTUPMjVBtlP5MZStUpfn5csWYIlS5YI1iEGS6tbnLTtiv9LGpIkDQEwz+6bwFoAXkLIeEmS\\n1DqZSZCNR3ixOuoAeAF8rmtDJyFkK4AG1oUKkQuF9uDjj/9v5LjbXYhp0/4NpzMdfn8lens/p16f\\nWmYH/mBzOs29RkWJHI1I5eQci+pq+ZlTyUogdn+WJMqFmppHqHYeekyY8AesW6eNyK1VFYp9C7VB\\nPws+33iqajAn51gUFJzOvI6mSlODPUGYi+gLCs6iErnycv2OXEwiZ47UbNxEnR0qKq43ELns7G+h\\ns/NflGs8TJVddfV9yMn5tnD7ZNUp39lBRHWSkXEgU3JBewe8sUaTTKuJa1XVnVi9+lvc9lglcrm5\\nx2DevO2IRLqRllYTr8NDDcCt9sJ0OtMwZcor3LrT0upNA0uLoqzsMhQVfR8ffshX2eblnYR9+/6G\\njo63Ro7V1T2OTZsuMpQtLZUzocyduwWDg5uRllY/sulNlcTbp1olIMRNJag+X7khBpp879QlcpIU\\nRUXF9di2LZH5xuerxty5m/D+++Lrns9XjenTl2DVqgXU82oixw+eLnpP8w2EXarVgoIzsWfPE6rf\\n8vq0YMECLFiwYOT4rbfeKlQft02iBQkhUwghLxFC2gghkfj/f7USVDcFvAUgAuBs3fFzAHwpSdIO\\nzrVKaGtNHiNCSA6AGgBGtx4d9JIeh8ONYHAK/P5KALxdnvVdZ8JDh92ZZGmAx9TIV5zIGTtmQ8Oz\\nI8as1iPsW7OboxFJr7cMBx3UjtLSn3AmlMRCSgtUKiqRS0trwMyZn2D27NUoLzc392RPKHzhtPkE\\nwUrCbh4dnBBiqq6Sy/F28OJq8lS9TkWvT083xmh0OoPUMBcOh4/al4uKzkd5+dUa4mW2UTKPIye2\\nGNKScCugOb/wJEo0tbE6PVtOztGYPXu1ULuswOPJHyFxAP3Zp059K24/Jw6eejE393hLdQGyA0V5\\n+c+5ZTyefFRV3TVC+AOBqdSUbU5n+oiTlcsVRHr6DM34SFWtbqfHJ2ssuVw5VI9/OyRyAwPrUFR0\\nHrxeORm9252HadPetixpdToDqqwzlBY4xGLeiWtczBWIZt9WdJ6sqrpNle7MS1Vz2wWhpyeEzAHw\\nPoBBAP+ATI6KABwP4DuEkEMlSaKLpWyAJElthJD7AdxACOkDsAKyt+yCeBvUbX0XQIUkSbXxa3cQ\\nQl4HcF18In8fQB6A6yCHJXnM7P5ffHGU5rfepZs1+SajPigokMOO8DqTx1Mysijl55/GSeUiqlpl\\ned3KCAYnIydn4cgudsKEP3LrsyqJpA0MQrwjjgWsaPJaL0tjHaISOULcyMiYK9xeFrHiqeISbSCg\\nTSYycaD3F3VqIx7S02djaGj7yG+PhxbrmqdaVZMgM1I6eqpVlyuLS7RcrmwEg1MNUlE5bhatLxnv\\nJSaR43sEiiAv72QEg9PR17dKqLwc6ogOmt2s3vuTlo1EW3/q0nV6XEnrEia+UxHXf42J8vIr0dn5\\nNvV9K+QtPX0GDjhgAwYHtyE9fSaVVLFCASnYXyRyAL1/y5l3CDWNl+i6ZDaPezz5mDNnNfr6ViEt\\nbRI8HjrR8niKqKnCAJnI8exa1e9ZUWsn01YFIv3ffG4Q+3YeTyEOOGA9OjreRkbGAQgEJgldlwxE\\nmcbdAL4EUClJ0o8kSbpBkqQfAaiKH797tBqowo2QMzT8DLKEbj6A70mS9KaunAPG5zotfu0pAF4F\\n8ABkG7+DJEniJ94EuLkFAd4u2jqRM4usD2gndN5kKCqRS0ur10hzsrIWGMjV5MmvYcqUNzFr1uco\\nLuan1dXnUTQDTZKibk9e3snU3bs67AhtcIlK5Kzaz9GzFYgQOcL8rkr7J0x4UnPc660wXZwVVFXd\\nAbWUsqrqTkobeKrVxDs2SwllnnzaTOLFvn7SpL9pfiu2mgpKSi6kfjOnM8DoBzQiZ5aqzMOVColI\\n5GpqHoTD4cLkya9Rz9NimvFsuGiSbtpCHQxSjHlHwCaKogiHjbZ9yRE5tlQqWYmVx1OImTM/xezZ\\nayjnijXlMjPnj9yntPQyTdm6ut9x7yPy/bOz2Wru0ZbIFRdfCACGECEi2U8S9ZqvXy5XJrKyDtOQ\\nOH2IpHHjfsm8Xh6z7ODa6nnE4ylgSnFFNygi2YzM7XethI4pQXHxj0aVxAHiTGMe5KwKGh1j/Pc9\\nkEnVqEKScVc8bZhfkqTpkiT9nVLucEmSqnXHhiRJulOSpMmSJKVLklQqSdLxdkkR2RI5a5Kp2trf\\nqq7lEbQ0wXJiKbQcDhemTPknCgvPQXHxj6lxoBwOF3JzFyI9faZpfbSUOjwQ4h5RKSsYPz6xN/B4\\n8tHQ8MxIahSHw4/KyttHoqwrx4xtFvNatSvFj0jKLRbxViaHoqJzUVPzMHy+KhQX/xhz524Wvn9a\\n2gRMnvwq8vNPQ3X1AygqokV9F5PI+f3VyM5WbMocaGh4XlN2NFWr+lhwFRU3Ii1tIghxo6zsKqSn\\nH0CduFmq1WQcXRwOL7Kzj2IGzVa+Y3r6AZw65HHK2thMmfJPwzHWJgEQk8gBQCAwzXBMgR19XR+4\\nF0iOyPHmrlRUlw6Hmxp7kufhW1v7MOrqHkdW1gLMmvW5qRTczN4VoNmnqttoJ5EzflNFy+JweOIe\\nxHJu1JoacxtgVS1Jtaeo6FyUl1+HjIwDUV39ADfdnrI5Ya1V+j7C0pyIOrG4XBnM7B719U/H72kf\\nkRsr2KVYTsZz9WsL/U6LLWURG6wVFTcgLa1eI3ngSTTUdgO8e4i75MtBIRsa/mxeUABWsw8ouURr\\nah5EV9f7yMs7GRkZczRlCgpO4wbqpQ0u7WLAM1y3i8jxJXIAe/FS2k+IE2Vll6Gs7DJqOTPk5R2P\\nvDyeJIn3HrTvcMqU19DT8xE8niJKIFLznIXJntf36UCgHgccsBaSJI1IrGn5DuWYU2KqVTMozgxT\\np76FtraXsW6dtu8pz19aeik2bKCnSVLeJ2viV9udKYjFeETOKJGjZVFg20xlp5Qqjge7Vauiqmh2\\n3cZ50evlp9UuKfkxSkp+LFS/2RwXDM7iqoftylMNsJxmEv2orOwyFBScCUKcQmnsEvWyx3he3inM\\ncw6HF9XVCceXgYGNzLJKn3Y6g1Qvbv3ayuozVoIx19Y+isLCc0CICy0tT8c9q48cCTVjl2p1LCE6\\nwy0DcCMh5B21VI4QEgDwcwCfjEbj9h9o7ZqqqrSZBPLzT9V4p2RlHQFA3M5j/Pi7jHfkDCJRiZxo\\n8Fq7YfW+svOGA2Vll6OsjB9rjYWxVK2yYe7FaCaRG32I2sjJBDcri76bFslZyD8vTuQS1yTeb3n5\\nVYawCg6Hl7pAJheTTknl5UBu7vFwONIQi8nRkNTOP0VF5yIYnIbly41SsAQ5N74LVg5ankSOJmWi\\n20DRn3fSpJdtiH1HR3ISOfYmtK8vNacNWnusBA42A+29q1FQcIaJGUPyEQ30oBEgfSQFlv0aD7z2\\nV1RcZ6Ee9vhTpNUsYqvfZLPWOythZeR0iXLw5oyMAwDoUzLyzQ/2RyInqlq9EXKojx2EkGcIIfcQ\\nQp6GHIdtMuRgu99IyCoctcDREf/4CWRnH4WcnIUA5B2yQvSs2oqJQiuRY0/MVlWcdsFqtgc7JGI0\\nhwkrzg72wFwwzZqIRGw37EAqceS09aRGfnmTochE6fUag1h7PIVUspPMoqnNC+pDQ8Ni+Hzj4ffX\\noq5O6x8VDE5FdvZR+iq4z8GSIPA8lH0+o7qPRiho46m6+j5kZ/PT/omCHmTWXomclbRjNNDGmZ0k\\n1kwi5/NVMO22aN8xFdA0ASImMOZgjxtrtna8HKnyPdiqVT2Ro9dlRSJnhq6uD7jnv7ZETpKkTyHb\\nyf0HckquqyAnsn8PwDxJkvhRKL/G0HcQuuE0wZQpb2D27DWYO3fLCNtP1vPKDOI2cl9Nh/P7a1BR\\nIT4R2yERo0vkxFJKWSVy48f/2lJ5NVgkd+ykpzwpgfh7SFWiYEdoj5KSS0b+DgZnIRCYyFisrVt+\\n6Eltfv5JmDdvK+bO3USVUtKkS8kQOZ5kgZbbUlwiZ58EiJYH2m5nB8V7P1nQY/zZlzJJvZmmweMp\\nYo51u0w5eCgp+UnKdfAlilbmCvOyokSOTcbts+6ibRK1bfiaEjkAkCRptSRJp0qSVChJkjv+/2mS\\nJBndg75BECFy8nEHgsHJGhH2aC3OohK5sYKa2DgcPpSUXILBQbZdhB52SMToxICoztunWi0qOk8T\\nv0sBz6hXAUslYy0Yb/LgT87i74FXdvLkVy21yVi32IJbU/MAamoeQWXl7Zg2zRggWIEVtUuiDda+\\nB91Gk0fk6NIaXqIcvbTR4fAz8jxb99K1Atqck4zakveOfT52ho7kYR+RM+ujhHgM6c0S50afyPFi\\nromCb09rhciZzys0Sbp8rUP3m95nhodbhdtjBn0WEmObvvo1Vw9Lo5vImEQIOYQQMpGMZVbYrwii\\nRI4GQhzUBV+N9HR2/DK/nx4CQkQiN1pGzTSUlV2N8eN/jcLCH2D69CVwu7PQ37+WWnbChEWGY6M3\\nsSVsHexUrXo8+Zg58xNNyieHw4eqKvMI3SyVzNgR8tElcg0NzyEv7wTLrVJQV/e4cFmHw42ysktR\\nWflLrhmDWa5ket3WvArpqn3rEjmeZIEQJ+rrnxn5XV5+LdV7kt6f7SNy6ekHaJ4tN/c4YfKtadGY\\nb0LtXa6CQbb6UnGWGYv5jhYI3B4bPHuywIg8L0tVm5NzjLZFDAIZDM4Qbo8ZzEyi9kfaYyWzwwWQ\\nY6+tBrAEwBoAuwkh/KBiX3PoFwGr0pu6useQnj6HeZ6X0onVYUQkcqmo/6zC4XChouLnaGh4asQ9\\nnKZWLim5hDrgRovIqYOr2hHcVQ1CnCgqOgdTpryBceNuxqxZK6iqLz1oXoZm7bMTfBs5K+/BuFDU\\n1z+NwsIzhWsoL7/GcEwfesQOJCeRs9Yn6OFv2ESO9R30IStKS3+m+V1UdC4OPHAv5s7dytw40CVy\\n9qlW3e4s1Nb+Hl5vGdLTZ2tSc1mBXYnjRWGWh9YqeJsOpf/QwpjYPd/l5Bxra30K6LmAZVhTrZrP\\nbaz68vNP0ZWjr3fWwqqYtcW+Tc9YQajFhJCzATwBmbydB+DY+P9rADxBCBGfvb9mMErkrA3C9PRZ\\nmDXrU4wbd5Ph3KRJL3NT+LCivItI5OwQracC2oJcV/db6oIyWjYjavXVaMWRy809FlVVtyAQYKbs\\n1YC1uIfD7Um3wRpGTyJnVeVQUGCcNkaD1NtpCM1CNDpgOMa3paFv0srKrhpJe+T1lqG8/FpDGY+n\\nAH6/MUWZAlrAXrsXp+LiH2L+/F2YNeszy6m5FIy1RE5xSLMLvBAiSj+mO13Y3cdTD/JMA29OsvLt\\nWM9bW/t7bn11dY8b7Axp80MwOB1eLz37z/8vEJ25rwOwWJKkc3XHnyaE/BlyCJLnjZd9/ZGKalUL\\n48Sdn/9dk2voA1REImc136ndKC39KfbufXrkd2GhHGuLRuRGTyKXkMTwVatjIw0D2N9reHjPmNzf\\nPhs5GiG3tjDTMxCMhtoimYXO2jW095oMkfN6izFnzmr0969DWloD3G5rMRkBoK3tL5Sj+5+UgaW+\\nzsszmxfFUFFxPXbuTGgmSkt/aku9Cng5NxXyQhsTds93dqRdo4GXAzVVZwenMwPFxeeZlDESZdqY\\nosWU/P8NoqN7AoBnGeeejZ//RkKvlkl20c/MPETzW8R9mxWJXC2RY02GonlWRwvp6XNQVCRr3X2+\\n8aiouAEAi8iNDpFSh3IYi8wOImDdSySYsD2wyxPNev5SY3ka+bH/W7DU2SwQ4uWaQ9BAS1vHV62y\\nCavLlYnMzPlJkTgAiEb7KfezT7VqF1gSXPMNrhjGj78bM2cuQ03NwzjkkH7LYZHMQFOnK1CejfaM\\n9hO50ZHI8b6DVVtxPaqq7tCFhzK+J1ooHp+vIqW2fFMhSuR6AbDciMri57+RsEsil5195AiZI8Qj\\nlEWBplYBtBI5dqYA8xQyowlCCOrr/4hDDunD3LmbEAgoQVSNXc6uiU2fG1Pr8DEWceTMwZJaRaN9\\nY3J/uySTdkjkaPB4+K7/IqiouF7zW73zN79/MSZOXGzZ45zmtZmMRM4OVFbeRjn69ZHI2TkeMzIO\\nQFnZZUIptayCN8cqzzAWEjlgdCRyDoeHmSc4dYN/rVMPjezl5Z1kOObxGLNz/I/IiatW3wRwFyFk\\nkyRJI9HyCCHzISej1yeu/8ZAT+SSlRgQQjBt2rvo7l4Kr7eMmp5HD5ZNh1YiZ5wosrKO2G88a4w2\\nDqOnWi0uvgDt7f8EEEUwOF3jSLK/qFZZxJsmRRmd+7vgcuUw0uGktstO5j1WVt6C7dtvAQDk5p5o\\nS9iJsrKr0N+/Dv39q1FS8hNhGy5CPDjwwN1J3ZOWDo/v+Tp6xKqg4Axs26bdBO6PBtwHH3wfdu2i\\nnTk9/u/rDJ7N1hsYTSIvY3+v//L4Px5E47A+j7G17LL+7OPGjcP27dvtb0ocVmzk5gFYQghphuy9\\nWgRZGrclfv4bCfts5GQSmJ29QLg8IQS5uSegvf0funr4Ejm7VBOjgdF0dsjLOwFz5nyBwcFtyM4+\\nWlcvO6zDWAToVMAirWMXR47A7c4XymtoHdbJwrhxv0JGxnxEIj3UHXgy8HjyMWVKMrHskl+cPJ5C\\nEOIZSbHl/H/s3XtYlWW++P/3vURZayGaSBwElEMeRqRfgqbmiAfE3JBijTaeSjo4mo6mTR5Kt0ob\\n85CnSppNzeDG9hR9v7Xza2UqWaCOOYZcnkfdiYgpMDqVJiNy8PP7Y+GSJazlUk5LvV/X9Vyynud+\\n7uezllzw4T42a+2whbIhE6sWLfxqe2KDPe92nT59zuG6eZp2t2johhWnshIRKVJKPYRlpmo/LKly\\nPpAN/JeI1JyydZeorzFyt6v2xTcddxM4GrvR9Bp2soOHRzgeHuE1zjtagqJxx8jV/v3TsePbjRaD\\nvfGTdf3evp3kRCmFl9eQOj23vtQloXdz86R9+9mcOpWMwWCkc+f3bK43b+5LeekrUDcAACAASURB\\nVHmx9bXJ1PG2n3UzBkPN/0dHW39pmnZnc/ond1WytrbquGfUZ4vc7ahtraXqs3lKS0/VuN62bXyD\\nxlQXjTlrtTpHS1A07qzV2t+rt/fjjRaDvVX46/o5XL1qf8N3V9S5cxrHjj1b7fWf6lRfSMh/0K7d\\nFJRqXmOT8s6d3+XQoQTr6/pc98oZjbEEi6ZpTUOPEryJuq4jV3c1ZyS5u18fR3RtX9fqnFmYtqnU\\ntmp2Q02ft32Go0SuabtWPT17Nuq+uLWN54K6fw61bRflynx8nuSf//yCn37KpG3bONq2Tbj5TTdh\\nbz2rtm2H0bHjWn766Wu8vYfTqlWfOj/rVlzr8tU07e7jVCKnLAN4XgHGAO2BG5uJRETuyqSwqVvk\\nalN9X7qWLbtz332D+PnnrwGIiPi8qcJySm0DwG9n5f1bVV7+k91rTZ3INfb3VH11rQYHv0Z+/gLA\\nsiZcy5b/X51ja0zNmnnQrdvHjfIspRQBAVMJCJjaKM+70c02Atc07c7l7E/uN4CpWGan/g9wzwy4\\naOoxcjcbpGyZDbuVX37ZS4sWfrWus+NqvLz+jR9/tEx0btbMkzZtBjX4M0tL8+1ea9xZq7Ulco27\\nxld9da126DAfs7kzZWXF+Pk97TIzpTUIDV1GXt4cwDI+78alebR7S0hICNOmTeOll166eWHtjuPs\\n6OSRwEIRGSYir4pI0o1HQwbZlFyxRe5GSjWjVauH74gkDiAsbCWtWvXGZHqAzp3TcHO7tQVbb4ej\\ngeyNO2u1toV0G3sCTe3duLf6OSil8PF5ksDAaY3yf6g5LyjoZTp3/jPt288jKupvTbBB/b0pPT0d\\nT8+mXYy9Njk5OUyZUr87W9yKGTNm0LNnT0wmE6Gh9reXu9GiRYsICAjAbDYzcOBAjhw5Ui/xZGdn\\n06NHD0wmEw888ACpqfb3zf3www8xGAwMHz68Xp7dEJxN5FoC3zZkIK7qTkjk7jQeHr8iMvJbevX6\\nX3x8RjbKMx0NxG/MxZNrT5Yat0XO3i91/b1991DKgL//s4SGJmM0dmjqcO4ZIuKSLdNt27bFaGy8\\ncbg3EhESExN5+umnnb5n2bJlrF69mpSUFHJycvDx8SE2NpaSkrqtuZmfn098fDy//vWv2bdvH3Pn\\nzmXatGl8+umnNcrm5eUxe/ZsoqOj6/TMhuZsIvcZ4NrvpIFcveraXauac65evWz3WmO2JrlC16q9\\nNet0Iqe5EqUa7qir7du306dPHzw9Pbnvvvvo3bs3KSkpPPvss5SUlGAwGGjWrBmvvWbZZaO8vJw5\\nc+YQFBSEh4cHvXr1YuvWrdb6srOzMRgMfPHFF3Tv3h2TyUSPHj3Izc11Kp6LFy/y1FNP4evra21l\\neuutt6zXQ0JCWLVqFQBJSUnW+AwGg/W4FivAunXrCA8Px2Qy0aVLF9asWVOnz+vNN99k6tSpdOrU\\n6ZbueeWVVxgxYgRdu3YlPT2dX375hQ8++MDmff/ud7/D19eXVq1aMXDgQPbu3euw3j/+8Y8EBASw\\nZs0aOnfuzPPPP8+ECRNYsWKFTbmKigrGjh3L66+/TkiIa+/najeRU0qFXjuAt4ExSqkFSqke1a9V\\nK3NX+vnnb2xe17bch+b6zOZf2b3W1IlcY3d72W+Ra+wZ2Zp256msrGTEiBFER0dz8OBB9uzZw4wZ\\nM4iOjmbNmjWYzWaKi4spLCzk5ZdfBiAxMZEdO3aQkZHB4cOHmTBhAsOHD+fgwYM2dc+aNYs33niD\\nvXv3EhoayrBhwygtvfk+zPPmzePw4cNs2rSJ48ePk5aWRkBA7RNcZs2aRVFREYWFhRQVFbF+/Xqa\\nN29Ov36WLSTfe+895s+fT3JyMkePHmXlypUsX76cd955x1pHXFwcnp6edo9WrW5ti7sbnTx5kqKi\\nImJjY63njEYj0dHR7Nq1yyaOoqIiNm3axL59+4iOjiYmJobi4uLaqgVg9+7dDBliu3blo48+Sk5O\\nDpWV11dQePXVVwkNDeWpp56q03tpDI7+BP8e2+XwFbAIWGinvOvtylwPzpx5y+Z1ScmBJopEq4uQ\\nkMUcOBBb67Vb3VS9Lq5erflDubF2dbjZ83SLnKbd3MWLF7lw4QKPPfYYwcHBANaWptzcXJRS3H//\\n9aV48vLyyMjI4NSpUwQGWpaOmjJlCpmZmaSmprJ27fWlWRcsWMDgwYMBS6tYYGAgH3zwAc8+63i/\\n4IKCAiIjI4mKigIgKCjIblmz2YzZbBlOcuzYMaZPn86KFSsYOHAgAMnJySxfvpzHH7esbdmhQwfm\\nzJlDSkqKdZzdn//8Zy5ftt/LUVdFRUUopfD1tV1Ky9fXl7NnLdvoff311xw4cIBz587h7m5ZDSEp\\nKYmNGzfy/vvvW5Po2uquniBeq7eiooLz58/j6+vL1q1b+fjjj9m/f38DvLv65+gn9zONFoWmNbA2\\nbWLw83uGoqJ1Na41Zovc5cvf1zjnKi1yjvcG1TQNoE2bNkyYMIEhQ4YQExNDTEwMI0eOtJs85ebm\\nIiJ07drVZkuysrIyBg26PmNfKUXv3r2trz08PIiIiHBqgP8LL7zAyJEjycnJITY2lmHDht10XNfP\\nP/9MQkICo0ePZtq0aQCcP3+e06dPM2nSJCZPnmwtW1FRYTP2z9/f0V6yjSM3N5eSkhK8vW0X375y\\n5Qp5eXkA1oknSinGjx9v06poz/nz53nmmWfIyMhwyYkrtbGbyIlIemMG4qrc3NpSUfFP62t//4mN\\nHEHNBYG1W6eUwt//+SZP5Nq2fYyCgtdtzrlKi9ydtjODdndz5W1Y09LSmDlzJps3b2bjxo3Mnz+f\\nDRs21Fr26tWrGAwGcnJycHOz/ZVrMtXPdopDhw6loKCAL7/8km3bthEfH8+oUaNIS0urtXxlZSWj\\nRo0iKCiIt9++vj3g1auW3zepqan06WN/0eq4uDh27Nhh97pSiosXL97muwE/Pz9EhOLiYmsrJkBx\\ncTF+fn7WWP38/Ni5c2eNPXuvde1Wb1G7ds7Pz69G12txcTFubm54e3uzc+dOioqKiImJsdZ77XNp\\n0aIFhw8fpmPHhtti73bcMX0pSqmXgAFAD8APWCQirzm8yfb+EcAC4FdAMfAesEREHGZKZnMnLl68\\nPmHX19f5WTf1oUWLpv/L525hr+uwMRM5s7lzjXOu0iJnMoU1ahyadieLiIggIiKCWbNmERcXR3p6\\nOvHx8TbjrAC6d++OiFBYWEj//v3t1ici7N6929pdW1JSwqFDh0hMTHQqHi8vL8aNG8e4ceMYOnQo\\nY8eOJTU1lebNa459ffHFFykoKGDPnj00a3Z9VJSPjw/t2rXj+++/Z9y4cXaf1dBdqyEhIfj5+ZGZ\\nmWntLi4tLWXHjh2sXLkSgMjISIqLi1FK2Z2MUNtSJ3369KmRdG/dupUePXrQrFkzevbsWWPs4rx5\\n8/j555955513XHLig91ETimVBvyHiJys+toREZHn6je0Gp4HLgCfApNvUtaGUupR4GMsydtMoDuw\\nBMuyKq84uvfGPK+xZxgGBEzlhx9WWV936vSfjfr8u4m9RK5xlx+p+Re4m1vbRns+2G+Rc3dv16hx\\naNqdKD8/n9TUVIYPH05AQAAnTpzgwIEDTJ06leDgYEpLS/nqq6/o3r07ZrOZjh07MnbsWBITE1mx\\nYgWRkZH8+OOPZGVlERYWxogRI6x1Jycn4+3tjb+/P6+99hru7u6MGTPmpjEtXLiQyMhIwsPDKS8v\\n55NPPiEsLKzWJG7dunWsW7eOzZs3U1paap1M0bJlSzw8PEhKSmL69Om0bt2auLg4ysvLyc3N5cyZ\\nM8ydOxe49a7VEydOcOnSJc6cOUNZWZm1pSw8PBw3NzfOnj1LTEwMS5cuJSHBslXejBkzWLJkCZ07\\nd6Zjx44kJyfj6elp/TwGDx5M3759SUhIYNmyZXTp0oXCwkK2bNlCbGwsffv2rTWWyZMnk5KSwsyZ\\nM5k0aRI7d+5k/fr1ZGRkAJYxhF27drW557777qOyspJf/cr+pLmm5KhFbiDwZtXXg7Cd+HCjBm8E\\nF5GuAMqSSb1wi7cvAbaLyLX7spVSnsA8pdRqEfmH/VubNpEzmULp1m0jRUXpeHpG4efneNCrZp+9\\nRK4x132qbTFeN7f7Gu35lhhqJnKBgX9o1Bg07U5lNps5fvw4Tz75pHVw/FNPPcXs2bNp1qwZkydP\\nZsyYMfz4448sXLiQBQsW8F//9V8sXryYOXPm8MMPP+Dl5cXDDz9cY4zc0qVL+cMf/sDx48cJDw/n\\niy++cKr71d3dnfnz53Py5EmMRiO9e/dm48aNNnVf+zm3fft2SktLGTBggE0d12J97rnnaNmyJW+8\\n8QavvvoqJpOJ8PBwfv/739/2Z/b888+zfft26+vIyEjAMju1ffv2lJeXc/z4cS5cuGAtM3v2bEpL\\nS/n973/PTz/9ZF2yxcPDw1pm06ZNzJ8/n9/97nf84x//wNfXl759+zJhwgS7sQQHB7Np0yZmzpzJ\\nf/7nf9KuXTvefvttm4T6TqNu7Ft2dVWJXDlOdq0qpQKBAuB5EUmrdj4YyAOeqW08oFJKRIScnCgu\\nXbq+lk9k5He0atWjzu9Da3yXLh0iJyfC5twjjxTRooWvnTsaRlaWbeIYGvoG7dvXPsOqIZw79ymH\\nDz9hc659+1cJDV3caDFomlKqxtime1V2djaDBg3i3LlzeHl5NXU4Wj1z9L1eda1OrQnOLgh8JwvH\\n0mJ4uPpJEckH/gV0reWeam5skbsXPrK7040bh7u7t2/0JK42jb0SfG0tcnoLJ01rWjqp1W6XowWB\\n29/K0ZhB36Jrf978VMu1n6pdr1VTj5HT6k/z5m0IDV0GWBa/7dDh35s4omsa94+D2sbIKaWXHtG0\\npuToDzp7C/C2atWKpUuXNmKUmityNEYun1sb++Z0hqOUigEynSiaJSKDbl6s4YhU3nBGt8jdydq3\\nn42fXyIi5TVa6JpKs2YtG/V5tbW+NXYMmqZd179//xqzXatzNEtUd8VqjhK5Z2m4SQx/Bbo4Ue5f\\n9fCsay1xbWq51gb40d6NixYt4syZYsrL4aGHLIdukbvztWjh06TPb93611y4sNP6ulWr3g5K17/a\\nJlyYTK43pV7TNAtXWIBXqx9ZWVlkZWXVa533wmSHIOAUNSc7dABOcpPJDn/7W2cuXz5uPd+z59/x\\n8HAmB9W02v3yy14OHBhKefl5fHxG86tffdCo4+RKS39g927bVei7d/8rrVs/0mgxaJqe7KDdKxp6\\nssMtLQisLCP9uwJtgRwRKanLwxuDiJxWSu0HxgHV18N7CigDvnRcg57soNUvT88oevfOp6LiAi1a\\n+Df6ZIfa1ovT23NpmqbdmZzOSpRSU4Ei4ADwNdC56vwGpdT0hgnP5vlRSqnfAL+pOtVVKfWbqsNY\\nrdw2pdT/3nD7q0B/pdR/KqX6K6VmAvOANY7XkNOTHbSG0ayZB+7u7Ro9iQPLHyOenj2trw0GEyZT\\nzR0nNE3TNNfnVCKnlJqIZXHgDcCTQPXfPju4nlw1pN8D/wf4EMvYvVFVr/8PUH3Qk4Eb3peIfAmM\\nBHoBm4EXgWRusquD5V492UG7+4SGLqV5c2+UciM0dClubnqyg6Zp2p3IqTFySqm/AxtFZE61MWo9\\nRCRXKRUP/FlE/Bo41kZ1bYzct9+258qV09bzvXufwmh05dVWNM05V6+WAwqD4Y7Zclm7i+gxctq9\\nwlUWBA4Btti5VgI07h5DjejGrlXdIqfdLQyG5jqJ07R7QEhICKtWrbp5Qe2O5GxWch4ItnOtM3Cm\\nXqJxSbZdq3qyg6Zpmlab9PR0PD09mzqMGnJycpgyZUqTPX/GjBn07NkTk8lEaGio0/ctWrSIgIAA\\nzGYzAwcO5MiRI/UST3Z2Nj169MBkMvHAAw+Qmppqc/3jjz+mZ8+etGnThpYtW9K9e3fWr19fL89u\\nCM5mJZ8DC5RS1f8HRCnlDczEMnburqQnO2iapmnOEJEmmcB0M23btsVorLl+ZGMRERITE3n66aed\\nvmfZsmWsXr2alJQUcnJy8PHxITY2lpKSui2WkZ+fT3x8PL/+9a/Zt28fc+fOZdq0aXz66afWMt7e\\n3vz7v/87f/vb3zh48CDPPPMMzz33HJs3b67TsxuMiNz0ALyBY1gW6P0GSzPVDuAclj1MWztTz510\\nWD4akR072so332A9rlz5h2iapml1c+1n7J0oOztbevfuLS1btpTWrVtLr169ZO3ataKUEoPBYP03\\nKSlJRETKyspk9uzZEhgYKGazWR5++GHZsmWLtb6srCxRSsnnn38uDz30kBiNRomKipK9e/c6Fc+F\\nCxdk/Pjx4uPjI0ajUcLCwuTNN9+0Xg8ODpaVK1eKiMiiRYts4rx2XItVRCQtLU26du0qRqNROnfu\\nLKtXr66Pj01WrFghISEhTpX19/eXJUuWWF9fvnxZPD095d1337Weu3DhgkycOFF8fHzE09NTBgwY\\nIDk5OQ7rnT17tnTq1Mnm3PPPPy+PPPKIw/siIyPl1VdfdSr2Gzn6Xq+6Vqd8xakBMiJyXinVA5gB\\nPAqcwLIG3VpgtYhcrMfc0sXodeQ0TdMam0pquJYtWXj7kywqKysZMWIEEydO5MMPP6SsrIzc3FzC\\nw8NZs2YN8+bNIy8vDxGhZUvLbPDExEROnjxJRkYGAQEBbNq0ieHDh/Pdd98RERFhrXvWrFm89dZb\\ntGvXjkWLFjFs2DBOnDhx09a0efPmcfjwYTZt2oSPjw8nT57k3LlztZadNWsWL7zwgvX11q1bee65\\n5+jXrx8A7733HosWLWLt2rVERkZy6NAhJk6cSIsWLazds3FxcezYscNuPEopLl68/bTg5MmTFBUV\\nERsbaz1nNBqJjo5m165dTJw40RqHl5cXmzZtok2bNqSnpxMTE8OxY8fw9fWtte7du3czZMgQm3OP\\nPvoo69evp7KykmbNava6bdu2jePHj7NkyZLbfk8NyemRziLyC/AfVYcNpZSbiFTUZ2CuouZkB921\\nqmmadq+6ePEiFy5c4LHHHiM4OBiATp06AZCbm4tSivvvv99aPi8vj4yMDE6dOkVgYCAAU6ZMITMz\\nk9TUVNauXWstu2DBAgYPHgzAunXrCAwM5IMPPuDZZ591GFNBQQGRkZFERUUBEBQUZLes2WzGbDYD\\ncOzYMaZPn86KFSsYOHAgAMnJySxfvpzHH38cgA4dOjBnzhxSUlKsiZyjvV/rQ1FREUqpGsmYr68v\\nZ8+eBeDrr7/mwIEDnDt3Dnd3y4LmSUlJbNy4kffff5+XX37Zbt3VE8Rr9VZUVHD+/HnrMy9evEhA\\nQABXrlzBzc2NlJSUGgmgq3AqkVNKzRaR5XauuWFZy+2J+gzMdejJDpqmaZpFmzZtmDBhAkOGDCEm\\nJoaYmBhGjhxpN3nKzc1FROjatavNEhRlZWUMGjTI+lopRe/e1/dd9vDwICIiwqkB/i+88AIjR44k\\nJyeH2NhYhg0bRnR0tMN7fv75ZxISEhg9ejTTpk0D4Pz585w+fZpJkyYxefJka9mKigqbsX+usPdr\\nbm4uJSUleHt725y/cuUKeXl5ANaJJ0opxo8fzzvvvON0/Z6enuzfv59Lly6xbds2Zs6cSXBwsDXh\\ndSXOtsj9h1KqUETer36yak25DMD13lk90ZMdNE3TtOrS0tKYOXMmmzdvZuPGjcyfP58NG2qf83f1\\n6lUMBgM5OTm4udn+yjWZTPUSz9ChQykoKODLL79k27ZtxMfHM2rUKNLS0motX1lZyahRowgKCuLt\\nt9+2iRUgNTWVPn362H1eQ3et+vn5ISIUFxdbWzEBiouL8fPzs8bq5+fHzp07a6zR1qpVKwD2799f\\n45yfnx/FxcU25YuLi3Fzc7NJCpVS1hm2Dz74IEeOHOH111+/oxO5ycB7SqlzIrIZrPuufgjEYhk3\\nd5fS68hpmqY1trqMY2sMERERREREMGvWLOLi4khPTyc+Pp7KSttenO7duyMiFBYW0r9/f7v1iQi7\\nd++2dteWlJRw6NAhEhMTnYrHy8uLcePGMW7cOIYOHcrYsWNJTU2lefPmNcq++OKLFBQUsGfPHpsx\\nYT4+PrRr147vv/+ecePG2X1WQ3ethoSE4OfnR2ZmprW7uLS0lB07drBy5UoAIiMjKS4uRilFSEhI\\nrfXUttRJnz59aiTdW7dupUePHrWOj7vm6tWrXLly5XbfUoNydrLDOqWUP/B/lVIxwHfAB8BQYKiI\\n7G7AGJvUjVt06a5VTdO0e1d+fj6pqakMHz6cgIAATpw4wYEDB5g6dSrBwcGUlpby1Vdf0b17d8xm\\nMx07dmTs2LEkJiayYsUKIiMj+fHHH8nKyiIsLIwRI0ZY605OTsbb2xt/f39ee+013N3dGTNmzE1j\\nWrhwIZGRkYSHh1NeXs4nn3xCWFhYrUncunXrWLduHZs3b6a0tJTS0lIAWrZsiYeHB0lJSUyfPp3W\\nrVsTFxdHeXk5ubm5nDlzhrlz5wK33rV64sQJLl26xJkzZygrK7O2lIWHh+Pm5sbZs2eJiYlh6dKl\\nJCQkAJa155YsWULnzp3p2LEjycnJeHp6Wj+PwYMH07dvXxISEli2bBldunShsLCQLVu2EBsbS9++\\nfWuNZfLkyaSkpDBz5kwmTZrEzp07Wb9+PRkZGdYyr7/+Or169SI0NJQrV67wxRdf8N///d824xld\\nyq1McQXexrLkyP8DfgF+Xddps656UDVd+JtvmtksP1JZWW53GrGmaZrmHO7Q5UeKi4vliSeekMDA\\nQDEajdKhQweZO3euVFRUiIjIlClTxNvb22b5kYqKCklKSpKwsDBxd3cXf39/SUhIkNzcXBGxLD9i\\nMBjks88+kwcffPCWlx9ZvHixdOvWTTw8PKRt27YSHx8vR48etV4PCQmRVatWiYhIYmKiGAyGGkf1\\n5UcyMjIkKipKTCaTeHl5Sb9+/eSjjz667c9swIABtT7z1KlTIiKSn58vBoNB0tPTbe5LSkqSdu3a\\niclkkgEDBsjhw4dtrl+6dElmzJghQUFB4u7uLu3bt5cxY8ZIXl6ew3i2b98uUVFRYjQaJTQ01GZJ\\nExGRV155RTp16iRms1natm0rffv2rdP7d/S9Tj0sP+LUXqvXKMtoxwwgDogXke31mlW6kGt7rWZl\\n2U6B79+/UrfKaZqm1ZHea/W67OxsBg0axLlz5/Dy8mrqcLR61tB7rdrtWlVKnQZqe7IbloFi/11t\\nFouISIe6BOKKav/gXW/Vbk3TNO3OppNa7XY5GiO3jdoTuXtIzYkOrrj9iqZpmnZnc/S7xd4sUaUU\\nr776qnXsmnZvuqWu1XuJUkoqK6+wfbt7tXNu9O9f3oRRaZqm3R1016rzCgsL7c4S9fLy4r777mvk\\niLRb0WRdq5re1UHTNE1req6wAK/muhyNkXsa+EJE/ln1tUMisr5eI3MJep9VTdM0TdNcl6MWuf8C\\negP/rPraEQHuukTuxjXk9GLAmqZpmqa5EkeJXAhQWO3re5DenkvTNE3TNNdlN5ETkVO1fX0v0bs6\\naJqmaZrmynRm4kDNyQ7649I0TdM0zXU4muxwEufXkRMRCaufkFyJ7lrVNE3T7mwhISFMmzaNl156\\nqalD0RqAoyam7Fs47sqtuvRkB03TNM1Z6enpeHp6NnUYNeTk5DBlypQme/6MGTPo2bMnJpOJ0NBQ\\np+9btGgRAQEBmM1mBg4cyJEjR+olnuzsbHr06IHJZOKBBx4gNTXV5vqf/vQnoqOj8fLyok2bNgwa\\nNIi//vWv9fLshuBojFxiI8bhovTyI5qmaZpzRMQld/9p27Ztkz5fREhMTOTAgQNkZmY6dc+yZctY\\nvXo16enpdOrUiaSkJGJjYzl+/DgeHh63HUt+fj7x8fE8//zz/OUvf2HHjh1MmTIFHx8fHn/8ccCS\\n6I0ePZq+fftiNptZtWoVjz76KPv37ycszAU7H0VEH7UcgFy+fFq++Qbr8de/BoimaZpWd5ZfP3em\\n7Oxs6d27t7Rs2VJat24tvXr1krVr14pSSgwGg/XfpKQkEREpKyuT2bNnS2BgoJjNZnn44Ydly5Yt\\n1vqysrJEKSWff/65PPTQQ2I0GiUqKkr27t3rVDwXLlyQ8ePHi4+PjxiNRgkLC5M333zTej04OFhW\\nrlwpIiKLFi2yifPacS1WEZG0tDTp2rWrGI1G6dy5s6xevbo+PjZZsWKFhISEOFXW399flixZYn19\\n+fJl8fT0lHfffdd67sKFCzJx4kTx8fERT09PGTBggOTk5Disd/bs2dKpUyebc88//7w88sgjDu/z\\n8/OTtWvXOhX7jRx9r1ddq1O+opuYHNItcpqmaU1CqYY76qCyspIRI0YQHR3NwYMH2bNnDzNmzCA6\\nOpo1a9ZgNpspLi6msLCQl19+GYDExER27NhBRkYGhw8fZsKECQwfPpyDBw/a1D1r1izeeOMN9u7d\\nS2hoKMOGDaO0tPSmMc2bN4/Dhw+zadMmjh8/TlpaGgEBAbWWnTVrFkVFRRQWFlJUVMT69etp3rw5\\n/fr1A+C9995j/vz5JCcnc/ToUVauXMny5ct55513rHXExcXh6elp92jVqtXtfrwAnDx5kqKiImJj\\nY63njEYj0dHR7Nq1yyaOoqIiNm3axL59+4iOjiYmJobi4mK7de/evZshQ4bYnHv00UfJycmhsvLG\\n4VQWV65cobS0lDZt2tTpfTWUO2aLLqXUS8AAoAfgBywSkdecuM8T+AMwFOiIZaDbEWC5iPw/R/fq\\nWauapmladRcvXuTChQs89thjBAcHA9CpUycAcnNzUUpx//33W8vn5eWRkZHBqVOnCAwMBGDKlClk\\nZmaSmprK2rVrrWUXLFjA4MGDAVi3bh2BgYF88MEHPPvssw5jKigoIDIykqioKACCgoLsljWbzZjN\\nZgCOHTvG9OnTWbFiBQMHDgQgOTmZ5cuXW7sZO3TowJw5c0hJSbGOs/vzI7FPWAAAIABJREFUn/9s\\nd+/X+lBUVIRSCl9fX5vzvr6+nD17FoCvv/6aAwcOcO7cOdzdLXuiJyUlsXHjRt5//31rEl1b3dUT\\nxGv1VlRUcP78+RrPBJg/fz6enp4MHz68Pt5evbtjEjngeeAC8Ckw+Rbua19V/r+ARUAlMAb4VCk1\\nVUT+aP9W3SKnaZqmXdemTRsmTJjAkCFDiImJISYmhpEjR9pNnnJzcxERunbtarNxellZGYMGDbK+\\nVkrRu3dv62sPDw8iIiKcGuD/wgsvMHLkSHJycoiNjWXYsGFER0c7vOfnn38mISGB0aNHM23aNADO\\nnz/P6dOnmTRpEpMnX/81W1FRYTP2zxX2fs3NzaWkpARvb2+b81euXCEvLw/AOvFEKcX48eNtWhWd\\n9eabb/Lee++xbds2WrZsWffAG8Adk8iJSFcAZVkD5IVbuDUPCBaR6u3TmUqp9sAcwG4ip1vkNE3T\\ntBulpaUxc+ZMNm/ezMaNG5k/fz4bNmyotezVq1cxGAzk5OTg5mb7K9dkMtVLPEOHDqWgoIAvv/yS\\nbdu2ER8fz6hRo0hLS6u1fGVlJaNGjSIoKIi3337bJlaA1NRU+vTpY/d5cXFx7Nixw+51pRQXL168\\nzXcDfn5+iAjFxcXWVkyA4uJi/Pz8rLH6+fmxc+dOmwQZsHbt7t+/v8Y5Pz+/Gl2vxcXFuLm51UgK\\n16xZw8KFC9m8ebO1tdMV3TGJ3O0SEXvtvzmA4z9ZarTIud5sJE3TtLuSOLuMadOIiIggIiKCWbNm\\nERcXR3p6OvHx8TXGWXXv3h0RobCwkP79+9utT0TYvXu3tbu2pKSEQ4cOkZiY6FQ8Xl5ejBs3jnHj\\nxjF06FDGjh1LamoqzZs3r1H2xRdfpKCggD179tCs2fX1UX18fGjXrh3ff/8948aNs/ushu5aDQkJ\\nwc/Pj8zMTGsCVVpayo4dO1i5ciUAkZGRFBcXo5QiJKT2XURrW+qkT58+NZLurVu30qNHD5vPYtWq\\nVSQlJbFp0yaHSa0rcCqRU0o5SniuYunyPCoi5fUSVePoDxx1XOTGHyS6RU7TNO1elp+fT2pqKsOH\\nDycgIIATJ05w4MABpk6dSnBwMKWlpXz11Vd0794ds9lMx44dGTt2LImJiaxYsYLIyEh+/PFHsrKy\\nCAsLY8SIEda6k5OT8fb2xt/fn9deew13d3fGjBlz05gWLlxIZGQk4eHhlJeX88knnxAWFlZrErdu\\n3TrWrVvH5s2bKS0ttU6maNmyJR4eHiQlJTF9+nRat25NXFwc5eXl5ObmcubMGebOnQvcetfqiRMn\\nuHTpEmfOnKGsrMzaUhYeHo6bmxtnz54lJiaGpUuXkpCQAFjWnluyZAmdO3emY8eOJCcn4+npaf08\\nBg8eTN++fUlISGDZsmV06dKFwsJCtmzZQmxsLH379q01lsmTJ5OSksLMmTOZNGkSO3fuZP369WRk\\nZFjLvPHGG8yfP5+//OUvPPDAA9YWPJPJVOeJHA3CmamtWJK1ypscvwCL6zqN1olYmlXFs6AOdfyu\\nKubRDsrIpUtHbJYf+dvfutidQqxpmqY5jzt0+ZHi4mJ54oknJDAwUIxGo3To0EHmzp0rFRUVIiIy\\nZcoU8fb2tll+pKKiQpKSkiQsLEzc3d3F399fEhISJDc3V0Qsy48YDAb57LPP5MEHH7zl5UcWL14s\\n3bp1Ew8PD2nbtq3Ex8fL0aNHrddDQkJk1apVIiKSmJgoBoOhxlF9+ZGMjAyJiooSk8kkXl5e0q9f\\nP/noo49u+zMbMGBArc88deqUiIjk5+eLwWCQ9PR0m/uSkpKkXbt2YjKZZMCAAXL48GGb65cuXZIZ\\nM2ZIUFCQuLu7S/v27WXMmDGSl5fnMJ7t27dLVFSUGI1GCQ0NtVnSRMSyXEtt8T7zzDO39f4dfa9T\\nD8uPKHGi+VopNQx4G9gPfAwUA77Ak8CDwL8DDwOTgFdEZMVN6osBnFkVMEtEBlU/UTVGrhwnZ63W\\n8uwBwJfAhyJidyqQUkouXTrEd991s54zm7vy8MOHb/WRmqZp2g2UUjXGNt2rsrOzGTRoEOfOncPL\\ny6upw9HqmaPv9aprdRq35ewYuRHAZhG5cbbo+0qpVGCgiDyjlLoKPAc4TOSAvwJdnHjuv5yMzylK\\nqZ7A/wO+AiberPzixWupmunMQw9B3766a1XTNE2rfzqpvTdkZWWRlZVVr3U62yL3I/BbEanRiqaU\\nigU+EhEvpVQc8D8iYqzXKG2fd1stckqpCCALOAAMFZErNykvv/yyj5ych6znPDwepGfP/Q7u0jRN\\n05yhW+Suu1mLnL1ZokopXn31VevYNc01uUqLXDMgjNq7Qx+oug5wpepwKUqpjsBW4Htg2M2SuGtq\\nLj+iZ61qmqZp9at///52dxUAx7NEdVes5mwitwl4XSl1DtggIpVVLWOPA4uBL6rKhQMn6j9MUEpF\\nAcFcTxq7KqV+U/X1F1K1TpxSahvQXkQ6Vr2+H0sC2hzLgsDhNywjkit2Z9vaZtB6QWBN0zStsbnC\\nArya63I2kZuGZUeF/wtUKKV+AtpU3f/XqutgWYbk9foOssrvgaervhZgVNUBEAIUVH1twHadkK7A\\ntSW3P6+l3ur32tALAmuapmma5sqcGiNnLazUEKA3lr1OC4HdtY2buxsopeTChb+Rm9vLes7TsydR\\nUXuaMCpN07S7gx4jp90rXGWMHAAishXLWLN7gm6R0zRN0zTNld1SIqeUegzLjghewI/ANyKyqSEC\\ncw03btGlEzlN0zRN01yHs1t0eWIZX9YPqAD+CbQFXlJK7QAeE5FLDRZlE9GzVjVN0zRNc2XONjG9\\nDkQCTwEmEfEHTFgmH0TScBMcmpietappmqbd2UJCQli1alVTh6E1EGczk98A80XkLyJSCSAilSLy\\nFyzbc/3G4d13LD1GTtM0TXNOeno6np6eTR1GDTk5OUyZMqXJnj9jxgx69uyJyWQiNDTU6fsWLVpE\\nQEAAZrOZgQMHcuTIkXqJJzs7mx49emAymXjggQdITU21uX7kyBFGjRpFWFgYBoOB11675d1AG5Wz\\nmUlbwN4neKTq+l3nxq5V3SKnaZqm2SMi3LBOqUto27YtRmODbbh0UyJCYmIiTz/99M0LV1m2bBmr\\nV68mJSWFnJwcfHx8iI2NpaSkpE6x5OfnEx8fz69//Wv27dvH3LlzmTZtGp9++qm1zL/+9S9CQkJY\\nvHjxLSWeTcXZzOQk8Jida3FV1+9CukVO0zRNs7V9+3b69OmDp6cn9913H7179yYlJYVnn32WkpIS\\nDAYDzZo1s7bklJeXM2fOHIKCgvDw8KBXr15s3Xp9AYjs7GwMBgNffPEF3bt3x2Qy0aNHD3Jzc52K\\n5+LFizz11FP4+vpaW5neeust6/XqXatJSUnW+AwGg/Wo3uq0bt06wsPDMZlMdOnShTVr1tTp83rz\\nzTeZOnUqnTp1uqV7XnnlFUaMGEHXrl1JT0/nl19+4YMPPrB537/73e/w9fWlVatWDBw4kL179zqs\\n949//CMBAQGsWbOGzp078/zzzzNhwgRWrLi+RXyPHj1Yvnw5o0ePxmQy3fobbmTOzlpNBVYqpVoC\\nf8GyhpwfMBp4HnipYcJrWrpFTtM0rWmoet5YvDoZMOC2762srGTEiBFMnDiRDz/8kLKyMnJzcwkP\\nD2fNmjXMmzePvLw8RISWLVsCkJiYyMmTJ8nIyCAgIIBNmzYxfPhwvvvuOyIiIqx1z5o1i7feeot2\\n7dqxaNEihg0bxokTJ27amjZv3jwOHz7Mpk2b8PHx4eTJk5w7d67WsrNmzeKFF16wvt66dSvPPfcc\\n/fr1A+C9995j0aJFrF27lsjISA4dOsTEiRNp0aKFtXvW3t6v1yiluHjxonMfaC1OnjxJUVERsbGx\\n1nNGo5Ho6Gh27drFxIkTrXF4eXmxadMm2rRpQ3p6OjExMRw7dgxfX99a6969ezdDhgyxOffoo4+y\\nfv16KisradasWa33uTKnEjkRWV211dVLQGLVaQWUAUtF5M2GCa+p6VmrmqZp2nUXL17kwoULPPbY\\nYwQHBwNYW5pyc3NRSnH//fdby+fl5ZGRkcGpU6cIDAwEYMqUKWRmZpKamsratWutZRcsWMDgwYMB\\nS6tYYGAgH3zwAc8++6zDmAoKCoiMjCQqKgqAoKAgu2XNZjNmsxmAY8eOMX36dFasWMHAgQMBSE5O\\nZvny5Tz++OMAdOjQgTlz5pCSkmJN5Bzt/VofioqKUErVSMZ8fX05e/YsAF9//TUHDhzg3LlzuLu7\\nA5bWxo0bN/L+++/z8ssv2627eoJ4rd6KigrOnz9vNwF0ZU6vIyciryql3sCys8O1deR2i8hPDRVc\\nU6u5ErNukdM0TbuXtWnThgkTJjBkyBBiYmKIiYlh5MiRdpOn3NxcRISuXbva/E4pKytj0KBB1tdK\\nKXr37m197eHhQUREhFMD/F944QVGjhxJTk4OsbGxDBs2jOjoaIf3/PzzzyQkJDB69GimTbPssnn+\\n/HlOnz7NpEmTmDx5srVsRUWFzdg/V9j7NTc3l5KSEry9vW3OX7lyhby8PADrxBOlFOPHj+edd95p\\n9Dgbw63u7PAT8GUDxeKCdNeqpmmaZistLY2ZM2eyefNmNm7cyPz589mwYUOtZa9evYrBYCAnJwc3\\nN9tfufU1/mro0KEUFBTw5Zdfsm3bNuLj4xk1ahRpaWm1lq+srGTUqFEEBQXx9ttv28QKkJqaSp8+\\nfew+r6G7Vv38/BARiouLra2YAMXFxfj5+Vlj9fPzY+fOnTUaXVq1agXA/v37a5zz8/OjuLjYpnxx\\ncTFubm41ksI7hd1ETinlOJ2/gYhsr3s4rkVv0aVpmtY06jKOrTFEREQQERHBrFmziIuLIz09nfj4\\neCorK23Kde/eHRGhsLCQ/v37261PRNi9e7e1u7akpIRDhw6RmJjoVDxeXl6MGzeOcePGMXToUMaO\\nHUtqairNmzevUfbFF1+koKCAPXv22IwJ8/HxoV27dnz//feMGzfO7rMaums1JCQEPz8/MjMzrd3F\\npaWl7Nixg5UrVwIQGRlJcXExSilCQkJqrae2Gad9+vSpkXRv3bqVHj163JHj48Bxi1wWN66IWztV\\nVe7O/AQc0i1ymqZp2nX5+fmkpqYyfPhwAgICOHHiBAcOHGDq1KkEBwdTWlrKV199Rffu3TGbzXTs\\n2JGxY8eSmJjIihUriIyM5McffyQrK4uwsDBGjBhhrTs5ORlvb2/8/f157bXXcHd3Z8yYMTeNaeHC\\nhURGRhIeHk55eTmffPIJYWFhtSZx69atY926dWzevJnS0lJKS0sBaNmyJR4eHiQlJTF9+nRat25N\\nXFwc5eXl5ObmcubMGebOnQvcetfqiRMnuHTpEmfOnKGsrMzaUhYeHo6bmxtnz54lJiaGpUuXkpCQ\\nAFjWnluyZAmdO3emY8eOJCcn4+npaf08Bg8eTN++fUlISGDZsmV06dKFwsJCtmzZQmxsLH379q01\\nlsmTJ5OSksLMmTOZNGkSO3fuZP369WRkZFjLlJeXc+TIEUSE0tJSioqK2L9/Py1btiQsLOyW3nuj\\nEJFaDyx7qjp92KvnTj0A+cc/PpVvvsF6HDiQIJqmaVrdWX793HmKi4vliSeekMDAQDEajdKhQweZ\\nO3euVFRUiIjIlClTxNvbWwwGgyQlJYmISEVFhSQlJUlYWJi4u7uLv7+/JCQkSG5uroiIZGVlicFg\\nkM8++0wefPBBMRqNEhUVJXv37nUqpsWLF0u3bt3Ew8ND2rZtK/Hx8XL06FHr9ZCQEFm1apWIiCQm\\nJorBYKhxXItVRCQjI0OioqLEZDKJl5eX9OvXTz766KPb/swGDBhQ6zNPnTolIiL5+fliMBgkPT3d\\n5r6kpCRp166dmEwmGTBggBw+fNjm+qVLl2TGjBkSFBQk7u7u0r59exkzZozk5eU5jGf79u0SFRUl\\nRqNRQkND5d1337W5np+fL0qpGvEOHDjwtt6/o+/1qmt1yleU1BjQrwEopeQf//iEw4evb1rh7T2C\\nbt0+dXCXpmma5gylVC0Tyu5N2dnZDBo0iHPnzuHl5dXU4Wj1zNH3etW1Oi2JofsKHdKzVjVN07SG\\np5Na7XbpzMQBvSCwpmma1hgcbe0VFxeHp6dnjaNVq1YsXbq0EaPUXNEtLT9y79GzVjVN07SG1b9/\\n/xqzXatzNEtUd8VqOpFzQLfIaZqmaU3NFRbg1VyXzkwc0lt0aZqmaZrmum4pkVNKGZRS3ZRS/ZVS\\nHg0VlKvQCwJrmqZpmubKnM5MlFJTgSJgP/A10Lnq/Aal1PSGCa+p2c4i0l2rmqZpmqa5EqcyE6XU\\nROBNYAPwW2z7GHcAv6ntvjudbpHTNE3TNM2VOZuZvASsFJHfATeuiHuUqta5u4+e7KBpmqZpmuty\\nNjMJAbbYuVYC3Fc/4bgW3SKnaZqmaZorczYzOQ8E27nWGThTL9G4nBtb5PSsVU3TNO3OEhISwqpV\\nq5o6DK2BOJvIfQ4sUEqFVjsnSilvYCaWsXMNSin1klJqo1LqrFLqqlJqwW3WE6KU+ldVHaGOyuoW\\nOU3TNM1Z6enpeHp6NnUYNeTk5DBlypQme/6MGTPo2bMnJpOJ0FCHv3ZtLFq0iICAAMxmMwMHDuTI\\nkSMNGKXFJ598Qnh4OEajkW7durFhQ8305p133iE0NBSTyUSPHj3YuXNng8fliLOZyXzgCnAI+ArL\\ndM63gL8DlcBrDRKdreeB+7GM0avLpnR/BH5yrg49a1XTNE1zjoi4ZM9N27ZtMRqNTfZ8ESExMZGn\\nn37a6XuWLVvG6tWrSUlJIScnBx8fH2JjYykpKbntOLKzswkJCbF7/dtvv2X06NE89dRT7N+/n7Fj\\nxzJq1Ci+++47a5mPPvqIGTNmMH/+fPbt28cjjzzCv/3bv/HDDz/cdlx1JiJOHYAn8O/ATuA48C2w\\nEGjlbB31cQDNsPR5LriNe8cChcB0LAloqIOy8sMPa+Wbb7Aex45NEU3TNK3uLL9+7PuGbxrsqKvs\\n7Gzp3bu3tGzZUlq3bi29evWStWvXilJKDAaD9d+kpCQRESkrK5PZs2dLYGCgmM1mefjhh2XLli3W\\n+rKyskQpJZ9//rk89NBDYjQaJSoqSvbu3etUPBcuXJDx48eLj4+PGI1GCQsLkzfffNN6PTg4WFau\\nXCkiIosWLbKJ89pxLVYRkbS0NOnatasYjUbp3LmzrF69us6fmYjIihUrJCQkxKmy/v7+smTJEuvr\\ny5cvi6enp7z77rvWcxcuXJCJEyeKj4+PeHp6yoABAyQnJ8dunVlZWQ6f/9vf/laGDBlic27w4MEy\\nduxY6+tevXrJpEmTbMp07NhRXn31Vbv1Ovper7pWp7zI6SYmEflFRP5DRH4tIp1EpI+IJInIxXrJ\\nKBuYUuo+YCXwB+CCM/foLbo0TdO06iorKxkxYgTR0dEcPHiQPXv2MGPGDKKjo1mzZg1ms5ni4mIK\\nCwt5+eWXAUhMTGTHjh1kZGRw+PBhJkyYwPDhwzl48KBN3bNmzeKNN95g7969hIaGMmzYMEpLS28a\\n07x58zh8+DCbNm3i+PHjpKWlERAQUGvZWbNmUVRURGFhIUVFRaxfv57mzZvTr18/AN577z3mz59P\\ncnIyR48eZeXKlSxfvpx33nnHWkdcXByenp52j1atWt3uxwvAyZMnKSoqIjY21nrOaDQSHR3Nrl27\\nbOIoKipi06ZN7Nu3j+joaGJiYiguLr6t53777bcMGTLE5tyjjz5qfWZ5eTl79+61iQtgyJAhNnE1\\ntntpr9U3gCMi8oFSaoJzt+gxcpqmadp1Fy9e5MKFCzz22GMEBwcD0KlTJwByc3NRSnH//fdby+fl\\n5ZGRkcGpU6cIDAwEYMqUKWRmZpKamsratWutZRcsWMDgwYMBWLduHYGBgXzwwQc8++yzDmMqKCgg\\nMjKSqKgoAIKCguyWNZvNmM1mAI4dO8b06dNZsWIFAwcOBCA5OZnly5fz+OOPA9ChQwfmzJlDSkqK\\ndZzdn//8Zy5fvuzcB3YbioqKUErh6+trc97X15ezZ88C8PXXX3PgwAHOnTuHu7s7AElJSWzcuJH3\\n33/fmkRXZ2kAc/zc2p5ZVFQEwPnz56msrKy1zLZt227tTdYjpxI5pdTXDi5fxdLCtRf4s4jcXirc\\ngJRS/YDxwEO3cl/NyQ6uN/ZB0zRNazxt2rRhwoQJDBkyhJiYGGJiYhg5cqTd5Ck3NxcRoWvXrjaJ\\nRFlZGYMGDbK+VkrRu3dv62sPDw8iIiKcGuD/wgsvMHLkSHJycoiNjWXYsGFER0c7vOfnn38mISGB\\n0aNHM23aNMCSqJw+fZpJkyYxefJka9mKigqbsX/+/v43jamh5ebmUlJSgre3t835K1eucOLECQBO\\nnz5N165dUUohIlRWVlJWVmadkKKUYvz48TatjXciZ1vkFNAJ8AdOAsWAL5b15QqrXscBM5VS/UXE\\n4XeeUioGyHTiuVkiMujmxRw+qznwn8AqETl2a3frrlVN07SmMEAGNHUIdqWlpTFz5kw2b97Mxo0b\\nmT9/fq2zGwGuXr2KwWAgJycHNzfbX7kmk6le4hk6dCgFBQV8+eWXbNu2jfj4eEaNGkVaWlqt5Ssr\\nKxk1ahRBQUG8/fbbNrECpKam0qdPH7vPi4uLY8eOHXavK6W4ePH2R135+fkhIhQXF1tbMQGKi4vx\\n8/Ozxurn58fOnTtrtLRd69pt164d+/fvt57fvXs3c+fOJTs723pP9W5gPz+/Gt2y1Z/p7e1Ns2bN\\nHJZpCs4mcquANUAPEcm9dlIpFQX8HyAJS4vcVmAx8PhN6vsr0MWJ5/7LyfgcmYllweK3lVKtq855\\nVP3bSinVUkQu1XbjqlVb+Okny9cPPQSBgTqR0zRN0yAiIoKIiAhmzZpFXFwc6enpxMfHU1lZaVOu\\ne/fuiAiFhYX079/fbn0iwu7du63dtSUlJRw6dIjExESn4vHy8mLcuHGMGzeOoUOHMnbsWFJTU2ne\\nvHmNsi+++CIFBQXs2bOHZs2aWc/7+PjQrl07vv/+e8aNG2f3WQ3dtRoSEoKfnx+ZmZnW7uLS0lJ2\\n7NjBypUrAYiMjKS4uBillN2ZqM2aNbNZ7uT06dO4ubnZLd+nTx8yMzP5wx/+YD2XmZnJI488AkDz\\n5s2JiooiMzOT3/zmNzZlRo0a5dR7y8rKIisry6myTnNmRgSwH3jKzrWngYNVXz8D/LOuMzBuEsst\\nzVoF1mGZoXrVzpFr5z45dWqZzazV77+fZXfmiaZpmuY8bjJr1VWdPHlS5s6dK7t27ZJTp07J119/\\nLQEBAfL666/Lrl27xGAwSGZmppw/f17+9a9/iYjI+PHjJTg4WD7++GPJy8uTnJwcWbFihXz66aci\\ncn3Wanh4uGRmZsqhQ4fkySefFD8/P2sdjixYsEA2bNgg//u//ytHjhyRJ598Ujp16mS9Xn3Walpa\\nmpjNZtm+fbsUFRVZj0uXLomIyJ/+9Ccxm82yevVqOXbsmBw6dEjWr19vM4P0Vn3//feyb98+mTlz\\npgQEBMi+fftk3759Ul5eLiIiZ86ckS5dusiGDRus9yxbtkzuu+8++Z//+R85ePCg/Pa3v5WAgABr\\nnCIi0dHR8uCDD8qXX34pJ0+elF27dsnChQtl586dtcZxs1mru3btkubNm8vSpUvl6NGj8vrrr0uL\\nFi3ku+++s5b56KOPxN3dXf70pz/J3//+d5k+fbp4enpKQUGB3Xodfa9TD7NWnU2eLgND7Vz7N+By\\n1dfRQGldg7pJLLeayHWqiqv6saQquRsNRNq5T/Lzl9yQyM2x+5+haZqmOe9OTeSKi4vliSeekMDA\\nQDEajdKhQweZO3euVFRUiIjIlClTxNvb22b5kYqKCklKSpKwsDBxd3cXf39/SUhIkNzcXBGxJBgG\\ng0E+++wzefDBB295+ZHFixdLt27dxMPDQ9q2bSvx8fFy9OhR6/WQkBBZtWqViIgkJiaKwWCocVRf\\nfiQjI0OioqLEZDKJl5eX9OvXTz766KPb/swGDBhQ6zNPnTolIiL5+fliMBgkPT3d5r6kpCRp166d\\nmEwmGTBggBw+fNjm+qVLl2TGjBkSFBQk7u7u0r59exkzZozk5eXVGsfNEjkRkU8++UR+9atfibu7\\nu3Tt2tUmubzmj3/8o4SEhIjRaJQePXrYTRyvaehETlnqcUwp9XcsMz5/U8u1T4EuIvIrpdQTwNsi\\nUvu85zqo6sYNxpLIZWDp0v2/VZe/EJHSqnLbgPYi0tFBXROANKCjiOTZKSP5+Ys5eXKe9Vz79q8Q\\nGvp6PbwbTdO0e9u1AeiaZaHaQYMGce7cOby8vJo6HK2eOfper7pWp5mUzo6Rew34b6XUAeAT4B+A\\nD/AboBuWhXYBBgN/q0tADvweSzcuWLZcGFV1gGXSRUHV1wbqaZ0QPWtV0zRNaww6qdVul1MJj4h8\\nCAwFLgGvAilV//4CDBGRjKqiLwG/bYA4EZFnRKSZnaOgWrmBIhJ2k7rSq+6rtTXuOj1rVdM0TWt4\\njrb2srcAb6tWrVi6dGkjRqm5IqcXBBaRTCBTWbIZb+C83NBkda178+5x419IOpHTNE3T6lf//v1r\\nzHatztEsUd0Vq93yzg5Vyds/GiAWl6O36NI0TdOamisswKu5LqcTOaVUCywzVDsDxhsui4j8R30G\\n5hr0Fl2apmmaprkuZ7foagfsxDJrVLg+6r963+Ndl8jpFjlN0zRN01yZs5nJG8A5oD2WJK4XEIpl\\nF4fvq76+C+lZq5qmaZqmuS5nu1b7AS8DZ6teXxWRfGCBUqoZ8BaQUP/hNa2ay4/oFjlN0zRN01yH\\ns5lJW6CwaqJDCdCm2rWvgQH1HJeLsJ21qrtWNU3TNE1zJc5mJj9gWQAY4AQwpNq1h4G7bNkRC90i\\np2mapt3pQkJCWLVqVVOHoTUQZzOTb7DsUQqQCryslNqqlPoCyyQBVOmYAAAcZElEQVSHjxsiuKZn\\nu66PbpHTNE3T7ElPT8fT07Opw6ghJyeHKVOmNNnzZ8yYQc+ePTGZTISGOj+kftGiRQQEBGA2mxk4\\ncCBHjhxpwCgtPvnkE8LDwzEajXTr1o0NGzbYXN+xYwcJCQkEBgZiMBhYv359g8d0M85mJvOx7OaA\\niPwReBEwA/7AcuAPDRJdExO5MZFr1kSRaJqmaa5ORBzu0NBU2rZti9F446phjUdESExM5Omnn755\\n4SrLli1j9erVpKSkkJOTg4+PD7GxsZSUlNx2HNnZ2YSEhNi9/u233zJ69Gieeuop9u/fz9ixYxk1\\nahTfffedtcylS5eIiIjgrbfewmw233Ys9UpEbnoArQF3Z8reLQcgx45NkW++wXr88MNa0TRN0+rO\\n8uvHvuo/e+v7qKvs7Gzp3bu3tGzZUlq3bi29evWStWvXilJKDAaD9d+kpCQRESkrK5PZs2dLYGCg\\nmM1mefjhh2XLli3W+rKyskQpJZ9//rk89NBDYjQaJSoqSvbu3etUPBcuXJDx48eLj4+PGI1GCQsL\\nkzfffNN6PTg4WFauXCkiIosWLbKJ89pxLVYRkbS0NOnatasYjUbp3LmzrF69us6fmYjIihUrJCQk\\nxKmy/v7+smTJEuvry5cvi6enp7z77rvWcxcuXJCJEyf+/+3deXhU9fn38fcnQMPmQkQIm4Fa1IJg\\nReujUgHZtCCCPqACLlTbulXFViqtW/GHirjUpy4/qS1UsYpaqqJF/KEWxe2HGBVEUVmDkETUqoBG\\nINzPH9+TOBlmJpMQMgm5X9d1Ljj7febkytz5rtamTRvba6+9rF+/frZ48eKk11ywYEHK+59++uk2\\nePDgCtsGDhxoY8aMSXh8y5Yt7f7776/0WVL9rEf7dilfqbRETlJj4DMqtotrEDZsuKfC+jffrMxQ\\nJM455+qC0tJSRowYQZ8+fVi6dCmLFi1i/Pjx9OnThzvuuIPmzZtTXFxMYWEhV1xxBQDjxo1j4cKF\\nzJo1i2XLlnHOOedw8skns3Tp0grXnjBhArfccgtvvvkm3//+9xk2bBglJZU3Qb/qqqtYtmwZc+fO\\n5cMPP2T69Ol06NAh4bETJkygqKiIwsJCioqKeOCBB2jSpAnHHXccAPfddx9XX301kydPZvny5dx2\\n221MnTqVe+757vsw2dyvsXPA7orVq1dTVFTEoEGDyrc1bdqUPn368Oqrr1aIo6ioiLlz5/L222/T\\np08fBgwYQHFxcbXu+9prrzF4cMVU54QTTqhwz7qo0uFHzGy7pGLiG4w1QKWlX2c6BOeccxn01Vdf\\n8eWXX3LSSSfRuXNnAA466CAA8vPzkcT+++9ffvyqVauYNWsWa9eupWPHjgBcdNFFzJ8/n2nTpnHX\\nXXeVH3vttdcycOBAAGbMmEHHjh156KGHOPfcc1PGVFBQQK9evTjiiCMA6NSpU9JjmzdvXl4l+MEH\\nH3DppZdy6623cvzxxwMwefJkpk6dyimnnAJAXl4eV155JXfffXd5O7tUc7/WhKKiIiTRtm3bCtvb\\ntm3Lhg1hFLQXXniBJUuWsHHjRrKzswGYNGkSc+bMYebMmeVJdKxQAJb6vonuWVRUtCuPs9ulO47c\\ng8DPgbm7MZY6z2x7pkNwzjmXQa1ateKcc85h8ODBDBgwgAEDBjBy5MikyVN+fj5mRrdu3SokElu3\\nbqV///7l65I4+uijy9dbtGhBjx490mrgf+GFFzJy5EgWL17MoEGDGDZsGH369El5zhdffMHw4cM5\\n44wzuOSSSwD49NNPWbduHeeffz4XXHBB+bHbt2+v0PavLsz9mp+fz5YtW2jdunWF7d9++y0rV4ba\\ns3Xr1tGtWzckYWaUlpaydevW8g4pkjjzzDMrlDbWR+kmcmuAMZLeAJ4ECokbZM3MptdsaHWP2bZM\\nh+Cccw1Cv36pS08yafr06Vx++eXMmzePOXPmcPXVV+/Uu7HMjh07yMrKYvHixTRuXPErt1mzZjUS\\nz4knnkhBQQHPPPMMzz//PEOHDmXUqFFMn574a7m0tJRRo0bRqVMn7rzzzgqxAkybNo1jjjkm6f2G\\nDBnCwoULk+6XxFdffVXNp4Hc3FzMjOLi4vJSTIDi4mJyc3PLY83NzeXll1/eqaStrGq3ffv2vPPO\\nO+XbX3/9dSZOnMiLL75Yfk5sNXBubu5O1bKx96yr0k3k7o7+7QAckWC/AZ7IOeecaxB69OhBjx49\\nmDBhAkOGDOH+++9n6NChlJZWbIV0+OGHY2YUFhbSt2/fpNczM15//fXy6totW7bw7rvvMm7cuLTi\\nycnJYezYsYwdO5YTTzyRMWPGMG3aNJo0abLTsZdddhkFBQUsWrSIRo2+G42hTZs2tG/fnhUrVjB2\\n7Nik99rdVatdunQhNzeX+fPnl1cXl5SUsHDhQm677TYAevXqRXFxMZKS9kRt1KhRheFO1q1bR+PG\\njZMef8wxxzB//nx+85vvBuKYP38+xx57bE092m6RbiKXvL9uA9KoUYtMh+Cccy6D1qxZw7Rp0zj5\\n5JPp0KEDK1euZMmSJVx88cV07tyZkpISnnvuOQ4//HCaN29O165dGTNmDOPGjePWW2+lV69efP75\\n5yxYsIADDzyQESNGlF978uTJtG7dmnbt2nH99deTnZ3N6NGjK43puuuuo1evXnTv3p1t27Yxe/Zs\\nDjzwwIRJ3IwZM5gxYwbz5s2jpKSkvDNFy5YtadGiBZMmTeLSSy9ln332YciQIWzbto38/HzWr1/P\\nxIkTgapXra5cuZLNmzezfv16tm7dWl5K1r17dxo3bsyGDRsYMGAAU6ZMYfjwMNvn+PHjuemmmzj4\\n4IPp2rUrkydPZq+99ir/PAYOHEjv3r0ZPnw4N998M4cccgiFhYU8++yzDBo0iN69e1cpRggJbt++\\nfbn55psZMWIE//znP1mwYAGvvPJK+TFbtmxhxYoVmBk7duygoKCAd955h5ycnJRtE3erXe32uqcu\\ngK1dO6VCl/Wvv16RtAuxc8659FHJ8CN1VXFxsZ166qnWsWNHa9q0qeXl5dnEiRNt+/btZmZ20UUX\\nWevWrSsMP7J9+3abNGmSHXjggZadnW3t2rWz4cOHW35+vpmFYTGysrLsqaeesp49e1Z5+JEbbrjB\\nDj30UGvRooXtt99+NnToUFu+fHn5/i5dutjtt99uZmbjxo2zrKysnZbY4UdmzZplRxxxhDVr1sxy\\ncnLsuOOOs0ceeaTan1m/fv0S3nPt2rVmZrZmzRrLysraaSiPSZMmWfv27a1Zs2bWr18/W7ZsWYX9\\nmzdvtvHjx1unTp0sOzvbDjjgABs9erStWrUqYRyVDT9iZjZ79mz74Q9/aNnZ2datWzd74okndrpG\\n2fAtscvPfvazpNdM9bNODQw/IqukF0csST0JMzzsB0wzsyJJPwCKzWxTzaeZmSPJtm3bxMqVV7B5\\n89u0b/8L2rU7L9NhOefcHqGsAboLA9X279+fjRs3kpOTk+lwXA1L9bMe7dulUaTTqlqVlE3ouXoq\\nIEKbuKeAIsLMDh8CE3clkLqoceOWHHzwvZkOwznn3B7Ok1pXXelO0XUDMBA4C2hLSObKPAOcUMNx\\nOeeccw1Gqqm9kg3Au/feezNlypRajNLVRWlVrUpaD9xoZncrTDi6DTjSzPIlDQQeM7NWuznWWiXJ\\n/C8k55zbPbxqNX2FhYVJe4nm5OSw77771nJErirqRNUqoU3c+0n2ZQHZuxKEc8455xKrCwPwuror\\n3arV1UCy0QGPAj6omXCcc84551y60k3kHgAmShoLlA1MY5KOBy6nAQwG7JxzzjlX16TbRq4R8Hfg\\nNOBbQlXqN0BTYJaZJR8Cup7yNnLOObf7eBs511DUiTZyZlYKnCHpbkIP1TbAZ8A8M3txVwJIl6Rf\\nA/2AI4Fc4A9mdn0Vzm9KGCJlDHAA8AWwCDjVzLbXeMDOOeeSysvLS9lT07k9RV5e3m69frqdHQAw\\ns4VA8plyd6+fA18CjwMXVOVESY2BeUAecCOh48b+wCCgEeCJnHPO1aI1a9ZkOgTn9gjpDgj8FnA/\\n8LCZFe/ekBIzs25RLI2AC6t4+hXAj4BuZrYhZvvjNRSec84551ytS7ezQyFwC7BO0jOSzoiqKuuL\\nC4FH45I4twdZsGBBpkNwVeDvq37x91V/+LtqeNJK5MxsCNAB+C2hSvIhoFjS9Kjnap0lqRPQCVgt\\n6c+SvpT0jaTnJB2W6fhczfBfXvWLv6/6xd9X/eHvquFJt0QOM/vEzO4wsyOB7sDdQH/gOUlrd1eA\\nNaB99O9EoAuh5+0ZhIT035I6Ziow55xzzrldkXYiF8vM3geuB64CNgBVSoYkDZC0I43lherEF6fs\\nGbcAJ5nZs2b2JDAUaA5cXAP3cM4555yrdWmNI1fhBKk/cBZwKtCSMITHTDO7pwrXaEoYAqQyX5vZ\\nx3Hnls31mtbwI5IOApYDs81sVNy+t4FCM/tpgvN8gCPnnHPO7Va1Mo6cpEOBMwljsHUE1gD/j5DA\\nfVTVm5pZCfBhVc+rplWEwYurZFc/WOecc8653S3dceSWEMZwewx4wMxe3n0h1Swz2y7pX8BxkpqZ\\n2TcAkg4ADgGezGiAzjnnnHPVlO4UXSOBp8zs290fUtIYjgA6EwbwnQU8SkgsAf4VlfIh6XngADPr\\nGnPuD4H/Bd4EbgOaAdcC+wGHmdnGWnoM55xzzrkak+7wI/9IlsRJ6itpes2GldCvCMnbw4ABo6L1\\nRwlThpXJIu65os4Z/YEdhCTwz4Sq3Z/EJnGSOkr6h6QvomFKZkfDl7g6RtJISY9LKpD0taTlkm6U\\n1DLTsbnKSZoXdWhKe5o9V/skDZH0oqRN0e/ERZL6ZToutzNJvSU9K6lY0leS3pT0s0zH1dBJ6iDp\\nTkmvStoS/d7bqY+ApH0l/UXSRkmbJc2PmrVVfo/qTFos6QfA2YROD3mETgn1+gtUUjNCFfI3hN64\\nADcQSu96llXJurpB0mvAx4TZOT4mzNwxCXjfzI7NZGwuNUmjCSXjbYEbzOzaDIfkEpB0PnAn8Cfg\\nGcIfyD8ClpnZ3EzG5iqS1INQ6/QacAfwNTASOB+40MymZTC8Bk1SX0IB0puEGsXBQBczK4g77mVC\\nJ9ArCHPB/54w1NthlU1mkHYiJ2kf4HTgHODoaPM7wDTC1F1fpfdYdZOky4BbgYPMbHW0rTPwETDB\\nzO7IXHQunqT9zOyzuG1nAX8DBpjZgkzE5VKT1Ap4DxhPKF2f7Ilc3SMpjzAn9ZVmdmem43GpSboR\\n+DXQKrbQQdKrgJlZ74wF58pJOo9QI1ghkZM0HPgncLyZvRRt2xtYTehUOj7VdVNWrUrKiorWHyFM\\n03UvoQTu7uiQ8WY2rb4ncZFhwOtlSRyAma0BXgGGZyool1h8Ehd5AxBhFhJXN90MLDGzRzIdiEvp\\nPKCU8Ie6q/uaAFsT1Bx9STXHi3W1ahiwoSyJA4jyqqdII/9I+oIl3Qasjy50EqEK60RC0d+1hC/M\\nPUl34N0E25cB3Wo5Flc9/QjtJ9/PcBwuAUk/IQxj5INw1329CeNvjpa0QtI2SR9JuijTgbmE/gZI\\n0p8ktZO0j6RfENqG357Z0FwaUuUfB0hqnurkVMOPXE74UpwLjIstAdlDB8vNAf6TYPvnQKtajsVV\\nkaQOhDZy880sP9PxuIokNSGU6N9iZisyHY+rVPtomQr8jjAe5yjgLkmNvLq1bjGzZdG8548TOgYC\\nbAUuMLPHkp/p6ogcQjVqvM+jf1sR2j0mlKrI9a/AJsJUVh9IukvSUdWN0rndRVILwniAW4FzMxyO\\nS+xKoClwY6YDcWnJIszc80szm25mC8zsYmAeIbFzdUjUAXE2sJTwnT2A8IfTtKhzkduDJU3kzOwX\\nQC4wFlhM6P3ymqT3Cb+U97RSuf+QuOQtWUmdqwOi6d6eJowxeEJlvXtc7YuG8Pk9cA3QNKr22Tfa\\nnR2tezueuqWsBua5uO3/A7SV1LaW43Gp3UT4Q/ZkM3vGzP4dNZB/lDALk6vbUuUfZfuTSvnL08xK\\nzOxhMytrG/c7QgPYiYQ2clMknRl9mdZ3ywj11PG6EXrZuTpGUmPCX6G9gJ+amb+nuun7QDbwIOEX\\n0n8IVQYGTIj+n9Z4Sa7WLMt0AK5KDiV0Itoet30RsJ+kNgnOcXVHqvyjwMySVqtCFXqzmFmhmU01\\ns0OBowg9V7sCDxB6tNZ3c4CjoyFHgPLhR3rj03jVOZIEPETo4DDczN7IbEQuhbeA46OlX8wiYGb0\\nf283V7c8Hv17Qtz2nwIfm1lxLcfjUisCekZ/3MY6Gijhu7ZWrm6aA3SQdFzZhmj4kWGkkX9Ua0Dg\\nmBs1IfRoPdvMTqn2heqAqFfI24QBga+JNl8PtCAMyJcyI3a1S9J/E6r7JwP/itv9sZmtr/2oXFVI\\n2oGPI1dnRdMd9gSuJnR2OI3QBnWcmc3MZGyuIkn/l1CNOh+4h/A9Nhy4ELjdzCZkMLwGL3o/AAMJ\\n31sXARuBjWb2UlQw8TLQEfgtYUDg3xFKWg+r7PtslxK5PY2kjsAfgUGE0oLngMvjR2B2mSdpNaG6\\nP5FJZuZTP9VxkkoJidx1mY7F7Sya7u4mwgwBrQjDkdzkYwDWTZJOILRf707oWLSSMA7gn82/6DMq\\n+qM10Tt40cz6R8fsS5iUYATh/b0K/NrMEg1LUvH6/n6dc8455+on7ynmnHPOOVdPeSLnnHPOOVdP\\neSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnXAMn6SxJa2PW\\nl0m6oIbvcbSk1yVtllQqqWdNXt/VPklrJE2vxnnDJV2+O2JyriHyRM451wtYDCCpBXAw8GYN32M6\\n0AgYChwDfFjD13e1r7qjyY8APJFzroZ4IuecO4LvErdeQCnwTk1dXFIWcBDwLzN70cwWmVlJTV3f\\n7TpJ38t0DM656vFEzrkGLEqyfsR3idyPgffMbGua5+8l6S5J6yWVSFouaXzM/nOA7YS5i6+VtEPS\\nqhTX+0N0zKGSXpC0RdIGSZPijsuWdLukpZI2SSqUNEfSwXHHtZV0f0x8G6LjWkf7G0n6L0krJH0j\\naaOklyQdG3edX0p6O+aYv0hqFXfMZZLek/S1pM8lvSFpeBqf4Zlx135AUm7M/qcl7VRCKilX0jZJ\\nl8Vs6yzp75I+iZ73LUkjknzG3SXNk7QJSDl/avRsq6MYF0n6SYJjWku6V9IH0XsriGJpH3PMDOAc\\noEMUQ/nPQ7rv1DlXUeNMB+Ccq32SVgN50aoBcyWpbD1mkucuZlaQ5BoC5hISwWuAdwlVp7dLam1m\\nVwNPA72BV4C/RMu3KUIrq657nFAdeyNwAnCNpFIzuz7anw3sBdwAbCBM6n4R8JqkQ8zsk+i4B4FO\\nwG+Aj4G2wACgebR/InAZ8HtCKeTewJFATsxzTgF+DdwBXAF0iO7bXdKxZmaSxhImvP4D8DLQDOgZ\\ne50kn+EvgXuBh6NY2hMmqj9KUi8z+xqYCTwUPdfymNPHRp/XQ9G1OgKLgKLomT4FTgdmSxpuZk/H\\nfcZPAH8FpgA7UsR4HvBHwvt4FPhBFG/LuENzCO/298AnQDvC5/5yFPtW4Hpgf8JnPIyQ4Jf9PKT7\\nTp1zsczMF198aWALcAgh0bgNWAr0iNa/BC6N/t8TaJziGicREoCz4rbfB3wD5ETrjaLjrk0jrusI\\nVbsT4rb/OYpt7yTnZRGSp6+Ay2K2bwJ+leJ+TwH/SLE/j1CieFXc9mOiZzo5Wr8TWFzFd5BFSLqe\\ni9veO7r2r6L1psAXwA1xx70FPB2z/legGNg37rj/AfITfMZJP5eYYwUUEKrFY7efFsU4vZLn6xgd\\nNzxm+wygIM3PZ6d36osvvlRcvGrVuQbIzJab2RJCadUCM1sKfE0oZXnMzJZEy/YUlzmOkBA8HLf9\\nQeB7hGSnuh6LW58VxXZo2QZJp0U9Yf9DSLa2AGWdNcq8AUyQdKmkQ9nZG8AQSZMl9ZbUJG7/IEIy\\n81BUDdtIUqPovE1An5jr/EjSnyQNkNQsjWc8GGhDVKJWxsxeAdYCfaP1EuAfhBK4smfvARwGPBBz\\n6gmEEtJNMbE2JiRyh0mKL0F7Io0YO0ZL/PuYTfjMK5B0YVRNvCnaX0AoAUyrejTNd+qci+GJnHMN\\njKSsmC/53oSqq0aEpGQ98Em0Xpkc4PMEyV4RIflJWa1YieIE6yJUayJpGCG5WwaMBo4iVNd9SijB\\nKnMaMAeYALwTtZW7Jmb/DYQSqmHAS8BnkqZLKou9TXTflcC2mGUrIbHcD8DMHgAujOKYB3wuabak\\nPJIru0dhgn1FVPz8ZgIHSOobrZ9FKKl6MuaYNsDZCeKcGu3fL+4eie4br130b4X3YWalwGex2yRd\\nAtxNSBxPIbS3/D+Ezy/2nSRUhXfqnIvhbeSca3ieJyrtIZSWzCSUopWtbyO0kzvezF5KcZ3PgRxJ\\njeOSudyY/dXVFlgTtw4h0YTQ9usjMzuv7IAoMa2QPJrZp8AlwCWSuhIa2k+S9ImZTYsSkluAWyS1\\nIVQX/5FQpTeakKwYoWTuiwRxliczZnYfcJ+kfYDBwO2ExCRZyWTZ55ObYF8u0ZAw0bVflFQAnCnp\\npSi2x8wstr3hZ4RkdAoheYq3IW49neFDypK9trEbo0Q/PjE8nVBN/NuY4zqncY/Y8yt9p865irxE\\nzrmG55eEko5bgRXR/48ENgJXRf//MZWPJfciof3bqLjtZxIasL+2CzGeFrc+mlCVuTRab87OVXtn\\nR/EkZGYfWeiA8R9iqmhj9n9iZtOB52L2zye08cozs/wEy9oE1/nSzB4jdAxIVJ1b5gNCSdcZsRsV\\neszmAf+OO/5BYCQwhFAyOTNu/zxCu8b3ksS6LUUsyXwMrGPn9zGSnQsCmhP+CIh1LjsnjN8SEuV4\\nVX6nzjkvkXOuwTGzjwAkXUtoxP5WNMRDa0Lj9XR7Bz5D6KF5b1SatYzQa/Vc4EYzq26JnIBfxLRF\\nOzG65nVmtik6Zh4wXNLthJ6xPwZ+RUjSiJ5vb0JS9ndgOSHJGAHsCzwbHfMEobdqfnRur+h+/w1g\\nZqskTQXuknQIIXktAQ4ABgL3RaVl0wiJ5muEHpsHE6o/n032kGa2I3oH90oqKxXtCEwmJHkz4k6Z\\nSegRei+wNkFp6bXA/wILJd1FKNFsRUgmu5jZz5PFkiJGUxj65T6FWRxmAV2BKwmdT2LNA34r6XeE\\n3rP9CQlfvPcI7/cCQqljiZm9Sxrv1DmXQKZ7W/jiiy+1vwBNCG2sBkXrlwFvVOM6LYE/Eao8SwgJ\\n06VxxzQidIq4Jo3rlfWo7Aa8QGjsvgH4Q9xxIgxl8TGwmVB6dRiwCvhrdMz3CAnZ0uhZvyAkOqfH\\nXOdy4FVCaeQW4H3CUCqN4u43NjpuU3StZdFzt4/2nx3FW0TosbuSUOLZMo1nHkPogfpNFMffgLZJ\\njl0UfT7/lWR/e0IP33XR+1hPSCbHxH3G24GsKrznS4DVhA4xi4BjYz/r6JimhDZyxYQk70lCyWKF\\nd08oefs7oSq4FFiV7jv1xRdfdl5kVt1ZVpxzrmZJuo5QstTEzJKObeaccy7wNnLOOeecc/WUJ3LO\\nubrGqwmccy5NXrXqnHPOOVdPeYmcc84551w95Ymcc84551w95Ymcc84551w95Ymcc84551w95Ymc\\nc84551w95Ymcc84551w99f8B6ssKwatUFoMAAAAASUVORK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"for step_size in np.logspace(-4, 2, num=7)[0:6]:\\n\",\n \" make_plot(log_likelihood_sgd[step_size], len_data=len(train_data), batch_size=100,\\n\",\n \" smoothing_window=30, label='step_size=%.1e'%step_size)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Quiz Question**: Which of the following is the worst step size? Pick the step size that results in the lowest log likelihood in the end.\\n\",\n \"1. 1e-2\\n\",\n \"2. 1e-1\\n\",\n \"3. 1e0\\n\",\n \"4. 1e1\\n\",\n \"5. 1e2\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Quiz Question**: Which of the following is the best step size? Pick the step size that results in the highest log likelihood in the end.\\n\",\n \"1. 1e-4\\n\",\n \"2. 1e-2\\n\",\n \"3. 1e0\\n\",\n \"4. 1e1\\n\",\n \"5. 1e2\"\n ]\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 2\",\n \"language\": \"python\",\n \"name\": \"python2\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 2\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython2\",\n \"version\": \"2.7.11\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 0\n}\n"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":398,"cells":{"repo_name":{"kind":"string","value":"jegibbs/phys202-2015-work"},"path":{"kind":"string","value":"assignments/assignment11/OptimizationEx01.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"21572"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"# Optimization Exercise 1\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"## Imports\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 2,\n \"metadata\": {\n \"collapsed\": true,\n \"nbgrader\": {}\n },\n \"outputs\": [],\n \"source\": [\n \"%matplotlib inline\\n\",\n \"import matplotlib.pyplot as plt\\n\",\n \"import numpy as np\\n\",\n \"import scipy.optimize as opt\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"## Hat potential\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"The following potential is often used in Physics and other fields to describe symmetry breaking and is often known as the \\\"hat potential\\\":\\n\",\n \"\\n\",\n \"$$ V(x) = -a x^2 + b x^4 $$\\n\",\n \"\\n\",\n \"Write a function `hat(x,a,b)` that returns the value of this function:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 3,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"6cff4e8e53b15273846c3aecaea84a3d\",\n \"solution\": true\n }\n },\n \"outputs\": [],\n \"source\": [\n \"def hat(x,a,b):\\n\",\n \" v = -a*(x**2) + b*(x**4)\\n\",\n \" return v\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 4,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"7204bd97cd003430289f171b6ba70d63\",\n \"grade\": true,\n \"grade_id\": \"optimizationex01a\",\n \"points\": 2\n }\n },\n \"outputs\": [],\n \"source\": [\n \"assert hat(0.0, 1.0, 1.0)==0.0\\n\",\n \"assert hat(0.0, 1.0, 1.0)==0.0\\n\",\n \"assert hat(1.0, 10.0, 1.0)==-9.0\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"Plot this function over the range $x\\\\in\\\\left[-3,3\\\\right]$ with $b=1.0$ and $a=5.0$:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 5,\n \"metadata\": {\n \"collapsed\": true,\n \"nbgrader\": {}\n },\n \"outputs\": [],\n \"source\": [\n \"a = 5.0\\n\",\n \"b = 1.0\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 6,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"6cff4e8e53b15273846c3aecaea84a3d\",\n \"solution\": true\n }\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAYUAAAEZCAYAAAB4hzlwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYXVWV/vHvSwBBxgQUkME0M3SggyDzEEEwMg8yOIKK\\ntK0toKAdtRtpJxBsRRvhByokKIOICMgcacKgoIAEwwxCmBMaQlAEGkjW749zqlIpKlW3qu65++xT\\n7+d56nnqVp177lqpyl21195nH0UEZmZmAIulDsDMzOrDRcHMzLq5KJiZWTcXBTMz6+aiYGZm3VwU\\nzMysm4uCWYYk7SDp/haPPUzSTVXHZM3gomDZkjRT0i69vtbyG2Arx0qaJukVSX+T9L+SfiVp1RbO\\nPU3SJ1uJo8VY50tau+txRNwUERu26/xmXVwULGdRflT9Gp+NiOWA9YEVge+3+Lx2UwXnNFuIi4I1\\nzUJvxpImSXpY0l8l3SNp3/LrGwGnA9uUo4A5A5444gXgYmBceY5tJd0maa6kP0rapvz6t4AdgFPL\\nc/+w/PqGkqZKel7S/ZIO7BHnZEk/knR5GeutXSMDSTeWh91Vnu9ASRMkPTFQnmaD5aJguev913Pv\\nxw8D20fE8sB/Aj+XtEpE3Ad8GrglIpaLiDEDvYaklYEDgD9JGgNcAZwCjAG+B1whaXREfBW4iXKE\\nERFHSloGmAr8HHgbcAhwWlmcuhwMHA+MLuP+FkBE7Fh+f9PyfL/sI8Y+8+wnJ7M+uShYzgRcIumF\\nrg/gR/QYLUTERRExq/z8QuAhYKsez2/lNX5Ynns68BTwBWAP4IGIODci5kfEBcD9wN69nttlT+DR\\niJhSHj+dYtRxYI9jLo6I2yNiHnAuML7Ff4eB8jRrmYuC5SyAfSJidNcH8Bl6vBlL+pikO3sUjXHA\\nSoN8jc+V518jIj4aEc8D7wAe73XsY+XXez63yzuBrXoVsA8Bq/Q4dnaP418Blm01yDbkaQbA4qkD\\nMGuzngXhncCZwM4UbaKQdGePY4YzGfwUsH+vr70TuGoR534cuCEidhvGa/aphTzNWuaRgjXZMhRv\\nzs8Bi0n6OOUkcWk2sIakJQY4T19vrlcC60v6oKTFJR0MbAhc3uPc6/Q4/vLy+I9IWqL8eLekrmWl\\nA72B9z5fTwPladYyFwVrmu5lqhFxL/BfwC3ALIo3ypt7HHsdcA8wS9KzA5xz4S9EzKGYJziG4s34\\nWGDP8usAPwA+IGmOpFMi4iVgN4oJ5qeAZ4ATgCV7x72I1z0emFK2hz4wyDw7sXTXGkKpb7IjaRRw\\nO/BkROxVrur4BcVQfCZwUETMTRiimdmIUYeRwlHAvSz4S2YSMDUi1qf4S25SqsDMzEaapEVB0hrA\\n7sBPWNBT3RuYUn4+BfBFOGZmHZJ6pPB94IvA/B5fWyUiupbmzWbBkj0zM6tYsqIgaU/g2YhY5NK5\\nKCY8PEFmZtYhKa9T2BbYW9LuwFLA8pJ+BsyWtGpEzJK0GvCmVSGSTqW4sGdm+aW5wPSImFZ+fwJA\\nxo+Pblg+zq9e8Tm/RTzu+rwu8bQpn8PKlGYCcyPiFPqRfPURgKSdgGPL1UcnAc9HxHckTQJWjIhJ\\nvY4/PiKOTxFrJzi/vDm/fDU5N2gtv9RzCj11VacTgV0lPUhxheaJfRw7tlNBJTI2dQAVG5s6gIqN\\nTR1AxcamDqBCY1MHkFottrmIiBuAG8rP5wDvTRuRmdnIVKeRwmBMTh1AxSanDqBik1MHULHJqQOo\\n2OTUAVRocuoAKjZtoANqMadgZmb1kOVIoecKgSZyfnlzfvlqcm6tyrIomJlZNdw+MjOzbh4pmJlZ\\ntyyLQtP7fs4vb84vX03OrVVZFgUzM6uG5xTMzKybRwpmZtYty6LQ9L6f88ub88tXk3NrVZZFwczM\\nqpHlnILEshG8lDoOM7NcSCwRwesDHZfrSGG2xKjUQZiZZWS7Vg7KtChcPRdYN3UUVWl6X9P55a3J\\n+TU5N2CTVg7KtCj8/VFgXOoozMwy0tJ7Zq5zCt8EXo/gP1PHYmaWA4nfRQzcQsp0pMDdtDgUMjMb\\n6SREiyOFTIvCwUvT4PZRw/uazi9zTc6vwbmtCfy9lQMzLQrXPgG8U2Kp1JGYmWVgHEWHZUBZzikA\\nSMwAPhbBnaljMTOrM4l/A94ewTEDHZvpSAEoql5jW0hmZm3U8kghy6JQ9v1m0NCi0OC+JuD8ctfk\\n/BqcW7OLQskrkMzMBiCxOLABcG9Lx2c8p7A2MC2CtVLHYmZWVxIbApdHtLYLRM4jhZnAaIkVUgdi\\nZlZjLbeOINOiIGlCBPMphkONm1docF8TcH65a3J+Dc1tE4o52JZkWRR68AokM7P+DWqkkO2cAoDE\\n0cA6EXwudSxmZnUk8QCwfwT3tHJ8E0YKXoFkZtYHiaWBtYAHW31OlkWhR9/vbmBcudlTYzS0r9nN\\n+eWtyfk1MLeNgIdaueNalyyLQg+zgQBWSR2ImVkNDWo+ATKfUwCQuB74dgRTU8diZlYnEicDcyI4\\nodXn5D5SAK9AMjNblEGPFLIsCr36fo3bA6mBfc2FOL+8NTm/BuY2MopCL16BZGbWi8RoYEXgsUE9\\nL9WcgqSlgBuAtwBLApdGxJcljQF+AbyTYiuLgyJi7qLPwwrAU8Dy5VXOZmYjnsT2wHcj2Howz0s2\\nUoiIV4H3RMR4YFPgPZK2ByYBUyNifeC68nE/5+FF4HlgbLURm5llZdCtI0jcPoqIl8tPlwRGAS8A\\newNTyq9PAfbt/bw++n6NaiE1sK+5EOeXtybn17DcBrXnUZekRUHSYpKmU1xvcH1E3AOsEhGzy0Nm\\n09o1CF6BZGa2sCxHCvPL9tEawI6S3tPr+0FxcVpv4yVNlnS8pONhv3fAhbt0fVPShJ4VP7fHXV+r\\nSzzOz/mNlPwiYlqd4hn641ETgE1gq+VVvFdOVvF+2X3cotTm4jVJ/wG8AhwOTIiIWZJWoxhBbNj/\\ncxkP/DzCowUzM4l3AHcBb4/o8w/rRUo2UpC0sqQVy8+XBnYF7gQuAw4tDzsUuKSP507o9aX7gXUk\\nlqws4A5qpZrnzPnlrcn5NSi3ccCMwRYEgMUrCKZVqwFTJC1GUZx+FhHXSboTuFDSJymXpA50oghe\\nlZhJcR/SQU+smJk1zCYMYT4BatQ+Gi6JXwIXR3B+6ljMzFKSOBu4JYIzB/vcJlzR3KVx212YmQ3R\\nOIbYNcmyKCyi79eYaxUa1Nfsk/PLW5Pza0JuEqOAjaG1O631lmVRWARfq2BmBv8APBfBX4fy5CbN\\nKYwC/gqsEsFLqeMxM0tBYl/g8Aj2HMrzGzNSiGAexdLUf0wdi5lZQkNeeQSZFoV++n6NaCE1oa/Z\\nH+eXtybn15DchrS9RZcsi0I/vALJzEa6Ia88ggbNKQBITASOjeC9qWMxM+s0ibcAc4HREbw6lHM0\\nbaQwHdhMQqkDMTNLYBzw8FALAmRaFBbV94tgFvAyxZKsbDWkr7lIzi9vTc6vAbm9G7htOCfIsigM\\n4HZgi9RBmJklsAXFe+CQNWpOAUDiq8AKEXwpdSxmZp0kMR04IoI/DvUcHimYmTWAxNLA+sCfh3Oe\\nLIvCAH2/24HNpTxzg0b0Nfvl/PLW5Pwyz208cN9wJpkh06LQnwieB54H1ksdi5lZBw17PgEaOKcA\\nIHEhcGkE56aOxcysEySmADdH8OPhnKdxI4WS5xXMbKRpy0ghy6LQQt/vNor1ulnKvK85IOeXtybn\\nl2tuEssBYxnGnkddsiwKLfgTMF5Keg9qM7NO2QyYEcHrwz1RI+cUACQeAA6IGH7lNDOrM4kvAGtH\\n8K/DPVdTRwrgeQUzGznaMp8AmRaFFvt+2c4r5NrXbJXzy1uT88s4t2HvedQly6LQIo8UzKzxJEYD\\nq1HceXL452vwnMIywLMU+4q/ljoeM7MqSOwCHB/BDu04X2NHChH8HXgE37PZzJptC9rUOoJMi8Ig\\n+n63k+G8QsZ9zZY4v7w1Ob9Mc3s3bZpkhkyLwiB4XsHMmq5tK4+gwXMKABJbAadH8K7UsZiZtZvE\\n24CHgDERzG/HOZs+UrgL2EBiqdSBmJlVYHPgjnYVBMi0KLTa9yv3FX8A+KdKA2qzTPuaLXN+eWty\\nfhnm1tb5BMi0KAyS5xXMrKnaOp8ADZ9TAJA4Atgmgo+njsXMrJ0kngK2j+DRdp1zJIwUbsMjBTNr\\nGIl3AG8BZrbzvFkWhUH2/e4B1i6vcM5Chn3NQXF+eWtyfpnltgVwewRtbfdkWRQGo9zi4m6K/cbN\\nzJqi7fMJkLAoSFpT0vWS7pF0t6Qjy6+PkTRV0oOSrpW0Yu/nRsS0Qb5cVpPNQ8gvK84vb03OL7Pc\\nmlUUgNeBz0fEPwJbA5+VtBEwCZgaEesD15WPh8vzCmbWGBKizXsedUlWFCJiVkRMLz9/CbgPWB3Y\\nG5hSHjYF2Lf3c4fQ98tqD6TM+pqD5vzy1uT8MsptLWAe8HS7T1yLOQVJYyl6/n8AVomI2eW3ZgOr\\ntOEl7gdWl1ihDecyM0utkklmqEFRkLQs8CvgqIj4W8/vRXERxZuSHmzfL4I3gOmQxx5ImfU1B835\\n5a3J+WWUWyXzCQCLV3HSVklagqIg/CwiLim/PFvSqhExS9JqFDfK6f28o4HxLFifOxeY3vUD7RoC\\nLvz47GfgsC2A6/v+vh/7sR/7cS6Pf70r7HvcQMeXnx9GYSYwbaDCl+yKZkmimDN4PiI+3+PrJ5Vf\\n+46kScCKETGp13MnDLaiS3wIOCCCA4YffbWGkl9OnF/empxfDrlJjAKeB9aPePMfzcOVsn20HfAR\\n4D2S7iw/JgInArtKehDYuXzcDjcBO5Sz9mZmudoEmFVFQYARsPdRTxKPAHtEcF/qWMzMhkLiKGDj\\nCP65ivMnn2jusBuBHVMHYWY2DDtSvJdVIsuiMIy1xDcCO7UxlEpktFZ6SJxf3pqcX91zK9vfLgpt\\ndAOwo+cVzCxTGwF/i+CJql5gpM0pCHgS2CGCR1LHY2Y2GBKfBraO6F5m2nYjaqRQXv13Axm0kMzM\\n+rATxXtYZbIsCsPs+9V+srnufc3hcn55a3J+dc6tE/MJkGlRGKYsJpvNzHpZh2Lbn0pb3yNqTgG6\\nq+2zwLuqnKwxM2sniU8A743gQ1W+zogbKZTzCjcCO6SOxcxsECpvHUGmRaENfb9at5Dq3NdsB+eX\\ntybnV/PcKp9khkyLQhvcQM0nm83MukisBSxDcW+Yal+rvzmFcmvr3SjeQMdSTHI8RvGX9jUR8UbV\\nAVah3GXwOWCDqjaVMjNrF4kPA/tF8IGqX2uRIwVJ/0Fx/889KarTWRRbXT8A7AXcLunfqw6wChHM\\nA36HRwtmloed6MB8AvTfProL2Cwi/iUizo6IayLiqog4KyI+TXEXsz93Isje2tT3q20LqeZ9zWFz\\nfnlrcn41zq0jk8zQT1GIiMsiIiQt1ft7klaOiPkRcVm14VWq1pPNZmYAEqtS3Kt+Rkdeb6DrFCTN\\nAI6IiFvKxwcAJ0bEeh2IrzISS1DcvWhsBHNSx2Nm1heJA4GPRbBXJ16vlXs0fwg4S9I0YHVgJeA9\\nVQbVCRG8LnErxR3gfpM6HjOzRdiRDixF7TLgktSImAF8G/gXimLw2Yh4surA+tPGvl8tW0g17mu2\\nhfPLW5Pzq2luHZtkhhaKgqSfAkdT3Bf0MOBySf9acVydUtvJZjMziTEUlwPc2bHXbGFO4WjgB1Ee\\nKGkF4HsR8ckOxFcpiaUorldYLYK/pY7HzKwniX2Az0Twvk69Zivto1OiR+WIiBebUBAAIngVuAPY\\nNnUsZmZ96NhS1C79Xbx2haQDJb21j++9VdLBkq6sNrxFxjahjaerXQuppn3NtnF+eWtyfjXMraOT\\nzND/SOEwinmE2yXNkHStpKnlEtU7KO4VemgHYqxaLSebzWxkk1ie4n32to6+7qLmFCSdBpwXETdL\\nWoVisgPgsYiY1aH4KiexDDAbeFsEr6SOx8wMQGIiMCmCCZ183f5GCg8CJ0t6DDgGeC0i/tCkggAQ\\nwd8prhTcKnUsZmY9dLx1BP1vc3FKRGxD0VqZQ3EB2wOSviZp/Y5F2IcK+n43ALu0+ZxDVsO+Zls5\\nv7w1Ob+a5bYzdSoKXSJiZkScGBGbAYcA+wH3VR5ZZ10J7J46CDMzAIm3AxsCN3f8tVu4TmFxijfM\\nQyj+mr4eOD8iLq0+vM6QWJzivs3jIng6dTxmNrJJHArs1Yn7J/TW35LU3SSdBTwFfAq4HFgnIg5p\\nUkEAiOAN4Bo8WjCzetgDuCLFC/fXPpoE3AJsFBF7RcR5EfFSh+LqV0V9v8spbiiUXM36mm3n/PLW\\n5PzqkJvEksCuFG3tjlvkLqkRsXMnA6mBq4HTJZYqr3Q2M0the+ChCGanePEB5xRGEombgW9EcE3q\\nWMxsZJL4L+DFCL6e4vUHXH00wtSmhWRmI9aeFO9FSWRZFCrs+10B7CGhis7fkjr0Navk/PLW5PxS\\n5yaxHrAcHdwqu7csi0KF7gZGUew3YmbWaXsAV0SQrK/vOYVeJE4DHo3g5NSxmNnIIjEV+FEEl6SK\\nIelIQdJZkmaXO692fW1MuRvrg+XOrCt2OCzPK5hZx5W7om4N/DZlHKnbR2cDE3t9bRIwNSLWB64r\\nHy+k4r7f9cBmEqMrfI1+pe5rVs355a3J+SXObVfg9xEkvR4saVGIiJuAF3p9eW9gSvn5FGDfzsbE\\nKxSbUHXs9ndmZhTzCclWHXVJPqcgaSzwm4jYpHz8QkSMLj8XMKfrcedi4p+BHSL4SCdf18xGJonF\\ngKeBbSN4JGUsqdtH/SrvDZ2ial0JTJQYleC1zWzk2RyYk7ogQD/bXCQ0W9KqETFL0moUu5cuRNKp\\nwLLAzPJLc4HpETGt/P4EgKE+Bq0Dl8+FPbYGfjfc8w3h8dHtzKeGj51f3o8bm1/POYXOvv4Zh8ER\\nl1eUz2FlSjOBaQve5/pWx/bRScDzEfEdSZOAFSNiUq/nTBgoseHHxbcARfCVKl+n79euPr+UnF/e\\nmpxfqtwkbgeOiej8TXXeFEvKoiDpfIo7u61McZ/k44BLgQuBtSgq20ERMbfzsbENcEYEm3b6tc1s\\n5JB4B8WFs6tE8HryeFKPFOqqnE+YBWweweOp4zGzZpI4HHhvBIekjgVqPtG8KJ1YSxzBPOAqimVi\\nHdXkdeDg/HLX5PwS5VaLpahdsiwKHeSrm82sMhJvAXamuJ9LLbh91A+JFYHHgVUjeDl1PGbWLBK7\\nAV+LYLvUsXTxSKEfEcwF7gB2Sx2LmTXSPtSodQSZFoUO9/3OBz7cwddrdM8WnF/umpxfJ3Mr78V8\\nEHBBp16zFVkWhQ77JbBbyg3yzKyRJgL3R/Bo6kB68pxCCyR+CUyN4MzUsZhZM0hcBFwTwY9Tx9KT\\nRwqt+Rnw0dRBmFkzlJ2HXSk6EbWSZVFI0NO8GthQ4h868WJN7tmC88tdk/PrYG4HAteWi1lqJcui\\n0GkRvEYxGeSttM2sHT5K0YGoHc8ptEhiS+BcYP2UN9U2s7xJrA3cCqxR/sFZKx4ptO42YD6wVepA\\nzCxrHwF+UceCAJkWhRQ9zXJ0cA4dmHBucs8WnF/umpxf1blJiBq3jiDTopDQucDB5UUnZmaDtTUw\\nj6LzUEueUxgkiRuA70dwSepYzCwvEqcBT0XwrdSxLIpHCoPXkRaSmTVLuSPqQRQdh9rKsigk7mle\\nBOwiMaaqF2hyzxacX+6anF/Fue0O3BPRfW/5WsqyKKQUwYvANRQV38ysVR+l6DTUmucUhkBiD+Ar\\nddoD3czqq+wsPAqsVf5hWVseKQzNtcC6EuumDsTMsnAwcHXdCwJkWhRS9zQjeJ0Kt71InV/VnF/e\\nmpxfhbll0TqCTItCTZwDfLS8GMXMrE9lR2Edig5D7XlOYYjKYvBn4AsRTE0dj5nVk8RJwOIRfCF1\\nLK1wURgGicOAD0X4Hs5m9mYSKwCPAJvXfSlqlyzbRzXqaZ4HbCwxvp0nrVF+lXB+eWtyfhXkdgTF\\nBPPMNp+3MlkWhboodzk8Bfhi6ljMrF7KK5iPBk5OHctguH00TBLLUwwPt8jprwEzq5bEx4FDInhf\\n6lgGwyOFYYrgr8BPgM+njsXM6kFiMYoOwkmpYxmsLItCDXuaP6RYnrpSO05Ww/zayvnlrcn5tTG3\\nPYBXgP9p0/k6JsuiUDcRPA1cDHwmdSxmVgtfAk7K8da9nlNoE4mNgGnA2AheSRyOmSUisS3wc4r7\\nub+ROp7B8kihTSK4j+Jm3IclDsXM0voi8F85FgTItCjUuKd5EnCsxKjhnKTG+bWF88tbk/Mbbm4S\\nGwLbAWe3JaAEsiwKdRXB74BZwP6pYzGzJI4BfhTBy6kDGSrPKbSZxD7AV4GtcpxkMrOhkVgVuJdi\\nLuG51PEMlUcK7fcbYHlgp9SBmFlHHQmcm3NBgJoWBUkTJd0v6SFJ/9bH9yckCKslEcynuKz9TXG3\\nqs75tYPzy1uT8xtqbhLLUexz9L22BpRA7YqCpFHAqcBEYGPgg5I2ShvVoP0c2Ehi59SBmFlHfAW4\\nMoJHUwcyXLWbU5C0DfC1iJhYPp4EEBEnJg1skCT2Bb4NjC83zjOzBipXHN0MbBLBM6njGa7FUwfQ\\nh9WBJ3o8fhLYKlEsw3EpxXDyKDLbJdEGVt5kaQywGrAyix51vwbMBp6J4KUOhWcdUv4e/DfwzSYU\\nBKhnURhw6CLpVGBZ6N6VdC4wPSKmld+fAJD6McSRwK3ShJlww/8O4vlH1zGfNj7OIj+IW4BxcNIh\\nsMracOhiwGpwzVhYYgzs/HfgGbj0NYj5sO/c4nn/vgZs8VL5+C1w9VhYciVp59fL41+G/5sDB/0B\\nmA77LAFXPRXx2vV1yj/3n99QHvecU2jx+QfAlevAQTMoa34N8zmsTGkmMK3ruEWpY/toa+D4Hu2j\\nLwPzI+I7PY6ZMFBidSHxDWC9CA5p/Tn55DcUdcxPYnHg3cCWwGblx3rAw8CdwF3AY8Az5cesRW1n\\n0ld+5V+Uy1OMLFYDVgXW7fFaK1Hc3vXO8uP3wAN1XNZcx59fuwwmN4llgfuAD0dwY6WBdVAdi8Li\\nwAPALsDTwB+BD0bEfUkDGyKJtwL3AIdHcF3qeGwBiXcC7ys/dqZ40/89C96Y747g1Q7FMhoYz4Ii\\nsRPFqPma8uO6COZ2IhZrjcSJwOoRfDR1LO1Uu6IAIOn9FHc0GwX8NCJOSBzSsJQXtJ2AJ52TKrcf\\nmQDsTVEIxgDXUrzpTo1gVrroFlaOLDZiQdHajmIkcTVwcQT3JAxvxCsnl28CNm3KXEKXWhaFgeQ2\\nfC3/g18OTIsYeNI5t/wGq5P5lf/2mwMfBg6G7m3OrwHuLK8rafNrtj8/iaWBHSiWah8IPE9xj/AL\\nIni8na81cCzN/f1sJbfyd+pa4IoITulIYB1Ux4nmxokgJI4CbpU4P4InU8fUdBLrAR8qP0YB5wI7\\nR3B/0sCGqJy/uBa4VuJYigLxYeBOibspCsQvI5iTMMyR4gPAKhTXUzVOliOFXEl8HdgggoNTx9JE\\nEksCB1Dc7Gg94BcUxeC2Ok7YtkN5c/iJFMXvfcCVwGnA75qac0pNnVzuyUWhgzzpXA2JtSiuCTmc\\n4t/3R8BvIng9aWAdJrEicChFUXyVojic6+sj2qepk8s91W6bi1bkuvdKuZ3uUcAZ5WqTPuWaX6va\\nkZ+EJHaV+DUwnWK553si2CWCi1MWhFQ/vwjmRvADignqYyhGEI9J/LC8M2BbNPn3s7/cJLYGPklx\\nq83GyrIo5CyCyygmnS8o18bbIEgsKfExipU436NYjbNWBEeWd78b8SKYH8FvI9iPYpnri8D1EpdL\\n7FhOlNogSKwO/Ar4eNNWG/Xm9lECZTG4CvhzBMekjicHEssDnwKOBh6kuMvdte6bt6ZcvfQxihHE\\nHIp/v0sjmJc0sAyU/3Y3Ar+KIKs92IbCRSERiTHAHyj2TJmSOp66kliNYp/6TwG/BU6O4I60UeWr\\nvFZjH4oWyErAd4FzFnV19khXjqp+RtFV+fBI+CMky/ZRE3qa5dLBfYDvlr3Kbk3Irz+t5CcxVuJ0\\nijtZLQtsGcEhORSEOv/8IpgXwcXANsAngD2BRyS+VN4TYEB1zm+4+sjtixRzNIePhIIAmRaFpojg\\nXor/mL8qe5YjnsQGEpOBO4AXKJbwfi6CR9JG1iwRRAQ3RbAXsBvF1hqPSBzX3yKIkURid4p25b45\\n33N5sNw+qgGJLwP7ATuN1GG8xKYUNyrZmWIr4lMjeCFtVCOLxPrAJIoR7JnA9yN4Nm1UaZTbWNxI\\nURB+nzqeTvJIoR5OBP4CnDnSVoZIbClxKcW2E7cDa0fwDReEzovgwQg+AbyLYonv/RKnjLRRbDlS\\nuhSYNNIKAmRaFJrW0yx7lZ+kuP3ocdKoCWkjqpY0aoLEThLXAhcBUymKwXebcKFV7r+fETwWwWeB\\nccA8YIbEGRJrQ/759UdaayJwIXB1BGeljieFLItCE5U9y72A/eCcL5ZbNjRKecHZRPj1fwM/AS4A\\n1o3g1JHaNquzCJ4ul0yvD/wv8EeJc2D/tRKHVoliRHT6D4CnYOQuFfecQs2Ue6ucC6wAHBDB84lD\\nGrZyGeS+wJeBt1Dcu/qXEbyRNDAblHIbjc9SLBG+CTghh9VgrZDYHLiEYpO7k0bKSqO+uCjUUPkm\\negLF5PNeue7sKbEMxa0APw88RzF3clkV21Vb55Q/1yOAL1Dcme67wFW5/lwlDgD+H3BEBL9OHU9q\\nWbaPmtzTLGiHCL5EURhulHhv6ogGQ2JViW9S3BN2F4pN2raJ4JII5jf959f0/EDvjuD7wNrAj4Fv\\nAPdIHC6xVNrYWle2M79CcUOv90Xw6+b/7AaWZVEYKcqJroOAcyU+nTqegUhsIvETiq2FxwDbRrB/\\nhLdxbqIIXo/gPIqbGH2WYmQ7U+I/JFZJG13/yi3HpwD7A1tH8KfEIdWG20cZkFiXYhO96cBxETyY\\nOKRu5VWwh1BsW706cAZwegTPJQ3MkpDYmKJd+AHgfygWFFxblz2WyiXfu1K0Mh8BPjaSLkxrhYtC\\nJsoJ6COzLOMYAAAICElEQVQp/sP9Bvh6BDMTxSJga4pCsD8wjaKNcE1d/vNbWuUGhl1/LKwGnAWc\\nnep3toxpR+CbwNuBr1EsdshyHqRKWbaPmt736yu/CF6K4NsUdxR7ErhD4rROXVhU9l83k/h3YAZw\\nDsVupRtFsF8EV7ZaEEbiz69JWskvgr9GcGYEW1LsrzQauF3iWolPS6xZdZxdJLYqr4mZTDFyGRfB\\nL/oqCE3/2bUiy6IwkpU3UjkO2AB4ieLCou9JjC9XLS3SOGn390tXHyRNe7909Thp9/6Ol1hGYh+J\\nM4EnKC7qWZmif7x+BN+JYFZ7MrOmiuCuCI4E1gR+CmwPTJe4S+LbEtsO9LsLg/v9lVhaYmeJyygu\\nkLyIYh+tc7wUun9uH2Wu3Fr6WGAPipuJ30yxZ8uNwJ+67kA2Ttp9G/jBj2Hdrud+Ch6+BY66O+LK\\nsj21AcWOkBsCWwDbAX8ErgAur9NchuWtLAJbU/ze7kExHzWV4uZJ91MsVvjLIH5/l6P4fd2x/BhP\\nMaK9ADgjglc7l13eXBQapFzxsQOwE8V/jH8AbgPmbMvm2/2OP63W+znbsNVzt3LrKxQjgAdZ8B/y\\nz8B1Efy1U/HbyFXeZ3tniq1eNio/1gAeBe7bjk03v5kZb7qSelvePfsW/vhEefztLPiD6JYI/t6p\\n+Jsky9tBSpoQEdNSx1GVoeYXwWwWDJW7buSzJbD8aGb9I8WE30LexqPPUFxt/FinJon988tbFflF\\n8DhFz7/H67AUxRzaRsvzt037et5KPPk8xeKL2yL4v+HG0fSfXSs8p9BgEcyJ4OoILpzH04/3dcwb\\nPPtUBI941ZDVTQSvRjAjgguDmQ/3dcw8nnk8gpvbURCskGVRaHolryK/J+CHnyq2JOh2OPzl8eLe\\nBR3ln1/eUuTXqd/fpv/sWuE5hRFknLT7WvC5ZWHpl+CVx+G/7464MnVcZq3w729nZFkUmt73c355\\nc375anJurcqyfWRmZtXIcqRgZmbV8EjBzMy6ZVkUmr4/ifPLm/PLV5Nza1WWRcHMzKrhOQUzM+vm\\nkYKZmXVLUhQkHSjpHknzJL2r1/e+LOkhSfdL2m0Rz5/QkUATcX55c375anJurUo1UphBcT/XG3t+\\nUdLGwMEUOyVOBE6T1FeM4yuPMC3nlzfnl68m59ZS0UtSFCLi/ojoa2/+fYDzI+L1iJhJsdfJln0c\\nt2KV8dWA88ub88tXk3MDmDDQAXWbU3gHxa0muzwJnbndpJmZVXg/BUlTgVX7+NZXIuI3gzhVX8uj\\nxg4pqHyMTR1AxcamDqBiY1MHULGxqQOo0NjUAaRWWVGIiF2H8LSnYKEbeq9Rfq236ZKO7/F4WsM2\\nsZqcOoCKTU4dQMUmpw6gYpNTB1ChyakDaKdyDmFCjy/NHfA5Ka9TkHQ9cGxE3FE+3hg4j2IeYXXg\\nt8C64YspzMw6ItWS1P0kPUFx4+4rJF0FEBH3AhcC9wJXAZ9xQTAz6xxf0WxmZt3qtvqoZZK+Ieku\\nSdMlXSdpzYGflQ9JJ0u6r8zxYkkrpI6pnfq7gDFXkiaWF10+JOnfUsfTbpLOkjRb0ozUsbSbpDUl\\nXV/+Tt4t6cjUMbWTpKUk/aF8v7xX0gmLPDbXkYKk5SLib+XnnwP+KSIOTxxW20jaFbguIuZLOhEg\\nIiYlDqttJG0IzAfOAI6JiD8lDmlYJI0CHgDeS7E44jbggxFxX9LA2kjSDsBLwDkRsUnqeNpJ0qrA\\nqhExXdKywB3Avg37+b01Il6WtDhwM8V87s29j8t2pNBVEErLAs+liqUKETE1IuaXD/9AsRKrMfq5\\ngDFXWwIPR8TMiHgduIDiYszGiIibgBdSx1GFiJgVEdPLz18C7qO4bqoxIuLl8tMlgVHAnL6Oy7Yo\\nAEj6lqTHgUOBE1PHU6FPAL5Beb2tDjzR47EvvMyUpLHAZhR/jDWGpMUkTQdmA9eXC3vepLLrFNph\\noAvgIuKrwFclTQK+D3y8owEOUysX+En6KvBaRJzX0eDaoI0XMOYgzz6sLaRsHV0EHFWOGBqj7DyM\\nL+cnr5E0oa/ru2pdFAZxAdx5ZPiX9ED5SToM2B3YpSMBtdkQL2DMVe8LL9dk4S1brOYkLQH8Cvh5\\nRFySOp6qRMSLkq4AtgCm9f5+tu0jSev1eLgPcGeqWKogaSLwRWCfiHg1dTwVU+oA2uB2YD1JYyUt\\nSbHb72WJY7IWSRLwU+DeiDgldTztJmllSSuWny8N7Moi3jNzXn10EbABMA/4C/AvEfFs2qjaR9JD\\nFBNCXZNBt0TEZxKG1FaS9gN+CKwMvAjcGRHvTxvV8Eh6P3AKxSTeTyNikcv+ciTpfGAnYCXgWeC4\\niDg7bVTtIWl7iq38/8yCVuCXI+LqdFG1j6RNgCkUA4HFgJ9FxMl9HptrUTAzs/bLtn1kZmbt56Jg\\nZmbdXBTMzKybi4KZmXVzUTAzs24uCmZm1s1FwawNyq2XH5E0unw8uny8VurYzAbDRcGsDSLiCeB0\\nFmzMeCJwRkQ8ni4qs8HzxWtmbVLuU38HcDbwSWB8RMxLG5XZ4NR6QzyznETEG5K+RHF/8V1dECxH\\nbh+Ztdf7gaeBRt2ZzEYOFwWzNpE0nuJ2nNsAny9v8WiWFRcFszYot14+neLmLE8AJwPfTRuV2eC5\\nKJi1x6eAmRFxXfn4NGCj8mb3Ztnw6iMzM+vmkYKZmXVzUTAzs24uCmZm1s1FwczMurkomJlZNxcF\\nMzPr5qJgZmbdXBTMzKzb/wcK7AmeBMy4QAAAAABJRU5ErkJggg==\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"x = np.linspace(-3.0, 3.0)\\n\",\n \"plt.plot(x, hat(x,a,b))\\n\",\n \"plt.plot(-1.5811388304396232, hat(-1.5811388304396232,a,b), 'ro')\\n\",\n \"plt.plot(1.58113882, hat(1.58113882,a,b), 'ro')\\n\",\n \"plt.xlabel('X')\\n\",\n \"plt.ylabel('V(x)')\\n\",\n \"plt.title('Hat Potential')\\n\",\n \"plt.grid(True)\\n\",\n \"plt.box(False);\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 7,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"bd49ce2f030e3366ee640213f26fdaa6\",\n \"grade\": true,\n \"grade_id\": \"optimizationex01b\",\n \"points\": 2\n }\n },\n \"outputs\": [],\n \"source\": [\n \"assert True # leave this to grade the plot\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"Write code that finds the two local minima of this function for $b=1.0$ and $a=5.0$.\\n\",\n \"\\n\",\n \"* Use `scipy.optimize.minimize` to find the minima. You will have to think carefully about how to get this function to find both minima.\\n\",\n \"* Print the x values of the minima.\\n\",\n \"* Plot the function as a blue line.\\n\",\n \"* On the same axes, show the minima as red circles.\\n\",\n \"* Customize your visualization to make it beatiful and effective.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 8,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"6cff4e8e53b15273846c3aecaea84a3d\",\n \"solution\": true\n },\n \"scrolled\": true\n },\n \"outputs\": [\n {\n \"data\": {\n \"text/plain\": [\n \" nfev: 35\\n\",\n \" status: 0\\n\",\n \" fun: array(-6.249999999999999)\\n\",\n \" nit: 2\\n\",\n \" x: array(-1.5811388304396232)\\n\",\n \" success: True\\n\",\n \" direc: array([[ 0.00105468]])\\n\",\n \" message: 'Optimization terminated successfully.'\"\n ]\n },\n \"execution_count\": 8,\n \"metadata\": {},\n \"output_type\": \"execute_result\"\n }\n ],\n \"source\": [\n \"opt.minimize(hat, -3, args=(a,b), method = \\\"Powell\\\")\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 66,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"text/plain\": [\n \" status: 0\\n\",\n \" jac: array([ -5.96046448e-08])\\n\",\n \" nfev: 36\\n\",\n \" x: array([ 1.58113882])\\n\",\n \" hess_inv: array([[ 0.05000928]])\\n\",\n \" success: True\\n\",\n \" fun: -6.249999999999999\\n\",\n \" njev: 12\\n\",\n \" message: 'Optimization terminated successfully.'\"\n ]\n },\n \"execution_count\": 66,\n \"metadata\": {},\n \"output_type\": \"execute_result\"\n }\n ],\n \"source\": [\n \"opt.minimize(hat, -3, args=(a,b))\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"235361d4c954cf9fd6a8ecef309b3a44\",\n \"grade\": true,\n \"grade_id\": \"optimizationex01c\",\n \"points\": 4\n }\n },\n \"outputs\": [],\n \"source\": [\n \"assert True # leave this for grading the plot\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"nbgrader\": {}\n },\n \"source\": [\n \"To check your numerical results, find the locations of the minima analytically. Show and describe the steps in your derivation using LaTeX equations. Evaluate the location of the minima using the above parameters.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": false,\n \"nbgrader\": {\n \"checksum\": \"d7d37614ffa0d469a42ff3fd121335f2\",\n \"grade\": true,\n \"grade_id\": \"optimizationex01d\",\n \"points\": 2,\n \"solution\": true\n }\n },\n \"source\": [\n \"$$ V(x) = -a x^2 + b x^4 $$\\n\",\n \"$$ V'(x) = -2a x + 4b x^3 $$\\n\",\n \"$$ 0 = -2(5.0) x + 4(1.0) x^3 $$\\n\",\n \"$$ 0 = -10 x + 4 x^3 $$\\n\",\n \"$$ 10x = 4 x^3 $$\\n\",\n \"$$ \\\\frac{5}{2} = x^2 $$\\n\",\n \"$$ \\\\sqrt{\\\\frac{5}{2}} = x $$\\n\",\n \"$$ x = +- 1.5811388301 $$\\n\",\n \"I simply set the derivative of the function equal to zero, plugged in the values of a and b, and solved for x.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": []\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.4.0\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 0\n}\n"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":399,"cells":{"repo_name":{"kind":"string","value":"jgarciab/Stats_Python"},"path":{"kind":"string","value":"Statistics 2014-09-29.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"482112"},"content":{"kind":"string","value":"{\n \"metadata\": {\n \"name\": \"\"\n },\n \"nbformat\": 3,\n \"nbformat_minor\": 0,\n \"worksheets\": [\n {\n \"cells\": [\n {\n \"cell_type\": \"code\",\n \"collapsed\": true,\n \"input\": [\n \"__author__ = 'Javier Garcia-Bernardo 2014'\\n\",\n \"\\n\",\n \"# Math\\n\",\n \"import numpy as np\\n\",\n \"\\n\",\n \"# Stats\\n\",\n \"import scipy\\n\",\n \"\\n\",\n \"# Plot\\n\",\n \"import pylab as plt\\n\",\n \"import matplotlib\\n\",\n \"\\n\",\n \"# Multiple comparisons\\n\",\n \"from statsmodels.stats.multicomp import pairwise_tukeyhsd\\n\",\n \"\\n\",\n \"# Kernel Estimation\\n\",\n \"from sklearn.grid_search import GridSearchCV\\n\",\n \"from sklearn.neighbors import KernelDensity\\n\",\n \"\\n\",\n \"# Bootstrap\\n\",\n \"import scikits.bootstrap as bootstrap\\n\",\n \"\\n\",\n \"%matplotlib inline\\n\",\n \"\\n\",\n \"def customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8):\\n\",\n \" '''\\n\",\n \" From stackoverflow. User gcalmettes \\n\",\n \" '''\\n\",\n \" for c_spine, spine in zip([c_left, c_bottom, c_right, c_top],\\n\",\n \" ['left', 'bottom', 'right', 'top']):\\n\",\n \" if c_spine != 'none':\\n\",\n \" ax.spines[spine].set_color(c_spine)\\n\",\n \" ax.spines[spine].set_linewidth(lw)\\n\",\n \" else:\\n\",\n \" ax.spines[spine].set_color('none')\\n\",\n \" if (c_bottom == 'none') & (c_top == 'none'): # no bottom and no top\\n\",\n \" ax.xaxis.set_ticks_position('none')\\n\",\n \" elif (c_bottom != 'none') & (c_top != 'none'): # bottom and top\\n\",\n \" ax.tick_params(axis='x', direction='out', width=lw, length=7,\\n\",\n \" color=c_bottom, labelsize=size, pad=pad)\\n\",\n \" elif (c_bottom != 'none') & (c_top == 'none'): # bottom but not top\\n\",\n \" ax.xaxis.set_ticks_position('bottom')\\n\",\n \" ax.tick_params(axis='x', direction='out', width=lw, length=7,\\n\",\n \" color=c_bottom, labelsize=size, pad=pad)\\n\",\n \" elif (c_bottom == 'none') & (c_top != 'none'): # no bottom but top\\n\",\n \" ax.xaxis.set_ticks_position('top')\\n\",\n \" ax.tick_params(axis='x', direction='out', width=lw, length=7,\\n\",\n \" color=c_top, labelsize=size, pad=pad)\\n\",\n \" if (c_left == 'none') & (c_right == 'none'): # no left and no right\\n\",\n \" ax.yaxis.set_ticks_position('none')\\n\",\n \" elif (c_left != 'none') & (c_right != 'none'): # left and right\\n\",\n \" ax.tick_params(axis='y', direction='out', width=lw, length=7,\\n\",\n \" color=c_left, labelsize=size, pad=pad)\\n\",\n \" elif (c_left != 'none') & (c_right == 'none'): # left but not right\\n\",\n \" ax.yaxis.set_ticks_position('left')\\n\",\n \" ax.tick_params(axis='y', direction='out', width=lw, length=7,\\n\",\n \" color=c_left, labelsize=size, pad=pad)\\n\",\n \" elif (c_left == 'none') & (c_right != 'none'): # no left but right\\n\",\n \" ax.yaxis.set_ticks_position('right')\\n\",\n \" ax.tick_params(axis='y', direction='out', width=lw, length=7,\\n\",\n \" color=c_right, labelsize=size, pad=pad)\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 2\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Interaction between parameters (Observed vs Expected). \"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Chi Square\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"About 25 percent of the U.S. scientific workforce consists of foreign-born scientists, in both industry and academia.\\n\",\n \"\\n\",\n \"We have 3 Americans and 4 Internationals. So the obvious question is: Does Mary hate Americans?\\n\",\n \"\\n\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"%%latex\\n\",\n \"$$ \\\\frac{\\\\sum{(Obs - Exp)^2}}{Exp}$$\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"latex\": [\n \"$$ \\\\frac{\\\\sum{(Obs - Exp)^2}}{Exp}$$\"\n ],\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 4\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"p-val = \\\", scipy.stats.chisquare(f_obs = [3.,4.], f_exp = [7.*0.75,7.*0.25])[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('p-val = ', 0.049534613435626491)\\n\"\n ]\n }\n ],\n \"prompt_number\": 40\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"YES! But wait... This test is invalid when the observed or expected frequencies in each category are too small. A typical rule is that all of the observed and expected frequencies should be at least 5.\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Fisher's exact test\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"p-val Exact test =\\\", scipy.stats.fisher_exact([[3, 75000], [4, 25000]])[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('p-val Exact test =', 0.070570483471531401)\\n\"\n ]\n }\n ],\n \"prompt_number\": 41\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Math says Mary doesn't hate Americans... until Jess leaves:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"p-val Exact test =\\\", scipy.stats.fisher_exact([[2, 75000], [4, 25000]])[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('p-val Exact test =', 0.03760622581012793)\\n\"\n ]\n }\n ],\n \"prompt_number\": 42\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Compare 2 independent samples\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Imagine we want to compare if there are difference in GFP expression between two populations of cells.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"def median_test(samples1, samples2):\\n\",\n \" \\\"\\\"\\\"Adapted from https://gist.github.com/wanderview/8285920\\\"\\\"\\\"\\n\",\n \" median = np.median(samples1 + samples2)\\n\",\n \" samples1 = np.asarray(samples1)\\n\",\n \" samples2 = np.asarray(samples2)\\n\",\n \" below1, above1 = np.sum(samples1<=median),np.sum(samples1>median)\\n\",\n \" below2, above2 = np.sum(samples2<=median),np.sum(samples2>median)\\n\",\n \" \\n\",\n \" below_exp = (below1 + below2) / 2\\n\",\n \" above_exp = (above1 + above2) / 2\\n\",\n \"\\n\",\n \" result = scipy.stats.chisquare(\\n\",\n \" [below1, above1, below2, above2],\\n\",\n \" f_exp=[below_exp, above_exp, below_exp, above_exp]\\n\",\n \" )\\n\",\n \"\\n\",\n \" return result[1]\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 43\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" x = [np.random.randn() for _ in range(200)]\\n\",\n \" y = [np.random.randn()+0.6 for _ in range(200)]\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\\n\",\n \" \"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3V1zG9edJvCnIZGy3ogGKMu2YidEg5PMzqYqIgDmIqmt\\nbAmAp2q3pnbKFCHXXpts+l4SoE8ggf4AFkF9AQqAM1PJxURsyNlN1eyOSYLeSSpxxeEBJ44sWQrB\\nBsd6M0mcvdAAEQiQQlMNdoN8flWsMk/3Qf9NEHzUfU6fVqSUEkRERDbyOF0AERHtPwwXIiKyHcOF\\niIhsx3AhIiLbMVyIiMh2DBciIrLdYacLAADDMGAYBvr7+7G0tIRwOIyxsbGGfYrFIhYWFuD3+yGE\\nQCgUQjQadahiIiLaiePhYhgGFEXBtWvX6m2RSASmaeLSpUsAACEEUqkUbt26Vd8nkUhA0zQEAoE9\\nr5mIiHbm+GWxqampprZYLNbQnk6nMTEx0bCPrutIJpMdr4+IiKxzPFwURYFhGA1tUkr4fL7699ls\\nFqFQqGGfcDiMXC63JzUSEZE1ihuXfwkGg3j//fdx8eJFmKYJv98P0zTR19fXsJ/H44EQAgMDA84U\\nSkRELTl+5rJVJpNBJBLBxYsXAQDlchkAmoKlRgixZ7UREVF7HB/Qr8nn85idnYWiKJiZmam3m6bp\\nYFVERLQbrgmXkZERjIyMoFKpIBKJYHp6GkNDQ06XRUREu+C6y2Jerxe6rr/0PSyKomz7RUREneW6\\ncAGAaDQK0zRx+/ZtaJoGAFhbW2u5b227FQwYIqLOcjRchBDw+Xz49NNPW243TROqqkLTtKaBeyEE\\nVFXddqaYlLLlFxERdZ6j4WKaJoLBYNPZRy1Iave2xGIxzM3NNexTLBYRj8f3plAiIrLE0XAJhUK4\\ncOFC0xlFOp1GMpmsn5Wk02lks9mGfTKZDNLp9F6VSkREFrjiJsrp6WksLS3VF66MRCJ47733GvZZ\\nXFzEzMwMhoeHIYRAOBzGuXPnLB+rNt7igv9tIqJ9yxXhspcYLkREneea+1yI6Jn79+9jY2PDUh9F\\nUXD69GkcOnSoQ1URWcNwIXKRzc1N/EPhHyBPWDuz3vh6A4lYAq+++mqHKiOyhuFC5CJSSkhF4sx3\\nz1jq9+VnX3aoIqLdceVNlERE1N0YLkREZDuGCxER2Y7hQkREtmO4EBGR7RguRERkO4YLERHZjuFC\\nRES2Y7gQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4EBGR7Rgu\\nRERkO4YLERHZ7rDTBRDtNSnlrvopimJzJUT7lyvCJZ/PQwiBpaUlCCGg6zpGRkbq22ttqVQK4XAY\\n5XIZmUwG8Xgc0WjUwcqp21SrVczM/AKVStVSv95eib//+x/B7/d3qDKi/cXxcMnn89A0rR4mlUql\\nHiBjY2P1/QqFAgqFAgBAVVXcuHGDwUKWSSmxtgZ861v/3VK/L7/8F2xsbHSoKqL9x/ExFyEEhoaG\\n6t97vV4kk0noul5vUxQFhmHANE0IIVAul/HOO+84US4REbXB0XAxTRMzMzOoVCoN7bUzkuXl5Xqb\\nlBJ9fX0YGBjYwwqJiGg3HA0XVVUhhECpVHKyDCIispnjYy7lcrmpzTAM+Hy+hrMUIQRM06z38fv9\\nDYP+RETkHo6HSytTU1O4cuVK/fvaDJ3nwySRSDS1ERGROzg+oL9VJpPBqVOncPHixXqb1+ttmDkG\\nALquI5lMbvs6iqK0/CIios5z1ZmLEAKZTAbz8/Mv3DcQCEAIgbW1NfT19e1BdURE1C5XnbmkUinc\\nvn27qX1ycrKprXapTAjR8rWklC2/iIio81wTLhMTE5icnGw6CxFCIJVKNUxLBv4yEUDTtL0qkYiI\\n2uSKcJmenkYqlWqYHVYoFFAqlaBpGqampprubzEMA+FwmJfEiIhcyPExl1wuB+DZmUjtbKRcLiOX\\ny+H69esAnl0CK5VKCAQCAJ7dfJnJZHDjxg1niiYioh05Gi6madanFG8VDAbr/z0yMoJ8Po9cLoeV\\nlRWYpolcLse79YmIXMrRcFFVFdVqe6vT8n4WIqLu4YoxFyIi2l8YLkREZDuGCxER2Y7hQkREtmO4\\nEBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuG\\nCxER2Y7hQkREtmO4EBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGS7w04XAAD5fB5CCCwt\\nLUEIAV3XMTIy0rBPsVjEwsIC/H4/hBAIhUKIRqMOVUzdSkqJ335exL/df2ypn7laQvzrV3H69OkO\\nVbb3VlZW8Ku5X6GKqqV+/Sf78ZMf/6RDVdF+4Xi45PN5aJpWD5NKpYJwOIxyuYyxsTEAgBACqVQK\\nt27dqvdLJBLQNA2BQMCRuqk7VatVPHh0F0e+O2ip32r5Hh4/thZIbvfw4UPceXIHp9461XafzY1N\\nlP5Ywk/AcKGdOX5ZTAiBoaGh+vderxfJZBK6rtfb0uk0JiYmGvrpuo5kMrlnddJ+ouDI0WOWvjye\\nQ04X3RGHew7j2IljbX8dPX7U6ZKpSzgaLqZpYmZmBpVKpaG9drlreXkZAJDNZhEKhRr2CYfDyOVy\\ne1InERFZ42i4qKoKIQRKpdK2+5imCdM04ff7m/oCfwkgIiJyD8cvi5XLZZw9e7ahzTAM+Hw+DAwM\\noFwuAwD6+vpa9hdCdLxGIiKyxvFwaWVqagpXrlwB8OzMhYiIuovjs8W2ymQyOHXqFC5evPhSr6Mo\\nik0VkVV3797FxsaG5X5vvPEGDh923a8kEe2Cqz7JQghkMhnMz887XQrtUrVaxc9+tgAp37LUb339\\nAUZHe/Haa691qDIi2kuuCpdUKoXbt283tGmaBgBYW1trOe5S276VlLJlO89oOq9a9eBb3/qBpT5f\\nfvlJh6ohIie4ZsxlYmICk5OTTQGiqio0TWsauBdCQFVVDAwM7GGVRETUDleEy/T0NFKpVENQFAqF\\n+hTlWCyGubm5hj7FYhHxeHwvyyQiojY5Hi61GyHL5TKKxSKKxSIMw0A2m60v7ZJOp5HNZhv6ZTIZ\\npNPpPa+XiIhezNExF9M0kUgkWm4LBoP1//Z6vUin00ilUhgeHq6vNcZLYkRE7uRouKiqimq1vRVZ\\nh4aGGtYgIyIi93LVbDGi/eT+/fv4p1/9Ezarm233kVLi8eb+Wn2ZDiaGC1GHPH36FI96H+F17XVL\\n/fo9/R2qiGjvMFyIOkjxKDh0eH8u10+0E8dnixER0f7DcCEiItsxXIiIyHYMFyIish0H9KlrPX78\\nGF988YWlPuvr67s+3r1799DT09P2/lsf3010kDBcqGutrKzg5z+/i2PH3mi7T7XqwSFP+/vX9Ppe\\nwcLqAj5f/9xSv75TrZ+gSrTfMVyoqx0/7sWZM99te//NzU2c/ML6fSTHTp7AG99+DapXtdyX6CDi\\nmAsREdmO4UJERLZjuBARke0sjbkMDg5afkywlBKKouDzz60NhBIRUfeyFC5DQ0MolUooFov1tkAg\\ngHK5XJ92qapq/SFfNXxuPe0Hm5ub2NjcsNTnkOcQf//pQLIULleuXEEkEkEoFML09HTD81WKxSLG\\nxsawvLyMXC7XFDBE3UyiF3OfLFvqU5US3/veqwhq3+lMUUQuZilcrl27BlVVUSgU4PV6G7aFQiEs\\nLCzA5/MhlUphZmbG1kKJnNTvDwCw9g+mytoDbGx83ZmCiFzO0oC+YRiIx+NNwfK8WCwGwzBeujAi\\nIupelsJFSgkhxI77lEqllyqIiIi6n6VwicViWFhYwEcffdRyez6fR7FYRDgctqU4IiLqTpbGXNLp\\nNAzDwOjoKM6fP494PA5N07C0tITZ2Vnkcrn6fkREdHBZChdN01AoFJBMJpHNZpHNZpu2T01NNcwi\\nIyKig8fywpWhUAizs7MQQqBYLEIIAU3ToGkaQqHQrgvJ5XLw+XyIRqMN7UII6LqOVCqFcDiMcrmM\\nTCaDeDzetC8dLA8fPkTpj7/G2qMnFnpJVOVmx2p6WVJKiNIfsb5urcaV5QconijC27f9ZJutHj16\\nhKqsWi2RqC27XhX51KlTiEQiL5w91g7DMDA+Pl6/rLZVoVBAoVAA8OwmzRs3bjBYCGtrayg9/Fc8\\netXaM1qOvXWyQxW9vGq1it///gEOH7Z2b8zav6/gs8ef4eQha/9v/WesrxBN1A7L4bK4uIixsTEU\\ni0UoioLZ2VmcO3cOg4ODmJiYwMWLF9t+rVKphHQ6jXA4DL/f33IfRVFgGAYikQjK5TIGBgaslkz7\\n2OHeI/D2v+p0GbZSoMDbZ+3/aXOjjP7X+i2duRB1kqXZYqVSCeFwGMViEdFoFFLK+raVlRVcvnwZ\\nw8PDbb9eIBDA9evXMTY2tuN+Ukr09fUxWIiIuoSlcKnNAltYWGgazF9dXcW1a9ewsLCAK1eu2Fch\\nERF1HUuXxW7evIlYLIahoSGYptm0/fLly5iZmUEul8PVq1dtK1IIUT9euVyG3+/HyMiIba9PRET2\\nshQupmkiGAzuuI+macjn8y9V1PNqYzHPh0kikWhqIyIi97C85P78/PyO+ywuLr7UlOStvF5v05iM\\nruvQdX3HcOEy53TQPH36FI8ePeroMTbWN/DN+jcdPQbtD5bC5cKFC0ilUvj4449bBkgikYAQApcv\\nX7atwFYCgQCEEFhbW0NfX19Hj0XUDTye4ygu3Adwv6PH2dzcgHK3AvzPjh6G9gFL4VIbU4lGo4jH\\n4wCeDfJPTU3BMAysrq5C0zRcu3bNtgInJyebwqp2qUwIgbNnz7bs9/xMtufxjIb2I1V9E8CbHT/O\\nN988wcq//d+OH4e6n6XZYsCzmWLXrl3DJ598AgCYnZ1FNptFtVrF5cuX8Yc//MG24oQQSKVSWF5e\\nbmgvl8sAno3vEBGR++zqDv3Lly/XzyaEEPD7/VBV1dbCgL+sVbb1/hbDMBAOh3lJjIjIpSyduUxP\\nTzctt69pmm3B0upSlt/vb3hGjGmayGQymJ6etuWYRERkP0tnLrquw+fz4Z133rHl4JVKBVevXoUQ\\nor5AZSwWQzwer88EGxkZQT6fRy6Xw8rKCkzTRC6X4936REQuZilc3nvvPdy4cQOffvrptgPpVni9\\n3rYG/3k/CxFRd7EULplMBoODgwiHw5iamkIkEoGmaRz7IGpBgYKvvjLx8OFnbfeRUmJ9o4NFEe0R\\nS+FSmwIspcT4+Hi9/fnpvVJKKIqCzU33PjODaC+cOOHDk6e9WFuz1k/17vpJGESuYem3uN1nqPBe\\nEiLA4zmEY0d5Vk8H047hkkql8MMf/rA+gL91JWQiIqJWdpyKPDk5iZmZmab26elpvP/++x0rioiI\\nupvlO/QB4NatW8hkMnbXQkRE+8SuwgXYfu0uIiKiXU9L4aD9/rexsYGVlRVLfarV6q6P1+oBdDtZ\\nszoNi4j2DOc80ra++uor/PSnv0VPj9diT+ur8/b2nsYvf3kfQKXtPqurj9DTc8LysYio8xgutC0p\\nJXp6TuHMmaGOH+vUqQEAA5b69Pb+CV9Uv+xEOUT0knY95kJERLSdF565GIaBCxcuNLQVCgVIKZva\\nn9dqCjMRER0MLwyX1dXVbW+e3OmmSoYLEdHBtWO4zM/P71UdRES0j+wYLqFQaK/qICKifYSzxYio\\nbYpHwaPNh7j5s5uW+vUc6kHsv8Rw8uTJDlVGbsNwIaK2eTyH4P+rU1DetHYT9T1xD0+ePGG4HCAM\\nFyKy5HDPYbxy7BVLfTyHeNfDQcN3nIiIbMdwISIi2zFciIjIdgwXIiKynWsG9HO5HHw+H6LRaNO2\\nYrGIhYUF+P1+CCEQCoVa7kfd6+uvV/HwYfsrItf6EJE7uSJcDMPA+Pg4crlc0zYhBFKpFG7dulVv\\nSyQS0DQNgUBgL8ukDhJffIrlJ79GT+8RS/2Oeo93qCIiehmOhkupVEI6nUY4HIbf72+5TzqdxsTE\\nREObrutIJpO4edPajVzkXhISJ/wqTnh9TpdCRDZwdMwlEAjg+vXrGBsb23afbDbbtAxNOBxueZZD\\nRETu4OoBfdM0YZpm01mNqqoAgOXlZQeqIiKiF3F1uJTLZQBAX19fy+1CiL0sh4iI2uTqcDFN0+kS\\niIhoF1wdLkRE1J1cMRW5ExTF2qqt+93c3P/D4uKfLPaSAAY6UA0dNJvKJn46+1PA4sfyRz/4Eb7/\\nN9/vTFHUUa4OF03TAABra2stx11q2+nFvv76Gxw5EoLP97qlfgxpssNbf/0WpJSW+ty/cx+Pnzzu\\nUEXUaa6+LKaqKjRNaxq4F0JAVVUMDAxs21dK2fLrIFMUxfIXkV2s/u55PK7+80Qv4Pp3LxaLYW5u\\nrqGtWCwiHo87VBEREb2Iq8Kl1ZlFOp1GNpttaMtkMkin03tVFhERWeTomEulUsHVq1chhIAQArqu\\nIxaLIR6PY2RkBADg9XqRTqeRSqUwPDxcX2tsp0tiRETkLEfDxev14tq1ay/cb2hoCENDQ3tQERER\\n2cFVl8WIiGh/YLgQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4\\nEBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGQ7R5/nQkQHw71797FSXrPUx3ywite/83qH\\nKqJOY7gQUcd9ebeMe/dO4Ejv0bb73L9Twf1jZgerok5iuBDRnjh69CSOH/O2vX/llQcdrIY6jWMu\\nRERkO4YLERHZjuFCRES2Y7gQEZHtumJAXwgBXdeRSqUQDodRLpeRyWQQj8cRjUadLo+IOmT9m3Ws\\nrq5a6tPT04MTJ05Y6vPkyRM8fvzYUh8AOH78OHp7ey33Owi6IlwAoFAooFAoAABUVcWNGzcYLET7\\nWM+RI1gyP8fNj2+230kC3sNevPs/3rV0rH+e+2d8du8zHDp0qO0+69+s48f/6ccY+sGQpWMdFF0R\\nLoqiwDAMRCIRlMtlDAwMOF0SEXXYK8dP4PR3gDN/dabtPhvrG1j7zNrNmgCwvrkO71te9Pn62u5z\\n/859VKtVy8c6KLoiXABASom+vj709bX/5hMRkTM4oE9ERLbrmjMXIQRM89lSEOVyGX6/HyMjIw5X\\nRURErXRFuPj9fgBoCJNEItHURkRE7tAVl8W8Xi/GxsYa2nRdRzKZdKgiIiLaSVecubQSCAQghMDa\\n2lrLQX5FURyoimh/U6Dg0eMqPvnkt5b6ra09xuEefiYPkq4Il8nJSVy+fLmhrXapTAiBs2fPOlEW\\n0YHj8RyC6v0+Hj/ZtNSvpxd45ZXjHaqK3Mj14SKEQCqVQiKRaLi/pVwuAwA0TWvZT0rZsp1nNEQv\\n58iR9p/JQgeX68dcNE3D1NRU042ThmEgHA7zvhciIhdyfbgAzy6BlUql+vemaSKTyWB6etrBqoiI\\naDuuvywGPJtunM/nkcvlsLKyAtM0kcvluAwMEZFLdUW4ALyfhYiom3RNuOylBw8eYH193XK/1157\\nzdKqqkRE+xXDZQspJf7xH/8Fm5tvWOq3vl7G+fMevP766x2qjIioezBcWlhfB958M2ypz5dfzneo\\nGiKi7tMVs8WIiKi7MFyIiMh2DBciIrIdw4WIiGzHcCEiIttxtliXkVLi5z//JSqVDUv9fvf7z1B+\\nNIejR62txRZ8Ywjffus/W+pDdBAoHgWf/v5T/G75d5b6ve57HbH/GutQVe7BcOkyUkrcufMIp09b\\n++XsPVpFj/8OjvQda7vPv5srePS0YrVEogPh1TdexXq/tZut179Zx53lOx2qyF0YLl2qp+eIpf0P\\nH+7FoUOHcbinp+0+hw4dBqpWKyM6OHp62/881TzBkw5U4j4ccyEiItsxXIiIyHYMFyIish3DhYiI\\nbMcBfdrR48df4+7dpY4f5+nTh0D7E9nogHj46BHu3rvb9v6bG5uo3Kvg9u3blo5TWi7h6PeOWi2P\\ndsBwoW0dPX4S954I3FsVHT+W7AXUY6c7fhzqHkePnsTdu09w927793RJKbH24Cn+9c7/snSszWoF\\n/+2vh6yWSDtguNC2eo4cQf+ZbzldBh1QvT2voN//luV+p/q/bblPefUzHO7hn0M7ccyFiIhsx3Ah\\nIiLbMVyIiMh2DBciIrIdR7C6kJQSUkrLfYioe+3lZ1hRlJd+ja4Jl2KxiIWFBfj9fgghEAqFEI1G\\nnS5rz0kpMf+b/41f//FPlvptVtdxcqC/Q1URUSf96v/8Cr8p/QYKXv6P/k4kJN7sfxN/97d/99Kv\\n1RXhIoRAKpXCrVu36m2JRAKapiEQCDhY2d6TUuLx5kOc+RtOESY6KL5+/DX6tD70+aw9j8mq9W/W\\nYX5u2vJaXTHmkk6nMTEx0dCm6zqSyaRDFRER0U66Ilyy2SxCoVBDWzgcRi6Xc6giIiLaievDxTRN\\nmKYJv9/f0K6qKgBgeXnZgaqIiGgnrg+XcrkMAOjra32tUYjOr3tFRETWuD5cTNOewSUiIto7inT5\\nDRDFYhGRSATVavPD3D0eDwzDwLlz55q22TFPm4iI/sJKXLj+zIWIiNzByj/aXX+fi6ZpAIC1tbWW\\n4y617Vttl7C1H47LT9i2xfqd0821A6zfaful/na5/sxFVVVomtY0cC+EgKqqGBgYcKYwIiLaluvD\\nBQBisRjm5uYa2orFIuLxuEMVERHRTlw/oA8AlUoFo6OjDcu/vP3228hkMpbPXPbLqSnr33vdXDvA\\n+p120OrvinABgMXFRczMzGB4eBhCCITD4ZazxF7koL3BbtPN9Xdz7QDrd9pBq79rwsUuB+0Ndptu\\nrr+bawdYv9MOWv0HLlyIiKjzumJAn4iIugvDhYiIbMdwISIi2zFciIjIdgwXIiKynevXFiNyg2Kx\\niIWFBfj9fgghEAqFEI1GnS7LklwuB5/P13V15/N5CCGwtLQEIQR0XcfIyIjTZbXNMAwYhoH+/n4s\\nLS0hHA5jbGzM6bJ2xTRNpFIpXL9+/YX7MlzQ3W9+t3/watz8h08IgVQq1bBCRCKRgKZpCAQCDlbW\\nPsMwMD4+3nWPBs/n89A0rf47XalUEA6HUS6Xu+IzahgGFEXBtWvX6m2RSASmaeLSpUsOVrY7yWQS\\nq6ur7e0sD7jZ2VlpGEZDWzgclpOTkw5V1L5cLieLxWL9e9M0ZTAYlJlMxsGqrJudnZU+n08WCgWn\\nS2lpfHxc5vP5hjbDMOTo6KhDFbVPCCF1XZeZTEYGg0HX/oy30+pzmMlkpKIoDlRj3fnz55v+viST\\nSRkMBh2qaPeWlpbk6OioTCQSbe1/4MdcpqammtpisVjLdrcRQmBoaKj+vdfrRTKZhK7rDlbVvlKp\\nhImJCZRKJfj9fqfL2VY2m0UoFGpoC4fDXXEWEAgEcP369a74V/5WpmliZmYGlUqlob12dru8vOxA\\nVdYoigLDMBrapJTw+XwOVbR7hUIB8Xi87Tv0D3y4dOubvx8+eN3wh880TZim2RR+qqoC6I6fc7dS\\nVRVCCJRKJadL2bWbN2/i6tWrDW25XA4XLlxwqKLdKRQKiMVilvoc+DGXmzdvNrXlcjm8//77DlTT\\nvuc/eGfPnnW6nH2rXC4DQMsH1QHPzh75TKHOqf38n2cYBnw+X1f+3DOZDCKRCC5evOh0KZYIIRCN\\nRi2ti3bgw2Wrbnrz99sHz41M03S6BNpiamoKV65ccboMS/L5PGZnZ6EoCmZmZpwux5J8Pr+rqwsM\\nl//QzW/+87rxg0fUrkwmg1OnTnXFP/6eNzIygpGREVQqFUQiEUxPTzeMl7rVy/zjiuHyH7r1zX9e\\nt37wiNohhEAmk8H8/LzTpeya1+uFruuIRqMtrzy4TTabbThrqS273459Ey5CiLb37e/vh9frbbnN\\niTffjtqd/ODZ9bN3I03TAABra2stx11q26nzUqkUbt++7XQZLy0ajcI0TRQKBVfe11WzuLiISCTS\\n0HbgxlxKpRJSqVTb+w8PD+94A9Nevvl21e7UB8/un73bqKoKTdMghGiYOCGEgKqqHNvaIxMTE5ic\\nnNx2YoUb1Z6Y+/HHH7ecdLN1pqfbzM/PY2lpqWGYoFgs1m8qHh4e3vGG7X0RLoFAoOWsrxdxw5u/\\n29qf5+QHz4763S4Wi2Fubq7hd6RYLCIejztY1cExPT2NVCrVEOSFQsH1KySYpolgMNh0dls70996\\n75TbtBrE/+CDDzA/P9+w4sB2DvR9Lt3+5gPbf/C6+d4At0mn08hmsw1tmUwG6XTaoYp2z8plDTeo\\n3ahaLpdRLBZRLBZhGAay2ayrgwV49vfjwoULTT/zdDqNZDLZlWe9f/7zn/mY43Z98MEHGB8fbxgH\\niMfjiEQiTTc/uU0ul8Pq6irC4XC9rVwuI5fLtbWwnJsMDg5iamrKtdegFxcXMTMzg+Hh4foZ77lz\\n55wu64UqlQquXr0KIQRyuRw0TUMsFkM8Hnf9GnStbl6tCQaD+Pzzz/e4ot2Znp7G0tJSfe3CSCSC\\n9957z+myLCmVSkin07h58yYqlQrGxsag6/qOk54OfLgA3fnm74cPXjf/4SOinTFciIjIdgd6zIWI\\niDqD4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4EBGR7RguRBYUi0V4PJ6m1WK3MgwDHo8H\\niUTC0uuPjo7C4+HHkroff4uJLAiFQlBVFYuLizsubFpbi+zdd9+1fAwrz8wgciuGC5FF4+PjkFLu\\nuBr0zZs3oSgK3nnnnT2sjMg9GC5EFl24cAHAs0dKt1IsFlGpVHD+/Pm9LIvIVRguRBYNDQ1B07Rt\\nL43VHq5UCyHg2WMcRkdHEQwG4fF44Pf7kUgkWj4a4fnl/uLxeMsxGNM04fF4MDEx0bRtcnIS4XC4\\nfpyJiQk+goH2HMOFaBd0Xd/20lgmk2m4JCaEwODgID766CMMDg5C13VEIhHkcjmEw+EXPpRupzGY\\nrdvC4TBSqRQ8Hk/9OJlMBsFgEIuLi7v4PyXaHYYL0S7ULnltvTTW6pJYOp2GoiiYnZ3FL37xC3z4\\n4Ye4deuB1ym+AAACm0lEQVQW0uk0TNOEYRi21DQ5OYnFxUUUCgXMzc3Vj7OwsACg9ZMFiTqF4UK0\\nC4FAAENDQ02XxlpdEpuYmEA2m216uFjtQUurq6u21HT16lXE43GEQiGYpln/CgQCiEajKBaLWFtb\\ns+VYRC9y2OkCiLrVu+++i8XFRWQyGVy6dAnAs6eDbp0lNjQ0VA8S0zQxPz+PYrG47YSA3apUKpid\\nnYXP52u5XVEUlMtl9PX12XpcolYYLkS7ND4+jmQyiZmZGVy6dAlCCJRKJYyOjjbsZ5omkslk/RGx\\nwLOxkXA4bNtAuxACwLMJAMlkctv9tgseIrsxXIh2yev1IhQK1S+N5XI5AM8G+58XjUaxuLgIXdeh\\n6zrOnj0LACgUCvU+VpXL5Ybva4+8VlW16fIbkRM45kL0EmqzxjKZDGZmZqAoSsMfd9M0sbi4iNHR\\nUXz44Yf1YAEapxxbVSwWG75XVRVer3fbyQE+nw+Dg4O7Ph6RVQwXopdQWztsamoKi4uL2944uXXQ\\nvnapDGgOmeenF6uqCiklCoVCy77P03Udq6urTeuZTU5OolKptLwnhqhjJBG9lHg8LhVFkYqiyEKh\\nsO320dFRmU6n5fj4uPT5fPLtt9+WiqLIYDAoDcOQUkp5/vx5qShKvW8ul6u/tq7rDX19Pp+cmJho\\nOFYwGKy/5vnz52UoFJKKoshIJNLZHwLRFgwXopdUCwCPx9Nyu2maUtd16fP56n/o8/m8lFJKXdel\\nx+Oph8To6GjT62QymXpo+P1+mUqlpJSyZbhIKWUymZThcFgqiiIHBwfr+xPtJUXKl7jwS0RE1ALH\\nXIiIyHYMFyIish3DhYiIbMdwISIi2zFciIjIdgwXIiKyHcOFiIhsx3AhIiLbMVyIiMh2/x/lFxwk\\ni6G8+gAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 44\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Check Variance\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"pval Equal-Variance = \\\",scipy.stats.levene(x,y)[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('pval Equal-Variance = ', 0.34631004235050145)\\n\"\n ]\n }\n ],\n \"prompt_number\": 45\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Equal variance. USE: Mann-Whitneyu test\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Use only when the number of observation in each sample is > 20 and you have 2 independent samples of ranks. Mann-Whitney U is significant if the u-obtained is LESS THAN or equal to the critical value of U.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"Mann-Whitney U test.\\\", scipy.stats.mannwhitneyu(x,y,use_continuity=True)[1]*2)\\n\",\n \"print(\\\"T-test. Only if normality\\\", scipy.stats.ttest_ind(x,y)[1])\\n\",\n \"print(\\\"Median test\\\", median_test(x,y))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Mann-Whitney U test.', 3.337747132801931e-09)\\n\",\n \"('T-test. Only if normality', 1.7455489694871835e-10)\\n\",\n \"('Median test', 1.5440498291101365e-05)\\n\"\n ]\n }\n ],\n \"prompt_number\": 46\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" x = [np.random.randn() for _ in range(200)]\\n\",\n \" y = [np.random.randn()*2+0.2 for _ in range(200)]\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3f9vG2d+J/D3yLEdy7Y4HNn54r1tTUq9ot1+sUgq2OsV\\nh0NI5rcD2siSFijaAkWkYX4+W2SAux/uJ4sKDrjfEg39D0giAxyaxV0sjhfFAkUvlkbutrft7loP\\nlWSTza4taqjEF8eWNfeDQMIjUtJQHnJmpPcLEBI9fEh+LJF8a55n5nkky7IsEBERuajH6wKIiOjo\\nYbgQEZHrGC5EROQ6hgsREbmO4UJERK5juBARket8Fy6maSKTydjahBBIp9PQdR2maUIIgVwuB13X\\nPaqSiIj284LXBeyWzWaxsbHR1K7reiNMZFnGzZs3kUwmu10eERE54KtwEUJgY2MDkiTZ2iVJQrlc\\nRiKRQLVaxeXLl70pkIiIHPHVsJiu60in02i1aIBlWejr62OwEBEFgG/CRdd1pFIpr8sgIiIX+GZY\\nTAiBZDLZ8qilfrtpmgCAarUKRVEwMjLSzRKJiMghX4RLqVTCxMTEnrcrigIAtjAZGxtraiMiIn/w\\nfFisfjSyn1Ao1BQ+qqoim812qiwiInoOnofLwsKC7ehj95lie4lEIhBCYHNzs+XtkiTt+UVERJ3l\\nabisrKwgkUjY2lrNuczMzDS11YfKhBBtPy8DhoiosyQvNwsrFApYXV21tRmGASEErl69iuHhYQwN\\nDWFwcBBCCNtpyEIIDA4OwjRN9PX1OX7OerBwjzQios7xdEK/1ST+u+++i6WlJUxPTzfaZmdnm65v\\nKZfLiMfjbQULERF1h+dzLrs9ePCg6ahCURRUKpXG96ZpQtM0FAqFbpdHREQOeDos9qxKpYJ8Po/5\\n+XnUajVMTExAVVUMDQ0B2DldWQiB9fV1mKaJXC53qKv1OSxGR929exX85CefOu5/5kwPUqnv4+TJ\\nkx2sio4b34RLtzBc6Kj7+ON/xPLyi1CUVx31r1b/D/76r/89ent7O1wZHSe+uIiSiNx1+vQZ9PY6\\nm4/c2PDd6DgdAXxVERGR6xguRETkOoYLERG5juFCRESuY7gQEZHrGC5EROQ6hgsREbmO4UJERK5j\\nuBARket8d4V+fd2w999/39ZuGAaWl5ehKAqEEIjFYkgmkx5VSURE+/FduGSzWWxsbNjahBDI5XK4\\ndetWo21sbAzRaBSRSKTbJRIR0QF8NSwmhMDGxkbTTpH5fB6ZTMbWpqoqstlsN8sjIiKHfBUuuq4j\\nnU43rVi8sLCAWCxma4vH4ygWi90sj4iIHPJNuOi6jlQq1dRumiZM04SiKLZ2WZYBAGtra90oj4iI\\n2uCbcBFCIBKJNB21VKtVANhzO2MhRMdrIyKi9vgiXEqlEiYmJlreZppml6shIqLn5Xm4MDyIiI4e\\nz09FXlhYsB217D5T7LDcehwir92/fx8ffvgxnjxx1v/pUwu9vS91tiiiA3gaLisrK0gkEra23XMu\\n0WgUALC5udly3qV+O9FR9fjxYzx+/CpefXXI8X34xxV5zdNwWVpawurqKubm5hpthmE0LpocHh7G\\nyMgIotEohBC4cuVKo58QArIs4/Llyy0fe3dI1fFNR0HF1y4Fiafh0moS/91338XS0hKmp6cbbalU\\nCnfu3LGFi2EYSKfTXamTiIja4/mE/m4PHjxoOurI5/NYWFiwtWmahnw+383SiIjIIc8n9OsqlQry\\n+Tzm5+dRq9WQyWSgqiqGhoYQCoWQz+cbQ2X1YbO9hsSIiMhbkrXX5MQRVR+3Pmb/bAqwzz//HB9+\\n+GtcuhQ7uPOhHl/HX/3Vv0Nvb29HHp+OJ98NixERUfAxXIiIyHUMFyIich3DhYiIXMdwISIi1zFc\\niIjIdQwXIiJyHcOFiIhcx3AhIiLXMVyIiMh1vlhbrFwuo1wuo7+/H6urq4jH47YVk4UQUFUVuVwO\\n8Xgc1WoVmqYhnU4jmUx6WDkREbXiebiUy2VIkmRbYj+RSMA0TVy/fr3Rpus6dF0HAMiyjJs3bzJY\\niIh8yvNhsdnZ2aa2VCpla5ckCeVyGaZpQgiBarWKN998s5tlEhFRGzwPl3pwPMuyLITD4aa2vr4+\\nLrNPRBQAng+Lzc/PN7UVi0W8/fbbHlRDRERu8DxcdtM0DYlEAteuXbO1CyFgmiYAoFqtQlEUjIyM\\neFEiEREdwDfhUiqVsLi4CEmSMDc3Z7tNURQAsIXJ2NhYUxsREfmD73airNVqSCaTKBQKGBoa2rOf\\nrutQVRX37t1reXt9x8m9+OyfTbQn7kRJQeT5hP5uoVAIqqoeeJpxJBKBEAKbm5tdqoyIiJzyXbgA\\nQDKZhGmauH37NgBgZmamqU99qEwI0fIxLMtq+UVERJ3nabgIIRAOh3H37t2Wt9eva8nlclhbW7Pd\\nVq1WAQDRaLTTZRIRUZs8ndA3TRMDAwNNAVE/GonFYrh8+TJmZ2ebrm8pl8uIx+Po6+vrVrlEROSQ\\np0cusVgM4+PjTcNV+Xwe2Wy2ESiKoqBSqTRuN00TmqahUCh0s1wiInLI81ORr1+/jkKhgNXV1cbC\\nlePj43jrrbcafUZGRlAqlVAsFrG+vg7TNFEsFnm1PhGRT3keLgBsKyDvhdezEBEFhy/PFiMiomBj\\nuBARkesYLkRE5DqGCxERuY7hQkRErmO4EBGR6xguRETkOoYLERG5juFCRESuY7gQEZHrfLH8S7lc\\nRrlcbqwtFo/Hm5aEMQwDy8vLUBQFQgjEYrEDNxQjIiJveB4u5XIZkiRhenq60ZZIJGCaJq5fvw4A\\njT1dbt261egzNjaGaDSKSCTS9ZqJiGh/ng+Lzc7ONrWlUilbez6fRyaTsfVRVRXZbLbj9RERUfs8\\nDxdJklAul21tlmUhHA43vl9YWEAsFrP1icfjKBaLXamRiIja4/mw2Pz8fFNbsVjE22+/DWBnYzDT\\nNKEoiq2PLMsAgLW1Ne7rQkTkM54fueymaRoSiQSuXbsGAKhWqwCw53bG9S2RiYjIPzw/cqkrlUpY\\nXFyEJEmYm5trtJum6WFVRER0GL4Jl5GREYyMjKBWqyGRSKBQKGBoaOjQjydJkovVERFRO3w3LBYK\\nhaCqKq9hISIKMN+FCwAkk0mYponbt28jGo0CADY3N1v2rd++m2VZLb+IiKjzPA0XIQTC4TDu3r3b\\n8nbTNCHLMqLRaNPEvRACsizzTDEiIh/yNFxM08TAwEDT0Uc9SOrXtqRSKdy5c8fWxzAMpNPp7hRK\\nRERt8XRCPxaLYXx8vGm4Kp/PI5vNNo5K8vk8RkdHbeuNaZoGTdO6WS7RkbS5uYFPPvkEZ86ccdT/\\nzJkzePnllztcFQWdZPlgIqJQKGB1dbWxcGUikcBbb71l67OysoK5uTkMDw9DCIF4PI7XX3+97eeq\\nn0Xmg382kSOff/45Pvzw17h0KXZw50P4n4v/Bd/7D/3o7e09sO/Wky1c6LmA8f803pFa6OjwxanI\\nu1dAbmVoaOi5Tk0motYsAC999yX0ya0vVH7Wt998i61PtzpfFAWeL88WIyKiYGO4EBGR63wxLEZ0\\n3FQqFWxvbzvqW6vVOlwNkfsYLkRd9u233+J//+9/hSRddniPMzh37kIHKyJyH8OFyAOSdALf+c7v\\neV0GUcdwzoWIiFzHcCEiItcxXIiIyHUMFyIich3DhYiIXOeLcCmVSnj33XeRyWTwxhtvoFQq2W4X\\nQiCdTkPXdZimCSEEcrkcdF33qGIiItqP56cil0olRKNRjIyMANi5YCwej6NardrWHNN1vREmsizj\\n5s2b3K2SiMinPD9yEULYFqQMhULIZrNQVbXRJkkSyuVy46ilWq3izTff9KJcIiJyoK0jl8HBwcaS\\n9U5ZlgVJkvCLX/yi6TbTNDE3N4fJyUmEQqFGe/2IZG1trbGni2VZ6OvrQ1/fwSu3EhGRt9oKl6Gh\\nIVQqFRiG0WiLRCKoVquN9Y9kWUYkErHdb69AkmUZQghUKhVcuXKl3dqJiMin2gqXd955B4lEArFY\\nDIVCwTacZRgGJiYmsLa2hmKx2BQwe6lWq01t5XIZ4XC4cdQC7AyfmabZuI+iKI15GiIi8pe2wmV6\\nehqyLEPXddswFrCzZfHy8jLC4TByuRzm5uYOXdTs7CzeeeedxveKogCALUzGxsaa2oiIyB/aCpdy\\nuYx0Ot0ULM9KpVIol8uHLkjTNFy4cAHXrl1rtIVCoabdKlVVhaqqe4ZLu3NDRMeWBXz62ec4s948\\nirDb40ePcWr9ZBeKoqBrK1wsy4IQYt8+lUrl0MUIIaBpGpaWlg7sG4lEIITA5uYmJ/mJnsOLL34X\\nn3yyhZOnTh/Y99EjC2fWf9OFqijo2joVOZVKYXl5GR988EHL20ulEgzDQDweP1QxuVwOt2/fbmqf\\nmZlpaqsPle0VdpZltfwiIrve3hDk0MuQ5YO/+s73e10uBURbRy75fB7lchmjo6O4evUq0uk0otEo\\nVldXsbi4iGKx2OjXrkwmg5mZmaajkPrV+GNjY7YJ/vqJANFotO3nIiKizmorXKLRKHRdRzabxcLC\\nAhYWFppun52dtZ1F5kShUEAul7OFh67riEajjcd89jZgZ/4nHo9zSIyIyIfaXv4lFothcXERQggY\\nhgEhRCMEYrFY2wXUj3aq1WrjaKRaraJYLOL9998HsDMEVqlUGqc3m6YJTdNw8+bNtp+PiJ7Pt99u\\n4R/+4a7j/r/926/g1Vdf6WBF5EeHXlvswoULSCQSB549th/TNBunFO82MDDQ+P+RkRGUSiUUi0Ws\\nr6/DNE0Ui8Wmoxki6qyTL5yG1PNd/PSnzuZevvpqHZL0a4bLMdR2uKysrGBiYgKGYUCSJCwuLuL1\\n11/H4OAgMpmM7RTig8iyjO3tbUd9eT0LkT+cP9ePixe/67C3BWCjk+WQT7V1tlilUkE8HodhGEgm\\nk7azr9bX1zE1NYXh4WHXiyQiomBpK1zqZ4EtLy83TeZvbGxgenoay8vLtqvriYjo+GlrWGx+fh6p\\nVApDQ0ONdb6eNTU1hbm5ORSLRdy4ccO1IonIJyTg0ZOH+L8//7Gj7qb5a1y8yDM6j6O2wsU0TdtE\\neyvRaLRpJ0kiOhpOnjqNF149iS+tVUf9f/P0E/xOdf/PDDqa2l5y/6ClWVZWVg51SjIRBcM5Oey4\\nb612v4OVkJ+1NecyPj6O5eVl/OhHP2q5MOTY2BiEEEilUq4VSEREwdNWuExNTWFoaAjJZLJxfUo+\\nn8f4+Dj6+/tRLBYRjUYxPT3dkWKJiCgY2goXYOdMsenpaXz88ccAgMXFRSwsLGB7extTU1O4d++e\\n60USEVGwHOoK/ampKUxNTQHYWVhSURTIsuxqYUREFFxthUuhUEB/fz/efPPNRpsbqxKXSiUIIbC6\\nugohRMtNwAzDwPLyMhRFgRACsVgMyWTyuZ+biIjc11a4qKqKcDhsC5fnVSqVEI1GG2FSq9UQj8dR\\nrVYbu0/Wl92/detW435jY2OIRqONxSyJiMg/2ppzeeutt7CxsYG7d52viHoQIYRtif5QKIRsNgtV\\nVRtt+XwemUzGdj9VVZHNZl2rg4iI3NNWuGiahunpacTjcdy8eRN3797F5ubmoZ/cNE3Mzc2hVqvZ\\n2uvDXWtrawCAhYWFpmtn4vF4Y7l+IiLyl7aGxepbC1uWhcnJyUb7s9e8WJYFSZLw9OnTAx9PlmUI\\nIVCpVHDlypWWfUzThGmajed+9r7ATgBx6X0iIn9pK1ycTqC3usByL/UNwp5VLpcRDodx+fJlCCEA\\nYM8dJ4UQDBciIp/ZN1xyuRxee+21xgT+7pWQO2V2draxsnKrBTKJiMjf9p1zmZmZwdzcXFN7oVDA\\n22+/3ZGCNE3DhQsX2tp0jIiI/OVQF1HeunULH3zwAd577z1XixFCQNO0AxfHdKKdoTki6gxJkvD5\\n/c/wt4t/66j/iZ4T+JP4n/Ci7CPgUOECwLYLpVtyuRxu375ta6tfpLm5udly3sWNiziJqDPOhmTg\\nwgN8HfraUf/q51X88cM/ZrgcAYcOF7ePDDKZDGZmZpoCRJZlRKNRCCFsZ5QJISDL8p6T+XuFH49o\\niLpH6ulB77lenAudc9R/8zeHv7SB/KXthSs7oVAoIJfL2YJC13VUKhUAQCqVwp07d2z3MQwD6XS6\\nm2USEZFDnodL/ULIarUKwzBgGAbK5TIWFhYaS7vk8/mmM9U0TUM+n+96vUREdLBDD4u5wTTNxr4w\\nuz27nXIoFEI+n0cul8Pw8HBjrTFe30JE5E8Hhku5XMb4+LitTdd1WJbV1P6sVqcw7ybLMra3tx2U\\nubPF8rNrkBERkX8dGC4bGxt7Xjy530WVTsKFiIiOpn3DxY3rTYiI6PjZN1x2r0RMRETkhKcT+kTk\\nvl9+8XNUfuV8z6XaN/fRL13qYEV0HDFciI6Y//eNiYfnNnBOVg7uDECRXsULp051uCo6bhguREfQ\\niRMncer0i16XQceY5xdREhHR0cNwISIi1zFciIjIdQwXIiJynW/CpVgsQtf1pnYhBNLpNHRdh2ma\\njXXFWvUlIiJ/8EW4lMtlTE5O7rnXiq7rSKfTUBQFiUQCr732GpLJZJerJCIipzw9FblSqSCfzyMe\\nj0NRWp+TL0kSyuUyEokEqtUqV0ImIgoAT49cIpEI3n//fUxMTOzbz7Is9PX1MViIiALCF8NiRER0\\ntATiCn0hBEzTBLCzY6WiKBgZGfG4KiIi2ovvw6U+F/NsmNR3r2TAEBH5k++HxUKhUNOcjKqqyGaz\\nHlVEREQH8f2RSyuRSARCCGxubqKvr69ln71Oayby2tbWFj7+px+h95M1x/cZvPQaBi5f6VxRRC7z\\nfbjMzMxgamrK1lYfKhNC4MoVvuEoWJ4+fYpH1kNc+r1XHPX/amMd3z5+2OGqiNzl62Gx+tX4a2tr\\ntvZqtQoAiEaje97XsqyWX0R+IUmSoy+AR+EUPL4Ol2g0itnZ2abrW8rlMuLx+J5DYkRE5C1fhUur\\nIwtFUVCpVBrfm6YJTdNQKBS6WRrRgba3tx19bW1teV0qUcd5OudSq9Vw48YNCCEghICqqkilUkin\\n043TjEdGRlAqlVAsFrG+vg7TNFEsFnm1PvnK9H//H/jHn//c8Ykk3/ac6HBFRN7yNFxCoRCmp6cP\\n7MfrWcjv7ps1vPJH38e5vrDXpRD5gq+GxYiI6GhguBARket8f50LEQGWtY2trSeO+m5b2x2upj3W\\n9ja2njo7iWH7qb9qp8NjuBD53AsnT2Lty5/gs+pPHfXftp7ixe+c63BVzrxw4iSEMLG2ZjrqX/v8\\nAb7/W9/Hd77znQ5XRp3GcCHyud7zfej9/WBe03X2rIyzZ+OO+5uf/wOePn3awYqoWzjnQkRErmO4\\nEBGR6xguRETkOoYLERG5juFCRESu883ZYsViEeFwGMlksuk2wzCwvLwMRVEghEAsFmvZj4iI/MEX\\n4VIulzE5OYlisdh0W31Pl1u3bjXaxsbGEI1GEYlEulkmERE55OmwWKVSQSaTQaVSaewuuVs+n0cm\\nk7G1qaqKbDbbjRKJqMseP36Mhw8fOvp69OiR1+XSHiTLJ9szDg4OQtM0vP7667Z2RVFgGIZtiX3T\\nNKEoCra3218qor4kuk/+2XRE/Of/+t+w/UqEqyI/p7Wf3cEf/PZZyLLsqP+p7VP4iz//C5w6darD\\nlVG7fDEsthfTNBtB8qz6C29tbY37uhAdIX0XFbz8PRn9/f2O+n/xj1/wD0Wf8vXZYtVqFQD23M5Y\\nCNHNcoiIyCFfh4tpOlvsjoiI/MXXw2LPw+l2s0RE5D5fH7kQEVEw+TpcotEoAGBzc3Pf21uxLKvl\\nFxERdZ6vw0WWZUSj0aaJeyEEZFnmmWJERD7l63ABgFQqhTt37tjaDMNAOp32qCIiIjqIryb0Ww1b\\n5fN5jI6OYmJiotGmaRo0TetmaUR0BNRqtbYuvj579iwv0DwkT8OlVqvhxo0bEEJACAFVVZFKpZBO\\npzEyMgIACIVCyOfzyOVyGB4ebqw1xiExImrHw4cPMf+/5rF9ylm4PHn8BH/6+3+KK390pcOVHU2e\\nhksoFML09PSB/YaGhjA0NNSFiojoqLIsC9svbOPS9y456v/rX/76UEtM0Q7fz7kQEVHwMFyIiMh1\\nvprQJyLyk0ePHuHBgweO+yuKgp4e/s0OMFyIiFrqPdeLn3zxE/zzl//sqP/TR0/x5//xz/HKK690\\nuLJgYLgQEbVwXj6P8/J5x/2/+BmX/38Wj9+IiMh1DBciInIdh8WIWnj06BFqtZrj/ttPn3awGtrP\\n/fv3cfLkyQP7ffPNN12ohuoYLkQt/MvP/gU//pcf4/SZ0476f31yE6EX+HbquvPAD5d/6Lh7z3kO\\n1nQL3w1Ee+i92IuX/83Ljvr2V9dhbfPt1G2Xos6utqfuC0SMCyGQTqeh6zpM02ysL6brutelERFR\\nC4H5U0vX9UaYyLKMmzdvIplMelwVERG1EohwkSQJ5XIZiUQC1WqVKyITEflcIMIF2FnRtK+vD319\\nfV6XQkREBwjEnAsREQVLYI5chBAwTRMAUK1WoShKY0MxIiLyl0CEi6IoAGALk7GxsaY2IiLyh0CE\\nSygUwsTEhK1NVVWoqrpnuEiS1I3SiMhlm19tYttytgNkj9SD/v7+Dlfk3IMHD7C1teWo74kTJ3Dp\\n0tG9TicQ4dJKJBKBEAKbm5uc5Cc6Ik6dDuNn/1oD8LWj/hbWkUr2OVr+pdNeDL+Iv//074FPHd6h\\nBvzN6N/4ovZOCES4zMzMYGpqytZWHyoTQuDKlStN99lr6Wse0RD517mzCnBWcdy/WjU7WE17lJcU\\n4CXn/b9Y+aJzxfiA788Wq1+Nv7a2ZmuvVqsAgGg06kFVRES0H9+HSzQaxezsbNOFk+VyGfF4nENi\\nREQ+FIhhMUVRUKlUEIlEAACmaULTNNy8edPjyshLn332GZ52aKn7zc3Njjwu0WFsb2/js88+a2un\\nywsXLuDcuXMdrGp/gQiXkZERlEolFItFrK+vwzRNFItFLgNzjD158gQ//PEPIcmdm0OTX5Y79thE\\n7fjqq6/w4d9/iBdCzj6yH371EOnvpfGHf/CHHa5sb4EIF4DXs1AzqUfCpYGjeyon0bNeOPWC49f7\\nrz79VYerOZjv51yIiCh4GC5EROS6wAyLkfeePHmCTz91eoXYjldeeQVnz57tUEXOPdl6ggcPHnTs\\n8be2tnCCf6oRNTBcyLGNjQ388OMf4pR8ylH/h+ZD/Nlrf4aBgYEOV3awr7/6Gh9//BucOuX8Ar32\\nXETY4c+F6DhguFBbTveedrxv+RfCX1cgnz7VC0X5rtdlEB0LPJAnIiLXMVyIiMh1HBajjrp//77j\\nq+glSUI0GsWJEyc6XBWRP9y7d8/R6/3Ro0ddqMZdDBfqmNDFEO4+uAs4XLh2a2MLf/nSXyIUCnW2\\nMCIfOPnySfzdJ3/nuP+Zl850sBr3MVyoY86eP4uz552fhvzFQ3+dAEDUSRcvXfS6hI4KTLgYhoHl\\n5WUoigIhBGKxGJLJpNdlERFRC4EIl/qeLrdu3Wq0jY2NIRqNNlZKJiIi/whEuOTzeWQyGVubqqrI\\nZrOYn5/3qKruME0Tn/3yM8f9JUnC7/7b3z2yW6cSPcsC8NkvP0dPj7MTX8/2nsHFi0d7OKruNw9+\\ng3/6539y1FeSJPzO4O/g9OnTrj1/IMJlYWEB77zzjq0tHo+jWCx6VFH3fPnll/jopx+hL+xsU7Rv\\n17/FpVcvNbaBJjrKTp38Lfz8548d9X269QRy+MtjES7KRQWr91ex+qtVR/2/efANXrr4El56qY19\\nmg/g+3AxTROmaTZ9WMryzl4ba2trR35fl/Oh83j1t1511PeLrzkpTsfH+fP9jvs+fvwNgFrnivGR\\n02dOO/7MADpzMo3vL6KsVqsAsOd2xkKIbpZDREQO+D5cTNPhRRJEROQbvh8WOyxJ2n/724NuD7IM\\nMgd38qkg104UZE7ee5ZlOX483x+5EBGRP7TzR7nvj1yi0SgAYHNzs+W8S/323fZK2PoPp50E9hPW\\n750g1w6wfq8dlfqd8v2RiyzLiEajTRP3QgjIsnzkzxQjIgoi34cLAKRSKdy5c8fWZhgG0um0RxUR\\nEdF+JCsAx2i1Wg2jo6O25V/eeOMNaJrW9pHLUTk0Zf3dF+TaAdbvteNWfyDCBQBWVlYwNzeH4eFh\\nCCEQj8fx+uuvt/04x+0X7DdBrj/ItQOs32vHrf7AhItbjtsv2G+CXH+QawdYv9eOW/3HLlyIiKjz\\nAjGhT0REwcJwISIi1zFciIjIdQwXIiJyHcOFiIhc5/u1xYjo+RmGgeXlZSiKAiEEYrEYksmk12U5\\nUiqVIITA6uoqhBBQVRUjIyNel3Uopmkil8vh/fff97qUthiGgfn5efT392N9fR2qqiISiex7H4YL\\ngHK5jJWVFQDA+vo6BgYGMDEx4XFVzh3mF+9HQXzjBeGDTwiBXC5nW+FibGwM0WjU96+TUqmEaDTa\\n+JnWajXE43FUq9VAvUfrstksNjY2vC6jLcViEeVy2fa+VFUVs7Oz+9/ROuaWl5etYrFoaysWi5am\\naR5V1J6FhQVLVVVb2+TkpEfVPJ/JyUlrdHTU6zIcKxaLlmEYje9N07QGBgZ899qZnJy0SqWSra1c\\nLgfiZz0zM9PUpmmaJUmSB9U8n9XVVWt0dNQaGxvzuhTHNjY2rHA4bGubnZ21BgcHD7zvsQ+X3R/M\\ndUF44z3PL95vgvjGC8oHXzgctiqViq1tY2PDd3XutrGxYcXjccs0TVv76uqqJUlS07/J7zRNszRN\\nC8RnS93U1JSVy+Wa2p387I/9hP7S0hIqlUpTexC2V75x4wZUVbW1TU5OYnFx0aOKDk/XdaTT6cAs\\njWGaJubm5lCr1Wzt9XmMtbU1D6pqZpomTNOEoii2dlmWAfinzlZkWYYQouX7M2h0XUcqlfK6jLYV\\nCgUMDw83tTtZMPjYh0sqlUI6nba9gMvlMsbGxjysypnn+cX7SRDfeEH54KtWqwDQcqM9AE37JPlN\\ntVrFlSsbtO6CAAAHsElEQVRXbG3lchnhcDhQr3MhBCKRSGD+eKozTROhUAiFQgGlUqnxXyeO/YT+\\n9PQ0yuUyBgYGMDs7i0gkglqthrfeesvr0g707C9eURRUq1UoiuK7CeWDCCGQTCYD98arf3A/y28f\\nfEE4Am/X7Ows3nnnHa/LcKxUKgXy5IP6Hx4rKyu4du1aoz2Xyzk6oeLYhwuwMzT2xhtvQFVVxGIx\\n6LrudUkHet5fvF8E9Y23l6B98AWNpmm4cOGC7TXvZ0EO93rtu7eSHx8fRzKZPPB9e+yHxYCd4aWZ\\nmRksLi429orx+3DHfr/4bDbrRUltC/Ibr5WgffAFjRACmqbho48+8roUxxYWFmwjCe3uQ++l+mfL\\n7s+YoaEhmKZ54HzdkTlyaWfsuL+/H6FQCACQyWSQy+UawxiVSgWjo6NIp9O4d+9eJ0ptcpjanfzi\\nuzU0c9if/cLCgu2vH6/eeIetf/djaJqGpaUlN0t7bvXXx+bmZst5l92vHz/L5XK4ffu212U4trKy\\ngkQiYWsL0tBv/aSP+n93E0Ls+xlzJMKlUqkgl8s57j88PIzr1683/nJ+9gcUCoVw69YtJBIJ6Lre\\n8auYD1v78/7i3dJu/a+99hquXbsGwzB88cY77M9/N79+8MmyjGg0CiGEbWJcCAFZln0zN3SQTCaD\\nmZmZPU9M8KOlpSWsrq5ibm6u0WYYRuOi1uHhYd/Pj9ZfO61eJwf9YXKsNwvTdR2GYbT8sKhPkvv5\\nlz84OAhN05q2e+7p6elauBxWoVDA6uqqra3+xrt69Wog3nh1u49+/SaTySAej9uOEovFIhYWFmwf\\nfH5VKBSQTqdtP19d1wOxwsBu7777LpaWlgLxcwd26gVg+4w0DAPpdBrr6+v73vdIHLkcVjQaxcLC\\nQsvbTNNEOp3uckXtUVUVy8vLtnAxDMNXZyvtpdVkYP2NNz097UFFh1MoFJqCxW8ffPl8HqOjo7af\\nuaZp0DTNw6qcKRaLAHbOzKufnVetVlEsFgO1TFDdgwcPAjU0Njk5iXg8bguXXC6HQqFw4H2PdbjU\\n3/y7h7+EEFhfX/f9B/Tz/OL9KGhvvKB88IVCIeTz+cZQTH1Yxu+vb9M097zebGBgoMvVPJ9KpYJ8\\nPo/5+XnUajVkMhmoqoqhoSGvS9tXKBTC4uIiMpkMBgYGsLq6ilwu1zRa0sqxHharqw/R9Pf3A9gZ\\npw7K6bH1F239Fz82NuboF+8nu994ExMTvn/jtbrqvW5gYAC/+MUvulwRkb8wXIiIyHW8zoWIiFzH\\ncCEiItcxXIiIyHUMFyIich3DhYiIXMdwISIi1zFciIjIdQwXojYYhoGenp6mRTd3K5fL6OnpaXtH\\n09HRUfT08G1JwcdXMVEbYrEYZFnGysoKarXanv3qa9b94Ac/aPs5grTnB9FeGC5EbZqcnIRlWZif\\nn9+zz/z8PCRJwptvvtnFyoj8g+FC1Kbx8XEAO1sat2IYBmq1Gq5evdrNsoh8heFC1KahoSFEo9E9\\nh8bqe3XUQwjYWWl7dHQUAwMD6OnpgaIoGBsba7md9rPL/aXT6ZZzMKZpoqenB5lMpum2mZkZxOPx\\nxvNkMhnfb9tNRw/DhegQVFXdc2hM0zTbkJgQAoODg/jggw8wODgIVVWRSCRQLBYRj8f3nbsB9p+D\\n2X1bPB5HLpdDT09P43k0TcPAwABWVlYO8S8lOhyGC9Eh1Ie8dg+NtRoSy+fzkCQJi4uL+Oijj/De\\ne+/h1q1byOfzME0T5XLZlZpmZmawsrICXddx586dxvMsLy8DaL1BG1GnMFyIDiESiWBoaKhpaKzV\\nkFgmk8HCwkLTPjv1/Wo2NjZcqenGjRtIp9OIxWIwTbPxFYlEkEwmYRgGNjc3XXkuooMc650oiZ7H\\nD37wA6ysrEDTtMZuoMVisekssaGhoUaQmKaJpaUlGIax5wkBh1Wr1bC4uIhwONzydkmSUK1W0dfX\\n5+rzErXCcCE6pMnJSWSzWczNzeH69esQQqBSqWB0dNTWzzRNZLPZxk6bwM7cSDwed22iXQgBYOcE\\ngGw2u2e/vYKHyG0MF6JDCoVCiMVijaGxYrEIYGey/1nJZBIrKytQVRWqquLKlSsAAF3XG/dpV7Va\\ntX1f33JZluXAbXNNRxPnXIieQ/2sMU3TMDc3B0mSbB/upmliZWUFo6OjeO+99xrBAthPOW6XYRi2\\n72VZRigU2vPkgHA4jMHBwUM/H1G7GC5Ez6G+dtjs7CxWVlb2vHBy96R9fagMaA6ZZ08vlmUZlmVB\\n1/WW932WqqrY2NhoWs9sZmYGtVqt5TUxRB1jEdFzSafTliRJliRJlq7re94+Ojpq5fN5a3Jy0gqH\\nw9Ybb7xhSZJkDQwMWOVy2bIsy7p69aolSVLjvsVisfHYqqra7hsOh61MJmN7roGBgcZjXr161YrF\\nYpYkSVYikejsD4FoF4YL0XOqB0BPT0/L203TtFRVtcLhcOODvlQqWZZlWaqqWj09PY2QGB0dbXoc\\nTdMaoaEoipXL5SzLslqGi2VZVjabteLxuCVJkjU4ONjoT9RNkmU9x8AvERFRC5xzISIi1zFciIjI\\ndQwXIiJyHcOFiIhcx3AhIiLXMVyIiMh1DBciInIdw4WIiFzHcCEiItf9f6rq2MGELdn3AAAAAElF\\nTkSuQmCC\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 8\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Non-Equal Variance and Normality. USE: T-test\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Check Normality\\n\",\n \"The Shapiro-Wilk test tests the null hypothesis that the data was drawn from a normal distribution. Bad if sample is big (small differences make it non-normal). QQ plot\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(scipy.stats.levene(x,y)[1])\\n\",\n \"print(scipy.stats.shapiro(x))\\n\",\n \"print(scipy.stats.shapiro(y))\\n\",\n \"plt.figure(1)\\n\",\n \"ax = plt.subplot(1,1,1)\\n\",\n \"(osm, osr),(slope, intercept, r) = scipy.stats.probplot(x, dist='norm', plot=None)\\n\",\n \"ax.plot(osm, osr, 'o', osm, slope*osm + intercept)\\n\",\n \"ax.set_xlabel('Quantiles',fontsize=20)\\n\",\n \"ax.set_ylabel('Quantiles Obs',fontsize=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\\n\",\n \"\\n\",\n \"ax2 = plt.subplot(1,1,1)\\n\",\n \"(osm, osr),(slope, intercept, r) = scipy.stats.probplot(y, dist='norm', plot=None)\\n\",\n \"ax2.plot(osm, osr, 'o', osm, slope*osm + intercept)\\n\",\n \"ax2.set_xlabel('Quantiles',fontsize=20)\\n\",\n \"ax2.set_ylabel('Quantiles Obs',fontsize=20)\\n\",\n \"customaxis(ax2, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"3.45647037494e-13\\n\",\n \"(0.9944772124290466, 0.6720660328865051)\\n\",\n \"(0.9897152781486511, 0.16231410205364227)\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZ0AAAEsCAYAAAAYSW5yAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X180/W5+P/XJxRoEWjSosObKU2KHm9Q2gQ9OuccTVsV\\n3I20RT0729mEpugB93PQFBVPhzpocecIjpumbkd3tim0ZftO6oQmqHXTKb1TmTChn8LUiQptUlTu\\n+/n9kSZt6G0gTZr0ej4ePrCffBKuFJqL9/t9va+3ommahhBCCBEGukgHIIQQYuSQpCOEECJsJOkI\\nIYQIG0k6QgghwkaSjhBCiLCRpCOEECJs4iIdwNlyOp04nU6Sk5Npbm7GbDYzf/78SIclhBCiF1Gd\\ndJxOJ4qisHLlSv81i8WC2+1myZIlEYxMCCFEb6J6eq2srKzHNavV2ut1IYQQkRfVSUdRFJxOZ8A1\\nTdMwGAwRikgIIUR/lFhrg2MymViwYAGLFy+OdChCCCFOE1NJx+Fw4HK52LhxY6RDEUII0YuoLiTw\\nqaqqoqamBkVRJOEIIcQwFlMjHY/HQ0ZGBuXl5aSlpUU6HCGEEKeJ6kKC0yUmJmKz2cjIyOjzHkVR\\n+vxPCCHE0IqppAOQkZGB2+3G5XIF/VxJPEIIMbSiNumoqorBYKCpqanXxz0eT6/XNU3r9T8hhBBD\\nL2qTjtvtxmQyYTQaA66rqgpAenp6JMISQgjRj6hNOunp6cydO7fHKKWkpAS73c6UKVMiE5gQQog+\\nRX31Wnl5Oc3Nzf6GnxaLhXnz5gX9Or71nCj/dgghxLAW9UknVCTpCCHE0Iva6TUhhBDRR5KOEEKI\\nsJGkI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGkI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGk\\nI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGkI4QQI5T7qJvfvfu7sP6eknSEEGKE0TSN5959jivW\\nXsFf/vEXOrSOsP3ecohbJznETQgxEjS3NnPvi/fy/j+bOe/Nr5Nw6BLGjj3JokVZzJp105D//nFD\\n/jsIIYSIuOOnjrPqL6v4n7/+D99OzmNveRpv7V3pf7y5+SGAIU88Mr0mhBAxrnZ/LdM3TOfNj96k\\nPr+eDzcloXZLOADNzY/z1FM1Qx6LjHSEECJGHfzyIIU1hdSoNay5ZQ3f+ZfvoCgKx471/tF/9Oio\\nIY9JRjpCCBFjNE3jmaZnuGrdVUwcO5H37n2P717+Xf/a9dixJ3t9Xnz8qSGPTUY6QggRQ3Yf3E3B\\nlgI+P/451XdXY77A3OOeRYuyaG5+iObmx/3XTKYHWbjwliGPT6rXOkn1mhAimh05cYSfvfYzNtRv\\n4JGbHuHeGfcyStf3dFl1dS1PPVXD0aOjiI8/xcKFmWGpXov6pFNVVYWqqjQ3N6OqKjabjTlz5gT9\\nOpJ0hBDRqqa5hgXVC0g7P40ns5/kwokXRjqkPkX19FpVVRVGo9GfZDweD2azmdbWVubPnx/h6IQQ\\nYmh98vknPLDtAV7/4HV+cesvmHXprEiHNKCoLiRQVZW0tDT/14mJidjtdmw2WwSjEkKIodWhdVBW\\nV8a09dO4aMJF7FywMyoSDkRx0nG73WzcuBGPxxNwPSMjA4B9+/ZFICohhBha737yLlf+/Grszz3K\\nxa/MoemJ0bxSUx/psAYtaqfX9Ho9qqrS0tLC9OnTIx2OEEIMqS+Of8FPX/0pjrfKGfPn6/FsfYd6\\nzTtuCFc3gVCI2pEOQGtra4+E43Q6MRgMTJkyJTJBCSHEGaquriU7+2FuvrmY7OyHqa6uBWDL+1u4\\nct2V/PPwP5n+xg/47KUXQev6+A5XN4FQiNqRTl/KyspYunRppMMQQoigVFfXcv/9WwP2zvz9n4v4\\nWfMjfKp8xNPfehqr0crNa4p7fX44ugmEQkwlHYfDwaRJk1i8eHGf9/hKo4UQYjhZs2ZbV8JRTsG1\\na9l/03PEvXM5Oze8S3xcPBDZbgKhEDNJR1VVHA4HdXV1kQ5FCCH6VF1dy5o12zh2LC7gSAF/P7Tz\\n6+F2GxybAP/7Ghdd+bw/4UBkuwmEQswknaKiIrZv3z7gfX1t/pQRkBBiqPU2heYrAhg17gu45X64\\naiPUlMLb/w4oPUYwvmKBp55a1q2bwC1RUUQAMdCRAKCgoICioqKzKh6QjgRCiKGWnf0w27Y9dtpV\\njWvuyuWjq2o5tusCDle54Egy4B3BrF4dPQllMKJ+pFNeXt4j4bhcLoxGIykpKZELTAghTtPjSAH9\\nPrjtP9lz4Zu89G+bad+p8dRnT0blCGawojrpVFZWAt7S6dbWVv//V1ZWsmHDhkiGJoQQPdZv2tu9\\nn1PoTsD1/wNfK4U3HuBrrVfz9Uu+DpdEx16bsxG1ScftdpOXl9frYyaTKczRCCFEoN7WbyZPvoek\\na+6k9Yb34PAFUP4mpqRfcv/q6CgCCIWYWNMJBVnTEUKEUo/1m/g2sBYx+srfcPkH2eg/mkZCfEfY\\njhQYLqJ2pCOEEMNZ1/qNBtOeg6yfwO7vcm3dQv7sXBnR2CJJko4QQoRAr+s3SXth1gI45zN4/g/w\\n0XWMz14W6VAjSpKOEEKcge5Jpr39Qz7+eCIHDvy398FRxxiffQNK1jS02sfgzfuhIy6qNnEOFVnT\\n6SRrOkKIwepZJPAw0Ll+M+UVmF0ABy/jyn8kcNGEqWE/Eno4C9lIp729nYkTJ4bq5YQQYljpPrLZ\\nuXMXhw5t7PZoHIw7CFmLIWU7/GkN7P4Ok75RzEsvFUcq5GEp6KMNGhsbWbBggf+QNI/Hg8ViQa/X\\nM2rUKOnwLISIOb6RzbZtj/Hqq8UcOnR5t0c1SKuDe6+EI0mw9m+w+ztA9DThDKegko7L5cJsNlNW\\nVobb7QbAbrfT0NBARkYGU6ZMobS0lM2bNw9JsEIIEQkBHaAB6Oz0fO578MNvgKUZfjMbtv43HJ8A\\n+JpwZoY/2GEuqDUdi8VCQ0MDNTU1/mOhdTodVquVbdu2AWAwGEhNTWXHjh1DE/EQkTUdIcTpfFNq\\nb775IR7PM10PxNXATcVgfh9eKYa6AiZ/ZT4XXJDAhAnnyvpNP4Ja01FVlZycHH/CaWxsBMBms/nv\\nycvL87enEUKIaBVYLPBw1wOmbTDrXvj4qxg23sDVKZ8Rn1XMwoX/IUlmEIJKOm63O+AIAKfTCUBm\\nZtcQsrW11T/1JoQQ0SpwSi0Lxt8P2Z/CRW9C9VpM2musXhd7DTmHWlDTa2azmX379nHo0CEAUlNT\\nAdi7d6//nqSkJJKSkgKuRQOZXhNCQC9TakoHmMvgm0uh4UomNqVwvSVFps/OUFCFBDabjba2NqZO\\nncqMGTNQVdU/teZyuUhNTcXtdpOTkzMkwQohxFDqXqXm8VwEX3kb7rkBrv4tPPtncP2F6y0pvPTS\\no5JwzlBQ02v5+fk0NzfjcDhobm4mJyeHJUuWALBt2zZUVcVqtbJy5cjtKySEiB6ndxXYu7eVw4c3\\nw5jP4ea9cM0N4FoNjT8CTScdBUIgZB0JVFUFwGg0huLlwk6m14QYOaqra1m27Nfs2jWao0fXA7XA\\nVmA0XGqG2xbC/ptg2xz4oo7ExA/413/9qkyphcAZJ519+/ahqiputxuj0YjRaIzqjgSSdISIfYHJ\\nJhl/6xoehokFcKsVztWgej20zPQ/Lzt7GS+99GhEYo41QbfBaWxsZP78+TQ0NARcVxSFnJwcSkpK\\nAo6OFkKISAtMNpPxJpti74O6k3BtHXw9Dd66HarOhZNdCUem1EIrqJFOS0uL/1TO9PR05s6dS0pK\\nCqqqUlNTg8vlwmAw0NLSEnWjHhnpCBGbuvbbKHQlm2LgYbjg23C7DY60QfVWOHQp3qm2GmAUycm7\\nefbZe2VKLZS0IOTm5mqKomgOh6PXx8vKyjRFUbS8vLxgXnZYALQgvx1CiGFqy5ZXtaysh7Qrr8zX\\n4uJma6Bp8F+dvz6kMdatcet3NX5yjsbVv9bgFQ0e7Hzc+5/JtFTbsuXVSL+VmBPUSCcpKQmj0Uhd\\nXV2f95jNZtrb29mzZ08IUmL4yEhHiOjlq0L76KPP2L//A44du4gTJ76HvzjAN7LhUbhiOdzyc9gz\\nF5zfhiNvEh+/nwsuOI5enyxtbIZY0B0JfNNrfTEajdLwUwgRNl3TZ9l4k8y5eKfRHga6tbDRT4NZ\\nUyExHip/Bv/4hPj4TVyRPoHly+dJggmToJJORkaGv/VNX1wuF2lpaWcVlBBCDNayZc/T3LyOriRT\\n3PlI58ebbibc8E244V14/Q54YxLxo9+SZBMhQXUkKCsro6Ojg+zsbP95Oj4tLS1kZWXhdrspLy8P\\nZYxCCNGr6upadu36vPMr37+hT3b9+tW/QMEiuORLKL8T/nwByXqVysp51NevlYQTAf2OdLKysgIa\\nfAIkJydTU1ODyWTCaDSi1+txu92oqoqmaaSnp+NwOFi/fv2QBt5dZWUlBoPB3/1aCDEyrFmzjaNH\\nL+78ypdssiDhAbDugamrYesv4W+5gILJ9CCrV0s1WiT1W0hgMBhQFCXoxXVFUWhtbT3r4AbD6XT6\\nj1OYOXPmwE/ogxQSCBFdqqtr+d73fonbfQ/etZxs4CW4+grIvB92GYmrnUSCMo5LLvkqF144QYoD\\nhoF+RzptbW3hiiNoLS0tlJSUYDabSUpKinQ4Qogw8FWp7d79dz78cCIdHV8FOpNI8vMw64+Q8AXx\\nf5jBN1KvY+HzkmSGm5D1Xouk1NRUHA6HjHSEiGGBVWprgY1ALYyqhhvHwXVPQe1DGA9+wponb5Nk\\nM0wFVb3W2NjIxo0baWlpwe12o9frMRqNzJ07l+nTpw9VjEIIcVqV2uXei1NOwezn4LNxsOHfMYx6\\nizX/t0ASzjA2qKTTV781H980V3l5uSQfIUTI+Hqmvf/+x3zxha+1VhyM80D29+GSV+FPv4C/fwuA\\na7OXScIZ5gZMOi6Xy38cdXp6OjabDYvF4u+5VldXR1lZGfX19ZjNZmpqas5qmksIIQCKi9exYsUr\\nHD8+FZjsvah0QNoOyHgd3r4M1v0Njo8HICHBxsKF/xa5gMWg9Lum4/F4SElJwe12U1ZWxvz58/t8\\nIYfDQUFBAQaDwX+cdbgEs6Zzegn46WRNR4jI8o1umppa0bQr8DfpPDcFZj8MoybAlhvgwPfxNeZM\\nSNhFYeE3KC6+N6Kxi4H1O9JxOBy43W4KCwv7TTjQdaroqlWreOKJJ1i8eHFIAxVCxKbAKTQPMBW4\\nELjIe8PoL+GmGkh/H175HtSNA+0gsI5zzlG48cZUFi68T6bVokS/Ix2z2UxTUxOnTp0a9AvqdDoy\\nMzPZunVrSAIcDKleEyK6BCaaeEDf+cjneKvSioGTkNoMt70F/5wCL10Fn6/2v4Z3o+ctkmyiTL8j\\nHVVVgz5+OiUlpd8u1EKIka26upZ5857lwIHJ+Ndq/Do/ksa3wS3vwgV1UD0Lmp/De87NMkaPbmHa\\ntESWL58rCScK9dt7zePxBJ10jEYjbrf7rIISQsSuZcue58CB8/E254wL/E85DjPWwoJnofUYrKuC\\n5nOAu1CUpzCZ/sHvf58vfdOiWL8jncTExKBHLXV1dej1+oFvDDGZFhNieKuurmXRotWo6mjgvM6r\\nJ7tumHwAZr8Opz6HZ16Hzw4CNSjKF6SlJcnIJkb0O9KxWq20tbXR1NQ0qBdrbGzE4/GEpfGmx+Oh\\nqKiIvLw8VFXFZrNRUFBAVVXVkP/eQojBqa6uJT19HvHxM5k9+0lUNQ5IJaA555h/QNYf4Hu/hXoj\\nPPNr+Ow5YDtjxuzikUe+LiObGNJvIUFDQwMWiwWTyTTgSaAejwez2YyqqtTX10fdmTpSSCBEaHXt\\ns5mAt0BgKt7JlZnAs8BkuOxauNUG+ybCtq/Al2PQ6c4hIWE8l11mkNFNDOp3ei09PZ358+dTXl7O\\n1KlTKSkp4Y477uhxX1VVFXa7HVVVycnJibqEI4QIna5ptFPAVZ1Xu591cxNM/BRu+wlMegr+cD0T\\nDiXw3KYHJMGMAINq+Jmbm+uftjIYDBiNRoxGI6qqoqqqvxt1Tk4OmzZtGtqIh4iMdIQ4c74S6Pfe\\nUzl2TA+Mxt8fDfBPp+lmwnU/g683wZuL4M92EsYsoqLi3yThjBCD7jLtdDopKSnB5XL1eMxqtWK3\\n26P6EDVJOkIEr2tUowEGAqfRuhUJkAUXPgGz34IjF8GW66D1XMaM2cnSpTOlk8AIckZHG6iqGtBl\\nOhZI0hEiON5D1Mpxu4/jTTQQOI2WBTwLY49Dxntw+T7YNg3enQycwmQax+rV98gIZ4SJifN0QkGS\\njhCDV11dS25uCUeOpBG4NNytKo2X4MoxkL0K3k8G5+XEo+eKKyZJgcAIJkmnkyQdIQanq6NAO3Al\\nPabReBYMY+G2epjYAltmM+aTdplGE0CQh7gJIcSaNds6Owp8QcA0GsCoF+EGHVz/K/jLv8AbX8eU\\ncorVmxfJyEYAknSEEEE6dsz3sTEe+BjYCvwALi6F2ZvAncCYZzO46sIpLP+jTKOJQJJ0hBBBaW//\\nFEgCvg88Cwn7IfOHkHoAXvoXHsn9ET/97X0RjlIMV7Km00nWdIToW899OAbgK3ANkLkG/nYlo1+b\\nzIM/yZZ1G9GvkCWd9vZ2Jk6cOPCNw5QkHSF611UaPQb/eTfJv4HZhTD2KGy5ngmHR/Pcc9JRQAys\\n34afvWlsbGTBggXs27cP8PZcs1gs6PV6Ro0axdKlS0MdoxAighYtehq3+xLgfIibCjf/F9zzY9ht\\nh6c/hX9Wk54+XRKOGJSgko7L5cJsNlNWVuY/M8dut9PQ0EBGRgZTpkyhtLSUzZs3D0mwQojwKi5e\\nh6p+CcRByj9gwXo4bydsaII374cO77JwfPzgTxcWI1tQ02sWi4WGhgZqamr8LW90Oh1Wq5Vt27YB\\n3t5sqamp7NixY2giHiIyvSZEl4CmnecA2c1w8QfwYhG8fxjvAWxeCQk26Z0mBi2o6jVfF2lfwmls\\nbATAZrP578nLy6OysjKEIQohwqW6upZ77nmcTz4ZB8poMB+HmU5oSoW134ITh4FsYBkwijFjdlJY\\nOFMSjhi0oJKO2+32jwjA2wQUIDMz03+ttbVVjqsWIgp5CwaexO0eB+edC7NfAqUDfr0WPvkLoABN\\nwE4gDpNpPKtXy6ZPEZygptfMZjP79u3j0KFDAKSmpgKwd+9e/z1JSUkkJSUFXIsGMr0mRrLi4nU8\\n+ugLdIwaB9/4BNIa4eWboN4OWg3e0U0NMAqd7m2WLcuU0mhxRoIqJLDZbLS1tTF16lRmzJjhPyYa\\nvEUGqampuN1ucnJyhiRYIUToeRPOK3SYjsO92yDRDevnQ91SSTgi5ILep2O323E4HHg8noBD2+x2\\nO6tWrQooKogmMtIRI9X482/li6/vg/M/gepp0Pwo/uOkuyUcOftGhELINoeqqgoQtefrSNIRI80f\\nt7zMj9b9fxy6ahfUXwe1y+DkeuA84G7g13ibep5g8mQdTz/9n7J+I87aGSed9vZ2WltbMRgMJCYm\\nhjqusJOkI0aS1Zue5icv2zl1dBRsMcNBM/AYUAusBo4D4xg16nMefniWjG5EyJxRRwJfBwKTyUR9\\nfT3gLSp44oknQh6gECJ0Dh87zHfW5/Hjuvs49dcb4JkFcPB24H3gIeAmoAp4AYNhEv/v/9kl4YiQ\\nCmqk09LSgslkAiAjIwOXy4XT6WTmzJkYDAY8Hg9mszmsG0MbGhqor68nKSkJVVVJT0/37yMKhox0\\nRCzTNI2Hf/s4K5sep2PveVBzDXyZjvc8nMeAdUA13l0UY0lI+JKKikKZThMhF9Q+nZKSEgDq6+tJ\\nSUkhKSnJ/1hbWxulpaUUFRWxdOlSVqxYEdpIe6GqKkVFRQGFC3l5eRiNRlJSUob89xciGux37yfr\\nydt5/5AKL1hg/zeAvXQdwPYQ3g4D3hGNt8OArN+IoRHUSCcpKQmLxcK2bdtwu90kJSX5Rzo+ZrOZ\\n9vZ29uzZMyQBd2ez2cjOzuaOO+7wX3O5XJSVlfmr6gZLRjoi1pw4dYLVb67moT89wvHaS+AvV8Kp\\nqzof/RDQOL1CTVGaeOSRLJlSE0MmqDUdt9vtn17ri9FopLm5+ayCGqyKigrS09MDrpnNZmnDI0a8\\nv374Vy79+eU89KuVHF/3NaidC6fG4x3dnMR7ABvAJ8B64B8oSr0kHDHkgko6aWlp1NXV9XtPY2Nj\\nj0QwFNxut3+01Z1erwfwH70gxEhSVPwEo797Mdc/eRP7/s/A8V/+K7R+DW+iOYJ3Oq3bEdOcD1zG\\nmDFf8Mgjt0rCEUMuqKQzd+5c6uvrefnllwN6sPnk5eWhqipWqzVkAfaltbUVoM+D43z7hoSIZdXV\\ntZhMc9CN+ibKNBMlny/j5MlRsDYTdmYDk+hauzkB/A5vsvGNcHYxefJ7bN68SBKOCIug9+mYzWYa\\nGxvJzMykpqaGzMxM9Ho9TqeTtrY2jEZjWPquNTQ0YLFY6Ojo6PGYTqfrsdY0EFnTEdGmuHgdjz32\\nAqcmKjDrHZjQDi/cAR8eAS7vvGsXcB/ekU02XXtw4klIOE5hoRwvLcIrqOo18FaulZaW+qvTampq\\nAEhMTKSwsJCVK1eGNsIQ622EJkS0KS5ex08f2wo3fAjXN8Ofr4e/XggdU4B9eEc3AN/AO7q5G2+x\\nwDSgibvuMvK735VEInQxwgWddAAKCwspLCwEvNNYSUlJ/rUUIcTQKi5ex0+f+T8o2Aut8VCWDx49\\n3lFN97WbZ/FWqF2Ndx9OPIpykDvvvFISjoiYkPVeCzdfEYHb7e6xrqPT6VBVlSlTpgz69WR6TQx3\\n1dW13LeklP2XvgPGQ/DSrbBLB1zaeccFwCt4E4/0TxPDU79JR6fT9Tkd5Xta9w9rRVH8v546NfRn\\npqemplJZWcn06dP911RVxWKx+AsNBkuSjhjO7rq7kOd3ucD6N9g5HbZfCMfvB57EO2ExAe+emwvx\\ndhbwABOBc5gwoYMHHsiQtRsxLPQ7vTZnzpwzetFwrZtYrVZ27NgRkHQaGhoCTjIVIpoVF6/j8bJy\\nTt7yAVw7Gn5rhY+nAwfwFgf8GG9xQEvnf+OIjx/PFVdMYfnyuTKqEcNO1E6vAXg8HnJzcwPa4GRl\\nZeFwOIKaWgMZ6Yjhpbq6lh/lL+fTyz4CiwqvzoQdM0B7H2+7mmc777wAGAWcQq9v4Te/yZdEI4a1\\nqE464N2MunHjRv9JpmazOahSaR9JOiKSqqtrWbRoNfv2tdHRcQyMGsx+Gz6+GF66Cg5f1nnnAeAr\\neMuffes1J0lIOCINOkVUGNSaTnNzM1OmTOl3jccnnGs6oSRJR0SKf7/NqQlwThxkvwYXH4ZqC+y5\\nka69Ns92e5aMcER06ndNJyMjA0VRMBgMwODXeGQvjBAD841uVPUkKBPA/DnMfBUaU2Dtv8OJZryV\\naL69Nj/AO7r5GPiE0aMTmDbtPJYvl4QjokfUT6+Fiox0RDjdfbed557bA3TAeefD7VXAWHhhNnza\\nBqTSVQI9FW9VWi0QDxzkrrtkr42ITkElnfb29j57nUU7SToiXLwJ530YPRVufhGmt8D2y6EhGzQF\\n77qN79gBXwl0HDCKyZPjZK+NiGpBNfzU6/U8/fTT/d5TVFREcnLyWQUlRCyqrq5l8uRsnnvuXbg0\\nAe5zwITDsO63UH8xaHvwTp35/uHzCfAaMIm4OI3/+i8rH3+8SRKOiGoDtsGpqqryb/oE/EdD90bT\\nNCorK2lrawttlEJEsa61m8MwQQd578FX2uGPt4E6DthB4H4bL0U5h3HjJnDZZeNZvvweSTYiJgw4\\nvabTBTUYArybNrvvnYkGMr0mQq0r2XSAEgfX7oWb3oe6KfDak3Dy+W53SzWaGBkGTDrdT+HMy8sj\\nPz+/3/NyDAYDGRkZoYswTCTpiFCqrq7le98rx+0+DOcnw+1/guMdsOU7cPBq4B26eqN9DCjdqtGk\\nk4CIXUEVEmRmZlJUVBSVSWUgknREKJlM30f96CvwzS1w1QdQMxPejgf+E2/7mu7VaJ9x111XSTWa\\nGBGkZLqTJB0RCsXF61hZsoljKcfglvegORlqvgNHvoO3Oaev+3MN3um0t7nrrksl4YgRI+ik43K5\\nqKiooKWlpd/7tm7delaBhZskHXE2qqtrueeex/nkmA5uexsMX8CWb8P+MXSVP8vJnUIElXSqqqrI\\nzc0d1L29HSM9nEnSEcGqrq5l2bJf8+67uzjZMQmufx++th/euB5evxhOdS/CUfD2SRtDXFwbDz10\\niyQbMSIFlXRSU1NRVZWampqYW9eRpCMGo6si7QDeqTIFLjoEt++Gw3FQPQfaJtJ1cqeCt1AgDojD\\nZBrP6tVS/ixGrqCSjk6nIz8/nw0bNgxlTBEhSUcMxFuR9iRudxygQPxFYP0DXPYpbM2Gnb5TPLPw\\nFgtk41u70eneZtmyTBndiBFvwM2h3SUmJkozTzFiLVv2PG73aCAVpu2GLAfsvhDW2uBoPF290jS6\\nJ5y4uHd56CFJOEJAkCMdu91OeXk5+/bti7kebDLSEX3pmlIbDUnHYdbbcM7n8MJt8NGXdB07cHqv\\ntDgmTx4lvdKE6Cbo6rXc3FyampooKSkhPT29z5Y40ZaUJOmI7nxFAu+9p3Ls2EQYFQdf+wz+9a/w\\n2tfhzQeh47dAG11l0L5D1U4webJOko0QvQgq6fgSjNvt7v9F5RA3EaW6RjUaYAAOwZQJMPtPcPBf\\n4E/jwTMR73EDvtM7VSAeRTmH8eM7eOCBDJlKE6IPQa3pDLZcWtZ9RDTynuC5nVOn4oCpMO5LyHoV\\nUj6DP2XB7gq8XQRWA2/gbWUzGpPpq1KRJsQgSUeCTjLSGdmKi9exfPmLaNp0YBSkNUGGC969EF7+\\nFhy/HW9F2uP+5yQk2Kio+DdJNkIEIaiRzmC4XC4qKytZv359qF9aiCFRXV1LaemraFoynNsGs1+A\\nuJPw27nwsQK00lUCvQwYhaI0UViYJQlHiCAFPdLxeDw4nc5ez8zRNI2SkhJaWlpkTUdEjfT0e2l8\\n1wA3/R4DNvXdAAAdNUlEQVTM++HV+bDDA5p0FBAi1IIa6bS0tGA2mwcsJMjPzz+roIQIl+LidTS2\\n74J734aP9bDhW3D4HOAOuo4dOCIHqgkRIkGNdPLy8qisrKSkpIS0tDRsNhtmsxmbzYamadjtdiZN\\nmhR1zT5BRjojha8U+v33P+YL5TPI/idc9AW8uBT2/L3zLhnVCDFUgi6Ztlgs/lNBS0tLqaioYMeO\\nHYC3lNpoNPL0009zxx13DE3EQ0SSTuwrLl7HihWvcPzEeDDvhm82QIMFah+BE6/SVQLt3WtjMp0j\\nVWlChFhQZ1G73W5MJpP/6/T0dOrr6/1f6/V6cnNzWbFiRegiHITKykpcLldYf08RXYqL1/HoozUc\\nNyTCPVvh6g/g2R+B62Y4kUVX25qLgFTS0vTs3fusJBwhQiyopJOSkoKqqv6vLRYLAE1NTf5rJpMp\\nIBENNafTSX5+vuwNEj1UV9eSnj6P+PiZ/HTFi3RYP4Hv/w4a0uF/fwSfJuFtzvkQcBPwKFBMQsKn\\nPPro9yMauxCxKqikk56ejtPpZPv27YB3ZJOYmEhZWZn/nrq6OvR6fWij7EVLSwsFBQW0tLT02YpH\\njFzV1bXMm/csjY0axy45Aff+Gc45DOvyoeEa0E4R2A16GVCMTvddCguvkRGOEEMkqDUdVVVJTU1F\\nURQqKiq44447sNlslJeXk5ubS1tbm3/kEc7jD1JTU3E4HMycOfOMX0PWdGJLevq9NDbHwa3b4LzP\\nYMst0GLD25jTx3eap7cb9JgxO1m6dKYUDQgxhIIqmTYajezdu5eSkhJSUlIAKCkpoa6ujoqKCgCs\\nVislJXLeuwif7hVpR44co4Mv4dojUPB3eOtaqPoOnLwN76jmB3SVQregKO90lkIbWL58kYxwhBhi\\nIWuD49u7E46ptdPJSGfk8k2jHTjQeeGCz+D21+BoImy5FQ4lI4eqCTF8hKwNTiSSzZmQgoPYsmzZ\\n8xw4cD6MPQozX4Urd8G2THjnx3SNaAITjncaTRKOEJEQVNIpKCgY8ENb0zQURZHea2JI+abUGpu+\\ngCs+g1u2wp5UWHsfHBkNfAPvJs9fA03ATnS60Uyf/hWZRhMigoKaXtPpBi528414WltbB/Wa3Uuw\\nB5KcnExiYmKP6zK9NjIEHqw2BfTjYNZLkNjunUr7x1c77/RNp0lHaCGGm6BGOn0lktbWVhoaGrDb\\n7aSmpg66DU5LSwtFRUWD/v1nzJjBkiVLBn2/iA2+ZLNz52FOnBgPumS48VK4YTm8/j144zicGoV3\\nKg1O7wg9ZsxOCgtnSsIRYhgI6Xk6vjY4NpstrF0JZKQTu4qL11Fa+g5HjkzyXvjqB3D7n8BjhheN\\n0LYW78FqvvWbY0AHOt14EhLGd1alzZWEI8QwEdLzdHxtcBwOR9hb4YjY42td09Hxe0iwg9UJU/fA\\nViv8rQp4DW83gcfxdhQAk+lBVq++RZKMEMNUyA9xUxSl17N2hpqMUKJbdXUta9Zs46OPPmP//g84\\nebKDo0fjgWvg6t9A5lrY9S+wNh+OfQt4mK41m2Uoyl7S0pJkVCPEMBfS6TWXy0VmZqZ/E+lQ8ng8\\nrFixAlVVqaysxGg0YrVayczMZM6cOUG/nkyvhZ8v0eze/Xc+/HAiHR0/wNsxYDKgQLIHZm2BBD1s\\nKYCP3up8pnQSECJaBV291l/JtO+lysrKmD9//tlHF0aSdIbe6aOZY8cu4sSJ7wFrgY14Ry/AqGVw\\nYzZc9xa89kN4cyJ0rKBr7UaVNRsholRQ02sZGRn9Pq7X67nzzjvPaKQhYltXQcDdeKvLzgUew5to\\nLu+8Kw6mtMDsq+EgUPYseJroXomm0x1i2bIcGdUIEaWCSjo1NTVDFYeIMaePaj7/fCzwe7rWYoo7\\n74wDTsK4zyB7M0zZDy/+Gv5u4PROAgkJuygslE4CQkSzkBcSiJGre6JRVeW0UY3vr5rv15PeX5QT\\nkHYCMqbA27Nh7XQ4/hZdRQI1jB7dwrRpiSxffp9MowkR5YJKOi6Xi5qaGhobGwHvdJrRaGTu3LlM\\nnz7df9/mzZuj7rhqceZ8mzd37RrN0aPr8Y5mfFNnvlFNZ5Lx/5oF5+bD7L/CqEPwf2vgwD7gU+AN\\n4uO/S0LCRFJSxrN8eb4kGyFixKCSTmNjI7m5uX22rCkpKcFsNlNRUUF9fT25ubmUlpayePHikAYr\\nhp/q6lruv38rzc2T8SYa6H1U4zuhMxtGF8JNcZC+CV65nri3LyFh7ItcctVXufDC81i4UNrVCBGr\\nBkw6jY2NmM1mwHtyqM1mw2Kx+I+urquro6ysjPr6ekwmE5qmYbVaJeGMANXVtfzgB2s5dGgjXWs0\\n0Ouoxrc+k7oBbtsC/5zAhS/M4qpLjCzcnClJRogRYsCS6aSkJNxu94Bl0KWlpRQVFaEoCq2trb02\\n5hzOpGR6cHqu20zGm3B8U2rgLW32FQF0Nt4c/3u45WGUC/+BcffNrF64RBKNECNQvyOdVatW4Xa7\\nKSwsHHDfzaZNmwDvh3ZFRQXz5s0LXZQionommg0ErttA1/RZV0uahIS1nPsVHYemmDl6/S4u/iyN\\nVTP/hzlPZkXibQghhoF+Rzpms5mmpiZOnTrV74s4nU6ysrLYtGkTeXl5mM1mduzYEfJgh5KMdAL1\\nn2jAO7oppmtU83jn/9cQH7+fK66YwH8UpfMbj4Mxo8awYdYGrjzvygi8EyHEcNLvSEdVVYxG44Av\\nYrVaaW1tRa/Xk5aWFtQZOWL46SoOeJzARNP9r4tvvcY3RebdvJmcvIcNv/oP3hhbw2PvPsjPZv6M\\nH6b9EJ0y8FlMQojY1+8ngcfjGVTSga7D23xrQCJ6rVmzrTPhQO+JBrqm08CbeB7FZDrOgiev5ieq\\njYNHDrJzwU7uSb9HEo4Qwq/fkU5iYiJ1dXVBvWBdXZ0/AYnodOzYQImm+7rNXEym80lK6eB4RiOb\\n3J/yzLef4Zsp3wxfwEKIqNHvP0GtVittbW00NTUN6sUaGxvxeDwD9mgTw9vYsf2NaLJJSJjLVVf9\\nmOzsGp7fZOOHjov5242/49bpmbxT8I4kHCFEn/otJGhoaMBisWAwGGhpaWHixIn9vlhqaiqqqlJf\\nX09aWlrIgx1KUkjQJXBNB6CWhIS1mEznc+GFE1i40Luv5q2P3sK2xUZyQjLrZ61navLUiMYthBj+\\nBtynY7PZKC8vx2QyUVJS0mt7m6qqKux2O6qqkpOT4y+fjiaSdAJVV9fy1FM1HD06ivj4U/5EA+A5\\n6uFB14Ns3r2ZJzKf4O5pd/d75IUQQvgM6jyd3NxcqqqqADAYDBiNRoxGI6qqoqqq/6TQaE04IEln\\nMDRNY9PfNvHAtgeYNXUWK60rSUpIinRYQogoMuhD3JxOJyUlJbhcrh6PWa1W7HZ7VK/ljPSk49uX\\nc+xYHGPHnmTRoqyAjgFqm8p9L97Hh+0fsmHWBr528dciGK0QIlqd0XHVqqridrv9XaZjwUhLOt2T\\nTHv7h3z88UQOHPhv/+Mm00OsXp1N5i3/yhOvP8F/v/HfLLlhCQ9c/wCjR42OYORCiGh2RkknFo2k\\npNOzUKD7BtAu1+b8gM+/WccU/RR+cesvSDGkhDVOIUTskUPcRojuI5udO3d1dob2Oe2vQcIhyLTT\\nNPX3/PbmXzHn8jlSKCCECAlJOiNAz5FN8Wl3+PblaHDN/0FmIfwtlxvftpHzs5zwBSqEiHmSdEaA\\nwLY2ENhlACALkgtg9vsQ74bfvYAp4fc8sPqWcIYphBgBojrpVFVVoaoqzc3NqKqKzWZjzpw5kQ5r\\n2AlsawMB7WzijsKNLpTrnuHCZgvG/bNJmPZHFi68Rc67EUKEXNQmnaqqKoxGoz/JeDwezGYzra2t\\nA579M9IEtrUBX9+0idd8kxPZ7zDhyLmUXvcbfrBSptKEEEMratv/qqoa0GonMTERu92OzWaLYFTD\\n06JFWZhMD3VdOOdTxn//XsbO3cXGHz3DJ2t284PvSsIRQgy9qCyZdrvdWK1WXC5XwLHYqqr6+79N\\nmTIlqNeM9ZLp6upa1jy1jRbD2+w3bWf2Rd/i2R+VM37M+EiHJoQYQaJyek2v16OqKi0tLUyfPj3S\\n4USFS2Yk8XneyyR1nKJi9utcM/maSIckhBiBojLpALS2tva45nQ6MRgMQY9yYsnp7Wzy77uJHeO2\\n88vGX/LoNx8l35wvh6oJISImapNOb8rKyli6dGm/98TyJsce+3Gmvsj21/L42sUW3l3wLpPHT45s\\ngEKIES9mko7D4WDSpEksXrw40qFEjH8/zoR/wi33w/mNnPz9JuJTX2PyQkk4QojIi3jSUVV10Pcm\\nJycHFA50fw2HwzGoo7X7KhSIhRHQ0WM6uPYX8I2fQr0Nfv9rOJnA0Ytej3RoQggBRDjptLS0UFRU\\nNOj7Z8yYwZIlS3pcLyoqYvv27aEMLeo0fNxA04yn4eBU+N9aOHi5/7H4+FMRjEwIIbpEZcl0dwUF\\nBRQVFZ118UC0lkwfPnaYR15+hN/t/B13nftDXnhUh9r8M//jJtODrF4t3QWEEMNDVCed8vJyMjMz\\nAxKOy+XCaDSSkhJcG/5oSzqapvGH3X/g/pfuJ8OYwarMVUwaN6nfY6aFECLSojbpVFZW0tbWhtls\\n9l9rbW2lsrKSDRs2BP160ZR09rv3s/BPC3n/0PtsmL2Bm6fcHOmQhBBiUKIy6bjdbpKSknp9zGQy\\nsWfPnqBfMxqSzolTJ1j95mpW/nkl9193P4VfK2Rs3NhIhyWEEIMWlUlnKAz3pPPXD/+KbYuN8845\\nj9xxP6TK8Z5/A+iiRVkyhSaEiAoRL5kW/XMfdbPUuZQ//P0P/Dzr50zcfyE//nHg+TjNzd5mnpJ4\\nhBDDnfRDGaY0TeO5d5/jirVXoKHx3r3vcfe0u3nqqZrTDmSD5ubHeeqpmghFKoQQgycjnWGoubWZ\\ne1+8l48Pf0xVXhXXf/V6/2M9D2TzOnp0VLjCE0KIMyYjnWHk+KnjPF77ONc9fR3WFCv1+fUBCQd6\\nO5DNSzaACiGigSSdYaJ2fy2pT1zKk1XPkLr9eziXe9j20hs97utxIBveDaALF2aGK1QhhDhjMr0W\\nYQe/PEhhTSF//NsW4pxf5+DLlRzEW0nXW4GA7/+fempZtw2g0nFACBEdpGS6U7hLpjVN49m3n8Xu\\ntHPnlXey86kxbP/Tqh73ZWcv46WXHg1LTEIIMdRkpBMBuw/upmBLAZ8f/5wX734R8wVmbi4p7vVe\\nKRAQQsQSWdMJoyMnjrBs+zJu/NWN3HH5Hbw5703MF3jb+EiBgBBiJJCkEyY1zTVMWz+NXQd38XbB\\n2yy6bhGjdF2jGCkQEEKMBLKm0+ls13Sqq2tZs2Zbj9Y0Bz4/wANbH+D1D15n7W1rmXXprH5fQzpE\\nCyFimSSdTmeTdKqra7n//q0BnQKMpge59eHjbPrs1/xw+g955BuPcM6Yc0IWrxBCRCNJOp3OJulk\\nZz/Mtm2PdV0471243YZe/wG1S15k2lemhSpMIYSIalK9FgL+1jSjv4CbfwrTn4Htj3H1+I8k4Qgh\\nRDdSSBAC/sqz6/8HJnwE696F+nwS4jsiG5gQQgwzMtIJgUWLsmhufojm1x4FzZvHvZVnt0Q4MiGE\\nGF5kTadTKKrXpPJMCCH6J0mn03A/OVQIIWKBrOkIIYQIG0k6QgghwkaSjhBCiLCRpCOEECJsorpk\\n2ul04nQ6SU5Oprm5GbPZzPz58yMdlhBCiD5EbdJxOp0oisLKlSv91ywWC263myVLlkQwMiGEEH2J\\n2um1srKyHtesVmuv14UQQgwPUZt0FEXB6XQGXNM0DYPBEKGIhBBCDCSmNoeaTCYWLFjA4sWLg36u\\nbA4VQoihFzNJx+Fw4HK52Lhx4xk9X5KOEEIMvagtJPCpqqqipqYGRVEGlXB8yeVMHxdCCBEomH+s\\nx8xIx+PxkJGRQXl5OWlpaX3eJ0lFCCFCb7CpJOIjHVVVB31vcnIyiYmJvT6WmJiIzWYjIyOD1tbW\\nPl+jr29MrE+vyfuLbrH8/mL5vcHIeX+DFdGk09LSQlFR0aDvnzFjRr97cDIyMnC73bhcLjIyMkIR\\nohBCiBCKaNJJSUlh06ZNQT9PVVXMZjMvv/wy06dP7/G4x+MJRXhCCCFCLCr36bjdbkwmE0ajMeC6\\nb6ouPT09EmEJIYQYQFQmnfT0dObOndtjjrSkpAS73c6UKVMiE5gQQoh+RXX1Wnl5Oc3Nzf6GnxaL\\nhXnz5p3Ra42UxT55f9Eplt9fLL83kPfX4/5oTjpCCCGiS1ROrwkhhIhOknSEEEKEjSQdIYQQYSNJ\\nRwghRNhI0hFCCBE2Ee+9JoToW0NDA/X19SQlJaGqKunp6THX4qmyshKDwRBz7wu8XfBVVaW5uRlV\\nVbHZbMyZMyfSYYWM0+nE6XT6t62YzWbmz5/f73Mk6fTjTL6h0STWfyB8ovVDTVVVioqK2LZtm/9a\\nXl4eRqORlJSUCEYWOk6nk/z8fCorKyMdSshVVVVhNBr9P1Mejwez2Uxra2tMfI44nU4URWHlypX+\\naxaLBbfb3W+PTDTRq5qaGs3pdAZcM5vNWmlpaYQiCq3KykqtoaHB/7Xb7dZMJpPmcDgiGFXo1dTU\\naAaDQXO5XJEOJWj5+flaVVVVwDWn06nl5uZGKKLQUVVVs9lsmsPh0EwmU1T++Qykt88Kh8OhKYoS\\ngWhCLycnp8dnpN1u10wmU7/PkzWdPpSVlfW4ZrVae70ejVRVDTh3KDExEbvdjs1mi2BUodPS0kJB\\nQQEtLS0kJSVFOpwzUlFR0aOPoNlsjolRQUpKChs2bIiJf/H3xu12s3Hjxh7Nh32j7X379kUgqtBS\\nFAWn0xlwTdM0DAZDv8+TpNOHM/2GRoOR8AMR7R9qbrcbt9vdI2Hq9XogNv6MYpler0dVVVpaWiId\\nypDZtGkTK1asCLhWWVnJ3Llz+32erOn0obcjFyorK1mwYEEEogmt7j8QvR0NISLPdxDhxIkTe31c\\nVVVpbDvM9XaYpNPpxGAwxOSfncPhwGKxsHjx4n7vk6QzSIP9hkaLkfYDEW3cbnekQxBDoKysjKVL\\nl0Y6jJCqqqqipqYGRVHYuHHjgPdL0hlAsN/QaBaLPxBCDBcOh4NJkybFzD9cfebMmcOcOXPweDxY\\nLBbKy8sD1otPJ0lnAMF+Q6NVrP5ACDEcqKqKw+Ggrq4u0qEMmcTERGw2GxkZGb3OpPjEfNLxnSY6\\nGMnJySQmJvb62GC/oeEWivc3nH8gQvXnF218p+K2t7f3uq5z+qm5YngrKipi+/btkQ5jyGVkZOB2\\nu3G5XH3ui4vppNPS0kJRUdGg758xY0a/m5oG8w0Np1C9v+H6AxHqP79ootfrMRqNqKoaUOyhqip6\\nvV7W3aJIQUEBpaWlfRaFRCNVVTGbzbz88su9FiOdXhnbXUwnnZSUlF6r0AZyNt/QcDrT99fdcP6B\\nCMX7i2ZWq5UdO3YE/B1saGggMzMzglGJYJSXl1NUVBTwjwSXyxX1XSXcbjcmk6nHiNs3M3H6/rLu\\nZJ9OL87mGxpN+vqBiOW9BdGkpKSEioqKgGsOh4OSkpIIRTR0tBg8wNi3ibe1tZWGhgYaGhpwOp1U\\nVFREdcIB72fg3Llze/y5lZSUYLfb+x2Jy3HVfVi1ahX5+fkBawSZmZlYLJYeG6KiUWVlJW1tbZjN\\nZv+11tZWKisr2bBhQwQjC73U1FTKysqGxZRosBobG9m4cSMzZszwj8BnzpwZ6bDOmsfjYcWKFaiq\\nSmVlJUajEavVSmZmZkz0/+ttY6+PyWRiz549YY5oaJSXl9Pc3OzvT2mxWJg3b16/z5Gk048z+YZG\\ng5HwAxHrH2pCRCtJOkIIIcJG1nSEEEKEjSQdIYQQYSNJRwghRNhI0hFCCBE2knSEEEKEjSQdIYQQ\\nYSNJR4jTNDQ0kJubi8FgQKfTYTAYMJvNrFq1KtKhnZHMzEx0uq4f9dzc3ICvhQgn+ZsnRDc2mw2L\\nxUJVVRU6nY7MzEwmTZpEU1MTdrudpKQkGhsbIx1mryorK9HpdFRVVQVcVxQFRVF6XBMiEiTpCNEp\\nNzeX8vJyDAYDDQ0NHDp0iK1bt7Jnzx5OnTpFYWEhbrcbs9k8bBMP9EwoFRUVNDc3RygaIQJJ0hEC\\n71HdVVVVmEwmWlpaeu0uvnLlSsrKygBvghquTm8ykpiYKEchiGFDko4Q4O/cXFJS0u8xD/Pnzyc9\\nPR1VVXG5XP7rp6+b+LjdbnQ6HQUFBQHXVVUlNzcXk8mETqcjKSmJvLy8Hh2+bTabv0+e3W73rzOl\\npqYGTKNlZmaSl5cHdK3ZtLe3B3w9kNLSUsxmsz+egoKCXjuOOxyOgPssFkvA90KI/kjSEQLvkQ4G\\ng4E77rhjwHttNhsANTU1Adf7Wyfp/piqqqSmprJ582ZSU1P960iVlZWYzeZez2vyTf3deeed5Ofn\\n+5OW78O+qKiI/Px8f3wOhyMgeQ60hmM2mykqKkKn0/njcTgcmEymgKlEu91OQUEB+/btIzc3F6vV\\n6j/jZzhPOYphRBNihGtubtYURdEsFsug7m9oaNAURdGysrL816xWq6bT6Xrc29bWpimKohUUFPiv\\n5efnazqdTnO5XAH3lpaWaoqiaJWVlQH3Koqipaamah6Px3/d6XRqiqJoNpvNf62iokJTFEWrqqoK\\neN2cnJyA2E7/uqSkRFMURdu+fXuv79NsNvuv6fV6LTU1NeA+Xyzd36MQfYnpk0OFGAy32w3Q49C+\\nvpztAVwFBQVkZ2f3OBcnLS0NgLa2th7POX3az3c20JkeuKd1W/dZsWIFmZmZpKen+78X4H2fGRkZ\\nuFwu2tvbmThxIh6Ph9TU1IDXysjIoKGhAb1ef0axiJFFko4Y8Xwflr6TYQfiu+9MP2TT0tL8Ccbt\\ndlNXV0dDQ4O/SKE3Q3larcfjoaamBoPB0OvjiqLQ2trKxIkTycnJobKy0j8taLVaSUtL67XwQoje\\nSNIRI55vhDPYpFNXVxfwvGC53W7sdjubNm3yr9+YzWbMZnOfI5e+Dt07U741Ht97zszMxG6393m/\\nLyFt2rSJVatWUVZWFnB/fn4+JSUlASftCtEbSTpCAFar1V823dvJok6nE6vVCuAfkcydO3fA121t\\nbe1xLSMjg8bGRmw2GzabzT9KcLlcVFZWns3bCJovmen1+kEfg71kyRKWLFlCe3s7NTU1lJWV4XA4\\nqKur8ydkIfoi1WtCgP9f7b39a9/tdpOVlYXFYqG0tJTGxkbMZvOgppQaGhp6vFZjYyO5ubmsX78+\\n4DW0MB7i6/u99Ho9iYmJOJ3OXu8zGAz+NRxVVbHb7f6KuYkTJzJnzhy2bdvmX9fxlWkL0RdJOkLg\\nHX3k5OT4y5m7l//q9Xo2bdpEQ0MDRUVFKIpCRUVFwPP1ej2apgXsV/FNo/Xm9GKB7veebfIZzPO7\\nl1DbbDba2tr8+3x8SktL8Xg8AXuMVq1a5S8Z705VVRRF6XePkxCAlEwL0V1ubq6mKIqmKIqm1+s1\\nq9Wqpaen+6/pdLoeZc2apmmVlZX+e2w2m5afn68ZDAYtKytLMxgMAaXNmZmZmqIoWm5urlZSUhJw\\nr6Iomslk0pxOp6ZpXSXT3culfU4v2/aVLptMJs1ut/uv5+TkaIqi9Pm1pmmayWTyPzcnJ8f/nk8v\\nI/fFbjAYtJycHC0/P1/T6/WaTqfTioqKzuA7LkYaSTpCnKahoUHLzc3VkpKSNJ1OpyUlJWkWi0Ur\\nLy/X3G63/4P39P0wDofD/+GdlJTk/xA2GAwBe1jcbrdms9k0g8Hg/2D3vZbNZtN0Op3/ft/Xg0k6\\nmtaVFJKSkvzXcnNzA/blnP61j91u18xms39fUF9JxG63ayaTKeB7c/r3Qoi+KJoWxolkIWLEE088\\nweLFiyMdhhBRR5KOEEKIsJFCAiGEEGEjSUcIIUTYSNIRQggRNpJ0hBBChI0kHSGEEGEjSUcIIUTY\\nSNIRQggRNpJ0hBBChI0kHSGEEGHz/wNYFsApVCsHzQAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZ0AAAEsCAYAAAAYSW5yAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X18k/W9//FXwl0RoUkKivc0qfc3o02LujlvaNq66dk5\\nB9qinnPmzpk01Q386YAWkcnx5mCL2xkylbbsbLodHbR1N1onbYLas+mmbYKKikCu1Ptb0qsdyF3b\\n6/dHmtD0PiU3Tfg8Hw8ewJUr6beF5t3v3eer0zRNQwghhIgBfbwbIIQQ4vghoSOEECJmJHSEEELE\\njISOEEKImJHQEUIIETMSOkIIIWJmYrwbEAkul4stW7aQlpbG3r17sdvtpKenx7tZQggh+kn40Kmr\\nq8PhcLBx48bgNbvdTlVVVRxbJYQQYjAJHTqqqlJSUoLP5wteq66uZtu2bXFslRBCiKHoErkiQVlZ\\nGXq9nrVr14Zcb2trY86cOfFplBBCiCEl9EKCmpoacnJyBlyXwBFCiPEpoXs6er2epqYmFEXBZDLh\\n8/kwmUwsXLgw3k0TQggxiISd01EUBQC3282yZcuC18vLy/H5fCxevDheTRNCCDGEhB1eU1UVALPZ\\nHHJ90aJFlJWVxaNJQgghRpCwoRMIm/6hk5mZiaqqtLW1Dfo8nU435C8hhBDRlbChYzAYQn7vLzD8\\nFg4JHiGEiK6EDR3w93KGCpf+PaAATdMG/SWEEMcbj8/DQy8/FNOPmdChY7fbaW1tDbnmcrkwGo2y\\nbFoIIYagHlRZ3ricSzddyuHuwzH9wTuhl0x3dHRgtVrZs2dP8Fp+fj6lpaUsWLAgrNcKDK0l8JdD\\nCCGG1dXTRXVrNfe+dC9fm5rNoT9lwD4DU6Z0sXRpPtddd2XU25DQoQPg9XqpqKjAYrHg8XgoLi5m\\n/vz5Yb+OhI4QIpn9afef+FHjjzh1+qn849SbWL/Sg8fzQPBxi2UV69cXRD14Ej50IkVCRwiRjHZ8\\nvoNljcvwql4eynuI68+5nmuvXU1j4/0D7i0oWM3zz98X1fYk9JyOEEKIwX2+/3NuffZW5j8+n2+f\\n/W123LqDfzj3H9DpdBw6NHhdgIMHJ0S9XRI6QgiRRA52HaTyL5Vc8MgFpExMYecPd7L00qVMmjAp\\neM+UKV2DPjclpTvq7ZPQEUKIJKBpGrVv1XLBIxfw8gcv8/L3X+a/r/1vTFNNA+5dujQfi2VVyDWL\\n5S6WLMmLejtlTqeXzOkIIRLVax+9xh1b72D/kf38JP8nzE8feTFVQ0MzGzY0cfDgBFJSulmyJE9W\\nr8WShI4QItF80PEBd227i23ebdx3zX3c/LWbmaCP/rzMsUjYKtNCCHG8qvvj85T98QHen93KmZ9m\\nsf47v6Aw89p4N2tUJHSEECJB9Gg93PnEXfz87Ufobv9HqPtflI4zKX9xFVMnnBCT4bFjJcNrvWR4\\nTQgxnr3Y9iJ3br0T764vUDfXwUeXhjweiz02kSA9HSGEGCcaGpp5+OFGDh2aGCxNc85lp7DCsYLt\\nn26nwlbBI0+9RXO/wIHY7LGJBAkdIYSIocGC5brrrqShoZnbb996tDRNSjt/M1yLtv1d7rpqJU8t\\nfIqUiSn8Ysrdg75uLPbYRIKEjhBCxMiAYAE8Hv9+mYcfbvRf1x+B7I1w5f107Pxnrv7r1ylbdfQ0\\n5KVL8/F4VvWrm3YXS5bIQgIhhBB9BIOlD4/nATZsWM3BQxPgnGchfxl0nAlPOODzi9GuWhNyf2Cx\\nwIYNq/vssbk2IRYRgISOEEJETf+htI8/3jfofV9O+BJv5la4aAts/Sns/hbgX9w02LDZddddmTAh\\n05+EjhBCRMFgQ2lTpy4KvenET+GaH/PmxU/yHxmLafyvKSh7vh18OJGGzUZLQkcIISKgf6/miy98\\neDyPhtxz4MAPmDq1lANH/hsu+xl8/Sekei1UzdvMon+8joaTmhN22Gy0ZJ9OL9mnI4QYq8F6NSkp\\n3+XgwSf63alx+rU2vpzbyomdp3LeR9dQvnhR0gXLcKSnI4QQx2iwBQIHD54ZetPpf4WCO+g0tvG8\\n/Q9cNeeqGLZw/Eiqow1UVaW0tDTezRBCHAcaGpopKLibq69ew6uvfjDIHfmkpNwKqe/BwpuguJBZ\\n76fxm6ueOm4DB5Ksp1NWVkZ7e3u8myGESHIDh9MG2bA5OZPUBUvpTj+fUz+cR8Y7/8Idt193XA2l\\nDSZpQkdRFNrb24NzM0IIES0Dh9PygVXAA6DrhsxfMsF2Bxee8Q0e/+6znD7j9Di1dPxJmtBxOp3k\\n5eXR1NQU76YIIZJQ39Vpr7/efzjN33s58ZJr0PLfYXLPZH5s/Qn/r7gk9g0d55IidJxOJzabDYfD\\nEe+mCCGSSCBoPvroCxRFx4EDG3sf6TeclvYu5D9E91nb+fW/bWLB+Qtk1GUISbGQQFEU0tPTZbmz\\nECJiAvM2jY3389Zbs/oEDgSH06b64Nrb4T+uIG3ffp78ei0LL1gogTOMhO/p1NfXs3jx4ng3QwiR\\nZELnbfq9VU64DHJq0V15Kqf4Lubct/+NH936T8f9IoHRSOjQUVU13k0QQiSpQ4f6vj129f6uwbl/\\nhPzl4Mvg67u+x59/t3Gwp4shJHTo1NbWhvRyRtOllW6vEGI4gXmcN97Y0+dqPsy+BQoUmPYZPLcB\\nCy+xcn1y1UWLhYQNHbfbTXZ2dsg1mdMRQoSj74q0zs4P6ej4Ox9/bOLgwceAZmAVnPhDmP84nPN7\\nJv1lDufsy+X0jD8nZV20WEjY2ms1NTV4PJ6Qay6XC0VRKCwsJCcnh4ULF4769aT2mhDHl9ANns3A\\nVvzHCdzvv2HiAfj6ErjsSaa8beYbPd/iztv+QYLmGCVs6Axm3bp1tLS0sHnz5rCfK6EjxPGjoaGZ\\nm29+hL17A+8Vd+MPmzWg+zFc9BTYVsKHl4KjgqsueYIXX1wTt/Ymk4QdXhvMl19+KaEhhBhWoIez\\nd+/5fa72vhWe0QYFl4OuB+qfhPevAAY/SE2MTVLs0/F6vZSWllJTU0N9fT2lpaW43e54N0sIMc4E\\nejj+IbWuow8YvoTCRVD4HLw6Gzb9LRg4/oPU8uLT4CSUVMNrx0KG14RIPn0rCrz33gccOnQ6R46c\\nCqwBmmHKH+GbEyHrMfjrXHjlT3CkBWgiJeU9LrhgOvfee3yddxNtSTW8JoQQ4A+b1auf4J13JnHw\\n4I34FwnMwj9vczfouyDzHbj6l7DndHjsFk7UdnLOxcuZPn0WKSmwZMktEjZRIKEjhEgqR1elzSYY\\nMjyAv3cDmI1QcCocuACebIJPsrBY7mL9+jIJmRiQ0BFCJLy+w2jvvvsxXV3PEAyZwNvczE8h/zpI\\n2wVNt8POA8AfSUurZP362yRwYkRCRwiR0NaseZTKyjc4cOAm/MNop/Q+0rtQ4IROuPqHcOFv4f9y\\nYPNb0D0ZoLeHI4ETSxI6QoiEE5iz2bXrE/bvnwT8nqPDaL3HDky4GubZ4IoW2JEBj+yBr94G7pNF\\nAnEkoSOESBiBsNmx4+8cOZIBzObo21jg9zw4fyHkvQ5fngS/vJFJHR+RkmLnrIvO4LTTpssigTiS\\n0BFCjFuBkGlr28f+/V9y5MiZaNqp+MOmt4JAcL9NF5zigoJ7YOoH8OxloJxNWtpOHv/dMgmZcSIp\\nNocKIZJPQ0Mzt9zyOG73ybS338bhw2lo2v/g/1k58PNyF5AP05fCP7XCTVfCmzfBxl2g/C8Wy2Ee\\nf1zmbMYT6ekIIcal1at/y6efnsLRZc+BsjV9KglM+iZ8/W649HVovQh+XoT+yDOcceZrnHfebKkE\\nPQ5J6Aghxp2GhmbeeWcfcFLvlYkcDZt80P0KLvkOzHfDB+dA9XeZtL+diy8+gXvvXS5BM45FLHQ6\\nOzuZMWNGpF5OCHGcCtRHO3jwbELma8gHVsGZ10LBy6D5oPYcprWfzLnn9nDvvSUSNgkg7Dkdt9vN\\nrbfeSltbGwAdHR1kZ2djMBiYMGECK1eujHQbhRDHiTVrHqWo6MneCtD5wCfAKv+fjb+F4r/Aguvh\\nlQtJ+d+ruef7N7Fv35O0tj4igZMgwir46XQ6ycvzV1t1uVzMnTuX0tJSqquryc3NRVEU2traqK2t\\nZcGCBVFrdDRIwU8h4mvNmke5774menp+x9HzbZphyia48jXIVND9dQ7nq3mccYqRJUvyJGgSUFih\\nk52djcvloqmpidzcXAD0ej02m43GxkYAjEYjGRkZvPbaa9FpcZRI6AgRPw0NzRQVPcKBA+cTrACt\\n/xNknQlX/yfsup6zPCfwSEWhBE2CC2tOJ3AUdCBwAmfW2O324D3FxcXU1dVFsIlCiGT38MONvYHT\\nO4eT8RXk/xb2Ab/+J9K6VB55/LsSOEkgrNBRVTXYIwBwOBwAwSE3AJ/Ph6qqEWqeECLZNTQ085e/\\neAALzDobCixgmAiND8Ou65k6tZTHa2WvTbIIa3jNarXS1tbG3r17AcjIyABgz549wXtMJhMmkynk\\nWiKQ4TUhYi+wAfTTzi/hGuACBzR/H1pOhO7J6PWvs3p1HmvW3BbvpooICWv1mt1up729nbPPPpuc\\nnBwURQkOrTmdTjIyMlBVlcLCwqg0djD19fWsW7eO0tJS8vPzqa+vj9nHFkKMXUNDM9/994f51NwG\\nP3gJuj+Bn2+Gv6VK4CSxsIbXSkpK8Hg8VFdX4/F4KCwsZPny5QA0NjaiKAo2m40HH3wwKo3tr76+\\nHrPZzMKFCwH/8m2r1YrP52Px4sUxaYMQYvQCtdTeetvDYYsObnLDZyfD/7wKez8FmoAJQDfnn3+S\\nBE4SCmt4bTiKogBgNpsj8XKjsm7dumDoBdTU1GC32+np6QnrtWR4TYjoCg6l6b+Agldgymmw9SLw\\nzsG/PDpUQcFqnn/+vpi3U0TXmEOnra0NRVFQVRWz2YzZbI5pRQJVVbHZbDidTlJTU4PXFUUhIyMD\\nRVGYM2fOqF9PQkeI6LrqH5bSPOkFMLfBtmtg++9A+wvwOP6q0Q8E7509+w42bfpnWTyQhMIug+N2\\nu1m8eDEulyvkuk6no7CwkIqKirDe7MfKYDCgKAper5e5c+dG/eMJIcZm3+F9VP6lkpe/tgleyYYN\\n18PhCfiH0QKh8gRwIxMndnPJJbPkcLUkFlZPx+v1YrFYAMjKymLRokWkp6ejKApNTU04nU6MRiNe\\nrzduddiqq6tZuXJlcIXdaElPR4jI6tF6+NETq3jknYfp8Rro3poBHd/sfTQf/9HSR3s3U6faqa39\\nFwmbJBdW6AQ2flZVVQ06UV9dXU1paSlFRUVs3rw5og0dLavVyo033siyZcvCep6EjhCR81LbS3y/\\ndjHvKx0ceWYefHRSvztmAwUEFg5MnryDlSvny8KB40BYoWMymTCbzbS0tAx5j9VqpbOzk927d0ek\\ngeGorq6mvr6erVu3DnlP382tg5HQEWLs9vj2sKJpBa5PXKS+msUbT50PBL7nemup8QT+Qp4T0esn\\nMXfuyTKcdhwJa5+OqqrB4bWhmM3m4Eq2WFIUherq6mEDRwgRHe0H2rlz651ctuky5p02j50/3Inx\\n40uASYSe9HklsAloAP7AN795kVSIPs6EFTq5ubnB0jdDcTqdZGZmHlOjxqK8vJxt27aNeJ+maYP+\\nEkKE70j3EX7+6s8575Hz2H94P2/d9hblV5Tj3PoqLtd2/LXUAr8GSknpjmVzxTgQ1vCaoihYrVbm\\nzZtHVVVVyCo1r9eL3W7H4XDQ2toa0+ApLS2lvLz8mFbNyZyOEKOnaRrP7X6OZU3LSDk0jYN/OJMP\\nWg9x4MAhenoO4D/x09TvWbIsWowQOvn5+QPmQDweD4qioNPpMJvNGAwGVFVFURQ0TSMrK4ucnBwe\\ne+yxqDce/JtB8/LyQgLH6XRiNptJT08f9etI6AgxOm9+9iZ3Nt7Jh50fkvnFNdSt/YIjh/uuVt0H\\nnM3AOZxDQArTps3g3HONMo9znBo2dIxGIzqdLuw3Yp1Oh8/nO+bGjaSuro729nasVmvwms/no66u\\njo0bN4b1WhI6Qgzvs32f8eMXfszv3/09q69czWfPaTxw7zY07cJ+dwbmb9YMeI2rrlrDiy8OvC6O\\nH8NuDm1vb49VO8KmqirFxcWDPjbSYgchxOgd7DrIz/76M9a+9CBTdp7B/ue+xpLlvwVSgZxBnjH4\\n/A3IHI4YQ0WC8cJgMIRdX00IMXqaprHlrS2UOcro/nAynb+cB74zeh/dB6QweMDk4y9ts4r+czhL\\nlvxztJstxrmwFhK43W42b96M1+tFVVUMBgNms5lFixYlfCkaGV4T4qi/ffg3vvfb7/PeR59y6JnZ\\n9HgygIv63DER2Anchj9g+gps/HwC2A90YbGcwPr135c5HDG60Bmq3lpfVquVmpqahA0fCR0h4P2O\\n97n+vxfy5r43wHkRvP410L4ArP3u7AI+BU7maMB8AhwAQK8/kalTT5QFA2KAEUPH6XQGj6POysrC\\nbreTnZ0drLnW0tJCVVUVbrcbnU5HU1MT8+fPj0njI0lCRxzPav/4PEs2l/PZ6W/Bqxnw8vlw+ILe\\nRz8ETu/3jMAQGsCpBM7AMRi8/OY3JRIyYkjDhk5HRwfp6emoqjpkvbWAQN01o9EYdrHN8UBCRxyP\\nunu6+ed7b+aZffWgnAbOOdB5GaHTve8APyB0GE2G0MTYDFuRoLq6GlVVWbFixYgncZaUlLB8+XLa\\n29t56KGHItpIIUTkbfNu47R7z+KZ95+Dp26E390AnafjD5y+lQSuAp4EbsZfR+1T4BVgHdOmfUVW\\nlolnn13Cnj2PS+CIEQ3b07FarWzfvp3u7tEvc9Tr9eTl5SVcDTTp6Yjjxa69u/jub/6DlvdddD9/\\nIbx9PhA48fcd/Bs7+w6fzQZOw7/RMwWd7ktuuOFCnnyyIuZtF4lvxM2hM2fODKtitMViQVXVhBti\\nk9ARyc53wMe//8rOs+//kZ7ms+DV86ArC/8qtIzeu04FXsQfPH0XCOhISZnGBRfMlIUB4pgMu0+n\\no6ODefPmhfWCZrN5VIU3hRCxcaT7CD94/Ef8Ylc1PTtOhReuha9SgPPxD5+diD9YADTgavxVoHcA\\nE5k9exqbNv1QgkZExIg9Hb1eH1avZSzPGQ+kpyOSSUNDM3evfpx3ul/n0JVvgToDtl4IX3wd/8+a\\nbfhXpPUdRtMROOcGJmKxnCgLA0TEDbuQwGaz0d7ezvbt20f1Ym63m46ODnJzcyPSOCFEeBoamrFY\\nFnL9Lfew/eI/ceiKXfB8JvxmMXxxBkcXCRzg6JHRgQUC+4GpWCwGnn32dlkYIKJi2J6Oy+UiOzsb\\ni8Uy4rxOR0cHVqsVRVFifrRBJEhPRySqhoZmVq9+grffVjg0aTLMfwfO2QsvfhNcJ0JPoCBnYO4m\\nH/gZ/uMHbiJwZDS8zo03niMLBERUDdvTycrKYvHixXg8Hs4++2yefvrpQe+rr68PBk5hYWHCBY4Q\\niWjNmkeZOvUarr/+p7jfPMKheZ/Abc1wYDr8/IfQcin0TOPo0ufA3M1W4P8BXwDrgJ1Mnermnnvy\\nJHBE1I2qDE5RURH19fWAf87GbDYHj6VWFCVYjbqwsJAtW7ZEt8VRIj0dkQgaGppZunQ9ivIBcAbQ\\nBRfrIPcF+MgIju9A++ccXY22m4EbOwNDaZOZOLGdVauuZc2a22L6eYjj16gLfjocDioqKnA6nQMe\\ns9lslJWVJfRcjoSOGK+OBs2nwAmAETgAZ6RBQQPoJsPWfHj/AP6w+RT/KjSAdo4Oox1d/jxp0lQu\\nvvgkWf4sYi6sKtMBiqKEVJlOBhI6YjwJzNO8+eY7dHUFgqb3FF/DLLA1wBk+cJ4Pb+aCFqgU0Pf/\\nb2A1WgcwA51uGiee2MOdd+ZKz0bEzZhCJxlJ6Ijx4Givpgd/aGjAZOBsmNINVzwLVg/8zQwvfxuO\\n+AgNGpClz2I8k9DpJaEj4iW0V3MS/hC5CP98zPmgUyCrHa5+AfbMgm3/AH8/D3/lgOm9rxIImkNA\\nilQPEONWwoeOy+WitbUVk8mEoihkZWWNaW5JQkfEUsgy50Mz8C8k1YALgQ+AdKANzIeh4Dk4kApb\\nV8Mnz+HvwZyNvx5aA4GgkXkakQgS9rhq8M8tlZeX09jYGLxWXFyM2WwmPT09ji0TYnChw2cmYAYh\\nvRoADsHMTyG/EWbqofE82HkG4MW/1Hk9/irP09DpUjCbZ8rwmUgYCd3TsdvtFBQUsGDBguA1p9NJ\\nVVVV2Eu3pacjomVgrwaOHv3cp1fD6XDCV3DVVrhIgT9nwKuXQfe/4Q+admAaMFnmaUTCSujQMZlM\\nuFwu5syZE7ymqiomk4menp6wXktCR0TDmjWPcv/92+juTgX24g+bQNBAsErAhJ0w72S44n9gRzq8\\nlAlfTQUUYCowlalTj7BiRYGsPBMJLWLDa52dncyYMWPkGyNEVdVgwPRlMBgAaGtrCwkjIWKpoaGZ\\n73//AT77bCIQqNDRhf9b7lDvnwGmwXmvQN7fYG8a/LIKvmwmsNR50qQ0macRSWXYMjiDcbvd3Hrr\\nrbS1tQH+mmvZ2dkYDAYmTJjAypUrI93GQfl8PoAhg05RlJi0Q4i+ggU3r7+fzz47AZhJYOny0bDp\\nLUdzypvwvefgGjc8dwU8aYEvNwMqU6dO5J57vs3hw7W0tj4igSOSRlg9HafTSV5eHuCfTwEoKyvD\\n5XKRm5uLoihUVlaSk5MTMs8SDaqqRvX1hQhXQ0Mz//qvNajqRPybOc/HP3wW6NX0hs30r2B+K2R8\\nCC9awD0LeiaSkpIqy5xF0gsrdMrKygBoampi7ty5AFRXV2Oz2YIryIxGI2vXro166IxVYO5GiEhq\\naGimqKiCAwcyOXpeTb8D0iZ1wdffhEvfhtbT4OdXw6GpsihAHFfCCp1AFenAPhi32w0c7fWAf8ly\\nXV1dBJsoxPh2001lPPXUbvx10fqfV/M46DS42AO5r8IHM6D666QcnMUFF0qvRhx/wgodVVVDegoO\\nhwMgOOQG/rmWWAx9BWq+DbWAYaiacEOtTpMekAhHaBWBWfhXpe3BHzj5wNvAk3BmJhT8J2g9UHcZ\\ns4/MYtNv5OhncfwKa8m01Wqlra0teBR1Roa/fPqePXuC95hMJkwmU8i1aMnIyKCuri441Af+3lh2\\ndnZwocFoyZJpMVpr1jzK2rUvcvjwdOBzwNr7yIf4qwrMBuPFYFsGp+8FxyWk7DmZshVyhIAQYa1e\\ns9vttLe3c/bZZ5OTk4OiKMGhNafTSUZGBqqqUlhYGJXG9mez2XjttddCrrlcrpCelxCRtGbNo9x7\\nbxOHD58DnAKkcfSQtO/ClMOQ9wwsvhk+mwU/v4Z7FtzMga/+KIEjBIAWphUrVmgGg0HT6XRaUVFR\\nyHWdTqfl5eWF+5JjpqrqgI+Xl5eneb3esF8L/4+oEWqZSBbPPvuSZjYv0PT6azT4ugbf1uCePr+K\\nNXhJQ/89jewCjWUmje/M1TjxTm3y5IXaPfc8Eu9PQYhxJWIVCQL7YmJ9vo7b7Wbz5s3BnpfVamX+\\n/Plhv44Mr4n+/Eugf9a7BHo6sA9IwX9iZ8CpYGmAgndg/0HYegl8eiKzZ+vZtEnmboTob8yh09nZ\\nic/nw2g0kpqaGul2xZyEjugvK+s23O69+Cs6g3/dzU7gNuBxmNUO+a+DaR80ngPvmtHp9nLDDRfy\\n5JMVcWu3EOPZmCoSBCoQWCwWWltbAf+k/kMPPRTxBgoRD2vWPMr27Sr+umeBigK9+25OeBqu2wvf\\n+xPsmQKPZqPbdRJZWSfyzDMrJHCEGEZYPR2v14vFYgEgNzcXp9OJw+Fg/vz5GI1GOjo6sFqtAyb3\\nE4H0dAT0PXqgm6NHDvT2dCZcDZfeBVe8AW9cAi9dAwcmYzB4+c1vSmQoTYhRCKunU1Hh/wmutbWV\\n2trakMfa29t58MEHaW1tjVn9NSEiKVDGRlEmAnPx77c5ArwLF7wMPyiCsybBL66H5y1wQMFieV8C\\nR4gwhNXTMZlMZGdn09jYGKzwHOjpBFitVjo7O9m9e3dUGhwt0tM5vg0sY9MF3A+nVkPBXTDlIGzN\\nAO/pchS0EMcg7IoEgeG1oZjNZurr64+pUULEytHhNI2QMjYz5kLuxWDeC9sqYPv3mJpyG7XP/osE\\njRDHIKzQyczMpKWlZdh73G43WVlZx9QoIaIlUL5m165P2L+/A5gFTMY/b7MHJn0F3/gc5v0UWhbC\\nhlPg8Afo9YWsWJEngSPEMQprTmfRokW0trbywgsvDFqrrLi4GEVRsNlsEWugEJFw9Jybn+F2a+zf\\nPxs4DbgQOB90E2Dux7DkEUh7Dap+BdvmwOET0Om2s3p1nlQUECICwt6nY7Vacbvd5OXl0dTURF5e\\nHgaDAYfDQXt7O2azOSZ11yJN5nSSV0NDM7fc8jiffrqPo3tuINjRP8sDBQ7oToOt6fDhycB+YDI6\\nnY8f//hbEjhCRMiYNodWVlaydu1aOjo6gtdSU1Ox2+08+OCDEW1grEjoJC//Jk8TA0aTTZ9D3jY4\\npQOazoO3LgeuBZqACUyevIOVK+dL4AgRQcdcBkdRFEwmEwaDIVJtigsJneQxcN7mdOA8gid4phyE\\nK/8Mc3fCyxnw1/nQdT3wBP4eThcWywlysJoQURCx2muJTkInORwdSgtc6TOkpp8P2avgyu3w7pmw\\n7VrYvxAJGyFiZ9jQ0ev1Qx5uFnha3zdrnU4X/L27uzsKzY0eCZ3EFujdvP76R/T0WPs8MhG4Bs5+\\nAPJd0DkHGs+Ezw4BB9DppnHCCdM591yj7LsRIgaGXTK9cOHCMb2onMIpYiV0n40R/xLoPv+tT/oY\\nCh6A1HehMQt2mYApTJ/ew1NPlUnICBFjMrzWS3o6iSXQs9mx4+8cOQKhq9KAafvgmmY43wsv5UBL\\nA/RMAmDqVDu1tbLJU4h4CGtzqBDjwZo1j1JZ+QYHDswGZhPy33jiN+CylfD1HfB6Bmz4dzj4T8C9\\nBFakrVgxXwJHiDgZ1ZyOx+Nhzpw5w87xBMicjoiW0ArQvwfW9D7SBWhw4Ttgc8Onp0PTbPB9BRwC\\nUpg2bYbM750yAAAfK0lEQVTM2wgxDgzb08nNzUWn02E0GoHRz/HInI6IpNChtInAxb2P9C6BPu0M\\nKPgxTOqCP1wLbf8bfO7s2XewadM/S9AIMU7InE4v6emMHw0NzTz8cCMfffQFHs8uDh1KR9NO7X20\\nTwXo1FrILYc5n8O2H8Drn4P2GaAnJeUEqQQtxDgUVuh0dnYyY8aMaLYnbiR0xoej8zU3AY/j32ez\\nmZChtMlXwDfuh5x34LXr4S/AYR/TpsnSZyHGu7AKfhoMBjZt2jTsPeXl5aSlpR1To0arvr6edevW\\nUVpaSn5+vhypkOAaGpqprHyJAwc2Ao3AKcD5vY92ge4wZB6BJUVgOAE2/gu8kI6+q5N77vkW+/Y9\\nSWvrIxI4QoxjI65eq6+vD276BP+poSaTadB7NU2jrq6O9vb2yLZyiHaZzebgPFPgqGyfz8fixYuj\\n/vFF5ATmbN588zO6ugIbOwP/NXvnbebMhIL74MgJ8NuH4KMPOVofTSpAC5EoRhxe0+vD6gwBYLPZ\\naGxsHHOjRmPdunUsX7485FpNTQ12u52enp6wX0+G12Kn75zNe+99wIED0+juPgeYRHC+hrv9N6ed\\nD3n/CSd3QdPN8Pb7wOcylCZEghoxdOrq6oJ/Li4upqSkZNjzcoxGI7m5uZFr4SBUVcVms+F0OklN\\nTQ1eVxSFjIwMFEVhzpw5Yb2mhE5sNDQ0c/vtW/F4CoCtQGClYyBo8v3Xp14OV5XBJV74y3fhb0bo\\nmiKVn4VIcCMOrxUWFgb/nJubS1FRUdRDZSQGgwFFUfB6vcydOzeubRHhefjhRjyeB/AHzAMcXSAA\\nkA/65yDnK7hyEbx9FjySRUr3Z0ydfoD09BO5996l0rMRIoGFVZGgqakpWu0Im8/nG3DN4XBgNBqH\\n7eXIHqL4OnQo8F+u35wNGpzTAflPgjoJfnUzaT0+Ht98m4SMEEkk7DI4TqeT2tpavF7vsPdt3bp1\\nzI0aq6qqKlauXBnzjyuG1n/+5quvAnOEgbDJh5N/CgVmmD4Vnq+CPd/yb+r8pQSOEMkmrH069fX1\\nFBUVjeresUzmH4vq6mrq6+vHHHYypxN5ofM3j+OvkxaYyymAE+th/n4452l46TxoTWPaVFkgIEQy\\nCyt0ApP0TU1NEZvXURRl1PempaWFLBzo+xrFxcW0tLSMuR0SOscu0Ks5dGginZ0fsmePj7///WmC\\nK9G43//bxCa4/L/g8lfQvX4a532ez5knzWTJkjwJGiGSXFjDa4qiUFJSErHA8Xq9lJeXj/r+nJyc\\nAcukwb8hddu2bRFpkxibo72aB4Bm/L2Z03sfDfw30+Ci34KtHD7OgZq3uPKSX/Oia008miyEiIOw\\nQic1NTWiE/Hp6els2bLlmF6jtLSUysrKpC3PM571na95992P6ep6pveRRvwr0wI9nC44/UO49nLQ\\nd8Hvfg3v+Xs0KSmJVY1cCHFswtr5WVJSwubNm+ns7IxWe8JSU1NDeXl5yGo1p9M54iIHcewCPZvG\\nxnzeemtmn0oCcPRnmXxI/SEUvgLFtfDaSVDzajBwZs++gyVL8mLediFE/ITV06moqEBRFKxWKxUV\\nFWRlZQ1ZEifaPY/AplWfzxdcPu3z+airq2Pjxo1R/dhisP02d/d5tAumdMIVz4P11/C3ufCHRei7\\n2zhhWjGTJk3r3XMjiwWEON6EFTqBgFFVNWTTaH/RPsRNVVWKi4sHfcxisUTt44qjBu63yQdWge5e\\nyDwE15wKnkJ47G34+2lYLHexfv33JGSEOM6FFTqjXS4d7Q2YBoMh5kuyRagpUwL7bAK/XwnmFig4\\nFQ5MZerv53J+6jSmZ9WQktLNkiXXSuAIIeQQtwBZMh2ekD04M/8X8j6GWW9D0zrMh1/j4fXfkpAR\\nQgwQ8dBxOp3U1dXx2GOPRfJlo05CZ3T67sXxHdjDp+e9ge+03Ux57VzmfH4FZ5xilP02QoghhR06\\nHR0dOByOQc/M0TSNiooKvF5vVOd0okFCZ2h9l0Yrio4Dhx+GnEfgm//FjA/O4rFFP+amf/pOvJsp\\nhEgAYc3peL1erFYrqqoOe19JSckxNUqMH6GbPlfBeTmQdyHsPQd+9RKdX1zAE+2rJXSEEKMSVuiU\\nlZWhqioVFRVkZmZit9uxWq3Y7XY0TaOsrIyZM2fKkuUkElwaPdsNBU/CtD/Ac4+AJz94z8GDE+LY\\nQiFEIglreM1kMpGdnR08FbSyspLa2lpee+01wL+U2Ww2s2nTJhYsWBCdFkfJ8T681neuZsqULi6/\\n/FReeeVjXtmxi7/nTIOz/wQvZIH7j9AT+rNKQcFqnn/+vji1XAiRSMKqSKCqasg+mKysLFpbW4N/\\nNxgMFBUVsXbt2si1UETd0eoC9/PSS2tobMzn/opWGg9O4e//+izsPxk2vAut5dBzT8hzLZa7pKqA\\nEGLUwhpeS09PD6kKnZ2dDcD27duDJ3haLBZqamoi2EQRbUerCwC6Hrj4J3TnuuGDy6H6l6C+AaQC\\n/hVpU6cuwmI5hdNOmy77b4QQYQkrdLKysnj66afZtm0b8+fPx2AwkJqaSlVVVXCJdEtLCwaDISqN\\nFdERrC5w5p+h4E7gI6jbAh98o/eOU4DVpKZ+wGWXncGSJT+QoBFCjEnYtdfq6+vJy8ujtraWBQsW\\nUFxcTFVVFT6fj/b2dhwOh6xeSzDdM76EomI4/a/gWAs73gbtG33uuBK4kssuk7kbIcSxCSt0zGYz\\ne/bsoaKigvT0dMAfRC0tLdTW1gJgs9moqKiIfEtFxHUc7OC//u+/eOPS32Bq+Rq+n++EIycAzUyc\\nWEpX19FViP65m2vj11ghRFKIWEWCwN6dRB1aO55Wr3X1dLHJtYk1L67h22d/m/vn34+7eQ8bNjRx\\n8OAEUlK6ueyyU/jrXz8J/l2qDAghIkFqr/U6XkJn656t/KjxR8yaNouf5v+UzFMy490kIcRxJKzh\\ntdLS0hErSGuahk6nS7jaa8nu7S/eZlnjMnb7dvNQ3kN859zvRL0auBBC9BdWT0evH3lbT2B4LXCw\\nWqJI1p7OF/u/YM2La9jy9hZWfXMVt+XcxuQJk+PdLCHEcSqsns5QQeLz+XC5XJSVlZGRkcHWrVsj\\n0jgxdoe6DrHh1Q1U/KWCGy+6kZ0/2EnaCWnxbpYQ4jgX0TmdQBkcu90e86oEqqpSXl4+5rpvydLT\\n0TSNp995mhWOFVw460Iq8yo5b+Z58W6WEEIAUVhIYLfbqaurY+/evZF82VF93Pb2drZs2TKm5ydD\\n6LR83MKdW++k41AHP8n/CTazLd5NEkKIEGENr42GTqcb9KydaFIUhfb29uN2YvzDzg9ZtW0VjZ5G\\n7rvmPv597r8zQT985ef+BT6XLs2XJdFCiKiLaOg4nU6qq6sxm82RfNlRfdy8vDyamppi+nHjbf/h\\n/ax7eR0bXt1AqbWUXT/cxfQp0we9t2/IdHZ+yCefzODTT38afNzjWQUgwSOEiKqwQkev1w/bmwgM\\nTZWVlR1bq8LgdDqx2Ww4HI6Yfcx469F6+PXrv2bVtlV886xv4ipxcZbhrCHvDz2IDeBu4P6Qezye\\nB9iwYbWEjhAiqsIKndzc3GEfNxgM3HDDDSxcuPCYGhUORVHIzc1N6LmYcDS/18wdW+9g8oTJ1BbV\\ncvkZl4/4nJAq0sBQ/+xyGJsQItrCCp3xNnxVX1/P4sWLw3pOos77eHweVjhW0PJxCw/mPsgNF90w\\n6s8lWEU6qGvQ+1JSuo+xlUIIMbywDnEbTwK13pKdelBlWeMyLt10KdmnZLPzBzu58eIbwwrPKVP6\\nh0w+sCrkihzGJoSIhbB6Ok6nk6amJtxuN+AfTjObzSxatCh4iBvA008/PerjqvseCjeStLQ0UlNT\\nAaitrQ3p5Yz2TXioYbjx1gPq6umiqqWKe5vv5TvnfIcdt+1g9omzR3zeYKvSli7Nx+NZ1WeI7Upm\\nz/4Vp576A6ZPn9Vb0FMOYxNCRN+oQsftdlNUVDRkQFRUVGC1WqmtraW1tZWioiIqKytZtmzZsK/r\\n9XopLy8fdWPnzZvHsmXLcLlcwVNLA5JlTkfTNP60508sa1zGqdNPpfFfG/na7K+N6rkDFwz4V6Wt\\nX1/A+vUFbNiwuk/V6O9JyAghYm7EzaFutxur1Qr4Tw612+1kZ2cHj65uaWmhqqoKt9uNTqdD0zRs\\nNhuNjY1Ra3RNTQ0ejyfkmsvlQlEUCgsLycnJCXsxw3jYHLrj8x38qPFHvKe+x0P5D3Hd2deF1QMr\\nKLibxsb7B7kuh68JIcYJbQRGo1HT6XRadXX1sPdVVFRoOp1O0+v1mqqqI71sxFVWVmrFxcVjfj6g\\njeLLERWf7ftMsz9j12ZVztIe/uvD2uGuw2N6nauuukcDbcCvq666J7INFkKIMRp2IcG6detQVZUV\\nK1aMuEosUH5G07TgKaKx9OWXXybcENvBroNU/LmCCx65gKkTp7LzhztZcukSJk2YNOzzGhqaKSi4\\nm6uvXkNBwd00NDQDgy0Y8JNVaUKIcWO4RMrKytL0ev2IydXU1KTpdDqttrZW0+l0WnZ2doQycWSK\\nomh2u10zGo2aXq/X7Ha75nK5wn4dYtjT6enp0Tbv2KzN+dkc7R+f+kft3S/fHfVzn332Jc1iuSuk\\nJ2Ox3KU9++xLQzy2Unv22Zei+NkIIcToDTunYzQamTlzJrt37x4xvFRVxWAwYLVaaWtri3nBz2MV\\nqzmdVz96lTu23sFXR77ip/k/5Zr0a8J6/kjzNg0NzSHHTssx00KI8WTY1WsdHR3MmzdvVC8UOLzN\\nZDKxffv2Y29Zkvmg4wNWOleyzbuN++ffz81fu3lAUc7RFOEcuNHTL1BN4LrrrpSQEUKMW8OGTmpq\\nKi0tLWG9YEtLSzCABOw7vI+KP1fwaMuj3JZ9G7uW7OLEyScOuG+o5c4QWoRT5m2EEIls2IUENpuN\\n9vb2Ufdc3G43HR0dI9ZoOx5093TzP+7/4dyfn4tX9bLdvp375t83aODAYPXRAkU4Q0sPLV2aj8Ui\\n1QSEEIlp2J7OypUrqa+vJzc3F6/Xy4wZM4Z9saKiouDzjmcveF/gzsY7OWHSCfxu0e+Yd9rIQ5Qj\\nDZsFBHo9oRs9pZqAECIxDBs6WVlZLF68mJqaGqxWKxUVFYOWt6mvr6esrCy4OTMzMzNqDR7Pdu/d\\nzfKm5bz+2etU2CoouqBo1Js7wxk2k3kbIUSiGtVx1UVFRdTX1wP+FW1msxmz2YyiKMFTOwEKCwvH\\nfFx0vEVi9dovXL/gy6++5PbLbidlYkpYzx1sTsdiuYv166UXI4RIHqMKHQCHw0FFRQVOp3PAYzab\\njbKysoSeyxkPZXBkubMQItmNOnT6UhQluC8n1kdTR8t4CB0hhEh2YwqdZCShI4QQ0Zewh7gJIYRI\\nPBI6QgghYkZCRwghRMxI6AghhIgZCR0hhBAxI6EjhBAiZiR0hBBCxIyEjhBCiJgZtuBnInC5XGzZ\\nsoW0tDT27t2L3W4nPT093s0SQggxiIQOnbq6OhwOBxs3bgxes9vtVFVVxbFVQgghhpKwoaOqKiUl\\nJfh8vuC16upqtm3bFsdWCSGEGE7C1l4rKytDr9ezdu3akOttbW3MmTMn7NeT2mtCCBF9CbuQoKam\\nhpycnAHXxxI4QgghYiNhezp6vZ6mpiYURcFkMuHz+TCZTCxcuHBMryc9HSGEiL6EnNNRFAUAt9vN\\nsmXLgtfLy8vx+XwsXrx4yOeO9vhoIYQQkZeQoaOqKsCAA+QWLVpEbm7usKETLQ0NzTz8cCOHDk1k\\nypQuli7Nl1M/hRCin7iHTqDXMhppaWmkpqYGw6Z/6GRmZqKq6rCLCYYaPjuWHlBDQzO3374Vj+eB\\n4DWPZxWABI8QQvQR19Dxer2Ul5eP+v6cnByWL1+OwWAACP7en6IoMV1Q8PDDjSGBA+DxPMCGDasl\\ndIQQoo+4hk56ejpbtmwZ03PNZvOQ4dK/BxRthw4N/mU8eHBCTNshhBDjXcIumbbb7bS2toZcc7lc\\nGI3GmC+bnjKla9DrKSndMW2HEEKMdwkbOiUlJQPK3ZSXl1NTUxPztixdmo/FsirkmsVyF0uW5MW8\\nLUIIMZ4l7D4d8M8JVVRUYLFY8Hg8FBcXM3/+/DG91rHu02loaGbDhiYOHpxASko3S5bkyXyOEEL0\\nk9ChE0myOVQIIaIvYYfXhBBCJB4JHSGEEDEjoSOEECJmJHSEEELEjISOEEKImJHQEUIIETMSOkII\\nIWJGQkcIIUTMSOgIIYSIGQkdIYQQMSOhI4QQImYkdIQQQsSMhI4QQoiYkdARQggRMxI6QgghYkZC\\nRwghRMxI6AghhIiZifFuwLFwOBy43W4A9u7di8ViYfHixXFulRBCiKEk7HHVLpcLr9fLwoULg9fq\\n6+vx+XxjCh45rloIIaIvYYfXqqurQwIHYOHChTQ1NcWpRUIIIUaSsKHT0tKC1+sdcF1V1Ti0Rggh\\nxGgkbOjYbDby8vJCgsfhcFBcXBzHVgkhhBhOws7pAGRnZ+NyuaiqqiI9PZ2Ojo4BQ26jJXM6QggR\\nfQkdOgD5+fk4HA6ysrJwOp2kpqYOe38gXIQQQkRGODGS0KFTU1NDTk4Oe/fupaioCJPJRFNTE+np\\n6UM+R0JHCCEib7RREvfQURRl1PempaUFezKlpaWUl5czZ84cADo6OigqKkJRFPbs2RN2O5J9eE0+\\nv8SWzJ9fMn9uIJ9ff3HdHOr1eikvLx/1/Tk5OSxfvjy4Qi0QOACpqak0NjaSnZ2N0+kkNzc30s0V\\nQghxjOIaOunp6WzZsiXs57W2tmKxWAZ9zG63y7JpIYQYpxJyybTZbMbj8Qz6mKqqWK3WGLdICCHE\\naCRk6AQWCjidzpDriqKwd+/ekGE3IYQQ40fcFxIci5qaGjweD2lpaQAYDIYxF/yUyb7EJp9f4krm\\nzw3k8xtwfyKHjhBCiMSSkMNrQgghEpOEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzMS1IoEQYngu\\nl4vW1lZMJhOKopCVlZV0JZ7q6uowGo1J93kB1NfXoygKHo8HRVGw2+1jPn5lPHI4HDgcDtLS0vB4\\nPFit1hG3rUjoDGMsX9BEkuzfEAGJ+qamKArl5eU0NjYGrxUXF2M2m4etpJ5IHA4HJSUl1NXVxbsp\\nEVdfX4/ZbA5+T3V0dGC1WvH5fEnxPuJwONDpdDz44IPBa9nZ2aiqyvLly4d+oiYG1dTUpDkcjpBr\\nVqtVq6ysjFOLIquurk5zuVzBv6uqqlksFq26ujqOrYq8pqYmzWg0ak6nM95NCVtJSYlWX18fcs3h\\ncGhFRUVxalHkKIqi2e12rbq6WrNYLAn57zOSwd4rqqurNZ1OF4fWRF5hYeGA98iysjLNYrEM+zyZ\\n0xlCVVXVgGs2m23Q64lIURQyMzODf09NTaWsrAy73R7HVkWO1+ultLQUr9eLyWSKd3PGpLa2lqys\\nrJBrVqs1KXoF6enpbNy4MSl+4h+Mqqps3ryZjo6OkOuB3nZbW1scWhVZOp0Oh8MRck3TNIxG47DP\\nk9AZwli/oIngePiGSPQ3NVVVUVV1QGAaDAYgOf6NkpnBYEBRFLxeb7ybEjVbtmxh7dq1Idfq6upY\\ntGjRsM+TOZ0hDHbkQl1dHbfeemscWhNZfb8h5s6dG+/miEH4fD4AZsyYMejjiqJIYdtxLvBv2JfD\\n4cBoNCblv111dTXZ2dksW7Zs2PskdEZptF/QRHG8fUMkGjkTKjlVVVWxcuXKeDcjourr62lqakKn\\n07F58+YR75fQGUG4X9BElozfEEKMF9XV1cycOTNpfnANWLhwIQsXLqSjo4Ps7GxqampC5ov7k9AZ\\nQbhf0ESVrN8QQowHiqJQXV1NS0tLvJsSNampqdjtdnJzcwcdSQlI+tBRFGXU96alpZGamjroY6P9\\ngsZaJD6/8fwNEal/v0RjNpsB6OzsHHReJ/C4SAzl5eVs27Yt3s2IutzcXFRVxel0DrkvLqlDx+v1\\nUl5ePur7c3Jyht3UNJovaCxF6vMbr98Qkf73SyQGgwGz2YyiKCGLPRRFwWAwyLxbAiktLaWysnLI\\nRSGJSFEUrFYrL7zwwqCLkfqvjO0rqUMnPT190FVoIzmWL2gsjfXz62s8f0NE4vNLZDabjddeey3k\\n/6DL5SIvLy+OrRLhqKmpoby8POSHBKfTmfBVJVRVxWKxDOhxB0Ym+u8v60v26QziWL6giWSob4hk\\n3luQSCoqKqitrQ25Vl1dTUVFRZxaFD1aEh5gHNjE6/P5cLlcuFwuHA4HtbW1CR044H8PXLRo0YB/\\nt4qKCsrKyobtictx1UNYt24dJSUlIXMEeXl5ZGdnD9gQlYjq6upob2/HarUGr/l8Purq6ti4cWMc\\nWxZ5GRkZVFVVjYsh0XC53W42b95MTk5OsAc+f/78eDfrmHV0dLB27VoURaGurg6z2YzNZiMvLy8p\\n6v8NtrE3wGKxsHv37hi3KDpqamrweDzB+pTZ2dnccsstwz5HQmcYY/mCJoLj4Rsi2d/UhEhUEjpC\\nCCFiRuZ0hBBCxIyEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzEjoCCGEiBkJHSH6cblcFBUVYTQa\\n0ev1GI1GrFYr69ati3fTxiQvLw+9/ui3elFRUcjfhYgl+Z8nRB92u53s7Gzq6+vR6/Xk5eUxc+ZM\\ntm/fTllZGSaTCbfbHe9mDqqurg69Xk99fX3IdZ1Oh06nG3BNiHiQ0BGiV1FRETU1NRiNRlwuF3v3\\n7mXr1q3s3r2b7u5uVqxYgaqqWK3WcRs8MDBQamtr8Xg8cWqNEKEkdITAf1R3fX09FosFr9c7aHXx\\nBx98kKqqKsAfUONV/yIjqampchSCGDckdISAYOXmioqKYY95WLx4MVlZWSiKgtPpDF7vP28SoKoq\\ner2e0tLSkOuKolBUVITFYkGv12MymSguLh5Q4dtutwfr5JWVlQXnmTIyMkKG0fLy8iguLgaOztl0\\ndnaG/H0klZWVWK3WYHtKS0sHrTheXV0dcl92dnbI10KI4UjoCIH/SAej0ciCBQtGvNdutwPQ1NQU\\ncn24eZK+jymKQkZGBk8//TQZGRnBeaS6ujqsVuug5zUFhv5uuOEGSkpKgqEVeLMvLy+npKQk2L7q\\n6uqQ8BxpDsdqtVJeXo5erw+2p7q6GovFEjKUWFZWRmlpKW1tbRQVFWGz2YJn/IznIUcxjmhCHOc8\\nHo+m0+m07OzsUd3vcrk0nU6n5efnB6/ZbDZNr9cPuLe9vV3T6XRaaWlp8FpJSYmm1+s1p9MZcm9l\\nZaWm0+m0urq6kHt1Op2WkZGhdXR0BK87HA5Np9Npdrs9eK22tlbT6XRafX19yOsWFhaGtK3/3ysq\\nKjSdTqdt27Zt0M/TarUGrxkMBi0jIyPkvkBb+n6OQgwlqU8OFWI0VFUFGHBo31CO9QCu0tJSCgoK\\nBpyLk5mZCUB7e/uA5/Qf9gucDTTWA/e0PvM+a9euJS8vj6ysrODXAvyfZ25uLk6nk87OTmbMmEFH\\nRwcZGRkhr5Wbm4vL5cJgMIypLeL4IqEjjnuBN8vAybAjCdw31jfZzMzMYMCoqkpLSwsulyu4SGEw\\n0TyttqOjg6amJoxG46CP63Q6fD4fM2bMoLCwkLq6uuCwoM1mIzMzc9CFF0IMRkJHHPcCPZzRhk5L\\nS0vI88KlqiplZWVs2bIlOH9jtVqxWq1D9lyGOnRvrAJzPIHPOS8vj7KysiHvDwTSli1bWLduHVVV\\nVSH3l5SUUFFREXLSrhCDkdARArDZbMFl04OdLOpwOLDZbADBHsmiRYtGfF2fzzfgWm5uLm63G7vd\\njt1uD/YSnE4ndXV1x/JphC0QZgaDYdTHYC9fvpzly5fT2dlJU1MTVVVVVFdX09LSEgxkIYYiq9eE\\ngOBP7YP9tK+qKvn5+WRnZ1NZWYnb7cZqtY5qSMnlcg14LbfbTVFREY899ljIa2gxPMQ38LEMBgOp\\nqak4HI5B7zMajcE5HEVRKCsrC66YmzFjBgsXLqSxsTE4rxNYpi3EUCR0hMDf+ygsLAwuZ+67/Ndg\\nMLBlyxZcLhfl5eXodDpqa2tDnm8wGNA0LWS/SmAYbTD9Fwv0vfdYw2c0z++7hNput9Pe3h7c5xNQ\\nWVlJR0dHyB6jdevWBZeM96UoCjqdbtg9TkIAsmRaiL6Kioo0nU6n6XQ6zWAwaDabTcvKygpe0+v1\\nA5Y1a5qm1dXVBe+x2+1aSUmJZjQatfz8fM1oNIYsbc7Ly9N0Op1WVFSkVVRUhNyr0+k0i8WiORwO\\nTdOOLpnuu1w6oP+y7cDSZYvFopWVlQWvFxYWajqdbsi/a5qmWSyW4HMLCwuDn3P/ZeSBthuNRq2w\\nsFArKSnRDAaDptfrtfLy8jF8xcXxRkJHiH5cLpdWVFSkmUwmTa/XayaTScvOztZqamo0VVWDb7z9\\n98NUV1cH37xNJlPwTdhoNIbsYVFVVbPb7ZrRaAy+sQdey263a3q9Pnh/4O+jCR1NOxoKJpMpeK2o\\nqChkX07/vweUlZVpVqs1uC9oqBApKyvTLBZLyNem/9dCiKHoNC2GA8lCJImHHnqIZcuWxbsZQiQc\\nCR0hhBAxIwsJhBBCxIyEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzEjoCCGEiBkJHSGEEDEjoSOE\\nECJmJHSEEELEzP8HWpCiemPQ0ukAAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 13\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"Mann-Whitney U test. NOP\\\", scipy.stats.mannwhitneyu(x,y)[1]*2)\\n\",\n \"print(\\\"Unpaired T-test\\\", scipy.stats.ttest_ind(x,y,equal_var=False)[1])\\n\",\n \"print(\\\"Median test\\\", median_test(x,y))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Mann-Whitney U test. NOP', 0.087346603341420845)\\n\",\n \"('Unpaired T-test', 0.25717460096222738)\\n\",\n \"('Median test', 0.18389510355041561)\\n\"\n ]\n }\n ],\n \"prompt_number\": 49\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Non-Equal variance and Non-Normality. USE: Median test\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" x = [np.random.lognormal(1,1.3) for _ in range(200)]\\n\",\n \" y = [np.random.lognormal(1.5,1) for _ in range(200)]\\n\",\n \" \\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAakAAAEsCAYAAAB5UUwwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U9sI9edJ/AvZbs94yRisbq9nvF6ZqSighnsHCKSYrAB\\ndgczTdKXAXYTy6J82pOlYvbcbrKBnBYLSCXn7lYxWGByk0gamACDXUtkB4M9LBCRxUyQnWy2zUdt\\n/k4yLaooJx13PFHtQWFFJVJqskWyHqXvBxDaevVK9bNU6m9X1av3Ao7jOCAiIpLQlN8FEBERnYch\\nRURE0mJIERGRtBhSREQkLYYUERFJiyFFRETSet7vAjqKxSJCoRASiUTP7ZZlYXt7Gzdv3sTBwQF0\\nXcfs7Kxne61Wg6qqEEIgGo2e+7WIiGgySBFS5XIZq6urKBaLPbcXi0WUy2Xcv3/fbdN1HZubmwAA\\nIQRyuRx2dnbc7el0GpqmeYKMiIgmi6+3+5rNJjKZDJrNJlRV7dnHtm2srq56Aso0TTx48MD93DAM\\nZDIZz366riObzY6mcCIiGouALDNOzM3NwTRN3L5929OezWYxNTWFtbU1T/v+/j5mZmYAAKqqwrIs\\n93PgJNxUVcXx8fGoSyciohGRfuBEPp9HPB7vau8Ekm3bbiCdpigKgJMwIyKiySTFM6mL2LaNYDCI\\nfD4PVVXRarWgqioWFxcBAK1WCwAwPT3dc38hhOcKi4iIJofUISWEAADU63XcuXPHbc/lcmi1WlhZ\\nWYFt236VR0REIyb17b5OAGma5mlfXl7moAgiomtA6iupTjidDalIJALbti/9vCkQCJy7TZLxJERE\\n15rUV1KdwQ+dP88SQrgBdnR01LPP2YDr10UBRkRE4yF1SAEnIdN5NtVrm6IoPfsIIaAoyoWDJhzH\\n6flBRERykD6kdF1HrVbztFmWhVAo5AZQMpnE3t5eV59UKjWuMomIaASkCqleVzGrq6vu9EcduVwO\\n+Xze/dwwDBQKBU8f0zRhGMZoCiUiorHwdcaJdruNtbU1CCFQLBahaRqSySRSqZT7HhRwMn2SYRgI\\nh8NoNBpIp9NdM1PU63VsbW0hHo9DCIFYLNbVp1+d51G89UdE5C9ppkWSCUOKiEgOUt3uIyIiOo0h\\nRURE0mJIERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0GFJERCQthhQREUmLIUVERNJiSBERkbQY\\nUkREJC2GFBERSet5vwvoKBaLCIVCSCQSF/azbRu5XA7379/3tFuWhVqtBlVVIYRANBp96tciIiK5\\nSRFS5XIZq6urKBaLT+2bzWZxeHjoaRNCIJfLYWdnx21Lp9PQNA2zs7NDr5eIiMbD19t9zWYTmUwG\\nzWYTqqo+tb8QAoeHh+56Tx2GYSCTyXjadF1HNpsdar1ERDRe0ix6ODc3B9M0L1xNt7Nk/O7uLra3\\nt912VVVhWRZmZmbcNtu2oaoqjo+PB66Fix4SEclhYgZOVCoVJJPJrnbbtt1AOk1RFADA/v7+OMoj\\nIqIRkOKZVD+EEEgkEl1XN61WCwAwPT197n6nr7AG8fd/Xx2o/5/+6R/hD/7glWc6FhERdZuIkCqV\\nSlhZWem5zbbtkR13f/9f99338PCfoKoHDCkioiGSPqRGGUJPo6p/2HffJ08eA3gyumKIiK4h6Z9J\\nFQoFLC4uup+fHdl3GYFAoOcHERHJQeqQqtfrWFhY8LSdfSalaRoA4OjoqOfX6GwnIqLJI/Xtvmq1\\nikajga2tLbfNsiz35d14PI7FxUVomgYhBObn591+QggoinLhoInzhpjzaoqISA5Sh1SvwRLvvvsu\\nqtUq1tfX3bZkMom9vT1PSFmWhVQqNZY6iYhoNKS63dfPy7OPHj3q6mcYBgqFgqfNNE0YhjHU+oiI\\naLx8nXGi3W5jbW0NQggUi0VomoZkMolUKuUZLAGcTKFkGAa2t7fRbrexsrICXdcRiUQAnDy/2tra\\nQjwehxACsVjswtkrLtK53fc3f/NPfe/z85/v4y//8gYWFiLPdEwiIuomzbRIMumE1H/+L/ef0vN3\\nHj36MZb/KoY3vvgfR1UWEdG1I/UzKb+pM6/23bf9SfdtSCIiuhypnkkRERGdxpAiIiJpMaSIiEha\\nDCkiIpIWQ4qIiKTFkCIiImkxpIiISFoMKSIikhZDioiIpMWQIiIiaTGkiIhIWgwpIiKSljQTzBaL\\nRYRCISQSia5tpVIJQgg0Gg0IIaDretdSHpZloVarQVVVCCEQjUZ7fi0iIpocUoRUuVzG6uoqisVi\\n17ZSqQRN09xQarfbiMViaLVa7sq9neXkd3Z23P3S6TQ0TcPs7Ox4/ieIiGjofL3d12w2kclk0Gw2\\noapqzz5CCHdhQwAIBoPIZrPQdd1tMwwDmUzGs5+u68hms6MpnIiIxsLXkJqdncX9+/fdK6KzbNvG\\n1tYW2u22p71zG29/fx8AUCgUEI1GPX1isVjPKzMiIpocUg+cUBQFQgg0m81z+9i2Ddu2u67EFEUB\\n8LsgIyKiySN1SAFAq9XC/Py8p61cLiMUCmFmZgatVgsAMD093XN/IcTIayQiotGQPqR62dzcxL17\\n9wCcXEkREdHVNHEhZZombt26hTt37vhdChERjZgUQ9D7JYSAaZqoVqtD+XqBQGAoX4eIiEZjoq6k\\ncrkcHjx44GnTNA0AcHR01HOfznYiIpo8ExNSmUwGGxsbXQMkFEWBpmldAySEEFAUBTMzM+d+Tcdx\\nen4QEZEcJiKk8vk8crmcJ3AqlYo7ND2ZTGJvb8+zj2VZSKVS4yyTiIiGTKqQ6nUV03kht9VqwbIs\\nWJaFcrmMQqHgTnlkGAYKhYJnP9M0YRjG6IsmIqKR8XXgRLvdxtraGoQQ7sSxyWQSqVQKi4uLsG0b\\n6XS6577hcNj972AwCMMwkMvlEI/H3bn8LrrVR0RE8vM1pILBINbX18/drigKjo+P+/pakUjEM8cf\\nERFNPqlu9xEREZ3GkCIiImkxpIiISFoMKSIikhZDioiIpMWQIiIiaTGkiIhIWgwpIiKSFkOKiIik\\nxZAiIiJpMaSIiEhaDCkiIpIWQ4qIiKTl6yzopxWLRYRCISQSia5tlmWhVqtBVVUIIRCNRrv69dOH\\niIgmixQhVS6Xsbq66i5weFpnbaidnR23LZ1OQ9M0d9HDfvoQEdHk8fV2X7PZRCaTQbPZhKqqPfsY\\nhoFMJuNp03Ud2Wx2oD5ERDR5Ak6vNdt9MDc3B9M0cfv2bU+7qqqwLMuzyq5t21BV1V0QsZ8+gwgE\\nAgCAr3z9G33v03z4HXwp8udY/NIXBz4eERH1JvXACdu23bA5TVEUAMD+/n5ffYiIaDJJHVKtVgsA\\nMD093XO7EKKvPkRENJmkDinbtofSh4iIJpMUo/v80nn2REREcpL6SoqIiK43qUNK0zQAwNHR0bnb\\n++lzHsdxen4QEZEcpA4pRVGgaVrX4AchBBRFwczMTF99iIhoMkkdUgCQTCaxt7fnabMsC6lUaqA+\\nREQ0eaQKqV632gzDQKFQ8LSZpgnDMAbqQ0REk8fXGSfa7TbW1tYghECxWISmaUgmk0ilUlhcXHT7\\n1et1bG1tIR6PQwiBWCzWNTNFP336xRkniIjkIM20SDJhSBERyUGq231ERESnMaSIiEhaDCkiIpIW\\nQ4qIiKQ10Nx9c3NzA8935zgOAoEAHj58ONB+REREA4VUJBJBs9mEZVlu2+zsLFqtFtrtNoCTWSLO\\nLtnOiVyJiOhZDBRS9+7dw8LCAqLRKPL5PCKRiLvNsiysrKxgf38fxWKxK6iIiIgGNdAzqfX1dSiK\\ngkql4gkoAIhGo6jVajg+PkYulxtqkUREdD0NFFLlchmpVArBYPDcPslkEuVy+dKFERERDRRSjuM8\\ndTn2ZrN5qYKIiIg6BgqpZDKJWq2G999/v+f2UqkEy7IQi8WGUhwREV1vAw2cMAwD5XIZS0tLePPN\\nN5FKpaBpGhqNBnZ3d1EsFt1+RERElzVQSGmahkqlgmw2i0Kh0LU8hqZp2Nzc7BpUQURE9CwGCing\\nZBTf7u4uhBCwLAtCCHcZ92g0OooaAZwM2qjX6wCAg4MDhMNhrKysePpYloVarQZVVSGEQDQaRSKR\\nGFlNREQ0WgOHVMetW7ewsLDw1NF+w2BZFtrtNt555x23rVQqIZ/Pu0ElhEAul8POzo7bJ51OQ9M0\\nvrNFRDShBp67r16vY2FhAYqiIBwOo1arATiZMumrX/3q0AsETlbZPb0IIgAsLi5id3fX/dwwDGQy\\nGU8fXdeRzWZHUhMREY3eQCHVbDYRi8VgWRYSiYRnufeDgwPcvXsX8Xh86EVWq9WeQ9tt23b/u1Ao\\ndN1ujMVi7mAOIiKaPAOFVGfUXq1W6xo0cXh4iPX1ddRqNdy7d294FQLukvKng6pcLiOdTgM4CSvb\\ntqGqqmc/RVEAAPv7+0Oth4iIxmOgkNre3kYymTx39N7du3cRiUSGfvXSmY4pHA4jn8+jXC6j3W7j\\n7bffBgC0Wi0AwPT0dM/9n/YCMhERyWmggRO2bSMcDl/YR9M0lEqlSxXVS7Vaxeuvvw5d1xGNRlGp\\nVDx1ERHR1TPQlVQkEkG1Wr2wT71eH8lQ9Hw+j42NDXf4eywWu/QUTIFAoOcHERHJYaCQWl5eRq1W\\nwze/+c2ef5mn02kIIZBMJodWIABkMhmkUinMz88jkUig2WxC0zSkUqmhHoeIiOQyUEh1njklEgl3\\n0IJhGFheXsbNmzdRLBahaRrW19eHVmDnVt7MzIzbFgwGsbOzA0VR8ODBA2iaBgA4Ojrq+TU6289y\\nHKfnBxERyWHg96RqtRrW19fxrW99CwCwu7uLQqGA4+Nj3L17Fx9++OFQC6zVauc+B9N1HbZtQ1EU\\naJrWNUBCCAFFUTwBR0REk2PgkAJOrqgODw9xfHyMDz/8EK1Wyx2CPmydCWx7sW3bff6VTCaxt7fn\\n2W5ZFm8JEhFNsIFCKp/Pdy3ToWma+z7SKHSmNDo9mg84uUo6ODhwr5IMw+h6d8s0Tc7ITkQ0wQLO\\nAA9hpqamEAqFcHBwMMqaesrn82g0Grh58yaAkxd1z04wW6/XsbW1hXg87o4AvH379sDH6gwK+crX\\nv9H3Ps2H38GXIn+OxS99ceDjERFRbwO9J/X222/ja1/7Gr797W9jfn5+VDX1dDaQeolEIlwmhIjo\\nChkopEzTxNzcHGKxGDY3N7GwsABN086d6YGIiOgyBgqpztx4juNgdXXVbT/9zpTjOAgEAvjNb34z\\npBKJiOi6Giik+l1AkLM2EBHRMFwYUrlcDp///OfxxhtvAEDX6DkiIqJRunAI+sbGBra2trra8/k8\\nvvzlL4+sKCIiIuAZX+bd2dmBaZrDroWIiMjjmUIKAOe4IyKikXvmkOLgCCIiGrVnDikiIqJRY0gR\\nEZG0GFJERCStp77MWy6Xsby87GmrVCpwHKer/bReQ9eJiIgG8dSQOjw8PPcl3ote7mVIERHRZV0Y\\nUtVqdVx19MWyLGxvb+PmzZs4ODiAruvuelOd7bVaDaqqQgiBaDTa91ROREQknwtDqrPqrQyKxSLK\\n5TLu37/vtum6js3NTQAniyDmcjns7Oy429PpNDRN8wQZERFNjokYOGHbNlZXVz0BZZomHjx44H5u\\nGAYymYxnP13Xkc1mx1YnEREN10SE1NraGnRd97Strq5id3fX/bxQKHRd+cViMRSLxbHUSEREwzcR\\nIZXP5xGPx7vaZ2ZmAJxcadm27a531aEoCgBgf39/1CUSEdEIDLSelF9s20YwGEQ+n4eqqmi1WlBV\\nFYuLiwCAVqsFAOeuECyEcAONiIgmh/QhJYQAANTrddy5c8dtz+VyaLVaWFlZgW3bfpVHREQjJP3t\\nvk4AaZrmaV9eXr70oIhAINDzg4iI5CB9SHXC6WxIRSIR2LbN501ERFeY9CHVGfzQ+fMsIYQbYEdH\\nRz37nA24Dsdxen4QEZEcpA8p4CRkOs+mem1TFKVnHyEEFEXhoAkiogk1ESGl6zpqtZqnzbIshEIh\\nN4CSyST29va6+qRSqXGVSUREQzYRIbW6uupOf9SRy+WQz+fdzw3D6Jrw1jRNGIYxlhqJiGj4pB+C\\nDgDBYBC7u7vIZDIIh8NoNBrI5XK4ffu2p49hGMjlcojH4+5cfrzVR0Q0uSYipABgdnbWM3dfL5FI\\nBJFIZEwVERHRqE3E7T4iIrqeGFJERCQthhQREUmLIUVERNJiSBERkbQYUkREJC2GFBERSYshRURE\\n0mJIERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0JmYW9NNs20Yul+uaFd2yLNRqNaiqCiEEotEo\\nEomET1USEdFlTWRIZbNZHB4eeto660ft7Oy4bel0GpqmYXZ2dtwlEhHREEzc7T4hBA4PDxEIBDzt\\nhmEgk8l42nRdRzabHWd5REQ0RBMXUpVKBalUCo7jeNoLhQKi0ainLRaLoVgsjrM8IiIaookKqUql\\ngmQy2dVu2zZs24aqqp52RVEAAPv7++Moj4iIhmyiQkoIgdnZ2a6rqFarBQCYnp4+dz8iIpo8ExNS\\npVIJKysrPbfZtj3maoiIaBwmYnTfqELo7OCLy3r8y1/ihz/84UD7vPLKK7hx48ZQ6yAiuiomIqQK\\nhYLnKmrY4TIMv/fSp/Dw8UM8/s4v+t7nydETvPHv38Brr702wsqIiCaX9CFVr9exsLDgaTv7TErT\\nNADA0dFRz+dSne1nnf06Hc8Sgi++9BJennkBr/7Jq33v85OHPxn4OERE14n0IVWtVtFoNLC1teW2\\nWZblvrwbj8exuLgITdMghMD8/LzbTwgBRVEwMzPjQ+VERHRZ0odUr8ES7777LqrVKtbX1922ZDKJ\\nvb09T0hZloVUKjWWOomIaPgmZnTfaY8ePeq6VWcYBgqFgqfNNE0YhjHO0oiIaIikv5I6rdlswjAM\\nbG9vo91uI5PJQNd1RCIRBINBGIbh3gLs3A7krT4ioskVcM4bPXCNdQZOfOXr3+h7n9bhT/Fnf/YJ\\nZv7kj/ve5ycPf4K/nv9rju4jIjrHRN7uIyKi64EhRURE0mJIERGRtCZq4ITsPvn1J/jFL/qfceLx\\n48c4Pj4eYUVERJONITUkL774Ej5sHKLR+EHf+7R+9BP8u9mf4Y//uP/BFkRE1wlDakg+9VIQn3op\\nONA+9o8/GlE1RERXA59JERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0GFJERCQthhQREUlrYt6T\\nKpVKEEKg0WhACAFd17G4uOjpY1kWarUaVFWFEALRaBSJRMKniomI6LImIqRKpRI0TXNDqd1uIxaL\\nodVquSv3dtaP2tnZcfdLp9PQNA2zs7O+1E1ERJczEbf7hBCIRCLu58FgENlsFrquu22GYSCTyXj2\\n03Ud2Wx2bHUSEdFwSR9Stm1ja2sL7Xbb0965jbe/vw8AKBQKiEajnj6xWAzFYnEsdRIR0fBJH1KK\\nokAIgWazeW4f27Zh2zZUVe3aF/hdkBER0WSRPqQAoNVqYX5+3tNWLpcRCoUwMzODVqsFAJienu65\\nvxBi5DUSEdHwTURI9bK5uYl79+4BOLmSIiKiq2ciRvedZZombt26hTt37lzq6wQCgSFVREREozBx\\nISWEgGmaqFarfpdCREQjNnG3+3K5HB48eOBp0zQNAHB0dNRzn872sxzH6flBRERymKiQymQy2NjY\\n6BogoSgKNE3rGiAhhICiKJiZmRljlURENCwTE1L5fB65XM4TOJVKxR2ankwmsbe359nHsiykUqlx\\nlklEREM0ESHVeSG31WrBsixYloVyuYxCoeBOeWQYBgqFgmc/0zRhGMbY6yUiouGQfuCEbdtIp9M9\\nt4XDYfe/g8EgDMNALpdDPB535/LjrT4iosklfUgpioLj4+O++kYiEc8cf0RENNkm4nYfERFdTwwp\\nIiKSlvS3+640B/jHf9xHu93f7UwAeP75AL7whc/hxRdfHGFhRERyYEj56NOfeQW2/VlMTb3a9z4f\\nffRdRCIfM6SI6FpgSPno+edvYHr6FhTlX/W9z+PH/JER0fXBZ1JERCQt/rN8whwe/hzf+z/fw2c+\\n85m+97nxwg189rOfHWFVRESjwZCaMP/vZ9/H//xBE9PB3gs89nL86BjhcBhTU7xwJqLJwpCaQDdf\\nuYmXX3m57/4/fvTjEVZDRDQ6DCkfOXDQ+JGFH/zsf/e9zy+etIHAH46wKiIieTCkfBR85WX86slH\\n+BU+6nufG6+9iN//1O+PsCoiInkwpHz0/I0beP7GjYH2+fiTl7jsPRFdGwypa+Af/uH7+G+P//tA\\nAydmZkK4ffvfjrAqIqKnu1IhZVkWarUaVFWFEALRaBSJRMLvsnz30Ue/RiiUxHPP9ffj/vjjX+DR\\nI2vEVRERPd2VCanO+lE7OztuWzqdhqZp7sKI19nU1HN47rnn+u5LRCSDK/PijGEYyGQynjZd15HN\\nZn2qiIiILuvKXEkVCgXcu3fP0xaLxdyl56+K3/wmgO9+tznQ86WPP/kE9e/9DwTQ34CLJ09+BeXT\\nBwD+6hmrJCIajisRUrZtw7ZtqKrqaVcUBQCwv79/ZZaRV0Jz+PhXvx5on9c+9woeP3fUd//HvzzC\\n40c/xI9+9KOBjjM9PY3p6f5nwrhKjo+P8dOf/hSO4wy0n6Io+PSnPz2iqogm35UIqVarBQDn/gUp\\nhLgyIfXC8y/ihecHXKZjwNeqAs8FYP/y+/i7b/9d3/s8+dUTzL82j7/4wl8MdrAr4ujoCN/4xncx\\nNfVK3/t8/PEv8YUvHODzn//cCCsjmmxXIqRs2/a7hCtl6rnnoL52C69+tv91rlo/bw18FfEsavUa\\nrO8PNvJQ/N8f449uzeOFF17oe5+XX/49fPGLg40MnZp6Ca++Ot93/3/+5x/CcVoDHYOut1arhb/9\\n2/+Ff/mXwfZLJv/NxA4guxIh9aye9lLsf/1P/2FMlchpw+8CiGjiDPsfq1dmdB8REflv2DPiXIkr\\nKU3TAJw8F+j1XKqz/azzEr/zTR7H7at+sab+yVgXa+oPa+qfjHWNYsq2K3ElpSgKNE2DEMLTLoSA\\noihXZtAEEdF1cyVCCgCSyST29vY8bZZlIZVK+VQRERFdVsCR6VrxEtrtNpaWljzTIr3++uswTXPg\\nKymZL6NZ09PJWBdr6g9r6p+MdY2ipisTUgBQr9extbWFeDwOIQRisRhu37498Ne5Lj/8y5KxJkDO\\nulhTf1hT/2SsiyE1Jtflh39ZMtYEyFkXa+oPa+qfjHUxpIiI6Fq5MgMniIjo6mFIERGRtBhSREQk\\nLYYUERFJiyFFRETSuhJz9w2LZVmo1WpQVRVCCESjUSQSgy3XcFmlUglCCDQaDQghoOs6FhcXpanT\\ntm3kcjncv39fiposy8L29jZu3ryJg4MD6LruWZJg3HWVy2XU63UAwMHBAcLhMFZWVrpqHmVNxWIR\\noVCo59fs59ijqu+iuvw67y+q6bRxnvdPq8mPc/6imkZ+zjvkOI7jNBoNJ5VKedqWlpYcIcTYaigW\\ni45lWe7ntm074XDYMU1TmjpXV1edpaUlT5tfNRUKBUfX9a76/KqrVqs5xWLR01YsFsf689vd3XVC\\noZBTqVS6tvVz7FHVd1Fdfp33F9V01rjO+6fV5Mc5f1FN4zjnGVK/tbq66pRKJU9buVzuOjFHaWNj\\no6vNNE0nEAi4n/tZZ6PRcJaWlpx0Ou1p96Omw8NDJxQKedo2Nzedubk53+o6+5dHx+njjaomIYSj\\n67pjmqYTDod7/oXSz7GHXV8/dY37vO+nptPGcd73U9O4z/l+ahrHOc+Q+q1QKOQ0m01P2+HhoecX\\nZZQODw+dWCzm2LbtaW80Gk4gEHBr87NO0zQd0zS7Ti4/arp7966Ty+W62k/XMe66YrFYz38dnv5X\\n5DhqOu8vlH6OPcr6etXl93nfT0iN+7w/ryY/z/nzahrHOc+BEzi532zbNlRV9bQrigIA2N/fH3kN\\niqJACIFms3luHz/rrFQqSCaT0tSUz+cRj8e72juTCftRVzKZRCqV8vwMy+Uy0um0bzV19HNsP+rj\\ned+/63rOM6QAtFotAOi5YCKArnWqRlnH/Py8p61cLiMUCmFmZsbXOoUQmJ2d7ZqTy6+abNtGMBhE\\nPp9HqVRy//SzrvX1dSiKgnA4jHw+j3K5jHa7jbffftu3mjr6ObZf9fG87891Pec5ug8nP3xZbW5u\\n4t69ewD8q7NUKnWN1unwo6bOiV2v13Hnzh23PZfLodVqYWVlxbfvVbVaxeuvvw5d1xGNRlGpVNxt\\nfp5n/Rxbpt8Dnvde1/mc55WUxEzTxK1btzwn5bjJ9BdXR6cmTdM87cvLy8hms36U5Mrn89jY2MDu\\n7q67XMxFt7KoG8/7btf5nGdISUoIAdM08cEHH/haR6FQ8Lyv0pmK30+dX9Szv7CRSAS2bY/lGWIv\\nmUwGqVQK8/PzSCQSaDab0DSNq0MPgOd9b9f5nGdI4Xc/+KOjowu3j1Mul8ODBw961jGuOuv1OhYW\\nFjxtZ+/N+/G96zx07fx5lhBi7HV1/qV7ehXoYDCInZ0dKIqCBw8e+Hqe9XNsGX4PeN73dp3PeT6T\\nwskPXtM0CCE8D3CFEFAUZeDl5y8rk8lgY2Oj62HjuOusVqtoNBrY2tpy2yzLghACuVwO8Xgci4uL\\nvnzvOsfs9fU1TRv796pWqyEcDvfcpus6bNv29Tzr99h+/h7wvL/YdT3nGVK/lUwmsbe35/lGWpY1\\n9ls1+XweuVzO88OrVCrQNA2zs7NjrbPXQ+N3330X1WoV6+vrbpsf3ztd11Gr1XD79m3PMTsjwsZd\\nl6ZpKBQKPbfZtu0e08/zrJ9j+1Ufz/unu7bnfP+vc11ttm13Td2RSqW6XkIbpUKh4Jim6dRqNfdj\\nd3fX81a333XevXu366VGP2rqTJ1z9pin32wfd126rjvlctnT1mg0nGw2O9aawuFwVx39HnuU9Z1X\\nl5/n/Xk1nTXO8/6in59f5/x5NY3jnOfy8afU63VsbW0hHo+7o1RO/6tllHq98NYRDofx8OFDX+ts\\nNpswDAPQlOBxAAAEhElEQVTb29tot9tYWVmBruuIRCK+1xQOh9FoNJBOp7uOOe668vk8Go0Gbt68\\nCeDkVtXZf5mPoqZ2u421tTUIIVAsFqFpmvui5ekBAP0ce5j1Pa0uP877fr9XwPjO+35rGuc5329N\\noz7nGVJERCQtju4jIiJpMaSIiEhaDCkiIpIWQ4qIiKTFkCIiImkxpIiISFoMKSIikhZDioiIpMWQ\\nIhoyy7IwNTXVNZP2WeVyGVNTU+5S2/1aWlrC1BR/del64JlONGTRaBSKoqBer6Pdbp/brzM551tv\\nvTXwMfxe34hoXBhSRCOwuroKx3Gwvb19bp/t7W0EAgG88cYbY6yMaLIwpIhGYHl5GQCwubnZc7tl\\nWWi323jzzTfHWRbRxGFIEY1AJBKBpmnn3vLrLKjXCTPgZCG4paUlhMNhTE1NQVVVpNNpNJvNrv1P\\nzwudSqV6PqOybRtTU1PIZDJd2zY2NhCLxdzjZDKZnsch8htDimhEdF0/95afaZqeW31CCMzNzeH9\\n99/H3NwcdF3HwsICisUiYrHYhc+2gIufUZ3dFovFkMvlMDU15R7HNE2Ew2HU6/Vn+D8lGh2GFNGI\\ndG7lnb3l1+tWn2EYCAQC2N3dxQcffID33nsPOzs7MAwDtm2jXC4PpaaNjQ3U63VUKhXs7e25x6nV\\nagB6r0pL5CeGFNGIzM7OIhKJdN3y63WrL5PJoFAodC0E11lc7/DwcCg1ra2tIZVKIRqNwrZt92N2\\ndhaJRAKWZeHo6GgoxyIahuf9LoDoKnvrrbdQr9dhmibeeecdAECxWOwa1ReJRNxAsm0b1WoVlmWd\\nO/DiWbXbbezu7iIUCvXcHggE0Gq1MD09PdTjEj0rhhTRCK2uriKbzWJrawvvvPMOhBBoNptYWlry\\n9LNtG9ls1l2mHDh5dhSLxYY2oEEIAeBkoEU2mz2333kBRuQHhhTRCAWDQUSjUfeWX7FYBHAyqOK0\\nRCKBer0OXdeh6zrm5+cBAJVKxd1nUK1Wy/O5qqoAAEVRum4rEsmKz6SIRqwzys80TWxtbSEQCHhC\\nwrZt1Ot1LC0t4b333nMDCvAONR+UZVmezxVFQTAYPHcQRigUwtzc3DMfj2gUGFJEI9aZm29zcxP1\\nev3cF3jPDo7o3AIEusPq9LByRVHgOA4qlUrPfU/TdR2Hh4dd8wVubGyg3W73fKeKyE+83Uc0YsFg\\nEMlk0r2COXurT1EUd3s6ncbCwgIajQYKhQLi8TiAkyHqmqYhkUgA8IbWW2+9hVKphFQq5U7H1Nn3\\nbPCtr6+jWCyiWCxibm4OkUgEQgjU63XEYjHcuXNnlN8KosE5RDRyxWLRCQQCztTUVM/ttm07uq47\\noVDICQQCzsLCglMqlRzHcRxd152pqSknk8k4juM4S0tLXV/HNE0nHA47gUDAUVXVyeVyjuM4TigU\\ncvc7LZvNOrFYzAkEAs7c3Jzbn0g2Ace5xE1vIiKiEeIzKSIikhZDioiIpMWQIiIiaTGkiIhIWgwp\\nIiKSFkOKiIikxZAiIiJpMaSIiEhaDCkiIpLW/wfN3Mv8uQph8wAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 50\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print('Mann-Whitney U test test. NO', scipy.stats.mannwhitneyu(x,y)[1]*2)\\n\",\n \"print('T-test. NO', scipy.stats.ttest_ind(x,y)[1])\\n\",\n \"print('Median test', median_test(x,y))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Mann-Whitney U test test. NO', 0.0087839417344925171)\\n\",\n \"('T-test. NO', 0.63251493042679674)\\n\",\n \"('Median test', 0.58075022224762773)\\n\"\n ]\n }\n ],\n \"prompt_number\": 51\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Compare 2 paired samples\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Imagine we want to check if there are difference in GFP expression after we add salicylate in non-growing cells.\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"USE: Wilcoxon signed-rank test\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" x = [np.random.randn() for _ in range(200)]\\n\",\n \" y = [np.random.randn()+0.2 for _ in range(200)]\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U1sG2eeJvCnaH3YsU0WabeT2I1esaT0zHT37JofCtBA\\nA7sTkgEGGMzBsqScZ2xRudsmfVigF1jAotKXvWwsyoM99GEhkcxpZxptFZ1ZoHeRji3KyU5nJh96\\nqaQnTie2SkXZ7diWxNqDhowpUjJLLrKK0vMDBERv1Sv+LYV6VPV+lGQYhgEiIiILuewugIiI9h6G\\nCxERWY7hQkRElmO4EBGR5RguRERkOYYLERFZ7sDPf/7zn9tdhKqqSKfTWFhYwC9/+Ut89dVXCIVC\\n1eNCCIyMjODUqVPw+Xy4c+cOUqkUJEmCoig2Vk5ERI1Idq9zUVUVkiQhEolU28LhMEZHR3Hx4kUA\\nm+EyMDBQPS7LMq5du4YzZ860vV4iIno222+LTU1N1bVFo9GadkmSoKoqdF2HEAKapjFYiIgczPZw\\nqQTH0wzDgNfrrWtzu93o6+trY3VERLQbXXYXMDs7W9eWzWbx5ptv2lANERFZwfZw2SqdTiMcDuPC\\nhQs17UII6LoOANA0DT6fD0NDQ3aUSEREz+CYcMnlcpibm4MkSZiZmak55vP5AKAmTEZGRuraiIjI\\nGWyfLbZVqVRCJBLB9PQ0AoHAtufl83nE43F89tlnbayOiIiaYfuA/lYejwfxeLxmanIjfr8fQgis\\nrq42PC5J0rYfRETUWo4LFwCIRCLQdR03btwAAExOTtadU7lVJoQw/fUZMERErWVruAgh4PV6cfv2\\n7YbHK+takskklpaWao5pmgYA267QNwyj4QcREbWerQP6uq6jv7+/LiAqVyPBYBB9fX2YmpqqW9+i\\nqipCoRDcbne7yiUioibZeuUSDAYxOjpad0WRSqWQSCSqgeLz+VAsFqvHdV1HOp3G9PR0O8slIqIm\\nOWK22PT0NBYXF3Hs2DEsLi4iHA7j3LlzNefkcjkIIbC8vAxd15FMJne1Wr8y3uKAfzYR0Z7liHBp\\nJ4YLEVHrOXK2GBERdTaGCxERWY7hQkRElmO4EBGR5RguRERkOYYLERFZjuFCRESWY7gQEZHlGC5E\\nRGQ5hgsREVmO4UJERJZjuBARkeVsfZ4L0V6ysrKCjz4qPvvELfz+l3Hy5MstqIjIPgwXIousrKzg\\n/ffX4PV+v+k+q6vL6O7+huFCew7DhchChw4dwbFjp5o+v1zeALDSuoKIbMIxFyIishzDhYiILOeI\\n22KqqkJV1epjjkOhEM6fP19zTqFQwPz8PHw+H4QQCAaDiEQiNlVMREQ7sT1cVFWFJEmYmJiotoXD\\nYei6josXLwIAhBBIJpO4fv169ZyRkREoigK/39/2momIaGe23xabmpqqa4tGozXtqVQK4+PjNefE\\n43EkEomW10dERObZHi6SJEFV1Zo2wzDg9Xqrn2cyGQSDwZpzQqEQstlsW2okIiJzbL8tNjs7W9eW\\nzWbx5ptvAgB0XYeu6/D5fDXnyLIMAFhaWkJfX1/L6yQioubZfuWyVTqdRjgcxoULFwAAmqYBANxu\\nd8PzhRBtq42IiJpj+5VLRS6Xw9zcHCRJwszMTLVd13UbqyIiot1wTLgMDQ1haGgIpVIJ4XAY09PT\\nCAQCdpdFRES74LjbYh6PB/F4/LnXsEiS1PCDiIhaz3HhAgCRSAS6ruPGjRtQFAUAsLq62vDcynEi\\nInIOW8NFCAGv14vbt283PK7rOmRZhqIodQP3QgjIsrztTDHDMBp+EBFR69kaLrquo7+/v+7qoxIk\\nlbUt0WgUN2/erDmnUCggFou1p1AiIjLF1nAJBoMYHR2tu6JIpVJIJBLVq5JUKoVMJlNzTjqdRiqV\\nalepRERkgmQ44F7R9PQ0FhcXqxtXhsNhnDt3ruachYUFzMzMYHBwEEIIhEIhvPbaa6ZfqzKo74B/\\nNu0xQghcv/4tTp36cdN97t79Aj/5yQpeffU/tLAyovZzxFTkrTsgNxIIBDg1mYioQzhythgREXU2\\nhgsREVmO4UJERJZjuBARkeUYLkREZDlHzBYj2gsMw8Djxw/x6NEfm+7z+PFDbGxstLAqInswXIgs\\n8uWXX+K9f7kO371C031Kpbs4cnQAP/1p8NknE3UQhguRRcrlMuBxwffDk033ebi0ivXyegurIrIH\\nx1yIiMhyDBciIrIcw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIco4Il1wu\\nh7feegvj4+N4/fXXkcvlao4LIRCLxZDP56HrOoQQSCaTyOfzNlVMREQ7sX37l1wuB0VRMDQ0BAAo\\nlUoIhULQNK3m8cf5fL4aJrIs49q1a4hEIrbUTEREO7P9ykUIgUAgUP3c4/EgkUggHo9X2yRJgqqq\\n1asWTdNw5swZO8olIqIm2Bouuq5jZmYGpVKppr1yRbK0tFRtMwwDbrcbfX19bayQiIh2w9ZwkWUZ\\nQggUi0U7yyAiIovZPuaiaVpdm6qq8Hq9NVcpQgjoul7t4/P5quM0RETkLLaHSyNTU1O4fPly9XOf\\nzwcANWEyMjJS10ZERM5g+4D+Vul0GsePH8eFCxeqbR6Pp2bmGADE43EkEoltv44kSQ0/iJzIMAxT\\nH0RO56grFyEE0uk0bt269cxz/X4/hBBYXV2F2+1uQ3VE1nN1deGff/87TP3Pqab7GIaBV3/0KkKB\\nUAsrI3o+jgqXZDKJGzdu1LVPTk7i0qVLNW2VW2VCCJw+fbquz3Z/3fHqhZzksNuDF39wAKd+eKrp\\nPstfL+Ph44ctrIro+Tnmttj4+DgmJyfrrkIqq/GfnpYMfDcRQFGUdpVIRERNckS4TE9PI5lM1swO\\ny+fzKBaLUBQFU1NTdetbVFVFKBTiLTEiIgey/bZYNpsFsHklUrka0TQN2WwWV69eBbB5C6xYLMLv\\n9wPYXHyZTqdx7do1e4omIqId2Rouuq5XpxRv1d/fX/3voaEh5HI5ZLNZLC8vQ9d1ZLNZrtYnInIo\\nW8NFlmWUy+WmzuV6FiKizuGIMRciItpbGC5ERGQ5hgsREVmO4UJERJZjuBARkeVsX+dC1GpPnjzB\\n/fv3Tfdzu93o7u5uQUVEex/Dhfa8jz/+DP/4j39Ab++hpvs8evQQf/mXP8Arr7zSwsqI9i6GC+15\\n5bKBgwf78NJLze9D9+WXn3Bre6LnwDEXIiKyHMOFiIgsx3AhIiLLMVyIiMhyDBciIrIcw4WIiCzH\\ncCEiIssxXIiIyHIMFyIispwjVujncjkIIbC4uAghBOLxeN2TJwuFAubn5+Hz+SCEQDAYRCQSsali\\nIiLaie3hksvloChKNUxKpRJCoRA0TcP58+cBAEIIJJNJXL9+vdpvZGQEiqLA7/fbUjftbd9++wDF\\n4l1TfTRNa1E19R7cf4BPPvnEVB9ZlnHixIkWVURUy/ZwEULUXKV4PB4kEgnE4/FquKRSKYyPj9f0\\ni8fjSCQSmJ2dbWu9tD+srt6F+omKfqO/6T73Ht7DC7K7hVVtOiofxed3Psfn4vOm+zz69hF+7Psx\\nYidiLayM6Du2houu65iZmcHY2Bg8Hk+1vXK7a2lpCX19fchkMrh8+XJN31AohGw229Z6aX854jmC\\nU/5TTZ9/4NAB3Fl+0sKKNvX09piqCwBKWglofWlEVbYO6MuyDCEEisXitufoug5d1+Hz+er6ApsB\\nREREzmL7bDFN03D69OmaNlVV4fV60dfXV72P7XY3vt0ghGh5jUREZI7t4dLI1NRU9TaYrus2V0NE\\nRGaZGnMZGBiAJEmmXsAwDEiShE8//bSp89PpNI4fP44LFy6Yep2tzNZJ7bexsYEnT8wPBBw61PwT\\nJYnIHqbCJRAIoFgsolAoVNv8fj80TUOpVAKwORaydXpws7/ohRBIp9O4deuWmbKoQ928+SEWFu7C\\n5TrQdB/DeIK/+qs/x/e///0WVkZEz8tUuFy+fBnhcBjBYBDT09MIBALVY4VCAefPn8fS0hKy2eyu\\n1p8kk0ncuHGjpk1RNh9Nu7q62nDcpXJ8q+0eUcsrGudYWyvj0KGf4Nixk033uXPnA5TL5RZWRURW\\nMDXmMjExAVmWkc/na4IFAILBIObn51Eul5FMJk0XMj4+jsnJyboAkWUZiqLUDdwLISDLMvr6+ky/\\nFhERtZapcFFVFbFYrGZNylbRaBSqqpoqYnp6GslksiYo8vl8dYpyNBrFzZs3a/oUCgXEYlwQRkTk\\nRKbCxTCMZ0793WnNSiOVhZCapqFQKKBQKEBVVWQymeqttVQqhUwmU9MvnU4jlUqZei0iImoPU2Mu\\n0WgUuVwO77zzDs6cOVN3PJfLoVAoIBqNNvX1dF3HyMhIw2P9/d9tu+HxeJBKpZBMJjE4OFjda4y3\\nxIiInMlUuKRSKaiqiuHhYZw9exaxWAyKomBxcRFzc3PVq5BmryhkWW56cDYQCNSN8xARkTOZChdF\\nUZDP55FIJJDJZOpuVSmKgqmpKYYAEdE+Z3rjymAwiLm5OQghUCgUIISAoihQFAXBYLAVNRIRUYfZ\\n9a7Ix48fRzgcfubsMSIi2n9M7y22sLCAcDgMWZbR39+P+fl5AJtbw/ziF7+wvEAiIuo8psKlWCwi\\nFAqhUCggEonUrIJfXl7GpUuXMDg4aHmRRETUWUyFS2UW2Pz8fN1g/srKCiYmJjA/P1/3YC8iItpf\\nTIXL7OwsotHotrPBLl26hEAgwCdEEhHtc6bCRdf1msWNjVTWvRAR0f5lKlwCgcAzt8NfWFjglGQi\\non3OVLiMjo5ifn4e7777bsOt60dGRiCEaHr7FyIi2ptMhUtlTCUSiVT3BEulUhgdHcWxY8eQzWah\\nKAomJiZaUiwREXUG0+tc5ufnMTExgffffx8AMDc3h0wmg3K5jEuXLuGzzz6zvEgiIuosu1qhf+nS\\nJVy6dAnA5kO7fD4fZFm2tDCixrrxD//wASTpw6Z73Pnq9yje1XH0qK/pPisrf8CPXmn+8ctEVMtU\\nuExPT+PYsWM12+1v95hholY4efJHAH5kqs/jtQ9w78hv4Xvx5ab7GJqB482fTkRbmAqXeDwOr9fb\\n8FkuRE7WaAIKEbWOqTGXc+fOYWVlBbdv325VPUREtAeYunJJp9MYGBhAKBTC1NQUwuEwFEWB2+1u\\nVX1ERNSBTIWLz7c5IGoYBsbGxqrtT99yMAwDkiRhY2PDVCHZbBZerxeRSKSmXQiBeDyOZDKJUCgE\\nTdOQTqcRi8XqziUiImcwFS7N/jI3e39bVVWMjY1tuydZPp9HPp8HsPlo5GvXrjFYHOaLL/4VX321\\nbKrP3bs6AOeOmn/zzQoePHjS9PnffvsQwNHWFUTUQXYMl2QyiVdffbU6gL91J+TnVSwWkUqlEAqF\\nqldFW0mSBFVVEQ6HoWka+vr6LK2BrPHxx1/ik0+O4NAhM7dIffB6v9eymp6H230c9+71mOx1BEeP\\nMlyIgGeEy+TkJIaHh+tmh01PT6NQKODtt99+rhf3+/24evUqgO+282/EMAy43W6O7Ticx3MCHo8z\\nw8Ks7q5eeNx7499CZAfTK/QB4Pr160in01bXQkREe8SuVugDqHkKZasJIaDrOgBA0zT4fD4MDQ21\\n7fWJiMicXYdLuxalVcZing6TyqaZDBgiImfadbi0i8fjwfnz52va4vE44vH4juHCFdnUKdbW13D/\\nwX1TfXp7e9HTbXbCAVH7OD5cGvH7/RBCYHV1lYP81NF6ug/iiy828Pvf/2vTfdbX19Dffxh/9qc7\\nPxWWyE6OD5fJycnqDswVlVtlQgicPn26Yb/txoR4RUNOcujQURw69Gem+ty/v4xyeaVFFRFZ45nh\\noqoqRkdHa9ry+TwMw6hrf9rMzMxzFyeEQDKZxMjISM36Fk3TAHBHZiIip3pmuKysrGy7eHKnRZVW\\nhIuiKJiamqpbOKmqKkKhEG+JERE51I7hcuvWrXbVAaDxrSyfz4disQi/3w8A0HUd6XQa165da2tt\\nRETUvB3DJRgMtvTFS6USrly5AiFEdYPKaDSKWCxWnQk2NDSEXC6HbDaL5eVl6LqObDbLbWCIiBzM\\n1gF9j8eDiYmJZ57H9SxE35FcLnz5ZQkr2gdN93l4/4/4iecR8B9bWBjRUxw/W4yIah057MXa+k9M\\n7ZLx6NEdrBgPW1gVUS2GC1EH6u7qNXX+ga5uAOutKYaogV1tXElERLQThgsREVmO4UJERJbjmAsR\\nNbS+vo6lpSXTj9c4cuQIXn7ZuY+vpvZguBBRQ/fv38evbv4KXXLzvybW19Zxsuskhl7m8oH9juFC\\nRNvqOdiDk8rJps9/+OAh8HULC6KOwTEXIiKyHMOFiIgsx3AhIiLLccyFOkq5XMb6+hOTfTZaVA0R\\nbYfhQh2l+MUH+PjOe5BcZi66DfS8dKhlNRFRPYYLdZSNjTV0n+iF5/j37C6FiHbAMRciIrIcw4WI\\niCzHcCEiIss5Zswlm83C6/UiEonUHSsUCpifn4fP54MQAsFgsOF5RETkDI4IF1VVMTY2hmw2W3dM\\nCIFkMonr169X20ZGRqAoCvx+fzvLJOpo2uoyfv2/f930+etr69jgNG7aJVvDpVgsIpVKIRQKwefz\\nNTwnlUphfHy8pi0ejyORSGB2drYdZRJ1vEOHj0Dy3MXdnrvNd+oBvneMs/Jod2wNF7/fj6tXrwLY\\nDJFGMpkMLl++XNMWCoUaXuUQUWOSy4XD7sPw+Dx2l0L7hKMH9HVdh67rdVc1siwDAJaWlmyoioiI\\nnsXR4aJpGgDA7XY3PC6EaGc5RETUJEeHi67rdpdARES74IjZYq0gSZLdJRAR7VuOvnIhIqLO5Ohw\\nURQFALC6urrj8UYMw2j4QURErefocJFlGYqi1A3cCyEgyzL6+vrsKYyIiHbk6HABgGg0ips3b9a0\\nFQoFxGIxmyoiIqJncVS4NLptlUqlkMlkatrS6fS2iy6JiMh+ts4WK5VKuHLlCoQQEEIgHo8jGo0i\\nFothaGgIAODxeJBKpZBMJjE4OFjda4y3xIiInMvWcPF4PJiYmHjmeYFAAIFAoA0VUTstFhfw2Ve3\\nTPXZKK+j9/svtKgiIrLKnl3nQs73aO0BDrzUjaOy11Q/yeWou7lE1ADDhWwlSQwLor2I72oiIrIc\\nw4WIiCzHcCEiIstxzGWP+2zxM+glc7tLf/WHr3Hc+xK6u7ub7qPr982WRg63tr6GLz7/EmUT2yY9\\nevgInvtHW1gVdQqGyx73wccf4BvpG/T09jTd5/3/+094RR6F13u86T6SJMPnMzfri5zt8aPH+Oif\\nS+jtfbnpPg8fbMD38JsWVkWdguGyD/hO+PDCkebXhnR1dcHjeREnTvy7FlZFnaC7qxuy50TT5x9A\\nF/Cw8UaztL9wzIWIiCzHcCEiIssxXIiIyHIccyFLPHnyCE+efGuqz/raE6D5CWnUIdbX1lEsFk31\\nOXz4ME6caH5sh5yP4UKW+HjxPXxx/yMcOHCg6T5llHHEyxlme0nPwYNYevgQ//m//fem+5SNMk4e\\nPYJf/Nf/0sLKqN0YLmSJDWMNL7zkxmG3x+5SyEa9vS/gT8L/yVSfhw9X8Wjxd60piGzDMRciIrIc\\nw4WIiCzHcCEiIst1RLgIIRCLxZDP56HrevVRx/l83u7SiIiogY4Z0M/n89UwkWUZ165dQyQSsbkq\\nos4gSRLufvMAv/k/Hzbdp1wuY2Ojt4VVbZIkF+4/XkXm7zOm+h33HMdf/OwvWlQVPa+OCBdJkqCq\\nKsLhMDRNQ19fn90lEXWUFw650dX1Y8DEDscuCfD6Wv8roqu7G/IrXhgvN1/bxsYGPl/6vIVV0fPq\\niHABAMMw4Ha74Xa77S6FqCP1dB+0u4Rtdff04NDhQ02fv762jsd43MKK6Hl1xJgLERF1lo65chFC\\nQNc3H3qlaRp8Ph+GhoZsroqIiBrpiHDx+XwAUBMmIyMjdW1EROQMHREuHo8H58+fr2mLx+OIx+Pb\\nhoskSe0obc/StDsolzeaPv/x42+BIy0siIg6SkeESyN+vx9CCKyurnKQ32I9x3rwycpv0as3//RK\\nHATkF7irLRFt6ohwmZycxKVLl2raKrfKhBA4ffp0XR9jmymXvKJ5tiOyGwcOvoxDB3kpQkS74/jZ\\nYpXV+EtLSzXtmqYBABRFsaEqIiLaiePDRVEUTE1N1S2cVFUVoVCIt8SIiBzI8eECbN4Ce/rJdrqu\\nI51OY3p62saqiIhoOx0x5jI0NIRcLodsNovl5WXouo5sNsttYIj2CAMG1tbWmj5/fW0dGyZmM1L7\\ndUS4AFzPQrRXuVwHsLoqIZ//p6b7bGxs4MDXf8TfjrawMHouHRMuRLQ3HXB14aUX62d87uTJk0dY\\n/vy9FlVEVuiIMRciIuosDBciIrIcw4WIiCzHcCEiIstxQL+D3L79O9y798BUnw8+/ATllzfQe6j5\\nB0Xdv/8turrNVkdE9B2GSwf56KOv8Pjxn6Krq6fpPvrKiygfXEfPt80/5c914CUcPHh4NyUSEQFg\\nuHSco0ePobe3+aB44bAH5RfW0XvIxA7HRETPiWMuRERkOYYLERFZjuFCRESW45iLBe7evWtq0z1g\\n83k0T548MdXn3r1vcPDgHfT0ND/mUt5YN/UaRJ1io7yBQqFgqk9PT0/1QYPN6urqwokTfMqqWZKx\\n3SMb96jKkyit/Gf/3d/9L6yvv2yqz3sf/j0eH/wWkqv5J2Mahgsezym4XM1fcBowIJ98EQe6+HcE\\n7R1lo4zF//dbHDDZz+Vaxc9+9ufm+jxw4W9G/gYHDph9tf2Nv3EssLZm4NSpkKk+7i8+xJFXvHDx\\nf1gi01ySC6/8+5+a7qdpN3HyhydN9bmzcMf06xDHXIiIqAUYLkREZDmGCxERWa5jxlwKhQLm5+fh\\n8/kghEAwGEQkErG7LCIiaqAjwkUIgWQyievXr1fbRkZGoCgK/H6/Za9TLpfxzjsqVlfNPZv7t7d/\\ni6O/v2uqz8P1Eo5IXlN9iKj9PvjgX/A/HvwKLlfzk28OH3bhzJnX0N3d2h1gf/Peb/DJF5+Y6tN9\\noBt/Hf1reDyeFlW1qSPCJZVKYXx8vKYtHo8jkUhgdnbWstcpl8tYXt7Aiy++bqrfQfcSjv7Q3Nx5\\nN45BMjGlmIjs8eDBOjye19Dd3dt0nz/8IY+NjY2Wh4u2qqH3B7047G5+o9mvP/7a9Lq83eiIcMlk\\nMrh8+XJNWygUQjabbcnrmZ3PLkmSqb9qiKizuFxdpn4vVNbTtYPrgMvc76w2leb4P511XYeu63Wr\\namVZBgAsLS3ZUBUREe3E8eGiaRoAwO12NzwuhGhnOURE1ATHh4uu63aXQEREJjl+b7FCoYBwOIxy\\nuVx3zOVyQVVVvPbaa3XH2nnPk4hoPzATF46/ciEiImcw80e742eLKYoCAFhdXW047lI5vtV2CduK\\nXZHbifXbp5NrB1i/3fZK/c1y/JWLLMtQFKVu4F4IAVmW0dfXZ09hRES0LceHCwBEo1HcvHmzpq1Q\\nKCAWi9lUERER7cTxA/oAUCqVMDw8XLP9y+uvv450Om36ymWvXJqy/vbr5NoB1m+3/VZ/R4QLACws\\nLGBmZgaDg4MQQiAUCjWcJfYs++0H7DSdXH8n1w6wfrvtt/o7Jlysst9+wE7TyfV3cu0A67fbfqt/\\n34ULERG1XkcM6BMRUWdhuBARkeUYLkREZDmGCxERWY7hQkRElnP83mJETlAoFDA/Pw+fzwchBILB\\nICKRiN1lmZLNZuH1ejuu7lwuByEEFhcXIYRAPB7H0NCQ3WU1TVVVqKqKY8eOYXFxEaFQCOfPn7e7\\nrF3RdR3JZBJXr1595rkMF3T2D7/T33gVTv7FJ4RAMpms2SFiZGQEiqLA7/fbWFnzVFXF2NhYyx4N\\n3iq5XA6KolT/ny6VSgiFQtA0rSPeo6qqQpIkTExMVNvC4TB0XcfFixdtrGx3EokEVlZWmjvZ2Ofm\\n5uYMVVVr2kKhkDE5OWlTRc3LZrNGoVCofq7rutHf32+k02kbqzJvbm7O8Hq9Rj6ft7uUhsbGxoxc\\nLlfTpqqqMTw8bFNFzRNCGPF43Ein00Z/f79jv8fbafQ+TKfThiRJNlRj3tmzZ+t+vyQSCaO/v9+m\\ninZvcXHRGB4eNkZGRpo6f9+PuUxNTdW1RaPRhu1OI4RAIBCofu7xeJBIJBCPx22sqnnFYhHj4+Mo\\nFovw+Xx2l7OtTCaDYDBY0xYKhTriKsDv9+Pq1asd8Vf+VrquY2ZmBqVSqaa9cnW7tLRkQ1XmSJIE\\nVVVr2gzDgNfrtami3cvn84jFYk2v0N/34dKpP/y98MbrhF98uq5D1/W68JNlGUBnfJ87lSzLEEKg\\nWCzaXcquzc7O4sqVKzVt2WwWo6OjNlW0O/l8HtFo1FSffT/mMjs7W9eWzWbx5ptv2lBN855+450+\\nfdrucvYsTdMAoOGD6oDNq0c+U6h1Kt//p6mqCq/X25Hf93Q6jXA4jAsXLthdiilCCEQiEVP7ou37\\ncNmqk374e+2N50S6rttdAm0xNTWFy5cv212GKblcDnNzc5AkCTMzM3aXY0oul9vV3QWGy7/p5B/+\\n0zrxjUfUrHQ6jePHj3fEH39PGxoawtDQEEqlEsLhMKanp2vGS53qef64Yrj8m0794T+tU994RM0Q\\nQiCdTuPWrVt2l7JrHo8H8XgckUik4Z0Hp8lkMjVXLZVt95uxZ8JFCNH0uceOHYPH42l4zI4fvhW1\\n2/nGs+p770SKogAAVldXG467VI5T6yWTSdy4ccPuMp5bJBKBruvI5/OOXNdVsbCwgHA4XNO278Zc\\nisUikslk0+cPDg7uuICpnT98q2q3641n9ffeaWRZhqIoEELUTJwQQkCWZY5ttcn4+DgmJye3nVjh\\nRJUn5r777rsNJ91snenpNLdu3cLi4mLNMEGhUKguKh4cHNxxwfaeCBe/399w1tezOOGHv9van2bn\\nG8+K+p0uGo3i5s2bNf+PFAoFxGIxG6vaP6anp5FMJmuCPJ/PO36HBF3X0d/fX3d1W7nS37p2ymka\\nDeK/9daYMo9qAAAFEUlEQVRbuHXrVs2OA9vZ1+tcOv2HD2z/xuvktQFOk0qlkMlkatrS6TRSqZRN\\nFe2emdsaTlBZqKppGgqFAgqFAlRVRSaTcXSwAJu/P0ZHR+u+56lUColEoiOveu/du8fHHDfrrbfe\\nwtjYWM04QCwWQzgcrlv85DTZbBYrKysIhULVNk3TkM1mm9pYzkkGBgYwNTXl2HvQCwsLmJmZweDg\\nYPWK97XXXrO7rGcqlUq4cuUKhBDIZrNQFAXRaBSxWMzxe9A1Wrxa0d/fj08//bTNFe3O9PQ0FhcX\\nq3sXhsNhnDt3zu6yTCkWi0ilUpidnUWpVML58+cRj8d3nPS078MF6Mwf/l5443XyLz4i2hnDhYiI\\nLLevx1yIiKg1GC5ERGQ5hgsREVmO4UJERJZjuBARkeUYLkREZDmGCxERWY7hQmRCoVCAy+Wq2y12\\nK1VV4XK5MDIyYurrDw8Pw+Xi25I6H/8vJjIhGAxClmUsLCzsuLFpZS+yN954w/RrmHlmBpFTMVyI\\nTBobG4NhGDvuBj07OwtJknDmzJk2VkbkHAwXIpNGR0cBbD5SupFCoYBSqYSzZ8+2sywiR2G4EJkU\\nCASgKMq2t8YqD1eqhBCw+RiH4eFh9Pf3w+VywefzYWRkpOGjEZ7e7i8WizUcg9F1HS6XC+Pj43XH\\nJicnEQqFqq8zPj7ORzBQ2zFciHYhHo9ve2ssnU7X3BITQmBgYADvvPMOBgYGEI/HEQ6Hkc1mEQqF\\nnvlQup3GYLYeC4VCSCaTcLlc1ddJp9Po7+/HwsLCLv6lRLvDcCHahcotr623xhrdEkulUpAkCXNz\\nc/j1r3+Nt99+G9evX0cqlYKu61BV1ZKaJicnsbCwgHw+j5s3b1ZfZ35+HkDjJwsStQrDhWgX/H4/\\nAoFA3a2xRrfExsfHkclk6h4uVnnQ0srKiiU1XblyBbFYDMFgELquVz/8fj8ikQgKhQJWV1cteS2i\\nZ+myuwCiTvXGG29gYWEB6XQaFy9eBLD5dNCts8QCgUA1SHRdx61bt1AoFLadELBbpVIJc3Nz8Hq9\\nDY9LkgRN0+B2uy19XaJGGC5EuzQ2NoZEIoGZmRlcvHgRQggUi0UMDw/XnKfrOhKJRPURscDm2Ego\\nFLJsoF0IAWBzAkAikdj2vO2Ch8hqDBeiXfJ4PAgGg9VbY9lsFsDmYP/TIpEIFhYWEI/HEY/Hcfr0\\naQBAPp+v9jFL07SazyuPvJZlue72G5EdOOZC9Bwqs8bS6TRmZmYgSVLNL3dd17GwsIDh4WG8/fbb\\n1WABaqccm1UoFGo+l2UZHo9n28kBXq8XAwMDu349IrMYLkTPobJ32NTUFBYWFrZdOLl10L5yqwyo\\nD5mnpxfLsgzDMJDP5xv2fVo8HsfKykrdfmaTk5MolUoN18QQtYxBRM8lFosZkiQZkiQZ+Xx+2+PD\\nw8NGKpUyxsbGDK/Xa7z++uuGJElGf3+/oaqqYRiGcfbsWUOSpGrfbDZb/drxeLymr9frNcbHx2te\\nq7+/v/o1z549awSDQUOSJCMcDrf2m0C0BcOF6DlVAsDlcjU8ruu6EY/HDa/XW/1Fn8vlDMMwjHg8\\nbrhcrmpIDA8P132ddDpdDQ2fz2ckk0nDMIyG4WIYhpFIJIxQKGRIkmQMDAxUzydqJ8kwnuPGLxER\\nUQMccyEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIcgwXIiKyHMOFiIgsx3AhIiLL/X/5\\nSxhgL1jXqQAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 52\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"The Wilcoxon signed-rank test tests the null hypothesis that two related paired samples come from the same distribution\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"Wilcoxon Signed-Rank test. Only if equal variance\\\", scipy.stats.wilcoxon(x,y)[1])\\n\",\n \"print(\\\"Mann-Whitney U test NO\\\",scipy.stats.mannwhitneyu(x,y)[1]*2)\\n\",\n \"print(\\\"Paired t-test. Only if normality and equal variance\\\",scipy.stats.ttest_rel(x,y)[1])\\n\",\n \"print(\\\"Unpaired t-test NO\\\",scipy.stats.ttest_ind(x,y)[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Wilcoxon Signed-Rank test. Only if equal variance', 0.0064134158222216931)\\n\",\n \"('Mann-Whitney U test NO', 0.0023466572817885658)\\n\",\n \"('Paired t-test. Only if normality and equal variance', 0.005920142900373267)\\n\",\n \"('Unpaired t-test NO', 0.004349070916356835)\\n\"\n ]\n }\n ],\n \"prompt_number\": 53\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Compare >2 independent samples. Same mean?\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Imagine we want to check if there are difference in GFP expression in three different versions of a promoter.\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"ANOVA (Parametric) or Kruskal-Wallis (Non parametric)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Analysis of variance (ANOVA) is a collection of statistical models used to analyze the differences between group means and their associated procedures (such as \\\"variation\\\" among and between groups). T-test\\n\",\n \"\\n\",\n \"\\n\",\n \"The Kruskal\\u2013Wallis one-way analysis of variance by ranks (named after William Kruskal and W. Allen Wallis) is a non-parametric method for testing whether samples originate from the same distribution. Mann-Whitney-U \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" x = [np.random.randn() for _ in range(200)]\\n\",\n \" y = [np.random.randn()+0.2 for _ in range(200)]\\n\",\n \" z = [np.random.randn()+0.4 for _ in range(200)]\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(z,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3W1sG3d+J/DvkHrykziknDhxHlYcqe2118NaJLXt9q4o\\nsCSDosChC8uSFu3bWFTe2yb9bl8czqbS97Eo41Cgb04SuVu0aO/WGjo9YLe7jSXKu3e7zSbRn0qa\\nOHYcUUPZsmw9zb1QxTVNSp6hh5yh9P0AAqyZ+Wt+lkR+NfN/GEnXdR1EREQWctldABERHTwMFyIi\\nshzDhYiILMdwISIiyzFciIjIcgwXIiKynPv73//+9+0uQlVVpFIpzM/P42/+5m/w5ZdfIhgMlvYL\\nITA0NITXXnsNPp8Pd+7cQTKZhCRJUBTFxsqJiKgaye55LqqqQpIkhMPh0rZQKITh4WFcvHgRwE64\\n9Pb2lvbLsozr16/j7NmzDa+XiIiez/bbYuPj4xXbIpFI2XZJkqCqKjRNgxAChUKBwUJE5GC2h8tu\\ncDxN13V4vd6KbZ2dneju7m5gdUREVIsWuwuYmpqq2JZOp/HOO+/YUA0REVnB9nB5ViqVQigUwoUL\\nF8q2CyGgaRoAoFAowOfzYWBgwI4SiYjoORwTLplMBjMzM5AkCZOTk2X7fD4fAJSFydDQUMU2IiJy\\nBttHiz2rWCwiHA5jYmICfX19ex6XzWYRi8XwySefNLA6IiIywvYO/Wd5PB7EYrGyocnV+P1+CCGw\\nsrJSdb8kSXt+EBFRfTkuXAAgHA5D0zTcvHkTADA2NlZxzO6tMiGE6a/PgCEiqi9bw0UIAa/Xi9u3\\nb1fdvzuvJZFIYHFxsWxfoVAAgD1n6Ou6XvWDiIjqz9YOfU3T0NPTUxEQu1cjgUAA3d3dGB8fr5jf\\noqoqgsEgOjs7G1UuEREZZOuVSyAQwPDwcMUVRTKZRDweLwWKz+dDPp8v7dc0DalUChMTE40sl4iI\\nDHLEaLGJiQksLCygq6sLCwsLCIVCePvtt8uOyWQyEEJgaWkJmqYhkUjUNFt/t7/FAf9tIqIDyxHh\\n0kgMFyKi+nPkaDEiImpuDBciIrIcw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFc\\niIjIcgwXIiKyHMOFiIgsx3AhIiLL2fo8F6LDZmlpCZ9++KHpdvLLL0P5rd+qQ0VE9cFwIWqgpaUl\\nbH/wAV71eg23efTkCb545RWGCzUVhgtRg504cgSvdXUZPr64uoq7dayHqB7Y50JERJZjuBARkeUc\\ncVtMVVWoqlp6zHEwGMT58+fLjsnlcpibm4PP54MQAoFAAOFw2KaKiYhoP7aHi6qqkCQJV69eLW0L\\nhULQNA0XL14EAAghkEgkcOPGjdIxQ0NDUBQFfr+/4TXTwVMoFLC1tWWqjSRJ6OrqKj06m4h+w/Zw\\nGR8fx+joaNm2SCSC8fHxUrgkk8mKY2KxGOLxOKamphpWKx1MGxsb+OEPf4rNTeOd7Ds0DA//IWRZ\\nrktdRM3M9nCRJAmqqpbd4tJ1Hd6nhmpOT0/j8uXLZe2CwSDS6XTD6qSDS9d1bG624PTpPzTV7s6d\\nH9epIqLmZ3u4VLvySKfTeOeddwAAmqZB0zT4fL6yY3b/WlxcXER3d3fd6yQiIuMcN1oslUohFArh\\nwoULAHbuhQNAZ2dn1eOFEA2rjYiIjLH9ymVXJpPBzMwMJEnC5ORkabumaTZWRUREtXBMuAwMDGBg\\nYADFYhGhUAgTExPo6+uzuywiIqqBY8Jll8fjQSwWQzgcLt0SqwWHh5IT3b17F4u3P8CX/2Z8bbGH\\nj5/gy1fewB/jz+tYGZG1HBcuABAOh6FpGm7evIlAIAAAWFlZqdrvoihKo8sjqtna2hoeuR+h7dQp\\nw2305ccorhbrWBWR9Wzt0BdCwOv14vbt21X3a5oGWZahKEpFx70QArIs7zlSTNf1qh9EdnO5XGhp\\nbTH84W5x210ykWm2houmaejp6am4+tgNkt2rlkgkglu3bpUdk8vlEI1GG1MoERGZYmu4BAIBDA8P\\nV1xRJJNJxOPx0lVJMpnE9PR02TGpVArJZLJRpRIRkQm297lcvHgRExMTWFhYKC1cOTw8jLfffrt0\\njMfjQTKZRCKRQH9/f2mtMU6eJCJyJtvDBUDFCsjV9PX1cWgyEVGTcNwMfSIian4MFyIishzDhYiI\\nLMdwISIiyzFciIjIcgwXIiKyHMOFiIgsx3AhIiLLMVyIiMhyDBciIrIcw4WIiCzHcCEiIssxXIiI\\nyHIMFyIishzDhYiILMdwISIiyzFciIjIco4Il0wmg3fffRejo6N46623kMlkyvYLIRCNRpHNZqFp\\nWukxx9ls1qaKiYhoP7Y/5jiTyUBRFAwMDAAAisUigsEgCoVC2eOPs9lsKUxkWcb169cRDodtqZmI\\niPZn+5WLEAJ9fX2lzz0eD+LxOGKxWGmbJElQVbV01VIoFHD27Fk7yiUiIgNsDRdN0zA5OYlisVi2\\nffeKZHFxsbRN13V0dnaiu7u7gRUSEVEtbA0XWZYhhEA+n7ezDCIispjtfS6FQqFim6qq8Hq9ZVcp\\nQghomlZq4/P5Sv00RETkLLaHSzXj4+O4fPly6XOfzwcAZWEyNDRUsY2IiJzB9g79Z6VSKZw8eRIX\\nLlwobfN4PGUjxwAgFoshHo/v+XUkSar6QURE9eeoKxchBFKpFGZnZ597rN/vhxACKysr6OzsbEB1\\nRERklKOuXBKJBG7evFmxfWxsrGLb7q0yIUTVr6XretUPIiKqP8eEy+joKMbGxiquQnZn4z89LBn4\\nzUAARVEaVSIRERnkiHCZmJhAIpEoGx2WzWaRz+ehKArGx8cr5reoqopgMMhbYkREDmR7n0s6nQaw\\ncyWyezVSKBSQTqdx7do1ADu3wPL5PPx+P4CdyZepVArXr1+3p2giItqXreGiaVppSPGzenp6Sv8e\\nGBhAJpNBOp3G0tISNE1DOp3mbH0iIoeyNVxkWcb29rahYzmfhYioeTiiz4WIiA4WhgsREVmO4UJE\\nRJZjuBARkeUYLkREZDnb57kQWWlra6v0aAajNjY26lRNpc3NTTx58gSP1h4ZbvP4yRrWt9pMn+vB\\ngwdYX1833U6WZbjdbtPtiJ7GcKED5e7du/jbv/0lWltPmGqn66/UqaJy9+7dw+LiMlpgfGWJYnEF\\nn7U9Nn2un/3jP+Lo8jJcLuM3KB5sbOD3/vzP8frrr5s+H9HTGC50oOi6jpaWl/Dqq312l1KVrutw\\nuY7ixHHjb97r619he934lU7pXE+eoP/ll9HW2mq4ze07d7jAK1mCfS5ERGQ5hgsREVmO4UJERJZj\\nuBARkeUYLkREZDmGCxERWY7hQkRElmO4EBGR5RguRERkOUfM0M9kMhBCYGFhAUIIxGKxiidP5nI5\\nzM3NwefzQQiBQCCAcDhsU8VERLQf28Mlk8lAUZRSmBSLRQSDQRQKBZw/fx4AIIRAIpHAjRs3Su2G\\nhoagKAr8fr8tdRMVi0v45JNP0NlpfJ2wlZWVms61ubWJjz76yFSbLYOPECeqB9vDRQhRdpXi8XgQ\\nj8cRi8VK4ZJMJjE6OlrWLhaLIR6PY2pqqqH1Eu1avPsh1E/+FbIsG24jNgQ6j3SYOk97Syv+w6NH\\nwM2bptr9tsuF1hbbX+J0SNn6m6dpGiYnJzEyMgKPx1Pavnu7a3FxEd3d3Ziensbly5fL2gaDQaTT\\n6YbWS/Ssk6+exKlXThk+/t5X97Dd+rWpc7hcLrzS2Ynffu01s+UR2cbWDn1ZliGEQD6f3/MYTdOg\\naRp8Pl9FW2AngIiIyFlsHy1WKBRw5syZsm2qqsLr9aK7uxuFQgEA9ryvLYSoe41ERGSO7eFSzfj4\\neOk2mNmnChIRkf1M9bn09vZCkiRTJ9B1HZIk4eOPPzZ0fCqVwsmTJ3HhwgVT53mW2TqJarGxvoEn\\n608MH7+1tQX+ZtJhYCpc+vr6kM/nkcvlStv8fj8KhQKKxSKAnb6QZ4cHG32jF0IglUphdnbWTFlE\\nttBxBHOzn6P96JLhNtpXK/gdl/EnQxI1K1PhcvnyZYRCIQQCAUxMTKCv7zePks3lcjh//jwWFxeR\\nTqdrmn+SSCRw85nhloqiANiZH1Ct32V3/7P2elQrr2jIKl1dfjzxvoSOY8cNt9GffIGOjl/UsSoi\\nZzDV53L16lXIsoxsNlsWLAAQCAQwNzeH7e1tJBIJ04WMjo5ibGysIkBkWYaiKBUd90IIyLKM7u5u\\n0+ciIqL6MhUuqqoiGo2WzUl5ViQSgaqqpoqYmJhAIpEoC4psNlsaohyJRHDr1q2yNrlcDtFo1NR5\\niIioMUyFi67rzx36u9+clWp2J0IWCgXkcjnkcjmoqorp6enSrbVkMonp6emydqlUCslk0tS5iIio\\nMUz1uUQiEWQyGfzgBz/A2bNnK/ZnMhnkcjlEIhFDX0/TNAwNDVXd19PTU/q3x+NBMplEIpFAf39/\\naa0x3hIjInImU+GSTCahqioGBwdx7tw5RKNRKIqChYUFzMzMlK5CjF5RyLKMbYOL6/X19VX08xAR\\nkTOZChdFUZDNZhGPxzE9PV1xq0pRFIyPjzMEiIgOOdMLVwYCAczMzEAIgVwuByEEFEWBoigIBAL1\\nqJGIiJpMzasinzx5EqFQ6Lmjx4iI6PAxvbbY/Pw8QqEQZFlGT08P5ubmAOwsDfNXf/VXlhdIRETN\\nx1S45PN5BINB5HI5hMPhslnwS0tLuHTpEvr7+y0vkoiImovp0WIAMDc3B7/fX/aMleXlZYyNjSGR\\nSODy5cu4cuWKtZUS1VGh8CW2t7dMtdncML5gJdFhYypcpqamEIlE0NfXV3Up/EuXLmFychLpdJrh\\nQk1jY2Md//Lh30E6Ya6d3rYNud34UyiJDhNT4aJpWtnkxmoURUEmk3mhoogaTZIA3xun7S6D6MAw\\n1efS19f33OXw5+fnOSSZiOiQMxUuw8PDmJubw/vvv1916fqhoSEIIQwv/0JERAeTqXC5dOkS+vr6\\nEA6HS2uCJZNJDA8Po6urC+l0Goqi4OrVq3UploiImoPpeS5zc3O4evUqPvjgAwDAzMwMpqensb29\\njUuXLuGTTz6xvEgiImouNc3Qv3TpEi5dugRg56FdPp8PsixbWhjR/M/n8cEvPzDVZnl5GQ/vdeP0\\naePr221tbeGrX36A9S87TJ1rs7UNL/d/G20dR0y1IzoMTIXLxMQEurq6ypbb3+sxw0QvavXxKtpf\\nb0fXqS7DbR7+60Os33ls6jzb21s4uv4Yf+I1N1rs9vIStrfMzY0hOixMhUssFoPX6636LBeiw6ba\\noBYi2mGqz+Xtt9/G8vIybt++Xa96iIjoADB15ZJKpdDb24tgMIjx8XGEQiEoioLOzs561UdERE3I\\nVLjsriWm6zpGRkZK25++PaDrOiRJwpbJe9HpdBperxfhcLhsuxACsVgMiUQCwWAQhUIBqVQK0Wi0\\n4lgiInIGU+Fi9M3c7L1oVVUxMjJSekzys7LZLLLZLICdRyNfv36dwUKHyoPVVdzIvm+qTXtbK/74\\nP/8RXC7TMw6IXti+4ZJIJPCtb32r1IH/7GONX1Q+n0cymUQwGCxbYflpkiRBVVWEQiEUCgV0d3db\\nWgOR03UcPY614zJ+9XXlYrH7Wf/6Hr4VCuLIEQ6VpsbbN1zGxsYwODhYMTpsYmICuVwO77333gud\\n3O/349q1awB+s5x/Nbquo7Ozk307dCi5XG50vfya6XZ3l+/XoRoiY2q6Xr5x4wZSqZTVtRAR0QFR\\n0wx9AGVPoaw3IUTp+TGFQgE+nw8DAwMNOz8REZlTc7g0agLZbl/M02Gyu2gmA4aIyJlqDpdG8Xg8\\nOH/+fNm2WCyGWCy2b7hw9nTzW19fx+qjVbQ9bDPcZu3RGtbWHuLBg4LhNo8fr9ZSHhHtw/HhUo3f\\n74cQAisrK+zkP8A++vUifvpvn8HTZfzN/6vP7uHlDz9F8YnxQNra2sSpBt7mJToMHB8uY2NjpRWY\\nd+3eKhNC4MyZM1Xb7dUnxCua5rG1raOj/RX4vL2G26wtu/HGsXsI+l413GZzcwPuJW8tJRLRHp4b\\nLqqqYnh4uGxbNpuFrusV2582OTn5wsUJIZBIJDA0NFQ2v6VQ2LnlwRWZiYic6bnhsry8vOfkyf0m\\nVVoRLoqiYHx8vGLipKqqCAaDvCVGRORQ+4bL7Oxso+oAUP1Wls/nQz6fh9/vBwBomoZUKoXr1683\\ntDYiIjJu33AJBAJ1PXmxWMSVK1cghCgtUBmJRBCNRksjwQYGBpDJZJBOp7G0tARN05BOp7kMDBGR\\ng9naoe/xeHD16tXnHsf5LETmbWETP7v9M7S4Ww23+WhZQ/+3v4033njDcJvl5WXM37wJmFwJvcPn\\nwx9FIqbaUPNw/GgxIqrN8VMeuE66IJlY5Gnl6xWsra2ZOs/jx49x7N49/P5LLxlus7W9jZ989pmp\\n81BzYbgQHVAutxut7a1ocRl/mbvdtS3P3+J241hHh+Hjt7a2gFVOXj3I+KAHIiKyHMOFiIgsx3Ah\\nIiLLsc+FDpz19ccoFO4YPn57e7vmcxWX7uPRgxXDx689fFDzuRrl17/+NVZWjP+fVldX4X34sI4V\\nUTNiuNCB0nH0OFZavkZ+9bapdi6P+ZfCN1pasfrxh6bbyceOmW7TKN846cHdD/4XhIk2G+sb8L36\\nO3WriZoTw4UOlNa2NhzrlHHC21X3c8nHT0Cu+1ka69VTXXj1lLnv3YPiA/jcx+tUETUr9rkQEZHl\\nGC5ERGQ5hgsREVmOfS7UEBsbGzuzsk22IaLmxHChhnj/hz+EtLxsqs0XP/1nPHqjp04VEVE9MVyo\\nIbYePkT01Cm0uN2G2/wCwOd8tj1RU2KfCxERWY7hQkRElmO4EBGR5RzT55JOp+H1ehEOhyv25XI5\\nzM3NwefzQQiBQCBQ9TgiInIGR4SLqqoYGRlBOp2u2CeEQCKRwI0bN0rbhoaGoCgK/H5/I8skAGtr\\na/jp7E+xsW1umPBHCx8j4v1WnaoiIqexNVzy+TySySSCwSB8Pl/VY5LJJEZHR8u2xWIxxONxTE1N\\nNaJMesra2ho+vPshOl/vNNXu868/x/Z2qE5VEZHT2Boufr8f165dA7ATItVMT0/j8uXLZduCwWDV\\nqxxqDHeLGx6fx1QbqU61EJEzObpDX9M0aJpWcVUjyztr0S4uLtpQFRERPY+jw6VQKAAAOjur34IR\\nwsxTJ4iIqFEcHS6aptldAhER1cARo8XqQZJ4l/95CoWC6au/R48eQdM0tC+1m263tLSE9rY2w202\\nuXAlUdM6sOFCz/fjn/wz/sc//m8cO26uc959tAWfrZi7qvzi88eYndPQ1mI8XJa1NrS1dZg6DxE5\\ng6PDRVEUAMDKykrVfpfd/dXoeyx4yCuacse7TsH/O2fqfp7C0Tn4fD2mwuXEiS/wdau5KyQicgZH\\n97nIsgxFUSpu3QghIMsyuru77SmMiIj25ehwAYBIJIJbt26VbcvlcohGozZVREREz+OocKl2KyuZ\\nTGJ6erpsWyqV2nPSJRER2c/WPpdisYgrV65ACAEhBGKxGCKRCKLRKAYGBgAAHo8HyWQSiUQC/f39\\npbXGeEuMiMi5bA0Xj8eDq1evPve4vr4+9PX1NaAicpJWfRtPfvlz3F1cMNxG13W8zIdXOp4kSUCx\\niH+YmDDXrr0d/+W7391zYjU5h6NHi9Hhpnhehse9iSPHT5hq5+KIQMdzuVz4056ePUd17uVn9+5h\\ng/OfmgLDhRzNJUkMiwNKkiRODTjAHNWhT0REBwPDhYiILMdwISIiy7HPheiA0nXg7t37cEn1/Rvy\\n0cNVbGEL7SaX6ulo78Abr79Rp6rIbgwXogOqre0U7n9V/5FV64+3sX78PvDQeBsdOlxfuhguBxjD\\nheiA6ug41pDzuFxuHOsE5C7ZcJvt7W08ePCgjlWR3djnQkRElmO4EBGR5RguRERkOfa5EJEtdF3H\\nw4cmRgEAeLS6anrJGLIHw4WIGk5ySdhwb+DHv/ixqXa37xfRrf1XnDx5sk6VkVUYLkTUcBIkvPTm\\nS+YbakVeuTQJ9rkQEZHlGC5ERGQ5hgsREVmuKcJFCIFoNIpsNgtN00qPOs5ms3aXRkREVTRNh342\\nmy2FiSzLuH79OsLhsM1VOccHH/wcn35aMNVmQdwBXI35+2ILm/hQ/AwtbuPnW99cg0t217EqajZb\\n2MI//cs/4fZHt021+4P/9Ad4880361QVVdMU4SJJElRVRSgUQqFQQHd3t90lOc7nn2tYW/tddHQc\\nN9ymtfUETpyYrWNVv3H8ZR+kIzB1rdyGI3C3ttatJmo+8ksyXKdd0GXjI8buf3kfKw9W6lgVVdMU\\n4QLsTLjq7OxEZ2en3aU4Vnv7URw5YjxcOjqOwvWoMY+ZdbvdaGlrg7tBV0p0MLlaXOg42oEjx44Y\\nbtPaxj9Q7MBXOhERWa5prlyEENA0DQBQKBTg8/kwMDBgc1VERFRNU4SLz+cDgLIwGRoaqthGRETO\\n0BTh4vF4cP78+bJtsVgMsVhsz3CRpMb0JexnbW0NX3zxhel2R44cwWuvvVaHiojqY2NjHYVlc6MV\\n3W43PJ2eOlX0G0/WnuCzzz5DR3uHqXbHjx/HK6+8UqeqDr6mCJdq/H4/hBBYWVlxbCf//fv38Xd/\\n9wWOHn3ZcJvt7U14PHn85V8yXKg5tLV1oFg8hmJx23AbXdfR0lLAmW/WP1xWllew+v9uYuPTzwy3\\nWd/cxOenT+OVs2frWNnB1hThMjY2hkuXLpVt271VJoTAmTNnKtrstbhdo69ojh3z4vTp3zV8/Pr6\\nYzx+fLeOFRFZy+1uxYkT5lYp1re3sfa4WKeKKnmPHMXvmrgb8ODRI8xxgcwX4vjRYruz8RcXF8u2\\nFwo7l+CKothQFRER7cfx4aIoCsbHxysmTqqqimAw6NhbYkREh5njwwXYuQWWz+dLn2uahlQqhYmJ\\nCRurIiKivTRFn8vAwAAymQzS6TSWlpagaRrS6TSXgXnK1tYWNjaeYGPjiYk2m7Wda3MDvB1NB52u\\n63jyxPjrCQBcLhdauWQRgCYJF4DzWZ7nFx/O4cviz9HWftR4I11H6ylzwzMfP1pF4dZP0LG1Zapd\\n58YGpBO8hUnNobWlBVtffIH/89d/bardens73vqLv0BbW1t9CmsiTRMutL8nm49x7Buvo1Ou77PF\\n9e1t+La28U1vV13PQ2SnjrY2RPx+0+3UO3ewZfIPr4OqKfpciIiouTBciIjIcgwXIiKyHMOFiIgs\\nxw59IrLFxoYOsWhuYdcvC0VouV+h44jxUY4r/3YXAAegNBrDhYgaTnK5cKTjdTx8YHyxSwCQnzyC\\n/34BR44YfxLlqw8f4c3TvWZLpBfEcCEiW7S1Gw+IXRubHfCeOIqjR0zM53r8BO2c2Nhw7HMhIiLL\\nMVyIiMhyDBciIrIc+1wcaGtrC3fu3DHVZls31zEKAJvr61hbfWCqzfrjxzhm+kxE1llbW8OmiSVW\\nVldXsX5ivY4VUTUMF4dpaWnD6uop/P3ff2mq3YOV4zh+2txiecWv7uL4L2+jvdVcO7mFvzZkD7fr\\nBBYX1wAYD4uV5SJOtxTwWxww1lB8l3AYl8uF11/vM93u068+xaZrw3S7U21tOCX7TLcjssPRozIA\\n2VSbRw/MLZtP1mCfCxERWY7hQkRElmO4EBGR5ZqmzyWXy2Fubg4+nw9CCAQCAYTDYbvLIiKiKpoi\\nXIQQSCQSuHHjRmnb0NAQFEWBv4anxQHAuUjU1PGSuwWJ//7fEAwGDbf51a9+hR/9z2s4dtRrtjzT\\nHknb+MafvYX2up+JqLm43G788/xt/Msv/q+pdp2d7Xjj9VdMtfnF0gpWdd3UY47v3L2HYsebkE0M\\nrFldfYDC44/xxjdeNVWf77gP3/2z75pqU6umCJdkMonR0dGybbFYDPF4HFNTUzV9zT/97W/C7XYb\\nPv5nH95GsVg0dY61tTWcbn2C/h5zv6C1mF/R0MIhwkQVXjr1BrZOmnsT3thch8t1DyfePGGq3e/p\\nm/gTrxft7cb/zPuHj/O47/oGfL5vG27z8OEvoW3n8M3f/4/Gi9OBr37+lfHjX1BTvBtNT0/j8uXL\\nZduCwSDS6XTNX7OltRUtbuP/fQlSTedxSRLcDXjTlyR2nxHtxW3itQ4A29vbkFwSXC5zrytJkuB2\\nu0394SpJElwuyWQbFyDBVBtd1w0fawXHvyNpmgZN0+DzlV8yyvLOWPfFxUUbqiIiov04PlwKhQIA\\noLOzs+p+IUQjyyEiIgMcHy6aptldAhERmSTpjb4RZ1Iul0MoFML2duXCjC6XC6qq4jvf+U7FPkmq\\nrY+EiIiqMxMXjr9yISIiZzDzR7vjR4spigIAWFlZqdrvsrv/WXsl7O43x+EXbHti/fZp5toB1m+3\\ng1K/UY6/cpFlGYqiVHTcCyEgyzK6u7vtKYyIiPbk+HABgEgkglu3bpVty+VyiEbNzbInIqLGcHyH\\nPgAUi0UMDg6WLf/y1ltvIZVKmb5yOSiXpqy/8Zq5doD12+2w1d8U4QIA8/PzmJycRH9/P4QQCAaD\\nVUeJPc9h+wE7TTPX38y1A6zfboet/qYJF6scth+w0zRz/c1cO8D67XbY6j904UJERPXXFB36RETU\\nXBguRERkOYYLERFZjuFCRESWY7gQEZHlHL+2GJET5HI5zM3NwefzQQiBQCCAcDhsd1mmpNNpeL3e\\npqs7k8lACIGFhQUIIRCLxTAwMGB3WYapqgpVVdHV1YWFhQUEg0GcP3/e7rJqomkaEokErl279txj\\nGS5o7h9+s7/wdjn5jU8IgUQiUbZCxNDQEBRFgd/vt7Ey41RVxcjIyAs9GtwOmUwGiqKUfqeLxSKC\\nwSAKhUJTvEZVVYUkSbh69WppWygUgqZpuHjxoo2V1SYej2N5ednYwfohNzMzo6uqWrYtGAzqY2Nj\\nNlVkXDqd1nO5XOlzTdP0np4ePZVK2ViVeTMzM7rX69Wz2azdpVQ1MjKiZzKZsm2qquqDg4M2VWSc\\nEEKPxWLqDI8fAAAH7klEQVR6KpXSe3p6HPs93ku112EqldIlSbKhGvPOnTtX8f4Sj8f1np4emyqq\\n3cLCgj44OKgPDQ0ZOv7Q97mMj49XbItEIlW3O40QAn19faXPPR4P4vE4YrGYjVUZl8/nMTo6inw+\\nD5/PZ3c5e5qenkYgECjbFgwGm+IqwO/349q1a03xV/6zNE3D5OQkisVi2fbdq9vFxUUbqjJHkiSo\\nqlq2Tdd1eL1emyqqXTabRTQaNTxD/9CHS7P+8A/CC68Z3vg0TYOmaRXhJ8sygOb4PjcrWZYhhEA+\\nn7e7lJpNTU3hypUrZdvS6TSGh4dtqqg22WwWkUjEVJtD3+cyNTVVsS2dTuOdd96xoRrjnn7hnTlz\\nxu5yDqxCoQAAVR9UB+xcPfKZQvWz+/1/mqqq8Hq9Tfl9T6VSCIVCuHDhgt2lmCKEQDgcNrUu2qEP\\nl2c10w//oL3wnEjTNLtLoGeMj4/j8uXLdpdhSiaTwczMDCRJwuTkpN3lmJLJZGq6u8Bw+XfN/MN/\\nWjO+8IiMSqVSOHnyZFP88fe0gYEBDAwMoFgsIhQKYWJioqy/1Kle5I8rhsu/a9Yf/tOa9YVHZIQQ\\nAqlUCrOzs3aXUjOPx4NYLIZwOFz1zoPTTE9Pl1217C67b8SBCRchhOFju7q64PF4qu6z44dvRe12\\nvvCs+t47kaIoAICVlZWq/S67+6n+EokEbt68aXcZLywcDkPTNGSzWUfO69o1Pz+PUChUtu3Q9bnk\\n83kkEgnDx/f39+87gamRP3yrarfrhWf1995pZFmGoigQQpQNnBBCQJZl9m01yOjoKMbGxvYcWOFE\\nu0/Mff/996sOunl2pKfTzM7OYmFhoaybIJfLlSYV9/f37zth+0CEi9/vrzrq63mc8MOvtfan2fnC\\ns6J+p4tEIrh161bZ70gul0M0GrWxqsNjYmICiUSiLMiz2azjV0jQNA09PT0VV7e7V/rPzp1ymmqd\\n+O+++y5mZ2fLVhzYy6Ge59LsP3xg7xdeM88NcJpkMonp6emybalUCslk0qaKamfmtoYT7E5ULRQK\\nyOVyyOVyUFUV09PTjg4WYOf9Y3h4uOJ7nkwmEY/Hm/Kq9+uvv+Zjjo169913MTIyUtYPEI1GEQqF\\nKiY/OU06ncby8jKCwWBpW6FQQDqdNrSwnJP09vZifHzcsfeg5+fnMTk5if7+/tIV73e+8x27y3qu\\nYrGIK1euQAiBdDoNRVEQiUQQjUYdvwZdtcmru3p6evDxxx83uKLaTExMYGFhobR2YSgUwttvv213\\nWabk83kkk0lMTU2hWCzi/PnziMVi+w56OvThAjTnD/8gvPCa+Y2PiPbHcCEiIssd6j4XIiKqD4YL\\nERFZjuFCRESWY7gQEZHlGC5ERGQ5hgsREVmO4UJERJZjuBCZkMvl4HK5KlaLfZaqqnC5XBgaGjL1\\n9QcHB+Fy8WVJzY+/xUQmBAIByLKM+fn5fRc23V2L7Hvf+57pc5h5ZgaRUzFciEwaGRmBruv7rgY9\\nNTUFSZJw9uzZBlZG5BwMFyKThoeHAew8UrqaXC6HYrGIc+fONbIsIkdhuBCZ1NfXB0VR9rw1tvtw\\npd0QAnYe4zA4OIienh64XC74fD4MDQ1VfTTC08v9RaPRqn0wmqbB5XJhdHS0Yt/Y2BiCwWDpPKOj\\no3wEAzUcw4WoBrFYbM9bY6lUquyWmBACvb29+MEPfoDe3l7EYjGEQiGk02kEg8HnPpRuvz6YZ/cF\\ng0EkEgm4XK7SeVKpFHp6ejA/P1/D/5SoNgwXohrs3vJ69tZYtVtiyWQSkiRhZmYGP/rRj/Dee+/h\\nxo0bSCaT0DQNqqpaUtPY2Bjm5+eRzWZx69at0nnm5uYAVH+yIFG9MFyIauD3+9HX11dxa6zaLbHR\\n0VFMT09XPFxs90FLy8vLltR05coVRKNRBAIBaJpW+vD7/QiHw8jlclhZWbHkXETP02J3AUTN6nvf\\n+x7m5+eRSqVw8eJFADtPB312lFhfX18pSDRNw+zsLHK53J4DAmpVLBYxMzMDr9dbdb8kSSgUCujs\\n7LT0vETVMFyIajQyMoJ4PI7JyUlcvHgRQgjk83kMDg6WHadpGuLxeOkRscBO30gwGLSso10IAWBn\\nAEA8Ht/zuL2Ch8hqDBeiGnk8HgQCgdKtsXQ6DWCns/9p4XAY8/PziMViiMViOHPmDAAgm82W2phV\\nKBTKPt995LUsyxW334jswD4XohewO2oslUphcnISkiSVvblrmob5+XkMDg7ivffeKwULUD7k2Kxc\\nLlf2uSzL8Hg8ew4O8Hq96O3trfl8RGYxXIhewO7aYePj45ifn99z4uSznfa7t8qAypB5enixLMvQ\\ndR3ZbLZq26fFYjEsLy9XrGc2NjaGYrFYdU4MUd3oRPRCotGoLkmSLkmSns1m99w/ODioJ5NJfWRk\\nRPd6vfpbb72lS5Kk9/T06Kqq6rqu6+fOndMlSSq1TafTpa8di8XK2nq9Xn10dLTsXD09PaWvee7c\\nOT0QCOiSJOmhUKi+3wSiZzBciF7QbgC4XK6q+zVN02OxmO71ektv9JlMRtd1XY/FYrrL5SqFxODg\\nYMXXSaVSpdDw+Xx6IpHQdV2vGi66ruvxeFwPBoO6JEl6b29v6XiiRpJ0/QVu/BIREVXBPhciIrIc\\nw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIcgwXIiKy3P8HynkIpHhL8JoA\\nAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 54\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"f_val, p_val = scipy.stats.f_oneway(x, y, z) \\n\",\n \"print \\\"One-way ANOVA P =\\\", p_val \\n\",\n \"f_val, p_val = scipy.stats.mstats.kruskalwallis(x,y,z)\\n\",\n \"print \\\"One-way Kruskal Wallis P =\\\", p_val \"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"One-way ANOVA P = 3.03067030652e-08\\n\",\n \"One-way Kruskal Wallis P = 2.7064432518e-08\\n\"\n ]\n }\n ],\n \"prompt_number\": 55\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \" np.random.seed(50)\\n\",\n \" x = [np.random.randn() for _ in range(200)]\\n\",\n \" y = [np.random.randn()+0.1 for _ in range(200)]\\n\",\n \" z = [np.random.randn()+0.1 for _ in range(200)]\\n\",\n \" i = [np.random.randn()+0.1 for _ in range(200)]\\n\",\n \" j = [np.random.randn()+0.2 for _ in range(200)]\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.hist(x,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(y,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(z,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(i,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.hist(j,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\\n\",\n \" ax.set_xlabel('Value',size=20)\\n\",\n \" ax.set_ylabel('Freq',size=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3VtwWneeJ/DvQaCbZXGRc3PSGXPkvs50jwUoM70121sV\\nRKZqamurNrKk7NO+xEL9blv4aV62ykap3dq3WMhP+7IrCTIzex8L3DtTPTu9bQs53Z100rYOysWO\\nb0IHdEMIOPvgFmMEkv7IwDnI30+Vq6I//8P5BYF+/O+SpmkaiIiIasikdwBERHT0MLkQEVHNMbkQ\\nEVHNMbkQEVHNMbkQEVHNMbkQEVHNmfUOYDdVVREIBHD16tWS8ng8jvn5eTgcDiiKApfLBa/Xq1OU\\nRES0H8Mll/HxcaysrJSUKYqCQCCA69evF8uGh4chyzKcTmejQyQiogMYqltMURSsrKxAkqSS8mAw\\niLGxsZIyv9+P8fHxRoZHRESCJCOt0J+amgIAzM3NYWZmpljucDgQj8dx6tSpYpmqqnA4HCgUCo0O\\nk4iIDmCYlkssFsPAwEBZuaqqxUTyLJvNBgBYWlpqRHhERFQFwyQXRVHgdDqxuyGVTCYBAN3d3Xte\\nR0RExmKI5BKJRHDu3LmKj6mq2uBoiIjoeemeXJg8iIiOHt2Ty+zsLAYHB4s/754pdliSJO35j4iI\\n6kvX5LKwsACPx1NStnvMRZZlAEA6na74HDuPV4MJhoiovnRdRHnr1i0sLi5ienq6WBaPx4uLJvv7\\n+zE4OAhZlqEoCs6cOVOspygKbDZbyfTkZ+01w5qJhYio/nRNLpUG8T/44APcunULV65cKZYNDAzg\\n5s2bJcklHo/D5/M1JE4iIqqO7mMuuz158qSs1REMBjE7O1tSFgqFEAwGGxkaEREJMswK/UQigWAw\\niJmZGaRSKZw7dw5+vx99fX0Ano7PTE9Po7+/H4qiwO124+233676PjvdYgb53yYiOpIMk1wahcmF\\niKj+DNctRkREzY/JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiI\\nak7XjSuJXhT5fL6q+iaTiTt4U1NjciGqs08//Rx/93d3YTKJdRRomoY33+zCX/zFT+ocGVH9MLkQ\\n1dn2dg5m8/fx6qtiB9ttbW1gdfUXdY6KqL445kJERDVniJZLNBpFNBpFT08PFhcX4Xa7Sw4SUxQF\\nfr8fgUAAbrcbyWQSoVAIPp8PXq9Xx8iJiKgS3ZNLNBqFJEklJ096PB6oqooLFy4Uy2KxGGKxGADA\\nZrPh2rVrTCxERAale7fY5ORkWdnAwEBJuSRJiEajUFUViqIgmUzi3XffbWSYRERUBd2Ty07ieJam\\nabDb7WVl3d3dOHXqVAOjIyKiw9C9W2xmZqasLBwO46c//akO0RARUS3onlx2C4VC8Hg8OH/+fEm5\\noihQVRUAkEwm4XA4MDg4qEeIRER0AMMkl0gkgrm5OUiShOnp6ZLHHA4HAJQkk+Hh4bIyIiIyBknT\\nNE3vIJ6VSqXg9XoxNTWFvr6+PevFYjH4/X7cvXu3quff2VLDYP/bdIR9/PEn+OUvO6paRJnP/wIj\\nI2/XOTKi+tF9QH83q9UKv99/4DRjp9MJRVGQTqcrPi5JUsV/RERUf4ZLLgDg9Xqhqipu3LgBAJiY\\nmCirs9NVpihKQ2MjIqKD6ZpcFEWB3W7H7du3Kz6+s64lEAhgaWmp5LFkMgkAkOXKXQ2aplX8R0RE\\n9afrgL6qqujt7S1LEDutEZfLhVOnTmFycrJsfUs0GoXb7UZ3d3ejwiUiIkG6tlxcLhdGRkbKWhTB\\nYBDj4+PFhOJwOJBIJIqPq6qKUCiEqampRoZLRESCDDFbbGpqCouLi8WNKz0eD95///2SOpFIBIqi\\nYHl5GaqqIhAIHGq1PmeLUaNxthi9iAyxzuXZHZD3wvUsRETNw5CzxYiIqLkxuRARUc0xuRARUc0x\\nuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRAR\\nUc0ZYlfkaDSKaDRa3HLf7XaX7ZQcj8cxPz8Ph8MBRVHgcrng9Xp1ipiIiPaje3KJRqOQJAlXrlwp\\nlnk8HqiqigsXLgBA8ajj69evF+sMDw9DlmU4nc6Gx0xERPvTPblMTk5ibGyspGxgYACTk5PF5BIM\\nBsvq+P1+jI+PY2ZmpmGxEhnVN/fvI/noUVXXOF5+Ga+dPFmniOhFp3tykSQJ0Wi0pItL0zTY7fbi\\nz7Ozs7h06VLJdW63G+FwuGFxEhnZl59+io5PP8Xxjg6h+qubm/jyBz9gcqG60T25VGp5hMNh/PSn\\nPwUAqKoKVVXhcDhK6thsNgDA0tLSoY47JjpqXrXb8fLvPxcHeaSqSNQ5HnqxGW62WCgUgsfjwfnz\\n5wEAyWQSANDd3V2xvqIoDYuNiIjE6N5y2RGJRDA3NwdJkjA9PV0sV1VVx6iIiOgwDJNcBgcHMTg4\\niFQqBY/Hg6mpKfT19ekdFhERHYLhusWsViv8fv9zr2GRJKniPyIiqj/DJRcA8Hq9UFUVN27cgCzL\\nAIB0Ol2x7s7jRERkHLomF0VRYLfbcfv27YqPq6oKm80GWZbLBu4VRYHNZttzppimaRX/ERFR/ema\\nXFRVRW9vb1nrYyeRuFwuAE8XVd68ebOkTjweh8/na0ygRERUFV2Ti8vlwsjISFmLIhgMYnx8vNgq\\nCQaDmJ2dLakTCoUQDAYbFSoREVVB99liFy5cwNTUFBYXF4sbV46MjOD9998v1rFarQgGgwgEAujv\\n7y/uNcbFk0RExqR7cgFQtgNyJX19fZyaTETUJAw5W4yIiJobkwsREdUckwsREdUckwsREdUckwsR\\nEdUckwsREdUckwsREdUckwsREdUckwsREdWcIVboEzWTdDqNXC4nXD+VSiGft9QxIiLjYXIhqtJf\\nX/9rbJo2hQ+fW1xcgm37z/H669+pc2RExsHkQlSlzHYGr/W9Jpxcvnx8D9oTniVELxaOuRARUc0Z\\nIrlEIhF88MEHGBsbwzvvvINIJFLyuKIo8Pl8iMViUFW1uOV+LBbTKWIiItqP7t1ikUgEsixjcHAQ\\nwNPBT7fbjWQyWbIVfywWKyYTm82Ga9euwev16hIzERHtT/eWi6IoJee0WK1WjI+Pw+/3F8skSUI0\\nGi22WpLJJN599109wiUiIgG6JhdVVTE9PY1UKlVSvtMiWVpaKpZpmobu7m6ePklE1AR0TS42mw2K\\noiCRSOgZBhER1ZjuYy7JZLKsLBqNwm63l7RSFEWBqqrFaxwOR3GchoiIjEX35FLJ5OQkLl26VPzZ\\n4XAAQEkyGR4eLisjIiJjMFxyCYVCOHHiBM6fP18ss1qtJTPHAMDv98Pv9++ZXEQXuBHVm6ZpyOW2\\nsb2dFar/tF6+vkEB2N7eRjYrFhPw9DNlsXAbGxJjqOSiKApCoRBu3bp1YF2n0wlFUZBOp9Hd3d2A\\n6IgOJ/nNY1ji/xOLDxSh+tu5LeTta8C/8dUtptXVVcx9toBP0l8KX9MmteG9f/Ue2tvb6xYXHR2G\\nSi6BQAA3btwoK5+YmMDFixdLyna6yhRFwZkzZ8qu0bTK222wRUONpuU1fNvUgj/pOSlUf3UjjX/M\\nPK5rTAVNQ761gJNnxGICgHsf30OhUKhjVHSU6L7OZcfY2BgmJibKWiE7q/GfnZYM/NNEAFmWGxUi\\nEREJMkRymZqaQiAQKJkdFovFkEgkIMsyJicny9a3RKNRuN1udokRERmQ7t1i4XAYwNOWyE5rJJlM\\nIhwO4+rVqwCedoElEgk4nU4ATxdfhkIhXLt2TZ+giYhoX7omF1VVi1OKd+vt7S3+9+DgICKRCMLh\\nMJaXl6GqKsLhMFfr05FU0ApYVpP43e9+J3zNl19/jcKjR1DX14XqL96/j3uP7+Pe/XvC93j0+BHH\\nXEiYrsnFZrMJv1m5noVeFNncNu5sb+LGyorwNQlJQqKtDd0tLUL17wD4RFlBx6/E40p+/hiZTAZd\\nXV3iF9ELS/duMSIqZ2ppwevPtN4Psra2hlc6O2E7dkyo/qOVFZhNZvQ4Xhe+h2r6TLgukSEG9ImI\\n6GhhciEioppjciEiopqraszl9OnTVa9w1zQNkiThzp07VV1HZFS/+u0dfJr+BhD8LHz+5SO8sSn+\\n/JIkAZsbiFfYrWIv+a0tvNbZKX4TojqrKrn09fUhkUggHo8Xy5xOJ5LJZPHAL5vNVlyPsoNbrtBR\\noma38UbfGZgE2/3bd77B9v1t4edvM7fidNdx/LCjQ/gaqbMTZtGAiBqgquRy6dIleDweuFwuTE1N\\nlRxPHI/Hce7cOSwtLSEcDpclGKKjpMVihskk9qVJEqz3LJPJBIvgtGIiI6rqq86VK1dgs9kQi8VK\\nEgsAuFwuzM/Po1AoIBAI1DRIIiJqLlUll2g0Cp/PB6vVumedgYEBRKPR5w6MiIiaV1XdYpqmQVH2\\nP5MikUg8V0BEjZTNZvHkyZPqLqp8mgMRPaOq5DIwMIBIJIKPPvoI7777btnjkUgE8XgcAwMDNQuQ\\nqJ4ePHiAv/m/f4PWY63iF3VoohPFiF5YVSWXYDCIaDSKoaEhnD17Fj6fD7IsY3FxEXNzc8UdjoPB\\nYF2CJao1TdPQerwVJ0+LH5pl++p+HSMiOhqqSi6yLCMWi2F8fByzs7OYnZ0te3xycrJssJ+IiF4s\\nVW9c6XK5MDc3B0VREI/HoSgKZFmGLMtwuVyHCiISiUBRFCwuLkJRFPj9/rJdkOPxOObn5+FwOKAo\\nClwuF7xe76HuR0RE9XXoXZFPnDgBj8dz4Oyxg0QiEciyXEwmqVQKbrcbyWQS586dA/BPRx1fv369\\neN3w8DBkWeZ6GiIiA6o6uSwsLODcuXOIx+OQJAlzc3N4++23cfr0aYyNjeH8+fNVPZ+iKCWtFKvV\\nivHxcfj9/mJyCQaDGBsbK7nO7/djfHwcMzMz1f4vED2Xuz//DTqVVeHtXzKffI07X6/jf/3DfxOr\\nn8vgztZj5Cx/LxzTZmYdre0taBFcePnw0WNk1sQOFiM6jKqSSyKRgNvtBgB4vV7EYrHiY8vLy7h4\\n8SKmp6dx8+ZNoedTVRXT09MYHR0taf3sdHctLS3h1KlTmJ2dxaVLl0qudbvdxQkERI2UW1rFn3S8\\nDkhiy8RkrQWOYxt4WTohVH9LymJzuwffSv9QOKZl9Ut09mjoaBfbMkbKmJBo4cQEqp+qZ4sBwPz8\\nPJxOJxwOR/GxlZUVTExMIBAI4NKlS7h8+fKBz2ez2aAoChKJBM6cOVOxjqqqUFW15F471wL/lICI\\nGsnWZRVuJWTVNVjXzLB12YXqb21toWvLDGuXWDICgMzmCro6gWNdYoeFLadSkFa5FxnVT1XvrpmZ\\nGQwMDOw5G+zixYvo6+urqkWRTCbLEks0GoXdbsepU6eQTCYBAN3d3RWvP2hRJxERNV5VyUVVVfQe\\ncPTqzrqX5zE5OVnsBlNV9bmei4iIGq/qLfdv3bq1b52FhYVDT0kGgFAohBMnTlQ9MWA3bvP/Ytra\\n2sLW1pZw/dXVVeTz+TpGZFyapmFrc0O4fmZjA6urq2htFd/NoLOzE2bzoSelUhOr6rc+MjKCQCCA\\nn/3sZxUTyPDwMBRFwcWLFw8VjKIoCIVCByYwor1E/+Ef8OX6Okyis6YePkR24wG+9d1v1TkyY2lp\\nMSHT1o7ffC2+F+D9TxP4+X/+OXp6eoTqZ3NZfOdffAc/+KMfHDZMamJVJZed2WBerxc+nw/A00H+\\nyclJRKNRrKysQJZlXLly5VDBBAIB3Nh1+p4sywCAdDpdcdxl5/HdNK3y7oJs0RxtW/k8HD/8ITq7\\nuoTqp27fxuZnL95mq2aLBW0nT+L4D38kfI3pxs/xh/Y/xJsn3xSqv/Rg6YVtFVKVYy7A05liV65c\\nwS9/+UsAwNzcHGZnZ1EoFHDx4kXcvXv3UIGMjY1hYmKiLIHYbDbIslw2cK8oCmw2G2eKEREZ0KHm\\nIl68eBErKysoFAq4e/cukskkVlZWDt1imZqaQiAQKEkUsVisuH3/wMBA2dqZeDxebD0REZGxVJVc\\npqam8NFHH5WUybJcXHNyGDvTlpPJJOLxOOLxOKLRKGZnZ4tbuwSDwbJNMkOhEHdfJiIyqKrGXPx+\\nP+x2e8WzXA5DVVUMDw9XfOzZKc9WqxXBYBCBQAD9/f3FvcbYJUZ62Mpmsba2DpNJbNJAbjtX9T0K\\nhRxW15LC9XP5bQCWqu9Tje3sFu59sYTCpthsvK+X76HnO6/UNSYyrqqSy/vvv49r167h9u3be66o\\nr4bNZkOhUBCq29fXx638yRA2N7NYXzPDZBZr+Ge322BpFf+oSS0tQBuwromv8Sq05WC2iG39cmib\\nGXR8+TWObWTFYnqwhOU/5gSaF1VVySUUCuH06dNwu92YnJyEx+OBLMt7rp4nOqosrW3CLReLuQ0t\\n2Yzwc0sSYLa0wtLWLnyNJmUhmer/h9za2YmXrGKf96WVdoivOKKjpqrksrO/l6ZpGB0dLZY/O71X\\n0zRIksQpiEREL7Cqkovo4VxcS0JE9GLbN7kEAgG89dZbxQH83TO2iI4CTdP2XHRLRIezb3KZmJjA\\n0NBQ2eywqakpxONxfPjhh3UNjqjeUuk0bt++i3RBvLVdqKIu0YvqUDvKXb9+HR999BGTCzW9p2OD\\n3ehx9Atf02r5Rf0CIjoiDn1aELsRiIhoL4dOLhy0JyKivfCcUyIiqjme4kPUAJvbWWB9TahuXhPb\\nteJ5aZqGtVQVJ72yK5yqwORCVGeWzk48qvKaFkt9P5qtLS1wrG/C8YX4keSpQgGtZrFdCYgOfAdH\\no1GMjIyUlMViMWiaVlb+rOnp6eePjugIaG1rR2sVW7k0gqlFQndHB17qEt+66YHZAkliTzqJOTC5\\nrKys7Ll4cr9FlUwuREQvrn2TSyPPsg+Hw7Db7WVbzCiKAr/fj0AgALfbjWQyiVAoBJ/PJ7wdDRER\\nNda+ycXlcjUkiGg0itHR0eLBYbvFYjHEYjEAT7fpv3btGhMLEZGB6Tqgn0gkEAwG4Xa7izsu7yZJ\\nEqLRKDweD5LJJA8IIyJqArqOzjmdTly9ehXnzp3bt56maeju7mZiISJqEpz6QURENdcU61wURYGq\\nPl3slUwm4XA4MDg4qHNURES0F8Mnl52xmGeTyfDwcFkZEREZh+GTi9VqLRuT8fv98Pv9+yYXbqz5\\nYtrMZLCRTmO7ILaFSnaLp7xXI7O1iY31DaG6W5kMtre36xwRGZXhk0slTqcTiqIgnU6ju1t8hTEd\\nfb/+zSIe329F+7HjQvXvL2Vhbumsc1RHRAvwxcMvoK49Eaq+9M1XkB601TkoMirDJ5eJiQlcvHix\\npGynq0xRFJw5c6bidXudN8MWzdFWyAPHj7+J47aXhOqvJTew3rFU36COCEt7Kzp7jqFLMHGbkiYU\\nGrQJJxmPoWeLKYqCQCCApaWlkvJkMgkAkGVZh6iIiOgghk4usixjcnKybH1LNBqF2+1mlxgRkUEZ\\nKrlU6spyOBxIJBLFn1VVRSgUwtTUVCNDIyKiKug65pJKpXD58mUoilLcoHJgYAA+n684E2xwcBCR\\nSAThcBjLy8tQVRXhcJir9akmtrczeJD4HJm02CA1AGg4AodmSRLya1k8vvuV+DXbgASOWZIYXZOL\\n1WrFlStXDqzH9SxUL+bOYzj2ygk4bDbha0yvv9H055ocaz+G09ppWFJdwtfYzetoM1vqGBUdJYaf\\nLUZUT6YWM7q6unHixMvC12Q7VuoYUWOYJBO62o+jtVV83DJn4ZRtEtfcX7+IiMiQmFyIiKjm2C1G\\nhqaqKgqCW7kAQCaTQSGbwfbWplD9XHZrzwW39Hw0Dchmt7G5Kfa7AIB8Po+Wlpaq7tPe3s7F0QbE\\n5EKGlUgkcPUv/wPa8+Jv048//xyv/9CKrWNiA/QbyXtYk5aB1147bJi0h/XMFuJLCfynaFSofqFQ\\nQOL/zOOff69f+B45LYf+f9mPN95447BhUp0wuZBh5XI52AudeFv+M+FrPk48wXeP/wg2u1iyuJu+\\nhc+2PztsiLQPDYBkd+Dkj38sVD+Xy+F3//MmfnxSrD4A/Pb+b6tq2VLjcMyFiIhqjsmFiIhqjsmF\\niIhqjmMuZFjZbBYP0su4+/hL4Wvy+XzV98llMlj+5oH4BRpnJhEdhMmFDGt9fR2LrRo6XmoXvib/\\n8gmYzOIHVHV22CHffxM9X1qFr2kx9XDqK9EBmFzI0MxmC06cEJ8m3NG1VNUffou5DbZjJ9Bz3H6Y\\n8IhoDxxzISKimjNMyyUcDsNut8Pr9ZY9Fo/HMT8/D4fDAUVR4HK5KtYjIiJjMERyiUajGB0dRTgc\\nLnts56jj69evF8uGh4chyzKcTmcjwyQiIkG6JpdEIoFgMAi32w2Hw1GxTjAYxNjYWEmZ3+/H+Pg4\\nZmZmGhEm1cjCwm8Qj4vP/FpauoOVxEPckW4JX7P+4BG+avkUbaljQvWzmxvo4ti8kLzZjI8frkAy\\nie399U02D6nKfcLo6NA1uTidTly9ehXA0yRSyezsLC5dulRS5na7K7ZyyNjS6QxaWv4YNturQvWX\\nl+142fQ7uDo9wvdo7bJBcnShtUNwhtmGBktOfHbZi+z4K6+g86UumAQTRntLAdZXxM/JoaPFEN1i\\ne1FVFaqqlrVqbL8/NXBpaYnHHTcZSTIJ73pr+v03ZJPgN+Wd55ckQBKeq8JmiyhJkiCZTDCZxF5b\\n0Xp0NBn6t59MJgEA3d2VT8tTFKWR4RARkSBDJxdVVfUOgYiIDsHQ3WLPgyuoifSX3dzE43v3hOoW\\nDrF1DxnXkU0uRKSvzrZOOL7sxEZULLloBQ2vSSfrHBU1iqGTiyzLAIB0Ol1x3GXn8Ur2OrqWLRqi\\nxmhv7UC3wwn51e8J1dcKGlJJHvx1VBh6zMVms0GW5bKBe0VRYLPZOFOMiMigDJ1cAGBgYAA3b94s\\nKYvH4/D5fDpFREREBzFUcqnUlRUMBjE7O1tSFgqF9lx0SURE+tN1zCWVSuHy5ctQFAWKosDv92Ng\\nYAA+nw+Dg4MAAKvVimAwiEAggP7+/uJeY+wSO/q2tzexvqliWf1a+JpcPgsLx9UMYTuXw5P7y5BM\\nX4ldoGnYvlfFoW1kaLomF6vViitXrhxYr6+vD319fQ2IiIwkm81iu7CFfJv4FFUzLGhpMfQ8lRdG\\nIZ/HxkYLcjmxLWC0Qh6p1K/rHBU1Cj+FZGgmyYSWFot4fVOujtFQtUwmE1otYnu3FQqcKXaUGGrM\\nhYiIjgYmFyIiqjl2ixEdEYV8HjlsC9clqicmF6IjQJIsWFnJAshWcU1r/QKiFx6TC9ERYLF0AOjQ\\nOwyiIo65EBFRzTG5EBFRzTG5EBFRzXHMhYiEaBqwtrYB0d11trI55KVNqE/Etu8pFAp49PAePvvd\\nZ8IxLT5ehGPVIVyfGofJhYiEmM3HkMmIr6I3S8fwBkzoWl0Wql/I53FXfYR7WbHDxQBgKbmE76a/\\nK1yfGofJhYiEVLMNDwAULAV0mTpwrK1TqH4un4ME4LjtuPA9LK3VxUSNwzEXIiKquaZILoqiwOfz\\nIRaLQVXV4rb7sVhM79CIiKiCpukWi8VixWRis9lw7do1eL1enaOiahQKBWQyG8hkNoTq53Liq82f\\npWkFaMI77JYfUEe1owEoaGK/i53DAre3xbawAYB8Lo98Pl/VNdWSJAlmc9P8qTSMpnjFJElCNBqF\\nx+NBMpnkQWFNKnb9f+PX/3gP7e3HhOpvrKfRhuq2KDFrBWzeEz9cDABaeLhYXUiSCauZZaxmkkL1\\nC/kCttva8T+ux4Xv8fDxV0DLDTz55MlhwzxQ3pzHwNkBWK3Wut3jKGqK5AI8/VbT3d2N7u5uvUOh\\nQ9rKZHD6pe/hzW+Jze5JJ5N4kBCflgoAJzrEEhfVn6W1DdV8N9Cgoef7f4SuP+gVvmbrs1/BZf0+\\n/vTknx4iQjHxb+LIc6PPqjXFmAsRETWXpmm5KIoCVVUBAMlkEg6HA4ODgzpHRURElTRFcnE4nq7A\\nfTaZDA8Pl5UREZExNEVysVqtOHfuXEmZ3++H3+/fM7lIHKQ1nM3NDPJraayuiA3wZjbW6hwRHQVr\\na2u4f/++cP2O9g7YHfY6RkRAkySXSpxOJxRFQTqd5iB/k1hffoLX76/hpW2xob5Mdhv5lpY6R0XN\\nzNxqxteZr5H7JidUP5fLocfcgx87flznyKgpksvExAQuXrxYUrbTVaYoCs6cOVN2zc6c+d3YotHX\\nsdY29BwT+zKwadnCcv5wa13oxdBitqC75xgcr4htXrmV2QJSdQ6KADTBbLGd1fhLS0sl5cnk064V\\nWZZ1iIqIiPZj+OQiyzImJyfLFk5Go1G43W52iRERGZDhkwvwtAsskUgUf1ZVFaFQCFNTUzpGRURE\\ne2mKMZfBwUFEIhGEw2EsLy9DVVWEw2FuA6OjTCaDf//v/hLZ1bTwNSv3v4DJ9Md1jIpeOCYJ9x6q\\nWFkV21sst52DXevAj93it1hKfA1lZhVdXeK9JD/60Rv40Y++L36TI6gpkgvA9SxGk81msfHgK/h+\\n8LrwNS33reh60lXHqOhF0+ZwwPLyy7AcEzwzZnUdG4nq9iFbW9tCe+EH6OwUG99V1YdQ1cdV3eMo\\naprkQsbU2dEuXLfNwrcb1ZZkkmAym9EiuGux6ZBT283mVlgsbUJ1qz1U7ahqijEXIiJqLkwuRERU\\nc+ynaAK5XA5PnlTXT1ztzgWZTAaSJKGtTazpv7q6ivXNDJZT4lu0rGa2YMpuYX1rU6h+Npfj1x+q\\nuUKhgJWVFeH66+vr6BQ+fI52MLk0gYcPH+K3f/VXsFnE+3L/+pef4jXXCMxmsQM1vlj6BH2m38H5\\n5ptC9dc3N/FoYwt/nxE/yfGOZMZJswmrogmj1QxTu/iYDtFBWixmbHZ24P99JX6g3OLyQ3Rtis+K\\npKeYXJpEj8WCvpMnhev/19wnePnlM2hvF5tFc//eQ7xm/gIewXusbWygp/s4TvQ6hWN68GgTndoJ\\nHDv+svCOnmgKAAANy0lEQVQ1RLVkamnB8ZOvwXHqD8SvuV3daaj0FDsdiIio5phciIio5phciIio\\n5jjmckS15Lax9KsbMJvFJgFsPFAgfYvHEZB+JACmfAEbjx4IX7OVXUOq0IKttg6h+vlcDhZJbBxy\\nx/rGBv7xF7P47Wd/L1R/YyONt/pfw09+UsUeM0cQk8sRdabbhtbVZbS0iP2KX81m8EZPT52jItqP\\nhFdbW6Flt4SvyGazsGXMaCuIdcJsZbNYQXXTils629H+0nHYe2xi93iUwr17X1V1j6OIyeWIOtbW\\nhmOd3cLJJbeRhqWFvaSkL4tgS7uoYEFbawva28Su07QCILbHZZHJbIGjuwcvO14Rqr+2pgIQO8r7\\nKONfEyIiqrmmabnE43HMz8/D4XBAURS4XC54vV69wyIiogqaIrnsHHV8/fr1Ytnw8DBkWYbTKb6I\\nT0Qul0Mmk6nqmu3tbViqWD0vSRKOHTsmXL9QKCCZTuNxh9igJQBsbmUhmTeFu8U2tzMoFKpbDZ/Z\\n2sLa2rpw/XwhX9XzE4nQCgXk8mLvrVw+j0JeQjYr3jdWyOexmVnD2npKqH5mYx1SywYePBCfmJDP\\n52G1WoXrA0BHRwdaDrnLcyM0RXIJBoMYGxsrKfP7/RgfH8fMzExN7/Xxx5/iF794KDzLan09ja/W\\nP8f33H8ofI+WTAZDXq/wm+mTTz7Bf5+Zx3znCeF75PMmHD++BJNJbAZYMvUEr52y44033hCqv57J\\nQPn1Q2ysJQ6u/HtSwQTLcbG9y4hESKYWqGoGQFao/tb2Nh4X8vjN4q+F75FZ3cDD24+gWhSh+qvp\\nFNrXVvBfVv6j8D3i9xPw/Ot/i7Y2sZls29tb+PM/l/Htb39b+B6N1hTJZXZ2FpcuXSopc7vdCIfD\\nNb9XNltAZ+f3ceKE2B/Zx4+/xN3tL3DyrbeE73F/fh6FKjbCKxQKcEiv4c9e9QlfU61PVn+NQkF8\\nlo5WKKAt344f9fyzusVEdBCLuR1AFS1uaQuWlk0cf/m48CWvv3YKJzYsaBec7pxqfYw3zUmclX8i\\nfI9PEl/C4eiH1fqSUP379+8gnzf2ZpqGH9BXVRWqqsLhcJSU22xPpwUuLS3pEBUREe3H8MklmXw6\\npW+v7eMVRaypSkREjWP45KKqqt4hEBFRlSRN08QP5NBBPB6Hx+OpOEZhMpkQjUbx9ttvlz0mSdzK\\nhIiolqpJF4ZvuRARkTFU86Xd8LPFZFkGsPexvTuP77ZXht15cQzeYGOcNdQMMQKMs9YYZ21V2xtk\\n+JaLzWaDLMtlA/eKosBms+HUqVP6BEZERHsyfHIBgIGBAdy8ebOkLB6Pw+er37oPIiI6PMMP6ANA\\nKpXC0NBQyfYv77zzDkKhUNUtl2ZrgjLO59cMMQKMs9YYZ21VG2dTJBcAWFhYwPT0NPr7+6EoCtxu\\nd8VZYgc5qr9IvTRDnM0QI8A4a41x1taRTS61clR/kXpphjibIUaAcdYa46wtJhciItJdUwzoExFR\\nc2FyISKimmNyISKimmNyISKimmNyISKimjP83mJEL4J4PI75+Xk4HA4oigKXywWv16t3WBWFw2HY\\n7XbDxheJRKAoChYXF6EoCvx+PwYHB/UOq0w0GkU0GkVPTw8WFxfhdrtx7tw5vcPal6qqCAQCuHr1\\n6oF1mVx2qebFa6RmeSM2ywd7hxH+UCqKgkAgULIDxfDwMGRZhtPp1C2uSqLRKEZHR+tyxHgtRCIR\\nyLJcfM+lUim43W4kk0lDfV6i0SgkScKVK1eKZR6PB6qq4sKFCzpGtr/x8XGsrKyIVdaoxOjoqDY0\\nNKR3GCXm5ua0aDRaUuZ2u7WJiQmdIqosHA5r8Xi8+LOqqlpvb68WCoV0jGpvc3Nzmt1u12KxmK5x\\njI6OapFIpKQsGo0a6n2oKIrm9/u1UCik9fb26v6a7aXSZyIUCmmSJOkQzd7Onj1b9pkeHx/Xent7\\ndYroYIuLi9rQ0JA2PDwsVJ9jLs9QFAUrKyuGO2hscnKyrGxgYKBiuZ4URUFfX1/xZ6vVivHxcfj9\\nfh2jKpdIJDA2NoZEIgGHw6F3OJidnYXL5Sopc7vdhmodOJ1OXL161VDf/ndTVRXT09NIpVIl5Tut\\n0qWlJR2iqkySJESj0ZIyTdNgt9t1iuhgsVgMPp9PeIU+k8szqn3xGqUZ3ojN9ME20h9KVVWhqmpZ\\nkrPZbACM9boZnc1mg6IoSCQSeodyoJmZGVy+fLmkLBwOY2RkRKeI9heLxTAwMFDVNUwuv3eYF69R\\nmuGN2EwfbCNJJpMAUPEgPABl5xjR/pLJJM6cOVNSFo1GYbfbDX32UygUgsfjwfnz5/UOpSJFUeB0\\nOqv64s0B/d9TFAVer9dwrZZKjPpG3PlD+axm+GDrSVVVvUM48iYnJ3Hp0iW9w6goEolgbm4OkiRh\\nenpa73AqikQih2rlM7ng8C9eozXDG3E3I3+w6egLhUI4ceKE4b6I7RgcHMTg4CBSqRQ8Hg+mpqZK\\nxi319jxffl745NJM3xyN/kbczegfbDraFEVBKBTCrVu39A7lQFarFX6/H16vt2IPgF5mZ2dLvnhX\\nM9npyCSXavqme3p6YLVaATzfi1etw8a4W73fiLWIsxEf7Fq9nnqSZRkAkE6nK4677DxO1QsEArhx\\n44beYQjzer1QVRWxWMwQC1QXFhbg8XhKyl64MZdEIoFAICBc/6233sL58+cRj8ef68WrRrUx9vf3\\n77uYql5vxFrFWe8Pdq1fT73YbDbIsgxFUUoGohVFgc1m41jVIY2NjWFiYmLPiRJ62jlJ92c/+1nZ\\n5AMAZTMu9XLr1i0sLi6WdMHH4/Hiot/+/v59F0gfieTidDoxMzNT9XXz8/PP9eI1IsZGvxEPG+ez\\nGvHBrkWcRjEwMICbN2+W/H7j8Th8Pp+OUTWvqakpBAKBksQci8UMs+OBqqro7e0ta5XutMR3r3nS\\nS6Vx6A8++AC3bt0q2VlgL0ciuRzW8754jdAsb8QdRv9gG1EwGMTQ0FDJ+zEUCiEUCukY1f6MOqty\\nZ+FpMpksdhknk0mEw2HDbOnkcrkwMjJS9hoGg0GMj48burX65MkT4d/9C51cKqnmxWuEZnojNsMH\\nuxK9f99WqxXBYLDYWt5pORvpd5tKpXD58mUoilLcM25gYAA+n88we8epqorh4eGKj/X29jY4mv1d\\nuHABU1NTWFxcLO4XODIygvfff1/v0CpKJBIIBoOYmZlBKpXC2NgY/H7/vhOKJE3vT5ZB7H7xzp07\\nd+CL10i734gej8dQb8RKq8x39Pb24s6dOw2OaG/P/qEMh8OQZdlwfyiJmh2TCxER1Ry3fyEioppj\\nciEioppjciEioppjciEioppjciEioppjciEioppjciEioppjciGqQjweh8lkKtvwdLdoNAqTybTn\\nivG9DA0NwWTix5KaH9/FRFVwuVyw2WxYWFjYd9PQ2dlZAMB7771X9T3qeewDUaMwuRBVaXR0FJqm\\n7bsr88zMDCRJwrvvvtvAyIiMg8mFqEojIyMAnh7hXEk8HkcqlcLZs2cbGRaRoTC5EFWpr68Psizv\\n2TW2cz7QThICnh6RMDQ0hN7eXphMJjgcDgwPDyORSJRd/+x2fz6fr+IYjKqqMJlMGBsbK3tsYmIC\\nbre7eJ+xsbGK9yGqJyYXokPw+/17do2FQqGSLjFFUXD69Gl89NFHOH36NPx+PzweD8LhMNxu94EH\\nvu03BrP7MbfbjUAgAJPJVLxPKBRCb28vFhYWDvF/SnQ4TC5Eh7DT5bW7a6xSl1gwGIQkSZibm8Pf\\n/u3f4sMPP8T169cRDAahqiqi0WhNYpqYmMDCwgJisRhu3rxZvM/8/DyAyofjEdULkwvRITidTvT1\\n9ZV1jVXqEhsbG8Ps7CzefvvtkufYOStoZWWlJjFdvnwZPp8PLpcLqqoW/zmdTni9XsTjcaTT6Zrc\\ni+ggPImS6JDee+89LCwsIBQK4cKFCwCensa5e5ZYX19fMZGoqopbt24hHo/vOSHgsFKpFObm5mC3\\n2ys+LkkSkskkuru7a3pfokqYXIgOaXR0FOPj45iensaFCxegKAoSiQSGhoZK6qmqivHx8eIpp8DT\\nsRG3212zgXZFUQA8nQAwPj6+Z729Eg9RrTG5EB2S1WqFy+Uqdo2Fw2EATwf7n+X1erGwsAC/3w+/\\n348zZ84AAGKxWPGaaiWTyZKfd46YttlsZd1vRHrgmAvRc9iZNRYKhTA9PQ1Jkkr+uKuqioWFBQwN\\nDeHDDz8sJhagdMpxteLxeMnPNpsNVqt1z8kBdrsdp0+fPvT9iKrF5EL0HHb2DpucnMTCwsKeCyd3\\nD9rvdJUB5Unm2enFNpsNmqYhFotVvPZZfr8fKysrZfuZTUxMIJVKVVwTQ1Q3GhE9F5/Pp0mSpEmS\\npMVisT0fHxoa0oLBoDY6OqrZ7XbtnXfe0SRJ0np7e7VoNKppmqadPXtWkySpeG04HC4+t9/vL7nW\\nbrdrY2NjJffq7e0tPufZs2c1l8ulSZKkeTye+r4IRLswuRA9p50EYDKZKj6uqqrm9/s1u91e/EMf\\niUQ0TdM0v9+vmUymYpIYGhoqe55QKFRMGg6HQwsEApqmaRWTi6Zp2vj4uOZ2uzVJkrTTp08X6xM1\\nkqRpz9HxS0REVAHHXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiI\\nqOaYXIiIqOb+P7yRB6q5iztCAAAAAElFTkSuQmCC\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 56\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"f_val, p_val = scipy.stats.f_oneway(x, y, z,i,j) \\n\",\n \"print \\\"One-way ANOVA P =\\\", p_val \\n\",\n \"f_val, p_val = scipy.stats.mstats.kruskalwallis(x,y,z,i,j)\\n\",\n \"print \\\"One-way Kruskal Wallis P =\\\", p_val \"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"One-way ANOVA P = 0.0142504270115\\n\",\n \"One-way Kruskal Wallis P = 0.0258559380048\\n\"\n ]\n }\n ],\n \"prompt_number\": 57\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Resistant to deviation (CLT)\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 2,\n \"metadata\": {},\n \"source\": [\n \"Compare >2 independent samples. Corrections\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.plot(1-(1-0.05)** np.linspace(0,21,11),linewidth=3)\\n\",\n \"ax.set_xlabel('Prob of screwing up with the labels',size=20)\\n\",\n \"ax.set_ylabel('Number of plots I make',size=20)\\n\",\n \"plt.title('Are line plots different than the histograms?',fontsize=14)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\\n\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAaEAAAEzCAYAAACYBryKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8G2eZL/DfKG25tfaMkgXK0iUeqed0ucaS3AXOAZZY\\ncrkUFmJLKbtAgY01KtcFkkih7EKXSyK73OEkkkK7LdfEMst9t5YULgvsbm2NWqALJfHI0NKFpbHG\\nLqX0Er/nj+mMNbqPLXsk6/l+PvokejWaeWY00uN5571wjDEGQgghxAYOuwMghBDSuygJEUIIsQ0l\\nIUIIIbahJEQIIcQ2lIQIIYTYhpJQB0un03A4HAiFQm1ft6qqcDgcWF5eNv1/M1ndbjKZRLFYXPd2\\ns9ks3G53zRjS6TQEQcChQ4dqPrdDvf2uLN/Mz3Cjt91ofVbOm3adM51AkiQ4nU44nU6EQiEsLS3Z\\nHVJ7MNKxxsbGGMdxzOFwtH3dpVKJcRzHlpaWGGOMRSKRtm/DagzNuFwuNj09ve7tZjIZ5nK5jOfl\\n++73+xs+t0O9/a4st3Is2x1Tu7fdbH2tfibtOmfsdvDgQeZyuVgul2PZbJZ5vV4WDAbtDqst6Eqo\\ng01PT2NiYgKMMeRyuQ3d1tGjRzd0/e3CNqBbW/m+l0ol+P3+us/tUm+/N+J4tMrObVs5X+2Ms12m\\np6cRi8Wwe/duDA8PIx6PI51O2x1We9iZAUl9U1NTjOM4pqoqc7lcTJIk0+scxzFFUZgoimxycpIx\\npl1ZjI2NMUEQmCAILBqN1l1/+VVI5RWJvm6Px8M4jmOBQICpqmp6byvbyWQyTBRFNjU1xURRZIIg\\nmPajcrulUon5/X7GcRxzuVxsYmLCWFYURcZxHOM4jsViMcYYY4lEwij3er1MluWaceTzedO+JBIJ\\n40pIj0FVVWMZjuOYJEnM6/Uaz/W/vJvt+1o+l0bHu9Z+1yvnOI5ls1ljPV6v1/S5lR+Hys+ilc99\\nPdu2cm42W1/leVPvPKgVZ6NzjDHG5ufnTfs/NTXFvF5vzc+2leOp74O+z5XrL9fofE4mk0xRFNOy\\nTqez4THsFpSEOtTY2Bjz+XyMMe1SXBAE0+v6iTo5OcmKxSJjjDGPx8NCoRArFAosm83WTF66ZknI\\n6/WyQqHAZFmuWk+r28lkMozjOOZ2u1kul2PpdNr0Za3criiKbGRkhBUKBWPZZDJprK+8amV+fp5x\\nHMcmJydZoVBgwWCw6hiVb0OPd2JiwoipVgxer9dUfVP5vNm+r+VzaXa8rVTHud3uuuvhed6II51O\\nM47jTMe3WRzr2baVc7PZ+so/s2bnQWWczc4xnudZJBIxzhWe543vYflnqyhKS8dzZGSEFYtFlkwm\\njcSnH4Py5Vs9n/X953ne+COn21ES6lD6CckYM07YbDZrej2VShnP8/l81UmbyWQansiNklD5F3di\\nYsL4q83KdvQkVCgUjDJ9Xypj0JctNzExYbp3U/6Doi+v/3WsqmrNH+pEImEkHJ0kSVVXQuVJKJ1O\\nG8uWJ6FW9n0tn0uj41253+VqJYJG65mcnDTdZwkEAqYrkmbvX+u2rZ6bzdZX67ypdx7UOmfKlZ9j\\nU1NTVVcXwWDQlITKP9tWjmculzOeC4JgShyBQMC4Qmv1fC6VSkwURRYKheocue5znt3VgaRaNpsF\\nAIyOjgIAhoeHAQBTU1PG/wGY7lXMzc1BVVU4nU7Tutbagsbj8Rj/7+/vX9d2du3aZfxfj39hYQE8\\nzxvlsizD6/Wa3jc8PIxoNFpznX6/H36/HwMDAwiFQggEAsbxKpfP5037or9XP8a1cBxXs7zVfV/L\\n51LveFvVaD379+9HNpuFLMvIZDLI5XJVx3w9cbTznGk1llbPA6D5OTY7O1t1/8/n85la15W/3srx\\nFEXR+L/T6TQ9Lz//W92PZDIJh8OBEydO1NzHbtQRDRNkWUYqlcL09DQmJydbugkfjUaRy+Wgquom\\nRLi5EokEAMDlcsHhcMDh0D6mkydPmpar/FKLooiFhQXTY3Fxse3xbdR2mMUbyDMzM8jlcuB5HtFo\\nFG63u+qHjeO4tt6YbmXf7fpcam1bp6oqXC4XDh06BKfTiYmJCYyNjbX12NTbNrC2Y9BofeVqnQf1\\nmm83299mr+sxbcTxbOV8npub64iGMu1kexJSFAWxWAzj4+MYHR3FgQMHkEgkmrbtl2UZgUAATqfT\\n+KHWH5deeukmRb8xstksJEmCoijGI5FIQFVV3HbbbTXf4/P5oCgKGGPo6+tDX18fZmZmMD4+3tbY\\n1rKdQqFg2jcA2Llzp2kZj8cDWZZNZdlsFi6Xq+Y6s9ksJiYmMDg4iCNHjuDMmTNQFAX5fN60nNfr\\nrVpvJpNpup+1rGXfN+tzaSabzYLjOMzOzmLfvn0YHBzctFZjG3kM6p0Hc3NzVcs2O8dcLlfVFfLs\\n7Gzd7bbzeLZ6Pp88ebJrWrK2yvYkFI/HEYlETGWSJNWthtG5XC7Ismz6odZ/rKempjYy5A2VzWax\\ntLSEaDSKnTt3Go/x8XHwPI8vf/nLNd/n8Xjg8XgwPDyMXC6HdDqNcDiMyy+/vK3xrWU7wWAQuVwO\\n2WwWwWAQkiRVLeP3+yGKIkZGRlAoFJBOpxGLxarOg/n5eeP/sVgMqVQKsixjYmICHMeZqjsAIBQK\\nQVEUhEIhY7m1nh9r2fd2fS7l+91KeSWe56EoilF7MDExgenpaSiKYimOtWx7o8/NZueBHmezcywc\\nDgMAIpGIsa56tTLtOJ5Muyff8n4AWnXcRnfX2HQ23IcyEQTBaEWk0288NlLeCqWV8m4hSZJxI7TW\\na/pNdofDUdWZT1VVo1WNIAimJr2VSqWSsY7y/+vrLv9MkskkGxkZsbwd/eZzKpViLpeLCYJg6mRY\\nuV1VVVkgEDBaRlW2/tFbtunlExMTTBAEY/l6nRJlWTaaW4+MjLBsNmtqHVceQ7PWcc32fS2fS7Pj\\nXbnf9cort125nmg0aoohm80yQRCM/WsWx3q2beXcbLa+ys+s0XlQGWezc0xRFOb1epkgCCwUCrGJ\\niQmjEUBlTFaPZ2VjjmAwaDoOrZzPgUDA9s7T7cYxZl9PLv1mpaqq6OvrM73mcDigKEpVtU0jqVRq\\n06s5SH3ZbBahUGjD7n8Q0k7FYhGZTMa4IgK0WhmHw7HlqsA6ia2t4/Qfp8oEpLOShHK5HHw+X7tC\\nI4T0GEEQEIlEwHEcgsEgZmdnjeoxsnFsvSfUzpZtsixjcHCwbesj7VGvuTMhnYbneWQyGcTjcTid\\nTrz5zW9GOp02dTEg7bcl+gml0+m6raiIffx+P86ePWt3GIS0bHh4GGfOnLE7jJ6yJZLQkSNHcOrU\\nqZaWbfSXuY23xwghpCfZWh2nNz+s17GssnliLaqqQpbluveVrKCqI0II2Vy2JiGe5yGKYlXbekVR\\nwPN8S40SstmsafiLZtijbfMrH4QQQjaf7Z1V/X5/Va9kfTSEVszOztL9IEII6VK2J6F4PF7Vgz2Z\\nTCIejxvP9XGaUqlU1fsVRWl5jClCCCGdxfaGCf39/YjH44jFYhgaGjLGkqusiiuVSjXv2Wzfvh07\\nduzYpGgJIYS0k60jJnQSPcHR4SCEkM1je3UcIYSQ3kVJiBBCiG0oCRFCCLENJSFCCCG2oSRECCHE\\nNmtOQsvLy1hYWKiaA50QQkhveOgh4KtfXd86LCehQqEAn88HnufhcrmMOdDdbjeuv/769UVDCCGk\\nozEGzM4Cb30rcPHFwKtfvb71WUpCxWIRXq8XsixjeHjY1Kfm7NmzOHjwIIaGhtYXESGEkI5z113A\\n4cPA058OXH458JnPAO2YNNlSEtKH0snn81VD7ZRKJRw5cgT5fB6HDh1af2SEEEJs9fvfA5/7HOD3\\nA097GvCe9wA//7l5mT/7s/Vtw9KICU6nEz6fDzMzM1BVFU6nE9lsFrt37zaW8Xq9WF5exunTp9cX\\n2SajERMIIQRYWQG++13gppuA6Wng/vurl7nwQmBsDLj6auCFLwQc62jiZmnsOH0g0UZEUcT09PTa\\nIyKEELLp7rxTSzyf/7xW9VaJ47Qrote/XrsP9IQntGe7lpLQ4OAg5ubmGi5TKBTg8XjWFRQhhJCN\\nd/YscOKElnxuvbX2Mn/+59oVz9/8DfDUp7Y/BksXUXv37kU+n8d3vvOdmiNah0IhKIoCv9/ftgAJ\\nIYS0z0MPAV/7GjA6qrVue8tbqhPQ9u3A296mtYK74w4gGt2YBASsYRRtr9eLQqGAQCCATCaDQCAA\\nnueRzWZRKpUgiiLOnDmzMdFuILonRAjZqhgD8nng5puBL30JuPfe6mXOPx94xSu06raXvhS44ILN\\niW1NUzlMTEzg8OHDpo6q/f39kCQJR44caWuAm4WSECFkq/n1r7V7PDffDPzXf9Ve5vLLteq2vXu1\\nK6DNZikJLS0tob+/31Smz2zK8zwArS9RJBLBLbfc0t5INxglIULIVnD//dooBjfdBGSz2lVQpac+\\nFXjd67Srnssu2/wYy1lKQpdeeiny+Tz6+vpqvh6LxTAxMQEAWFlZaU+Em4SSECGkW62sAN//vpZ4\\n0mmtf0+lJzxBuw909dXAX/7l+ppVt5Ol1nHz8/Pwer1ViWh6ehrj4+NQVRU8zyOVSlkKQpZl5PN5\\nOJ1OKIoCj8eD4eHhlt978uRJbN++HWfPnoUkSRgYGLC0fUII6Ua/+IVW1fa5zwG/+lX16xwH7N6t\\nXfHs2aP17+k4zIJMJsM4jmNut5sVi0WmKAoLBAKM4zjGcRyLRqNWVscYY2x+fp4FAgFTWTAYZIqi\\nNH3v1NQUkyTJVBYOhy3HwBhjAJjFw0EIIZvugQcYu+kmxp7/fMa0yrbqx//+34x9+MOM/fKXdkfb\\nnOVf3Xw+zziOY06n00g+gUCgpaRRSzgcZtPT06aybDbLgsFgw/eVSiUmCIKpLJFIMLfbvaY4KAkR\\nQjrZ6dOMvfvdjDmdtROP08nYW97C2H/+J2MrK3ZH27o1tY7TBzBdWlpCIpHA+Pj4mq/EnE4nZFnG\\nzp07jTJ9SKBG95Wi0SgcDgcOHz5sKl9YWDCtq1V0T4gQ0mkeeQT45jeBo0eBmZnq1887D3j5y7X7\\nPC97GfCYx2x+jOu1piQEaK3ivF4vduzYgUwms6Yffj3ZqKpa1djB4XBAUZS663U6nTh+/Dj27Nmz\\nhuirURIihHSKe+4Bjh8HUing7rurX3/a04BIBHjTm4AnPnHz42unhg0T3G53zZERdBzHGY0VnE6n\\n6bVWBjBdfHQc8Hqt7RolIVVV0d/fj1QqBafTicXFRTidToyOjjbdLiGEdBrGgO98R7vq+epXtaug\\nchynXe1ccw3wkpcA27bZE2e7NUxCTLtnVPd1QRAgCAIAc5PsRomrnKqqLS1XSVEUANo4dfv37zfK\\nY7EYFhcX11U9SAghm6lU0ppWHzumDSJa6U/+BNi3DwiHgTVUOHW8hklofn5+s+KwRE9eoiiayvfu\\n3Yvh4WFKQoSQjjc3p131fOlLwAMPVL/+ghdoVz179nTnvZ5Wtb27Ui6XwzXXXNPu1ZroyacyCQ0O\\nDkJVVSwsLNR9L8dxNR+EELLR/vAH4IYbgKEh7XHDDeYEdNFF2oCiP/mJ1vn0Na/Z2gkIsNhZFdCG\\n7tEHK63EGEM8HkexWMTRo0ebrktPIsvLyzXvC1UmGZ0+RJD+b6VG95IIIWSz3XmnVt32T/8E1LoL\\nsWuXdtXz13/doR1KN5ClJFQsFuH1epveywmHwy2tj+d5iKIIRVGwa9cuo1xRFPA83zCR6O+rtUy9\\n5AXUb/1GV0OEkHZ6+GFtyoSjR4FTp6pff8xjgFBISz7Pfa7W8KAXWaqOi0ajUFUV8XgcMzMzGBgY\\nwNjYGDKZDGZmZjA4OIhAIIBjx461vE6/34/Z2VlTmSzLCAQCDd8nSRLy+XzV+wRBoKsgQoht7r4b\\n+Id/0JpRB4PVCcjlAiYnteVuvhl43vN6NwEBsDZEgCAIpiF24vE48/l8xnN9FIPKERAaUVW1atie\\nQCDAisWiab2iKLJkMml6n8vlqnqflW2XA42YQAhZo3PnGLvlFsZe9SrGtm2rHs3A4WDsr/6KsX/9\\nV21ZsspSdZyqqnC5XMZzj8eDWCxmPOd5HsFgEIcPH265E2l/fz/i8ThisRiGhoagKApisVjV1Uyp\\nVDJVmfX39yOTySASicDlcmF+fh6xWAy7d++2skuEELJmZ88CN94IJBJArbk8n/xkYHxce1xyyebH\\n1w0sjZjgcrngdruNuYL0EQ9kWTbu6UxMTCAWi9FUDoSQLYkx4D//U7vXc+IE8OCD1cu8+MXavZ5X\\nvUqbsZTUZ+mekMfjQTabxalHKzl5nkd/fz8SiYSxzNzcXN1Wa4QQ0q3OnQOmprRGBM97nnY/pzwB\\n9fcD73gH8LOfafeBgkFKQK2wdCWkKIoxlM/U1BT27NkDSZKQSqUQDAZRKpWQzWYRDoctNU7oBHQl\\nRAip5Q9/0JpWf/SjQK3++16vdtVz1VXaxHHEGssDmCqKgng8jkgkYnQOHR4eRqFQAKC1dpuamqqa\\nBrzTURIihJT73e+Az3xGe9x7r/m1xzxG60j65jdrnU7J2q15FO1Ket+hbq2KoyRECAG0BgYf/ajW\\n4OCPfzS/Jgha4nnb24AnPcme+LaatiWhbkdJiJDeduutWv+d6Wmt8UG5pz0NeNe7tKkTem1Eg41m\\nedgeQBtmR5+GoR7qMEoI6XQrK8C3v60ln+9/v/r1wUHg4EFgbEybQI60n+VhewKBAIrFYsMrBo7j\\ncO7cuXUHRwghG+HBB4EvfAG4/nqtNVulK64ADhwAdu/u8dEMNoGlJCRJEhRFgcfjwfDwcN3laBw2\\nQkgnUlVtINFPfhL47/82v3beeVpjg/37gWc/2574epGle0IOhwMejwdzc3MbGZMt6J4QIVvXXXcB\\nH/84kEwCv/+9+bULLwQkSevjQ6MabD5LV0IDAwNNBxYlhJBOcfvtWpXbl79cPV32xRdriUeSgC5t\\n1LslWBoxwe/3I51Ob1QshBCybowB2ax2X2fXLuDznzcnoKc/XZtMrlgEolFKQHaz3ETb6/Vix44d\\niEaj8Pl8dZerNUldJ6PqOEK62yOPACdPalc+j/adN3nRi7TGBi99KeBo+5zSZK0sJaGlpSV4vV4o\\nitJ4pV3YOo6SECHd6fe/Bz77WeBjHwN++Uvzaw4HsGePlnwuv9ye+Ehjlu4JjY+PQ1EUiKJIreMI\\nIbb6zW+AT31KG826VDK/9rjHAW98o9bBtGz2GdKBLF0JCYIAl8tFreMIIbb5+c+Bj3xEG8X6oYfM\\nr+3YAbz1rcBb3qL9n3Q+y32AqXUcIcQOt90GXHcd8NWvVr/mcmlXPW94A/D4x296aGQdLN2eC4VC\\nyGazGxULIYRU+elPgdFRbQidygR0+eXaHD933qkNLEoJqPtYbh03MjICjuMQj8chimLd5ay0jpNl\\nGfl8Hk6ns6URGQBtSglJkhCLxeD1erG4uIhkMolAIND0vbVQdRwhneXnPwfe/36txVvl1/LKK7XG\\nBi94AQ2r0/WYBYIgMI7jmj4cDkfL65yfn2eBQMBUFgwGmaIoTd9Xvk1BENj09LSV3TEBwCweDkLI\\nBjh9mrHXvpYxh4MxLf2sPl79asZuv93uCEk7WbonFAwGW1rOSus4fYK8cpIkIRqN4uTJkw23kc1m\\n4fP5sLi4SKN2E9LlikXgAx/QGhxU9vB4xSu0qyKPx5bQyAayfT4hp9MJWZZNSURVVTidTqysrNR9\\nX7FYhKIoa6p6q4Wq4wixx113AR/8oDaKQeXQOi95idYYgfr4bF229htWVdVIOOX02VkXFhZsiIoQ\\nshnuuUdrTu12awOLlieg4WHgBz8A/uVfKAFtdbZO06RPjFevEYOiKA2r2RRFMaYVX1xchNPpxOjo\\naNvjJIS0z29+A8TjWifTBx80v/aCF2hVci96kT2xkc1naxLSE8ha6FdP5UknFApVlRFCOsO99wIT\\nE8CnPw088ID5tec+V0s+w8PU2q3XdO0wfv39/RgfHzeV6Q0aCCGdY3ERuPZaYGBAm0a7PAH5fFqV\\n249+BPj9lIB60ZaaNX1gYACKomB5ebluFR+Na0fI5lBVbSK5j30MWF42v7ZrF/CP/6j196GvZG+z\\n9UpI7+y6XHmGVrxey8TERFWZXkXXbJRvQsjGue8+4EMf0q58rrvOnICe+UxgehrI57Vm15SAiK1J\\niOd5iKJYlTQURQHP83UbJSiKglgsVtV6Tm/o0Ch5McZqPggh63P//do9n4EB4L3v1a6EdJddps1u\\nevvt2tQKNJ8P0TWsjnO73Wuuvjp9+nRLy/n9fszOzmLXrl1GmSzLDQdKFUURiUSiKklls1l4vd6u\\nm1CPkG72wAPAsWPAkSPA//yP+TW3G3jf+4DXvAbYts2e+EiHazScQitD9NR7tEpV1aphewKBACsW\\ni8bzUqnERFFkyWTSKEun06ahfUqlEvN6vaxQKLS87XKgYXsIseSPf2TsU59i7OKLq4fX2bmTsRtu\\nYOzhh+2OknS6hldCjUYsaJf+/n7E43HEYjEMDQ0ZVW2VVzmlUsl0VTY6Oorp6Wmk02mcPXsWqqoi\\nnU7T8D2EbLCHHgJuvFEb5eDuu82vXXKJVhX3hjcAF1xgS3iky9g+bE+noGF7CGns4YeBz31O689T\\nOZjJxRdrzbD37QMe8xhbwiNdaks10SaEtB9j2nQK114LzM+bX3viE4FDhwBJ0qbUJsQqSkKEkLpu\\nvRV45zu1zqTltm8HolFtIrknPMGe2MjWQEmIEFLlrru0K5wvfMFcLgjA/v3A294GXHSRPbGRrYWS\\nECHEoPf1qRxe5/zzgXe8Q6uSe3SQe0LagpIQIQQrK1qjg/e8R5tiodyePVpicrnsiY1sbZSECOlx\\n//ZvwLveBczNmcsHB7Vx32haBbKR2jZ4Rr3x3wghnalYBIJB4IUvNCegJz9Zm+V0dpYSENl4lpNQ\\noVDANddcY4zbtrS0BJ/PB57nsW3bNhw6dKjdMRJC2mh5WWvZdtllQDq9Wv7Yx2r3fE6fBt74Rhpm\\nh2wOS0kol8vB6/UikUgYE9JFo1HIsozh4WHs3LkTExMT+MpXvrIhwRJC1u7cOW0a7Usv1e7xPPTQ\\n6muveQ1w553aKAgXXmhfjKT3WBoxwefzQZZlZDIZDA8PAwAcDgf8fj9mZmYAAIIgwO12Y3Z2dmMi\\n3iA0YgLZynI5rb/PT35iLv+Lv9Du+zzvefbERYilKyFFUTA2NmYkoEKhAECb0VQXCoVoPh9COsQv\\nfgG88pXarKXlCeiSS7Q+QD/6ESUgYi9LreNUVTUNIprNZgHANO3C4uKiUVVHCLFHqaTNXPrpTwOP\\nPLJa/vjHA7EY8O53a/8nxG6WquO8Xi8WFhZw9uxZANp8QwBw5swZYxmn0wmn02kq6wZUHUe2gocf\\n1ub2ef/7gUfneASgzWB69dXajKdPeYpt4RFSxVJ1nCRJKJVKuPTSS41pF/SquFwuB7fbDVVVMTY2\\ntiHBEkJqYwz49reBZz8bePvbzQlIb4J9442UgEjnsVQdFw6HMT8/j2Qyifn5eYyNjeHAgQMAgJmZ\\nGSiKAr/fjyNHjmxIsISQaj/9qVa99mjbIMPAgDb8zp492pUQIZ2obfMJFYtFMMYgimI7VrfpqDqO\\ndJvf/Q74h3/Qml2Xzz950UXA3/+9dkVEc/uQTmcpCS0vL6Ovr28j47ENJSHSLR58EPjUp7TJ5coH\\nKnE4gPFxrUHCE59oX3yEWGHpnhDP8zh+/HjDZWKxGLZv324pCFmWkUqlMD09jcnJSeRyOUvvB7SW\\ne5FIxPL7COkWjAH//M/AM54BHDhgTkB+P3DbbVqjBEpApJs0vSc0PT0NjuOMK4R8Pg+n01lzWcYY\\n0uk0SqVSywEoioJYLGZ0dgW0vkaiKGJgYKDl9USjUUvbJaSbFApaZ9Pvfc9c/r/+F/CRjwAvfznd\\n9yHdqWl1nMNhfYzT8hEUmpEkCVdccQX27NljlOVyOSQSCZw8ebKldeiJjOM4nDhxwnK8AFXHkc50\\n771av54bbtCuhHSCALzvfdrMpuefb198hKxX0ySULhvhMBQKIRwOw+/3111eEARjRIVWOJ1OyLKM\\nnTt3GmWqqsLpdGKl/G5rA6lUCgCQyWRaTlyVKAmRTsKYNqLBO9+pJSLdeedpied97wPqVEgQ0lWa\\nVseV9/kZHh5GMBi0lGQaUVXVSDjl+EenblxYWDAlp1pyuRz8fr8xegMh3W5+HrjmGiCTMZe//OXA\\n9ddro18TslVYqmsrH7hUt555hBYf7VFXr8VdK2PQKYqCgYEBuoIhXe/hh4F4HHjmM80J6JJLgG98\\nA/jmNykBka1nTZPaTU5Owu12Y9u2bcY8Qtu3b8f1119vaT3rHWNuenoa4+Pj61oHIZ3g1lsBn0+7\\n//PHP2plDodWHfdf/wVceaW98RGyUSxP761P59Df34/du3dDFEUoioK5uTkcPHgQJ06c2JRpHGiQ\\nVLIV3Hcf8N73av1+yi/md+0CUiktMRGylVm6EorFYpBlGeFwGKVSCZlMBolEAplMBqVSCePj48jn\\n85syu+rU1BRGR0eN51yL7VM5jqv5IGSzff3rwNOfDnzyk6sJ6HGP04bamZ2lBER6g6UklM1mIYoi\\njh07VvP1RCKBgYGBlhsJ6EP81LuvVG8IoEKhAF/FN5TuCZFucc89wNgY8Fd/Bdx992r5FVcAd9wB\\n7N+vtYIjpBdYOtVlWUYwGGy4jN/vbzqqgo7neaM6b9euXUa5oijgeb5uy7i5uTnMz8+b+gTJsmz0\\nFxoaGjJdJZWrl6zoaohstJUVbZy3aNQ82sGf/AnwiU8AV11FHU5J77GUhAYGBpq2WMvn85ZGOvD7\\n/ZidnTUlIVmWTRPlVarVGGFychJzc3M0gjfpSHfcAYTD2kym5d70Jq36jfr8kF5lqTrO7/cjn8/X\\nbQWXSqUgy3LDzqyV4vE4pqamTGXJZBLxeNx4rqoqXC6X0Sm1lnvvvZeq5EjH+eMftRGtBwfNCejS\\nS4FTp4BfPda2AAAgAElEQVTPfpYSEOltlkbRVlUVXq8XxWIRLpcLfr8fLpcLZ86cQS6Xw/z8PHie\\nR7FYRH9/f8tBFAoFnDhxwpgoz+v1Yvfu3abtiqKIiYkJ7Nu3z/TeYrGIeDyOkydPYmlpCePj45Ak\\nCYODgy1vH6ARE0j7ffe72tXP6dOrZeefrzXDfs97gMc+1rbQCOkYlucTUlUV0Wi05lVJOBxGPB63\\nlIA6BSUh0i5nz2qjXN94o7n8+c/X7gk94xn2xEVIJ1rXpHaKokBRFIii2LWT2ekoCZH1Ygz40peA\\nv/s7bcI5XV+fNhJCOKx1QCWErGrbzKrdjpIQWQ9F0cZ7qxw8fnRU6wf0lKfYExchna5h6ziHw1G3\\n6TJjzPSa/lz/99y5c+2NlJAO9MgjwMc+po1q/cADq+VPfSrwmc8Ar3ylfbER0g0aJqF6fW2aoT43\\npBfMzmpVbLfdtlrGccDb3gZ88IPARRfZFxsh3YKq4x5F1XGkVb//vdbs+pOf1Dqg6p79bG28t8sv\\nty82QrrNmgcHWV5extzcHFRVNUY+aDb3DyHd7pvf1CaVu+uu1bLHPha47jptxGua5ZQQaywnoWKx\\nCEmSqsaH4zgOfr8f8XjcNPoBIVvBf/838I53ABX9qhEIAEePAi6XPXER0u0sVccVi0V4vV6oqgqP\\nx4O9e/caQ/lkMhnkcjkIgoB8Pt91V0VUHUdqWVkBjh8HDh4ElpZWy3fsAD7+ceCv/5rGeyNkPSwl\\noVAohHQ6jUQiUXP8tmQyiUgkgmAwaBpctBtQEiKV7rwT2LcP+MEPzOVveIM2zfb27baERciWYikJ\\nOZ1OiKKIubm5ust4vV4sLCzg7NmzbQlws1ASIjrGgGPHgHe/29zs2u0GEgmgbEQpQsg6Weq/rQ8k\\n2ogoivRDTrrWb38LvOIVWuMDPQGddx5w7bXAj39MCYiQdrPUMGF4eLjphHW5XK5qwjlCusE3vgH8\\n7d+ah9x55jOBz38eeM5z7IuLkK3M0pVQIpHAysoKrrjiCiwsLJheKxaLGBkZAaDdGyKkW9x/PxCJ\\naKMblCegd75T65BKCYiQjWPpnlAkEoGiKMhms+A4zjQzqqqqYIyB5/maVXazs7NtDbzd6J5Qb5qd\\nBf7mb8zTLTzlKcBNNwEWpsUihKyRpSQkCIIxPpyljXAcFhcXLQe3mSgJ9ZZz54AjR4D3v18b/003\\nNqY1PqCJ5gjZHDRsz6MoCfWOYhF43euAH/5wtezCC4FPfxp4/eup3w8hm2nNw/YQ0m0YA26+WRtg\\n9L77Vsuf/3zgc58DunxKLEK6UkckIVmWkc/n4XQ6oSgKPB4PhoeHm74vm80im81i+/btmJ+fh9fr\\nrdmJlpDFRUCSgHR6tWzbNq06LhbTmmETQjaf7V89RVEQi8UwUzYbWCgUgiiKGBgYqPs+vXHEkSNH\\njDKfzwdVVXHgwIENjZl0l2wWuPpq4J57VssuvVRrek0jXhNiL9snG47H44hEIqYySZIQjUYbvi+R\\nSFSV+f3+muWkN/3xj8C73qUNMlqegCQJKBQoARHSCWxPQlNTU/B4PKYyr9eLdHm9SQ0cx1V1nGWM\\nQRCEtsdIus9PfqIlmY99bLVsxw7ga1/ThuR5whPsi40Qsqph67iFhQUIgoD+/n7jeTtHx1ZVFU6n\\nE6qqoq+vz/Saw+GAoiiWtudyuXDNNddg//79lmOh1nFbw8oK8IlPaPd5HnpotfxlLwM++1ngyU+2\\nLzZCSLWGV0KiKCIWi5meHz9+vG0b1/sOVSYgnaIoLa8rmUzC5/OtKQGRreHuu4GREa0KTk9Aj3sc\\n8P/+nzYZHSUgQjpPw4YJ/f39OHnyJFwul3E1lMlkWlrxvn37mi6jqmpL62pkenoamUwGHMd13fQR\\npH2mprR7PaXSapnHA3zhC8Bll9kXFyGksYbVcfr8QJZXynE4d+5c0+VkWYbP58PKykrVaw6HA9ls\\nFrtbHLZ4aWkJw8PDSKVSGBwcXFPMAFXHdZvlZeDtb9eG2dFxnFYd9/73AxdcYFtohJAWNLwSCofD\\nCIVCUBQFi4uLGBkZwcGDB+HvwEG1+vv7IUkShoeHGw4RxFF3+C3jBz/QRj4oH0v3aU/TOp6+4AW2\\nhUUIscDSsD3BYBCRSKSljqStaHfDBEVR4Ha7kclk6sbYLAnRlVDne/hh4LrrgMOHtYYIute+Vht6\\n59GaY0JIF7DURHtqaqrqx315eXnNGy8fhbucoijgeb5uAlIUBYIg4Lbbbqv5+tLSUt1tMsZqPkh3\\n+MUvtGF2PvSh1QTE88CXvqRdAVECIqS7rKmf0OTkJNxuN7Zt2wae57Ft2zZs374d119/veV1+f3+\\nqmkeZFlGIBCo+x59hlexYrAvPZlV9jsi3Y8xbXTrwUGgfHb5F79Ym/H0qqvsi40Qsg7MIq/XyziO\\nYzzPM7/fz8LhMPP7/YznecZxHPP5fJbWp6oqCwQCprJAIMCKxaLxvFQqMVEUWTKZNMomJiaYqqqm\\n9/n9fhaLxazuEmOMMQBsDYeDbILf/paxK69kTEtF2uP88xmbnGTs3Dm7oyOErIelseNisRhkWUY4\\nHMaxY8eqXpckCalUCocOHcLhw4dbWmd/fz/i8ThisRiGhoaMseQqq+JKpZLpfs6BAweQSqUwPz9v\\nDGC6d+/elpqGk+7xrW8Bb3oT8D//s1r2jGdoTa9pxlNCup+lhgn6AKFnzpypu4zL5YLT6ez4mVQr\\nURPtzvKHPwD79wNHj5rL3/EOrUHC4x5nT1yEkPaydE9IlmV4vd6Gy/j9fsiyvK6gSG+74w7A6zUn\\noIsvBm65Bfj4xykBEbKVWEpCAwMDTYfSyefzDadgIKSREyeAv/gL4Oc/Xy179au1xgcjI/bFRQjZ\\nGJaSkN/vRz6fr9sKLpVKQZbljuzMSjrbww9rY75ddRVw//1a2eMfrw06Oj2tjYBNCNl6LN0TUlUV\\nXq8XxWIRLpcLfr8fLpcLZ86cQS6Xw/z8PHieR7FYNMaa6xZ0T8g+v/0tsHcv8L3vrZa53cBXvgI8\\n61n2xUUI2XiWkhCgJaJoNIpUKlX1WjgcRjwe77oEBFASssu//zswNmaedO6VrwRuvpk6nhLSCywn\\noXKKokBRFIiiWNVxtNtQEtpcjGkND/7u77SqOEAbePQDHwAOHQIctk+3SAjZDOtKQlsJJaHN84c/\\nAJGINsyOzukEvvhF4Ior7IuLELL5LHVWJWS9FAXYswe4/fbVMo9Ha3zQxkl7CSFdgio9yKb59re1\\n/j/lCeiNb9SmZKAEREhvoiRENtzKijb1wpVXAvpkuhdcoA1I+tnPUudTQnoZVceRDVUqaRPPfetb\\nq2VPfapW/Xb55fbFRQjpDJauhFKpFL7yla9sVCxki/nxjwGfz5yAXvxiIJ+nBEQI0VhqHedwOCAI\\nAs6ePbuRMdmCWse11+c/D4TDwAMPrJYdPKhNRnceXX8TQh5l6Upo3759KJVKdWc0JeShh4C3vU2r\\ngtMT0IUXAuk0EI9TAiKEmFn6SUgmk3C73fB6vUgkEvD5fBBFEX19fRsVH+ki99wDBIPAj360WnbZ\\nZdrwO3/+5/bFRQjpXJaq45xOJwBt6B7TSsomm2OMgeM4nDt3rk0hbg6qjluf738fCIW0ceB0o6PA\\njTcCF11kX1yEkM5m6UpoeHi4peXKkxLZ2hgDPvEJbQI6/e8OhwM4ckQro1OBENJIRwzbI8sy8vk8\\nnE4nFEWBx+NpKeFNT09DURTMz89DURRIkoTR0dE1xUBXQtbdfz+wbx/w5S+vlu3Yoc0JtHu3fXER\\nQrrHmm8TLy8vY3FxEYIgrGvUbEVREIvFMDMzY5SFQiGIothwcrzp6WmIomgknaWlJXi9XiwuLmJ8\\nfHzN8ZDWnD6tDb/z05+ull1+udYA4ZJL7IuLENJdLI+YUCgU4PP5wPM8XC4X8vk8AMDtdted7K6R\\neDyOSCRiKpMkCdFotOH7FEXB4OCg8by/vx/RaBSSJFmOgVjz9a9r/X/KE5AkafeFKAERQixhFiiK\\nwjiOYxzHMb/fzziOY7lcjjHGGM/zjOM45vP5rKySCYLAisWiqaxUKjGO4+q+p1QqMa/Xy1RVNZXP\\nz88zjuOq1tcKAMzi4eg5jzzC2LXXMqbdCdIej3kMYzfcYHdkhJBuZelKKB6PAwDy+TympqZMr5VK\\nJRw5cgT5fB6HDh1qaX2qqkJVVaPVnY7neQDAwsJCzffxPA9FUVAsFq2ET9bh7FngZS/TOpvqnvY0\\n4Ic/1AYhJYSQtbCUhE6ePAm/32+qBit38OBBDA4OIp1Ot7S+xcVFAKjbz0hRlIbv3bVrl6ksm81C\\nEATspCGZ2yqf10a/Lrtth5GR1XJCCFkrS0lIVVW4XK6Gy4iiiPn5+ZbX106JRKLlqzDSmhtuAP7P\\n/wF++cvVsmuv1aZl2L7dvrgIIVuDpdZxg4ODmJuba7hMoVCAx+NZV1BrkUwmsWPHDuzfv3/Tt70V\\nPfgg8Pa3A8nkallfnzYb6itfaV9chJCtxdKV0N69e5HP5/Gd73ynZofUUCgERVHg9/vbFmArFEVB\\nMpnELbfc0nRZjuNqPsiqu+4CXvhCcwJ65jOBuTlKQISQ9rLcWdXr9aJQKCAQCCCTySAQCIDneWSz\\nWZRKJYiiiDNnzrS0Lr1RgqqqVfeFHA4HFEVp6f5OKBTC8ePHWxrDrlnCsXg4tpzvfU8b/+13v1st\\nu+oq4Phx4AlPsC8uQsjWZLmfUD6fx5EjR3DrrbcCADKZDKamprCysoKDBw+2nIAArZWbKIpVDRAU\\nRQHP8y0loEgkgomJiZYHUWWM1XwQbfqFQGA1AW3bBnz848AXv0gJiBCyMdY9bI+iKHA6nUazaqsi\\nkQi8Xq9plIN0Oo2pqSmcOHGi4XtTqRQCgYApWeVyuaajLdTSy8P2MAZ8+MPAe9+7WvakJwFTU8AL\\nXmBfXISQrc/ylZBuYWEBp06dwm233YaFhQUsLy+vaT3xeLyqz1EymTT6JAGrrfJSqZRRpjcDX1xc\\nhCzLkGUZ2WwWU1NTlhNQL3v4YW3yufIE9IxnALfeSgmIELLxLI8dVygUMD4+DlmWTeUcx2FsbAzx\\neNxSP53+/n7E43HEYjEMDQ0ZY8lVrqNUKhlXK6qqIhQK1VxfsybkZNV992n3f8rbc7z4xdr8P2u8\\nsCWEEEssVccVi0XjR97j8WDv3r0YGBiAoijIZDLI5XIQBAHFYrHrJrrrteq4e+4BXv5yoHyS3Ne9\\nTmuAcMEF9sVFCOktlpJQKBRCOp1GIpGoOVJ1MplEJBJBMBhsej+n0/RSEvrpT7UheO66a7Xs7/8e\\nuO46mv+HELK5LM+sKopiww6rXq8Xy8vLOH36dFsC3Cy9koRyOW0KBv0W3nnnAYkE8KY32RsXIaQ3\\nbciwPY3GfCP2uekm4CUvWU1AF10EfOtblIAIIfaxlISGh4eRzWYbLpPL5eoOcErswRjwj/8IvOEN\\nwCOPaGV/+qfAv/2bNhApIYTYxVISSiQSWFlZwRVXXFE1zUKxWMTIyAhUVTU1pSb2evhh7Urnfe9b\\nLXvWs4D/+A/gOc+xLy5CCAGa3BMaGRmpGuZmfn4eiqKA4ziIogie56GqKhRFAWMMHo8HQ0NDOHr0\\n6IYH305b8Z7Q8jIwNgZkMqtlfr82Bfc6ZmQnhJC2aZiEBEEAx3GWf5g5jjPmCuoWWy0J3X231gT7\\nxz9eLXvDG7RBSc8/37awCCHEZN3D9mwVWykJ3X67loB+/evVsuuu05phUxNsQkgnsTxiAulsMzNa\\nFdx992nPzztP64B69dX2xkUIIbWsKQktLy83rW6jKbY33w03aOPAnTunPe/r04bgGR62Ny5CCKnH\\nUhIqFosIBAIoFosNq604jsM5/ZeQbDjGtNZvH/jAatlTn6pNwf2sZ9kXFyGENGMpCUmSBEVR4PF4\\nMNzgz2uaqXTzPPQQsG+fNu227jnP0Tqh/umf2hcXIYS0wlLDBIfDAY/H03DYnm7VjQ0TVBUYHQVO\\nnVotu+IKbR6giy6yLy5CCGmVpc6qAwMDCAQCGxULseBXvwL+7/81J6B9+4BvfIMSECGke1hKQn6/\\n35hMjtinUACe+1zgjjtWyz74QeoDRAjpPpb7CXm9XuzYsQPRaBQ+n6/ucjSf0Mb4l38BQiHg97/X\\nnp9/vtYq7rWvtTcuQghZC0tJaGlpCV6vt+ko2d3YOq4bklAyCbz5zatNsPv7gX/+Z202VEII6UaW\\nWseNj49DURSIotjW1nGyLCOfz8PpdLbU+q5SOp2GIAiW3tNNGAPe+17gwx9eLfuzP9OaYD/jGfbF\\nRQgh62UpCWUymba3jlMUBbFYDDMzM0ZZKBSCKIoYGBho+v5sNotwOLxl71U9+KA2CvYXv7ha5vEA\\n3/wmcPHF9sVFCCHtYKlhAoC2t46Lx+OIRCKmMkmSEI1GG76vWCwiEomgWCzC6XS2NaZOUSppTa7L\\nE9DLXgZ873uUgAghW4Ole0KSJEGWZczOzrYtAKfTCVmWTcP8qKoKp9OJlZWVltbhdruRTCaxe/fu\\nNcfRafeEFha0hPOzn62WSRLw6U9r48ERQshWYHlSO0EQcMUVV+C2227D8vJy3UcrVFU1Ek45nucB\\noGrivF6Rz2tNsMsT0JEjwNGjlIAIIVuLpZ80p9MJVVUBaPeH6mm1dZw+CGq95tyKovTcQKjf/Caw\\ndy/whz9ozy+4APinfwJe8xpbwyKEkA1hKQkFg8GWlmu1dZye0Ijm2DHgLW8B9FpIQQC++lXghS+0\\nNy5CCNkolpJQIpHYqDh63pEjwKFDq8937tQ6pl52mW0hEULIhrPcOq7bcRxX82EXxrRZT8sTkM8H\\n/Md/UAIihGx9lq6EIpFI0x9sxhg4jsPRo0ebrk8URQDaJHm17gvpr29VjAHXXgscPrxa9uIXA1//\\nOnDhhfbFRQghm8VSEkomk02X0Vu2tZKEeJ6HKIpQFAW7du0yyhVFAc/zG9IooV4T7M2+GmIM2L8f\\n+OhHV8tGRrRheB7/+E0NhRBCbGOpOm5xcbHm48yZMzh58iQGBgYwNDTUdOrvcn6/v6rfkSzLW3rK\\niJUV4O1vNyegK68EvvY1SkCEkB7D2qhUKjFBEFgsFmv5PaqqskAgYCoLBAKsWCya1iuKIksmkzXX\\n4XK5WDabXVPMOgCszYejpnPnGBsfZ0y7FtIee/Yw9uCDG75pQgjpOJancmhGkiSk02mcPXu25fcU\\nCgWcOHECQ0NDUBQFXq/XNPqBqqoQRRETExPYt28fAG1E78OHD0NRFKTTaYiiCL/fj0AggNHRUctx\\nb8aICefOAX/7t8BNN62WXXUVcPPNNA8QIaQ3tT0JRSIRJJPJlofc6RQbnYQeeQR4/euBL31ptex1\\nrwNuvBHYtm1DNkkIIR2vrU20c7kcksnklm/VZtVDD2lXPOUJaN8+SkCEEGKpdZzD4WjYiky/img2\\nAnYvefBBIBgEvvGN1bI3vxn41KcAR8/10iKEEDNLSajZpHE8z+Oqq65a0z2ZreiBB4BXvxq45ZbV\\nsne+E/jIRwAb+8cSQkjHaPs9oW7V7ntC998PvPKVwKlTq2WxmDY7KiUgQgjRUIXQBrjvPuClLzUn\\noPe9jxIQIYRUalgd53a7LY8kwB4dtuf06dPrCqxbLS1pCejf/3217EMfAt7zHvtiIoSQTtUwCVnp\\n68NxXM9PzbC4qE3HPTe3WvaRjwDvepd9MRFCSCdrmIRKpVJLK1laWsL4+DjS6TQA4ODBg+uPrMv8\\n7ndAIADcfvtq2ac+Bbz1rfbFRAghnW7dk0WnUilEo1GoqgqPx4OpqSkMDAy0I7au8ZvfAH4/cMcd\\n2nOO0yaoC4ftjYsQQjrdmhsmFItF+Hw+SJIEQJvwbm5urucS0K9/DfzlX64mIIdD64RKCYgQQppb\\nUxKKxWJwuVyQZRljY2MoFosYHx9vd2wd71e/Al70IuDOO7Xn27YBn/88cPXV9sZFCCHdwlJ1XC6X\\nQzAYNAYUTSQSTTuwblWKAuzeDfzyl9rz884DvvxlgPrpEkJI61q6ElpaWkIoFEIgEICqqojH4zhz\\n5kzPJqDTp7UrID0BXXABMD1NCYgQQqxqeiU0OTlpjAXn9/uRSCR67r5PuZ/9TLsC+s1vtOePfaw2\\nG+pLXmJvXIQQ0o0aDtvjdruhKAoAIBwOIxgMttx5tXw+oG7QyrA9P/kJMDysNccGgMc9ThuYtEcv\\nCAkhZN0aJiHHGod55jgO586dW3NQdmiWhGRZ6wekz1x+4YXAt74FvPCFmxUhIYRsPQ2r444cObKm\\nlVod6qfT3XqrNhKCPiBEXx/wr/8KPO959sZFCCHdriNG0ZZlGfl8Hk6nE4qiwOPxtNToYa3vq6Xe\\nldAPf6iNBXfffdpzQQBmZgCfb02bIYQQUmbdIyasl6IoiMVimJmZMcpCoRBEUWzYAGKt77Piu98F\\nrrxSm5YBAHbsADIZYNeutqyeEEJ6nu1TOcTjcUQiEVOZJElNZ2dd6/talckAL3vZagJ60pOA73yH\\nEhAhhLST7dVxTqcTsixj586dRpmqqnA6nVhZWWn7++opr4779reBPXu0qbkB4OKLtbmBLrvM8moJ\\nIYQ0YOuVkKqqRuIox/M8AGBhYaGt72vFV78KvOpVqwnokkuA73+fEhAhhGwEW5PQ4qPtnfv6+mq+\\nrvdRatf7WhEMAg8/rP1/YEBLQG73mldHCCGkAduvhDbzfa145BHt30svBb73PaCsto8QQkib2d46\\nrhNddpl2D+jii+2OhBBCtraeS0LNO9Jy+PnPgac8ZVPCIYSQrree9m22VseJoggAWF5ebvh6u95H\\nCCGk/dYzSo6tV0I8z0MURSiKgl1lHXAURQHP86bm1+14H1A/Y7cygGmvoGOxio7FKjoWq+hYrFrv\\nMG22d1b1+/2YnZ01lcmyjEAgsCHvI4QQ0jlsT0LxeBxTU1OmsmQyiXg8bjxXVRUulwupVMrS+wgh\\nhHQ220dMAIBCoYATJ05gaGgIiqLA6/Wa5iPSpxOfmJjAvn37Wn6fFXR5vYqOxSo6FqvoWKyiY7Fq\\nvceiI5JQJ6CTahUdi1V0LFbRsVhFx2LVeo+F7dVxhBBCehddCRFCCLENXQkRQgixDSUhQgghtqEk\\nRAghxDaUhAghhNim5wYwrSTLMvL5PJxOJxRFgcfjwfDwsN1h2WJ6ehqKomB+fh6KokCSJIyOjtod\\nlu1UVUUsFsOxY8fsDsU2sizj5MmT2L59O86ePQtJkjAwMGB3WJsum82iUCgAAM6ePQuXy4Xx8XGb\\no9oc6XQagiDU/H1c1+8o62Hz8/MsEAiYyoLBIFMUxaaI7JNOp5ksy8ZzVVWZy+ViyWTSxqg6Qzgc\\nZsFg0O4wbDM1NcUkSTKVhcNhm6KxTz6fZ+l02lSWTqd74juSyWSYIAgsl8tVvbbe39Gero6Lx+OI\\nRCKmMkmSEI1GbYrIPoqiYHBw0Hje39+PaDQKSZJsjMp+iqKgVCqte5DGbqWqKsLhsOkqMJlM4tSp\\nUzZGZY9kMllVMzA6OopMJmNTRBuvWCwiEomgWCzC6XTWXGa9v6M9nYSmpqbg8XhMZV6vF+l02qaI\\n7KGqKk6cOIGlpSVTuX45vbCwYENUnSGXyyEQCPRsz/jDhw9X/SESDoe39A9vPXNzcygWi1XlGznT\\ns90GBgZw7NixhlWO6/0d7dkkpKoqVFWtyu48zwPorR9enuehKErNL1gvy+Vy8Pv9dodhq1QqhaGh\\noaryRtOlbFV+vx+BQMD0PclmswiFQjZGZa92/I72bMOExcVFAEBfX1/N1xVF6akvmn48ymWzWQiC\\n0FPHoZyiKBgeHu7ZqyBA+5Hp7+9HKpWC0+nE4uIinE5nTzZYOXLkCLLZLFwuFxKJBAYGBrC0tGQa\\nVLnXtON3tGeT0Fa+hG6XRCKBQ4cO2R2GLaanp3um1VM9iqIA0Ear379/v1Eei8WwuLjYk8dnbm4O\\nIyMjkCQJHo8HuVzO7pBs1Y7f0Z6tjiONJZNJ7Nixw/Tj0yvoDxSNfhxEUTSV7927tycb7wBa9eTE\\nxAQymYwxfQxVY68PJSFSRVEUJJNJ3HLLLXaHYoupqSlTdVOvtozTk09lEhocHISqqj113xQAIpEI\\nAoEAdu3aheHhYRSLRYiiSLM5r1PPJiH9i7W8vNzw9V4Ui8V6sgkuoFU9+Xw+U1mv3hPSby7r/1bS\\nq+t6gX5VWH5/o7+/HzMzM+B5vmer5drxO9qz94R4nocoilAUBbt27TLKFUUBz/M9ezM+EolgYmKi\\n7o3GrW5ubg7z8/M4ceKEUSbLMhRFQSwWw9DQUE/dlNe/I7W+D730h1o+n4fL5ar5miRJPVuF247f\\n0Z5NQoDW5HJ2dtZ08GRZ7tnL61QqhVgsZjpxcrkcRFHsmSFaat1sn5ycxNzcHI4cOWJDRPaSJAn5\\nfB67d+82ymRZ7rlWk6IoYmpqquZrqqr27G8GsP7f0Z6tjgO0nr6VJ1YymUQ8HrcpIvvoHcsWFxch\\nyzJkWUY2m8XU1FTPJKB67r333p6tkguHw0gkEqayWCyGVCplU0T20L8DldVuiqLg7NmzPZOQa30P\\n1vs72vMzqxYKBZw4cQJDQ0NGa5fyv/p6Qa3OZjqXy4XTp09vckSdoVgsIh6P4+TJk1haWsL4+Dgk\\nSTINb9QL9OPgcrkwPz+PUCjUc98RXSqVwvz8PLZv3w5Aq47ayk3Vl5aWcPjwYSiKgnQ6DVEUjU67\\n5dXS6/kd7fkkRAghxD49XR1HCCHEXpSECCGE2IaSECGEENtQEiKEEGIbSkKEEEJsQ0mIEEKIbSgJ\\nEUIIsQ0lIUIIIbahJLROsizD4XDUfAiCgJGRERQKhQ3Ztr7+zZRMJiEIAhwOR88M5R8IBOBw0Fel\\nmVaPkyRJG3Y8N3LdlYLB4Jq3tVHf3fXEZJfuiraDCYKAYDBoPAKBAHbs2IFsNguv14vp6em2b5Pj\\nuHJn2qIAAAqYSURBVE2d60ZVVUQiETgcDkiSBEEQNm3bdtrs49ytKo9TOp2Gw+Goee6v93hu5Lqt\\nWOu2NvKc6rZztadH0W4nv99vGv5fl0qlIEkSxsfH2z4FwGaPuKTPH3Po0KGemnF1amoKpVLJ7jA6\\nXr3jVOtHsV3n7kaueyN1Q4ybha6ENtj4+DgGBgawtLTU9dMALy4uAtAm8+ol/f39PTNK8nrUO04b\\n+YNLP+bdj5LQJhBFEYwxLC0tAdDqbfVRq8PhMBwOh2lofFVVIUkSXC4XHA4HfD4fYrFY3fUrimLU\\nxzudToRCIUsJr5XtBYNBow5br3dvdk8omUzC6/Uacfl8vpozUFZuf2RkpGqqgGbHDAAmJiZM24tE\\nIsZx0I+P/hno9Pt3lfft9Pte+rbL69klSTJiiUajxrJut7tm9ZCqqggGg8ZyoVAIqqrC6/W2dF+g\\n3r0WVVXhcDgQiURMcUcikTWfE+06ToFAAKFQyFReOfvm0tJSS8evVoztXHej88YqRVEQDAaNc7nZ\\nsbfyOa01zla/h7ZhZF3y+TzjOI6FQqG6y/A8zxwOB1taWmKMMTY2NsYEQWDxeJxxHMecTiebnp5m\\njDFWKpWYKIqM4zjm8/lYKBRiLpeLcRzHvF5v1XpdLhfjeZ45nU4WCoWY1+tlHMcxjuOYLMtN4291\\ne9lslkWjUWNfU6lUw/UePHjQ2LdQKMSCwWDNuObn5xnP84zjODYyMsJCoRATBIFxHMckSTKWa3TM\\nGGPM4/EY+xCJRFggEDBtb2JignEcx9LptPGeTCZjLDMxMWGKqfwzHRsbYw6Hw3g9HA4zQRCMmCKR\\nCJMkyVhXNput2j+Hw2HaP5fLxVwuFxsZGWn6Gfn9ftP2daVSiXEcxyKRiFEmCAILBAI1zwlBEJii\\nKA231a7jlM1mjWMSiURM50s4HGYcxzG/328cv/Lzo/z41dLOdTc7bxqpPC/046F/1uXrEwSBqapq\\nLGv1u9tqnJUxtfo9tBMloXVqlITm5+eZ3+83Th7d2NiYcbIWCgXTe/Qv0eTkpKlc/9KV/wiU/3iX\\nSyaTNZNWLVa2p/8YNUtAemxut9tUls1mq3409WNRnlAYY8YXsjxx1ztmemI6deqUqVyWZeM46P8v\\nT2z6F5TjOBYIBIzyRCJh2s9aSYjjOOZ2u434yvevMnlyHMdyuZxRpqqqkejbnYSanRPl+1lLO4/T\\n1NRUzc+22fEr35961rru8v1q5bxppNZ54XA4TJ81Y7UTu5XvrpU49fOtfDutfA/tRElonfQk1Ojh\\ndDpZsVg03qOfKLV+zPUvUC36X0/lzx0Oh2ndOv1HvNlfvla2ZyUJVSZeXaFQMOLVf0Rr/RCn02nm\\n8/mMhNPomPE8z0ZGRpiqqqxUKpke+g+4qqpV++P3+5nX6zX+qtTp2ypPgLWSUOUPoL7f+v4027+N\\nSkLNzonyv8hraddxapYo6h2/RrUK7Vx3s/OmfN9qqdxfWZZrbrfW96aVz0l/zUqclUmole+h3ah1\\nXJsIggC/328qczqdcLlcdVuS+Xw+03O99VnlesqXP3XqlKlMFMWaN4P37t0LWZZRLBbrTs+9lu21\\namxsDOl0Gm63G5Ikwe/3Y3Bw0DQPvb79WnPRj46O1mxNWHnMAK3+P5PJ1G0yznEcFhcXEQgEkE6n\\nsby8jL6+PuRyOUSjUTidTmSzWSwsLGDnzp2QZRkulwt9fX0N99Hj8TR8fW5uDoB236LS8PBww/eu\\nB8/zDc+JfD7fcNbLdh+nepodv/VoZd2tnjet7t/g4KAx666qqpibm4Msy1XTo+uafXcVRcHOnTst\\nx8mVtRhs5XtoN0pCbVKviXYjoiianus/yi6Xq+7yuVzO+HEAtB+cWvTEo6pq3e2vZXutOnnyJCYn\\nJ5FIJBCNRo3ycDiMeDyO/v5+Y/v19qFeTLX2IRAImLZTyel0Yu/evUin08hkMsbxCQQCxpc7m81i\\nbGwMxWIRkiQ1jaXelOiVsdVazso+W1V5jHStnBMA2n6c6tnIFofN1t3qeWOlL5yqqohGo8Z08ADg\\n9Xrh9XprNiBo5bu73jhb+R7ajZKQTTiOq/ph1388zpw5U/M9iqJUva/eD4p+8tb7QVrr9qw4cOAA\\nDhw4gOXlZWQyGSQSCSSTSczNzWFubs74Ejb7UdTVikX/ged5vumc9vrVRyaTMfbd5/MZ65yZmTFi\\nqnX1YpW+Db1pe7lW97mRWusFVj/7euXNEuBmHyc7WDlvGmFlTcSHh4dRKBQgSRIkSTKuNnK5HNLp\\ndNV7W/nutiPOZt9Du1ET7Q6if+HrNZ8s/+HWKYpS86+sTCYDjuNaSkJWtteKYrGIaDRqrLevrw+j\\no6OYmZnB8PAwZFnG8vKyUbV26623Vq1D7xF//PjxhtvieR79/f3IZrM1XxcEAW6321hWFEVks1nM\\nzc2ZqpL8fj+y2SwymQwArOuHSacf35mZmarX2vHll2W5Zrmqqms+J4DNP052sHLeNKJXfamqikKh\\ngGAwiKNHj5qqu1idvkytfHfXE6eiKC19D+1GSajDhMNhzM/PV/WBkSQJS0tLOHTokKmcMVZVJZJM\\nJpHL5TA2Ntb0Ksbq9lrBGMPk5GTNqpryqyue5+H3+5FOp6sS4eHDh8FxXN37VZWxlkolo++IbmJi\\nAktLS6Z+NGNjY1AUBdls1rTuQCAAVVUxNTVV8x7VWoiiWHP/9H5RreJ5HoyxqnXUq55pdE74/f6W\\nqsHaeZxq/QiX37dYj/Ws28p506rKESPKP6fKWFv97q4nzla+h7azq0XEVtFKP6FKlS1YyqmqavST\\n8Xq9LBwOm/rxlON53tQHZGxszOhPUNkirx4r27PSOq68f8TY2BgLh8NGi6BYLGYspyiKsf1AIGDa\\nfvlyjY4ZY8xo8uxyuUzHoXIf9OaplS2o9OautZqrV25bb4FVq+VUZYu38vUGAgGjb1EoFGr5vNFb\\n0ulNjPV+SiMjI0wQBFOzY57nmSAIxqPynKhs3l5PO46Tvg6Xy8Wi0WjV8aul1WPSrnW3et7UUrm/\\n+jkfDAZZPB43fU76NvR+Sla/u63GWS+mZt9DO1ESWqe1JKFgMFizya1OVVUmSRJzuVzM4XAwn89X\\n84TRO+PJssy8Xi9zOBzM7XazUCjUsGnpWreXyWSYw+FoKQkxxlg0GjXW6XQ6mc/nq9mEVVVVFgwG\\njS+az+er2kazY6ZvT/9iu93uul8y7tH+RpVf9HrllduWJMnU+bhyHZXNrhVFYcFgkAmCwJxOpxGX\\nlb4ayWTSOD7l69DPAR3P88zn87FiscgCgYCxzVAoZLlJ7nqPE2OrP4JOp9Mo049fvW22+l1q17pb\\nPW8qVe6v/j3S/6gqP9/1uPTPai3f3VbirPUZtPo9tAvHGA2+RMhGyWazcLlcVc3kFUWB2+1GNBrF\\n4cOH27Y9/R7B7Oxs29ZJyEai1nGEbKBgMIjt27dXtUCMx+MAsK4mzoRsBZSECNlAExMTkCQJbrfb\\n6HybzWaNllQ0OjfpdZSECNlA4+PjcDqdOHz4sNEC0eVyIZlMYt++fW3fXrtanRGyWeieECGEENtQ\\nPyFCCCG2oSRECCHENpSECCGE2IaSECGEENtQEiKEEGIbSkKEEEJs8/8Befay03Pn2iIAAAAASUVO\\nRK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 58\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.plot(1-(1-0.025)** np.linspace(0,100,100),linewidth=3)\\n\",\n \"ax.set_ylabel('Prob of screwing up',size=20)\\n\",\n \"ax.set_xlabel('Number of trials',size=20)\\n\",\n \"plt.title('Be careful discarding experiments')\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAaYAAAExCAYAAAA3Egb4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X14I1d9L/DvaElIgKwlbXhJLi/rkZICIWTXktNAIMBa\\nclpeWsha2tCWQmEtGS5vbbMrbS+0fWhhV3Z6G96albQ3AXoL2JIXuFwCa0ublrf2xtYohQIhWY0W\\nCORpk7VGDoQEWJ/7x0QjjS3LGlu2JOv7eR49u3M0M/rN8a5+PnPOnCMJIQSIiIg6hK3dARAREdVi\\nYiIioo7CxERERB2FiYmIiDoKExMREXUUJibaEE3TYLPZTC+v14t8Pt/u0FaIRCLYsWNHw30URYHb\\n7W64j6ZpcDqdxv5er7dlMTarE2Jola2O32bj116n40+IWkLTNGiahlKpBJ/Ph0Ag0O6QVpiYmECp\\nVGrpOV0uF2KxWEvP2Y0xbES3x0+tx8RELbFz507s3LkTfX19CIVCUFXVeC+TycDlcsFms2F4eBjl\\ncrnuOdLpNFwuF5xOJ8bGxozyRCIBp9NptMaKxSIAQFVV+P1+RCIR4zfu1T7L7/cDAPr7+5HP502/\\noWcyGQwPDze8vvHxcTidTjidTiQSCaO8UCggEokY2+Fw2NhvYmKipde2VgzFYhEejwcTExNwOp1w\\nu92mlmvls9xuNxKJRN2WYb36S6fTpvpxuVzIZrOYnp5GOBxGIBBYEX+jn8Xya1NV1ahDVVXh8Xgw\\nNjYGp9OJ4eFhKIpinKe2Thudf7V6qPw72LVrV8OfF7WZINqAUqkkJEkylcViMTE8PGy873A4xOnT\\np0W5XBbhcFgEAoEV5ykUCsLhcIh8Pi9UVRUul0tMT08b57/33nuFpmkiEAiISCRiHCNJkhgbGxPF\\nYnHNz6rEmcvlhMfjMcpnZ2eF3+833nO5XKbYcrmcEZumaWJgYEA4nc4V50qlUsLlcolyuSwURRGS\\nJIlyudySa2smBlVVhSRJYmJiQgghRDgcNq6rNobK8W63e8XPcrX683g8Ip1Oi1gsJoLBoHG9kiSJ\\nZDJp7F+pi0bnqndtleMq701PTwtN04Qsy8LhcIhyuSwymYzxM2zm/PXqofbfwfKfl81mE+VyecW/\\nTdp6TEy0IZUv19qXzWYTiqIIIYSIx+MrEpHD4VhxnlgsJqLRqLGtKIpxDk3TjPJQKCTC4bAQovoF\\nVLHWZ603MYVCIVNsmUzGOG/tudLptHC5XEbclS+5VlxbMzGoqmq6XkVRjNgOHz5sOr4Sa61G9aeq\\nqrDb7cLtdhvXlUqlhNfrNe0vSZLQNK3huZZf2/LEVHsN4XDYFHcl2a91/tXqoXKOSvy1P6/anwW1\\n11Pa3WKj7aH21l0ul4PH40GpVEKhUEA6nTY66gFAkqS6x3s8HmN77969xt8/8pGPIJvNGueQZdl4\\nr/bvzX6WVaVSCYODg8Z2f39/3f3279+PhYUFBAIBLCws4MiRIzh06FBLrq3ZGGqvXdTMNlYsFk23\\n4+od36j++vv74XK54HK5sHPnzlXPI8syVFVd82dRe22NrsFut5u2K9e11vlXq4daIyMjKJVKK35e\\n1H4dk5jS6TQcDgeGhoaa2l9RFORyOTidTqiqioGBgaaPpdbbvXu36e8DAwPIZDJwu90YGRnB1NSU\\n8X69EXt2ux2FQsHYVhQFxWIRQghks1mcPn0aO3fuRCKRgKIodWNo9rOW0zSt4fuyLOPMmTPGdm0S\\nrqWqKnw+H0ZHR1EsFuH3+yHLckuurdkYNnINjeovk8kYfxaLRSMhLT+PqqpwuVzr/lk0Q5Kklpx/\\ntZ/X/v37WxInrV9HDH7IZDIIhUJN/3arqiqi0ShGR0exf/9+HDp0CPF43NTxSlurXC4bI/NmZ2eh\\nKAo8Hg8CgQAymQyy2Sw0TUM4HDYNFqgIh8NIJBLI5/NQVRXBYBClUgmlUglOpxM7d+6EpmlIJBJY\\nWFioG0MwGGzqs+x2u5EcNE3D0aNHG17bgQMHjNg0Tat7TkD/5SoQCKBcLhu/pUuS1JJrazaGZq/h\\n6NGjK/6/1au/aDQKABgbG8OJEydw7NgxhMNh4xhFUZBMJo39PR4Pdu7c2fTPfb1acf7Vfl7UAdp4\\nG1GoqirC4bBIJBLC5XKJbDbb1HGhUEhMT0+byjKZTN1Oddpc9fqYnE6nSCaTxj6ZTEa4XC4hSZIY\\nHh5etYM5kUgIh8NhdIxX+P1+4XA4hNfrNfpWstmsKBQKKzrwG32WzWYz/h4Oh4UkScLtdot0Om0M\\n1sjlcivOWRub0+kU6XTaNPCgtp/F7/cLSZKEw+Ew9Y204trWikFVVdMxy2OrHO92u0UikTD1uzSq\\nv1gsZoq5MngjnU4Lv98vAoGAkCRJeL1eUSwW1/xZLL+22jiXvxeJRIxBDEII0wCF9ZxfCCECgYDx\\nb2G1nxe1lyREZyx7URnCum/fvjX3dTqdUBTFdPuo8sDh0tLSJkZJ1J0qrcNK/1Y6nUYikcDMzMy6\\nz5lOpzE1NWW6nUbUCh1xK8+Kyu2i5R2idrsdAHD27Nk2REXU2UqlEoaGhoxnfeLxOILBYJujIqqv\\n6xJT5R587cigWlY7hYl6wcDAAI4cOYL+/n7jodODBw9u6JySJLFPhjZFx4zKa9ZaI6iIqL5Dhw61\\ndDj0/v37OYKNNkXXtZiIiGh767oW00Y1uvXQIeNAiIh6Wte1mCpPjC8uLjZ8fz14v5yIqP26LjHZ\\n7XZj2pNaqqrCbrebhpDXI/T5AVe8iIioM3RdYgIAn8+Hubk5U5miKMaU9kRE1L06KjHVa7lomgaX\\ny4VkMmmUxWIxpFIp036JRIKLjRERbQNtHfxQLpdx9OhRqKoKVVURDofh8/ng9/tNw1BLpZKp/6ev\\nrw+xWAzRaBSDg4PG3Hlr3cYjIqLO1zFTErVbJfGxOoiI2qujbuURERExMRERUUdhYiIioo7CxERE\\nRB2FiYmIiDoKExMREXUUJiYiIuooTExERNRRmJiIiKijMDEREVHThAAeegj4z//cvM/ouYUCiYio\\nsfPngZ/8BDhzxvwqFABVBR57DDh8GNisebOZmIiIelCl5XP//dXXAw/or0IB+NWvGh9/5szmxcbE\\nRES0jT3+uJ5s7ruv+vrhD/XXz3++vnPa7cBFF7U2zlpMTERE28CjjwI/+AHw/e9XX/fdBxSLwNKS\\n9fM961nAFVcAbrf+crn0l9sNOJ2tj78WExMRURd57DE9Af3Hf1Rf3/ue3idkVV8f8Fu/BVx5pf66\\n4orqa+fO1sfeLCYmIqIOtLSk9/V85zvAd79b/bNQ0PuHmmWzAbt3Ay96EfDCF+qJqPJ61rOAmjVY\\nOwYTExFRm/3853rSufde/VVJQr/4RfPneMpT9GTz4hfrSajy55VXbm5/0GZgYiIi2kLnzgH5PKAo\\n+iuf1wcnNNsKstn0W20veQlw1VXVP6+4Arjggs2NfaswMRERbZJHHgFyOWB+Xv9TUYAf/aj545/9\\nbODqq4GXvlR/XX213gq6+OLNi7kTrDsxlctl5HI5aJoGu90OWZaxe/fuFoZGRNQ9fv5zPfnccw8w\\nN6e/zp5t7libTU8411wD7Nmj/3nNNXpi6kWWE1OxWEQ4HEYmkzGVS5IEn8+HWCyGPXv2tCxAIqJO\\nc/68Phz73/4N+H//T399//vNDct+6lP11s/evcDAgP7n1Vdv/1aQFZIQzY/vKBaL8Hg80DQNAwMD\\nOHDgAPr7+6GqKmZnZ5HNZuFwOJDL5bqu9SQ9OTTFQnUQUY9YWNCT0L/+K/Dtb+utomYeTr3wQr0F\\n5PEAXq+eiK66avv0BW0WS4kpGAwinU4jHo9jdHR0xfuJRAJjY2MIBAKYnJxsaaCbjYmJiAB9EEKh\\nAHzzm8C3vqW/fvCDtY+z2fSkMzgIXHutnoiuvlpPTmSNpcTkdDohyzLm5+dX3cfj8eDs2bM4d+5c\\nSwLcKkxMRL3p/Hl9ePY3vgF8/et6Qmpm5uzLLgOuu05/VRLRM56x+fH2Akt9TJqmweVyNdxHlmUU\\ni8UNBUVEtFl+/Wt9dNy//Iv++uY3gcXFxsc85Sl6X9DLXw687GX663nP68yHU7cDS4lpaGhoxaCH\\n5bLZLLxe74aCIiJqlfPn9UR0993665vfXLt/qK8PuP766mtwEHja07YmXrJ4K09VVXg8Hlx77bWI\\nx+OmAQ6V0Xrz8/NQFIWDH4ioLYTQ+4QyGeD0aeCf/xkolxsfc9llwA03AK98pf7nVVfpfUbUHpYS\\n09jYGFRVRSaTgSRJxvNLqqpC0zQIIWC32+ve7pubm2tp4K3GxETUvR56SE9Es7P6nw891Hj/5z8f\\neNWrqi+Xi7flOomlxORwOCBJkuUvb0mSsLCwYDm4rcTERNQ9nnhCH6xw6hQwM6MPXmjk8suBffuA\\n17xGf/X3b02ctD6WEtN2xsRE1NlUFbjrLuBrX9P7ih57bPV97XY9EQ0N6a8rr2SLqJt0xFx5iqIg\\nl8vB6XRCVVUMDAxgaGhozeMymQzy+TwA4Ny5c3C5XHWfryKi7vOrX+mtov/7f4GvflVfcXU1F1yg\\nD1Lw+/XXwACwY8fWxUqtZbmPSVrj1w4hBCRJwu23397UOVVVxdjYGGZmZoyyYDCIWCyG/gbtbUVR\\nUCwWsX//fqNsenoaCwsL60pObDERtd/DDwNf+YqejGZm9FVZV3PFFcCNNwK/8zt6PxGfIdo+LCUm\\nWxPDVOx2OwA03acUDodx44034qabbjLKstks4vE4pqamVj1ubGwMx48fX1EeDAYbHrcaJiai9rj/\\nfuCLXwT+z//Rp/tZ7b/gxRfrt+d+93f1ZLTGI5XUxSwlJk3T6pYvLCxAURREIhG43W6cOnWq6QCc\\nTueK4eWapsHpdGKpwYyIXq8XqVRqRatqeHjY1PpqFhMT0dYQQp95+wtf0BPSffetvm9/P/D61wOv\\nfS3w6ld334J3tD4tHfygaRpkWUY4HMbRo0eb2t/pdELTNOxctsC8zWaDqqqrPg8VjUaRTqcxOztr\\nJKdMJoOzZ8/i4MGDlmNnYiLaPOfP6/1F09N6Mnrwwfr72Wz6rApveAPwe7+nLwXOQQu9p+Wj8sLh\\nMNLpdFNz5amqCrfbXbdlZLPZkMlksG/fvlWP93q9UBQF8Xgc/f39KJfLpj4nK5iYiFrrN7/RH25N\\np/XW0X/9V/39Lr5YvzX3+7+vt4ye+cwtDZM6UMtH5UmShFKp1NS+q90abNb8/DyGh4cRDocxMDCA\\nbDa7ofMR0cacP6/PPzc1pbeOHnmk/n5Op94ietObAJ+P0/2QWUsTUzabRSKRgCzLrTztqpLJJMbH\\nx3Hu3DkEAgF4PB7Trb161hpVSETWLC3p6xR9/vNAKrX6zNzPeQ5w003A/v36tD9P6YiHVagTWfqn\\nYbPZGn6xV26DRSKRjUXVhLGxMUSjUaMPqlgsIhAIwO/348yZM5v++US97j/+A/infwI++1ngxz+u\\nv8/llwMjI0AgoPcd8dkiaobl2cUbsdvtuPnmm5vu56m0rBYXF1cMfqh9f7nKLcDagRF9fX2YmZmB\\n1+tFNptdNdbV+pDYkiJa209/qiei//2/V58G6DnP0ZPRgQP6MhGcDJWsspSYZmdnW/rhtZPA7tmz\\nxyhXVRV2u33VEXm5XG7VdaHC4fCG+66IqOoXvwBOngQ+8xkgm63/nJHDod+ie/Ob9Ydd2TKijWj7\\nXV6fz4e5uTlTYlIUBX6/f9VjZFlGKpWq+56maQ2PJaK1CaEP7/7Up/R+o3rrF110kT6S7g/+QJ+B\\n4alP3fIwaZtqeyM7FoutSDKJRAKxWMzYrqycm0wmAcAY3LB8FJ6qqjh37lzXrQVF1CkefBD48If1\\n6X5e9SrgzjvNSUmS9NkX7rxTH+Tw+c/ro+uYlKiVOmJ28Xw+j8nJSQwODhqLEdY+v1R5cHd8fNz0\\n8GwymUShUMCuXbsA6LcG1zuJK59jol7161/rc9Mlk/rM3fX+C7zwhcBb3wr84R/qS4oTbaaOSEyd\\ngImJeo2q6smo0vpZrq9P7zN629uAa6/lDAy0ddrex0REW+c3v9EnS43H9dm769m3D3jHO/SHXy++\\neGvjIwKYmIh6ws9+preOEgn978tdfjnwJ38CvP3twBY9H0+0KiYmom2qMrLuE5/Qh3ufP29+X5L0\\nJSTCYX2OOs7EQJ3C0j/F4eHhNR9EtdvtcDqdsNvtCIfDHCFHtMV++Ut9RoaPf7z+Q7DPfjZw8CAw\\nOgq84AVbHx/RWiwNfvB4PCiXy1BVtekPCAQCmJycXFdwW4mDH6jb/fSnwD/8g95/VG9y/xtuAN71\\nLr3v6MILtz4+omZZeo6p8txQ5QHXhYUFLC0tYWFhATMzM+jv70cgEMDS0hLOnDmD0dFRpFIpnDhx\\nYlOCJyJAUYC3vAXYvRv4yEfMSelpT9Nv1X3nO/qs3wcOMClR57PUYgoGg8hkMigWi+jr61vxfr2F\\nAj0eD2w2G+bm5loX9SZgi4m6ydIScNddwK236glnuRe8AHjPe/TBDA7H1sdHtBGWWkzpdBp+v79u\\nUgL0/qWhoSEkEgmjzOfzoVAobCxKIgIAPPEEcMcdwEteoq/yujwpvfKV+jpIZ84Af/7nTErUnSwN\\nfujr61tzgtRyucxWB1GLLS7qQ73/5/8EHnrI/N6OHfotuj/9U8DrbU98RK1kqcXk8/mQyWRw+vTp\\nuu9ns1lkMhn4fD6jbHp6essWDiTabh5+GPjAB/Rbc4cOmZPSJZforaJiUR+Fx6RE24WlPiZN09Df\\n349yuQy/349AIACn02kMfkin0wBg3Lrz+/1QVRWpVKrpNZrahX1M1El+9jO9/ygeBx57zPzeZZcB\\n73+/PqhhlbvqRN1NWFQoFMTIyIiQJGnFy+/3C0VRhBBCzM7OCrvdLhKJhNWPaAsAYh3VQdRSP/qR\\nEO98pxAXXiiE/ohs9XXFFUIkk0I8/ni7oyTaXOuexFXTNMzPz0NVVciybLy6FVtM1E5nz+pDvT/1\\nKX2271rXXAP8xV/oC/FxAT7qBZxd/ElMTNQOP/qRvv7RnXfqE6zWuu46vX/pta/lzN7UWyzPjpXN\\nZpFKpVAsFhvud+rUqXUHRbTd/fSnekI6cWJlC+kVrwD+6q+AoSEmJOpNlhLT9PQ0AoHAZsVCtO09\\n/DBw7Jg+ddDjj5vfu+EG4K//Gnj1q5mQqLdZupXndruhqipmZ2cxNDS0mXFtOd7Ko820uAj83d/p\\nzyHVLlUOANdfD3zoQ8BrXsOERARYbDGpqopQKLTtkhLRZnn8ceD22/XbdssnVvV6gb/9W2B4mAmJ\\nqJblmR/WWvaCiPS57D77WX3wwo9+ZH7vJS8B/uZvgN//fSYkonoszfwQCoUwOTmJxcXFzYqHqOtl\\nMnpr6C1vMSel3buBz3wGuPde4I1vZFIiWo3l4eKBQAD33nsvYrEYBgYG4HQ66+63c+fOlgS4VdjH\\nRBv1/e8Dt9wCfPWr5vJLLwU++EF9poanPrU9sRF1E0uJqZKE1prIVZIknF++jnOHY2Ki9Xr4YeAv\\n/xJIJs3Ll198MfBnfwYcPgx02e9pRG1lqY+p2aHi7IeiXvCrX+nLl3/oQ/qouwpJAv7kT/Ty//bf\\n2hcfUbfizA9PYouJrPjKV/RlJh54wFw+NKQPC7/mmvbERbQdWJ75gaiXPfCAPrP3XXeZy6+8Uk9I\\nr3sdBzUQbVTDUXk2mw07duzA2bNnTduNXpV9iLaTX/wCOHJEH+pdm5T6+vSHZr/7XeD1r2dSImqF\\nhi2moaEhSJIEx5PrMze7phL7mGi7EAI4eVK/bfeTn1TLJQk4eFB/cPaZz2xffETbEfuYnsQ+Jlqu\\nUADe/W7ga18zl193nT7ogSvGEm0OSw/Y2mw2HDhwACdOnOBDtrRtPfGEPlXQVVeZk9IznwnccQfw\\nrW8xKRFtJkstJofDgXK5bGy7XC74fD4EAgHs27dv3UEoioJcLgen0wlVVTEwMND0fHyKomBqagq7\\ndu3CuXPnEA6H0d/fbzkGtpgIAL7+df1B2Pvuq5ZJEjA2pt+2e/KuNhFtJqtL3hYKBRGPx8XIyIiQ\\nZdm0tPrw8LCYmJgQxWLR0vn8fr+pLBAICFVV1zw2lUqJcDhsKguFQk1/di1wafWetrAgxMGDK5cz\\nHxgQYm6u3dER9ZYN9zFpmoZMJoPZ2VmkUilommZp5odwOIwbb7wRN910k1GWzWYRj8cxNTXV8HNl\\nWcbCwoJRlkgkMDExgQeWP1zSBLaYepMQwPS03pf0n/9ZLb/kEv123n//71zOnGirbSgxnT17FplM\\nBjMzM8hkMqapipaWlpo6h9PphKIo2L17t1GmaRqcTmfDc0QiEdhsNhw9enRFTLXnahYTU+956CHg\\nXe8CvvhFc/kb36gPbnjuc9sTF1Gvs5SY8vm80TrKZDKm93w+H/x+P3w+H/bu3dvU+SoJSNO0FZO+\\n2mw2qKq6apJxOp04ceKEqaW1EUxMvUMI4NOf1oeA1077eNllwCc/CbzpTe2LjYgszvzg8XiMv68n\\nES1XuQ232kzkjRKTpmno6+tDMpmE0+nEwsICnE5n089aUW968EFgdHTlEPBQCBgf1x+YJaL2WveU\\nRAsLC1hYWECpVMLi4uK6lrlYa5by1aiqCkBvwd1yyy1GeTQaxcLCAkZHR9d1Xtq+hAA+9Sm9lVQz\\nsBSyDJw4oS9rTkSdwdJzTEtLS5iZmcGhQ4fgcDgQi8Xg8/lgt9txxRVX4J3vfCdOnjxpTGG0WSoJ\\nTZZlU/mBAwcQiUQ29bOp+zz0EPCGNwBvf3s1KUkS8L73Ad/5DpMSUaex3GLy+Xzw+XzGtqIoyGQy\\nmJ+fx+TkJOLx+Kavx1RJSMsT0969e6FpWsMBEJwuqbekUvozSDWDN+F2A3feCbziFe2Li4hWZ6nF\\ntNzi4iKKxSJUVYWiKEZLptkBBJXEstosEssTT4Xdbjf9uVzlVh/1rlIJ+MM/BIJBc1J673v1pc2Z\\nlIg6l6UWU7lcNo3Kq00Asizj8OHD8Pv9Tc/aYLfbIcsyVFXFnj17jHJVVWG32xsO+64cV2+f1RIa\\nsHrSZEtq+7j7buCtbzVPuvr85+t9TLxtR9T5LCUmR818LH19fRgZGcGBAwcwNDS0autlLT6fD3Nz\\nc6bEpCgK/H5/w+PC4TByuZxpKiRFUeBwONb1HBN1vyeeAD74QeDWW/XBDhVvextw220ccUfUNaxM\\nE+Hz+cT4+LhQFEVomiZUVRWapm1o6glN01ZMSeT3+03TGpVKJSHLskgkEqbjXC7XiuOmp6fXFQc4\\nJVFXu+8+IfbuNU8ntGuXECdPtjsyIrLK8swP+Xweo6OjyOfzAIDZ2Vns27cPbrcbY2NjpuHbVs45\\nOTmJwcFBqKoKj8djaglVph8aHx/HwYMHjfJisYhYLAaXy4VCoYBgMLjuyWT5gG13EkKf8fu97wUe\\ne6xaPjysD3C4/PL2xUZE62MpMRWLRbhcLgD6IoLZbBaZTAb79u0zZh73eDyYm5vbtIA3CxNT9ymX\\n9ZnAJyerZRdeqD8o+573ALYNDe0honax9F83FosBAHK5HFKplOm9UqmEY8eOIZfL4ciRI62LkKiO\\n+XlgYMCclF74QuCee/Tnk5iUiLqXpRaT0+mE1+vFzMyMMc9dpcVU4fF4sLi4uK4ZvtuJLabuIATw\\nsY8Bhw4Bv/51tXx0VB/g8LSntS82ImoNS79Xappm3MpbjSzLKBQKGwqKqB5NA/bvB97//mpSuuQS\\n4POfBxIJJiWi7cLScPG9e/difn6+4T75fB4DAwMbCopouXweGBkBap+d9nj0W3lr/K5ERF3GUovp\\nwIEDyOVyuPvuu+s+kBoMBqGqqmnKIqKNEAJIJoGXvcyclN7zHuBb32JSItqOLA8X93g8yOfz8Pv9\\nmJ2dhd/vh91uRyaTQalUgizLOHPmzGbFu2nYx9R5fvlLfWXZO+6oll1yCfC//hcQCLQvLiLaXOta\\nwXZ8fBxHjx5FuWb9gL6+PoTDYRw7dqylAW4VJqbOcvas3p+kKNWyl75Un5T1yivbFhYRbYENLa0O\\n6PPaOZ3OdU9J1CmYmDrH7Cxw883myVff8hbg+HEOcCDqBZYSUzKZxK5du1q2nHknYWJqPyGAv/s7\\nIBIBlpb0sgsuAD76UX3pCs6zS9QbLCUmm80Gh8OBc+fObWZMbcHE1F6PPQYcPAh87nPVsssvB6an\\ngeuua19cRLT1LI3KO3jwIEqlEu69997Niod60I9/rK+PVJuUXv5yIJdjUiLqRZaeY0okEnC73fB4\\nPIjH4/B6vZBlGTt37tys+Gib+/a3gTe9Cfiv/6qWjY3pt+8uvLB9cRFR+1iekgiAsVKtcZKam/9C\\niE1fWn0z8Fbe1vvUp/RJWH/1K337KU8BPvEJvYyIepelFlOzK9NyNVhqZGkJOHJEnwW8YtcuvT/p\\nVa9qX1xE1Bk2PFx8u2CLaWv84hfAH/0R8MUvVsuuvhr40peA/v72xUVEnWNdiwMsLi6uGABx4sQJ\\nnD17thUx0Tb1s58BN9xgTkqvf70+tRCTEhFVWE5MY2NjsNvtGB0dNZWHQiG4XC6uxUR1ffe7wG//\\ntnkmhz/7Mz1JXXJJ++Iios5jKTElk0kkEgkMDAwgGo2a3puamsKePXsQi8Vw4sSJlgZJ3W1mBrj+\\neuDBB/XtHTuAeFx/mHbHjvbGRkSdx1If0/DwMObn57FQO1fMMi6XC06ns+uWV2cf0+a44w4gFAIq\\ngzQvuQRIp4Hh4fbGRUSdy1KLKZPJwO/3N9zH5/Mhl8ttKCjqfkIAH/oQ8I53VJPS856n9ycxKRFR\\nI5aGi/f39694hmm5YrEIWZY3FBR1t9/8BnjXu/R1lCr27AG+8hV9miEiokYstZh8Ph9mZ2dx8uTJ\\nuu9ns1lkMhmuYNvDHntMn8mhNikNDwNf/zqTEhE1x1Ifk6Zp6O/vR7lcht/vNxYJ1DQN99xzD9Lp\\nNOx2O4rFIvr6+jYz7pZjH9PGLSwAb3iDPs1QxR//MXDihD5LOBFRMyw/YKuqKiKRCKanp1e85/P5\\nEI/H0d/AuiSvAAAgAElEQVSFD6UwMW3Mgw8Cv/M7wPe+Vy37i78A/vZvuVwFEVmz7pkfNE2DqqpQ\\nVRV2ux1er7erFwtkYlq/H/5Qv1334x9Xyz72MeA972lfTETUvVo2JdHi4mJXzzLOxLQ++Txw443A\\nww/r2xdcAHz608Cb39zeuIioe1me+SGfz+Od73ynMf1QuVw2Wks7duzgzA895BvfAF796mpSetrT\\ngC9/mUmJiDbGUmLKZrPGWkyVYeORSASKomBoaAi7d+/G+Pj4qqP2aPv42tf0ltLior5ttwOZjF5G\\nRLQRlm7leb1eKIqC2dlZYwkMm80Gn8+HmZkZAIDD4YDb7ebMD9vYF74AHDgA/PrX+vazn61PO/TS\\nl7Y3LiLaHiy1mFRVxcjIiJGU8vk8ACBcs7JbMBiEqqotDJE6yec+BwQC1aT0/Ofrt/SYlIioVSzN\\n/KBpmmkRwEwmAwCmaYoWFhbWnB1iOUVRkMvl4HQ6oaoqBgYGml6UsDa2aDSK48ePWzqOmnfnnfoU\\nQ5VGpdsNZLN6ciIiahVLiWnv3r1GMgKAeDwOWZZNo/Gy2ayl55hUVUU0GjVuBQJ6q0uWZUvniUQi\\nKJVKTe9P1sTjwNhYdfvFL9b7lC67rH0xEdH2ZOlWXjgcRqlUwhVXXIHBwUGoqmrcxstms3C73dA0\\nDSMjI02fMxaLYaz2G+/Jz4lEIk2fQ1VVlEolLum+ST75SXNS2rsX+Jd/YVIios1h+TmmSCSCRCKB\\ncrmMkZERTE1NGeUTExOmgRDNcDqdUBQFu3fvNso0TYPT6cTS0lJT50g+OTHb7OysEY9VHPxQ30c/\\nCrz//dXtwUHg1CnA4WhfTES0vbXsAdtisQghhKWZxSsJSNO0FQ/n2mw2qKpqSlj1ZLNZyLKMTCbD\\nxNRit90G/OmfVrevu04fJt5l0yASUZex/IDtavr7+y0vd1FZcHC1GSOaGd2nqir6+/uZUFrsYx8z\\nJ6Xrr9dbSkxKRLTZLA1+aDWro/eWm56exujoaIuioYpPfhJ43/uq2694BfDVrwLPeEb7YiKi3tGy\\nFtNW22hSo/qOHwfe/e7q9stfDtx1F5MSEW2drk1MqVQK+/fvN7abHZEnSVLdFwF33AG8853V7Ze9\\nTG8pXXJJ+2Iiot7T1sRU6ZNarEy4tsr7y+XzeXi9XlMZ+5g25rOfBQ4erG5fe62elLp4wngi6lIN\\nR+WdPXsWDofDWI327Nmza46Ss8rtdiOdTmPPnj1Gmaqq8Hq9xuCI5ZLJJAqFgqlMURRjyqTBwUFT\\na6oZvTwq7+RJIBgEzp/Xt/fsAU6f5pBwImqPhoMfZFlGOBzG7bffbmwnEgkcrP3VeoN8Ph/m5uZM\\niUlRFNM0R8vVG/AwMTGB+fl5HDt2rGWx9YKvfQ24+eZqUrrqKmB2lkmJiNqnYWLq6+vD1NQUXC6X\\n0WqanZ1t6sTNJq9YLIZAIGBKNolEAolEwtjWNA0ejwfRaHTVUXiPPPJIT7Z2NuIb3wBuuqk6IeuV\\nV+pz3116aXvjIqLe1vBWXiKRWDFdUFMnlSScr/wK3oR8Po/JyUljmiOPx4N9+/YZ72uaBlmWMT4+\\nviLhFYtFxGIxTE1NoVwuY3R0FOFwGHv37rUcM9A7t/JyOeA1rwEefVTffsELgG9+E3juc9sbFxHR\\nmjM/aJoGVVWxsLCA4eFhHD58GD6fb80TN7NPJ+mlxPSDHwCvfCVw7py+/Zzn6K0nt7u9cRERARan\\nJAoEAhgbG7O8JEU36JXE9OMf67M4PPigvu1w6BOyXn11e+MiIqrY8Fx5i4uLq04p1E16ITE98og+\\ni8MPf6hvP/3p+ui7a69tb1xERLXW9RzTxMQE3G43duzYAbvdjh07dmDXrl249dZbWx0ftcijjwKv\\nfW01KV14IfDFLzIpEVHnsdxi8nq9UBQFfX198Hq9kGUZqqpifn4e5XIZHo8Hc3NzmxXvptnOLaZf\\n/Qp4/ev1YeAAIEnA1BRgYdksIqItY6nFFI1GoSgKQqEQSqUSZmdnEY/HMTs7i1KphNHRUeRyORw5\\ncmSz4iWLlpaAt7+9mpQA4B/+gUmJiDqXpRaT1+uFpmk4c+bMqvu4XC44nc6uazVt1xbT4cPAxER1\\n+6//Gvirv2pbOEREa7LUYlIUBR6Pp+E+Pp8PiqJsKChqjY9+1JyUQiHgL/+yffEQETXDUmLq7+9f\\nc/G+XC6H/v7+DQVFGzc9bV7o7/d+T19niROpE1Gns5SYfD4fcrncqqPvkskkFEXpuodrt5t//Vfg\\nj/4IqNyVfNnLgM99DnhKW5eFJCJqjqU+psqcdcViES6XCz6fDy6XC2fOnEE2m0WhUIDdbkexWDTm\\n1usW26WP6cwZPRE98oi+fcUVwLe/zfnviKh7WB4urmkaIpEIksnkivdCoRBisVjXJSVgeySmRx7R\\nk1JlbMqllwL/9m+Ay9XeuIiIrNjQzA+qqkJVVciyvOqift2i2xPTE08APp8+ESsAXHQRcPfdwHXX\\ntTcuIiKrNjwl0XbRzYlJCOCtbwX+8R/1bUkC0ml9SQsiom7T1qXVqTU+/OFqUgKA8XEmJSLqXmwx\\nPalbW0yTk/oKtBUHDwKJBIeFE1H3YmJ6Ujcmprk54IYbgMcf17f37dOXSr/ggvbGRUS0EUxMT+q2\\nxPTTnwKDg8BDD+nbv/Vb+vNLDkd74yIi2ij2MXWhX/4SeOMbq0nJ4QC+/GUmJSLaHtY9F0CxWESx\\nWISmacZw8e2wYGCnE0KfLXx+Xt/esQNIpfQHaYmItgPLiSmfz2N0dHTFRK2SJGFkZASxWAy7d+9u\\nVXy0TCwGfP7z1e2PfQzYhivdE1EPs9THVJmKCAAGBgZw4MABY2LX2dlZZLNZOBwOFIvFrms9dUMf\\n01136Qv+VUIcGwNuv729MRERtZqlxBQMBpFOpxGPxzE6Orri/UQigbGxMQQCAUxOTrY00M3W6Ynp\\n/vv1ZdDLZX37hhuATIYj8Iho+7GUmJxOJ2RZxnylg6MOj8eDxcVFPPDAAy0JcKt0cmJaXAR++7eB\\n++7Tt5/3PL2P6VnPam9cRESbwdKoPE3TjFt5q5Flec01m6h5S0vAH/9xNSlddBHwhS8wKRHR9mUp\\nMQ0NDSGTyTTcJ5vNYu/evRsKiqqOHQO+9KXqdjIJrLGIMBFRV7OUmOLxOJaWlnDjjTfi7NmzpveK\\nxSKGh4ehaVrdJTHIupkZ4AMfqG6///36AoBERNtZwz6m4eFho++lolAoQFVVSJIEWZZht9uhaRpU\\nVYUQAgMDAxgcHMTtXTZcrNP6mM6e1VtGCwv6Ngc7EFGvaJiYHA4HJEmy/GUtSRIWKt+oXaKTEtPj\\njwPXXw9UHhW7/HIglwOe85z2xkVEtBUaPmBbKpW2Kg6q8b73VZPSBRfoaysxKRFRr1j3lEQVi4uL\\nG36YVlEU5HI5OJ1OqKqKgYEBDDUxncH09DRUVTVuL4bDYezfv39DsbTbZz6jL1tR8fd/ry+XTkTU\\nM8Q6jI+PC5fLJWw2m5AkSdhsNuF0OsXExITlcxUKBeH3+01lgUBAqKra8Lh0Oi0URTG2NU0TLpdL\\nJBIJyzEIIQQAsc7qaJnvfEeIiy8WQp/bQYg3v1mIpaW2hkREtOUsL3vh9XqhKAr6+vrg9XqN55bm\\n5+dRLpfh8XgwNzfX9PnC4TBuvPFG3FSz5Go2m0U8HsfU1NSqx01MTODQoUOmsmQyiXA4jKWlJSuX\\nBKD9fUyLi/oyFvffr2+/6EXAPfcAz3hGW8IhImofK1ksEokISZJEOByu+34oFBKSJIloNNr0OR0O\\nhygWi6ayUqkkJEla9ZhSqSQ8Ho/QNM1UXigUhCRJK87XDLSxxbS0JMTNN1dbSk9/uhDf/35bQiEi\\najtLzzFlMhnIsozjx4/XfT8ej6O/v3/Nh3ArNE2DpmlwOp2mcrvdDgArnpWqfV9VVRSLxeaD72DJ\\npHnG8ERCbzEREfUiS4lJURR41ph2wOfzrVgSYzWVIeWrDZ5oNLXRwsIC9uzZYyrLZDJwOBxdtezG\\nv/878N73VrdDIeAP/qB98RARtZulxFRZ4qKRXC6H/v7+ps6naZqVj19TPB7HkSNHWnrOzfToo0Aw\\nCDzxhL790pcCt93W3piIiNrNUmLy+XzI5XK49dZb676fTCahKAp8Pl9LgrMikUjg0ksvxS233LLl\\nn71e73pXdbDD058OTE0BF1/c3piIiNrN0qg8TdPg8XiMBQN9Ph9cLhfOnDmDbDaLQqEAu92OYrGI\\nvr6+Nc+nKAq8Xm/dUXQ2mw2ZTAb79u1b8zyqqiIYDDZcjqNi+RRLy1mojg35zGeAt761uv2P/8h5\\n8IiIAIuJCdCTUyQSqTtRaygUQiwWayopVc7ldDqhadqKfiabzQZVVZvqLwoGgzhx4kRTD/p2QmK6\\n/35gYAD4xS/07be9Dbjzzk3/WCKirmA5MdVSVRWqqkKWZciyvK5zuN1upNNp00AGVVXh9Xqbmm9v\\nbGwM0Wh0wwMetuo5pieeAF7+8uqUQ1deqc+Dx+eViIh0lvqYkskkTp48aWzLsgyfz7fupATo/VbL\\nH8hVFAV+v7+peJYnpWw229HDyI8cqSalCy/Uh4kzKRERVVlqMdlsNjgcDpw7d65lAZTLZQQCAczM\\nzBhlw8PDSCQSRsKp9G1Fo1GMjo4CANLpNEqlkmn4+sLCAtLp9KrPWTWyFS2mmRngxhur27fdpk/Y\\nSkREVZYmcT148CBOnDiBe++9d8UzROvV19eHWCyGaDSKwcFBqKpa99ZcqVQykoemaQgGg3XPt9bS\\n7+3yyCPmwQ6vfa35+SUiItJZ7mMaHx/HkSNHEI/HjbnyNjq7eCfYzBaTEMCb3lRdIv1ZzwK++139\\nTyIiMrOUmCpTBy1/MLZ2pJsQApIk4fz58y0KcWtsZmJKJIBwuLp9113A7/5uyz+GiGhbsHQrr5k1\\nkoC1h2T3kvvvB97//ur2e97DpERE1MiGhotvJ5vRYvrNb/Ql0u+5R9++6ipgbo6zOxARNdL0cPFi\\nsYh7770Xi4uLmxnPtvKRj1ST0gUXAP/0T0xKRERrWTMxTU9Pw+l0wu12Y2BgAA6HA4ODg6suSUG6\\nuTngQx+qbv/N3wDXXNO+eIiIukXDW3n5fN54Tqi/vx+yLBsr1bb6eaZ2a+WtvMce06cc+uEP9e1X\\nvAL4538GduzY8KmJiLa9hi2mSCQCQF9OolAoYHZ2FqVSCUNDQyiVSqvOMt7rotFqUnrGM4BPf5pJ\\niYioWQ0T09zcHFwulzHbQkU8HgcAFAqFzYusS919N/Dxj1e3b7sN2MCMTUREPadhYiqXy3XnwauU\\nNTPJai959FHg7W+vbr/udeZtIiJa25qDH+x2+1bEsS0cOgRUxoQ4HEAyCfCRLiIiayzNLk6rm5kB\\nnrzDCQD4xCeAyy5rXzxERN2KiakFymXgHe+obr/pTcCb39y+eIiIulnD4eKVZS58Pt+K91Kp1Krv\\nAcDk5GTrotwCGxkuHg7r8+EBwKWXAt/7HidoJSJarzUT03otLS2t+9h2WG9iymaB2tw8OQmssiIH\\nERE1oeEkrvPz81sVR1f6+c+Bgwer2zfdBAQC7YuHiGg74CSuT1pPi+m9760+s+RwAN//PvCc52xG\\ndEREvYODH9bpm980P0j70Y8yKRERtQJbTE+y0mJ6/HFgz57qtEOvex3w5S/zmSUiolZgi2kdPvzh\\nalK65BLg+HEmJSKiVmFisui73wWOHatux2LAc5/bvniIiLYb3sp7UjO38s6fB17+8urif9dfD3z9\\n68AGRtUTEdEy/Eq14OMfryalCy/U58JjUiIiai1+rTbpJz8BPvCB6vYHPgC86EXti4eIaLvirbwn\\nrXUr741vBL70Jf3vL34xkM/rrSYiImottpia8MUvVpMSoM8izqRERLQ5mJjW8OijwLvfXd0OhYBX\\nvKJ98RARbXdMTGv44AeBn/5U//uznmUeKk5ERK3HxNSAopinHbrtNn1OPCIi2jwc/PCk5YMflpaA\\nl72sOjzc7wdOneIMD0REm40tplWcOGF+ZumTn2RSIiLaCg3XY9oqiqIgl8vB6XRCVVUMDAxgaGho\\n045by8MPA9FodTsaBa64YsOnJSKiJrQ9Mamqimg0ipmZGaMsGAxClmX09/e3/LhmRCJAqaT/XZbN\\nSYqIiDZX22/lxWIxjI2NmcrC4TAikcimHLeWb30LuPPO6vYnPgFcfPGGTklERBa0ffCD0+mEoijY\\nvXu3UaZpGpxOJ5aWllp+3Goqgx+uuUbg3/9dL7vpJmB62vKpiIhoA9raYtI0zUgmtex2OwDg7Nmz\\nLT2uGZWkdPHFwN///bpPQ0RE69TWxLSwsAAA2LlzZ933VVVt6XFW/I//ATz/+Rs+DRERWdT2FtNW\\nHtcslwv48z/f1I8gIqJVtH3wQyf66EeBiy5qdxRERL2p7cPFt5q05lOyEl7/+i0JhYhoW2j1GLq2\\ntphkWQYALC4uNny/VccREVHrrf0LvzVtbTHZ7XbIsgxVVbFnzx6jXFVV2O1201DwVhwHrJ7Z11oo\\nsJewLqpYF1WsiyrWRVWrkxLQAX1MPp8Pc3NzpjJFUeD3+zflOCIi6mxtT0yxWAypVMpUlkgkEIvF\\njG1N0+ByuZBMJi0dR0RE3aftMz8AQD6fx+TkJAYHB6GqKjweD/bt22e8r2kaZFnG+Pg4Dh482PRx\\nVrBpXsW6qGJdVLEuqlgXVZtRFx2RmDoB/6FVsS6qWBdVrIsq1kXVZtRF22/lERER1WKLiYiIOgpb\\nTERE1FGYmIiIqKMwMRERUUdhYiIioo7Sc5O4LqcoCnK5HJxOJ1RVxcDAAIaGhtod1paYnp6Gqqoo\\nFApQVRXhcBj79+837dNr9aNpGqLRKI4fP24q76V6UBQFU1NT2LVrF86dO4dwOIz+/n7T+71QF5lM\\nBvl8HgBw7tw5uFwujI6OmvbZznWRTqfhcDjqXk8z172huhE9rFAoCL/fbyoLBAJCVdU2RbR10um0\\nUBTF2NY0TbhcLpFIJIyyXqyfUCgkAoGAqayX6iGVSolwOGwqC4VCxt97pS5yuZxIp9OmsnQ63TP/\\nP2ZnZ4XD4RDZbHbFe81c90brpqcTUygUEtPT06ayTCaz4otpOxofH19RlkgkhCRJxnav1U+hUBCB\\nQEAEg0FTea/UQ6lUEg6Hw1QWj8eF2+02tnulLpYn54ra69yOdaGqqgiHwyKRSAiXy1U3MTVz3Rut\\nm55OTA6HQxSLRVNZqVQyfTlvR6VSSXg8HqFpmqm8UCgISZKMOum1+kkkEiKRSKz4z9Mr9XD48GER\\njUZXlNdee6/UhcfjqfvbfW0rYLvXxWqJqZnr3mjd9OzgB03ToGkanE6nqdxutwMAzp4924aotobd\\nboeqqigWi6vu02v1k81m4fP5VpT3Uj0kk0kMDg6uKK8sI9NLdeHz+eD3+03/RzKZDILBIIDeqota\\nzVx3K+qmZxPTwsICAGDnzp1131dVdSvD2XILCwumtawA/T+ew+HA7t27e65+VFVFf3//ivm+eqke\\nNE1DX18fkskkpqenjT8reqkujh07BrvdbqxqkMlkUC6XjUmke6kuajVz3a2om54dladpWrtD6Djx\\neBxHjhwB0Fv1Mz09vWK0VUWv1EPlyyKfz+OWW24xyqPRKBYWFjA6OtozdVExPz+P4eFhhMNhDAwM\\nIJvNGu/1Wl1UNHPdraibnm0xkVkikcCll15q+lLqBb36BbNcpR5kWTaVHzhwAJFIpB0htV0ymcT4\\n+DhmZ2eNZXUa3f6m1mFiIqiqikQigVOnTrU7lC2XSqVMz25txjLR3aCSkJYnpr1790LTtG3bZ7Ka\\nsbEx+P1+7NmzB0NDQygWi5BlmStkb5GeTUyV/4CLi4sN3+8F0WgUp0+fNpX1Qv3k83l4vV5T2fI+\\npl6oB6DaMV35czlVVXumLiqtx8qgDwDo6+vDzMwM7HY7Tp8+3TN1sVwz192KuunZxGS32yHL8oqO\\nOFVVYbfbTf8ot7OxsTGMj4+v6KjshfqZn5/H5OQkotGo8Uqn01AUBdFoFNPT0z1RDxX1rrP2vV6p\\ni1wuB5fLVfe9cDgMTdN6pi6Wa+a6W1E3PTv4AdCHhM7NzZlGpymK0jPN9WQyiWg0avqHks1mIcsy\\n+vv7t3391BvwMDExgfn5eRw7dswo2+71UBEOh5HL5bBv3z6jTFEUY6Qm0Bt1IcsyUqlU3fc0TTOu\\ntRfqop5mrnvDdWPxmattRdO0FdNm+P3+FQ+GbUepVEokEgmRy+WM1+zsrOmJ916sn8OHD694wLZX\\n6qEyLVUtv99veoK/V+oiHA6LTCZjKisUCiISiRjb270uXC7XijoQornr3mjd9PwKtvl8HpOTkxgc\\nHDRG3tT+xrgd1Xv4rcLlcuGBBx4wtnulforFImKxGKamplAulzE6OopwOIy9e/cC6L16cLlcKBQK\\nCAaDK66zV+oimUyiUChg165dAPTbWMtb2dutLsrlMo4ePQpVVZFOpyHLsvGwce0goWaueyN10/OJ\\niYiIOkvPDn4gIqLOxMREREQdhYmJiIg6ChMTERF1FCYmIiLqKExMRETUUZiYiIioozAxERFRR2Fi\\noo4yPj4Om80Gt9vdcD+Hw7HmPpvJ4XBgeHi4bZ+/XolEAg6HAzabreVLWfj9fths6/tKCQQC6z6W\\nth/+S6COpKoqJiYmGu7TzrWTJEnqurWbNE3D2NgYbDYbwuEwHA7Hqvum02nYbDbT0upr2WiddFt9\\n0uZhYqKOFYlEUC6X2x1GXd04k1dlGYIjR47g9ttvR19f35rHWEkWqVQKhUJh3fERVTAxUUcKhUIA\\n6i9NQeuzsLAAAE0lpAorCbivr2/brkNEW4uJiTpSIBCAz+dDOp1GNptdc//V+jc0TYPNZsPY2JhR\\nFg6HjdnVK7e0HA4HgsGg0UILh8NwuVyw2WwYHh5GsVis+7mqqhqf7XQ6EQwGV913fHwcHo/H2Hds\\nbGzFvoFAwIgtFArBZrMhmUw2vHZN00zxer1eRKPRFeet9ImFw+GGfUx+vx/BYNA4zmazGauR1ovv\\nxIkTpn2X108gEDBiW6uOaiUSCVN9eb3epv4t0DZgYXkOok0Xi8WEJEkim80KVVWFJEnC4XCs2M9u\\ntwu3221s+3w+YbPZVuxXKpWEJElibGzMKAuFQkKSJOH3+4XX6xXRaFR4PB4hSZJwuVxiYGBAuN3u\\nFeXLP9/lcgm73S6cTqcIBoPGvpIkCUVRTPsPDAwISZKE1+sVY2Njwu/31913ZGREOBwOox6cTqdp\\nPaR61yfLsnHuYDAoXC6XkCRJeDweY79MJiMikYiQJEkEg0GRTCZXPWcmkxHhcNiot9p9G8U3MjJi\\n+hkUCgUhSZKw2WxieHjYdN0Oh0NommY6b+2xhw8fNs4fDAZFIBBYtW5p+2Fioo5Sm5iEEGJ8fFxI\\nkmRaoE2I1iSm4eFh076VL/Tl5R6PR9hsNlEul02fX2/fRCKxIilUrun06dOmfRVFWbHvyMiI8WWe\\nz+frV1KNyrVMTEyYyiuJZXx83CibnZ0VkiQ1TEoVqVRKSJK0Iik2im95cgmFQsJmsxk/y4rKzzSd\\nTq84b8Xyn68QesJc/rOk7Ym38qijHTp0CLIsY3x8vKnbP1bEYjHT9tDQEAB90MXyciGE0UdTIUkS\\n4vG4qWx0dBQDAwNQFMW4VXb06FH4/X4MDAxA0zTj1d/fj6GhISiKYtwqq4jH46ZlqVeTTCbhcrlw\\nyy23mMqPHz+Ovr6+FfG1SjPxjY2NIZVKrVgcrrL4YqlUWvXYcrkMu91uKqvU1fKfD20/TEzU8Spf\\nroFAoKXnlWW5brnX6236+Hqd/QcOHABQHQVXLpcxOzsLh8MBp9NpemWzWUiStCLpNRND5fw+n2/V\\n62h1Mq8991r27t2Lm266CYDeD5bJZDA+Po5wOFx3/9oRgCMjI8jlcnC73ZiYmEA+nwcA7NmzhwMs\\negATE3W8oaEhjIyMQFGUNQcCbKXlv9FX9Pf3A9C/jCvJw+/3I5PJ1H1Vklat1ZJmrcq5XS5X3fdl\\nWYYQYkVrrBWaia8yKKOSkIeHh5FKpeDxeNY8dmpqymjRRiIRYxDE2NhYxz5CQK3zlHYHQNSMZDKJ\\nTCaDSCRijBhrxvKWSCtpmla3vJIwZFk2RrDZ7fYVt7RWI0kSdu7cueZ+leRw5syZVeNo9lxWNDqn\\nqBlePjQ0hHw+j3A4jHA4bNz6y2azSKfTa37OoUOHcOjQISwuLmJ2dhbxeByJRALz8/OYn59vzcVQ\\nR2KLibpCX18fYrEYNE3D6Oho0w9+KoqyaTGpqlr3Vtns7CwkSYIsy7Db7ejr60Mmk6l7jo1MrVRJ\\nTKsNoZ6fn1+1VbdZKj8XTdOQz+cRCARw++23m/qjxBrPRqmqikgkYlzXzp07sX//fszMzKzaJ0fb\\nCxMTdY3KwIJ0Or2itWK32yGEMH1Ja5q2qR3lQogV/SWJRALZbBYjIyNGqyIcDqNUKq1o6Y2Pj6Nc\\nLpuesbIqFAqhUCisuMUZDodRLpdx5MiRdZ8b2PgMF8sHONT+TBqde2Jiom5f1Ga1Aqmz8FYedZVU\\nKmX0qdR+sd18882Ynp6G3+9HKBSCEAKpVAqDg4MolUqbMoXQwMAAMpkMnE4nhoaGoKoq8vk8HA6H\\nacTfsWPHkE6nkU6n4Xa7sXfvXmNfj8ezYkSdlVhjsRimpqYQDocRj8fh8XiQyWRQLBbrnrtZlT6v\\nSCSCubk5HDt2rKn4Ku/Z7Xb4fD5kMhkEg0F4vV4UCgXjZ1KJXZZlYzRk5VhZlo1jK3XrdDoxNTWF\\nxcVFHD58eF3XRN2DLSbqKGtNBNrf3298MdXut3//fsTjcciyjEQigXQ6jXA4jFOnTq3Yd7XPsFIu\\nSRIGBweRy+UgyzJOnjyJxcVFBAIBFIvFFSPHzpw5g8OHD8Nut2N6ehqLi4vGl76V61+ur68PxWIR\\nofuEcIsAAACrSURBVFAImqbhxIkTcDqddc+9vB4aGRoags/ng6qqptZYo/iWv5dKpRAKhZDJZBCN\\nRqEoCk6cOIFTp04hFAqhWCwafU3Lj52ZmcHhw4fhdDpx8uRJI6mnUikcPXq0qWug7iWJzfhVkoiI\\naJ3YYiIioo7CxERERB2FiYmIiDoKExMREXUUJiYiIuooTExERNRRmJiIiKijMDEREVFHYWIiIqKO\\nwsREREQd5f8DTnDrXxe6gIwAAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 59\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Bonferroni\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Corrects for the number of comparisons that you WILL make (Set p-value before the experiment. Don't cheat)\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"%%latex\\n\",\n \"$$1 - (1-\\\\alpha_{new})^{trials} = 0.05$$\\n\",\n \"$$$$\\n\",\n \"Our Friend Taylor\\n\",\n \"$$1 - (1-trials \\\\cdot \\\\alpha_{new}) = 0.05$$\\n\",\n \"$$$$\\n\",\n \"$$trials \\\\cdot \\\\alpha_{new} = 0.05$$\\n\",\n \"$$\\\\alpha_{new} = 0.05/trials$$\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"latex\": [\n \"$$1 - (1-\\\\alpha_{new})^{trials} = 0.05$$\\n\",\n \"$$$$\\n\",\n \"Our Friend Taylor\\n\",\n \"$$1 - (1-trials \\\\cdot \\\\alpha_{new}) = 0.05$$\\n\",\n \"$$$$\\n\",\n \"$$trials \\\\cdot \\\\alpha_{new} = 0.05$$\\n\",\n \"$$\\\\alpha_{new} = 0.05/trials$$\"\n ],\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 60\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"print(\\\"p_min = 0.05/3 = %f\\\" %(0.05/10)) \\n\",\n \"print(scipy.stats.mannwhitneyu(x,y)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(x,z)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(x,i)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(x,j)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(y,z)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(y,i)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(y,j)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(z,i)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(z,j)[1]*2)\\n\",\n \"print(scipy.stats.mannwhitneyu(i,j)[1]*2)\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"p_min = 0.05/3 = 0.005000\\n\",\n \"0.0951349836324\\n\",\n \"0.176819928628\\n\",\n \"0.0515876890194\\n\",\n \"0.00138320106226\\n\",\n \"0.692955551073\\n\",\n \"0.817025225356\\n\",\n \"0.105130438032\\n\",\n \"0.500168565389\\n\",\n \"0.0464220325154\\n\",\n \"0.187879318583\\n\"\n ]\n }\n ],\n \"prompt_number\": 61\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Dunnett's_test. Compare with control.\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Still not implemented in Python. There are some non-official implementations in MATLAB though.\\n\",\n \"Assumes normality\\n\",\n \"\\n\",\n \"You can use bonferroni with p-min = 0.05/(n-1)\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Tukey HSD. Best\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \" Assumes normality\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"from statsmodels.stats.multicomp import pairwise_tukeyhsd\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 62\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"res2 = pairwise_tukeyhsd(np.asarray(x+y+z+i+j),['x']*200+['y']*200+['z']*200+['i']*200+['j']*200)\\n\",\n \"print res2\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"Multiple Comparison of Means - Tukey HSD,FWER=0.05\\n\",\n \"=============================================\\n\",\n \"group1 group2 meandiff lower upper reject\\n\",\n \"---------------------------------------------\\n\",\n \" 0 1 0.1404 -0.1341 0.4149 False \\n\",\n \" 0 2 -0.1942 -0.4687 0.0803 False \\n\",\n \" 0 3 -0.0337 -0.3081 0.2408 False \\n\",\n \" 0 4 -0.1121 -0.3866 0.1623 False \\n\",\n \" 1 2 -0.3346 -0.6091 -0.0601 True \\n\",\n \" 1 3 -0.174 -0.4485 0.1004 False \\n\",\n \" 1 4 -0.2525 -0.527 0.0219 False \\n\",\n \" 2 3 0.1606 -0.1139 0.435 False \\n\",\n \" 2 4 0.0821 -0.1924 0.3566 False \\n\",\n \" 3 4 -0.0785 -0.353 0.196 False \\n\",\n \"---------------------------------------------\\n\"\n ]\n }\n ],\n \"prompt_number\": 63\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"res2.plot_simultaneous(comparison_name=None,xlabel='diffs',ylabel='grups')\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"pyout\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAlMAAAGGCAYAAABfWgTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAHrtJREFUeJzt3c1TU2ueB/Bf7K4aV4q5/Qcocd9exJmq2UhdAizcXUTv\\nHyAvs0A34wVnM/amfWFWspgW/APmQugdVQqhO7OdQbh330T3U2K4K2eVWVjJgPISfAwJ8PlUWebl\\n5Dy/PCcn+eY5DyeZarVaDQAAvsiZVhcAAHCcCVMAAAmEKQCABMIUAEACYQoAIIEwxYlVqVTizJkz\\nMTY29tl9Q0NDcebMwS//tbW1uHz5cv167TFra2vR3d196Mc3YmZmJnK5XJw5cyYuX74cs7Ozh3r8\\nUWj0+TdDbbtu/9fd3R3r6+sNPb6R7X7ULly4ENlsdsdt2187+72OLly4sKMvLl++HAsLC/u297W2\\n39OnT2N9fT2uXr362TY5c+ZM/OY3v9nzsYVCIW7dupXU/sLCQlvuH5w+7feuAl/Z/Pz8Z7cVi8XI\\nZDKHWs/2s4jkcrl48uRJcm2fevr0aTx9+jRmZ2ejUqnE8+fPY2Ji4sAPx6PW2dnZlOd/GJVKJSqV\\nSrx//z7y+XwMDQ21tJ4vtba2FplMJjKZTMOBcLtMJhNra2v1/piYmIihoaF4+/btno/5Gq/fSqUS\\nc3Nz8e2338br16/r26KjoyOKxWL9+n51pxocHGz56xAihClOgU9HLYrFYvT19dWvf/otvVgsRn9/\\n/2frqd32zTffRLlcjomJiYj4+A17dHS0PtrV3d0db968+ezxxWKxPuLU398fW1tbO+6vVCoxOTkZ\\nxWIxvvvuuzh37lz09vbGkydPYm5urr5coVCor+fWrVv19ZTL5bh69WqMjY1FNpuN/v7+WFtbqy87\\nNTXVUL0zMzORzWY/u69cLkdfX19MTk7GP/7jP9aff0TE6OhoZLPZyGaz9XYaqXVqaiqy2Wxcvnx5\\nxzbaa33bnTt3Ls6dOxfnz5+PkZGRKJfLB/Z1bbtns9no7u6OlZWViPgYYrePWOVyufjLX/5y4Hbb\\n676Dnt92z58/j9HR0RgeHo7nz5/vukwjav0xPDwcnZ2dsbGxETMzM/WRq+3bcmNjo779att1YmKi\\nvh800v8zMzM7Rn1r2yLiY/+eO3cu/va3v+25b23/crK2thbZbDZ+/vnnXft0dHR0Rx0TExMxOTkZ\\nERE3b95suy8bnD7CFCfe0NDQjg+pQqEQt2/fjsOer3Z5eTkiIt69e/fZY2dnZ2NgYCAqlUp0d3d/\\nNkqytbUVt27dihcvXkSlUonOzs4YHh7esczq6mp0dXXFxYsXd9w+PDwcP/30U0R8/OC7detWzM7O\\n1r/1bw816+vr0d/fH2/evImNjY3I5/Oxvr4ey8vLO5bbq95KpRJjY2Px17/+Nd6/fx+dnZ07+m5l\\nZSW2trZ2jAYUCoVYWVmJt2/fxsrKSkxMTMSvv/7aUK2ZTCY2Nzcjn8/vCKfb1zc5ORm//vrrvtum\\nUCjUg1KlUtmzr2vbsNZm7fry8nJkMpn6aM6bN2/iu+++23dd+9233/P71Pz8fIyOjsbt27d3hObD\\n2P56XF5ejnK5HL/73e9ibGwsSqXSrttyu5WVlfj111+jUCg03P9zc3ORz+e/qN7tyuVy5PP5KBQK\\ncfHixV37tL+/v76tIj4e3vvhhx8i4mNAru0f0DJVOKHev39fzWQy1UqlUr1w4UL99trlTCZTrVar\\n1devX1evXr1av395ebna19dXvy+Xy9Xv2+0x8/Pz1e7u7h1tZzKZ6tbWVv3xMzMz1aGhoR3LbK+p\\nWq1Wnz9/Xm93L0+ePKmOjY3Vr5fL5fp6NjY2dqxzdHS0Ojk5+VlN+9VbrVarlUqlfvvIyEh1dHS0\\nvv7dnn+hUKjmcrnq2tpatVqt1tdzmFrX1tb2XN/2eqrV/9+u2/+dOXOmvvzz58/37evacygWi/U2\\nOzo6qmNjY9WZmZnq8vJy/fb91rXfffs9v+22t1V7fO15bH/tffo63K6jo+Oz/piamvqs77Zvy+3b\\nb/t2rVYP7v+a7Y/5tA/W19c/a6f2fGuv8fn5+Wo+n6/mcrn662S/Pq2192nffnodWuG3rQ5z0Gzn\\nz5+vH+p79+5dXLt27au3cenSpR3XOzs7dxx22tjYiEKhsGOS8adzRnK5XGxubn627q2trZibm4vh\\n4eHY3NyMzs7OHe1WKpX69e3r7+jo+GxS80H1XrlyJf74xz/GyspK/bHb29t+uWZwcDA2NzdjaGgo\\nNjc348GDB3H//v1D1VrdNrKy1/o+tb1/X79+HVevXo3379831NcREb29vbG2thZv3ryJXC4X+Xw+\\nfvrpp7h27Vp9lGu/dR3Uzl7Pb7v5+fn6Ia6IqM+T+9Of/rTr8rvJZDJRLBbrfb19ZHO/bbnd9tsb\\n6f9KpRIdHR0N17iX2kjmkydP4vHjx/v2aT6fj5WVlXj9+nWMjo7uqH376wpawWE+ToWhoaH4j//4\\nj/p8of18yRvz9g/22vXtH1C5XC5u3rwZm5ub9X/FYnHHY65evVr/cN/up59+qh9W++abb2JjY2NH\\nrV/yobZXvbVDPH/5y19iaWkpbt682dC68vl8/O1vf4vXr1/H8+fPY2Fh4Ytr3Wt9n7p48WL93+Dg\\nYHR1dUWxWIzLly8f2Nc1XV1d8eTJk+jr64t8Ph+vX7+O5eXluH37dkTEvus6TDt7qYWpt2/fxtu3\\nb2N5efmLDvVls9l6X9R8ybaMaLz/v8Sn+1ZfX188evQobt68GRMTE/v2aV9fX8zNzcXc3Fx9+0C7\\nEKY4FYaGhmJmZiaKxeJn8zw6OjrqIaZSqcSjR48Ovf61tbX6X+CNjo7G1atX49y5c/X7b926FcVi\\nMVZWVurLfDqHpqOjo/7BXluuUCjE5ORkfbLt4OBgzMzM1O8fHh7+og+Wvep9//59ffJwpVKJmZmZ\\nXUfLtisUCjE0NBRbW1v1EZhMJhM3b978olr3Wt+ntra26n/Btry8HGtra3H16tUYGho6sK9r8vl8\\nzMzMxLVr1+L8+fOxubkZr1+/jitXrkTE/tvtMO3splgsRjabjStXrtQnj/f29kZE1CfGp/iSbRnR\\nWP93dHQ09KVjt31r+7pqE9ZnZmZiZmYm/v7v/37PPr1582bMzc3Fmzdv6tsn4mP4+xqjZJBCmOJE\\nq71xd3R0RC6Xi1wuVw85tfs6OztjZGQkcrlcXLt2Lf7lX/5lxxv+9ss3b96M3/zmN/U/Za+pTWbO\\nZrOxtra243QMmUwmzp8/X59onM1m4+3bt1EoFD6r9/79+zE6Olpf7sGDB/H06dO4c+dOvdbt6zlz\\n5syOyeCffujt9Tz2qrc2gTqbzUZfX188efIkisVi/S/bdlvfjz/+GNlsNi5cuFCfzP7999/HpUuX\\nvqjWvdb3qdq5mbLZbPzwww8xMzMTFy9ejI6Ojn37urYNa/2QyWTqAbuvr2/HX5/tt90Oame/bRHx\\nMUDsdjqH2mTsT19jhz2VwH7bcr91N9r/XV1du/7V6na77Vvb29y+f/74449x//79+ujxp3166dKl\\n+Oabbz47N1XtrxGhlTLVvQ7mAw0pFAr1ww/HwXGrl/Y0NTUVHR0dn/1VajN1d3fHixcvdoxMTUxM\\nxD/8wz/sGvjgqBiZAuDQRkZGks6LdVjLy8ufHeKL+HiaBEGKVhOmINGnh0za3XGrl/Z0/vz5uH37\\n9hedtf2waueG+/TXDBYWFurzCaGVHOYDAEhgZAoAIIEwBQCQoGVnQL9y5Ur88ssvrWoeAKBhv//9\\n7+Pnn3/e9b6WjUz98ssvUa1WT/y/f/3Xf215Dcftnz7TX/qrvf7pM/2lz6r7DgA5zAcAkECYAgBI\\nIEw1WU9PT6tLOHb02eHor8PRX4enzw5Hfx3ece+zlp1nKpPJRIuaBgA4lP1yi5EpAIAEwhQAQAJh\\nCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAk\\nEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQA\\nQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBM\\nAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKY4lFKp1OoS2MXi4mIM\\nDAxET09PDAwMxOLiYqtLYg/2ITh5ftuMlS4sLMRPP/0UERHFYjFevHgR33//fTOa4oiVSqXo6elp\\ndRlss7i4GPfu3YuNjY36bbXLN27caFVZ7ME+BCdPU0amBgcHY25uLkZGRuLatWuCFDTRs2fPdgSp\\niI9hanp6ukUVAZwuTRmZiohYW1uLycnJWF1d3XOZhw8f1i/39PT4tnYMlEqlyGQyrS6DBrx69cq2\\nakPXr19vdQlAA0qlUsOH5TPVarX6tQuoVCrR29sbf/3rX+PcuXO7N5zJRBOapskePny4IwTTegMD\\nA7G0tLTr7S9fvmxBRezHPgTH0365pSmH+UZGRuLXX3+NO3fuxK1bt2JhYaEZzQARcffu3cjlcjtu\\ny+VyMT4+3qKKAE6Xphzmm5uba8ZqaQMOxbaf2iTz6enp+PDhQ5w9ezbGx8dNPm9T9iE4eZpymK+h\\nhh3mAwCOiSM/zAcAcFoIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAA\\nCYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAF\\nAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABII\\nUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAg\\ngTAFAJBAmAIASCBMAQAkEKZgD6VSqdUlsIfFxcUYGBiInp6eGBgYiMXFxVaXxB7sR5wGTQlTY2Nj\\nsbKyEhERhUIhJicnm9EMNJUPgfa0uLgY9+7di6WlpfjP//zPWFpainv37glUbcp+xGnQlDA1NDQU\\n8/PzERExMzMTY2NjzWgGOIWePXsWGxsbO27b2NiI6enpFlUEnHa/bcZKe3t7Y3R0NLa2tmJzczMu\\nXry463IPHz6sX+7p6Ymenp5mlANfpFQqRSaTaXUZNOjVq1e2Vxu6fv16q0uAL1IqlRoeWc1Uq9Vq\\nM4oYGxuLcrkct27dijt37nzecCYTTWoavoqHDx/uCPy0h4GBgVhaWtr19pcvX7agIvZjP+Kk2C+3\\nNGVkKiJiZGQkuru7d33TA/hSd+/ejY2NjR2H+nK5XIyPj7ewKuA0a1qY2tzcjNHR0WatHprOYef2\\ndOPGjYiImJ6ejg8fPsTZs2djfHy8fjvtxX7EadCUw3yFQiEeP34chUJhz/lSDvMBAMfFfrmlaXOm\\nDiJMAQDHxX65xUk7AQASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\\nCFMAAAmEKQCABMIUAEACYQoAIEFDYWprayvevHkTW1tbMTU1FW/fvm1yWQAAx0NDYWp4eDjK5XJM\\nTExEtVqNoaGhZtcFAHAsNBSmKpVK9Pb2Rrlcjh9//DGq1Wqz6wIAOBYaClPVajUePHgQXV1dsb6+\\nHpVKpdl1AQAcCw2FqefPn0c2m40HDx7E6upqzM/PN7suAIBjIVM9xDG7t2/fxsWLF79Ow5mMw4UA\\nwLGwX25paGRqYWEhLl++HCMjI3H58uX485///FULBAA4rhoameru7o7V1dU9r39Rw0amAIBjInlk\\nKpvN7nsdAOC0+m0jC126dCkGBgYin8/H8vJyRETMzs5GJpOJO3fuNLVAAIB21tDIVC6Xi97e3oiI\\nyOfzkc/no1KpxPv375taXLsqlUqtLoE9LC4uxsDAQPT09MTAwEAsLi62uiR2YR8CTpKGRqZ+/PHH\\nQ610dnY2Xr9+HX/6059iaGgo/umf/im+++67LyqwHZVKpejp6Wl1GXxicXEx7t27FxsbG/Xbapdv\\n3LjRqrLYhX0IOEkaClPd3d07rmcymfjv//7vPZcfHh6O5eXlmJiYiN/97ncnKkjRvp49e7YjSEV8\\nDFPT09PCFABN01CY2v6Xe8ViMYrF4oGPefz4cVy+fHnfs6U/fPiwfrmnp+fYfFMtlUqRyWRaXQYN\\nevXqle3VZq5fv97qEgD2VSqVGp6ScKiTdtb09/fH0tLSvsv09fXFwMBA/Nd//VfMzc193vAxPjXC\\nw4cPdwRB2sPAwMCur8uBgYF4+fJlCypiL/Yh4LjZL7c0NDI1NTVVv/zu3buGlh8YGIh//ud/jrGx\\nsVhYWIjBwcEGy4Uvc/fu3djY2NhxqC+Xy8X4+HgLqwLgpGtoZKpQKOw4TJLP5+P8+fNpDR/jkSmT\\nZ9vX4uJiTE9Px4cPH+Ls2bMxPj5uvlQbsg8Bx81+uaWhMPXmzZu4dOnSkRUFANBOks+A3tfX91UL\\nAgA4KRqaM9Xb2xvd3d2Rz+frtz1+/LhpRQEAHBcNhan+/v7o7+9vdi0AAMdOQ3Omuru7PztfVC6X\\ni+fPn8fFixe/rGFzpgCAYyL51Ajd3d0xNDQUvb299ZN23rp1K0ZGRg483xQAwEnW0AT0crm844eO\\n19bWoqurq6mFAQAcBw2NTJ0/fz7+7d/+rT4yFRGxsrLS1MIAAI6Dhkam5ufn43/+53/i0aNH8e7d\\nu5ifn6/fDgBwmn3Rb/N9lYZNQAcAjonkk3YCALA7YQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\\nCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASHEmYWllZicnJyaNoCgDgSGWq\\n1Wq1JQ1nMtGipgG+SKlUip6enlaXwS4WFxfj2bNn8b//+7/xd3/3d3H37t24ceNGq8tiF8d1P9ov\\nt/z2KAooFotRLBbj8ePHR9EcQFMc1w+Bk25xcTHu3bsXGxsb9dtqlwWq9nMS96MjOcyXyWSOohkA\\nTqFnz57tCFIRH8PU9PR0iyritDmSkam9PHz4sH65p6fnxCVV4GQplUq+HB4jr169sr3a0PXr11td\\nQkNKpVKUSqWGlm2bMAXQ7np6ehp+c+XoDAwMxNLS0q63v3z5sgUVsZ/j8tn/6SDPH/7whz2XdWoE\\nAI61u3fvRi6X23FbLpeL8fHxFlXEaXMkI1Pv378/imYAmspUhPZUm2Q+PT0dHz58iLNnz8b4+LjJ\\n523qJO5HTT81QqVSiXw+Hy9evIgrV678f8NOjQAAHBP75RbnmQIAOMB+ucWcKQCABMIUAEACYQoA\\nIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCm\\nAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEAC\\nYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEA\\nJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEjQ9DC1sLAQU1NTzW4GAKAlMtVqtdqS\\nhjOZaFHTAACHsl9uafrIVKFQiMnJyWY3A8dWqVRqdQnsYXFxMQYGBqKnpycGBgZicXGx1SWxB/sR\\nrfTbZjeQyWSa3QQca6VSKXp6elpdBp9YXFyMe/fuxcbGRv222uUbN260qiz2YD+ilUxAB9jFs2fP\\ndgSpiI9hanp6ukUVAe2q6SNT+3n48GH9ck9Pj28VnEqlUskI7jHy6tUr26sNXb9+vdUlcMKUSqWG\\nDx8fSZja641ne5iC06qnp8d8jzY0MDAQS0tLu97+8uXLFlTEfnye8LV9Osjzhz/8Yc9lmx6mBgcH\\nY3BwsNnNAHxVd+/ejY2NjR2H+nK5XIyPj7ewKqAdtfQwHxAOb7ep2iTz6enp+PDhQ5w9ezbGx8dN\\nPm9T9iNayXmmAAAO0NLzTAEAnGTCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkA\\ngATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECY\\nAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJ\\nhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUA\\nkECYAgBIIEwBACQQppqsVCq1uoRjR58djv46HP11ePrscPTX4R33PhOmmuy4v0BaQZ8djv46HP11\\nePrscPTX4R33PhOmAAASCFMAAAky1Wq12oqGr1y5Er/88ksrmgYAOJTf//738fPPP+96X8vCFADA\\nSeAwHwBAAmEKOLEWFhZiZWUlZmdn91xmYmLiCCuC062RfTIiYmpq6ogq+jqEKdqKD7/9HdQ/jb5R\\nnQZra2sREdHb2xsREevr658tMzMzEwsLC0daVzs76PUzOzsbs7OzMTk5ecSVta+D+qxQKMTKykqM\\njY0dcWXtp5F9MiKiWCzG8vLykdX1NQhTTeSN6XB8+O3voP5p9I3qtJibm4sLFy5ERERnZ2cUi8XP\\nlhkZGYnOzs6jLq0tHfT6WVlZiXw+H8PDw1Eul2NlZeXIa2w3jfTZyspK9Pb2Rrlc3nPy8mnRyD4Z\\nEZHJZI6yrK9CmGoSb0yH58Nvfwf1T6NvVKdFpVKJbDZbv/7u3bsWVtP+Dnr9lMvl+m2dnZ1RLpeP\\nvMZ2c1Cf9fb2xr//+79HRMTm5mZcuXLlyGtsJ43sk+vr6/XPzeNEmGoSb0yH58Nvfwf1j/77nD9W\\nbtxBr5/h4eEYHh6OiI9fFq9du3ak9bWjRva5ra2tmJqaigcPHhxlaW3roH1yc3PziCr5un7b6gJO\\nqkbemGrW1tbihx9+OLLa2pkPv/0d1D/67/91dHTU35jfv38f33zzTYsran+NvH7W1tbi6tWrp36U\\npeagPjt//nzcv38/+vv7o6urKy5dunRElbWfg/bJ4zoqFSFMNZU3ps/tNn8sm83G4OCgD78DHNQ/\\n+m+n27dvx+rqavT29sabN2+ir68vIj5+0eno6Ghxde2n0dfPyspKPHr06ChLa1sH9dna2lpkMpn4\\n9ttvo6urKwqFQty/f78VpbaFg/bJcrkc5XI53r17F5ubm7G+vh7ffvtti6tujMN8CWoTyLf/q02O\\n9sa0u9qhgu3/BgcHI+LjjlY73PnpjsbB/bPX/adV7U14ZWUlOjo66l9Y8vl8fZlCoRCrq6vx4sWL\\nltTYThrZ/2ZmZuphwDzPg/tsZWWl/jlQqVQil8u1ptA2cdA+OTg4GIODg5HJZGJra+tYTUR3BvQm\\nWV9fj9XV1RgeHo6pqano6+uLK1eu7PhWPDMzEyMjIxER9b/4OO1mZ2frc8hqh0K7u7tjdXU1Ij5+\\n+I2MjMTTp0/jzp07rSy1JQ7qn93uh0bt9/oqFotx69atyGazsbm5GYVCIb777rsWV9x6+/XZ1tZW\\nzM3NRcTHebKn6YvzaSNMNZE3JgA4+YQpAIAE5kwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKOLYu\\nX74cERELCwsxNTUVERF9fX31k3BuvwzQLH5OBjj2amfRL5fLkclk4s6dOzsuAzSTMAUcG5VKJYaG\\nhiKTyez4fb3az8JUKpVYXV2NhYWFWFpaitXV1fjzn/8cV65cidHR0frjZmdn4/z58y18JsBJIkwB\\nx8ajR4/i9u3bcefOnR2/MF/7Da+JiYkol8sxODgYXV1d8ebNm/j+++9jamoquru749GjR/XfSxOm\\ngK/FnCng2FhfX6//KOr2X5Pf7Ycctt82MjIS1Wo1+vv7Y35+PrLZbPOLBU4NYQo4Nrq6umJ5eTki\\nItbW1hp+3NzcXNy+fTuWlpais7MzZmZmmlUicAo5zAccGw8ePIihoaGYn5+Pjo6OyOVyEfHxMF/t\\nUF/t/+2Xu7u7Y2hoKDo6OiKTycT8/PzRFw+cWH7oGAAggcN8AAAJhCkAgATCFABAAmEKACCBMAUA\\nkECYAgBIIEwBACQQpgAAEvwfvrS5X6uMz9QAAAAASUVORK5CYII=\\n\",\n \"prompt_number\": 64,\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAlMAAAGGCAYAAABfWgTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAHrtJREFUeJzt3c1TU2ueB/Bf7K4aV4q5/Qcocd9exJmq2UhdAizcXUTv\\nHyAvs0A34wVnM/amfWFWspgW/APmQugdVQqhO7OdQbh330T3U2K4K2eVWVjJgPISfAwJ8PlUWebl\\n5Dy/PCcn+eY5DyeZarVaDQAAvsiZVhcAAHCcCVMAAAmEKQCABMIUAEACYQoAIIEwxYlVqVTizJkz\\nMTY29tl9Q0NDcebMwS//tbW1uHz5cv167TFra2vR3d196Mc3YmZmJnK5XJw5cyYuX74cs7Ozh3r8\\nUWj0+TdDbbtu/9fd3R3r6+sNPb6R7X7ULly4ENlsdsdt2187+72OLly4sKMvLl++HAsLC/u297W2\\n39OnT2N9fT2uXr362TY5c+ZM/OY3v9nzsYVCIW7dupXU/sLCQlvuH5w+7feuAl/Z/Pz8Z7cVi8XI\\nZDKHWs/2s4jkcrl48uRJcm2fevr0aTx9+jRmZ2ejUqnE8+fPY2Ji4sAPx6PW2dnZlOd/GJVKJSqV\\nSrx//z7y+XwMDQ21tJ4vtba2FplMJjKZTMOBcLtMJhNra2v1/piYmIihoaF4+/btno/5Gq/fSqUS\\nc3Nz8e2338br16/r26KjoyOKxWL9+n51pxocHGz56xAihClOgU9HLYrFYvT19dWvf/otvVgsRn9/\\n/2frqd32zTffRLlcjomJiYj4+A17dHS0PtrV3d0db968+ezxxWKxPuLU398fW1tbO+6vVCoxOTkZ\\nxWIxvvvuuzh37lz09vbGkydPYm5urr5coVCor+fWrVv19ZTL5bh69WqMjY1FNpuN/v7+WFtbqy87\\nNTXVUL0zMzORzWY/u69cLkdfX19MTk7GP/7jP9aff0TE6OhoZLPZyGaz9XYaqXVqaiqy2Wxcvnx5\\nxzbaa33bnTt3Ls6dOxfnz5+PkZGRKJfLB/Z1bbtns9no7u6OlZWViPgYYrePWOVyufjLX/5y4Hbb\\n676Dnt92z58/j9HR0RgeHo7nz5/vukwjav0xPDwcnZ2dsbGxETMzM/WRq+3bcmNjo779att1YmKi\\nvh800v8zMzM7Rn1r2yLiY/+eO3cu/va3v+25b23/crK2thbZbDZ+/vnnXft0dHR0Rx0TExMxOTkZ\\nERE3b95suy8bnD7CFCfe0NDQjg+pQqEQt2/fjsOer3Z5eTkiIt69e/fZY2dnZ2NgYCAqlUp0d3d/\\nNkqytbUVt27dihcvXkSlUonOzs4YHh7esczq6mp0dXXFxYsXd9w+PDwcP/30U0R8/OC7detWzM7O\\n1r/1bw816+vr0d/fH2/evImNjY3I5/Oxvr4ey8vLO5bbq95KpRJjY2Px17/+Nd6/fx+dnZ07+m5l\\nZSW2trZ2jAYUCoVYWVmJt2/fxsrKSkxMTMSvv/7aUK2ZTCY2Nzcjn8/vCKfb1zc5ORm//vrrvtum\\nUCjUg1KlUtmzr2vbsNZm7fry8nJkMpn6aM6bN2/iu+++23dd+9233/P71Pz8fIyOjsbt27d3hObD\\n2P56XF5ejnK5HL/73e9ibGwsSqXSrttyu5WVlfj111+jUCg03P9zc3ORz+e/qN7tyuVy5PP5KBQK\\ncfHixV37tL+/v76tIj4e3vvhhx8i4mNAru0f0DJVOKHev39fzWQy1UqlUr1w4UL99trlTCZTrVar\\n1devX1evXr1av395ebna19dXvy+Xy9Xv2+0x8/Pz1e7u7h1tZzKZ6tbWVv3xMzMz1aGhoR3LbK+p\\nWq1Wnz9/Xm93L0+ePKmOjY3Vr5fL5fp6NjY2dqxzdHS0Ojk5+VlN+9VbrVarlUqlfvvIyEh1dHS0\\nvv7dnn+hUKjmcrnq2tpatVqt1tdzmFrX1tb2XN/2eqrV/9+u2/+dOXOmvvzz58/37evacygWi/U2\\nOzo6qmNjY9WZmZnq8vJy/fb91rXfffs9v+22t1V7fO15bH/tffo63K6jo+Oz/piamvqs77Zvy+3b\\nb/t2rVYP7v+a7Y/5tA/W19c/a6f2fGuv8fn5+Wo+n6/mcrn662S/Pq2192nffnodWuG3rQ5z0Gzn\\nz5+vH+p79+5dXLt27au3cenSpR3XOzs7dxx22tjYiEKhsGOS8adzRnK5XGxubn627q2trZibm4vh\\n4eHY3NyMzs7OHe1WKpX69e3r7+jo+GxS80H1XrlyJf74xz/GyspK/bHb29t+uWZwcDA2NzdjaGgo\\nNjc348GDB3H//v1D1VrdNrKy1/o+tb1/X79+HVevXo3379831NcREb29vbG2thZv3ryJXC4X+Xw+\\nfvrpp7h27Vp9lGu/dR3Uzl7Pb7v5+fn6Ia6IqM+T+9Of/rTr8rvJZDJRLBbrfb19ZHO/bbnd9tsb\\n6f9KpRIdHR0N17iX2kjmkydP4vHjx/v2aT6fj5WVlXj9+nWMjo7uqH376wpawWE+ToWhoaH4j//4\\nj/p8of18yRvz9g/22vXtH1C5XC5u3rwZm5ub9X/FYnHHY65evVr/cN/up59+qh9W++abb2JjY2NH\\nrV/yobZXvbVDPH/5y19iaWkpbt682dC68vl8/O1vf4vXr1/H8+fPY2Fh4Ytr3Wt9n7p48WL93+Dg\\nYHR1dUWxWIzLly8f2Nc1XV1d8eTJk+jr64t8Ph+vX7+O5eXluH37dkTEvus6TDt7qYWpt2/fxtu3\\nb2N5efmLDvVls9l6X9R8ybaMaLz/v8Sn+1ZfX188evQobt68GRMTE/v2aV9fX8zNzcXc3Fx9+0C7\\nEKY4FYaGhmJmZiaKxeJn8zw6OjrqIaZSqcSjR48Ovf61tbX6X+CNjo7G1atX49y5c/X7b926FcVi\\nMVZWVurLfDqHpqOjo/7BXluuUCjE5ORkfbLt4OBgzMzM1O8fHh7+og+Wvep9//59ffJwpVKJmZmZ\\nXUfLtisUCjE0NBRbW1v1EZhMJhM3b978olr3Wt+ntra26n/Btry8HGtra3H16tUYGho6sK9r8vl8\\nzMzMxLVr1+L8+fOxubkZr1+/jitXrkTE/tvtMO3splgsRjabjStXrtQnj/f29kZE1CfGp/iSbRnR\\nWP93dHQ09KVjt31r+7pqE9ZnZmZiZmYm/v7v/37PPr1582bMzc3Fmzdv6tsn4mP4+xqjZJBCmOJE\\nq71xd3R0RC6Xi1wuVw85tfs6OztjZGQkcrlcXLt2Lf7lX/5lxxv+9ss3b96M3/zmN/U/Za+pTWbO\\nZrOxtra243QMmUwmzp8/X59onM1m4+3bt1EoFD6r9/79+zE6Olpf7sGDB/H06dO4c+dOvdbt6zlz\\n5syOyeCffujt9Tz2qrc2gTqbzUZfX188efIkisVi/S/bdlvfjz/+GNlsNi5cuFCfzP7999/HpUuX\\nvqjWvdb3qdq5mbLZbPzwww8xMzMTFy9ejI6Ojn37urYNa/2QyWTqAbuvr2/HX5/tt90Oame/bRHx\\nMUDsdjqH2mTsT19jhz2VwH7bcr91N9r/XV1du/7V6na77Vvb29y+f/74449x//79+ujxp3166dKl\\n+Oabbz47N1XtrxGhlTLVvQ7mAw0pFAr1ww/HwXGrl/Y0NTUVHR0dn/1VajN1d3fHixcvdoxMTUxM\\nxD/8wz/sGvjgqBiZAuDQRkZGks6LdVjLy8ufHeKL+HiaBEGKVhOmINGnh0za3XGrl/Z0/vz5uH37\\n9hedtf2waueG+/TXDBYWFurzCaGVHOYDAEhgZAoAIIEwBQCQoGVnQL9y5Ur88ssvrWoeAKBhv//9\\n7+Pnn3/e9b6WjUz98ssvUa1WT/y/f/3Xf215Dcftnz7TX/qrvf7pM/2lz6r7DgA5zAcAkECYAgBI\\nIEw1WU9PT6tLOHb02eHor8PRX4enzw5Hfx3ece+zlp1nKpPJRIuaBgA4lP1yi5EpAIAEwhQAQAJh\\nCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAk\\nEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQA\\nQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBM\\nAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKY4lFKp1OoS2MXi4mIM\\nDAxET09PDAwMxOLiYqtLYg/2ITh5ftuMlS4sLMRPP/0UERHFYjFevHgR33//fTOa4oiVSqXo6elp\\ndRlss7i4GPfu3YuNjY36bbXLN27caFVZ7ME+BCdPU0amBgcHY25uLkZGRuLatWuCFDTRs2fPdgSp\\niI9hanp6ukUVAZwuTRmZiohYW1uLycnJWF1d3XOZhw8f1i/39PT4tnYMlEqlyGQyrS6DBrx69cq2\\nakPXr19vdQlAA0qlUsOH5TPVarX6tQuoVCrR29sbf/3rX+PcuXO7N5zJRBOapskePny4IwTTegMD\\nA7G0tLTr7S9fvmxBRezHPgTH0365pSmH+UZGRuLXX3+NO3fuxK1bt2JhYaEZzQARcffu3cjlcjtu\\ny+VyMT4+3qKKAE6Xphzmm5uba8ZqaQMOxbaf2iTz6enp+PDhQ5w9ezbGx8dNPm9T9iE4eZpymK+h\\nhh3mAwCOiSM/zAcAcFoIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAA\\nCYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAF\\nAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABII\\nUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAg\\ngTAFAJBAmAIASCBMAQAkEKZgD6VSqdUlsIfFxcUYGBiInp6eGBgYiMXFxVaXxB7sR5wGTQlTY2Nj\\nsbKyEhERhUIhJicnm9EMNJUPgfa0uLgY9+7di6WlpfjP//zPWFpainv37glUbcp+xGnQlDA1NDQU\\n8/PzERExMzMTY2NjzWgGOIWePXsWGxsbO27b2NiI6enpFlUEnHa/bcZKe3t7Y3R0NLa2tmJzczMu\\nXry463IPHz6sX+7p6Ymenp5mlANfpFQqRSaTaXUZNOjVq1e2Vxu6fv16q0uAL1IqlRoeWc1Uq9Vq\\nM4oYGxuLcrkct27dijt37nzecCYTTWoavoqHDx/uCPy0h4GBgVhaWtr19pcvX7agIvZjP+Kk2C+3\\nNGVkKiJiZGQkuru7d33TA/hSd+/ejY2NjR2H+nK5XIyPj7ewKuA0a1qY2tzcjNHR0WatHprOYef2\\ndOPGjYiImJ6ejg8fPsTZs2djfHy8fjvtxX7EadCUw3yFQiEeP34chUJhz/lSDvMBAMfFfrmlaXOm\\nDiJMAQDHxX65xUk7AQASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\\nCFMAAAmEKQCABMIUAEACYQoAIEFDYWprayvevHkTW1tbMTU1FW/fvm1yWQAAx0NDYWp4eDjK5XJM\\nTExEtVqNoaGhZtcFAHAsNBSmKpVK9Pb2Rrlcjh9//DGq1Wqz6wIAOBYaClPVajUePHgQXV1dsb6+\\nHpVKpdl1AQAcCw2FqefPn0c2m40HDx7E6upqzM/PN7suAIBjIVM9xDG7t2/fxsWLF79Ow5mMw4UA\\nwLGwX25paGRqYWEhLl++HCMjI3H58uX485///FULBAA4rhoameru7o7V1dU9r39Rw0amAIBjInlk\\nKpvN7nsdAOC0+m0jC126dCkGBgYin8/H8vJyRETMzs5GJpOJO3fuNLVAAIB21tDIVC6Xi97e3oiI\\nyOfzkc/no1KpxPv375taXLsqlUqtLoE9LC4uxsDAQPT09MTAwEAsLi62uiR2YR8CTpKGRqZ+/PHH\\nQ610dnY2Xr9+HX/6059iaGgo/umf/im+++67LyqwHZVKpejp6Wl1GXxicXEx7t27FxsbG/Xbapdv\\n3LjRqrLYhX0IOEkaClPd3d07rmcymfjv//7vPZcfHh6O5eXlmJiYiN/97ncnKkjRvp49e7YjSEV8\\nDFPT09PCFABN01CY2v6Xe8ViMYrF4oGPefz4cVy+fHnfs6U/fPiwfrmnp+fYfFMtlUqRyWRaXQYN\\nevXqle3VZq5fv97qEgD2VSqVGp6ScKiTdtb09/fH0tLSvsv09fXFwMBA/Nd//VfMzc193vAxPjXC\\nw4cPdwRB2sPAwMCur8uBgYF4+fJlCypiL/Yh4LjZL7c0NDI1NTVVv/zu3buGlh8YGIh//ud/jrGx\\nsVhYWIjBwcEGy4Uvc/fu3djY2NhxqC+Xy8X4+HgLqwLgpGtoZKpQKOw4TJLP5+P8+fNpDR/jkSmT\\nZ9vX4uJiTE9Px4cPH+Ls2bMxPj5uvlQbsg8Bx81+uaWhMPXmzZu4dOnSkRUFANBOks+A3tfX91UL\\nAgA4KRqaM9Xb2xvd3d2Rz+frtz1+/LhpRQEAHBcNhan+/v7o7+9vdi0AAMdOQ3Omuru7PztfVC6X\\ni+fPn8fFixe/rGFzpgCAYyL51Ajd3d0xNDQUvb299ZN23rp1K0ZGRg483xQAwEnW0AT0crm844eO\\n19bWoqurq6mFAQAcBw2NTJ0/fz7+7d/+rT4yFRGxsrLS1MIAAI6Dhkam5ufn43/+53/i0aNH8e7d\\nu5ifn6/fDgBwmn3Rb/N9lYZNQAcAjonkk3YCALA7YQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\\nCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASHEmYWllZicnJyaNoCgDgSGWq\\n1Wq1JQ1nMtGipgG+SKlUip6enlaXwS4WFxfj2bNn8b//+7/xd3/3d3H37t24ceNGq8tiF8d1P9ov\\nt/z2KAooFotRLBbj8ePHR9EcQFMc1w+Bk25xcTHu3bsXGxsb9dtqlwWq9nMS96MjOcyXyWSOohkA\\nTqFnz57tCFIRH8PU9PR0iyritDmSkam9PHz4sH65p6fnxCVV4GQplUq+HB4jr169sr3a0PXr11td\\nQkNKpVKUSqWGlm2bMAXQ7np6ehp+c+XoDAwMxNLS0q63v3z5sgUVsZ/j8tn/6SDPH/7whz2XdWoE\\nAI61u3fvRi6X23FbLpeL8fHxFlXEaXMkI1Pv378/imYAmspUhPZUm2Q+PT0dHz58iLNnz8b4+LjJ\\n523qJO5HTT81QqVSiXw+Hy9evIgrV678f8NOjQAAHBP75RbnmQIAOMB+ucWcKQCABMIUAEACYQoA\\nIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCm\\nAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEAC\\nYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEA\\nJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEjQ9DC1sLAQU1NTzW4GAKAlMtVqtdqS\\nhjOZaFHTAACHsl9uafrIVKFQiMnJyWY3A8dWqVRqdQnsYXFxMQYGBqKnpycGBgZicXGx1SWxB/sR\\nrfTbZjeQyWSa3QQca6VSKXp6elpdBp9YXFyMe/fuxcbGRv222uUbN260qiz2YD+ilUxAB9jFs2fP\\ndgSpiI9hanp6ukUVAe2q6SNT+3n48GH9ck9Pj28VnEqlUskI7jHy6tUr26sNXb9+vdUlcMKUSqWG\\nDx8fSZja641ne5iC06qnp8d8jzY0MDAQS0tLu97+8uXLFlTEfnye8LV9Osjzhz/8Yc9lmx6mBgcH\\nY3BwsNnNAHxVd+/ejY2NjR2H+nK5XIyPj7ewKqAdtfQwHxAOb7ep2iTz6enp+PDhQ5w9ezbGx8dN\\nPm9T9iNayXmmAAAO0NLzTAEAnGTCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkA\\ngATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECY\\nAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJ\\nhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUA\\nkECYAgBIIEwBACQQppqsVCq1uoRjR58djv46HP11ePrscPTX4R33PhOmmuy4v0BaQZ8djv46HP11\\nePrscPTX4R33PhOmAAASCFMAAAky1Wq12oqGr1y5Er/88ksrmgYAOJTf//738fPPP+96X8vCFADA\\nSeAwHwBAAmEKOLEWFhZiZWUlZmdn91xmYmLiCCuC062RfTIiYmpq6ogq+jqEKdqKD7/9HdQ/jb5R\\nnQZra2sREdHb2xsREevr658tMzMzEwsLC0daVzs76PUzOzsbs7OzMTk5ecSVta+D+qxQKMTKykqM\\njY0dcWXtp5F9MiKiWCzG8vLykdX1NQhTTeSN6XB8+O3voP5p9I3qtJibm4sLFy5ERERnZ2cUi8XP\\nlhkZGYnOzs6jLq0tHfT6WVlZiXw+H8PDw1Eul2NlZeXIa2w3jfTZyspK9Pb2Rrlc3nPy8mnRyD4Z\\nEZHJZI6yrK9CmGoSb0yH58Nvfwf1T6NvVKdFpVKJbDZbv/7u3bsWVtP+Dnr9lMvl+m2dnZ1RLpeP\\nvMZ2c1Cf9fb2xr//+79HRMTm5mZcuXLlyGtsJ43sk+vr6/XPzeNEmGoSb0yH58Nvfwf1j/77nD9W\\nbtxBr5/h4eEYHh6OiI9fFq9du3ak9bWjRva5ra2tmJqaigcPHhxlaW3roH1yc3PziCr5un7b6gJO\\nqkbemGrW1tbihx9+OLLa2pkPv/0d1D/67/91dHTU35jfv38f33zzTYsran+NvH7W1tbi6tWrp36U\\npeagPjt//nzcv38/+vv7o6urKy5dunRElbWfg/bJ4zoqFSFMNZU3ps/tNn8sm83G4OCgD78DHNQ/\\n+m+n27dvx+rqavT29sabN2+ir68vIj5+0eno6Ghxde2n0dfPyspKPHr06ChLa1sH9dna2lpkMpn4\\n9ttvo6urKwqFQty/f78VpbaFg/bJcrkc5XI53r17F5ubm7G+vh7ffvtti6tujMN8CWoTyLf/q02O\\n9sa0u9qhgu3/BgcHI+LjjlY73PnpjsbB/bPX/adV7U14ZWUlOjo66l9Y8vl8fZlCoRCrq6vx4sWL\\nltTYThrZ/2ZmZuphwDzPg/tsZWWl/jlQqVQil8u1ptA2cdA+OTg4GIODg5HJZGJra+tYTUR3BvQm\\nWV9fj9XV1RgeHo6pqano6+uLK1eu7PhWPDMzEyMjIxER9b/4OO1mZ2frc8hqh0K7u7tjdXU1Ij5+\\n+I2MjMTTp0/jzp07rSy1JQ7qn93uh0bt9/oqFotx69atyGazsbm5GYVCIb777rsWV9x6+/XZ1tZW\\nzM3NRcTHebKn6YvzaSNMNZE3JgA4+YQpAIAE5kwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKOLYu\\nX74cERELCwsxNTUVERF9fX31k3BuvwzQLH5OBjj2amfRL5fLkclk4s6dOzsuAzSTMAUcG5VKJYaG\\nhiKTyez4fb3az8JUKpVYXV2NhYWFWFpaitXV1fjzn/8cV65cidHR0frjZmdn4/z58y18JsBJIkwB\\nx8ajR4/i9u3bcefOnR2/MF/7Da+JiYkol8sxODgYXV1d8ebNm/j+++9jamoquru749GjR/XfSxOm\\ngK/FnCng2FhfX6//KOr2X5Pf7Ycctt82MjIS1Wo1+vv7Y35+PrLZbPOLBU4NYQo4Nrq6umJ5eTki\\nItbW1hp+3NzcXNy+fTuWlpais7MzZmZmmlUicAo5zAccGw8ePIihoaGYn5+Pjo6OyOVyEfHxMF/t\\nUF/t/+2Xu7u7Y2hoKDo6OiKTycT8/PzRFw+cWH7oGAAggcN8AAAJhCkAgATCFABAAmEKACCBMAUA\\nkECYAgBIIEwBACQQpgAAEvwfvrS5X6uMz9QAAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 64\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Compare >2 independent samples and >2 different parameters.\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Imagine we want to check if there are difference in GFP expression for 3 different versions of a promoter in three different media. Create models, explaining the contribution of each factor.\\n\",\n \"\\n\",\n \"The two-way ANOVA can not only determine the main effect of contributions of each independent variable but also identifies if there is a significant interaction effect between them.\\n\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Fitting distributions\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Kernel estimation \\n\",\n \"\\n\",\n \"Adapted from: http://jakevdp.github.io/blog/2013/12/01/kernel-density-estimation/\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Smooth histograms.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"from sklearn.grid_search import GridSearchCV\\n\",\n \"from sklearn.neighbors import KernelDensity\\n\",\n \"\\n\",\n \"# The grid we'll use for plotting\\n\",\n \"x_grid = np.linspace(-4.5, 3.5, 1000)\\n\",\n \"\\n\",\n \"# Draw points from a bimodal distribution in 1D\\n\",\n \"np.random.seed(0)\\n\",\n \"x = np.concatenate([scipy.stats.distributions.norm(-1, 1.).rvs(400),\\n\",\n \" scipy.stats.distributions.norm(1, 0.3).rvs(100)])\\n\",\n \"\\n\",\n \"grid = GridSearchCV(KernelDensity(),\\n\",\n \" {'bandwidth': np.linspace(0.1, 1.0, 30)},\\n\",\n \" cv=20) # 20-fold cross-validation\\n\",\n \"grid.fit(x[:, None])\\n\",\n \"print grid.best_params_\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"{'bandwidth': 0.19310344827586207}\\n\"\n ]\n }\n ],\n \"prompt_number\": 65\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"kde = grid.best_estimator_\\n\",\n \"pdf = np.exp(kde.score_samples(x_grid[:, None]))\\n\",\n \"\\n\",\n \"fig, ax = plt.subplots()\\n\",\n \"ax.plot(x_grid, pdf, linewidth=3, alpha=0.5, label='bw=%.2f' % kde.bandwidth)\\n\",\n \"ax.hist(x, 30, fc='gray', histtype='stepfilled', alpha=0.3, normed=True)\\n\",\n \"ax.set_xlim(-4.5, 3.5)\\n\",\n \"ax.set_xlabel('Value',fontsize=20)\\n\",\n \"ax.set_ylabel('Norm Freq',fontsize=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAaEAAAEsCAYAAABqhgzEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3elXG1maJ/5viH2xFBLgDW8EeMvVSJBV2VWdlWVEZ1dP\\nLT0mjfNM1Zx+Y1vk9Jl3tlHOP2CLrBfzrhKRPfM7NVN9GiOq5pyeOlNlhHOrrFxAwk7b6ZUQ3o0B\\nKQQYzCLF70WkQhKSQAJJEYLncw4npZDi6iYWenRvPPe5jCiKIgghhBAFaJTuACGEkI2LghAhhBDF\\nUBAihBCiGApChBBCFENBiBBCiGIoCBFCCFFMvtIdAAC32w2XywWDwQCe52E0GtHU1JRSG4IgwGq1\\n4oMPPkh724QQQjJD8SDE8zysVisuXLggH2ttbQXHcaipqUm6nfb2dvh8voy0TQghJDMUn46z2Wxo\\na2uLOmaxWNDe3p50GzzPw+fzgWGYtLdNCCEkcxilKyYYDAa43W7s2bNHPiYIAgwGA4LBYFJtdHV1\\nAQD6+vpw/vz5tLZNCCEkcxQdCQmCIAeFSCzLAgBGRkZWbKO/vx9mszkjbRNCCMksRYOQ1+sFAGi1\\n2riP8zy/Yhs8z6OmpgZLB3TpaJsQQkhmKT4SWove3l6cOHEiI20TQgjJPMUTE1aLggwhhOS+nA1C\\nPT09aGlpke8vzYxbLYZhEv4QQghJL0WDEMdxAIDJycllH19qaGgIDQ0NUceWXhNabdvLoUBECCHp\\npehiVZZlwXEceJ7HoUOH5OM8z4Nl2ajU6kiDg4MYHh5Gd3e3fMztdsuLUxsbG9HS0rKqthNlrFMA\\nIoSQ9FO8YoLZbMbAwEBUoHC73Whubk54TrxkhPfffx+Dg4M4d+7cmtomhBCSPYpfE7LZbOjp6Yk6\\nZrfbYbPZ5PuCIKC2tlZelBrP+Ph4zCgmmbYJIYQoR/GKCYB0jae7uxuNjY3geR4mkwmHDx+WHxcE\\nARzHoaOjA8ePH4861+PxwGaz4fz58/D7/Thx4gQsFgvq6+uTajtZoek4Ffy6CCFk3VBFEMoFFIQI\\nIST9FJ+OI4QQsnFRECKEEKIYCkKEEEIUQ0GIEEKIYigIEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQo\\nhoIQIYQQxVAQIoQQohgKQoQQQhRDQYgQQohiFN9PiBA1CgaDuHXr1rIFa6uqqlBZWZnFXhGy/qgi\\nCLndbrhcLhgMBvA8D6PRiKamphXPczqdcDqdqKiowPDwMEwmU9SGdzzPw2KxwGq1wmQywev1wm63\\no7m5Oan2ycY1OzuLoaEhVFRUxH18amoKO3fupCBEyBopHoRCW3JfuHBBPtba2gqO41BTU5PwPKfT\\nCYZhonZSbWhogCAIOH36tHysv78f/f39AKTtxD/88EMKQCQpBQUF2L17d9zHnjx5kuXeELI+KX5N\\nyGazoa2tLeqYxWJBe3v7sud1dnbGHDObzVHHGYaB0+mEIAjgeR5erxdHjhxJT8cJIYSsmeJBqKen\\nB0ajMeqYyWSCw+FY9rxQgIkkiiL0en3MMa1Wiz179qSlv4QQQtJH0ek4QRAgCAIMBkPUcZZlAQAj\\nIyMJg8f58+djjjkcDrz77rtp7ychhJDMUDQIeb1eAIBWq437OM/zSY9g7HY7GhoacOrUqZg2BEGQ\\nX89gMKClpWX1nSaEEJI2io+E1qq3txd9fX1gGAbd3d1Rj4VGWJFBp7W1NeYYIYQQZSh+TWitWlpa\\n8MEHH+DcuXNoaGjA0NCQ/JhOp4tK2QaSS3oghBCSHTkfhEJ0Oh0sFsuK6dc1NTXgeR6Tk5NxH2cY\\nJu4PIYSQ9FM0CHEcBwAJA0Lo8WQ1NTVBEARcvHgRANDR0RHznNAUHc/zKbVNCCEk/RQNQizLguO4\\nmIDA8zxYlk2YlMDzPPR6PS5duhT38dC6IKvVipGRkajHQskQiQKcKIpxfwghhKSf4hUTzGYzBgYG\\ncOjQIfmY2+1Gc3NzwnMEQUBtbW1MIAkFM6PRiD179qCzszMmkDmdTphMpoQZeYQQ9fJ4PJidnU34\\neHl5OXbt2pXFHpG1UvyakM1mQ09PT9Qxu90Om80m3w8Fna6uLgBSkDl27FjMCMVms6G9vV0OPAaD\\nAR6PJ6odu90ut0MIyS0ulwt3797FgwcPYn48Hg8uX76sdBdJihQfCel0OthsNlitVjQ2NsrTaEtH\\nMD6fLypB4PTp0+jq6sLw8LBcwPTYsWM4fvy4/JyWlhb09vbC4XBgYmICgiDA4XBQ9QRCctjOnTtR\\nUFAQc3xmZgYPHjxQoEdkLRQPQgBQX1+P+vr6hI+zLCtfy4m0NP06HloPRAgh6qX4dBwhhJCNi4IQ\\nIYQQxVAQIoQQohgKQoQQQhRDQYgQQohiKAgRQghRDAUhQgghiqEgRAghRDEUhAghhCiGghAhhBDF\\nUBAihBCiGFXUjiMklzx6lI8vvqjA9HQZrlwBtm8H6uuBrVuV7hkhuYeCECFJmp8HPvqoHLduFWF6\\nOg8FBQUoLATu3we++gowGoGf/ASIU+CZEJKAKoKQ2+2Gy+WCwWAAz/MwGo1oampa8Tyn0wmn0ylv\\n5WAymWIqa6+2bUIizc0x+MMftBgbS/wn43YDDx8Cv/oVsGlTFjtHSA5TPAiF9g+6cOGCfKy1tRUc\\nx6GmpibheU6nEwzD4Ny5c/KxhoYGCIKA06dPr6ltQiIFg8Af/7gpKgBx3DO88soCXnyxGoODwM2b\\n0vHRUeD/+/+Af/ongDbvJWRliicm2Gw2tLW1RR2zWCxob29f9rzOzs6YY2azOer4atsmJNJXX5Xi\\n4cPwHNubb07jRz8ax/bt89i7F3jnHeDnPwc03/01TUwA//qvwNycQh0mJIcoHoR6enpgNBqjjplM\\nJjgcjmXPYxgGTqcz6pgoitDr9Wtum5CQhw/zMThYIt///vdn8PLL0dGFYaTrQUePhgPRkydAb680\\niiKEJKZoEBIEAYIgwGAwRB1nWRYAMDIykvDc8+fP4+zZs1HHHA4Hjh07tua2CQGAQAD45JNy+f6u\\nXQtoaJhN+PyDB4Gf/Sx8/9Yt4JNPMtlDQnKfokEotGW3NsHkOc/zSbdlt9vR0NCAU6dOpb1tsjHd\\nuWPAxEQeAKCgQERT0zQYZvlz6uuBH/4wfP/TT4Hh4Qx2kpAcp/hIaK16e3vR1taGoaEhdHd3p7Vt\\nsnHNzQE3blTK9197bQbl5cnNrR0+DHCcdFsUpWm5yclM9JKQ3Kd4dtxatbS0oKWlBX6/Hw0NDejq\\n6kJ9fb3S3SI5bmBAg7k56c9Dqw3i1VefJ32uRgP8+MdeXLkyj2fPpO95//2/L+Af/1FAXl5ybRQW\\nFmLv3r0p9xsApqencffu3WWfw3EcSkpKln2OEh4/fizPYsQTCASy2BuSDTkfhEJ0Oh0sFguampqW\\nfROvhFlpvoWse8+fA199FY4WjY0zSQePEK/3PjjuIb78cj+CQWBqCvjjH+fQ0DCx4rmiKGJsbGzV\\nQWhsbAxXr16NuR4a7psXLMuiurp6Ve1n0u3bt+Hz+VBaWhr38crKShTQauB1RdEgxH03ZzE5ORn3\\n2k3o8WQ1NTVBEARcvHhRzopLV9tk43C5pEAEADpdAAcOrC7Xet++IrBsAT7/XPpAffhQh1df1aO2\\ndn7Fc8fGxlb1miFarRa7du2K+9jz58mP6pRQVVWFiooKpbtBskTRa0Isy4LjuJgkAZ7nwbIs9uzZ\\nE/c8nueh1+tx6dKluI8LgrDqtkVRjPtDNoZAQCrBE9LQMCunXa9Gff0samrCQcfpLIfPp/jKiJx3\\n+3Yh/u3fdPiXf9HjT38qx9QU/U5zleL/cmazGQMDA1HH3G43mpubE54jCAJqa2tjRjOhgBMaBa2m\\nbbKxXb8eTiIoKlrEvn1rW3HKMIDZPA2dTrqWMT/P4E9/0mJhYa093bguXy7Gn/4kVbCYmdHg9u0i\\nnD+vo0CUoxT/V7PZbOjp6Yk6ZrfbYbPZ5PuhoNPV1QVACjLHjh2LGaHYbDa0t7fLo5xk2iYk0pdf\\nhm/X1fmQn4YJ6+JiEX//91PIz5fer+Pjebh4sRw0wE7d2Fge/vKXspjjMzMa9Pez9DvNQYonJuh0\\nOthsNlitVjQ2Nsr13pZOl/l8vqikgdOnT6OrqwvDw8NyAdNjx47h+PHjKbdNNiae5zE7G158Oj6e\\nD7c7VHFjEa+/PgEg8f4MgiDg2rVrcR+bmIhOQNi8OYA33niGixelxa+3bhVBqw3i9ddn1vT/sNH8\\n5S9lchWKLVsW8eqrz+F0liMYBJ48KcTdu1Q5NtcoHoQAoL6+ftm0apZl42a8La2YvZq2ycblcrmw\\nadMm5H2X+vb11xWYmpL+JGpqplFTsznhuXq9HqOjo3j06FHC52zeHH3+Cy/MYWwsH1euFAMABgdL\\nUF4exMsvqztRQC1GR/Pw4IGUGafRAM3N09DrA5iYyIPLJaWbf/utAaKIFRcVE/VQRRAiRCk7duxA\\nQUEBFhcBn88AnU769HrjDQZVVcUJzysqKkqYfZYIwwBvvPEMU1MajIwUAgA+/rgMogi88goFopVc\\nuhRe17R37xz0euk6m9E4i2++KcbCAiAIRfB4wouFifopfk2IEDXg+UI8fy4FIJ0ugB07MpM5oNEA\\nb701hS1bFuVjn3xShs8+KwWtw0xsfp4BzxfK9w8dCk+jFheLUWn0Q0NZ7RpZIwpChAC4fj086jlw\\nYC6j0zmFhcAvfjGJbdvCgejSpRL8/vc6jI6muCp2gxgeLsTiovSPUlW1iM2boyP2iy+GR5I3bki7\\n4JLcQNNxZMObnmZw/750rYFhgIMHM78RUFGRiJ//fBJ9feXyN/wnT/Jx/jyL7dsXMDdXhRs3gJIS\\naTuIYFCqQ1dQABQXAxUVSEvmXq64fbtIvr1vX2yEqawMgGUXMTkJLCxIFcxfeimbPSSrldLbuK6u\\nLuWyNqIogmEY3L59O6XzCMmWO3eK5NTe6uoFbNqUnU2ACgtF/MM/TMHlKsHXX4en4x49KsCjR1uX\\nHY1pNMCuXcChQ8DLLyPlskK5ZH4eckICIF0PWophgLq657h3T7p/4wYFoVyRUhCqr6+Hx+OB2+2W\\nj9XU1MDr9cLv9wOQMtmWbp1N9diImt25E/6WHe8DLpMYRqrKUFs7hy+/LAPPFya1EV4wCIyMSD+f\\nfQb89KfAet2x/uHDAjlAV1QEEn5J2LPnOQBpVDk8LP2O1lLtgmRHSkHovffeQ0NDA4xGY0y1arfb\\njRMnTmBkZAQOhyMmEBGiRlNTGjx+LP0ZaDRIqq5bJuj1QfzkJ1OYnmZw924hPv/ci337pBp2Go30\\nwzDSVNP0NBC5YmFiAvjtb4E33wTeeEOR7mfUvXvhhITduxP/+1RULKKkRIo6s7PAw4fAzp0Z7x5Z\\no5SC0Llz58CyLPr7+6HT6aIeMxqNcLlc0Ov1sFqtUXv7EKJWw8PhUdDOnQsoKVF2yX15uYgXX5zD\\n7OxD/Kf/lPh5U1PApUvA559LgUoUgY8+Ap49Aw4cyF5/s+Hu3fBU3O7dibMWGQbYtu2ZfP/OHQpC\\nuSClwarT6URzc3NMAIpkNpvhdDrX3DFCsuHOnXBWXF1ddqfi1mLTJuBv/xb4538GIguAfP018Je/\\nqG+foNXy+zXw+8O7227dunzq/LZt4QoUK2ypRFQipSAkiuKK22J7PJ41dYiQbJmeLsDTp9K37Lw8\\ngONyL6930ybgP//n6IvwLlcRbt2Kv619rnn0KDwK2r59ccWMwKqqcBB68ABYXFzmyUQVUgpCZrMZ\\nLpcLv//97+M+3tvbC7fbDZPJlJbOEZJJDx+GP6h37pxHcXFuVr/MywOOHImehhscrMLTp7mfMhe6\\nXgcA27evvIA4P38Wc3OP8PTpUzx69BQffXQTV69elX/Wuk8TSb+UrgnZbDY4nU4cPXoUb7/9Npqb\\nm8FxHIaHh9HX1weHwyE/jxC1e/QoXOxSqYSEdNFogJYW4H/8D8DnA4JBBn/+8yYcOyagsHDl89Uq\\nciS0bdvyQaikpAQsy6K4+CkePJD+ba9cmQQgAACmpqYwMzODqqqqjPWXpC6lIMRxHPr7+9He3o6e\\nnp6YbRI4jkNnZycVDCWqNzsLTEyUoKJCuqC9XNZVrigoAN5+Gzh7VhrRCUIevviiDD/60bMVzlSn\\n2VkGPp80msvLAzZvXn5ujWEY7NixA6++WoSxMalaeSBQil27pBHv6OhoZjtMViXlNddGoxF9fX3g\\neR5utxs8z4PjOHAcJ28mlyq32w2XywWDwQCe52E0GtHU1LTieb29veB5HsPDw+B5HhaLBS0tLfLj\\noWNWqxUmkwlerxd2ux3Nzc1JtU/Wrzt3pNECIG0JUFaWm1NxS1VUAIcPz+J3v5PuX7lSjAMH5qJq\\n1eWKyKm4zZsXUVCwzJMjRE7bPX6cT1W1VW7VhT8qKyvR0NCwYrbcSkJ7/Fy4cEE+1traCo7jll1r\\n1NvbC47j5KDj9/vlQBO5xUN/fz/6+/sBSAtpP/zwQwpABDdvhm/v2ZP7o6BIBw7MY/v2GczO6r9L\\n3S5Da6s/5xZuPn6c/FRcJK02iNLSIGZmNJifZyAIeXLFbaI+Kb8th4aG0NDQAJZlUVtbC5fLBUAq\\n6fPrX/865Q7YbDa0tbVFHbNYLGhvb1/2PJ7no6b9dDod2tvbYbFY5GMMw8DpdEIQBPA8D6/XiyNH\\njqTcR7K+BALSSChkvQUhhgEaG5/KO7mOjeXj+vWiFc5Sn9UGIYaJnrp7+nQDFdnLQSkFIY/HA5PJ\\nBLfbjaampqjttScmJnDmzBk0Njam1IGenp6YaTyTySQnOcQjCAK6u7vlUkEhoRHOyMiIfEwURWi1\\nWtpNlcju3ZMWeAJAeXkAlZXq/JYcmdW19OfBgwfLnrtp0yJMpvB2B199VYqFzOxOkRGBgLSVd8jW\\nralNJ0YGodFRCkJqllIQCmW9uVyumKQEn8+Hc+fOweVy4b333kuqPUEQIAgCDAZD1HGWZQFEB5Ol\\nj/M8T2uSyKrcuhW+vWdPZrdtWK3t27fj8ePHcX88Hg+uX7++YhuHDs2irEyqs/bsmQaXL+fOIlav\\nN0/eumHTpiBKS1O7ZkcjodyR0r/O+fPnYTabUV9fD0EQYh4/c+YMuru74XA4cPbs2RXbC23ZrdXG\\nX1jH83zCEUy87b6dTif0en3UOTzPy331er0wGAxRyQtkYxHF3LgetH379oSP+f3+mFmAeAoLgdde\\nm8FHH0mZYm53Sc7s4Do2Fp2UkKrIRIyxsTzaMFDFUgpCgiCgtrZ22edwHIfe3t6k20unzs7OqFFY\\naIQVGXRaW1tjjpGNY2IiXPwzPz+I7dvnASSZdpWDXnhhDkNDJRCEPMzNMbhypRibNq18ntIiRy+r\\nCUKlpSI2bQpiakqDxUUGXm/uL9xdr1Kajquvr8fg4OCyzxkaGlp1qvZa2O12VFZW4tSpU/IxnU4X\\nlSkHrJz0wDBM3B+yPkSOgrZunV73G8NpNIi6NnTpUrE8zaVmaw1CS88bH1/n/9A5LKUgdOzYMbhc\\nLnz00UdxP5hbW1vB8zzMZnPaOpgMnudht9vx5z//ecXn1tTUgOd5TE5OZqFnRG0irwdt2zatXEey\\naP/+OZSXS9eGZmY04PnVL6nIhkAAmJgIj1yqqlYXhCoqIoMQjYTUKqWvB6FrPk1NTWhubgYgJSt0\\ndnbC6XTC5/OB4zicO3cuqfY4jgMATE5Oxr0uFHp8JVarFRcvXow53tHRgTNnzkQdC03R8TyPQ4cO\\nxZwTmfEXiUZDuW92FvLOm1LZ/ykA2xTt02rNzs7i6tWrcR9ber0oLw8wGmfx6adlAIDr1/W4e/c+\\nfD5f3PPz8vKwf/9+aBRaWOTzFcijNZ0usOrtNaqqwheCxsfzsW9fWrpH0izld5nL5cK5c+fw9ddf\\nAwD6+vrQ09ODYDCIM2fO4E7kAowVsCwLjuNiKnPzPA+WZZNKq25ra0NHR0dMEAstgl2aYRdKaEg2\\nwJH14/ZtRGzjDRQX5+bV6vLycpSVlSXMnpuZmcHmzZujznnhhefyhznD6HHjRiDh+ZcuXcLs7Gy8\\nl86K8fFwsbvIQJKqyJHQxEQ+Eny/JApb1UTpmTNn5BEGz/MwGAxyWnWqzGYzBgYGokYlbrdbHmkt\\np6urC1arNSpY9ff3y2WEOjs7YwKZ0+mEyWRKmJFH1q/Iqbh9+4BcLSWWl5eHHTt2pHROQYEUiFyu\\nEhQVFWF8nMMPfhB/SjrdCUOpmpgIB6HVXg8CpMoJhYUi5ucZzM4ymJ3NQ0nuZKlvGCmNhLq6umK2\\nceA4btUBCJCm85auObLb7VGVuENZeV1dXfKx0GJWr9cLt9sNt9sNp9OJnp4eudyPwWCIWkskCALs\\ndntUO2RjWFolYf9+5fqilJdeei6vibp3r0AuDqo2kSOhtQQhhgEqK8Pne73rNwsyl6U0ErJYLNDr\\n9WktfaPT6WCz2WC1WtHY2ChPoy0dwfh8Pvm6jCAIcqr1UpEp5C0tLejt7YXD4cDExAQEQYDD4aDq\\nCRtQZJUEnQ5YMlu1IWi1QdTUzIPnpQ/5b74pVl2F7cVFKVgUfVdlaLVJCSEVFQF5OwivtxCAOteF\\nbWQpBaHjx4/jww8/xKVLl+Je1F+t+vr6Zbd/YFk2anEqy7IIBoNJtU3rgQgQnZq9f//Grar8yivP\\n5SB040YR/uZvniVdnTobBKFQrm6u0wXWvNFg5EjI56MgpEYpBSG73Y66ujqYTCZ0dnaioaEBHMfR\\n9RWiakurJGzkLKkdOxbAsgEIQh7m5xkMDxfhwIE5pbslk0YrkrVMxYVE1gWk6Th1SikIhdKbRVHE\\nyZMn5eOR6cuiKIJhGASoTgZRifFxabdRQCpls5FnYxlGqqLw17+WAgCuX1dXEIpMSkhHYVmDIRzI\\n/P4CKt+jQikFoWT34aE1NURNIkdBdXVY91USVrJ//3N88UUpRBF48KAAfr8GOl1y09uZFhmE1no9\\nCJC+dGi1QUxOaiCKDCYnN/g/vgot+y9itVrx2muvyYkIS7PYCMkFS1OzN7rychG7d89jZET6wL9+\\nvQjf/75y64JCgkFpoWpI5PWctTAYFjE5Kf2/+nwUhNRm2RTtjo4OdHd3xxzv6urCu+++m7FOEZIu\\nMzPA/fvSbYYB9u5Vtj9qcfBgeAruxo1iJJnnk1ETE8DiovSRVFYWTNuW65G7qgoCXRdSm1XV5bhw\\n4QLsdnu6+0JI2t26Fa6SsGMHUFambH/UoqZmXq6gMDWlwcOHyn84P3kSvp2OqbgQgyEchGgkpD6r\\n/hdJVGONELV49OgR/vznAJ4+lRadcNw0rl6dkR/fyMkzeXnAvn1zuHy5GABw61YRdu5UduvVx4/D\\nt9dSrmcpGgmp26orFFLyAVG7q1fv4JtvnmFqagpTU1MoL78bVSNt8+bNKFDTIpks27cvPCU3PFyI\\nxfQNPlYlciSUrutBQPRIyO/PV8XUIwmjsSlZt+7dK0VxcRlKSkqwefMiXnwx8W6lG9GWLYvQ6QLw\\n+6UN7+7eLURtrTKLOUVx6UgofUGoqEhEWVkQz54BgQADnw+oqEhb82SNlKnVTkgWjIyELwDt3Usr\\n5ZdiGGDfvvDv5datIsX6MjkpbbUBAIWFQWi16R2uRI6GxsfT2jRZIwpCZF2anQUePQqXTK6rU8+C\\nTDWJnJIbGSnA/Lwy0+yRoyCDYT7tZZUig9DYWHrbJmuz4nSc0+nEsWPHoo719/dDFMWY45HipXYT\\nki3Xr0vrTvLypGmndH+zXi8MhgCqqhYxNpaPxUUGw8OFK5+UAdHXgxYApLfCt16/CECKbBSE1GXF\\nIOTz+RIuUl1u8SoFIaKkS5fCt/fupVHQcvbtm8fYmPRRcPt2kSJljZaOhID0bvwjZchJ/48UhNRl\\n2SA0ODiYlU643W64XC4YDAbwPA+j0ZhUiaDe3l7wPI/h4WHwPA+LxRJTNXu1bZPcNT4e3sZbo4me\\nciKx9u6dw+efS7Xk7t8vwNat2d9nKDIISSOh9AYhaTpO+rgbH5cSISjBVx2WDUJGozHjHQjtH3Th\\nwgX5WGtrKziOkzeni6e3txccx8lBx+/3w2Qywev14sSJE2tqm+S2yFHQzp2zaVt5v15t2hTE9u0L\\nePSoAMEgcP++LquvPzMjJSYAQF6eCJ0u/euVSkpEFBUFEAjkY34emJoCqPi/OiiemGCz2dDW1hZ1\\nzGKxoL29fdnzeJ6P2oNIp9Ohvb0dFotlzW2T3BUIRAehffvUtWmbWkWOFu/fz+6nc+QoSK+fhyYD\\nn0oMA2i14bTviYn0vwZZHcWDUE9PT8yIy2Qyydt3xyMIArq7u+H3+6OOh6bZRkZGVt02yW3ffgtM\\nT0u3S0oC2LnzubIdyhF1deEP//HxUghC9l47MilBuh6UGVpteIRFQUg9FA1CgiBAEAR5n6IQlmUB\\nhIPJUizLgud5eDyetLdNcpcoAn/9a/j+gQNTGflWvR6VlIjYtSscAL79Nnu/uMiRUEVF5oKQTkcj\\nITVStGJCaMvuRDuz8jyPPQlSdSK3+w5xOp3Q6/XYs2cPeJ5fddtEHZ4/f447d+4s+5ydO3dCp5Ou\\nYdy9G/5Ay88H9u+fAhUFSd7eveHtHa5d06C5OTuvSyOhjU3Rv1AhzWP+zs5OvPfeexlpm2Tf5OQk\\nrl69isrKyriPe71eFBYWykHo88/Dj736KlBSQmuDUsFx88jPl5I4nj5l8PQpsHlzZl/z+fNwBQON\\nBjAY0r9GKISCkDqtm6+JdrsdlZWVOHXq1JraocKs6lJSUoKdO3fGfWwxouLm/fvA7dvSbYYBXn8d\\nuHYtGz1cPwoLRdTUzOPhQ+n+1avA4cOZfc1Hj8K3t2yBHAQzITIxweeTkljysp+NTpZYVRCanJyM\\nOx0WKZtTXTzPw263Z21dE1EXUQT6+8P3X34ZSDB4IivYu3cef/mLdPvKFeDHP87seppQwAOA7Rmu\\nL1tQIKKsTCrfEwwCgkCFTNUgpSDk8XjQ3NwMj8ez7H5CDMMktVcLx3EApKAW79pN6PGVWK1WXLx4\\nMS1tJ/rrVOYXAAAgAElEQVT/ohGSeg0PA6E8E40GePNNJXuT23bvnkdBgTSN6fNJI5Xq6sy9XuRI\\nqLo6nNmYKUuTEygIKS+lIGSxWJKqOpDsBzbLsuA4DjzP49ChQ/JxnufBsmxSo6m2tjZ0dHTEBJp0\\ntE3Ub3ERcDrD941GYElCJElBfj5QXT0p379yJbNBKHIkVF0N3LyZudcCAJ1uQV4YS9eF1CGlIOR0\\nOmE0GtM67WU2mzEwMBAVKNxuN5qTSM3p6uqC1WqNCij9/f1yRYS1tE1yg8tVgtDMcHExjYLSYdcu\\nv5xleO0a8Hd/h4ykuk9NhSslFBQAVVXZCEKL8mvSlg7qkNJbq6amJu0f4DabLaYQqt1uh81mk+8L\\ngoDa2lp0dXXJx0ILTr1eL9xuN9xuN5xOJ3p6euSSPMm0TXLX1FQBXK5wjbGmJqC8XMEOrRObNz9D\\n2XdbMU1NSanvmRA5Ctq2LTOBbilaK6Q+KY2EzGYzHA4Hzp49m7YO6HQ62Gw2WK1WNDY2yvXelk6X\\n+Xw+eZpPEAS0trbGba+2tjbltknuEUXg66+rEAhI74nqasBkUrhT64RGAxw8GMQ330j3r14FMlFq\\ncen1oGygIKQ+KQWhzs5OmEwmvPXWW2hvb0dDQ0PC5yZaJBpPfX19VB24pViWjcrGY1kWwSQ3il+p\\nbZKb7twpxOPHedDrpeytn/40O9+kN4oXXwwHoW+/Bf7hH9Kfzrz0elA2bNoUgEYjZcdNTQHz80Ch\\nMlsoke+kFIT8fj/8fj+GhobQ19eX8HnJZscRshrz8ww++6wMgDS5/9pr0nQOSZ/qahEsK6Uxz84C\\nd+4A+/enr/1gMLvp2SHSgtjw9aCJCXrvKC2lIHTixAnwPA+O49KSHUfIanz1VQmePZOGPaWlQfz4\\nxwp3aB1iGOCllyCvGbp6Nb1B6OlTqVoCIF3H0+vT1/ZKKiooCKlJSkGor68v7dlxhKRifDwP33wT\\nTkb44Q+fobi4SsEerV+RQejGjfROXUUmO+zend0N5iLXBtF1IeWlPItO6c1EKaIIfPJJGUKXA7ds\\nmcG+fZkreLnRbdkipU0DwMKCFIjSJbTzLQDs2pW+dpNBQUhdUgpCra2tcEauDCQki27cKMKjRwUA\\npIvkjY1jtEVzBjEM8Mor4ftDQ+lpVxRjR0LZREFIXVIKQp2dndDr9Xjrrbdw6dIlTE5OJvwhJJ3m\\n54G//rVUvn/o0CxYNv3bQJNor74anirzeKRSPmvl9YbL8xQXZ75S91KRQWh8XAqKRDkpXRMyGAzy\\nFgmUHUey6fLlEszMSN+ZysqCaGiYicquIpmh1QJ1deEK5UNDa6+sHTkVt3Nn9lPry8uBoiJgbk76\\nmZmBvDiXZF9KQejo0aNJPY+y40g6zcwwcLvDyQjf+94Mre3IIqMxHIQuXZJKI60lcERuiJztqThA\\nGtlVVIQXy05MUBBSUsqLVQnJNperBPPz0hcbgyGAgwfnFO7RxrJvn/Qh/eyZVOuN56XR0WqIolT1\\nPCTJQvlp4/P5cOXKFUxPazE6WgwA+PLLSfj9Ur74nj17sGnTpux2aoOjNeZE1Z49y8eVK+FR0Ouv\\nz1BlhCzLy4tOUFjLCo3Hj6VgBkiBLZtrdPR6PfLy8jA6OgpRHMezZ8/w7NkzjIxMYXR0FNevX8c4\\nVTXNupRGQl1dXaioqMCRI0cy1R9Coly/bkDo8uK2bYuoqaGUbCUYjcAXX0i3b96UKimwbOrtRI6C\\namuzuz6osLBQ3qV3ZqYIHo9U7bagoBg7d5Zhfp7eW0pI6TulxWLBiRMnMtUXQqJMTzPg+fAn3Wuv\\nzVBKtkKqqqSgAYSKx66unTt3wrcjag1nHcuGE6cEgfb4VlJKQej48ePw+Xy4dOlSpvpDiGxwsECu\\nkr1lyyJ27qSUbCV973vh2263lDafiunpcGYcw6gnCPn9GiRZD5lkQEpByG6349y5czCZTPjwww/l\\ntUJr5Xa70dXVhd7eXrz//vvo7+9P6XyHwxH3HJ7n0dzcjP7+fgiCIG/lkGr7JPtmZoBLl8KzxQ0N\\nNApS2t694V1rnz+HXGU7Wdevh9fk7Nql7N5PRUUiSkulyLO4yGB6mi40KiXldUIAIIoiTp48KR+P\\nTMkWRTGldUKhwHDhwgX5WGtrq7w76kqcTidOnjwpb3K3VH9/vxx0WJbFhx9+uGzxVaIOX34JLCxI\\n76vKygBqamJHQaIo4smTJ5ibi58tNzU1hYrIlYlkTRhGqlj+pz9J9z//HKivT36Lh2+/Dd9+8cX0\\n9y9VLBuQ157RlJxyUgpCyX54p7JOyGazoa2tLeqYxWJBe3s7zp8/n/A8j8cDm80Gk8kkB8d4/XA6\\nnWhoaIDX66XN7HLE8+fR1xxMpvijoC1btsDr9WJ0dDRuOyUlJZRum2b19cAnn0jbO/h80mgome26\\npqeBkRHpNsMABw9mtJtJYdmgvFZIEPJorZBCUgpCS7fKToeenh689957UcdMJlPCkU1ITU0NPvjg\\nAwBYdrtuURSh1WpT2mSPKGtgIFzmf9OmedTVxf9SU1ZWhjL65MiqoiLg9deBixel+599JpX2WSlt\\n/tKl6Kk4NXw3WJqcQG8lZax5InQt14QEQYAgCDEjGfa73M+R0FcnsmEsLIRTgQHghRcmaF2Qynzv\\ne0DJd0u3vF7A5Vr++aIYvbbIaMxc31JBGXLqsKo/7/fffx91dXXIy8sDy7LIy8tDRUUFfv3rX6fU\\nTmjL7kSjFJ7nV9O9mDZ6e3vR29srJz8Q9RoakpISAGDTpiB276ZiuGpTVAT8zd+E71+8KE3PJXL9\\nurSuCJCC1wsvZLZ/yYoOQvRNRykpTccBQENDA9xuN3Q6HQ4fPgyO48DzPAYHB3HmzBl0d3djYGAg\\nqbZCxVAzJTTCamlpkY+1trbGHCPqEAxGj4IaGxdSTgMm2fH970sjoND23xcuAL/4RezzpD2gwvdN\\nJqCgIHv9XI5OFwDDSH2cnMyTlwOQ7EopCFmtVrjdbpw8eVK+HhPJYrGgq6sL7733Hs6ePZu2Tq6W\\nTqeLWVxrsVhgsVgSBiEqvqqcb78NbxVQWgq8/PLiilM9JLtEUcT169cRCATAcUX4f/9PB0DKmAsE\\n/Ni7NzpT8erVEnzzjXQBqKBAhFY7DkHYIU+5Kyk/XxptT05qIIrA9LRKouMGk9IY1Ol0guO4uAEI\\nkAqc1tTUqHrju5qaGvA8T3seqYwohreSBqRUYKqUrT4LCwu4dOkSRkdHUVJyD5s3j8o12P7v/9Xg\\nyhUBo6Oj39Vi86GvD/Lju3Y9hMdzDU+fPlX6f0MWOSU3OUlBSAkpBSG32w2TybTsc8xmM9xud1Lt\\ncd+V0E0UELg1ltjt6OiIORaaokt0vUkUxbg/JLN4HnjyRLpdUCAFIaJOeXl52LlzJ3bt2om335bq\\nrmm1WpSWsvjqq4N4+HA/BGEvBgYOorSUhVarxe7dZfjJT8pVl6UaGYSmpuhbjxJSCkKhUcRyXC5X\\nUotMASkLLnRNKRLP82BZdk3rekKLYJdm2IWSIdYa4Eh6ff55+HZ9vTQdR9SvsFDEz342JVcfCASA\\ngYESfPxxGWZnpantoiIRf//3U8hP+Qp05tFISHkpBSGz2QyXy5UwC66rqwtutxtmszmlNpcmMrjd\\nbjQ3N6fStRgcx6GzszMmkDmdTphMJtV9I9vIHj2SRkKAtN4kMvOKqJ9eH8CRI35UVS3GPFZaGsTP\\nfjaJykp17rRMIyHlpRSEbDYbampqcObMGezduxfvvvsufv3rX6OtrQ179+6FxWIBy7LLLh6N1+bS\\nRbB2uz2qDUEQUFtbi66uroTtxJsyMxgM8ERs4ygIAux2+7LtkOyLHAW9+OLqtgggytLrgzh61I+3\\n3prC/v1zqKubxw9+8Ay//KWAbdtig5Na0EhIeSkNkFmWhcvlQnt7O7q6ujAcuTkIgJMnT8Jms0Gn\\n0yXdpk6ng81mg9VqRWNjozyNtnQE4/P5ojLX/H4/zp49C57nwfM8LBYLzGYzmpub5cy3lpYW9Pb2\\nwuFwYGJiAoIgwOFwUPkelRBFEV98cRMffcRCFKV/2zfemMA330gfWjOhBUMkq0RRxI0bN1AQJ5c6\\nEAgkvEaalwfs2zePfftyJ69+06Yg8vKkacTnz/ORoAwhySBGXMNV91AA4Dhu3V9jCQVASlJIn/n5\\nefy3//ZXPH26CwBQXT0Ls/lJ1HPKy8tVkc67kYyNjSUsCgsABQUF2LJly6ra5nketbW12LdvX9zH\\nP/30U+Tn52e18OzvfsfC682Dz+fDf/2vRfj+93dl7bXJKharRtoIwYdkzvQ0cP9+BaqqpOtzZjOw\\nY8cOhXtFqqqqlO5CVrFsAF6vVLbH56PKCdm2bBCqq6tLefFmaCuH27dvr6ljZP37+msmatO66mra\\ntI5kH9WQU9ayQWhiYiLphhiGyXgZHrJ+zM0BLlf4C47ROEub1hFFRAYhGgll37JByBeqobICv9+P\\nEydOyNsvnDlzZu09I+ua2w08fy5FHZYNgONy52I2WV9oJKSsNS8f6+rqQnt7OwRBgNFoRE9PT9KL\\nVcn65/F4MDU1FXUsGAT+8IdK+P1SEDp0aJa2a9hAHj9+jOehDaOWmJqagl6vz2p/lo6ERBE0Ks+i\\nVQchj8eDo0ePwu12g2VZdHZ2xhQLJeTKlSsoKChAYUQhuLt3S/HkSTkAoKqqDAcOUF7sRrF161Z4\\nvV6MjY3Ffby4uDjrC8lLS0UUFkpZr/PzDJ49A8rLs9qFDW1VQchqtcp12d5++210dXWltDaIbCzb\\ntm1DSWgXNABffaWFViutQWlsnEVBAU3FbRSlpaUoVVlNJoaRRkOhXeInJigIZVNKQai/vx9Hjx6F\\nIAhyWZympqZM9Y2sQ6OjeXj0SApAGg3w0kvL7IZGSJZETsl5vcDu3Qp2ZoNJaibe7/ejtbUVzc3N\\nEAQBNpsNd+7coQBEUnb5cnhEtHfvHMrLafEvUV5kEEohKZikwYpB6P3334der4fD4YDZbMbw8DBO\\nnz6djb6RdWZ6msGdO0Xy/VdfpVEQUYfIIJTgchXJkBUXq4a2WTh58iSOHj0Kj8cTVRQ0kcOHD6en\\nh2TduHGjGIHv/ta3bVvEli3qrKxMNh6DIfxeHB9XsCMb0LJBKHKfH7vdDrvdnlSjDMMgEKAPGBIm\\nisC1a8Xy/Zdfjp+iS4gSWDYgV4fxeoHFRahy/6P1aNlf87lz51bVaKqlfsj6d/9+ASYnpdnf4mIR\\ntbWUlk3Uo6AAKC+XykaJojQa2rpV4U5tEMsGoWxVPnC73XC5XDAYDOB5HkajMaWkB4fDAb1eH/ec\\ntbZN0iNyFHTgwHP6lklUR6udl7dyGBujIJQtin8UhPYPunDhgnystbUVHMclVXnB6XTi5MmTcsmg\\ndLZN0mNmRgOeDy9WffFFGgUR9dHp5vH0qXSbkhOyR/FiKTabDW1tbVHHLBYL2tvblz3P4/Ggra0N\\nHo8HBoMhrW2T9Lp5swTBoHR7+/aFqIvAhKgFy4YXTVMQyh7Fg1BPTw+MRmPUMZPJFHdkE6mmpgYf\\nfPDBsqWCVts2Sa/bt8NTcTQKImql01EQUoKiQUgQBAiCEDOSCe2kOTIyosq2SfIEoQher1QhoaBA\\nBMdRECLqpNXOy4VLQxlyJPMUDUJerxcAEhYsjEwRV1PbJHl3726Sb+/ZM4+IOqaEqEp+vgitVpo3\\nDgalQEQyT/GRUC62TZIjisC9e+EgtG8fFSol6hZ5vZKm5LJD8WtCasMwTNwfkrqHD4HpaWnoU1Qk\\nYtcuCkJE3SKDUChTjmQWBSGSMVeuhG/X1s7T2iCiehUVQfk2BaHsUDQIcRwHAJicnFz28Wy2LYpi\\n3B+SmmAQuHYtfH/fPkpIIOpXWRkeCYX2FyKZpWgQYlkWHMfFJAnwPA+WZbFnzx5Vtk1WNjICTE9L\\nt0tLA6iuXlC0P4Qkw2AIyFvNe72QKyiQzFF8Os5sNmNgYCDqmNvtRnNzs6rbJsuLnIrjuOfyHzYh\\napafD1RVhe/TaCjzFP9osNls6OnpiTpmt9ths9nk+4IgoLa2Fl1dXQnbiTdllkzbJP0WF4Hr18P3\\n9+6litkkd2zZEr795Ily/dgoFL9UrNPpYLPZYLVa0djYKNd7Wzpd5vP5orLU/H4/zp49C57nwfM8\\nLBYLzGYzmpub0dLSklLbJL3u3AGefxd3ysvnsXlzACp4qxGSlK1bgW++kW7TSCjzGJGuuiclFADp\\n17Wynp5wUkJe3l/xs5+VoqSkZPmTCFHY8PAwDh48CFGswW9/Kx2rrgaWqQxG0kDx6TiyvszNATdv\\nhu/v3h0/O5EQtYrcwmF0FHLxXZIZFIRIWt28Ga65tWVLdGViQnJBaSkQqva1uAhMTCjbn/WOghBJ\\nq8isuJdeUq4fhKwFJSdkDwUhkjYzM8DwcPg+BSGSq5ZOyZHMoSBE0ubbb8Pz5zt3Anq9sv0hZLUi\\ng9CjR8r1YyOgIETShqbiyHpRXR2+/fChVBGeZAYFIZIWfj9w9650m2GAF19Utj+ErIVOB5SVSbfn\\n5oDxcWX7s55RECJpcfVq+DbHAeXlyvWFkLViGGDHjvD9hw+V68t6R0GIpEVohTkAvPyycv0gJF0i\\np+QePFCuH+sdBSGyZqOj4QyiggLg4EFl+0NIOiy9LkQyg4IQWbPIUdD+/UBRkXJ9ISRdIoPQ6Ciw\\nQLuRZAQFIbImwWB0VtwrryjXF0LSqbgYqKyUbgeDlKqdKVTamKzJ4OAYbt2SdqMsKQlienoMly+H\\nH5+jXcFIDnnw4EHUbswLC1o8eSIV3/3oo2f45S93oaCgQKnurUuqCEJutxsulwsGgwE8z8NoNKKp\\nqWnN54W2eLBarTCZTPB6vbDb7Whubk6qfbKyjz/2QRCCKCwsxO7dk/D5ogttVVRUoLi4WKHeEZK8\\nLVu2QBAEjEfkY5eWPsfMjLTL3cDAGP7xHyvAsqxSXVyXFA9CoT1+Lly4IB9rbW0Fx3GoqalZ83n9\\n/f3o7+8HIG35/eGHH1IASpPZWWB4uAQlJUGUlZXhBz8QsWULbdlAclN5eTnKl6wt0Go1uHJFqmbq\\n880iEFCiZ+ub4teEbDYb2traoo5ZLBa0t7ev+TyGYeB0OiEIAnieh9frxZEjR9LX+Q3um2+AQEDa\\nZ6mqahGbNy8q3CNC0kurDUKrlWpRLS5q8OQJs8IZJFWKB6Genh4YjcaoYyaTCQ6HIy3niaIIrVZL\\nu6mmmSgCLlf4/osvPgdDf59kHaquDqfF3bun+EfmuqPob1QQBAiCAIPBEHU8NOc6MjKS1vNI+ty/\\nDzx9Kt3Ozw9i/37aN4isTxSEMkvRa0JerxcAoA3tILUEz/NxRzCpnMfzPARBkM8zGAxoaWlZY8/J\\nwED4Nsc9Q2EhZQyR9SkyCD14oMHiIpCv+NX09UPRX2UoOGTqvNBIKTLotLa2xhwjqREE4Nq18P0D\\nB6YB0L4NZH3SaoPQ6QIYGwMWFhjcuyfVRyTpsa7HljqdDidOnIg6tlLSA8MwcX9I2BdfhPcNqq6e\\nQ0UFTcWR9W3PnvBo6NYtBTuyDq3rIBRPTU0NeJ6PWpBGkjczA7jd4fuvvDKlXGcIyZI9e8JftG7e\\npP2F0knRIMR9N6ZNFBC4BGPeZM/r6OiIeSw0RcfzfNxzRVGM+0Mkf/lLuIbW1q3SSIiQ9W779gXk\\n50vDf58PmJhY4QSSNEWDEMuy4DguJiDwPA+WZROmVSdzXmgx69JMuVBSQ6IARxLz+4Gvvw7ff+MN\\nUFo22RDy84GtW6fl+zQllz6KT8eZzWYMRKZaQSrH09zcvKbzOI5DZ2dnTCBzOp0wmUwJM+tIYh99\\nBCx+tx61upq2bCAby7Zt4SD07bcKdmSdUTwI2Ww29PT0RB2z2+2w2WzyfUEQUFtbi66urpTOMxgM\\n8Hg8Ue3Y7faodkhy7t0DLl0K3zebaRRENpbq6mloNNLU/IMH0rQcWTvFs911Oh1sNhusVisaGxvl\\nabSlIxifzxeVpZbMeS0tLejt7YXD4cDExAQEQYDD4aDqCSlaXAT+/d/D9/ftA5Yp60fIulRUFEBN\\nTVDe4O7qVeBv/1bZPq0HjEhX3ZMSCoAb8dd18SLw6afS7cJC4J//GdDppPtfffUV5ubmsGXLFuU6\\nSEgWXLt2DVu2mNHXJ03lV1UB/+W/0IzAWik+HUfUbXgY+Oyz8P2mpnAAImSj2bs3iNB2QmNjtO13\\nOlAQIgn5/cDvfx9eE8FxQGOjsn0iREmFhcBLL4XvDw4q15f1QvFrQkSdZmeB//2/Aa93Dj6fD6Wl\\nQezdO4ErV4JRz/N6vSgrK1Ool4RkX0MDMDQk3b56FXjrLaCEttFaNQpCJMbcHPCv/ypNN8zMzMDn\\nG8cbb/gxM/McMzPRzy0sLIReT3XjyMZRXQ1s3w48eiQl7QwMSGvmyOpQECJRQiOgyLnuN9/0wWTa\\nrFynCFGZ730P+MMfpNtffgl8//vSVB1JHV0TIjJBAP7n/1wagGaxZ8904pMI2YBeegn4bvsyzMxE\\nb/BIUkNBiAAA7t4F7PbwRnUA8NOfAocOUW04QpbKywN+8IPw/c8+k2YRSOooCG1wogh8/jnw299C\\nvt6TlwccOSJdgCWExFdfHz0a+uQTZfuTq+iaUA4YHx/Hw2UWJGg0Ghw4cAAFBfF3N71+/Trm52P3\\n/Jme1uDjj3W4fz88mV1SEsRbbwkQxQVcvgz4/f4NuUCXkKVEUcTNmzdRXFwsH9u1qwg3bkiR6I9/\\nzIPRWIXNdPk0JRSEcsCDBw8wPDwMNvS1a4mxsTHs2rULujirSEVRhNvtxtatW+VjgQBw44YOly+z\\nWFhYBCBVJa2snMOPfvQUBQWLGB8Pt0HVEAgBqqurMT09jenp8DVSrRbYtCmI0dFiTE9P4w9/qMLx\\n49JsAkkOBaEcwbIsduzYEfcxv9+/7LkMw2DHjh0IBoHbt4swMFACny8PJSXS+gaGAUymWbz22gLy\\n8rYu2xYhG5Ver4+7HOE//sc8dHdrMT09jcePgY8/liqLkORQEFrnAgFgYqIEf/1rKW7eLML0dPRl\\nQIMhgDffnEZ19aJCPSQkt1VUBPD6689w/750/7PPgG3bgBdeULZfuYKCUI4RRelajs+Xh5kZDWZm\\nGNy6VYVgMB95edJC08gfvx8YGqrDtm3RS7qLikQ0NMzi1VdnaeqAkDU6dOg5Pv44PE33hz9IU3UJ\\nJi9IBFUEIbfbDZfLBYPBAJ7nYTQa0ZTEeDaZ81bbtprMzGhw+/YmXL68CY8fF2B2Nrps79hYJWZn\\n8xBxvVS2NKegtDSIl156jkOHnqOoiBIOCEkHhgFee+0enj37G0xMAAsLwP/6X8CvfgXs3Kl079RN\\n8SAU2gfowoUL8rHW1lZwHIeaZTatSea81batBsGgVMF6cBD49NMqPHs2C602/pJsURQxMTGBvARD\\nmtLSORw4MIfa2jns3r1AIx9CMqCoKIBf/AL4l3+RUrbn5qRAdOQIcOCA0r1TL8WDkM1mQ1tbW9Qx\\ni8WC9vZ2nD9/fk3nrbZtJU1PS8URXS6pggEAiGL0yKeoSERFxSLKy4MoLQ1ifl5EIPAIBQVBFBYG\\nv/uv+N1/A9Bq87BlC1U9ICTTKiqAf/onad3ds2fA/Dzwb/8G/PCHwJtvAvmKf+Kqj+Kb2hkMBrjd\\n7qjdTgVBgMFgQDAYXNN5q207nkxuaieKgMcjjXpu3JBGQZGePHmCTZu8MJnKsHv3AvT6AG2kRYjK\\nDA4O4pe//CUAqfjv734X/iIJAJWVwN/9HbB3L22EF0nRuCwIghwUIoXWw4yMjMTdijuZ81iWXVXb\\n2SKKwOPHwPXrwLVrgNcb+5ySEmlVdmHhGAKBpwlTtAkh6lJVBZw8CfT2StPqADA+LlWn374deO01\\n4OBBoKhI2X6qgaJByPvdJ69Wq437OM/zcQNFKuel2nYmBIPA5CQwMSF9Q7p3T/qZTjBDtmuXVDLn\\nhRek4fulSwFMTGSlq4SQNCktlRITBgcBp1O6RgRIW0D8n/8D/PGP0t96TY2U0l1RIe1avNFGSYqP\\nhDJ13mrbXsm//7s0igkGE/83GASeP5cKGob+Gwgs325REfDqq1LwobIfhKwPDCPtRnzggFSjcXBQ\\n2oMIkDLohofDIyVAqrRQVibNgpSWAgUF0jGNRvpvXl50kIoXsJI9lk3/4T8kfowuky3BrPCv9fOf\\nb7CvKYSQpP3qV79SuguqtNy1dKqiTQghRDGKjoQ4jgMATE5Oxr12E3p8NeeFEhBSbTubyYKZzLhL\\nJ+pnelE/0ysX+pkLfQSU6aeiIyGWZcFxHHiejzrO8zxYlk2YOJDMeattmxBCSPYoPh1nNpsxMDAQ\\ndcztdqO5uXnN5622bUIIIVkiKkwQBLG5uTnqWHNzs+jxeOT7Pp9P5DhOtNvtKZ2XzHOUBEBUwT/B\\niqif6UX9TK9c6Gcu9FEUlemn4hUTAGBoaAjd3d1obGwEz/MwmUw4fPiw/LggCOA4Dh0dHTh+/HjS\\n5yX7HKXQPHF6UT/Ti/qZPrnQR0CZfqoiCG1U9MZML+pnelE/0ycX+ghQECKEELLBKJ6YQAghZOOi\\nIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohiqok0IieJ2u+FyuWAwGMDzPIxGI5qampTuVlwOhwN6\\nvV61/QOA3t5e8DyP4eFh8DwPi8WClpYWpbsVw+l0wul0oqKiAsPDwzCZTDhx4kTGX5eCkIoJggCr\\n1YoPPvhA6a7EUOoNm6pc+QAIUfpDled5WK1WXLhwQT7W2toKjuNQU1OjSJ8ScTqdOHnyJBwOh9Jd\\nSai3txccx8nvOb/fD5PJBK/Xq6q/F6fTCYZhcO7cOflYQ0MDBEHA6dOnM/vi2SzPQFJz8uRJ8ejR\\no0p3I0ZfX5/odDqjjplMJrGjo0OhHsXncDhEt9st3xcEQaytrY0q/6QmfX19ol6vF/v7+xXrw8mT\\nJ0wl0CUAAAg5SURBVMXe3t6oY06nU1XvQ57nRYvFItrtdrG2tlbR39dK4v1N2O12kWEYBXqT2Ntv\\nvx3zN93e3i7W1tZm/LXpmpBK8TwPn8+34iZ7Sujs7Iw5Zjab4x5XEs/zqK+vl+/rdDq0t7fDYrEo\\n2KtYHo8HbW1t8Hg8MBgMivalp6cHRqMx6pjJZFLVaKOmpgYffPCBqkYS8QiCgO7ubvj9/qjjoVHu\\nyMiIAr2Kj2EYOJ3OqGOiKEKv12f8tSkIqVR/fz+am5tVWeZDyTdssnLpA0AtH6qCIEAQhJhAGNqb\\nS02/s1zAsix4nofH41G6Kys6f/48zp49G3XM4XDg2LFjGX9tuiakQv39/TCbzTEf9Gpx/vz5mGMO\\nhwPvvvuuAr2JL/ID4NChQ0p3Jyd4vV4AiLsJJCCNLGkfrtSEfqeRnE4n9Hq9qn+XdrsdDQ0NOHXq\\nVMZfi4KQCvE8j6amJlWOguLJ5hs2Fbn6AaAUQRCU7sKG0NnZiffee0/pbsTV29uLvr4+MAyD7u7u\\nrLwmBSGV6e3tVXxaJllKvGHXSs0fAGT9s9vtqKysVN0XtpCWlha0tLTA7/ejoaEBXV1dUddVM4GC\\nkIrk2jdRJd6wa6H2DwCyvvE8D7vdjsHBQaW7siKdTgeLxYKmpqa4MwrpREEoA3ieT/q5FRUV0Ol0\\nAKTMpMhRUKYz41bbz6Uy/YZNRz+z8QGQrt+nUjiOAwBMTk7GvS4UepysjtVqxcWLF5XuRtKampog\\nCAL6+/szum6NglCaeTweWK3WpJ//2muv4dSpU3C73WhoaIh6LJPXhFLtZ2Nj47KL1jL1hk1XPzP9\\nAZDu36cSWJYFx3HgeT4qmYPnebAsS9fR1qCtrQ0dHR0Jkz6UFNpx+qOPPoqbxLM0wzTdKAilWU1N\\nTdzssZW4XC4MDw9HXVtxu93yCvbGxsa0rvRfbT+z/YZdbT8jZeMDIB39VAOz2YyBgYGof1u3243m\\n5mYFe5Xburq6YLVao4J4f3+/aqpQCIKA2tramJFuaGS/dN1YulEQUol4yQjvv/8+BgcHo0ppKE3p\\nN2yq1P4BoDY2mw1Hjx6Nej/a7XbY7XYFe7U8NWeRhhb5er1eeara6/XC4XCophyX0WjEsWPHYn6P\\nNpsN7e3tGR8BUxBSsfHxcdX9gSn9hk1FLnwAxKPkv7lOp4PNZpNH36GRuJr+Xf1+P86ePQue5+V6\\ngGazGc3NzaqqCygIAlpbW+M+Vltbm+XeLO/06dPo6urC8PCwXA/y2LFjOH78eMZfmxHV9ilH4PF4\\nYLPZcP78efj9fpw4cQIWi0VVmWdL37ANDQ1ZecMmK97K/5Da2lrcvn07yz1KLPJD1eFwgOM4VX6o\\nEpIJFIQIIYQohmrHEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohgKQoQQQhRD\\nQYiQLHC73dBoNDFFapdyOp3QaDQJV9oncvToUWg09OdMcg+9awnJAqPRCJZlMTQ0tGyR156eHgDA\\nO++8k/JrZHrrD0IygYIQIVly8uRJiKK4bLXt8+fPg2EYHDlyJIs9I0Q5FIQIyZJjx44BkLYYj8ft\\ndsPv9+Ptt9/OZrcIURQFIUKypL6+HhzHJZySC+0lFQpWgLRFxtGjR1FbWwuNRgODwYDW1lZ4PJ6Y\\n8yPLQDY3N8e9RiQIAjQaDdra2mIe6+jogMlkkl+nra0t7usQkk4UhAjJIovFknBKzm63R03F8TyP\\nuro6/P73v0ddXR0sFgsaGhrgcDhgMplW3EBwuWtESx8zmUywWq3QaDTy69jtdtTW1mJoaGgV/6eE\\nJIeCECFZFJpqWzolF28qzmazgWEY9PX14c9//jN+85vf4MKFC7DZbBAEAU6nMy196ujowNDQEPr7\\n+zEwMCC/jsvlAhB/w0VC0oWCECFZVFNTg/r6+pgpuXhTcW1tbejp6cHhw4ej2gjtK+Xz+dLSp7Nn\\nz6K5uRlGoxGCIMg/NTU1aGpqgtvtxuTkZFpei5ClaGdVQrLsnXfewdDQEOx2O06fPg1A2gV2aVZc\\nfX29HHAEQcDg4CDcbnfCxIbV8vv96Ovrg16vj/s4wzDwer3QarVpfV1CAApChGTdyZMn0d7eju7u\\nbpw+fRo8z8Pj8eDo0aNRzxMEAe3t7fIOu4B07cZkMqUtYYDneQBSIkN7e3vC5yUKUISsFQUhQrJM\\np9PBaDTKU3IOhwOAlLQQqampCUNDQ7BYLLBYLDh06BAAoL+/Xz4nVV6vN+p+aAt0lmVjpv0IyQa6\\nJkSIAkJZcna7Hd3d3WAYJioICIKAoaEhHD16FL/5zW/kAAREp2Knyu12R91nWRY6nS5hkoNer0dd\\nXd2qX4+QlVAQIkQBodpwnZ2dGBoaSrhAdWnyQWiKDogNRpFp1yzLQhRF9Pf3xz03ksVigc/ni6lX\\n19HRAb/fH3dNESHpQtNxhChAp9PBbDbLI5ClU3Esy8qPt7a2oqGhAcPDw+jp6UFjYyMAKYWb4zg0\\nNTUBiA5K77zzDnp7e9Hc3CyXCwqduzSwnTt3Dg6HAw6HA3V1daivrwfP8xgaGoLJZMKpU6cy+asg\\nG51ICFGEw+EQGYYRNRpN3McFQRAtFouo1+tFhmHEhoYGsbe3VxRFUbRYLKJGoxHb2tpEURTFo0eP\\nxrRjt9vF2tpakWEY0WAwiFarVRRFUdTr9fJ5kdrb20WTySQyDCPW1dXJzyckkxhRXMMEMyGEELIG\\ndE2IEEKIYigIEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohgKQoQQQhRDQYgQ\\nQohi/n9FsuBR8keiKwAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 66\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Fitting\\n\",\n \"Adapted from Saullo Castro, StackOverflow\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"What is the best fit to our distribution? \\n\",\n \"\\n\",\n \"For discrete distributions you can use ChiSquare (Observed and Expected) to see which one fits better. For continuous distribution you can take intervals and use ChiSquare (below).\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"size = 30000\\n\",\n \"x = np.linspace(0,15,size)\\n\",\n \"y = [np.random.lognormal(1,0.8) for _ in range(size)]\\n\",\n \"h = plt.hist(y, bins=np.linspace(0,15,50),normed=1,fc='gray', histtype='stepfilled', alpha=0.3)\\n\",\n \"plt.figure(1)\\n\",\n \"ax = plt.subplot(1,1,1)\\n\",\n \"dist_names = ['beta','rayleigh', 'norm','lognorm','expon']\\n\",\n \"\\n\",\n \"\\n\",\n \"for dist_name in dist_names:\\n\",\n \" t = []\\n\",\n \" dist = getattr(scipy.stats, dist_name)\\n\",\n \" param = dist.fit(y)\\n\",\n \" pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1])\\n\",\n \" ax.plot(x, pdf_fitted, label=dist_name,linewidth=3)\\n\",\n \" \\n\",\n \" init = h[1][0]\\n\",\n \" for value in h[1][1:]:\\n\",\n \" t.append(np.mean(pdf_fitted[(x>=init) & (x < value)]))\\n\",\n \" init = value\\n\",\n \"\\n\",\n \" \\n\",\n \" print(dist_name+\\\" Chi stat = \\\", scipy.stats.chisquare(f_obs = size*np.asarray(h[0]), f_exp = size*np.asarray(t)))\\n\",\n \" print(dist_name+\\\" p-val KS = \\\", scipy.stats.kstest(y,dist_name,args=tuple(param))[1])\\n\",\n \" scipy.stats.probplot(y, dist=dist_name,sparams=tuple(param), plot=None)\\n\",\n \" \\n\",\n \"\\n\",\n \"ax.set_xlabel('Value',fontsize=20)\\n\",\n \"ax.set_ylabel('Norm Freq',fontsize=20)\\n\",\n \"plt.xlim((0,15))\\n\",\n \"\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.legend(loc='upper right',fontsize=16,frameon=False)\\n\",\n \"plt.show()\\n\",\n \"\\n\",\n \"fig = plt.figure(2)\\n\",\n \"\\n\",\n \"i = 1\\n\",\n \"for dist_name in dist_names:\\n\",\n \" i += 1\\n\",\n \" t = []\\n\",\n \" dist = getattr(scipy.stats, dist_name)\\n\",\n \" param = dist.fit(y)\\n\",\n \" (osm, osr),(slope, intercept, r) = scipy.stats.probplot(y, dist=dist_name,sparams=tuple(param), plot=None)\\n\",\n \" plt.figure(i)\\n\",\n \" ax = plt.subplot(1,1,1)\\n\",\n \" ax.plot(osm, osr, 'o', osm, slope*osm + intercept)\\n\",\n \" ax.set_xlabel('Quantiles',fontsize=20)\\n\",\n \" ax.set_ylabel('Quantiles Obs',fontsize=20)\\n\",\n \" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \" plt.legend([dist_name])\\n\",\n \"\\n\",\n \" plt.show()\\n\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('beta Chi stat = ', (3859.8620361298576, 0.0))\\n\",\n \"('beta p-val KS = ', 1.6315016931288011e-47)\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"('rayleigh Chi stat = ', (30796.145832321308, 0.0))\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"('rayleigh p-val KS = ', 0.0)\\n\",\n \"('norm Chi stat = ', (52091.666972563071, 0.0))\\n\",\n \"('norm p-val KS = ', 0.0)\\n\",\n \"('lognorm Chi stat = ', (178.17135553030289, 7.4331840876546572e-17))\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"('lognorm p-val KS = ', 0.98944659461564122)\\n\",\n \"('expon Chi stat = ', (13627.328442541573, 0.0))\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"('expon p-val KS = ', 5.139587050053985e-318)\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAaEAAAEsCAYAAABqhgzEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4W8W5/z9H8r5psbMnJJZF2coS20lbCjRN5EAptIXE\\nDgVKgSaW6S0tF5LYob23pffXxnYoSykQy7nQ0hYwlqHLU0piORRK0wvEStghsSVnX21J3led3x+K\\njqx4lS1bTjKf59ETz+jMO6Ml+p6Zeed9JVmWZQQCgUAgiACqSA9AIBAIBOcuQoQEAoFAEDGECAkE\\nAoEgYggREggEAkHEECIkEAgEgoghREggEAgEESMq0gMAsNvt1NbWotfrcTgcZGZmsmzZshHb2Ww2\\nbDYbqamp1NfXk5WVxZo1a8JiWyAQCAQTT8RFyOFwUFRUxLZt25S6vLw8DAYD6enpQ7az2WxIkkRx\\ncbFSl52djdvtZt26deOyLRAIBILJIeLLcSUlJRQUFATVmc1mCgsLh21XVlY2oM5kMgXVj9W2QCAQ\\nCCaHiItQZWUlmZmZQXVZWVlYrdZh20mShM1mC6qTZRmdTjdu2wKBQCCYHKRIhu1xu93o9Xrcbjcp\\nKSlBz6lUKhwOBwsWLBi1vYyMDO655x7Wrl0bdtsCgUAgCD8RnQk1NTUBDBAJPw6HY9S2LBYL2dnZ\\nrF27Nuy2BQKBQDAxRNQxwe12j9tGVVUV1dXVSJJERUVFWG0LBAKBYGKJuHfceFmxYgUrVqzA4/GQ\\nnZ1NeXk5CxcujPSwBAKBQDAKIu6YEC40Gg1ms3ncZ4AkSRryIRAIBILwElERMhgMADQ3Nw/7/GhZ\\ntmwZbreb7du3h902IIRIIBAIwkxERUir1WIwGAY4CTgcDrRa7ZDeaw6HA51Ox+7duwd93u12j9m2\\nLMuDPgQCgUAQfiK+HGcymXj33XeD6ux2Ozk5OUO2cbvdZGRkDJjN+AXHfzZoLLYFAoFAMInIEcbt\\ndss5OTlBdTk5ObLT6VTKLpdLNhgMssViUepKS0tlt9sd1M5kMslFRUUh2R4tgDwF3i6BQCA4q4jo\\nYVU/u3btoqKigkWLFuFwOMjKymLp0qXK8263G4PBQGlpKatXr1bqy8vLqa+vVwKYZmdnBz0/Gtuj\\nxb8fNAXeLoFAIDhrmBIidCYgREggEAjCT8T3hAQCgUBw7iJESCAQCAQRQ4iQQCAQCCKGECGBQCAQ\\nRAwhQgKBQCCIGEKEBAKBQBAxhAgJBAKBIGIIERIIBAJBxBAiJBAIBOPE4XCgUqloaGgYty2r1UpV\\nVdX4B3WGcMYntRMIBIKziYqKCiRJYsWKFZEeyqQgZkIh4vV28emnd/Pee9fR2Xkg0sMRCASCMxoh\\nQiHS1LSNo0efxeXayq5dV0d6OAKBYApRX19Pbm4uer0eo9HIpk2bBlxjsVjIyspCpVJhNBqDlt6y\\nsrKoqqrCarWiVquVerPZTEZGhtJmMLtnKkKEQqSt7UPl766ufXR2HozgaAQCwVQiNzcXlUrFli1b\\nMJlMFBYWUlRUpDxfWlpKQUEBy5cvx2q1kpmZSW5uriJE27dvx2QykZOTQ319vWKzsrKSe+65B6vV\\nqtg9W/aNxJ5QiMTEzAoqHzmyhfT0n0VmMALBOYD0kDThfcg/DU90/JycHCoqKgC4+eabAZ/wFBcX\\nA7Bx40YKCwvZuHGjck1eXh6FhYWsWLECjUaDRqNBkiQl+7PH42HLli2KvZtvvhmbzYbT6QzLmCON\\nmAmNkyNHyvF6eyM9DIFAMAUwm82Dlnfv3o3dbsfj8ZCfnx90TV5eHg6Hg+bmZqXOnzoGYNu2bYoA\\nORwOLBYLDoeDxsbGiXoZk4qYCY2T7u7DNDX9jbS0b0Z6KAKBIMLo9fqgcnp6OgBNTU00NTUBkJGR\\nMaCdJEk0NTWRkpICBOcts9vtrFmzhl27dmEwGMjMzESr1U7US5h0hAiFgcOHNwsREggmiHAtlU0G\\np89OHA4HAAaDQREOu90eJCJ+wfEvv0FgJuR2u8nOzsZsNlNVVaVcYzQaJ+olTDpiOS4MNDVtpaPD\\nEelhCASCCFNWVjagrNPpWLBgAQaDAfB50C1YsEB5bN68mcLCwqB2fmHauXMnACUlJUEidbYsxYEQ\\noTAhc+RIeaQHIRAIIkxNTQ15eXlYrVZyc3MpLy+npKQEAK1Wy/r168nNzaWoqAir1YrZbGbTpk0s\\nX75csSFJEna7nZqaGhYtWgTA6tWrsdlsWK1WMjIy8Hg81NbW4vF4IvI6w4osGBWADMiHDz8rv/46\\n8uuvI//znzrl77femi739XVFepgCgSAC1NfXyyqVSnY6nXJOTo6s0+lko9Eol5eXD7i2tLRUzsjI\\nkCVJGvQam80mZ2RkyCqVSpZlWbZarcr12dnZck1NjWyxWGSdTidv2rRpUl7fRCLJsnzmLLhGEP8a\\n7eHDz/LZZ3cBMH36bbjd/6C7+xAAF19cwfTpeREbo0AgEJxpiOW4cSBJUcyevUYpHz68OYKjEQgE\\ngjMPIULjZNas1YAvvIbb/TptbZ9EdkACgUBwBjElRMhut1NeXk5VVRWbNm2ipqZmVO381/vDYJwe\\nxsLhcJCTk0NNTQ1utxuHw0FRUdGo7Y+G2Ng5pKXdqJQPHfpN2GwLBALB2U7Ezwn5hWHbtm1KXV5e\\nHgaDQTnoNRhVVVUYDAYl3LnH4yErK4umpibWrAkskdXU1Ciio9Vq2bJlC8uWLQvra5gz54ecPPkn\\nAI4e/R0Gwy+JitKEtQ+BQCA4G4n4TKikpISCgoKgOrPZPMBv/nQcDgcLFy5UyhqNhsLCwqCwGZIk\\nYbPZlFlQU1OTEv4inGi1S0hM/DwAXm8bR448G/Y+BAKB4Gwk4iJUWVlJZmZmUF1WVhZWq3XINm63\\nm4qKigE+8v4ZTv/shrIsk5KSEnTQK9xIksScOfcq5UOHnkCW+yasP7fbzdGjRwd9+EODCAQCwZlA\\nRJfj3G43brd7QLwlf0iLhoaGQcVDq9XicDhwOp1cccUVkzHUEZkx4zYcjiJ6e110djpobPw7aWk3\\njNnevn37OHr0qFKWT8rIx2TQwb7Ofaij1MTGxga1kWWZ7u5ucnNzx9yvQCAQTCYRFSH/Xbs/aN/p\\nOByOIWcwg93x22w2JURGfxtut1tpo9frJyRtrlqdyKxZ3+PAgYcB32xoPCJ04MABPB4PSfuSkDfL\\n8EHguZnnzUTzfQ3x34hHUgWi7Xq9Xt5///0x9ykQCASTTcRnQuGkrKyMDRs2KGX/DKu/6OTl5Q2o\\nCxezZ/8HBw48AnhxubbR1vYJiYkXjdleyo4U+kr74PRMEfvBU+Sh8++daDdpUaVEfFVVIBAIxsRZ\\n8+tlsVhIS0tj7dq1Sp1GownylIORnR4kSRr0MRri4xeQlvYNpTwed23vDi99xf0EKBqiLopCSgiM\\npeuNLhrvbMTr9o65H4FAMDXR6XSUl4cWk9Kf1TXUfiKZLvysECF/oqetW7eOeG16evqABFLhpL+D\\nwtGjv6O3N/QAg90nuvH+0guntCXqwiim/X0a016ZxvQ3p5P43UTl2t6Pe2kyNyF3iehLAsHZRCg3\\nwH5ycnKUaN0T2U84iagI+d+soQRhtG9mUVER27dvH1BfWlo6oM6/ROfP83E6siwP+hgtWu1XSUi4\\nBPC7az8z6rZ+6h+oh1PapZqpQr9FT9Rc38qpKklFyoYUNL/QwKnvTc97PXj+2xPSOAUCwdnH1q1b\\nWbp0aaSHERIRFSGtVovBYBggCA6HA61WOyq36oKCAkpLSwc4N/gPwfZ314aAQ0OodwujRZIk5s79\\noVI+ePDxkNJ/t33cxrE/HFPKmv/RoE5TD7guYUUCKRsCr7njzx10vtw5xlELBILxoNPpqKqqorCw\\nEJVKpdxYm81mMjIyUKlUGI1GZdmrsLBwgFcwjLycZrFYyMrKUuydHiVGpVINWMIzm83o9Xql/9LS\\nUrKzs4OukWWZwsJCZaz+vfPJIOLLcSaTiXfffTeozm63k5OTM2Lb8vJyioqKgsSqpqYGp9OJwWCg\\nrKxsgJDZbDaysrKG9MgLBzNm3E50dBoAXV37OHmyaoQWAfb9Yp8vaQQgXSkRd3XckNcmfCeB+JXx\\nSrllYwvqYwMFSyAQTCySJFFWVqYIUUpKCrm5uVRWVnLPPfdgtVoxmUwUFhZSVVXFLbfcgtvtxul0\\nKjb8ZyOHEoDS0lIlRJnVaiUzM5Pc3NwBQtR/ac2f0+jBBx+kpKSEiooKiouLg66RZZmNGzfS0NBA\\neXk569evx2q1UlRUFM63aEgiHranpKSE3NzcIAcCi8WCxWJRym63m6ysLIqKipTr/B9Y/9ztTU1N\\nWK1WNm/2RbPW6/U4nU4l/I/b7cZisYS8cRcqanUCs2f/B/v2PQTAgQO/Ytq0vBHXXbsOdXH8xeNK\\nWXXX8PcIkiSh+bGG7tpu+px9yO0yKZtTkO+VI7rGKxCca8iyTG1tLU6nU7nB9Xg8bNmyRYnScvPN\\nN2Oz2XA6naxYsQKtVovVamXdunUAVFRUDHuDvHHjRgoLC9m4caNiLy8vj8LCwkG9fR0OB1VVVVit\\nVmUMJpMJnU434NrU1FQqKioAWLp0KQ6HA7vdPs53ZXREXIQ0Gg0lJSUUFRWxaNEiZRnt9BmMy+UK\\nyrs+1N1CRkaG8veKFSuUD6GxsRG3243Vap3Q6Al+5sz5Pvv3FyPLXbS0vIvH80+02muGbXP0d0cV\\nZwRpoYTqopEnqlK8hLZUS+MtjdAHMZ/EcOyPx5h5+8xwvAyBIPJMxg3VOPdTJUkiLy8vSED6x8N0\\nOBzYbDYcDoeSmttkMlFRUaGIUFVVVdDNd3/sdjsej4f8/Pygen8W1+bm5gHiZbPZAIJClWk0Gkwm\\nEy6XK2jsK1euDGqr0+nCfoRmKCIuQgALFy4MigN3OlqtNuhwqlarxesdnVvyRJwHGg0xMdOZOfO7\\nHDni+1IdOPDwsCIke2WO/O8RpSzdOPr/eDGXxpB4ZyJt/9sGQP3aetJuTCNKMyU+XoHgnKD/DTD4\\nhGPNmjXs2rULg8FAZmamEg0GYNWqVeTm5tLc3Mw777wDDL0U5983P70P8IlIU1PTABGqr68P6s9P\\nenr6gMP+qampo3iFE0PE94TOZubNu1/5u7Hxr7S1fTrktc1vN9Pp8DkWROmikK4J7e4v6Z4kVDN8\\nH2fPsR4aftYQ+oAFAkFYcLvdZGdns3jxYhwOB3V1dbz00ktBzgj+G+Tq6moqKyuHXYrzO1LZ7XYc\\nDofyqK+vp66ubtDVnYyMjEFnMw6HY0ot1wsRmkASEi4gNTVwePXgwUeGvPbkKyeVv9NuTkOKDe1L\\nokpSkbw+WSkfevIQHY6OkGwIBFMSWZ74R5jZuXMn4Nvz7i8Q/qU4PyaTiRdffJHKysqgDACn4xeh\\n+vp6FixYoDw2b9485OF7vwdc//xpbrc7rPnUwoEQoQlm3rxABIejR5+ju/vYgGtkWQ4SoWk3TRtT\\nX7HXxdJ9QbfPZo+M87+cI7QQCATh4PQzeosWLQJg9erV2Gw2rFYrGRkZeDweamtrlQwAfu82j8cz\\nrFu0Vqtl/fr15ObmUlRUhNVqxWw2s2nTJpYvXz5om8zMTEwmEzk5OWzatAmLxYLJZBpwPCXS5wuF\\nCE0wGs1VJCcvBkCWuzh06KkB17R/3E5HnW/Wok5So102cB13NEiSROutrUr5+PPHadndMiZbAoFg\\n9Jy+vKXRaKisrMRut7N8+XJKSkooLy+nrKyMnTt3Kmd5/MKTmZk54rGR4uJiSkpKsFqt5OXlsX37\\ndiwWC6tXrx6yzbZt28jPz2fjxo1s2rSJBx98EJPJFLQsONjS3GRGUZDkSMvgGYL/Azl8+Fk+++wu\\nAGbM+C4XXfTbEdseP17Jxx/7vmxRUal86Uv7UKsDoXf2P7wfxzrfxuO0ldO4pPIS3nrrLSRJIi0t\\nbdRj9EfRvvj5i2n8i2/ar79Oz2V/v2zUNgQCweSiUqlGFJOx4nA4Bsx8cnJyMBqNPP3002HvbyyI\\nmdAkkJZ2E3FxvrNKvb2NHD4cfKLZvT2weai/buAp6lCQZZnEHyUqn2zTa03U/aWOQ4cOTZrLpUAg\\nGB1+N+qJiFDgdrsxGo3s2rUrqH7nzp2DetlFCiFCk4BKFcW8eeuU8oEDm/B6u+jq6uL44eO43wiI\\ng/dyLydOnKCrq2sM/ahITk7mo7aP6PlKj1Lf8PMG3nnnnQGRKQQCQWTweDxYLBbMZjM5OTkTEsFF\\nq9ViMpnIzc2lpqYGm81GTk4Ozc3NA84bRRIhQpPEzJl3ERPjO0Da3X2Yo0efw+Fw8Gb5m3jbfWee\\nvNO97Dy0kx07dtDc3Ex8fPxwJgfFaDTyuc99jtnrZisBTqNqo5jdMpu+volLOS4QCEaPLMsUFRVh\\nNBopKyubsH4qKyuV8D55eXmoVCrq6+snNGxZqIjTjJOEWh3H3LkP4HD4ZkT79xeTkvIntM6AE0Li\\nVYnMuXBOWPqLMkQR97U4Ol/1nT3qfqYbJicUlEAgGIHTD+BPFBqNhpdeemnC+xkPYiY0icyeXUBU\\nlC9uU2eng87O11B9GPgIYr4QE9b+kgqSlL/73uhDckydA2oCgUAAQoQmlaioJObO/ZFSbmuzIO0J\\nOCfGLAyvCEV/Lpq4nEAU7qgXxcRXIBBMLYQITTJz5tyLWu2bofT11SFd9m8AJK2Eel740zAkfT8w\\nG1L9S0VHvYiiIBAIpg5ChCaZ6Gg9s2ffE6i47Y+ATMxlMRNyOCz6omhir4oFQPJKHHjkQNj7EAgE\\ngrEiRCgCzJ37n0iSTxi46FPIqiX6sugJ6y/xe4GDsUefPUr3ye4J60sgEAhCQYhQBIiNncWsWd8L\\nVNzxHFGXT9x+TcwXY1Bd4PuovR1eDj91eML6EggEglAQIhQh5s5aBz2nhOeyD+Ci2gnrS5Ikor8T\\nmGnt//V+GvY0sH//fuXR0iJizAkEgslHiFCE8DakwavXK+U2fjOh0WyTrk/CO+3UodhGL589/hkf\\nfPABH3zwAW+//TaffPLJhPUtEAgEQyFEKEK0vd8Gf7wNun0zlJ6e3XR1vTVh/cUkxKBdHTgYm/C3\\nBDLSMzAajUyfPn3C+hUIBILhEAdHIkTrB61wYjr87etw0598da1PEBt71Yhecp29nVQfrGbHsR3s\\nce/B0+0hVh3LjPgZXJF2BVfPuporUq8YYCd+ZTwtT7YgN8v07eujs6aT+OWhhwYSCASCcCFmQhGi\\n7f023x/P3wpe3yHVnp736ep6Y8g23X3dbPlkC1/5y1dY93/reMX5Ch+5PuJg20Hqm+vZcWwHT330\\nFN+2fZvrX72eyvpKeryBQKaqRBUJtyQo5fbn2ifmxQkE5xg6nY6qqipKS0sxGo3o9fpBI2OXlpaS\\nkZGBSqUiOzt7QJZTv53CwkJUKhUej0epM5vN6PV6jEYj5eXluN1ucnJyUKlUGI3GKZcxdbSIfEKj\\nZDz5hAZjx9wddB/yuUrHV2+hI+qPAERHX0JqqnXALGZfyz7ufete9nj2hNTP/OT5/CzrZ3xp5pcA\\n6DvWx/Flx6HX93yaNY3GtEbi4+NZvHjxmF6LQDCRSP/4x4T3IS9ZMq72er0eg8FARkYGZrOZ2tpa\\nCgsLWb9+PcXFxQCYzWbKy8spLCxk0aJFvPjii1itVqqrq1m2bJliJzs7G4fDQW5uLhs3bkSn0yFJ\\nkhJxu7i4GJvNhlar5cEHHyQzM5P169fjcDgmJR5duBEiNErCKUI9jT38K+1fAMjRMtN3qjnRtBzw\\npW/Q6Z4iLm6pcr39hJ2CNwto7mlW6uYmzmWFYQWLpi1iWvw0Ovs6qW+u519H/sVrB16jrbctqM9c\\nQy4PZj5IfFQ8rnUuOv/qC2wa/414Ou/vFCIkmLKcCSKk0+lIS0tj7969Sl1eXh5ut5tt27bhdrvR\\n6/UDktdlZ2cDvhw/fjsqlQqn06lEutbpdCxevJitW7cC4HQ6ycjIoLCwkI0bNwJQU1NDTk4Obrd7\\nSkXIHg0h7QkZjcaQT/XLsowkSUEfzunY7XZqa2vR6/U4HA4yMzOVO4PhqKqqwuFwUF9fj8PhwGw2\\ns2LFirDYnkhaPwik4Jbny0TFziAx8Rba2n4HQEvLE8TGLkGSVLzX+B5r3lijiEqMKob7L7+f28+/\\nnShV8Md3gfYCrj/veh7MfJA/7P0DWz7ZQkuPz/W60lHJB00f8MRVTzDzuzMVEer4ewfcAcybhBcu\\nEJylSJLEypUrg+p0Oh0ejwcIiMzpS3T5+fkUFBQE2cnLywsSEkmSyMnJCbILDFp3JhKSCC1cuBCn\\n04ndblfq0tPTaWpqUt5srVZLenp6ULvhhMvhcFBUVMS2bduUury8PAwGwwA7/amqqsJgMCii4/F4\\nyMrKoqmpiTVr1ozL9kTT9mFgliKn+yaiiYlraGurADrp7f2Ezs7XcHmvoODNAkWA0uLSePrqp7k0\\n9dJh7SdGJ2K+2MzN6Tfz89qfU32wGoBP3Z+ycttKnrzqSRZkLaCntgd6gD8DP5iIVyoQjJ/xzlIm\\ni9TU1CGfczgcAANmKXq9L5Nyc3Oz8txUyno6GYTkmLBhwwbsdjuZmZnU1tbi9Xqpr6/H5XKxc+dO\\nFi5ciCRJWK1WamtrlYf/LmAwSkpKgu4EwLd2WlhYOOxYHA4HCxcuVMoajYbCwkLMZvO4bU80HZ8F\\ngojK83wipFankZj4HaW+ueUx/vNfP8TV5QJAF6vj2a8+O6IA9Wda/DR+/eVf8/NFPyda5XMF93R7\\n+N4b36PhhobAhX8BuVOsygoE4ca/22EwGACf2PTHv4dzpi2hhZOQRKi4uBitVktNTU2QAABBwlRU\\nNPrsaf7Mf/3JysrCarUO2cbtdlNRUaHMvvz4l9kaGhrGbHsyaP8s4JXmFyGApKTVSJLvy+jt28/8\\n2A8BiJKi+M1Vv+F8zfkh9yVJEnkZefxh2R9Ii0sDoKuvi7vku+iacSqFuAf6toqsqwLBROHf+6mo\\nqAiqLysrIysrKxJDmjKEJEL+HOUajWbIa0wmEzabbVT23G63smHXH63Wd6jSLyano9VqcTgcOJ3O\\nsNueDNr39BOhuQERUqk0JCUFcr/fMR/iVLD2irVkTRvfF/Xy1Mt5ftnzzE2cC0CPqodnrnhGeb7n\\nxZ4JjdggEJzNjPR/R6vVkp+fj9lspqioCKvVSk5ODrt376akpGRYO2f7/8uQREiWZWVtcyiGE4bT\\nGWkqOlxfTU1NXHHFFUF1NpsNnU7HggULxmV7Iunr6KNr/6kZiAqYFfx8fMKtuHt8S2epsfDDC2Zz\\nx+fuCEvf5yWfx/Om55UZ1d8W/o32GJ8gyg4ZV40rLP0IBOcag+17S5IUVL9582ZKSkqwWq2K51x1\\ndTVLly4d0c5Yx3AmEJJjgslkoqqqipdffpmbb755wPNVVVXY7XZMJtOo7Lnd7lC6H5GysjI2bNgw\\nIbbDRcfeDjh1Y6Oeo4bTMjhsO/gG1Y4e1l3gK1833Q2yB6TweL9Mj5/OM0ue4fbtt7OPfbx2xWvc\\n/I7vszz46EH0Jv0IFgQCwekMdj5n8+bNA+rWrVvHunXrQrJzep1Wq8Xr9QbVZWZm0td3Zi6phzQT\\nKikpQaPRkJuby6pVq9iyZQvbt2+nvLycvLw8cnNzlesmG4vFQlpaGmvXrh2XHf/dy+mPcNF/P0id\\nHpxJtcfbw2PvP8ZrR2HfKQc6iXZaW8vC1j/4HBZ+u+S3zEmcw8tfeBkvvi9006tNQeMTCASCiSYk\\nETIYDNTU1LB06VIqKyvJz8/HZDJhNpuxWq0YDAaqq6sHOC1MNA6HA4vFohzmmsp07Al4xkWlB09E\\n/+T8E/ta9+EFnj8QiOnW1vZH+vrCmwNoVuIsnl3yLO2z2/n35/6t1Nc/Uh/WfgQCgWA4Qg5gmpmZ\\nSXV1NQ6HA7vdjsPhwGAwYDAYBniijUR/t8XB9m78z49EUVER27dvD4vtoTYBwzUbCpoJLQjMhLyy\\nl2c+DTgKXDrzHqKja+jpeQ/ooaXlcbTa8M4wz0s+jyevfpJHP3uUL+/5MgCHf3sY901uorWBdcLP\\nfe5zAxw8BAKBIByMOYBpWloa2dnZmM1mVq5cGbIAgW9t02AwDHAScDgcaLVaFixYMKKNgoICSktL\\nBwhNOGxPBP1FqP9M6B+H/4GzxefUkRSdxLeNt5KcfL/yfEfHn+nu/iDs48lMy2RV3irqZ/hmQLHd\\nsby55U26u7vp7u7m0KFDZ2Q8KoFAcGYQsgjt2rWL7OxstFotGRkZ1Nb6MoIajUYefvjhkAdgMpl4\\n9913g+rsdntQSIqhKC8vp6ioKEhQampqFA+98dieKDrqAstx/WdC/WdBt2TcQlJ0ErGxXyA2NuA5\\n09xcPCHumjcYbqB5ZeAQ3fnV5/NOyzvMmDGDhISEYVoKBALB+AhJhJxOJ1lZWdjtdpYtWxb0g9jY\\n2Mj69etZtGhRSAMoKSmhsrIyqM5isQQ5N7jdbjIyMigvL1fq/AdOm5qasNvt2O12bDYblZWVSkie\\n0dieTHo9vfQ2+cJXq+JUqNJ8b/8e9x52nvBFlYiSovjO5wKRE1JS1uFfNe3pqaWzc2L2va5bcx1t\\nyT5viOnN09n23DY+cYlsqwKBYGIJaU/I/+NdW1tLenp60D6By+WitLSUoqIiNmzYoER3HQmNRkNJ\\nSQlFRUUsWrRIifd2+nKZy+VS9mXcbveguTogOO7SaG1PFh3OwCwobkEcksr3eqocVUp9ztwcZiTM\\nUMpRUekkJt7WL7jpw8TFfRVJig3r2FRxKnS36+h+2pde4hs7vsEPFv2ARy54JKz9CAQCQX9CSuXg\\nz3XRPzS5zWYLOmyVlZVFc3PzsFGzz0TCkcrhxCsn+OjmjwDQf01P9K+iqd9Xz3d2fQd3t+9c05av\\nbOGqWVcFtfN6PRw/vhxZ9oUpSk5eS1LSasJN34k+ji09htTje63fX/19tJdq+d3Xfsf554ceMkgg\\nEAhGIqTlOP+y2HAYDAbq64Wb72B0OjuVv+PS4wD4P9f/KQI0O2E2V868ckA7lUpDcnIgzHVr69P0\\n9TWGfXzCZBzpAAAgAElEQVTqaWoSvh7YA8r9dy7/dv2bP+z5Q9j7EggEAghRhBYuXDhsRGzwOS6M\\nxVPuXGAwEbKdCMTZuyn9JlTS4B9JQsItqNU+t3JZbqO19dcTMsbEOxOVv6/5+BpmuGaw0b6R3Ud3\\nT0h/AsHZgE6nC9qzFoyekERo1apV1NbW8vrrrw96biYvLw+HwzHqsD3nAh6Ph9dff53t27dz8N2D\\nSn1dax3v73kfuzuQm+mbC745pB1JiiYlZb1Sbm+vpKfn07CPN/rCaGK+FAOAWlaz4u0V9Hh7WGVd\\nRWt36witBYJzk3BHVjmXCEmE1q9fz8KFC1m2bJniGFBSUsKqVatITU1Voib4c6oLoLW1FZfLRUJC\\nAqpjgbc7Lj2Oj/s+pkfuAeBi3cWcl3zesLZiY79CTMyXT5W8eDz/MyEu24l3BWZDX7d/ncSORPY0\\n7uE/Xv2PsPclEAjObUI+J1RbW0txcTHvvPMOANXV1VRWVuL1elm/fj11dXVhH+SZTkxMDFqtFvlo\\nQDB0F+n4Z+M/lfJ1864b0Y4kSaSkPEh/l+2Ojr+EfbyxV8cSZfT1kdCdwA32GwB47r3neOGDF8Le\\nn0BwNlJaWkpGRgYqlYrs7GxqamoGXGM2m9Hr9RiNRjZt2kRpaamSewh8y3xVVVWUlpZiNBrR6/WD\\negaP1JffTmFhISqVCo/Ho9T1H0N5eTlut5ucnBxUKhVGo3HQcYeTMUVMWL9+PS6XC6/XS11dHU1N\\nTbhcLjEDGgbvSS+c2hKSUiTa4tt46+hbyvOjESGA6OgMEhPvVMotLZvwelvCOVQkSQraG7qt9jbU\\nfb6Dtd9/9fscbD44VFOBQABK3qC8vDxlhSgnJyfoBz03N5fy8nIefPBBSkpKqKiooLi4OGhZT5Ik\\nNm7cSG1tLRaLhQ0bNmC1WoMSh46mL0mSKCsrU4TInxNuzZo16PV6pZ3ZbMZgMHDttddis9nQarVK\\nYOqJIiQX7fLyclJTUwdN43C2M1YX7UOHDrFr1y7mt86n8ds+j7aoi6N497F3uX+HLyzPxbqLefna\\nl0c9Fq+3jRMnrsfrPQZAQsIdaDQPhvqShkXukjm+9DjeRl+EbcvtFl4w+mZBy9KXse0724Z0ohAI\\nwsk/pH9MeB9L5CXjaq/X6yktLWX16tXK8RWLxcLq1YGjFP4Zzs6dO3E4HBiNRqxWq/J76p+dZGVl\\nKZFedDodaWlpQUde/LmI+h+VGa4vvx2VSoXT6VRCnOl0OhYvXqwEfnY6nWRkZFBYWKic86ypqSEn\\nJwe32z1hKchD+hUxm82sWbNmQgZyttN3MJDrI2pOFG8cfkMpL52zdLAmQ6JSJZKSUqiU29v/SE/P\\nZ+MfZD+kWImEWwPu2vm785FknxDXOGv4zTu/CWt/AsHZgv+H//Rls/z8fOx2nyOSP/t0/xt6jUYz\\nwKlLkiRWrlwZVKfT6ZSb4tH05beTl5cXJCSSJAWFMNPpfDnLBqubSEISodWrV+Nyudi9W7jrhkrv\\noV7lb9UcFW8dCSzFXTPrmpDtxcV9jZiYL54q9eHx/DzsTgoJ305Ajjll80MoTg4stxbaCvn4xMdh\\n7U8gOBvwB00+febgjzDj8Xior69Hq9UOaJuenj7g/3FqauqY+2puDsSEHOmMZ6QIKWyPxWLBaDSS\\nlZVFWVkZ2dnZGAyGCZumnU14jwYyIZ7QnKCxy7c0p4/V83n950O253NS+C9Onvwm0Ks4KSQkDO3m\\nHSpqvZq+ZX1E/d33Nbn29Wt5/obnee/Ye3T2dvKdV77Dv7/3b2LUMWHrUyA4nfEulU02Q6WR8Uej\\n12g0ZGRkDJr92eFwjMrV2y9UI/V1Jvw2hzQT0uv1FBf7Ijnn5+eTmZmJVqtFrVYrD5VKhVqtHtnY\\nOUbfkcBy3IfRHyp/XzXzqjHvrficFO5Qyi0tpXi94U1r3ntTYAbn+puL3176W0V07Efs/PyNn4e1\\nP4HgTMe/H1NRURFUX1ZWRlZWVtA1/Z0H3G53yJ5oo+lrqhPSTGjZsmWjuk4c2hpI39GACP2Lfyl/\\nXz3r6nHZTUr6Ph0df8PrPYbX20hz8ya02l+My2Z/5LkycUvj6Nzuc+2Lfy6ejXdu5IFtDwCw8a2N\\n3PC5G/ji3C8OZ0YgOGfQarXk5+djNpupr68nOzubsrIydu/eTXV1NeBLDmoymcjJyaGkpASNRoPF\\nYhmQbHOkJfbR9DWUnYk4YzgWhhWhoqIiFi9erGyenZ4WQTB6+ovQDnYAICENCFYaKipVEhrNf+Ny\\n+Q6SdnRUER9/I7Gx4ROFjhs7kLb7biyO/O4IV958JVmpWdQ21uKVvdz5pzvZZd5FfHT8CJYEgnOD\\nzZs3k5GRQVlZGaWlpWRlZVFdXR0U7Hnbtm0UFBSwceNGUlNTKSkpYdu2bUo+NBj8hv706Ayj6Wso\\nO6NhoicVw7poq1QqcnNzB0z1ysvLsdvtPP300xM6uKnEuFy0/72LpNwkAOQomWUPLkNWySG7Zg+H\\ny/VDOju3AaBWz2fatD8jSXHjttvR0YHb5YYCYM+pyjvg6LePcte7d9Hp9c2Q1n5pLZuWbxp3fwLB\\nuYLD4Rgw88nJycFoNJ5Tv61j2ozYtm0bFosl3GM5a5FOBu4k2nRtyCqf7i+aHloCwOFISfkxkpQM\\nQF/fPlpbN4fFbnx8PLNmz0JrDnjySH+WuHza5dw1+y6l7lf//hU7DuwIS58CwdmO2+3GaDSya9eu\\noPqdO3dOWS+2iWLMpw2nynrimYCqMfA2H005qvz9helfCFsfavUMkpMfUMqtrVvo6dkzTIvQiLs2\\nDvU8n8OJ7JFpf6md5anLuWaOz71cRuauP99FR0/HcGYEAgG+vRyTyURubi41NTXYbDZycnJobm4m\\nPz8/0sObVMYsQsL5YPRIJwLv1b6Efb46JLKmhdd7JSEhj+hofxqNXjye/0KW+4ZtM1qkKInE7wVC\\n+bT9tg2pV+KRJY+QHOObge1p3MNPtv8kLP0JBGc7lZWVZGZmkpubS15eHiqVivr6+jPCrTqciLgr\\nk0D/5bjjKccBuFB7IZoYTXj7kVRoND8HogHo6XmP9vY/hs1+wk0JqKb5vjLe416iX49mbvJcfrX8\\nV8o1j/7fo/xr/7+GMiEQCE6h0Wh46aWXaGpqoqmpia1bt7JgwYJID2vSESI0CahOBt5mvwgtnr54\\nQvqKjjaSlBSYzjc3P0Jvb0NYbEuxwYFNY1+JRe6TWZ25muUZywHfstydf76T9p72sPQpEAjOboQI\\nTQL9Z0InUk4A4XVKOJ2kJDNRURecKnXidj8YtmW5hFUJSCm+16M+oqblry1IksSWG7eQEutbRqhr\\nquPHNT8OS38CgeDsZsTDqjabjVWrVgXV1dTUIMvygPr+nO7WfS4TJEIanwhdkXbFxPUnxaDVbuTk\\nyTx8IX3stLU9R1LSXSO2HQlVkorE2xJpfdqXZfXkEycx5huZp5nHI8sfYfVffZF8H3/7cW6+6Gau\\nnj++w7gCgeDsZsRzQmPF6/WOfNEZxHjOCe25YA9Sm6/9TWtvInFGIjU3TmyiKICWlt/Q2uqPdh3L\\ntGmvEBVlGLbNaOhr6uP40uNKfqRLX72U1K+lIssy1z9/Pa/VvQaAUW/kvYL3SIhOGMaaQCA4lxl2\\nJuQPEz7R2O12amtr0ev1OBwOMjMzRx0iCMBqtaLT6Qa0cTgcSsKnrKwsmpqasFgs5OTkhGR/PHjb\\nvIoAdau7cSe6uTL1yknpOynJTGdnDb29nwBduN0bSE19HkkaX2w/tV5NQl4C7c/59n32b9xP6tdS\\nkSSJ8hvL+fxTn8fT5aGuqY4Hax7kseseC8OrEQgEZyPDilBmZuZwT4cFh8NBUVER27ZtU+ry8vIw\\nGAykp6eP2N5ms5Gfn4/Vah30+ZqaGiUooFarZcuWLZMmQAC9RwIBQE+knAAJLk+9fFL6lqRotNpi\\nTp5cCfTQ0/MebW3PkpS0esS2I5F0VxJtz/vctD3/9OB+w432K1rmpszl0Wsf5e6/3A0EluWumR96\\nugqBQHD2E3HHhJKSEgoKCoLqzGYzhYWFQ7Tw4XQ6KSgowOl0KrkzTkeSJGw2G263G4fDQVNT06Rn\\nhe09FhChxmRf+obLUi+btP6joy8gKek/lHJLy+NhSYCnnqWm5ys9SrnhoQbl7zuvuJPrz79eKd/1\\n57to7W4dd58CgeDsI+Ii5D+w1Z+srKwhZzZ+0tPT2bx584iZXmVZJiUlJWL+930nA15prkQX0apo\\nLtZdPKljSEpaTXS0P2dRD273WmS5c9x2O3M74dTKnvt1Nw1/buDEiROcPHmSki+XoI3zhfpxuBwU\\n2YrG3Z9AIDj7iKgIud1uJUd6f/wZBxsaGiIwqvDSe6JfPp4kFxdqLyRWHTupY5CkKLTaUsAX0LS3\\ndy/NzQ+P227S+Ul0L+lWynU/qWPHjh3s2LGDD//9IQ8vC/Tx5LtPst25fdx9CgSCs4uIitBI2f/8\\nqWvHg8PhoKqqiqqqKsrLy6mqqhq3zVA4fSZ0aeqlk9q/n6goAxrNBqXc3v4HOjvfGJfNOXPmMKdo\\njrKzGPVhFOmedC688EJUKhW3XHQL37jgG8r1d//5blq6WsbVp0AwlbFYLGRlZaFSqTAajcrvjc1m\\nQ6VSBQUstVqtqFQqGhoacDgcqFQqnE4nubm56PV6jEYjmzYNjExfWlpKRkYGKpWK7OzsAYnwdDod\\nVVVVlJaWYjQa0ev15OXlTewLHwcRnwlNJP4Z1ooVK1ixYgVr1qyhoqJiUoWo70Q/EUpycYnukknr\\n+3Ti4/OIjQ04ZXg8D9LXd3JcNqPmRRH/rUAeodbfBPZ+JEmi7IYy9PG+z2GfZx/rqteNqz+BYKpS\\nWlpKQUEBy5cvx2q1KnHhqqqqMJlMrFy5ktzcXMD327dmzRpKS0uDtgpycnJQqVRs2bIFk8lEYWFh\\nkBD5vX3z8vKwWq0YDAZycnKChEiSJDZu3EhtbS0Wi4UNGzZgtVopKpqaS+LDnhOaaOx2O9nZ2YOe\\nKVKpVNhstqDETENhNBqxWCyjurampgaz2UxdXd2gz48UmDXUc0LvmN6hvcbnyvyTVT/hgfsemPQ9\\nof54vS5OnPgGXq/v0Gxs7FfQ6TaPKyBt74FeTnztBJxaedT/Ts+ncZ9yww03kJCQwAsfvMCtL9+q\\nXL/19q1KmB+BYCT+8Y+JD5a8ZMn4fwZ1Op2SpM5PXl4edruduro6PB4P6enpbNiwgbq6OrZv387e\\nvXsB34qN0WgckL+toKBAiS/n37qwWCysXh3wcPWn+PYfqdHpdKSlpSm2/eNwu91BXshThTHNhJqb\\nm2loaBj2MVVJT0/H4XDQ3Nw8Kf11Hw/smTQnN2NMMU5Kv0OhUunQaouVclfXG7S3/2FcNgfMhp5o\\nhX7/p2/5/C3cfFHAK/F7f/kenk7PuPoUCKYSdrsdj8czIA1DXl6e8nuj0WgoKSmhsLCQLVu2DJqp\\n+vQoNGazGbfbTUNDgyIypy+t5efnY7fblbIkSaxcuTLoGp1ON67XN5GEJEJOpxOj0YhOp8NgMAz5\\nGG1SJn9WwaEE4fSsg6FSWlo6oM6/RDfUfpMsy4M+xkrX8S7lb81MDTHqmDHbChexsV8mMfFOpdzc\\nXEpPz4fjsplUkKTsDXXv7Cb6o2jlOUmSePrrT5OWkAbAweaD3L/1/nH1JxBMJfy/J/69Gv8jLy8P\\nSZKU/W+/N29mZiZXXDEwdNfpv3n+s5IOh0Pp4/Q9dP9vWv/f0dTU1HC8rElhxNhx/TGbzaOKaDDa\\npR2tVovBYMDhcAR9IA6HA61WOy63av8h2Ly8vCA7/i/DeAVuNMiyjNQUeC9mzps54X2OluTk++nq\\nevtUNIUeXK7/JC3tZVSq5DHZi5obRfxN8XRU+pLaJb2QhFwYEO/pidN56vqnyLP67uKe2f0MKy5e\\nEXSeSCAYjHAslU00/t8Tu92uePdCIPmn/zeotLQUrVZLbW0tVVVVrFixIshOfX39gN9Cv33/tkVz\\nc3OQEI3k4DXVCUmEbDYbmZmZYQ3nYzKZePfdd4PeeLvdTk5OzrjsGgwGysrKBgiZzWYjKytrUj6w\\nXk8vqh7fZLMjuoPzZ54/4X2OFkmKQad7lJMnVyDLbfT1HcDjeRCt9tdj3h9KvieZjj91QA9E10Xj\\n+quLxFsCqR9yL8ll1SerqPjIt+a95q9r+PCeD9HFT92lAoFgNPhFqL6+PkhYCgsLcTqdvPTSS8qN\\nsc1mY9u2baxZswaTyYRGE8grVlFREdS+rKwMSZJYsGCBIm4VFRVB5yPLysrIygpvgszJJKTluPT0\\n9HGLw+mUlJQMWBu1WCyUlJQoZbfbTUZGBuXl5UPaGWzJTK/X43Q6g+xYLJZh7YSTnmOBiAJNSU1c\\npLtoUvodLVFRC9BofqGUOzuraW///ZjtqWerSbw1IDoHHzqItzfY6eQ31/+G6YnTATjccpj7tt43\\n5v4EgqmCVqtl/fr15ObmUlRUhNVqxWw2s2nTJpYv9znh5ObmkpOTw9KlSyku9u3Lnh4ZpqqqSvF8\\nM5vNlJeXK7+FWq2W/Px8xUPOarWSk5PD7t27g34vI+hrNiZCEiGTyTRiJINQ8W/WFRUVUVVVxaZN\\nmygqKhowg3G5XEF36B6PR1lu8wcqLSgoCHK/XrFiBXa7XbHp/+AGW4udCNoOtwXGn+g7qDrViI+/\\njoSE25Ryc/MmurvfH7O9pIIkpETf59T5aSfHnjsW9HxaQhqbv75ZKT/33nP85bO/jLk/gWCqUFxc\\nTElJCVarlby8PLZv3654slksFnbv3k1ZWZlyfXl5OeXl5ezevVupq66uxu12k5+fz/bt2yktLWXt\\n2rXK85s3bw7qw+12U11dHeQZPNhKhiRJ4/KAnUhCdtHOysoiLS2NwsJCxTVwMM7U9cmhGEsqh53l\\nO2nN952b2XnJTm6sunHCxzkWZLmbxsZbFecEtXo2aWkvo26PInbPHmLr6og6epToo0eJOnYMVXs7\\nUmcnUmcnqNXIsbF4Y2PxJifTO306h/d9hePv+M5Dxc6JZnHdF1HHBUfuvv3l2/njB77U4zMSZ/DR\\n9z8iNeHM2UwVCMKJ30XbbrdP2k3yVCGkPSGPx4PH42HXrl1UV1cPeZ0kSfT1hSeT55nMYedhUjgl\\nxlP499WXBO8xTh7/JrLURl/fYbq2LeHy+zuRxpAWKom/4uKP9KCn61APh2few7wcF1x1FVx9NVx2\\nGb/+2q+pcdZwtPUox9qOce/f7+X5Fc+H/8UJBIIpTUgitGbNGhwOBwaDISzecWcmo584Nh5oVEQo\\ndtrkxosbLTEOB8mvvUbya68xfVobH/0/X7378k6cd4NhS+g2o+hkPr+njh8BsM/zdWZZbyPKv5Sr\\n06H/2tf4W/Z3WNqxCU88vPDhC6y4aAUrLl4xjGWBQHC2EZIIVVdXh9077mym7UhgTyhpZlIERxKM\\n1N5Oyt/+hvbFF4n76COlftoeOO+PsP/UFtH+2yCuZSZJrVl0n3cevTNm0DtjBt6UFLxxcchxceD1\\nInV2ourqQu12E3X8OFHHjtH33sfE7jxBV+80etGwn29j4JSiuVzw/PNkPg8n1RKvGWR+fzn8Z3QB\\nV8+/WnFcEAjOJc7um/ehCUmEgLB7x53JjPSl6TseWJJMm5020cMZkahjx9A98wyal19G3TIwkKg3\\nNpbpn2TSdOwIrTMaANh7TzOpqWaioz8XUl+HDx+m5+89xJwKe7VffQvq7BPM2PtP4k6dawCI6pO5\\nYS/csBc8fz3J/9kWsfzhV5AmIaGiQDBVMBgM5+wWRkjecXl5edhstokay1lFd183Ma5AdIRIHlSN\\nOnyY6Q89RLrJhP53vwsSIG9MDC05ORz+1a+o27GDQ//7LImXVaBWnweALLfjcv0Arze0MDuzZ8/m\\nvLvOI/rSU5ET+tQc0RfhePNNthYXw0MPwWmOLZouuPb1/UhZWb69o5degp6eQawLBIKzhZBEqKys\\nDJ1Ox7XXXsvu3btpbm4e8nGus6dxD9rWwMnphOkJkz4GVWsraQ8/TPq116J74QVU/X7Qu+fP53hh\\nIfVvvsnhJ56g5etfR070nfFRqTTodL9Bknxj7uvbj9v9ALIc2p2apJJI2RDwkuz8eyfdu3pwL1gA\\n//3f8O67UF8PDz3EiVma4MZvvQWrVoHBAL/+NXR0jO1NEAgEU5qQXLT1ev2o0i+cjd5xARftZ/js\\ns7sBmDnzTi688NlBr3/pw5dIWZhCXK8vkdyMnTNQJU1S5oy+PjRVVaQ9/jhRjY1BT3VcfjmN99xD\\n2zXXgGr48XR0bMXt/pFSTky8k5SU0MPBu+530fmqL5Nr1CVRHPrxIVZ9OzhQY0d3O6uLLubr1fvI\\n/RiiT/fKmzED1q6FggJImjr7awKBYHyEtCfkz4UxEufqBlt/Ptv/GVf3Xg1Ab3SvcoBzoolxOJj5\\n4x8T3y95FvjE5+QPf0j7lVfCKD+f+Phr6e0toLXVd7i0re23qNULSEy8JaQxJT+QTKetE7qh96Ne\\n4t6Kg2+f1ldMAmvXvcIXdF/gAU8P5p2w9v1EklynnDuOHYN166CkBH7yE58YxU5Nj0OBQDB6IppP\\n6Ewi1JnQ6idWc/sPbwegPbWdjH+NLrL4mOnpQf/MM6Q++SSq7kD6iJ5Zszhx//203HDDqMWnP7Ls\\nxeX6EV1d/nNhavT6MmJjrwrJTvOjzbSV+QSlT9fHkgNLUCeqB1xX8lYJRTW+2VZir4oPYu4j3fIS\\nHDwYfGF6Ovzyl5CXN+KMTiAQTF3E/94J4lhDIFyNrJ1YnY8+eJDzbr+daY8+qgiQHB3Nye9/H+er\\nr9Jy441jEiAASVKh1ZYQHe3PCNuHy3UfPT2DJwUciqQ1Saim+b5uapeafRv3DXrd2ivXcs38awBo\\ni/KSo/kzrR/vhrIymD8/cKHTCd/+NixeDP/8Z8ivSyAQTA1CEqHy8nJefvnliRrLWUOvt5fWw4E0\\n11G6kD3hR03Sa68x/1vfIv6995S6js9/ngarlcYf/hA5Pn6Y1qNDpUpAp3sKlcrn4SfLrbhcZvr6\\nGkdo2c9Gkork+wJpIg5sOkD7Z+0DrlOr1Dz3redIifU5NNS76vnP14sgPx8++wwefRRO5U8BoLYW\\nrrkG7rgDjh4d4ysUCASRIiQRMpvNQSHEBYOz37Of5JbAD65KF/4Jp9TdzYyf/Yw5992HutUneHJU\\nFCceeID9L75I9wUXhLU/tXoGev3mfh5zh3C5vo8sd47aRvxN8URd7hNkuVtm7w/2Dhrxd752Pk9d\\n/5RS3rJrC3/69E++PaD77vN51BUVQVxcoNHvfw8XXACPPw69vWN8lQKBYLIJ6ddx9erVuFyuoKiv\\ngoHsbdyLri2QIyfcy3Hqxkbm3nkn2hdfVOq6585l//PP07RmDURNzMwrOvpCtNpH8H9tenrew+V6\\nAFke3Y++pJJI/q9kZMn3frhsLk68dGLQa2+99FZWXRLwoPveX77HAc8BX0GrhY0bYc8e356Qn+Zm\\nn0hlZsLbb4f+AgUCwaQTkghZLBaKi4vJyspiy5YtylkhQTB7m/aibw0sGYVThGI/+YT5K1eS0C+n\\nfPN117HvlVfovOyysPUzFHFxS4LctLu6avB4Hhp1DpPoi6LpuDZw5qfuP+vobR4oYv6U4PNS5gHQ\\n1NHErS/fSq+337Xz5kFFBVRX+2ZBfj74AK68Eh54ANoHLvkJBIKpQ0gipNfrKS4uRpZl8vPzyczM\\nRKvVolarlYdKpUKtHuj1dC4xYCakC48IJdXUcN6ttxJ95IjPrkrF8fXrOfLoo3iTx5aWeywkJt5B\\nYuL3lHJHRyWtrU+Mun1rXisxM33RJLqPdNPws4ZBr9PF63hhxQuoJd/36a39b/HQPx4aeKHJBO+/\\nD8XFkHDqULDXC488ApddBv/4x6jHJhAIJpeQ1m2Gi5zdn3P9nNDepr0YW41KORwzIU1lJTN++lOk\\nU3nm+5KSOPLII75DpxEgOfkBvN6TdHT8GYDW1qdQqdJITLx1xLZygkzGIxl8cusnABz89UFm3DGD\\n5CsGCumXz/syDy15iJ+8/hMAfvHPX7BkwRKWGU77LsbEQGGhL8pCfr5vdgS+/aOvftVXt2kTnGV5\\nrgSCM52QROj0NNyCwdnbtJdb2wI/xl7tGJLy+JFl9GVlTHvsMaWq+7zzOLR5M92n8tpHAklSodH8\\nP7xeF11dbwLQ3Pw/qFR64uOvG6adRE9PD3vm70HKlJDtMvRB7S21qDermT5rOhec5lRRdFURrze8\\nTo2zBhmZ21+5nfcK3hs82vaCBbB1K/z2t3D//eCP8GGxwLZt8Nxzvrh0AoFgSjButy2xJxRMT18P\\nTpcTXWsYHBO8Xqb/4hdBAtR5ySXsf+GFiAqQH0mKRqt9jOho/16UjNu9jq6ut4Zso1KpMBqNvmXb\\ntWrwx3j9DLr/0E1DQ8OANmqVmt/f9HumJUwD4GjrUe545Q688hDiLklw113w8cfwrW8F6hsa4Ctf\\ngQ0boN+BXoFAEDnGJEKbNm3CaDSiVquVPaHU1FQefvjhcI/vjKPB3YC6W01ity8YKNHAWEKdeb3M\\n+NnP0P3hD0pV25e+xP7f/Y6+1KmTplWlSkCvL0OtTj9V00NT0w/o6npnyDY6nY60tDSmZU4j+QeB\\nJTj179VIBwZfyp2VPIvf3/R7pby1fiu/2vGr4Qc3axa8/DK88ILPow5Aln17R1/8ok+kBAJBRAk5\\nbE92djZ2ux2NRkN2djYGgwGHw8HOnTvxeDxkZWXx7rvvTtR4I8Zow/a8uvdV7n7ybl583Oc+HTUz\\nCne5m/PPP3/0nXm9zPjpT9H2W/5s/trXOFpSghwTM0zDyNHbe4jGxtvxen1OE30ksDPhKfZKF3PS\\n66XN66VdlmmTZTpkGQnfHZC6V2a9uY95e3x2DnxeZnfVXGbHx3FebCznxfn+nRkTgyRJFFYXUrqj\\nFKNMLa0AACAASURBVIAoVRRv3vkmX5r3pZEHePAgfPe7sH17oC4uzheL7t57xxxRQiAQjI+Q9oSK\\nioqw2+3k5+ezefPmAc+bzWbKy8vZsGEDGzduDNsgzyTqmurQtwXcs9XTQvQUHESAPN/8Jkd/+UuY\\nQl6HXbLMJz09vN/Tw2c9PdT3xtLh3cT/40ek0Yiadi5p/w/+l0fYy/AJ8R5aB5sLIKoP5n0o8fKT\\nh3jkpuBrktVqLklM5OJ5dzL/kl72Hayht+VTcitzsZvtI2djnTvX56zw+OO+5biuLujshB/9yFf/\\n29/CFJphCgTnCiHNhLKzs3G73dTVDR03LCMjA71ef9bNhkY7E7r31Xux/97OL178BQAJX03g+P3H\\nRzcTkmVm/OxnaCsqlKqpIkAtXi/vdHfz764udp0SnsGOqM6ngce4Dy2+JHgeUriPx2ggfZCrA9z9\\nv/CdUyuPHXFw9zNwdNYIg/L2Qmsdc/Cw6Qt3sFyfRmp09Mgv5sMP4bbbfG7dfubO9S3bXRVaYFaB\\nQDA+QpoJ2e32EdM5mEwmtmzZEtIg7HY7tbW16PV6HA4HmZmZo3YHB7Bareh0ukHbjNd2qNS56oLO\\nCIUyE0p79NFgAfrWtzj6i19ERIBkWebDnh5e7+riX11dfNjTw2gyRJ2Q0nla/Rj39f6QeFrQ0EyZ\\ntA5nUhnq6PNJlCTiJAkV4D316JNl2n7kpeMtN/ENMvGd8MSvYvjjliT29XbT0NmJa7BQPKooSLmQ\\nQ8Ctn3yGxGcsTk7mWr2e6/R6FqekoB5sme3zn4d33vHNiB591Fd38CAsWQI//7kvJJCIzC0QTAoh\\niVB6ejoOh2PYa2pra0lPH/6utz8Oh4OioiK2bdum1OXl5WEwGEZlx2azkZ+fj9VqDbvtseB0OVnU\\nukgpR6WN7i3WPfMMqRaLUvZ84xuTLkC9skxtdze2zk5snZ0c8Q7vWr5AreaymBg+Hx2NMSqKjKgo\\npqtUSNJMurv/l6amu5DlNmLkRi5qy0evf5bo6CFi2sWA+2dxtN/djuSVSKvt5rHXNMwvmo8syxzr\\n7ubDtjY+bGvj/bY23m5u5uPToiHIwNstLbzd0sLP9+1jZkwMK9LSWDltGldrtcGCFBvrO8z61a/C\\nnXdCUxP09cGPfwyvv+6LRTczcinZBYJzhZBu90wmE7W1tUN6wZWXl2O32zGZTKO2WVJSQkFBQVCd\\n2WymsLBw2HZOp5OCggKcTif6/lGVw2B7rMiyzD7PvpBnQikvv8z00lKl3PrVr06qAH3W00NxczNL\\njh/nu01N/L69fYAAScAl0dGsSUykXK/n7RkzeG36dEq1Wu5ITOTK2FhmqNXKsmVMzGXo9RYl4KnX\\n20Rj43fp6flkyHGoL1HTd2tgvtXw3w207GpBkiRmxsZi0uu5b948nrnwQj5avJiTV36J7JOVsO85\\naP4ITks/frS7mycPH+ar773H7B07+MGePdS2tASHGLrxRti9G7785UCdzQZXXOH7VyAQTCgh7Qm5\\n3W6ysrJwOp1kZGRgMpnIyMigrq6Ompoa6uvr0Wq1OJ1ONBrNqGzq9XrsdjsLFiwI6kev1+Md4U7c\\nj9FoxGKxsHTp0rDb9jOaPaGjrUeZ9atZ/PSln7Lk4yUAzHhiBvUL6ofcE0rcvp05996LdCodent2\\nNge3bEHuHyF6AnB5vfylo4M/tbfzyRBRpzWSxFfj4lgSG8sXYmPRjWGJqrvbTlNTPrLsi/QtSRr0\\n+i3ExFw64NqWlhYO7jtI2kNp9H7gG5PaoEbzogYpTmLmzJlMmzYtqE1jeyNZliz2efZBVDLz5t/E\\nksx1bHV5ON7TM+iYLktM5O5Zs7ht+nTS/N6G/7+9Mw9vqkr/+Odma5suWVt26Aa4sxRUUEal1FEc\\ndRRBxHGZUSj6Gx1nFClu4w4FddyBojI6bkCLOjouQMVd1hQVEISm7FuXJG3TNcn9/RGaJm1SWmib\\nFs7nee7T3nPvOXmb5txvzjnveV+XC/75T29g1IYuIUnwxBPeaTsxPScQdAht6ll6vZ6NGzcydepU\\nCgsLWbhwIffffz85OTkUFhYybdq0NgmQ3W73iULT1wGCblxsLR3ZdiiKbEUAASMhVXzo6biILVvo\\nfe+9PgGqOe009s+f36ECtLm+nll2OxcdPszs8vJmAhSvUDBFq2Wx0ch3PXowR6/nsqio4xIgAI1m\\nOEbjYiTJGy5Hlh2Ulf2Zurrmkdi1Wi2x+lhq/lGDHOkVArfVTcnTJezYsYOioqJmdUxaE3mT8ohQ\\nRoCrgr2Fb1H/61PsHzWKL4cM4c7evenRxFnhZ6eTe3bupPePPzJl61bWOBzeyONPPeWNtpBw1NNO\\nlr2pxK+6Cmy24/r7BQJBy7T5yaLX61m4cCEej4edO3eyYsUKdu7cicfjYcGCBa0WIICysjIA4kLE\\n8zrW+lO42g7FLvsugIBoCUpz8Ck11aFD9LnjDhTV3ojSdX37su+11zokEGmdLPNxdTXXl5RwXUkJ\\nH1RX4x8vIAIYHxnJIoOB1QkJPKLTMSoiAnU77Z3RaM7GZPo3kuT9bMhyJWVlf6G2dk3AfUqlkr59\\n+9JvVD/0s/S+csWHCozbg0+5AqT1TuPl8S/7zt/f/D7P/DCXSwwGXhk0iP2jR5M/ZAg39ehBlJ+Y\\n1ssy7x05wqiCAs7buJF3Dh+mLj3dOz3nH5Pvf/+DtDQoKDjRt0IgEDThhOYYkpOTGTduHMnHGULG\\n3hDXqwPoyLZD4ROhY6wJSU4nfe64A/WRIwC4Y2PZn5OD22xuV3ucHg//rqwk48gRZtjt/NRkeuos\\ntZrHdTq+69GD5wwGxkRGouqgTZtq9RmYTG+hUHjFRJarKCubSk3NyqD3R02KIuKSiMaCOeA5FHoK\\n9fbht5OZluk7fyD/AT7e/jEASklirMHAW6efzsHRo1k4aBDnNRH7dRUV/OnXXxmwZg2z6+pwfPEF\\n3Hdf4w1FRTBqFLzxRlv/dIFA0AItum6lpqa2OSK2LMtIksSOHTtOyLDuSJG9CLVLTWzN0QecEpQG\\nJezxu8ntpvd99xH5q3eBXlapOPDii+0aC87m8fC208nbTieOJkt+amB8VBQ3arWc08nRF9TqwRiN\\nb1FW9hc8niNAPTbb39DpHkOrDXT9lyQJ/dN6iq8p9opPOdQ9VIfncg8KdfDvTi9e/iK/lvzKN7u/\\nQUZmyvIprLltDWcmnOm7R6dSMa13b6b17k1BRQUv7t/Pu4cPU3f0fTpUV8cDRUVk79nDX++4g3tG\\nj8Z8yy1QUeHd4HrbbfDDD/Dyy4GZXQUCwXHR4kiotLSUkpKSVh2lpaUUFhZitVopLCzsLPvbHUmS\\ngh6tYZd9F3pn4zSSJl6DpAisG//cc8SsXu07P/zoo1SNakXYmVZQ6naTXV7O2CNHeKWyMkCAzAoF\\n98TE8FVCAtl6facLUANqdSom07solQOOlnhwOB6msjKnWWI8hUGB4TkDHB1Men7xUPRA83WhBjRK\\nDbkTc0nUJwJQWVfJVe9fRWlVadD7h8XGsvi009g7ahRPJiXR2+89cbjdPLVnDwNMJv6Rn8+B0aMb\\nK77+utebLsgalUAgaBstipDNZmvVsWvXrgC37Pvvv79VL94wjRcqEvfxTvN1dNuhKLIHRs9W9whc\\nEI/99FOMr7/uOy+dOhXHdded8Os6PB7+VV5ORnExi51Oqv0e5v2USh6NiyM/IYHpsbGYukDoH5Wq\\nLybTu6hUZ/jKKiqeo6JiDnKTyNia4Rpi/9E4dbb3mb2UfFwSsu346Hg+mvwR0WpvAFmrzcrEZROp\\ndwf3lANI0Gh4cMAAis4/nzcGD2ZQVJTvWpXHw7+cTlKefpoZzz9PScMao8XiXSf69NM2/e0CgSCQ\\nE/Y7XbRoEUlJSeTm5jJ8+HAKCwuZM2dOq+rq9XpfAFR/rFYrer0+wLW6rRxv27IsBz1awu12s2Pn\\nDnbbdwfEjXPFujh06BAAmu3b6fngg75rlRdfTMnf/36cf93RNjwe5ldUMO7IERY6nVT52XmaSsWz\\nej2fxcczOTqaiC4WoFOpNGEyvYVGc76vzOl8E7v9PmS5NuDe6D9HQ+NtbL1pK3vW7OHQoUO+o84v\\nNcM5Pc4JiLi9etdq/vb53475f9QoFPy5Vy+2nnsuS844gyHR0b5rNbLMM0OGkLx8OY/9+c+Ua7Ve\\nj7k//AEefdSbyVUgELSZ4xahoqIiRowYQWamdzF44cKFbNiwoc2RCMaNG9cszpzFYiEjI+N4TeuU\\ntv2prKxkxQ8rqPfUB4yEnBonR44coYdGQ5+77mr0hBswgIPz5h333pM6WeZNp5OM4mJeqKykwu/h\\nOlil4hWDgQ/MZq6IiuowR4P2QKGIwWhcSGRk4/+jpuZTSktvxe0u85VJComYJ2PwmL0Peo/Dw47r\\nd7Duq3WsW7eO1atXs3fv3oC2rzn9Gh6/+HHf+fwN83n2x2OkfjiKUpKYlJBAwYgRfHL22aTFNObi\\nqFAqefTmm0l+/32emTSJGpUKHnvMK0ZlZS20KhAIgnFcT8GsrCxSUlKwWCxcd911FBUVMXXq1OMy\\nIDs7u1nG1pycHLKzs33ndrudlJQUFi1aFLKdYN9yW9N2e2HDu4/E3zNOl6gjOTGR059+Gs0er3eC\\nR6tl/8svH5crtizLrKyp4criYmaXl2Pz+/adqFTynF7PB2Yz6ZGR3SbFuiRFoNc/j1bbmIm2vr6A\\n0tLrcbkaR7GxfWOJnx/vS4Kn3KMk/o14Bg0chF6vD/r/f+h3DzH5rMm+8xkrZ7BsS+uzA0uSxBUm\\nE+vT0sg780xO12p910pjY5lxxx2c9tZbLLnkEuTPPoMRI4Qbt0DQRtokQvn5+RiNRubOnUtycjIr\\nV65k6dKlbdob1BSdTkd2djZZWVnk5eUxb948srKymk2X2Wy2gAerw+EgKyuLSZMmYbVayczMZPr0\\n6eTl5bW57faguL4YCNwjpDApML3yCjFff+0rO/j009S1JbfQUTbX13NTWRl32WzsdjeGp+mjVPK0\\nTscn8fGMj4pC0U3Exx9JUhIX9zBxcQ/gDRAEbvdeSkpuCEiOpzlbg+7xxs9a7cpaKudXttCuxOKr\\nFzOmf2M675s+uInv93zfRvskro2P55eRI3nztNNI9POK292zJ5MfeYQLXnqJtZGRMHo0vPlmm9oX\\nCE5lWhW2x+FwMHXqVF+Q0OzsbGbMmNHhxnUlWgrb43A4uOPdO3jvyHs8lPsQ6Zu9UboTppZw+muT\\nkI6+xaVTp1Jy771tet2DbjfPV1Tw0dGpvAbiJIk7Y2KYEh2NphsKTyhqavKPrgs1/L1qdLpH0Won\\n+O4pn12O802n77z24VpSbk4hNTU1aJtl1WWMfn0020u3A2CMMvLjbT8yyNRynqNQ1Hk85Bw4wKO7\\ndlHaJOLEDfn5zMnJof+ECd4I3RERIVoRCATQipHQvHnzMBgM5ObmMm7cOAoLC085AWoNpS6vG7D/\\nSCh+6QKfADnPO4+Se+5pdXt1ssyCykouP3IkQIBUwM1aLV8kJHBrTMxJJUAAkZHpmEz/QaFoiBFX\\nj8PxIA7HU8iy18MtdkYsmlGN7tSaeRrqttQFac2LMcrIpzd+SrzW22ZZdRmXv3M5xc7i47JRo1Dw\\n17592XneedzXr19AZIn30tMZ/NZb/LO6mur0dG+KCIFAEJIWR0Kpqak+77Jp06YxceLEVq81NA0m\\n2t051kgo/fV0NlZsZPEri0ksTgRgBLcTQyEuo5FdH36IO+EY2T+P8m1tLU86HAHTbgDpERHcFxdH\\nkqpNGTi6JW73AcrKpuNy/eYr02jORa9/HqXSiMfmoWRiCe593vdIEa/g3PXnEjkg9AbSdfvXcfG/\\nL6ba5RX1Eb1H8OXNXxIbcWKhkgqrq5lZWEheSaDreOLBg7z41ltcOWMGnGT9QSBoL1oUIcVxem9J\\nkoTb3ZoUaN2HY4nQ0AVD2VWziw+zP0RX7V23GMW1RGBj76JFVI0ZE7LtBg643cwuL2dlTU1A+WCV\\nillxcZx/ik3teDxOHI5Z1NQ05oNSKntjMLyMWn0G9YX1lN5Qilzu/Qhrz9Ay7PthqPWhs6t+tO0j\\nrllyDTLeOmOTxvK/Kf8jUnXi0Q++tdv5+86dbKwMXKf6w48/8oJWS/Ldd3sjcwsEAh8tfqVu7X6f\\npnQXz6z2pLS+FKVb6RMg8KDGQenUqccUoDpZZrHTyfyKCvzlJ1aS+FtsLJO12i7tat1RKBTR6PUv\\n4HQupKLiBUDG7T5ASckU9PoniEq5EsPLBkr/UorkkqjaWsWWa7dwzufnoNAE/wJ19WlXM/+K+Uz/\\nnzfP1JdFX3JD3g0sm7gMleLERphj9HrWpqXx+sGDzPrtNxoctj8ZNYqVdXXMmjuX+zMzidLrW2xH\\nIDiVaFM+oVOZlkZCh0oP0evlXiQdMfHGq17nDTU2hg99nD3/+Q+oQ38z/6G2lseCTL39MSqK+2Jj\\nMXeBCAddgZqar446LDSOMrTaycTFzWLPG4fQzGtcI+rxpx6c9uZpzUIm+TP729k88OUDvvNbh97K\\n61e9jkJqn7xBpfX1PLB5M4tsNmS/GYWk4mJeTk1l/LBh7fI6AkF3R2TqagcOVh4EYM4Kv5A9inIO\\nPPtsSAGyeTxk2e38pawsQIBOU6l412Rijl4vBMiPyMiLMZuXolQ2hluqqnqfkpLJeMbuJe7vjSk7\\nDr99mB1372gxQkLWhVncN6oxSva/N/2bGStmHDOqQmsxqdUsHDaMNUOGkOaXi6goPp4rHA4mf/45\\nh2prW2hBIDg1ECLUDuyr2Mf1v0D6zkYRklNNuPr0aXavLMv8r7qaK4qL+dDP6y1WkngoLo5cs5nh\\nYQou2tVRqZIxm5cSGTneV+Zy/UpExF2obv2OXtN6+coPvHKAoodCBxiVJIm5GXO5bdhtvrLn1jzH\\nY18/1q42n2sysfaPf2S+3Y6hosJXviQyktO//prX9u3DIyYjBKcwQoTaAYd1C/P/B/U0xo2TBzXP\\nDXTQ7eYOm4177XbK/KIdjI+M5LP4eP4UHX1Krv20BYUiBr3+WeLi/ok3MQVIUjVlZX9D+seLmKc0\\njoj2PL2HPXP3hGjJK0QL/7CQCac37kF67OvHeOLrJ9rVZqUkMf2Pf2R7//7c/MMPvnK7RsPUnTu5\\neN06tjmdLbQgEJy8CBE6UTweRj2ag6EG6vBLZmdqnErzyDLvOJ1cUVzMV35TMD0VCl41GHjOYBBT\\nb21AkiSio2/AbH4fpbKfr/zAwVep/tutxN3SmLrBOtPK/gX7Q7alVCh559p3uCz1Ml/ZI189wlPf\\nPNXudscPGcKbd97JytxcUvY32vRtdTVD1q/nsV27qBWBUAWnGEKETpSXXyalwDvtU+snQgqz963d\\nWV/PjaWlPFFeHhDleopWyyfx8YwVidGOG7X6TMzm5bjdF/jKnFW/4LhlMu67loDkfaDvuGMH++eH\\nFqIIVQQfXP8Bl6Zc6it7aPVDzPnu+LxDW0SvZ9yLL/LL3r3MeucdVEcjLtQBj+7axdANG/g2DFmB\\nBYJwIUToRLDbYeZM3+mm+EYR8pgkXqmo4JqSEgr80monK5W8azLxiE5HzHHuwxI0olDE0qtXDlrt\\nA4BX0CXJhfLaBTD/fjB7oyLsuHMH+14KHb0gUhXJh9d/yLjkxrxYs/JnMff7uR1hNFFZWTw9cSIb\\nZ87kvK1bfZe2VVXxu02bmLZ9O/b60DmQBIKTBfEUPBG+/RaObizd1AP2xjSK0Gx1JS9VVtLwGFED\\nd8bE8GF8vHA8aGeUSiU63c3Exy8PSJTH4I3I/74NLvkSgJ1372Tn7J1UVFRQUVGBs8k6TJQ6io8m\\nf8TYpMboBjNXzeTJb55sN6+5AC69lHOWL+f7xYt56YUXiPWzZ9HBg5yxfj3Li48vtJBA0F0QInQi\\nlHjXHmpU8KdrQVdl8l3aHNc4tz9ErSbPbObu2NiTLtZbV8LrPfc+0dHTaIjGLUVXwCNPwKP/BEMZ\\n+x7Yxzd3fMMXX3zBJ598Qk2T6BRatZaPb/iYixMv9pU9vPphZq6a2TFCNGAAym+/5a9mM1tvvZU/\\nfvut79LBujombNnCNZs3s1+4cwtOUoQItQOPXAxbTj8PQ21/X5nNAFpJ4oG4ON41mRjUwoZVQfsh\\nSRri4v6ByfQflMrejRcu+gYW/xnGrST6HS0DPhuAAgWeII4AWrWWT274JGBqbt4P87jzf3fikTvA\\ncSAyEhYtou/s2Xzw1FPkPfIIPUsbnSs+LCnhjHXrWLB/v3DnFpx0CBFqK00eWnvHjOKZ2x5CccYc\\ndOWNHm5n9tTwsdnMzdHRKMXop9PRaEZgNn9EVNTExkJdOTz4NDz9AM7/7iL21Vg89cFFJVoTzcc3\\nfMzVg6/2lS3YuICbP7iZencHrdXcfjt89x3X7t7Nr7fcwrSPP/ZdKne7uWPHDi7atIlfhTu34CRC\\nhO1pJb6wPYuvZ3viEgCcv/ThT2e9iV1SYiiD5Ue3m7h0En3X9DglY+h1RWprv8fheBi3+0BjYWU0\\n5Ewjru5GhuQNRRkd3EW+3l3PX/77F97++W1f2VWDr+L9Ce8TpY7qGINLSmDKFFi5km/OOYep997L\\nb/0bR9kaSeLBAQPI6t8fjXBuEXRzxCe4rSxvzNz6zdlnY5e8Dy9DY2QWIs1KIUBdiIiICzCbP0ar\\nvbGxMMYJ//gX5Vf/iY03vU/d4eD5iNRKNW/+8U3uGHGHr+y/2//L2LfGUlJVErTOCWM2w2efwYMP\\n8ruff+an22/nobfeanTnlmX+uWsXwzds4EeHo2NsEAg6CSFCbWTlkCHNC2sOYdi4yHeqMIm3tauh\\nUESj0z2MyfQ2SuWAxgunb6Pq/25mzQs3cvDHnVRWVlJZWRngsKCQFLwy/hWyLsjyla3Zt4bRr4+m\\nsKywYwxWKuHJJ+Gjj4iMiuKJxYuxTJsW4M69paqKCwoK+Otvv1HeJMOrQNBdEE/LNvJeerrvdwkY\\n6dkN6/+M4dARX3nDRlVB10OjGUF8/EfExNyJ7D6aukHpwXNpLtsOnss3r/+Tzz//jM8++yygniRJ\\nzB43m5cufwnpqOfdjrIdjHp9FOv2r+s4g6+6CjZsgGHDOLuoiO/vuosXXnqJ6KMiKQOvHDjAmevX\\n83FJB43MBIIORDwtT4ArjCbOrvgGPDUYnH7REsRIqEsjSZHExt5NQs9PUDlHNZYbbWiHPEeCYjZu\\n16+UlJQ0OyYnT+adq9/xJcErrirm4n9fzEfbPuo4gwcOhB9/hL/9DaXHw93Ll7P1llsYv2aN75Z9\\ntbVctXkz12/ZIqJzC7oV4mnZRlSuxrQL8Rq1L42DsbIxeKl/3DhB10WlSsSc8gax1c9AWWPAWY+x\\nAJPpISzrJvH99//lu+++8x1fffUVCaUJfHnzl5iivPvCql3VXLPkGp7+9umO2UsEEBEBzz8PH38M\\nJhP9jxzhk1mzeO/xx4n3y+S6tLiY09ev542DBzvOFoGgHREi1EYeiwxMsX2o8hBA4EhITMd1GyRJ\\nIib5D5h7fIriq+vB5f0CISlkNNrV6OL+St++X3LaaYmcfvrpDBgwALfbzah+o/jhth9INnjzG8nI\\nPPjlg9yQdwNV9VUdZ/Af/gA//QQXXYQETF69ml9vvJFbv/zSd4vd5eK27dtJ/+kndlR1oC0CQTvQ\\nJZ6WFouFRYsWkZeXx7x588jPz2+XelarlYyMDPLz87Hb7VitVrKyslrdfjB6paQGnDeMhAyVYjqu\\nO6M2x5Ew4VEil74P349uvCBVU1n5EkeOXE5V1XJkuXEkPMg0iLW3rw2IrrBkyxLGLB7DXsfejjO2\\nTx/Iz4fHHweFAlN5OYufeIKV995Lsl/OotV2O+ds2MCc3bupF9G5BV2UsO8TslqtTJ8+nRUrVvjK\\nJk2aRHZ2NklJSSdUz2q1kpraKBp6vZ7XXnuNa6+9ts12Bkvv3aPHLZy17D94ZA85C3IYeGggAKZl\\nJjRni/hw3ZWqD6pwfPglTH0VUqwB1yQpibq6Gxk37nHfZ6LeXc89n9/Dqxte9d3XI7oHyyYuY8yA\\nMR1r7HffefcU7fWKXlVEBI/dfTfPjh+Pf8L4IdHRLBo8mJFxccHbEQjCRNi/smdnZzN9+vSAsszM\\nTGb6Rac+3nqSJLFq1SrfKKisrOy4BCgUNa4aXxgXo7NxTUhhDPvbKjgBtNdoMT/wexRPvg7P3Atl\\nfhlz5SLU6iexWM6lrGwlsiyjVqp55YpXWHDFAlQKr8fdYedhLnnzEuZ+P7djQv00cOGF3um5G27w\\n2l5bS/a8eayfNo3hfnuIfnI6Od9i4R87d+J0u0O1JhB0OmEfCRmNRiwWC4mJib4yu92O0WgMGter\\nLfWKioqwWq2k+7lVHy/BRkLquCu58OOPkTwSK59cidLjXU/o+VNPpAixWbW746nw4HjAQc13ZTBx\\nGUxaCtGBayx6/cUkJT2JTufNafTN7m+YsHRCwEbWKwddyb//+G+MUUY6lPffhzvu8KYYAVwKBS/8\\n9a88fM01VPvdlhgZyYJBg/i9sYPtEQhaQVi/stvtdp9w+KPX6wHYtWtXu9Zrb6pd3q4dVx3nEyAp\\nThICdJKgiFWgf1GP7sFeSMtuhSnvwvvXQ23jVKvd/hUFBReyadNYbLbVjOk/Bss0C6P7Na4rffzb\\nxwxfOLxj9xMBTJ4MmzfDpd7kfCqPh3tffJHNt9xChl+ivF01NVz288/8aetWiuuCR4oQCDqLsIpQ\\nWVkZAHEh5qmtVmvQ8rbUs1qt5OXlkZeX53NiaC+q670iFOCUIDzjTiokSUJ7nRbzB2bUA8ywcDr8\\n6W3475Xgbvxf2+2r+emnsVgsF6B1bWH1zau5d9S9vuu7Hbu58I0LeeaHZzp2eq5PH/j8c3j5ZYjy\\nxrZL3rOHL665hjffew+jXzipd44c4fR16/jPoUPCnVsQNsI+EurIeg0jpQkTJjBhwgSmTp3KKdIS\\nBgAAIABJREFUkiVL2k2IGkZCAXuEzGKP0MmIKlGF6V0TUVOjkMvM8K9/wM1vwWeXIfuJUUXFj/zy\\ny+X88tMFzBx2IR9MykMXoQOg3lPPjJUzSH8rvWO95yQJ/u//oKAARo70FgE35+SwbcIEbjx0yHdr\\nqcvFzdu2cdnPP1NUXR2iQYGg4zipv7brdDqmTp0aUNYap4fW0rAfxF+ExEjo5EVSS+jv1WNeYkY1\\nSAUH+sDcmUh/ehs+uRIawgABFRUb2LLlGnqVz+LrCfcxus9w37Wvdn3F2fPP5v3N73eswYMHww8/\\nwJw53s2uQHxpKW/fcAOfvvoqA/xGRStsNs5av56nd++mVrhzCzqRU+6JmZSUhNVqpby8POh1SZKC\\nHsFomI4TInRqoTlbgznXTMzdMd687Yd6wbP/gMnvwufXIsmRvnurq3/Dtv9hsk/bzRu/G4NJ4/0s\\nOWod3JB3Azcuv5HSqtIQr9QOqFQwc6bXg+6CC3zFly9bxubx47nHavU9BKo8Hh4sKuLMdev4RMSh\\nE3QSYX1iJid7d5uHEoSG68dbb+7cuc2uNUzRhVpvagvVLm8QSTEdd+ohaSRi74zFvNyMesjRrLkl\\n8ZB9F/KEd3CtmojHpfXd73KVkiR9S+4oFY+fFUNStLf83V/e5YxXz2DZlmUduy4zeDB88w28+CJE\\ne188pqqKf912G2see4whfm7bhTU1XLl5M1f8/LOIuCDocMIqQnq9nuTk5GaCYLVa0ev1Ae7Xba3X\\nEB2hqadcg1NDKIGTZTnoEYyaICIkRkKnFuqBakzvmdA9oUPSHx0x24yonroTxYRlqNf8HQV9/GrU\\nM8ZUyRsj4IWhMDYebFVHmJQ7iWuXXsuBigNBX6ddUCjgrru8HnTjGlOXj/zqKzZceikv5+ej90uS\\n92lZGWetX88sq5VKkSpC0EGE/Yk5btw41q9fH1BmsVjIyMg4oXrJycksXLiwmZCtWrWKtLS0kJ51\\nbaHmqGNCQNy4+LC/pYJORlJIaCdqSfg8Ae0UbWOvKtdSP+sqPFe/iWv1Q6hV5wTUO0cHD58BS86H\\n25Pgx6IPOeOVM3jN8lrHetAlJsKKFbB4sTeBHl537v978kl+mzSJqYcO0TABXSfLzNmzh9PWreO9\\nw4eFF52g3Qn7EzM7O5tly5YFlOXk5JCdne07t9vtpKSksGjRojbVMxqNFBUVBbSTk5MT0M6JUOv2\\n7rEQ03ECAIVege4RHeZcM+rh6sYL5UpUj6fjvu4l+u37gHjzRCSp0YnBoIEb+8M758H9Ax0s/mEq\\nY94YxcYDGzvOWEmCW2+Fbdtg2jRfcfzhw+TccAPrnn6a8/0EZ39dHVN+/ZULCgr4QWRzFbQjYY+Y\\nAFBQUMCSJUsYOXIkVquVtLQ0xo4d67tut9tJTk5m7ty53H777a2uB5CXl4fVaqW0tBS73U5WVlbI\\nab6WCBYx4bNDMHc7fDjvQ3ROrxtuwrcJKOOFEJ3qyLJMbX4t5c+W4y4KDJMTmRxJn0cicY35L4cO\\nL6K2dl+z+mV1sOowxJgmMvPi+Zi0po41eM0ab7SFTZt8RR5J4j/338/M8eM53MRj7rr4eOYkJ5Ny\\ndC+SQHC8dAkR6g6EEqFntypZ9cSqozdBz196IqlExASBF9klU51Xjf15O5It8HMRmRhJvwd6o/7D\\nBg4eWYDNtjJoGzsqlcSaJvHHtBeJ1JiD3tMuuFzw6qvw0EPgF43bERfHE88+y0sDB1Ln97hQSxL/\\n16cPDw0YgEmtDtaiQHBMwj4d190JWA8yKoQACQKQVBLa67XUvF5DzY01yDGND/GaXTXsmGZlyxAD\\n0Z+/StqZW+jXbyYKVUJAGwNj3PSsfY9vvktg5ZoLOHIkD7e7pv2NVang7rth+3bvVN1RdOXlPDN1\\nKr/ecQfX+20Ur5dlnt+3j9S1a3l2715qRGBUwXEgROgEESF7BK2h/6D+mO8xE/NxDJr/04Cu8ZpU\\nLLEvax+bBpZCzlRGDijkrLM+oT5yNPV+s2AahYy65ge2br2Ob7838+uvt1JW9gUeTzt7rvXq5XVa\\n2LABxjSmokj+9Vfev+YafszO5oL6el+53eXivsJCBq5bx6IDB0TuIkGbENNxrSTUdNzXH5/HnHfn\\nAKC5QIPp9Q6euxecFHicHqrer8L5uhNPWZOHtgqir4gm7rY45NPsfH/gCaj4jJSY4A93tdpMfPxE\\nEhImo9NdgCS145qkLENeHtx/P/g5+cjAB7fcwsybb2anIvDLV0pkJI8mJnJDjx4oQ2z0FggaEF/d\\nTxDhGSc4HhTRCmJuiyEhPwHpHxKe3n4C4wLnR04OXnWQPZc5uPjnF8gYWsTnzsm8vUdif5MQb/X1\\nJRw4MJ9Nmy7ihx96sW3b7ZSUfNI+U3aSBNddB1u3esP/HN3aIAHXvvkmW37/e1747DP8JxALa2q4\\nads2zlm/nrziYuHWLWgRMRJqJaFGQgdzbuIvq73n0bdHE3efyFwpaDuyR6b2q1qcbzip29A8vYIn\\nykPN72rYd9E+Fke8gY21pCfAxfEQHxG8TaUyBqPxcszmazCZxqNS6YLf2BZKSyE7G156CWoaRc4Z\\nGclLs2Yx93e/w9akyvCYGB4aMICrzWYUYmQkaIIQoVYSSoTqn/k7V228CoC4h+KI/lN02GwUnBzU\\n/VKH8y0nNV/UQJB0P+qz1ZSOLeUZwzN8z7ecrYNLEuBCE5hCCJIkqdHrL8JovByjcTxa7eCQMRFb\\nxf798OST8NprXq+6oziio/nXzJk8N2YMFU2qnKnVMmvAAK6Pj0elEJMwAi9ChFpJKBHSP/I0o3aM\\nAsDwsoHIcZEh2xAI2oLH5qHqwyqqllTh3tXc80xWyqguUfHhGR/yUuxLuNT1nB4HY8xeQeqrDdLo\\nUSIjE32CZDBcglJ5nF+edu6ERx+Fd9/1rh8dpSQujnn33cdLF15IdROxS46MZGb//tzSsycRQoxO\\neYQItZJQIjTwnkWkHk4FwLTMhOZsTcg2BILjQZZl6tbWUbWkippVNVAf5KY42DJ0C+/0eYcNyRuo\\nV9eTqIULzZDeQ0OiNnQGVUmKQK//HQbDpRgMY4mJGYoktVEctm6F2bO9YuTnHXfYYOBff/0rr158\\nMRVNBKe3RsPf+/bl9l690It9RqcsQoRaSSgRGv2XD9FVH42W8E0CygThnCDoODx2D9WfV1P9YTX1\\nm4KpEdRF1fHdwO/46rSvWJe6jlpNLWYNXBiv4ZoBvegfUQIeZ8jXUKmM6PUXYzCMRa9Pb9vUXWGh\\n14HhzTfBz43bFhPDS7feygtXX02ZShVQJUap5M89e/K3vn1FBIZTECFCrSSYCK04oODSG/MB79RI\\nr597ISnFwqug43G73WxduZVhpcMofqeYGmtwT7gadQ3rUtaxdtBa1gxcQ1lsGSoJrks5jcnJSfRU\\n7qa6amuLr6XR9EKvH4vBcAk63YVERQ06tijt2QPz5nnXjPwcGCojI1lw3XU8O2UKh5oIjgRcZTLx\\n9379+J1Od2JrVoJugxChVhJMhL7eHcVFt34KgNvspu93fcNmn+DUwuPxsGnTJhQKBcigsqqIXBtJ\\nxNoIVIdVIev91vM31gxaw9qBa9nWZxvRkdHccublTEjqT7xyH3bbaurrD7f42mq1mbi4C9DpLkSn\\nu4DY2DQUihDT0MXFsGABvPwyHDniK65Rq3k7I4Pnb7mFLQkJzaoNjYlheu/eTElIIFYV+u8RdH+E\\nCLWSYCK0doeB86YtB6B+cD39P+ofNvsEAvCuH9k32nF+6iTGEkP1tuqQ9zqiHFiSLRQkFWBJskA/\\nuPHsKdxy9iXEyTux27/Ebv8Kl8sesg0AhSKS2Nhz0ekuIC5uFLGxI4mI6Bl4U20tvPcePPcc/PJL\\no73AyhEjeH7KFD4bNqxZ2zFKJVMSEsjs3ZvhsbFtei8E3QMhQq0kmAj9tLUXQ/7vXQBqR9WSuDgx\\nXOYJBD6cTidbt25FoVCg2q8iYlMEkZsi0WzXILlDT3EdjjtMQVIBBUkFuM53kXFBBhNOv4Ye6grs\\n9i9xOL7D4fgel6vsmDZERPQjNnYkcXHnEhs7ktjYNO8+JVmG/Hx44QX49NMAJ4Zf+/fnhQkTeOvy\\ny6kO4qgwIjaWzF69mJSQQJwYHZ00CBFqJcFEaPtPSQy+5w0Aqv9QTfIzwbO1CgRdAU+Fh9ofaqn9\\nupbab2rxlLQc4+2g/iCb+22mZFAJCecnMGnyJM7qcyZVVdtwOL4/KkrfUVNjbbGdBqKiBh8VpRHE\\nxAwl2mZAvXiZd93o4EHffbaYGN76/e9ZeNVV/Nq/+exClELBH81mburRgwyDQew56uYIEWolwURo\\nz/oz6H//KwA4b3WSmpUaNvsEgrYge2Rc213Urq2lbk0ddevrkJ0tPwqqNFUUDSii5swazGlmUkam\\noDFokCQb/fo5qKz8kfLydVRWFuDxhJ4G9CciYgAx0ecQsz+KmM9+IyZ3E5GHQJK9U3XfnX02C6+8\\nktyLLqJW03zdqYdazZQePbipRw+GxsQIZ4ZuiBChVhJMhIq/G0H8w/MAKJ9ZzuA/Dw6bfQLBiSC7\\nZOo311O3pg7nj05cBS4UdcceYdiNdsoHlHPO+HPo/7v+xKbFojRIVFVtobx8HTbbj1RWbqS6egvQ\\nulQPSlcEMUUKordWo90F0buhtjSGd8+7jH///jJ+SUkJWm9wVBTXxcdzXXw8Q4QgdRuECLWSYCLk\\n/HIM0U88DoD9OTunjz89bPYJBO2JXCdTv62eyg2VHPrxEKqfVcQ6WucY4O7txjDSgH6Inl8qf8E9\\nwI2nRzWqiF2oVDtRqYpQKnehVu8HWp+GQlUO2j1QUxZLQexZ/DclnYK4sykmHq+DdyMpkZE+QUqL\\njRWC1IURItRKgomQ5/NLUWTPAqD07VLOGnFW2OwTCDoSWZap2lvFb1//RunaUiK3R9LvQD807lZG\\nCIkAVYoK9UA1qkEq6vrUUWm2cf6VvXFW/Uxl5U9UVm6isvInXK7SNtlW59KwV9GXvYp+7KMv++nj\\n+2nDQL+ISMYbjVxhMjHWYCBaKTaUdyWEi8kJoJC90xWqBBWIkHGCkxhJkojuH82wm4bBTV5RKiwr\\nZO3atez7cR8xRTGkHkgl5XBKcGGqBddWF66tjSMfNVoKtOVEDTwd7aA0dIO19BgUiXqgA3ev7dRK\\nv1FVtRWncytVVb/idjcNiepFo6ojBSspNHeQqCKK/bV92H+wD/892Icc+tEzJpXhpjMZl3AmqVox\\nSgo3QoTagYjEEKGLBYKTFEmSSDWlkjo+FcZDtauagpIClu9fzt6f9yJvl0k8nEjSkSQSjyQSXxEf\\ntB1PlQfnT06cPzUNI6RDHT+aqEHpaFOiMCRFoE61I/fdhdtUSJ16h1egHD/jkoKLE4CWagayk4Hs\\nbCys9B57div4iXhc6n7ERiXSN3YgCTGpREYmEhk5gIiIfqE34QraDSFC7YAmUXxQBac2UaooRvcc\\nzeieoyENKuoq2FC8gbVH1vJOyTvs3b+Xvof6knQkyXcMKB7gi7sYjPrieuqL6yn/vtyv1AgYkVTn\\nEtE/guikCCJOq0E58CDEbcFTsxZX3c/URu2nurcHd0xom5V4MHMY6g9D/QZs5TTJhSSh0fQmIqLv\\n0aOP79Bo+vjKlEoR7+5EECLUDkQOEnNxAoE/sZpYLulzCZf0uQSAWnctW8q2UFBawKaSTbxd8jYl\\nNSXEVcXRt7Qv/Ur7eX+WeH/2LetLhCv0DIPskqmx1nhj5uWDV5zGHD28KGPdaOP3ozT+hMK4Ffoc\\noGaAnfLEOtwJVWijykO07nsV6ur2U1e3n4qKtSHvUqkMzYRJo+mBRtMDtbqH73elUkz9BUOIUDsQ\\neboQIYGgJSKUEQyPH87w+OGAd01pn3MfW2xb2Fq2la22rSy3LcdW6x2LSB6JhPIE+pb2pZetFz3t\\nPX0/e9p7YnQaj/ma7golVRX9wdofuLLRloZf1HWQcJC6AXupSiqmKrEUeh5GbTpElO4w0VElSNKx\\n/bZcLhsulw2nc3OL9ykUkQGi1FSkvOdmVCoTarUJheLUSG/RJUTIYrGwceNGjEYjVquV4cOHk56e\\n3i71jrftUGzcuIGYJkN8S5kFuadwMhQIWoskSfSL6Ue/mH5c1u8ywCtMh6sPs9W2lS1lW9hm38ZO\\nx04slRZkAvtXZF2kT5B62nrSy96LBEcC5nIz8eXxmCvMKOVjeMHVa2D/ADT7B6D5AfRNr6vqIb4Y\\nzCUQX4wnvoT63iW4e3jLlMYS1HElKJSt2//k8dRQW7ub2trdrbpfqYxFrTajVpt8wuQ9gpepVAaU\\nyu63PyrsImS1WsnKymLFihW+skmTJpGcnExSUtIJ1TvetltCb9bj8o+aHwEpF6ag0oT9rRQIujWS\\nJNFT25Oe2p6M7TPWV17jqsFaYaXQUcgOxw52lu+k0FHIbs1udiXsCtqWwqNA79R7BclPmOLL431l\\nRqeR6NoWMsq61HCwt/cAFPiNonxGe0Bv9wqV/2EsA4MNDDZko/enFFHbpvfD7a7A7a6gpqaoDbUU\\nqFQ6VCq939H0XI9SGfwepTIWhaJzn2Vh3yeUmZnJ73//e6699lpfWX5+PgsXLmTp0qUnVO942w5G\\nw7eL1WtmQnW2t/Czy1CvfAjze+Y2tSUQCE6cWnct+yr3sbtyN7srdrOnco/v54GqA3jklmPjAWjq\\nNRicBgyVhoCfxkojxkoDfW0GEipNRFfrUbpOJIq3DFHVXmHyE6hmR1x546E8tv0dgSRFoFLFolTG\\nolTGBPz0ljeUBV4PrBODUhmNQhGNUqltMVNv2EXIaDRisVhITEz0ldntdoxGIx5P6H9Ca+odb9vB\\naBChz7+/h4i6572Fn11GdOnjxM2Ia1NbAoGgY6lz17HPuY+9lXs5WHXQezgPcqDqAAerDnK46jAu\\nufXRGgCUbiVxVXGklsRx5qFYBhbrSCyLI6HCAIp+OCN741QbcRGHVB9FVJWauHLQBE+A2zKSB6Kd\\nXjHSObyHv0D5nzf8HlMJUcGTG4abiy8OLTNhnUOy2+0+UfBHr/fOzu7atStAQNpST6/XH1fbx6LW\\nXRMwJNcME+7ZAkFXQ6PUkByXTHJc8Mj2bo+bkpoSDlQd4IDzAEeqj1BSU0JxdbH3Z00xxdXF2Osa\\ncym5lW5ssTbWx9pYH2Q231AFg0ohyQ7JNujjjKQ0oh910anYdMnsM/anNKYH9igzsieamEqvzjQc\\n/ucxlQqinbHEOGLRHuyDorVDBaWrsTH/o2lZqPOo6k4fgYVVhMrKvHlJ4uKCjySsVmtQoWhLvba2\\nfSxch91wdPbNo/CgOV+IkEDQ3VAqlPTQ9qCHtgfDzM2T6TVQ566jtKa0mTDZa+3Yam3Y6xp/2jV2\\n1modrO3XULsG2AHsQOOCAXZIOgADysFcG41a0wtZ25uamJ7Ye/bmt/ie7Deb2W82U6bz2z8lQ0St\\nVx+aHtqqxt8jayCqWkVUte7ocfRaOUQd9v4eURt4NNcbGTR13ob9G/c/D1YeWdP4e8N5g1ERdS3+\\nL8I+Euqoesfb9rGIPfSjT4Qq9BX0iRG5TASCkxWNUkOv6F70iu7VqvtdHhfldeU+cXLUOaisr6Si\\nvoKKugrf71vqG3+vrD9Ied3X1FeVY/ipmjMrwFirQSuZUavMSBFm3JFmqqPNVMUYcWp1OGL1HOih\\no1ivpz5IAsDWonR5dUJT1yBMEhG1EUcPQzPR0tT53V8GkQdAXe89b/rT93u9G/aHtkG4dDXhWO6N\\nl97lvxfgR8g6rWMNEggEpwxlQCEAdcCBo0fH4QacR4+OZAqh5xPF13iBQCAQhI2wjoSSk72LhuXl\\n5UHXbhquH0+9BgeEtrYdylmwYYTUnTJfCJs7nu5mLwibO4PuZi+Ez+awjoT0ej3JyclYrYEh2K1W\\nK3q9PqTjQGvqHW/bAoFAIOg8wj4dN27cONavXx9QZrFYyMjIOOF6x9u2QCAQCDoJOczY7XY5IyMj\\noCwjI0MuKiryndtsNjk5OVnOyclpU73W3NNaALkLvF1tQtjc8XQ3e2VZ2NwZdDd7ZTl8Noc9YgJA\\nQUEBS5YsYeTIkVitVtLS0hg7tjF2lN1uJzk5mblz53L77be3ul5r72kNYo63c+huNnc3e0HY3Bl0\\nN3shfDZ3CRHqDogPVefQ3WzubvaCsLkz6G72ghAhgUAgEJyChN0xQSAQCASnLkKEBAKBQBA2hAgJ\\nBAKBIGwIERIIBAJB2BAiJBAIBIKwIaJotwKLxcLGjRsxGo1YrVaGDx9Oenp6uM1qkby8PKxWK4WF\\nhVitVjIzM5kwYUK4zWoVdrudrKwsFixYEG5TjonFYmHp0qWYTCZKS0vJzMwkKSlIxrMuwKpVqygo\\nKACgtLSUlJQUpk6dGmarmpObm4vBYAjax7piX2zJ3q7aD1uy2Z9O6YuduTO2O1JYWNgs6sLEiRNl\\nq9UaJouOTW5urmyxWHzndrtdTklJCYg40ZWZNm2aPHHixHCbcUyWLVsmZ2ZmBpRNmzYtTNa0zMaN\\nG+Xc3NyAstzc3C73mVi5cqVsMBjk/Pz8Zte6Yl9syd6u2g9bsrkpndEXxXTcMcjOzmb69OkBZZmZ\\nmcycOTNMFh0bq9XKsGGN2SJ1Oh0zZ84kMzMzjFa1DqvVis1mO2Zep3Bjt9uZNm1awDfEnJwcvvzy\\nyzBaFZqcnJxm38AnTJjAypUrw2RRIEVFRUyfPp2ioiKMRmPQe7pSX2yNvV2tH7bGZn86rS92qMSd\\nBBgMhmax5mw2myxJUngMOgY2m01OS0uT7XZ7QHlhYaEsSdJxxc3rTHJycuScnJwuPxK6//775ays\\nrGblXfX9TUtLCzpiaDqy6AqkpKQE/ZbeVftiMHu7ej8M9R7701l9UYyEWsBut2O325t9a2jIVbRr\\n164wWNUyer0eq9VKUVFRuE1pM/n5+YwbNy7cZrSKRYsWMXLkyGblXTVFyLhx48jIyAj4XKxatYpJ\\nkyaF0arW0936Ynfuh9C5fVE4JrRAWVkZQNCkeOAdrnbFh06D3f6sWrUKg8HQJe1twGq1kp6e3i3i\\nbdntdnQ6HYsWLcJoNFJWVobRaOwSi87BmDNnDqtWrSIlJYWFCxeSlJSEw+EICAjclemOfbG79kPo\\n3L4oRKgF7HZ7uE1oNxYuXMisWbPCbUZI8vLyuqSnVjAaEiUWFBRw3333+cqzsrIoKyvrsn/Hhg0b\\nuPTSS8nMzGT48OHk5+eH26RWc7L0xa7eD6Hz+6KYjjsFyMnJwWw2BzwwuxLd7QHTYG/TFPHXX399\\nl3ZYWbRoEXPnzmXlypW+tCbddbqoO9LV+yGEpy8KETrJsVqt5OTk8MUXX4TblJAsW7YsYBqrq3vG\\nNYhPUxEaNmwYdru9y61PAEyfPp2MjAyGDh1Keno6RUVFJCcniyzDnUR36IcQnr4oRKgFGh4y5eXl\\nLV7vymRlZXVZt2HwTmmNGDEioKyrrwk1LIY3/GxKw3RdV6Hh263/OoROp2PFihXo9fpuMS3X3fti\\nV++HEL6+KNaEWkCv15OcnIzVamXo0KG+cqvVil6v7/KLi9OnT2fu3LkhF3O7Ahs2bKCwsJAlS5b4\\nyiwWC1arlaysLEaOHNklF/sbPhfBPgNd7YG4ceNGUlJSgl7LzMzsFtOh3bkvdod+COHri0KEjsG4\\nceNYv359wAffYrF0+WmMRYsWkZWVFdA58/PzSU5O7lJhZYItgM6bN48NGzYwZ86cMFjUOjIzM9m4\\ncWNAqniLxdIlPZ+Sk5NZtmxZ0Gt2u73Lf5Yb6I59sbv0QwhfXxTTcccgOzu7WQfOyckhOzs7TBYd\\nm9zcXMDrImqxWLBYLKxatYply5Z1uQ9+MEpKSrr8lNy0adNYuHBhQFlWVhaLFi0Kk0WhafifN512\\ns1qtlJaWdjnRhODTQF25Lwazt6v3w9b0sc7oiyK9dysoKChgyZIljBw50udV5P8NuCsRbENfAykp\\nKezYsaOTLWo9RUVFZGdns3TpUhwOB1OnTiUzMzMg9ElXosHelJQUCgsLmTRpUpf9XID3W3lhYSEm\\nkwnwTnF1FXdyh8PB7NmzsVqt5Obmkpyc7Ntg6z8F1FX64rHs7Yr9sLXvMXRuXxQiJBAIBIKwIabj\\nBAKBQBA2hAgJBAKBIGwIERIIBAJB2BAiJBAIBIKwIURIIBAIBGFDiJBAIBAIwoYQIYFAIBCEDSFC\\nAoFAIAgbQoQEgk7AYrGgUCiaRSluyqpVq1AoFG1Ouz1x4kQUCtGdBd0P8akVCDqB4cOHo9frKSgo\\nwOFwhLyvITba5MmT2/waXT0Pk0AQDCFCAkEnMW3aNGRZZunSpSHvWbp0KZIkce2113aiZQJB+BAi\\nJBB0Etdffz1As+jbDVgsFhwOB9ddd11nmiUQhBUhQgJBJzFs2DCSk5NDTsk1JBNrECvwpluYOHEi\\nKSkpKBQKjEYjkyZNoqioqFl9/1jEGRkZQdeI7HY7CoWC6dOnN7s2d+5c0tLSfK8zffr0oK8jELQn\\nQoQEgk4kMzMz5JRcTk5OwFSc1WolNTWV5cuXk5qaSmZmJiNGjCA3N5e0tLQW15ag5TWiptfS0tLI\\nyspCoVD4XicnJ4eUlBQKCgqO4y8VCFqHECGBoBNpmGprOiUXbCouOzsbSZJYuXIlX3zxBfPnz2fF\\nihVkZ2djt9tZtWpVu9g0d+5cCgoKyM/PZ/369b7X2bhxIxA846ZA0F4IERIIOpGkpCSGDRvWbEou\\n2FTc9OnTWbZsWbOkbQ2JxWw2W7vYNHv2bDIyMhg+fDh2u913JCUlkZ6ejsVioby8vF1eSyBoiirc\\nBggEpxqTJ0+moKCAnJwcZsyYAXhTQTf1ihs2bJhPcOx2Oxs2bMBisYR0bDheHA4HK1euxGAwBL0u\\nSRJlZWXExcW16+sKBCBESCDodKZNm8bMmTNZsmQJM2bMwGq1UlRUxMSJEwPus9vtzJxioyS5AAAC\\nGElEQVQ505diGbxrN2lpae3mMGC1WgGvI8PMmTND3hdKoASCE0WIkEDQyeh0OoYPH+6bksvNzQW8\\nTgv+pKenU1BQQGZmJpmZmQwdOhSA/Px8X522UlZWFnBuNBoB0Ov1zab9BILOQKwJCQRhoMFLLicn\\nhyVLliBJUoAI2O12CgoKmDhxIvPnz/cJEAS6YrcVi8UScK7X69HpdCGdHAwGA6mpqcf9egLBsRAi\\nJBCEgYbYcAsXLqSgoCDkBtWmzgcNU3TQXIz83a71ej2yLJOfnx+0rj+ZmZnYbLZm8ermzp2Lw+EI\\nuqdIIGgvxHScQBAGdDod48aN841Amk7F6fV63/VJkyYxYsQICgsLWbZsGSNHjgS8LtzJycmkp6cD\\ngaI0efJk8vLyyMjI8IULaqjbVNjmzJlDbm4uubm5pKamMmzYMKxWKwUFBaSlpXHfffd15FshONWR\\nBQJBWMjNzZUlSZIVCkXQ63a7Xc7MzJQNBoMsSZI8YsQIOS8vT5ZlWc7MzJQVCoU8ffp0WZZleeLE\\nic3aycnJkVNSUmRJkmSj0ShnZWXJsizLBoPBV8+fmTNnymlpabIkSXJqaqrvfoGgI5Fk+QQmmAUC\\ngUAgOAHEmpBAIBAIwoYQIYFAIBCEDSFCAoFAIAgbQoQEAoFAEDaECAkEAoEgbAgREggEAkHYECIk\\nEAgEgrAhREggEAgEYUOIkEAgEAjCxv8D35NEikcC+EAAAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtwW9d59/vvhmRJtCQSgOT7jQSgNBe/rkiQaZImvogA\\nZZ70PT2WCMppO6dzphbBNMdO54wt0IlzrDZNZEjuO8f2NDZBnzmTpvO2JEH7bRtWlgjItvr2ShJQ\\nU6duKnJDsR1bjiVyg5KsiyXu88cmNgkCvIAXAASfzwzHxMYmuAhv8cdnrbXXUnRd1xFCCCGKmKXQ\\nDRBCCCHmImElhBCi6ElYCSGEKHoSVkIIIYqehJUQQoiiJ2ElhBCi6K0tdAMWIxAI0NDQgNvtxmq1\\nznheLBZjcHAQu92OqqrU1NRQX1+fx5YKIYRYjBUdVrFYjEOHDmV9zul0cvLkSVRVpa2tjaNHj5rP\\nNTc343A4qKqqyldThRBCLMKKDiun08mhQ4cyqqq+vj7q6uoACAaDtLa2pj3v9/sJBAJ0dXXlra1C\\nCCEWbkWHldvtZvv27VmfSx3v7u7mySefzPi6cDi87O0TQgixNJRSW26po6ODvXv3AqBpGna7HU3T\\nKC8vTzvPYrGgqiqVlZUFaKUQQohclNRswGg0Sm1trfl4ZGQEICOoUlRVzUu7hBBCLE5JhVUsFqO6\\nutp8rGlaAVsjhBBiqZRMWIXDYZxOZ6GbIYQQYhms6AkWUz3zzDMcO3ZsSV5LUZQZnyuxIT4hhFgR\\nSqKy0jSNWCyWMTblcDgAGBsby/p1qedzMVuQCSFEKbn//v0oChkf99+/P+9tKYmwikQiWVewsFqt\\nOByOjIkUqqpitVpnnAmo63rWDyGEWE3Wr7+a9fiGDdfy3JISCav+/v4Zx6s8Hg/9/f1px2KxGF6v\\nNx9NE0KIFeuxxxpwOr+ddszp/BaPPpr/358lcZ+Vz+djbGyMI0eOZDyXTCbx+Xxpyy01NDQQCoVy\\nvscq1QVYAm+ZEELMS2/vcV54oY9Ll9awYcM1Hn3Uy1e/em/e21ESYdXa2oqiKLz44otZn4/H43R2\\ndlJXV4eqqrjdbnbs2JHz95GwEkKIwiiJsMoXCSshhCiMkhizEkKIQnvvvfeoq6tjzZo1KIqy6j7W\\nrFlDXV0d77333rK8vxJWQgixBB566CF27drFxYsXZ5xRXMofFy9e5KGHHuKhhx5alvdXugFzIN2A\\nQoiZrFmzhosXL7Ju3bpCN6Vgrly5QllZGdeuLf3UdgmrHEhYCSFmoiiK/G5g+d4H6QYUQghR9CSs\\nhBCihIXDYZqbmxf0tRZL8UREySxkK4QQxai39zjPP3+Uy5fXsn79VR57rCHnm2oX8xqlsp5p8cSm\\nEEKUmN7e43zzm0c4evSPefPN/Rw9+sd885tH6O09ntfXAGhubsZisVBbW0sikTCPRyIRnE4nFouF\\nhoYGkskkgLkk3ZYtWwAIhULY7fasr5EPElZCCLFMnn/+KMPD30s7Njz8PV54oS9vr6HrOuFwmIaG\\nBjRNo7a2Fp/PBxg7VjQ3N/Pyyy+jaRoOh4O9e/cC0NdnvP7Zs2fRNI3W1lZef/11RkdHcTgctLe3\\nz/tnWArSDSiEEMvk8uXsv2IvXVqT19dwu9088sgjALz00ktYLBaSySRdXV14PB4eeOAB8zm73Z7x\\n9VarldHRUSoqKgCw2Wx534ldwkoIIZbJUmyxsRSvUVVVlfY4tXXS8PAw4XA4LaBmGuP6/ve/TzQa\\nNc9dyH6AiyHdgEIIsUyWYouNpXiNbHv6OZ1OXC4XTU1NjIyMmB+RSCTj68PhMNFolGPHjnH06FGa\\nmprm/b2XilRWQgixTFIz9l544TtTtth4MKfZgEvxGrFYjJ6eHurr6wkEAni9XsrLy/H5fAQCAaLR\\nKG63m0AgQCKRSNtSCWB0dBS73U55eTmaphEKhfJeWZXEChaxWIyuri62bNnC2bNn8fv9aWVvLBZj\\ncHAQu92OqqrU1NRQX1+f8/eRFSyEEDMp1hUsenp66OvrQ1VVIpEIXq+X7u5uysvLAYhGo/j9flRV\\nzXiuubmZnp4erl27RkNDAwMDAzidTp555hl8Ph/hcDhju6Xleh9WfFiFw2EikQgvvfSSeczv95sz\\nVVRVpbW1Ne0vhebmZoLBYEY/7lwkrIQQMynWsMo3WW4pC03TaGlpSQuqUCjEsWPHzMfBYJDW1ta0\\nr/P7/QQCgby1UwghxOKs6MoqEAhgsVg4cOBA2vFTp06ZW9bb7XZisVjaFvaapmG32xkfH8/p+0ll\\nJYSYiVRWBqmssujo6KCuri7jeCqYNE0zg2kqq9UKGKEmhBCi+K3o2YCaplFRUUFHRwd2u52RkRHs\\ndju7d+8GYGRkBMAcLJxOVdW0iksIIRbKYrFw5cqVVb+f1XItfrtiK6vUfQPxeJy9e/eye/du9u7d\\nS39/Px0dHQB5v8NaCLF61dTU8Oyzz3LlypVCN6Ugrly5wrPPPktNTc2yvP6KDatUEE2f679nzx6Z\\nPCGEyLtXX32VV199lbKyMhRFWXUfZWVl5nuwHFZsN2AqpKaHVXV1NZqmLWo8qlSW1BdC5M/tt99O\\nf39/oZtRslZsZZWaJJH673SqqppBNjY2lvWcfN+BLYQQYmFWbFjB5GKMMz1ntVqznqOqKlardcbJ\\nFbquZ/0QQghRGCs6rPx+P4ODg2nHYrEYNpvNDCKPx5NRmsdiMXNjMSGEEMVvRd8UnEwmcbvdDA0N\\nmccaGhpobW1l165d5jk+ny9tuaWGhgZCoVDO09blpmAhhCiMFR1WAIlEgmAwiNPpZHh4mObm5oyF\\nFePxOJ2dndTV1aGqKm63O+Oc+ZCwEkKIwljxYZVPElZCCFEYK3rMSgghxOogYSWEEKLoSVgJIYQo\\nehJWQgghip6ElRBCiKInYSWEEKLoSVgJIYQoehJWQgghip6ElRBCiKK3YvezEkKIlai39zjPP3+U\\ny5fXsn79VR57rIGvfvXeQjer6ElYCSFEnvT2Hueb3zzC8PD3zGPDw98GkMCag3QDCiFEnjz//NG0\\noAIYHv4eL7zQV6AWrRwSVkIIkSeXL2fvzLp0aU2eW7LyrOiwUlUVr9dLNBpF0zRUVaWtrY1oNJp2\\nXiwWo6Ojg56eHg4dOpTxvBBC5MP69VezHt+w4VqeW7LyLNmY1djYGOXl5Uv1cvMWjUbN8LFarbz8\\n8svU19ebz6cCbOrmi83NzTgcDqqqqvLeXiHE6vXYYw0MD387rSvQ6fwWjz76YAFbtTLkHFbxeJxQ\\nKEQgEKCyspJkMkl9fT2xWAxFUdi3bx8HDhxYjrZmUBSFSCRCbW0tIyMjWXf+DQaDtLa2ph3z+/0E\\nAgG6urry0k4hxOoz26y/F174DpcurWHDhms8+uiDMrliPvQcRCIRXVEUXVEUPR6P67qu636/X1cU\\nRfd4PLrD4dAtFove09OTy8sumKqqeiQSmfUcm82mJxKJtGOjo6O6oig5fz9Az/EtE0KsQj/+8Zu6\\n0/ktHXTzw+n8lv7jH79Z6KatWDmNWQUCAQD6+vrYvn07AKFQCI/HQ19fH8PDw5SXl+etspqLpmlo\\nmobdbk87brVaATh16lQBWiWEKHUy62/p5dQNqKoqTU1N5phQPB4HjG61lObmZsLh8BI2ce42aZoG\\nwMjICHa7nd27d5uPgRnH0lRVzdp1KIQQiyGz/pZeTmGlaRqKopiPI5EIAF6v1zw2MjJihsdyS1VM\\nqXACIyxTx/LVDiGEmEpm/S29nLoBq6urzYACaG9vx+FwpFUu0Wg0b7PsKioq2Lt3b9qx1OQJIYQo\\nlMcea8Dp/HbaMWPWn3eGrxBzyamy8vv9tLa2sm3bNqxWK6qqEgwGASOk/H4/mqbR0tKyLI2dj6qq\\nKlRVZWxsbMGvMbV6FEKIXMmsv2WQ64yMffv26VarVVcURff5fGnHFUXRvV7vks4AmU0wGMw4lprp\\nF4/Hzc+TyWTGeYqiZMwSTGFi1t9MH0IIIfJL0XVdX4rQU1UVAIfDsRQvN6/v53K5MiZJpI5rmkZ5\\neTkul4twOGzOXkydk7o3KxepimuJ3jIhhBDztOAVLE6dOmXOxHM4HBljV8vN4XDQ3t6eMZsvEong\\ndrvNtng8Hvr7+9PCKhaLpU0KEUIIUdxyXhswHo9TW1uLw+HA4/HQ1NRETU0NNpuNPXv25PXeJbvd\\nTiKRMB9rmkYoFKKjo8M8FgwG6e7uTvu6UChkjrUJIYQofjl1AyYSCZxOJwA1NTXs2bPHnNDQ19dH\\nNBrFZrORSCTyVmX19PSgqipnz55F0zTa2toyqq14PE5nZyd1dXWoqorb7WbHjh05fy/pBhRCiMLI\\nKaxSN/y2t7dnTBkHo2JpbW3F5/PR2dm5pA0tBhJWQghRGDmFld1ux+FwMDAwMOM5brebsbExTp48\\nuSQNLCYSVkIIURg5jVlpmmZ2A87E4XCYMwOFEEKIpZBTZeX1eonFYpw9e3bGc+ZTfa1UUlkJIbKZ\\nbTsQsTRymrre3t6O2+1m586dGdPGE4mEuYLF1Nl4QghRynp7j/PNbx5JW2V9eNhYakkCa+nMWlk1\\nNDRkLD00PDyMqqooioLD4cBqtZpbyuu6Tk1NDXV1dbz44ovL3vh8k8pKCDHdzp1PcfToH2c5/h1e\\ne+27BWhRaZq1surv70dRlIxfzhUVFQCcOXOGM2fOAJPbcKTCrBTDSgghppPtQPJj1rAaHR3NVzuE\\nEGJFku1A8iPnFSyEEEJMku1A8iOn2YCplSASiQSapmG1WnE4HOzZsydt7b1SJWNWQohsenuP88IL\\nfVO2A/HK5IolNq+wisfj7N27l1gsNuM5brebjo6Okg4tCSshhCiMOcMqGo2aK5TX1NTg9/upra01\\n1wQcGBigvb2deDyOoij09fUtaN29lUDCSggBcl9VIcwaVslkkqqqKjRNm3E9wJTUuoA2m23Wm4ZX\\nMgkrIUS2+6qczm/z3HM7JbCW0awTLEKhEJqmsW/fvlmDCqClpYUnnniC0dFRnn322SVtpBBCFFJv\\n73F27nyK++/fz+/+7p+mBRXA8PD3eOGFvgK1bnWYtbJyu92cOHGCa9fmPwXTYrHg9Xo5cuTIkjQw\\nF6ktQl566aW047FYjMHBQex2O6qqUlNTQ319fc6vL5WVEKVnapfe2Nh7wDrKy280P79y5RqqqnDx\\nYur3yv6Jj3T33befN97IPC6Wxqz3WamqmvM29VVVVQVbFzAQCGTcG6aqKm1tbRw9etQ81tzcjMPh\\noKqqKt9NFEIUkfQuvePAEWD6508BU1eokPuqCmHWbsBkMplzWDkcDjRNW1SjFkJVVUZHRzOWhwoG\\ng7S2tqYd8/v9BAKBfDZPCFFkenuPT+vSO4oRTtM/n/43fQMg91Xl26yVVUVFRc5V0sDAAFardVGN\\nWojUrMW+vvR+4+7ubp588sm0Y263m3A4nM/mCSGKSKqiOnv2M1OOrp3h8+mVlDGJYsuWh7n77k9P\\n3Ff1oEyuWGazVlYej4fR0VFOnDgxrxeLx+Mkk8kFjQctRjQaxePxZBzXNA1N07Db7WnHU2F66tSp\\nfDRPCFFknn/+6ERFNTWIZvo8WyX1Gj/84e/zxhv7ee2170pQ5cGsYZWqSHw+35wvlEwmzfOmVzLL\\nTVVVqqqqMiY+jIyMAJOL7Gb7OiHE6jO5+OzUIJrp83uBnZSV7eHuu/+AnTu/w3PPSSWVb7N2A9bU\\n1LB37146OjrYtm0bwWCQXbt2ZZzX09NDIBBAVVWampqorq5etgZn+94zTasvxNiZEKK49fYe5623\\n3p54lAqc7wBr2LTpBJ/61DfYvPkGxsY+RFGMz42uvm9IQBXQnJsvtre3MzIyQk9PD01NTdhsNhwO\\nh7l9fWpiA0BTUxNdXV3L3uiU5Qqj6ZM0hBClYXKs6hsYldP3MALrXpzOb/HccwEJpCI1r52Cu7u7\\niUQiBINBotEog4ODDA4Oms97PB4CgUDex6q6u7vTqioJGSHETFKz/86e7Zxy1Kiotmz5D5577vcl\\nqIrYvLe193g85iQGVVXTVl0vhHg8Tm1tbdqx6WNWqbaNjY1lHbeaqe0z3fQrYSjEypR99t+9pLoB\\n7757vwRVkZt3WE1VqICaamBggOHhYTo7J/9KisVi5k3AdXV17N692+yunLoavKqqWK1WKisrC9By\\nIUQ+pVdUT2U9R27oLX4LCqtikG1SxaFDhxgYGOCZZ54xj3k8Hvr7+9PCKhaLmSvJCyFKV2ZFlZrl\\nN3UR2m/x6KMPFqJ5IgcltVPwmTNnMrrwgsEg3d3dacdCoRDBYDCfTRNCFEDm/VTGNHRjrGo/W7Y8\\nLNPQV4icdgouVolEgmAwSFdXF8lkkr179+L3+80p9Kkdjuvq6lBVFbfbvaA9t2QhWyFWjt7e4/zO\\n7/y/aNoPSV/rz2DM/pOgWilKIqzyRcJKiOLX23uc73znz3j77eu4dGkLk4vQHgf6SM3+++EPZfbf\\nSiJhlQMJKyGK2+Qq6gpGSElFVSqWLKxmmh5eSiSshChuNTW/Tzz+A9L3nJqsqGy2n/GjH31dgmoF\\nynmCRTwe5+tf/7q5CGwymaS2thar1cqaNWvyvi6gEEKAUVW9/fb5iUdTF6K9F/gusJ/Pf94lQbVC\\n5RRW0WgUt9tNe3u7udRRIBAgFotRX19PZWUlBw8e5JVXXlmWxgohxEyef/4oly7dOfFI9pwqNTl1\\nA9bW1hKLxejr6zOXVrJYLHg8HnMnXpvNhsvlor+/f3laXEDSDShE8br//v28+eYO0nf77UNRhqmu\\ntvFHf7RHqqoVLKebglOrqqeCKh6PA8bOuynNzc2ysaEQIq8mV1LfP3HEWPMPYPv26xkc/NMCtUws\\nlZzCStO0tPXxIpEIQNpqECMjI7I1hxAib/bv/wEHD/6Eixenr6RudP1997v/eyGbJ5ZITt2Abreb\\nU6dOcfbsWQBcLhcAQ0ND5jl2ux273Z52rFRIN6AQxWX//h/w3e/2MT7+6sQRuZeqVOU0wcLv9zM6\\nOsq2bdvM1SBSXYDRaBSXy4WmaTQ1NS1LY4UQorf3ODt3PsVdd/n4wz88yvj4r055dnLm3913f1qC\\nqoTk1A3Y0tLC8PAwoVCI4eFhmpqaeOKJJwA4evQoqqri8XjSFpIVQoilMnnT707gJLCd9Gnqk2Ql\\n9dKyZDcFq6oKFMf2IctFugGFKKzJm36fwvhb+yrGNPX0VSrKyvx0d/+2VFYlZMFbhIyNjTEyMoLN\\nZqOioqKkQ0oIUVi9vcd57LHnUNXrJo5MD6rUSuprsFj+lX37vBJUJWZBK1ikVqxwOp3m9vYul4tn\\nn312yRsohFjdenuP88gjP0RV1wKuiaPTg8qYVGGx/Cvf+Y6X/ft/v0CtFcslp27ARCKB0+kEoL6+\\nnmg0SiQSYceOHdhsNpLJJG63O683BEciESKRCFu2bGF4eBi3252xMWMsFmNwcBC73Y6qqtTU1Jj3\\niuVCugGFyL+dO5/CWHNgLZC66Xcn04OqrOxt9u27T4KqROXUDZjasHBwcJCqqirsdrv53OjoKAcP\\nHqStrY0nn3ySAwcOLG1Ls4hEIiiKkjaho7a2Fk3TzIkfqW3uUytsgHHjssPhoKqqatnbKIRYnMuX\\nU7+mrpK6f8oIqDPAD9i4UeHLX3bx6KPfkK6/EpZTN2BXVxcej8fc1HC6ffv2UV1dnbcVLNrb2zOO\\neTyetOPBYJDW1ta0c/x+P4FAYNnbJ4RYvLGxXzLZ7fdtJqent1NWVkFn59d57bXvSlCVuJzCStM0\\nsxtwJg6Hg+Hh4UU1ar4URTFX0UjRdR2bzWY+7u7upqamJu0ct9stS0IJUaR6e49TU/MImzZ9FUX5\\nMvH4B8AHpE+k2M+6dU3s2/erElJ5kLyULPjwR07dgNXV1QwMDMx6TjwezwiH5dLV1ZVxLBwO8/Wv\\nfx0wwlXTtLTuSgCr1QrAqVOnqKysXPZ2CiHmZ//+H3DgwBtcubIZuBnYBHRirEzxZ8CLwDo2b07y\\nF3/xf0lQLRNd1zlx+gSHhw5zeOgwJ06f4Ke//1PurLhz7i9eJjmF1Z49e2hra+P111/PGkjNzc2o\\nqsq+ffuWrIG5CIVC1NbW8vjjjwPGOoXAjJtCqqoqYSVEge3f/wP+5E9+zPnzY8AW4L9MeTb1K+pe\\nJseroKZmvwTVEhu9OEqf2sfhocO8NvQam9dtptHVyLe/8m3uu+s+yq4rK2j7cgqrffv20dnZSX19\\nvbl4bTAYpL29nUgkwujoKA6HI+8rWPT09NDX14eiKHR2dprHZUFdIYpXb+9xfu/3vseHH24GbgHW\\nYaxIMZWsTrFcxvVx4h/Ezerp3z78N75y11dodDXy1Feewmmffcgn3xa0gsXBgwc5cOAAyWTSPFZR\\nUYHf7y/oUkvJZJL6+no6Ojqorq4mFotRW1vL+Ph4xrkWi8Wcdj/d1JXlsyl0360QK13q3qnTp38J\\npNb2exe4Y9qZsjrFUhq5OMLR4aMcHjrMkaEjWDdYaXQ10ritkXvvupcNazcUuokzWtAKFvv27TO7\\n+lRVxW63m+NAhZQKzPr6erMLUAhRfB577GVOn74TuMbkr6HLGOH0wylnpq9OsW7dW+zbt0OCap7G\\n9XEG3x/ktaHXODx0mLd++Rb3Vd5Ho6uR/fftp8q2cm7fWbK1AYuFqqq4XC4ikQg1NTXY7XY0TcsY\\nt7JYLDmPWclNwUIszmTXnx34FeBtYNvEs6eBmzDC6c8wZgBeBK5n48ZyfuVXZLff+Tjz8Zm06mnr\\n9VvN6unLd365qKun2cxaWVkslhm7xFK/sKf+AlcUxfzvtWvL26esqiput5vXX3+d7dun93Mb41VW\\nqxWHw4GqqmnnqKqK1WqVyRVC5FGq6+/DD9cBTozxqPuAN4DNE2edxrjh93bgFqzWBH/+5y0SULO4\\nNn6NgfcHzOrp7TNvc3/l/TS6GvnuA9+l0lpZ6CYuiVnDavfu3Qt60bnGfJZC6p6v6QvoplZ/T81W\\n9Hg89Pf3p4VVLBZL291YCLF8JhehHQN+DaPrL9XdpwP3A70Y3YDjwC/ZuHHzRCUlQZXNRxc+4sjw\\nEQ4PHebo8FFu2ngTja5Gvl//fX79jl9n/dr1hW7iklvR3YCHDh2ipaWFiooK85jX66W2ttZc7imZ\\nTOLz+dKWW2poaCAUCuVcWUk3oBC5+a3fCvAXfxEH1mDcM/U5jK6/qfdOXQDWYbF8xF//dZuEUxbX\\nxq/xL7/4F7N6+s+z/8kDVQ/Q6GrkQdeDBb3/KV9WdFgBdHR0MDw8bC5kW1tbyyOPPJJ2Tjwep7Oz\\n09zd2O12Z50FOBcJKyFmNjkedQ6jYroM3AlM/St/G3Ar8BPgpSnHH+Hpp2tkEdopPjz/oVk99Q33\\ncevmW82xpy/d8SXWrVlX6Cbm1axhlRqzGh4eprKyctYxrJR8jVkVgoSVENn19h6nufmP+fhjC5D6\\nHWEB6oBTE4/XY4xT3QzchlFZbQA+4mtfu5v//t+D+W10kbk6fpV/fu+fzeppaGSIeke9WT3dXn57\\noZtYULOOWdXX16MoirnW3nzHsPIxZiWEKA779/+AP/qjv0LX1wPXT3mmDCOcLk48vh1jrOrPABUj\\nvDZSXb121QbV6fOnzXDqG+7jzoo7aXQ18t92/je+ePsXuW7NdXO/yCqx4rsB80kqKyEm9fYe57d/\\n+zskkxuAcoxxqanToi8C3wD+n4nPN2N0A07e4GuzfYMf/Wj1TEe/On6Vf3rvnzh80lg1IqEl8Dg8\\nZvV06+ZbC93EopVTWI2Njc24zt5qIGElhMGYOBHD6JxJ/U74mPTK6j6MsanfAp7DmJa+DtiIoqzH\\n4djEc8/9XskH1fvn3jerp6gapdJayYOuB2l0NfLFO77IWsuC1mZYdXIKK4vFQigUypjAMFVbWxsd\\nHR2cPXt2SRpYTCSshID77vs/OH78NJMhVYbRpZfAGKdKDQPcBdzD1LGpe++9kTff/P/y3OL8+uTa\\nJ/zje/9oVk/vJN/B6/TS6Gpkp3Mnt2y+pdBNXJHmjPSenh7zZl/A3B4+G13XCYfDjI6OLm0rhRAF\\nZ1RTr2GMPW3CCKnUH6W3A7+N0cU3NnHsJ8A7wPWUlY2yb99XS3a233tj75nV07HEMZw2Jw+6HuRP\\n/5c/5ddu/zWpnpbAnJWVxZLT/oyAcSPu1PuaSoVUVmI1MkLqbwE7RjffTcAoRrV0FaP7b3WNR125\\ndoV/ePcfzOrpF+d+QYOzwayebtp0U6GbWHLmDKupO+o2NzfT0tKCx+OZ8XybzUZ9ff3StbCISFiJ\\n1ebuux/ipz8dwQiptUyOSZ3DCKu1GIGV2o5nI3AdN9+8lpdf/j9LKqjeTb5rbqfxeuJ1PrXlU+bY\\n0+dv+zxrLGsK3cSSltOYldfrpa2trWTDaC4SVmI1uesuL++8sxYjkDZOHL0ANAJ/g1FNXcOosoyQ\\nstnG+dGPSmMH3yvXrvA/3/mfZvX04YUPzeqpwdnAjRtvLHQTVxWZup4DCSuxGhgTKPox9pbahDEl\\n/cLEs+uAGzAmToQxxq3KgPM8/fT/uuLHpH6u/dysnt449Qaf2foZs3qqvbVWqqcCyjmsotEo3d3d\\nJBKJWc87cuTIohpWjCSsRCkzxqZ6MbaWvx5jtt85jLD6LPBPGEE1jhFaG4BLXHedxquvfmtFVlOX\\nr17m7975O7N6OvPxGXa6dprV09brtxa6iWJCTmHV09ODz+eb17nZdudd6SSsRCmaDKnNgBWj268M\\n40beK8Al4FMYEyxexwiyzazUsanEaMKsnt489SZ333i3WT25b3VjUXKfVCaWX05h5XK5UFWVvr6+\\nVTluJWElSo0xgeI0RkgpGN1+Fozp52UYVZU28bFl4vnz3HvvzSvmfqlLVy9x/OfHzepp9NKoGU5e\\nh5ct128pdBPFPOR8U3BLSwsvvfTS3CeXIAkrUSp6e4/zm7/5B1y7dhNGSG2c+O95jIDaitEFOI6x\\nevpajBt/x1bE2NTwyLBZPf3dz/+Oe266xwyo6luqpXpagXK6U62ioqLoFqnt6elBVVWGh4dRVRW/\\n35+x4G6O2OWHAAAgAElEQVQsFjNvZlZVlZqamlVZGQoBRlD9xm88jnG/1CYmQ4qJYyrGyuibMVZM\\nNyZZGGNTTxVll9/FTy7y5s/fNKunc1fO8aDrQX73V3+XP3/oz7GV2QrdRLFIOYVVS0sLHR0dBIPB\\nolgjsKenB4fDYYZTMpnE7XYzMjLC3r17AWPn4La2trSblJubm3E4HFRVVRWk3UIUijE+9S9M7dIz\\nwuoaRtffbYADOIFRXW0FzvO1r3226FZGP3n2pFk9/f07f8/2m7fzoOtBOps6+dWbf1WqpxKT82xA\\nn8/HiRMnCAaD1NTUzLj0Uj7C7NChQzzxxBNpxzo6OvD7/eYED7/fz86dO9m1a5d5TjQapb29na6u\\nrpy+n3QDipWqt/c4//W/Poqur8OYkp6ajq5hbJR4G0ZYnWGy4jrP5z63gbfeerVArU738Scf88ap\\nN8zq6eNPPjY3I/Q4PFg3WAvdRLGMcgqrVDBpmjbrefnYfFHTNDweD9FoNG1be1VVzYkglZWV2O12\\nYrFY2hb2mqZht9tznrEoYSVWGuPG3g8wxptSN7GuwaikLmFMP7+IEVTlpGb5bdjwMeFwYaej67rO\\nf579T7N6+od3/wH3LW5z7Omem+4pumEJsXxy6gac77T1fFxAVqsVVVVJJBJs37496zmappnBNP1r\\nAU6dOpUWYkKUihtv/AoffTSKcT/UTRP/3TTx7BmMgEpVIhbgFowp6ee5996tvPnmK3luseHClQu8\\nfup1s3q6cu0Kja5G/G4/XU1dVGyomPtFREnKKaza29uXqx0LMjIyknEsEolgs9morKxEVVVg5i7J\\nVPUlRKkwpqKfxAinOyaOpqagn59y5p3AuxOf2ybOGePpp38zrzP9dF3nP878h1k9/dN7/0TtrbU0\\nuhr5q4f/irtvvFuqJwHkGFbzEY1GCYfDvPjii0v90vPS3t7Ok08+CczdXSlEqZgMqTVMhlSqkrqI\\n0e2XBD7BmFxxDmO/KWMVChjh6af/t7wE1fkr5zmWOGZWT+P6OI2uRr5R9w16mnsoX1/4yVui+OQc\\nVslkkkgkknXPKl3XCQaDJBKJgoRVKBRi69atPP7444t6HflLTqwUs4dUqpK6iBFI1on/foDR5adg\\nrJh+flmDStd1/v2jf+fw0GFeG3qNf/7FP/P52z5Po6uR3t/q5bM3fFb+zYk55RRWiUQCt9s9Z8XS\\n0tKyqEYthKqqhEIhBgYG8v69hci3yYkTCjOH1FWMzRHXYFRRv5g4fhtGWJ3j6ad3LEtInbt8jmgi\\nyuGTh3lt+DUUFBpdjTz2a4/xQOUDbF6/ecm/pyhtOYVVIBBA0zSCwSDV1dX4/X7cbjd+vx9d1wkE\\nAmzdurUgK1y0tbVx7NixtGMOhwOAsbGxrONWqeenm2m2n/z1J4rB2rX3cO3aODOH1HmMaenuicen\\ngZPArUxOSb/GW28t3WLTuq7z1i/fMqun/vf7+cLtX6DR1cgffOEP+PTWT8u/H7EoOU9dr62tNW+w\\nPXjwIN3d3fT39wPGGJHD4eDll19Ou69pubW2ttLW1pZ1soTL5SIcDqfNGFRVldra2qwTNGYjU9dF\\nIU3O8JsppD7EGJv6PPAfGPdQpbagP8+dd17l5z/vW7L2jF0eI6JGzOrpOst15n1P91fez6Z1m+Z+\\nESHmKafKStM0nE6n+bimpoa2tjbzsdVqxefzceDAgbyFVUdHR0ZQRaNRc4UKj8dDf39/WljFYjG8\\nXm9e2ifEYq1fv50rV65OPErtMQWZIXULRrffP06cdzNwnrIylY8/Hlx0O3Rd5ycf/sSsngY/GORL\\nd3yJRlcjj3/pcT615VNSPYllk1NYVVVVmdPBAWprawE4ceKEGQZOp5OOjo4lbOLMwuEwYExhT1VJ\\nIyMjhMNhsysyGAzi8/nM5ZfAmIgRCoXy0kYhFmqyuw/Sq6lUSL2PsdDsbRgh9R7GTb13YoxJLX4q\\nunZJS6ueytaW0ehq5IkvPcEDVQ9w/XXXz/0iQiyBnLoBfT4fr7zyCn19fezYsQMAm83Gww8/bM7+\\na25uJhKJ5NzFlqtsN/umOJ1OTp48aT6Ox+N0dnZSV1eHqqq43W6z/bmQbkCRDzOHFBhB9T5GJbUF\\n+Bhjtt9mjPulUhMnFhZSuq5z4vQJs3qKn47z5Tu/bHTvuRrZtmXbIn4yIRYup7BKLWWkKArd3d3s\\n2rULv99PR0cHPp+P0dFRIpFIyW4jImEllpui3D3x2UzjUu9jdPf9EmNjxDKMxWaNiutrX7sn5wVn\\nRy+O0qf2mQG1ed1mGl2NPOh6kPsr76fsurLF/EhCLImcF7JVVZVgMEhrayvV1dVomkZ9fT3xeBwA\\nj8dDd3d32np9pULCSiyXuWf4vYex4OxmjCnpa5laSd155/i8J0+M6+NG9TRxU+5PPvwJX7nrK2b1\\n5LQ7534RIfIs57CaSereq9S6e6VIwkosteuvd3Px4uWJR9kmT6SWRLod42bea0yu9zf/XXtHLo5w\\ndPgoh4cOc2ToCNYNVrN6uq/yPjas3bCUP5YQS27Jwmo1kLASS2Xypl7IPnkiFVKfxpiGDrmMS43r\\n48Q+iJnV01u/fIv7Ku8zA8phy36PoRDFKqewam1tnXNqqq7rKIpSsLUBl5OElViszGnokF5NZQup\\nraS27oBRfvzjP8y6dceZj8+kVU9br99qhtNX7vqKVE9iRcsprCyWuXfeTHUDLvdswEKQsBILNTlx\\nAmYel3qXXELq2vg1Bj8YNKunt8+8zf2V95sBVWmtXK4fR4i8yymsZloTcGRkhFgsRiAQwOVyceTI\\n0i3jUkwkrESu5h9SMBlU6SH19NM+s7vvowsfcWT4CIeHDnN0+Cg3bbzJ3Izwy3d+mfVr1y/rzyNE\\noSzpmFVquSW/38+BAweW6mWLhoSVmI/0SRMwd0htwbipF6YH1V/9zf/NjdvLzOrpZ2d/xo6qHWb1\\ndGfFncv5owhRNJZ8goXf7yccDnP27Nm5T15hJKzEbOYfUqlp6Osw7pWCtPulNp7lC79TRqW3nL7h\\nPm7dfKtZPf36nb/OujXrlvtHEaLoLPnmi4qiZN3rSohSlb2rD2aupGAyqBSw3Aq3XQHXSdZ97peU\\n3WbhVkc99VX1HPIe4vby25ex9UKsDEtaWUWjUbxeLw6Hg6GhoaV62aIhlZWYavbxKMgMqSmV1KZP\\nwLUOXBo4PkQ5t4Z9u75Jo6uRL93xJa5bc91yNl2IFSenyspiscw6dT31SzwQCCyuVUIUsflNmoDJ\\nkNoMljG4fRRcF2DbZbBeBNWOfcTOvz31z9y6+dZlb7cQK1lOldVc22pYrVYefvhhdu/eveiGFSOp\\nrFav3t7j/MZvTL0Bd65JE8Dme8D1JrjOg+MCaBth6BY4WcGXqz7N373xw+VvuBAlQlawyIGE1eqT\\nXkXBrCFl0eGOj41w2nYeKj6B4Rtg6HYY2gTnP0LX38pPw4UoMSURVuFwGJvNRn19fcZzsViMwcFB\\n7HY7qqpSU1OT9bz5kLBaPdJD6gYgtfrDtJDarBrB5DpnVE8j64xgOumEX9wG4x+jKO8yPi4hJcRi\\n5DRmFY1G6evrM1dYt1qtOBwO9uzZk7YT7yuvvJK3nYJTW5KkNmKcSlVV2traOHr0qHmsubnZ3EVY\\niKlmrqLKgDXGp2vG4I5RcE2E1OarMLwRflYOf3sLnHcwucbfz6SSEmKJzCus4vE4Pp8vbZfgqYLB\\nIG63m+7ubgYHB/H5fBw8eJDHH398SRs7VSKRML/vTJswprYymcrv9xMIBOjq6lq2tomV4+67H+Kn\\nPz057ei0rr7yEdj2Ibg+gqozcHYdDG2Gv7kVflEGusLkiunnWbPmZ1y9+pO8/QxCrAZzdgPG43Hc\\nbjcANTU1+P1+amtrzS3uBwYGaG9vJx6PoygKuq7j8XjSqpnl5nK5CIVCGbv/2u12YrEYlZWV5rHU\\nDsPj4+PkSroBS8fMVRSw5nq48wy43oFtZ2DTJRjaaHTvDd8BF85N+zojpNat+4DLl08sf+OFWIXm\\nDCu73Y6mabS3t7N3794Zzzt48CBtbW0oisLIyEheN1/MFlapUNI0jfLy8rTzLRYLqqqmhdh8SFit\\nbLMGVIUC206D6zRUfgRnNsLQOji5Cd4vA/0zTC4wu/jdeYUQuZm1G/DQoUNomsa+fftmDSrA7FbT\\ndZ3u7m4eeeSRpWvlAqRWfZ8eVCkLCSuxMmUNqTXjcNcFI5y2nYbrL8PQVvjpDfDX5fDx9H8a/8HU\\nKgrelfEoIfJo1rD6y7/8SxRF4Zlnnpn1RSKRCLFYjK6uLpqbm2lvby94WM20QrxYHbIGlPVjo1vP\\n9a9G9fTLjTB0A7x6N3yQnBh7ugZUYqzfN+VrzZB6W0JKiAKYNaxUVcXhmHtHUY/Hw8jICFarlerq\\n6hknYqwUc20wKYpTRkCtHYe7NhoTI7b9PWy4AkM3w7/dAP/jM3DxDEY4jQFT/5+/R+auvA/MuCuv\\nEGL5zRpWyWSSz3/+8/N6odSmi3a7nRMnZJBZ5EdGQNmuwLa14DoDd43Ah1YjoHpuhdPlE9XTu8CH\\nE19QBlyc8gJTq6h3pIoSokjMGlYVFRUMDAzk9IIDAwNmcBVSqiIcGxvLOm41W8U40wQKqbiKQ1pA\\nrR2HygvgUmDbR7DumhFO/+qAV78IF1NbcLyLUUEBfBH4x4nPLyJjUUIUv1nDyuPx0NPTw4kTJ9Ju\\n+p1JPB4nmUzS1NS0ZA1cqNQNy6qqprVdVVWsVqtMrlhh0gLKfnli1YircOeoUTEN3QrdLqOS0i9M\\nnHiF9G05Uv4RCSghVpZZw+rJJ5+kp6eH+vp6EonEjDPrUnw+n/l1xcDj8dDf358WVrFYbM4FeUVx\\nMAPqunHYdmFizb1LcN01OLkV4pXQcyNcWsfkGn0XyB5QKTJZQoiVyDLbkzU1Nezdu5fR0VHcbjev\\nvPJK1vN6enpwuVyoqkpTUxPV1dXL0tjZZOu6CwaDdHd3px0LhUIEg3JPTLFau/YeFOVzKFu3wRfO\\nwu/8HB7/T/j1c3BuK3R+Cf7kN+Cvvwj/boVLV0hVR5Mf2dwBfGbi87fR9cMSVEKsIPNayNbn89HT\\n0wOAzWbD4XCYXWyqqpo7Azc1NeVtGaNkMsmBAwdQVZVwOIzD4cDj8eD1etO2KInH43R2dlJXV4eq\\nqrjd7oyVLuZLbgpeHopyt1E9VV0wFoTddh7WWODkDca9T+pdcDm1GWG2/aJmIl19QpSKea+6HolE\\nCAaDRKPRjOc8Hg+BQGDBq5mvFBJWS0dRPgdbr8C2c0b33u0X4X2rEU4nb4Bf3szkdHIJKCFWuwVt\\nEaKqKpqmmZMYVgsJq4VTlLuNmXpVFyb3e1KAkzcZN+YmtsDlqbNIJaCEEJNKYj+rfJGwyo2ifA5u\\nuDwZTrddNFYpH7rdmCDx0SaMm29TJKCEENlJWOVAwmp2ZvXkmKieXBPhM3SzEU6JLXBlLZMbGIIE\\nlBBiPiSsciBhlc6YWq7DjVOqp1svwnup6ukGY/XytOoJJKCEELmSsMrBag8r876n9anqaWJyxLgy\\nUT3dAKfsc1RPIAElhMiVhFUOVmNYmdXTTZcnp5XfcgnetRkTI05uhbOLrZ5AAkoIMRsJqxyshrAy\\nq6cN18BxfnLs6ep1k+F0yg6fTF//MdfqCSSghBDzJWGVg1ILq/QVy3W4+dLk2NPNl+Ad++R9TyM3\\nTftqCSchRP5IWOVgpYdVxnYaG66Bc0r1dGXdZDidssPViiknLyScQAJKCLEUJKxysJLCKnOnXECZ\\nWj1dgZvOwc8nqqehrXNUTxJOQojCkbDKQTGHVdZwAii7Cs4L4Bo3NiS8tHZi7OkO+PkNcHXNlJOl\\na08IUZwkrHJQDGE1YyiZJ+hwS8XEVu5n4MZzRpfe0O0wdBOMpqaUTw8mkHASQhQrCasc5Dus5gym\\nlOtvAucZo3JynYGP10/c93QzvLN1onpa6JgTSEAJIQptVYRVLBZjcHAQu92OqqrU1NQsaIX45Qyr\\n+QXTHRMn63Br0gimbR/B1gtw6gYjoIZuBi1b+xYWTmvW/IKrV3+Sw9cKIcTSm3Wn4FKgqiptbW0c\\nPXrUPNbc3IzD4aCqqirv7Zl3tZQKppTrr4DrLLhOg/NDuLDB6NaL3gPvlMG11D6aOlI1CSFKTclX\\nVn6/n507d7Jr1y7zWDQapb29PeeNInOprOYfSpARTADKRrhtxAinbadhyzlI2I3JEUNbIVk25WQJ\\nJyFEaSv5sLLb7cRiMSorK81jmqZht9sZHx/P6bVmCqsFV0umiUkPGy+B68OJ6uk0nFs/uWrEuza4\\n9ouc2ivBJIQoFSUdVqlQ0jSN8vLytOcsFguqqqaF2FxSYQWfm+PMOULJbMT4RPX0rjH2ZP8Y1C0T\\n9z19AmPXZX+ZWb+vhJMQovSU9JjVyMgIQEZQpeQaVtllC6ZNWY4BnIdNl41p5a4z4DwLyQ0wtB6O\\n2OHd240VzAGYLagklIQQq0tJh5Wmacv0ylMDKlswTZkmbhmH25MT9z29D9YroG6CoU1wpArOzVU9\\nSTAJIURJh9VCTXb3zWS2vZqAzerkenuO86CtM8Lp8M3w3vVTqqfpJJiEECIbCasFmbZmnkWHOz6e\\nXLG84hMY3ggnJwLq/PTqSUJJCCFyUdJh5XA4ABgbG8s6bpV6frqZ5pxMVlzvwuZPjGBynYeq8zA6\\nUT313gK/KJuoniSUhBBiKZR0WFmtVhwOB6qqsn37dvO4qqpYrdaFT664R4MHTxvV0882w9/eDOcd\\nSDAJIcTyKOmwAvB4PPT396eFVSwWw+v1LvxF//2z8G9fAP2CLEckhBB5UNL3WQEkk0l8Pl/acksN\\nDQ2EQqGcK6tiWHVdCCFWo5IPK4B4PE5nZyd1dXWoqorb7WbHjh05v46ElRBCFMaqCKulImElhBCF\\nYZn7FCGEEKKwJKyEEEIUPQkrIYQQRU/CSgghRNGTsBJCCFH0JKyEEEIUPQkrIYQQRU/CSgghRNGT\\nsBJCCFH0JKyEEEIUPQkrIYQQRU/CSgghRNGTsBJCCFH0JKyEEEIUvZLYKTgcDmOz2aivr894LhaL\\nMTg4iN1uR1VVampqsp4nhBCieK34sIpEIrS0tBAOhzOeU1WVtra2tF2Cm5ubcTgcVFVV5bOZQggh\\nFmHFdgMmEglaW1tJJBLY7fas5wSDQVpbW9OO+f1+AoFAPpoohBBiiZTETsEul4tQKJSxVb3dbicW\\ni1FZWWke0zQNu93O+Ph4zt9HdgoWQojCWLGV1Vw0TTODaSqr1QrAqVOnCtAqIYQQC1GyYTUyMgJA\\neXl51udVVc1nc4QQQizCip9gMRNN0xb8tanuvoU+L4QQIt1ih09KtrISQghRPBb7R37BK6tcuuO2\\nbNlCRUXFMrbGMNNfADLBYpK8F5PkvZgk78UkeS8mLUVvVEHDKpFI0NbWNu/z6+rqeOKJJ+Z1rsPh\\nAGBsbCzruFXqeSGEEMWvoGFVVVVFV1fXsry21WrF4XCgqirbt283j6uqitVqTZvOLoQQoriV9JiV\\nx+Ohv78/7VgsFsPr9RaoRUIIIRaiZMIqW79wMBiku7s77VgoFCIYDOarWUIIIZbAil3BIplMcuDA\\nAVRVJRwO43A48Hg8eL1edu/ebZ4Xj8fp7Oykrq4OVVVxu90ZK13MlwyYTpL3YpK8F5PkvZgk78Wk\\npXgvVmxYCSGEWD1KphtQCCFE6ZKwEkIIUfQkrIQQQhQ9CSshhBBFT8JKCCFE0Vuzf//+/YVuxEoQ\\ni8X48Y9/zKlTp+jt7eXSpUurcskmVVVpbm7mtttuw2638/777xMMBlEUZVW8H+FwmA8++CDrz7ra\\nrpGZ3ovVdo309PTQ29vLj370I55//nmuv/56PvvZz6ads1qujbnei0VdG7qY0/DwsO71etOO+Xw+\\nXVXVArWocIaHh3VFUcwPm82m9/T0FLpZedHX16fbbDY9Go1mPLfarpG53ovVco2Ew2E9FouZjzVN\\n051Opx4Khcxjq+XamO97sdBrQ7oB5yEYDNLa2pp2zO/3EwgECtSiwlEUhUgkgqZpqKrKyMgIu3bt\\nKnSzllUikaC1tZVEIpGx83TKarlG5vNerKZrRFVVqqurzccVFRUEAgH8fr95bLVcG/N5LxZ1bSx5\\nvJYgm82mJxKJtGOjo6O6oiiFaVABqaqqRyKRQjejYJxOZ9ZqYjVeIzO9F6vlGhkdHdXdbreuaVra\\n8VT1kLoeVsO1Md/3YjHXhlRWc9A0DU3TMv6KtFqtAJw6daoArRLFRK6R1clqtaKqKolEYsZzVsu1\\nMZ/3YrEKvvlisRsZGQHIuicWGKXvattuRFVVNE0DjPfHbrenrce42sg1kmm1XCOp//dTRSIRbDYb\\nlZWV5uayq+HamOu9SFnotSFhNYfUmyoMqb8Qp15czc3NGcdWE7lG0q32a6S9vZ0nn3wSkGtj6nsB\\ni7s2pBtQ5KSiooK9e/emHSvFwWKxcKv5GgmFQmzdupXHH3+80E0puGzvxWKuDQkrsWhVVVWoqsrY\\n2FihmyKK1Gq4RlRVJRQKceTIkUI3peByeS/me21IWM0hdaPaTG9kKd7YN5uDBw9mHEuV9qn++dVG\\nrpF0q/UaaWtr49ixY2nHVuu1ke29gMVdGxJWc7BarTgcjow3UlVVrFZryQyOzoeqqrS1tWXMYEoN\\nrJbqP7y5yDUyabVeI62trRw8eDBjIsVqvDZmei8We21IWM2Dx+Ohv78/7VgsFsPr9RaoRYXhcDho\\nb2/P+AcWiURwu90zznhaDeQaMazGa6Sjo4O2tra0nzkajZrTuFfTtTHbe7HYa0PCah6CwSDd3d1p\\nx0KhEMFgsEAtKhy73Z52L4WmaYRCITo6OgrYqvzSs2yuvVqvkWzvxWq6RsLhMGBUB7FYjFgsRiQS\\nobu7m6qqKmD1XBvzeS8Wc23ItvbzFI/H6ezspK6uDlVVcbvd7Nixo9DNKoienh5UVeXs2bNompbx\\nl1SpSSaTHDhwAFVVCYfDOBwOPB4PXq83bbrtarhG5vterIZrJNvNvilOp5OTJ0+aj0v92sjlvVjo\\ntSFhJYQQouhJN6AQQoiiJ2ElhBCi6ElYCSGEKHoSVkIIIYqehJUQQoiiJ2ElhBCi6ElYCSGEKHoS\\nVkIsQCwWw+fzYbPZsFgs2Gw23G43hw4dKnTTFsTr9WKxTP468Pl8aY+FKDS5GoXIkd/vp7a2lp6e\\nHiwWC16vl61bt3LixAkCgQB2u514PF7oZmYVDoexWCz09PSkHVcUBUVRMo4JUSwkrITIgc/no6Oj\\nA5vNRiwW4+zZsxw5coSTJ09y7do19u3bh6ZpuN3uog0syAyi7u5uhoeHC9QaIeYmYSXEPEUiEXp6\\nenA6nSQSCbZv355xzjPPPEN7eztgBFuxmr7KWkVFRcmt3SdKi4SVEPOUWiU7GAzOup3B3r17qamp\\nQVVVotGoeXz6uFCKpmlYLBZaW1vTjquqis/nw+l0YrFYsNvtNDc3p61aDUa3ZGoR0UAgYI6juVyu\\ntO4+r9dLc3MzMDkmldoUcL5jVAcPHsTtdpvtaW1tzWgPGKuKTz2vtrY27b0QIlcSVkLMUzQaxWaz\\nsWvXrjnP9fv9APT19aUdn20caOpzqqricrl45ZVXcLlc5jhZOBzG7XaTTCYzvj7VRfnwww/T0tJi\\nhl0qJNra2mhpaTHbFwqF0kJ3rjEqt9tNW1sbFovFbE8oFMLpdKZ1eQYCAVpbWzl16hQ+nw+Px2Pu\\n31TMXaOiyOlCiDkNDw/riqLotbW18zo/FovpiqLoDQ0N5jGPx6NbLJaMc0dHR3VFUfTW1lbzWEtL\\ni26xWPRoNJp27sGDB3VFUfRwOJx2rqIousvl0pPJpHk8EonoiqLofr/fPNbd3a0riqL39PSkvW5T\\nU1Na26Y/DgaDuqIo+rFjx7L+nG632zxmtVp1l8uVdl6qLVN/RiFysbbQYSnESqBpGjD/bdlTm80t\\nVGtrKzt37szY86i6uhqA0dHRjK+Z3j1ZX18PkLWbbj70KeNaBw4cwOv1UlNTY74XYPyc9fX1RKNR\\nxsbGKC8vJ5lM4nK50l6rvr6eWCyG1WpdUFuEkLASYh5Sv2RVVZ3X+anzFvrLubq62gwmTdMYGBgg\\nFouZkzeyqampWdD3mo9kMklfXx82my3r84qiMDIyQnl5OU1NTYTDYbP70uPxUF1dnXVCihDzJWEl\\nxDykKqr5htXAwEDa1+VK0zQCgQBdXV3m+JTb7cbtds9YKc20U+tCpcawUj+z1+slEAjMeH4qyLq6\\nujh06BDt7e1p57e0tBAMBqmoqFjSdorVQcJKiHnyeDzm9PWpW7inRCIRPB4PgFkB7dmzZ87XHRkZ\\nyThWX19PPB7H7/fj9/vNqiQajRIOhxfzY+QsFYJWq3XeW7E/8cQTPPHEE4yNjdHX10d7ezuhUIiB\\ngQEzyIXIhcwGFGKeUlVCtupC0zQaGhqora3l4MGDxONx3G73vLq+YrFYxmvF43F8Ph8vvvhi2mvo\\n0+6PWk6p72W1WqmoqCASiWQ9z2azmWNUqqoSCATMGYjl5eXs3r2bo0ePmuNWqenyQuRCwkqIeaqv\\nr6epqcmcVj51GrbVaqWrq4tYLEZbWxuKotDd3Z329VarFV3X0+43SnX3ZTN9EsXUcxcbWvP5+qlT\\n2f1+P6Ojo+Z9WikHDx4kmUym3SN26NAhc+r+VKqqoijKrPeoCTET6QYUIgddXV00Nzeb9ztVVFRQ\\nW1vLyMiIGV6KoqDrOoODg2mrQjz88MP09PTg9XppaWlB13W6u7upq6tjdHQ0rZJJdTk2NzdTW1vL\\n8PCweS4YM/8cDoc542++UuNKgUCA/v5+nnnmGfO56QE29fEzzzxDOBw2J05UV1ejqqpZQT7++OOA\\nMUaXarvdbqe+vh673U5XVxdjY2Ps27cvp/YKYSrQlHkhVrRYLKb7fD7dbrfrFotFt9vtem1trd7R\\n0cmP4fMAAADLSURBVKFrmqZ7vd6s9zOFQiHd6XTqiqLodrtdb2tr03Vd1202W9o9SJqm6X6/X7fZ\\nbOb9XanX8vv9usViMc9PPZ56j1XK9Hu9dF0322a3281jPp8v7b6q6Y9TAoGA7na7zfu6Uu3Pdp7T\\n6Ux7b6a/F0LkQtH1PHaCC7GKPPvss2bFIYRYHAkrIYQQRU8mWAghhCh6ElZCCCGKnoSVEEKIoidh\\nJYQQouhJWAkhhCh6ElZCCCGKnoSVEEKIoidhJYQQouhJWAkhhCh6/z9oWFi7XbkdAgAAAABJRU5E\\nrkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X1wG+dhLvpnoW9ZJgFI/pZoEqCbJnEaEQDjk1RxPCJA\\npZOkrSWCcjJn0tuOSTC51845c20BSuJEnpxGguR/Yk9tE1TnnJzeSSIStM+9EU8rEVBiVUkmIblQ\\nmzjuxMaClmTLsSVgQcv6ssS9fyx3iSVAEiBBAASe3wxGxGKxfAmt+Oj9FhRFUUBERFTBTOUuABER\\n0XwYVkREVPEYVkREVPEYVkREVPEYVkREVPEYVkREVPFWlrsAi+H3+9He3g6n0wmz2TzreaIoYmxs\\nDFarFZIkweFwoK2trYQlJSKixVjWYSWKIg4dOpTzNbvdjtdffx2SJCEQCOD48eP6a52dnbDZbGhq\\naipVUYmIaBGWdVjZ7XYcOnQoq1Y1PDyM1tZWAEAwGERPT4/hdZ/PB7/fj/7+/pKVlYiIFm5Zh5XT\\n6cTWrVtzvqYdHxgYwN69e7PeFw6Hl7x8RERUHEK1LbfU19eHrq4uAIAsy7BarZBlGXV1dYbzTCYT\\nJElCY2NjGUpJRESFqKrRgNFoFC6XS3+eTCYBICuoNJIklaRcRES0OFUVVqIooqWlRX8uy3IZS0NE\\nRMVSNWEVDodht9vLXQwiIloCy3qARaYDBw7gxIkTRbmWIAizvlZlXXxERMtCVdSsZFmGKIpZfVM2\\nmw0AMDExkfN92uuFmCvIiIiqxUMP7YMgIOvx0EP7ylKeqgirSCSScwULs9kMm82WNZBCkiSYzeZZ\\nRwIqipLzQURUK9asuZHz+Nq1N0tcElVVhNXIyMis/VVutxsjIyOGY6IowuPxlKJoRETL0uOPt8Nu\\n/5bhmN3+TTz2WHl+d1bFPCuv14uJiQkcO3Ys67V0Og2v12tYbqm9vR2hUKjgOVZaE2AVfGRERPMa\\nGjqJ554bxtWrK7B27U089pgHX/jCg2UpS1WEVU9PDwRBwAsvvJDz9VgshiNHjqC1tRWSJMHpdGL7\\n9u0Ffx+GFRFReVRFWJUKw4qIqDyqos+KiGihzp07h9bWVqxYsQKCIPCxwMeKFSvQ2tqKc+fOLcnf\\nE8OKiGraww8/jJ07d+LKlSuzjgTmY/7HlStX8PDDD+Phhx9ekr8nNgMWgM2ARNVnxYoVuHLlClav\\nXl3uoix7169fx7p163DzZvGHtzOsCsCwIqo+giDw33QRLdXnyWZAIqIqJIoimpub8zovc7eK2UiS\\nlNf1lgrDioiohtntdgSDwXIXY14MKyKiHIaGTmLHjm/joYf2YceOb2No6GRJryFJEjweD/x+v17z\\nCYVCsFqtMJlMcLlcSCQS8Pl8OHTokP4+v9+PQCCQtY5pJBKB3W6HyWRCe3s70uk0ACAej8Pv9+vn\\nad+jubkZoVAoqzYVCAT012OxWMGfyYIplDcACj8youqS69/00aOvKHb7NxVA0R92+zeVo0dfyfu6\\ni71GPB5XBEFQenp6lEQioaRSKUUQBOX06dOKLMuK1+tV/H6/Eg6HFY/Ho7/PbrcrsVhMGRsbU+x2\\nu6IoipJKpRSLxaKcOHFCSafTis/nU7xer6IoijI2NqY4nU79e1osFiUWiymyLCsOh0Npbm42lOfQ\\noUOKoiiK3+83fN+5Ps9i4G/eAjCsiKpPrn/T7e3fMoSM9tix49t5X3ex19DCIZMsy/rX3d3dSk9P\\nj6Ioin6eFjaKohjCqre3Vw8nTeZ5Wljt2bNHCQQC+jnhcFi/Rua1FUVRRFHU35dpqX5HVs1+VkRE\\nxXLtWu5fjVevrijpNWZuY/T9738f0WgUVqsVAPQFvN1uN6LRKMbGxuDz+bKuE4/HEQ6H9fcBubc7\\nSiQSaG9v1583NTUZXs98v1LiEZTssyIimqEY22MUe4uNcDiMaDSKEydO4Pjx4+jo6NADw+PxoL+/\\nH/39/di9e3fWe5ubm9HR0YFkMqk/IpFI1nk2mw1vvPGG/nzm9krlxLAiIpqhGNtjFHuLjVQqBavV\\nirq6OsiyjFAohGQyCQDo6OhAf38/EokEtm7dmvVer9eLSCSCaDQKWZbh8/kMgyo0u3fvRigUQiwW\\ngyzL2L9/f8VsOMtmQCKiGbRtMJ577qmM7TE+X9D2GMW4RmZQdHV1YWBgAFarVR9u7vV6ceLECWzf\\nvh0bN27M2qdPe7/ZbMbAwAB8Pp8+yjAcDmed19LSgmAwiLa2NmzcuBF79uxBb29vzvLker6UqmIF\\nC1EU0d/fj40bN+LixYvw+XyGtlZRFDE2Ngar1QpJkuBwONDW1lbw9+EKFkTVp1pWsHC5XDh8+HDO\\nmlW+EokEZFlGS0sLALXpMRQKGfYDnM9SfZ7LvmYVDocRiUTw4osv6sd8Pp/+vwFJkhAIBAwfdmdn\\nJ2w2W1bnIRHRcjQ8PDxrE2AhUqkU3G43EokE6uvr0dvbm7MPrByWdZ+VLMvo7u42BFUoFMKJEyf0\\n58FgED09PYb3zdZeS0S03ITDYezevRsDAwOLvpbD4cDevXvR1NSkT/x99NFHi1DKxVvWzYB+vx8m\\nkwn79+83HB8fH9e3rLdarRBF0bCFvSzLsFqtmJycLOj7sRmQqPpUSzNgpeBCtjn09fWhtbU167gW\\nTLIs68GUyWw2A1BDjYiIKt+y7rOSZRn19fXo6+uD1WpFMpmE1WrFrl27AEAf1llXV5fz/ZIkGWpc\\nRFR7TCYTrl+/zv2siuD69eswmZamDrRsa1baZLVYLIauri7s2rULXV1dGBkZQV9fHwA1zIiI5uJw\\nOPDMM8/g+vXr5S7Ksnb9+nU888wzcDgcS3L9ZRtWWhDNXI5k9+7dHDxBRHl7+eWX8fLLL2PdunUQ\\nBIGPBT7WrVunf5ZLYdk2A2ohNTOsWlpaIMvyovqjKmXGNhEtvc2bN2NkZKTcxaB5LNualTZIQvtz\\nJkmS9CCbmJjIec7MoCMiosq0bMMKUMNmtoUWbTYbzGZzznMkSYLZbJ51cIWibp2S9SAiovJY1mHl\\n8/kwNjZmOCaKIiwWix5Ebrc7q4ovimLWGlpERFS5lvWk4HQ6DafTaVjSvr29HT09Pdi5c6d+jtfr\\nNSy31N7ejlAoVPCwdU4KJiIqj2UdVoC68GIwGITdbkc8HkdnZye2b99uOCcWi+HIkSNobW2FJElw\\nOp1Z5+SDYUVEVB7LPqxKiWFFRFQey7rPioiIagPDioiIKh7DioiIKh7DioiIKh7DioiIKh7DioiI\\nKh7DioiIKh7DioiIKh7DioiIKt6y3c+KiIhUQ0Mn8eyzx3Ht2kqsWXMDjz/eji984cFyF6uoGFZE\\nRMvY0NBJfOMbxxCP/71+LB7/FgBUVWCxGZCIaBl79tnjhqACgHj87/Hcc8NlKtHSYFgRES1j167l\\nbiC7enVFiUuytJZ1WEmSBI/Hg2g0ClmWIUkSAoEAotGo4TxRFNHX14fBwUEcOnQo63UiouVqzZob\\nOY+vXXuzxCVZWkXrs5qYmEBdXV2xLpe3aDSqh4/ZbMbhw4fR1tamv64FWObmi52dnbDZbGhqaip5\\neYmIiunxx9sRj3/L0BRot38Tjz32+TKWqvgK3s8qFoshFArB7/ejsbER6XQabW1tEEURgiBgz549\\n2L9//1KV1yCRSCCRSMDlciGZTObc+dfn82HHjh36zsGAGnC9vb3o7+8v6PtxPysiqhSZIwAnJs5B\\nENbg1ltvw9q1N/HYY56qGlwBAFAKEIlEFEEQFEEQlFgspiiKovh8PkUQBMXtdis2m00xmUzK4OBg\\nIZddMEmSlEgkMuc5FotFSSQShmOpVEoRBKHg7wdAKfAjIyIquqNHX1Hs9m8qgKI/7PZvKkePvlLu\\noi2Zgvqs/H4/AGB4eBhbt24FAIRCIbjdbgwPDyMej6Ourq5kNav5yLIMWZZhtVoNx81mMwBgfHy8\\nDKUiIlqcWhkBmKmgPitJktDR0aH3CcViMQBqU5ums7MT4XC4iEWcv0yyLAMAkskkrFYrdu3apT8H\\nMGtfmiRJOZsOiYgqWa2MAMxUUFjJsqz32wBAJBIBAHg8Hv1YMpnUw2OpaTUmLZwANSy1Y6UqBxFR\\nKdXKCMBMBTUDtrS06AEFAL29vbDZbIaaSzQaLdkou/r6enR1dRmO+Xw+vbmSiKgaPf54O+z2bxmO\\nqSMAPbO8Y/krqGbl8/nQ09OD++67D2azGZIkIRgMAlBDyufzQZZldHd3L0lh89HU1ARJkjAxMbHg\\na2TWHomIKo020u+5557C1asrpkYAfr76RgBmKnRExp49exSz2awIgqB4vV7DcUEQFI/HU9QRIHMJ\\nBoNZx7SRfrFYTP86nU5nnScIQtYoQQ2mRv3N9iAiotIqeJ7VbCRJAgDYbLZiXC6v79fc3Jw1SEI7\\nLssy6urq0NzcjHA4rI9e1M7R5mYVgvOsiIjKY8ErWIyPj+sj8Ww2W1bf1VKz2Wzo7e3NGs0XiUTg\\ndDr1srjdboyMjBjCShRFw6AQIiKqbAWvDRiLxeByuWCz2eB2u9HR0QGHwwGLxYLdu3eXdO6S1WpF\\nIpHQn8uyjFAohL6+Pv1YMBjEwMCA4X2hUEjvayMiospXUDNgIpGA3W4HADgcDuzevVsf0DA8PIxo\\nNAqLxYJEIlGyWtbg4CAkScLFixchyzICgUBWbSsWi+HIkSNobW2FJElwOp3Yvn17wd+LzYBEROVR\\nUFhpE357e3uzhowDao2lp6cHXq8XR44cKWpBKwHDioioPAoKK6vVCpvNhtHR0VnPcTqdmJiYwOuv\\nv16UAlYShhURUXkU1Gcly7LeDDgbm82mjwwkIiIqhoJqVh6PB6Io4uLFi7Oek0/ta7lizYqIyilz\\nW5A1a27g8cfbq3sicIaChq739vbC6XRix44dWcPGE4mEvoJF5mg8IiJavKGhk/jGN44ZVluPx9Ul\\nl2ohsOasWbW3t2ctPRSPxyFJEgRBgM1mg9ls1reUVxQFDocDra2teOGFF5a88KXGmhURlcuOHd/G\\n8eP/Lcfxp/Av//K9MpSotOasWY2MjEAQhKxfzvX19QCACxcu4MKFCwCmt+HQwqwaw4qIqFxqcVuQ\\nTHOGVSqVKlU5iIhoDrW4LUimglewICKi0qvFbUEyFTQaUFsJIpFIQJZlmM1m2Gw27N6927D2XrVi\\nnxURldPQ0Ek899xwxrYgnpoYXAHkGVaxWAxdXV0QRXHWc5xOJ/r6+qo6tBhWRETlMW9YRaNRfYVy\\nh8MBn88Hl8ulrwk4OjqK3t5exGIxCIKA4eHhBa27txwwrIioHGp5fpVmzrBKp9NoamqCLMuzrgeo\\n0dYFtFgsc04aXs4YVkRUarnmV9nt38IPfrCjpgJrzgEWoVAIsixjz549cwYVAHR3d+PJJ59EKpXC\\nM888U9RCEhHVoqGhk/ibv/kHQ1ABQDz+93juueEylao85qxZOZ1OnD59Gjdv5j800mQywePx4Nix\\nY0UpYCG0LUJefPFFw3FRFDE2Ngar1QpJkuBwONDW1lbw9VmzIqKlojX1vfXWe3jzzbO4cWMS165t\\nhqJsBrAv6/zPfW4ffv7z7OPVas55VpIkFbxNfVNTU9nWBfT7/VlzwyRJQiAQwPHjx/VjnZ2dsNls\\naGpqKnURiYiyTDf17QDwQwAtAAQA/w3At3O+p1bmV2nmbAZMp9MFh5XNZoMsy4sq1EJIkoRUKpW1\\nPFQwGERPT4/hmM/ng9/vL2XxiIhm9dRTP5lq6jsO4C4Af4/pukQ7gNqdX6WZM6zq6+sLriWNjo7C\\nbDYvqlALoY1anNlENzAwAIfDYTjmdDoRDodLWTwiopyGhk7itdcuTT1biemQ0laseBDADgBPAdiH\\njRsfwQ9+8PmaGlwBzBNWbrcbqVQKp0+fzutisVgM6XR6Qf1BixGNRuF2u7OOy7IMWZZhtVoNx7Uw\\nHR8fL0XxiIhm9eyzx3H1asPUsxuYDqnMGtWDAL4Hu/06fvjDr9dcUAHzhNXevXsBAF6vd94LpdNp\\n/TztfaUiSRKampqyalXJZBLA9CK7ud5HRFRO6gK1WjC1Azg/9fV0jWrVqv8Mh+P/rMkalWbOsHI4\\nHOjq6kI8Hsd9992Hl156Ked5g4ODcDqdkCQJHR0daGlpWZLCzva9ZxtWX46+MyKiQkxMvIvpYBqG\\n2gx4GibTl2Cx/CMcjiRefrkbY2P/ULNBBeSx+WJvby+SySQGBwfR0dEBi8UCm82mb1+vDWwAgI6O\\nDvT39y95oTVLFUYzB2kQES2FoaGTOH/+GtSa1N9DDS3gzjv/Kw4ffrimw2mmvHYKHhgYQCQSQTAY\\nRDQaxdjYGMbGxvTX3W43/H5/yfuqBgYGDLUqhgwRLSdPPfUTvPPOPwI4CXUAxQoAN3HXXe8zqGbI\\ne1t7t9utD2KQJMmw6no5xGIxuFwuw7GZfVZa2SYmJnL2W81W9tkm/TIMiahYjKMAH4RWqwKAurp9\\n5ShSRcs7rDKVK6AyjY6OIh6P48iRI/oxURT1ScCtra3YtWuX3lyZuRq8JEkwm81obGwsQ8mJiNRa\\n1fQoQKNam/CbjwWFVSXINaji0KFDGB0dxYEDB/RjbrcbIyMjhrASRVFfSZ6IqNSma1WPYLq/SrV2\\nbQ8ee+wr5SpaxVq2YZXLhQsXsprwgsEgvF6vIdxCoRBCoVCpi0dEBCBzbpXW9DfdX/XRj95gf1UO\\nBe0UXKkSiQSCwSD6+/uRTqfR1dUFn8+nD6HXdjhubW2FJElwOp0L2nOLC9kSUTF84hP/Bb/73U4A\\nxzCzVhUOf4VhlUNVhFWpMKyIaLH27Xse3/veMCYnX4Y6CnAYWq2qpeU8RPFweQtYoaqqGZCIqJIN\\nDZ3EwYOvYHLyv2Lm3Kp163z43ve+Ws7iVbSihdVsw8OJiEj11FM/wZUrH0WuviqbDWz+m8Ocyy3l\\nEovF8LWvfU1fBDadTsPlcsFsNmPFihUlXxeQiGg5mB4BmLma+vegbqz4PWzefHu5irYsFBRW0WgU\\nTqcTvb29+lJHfr8foiiira0NjY2NOHjw4KxrCBIR1arpEYDZ+1OtW+eruf2pClXQAAuXywVRFDE8\\nPKwvrWQymeB2u/WdeC0WC5qbmzEyMrI0JS4jDrAgooV66KF9eOWV7VBHAGqL1q6AIPw7vvMdN/bt\\n+3p5C1jhCqpZaauqa0EVi8UAqDvvajo7O7n1BhHRDNmrq6t9VVu3WhlUeShogIUsy4b18SKRCAAY\\nVoNIJpPcmoOIKMO+fc/j1VcvINfq6hwBmJ+CmgGdTifGx8dx8eJFAEBzczMA4I033tDPsVqtsFqt\\nhmPVgs2ARFSooaGT2LnzWVy/HgbnVS1cQc2APp8PqVQK9913n74ahNYEGI1G0dzcDFmW0dHRsSSF\\nJSJaToaGTsLrDeL69funjhhHANbVbS5b2ZabgpoBu7u7EY/HEQqFEI/H0dHRgSeffBIAcPz4cUiS\\nBLfbbVhIloioFg0NncSjj/4QV66sx/RwdSOurp6/oi23pA2qqITtQ5YKmwGJKF87dnwb6iDpNwB8\\nHTPXARSEv8NPf/p/cCJwnhYcVhMTE0gmk7BYLKivry92uSoSw4qI8jE0dBK7dj2La9fuB3AOwB0w\\njgJ8DTbbDcTjg+Us5rKyoBUstBUr7Ha7vr19c3MznnnmmaIXkIhoOdGa/65duwa1+e+rAN5B5sCK\\n1asn8eyz3yhnMZedgvqsEokEnE4nAKCtrQ3RaFR/7eLFi9izZw+OHDlS0gnBkUgEkUgEGzduRDwe\\nh9PpzNqYURRFjI2NwWq1QpIkOBwOfa4YEVExPfvscbzzzl1Qf72eh9r89zdQwwoAfou9e9vZ/Feg\\ngsIqGAwCAMbGxtDU1ASr1aq/lkqlcPDgQQQCAezduxf79+8vbklziEQiEATBMKDD5XJBlmV94Ie2\\nzb22wgagTly22Wxoampa8jISUW25dk37tXob1KWV/ieAFwCsBrABLS2bOAl4AQpqBuzv74fb7dY3\\nNZxpz549aGlpQTgcLkrh5tPb25t1zO12G44Hg0H09PQYzvH5fPD7/UtePiKqPWvW3IDa/NcOtVZ1\\nGMCPAfwQ69bd4CTgBSoorGRZht1un/Mcm82GeDy+qELlSxAEfRUNjaIosFgs+vOBgQE4HA7DOU6n\\ns2SBSkS1Y9++5xGNHgPwGqbXAHwKwD6sXLkLe/Z8ks1/C1RQM2BLSwtGR0fnPCcWi2WFw1Lp7+/P\\nOhYOh/G1r30NgBqusiwbmisBwGw2AwDGx8fR2Ni45OUkour3la/48eMf/xuAzQC+gZnNf5/4hIXN\\nf4tQUM1q9+7dGBsbw89+9jPDGoEabRFbt9tdtAIWIhQKweVy4YknngCgrlMIYNZNIbngLhEt1r59\\nz2P16s/gxz/+LYB6AJ+EulLFdPMf8A9crWKRCqpZaaP92tra9MVrg8Egent7EYlEkEqlYLPZSr6C\\nxeDgIIaHhyEIAo4cOaIf54K6RLSUPve5v8XJk+cBWAFsmjrK1SqWQsHzrMbGxnDgwAH85je/AQAM\\nDw9jYGAAk5OT2LNnT1kWsN21axdefPFFHDhwAC6XS9+6ZKEEQcj5ICLS7Nv3PE6efBdqbWojgCtT\\nj+zNFU2mv+Pmiou06OWWJEmC1WrV+4HKra+vD36/H8lkEqIowuVyYXJyMus8k8mESCSC7du3Z702\\nXzBxBQsiWr/+r3DlijaY6yrUpr+fArgXwFcwPQn43/DlL/8JfvSjYHkKWiUKrlnNZLPZKiaoAHWy\\nsizLOHHihL5O4cTERM5zZ1vHUFGUnA8iIkAdTHHlyhpM16Y2AHgLwJcA/AFAEMBrEIRf47vf9TCo\\nimDOsDKZTFixYkXOh8lkMryufa39udQkSYLFYsHp06dzvi7LMsxmM2w2W9ZACkmSYDabORKQiAo2\\nNHQSP/nJ7wAIAD4HYGLq8Q7UFSseBODALbesxE9/upcjAItkzgEWu3btWtBFS9G/o835mlk70oJJ\\nGz7vdrsxMjKCrVu36ueIomjY3ZiIKB/qRorfh6LUQw2qf4damwoDuADgjwBWw26/FT/4wdc5p6qI\\nirZFSDkcOnQI3d3dhlXfPR4PXC6XvtxTOp2G1+s1LLfU3t6OUChUcM2Kq64T1a6hoZP467/ehxs3\\nzAA+hNo/9TzU3X/XQu23OgtF+UUZS1m9lnVYAeqAing8ri9k63K58OijjxrOicViOHLkiL67sdPp\\nzDmwYj4MK6Laow5P/x2AWwHcMnV0NdS1/17MONMHm+0Ct/1YInOGlclkgiAIiMfjaGxs1J/PRVEU\\nCIKAmzerb04Bw4qotqhBpfV5b4QaUlenvk5NPddqVRdx9OhTbPpbInP2WbW1tUEQBH2tvXz7sDgn\\niYiWu6Ghkzh58h0A2go4NwF8AGA91C0//ufUcwXARmzY8D6Dagkt+2bAUmLNiqg27Nv3PJ5++ocA\\nGqDOlQLUEX83oA6ibkRmE6AgPIrvfMfBkX9LqKCwmpiYmHWdvVrAsCKqfmpQ/S9MNzxpYfUXAH4O\\nIA3gfQBmAOthMl3GU099kUG1xAqaFGw2m3H48OE5zwkEAti4ceOiCkVEVA5DQyfx9NP/L9TBFBsA\\n3IHpeVQxAA8BsAD4EwACPv7xm7h5838zqEpg3oVsBwcHIQiCXpvQtofPRVEUhMNhpFKp4paSiGiJ\\nDQ2dxJe+9DTUGtN1qH1U/QD+FsDvAJwGcA7ABgjCu3jkkU9wZYoSmrcZ0GQqfEUmt9ttmNdULdgM\\nSFSd1L2ofg7gHqhzqD6A2j/1EQB9GWc+igcfvIlXXvnvpS9kjZs3rDJ31O3s7ER3d/ec+1VZLBa0\\ntbUVr4QVhGFFVH3UPqqXoA5DNwG4DLXRqQ7Ae1BH/20AcAm33XYJ7777r2Uray0raICFx+NBIBCo\\n2jCaD8OKqPoIwuehBtJKqOG0CmpQvQ91cMUtAC6hoeEG3nxzuGzlrHUcul4AhhVRdVmzZiuuX2+G\\nOql3EuoK6rdBHfE3HVSC8EdMTorlKygVtlMwAESjUQwMDCCRSMx53rFjxxZcKCKipTQ0dBJf/OLX\\nAWyB2j91FeqAivVQa1QWTK9MMYnvfOfR2S5FJVJQWA0ODsLr9S5VWYiIlpw6mOIY1KDS9qFSoA6u\\neA/qSEAB6gCLS/jud/+KQ9MrQEHNgM3NzZAkCcPDwzXZb8VmQKLlTR1MEQawBtqgCbX5TwCQhLrm\\nn3p8xYo/4sYNNv1VioLCymQyobu7Gy+++OL8J1chhhXR8iYIO6D2Q62AGlSXofZRTUANsFugNgum\\ncPTo97nWXwUpqBmwvr6+4hapHRwchCRJiMfjkCQJPp8va8FdURT1ycySJMHhcNRkzZColq1f7wTQ\\nhOn+qRtQg+pdqOG1BmoT4BV897tfYVBVmILCqru7G319fQgGgxWxRuDg4CBsNpseTul0Gk6nE8lk\\nEl1dXQDUnYMDgYBhknJnZydsNhuamprKUm4iKq177/XgypXbodaarkCtVbUAGIc6t2oD1CHrKRw9\\n+jSDqgIVtDxFMBhEW1sbnE4nXnrpJYyPj2NiYiLnoxQkSUJLS4v+vL6+Hn6/Hz6fz1Dmnp4ew/t8\\nPh/8fn9JykhE5VVf/wDOnNECSYba5NcIdfmklVBrVzcgCH+AovyMQVWhCuqz0tYElGV57ouWYPNF\\nWZbhdrsRjUYN29pLkqQPBGlsbITVaoUoioYt7GVZhtVqxeTkZEHfk31WRMuHunHiCNRRf1pf1GUA\\n6wCcB3A3pgdZnIWi/K5cRaU8FNQMmO+w9VL0a5nNZkiShEQiga1bt+Y8R5ZlPZhmvhcAxsfHDSFG\\nRNVh5co/w82bk5genn5p6nEH1D6qezKOJ3H06PPlKirlqaCw6u3tXapyLEgymcw6FolEYLFY0NjY\\nCElSt6OerX9Nq30RUfUQhPuhhhQwHUgygE8CeBXqYIoVUAdYXMHRo4fY9LcMFL6k+jyi0Si+9rWv\\nFfuyeevt7cXevXsBzN9cSUTVY9++5zOCagOmg+qPAK5BHUxxD9T+KrVZsKFhJYNqmSh4uaV0Oo1I\\nJJJzzypGnaYPAAAfmUlEQVRFURAMBpFIJPDCCy8UpYCFCIVC2LRpE5544olFXafShucT0dzq6x/A\\nxMQHMDb7AWpQrZn6+i2ok39vAriE1av/iDffPF3ysi4X6atp/Orcr3DqzCl8ePNDBD3l3buroLBK\\nJBJwOp3z1li6u7sXVaiFkCQJoVAIo6OjJf/eRFQ+am3qHgBWGGtT16Hu+AuoNavN+ut1dUmk0wyq\\nTOcmzuHUmVP6I56Ko/XuVmxr2Ia/uO8vyl28wsLK7/dDlmUEg0G0tLTA5/PB6XTC5/NBURT4/X5s\\n2rSpLCtcBAIBnDhxwnDMZrMBACYmJnL2W2mvzzTbaD/WuIgqy3Sz3y1Qa02XoO7muwpqUL0PdZ+q\\nO6AF1YMP3olXXvnn8hS4Qkwqk/j9e783hNPlDy9jW8M2bGvYhq9+8qtoubMFq1asKndRdQUPXXe5\\nXPoE24MHD2JgYAAjIyMA1D4im82Gw4cPY+fOnUtT4hx6enoQCARyDpZobm5GOBw2jBiUJAkulyvn\\nAI25cOg6UeUw9k9pzX5nodagzkNd829mberX5Shq2V29cRWjb4/qwfTLs7/EpvWb9HDa1rAN91nv\\nq+j/kBdUs5JlGXa7XX/ucDgQCAT052azGV6vF/v37y9ZWPX19WUFVTQa1VeocLvdGBkZMYSVKIrw\\neDwlKR8RFVfu/ikZai3qTwH8B9RalQXqlh8T+PKXt+JHPypvn0spJa8k8cuzv9TD6fQ7p/HR2z6K\\nbVu24e9a/g7/+Jf/iDs23FHuYhakoLBqamrSh4MDgMvlAgCcPn1aDwO73Y6+vr4iFnF24XAYgDqE\\nXaslJZNJhMNhvSkyGAzC6/Xqyy8B6kCMUChUkjISUfGotSnAGFTnoG7xsRlqUG2CGlarAFys+uWT\\nFEXBm+k3DU16Z9Jn8MDmB7BtyzY8/dDTeGDzA9iwekO5i7ooBTUDer1evPTSSxgeHsb27dsBABaL\\nBY888og++q+zsxORSKTgJrZC5Zrsq7Hb7Xj99df157FYDEeOHEFrayskSYLT6dTLXwg2AxKVx/33\\nP4xXX30d2fOnzkLtkwLUARVbUO2rUtycvInfvvtbQzjdVG6qzXlb1Ca9T975Saw0FTzYu6IVFFba\\nUkaCIGBgYAA7d+6Ez+dDX18fvF4vUqkUIpFI1W4jwrAiKj1jUGm1A61G9RGotSkBmf1Tt912Ce++\\n+6/lKG7RXf7wMn7z1m/0YPrVuV/h7lvv1oNpW8M22Cy2iu5vKoaCwgpQA0tbHLalpQWyLKOtrQ2x\\nWAwA4Ha7MTAwYFivr1owrIhK6957PThzRqshzBxIoa1EUYfpZr806uouLeuBFO998B5+cfYXejj9\\n9t3f4s/u+DM9nD6z5TO47Zbbyl3Mkis4rGajzb3S1t2rRgwrotKZ7p/66NSfWrMfAHwawK+mvp5u\\n+ltuNSpFURBPxQ1Neu9cegef3vJpPZxa72nF+lXry13UsitaWNUChhVRaRjX99OchdrcB6gDKpZf\\n/9SNyRs4/c5pQzitNK3EZ+/9rB5O999+P1aYVpS7qBWnoLDq6emZt11UURQIglCW5ZaWGsOKaGmt\\nWbMV16/fgLF/6g9Ql0jaDLWfCsgMqtWrz+PatcpcjeLS9Uv49blf49SZU/jXM/+K37z1G9xrvtfQ\\n39RQ31D1/U3FUFBYmUzzr3urNQMu9WjAcmBYES2NoaGT+OIXvz71LNdE33VQd/jNnD/1Pr773b/C\\nvn1fn3m5snnn0jv4xZmp/qazp/Dae6+h5a4WPZw+veXTsK7LPYqZ5lZQWM22JmAymYQoivD7/Whu\\nbsaxY8eKVsBKwrAiKj7j3Ckge/6UNtHX2Ox39OjzZZ0/pSgK/nDxD3ownTpzChcvX8RntnxGrzW5\\n7nZh7cq1ZStjNSlqn5W23JLP58P+/fuLddmKwbAiKh6T6X6o/5RuA7AWxmHp2kCK1VDnT2VO9E2V\\nZaLv9ZvXETsfM4TTLatuMSxZ9LHbPgaTUPSdlwhLMMDC5/MhHA7j4sWLxbxsRWBYERWHsTa1DuoQ\\n9Mxmv0zlGUgxcW0Cvzr7Kz2cRt4aQbO1WQ+mP9/y59hSP3MQCC2Vok9xFgQh515XRES5m/yuQB1A\\noYWUtlq6dl5pguqtibemR+mdPYXXL74O190ubGvYBv+f+/HpzZ9G/drqmz+6XBS1ZhWNRuHxeGCz\\n2fDGG28U67IVgzUrooXJPYACUEPoCoALM96Ra1uP/1608kwqk3jtvdcMTXrvX3vf0KTnuMuB1StW\\nz38xKomCalYmk2nOIZbaL3G/37+4UhFR1Zh9AAUwXZvSBlFo52nnvFaU2tS1G9emt8g4ewq/OPML\\nWNdZsa1hGz537+fwrc9+Cx/Z+BEOIa9gBdWs5ttWw2w245FHHsGuXbsWXbBKxJoVUf6mQ2quARSZ\\nitfkl7qSmt4i4+wpxM7H8Keb/tTQ33TXrXct+PpUelzBogAMK6L5rV/vxJUr16ae5TOAQjtv4ZN8\\n35TfNPQ3jcvjeOCeB/RweuCeB3DrmlvnvxBVrKoIq3A4DIvFgra2tqzXRFHE2NgYrFYrJEmCw+HI\\neV4+GFZEs8sOKWApBlDcnLyJV9971bBk0bWb1/DZhs/q4fTJOz5ZUVuy0+IV1GcVjUYxPDysr7Bu\\nNpths9mwe/duw068L730Usl2Cta2JNE2YswkSRICgQCOHz+uH+vs7NR3ESaixbv99s/ivfe0EcCZ\\nIQXkHkDxPnIPoPjnnNe/8uEVjLw9YtiS/Y4Nd2Dblm3w2Dx4+qGn0WxtZn9TlcsrrGKxGLxer2GX\\n4EzBYBBOpxMDAwMYGxuD1+vFwYMH8cQTTxS1sJkSiYT+fWfbhFHbyiSTz+eD3+9Hf3//kpWNqBZM\\n90kBuUMKWMgAiguXLxi2ZP+3P/4b7r/9fmzbsg1dji78j7/+H7j9ltuL/vNQZZu3GTAWi8HpdAIA\\nHA4HfD4fXC6XvsX96Ogoent7EYvFIAgCFEWB2+021GaWWnNzM0KhUNbuv1arFaIoorGxUT+m7TA8\\nOTlZ8PdhMyBRoSElQF0ySTvX2OSnKAoScsLQpPfW+2/hP23+T/p6ep+651O4ZfUtS/kj0TIwb1hZ\\nrVbIsoze3l50dXXNet7BgwcRCAQgCAKSyWRJN1/MFVZaKMmyjLq6OsP5JpMJkiQZQiwfDCuqZYWF\\n1ExTQWWawC22t/D9/6dbDycAhi0yPnHHJ6puS3ZavDnviEOHDkGWZezZs2fOoAKgN6spioKBgQE8\\n+uijxSvlAmirvs8MKs1CwoqoFi0qpFbdBWy+DjS8ATScx60fNWFL/Ra8+u6r+NKffAlBdxCN5kb2\\nN9G85gyrn/zkJxAEAQcOHJjzIpFIBKIoor+/H52dnejt7S17WM22QjwR5WdBIXXLDaDhMtBgAhom\\ngNv+A3hnNfY88pi+JfvG9RuXtuBUleYMK0mSYLPZ5r2I2+1GMpmE2WxGS0vLrAMxlgv+L49qlTGg\\ngLlDSgE2XgcargINl9SQWj8JnN0EnLkVOFaPy2+8hXWr1pWk7FTd5gyrdDqNT33qU3ldSNt00Wq1\\n4vTpyty1k4hyyyukTJPAXa9P1ZymHh+agDPrgTP3AL+6B3jPBCjnlsUW87S8zBlW9fX1GB0dLeiC\\no6OjenCVk1YjnJiYyNlvNVeNcbYBFKxxUTWZPaAAYAOw5kNg8zjQkAIa3gHuvgLIq4A31wOv1gP/\\ncieQtqMc23dQ7ZkzrNxuNwYHB3H69GnDpN/ZxGIxpNNpdHR0FK2AC6VNWJYkyVB2SZJgNps5uIJq\\nUnZAAXpI3boCaLgANFwEGt4FNn4AnF+j1px+uRE4ux64uiLjPcVdbJZoLnOG1d69ezE4OIi2tjYk\\nEolZR9ZpvF6v/r5K4Ha7MTIyYggrURTnXZCXqNpkhZSwGdj0wVSt6fdqQK25Dpw1A2cswP/eCLx9\\nD3Bz5q63DCkqjzn3X3Y4HOjq6kIqlYLT6cRLL72U87zBwUE0NzdDkiR0dHSgpaVlSQo7l1xNd8Fg\\nEAMDA4ZjoVAIwWCwVMUiKhtBuF9/YMUksHkD8JkbwJffBZ78GfCVGNDwvjoY4kctwKH7gB/fDvxi\\nlVqLMgTVFgAfnfr6NSjKPzOoqKTyWsjW6/VicHAQAGCxWGCz2fQmNkmS9J2BOzo6SraMUTqdxv79\\n+yFJEsLhMGw2G9xuNzwej2GLklgshiNHjqC1tRWSJMHpdGatdJEvTgqmSqfXoNbeBDZrAyFuAndP\\nABdvBc5sAs5sBM6sA95fO/Wu2SbyAuXaUp5oprxXXY9EIggGg4hGo1mvud1u+P3+Ba9mvlwwrKgS\\nCcL9QN2HU8H0gfqn5Qbwdr3apHfmLuDcRuDatYx3MaBoeVnQFiGSJEGWZX0QQ61gWFElmFQmseLO\\nPzEOIV81OVVrmupzOn83MKk14823FJKGIUWVqyr2syoVhhWVw9UbVzHy1gge/M8dajBtuQxcXjk1\\nv2mzGk4X10PdJ0pzKeNr1qJo+WNYFYBhRaVw8fJF/PLsL/GX/9ffquF051XgvbVT4bQeONMMfLBm\\n6uwNGe9kQFH1YlgVgGFFxaYoCsblcZw6cwpf/fY31HCq/xA4t246nN5aB1xvzHjXQgIKYEjRcsaw\\nKgDDihbr5uRN/Psf/x2nzpzC4898Ww0nARm1pvXAH9cCkw0z3smAotrGsCoAw4oKdfnDy/j1uV/j\\n1JlT+M7hILD5CvC+1t90i/pnahWAucIJYEBRrWNYFYBhRfN574P3cOrMKez8L11qren2q2pNSas1\\nnV2vDo4wrMMHzB1OAAOKah3DqgAMK8qkKAriqTjua/vc9BDyDTfUQNLC6e116srkiw6nTwP41Yxj\\nDCiqHQyrAjCsatuNyRtYteUjxvlNk1BXIdea9d5dAygzm/SAxdecAIYT1TKGVQEYVrVFWPNRtY9J\\nC6Z7prbIyBwMkbZBHSGRaWYwAQsLJ4ABRaRiWBWAYVV9DKuRb/jQWGvadA04nzGE/FwzcGX1jCvk\\nE0wAw4locRhWBWBYLU+593BSgE3XjeG07qa6wOuZ9cCZJuB8HXBjRcZ7ih1MAMOJKD8MqwIwrCpX\\n7kDKsGISuOvqdDBtuQxcXz210OvUenoXNgCK1qS3FMEEMJyIFqYmwkoURYyNjcFqtUKSJDgcjgWt\\nEM+wKo95gyiXNTfVQGpYqW4wePcEkFw/FU5Tj4lNc1yAwURUSebcKbgaSJKEQCCA48eP68c6Ozth\\ns9nQ1NRUxpLRgkIopy1A3dWpXW+nHtbLwNt1wJk7gFMfB85uBK6tmvG+XIGkYTARVZKqr1n5fD7s\\n2LEDO3fu1I9Fo1H09vYWvFEka1b5KV4IAdnzkwAICnDbpYxwSgOrb2RsLLgJOG+Z2ul2oYH0pwD+\\nY44yMZiISqnqw8pqtUIURTQ2NurHZFmG1WrF5ORkQdeq1bAqbvhocoRQThuAlTeBu1NAwwX1seWi\\nOirvzKapxzrgwi3IHkIOFF5DyrQJ6rYbqwCkcPTo0/jCFx5cxPWIaKGqOqy0UJJlGXV1dYbXTCYT\\nJEkyhNh8qimsbr/9s3jvvdQSXLmAEJrNuuvAlgtAw0Wg4Y/Ane+rYaT3N5mBS2sz3rCYQAJYUyKq\\nfFXdZ5VMJgEgK6g0hYZVtTCZ7kf+eZtv+GjmCCEDrXlOAepn9DeZrwBvmdVQ+nk9cO5O4Lo2hPxD\\nAO8VWCaAgUS0vFV1WMmyXO4iVJz7738YilJIAOUbPpq5+oig9jfd/j7QIE0PI1+hTK9AHrsdeGct\\nMJmrSW8+DCSialXVYbVQWnNfNXr11asoLIDmCZ8sM5rkVk0Cd18xzm+6NLVFRnwD8LPbgeRq5O5v\\nysQgIqplDKuao/3Cz1eB/UHrb0zNb5p63HEVeHdqi4wxC/C/7gE+yLztGEJENL+qDiubzQYAmJiY\\nyNlvpb0+02wDKKqjxqWGQnEogEVbT+8D9c9bbwDn1gNn7gKiHwfeWgN8+DZDiIgWparDymw2w2az\\nQZIkbN26VT8uSRLMZnNNDq74+MfX4tVXVwO4OfXI1xbAtB644zzQkEDH/70Np86cggABn733s9i2\\nZRu2NWzDJ+74BFaaqvq2IqIyqPrfKm63GyMjI4awEkURHo+njKUqn9/97mXcf//DePXVN5DZBNfQ\\ncANvvjlsOPfS9Uv6luynzp7Cr88NY0v9Fmzb8pfY1rANB90H0WhurJIaJxFVsqqeZwUA6XQaXq/X\\nsNxSe3s7QqFQwTWrappnlcs7l97BL878Qg+n37/3e2y9c6tea/rMls9g4/qN5S4mEdWgqg8rAIjF\\nYjhy5AhaW1shSRKcTie2b99e8HWqKawURcEfLv5BD6ZTZ07hwuUL+MyWz+jh5LrbhXWr1pW7qERE\\ntRFWxVJNYfXo//cohqVhbGvYpofTx2//OEyCqdxFIyLKwrAqQDWF1dUbV7F25dr5TyQiqgAMqwJU\\nU1gRES0nbPMhIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7Ai\\nIqKKx7AiIqKKx7AiIqKKx7AiIqKKVxU7BYfDYVgsFrS1tWW9JooixsbGYLVaIUkSHA5HzvOIiKhy\\nLfuwikQi6O7uRjgcznpNkiQEAgHDLsGdnZ2w2WxoamoqZTGJiGgRlm0zYCKRQE9PDxKJBKxWa85z\\ngsEgenp6DMd8Ph/8fn8pikhEREVSFftZNTc3IxQKZW1Vb7VaIYoiGhsb9WOyLMNqtWJycrLg78P9\\nrIiIymPZ1qzmI8uyHkyZzGYzAGB8fLwMpSIiooWo2rBKJpMAgLq6upyvS5JUyuIQEdEiLPsBFrOR\\nZXnB79Wa+xb6OhERGS22+6Rqa1ZERFQ5Fvuf/LLXrAppjtu4cSPq6+uXsDSq2f4HwAEW0/hZTONn\\nMY2fxTR+FtOK0RpV1rBKJBIIBAJ5n9/a2oonn3wyr3NtNhsAYGJiIme/lfY6ERFVvrKGVVNTE/r7\\n+5fk2mazGTabDZIkYevWrfpxSZJgNpsNw9mJiKiyVXWfldvtxsjIiOGYKIrweDxlKhERES1E1YRV\\nrnbhYDCIgYEBw7FQKIRgMFiqYhERUREs2xUs0uk09u/fD0mSEA6HYbPZ4Ha74fF4sGvXLv28WCyG\\nI0eOoLW1FZIkwel0Zq10kS92mE7jZzGNn8U0fhbT+FlMK8ZnsWzDioiIakfVNAMSEVH1YlgREVHF\\nY1gREVHFY1gREVHFY1gREVHFW7Fv37595S4ELS+iKOLo0aMYHx/H0NAQrl69WpPLV0mShM7OTtxz\\nzz2wWq14++23EQwGIQhCTXwe4XAY58+fz/mz1to9MttnUWv3yODgIIaGhvBP//RPePbZZ7F+/Xp8\\n7GMfM5yz4HtDoQWLx+OK2+1WIpGIkkqllHg8rvj9fiUSiZS7aEsmHo8rHo/HcMzr9SqSJJWpROUT\\nj8cVQRD0h8ViUQYHB8tdrJIYHh5WLBaLEo1Gs16rtXtkvs+iVu6RcDisiKKoP5dlWbHb7UooFNKP\\nLebeYDPgIkWjUXg8HlitVrhcLnzqU59CW1tbuYu1ZILBIHp6egzHfD4f/H5/mUpUPoIgIBKJQJZl\\nSJKEZDKJnTt3lrtYSyqRSKCnpweJRCJrF25Nrdwj+XwWtXSPSJKElpYW/Xl9fT38fj98Pp9+bFH3\\nRvFytfZIkqREo1ElnU4riUSi3MUpCYvFkvWzplIpRRCE8hSojCRJqupa9HzsdnvO2kQt3iOzfRa1\\nco+kUinF6XQqsiwbjms1S+1+WMy9wZrVIimKgrq6uppYxV2WZciynPW/SLPZDAAYHx8vQ6mokvAe\\nqU1msxmSJCGRSMx6zmLvjbJvvkjLRzKZBICc+4MBajNALYR2JkmSIMsyAPXzsVqthrUpaw3vkWy1\\nco9of/eZIpEILBYLGhsb9Y12F3pvMKwWqVZuRAD6z0kq7X+ImX/fnZ2dWcdqCe8Ro1q/R3p7e7F3\\n714Ai783GFaLUOs3Yq2rr69HV1eX4ZjP54PP5+PfPwGo7XskFAph06ZNeOKJJ4pyPfZZLcJsN2K1\\njXqi/DU1NUGSJExMTJS7KFShauEekSQJoVAIx44dK9o1GVZQP9h8H+l0es5rVfONqE3cm+1nq8ZJ\\njnM5ePBg1jGttq21z9ca3iNGtXqPBAIBnDhxwnBssfdGzTcDJhIJBAKBvM9vbW3Fk08+CUC9Effs\\n2WN4PfNG3Lp1a/EKWgHMZjNsNlvWzyZJEsxmc011nEuShEAggM7OTsPPrXUy19ovZQ3vkWm1eo/0\\n9PTg4MGDWQMpFntv1HxYNTU1ob+/v+D31eqN6Ha7MTIyYrjZRFGEx+MpY6lKz2azobe3N+sfWCQS\\ngdPpnHXEUy3gPaKqxXukr68PgUDA8DNHo1HYbDY0NTUt6t5gM+AC1eKNCKgz0AcGBgzHQqEQgsFg\\nmUpUPlar1TCvRJZlhEIh9PX1lbFUpaXk2Gi8Vu+RXJ9FLd0j4XAYgPofdlEUIYoiIpEIBgYG0NTU\\nBGBx9wa3tV+EwcFBOBwO/S9ClmW43W4cPny46poAM8ViMRw5cgStra2QJAlOpxPbt28vd7HKYnBw\\nEJIk4eLFi5BlOet/ldUmnU5j//79kCQJ4XAYNpsNbrcbHo/HMLqtFu6RfD+LWrhHck321djtdrz+\\n+uv684XeGwyrRaqFG5GIqNwYVkREVPHYZ0VERBWPYUVERBWPYUVERBWPYUVERBWPYUVERBWPYUVE\\nRBWPYUW0AKIowuv1wmKxwGQywWKxwOl04tChQ+Uu2oJ4PB6YTNO/Drxer+E5UbnxbiQqkM/ng8vl\\nwuDgIEwmEzweDzZt2oTTp0/D7/fDarUiFouVu5g5hcNhmEwmDA4OGo4LggBBELKOEVUKhhVRAbxe\\nL/r6+mCxWCCKIi5evIhjx47h9ddfx82bN7Fnzx7Isgyn01mxgQVkB9HAwADi8XiZSkM0P4YVUZ4i\\nkQgGBwdht9uRSCRyrv944MAB9Pb2AlCDrVLNXLimvr6ey4RRRWNYEeVJWxk6GAzOuap+V1cXHA4H\\nJElCNBrVj8/sF9LIsgyTyYSenh7DcUmS4PV6YbfbYTKZYLVa0dnZaVjFG1CbJbVFRP1+v96P1tzc\\nbGju83g86OzsBDDdJ6VthJdvH9XBgwfhdDr18vT09GSVB1BX0s48z+VyGT4LokIxrIjyFI1GYbFY\\nsHPnznnP9fl8AIDh4WHD8bn6gTJfkyQJzc3NeOmll9Dc3Kz3k4XDYTidzpw7VmtNlI888gi6u7v1\\nsNNCIhAIoLu7Wy9fKBQyhO58fVROpxOBQAAmk0kvTygUgt1uNzR5+v1+9PT0YHx8HF6vF263W9+z\\nqJKbRqnCKUQ0r3g8rgiCoLhcrrzOF0VREQRBaW9v14+53W7FZDJlnZtKpRRBEJSenh79WHd3t2Iy\\nmZRoNGo49+DBg4ogCEo4HDacKwiC0tzcrKTTaf14JBJRBEFQfD6ffmxgYEARBEEZHBw0XLejo8NQ\\ntpnPg8GgIgiCcuLEiZw/p9Pp1I+ZzWalubnZcJ5WlsyfkagQNb9TMFE+ZFkGkP8O0NoeZwvV09OD\\nHTt2ZO3z09LSAgBIpVJZ75nZPNnW1gYAOZvp8qFk9Gvt378fHo8HDodD/ywA9edsa2tDNBrFxMQE\\n6urqkE6n0dzcbLhWW1sbRFGE2WxeUFmIGFZEedB+yUqSlNf52nkL/eXc0tKiB5MsyxgdHYUoivrg\\njVwcDseCvlc+0uk0hoeHYbFYcr4uCAKSySTq6urQ0dGBcDisN1+63W60tLRU9YaktPQYVkR50GpU\\n+YbV6Oio4X2FkmUZfr8f/f39ev+U0+mE0+mctaY0206tC6X1YWk/s8fjgd/vn/V8Lcj6+/tx6NAh\\n9Pb2Gs7v7u5GMBhEfX19UctJtYFhRZQnt9utD1/P3LZcE4lE4Ha7AUCvAe3evXve6yaTyaxjbW1t\\niMVi8Pl88Pl8eq0kGo0iHA4v5scomBaCZrM5763pn3zySTz55JOYmJjA8PAwent7EQqFMDo6qgc5\\nUSE4GpAoT1otIVftQpZltLe3w+Vy4eDBg4jFYnA6nXk1fYmimHWtWCwGr9eLF154wXANpYQbe2vf\\ny2w2o76+HpFIJOd5FotF76OSJAl+v18fgVhXV4ddu3bh+PHjer+VNlyeqBAMK6I8tbW1oaOjQx9W\\nnjkM22w2o7+/H6IoIhAIQBAEDAwMGN5vNpuhKIphvpHW3JfLzEEUmecuNrTyeX/mUHafz4dUKqXP\\n09IcPHgQ6XTaMEfs0KFD+tD9TJIkQRCEOeeoEc2GzYBEBejv70dnZ6c+36m+vh4ulwvJZFIPL0EQ\\noCgKxsbGDKtCPPLIIxgcHITH40F3dzcURcHAwABaW1uRSqUMNRmtybGzsxMulwvxeFw/F1BH/tls\\nNn3EX760fiW/34+RkREcOHBAf21mgGU+P3DgAMLhsD5woqWlBZIk6TXIJ554AoDaR6eV3Wq1oq2t\\nDVarFf39/ZiYmMCePXsKKi+RrkxD5omWNVEUFa/Xq1itVsVkMilWq1VxuVxKX1+fIsuy4vF4cs5n\\nCoVCit1uVwRBUKxWqxIIBBRFURSLxWKYgyTLsuLz+RSLxaLP79Ku5fP5FJPJpJ+vPc+cY6WZOddL\\nURS9bFarVT/m9XoN86pmPtf4/X7F6XTq87q08uc6z263Gz6bmZ8FUSEERSlhIzhRDXnmmWf0GgcR\\nLQ7DioiIKh4HWBARUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVj\\nWBERUcX7/wEMgOSMA0DVtAAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X1QW2eeJ/rvEY6xnQQk2c6bkwCCTPcm7hkjQXdPd8d4\\njYT7TurWdGyEk92aOzW1AZG+N+47VY6FO+s7ns102cKZ2hnn3iSI3N3bO3t7Agh3za1Q2wbJE9wv\\n09uA5N5+b0cHiJPYcWxxhN8dm3P/OJyDDhIvB4Te+H6qKKOjI/FDAr5+zvmd5xFkWZZBRESUw0zZ\\nLoCIiGghDCsiIsp5DCsiIsp5DCsiIsp5DCsiIsp5DCsiIsp5a7JdwHJ4vV40NDTA4XDAbDbPuV84\\nHMbIyAisVitEUYTdbkd9fX0GKyUiouXI67AKh8M4duxYyvsqKytx9uxZiKKItrY29Pf3a/c1NTXB\\nZrOhoqIiU6USEdEy5HVYVVZW4tixY0mjqoGBAdTW1gIAfD4fWltbdfd7PB54vV50d3dnrFYiIlq6\\nvA4rh8OBbdu2pbxP3d7T04ODBw8mPS4QCKx4fURElB5CoU231NnZiebmZgCAJEmwWq2QJAklJSW6\\n/UwmE0RRRHl5eRaqJCIiIwqqGzAUCqGmpka7HYvFACApqFSiKGakLiIiWp6CCqtwOIzq6mrttiRJ\\nWayGiIjSpWDCKhAIoLKyMttlEBHRCsjrBotER48exalTp9LyXIIgzHlfgZ3iIyLKCwUxspIkCeFw\\nOOnclM1mAwBMTk6mfJx6vxHzBRkRUSHYseMwBAFJHzt2HM5aTQURVsFgMOUMFmazGTabLamRQhRF\\nmM3mOTsBZVlO+UFEtBoUF99JuX3dursZrmRGQYTV0NDQnOernE4nhoaGdNvC4TBcLlcmSiMiyjv7\\n9jWgsvIV3bbKym/jpZey93ezIK6zcrvdmJycxMmTJ5Pui8fjcLvduumWGhoa4Pf7DV9jpR4CLICX\\njIhoXn19p/H66wO4ebMI69bdxUsvufDMM9uzVk9BhFVraysEQcCbb76Z8v5IJIKuri7U1tZCFEU4\\nHA7s3LnT8NdhWBERZUdBhFWmMKyIiLKjIM5ZERFl0q1bt/DKK6/goYcegslkgiAIq/6jqKgItbW1\\n+PDDD1fkNWdYEREZ9Kd/+qf41a9+hZ/85Ce4ffv2nB3Eq+njxo0bePbZZ/Hss8+uyGvOw4AG8DAg\\nEQHAPffcg8nJSaxfvz7bpeSU27dvY/369bh7N/0t7gwrAxhWRAQofwv4dyC1lXpteBiQiIhyHsOK\\niIhyXsFMZEtElAv6+k7j+PF+3Lq1BsXFd7BvX4Phi2nT8RwFR6ZFAyDzJSOiuf4OvPvuoFxZ+W0Z\\nkLWPyspvy+++O7jo517uc0SjUdlut8vt7e2yxWKRKysr5XA4rN3f09Mj22w2WRAE2e12y5IkaY9z\\nOp3ygQMHZIfDIYuiKNvtdtnj8cgWi0V2uVzyyMiI9tj29nZDr81y8TAgEVGaHD/ej2j0O7pt0eh3\\n8PrrAxl9jkgkAkEQEIvF4HQ64fV6ASiTeDc1NaGzsxMTExMAoN0HKKutT05OIhAIQJZlRCIRNDQ0\\nYHR0FNFoFE6nE5FIBAMDA7rHZQLDiogoTW7dSn1m5ebNoow+h9lsxv79+wEAHo8HsVgMgLJIrcfj\\nwc6dO1FaWgqfz4fu7m7dY998801t3lSz2Yzdu3ejtLQULpcLHo8HJSUlqK+vBzD38ksrgWFFRJQm\\n6VhaIx3PYbVatc/lhDbyWCymW8evoqICkiRpt2ev8Zf4PGazWXc70xhWRERpko6lNVZyeY6NGzci\\nGo1qtyVJSrkWYC5iNyARUZqoHXuvv34oYWmNrxvq5EvHc8xlz549qKqqgtvthsPhQHNzM/bu3bvs\\n582EggircDiM7u5ubNy4EZcvX4bH40FFRYXu/pGREVitVoiiCLvdrh1zJSJKp2ee2b7sYFnuc6iz\\n7cy+bbPZ0NPTA4/HA1EU4Xa74fP5Fnxcqtuz71tpeT/dUiAQQDAYxFtvvaVt83g86OjoAKB0v7S2\\ntuoWX2xqaoLP59MF2mJwuiUiAjjd0nw43VIKkiShpaVFF1R+vx+nTp3Sbvt8PrS2tuoe5/F4Mt52\\nSURES5fXIyuv1wuTyYQjR47oto+NjWmtl1arFeFwWLeEvSRJsFqtmJqaMvT1OLIiIoAjq/lwZJVC\\nZ2cnamtrk7arwSRJkhZMidTul7GxsZUukYiI0iCvGywkSUJpaSk6OzthtVoRi8VgtVqxZ88eANAu\\nhCspKUn5eFEUdSMuIqLFWLNmDW7cuMH1rGa5ffs2TKaVGQPl7chKFEUAyrQizc3N2LNnD5qbmzE0\\nNITOzk4A0F3sRkSULvX19XjuuecQjUZx507qi3hXm9u3b+O1116D3W5fkefP27BSg2j2Fdd79+5l\\n8wQRrah/+qd/wtatW/G1r30NxcXFEARh1X+sX78e3//+9/H9739/RV7zvG2wUM9FhcNhbNu2TXef\\nyWSCKIqIxWKoqalJ2UhhMpkQDAaxc+fOpPsWun4gT18yIqK8lbcjK7VJYq6pQkRR1EZdc022OHtU\\nRkREuSlvwwpQwkY9d5XqPrPZnHIfURRhNpvnbK6QZTnlBxERZUdeh5XH48HIyIhuWzgchsVi0YLI\\n6XRiaGgoaR+Xa/mTQhIRUWbk7TkrAIjH43A4HHj//fe1bQ0NDWhtbcXu3bu1fdxut266pYaGBvj9\\nfsNt67womIgoO/I6rABgdHQUPp8PlZWViEajaGpqSmqaiEQi6OrqQm1tLURRhMPhSNlYsRCGFRFR\\nduR9WGUSw4qIKDvy+pwVERGtDgwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwr\\nIiLKeQwrIiLKeXm9rD0REc2vr+80jh/vx61ba1BcfAf79jXgmWe2Z7sswxhWREQFqq/vNL71rZOI\\nRr+jbYtGXwGAvAssHgYkIipQx4/364IKAKLR7+D11weyVNHSMayIiArUrVupD57dvFmU4UqWL6/D\\nShRFuFwuhEIhSJIEURTR1taGUCik2y8cDqOzsxO9vb04duxY0v1ERIWouPhOyu3r1t3NcCXLl7Zz\\nVpOTkygpKUnX0y1aKBTSwsdsNuPtt99GfX29dr8aYImLLzY1NcFms6GioiLj9RIRZcq+fQ2IRl/R\\nHQqsrPw2Xnrp61msamkMj6wikQhefPFFjI2NAVBW4q2pqYHZbEZRUREOHjyY7hrnJAgCgsGgNqqK\\nxWLaCsEqn8+H1tZW3TaPxwOv15uxOomIMk3tAly37hI2btyLrVv/d+zadQh///dfz7vmCgCAbEAw\\nGJQFQZAFQZAjkYgsy7Ls8XhkQRBkp9Mp22w22WQyyb29vUaedslEUZSDweC8+1gsFnl0dFS3bWJi\\nQhYEwfDXAyAbfMmIiDLu3XcH5crKb8uArH1UVn5bfvfdwWyXtmSGRlbqaGRgYADbtm0DAPj9fjid\\nTgwMDCAajaKkpARHjhxJd6YuiSRJkCQJVqtVt91sNgOANjokIiokhdQFqDJ0zkoURTQ2NmrnhCKR\\nCADlsJqqqakJgUAgjSUuXJMkSQCAWCwGq9WKPXv2aLcBzHkuTRRFlJeXZ6ROIqJMKaQuQJWhsJIk\\nCYIgaLeDwSAAwOVyadtisZgWHitNHTGp4QQoYaluy1QdRES5pJC6AFWGDgNWV1drAQUAHR0dsNls\\nupFLKBTKWJddaWkpmpubddvYPEFEq92+fQ2orHxFt03pAnTN8YjcZ2hk5fF40NraiieeeAJmsxmi\\nKMLn8wFQQsrj8UCSJLS0tKxIsYtRUVEBURQxOTm55OdIHD0SEeUbtdvv9dcP4ebNIqxbdxcvvZSn\\nXYAqox0ZBw4ckM1msywIgux2u3XbBUGQXS5XWjtA5uPz+ZK2qZ1+kUhE+zwejyftJwhCUpegCtNd\\nf3N9EBFRZgmyLMvpCD1RFAEANpstHU+3qK9XVVWV1CShbpckCSUlJaiqqkIgENC6F9V9ampqtAaM\\nxVJHXGl6yYiIaJGWPIPF2NiY1olns9mSzl2tNJvNho6OjqRuvmAwCIfDodXidDoxNDSkC6twOKxr\\nCiEioty2pBksampqYLPZ4HQ60djYCLvdDovFgr1792b02iWr1YrR0VHttiRJ8Pv96Ozs1Lb5fD70\\n9PToHuf3+7VzbURElPsMHQYcHR1FZWUlAMBut2Pv3r1aQ8PAwABCoRAsFgtGR0czNsrq7e2FKIq4\\nfPkyJElCW1tb0mgrEomgq6sLtbW1EEURDocDO3fuNPy1eBiQiCg7DIWVesFvR0dHUss4oIxYWltb\\n4Xa70dXVldZCcwHDiogoOwyFldVqhc1mw/Dw8Jz7OBwOTE5O4uzZs2kpMJcwrIiIssPQOStJkrTD\\ngHOx2WxaZyAREVE6GBpZuVwuhMNhXL58ec59FjP6ylccWRFRrlOXBrl1aw2Ki+9g376G/L4YeJqh\\n1vWOjg44HA7s2rUrqW18dHRUm8EisRuPiIgyo6/vNL71rZO6GdejUWXapXwPrHlHVg0NDUlTD0Wj\\nUYiiCEEQYLPZYDabtcUPZVmG3W5HbW0t3nzzzRUvPtM4siKiXLZr179Hf//fpNh+CD/4watZqCh9\\n5h1ZDQ0NQRCEpD/OpaWlAIBLly7h0qVLAGaW4VDDrBDDiogolxXi0iCqecNqYmIiU3UQEdEyFeLS\\nICrDM1gQEVFuKsSlQVSGugHVmSBGR0chSRLMZjNsNhv27t2rm3uvUPGcFRHlur6+03j99YGEpUFc\\ned9cASwyrCKRCJqbmxEOh+fcx+FwoLOzs6BDi2FFRJQdC4ZVKBTSZii32+3weDyoqanR5gQcHh5G\\nR0cHIpEIBEHAwMDAkubdywcMKyLKZYV6jRWwQFjF43FUVFRAkqQ55wNUqfMCWiyWeS8azmcMKyLK\\nVamusaqsfAV///e7CiKw5m2w8Pv9kCQJBw4cmDeoAKClpQUvv/wyJiYm8Nprr6W1SCIimt+hQ+/o\\nggoAotHv4PXXB7JUUXrNG1bvvPMOBEHA0aNHF/Vk6hpRAwPZeXEkSUJra2vS9nA4jM7OTvT29uLY\\nsWMIhUJZqI6IKL36+k7Dbn8B69btRCSSeuXzQrjGCljgOitRFA0vU19RUZG1eQG9Xm/StWGiKKKt\\nrQ39/f3atqamJthsNlRUVGS6RCKitOjrO40XXvguLlwAgM0AqlLuVwjXWAELjKzi8bjhsLLZbJAk\\naVlFLYUoipiYmEiaHsrn8yWNtjweD7xebybLIyJKq0OH3sGFCw8DeBjAvwLQAEB/jdW6da0FcY0V\\nsECDhcVigclkMtQwsZTHpIM6ee7AwAC6u7u17VarFeFwWDfpriRJsFqtmJqaMvQ12GBBRLmgr+80\\nGhvfxs2b6mDiDoC/AXAawACAIgB3UV19HuHw29kqM63mHVk5nU5MTEzgzJkzi3qySCSCeDyO+vr6\\ntBS3WKFQCE6nM2m7JElaMCUym80AgLGxsUyUR0SUVseP9+PmzcehhNQdzIyqtgN4FcBhrF9/Ea++\\n+r9kscr0mjesDh48CABwu90LPlE8Htf2Ux+XKaIooqKiImnEE4spJxzVSXZTPY6IKN8oE9Y2ADg/\\n/XESwC4AhwAcxtq1jThw4I8KomVdNW9Y2e12NDc3IxqN4oknnsCJEydS7tfb2wuHwwFRFNHY2Ijq\\n6uoVKXaurz1XW302zp0REa20ycmLUEZRfw5AAHAGwN/CZPoN7PZPceLEPhw+/M2s1phuCy6+2NHR\\ngVgsht7eXjQ2NsJiscBms2nL16uNDQDQ2NioO1+00lYqjGY3aRAR5Yq+vtM4f/4WlMN+34ESWsBD\\nD/0l3n772YIaTSVa1ErBPT09CAaD8Pl8CIVCGBkZwcjIiHa/0+mE1+vN+Lmqnp4e3aiKIUNEhU7p\\nAvy/oTRTHILaTPHww1cKNqgAA8vaO51OrYlBFEXdrOvZEIlEUFNTo9s2+5yVWtvk5GTK81Zz1T5X\\ntx/DkIiyqa/vNH7zm6vTt7ZDHVUBQEnJ4WyUlDGLDqtE2QqoRMPDw4hGo+jq6tK2hcNh7SLg2tpa\\n7NmzRztcmTgbvCiKMJvNunZ2IqJcN9MFmKxQLv6dy5LCKhekaqo4duwYhoeHddNDOZ1ODA0N6cIq\\nHA5rM8kTEeWLjz++CmA3Zs5XKe65pxkvvfRn2SorI/I2rFK5dOlS0iE8n88Ht9utCze/3w+/35/p\\n8oiIluX8+fOYOfQ3c76quPjjgj5fBRhcKThXjY6Owufzobu7G/F4HM3NzfB4PFoLvbrCcW1tLURR\\nhMPhWNKaW5zBgoiyqbz832J8vByJoyrg23jqqcv45S87slNUhhREWGUKw4qIsqWv7zR27z6O27f3\\nIXFKJcCFXbsG8IMfvJrdAldYQR0GJCIqVIcOvTMdVCeROLJau7bwz1cBaQyrudrDiYho+X7/ewmp\\nzlfdc8/Fgj9fBSww3VIqkUgEL774ojYJbDweR01NDcxmM4qKijI+LyARUaHr6zuN69evTd+amawW\\neBVr127IWl2ZZCisQqEQHA4HOjo6tKmOvF4vwuEw6uvrUV5ejvb29jnnECQiIuOOH++HLG/G7PWq\\ngG+jvPzebJSUcYYaLGpqahAOhzEwMKBNrWQymeB0OrWVeC0WC6qqqjA0NLQyFWcRGyyIKBt27DiM\\nwcGdAL4L4BHMHAL8Hb7//f+NhwFnU2dVV4MqEokAUFbeVTU1NXHpDSKiNNLPsj5j69aSVRFUgMEG\\nC0mSdPPjBYNBANDNBhGLxbg0BxFRmvT1ncbo6BWkmmW9kBZXXIihw4AOhwNjY2PakvVVVVUAgPff\\nf1/bx2q1wmq16rYVCh4GJKJMs9u/iUjkDcxest5mO4to9J3sFpdBhg4DejweTExM4IknntBmg1AP\\nAYZCIVRVVUGSJDQ2Nq5IsUREq80vf/np9Gf6LsBPPjHczJ3XDB0GbGlpQTQahd/vRzQaRWNjI15+\\n+WUAQH9/P0RRhNPp1E0kS0RES3P48Bv47LMbKe+7detayu2FKm3TLalNFbmwfMhK4WFAIsqkkpLd\\nuHLlFoBtmD0f4L33/hxXr/ZlqbLMW/IMFpOTk4jFYrBYLCgtLS3okCIiyrTDh9/AlStrAFgBXEDi\\nrBXABfzBHzyczfIybkkzWKgzVlRWVmrL21dVVeG1115Le4FERKtNX99pHDnSD0AAkKrjT1pVnYCA\\nwZHV6OgoHA4HAKC+vh6hUEi77/Llyzhw4AC6uroyekFwMBhEMBjExo0bEY1G4XA4khZmDIfDGBkZ\\ngdVqhSiKsNvt2rViRES55vjxfty+XQrgSwC+B+X6qoHpe3+B55//3Kq5vkplKKx8Ph8AYGRkBBUV\\nFbBardp9ExMTaG9vR1tbGw4ePIgjR46kt9IUgsEgBEHQNXTU1NRAkiSt8UNd5l6dYQNQLly22Wyo\\nqKhY8RqJiIy6dWsNgFsAvgngjemPdQBuorh4Et/7ni+b5WWFocOA3d3dcDqd2qKGsx04cADV1dUI\\nBAJpKW4hHR3Ji405nU7ddp/Ph9bWVt0+Ho8HXq93xesjIlqK4uI7AO6DciHwNwG8A+D/AWDDk0+u\\nzv4AQ2ElSRIqKyvn3cdmsyEajS6rqMUSBEGbRUMlyzIsFot2u6enB3a7XbePw+HIWKASERn10Ue/\\nAjCBmcaKwwAO4d57xVV3rkpl6DBgdXU1hoeH590nEokkhcNK6e7uTtoWCATw4osvAlDCVZIk3eFK\\nADCbzQCAsbExlJeXr3idRESLVVf3F/jVrz4DcADAfwHwPoC1AO7Dgw9i1Z2rUhkaWe3duxcjIyP4\\n53/+Z90cgSp1Elun05m2Ao3w+/2oqanB/v37ASjzFAKYc1FITrhLRLmkru4vcPr0BQAbocxY8TaA\\nf4Qy2/r/hYmJ4myWl1WGRlZqt199fb02ea3P50NHRweCwSAmJiZgs9kyPoNFb28vBgYGIAgCurq6\\ntO2cUJeI8sVMUJVCaa5I5XYGK8othq+zGhkZwdGjR/Gzn/0MADAwMICenh5MTU3hwIEDWZnAds+e\\nPXjrrbdw9OhR1NTUaEuXLJUgCCk/iIhWQl/f6emgug/ANcw0VyRaPQstprKkGSwOHDiAAwcOAFAO\\npVmtVu08UDaVlpbC4/Ggvr5eOwRIRJTrjh/vhxJQtwE8CSAKQEbirBXr1p3Fq6++lL0is2zJ0y2p\\ncm2apfr6ekiShFOnTmmNHpOTkynPW81V+1xz/3F0RUQrIRIZhzKiApQ/y5UAhgBcBHAPgEkEAv/H\\nqm2uABY4DGgymVBUVJTyw2Qy6e5XP1f/XWmiKMJiseDMmTMp75ckCWazGTabLamRQhRFmM1mdgIS\\nUdb19Z3Gp59egjLn3xSAs1C6/7ZDmcAW+Ku/2r2qgwpYYGS1Z8+eJT1pJkYg6jVfs0dHajCpoyqn\\n04mhoSFs27ZN2yccDutWNyYiypYXXvg/ocwB+CiAcwA+AnAVwAYAV/H883+Ew4e/mcUKc0PalgjJ\\nhmPHjqGlpQWlpaXaNpfLhZqaGm26p3g8DrfbrZtuqaGhAX6/3/DIikuEEFE6KR2AMSgjqpehXFd1\\nDep1VSbTb3D37qlslpgz8jqsAKCzsxPRaFSbyLampgYvvPCCbp9IJIKuri5tdWOHw4GdO3ca/loM\\nKyJKlwceeBqffnoflFHVegCbAbyVsIcHNtslRKO9Wakv18wbViaTCYIgIBqNory8XLs9H1mWIQgC\\n7t69m/Zis41hRUTpUFbmwgcfyAAsAK4DeAjK9EproU5YC1zGu+8eWvXnqlTznrOqr6+HIAjaXHuL\\nPYfFrjkiorl98MEaKKOpa1Ba0/8cM4cAZQAbYTJdZFAlyPvDgJnEkRURLVdp6ZcwOfk4gBsAPoMy\\nivoDAJ0Je72A55/fuCqXApmLobCa63ql1YJhRUTLMTOlEqCElA1KB6AEZT7A+wBcxfbtD2Fw8D9n\\nqcrcZGi6JbPZjLfffnvefdra2rBx48ZlFUVEVGj0UyrdgRJWcQCPQ7kI+AEAN/DUU+sYVCksOINF\\nb28vBEHQRhPq8vCpyLKMQCCAiYmJ9FZJRJTn9u71QR05KUvUuwCIAB6c3i5xRDWPBQ8DmkyG57qF\\n0+nUXddUKHgYkIiWQjn8F4dynkoCsBWzz1Ft2PArXLv2L1mpLx8sOLJKXOCwqakJLS0t865XZbFY\\nUF9fn57qiIjynHL47zyUP7eXoRz2+wWA/wkzI62L6O7+j9krMg8YarBwuVxoa2tbtWHEkRURGfXw\\nw024cEEG8CmU66huQWlXv3f69hVs376Fh/8WwNZ1AxhWRGSUIOyGcvgvDmX+vzhmwuoqgI8hyz/P\\nXoF5wvASIaFQCD09PRgdHZ13v5MnTy65KCKiQmAybQVQDuASlD+3k1BmrVBnqZjC9u32rNWXTwyN\\nrHp7e+F2uxe179TU1JKLylUcWRHRYm3Y4MCNG0o7uhJMxQCuYKb77yrWr7+I69dHslhl/jDU6uf1\\negEoS9lPTU3N+0FEtFrV1f3FdFCpy9Q/CmUV4JmgAs4xqAwwdBhQFEW0tLSs2gYLIqLFmLn49yqU\\noPoUwCYo56muAbiOp556InsF5iFDYVVaWppzk9T29vZCFEVEo1GIogiPx5M04W44HNYuZhZFEXa7\\nnYFLRCti69ZnMRNUHwL48vQ9N6GsBnwHwGX88peD2SkwTxkKq5aWFnR2dsLn8+XEHIG9vb2w2Wxa\\nOMXjcTgcDsRiMTQ3NwNQRoNtbW26i5Sbmppgs9lQUVGRlbqJqHD96lc3pz/7GMAWAD8D8AhmAuxj\\n/NVfceVfowyds/L5fKivr4fD4cCJEycwNjaGycnJlB+ZIIoiqqurtdulpaXwer3weDy6mltbW3WP\\n83g82vk3IqJ0eeCBp6GE0idQlqW/PP2vAGXpjyk8/vgDXKZ+CQx1A6pzAkqSNP+TZmDxRUmS4HQ6\\nEQqFdMvai6KIqqoqiKKI8vJyWK1WhMNh3RL2kiTBarUabgRhNyARzUVZUFE9WPUJlO6/W5jdVCHL\\nv8xShfnN0GHAxbatZ+K8ltlshiiKGB0dxbZt21LuI0mSFkyzHwsAY2NjuhAjIloKZY2qDQDMAH4/\\n/e9tKCsAq0El4fnnn8lekXnOUFh1dHSsVB1LEovFkrYFg0FYLBaUl5dDFEUAmPP8mjr6IiJaqn/z\\nb7yYnLRCWfn3KpSOv+vT98oJH9e5mOIyGJ9SfQGhUAgvvvhiup920To6OnDw4EEACx+uJCJarn/8\\nx59DGT3dhtL9pyxLr6xR9SCUqZU4U8VyGZ5uKR6PIxgMplyzSpZl+Hw+jI6O4s0330xLgUb4/X5s\\n2rQJ+/fvX9bz5Fp7PhHlJkHYCuBfQRlR3YDyJ/UWgItQmiruAriKoqLzGBzkFHTLYSisRkdH4XA4\\nFhyxtLS0LKuopRBFEX6/H8PDwxn/2kS0+ihB9RjUdnQlmD4P/YKKSlPFnTtsqlguw9MtSZIEn8+H\\n/v5+VFRUoLGxEQMDA+jv70d1dTVcLhfeeuutlap3Tm1tbTh16pRum81mA4A5W+nV+2eTZTnlBxER\\noE5Q+xiUQLoEJajWA/gt2P23Mgy3rtfU1GgX2La3t6OnpwdDQ0MAlHNENpsNb7/9Nnbv3r0yFafQ\\n2tqKtra2lM0SVVVVCAQCuo5BURRRU1OTskFjPmxdJyIAEITEhRPPQTlHdRkzAcagSjdDIytJklBZ\\nWandttvtGBmZmYjRbDbD7XbjyJEj6atwAZ2dnUlBFQqFtCVMnE6nFqaqcDgMl8uVsRqJqHAoh/8S\\ng+qPwaBaeYbCqqKiQmsHB4CamhoAwJkzZ7RtlZWVugBbSYFAAIDSwh4OhxEOhxEMBtHT06NNpeTz\\n+dDT06N7nN/vh8/HFlIiMkZ/nkodUf0LZgcVr6dKP0OHAd1uN06cOIGBgQHs3LkTAGCxWPDcc89p\\n3X9NTU0IBoOGD7EZlepiX1VlZSXOnj2r3Y5EIujq6kJtbS1EUYTD4dDqN4KHAYlWr5mgug/Ab6As\\nSX8byrma1aQVAAAgAElEQVSqTeAaVSvLUFipUxkJgoCenh7s3r0bHo8HnZ2dcLvdmJiYQDAYREtL\\nS1aaLFYaw4poddIH1dXpjwko7emPgof/Vp6hsAKUwFInh62uroYkSaivr0ckEgGgnCPq6enRzddX\\nKBhWRKuPybQVsqw/zKecp/rt9DYGVSYYDqu5qNdeqfPuFSKGFdHqsnXrs9NLfswOquTzVAyqlZW2\\nsFoNGFZEq0tyizqDKlsMzWDR2tq64FREsixDEISsTLdERJQu+qmUzkE5N5UcVFxIMTMMjaxMpoU7\\n3dXDgCvdDZgNHFkRrQ4zDRWAElTrocz9dz8AC5QFFa9g8+bruHjxh9kpcoVc/+w6fvrhT/He2HsY\\nHB/ENz73DfzlH/9ltssyFlZzzQmoXufk9XpRVVWFkycLc8JGhhVRYTt8+A389V+/gZnR0++hTKVU\\nNL1H4vL0hXH479rta/jJuZ9o4XTmwhl84cEvYEfZDtSV1+Grj30V9xffn+0y03vOSp1uyePxZHQW\\ni0xhWBEVLmU0Bcw+zDczqiqM81RXbl3Bj8/9GINjg3hv/D384pNfYNtD27CjfAfqyurwlce+gnvX\\n3pvtMpOkvcHC4/EgEAjg8uXL6XzanMCwIipMSlBtgTKpT2E1VMRvxvGjD36EwfFBvDf2Hn796a/h\\neMShjZy+/OiXseGeDdkuc0GG17NaiCAIKde6IiLKRTPnp+6FcpFv4ogqOaieeuqJLFW6OBM3JvDD\\nD36IwbFBDI4P4reXfosvbvkidpTvwDHXMXzp0S9h3Zp12S7TsLSOrEKhEFwuF2w2G95///10PW3O\\n4MiKqLAkz0wBzHT+fQjlXNXMearNm6/mXEPF5euXcXr8NAbHlXB6P/Y+vvzol1FXVocd5TtQ+0gt\\nitcUZ7vMZTM0sjKZTPO2rqt/xL1e7/KqIiJaYclBJQG4AmUBxd9C3/k3ieef34bvfS/7E2BfvHZR\\nCafpkdOYNIavPPYV1JXV4Y0/eQOORxxYW7Q222WmnaGR1ULLapjNZjz33HPYs2fPsgvLRRxZERWG\\n5KA6N32POqLaBCWs7gEwgXff/Ws888z2bJSKC1cvaME0OD6IjyY/wlcf/6o2crI/bMcaU9rP6OQc\\nzmBhAMOKKP/NHVSq7DZTfDT5kRJM0wH1ybVP8PTjT6OurA515XXY9tC2VRFOsxVEWAUCAVgsFtTX\\n1yfdFw6HMTIyAqvVClEUYbfbU+63GAwrovw1d2t6oswH1bn4Oe0ap8HxQcRuxLC9bLsSTmV1+MMH\\n/xBFpqKFn6jAGYrnUCiEgYEBbYZ1s9kMm82GvXv36paNP3HiRMaWtVeXJFEXYkwkiiLa2trQ39+v\\nbWtqaoLNZtMWZySiwpdLQTUmjc2E09ggrty+ogXTvi/tw9YHtsIkGFoXd1VYVFhFIhG43W7dKsGJ\\nfD4fHA4Henp6MDIyArfbjfb2duzfvz+txSYaHR3Vvu5cizCqS5kk8ng88Hq96O7uXrHaiCg36Gek\\nADIdVLIsQ5wQtWucBscHcfPOTe0C3P1/vB9Pbn5ywTlXaRGHASORCBwOBwDAbrfD4/GgpqZGW+J+\\neHgYHR0diEQiEAQBsizD6XTqRjMrraqqCn6/P2n1X6vVinA4jPLycm2busLw1NSU4a/Dw4BE+SN5\\nNAWsdFDJsoyzsbPa7BCDY4OYkqe0cKorr8PnNn6O4bQEC4aV1WqFJEno6OhAc3PznPu1t7ejra0N\\ngiAgFotldPHFVGGlhpIkSSgpKdHtbzKZIIqiLsQWg2FFlB9Sz0gBpDuoZFnGby/9VjvfNDg2iCJT\\nkdapV1dWhyprFcMpDeY9DHjs2DFIkoQDBw7MG1QAtMNqsiyjp6cHL7zwQvqqXAJ11vfZQaVaSlgR\\nUW7Tj6Zmz0iB6dtywj7GgmpKnsKvP/21rpV8/Zr1qCuvQ4OtAd/Z+R1UmCsYTitg3rB65513IAgC\\njh49Ou+TBINBhMNhdHd3o6mpCR0dHVkPq7lmiCeiwpS6iQLQj6aSg6qkJIZ4PHVQTclT+MUnv9CC\\n6fT4aZQUl6CurA7PPPEM2l3tKDeXp/+boSTzhpUoirDZbAs+idPpRCwWg9lsRnV19ZyNGPmC/ysi\\nyh/6kAKSZ6RIlBhkv0kaTd2duouff/JzbeR0evw0Nm3YhLqyOjz7+Wfxd7v+Do+VPgbKvHnDKh6P\\n44tf/OKinkhddNFqteLMmTPLr4yIaB4zIQXM3UShzkiRuM/MYb87U3cQOR/RRk4/+uBHeOi+h1BX\\nVoe9T+3FG8+8gUfufyQT3w4tYN6wKi0txfDwsKEnHB4e1oIrm9QR4eTkZMrzVvONGOdqoOCIiyj7\\niou34fbtO9O3Zo+mAP1hvw+hCynTr/HT8f+E98bew5/8v3+CH5/7MR4reQx1ZXX4sz/8M3T+z514\\n6L6HMvONkCHzhpXT6URvby/OnDmju+h3LpFIBPF4HI2NjWkrcKnUC5ZFUdTVLooizGYzmyuI8kzy\\nSApIPZpKaKIo2gI8chMojwJlH+P+J01oebcFdWV1+HfV/w7f/cZ3sfnezZkon5Zp3rA6ePAgent7\\nUV9fj9HR0Tk761Rut1t7XC5wOp0YGhrShVU4HF5wQl4iyi2pz0sBSaOpoilgyw2g/BpQPgVs+R0Q\\n24C1H69H1yv/FU8//jQ2btiYucIpbead08Nut6O5uRkTExNwOBw4ceJEyv16e3tRVVUFURTR2NiI\\n6urqFSl2PqkO3fl8PvT09Oi2+f1++HzZn+afiBYmCFsTJp5VD+eph/yuAmvGgfLfAnUXgT8fBby/\\nA3bFgHVm4KdlwH+sgvxWHLf+vwv4xue/waDKY4uayNbtdqO3txcAYLFYYLPZtENsoihqKwM3NjZm\\nbBqjeDyOI0eOQBRFBAIB2Gw2OJ1OuFwu3RIlkUgEXV1dqK2thSiKcDgcSTNdLBYvCibKjDmbJ+6J\\nA49KQPmYMnp6+CZwsRgY2wCM3wt88ARwy4J8XH6e5rfoWdeDwSB8Ph9CoVDSfU6nE16vd8mzmecL\\nhhXRytEHFAA8Bqy9Azx2Eyj7GCiPAQ/FgU/WAWP3Kh/n1gO3i5DtZT1o5S1piRBRFCFJktbEsFow\\nrIjSTxdSxXeBx+5Vgqk8DjwQB86XAONF0+G0Afgs8ewFQ2q1KIj1rDKFYUWUPoKwFVh3F3j8OlBm\\nUgJq8zXgYwswthkYuw/40Azc+TjFoxlSqw3DygCGFdHyCBs+r4RT+XWg7Bqw8TPgo1Jg/CEloD6y\\nAnduTO+ttqJvBHB5+nOG1GrFsDKAYUVkzKXrl7C5xq4EU/l1wHIb+HA9MPYIMGYFPt4C3DVhpgUd\\nSJ4ZHQDWA9gENaief/4P8b3vsat3NWFYGcCwIprfxWsXMTg2iKYDrUpAlX6mnGca3wCMVQAflwJT\\n6rIdwNxLdyTiaIoYVoYwrIj0zl85r63j9NYP/jNw/2fABxuUZojxDcD5J6bDCZgJKMBoSAnCOUxN\\nMaRWM4aVAQwrWu0+nPxQm5G8s/+7wL13lOubxqcD6sI6QH484RGpAgqYO6Q4iqLUGFYGMKxotfkg\\n/oGyRPvYe/hPp/6r0r03njBy+mQdIAuYmQYJWFxAFQG4m3CbIUXzY1gZwLCiQibLMsakMQyOK+H0\\n3fe+B6ydUkZOY9MB9WlxinACjI+gVDMhtXnzVVy8+MM0fCdUiBhWBjCsqJDIsozoRFQ7rPcPP3wH\\nKJJngml8gxJOWCicgKUGFEdRtFgMKwMYVpTPZFnG7y//Hp//+r8Gyq4rc+sB+pHT5bUwHk4AA4pW\\nGsPKAIYV5RNBeArYfGsmmMquA1OCfuQUW6lwAhhQlE4MKwMYVpRrdPPqCbISTmowlV8Dbpv0IyfJ\\nBiWcZktHOAEMKFopqyKswuEwRkZGYLVaIYoi7Hb7kmaIZ1hRpiXPRJ54pww8eFM/crpZNL1cxmPK\\nDBHx9bMeNDuUVAwnym3zrhRcCERRRFtbG/r7+7VtTU1NsNlsqKioyGJltFrNG0DzPlAGHro5E0xl\\nN4Fr9wDjVuDXFcB/swKT66Z3XmwoqZYaTv/NwDdAtHQFP7LyeDzYtWsXdu/erW0LhULo6OgwvFAk\\nR1aUyGTaihX9UTBtAR6eBMomlBnJH58ArhQrI6ZxKzD2KHB19shJtdxQUnHkRLmh4MPKarUiHA6j\\nvLxc2yZJEqxWK6ampgw9F8Mqf614sCza7EaGBKYp4JFJJZjKYsBjEjC5YXq5jM3A+Cbg2rqEB8wV\\nSIDxUEqsj+FEuaegw0oNJUmSUFJSorvPZDJBFEVdiC2EYQX09Z3GoUP/Bb///XlcuxYHMAUg8fW4\\nM+sRd2d9PgXANGt7PpondOaVcHiuaAp4JAaUf6p8PBoDJu6dDqbNwPh64PraeZ5rqYEEMJQo3xT0\\nOatYLAYASUGlMhpW+aCv7zSOH+/HrVtrUFx8B/v2NeCZZ7anvH9y8kMAa1FS8oD2+e3bd3HhgoT7\\n7luDy5cnAGzA1NRnkOUbuHPnFj77zAJlfaFiAPfP+uo3ACT+cb2NmR8xNcTWTm8vmr49O+xWwlKD\\nZT5znROax5q7wJYPlFFTeQzYEgdi9wJjFuBnW4DAVuBG4uu3nDBSMZSoMBR0WEmSlO0SMqqv7zS+\\n9a2TiEa/o22LRl8BADzzzPZZ958GcBJA4ue7pv/9t7h8+bsAqqe3fXf62S4DUJsDrgK4Z1YFs3+c\\nEkdP2RyNLiFYFjTfIbhpa+4Cj0rTS7THlEN8n96jtJD/9D7ggweU7j0ASoB/ssRaGEhU+Ao6rJZK\\nPdyXb44f79cFFQBEo9/B668fwjPPbJ91fz+UoEr8/N8n/PswgL9J+BxQRkfqj0yqE/uzX7fEc4LZ\\nDKtFBIthKUY990wBj12fWWjw4ZvAxWKllfxH9wPnHgRuFSU/bkEMIyKGVQG5dSv123lz+n/v+vtT\\nfT7739mf38LM4bwbSHZ91u1cGVml43BaCmvvAo/dmG4lv6a0lV9Yp1yEe3ozcG49cHuucGIAERlR\\n0GFls9kAAJOTkynPW6n3zzZXA0Wuj7iKi2c3NyjWrbub4v5Un8/+d/bn9wE4P/35Z0gOrBvQh9Lt\\nWc9zF8q5qsTtmThnlSbFd4HHE0ZOD9wCzpcCYw8C75UD565Bvv3rbFdJVJAKOqzMZjNsNhtEUcS2\\nbdu07aIowmw2F1xzxb59DYhGX9EdCqys/DZeeunrKe5vAPAKlMN+6ue7Ev797qzPEwlQRllXoD/U\\nByghlmh2N+BnyF43oLHRjHRTwg/Hf6ishDs+iN98+hvUbqlFXVkd6srq8OVHv4z198x1nRMRpVNB\\nhxUAOJ1ODA0N6cIqHA7D5XJlsaqVoXb9vf76Idy8WYR16+7ipZe+rm2fff/k5CcQhP8V99+/efrz\\nLty6dQcXLryB++4rwuXLZwD8DrL8GaambkKWBdy+fQfABqxfX4rPfa4c/+E/7NV1G+az2I0YTo+f\\n1pbMOBs7iy9t+RLqyurwtw1/iy9u+SLWrVm38BMRUdoV9HVWABCPx+F2u3XTLTU0NMDv9xseWfE6\\nq8Ly6bVPlXCaHjmJEyK+8thXtJFT7ZZarC2a7zonIsqUgg8rAIhEIujq6kJtbS1EUYTD4cDOnTsN\\nPw/DKr99cvUTnB4/jffG3sPg+CDOTZ7DVx/7qhJO5XVwPOzAPUWz2/GJKBesirBKF4ZVfjl/5by2\\nRPvg+CDOXzmPrz3+Newo34G6sjpUP1yNNaaCPxJOVBAYVgYwrHLbh5MfYnBsJpwuXb+Ep8uexo6y\\nHagrr8MfPfhHKDIt5TonIso2hpUBDKvcMi6N60ZO8ZtxbC/bro2cvvDgF2ASTNkuk4jSgGFlAMMq\\ne2RZxqg0qnXqvTf2Hq5/dh115XXayOnJzU8ynIgKFMPKAIZV5siyjPdj72udeu+NvYc7U3e0Tr0d\\n5Tvw+U2fz/kLtYkoPRhWBjCsVo4sy/jd5d9pI6fB8UEIEFBXPhNOT1ifYDgRrVIMKwMYVukjyzJ+\\n/emvtWAaHBtE8Zpi3cjJZrExnIgIAMPKEIbV0k3JU/jlxV9qI6fT46dx39r7dCOncnN5tsskohzF\\nsDKAYbV4d6fu4n988j+0kdMPx38I8zqz1qlXV16Hx0sfz3aZRJQnGFYGMKzmdnfqLs5cOKO1kf/o\\ngx9h872btU69urI6bCnZku0yiShPMawMYFjNuDN1B+HzYS2cfvzBj/HI/Y9oI6ftZdvx8P0PL/xE\\nRESLwLAyYDWH1Wd3P8Pwx8NaG/lPzv0EZeYybeS0vWw7Hrj3gWyXSUQFimFlwGoKq1t3bmHo4yFl\\n+qLx9/DTD3+KSkul1gzxdNnT2LRhU7bLJKJVgmFlQCGH1c07N/HfP/zv2sjpZx/9DJ/b9DktnL72\\n+NdgXW/NdplEtEoxrAwopLC68dkN/MuH/6K1kg9/PIwnNz+pC6fSdaXZLpOICECBhFUgEIDFYkF9\\nfX3SfeFwGCMjI7BarRBFEXa7PeV+i5HPYXXt9jX85NxPtFbyyPkIvvDgF7SLcL/6+FdRUlyS7TKJ\\niFLK+8V8gsEgWlpaEAgEku4TRRFtbW26VYKbmppgs9lQUVGRyTIz7sqtK/jxuR9rI6eff/JzVD9U\\njbqyOhzafghfeewruG/tfdkuk4hoUfI2rEZHR+Hz+eBwOGC1pj6X4vP50Nraqtvm8Xjg9XrR3d2d\\niTKz4tL1Syj/u3I4HnGgrqwOr/7rV/HHj/0xNtyzIdulEREtSUEcBqyqqoLf709aqt5qtSIcDqO8\\nvFzbJkkSrFYrpqamDH+dfDoMePPOTaxbsy7bZRARpUXBLv4jSZIWTInMZjMAYGxsLAtVZQ6DiogK\\nScGGVSwWAwCUlKRuGhBFMZPlEBHRMuTtOauFSJK05McutCwFl60gIjJmuadPCnZkRUREuWO5/8nP\\n+sjKyOG4jRs3orR05S9Unet/APnUYJEK688u1p9d+Vx/PtcOpOdoVFbDanR0FG1tbYvev7a2Fi+/\\n/PKi9rXZbACAycnJlOet1PuJiCj3ZTWsKioqVux6J7PZDJvNBlEUsW3bNm27KIowm826dnYiIspt\\nBX3Oyul0YmhoSLctHA7D5XJlqSIiIlqKggmrVMdyfT4fenp6dNv8fj98Pl+myiIiojTI2xks4vE4\\njhw5AlEUEQgEYLPZ4HQ64XK5sGfPHm2/SCSCrq4u1NbWQhRFOByOpJkuFqtQTnKy/uxg/dmVz/Xn\\nc+1AeurP27AiIqLVo2AOAxIRUeFiWBERUc5jWBERUc5jWBERUc5jWBERUc4rOnz48OFsF0FUyMLh\\nMN59912MjY2hr68PN2/ezJvpvkRRRFNTE7Zs2QKr1YqPP/4YPp8PgiDk7PcQCARw/vz5lPXlw3sx\\nV/358F709vair68P//AP/4Djx49jw4YNePLJJ3X7LPk9kGlJenp65GAwmLQ9Go3KTqdTDgaD8sTE\\nhByNRmWv15ty32yZq3ZZluWRkRHZ7/fLgUBAbm9vz6m6Z8uH1zoajcoul0u3ze12y6IoZqkiY6LR\\nqCwIgvZhsVjk3t7ebJc1p4GBAdliscihUCjpvnx4LxaqP5ffi0AgIIfDYe22JElyZWWl7Pf7tW3L\\neQ8YVkuQzz9Q+f7LnCjXX2tZluWWlpakmoLBoOx2u7NUkTGiKMqhUEiOx+Py6OhotsuZkyiKssfj\\nkf1+v1xZWZny5zuX34vF1J/r70V7e3vSNr/fLwuCoN1eznvAsDIgn3+g8v2XOZVcfa0TWSyWpNom\\nJiZ0v8C5TBTFnBqpLsZcP9/58l7M97clV9+LiYkJ2eFwyJIk6bar/6FUX/flvAdssDCgoqICb731\\nFpqbm+fdT5ZllJSU5NTM7oupvaenB3a7XbfN4XAgEAisdHlLlouvtUqSJEiSBKvVqttuNpsBAGNj\\nY1moanXie7GyzGYzRFHE6OjonPss9z3I+uKLlBsW84OUi4GQy2KxGACkXE8NUE6Y58NrKooiJEkC\\noHxPVqtVN/9mPuB7sfLU1zhRMBiExWJBeXm5ttDuUt8DhtUKyOUfqLnk6y9zLr/Wal35TP3PS+Jr\\n2tTUlLQt1/G9yI6Ojg4cPHgQwPLfA4ZVmuXjDxSQn7/M+fpa55PS0tKkQ8cejwcej4evcYbl23vh\\n9/uxadMm7N+/Py3Px3NWaTbXD5TX681SRYWLr3V2VFRUQBRFTE5OZruUVS9X3wtRFOH3+3Hy5Mm0\\nPeeqHFmpx04XY+PGjSgtLV3W10v8gZrrMNtiZbr2TEjn95TO13q51Asd56olVy7knE97ezsOHDig\\n26aOaEVRxLZt27JRlmF8LzKrra0Np06d0m1b7nuw6sJqdHQUbW1ti96/trYWL7/88qL3X8kfqJWs\\nPVu/zMv5nnL9l9dsNsNmsyXVIooizGZzTp4DTCSKItra2tDU1KSrVT2/mQ9/4FV8LzKntbUV7e3t\\nSX9HlvserLqwqqioQHd394o890r/QK1k7dn6ZV7q95Qvv7xOpxNDQ0O61zQcDsPlcmWxqsWx2Wzo\\n6OhIeu+DwSAcDkfWR65G8b1YeZ2dnWhra9PVGQqFYLPZUFFRsaz3gOes0ihffqDmov4gJcrVX+Z8\\nea19Ph96enp02/x+P3w+X5YqMsZqtequnZEkCX6/H52dnVmsamFyigXQ8+m9SFV/rr8X6vWYsVgM\\n4XAY4XAYwWAQPT09qKioALC894DL2i9RVVUVOjo6UF9fr9ve29sLu92uvTmSJMHpdOLtt9/O+mEp\\n1Vy1x+NxuN1u9Pf3a9saGhrg9/tz8jBJPrzWABCJRNDV1YXa2lqIogiHw4GdO3dmu6xF6+3thSiK\\nuHz5MiRJSvqfcy6Ix+M4cuQIRFFEIBCAzWaD0+mEy+XSdcrl6nux2Ppz9b1IdY2mqrKyEmfPntVu\\nL/U9YFgZkM8/UPn+yzyXXHytiSj9GFZERJTzeM6KiIhyHsOKiIhyHsOKiIhyHsOKiIhyHsOKiIhy\\nHsOKiIhyHsOKaAnC4TDcbjcsFgtMJhMsFgscDgeOHTuW7dKWxOVywWSa+XPgdrt1t4myjT+NRAZ5\\nPB7U1NSgt7cXJpMJLpcLmzZtwpkzZ+D1emG1WhGJRLJdZkqBQAAmkwm9vb267YIgQBCEpG1EuYJh\\nRWSA2+1GZ2cnLBYLwuEwLl++jJMnT+Ls2bO4e/cuDhw4AEmS4HA4cjawgOQg6unpQTQazVI1RAtj\\nWBEtUjAYRG9vLyorKzE6Oppy/sGjR4+io6MDgBJsuWr2xDWlpaWcpopyGsOKaJHUmaF9Pt+8s7o3\\nNzfDbrdDFEWEQiFt++zzQipJkmAymdDa2qrbLooi3G43KisrYTKZYLVa0dTUpJt5G1AOS6qTiHq9\\nXu08WlVVle5wn8vlQlNTE4CZc1LqCrOLPUfV3t4Oh8Oh1dPa2ppUD6DMpJ24X01Nje61IDKKYUW0\\nSKFQCBaLBbt3715wX4/HAwAYGBjQbZ/vPFDifaIooqqqCidOnEBVVZV2niwQCMDhcCAejyc9Xj1E\\n+dxzz6GlpUULOzUk2tra0NLSotXn9/t1obvQOSqHw4G2tjaYTCatHr/fj8rKSt0hT6/Xi9bWVoyN\\njcHtdsPpdGpLzeTyoVHKcTIRLSgajcqCIMg1NTWL2j8cDsuCIMgNDQ3aNqfTKZtMpqR9JyYmZEEQ\\n5NbWVm1bS0uLbDKZ5FAopNu3vb1dFgRBDgQCun0FQZCrqqrkeDyubQ8Gg7IgCLLH49G29fT0yIIg\\nyL29vbrnbWxs1NU2+7bP55MFQZBPnTqV8vt0OBzaNrPZLFdVVen2U2tJ/B6JjFh1KwUTLYUkSQAW\\nvwKxusbWUrW2tmLXrl1Jy7NUV1cDACYmJpIeM/vwpLpeWarDdIshJ5zXOnLkCFwuF+x2u/ZaAMr3\\nWV9fj1AohMnJSZSUlCAej6Oqqkr3XPX19QiHwzCbzUuqhYhhRbQI6h9ZURQXtb+631L/OFdXV2vB\\nJEkShoeHEQ6HteaNVOx2+5K+1mLE43EMDAzAYrGkvF8QBMRiMZSUlKCxsRGBQEA7fOl0OlFdXZ1T\\nC2JS/mFYES2COqJabFgNDw/rHmeUJEnwer3o7u7Wzk85HA44HI45R0pzrdS6VOo5LPV7drlc8Hq9\\nc+6vBll3dzeOHTuGjo4O3f4tLS3w+XwoLS1Na520OjCsiBbJ6XRq7euJqyurgsEgnE4nAGgjoL17\\n9y74vLFYLGlbfX09IpEIPB4PPB6PNioJhUIIBALL+TYMU0PQbDYvetXol19+GS+//DImJycxMDCA\\njo4O+P1+DA8Pa0FOZAS7AYkWSR0lpBpdSJKEhoYG1NTUoL29HZFIBA6HY1GHvsLhcNJzRSIRuN1u\\nvPnmm7rnkDO4sLf6tcxmM0pLSxEMBlPuZ7FYtHNUoijC6/VqHYglJSXYs2cP+vv7tfNWars8kREM\\nK6JFqq+vR2Njo9ZWntiGbTab0d3djXA4jLa2NgiCgJ6eHt3jzWYzZFnWXW+kHu5LZXYTReK+yw2t\\nxTw+sZXd4/FgYmJCu05L1d7ejng8rrtG7NixY1rrfiJRFCEIwrzXqBHNhYcBiQzo7u5GU1OTdr1T\\naWkpampqEIvFtPASBAGyLGNkZEQ3K8Rzzz2H3t5euFwutLS0QJZl9PT0oLa2FhMTE7qRjHrIsamp\\nCTU1NYhGo9q+gNL5Z7PZtI6/xVLPK3m9XgwNDeHo0aPafbMDLPH20aNHEQgEtMaJ6upqiKKojSD3\\n798PQDlHp9ZutVpRX18Pq9WK7u5uTE5O4sCBA4bqJdJkqWWeKK+Fw2HZ7XbLVqtVNplMstVqlWtq\\nauTOzk5ZkiTZ5XKlvJ7J7/fLlZWVsiAIstVqldva2mRZlmWLxaK7BkmSJNnj8cgWi0W7vkt9Lo/H\\nI5tMJm1/9XbiNVaq2dd6ybKs1Wa1WrVtbrdbd13V7Nsqr9crOxwO7boutf5U+1VWVupem9mvBZER\\ngrv7PukAAABUSURBVCxn8CA40Sry2muvaSMOIloehhUREeU8NlgQEVHOY1gREVHOY1gREVHOY1gR\\nEVHOY1gREVHOY1gREVHOY1gREVHOY1gREVHOY1gREVHO+/8B5wKzyrvpMy8AAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8G/WZ+PHPKIEkHLakQKGcsWR6UhpbMj23tJFk03K1\\nieVAu9tCwZbbXej+9geWuX6ldEsih+4u0CVYpt1td7etYznlcltsKZTQctmWoIVyBI0CpS0txB55\\nAznt+f2haGJZsmP5kmw/79dLr0Qzo/FjJ9Lj53squq7rCCGEELPMVOgAhBBCLA6ScIQQQswJSThC\\nCCHmhCQcIYQQc0ISjhBCiDkhCUcIIcScWFroAADC4TCxWAyAXbt2Ybfbqa+vz7gmGo3S39+P1WpF\\nVVUqKytxuVyFCFcIIcQUKIWehxONRkkkEqxbt8441tnZycDAgJF0VFWlsbGR7u5u45q6ujoCgQBl\\nZWVzHrMQQoj8FbxJLRgMZiQbgHXr1tHT02M8DwQCNDY2Zlzj8/nw+/1zEqMQQojpK3jC6evrI5FI\\nZB3XNM34e0dHB5WVlRnnHQ4HoVBo1uMTQggxMwqecNxuNx6PJyPphMNh6urqgFTi0TQNq9Wa8Tqz\\n2QzAzp075yxWIYQQU1fwhLNx40bMZjN2u522tjbC4TDJZJKrrroKgIGBAQBKSkpyvl5V1TmLVQgh\\nxNQVxSi1vr4+qqur8fl8VFZWEolEjHOjm9aEEELMXwWvcADa2tpoaWmhp6cHVVVxOBw5+3WEEELM\\nXwVPOI2NjXg8HlavXo3L5SKRSGCz2fB4PNO6r6Io4z6EEELMvYImnHRz2apVq4xjpaWldHd3Yzab\\n2bZtGzabDYChoaGc90ifz4ckHSGEmHsFTTj9/f3Y7fac53w+H5qmYTabsdlsWYMDVFXFbDZnJKvR\\ndF3P+RBCCFEYBU04NpuNeDye85ymacbcG7fbTW9vb8b5aDQ67WY3IYQQc6egCSe9LM3oUWmQql52\\n7dplVC+BQICOjo6Ma4LBIIFAYE7iFEIIMX0FX0sNUqPU4vE4K1euBFKTOscu3hmLxWhvb6eqqsoY\\nybZmzZq8v1a6/6YIvm0hhFhUiiLhzCVJOEIIURgFHxYthBBT8frrr1NVVcWSJUsmnAYhj8k9TCYT\\nJ598MjfeeCP79u2blX8zSThCiHnpC1/4AmvXrmXPnj3jjkqVx+Qf+/fv5/HHH+f555/nkksumZV/\\nM2lSE0LMS0uWLGHPnj0cffTRhQ5lQdmzZw8lJSUcOHBgxu8tCUcIMS8piiLv41kyWz9baVITQogZ\\nFI1GKS8vL3QYRUkSjhBCiDkhCUcIsaB0dW2npuYmPv3pW6ipuYmuru0FuUdaKBTCbrdjMpmoq6sj\\nmUwa54LBIFarlfLycoLBoFEZpecabtq0yTgfi8UmvKeqqng8Hpqbmzn77LNxOp00NjZitVqprq4m\\nGo0ar9m0adOUv59p0RcZQF+E37YQC06u9/FDDz2q2+036KAbD7v9Bv2hhx6d9H2ne4/+/n7dbrfr\\nuq7r8XhcVxRFj0QiuqZputfr1X0+n3HOYrHosVhM1zRNr6ys1MvLyzNet2nTJl3Xdd3n8+kej2fC\\ne6qqqiuKojc2Nuq/+tWvdEVR9M7OTl3TNN1ms+kWi0VPJpN6OBzWFUWZ8HuYrc/IRffJKwlHiIUh\\n1/u4uvrGjESRftTU3DTp+073HqMTTiAQ0BsbG41zqqrqFotF13Vdb2pq0pubm41zoVAoI1Glr9N1\\nXY9Go7rD4ZjwnumEk+v1Pp8v42spiqInk8lxv4fZ+oyUJjUhxIKxb1/uTYz37l0yp/dIGxgYyNhC\\npayszNiWJZFIZKyWn15bMs1qtRp/10eNGJvonqOPj3692WzOeF4oknCEEAvGsmUHcx5fvnx4Tu+R\\ntnLlyowV8dNbrkAqObzyyivGubFbsEzlnsVOEo4QYsG45ppq7PYbM47Z7Tdw9dWT38pkJu6Rtm7d\\nOoLBIJFIBE3TqK+vZ/369QCsX7+eYDBILBZD0zQ2bNgwqc0hJ7pnsctdOwohxDx0wQWfAuCuu25m\\n794lLF8+zNVXn28cn6t7pBOHzWajo6MDn8+Hqqp4vV5jW5WKigoCgQAul4uVK1fS1NREa2tr1j0m\\ne8+33nor4zXjvT7XublS8JUG/H4/1dXVOByOCcvCaDRKf38/VqsVVVWprKzE5XLl/fVkpQEhFob5\\nvtJAIpFA0zQqKiqA1FDnYDBId3d3gSObvZ9twSucaDQ67phwu93Ojh07UFWV5ubmjH+Iuro6bDZb\\nVkebEELMB4ODg7jdbhKJBKWlpbS2ts6bprGpKngfjt1uJxqNoqpqxqO1tdXY5TMQCNDY2JjxOp/P\\nh9/vL0TIQggxbZWVlVx//fWUlZUZkzuvuuqqQoc1qwrepNbW1pa1u+fY41arlWg0amw5DamRGVar\\nlZGRkby+njSpCbEwzPcmtWI2Wz/bgiecXEYnm3Ri0TSNkpKSjOtMJhOqqmYkoiORhCPEwiAJZ/Ys\\nmtWiI5EITqfTeD4wMACQlWzSJjt2XQixsJhMJvbv31/oMBacPXv2sHTp7HTvF13CiUajxqgNwJhB\\nK4QQo1VWVnL77bdL0pkhBw8eJB6Pc+mll05pBPBkFFXCSa+AKoQQR/Kzn/2Mn/3sZ6xYsQJFUeQx\\nzceyZcv45Cc/ydlnn839998/K/9mBR8WPdrGjRvZtm3bjNyrUBObhBBz47TTTqO3t7fQYUyLrut8\\n6MsX8/y7n4Kn/wEeux5GjgKgpuZmfvnLbxc4wplVNAlH0zSi0WhWX016MbqhoaGc/TijF6sTQoj5\\n4vWh16l/sJ5XT3oGftQDf/lwxvmpLBZa7IqmSS0cDudcacBsNmOz2bIGB6iqitlsHneEmp7aeiHr\\nIYQQhaTrOj+I/YCK1go+ftrH+ehzl2clG5jaYqHFrmgqnN7e3nH7b9xuN729vaxevdo4Fo1G8Xjy\\nX0xPCCEK5Q/JP9DwUAN/2f0XIl+OcM5J59C1ezuJV24kHv+OcV1qsdDzCxjp7CiaeTher5ehoSEe\\nfvjhrHPJZBKv15uxtE11dTXBYDCvOTgg83CEEHMvXdU0R5r5xke+gf8Tfo5acpRxvqtrO3fd1TNq\\nsVBPXouFzhdFk3AaGxtRFIXNmzfnPB+LxWhvb6eqqsrY73vNmjV5fx1JOEKIufRa8jXqH6znrXfe\\n4j8v+U8+dNKHCh1SwRRNwpkrknCEEHNB13W+H/s+10eu5x8/8o80faIpo6pZjIqmD0cIIRaK0VXN\\nti9vW9RVzWhFM0pNCCHmO13XaetvwxF0cN6Z5/HklU9KshlFKhwhhJgBr2qvUv9gPYN7B3nkK49w\\n9rvOLnRIRUcqHCGEmAZd1wn2B3G2OfnMqs/wxJVPSLIZh1Q4QggxRa9qr3LVg1eh7dWkqpkEqXCE\\nECJPuq7T2teKs82Jq8wlVc0kSYUjhBB52Knt5KoHrmJo3xCPXv4oHzjxA4UOad6QCkcIsWB0dW2n\\npuYmPv3pW6ipuYmuru0zdu8RfYR7+u6hqq0Kj83D41c+LskmT1LhCCEWhK6u7XzjGw9nrEkWj98I\\nMO1lYnZqO7nygSvZvX+3VDXTIBWOEGLOzUYlcued3RnJBiAe/w533dUz5XuO6CNs7t1MVVsVNfYa\\nfvPV30iymQapcIQQc2q2KpF9+3J/nE11X5nEYIIrH7iSdw68w/bLt/P+E98/5dhEilQ4Qog5NRuV\\nCMCyZQdzHs93X5kRfYS7e++mqq2Kz5Z/lt989TeSbGaIVDhCiDk105VI2jXXVBOPT29fmcRggq8+\\n8FX2HNjDY1c8JolmhhVNwolGo2zZsoWVK1eya9cufD4fZWVlGef7+/uxWq2oqkplZSUul6uAEQsh\\npmKmKpGx0s1xd91186h9Zc6fVDNduq/mm7/6Js2fbOb/fPT/sMS08LZ4Ljh9hiSTySm/tqOjQ/f5\\nfBnHGhoajL/H43Hd4/FknPd6vbqqqnl/LUCfwW9bCJGnhx56VLfbb9BBNx52+/X6Qw89WpB44gNx\\n/bz/OE//2L0f019484WCxLBY5P3JG41G9cbGRj2RSOi6ruuapukOh0NXFEU3mUx6c3NzXvcbHBzU\\nLRZLxrHW1la9vLzceN7Q0KB3dnZmXBMOh3Wv15tv+JJwhCgCDz30qF5Tc5N+3nnf1GtqbipIshke\\nGdbveuoufWVgpX77b27XDw4fnPMYFpu8NmCLRCJ4PB4g1cS1evVqGhsbCQaDuFwuVFVl586ddHR0\\nsHbt2knd0+/3YzKZ2LBhQ8bxnTt3GttHW61WotFoxnbSmqZhtVoZGRmZbPiAbMAmhID4QJwrH7iS\\n/cP7+Y9L/oP3nvDeQoe0OOSTndKVTDgcPpyxFCWjuctsNutOp3PS97RYLFnVy2iDg4O6oig5m+wU\\nRTEqrclCKhwhFq3hkWH9zifv1FcGVurfffy7UtXMsbwGDaiqSm1trdFZH4vFAPD5fMY1dXV1hEKh\\nSd9T0zRKS0tpa2vDarUyMDCA1Wpl3bp1AAwMDABQUlIybkyjKx8hhMjllYFXuPKBKzk4cpDHr3yc\\n96x8T6FDWnTySjiaphlNUgDhcBjAaGaDVILQNG1S91NVFUglrmuvvdY43tzczMDAAPX19ZO+lxBC\\n5DKij/C9p7/HrY/eyo1/cyPXfOQaGYFWIHklnIqKCiPJALS2tmKz2TKqj0gkkjGceSLpZGKz2TKO\\nr1+/HpfLRX19fT7hCSFEhlcGXuGr93+VEX1EqpoikNdKAz6fj8HBQc466yyqqqpQVdVoTotEIpSX\\nl6NpGrW1tZO6XzrRjE04FRUVaJrGzp078wkvg6IoOR9CiIVvRB/hjifv4KP3fpS171/Lo5c/Ksmm\\nCORV4TQ0NBCPxwkGg8TjcWpra7nuuusA6O7uRlVV3G43GzdunNT9zGZzxp9jpSd4AgwNDeXsxxmb\\nrIQQi9uOXTv46gNfBeCJK5/grJVnFTgikZbXsOiJpPtj8k0A5eXlBINB1qxZk3HcZDIZAwLKy8sJ\\nhUKsXr064+s5nU5jUMFkybBoIRamEX2EO5+6k3/e/s/c/KmbufojV2NSZLnIYjLlpW127tyJqqpo\\nmobNZsvqy5ksn89Hf39/RsKJRqNYLBZj9Jnb7aa3tzcj4USj0YzBCkKIxUuqmnki33HU0WjUmI8z\\n+mEymfS6urq858Vomqbb7faMYx6PJ2NujqZpWUvbeDyevL+Wrss8HCEWkoPDB/V/efxf9JWBlfod\\nT96hD48MFzokMYG8mtQSiQR2ux2AyspK1q9fT1lZGaqq0tPTQyQSwWKxkEgk8qp2EokEgUAAu91O\\nPB6nrq4uq4ktFovR3t5uDFZwOBxZ10yGNKkJsTC8vOtlrrj/CpaalvL9i79PubW80CGJI8gr4aQn\\ndba2tuYcshwMBmlsbMTr9dLe3j6jgc4USThCzG/DI8Pc8dQd3PbYbXzzvG/y9+f+vfTVzBN5JRyr\\n1YrNZqOvr2/caxwOB0NDQ+zYsWNGApxpknCEmL9eeuslvvrAV1lqWsoPLv4Bdqu90CGJPOT1a4Gm\\naUaT2nhsNpsxYk0IIWbC8Mgw3338u3ziB5/gsrMv45GvPCLJZh7Ka5Say+XKWGkgl0gkQkVFxbSC\\nEkKItBffepEr7r+CZUuW8XT909gsMvduvsqrwmltbWVkZISampqsVQASiQTV1dVomkZbW9tMxiiE\\nWISGR4a5/fHb+eQPPsnffuhv2faVbZJs5rkJ+3Cqq6uzloOJx+OoqoqiKNhsNsxmM5qmoaoquq5T\\nWVlJVVUVmzdvnvXgp0L6cIQofumqZvnS5Xz/4u9LolkgJkw4FosFRVHy/nBWFCXvFQDmiiQcIYrX\\n8Mgw//LEvxD4TYBbP3Mrjc5GGYG2gEzYhzM4ODhXcQghFrkX3nyBK+6/gmOOOobe+l7KLJNbdV7M\\nH/KrgxCioIZHhmn5TQt/8x9/w1c+/BXCXw5Lslmg8hqllp7tn0gk0DQNs9mMzWZj/fr1GeucCSHE\\nZEhVs7hMauJnLBajvr6eaDQ67jUOh4O2traiTzzShyPEzOnq2s6dd3azb99Sli07yDXXVHPBBZ86\\n4usOjhzku49/l9ufuJ1vf+bbNDgapK9mEThihROJRIxVmSsrK/H5fDidTmMNtb6+PlpbW+nv78fh\\ncNDT0zOlNc6EEPNLV9d2vvGNh4nHv2Mci8dvBJgw6fz+zd9z+X2XU7KshN76XlaZV812qKJYTLSy\\np6ZpusVi0RVF0YPB4ISrgLa2tuqKouhWq3XKK4nOBWS1aCFmRHX1jTroWY+amptyXn9g+IC+4bEN\\n+gktJ+j39N6jj4yMzHHEotAmrGGDwSCaptHU1JRzsc7RGhoauO666xgcHOT222+fwZQohChG+/bl\\nbiDZu3dJ1rHn//o8H//+xwmrYXrre/E5fbLl+yI0YcL56U9/iqIok94yOhAIANDT0zPpAFRVxePx\\nEIlEjAmkzc3NRCKRjOui0ShtbW10dnayadOmrPNCiLm1bNnBnMeXLx82/n5w5CAbHtvAp3/4aa6q\\nvIqev+uRJrRFbMI+HFVV894yuqysbMLVpHOJRCJGAjGbzdx77724XK6MOJqbm+nu7jaO1dXVYbPZ\\nKCuTUS1CFMI111QTj9+Y0Ydjt9/A1VefD8Bzf32OK+6/AstyC331fZxpPrNQoYoiMWHCSSaTnHvu\\nuXnd0GazsW3btklfrygK4XAYp9PJwMCAsa30aIFAgMbGxoxjPp8Pv9/Pli1b8opPCHFkkxl9ln5+\\n1103s3fvEpYvH+bqq8+n5rMf57bHbuNfn/xXbltzG1dVXiXNZwKYxNI2JpOJXbt2TfqG+b4mkUig\\nqmpGRTOW1WolGo1mJCNN07BarYyMjEw6NpBh0UIcSa7RZ3b7jdxxR80Rhzw/99fnuPy+y7GusHLv\\nxfdyRukZsx2umEcm7MNxu90MDg7yzDPPTOpmsViMZDI5YfLIl6ZpRnIZzWw2A2StWi2EmJ477+zO\\nSDYA8fh3uOuu8ftmDwwf4Dvbv8NnfvgZGp2NPPy3D0uyEVkmbFK7/vrr6ezsxOv1HnEHz2Qyidfr\\nNV6XD1VV0TQNgIGBAaxWK+vWrTOeA5SUlIz72lzNcEKIqcln9BnA7/7yOy6//3JOPOZE+hv6JdGI\\ncU1Y4VRWVlJfX088Huess85i69atOa/r7OzE4XCgqiq1tbV5bcCWrlzWrVvHunXrqK+vp729nc7O\\nTgAjEQkh5sZkRp9Bqqr55+3/zJofreHrzq/ziy/9QpKNmNhkJuvU1tbqiqIYEzudTqdeV1enO51O\\n3Wq1Gue8Xu+MTA4Kh8O63W7XdV3X+/v7dUVRcl6nKIoeiURynuPQBM/xHkKI3B566FHdbr8hYzKn\\n3X69/tBDjxrXPPvGs3pla6Ve8181+mvaawWMVswnk1q8s6Ojg3A4TCAQIBKJ0N/fT39/v3He7Xbj\\n9/tnrO8mvWzO0NDQjNxPCDF5440+u+CCT3Fg+AAbf72RO5++k4A7wBWrr5ARaGLSJrV451jpPpf0\\natHT0dLSQlNTU8ax9CCB9Mg0q9WKpmlZ/TgmkynvPhwZpSbE1Dz7xrNccf8VnHTcSbRd1MZpJacV\\nOiQxz0wp4cwUVVUpLy/PShrp4+kkU15eTigUyliJWlVVY+5OPiThCJGfA8MH2PDrDdz19F20uFu4\\nfPXlUtWIKclrP5yZZrPZaG1tzapQwuEwDofDqGjcbje9vb0ZCScajRqrWAshZsezbzzL5fdfzruP\\nezcxX0yqGjEtBd+Awmq1kkgkjOeaphEMBmlrazOOBQIBOjo6Ml4XDAaNtduEEDNr//B+vvWrb+H5\\nLw/f+Mg36PpilyQbMW0FbVJL6+zsRFVVdu3ahaZpNDc3Z1U96d1Gq6qqUFUVh8MxpX13pElNiIk9\\n88YzXH7f5ZxacirBC4OcWnJqoUMSC0RRJJy5JAlHiNz2D+/ntsdu4+7eu9nk2cSXP/xl6asRM6qg\\nfThCiOKQrmpOKzmNmC8mVY2YFTPWhyNzZoSYf/YP7+ebj3yT6v+q5p8+9k88eNmDkmzErMk74cRi\\nMb72ta8Zi2Ymk0mcTidms5klS5bkvY6aEGLudXVt52Nrr8LafAZ33/djbi+/R5rQxKzLK+FEIhEc\\nDgetra3GGmd+v59oNIrL5WLVqlW0tLSMu+aaEKLw7nswwt/94AaeLH+At7s38dadL3Prdf10dW0v\\ndGhigctr0IDT6SQajdLT02MsY2MymXC73cZunBaLhfLycnp7e2cn4mmSQQNiMYv+Ocp5//pZdr9+\\nLjzUCv97inGupuZmfvnLbxcwOrHQ5VXhpFeDTiebWCwGpHbfTKurq0NV1RkMUQgxXfsO7uPmbTdz\\n/n+fz2mvfgJ+8kBGsoHxtx8QYqbklXA0Tcto4w2HwwAZM/4HBgZkSwEhikj/n/pxtjl59i/P8mzj\\ns5yhfQDI7qsZu/2AEDMtr4RTUVFhJBmA1tZWbDZbxqKakUiEsrKymYtQCDEl+w7u46ZtN/G5H3+O\\n5k80c/+l9/Pu49/NNddUY7ffmHGt3X4DV18tS0WJ2ZXXPByfz0djYyNnnXUWZrMZVVWN5WUikQg+\\nnw9N02hoaJiVYIUQk9P3pz6uuP8KbBYbz/ie4d3Hv9s4N9H2A0LMprxXGvD7/QSDQZLJJLW1tWzZ\\nssU4vmnTpowBBMVIBg2IhWzfwX3c+uit3Bu7l3+t+VcuO/syGeosisaMLW2THigw3f1xZpskHLFQ\\n9f2pj8vvu5xyazn3XHgP/Y++zJ13drNv31KWLTvINddUSxUjCmrKS9sMDQ0xMDCAxWKhtLS06BON\\nEAvVvoP7+Naj3+L7se/zbzX/xqVnX8rPf/4Y3/jGw8Tj3zGui8dT/TaSdESh5F3hxGIx6uvriUaj\\nKIpCT08Pa9asoby8nMbGRq699trZinVGSIUjFpLeP/Zy+f2XU3LAyrIeB+w2s2zZQd58c4BY7O6s\\n62WujSikvCqcRCKBw+EAwOVyEYlEjHO7du2iqamJ9vb2aU36TG9PcM8992Qcj0aj9Pf3Y7VaUVWV\\nyspKYz6QEAtJV9f2jKawj33sFJ544k8Zz3/95Gu8fMqv+cu7n+Gio+qI/ffJqPHbjHssX/7lnPeW\\nuTaikPJKOOkRaf39/ZSVlWG1Wo1zg4ODtLS00NzczPXXX8+GDRumFJDf72dwcDDjmKqqNDc3ZwxG\\nqKurw2azyRBssaB0dW0f0xS2nW3bfszBg/cYzyMv/hvDF74Eu94Ld8T5+cg17NlzW8Z99u49I+f9\\nZa6NKKS85uFs2bIFt9tNRUVFzvNNTU1UVFQQCoWmFIyqqgwODmaNqgkEAjQ2NmYc8/l8+P3+KX0d\\nIYpNV9d2ampu4u/+7u6MfhfoPpxslu4FdzPDdY/Do/8P2jvh7ZPYs+f9Oe5YzfLlX8s4InNtRKHl\\nVeFomobdbp/wGpvNRmdn55SCiUQieDweenp6Mo53dHRkrULtcDimnNiEKCaZVc0tY84eeoue+hR8\\n/gp4E9j8LLx90qhrDua466d4//t/xLveJXNtRPHIK+FUVFTQ19c34TWxWIzKysq8A4lEIrjd7oyV\\nDCCV5DRNy2i+AzCbzQDs3LkzaztqIeaTO+/sHlXVjEkeS/fCp/2w+ofwizvh+WeBk8bcoZoVKxrZ\\ns+dwv6fdfgPf/vaXJcGIopJXk9r69evp7+/nkUceyTmZLL1wp9vtzjsQVVUpKyvLGj02MDAAkLF8\\nztjXCTGf7ds3+ve+auDQsjOnPQm+n6Cs7IDNv4Xn64Aali7NbF62239JU9M51NTczHnn3UJNzc3c\\ncYdUM6L45FXhpEehuVwuY8HOQCBAa2sr4XCYwcFBbDYbGzduzCuIzs5O6uvrc56ThUDFQpUejfbb\\n374y6uinYOk++MzHUVbHOOf1z/H597l4UrvLaBr76EfP4cknpalMzD95T/zs7++npaXFGIWW7m8p\\nLS2lqakp72QzWwlFlvMQxSyz32Y7qarmO6mq5pJrOPZtaP34T/nS5y8pcKRCzJwprTTQ1NREU1MT\\nkGrSslqtRp9Kvjo6OjKqG0kUYiFLVzW9va8wOPjTQ0fTVc3HUFY/yzmvf5bvfOkbUrWIBWfKS9uk\\nTWdJm1gshtPpzDg2tg8nff+hoaGc/Tjjff3xVhKQhCYKZdzRaKc9AZ+/Gt74MB+NfZLHezYVKkQh\\nZtWECcdkMo37AZ3+QB+9VIyiKMafw8NHnmDW19dHPB6nvb3dOBaNRo2JnlVVVaxbtw6bzYaqqqxe\\nvdq4TlVVzGazjFAT80JX13a+8pV/Z9eu9P/1g7B0D6y5GT70P/CLu+D3tZTU3FzQOIWYTRMmnHXr\\n1k3pppOtInINFNi0aRN9fX0ZfUFut5ve3t6MhBONRjN2GhWiWKUrm127Rk3QPP0UuOQ0eMOTGoH2\\nzomHJmaeX7hAhZhlEyacjo6OuYrD8NZbb2U1hwUCAbxeb0aCCgaDBIPBuQ5PiLwdnmdzExz1Dnzm\\nZvjQj+Hn/wgv7MdiuZZz/+YMGW0mFrwZ2w9nuhKJBIFAgC1btpBMJqmvr8fn8xnL6MRiMdrb26mq\\nqkJVVRwOB2vWrMn768hq0WKupAcIPPXU6yST/wmn/zt8/v/Bn6pTTWjvnIDdfoPMmRGLxoQJJ92H\\nE4/HWbVq1YR9Omn59OEUgiQcMdu6urZz880/4oUXjmLv3s1wlB/WHICzfwo//zq8sA9YwsqVL/LD\\nH35dko1YNCZsUnO5XCiKgsViASbfpyMjwcRidXgk2snAP8MZv4ZLfgx/KjnUV3MCwKHKRpKNWFyK\\npkltrkiFI2ZLxki0o26ENe/A2e3Q9e/w4kqgh9LSP/DRj57O1Vd7JNmIRSevhDPeXJj5RBKOmA2H\\nK5uj4Aw3XHIx/PGzqQU396w0rpMdN8ViltfinWazmXvvvXfCa5qbm1m5cuWE1wix0Nx5Zzfx126E\\n838O3jro+b+wdVVGspH9aMRid8SVBjo7O40JnYCxzXMuuq4TCoWyduwUYqH7y/I/QuOH4Y9lcPcn\\nYM+NpNZvGhM6AAAgAElEQVRIu5nly1/lAx84nltvXS/NaGJRO2KTmsmUVxEEpCZqjt4OuphIk5qY\\nKV1d2/mX7z3EMyt/wcBJO6CrHV66hFSi6UFGogmR6YgJZ/SumnV1dTQ0NEy4343FYsHlcs1chDNM\\nEo6YCV1d22n4Tht/qnoE/mCBX26APU8Ah7eHljk2QmTKa9CAx+Ohubm5qBPKkUjCEdP19v63Kav/\\nGG+esAu6PgEvbTl0RiobISYiw6KFmKSuru38478FiJ/9K/RX3wW/7Ic9d5Kx8vMh5513C7/6VfZx\\nIRazvLcniEQidHR0kEgkJrzu4YcfnnJQQhSb0AO/5Cs/+ifeOed1eOgCePk9gBU4mPP65cuLc6UN\\nIQopr4TT2dmJ1+udrViEKEobfnIHN/XeyMiwDe5+FfbeAawhtUtnDcZunYfIqs9C5JZXwvH7/UBq\\nW+n53I8jxJGkR6A9XbKV3af9GbouOVTVWEhVNem+mR7gLeBSjj1W4ZOfLJdVn4UYR14JR1VVGhoa\\nJNmIBa2razsNt7WmRqC9ugzufh32fpfDzWfVHK5qUolFRqQJcWR5JZzS0tJZWZgzHA4TDodZuXIl\\n8Xgch8ORtTlbNBo1Jp2qqkplZaUkPjHjdu/fzdce/Cf+9NE34MG/gR3vJ1XVVAM/JLP57GaOOirB\\nhz5UKpM6hZiEvBJOQ0MDbW1tBAKBGVtTLRwOoyhKxg6fTqcTTdO47rrrAIwtp0dPJq2rq8Nms1FW\\nVjYjcQjxSOIRrnzgSvZTCnf/7lBfTbqqSSeTHwGXsXTpMOeccyK33togiUaIScprGYFAIIDL5cLh\\ncLB161Z27tzJ0NBQzsdktba2Zh1zu90ZxwOBAI2NjRnX+Hw+o09JiOnYvX83X+/6Ol++78t873Pf\\n45SnPwZ703016eYzSCWde1mxooT77vsH+vv/XZKNEHnIax5Oeg01TdMmvmkeG7DV1dVht9vZsGGD\\ncczv97Nt2zZ6e3uNrxuNRlm1apVxjaZpWK1WRkZGJhu+ERvIPByRsi2xjS/+9Esc2HE8e+9fxTsD\\n7wAnAh8gNQLt4UN/piZ0rljxAk1N53HLLV8vYNRCzE95NalNdkh0Pv08W7ZsyToWCoX42te+BqQS\\nSzq5jGY2mwHYuXNnRiISYjL+d9//sv77f0v3zh6Gf7YaXnn/oTO7gXYOrxrwFnD3qBFofy9VjRBT\\nVHQrDQSDQSKRCO3t7UCq/6a8vDxnJWMymQiHw6xZs2bS95cKZ/Eytn7e+zv21jwL6knQXQl7Pzjq\\nqqXIygFCzI68Vxo4kkgkQigUYvPmzXm9rrOzk56eHhRFMZINHLn5Togj6erazjXX3IH6+n6o3gFn\\nvQ4PnguvfIrst4CsHCDEbMm7wkkmk4TD4Zx73ui6TiAQIJFITLoPJ9f9XS4XbW1tVFRUEI1GcTqd\\neVc4R2rWkwpncejq2s5VV/2QN46Jw8XPgLoKHnbDvuMOXTE2wVST6rc5vHLAihU+Ojq+JE1pQkxT\\nXhVOIpHA4XAcsepoaGiYckClpaX4fD5cLhcDAwNTvo8QADd860e84YzBWXF44CKIlx86M3oS5w9H\\nvSI9SOBmYAlHH/0cTU1rJNkIMQPyGhbt9/vRNI1AIEB3dzdlZWXU1tbS09NDd3c3FRUVeDwe7rnn\\nnmkF5XK50DSNbdu2YbPZAMYdap0+P5au6zkfYnHo6trOuz/5SX77iZ+AAtxdD/FVpBJNerjzn0kl\\nmK+QuugN4AkUZRPHHhunsvJNtm69RkakCTFD8ko44XAYt9vNddddh9vtxufzkUgkcLlcuN1uIpEI\\nvb29bN26dVL3U1UVi8XCM888k/O8pmmYzWZsNhuqqma91mw2ywg1kaXjgV/g/VE9b1TF4EEnPPg5\\n2HcxqQSTfqQTzV+AzUASu/0EHnroFkZGHmT37h/LPBshZlheCUfTNOx2u/G8srKS/v5+47nZbMbr\\n9WbMqZnM/cZWKenkUllZCaQmgqbn5KRFo1E8Hk8+4YsF7pZb7ubo93+YukfWsmfPMbD5aoi/j4kr\\nmXeorLTy0ENX88orP5QEI8QsyivhlJWVZVQaTqcTIKNCsdvtGUloIpWVlaxfvz6rqSsQCOD3+43q\\nJRAI0NHRkXFNMBgkEAjkE75YgG655W5WrPgMyvIKvhW9jQPnvwIPfgQevAT2LSU1iXN0JXMAWEVF\\nhU0qGSHmWF6j1LxeL1u3bqWnp8cYGWaxWLj00kuNYdB1dXWEw+G8Ovzb2tqIx+PG4p1Op5Orrroq\\n45pYLEZ7eztVVVWoqorD4chr/k2azMOZ34whzuobwB7gRLDvgYt7Yccp0LMW9r0GnMXhAQEnM3rU\\n2ckn/x/uvfcLkmSEmGN5JZz0JExFUejo6GDt2rX4fD7a2trwer0MDg4SDodpaGiY9sCB2SIJZ/7q\\n6tpOXd3tvPPOgdSBZcNQ8wrYBuCBc0E9BVhFqgntIKlEU0Nqwc23gQPY7cdyxx1XSrIRogDynoej\\nqqqxmGZFRQWapuFyuYjFYkCqv6Wjo4PS0tJZCXi6JOHMT7fccjff+tbPSG3rDJT/GS6Kwo5TD1U1\\n6abesw79Wc3hRHM0cBwVFfuIRu+d48iFEGkztrRNem5Oeo2zYiUJZ3655Za7ufXWe9H1E4HjYfnR\\nUN0Ltj/DA87U8jScBZwCPJi6huORZjQhik/RraU22yThzB9nn/0Fnn9+ADgu9Sh/Ay7qhZdPgZ5z\\nYL+bw0nmLOBUIDTqDsewfPmxfOADJ8gGaUIUgbwSTmNj46SWjFEUJe+11OaKJJz5IZVs9gMmWH48\\n1PTCqjfggQ9D4vhDV50JnMPhJHMMcDR2+/HSTyNEEcor4ZhMRx5FnW5SK9ZlaSThFLcvftHPT37y\\nS1JNZCfBWSpc2Heoqvke7O8ANFJzaXTADBzDihUHaGqqkVUBhChieSWc8dZQGxgYIBqN4vf7KS8v\\n5+GHH56xAGeaJJzilEo0Pyc1KOAYWL4CamKw6i/wQD0kXiZV0XyR9GZo8CyXXfYefvxjmY8lxHww\\no304mqZhs9nw+XyTXm1grknCKS5dXdtZu/b/sn//MaSaxJbCWUm4sBdeOhfCI7D/fUAFqaazFcAK\\nTKZ3uPnmC6WiEWIemfFBAz6fj1AoxK5du2bytjNGEk7xSA11/gmpQQFLYflRcH4Mzvwr3H8R7Dye\\nVKL5H6AUOBbYzWWXnSNVjRDz0IxvwKYoSs69coRI6+razpe+dDPJ5NGk+mCOhbP+lBqB9uJJsNkN\\n+82kkswvgNOBIY455nXefvuJQoYuhJiGGU04kUiEYDA47pYBQpx5pofXXttDqvnseFiuw/m/gTMH\\nYOslsPPPwFHAX0kNDlgJ7OWoo0bYskWqGiHms7wSjslkmnBYdLqZyu/3Ty8qseCkBgV0kRp9ZgGO\\nhvf8AS78HbzwAdh8Juw/ntTAgEcwEhL7Ofnkpdx77w0yzFmIeS6vPpwjbQdgNpu59NJLWbdu3bQD\\nmy3ShzP3UnNq3iA9hJnlOnz2aTh9FzzwQdhZQWp02iOkKprjkL4aIRYeWWlAzKp3vetvePPN40jt\\nQ3MsvOdVuPC38MIJEH4vHLAA/0tqmHNqUMAZZxzk1Vd7Chm2EGIWzPiggano7OxEVVXi8TiqquLz\\n+bKqpGg0Sn9/P1arFVVVqaysxOVyFShiMRmpZHMscBysOADnPw6nD0Dn2fDqsaSa1iTZCLFY5JVw\\nIpEIPT09xsrQ6e2f169fz+rVq43rtm7dytq1ayd1z87OTmw2m5FgkskkDoeDgYEB6uvrgdQK1c3N\\nzXR3dxuvq6urw2azUVZWls+3IOZAarjz3aRGlx0L71Xhgufh96fCZgccOJlUonkVOAEZ7izEIqFP\\nQjQa1e12u64oyrgPp9OpJxIJPRQK6Yqi6Js2bZrMrfWWlpasY8FgUFcUxXje0NCgd3Z2ZlwTDod1\\nr9c7qa8xGqn1UPJ+nZickpJzdajQoUZnxcU6a0/RuWaZzpkf0OEqHT6vg1OH83Wo1eF8/bLLmgod\\nthBiDhyxDycWi+FwOIDUltA+nw+n02lsN93X10drayuxWAxFUdB1HbfbnVGNjEfTNNxuN5FIJGP/\\nnPRGb6qqsmrVKqxWK9Fo1NhyOv1aq9XKyMhIXglW+nBmXlfXdi655B8ZHt4PnAYo8N4kXBCF31sh\\n8kE4cAAYAk4iPShAms+EWFyOmHCsViuaptHa2mo0ceXS0tJCc3MziqIwMDAw6Q3YrFYr27Zty2iS\\nG51wzGazEUNJSUnGa00mk5GUJksSzszp6trORRddfehnuRQ4CVYshc8+C6ftgvsq4TUTqeVo9h/6\\n8xhgNx/84HKee+5nBYxeCDHXJlz+edOmTWiaRlNT04TJBmDLli1A6oO8o6Nj0gEMDAxkJBuAcDiM\\nxWJh1apVxqrTY5NNmqqqOY+L2XX22V/gwgv/AV1fSWofmpPgfUn4eg+8bYLNH4LXPkhquPMuYBnp\\nZHPZZedIshFiEZow4fz0pz9FURQ2btw44U3C4TDRaNRIOq2trdMKqrW1leuvvx4Yf4VqURhf/KIf\\nRTmb559Pkko0ZlhxFKx7HjzPQsdZ8LAVDiwDdpJKNB8ktUzNkAwMEGIRm3CUmqqqk1qmxu12MzAw\\ngNlspqKiYlpVRzAY5IQTTuDaa6+d8j2AI24UJ/JzeOQZpEafrQCWwPsScMFz8NzJcM974cDxh879\\nGXiH1PybYVKVzWpJNkIsYhMmnGQyybnnnjupG6U3XrNarTzzzDNTCkZVVYLBIH19fVN6vZgdxxzj\\nYM+efRgDAjgOjknCZ38HpySh43R47XjARqqqeYfUEjapwQGf+tRxPPro5JtZhRAL04SDBiwWCyaT\\nKa+tBqbymrS6ujruvffejP6a9Gg0GTRQGEuXnsPw8LtJtb4elzr4/lfgc7+H35XCI6fAgXJABQ6Q\\nWprmeOAoli9/h1BI1kATQqRM2IfjdrsZHBycdMUSi8VIJpNTWgGgsbGRlpaWrKSSnlw6tpkuPYIt\\nn2QjJu+WW+5GUc5mePhUUgnkODhmAGp/Da4XYMvp0P0pOGACXiI13Pl9wArOOGMvur6VPXt+KclG\\nCGGYsMKJRqM4nU4sFguJRGLckWJp6aHM/f39VFRUTDqItrY2PB5PRvKIRCLGSgKNjY04HI6MkXKh\\nUIiOjg7a29sn/XVAKpzJUJSzD/3tdNLNYrz/Dfjc8/C7Ethmh4MmUqsFHL5myZI/cvDgbwsUtRCi\\n2E1Y4VRWVlJfX8/g4CAOh4OtW7fmvK6zs9NINrW1tXklm1AoBKSGR0ejUaLRKOFwmI6ODmPZmkAg\\nkDXUOhgMEghIB/RMOuYYx6FkcypGIjlmAGqfBtfvYcsq6P4gHHwb2MfoZPOpT50syUYIMaFJrRbt\\n9Xrp7OwEUn00NpvNaOZSVdXY4bO2ttYYGj0Z6f6ZXOx2Ozt27DCex2Ix2tvbqaqqQlVVHA4Ha9as\\nmfTXSpMKJ7fMquZYQIEPvAKffQ5+a4ZHVsPBP6eOcxqyWoAQIl+T3p4gHA4TCASIRCJZ59xuN36/\\nf16s3iwJJ1sq2Zx+6NmhquaC38NJg3BfOby+hNTQ5sMVjaL8gZGR5woVshBiHprSfjiqqqJpmtGh\\nP59IwjkstX3AIIcTCamq5nPPw7Ml8Mi74eBxpJrPDq+BJn01QoipkA3YFqmsgQHH7koNdT5pEO47\\nFV5/D/B65jXs5sQTd/PXvz5WiJCFEPOcJJxFJrXd8w4ymtA+uAM++zw8Uwq/uggO9h46dzjRHH30\\nn9m3b2oTeoUQAiThLCrZVc1e+FwvvGsQ7rPBH5dknmc38Ad0XfpqhBDTN+GwaLEwnHmmZ9TAgEOj\\n0D64A77WDYPD0Pq5Q8lmCaOTzRlnHJRkI4SYMVLhLGBdXdu58MKvH3o2qqq5oBdO1OC+U+CPK4E9\\npLZ6Ti1JA4OcccZSGe4shJhRknAWqMzmM4Bj4exX4PwXIFYCj54IB48iNdx5CaMX25TN0YQQs0ES\\nzgKUSjYnAsvJqGpO0OD+U+CPxwLp71/6a4QQc0MSzgKSWdWsAExw9g44/8VRVc2xpJrQ0telkk1J\\nyQDJ5FMFiFoIsVhIwlkgskagHTcIF/wOViZT82r+dAxS1QghCkkSzjyX2q9mhIy+mg/tgJoXIFqa\\nqmqGlwP7D52XqkYIURiScOax7KpmL1zw9KiqpgJ4MfMaqWqEEAUiCWce+uIX/fzkJ11kVzUvQvRQ\\nX81weoqVJBohRHEomoQTCoWwWCw5V5yORqP09/djtVpRVZXKysopr0w93xNOdlWzBy7sBUsS7j8V\\n/nQWudZAk2QjhCi0pYUOAFJbHzQ0NBibsY2mqirNzc10d3cbx+rq6ozdQBeLw4nmNFJ70hwL57wM\\n1S9Cfwl02A5VNa+TmsBpAY4BhvjmNy/hllu+nvvGQggxRwqacBKJBIFAAIfDMe5GbIFAgMbGxoxj\\nPp8Pv9+f12Zv81nuquaxVFXzP6fBn1eMunp0VfOiVDVCiKJRNE1q5eXlBIPBrF08rVYr0WiUVatW\\nGcfSO4WOjIzk/XXmU5NaztUCznkZal6CvlLYfsKovpr0ddKEJoQoTkXRpDYeTdNybkNtNpsB2Llz\\nZ0YiWkiyqprj98CF28G8G/57oqrmBUk0QoiiVNQJZ2BgAICSkpKc51VVXXAJJ2dV8+GXoPol6C2F\\nLatg+ERg16jrpKoRQhS/ok44mqYVOoQ5NW5VUzoE/3UavJGuanYhVY0QYr4p6oQzHem+mvngyFWN\\nTfpqhBDz3oJNOPNFzqrmou1Q8r+HqprjSG0hMOoaqWqEEPNQUSccm80GwNDQUM5+nPT5XMYbhVYs\\nlU/Oqmb1i+B5GZ4uhfayQ1VNdrI58cTd/PWvkmyEEPNLUSccs9mMzWZDVVVWr15tHFdVFbPZPC8H\\nDBxONDB+VSMj0IQQC4/pyJcUltvtpre3N+NYNBrF4/EUKKKpy6xqTseoahp74I9A0DZusjn66D9L\\nshFCzGtFVeHkagYLBAJ4vV7q6+uNY8FgkGAwOJehTVsq2aSbz46DknfgokfhuN3wo9PhL8tHXS1V\\njRBi4SnoSgPJZJINGzagqiqhUAibzYbb7cbj8bBu3TrjulgsRnt7O1VVVaiqisPhyFqRYLLmeqWB\\nrEEB6FDxErhfgqfM8OsTYWR0v5KMQBNCLExFs7TNXJnLhJOVbErehIueT1U19506QVUjiUYIsfAU\\nVZPaQpFzBFrFi+B+AZ5aCb+2jVvVrFjxV955R5KNEGLhkQpnxu8/tqp5By5+Go7ZndqvRqoaIcQi\\nJQlnxu6bo6qpfBFcL8OTFvjNCaOqGkk0QojFRxLOtO+XY15N6Ttw0VNwzNupvpq/SlUjhBCScKZ1\\nr3yqmvR1kmyEEIuTJJwp32fMvJrSd+Dip2CFVDVCCJGLJJy8X59jXo3jRVjzMjxhgcelqhFCiFwk\\n4eT12jHJpvRNuPg5WP52agSaVDVCCDEuSTiTek2OvhrHC7DmJXhipVQ1QggxCZJwjnj92Krmbbjk\\naVj2Dtx3CrwpVY0QQkyGJJxxr8tR1ThfgM/sgMct8ITMqxFCiHxIwsl5zZiqxvx2agTa0Xvgfqlq\\nhBBiKmQttVGyqhrlWHD8/lBVY4UnTpY10IQQYormTYUTjUbp7+/HarWiqiqVlZW4XK687zNehZOz\\nqrnkKThqT2pezVvLRl0tVY0QQuRrXlQ4qqrS3NxMd3e3cayurg6bzUZZWdm07p2zqnH+Hj69A35j\\nhSfHr2ok2QghxOTNiwrH5/NRU1PD2rVrjWORSITW1la2bNmS171GVzhS1QghxNyZFwnHarUSjUZZ\\ntWqVcUzTNKxWKyMjI3ndK51w4INkVTWfeQV+bU3NrdGlqhFCiJlU9E1qmqYZyWU0s9kMwM6dOzMS\\n0eQdSiKW3XDxI7B0D/zgzAmqmhck0QghxDQUfcIZGBgAoKSkJOd5VVWnlnCUY6Hqefj0K/DYob4a\\nqWqEEGLWFH3C0TRtdm78lW2wZC98/0zYJVWNEELMtqJPOFN1uK9mHP85eOgvr4w58Xx+9xFCiEVi\\nul3+phmKQwghxAI33V/Ai77CsdlsAAwNDeXsx0mfH2u8TDzTW0zPFolz5syHGEHinGkS58yaidae\\noq9wzGYzNpsNVVUzjquqitlsnuIINSGEEHOt6BMOgNvtpre3N+NYNBrF4/EUKCIhhBD5mhcTP5PJ\\nJF6vN2Npm+rqaoLBYN4VznwrXyXO6ZsPMYLEOdMkzpk1E3HOi4QDEIvFaG9vp6qqClVVcTgcrFmz\\nJu/7LKZ/3LkwH+KcDzGCxDnTJM6ZtagSzkxZTP+4c2E+xDkfYgSJc6ZJnDNLEo4QQoh5Y14MGhBC\\nCDH/ScIRQggxJyThCCGEmBOScIQQQswJSThCCCHmRNGvpTZTotEo/f39WK1WVFWlsrISl8tV6LAA\\nCIVCWCyWnPEUQ9ydnZ2oqko8HkdVVXw+H+vWrSu6OMPhMOFwmJUrVxKPx3E4HNTX1xddnKNpmkZz\\nczP33HNPxvFCx5n+d25ubsbhcDAwMEAwGMTj8WTEUeg4R8exZcsWVq5cya5du/D5fJSVlRVNnH6/\\nn+rqahwOh7F5ZC6FjhNS76NYLAbArl27sNvtM/c+0heBeDyuezyejGNer1dXVbVAER3W09OjWywW\\nPRKJZJ0rhrhDoZAejUaN55qm6Xa7XQ8Gg0UVZ09Pjx4OhzOOORwOvaWlxXheDHGO1dDQoHu93oxj\\nxRBnPB7XFUUxHhaLRe/s7Cy6OHVd1zs6OnSfz5dxrKGhwfh7McTpdrszfp6jH+Xl5UUTZ39/vx4K\\nhTKOhUKhGXu/L4qE09DQkPVmCYfDWW/0uaSqqu7z+fRgMKjb7facCacY4h79gZ0WDAZ1RVGM58UQ\\nZ21tbVbC8fv9ut1uN54XQ5yjxeNx3ev16nV1dRnHiyFOVVX1SCSiJ5NJPZFI5LymGOIcHBzULRZL\\nxrHW1lbjQ1zXiyNOn8+nx2IxPZFIZDyCwaAei8WKKs5cRscwnTgXRcKxWCxZb5rBwcGMD81CGi/h\\nFDruwcFB3eFw6JqmZRxP//abjq3Qcep66g3R3NyccaypqUl3Op3G82KIc7RgMKgHg8GsN2oxxKmq\\nalYCH6sY4mxqasr6d9d1PSOuYohzdIUw3vFiiNPhcOSsVEZXNNOJc8EPGtA0DU3TsFqtGcfT7ag7\\nd+4sQFRHVgxxm81mVFUlkUiMe00xxAmwZcsWNmzYkHEsFAqxfv36ooozLRKJ4Ha7s44XW5zjKZY4\\n29raqKqqyjqeXtS3WOIc2wcCqdjTx4slTrfbjcfjyXjPh8Nh6urqZiTOBT9oYGBgACDn5m2Q6hwt\\nxj11iiXudByjhcNhLBYLq1atMvYpKnScYwWDQZxOJ9deey1QPD/P0V/P5XJlrUtVTHGqqoqmaUZc\\nVqvVGCxSLHFqmkZpaSltbW1YrdaijXOsSCSC0+k0nhdLnBs3biQcDmO322ltbaWsrIxkMslVV101\\nI3Eu+ISTfsPMN8Ucd2trK9dffz1QfHF2dnbS09ODoii0t7cbx4spzs7Ozpy/8ULxxJn+DXb0aMT0\\nb7nr1q0rijjTv+zEYjHjFwuA5uZmBgYGqK+vL4o4c4lGo1x33XXG82KKs6+vj+rqanw+H5WVlUQi\\nEePcdONc8E1qYmYFg0FOOOGEjDd4MVm3bh333HMPGzduxOl0GsM7i0UxfbBMpLS0NCsp+nw+/H5/\\ngSLKlv5Zjt1mfv369UUV51ihUAi73V7oMMbV1tZGS0sLPT09xlYwEzWr50MSjpg0VVUJBoM8/PDD\\nhQ7liEpLS/H5fEUz1yqto6Mjo2qYiX3i50pZWRmqqjI0NFToUIDDiWZswqmoqEDTtKLp7xpr48aN\\nOfvvikFjYyMej4fVq1fjcrlIJBLYbLYZ2115wSec9H/G8d4kY/+zFotijLu5uZlt27bljKOY4kxz\\nuVxomsa2bduKIs5YLJbRbg/Ze4sUQ5wALS0tWcfSzWyqqhZFnOmO6vEmUhZLnKNpmkY0Gs3qAymG\\nONMV4+g+mNLSUrq7uzGbzTPyPlrwCcdsNmOz2Yz23jRVVTGbzUU5YACKL+7GxkZaWlqy3ijFEKeq\\nqlgsFp555pmc5zVNK4o4+/r6aG9vp7m52XiEQiGi0SjNzc10dnYWRZyqqtLc3JxVIaQ7jG02W1HE\\nmY5lbAyjzxVLnGnhcDhngiyGOPv7+8dt6vP5fDPyPlrwCQdSQ/16e3szjkWj0RkrE2dLscTd1tZG\\nc3Nzxn+mSCRitOsWOk5N07Db7Vm/XaXfFJWVlUURZ319PRs3bsx4eDweHA4HGzduNJraCh2nzWaj\\ntbU168MjHA7jcDiMXzoKHSekPgj7+/uzYkiPooTiiDOtt7d33A/1Qsdps9mIx+M5z2maNjPvo2nO\\nE5oXNE3LWorB4/GMO4N6rtnt9pyT7Ioh7o6ODj0YDOr9/f3Go6enJ2NGcjHE2dLSkjVB1e12Z0wK\\nLIY4x2pqasqa+FkMcYZCoYwJgOlJwOlZ8bpeHHGml1oaG8PomfDFEGdabW2tXl1dnfNcMcTp8/my\\nPovi8bju9/uN59OJc9FsMR2LxWhvb6eqqsoYebFmzZqCxZNMJtmwYQOqqhIKhbDZbMakq9GdyoWM\\nO9cErzS73c6OHTuKIs60trY24vG4sXin0+k05g8UU5wAiUSCQCDAli1bSCaT1NfX4/P5qKioKJo4\\n04u27tq1y1hkdGzVUwxxpn+WdrudeDxOXV1dVgzFECekmqYVRWHz5s05zxdDnKPfR5Bq7hs7YnGq\\ncS6ahCOEEKKwFkUfjhBCiMKThCOEEGJOSMIRQggxJyThCCGEmBOScIQQQswJSThCCCHmhCQcIYQQ\\nc0ISjliUotEoXq8Xi8WCyWTCYrHgcDjYtGlToUObEo/Hg8l0+O3s9XozngtRDOR/pFh0fD4fTqeT\\nzvSYbmQAAAXOSURBVM5OTCYTHo+HE044gWeeeQa/34/Vai26fXTSQqEQJpOJzs7OjOOKomRtdTCf\\ntj4Qi4MkHLGoeL1e2trasFgsRKNRdu3axcMPP8yOHTsYHh6mqakJTdNwOBxFm3QgO5l0dHSMu/Ci\\nEMVCEo5YNMLhMJ2dndjtdhKJBKtXr866ZuPGjbS2tgKp5FSsxq5IVVpaWrRbbQiRJglHLBqBQMD4\\nc+y+PqPV19dTWVmJqqoZ+7mP7SdJ0zQNk8lEY2NjxnFVVfF6vdjtdkwmE1arlbq6uqzten0+n7FI\\nqt/vN/qVysvLM5rOPB4PdXV1wOE+mvRGWJPts2lpacHhcBjxNDY25tw+OBgMZlzndDozfhZCTIUk\\nHLFoRCIRLBYLa9euPeK1Pp8PgJ6enozjE/WLjD6nqirl5eVs3bqV8vJyo98oFArhcDhIJpNZr083\\n91166aU0NDQYCSv9Qd/c3ExDQ4MRXzAYzEicR+qzcTgcNDc3YzKZjHiCwSB2uz2j+dDv99PY2MjO\\nnTvxer243W5jv5NibmYU88B0908QYj6Ix+O6oii60+mc1PXRaFRXFCVj7xK3262bTKasawcHB3VF\\nUfTGxkbjWENDg24ymfRIJJJxbUtLi64oih4KhTKuVRRFLy8v15PJpHE8HA7riqJk7D3U0dGhK4qS\\nsd+Lrqf2WRkd29jngUBAVxRF37ZtW87v0+FwGMfMZrNeXl6ecV06ltHfoxD5WlrohCfEXEjv1z7Z\\nveHLysqm9fUaGxupqanJ2iMkvd/N4OBg1mvGNvW5XC6AnE1ek6GP6ufZsGEDHo+HyspK42cBqe/T\\n5XIRiUQYGhqipKSEZDJJeXl5xr1cLhfRaDTn9shCTJYkHLEopD8ox+7FPp70dVP9gK2oqDCSi6Zp\\n9PX1EY1GjQEJuaS38J0NyWSSnp4eLBZLzvOKojAwMEBJSQm1tbWEQiGjKdDtdlNRUZFzkIUQ+ZCE\\nIxaFdGUz2YTT19eX8bp8aZqG3+83dvSEVB+Kw+EYt2IZb3fVqUr36aS/Z4/Hg9/vH/f6dDLasmUL\\nmzZtorW1NeP6hoYGAoEApaWlMxqnWDwk4YhFw+12G0OjR2/jnRYOh3G73QBGJbJ+/foj3ndgYCDr\\nmMvlIhaL4fP58Pl8RnUQiUQIhULT+Tbylk5kZrN50tsVX3fddVx33XUMDQ3R09NDa2srwWCQvr4+\\nIxkLkS8ZpSYWjfRv67l+y9c0jerqapxOJy0tLcRiMRwOx6SakaLRaNa9YrEYXq+XzZs3Z9xDn8Md\\n3dNfy2w2U1paSjgcznmdxWIx+mxUVcXv9xsj40pKSli3bh3d3d1GP056KLYQ+ZKEIxYNl8tFbW2t\\nMWR59BBfs9nMli1biEajNDc3oygKHR0dGa83m83oup4xHyXddJbL2IEBo6+dbuKZzOtHD5P2+XwM\\nDg4a83jSWlpaSCaTGXOINm3aZAwLH01VVRRFmXAOkxATKuQQOSEKwev16oqi6Iqi6GazWXe73Xpl\\nZaVxzGQyZQ1d1nVdD4VCxjU+n09vaGjQLRaLXl1drVsslozhyx6PR1cURfd6vXogEMi4VlEU3W63\\n6+FwWNf1w8OiRw+JThs7NDs9PNlut+t+v984XltbqyuKMu5zXdd1u91uvLa2ttb4nscOFU/HbrFY\\n9NraWr2hoUE3m826yWTSm5ubp/ATFyJFEo5YlKLRqO71enWr1aqbTCbdarXqTqdTb2tr0zVNMz50\\nx853CQaDxge31Wo1PoAtFkvGHBVN03Sfz6dbLBbjQz19L5/Pp5tMJuP69PPJJBxdP5wQrFarcczr\\n9WbMuxn7PM3v9+sOh8OY9zNeAvH7/brdbs/42Yz9WQiRL0XX57BRWYh55Pbbb+faa68tdBhCLBiS\\ncIQQQswJGTQghBBiTkjCEUIIMSck4QghhJgTknCEEELMCUk4Qggh5oQkHCGEEHNCEo4QQog5IQlH\\nCCHEnJCEI4QQYk78fw4CAYBE2TLbAAAAAElFTkSuQmCC\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtUW/ed7/33lu3YTmKQ5FycpG1AIp0mcbBBuLPOc86T\\ndIwE6bSdrrERTtKSeU6fGJHpak7PPIlFmrpxL7MccM9ZJ+mZJIhMZxoybQGRmWnjmdpIbuOZdmaO\\njWTTpGnjsCH3q2GLOvEltvfzx2ZvEAgsgZAEfF9rsWK2Nls/tmM+/Pb3d1F0XdcRQggh5pkt3w0Q\\nQgixNEjgCCGEyAkJHCGEEDkhgSOEECInJHCEEELkhASOEEKInFie7wYEg0FqamrweDzY7fZpz4vF\\nYvT19eF0OlFVlcrKSqqrq3PYUiGEEHOR98CJxWLs2bMn5Wtut5tjx46hqirNzc3s37/feq2+vh6X\\ny0VpaWmumiqEEGIO8h44brebPXv2TOnd9Pb2smnTJgBaWlpoampKej0QCBAMBunq6spZW4UQQsxe\\n3gPH4/GwcePGlK+Zx7u7u7n//vunfF04HJ739gkhhMgOpRCXtmlvb2f79u0AaJqG0+lE0zSKioqS\\nzrPZbKiqSklJSR5aKYQQIhMFN0otGo1SVVVlfT48PAwwJWxMqqrmpF1CCCHmpuACJxaLUVFRYX2u\\naVoeWyOEECJbCipwwuEwbrc7380QQggxD/I+aGCihx56iAMHDmTlWoqiTPtaAZathBBi0SuYHo6m\\nacRisSm1GpfLBcDo6GjKrzNfz8RMYSSEEEvBpz61C0VhysenPrVr3t6zYAInEomkXGnAbrfjcrmm\\nDA5QVRW73T7tCDVd11N+CCGEgJUrz6Y8vmrVuXl7z4IJnEOHDk1bv/F6vRw6dCjpWCwWw+fz5aJp\\nQgix6NxzTw1u9wNJx9zur/GVr8zfz9WCmYfj9/sZHR1l3759U15LJBL4/f6kpW1qamoIhUIZz8Ex\\nH6cVyLcthBB5s3fvQb73vV5OnVrGqlXn+MpXfHzmMzfP2/sVTOA0NTWhKAqPPfZYytfj8TidnZ1s\\n2rQJVVXxeDxs3rw54/eRwBFCiPwomMDJFQkcIYTIj4Kp4QghxHw5ffo0DzzwAOvWrcNms6EoinxM\\n+rDZbKxbt44HHniA06dPz8vfgwSOEGLR+/znP8/zzz/Pr371K86cOTPtKNal/HHmzBl+9atf8fzz\\nz/P5z39+Xv4e5JGaEGLRW7FiBaOjo6xevTrfTSl4J0+epKioiA8//DDr15bAEUIseoqiyL/5DMzX\\n/ZJHakIIIXJCAkcIIUROSOAIIZa0vXsPUlv7dT71qV3U1n6dvXsP5vwakUgEt9uNzWajpqaGRCJB\\nOBympqbGOsftdhONRunp6SEQCOD3+7HZbFRVVTE4OGidZ666b7PZqK+vJ5FIAFjzF/fs2YPT6aSs\\nrIx4PJ7x9zon+hID6Evw2xZiSZvu3/wzzzyru91f00G3Ptzur+nPPPNs2tee6zVGRkZ0h8OhHzhw\\nQE8kEnogEND9fr+u67ru8Xj0cDist7S06PX19bqu63p3d7euKIre3t5une/xeHRd1/WBgQFdURQ9\\nGo3qmqbpfr9fDwQCSa/t2bNH13VdDwQCus/ny+h+zdWS+8krgSPE0jPdv/mamgeSgsL8qK39etrX\\nnus12trarIAxORwOXdd1XVVV3W6362VlZXoikdB13QicqqqqpPMVRdE1TdNbWlr0pqYm67iqqta1\\nBgYGrD/ruq7HYjErqCabr5+RBbUfjhBC5NLp06l/BJ46tSxn1xgYGCAcDuN0Oq1j5mja0tJS3G43\\nbrc7aeuW0tLSpGuYK+oPDw8nbdlSWlqatGvyxPfQ8zBqT2o4QoglKxtL9M/1GmVlZdTV1TE8PGx9\\nRCIRgKT/TqzTpNquxe12s3btWgYGBqzjmqal3PYlXyRwhBBLVjaW6J/rNerr64lEIkSjUTRNIxAI\\n0NzcDBiLGj/xxBM89NBDBAIB62tisRjt7e3W+R6Ph6KiIrZu3UooFLKutX37drZt25b29zLf5JGa\\nEGLJMpfi/973dk5Yov/WjJbon+s1iouL6e7uJhAIoKoqPp+P7u5uWltb8fl8bNy4kY0bN9LS0sLT\\nTz+Noih4vV56e3utsOnu7gaMR2sTr+X3+2lpabHea/Jux7ne/VhWGhBCLHqLaaWBcDhMV1cXXV1d\\n8/YestKAEEKIBU0CRwghFhBzO4GFSB6pCSEWvcX0SC0X5ut+FcyggVgsRldXF2vXruX48eMEAoGk\\nseaxWIy+vj6cTieqqlJZWUl1dXUeWyyEECITBRE44XCYSCTC448/bh0LBAK0tbUBxhjz5uZm9u/f\\nb71eX1+Py+WaMgFKCCEmW758OSdPnpT9cNJw8uRJli+fn2jIew1H0zQaGxuTwiYUCnHgwAHr85aW\\nFpqampK+LhAIEAwGc9ZOIcTCVV1dzW233cbAwABnz6aeqLnUnT17loGBAW677bZ5e3qU9xpOMBjE\\nZrOxe/fupONDQ0OUlJQAxnIMsVjM+hyMoHI6nZw/fz6j95MajhBLz+nTp/nWt77F97//fd55552M\\nf24sBTabjSuuuIIvfelLfOMb32DlypVZf4+8B47T6eSJJ55gy5YtKV83g0XTtKS1hMC4QaqqJgXR\\nhUjgCCFEfuS9hqNpGsXFxbS3t+N0OhkeHsbpdLJ161YAhoeHAaaEjSnTwBFCCJEfeQ0ccwG6eDzO\\nvffeax1vbm5meHiY7du3J610KoQQYuHK66ABM0wmLqcNsG3bNhkQIIQQi0xeezhm0EwOnIqKCjRN\\nY2hoaNbXXqgzcYUQYrHKaw/H3Kdhuv0aVFW1wmh0dDTlOZPDSgghRGHK+zwcc6e66V6z2+0pz1FV\\nFbvdPu2AAd3YPnvKhxBCiPzIe+AEAgH6+vqSjsViMRwOhxUmXq+XQ4cOTTnH50t/kyQhhBD5lfd5\\nOIlEAo/Hw0svvWQdq6mpoampyZqbk0gk8Pv9SUvb1NTUEAqFMh4SLfNwhBAiP/IeOACDg4O0tLTg\\ndrsZGBigvr6ezZs3J50Tj8fp7Oxk06ZNqKqKx+OZck46JHCEECI/CiJwckkCRwgh8iPvNRwhhBBL\\ngwSOEEKInJDAEUIIkRMSOEIIIXJCAkcIIUROSOAIIYTICQkcIYQQOSGBI4QQIickcIQQQuSEBI4Q\\nQoicyFrgTLdfjRBCCAGzCJx4PM7dd99t7caZSCSoqqrCbrezbNky7r///my3UQghxCKQ0eKd0WjU\\n2oMmFouxceNGmpqaCIVCVFdXo6oqQ0NDdHd3W1sLFBpZvFMIMRd79x7kkUf2c/r0clauPMs999Tw\\nmc/cnO9mLQgZBU5VVRWxWIze3l6qq6sBsNlseL1ea68ah8NBWVnZlA3TCoUEjhBitvbuPch/+2/7\\nGBj4S+uY2/0ADz9cK6GThoweqamqSl1dnRU28XgcMHbtNNXX10+7ZbQQQixkjzyyPylsAAYG/pLv\\nfa83Ty1aWDIKHE3TrB4CQCQSAUja6nl4eBhN07LUPCGEKBynTy9PefzUqWU5bsnClFHgVFRUWCED\\n0NbWhsvloqioyDoWjUYpLS3NXguFEKJArFx5NuXxVavO5bglC1NGgRMIBBgZGeG6666ztno2H6dF\\no1HKysrQNI26urq0r6mqKj6fj2g0iqZpqKpKc3Mz0Wg06bxYLEZ7ezs9PT3s2bNnyutCCDHf7rmn\\nBrf7gaRjbvfX+MpXfNN8hUiiZ2jHjh263W7XFUXR/X5/0nFFUXSfz5fR9QYGBnRFUawPh8Oh9/T0\\nTDln8nX9fr+uqmqmzdcBfRbfthBC6Lqu688886xeW/t1/ZZbHtRra7+uP/PMs/lu0oKR0Si1mZgD\\nBVwuV0ZfNzg4yODgIFVVVQwPD1NSUjLlnEAgQG1tbdJQ62g0SltbG11dXRm9n4xSE0JciAx9nh+p\\nK2BpGBoaQlVVNE3D5XJNqeVkQtd1ioqKpv367u7uKRNKPR4P4XB4Vu8nhBDTSTX0eWDAeIwmoTM3\\ns1ppoKqqCpfLhdfrpa6ujsrKShwOB9u2bbNWIMgWTdPQNA2n05l03G63A2T9/YQQS5sMfZ4/GfVw\\nBgcH8Xg8AFRWVrJt2zZKS0tRVZXe3l66u7uJRCIMDg5m1Nsxe0pgDKt2Op1s3brV+hyY9nqqqqZ8\\nDCeEELMhQ5/nT0aBEwwGAWM49Pbt25Ne27FjB6FQiKamJrZv305nZ2da1zR7LmbAgDF51Dwmc3qE\\nELkkQ5/nT0aP1CKRCJWVlVPCxtTY2EhFRQWxWCztaxYXF0+5XiAQsMJtthRFSfkhhBAzkaHP8yej\\nHo6mabjd7hnPcblcPP3003NqlPmYTrY8EELkmjkw4Hvf28mpU8tYteocX/nKrTJgIAsyGhbt8/mI\\nxWIcP3582nOcTicul4vDhw+ndc3W1lZ27NiRdMwcJBCLxSgpKcHpdKJp2pQ6js1my7iGI8OihRAi\\nPzJ6pNbW1sb58+epra2dMjpscHCQmpoaNE2jvb09reuZqwpMvpY5UMDlcmG323G5XFMWBFVVFbvd\\nLgMGhBBigZjxkVpNTc2UusfatWvp7e3F7XZbgWAuSaPrOpWVlYRCIR577LELvrnL5aKtrW1KaEQi\\nETwej9Wj8Xq9HDp0iI0bN1rnxGKxpEVDhRBCFLYZH6k5HA4URcn48ZOiKFYv5UJ6enqorKy0FvzU\\nNA2v18sTTzxhBUwikcDv91t77oARhqFQKOMejjxSE0KI/Mja0jZz0dPTg6qqHD9+HE3TaG5unhIk\\n8Xiczs5Oa9FQj8fD5s2bM34vCRwhhMiPggicXJLAEUKI/MhoWLTZyxgcHETTNKugv23btqT6ihBC\\nCDFZWj2ceDzO9u3bZ5zQ6fF4aG9vL/jgkR6OEELkxwUDJxqNWqPBKisrCQQCVFVVWZMzDx8+TFtb\\nG/F4HEVR6O3tnVVtJVckcIQQIj9mDJxEIkFpaSmapqVcP20icx01h8Mx48TQfJPAEUKYZN+b3Jqx\\nhhMKhdA0jR07dswYNmCsozYwMMCePXv47ne/y7333pvVhgohRDbJvje5N2MPx+PxcOTIEc6dS3+V\\nVJvNhs/nY9++fVlpYLZJD0cIAVBb+3X27/9OiuM7+dnPvp2HFi1+My5to6pqxltGl5aWpr2OmhBC\\n5Ivse5N7MwZOIpHIOHBcLpfsYSOEKHiy703uzRg4xcXFGfdWDh8+bG3/LIQQhUr2vcm9GQcNeL1e\\nenp6OHLkSFrza+LxOIlEgrq6uqw1UAgh5oPse5N7Mw4aiMViVFVV4Xa7OXbs2IwXSiQSeDweVFWl\\nr6+PioqKrDc2G2TQgBBC5MeMj9TM7aQHBga47rrrpt3Js6enxwqburq6gg0bIYQQ+ZPW0jZ+v5+e\\nnh7A2LLA5XJZm6KpqsrIyAgAdXV1dHV1zW+L50h6OEIIkR9prxYdiURoaWkhGo1Oec3r9RIMBqmu\\nrs56A7NNAkeIpUlWFci/WW1PoKpq0mrRC4kEjhBLT6pVBdzuB3j44VoJnRyS/XCEEIvSxB7Nc8+9\\nwPHjnVPOkVUFciuj/XCEEKJQTQyY0dHXePPNIt5663+Ovbor5dfIqgK5VXCBY24x/fjjjycdj8Vi\\n9PX14XQ6UVWVysrKBVEzEkJk1+RggYs4c+Ycqqpw8qT5c+PrwMR10mRVgUJQcIETDAatUW8mVVVp\\nbm5m//791rH6+npcLhelpaW5bqIQIsfMkHn99XcnBMtBYB/wl0wNmMk/2mqAB8bONRirCtw6vw0X\\nSQoqcMwh1madxdTS0kJTU1PSsUAgQDAYLPhh2EKIuUku+E8Mlv2MB8jkH2WTezTGwIC1a29j/fpP\\nyKoCeTLjxM9cM3cXnVzQ7+7uprKyMumYx+MhHA7nsnlCiDx45JH9E0aXTQyWiX+eHDBmj2ac2/0z\\nfvCDP+cXv9jFz372bQmbPMha4IyOjs7p66PRKF6vd8pxTdPQNA2n05l03FwgdGhoaE7vK4QobMnb\\nCJyd5s+TA+Zm1q17k8rKL3PLLbuord3Jww9LjybfMg6ceDzO3Xffbf2gTyQSVFVVYbfbWbZsGfff\\nf/+sGqKqKqWlpVN6N8PDwwAUFRVN+3VCiMUreRuBicEy8c83A7WsXr2N9eu/Sm3tTp544v+hr++v\\npEdTQDKq4ZiPvMCooYBR5I/FYlRXV6OqKq2trWzatIktW7akfd2enp5pt7CWvXWEWLr27j3Iu+++\\nxapVd3Pq1GOYtZjVq7fhdl/FihUnUJQvs2bN5WN1mS9LsBSwjAInGAwC0Nvba21XEAqF8Hq91ggy\\nh8PB7t270w6c+QqUyQMPhBALy/hggScwRqTtZNWql7nhhjV861sSLAtRRoFjrgZtzn+Jx+PAeG8H\\njOHKmRTzu7u7k3o3EhRCLG3mEOhDh15iZOTHY0dvBm7m1Cm4/PKdEjYLVEY1HE3TkgIhEokAWI/Z\\nwKi5pNtricfjVFVVJR2bXMMx12qbblDCdGu56bqe8kMIUbjMXs3+/d9hZOQTKc+R1QEWrox6OBUV\\nFVbIALS1teFyuZIK+tFoNO3JmIcPH2ZgYIDOzvE1jmKxmDXRc9OmTWzdutXaCmHirqOqqmK32ykp\\nKcnkWxBCFKi9ew/yZ3/2VxPWPJPVARabjAInEAjQ1NTEddddh91uR1VVWlpaACNoAoEAmqbR2NiY\\n1vVSDRTYs2cPhw8f5qGHHrKOeb1eDh06lBQ4sVgsqWclhFi4zJ7N8ePXTzgqqwMsOnqGduzYodvt\\ndl1RFN3v9ycdVxRF9/l8mV5yyvUnXlfXdV3TtCnX9fl8+uDgYMbXB/RZfNtCiHlUU/OADroO5n/N\\nj2d1+LrucNyp19Z+XX/mmWfz3VQxB1nbnsCcDzPb/XEGBwdpaWmhq6uLRCLB9u3bCQQC1nbV8Xic\\nzs5ONm3ahKqqeDweNm/enPH7yPYEQhSeT31qF88+u4vk9dEMbvfXZNLmIjHrwBkdHWV4eBiHw0Fx\\ncXG22zVvJHCEKCxTazcHgV5gGWvX/pYf/ODPJWwWiVmtNGCuLOB2u+nr6wOgrKyM7373u1lvoBBi\\n8Rqv3XyZ5FUDvo3bfUbCZpHJKHAGBwfxeDzWygITewnHjx9nx44dbNq0KeuNFEIsPmbPxliY01ia\\nBnYCu1i79jZ5jJYD5/Xz/Hzw5yROJXLyfhkFjjkira+vj+7u7qTXRkZGeOihh+jr65v1empCiMVv\\n796DVFbeRV3djyaNSjN6NrCL9es/IWEzj37z7m+4P3I/Jf+rhP++77/zSuKVnLxvRoHT1dWF1+u1\\nCvmT7dixg4qKCtk2QAiRkvkILR5fN7Y2msy1yZV33n+Hh//9YTwhD74OH2fPn+WZO57hSNMRbrry\\nppy0IaN5OJqm4Xa7ZzzH5XLR09Mzp0YJIRan8b1tdo0dkbk28+nkhyf5x9/9Ix39HfzylV/yJ3/w\\nJzxU/RCbSzezzJb7FRsyXmng8OHDM54Tj8enbJYmhBAwcW8bs2djPjbbiTkq7eGHZaDAXJzXz/Ps\\n0LN09Hfw97/9ez55zSdpKG+gs66TSy+6NK9ty+iR2rZt2+jr6+PnP/95ykU26+vrUVU15UZqQggx\\nvrfN5L1sZFTaXL3w7gt8Lfo1Sh8u5av7vsoNl9/A83/+PPu+uI8vln8x72EDs5iH4/F4iMfj+Hw+\\nent78fl82O12IpEIIyMjuFwuXnrppflq75zJPBwh8mfXrkdpbe3n5MnHMefbjG85sE3CJkPvvP8O\\nP/r1j+jo7+CN37/BF276Ag0bGii/sjzfTUtpVhM/W1tb2b17N4nE+FC64uJiAoFA0hpohUgCR4jc\\n27v3IDt3PskLL6zg1KnbMSd2rl79Ajt23MKuXX+e7yYuGCc/PMlPfvcTnux/kl++8ks+9wef487y\\nO/NWl8nEnJe2UVUVp9OJ3W7PVpvmlQSOELk1vpGaAnxnyuu1tTv52c++nfuGLSDn9fMcfPkgHUeN\\nukzV1VU0lDfwp9f/aUE8KktXRoMGUpnt2mlCiKVh584fMzDwKOMj05LJ/jbTe+HdF+jo7+Dvfv13\\n2FfZaShv4Nubv83Va67Od9NmZcbAsdls0+7AafYQJvYYFEWx/nvunIyjF2KpMh+hvfjim7z/vrlf\\nlsy5Scc777/Dj5/7MR39Hbw++jp33HQHP7ntJ2xYtyHfTZuzGQNn69ats7qobBMtxNK1d+9B7rrr\\nB7z11jpg3YRXZM7NdMy6TEd/B//6yr/yuT/4HH+5+S+pLq0u+LpMJrK2PcFCITUcIebH3r0HeeSR\\n/fzyl8/z/vs3YtRrdgGbGd9ywBiZpigDVFQ4lvTItPP6ef7l5X+ho7+Dp194Gs/VHu4sv3PB1WUy\\nMecajhBCjA93vgN4hfEfLWeZPLkTYOPGi+nr+6uct7MQ/Pa939Jx1KjLFK0soqG8gV/f/WuuKbom\\n302bd2nVcAYGBigpKZmxpmOSGo4QS8vevQdpbX2Wkyc7ga8DH2O8XjPxMZoRPG731/j2t+/MR1Pz\\nZmJd5rXR1/jCTV/gH2/7x0VRl8nEjIFTXV2Noig4HA4g/ZqO1HCEWDoeeWQ/J0+aqz4vx3iE9gOS\\n6zU7WbFikJtuKl4yj9FOfniSn774Uzr6O/iXl/+Fz378s3znj75Dtaua5bal+XBpxu+6t7c36fPJ\\nWxJkSyQSIRKJsHbtWgYGBvB4PGzfvj3pnFgsRl9fH06nE1VVqayspLq6el7aI4RIn7E+mtmjmfgI\\n7UngduAi1qxJ8KMf/cWiD5pUdZmG8gZ+uOWHrFm5Jt/Ny7uMYnZ0dJSioqILn5iBSCSCoihJKxRU\\nVVWhaRr33XcfYEwubW5uZv/+/dY59fX1uFwuSktLs9oeIURmRkffAW7D6NHUkuoR2sMP/7+LOmx+\\n997v6Ojv4Kn+p1izcg0N5Q30393PR4o+ku+mFZSMFu+02+088cQTM57T3NzM2rVr075mW1vblGNe\\nrzfpeEtLC01NTUnnBAIBgsFg2u8jhMgecxO1Vas2E4+/hTEKrRZjyZr3UJTPcu2126mt3blod+58\\n9/13+d5/fI9Ptn+ST/3gU5z88CT/cNs/0N/Uz47/vEPCJoUL9nB6enqsCZ2A9VgrFV3XCYfDjIyM\\npN0ARVGIRCJJj8d0XbfqRmA8ypu8i6jH45GN3oTIg127HmX37l9w5swa4HKgE3O4szEK7Qo2bjxH\\nLNaez2bOi1NnT1nzZcy6zLf/6NtLui6TiQvOw7HZMuoEAUYPZeLjr0y53W7uvvtu7r33XjRNw+l0\\nomnalMd5NpsNVVUpKSlJ+9oyD0eI2dm79yD33PMwqnoOWD92dDmplqy55ZZd/OIXU48vROf18/zr\\nK/9Kx9EOel7oofKqShrKG9hy/Rapy2TogpHc1dVl/bm+vp7GxsYZ97txOBxzKuaHQiGqqqq49957\\nARgeHgaYtnaUaeAIIdKTvDxNAqM3cxEwcTvixbtcjdRlsu+CgVNXV2f9ubq6Gr/fPy+jw3p6eujt\\n7UVRFDo7O63jmqZl/b2EEDPbu/cgX/xiO5p2EcbyNJcC12H8yJgYMlOXq1m9OsBXvvKFHLY2e977\\n4D1+/NyPefLok7w6+iq3r7+df7jtH9hw5QaZ7pEFBbe0TSKRoLq6mvb2dioqKojFYlRVVXH+/Pkp\\n59psNiKRCJs3b57yWjoTVIUQqbndd6KqH5twZOLKATUY82zACCNzsMAyLrroOe6/f/OC2t/m1NlT\\n/PR3xnyZgy8f5DMf/wwN5Q14XV6py2RZxnczGo3S3d3N4ODgjOft27dvVg0yN3Krrq62HqcJIXJn\\n165HUdUPSP7xMHHlgH3An2HMszkCHGXVqku44YbL+Na37lkQI9LO6+f55Su/5MmjT9LzQg8VV1Vw\\nZ/md/N2Wv5O6zDzKKHB6enrw+/3z1RZLdXU1mqZx4MABKisrgennAE23H890PRjpFguRWvKggFVM\\nfXT2A5KHP3+Eiy7SFlSP5sXjL9JxtIOnfv0Ul6y4ROoyOZbREDRz3ktvby/nz5+f8SMdqqricDg4\\ncuRIytc1TcNut+NyuVBVdcrX2u12GTAgRBaYNRtVXQ5sxKjZvDnhw+zVvA08BvwWt3uQp5++p+DD\\n5r0P3uN//5//zR8+8Yfc8re38P6H7/N0/dP8+u5fE/wvQQmbHMqoh6OqKo2NjVkbNKBpGm63e0ov\\nxQwXs3fj9Xo5dOgQGzdutM6JxWL4fL6stEOIpW7nzh+jadcyPijgTowejYIROC+T/OissNdDO3X2\\nFM+8+AxPHn2SZ19+ls9c9xm++alvSl0mzzK688XFxVl9JFVZWcm2bdumPP5qaWkhGAxavZeWlhb8\\nfn/S+mqhUIhQKJS1tgix1Oza9Sj/4388w4kToxhDnq9gfFCA2aMxHp3ZbEfZudNX0L0Zsy7T0W/M\\nl9m4biMN5Q08teUpilZmd0kuMTsZjVILBoO0t7czNDSU1TXV2tvbGRgYsBbvrKqq4q677ko6Jx6P\\n09nZyaZNm1BVFY/Hk3J02oXIxE+xlJlza44e7ef8+Y8COsbvnacx5teYYTM+8qzQw2ZiXebiFRdz\\nZ/md3HHTHXy0+KP5bpqYJONh0X6/nyNHjtDS0kJlZeW0y9xke5HPbJHAEUvJ+ECAt4AzwNUYy8+c\\nBiqAYxjza97CCJ/kYc6KcoRvfKOm4MLmvQ/eo/O5Tjr6OxjShrh9/e00bGigYl2FDAwqYBkFjhku\\nF5qMWcgbsEngiKXCGAjwv9C0k2NHlmEMCDgGrAZKgKGx/5p72CjA+xgrCgzz4IOfLpiwMesyHf0d\\nPDv0LH983R/TUN6Az+2TuswCkdHfUrpDouU3DCHy7557nkDTVgArxo6swvgnvxo4iVGvMf9rDgAw\\nF+A8R0XFiryHja7r/PLVX9JxtIPwC2E2XLmBOzfcScefdkhdZgEquJUG5pv0cMRit2vXo3znO3/D\\nuXPXYgxvNp0CyjB6OLcAv8AIm+UYj9XGl6dxOL5MR0f+RqIdO37MWsds9YrVNJQ38IWbviB1mQUu\\n64ETjUbccIxeAAAgAElEQVQJh8M89thj2bxs1kjgiMVq796DfOELO0kkzJ7MpZPOWINRpxnBGJFW\\nDuwFEhi9oEux2VZSWnpJXjZMO/7BcTqf7+TJo08yqA1yx/o7pC6zyGQcOIlEgkgkknLPG13XaWlp\\nYXBwUGo4QuTQHXcE+dGPYhi1l0sxHputBN7FeGwGRuCswajTqGPnrGb16g/ZsaM2L4/PTp89bdVl\\nfjH0Cz593adpKG+gxl0jdZlFKKO/0cHBQTwezwUHDTQ2Ns6pUUKI9Blh0w84MUIEjJD5CPAF4GGM\\nUWgJjBC6BEVx4HJdmpeeTKq6TEN5A0/+6ZNSl1nkMgqcYDCIpmm0tLRQUVFBIBDA4/EQCATQdZ1g\\nMMhll13G448/Pl/tFUKMMYLm58BljPdqzN6MWaPRgR7ra/JZmzl2/BhP9T/FU79+ipXLVnLnhjs5\\nEjgidZklJONh0VVVVdZunq2trXR3d3Po0CHAGC7tcrl44okn2LJly/y0eI7kkZpY6HbtepRvfrMN\\nuArj8diVGHWZVRhB81PgWsZrNMuBZTgc5+no+Iucho1Zl+no70AdUY35MuUNVF5VKXWZJSijwLHZ\\nbAQCAWtAQCQSoaamJmmxzkAgQCwWs0Ko0EjgiIVs/fo/5fnnh4GLgSLgPMYavL/HCBxzMEAYs0az\\nfPlJHnjgMzmr0Zw+e5q9x/bS0d/BgcED4/NlXD5WLFtx4QuIRSujR2qlpaVJqzZXVVUBcOTIEWth\\nTbfbTXt7exabKITYu/cgW7b8f5w5cxlG0FyCETAjGCsD/BTjn/O7wD9jrI32e26+eQ3PPhue9/bp\\nus6vXv0VHf0dhH8T5qYrb6KhvIG//fzfUryqeN7fXywMGW1PUFlZSSQS4cCBAwDY7XaKi4tpa2uz\\nzjl8+DB2uz27rRRiibrjjiCKUslnP/u1SWHzPka95kPgdeBzwHsYc21WAgkefPCzPPvs38xr+14a\\nfokHf/4gZd8rY/tPt3Nt8bXEAjF+/mc/50sVX5KwEUkyeqSmqiplZWUoikJ3dzdbtmwhEAjQ3t6O\\n3+9nZGSESCRCY2NjwQ4ckEdqYqG45Zb/ysGDKsbjs+WMBw3ADcBRjBrOGuAPMFcIgBd48MH52xTt\\n+AfH6Xq+i47+DgZGBrjtxtto2NCA5yqP1GXEjDKeh6OqKi0tLTQ1NVFRUYGmaVRXVxOPxwFj75ru\\n7m6KiwvzNxsJHLEQGLWaUxhBswojTMw1zo5jrAzgBP4VYySaHbh43ubUTK7LfLpsfL6M1GVEurK2\\n0oA5N6fQH6dJ4IhCZgx13gt8FGOo8zKMR2fnMXo1A2N/fhsoxuj1nODmm9dl/fGZruv822v/RsfR\\nDrp/023VZbZev1UelYlZkbXUhCgQV1zxf/Puu2cxeiuXYvRozMdkZzGGOjuBQxhBs4JVqz4gHP5a\\nVoc6vzT8kjFfpv8pVixbYa1jdq392qy9h1iaMgqcpqamCz6j1XUdRVFkLTUh0mTMq3kUo1ejYITN\\naYwBAKcwhjcXYawUsAyzV3Pjjat47rm/z0obhk8OW/vLSF1GzJeM5+FciPlIbXh4ePatmkcSOKKQ\\nGGHzNxirBRRjPC47MfbqVcCrgIYRNA7g4qzNqzl99jT/dOyf6OjvIDoY5dayW2kob6DWXSt1GTEv\\nMgqc6dZQGx4eJhaLEQwGKSsrY9++fRk1oqenB1VVGRgYQFVVAoEAW7duTTonFovR19eH0+lEVVUq\\nKyuprq7O6H1AAkcUDqNecwRjdsIajFrNOYyVA97E6NUUMXGwwO2338gPf9gy6/ecXJdZf8V6Gsob\\nqLuhTuoyYt5lNPFzugEBdrsdl8uF1+vF5XJx//33s3v37rSu2dPTg8vlsgImkUjg8XgYHh5m+/bt\\ngDEyrrm52VpSB6C+vh6Xy0VpaWkm34IQeTc+MGANcA3GY7QTwE3AwbFjVwG/wxx9BiM8+OCfzLpX\\nMzA8wFP9T9HR32HVZfoa+6QuI3Iq64MGAoEA4XCY48ePp3X+nj17uO+++5KOtbe3EwgErCVzAoEA\\ntbW1SeuzRaNR2tra6Orqyqh90sMR+TJeq1mN8QjNrI3owDqM3/+cGLtuXolRy5n9CLThk8PWfJlj\\nx49x2/rbaChvoOrqKqnLiLzIeuA0NTURCoWS1lebjqZpeL1eotFo0rwdc4KpqqqUlJTgdDqJxWKU\\nlJQkfa3T6UzrfSaSwBG5ZsypOYbxWOzKsaOXYgTOuxi9m40YI9HeHnvt96xe/Q4ffNCX0XtJXUYU\\nsqzucBSNRgmFQrhcrrTOt9vtqKrK4OCgtRbbZJqmWeEy+WsBhoaGkoJIiEIwvvbZSYwezUcYH4EG\\nRsgogB9jHbQ+xns1v+fyy0/wzjvphY2u6/z7a/9OR38HXc93ceMVN9JQ3sD3P/997KsKe16cWFoy\\nChybzTZjV9zsNQSDwbSvmWo0WyQSweFwUFJSYi0WWlSUemMmsxckRKEwlqSJY2zbbO71cglGwLyP\\n8QgtMfbfOMY6aAcxVhR4l4997Cwvv/wvF3wfsy7z1K+fYpmyjIbyBg43HqbEXpL170mIbMgocC40\\nKsxut3PbbbdNGWGWqba2Nu6//35g+pFxQhSa8RrNFRhFfxjv0ZhBcx4YBtZizLHpA14bO+/tsbDp\\nnfY9Rk6O0PV8F0/2P2nVZX645YdSlxELQkaB09s7/T+EbAmFQlx22WXce++9c7qO/OMTuTIeNMsw\\nejSrx/4M43NqRjGGPbswgudNjNFn64CLUZQTfOMbn0s5Cu3MuTNWXSaiRqh119L8n5u5texWqcuI\\nBSWrNZy5UlWVUCjE4cOH890UIS7IeHR2CCNcJtZozPk0YEzaPIsRLlcAxzAmcH4MWIHNluAnP2me\\nsjTNxLpM92+6ueHyG2gob+Cv/+SvpS4jFqyMAicajdLb22utDG3Ov9m2bVtS0f/pp5+e1RbTzc3N\\n1l47JnMAwujoaMo6znQDFKYbhSY9H5ENy5eXc+6cgjFnxsZ4jeYERuCYgwKuxXhkpgEfAFdjDne+\\n/fYbpkziVEdUa76MTbHRUN7Aoe2HpC4jFoW0hkXH43H8fn/Sbp+TeTweuru76evrw+/309ramtFj\\nsaamJpqbm1MOACgrKyMcDieFmqqqVFVVZbyEjgyLFnOlKOuZOhjAfHR2HKNH4wJeBs5g9GjWACu4\\n5JLTdHYGk3o0Zl2mo7+DF4+/yLYbt9GwoYFNV2+SX5DEonLBHk48Hsfj8QDGjp+BQICqqipru+nD\\nhw/T1tZGX18fbrcbXdfxer0ZhU17e/uUsIlGo9ZKAl6vl0OHDiUFTiwWw+fzZfCtCjF7e/ce5LOf\\n/TJG/cXcOgDGgyaBMTDAfNz1O4zHbEZvZvXqN5Lm1Jw5d4Z/PvbPPNn/pFWXCf7noNRlxKJ2wR6O\\n0+lE0zTa2tqspWZSaW1tpbm5GUVRGB4eTnsDtnA4zMjIiBVqYAyVDofD1q6hiUQCv9+ftLRNTU0N\\noVAo4yHR0sMRmRgfEGAyw8YMGvNR2cUYi2++jjG8+TLGH52V88MftqDrOv/x+n/QcbSDrt90cf1l\\n19NQ3oD/Rr/UZcSSMGPg7Nmzh2AwyI4dO3jooYdmvFBVVRWxWAwwRprdddddF3zzVBM6TW63m2PH\\njlmfx+NxOjs72bRpE6qq4vF42Lx58wXfYzIJHJGO5KC5HCNEYDxs3sYYGLAMYzDA6xjzbqYuSWPW\\nZZ7qfwpFUaz9ZUodsg6gWFpmDByPx8ORI0c4d+7cdKcAxkTNmpoaurq6qK+vx+PxcOjQoaw3Nhsk\\ncMRMxhfWhPEBAZOHOb8NrBz7/PcYNZzxx2cf+9hZjvy2i+7fdNPR38Fv3/utUZcpb+CT13xS6jJi\\nyZoxcBwOB5dddllST2M6mqZht9vxeDwMDQ2lvXhnrkngiOmMr3k2eeTZxGHOb2MMCBgYe228R3P9\\n+ovY3f0lOvo76FV7qXHX0FDewK1lt3LRsoty/v0IUWhmHDSQSCT45Cc/mdaFzLXNnE4nR44cmXvL\\nhMghY3vnSzBqNJNHnp3EGH2mA5/ACJtijJFny+EalU13XcrgJYf57r8Nc2f5nTzxJ09IXUaISS7Y\\nw7HZbBn1VmbzNbkkPRwxkTGf5jxGr8ac5zVxQID5yOwPMEae6cBlYF8G5W9C+ctcfY2Tpv/UyBfL\\nvyh1GSFmMOOe0V6vl5GRkbR7LPF4nEQiMaudOIXIpV27HkVR1o+FzUcxeisnxj40jK2dT2DUZnTg\\nt7DqSvCshP/aj9J4kC8HN/PvwQO8FnyFnbfslLAR4gJm7OHEYjGqqqpwOBwMDg5Ou2KzydzDpq+v\\nj4qKiqw3Nhukh7O0jS9HA+OTN82RZ+9hPD4zVxB4DZadh7LVUP42uN9m+StrCO/8Gz593aelLiNE\\nhmbs4VRWVrJ9+3ZrnszTTz+d8ryenh4rbOrq6go2bMTSdccdQRRl/VjYXMP4fBozbDSM1ZvXAufh\\nmhfhj38PfzEA/9cgq95YwfA33uHDvxvm85/4vISNELOQ1tI2fr+fnp4ewKjRuFwuXC4Xqqqiqioj\\nIyMA1NXVZbzlc65JD2dpSR7mPN1yNG8A58C+Fsp/C+UnQLHB0XXwawV9+MVcN1uIRSntLaYjkQgt\\nLS1Eo9Epr3m9XoLB4IKo3UjgLA3Jj85S7bYJ8CqsOgc3/B42JOCyk/D8NdDvhtcuAl5D15/LddOF\\nWLTSDpyJVFW15t2ku510oZDAWdyMhTVN0wTNsmEoexPKz4D7XVAvhaPF8NL1cK4IODG2xfOFd90U\\nQqRvVoGzkEngLE4rV27kzJmzY59NHAwARtDocM0glL8H6xNwfA0cXW30aE5djrEW2u958MHPp9wE\\nTQgxdxI4YkEbn0cDKYPG/gGUv2QEjQL0XwH9q2HkIiYuxLls2eucPduf49YLsbRI4IgFKfnR2aSg\\nWTUCN7wFG16Gy0/Cc0XQfy28dgYjdSRohMgHCRyxoFx8sYeTJ0+PfTYhaGznoWwINrwB7ndAvQT6\\n7XDsWjg3MuF8I2gU5VXOn5cBAULkkgSOWBBS92gugatHYMNLsP4tOL7cKP4/Xwyn7BjL0pjnm/Nt\\nXpWRZ0LkiQSOKGgpg6ZYgfJXYMMQ2HQ4OtabGbkKY5HNiedL0AhRKCRwREGaEjQrP4QbNSh/Ga5I\\nwPPr4OhyeG01Rl3GtJpUu20KIfJPAkcUjOLiP2R09P3xA7ZroOw9KH8Hyt4CdS30Xw3HTsG5VKsy\\nyWAAIQpZwQROOBzG4XCkXK0gFovR19eH0+lEVVUqKytnvaqBBE7hSe7N6HB1MWx4HW58G4Yvhf4r\\njR7NybfHzlnG+IZoIEEjxMIw4wZsuRKJRGhsbCQcDk95TVVVmpub2b9/v3Wsvr4el8tFaaksB7+Q\\nJQVN8WVQ/oYxyswGHL0W/roERi7G2Crg7QlfaYbNeNBcfvlbsjKAEAUur4EzODhIS0sLHo8Hp9OZ\\n8pyWlhaampqSjgUCAYLBYMEvFCqmSgqZlefghuVGb+aKY/D8R+AfPjm2jpmCETTHmalHAy/IYAAh\\nFoiCeaRWVlZGKBRi8+bNScedTiexWIySkhLrmKZpOJ1Ozp8/T6bkkVru7dr1KN/85qPGJzYdyk4Y\\n65iVvQeDVxi9mWNrJtRlXp3mShN7NLLWmRALTUE8UpuOpmlWuExktxt7xQ8NDSUFkSgs470ZHa4+\\nBeXnYP2bMHwx9JfC3k/CyTNj50wMGcX4Gst40Fx00TFOn05vB1ohRGEp6MAZHh4GmHanUVVVJXAK\\nkBU0xWegXIfyN42dM/tL4PubjYEAnADOkDpozLAZD5qioldIJP4jV9+CEGIeFHTgaJqW7yaIDCjK\\neqMuUzEKG07CFSeMusxPNsGrawFzyLMxEXMqHZmsKcTiVdCBMxdmrUbML0VZb9Rl3CegToOyD2DQ\\nCf/+CTi2Ds6dHDvzfZJD5iPAaxM+l4EAQix2izZwxPwxHpmN1WVu1Yz9ZUbWwNGPwF43nFyJERwn\\nAY3xNc0meg1YAzgY34vmj2QvGiEWsYIOHHM30dHR0ZR1nJl2G51uFJr0fGbHGmlWfAb+S8LYknmZ\\nzZj5//0bYfjKsTNPAB+Sfm/mFenNCLFEFHTgmFtYq6rKxo0breOqqmK322XAQA5YdZkbRuHPNLjy\\nQ/jNOvjJRnjV3MIZrO2bU9ZmXkNqM0KIgg4cAK/Xy6FDh5ICJxaL4fP58tiqxS2pLrNVg+vG6jL/\\n5+PwYimcWzZ25okJX3XhuTNSmxFiaUu1AmLepHoM1tLSQnd3d9KxUChES4usAJxNu3Y9iqLciHK1\\nG259E/7iRbg5AS9/BB6+FTpvhhfKxgYBnGB8pJn58Z8mXfGjwPVjf34BXf9nCRshlri8rjSQSCTY\\nvXs3qqoSDodxuVx4vV58Ph9bt261zovH43R2drJp0yZUVcXj8UxZkSBdstJAMkVZb9Rlbhqryyy3\\nwdGrjdpMUl3GNLEn8wngtxM+l8dmQojpFczSNrkigTOhLnP9qBEyV54x6jJHr56mLjPdSDMw9p5Z\\nA6wARnjmmW/ymc/cPL/fgBBiQZLAWSKS6jLlGlx3AoYuM0LmxRI4Z5bzpuvNzDTSTHozQogLk8BZ\\nxKz5MledMkLmplEYuQT6r4Hn1sFJc426dIr/ICEjhJgLCZxFxlrHrOhDI2TKE7AiVV0G0ntkBhI0\\nQohskMBZBKyQmVKXudLozbySqi4D8shMCJFLEjgLlBUyNh1cJ4yQue59GHIavZljpXA2k/kyICEj\\nhJhPEjgLSNL+MlZd5gRoq42Qeb4MPlg5dk66IQMSNEKIXJDAKXBJWzIXfQg3abDhA1hxzqjJ9JfB\\n8TVjJ0jICCEKlwROgUkKGICLxtYxKz8F634/Vpcpg1fWYtRlJGSEEAuDBE4BmBIyVl3mQ7juXaMu\\n0++CF68aq8tIyAghFh4JnLy1Y1LIoMM6O2x4Hda/BYlVcLQUnv/oWF1GQkYIsbBJ4OTsfScHzJii\\ny+GmN2DDG7DiPPR/DPqvHavLSMgIIRYPCZx5fa9pQuaiq+D6t43ezLoT8MI1cPRj8Ooq0CduECch\\nI4RYPCRwsn79VCHzUbCdB9dxKH8DPv6esY5Z/7Xw4poJ82UmB8xa4PjUa0nICCEWIAmcOV9vml4M\\nH8Woy/weNrwL61+FxGojZJ5zwgcXjZ13oV7MaowVmY2Quf32cn74Q9kLSAix8EjgZPz10wUMGCED\\nrDkF5ceh/GW46Cz0X2V8HL907Dx5VCaEWHokcNL6mpl6MWMuOgvXa7DhFbhqxJgvc/RqeNUB+mvT\\nfP3ka0nICCEWLwmcac+bphYzke1iKH0HNrwMH38LXrbD0Wvgxcvh7BtptEZCRgixdCyYwInFYvT1\\n9eF0OlFVlcrKSqqrqzO+zkyBc+GQuRSjLpMwHpfd9AqMrjJ6Ms9dBR+8fYF3l4ARQixdyy98Sv6p\\nqkpzczP79++3jtXX1+NyuSgtLZ3TtdMLGWDNSSjvN0aZrTxrrGP2g4/Ce+ZimdOFjYSMEELAAunh\\nBAIBamtr2bJli3UsGo3S1tZGV1dXRtcyezhw46RXUoTMRWfh+gEjZK4ehd9cAv12eOXiSfNlJpOQ\\nEUKIyRZE4DidTmKxGCUlJdYxTdNwOp2cP38+o2slB06KkFF0cA0ZM/8//i68vAqO2sfmy9imuaoE\\njBBCXEjBB44ZLJqmUVRUlPSazWZDVdWkILqQ8cC5FStkAK4cW17mpjdh1AZHi+G5Yvgg1VNHCRgh\\nhMhUwddwhoeHAaaEjSnTwBl3Kax5zwiYDa/DytPQXzypLjORhIwQQsxFwQeOpmnzc+GGn8PVGryw\\nBv7psmnqMhIyQgiRLQUfOLM1/uhsGh3mGmXa2Ecqz2d2TSGEWMTmWoGZrgouhBBCJJnrL90F38Nx\\nuVwAjI6OpqzjmK9PNl0SF8oGbBci7cyehdBGkHZmm7Qzu7LxhKfgezh2ux2Xy4WqqknHVVXFbrfP\\ncsCAEEKIXCv4wAHwer0cOnQo6VgsFsPn8+WpRUIIITJV8PNwABKJBH6/P2lpm5qaGkKhUMY9nIXW\\nfZV2zt1CaCNIO7NN2pld2WjngggcgHg8TmdnJ5s2bUJVVTweD5s3b874OkvpLzcXFkI7F0IbQdqZ\\nbdLO7FpSgZMtS+kvNxcWQjsXQhtB2plt0s7sksARQgixYCyIQQNCCCEWPgkcIYQQOSGBI4QQIick\\ncIQQQuSEBI4QQoicWLZr165d+W5ELsRiMZ555hmGhobYu3cvp06dmnYdtnxRVZX6+nquueYanE4n\\nb7zxBi0tLSiKkve2hsNh3nzzzZTtKKR7O107C+ne9vT0sHfvXjo6OnjkkUe4+OKLueGGG5LOKYR7\\neqF2Fso9jUQihEIh4vE4HR0dvPnmm3g8nqRzCuF+XqidhXI/J9I0ja9+9at89rOfTTo+6/upLwED\\nAwO6z+dLOub3+3VVVfPUotQGBgZ0RVGsD4fDoff09OS7WXpvb6/ucDj0aDQ65bVCurcXamch3Ntw\\nOKzHYjHrc03TdLfbrYdCoaS25vueptvOfN/T3t5ePRKJJB3zeDx6a2trUjvzfT/TbWe+7+dkjY2N\\nut/vTzo2l/u5JAKnsbFxyl9cJBKZciPzTVVVPRqN6olEQh8cHMx3c3RVVfVAIKCHQiHd7Xan/EFe\\nCPc2nXYWyr2d+APGFAqFdEVRrM8L4Z6m085CuKd1dXVTfpAHg0Hd7XZbnxfC/UynnYVwPycaGBjQ\\n/X6/Xl9fn3R8LvdzSdRwuru7qaysTDrm8XgIh8N5atH0dF2nqKioIFbBLi0t5fHHH2f79u3TnlMI\\n9zaddkL+762maXR2dpJIJJKOV1dXAzA0NATk/56m207I/z1VFIVIJJJ0TNd1HA6H9Xm+7yek107z\\nWKH8+49Go/h8vikrC8zlfi76wNE0DU3TcDqdScftdjuQ/I9HZEbubWbsdjuqqjI4ODjtOYVwT9Np\\nZ6Ho6upi9+7dScfC4TDbtm0DCuN+ptPOQhONRvF6vVOOz/V+FvwGbHM1PDwMkHLzNjAKdYXw24RJ\\nVVU0zdjyenh4GKfTydatW/PcqtTk3mbOvGcTRSIRHA4HJSUl1r5P+b6nF2rnxPbk+55OFAqFqKqq\\n4t5777XaBPm/n5NNbufE9hTC/VRVlerq6im9m7nez0UfOOZf3kJg/tYw8X+w+vr6KccKhdzb7Ghr\\na+P+++8HCvueTmwnFNY97enpobe3F0VR6OzstI4X2v2crp1QOPezp6dn2sfTc76fWakuFbC+vr6k\\nQudEiqKkLDAXkkgkklRYzJdUxfhCvLfTDRpIpRDubVtbm15TU2N9Xoj3VNentnM6+b6nmqbpHo/H\\nGmFXqPdzcjunk+v7OTIyoofDYevztra2pMEAc72fi76Gs9CVlpaiqiqjo6P5bsqik+97q6oqoVCI\\nffv25eX905VJO/N9T4uLiwkEAtYAh0KVbjtzfT+7u7uTelPmlgTZsugDx5yMNN1fWL4nVE7U2to6\\n5ZjZzTaf7RcSubdz09zczIEDB5KOFeI9TdVOKMx7CsZoOk3TOHDgQEHeT9PEdkL+72c8Hqeqqirp\\nmD6phjPX+7noA8dut+Nyuab8hamqit1uL5iitqqqNDc3TxnlYRbpCumHt0nu7ew1NTXR2to6pfha\\naPd0unYWwj1VVRWHw8GRI0dSvq5pWkHcz3TaWQj38/Dhw3R2dtLc3Gx9hMNhYrEYzc3N9PT0zPl+\\nLvpBAwBer5dDhw6xceNG61gsFsPn8+WxVclcLhdtbW1T/sIikQgej2faUSH5Jvc2c+3t7TQ3Nye1\\nJxqN4nK5KC0tLZh7OlM7C+GeapqG2+1OuYwRYM0Vyff9TKedJSUleb+fqQYK7Nmzh8OHD/PQQw9Z\\nx+Z0P7NSaSpwmqZNWYrB5/MVxGzeicLhcNLyECMjI7rH49Hj8XgeW2Vwu91TZkrreuHd2+naWSj3\\ntru7Ww+FQnpfX5/10dvbqwcCAeucQrin6bSzEO5pa2urrmla0jGv16s3NzdbnxfC/UynnYVwPyfb\\nsWPHlBUE5nI/l8wW0/F4nM7OTjZt2oSqqng8HjZv3pzvZk3R09ODqqocP34cTdOm/IaZS4lEgt27\\nd6OqKuFwGJfLhdfrxefzJRUW831v021nvu9tqglzJrfbzbFjx6zP83lPM2lnvu8pGD2xgYEB1q5d\\ny8DAAFVVVdx1111J5+T7/9F021kI9xNgcHCQlpYWurq6SCQSbN++nUAgQEVFBTD7+7lkAkcIIUR+\\nLfpBA0IIIQqDBI4QQoickMARQgiRExI4QgghckICRwghRE5I4AghhMgJCRwhhBA5IYEjlqRYLIbf\\n78fhcGCz2XA4HHg8Hvbs2ZPvps2Kz+fDZhv/5+z3+5M+F6IQyP+RYskJBAJUVVXR09ODzWbD5/Nx\\n2WWXceTIEYLBIE6nk3g8nu9mphQOh7HZbPT09CQdVxRlylLy2V5aXoi5ksARS4rf76e9vR2Hw0Es\\nFuP48ePs27ePY8eOce7cOXbs2IGmaXg8noINHZgaJt3d3QwMDOSpNUKkRwJHLBmRSISenh7cbjeD\\ng4NJq92aHnroIdra2gAjnArV5BWpiouLC2Y7CCGmI4EjloyWlhbrvzMt9759+3YqKytRVZVoNGod\\nn1wnMWmahs1mo6mpKem4qqr4/X7cbjc2mw2n00l9fT2Dg4NJ5wUCAWuxzGAwaNWVysrKkh6d+Xw+\\na497s0ZjboSVbs2mtbUVj8djtaepqWlKewBCoVDSeVVVVUn3QojZkMARS0Y0GsXhcLBly5YLnhsI\\nBADo7e1NOj5TXWTia6qqUlZWxtNPP01ZWZlVNwqHw3g8HhKJxJSvNx/33XbbbTQ2NlqBZf6gb25u\\nprGx0WpfKBRKCs4L1Ww8Hg/Nzc3YbDarPaFQCLfbnfT4MBgM0tTUxNDQEH6/H6/Xa+13UsiPGcUC\\nkB2RoP4AAAQ+SURBVKVtE4QoaAMDA7qiKHpVVVVa58diMV1RFL2mpsY65vV6dZvNNuXckZERXVEU\\nvampyTrW2Nio22w2PRqNJp3b2tqqK4qih8PhpHMVRdHLysr0RCJhHY9EIrqiKEl70HR3d+uKoug9\\nPT1J162rq0tq2+TPW1padEVR9AMHDqT8Pj0ej3XMbrfrZWVlSeeZbZn4PQqRqSWx46cQmqYB6W/V\\nW1paOqf3a2pqora2dsoeIeZ+IiMjI1O+ZvKjvurqaoCUj7zSoU+o8+zevRufz0dlZaV1L8D4Pqur\\nq4lGo4yOjlJUVEQikaCsrCzpWtXV1cRiMex2+6zaIgQskS2mhTB/UE7ei3065nmz/QFbUVFhhYum\\naRw+fJhYLGYNSEjF3BJ5PiQSCXp7e3E4HClfVxSF4eFhioqKqKurIxwOW48CvV4vFRUVKQdZCJEJ\\nCRyxJJg9m3QD5/Dhw0lflylN0wgGg9aOiWDUUDwez7Q9lul22Zwts6Zjfs8+n49gMDjt+WYYdXV1\\nsWfPHtra2pLOb2xspKWlheLi4qy2UywdEjhiyfB6vdbQ6IlbT5sikQherxfA6ols27btgtcdHh6e\\ncqy6upp4PE4gECAQCFi9g2g0Sjgcnsu3kTEzyOx2e9rbKt93333cd999jI6O0tvbS1tbG6FQiMOH\\nD1thLESmZJSaWDLM39ZT/ZavaRo1NTVUVVXR2tpKPB7H4/Gk9RgpFotNuVY8Hsfv9/PYY48lXUPP\\n4Y7u5nvZ7XaKi4uJRCIpz3M4HFbNRlVVgsGgNTKuqKiIrVu3sn//fquOYw7FFiJTEjhiyaiurqau\\nrs4asjxxiK/dbqerq4tYLEZzczOKotDd3Z309Xa7HV3Xk+ajmI/OUpk8MGDiuXMNnnS+fuIw6UAg\\nwMjIiDWPx9Ta2koikUiaQ7Rnzx5rWPhEqqqiKMqMc5iEmFE+h8gJkQ9+v19XFEVXFEW32+261+vV\\nKysrrWM2m23K0GVd1/VwOGydEwgE9MbGRt3hcOg1NTW6w+FIGr7s8/l0RVF0v9+vt7S0JJ2rKIru\\ndrv1SCSi6/r4sOiJQ6JNk4dmm8OT3W63HgwGreN1dXW6oijTfq7ruu52u62vraurs77nyUPFzbY7\\nHA69rq5Ob2xs1O12u26z2fTm5uZZ3HEhDBI4YkmKxWK63+/XnU6nbrPZdKfTqVdVVent7e26pmnW\\nD93J811CoZD1g9vpdFo/gB0OR9IcFU3T9EAgoDscDuuHunmtQCCg22w263zz83QCR9fHA8HpdFrH\\n/H5/0rybyZ+bgsGg7vF4rHk/0wVIMBjU3W530r2ZfC+EyJSi6zl8qCzEAvLd736Xe++9N9/NEGLR\\nkMARQgiREzJoQAghRE5I4AghhMgJCRwhhBA5IYEjhBAiJyRwhBBC5IQEjhBCiJyQwBFCCJETEjhC\\nCCFyQgJHCCFETvz/iVvBSPNrLTUAAAAASUVORK5CYII=\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 6\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Central Limit Theorem\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.hist(np.random.rand(10000),fc='gray', histtype='stepfilled', alpha=0.3)\\n\",\n \"ax.set_xlabel('Value',size=20)\\n\",\n \"ax.set_ylabel('Freq',size=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\\n\",\n \"\\n\",\n \"x = [np.mean(np.random.rand(100)) for _ in range(10000)]\\n\",\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.hist(x,fc='gray', histtype='stepfilled', alpha=0.3)\\n\",\n \"ax.set_xlabel('Value',size=20)\\n\",\n \"ax.set_ylabel('Freq',size=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\\n\",\n \"\\n\",\n \"print('Real STD: ', np.std(np.random.rand(10000)))\\n\",\n \"print('STD estimated *sqrt(n-1), n = 100 : ', np.std(x)*np.sqrt(100-1))\\n\",\n \"print('STD estimated *sqrt(n-1), n = 50 : ', np.std([np.mean(np.random.rand(50)) for _ in range(10000)])*np.sqrt(50-1))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAbEAAAEsCAYAAABNKI0sAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U9TI9t9//GPuNd/4puCRjNVqVQWgRaVSnkFEniTHUiz\\nmMoiZQxzH4BByn7uleYRDMLZ+yL5ARgkvDdIY2+SRUAtJ9lM1bWOKC9crsQjWqT8Nzb9W8wPzQjE\\njCQErTO8X1XUXJ3+tnTUIH1ud58+HQmCIBAAABaaCLsDAAAMixADAFiLEAMAWIsQAwBYixADAFiL\\nEAMAWOvjsDtwoVwua3p6WisrK1eW7e/vyxijRqMhY4zS6bRWV1e7ajzPU61WUzQalTFG8Xj8ynP1\\nUwMAsMdYhFilUtHm5qbK5fKVZfv7+3JdtxNa7XZbiURCrVZLGxsbkiRjjHK5nA4ODjrrra+vy3Vd\\nzc7O9l0DALBLqIcTm82mMpmMms2motFozxpjjBYWFjqPp6amlM1mlU6nO235fF6ZTKZrvXQ6rWw2\\nO1ANAMAukXGZsWNubk6FQkHLy8udNt/3lUwmVa1WNTU11Wk3xmhubk7GGM3MzCgajcrzPM3MzHSt\\nG41GdX5+Lkl91QAA7DLWAzscx5ExRs1m89oa3/c7YXR5XUk6OTnpqwYAYJ+xDjFJarVamp+f72qr\\nVCqanp7WzMyMWq2WJGlycrLn+saYvmoAAPYZ+xDrZWdnR8+ePZP0ek/sffqpAQDYx7oQKxQKevjw\\noZ4+fRp2VwAAIRuLIfb9MsaoUCjo+Pj4zl4zEolcu2xMxsQAwL1l1Z5YLpfTixcvutpc15UknZ2d\\n9VzHdd2+aobxroADANw+a0Isk8loe3v7yuAMx3Hkuu6VwRnGGDmOo5mZmb5qrhMEQc8fAED4rAix\\nYrGoXC7XFTbVarUz9D6ZTOro6KhrHc/zlEqlOo/7qQEA2GWsQqzXHs7FVFStVkue58nzPFUqFZVK\\npc50Ufl8XqVSqWu9QqGgfD7fedxPDQDALqHO2NFut/X8+XMZY1Qul+W6rpLJpFKplFZXV3teoHwh\\nFovpyy+/7Dyu1+va3d3V0tKSjDFKJBJds3/0W9Ovi/NhHFoEgPCMzbRTtiHEACB8Y3U4EQCAQRBi\\nAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAA\\naxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGt9HHYHAAB34+joSH/4wx9C\\n7UMkEtE//MM/jOz5CDEAuAfOz8/15Zdf6m//9m9D7cevfvWrkT7f2IRYuVzW9PS0VlZWrizzPE+1\\nWk3RaFTGGMXj8St1o6oBgA/Zw4cPQ339drs90ucbixCrVCra3NxUuVy+sswYo1wup4ODg07b+vq6\\nXNfV7OzsSGsAfHh+//vf609/+lPY3dA3vvENTUwwDGHUQg2xZrOpfD6vRCKhaDTasyafzyuTyXS1\\npdNpZbNZ7e3tjbQGwOj893//t372s5+F3Q39+te/1le+8hVFIpHQ+vDHP/5R3/rWtzQ3NxdaHz5U\\nkSAIgrA7IUlzc3MqFApaXl7uao9Go/I8TzMzM5023/cVjUZ1fn4+0ppBXHwgxmTzYUz86U9/0qtX\\nr8Luhj766KPQDxsZY/Sf//mf+pu/+ZtQ+/HRRx/pk08+CbUPzWZTruvq7/7u70Lrw/n5uX74wx8q\\nkUiE1gdJajQaevz48ciebywOJ17H9/1O0LzNcRxJ0snJiRzHGUnN2+EGDOuXv/yl/vVf/1Xf+MY3\\nQu3H7373O62uruorX/lKqP342te+psnJyVD7gA/bWIdYq9WSpGs/BMaYTviMqga4qcnJydAPG/3s\\nZz/jKAHuhbEOMd/376wGN/Pb3/429C/NiYkJ/cVf/EWofRgnv/3tb/V///d/ob3+H//4x9BeG/fH\\nWIfYOAjzZLAtfvWrX+mnP/2pPvroo1D78ec//1n/9E//pK9//euh9mMcfPWrX9Xh4WHY3Qj9vBw+\\nfIQYbuz8/FyffPJJqCetJek//uM/hhqk8yH65je/GXYXcMlvfvMb/c///E9or/+hfjbGOsRc15Uk\\nnZ2d9Tyf5bpuZ3DGTWuuc90hMvbQAPRrcnJSv/jFL/SLX/wi1H785V/+ZaivfxvGOsQcx5HrujLG\\naH5+vtNujJHjOJ3BGKOqAYDb8ODBAz148CDsbnyQxv7y8WQyqaOjo642z/OUSqVGXgMAsMtY7Yn1\\nOnSXz+e1tramjY2NTluhUFChUBh5DewWBIH+7d/+LdQBJr///e9DH6UJ3CehztjRbrf1/PlzGWNU\\nLpfluq6SyaRSqZRWV1c7dfV6Xbu7u1paWpIxRolE4srMHqOq6Rczdrzxy1/+UrVaLfSBHb/5zW/G\\nYlj3J598oq9+9athdwMYS6OesWNspp2yDSH2xriEGIDxd6+mnbJB2MNWI5EIIyUB3FuE2A398Ic/\\nDPX1P/74Y/3jP/5j6HP1AUAYCLEbCntG6P/6r//Sy5cv9bWvfS20Pvzv//4vh1UBhIIQs9xf//Vf\\nj8WtP/7qr/4q7C4AuIcIMcsxNx2A+2zsL3YGAOA6hBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQY\\nAMBahBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQYAMBahBgAwFrW3Nm5\\nUqmoXq9Lkl69eqVYLKaNjY2uGs/zVKvVFI1GZYxRPB7XysrKwDUAADtYEWKe56ndbuuzzz7rtO3v\\n76tYLHaCzBijXC6ng4ODTs36+rpc19Xs7GzfNQAAe1hxOLFQKGh1dbWrbXV1VYeHh53H+XxemUym\\nqyadTiubzQ5UAwCwhxUhdnx8rGazeaXd9/3Of5dKJcXj8a7liURC5XJ5oBoAgD2sCLFkMqlUKtUV\\nZJVKRevr65Jeh5nv+4pGo13rOY4jSTo5OemrBgBgFytCbGtrS47jKBaLqVgsqlKpqN1u67vf/a4k\\nqdVqSZImJyd7rm+M6asGAGAXKwZ2SK8PKT569EjpdFrxeFzVarWz7O3DitfppwYAYBcr9sQkqVgs\\nant7W4eHhzLGKJFI9DxPNmqRSKTnDwAgfFaEWCaTUSqV0vz8vFZWVtRsNuW6rlKpVNhdAwCEaOxD\\n7OIw4MzMTKdtampKBwcHchxHL168kOu6kqSzs7Oez+G6bl81vQRB0PMHABC+sQ+xWq2mWCzWc1k6\\nnZbv+3IcR67rXhmcYYyR4ziamZnpqwYAYJexDzHXddVoNHou832/c91XMpnU0dFR13LP87oOOfZT\\nAwCwx9iH2MV0UG+PRpRe70G9evWqsweVz+dVKpW6agqFgvL5fOdxPzUAAHtEAktO8BSLRTUaDT14\\n8EDS64uUL08AXK/Xtbu7q6Wlpc4IxuXl5YFr+nExQvHly5dDviMAuH8ajYYeP348suezJsTGDSEG\\nAIMbdYiN/eFEAACuQ4gBAKxFiAEArEWIAQCsRYgBAKxFiAEArEWIAQCsRYgBAKxFiAEArEWIAQCs\\nRYgBAKxFiAEArEWIAQCs9fEgxXNzc53Z2/sVBIEikYi+/PLLgdYDAOB9BgqxhYUFNZtNeZ7XaZud\\nnVWr1VK73Zb0+j5fFzeyvDBo8AEA0I+BQuzZs2daXFxUPB5XsVjUwsJCZ5nnedrY2NDJyYnK5fKV\\nIAMAYNQGOie2tbUlx3FUrVa7AkyS4vG4arWazs/PlcvlRtpJAAB6GSjEKpWKUqmUpqamrq1JJpOq\\nVCo37hgAAO8zUIgFQSBjzDtrms3mjToEAEC/BgqxZDKpWq2mH/3oRz2X7+/vy/M8JRKJkXQOAIB3\\niQRBEPRbbIxRIpHQ2dmZvvOd7yiVSsl1XTUaDR0eHqpcLkuSarXalXNmH5qLEZcvX74MuScAYI9G\\no6HHjx+P7PkGGp3ouq6q1aqy2axKpZJKpdKV5Ts7Ox98gAEAxsNAISa9HoV4eHgoY4w8z5MxRq7r\\nynVdxePx2+hjh+d52tvb04MHD/Tq1Sul0+muofye56lWqykajcoYo3g8rpWVlSvP8b4aAIAdBg6x\\nCw8fPtTi4uJ7RyuOSrlcVqVS0RdffNFpS6fT2tnZkfT6UGcul9PBwUFn+fr6ulzX7QRdPzUAAHsM\\nPHdivV7X4uKiHMdRLBZTrVaT9HpKqn/5l38ZeQclyfd9bW5udgVYoVDQixcvOo/z+bwymUzXeul0\\nWtlsdqAaAIA9BhrY0Ww2FYvFJEkrKyuqVquqVCpaXl7W9PS02u22EomEjo6ORtrJbDariYkJPX/+\\nvKv95OREMzMzkqRoNCrP8zqPpdfhF41GdX5+3ndNvxjYAQCDG/XAjoH2xPL5vKTXow8vD+o4PT3V\\n1taWarWanj17NrIOSlKxWNTS0tKV9osw8n2/E0ZvcxxH0uuw66cGAGCXgUJsb29PyWTy2tGHn3/+\\nuRYWFjpD7UfF931NTU2pWCxqf3+/8++FVqslSZqcnOy5vjGmrxoAgF0GGtjh+37ncOJ1XNftCpib\\nugiXer2up0+fdtpzuZxarZY2Njbk+/57n6efGgCAXQbaE1tYWNDx8fE7a+r1+kiH2l+Ej+u6Xe1P\\nnjy5kwEZkUik5w8AIHwDhdiTJ09Uq9X0k5/8pOcX+fr6uowxSiaTI+vgRXhdDrGFhQX5vs+5LAC4\\nxwYKsYtzXisrK1pfX5f0erDHkydP9ODBA5XLZbmuq62trZF18GLgxcW/l11cbC1JZ2dnPWsuLsZ+\\nX00vQRD0/AEAhG/g68RqtZq2trb07//+75Kkw8NDlUolnZ+f6/PPP9fPf/7zkXfSdd1rB164rivH\\ncXrWGGPkOI5mZmb6qgEA2GXgEJNe75Gdnp7q/PxcP//5z9VqtTpD7G9DOp3uXFR9wfM8TU9Pd8In\\nmUxeuT7N8zylUqnO435qAAD2GOhi52KxqAcPHujb3/72bfbpiouLqN/ey3v06JEymUynL+12W2tr\\na11TSj169EiFQqETdP3U9IuLnQFgcKO+2HmgEJuYmND09LRevXo1sg70q9lsKp/PKxaLqdFoaH19\\nXcvLy1019Xpdu7u7Wlpa6tw2ZpiafhBiADC4UENsc3NTP/jBD+R5nubn50fWCRsRYgAwuFDvJ1Yo\\nFDQ3N6dEIqGdnR0tLi7Kdd1rZ8EAAOA2DRRiF/MOBkGgzc3NTvvb14wFQaBIJKI///nPI+oiAAC9\\nDRRi/d48khktAAB34Z0hlsvl9K1vfaszAvDyzPUAAITpndeJbW9va3d390p7sVjUP//zP99apwAA\\n6MdQFzsfHByoUCiMui8AAAxkqBCTxPyBAIDQDR1iDN4AAIRt6BADACBshBgAwFqEGADAWu+92LlS\\nqejJkyddbdVqVUEQXGl/W6+h+QAAjNI7JwCemBh+R+38/HzodW3ABMAAMLg7nQD4+Ph4ZC8EAMCo\\nvTPE4vH4XfUDAICBMbADAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGCt9047NY5831cu\\nl9MXX3zR1e55nmq1mqLRqIwxisfjWllZGbgGAGAHK0Msm83q9PS0q80Yo1wup4ODg07b+vq6XNfV\\n7Oxs3zUAAHtYdzjRGKPT09MrN+XM5/PKZDJdbel0WtlsdqAaAIA9rAuxarWqVCqly/MWl0qlK9Nk\\nJRIJlcvlgWoAAPawKsSq1aqSyeSVdt/35fu+otFoV7vjOJKkk5OTvmoAAHaxKsSMMZqdnb2yF9Zq\\ntSRJk5OT167XTw0AwC7WhNj+/r42NjZ6LvN9/73r91MDALCLFSFGAAEAerEixEqlklZXVzuPL49M\\nvE2RSKTnDwAgfGMfYvV6XYuLi11tl8+Jua4rSTo7O+v5HK7r9lUDALDL2F/sfHx8rEajod3d3U6b\\n53mdC5eXlpa0uroq13VljNH8/Hynzhgjx3E0MzMjSX3VXHY5MC+wNwYA4Rv7EOs1mON73/uejo+P\\ntbW11WlLJpM6OjrqCijP85RKpQaqAQDYY+wPJ/by61//+soeUj6fV6lU6morFArK5/MD1QAA7BEJ\\nrjteNoaazaby+bz29vbUbre1sbGhdDqthYUFSa/Pn+3u7mppaUnGGCUSCS0vL3c9Rz81/bg4nPjy\\n5cubvzEAuCcajYYeP348suezKsTGCSEGAIMbdYhZeTgRAACJEAMAWIwQAwBYixADAFiLEAMAWIsQ\\nAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMA\\nWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFjr47A70K/9/X0ZY9RoNGSMUTqd1urqaleN53mq1WqK\\nRqMyxigej2tlZWXgGgCAHawIsf39fbmu2wmtdrutRCKhVquljY0NSZIxRrlcTgcHB5311tfX5bqu\\nZmdn+64BANjDisOJxhgtLCx0Hk9NTSmbzSqdTnfa8vm8MplM13rpdFrZbHagGgCAPSJBEARhd+Jd\\nfN9XMplUtVrV1NRUp90Yo7m5ORljNDMzo2g0Ks/zNDMz07VuNBrV+fm5JPVV069IJCJJevny5fBv\\nDgDumUajocePH4/s+cZ+T8xxHBlj1Gw2r63xfb8TRpfXlaSTk5O+agAAdhn7EJOkVqul+fn5rrZK\\npaLp6WnNzMyo1WpJkiYnJ3uub4zpqwYAYBcrQqyXnZ0dPXv2TNLrPbH36acGAGAXK0OsUCjo4cOH\\nevr0adhdAQCEyIoh9m8zxqhQKOj4+PhOXu9iAAcAYPxYtyeWy+X04sWLrjbXdSVJZ2dnPddxXbev\\nGgCAXawKsUwmo+3t7SuDMxzHkeu6VwZnGGPkOI5mZmb6quklCIKePwCA8FkTYsViUblcritsqtVq\\nZ+h9MpnU0dFR1zqe5ymVSnUe91MDALCHFSFWLpclvR5q73mePM9TpVJRqVTqTBeVz+dVKpW61isU\\nCsrn853H/dQAAOxhxYwdly9QvhCLxfTll192Htfrde3u7mppaUnGGCUSCS0vL3et009NP5ixAwAG\\nN+oZO8Y+xMYVIQYAg7t3004BAHAdQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1C\\nDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwA\\nYC1CDABgLUIMAGAtQgwAYK2Pw+7AXfM8T7VaTdFoVMYYxeNxrayshN0tAMAQ7lWIGWOUy+V0cHDQ\\naVtfX5frupqdnQ2xZwCAYdyrw4n5fF6ZTKarLZ1OK5vNhtQjAMBN3KsQK5VKisfjXW2JRELlcjmk\\nHgEAbuLehJjv+/J9X9FotKvdcRxJ0snJSQi9AgDcxL0JsVarJUmanJzsudwYc5fdAQCMwL0JMd/3\\nw+4CAGDE7tXoxGFEIpF3Lv/7v//7O+oJAHwYgiAY2XPdmz0xAMB4eN/OwSDuzZ6Y67qSpLOzs57n\\nxS6WX3bd/zFc/BJG+X8UtmJbvMG2eINt8Qbb4o1RBph0j/bEHMeR67pXBnAYY+Q4jmZmZsLpGABg\\naPcmxCQpmUzq6Oioq83zPKVSqZB6BAC4iUhwj/Zv2+221tbWuqadevTokQqFwsB7YhweeINt8Qbb\\n4g22xRtsizdGvS3uVYhJUr1e1+7urpaWlmSMUSKR0PLy8sDPwx/lG2yLN9gWb7At3mBbvEGIjQn+\\nKN9gW7zBtniDbfEG2+INQgwAgP/vXg3sAAB8WAgxAIC1CDEAgLUIMQCAtQgxAIC17s3ciYPwPE+1\\nWk3RaFTGGMXjca2srNzaeuNs2Pe0v78vY4wajYaMMUqn01pdXb2DHt+eUfx+fd9XLpfTF198cUu9\\nvBs32Rae52lvb08PHjzQq1evlE6nNTs7e8s9vj3DbotKpaJ6vS5JevXqlWKxmDY2Nm67u7euXC5r\\nenp6oL+HG32uAnRpNBpBKpXqaltbWwuMMbey3jgb9j2Vy+XA87zOY9/3g1gsFhQKhVvp510Y1e93\\nc3MzWFtbG2XX7txNtkWpVArS6XRX2+bm5kj7d5eG3Ra1Wi0ol8tdbeVy2erPSBAEweHhYTA9PR1U\\nq9W+6kfxuSLELtnc3Az29/e72iqVynu/eIZdb5wN+562t7evtBUKhSASiYy0f3dpFL/fRqMRrK2t\\nBevr66Pu3p0adlucnp4G09PTXW07OzvB3NzcyPt4V4bdFpeD/IKt3xfGmCCdTgeFQiGIxWJ9h9go\\nPleE2CXT09NBs9nsajs9PX3vF/Cw642zYd7T6elpkEgkAt/3u9objUYQiUSuPJ8tRvH7LRQKQaFQ\\nsPaL6sKw2+Lzzz8PcrnclXZb/yaCYPhtkUgkeu5tXN4rsdEgITaKzxUDO97i+75831c0Gu1qdxxH\\nknRycjLS9cbZsO/JcRwZY9RsNm+7i3dmFL/farWqZDJ5G927UzfZFsViUUtLS1fabb0N0k22RTKZ\\nVCqV6vqcVCoVra+v30pfx9GovjcJsbe0Wi1J6nnTTElX7kV20/XG2U3eU6vV0vz8fFdbpVLR9PS0\\nlV9Yo/j9GmM0Oztr/dx5N9kWvu9rampKxWJR+/v7nX9tdZNtsbW1JcdxFIvFVCwWValU1G639d3v\\nfvdW+jqORvW9yejEt/i+f6frjbNRv6ednR09e/ZspM95V266Lfb39z+IUWfS8Nvi4gupXq/r6dOn\\nnfZcLqdWq2Xl9rnp38Xx8bEePXqkdDqteDyuarU6op7ZYVTfMeyJ4dYVCgU9fPiw68vrvvgQ/wdn\\nGBfbwXXdrvYnT54om82G0aXQFYtFbW9v6/DwsHNbqA/pMPxdIcRwq4wxKhQK+vGPfxx2V0JRKpW6\\nro+7uA3FfXMRXpdDbGFhQb7vW3ne+CYymYxSqZTm5+e1srKiZrMp13W5y/wQCLG3XHzAzs7O3rl8\\nVOuNs1G9p1wupxcvXoysX2EYdlvU63UtLi52tdl+TmzYbXFxsv7i38tsPG887La42Ct9+/zw1NSU\\nDg4O5DjOvTmsOKrvGELsLY7jyHXdKx8oY4wcx7l2UMKw642zUbynTCaj7e3ta0/c2mLYbXF8fKzd\\n3V3lcrnOT7lclud5yuVyVg5quMnfRa/13l5mm2G3Ra1WUywW67ksnU7fm0PQo/reZGDHJclkUkdH\\nR12j6zzPe+9u/rDrjbObvKdisahcLtf1h1itVuW6rpVTDA2zLXoNVvje976n4+NjbW1t3Uo/78Kw\\nfxfpdFq1Wk3Ly8td69k6alUablu4rqtSqdRzme/7Vn9nDGok35v9X8J2P/i+f+WCw1Qq1XVB3unp\\naeC6btcUMf2sZ5tht0WpVAoKhUJQq9U6P4eHh9fOUmCDYbfFZZ9//rn1Fzvf5DMSi8WurHd5xgab\\nDLst0ul0UKlUutZrNBpBNpu91f7ehVgsduW9BcHtfW+yJ3bJ1NSU8vm8crmclpaWZIy5skchSaen\\np10n6ftdzybDbAvf96+9YPO6Qyg2GPbv4kKz2VQ+n9fe3p7a7bYymYzS6bQWFhbu6B2Mzk0+I4eH\\nh8pkMorFYmo0Gsrlcl17ZrYZdlt88cUXKhaLOjw81IMHDyS9Prxm6x56u93W8+fPZYzpTPh9cUH3\\n2wObbuN7MxIElp9pBgDcWwzsAABYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiL\\nEANC4HmeJiYmrsxyf1mlUtHExMTAt61fW1vTxAQfb3z4+CsHQhCPx+U4jur1utrt9rV1FxPFfvrp\\npwO/xn29dxnuF0IMCMnm5qaCINDe3t61NXt7e4pEIvr2t799hz0D7EGIASF58uSJJGlnZ6fncs/z\\n1G639Z3vfOcuuwVYhRADQrKwsCDXda89pLi7uyvpTdhJr28YuLa2plgspomJCUWjUa2vr6vZbF5Z\\n/+25vVOpVM9zZL7va2JiQplM5sqy7e1tJRKJzutkMpmerwOEiRADQpROp689pFgoFLoOJRpjNDc3\\npx/96Eeam5tTOp3W4uKiyuWyEonEO8+tSe8+R3Z5WSKRUC6X08TEROd1CoWCYrGY6vX6EO8UuB2E\\nGBCii0OFlw8p9jqUmM/nFYlEdHh4qB//+Mf6/ve/r4ODA+Xzefm+r0qlMpI+bW9vq16vq1qt6ujo\\nqPM6tVpNUu87VgNhIcSAEM3OzmphYeHKIcVehxIzmYxKpdKVm0he3Fjz9PR0JH16/vy5UqmU4vG4\\nfN/v/MzOzmplZUWe5+ns7GwkrwXcFHd2BkL26aefql6vq1Ao6LPPPpMklcvlK6MSFxYWOoHl+76O\\nj4/led61A0OG1W63dXh4qOnp6Z7LI5GIWq2WJicnR/q6wDAIMSBkm5ubymaz2t3d1WeffSZjjJrN\\nptbW1rrqfN9XNpvV3t5eZ68tkUgokUiMbMCFMUbS64Eg2Wz22rrrAg64a4QYELKpqSnF4/HOIcVy\\nuSzp9aCPt62srKheryudTiudTmt+fl6SVK1WO+sMqtVqdT2ORqOSJMdxrhy2BMYR58SAMXAxSrFQ\\nKGh3d1eRSKQrRHzfV71e19ramr7//e93AkzqHko/KM/zuh47jqOpqalrB4lMT09rbm5u6NcDRo0Q\\nA8bAxdyIOzs7qtfr117gfHnwxsUhRulqmL09bN5xHAVBoGq12nPdt6XTaZ2enl6Zr3F7e1vtdrvn\\nNWVAWDicCIyBqakpJZPJzh7Q5UOJjuN0lq+vr2txcVGNRkOlUklLS0uSXg/Bd11XKysrkrpD7dNP\\nP9X+/r5SqVRnuquLdS8H49bWlsrlssrlsubm5rSwsCBjjOr1uhKJhJ4+fXqbmwIYTABgLJTL5SAS\\niQQTExM9l/u+H6TT6WB6ejqIRCLB4uJisL+/HwRBEKTT6WBiYiLIZDJBEATB2tralecpFApBLBYL\\nIpFIEI1Gg1wuFwRBEExPT3fWe1s2mw0SiUQQiUSCubm5Tj0wTiJBcIMD6gAAhIhzYgAAaxFiAABr\\nEWIAAGs9DzJCAAAAJElEQVQRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGv9P1QePcgzjpnd\\nAAAAAElFTkSuQmCC\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAbUAAAEsCAYAAABEwy1WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3b9zG+lh//EP+D2f4x9DLKC7xvFMyCUdt0cs6OZciYCr\\nVMcjdH+ASdBdCp2A69xJoNO4sgmqc0UBcGOnCAUo40nSmOIiPwoVPj5gksnlrhC4ZJz4PLrTfgsN\\n1gIBSgAJENjl+zWDsfHss7vPg4enD3b32UXM931fAABEwMykGwAAwKgQagCAyCDUAACRQagBACKD\\nUAMARAahBgCIjDcm3QBJqtfrqtfrunHjhg4PD+U4jtbX17vquK6rg4MDJZNJGWOUSqW0srIyljoA\\ngHCaeKjV63XFYjHdu3cvKEun0/I8Tx9++KEkyRijYrGovb29oE4ul5Nt25qfnx9pHQBAeE389OP2\\n9nZPWSaT6SovlUra3NzsqpPP51UoFEZeBwAQXrFJP1Ekl8tpYWFBd+/eDcoKhYIePXqk/f19SVIy\\nmZTrupqbmwvqeJ6nZDKp58+fj7QOACC8Jh5q/SwsLOhHP/qRbt++HYSO53manZ3tqjczMyNjjCzL\\nGkmdl8MOABA+Ez/9eFa5XFY6ndbt27clSe12W5J6gqjDGDOyOgCAcJv4RJGOWq2mhw8fKhaLaXd3\\nNyj3PO+1646qDgAg3KYm1FZXV7W6uqqTkxOl02nt7OxoaWlp0s0CAITI1J1+jMfjyufzU3PvWCwW\\nO/cFAJguUxdqkrSysiLP8/To0SPZti1JOj097VvXtu2R1RkWwQYA02WioWaMUSKR0D//8z/3Xe55\\nnizLkm3bPRM5OjMa5+bmRlanH9/3+74AANNnoqHmeZ4WFhZ6jpI6wZNKpSS9uBm7c89ah+u6ymaz\\nwftR1QEAhNfE71P7yU9+oo2NDcXj8aAsm80qnU4HN2SfnJxobW2t6/FWP/jBD1Qul4MjrFHVGVTn\\n1CNHbZgWvu/r97///dj3E4vF9M1vfnPs+wEuYuKhJkk7Ozs6PDwMHmicTqf1wx/+sKtOs9nU7u6u\\nlpeXZYyR4zi6efPmWOoMglDDtPnP//xP/eM//qO+8pWvjHU/X3zxhbLZrG7cuDHW/QAXMRWhFkaE\\nGqbNf/zHf+jf/u3ftLi4ONb9PHnyRO+++67efvvtse4HuIipnP0IAMBFEGoAgMgg1AAAkUGoAQAi\\ng1ADAEQGoQYAiAxCDQAQGVPz0zNAlH322Wf64osvxrqP4+PjsW4fCANCDRizL774Qo8ePbqSR0sl\\nk8mx7wOYZoQaMGa+7ysWi+kv//IvJ90UIPK4pgYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACR\\nQagBACKDUAMARAahBgCIDEINABAZhBoAIDIINQBAZBBqAIDImIqn9NdqNRljdHh4KGOM8vm8VldX\\ng+WdsmKxKMdx1G63VS6Xlc1mtbKyEtRzXVcHBwdKJpMyxiiVSnUtH7QOACCcJh5qtVpNtm0HIXZy\\nchIE1/r6elCv0Wio0WhIkizL0v3797vCyBijYrGovb29oCyXy8m2bc3Pzw9cBwAQXhM//WiM0dLS\\nUvA+Ho+rUCgon88HZbFYTPV6XZ7nyRijdrut9957r2s7pVJJm5ubXWX5fF6FQmGoOgCA8JpoqHme\\np93dXZ2cnHSVd47Ajo6OgjLf9zU7O6u5ubm+26pUKkqlUl1ljuOoWq0OVQcAEF4TDTXLsmSMUavV\\nutR2PM+T53k9P2VvWZakF+E4SB0AQLhN/Jpau93uKavX60okEl1HZcYYeZ4XrJNMJoPrcJ1tzM7O\\n9t2HMSbY1iB1AADhNPFQ62d7e1sfffRR8L5zdPXyjMhcLheUdcLuVQapAwAIt4lPFDmrXC7rrbfe\\n0u3bt4OyeDzeNRNSuroJHrFYrO8LADB9pupIzRijcrmsx48fv7bu/Py8jDE6PT29gpYBAMJgqo7U\\nisWiHj161FO+tbXVU9Y5JWmMkW3bknRuwNm2PVCdfnzf7/sCAEyfqQm1zc1NbW1t9Uzk6NwwfXZ2\\nYmdyiG3bsixLtm3LGNOzrmVZmpubG6gOACDcpiLUdnZ2VCwWu4Kl0Wio1WrJtm1tb2/3hE69Xpfj\\nOEEIZjIZ7e/vd9VxXVfZbDZ4P0gdAEB4TTzUOjc+t9ttua4r13VVr9dVqVSCR1clk8mue9k8z1O5\\nXNbOzk5QViqVVKlUurZdLpdVKpWGqgMACK+YP8ELRP1uhu5YWFjQ7373u+B956HHT58+led5PUd2\\nktRsNrW7u6vl5WUZY+Q4jm7evDl0nUF0ZkByfQ2v8+zZM9Vqta7HwYXZkydP9O677+rtt9+edFOA\\nHhMNtTAj1DAoQg24OhM//QgAwKgQagCAyCDUAACRQagBACKDUAMARAahBgCIDEINABAZhBoAIDII\\nNQBAZBBqAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAAkUGo\\nAQAig1ADAEQGoQYAiIw3Jt0ASarVajLG6PDwUMYY5fN5ra6udtVxXVcHBwdKJpMyxiiVSmllZWUs\\ndQAA4TTxUKvVarJtOwixk5MTOY6jdrut9fV1SZIxRsViUXt7e8F6uVxOtm1rfn5+pHUAAOE18dOP\\nxhgtLS0F7+PxuAqFgvL5fFBWKpW0ubnZtV4+n1ehUBh5HQBAeMV83/cntXPP85TJZNRoNBSPx4Ny\\nY4wWFxdljNHc3JySyaRc19Xc3FzXuslkUs+fP5ekkdUZVCwWkyRN8ONDSDx79ky1Wq3ry1uYPXny\\nRO+++67efvvtSTcF6DHRIzXLsmSMUavVOreO53lB8JxdV5KOjo5GVgcAEG4TP/3Ybrf1zjvvdJXV\\n63UlEgnNzc2p3W5LkmZnZ/uub4wZWR0AQLhNPNT62d7e1kcffSTpxZHa64yqDgAg3CY++/Gscrms\\nt956S7dv3550UyT96doZAGD6TVWoGWNULpf1+PHjSTcFABBCU3X6sVgs6tGjR11ltm1Lkk5PT/uu\\nY9v2yOr04/t+3xcAYPpMTahtbm5qa2urZyKHZVmybbtnIocxRpZlaW5ubmR1AADhNhWhtrOzo2Kx\\n2BUsjUYjmOqfyWS0v7/ftY7ruspms8H7UdUBAITXxEOtWq1KejG133Vdua6rer2uSqUSPLqqVCqp\\nUql0rVcul1UqlYL3o6oDAAiviT9R5OzN0B0LCwv63e9+F7xvNpva3d3V8vKyjDFyHEc3b97sWmdU\\ndQbBE0UwKJ4oAlydiYZamBFqGBShBlydiZ9+BABgVAg1AEBkEGoAgMgg1AAAkUGoAQAig1ADAEQG\\noQYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACRQagBACLjjWEqLy4uBk+nH5Tv+4rFYl0/IwMg\\nvHzf17/+67/qzTffHOt+vvnNb0bmlw1wdYYKtaWlJbVaLbmuG5TNz8+r3W7r5OREkmRZVvDjnh3D\\nBiGA6fUXf/EX+sMf/jDWfXz55Zf6+OOPCTUMbahQ++ijj5ROp5VKpbSzs9P1B+e6rtbX13V0dKRq\\ntdoTbACi4Rvf+Ia+8Y1vjHUfz54902effTbWfSCahrqmdu/ePVmWpUaj0fMNKpVK6eDgQM+fP1ex\\nWBxpIwEAGMRQoVav15XNZhWPx8+tk8lkVK/XL90wAACGNVSo+b4vY8wr67RarUs1CACAixoq1DKZ\\njA4ODvTLX/6y7/JarSbXdeU4zkgaBwDAMIaaKFIqlVSv17W2tqb3339f2WxWtm3r8PBQDx8+VLVa\\nDeoBAHDVhgo127bVaDRUKBRUqVRUqVR6lm9vbzMNFwAwEUOFmvRiluPDhw9ljJHrujLGyLZt2bat\\nVCp14YZUq1UlEgmtrKx0lRtjlM/nVSwW5TiO2u22yuWystlsV13XdXVwcKBkMiljjFKpVM+2BqkD\\nAAivoUOt46233lI6nX7tbMhB1Ot1bWxsBKcvz2o0Gmo0GpJe3Nx9//79rjAyxqhYLGpvby8oy+Vy\\nsm07uF9ukDoAgHAb+tmPzWZT6XRalmVpYWFBBwcHkl48Qutv/uZvhtpWq9XS5uamWq2Wkslk3zqx\\nWEz1el2e58kYo3a7rffee6+rTqlU0ubmZldZPp9XoVAYqg4AINyGCrVWqyXHceS6rlZWVuT7frDs\\n6dOnunPnjpaXlwfe3vz8vH7+859rfX39lfV839fs7Kzm5ub6Lq9UKj2nPh3H6TryG6QOACDchgq1\\nzqzGg4ODnkkix8fHunfvng4ODvTRRx+NroWv4XmePM/rOdKzLEuSdHR0NFAdAED4DRVqDx48UCaT\\nOXd24507d7S0tDTyox9jjGq1mmq1mnZ2dlSr1YJl7XZbkjQ7O3vuuoPUAQCE31ATRTzP08LCwivr\\n2LbdFTqX1Tm6Wl1dDcpyuVxQ5nnea7cxSB0AQPgNdaS2tLSkx48fv7JOs9m81NT+s+LxeM81t6uc\\n4BGLxfq+AADTZ6hQu3Xrlg4ODvT3f//3ff9hz+VyMsYok8mMrIH9zM/Pyxij09PTse4HABAuQ4Va\\n55rZyspKcAqwVCrp1q1bunHjhqrVqmzb1r1790bWwK2trZ6yzinJzo3fks4NuM6N4a+rcx7f9/u+\\nAADTZ+j71A4ODnTv3j399re/lSQ9fPhQlUpFz58/1507d/Txxx+PrHGdG6bPzk7sTPywbVuWZcm2\\n7Z7JHsYYWZalubm5geoAAMJv6FCTXhyxHR8f6/nz5/r444/VbreDKf2j1HmW5NnQqdfrchwnmM2Y\\nyWS0v7/fVcd1XWWz2eD9IHUAAOE21OzHnZ0d3bhxo+uJHq86dTesfqf1ksmkWq1W8Cgrz/NULpd1\\n//79oE6pVNLa2lrXhJJyuaxyuTxUHVw///d//6f//d//Hes+vvzyy7FuH8CfxPwhLhDNzMwokUjo\\n6dOnI9n5ycmJ7t69K2NMcD0uk8kom812TeGv1Woyxujp06fyPE/FYrHn6K3ZbGp3d1fLy8syxshx\\nHN28eXPoOoPqTJTh+lq4/cM//IM+/fRTfeUrXxnrft544w195zvfGes+ouTZs2d68uSJ1tbWJt0U\\nhMxQobaxsaH79+/LdV29884742zX1CPUouE3v/mN3nzzzXOfPYrJINRwUUOdfiyXy1pcXJTjONre\\n3lY6nZZt2+c+qQMAgKs0VKh1vs36vq+NjY2g/OV71nzfVywW4zoCAODKDRVqg/6gJk/cAABMwitD\\nrVgs6nvf+14w2/Hsk/kBAJgmr7xPbWtrS7u7uz3lOzs7+tGPfjS2RgEAcBEXuvl6b2+P+7sAAFPn\\nQqEmMZUdADB9LhxqTAYBAEybC4caAADThlADAEQGoQYAiIzX3nxdr9d169atrrJGoyHf93vKX9bv\\nVgAAAMbplQ80npm5+IHc8+fPL7xuGPBA42jggcbTiQca46JeeaT2+PHjq2oHAACX9spQS6VSV9UO\\nAAAujYkiAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMl77mKyrUq1WlUgktLKy0rPM\\ndV0dHBwomUzKGKNUKtVTb1R1AADhNRWhVq/XtbGxoWq12rPMGKNisai9vb2gLJfLybZtzc/Pj7QO\\nACDcJnr6sdVqaXNzU61W69xn75VKJW1ubnaV5fN5FQqFkdcBAITbKx9ofJUWFxdVLpd18+bNrvJk\\nMinXdTU3NxeUeZ6nZDIZPDR5VHWGwQONo4EHGk8nHmiMi5rqiSKe5wXB8zLLsiRJR0dHI6sDAAi/\\nqQ61drstSZqdne273BgzsjoAgPCb6lDzPO/K6gAAwm+qQw0AgGFMxZT+adaZEAIAmH5TfaRm27Yk\\n6fT09Nzlo6oDAAi/qQ41y7Jk23bPRA5jjCzL0tzc3MjqnMf3/b4vAMD0mepQk6RMJqP9/f2uMtd1\\nlc1mR14HABBuUxVq/Y6ASqWSKpVKV1m5XFapVBp5HQBAuE30iSInJye6e/eujDGqVquybVuZTEbZ\\nbFarq6tBvWazqd3dXS0vL8sYI8dxep48Mqo6g+KJItHAE0WmE08UwUVNzWOywoZQiwZCbToRario\\nqTr9CADAZRBqAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAA\\nkUGoAQAig1ADAEQGoQYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACRQagBACKDUAMARAahBgCI\\njDcm3YBBGGOUz+dVLBblOI7a7bbK5bKy2axWVlaCeq7r6uDgQMlkUsYYpVKpruWD1gEAhFMoQk2S\\nGo2GGo2GJMmyLN2/f78rjIwxKhaL2tvbC8pyuZxs29b8/PzAdQAA4RWK04+xWEz1el2e58kYo3a7\\nrffee6+rTqlU0ubmZldZPp9XoVAYqg4AILxCEWqS5Pu+ZmdnNTc313d5pVJRKpXqKnMcR9Vqdag6\\nAIDwCk2ovYrnefI8T8lksqvcsixJ0tHR0UB1AADhFpprasYYeZ4nSWq320omk1pdXQ3eS9Ls7Oy5\\n63aO8AapA2DyfN/Xp59+Ovb9xONxfe1rXxv7fnA1QhFqnaOrTohJLyZ4dMo6Yfcqg9QBMB3eeOMN\\n/dmf/Zl++9vfjnU/n3/+ub7zne9oaWlprPvB1QlFqMXjca2vr3eV5fN55fP5rqADEA2xWEzf/e53\\nx76fTz75RL7vj30/uDqhCLV+5ufnZYzR6enpWPcTi8XGun0AwOiEYqLI1tZWT1nnlKQxRrZtS9K5\\nAWfb9kB1AADhNvWh1rlh+uzsxM7kENu2ZVmWbNuWMaZnXcuyNDc3N1Cdfnzf7/sCAEyfqQ8127a1\\nvb3dEzr1el2O4wSzGTOZjPb397vquK6rbDYbvB+kDgAgvKY+1KQXpxpbrVbw3vM8lctl7ezsBGWl\\nUkmVSqVrvXK5rFKpNFQdAEB4xfyQnEur1Woyxujp06fyPE/FYrHn6K3ZbGp3d1fLy8syxshxHN28\\neXPoOoPoTCAJyceHc/zmN7/Rm2++2XNTPq6HTz75RPF4vOdJQwiv0ITatCHUooFQu94ItegJxelH\\nAAAGEdr71BBtx8fH+pd/+ZexHwk/ffpU3/72t8e6DwBXh1DDVPqf//kftdttfetb3xrrfr797W8H\\nD7UGEH6EGqbWV7/6VSUSiUk3A0CIcE0NABAZhBoAIDIINQBAZBBqAIDIINQAAJFBqAEAIoNQAwBE\\nBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAAkUGoAQAig1ADAEQGoQYAiAxCDQAQGYQaACAy\\n3ph0AwBgkj7//HM9ffp0rPuIxWJKJBKKxWJj3Q+uYai5rquDgwMlk0kZY5RKpbSysjLpZgGYgK9/\\n/ev6r//6L3322Wdj3c8f//hHZbNZ3bhxY6z7wTULNWOMisWi9vb2grJcLifbtjU/Pz/BlgGYBMuy\\nZFnW2Pfz5MkT+b4/9v3gml1TK5VK2tzc7CrL5/MqFAoTahEAYJRi/jX6+pBMJuW6rubm5oIyz/OU\\nTCb1/PnzobbVOTd+jT6+wL//+7/ryy+/HOs+2u22PvvsMy0uLo51P8BVePLkib7//e/rrbfemnRT\\nIu/anH70PC8IsJd1Tj0cHR11hR36e/bsmf7pn/5JiURi7Pvi+gOAYV2bUGu325Kk2dnZvsuNMYTa\\ngGZmZmTb9qSbAQA9rk2oeZ436SZciWFPo07b9oGoarVa+vTTT8e6j69//evX/gvntQm1i3rdfSXc\\ndwIAwxnnXIRrNfsRADB54zwYuDZHap1D8tPT077X1c47ZD/vG0XUZz/Sv3CLcv+i3Dfp+vRvXK7N\\nkZplWbJtW8aYrnJjjCzLYpIIAETAtQk1ScpkMtrf3+8qc11X2Wx2Qi0CAIzStbr5+uTkRGtra12P\\nyfrBD36gcrk89JHadTlFQP/CKcr9i3LfJPp36e1fp1CTpGazqd3dXS0vL8sYI8dxdPPmzaG3wx9e\\nuNG/8Ipy3yT6d+ntX7dQGxX+8MKN/oVXlPsm0b9Lb59QAwBExbWaKAIAiDZCDQAQGYQaACAyCDUA\\nQGQQagCAyPh/P/7xj3886UZMmuu6+vWvf62joyP97d/+rT7//POBfr6hXq+rXC6r2WzqF7/4hf77\\nv/9bjuMEy40xyuVy+vM//3Mlk0l98sknKpVKisViV/rzEBft38s8z9Nf//Vf66/+6q9Gvu3LGFff\\nwjx2g7Z90mN30TYM0r8wj9/L6/70pz9Vs9nUr371Ky0sLHT9OG9Yx+/ldc/r36XGz7/mDg8P/Ww2\\n21W2trbmG2Neud7Dhw/9er3eVeY4jr+1tdW17VgsFrwSiYRfq9VG1/gBXLR/Z21sbPhra2tj2fZF\\njbtvYR27Qdo+6bG7TBsG7V9Yx8/3fb9Sqfj5fL6rbGNjYyTbHpVx9++i43ftQ21jY6Pnw6rX6z3/\\nyJ31/vvv94RaoVDwFxYWgvfGGL/RaPgnJyd+q9UaWZuHcdH+vezw8NBfW1vzc7ncyLd9GePsW5jH\\nbpC2T3rsLtOGQfoX5vE7Pj72E4lEV9n29ra/uLh46W2P0jj7d5nxu/ahlkgkej604+NjPxaLvXK9\\ntbU1v1gsdpXduXPHT6fTwXtjTE/wXbWL9u9l5XLZL5fLPX+so9j2ZYyzb2Eeu0HaPumxu0wbBulf\\nmMfvzp07Pf+2+L7fta0wj98g/bvM+F3riSKe58nzPCWTya5yy7IkSUdHR+eu++DBA929e7errFqt\\n6tatWyNv50Vdpn8djUZDmUxmLNu+jHH2bRqM8/Od9NhNSxvG6TL929nZ0fLyck9556Hr0/DZjbN/\\nl3VtfiS0n3a7LUl9fzRUenGxctAPulwuK51O6/bt2z3b8Dwv2F8ymdTq6urFGz2EUfTPGKOVlZWe\\n57SN8rO7iHH27eXlYR27V7V90mM3ijYMMjZhHT/P8xSPx7Wzs6NkMhm58Xtd/17exkXG71qHWucD\\nu4xaraaHDx8qFotpd3e3a1nnW8zLA5HL5XrKxuWy/avValpfXx/Lti9rnH2Twj12r2v7pMdOGm//\\nBq0zThftX+dHjJvNZtcX5GKxqHa7rfX19VCP3yD9ky43ftf69OMorK6u6uc//7nu3bundDqtZrMZ\\nLIvH4z3/cObzeRUKhatu5tCm4T+ccRmkb2EeuzC3fRCD9C+sn0Hnb/PstPVbt25NfdsHMWj/LjN+\\nhNqIxONx5fN5raysvLLe/Py8jDE6PT29opZdTKVS6fpG1Pm5iCi4aN/CMnb9hLntgxikf2H4DDr/\\n2J/9R39paUme54X+WuNl+jfo+F3rUOt8sOd9SMPeyLiysiLP8/To0SNJ0tbWVk+dzmF15zB8nC7a\\nv2azqXQ63VV29rrTqD+7YY2zb1J4x056fdsnPXYv72Mc/Ru0zjhdtH+diRad/z0r7OM3SP+kS47f\\nheZMRsjCwoLfbDa7yg4PD3vuozi73LKsvuvFYjG/VqsF///slNdO+cnJycj68CoX6V+5XPYLhULX\\nK5vN+gsLC36hUPCr1eqFtz1K4+pbmMdu0LZPeuwu2oZB+hfm8eus12g0espf7lNYx6+z3qv6d9nx\\nu9YTRSQpk8lof39f77zzTlDmuq6y2ey563iep4WFhZ5vI51vEKlUSnNzc9re3u6ZAVSv1+U4zrmz\\nhkbtIv3rN4HiJz/5iR4/fqx79+5datujNM6+hXXsbNseqO2THruLtmGQ/s3OzoZ2/KQX144ODg50\\n8+bNrvUSiUTQp7COnzRY/y41foNlcnR5ntfzqJdsNtv1LeH4+Ni3bdsvl8tB2dbWlu95Xtd6mUym\\n66bCarXa9ciY4+Nj33Gcnm8343TR/p11586dnhuUB9n2OI2zb2Eeu0HaPumxG7QNF+1fmMfP87yu\\nJxN11nv56R1hHr9B+neZ8Yv5/jk36VwjzWZTu7u7Wl5eljFGjuN0fYvwPE+2bWtra0s//OEPg/Kd\\nnR0dHh7qxo0bOjw8VDqd7louvZg6bozR06dP5XmeisXi2O8hOeui/ZOkVqulUqmkBw8e6OTkROvr\\n68rn81paWhpo22HuW5jHbpC2T3rsBmnDZfoX5vHr/G0uLCzo8PBQuVyuZ2zCPH6D9O+i40eoAQAi\\n41rPfgQARAuhBgCIDEINABAZhBoAIDIINQBAZBBqAIDIINQAAJFBqAEAIoNQAybAdV3NzMz0/GLA\\nWfV6XTMzM8EPJA5qbW1NMzP8543rh796YAJSqZQsy1Kz2dTJycm59SqViiTpgw8+GHofUfoNPGBQ\\nhBowIRsbG/J9Xw8ePDi3zoMHDxSLxfTee+9dYcuA8CLUgAm5deuWpBc/s9GP67o6OTnR+++/f5XN\\nAkKNUAMmZGlpSbZtn3sKcnd3V9Kfwk968Zt9a2trWlhY0MzMjJLJpHK5nFqtVs/6Lz+rPJvN9r3G\\n5nmeZmZmtLm52bNsa2tLjuME+9nc3Oy7H2CaEGrABOXz+XNPQZbL5a5Tj8YYLS4u6pe//KUWFxeV\\nz+eVTqdVrVblOM4rr81Jr77GdnaZ4zgqFouamZkJ9lMul7WwsKBms3mBngJXg1ADJqhzavHsKch+\\npx5LpZJisZgePnyov/u7v9PPfvYz7e3tqVQqyfM81ev1kbRpa2tLzWZTjUZD+/v7wX4ODg4k9f/1\\ncGBaEGrABM3Pz2tpaannFGS/U4+bm5uqVCo9P6bY+VHT4+PjkbTp7t27ymazSqVS8jwveM3Pz2tl\\nZUWu6+r09HQk+wJG7Y1JNwC47j744AM1m02Vy2V9+OGHkqRqtdoz63FpaSkIMM/z9PjxY7mue+5E\\nk4s6OTnRw4cPlUgk+i6PxWJqt9uanZ0d6X6BUSDUgAnb2NhQoVDQ7u6uPvzwQxlj1Gq1tLa21lXP\\n8zwVCgU9ePAgOKpzHEeO44xsAocxRtKLiSWFQuHceucFHjBphBowYfF4XKlUKjgFWa1WJb2YRPKy\\nlZUVNZtN5fN55fN5vfPOO5KkRqMRrDOsdrvd9T6ZTEqSLMvqOc0JhAHX1IAp0JkFWS6Xtbu7q1gs\\n1hUqnufZLzsPAAABcUlEQVSp2WxqbW1NP/vZz4JAk7qn7g/Ldd2u95ZlKR6PnzvpJJFIaHFx8cL7\\nA8aNUAOmQOfZjtvb22o2m+fecH12MkjnlKTUG24vT9O3LEu+76vRaPRd92X5fF7Hx8c9z5vc2trS\\nyclJ33vagGnB6UdgCsTjcWUymeAI6eypR8uyguW5XE7pdFqHh4eqVCpaXl6W9GLKv23bWllZkdQd\\nch988IFqtZqy2WzweK7OumeD8t69e6pWq6pWq1pcXNTS0pKMMWo2m3IcR7dv3x7nRwFcjg9gKlSr\\nVT8Wi/kzMzN9l3ue5+fzeT+RSPixWMxPp9N+rVbzfd/38/m8PzMz429ubvq+7/tra2s92ymXy/7C\\nwoIfi8X8ZDLpF4tF3/d9P5FIBOu9rFAo+I7j+LFYzF9cXAzqA9Ms5vuXOCEPAMAU4ZoaACAyCDUA\\nQGQQagCAyCDUAACRQagBACKDUAMARAahBgCIDEINABAZhBoAIDL+P0MVIng+hRl9AAAAAElFTkSu\\nQmCC\\n\",\n \"text\": [\n \"\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Real STD: ', 0.28883809877618805)\\n\",\n \"('STD estimated *sqrt(n-1), n = 100 : ', 0.28733455295932581)\\n\",\n \"('STD estimated *sqrt(n-1), n = 50 : ', 0.28646705134779565)\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\"\n ]\n }\n ],\n \"prompt_number\": 13\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 1,\n \"metadata\": {},\n \"source\": [\n \"Bootstrap methods\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Calculate CIs\"\n ]\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 4,\n \"metadata\": {},\n \"source\": [\n \"Peasants way. Parametric\"\n ]\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Calculate confidence intervals with SEM --> >20 replicates pufff\\n\",\n \"Lower Limit = Mean - (t-statistic for x df)(SEM)\\n\",\n \"Upper Limit = Mean + (t-statistic for x df)(SEM)\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"%%latex\\n\",\n \"$$\\\\mu = \\\\left[\\\\mu + t_{1 - \\\\alpha/2,n-1},\\\\mu + t_{\\\\alpha/2,n-1} \\\\right]$$\\n\",\n \"$$$$\\n\",\n \"$$\\\\sigma = \\\\left[\\\\sqrt{\\\\frac{(n-1)\\\\cdot \\\\sigma^2}{\\\\chi^2_{1 - \\\\alpha/2,n-1} }} \\\\sqrt{\\\\frac{(n-1)\\\\cdot \\\\sigma^2}{\\\\chi^2_{\\\\alpha/2,n-1} }}\\\\right]$$\\n\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"latex\": [\n \"$$\\\\mu = \\\\left[\\\\mu + t_{1 - \\\\alpha/2,n-1},\\\\mu + t_{\\\\alpha/2,n-1} \\\\right]$$\\n\",\n \"$$$$\\n\",\n \"$$\\\\sigma = \\\\left[\\\\sqrt{\\\\frac{(n-1)\\\\cdot \\\\sigma^2}{\\\\chi^2_{1 - \\\\alpha/2,n-1} }} \\\\sqrt{\\\\frac{(n-1)\\\\cdot \\\\sigma^2}{\\\\chi^2_{\\\\alpha/2,n-1} }}\\\\right]$$\"\n ],\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 68\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"x = np.random.randn(20)\\n\",\n \"print('CI for mean with SEM = ', np.mean(x) + scipy.stats.t.isf([0.025, 0.975], [19])[::-1] *scipy.stats.sem(x))\\n\",\n \"print('CI for std with SEM = ', np.sqrt(np.var(x)*19/scipy.stats.chi2.isf([0.025, 0.975], [19])))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('CI for mean with SEM = ', array([-0.53678197, 0.49794991]))\\n\",\n \"('CI for std with SEM = ', array([ 0.81939658, 1.57370483]))\\n\"\n ]\n }\n ],\n \"prompt_number\": 6\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 4,\n \"metadata\": {},\n \"source\": [\n \"CLT make it easy. Non parametric, taking samples with replacement\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"import scikits.bootstrap as bootstrap\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 70\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"CIs = bootstrap.ci(x, statfunction=np.mean,n_samples=100000) \\n\",\n \"print('CI for mean with bootstrapping = ', CIs)\\n\",\n \"\\n\",\n \"CIs = bootstrap.ci(x, statfunction=np.std,n_samples=100000) \\n\",\n \"print('CI for std with bootstrapping = ', CIs)\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('CI for mean with bootstrapping = ', array([-1.00376369, 0.02051702]))\\n\",\n \"('CI for std with bootstrapping = ', array([ 0.86606787, 1.59350777]))\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\"\n ]\n }\n ],\n \"prompt_number\": 71\n },\n {\n \"cell_type\": \"heading\",\n \"level\": 3,\n \"metadata\": {},\n \"source\": [\n \"Anything you want\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"np.random.seed(105)\\n\",\n \"size = 100\\n\",\n \"x = [np.random.lognormal(1,1) for _ in range(size)]\\n\",\n \"y = (np.random.randn(size)*np.std(x)+np.mean(x))\\n\",\n \"print('Mean = %f STD = %f Median = %f' %(np.mean(x), np.std(x), np.median(x)))\\n\",\n \"print('Mean = %f STD = %f Median = %f' %(np.mean(y), np.std(y), np.median(y)))\\n\",\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.hist(x,bins=np.linspace(-5,20,10),alpha=0.3,histtype='stepfilled')\\n\",\n \"ax.hist(y,bins=np.linspace(-5,20,10),alpha=0.3,histtype='stepfilled')\\n\",\n \"ax.set_xlabel('Value',fontsize=20)\\n\",\n \"ax.set_ylabel('Freq',fontsize=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"plt.show()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"Mean = 5.135465 STD = 6.925996 Median = 2.494636\\n\",\n \"Mean = 6.227468 STD = 6.899373 Median = 6.389744\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAH0pJREFUeJzt3WFsG+ed5/EfGTsN0lYa0m66TbE9cWTc3fZwrUlKeXG4\\nuwUsMtjDAvvCiuS8uzeRyb63Tfpd39l0+uLQN4movOsBhUwqWNy22ItMZRcHHLBbWcMsbrd32FiP\\n1NZN0ktMjdTETuLacy98pD0mZZuSPDMSvx9ASPjMDPnn+LF/mmeemYl5nucJAICnLB52AQCAwUDg\\nAAACQeAAAAJB4AAAAkHgAAACQeAAAAJxKOwC2hzH0eXLl3XkyBHduHFDhUJBqVTKt3xlZUXJZFLG\\nGGUyGU1MTIRYMQCgH5EInHq9rkajoTfffLPTVigUNDs7K0kyxqhcLmtxcbGzfHp6WrZt+0IJABBd\\noQ+pua6r06dP+8KmWq3q3Xff7byuVCoqFou+7QqFgkqlUmB1AgB2Jxb2nQZKpZLi8bguXLjga19f\\nX9fIyIgkKZlMynGczmvpXlAlk0ndvXs3wGoBADsV+hHO3NycxsfHu9rb4eK6bidcHmRZlqR7wQQA\\niL7Qz+G4rqvh4WHNzc0pmUyq1WopmUxqcnJSktRqtSRJQ0NDPbc3xviOfAAA0RRq4BhjJEnNZlNn\\nzpzptJfLZbVaLc3MzMh13bDKAwDsoVCH1NphYtu2r/3UqVNMCACAAybUI5x20DwcOOl0Wq7r7ur8\\nTCwW23YZT2QAgOCFeoTTPvHf/u/DjDGdMNra2uq5zsNh9SQeFUYAgKcj9Flqtm13zuX0WmZZVs91\\njDGyLGvbCQOe5/X8AQCEI/TAKRQKWllZ8bU5jqNEItEJk1wup+Xl5a518vl8UGUCAHYp9As/Nzc3\\nlc1mde3atU7byy+/rGKxqJMnT3bWmZqa8t3a5uWXX1a1Wu17SnR7OI2jHQAIVuiBI0lra2uqVCoa\\nHR3V6uqqpqendeLECd86zWZT8/PzGh8flzFG2Wy2a50nQeAAQDgiEThBInAAIByhn8MBAAwGAgcA\\nEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAI\\nAgcAEAgCBwAQiENhF4BounPnjn71q19F7rlBhw8f1ne+852wywCwAwQOevrss8/01399Tc8888dh\\nl/KQX6pQ+OPOg/QA7B8EDrZ16NBX9OKLfxJ2GT7Xr6+GXQKAHeIcDgAgEAQOACAQBA4AIBAEDgAg\\nEAQOACAQoQeOMUb5fF5LS0tyXVfGGJXLZS0tLfnWcxxHc3NzWlhY0Ouvv961HAAQbZGYFr20tNQJ\\nEMuy9NZbb2liYqKzvB1Ci4uLnbbp6WnZtq1UKhV4vQCA/oV+hBOLxdRoNDpHN61WSydPnvStU6lU\\nVCwWfW2FQkGlUinIUgEAuxB64EiS53kaGhrSyMhIz+W1Wk2ZTMbXls1mVa/XA6gOALAXIhE4j+K6\\nrlzXVTKZ9LVbliVJWl9fD6EqAEC/InEOxxgj13UlSa1WS8lkUpOTk53XkjQ0NLTtttsdGQEAoiP0\\nwGkfubQDRro3IaDd1g4iAMD+FvqQ2vDwsGZmZnxtezEhIBaL9fwBAIQj9MDpJZVKyRijra2tsEsB\\nAOyR0APn0qVLXW3tYTZjjGzblqRtw6e9/GGe5/X8AQCEI9TAaV/Q+fBMs/ZEAdu2ZVmWbNuWMaZr\\nW8uymDAAAPtEqIFj27ZmZ2e7QqPRaCibzXZmpuVyOS0vL/vWcRxH+Xw+qFIBALsU+pBaMpnU2tpa\\n57XruqpWq5qbm+u0VSoV1Wo133bValWVSiWwOgEAuxP6tOjJyUktLCyoXq/rxo0bcl1X9Xrdd9Qz\\nPDysSqWicrms8fHxzlAcw2kAsH+EHjiS/xqc7aTTaaXT6QCqAQA8DaEPqQEABgOBAwAIBIEDAAgE\\ngQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIED\\nAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACMShsAt4mOu6KpfLevPNN33tjuNo\\nZWVFyWRSxhhlMhlNTEyEVCUAoF+RC5xSqaSNjQ1fmzFG5XJZi4uLnbbp6WnZtq1UKhV0iQCAHYjU\\nkJoxRhsbG4rFYr72SqWiYrHoaysUCiqVSkGWBwDYhUgFztLSkvL5vDzP87XXajVlMhlfWzabVb1e\\nD7I8AMAuRCZwlpaWlMvlutpd15Xrukomk752y7IkSevr60GUBwDYpcgEjjFGqVSq6+im1WpJkoaG\\nhrbdDgAQfZEInIWFBc3MzPRc5rpuwNUAAJ6G0GepPa1AeXjiAQAgXKEf4dRqNU1OTnZeExQAcDCF\\nGjjNZlNjY2O+tofP4di2LUna2trq+R7t5Q/zPK/nDwAgHKEOqV29elWrq6uan5/vtDmO07nQc3x8\\nXJOTk7JtW8YYHT9+vLOeMUaWZWlkZCSEygEA/Qo1cHpNFHj99dd19epVXbx4sdOWy+W0vLzsCxzH\\ncZTP5wOpEwCwe6Gfw3nYJ5980jX0ValUVKvVfG3ValWVSiXI0gAAuxD6LLW2tbU1VSoVXb58WZub\\nmyoWiyoUCkqn0xoeHlalUukMs7WH3BhOA4D9I+YN2Jn09iy4Afvafdva2tJPf9rUiy/+adil+Fy/\\n/jMVi3/ObEZgH4rckBoA4GAicAAAgSBwAACBIHAAAIEgcAAAgSBwAACBIHAAAIEgcAAAgSBwAACB\\nIHAAAIEgcAAAgSBwAACBIHAAAIHo6/EEx44d6/suvZ7nKRaL6f333+9rOwDAwdJX4KTTaa2trclx\\nnE5bKpVSq9XS5uamJMmyLKVSKd923EoeANBX4Jw/f15jY2PKZDKam5tTOp3uLHMcRzMzM1pfX1e9\\nXu8KHQDAYOvrHM7FixdlWZaWlpZ8YSNJmUxGKysrunv3rsrl8p4WCQDY//oKnEajoXw+r+Hh4W3X\\nyeVyajQauy4MAHCw9BU4nufJGPPIddbW1nZVEADgYOorcHK5nFZWVvT222/3XL6wsCDHcZTNZvek\\nOADAwdHXpIFKpaJGo6GpqSm98soryufzsm1bq6urunLliur1emc9AAAe1Ffg2LatpaUllUol1Wo1\\n1Wq1ruWzs7NdEwoAAOgrcKR7s9GuXLkiY4wcx5ExRrZty7ZtZTKZHRXRaDTUaDR05MgRra6uKpvN\\namZmxreO4zhaWVlRMpmUMUaZTEYTExM7+jwAQPD6Dpy2o0ePamxs7LGz1h6n0WgoFovp4sWLnbax\\nsTG5rquzZ89KkowxKpfLWlxc7KwzPT0t27a53gcA9om+76XWbDY1NjYmy7I0OjqqlZUVSfdue/Oj\\nH/2o7wJmZ2e72nK5nK+9UqmoWCz61ikUCiqVSn1/HgAgHH0FztramrLZrBzH0cTEhDzP6yy7ceOG\\nzp07p/Hx8b4KiMViXdfteJ6nRCLReV2r1bqG67LZbGeSAgAg+voKnPbss5WVla4JAxsbG7p48aJW\\nVlZ0/vz5J37Py5cv68KFC762er2uU6dOSZJc15Xrukomk751LMuSJK2vr/fzFQAAIekrcC5fvqxc\\nLrftLLRz584pnU7v6sijWq1qbGxMZ86ckSS1Wi1J0tDQUM/1H3chKgAgGvqaNOC6rkZHRx+5jm3b\\nWlhY6LuQhYUFXblyRbFYTPPz877PBADsf30/nuDq1auPXKfZbO5oevTk5KQmJye1ubmpsbGxrrtR\\n94tHIgBAtPQ1pHbq1CmtrKzob/7mb3r+gz49PS1jjHK53I4LGh4eVqFQ4BobADhg+gqc9jmaiYkJ\\nTU9PS7o3keDUqVM6cuSI6vW6bNv2XVOzExMTE3JdV++++65s25YkbW1t9Vy3vfxhnuf1/AEAhKPv\\n63BWVlZ08eJF/eIXv5AkXblyRbVaTXfv3tW5c+d07dq1J34vY4wSiYTee++9nstd15VlWbJtu2ty\\ngDFGlmVpZGSk368AAAhB34Ej3TvS2djY0N27d3Xt2jW1Wq3OtOh+tCchPHyU0g6X9rmgXC6n5eVl\\n3zqO4yifz++kfABACPoKnLm5ua5HE9i23bkmpl+ZTEanTp3qGuqqVCoqlUqdo5dKpdJ13U+1WuWu\\n1ACwj8S8Pk5sxONxJRIJ3bhxY0+LmJub0+rqaufmnWNjY3rttdd86zSbTc3Pz2t8fFzGGGWzWZ04\\ncaLvz2pPduB8zqNtbW3ppz9t6sUX/zTsUnyuX/+ZisU/ZxYisA/1NS36tdde01tvvaX33ntPx48f\\n37MiHr4zdC/pdJrHHgDAPtZX4FSrVR07dkzZbFazs7MaGxuTbdvb3gUAAIC2vgKnfT8zz/N0+vTp\\nTvuDwxue5ykWi+nOnTt7VCIA4CDoK3Ce9GJMxtcBAA97ZOCUy2W99NJLOnnypCR1zRQDAOBJPXJa\\n9KVLl3w30mybm5vTD37wg6dWFADg4NnRhZ+Li4uqVqt7XQsA4ADbUeBIXMcCAOjPjgOHiQEAgH7s\\nOHAAAOgHgQMACASBAwAIxGMv/Gw0Gjp16pSvbWlpSZ7ndbU/qNd0agDA4Hps4GxsbGx7weejLgQl\\ncAAAD3pk4Fy9ejWoOgAAB9wjA6f9xE0AAHaLSQMAgEAQOACAQBA4AIBAEDgAgEAQOACAQBA4AIBA\\nEDgAgEA89k4DQVhYWJAxRqurqzLGqFAoaHJy0reO4zhaWVlRMpmUMUaZTEYTExMhVQwA6FfogbOw\\nsCDbtjsBs7m5qWw2q1arpZmZGUmSMUblclmLi4ud7aanp2XbtlKpVCh1AwD6E/qQmjFG6XS683p4\\neFilUkmFQqHTVqlUVCwWfdsVCgWVSqXA6gQA7E6ogeO6rubn57W5uelrbw+Vra+vS7p3k9CHb7OT\\nzWZVr9cDqRMAsHuhBo5lWTLGaG1tbdt1XNeV67pKJpNd20r3QwkAEG2hD6m1Wi0dP37c19ZoNJRI\\nJDQyMqJWqyVJGhoa6rm9Meap1wgA2L3QA6eX2dlZnT9/XtK9IxwAwP4XucCpVqs6evSozpw5E3Yp\\nAIA9FPq06AcZY1StVvfkwW+xWGwPKgIA7JVIHeGUy2W9++67vjbbtiVJW1tbPbdpLwcARFtkAqdY\\nLOrSpUtdkwMsy5Jt212TA4wxsixLIyMjPd/P87yePwCAcEQicObm5lQul33hsbS01JkuncvltLy8\\n7NvGcRzl8/kgywQA7ELogdO+eLPVaslxHDmOo0ajoVqt1rltTaVSUa1W821XrVZVqVQCrxcAsDOh\\nThpwXVfT09M9l42Ojnb+f3h4WJVKReVyWePj4517q203nAYAiJ5QA8eyLN29e/eJ1k2n0757rgEA\\n9pfQh9QAAIOBwAEABILAAQAEgsABAASCwAEABILAAQAEgsABAAQiUneLBh7nzp0/6PPPP4/U3cDj\\n8bieffbZsMvYFz7//POwS+hy+PBhPfPMM2GXMRAIHOwrzi//pw79t48iFTiHvEOa+k9T2z6VFvf8\\n9re/1V/9j79S7Jno/Nl5nqeRoyP6s4k/C7uUgUDgYF/5/M4tfet731I8Hp3R4A/+6QPduXMn7DIi\\n7+7du4oNxfTisRfDLqXj5qc3dfPjm2GXMTCi87cWAHCgETgAgEAQOACAQBA4AIBAEDgAgEAwSw09\\n3b59W6u//idtfBqt30lu3/2Dfvm/VyM1LXrD3NAX/+6LsMvw+fDDD3XtV9fCLsPn5s2b8jwv7DIQ\\nIgIHPd26dUvXt97Xl998PuxSfI78q+/pdx9Fq6bf/fo3unXrVthl+Hz4uw/V/F1TQ4kIXRt0SDry\\n7SNhV4EQETjYVjwe19cT0foH4uuKVj2S9Ek8mlepP/+153Xkm9HbXxhc0RovAQAcWAQOACAQBA4A\\nIBAEDgAgEJGZNFCv15VIJDQxMdG1zHEcraysKJlMyhijTCbTcz0AQHRFInAajYZOnz6ter3etcwY\\no3K5rMXFxU7b9PS0bNtWKpUKskwAwC6EOqS2tramYrGotbU1JZPJnutUKhUVi0VfW6FQUKlUCqJE\\nAMAeCTVwUqmU3nzzTc3MzGy7Tq1WUyaT8bVls9meR0MAgOiKxJDadlzXleu6XUc/lmVJktbX1zUy\\nMhJCZYDf9evXdfv27bDL6HBdN+wSgC6RDpxWqyVJ2z661xhD4CB0h498RcsfL+v5z6J1y52jf3Q0\\n7BIAn0gHDr+lYT94fujr+ta/+Ja+9rWvhV0KEGlchwMACESkj3B2I0q3rwcARPwIx7ZtSdLW1tYj\\nlwMAoi/SgWNZlmzbljHG126MkWVZj5ww4Hlezx8AQDgiHTiSlMvltLy87GtzHEf5fD6kigAAOxGp\\nwOl1BFKpVFSr1Xxt1WpVlUolqLIAAHsg1EkDm5ubunDhgowxMsaoUCgol8spn89rcnJSkjQ8PKxK\\npaJyuazx8fHOvdW4/gYA9pdQA2d4eFgXL1587HrpdFrpdDqAigAAT8uBnRa9n9y+fVsff/xx2GX4\\nRK0eAPsfgRMBH330kf7yL/9Zzz5rhV1Kx61bnyoeT4RdBoADhMCJiGefPaoXX/x+2GV03Ly5pa+3\\n/k/YZQA4QCI1Sw0AcHBxhBMBn376qdZ+/b+0dfNW2KV03LlzW3d1N+wygKfu95/+Xn+3/Hdhl+Hz\\n3Fee0/HvHQ+7jD1H4ETA1taWzGf/oJvf+DLsUu47JH31W8NhVwE8Vc89/5xuvXBLv/zsl2GX4vPF\\n+1/o+//2+wfunpAETkQc/spzGj7yjbDLAAZKPB7XkW8eCbuMLtc/uB52CU8F53AAAIHgCAfYpT/c\\niekXy/8cqeGPeEz63vdGlEgwtR3RQeAAu3T0yL/UXS9aEyxc9zf68naEzgkCInCAXYvHn1Fcz4Rd\\nhk88xmg5oofAAQ6o21/e1s2bN8MuI/IOHz6sw4cPh13GQCBwgAPo0KHn9Y//+H8luWGXEml3vTt6\\n4YVDGsv+m7BLGQgEDnAADQ29IOmFsMuIvC++uKkvvzSPXxF7goFeAEAgCBwAQCAIHABAIAgcAEAg\\nCBwAQCAGdpbaO3/7TtgldFy/fl3iUQAA/r/bd27rnb99J1K3SzoUP6SJ/zixu/fYo1r2nU+e+yTs\\nEjo+TXyqr30jGXYZACLihT95QTf+cCPsMnw2f7OpCRE4OzKUGAq7hI4v7nyhQ4c/DbsMABHx1a9/\\nNewSunz6we7/jRrYwAGANs/zwi6hS5SG0/bKvgkcx3G0srKiZDIpY4wymYwmJnZ3eAdgsMWfeUaf\\nfPK5/vs7V8MuxeerX43rP/z7zIELnX0ROMYYlctlLS4udtqmp6dl27ZSqVSIlQHYzw4f+or+6Jtj\\nYZfR5ZMby2GX8FTsi2nRlUpFxWLR11YoFFQqlUKqCADQr31xhFOr1XT+/HlfWzabVb1eD6kiAHi6\\nXNeN1JDa73//+12/R+QDx3Vdua6rZNI/bdiyLEnS+vq6RkZGQqgMAJ6Wo/r7v/847CJ83LVfS/95\\nd+8R+cBptVqSpKGh3tOYjTEEDoAD5eiR6J2b3lz7aNfvEflzOK7LA6QA4CCI/BHOTj1u7PMv/vVf\\nBFQJABwM//W/vL6r7SN/hAMAiIbdTmKI/BGObduSpK2trZ7ncdrLH7bdlcPtHRbFK4uDxr64j31x\\nH/viPvbFfXsxYy7yRziWZcm2bRnjf+64MUaWZTFhAAD2icgHjiTlcjktL/uvvHUcR/l8PqSKAAD9\\ninn74Fhxc3NTU1NTvlvbvPzyy6pWq30f4XCIfB/74j72xX3si/vYF/ftxb7YF4EjSc1mU/Pz8xof\\nH5cxRtlsVidOnOj7fehA97Ev7mNf3Me+uI99cd9ABc5eoQPdx764j31xH/viPvbFfQQOAGDf2BeT\\nBgAA+x+BAwAIBIEDAAgEgQMACASBAwAIxDM//OEPfxh2EQiW4zj62c9+pvX1df385z/X559/vu09\\n6Q4yY4ymp6f17W9/W8lkUh988IEqlYpisdjA7I96va4PP/yw5/cdtH6y3b4YtH6ysLCgn//85/rJ\\nT36iH//4x3r++ef13e9+17fOjvuGN+BWV1e9XC7nNRoNb2Njw1tdXfVKpZLXaDTCLu2pWF1d9fL5\\nvK9tamrKM8aEVFF4VldXvVgs1vlJJBLewsJC2GUF5sqVK14ikfCWlpa6lg1aP3ncvhiUflKv1z3H\\ncTqvXdf1RkdHvWq12mnbTd9gSE3S0tKS8vm8ksmkxsbG9NJLL2liYiLssp6KSqWiYrHoaysUCiqV\\nSiFVFJ5YLKZGoyHXdWWMUavV0smTJ8Mu66lbW1tTsVjU2tpa16Pb2walnzzJvhikfmKMUTqd7rwe\\nHh5WqVRSoVDotO2qb+xdNu5PxhhvaWnJ29zc9NbW1sIu56lLJBJd33NjY8OLxWLhFBQiY8yBPZJ9\\nUqOjoz1/qx/EfrLdvhiUfrKxseFls1nPdV1fe/sIr90fdtM3OMLRvVs1DA0NHfhHHbiuK9d1u36T\\nsyxLkrS+vh5CVYga+slgsixLxhitra1tu85u+0bkH8CGvdNqtSSp54PspHuH0wc9dB9mjJHrupLu\\n7Z9kMqnJycmQqwoX/aTboPST9p/9gxqNhhKJhEZGRjrPJdtp3yBwNDidqf0dcU/7t7QH/6ynp6e7\\n2gYN/cRv0PvJ7Oyszp8/L2n3fWPgA2fQO9MgGx4e1szMjK+tUCioUCjwZ4+OQe4n1WpVR48e1Zkz\\nZ/bk/Qb+HM52nemgzcbBk0mlUjLGaGtrK+xSEGGD0E+MMapWq3rnnXf27D0PTOAYY574Z3Nz85Hv\\ndVA7U/vCrO2+10G8iO1RLl261NXWPuJtj1UPIvqJ36D2k3K5rHfffdfXttu+cSCG1NbW1lQul594\\n/fHxcZ09e1bSvc507tw53/IHO9Px48f3rtCQWZYl27a7vpcxRpZlDdSJYGOMyuWypqenfd+7fdJ0\\n0P5RfRD95L5B7SfFYlGXLl3qmhyw275xIAInlUrp8uXLfW83iJ0pl8tpeXnZ11kcx1E+nw+xquDZ\\ntq3Z2dmuvyCNRkPZbHbbWTiDgn5yzyD2k7m5OZXLZd93Xlpakm3bSqVSu+obB2ZIbScGsTNVKhXV\\najVfW7VaVaVSCami8CSTSd81B67rqlqtam5uLsSqguf1eOjvoPaTXvtikPpJvV6XdO+Xbsdx5DiO\\nGo2GarWaUqmUpN31jYF/xPTCwoIymUxnZ7quq1wup7feeutADac9qNlsan5+XuPj4zLGKJvN6sSJ\\nE2GXFYqFhQUZY3Tjxg25rtv1m91BtLm5qQsXLsgYo3q9Ltu2lcvllM/nfbOuBqGfPOm+GIR+0uuC\\nzrbR0VG9//77ndc77RsDHzjSYHQmAAgbgQMACMRAn8MBAASHwAEABILAAQAEgsABAASCwAEABILA\\nAQAEgsABAASCwAH64DiO4vG4xsbGHrleo9FQPB7vPFvpSU1NTSke568lDiZ6NtCHTCYjy7LUbDYf\\n+ZiL9r2mXn311b4/IxaL7bg+IMoIHKBPp0+flud5j7xD+eXLlxWLxXTy5MkAKwOijcAB+nTq1ClJ\\n95713ovjONrc3NQrr7wSZFlA5BE4QJ/S6bRs2952WG1+fl7S/WCS7j17aWpqSqOjo4rH40omk5qe\\nnvbd9r7twdsb5vP5nud0XNdVPB5XsVjsWnbp0iVls9nO5xSLxZ6fAwSNwAF2oFAobDusVq1WfcNp\\nxhgdO3ZMb7/9to4dO6ZCoaCxsTHV63Vls9nHPvL8Ued0Hl6WzWZVLpcVj8c7n1OtVjU6Oqpms7mD\\nbwrsHQIH2IH2cNnDw2q9htMqlYpisZiuXLmid955R2+88YYWFxdVqVTkuq4ajcae1HTp0iU1m00t\\nLS1peXm58zkrKyuSpJmZmT35HGCnCBxgB1KplNLpdNewWq/htGKxqFqt1vWAqnQ6LUna2NjYk5ou\\nXLigfD6vTCYj13U7P6lUShMTE3IcR1tbW3vyWcBOHAq7AGC/evXVV9VsNlWtVnX27FlJ9x7R+/Ds\\ntHQ63QkX13V19epVOY6z7aSDndrc3NSVK1eUSCR6Lo/FYmq1Wgfy0enYHwgcYIdOnz6tUqmk+fl5\\nnT17VsYYra2taWpqyree67oqlUq6fPly52gom80qm83u2cl8Y4yke5MMSqXStuttF0ZAEAgcYIeG\\nh4eVyWQ6w2r1el3SvQkFD5qYmFCz2VShUFChUNDx48clSUtLS51t+tVqtXyv28+ityzriZ4tD4SB\\nczjALrRnq1WrVc3PzysWi/n+wXddV81mU1NTU3rjjTc6YSP5pz/3y3Ec32vLsjQ8PLztBIREIqFj\\nx47t+POAvUDgALvQvlfa7Oysms3mthd7PjwxoD3MJnUHz4NTnS3Lkud5Wlpa6rntgwqFgjY2Nrru\\n33bp0iVtbm72vGYHCBJDasAuDA8PK5fLdY4sHh5Osyyrs3x6elpjY2NaXV1VrVbT+Pi4pHvTpm3b\\n1sTEhCR/AL366qtaWFhQPp/v3FKnve3DIXbx4kXV63XV63UdO3ZM6XRaxhg1m01ls1mdOXPmae4K\\n4PE8ALtSr9e9WCzmxePxnstd1/UKhYKXSCS8WCzmjY2NeQsLC57neV6hUPDi8bhXLBY9z/O8qamp\\nrvepVqve6OioF4vFvGQy6ZXLZc/zPC+RSHS2e1CpVPKy2awXi8W8Y8eOddYHwhbzvF0MJAMA8IQ4\\nhwMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAjE/wMyYvNEF9d8ygAA\\nAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 72\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"y2 = [np.median(np.random.choice(y, size=size, replace=True)) for _ in range(100000)]\\n\",\n \"y2 = np.asarray(y2)\\n\",\n \"ax = plt.subplot(1,1,1)\\n\",\n \"ax.hist(y2,bins=np.linspace(2,11,10),alpha=0.3,histtype='stepfilled')\\n\",\n \"ax.vlines(np.median(x),0,25000,linewidth=3)\\n\",\n \"ax.set_xlabel('Value',fontsize=20)\\n\",\n \"ax.set_ylabel('Freq',fontsize=20)\\n\",\n \"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\\n\",\n \"print('Bootstrap: ',float(len(y2[y2<=np.median(x)]))/100000)\\n\",\n \"print('Median test: ',median_test(x,y))\\n\",\n \"print('Mann: ',scipy.stats.mannwhitneyu(x,y)[1]*2)\\n\",\n \"print('T_test: NOT NORMAL!',scipy.stats.ttest_ind(x,y)[1])\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('Bootstrap: ', 0.0)\\n\",\n \"('Median test: ', 0.16201071261586195)\\n\",\n \"('Mann: ', 0.0089697635496793649)\\n\",\n \"('T_test: NOT NORMAL!', 0.2677343915603817)\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"display_data\",\n \"png\": \"iVBORw0KGgoAAAANSUhEUgAAAbcAAAEsCAYAAABANv1rAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3c9vI2d+JvCnNE5mPD/EYrUnseFglyzqsJnLtljUHBZB\\nshBJI4ccgtaI7T/AUnFuObSb7JtzalHJJbnYLPkQYJADRXIu4xkgUrHnkhlgI7FoIHMI4NFL7cbu\\nARI3VdQMDMeJu/YgVI1KpLrFbopvsfr5AISbL78kv6YkPqy33ioqnud5ICIiipEF2Q0QERFNG8ON\\niIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2XpLdAADYtg3btnHjxg0cHR3BMAxsbGwEtwshYJom\\nqtUqDMPAYDCAZVkoFovI5/NBneM46Ha70DQNQghks9nQ7dOsISKiCPMk29/f92zbDo0ZhuFtb28H\\n14+OjjxFUYJLMpn02u126D5HR0desVgMja2vr3tCiKnXEBFRtEmflqzX6yNjhUIhNK4oCmzbhuu6\\nEEJgMBjg1q1bofvUajWUy+XQmGmaqFQqU68hIqJokx5ufnCd53keksnkyNji4iJSqdTYx2k2m8hm\\ns6ExwzDQarWmXkNERNEmfZ/b7u7uyFir1cL3v//9Kz+G67pwXReapoXGVVUFABwfH0NV1anUXBau\\nREQUHdLD7SLLspDL5XDnzp3QuBACrusCAAaDATRNw9raWnAdABYXF8c+phAiCKVp1RARUXRFJtza\\n7Tb29/ehKAoajUboNn9Lyg8zACiVSsGYH3pPMq0aIiKKPun73Hxra2t47733sLW1hVwuh16vF9yW\\nSCRChwYAXORBRESXi0y4+RKJBEzTfOpxZel0GkIInJ6ezqizyymKcumFiIhmL3LhBgD5fB6u6+LB\\ngwcAgO3t7ZEaf6pSCAFd1wHg0qDTdX1qNZNiwBERzZ7UcBNCIJlM4sMPPxx7u39cW7VaxfHxceg2\\nfxGJrutQVRW6rkMIMfL4qqoilUpNrWYcz/PGXoiISA6p4ea6LjKZzMgWkR8u2WwWuq6jXq+PBItt\\n2zAMI1jZWCgUcHBwEKpxHAfFYjG4Pq0aIiKKOHknRzmzvb3tua4bGisUCl61Wg2ut1qt0OmvTk5O\\nPMMwvF6vF4y5rjty2qxisej1+/2p11wVAC8CLzER0QtH8Tz582c7Ozs4OjoKTpycy+Xw1ltvhWra\\n7TaEEHj06BFc10W1Wh3Zmuv1emg0GlhZWYEQAoZhYHV19VpqrsLf3xaBl5iI6IUSiXCLK4YbEZEc\\nkVwtSURE9DwYbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2InM97kR0dP95je/wb/8\\ni0DUDp1MJr+FpaW07DaIAgw3ojniui7+8R9Psbj432S3Evjii8/x7W//X4YbRQrDjWjOfO1r38C3\\nvx2dcPvss18DeCi7DaIQ7nMjIqLYYbgREVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcUOw42IiGIn\\nEse52bYN27Zx48YNHB0dwTAMbGxshGocx0G324WmaRBCIJvNIp/PS6shIqLokh5utm1DURRsbW0F\\nY7lcDq7r4u233wYACCFQrVaxt7cX1JRKJei6jnQ6PfMaIiKKNunTkvV6fWSsUCiExmu1GsrlcqjG\\nNE1UKhUpNUREFG3Sw01RFNi2HRrzPA/JZDK43mw2kc1mQzWGYaDVakmpISKiaJM+Lbm7uzsy1mq1\\n8P3vfx/A2YliXdeFpmmhGlVVAQDHx8dQVXVmNalU6hn/T4mIaFakb7ldZFkWcrkc7ty5AwAYDAYA\\ngMXFxbH1QoiZ1hARUfRJ33Lztdtt7O/vQ1EUNBqNYNx13afed5Y1REQUfZEJt7W1NaytrWE4HCKX\\ny2FnZwfLy8uy2yIiojkUuWnJRCIB0zTn6rgyRVHGXoiISI7IhRsA5PN5uK6LBw8eQNd1AMDp6enY\\nWl3XZ1pDRETRJzXchBBIJpP48MMPx97uui5UVYWu6yOLOYQQUFUVqVRqpjXjeJ439kJERHJIDTfX\\ndZHJZEa2iPxw8Y83KxQKODg4CNU4joNisRhcn2UNERFFm9Rwy2azuH379shWTq1WQ6VSCbaUarUa\\nms1mqMayLNRqtdB9ZlVDRETRpngRmD/b2dnB0dFRcOLkXC6Ht956K1TT6/XQaDSwsrICIQQMw8Dq\\n6qq0mqvwF5VE4CWmmPj444/xwQf/jtdfj85K4s8++zVeeqmLtbX/LbsVokAkwi2uGG40bQw3oquJ\\n5GpJIiKi58FwIyKi2GG4ERFR7ETm9FtENJ8URcGnn36GDz74mexWQr75zZfwJ3/yXZ4t6AXFcCOi\\n5/Lyy9/El1/+L/z619FaOPXxxz/HH/+xx3B7QTHciOi5ffObquwWRgyHDLUXGfe5ERFR7DDciIgo\\ndhhuREQUOww3IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5ERBQ7kTi3\\nZLvdhhACR0dHEELANE2sra0Ft/tj1WoVhmFgMBjAsiwUi0Xk8/mgznEcdLtdaJoGIQSy2Wzo9mnW\\nEBFRdEkPt3a7DV3XgzAbDodBgG1sbAR1nU4HnU4HAKCqKt5///1Q4AghUK1Wsbe3F4yVSiXouo50\\nOj3VGiIiijbp05JCCCwvLwfXE4kEKpUKTNMMxhRFgW3bcF0XQggMBgPcunUr9Di1Wg3lcjk0Zpom\\nKpXK1GuIiCjapIab67poNBoYDoehcX+L7Pj4OBjzPA+Li4tIpVJjH6vZbCKbzYbGDMNAq9Waeg0R\\nEUWb1HBTVRVCCPT7/ed6HNd14bouNE0beXzgLCSnVUNERNEnfZ/bYDAYGbNtG8lkMrSVJoSA67rB\\nfTRNC/bT+Y+xuLg49jmEEMFjTauGiIiiS3q4jVOv13Hv3r3gur8ldX4FZalUCsb80HuSadUQEVH0\\nSV9QcpFlWXjllVdw586dYCyRSIRWTgLRWuShKMrYCxERyRGpLTchBCzLwuHh4VNr0+k0hBA4PT2d\\nQWfyvfPOO2P/TUREoyIVbtVqFQ8ePBgZ397ext27d0Nj/lSlEAK6rgMATk9Px+4v03U9WBTyvDXj\\neJ43dnyaW29/+Zd/Gfyb4UZE9GSRmZYsl8vY3t4eCRX/oOqLKxX9RSR+KOm6DiHEyH1VVUUqlZpa\\nDRERRV8kwm1nZwfVajUUHp1OB/1+H7quo16vjwSLbdswDCMIw0KhgIODg1CN4zgoFovB9WnVEBFR\\ntEkPN//g6MFgAMdx4DgObNtGs9kMTnelaVroWDjXdWFZFnZ2doKxWq2GZrMZemzLslCr1aZeQ0RE\\n0aZ4l+0wmoFxB0z7MpkMPvroo+C6f3LlR48ewXXdkS09AOj1emg0GlhZWYEQAoZhYHV19VpqrsLf\\n5zaNl/j8/juJPzKS7OOPP8YHH/w7Xn99+enFL7hPPvkJNjf/FAsL0j/DkwRSwy3uGG40bQy3q2O4\\nvdj4UyciothhuBERUeww3IiIKHYYbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2GG4\\nERFR7DDciIgodhhuREQUOww3IiKKHYYbERHFzkuyGyCKqn/914/xz//8/2S3EfLFF/8BICm7DaLI\\nY7gRXeLTT130+wkkk6/JbiXk937vG7JbIIo8hhvRE/zu734d3/rW+G+LJ6LoikS4tdttCCFwdHQE\\nIQRM08Ta2lqoxnEcdLtdaJoGIQSy2Szy+by0GiIiii7p4dZut6HrehBmw+EQhmFgMBhgY2MDACCE\\nQLVaxd7eXnC/UqkEXdeRTqdnXkNERNEmfbWkEALLy8vB9UQigUqlAtM0g7FarYZyuRy6n2maqFQq\\nUmqIiCjaFM/zPFlP7rouCoUCOp0OEolEMC6EwNLSEoQQSKVS0DQNjuMglUqF7qtpGh4/fgwAM625\\nKkVRAADTeIn9x5rW49HT9Xq/wOHhN/Dqq9xin0effPITbG7+KRYWpH+GJwmk/tRVVYUQAv1+/9Ia\\n13WDcLl4XwA4Pj6eaQ0REUWf9I80g8EAN2/eDI3Zto1kMolUKoXBYAAAWFxcHHt/IcRMa4iIKPqk\\nh9s49Xod9+7dA3C25fY0s6whIqLom2i15NLSUmjfz1V4ngdFUfDRRx9dqd6yLLzyyiu4c+fORM8j\\n06SvCRERXa+Jwm15eRn9fh+O4wRj6XQag8EAw+EQwNn+qYtL5q/65i+EgGVZODw8nKQtIiKikInC\\n7d69e8jlcshms9jZ2Qkt4XccBxsbGzg+Pkar1XqmY8Kq1SoePHgQGtN1HQBweno6dl+YruvBgo9Z\\n1Ixz2epFbtEREckx0T63ra0tqKqKTqcTCjYAyGaz6Ha7ePz4MarV6sSNlMtlbG9vj4SKqqrQdX1k\\nMYcQAqqqIpVKzbSGiIiib6Jws20bxWIxdEzaRYVCAbZtT9TEzs4OqtVqKDw6nU5wiEChUMDBwUHo\\nPo7joFgshp53VjVERBRtE4Wb53lPXQ7/pGPWxmm1WgDODglwHAeO48C2bTSbzWBqs1arodlshu5n\\nWRZqtVpwfZY1REQUbROdoWR9fR3tdhutVgu3bt0aub3dbmN9fR2FQiF0bsbLjDtg2pfJZEIrLHu9\\nHhqNBlZWViCEgGEYWF1dDd1nljVXwTOUzDeeoWS+8QwlL7aJws1/oz89PcX3vvc9FItF6LqOo6Mj\\n7O/vB1th3W53ZJ/ci4jhNt8YbvON4fZim2i1pK7r6HQ6qFQqaDabI9N3uq6jXq8z2IiISKqJv/Im\\nm81if38fQgg4jgMhBHRdh67ryGaz19EjERHRRJ75+9xeeeUV5HK5p66eJCIimrWJJ6N7vR5yuRxU\\nVUUmk0G32wVwdmquv/7rv556g0RERJOaKNz6/T4Mw4DjOMjn86GFDY8ePcLdu3exsrIy9SaJiIgm\\nMVG4+cd6dbvdkcUkJycn2NraQrfbDc7oT0REJMNE4ba7u4tCoXDpasi7d+9ieXk5OCSAiIhIhonC\\nzXVdZDKZJ9b4x70RERHJMlG4LS8vP/XraHq9Hg8JICIiqSYKt9u3b6Pb7eKnP/3p2K9zKZVKEEKg\\nUChMrUEiIqJJTXT6LQAwDAO9Xg/FYhH7+/soFotQVRW2bePk5AS6ruOXv/zldfU7V3j6rfnG02/N\\nN55+68U28U+92+1ia2sL//RP/wQA2N/fR7PZxOPHj3H37l0GGxERSfdMZyi5e/cu7t69C+DsZMqa\\npgXfYk1ERCTbRFtuOzs7+OEPfxga03WdwUZERJEy0ZabaZpIJpNjv8uNiIgoKibacnvrrbdwcnKC\\nDz/88Lr6ISIiem4TbblZloWlpSUYhoF6vY5cLgdd17G4uHhd/REREU1sonDTNA3A2VL0zc3NYPzi\\nMnVFUfDll19O1Eir1UIymUQ+nw+NCyFgmiaq1SoMw8BgMIBlWSgWi6Fax3HQ7XahaRqEEMhmsyOP\\nNa0aIiKKtonC7apv8uMO8H4S27axubl56TkpO50OOp0OAEBVVbz//vuhXoQQqFar2NvbC8ZKpRJ0\\nXUc6nZ5qDRERRd8Tw61areK73/1usIDk4jcBPK9+v49arQbDMIKtwosURYFt28jlchgMBkilUiM1\\ntVoN5XI5NGaaJiqVCnZ3d6daQ0RE0ffEM5QsLCxgfX0djUYjNL6zswPHcfDuu+9OrZGlpSVYloXV\\n1dXQeL/fhxDiiVuNmqbBcZxQ8LmuC03T8Pjx46nWTIJnKJlvPEPJfOMZSl5sz/RT39vbg2VZ0+7l\\nmbiuGwTQef6xd8fHx1OrISKi+fBMZygBZrv1IISA67oAgMFgAE3TsLa2FlwHcOmKTSFEsCU2rRoi\\nIoq2Zw63SReNPCt/S8oPM+BskYc/5ofek0yrhoiI5kPkJ6MTiQQ2NjZCY/4ij6hQFGXshYiI5Ih8\\nuI2TTqchhMDp6ansVoiIKIIiH27b29sjY/5UpRACuq4DwKVBp+v61Gou43ne2AsREcnx1H1utm3j\\n9u3bobFOpwPP80bGz7t4+MCz8A+qLpVKocUc/iIS/9Rfuq5DCIGbN2+G7quqanC/adUQEVH0PTXc\\nTk5OLj14+0kHdU8j3HRdR71eHwkW27ZhGEawsrFQKODg4CAUSo7joFgsBtenVUNERNH3xHA7PDyc\\nVR8Axh9eoGka+v1+cPor13VhWRbef//9oKZWq2F9fT208MSyrNCxeNOqISKi6HviGUqu23A4xP37\\n9yGEQKvVgq7rKBQKKBaLoaX/7XYbQgg8evQIruuiWq2ObM31ej00Gg2srKxACAHDMEbOdjKtmqvi\\nGUrmG89QMt94hpIXm9RwizuG23xjuM03htuLjT91IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLY\\nYbgREVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcUOw42IiGKH4UZERLHDcCMiothhuBERUeww3IiI\\nKHYYbkREFDsMNyIiip2XZDfga7VaSCaTyOfzI7c5joNutwtN0yCEQDabHambZQ0REUVbJMLNtm1s\\nbm6i1WqN3CaEQLVaxd7eXjBWKpWg6zrS6fTMa4iIKPqkTkv2+32Uy2X0+31omja2plaroVwuh8ZM\\n00SlUpFSQ0RE0ad4nufJbgIAlpaWYFkWVldXQ+OapsFxHKRSqWDMdV1omobHjx/PvGYSiqIAAKbx\\nEvuPNa3Ho6fr9X6Bw8Nv4NVXudU+jz755CfY3PxTLCxwacGLKNI/ddd1g3A5T1VVAMDx8fFMa4iI\\naD5EOtwGgwEAYHFxceztQoiZ1hAR0XyIdLi5rhupGiIimg+RWC05787vDyMiIvkiveVGRET0LCK9\\n5abrOgDg9PR07L4wXdeDBR+zqLnMZasXuUVHRCRHpLfcVFWFrusjizmEEFBVFalUaqY1REQ0HyId\\nbgBQKBRwcHAQGnMcB8ViUUoNERFFX6TCbdz0Xq1WQ7PZDI1ZloVarSalhoiIok/qGUqGwyHu378P\\nIQRarRZ0XUehUECxWMTa2lpQ1+v10Gg0sLKyAiEEDMMYOZPJLGuuimcomW88Q8l84xlKXmyROf1W\\nHDHc5hvDbb4x3F5s/KkTEVHsRPpQACKi5/HZZ5/hK1/5iuw2Ql5++WXZLbwQGG5EFEv/+Z+L+Pu/\\n/z+y2wj5ylc+x/r6HyGRSMhuJfYYbkQUS6nUH8luYcTDhz/Dl19+KbuNFwL3uRERUeww3IiIKHYY\\nbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2GG4ERFR7DDciIgodhhuREQUOww3IiKK\\nHYYbERHFzlx8K4AQAqZpolqtwjAMDAYDWJaFYrGIfD4f1DmOg263C03TIIRANpsN3T7NGiIiiq65\\nCDcA6HQ66HQ6AABVVfH++++HAkcIgWq1ir29vWCsVCpB13Wk0+mp1tD0ffzxJzg5GcpuI+TTTwcA\\nviG7DSJ6BnMRboqiwLZt5HI5DAYDpFKpkZparYZyuRwaM00TlUoFu7u7U62h6fvww2P0+4v46le/\\nLruVc16Hpr0quwkiegaK53me7Caept/vQwjxxKlBTdPgOE4o+FzXhaZpePz48VRrrkpRFADANF5i\\n/7Gm9XhR88EHP8Pp6R/iW9/SZLdCdG0ePvwZ1tf/EJrG3/PrFosFJa7rBgF0nqqqAIDj4+Op1RAR\\nUfTNxbQkcLYvzHVdAMBgMICmaVhbWwuuA8Di4uKl9/W3xKZVQ0RE0TUX4eZvSflhBpwt8vDH/NB7\\nkmnVEBFR9M3FtGQikcDGxkZozF/kEQWKooy9EBGRHHMRbuOk02kIIXB6eiq7FSIiipi5CLft7e2R\\nMX+qUggBXdcB4NKg03V9ajXjeJ439kJERHJEPtz8g6ovrlT0F5Houg5VVaHrOoQQI/dVVRWpVGpq\\nNUREFH2RDzdd11Gv10eCxbZtGIYRrGwsFAo4ODgI1TiOg2KxGFyfVg0REUVb5MMNOJuC7Pf7wXXX\\ndWFZFnZ2doKxWq2GZrMZup9lWajValOvISKiaJuLM5QAQLvdhhACjx49guu6qFarI1tzvV4PjUYD\\nKysrEELAMAysrq5eS81V8AwlV8czlNCLgGcomZ25Cbd5xHC7OoYbvQgYbrMzF9OSREREk2C4ERFR\\n7DDciIgodhhuREQUOww3IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5E\\nRBQ7L8lugIjoRfLw4UMMh0PZbYS8+uqrePnll2W3MVUMNyKiGfnqV/87fvazIYDPZLcS+OyzR/jz\\nPwfS6bTsVqaK4UZENCM3bvwBgD+Q3UbIw4e/kN3CteA+NyIiih2GGxERxQ6nJcdwHAfdbheapkEI\\ngWw2i3w+L7stIiK6IobbBUIIVKtV7O3tBWOlUgm6rsduhysRUVwx3C6o1Wool8uhMdM0UalUsLu7\\nK6mr6fq3f/s3fPHFF7LbCPnii/+Q3QIRxYjieZ4nu4ko0TQNjuMglUoFY67rQtM0PH78eKLHUhQF\\nADCNl9h/rGk83t/93U/w+eevhR5TtsePFfz+7/8P/M7vfFV2K0QvlIcPf4E33vhG7GamuOV2juu6\\nQZCdp6oqAOD4+DgUevPqv/4LeO21/4mFBa4nIqJ44rvbOYPBAACwuLg49nYhxCzbISKiZ8RwO8d1\\nXdktEBHRFHBacgqetu9q2vu2orSvjIjoOjzv2gJuuRERUeQ874d4brmdo+s6AOD09HTsfjf/9osu\\n+4QxzdWS0xTFvtjT1bCnq4tiX+zpaqYxO8Utt3NUVYWu6yMLR4QQUFU1FisliYheBAy3CwqFAg4O\\nDkJjjuOgWCxK6oiIiCbFg7gvGA6HWF9fD51+64033oBlWRNvuUVxcx+IZl/s6WrY09VFsS/2dDXT\\n6InhNkav10Oj0cDKygqEEDAMA6urqxM/ThR/aYBo9sWeroY9XV0U+2JPV8Nwi7go/tIA0eyLPV0N\\ne7q6KPbFnq6G4UZERDQGF5QQEVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcXOV9555513ZDcRR+12\\nGz/+8Y/xgx/8AH/7t3+Lr3/96/jOd74jtSfbtmFZFnq9Hn7wgx/gV7/6FQzDkNrTea7r4i/+4i/w\\nZ3/2Z9J6EEKgVCrh9ddfh6ZpePjwIWq1GhRFufTcorPkOA7+5m/+Br1eDz/60Y+QyWSQTCal9FKp\\nVLCwsABN0/C1r31NSg/j2LaNdruNn//85/jRj36Efr8v/ff84s/txo0beO2112beR6vVwq9+9aux\\nv8uO4+CDDz7A8fExfvzjH+Pzzz+fye/8k3qapGaER1PXarU8x3GC667replMxrMsS1pP+/v7nm3b\\noTHDMLzt7W1JHY3a3Nz01tfXpfZwdHTkKYoSXJLJpNdut6X25Gs2m55pmqGxzc1NSd14XqFQCL1W\\n5y9LS0tSeup2u16r1QqNtVot6X97xWIxNGYYhieEmHkfyWTS63Q6I7cdHR2N9Li+vn7tPT6pp0lq\\nxuG05DUQQmB5eTm4nkgkUKlUYJqmtJ7q9frIWKFQGDsugxACJycn0r+rTlEU2LYN13UhhMBgMMCt\\nW7ek9gScbdVubm7ivffeC8Ysy8KDBw+k9ZTJZOA4DoQQoUu9Xkez2ZTSk2VZWFtbC42tra1hf39f\\nSj8AYJomyuVyaOzevXsz+9vr9/sol8vo9/vQNG1sTa1WG+nRNE1UKhVpPV2l5kkYblPmui4ajQaG\\nw2FoPJ/PAwCOj48ldPXbN+3zPM+TNqV1UafTQbFYjMRZEjzPw+LiYqS+BeL+/fsjH442Nzelvmkb\\nhoGbN28ilUqFLgBw8+ZNKT0dHh6i3++PjLuuK6Gbs+ft9/vIZrOh8eXlZWxvb8+kh3Q6jffeew8b\\nGxuX1jSbzZEeDcNAq9WS1tNVap6E4TZlqqpCCDH2D0ym3d1d3L9/PzTWarVw+/ZtSR39VqfTQaFQ\\nkN1GpO3s7GBlZWVkXGYAj3vT2dnZeeY3o2koFAooFouhvz/btlEqlaT043991sUtD//66enpzHu6\\nyHVduK470qOqqgDkfSB/Xvyy0mswGAxGxmzbRjKZjMzWgGVZyOVyuHPnjuxWIIRAPp+PxFYbcNaP\\n/0l/MBhA07SRqa5Zc10XiUQCOzs70DQtMn2d1+l0kMvlpPawtbUF27aRyWRQr9eRTqcxHA7x1ltv\\nSenHXwAxGAxCX4Dsv0dcHJfB7+WyPoQQkXnfmgTDbUbq9Tru3bsnuw20223s7+9DURQ0Gg3Z7aDd\\nbkv9pH+R/+n1fGj4n/plBYn/6b/X64U+jFSrVQwGg8i8fo7j4O2335bdBg4PD/HGG2/ANE1ks1l0\\nOh1pvaiqikKhgG63GwoI/2caheCQNWV73TgtOQOWZeGVV16JxFbS2toa3nvvPWxtbSGXy6HX60nr\\nJYp/VIlEYiQsrnPH+lX4r9PFZdC3b9+W2td5rVYLmUxGdhsAzqZGt7e3sb+/H3xllczdBPV6PbR4\\n5Pz++GdZKEFXwy23ayaEgGVZODw8lN1KSCKRgGmayOfzY6dRZ6HZbIaCRPZKycuk02kIIXB6eipl\\nCskPtYvhtry8DNd1cXx8LP3T/9bWltSVm75yuYxqtRq8Hv1+H+vr6ygWi/jlL38ppad0Oo1ms4l2\\nuw3gbGvusp8pTQ+33K5ZtVqNxB/9OPl8Hq7rSpm26fV6I/tnorDPbdwKNv/TtT+VNGv+jn3/vxfJ\\n6svnui4cx5G+78jfwj0f9IlEAnt7e1BVVer0ZCKRwNraGtbW1pDP54OfmezXDPhtwF62uGVeA5hb\\nbteoXC5je3tb+i+wPzXz05/+dOwS7YuHLczC4eEhjo6OQvv9/GOmqtUqVlZWZr6Py3/uUqkUeoP0\\nt2xl/pHrun7p/hnZbz62bV8avLPU7XYvnRo1TTNS0+CO42B9fV12GwB+uyUphAi9PwghoKqq9FmB\\nZ8VwuyY7Ozuh6RHgbDWZrutIp9Mz7cV1XWQymZE3Qf/T48XjW2Zh3CKIv/qrv8Lh4SG2trZm3g9w\\nFhL1en2Pi9RWAAAFoUlEQVTkj9m2bRiGIfVDimma6Ha7WF1dDcYcx4nECtyDg4NI7G/Tdf3Sg8dd\\n10WxWJxxR2eKxSJu374dWrFpWdbIcacyFQoFHBwchMLNcRxpr9k0cFryGvgHPg4GAziOA8dxYNs2\\nms3mzIMNOAuv27dvj0z71Wo1VCoV6W+Ovk8//VT61KSmaaHFB67rwrIs7OzsSOzq7IDti2e0qFar\\n0vsCzj4kRWFhhP+3dXH6UQiBR48eSfs9TyaTwUkcgLOp73K5LK2fcX9jtVpt5IOBZVmo1WrSenqW\\nmvMUT/a7ScyMOxjSl8lk8NFHH824o9/a2dnB0dERbty4gaOjI+RyOWnH/5zX7/dRq9Wwu7uL4XCI\\njY0NmKYZOoXZLLXb7eAN0XXdkS1wWfzXKZPJ4OjoCKVSKbQlJ0u5XIaiKHj33XdltwIg/HsOnE27\\nyTxcot/vo9Vq4dGjRwCApaWlmf7dDYdD3L9/H0IItFot6LoeHOx+fuq/1+uh0WhgZWUl2JVxXb9f\\nV+npqn1fhuFGRESxw2lJIiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5E\\nRBQ7DDeiiHIcBwsLC0/9dmvbtrGwsBB8qepVra+vY2GBbwEUT/zNJoqobDYLVVXR6/We+M0N/jkB\\n33zzzYmfI6rfoUf0vBhuRBG2ubkJz/Owu7t7ac3u7i4URcGtW7dm2BlRtDHciCLs9u3bADDyjQA+\\nx3EwHA7xve99b5ZtEUUew40owpaXl6Hr+qVTk/6XvfohCJx9xcv6+joymQwWFhagaRpKpVLoq3x8\\n58+bXiwWx+6Dc10XCwsLKJfLI7dtb2/DMIzgecrl8tjnIZo1hhtRxJmmeenUpGVZoSlJIQSWlpbw\\nwx/+EEtLSzBNE7lcDq1WC4ZhPPVb15+0D+7ibYZhoFqtYmFhIXgey7KQyWTQ6/We4f+UaHoYbkQR\\n5085XpyaHDclWavVoCgK9vf38Q//8A949913sbe3h1qtBtd1p/btz9vb2+j1euh0Ojg4OAiep9vt\\nAhj/TetEs8RwI4q4dDqN5eXlkanJcVOS5XIZzWZz5Esm/S9+PTk5mUpP9+/fR7FYRDabheu6wSWd\\nTiOfz8NxHJyenk7luYiexUuyGyCip3vzzTfR6/VgWRbefvttAECr1RpZJbm8vBwEmeu6ODw8hOM4\\nly5IeVbD4RD7+/tIJpNjb1cUBYPBAIuLi1N9XqKrYrgRzYHNzU1UKhU0Gg28/fbbEEKg3+9jfX09\\nVOe6LiqVCnZ3d4OtPMMwYBjG1BZ6CCEAnC1AqVQql9ZdFnxEs8BwI5oDiUQC2Ww2mJpstVoAzhab\\nnJfP59Hr9WCaJkzTxM2bNwEAnU4nuM+kBoNB6LqmaQAAVVVHpj+JooL73IjmhL9q0rIsNBoNKIoS\\nChfXddHr9bC+vo533303CDYgvOR/Uo7jhK6rqopEInHp4pRkMomlpaVnfj6iaWC4Ec0J/9yR9Xod\\nvV7v0gO3Ly4a8acqgdGQO7+8X1VVeJ6HTqcz9r7nmaaJk5OTkfNZbm9vYzgcjj0mjmiWOC1JNCcS\\niQQKhUKwxXRxSlJV1eD2UqmEXC6Ho6MjNJtNrKysADg7VEDXdeTzeQDhsHvzzTfRbrdRLBaD0375\\n970YmFtbW2i1Wmi1WlhaWsLy8jKEEOj1ejAMA3fu3LnOl4Lo6TwimhutVstTFMVbWFgYe7vrup5p\\nml4ymfQURfFyuZzXbrc9z/M80zS9hYUFr1wue57neevr6yOPY1mWl8lkPEVRPE3TvGq16nme5yWT\\nyeB+51UqFc8wDE9RFG9paSmoJ5JN8bznmIwnIiKKIO5zIyKi2GG4ERFR7DDciIgodhhuREQUOww3\\nIiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLY+f/e58P1vQLe8QAAAABJRU5ErkJggg==\\n\",\n \"text\": [\n \"\"\n ]\n }\n ],\n \"prompt_number\": 73\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Back to the important question today. Does Mary hate American? BOOTSTRAP\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"x = np.random.rand(100000)>0.75\\n\",\n \"size = 10000\\n\",\n \"simulated = np.asarray([np.mean(np.random.choice(x,size = 7)) for _ in range(size)])\\n\",\n \"p = float(np.sum(simulated>=(4./7.)))/size\\n\",\n \"print('p-value: ', p)\\n\",\n \"\\n\",\n \"print('CI for p with SEM = ', p + scipy.stats.t.isf([0.025, 0.975], [size-1])[::-1] *np.sqrt(p*(1-p)/(size-1)))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"('p-value: ', 0.0688)\\n\",\n \"('CI for p with SEM = ', array([ 0.06383821, 0.07376179]))\\n\"\n ]\n }\n ],\n \"prompt_number\": 9\n },\n {\n \"cell_type\": \"raw\",\n \"metadata\": {},\n \"source\": [\n \"Compare with the result of the Fisher test: 0.07057048347153140\\n\",\n \"\\n\",\n \"We can get confidence intervals with the CLT (It's normally distributed because we calculate p many times)\"\n ]\n }\n ],\n \"metadata\": {}\n }\n ]\n}"},"license":{"kind":"string","value":"agpl-3.0"}}}],"truncated":false,"partial":true},"paginationData":{"pageIndex":3,"numItemsPerPage":100,"numTotalItems":47214,"offset":300,"length":100}},"jwt":"eyJhbGciOiJFZERTQSJ9.eyJyZWFkIjp0cnVlLCJwZXJtaXNzaW9ucyI6eyJyZXBvLmNvbnRlbnQucmVhZCI6dHJ1ZX0sImlhdCI6MTc1Mjg4MDAwOSwic3ViIjoiL2RhdGFzZXRzL2NvZGVwYXJyb3QvZ2l0aHViLWp1cHl0ZXIiLCJleHAiOjE3NTI4ODM2MDksImlzcyI6Imh0dHBzOi8vaHVnZ2luZ2ZhY2UuY28ifQ.QvLNb3Xdw9mp2EP5cIaXPc1-fRwz3RZreOdQDPNQD9RHeTLJgG5Bic4kyM8iFF6SU3HkVOTBLmqcFDptCI_jCQ","displayUrls":true},"discussionsStats":{"closed":2,"open":0,"total":2},"fullWidth":true,"hasGatedAccess":true,"hasFullAccess":true,"isEmbedded":false,"savedQueries":{"community":[],"user":[]}}">
repo_name
stringlengths 6
92
| path
stringlengths 7
220
| copies
stringclasses 78
values | size
stringlengths 2
9
| content
stringlengths 15
1.05M
⌀ | license
stringclasses 15
values |
|---|---|---|---|---|---|
dsacademybr/PythonFundamentos | Cap04/Notebooks/DSA-Python-Cap04-Exercicios-Solucao.ipynb | 1 | 8978 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# <font color='blue'>Data Science Academy - Python Fundamentos - Capítulo 4</font>\n",
"\n",
"## Download: http://github.com/dsacademybr"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Versão da Linguagem Python Usada Neste Jupyter Notebook: 3.8.8\n"
]
}
],
"source": [
"# Versão da Linguagem Python\n",
"from platform import python_version\n",
"print('Versão da Linguagem Python Usada Neste Jupyter Notebook:', python_version())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Versão da Linguagem Python\n",
"from platform import python_version\n",
"print('Versão da Linguagem Python Usada Neste Jupyter Notebook:', python_version())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercícios "
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[27, 64, 125]\n"
]
}
],
"source": [
"# Exercício 1 - Crie uma lista de 3 elementos e calcule a terceira potência de cada elemento.\n",
"list1 = [3,4,5]\n",
"quadrado = [item**3 for item in list1] \n",
"print(quadrado)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['A', 'a', 1]\n",
"['DATA', 'data', 4]\n",
"['SCIENCE', 'science', 7]\n",
"['ACADEMY', 'academy', 7]\n",
"['OFERCE', 'oferce', 6]\n",
"['OS', 'os', 2]\n",
"['MELHORES', 'melhores', 8]\n",
"['CURSOS', 'cursos', 6]\n",
"['DE', 'de', 2]\n",
"['ANÁLISE', 'análise', 7]\n",
"['DE', 'de', 2]\n",
"['DADOS', 'dados', 5]\n",
"['DO', 'do', 2]\n",
"['BRASIL', 'brasil', 6]\n"
]
}
],
"source": [
"# Exercício 2 - Reescreva o código abaixo, usando a função map(). O resultado final deve ser o mesmo!\n",
"palavras = 'A Data Science Academy oferce os melhores cursos de análise de dados do Brasil'.split()\n",
"resultado = [[w.upper(), w.lower(), len(w)] for w in palavras]\n",
"for i in resultado:\n",
" print (i)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['A', 'a', 1]\n",
"['DATA', 'data', 4]\n",
"['SCIENCE', 'science', 7]\n",
"['ACADEMY', 'academy', 7]\n",
"['OFERCE', 'oferce', 6]\n",
"['OS', 'os', 2]\n",
"['MELHORES', 'melhores', 8]\n",
"['CURSOS', 'cursos', 6]\n",
"['DE', 'de', 2]\n",
"['ANÁLISE', 'análise', 7]\n",
"['DE', 'de', 2]\n",
"['DADOS', 'dados', 5]\n",
"['DO', 'do', 2]\n",
"['BRASIL', 'brasil', 6]\n"
]
}
],
"source": [
"resultado = map(lambda w: [w.upper(), w.lower(), len(w)], palavras)\n",
"for i in resultado:\n",
" print (i)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[1, 3, 5, 7], [2, 4, 6, 8]]\n"
]
}
],
"source": [
"# Exercício 3 - Calcule a matriz transposta da matriz abaixo.\n",
"# Caso não saiba o que é matriz transposta, visite este link: https://pt.wikipedia.org/wiki/Matriz_transposta\n",
"# Matriz transposta é um conceito fundamental na construção de redes neurais artificiais, base de sistemas de IA.\n",
"matrix = [[1, 2],[3,4],[5,6],[7,8]]\n",
"transpose = [[row[i] for row in matrix] for i in range(2)]\n",
"print(transpose)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 0]\n",
"[1, 1]\n",
"[4, 8]\n",
"[9, 27]\n",
"[16, 64]\n"
]
}
],
"source": [
"# Exercício 4 - Crie duas funções, uma para elevar um número ao quadrado e outra para elevar ao cubo. \n",
"# Aplique as duas funções aos elementos da lista abaixo. \n",
"# Obs: as duas funções devem ser aplicadas simultaneamente.\n",
"lista = [0, 1, 2, 3, 4]\n",
"\n",
"def square(x):\n",
" return (x**2)\n",
" \n",
"def cube(x):\n",
" return (x**3)\n",
"\n",
"funcs = [square, cube]\n",
"\n",
"for i in lista:\n",
" valor = map(lambda x: x(i), funcs)\n",
" print(list((valor)))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1024, 177147, 16777216]"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Exercício 5 - Abaixo você encontra duas listas. Faça com que cada elemento da listaA seja elevado \n",
"# ao elemento correspondente na listaB.\n",
"listaA = [2, 3, 4]\n",
"listaB = [10, 11, 12]\n",
"list(map(pow, listaA, listaB))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[-5, -4, -3, -2, -1]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Exercício 6 - Considerando o range de valores abaixo, use a função filter() para retornar apenas os valores negativos.\n",
"range(-5, 5)\n",
"list(filter((lambda x: x < 0), range(-5,5)))"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[2, 3, 5, 7]\n"
]
}
],
"source": [
"# Exercício 7 - Usando a função filter(), encontre os valores que são comuns às duas listas abaixo.\n",
"a = [1,2,3,5,7,9]\n",
"b = [2,3,5,6,7,8]\n",
"print (list(filter(lambda x: x in a, b)))"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"05/07/2021 12:12\n",
"05/07/2021 12:12\n"
]
}
],
"source": [
"# Exercício 8 - Considere o código abaixo. Obtenha o mesmo resultado usando o pacote time. \n",
"# Não conhece o pacote time? Pesquise!\n",
"import datetime\n",
"print (datetime.datetime.now().strftime(\"%d/%m/%Y %H:%M\"))\n",
"\n",
"import time\n",
"print (time.strftime(\"%d/%m/%Y %H:%M\"))"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{'a': 4, 'b': 5}\n"
]
}
],
"source": [
"# Exercício 9 - Considere os dois dicionários abaixo. \n",
"# Crie um terceiro dicionário com as chaves do dicionário 1 e os valores do dicionário 2.\n",
"dict1 = {'a':1,'b':2}\n",
"dict2 = {'c':4,'d':5}\n",
"\n",
"def trocaValores(d1, d2):\n",
" dicTemp = {}\n",
" \n",
" for d1key, d2val in zip(d1,d2.values()):\n",
" dicTemp[d1key] = d2val\n",
" \n",
" return dicTemp\n",
"\n",
"dict3 = trocaValores(dict1, dict2)\n",
"print(dict3)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"g\n",
"h\n"
]
}
],
"source": [
"# Exercício 10 - Considere a lista abaixo e retorne apenas os elementos cujo índice for maior que 5.\n",
"lista = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']\n",
"for indice, valor in enumerate(lista):\n",
" if indice <= 5:\n",
" continue\n",
" else:\n",
" print (valor)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fim"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Obrigado\n",
"\n",
"### Visite o Blog da Data Science Academy - <a href=\"http://blog.dsacademy.com.br\">Blog DSA</a>"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.8"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
mne-tools/mne-tools.github.io | 0.20/_downloads/05c57a644672d33707fd1264df7f5617/plot_time_frequency_global_field_power.ipynb | 1 | 7227 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n\n# Explore event-related dynamics for specific frequency bands\n\nThe objective is to show you how to explore spectrally localized\neffects. For this purpose we adapt the method described in [1]_ and use it on\nthe somato dataset. The idea is to track the band-limited temporal evolution\nof spatial patterns by using the :term:`Global Field Power(GFP) <GFP>`.\n\nWe first bandpass filter the signals and then apply a Hilbert transform. To\nreveal oscillatory activity the evoked response is then subtracted from every\nsingle trial. Finally, we rectify the signals prior to averaging across trials\nby taking the magniude of the Hilbert.\nThen the :term:`GFP` is computed as described in [2]_, using the sum of the\nsquares but without normalization by the rank.\nBaselining is subsequently applied to make the :term:`GFPs <GFP>` comparable\nbetween frequencies.\nThe procedure is then repeated for each frequency band of interest and\nall :term:`GFPs <GFP>` are visualized. To estimate uncertainty, non-parametric\nconfidence intervals are computed as described in [3]_ across channels.\n\nThe advantage of this method over summarizing the Space x Time x Frequency\noutput of a Morlet Wavelet in frequency bands is relative speed and, more\nimportantly, the clear-cut comparability of the spectral decomposition (the\nsame type of filter is used across all bands).\n\nWe will use this dataset: `somato-dataset`\n\n## References\n\n.. [1] Hari R. and Salmelin R. Human cortical oscillations: a neuromagnetic\n view through the skull (1997). Trends in Neuroscience 20 (1),\n pp. 44-49.\n.. [2] Engemann D. and Gramfort A. (2015) Automated model selection in\n covariance estimation and spatial whitening of MEG and EEG signals,\n vol. 108, 328-342, NeuroImage.\n.. [3] Efron B. and Hastie T. Computer Age Statistical Inference (2016).\n Cambrdige University Press, Chapter 11.2.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Authors: Denis A. Engemann <[email protected]>\n# Stefan Appelhoff <[email protected]>\n#\n# License: BSD (3-clause)\nimport os.path as op\n\nimport numpy as np\nimport matplotlib.pyplot as plt\n\nimport mne\nfrom mne.datasets import somato\nfrom mne.baseline import rescale\nfrom mne.stats import bootstrap_confidence_interval"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set parameters\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data_path = somato.data_path()\nsubject = '01'\ntask = 'somato'\nraw_fname = op.join(data_path, 'sub-{}'.format(subject), 'meg',\n 'sub-{}_task-{}_meg.fif'.format(subject, task))\n\n# let's explore some frequency bands\niter_freqs = [\n ('Theta', 4, 7),\n ('Alpha', 8, 12),\n ('Beta', 13, 25),\n ('Gamma', 30, 45)\n]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We create average power time courses for each frequency band\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# set epoching parameters\nevent_id, tmin, tmax = 1, -1., 3.\nbaseline = None\n\n# get the header to extract events\nraw = mne.io.read_raw_fif(raw_fname)\nevents = mne.find_events(raw, stim_channel='STI 014')\n\nfrequency_map = list()\n\nfor band, fmin, fmax in iter_freqs:\n # (re)load the data to save memory\n raw = mne.io.read_raw_fif(raw_fname, preload=True)\n raw.pick_types(meg='grad', eog=True) # we just look at gradiometers\n\n # bandpass filter\n raw.filter(fmin, fmax, n_jobs=1, # use more jobs to speed up.\n l_trans_bandwidth=1, # make sure filter params are the same\n h_trans_bandwidth=1) # in each band and skip \"auto\" option.\n\n # epoch\n epochs = mne.Epochs(raw, events, event_id, tmin, tmax, baseline=baseline,\n reject=dict(grad=4000e-13, eog=350e-6),\n preload=True)\n # remove evoked response\n epochs.subtract_evoked()\n\n # get analytic signal (envelope)\n epochs.apply_hilbert(envelope=True)\n frequency_map.append(((band, fmin, fmax), epochs.average()))\n del epochs\ndel raw"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can compute the Global Field Power\nWe can track the emergence of spatial patterns compared to baseline\nfor each frequency band, with a bootstrapped confidence interval.\n\nWe see dominant responses in the Alpha and Beta bands.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Helper function for plotting spread\ndef stat_fun(x):\n \"\"\"Return sum of squares.\"\"\"\n return np.sum(x ** 2, axis=0)\n\n\n# Plot\nfig, axes = plt.subplots(4, 1, figsize=(10, 7), sharex=True, sharey=True)\ncolors = plt.get_cmap('winter_r')(np.linspace(0, 1, 4))\nfor ((freq_name, fmin, fmax), average), color, ax in zip(\n frequency_map, colors, axes.ravel()[::-1]):\n times = average.times * 1e3\n gfp = np.sum(average.data ** 2, axis=0)\n gfp = mne.baseline.rescale(gfp, times, baseline=(None, 0))\n ax.plot(times, gfp, label=freq_name, color=color, linewidth=2.5)\n ax.axhline(0, linestyle='--', color='grey', linewidth=2)\n ci_low, ci_up = bootstrap_confidence_interval(average.data, random_state=0,\n stat_fun=stat_fun)\n ci_low = rescale(ci_low, average.times, baseline=(None, 0))\n ci_up = rescale(ci_up, average.times, baseline=(None, 0))\n ax.fill_between(times, gfp + ci_up, gfp - ci_low, color=color, alpha=0.3)\n ax.grid(True)\n ax.set_ylabel('GFP')\n ax.annotate('%s (%d-%dHz)' % (freq_name, fmin, fmax),\n xy=(0.95, 0.8),\n horizontalalignment='right',\n xycoords='axes fraction')\n ax.set_xlim(-1000, 3000)\n\naxes.ravel()[-1].set_xlabel('Time [ms]')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.8"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | bsd-3-clause |
daviddesancho/mdtraj | examples/WebGL-Viewer.ipynb | 4 | 3145 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Interactive WebGL trajectory widget\n",
"\n",
"Note: this feature requires a 'running' notebook, connected to a live kernel. It will not work with a staticly rendered display. For an introduction to the IPython interactive widget system and its capabilities, see this talk by Brian Granger\n",
"http://player.vimeo.com/video/79832657#t=30m\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's start by just loading up a PDB file from the RCSB"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from __future__ import print_function\n",
"import mdtraj as md\n",
"\n",
"traj = md.load_pdb('http://www.rcsb.org/pdb/files/2M6K.pdb')\n",
"print(traj)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To enable these features, we first need to run `enable_notebook` to initialize\n",
"the required javascript."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from mdtraj.html import TrajectoryView, enable_notebook\n",
"enable_notebook()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The WebGL viewer engine is called iview, and is introduced in the following [paper](http://www.biomedcentral.com/1471-2105/15/56): Li, Hongjian, et al. \"iview: an interactive WebGL visualizer for protein-ligand complex.\" BMC Bioinformatics 15.1 (2014): 56."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Controls:\n",
"# - default mouse to rotate.\n",
"# - ctrl to translate\n",
"# - shift to zoom (or use wheel)\n",
"# - shift+ctrl to change the fog\n",
"# - double click to toggle full screen\n",
"\n",
"widget = TrajectoryView(traj, secondaryStructure='ribbon')\n",
"widget"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can even animate through the trajectory simply by updating the widget's frame attribute"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import time\n",
"for i in range(traj.n_frames):\n",
" widget.frame = i\n",
" time.sleep(0.1)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| lgpl-2.1 |
ngcm/training-public | FEEG6016 Simulation and Modelling/07a-Finite-Elements-Lab-1a-50-lines.ipynb | 1 | 285843 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Finite Elements in 50 lines\n",
"\n",
"Taken from the Matlab code ([see this link](https://www.particleincell.com/2012/matlab-fem/))."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<link href='http://fonts.googleapis.com/css?family=Open+Sans:100,300,400,500,700,800,900,100italic,300italic,400italic,500italic,700italic,800italic,900italic' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Arvo:400,700,400italic' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=PT+Mono' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Shadows+Into+Light' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Nixie+One' rel='stylesheet' type='text/css'>\n",
"<style>\n",
"\n",
"@font-face {\n",
" font-family: \"Computer Modern\";\n",
" src: url('http://mirrors.ctan.org/fonts/cm-unicode/fonts/otf/cmunss.otf');\n",
"}\n",
"\n",
"#notebook_panel { /* main background */\n",
" background: rgb(245,245,245);\n",
"}\n",
"\n",
"div.cell { /* set cell width */\n",
" width: 1000px;\n",
"}\n",
"\n",
"div #notebook { /* centre the content */\n",
" background: #fff; /* white background for content */\n",
" width: 1200px;\n",
" margin: auto;\n",
" padding-left: 0em;\n",
"}\n",
"\n",
"#notebook li { /* More space between bullet points */\n",
"margin-top:0.8em;\n",
"}\n",
"\n",
"/* draw border around running cells */\n",
"div.cell.border-box-sizing.code_cell.running { \n",
" border: 1px solid #111;\n",
"}\n",
"\n",
"/* Put a solid color box around each cell and its output, visually linking them*/\n",
"div.cell.code_cell {\n",
" background-color: rgb(256,256,256); \n",
" border-radius: 0px; \n",
" padding: 0.5em;\n",
" margin-left:1em;\n",
" margin-top: 1em;\n",
"}\n",
"\n",
"div.text_cell_render{\n",
" font-family: 'Open Sans' sans-serif;\n",
" line-height: 140%;\n",
" font-size: 125%;\n",
" font-weight: 400;\n",
" width:900px;\n",
" margin-left:auto;\n",
" margin-right:auto;\n",
"}\n",
"\n",
"\n",
"/* Formatting for header cells */\n",
".text_cell_render h1 {\n",
" font-family: 'Arvo', serif;\n",
" font-style:regular;\n",
" font-weight: 400; \n",
" font-size: 45pt;\n",
" line-height: 100%;\n",
" color: rgb(0,51,102);\n",
" margin-bottom: 0.5em;\n",
" margin-top: 0.5em;\n",
" display: block;\n",
"}\t\n",
".text_cell_render h2 {\n",
" font-family: 'Arvo', serif;\n",
" font-weight: 400;\n",
" font-size: 30pt;\n",
" line-height: 100%;\n",
" color: rgb(0,51,102);\n",
" margin-bottom: 0.1em;\n",
" margin-top: 0.3em;\n",
" display: block;\n",
"}\t\n",
"\n",
".text_cell_render h3 {\n",
" font-family: 'Arvo', serif;\n",
" margin-top:16px;\n",
"\tfont-size: 22pt;\n",
" font-weight: 600;\n",
" margin-bottom: 3px;\n",
" font-style: regular;\n",
" color: rgb(102,102,0);\n",
"}\n",
"\n",
".text_cell_render h4 { /*Use this for captions*/\n",
" font-family: 'Arvo', serif;\n",
" font-size: 14pt;\n",
" text-align: center;\n",
" margin-top: 0em;\n",
" margin-bottom: 2em;\n",
" font-style: regular;\n",
"}\n",
"\n",
".text_cell_render h5 { /*Use this for small titles*/\n",
" font-family: 'Arvo', sans-serif;\n",
" font-weight: 400;\n",
" font-size: 16pt;\n",
" color: rgb(163,0,0);\n",
" font-style: italic;\n",
" margin-bottom: .1em;\n",
" margin-top: 0.8em;\n",
" display: block;\n",
"}\n",
"\n",
".text_cell_render h6 { /*use this for copyright note*/\n",
" font-family: 'PT Mono', sans-serif;\n",
" font-weight: 300;\n",
" font-size: 9pt;\n",
" line-height: 100%;\n",
" color: grey;\n",
" margin-bottom: 1px;\n",
" margin-top: 1px;\n",
"}\n",
"\n",
".CodeMirror{\n",
" font-family: \"PT Mono\";\n",
" font-size: 90%;\n",
"}\n",
"\n",
"</style>\n",
"<script>\n",
" MathJax.Hub.Config({\n",
" TeX: {\n",
" extensions: [\"AMSmath.js\"],\n",
" equationNumbers: { autoNumber: \"AMS\", useLabelIds: true}\n",
" },\n",
" tex2jax: {\n",
" inlineMath: [ ['$','$'], [\"\\\\(\",\"\\\\)\"] ],\n",
" displayMath: [ ['$$','$$'], [\"\\\\[\",\"\\\\]\"] ]\n",
" },\n",
" displayAlign: 'center', // Change this to 'center' to center equations.\n",
" \"HTML-CSS\": {\n",
" styles: {'.MathJax_Display': {\"margin\": 4}}\n",
" }\n",
" });\n",
"</script>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.core.display import HTML\n",
"css_file = 'https://raw.githubusercontent.com/ngcm/training-public/master/ipython_notebook_styles/ngcmstyle.css'\n",
"HTML(url=css_file)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import numpy\n",
"from matplotlib import pyplot\n",
"from mpl_toolkits.mplot3d import Axes3D\n",
"from matplotlib import cm"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Create a square grid\n",
"m = 11; n = 11\n",
"x = numpy.linspace(0, 1, m); y = numpy.linspace(0, 1, n)\n",
"X, Y = numpy.meshgrid(x, y)\n",
"p = numpy.vstack((numpy.ravel(X), numpy.ravel(Y))).T # locations of all nodes\n",
"triangles = numpy.array([[0, 1, m+1], [0, m+1, m]]) # First two triangles\n",
"triangles = numpy.kron(triangles, numpy.ones((m-1, 1), dtype=numpy.int)) + \\\n",
" numpy.kron(numpy.ones(triangles.shape, dtype=numpy.int).T, numpy.arange(m-1)).T # Replicate vertically\n",
"triangles = numpy.kron(triangles, numpy.ones((n-1, 1), dtype=numpy.int)) + \\\n",
" numpy.kron(numpy.ones(triangles.shape, dtype=numpy.int).T, m*numpy.arange(n-1)).T # All triangles\n",
"b = numpy.hstack((numpy.arange(m), numpy.arange(m, m*n, m), \\\n",
" numpy.arange(2*m-1, m*n, m), numpy.arange(m*n-m+1, m*n-1))) # Boundary nodes"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"N = p.shape[0] # Number of nodes\n",
"T = triangles.shape[0] # Number of triangles\n",
"K = numpy.zeros((N, N)) # Should make this sparse\n",
"F = numpy.zeros((N, 1))"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Loop over the triangles; assemble the stiffness matrix and load vector\n",
"for nodes in triangles:\n",
" Pe = numpy.hstack((numpy.ones((3, 1)), p[nodes, :]))\n",
" Area = abs(numpy.linalg.det(Pe)) / 2\n",
" C = numpy.linalg.inv(Pe)\n",
" grad = C[1:3, :]\n",
" Ke = Area * numpy.dot(grad.T, grad)\n",
" Fe = Area / 3\n",
" nodes2 = numpy.outer(numpy.ones((3,1), dtype=numpy.int), nodes)\n",
" K[nodes2, nodes2.T] += Ke\n",
" F[nodes] += Fe"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Set Dirichlet boundary conditions\n",
"K[b, :] = 0; K[:, b] = 0; F[b] = 0\n",
"b2 = numpy.outer(numpy.ones(b.shape, dtype=numpy.int), b)\n",
"K[b2, b2.T] = numpy.eye(len(b))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Solve\n",
"U = numpy.linalg.solve(K, F)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqsAAAHMCAYAAADyAuGOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYVOX1wPHve+/02b6UpXdUUEGxiw0VsGFFwa5YQERN\nNGI3scQWjcYSsST2ghU1dpP4M1Fib9gAQQWlSNs29b7v7487s+yyu2ybmR3lfJ5nnnvnlpnDsDNz\n5ty3KGMMQgghhBBC5COrswMQQgghhBCiOZKsCiGEEEKIvCXJqhBCCCGEyFuSrAohhBBCiLwlyaoQ\nQgghhMhbnhb2y1ABQgghhBAiF1RTG6WyKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHyliSrQgghhBAib0myKoQQQggh8pYkq0IIIYQQIm9JsiqEEEIIIfKWJKtCCCGE\nECJvSbIqhBBCCCHylqezAxC/XsYYEokESqlmj0kmk9i2vdFjxHqO42BZlrxerWSMAZDXq5Xk9Wob\nYwxaa2zb7uxQfjGSySQez8ZTD4/HI3+DogFJVkXWJJNJampqiMVidV+CQgghRHMCgQAlJSWdHYbI\nM5KsiqxSSmGMoaSkBKVUo1/LxhgikQixWIxwOIzP5+ukSH8ZjDFUVlbi8/kIBoOdHU7eS/9gKi4u\n7uxQfhEqKysJBALyPmyFWCxGJBKhqKgIy5IWdRuTSCSoqanB6/USCoUafQ9orQG3oipVVdEU1ULF\nS8phot3SH1CRSISCggKqq6s7OyQhhBB5KBwOU1RU1NlhiM7X5C8VqayKnCooKKj75dzUr+va2lqS\nyWTdcaJpyWSSqqoqCgoK8Hq9nR1OXquursbj8RAIBDo7lLwWj8eJRqOSMLTAcRwqKyvlvdeC9FUN\ny7IIh8ONqs9STRVtIZVVkTWJRILq6mqi0WhdZbWgoABAqqxCCLGJk2qqaIJUVkVuGWOIxWJ16xsq\nKCigpqZGOl8JIcQmJBgMUlxcLNVU0WqSrIqsUUrh8/nqOiI0xRhDYWFhk5eB0sluJBIhGAzi9/vl\nw60J6aYThYWF8vo0Y926dYRCIbls24xkMkl1dbUkEM0wxlBdXY1SinA4LK/RBowxxONxamtrCQQC\nBAKBBq+RMQZjDJZl4fV6pUOaaDNpBiCypn4HK7/fTywWw+v14vP5qKmpadQ0QKqsQgjx6yWX/UUr\nSDMA0Xm8Xm/deKu1tbVNHpOuslZXV0vSKoQQvwKBQIDi4mKppooOkWRV5FQgECCZTBKNRolGo432\npy8XNTcua/pypcfjIRQKyQdgPVprKisr65pMiPWMMaxdu5aioiKZbWgDxhjWrFlDaWmpXN7eQDwe\np6amRv5uNpAuOiQSCcLhcIPmNenPcJCe/iJzJFkVOZcekir9AZZIJBoNU5VOSpsTj8eJx+PZC/IX\nrKamhpqams4OIy+tW7eus0PIW2vWrOnsEPKW/N00r6qqqsnt4XBYJi4RGSPJqug0fr+fRCJBIpEg\nmUw2eYyMGCCEEL8c0tNfZIMkq6LTBYNBEokEjuM0WS1Nt2Vt6jKc1ppIJILjOITDYblUlxKPx4lE\nIhQWFkpTiZR0Mwn5Il0vPX1vQUGBvHdSjDFUVVXh8/lkIokUrTU1NTUopZptfiU9/UU2SbIqOl16\niKt4PF5XYXUcp8Ex9Yexak5zl6M2ZZWVlZ0dQt6RS7qNyXunseba1W/qmvtMCYfD0lZeZI0kqyKv\nBIPBuuGuoOnJBIqLixtti8ViaK2ljVQ9tbW1eDwefD5fZ4eSN6qqqgiFQlJFTElXVpt6T22q0h1A\n00PqiZY/X8eNG8dbb72V46jEpkTq9SKvpC/PhkIhgGaHuRJCCCHEpkGSVZGX0u2e0peV0mO0CiGE\nEGLTIs0ARF5LD2mVbrMKTVdb99hjH5YuXUEoFM5pfBuKRKqorolQVlqObXfu1J4rVi0jFAgSDnVu\nh6KamtXUJhKUFpTi8XRuk4QVq38kHAgRCnbua1JVtYaYTlASLun012T5qh8pCHb+a1JZuYqEdigp\nLOnU944xhhUrf6SosJBAoHOnVl23bi2OE0uNgdu5taWhQwfz5JOPNrmve/fuOY5GbGokWRW/CIFA\noG5s1Q3HZAVYs6aadeuqqKw0GHMuUJH7IAG4BTyrWbFyGZgRwHVAZ7SPdEDtRXWoL1U/L4HkpcD4\nTogD4AToFmPl6gUoBmP0X0GV5j4Mo8GMoKrLICp//haSU8BzSu7jAEicAeU/snLtUjA9Qf8FVL/O\niYVtqfL0oHL1MogfDczopDh+C8HPWLFqGZh+oK8BunVCHAYYw9oqjapcjdEnAKM6IQ6AOcDzLFu2\nEtgGGNlJcdRSXf1cg8/e0tKG7+Hmknq5IiYyQZJV8YuR7hTTVIchvz8A3ADcB1yGUtMx5mCamWY4\ni2IQOhFCE1FrjobkERjnVmCfHMfxCXgKMOM+Ri28E/PxBSjzNMZ5FuiS00gsfxw9ahoMOQD18hmY\nxftBYgaoKyGXw9yY1aAszG8+hI9nw7MzsJw5aOfvYO+euzgAKEBtcQBmr5lYL12I/ugI0GPBPAhW\njjv2WH7MpBdh+ceoV85GJZ5HR28CjsxtHIzALnFwtr8X65Pz0EuOAecA4GYgt0NIKbsIU/4cJN6C\ntb9HqTcw+gqga07jgEHYdk8c51TgGizrB7SeBOT6CpI7WkT9z976E4+01MHq5Zdf5pxzzkFrzZQp\nU5g5c2ajY8466yxeeuklwuEw9913HyNHdlZiLvKRtFkVvyI+jLkRuBS4G8uaDizLaQS2JwJ2T/Bu\njun6PhRdDOpklJoI5LKz2EeocG+wbMyQ6XDgN6ieXcEzELgqh3GAsiuhsBcU90Uf9QJMfApV9BCW\ntx/o13IYyffgC4FSsM1RcMl3sMfxYPZD6dGgf8xhLClFFeij/g5n/w9rwDrw9gLnd6B1zkJQlg9i\nlbDF4ZgZizB7zgT/qVj+YcB7OYsDNsPU/ADhvuhdZsPeb6LKF6O8w4EbcxgHWKoQnKWYgvOgxwJU\naEtQxwLXA7n7v4FyIALsDjwGDEKp24F3cxhDx2itOfPMM3nllVeYN28ejz76KF999VWDY1566SUW\nLlzI/PnzmTVrFlOnTu2kaEW+kmRV/ArtjjFPYUwQOA6lnsW9tJd9hqibrIJbxSs4CyrmoQIOytoa\neDInccAXWIWD1t8N9kCPfgZ2nQ3B27G8g4GPcxKJ1tVQ1Gv9hoH7YqbPx4w+E+xDUWo30CtyEMmP\nKH/h+rveIHrfy+HC+ajhfUEPhfhJoBM5iGUDPbZET/snnPAkqvxZlK8H6Hty8tRuspoae9b2Yraf\nAWd9D9sdBJ49UZ7RwPc5iGRrdKTej8vy7TD7/g+z032o0INYvq2A53IQBxhTDMlF7h27Al36CHR9\nDeVbgLIPBV7NSRzQBa3TY70Wo/VVGHMJ8BaWdS+Q/9Mqv/vuuwwZMoR+/frh9XqZNGkSc+bMaXDM\nnDlzOP744wHYcccdWbduHcuXL++McEWekmRV/EoFOqXKakwt2D0abvT0Q5f/C1NyE6jzUNb+wOos\nR7IAXTC08eae4+HAhTDkMLB3BTUZaHqq20wxyRoo7N1wo+3D7DITzvgaNbgb2IPAOTfLFcUfIVDU\neHNxT/Qxj8AZ/8Kq+ASlekDi1izGsRGb7YuZ+RXm4GsgMBPLMxj0/2X1KRV+iK5tuDFQjB5zHUz/\nGmuL/uDZAtQRQHUWI9kKklUNfywoBb0Pxhy0ELPVBeA9G8s7Gvg0i3GAdnpimfkNN/p3xnT7DFP8\nR7BuwbJPAr7LahxQjjEbToTyy6qyLl26lD59+tTd7927N0uXLt3oMb169Wp0jNi0SbIqfuVyW2U1\nOtI4WQX3Szd8IvT4BhXshrJGAXdnLQ7btxJTMLjpnZ4QesT1MO5dVOk3KG8PYHaWIqkEJw7hZtr6\nFfVCH/EUTH4BVfIslrcP6BeyE4pZjgqWNL+/7/bo33yAOeI28F+JxSBwspsoNsmyYYeT4ZLvYY9j\nwd4Py9oR9KKsPJ0x/vWV1Q0V9cY55CE4+R2sfj+DrxdwLtm5FO4HOwSRnxrvsryYoTNgwncwaDzY\n+6cqnCuzEAfAUFTym8ablQXh06DHIgjvDepU4DIgWzNdlQDxJh7/l1llFaK9JFkVm4BcVVlrwcTB\n2kgnDLsCXfYcpvQ+sK7DsvcEMl9BMFYlhPtv/KDi4Zix72G2uRo8p2B5dgIyfTn+YwiWul/yG9Nv\nD8y0rzB7nAeeyVjWTlloQ/ozKtTCKARKwTaT4NJ67VmdTmrP6g+jx/4eLloII4eBvSWYQ0FnuLrp\nBJtPVtO6b40+7t9ue+PyF1D+CuCvmY0DsOwwRDbyfvCVoLe5Cfb/AtWrHDyjcEcviGc4kq3QiY38\nOLBK0cV/hW5zsQI1KOsIstPExwYKgIXN7M//KmuvXr34/vv1zUiWLFlCr169Gh3zww8/bPQYsWmT\nZFVsQrJdZV0IVlHLiRlA6FDosRBCI0DtgttxI3O0U9VysgpurINOg4MWQK++4BmMWynKlE+xCnu2\n7lDbi9nxNzB9AQwdCPZQcKZnsGnASgiVte7Quvas36CG9wEzFOIng85uk4kmZbkTlk6EGjcDaM7A\nfTDTvsSM/xOELsfyDwBeykgcAEoVQG0rfrwV9Efv+jTs9QZW2Zco7zDglozFAaMwiR+hpWGXfFuh\nu7yDKZ0F1kNY9tHAFxmMAyyrFFi8kSPyu8q6/fbbs2DBAr777jvi8TiPPfYYEyZMaHDMhAkTeOCB\nBwCYO3cuJSUlMnaraECSVbGJyWaV9TssTxs+YK1SdMmD0OUZsO/HsncE5rd4WsvikKyGcBvG7Qx0\nc3tg7/YMKvR3LN8AMtMT/BtUcd+2nVLQHX3oI3DMq6jyN1DenqCfykAsa9Ch8radUtwLfeyjMO2f\nWBUfoVQFJG7LQCztkLVOWCWoaBvaUCsLtj4ezvoOM/p08B2J5RsJzOtwJCZZDLVLWn9Clx3RYz/A\n7Hg3BO/B8o0AXuxwHNDH/XfqVS0fqhSEjoQei6FgMqizUeo8MtW+V6muQGtek/ysstq2zW233cbY\nsWMZPnw4kyZNYosttmDWrFncddddAOy///4MGDCAwYMHc/rpp3PHHXd0ctQi30iyKjZR2aiyfo/y\ntOPSVWAfqFgA4XGgxgAX0rE2gZ+BpxDsdoxNWbE35sD5mKHHgL0HqMPp2CXWRZiS/u07tc8umNPn\nwZhLwXMSlrUd6A50aFHrMG1NVtP67oD+zYep9qxXpNqz/qf9sXREXSesa+t1wnqzAw9YhhVpRVK2\nIW8Qs8sFMGMRjNgVPNuj7H2Bn9sdiU52R0XaOPKAUtDncDhoEWb4OeA5A8u7Ox2tcCqrEJzFrT/B\nCqOLroWKz1DBIrAmApn4MdEdaG0zlPysso4fP56vv/6a+fPnc8EFFwBw+umnc9ppp9Udc9ttt7Fg\nwQI++eQTtt12284KVeQpSVbFJizTVdZlYLexiphmhdHFt0HXN1Ce17DsbYGP2hnHx1jhPi0f1hw7\ngNnqKhj/IVb5UreyyUPteijl+Qld1L/9sVg2ZrvpMONbGLYl2MPAmdKuy/GWtwYCxe2PJd2e9ZLF\nsPtxYMahnN1AN9EhKNssG3Y4qV4nrP070AmrHNqTrKaFuqDH3w6nf4YaHAZvf+AE2vcjpz9WbTs7\nktk+zObnwoTFMHAvsMem2pK2b+QNSxVCcnHbT/QMQpe/AmWzUZ43sOyJdKTK6TjdafsPgPyssgrR\nXpKsCpGxKusqnI5OmenfCVPxJRQcD2oCMI22V1m/QBUNavmwlhRtjt7nHcyoG8F7JpZnO9raGczy\npSYE6KhQF/RB98Hx/0Z1fS/VNODhNj2EsqOwsdEAWssXcjs+XfA1anhPMEMg3r4EusMy0gmrGya6\npuOxlA1CH/ksHPcGqse8VCesK2jb3+9QTHUHh4Pyl6G3vRX2+xTVMwSebYDf0tYh2rSuN9ZqewTH\nYyoWYArPBnUpyjoDaM+PgnJsuz1NCvKzyipEe0iyKgSQiSqr7aldPyFARyg/uugq6PYOyjcPy94S\naMsQSt+iCzbreBzgVhMHnAAHLYQ+W4Bnc+B8WpuAGLPBhAAd1XN7zGkfY/a9GrzTsawRoBe07lwV\n61hldUMlvdHHPp5qz/pBqj1rJ7W1S3fCOuddrIGVqU5Y57WuE5bqBpEWRgNoi147Yqa8hzn476ji\ne7ECvYHW/rDYEl2boZEXCgejd3sB9nwZVfphqhPWrFafbnQvLN3BNuTKhymc6Q5ZF9oM1NG4s3G1\nJYHvQsdmv5Mqq/jlk2RViAY6UmVtZozV9vJtjen2MaboXFDHuDdiLZ5m+37GhDNQWa3PX47e6UHY\n4x+o8BOpDlj/bfE07VRnprJan7Jgm1PdtpJb7Qz2CHCOAb3xy86GDCeraX13QP/mI8zht4L/ciwG\nd1571orh6KlvwIlPocrnpDph3dvCST0xLQ1d1VZKwWYHY6YvQI+5BPxnYvk3p+W/mW0gtqrlXvht\n0XVXzLhPMNvfBoFbUp3BXm/FiZs1PdZqe9g90aWzoesrKO8XKPsw4I1WntwFrTecGKCtpMoqftkk\nWRWikfZVWbWJZKayWp/yYAp+B90/wfKvQVlbAc9v9BRjrWvdsFXt0W13zAFfw+ZTUm0CD6L5qk8S\nErXQ2qGr2ipYit7/Tjjxv6iKr1JNA5pPzIyOZ6YZQFOUgm0nwyXfwW7HpNqz7g46+7OmNWnoPvU6\nYZ3fQiesXph4lmamsr0w6gw4+3vMDkeAdyzKuzPQ3OX1clAeiHegDW1TlIJ+k2DCYsyw6eA5Gcu7\nFxsffaOFsVbbw78rpvs8TNEVoG7Esk8GfmjhpHKMydSkA1JlFb9MkqwK0ay2VVmbnb0qE7yD0V3e\nxpRcDepMlDoYqGzyUO1UQUH/7MQBYPvQwy+D/T5BdVmH8vam6V7PX4I3CJ52jErQFhUjMVPex4y/\nCXy/w7KHg27cE9zoeHYqq/X5Quhxf3Dbsw6rAD0Y4qd0TnvWVnfC6uv+qMgmfyFmz6tg+nzUsKHg\n2RLUITT1N6w84daNtdoedgCzxUy3E1b/ncHeC2VNApoaZ3YUJrkss1VeAGVDwTR3FqzQnqCmAH+g\n+Q5ppbhXVDKVsEqVVfzySLIqxEa1tsoaBRMFq1v2QlEWhE+Hiq9QwSDKGgk8sMFBMUjWQKidoxK0\nReFg9Jg3Mdvd5iaJ3pE0nCv9E1Q4RwN7K5Ua+3MxjNwbrO1BTwRd7ws+GYNglpPVtJLe6ONmw7Q3\nUN3f69z2rC11wrJK3IQsma0pQ+sp7ImecD9MeRdrQDX4egNnUb/zk2WF2zbWanv4u6C3uxPGf4Sq\nsMAzEriAhm1Je7qJpc7SlK52GbpkFnR7O3XV5HCgqfGEPUAIaOOQXi2SKqv45ZBkVYhWaanK+m1q\n9io7+6F4eqHLXknNmvN7LHsf1s+R/il4i8H2Zz8OcJPE/kfDQd9Cv1FgDwfOxv3S/xKruANDaLWH\nvwg99i9uMtRzSappwO1uZdOJg78ot/H02xHz248xh//Fbc9qhoDTclvfrGjQCWtdw05Yth+iGW63\nujHdhqOPeR2OmoPq8hrK34O6Gah00canXM2kos3Qe7wMuz+HKv4PyrsF8Le63coqaN/wVW3hG4Hu\n+i6m5Haw7seyjwW+bnCIUqXAt1l4cqmyil8GT2cHIMQvR7rK+n/AdVjWq2h9GVABLEbZ3TI6eetG\nKQWho8C/N1ROg5rtwfwGCGCF+3RoSoF28ZWit78X+k9BzT0eFX8KHe8HJUNzHYmr23D0iW/DvMfh\npeng3AjGhlg1YMBot5poDJBe16l99da1cZeYVM/6essG69Q7Rzd8DoCyQXDcbPQ7d8Bne4L2YVZ7\nYdF/U9PzKvdmpeoHSq3fvuF63XEbrNc/zlJN7LfcY8Jd0cfOhoX/hufPhdoHIKGhehkESsHyrI8j\n2/rvhZk6Dz5/DF77LVbyJpyYDyIttePMsO57Yvb7HBY/Ah/9Bsvcjo7/GUsV4jiLgR2y+/xKQXgy\nBA+C6iug8kwUIzHmcqAAy+qK42S6slrf7sAI4AaUuh1j9iTr/2Yh2kCSVSHabHeM2QG4GLfKOh1j\nlmN5e+HkKgStgWowMXT4KrC3h3WXAwrNZrD4Ybd3vBN3l41uiXrLBJhE43WTdCuSJgkmgVIapZIo\n5aDQgIPCgbp17a6Hkzj2Oiz1Hmr+BwRmveB+GZtUgpdKEk16HTbYRt2xxqy/7x6aOq7J7WC0Wb8t\n/dgKMKuxvQp9WSlGgWVZ7vbUAekcsMH99LnpHelcse5Oai21cf05jfeltysFlPqIVUbxLJhD/PNn\n8ZcG3eNMOu2tW6n370utp3bXvWbpu6beOeC+Put3Nmx2WW9ferPHDzy4LYlovZ85qX+HUu4/XFmq\nye0olXqZUv9upVDU25d+DdOvhbI22JZahg1O7Gcsr4Oz4Hqs5fejLE8qAV9/M9ju0ligbIxxbxjb\n7ZylPG7CrTxgedcvLS8oL1i+1P36y3q34ZeilzwJKw7HSfqg5nG3eY8KgyoAq9C9ikJB5pN6qwBd\ndD0ET0OtmwqxIzH6CNxZrLLdWc+tsro/xq/Bsj5D60lAOMvPK0TLJFkVok00bqeQtRhzHPAfjLkN\nSOLE+8Oa88FEcNuwRtx2rCa2/mYlUHYCZSVRKgnKAdJLB2PqLY0GnVrX7nqDm2WD7XFvHh+UFEHl\nKqzIPPS7xxMa0gfl8aA8tnvz2u59b/q+Z/19b8MlXj/KG06t1zvHY0PduXaTN1LLH2fciBWpIV67\nln6Td2Tw0aNQtuUmPZZCWe56etv67Q23udstLHuD8+odR71jGzyeUiil+P7Fz3nnmHvot3mQ776J\nMfr68YyY0nlTOj5x4MOURpbx0+IEtVGLPe6ZyID9MjQ2bjvc1+tq+gwL8fXbq+h2wCi2e2Cq+3+p\nDUZrjKPdHwLaYFLb0KZue9399M3RoBuf425ffxz1Hjt9f9G9/2bZsx9gqpdhRo4gMONklNaQTGKS\nDiSTkHQwjrusu59MQiIJiQQqsX6dRAKTSLidyOq2JzHJJCaRhGQCEqnzk6ntZQ4U9cNZvRZT+yKs\nfAYCJet/0DlJMI6bSKcTamWDZaOUXXdfKRuwUcrC/bq1UzcPxnjA2GjtBe0F5U/dAu5Yy1Z/8EQh\n/jccJwAEgeeAIqAEKE7dSshsi76mqqxbZPDxhWg7SVbFr5DGHU5pHbAmtazCTTKrgOrU/lrc9llR\nlJXEspK4HT2SGJK4SWMCY9LVxSSQAOzUF0oAZYVQ1gB0fBE430Lyduxt9wZ/EHwBjK8c/AGML4jx\nBcDrx3j9GJ/fTTC9fkiv+/zufa8fvL6m1+vO89Uv89XxnL4NPbcN8PNb30AsRv/HLyO89eDsv+RN\nWPnbWzjqulEoBQ9MfY81/1vEXs+dTmG/8pzHEl8TobiLl9vf3pzXHl7FLTNe5JNb3mHCnKMpGVCa\n83gABm0d4saXe/HELSu4d+IDdN2mD/s9cyyhLgU5j8XyWOz3m4Ecd/OWzDrpY17tfQabX3csA6bs\nmfNYKr9YSuzLHxh9+6H88/jHiJ5/Ob4H7sC3x845jyX26LPUnnclBhtlQuijXoTyIe5OY8BJgBNz\nO+85cXBimGbW2XC90b4oVjICySgqGYVkNSS7QHIczqqFsG4pODeiVNfUUFYx3M+jJO5XuZsMK+VB\nqfS6t26fMV43MSaI22ErCBTgVk4LU7ci0gmw1jOBD4FrUeqj9dV6ITqBJKviV+HHH38ANcOtdhAH\nLFC+uoQSFUZZYbfDhFUIViFG9cBQjKEIo8I4VuoynwqDFV5/2a/B/XCDTlTpFo1q9Q6YUX1Qn7yJ\nqV6DPvtWqOjg1KvtYMcr6bHfDmx/78l8cdmzfLXzNMom7UO/u3/nXvrOIR2NUlDuZ9g+FQwf24PZ\n537MnOFXMvjU0exw42E5jSe+tpZA2EYpxdhju7DzgSXMOn8p9215K5tNHsG4uw7K+esD4PEqJp/X\nnX0ml/LnM5fy4IBrGX7maHa5emxO47G8NrEahz7Di7jyf7vxn4eWcP9Z9/PdzS8x6ulzKBySpSHZ\nmhDqU07NhnbdAAAgAElEQVR0dS09dhnApC/P55M//Zv3DzyG+O67EHriLqxQKGexqK7lKNvGvPUx\n6qpL4e6RMOpM2Pc698eix+fe/IUZeb5m25p/8hDqpQswcQdFCca5GTfRBHBwE1f3io4xtalkNpra\nFqnbBxGUqq27udMn12KMe4wxEYyJ4X6GxnE/3WyMiVNTk4POo0I0Q5JV8atQVtaNZStWonybYcqe\nAs+Aun1mg2U2WHYEZ4fxmEsehksOgROHo6bdgJkwtckKaLaoaA2+LgXYAR9bXX8kvSfvyP+OvpPP\n+xxB/8cup2i3ETmLxYkmCJf5AAiV+Djx3h0YPWUA9xz3Dk8/9RGjH51Cxa4DcxJLfG2EYGh98ldY\n4uG8u/pxwKnlXHPC19zV8yvGzDqYoQdvnpN4NtS1l48/PjOA99+o5JqT5/LgQx8w5oFJ9NkrwzOR\nNcPy2cRq3RbXSil2O64P2x7Unccu+Ip/j7yAHkfszLb3noLlyf5XRrBfF2Lr3BmbbK/NthfuzaCj\nRvLvKbNZ2WcbPNdcSvC0Y7MeB4DVpQwTjaJCIcwfb0QdfDicfiJq/tMNq6zZFijGsr04FZ/Dmsmo\n6GSMvhIYidusIJS6tayuX2GrJHET3Z8IhX7XjsCFyAwZukr8KgQCIdCPQqIIlo2AmocyP5j3xlhR\nCBe7l/xveBkueRjuvRTrrN1h2Xctn58hOhbF33X98Eyl2/Rj7GdXMfTMvZg//jwWHHYJOr7xaUkz\nJRlbn6ymDd6lK1d9eQB7ndqf18bewusTZpGMZj+eeGWUQLhxZWiL7Qv4+2fDOeGibrx87Gwe2fUe\nalZkaTanVthu7yIemz+MidNKeOHAv/HMmLuJrs3ygP24ldV4bcPugeESH1Pu3Jrfv7Ub5uPPeLXn\nGfzw+DtZjyXcvwuJ6niDy87FA8uZ8M+p7DnrMJyLrqBm5BiSi7L/vlJd3WS17v6Ou8DbH6MO2Nut\nsr42M+sxAOAvdiueVgm67EUovgTU+cCdWX5iD27zgLJOufIgRJr89YlfkQBGPw3mBtTaM7FWHwzO\nzzl5ZmNiUFBvwPnRB2OeWIIJhN0q65y/5iR51rEY/q4NL0laHpvNLzyQsR9dgVqylM96Hc7qOdmf\nuz4ZdQiXNx7v1eOzOejS4fz+k/3xrV7OE70u4pv752Y1lkRllFBh05cxbVtx+FndeXj+1gzsEeXe\nQX/mzYtbO2975nl9Fsdf1J2HvxxOr9Aa7u97DXP/0Jq57NtP+T3EapqeZWvAtiVc89GeHH3VUD47\nbRZvjrqY2u+z977ylRaAgmRtwx8xSikGHzmSY7+9iEE7lVMzYi+qZ1yC1tkbqM3qUoaJRBs8R12V\n9bFnUQsewrpjCKza2LStGRAodmdgA1AKU/Bb6PoG2K9g2afjVj+F+PWSZFX8Ck3E6A8h9iMsGwKR\n57P/lCbuVlbry3WVVWucSBx/Mx10CodWMGbuJQz/wyEsPvYKvt77NySrs1O1S1ZWox1NoKD5y8bd\nBxcy8629mXzzNrx/9uM8v9211PzY1LSXHZeoihIs2PjHXXmFjyueHMjVzw7m2wff5e7+N7Lkv9kc\n23LjKvr6uP6FgVw5uz8L7nqLB/pfw4//XZyV57L83rpmAE3utxRjTuvPzQv3ZdiW8M9h5/HRtL9l\nLVH0BLxEVzf9t+kvCbLHXUcw4fWpBF/9B5H+2xL/V3YmWlB+P/i8sLTxuK85rbL6izHOBlcg/DtB\n96/A1wNlHQV8lr3nF6KTSbIqfqVK0M6roGfCqmOw1h4HuvE85JlinCaS1bRcVVnXLEfZCk+o+dmr\nlGUx+IwxjP/yGoJWnM/6HMGKv72Y8VBii5fhL/A2HGe0qXiUYpfjBnDtwgkM2tzHM5v9gfcufC7j\n8SRq4oQKW/dxN2rvYh6evxUHn1TMk2Pv46n9HyJeHct4TK210/hiHl84nENOLGTOvnfz7Li/EavM\n7NSonrCXWFXLowQXdfEz7f5tuPj1XYj+6z1e73UGPz73YUZjATdZja3eeLWwYqd+HPXF79hmxo5E\nJhxH9X5Ho6sz34TDKi6CRU3PHpWzKmug2B05YEN2Gbr8FSg+H9S5wL2Zf24h8oAkq+JX7jQw70Dt\nh26VNfrvrDyLceINmwFsKBdV1iXz8Ra1rpNFqHcZu716LqPuOI6lv/0LX+5wOvEVazIWSnzxckJF\nvpYPTCko93PKQztx1vO7s+Th//JU/0tZ+d7ijMWTrI4RbGWyCuDzW5x4eU/u+2xLCqMruavPn3j/\nluw2VdgYf8Di5N9X8MDnw+iqV3B/36t5//o3M/b4nrCPSCuS1bQhO5Vxw7wxHHbhQD465i+8tcvl\nRJdlripu+73EmqmsNjjOa7PNzDFMmvc7uiZ/oqbftkTuuD9jcQDYZaXw3aKNHpP1Kqu/KDXBRxNN\nNZSFKZgJXV8F6zks+wzcnv9C/HpIsio2AT3QzlvgnAg/H4i17kzQGW7jlYg1X1mtL5tV1qUL8Ze3\nfoxOpRR9J+/E/guup7R/MZ8PnsyP1z+akVDiS1YQLmu+wtuczffszh/nH8hux/Xm5T1v5p9H3EMy\n3nRbyrZwauMEC9o+KkPPgQH+/MZQZt7Tj/evfJ2/b/4XVs5b3uF42qvXQD9/fm0wlz3Yj3k3vcFD\ng69j2Xsdn5rUV+AjWt22+dcsWzH+rIH8ef4+DOod4/Uh5/Dp7x7JSNMAO+Aluqr1c9QX9S/joNdP\nZ6+7j8C5/GpqRuxFcuHiDscBYHXrAktafo2zWmW1bLB9oH9q/hj/rlDxJfhKUfYk4MvMPLcQeUCS\nVbEJmQnmX1DzImr5FhB/PzMPq2vcGaYCrRz/MVtV1hXfE6g3EkBr+bsUstPsaez82FRW3vAwXww/\ngeiijXwptkJ86SoKmuhc1Rpev80hV27FZR+Mg++X8GSvC1n4+AcdikfFk02OBtCqc5Vij8PLeGzR\nCHYf7+fhHWbx/DFPopM5m1y3kdEHlfDEt1uy38QQz+x5J88ddB/x2vaPquAt9BOrbt+PgpKKAGfN\n3o7zX9iJtU+9yRt9Z7D89Y61n7RC/mbbrDZHKcWgI0Zw7LcXMXiXrtRsM4bqMy7ocPJs9egKy1r/\nfshaldUXBmfpxo+xu6LL/4kqPAvU2UBmq8xCdBZJVsUmZhDaeR+THAsr9kBVXgom0bGHTP7gzljV\n1vFUM11lXbGEQEUrqrvN6LH/CPb/9noqRg/gi61O4Pvz/9rux0osW0Vht0C7zwfosXkxF83dl4nX\nbM3cUx/iHzvdQO2K9rU7NrEEgVDHPu5ChTYzbu7DX98ZRuLLxdzZ43q+eLTzOrUEQhanX9OD+z7e\ngqLKn7i/11V8dEv7Ohr5iwJEqjpWwR62Rxdu+npvDjyrD+8d8if+s9dVxFe3rw2pFfa3qhlAU/zF\nQXafdTgH/3MawX+9Sm3fbYi//n/teiwAVdENVrStmp6NKqvyF4DzYysOtNCFl0KXf4D1JMqagTtp\ngBC/XJKsik3UtWBeQFX/DbViJCS+aP9DOUsh2M4pMjesss7oQJV19TICPdqfrAJ4C4NsO+sEdnv5\nXCoff43PBx5FzacL2vw4iZVrKerW+jarzbEsxW6nDOKaBQfRpw88PfhyPvxD2zuEmUQSfweT1bRB\nW4e46/0tmPrHnrwx9Vke2u5OKpesy8hjt0efIQFu/fdgLrynDx9f9TIPD72BlZ+2rTLuKw40O3RV\nW3i8FgedP5gbv9qH3oWVvNZ/BvN+/1TbH6c0THRl65sBNKX7Dn2ZNO88Rv12FyKHnkj12Enoqqq2\nP1BFV6y1q9sVQyarrMpfDM6y1p8Q2BMqvkT5QqlmAd+0+7mF6GySrIpN2Ai08wkmPhyWb4+qvgFM\nOy4Z6p9QoQ5Ot5iusoYK2l1ltSpX4qtoezOApnQdPZT9vr6GfhNH8dXO01h08rVtupyqV1dS0K19\nzQCaUtQtwNQndmX6U6P5dta/eHrw5az6ZEmrzzeJJMFw5j7uLEtx4KldeXTh1gzfwuHvm/+F189+\nKatjfm6MUoo9Dy/liUVbss8EP0/ufBv/OOzBVk+44C/2b3ToqrYq7x3kvOd24JwntmPFvS/zev8Z\n/Pzf1idL/i4FRFd0LFkFd4zhkeftyeQvfkc3tZKafqOI3Pq3Nj2GKi/DirQ/lkxVWVWwBPSKtp1k\nd0d3eRNVOBXUmcAjbX5eIfKBJKtiE2cBd4J5BCpvQK3cCZIb7/nbiLMctbGRAFrLH8Bc/1K7q6ye\n2NpGEwJ0hB3wsdV1Exnz34uJzf2Ez/scwbp/f9Sqc63qmkazV2XC8H17cO3Cg9jpsApe3OUG3jzm\nPnSy5YqgzmBltb6SLl4ufnAAf3plKMte/IS7+9zIotcWZvx5WitUYDP9Tz259/3N8f30A/f1vJpP\nZ/2vxfP8pcGMVFY3NGJcd25esA/7nlTBO2Ov5u3x15GsbrmneqCihMjKzA1DVdivjANfPZW9/jYR\nfeV11Gy1B8n5rXufW13LobbjiXOHq6zBUnBWtuOJbXThFdDlObAewbLOAXIzi50QmSLJqhAA7IZx\nPoV4GSzbCmrubn1l01mBKijNXCjtrLJa8RoCGUxW00pH9mPsp1ey2Vl7s+CA81lw6MUtTtmqaiNZ\nSVYBfEEPR1w/govnjiP+xbc80etiFj/z8UbP0Qnd7g5WrbHVroU88MWWTD6nnOcOfZjH9/o70bWd\nN6tQ/y2C3Pn2EM69vRfvXfgCjwy/kVVfNN/u0l8aJBbJfLIKboe5wy/fjBs+H0MXZwWv9j6Dr294\nYaPnBHqWEPm54wlifUopBh22Ncd+exFD9qigZtu9qZ56fovV8A2nXO1QDB2psgbLwLSvOQIAgb2h\n4guM18ayJwGd96NKiLaSZFWIOj6MeQTMX1FrL8BatS84rWj7Z1ZBUVlmQ2lHldXEavF1yXyyCu7l\n1M1m7s/Yj69A/fiTO2Xrs281e7yORts1dFVb9N6qhEs/GMchlw/jP8ffx4u73US0mQ492nE63MGq\nJR6vxaTfVfDgl1vRI1zF3f1u5J0/tr9jT0cppdh3chlPLt6S3cfYzN7+L7w8+dEmhwILloVIRLM7\nukG3AWEuem1nznhgG77/0zO8Mfgc1ny4uMljg73L2jwaQGv5igLsdsdhHPzvaYTeesPtgPVK82PW\nWl3K0BlKVtMaV1kvaPEcHSgDp4NjIds9MF3/AwUngToDmN2xxxMiRyRZFVllsjFTU9YdgNEfYWIR\n+GlzqG3hA12vxmQ6WU1rQ5VVR2MZbQbQlMIhFYx552K2vOIQFh93JV+PaXrKVh2Lt3voqrawLMVe\nZwzhj98cREVZgqcGXMYn17/W6DgnobPSDKAp3fr4ufaFwVz+6EA+v/Ut7h10Mz+938KQQ1kULrI5\n59be3DV3c8z8b7m/51XMu7/hsG2BLiES0dy0t91uQg/+smhfdj+8jP+Mvpy5h9zUqG1tsF8XYmuz\nk6ymdd++L0d9di7bnbsrkYknUbPPRHRl49EmVNdyTCTzg+w3rLI+2GKV1QTLQWVgFj7lQRddC+VP\ngnU/yjoXyE5VXYhMkWRVZI0xhljMHTIl3sJl4/xTgNHPg7kSteZUrNWHg9PMJTi9Fp2tZBVaXWV1\nonH8Waqs1qcsi0HT3ClbQ57UlK33/qPBMcloMmvNAJpS0iPImXN247RHdubrG1/hmc3+wJov11fF\nnaTOaAer1thp/xIeXbg14yaGeXz3e3nm0EdJRjs4TFoHDNoqyD3vDeWsG3vwzjnP8ujWf2bNfLcN\nZLA8RDKeu85h/pCHydcN45qP9qTg5+95rec0Ft6x/kdGwcBuJKqyP9yS5bEZce4eTP7yfLr71lLd\nfzsit9zT4BhVVAjaQa/N3AxdDR6/tVVWfzGWncEEPjgeun8O3kSqWUCGZ9QTIoMkWRVZo5TC73er\na+l2YZFIhGQrOsTkj2Mx+n2IfutO1xp5udERylMFmWyz2pyNVVmjtehEEl9pKycmyIBQ7zJGv3Iu\no+48nqXn3saX26+fsjWR42Q1bcQBvbju2wmM2q8LL2x3HW+d/BBaa5ykyVlltb5AyOa0a3txz0fD\n8S3/iVm9buDjezo2wUFHKKXY74Rynli0JTvtDI+NvJlXT3gCO2BjtCGZyO1oBj03K+Tyt3bllDu3\nZsGlj/KvYeexbt4SfGUFGAPJSG6S+8I+pRzw8insfd+R6D/eQM3w3Ul+7bbpVEqhCgtgUfbaeLaq\nyhooRqkMV3g9vTFd50LB0aBOA57J7OMLkSGezg5A/Lqp1ED5gUCA6upqPB5PXZU1XXXNf+Vo5w3g\nNlg1EavgSHTRLWC5Y6tadhSnNVOtZkK6yvqfOXD9FKzXHkFf8hBUr8NTEEBZuU3IlFL0PWpHuu89\njI/OeIjPB0+m2/lHo5OaYJE3p7Gk+cMeJt28DTsd35d7jp3LEz0uJBHTxGo1a1bE0dodocxo0Nqg\njQHtTkKmtUntM+5xpv621Lpx95v0OQbQpu449z717rvLoy/oztsvrOXFac+jbEVZtIA3n16DskBZ\nbpMGy1IoRb1tqWTJUu66BZYC6u4rLOUeR4NjVOox3G3u/tRzpPaddHl3dj+siD/P+IL7es4DBZUr\nYhR19WN5wMrR35JSip2P7MXI/brxxMVf88YOF1MxYXssv010dS0FvXL03gIGHrIVvfcewrsXvsQX\n2+2LPekwQrOuxy4rIbn4W9hmVFafX+24C+btj1FXXepWWUfNgH2vdXcGisnK4P7Kiy66Ebx7wapj\nUMzFmKuR9EDkE9VCm8JfYoNDkScSiQQ1NTVEIhEKCgqorq6moMBN8Kqrq/F6vSQSCSzLwuv1EovF\nGhy34dJxHCKRCMXFjb+8hg/fmcWLbwZGZPlftQTLnoimGsofB/9o7KohOGdfDWOOzPJzbyAWRV16\nKObTt2C3wwh/9RIHfPenZg/XWqPjSZLVMZI1UZzaOMmaeGoZQ0cTOLUxnEgcJ5rEiSTc9VgSHY3j\nRBPoWBInnkRHE+h4Eh133GUsgXIcahevIPZzNUZDr8GFWCqd2LkJoTGm7r4x9bellia9TG/bcDt1\nt7rEMX2/ifX0nGIeK5VEArYFKHefYv163bbUSen1Dfc1dV+lNqomttc9Xr1tKysN2oG4hl5l7sb0\nR3Hdv4mGSzCN9tHomPX32ci21MM1WFrKfY0STr14VTphdvcrteF2VW9bKkFW9bent6WTcNVgnfS2\nekl5bVWC6tVxHAO+rkWEK4pQHhs8FpbPg+Wzsf02dmrdE/Bg+z1Yfo+7HvBiBzx4gl48QS920Isn\n4MUT8uIN+9z7IS/eAr97TIEfT8DTKDlf+eES3jjuUWpWxUh4AugTp2LNOLfZ91emmf+9DaefiDIh\n9FEvQtVPWLMnoctaMYtVeyW/R62agHJWoJ2bgV6pHT9TWHgqy5YtbvK0cePG8dZbzXe4FKINmpwK\nUn46iU7j9/tJJBL4fD4SCfdyXzTV6zZ/O2b1RjvvAFfAynFYRadjiEJrx1nVGqrXQtUaqFwNNWuh\neh3UrIOaKqithEg11FZBtMa9xWohGsFKRrCdGMqJoZwEJBMoncAJ2ej/zsYxcV4qOyVVFTRoJ1Ud\n1AbHAe24VTfbBttW2B7weBUej3KXXoXX5y59Pnc94AOfT+Hzu/d9ftz1IvD7wRdQ+HwGX0Dh9YHX\nZ/PdghCPz6pl5aIqhg+AMw9xE0TbTi1TN4+9ke0bbEsf52lme4PHq7dNKVhbDeWHwF69LT5YafjT\nRMOUXbPxt9H6v9kDb4PYavi2ShHXitlnaXYeko2YWq/oFNi2t+LDpYZLz4LfnASOA45uvEwm0/dN\nvX1mg331lvXWk04zj7vBY//hVlj2UyWmuobxM/pjexTJqCYRc0jENMmYIRHTJKo0yVU6tU0TTWgS\nMUMy7pBMGJJxTTKucZIaJ+E2ddBJ495Puu8To1MVaVth2elKtrtuaY2PSqJ/ugr+dgeWxwseD9ge\njMcLXh/G50N7fRAMpm4hCBdAOOwuCwqgsMi9FRVDcQkUp5clWJ7GX8WNqqyDJmB0ltv+e/piur2L\nqjwXqqaAmQ4clN3nFKIVJFkVnc7j8eDxeKiurq6rbtTWuh0JOmtGINDAKmAZ8BOwEvg5tW0NsA7M\nYHTlnSivxnvTCVheP0onME4SnCQm6WAcB5N00KmlSWqUx8LyupUgtwqUqvYEfdhBP56QD0/Yj6eb\nHzvsww77scPF2KGu2EEfdtCHJ+Sek76/8N43Wf3c/4hUJzl+RiHHnxXG51e436Vuoun1upeBs+3F\n2TXMfTrC/acZjrlDccWDijlXaLYcmPWnblJVLfgseG1/zWMLYdrj8Nc3LV6YrqnI3RXmRrYsVfxj\nb8M1nyv2+SOMGwmPTQdfJ30q25biromG+SvhxNvhvicsXrhXM6BP58Rz39M2Rxzu8Ok8w+u3LeLk\nv27Frkf1zMpzaW1wErpecpu6n1p/aOY3fPDqKuyaSjwzz8YeOhAiUUwkiolE3PXaKKq2FqprMTUR\nqPoJs7wWU1OLqXWP09EYJhrFROMQj2NicUgm0bYNHk+qguwulV1vGQ5hFj+PMRq1dipGVYBVDKrI\nXVpF69dVUep+wfqyflsoH7r4VvDuDauPA94B85uMv+ZCtIUkqyKv+Hw+4vE4gUCASCRSl7S2vlOW\nBtbiJpjLgRWsTzJXp/ZVoqxalCeKUjFQMYxJYEwcoxOg46BjoDzgCaG8BShvIXiLUb4S8JVifH3R\n3hHgLUV9fQnO6lUUbt2HYZceiqcg0CCRtINe7JDfXQa8WWlX+sPsd9l13zCHHu/noilr+eTdBDc+\nVELXity/xdeuMoQDit02M3x9g+GypxU7TofjxsIdZ6faT+ZQVa3bDEApmDwYxvaGGW/DkEvgd+Ph\nsgNyG099PhsuH6GZ1B+O+4+i13S48xTD4dvnPhbbglgSDhgGCy+C816ArcbDtOPghpaHAc24wjDY\nHnhljuaBR+CcUz7h9Vk/MPP5UQTCmf27tiyF5bfxNjPaWrcBIfrsXUrFzgP44OqbMKceT/im32fk\nuY0xEE0nvtH1SXBtpF5CHMX8vJqacy7H1D4ITgWWXeR+fhHDEMeYOKQ+xzBxIAkqACqMsgtQVhHK\nKga7FFQpWpVhKHUT2wZJbir59e8I3eeiVh8FyamY9kxFLUSGSLIq8pJtu7MNhcNhampqiMfjdVXW\n6urGA7//+NN3YO0HOpG61h1EeQvAW4jyFqWSzBKMryfauyXGW4LxFoG3GBos0+uFYLkdhAwbv8Cr\nFv6e/vdcwNJzbmXepc+w0xNnUDikItMvyUbF19ZSVKzY5+Ago8f5mX7oGvYfvpyZN5QweWqorqNb\nLqxbqylIfekHfXDDJM2kHWHyHYp+kxVP/l6z4xY5C4eaKHjrJcjlAXhkjOa1H+D4N+ChuRZzztBs\n0SN3MUHDv6nNimHu/oa7voET74CbByieP9dQEs5dPFYqWQUoCsBdR2iO3xaOeUTx5D8UT92p2XZ4\n7uIpLIB1le6PjBOOgX32gpOmruWMPm8wJYtV1qaESmziVXFGXbIPvccN5eVD76Pm1X8SfHU2Vs+O\nvdeVUhAMooLBjR5namqpmXEJats/Yz48D+0cAWxsytYomOVgfsLoFZi6q0PpH+1LgWosOwIqijsF\na+Ok1+AAhpqaQJOfvQB9+nRS+V1sMiRZFXktnWSFQiESiQSxWIxAINDouLLS7iz7eTlW153Ru8yG\nQNf1HUqyHKNxHApHb82W3z/Bt5Ov4NVtLmfEtUcyaPqYnCWJiXURCnukR16wuPelcl6fE+GiKWt5\n7uEINz5cQq9+uXm7V67RFAYb/rtHDYB51xj++LxizG/h4NHwwEy36V+2VUfB28RMq/v2gQWT4aL3\nYbur4bhd4I5Juav8bviXYSmYuhkc3AdOm6vodxb8YaLhnPG5ice2FPFkw3fL6IHw9UzD719T7DYR\nDj8A7rsuN69RUYGhct36+7165qbK2pRQkQcTcRO17tv35eivZvLWGU+zcNhovDddSfDkyVmPgWAA\nkknMwNOheAT830Eo512M8zhNf5UHgH6pW/N0ixOXVQPzCIePb/DZu2FH10cffbTJs/O3/4H4JZFx\nVsUvRro9a7qNa/1bIBCE5POwKg7/2Ax+ejVncRnHwQr5sTweBj9xBYOeuJJ5f5jDm3tcS+2SDszl\n3QbJqgiFJQ237XNwkP9b0p1woWL/4ct55K81OfniqK7UFDb+PYHXA5cfqnnvCvhigaLPJMVr7zc+\nLuPx1IKvmba6YS/csrPmzQnwr08VfS+0+E8rp2rPlh4heH6M5oHRhquehC1nWixakf3ntRXEmkhc\nAl64dn/NO2fBh3PV/7N33nFSU20bvs7JtC0UQRHpvUpVUKRILxaqBZQPK6iIDVRQLCg2VKyIAr42\nREDRVxQF7CKIgKIoHURpCiJK2zYzOef7IzPL7LKzO315NdfvF5JJTpKH2cnkzj3PeQ5Vz5R8+nXy\n4ymXqTmSVXBd0GVduwoqqgNcX/1Tls1NYu/4AJ4yBjpkQAdnppuurw2h68sX4xtzN1m9BqOSPPCJ\nkIGeg/5DcNJZ0OcnKHcA6WwDJPM9yARqIoQs8J2blZWVP3Xo0OFoFY9CE8CiRYto1KgRDRo0YNKk\nScec4Y033qBFixa0aNGCDh068NNPPyXx/2Pzv4gtVm3+QWSg/MvAexcsHYhcPQrM5Ndy1X4TmXY0\n2a18nzNotnMeXncZFjW5k+2vf510kShycsksc6wgC7qsk2dV4Km7DzGk0352b0/uoAyHD2rKFfOL\nZpOq8N1EzW19oP89cP54QW4S7/PZeVZuaHGcXgnWXqgZ2UjT62kY8AJ4S3nsin414OdB0K4MNBsL\nY2ZZxSSShWEcTQMoiuZV4IfRmtHtNX2Hw7lXC3ITPwppPmUyNIeL/tU532V9/EHF9KvXcF9Xq3Nh\nsohG/kwAACAASURBVEjLdKCK+EDUHdScIetuo3zWLrJrtsa3bGXSYgDA5QSvNfAG6VXQ3b+Bmt0R\njg7AJ8k9d4wopRg1ahSLFy9m3bp1zJ49m40bNxZoU6dOHZYsWcKaNWu46667GD58eClFa3O8YotV\nm38go8G/BrZ9iFjYDA6uT96p/F5QGuEqWABfetw0+HgyNZ6/ldU3zOLrfs+Q9+fhpIUh8rxklAl/\nOee7rJnJd1mzDmvKeopXVYaE0X00Pz0E+/cLql0keHtJUsIhKxfcRsnpGE4D7myl+f4C+O13QZXb\nBfNKb7ApAMq5YEY7xeIe8M5SQe2bJau2JedcVhpA8W0cBtzWRfPjGDiwQ1D1LMHcBcmJp0wG5OWG\n/7sd47LW+JSlSXJZPWWMIsUqQGa18gxYej2tR7cnu/dgsm68KykxAAiXC/L+PrrCcKPa/AdaTQLj\nCuCBpJ07VlauXEn9+vWpWbMmTqeTwYMHM3/+/AJtzjzzzPy0gjPPPJPdu3eXRqg2xzG2WLX5h1IX\n5duKPtwOFrdBbJlytEJ6IvEfsMrLhMlNPfHSHjT7ZS6H9+aysME4flvwQ+JjAMjzklGEsxpKqlzW\n7MOKsmmRvdd1KsGyuxUPXai5fBJ0GS04ksDhzwGyc0t2VkNpUB6W99c81EZzxSvQ6XHBgQTHFC3t\nT4aNAzSX1YTOE+GiKVY90kRiyKLTAIqi7omw9HrFpD6a4eOgw0WCA4cSG09GGuTllfyQEXRZJz+o\nmJEklzWtjAOzGCUvpKTV2K70XzISx3vzyWrSHnNn4oWz8LjBd+CY9breNdD1U3C/hnQMAI6fIa13\n795doANWtWrVihWjL774In369ElFaDb/Q9hi1eYfjAReBfMdWDMB+WUvyN2X2FPk/XWMq1oYR/ky\nNFrxApUnXMk3Q15g1WUv4juck9AwlNdPemZknbmS7bJ6cygyZzUcQsCILrBxEri0lcv68qKEhUN2\nHrijEKtgdXYa0Rg2D4ayfkHNOwTPfp64mGLBbcD9LRWrzoOtWwVVRgnmJ9D5NWTxaQCFEQKuPgM2\njYMTvIJaHQTPvpa4eDLSweuN7DOdbJc1rYwD01eykq90WnWGbLiNOu0rk9WsEznTXk9YDADCXbRY\nBeDEM6HPWnS5LKTzNGBXQs+dCj7//HNefvnlIvNabf7d2GLV5l9AL7TvV9iXFeh8tThxh/b+jXQX\nL1aDVL7xAk7dNIt9q3ezsME49i3ZlLAwlNdfbBpAYZLpsnpzICNMvcriqFoBFt2qmHqZ5pYpcMb1\nkj/D3JejwRKrsVVlOCUDFvRWvNJZM2E+NL9fsiM1febC0qQ8fHue5t5mMHQKdH5QcCgBzq9Dxpan\ne0pZeP9KxcsXayZMhhbnSnb9Hn88mekQbZ+lZLmskYpVAGeGm87/uYhurw3GP24CWd0vRCUouVek\necB3MHyDtMrobl9DrXMQjo5AAr/rYqRq1ars2LEj//WuXbuoWrXqMe1+/PFHRowYwXvvvccJJ5yQ\nyhBt/gewxarNv4TMkM5XgwKdrxJwA/EdQLpdETd3VTmRJj+9wgnD+7HknCdYc8tszAT0LjJ9/hLT\nAIoiGS6rPxcyo3BWQxEChrSDLY9D9bJQdyg8NS+ucMjxRu+sFmZAbfh5CJxWDprcC3f8N77jxYsU\ncH0jzcYB4DkiqHGjYOrH8R3TkDriNICiGNDMGkygZTlo1APufjK+eDLSweeL/rOYDJfVk2lgeqPr\n3VanfzOGbLidCv69ZNc6De+Xy+OKAUCmecBXQr6F4UKdPg1OewKM4cD9cZ83Htq0acPWrVvZvn07\nXq+XOXPm0Ldv3wJtduzYwaBBg5g5cyZ169YtpUhtjmdssWrzLyO081Xz+Dtf+Q4hPZGL1SDV77+K\nJt+9yM75a1jcdDx/f789rjBMnyIzCmc1lES7rF6vjslZDeWksjDvBsXr18IDM6H51ZIde2M7Vk4u\neOIUqwDl3fDy2YoP+sDrywR1xkt+2Bn/ceOhagYs7Kb4TzvNXXOhxR2SHftjO5azhGoAkVA+DV4d\nrHj/SnhpFtTrLFm7ObZjZaaDL454EumyppVx4PdFX4oho0o5+n1xHafd1omc8y7lyHVj4xpCWqSl\ngS+yjpq6zlXQ7XNwz0IY5wO+EvdJBoZhMGXKFHr27EnTpk0ZPHgwjRs3Ztq0aUyfPh2AiRMn8tdf\nfzFy5EhatWpF27ZtSyVWm+MXW6za/AtJYOcr38ECZauiIa1hDZpsnU16z7P4rMODrL9vPsofm7Xl\n96mYnNVQ8l3WjPhcVr9X549gFS/nt4afJ0Pr6tD0SpjwSvTHyPUmRqwGObsKbBmsubAGnDUJLnsl\nuSWlSkIIGFQLtg2E09KhyW0wdk70x3EYOmHlurrUgy3joG89OGMAjLgr+vcoIw38MTiroSTKZXVn\nGCi/RsXQq01IScvbOjNw2ShcHy0kp3EH/Ntje8oR6ZGLVQAqtoFz1kF5XyCPtXSernr37s2mTZvY\nsmUL48ZZY/dec801jBgxAoAZM2awf/9+Vq9ezffff8/KlUkuAWbzP4ctVm3+pSSo85XvMEZ6jL95\nYw10UOv50TT4/Bm2Tl/CJ6dN4NCm6BP+/F4dcQer4vB4JP9ZdNRlvSQGl9XvU3E7q6GUS4dXhivm\n3wzT34cGwySborjnJlqsAngcMOkMxfL+8N1mQdWxko+TWCEtEsq74aWzFB92gzlfWmWuVv8a+f4O\nI740gMKku+CJvoolI+HLzwQ12kuWRjEIRGYG+PyJ6fgXr8sqpcDhkmTvCVP4NQJObFmVwetuo26X\nqmQ370zOc69EfQyRkQb+KGPwVEJ3Xwa1+4KjI/BB1Oe1sSltbLFq8y8nzs5XvsPI9PiVWZm2jTl1\n+5sYDevx8WkT2PrMx+gIrSh/rhfThLT0xA3tGnRZ02NwWf3+2HNWi6NrU9jyGPQ+FU67Bm6aEplb\nl+MFj5GcmrItToQ1F2huPVXTfyqc86wgO7kDGZVIp8qwqb9mcDXoeB9c8lxkZa7cDshJwi/Fp1WH\ntbdprmuj6TUMBo6MrONURlp8aQCFiddldaUZZO+Jr1ayM93F2dMvoMfsofjvfpCszgNR2VH0jktP\nAzOr5HaFkU7UaVPh9GfAuBa4J/pj2NiUIrZYtbEJ7Xz1VZSdr/yHkXE4q6FIh4O6b06g7tsPsG7i\n+3zR6RGyd5acgJi79yAutwhb6zVWYnVZff74c1bDkeGBZ4YqPh0H7y8V1L5UsrqEnMg8X+Kd1VAM\nCWNaaNZeBFl/C6qNFcz8JnnniwSPAx5upVhxLqzfIqh6g+DDEkr8uh2Q60/sZyiI04Dx3TWrR8PO\nTYKq7QTzSxhwKTMdfEkQz7G6rO4Mg5x9sTurodQ6rwmXbLydivIvsmqfjvezpRHtJzLTwR+DWA1S\n+3LovgQ8byGMc4BSfrKysYkQW6za2OQzGswoO1/5j2BkJNZGLN+rLc12zsOXXpZFTcazfeayYl3N\nvL2H8KQlR2RA9C6r36+T4qyGckY92DBJM7SdpuPNcNmk8C6rJVaTO9wtQO2y8MX5iqfaaUa9AWc+\nItmXvEHLIuLUE+C7czXjm8JFT0O3hwVHwjyHuZ3JE6tBGlaCFTdo7usBQ2+CrkNF2CFV0wPOqpnA\n1IQgsbisngwHOfviEIqFSK9clr6fXUPb8V3I6TeMrKvHlNz5KiMdzDjrlFU4DfqsRVSQgTzWX+I7\nno1NCrDFqo1NAaLsfOXPQiZYrEJguNaPJlNj+m2svvENvu77NLn7ii5Zk7v3EGkZyb2Uo3FZfWZs\ndVajxe2EBy/QLL8Hvl0nqHaxZMmaY9vleSEtBWIVLBE0rAFsGQLVDKg7HiYlcICDWDAk3NhYs2EA\nyIOC6jcIpn92bDtPEp3VUKSEkWdpNowFxwFBjfaCF+cWEbcBTgf8lcS6toVd1gldwrusaWUc5P6Z\nOLEKVuer5jd3YtA3N+L68hNyGrbD/0v4yiA6MwP8CSiq6zkJ1XUJ1BkIji7Ae/Ef08Ymidhi1cbm\nGAp3vuoZvvNVksRqkBOHdLeGa/3Ty8KG4/jt/e+PaZP35xHSM1NzKZfksiql8PlTI1aDNK8Bax7U\n3NhD02ccDJxQMCfS5wd3ir/pKqXBvB6KOd1g8mJocq9k6x+pjaEw1TPgo+6KaWdoxs2CVuMlu0KE\noMcFuSmsblStPCwernhhoObWB+H0fpI9hS4ztxv2xViKK1JCXdYTdXiXNb2sk9z9iRWrQSo2O4XB\na2+jfq9aZLXsSs5TM4qONT0NSMwAA0gHqvWz0GYqGKOAOxJzXBubJGCLVRubsFidr/Qf2eE7X5nZ\niCSKVQgM17r8earcP5xvLp3GqmEz8B06Olyr988jUY1eFS/FuawH/9YYhuXmpRKHAePO03z/AOzc\nLag2WLAgUIPd5xdxDwoQK+fUtAYT6HwStLgfbppb+mWuLqoNPw+CZm5ofCuMf8va5nFCboqHlBcC\nLm4FP98B9d1Qvws8+PzR7eke2PdnamIpyWVNL+cg7+8EuJphcKQ56Th1IL3e/D/MBx4lq2Nf1JFC\nORJpHqRIcJ5praHQ/SvwzEc6epMwMWxjk0BssWpjUyyZaLOYzlcqG5mZlpJITh41kFM3zmLf97+x\nsME4/vhyIwDevw5TpmzqL+WiXNb9e008kY0+mxQanAIr7tXc2w8GT4SetwvyvAJXKYlVgDIumNpB\n8en5sOA7Qa07JXtLOZf1BDe81l7xXld49ROoe4vk76zUi9UgFTNg9lDFvGHw7Axo1F2y5RdI8wj2\np3B42+Jc1vRyTrwHky/kavZpzJCNYznRc4SsOm3wLv7yaHweDyLRYhWgQis4Zy2c4Arksf6c+HPY\n2MSBo7QDsLH532A0mP1gWw/Ebx+hO/4XyjVFijxkWvQjWMVKcLjWXRNeZum5T1Lnyk54s3LJLFc6\nz50ej2TGhyfw4Zs5TBh5kPIVJQ4BP+0Arwl+08ph9fqPLvuVNff5A3MTTBWy3QSfstr5TauDjT/k\ndf56HZiro3NTWetNU9OiBnyyWiPRPPoHvPsLaKwU5GDiggpZDmYz5M8JbhPWPqFtERB8rUPbFrG/\nFvnb3MAfB032HYD1aD7aKZGBKg4i8I+wjm6tCyyEf12wrbCizW8kwuwrQ5ZrZ8K3+xVvrQBDmvSa\nBg5p5ZY6JBgiMA9OwnKyHfLoZITMnfLodqdxdFtwvdOwlp3BY4Ssy3DB7EvhsS81zc8BLTRbtsDe\nP6y+RenpVlzJJuiyvvYG3Hz1Gj55YSenNMjE+2dqXMf0SmU4/5MRrJ2yjOUXXIF3UF/SX3oCkeZB\nJGskKveJqK5fINfcDlu7gf8JYGByzmVjEyW2WLWxiRir8xW+K2BxW0TLR5DkJax0VSjK68V/IAvz\n4BHMg1mYh7IxD2ejDltzmeHhhGG9+Pk/izGz88itZnDLpSZ+L/i8Gq9X4/dZIwCZPlA+S/SZflB+\nUGZw0kfnCpSy5jowN/Nfg9KBNtoShUqT/1oKS5RkHVQoBc3HQznDEjaSwHaENRdgBNcF1hvCeu0I\ntDcEGELgyF+2vqxkYG4E2hqBZSfgEeBA57eti+asSvDSH5rfs+HvbPg/IINCIq6YyUIXsU0f0664\n4xVe/x9gM/DLIcVgB7SSwTMdO1FoXuSkI2gT5jgKOEvCNuAjE5Zuhs6VoXamxK8DDwVaBObg02Bi\nPTQE16nA3NRH15laW5+V4BR8kAiux3qtlLWsQtorrXEBR3xw/4Nw90Trb28qS3QbATEtZcFlKcXR\nZRFYNo5uMwKvQ+eGoTEcYEiN4dA4HOB0gstpzc84Hb5c+hebvv4Lo2IZfp63BsPjxJHmwPA4MTwO\nHIG54XHi8Djyl2Uc+TBCCJrd0IGqXeuxaMAr5NQ/EznyKtBJTCyWDlSrJ6BCG1g5HPzfAI8m73w2\nNhFii1UbmxJRwBFgD/AHMADMTPT3t+N3KvbPVmR9twmVkxeYvOicPKTPBz4/wuezqrL7/Wi/ifb7\nwVQo00T7FcoMTH5liUa/QmswnBLDKXG4JA6XgdNt4PQYODwGLo9BRppB5U4nseXrPez/3c9n83K4\nuJ0kww0uh8aVrnE7Aq5VcHKAKzAvsD5knauYbUVtdxhHXbtZy+DGF0EgaJwmeL26oma+8RyuR35y\ne+q/d8BgaJ7Jail5QynuAy5J6hlLZhHQVAgqAy/6NX8YMMsFrlJMzPrUhG+EZLgHJu1VVHQqXjkt\nNU5mODotNfhLmvz6F9xyNdx/s3Up+YKTr/CyxucHrw98Pn10W5FtA+0Kb/NbFSS8PmFNXqjWT7Bm\nvcnaLYf57PLZuE8sC6ZGmybKVPnXsQ5cx9o0UT6FkALpNJBOA8NlYLgd1hQQtQ6PE0eaE0eaCyM9\nsJzuxJFhzY00J4bHSZNr2/Hjk1+Sc+8jmMIDv38MzkxwZIKjzNFl6T56McZDzSFQtgl82Qfp+x7l\nfzH+Y9rYxIEtVm3+YSjgELAX2IclLvcDfwWmg4HpEHAY4chFGrkgvSC8aHxo7QXlt+ZBWxLA4QFn\nOsKZjnBlgqs5/PkDR75ei+e3Xzm12ym4Kkmc6QaudAOnx4PTYwQmmb/sKGJdwckSqZEW+Z/c41Ma\n5+3lmw2SlT9r3hylaVI10e9rZGTlwSkuybf1FP1/haYb4bGqgmsr6ITcQ2NBAZWAp5TiY6yxe2YG\nhOsJpRMSYDnIg7WmA3C/FtTJgxlOTZ9S+lZ2YD023JOuGOiCi/cIqi8UzDtT0a5i6cTklnBeYzin\nMVz8OryzWPLxq4oqJ6fi7KFeNDzzKjw6Ox1cDo5kK8784i4y64YPRCmFyvXiO5CD72A2vkM5+A7l\nYB7KxXckB//hXPxHcvFn5WFm5WFme/Fm5+H/04u5MwuV40PlWepZ+0yc5cqgpUHuviOYXw1AGJmA\nH618ltuqvJbFbrjBSEM40hEBESucZcBZFpxl0c7yKEe5giLXUcaa57/OhLQq0PNb+GYI4q+epdox\n0MbGFqs2/wh2//4LGO0scSnkscLSnYlwl4XApNynoF1l0a4ymK5MKDCVKfQ6E4yjeamhtzDPS7U4\nuW059ny8AWHAoEktcKWl9rLy5Sqa1YU371EMewTa3AsTBgrG9NYpd8VyvOAS4JGwqI5m/gG4ahe8\ncUAWcllTh9JWuoAAegJtgIeANkJwh9ZclfqQClANeEFp3hWCoXnQ3hS86dR4Uvy3M7DeK4BTHfBD\nec3DOYLuS2BQNUrFZfUYVqevTnVh81i4/r/QqDs8dDuM+r/UxuJ2gTvNYMK3ZzNrzHq+aDmWxpMu\npe7IHkW2l1Ii0z040j2kVUnMY9G+LzfwzaDnUOknIw5rlHc5UCGkRRaY+8Dci/buQ7Mf62H978B0\nANgOHEYY2QiZh5B5IPLQWKJXByaUJYCVVoAm20zySB82NsVgi1WbfwQnVqjM7/v3IGt3RQ2YA55y\nQGFvJAlok3pD29L2iYF80mMK65p8yPX/7UiNlqnz7LRP4XZaQuL1O+GLH6ye8G+tFMwZqalTKWWh\nkO0tWNO0X3noVVaXqsuqKPhFdwLwmFJ8DtwPzJGSWUqRwrfpGCQwUGvOAiYqQZ1ceM6lGZDCb+ig\nsxrEKUrfZXXLo7Vfy3jgtSGK99fBsMdg1nzBopc15cqkKBYXKJ/C6Ta4fEozmvc+iSlD32DvO6s4\n88Pbka7k/7Gk00BIib5qNWL+UMS2Bui8D4AzAi0yAlOtEo+lTWsqmWxgHRnp58YYtY1N/Nilq2z+\nEbjdaeB/F3bsgecbw2/fpubEWiGdBmVrnciAzfdyYu+WPNz+IxY9ugGlkpuLGUR5LbEapHNL2DFb\nU7kSNL8TXvhMFDsIVyLJ8YG7kBINuqyzasDdv0OnbZLtKRySXFH0F10X4F2gKtAOeL6INqmmMjBF\nKa7VmqvzoHee4EiKfn41AFXEo13QZb3GaQ0rP2xV6mrFeiTkFCqndX5T2DwOKvgEtToK5i5ITSxu\nl9URMUjr8yrz+LquZB7Zy8c1R/H36l+THoNwGmilwZmOGvQ2dLgVnN2AqUk8azpQDSFsuWBTetif\nPpt/DqIcSn0PWUPg1bMRK54sfqjURBAQq2D13m3//GB6LL6BhZM3M6njJ/y1K3lFxPND8BcUqwAu\nF7z3gOaNu+CuedDtEclvfyc9FHK94UeL6lcedjXRZAhN043w/P7UiOhgGkBRlAMeVIqHgKeBzlJS\n/AjxyUcA5wFvADlKUC9X8EYKRpYyCH+5BF3WFSfAd3sE1RdKlid5ZCmw0gDyivi/n5QJC65UPNVX\nc/U46H2FKDBqWTJwu6xrLZQKVdOYsKwDva+pztKO97JuwttJjUE6HVZpDgAh0GeNgwvmgWsciKFJ\nPbeNTWlii1Wbfx7GZFAL4MsHkXPOhZwkqjRt5ovVIJU71GPQjgfITa/I3U0+YNVbO5J3fo6mARRF\n37NgxxwNLk2j263e+skUiDk+q4RUOErDZdVahxWrQTpguaz1A8tPJjekiDgJeEIpbtKam7zQNU9w\nIImOpgPLhS6OVLusbqnDDlQgBFx2Oqy7DQ7tElQ7S/Dp10mMpZCzGkQagkETGnLHonbsfu5DlrS9\nG++h5DykSqdx7Bterzdc/R2i3DKkqwVW5RIbm38Wtli1+Wciu6B922DHH1ZawO6VyTmPUgjnsVLI\n4XbS6+NRtHn6Il65eiUzLl1OzuHk2GOqCGc1lHQPfDZZM/VmGDVT0O8pyb5DSQmFXF94ZzWUVLqs\nivDOaihlgAlK8TjwItBRSrYnJ6SIEUAvLJdVKkHDXMHLSXJZHSKy/O5UuqxpUuMtIa+yxgmw9HrF\nuLOh79Vw6ejkCOhwYjVIo44n8sSmblSpmMOndW5i76drEx6DcBpoXcR/rmJ99Ig1UL0ywl0XSPy5\nbWxKE1us2vxzkWVR6lvIvgxe64L45rEk2IoK6Qx/GTW4oh0DNk1g65ocxjdcwNbl+xJ8/kAaQAS9\n7If2gF/e0PyRAw1uh/dWJzwU8kpwVkNJlcsaqVgNcgaWy9oc6Aw8nPiQoqYi8KhS3K41Y73QIU/y\nZ4IFWWg1gEhIhcvqFpq8CIaAlRJGn61ZdTP8sEpQs4Pkh/UJjsUFpln8fzCzgouxH57BRfc2YGXf\nx1h97X8SGoMM5qwWGWBZ1JCFiDZXgbMd8HpCz21jU5rYYtXmn48xCdQiWDIJObsX5CRusHGt1DFp\nAIVJr1yWfmvvosb/tWdy98959+6fMP2Ju6srUxfrrIZSPhO+maK4/woY+gJc+rzkYAJ/sbQ6WEX3\nQJBsl1UXk7MajnTgTqV4BpgtBGdKydbEhRQzXYA5QDkFjXNgagJdVqsaQHRvfLJdVo+EvIh6rFs0\nqQw/jNZc1lLT/kK45cHExVKSsxpECEGvG2pz37KOHF64gs8ajyF3z4GExCCKSgMo0ECiujwE/V4F\n57XAdQk5r41NaWOLVZt/B7Ij2vcr7DwAUxvBruWJOa7WJYrVIG0n9afPV6P54qVfmXj6Yv74+XBC\nQlD+yMVqkBsGwObXYO0eqH8bfLouIaHgjcJZDSWZLmvh0lXR0Bp4R2vaAT2ACYkJKS7KAxOV4m7g\nfi+ckSfZk4Bnn0hyVsORLJfVbYDfjO4D5TTggd6az6+Dt98VNOgq+WVn/LF43JGJ1SC1WpbnsXVd\nadrazacNR7NzbvzfOdLpQEfyJNd4IFyxHDLnI51nAiksv2FjkwRssWrz70FmotRKyBkBr3dHfD3p\naM/aGInEWQ3lxNY1uGD7RIzaNZjQYiFLX9oW2c2nGJRZfM5qOCpXgDUzFDcNgn5PwbWvSLLz4gqF\nPD94onRWQ0mGy6q1juuLLg24VSmmAvOFoI2UbIgvpITQActlraLg1ByYHKceMYivJnEyXFaXBL+K\nrShv2xqwcayma3Vo1gcemRZfLG4XUZej82Q6uH5Wa658rhlrrprGygufRsWh4q00gAj3P7kZXPMT\nVHYg3bWBn2M+r41NaWOLVZt/H8YDYH4MSycjZ/WA7D9jP5aOTqwCSIeDbv8dTvtXL2POmO+Z0m8p\nR/6KXSVGkwZQFOOHwk8vwmcboeHtguVbYj9Wng88cQ7DkGiXNdqc1XA0B97Wmi5AH2AssTuRiaIs\ncLdSTAQm+6B1rmRHjEFFm7MajkS6rC4B/ijSAAqT7oIXBin+exk8/jy0Ok/yZ4xZQFbOamz7dhxa\nnUd+6Ixev4nPat/E4S2/x3Qc4ZDoEvJmC5BeETXsC2gxEJytgPkxndfGprSxxarNvxN5lpUWsDvb\nqhawY2lMh9FKIx2xXUa1B7Vi0C8T+f03GN9gARs+2xPTcZSKT6wC1D4FNr+muLibpvskuG2OLLK+\nZUl4/bGlARRFolxWTWLEKoAbuEkpZgCfCcHpUrImQceOhzOAuUB9Da1y4IEYnn0irQYQCYlyWd1G\n7M5qKD0awpZxUM8DdTsL/vNWDLG4wIwiDaAwletl8vD3nTmrX0W+bH0HW55dHPUxpNMR/ROFdKB6\nPQt9ngHnJcAdUZ/Xxqa0scWqzb8XmY5SyyHnenijF3LZg1GnBUSbBlAYd/l0zvt2LA3H9OSZvkuY\nc/P3+KLpUYJ1A42kGkAkPH4trJgCb62CZncK1kRZu8lvClwJ/FZJhMuqdeLHlW4CvKU15wD9gJsp\nfZc1AxirFJOAaX5oliv5OYqgrBGsEku8LqtLQjRGYnGckA5vDVPMuEAz+n7ofIkgO4rOhfE4q0Ec\nLsmwZ07lprmns+XuOSzr9hDKG0G5gwAimjSAwrS4HIZ9AekvIoyuQOTntbEpbWyxamNjTADzc/Sy\nZ5Cvd4OsyMtLaRV5B6viaHlHL87/7g5WvbuHCc0X8tv6gxHvG28aQGFOrQPbZik6tdacdT9MnC8j\n/inWbwpcCXJWQ4nHZQ033Gq8OIHrlOJl4BshaCUlKRrkt1haY+WyttDQNgfGR+iyxtPBqjgKDmPE\nRQAAIABJREFUu6w1Fkq+idBldcv4BWJhLmoJG8eCPCCo3l7w3qcRxuJKnHBudU5lHl/flbI5e/m4\nxij2r4osn1QY0rK/VYxCs0obK4+10gGkux6U+nhtNjaRYYtVGxsA2Rbt+xW922elBWxfEtl+cTqr\noZRveDIDtt1HmTMbMbHNYj59ZlNEna/MBKQBFEZKeHEMfPI4PP8ZnHaPYFMEaXamH9xJEKsQu8uq\nKXkEq3hoAMzRmkHABVjFgkrbs0oDRivFZGCWKWicK1lfgtCySlclj6DLOsIJ3ZbAZd+W7LK6JMTx\ny3tYTikLn16jeKA3DLkR+l8H/hL+aIlwVkOpUCWNe7/qQJ+RNVjeeSLr7plX4j5CCEuweuOoN5dZ\nGX35cmjcBeFqCkSo1m1sShFbrNrYBJFpaL0Ucm+B2ecgl9wHqvi7k1a6yBGsYg5BSjq9Oowu74zg\n3fvXM7n7Fxzcm1PsPqYi4WI1SLumsGO2omFtTeu74KnFoliB4UuSsxpKtC5rLHVWo8UJXKUUM4G1\nAZc1iSN/RkxzYLbWtNPQIQdG54YXiMlyVkMJdVm//b1klzWRaQCFEQKua6dZMwZ2bBRUP0vydTED\nZTgCuSTRpukUhzQEA+9pwB0fteO3Fxby5enjSxyqVRgC/HEWR3a4Uee/DN0fBGdfjo+hL2xswmOL\nVRubwhjjwfwC/c3zyJmd4cjesE3jzVkNR7VeTbhwx4Mc9KUzvuEHrFmwO2xb0wRPgnJWi8LhgDfv\ngf/eDw+9Dx0ekGwPU0BBmclzVkOJxmVNVDWASKgDzNKaS7TmEuBKSt9ldQOjlOJZ4D0laOSV/FCE\n3kpGzmo4InVZ3dL65SCZ1DsRVt2kuaGdpsdQuHp8MYLegJxDiR/vtmH7ikze2I3qJ3v5tPaN7Pno\np7BthWGAr/gH2EjRp42EIQvB/SjCOJ/Sz7y2sSkaW6za2BSFPN1KC/hdWGkBv35eZDNtJiZntSgc\n6S76LLmFlg/0Y9qQr3n16pXkZR8rfZLprIbSsw3smqMpX17TdBy8+MWxo9f6FQntYFUSkbisiawG\nEAkGMExrZgO/CkELISj605NaGgOva003DV1z4dq8gqIs+GdL4OBqxRKJy+qSiR/CtSgMCXd20yy7\nAb74TFD3bMmGIoYsczgg53ByHj8yK7i4bUFbLr6vIasGPM7qa4oeqlUYMn5nNZSaneCaNXDCz0hX\nIyBxI/zZ2CQKW6za2IRDetB6CeTdDnPOR355T8G0AL8XBEgjuZdRk1Fn03/d3axdcpC7Gn/A9tVH\nbyZ+v0IpcKVArAK4XPDhI5pXx8LtcwU9H5WEjiRpmiQ9DaAwJbmsqRarQWoAr2rNlVgO61AhSn0c\nIRcwXCmeB740BfW8kpUB7SWEdUNIdYzFuaxWzmpyndVQWlaFdbdpBjSE0/vB+CcKbnc6IDdJYhWs\nnNSeo2pz//JOHF5c9FCtwiET5qzmU64G+upvoV4LhKs+kKAR/mxsEoQtVm1sSsIYB+ZSWDED+VpH\nOBKoh+rPRsjUXEKZNSowYPO9VD6/NY90/IQPH16PMhXeI34MaQmNVDLobNgxW5MnNA1vhzdXWOtN\npVOSBlAU4VzWVKYBFEYCg7VmLvBHwGVdWEqxhFIfS0ifp6F3HlyRZzn0EsgthXjCuazuJOashsPt\ngCf6KhYNh5dmQdNekl2BzoUuJ+QcTnB5giKo2bwcj63ryqmnu/ms0Wh2zj6aAS0cBviT8FdypqMG\nvonoNBacPYApiT+HjU2M2GLVJqmYge6z8QwxeFwgW6J829G/e6y0gG2fgC/H+kkuhbSbcjE9PrqR\nxU9v4eH2n/DbhoM4SkmJZabDkqc0T1wPI14SDHxG4vPrlDuroRTlsqbKWdVYwtgfmLyBKReoCExV\niqu05lrgG8CnNTmB7cEpL7CPL3AMM3DMZHiLDuBypZgOfGsK6uRJFJBbipdqYZf1jrXJz1kNR8c6\nsHksnF4RmvSEZ18Fl1OQdyQ1WcieDAcjZ7bmqqnNWTNiOisGPoVSCulIXM7qMQiBanc7XPg2uO4E\ncUlyzmNjEyWJrpVtY1OAoFjNybG+XLOyspABN9Lr9ea3kSlyKONCutB8BnmT4c3+iGZDrJ65caCU\nQnn9+HN8mMEpN/A614fKCyznWeuV14+Z66PxmB6sf/pzJnX6GKFh7Ayr9I7ftHIOTdNaNlVgnRlY\np6x1ZmCbWei1yp8Ephbo4GsNWluVALQOXWeNo1A+TfP5GkWuFy7aBh6HJRK1Piq0dGBChyyj83NM\nj647ti2h7cNsO3ZZs+Kw1b5zyHtenPQpSRbFI5tCPyl5wHvAu4FjBrfFevySPoVFbS+wTlt/TAnU\n+MsS96LQBJaDX+B1gWWR7/AX3l54f6t1oXai4D4ZApb/YQn3DlMk6W6BQ1r5pQ4RmAcmI3/S1joB\nDqkDbay5M9hGFJoXsywFnNNQITTc9AA4HZofP9mLMAQOp0A6JA6nwHBKpEPgyJ8XtU5iOAXSEIgo\nfgppf0k16p1xAo/3W8GntW9CeX3gT5JYDVK3FwxfjZjVE5HdHOV9O7nns7EpAVFCHcfSeaS1+Ufg\n8/nIysoiJyeHzMxMjhw5QlpaGlprcnNzcTqd+Hw+pJT5zmtwObjN4/GQm5tLRkYGSilycnIoV67c\nMedq2vQsft35EojWgYS3XOBwyJQVMg9MOiewnANkB+ahHlcu6DwwvAjpD0w+ECZaH0GZB3AZR8is\nkA5YZay0UmitUaalpJTSgfU6sMwxcyGtuqbSsG5khiEwHIFlR8HJ4QzcCAM3yZwsH7vW5+BTcNYp\nkhM8wrrZipAbugjc0IXOX3YIbbUJrHcG9ilwIxfWzbqo9eHW/d9H4NdQAbgRKMNR8SHjWI5n/85A\nuhBUAC7UmhM4VrwV9zrSttE8tnwJfAhUCry+HjiphH10oXnh9cW1i6QNwNhATLlCMM2paeuwnF2l\njzrHwYcBFfK68HL+Oh1+eyT77dEw2gvKgJqV4JyWIQ9fynr4KvCApo8+fOU/mIVO2jq29dAVeCAL\nWacIPKBpbT2cBR7IrLlm70GFV4Ir3Y0zzXn0mg9cy1pptA693nX+NqU02rQezqxrXuRf89IhkIa0\nrnuHwDAsYWs4rXWG03qY377mAIZTYKbXwDi5GTg94EhDOzxgeNCONLQjDQw3ONxguKzl/NeBdY4i\n1oW+Du7rz0W+czF6xyrSnYI//ih6SLtevXrx1VdfFbnNxiZKivwqtZ1Vm5RiGEd/kHW73fh8PtLT\nLbF35MgR3G43OTk5+c6Dz2eVicnKysrf79ChQ8cc98ChvUC7wB3HDwgwHCCdYFiTMFzWssONcAS+\nkB1uhNMTWPaAMw3tLGvdAJwetOEBpwdtuNEh+2C44MAuzMVjObAni/4jT6bzhRVCxGRwTr6jYi2H\nbguIUhm7O7t+xWFu77yBU0+UbP5TMbs7dK8W8+HixmMIJvs1D0nJI0rxANa49aWJAG7XmjeE4Dng\nXCE4Q+uoxGWyuAZYCjwI9AT6EF70xiKKo0UAj2KJ6aFeGGjCdJf1MFUa7FSW4/pFb7jgC8GC1YKP\nxilqnpiIo4f68ZHRaKykUtsyrProMHUvbEnXF/pHfVZlmvjzTMwcH/5sP/5cL/5c/9FfVPLM/LmZ\n58ef60N5Tfy5fqrl+fnusa8w/96JedAP4hysh+u/A3Ov9YAtvQjDZz1gCz9a+BHCBPzoYHKJNq1l\nbYJWaB1YVsF1JmiNEhK0SbbpKfK7F6BOnTpRvw82NtFgi1Wb44qgmHW5XHi9XtLS0jhy5AgZGRmY\npklubi6ZmZnH7Pf+/Lfo3Os8RN2z8Q+eCZ6yx7QpzmmKiV3f4VjmpvOk7iwcsxBvDtz4THXcaam7\ns/t8VoeQ1XcpHloI/T+EyxpKHj9TkVZKV3cl4AuleAq4FeglJWOUIr10wgGsXvBXac1a4B3gBym5\nWClOKMWYwPq5/WygITAX+A64AShfmkFhld7qANytBPXzBG+6FKeVQm50UJi3PQk29Nfc/K3g1Nth\n4kVwc+/UxyMltDu3HFfdV4VxfX/gjcZb6ff5CDIqH/t9E/YYhoEr3YB0l5XMHCXrXvqe3DPvQqyY\ngchajvItA1nE95229GbUhOZnKC9wBMTPZKSdV+C7t0yZMgV2e+2114o8XCSj8NnYlMT/QKKgjU1g\nmMGA2yqlPGZq2rQpZvZB1OZlOJ5uA/s2Jz8opRBC0HLE6Vy+7ga++TyPy09dy7a1CayBWFIIfpXv\nzN7ZB9bcA4v3QJO5gu/2pSyMfLQ++qVyM7AEWAf0xxJipUFoTuipwDitcWrNE8A3QhwXuU6VsVIB\nagMTgE9KKQ7B0bLwdbAqBvQGeuTCqGJGv0oWkqMPlhlOmNFO8ebZcP88OPNeSQmDPSUcQ1rGY73m\n6cxc15iWpwlmNXyMTXPXpCwGIQWUr4Ye8yPUqYFw1gNVzNBb8SBdICuAqIYQosB3blZWVv7UoUMH\nK/2hiAlg0aJFNGrUiAYNGjBp0qSwp1u1ahVOp5N33nknOf8fm/9ZbLFq849CsQlx0IF4qg389N8k\nn8y0bhxA2RrluWLzjVQ8uxHXnrGed5/7IyWOgmlaeaVB6p4EWx9QnHuaptN8uO87mbIi72AJi9Av\nlerAV0oxDLgJmCQlSe4aUiJBl/Vi4CNgmpT8XcoxgfUzV09gKPAx8LAQHE5xDKFiNRjTVUrxHLA4\nMPrV2hR+nkLFapA+1WDzAKjog1o3CeatTGE8AkzTiigtw+Ce12sy5rlqfHHVmyy86I2UVD0RAuup\nwVMGdeX7iC7Xg6MTqGlJP3csKKUYNWoUixcvZt26dcyePZuNGzcW2W7cuHH06tWrFKK0Od6xxarN\nPwtZEZ/4EakHIGYPw/nBbWAmqdSMNgskEEopOeel/pw/bwgz7vmNcedu5dBfyS1zo/yaolJepwyG\nL26FaRvh9HcEWw4c2yYZFBarQcYCnwKrgEFC8GNqwskXOkXleR6vLmsNrFSASsA9QKq7rRT1HjQE\nZmpNJw2dcuD2vNTEIkXR8ZzogQVdFZNP11z+PJw3WeBLQUUpQ1ij1oXSa2hFXvq+Mblrt/J6nUkc\n+Hl/mL0Tg5Di6O/7UqJ63Av/Nxect4IemtRzx8LKlSupX78+NWvWxOl0MnjwYObPn39Mu2effZYL\nLriASpUqFXEUm387tli1+echDEz5ClpNwb9sOq7pXeDw3sSfR5lFlqCp26c+V/0ymp1/ehja8Cd+\n+LLoTgmJwO/TYQcEaFMLdjysqFdd03IePL/+2KFIE43W4TsA1QGWK8VArRkJPCklydY8QZ8rXEzH\nq8vqAs7XmguB+cBjQpCKX7wLO6uFYxqpFE8Db5mCJrmSzUk2EiXHDukbRAi4oh781A/27oLqNwiW\nJTn7R0qrRFxhqtf38PL3jehyXhpzWz7Jj89/k7wghCg4kh5Ak3Phlu8Q5ZYhjWagkvedEy27d++m\nevXq+a+rVavG7t27C7T57bffePfdd7nuuuvsHFebIrHFqs0/F8dlaL0MtXMLxuTm8GuChxDUKuzQ\nUZ6yHoauvIZTb2jP2HM2M2P8bvz+xH8JK9OqIRkOhwPmXQNzR8Bdq6D7B5Lfs8K3TwQlfancCyzE\n6nF+gRCsT2IskWqp49VlrYflsmYAdwlBEiVQxDQF3tCaNhra5cA9SXziiOQGVbsMfHOO5qaG0PNh\nuPal5OXWGlKgwlzHLrfklinVuPeNWqwYt4D5vV7C70283Ws5q0XEcFKD1OSxJoGbb765QC6rLVht\nCmOLVZt/Nsap+MVmDF9t5PSeyKXPhLdqoiUkZzUcHe7pzODlI1jwygGubbuBPdsTe2c3/RSZBlCY\n85rD9oc1/jRNo7nw9raEhpFPuDSAwjQCVihFb60ZDkyREl8S4ommM/Tx6rKmARdoTd/AsK1PCJG0\nIVEFkb1nbuAmpXgceMUPzXMlvyRBIBaVs1oUhoQ7mmmW9YGPvxXUHyPZ8nsS4hHWA2JxdDi/PDPX\nNcHz9+/MrPUw+9b8ltAYhCzCWQ1yHOaxVq1alR07duS/3rVrF1WrVi3Q5ttvv2Xw4MHUrl2befPm\ncf311/Pee++lOlSb4xhbrNr88xFl8fI1gqth4d24Zw+GvATYi9oM+xN8KCc3r8zw7aOh6ilc3mwt\nn7/1V/znDqDMonNWiyLTA1+O0Tx2IVz5hWDIp5KDCXbFohnaVAIPAQuAxcDFQpDoX3FDKwFEyvHq\nsjbBclmFEIwXImnVFaLRnC2A2UBTDafnwCPexMYio4ynZUVY109zTiVoNR4eSrDeCe1gVRyVqrl4\nYXkD+l9VnrfbT2XFg58lLAYr9aiYd+U4y2Nt06YNW7duZfv27Xi9XubMmUPfvn0LtNm2bRvbtm3j\nl19+4YILLmDq1KnHtLH5d2OLVZt/B0JiyidR5iv4136E8+nW8Ze3UmbYNIDCSIfBwPcvpcuz5zPp\nql95+LJfycmKpQhiQcwoxGqQER1h00TNuixoMAe+2F3yPpGiA0N2RsOpwLdK0V5rrgCmJ9BljVVk\nHq8uayZwiVL00pqZwDNCkEh9WIIMKpI04DaleBh41get8yS7E+SyxnKD8jjg2baK+V3gyfeh9XjJ\nnwlK4ZQyvKlZGMMQDJ94Co8uqMv6Jz9n3llT8WbH/9cq1lkN5TjJYzUMgylTptCzZ0+aNm3K4MGD\nady4MdOmTWP69OnHtI9mKFqbfw+2WLX5d+EYgKlXwoFsjKfbwo9x1PPTqsQ0gMI0u6wlV2y8ke9W\n+Lms6Vq2romv24zfp2MaAatyOfjxHsXIrnDeIrh5uSQ3Ael1sTiZYH0RPYFVsP9d4BIh+Dn+cKIW\nXoU5Hl1WAbQERgLZAZc1dVU+w3M6MAeoraBFDjyVABVtEPsDR7cqVomrOgbUGy2YuTQB8Ugwo8w9\nb925DLM2NqVy+iFm1nyYXUvizMERWPnykXCc5LH27t2bTZs2sWXLFsaNGwfANddcw4gRI45p+9JL\nLzFw4MBUh2hznGOLVZt/H0Z9fGIjhm6DMfcKnB/cGlt5KxVZGkBhylQpy5Ubb+SU3qcy8qz1vPXU\n3pg7FCjTKqcTK/eeD9/dBe/thFPfEvzwZ+zHgshzVsPRGvheKVppzTDgZSGiyjstjEn8w5Mery5r\neeBypegEvARMFSJuRzoWZzWUDGC8UtwHTPLBGXmSP+I4YKQ5q+E4wQ3zzlY8f4bm+pegxyOC3DhE\ntBGFsxpK+RMdPPlxXS4bexIL+vyHJbcsiDkGIWXkYhUK5rEanUAd62ba2Bzv2GLV5t+JyMDLR2g9\nGvX1i7hndI2+vFUMzmoovV44n/7vXcqrD+xhTI8tHNgXvdRQpkbEeRU3PNkaSKBbc037d+Hh7wVm\nnAIjHiTwHJZLN1cI/k8Itsd4rET2+Qm6rK7jyGWVwBlacw2wXwjGS8m6OI4Xr1gN0g4rl7WSgqY5\nMC1GFR2vWA0ypA6s7w85fwpq3Cj4LMY3SYrYKw0IIRh8ayWmfNmAHW+uYk7zJ8n9K/pfVoQkesUc\nzGMdNgecY0o9j9XGJlpssWrz70UIlLwX03wL//YfcT7RAn5ZFvn+OvKc1XDU6laXq38dzR/ZmQxt\n9BPffXowqv2j6WBVHFLCtEvho5vhmfWCM94VbIshxS10uNV4ORPLZa2vNZcAs4SIWkglWky6gCuP\nQ5f1ROBqpWgLTAemC0EsWR2JEqsAZYH7lOIu4B4vdMyT/BXlwRMlVgGqZcCS3oo7msL5j8OwF6IX\nnpFUAyiJRqdnMGtDExrW8zOz7iP8/F50xdus0lUx/pWanBeSx9r8uKrHamNTHLZYtbFx9MAUa5De\nMhj/6YP86qnIyluFGRQgWlyZbi75+mpa3XY2d/bbytRbd+H3RXYz8vsiK10VKe3rwc6HFVVPgeZv\nwYwN0VX6ijcNoDAO4EXgNeBV4Aoh2BXF/or40wCK4nh0WQ2gk1JcBewKuKybYjhOov8fHbFc1nQF\njXIFr0XhsiZSrIJ1rdzSRLPqPFi5VlD7ZsnanZHvb0gSUi85o6zBA2/X4obHqvLxJbP46LI3Ix6q\nNeIOVuE4qQF6zBqoUy2Qx/pD7MeysUkRtli1sQGQNcnjRwx6Ij+6P1De6kjx+yiV0J6r7cZ15JIV\nI/ho7iGGn7aB37aVXE1TmRpHgq9ihwPmX6eZeSWMXSHos1DyR05k+yZarAbpBHyvNVWAwcBbEYrD\nZArI49VlrQxcqxQthGAq8JKUUeX9JqOefnngYaW4TWvGeKFbnuBQBCcKXl6JLvLfpDz82FdzcTU4\n4x64663I9jPkscOtxooQgvOursiMlY04+PUG3mjwOId3RvDLihDE/cn2lEVduQDReSQYHew8Vpvj\nHlus2tgEEWl49VuY/rvxr/sI9zOnw96N4dtrM7G2JnBS05O5evtonPWqc2XztXw8q/geT1bpquSU\nehnQCn59SHPYoWkwG977teR9Yq0GEAku4DWtmQZMA66WkpLqvieig1VJHI8uqwPobpr8H7AFuMsw\n2BrBfiLJsXcD3gC0EjTIFcyNwGUVgD8JCtplwKOnKRb3gP98DM3GSfYcKH4fQxJXPndR1G6Sxms/\nNqZdZydvNH2cda9+W2x7Kw0g/rJ3SInqOcHOY7X5n8AWqzY2oQiBNm7BVAsw//oDx3Pt4Md5RbeN\ns4NVOKSU9H9nMN1nDOCJ63cw8ZJfyD5c9M1JmRqZxKu4bDosu13z0EAY+hkM+1xyuITe1Mn+UumJ\n5bKW15oLsUpdhRNYSR66Pp/j1WWtAVyvFA2EYArwWgkuayJzVsNREXhMKW7Qmuu90CdPkF3MSQXE\nlH8bKR1Ohk0DoGUaNBwD04up32/pxMTLeXeaZOyL1bnzpRosveG/LOj7Kspf9P9aCAEqgTHYeaw2\n/wPYYtXGpiiM9vjlWhyqOs55w3F9MObY8lZKxdu/qliaDGnGlZtv5qc1mv9r/BObvjt21C2VeHO3\nSEZ2ho33w+qD1kACS8NYmslKAyiMB5ijNVOwCuOPlJJ9YeJJZYnx49FldQHn+v1cDKzFclnDVfpM\nwA/MESGAPsAs4LAS1MsVvB9GkSbLWQ2lrAtmdlC80h5unwWdJgqyi8jCkUlwVkPpcsEJvPZjE9ix\nk5m1J7F/w7EVShLmrIZi57HaHOfYYtXGJhyiCrn6W4TuBytfxTOjCxzac3S7NpPirIaSUSmTy9eN\nouagltzQaQNzHtuDCnFVTH9iqgFEQpXysHaC4spO0OsDuPUbSV6he2aqxGqQc7FcVofWDAI+pKDY\nSpWzGsrx6rLWxXJZa0nJM0IwyzCKdFlT+Z6dBDytFMO15vI86Jcn8BYKIBViNciAmrCxPziPWCWu\nPvi+4HZDgEpAB6viOKWWmxdXNaT3xWV4q82zfPfEVwUbxFMNoDjsPFab4xhbrNrYFIdw4dWv4PU+\njH/Hj7iebgXbAkPhaBV36apI6f70OQxaNIzXH/uDm7tsZv8e67d4ZWqMFF/FD/aHlXfCvO3Q/C3B\n2r+Obku1WAVIB97RmkeBx4TgZinZH9hWGmI1yPHosqYBA3w++mvNaq252+Hg15DtqUgDKIwA+mFV\nfPhdCerkCj72F9yeZH1YgMrp8EkPxcSWcPEzcOGzYAZUvSGPLicTh1Nw/eNVeOidOnw/cTHvdJmO\nPzCagYin2GtJ2HmsNscptli1sYkEYzh+PoEcE+cr52F89SQof9Kd1VCqd6zF8O2jOaDLMazxWlYs\nOoBZCmIVoGkV2Pag4qzGmjPegcfWCJRO/c/uoQwCvtWaPK0ZCHxM6cYDx6/L2gTLZa0sBE8LwZyA\ny1qa79UpwFSlGAZcnAcX51qOqiS1YhWsZ9DrGmpWnw+btgpq3CT57pdANYBE5ouWQNueZZm1oSnl\n/X/yWs1H2LNyR+A7J8mPFIXzWLWdx2pTujhKOwAbm/8ZZBu8ei0e3Rfjs4fBUw5xcmpDcKa5GLzk\nSlY9+TX3XPAplaq7qFdKCkNKePkyuKIdXDgd3t4m0OhSfQIuC7yvNbOAe4WgAURXKDZJnAo00JrX\ngSeAqqUcD0AmcLHPxxohWKQ1ax0Ocv3+uIa3jRcJXKA1ZwL3KkGdPPCjU5YGUJgG5WD1eZr7fxR0\nuh8qlDVpUjO1MVSs7GTKl/WZ+dBeZnadhkhPg6YpeEMCeazi9cGIbWeh1PHjbZmmydy5c9m2bRvV\nq1dn5cqV3HrrrdSuXbu0Q7NJEqKEMclL/1ve5n8Wn89HVlYWOTk5ZGZmcuTIETIzMwHyl4tbV3hu\nmv/P3nmGR1G1Yfg+Z2ZLCqGL0kHpiICKAhYUFQEVEQuIDVGxVyyoIDaKgohiQcUOoiIioqCC0gRB\nQKnSBQRsiJSQbLac8/2YXdgkm2Q3W+IHc1/XXDs7c2bmze5m5pln3vOeALm5uZQvX77QsRo3PYHf\ntm8DkZ6qvw4CHgwjgDREmThSGvD7NIamTNzVQmir84mgbB26EBoOCq//Skxw6KSqgMfKMpAw9gCT\ngD+xPjNH2YYDWJ+TF0vAGoBplG08eYGgnynA5S6bfzhvnrLSVYUBhiM1aUhag9+DMNxk7/snYpNO\nnToxb968iOuSwbJly2jevDmTJk3C6/VSt25dTj31VNxud8pisEkaEX/UtrNqc1ig/CZIB9RvA1e8\nBY605B900TiYNQChA1zz8DFcclvVlCuit5/YyfRX/8bng/ubw11NUlMdoCgqfwDlhKAGMEBrqpRd\nKABsA27BEl81paSLUqTqdqY4FgHzgMFlHEckHFjpC48CHco2FMAaAataJngFjLsGmh5ddrH0nyz4\nZovE59Oc+lhHGvVomvIYpl/3GdsW/4vQJlq9BbJ58g8q/yTD2S35x4mS1q1bA7Bw4ULuvfde21E9\nArDFqs1hgcPhgsBk5JZb0WPPRd84AyrWSu5BXeWoeGxVThtxPhOvHM+aRbk8+l5tsiq+Aez9AAAg\nAElEQVSm7t8qvZzBifUNHr0oQM8XBd/9KfjgdEXNjJSFkA8DWOHWXOUT3OyH+7DqopaVfi6HJbye\nBMYAr2N15mlSRvGEcAA1hKCH1kwQAo8QXKkUdcs4rmFCMEBr9grBYK1pJwRvaY2zDGMSwNyL4NW1\nksvHKm47C57pUTaxpLsk7S6swCmdK/Dsjd+yY+42Lp58OTKFtq/pcsApNyKcbvTsXhAYBo7bk3tQ\n7U5pfn5J/Pjjj9SvX5/Vq1dTr1495s2bx+mnn17WYdkkkf/Cw0Mbm8QgqqB86+Gf+jDieNg0J7nH\nkxKtNHU7NeTqXwew5Q83vRuvYeWCEoZpTWQIhiCgoWMz+O0FjauSpukUmPhrykLIhwDSBHzt0ox2\nwvNC8EAZdioKjS2fCTykFBdhDSLwsZTklFFM4RwN3KU1p2rNG8BEyraCAVg3HJdozUfA30LQUgi+\nK8N4FJBuwrA2im8ugPELoOljkm27S9w04QS01Ru/Y8/KvLWiOXrbdt6o8xx/rfyj5I0ThFYapIE6\n/0m49mMwHkEELk5ehYD/IDNmzGDy5Mm0a9eOKVOmJHTYa5v/JrZYtTm8kBLN55D3ELzeBTH3+eR1\nsBHy4L5dWW4uX3Inx93QnrvP3cA7T+Wvh5ospHHoGuV2wswBmhf7wM0/CC6bI9mTl/QQ8hHeT7m3\nA9a5NQEJPaFMBE/BE1wHLJd1P/AC8EuqA4qAAZytNbcDO4VgmJT5ykmlkvDqCdWBcUrRF7g+OCVz\nJKniYjKDX2S7o2FdTzi1EjQbDKNnpTYWpaz/OYBj6rkY+2MTulxdgQ/avs6Cp5N8cxxEa22dewCa\ndIb+y6HieqRoAGpnSmIoawYOHMiNN97IU089xcUXX8xpp51W1iHZJBlbrNocnhgPQeBLmPEEcvyV\n4MtN/DGEUaiMTfunO3Hxt/348MXd3H7mBv75I4rBz+PAMEShkRevPR02PqfZ6IcGn8K3RYw2lQwK\nFtWpIGG2SzHcCcOF4FEp2Zu6cIDCvURtl7VoCtbJlUBPrfkA2Bx0WReUQUxmWFCZDnjzTMUHHeHx\nqXDqMMm+FH2BAQ0y7HG46ZDcNKwGQz9vwIpR8xh/ymvk7U/uHaJWYWIVoFJd9D3LoHl7BE3BPy2p\nx7exKQtssWpz+CLPRPvWwpofEaNOgn9/S/D+jYim7TGn1OaarQ+xx6jMVU1Xs/jr5NUoNEwRcfjH\nKlnw0xDFXRfARbPgzh8lnhTYYkVVgLzeAWvcmj1Bl3V+8kMBLNeyKDpgu6yRiPRAtRbwrtb0Bq4E\nbiZ1QloDZoSgLqhjuayVNdR9WDBpafJjCSgwIvyoWp+Vxbtrj6d6xVzeqPccv369MWkxhNIA8uFw\no3q9C92eBa4A791JO76NTVlgi1Wbwxt5VPLyWIVEF5EnZrqdXDK7Hy0f7cTDl2zm5ft34vclPi1A\nGqLYVLVHu8GyITDtD2g+VbA8yXl+xZUrryJhgUsxyAlPAI9Lyf7khnMwZ7UobJc1P8UNomAA1wRr\nxa4UgpZSsiRFMUUSqwBV02Da+YqRbTV93oauYwTeJN6UKQWyiGAqVHHwzPTjuGHwMUztPoEZN0xF\nJSGP1BKrkS/d+pQb4fZ5kP4hUp0M6r/wa7axiR9brNoc/iQrj1UYFHoGX4AT7z2dyxbdwfSJ+7nh\n5HX8viWxjwilAaqEv6XhMbDxOcXZrTXtvoRhqyK7sYlAiJJF1W0OWJUGOyX0AhYnJxQg+hNcB2yX\nFQCti3WjAeoBE7SmB3ApcBfJFdIF0wAKIgT0aQQrL4O//4baDwnmrk9OLAXTAArHIuh++1G8/ENT\n/vp2DW83fpF92xOc+KKh2F92zdbwwGqonYUQ9UD9nNjj29iUAbZYtTlySHQeq5RRad7Kzapx9a8P\nQu1aXNtiDbM/SVzfeMOwLqAlISW81he+egieXwttpwu2JMnWjKZf2dESfnQp7nVY9TyHJcnRFEQ/\nsontshbOWS0KE7hBKd4GFgnBiVKyIknxQJFGYj7qZsHCbpp7m0PnF+D6dxPfQd56Al9yz/Njj0/n\n7VXNaHOGk7ebvsjyccsSFkOhnNVIpFdC3fQN4oybQZ0GvhcTdnwbm7LAFqs2RxaJzGMVBiWMAHfo\nsKbJBVOvpf3o7jzdZxvDbviNvNz4r6TSiM0lPa0RbHtRc1R1OP4zeHtjYoslxDpqeX8n/JQG64Xl\nsibukn4onljpwJHrssb6U2gATNSarlpzEfAgiRXSiti+Q0PCAy01C7vD/DWC+o9IViewg7xfFU4X\nLQp3usEDb9Th4bfrMveeL/ik8/sof/yD2WqlolPvUqI6PQ7XTQLjUUTgoiOqvJXN4YUtVm2OPBKV\nxxpWuipamvU5iV6r7mPhd16ubfELW36Jz901HMXnrEbCacK0/ppx/eCeJYKLvpPs8sQVxkFicTJD\n1JLws1txo2mJnZFSkqBwSsxZLYoj2WWN9aLgAG4JxjNLCNpImTCBH6tYDdGiMqy8TNOjDrQZAo9M\nSVA8yurUGAtnXFKJd1Y3x9z1B6/VHskfy+JTz1pjpSBFS+Pzg+WtNiHFcUdMeSubwwtbrNocmSQi\nj1UWLl0VDVm1K9B7w/1ktWvCDSevZdob/0Tt0BbEMESpndHLT4Vfn9f8ZULDT2HG9tLtJ5xYndVw\nBrlgURosF3ClEKyMP5y4T3AdOLJc1mjTACLRBPhYazoCnYFBCYintGIVwGXAyFMV07vAuLnQ/HHJ\nzj1xxqMt9zZWjqrl4uUfmtD9xkp8ePobzBv0baljiCoNoCCV6qLvWQotzgyWt5pa6uPb2JQFtli1\nObKJJ49VytLZdoCUkvPeuZxzx/fmxft3MPDyrRzYF/sjQqPkPl7FUiEDFj2ueKQ7XDYHbvpBkhNH\nb+poOlgVx3ESVrkVVxqae4AXpSSeLmmJOMEdaS5rPAOHOoE7leJVYKoQnCIlm+LYXyL+njOqw/qe\n0CoLGg+CV+IoCKJ0bKZmOIYh6PN4dZ79qhG/jF3I+ye+imdP7E9WiqsGUCwON+qKt9AXjwR6gfeu\n2PdhY1NG2GLVxqbUeaylc1bDObZbU3pveIBf1hn0brKGtUsOxLS9lbMaf9LpfV1h1XCYvRsafyr4\ncVfp9hOPsxrOEBd8nwYLBVwlBGtLuZ/SpgFEogP5XdbSxpRIEu2yJuqzOh74RGvaAucAQ0q5n3ic\n1XCynPDeWYr3zoIBn0D7ZwTZpcg1seqsxhdRi9PK8d7a46lbw8u4+qPYOG1dbDvQcShmgDZ94fb5\nkP6RXd7K5v8GW6za2EDp8liN6DtYFUd6lUx6rbiHWpeexO1nrmfic39FvV/DjD1ntSjqVIX1IxXd\n22k6zIDByyX+mPctEpZD2UTCGqfiImmJsbFSEut4YIk+wYW7rJ9yeLqsifrM3MD9SvEi8AHQXkq2\nxriP4uq+loZu9ayBBDL8gjoDBJ/+FNv2ARVdNYCSKFfR5OnPjuXmYTX4oueHfHHN5KhrspYqDaAg\nNVvBA2vCylslumujjU1iscWqjU2IWPNYhZHQrvRnjr6QC77syztD/uLe8zaxZ1fJz+MNs/Bwq/Ey\n+hqYMxBe2wQnThNsiGEArkQ5qyGkhFFu+NYNs4BrhGBDjPtI/FAMh6/LGk/OalG0whL2J2B9bqNi\n2DZRzmo41dLhq86KoW00V78J3V4R+KNMfVE69g5WRSGE4MKbqjL2x2bs+WEDbzUYzd4tJZe10/Hk\nIoSTXtEqb3XmLaDOAN/o+PdpY5MkbLFqY1OQaPNYhYw7DaAgNc+sz9VbHuL37HL0bryan+YUXwxV\nmvHlrBbFSfVh22hFg/qallPh1XXRdeRKtFgN0dKA9S7FWYbmFuAtKYlGXyTgkl4kh6vLmoyLQhrw\niFI8B7wOnCkl0fRJT4ZYBSu3+qYmsPxS+G0n1BogWbg5ingijHQaL3WbpPHmimac1imNd44fw7JX\nfiy2falzViMhJeq8wXDdJ2AOQgQutMtb2fwnscWqjU0kosljlUZCa5SGcGa6uXThbTS9uwP3d9nI\n6wN/J1BE5X/DSLyzGsI0YdJd8MEd8MjPcN5MyZ8l9AeJt4NVcUgJr7rgKxdMA/oIwa8lbJNMsRqi\nA4ePy5rox+4FaYMl7BsApwEvl9A+WWI1xLHl4cfumjuaas55DvqNL16rqQSlARTE5Zbc83JtBk6o\nz4IBM/jonHfwFzFurFW6KsGX7sad4L4VUOnXYHmrBJQGsbFJILZYtbEpipLyWGXsdVZj4ZRHO9J9\n3q1MGbeHm9ut56/t3kJtDCNxOatFcVFr2PqCxpOhafQpTN1WfPv4y54Xz8kmbHIpTjY0NwLjhSjy\nmKk6wR0uLmsy0gAKkgk8rhTDsMR9Ryn5q4i2qfD4DAkPt9LMvxi+WS5oMFCy4c/IbQNKx93Bqjja\nX1iRd1YfT3rOLt6oPZKdiwqLRq2TYO8CVKpjlbc64SyEbgb+zxJ/DBubUmKLVRub4igujzWGEaxK\nS7XWNbh6ywA8FY7m6mZr+H5a/kKRpjM5aQAFyXTDvIGaIb3gqnlwzfeS/RF6OwlSE4+U8LYLPnPB\nxwJuFILiajikICTg8HBZU3VRaI8l7GsCbYE3I7RJttMbTqsqsOZyTdca0OopeOKLwm0C2hqII5lU\nreHkxXmNuez2Knx89pvMfvCb/A0S0cGqKEwX6vJx6O6jgCvBe2dyjmNjEyO2WLWxiYZIeazCSIn1\nYzpNun3VlzZDu/JYry2Mun073jzrwNKQKRGHIW49B9aOhKXZ0OhTWFDAEpNJTAOIxOkmbHZpGktN\nH+AjEbkaQQo/ov97lzWVF4UsYIhSPAEMBTpJSXgXowCpE6sAbhNeaKf4/HwYMxNOeFLyV1gHQ6Wt\n2sbJxjAEVz96DM/NasyGdxfz7gkvk7Pb+hUlzVkNp831cMf3kDEJqU4ClZ3c49nYlIAtVm1soqVg\nHmv2H0l3VsM54da29Pz5Hr6blsv1rdeyfaMHwySlMQBUrwirn1Fcezac+zU8uEziDT6HT1YHq+Iw\nJUx0w4cueF/ALRE676T2E7LowP+fy5pKJzOcDljCvhJwshBMCC5XWHnQqeasGtZAAk3SocFAwbjv\ng/Ho5OSsFkWzUzN5b+3xNGwQ4M1jR7H+0zVoBSm5dNdoCfevhjoVEeJUlEp2go+NTdGYZR2AjU04\nIeHlD9aSycuzxi/Kyck5WIdw7969hbbbsXMz0A4wQBoIYVjOp5AIgvMY1jwGaAOtTdAmKBOlHBAw\nQbgBF1aVSBdWP+bwKR3lvRP+fgne7UnAGWDrNxsw0hyYLgMjzcR0OzDdDhzpDqTbxHSbyAT13q1w\nbGWu2vwgM674gD4t13DJ7VUJlFHn3aFXwJXtoOsz8Pk2wScdrO+urPoSn2vCZqm5wgvXArcJQTet\ny0R8hQi5rLOxxNhxUtI1+DsuCwEdIuSyzgHeAJoDl5OanNWiqAiMUIpvsIZqnSAEI8rw+6vggokd\nFZM2Qd8P4b0fBF6fSqpY1VoTCEDApwn4Nf7g6x2jazHt9b95v+fHaCGgwW+wbTH486wp4D00Hz4d\nXO5B+HMRPg/4cxF+D/iCk9+D9nkObqMPbudFB7wovxfy9pHjd0U89wI0atQoaZ+JjQ2AKMGVKcvz\nqc3/OT6fjwMHDpCbm0tmZibZ2dlkZGSgtSYnJwen04nX68UIFtcPL4ptGAaBQOBgm7S0NLTWeDwe\nsrKyCh2rYcOT2Pn3TkSNE9GdX7Zyuvx5EAieeAN5h94fXB52Mg8t9+ciAh6E34MIeKzH/X7PwUn7\nPQe3Ufv/RAb+Rfk1mZWdaKVRAY3yawIBjQ5olNJoZYUjpEBKUWA+bBICYQRfC62XIIPrpUQYggO7\nDpC3Jwfhhxa1BVKAlNp6FVbHkYKTWWDeNILzxqH3+V5D8wY4jMLLQ8tGfwW/bAdnAF5wQgtpiR6J\n5dSFzx98Lwqvi2ZeULLbNs0PN3kFdYVguVKMpuzvzLOBMVLyl1LUAjxCcHuKXfFI/IElDD1CsF8p\nJgO1otxWBycV43xJ7f4BhgjBH1qjgEWXWfmiAW0V5g/NKx22vMC6iO+LaVNwX34NfgV+LdieDRM3\natwG1D8pg9qNM/B7LTHpC776vUGB6VXWe5/G79f4fQoVEp4Bq03Af+g8oQIaFcA6Zyjrty2k5eAK\nwcHzQOjc4c0L4PO7EY4MhHSQ7yYcE3TwZlw50MpEBxygHCAK3oS7yX8jngEiHUi35skAymHdcuWQ\nmd6dP/44VN8rMzMzut+I1syYMYO7774bpRR9+/blwQcfLNRu9uzZ3HPPPfh8PqpWrcp3330X1f5t\nDjsint1tsWqTNHw+H3v27MHv9yOlPChGhRBorTFNE7/fj8vlQkpJbm4uGRkZHDhw4KC4DX8NBALk\n5uZSvnz5Qsdq1qwdW7aMQDpvRpd3oXvNgPLRXnJLyT8b4bVGZFZOp3p9F3dNOolK1dMKNVNBERvw\nKetC5QufV0EXRR10U6xlh9qGLnbh2/h91sVu5/p9fDt6Mx4/XNQM2tYJuwAr8CkIaIE/YF10/cHl\nfgV+JQ7Oh7+Gts+3XFs9oUP7DeRray33+DV79x4Sk+FDneqC87qI5VG8DyFKmBRWzqMGHGHbREIU\nMV/UsuLeR9w+TF1na40MxpcpRKGTbPg5udC6Et6XdhsF+LBiD8keTfHfQcHvIvQqolwWcZ0IX2ad\nJ3yAywEOh3VDJoT1eYZudkRwmRQEb/o42O5Qe6tTXujVahu8sZMghEYaYAiNCN3QGflv8KSEb5ZC\nng9cldOpdeHxGC4T6TAwnCbSaSBdJobLxHAaGC4H0mW9Gm7z0KvbEZyseTPNgRGcTLeJNIu/rZpY\nayAH5PHw+08QeAHkdcW2Twj6d8qlt8onVsPp1KkT8+bNi7hOKUXDhg2ZNWsW1atX5+STT2bixIk0\nbtz4YJu9e/fSrl07vv76a2rUqMGuXbuoUqVKUv4Um/88EU/TZW022BzmhC7SLpfroBgVQpCdnY3b\n7SY7OxuHw1GofemohPKuR+y+AF47Aa6YCrVPi/MvKAZHGlJKzt02hoWdn+H+pt9y+4QTadXl6HzN\nZNAVMR2Jf8C6a2sO347ZzCM3wfNvwHFVJUM6K1z5/rMjyYvkUGOQoKqh2bgfhmYKbnFbgiCR6JAL\nBvixXkPziqAQx/pr/UDD3eAEKgN3AVUoLLoKpi6oAq8FRVukZeFtC64vKEBnAt9iCdcrsBJYQh9T\nwV9J6H3B9eHtCgr1gsuKaxe+v8uADAk1XTC2BtR1Bv06eUjEhs9LElefvjCaXzzQbiOccJxk1XbN\nGw9oLmpnrSsLalwh6PBYa757eSN/f7uOjjNuo2KTY1Iag/IH4OxHwbsPpl4Hgc9Af5LMLyIuFi9e\nTIMGDahTpw4APXv25LPPPssnVidMmECPHj2oUaMGgC1UbQphi1WbpGKaJj6fDyPYhTY+MRoNEh34\nEgJPwIROiHNHoE+8JTmHcqSjAwrpNGk/62E2vPgVo6/4gLP71OXKEU0xncm/eLizTPx+eOoe6H0h\ndOkDU1cJJl2rOaF60g9fCNMQDD9e41PQZwmMz5OML6eol8DOy0KAISyx5IzUoMDHbgIr0uBGn+Bh\nv+YWIbg46G6WFZuBP4Sgt9Y8IQS/CcFApahchjGBJWBXN4a+2wWdNmtG1BD0q6TLpJMTgFeDKQXf\nDVC8+q3gyqeg44mCTx7TlGBAJgWfX1OzRQUG/3w+nz68kmknD6fZA+fRelCXlMWg/QocaXDsuXB0\nK8RH3RB766N8s0Aem7I4omXHjh3UqnXoKVfNmjVZvHhxvjbr16/H5/Nx1llnkZ2dzZ133snVV1+d\n6lBt/sP8N2/FbGziZhD4JsPMAchpN1h5ponGkY4Oy7NtcEcnzlw2lAWf/cOAVrP5Y2Pyy724y5kE\nApbb2OQ42DRH0eFsTbsX4elZIuWdr6QU5AXggmNgexdNpUqa43fDS7nJG2mrxJgAU8BUl+Y9F7wN\n3CwF/4Uxeq4GftQaD9Ad+JKyzb3SQAUDZtTXjK8Nj/4OZ2yWbE3Cv0805KlDj+9v6ahZ/jTs+B1q\nXiGY/XPq4/H6wJVpYjoNLhvRkrumncmGF2fxeetheHanpryT8isw3dabivXRNyyFEy4AoyWoN1IS\nQ6Lx+/0sW7aM6dOnM2PGDJ588kk2btxY1mHZ/IewxarNYUwntHcVrPkG8XZ7yC5iWJrSYjhBk0+w\nlmtwDGf/OhrRtBEPtZzN/PHFlaqPH9OUCAm+YIF+KeH1p+Gb92DMQkGb0YJNu5IaQv54pOWGAbgM\nmNZOM/FUGOyB0/ZKfi2D6jcCKx0AoIsJm92aekJzHTCxmNGvUkUF4HOlGAo8KwS3FzOiU7JRgCvo\nonarANubajKEptlaePUfkcwB2yLi1WCE5ZEcWw0WDdbc1xm6PgxXDUntUPa+AKSVO5S21LhDNYas\nv5CadSSTj32MTR8uTXoM2h+wnNUQhhPVaQx0fx/MexH6QlCRh2otC2rUqMG2bYeGvdu+ffvBx/0h\natasSadOnXC73VSuXJkzzjiD5cuXpzpUm/8wtli1OcypicrbBH9lwNjj4fcEXkyCPTiUL7/ckVLS\n5uO7OGFcP8bdupKXrlqG50DyLh6GhLwCzle71vDbAkXtxpoTRsKrC1MjNAwJ3gLioaxdVimsjmAh\nnBI+dsPHLpgo4AYh2Jq6cIrkcmCZ1git6QF8Rmpd1tDXZoZdFdyybF3WPG2lfIRjSLi/i2bxYFi2\nVlCnl2TZ+tTE4/ODK0ysAmRUdHLr5PZcObo1C294j5kXvoryJ+//XQUUGIU7ctKoG/RbCVW2IR31\nQW1IWgyxcPLJJ7Nx40a2bt2K1+tl4sSJXHTRRfnadOvWjfnz5xMIBMjJyWHRokU0adKkjCK2+S9i\ni1WbIwAT7Z8NOdfCO2fAyvcStmdhSLQvsjdX64q2dFz3HKuX5XF/02/Z8vOeiO3ixTAKi1UA04RP\nX4EJL8CjX8E5YyW/7yvcLqGxSMiL8HGUpcsqIKJ72jE4+lULQ9MXeE8IytqPygQ+1ZrngdFCcJOU\n/J6iYxc3WlRZuaxeXfSIUc1qwvKnNNedBqffBbe9kHyX1R+AtPKOQsuFELS7ph6Pr+gCO39nUu2B\n/L1kW4Q9xI8OhKUBFKRCHXTfH6HlJWC0BvVqUmKIBcMwGDNmDOeddx7NmjWjZ8+eNGnShLFjx/La\na68B0LhxYzp16kSLFi049dRTuemmm2jatGkZR27zX8IWqzZHEM+C71344jbkN/dAAkZkERGc1XDc\nR1fg7DUjKdf5FB5rP48ZL2xO+IhTRYnVEBd1hG3zNYEKmsbD4eMkPl0zIzir4ZSFyyqhSBFqSnjP\nBdNcMEUI+gjBpuSGExUXAT9pTZbWXAZ8XMQwsonET/EXhLJwWb3ayoMuCocJT/ZQzH0Upi8QNLha\nsi5JmTf+YG640110b8Gq9TJ5ZNG5nN2vHjPOfI5F901OeBw6oMCZXnQDw4k673m45AMwH0TQpczT\nAs4//3zWrVvHhg0beOihhwDo168fN91008E2/fv3Z/Xq1axYsYI77rijrEK1+Y9ii1WbI4we4FsK\nP32IfP9syP235E2KQUiJ8pV8IWj9al9OntKfjx9fz/Aui8jenbirvCFFsWIVID0dZk/QjBoEN34s\nuOw9yb9JGLDekJq8ElRVql1WQcl5qe1M2ORStJOafsA4KfElL6SoSAcmas3LwFigr5RJ7RSmiG6o\n1VS6rHnKcutL4sR6sGaY5sIT4MR+MPDNJMTitQbAKKmiiWFKLnqsOfd/ezY7PvyBKc2e5MDOxDxV\n0doabASzGLEaouEFcPMqqPoH0lEP1C8JicHGpiywxarNEUgDVN5m2JkLY5vDX6tLvyspikwDKMjR\n5x5Px19fYOc/adzXeBZr5/9T+uOGh2CULFZDXH8ZbJyt2ZwHDYfBzATn+pmGLtZZDSdVLqsURTur\n+dpJeN0NX7thBnC1EKxLfDgx0xlYrjXVgjVZxyfJZQ0Q/QUhVS6rV1sCMaqYnPD8VYov+8MbX0DT\nPpJtCexTmeeLTjiHqH9KFZ5a25VGJ2YypckTrHvj+7hj0KF/EDNi0bbClK+F7rMIWl8OxsmgxsQd\ng41NWWCLVZsjFDfKtxj2d4U3T4G1U0q1F8tZjd4WdGalc8biJ6l+axeGdlrAJ4PXoQLxKbSS0gAK\nUqUSLJ2quPdm6P423DJZkpMgoeGIQaxCalzW8GoA0XCSARtcivOk5jbgVSnJS2xIMeME3tOat4B3\nsIT0lgQfo7ic1aJItsuaV0zOalGc0Rg2PAtt60Gz62HkRwmKxRd7LO5MB33fPYXr3zqFpfdN4quO\nL+D3lP6fTfkCiII9zkrCcKDOGQk9PgLHowjOK/O0ABubWLHFqs0RzmvgewmmXIWcMwh0bJ6VELGJ\n1RDNBvfgtDmPMWPsbwxuP5/dO3Jj3keIWJzVcAbcDCumw6zfoMkzgsUJ6A/ikOAphe2XTJdVkr8a\nQFTbSBjjhjlumCPgKiFYlZhw4uIsLJf1OK3pDbyTwE5hsTir4STTZbWc1dh/CJluGHeD4uM7YMh4\nOPFmya44n8RbzmrpRkc48ZJaPPlLV9J9e5lU+1F2zi7dIw3lCyBKO1JVgy5WWsBRu5GOOqDieKJk\nY5NibLFqY8O14FuAXvQqcuIFkLc/+k1jSAMoSMWT6nPu1jFkZ1ajf7NvWfbFH6XajzQknlJaf/Vq\nwfpZiku6ac56BR6dISjlnwOAy4Q8VboLerJc1mjTACJxvAG/OBU9DM3dwGgp8cQfUlyYwBvABKw6\nsVcmqFNYaZzVcJLhssaSBhCJ81vAxhFQvxIce5XgjS9Kv688H8g4YqlYPZ37Z5/NBQ81YVbXl5l3\nw3hUjOULtC+AiGf84qya6D4/wElXgXEKBJ4v/b5sbFKILVZtbABogc7bCNt+QzseIQUAACAASURB\nVLzeEnZHN3qK5ayW3tuSTpN2Mx+m4VO9eKHnEt65YyW+SLWfittHKZ3VcEY9AvM/gnd+FrR8TvBL\nKXP9nCZ4dHxjcybaZY2mg1VxSAnPuGBBGiwV0EsIymDwpEK0A35WihO05hrgtTg7hcUrViHxLmue\nAqMUzmo4FTPg49sV427Q9H8FTrtLsK8Ug03leUvvrIaQUnDevY14eOG57Jm9iikNHmffpr+j3l75\nAtYPMq4gTNTZw+GyyeB8HCE6giqjIcpsbKLEFqs2NgfJQnmXo/e0gddbw6avS95EFl1nNRaOu/08\nOvw8nAWf72ZAqzn8viH6q2kixCpAq2awdb6iVRvNSc/DqLki5rqVLgM8CXBDE+myFlVnNVYaS1jl\nVlxraO4HRkhJEgoqxIQEXgYmAVOAK+LoFBbAcqETQaJcVq8Gh5mYfJBL28C6ZyFDCur2Fnw0O7bt\nLWc1MR9QrRYVeWJVF1qdX4WpLYewcuSsqLZT8Tqr4Rx7HtyyGlHtANJRF9SKxOzXxiYJ2GLVxiYf\nEvQH4H0aPu6OXPgMxV1lS5uzGonMY6vRcfNoZPPGDGg1m3nvRVcwUhoyIWIVLNPm/ZEw9Q0YNhtO\ne0myLYbqXm5H6dMAIpEIl7W4Oqul4QkXLEmD1QJ6Aj8mcN+l5STgJ6VopzXXAy8JQaw/CctZTdx3\nlwiX1aMttz5RVCsPM/orRvbS9H0WOj0oiLa/kyVWE3fJdLgNer90IrdOas/qp7/gi7Yj8O4rPnc9\nrpzVSJSrjrr2e2jTB4x2EHg2cfu2sUkgtli1sYnIHeCbiZ47HPnpFeAr4iKSQLEKwaFaP7qTE8b1\n4607VjLmyqV4souXWtJMjLMaTse28NsCTflammbPwttLitXsB3GbkJvgukrxuqwijpzVoqgnYblb\ncZsDHgaGSEkpniwnFAmMAqYCM4TgUiGIpQtNItIAIhGPy+pB4EqgWAXr99DnDFg9FA7sE9S6QvBV\nFHcceb7iBygoLc07Vefp9RdQtYKPT+oNZNu0orvyJdRZDSENVIen4YrPwDUUwVl2WoDNfw5brNrY\nFElbtHcdbPgJMe4k2BvB6RQS7U98RftaV7Tl7PWj+GW5n/4lDNUqzcQ5q+E4nTD9Tc0bw+HeqYIL\n35L8XYIic5uUOChAaSmty1qaagDRMsAJK9Jgi4QrgIXJOUxMtACWKMV5WnMTMCrKTmGJTAMoSGld\nVo8WuAqPbpoQaleBuY8oBnaDSx6DSweDv5i7mjyfdWOYDMpVcXPXl2dw6ZAWzO35Bt9d8WbEzlfK\np0Ak6bJdryPcsgZxjC9YLWBZco5jY1MKbLFqY1MsVVDedbC7HrzWArbNy7c21jqrseA+qjxnrX6W\n8l1PtYZqHR15qFaRBGc1nCu6wpZ5mt0OaDQMPi/GrktzQoz9w2KiNC6rJHHlnSJRQ8ISl+JBBzwG\nDJaSfUk8XjRIYCgwHZgL9BCCkkbZTZazGk6sLmui0wAKIiXceZ7mpydh4zZB7V6S74swNhOdBlAQ\nIQRn9juOQcvOJ2/1ZibXHcjuVTvytUl4GkBBMo9GXTMHTu0HxhkQGJq8Y9nYxIAtVm1sSkSiA9PA\n0x8mnI9Y+vLBNVokpoNVcbR65XraTL2fj5/cwPDOi9j/T35lmixnNZyscrDgY8UT90PvCXDNRMn+\nCHad2yxdndVYicVlTUYaQCTudsKqNNgVdFnnpOCYJdEEWKwUF2vNrcBwKSkqKzIVYhVic1nztMCd\nJGc1nIbHwJLHNbedrTnvfrj+WQp1LszzWjeGyebohlkM+ul82l9Zky9OeZalg6YdXKd8AesHnUyk\ngTpjMPScBu4RCHEG6LIu2GZzpGOLVRubqHkEfFNg5iPIaX0h4AWMuEpXRUu1js05d8uL7PzXGqr1\nl7m7Dq6TjuSL1RC3Xw1rZ8JPu6HhcJi3Of/6NAfkJeuZewGidVkT3cGqOI6WsMCleMIJQ4XgYSmJ\noX9a0hgMzAKWABcHXwtipQGkQq5aROOyerQ1jGoqMA14pJtm4WMw/2dBvSslK8IK2FppAKm5ZJoO\nSY9hJ3DPjA5sHjubqS2H4NmVbTmryUoDKEjdDnDLL4jqIBxtUCq5N+U2NsWRxAcsNjapY8fOTSDb\ngXQgpAOEAyEcCJyAE5QTFXChA2lAJpAVnCoGp0pAZaBqcDoaKE/h+7lz0d7ViDXtEH+0RatA0p3V\nEGammzMWPcmaxyczrPNnXNi/IZcMaohwJDcNoCDVq8HKGYpBz0Pn1+GmtpIhnRVuB6Q7iGm41UQQ\ncll7LILj/4ThmYJb3Ppg/qUEUhwS/RxwmaG52CfoqeB+oCOpcS6L4lhggVIMA+4GzpeSe5QiI7i+\ntCNYxUPIZf1sD/TdDuP3SN6vpagTFKgeBWkpvkq1qA2rhmoGfiJoewf0uxCeuyW1YjVEw9OP4un1\nF/DuDT8y+bhBHHvD6dHlrGpt3Ux794M3u8BUcNl+pHcvIm8v5O2FvH3ovP2Ql432ZqN8ByBvNzl+\nV/L/YBubIrDFqs1hwVFVa7Ljz52I8o3QJ74EgPbtB392oUn49iD8exG+f8G3Fe3bB779aF822p8D\ngVwIeEAHQDojCGAHWjnQf63D7/SyeuAkNo/9Ful2YKQ5MdOdGOkujHQnRoYLM8OFmenGLOfGkZmG\nkeXGUT4NR1Y6zgrpmBXSMWOwj5o+dgnHXNiar7sOY/lXf6KUIrcMOu8+cTf0ugC6XA9TVwsmXaOD\nzmrqYwm5rNN+hz5LYHyeZHw5RT0jtc5qOJUkzHUp3pHwgE8wQwgeUooqZRBLOA8BvYErsVzWJ4C2\nBNMAykhNd6sAnbI0F2+BZmthRA1Bv0qavBQ6q+E4TRh+haL7iXD5GMHnCwU9TlcIR3wfUMCv8HkC\nwenQvD/CMm/uoXV121Tkj417WfN88Dzz+bWQtw88QWHp3Y/2ZqN9OVblkkAeIMBwBM9fToQwrXMY\nTtBOtHKiA260Pw1FOayb92OwkkcqBacqwQky0rrH9bfb2MSDLVZtDgscDif430fsewAW9ER3mAGV\nT47YVgenElE+S+D6stFBoRt6JSiE1cr7yN26C//u/TTs1RrlDeDP8eL/5wCB33zk5Xrx5/rwe3z4\nPX4CHh+BPL81ef0EvIFgBy2BNCXClEjDmoQpEYZEGsbB5cI0kKaBcBiY1SqxdeVOfDl+5vhh2Fhw\nmGGTw3p1OvK/LzQffO8san1w3ogw1GST42DTbMUtj0H7MXBGffDGM9xUnERyWYUAf9mFxLUO6G5o\nevjgSgX3lF0oB6kFzFOK54EHgLOk5HSlytT5jeSy/uvXtItSrCoFvkDY5Ldevf4Cy8PWhU/52oXN\n9ztLM3K65oVPwMg4wIf3/oQ3J2BNuQF8OX68uYHg5D8kQPMC+L0B/F5FwKsI+BVageEQ1v+4eej/\nXBrW/7owDYRhIEwDTBNME+0w0Q4HOqMmzgZZ5P36B3r5h6A7AadySFhWBo4KmzIP3qVFfc4rkt8R\nZXUnY2ODLVZtDisyUb554L8FZpwI7SdC9S6l3510gLOiNRWB8dvLOHq0Qk/+nN+//5VOn1xLVt1K\nMR9K+QMEPH78Hh8Bj7/AfEjoBudzfWHrW7B81ByWrNrPjyuhcUOBwxQEAoJAAAIB6yJ+8FWBUhql\nQAXC5rW1/uD7g20PvQqssdFNwxKuoVeHCaYhMJ2a7zZCIKBpNktgCoEhwBBWSSRTgCEEhrSWmcF1\nockMezUPbqPDlgXn0RG3Dz9Wp2qaCg54cLtG6ABzTfD5rL+h0BS8BkdcV2CiwGu0E8BDpmYGMMoP\nBlBNa+ZxSEiExIQuYoq0Lt72RwP3Ai8oxVdAVkAxdpflsga0NSnyvw9g/V78hCZBQAdfg+0OLTu0\njV9TaFkg3zKNCi4/2qFZuF+hgeemw9vzBf4A+AIafwBrCv6uA8HfqMb67g1pvUoZnIRVH9WaF4eW\nh5YZYa9G+CsYplWuqm4zzW9bfOz6y8/MlzaQeXZrHFXKIyu5kTVdyMw0jIw0jMw00sqlkZmZjpGV\ngVE+HZmVgVk+A6NCJtLtikv07f5kDttuG4e/Wh/U6mcg0BC4r9T7s7H5f8EWqzaHGRL0WPC/Dd9f\njmz6AKrpo0mrTai0E1m7Bq4tS9l/SV8+PH4EZ756KQ17t44tatNAZho4MmPPC9uzYReurZvJ2eVh\nx+Z9jHtFc2EcGj0SSoHXCzk5kJMLuR7IzbXeezyQ49F4PLDsJxjxPKzfr2lZQ9OzpbW9Lygq/JpD\nYkOHiY6wdQEFPn1IhARUUNAERbM/XEjroNDWoJRAaauTTmhZ/aNg/d+KSX6YIqB6pkSI/B15tM7v\nOoXWhYs7dOH34W0Kb6cLt9OgDaggNHt8mh1AXyDTKfM9fj8ohoX1ToStiCSYQ2/ChTdh84W2CV8u\nQKCpgeDv3AD7fXDPDqhTVeJ2WoJNCDCkRgqNlMH3BgdvOgypMSSY0lpvyuA6ad3QOMOWmYY1f/BV\nBm94wt6bofcGDJoMuz2QY0juHlKOWvVN3GkCV5rAnSZwpwvSMyTudKsusExiWach9+7ji5+rk169\nEtun/kSNYf2odmtqH42r3DwQTlSzx6Da+TD/EqR/Oso3C6iW0lhsbFKJLVZtDlOuA38r9C+XI/9Z\nhGo7ERzlEn4UrZzoXA/SNMmY+g55H3zKnFsfYMuU1Zz5xqW4yqcl/JgFcVdMQ/0KQ5e254sXt3Dt\nTWvpdI7gpecUlWI3eSMiJbjd1lTcLhs1gFdegxlvwuW3SV5ZqJnQW9OmdmLiKJ7IDztvnCRZ8afi\nt10SITXjT1e0qpyKeIpmxCp4eTMcyBNUS9e8f5amaYK+q9Ly8SZ4YJnkqKqwbqvi1T5wxalll8cK\nMOwLwf1jKjB1vIen797Lg89WoNfN6WXySHr/Xo3rqCzavH8TNT5bxuLrXuPf97/huBnPYGZlpiQG\nlZuHJljLq8op0HUtLOmH2N4Q7R8DXJ2SOGxsUo1dusrmMOYEtO9H+GsrYnoL2Lcu8Ycw0uFAzsG3\nrl7dydywiO3rc/ig0XB+//7XxB+zAK7K6eTut5LTut5Rl+c3nsWKrZk0bgWff5n0w+ejahXw5EHb\nVrB1vqJTJ81Zr8AdUyQH8lIbS4g0E47Kgu0vKk5toTltOty7RJJTFr2uwqiaJdgxXNOwjubkyTBo\niSyTzmkhvAFwOQWLXlKMvA1ueUdw/gjJzjKsvZWTB0dVNxg3vTIjx1fi+YH76HXGP+zYmvovb98e\njaNCOgA1urWm87phZFY0WVnncnZ9OCslMaicPDRhSbyOcqi2E9BtxoJ5G0J2BXwpicXGJpXYYtXm\nMCcL5ZuLzjkFvjoJdnye2N0b6YgD+cusyyqVyPjpW1Sf6/j8vNdY/OgMVBKGZA3hrpRO7r5DF6gK\nR7kYurQ93Z9owjU3CXpdJ9m9O2mHz0elilbnFKUsN/alwbDsc/h6Gxw3FGauT00c4bhNjddvxfPm\njbDoCfj8TzhuMszcmfp4wjFNmHgDfHsvvLMJmnwoWPhH2cSSp6xH7wB9O8PWCZo8NI0egNdnU+xI\nU8ki16upWMW6TJ3TLY2526uRkSno0uxPJrxyIOKIbskie6/CWTH94Hv3UVm0n3Y3rUb1YtsNw1l/\nfn+UJ7l3ZCo3j4CKkCpUpyd0WQkV/0I6agM/JjUOG5tUY4tVmyMD/TL4n4QFvZCrBoFOUOXNAs5q\nOBlPP0jGvKmsfOsnJp00mr2b/0nMMQuQVjWT3OzCTlPXO+oyOsUuq2lagicnTL83qg/rZipuuR66\nvw29J0h2R/7IkoLb1OSFfTzNa8GG5xQ3dYLu38GV8yT/lPEAPafUh1+fVnQ7SXPONLhlvmR/isuR\n5QXyV3zIyoTZozRvPQADPhKc/pRk81+pjcnjg8pHHbpMud2yzFzW/fsUzkr5U4mEENS97jQ6rR6C\nuW8PK2tfxt5vIg25kBhUTh5auyOvzKiDPucHaHILGB2wqvva2Bwe2GLV5gjiGvB/iV77KnJOZ/Du\njX+XZiY6u2jlZbZsTvqvS9hftzkfthjB2reXJNwNSjsqE8+ByBfscJf12hS5rA4HHIgwpueg22Hd\nLFibA8cOgY+Xp8atc5tWB6+CDL4E1o2E9X44djKM31w27mEIKWHU5bDiMZi7C479AL7YmrrjewNg\nmoU/gEvPhO0facpX1Bz/MDw3XRBIwSgLSlnlpELOajhl4bIe2K9wVomcm5pRuzJnzR9A04e7svHi\nAWzq+Tiq4HitCUAfyAUzvegG0kA1GwRnfwtpE5CO5sCfCY/DxibV2GLV5gijOdq3BHb9jph+POz9\nJb7dOTLQOcXbhNI0yZw8Dve40cy7+zO+uuQd8vYUNUJ77KQdXQ5vbvFpBqnMZXWYkH0g8rrq1WDp\nVMWwAXDTJEHncZIdCbhnKA6nAb5A5A451SvCkqcUI6+GOxYLOn4j2Zqd3HhK4tiqsHqwov/50GsW\n9PhG8lfifi5FkhcARwSxClZh/i+GaCY/Ds98CScNEvyyI7nx5HqDVQGKGDUq1S7rgWyFqwixCiCk\npMHd53Hu0sH4V69nVa1Lyf4xzvNLAXS2x3qaUxKhzlc1WiDMhsB7CY3DxibV2GLV5ggkE+Wbjc49\nHb4+GbZPKf2uzHLoItIACuK67EIyNy5i59YAExoOY+fcTSVvFAVp1crhy1MlOkupcllNU0R0VsPp\n1wu2ztd4MjWNh8OrCwVJMKIAcJngL0KshujbAba/qHFU0jSdAs+tTo17WBwPdILNQ2CnggYfwDvr\nkuv8ehUYRYjVEJ1Ohu0fahrX15w0CJ6YIvElSR9m5x3KoS2OVLmsuQcU7qNKriiS1bg65/70OMfd\neDrrOtzJlltHJcxlVQc8xTur4didr2wOI2yxanPkol8E/1BYeBVyxYDS5bGa5dA50Sc8ykoVyVjy\nNdx8I9M6v8Gih74kEOkZdQw4050IIfB6oos/2S6rwyEoJjPiIFnlYPYEzdsjYeDX0HaMYMPfiY0F\ngmJVlVzqKN0NXz2omXwPPLMWWn4uWJGijmlFUSUTFj6oeLk33PuD4MzPJb/uS86xPAFwOUpuZ5rw\nwaMwcwS8NgeaPyxYtiXx8RzIA4cZXYmqVLisebka19Hlo2orTYOmgy/mrLkPc2D6fNY0uJLcddvi\njiFwwANmjGWy6vSELqvszlc2/9fYYtXmCKc3+Geg17+JnH0uePfEtrkjC50b+zPa9MH3kbHwS1aN\nX8Gk1qPYu3FXzPsIx3RKPPujvzgn02UtLg0gEj06wY6FmuoNNC1HwtBZ1mhFicJpWAMJREunFrD9\nBU2rppq2X8IDSyW5ZVzmqvcp8NtwTblKmuYfwYjlIqa/KRpyAyIqsRqibTPY9oHizNaa05+E/h9I\nchPYKSzbYwnjWEiWy6q1xpuncVeLTqyGqHRiXTqtGULNrs355cQb2D74rbjiUDmlEKsAGbXtzlc2\n/9fYYtXGhqZo31L4ZzdienPYuzr6TR1Z6NzSdSU3mzcm/delHGjUig9bjuSXcYtLfWE1HPJgrdVY\nSIbL6nCWnAZQEKcTPn0Fpr8NYxYJjh8h+Gl7/LGA5awGYhS/pgnv3gwLH4dPfocGnwq++z0x8ZSW\ndCd8cbtm6m0wcpWg5STB8vjucfLhUbGJVbA6hb12Lyx6CT5dBo0eEMxPUDnjWJzVcJLhsubmaGuI\nYbez5MYFMNOctHyhN6dNu5vdr0xmzfHX4t1Zui+u1GIV7M5XNv/X2GLVxgaAdJRvFjrnbPj6FPjt\nk+g2c5ZHx1FbUUpJxkev4X7nJeb3n8aMbm/jKUVdJ9NpkLu/dHZkol1Wh4Oo0gAicUYb+G2Bon0H\nzWkvQf9pktw40+xcJqXOP21RGzaNUlzbUXPht3DN95J/y2hwgxAdm8CO4YqTG2naTYEHFiXG+fUE\nBKXQYgA0rw+bxit6dtSc/yzc/LZkf5ydwrI9YDpKP1JVIl3WA/s1pjO+UbOO6tCEzhuGU7VlDVY1\n7s0fL0Z5jgkjcCAPHFlxxVG489W78e3PxiYF2GLVxiYfz4N/BPxwHXL5A6BKEICO8ui8+NWLq3tn\nMjct5vedMKHRMHbM3hjT9qV1VsNJlMvqcuqiSs9GhZTwxtOw6FP4dD00HCaYE0dfNGccYjXE05fB\n2hGwMg+O/QQ++rXsy1y9dS0sfAg++Q0aThTMiXOAA48/upzV4nimH6wcB3M3wHH94euVpd/XgTxw\nOOK7RCXKZT2wX2HGGQuAIyuNk9+7kVPe78fvg95g7ak349+zP+rtVa4nMcNG5+t8dTtCdsHufGXz\nX8YWqzY2hbgc/N/AhneRs88BbzHjTToroPMSk6gnK5QnY/EMxB238MUF41jYfxoBb3QXVukw8WTH\nn+iZCJfV6dKldlbDad4QNs1WXN1T03UcXP+hZG8p3DqXAX4Vv7KsWQl+eloxrDf0+0Fw3kzJbzHk\n5iaDFjVh01OKq9trLpgO182W7CnlvZNHQVqEwZFipd4xsOYtxZ2XQo8XoPcrkt2lKAeWnQemKz43\nM0S8LuuB/RojAWI1RI2LWtF5/TDKVXGxst4V7PpgZlTbBTxecMSWN1ssBztf/W13vrL5T2OLVRub\niDRE+ZbBP/vgy2bw74rIzRwV0d7EOhLpj95Nxg8zWPPRGj5uNYp/15U8bJB0mnE7q+HE47KmuRMj\nVkMMuQ/WfA1L/oX6Q+CzVbFt7zRJaFmsm86G38ZodHlNk0/hhV/KvszVkO6w+nH4eT/UnwCTN8e+\nD48f0kqZBhCJR3rDunfgl78sl3VyjDroQB44EiCeQ8Tjsh7I1hiOGHt7lRRP1SzafX4XrV+4km03\nPcP6c+8tcbhWlZuXWLEKducrm/8LbLFqY1MkbpT/G8g9H2a2g60TCzdxVgKfL+F1Hc2mDUnf/CM5\nx7fh4xNHsWbsD8UeQ7oSK1ah9C5rRgbsy06MIxaidnVY8aVi0D1wzURBt7ckf0b59NTKWU3s95Pp\nhpkDNB/eCU+vhhO/EKwqxoBPBbUrwc8DFU92h+vnCLpOl+yMwfn1BMCdQHEIUL0KLBureKovXP+G\n4MLnJH9EWXAj2wOOIkYWjYfSuKwH9iukM7FiFazhWutc3Z7z1wzBkbuflbUuZc9Xi4tsr/J84KyQ\n8Djszlc2/3VssWpjUyIjwD8KFt+I/OleUGGi0HSDEOBLfL6XlJKMCS/jHv8qCwZMZ/oFb+L5J7L6\nkG5HTKWrYiFWl7VcZuLFaoi7roNf52p2OTQNhsJbi0vOHXUZ8eesFkXXVrDjRU2zhppTvoCHf5J4\nyrjM1W0dYMtQTbZT02givLoGotHq3kBindVwbu0GWz7Q7PZqGj4A78wr+XvL9oAryvr3sRKry3pg\nv06KWA2RXqsyHeY+RLOBF7LpkkfYeNljKH/heLTXZ90gJ4tQ56uaJ9idr2z+U9hi1cYmKnqAfyZs\n+gD53VmQ98+hVaZZ6vJV0eC68DwyNi/mj10OJjQcxm8z1xdqI9yOUlcDiIZYXNZy5ZInVgEqVYDv\nP9KMHQr9vxCc+bLk13+Kbp/oNICCmCaMvxXmDoIPtkOjKYJ5ZWxKVUiHOfdp3u4DA5cK2k4RrC/B\n0fQENBlJcDIPxpQJ37+geeVuuGeC4Oxhkm3FVHDalydwZybvdwTRu6wH9iurvloSEVJy3J3ncu6y\nx1HrNrGq9mXsX7QmXxtLrFZMahw4yqFOHW93vrL5T2GLVZv/G0IXEaVUoSkZwysWpgHKtxR258H0\n5vDvzwAI04AkilUAmZVFxsIvEPfdyfSL3+b7e6YSyDvkvJiZLnL2JE+shgi5rMuLcVkrlIf9Keh4\n1OtCazCBzBqa5iNg5JzIuaMuEwIp+H2cWA9+fV7R80xN55lw/YLSd3ZKFD1aw47hmprVNa0mwZPL\nBEUNmOYNJKaDVUn0PscastWRpmn6ELz0TeShdvfmCDLLJf8SVchlPb2wy3pgv6bUdb1iJKvRMZyz\nbDDH9TuT9WffxZabR1rnOKXQ/gA4kpAGEImwzlfCcRJKBSKee5VSOBxxlpGwsSmB5D3XsLFJACER\n6vF48Acfi2VnF+5avGPHr0AnEC6EcIBwIoQTcCJwoZQLrdKALKACUBGoBFQBqgJHAf9j77zDpCi2\nPvxW9aQNwBIkLDmDElXAwDUjiooB9IJZ8SIqekW9FwNes2LWTzFgABNiFgNBEAwoUVAk57BkWDbN\n7qSu+v7omQ2wYXZ3Zhal3+eZp1N1z9ma2Z5fnzp1Tnp4vbx/Cw8qNB1Co2FmX+j9OhgOdH41k0pG\nSfLdIwldfC6rz/0nW6at4pwvrqVe50a4anvIr8pU+SqQ1tDN2N9O5tuXNnP18NWcc5Zg3HOKeuHR\nyTp1ICcvMXmdPB6Y+rZm5ly4+g7BO4vggys0XZsUtYlnGEBpPDkEbj4LBj4LbT6HN0+CS1om7v0P\nxuWAz26Eueth6BuCd9fApDM1vRqWbOePs2e1OMke+O4pzde/wrCnYeJcwQcjNB2KfW65PkFK7fh6\nVotz1oVJ9O3v5paLDzDgmN2MfjqNoSOSEULgzdXopAR1DuFyrQ9cSJMLuvPr4HGsbLeQ1p8/Cg7D\nyltWGbSGkBeC2RDMCb8OXs9GBA8ggwcgkIkOZEEgGx3MQQdzIJhFvukuce9t0qRJibcRovTPKjGO\nBJu/O7ZYtTksUWFXS36+Na1cSonH48Hn81G79qFJsRs3Tidjxx6E0QCd9hqIZLTKAZ0NKgd0Dqgs\nJAcQ+gCozWjzD1DZaJWDVnmg8oEA4LREr3QWCV7hAu1CqaSw6K0DZidYOBydLAnNX4LOyoEkDyI5\nCZHkQSR5rO3K1oysAEfHtiSvX0jBtf/m014vcNJTF+BKS8J7YG9M36cizru1FSf/swlPnruYTj1z\neOtVuGAA1E2jWnlWq0K/vlYxgevuhhNehNtPFfyvn8btiE2e1crSsgH8kzsblwAAIABJREFU8YRi\n3Ey4/iPBG+sFb56gaJqSWDuK07cdbHlCMfIjOO0rGHa05IleipSwU8xvkjCxGuGCkywv65DHoecY\nuP9iwV3nahwG5BRAkzqJHfyLeFlnTSng3mFZfDWpgGffTyMnC4xaSQmxQZkKsyCAWRDA1aAWJ39x\nK3+M+pDVJ90MCNj2eQnBKYIHkIFMCB6AQBY6kBUWmXmWSDV9IBxghO9j4fuawLqnadODCiWhqYVJ\nGtAU6EbRg3wjQJKSfHmJe6/XWzR80r9/f37++ecy/6bp06dz++23o5Ri2LBhjB49usTxnJwcrrzy\nSrZu3Yppmtx5551ce+21setUm788tli1OawIhicqRUSqx+OhoKAAl8uFWU7NTIfDCepJYDzsvxTq\nfwZJ/Q9pV6Fm0SboXFA5aJWN1jnFxG5E+GYhyUToWmizDsqcj3fkvSAkAtCmiQ6FIGRCKGRNwHI5\nES4Xwu1CeNwIjyVmRXISMiUJkpMRKUmI5GRISUanJENqstXGExa9SUXnkOTBPepGZO9jmXfv4xgO\nQbuuyQR8JoZTYhiJ8UhFYlm/fWkz1wxfTf+zBKefosjLT7w3xeGA956BUdfBJSMEk5bAB5drjm4c\n35jV8rilH1x1subC56HTFzD2eMFNHWvO0yQlvDIUbjsdLnoFPv4Q3j0dzm4OwRoQq2CFgn7+IPz0\nBwx5VPDeXPjwZk2eD2rXSZxntTgRL+vNF1le1kbNHIhOBt6t+wuFpJkfwCwIFm0XWw/lh497/Zh5\nAUxvgFC+H9PrJ+T1W8d94XN8AUx/CNMfRAdNtKkQTgPpMBCGRDgMhGFgJCehvAXoBcOQoh7oVFQw\nGU0qJrWxRoc6AvWxBGZDoLH10h4IQeSbV/lv4K4yPacVoZRi5MiRfP/996Snp9OrVy8uvPBCOnXq\nVNhm3LhxHHPMMXz11Vfs27ePjh07cuWVV+KI8YO+zV8X+5tgU+OYplk4xB9ZpqSk4PV6MQyjEldy\noNWLwPuw73xknf+gUu8HUYlrCANEGsjy48KKax+xvxm6TivYuxR5yyj0v+9ChmO4lFLg9UJWJjo7\nG52TBdnZkJsLuTnW0psL3jzLHbnXC1sPQEE+wu9HBgOIUMDKNhAKgRlCh4IQMtGmJYiVKQl6faz6\npYArUr9DmZY+loZAOgSGQ2A4JIbTWjqcEsMlcLokhlPidEkcbmu/0x1ed0mcboHTHdkncLglLo/A\ncEocLoHDZV3T4ZKkpDkZ8mRnPn1gLV99q0hN1sz6BQwDDGktHUbJ7RLr0hKbxbcPbhM5v6JR0GOP\ngY0/Kv4zFs4eD5f2kIR0zSVCrZ0Mc+7TTPkN/vUGvL1ecGzdmh0a7dQYVj+seGwqDJoG57eS5AVV\nlcSqUpbn2lRgmsXWlfW8dvC+4u1CxY45HPDhGMU9b8AJD4KUJk0zQnz3RQHBgCYU1AQChNetZTCg\nCQYh4IOAH4IB8Ps0AT8E/JpgwFoG/JpgUIfbWOvBgCYU0IRC1nYo/DJNMEPWUisQEnZuC+Jb9zvT\nZ61EOh0Iw0AYDjAMhOEEw4l2ONGGC2W4MA0P2pkE7iTw1AZPKnhSoGEqJNWClNqQXNtaptaBWnUh\ntS7UqgfJqWgpOeTRfMOfiFtPRToHoryfgRoGjKj+lyHOLFy4kPbt29OypRULM2TIEKZMmVJCrAoh\nyM21ctHl5uZSv359W6jalMD+NtjUGIGAVfnJ5/MV3piSkpLIy8ur8lO8xZWge6Nz/4v0zUbV+xSM\nhhWfVkWk9GCeOApqN0NPGARTPkWPfwfRuQtSSmt6fK1a0Lzy19ZU7AWRgPryU8w7b8HlEtTvfBSn\nvD6I5Ma1CHoDmPlBgt4AoYIgofwgwXw/ZkHQ2i4IWd4gn0nIF8T0hQj4g5h+E9MfQuWGMPdb62bA\nRAVMCAUhpCwPsqnQIUttaFNh1K6FiwL8Xh+DbwWnSyIdEq0ArdHaimGzlqBU0XrxY0oV7VPaEg1K\nF6U7ksISEVJY4jXyMg5ed8HkJQqtoeXtAiEoelG0bl1TlNjPQW2Kr8sS+8u4bvE2wrK1U3PN/LWK\n5ZmQ7NKc8YJh/Z2E/z4o2R8ctNSgKdZ/lN2Wg/ap8MrB75Pk0Xy+QRFUMOhBcDhEWEBqlAqL0fBn\nEvlcVGQ7/HlE/r7if2vhurTESIk+KtwWhW0QonA7tQ7kZgf5+sMCpk8xcddJKeXJRaINBzgNhMuJ\ndBpItwPpsl5GLQfS7cRwO5AeJ4bHhZHkwuNxkJLkxEhyWfuT3ThS3BhJThzJboxUF45kN44UF9Lj\nQkrJnJMew7cpiJm9F3X90+iBI4q+OInCm40wPKg6E8F9GWReiRSfosyPseLvD0+2b99O8+ZFN79m\nzZqxcGHJXLIjR45k4MCBpKenk5eXx0cffZRoM20Oc2yxapNQQqFQofc0EpeanGxNYgjGNFdpB7Q5\nGfRdsKsz1P8CPKfE8PrF8YAvG44ehBq5Fb66HgacgbxlFOrfdyESMVO2dRuEwyAlYwkHht7EZ31e\n5Nj/nknPu0/HcCf239z0h3g9aTSNzjiarHlruPDeDlzwn3Y4XLGJPwyFFKGAIuQPLwMKM7wMBbW1\nHgzvD2pCQcVTA+az1y9JqS0ZeldDGjR1WcJNgVbaEl3hpVYRcWypQWtfUZsSYlqFBXZEuBUe18WO\nlxTirRUsnpXDmiX5zFljcsKAOnQ8LsUSbxFhJy3xTDFRLqQo1iayLYodP/h8QAprKUAWPz98/eLX\nfODS9eQqJ8kpLi55rBsN26ZaXvSw1126Il55y9tuuCwPvOGQ1Xy4LJ3b6n+G87Te5E5fSMPBx9Hl\nycE4U2sgTgHw7c2BYc9Aci14ahhy5iTUmPehcQJnznmzETKckSBpADReB9k3IAqOR6vHgSGJsyXG\nzJgxg549ezJ79mw2bNhAv379WLZsGampqTVtms1hgi1WbRJCxIsaCAQKvagejycGXtTy8KDVy8AE\n2Hcuss69qNR7rF/mGKJVWKyC5SK6aCJk3HSIlzWutG6HzstDuN2kfDGB4K+L+OPyEayasJAz3x1C\n+ilt4/v+xTDcDqTT4Lh3byJv/S5mXDWO78dvZsTbPely5lHVvr7DIXE4JFQiYbw72eDin29m/n0z\nGD9mPUPuaMzV9zbCnVQz2ftS0wxydBotz+vAkmfmYhgGo15pwVFNE5MeqTS0hkGbHuaX6z7gvREL\nOe+eLpzz3044XJUJxYkdvtwg7V+5AzPHy8YL7mFbu9H0fu9fNO4X5/+lUvBneiG9DXQ5Cd2rP4y5\nCK49BnFTAr2sedmgi+UWM+qj6n0B+R9C5o0IJqP1JCr1j5EAmjZtytatWwu3MzIyaNq0aYk2EyZM\n4J577gGgbdu2tG7dmtWrV3P88ccn1Fabwxc7z6pN3NBa4/f7C9fB8qK64pxc+1CuA/0COud55P5+\nYJaTibwKqFAK+A6qtdmsD2rkVnTqCegBZyCeeQIdhypXEWTt2mAY6OwcAJwn9SJ54yKCl/6Tb857\ni9lXfVhm9at44KrlIW/jHo46pTNnbXmZBledxbMXL+S5ixeRuSMxKbaK4/QYmP4QA7+9jotm38g3\nk/K5rO1y5k3NTrgtxen7v9O4YdMoMrJSubLjMj5+bhehUOLjWUNBBRrc9VI46+sR9JtxK9+/vokx\nnaey7pfEZpkACBSEUKbGcVQaSe2bc8zq96l/62B+veRlFl7xOv7MQ9PXxQutNcGcfGjWwdrh9qCf\nng5jPoC37kfeegrs2hJ/Q7zZ1oPxwSQPhSarER4DIbsD0+JvSyXo1asX69evZ8uWLQQCASZPnszA\ngQNLtGnZsiWzZs0CYPfu3axdu5Y2bdrUhLk2hym2WLWJG0KIwmTRbncCso2Xy9Fo9REE9lphAf5f\nY3dpmYb0lVJCKeJlvXI2esJEOOME9KrlsXvfgxAeD3pfUVkpKSUpT95H6oq5bF5VwPttH2f1O4sT\nkvfQnZZEwdaiPuny6GWcufFFtu5P4Y4O3/PtsxswQ4mb9ORKMvBlWiK5SZ8WXLVhNB1uOZ0Hhm7m\nznM2sGtLzWXvT66fwpAfr+f8T4bywTP7uObo5Syfl5tQG3z5CodLWDHWQOO+7Ri05VEaDjyO5/rP\nYeKwheRnBRJmj/dAAKfHKLQHoOl9V9NlzQfsX72fqW3/y7ZPFyXkuxzy+i3PaVqDkgf6Xoj+JAOd\nlGJ5Wae8WnEN2ergzUaFyvCaGumo+rMh7TEQN4K4Cqjhur9hDMPg5Zdf5uyzz+aYY45hyJAhdO7c\nmddff53x48cDMGbMGH799Ve6detGv379eOqpp6hX7/CNw7VJPLZYtYkrsrIJrOOKB2W+Cuo82NsP\nmfdUbH5cZD1EQRm1RyFhXlbp8aD2HmqH0awJKQtn4HzhCebe8Q1fnjyOrLXx9ZZ56qVQkFHSFk+D\n2vT96X8c/+kopjy3hTs7z2b13HLqpMYQV5KBP7Nk8tc+953ONdvuY7fZgCuPXsnER3YR8Ndc1oC2\n57bnXxl30fDsLtzZby1jr91MTmZiBIfPqzAcJf9XpZSc8PxgLlpxP6sXebm7zVcs+nhLQgSiNzOA\nw3NolJorvQGdf3uD9LE3sfiGCfwy4HkKdhwo5Qqxw783F6Os6lUJ9LKK3AOgapXTQKBTRkDjPxCu\n3QijGzA/LrZUlnPOOYc1a9awbt067r77bgBuvPFGhg8fDlgFBmbMmMGyZctYtmwZQ4cOrUlzbQ5D\nDiclYWOTIP4F+ll09pPIzHNAVfPHTtaHggqukQAvq0hKQu8tW/x5rr6UlG1LyWzYgY97PsuiB2aU\nKNkaS5KPSsG3s/Ri9I3P6c5Z216m1vl9GXvuPMZdsYTsPfH1bLpTHPizDy2J667t4aKZwzh/xr/4\n/K1chrRfwaKZOXG1pTyklPR7+TyuXXErfywTDGnzB1Mn7I27QPTlKwxH6XGXtVrWZ+Cy++j++MW8\nc+Ninj3rB/Ztju8wvDczgOEue2JioxsH0nXLx3jzBdM63sPGN36MWx9ZYrWCkaEEeFlF7v4KU+oB\n4GiLPmoBovYoEJcCtxBFhmkbm8MaW6zaHKF0RavJ4M8IhwUsrPiUsjAaoisSqxHi6WVNSkbtK8fD\ni+V9Tf38LZJnfc6f7yxjUoexbP9xQ2zevxieo1Lx7yk7HlRKSffnr+TMNc+zZr3B7e1m8t24TSgz\nPoLDnVy6WI3QrG8rrt58D62u7ct9gzdx94Wb2JORuGHvg6nTMo2rltzEaS9dwCv/2cGI3qvYtCJ+\nZcH8+QrpKP/noPOIfzB422PkOepw/zFTmf7UqriFcngz/cik8gWio04tOv74f7SacA/L7vmUOSc/\nTt6GPTG3JbAvF+GOonpVnL2sIifTejCOqrGBSh0NDRcgnEuRRk8gfiFINjbxxharNkcwyShzPJhn\nwt7TEXnPV80bIhsVZQOIqn18vKwqORW9L7phdWefnqRsXExwyOVMPf8tZl0xiYJ9sfOWeRqm4t9b\ncdxlUnpdTlnwCD0m3sInj6xndLc5bFgU+2FdT6qBP6tssRrhpIf7cfWme9iaU4fLO63ggyd3EwrW\nXAL/Llf1YPiO/yDatuTG3it55c4MCrxlV3KrKgVe85AwgNJwpXo4e8ZIzvzqJqa/uJ7/dZnKpkWx\nD+XwZgascsVRUG/waXTL+AzV4ChmdBvDmqenoWJYX9e/NxftqkSd3Hh5WXMyQTaouF1xXF3QjZZB\n6pUgzgXur74dNjY1gC1WbWy4GfRYyH4EmXkBqNKHr8vEaIz2V2HoOMZeVpVWD3ZXLtNByhP3kLrq\nF7au9fNB2ydYPTE2k1Y8RyUTyo7eE9j0kl702/EqzpOP5ZHTfmH8DX+Qlxk7z6Yn1UkwN7pQA0+9\nZC6ZM5wBU65l8stZDO24giU/JHbCU3EcLgcDJ1/K0HnDmfONjyGtl/HzlwdiOuztz1dIZ/SZDNPP\n7MjgbY+RdlpXnjrte96/aTEFObGLw/ZmBtDJ0QtE6XHT7qsnaPfVWFY/9x0ze/yPrD+3xcQW/75c\nQu7alTspDl5WnZsFsgrFTYQLVfsJOGo2wvE10ugNbK6WLTY2icYWqzY2AByLVh+Cfz3sOhoCS6I/\n1WiK9lfRK1mal3VlFb2sRzVE79xdeRPSG5OyYDqucU8z965v+eLElziwpnrDqe56yWhv5cSmlJJj\nx9/A6Suf5s/fQtzWZiZz3t6CUjEQz6kGgbzKxcW2OLM9V225h/RL+zD6gg3cf+lm9u2MX/qximjU\nrTHXrbmNnqNP54lrN3PX2evYuTk2sb4+b8VhAAcjpeTk14Yy8Pd7+POnbO5u8xVLvoyNQMzb50fX\nqXxC+DpnHkfX7Z/j7Hk035/wCMvv+wzTX73PzL8rBzMlyuH3g4mhl1V7s8FoVDU7ANx90I1WQ0o/\nEKcAz1X9WjY2CcYWqzY2haSizLfA/Afs+QfC+3J0PyyOZhCsZjxhcS/reacjnn688l7W9HTUrqrP\n8ndffjEpGX9wIP1oPun5HAvvn07IV7Ufek+9ZMyCqnlGU1oexalLn6DLuBv4YPRqxvT6iS1/VC8f\nqifVQSC38vZIKfnHk+dy1Ya7Wb8zhaEdlvPR83tqJBdqhN53nsS/tt3FAVmfa4/5k/ce20kwUL1h\nb1++QlTCs1qcOu0bceGK+zlmzHm8fe0CXjjnRzIzqvf/kLs7gKNBFJOJSkFKSZt376PTTy+z+YOF\nTO90D/vmra+yLb6d2VCvcZXPj5WXVefngpFedTsAZDKqzqvQYAoY45HGKUDlH3BtbBKNLVZtbA7h\nNtCPQtb9yAOXgKpgiD8yQzdYcUxk+deJeFnnoCe+U3kva7MWqD3Vix+ULhepn75B8pzPWf7+cia1\nH0vG7HWVvo67XjKmr3rD+C2uOJmzd76K2bkz/zvpJyaO/JP8Kg41e2obhCrp6S1OcsNUBs29ibM/\nuor3nt7PlZ1XsuyXxCWmPxh3LTeDZ1zFxdOu5vPXD3Blxz9Z+kPVsxj48hXSVb2Chl1uP4PBWx8j\nM5DMmE7fMPOFNVWOHc3d48fZqGpiNULKcR05euNkal1yOj/1e5qlN79HMK/y/6O+XTlQv5oiEarv\nZfV5rQfjWOA50yrXmtQNZB/g7dhc18YmTthi1camVHpbYQG+lYhdx0Dgj/KbO9zgj1E1pKp6WZu3\nxNxffjaAaHH26knKhkWYV13FtAsnMGvo+xTsjV6ceeonY1bRK1sc6XDQ6/2bOe23J1g0J5/bWs3k\nlw8zKh2v6U41COVX357WAzpxdcZ9NBhwLHf0X89DV2zhwJ6aCw1ocUorhm2+g5aXHc/dF6zjwcs2\nkrm78vb4vCZUU6wCuGoncc7sf3PKxzfwzdg1PNh9OluWVv47mbvPh7NJFYfeiyGlpMWzI+m89C12\nzFnHtHaj2fVd5cJsfHuyoVGLatsCVN3LqhQE/SBjIJojyDqoupOg7rsgH0Ua5wI1l7bNxqY8bLFq\nY1MmtVDm22izF+w5CeF9vUxPiJAu8FVyYlZ5VMXL2rYdKju2E4GSHx1N6pp5bN1g8n67J1j15oKo\nhKKnXjKhasYKFqdWp3ROX/E0HcZewdsjl/PgyXPZvir6v9WdbKBjlFNWSslpL17AlWv/y8r1Hv7Z\nbjmfj9uLGae0W1HZ82Q/hq27nfXb3FzefhlfjttTKXv8+QrhKjuvaWVpMaALl25/jOReHRnbdxaT\nb1+K3xt9/+dl+nE1q8JkojJIat+cY1a9R/1bL+XXwS+z4PLXoi7Z6t+fB+mtY2YLUHkva34uGE6Q\ncShVnXwRNF4L7gYI2RP4PPbvYWNTTWyxamNTIXeCfgiyRiMPXAaqlB85w1W59FXRUhkva5OmEAyi\n/bFNsC8bNyRl/lTcrzzDL3dP5/M+/0fmqvLj3Nx1Lc+qUrHNw9lm+Jn02/4K3iatuff4H5j0n5X4\nohBB7hQDHYhtyqfU9NpcuuAWzpg4lLce2cs13VaxcqE3pu9RKXsa1+Lyef/inImDeOvh3dzQYyVr\nl0Rnj8+rICm2QkgaBqdMuIrzF47mt6n7uLvNVyybuj2qc/Oz/Lhbxk6sRmh631V0WTuJzLWZVsnW\nTxZW+PAVOOCF9HYxt6VSXlZvNjjjIFQjGA1R9b5Bp70AYhRCDgaqGdZkYxNDbLFqYxMVJ6LVB+Bb\nitjdBQIlvZxCuGIXBnAwUXpZpZSIJA+qnCpW1cE99CJSMn4nu2VXPj3+BRbeO63MCViOJCdCSgL7\nYx/X6fC4OOGz2+n7y0PMnZLFv1vPZNEXO8oVHe5kAxWIT7Wudpd04ZodY6jVtwu3nbGOJ67bSvb+\nmqvL3uGSo7lx+12k9GrPrf9YxXM3bSUvu3x78nM1juT4iKG6xzTh4rUP0GHU2bw+dB4vX/gzWTsL\nyj3HlxvE3SqGQ97FcDWuT+fFb5D+5E0s/tfEcku2qmDIyibQJMae1eJE42XNy0YYFVTRqi5CQMo1\n0HgFwhVAyO7A7Pi+p41NlNhi1cYmatJQ5jvoUDfYcwJ4iyYlCOGOj2e1OFF4WYXHg94Xv1rp0uUi\n5aPXSf7hC5Z/tIoP2j3BtllrS23rrOXGuzH2FYUi1O3RijPWPkfLuwfx6vV/8NiZ89i9oXRPoivZ\nQAVjn0w/gpSSM1+/hKEr7mTJHw4ubbOcr8bvi0narSrZ4zAY8PZFXPX7LSyYazKk9TK+n7y/TEFf\nkKtwpsbRcwd0v/tsBm16mN37ndzb4WvmvLKu1P4JBUzMoMKRXv2Y1fJoNHwgXbd+grdAWiVbx/9w\nSP/49+dheJzgqH48b7lU5GX1ZluhRonA0QLV4Ceocz+Ia0BcD9Tcw5eNDdhi1eZvQrxrp5dkNOj7\nEFl3IA9cASof8MRfrEKFXlbhiZ9ntTjO47qTsm4B6rrrmH7xO3x36Xvk7ykZQ+quk0T+lsoVKagK\nHe4YwNnbxpGZ1IT/dpvNJ/9bTcBXUpi6UxxxFasR6rSsyz+X3Mapr1/Ka2N2c/2xa1i7NH5lUiui\nXvv6XPPnLZz4RH+eu3kbt/5jDdvWHurV9OYqnLWiqxhVHTz1Ujl37h2cPPEavnhwBY8eP4OM5SVj\nvb0HAjg9DqSM/8+To3YqHX940SrZeu/nzDn5MXLXF4W4+PfmYrjj7NEsTlle1kSKVQAh0am3QaOl\nCOcmhDwLpeL//2NjUxZxfly0sUkMOTl7gRuwvtJOhDAAB0JYL2u/A60dKOUC3IAHSAZSwq9aQCpQ\nG6gTXqaFXwf/UJyCVscgCv6N8HXFNGT8wgBKI+xl5avr4bzTkTePQt3+H2RSMnpfbDICREPyQ3eh\nbrmWjIuu4YN2T3DyMwPpfENvhJQk1U+hICMxtjhSPZz07X/YP38dsy9/mTlvbWb4mz3pca6VRN2d\nbKBCifux7TikO+0HH8OsG77g5r6/0/+qBowY24RaaTVzy+15Yy+6XtODr4d8yrCeK7j09iZcPaYJ\n7iRLEBbkmTjTEyfKWg/qScsLu/LT1e/zWJ8ZnHlLJwY+dAyuJAfe/QEc7sT2U73Bp5F2wYlsvOwh\nvut+P10euIj2d/QnsC8P4Ym/iC9BxMs6dwo8NQw5cxLqxPNAR/H5aAU6H3QeaC8or7XUecXWi7YF\nOQhyETobVC6oPLTKA52HVl60KkDrfNAF5OcnuB9sbIphi1WbvwW//baANm06A05gFFp3BHxoXQBE\nXr7wKx8oQMp8hMgHsoAdhW21LkBrH+AHAkAQsMQvGIXiVwgDtIE2syHkg2WTkNlbUI4kcHjAcFsp\nrQxXyXWHu+xjZa0LcegfHfGyZtyEnjgIpnyKCoZQ++LvWS1hRsMGpPz6Lf5PvmbeyNGsHD+fM94Z\nQlKDFHxlxALGi/ontOfMjS+y6tEveXHIFDqf3IDrX+uKK9nADMV2sldFSIeDsydeyoExpzNj0Ht8\n33o5/36hOedcXS+hdkRweJxc/OVQdizKYNqQT5g2cRmj32pFn3PS8HkVztqJFSPS4eC0Sdey//cz\n+XHQm8z7YCPD3jkRp0diuGOXmSBqe9xu2k15nOzZS1hz5SNsfvcXml5yHMKVHP1FtIZQ0EozFfBD\nKFByPeC3touvB/0QDJS6rvtfg/56PKyYh+lIwTAvApWLLhSW+ZaYVAWg/Vj3KicIJ4Qf1AVOEAaC\ngx7aTQcaD5pkIAnrQb0hRQ/skVcaoEhJ+XdM+9vGpjKICoZPa65Mi81fnmAwiNfrpaCggNTUVPLy\n8khNtUooRtbL23fw0jRNCgoKqFOnziHv5ff7qVevHvBP4FvgdOA2rJtwddFYwjUieAtKWf8MWAsE\nwNHRquEtg0gZBGEiRAgr7ssMv0JorQATrU3QJmhlrauibVTIWgoDpCOcvsYBhgthuMBwIhxutHSi\n96wECbJ5Oq6O7cDpQDidJZbWy1rXTgc4nFZ+TYcD4TCs2DyHAxwGwrCWJY8ZCEf4GpH1Yse0UvhG\nP4Za8juu2h7STuhAt+euQEiBkAKkQBgSIWXRtpQIw1oSbmftC2+XJtSjIJDlZdGgFzgwfy0nX96c\nBZ/t5F+ZD1bvq1ANVkxczPy7viG9lZO23dwsW+HmigXDa8yeuQ//wJJn5tLz1NpsXVNA+ohz6HrH\nmdW+rtYarTQojVYKbVrbWqnC/cpU4eNFrz+emMHGd+fTsE0q2ZmaljNehJCJLuNV1rHy9qtgCAIh\ndDBktYusB010MGS1DU+qypq1GKGV9V1v0bVQROqw8NShAASDYAYhFLKWygQhwTBAhl/CQEjDerjE\nsB5yhQFCIiIPwTr84KsdoBwo5QTTAcIDwg2BFaC2WG05B2iGNRIUGQVKo2g0KB4+qH3UqvUvdu3a\nXOrR/v378/PPP8fhfW2OQEq94dti1SZu1IxYfRBLPH6NVUbwQaBnAv7aH5HyZZTqDWIWMmUgqvZz\nYFSjTGMEFQLyrUpaKrdoGK9waC8/vC8f8r+G4CLAD3WOgQYnW8Lu9ASdAAAgAElEQVRXBa2XDoYF\ncGQZspYihMAMC2tLRAtMQCFQUPyli5Y6sq0VaG0JcK3QpokMFaCVRjgkQkjQ4djiyD1H66LtwmOH\n7ges25cIC14RFrCimAAWBy2lLFwP5hTglCZKadwNaiEQRdcrfu3ILbJwvyjaLlwtOrewyUHrJa5T\neKJ1rlKKfX/uwOEUSJeDuu0bFvaHVgDa2tTF13Wku0quE+kv0ET6kGL9W7TfOkcfdF0I+YP4M70o\nBUaKG1eKp1BUah0WnMXFZ2RdE14WfVZaA5EJU8X7ovDzKrlu9U3J/RqNME201iinC2m4rO+OEJYI\nFOHPFVm4bU29sF4ao9jSQGOgtURrh7VPO6yHPRFZOostwy/htB4KhRN2zYDs1ZadKdeDqzeIVJAp\nIJJB1CralrWBVOt6McbIuh4zdyNC+NB6GUKMROuBlPG7HgdssWqTMEr9UtthADZ/Q5KAy4BVwD3E\n1staFvWxvK//AX0dFNwP3naItAfRKf+2fviqinQAtcM/hhXgOg554GpU6D5E/sOwexb6uHGQfk6F\np+qDltXFXPsS/P6Y5Z1KTUOfMw7a9Kv8hZRpCWoVRCtLXGsV8WSFir1MS4SbERFuFu73F2TC5/8k\nuFuBywOnjoKGncPCLhweoBTFFF9YLIePRdrpYsfRYXFWiXZoaKkJ/vkFYttCdi3ZAW3/AUcPDIum\n8KSiiCCTkft2RLBFBJ4oalvYrpRjEaFXuL9YOymL9k+6mpBXEfKFoO+90OKUsFfQEfYQusLLsMiT\nhhWeUrgdebnC1w13x0HLqPjpYfhxIiKUi1m7JbrPO9aDVw1gzF2Pmd0bSIL8d5CGgar1FMjUxBpi\nbgWaofVNwE/Ak0g5A6X+B8TggdjG5jDHFqs2f2M6A62Ar4AhxNfL2gClfEXr5qvAfETOM5D7Erru\nm+CpglCrLI7WKJULDEEHL4Pgo4hf/omo1x113DhI6xp/GyIkNcVwpmD61oF/NHwyGNmkB6r/S9Co\nW/TXiQynUo0JQJGZzKEdYA6HmY8iu1yAOu9pqNu86tethj16yzxcSQMJ7fgRR95OAhe+DB3PTrwt\nlkGg50DoM5g7FtlmgfU51YlRmdFKILM3oeiNDr4LmVfBjF7IjiNRxzwIjkrEj8YAnbsBOAW4DvS1\n4L0SvO2g3rvgSdxnpUPbgV7hrVPQujdwH3BVDXhZbWwSj526yuZvThJWHOuZWF7WJ7HCBGJNPawY\n1uL5CE9AmR+jQ6fB/kHI/QMgtDkO710Mo1k4lZYP69/7f+jQCtTeNPjuBOSCa6BgZ3xtiJDcDKXz\nwnY8DYGdqK0NYcKJyC+vgJyMxNgBYU+gG0QmyElgrkEv3wFPdkR+Oxp8NVMTPcCXKPNnyK6NfPdS\nXG+dA3vW1IAh+SBagPEYmJvRG3Lh1c6Inx+FUGwrolWEyNoMtAVcoD8Ccy6s/xy+aQc7pifUFuXN\nAI4Nb7VFmfPAvAH2DbLS1pmJyXahQruBlsX2eND6WeB+YDxS3gLsSogtNjY1gS1WbY4QjgZuAdZh\neVmXxvj6kXRY2w7aL4HhoD5G+/bDrqMROWPCgjIOCBfINOD3YjuTQU8E81fYugq+bodc/gCE4lwa\nNKkpusR7JIP+BIKr0Ku2wrgOyO//m5j8tACuZCBc7lM2Q+ufwJwDv06BR1rAr69YIQSJxuhCQCxG\nmZ+hN65GPH8cjin/hvwEZVII+cNhDOEsBbIemtlgTkXMfxPxcltYPy0xtgAqJwNrVCTCsajAeii4\nCX65DDn34sQ8cIXyIZQHHByCcAfo+VCwHHa1g/zP4muHVla8Om1LOXgKWn+G1klYXtYp2FNNbP6O\n2GLV5ggiCUuongHcTay9rEKkARvLOFoLrZ4D/Twi7z3Y1dr6kYtDMQPpbAEsKeVIc1RoOpgfwZr3\nYUoL2Ph20RB5rPE0AhVJFVacFujQzxD6EX77Bv6vBWLRS2AG4mNHGOGuTaFYjSD7oEKrITAO+e2j\niCfawspv4vK5VIjjLIJsQuv/Qy/8EPF4a8Qv4+IvoAuyrRRpByfhl6eiQpvRecMRnw1BTuoPB8r6\nfscOnbcL6F7KkfshtBG9Yw980wGxblxRrHA88G5BOGpRerRcE5Q5B9S9iAPXI/efD2acBLTaaz2E\nUlYIhO1ltfn7Y4tVmyOQY4CRWKmmYudlFaIBh3pWD6YLypwE5mWIAzcg9/WF4MqYvH+hHc52WJPL\nyuIkVGARBO5HLLkbMa0z7Po+pjYA1oQbZx1gWRkNeqH8K8H/FuKHJxEvtYFV8RHwAMJThzJ/xOUV\nqEAGOus6xPtXIV86CTJi7X2PAiHAcT0m29GhW2DqGIynO8GamfF7T1+WNTGqLIz/oUPb0FsEvNYF\n8cP9EIxHKA2WlzeYT0nPanEaoM1fIPQu/PEwYkZPOPBHfGzxbkYYFU2kuh6tlqJ9mbCzo1WCOdbf\nX3MnQkYzOdT2str8fbHFqs0RShIwlFh6WYVoxCGeuzIZglafovxu2H08MnskqNgMh5uyI7A5ipZX\no4Mr0Tn94OeLkXPOhOzYCmeZ1JiyxWqEwShfBjp3JOLr4cg3e8K2X2NqB4Dw1AW9p+wGUoLxIDq4\nE7WtNbzcF/n+UDhQ0QNIHBBOcDyG1lvQ2cfDxEtwvHF2fOJZC7IRRgWT12RtNNNBfY9YOAleag1r\npsRemOXuAGcKFc/9vRgd3I4+0A1mnoRcejsE82Jri3czqLQoGqah1Tegn0Nk/Qe571QIbYqdHeYO\nhIg2k4ntZbX5e2KLVZsjnIiXdQ3V9bIq1QjYW4kzPKAfAf0GeGfAzpaQ93b1hzaNNkhHtFWsJPAI\nhJahdnusmdeLboCC3RWeGQ0itQVW30bD3Wj/btSu3vBBf+Tk82D/2pjYAUBSXaL6fKSn2CSs7fBk\np5qbhCVro4zJIFagN3nhuZ4YU26LbTyrLxshoqw7L09EmRsg/w7El9cg3z8D9q+LnS25GUgjJcrG\nDuA9MBfAhmnwTVvY/nXMTBF561GBoypxxiVo9Sfa74ZdXRB5z1s5jquLuRNR6bR7tpfV5u+FLVZt\nbEgCLgdOw/KyPkVVvKxaN0DKqgiaVihzIqhbEDn/QezpAf6FVbhOGEcroLJ21Ab9Hpg/wZYl8E1b\nxMpHIVQ9b7NOaUXZcbyl4QDGQ3ALeoOG8T2RU28Ebzke0WhtSaoHVKIUbeEkrNk1PwlLtsCUv4CY\nBQtnwGOtEL/GKJ61IAtR2bRgxn/RoQz0tlQY392aKBeIwYS9nO0IUauSJ3VBBdeA707Er1cifzof\n8qufaULmraX0SU3l4UHrj0C/AzljEXuPr36Yj7kDM1SVlF22l9Xm74MtVm1sCumK5WVdRdW8rA0Q\nojo/2APQ5ufoQCvYewYy6yowqyDSHK1QZlWHRFujgrMg9B5i1VvwVQvY9F6Vvb0qqRXC2FGFM+uh\n1VQILYFlv8FLbRA/PxKOZ6waytMAqIJH8pBJWO1qbhKWcRKmWAPmOMS3jyKe7Fj9eFZfNihP5c+T\nqWjxNai58NuX8H8tYcXH1euX3O2oQBTFL0rlv+jQFvSuPPi2E2LN89WaPGjlWK1qMYIz0OafaH8b\n2N0LmfsQ6KpNIJRswSo6UlUO9rJ+ie1ltfmrYYtVG5sSJAFXUDUva3209lXcrFwcwGjQ70L+UtjZ\nNjycGIz+EkZzq/Qq1YnhOxUV+A38oxG/3YGY1gX2/Fj5yyQ3QzqrE4vbERVcDMGvEPMmwovN4fe3\nqiZCPHURRm7VTSmchHWNNQnr5ZNrZhIWgONKlN6Ozh4CEwcjXu8He6sYMuHLRptVEKsR5LEocy34\nH0B8MwL5zsmwt2reRJmzBR1qUnVbSEObP0DoY/jzKcT0rpD5W5WuVDLHalVwAG+A/gJy30Ds7gKB\nxZW+ijC3Uf0qVcW9rG/YXlabvxy2WLWxKZWIl3UF0XtZ6xerYlVdGqHM10Hfj8h5ErGrI/hmR3eq\ncIBRj9hkObjemoSV3Rd+vAD5Y3/IqcQkn6SmaF0NgVjIGSj/Bih4CvHdfYhXOsL66ZXz4nnqIBzV\nnMUuJRgPWZOwtraq2UlYUoLzMRA70RvrwrM9EV/cCgVZlbtO/gFUINo40fLsuRUd2oHang5v9kJ+\n92/wVy4cRWRtAlpX3xYGWBOwsk+CWacgf7sZgpWwJZgHZgFWfubqcjzK/B0d7At7TkXm3FGpPMs6\nmAHEqsqa7WW1+Wtii1UbmzKxbuhWucVovKwNwsdjmfvxZJT5CTp0Iuy/EJk5EEJbKzzLyrX6e4Xt\nosMAxkLod/QuDdN7IhePAF8Uk5WSm6JULIsPDEP7d6APXGbl/nynL+wsLadsKbjTEDJGKZcOq0lY\nyeD8GORy9KLf4JGWUIn8rLJgP4h6MbLFA/JTUAvg95nwf61g2XtRP1To7K1Ah9jYggTeBHMpbPoR\nvm4D2z6Pzpb8SI7VWP1ESuAZ0DMhbwpiVwfw/RDVmYdWr6outpfV5q+HLVZtbCqkO5aXdTnle1nd\ngJPo01dFiwRutqpgFeyEXZ2RuQ+AKlt4WblWV8fYjjS0mmxVfdo8D75ujVg5FsxyvMlJTcNVgGIp\n4CXwODqwA5XRAt75B/LzyyBrS/mneeqgiXHp0BKVsL6yhGKNTcJqDfJX0FNg6nMwtgOsnVXhaSI/\nE6gbY1u6oMyVEBiLmD4K8XYv2FVxPlSVuxNrVCOWdEAFV4D/f4j51yN/PBu8FXxX8jYjjcpO9IqG\nTihzEdq8DPadj8waVn7KOq1AZQFt4mCL7WW1+etgi1Ubm6hIAq4G/gGMpiwva/lVrKpLbbR6AfQz\nkDsBdrWB/C9L9RRZuVYr+EGuMu1RwTkQehux6lX4qhVsmVy6x8qRDNINrI+DHcmgP4TgOvTqPfBq\nZ+TMO6wk96XhrgM6TnXuZW9UaNVhMgnrNGA95IyGiUPgtbNgbznppfIzsUYF4oAcjg7uQO/qABNO\nQk4bAQVlTHLTCgoygR7xsYXb0KGtVqrdb49GrH4KVBmx4N7NaLOqE72iYQzoXyF/AexsCwXflN5M\n7bdy7hIP4Qy2l9Xmr4ItVm1sKkUPLC/rn5TmZbWqWFU8TF89uqHMD8G8CHHgWuT+UyF4kBfVaIMR\nda7VqnIWKrAUfLciFt2CmN4d9s49pJVIakjsQhJKIz08qWYuLJ0JL7ZALHjOqoZUHE8aWsW3pCvy\n8sNjEpYQ4LwRxHbY3AWe7QllxLPq/ANAo/jZIl1WyIRaAn/+ahUU+P2tQzNMePeC4QLqxM8WaqPN\nmWBOQSx/ETH1GNg3/5BWwrseFYxjnwDQDGX+BOp2yLwcmTkIzINCa8ydCFmVtFWVxfay2hze2GLV\nxqbSJAPXACdzsJdViIZAVVI1VYUr0eozlE/A7mOR2beDCsdMGq3QOlHxkzehg6vQWcfCD+daeS5z\nizypMqU5ENvKWKVzLMr/JwTeQfz4ArzUClZ8VOTddNeJv1iFw2sSlnCD4wUw1sPCTfBoa/ilZJiC\nLsgGEW9hBsiOKHMZBP8P8d3diPE9YEex2fG52xGOGEz0ioqzUMFt6Nx+MPtM5KJ/QaBIyMvcNUC7\nBNlyM6jfwLcVdrWD/A+KvrPmzkpUr6outpfV5vDFFqs2NlXmWCwv6zIiXlalGgOxqf4UHR7Qj4N+\nDbzfWFWwvO+AoyVKxbj8ZLk4gOcgtBS9swCmdUMuGQn+TEhpSXzCAMriYpR/K+Tdhfj2FsT4rrDl\nJ/DUATNOYQClUWISVkaxSVixyI5QSURjML4BNQu+fRXGdoS13wOg/TlAddJFVRJ5NTq4E733OHj3\nVOTX10P+PsjJQMrUxNmBBMaBuRy2LLAmYG2xHm5U7kaqnmO1KtRHmTNAPY44cCtyfz8IbbNKrVKN\ntGJVojQvq41NzVJRAWYbm8MGpaxhw1Do0MkrphmDsoZVIhm4FvgNGI3WaQiRiq5iAvCq0xxlvgFM\nRWSNAkcztPZilReNZ+zdwaSg1fvAath4C2x4B7NWOyAVYj25qUJGov0jYM8d8OF5yOYnolQIyASR\nKA8eII5Cq1mgF8KvN8Cv46FpvOIyK8A4DvQyyP0IJlwBLbtaoQFaxS+etzQEIF4DczSsHAIr20Dz\nk9FmTXxP0lHBRcB4xKIRiA2vorxbsSZ6JdqWS9DqbPBfD7s6g6snZsgDJPp+ItH6CWAu8AxCTEEp\nVeq9FyA5ORGhCjZHMkKXPwHADlqxqTLBYBCv10tBQQGpqank5eWRmmp5TiLr5e0rvnS5XAQC1g3b\nMIxD3kspRfv2HcnLq4HUQSVwAxrDqLl/Ha11+OVASoUQokZtUdINph9D1qwdGtBCInVN94lCOZMw\nVBAzGKu8vFVESJAOMEMYRs35LrRWKEcSBPIwDGcN2qHRCDQSiVnz3xPtQeBFypr8bDRaC1JT67B+\n/YrC/Y0aRRc6UoHGsLE5mFL/6WzPqs1hTcRjapombrcbv99fKG6L4/f72bx5I0lJiYrvOvzJz8/H\n4XDgcrlq2pTDhtzcXJKTk0t94DkS0VqTk5NDnTrxnNT01yIUCuHz+Uq9zxyp+P1+lFIl7q9eb1H+\n5P79+/Pzzz+Xeu6wYcP45ptvaNSoEcuWLSu1zW233ca0adNISUlh4sSJ9OhRQyMPNoctdsyqzWFJ\n5Gnc57M8Tx6PByntr6uNjY3NX4nrrruOGTNmlHl82rRpbNiwgXXr1vH6668zYsSIBFpn81fB/vW3\nOSzJz7fKEUZioSLDcenp6WWe06BBnHJF/oWpWzfGyd7/BtSuncgY3sOf8v6njlSiHeI+kqjq/bVv\n377l3oemTJnC1VdfDUCfPn3Izs5m9+5ETlK1+Stgi1Wbw4qIJ9XtdgNFIlVrzdKlNZCv0sbGxsYm\nbmzfvp3mzZsXbjdt2pTt22NdBdDmr44ds2pT42itC2eZRsSpw1H01UxPT2fUqFGsWrUKsOKjDiZy\nXmnHjlQiYRN2nxQRiVW1+6Qkdn8UYd9LDqWiPtm8eXMCrbE5ErHFqk2N4/P5CmNU3W43waBVAjE9\nPZ3vv7dyQXbs2JFnnnkGwzDKDOQXQpR57EjF7pNDsfukJHZ/HIrdJ4cSrz5p2rQp27YVFczIyMig\nadOmMX8fm782dhiATY1RPBXVwbP4I+EATz/9NAA33nijPcHKxsbG5i9IJJ1eaQwcOJB3330XgPnz\n55OWlmbHDNscgu1ZtUk4xdNRASVSK2mtSU9Pp3fv3gB8++23dpohGxsbm78ol19+OT/88AP79++n\nRYsWPPTQQwQCAYQQDB8+nAEDBjB16lTatWtHSkoKEyZMqGmTbQ5D7KIANnGjtKIATqeTUCiE1pqU\nlBS8Xm9hPsPatWszatQonn/+eTZt2kTr1q3RWiOEKHwqL75+MOUdO1Kx++RQ7D4pid0fh2L3yaHY\nfWKTIEotCmCPq9okhIgXtXhi6eIz/RctWgRYsakArVq1KvU65d0s7Rvpodh9cih2n5TE7o9Dsfvk\nUOw+salJbM+qTdwIBoPk5eXh8/kKn8oPLq0a8aauWrWK6dOnl/CkHry0sbGxsbGx+Vtje1ZtEovW\nGr/fDxQl94+Qnp5ewpv67bfflnsdGxsbGxsbmyMTW6zaxA0hxCHJ/SH6mf62SLWxsbGxsbGxxapN\nXCkuUiPe1PPPPx+gXG+qjY2NjY2NjQ3YYtUmQRT3pn700UcAZeZNrcijOn36dDp16kSHDh148skn\nS21z22230b59e3r06MHvv/9eDcv/GlTUJ5MmTaJ79+50796dvn378ueff9aAlYkjmu8IwKJFi3A6\nnXz++ecJtK5miKZPfvjhB3r27EmXLl04/fTTE2xhYqmoP3Jychg4cCA9evSga9euTJw4MfFGJpBh\nw4bRqFEjunXrVmabI+2+anMYEUnWW8bLxiZqpk2bpjt27Kjbt2+vx44dqwOBgD5w4IAGdO/evTWg\nR44cqdu1a6cBvXTpUm19BQ89tyxM09Rt27bVmzdv1oFAQHfv3l2vWrWqRJupU6fqAQMGaK21nj9/\nvu7Tp0/8/ujDgGj6ZN68eTorK0trbfX137lPoumPSLszzjhDn3feefqzzz6rAUsTRzR9kpWVpY8+\n+midkZGhtdZ67969NWFqQoimPx5//HF99913a62tvqhXr54OBoM1YW5C+Pnnn/XSpUt1165dSz1+\npN1XbWqMUvWo7Vm1iQlKKUaOHMmMGTNYsWIFH374IcuWLePhhx8GKPSmbty4kXXr1gEwYsSIMs9d\nvXp1qe+zcOFC2rdvT8uWLXE6nQwZMoQpU6aUaDNlyhSuvvpqAPr06UN2dja7d++Oy999OBBNn5xw\nwgnUqVOncH379u01YWpCiKY/AF566SUGDx5Mw4YNa8DKxBJNn0yaNIlBgwYVlrps0KBBTZiaEKLp\nDyEEubm5AOTm5lK/fn0cjr9vHZ2+fftSt27dMo8fafdVm8MLW6zaVJvp06fTunVrdu7cyeTJkwtv\n/p999hmdO3cG4LnnngNgxYoVLF26FIDs7GyGDh1KgwYN2L17d4XiAmD79u00b968cLtZs2aHCK+D\n2zRt2vRvLc6i6ZPivPnmm5x77rmJMK1GiKY/duzYwZdffslNN910REzki6ZP1q5dS2ZmJqeffjq9\nevXivffeS7SZCSOa/hg5ciQrV64kPT2d7t278+KLLybazMOKI+2+anN48fd9TLSJK9OnT+f2229H\nKcX+/ft57LHHWLx4MR9++CEXXnghzZo14+mnnyY/Px+gUKDefPPNnHbaaQBs27aNHj16cO+99/LE\nE08UXrtZs2YsXLgw4X/TkcCcOXOYMGECc+fOrWlTapTbb7+9RJzikSBYKyIUCrFkyRJmz56N1+vl\nxBNP5MQTT6Rdu3Y1bVqNMGPGDHr27Mns2bPZsGED/fr1Y9myZYW5om1sbBKHLVZtKk1k2P77779n\n27ZtDBgwgEAggJSy0Cu6b98+srOz2bx5M0IIdu3aBUDnzp2pV68ea9eu5Z///Cfz5s0rrFoVDU2b\nNmXr1q2F2xkZGYXDlsXbbNu2rdw2fyei6ROAZcuWMXz4cKZPn17ucN9fnWj6Y/HixQwZMgStNfv2\n7WPatGk4nU4GDhyYaHMTQjR90qxZMxo0aIDH48Hj8XDKKafwxx9//C3FajT9MWHCBO655x4A2rZt\nS+vWrVm9ejXHH398Qm09XDjS7qs2hxd2GIBNpTh4yH/37t106tSJNWvWsHXrVpo1a8akSZN46aWX\nyM7OLpwxGggEqF+/Prfddht79+7lgQceYNeuXXTu3BkhBIFAoPA9yrsJ9urVi/Xr17NlyxYCgQCT\nJ08+RGAMHDiQd999F4D58+eTlpZGo0aN4tQjNU80fbJ161YGDRrEe++9R9u2bWvI0sQQTX9s3LiR\njRs3smnTJgYPHswrr7zytxWqEF2fXHjhhcydOxfTNMnPz2fBggWFYTx/N6Lpj5YtWzJr1iwAdu/e\nzdq1a2nTpk1NmJswIpNZSuNIu6/aHF7YnlWbCilvyP/6668nJSWFuXPnsmrVKhYvXozT6cTtdjNq\n1KjCSVT79u2jVatWtGrVCp/Px8yZMzEMg1WrVvHUU0/x+OOPs2XLFpo0acLkyZP58MMPS7XFMAxe\nfvllzj77bJRSDBs2jM6dO/P6668jhGD48OEMGDCAqVOn0q5dO1JSUpgwYUIiuyvhRNMnjzzyCJmZ\nmdx8881orXE6nX/bUIto+qM4xXMBJ4IVK1bwxRdf0K9fP/r06cOQIUOYPHlyXN8zmj7p1KkT/fv3\np1u3bhiGwfDhwzn66KPjaldNEU1/jBkzhmuvvbYwldNTTz1FvXr1atjy+HH55Zfzww8/sH//flq0\naMFDDz1EIBA4Yu+rNocXooJYLTuQ6whHKUWHDh1KDPk/+uijLF++nDZt2rBt2zamTp2K1prXXnuN\nC/+/vXsL0bra/zj+aQ7aMJogDemYZnkAERkNLDPQQVLLLubCIMykE4zRRXQxkFk3IYRSFxUReSip\noCIhqMQLszJNGkqGSqh0hgYd1GY0m8lDjafZV/rf/Xeb/d9/2M3a+nrdPjdrPTfPm+/vt9bT1JSz\nZ89m8uTJefXVV7N48eIMHTo0vb29aWhoyLRp07J27dpUVlZm9OjRef755zN9+vQ0NjZmyJAhF384\nVqxYMdhbh/+I1tbWfPbZZ5k7d26uvvrqrF69Ohs2bBjsZQGU4E+nB14D4J/6vzzy//zzz7N///78\n8ssvGTlyZK688sqMGjUqXV1dWbJkSY4fP56ffvop/f39GTp0aLZu3Zrz58+nvr4+jz32WJqamjIw\nMJBhw4Zl7969aW9vF6pc0mbNmpW2trbMmjUrra2tmT179mAvCaBoYpU/deEQ1RNPPJElS5bk7bff\nzsGDB1NbW5uKiop0dHRk586d6e3tTU1NTaqqqjJnzpzU19envr4+SVJbW5va2tqsXLkyNTU12bVr\nV2pqanLbbbfl7NmzmT9/fu65557Mnj07+/bty7hx4zxa4rJQW1ubJPniiy9y6623DvJqAMomVvmD\nC39BOH78+FRWVqauru7iKf+9e/fm559/zo4dO/Lbb79l/fr1OXLkSMaNG5cPP/wwI0aMSE9PT/bs\n2ZP+/v4MHz48R48ezTvvvJM1a9Zk3rx5efnll7Nt27acOXMm8+fPzw8//JDXXnst/f39OXDgQB54\n4IHB/grgP27cuHHZtGlTPv7443/rNgyAy5FY5aK//yepZ599NkePHs2ZM2cuPvKvqKhIZ2dnTpw4\nkc7OztTU1KS+vj5z585NV1dXKisrs3DhwlRVVWX06NFpb2/PwMBAenp68tRTT+XTTz/N2rVrc+LE\niUyaNCnr169PW1tbbr/99sHeOvxlNmzYkMbGxjQ0NKSpqWmwlwNQPLHKP0xTr7vuulRVVWXChAnp\n7OxMR0dH1q1blzfffDOnTp3KsWPHMnXq1IwaNSoHDhzIpr8v2rUAAAVmSURBVE2bct999+Xw4cOp\nqKjIsGHDUlFRkbFjx+ajjz7KtddemwcffDCVlZX59ttvc/PNN2fhwoVZtGjRYG8d/nI33HBDjh8/\nns2bN2fVqlWDvRyA4rkN4DL396f9W1tb88gjj2TXrl3p7e1Nc3NzGhsbU1dXl1WrVuWqq67KsGHD\nUltbm0cffTRvvfVWjh07ltdffz1r1qzJu+++m+HDh6e+vj5z5szJCy+8kJqamjz99NPp6elJV1dX\nPvjgg8HeMgBQJrcB8Ef/+7T/hWnq+++/n5kzZ6a7uzvbtm3Lc889lyRZt25dpk2blpMnT6a7uzv7\n9+/P999/nyeffPLioapPPvkkbW1tqa6uzurVq3Py5Mls3bo1TU1NQhUA+LeZrF6mLkxUW1pasnv3\n7uzevTsrVqzIM888k8bGxrz44otZsGBBtm/fnurq6ixcuDCHDh3KkCFDsm/fvlRVVeXHH3/MNddc\nk9OnT2dgYCBDhgxJb29vOjs7M3/+/IuHr5YuXeo6KgDgXzFZ5X98+eWXmTRp0h9O+3d2dqa7uzvH\njx/P6dOn09bWltWrV2fevHlpaWlJX19fli9fntOnT+fcuXPZvn17Jk+enMbGxlRXV2fKlCnZt29f\nrr/++ixbtiwPP/xw9uzZI1QBgP83sXqZOnjwYMaOHZsxY8ZcPO1/+PDh3Hnnndm8eXOmTp2aurq6\nzJo1K319fdm4cWPGjBmTKVOmZGBgIP39/bnjjjvS0dGRU6dO5ZZbbskrr7ySpUuXZvr06fnmm2+y\ncuXKwd4mAPBfTqxe5mbOnJmOjo4cPXo0586dS1tbW3bs2JH29vZMnDgxSbJixYocOnQoSbJnz55M\nmDAhM2bMyJEjR9LT05P29vaMHz8+DQ0N+eqrr/L111/nvffey4gRIwZzawDAJaBqsBfA4LgwUa2s\nrMxLL72UZcuWZWBgIC0tLZkyZUrWrl2bX3/9NV1dXbn77ruzZcuWrFu3LocOHcr999+f9vb2jBw5\nMqdOnUpfX1/Onz8/2FsCAC5BJquXqQsT1f3792fevHkZM2ZMdu7cefH90uXLl+fxxx/PG2+8kSS5\n9957c+ONN+a7775LY2NjWltb8/vvv6empiaLFy9OQ0PDYG4HALhEmaxepi5MVBcsWJDz58/noYce\nujhRveKKK9Lc3JxFixZly5YtmThxYmpra7Nx48YkyU033ZS77rorM2bMSHV1dWbMmJHm5uZB3hEA\ncClydRUAACVwdRUAAP9dxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECx\nxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQ\nLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAA\nFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoA\nAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEK\nAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEus\nAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECxxCoAAMUS\nqwAAFEusAgBQrKp/8fkVf8kqAADgT5isAgBQLLEKAECxxCoAAMUSqwAAFEusAgBQLLEKAECx/gY6\nEBM6fyeF9QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10e050278>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot result\n",
"fig=pyplot.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection='3d')\n",
"ax.plot_trisurf(p[:,0], p[:,1], U[:,0], triangles=triangles, cmap=cm.jet)\n",
"ax.view_init(elev=90,azim=0);ax.set_xlabel(r\"$x$\");ax.set_ylabel(r\"$y$\");"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtgAAAHuCAYAAAClGHsoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvTuofVG3HzTG+S5WRu+Hjy+QqJDrCxRJJZaigaiFaQQf\nXaoUSW1rI4iFIJJCA8EQgijYmEJELbWQCEpIiBK9GuNNuIKJhXa5Z1is+fiN15xzPfbeZ5+zBvz/\ne63xmo8115y/Nc5Yc7GI0E033XTTTTfddNNNN910DX28ugI33XTTTTfddNNNN930negG2DfddNNN\nN91000033XQh3QD7pptuuummm2666aabLqQbYN9000033XTTTTfddNOFdAPsm2666aabbrrppptu\nupBugH3TTTfddNNNN910000X0sMBNjP/SWb+bWb+8wOdf4+Z/zIz/4/M/PsfXaebbrrppptuuumm\nm256FD0jgv0fEtEfzITM/M8T0W+IyD9ERH+EiP79J9Tppptuuummm2666aabHkIPB9gi8t8Q0d8c\nqPwhIvrTRfe/I6K/k5l/9eh63XTTTTfddNNNN9100yPoK+Rg/x4i+qtw/luFd9NNN91000033XTT\nTW9Hv/bqCuwhZr6/637TTTfddNNNN91001NIRPiI3VcA2L9FRH8fnP/ewgvpD/C/9PAKvQV9fIU/\nPryehIh+8/Mv0G/84h9/dVVeTkJEdGga+J70m7/zF+j33ePiJkP3uLjJkWzj4qevI1L+u5cRIhIh\nEqH/Wv7Twy6eBbCZ8mv2Z4nojxLRf8LM/xQR/T8i8ttPqtf7ERMRfxDxz74FGphkIhIm+fjZ/UFE\n96xIZVxU+mSiHzwu8IHr5/bCRoIH97ho9HN7wVAZFz9+HblzBDaSazri4QCbmf8jIvqniejvYub/\ng4j+DSL624hIRORPiMh/zsz/AjP/L0T0/xHRH350nd6WmLbINfOPBtht6DP8+6ET4waifmbbQ4Ku\nkN9hkl/84L/01L6Qe91UffHTx0Wle1x0EvnR68j91FWoRK2vujMeDrBF5F9b0Pljj67H29PHRwGT\n/GMBtgPW5fiXv/a7f1zKTNgXP5RUXwDzl7/2qx+3YKq/7CjmDybsi88fPC6I3Lj4Wb0QUO0Y4R+5\njrSnLKZ7npDrnzi/Qg72TSNSUWsqwPrnAWwEDgLgmojo1z9+94+aG1Su9c8aBjGF94LQr//iZ40L\nIor74qI/d74dRX3BP3RcRBOFyA/sB6AKLMvxz1pHSktlwxWMIPvndMJGLWItlz9o3AD7q1LLtSaI\nWtOPA9gqIsdEQqzXip/RDUSEUagssfbnzIzTvvg5XbFRmxsC+ml9QZT3xedzq/ElqPaFHQc/MoIN\nfaGi+T/sJoFNMfhHThCF6nV/0IPFDbC/ImHUmsgD7B+SIhKnhBhA9f27gYhMrrVdL1sUhn9Ed4S7\npbiG/4SeWNw55iePC0v8M/piiT6/f09EmIktuM4UvyOZdrJ70vCn35KyXOs7ReSbk821JvpxANsC\n675wsjmvrO/dF8OUEHP+ndeJMI80OlfK35hW8+9/ystsK33x+UP7IkSaz6jIFyEJDoHHx7Y5fhsS\nyLXGdBApv9+79YZqrvUTJoIbYH8VsrnWFIFq+vYpIj4lhBS4pnbef+WbTg8uIhf9pfeHBB/S3VLS\nBn9fGLV75xj5rnfIgb7g79sXG0W51jH7u6ZFuFZB+zngEX3brqD+dB3kWvOGsBnzjr9zDrbNtSaK\nd0+5c7C/EbVc6yRCHUWvbR7yNyALrImIJEgH+Qk52C6/mGgJXJc4xbeiUV8o+il/8m0P2TvoO0ew\n9/bFd45gZ7nWlYIc7O9L0BcWXFe+Ov+mnVFeYtwwpW3jAxDlV6WVXOs7B/ubEfO2XRSCZgTYaST7\newFsBaIauK688l8Svf5O/UAU51orGqZHfK/OmOXUjv+q+70Sh5byi1Pj79QThY426ZvlYI8wAc8A\nw3ccF5VsrnHUF5Icfwdyudb9fxRqfmV+o84QMg9PFWCYLWSaLDo+TjfAfhXZrfdcxPr7A2wLrKNc\n4ziKbfXevzOGkWkbmBqC7Pen3e0M//z9jdZM+KvOIfo2HVHoTF98twg29sXofa0ZwPxOtPoSowLY\n32US7bnWJNTSP2qudUsT6drfbfnodCTX+n7J8c0Jo9YZqJ7JvkGKSE8JAXBdeeU3SgcJX/h783z0\nG1x3Wsm1dnNg2Afvn2u7O784dfQNkNRVD9LfIAd7u5rsmcDigazzv8G4QMLgI5y3oTMM9z+qUk+i\nlgLBDlzrcVFRtpF9pxxsaf/1p4kw1zpo6DWB60Y3wH4mRVFrFaX+/gBbAetyHL3IqAIKRqZ+3/gR\nPEqNaTLX/kSm5O87M4a51o03MMxk7x7BxnvkLL11RxS6qi++QwTb9kXQoGn0esR/K2LVDpfdYOaB\nSL79vntnsD5iovb5d3zQUGj73SfJgCQA1E5nydEFlbkB9nNomGtNwN8Bvt8QVCKIsl9jJIZXMFQU\nm8gCbGv7hl2xfe8iy7VeBtT2/B17YpJfPMMSaZPfM9f2VK51Su/YEw+iN83BTpf7UeR6ZvzuaRFB\nxBqb5Pa7NnL1AuQbAk0M1LbUD64YczuxzSWqke3eeBejesdhoXKtAWS/+OHyBtiPplO51sh/X4A9\nzLUu/Dj/GuwCeT1+pz/6qoeIoNozMD0F229EYdrLkWh1xH+z4Ez/y85jnL/TMEnToa6gd/2SY4SU\nAkoDsd8tB9s+WAR/ybR9kUaviUje7mHD5FpbGYJrbqzwQeLdWu5olmt952B/Q1qJWk9lyAfZG6WI\nhLnWC+Da6lReqPsmnZGCKAY55fLp+RstmGF+8eAyDte/XWG7L0oPfY/g3bZvfGBf8DfpixWgNGvo\n53v1RKMFcL2sEx1/aZrkWsvGYFBFII46ZHXq77v0hcq1Rh5pXsaP2skJ/yDdAPsRNM21Rr4F0pTw\n3wtgW2DdeUk0uvWPsVe/ie0XpyzXOkwHWADbeZrE14/lt/l7B7g+JHuDRULdIw8u6B3GBRE9vi8+\nv35fNFrItUbZMI1kwf1XpF51PfEhgBSjzOa8Hdr7QAHsN5gwiFSkoR8JAGg2UWrx+sy9Q96VXK51\n0Jawec/90+YNsK+k5Vxr5I/AN/KNj4/XNHGF8pQQANABSB5vyRfYGvuvSOFDRaUZmDa8ESCvJ195\nygzrn/HQ7hD4/uIDg+iJVfza4+KpxG/aF1EEtlAYnbW2Efud0iJMGzEIa+UjwJ1gz6+PNWv9mHSu\ndf0aY6iqO02q7Yy+8rAQ8g9DV6WHPIBugH0FMVH8NUY6BqpHNl84gp0Da1KzoX/BscReDT/62IxP\nMbms+peSi8jNgDLwZoBbzPng9EtQj1oD8who3sP/ogtmmib08EK/MD2zL756BDtCShHZ6OzMJkop\n+aLjImwPTqMVYKKOnWYt4C7n6tq/C8CGFA8OBMMYA6aHvDu5XOsAaC/72sk/SDfAPktMPSUki1qv\npHvssoHfL0I2JeQsuLY6FOmwVfwaFKa3VJmt6lm50flq82iYDlJpctmmAbah/Kv1RKGX3LdftC9e\ncd9+2RzspC8mlZ1/rXEg+sppESsPBHKh/MtF8yHcXsG1Aswbo/31AoPVQlv0GvK0MfK96ZinFPz9\nasMC01kYeeRvG6y71Z3xq+zC9t8A+wztyrVG/ghIIz8B3wR2LyYVkcOowvDFxGCbPqpznAbSEVD/\nqtv0qchzBHoD8DyKRo9SQjKfX68v5hUcRuyNLJz7IjsX7XkdpX2xSmcb8tUWTKLXzV9fMoI9ANej\nysoCLhxc+68ZwWbf7lJPgaUh0om24FOsAcDmL/SwseHJDo47Hux15JJH3b/QKOYLjZsVd48mRWSE\nJL/QHSIF8Y8iztNo9IlI90m6AfYRYppHrWfgeAWUE+oYHx+vvwksoOyAsM9s+/a71og5slXnaPti\niuqv5AlQvlrn6/RFIFgA0MrHil0q/xq5tmlfPJW+xt7PX+F6fJXAREqLaSFEZljtsGvsLxe1JQec\nbX65LOh0RQh0DnSIAvD9KkLQX/8rALqCbv9gJOEd3sA171wkv8KwEOnguvEov1Bf5foZugH2HmKi\nNNc6A84jUD1NEZn4exHlUevyXwaQo8g1x7aZbJR+8QpS0ckA/Lr7PgHIoyi3KmsBhL+KhpHa6GFh\nIItsl6PXRETy2h1VTketm/3ZmhCRfJG0iK8Abl+8NR3EIGcKI600qLcMuom+EKokX1f7F6ioqoOI\n9O7zr9AVkO7R0kFqRyC4ZtSVFs2GUPd2iGkgaFPLyn5f3RduA3MrT2QRP7tJntTGG2CvEtOBXGvk\nX2jzQoAdgmsLjh3oJmqR6wBYq+hvomP9a90X94WpwiyCOwPTw+itBe1fALMQBdew0iJ4Vn5O2A99\nPYnSvnghvao28tLSA3p5VUZPmoloBrolPJz7fzWQqgTAj+FcMrnhYVQ7kqNOCtpfFs2HJyULrmvU\nmrJha8D15Hrygs5LqUWsJeBnNjv5M9nFdAPsFTqca438EZDO+F8HYOfAmlo9I8A5zasmam2JX4Cs\n52x8ou4L+gKLnYHgREf5Guiocic6z6Y0UjsCvpnsiE1mZxfTJ9BlUWuiayufRDsfTi98+E3pBV9y\nHEato9QFZAVysScWfC74945eQAgsK0vM7ZMA5QxMK1AO1La2i8oP9J9DQnGudf2/J370XOvals02\n6MJiDWkjxVZ35WhgvIDcvtZWPpHt4T+RboA9IqaTudbIvxiUPxFgK0A5A73t10SsjUyfr/tU5/b4\nCaSik3bhmwHkqK5nfdjF6Ik0i9SHdCWIHsqem4Od9sWXoC9bsefTV/rLws7INVFwJY9Gr4mIPl/Y\nFwbfMfB2Ra7hYPhQEj1wi1F4JpkJY4suSwPDxGaHEPe3IDwK/sTRgHvWruY4Fj2L0lzrTH+VvwDY\nn0A3wI6IiY7nWiP/iA0cD8H74+8CG7XuPD3r7QHX04/JGBmhjM289MSJQEUng3KnLygeAdcrfl6w\nRh6JWhMdB9CH7J69YF55P15+TZ8dyvlCINbS57Pz0ZO+OBC5ruzIR9rjo8a+YhuR6KHB8qLo88TP\nzEfIe1UEG4CzyrWGi6lzrbdodU8d0eqt7vAb6fLEpv0+qy+GudYS/oWjikIbW2/b1hn/AXQDbEtM\nJ3Otkb8KpDP+6wC2BddRhNkB3toO5CldDvkrtrZcbfukvjBFqcg+Eht5oLO0n3WiM/L7aGjzSRSP\nvVnBRwH0zPcLsZx62LyJvjSwrhQ/Hz+mIEujBX0ScBtiYZlghSxQ+WCAEQYVcYqvbTYgyaaI2PnB\n7QgCOuoBhbyOxXD9+NGjwgBGBYKhci7SvjVWLXUI0IepHsGfCV7wTOUozbXO9Cey3eUfsDlIN8BG\nuiTXGvlHQDnynw+wc2Bd25UAzgRAu68xOt4OW8s3fq8mB6B3guRUb0Un0rPg2ulsmXePoPYHyoW2\nWP64znNZ+rAx8vfASTTtiyvoQev8o+CD/cP1l6eH52AnfTHCQbQAoI/a1rIj9tMileXXgGLXH4Wn\nApQJUKZER9yB1nF/AUj0r6UYQEv7P/jUOdO2Nzdzb3OpI4Om3u9a+7BR7MkQfA4Nc60nT4p7QfYX\neJi4ATbRNupemmuN/EXw/QCArQBlA9LcebQAetvv+n7XlPj0v4O87osprGeVTcBwCAgjwJnojCLU\nDmTbxSao2ln6HDmeFTiRn/ta40j+wAeNl69Se+lr7An+JejZf3FY6fgJrpgB6ClQTiPYD1xDAgbD\neQSEOeDJTp1IjjrsmPX4QXeImTCmudYsUE8PmzUHtdBnHTMayi/TI26RPbnWRyLWdqDM9Hc5P04/\nG2Az0ZZrTesAeSWyfAqgw/GsnIvIRq077yC4ph37XSNgXADYIf9C6nXx4DoFVzt0UnBdeENwHfEs\n+A9MjpLri6wOiexs5FrXYaftxQtm2hdX0UNx37V/1+g9+3ZPGg/cBzvoi4WQYfgBFONjGr2eXYY0\ngv3wP/O0ujVwzUbHTrMndFLwXM7drfvoCDYA59O51kf2uwafrX+k26a/V/fF6r7Wo+tjr/eMj7KI\nH7YxFRymnwuwmY5HrQ+ndVzp65rFzYLrDhD7jLUvOr1oi9VvtmYmnfls7Gv6Qv312ALXCbBd0XmG\nj6sgz6Fc6x2yK8D3VHYRqbH5pnTtsvHGfXF51aObeKAeRVYTmfM8CtDtKLP5v2hQhFFrqHzBh0Pg\nbLGndT7TcdAoANijil8VzRf8cwQAaIkAtKpC31ZP4cfaecytD6OUmKjbGq+Ut/Isdikt5VoHjQl9\n7eQP63XA5iD9TIC9K9f6CjA98o/8EfA2/j/OdYECyGzOrwbXgSz+1QA7i5jb37YzyUEaRo15Llc+\nDsqbzgIIH/u4qC8yNwvuT6d9rPiY+jm/lCxFz6+gh696bwKIn7HwPeODIgvtWMmbnqksAeSBzjWf\nSh8AJDEj74Acp/0wck3As5HN0bkt6pKu6NFi3bb6BLAYncZ2Qx42AnZnG1eI2gKGNjO6rC9oPzA+\narOHn9L1E9DPAtjMRB8r4HgEgpFvQTAlfOv/SLmBj4PUgQPvAMfUwbUDuODP2eBvnDoi9SAB0Fi3\nZRC6SO1DOInfK8D1kHf1+QkK+3ZQxjIANfIj0et06hvYnumatC+upmeUccW68S71fHAZqXkWJU7k\nYdQ3shv4ttHr9BJdGf1zBJMkTv+DiHU954l8CK4r76rzs+kyQn2Nrm2DqDVRdn0ScG0vrrUv4LqB\nb0NsbLuNrXTWmIMk1ME1Tt7qTxgA/AXOrczxidTbntggMXqU6A2ftFb11ulnAGwm2rev9UiGfCMj\nivlHouArIH0ntTEPqRhDcI1lzMC1AchelxPQ3v37MrV9CsAPkH3IcDLrm3fKBzpDYGrny8DHUH6A\nVF8E9RlS1O6D9qGfA/bVy5HpcdgXV9MTitjo7ELxhIquRtdOl/OAvhjUHXHCYKjGc1B4EtRCUrWx\n4IocbFP3tlsHxzoM55LJK4+MjpXj3BP18S6ATccJwLEqH/OfDYDeQDh0BMi6LgBohrIo0rU6Hdi3\nvlO65iLg79G+cLnWyVOlvRFQzY6bGR9lET9qS8Z/AH1/gH0man1lukdqw72eDwTYClwznNcyyPKK\nXat35zuAWO3Z8qtuYO/KwVkay67nnPD3r8zhftxQ9gzgdj9juarrxN8MlKflIe/ApCFtTA38WpuJ\nPLN31dthnzZt4GPnLVL6d6/VCXpWUUcXk2f2xZMWvEP3CBHNbwZNHMhD1SDIuOLfAs/QduLj0JaF\n2VwTlRHoqNk6kbeiJvIIdGcPJkzB88RZgA2o3udab6W67mq6olJ0PH70kW290m1nDbOybkO0Kjae\n0T1N7Sky4mf6O2WHrs+Fvg7S9wbYl+VaGz0LdF+RZrKYg91vbADWpSo5aCUAwhr4enDMCR9543JQ\n7mVQh6z8RaSi2j4DwrSgs1N+hY95PQ/0xdBfQjPwu9NH6GvmYyhf35pu+YHhSnpmWc8tbB9lUa2H\nlXdRQZN6N8zBA7UABTmAGBiy1YlsJz42R3v6IkdvmA6isNZMJ5FXJRnJoRxBnVGVhwB7Z18IUY0u\ns5VRlmtddXVjGA9KRccvXeqBFeXinxrlu7qi9EX0xBecOrtQlpx8AcC8l74nwD4TtZ7yRyAY+aNy\nkT8olwK9HRHsEFxbQGtBa9EPAXNg2/lQFvLUr7fVoJ8Dm4GtPR6Qeliwi5r1EQG/ic4VAD3k7T1f\nIHe9F30d/dT5q2xXuma4x/ej6NnlLRb5knXqyYWu7pyRqg3sR76zIN+KrS03Up19qGYXP6Q62ZMa\nTNNc6wWdFR9hxHzkI7PJzlfTZerkydtxB9IddPtrsTFa9SAyzWjbWxNWsi6D+CJlfhHZyxQrkO8h\nIQ+SFdBe4NOF/P3hlIv0xvS9ADYT7c61JqN3BlQvR6ORH5R7EmA3ADWIWscAGmes/juMREf2oe3j\nyh6Bh3Zvc6z4MnB9lc4OsOYeZFb9JLLlyO8O325aO+x7nIM97ItH0pOL22g1H/3JlRtFVx9V5HLe\ncTQRxOwqi+5fBvlwzp4N1mB6nJWt7HcXaopOotJZrnWVE811XN0tLlzQmQHwmc30Yz7oE6LWUk9g\nh5D2Hh6T/xpjLavpirIl9IH1kl4HDeq5fwLe6KKt65NIVn+nD3vBBXKdRXn/j66LHSszfpWFT507\n+Q+g7wOwl6PWyB/JkB/ITgH2RRua1DWgEFxXXRtdBlkEjrUuex78pnnNpmynY+VR2a3vYv/Dh90k\nau3sAnnzMdE5fP4onwGpvthjP+jft7APKO2LR9MLipwVLUPpA+lJC9z+coO+mNiciVzP7KPyHb7Y\naT/lo+9Ab5hqUc55JF/R2Xt+0sf0AYeoATMLcKtIEZMC1xaYd8dm3VO6/ikhLmdQd2t85r7LBvPy\n+JL+M7TZUcaIToz7q+h7AOyH5FojP/C9N93jdH1MuSYHu42ZQdSaaB84dtvvVb9GN9zqzulyWn47\nyGTQBuUTZUCq7WZGcvbmPJQDT8x56mOgk8oLbwbqR3L70Z02lw3alFIiH9b/RBnhvHewjpFgV70f\nQa8ql77gp9JfBrB3XoQoEmrkZyLX0+hz9TFwc+Wn0tXfOkzE8dIdQgKdrM9a5HbQppVdRGTkI7wI\nMgfHTPEOIVNw3MF3A+xKN7Fv5YwHzqmpJuwKMcB48tSH/L1A9yr+KQouygF6b4B9Jmo9BcFGRoHv\nlSjzSkT8qO9CIbhubamyBPAqHuqy46/td81GN5bPgLz/9fVxx1l7bDlIth8HOpeC60RnKKegDa79\nDMexj+HsG9Vzp60qf8UukS8B4sWVJO2LZ9Cryv2K9Gqkv1r+QkQzvKyifoZ+nf2kbhGQbj5WIrAL\n/tQEgNN89KCQgOtUPtBRrm29Bn6R53wYnfFLjhFgLBVDELyca63XSK7ovoFwqyWoTqrj0NZpjS58\nrTz5/lklITqXaz25IU6B5kdOJtf4fk+AzUT7cq2Rv2pjAS7N+VcC8QWbBhoGUesYQJ/41DkNPhZj\nbL19XqcoCj61Rd12bmfrObAOdd7FB/vTNs9xIByR7ctEviJzPhbLtrQEjCO5SO+Ldt+8kF5ZPPTF\nVpcXVubFAJs/RVfD9sWsfgCuQ9UDQPeMvOHIA7Ys4kU2khrho0Bnlzyqz+x8QcdFqI1Oxceh3ALI\ncoG5sarCYq41PjiIbCmYTbf733Tha4y1r+o4C/wy+K+6agw0H+Xz6wu6Kl+7HdsLmfTdXr6V7eFH\n4yK7GffyH0BvCrAr2CTSV2SFv2oD5VibjL9so4vXk/zIpgNQ+Sg5Ih/GLAC5HsxyyG9lRjJO5ANZ\nBM6X/Tr/ua0DUBMQml6HE+cr4PnhPoTocwQmjwDVF9oeBtfFeNgXz6RXV6EuuF+hL14MsMO/wjml\nmZOVgp7jY3pFBz7kd8pBBmoye+Dxgs7MN1+g4/phrw72hQXd5lcB+YJaRdgBV6WLQL+B5yIQjsGv\n06UAgKtqrOmahwlGnhCx6ouC7KUqce8jlFXk7/ilYIlkO20cH/7tssF2ZDZF91MIr8deej+AfXaR\nOGKe2RwBFSP+gk0FHREYC8cBdxt0tqRrgbKp4FA3A/VGphb+1AfU2dkSyYfpjJ3ANQVyO3TEnKfy\nEzpDORHJB43vjxMg+PA2ey/wKyTbg2e6+j+ZvgCuHdz1z6VXV0EjI09C+fWqQGUi1+XExSkfWZ/w\nWB7l7royR2Pv4/GXo1XR1iWqW6KjmhnoMBs57dfhoC+y7nVtqv5N3eo9p4YF2KQR6WoLqSHCFOR6\ni65kJnO2HTSqpb3WYTTupp2ygx+VcZSPsuzeW+U32fm74/0A9lnKJp0RnwLZjG9ljh+hKhoOJKkg\nXKWQUPJbbm+sg9LhCTge+1/dks/7rbq+/LAO1i/65DJzJIA1PV/RwTpNdFJ54Z0Fzis+2kI0e6X8\nDOB9A/vaF1Nw8Sx6ZR1Y+uJ91QdWztDLrgmgidnG5xkgQLMjcgReI5AQ2Rs5Z2uMtR/JiIg+gopa\nVnQ+q+8qmEb2AFyP/LoHlaivMh3pv2LLcu7GA0OIiE0uzGavC3dVZO4BVQgtS/HrrauutiWptei2\nquZMALqDNJfaiqgjztARvLWLbwcBnQfa7oXO4/SDAPbFMzsnJ1kxh/nw0Rfm8lInyGe/KzoDmyk4\nDv0w6Hr5+AXK8h+CV1X25l8gNWa6N/QKQKWdOicAedOZ1Hs1Z7um5S8BmJH8CnD7Mvm2eDCMlS8B\nsF9Fdo5Y3v/5QfTCBx5V7AdRunKOgOlEPgS9K1G3QJ4+K4+w3grV8o98Kt1QuHsHyoNicSyIOedI\nPtCJ5ES971w0Vi3V2mjcpQNpAcfRZbaQWc3TgroDewWO48vf7MG/+ny7gd1Kl6iAe4MtIgoT3cn1\n/zE6OKiXQLl78kmKvwhZF/pBALvQVQD4Sl/ZoK7gkYnogyGCPaiTLSgAzxI40OByk+db6vmilrf0\nWwTXoS0X/xY8XARUH6IT2Fz2cZvykIF9deaLiWE9TtpHsnD6OuVb3Fh5eQT7ZWXHC6DdvvGp9JJr\nYUOkhUYR7BlwTeTc/kvsV2RGzlZm7VOAMJA1sDXQM2JXZQRlcO7mCRyGVqeCP1sP6XNZA9GJDts+\nHQDpMDpOfh1cHaJuONfArxGElwOixrgzSY9id4P+8CA6jcTqiphIdDED/7U8jHhvutUZD4dPo+we\n2cPP7oejfJRl98yELxC15ulEsE7vDbCXnlwMnwLZUb6VTfmc61ebMsMI0QagSl6tApw028kj4C/r\nmjo6XR74YA3wLOgb5lrzpK5J1BqPrS2ZcvboPMDHleWoSG30G9FsBXmC7W5wPSxXVF+wDfm96qW+\nlxSr+8KLr4vK7KJXPehk5a6M4xnIpoHOSD5aR0DOE3nqI5TbBw1QmvRFA7JJW9vymIAoVbTRsZHl\nplN4Ys5t9dtwtjoITiOdKKXAtAeLWsF6LTUjALmbrjhe9cFogODb1Coazhuol15R+wu1DFsMfdEO\nhcZBmiuqvVitAAAgAElEQVToCG5jy0j0j/hu2xCC34vovQF2NhBO8RcmIE6EV9SHqbysRtS232PQ\nZfhH898IBKe6WJ8BCPb8hMdYPg902eia8pnjPrDHpu6r5w/ZASTweXYLvgqgorXSjYuMErl7sNnh\nw81HO3ykc9m0HaKHFJv8Ri46r6BHL1COTF+E9PRKvYDgemfN/Uj46CKzDcBstO6H5Y8Ad1btCM3t\nIaGtvQ03sEaNUV/Ysmx/mPN2i8XIU/MSnZOvjcQ6Sb3bdnkLPrSLreNioFv3xBZl230y8KTDB9H1\n0VqVx6BLpKLZ3Zuq//jz7dL6O/2r1rDDcQBlx0DuKa1WKOIT6ZxqSfggK21Sgwt3D1Ggw7QvyLW+\n+pNc7w2wn0HZYFvmRzNxpI+51tSQ1DYp2n9ENhrsf3EW1L9tz2ngO4A18N+exy3PlePrMAXsyt9C\n1DoClbPznTpD8Gnn68TvTGcEUnFc9HabUEmbQIM6jso+KX8+uO6RWrfN9wAIPI2eWqYPl6XFv+Jh\n41XXYESzvOMEJzQZHZTbsRnIeCJXZMFCImtzRwGAap7+HIAscKU0TP+4qG3QfzOdKE+a4Tzc1WKm\nA+cWfw3nyoUxGwVUox1BvC6AZ6srtL2gbvhadwPO6sVG1K1gU/KhyPC/S2upx6P27wXA0+NaHxy0\ntQF2oGDdQNYaYvlJW6TUVzS6fsRU9fMAdtaLR3p3r69s8FbgxFRyrSuC6DYq/zoCZJTM+0d0EbRl\n+plu4/NEl1Mfu6LWtW9M3cK6ZvIVnagvZjqTei3p2HZbvajvMtoxXocPFTtlu0D4QCYs/RawK5y1\nnS0U707B7jnDbn32LiJPA9cx2k0fJ0YR7BXQCnKOZNZ+BLbFs9rJ6Hlo1LdC/d0MvIkjxMUNcocU\ngjQo21Yh7QYDOOu5u4VxzhjhtYxnzht4VP0JlbcPAoavVTQQ820NwK+yFCxdeeRaWQDKNu1GKHpz\nCiskvdxqq357Z9R2hh8AmlE2Nvfww4FFcedk/Gzw2UCCe+AqjS6dwKBUr9CVUez3BtijJ5TRJJle\nnBmfNd/aRBOa1UcbGeRaAwgNKQFYoZ3T4ZCv9rtGABv4j1JENl3O/ULdHIBr5SxGravfCEhF4C7R\nmYHqGTgcpZcMQar1HegIE7H9kBARueh1PZ6ByhngeYB8CahP5dJ3j7K3BJuFCybvp6ZgP62s4Nrv\nsXsWPbPv99Aogp2BhCqjRL4y1w9kHMn3rF8oLykhas6GgJ5q4yRFRMjjFSt3YNmCaTiw7ZTAhuE8\nkhPUSWzfGh2JrufgGkfL/9IwrqB4wb5dQgC/Ijn43vgFAILNdIcQZ8+qb9VYsnWHchxdga1WATfW\nZZUyXSGyudZqzTg6rU7ovQH2DHwu8xPBZf5jdsu1/mBSEVvzz/M9iM1+PTge/BKRBd/RR18icLzp\nsuNrXe68yBbbSjSMYOODyENeUFzRiQDlFTqlXWxldYZ0vOA3otnsYRfGA7ZIl4BrBNDcFxtvF6xw\nV8+WI3pGWdGe76v0rAj2U3D8uJChdGUsjhzUKW4GxKOKBGVP97RGPyNgU+UC83CV45/Pl1FjQrZ/\nOGhD0O6hju1TC7jg3M2JEVBEEGmR46D9u4dua4dkze6xUaiPjhyL0YW2MJHdIcTrStN1O4RA1LqW\nZFNY8GGmdctwfGDpo5vF6IVpH3XBqY2FCtXjVmkjU/tDmotqr3H9U47qwxESv47eG2BP6YJFJXNx\nmO9zrcXoKXkFpYw2i3XHcm35hmLQO7B1uuz42me/yb0O96+KMQV9EIBtlK8A1tH5gs4zdgixbfa/\nAbjEX0nKGNQ5rcdBW+fjaH2oR607XvAAk9sEi+d0Hkh8KRrvELLSzKtf3hkU9FBqAahBOaeqMPKN\nt5/VyaJvA7nDG3vrA476rhoeaKh4HYK7I/tgH7iv2M5LgY+ZDqu2UPjQse0FrRg7nvJnGt1Zq1oD\ntKx39HBVBAQLgJmLbbt+dQlVudYMuqUP1J7YrMqqJXMbXGtw2PXDqrI1HN0HowdOJZNclt136f0o\n8M+q6go9Yur6BgB7NiOaFZcjPpFOespsqiyzkX6oqtTuhr6Xc4taAzCtXwxh64DNv3VAqyYlpcvq\nPPRRdCLwnfkY1sHqljaPotZZiogC4/byR8OBze2U6LQ2XKDT9CY6RKT2te5yM9GwkTleUtaorkb2\nJcB1eZD4UDqmvcpP8OBBRCkivZIeWkRZGDgvZrmJj45gPxy/SwcaSVOWqjDrsBGwaAAol6UVMcWe\n+hpji+whsN7+E9H3gt2d0c+BO8eF6Z8QjJml0AEsu/ROdFw1I/BNRO176O4asj5Mrm+E/zJMGF2+\nfJu+yrMwmHREWVA7IwDX1pZJIfVWLjycqE+1Y/lYAvqLyrf4KKtnW1RqZVWtaB7VDmSjD92AuY5a\nZ7nWaFhrPJoA9tN7A+zs+o74FMimT0FGtsJHWRnM9MFJOghrsGj4z0oRicBxtPXepuvrsHeHkD1R\n6zMR7OXIcaKTAkYrT3Tc7RrUz+9rHYDGmSzqi0nZV8unOG4oj6LWG58cr56LOYdyXrVN3yU02df6\ngL+H0mX1TEhobYu9GUWfB7f2o7UjkmfzflInhxv2UukLUescm/OsQkC2P629UH/3ocqNOwT4HOjY\nD9tEqSK7nlcCcK12EOHgd2CflelVxfNq/W27KB5KdZ2xILe7E2WLuks7hIiQ3RVGjTXTT0wU98fR\nezkDv1k5I/7MhkYygZPk5dAz998Oem+AnV2YL8aX8gKjAtdVH/5lOdjhv1Wy4IziIReB6xSIL26/\nF4H7WdT6SAR7NEGE4NnKBzqXgmsjV+1G+QhcT3iHU0QW5OfA80Rec63ZqCUvMdpzV8Zo4v7qZPf4\nrmynKBM5yB4ZzX/YQiX5/ec0gw6L6ORLjruj16ZOpyLXCLZAR4TNuS5jeE5mrsFTCwKtPKo66HBg\nM93WD9rAcG77JdqVrTEqr8lmnW4asaqCQDnYYk9XWxojelnRp44U9SJDXZVrzQSfOfdfYzyCX5uD\n8F5AQTBgJJCpgQQ1q3OSejI0F17nzugau8aK5jeRb8idg/1sUnez5Wf6Iz7mWuvBj8ZjHuU8C7LU\nL3v+1MbbxgCZnY0s2G7nPI1a4/Fwmz70MUciX0pHiMquMUbeZu1AhvLsms4Wh8nCMZKfAtcjv9Ce\nNt+SqPONR+pLjaLkps9W6nSGHuXXXttRkTyRO9cPDNc8rD9i164lohfMYUtXxvHIAdrPwLbRyZaY\nKf4DIGHXi23+7ChYPWgIyKs+zhGTHOxwOkHwB/UdRqatDmInOLc6Chsj/hJKotYc8GzlJ4S4kPwl\nxmIdnzX4xRU9e25SudsAoDvInt23cG2xCRVzk64TNoxJP/C4Rj6a1PWRhJ/pGz4J/Iuvk791B1sf\nXkTfF2BnPXcECIz40Q1cQR8z0ccHnOt/UepHmg4S2WLd6oQUALPV6LLXtX7Z8xf8Xha1jurkroE/\n/0q7iIz3tZaBbGSXyCwNZGcA9NGoed3XGodV7YPotgr9ZecQIHkL2rlDyO6XFh/VGZfj9rHDOKh2\nYdsGD6kueu1X7MAosd1TH7uvdU3fM+hB7I0YgaegbmfJBhajPpzpuB1EMp06f7prwQEv0NtBuvjN\nmeJxVxLJcnpJeakRaRWl9lp9fZPga4yUf40R62Y/IpNt1BHOobNgTUR7gfERG/fAJYCr7TXAq+cH\nh71e3ea6Se29AfbqRVjlW9kKH2X1qR1yrTdgWI4rckCe+6iM54e609Ffhs8QgGkf6ZZ8hu8Ae/mx\nulJ94F7OqGeOm+/gmOwx+piArofsADKTGx3bzi4bgWoJeCCzPPSf0Vm50YkBz8yBzi+2kegIL7FB\nKNMPzWSOztLlLoVG6Cssjhd0XDGXI+Edhe+gwWIctsBE+aatvOAlx0si19naggoFXKcvMtZ50qxr\nyykiHx6g2baJvbUCoOxwve0fqwPR1VSuCiW/r3U9Zgoq4NuB69RwkOwBlq18KtkRourldkYhauDa\np3l08N18QjGqJTCgHN4kbxfJppT1U/jng/oTyBrfONVPGKQbzWBjGlEJ73uWrV9dZUWbYvFB0x5B\n7w2ws156Eb/lWteUkBD8mC8Ugj8FUFfrsPqL5dRBDDoeSLOeHJQtATqKbOtDgQfJWUQ6AtsZ8J6C\nyqjPBjoy0ZGAh+fZXN78MwU7hJBeiVxfJ+Aa7UbXJ6Od8lnb9vuXNvQsSIZ1Q7uyedjlRC8xxh8T\nHQ8bPokmUetYdKxNl+dgX9q1gh+aS8ljFXbMWSvl4EuOw9zpAeA+NARLX/h5yb/I2M/ZnKOcA/28\n6kgIl0ZydIhz0ChyLRN5s68FWfTIRO0tzFAWVHCGMgGEZZS5JYb2mAcCnKuiYbaaa83lJgnBM4wb\nrAe2qw0Hc+z6YE/jn81XUeuN7FrQ+dnF3Ms/Ru8NsIloPqUu2mdupvwg1xpkDqTh5KZAo9GNgGn7\nF3xJkcEuKkfJ4sh0n9TZyaZpJqoO10StHTjP/NlrFJxPgeLgOkU2Kw9D4QND+00A9FSW8LIFZVC/\nmfxacN2j1h7rieOtRLWH/b8rXPNsmu8QEooCtLbcxKsj2Ff2rVD/YmksDpjs+m+lhXzxlxwZZVEl\nbD8NQHyTux1CNoO94DqsD54v7IMdVEP5mL20KLbf6tIiubwy4lxrO1EIyJQDU5dZx3vSTdEP+ep5\ni6ndX1kpbYdumKeP5Frb5zyVax3We9SmgdJQuOLdHhO5pyD18IdPXkLh5Ij9lO6ooiPZEvBsTR5J\n3wBgJ5T13hEA4vjcfqa51rSeVx3aJ7wYtPUyW/1SHdOupstOR4NOTv2ejVqHgDSqsz221+fs+URn\nBVx/RnVvxwcA9Cpv5/iWiTyShdPrwFZYVGaTm/QYJzxRY65NoDyxKToof8oMupNq3vnKkHPySTh0\nbP/VOgOA0WjsXF3s2a3+XNTMyEbdPIrO1UNGPQZMgfdFH/xiHIi5Uet9o++U3oBpLn+tz4jHFEf4\nA97a1xql38wKrwEP7RvPdO7oeoyuBUcqtf8CsFbKHu4Iwv1adh785SbKteY411qVzzSM8o/yrtny\nsYAjCHShT3fZEMhE+r8m8mN337yajP1ozB+k9wbYqxdnlW9lA74QbZO1y7Um9S8DxzHf26dgfEYp\n8AqGZZ2ohzuEdLkF19V2NWptgfTyC4+Zv2iCMPTUHUKY+kKO8kFqRz+egW8JeJT3RUQLOtf4yaLW\nPmK9+dMjc2YzPH9WiGKZ8qj1UlefAtdUtvL6GtRA4wTspjUOUkOWW3fk64VYyF6gUGU0kBeZz7XW\ndoITL4Kl5oPJrVmjjvkwYtOGOuRclJkMcDM6sNQcACoFwlbb5gMrFvhdKmviY+onL6CbSTtxudZW\nz9RKe/eRWKvHgSzSPTJkd/dP3IiAH6yBo/tDQKH2a2LMjkdwT5i1ZVjh6+bK9wbY2eiY8u3KvM9P\n39f6g3yu9YZ0FNgmLnp4gxc9sqtu1Sv/6mRr0bUFWdnvgo5LIYl4oxcezQ4hDhir/tHHFmxnwDuS\n2y5x7bVt2aMT2OzaIQTlw32tB4B5CLYl4BHFyDWvc0TnwbWoqPXaS4xdHumEANP49eNgpSGPJiHC\nCP6A8sUunvD3te6L9AX1KTGWdgrX221fM8ePltyQrnjJkYIqWLdZcAYVAHz1uZXLOdz7TY7KYFMO\nms0IZLv2cSpzXQ1yAZ7VGX1cJksJcV9jVEIyYDuQKVqQORqPqSEvqF9ua8CitWUizPXBbkKMirhR\nYcjS33Vs4LF1xkT6xdHWnsEdlKHyK/jugbJU3vQp7I4PLrKtECUpKtuiT1x/nKH3BthHKLu/pvzJ\nvtZgH93TfV7outEuGSMw2v+ZT6xjGVDfFEAzkfswQ6jLgV8s6/qo9f4INvtF017LyflZcN0WNtfP\nI2AN8uA6LMmsXzGyiLJxXugacN0vyRXg2j1oBH5dvXiyUDyFBqutoRz3JeB65TopN6/uizFJeoJs\njvtSwsOYLviSI6POCIyPKiMUfo0xdGl9sQexyrABlHpuFqd6eiaaX11b9GLOQzl5Xphr7XgLMqQM\n3EXtCBQjmOsul1hgVy36va9fWtwOsuGTfo0Rz2E8sGm73ZoPj0fpIqrdFbHvnWMyOgK+WwMlmv6J\nQoA8AM0vou8LsEeDI5MN+DrXOs6rznKtl3Tr4hH8C9NJFts/3qZvpFvqHthGudaPyLtejWAvp20k\nOjYogjqzAIiwrO8QgrZHAHRUB3dtbIXjek/5B2wkqLeU/1md2zVfHAboOtJ4DieMrvuVC8QR2rVD\nSL4ArADvtengVZ0h0+VNyzlvUPaQsOdp4+ovOdqiI+Br5fVeMGhtvN0eh6Dapo2Mv9pomjfptrA7\ngMlkgDH6FCOvOnC+9DXGqOyRTBUQNSAmwYPV4YRb6jFcT/hkuNpesMjibfrqQbxDiD1fkUW6y3dK\n1ndZ39OAb2URv/kQWs+1jiooro455Mnmk1y0l94bYA+fgALZ7CI7frm0mGtNAfBrQIwdAIw+Kx4e\nzwCUpQh4tl/2fDh+9NcYV4F32IeWv2Dn+gjOQ3ANvKPgOo9ag9f0GkjAi/R28qK+SOof0TB6PbSV\nFlSyedPkeLSU7nE6RWTWFw+joC6GVqt1aQT+BdH8lRLFncRW4+j1jrZd+JJjKMsuLqxJUWRZRM8J\ndgtCLS/rUCtPQptpxT6wYqaeo/NoXTXrqXsfgkBHtsoLPnWrqKloIK30SANYMjLV0ejDVDa7VlV/\nwOymcP0A2DGkuQj8X220e/2ZmRQ8F6AeHdcxVZdv9Zn56CGmHKfDde+8OcJh6poM9IP7eJ5rnfER\nnNve7JKcf91c+d4AOxsI2ajZpU8l15oKuKYtQteATOURkeHnPOTbvGWhOApOUE73MU0RwclZ8Xo/\nKEAFssjPI6PWT9+mb6AfAnJzLhiddH04Ac+nIttZmRQsJAENZEfBNe6KMUsH2ZtnveulRsub9cVD\nSKZlKvHeD8wEdstNXMr9uYoQUIy1uk4+P2+AIYs26WV12spXveSIX2Osc20976eFF/SFiQSsbMk3\n1Vn4VLqpmpdDGQzngkrgoH+NEZQQXDu8Yydv1GPdLdntFPod6E/MqBdfALUoRd1kmAtVG71NVCY0\n1edWQ2VGOdmuUuU47YLRTWQeBJNG7+PbXOtSsVmudcbH4irX3wbPSSd5b4B9hLLBw/1AAUCXaw2X\nlNGYtS68qNheeKx87vodaHIsa/b4b0cDFSjrtv7FxtHe2nxZ1Hp3ukjEs8e2P6L+WdCZp5pIUr8R\nKM4BdZRSsWLXV7JIlgyOwZg5Bq6lg2vW/Oe9xDj2uY4+z9LJHUIcw/fFzM+0nGdGsBeQrriTuH5p\n5Hpil9JqR0Zu/So991vA9exrjETU0z3KtYo/hS5wbipXt31TNrUQ8c1iolnqkB+bFLZ7uv1eaZCO\nWpOffHhBRrN6c/9x13FhYLI9lEhcTvpWe/4jMwJg0dQ/6Pto+Vip9VFZToN7quW3VO8VcBs+DghE\n/raYCq5LJ3EF2tLlbZqvLouNXR6IpNuDjdcbN/FKjP19AfaRUVcBIFNLCYlTE+yOIAQAERYEBf70\nQqHBuanT0qps7BKg5aPUCHK7D1G2oGci7VeA513gfMXfZDa6ZocQcf2zHR8D1yFvJFv0KxmQGoz5\nlFKbHhW4AlxHZa1Eq4erEAfyh5DYWzusjhZEkZmclM5BoMwPj2BDZGlSlAbXSefF2oYOtGmWIlKL\nnLke6UQgF+b7KLI8/eLitJ+8zZQ46N2CmdQ5jXlMMH8GQLvd/ipqTf3ai9ZfkbnhHLV9b3+0eq0q\n6/t4mmtNRP01yeRrjOgZMKn69koB8LiNYpjPXsrngF9Bf9g9w3caogsSHLfxHFWmNOhErvWSbis+\n0308vTfAzkZI9PSMfCtTudZEOlWDadfLikwU7Ycd25/jqXYEv27Bq7x6x9Wb1wCT9qDwoKg1Hluf\nzv9A7vrCtnfx/NAOIUR0DlyPbBd5Vh71hSXb9oncattc6/YnuHZOcC4Br3PjlxbFnKPc1JZRamyE\n6PLPgysq4ZZJEXtrsCfvepfvR0ewhdJ12ZasLhtLqFM11TRtndqUotQP0OcFY2II3Pp97XKtBeaT\npgp/McWvAbobShIbKNekU4g6CipsHzaidTNCgdR5K8NK1ZXJT7juwrHRN+rRhW686+75zZMfY1T5\npUxfnyT9YLL9nnWDwWIF1olUikj4xctaxTokAiyc3S+7p80RDrN8ob79Xi1P9UldT7jh9GrIRRt1\nGbyIO+pnUeZ7nHa2NIss03sD7GwgcKKQLQANnGwHEehol9Is+mo0DkDQdgNUdBKVi3rAR+AE/6Ih\ngM+Cuu7Agnp4fn84OAKeXxXBdtfVXiPKdey8jrQctXbXPbMDv4nM2Q/LMb/Dhd/L9oDrM7nWXif7\naIwk+kU2uM7OhokeByrHwDoVHcidVnpn9sN+VAS7RqWyuXVUn+geXLPOC5zRaJu+WuTI9QhMVGIE\nQ+zE/Zz1uVnbLc8CbzV/Vx2sm/jLrlJIPu348hU1zfJ1NOVXebud2crYz1Wo51JIyFUyzS3fMySM\nPgf87VA3sDeFm+5WH4EUEYZoNnyN0Uxq0XS+V2bpirt8eIdkQkmEyEr2tY4fYkTxlS6OMePDtz+p\nsMmbfxS9N8AeUTbSuB+0CSqMWlP7lwLh4F/kQ+uCb4p95D6ND6Lpr8+rhgkfZHXyXt3XuvkOjlud\ng2Pbbusz8+H6C33MZiCYMEO54V22Q0gwSw7zriPeSBbwDu8EksoGO4SwMWvnuo/gliN4VJ2vHBwc\nrtrsXXCXaAyso+p0wWPA9SpdvSf4irdz4HrgayFdIqVHveRIm8zmWhNZXj03bTB2s+32KsjYpRPV\nN1GImtkwFFZdvAGjEoDOTSgeeONEYRvhXnIUsE1rmchMA+zDTEoeAIqRx13tv8aINbPPGKmsOM+m\ntuhZ5RThdUuFwXF5oHC1UeB7DIQj/hoPy/A1Xqdr58n3B9hHQEMFZUyDXOvKZ81n+Ppis+GYX8+r\nMfBFycjoAZ84+GfE6teiGi2zwJqIvlTU+pIINtraPiiUzc/H9rUegWoJeCAL/UF5oe2gLgdecoxl\n2dcYe72viFxHdkvR61bvoC+y8zO0a1/rwPaK8s/QhRFsu6Wck8/qMUwL2elvL826AbHBii2AxT6n\nbIruRcamgwZgVw7SLzISk04jQZ3SryFotM6Mz6RZ6Fbb+IcGImp7OYsCxbAehQ8APJY5nvE7koXN\njtvLeGD60FrovpF+WbgbcJIOYn06mfT5rx3XcQLXYjXv+lgO9uSOG6F4h/6lFIaj0fvnWq59vhpW\nIvIRiRLdJ9CbAuw6AvVpOwkmhE3/eK51xnc8ivTO8SJ+tE1fK7u1ves4QNl4r41aW/+ZP+tD+bN3\nS3D3nN4hhAIZyk3fTm33RrJXeGz8ZjSdXWBXDEb1GFh3Hd0XDHIXdQh1JnVkc7hic5qC67un2CBP\neIWcXmK43OQLI9hRmdmUq3RM5HnmJ9KTTAl0L2npzIkFKziQJZhvmw53e4ZihKgFQMKiOAAv2t1u\nil74zCsQllvPudRfyfF6GwC68VjzRrLMb1anjJfIxPIbuJUeQXb1EV9/4zzBwO5+aTKmh+ZdT/ul\nFpwSDFwXrS6tST4IFeZam37q64TW7Q8ahg/ePa/z7xzsI5SNg4R/NNeayFw2nNQM2Ilyrfsx8JWM\njR7wUZ+Nvm2fakv3qepZ6x5ErXv9/bHyY443f/HxzGfoP5Gnx7Y77LWbysX1z3Y8As9ERDKWAc+l\n6jj9Vb8DHxK01dJEXqPWqJu+yEhEGI1ksFGj0fW/aLa65Xq/sbFxbmxZbIo/9ZJj34YwopDP9nQ+\nUa9U0fkJbKaX/WQEexa1ni5LwipNJdO1RVg9VqG7WHfY0pUOHwKQgp7rC+BFtwGF0k/ctRsg3PpI\n/M3SzqFdxaZjNoHzbqd6NNhdQwzSsjnYM1JATrtq8javKwTJ8aCoMseDX7PWhl/PTHmL43w2YLl0\neUWrDPdAuxVY9X+fNhnduGJXZFF1nynT/ZPMP2JkjV8GphNpP239UNHtpMyAzwHft2nuZ41/jN4b\nYI8IerrddyVq3YElrOwMelGuNXVbIuSztifgU8Q3dQpkDgC6xomuu/uFehqZlHY8Omq9G5zvtFPH\n0UyxwBOSMiaMHBc7K0N5dM1O257kHZ5Re9Sala6Yc3Bl84rZyOGgnwcTIZSV1nXlGtt+ORy13ew+\nhv01W6CCxWSRnO7AeNnvwb5YtZL0hAjno9TnUkHsG7y3WWdecgQA6fa1NrYdm5i5WIxN4N6Ba0Xg\nbM+gGrgaiquOfXoRCtNt28TMhtf0OOChnl/89PzOcduv6A/CNqhDdaT5m4zVmdezTVV6FcCT7lNM\nEWldEzhfTRexAyrtMnt9LGUyBNwl3cOr5UD4nC6UbWgVHijhRTj7TQF2MiLbI33pIaYWqVW51urf\n+lZ7eUoHL+rt1c14sNDUmxFHjOW1c9a+CHwHx22SD46b/+CYBv6tjvXp/A/kqo+Qqn3Aq3Tqa4wU\n2A71T/DO6FOgF1Cca10mN2PnosahjgGXUdmp33WboQ9JfMxoEYh214G+rVfoYXExCI2zhWdEBzpD\n4px5XQv0zq4oEasZ1STY1zjQFfenZ1YK7EoKaBS1nYGKxa8x9o+7WF63G77EWOsw0dn9UqOlyZAQ\nPMB+rssvlsekwTPWp/EmFyvghVvyPZ064mbVHlF1i8A0UdwlhOeFicd1aEtw3JzXIYYPIUYnTBdJ\n6tL44SRkWqAehqSlWuvY0vyri8iffblRT+8wB0L14mcvWdJ7BL0pwB4QgqsPDoB1OSg/HSDXfwgW\nO9/nattPnWsfVldHy6s96lsexz5qHZPm559QvyZqfQU4n5a1098MeKkFv85kbGUXA+7ahqGtBLx6\nLFl1lxUAACAASURBVAHPyKxtG9+rJDjEO6+6NK6inSiOvKB4hc3GNHW2fbVrBp2v4s5d4H8lLYRo\n/TJdkR4S+hlQ9AKb01ngrnwcZbNarZt1dgB5jT40k06qtPQ1Rr3v9eSris6mnjPheNY+WD9kKHkp\nM2xS96nk0T7YZvnw4BqeXBvYZFBWxWmHmLPsZLrG1a+/JGLKBFcZklwg194CWln6taq8VkUmGn2N\n0Z5PZfrSz+u6U7ZK4Uu2UQFKLhRHrTfUrXhlLGR1ZaVH3j6oSue9/GlM0XsD7OQKKdCcdHn+RwbP\nzy9ZpuuHWKa/wg/LT4G0dnlmh5DdwHjRZ+bftmf1eDVFRO0Qoma3A2B2j20oewBPTH0HhBF89dI/\niVo/q3w7F3XudcTZVB2bf+t9ZB+e6X6jlyvV3XF4dfGA3hUT2Vi9xfLPgfCjC8ha5URkCELj0oN5\ncHEs5svsir8DF3wUwc7AA5OOHpLfi9nO8Yilo/NYh2Mbog42GY2DOo/ObbtsX4Bvg9vbraZ2CGGi\n5ZcRAbjm+p3Hkd/WBo7btWc4ZNcvqqN7xq2C+GuM9jyUCTQDgDsXBZva0eY/c0xUHwT8ceRnidzE\nA61QW5R8Vvzc5L5H1B0Bep6n7TNd1M/mAzHcXY2n7CXNI/TeAJvI3yTMLWrdwJfNteZ6zI2X8Y/p\nen37L0oD2f0P2m9TRGpfrEatrwDPpyLYZ3zY+cCcC4lPYWm/EvDq8UhWbB1v4rfpy8DvhDeQzd9l\ng1xr1nwiy6NJukdm02WRPAK0R2xUX6pz8ig+JKEZCAw9BMxl0Jw6jYoIfC7YxjSu3/GotZesR67n\n9eoakcMDC+HSU1AfT3Fqhx6L0rZ22GQ26qyqWl8KRrTcypHYptqFNlBn/aRMHVck6DPrUntvWn9M\nfaJRPGPleKgPdXU+4G4a+Qhp8QYxPjIrm13NcA1S8LwiK+UrsFy6JMvJdjg3KQyBe1ihnNUrOnpg\nUWNVwqnZ3bUwFqe6wI+rsB7R3k/XgWuiJwFsZv7niOjfpS028idF5N828r+DiP4MEf39RPQLIvp3\nRORPDZ2aiaQB6bO51pSD3zwvmwNepKd183LmvHAYtPqztiFaBsnNd3Bs/RzNuw7LOuMD7yw7iZzZ\nIcTxjDy1rWVntjPeQfDN5NqPtOdrjBvvPLh29aUkr9fyQr87bJhoDJ7DVSF06+yszi4/NrqSEGc6\ncZvGdZ5oiBAnUesobtSFHNYoSiWKam13NsmuFm/KXid4muSBHyIav+QIIsyFrS0Po9bpS4wAAwAw\n9XM257ZtkY1vm7WxXTLU/3C3ZmdI/92da+1SSIzfCq4Vr/+mdaqFjcDfKkXXEvgq1xr3Z2bfbArO\nV2V7fFCit0e2TMpJOak86bI6A0TPQJbfL7c4HnLx0qpca8Xfp3t2uBylhwNsZv4goj9ORP8sEf01\nIvpzzPyficj/BGp/lIj+ooj8i8z8dxPR/8zMf0ZE/lbuePsRorKvNZPPta7HARAmBIis9Qh0yfBh\nBrDgs/nsjQ/r7I6BohtjBKZVHWuZH7pue0Dyo9NFonqfPg76suWR7U4J2aw9z8iza8lQdujb2A/1\nJrxIHo4r6UOcNT8G1sVGnaP8PPCO5WPe3vOYgmuPPkam0Q4omerA/jCdsA+zWaNVytkNID1Mscpf\n4keV7ZBUXg2TduzK7z7HfoiIZLY1Hdt+4bCf7NcY41zqwCcRKQCKfjHa4GyMz6qaobNFGj7UoM/m\nmwMe6rF3qurFAa+L3HaSB9q0RBO//aGiByWseXQ8lAnMUcEDRrYTSFsuov4mUukiVmfqM6L0RqyN\nkMB+Q93eNJ8zI11evd7wCfqxz3juG/terMMCPSOC/U8S0V8Wkb9CRMTM/zER/SEiQoAtRPS7yvHv\nIqL/ewiuq1FFDLztteb7JP1mUBD1ZDcH1MlE8XFuVD5gwsc7kj3gDAGiAf9aluhCHV4RtX6Y/70+\nzF11aoeQvTnXe/1H4HqoH9UxkUWP6riVHtZBnXd+DlozG13GURu6wMa2PUwzmVC+6GQzyRrt+VT5\nY+qgNd1DYEBpjVVIE3QXKyOB/bAOkd+DC6CN1FfM0OafdlzWCbP/t00HiW1IXSufMiOJDTaMfRsN\nircR9d6gxXOXgy1Nnketg3tQLaai5yIHmAXqAH3ZzOBeDvPdJPFb6xt1yg6qfiTfes+eR7JIj5h8\nbjX3yz5K7WhDKijkinSRsA+avlT83JhLudbtuuKYsfbIQ/tMd+N4Xax41qDn0zMA9u8hor8K5/8n\nbaAb6Y8T0Z9l5r9GRH87Ef3LI4fbdeY4al2ONY8THvd5bEE35vUyNY+nvLlu54e7ixDU/QVR68y/\n1Vl6yXHge3pc60BZrvVO0Hy1bSjbanx1nfq6I21y1QGz/CXGYqV4Wmf0EiOW4OUWvGsd/xKjlau2\nVsI+DMq1NZitu6n4LLjeYbCnDvtI1E9Wjl/eXEX6fQtGK/6qvb1GOZDXfuFRMSyQR76CwhCv2qh1\nk7PRZ83UOpLkn4+AsQfbm04A7O39oIgHHwNKegYfNiqAYjhn6hMKIw/1OOCB7UxGO/ySkSleoDei\nUL8ObESsczAdyex9ZJ9V1HNEYmdqdrksozaXq2chUfcjzrqeR6Q/wdPrEvNE8TI+XpHIZ9U9OzSu\nxOJf5SXHP0hE/4OI/DPM/BtE9F8x8z8hIv+vVRRzVu8HvDEFF6MikzqLsuXrc6I6mYnXU6/omoly\ndEy6fupFF+RXgDj1B2+UM10Onq8A57sj2Cfq2K43LhjNz/PAtSi9M+UGvJm89AOCFyZyINUBUO6y\nxlI686h2OHtNotrOJqgHmXrYdbWfRz6D/o+qmYuKgqzpjfxd8bn0AcDetXgMlOfgtMxRiz5Df7Kg\nE/i18/7C27yDOpUJtc33tawymsLt90AfkUex6wAd5nbqdoJMXE9UOThm4eM1xW8/73bdRGCdg/Yy\nVoaDPz5Iv5FQxqRBLoG88TjgBXp2HdvLc35F992s/MjWlvW5XVc26vWYAleHZUI+gJHYRT4eLRPU\nU9OomVMrnDI56mqqctdAYj7cUzrlReJO2uWbwt1UFJxrevDF2emEOKdnAOzfou3lxUq/t/CQ/jAR\n/VtERCLyvzLz/0ZE/ygR/ffW2W/KXywjgOmX9PfSr//iV75EHEUDZvgntqob3YSWX53A3dIBcp/E\n28QIe+koIE1w9VVZG0/sgKuT4bE1phd7kkIf7I8l4RPRJQ8AYX+w+X0VL5RJro/ynbZMRGxBdjvu\nPtWw4WDiVEVLaLP9SGyTfAp9bNPryJGNGes8sSES+ggeDjIK1RLbPTl9q+UPfaf1WPeZTnVA01Yl\nLzXu8rX4YuPQnwl07PG1/bWbVT/rvaTxHOWsz80NkdtIaCOmDXYbQCIJbEihj3DrQLhX9L7c5Hx+\nlmgJ4wMDtmPIQ6QS6RX5oi3vsiUtv8C2zSJCWjY5FoG6G50G6gLbBgfq9YDj5tMcN5/BcYMmcEyJ\nn/pRmMhPPW77eyfrNnYXkxnLH0T86e224QvX/oNIPqu4+5Ai48+i+yHlAcjwS1n0WerwIUSf0vRI\n0Af19y8+eNvf/FM2e9E+/sbf+m36m7/zf22Cz/W5PqJnAOw/R0T/IDP/A0T014noXyGif9Xo/BUi\n+gNE9N8y86+I6B8mot+MnP2+j3+MWqrER7tUitR7FjBOXNoWXHi1oDM7sNduTQteWEeT60KPkV5u\nxz3NhMEG00zaXAgpKc2+6n58tHOsY2t7wK9+JDi2flpfTfzbsjJZrX9UdrsG5tjWA/vV9bG98SOK\ndNbfkvCy1ej1Sb9aTwJel32wTF9AjAAfpnd4m8p7hN9RdPy4X+YKrtcnx5UhhP7fw6+0By73gtzQ\nKmJyOK73LD8WVB6qA5HzsacO0TuO1n7f+ZaaodKbhCbnrK61ljNRAcLeB7fSrU1eh+6PCOZY2TIs\nT1MFf4oXXOdQjzpAxAW2Ri3Z2AZ/WR7a1iqwkZG2Xb43nE9Yx61fgrYFOsOXD6HdbPqAk2MiUtlL\nNl879AnFNpliDI6xDvBQhzJ7vNVJpnq9HuZ6WR+qn2HdxCU0jK77GaO1g4h++Ytf0S/p7yH+3MD9\n//75l5z+Kj0cYIvI7zDzHyOi/5L6Nn1/iZn/yCaWP0FE/yYR/Slm/vPF7F8Xkb9xuMyQG99EkW42\nYZ9/R9bzASYkunDpuQBsElWX0QKwZ7F4hOwRZaiHJ6YJKAULB0rBYwh26+8A2KJ8b/koT22T+oGM\nWbbFkhdeUjTlL0eH4cBGobXOxKbwVJFRGgYbG9WWUjfrh6R8vFWKeA16pcvrq19sPFX+NkNUELXy\ntcShBr7zMTFI518ElYsVUfNj0p8rvbyt3xwqi9GyaRQ9zaINZurrtJRz8N0OK9izI1HgfzuPY23s\n1YarWEBjs6nXudWhXK8k3UWYF4JziHoiWSnH+hm8yKhtSX9Qxsjaohf6rTzObUsfKVsoa7t8DMts\nPr4smG3gnMiBWexrC5Dr8fCFxno5mfSDUR9O7RhvCzHHZPw4n9hrYi7DjAbK3MowTlWBve5bO/q1\nbZe0dS64Mn2lb03RfOMDM4s2h5A/jvzP1c9fzekpOdgi8l8Q0T9ieP8BHP912vKwH1eH+p/ruawr\n28oEE6bWl0Bfl7OgiwpuIi4iZqIPJvmokwFOCnT4WM1fRr70YmKggz7t/Ihts+3cJfuAMm09yBxP\neTLRk4Cn5TIsQyZ1kYC3Wr8ataYGJh0oVWcZABdzjnI/Imd53a/x+Ul1L6Ht1jubHhLUcc1dqc/a\nUpX6PFE+kx4TRBFYiymstU/cdff20GdgPyzb+s3KXymbcI0XP3CUr00z/kqj8qJAlU05aTaAhhQG\n5PrTkY8qUrY5v/kEYMD1fyESAAgdfHUEYgGe3hox3uZM0+y6GblTRwTlzdQX9uoh+uDePwqkNb3m\nKLAlGkWt659M0zFnqvtKWTT1XyaLbonMEI8tlspkAHj7deiAV+v18d58lhtJPagU4+ivAGzHWxsi\nZhy1ooEhsqW2yPj67KGv8pLjE8ij6+hdVIH/9SWwV01baL7mSaAbvXvbJ3IotYJpmk93tuRlGSeL\nW1tA4uOtfuYYQSIcn3oBEvkWXE8pAKimfcd5TwbXuDhWYF0WWfxV1cS6qHPUyWxqWZFN9xn7PbLl\n3zGbD9sHg7ZGFKuNHgJm/lbhX9ye2OcK1THh67AHkK5w9wD2lf4Q4tgjLrzK50rZXFMxh/q2dlFt\nZzrR+zwzndAGQHms43cL0S9pwpckucsrYBfpGfkfO/7CskQIclXIlfRFqPJg0wHCtiC4drZEQ/BM\nIMeFk2nrA6W/1qwI6JvLpXTsS3Q2iow+MaJto9vtFqjrIIBiMceU+DHv03Y/RGSGU0hjedaJho/X\nJnzqsnPF1gCd1sHwv9ZtdexhcVN38bqVX7ci3DF3r9C3BNjR5Y550Q6LG3nYnOmu7vKo+WNeWcA+\nPtQKvHLpR/PFFTKrd0Rm+3hFxh9dqOrJYMSGf5o3BsCyYnvA79j2s+xOKY2tQPZOsOzSLhyPpmB6\nHJGelTsC/rNye9S6ylsEO3kwiChWE6+z4M9P/AO90F9Q7gL1qHX3oeaTCZgaS6NWRaA7csyqInk5\n4uXRdmxDH522eaMjs5GNqCM/z28gRiNd2xe2xzvwqUA52p5Qz5bepp5zO7fjuudmF48AuDYAyNSi\n6Cb3+xwNVozpAlxW3lQvAmbmpC0MIKu2EfCmAqzVgmHKTUhNVayPOeET0TAP2vnJFkMDxIna5XTH\n1o/1ie1QekTppYyaPqNIN7oTY9yDPJnykB/xproi2wuPxPA+gEz7Y5W+JcCO+2Z1eBDl0RnPFzxQ\nAJBjPbPaSLt7YEgwlRc4pSKorsK0DQCIbDuQmRw7QAjy1eiz1RF7DP7xOrhFa/W49EXjsei+iCji\nh7xgpNg+SniyAqAnPpbANcyKKteayEWvV3KwNa+eZwA5szkCxNdsojr7l3JKX1C9DTSorrsirERO\nwyEUrr9rM+7hKPe+NR9oBKzh72QLL3KlLbQR5MWXwiSwDfUyf6s526bMGjiJFu4obKznZp+tLiop\n1AKIUhZX30VucpPbfCHWprKlA2WhLi91FtIAvefmcjNAGxsJry2rfykQIvqcjrARrKoVZ69SQUor\nWbvC1JcOio2tAqFMrdLhS47Q11GuNZc7wQIo0OmLjSHUmRzzQCcEwrU/VFvxuufHChibY+szmIbD\n90WHa5Q9Lrt39MqBWmYT+GuncK8P37XB9QL5H9R2/FBtKU8T2r760Gij9cNF4JromwLsiKI+i4Bw\nE5iVMgLImseGRzGv+A7rg7nWxE4vBOlB1VcoTG0ox5Ich4A6OG7+J8fEGry7Y6sbtY6J5oBWBjIj\nD/VE8dxcfOVLjkn5mGtdQSmeH83B7jpHAHi3i/1mwHlQFzPDWZ0P7ikhFUCyPa+T8tmXDJXCyt23\n4HtSp3XfkCak7ON6Hn/J0YwgWevXNOXD+CKy/rzVCOZVBYNR1Cyt6pJM92jpWxdEqM1R+LXGdlxG\np1nBOwgGG1V5djbeztjI1vfC3Fou1D+Aw+CJ7d6CRwgdLvDY8ZhGedrKWeiXaZSnLWrBIcLRYde2\nkLKBVf0TqfQNlZsPoNj9ZYH7VLCaSrL3hUfCbhEDMts9w31NC5axGUX3ZtDDKR8vWbsv3Fg5GJ0G\nvuKWXOvW57XdV9wPhr4hwI5eOSGq043lVQuvux153c5neEGlavmL7z/rKcBtlz7Jtc6OY+A9lq3q\nPVvm9LhMHIxAu0ZpDfjGyTEEp2d5etbxDyYy8SeTMiTgddtZrvXeHOy6yGKZUTRVQQkYl3hwZDeR\nZmdmZQfYA5sWtSZofwPV1MZITxlZnzCHi4rt02Wvge6gTut+pV/vcu7tzaeeV0PrBPejqLNSSVtK\n5iCCqYZ8zkTT2rPU6Zf33HI69Yfzd2grRPkWeZudtYq2yYtTOySwKT6DrfeIul209Z57OZL0vYT5\ntuNt+gANpjIjZzITJNH6jiLcK6sWPOkytI0WRt2d/aGiyAR0GjBF212jTrXoYTKrd0iG7UdZCeDZ\nKSm74hFw3fS7VPP0EZ7ZJNoYfONDuobilhfPSnGu9fZH8GxOvxZkf0OAvesVo5O6mf26bt3Xuket\nyyVmkJfzIbBcOGbjm6tPc2x11V87GW42c1x/7K2QPSxUmdKraefYXijb9cGUPAhEfx5AZHqJbTSr\nNd4JcA251lx0W7MtT+Vgm2oGdX+8joRyKnXMfcR2HzXX2oDq6o+p312tb8Q+Nuc019MQbJWU7iWR\n6yhqLcHQ8oB7FpwJxaZSK7uB4FyQ6mQvOoHdyrzcsJdJNsU5ZRsZuNuGr9wMjMfb9ml9ne5Rz6E+\npsnSEJ6xKQVsKSPdpsuLTyEn75VgQOu2otiy0YVyykYW2Fe0hqgegS+bxqrJX0CPYGEyMgJ5lTVe\nl6mX7wctGCrVJkhvjl3M7LVHHRuZRp0wop0cE1EYJZeiA5lFuqgGJPFugP80xh0eq/FZq43zkNPr\n10WNFqxrsxdfneLDYgtivVVltW/ptJl9ybVuEfvSkfjw1dO6rgPZ3xBgG2qDcX1pXN3vOucZfrtR\nmGBItVOMfqiyW+qBrc9o8lskHNDJDeX4VQbHZI6P7Bbijg3ZF7TUma2LbdMpngbnMtVHXgDsrd/Q\nNsq1JviVMrEEKSJM0wj2PtD7LJvNztvADiEkug+Qh32C54u3yFDtYGqI000A9r5ZSUzUMQLXG9/6\nnr3kqC0zsiWskdeNW73sU0rLlRsdRU5Bc1C0tkoCIWbOtTOST/fQ8zoRpnugja5YXfiblvHr9rWu\nvpn7RghEJe9Y2sOMVB5g3M+9QMLVF8B0BN6j7SkauAaZ9TH6oMzSDiE1JUaar4gvtV9qkUmbbe4z\nHnPCr1WM+M0n1Hv6cmJwTKT9mKmh/HC3qWxzWXZ8/ymhgTHW2+jauyXm57r2+TFFbi1qnZRTZXeK\nyLWklqEGxCtlk6m9TBlv48eAkYkh11pFi4koCLK0UmZDYCRflaWL00G9qY/yd/8IuKuXGoGPPNeu\n+R1aeEGPRCA49GFmNYV0DoLrxVzrUznYtkk4y6hz9DECxnQoKj3LtW5fYyQisiA7ANRWL2tLREO1\nAwDb6Z0C1wLXeDv39h5Q22u9Z1u9q/X0cIhXc6eXOGv4zAHe/sdnXb8cNKPG8Fz0WPIpIrV/JdGJ\n0z1QXgH3KI0k+iJknSO5AXNAo5NODYdltMiASwSFIbgOALSulikgAubR1aoLI6acFNUNNHJbQ1vz\nHTg3fCxcwlLjNifHbe0OdBjKZSL1cFWfA+xxBeKSHBMFRRnwbKb3wludyeYUDbHO03chGT72t/0L\n0FC3cOJhimNL51q3Z9P6MjL01dL8c4DeHGDHXZJtv+dzrTdCPnZ4PVMLFdwkZHRjPbMMbgig149L\n+fWGUaALCmIAoC2kCborx7b84NjaqRcUbWfgZO/6wx87GcOk0dzpvaXNsuV5TDQGtMUulRl5qDcA\nxatlPCjXWuXissyjxKbu/VzMOVYRFkvTBnWnmfvC5WErHYltqEfwsb217uoBgyjh9b6Z0eqkmuod\nzM9e04O/ZpRzaxs/UHm9019yBGC8B1xnPpbLBSWdR+6WUw9yQz2/lHaZ99n9dk2tX4EvlCB2x486\nPlEf5cWb4Y3Pmfij7mtN5aMzG5Bv/cBMLP4FsTbfRoOwdQ9ojlHUkMcjPZRV8J1FtqmMHcWr6+UW\nnW4heu6/Ys7jX2zzoE14DVzd9TEnxxEonx1T6Zrw2NYVuhJYUAe/w45jrBwTtK1eG6WHnYbsiF8P\n4M7CwYn8D3a7l7AqoDYI1kkYa/1hT1RGFfKvpDcH2PFzh41udF1y/PhjM3ZK2qcbPVsJk9khxAJR\n9GlqzRTKdhOOWSh/mGPN8XHTS46Jqf/Zjak/oTPowXGdATRw1rJ6/NyXHFd4MwA+egBIcq0tkDa8\nTPcRedF5/rWY89znSl1GUWuVgz7VkTJcTgLsndFrp3Micj2OWkcPQzZ8YCLYZ7bpU8hgbQ7SM3Cd\nOGJwPatZw14GyWxnvUfwiwJdU0uiyntAbc9NLbmuwx3xqHWZ4WMvHYX49A6VYEvLNtvHxwqghHyC\nDcjra9WNfcM/hj0/uzIRmiZznTkoGgEPK1Wfa80ATKEfqtz8yVPApuXT1mvTyuxdFwL9Ca2qZvh7\nJDPYux1P9SSYo81YavawlWT12KLrpswVyvrDbymRIbC+6nPAW+HHUWuup4RzIb44KYpfb6X4XjlK\nbw6w1ynPq454x3UBDvVzZvcWfwyoWf2YFdQD76RuV8geUQaCc2ILlEVH762O4RPyLRmA6HmoJwHP\n2HMgYyNDOYAex0NA5HKtdc51XZ+WU0SYBmA5AmX1PJjM2NjAQRvZZrjWkzylREAHqfQFUeuHTc08\nUBieOq9+KO+LiNLF5AHgem3h8i8xatv8pcaR3uLW1cZbZciw8tP0E7Dfu3Tp7e+2xQ9b284EewpB\nhCk3qOqeeXCrE45pWye0gboYGx/1rvLYZsMJTPTR24v9wiIl77pxtmg21436es5xLWF3DnZEEVpc\n4nEAqFG/nLDxUfSEuOeUWx2mIHLd5WGrhSiUmHJtfnR2zMlxm/smx0SU7pXtcrupfEQIcWapDC5x\nGuDqGUbNFb4XVBM9XxzP+sHSxPHieuSzxSzXuo50X4baxlS66aPoWwLsaDBkPAsHGI4aHya/oa6a\nRAlyrTuQqSCTi7wCAZX+0ZzD3ckEEd9SUEcdS8cykKf7U5M+bn5614THoQw+c64XfNAM1+rBAm/b\nY/2c4gXgfNnHyPZcrvWpHGzTj7No9Tzq3GXH5IOotQPYWZrIuRxsomh45bPu3O8+cN79+qi1Hj6x\n35hvc7DHq8hYyhMdCY4qg10nTNczQZzVl10d6TK7g3BtcQfXHUhk8bCo9ntfcuyVbbVp5wiGoQ/t\nAwfIN7Ckq1qj1luu9dZutc+11OAEgOkCLNWrnwbBnHuxrfR1utgagTo1tiirtkGudZXhIzW1UeCR\nfNq8rNyIDJjFHT6QX9dFTo4bNhC43MExcb8udq/s1mVMRJ9QZYZE1FYvk2mNID7ojpShjqHDEOtA\nRRnKr43Sepux0isd1N0zDBFsNFYJGvQpCir1DXTE7amNd3irdjQeLqI3B9jZXbHIF2oTk6Xo+Sd+\nJvL8OkZs1GjLtS7Dgw1/VF+cjJM6ZKTmEAYfDDJz3Oy4y7A9bI7bhALHtant+EOP3e5TdJn1gI0P\nw3f/bLcs8WSgJ7EtEc2BtwS8jT/Mtebt5g8j04ZP1MGYAqBmaMxTRDKbDBQfSRkJyiCIWq9EqKOI\n9TRFZI2c3gB5DH0ezMeu/fNRjr29iVqH5fhZCG1mKSLDdSXLvV7Y8s72icF4cUXUYNG7g2wqfVYT\nxc/rIpnSxK5VCRllEdfn8OZPXeSbfKuv2u6Nqk6dYIN9rYlarnVl9OeVAhVaWkhUV/ORHUMc3shk\nOosNr+oBADYTOI5HC468basMLFTSG9KbXh40arWgM+o6HoCljK9+d9BIPVsuRrJDegDWm0zd7Oaa\nc7dz3qJrGxAC02oXbV9osp7UvcKhXr9R8OVT9XBSHLZm4Jr2+VnmfzNv1lOzXWs2P7ZGXoyw3xxg\nx3dIlIMd/2HCQT6j2/npt4T0TBrmWhN1sNqOscg6Shn08B8lvAUaDZdV2dLClclwhxCiUn/RvMbv\nMuWjtTmr8eymSNAW3qiOZ/Uy0AzyVEZko9ZUfrMo9Ozyd76O6k539GDTRCgX69uHdAD4mo5/0OiT\nfQa2y9cYST8UuKg19lErIte1EW1iX25GTu1o7vTOtJJNbxy1duDajPVVu9UUkdXlpW13dpXPiqlY\nz986l7PmVldwbf8sjnb6KMIWvn7cvHh5RwfhC4fBg4Ty6WyIVnYIUQnDTR+QR0MdpnQVmVBVDpJj\nOQAAIABJREFUafQRXb9oSR3ywGkEXDEazZTocV9HsV2t6fpmFuegXmOB8ky55jdMLVm4a0eYPGri\nTBZdxkhWsV+oB/2mPmtX5xW8R+z8D/fdVYRz0pyX2JuHMGcvskXxIde6Blbq/dr7yuRa27lFVYst\n4xS9OcBOaHQXKDWvJHjAyLPLVyW48blPBG3eKKNczx16wq9zSLVburwddajj4R7VwJOB3WjnkAxc\nu2Prg4gaeMa5n/s/tVcvm38knqfkup7X8ubgeWSbRa31PtcHUkICvemXHBWvnk9AeWijfUZlDaPW\nrV3lmEybWhcmoDqIevsUkbWJcnVtudYf/AWinHtbP0NxCOIXAPbioqFxWt6SdF9tsbVY6w+h7cuC\nfQGcfDCGACQF5cQgOa6R7VHXMib9FwAmE8Hui7y3achH60BU28qF6tatW6522yGEovSPHuGvpWHK\nhI3/L68vEY2A9qpsBq6xgkxEELVWzxegq587usB9Q9nYOJC9QCO1VZm7p1f0sJ1k5lYE16ObgCl8\nJka/yxVq/U0uJ9yBe4YHhJbzAjihRpkZ+EUJh003lH251mC61anYXIejU/qWADuaRLKt+8jwcx7w\nRQ/w7WuMXP/GSy3XusphmPRILqtBg8NE8/VNI8hXPKsTyBjOzXE7D463NsbHxKSi0zYC33X1EkdW\nDxciZxvwUGbJzkyOh3oS8FD/BLh+UK51zC880x7d7FEKSe8LN1mxkQd9uZRrbVJZPGiOeFm0uuuG\nEWyCyXxAi+vqheBa+oMW8pyfYIFgf31WI9pRMMHXzJwkbU59GZulHqsLcFthYS5Qran/M9hF86AY\nu3ldRvMnER2MUAc2TSewaYADVq94w+0W5a9AmgsIVbi0APMKM6Xx+vr4GXWKWjzLSeWhjImG0Wnv\nLCiItBzVXa517R8hG6XWH5XpddgFoKX956sJbY7SIuqxEFw+0x8IRC2GEHNM0AxcfpTbtohiFcR0\nZ/w+ga74Gm2Xu3ZqqWOpg0C0uY1vKfUBvd52UXptHW4diL6wQ6RnZ0I/s3lA63nVNrWu69jfR4Ht\nNwfY8QDJFxPWo5RiSNF5GR/OP4gEXt7bFguuaKHLPiq/6qANK/uMr7e0WyM7xQXzQiqjRDeVlWZj\nXbdz+GQp6rSSRdsFfmuhbsrG/mDDP8JTsgCcKz0JeLU9cdRa7V/NRNOIdMInp9d5qnugTvq8yuWU\n/tzGR60Z7qT1Fxj78dJLjrAwjWhJ5zKgDuOinEe2q+A61Q38iszboO+rZG4VXSbWpBa4tHwL3NtE\nFEetdQ7xJusLbj+vcga76qf73US+VqKOIM+3mejKKiBVy6qDtOEE0e0k2Btb9OfTpZ1gBwoUUn4r\noIT+2iK8CKORjL2VRtc4AqMhj8d6BuwqOdra6vF2HV2udb02CUDK+Eu/FLQvbNP4mJFvFkcmzXfR\n6OCY2r3GeHthRwX8YhdcWxVpRqvo+nqXyeWWJZ5FZZbXbi8xvHoknxuQbpa6+5tdvf/a7WfTQ7rP\ndi4om8+Te+jNAXZ22cnxl/awFgr+9MntAuLgFCaiX7Df15rRnV3yfL26DC4vp6pdwEYvORbDS1NI\nqoyMrau/Pxei+GuMRarqgGsI63/NJ9t/kvCDtpM5HvJkIJfExtTH2S7mWlt+1vRl/ixFpLdplu7h\n5+Y5cI/9TnYIYXNebHrbBlHsyTlx1A5PCyoXAGzpD1bl3NuYaAvq8Zqe9mkWtJXOaJbaJzgJG5rq\nJ84rntQ9oudiXFyVXgWfTk8tmaZeqznY1MvgvTo1dSPS4V4bgwwqmBSSEgyuO4QUq9Jfdb7ceNza\nygVw98BikZVoY08S2YwxtTXMwR5RjrIM4oGC2OqZShTbmmudrjlQxh4wfcVLjiO1qIlHZNjEevm2\nw77VXh/DetcQhWzKf2b79K3fqm/biD48jVE/3uogcYMWGt7soby6LmDZdj6r+1q3FzdLI9rQVS90\n2nnVJQmpUhiCDqyOdt4XA3pzgB1R/ixPZMeRvTQZr/+/gUmm+nm17pfd5WTqS77+c005L1GLtthw\n1WPwzO1fl2HJE8IJ39w4LrUDipOlY/Fb7zERAlAfdRfNaxNJsbM81Y5s4M9uiGhWIc07Gq2Gds1z\nrXUqBJXfWUpIpOf5xf/uiDS0zdn0+ox8xjbjXOuVKDVhn7XJ06bEoL21pWVKVaOI/bpbwr5o587f\nBCBDe4d6pPXsmjeu5ZxO+yiAp9862wyp12eday2gp8sIcrKNXp+hxxnouleDlxyFyH7AxdwxlH8K\nvfis0wd3ed2juk6sOhJdffbz3oGmhtF+Y9He5ab/x6Tbq1kgM9ULZejAvnhYf6SmGlSd7VfM+egl\nxhRMBxSz454Z9Ve0XJyS1csmcGy0/JQU7xTD8L9dvuJamYqoWaaMXZPDsvHxQnK5NLrA+tIuU79m\n/YGhl6R2CIF5vf3lxt4GLL1KOPSxfmHb9G2DNlfS+wLs3aOe0+itA4HMDnAS0xatLvtaV1kDhu2c\ntd9yl2xlcPeFMhxh7RcGMtpgPQNaHR+SHI9k+jgA16iF9a3EEreBzb+Ix/2m8DKwIXO8xJOJnkz8\nPTPXepIiQpp2n5vZ/kjKyXrUmgYAGs5bOXtTRNbuhvR2CgSjaUeTTQfp9dX+5uC6/3jgvJyDveMT\nwCn4CB42lrxWJdY10x8wZ6Ws//pXF3AGH5kentf/oZeC8LS9Aj5FpP7X9ftiXIA+VL/Jy8rdz6uc\niblHlusHYWp9BXjtnDqQqNCj2ZcjgfqhDic6n8OtZeCipTIjZyK/GwgD2I1AubpBoNSOkAUMGNqM\nhmzsVZVUedSG8p61MusplNkem8la/QqjR61BrwwedS8rfbzjSaWBRPVe5emLmPPXrsDG97r1zPRO\ni1r35ZmIkoiz8a1s/Hwb1QzcXE7vC7CJKBv2Ubf6JQd44U3OpAZvOY0BJ0z8dYx0BJHUJa6/9ZlS\nr546Zib/cFDdQR1Rz9o4PXUs7RjrWwEO9lG7tWo9oEnYp5s/WG4bj9xDkeJl/aP4EvBQ7wC4Blme\na13l2wSCOj6ibfkEPvR5zq+A14wurKtpYxvd6rz3i+oyNRwlGJ4lUgvt3cyyiHQvY1dEu/Xp2L6O\nqRUKh1HAHN2OmnzU2tp7YBzMCmHedR6x1romursYzg8XW4s4yd/jM599jG2+ejkdMlXlCgl1fZh6\n/nFVLXrdNG2Hmlui+uG564QK6KyO7hedEkJhykj/smJta7+fW70jkFQU9WuLGOXelIS4vPTFYJ1A\nqOj+UE0qJ/7yF96iPPRNsK81d/3yq/mlk0r/4XnOD5o/6o5sqmDqz5VYf2g6+uzXSh8T6euq8qEt\nkFQdRtFzbdFnz1NtMY1M2hhkxYbH9qVc4oZj9VojgC2gv/qOOWK214SjSa51mxca6K51s3/1qscZ\nyIZ96UXzr6Q3B9ijOyWcXqd89wdCrl9j3JZurpEGmBO8X1sjBU3y4zqpDu4LGfCOnO/TFR21pn7s\n9rZm8w9nD8UHyviU8NDG6hzlKZmb8UDveK61i86GvEx34CNIEWkTPRHlYLqPfs+rBwD2zLVQ+1qn\nUWtT5+JT69LxiLYpu/paITe0TqSF2AcIa7sacV77mEzmb9PVM13eF6Ne8iUu2rahVP8a6OdXTOlo\nJi1qC64k0CPQq/Nm5I+8v7wNuIRj+XW8ljZIH39dhzTQNWBk+ytlqd9w3zki9XdrMrpD0Aq6C3+x\n+Igua7akOh73+yQCrkkedsu1ZrxLYgQcfc9CdYH6hXYDyF7O1zbX05bXxNV1cEy1uXBM2E3mePsa\nY2krlCEwDtrlhWvcgl6tkHKfke7r/ljYFwEduZcumwyXOvwF/gqhwHOpi1ofhEraUy+qOxSCylPf\nIYThthDoW+DXdbV2drs9kF87WXUetmabY3Ec9MqMO2MHvTnAjijKwdZvonduxIOljOtEYPQKT+Uw\nNz4H/OqrHuM/hhvc/w5TIhbILRYHZDVq3RcyqGNN3UBHUM8mRR5bXUgdAb7K6cZ+yfrD+p3yZCCX\n1GY919pEYuGXzPmIH9mn/DQHu7cpCmYeejmSeqQ2jFq3CKyJLLvzzlPtr+fKl+krtD2Qgx2r2Nlj\nhbY65VHrID3E/rWB7Pl1duM/lmKNLbOuWAOdwBGmjEW51hilrn7jnGxd9y6zLfdtlFDP9IOqa185\nonam8yWgqgaGYK7cUkKkv7DI1FpaX1isKSNbekipTZk/64ud28NKiclJry3iiFYL1jq1ecupEWGu\nN/mbwQJVtDXgpYPrqt/R6/LuIIOCp+0CkxCkJ+Tuv0XZUFfKfVwuXp+ruha7esGLfll9M9mkjbHB\nPopS8vqVye5AoXZjFL1WVenDhAjeY4Aa+r90aRtLmc2j6H0B9qB34qFhLn+ZFMOJlDnIte5gzC+d\ndgEqkwaRmaTY6NX/1+6IEMSa43SXENYyq5e98Ng+Zc5Ghm1GX7Z1bj0zd4lt4XDEZ5Eow418pH9n\nM3KOZPX3c0uBYAPy4Pz5fNIA37S9n18LrrOoNZGuaztvPnJQHJ5D+6YRcJeDPaZQHkaOZ376tYgX\nkhWQ3G3z8+BaJXq2zFlAM51ODbie3J5EhBG27TycH9UMSPkxbE3XZbH9mj9jwL5vAlxDRz+Fvg0M\noQ5YuZfQkADyNNgm+L/tHNJytqE3SxFFo9ljBrP0UkiI6HN0NRsSB53e7aYjOZYV3oZ19CIRRa3F\nnBuninLdge3UbdwfdjxYMEfmfKgreA6BP4g6Wf2Np2cXPQ2wK7eXbWcF1OOAV09YVbYP1X5RVWZt\nfXAi6XXj/rBITC2Hus1MO3Otw7/WiSlzMu9zdDyZG8/Q+wJsIsq70vPjJajyYPAygkiv165FHSN1\nMELqSFSX+Bom9Ww+Q6Mh5VOSlkUThD6W2qzeJ1wWeGw76GxrhrTjZludVgCIfQy643zrDvTCqD42\niixvBTyPeHnUmqFeDgRPc62jSDcRwy+Zc89HcJdMQtT7wA6p/eB6ErVuPAt+tU4tW52jvrGPUmJc\nGajLtt6eslkil3v98iyu7KeLwkyPcz0LnO3swoGeEFH65cWEViLexqC/uE1E7nPEhICig+P2qWPq\nfYDAo+ddez0S3bt612xVipu3TdWNhelx0feJ1D9XY8nSx1sDlB/ACIC0G6ANd/eofwUu8VidXaOx\nDi+kkWyK5BeV1pTSFsUD/XLzZxudNJVSXwTObK8daf24SrqQqOpNNxNOyM2hizKql7y2m40WgkMw\nZAtIVAdwwg8qkoDPlTt91c7OVbGeEMlnGQB4lxIcG77U+0rUebcRY6/rQE4m+iE50T9Lbw6w83uf\nDJ/hyIJMItpePim51lxW5zp+281IRDXPLpPhmG+RHOau5/6xAo3dBio5+kf6OHvBkRj6AxeCoK+m\nO4RgW6ydqVsH10k9WhkybvOIb2l050ezIYIPq3dprjVEZacAcubD6hGNt+mr5KPcXW9su/Y1xqCN\n01SRiDcA4Rz3wZ4c7NmiMpVDysoasO5oAif/sY3xzZneGGD7M02ul0RzZ0tOBZy6R3SfbJBR+2SI\nTuv52egRt1o0iXDP74Qy/ILNUBstqaeYI14qpspRcxmAZdVNVUe2tURK/mi6r3W9llWHuIxf7n8x\nJ2r4tRcj/YW+1rp+0HvAyAMKc7AVFWsDjHs/lcphIdWEt0bqx2HraEOc9dPvVryWP10Kg3QTlMf5\n2kl7ok5jWB6CdjLYs+qb4tp0viqyXDg2clUm3DXoX9ASxh53Myip1yN6WHPPelhxvC0MXw19TBVl\nzVd/tS651u2z7uUahrnWlV8bX+sZ5Fojn6DvVOMbR918gc1sxlunNwfY0Tui9UJ7vn3Lu028zCR+\nLLZRF+da68uAl1Dxm+3IZu04Og8JFwTGeoMsOE5zrYnwjjd8sLV1VZcA5NOJPSnH8qB857fxZC5T\nvF760tcY4VfvAjIG5WTOR/zI3vOp1Vd1j5nl1yLUpo9pErV2ADriQX1bNy+C9NpeVSbok+n/sgL5\n2FdOs2i37ov1XGt113Out4ntQmB8Q5tD/4N67Nqmb70ztjn1Q6OOeC40kFsIouoWeuvaIwTXej6C\nrXsg0LPdwESqazgCKsAr/7VdC2BeEmHiOjBK+1QkmoTUvtbKKfJGi3yio5sOlR9d99l1NrY694eo\nrhcGpAgRnc61dr+lzXX7wgSUH8ZG6maB8171XtfSJHsJ1V7nEiMRH7W26xM32zqntWoJG7VyR0l3\n0A7L/KfuOabwJUf8I4Ttipii+WbEL7IGrqXp2uWIe8eZNJho3guKxns3mGNRmfXpQ+jNAXZE8bIa\n8srfd4/lWpuJvD7B1bstADLOph1Fw6BOonEbsuPjerItDkw9mk6laqz3r24TCnd5+/Mo6pVfG9lu\nEXvS9nmKSL8mx1JEomM7saHNmX2tKQXgc36177/r/AJgoxzdtjroebz/RACwlrESte533SFATX38\n5PbgnymxN7aLaRHzBaXWXZftbY+BX6Lkul1Yxr5t+ib9Jpt3JpjvCBb88r//sy1XY5j1tF6tufsT\nMfjB6u2eB4NusCWJkeodQij4qEyZrCqQLHM3Y33LuGkPAS3XulMzhx4w3/Vo+rXX+nmX92O9qR/a\nCxF9jq5zGuo0MihQba0X9iUBzyNjMee1let3aCHvRv/OPShy9+qKDFA4tqDlWpsuLCACu67x631C\n1NdNnC7q3aMi6LUKONGr+y6nfhdH/QEVkIAPV7E3RIg/e537Fnti2qjnHxzb27koH31Zs3esH55h\nO2XeF2fprQF29HzilqQ2abHiI5jDocQFFeI8UcY+9S2nqD/Mcz3mPhHWYto5xza1DuE/qNzIhoBv\n9HFidjd0a7c03yhro57t8C089qPT5ks3f6rOfr9ravUXx1eXjSXm2xpGd80wDaT7WY9abxOBAtnL\nudaWDz7M7x7+1hQAW6of9ke3Z7nWxOYc21R9YLtBVwPiFX/9zl5PEaEprU2wvS/qubXN0jRsPaZp\nIJkeL+ol/iaQeVmnz6duFgGVNuuYXsG/Ik70En9d96ienbRg7qxGOOcJUQ1JIliuh1vUunzERTq+\nbGkf7qVFakBageWS8kKUAfNanxEw9+0Y8cLnTzZ6FqCaPkbXNW1Hp2xI+DXGDYwLtfDp4FcCvji9\noK7Zb9SCtlB5sl1pu4fseQN/rGTxUedE3ds8QAGszfqPaL6Zzjd2ZOyrEvsP14+RntD2Ku02fzYd\ndU1EnTPw9Xn1Lduxu64S+PDzI3aI8/EAemuAbQc58rBr1c1RotZU9rWmOlm5G4/NOXWgPrFBQjC5\nauNoohIB4CZjOGdSQBx3CNE51WbRQ3+mNDexVw2/jnWPySTnffnl0tmZ9in+Lt7/z977+173/Hhh\n9v2yFBApgNBSBCUSiqCgQKKAhoIEKUqXNso/kIZ/JBISUZQUIKVKQ0MBFdAg0VBsh5TsSqAoUdgU\nm1WUciX2c51ixvbLP2bOnHvv+9nv+xHz6P2cOR7b4/nl8fH1mfNGrHUTDqHXCO9gK9w9PBuXndc2\nK0VTUKkLsjK+9zXGhRc73wdeUFYM6IbW5Ft7rLOsRHkzqel65Ul6YPA6I59uNVcZTo3hlif3uOcG\n9n4H6eyxjCC0PiHEdfHiIzGUXwSsMdmGV2Rfy5nLcptWZT2eyp2PQxPbw013LbzWRmSWFsKSBRCP\nWIg4aEmFDS7hUMw6HrlcARZZtZ2BMQ5ZUUiUK3qtFVwtW7G54nCZuTxOQqmJs1oJTZ+x7XateNp8\nuYLXJpSuPLrH+aFZgbkNdYTIEIZVC91r04goPAzp/jr4O23Q9wfD14idoB1O3Ycdju8uqNeaob0C\njm88Ohl/6WI4EQTWHXGQIcqsZeLtlgQvqf5y9hXpWxvY1HaRwP84hETEXIw4xFvFWuNEr7wTv0yD\nq2XZikVqZd0nw+GKb/NWV/H8i17x2X8BpnigFfIfDdrOw97yKnxg5Xf8V2VdKvDEO+Dd8VqvPdAr\no5zS/dYD3eCdw8nakfsiKBibnhLuFfaa19phoV16j32E/JZx2gm3pQXelMZlatkr5bkvn33Bfl9p\novbJG9DK65zpiLx9Edf7t8PLde7qkO7p9UYa6zVvqbjZJl0bWqG7XjSpW7wJi/o2Wi7uQd/gqcwZ\nrzNEiYKtu0IlVoNsnmtNarDp44KeY+1eZsVhmgad7lkJh4jAsz1kZuPvojk+4KTmxFHhZfljuQLQ\nOmPPp5fI7EVGFnthtYu17p4xLuHaT165tTavHp956+YkVvEKTS6dlPL4a4E9E016m5ZB97D/nwS0\nkqqeoUH5oD2ouysJdZyt+fuaodNVUHYVa02uo4lArRhNJ9vCGJ6d3/1AfWUxJdX+JembG9g1CSoE\nhTETPR72NUab04rDMHylLHmrgcbu518bptHyXP8FY/QCt6sH9qGYt/6RPtYa1Daxb+plC436wPVT\n8oyisqrbMSVPmPPqTiTazv+uHzB/I9aa5vXEwHVDkl4ICVHDCY1P73O81z7PeEt4juWtGrv1XN07\n1zr1g94T3if67X1Hv7o/w8U53KV1UfZav2BY23/nhnTFe6PuBm9nX+/Wl/0K742iaBpHL9GwwXzV\nup0WPUbZPHTPWvUsCeKx4xFJeDkL8XK7XB+lzYFocexegqk9YN7deUUkMMQs+lnDHMxAxE5B5lxl\n6243x/tdwkrajLwp42S5aD+kCSW04rY+33oPP5f20j7K1axwNAt91+Z1rjIRPUEOdjZ6BjrOd83g\nrzi5TrTrFYAPWMDmaMjX04DXONa48KRgOsB0jsk7G26G9RR9Mh7ntkPbdbpPdzZO/UEj8SVSm3fN\nzEB+Dc0uuW6Cmw8b29/cwO6f4MO2Yzslql/4qdOMHZ/wuswzV79VZR8nKS6PqtznNlT0sSzwa767\nb0UE40J/yVzHWo/2tOEZ0HehfoY/gr6asBhukmAJjn/xxceGF2/+mj4glCuU3/Faj9Fpvc4vG9bA\nY8X7BfhoYjKwLdcb1+a1DrxnXvkx3qe69T7gprION8kc+gfrWoaoxHozbtfW2ic5SegD2D5Cf1U+\nCQ/kq/WtDeQWjw/xGpk4YK3Mn0V/xJ2eRsujTkSdhxttwJOMhxJCJUxLPMMUDhhZn+YteKdHM5XJ\nQbpBg86bxhIoPFqfaz3umchjh8k93GoJcOhPvUP6KJXYn+PqAWixHO8j11z+7DpFCz0TsmpkhdAQ\nuBoc+rNfNbiCz+G9sr+ZYNi6iYFrYpcP8cOE+kbnCTDHsmBtY8Vp7uo+MsfD5oOxx/kDLGzYwLZg\nrw7XDxRVUXNi6uP2SSgY1yiT4ktsC0MfII3/L949SmNyJ6EIeifR9Ctf12RtxqfTNzew18lPCJmK\nMXuiDTObJHmzABpe0yg88o66ZkdzN+0M71omdq51NFglwlBWiM/WPzeuvawzinO4RwlBCbxSWQuP\n8hZ4Triyi14+OyGE0j2Tb7qcjL7OM4tbywnuXXg2Lnm2LYQTWH5hXB/FWicZuJFJ+xDpC7/ab19Z\n5xjCc435kte6i2fv8Ip5ofPrjC7g8Qn/ym/lFSxJ5tbLsfZouq690WiEWPhAwAtVTUgXUykBb/0Z\ndUp467IC9OpmCE3SGbMv9KuJw+E2Y35VcsPxXhGZvcPaOre1RmiJG9tWPjPaSqOXZPyw8oJeSaK7\nbaHmeJ+4ewLFhmE/WEU4w9BK9etw5kxB4areyZOXIOPV2UupbvB/96VH7KRiNE88DnjaVmBhA9mw\nFR2tNJ5mF0Y663dyOgNLwktNaWFyiGeonU5RPQAtECFanhAS9ZfXI7XfJk1u34qmSNvSrJIc4r2f\nvrGBrZ3EfsuLWGvdLKZCuYy1Zs37LlgfyoGGgcYtBMCd/2G9iHP1R/syyXythyTiYd8VGPZJVcnW\nL2njC31CibbM3nODp6YFLRMFwzzXDRrm7tcYKd3vQ0bIjUO7Kt9VfRFOhZ6W8L4+5x26qMCm15qS\n/LTyWid5lUeAifNgvMc6Vg8JiX5739EvPOlH2nPI9soJIZn96vPnBe8H8xv7/sHaU5vGeDGVzXDC\nkDdLxSPqjGumsrkJJ7rBPd7PlnHSAhK2+jJyfo8nF/WTory8LUOXY1iH9800rmYcdTC2vGFW93X4\nR2fxrdIbZoHan/P20elUFAOMMjHvdMTBlwYHfFTSnfzhRnbT5HAdTP1EEird2dI1/XO84+DQiE+T\nGKKAqPN/rgyaKKQxjxLch58L/qWoxguloVBHx/IIFhetz+tZZg9478Zat6bC6hc5kKlc17/i7VLo\nsy9K39jAbjzPzH2sNeLk7rfd5IaH23eg7dhU5U/tDL8c3yJTj5NPCNFfNS9jrQP/SucixJcYcR0O\nGNCCXIy8lF+Gzc14+eBBCziWU8I12CdircG7ujSQqyG9gmsfXNd3Ku/kv43Bpui1Rp56j3KTl11/\nOCa1qeUHBjHTIb/GwF7yq7LsEvZdv0GceJVrXVljrOiyeMFQTtqfV3iAs+N/5cHG73bAao84Y4XG\nGtUQusKbsKATzfC8wAN+hqvezyu8Jp9TCGuWyYfthswyReulGFEnhnSucMcvw9Da2eGhLE1bG/IW\nwQzZocA5zAn/jLkS4IuZyEpTD9dHqRyP7fh53NZw9WIHscIhL2l6LFO3nUz11MKzzChgeUXR4ImT\n9ONSPpO+lPSV8gta/PmE539mXAPI+noTa01xeWxjrTPcZJIwtpLraWnWyWbb4bx4JX1jA9snrxt4\n487ngr+oImDU4M93ZjQSEX7qnAMNhzrYaDCWe0rCpFZGMCKZhfCEEbvy8IJsPdq0gJX+mApw1k1Q\nv9Y1+iLycsNcIizVfRpbHcYjaqJIl1Lhnxt3lThd6cRrneFKN8Y5GL83DOgePnhRx3tV5zF8wloj\nzfvilteayfLGn9M9tgv5FYMc+mPJD/oK+bX8oX6Swr+2P/UFnXutwz0j3gkd4OXxWOD20yCSAAAg\nAElEQVQVugA8oat46/1jHp/3UHrTIpPeW6Q58zDrZpgkKXhaj/HXzTFzVrxsqLk0OScLPG9zxUvN\nNxL3Wmuoh7ZvQAZs3kOoB09PusIYcAM/7WsGfkqP/EwWtAudRs1ZISzHe8Xty7XZbQy2lvP4z41T\nMNrRaG26s3bu6oXG9by8tncqr+O0kD1zNjnAriPO5FxeUNQqrP8QNvnFFwYnWA1VoNCuR0S7xbmb\n+BM3PQNDuGpvSTrexkD6WGtohLadVHaEG9NGxwUasX5HmqrrlEZyMeWRuoZ/Pn1rA5uEhre6i7WO\naKQz141hn+QRL5XZzo/8epq8o8siH/ltlP8uoVy2yKSPtfbSgB/kglVT5ihT9FIZDHlJhGEdCMOy\nT8BzObTnpVjrd+EmUjYwG8PxDXg2Lk0GbrqC4WuMJ0YutgvrgJjjtYc506b+x7qLLJ/jF5Vz7Auf\nMteGqcqgSHnlc4cXeAIerJVlHbSpgw/qWLYjaRm4RT1Yj96TRMIUdIlJb7twxaOEN4vXeEl3dqI3\numrLIzCDnplNFFs8YD2iPjdLS/uEwSISZ9adQxcsr1QH0rsypujqQ3rsAKDPjWeqVnC+bZ5Axf7r\nVkk0atex1nofxTwLD1ldhV4KG9ldFwmWafplCjpjFiAuhaI4QeP6J9L4e0pw32aTIu/G9w5cy06M\nDW0oTGt6CvGTXK9qu8Cwrfqn02lUjGFvc9WLkV8SkaiuD9oOrfGKPC4JXk7f1sAexiSPz5yz/w1j\njiFPRI8F3Gg40c86dFWE+4lHPY0Z+IUmwUt7mrxuQlnPE8BZ+yL3AVEwmlObja70hdYnDT+VSyo/\nauqF/qJGplz39iXHJFPgn3ryK2OtK9yVcAjVCPWdeLbJphqnawengsdUQ0Tueq2VxmGq2O6FjST6\nlt/Ez7jk9IU3NbK29FOOMD+m15r9noyPl2O6NHr5Hl3E23ii+a5c1/WFT6XrT7lGwzS1waRhM6GQ\nGyst4NGkHP3BUFaDBgxPIl6sSfGAjiMeTvFWb+7KGp0hlM+1JusRkelVnm1THJ5yKUxtXIWpqhqw\nkWNxL7SFxJkdM2UQfQiZfmjm9FIjvNBH7h3H5uHLh/tzsGOPyaSoXmvZxGBfGdnX15VxHOEc5KnX\nSk/eTctyu/4C/cA6fvMFTMF+m309PbmxB/3s8rwmxRgrDB4qBWjDaGjT4qStdaSvf4Y6Glo6SewL\n7en7loZlxedEmXMXyGyIxfDsOdJoKJbN+ZSfYbUF9cVq6IyW5qylZT58MH1LA1t0p7Q15gvMY67Y\nB11gUjKHWCGnYRt0KbzINj2f0qBITxYyLeivGorKw1L6CpJ6ra00L9NI3r3dS4hXNmDEu6BFxQFw\nSdj353KPPUMERznP4+Zuh27MNvHou6/xenf1reS4lleVS6xPSF+6Yjo513q2j1J79R7roNRG5Acw\no+d0j+075BdlTbStrMhHiPkxcZ4mg86luO3ENUPkfUNMCXdjGK/q4Ip7myc7LOIu5M51mJIi0BV1\nxW691qCHKt56laOE67jruMIl9KTzynSRJra6wwuaU/U+KvqwuxPpzm9GfznXetCKzVHHCZsAWhjW\niWz8yThGLe7yolxqQXDkV3BrmT+6+IrQU09qX9ZU4f5AkK2UjkfPd8Wj8tzx2NPGq5T+tIkNLGEu\nqe2Q22KkcQ5jWIfOS1vCnEeHbYo4LIrzNTBpciikDON6Etm0Cw/ZmHzcI82wYTJNazATzTAsFzaU\nXeVv0hDeS4/3TvqWBjYTmeEcZqY4KMeM2VV3Ce1do6lwUvj8uUsCTazXrwv4U0YYS8d/VS9R5PWk\n4akWoXCM3iKdK7hDjNWsewHevrux40ObssdAmM9ctvcwUfH6ruCdUUxwX43lM74O3xvitIH3slE1\n0ImI6UkPdu/UOuRi8qZUl94TEQW+V/z0/oTfwnj/oLwj5u+X0DcEPDBtPdVMqUwSXuWJeJFHV3fP\nsxjO3OP1dUf4U+9BHTpWTOdlcXPGRSoJK0q1w3PcW6EqQCsFL9Y1fuUeD15qKGvogRg9W/y0tk0A\nZvck9sDgBiqUETf3cxuCPsT4bv0VIG9vlV/cMuJ9NJhr+cD5w/kWAtOsQ/WyxPs9HPoPrtTQ21Zn\nbdJtzj33eK1w2BZF6We/CIwRXDs4FTyiX36Zc/QRJo5OHxe4wFf4COdaltMSjmdGB/DEd96qU7Fe\nxkLJ0rhCCDoFN0V9USXYJzwC+B/kNsmTxgas8ECjkyfC9fShyGPyz6Ens94Say0JP9AM/pzqRXlA\nrQ7n1HPuw0+ggY8J3U3f0sDeJW7WQYtHuCUkGvZr9CkgzeqnNzibFOVh9J0gDTtNqJ7nCzIDoPNo\n8M7b9Fmb30mjfqmwKZdCun6MGzC1xnUIVyn8JfHCOtxw2IdQkPXfOZynMRevHX5XX4HDn84ghiul\n+z3cu9j+WOhXjysD+MwDbPwvDeoNP8B1eVf06b6V5x6/B8xXn1bnBnZeZku8HT/u4c4jm6ANHh/i\nLfj9MZIkMbX5XZlQbIsZvUKhV/KP0tmzjY7CiKdST7NTnD6a4mS/0iAPrQd1LJ584SqKiehZ7Z/W\nSEpSLvG8Rmsj2AFseOilHkohnHjAgK+GILvPWfsaH9hEVCdpn3BwlO/46UN4NwcaFb1I2th4De1c\n7U6zWOavzTns4wgeWJ3I4Q9RCg+nyDSty73CFQR1OLxbcd2Hz6slgXVIGIz6NdCkf+YEQV2gWW8j\nrBopoCzBUTqdM2Fty4omr23XbdBs4OF6KNLE+e1lEmmM19AKFvojQrx7E/gg/XQG9nV3lKnnGrAZ\n7d1mhDQlPrulmdv/iibDjQZ4pZhz/WOlU2tnGp5CCY/VQJcEi/3AKc5aFx3GWYdf1Wa9zNoesjp4\nloWJPnn4z2LQZ1anU2gdYXNhmacfhB5aXtEz3V/JV9vNKy/hfX0dPHuzEd7JyVaPDOOaRWeY9V29\ndxhBWbzf0d/A4aaOl4z42Dc9P8UX/+x72Jhm/1le04X3OdPB/It0maavrxrFOl9epEv1ZRWmYUMi\nkkuI6ArmW5LHm+IWpnL7VsZFCl/DGLOaTXEOmAR6AbhIg6e8a23NxkrzoWvlJQaNATClNU8u0LoX\nOtGH+zte51FJL0/yYnfyQAjLip96cfOcukpCVObXNXakWvE4gztPM5w19InBUE5V93D3kvdrISx1\nw+lkbD6InmY25MI65FRH5GG0gncwq6Xvs9bjraTSSUY2OdgUEe41cNXuSmXc4WLFk5YZaWRJw5lm\n1stqlZd6dT8A+BxnozEe2oY1Df3Sj/Xd9PMY2KCQVxFCUf3iXIuq2Jdb3DCcRg2fVAZbkBrMagTo\nGo00Umq2WD5V7rqBPYj4wTNmsGlbA+rU54+DSYWlFW0YnPA0xwv+07A+/bWiCJL0KpuSBngWF1IP\nr56SbJJc82l2B8LNsG4ED9ITQtC4Bl3FWR+6x58AN8KyVxl4GL+dV5mSgfyOl/rca/3gp4fGpM0Q\nN6fY7xs8PsRb8ePX6rV77vDi+Pf88QFH77GU2nwt88WQcxmP21LAE/cbrvDQ4xTfMiHS84AjXvTU\nRf7Rm01T/vxrb15Ref/oy6E2acrNboBQDVAvJj2+9Ai02CvDkPaWCUVVpfQs0YgfvNzIZmJ6mkde\nd6GVJuv1agfP/YGjsMLt+lPbgrKFhwRsf+LT8WCgjTzG/VN0nFA7LtJlhyR7I+CDlHlCakYXO94S\nEVrK4Txs0H3Oi8N6z6yx8t5rnfvhzizwEUtAaFecJXnNW5muc+n1ga98qFe7AmK3o12GNLNeoKFZ\nr8yK+Wmq9+308xjYYX2vFkzaZIyGUTfAL4N5IwH+QuEFSOnglucFTQOfk1JgomlcUlmzWbZ9kyP2\ntouaBZSMDfs/8bESzjDgz1JqCKeXIF1Y98PjPV7qFNNZ74eCuAGoV2rh3obMV9scjL8GTgdwl8/l\nIJADvdaPOYX8h40rD/Y9LzVB2ftx2hf8wv2dOsFrnXF9yIhMHkwLPKaEmz0aFwYy93jaH5GukY0v\n+C/l0n7jgFdX3L1UHmbhxk9mxg2NTTZdxxmPAIOJwDDlIK+eO5354wbcyUHTzujCatFI0+dru5/1\nKcxUMxMYt9N4YzVuO36KOfnNio1eXWniBqW60RjoNVTNPK4hBiXD5lX3NG2v+Jywfi2/atxMoUqm\n/Skfo72cXtyP3mUHmLzhtJEZg7uFd3z1Gr3WgF7WEDbRkBCm8AkI9AJ4HOG+vhdwKHP72ktx6L20\nSs+LuyKn9PTLBE+UsVuiUDqcemACvMs776XhAfzTGOLHZ5zH4BBPIRnXMR8k8Rjy2K/zKiMN/vTL\n0/YTl/+8a7r08xjYmjZzBfur9p2vEtxMVjHYOi2tTGk4xWDPculotExjpozHrGue8U3M8b1JLtMy\npfNZUTElGdOQTNskOpQt7rxl2TU6A3Ak8QIciLUOP7M1sgbF9tJ1xvgRrNztz1kn8LlxWnhOvAY4\n1NXxfrDQr0iCIct6vwm3cDa9Bzifcz3qXnmY+zqu+H36aD/1Whfe4u3FLiSKcMV/By/euxyXeB0/\nPsQr/OJDIKdyXE+r/BUeG0dZlNUNE+m6+GwzkmWFF++naRRk6OhQj2Lqfj4P5RTbfX2/DnXxe939\nm3JROwe8thJ/rxLS/oleWacFO/LCax3auttCThIaOsqeMxxuwtXx74R2COncjgU+lxxeYq21rxjP\ntG27ZvQPZlbzZlWWJ2ILVxCXsjCjsDhNrmAc67YRBE/8Sv3F7xzQStpvvfsylU8c0PNodKBMeOGx\n0o9QlmkmL7t/CvFz/qIjle6d9PMY2AfKAoctzHvu8CpNyPKcHtzRcKB5Kdaayby63Th/BNbIvqeT\ndV/B6g+01obK8cwrPuDjO0Lie8XML9dA1sGZ7TbJ8sofgF/i2sY0rmzXGF+sRqUZ1yQhRJ8g7/fo\nTYZyxvuVcU3HxjUx1j3LXvVsB1l8qwxea3Zcf9ggS7Aay31Q5GFMEl6aQMcGdzZsFI8j3i1ZoijU\nea1D/nzyx2QbDq7QKDgamQFPONxzkhz9ze7UmBj6k63RTbwJ82Ud8YjAMKvNCDpP/6aodq/eYoVp\n/RrzzFMCIXaPWeLH7DhEZHalmBhahxqBTktQx1ByiwYxZkA4wxF6sD5+q+GO3nafYfmPG9gKN8Jj\nSMYp7whPDxJ4D7HW3SklFe5ea07zhwjn69UC8XGyNIkZyhUeH+RgrSfvlf16aRd3thkQt10oNKMT\n8EMdzcO6DxrnktTaxc6qHeYdF8A9CYTIzrEJPLQf55gNvCSB4Urg4TRjf0Tehjf3juC1nnMDY62F\nxMsA75308xjYoIvWHl5cVkgzZ/BUqj7ocWa7AhQPIwk0CCeiqQzU41ppBGSe8AeZ19oWkipmA7Hn\n8Y9OYNimyWqW4dcaHeZ8bCICP5ycBgP+tvkBnzAKyVBGReIvMQIwqcYRku4eTOWJ97sPvBiPdL0O\nGwm6zodkA8cG8gWcEvzB8BKjyk1odOpfMmI7o9bYNt7pcN/wW/IHem74Md5Pej7gx7Xu4bUG2gYH\neRLww64lkLHDC7hHIRuVf2tcdxvfRg4GnI6/G9ZVbg6U+/wVHt8p02PWggzNiSBU8UhOvNbaQ9Gw\nRv3T7Y3cwHosSbm+xGOFZ7mADaOlEr2pY0vI9EwYKmL00hibgvdUvdbDehjv6/imRW5xaFvuWQ/9\nrpq9x1f4CI9WFsbyn8uy4qH3czx4fG0Oo0tmN40taPHTBlsVceStahplQR+IgR1bnMjB7LhWofJo\neoIJjGrORVX2bnHn2IiOg8qGv9qCjYJhHK5oJhLuX9pvapMl24gBjrMy9IWNFaf2Kw3+P8oCRHlD\nrDXN+xxrHfAA/k76eQzsmcZ4rhYphxwqazVgdSyNWaJ2xZlMvTmrPKYnycOVRs0Bg5thjXrwrhpM\nretWKVFZfTatQHsEDM6yFM2QqolRlEZli9J7Ij48eN3B+OQpM+bfTmvPc9LbsND1fioTeziTSzg3\neA4nUEKd1xqaTslri17sTYgIIT17+9deYvqw17mTJz3stPQ+Tu61Blrtj4zbz8B0X1cYepXirL4w\nsrnHy3UUnnlvW8jd0XFT1uXxJSmx/2PLs4Ez1mXCkwUe8NOxU5MS+atUOt1trWPL4WFGCE1p1Jtx\nI0R9EfRyyuMRvfpHTCEGm4jcAwq0MQZbYWIvSBkvclqaOMPb7X1k3myrV+x0J+n4ETk9u0HdnRDy\noGFcm8eXNJ5cacfLnqtd8l5KSvLqmoys4HbexF7TEp718uhvNQRZ2Oj0fSjzesKMWrUsNHGFYCGL\naSFbHQ60tQ5ljP/Ztlr37/iiY9JPOllAjzpcaYC+yLzvi749wI6kcgr7HKV+TA/fTLbn5dCgcS9x\nndsQi+HQ5IGx1tqlIZb7l/nNd5JYtsi/k34eAzsp16sUNhaf4Q193kiUhq04bc9hu9vSqMwWa03+\nwEcQiE8cf1laeuhP00UvrYzXZtVKgCsMlEM7LtL02yyZXuvsUWgfM5hiv6CYjDenV1vl4LG+plvV\nN+Bzle5isM3DHnlErzV6h1f30dDUfov3OEOzgZzwuaHnhr54rH38Kr9E3/Kr8gevdTK848MAtsnn\nDK7IPGVWnm67z5vWku4CjyNepKtznFd4PIyoWvc6X3/yrbtHfrkQ8RD7VTzE0GdJxSsb7swhh95r\nzaFfI4+af9odpE6d5h22saHcqHFLIBgXpPaFr3WR5GHVh2nrAzzjGbzDgm2f9Obpd2MbOia2Jw03\nqGYorGO4YbGFK6zAZx9IMpYRrkcNZu99/BVgDX9avUzqKc0vwmFI3OzYo8SYCVtEZFi2UPVyR3sb\n6mdE9TTnRtgfJtxhQNvZzfY0VzXTp9JK75gMeDW8Tn9ORKDxfls5EiTqzkxjvGQbaz1ofA2czold\n+nkM7PwEs5w8vhxsLpo+g6db14lBiUcaNhrTgZkG4XOSi8YmCrlLRZuhSkAnAds8Sav7qjNgfnAu\nifDe0F1wBc1ReHG3kWdeIFvQ8ui1jga6Pon6X1yYGG7BxiPBVZltcSVcKd2/Die6DldBePVa93nH\neQi0CboVYUQoW+jieZ8N12ucYFRbnSuvdzLyueFXvN7Jax2M6/iAgDCiNzzYgJuXwcqorjwdPvrk\nE/WPdj4y75Y25Rc6IOeRBm00NBwLXqLhWbsk+c1YJLQF1bPrPAMeRX4BT/xBGO2KXb71YC/vvQXo\n0bZy9j5ybzGZfaA45Z5imIf26dbrbV5r4Gd06rUmoxFSs8PpYh7HDTY8gl8hbqXMIz5InMErR2Iq\nL1FuTwhhoXGmbWjgZYtKxARSpQ4xGLBNy9uAOncRHr3Yo5yBJuA28CCqcIUp7ySjGzaItOqXhXVZ\n+hU55TWrNNKOXfZAB8nsV9xMIxdea3IdBTQnsdar/Dvp5zGwZ1IFNlK7ZClvadKvCrIwB840kujj\nigk0Kg8jnMIJIczAGxZs+GLjfY3XroVO70RY3uwQ1TfHLJK2vNvI1XBCPVMWE1PxWqetOzUEV6Rc\nX6cSdqUsdm1DN3xrLfWvhmINr6uUF/hM02udPdSERrsb4QHnZohI8XJzwqHRZ+HeaHf0X+C1TnTZ\nmM4wzdexuWk0c4/nuHG9tDxhnt6qO8n8WKiDVR7ve/OFE24yc8C60KXR4Q39MfFsjUupm0mAh2/H\nHtoBeOR4NPmrOIYHxjXqq12+/erxUlFqwbx6bEFDC7joVdF7FUKJ0GpEz4zSgKI0oxSMbbyPyhT5\ngFyNxbDTY5f7RoF7W3gauxiqsYJrdryQyNR5sw1OZ15r162Se6GXedMPGY0TAv76YOBm82QkDrx8\nfnCiMa+3jl/mP+vdeq3jT99JrNUMqG26gjNUnrWKC4U1+vnVJFmbdLoV/4d6LKZa+2/SQKw1Neda\nC9QZjPvsVXgz/TwGNvulbiYJieI0MQO3kDWx1goHGl08wxtxEmtNpKEBpkuZfS0w+QuHrbuxbo7n\naTdrYtnS86yyWEnddBIn/z+JbU+TTN5W81gzeK8Z4CsZKfbV8ioX18out4UXtNdw8g0XvNbD0PBz\nrZkIPiBDbly+ESLiXbDCGfJG/EN6xnuHZfq91xq8zznWugkLQcM+w4je9WDruGF6wUDmihfqaGhL\nHRASUrfLszyuUZQka4NVWfEwpTw3+XF/chRfwqOIZ+2Qiqdlp/nWgy3pfsrq9+5NxsfugF/u88uJ\nEcfuhQxDoJ5oTFYZ1bMd0qVBEGnu7CDHOw5T8jALLY+NoN5bvqoLwzyUd+u1Zq/WvKDAE/NWzweM\nqdAAS9zWEVZz3XYGXSPTWAeLMbQJqIrL+fcEhfNB0r2LwlB6qFMev2oJ6Apqw3bQo228KXq6Aa6/\n+NYyMa+1jTWT9Z3VRU5j/SapjW+kn8fAnum6P9gWXJx//QSzbeCCJmw4F7HWAvEKEtlAnhdwuMe/\nABsztzy8MkHdsOEaD2wPTDICWQ1BvH0onGib46qWeEtqWNef5tDo2Iymd/FZiMhE7vDHQ9HwnLhh\nCHUkvqHu2HqiuTV2P4OikRop8DPnYm+1s6DhTF5OV7CoVCJMAiz2oZg8A+aj61OkGrq0rCN7qZOR\n3tR55LU2OjTAsS8c5n1MdGLQnuIR9E/Gi/d1HnOLV+89HGQl53m+pm73WMNiSXfX45mJLBWPyFu9\n9VoTQZieG9fI4zT/NIn7xKS6T+WMo+ePBnNNq4cVxm/YvkjvL24FI3saCeGeHKa8BmzwsnOt0U0a\njmVjgHmPRkM39vOiE46uNVxDGwoN5joemCo8n0ziV4T7Q1Ba6PZrJMNU7Wp3WBciwgFNdXglZ+zn\nkkv9HcSQVAcDrVur0WM96XKVxZBwmVFgKR6p1BhjI3GD0OtiHlhVLa4t/jBXwifMkyy9HhMKq1Fc\n1NiXMs62tjIH14d9xJFGlvfSz2Ngw0CvYrBxrdmvfUH3cOIBm0JDMxRMohFVlEx61E6OtXYlPLeW\nu7vFovnnaYFtilAKPEKkgeEalwgD3kTzyRW+xtjMdMpGSSvzpj8KzvYq5covwWeb5pXTfYYzTU8t\n2zuu06gCI5jhBw+KeOE6/9DrS/Ma7x1GUBbvaRPucW0kF1pu6nrVa72KwQaY1o2vN4RNC4Y/K3Ol\nReCll7rjxas6T2SIxnW/2dzLS5F8Gimp3hZvnlTBAS+2yA3fem4IT+JYI3ovr04IuR9rvcqfxGDj\nUXloR7gxN808ySEITP5ZczzpwyFz0wCuqnQby0UijvnCvWPINyOKdMG4auojoof4mMnUy+XklE0/\n9XD02teXEc/gOBYzD+El4VxrMOJzJM7JvDhKTESdYRoYsV10eAJqEzvJQEbE2SflF4mAIIlgeZIx\nHC/TaboX0qLzOm3STcfWM01dmay91ptYa/4laiaMivJ8hHeT4wM9RUQ/k4E90y4GG9Vh3lgcnWEt\nxXfgJeFLoREbdNObwWvNiU7zYTeH/ALeDX9ZdTV10BNF0/UVtiHiSGwbUrI0J4TMBaH6AY1uyHNX\nRo3e43Rtio7hjBlf5euvMVYZGNsGZcuvMdrfhKkXeyqVeC/u7VZeN2KwCesxeRN94eewQG/6vzfI\nGcb53GudDOjkzSfq8LLhjt0u6d7bQIv7ng6VeEPHL9LNNt49IWSVx/uqvfo8b8oi3pjzkQb90BNP\nKp4bqZmfGpEUDIJ3vdaYP4vBnmtaUhGTe5knztzvfWfhURbOudY9QfkpDsFJGQwGpcEGffgaY4nn\nTnKvPJQNPr4bYBsX0/Lav1x4Fy7+cirEZ6/g9nl1lVS0vx+UPeXjVszoDqEFYYbpvIDfJ5ae3X0q\nVF0/a992dGIYhU+nBcrWmectEQxssne6sKJlKotisuzhGIPdl4i3SdtsqKgX8f9RxlYvtH8Raw1V\n2VpiIPG8pDGIfO/01C79PAY2+2X1pIY/96miGzebWGuy+TC4zsXa0ei2bnA77kGAD/KEkS2/UUXO\ntSzCu2kf2mg44jcdHcqKEjDQQu0aXoIGhPUXzGBhokf2Wpcgs84AiWU5MRHFeGRvwwmcAnyOoGsB\nygZdhtMlfOR5bi7hXGtG+dE4Vj4AM9kyXCKcvHsJ67D+EoMR4O69zMjvHQM+G783Y61LvqNxuU49\n2PEe5sUBbZ6rO9qI2xj2HE8IwTGqdd/Lr3RiljWbzGoZFt0JGhJNatS/wxiNm6fY/1nHxjYLcehL\ntNEo52UBb/JnMdhM+PEWow/1TM8rHOvl/BQWvdY5EGbttcaEJ4TA6SOsnl6AdXgqFxOJzI/QQBve\nSkn0eDWLN1296adGudt0E6j8TQgtg3udFFonAT3V++5DM13v9DCcaSMbwzrUGKwM7GVVRpjyUUWd\nVq9NNNTMQI2TuXnJ8a1k/RrHqjsFRoW1ZgcaKe/2Xsdae3PejbVGeFQU7PAPpJ/HwM4LfIEStryw\niOPiL/BdWYY/eHiukznhMjSyzFtfN2z5+PJj5FPbdw0zOGcYTLhCLwu4l7X1sxA/cLNM295cPNrm\n8jOTpaTEGvnbsu1V5WLyEI41Pjfw9bnWlWf+GuO1wUwJT+8R7moWZ1v2EhcDmIgIyuL9gp7xfuJz\nQ5893Fz5HXmtG1iu84o+TgdJ9y4jJl7gEeHGuafLdRY+iPdFXmvMVw/2mK8oMXr57H/71c3MZlex\ntrHG1pkZzV5/Zw5hbc5v4i1CQiL9zPMC3uRbD/YyuZTYT3YvZGsdbTjcMojI4rQF+U3DwbaNhdda\nUI9UCch1l25CCRaaEseKsyEBKqyz/Qt8SugPIk6guZXkoX+AB/JS+FP0QeZBPP8Zv8lQsoxUHWBd\n/ijd+FVA+S9hgrA0PoF2rrbciQLyFKdcr4Hy5O3Fzrwuekh03jr1eufuT3NRHerrRNfVnAXi8AGe\n+h/xINba15L3RPRag07OfXrY7LvppzCww6BxyTR4K6U5J7VOQlXc7CZEXagc+besYzMAACAASURB\nVD2cLsRxp93e8LnKsm2fAvJfgE8FW+CzLTojoUyUzuoQePmRPGO4wEOnc8DXWGuQhSnIhZu50uR2\n9aEjXs8qNC7srsskyysfwRe4upnZdfM1RsrnWrsB+zAcMWO0wGaoyIjbjt5c0noY7x3ms1c9zJ5f\ne51pU0fH88RrHftjCSNqjOv1Mjg9ReTYyOY3aFvcF7zWvIBf5E+cMlUPocZMes/UxyipOlECtY69\n40XvMG6QmpIt95H82Zccp0EM+7DaNdpu9CIT0KpuvX/ONfAQoQfr7He84KE2GDkeq1cdYEH2Cgu9\nI94XnXe5uwrz9DoC4XygOIXH+oQwZMQqM3wFDeF5ekItzl+I7Kt/zHCKSHx8LOtsuwHrwKWVzqoS\nYJbZgnPGbKRsZRwzcw3g4m681uTtHjCc3bq60gridH/8kiM0BztL0XIH6iJONB42KYUH23iT7/OJ\npvBSmuC1FvBOA94SDnLs8h9IP4WBXed+nHgOxZ6DxcACPKKvJ284u1hrsTPWgAe7NGhk4zzvzrse\nvBnyUY6SVuvmEwllhf+xbZhWX2NE7LGgJC7WBe5OLp688pXuwlteTOr14XSNYSV+rXyuvsYIxmSK\nMY5/C9hViEj6oxUO+8xH3plHZzBHL7a2pfI7Pdd69yIjdfhL2JmBXf0+1czs6AjanPH2dWp/ZNov\nzHOWps8jDR4FhzkhDp78UTZLxfsvmjQU8aDv/IXvKBNTlKnkZQHf5FsPdlE17EJhoSQcM1gSbncs\nHfCzfjEv9YDUo/ekOq+XMt+Hc9tTpdWXMFnAIjx6qXV2VK/1oHuK2o/jRUZWoxqNcSo9X/MT0Mkf\n2sINrLlr0GJJmsuWhPs6rOtj/5fJ255r7XR92zgNRtZsu6RzteuHygXXehQ9nneNfKJO8X4Maxti\nrWXyYDjX2sb/INY6nhyyWNcfDA8h+kkMbCJKeoxd94WUNhmj4VZfDjhHuE5UiNWQh3IX42vnZMsw\nGHTSqDHNJp8EOC5QsUd7h498nfbS3FXDHEo4w7CL8oMFNV5r4A+bLTHR4yEOTzS1xrmAWtxruo+l\ntB/qgOFTNl6v4epZjl3R/s1htitVz2wP6/6Sd/nUAx3uET96lSnIIXOu3vRadwb0yqjmezCTT7pz\nsPO9t0eBR3h4zzf4h/7ngot4n87XFV1T2Tq5L8OY51EG3mi2FW3zSTq8WaDqWtOlwYR5PsBJ+QcY\nZqDOkwd72jPijwFo4xDgqifaP+tN4XS4wVfmfnDqtQZ5cDBjp+/hebjL4Pp6fzWFw0rMGz3auoq9\nxmukJxuHOVKNzHHf6z22BANw1TF5hmxbW/GKbJiN/FgnTYAx4MO6QD7KiwEY+OfoZzAgcv/ceslR\nZcwAiWNpeJ3u8z2ijj94l9M8sm9fEAWvdTwhRMsY8nIAnxxwfoRpMCbhvV5ap5/HwJ6p9GGL0Snf\nBq7zf4ZxECfexWvtGt/qZecdvdaO0L2HUNboKp/bfQmTIBuys+2QMwwMCM4wbY8bYEXxhI1aYhk1\nuPOPIV9CRKAN919yHHKYvHCf4QRwX9nzov1U4Nex1o9w3+H1dEvvt8Le8DC3YSOJvucZ+xV53jnX\nOsBw/ABGHd6KFtx/PmUag7fdHKLh7Ze6EZ55vLGPqxxpCh3l7+CuVl2zApPEbiSP6TFg2GPBG01E\n3NEhHqiITs9Ign8y/2x0Z7ZDHAbSgLEG7565xGpMhhZ0Egj0BdJgxQvBrPOSsB4HkXD3beSQ2xvb\nrWkWmjTbsjCyR2tr/yDcX9Rc9cfo+BoWosZa9opmH73PToXq3ephw8aZGWgqVu0b3UdSiUQdYKuj\nXRDdSp/3vJLGCkq6Zzbm9dsWh9v1upMeT6I+cK/1lFb1xIy1JsSdePYQL8i3h7sYyUZp8st230zf\n3MCGbtB55SuimWM+i3HI8TQRn9dNeAjwkHkgMbPru5FnyBsp0TTS8dSNEOOc8uYJ6nC635p2aYce\n1qMEeNTjgIEy0VRlKBsT4YuLMXYVlXlW7H7fKbEs37ZJWTeFazSe8X4HH82ZMsCV7V4arzUagiew\nbCxewASMbYp1U+Cv97Ip93oMlzOu9w0Dv3jiyOiL++daQxu5gc3+r32IxncsD3MC2hjh3ZzTdu3x\nVnWUOjnTZZpNng9wrvLN6RRE+f2PuK2gv5mJwLs4IKoROEAHzFd4xLNagv5Ya4WSlwOcTf5Kc/Ya\nSQ1FL1c9qDL5ffRSM7tnWw0G81zjL5TYGVpxhlEq28Ib4zwZ8w8YLZVRKI4H/lEDW+EWOFNwaotd\nZ6w1C7GGUUzi87AQDt12lT9NvM1ph/Rnsei20fKDCVT5dYLmSYH2TV8WaVWJ3TEbVz024bighOCB\nitKvEnOyY6x19i6vxhpirUdLxMoMXWZPePWQl9AM+8Uk5d+eKJv0zQ3sOll2fWX3qhjnaGQaorEd\n2GAhzYNJHvMMTobtlaEugK9iraPXuu6gsoBbqRmys27csadRWzzjPGUIK53c0C9xmuJ1BFNC2yDa\nDbmk5N0AR547uoOyna4Ii5zSwl2xiQScGWyqfVD0WttLhyTTW00UXkak7MXevew4YDDchpdjwNHA\npFlnuAcYAe5J+EfkN/EZed/wWifZ2nJaGc49XsenjtnK5yMJr874+zyy1zrzX8NO8ndwBbz5LmX+\nkd1NasXbnXfNCzyye6LWa406ziShxO/r8nrfGY59mXtXtUV2L3hPRHhk3qwVj/xjmkfldUesaGdQ\ngncwhGfVyA2sSSuv7SqtzLMe3nut8YQQlWD8ZdfAWoYrHDrGOUzmSu02DpjYWh7GCyTmWIgfWaHJ\nKqxuQ63aJoYKr1Y/2WIT++8gZQWTt8Hmii+qbkx8H3WlAbjqyyGrhBNCTBwM3wD6HdyaBe0PJ+h8\n0KDO6Zsb2JBgoFceXhuCqd+chm2yxPdT2GKtRYjoAYYnxbpGvsKtDpt57JN9AzdGbQz2jX6Brohr\nUiqMVKZYYuseZrA1MYRuTKMM70NKBksO+wh/mVfzN+XKRiale0bcLRy90eOqcGrgBAb0I8iBhiWB\ngSkBh9J98OgqzWnISPjTrYuae4e5AejKCY3fSA/9QdLfUxdr3RjBp57sF+KyrU0pjg62mQTPRjjc\nw3y/5tUY15zrqvmrcjrgcZJHmGzyHPJsGL4fZeO6/4BHjbXmIgOnfDa42zwf4GzyRSUlRDcA2Ixn\nMxIZkJDWYBwraAzk8bN4GtSQOnMVYKG+yr+rc8WWYUwvLajuCrf15JHRF7uPyvi9MlB69sGa9wNV\nPBrGXhpML9mSr2mccxgwcrU+qClvc82w7OFc1rPh1012wtnLJ07aRReSzzKju8K9SLiAmjUU9GiY\nB9L8KgFwzjSSvNZE9uEg0qmi+8+cB5Z3uK9HMuXlXmv2M7cD/ufTT2FgB0XK3TaKeFxp5v+7WGu1\noMbLKpzq0nyF40KTNs8tvDRhlW/6AHtAAB+VjQJafT2N205Xu9d6ZzynxZaN8As6bsvWdXh+fa08\nT3A9dbDgtSaZLykKla8shjAOcnx6F5budWxAXiZKYR7Rq8rw9+NOCEnG9MoQhzw1sC3N7Is4fldG\ncbd99QZ4nA/JAGchPLXjahnfXfKv0NX9o1pcaDoP3aEGZYyqjnp047VWPJgvW+O3kczycoBzkme/\nN9tD1I5Rr3S0bYgIvNC6yTu99pvSc+A/IO61hj63DkhjoUKFGHBshXhj8mknQenDqNvmgro5946a\nqu6tr3BI03gOnzCfoR7hOEAUgcZJLgOm51pHMbVPODi+Jl9tPpOH4Ri//dysL/qmPmpKrXsuU+Il\nOKKwGiSi2UQrhHnlzrXVxuwv7llnp7Kpa36dFo2OTUzrSwp83Etcw6pWZHRGjLX29U7KR/EmHMfF\n9LMsxguXgDiQFzhnY32evrmBDcMKijNPSsfWUUOaFEoB00SI5mfOyawQp2vqTXBxlr7l8Ho8Pzy2\nLb+iZDjjQQ9yhOvmcmowc7oPq6al3S3/pjUL5KCfwlXKdR+DDTJeeq2hWQaLX2x8TENjhJBk+MxT\nzXewkjceySjdhIgEw5XTPZH1DfK99FpT9jzrdWF0M+RD3QsDeuHVpgZWN26BPBkNZTze4zk8P4z5\nA05fV6b/cfm8BQ9I1AbDFMybJJMeY8oXeL3XWoA/8lAJXL5lPtuOb+TX+gWw1IIORQoDHLUYZh9Z\nGVqBNBoQvsY424QGaIW5wV7Ou9arZBjSn8Be2XGwJ9dhIOp1RHT7lRdP+bByjvcwU+pKyvt7t99f\nj/axwQkTiRE2WYRHBIaLRECoyURmKjJsj+Lry6pgUEfGPUq4ehDs44RT3sdbYNwZ8JCGwxKKXus5\nS2F5efy92DziKeIqBhvxtRn/Pgb7drItwHSfrl/K95T63RY8HEaPNA8m4mHCjDNKMx05nKMMg5nN\nI8gnuMm0mvjnCyLopBusjK7EaDrdpdeaVU/MCW1/+b4RZYkr+/AQdvrTEBHmDBuDnc+3drjTan0P\nFvoVdYZeMhhzKEfAa+iI1uEft8NEptKxevyaYWT0rsYZYG5g+/hfe60PjeVlXmW7T3PXwM6r77VP\nnaNhTQW3y1/iLvjdqQPzVcdU4wJNZNNnAJGCp5hqapEZ1ornHFTXxbzL9+Pyeq9/xNG4JRL7iIza\n2UJkBnKIs2awJ9TLPXWJfY2RoeXQAaH3V7beXfiNtAoR6Yzmu/Aca+0zhO2foruhxcloy+XUlq/W\nyip/BaNcjgaEwRIHznAvK7wl/0nA7x4gZFM2JjDwOvmYzAdSWF8S22+GrxrJYfqL64JNrLXnQerD\nGGxNGGvNC3gYsw8a10Tf3sAeqc5pX3HhJcOwJUYiNydoxFozUXhRkBnyPVxYoN4kwxxdhaNhK5MP\nwv2DNsmDDvnyZzzZZcH2s9dDullgH2ReqiZ5ajaj1XbGjbRXELEObuRa4V7O9ld0RdgH5Pgavsao\n3RAMX0oGMA4NGsN4Lw2vN4zrFCICUxTuswEN+MmArl5rHetXYq1jvcUY5g62MKC5wijTtzHY3v4I\nl0O8Cs/GdU9zXk5E/kB4gntYnl9eXOXzEXvKpb7U6HCrZxrXH/FaY55v4m/y2UfQa50JlRhYwESk\nX0Mk8lAKNayV17BzpteaRt8PPLSrJNTT9lD3ERvawbAxqWVSYXdCRPyjME5ioTLzSnObkAIXEnk0\nop8ocK63kq+vbAQ3Ero9F2XxYYVMH1kKk6zZABNvAT61nzJuU5Yn9cwc2Y+cqoUrepdpjq8614at\ngLi+p+BJa2PKi51rreLmWGsS57mKtUZ4/amLQ6w1xmD3+Cn/gfRTGNj9GmMvQzxiohux1kXBT8JS\nJ6tqAn4uhgP1TutOcCp19anMAWnwpddj5pnCtZgZtl7rvDuBsVx+Vt/QEUxs4M+ndJrH3RuYMMWF\nTvM+wznBdU6UsA++Ptca7x94v8Bx/vmeKBiKhDBawzjD/JEx3hOh4Upaxg0NJxyKXmtKdJeG9KVx\nfdBWXrQf/nS8H2Vu+RzC+zqFzulqnPc6f1Wucr/NY5GPybQh6Ec0J1VH9XhEZGYYiepV77utkXtR\nbvkv2P/065kCf2YUonzTCNDZYfKgfiYCC2MUWozswmsNF9h8ACGEoUBN2Qi3n10BZlYvwqDuFL/L\nuVfzALVXrzs+VoyrP2D5g0dcYYvRMzajD8qzRRj4k1kQca7nTF0p2P0FC4bDYdC3UvF8klWNg/kg\na/OSYyjerHDDnbR31g0+OAdzAfikGWlUcX4TWQw13H8q1hrhILxlotcaEHZmxgfTNzewdaGTj7Jp\nTCJiBn0Fi3ZOVDU0xwkhcWIrnagSS3oL4SqKGt+dPsx5WcCP85f9QnPDq+jdJoizVphmdMyczZzy\nE8+XNqySjKuxV7ksClToaniIpHunzR+UMU9sgtMFXPuGbQ6BwWx/UsVicQe/3WdvcjaahYqhuX0Z\nMt/3MIyFDm2FMauGtCvT6rV23BprnduVHiSuYAQPF7k93MA6vNKumMcppvN0t0WtjOtCw2EKNjR9\n/o8Kt65W152Og+Zk0K4zz4ZnWDJ43/Vav6P6OjV4ms+fSs/6ka19HMrd2Icj90QfM/VPY62nt1fL\n2csVZszzZhHcg9Di4EWFXuUr2Lq1D62VQVboq/zHN+BjVjya8A5OzeRgjLLE68DlxKN2lcH9EvIP\n8rHv10+/qQbPNO4TpWuZQpiCJrA3vFAcZkhpVw6/LgAuGA64MvskwCfSXqe0EkbzCM+7xsEXC+8R\n8GpzPL6P5SjWWuEnsdbdedeY/6OIu8b0zQ3sOllwPeActjOoM/zBRPNca/u8OZkemLoKlC0s4vDF\nKYZxYvihNaxmDllp4Cv8Jbwr3ybxPsglLMQPSl7rSROqnxOaqdE0u5kKZS3tzXTcZnL9pv+BJvfY\na+d512t9jnfG63HKaxMiYt3Mrr7R4LVyw5cW9y2vdcB/0+g+gBHk66fSRxvz1Mmb6xp3tmW1LJv8\nVXnI84f5BTpv49YYlbSxkurBBBftaee927tW+9kyL9c4ryQzKuHPQh3IR9xOxwALbtTNbqiYFzlb\ndyB8awAlGFNv/KhrPcMoKXBEkQa2ECN8qhsGqh6518HFLBY8is8fIhqhjFaZ4f1K+AxL99p3nPok\nNVjacThMqWrO8DkeBR4MgKw0LjSQpPuU7zRb2zzBy/32r/SKCaB9AvdscJgFXxRrjXCTE82MBTy8\nxLyCfyB9cwMbkq43RsWfFfPYeg1urkkwOnOstfFHz4PD68djpMB19uAkr9vdanU08O2TaJwg0qwK\nW/cwU3uvtd9nqUNdgMsNbfnDqpe4s96OHviED+zsrnhrxrRf2a4eax0//OLV4odfIlxM9Mfcf9Wr\n7fcdr5p//S95sMu9w9AY9fbH8hprreUXBvFdz3TH+9BgpwamMoRxhzbHOXGC5w8vEe86f4Sb18WH\n66jbBieohr2Zibk0cEltq6TFeJO/Kg9543+NTzfz2YPdqV8z7ufDdziij6JxbhLpAO4M3Ay/MpIR\nngcwwJOBn2EBjqA8wunagN3IngoNz7W2vsh03MjPfZWhDq+GDF1XfJorRb44h/Ckj3atNHaVl/W0\nvpE28MIP+lqIPEidRliRYD15f+9mfYOLfNu0sxt6eevagz0fxi2eUY5jIB+PtY7wObaTDxHMB+IX\nYrCZPmlkf38DO80X3CoFcGAtXJ5rrfqDaBxmjwH6FgbCfpEmb7JZHngx8IpxBGd/jSXmRjMDLBvA\n9Yew4bVmMEbqQrafYIz3vE+4+cPLVauPezOaQ6q4q5/tMlUbR53g2LS2eqpfY7zjtX6AcYdfaHwg\nDtC0X3oEPng6R+Bt+RiugXCFkcmr7Y2Gq91PGFmd9YQQYgq8XzOMbxrdp/WFNl95sL3deR5Ri6/9\nkXE/mOcv4JnuEd4boB5R63eD0jZWQa0Q6fkif1Vu+W7PSzK/k4oHezIPRjNTOAKPGY3scf9EJwcT\nhc4Bs0TbhPxlBdvB38Vd/A0h1RodVzaD2RM3dAp7io6bnmvNVlhCQRSeeI9em302+59cJKPp503z\nMKi0dJa6H4VdvryHQU5SY9DQyAu7aXXROJLxqnDS9l7HJ6NsGtmJCftpWMTasQAf24fr3yGD+BMt\nkohYn2L3abiHVqEclTfCSxuBf1iHLb7EYfuUcmnSNzewVSHkBSlzcbMfr0ceax04TDoZ/5FeaANf\nxVojPOxAHOvK+Q5fFvCR6kKpm5AUpwoRrtXhtX485kyzv34GZ3UwgLKgc9yWTu8XdJzx2vtuhSis\nXrmB82yDea2ZwChH44/ACGxgZnzjvWx4ScPrzJB/J0REx2KUe5/48I/F8ta51h2eydng8YK2hI+s\nedMSr2xfaX5hmSQ8nzePgrvOX5X/UeWv95B8YoZtgbZkggqitXrCvZcgv8O9k6c38sWDjQJmGDKA\nhosMIzuk3DmGq3BU/g2MKMQRn/C+n1J9WZ7NFb3EtkfhJsXk1pIZiRezbhHPm5Cu+SDaIfpJYv1/\n8gx7GYNPXPCK2nfC4EVFMZxUR5NMIwn5H3HBXjfXx/dcDyBtjMEeN1MehljrGb/fea3N6QHj4vke\nbg49iXUjXEU0w97yVHBqvTH/yTmT0zc3sEcKShR2OpzL8mCSGWsdwz2A/gAejv0r4SF7eHgSBd2m\n8LT2WvyBeK5xu3lzGWvNs0x1BRN1Lzm6aGgwJ9zEx/hiWuKuy6z/Gm1TvRFjBeU33ony1xjJXzS0\nK8X72d7sWXbjLhqsTMoj8044oWkrWO6CHawzPn28rmKtb3ut6QVD/MIbfWy8h7Y67DQGuxrd9w3r\nNs9v0L7IZ1XGpQfGOhCACuDlr68RO6+LfaxZZXQUU83k63mF8+5G6B7s8Tghk3t7j15rSl7rjTxM\ndN9Dbf2T6li19wNwXiD3u0tzQoiMVWY/x+aBL1cu9jgxBQc6TafYOkTEJcf5eB0igu1u8qkrqr6I\nPVLOUQ4bEVqGzsO0jNGGFgR6sQWXcMsc3NkCsBnKFW6fCrb41cUD/SkyftKYZTb8EDsdvdZSxmCM\nJ6yGBp75W5gJyqiVXdX7hembG9jsizUo5rHFmmKeIRVq3I11zBD6AZ4bMKY7+KjLN+n6AqQEuKe8\nqFBe39qk0JxNg/dirWOtVfFm7eO0Vy9ELsu03ndm+Rz7qxCRHGuNoRnVa515SnMvqU6JtMHQQxpp\naKTeG+3uPhuxHRzaTD6u2RAm6mKtG4P2jgHNuR82vI/qQ3iE0ao+mFuKF+8nbZhU82EjTrNtvsB4\njXs7z5/hU7/a55rSNZP7sHWj2m3nXb4zsomisdPykGveygdluZt/dhKH4wWiweZAoQerPw4MZVYj\nOZ51nSZVr/5RuC1csoKPnXMKXxqRPlr6OCEkBtbYWPscOg1T206UMF4+p5SvxtiSdrHF30rAHnk3\nZkcfyjS+mVychENkModmlvbu99IuRMRAMHkDmhsHlffqXOvMHRVGxpWEWyVo+CIKhz64Z1KCgRtk\nSevE8kL8xLlAZKe/EPk8sDwHuHVDOtd6BdeKMKaaAU4Aj/WibDtb5TPpmxvYRCQcTinyY/loeK3B\nDSqqDRXP8r6AYhhHhcus0/OU8hzgnvrJvdoMtmm1TmAlFLOX3Qipisd5bo1rifecaJtae7HbTeHK\nyG/S4fNHVW0XXuuJc8vA1fu7oR1vhYQkHIovUFLII73f3/NaHxrdl4b4ohxhd41ua5PD0EjWcV/f\ny1te6zu4lm827bf4bfI7o3NudVS81g09X+Svyl/JfzJ1p4ig3Go8qwn4JJl7DPRqsDoczsUyV8N4\nWqlIHI7kIJegPUts0TNWVeotNWRbReuwxzRy7Jg+NaAt8DlSWP/0L9FAHZBMlhfSkVd8cS2tfSeN\nBcEJFM+oXq8YSfdezk47+YWwm1AZN/nFvcp1iXudGDPWv0L68ENMMwgfqjc08dZD/9nReiqSsrZ1\nR8lrnRCxqSpjygeEUC90xVX+A+mbG9ijN9rP+I5zzuzhUte5eZzZdMgRfO7aY+IMCwDytMwjbZe3\nh7yUP6HVvxyGEurWCctTcZrrdc42nl6GoNS9b1FN8cRH2spLQDbcLIAXjEvBTfcVL/YDnvii10Hu\nV7L7jdeaoVrqYCfXQ7ryJ8smLv9UzpUMtjbUk1uN0bdjrb/AG701ugusaWtpp8+8OWPS/ewbll8b\n4/pL8u0vavG7jXOaBG+zY67znTlIlDbVCx7Ee5zF/no7356DzWofTQ+uOUn0XOuhRYMtlP9sL4ce\nkVBLEqr0FgVPEfZC+8LOzug6g3GwYvqriyTEcnKuNRGDYdzFvQrgYFx35d3BE2/o4V3+7ikinDKc\nce54rXHBt1KMe7cLU9niAaXTZOE+b+kFd5FUXpbyHCjQk9FrPVZCN94ruDp09EIXcLMdoF28gBel\nRLEdK5y8VN9N39zAJlPMOuqfirVG+N1Y63pEn/PPcAG4FPyDPNwWE1m91tswDjBEmKiNn27otp7u\noq3AUD6k41KW7vVnR6Lo3WVYoJMRT3lfjbVGw+3RwMr9i7zve8w73snohBARHesv8VrTxlhe8Vnm\nT2F7A/vKg62K/+1Ya2qX9q8Vv/qpdDaoLkvVBJ0+2eURn4nwF9xb+9lyn/vghqdx+Wgc2wZMEB7R\nPWWoYAALulOBGK+Y6Vu4Wo8NLuJ38K5vDo0EDrloXWtfPEl/11g1hsZk7V5WDNcToQ5wMu8N3Z1p\n04eIcJ3g3cRpVozPssnj4ii+evI88IUj/Ry751Pvaa7tRdlVgqHVbhYmoqd4SIbg2gfJYH10cCG6\njLVGuBJHnaV5tA0iPma5xTnpiNfStzWwxwAxhVNEHlomNv8tpnoaIq7PdPJSGtkT+MxMOOpIaeAC\n+AJ8xNaPGP/upJHI36suHQKzx0S+MJhxiccE94nP3bjrUGXW1ccpK/UNGpP/XDsNz+0JIQbb4DBR\nMC4znjVNGlpJtBLxJl131N6lwc0NDLoH5SI6/BpjBytt3RnP0J+lb1awKGvo48K7aV/hUedpNLDn\nw8ZiSl3l7+C+lAc98Ametrl1eRm9gf3T4i3yaA60qnJb70E90KDVvniadw/2kFZlFr0LXmtqPNYx\n1roYLoK1JUWeW7jyWNceBUOBN3jY6ARr8Mp5FBoakkNFcpX6U2tXRajrKnHM5m46rmvN/VXbaUgG\n+7/2aQ4VgjYIUI5L7oPJVdZl4Z4Tz6bOWHdTxhHhvD9mzWgCzdyPjLXW/CrWGuH1yT7CjzzYH04/\nxMBm5v+SiP57GvvZ/ywi/12D8zeJ6O8S0W8Q0f8jIv/ZjmdQnMzjbGvzWvskNzx2Uy96m2fhAo7z\neZWPdXGplwAe+Wecw/wmnXitl4Z3vrdqm9mXcHnJC/5QXVzhBp4rftCPzfXB8Vzr9uxpNThZvbtu\n/IYzrA1GDY/MmxJvmrwJeFOiRRxKvAnkW9AR2biP7tG+Vrrota5hI2gwvb2cpQAAIABJREFUJ1gw\njF80xKGPj7zUvMBbyEcNDE8R8TTHKE3lV/KLpf2R/Mc92JMhkxuFPA1rYu/Dq/2nyweY3ODBZ/V8\ncvPzGGz/eEysGG7Q9sUkZHafGubjC4YEYbkbGJHHPCOMeJzOwQkGsnpe46YplacHgS1MvEE0hGQa\nDyEye2t9rjWlMA5ewMmeJUpYCHav4fKSh8O5wmF4dKbj8F2ulW6O4URFbFz4Rp4mSjneipfVlAYo\nbotc+W7RpAOep3CKy1Pcmyyw9g9iraPXejDw/Bqe69rlET8QBnkyztemLzewmflBRP8jEf0tIvq/\niei3mPkficjvAM5/SET/ExH9FyLyu8z8Z3c8cSsQiLU+iqkmiJ0mgnyEa6G/0ZzXW15smw2i65eL\n8vtp5bWGe+qW4x1DPOOf85qVb9b4Fa8+8ZQzG3wPii/8Ze9ugQlBqIXeE7Hgh2Ccf73fwWY+h4wk\nnL0Hu4N1ONFgJTr0Wgd4Ku+M2rsx1Z8wuhew9kGBXOnjnGL6sNe63dzfzH8BTzSgfXP6oNfaeJ7z\nOMrLWuO8km/PwTYPM7QmTB2QzAwChAmlniCzKhNshB10vacNTTAi4IPplR0k0nCBD6N/WFUcraJS\nH47UAmZGN1pjc3KXlwKRV4Y1OMGznXFWdMvNpw0RWX72E37eEMh7P3VtwbCOLI8Az8l3h3vSrnZq\n7PsgpjHepj/eiLVGODvrwesCrqKsYq0RXpRSkCHmX1o+L6Qf4cH+a0T0r0Xk/yQiYuZ/QET/FRH9\nDuD8N0T0D0Xkd4mIROT3dwyZaMZas+lF2z5QN7JvK+F8bF1NTHbkHsLHS4ICeYR7PcafgZfC2eE0\n+Qn8ji0A737fLvSU+XHgzZy/xpgVn8sWXkQ8nGkM/Vvk0jKK97wqC/XfoFtunS4L8+tfYzzC2fIC\nPvaXeXe8LuhOYI0B+yVea2wzwkofdLTvG9MrGC3qsznFn4m1xvynvcyW5w/zI19V0cPsRrfinuYL\nTO7z2OW/KvmYsRtmBsPOqUb1mEdqYrhNlQ+TsPwCDoOShHsB3nXYsiOjgRVfV1P5HhRnUMN3e537\nGfRZ5bcwmtuGqmJXI115N/tbEpYJ3zzocWrdBAM14ZxpFC23i1MVDOAGd5kSn9b6P+BTmrbj07Bk\nml5rMZl8mE2jbGKt8WM8rmtYT68hSrHWOAbQATL6jyfcZk+Cl3YTL2LCf4SmGelHGNj/ERH9X3D/\nb2kY3Zj+IhH9BjP/cyL6D4jofxCR/2XFUI/YYxkTgEjXHUM+wpkonVM9eDGxx0gPwOx+hrxAnmDC\nS9AlDAZ9t2sySfGQG9cEdxkm9wfZE7X8yj8HQeFK7b0ZGkUxEZXfYghFaQxaSfdZ/7TyJFka/bmi\nW6oE0NHjwUIsJCPU1bSJAcYGQ70ScQhwolwNDiinMbwZh5b1e3smb+OBcCp9nutnUg/+yvj9oGFd\nYF9rtNOqLYX3MIYIcOo4vJYPY3KX7hN1v5BXvSQcj6qjT+R9//0MP8h08dfv8FaGIhiCMUyx8eGU\nBKMKi6OR8oxCazkY5gK8GXgL1MdQn4AMnGXlFGYCfBjl5xR6MmBPepLOBhamBxOJPOnJTI95NOFT\nRriaCNOTmB409sORb3CY6SFEz9kPDysffe68yemITRLnPcZtwJU30UOIhIWeJi8Z/Dm7fWyVY5we\nxgP5aX7G2896SbcmXOARSLrxuFmYyyjYB8PI2+AmvmOKprLioQfcFR8GXLmus9yLEMZAa+jpkI/8\nB4TpLBNtdsj7r+r2zrDysnyF59PYdD/0fA/vZejycDrKnEPLPL2Xfl1ecvxjRPRXieg/J6I/SUT/\nkpn/pYj8m4z4vz//19l4pj/9+E36U7/x544r0e12VTrKEbfJi08KPSd75Any7BNBYFLoC5mTjw34\nnCEVTj5zBATpDOVlAjzcD5a9cJE4/ukyP0mMme5vK0t+MIh0G7/LdbLOPkG8QhHbZ3W8MB5+LWPD\nu7yZn+7JVb3yxq9LHlR6no554GpJsCKUePawvvpjz3hwjfABe8BnRfL1rTx/iE+X5wOcl3hHk+Bj\nKamXS/35gfw7POwUEfREE4WHhAyXDJ82V4Wjgax/aLgDjSTaV+BofBs81acyMCcealyODWo/b7iB\nz6T6bRrNuh/UY/EGH4e6B9R50JDFqpRQs89h/N6olw4S1b++MeOvFlFfaoGMgwbywl4mUMCYwv68\nwm1ojQ4mW8HF2Qz3Zh/gRJ19mXClpc2TWcZTCJMrW2XFQDfhw3SpcN+bxXipOTOGfI4Lwh80nrqY\nxhPZlEMeRPwc9Y88F/ignXNwPlXpF6srnIgfQvIc9TARyXOWk9D/++9+j/6/X36P9CHjnfQjDOzf\nJaL/GO7//IRh+rdE9Psi8gdE9AfM/C+I6K8QUTGw/8Kv/vIItXgw0WO1YfjElADNkxTxI1zC/wBn\nwJ87os9lgXwPN14M8tia4gB3R4h72YXH5nCkB0xIWTVzjduVhck2lZVZBbEs37vneoNrL2KttkkC\nGWbZqU7cpWy12FV6eEipv1Cp3OZ9g67A1LN7EmKxKV95hzsYL/COPN3K4wqm7RXvoyvYouu+IvEn\n8xzhH+O9W9YfTNkceCsvEZ41wiu8My+i2E/HXYSMX4ILgdV3JlAHv97Gxm0DxxfQMknMe49xgLr+\n8pcXJVBFuqrbjR9LOt/a9wrckTlwmqQwsAzhKeXFyFqr5Z6F61VC0xxSMa5zjeO+oCjdNHKrhHUE\nrD8TrTNfjQDkGlp5Yh3diogriBfwLGe0omIPGhweCvCT6Bzg0CqcIwK8DuHjKjPvffBnfvXn6M/w\nbxL94ZOYhP4P+e2mXWcpHxX7Fem3iOg/Zeb/hJn/OBH910T0jxPOPyKiv8HMv2LmP0FEf52Ilq3y\nAVktim6K1qne4UdIXdA4CUDHNIPaw3EyMfDp4PZuopB7sx/3fLVhOV+QNUsf0hRm/l3idnyZvFH6\nt8Jt+EQZJOxR+/SidZFttreMFOlvL6/SwCOvB4248/PFvOm4VRs7eLuhLOByA46wGcdnU0fGht7C\n5k+a+QVXojjl3vrjNH0/lecKp03+mDdTKvngX3pRhD+VlwrnlL/DjxKPPH4v9ZB8Gi4NXBr8Bazw\nF1sbngSccrn1L6ZTPXaLB5/zDvqDb/ES0r543OwNCazy3tjh+l3qkDBwecCaegJdQ2vNFagLFGzG\nnfd64s11yu3p4VcYpR9UNm0z9KNcwItJdgg3GE+o5kXGOd8fWCJf7sEWkV+Y+W8T0T8jP6bvt5n5\nvx3F8vdF5HeY+Z8S0b8iol+I6O+LyP+25KmZgw7YmWtnuMmUtAHjZvB6uCghR9k7uE8gji9dPghe\nzhQ6arzKQ/CUqEdkbHBdAryPZWJHbcwixnoSbuFDds9msQxegW/CJWiL/tR0a1NMf5TzYs3of+0i\n3/QiXApP60MdKuDtU0Qqfuj/2IORpxB+uAZpykZ7BLtDk73YCUYE3m29XnjIOcJGhy12VG5ghP0a\n0wf05DLlvn8pn+bap3h/YoO4SqiJPpIXz3eah094UOQRtVFM2EVH9sUuXdsYr8Nv8uhUfI4pfT3f\nh4AEGMRSuiyZzke16kMOOEIz7FJDPoTIw0nE1QL5HkGBe+T9LPvRuZ5oKUENZTxMxck3vcdu3NYe\nrz09/8sxSgEzu8DYhUq0dhLKC5ryDsVqXlnCeZKeJTIctwD/dbyHs5N7D+I2Ynkh+kXqtvNG+iEx\n2CLyT4joLyXY30v3f4eI/s41M+o16iJV5bwi2MRgCxi+YCDtYrAR7i8+M8UP3yS42hRMlpcHj3AY\nlO+dgcfX/Wsh9MamolaI3RNfxQ0TP5TjysoygUEfBT1OcZNIcH0hEawdBkHrC4wJDvzNUGQ0dtwg\ndbjX6XDvS4ej4Urzk+/6Umc2NheG6QnsyKjN5QnWeGFC5+T5UHgTGO7pr8BlnhDSPzSEat/NN+P8\n1Txf4s0R9mVJdRzUvdSfVziaB55HvBd53HB324TRBuLYxmM47hGfgAcBE84FPB/IMPrWNhxap1XD\nZI+j8bw4kEHQDpYaai8oTZTwwtNG5CJqM4kmb6ER5js9VgPhbUNKfCFb/+5mnCr3cW87UaHN/aSH\nJCzK4WXIEg5b4oRGZ4gwrM+u7n06MMFoxd321mYBC7uha2dxA1yHlCwvkI9w0bh8naI8+kP0YY1p\nnJbylKgH7sy7Rfp1ecnxPIXdZDW8ONEQutdKIdYa/y+74NfHWhOTn/GNOBPvPHXGzKJsR5cNpWDF\n5MeWhYEF9zrJI681XTB0s3GngWjc3YvJ6AFrlGDk/XIVG922CXH1ypVXu1Ehv83OahsOgRd4YvDo\nE2a6YZj+esKX2rqFi62Pj2jDw8SfyvMN3CN+6CGMvrI7xulH8/IGLbTvTj7YeYlvTka7QvjYlOr2\nqguYLPAWRhxLhY1jyqCH9FfRhOn5kxcUG1oRqh+bESJ94X/eW6hj4D25BxwC2o3XeuIRJ68njLrK\nqsdaDydX/r3Wu6jqmoiZDwAkYphA3tdDnw1aSWXjov2QKzXzs4hRf5nAkeugUBi81rMlzBvveTf5\nc1/s8dtYa4TfiLVGOFvx67HWBg9ea2jDB9b+9zOwg0blZiYRrYd9v3tXpQyKLmhx9s2DYSMBODoL\neq+1wzuvtTw8irTo01sDDz8WFTsuLwpsdVMmFZdotKPjEysTmPhNmd7bClHrQ4gfOIIfmPV8cd3V\nsaR1j7XeR54H9Saa7EnHL0OeJ4kyKCzLhm1ufyMTGJvMp4HhwwvCCh8JfO68CDlWCAO8/uVmvpzn\nD/HRPB/g3OTHLZVCBuzKOP11y0d9vM/jtHZee31RVOIlNuwJRWqFN1baSoxPwKUWmdd60bJbKmST\nLrUxDsaRN9olW+7bgWfD265s285T5s4GBmUrRitfM57LJBQUtKSywGcx+5lIShlR+Rl95uM4q35d\n4Mrkg6eGtLib9rUt6AcVP5kTuafFOsWyc7HZtw+EK74Or52LvYHHo/dueK0v5+p1+n4G9k3NcNU/\nnWkQ876zCtR/FYMtQC7Ax8wK2LnDh2/mN6+Z/MxsP6tbSW4ueJBlT7brLUnWCy7rTLe4Z6LwkRvl\nwx0dxOLO5u5fgHwjNcffHRCtwd0G0NKc8BAii7UWwjO/uVw/lRrNsmL+CTjnG1njkhCFtmaD/UCG\nNxPv8nyAk/J3cLt8/IGNW7wPrpaQtvqzM/wu8ndwc544ZtsXqXr0w/65GD081BfxbNdPNHiwL8Io\n82HfMBIfbngPgyKZNfC1yWK4bhvfKUWHOUf0GcObP6pap4HEog6jiaNeXJl8ZHKSqe9VFYhbUGz9\nBIaX0cG+JPAxRvZQiKyeS9PeSnO8gU/p7/YeNJoZwQS8FrgdH6TLsdZEPufEd9levnvprlWiY1Tz\nUuBKFT9q4/bHFdy+nULkLzHC0hjLTQ20z2nL72dg3zKCukXEi/IUgy1gBB/GWhPgb2OtJ38bXCH/\nMqVNDba22pijzny5B5iiURtxOeN6jxQ+bizPTuANbuCDjdBFL8aHWeBg65UMrXq8l27NJam37OPY\n81rIF2ii1ufkDWaan2pPxsOKV3sk3+QbYERkn4XPNIafYGDIB96Kx4k3NTQCtFo34iIf5E3gtRYO\nYTI8N9cAg35abSEfz/PrtC/RlfrWk/mVrTOrnC6/pJOK2+Xzar6q74rOZbh+4Mya7jjdUTuSb7iB\nX/BtrUA2I0Rh+pGZ0isS6XzOdaZfd1Z0NuMcBzl6n2PQg9zCERNdqPdKn12FhnF952wla+Tl+Arh\nL0KRPvd7CtEJdGlmz0XNpYzMwBCgpixFccWOMjXYNUJS9Mxs8lFo5TlIK/0UU+Kl++ZsM5oNnocX\nGqFZfoRjB5cAtzBU8FqTeq1BNM936+G99P0M7Na6yClPZIRHJhL+BzgPiBh6H2uN8ONYa1Ukc3S7\nWOuRh7aFmXxv+EOrMcyjsMk+n6xYEdzjav9EugWuQH4CmMm/9ERE+jCQY7Zz1/jfOlyAE772eX2h\ncIHf0BLQmsIocMSXHo4dlr3U5EpC9bddm/b9kaRV5Udw1JQdshDlOVH43bF63kvtpsIL+CJ/B7fN\nW31dh31mJuTt+rSH77zUeFW+o6OUvysv9lKL+7IhfQfXjeVjvlJHeP/VubhPVqMQgas9tefnpMOQ\n9P730IWAoyEaTMQyf6XVD7AJ7sCrk0W6WN6I85xkTGzxuyxRXrwG3XkwjlHKXBjHcvWY161dCV7r\nTBcpWs8z0poxHTciURmBtjcrVysownEm9A+1uFI9a48dAsEwAU7GTwRmg7jEFT4IFb73WkNIZ1mP\nZ6vgJH0/Azu0/Hr3jv3XD789UwvMPSE6ibVG+CdjrTFf2v2OLWFWWuyBmh/3rUeblc9slN4DH1SO\nVXBd9BL48OwK/KkvypAU7MsrYNGBQfOedPKJNhbgubpGPg/SE0Kge3jOEDWs4Epw5fLXe3bDEL4M\nn/HPb/NZ8X7SOCEk19XFXfex2NhFv875Y1xGWPVZr2hfWSwr9bPFlb3a6rTNDrenk1Yeh50pyKyd\nSsrqMMCTBFnF7eBYYScE8mZABO+LAKoYHmww2LtJhk+ui+WYMcX9boqzH9eLN2xYGSfiLtZaZwl0\nhxSjdVXHFdJiNYQxWJlqTQ9whxsGlrCXBO8vvNZudAscx3dnZecUO4cB3nNpOpMpxFRHD3aFa0y1\n59dw81Qfea2lFS+26730/QxsWF8vkC5NybRzuYFMDPlrOMZLqz4gg0PBg+ZnOgXC7tjzTCTBAMW/\nFXz95x5f0LLGa0WTy3KvS8xrPS1fm9WFjsl5M/CqMkD+xRQ2CVDSyx8LQl4KXIdCebAeCQQ8GZQP\nA584nDNU4jKWWg7/KF1X+UMYL/B4Qdu94Mi6NaQ6FrztFwVS43phWC8eID6ZlnPiaN7U/B3cUY9q\nFy/NbWT4v6QXOqToy43SNVxu6BKPbfkmr00QYXowwrLBHX/4xoQQbmBvpeYUD0LDeCfMDgZw5KQn\nhITWZ+PaDL6PtZLi6CQQToTLnk04umGGsDm439RvTjKNtWaa8d766N32yotjvxnPwrBfpYHM1DY3\n7UT2jXbItCYDhKlOfF7wKf0QN6ttHl8jKK8UrPI6PnNcjS7BlS4erUdmY3Rws8+ZtrHWnu/nVreS\nX0nfz8Am6I+Dnal++YcLfDVvPc9bOMpjphNObsARnrHW+tSNLxygrJ8aYYIJVPhlbSAxL00ZL3BD\nUS2zlGOMbfFVT/U2/4m+CdaOpPvm2t3m00IOr5zomMdx548JY7jefJZ67+9OXasx6OAcs319w2s9\n+iHGZdsYEV5zvq/yQE38sPxLdDz6xmHc4u74vG1eZTvolTwY16/y8LmgMCm43T3Cc5Nuq5I7ndni\nLozuC+Nas35CyICYibT00PabyatzGLlZuapPVWvSwbnCj3jwkjeR9odqi1Un1vavhuaKFvuhxZ1G\nbvZHVdcJl/+NMX6AZvMJdcyjoT5Cj3GkRl4gr/DepSNtNufL2LX4c42iDrnIhxdcgWcHZ60IQ4ye\nMo7fSzIJEeFn2JXdbR1wmH7Ep9I/nrzTVpPAb+LgCXWDTQCPgzfgdVAjHOVhXV042BgM9AB8hsXF\nadngTrLugYOUGC/VZ7xn4mj9XGzlwZ8WrCYuuIRFml8a7MkgV9Ati+GmeWEKPM6Jc14dTuKligfm\nks4du3b25EdSnhPX6CsY5z/ewwJ94asvSJJtqjqzWOBPYfonTZ03mneS2lWT1+xF/rZBwx5+4+Xr\nll295PjOn6kDXuRTPV2eAP+S34J35Lt+32JV1vXJ7bQi3FVyCW8mMWw61ifmlJANz0ZxvLwgNrps\ne48bpsok9b7Q7GDx/slqt4MyyhMMZDhSp20/1fYteWRlBCbtvt8k0fov26b4Al3sE//U91gwovm2\nYas89fColAJcFvCIP1ckwOUCXp2aa7i9Wj+dmvIUEAkdNDBFcG2Fdn92s/3mHuzrSVAHr8LDCwBl\nUHu4yxDl6eDDaz0DjAWO3BOUI5mYn3qskjjB9hMoP3wsHjNTGc96urJKCxuEibUyrhcpbCLXqee1\noe929O01byaT/wWenophT7lCMZasM7qP/yhdEwzCUeJpIXC6B8KmvArz8RZvL+mDqLazwuxUEcE6\nGq/1ar5yA+vw8nB8Or9SPRf5Y1wmyuda53m8Nqg7+HvKZE7LPi8HOCCBHOAOxPUaXbw2fdSOTPNS\nz6wq/AS8gT3FV9D4nxu82bPSwEqvr+bf9Ski3YuFxGThceHjMmrghP+H13S5JlAHTrE5iS9zU9Zj\n/5jSkWzadOiP3AuxN5DmKm1mDIZqXOHmsu7z5S0fsGPsmUPxBWLN46oT6uGXK6AYJg7nBbzDr87O\nNRzVPNoXeWtdeq2h74SkPJ8I8PqUqdWlb+7BBuAiv/opouJzM6hruH+JKMpjvjXU3jPWWp9EDX8a\nMjob6gPnXW3dpOwCa7ZpzJuCY6IqUL33tnCkWz09c8xUc7qPLQ21C42j2ujTab3b8QmepOLkAbej\niQQMXpsTc37ghErXr1ICR4nrrQ01NX952iFRSOilnf8zeqi5qYuburjI8G5azOBbxjWn/Anv2Hdc\neODKq31f++ETf11bXBde4Bz2TcAVbYu3KuIwQDtZ+37D9PI8KQZszib9IAtY9wABhoT3cTjfKuC9\nJUObbuJwA7P7C5jpO4n3AS/ePzWXvNP9Kliq0mY95fbsklQ6Y5YWBOXxlJCPhU47fr3CF8izk8Rt\nBmaGd5846EkUDnUKtflF2iiuC/s/5Gu4rhS4Ln6xPEEev5SNz08yjGtK04JhLiQluw6ze0kjLNM3\n92ADsOQHYBWD3dF+Saz1BLax1ggnuv9RpcOEbakv/kRFLbkMNEk+ozlSN3xBcfBDtLtckRR5zvL4\nIuVJzDC9m9exEFp6VdZGV+wXphFrXX76Zry60Z2jdPDK+UpdWj80tDDG8hUsPDFsYbYhNN5yOymF\n4OVFawRTkJMb2EXidP1Ifq0+lvkj3IYvpS0yU352K9gn7HnLywK+yJ/g4pTDctRNHFClzIrdPfZZ\ngJWppYs8C8dZgFjRDl4qXcPV/kZjkhGXQwbgZxvHsb2d09R7el710fiz723+AuLAilseOmy0KZye\nKeBIv8l3fZ0vs3E8HbzvkHOHTY5ZDuMie9ysAWwYhV72Wtu51jaouGJwUl7lo+Rddpc3H7nEKbqC\nA2Fom0kvIGWAgy/+KcS/iLEiyNpXIYmSc/VzLzFepW9pYLuCB8smzBkdDX+jmIj83E3iFp+J0sdj\nItzWui7uWa8fzydu8cxYa/wwlxrqJj/CKeiSuJu/lWACF3YbDZu8K+Fpu9ClFYJ0DGOR1C9rX8FR\nf/HjNWhMd/Iru7mysieEk8yrOEDOvKCu9soNHuw4WgD18OyLB83PnWuIRriSHxCjU3uWj1kSr+WP\n6dKj/KPg3p/UJDe49Z5m/ziPbJDn/PXfu4lfzN+m42BazHJucXd8dmWXRtAPyqtMXT5sqEH+uiG+\nukGidsK6lqpwoyLfqjzAR2tC+8TnRDAPZdWrOxilMl2zbHKtHQezTlN5Mbxj/eEYwJkGkX+1ER+W\n8MRs3QthzxKi5+TtG+TBKof2aL3boVR93k6sri9XZWx7oLWFO9xIJ7ksTEovcycgtgkElgWc0NWz\n0yCNrEE0b1+G2y+07N25gxt7OMmDj+A0ZHiCUyada+15hzN0Jyc75avStzSw3QiFyRF3LMcNc6/i\nC+BLA0eDF+vt4MI83JNEBHqpGOqWD63hsLjDw8BbyWdW5dQoB5zFPBrCnHHD1hTvke7h7Y71YEwU\nLvuIs2rOvRR9CCEfNpKKw8u8GK0bwmSGsbaZJy6eax0YlqvQVZjIJb39kV+5gVld1OA3MOOTE24g\nDquGOJ4QovfiZTnIEnfIXbz9xR6bUd7Kr9TNO3XyaD+WVnxO91d33Ur3VYir9+W8nON3JkXQPBAW\nUTVKLfN7SfeY+jnDCaP2ymFaTUnJN5zgHcxv/YSQPJpzQ0lSUyi7UXcnALK361x/cK8e5LE02b3Z\nLP6dCKFxzKwQeJJHA8WMrvXciRKyjbeJxpS81BRPKAQOPP/PzVuml22vxRwSonKMnmDxSkP4vWRa\nPNc6/fR9HWt91euN/JaXJdw4wXTZwZGl6xWQfgWfXmt7D8HmksC84mhjhLrXx3h+On3LGGxLK3ts\nZRMIUVY6DHBu4HdjrTUvWM3KgM8J5nl4GHgrQYP0L5dt7g29HNWQO1aARr2udSswnspj8uvOu+aE\nc3cPXKbLdZWViGDzLmlqrHX2PldDrF4Vn87+8vDYX8djA9PQlIC3eCGS6guRvlDyjjD8UKwWBL7k\nMhUji0A78CXL3D6Qv+B/bqqEbY8XcLjmMdzmdY6n0oqfMfyub+O+5UeyXeXlHn7um9BPIovyOP+x\nTMvzWJ+sE0y8vDmEd7p0V1mAo+7T+SWeN1xpeKgOgT5QPt3a5rO+2emP2OQ8LlGvZd1FACPggfrQ\n8+P+Saoi2DdO/TlY2F9vSdeip08+LpPTBUmeh57i5mAx1BzzOIaDX/6VrsZpL2OtJxylc9kqvDZw\n1VjpUTZ5XualwHW+e/4Qrh+M4WFQE0lyooL8DC3B/LqlH0/f0oNtaTHYnzzv2lTCpddan9rn1BYC\nDzaNBWH5CS+C+62Xv5sGJ0bh8bcSb22pdTwhbnBtMXiZKQDqz7WOx9rfzYOCeidxvkq83+IuaMJV\nLBykf07KxiduNpJYznKZVubqupstOERXcJ342WuMP01zxneBde+YK4KWXmv2fGSQ29GthDNYHpqv\nzh/hTk/96lzriN9tk7TA3Zdpiqv1hbyc4V+uZJtKWUugnkBaSffof6px2CsNmqfua6pkUu4UtOSb\n9Q6fTwgZOQVqO7w9IhVGQHm+c5xvNvc0NWh5hr1Qu03IfvVzeDZfbxOtAAAgAElEQVSaVVvUWOvB\nk0MPlKt502lpZL+7x5b9O8+m/Olzge30YOVeeq0tHKSuQIE8Hee3Db3Mr2OwfT7bkIjvb8ex1k+J\nkZjTFlh9FTKcPAJg+0Um03xB+t4G9iIGG8MrMAYbY7MVf4yDQJ4D/CTWmpSlicJRn67gVjanFMyE\nOjXeTKzs8mzqV4xtb0rHRPhyYqaziWv0lW/cMvdwTjgFZdk1L6yWrKFf4MtqfdjxdxA7bdeJC/sa\n/hF5XxRPN9Dy8ooec2ryH4AtPNk+t7SfJMgbOjjEWvtWGj1tGEKifBLs4u+V1G57vIBD/qqciMC4\nxvIoKadc345d2T7pKHx13lRuk1+Hl8QHLi+r5kLEOjITADvWHzMLguOEG86al29JTUSzdK1R6xRL\nEt5NWfuo3O6Yvjg2EqATh3U7noaUhokAxdXcMe2hmy4TkWQttGyMd70QuZb4RKrjIW0ZGiHxPryi\nKx0dUVwJROhNWpiK7uVP8C7fjfa6j2BkwoDp/CRV5Qbfx2DT0PtK+kKs9WiveMTSnDCirRPoVVjY\nZfQEEKQb3c+l721gL363ffe8awF8NIRNEUCsdVwnYpuxGuoIV0bBlJxlohVgPWWLiSbMLkUlTKEd\n+reLecbYx1JjE84hrMp4rVLdvHD4iZc7vGDJcdhTk9o/Kvn0s6fqRB0y7RuAk8EJ4CAXgdfaOzFa\nHPrCoqw82zmN0UZZt6gtAmq7WvQ2HPaT8YdeazTMvd/DnCpx4DMftCRaJuf4+CDTNeHT+W25rY9x\nk7uSy/9YxgmvK6GClXGJFgYvYHR5S4tptNIidaTgk8ZWz93TQXoheFkiCS9Cx7QJFgEFIxnfDciG\ncxBwNwsYaMf1SWy/bKKorl9qvZLLcoO1rDPw2wH1euNNps+wPGLkRpd5mQRQVVY3pBBPDP1B5rWG\nWm39zP7C919yiLj2VF5peXQy/706DhortTxSCmbAg82zH2RBZ/cyzYV0QgjPTjIPdruSRz7HYMsW\nJ8ndpWiw+FRKcGsJDHN4oRXGSfC9C9hGe681x7UBhvqRAV/sF+jDzfb4ifS9DezFHEOvdfRgE7Wh\nGglevdYcV+M0ru1LS6R65PqlyLIBpYeEbqxfGX9cyFZ7YiT26visnHAy4naWlOYsw1jBHC8dYqoD\nF5SsbscV50elg17WByW0TMBgZqJgrBNNBd+WNR5twIvn+FYjm/Mf3+mrzW67YtLBW1ypsrB32tor\nHY/qY2rKuGl3wK9/nag/Oh8fpl43rjuqc/g6ZS3Q2W1qJ3W4K3ost5ed2MtUv6DEK5NAsf9/9t4e\nZLvn+Q+auf9YCgYkARWFEFBI61srImqlCELSimATBSsre23EwkZRbFKkEETTqL02VhbxLRDxDTEW\nabTxz/cai92Z+czbnnOu+3q+yf3DfTjP2TM7M/s2Oztn7jl79b2bjt26XtNmtLbGaoKrXLeWFm46\nTRMAhn9INZTwhR5XetJx4QJ3wLCBTEY39uFiqOK8XnujObbWYMiPaP0aowmGDcHeUOCe989zc/Pq\nj+lI246F6q6OR+ylf6ztZW50x79WeIXrWe2B/DcErwnl4gbOkD/+JQCwAik0N8hvM/n4vrryEnBM\nD6BOALi0Xmux7dZwCXikJgdDPY3E+KHmL0g/0sBGhR+AIV+Vnb/UwJF7BQ6xXcCii7XeMuIbjxnk\ntI1zN9R1ZynrN61HbFfp7xuJ80IJukdm3FJjYzwTrTfttMpKT/mJSs7wJvW76SHdHL28x2WDuuHF\nJOtcayi2OLG96v3jnXqFuOtsuF/QTGW3wj26jxmffOBYYK8dMaXzr3MfZcpMpzKeiS6Vzel6bq+3\nnPfzVypoMjAi/mR01/y7Ze/oj3ml1vxYbpthbI3p2wKJGsRLUEMgrvOpp4qc9cilCmlCNcbTvTp4\nUvQi6mePo8bll/f2XSSxUUuk69epr31ZLyu9eSeX+RgvTUz7hBFJ3WIzilbs+Re5sSiHjxfZKzzd\nQz/T3JURaFKLdOKTpKj7NcYJVyXc1DdvOgE+Ky+aD6sizoJAngzragafp5lS9rw7onuUBc0ByAvZ\nX3SZlmENsdaGzzTGWtuvPyKN9bNpL9L/4vQjDWxfS2bFJPnRDZyDjhSDUwjh8DAN5eOx1stLzSQ7\n1jp6rYHHqs6nFNcWe0bCs9Iw5CkWUoZlBlfJFbXT+vhAT7wM63jgtbYj/RRulNVoqj2b8n2Xvp+a\nOtoPFyU9L7xlWOtPne9nM2SHOGHZPzIDd7b7BS3ph4Lna+xqLkzTXIbkCp6Mh6BMifwjRuk+bGSy\nn18nMk92NiyKJ1sQBmX4F4RhPH7XPMdn7V2E3CvLiQf4DL0uw3RtSM0GdcGVCL/jmY5l809ldLhT\nP6bU2mRNuhy7S+Ma2gOdsd6h1xMbBU6ZuAZ1nQyNfQK/lbpP03fbdLkyhQ8PtcndGnnpcw738JUO\n92Sf5zvU75vrvD6y7I5IIaFhm3sGefZnAez4J3QKtG5DIP84ariTNkbFmO+82Z3J2Y/FLEj9X5JU\nfvOxfBAZoKMirvXMhyWyfuZch0wwT/CiLlGvwHrpv+0QooCn7Zr/GvbJ9COP6bOBGWKwER5QLuAM\ncFYkONd63YX0lVMn25KAd7FdpJKEAmlooOnUxT0hMAELFkemRUGrZUqnxwxp3zQmTLtLuiAQTlE9\nzP05wSr9up3H4IlRxJf5aPR+EbnXmhtmRFQ+cDzg1jvQUD82U+JydcYnhmI0Xm5uYCTNS8COO2eN\nntxrqTS4g2kRrD28woB9Lz2RhTv5o7yErq7S3AuGnnIpCYuV+tGpfPpWVZqr9HQc2vKtB7LMIS7q\nnJ5PZ2o4PJfldKfHKGvdiE2i7EBpYIgnph4XDCyGUt9+gUy6BvHPOu95WdtnqJ/sGdrLix/+UBT+\nRc3nSHWfMhMSEnqJgPZwOOULhch4uK2aHdr+JAV6bzTuFPqqbVeW7Ibt5ldctmfsJu6l67nuq1X2\np3014pzWE/bpfuoNU/xOih3osgNEGCIZPmRM3jsJjEA6ce4ZJJbz9IGcBUWSNVCm+Vz64R5s8vEo\n+S1uAJcGLoCvsdZw3ObChfkQkwqyiXMFGmOwS3uBxtJA0/Z3THzASmXmMqUtt+yKPwyg07JmEZ8j\nrwBHulB//PPjvf409Jzhd1KHewHbMoInhBAYmdTdVd7yvdtE0sWhvns080XpnmDc4ZGLQAtL48RR\ngVeDXcWkC1mhgJ/rm/HzNXv8wzL71XmOz0STZxr/77FPfDLW1J6Oz510VKlUV2XBleh11rnNuKtM\nIm1oRW1DZ04V2Wnp+nSpPdxmuCZsYB5hVjYhKiNajt7bOtQ2DIetfSpXuHHaTnX4U/I2BS3OHr4R\ng/ngVxt3NSGmduONXmvmHUqC924kYuuG0bq1wxx3jlvbSpK8Ene9GUl6Bnl3gxErVg51Vd85LUQa\neMf/Xnqyt+qISJx38dLuKD4RWT9zrmUQN723F+8FHrmH6zLTNG2LbaGyFp6OzJP0Iw1sE1UU7CBX\nLtQe0yxtDLYabLZIMdZ6b99qWxGrYBBhaEr9KJKCdkFFRaks0F/1d0y1tBWasODT5sQBaYH09dr6\nEaQU+CQ4q/4Qt3QOeb6BY3lsr8G3sRi8Hvk542UYDkpY3Xss3HOdUyDdBrjfFR7v3RVpG5o794l/\nC2cwfu/SiI1F/jDRRwG2vjBeUMauMDnzakd4WgHOa0rnbelefixv1M/qTYfPDW7ErmVz6stOFNcJ\nR7rLj+XJsNbU/RIjh5I8uzLWcWprX3ZfLk5JxoceJkQ77HC1wgIdLCwxmYZh4HRXQvxYxsNIzz3q\ny7BK/w55x4QzGsv559GJ/OUI4t/NcNpyLkIvglhr7RdT/55hw8Q2XOsuLV4eQm0bhZY+TJlEFXCS\n3tVjvlnNlvi91dyKtYbTQroAqjl46mn+1OZsK1T4At0/is/+wvmSdaWhFfF90+SBUA5BVgNN1zNx\n2EGp3BmNd9OPNLAFM83IVq81EZHHYwvgq9eamMw7zUTmtV75/qNIJv8zhtHoE6d53G1APM9P4vv+\ntEvKrWpAcHkrroZi4deffHCfdNxqhaJPY9qiMw4XnKbHjY3WGSF+eT36rHXxXmka84y9i+1RXFUK\n22udwz4YGjDeN25S/WcabQD091ZdXTpZBJLyAOOhPI1/iKumZKyfyqzJSdtxncuO7u4FbD+fL7I4\nGdZXZVMdfCh7wmdake/ls8pV7xpqBP+/a0WFc8JfzwJ5rQN5O3Z/hnaSrZSu7CLGjhoQN5faFTvX\nmmHFCyKlGZIGRgQfPnqZG3TdYj8pgvf2kUuZYLJTutQoX/py3V+0n8kNMN4bKwvEWKudpduT4Vaa\n3FOdjUqzME7qsssHJPJOx/3UpQ5XQ5T3vFKIlm2Bu2CdW+S8CuoOpbR51+SEE1fASYtcp6MReuck\nD5tjIf7tReZ5nrzWIcyUIC/RJrB87aUaerldbgBSpflw+pEGti9wjkDNQthFNIzBNGTgxUzyhcJO\nS2iCoc6QF9eN+ravNMYm/anKaBiMe4dHMcGW3AuqmFM2bLEWdu20rQX0WtcW9fHa2YN9B6fLt1uD\nar+iBR+ko3ZIOKAp9ENG3Gh189A3av8KOt/DsO7+obEd7/0Hjle4cImE5WDjR96GcvHe/IphjHhM\n+YQQjNWOAwh3bmChjCIvksZgBbpvaMFpa7nKj+WcYTzgZwzNx870WBPnnvIen95AvpPvDC2cTi+X\nQOdokp6VLq5/NGTGem8830n9qHrL0z4cUTLI7IE0C1NICHEqWzApeM6tfPOT8R4OQAmnyM3cOg48\nSmAp5dl0Biuklkn2J16Sutt/lDgoL8m0qi0uOwf8Y7qklYqU11ZjzlH3Co1e67U1CF15rSWcXoM2\nwHmVdjiTb/f91PjOVS52t9GkMSObyc61jkYZ4nA813xnVh5pIOSEGcJP8qTt8dx7i9Mrr+9ZVnfS\njzSwg4Jv5KeLtUZ49Fqvu+kMy/uRfURRJvDDrPxDNuOmcKC5Su9sHk6bKQVu0UDCsI4uxKML5chG\nFkO+bwOqps5Au+zQ88R4l/mZiAi81Hrpc6WNeQ53MV6Fhl0B9eq/H4vrrmdDffPSudZ2mQyI0fnf\n+CTCtZ1hH21OCNn9Did+BHgtix2Ck0UYaJXucFLI6erG7lt5zrBzrHXp5viUqXp8hPclM77+3+mn\nq3xWs7Z1M5b3PxqD6z9u81HOrUyqqdDhI7w3H8465VTKE0IDswAKhpZgTCESo/K3ShiX2oJBCKLW\nEfh1bXu8UUAomm9UYb7Gv/BZI6Iceqw1LS9kG1OdDivcw8VqLDG5CrJ25AMOOT3vrpcxqJJxOUyn\nMT4arY1xC4oOd771XLWM4cB8SMKZaO/n76R5hApXNMhwOwXD91astR0gEfmiToh8E6/SrsrrRPMr\n0o88RcRSiKXVDBhDRGC/grG0Z0i+fCtWoxv+MhE+LND5dbsUYq0h9SamPzR27aVOvNaZ/RZ/LDNL\nhi12l4iW0aTDh19Ew/me+jbOinNZ74cUwGx7XhANoHynddTeH7H4kXiS7/s4PvFfbbw+Pg9pGp4D\nDd/m7xemUMYHulK2DWEmO4owf5hYBhA1Jt4bLzd6q7G/aTIKXZ+erY4neRzTHN++yqvPioFDxI34\nHZ9c1j3fLWvneD/czVOT10XIMFDr5ptZHJPJFMjmRuSTy7rnu2UT/mkNRCRpCWGX8bFQfUmwZvQu\nDSywL5sJ5XHNa+Ye7CxDTaXpuYGFEDY9IWRp0LKaUViJipCN6jik1Op9y6eK9HQP02GfmQ1bf4aD\nxrZNIfAsZmfkU7i8SsxV/SkJJ2J9h7b2pYPjnK48KgtcE9s7r7HWwNpOjmGYQ+MrTR3Qbr7uQZC7\npjuPzYg3088zsKvMrKzlOb7smGHrcIy1BrkgNTaNE2paXNeW5zJxTAEhFXCgd9ZnJXCtIjql2NA1\ni1o/qnN9h1bfwWvNsa5VX2dM5fZNXu6aCkzbeEzTxg3qWTdTnSaGcBDKYRl1f6j1JY2swwP3in+d\n6tjdo4mb58WAtcUCIm+DNBjitGOtmzIGnNCuWqmVt7xO1zU+vZm3tpXlnE3rOt5V/u7NSOZ6H/de\nmvac43rRu1TzwtdKN5Yy8JIGt6iZVHYyNBs+F1dJcuDRvAjrWARe+S8/bVmqdBvRtd6Dl+32iSDX\nKfQP3oldf3GAa7PDH7yUF+92q+5gHx/eyDnkjZKMlPvm2X6gPtFYOuvadnxbIYl7XJyj+Ey0xwGU\nJaMTy0IxHU4bjjrN66ufQGccfap6ZtJClfYqFU6C+eSR3hl+vUwe2pdylRfNQyX4l/Ggf+HjeDIe\noeLU3mb+73T4Q+nnhYiEmeaQ9YVeQzuYqI+1pkOsdXjf40CDcHx79g8HXSoMm0GduKa2H7OJcM/b\nMYG3LjSOvJWL32AkS/+RYhfwwojDA9yo7/F8lGCu3k9ZYapxDbztjord7zEcJG0gLU3m3eCVzQfb\ne3EVHrAZMG4EGPPcw7oTQuL8wryhpsOydo7cM57F9iwLTHljfZLqNjPnO/Vy2o7yU8+/29ZiJVO7\n+rLM+YS70tPRC7NhU42fdXW/xrj+x9XuvCLENYCEevAzxigRHPjk1nJbMsvUpEIKttTHcIoU0frT\ntildWAMCLbYgUAYDWeU64mMZB3yKvLpfdOziK7TDh+WlTWNga6wArh+Ki3lid6w1GNrlPcPu+pdi\nCNPs8PBRyGh6nvEeWbyxUWTVW/j0Kw491mtc9oC5wIDV4CumCzfJUc53cIh7/tf5JqEyBFHTWGvP\nO47oN0BMHmutc2xzI/bxqdCWKdlPlvfxZCcMNKH3Ag1O6yRrplD4O6WfZ2Drwr/Mx1hrYiL62vKy\nn5eMNLHWtrGynZSk86g0YBk4z5TXZDRE4UXAazmv6ZNurGlvUWa9JKWty1DHgImIBZ6dVhrP9hoP\nbE2ff9ebXXGSKuD4LBNeSM0Cw48RgTbe4U/6sNHQVjQ6tNkQK7S7UpsSvTYtfgzJRu00lOm6K/C4\nkdJ+ReQGN5ZUIxzyUxlnmJeBVgxNmQzvyv9JWenu/XySM5zPiI//z9jclQS56Wdt9i9VOB/LbkmF\nJZshiYauymXeoicTQrErbuIjWNZru0/++tqkb2O4RhQCPyEkjo/rVXZaONc6tFny6FT80MaEz7Gw\n8mr5UztEnewLRbOECfYuYGN209aFzcbWVs6EXWWsJFZASw5icRN3vfWn3hloaaJJd4bn0PnQ/lzg\nz1ex1kT4V3Wc3zoDHW3IZ+Wh+Yb/vfyQ0ktaoD7FSb/g2wzVHezrauWX9KihPn0USYWmkfhCX1ZQ\nS4PzO6yYj6SfFyISZEmCXNlwsv86lDCRfKU3Z6JzrDUoexJQ94LzwglP81XRBJOyUUKtXpKL8jGJ\nxYCtC39NTI1n/PPmM6M4Gu8rX0JLmtSB7wh1a8wzlsdqLb91EYaBKIL+uc5+jRG7CPf1Zo1/1rzf\nbjIasWEvdRzoMN2qb0LqTvrAbxRox50T0RfE1ts4mhem2UANP4VpKEzi/Exl1oFUt18Dr4uybmi6\nfJAflY84iGV4ufw/Y3OTmyBPFH2P+/5WEShF7KNTLfPwqW7d9S+Dum7qGq0vRpTgmdfp6nH7Oiqu\nx0h3yb+9gpkUOcZaA7XfC3+JKKlsavvTHeE+vs8vkere/dcvU2D6gzP6261x7fT3vVLZe5J1aX/3\nALCiey/FvK66K/1t+onyuA+rdMuFf48krsNECF/WcD04l97BlPe8gLNVd/i1x2GvnvN3Uidxu3UM\nNfHuiZAb16DHicSMYyKyrWeNNeyNRJCPayWPY+4Werq7uS0wuSj/YPoD9GCzv5JsK4qJGq+1j7N7\nrTl4sFfhWt5CSA+Eu6rTySBeF7ezWY5LUqZHVZCfxfNBy2uPnewy9GPCkYgTWw60NyT2vBBq3SEv\nNA8NUcQJ920wa8hEOiGk+1nzuFkcaIC2bPwHGi533LRrzCLfvjaPrYCCtxkVVvZaaz+tDZQ80tBG\nDMTEOzcwGNO4yUT+3UtUzyOVZXhStrfyZXlOhvWp7Lglh7omTtd19M9XuERxOVDKu1hEbaTzIuEZ\neUxlOcyD5uesWwvu2UDItCNesGlthSbdo3f1fqpgyD4mbm82qIjQk82gF9EzHcJBKOBnY1uwTGJr\njVfX4TZEpMevsgMhQLz6iuzMnuPd3+yBJuyCy0TVBHc2iNVe/7EZDs/nlKWxL+3rrQgYGKUc1Gud\nz1xxDJULh+dZpCtaxOEDjsz8+/yNlJSEhmZ4HsR2x1oT04XXmhqvtfQeaJBX5GWKHdpm4SStbDQn\nDKn8/g7ph3uwQUABrrHWKhO64NeXuktNxA8hhdR1PdOQQjae2CSJF5CqIZw+EYd3q3v+xbG78OGZ\nlxGkHmY1jKKquxOmAUZnF8ftjNtl/HBpl7rfY1jpmGavNeOd3KAd5yDTCI7bga7rQtiBZrrn44iE\ncYP4YqI/YvdDoec2+Is4MLF7DOdwP9P8IWSGN80KvL55wcNV/o7XGkS8lMGoUJdyWXwBzbX+Pqld\np1tsOfzz9ldILUMp6fnEMuTDqRYa4PXq+PSyFOYbrswgaHGwyh0lv8TimEZjOT50e0DFz/XcT98z\nHEzvmV7D/fKLeJsMURvkuYX5ZbyTq5TDHTkVL/lwz704raTjeLbDBzPrpsI2DwRUvkTbAZhmCyJD\nI1Wz/wH/kJ/w587cS+lYPGng8hKi33ZQkfD+S+aeLyGyORSfD9QxpHRQDwcaKrx0cXY0ef1E7YB9\nc4xfnf4APNhuSNscDLHWusiFgAdtHmk3dRoyGi3TSbuOu1b+ZqK282q4w5yH+u9g7Nf8aEww+U6w\n8gx5x3Magw01xoT1TUa4jLDbeXh5SEF3zd2t3+lca9xcg6LfQ7PulebeZuF/XrWhph434jQ07G2q\n+MC3TBRa7xJ4OI5K+/LHqFpizjCt01YRBbnTDuUyRgQvq0Z6xs90bQfHMr6Zj9W9Hw5y4pOxvs/n\naVvjE87QWiLR08MbS+DZ89EMUJruZ9EVv+OjWjHi3uOT00lCrvByaEiM49S9poxYwvA1FCtr8G3A\nUhl39VHQSWGz65qB/LsmYjM6Wz+TMXZ9Dwx8mCQbLuGZoqfZho1hqA405a50YnBt0zdMyNpRF2SK\nA6byDkrboHF1GinA78ZaS8KJdQ60ckGbUjde7Rh287fzIrI/YoRn8vkzEcFY67TIww/QCAwrerrF\n2xf+xp9o8nrNNEX07yqLD6SfZ2Czi7vnt4G8z7VmWXFCqN8874IZjGyBDxoDTVRk9pU1MeQJdF4T\n7hF15Ty3ne6+lSJHZiH6cul894PDhYfSO9M+y9fUdTvATpsHBnYF6hVf/MUUz7VmvG/DO9+zURmu\nbWg39+XRklCHhqXYvaGNF438C64GAdK6nz4UXOMwh39g3XnObe5LGMu+cwML9wqLqcOnpq1DWXOh\nJOR8vutTT8cNbsQ+8UlFDZ85zWW15InqUD3EJPbXfk91Y/J8v2nNP79x+BEY6fjM/ZjLJt1S4YWH\nRAkXGwy35DBEBEfOvHmcPsdD65IbfE3c4Gv7rCz1Yu89j08K6ZJ6lUFPEe99jTQc5gvtWrexxfXp\n2gvXSuT9zdKJRgoNRRqJIx076Guxo6mDdV5Btq2Et41Iox5rVbN6QojHXetHjP6ChVKvISa4chzL\nV81Im37tUeeHEm1emdysSqYTLXYaRkdg1F9C/Ju43Bih1Fhry0vZUkyXADzyAnptfmmP5qvQFz2O\nKE/WyDfTzwsRwcn21bGN6yUXfqKP72YSSBY8Hq+34IqHNGG7CDTwgDR5gbIjdXM7e7dxS7uX3CBe\nH5W4l1qtk/2xSbJYOFgvDIbAlamy62rgJ9/b43SD3BYqr3FwQ3lpRr8n/JGjpMvBPNwr7fPUS8nd\nJOm+8pznE9zYNu2k4Rzdn+K3LHWj1Qbd81jWh5IkutuJRxLk2+WjpNawBC+rkp/DEiKnvh4d11o2\nh8Vk3NOF9ZcyW+eQV20V5CAZenRdhmsqjkmnDeNaqWWz7H9TgxQe9mKI6hcRpF9LJFjmtOGbh9ze\nY8xnvyvgGAV+H4sf7fWbBUUG5VY1i4VbovXJcWInmlavKk2irW3te4I8Is27CcZhKyyB/HpmP0Z3\nlPp7sdaFdtflx/SC0mxo3823I5TQhYjo9SKVBzvCmGFuYWEX24q7AykiPNDkVrnwJ3qAQ5Kcm7r/\ni9MP9mBvA3cb1upNVo+M7rvBA709iyrE7oEWe/FjYqCXsjAqTZwtp4EtWqiej11oGF8+tcGkm68E\n/GZQtnLz7sa4L1zWXk1UqohDtMczhWqUMBDKSxR7n4y8ptVdT0aYGQa13A2MZUjrLxBCAdxzqAhs\nstPd+vCAJtRFrVHZXdqP3Oz2annqBv+iL9pea934FV/cY7wqwBcI2BZhjoPxgPUCr+LJlorvxoPY\nfIa2y9CvFj7ja2pFAEp73csF91SWOZWy9iWk1p/LnsBnPl4mtOakqJpdKhnXcnS7TDlV3P0sVRd0\n9d8re2ZA5T4s55pC1YtoSh4o9l0iNzmUrblFXrkVp7KuZ3KQlnnkpjLUq+rA9Vhr397Uqa/faPqd\naXm8GUcu3OvacxqrF+rvaZSSC9yO59uVVpqOV9/GMGLpHaCcaw1ea5SoTuq7VdWtqEI71XuH9na9\nQ8KXuB1rbTIuUKuQ8fU5lN32PQNGI4aHNMAwSTi0NtDgXoU0ecX4OIQQlYR2YzTeTj/PwMZVsf3v\nEEO/BI1huFHvpVjrk6fb4ICX84HGmsehzGnmKfT2XZSfStWIm1tk8EscZUmTVHqeG8k983+WCt1x\nHzl5rbFtDVMNtcjhHPulrNLK8Qr1CRkv8/QcL60v9uHe5e3zZaG7DxsO29XFWu88O8wTU9RWWOT8\nJ3zGi7s/TnY83kvNUgXYOX650pdRGKjOfLp6Jz4z9Mypx+iEt0cAACAASURBVN+cRMImhluxchQr\n0w0uSBFAchnOMwc+OKPxz9m1R/OPyeQ6YktybyX0BuH7LlSp21hrNS5qGbdl0OsSWAytuCjLa0Oo\nw4eejZ7taU35BuZe680H4yeBOv74Wje6RKWZe7At1jr0504SyMGefKkm+s3iikxtgCjDuEPCqkwn\neOCqv6QNM+xYaI9E01HXcE+bdzhOOPp/o9GLpNkC2bHWFuoIBJrXWOug6vlMg/BA08hwT3+msX5Q\nT4MdviuF76RLA5uZ/xIR/d9E9F8R0X8pIv/DL2zPZULHAr+IhEGNMrV5/iKS1yJj5HGgoS8iei0g\nkzQfNPqMVxrnPdVp6Wv3oytDgwXg8tV9GRvVQVzynWQdcDhtqeLjcOJzL/8smYrUDGe1KaSGKzP8\nATLte+suA3y3bu95FUd6muau+1P4cGdsT0/b8ujuMEbEvD2Daxz01xir/CyYrZogSKd56lX4ccNv\neAmW9ftfquMqTby2kQJrEGn65cgNbt42z+2clvk1buzA5/iqbHfzGo2le2XzZpZnXCXN8mFTOx37\n58/Yl+ync9zzD990rV9hDS6/tkmXD3hBOeQy3TR2mSR83rrU8VPPtEywN7nM8b9I6KVlkvC1fYBf\n77FMS/YI2Fgqpt15fdLzYgLPs4RmhjvS2t33j1p2uGt39733VHd37VUdhY7G5FNjqylLFUpUhL/r\nPa44eRWVFQS9yzLzyTwtOyaJLjOZvUVM/s3aHkAGvEizawAao5eOXkz0Iz18MNnRA02hF6gf6Qca\nXZbjHx5vpksDW0T+HDP/GSL6R4noX2Hmf5yI/hMi+tdF5P/9XvXPU1biV3AiiroHcI+iZjS+UUvg\nFT8OcJq9mJK+W8YfB725nJoLEeskWnCLeQ00+ffMXFnmXrxrcN/N3+X/rG17wAjf3R2ecYzFL01H\n6RqacE1TaZXmHp3Tgk+Q9Snz6NrTrQQt6leJyvFd/GBgYFlnyNDehvJHYzbPg8HQ8nIl/Z10msXs\nY5xWAelGBCuBKIxqWA1exg3uic/6v27bU7ovo++kwvlWdQL/H3g9qPcW7TeH4h4pzswddDTGoI7T\nRjfyr2Uon93yaZe5FWlYyMUXI8DLDh9o7xQM6Rg2wrG+lkem9XLeltXpLmYZnlJeWffzU/DVY5k4\ntOw5bNsqXTvihxlzXiB/E8/snIFGmIl98oF+TTAa6atsT/zGcyMf4NCGJRcRvmhW47QqYlpHEX4j\n3fFg/yNExCLyF4noLzLzP09E/w0R/QUi+re+VfvvldJGeyV4smmMGOkt3wRQMMALDSd68g8mgN5p\nuKfRIzGa9udl+ggmBzxuYORtijABmIT/2R7w/VtGWiyxFw+A+gedNfVqa9hFE7LvLf5naa5oiUV8\nSdIXJHzR4pY3wiTxwDtXuPXmtcfoqaJWzdIVqRaM+PGHNoDUPlxImwf+GRzL8p/bGaQEyzCsJf9J\nHfeoxOu9Las3QrJ3GUaDcBTqdupjm7eyXZr45LLs5a3nEeQyXWdetttw8WfUO08Znkt7qJZJKMr1\n9Pr5up67Za0RUQibMlTiCY7BW3fwozUR8UtQm0SY0RX+ZpUAS+CV2inES1v4l3O6ER2v9MVGuh9o\ndNov7rLjuMWe653wbmXifTzQvuwu4fk349nNV05c8tLA5YB/ygetteOu1avuE8gQH/6sDdkxV3Bk\nzcMj3ZlU8YgGSqmLJOxaVmliT90+gRhr30oIT4bhUCYBD+H2zdlL/CjCb6Q7Mdj/BBH9MTP/q0T0\n/xDR/0JE/xcR/dVv1/57JXGDZBKF8iaOuhjpAd55sG0mE83Kc6JXmv1mLm7TSEfDhB15K3W91ybj\nZW+Yd2gT5OjZ1j7YB5Nbund+wXbnmWiNAJofTKYqQO9QumvNsSz9upiQ/5mLunvrR115pbW77D+f\nnT7UygwE7qmSlgi2YJUViBHP/b+VRsRGC1qRl1WMSKfGX/Q+J/ypLHmmff1KKQvsKM79/dRJ88wH\nJLHH5YzrT/iMqyTjusxNZZP3m6i8BD1Ktden8czScI3rTzKW0VDWy17/cx649g9fMzCRSIPD5IYc\nlpXB3sngaRXCGg31oDrHDSZM2lYyJvdYpPheHyOvsE6IXgL8qwCW1K/vM26kaTaSDteayRT/du9d\nDPfCn1u+Xfv1ZeFlNI0XfrenG5a7sGe4KCvcw7u8qDapOoQoGtGdLrFxk4hzW3uK306Sgd87JIGP\n9FBt+EZC0gxLpDEnRaYX1xUcaCTQ2BYsRPySebt6mO4Y2P8xEf3tIvJvKoCZ/0Ui+mvfq/oTaZrW\npIhMieWtyPGXfGWajc8gqDCLSLPyeBQN0uBRNK48VxwgBV7GGRSv6M/u2Z9t7m2ZjzbW0YqYtr/6\n8eSqs+LbCMHCuk2bVs064/vU4KskRWxwLfVbgdPMHmlKfZLqxT7Q6pZr90wDdz8OSV9S+r5cpwNm\nKzzZTExl5eNHDjIeeajBMJSFU3fA33/ghUPxRDpOm8Mq4xY308XnGqoRNrSmrR1fXUEd7hQqYviS\n4c+fa5mk5zt8pBgrUjHGWk5lmVdXR/a+fixlIxrq21ojXbZ4Uyt55HU6gUQk17PrDi8KK/+SFb8d\nPwG/vijdt9a5hRtodhhG/43LRHvlOU/3YJyvEBEbQryTfipVP+EOw/zN1LGY2Aa3zFbyy1O9G77z\ngieKmC7pNc2tOHDfUFKa9oYEN7V8wqfgTV6o3WsB+QZJkjzYDOpfYItgyCMN+94YPqhUGyrRMAev\n9WlPeJLuxGD/lQb273+g7g+kaQiYsmyZN3jA3/OQaFjnOjmOfWMLDoE2VpsIY7gjDSd6aKciM1Mg\n3rzvpEFl9zAVxn05nkt5jjrvzh7QP1AjrS0h3guN2c7GRK+1nyvuXut4hJaOzR4o0sG8m3RxSXg0\n8IR/ogl3jkzUyhlpODxHPInVb/76wqHPspuG0RP3lcMm7JBRMBEfdkbJZdAIfzGCndS1ZVO2O6J4\n4ZgA3sdcNrw2nX+I7Ar7rmS8j8tDGVt3wp4C+JlP7O25jIBXbjvb2L+XTuOQy+TWk5hRE8ukwV1P\nFfeqLHN0SNb5crzuG54zvir9pl4ziGPIRg4HkRE/ho+slO5SYS/DZ/KwAlT2Sfk3V3x9pUv8QqOT\nI6nOdBdtn+HPdGJ3chmDe0f3sucv4J/7Rt6GJ9vL46Rz4XmFdzqmfHsl2kYGAUwhJDsvCcdgTT3n\nJO1jXWkRoXqwwfzfc8aKqGhAIyLJA615CfT6R2EigfwuF2inOP/ltX55XLbcH42r9POO6buRmIhO\nsjNuqAzlDMBMzy7swfBWIwjoLQ+7HtKYEa/wXZ17rbv+mJh9JnWDwV1hzXMDR5WgRUfPNtI29Vqs\nddflIWSmH6GMmDZBdmN13SU8m+DAXWPWdLFbceHlPMY47eluLV/+qC/bPxWKiuiZwTgiqxHcDhmb\nYiv4m2F0yOWBm2AR/+y1JtJYa7Z2rfR0TxTSVdulJCMG4fRc+cQypMJR6PkgpzhiEx/9rz9foM9F\n/A6zL5t4RQpJCLP3+9yGvp6+zNfJkoxJe5VkjeUGfh/f4n4perIjH6CTDFMl0eEvRRL5P/Bag8Ee\n2wr54W7LXbjHu6RheB7qst7q3MUdIt89r97q2Wv9Ij1xbm+ymaGsdjpzVCiuhHtDNeLMRm7im/ry\nbRjrSooaSSBPRBTO1g7cZptiLDkYpMFkadR8MLEE8aTQLP12I9ZaNwRxu6GPtd54L7GjCIXYjfNT\nnx+kP0gDu+i+MFrTnwo56rZEjwYuxlpLQyMNL421RhrnBQpIiOiLTFFM7bmTroTeYCps7AgcKFSN\ndQbSRT7EWhNlr7Vb1KdY67w64XlYCefFcW8gFcuNa6524XAmNJf71CIpj9pd3nVirPWKjuHL+tvG\nFHij9YJGmvFlwOeQ6bTqqc7GJJxirYmChzjK6aa/qSEXJcovpgjPI9CdVux84ye8uYVYby3rP3CM\nfLwetNdatXczSZO7xtXnKstTmYwltQ1SyvpWim2Oc6/leJ082L23Opd58pU/0oUQj/OHiYifTBdd\nKKHe4LX+YPL6YaO4uR+Z4Vx06InHpkm0hceB5mVt1T1V0pjlhqbx/VhiEIL6sSKR7Xih7m7OG417\ny/g3r3X+cGfUe/7UjsRhG3aYtPM7xk1rqSSeEmls+oU81looea2nWGtZISEE+y2JydOnZv2HG9jT\ntAsYbojSbIo4w/BRkCR4MBtTrLXTwGYJsdZqZDo9bJYMggKx1saj9IFi35riR6kRfM5STS70COcT\njvQ4Cy9tmVz5R6/1vAVPKevvW/SJqMZMo8+o3yOyceNKQJbc2J0uvNV6j15rNK+6makb/TgIXmlG\nPnxQhcZchy8AtopvnB6iPNxrrTspAT5R8FprgofQ99sbP5q83XBxg9s8c+QlDgbcnpdrpth0HZXM\nh4gIT42J+DH/qc0Cpa4vg2fcNJvNui+JZZlvhpjMi/JSw6pvl2RATm0cNBLm9eCZYoCL5hNdEdBs\n6DTaBHhFrzXUt2EvEnptT272Wq84aIK28uMLx9dDNLSe5g7j4kPJgba/e7+VWD3APQ0VGqH1A4Ta\nV2Vl+ay827nFxLfy0sA7wznkhc4G8kP+GceNeUoLIe9YSNcNQoLb4wmf7K/BXhPUq/sf0dpDLC/G\nUohhS5AQa73FwI1s5rCtWGjItslkx1qbaYHtwo8im948TT/cwJ6GgMsI6QbmeSiAWGslVXik3/nt\nQaw0Ed55uhe90ng7ZcdaWzwt8GaiqPsbOe4E4hZMhROslrj0liTr+KHZkGOwBfDVay3NCSH+8uFe\n6xJrHTydw4nDN1ZBLW4G8dZq4pRLUZDiNqHvj1UOY6U08Ihe6+j9bsbh7XSgHzzNMnnsH3imI/84\nz9IOJLDLnNLYTiP1JN0fVXjxZqSNsnIhxUYccVeSpoyoGtfdNnnXdjg938cFY1nwJg1uwG6x+jY0\nZaLczgtY4P742gZAhbuhWxIPRjAPBjInI30bBWJrLm9meZ2o15p83yrt+pTZ0O+LVlQEj+Gak83R\n1oEe9tHx7Cr26zdSQw3mJ9w5PQ/9uFhdMsCvcExe87GmHQ4Jeez8AafspfvJFFSWoXdkQdrHNi5A\nHAG3jWKFCbREYF8VivwF6IUsnMPzSrcIFc/4ixC/9EhbqIsBB/MfSD/cwD6kZuNt1yZujFzhtvnB\netQYbKSxPDv8GGttNLw810S4jghe45p231OUHUaASQPjDBMoqtteXSz3vNYmzBmHiboQhdPcoZ7M\nurjqVrH/ix18uOMqbiNFTCvgXWlAA+j4tviRDseo2wtQ/2Oo0rgH5dSKEDfjv83GA740+FWwpOV/\nGWu95SUcLEJWZLDb/W5Tb7Cq5OYqu9hpbWnFdT5Yk66g+Gyj3eCSRVrlbfS9NK2zfiSvjGLMZj5R\nbmc+ueaJT/Zah7KW9x35OI3mrE2n8JFqxMAiv1mmvOwuuT5eYaQUvcXtC0EHe3i97L7r27pnfAlp\nxkVpX5vmdcnDveETrd5/IwupJV9zVT5yvsiGyXGdI+QZ67kHDzwbr7Xm9QTXqI0iz6ynEKre76BJ\nbM/MCvNNTbLVdKuLQIXbN0gDDzB3tNOLJ/LfHm2FO08J/KPXevO3E0LiJimEnvXq7vtu+sM1sNMI\n9QvA8dCbrHD80PHSA600JhXnWGvaAoIGubbOeSye4ZSIYebfEgaGa+SVt3tcxhJwiMj+DNPGWm9j\n8XSudWwBrkiOz5JQE8c5OW+vPd4Ls+1FKR8+JhrsTccXQ0tqiAiHDx8jMWgge6bG4uw0GA9wGsdw\nHNswHTBvsKEFLWqbg6RmplHRyQ/hI8AyVTH1bepGTNcrJY/Y1TPKbY/L6bnH91msq40oqIS+Hcck\nTW49ZR5yWTbxihS/qp7Oa301Dp1BVa/hiD05l3Vap4RzBJr7ZbEDVVOZ19pwdWNRGOY72L2dYxxf\nO5UjIYo3OdxbWufR0sDd63A6/dGcl32417TnSQrqtNPw9/LHDw55gIf9KRkcVzyRtnyAsgfCYr/3\nJhaEHMbt7sAl1d6VEUk1rsVbvvJAs8cd9xbuaHCbOHqt9wrh/ayFisOJ99SfN9IPN7CrYjN4crep\ngeNPmMWwBIczUmB8aY61trzci7U2r7UuGi+MeoEhn3rzhuLoRopPhdq6ZtG1HukLHCJybzDCmZrQ\ng7htlA7f3xtavpkVEdWTQgKN9DRTHfq1BRjM4d62a8Va26Lf1qXsMVo/E7xwTc54/zC6E6XmT2tk\n6kCHn2DssKDw2wEUCB/JmxAMijEW41WmeOrGo+Vw0BnD+K3nPKLaTg6U3hNcu/iHXG54U8DCLVN5\noXHdbeuX6dl+eSCYMZ4b19LgVqjpRFFeqDtrfXfyH0nSGd3i+rwSUP3yVhV/lD/kdX1CSLKTqLka\nuCd+82p48DZ4zcWY7omu7nfNZaEi7EOId4pea7uBmrkKIeoalXegj+ZtItTgXXmFv+s5jzHb3Rzd\nSKJt7IQpwTf+Ok0rwcnbgp5ia7uArhNtXdSOWW+i7l1OL4b8pkmx1t5GEAv0ksN8v6VbD+mHG9j9\nEOD50h1+2NKF3LDeNF4OHqZgR7DJMMZM468xKo2Gkxi9xloT0lE07nMbKcpsl7ruZtgdnArzOOol\nuCsvO9/GWm8unVmRY629IhTt9TxFrCa0NvULJNUBe1v8mNFb2G8HgKO0ssan46XmReEfvNbRrMjz\nT5RHNCkD7UsdqUM6YLV/z1MtWFW940vEJ+9/KWOEpa1WXM+X5jYC27203BuDOl517PvwjumDxVk1\nX8MnmdW/HjzVC13KNE+e5zIZyiU9v8frHa91x7vYC+HqQj1OZdWQqWEcGLbRwBp8T7qRxHpedprI\nV6w/GLCdrFVtttp1NS44hkLHMVHVGu4SnjH+nNq7tHDvo/M3wzoZ1PfMowOOdTxq2jsxz2ACvk8b\nPMxC4Qdm7ANInTjeOLlPUp5vv2ikxXW16kogq3gPPY/kzSuEAJ9EY8E+UA3v8bBtRGlEiF7r9ZN0\nf9VKlD2DYc3UOhE/kX64gd2nMkRJhqXLZxHaNGocV5oIt7dQhjdSMLTlC2KtQx0C+SzGuFinDuXW\nn2GPEmg2doAVdovO/vwC8EzLZoznnp2Ee1zxbeqLffGe6H2Lgq0DlTfeE/+whQoV73WkXbhfTOGj\ntdjeizeIgFLV+mWakO1kkAZ/VxyccflLpF3GhzLkRbS0HJoId4V6kpoJ3humPJRF49f3c/gwOpSd\nw0SujPdAt2WkbsGfStcjJwO8w6+reaL+TKx1wBtamfPjJauW2SPcfYRYy7zCtEAF2wC8Cv+7J4RQ\nqo9BSNDI1oWIxnoywvsF0abm70q3adoqOr0YPnCEfRbvBOdaE3ufs0B0AnInlbFE4DkvDfy2R5pv\n4GQ+stsZ7rntuQ0XKcnEld4p5UwprrryLea+0chA38RaM3lYJROcEOLjoCPp5oafd63sx45/M/1B\nGthliIJ81i//W3rUPYnG8/BnC1jjzBw90l9Ax7mOvhGfneY5HW0YptVH8E5T8GYT4VnW8XOwQ6x1\nqamuvtqusDLnxpca0XTaJWl/yfdFw5HHfhHqP4T0X+q02Gxe4xFitQNu8lrLrkP3Y6gc7dMQ15/6\nS6nN/YicRivBSmiHDlNXBjVDWQjLan+tB4pJJUTmpjbpASrhGHXpblnGU5npyx7+1DnH0ZnydxNu\n1TXJG09SSk9lGVrLMvXO66YaDJWpdd9MqJwznJqyMGk+wm7fJM80hhiiAZz3AN9EQkV2rjXuKwK2\n1HgNseME7XxwWZft+YRPyTDOhjPygOFsJ8FxX/se4jGnFNTNA02hA3QD7RonGCBAF+Fm85mH2vMK\nz+Ek9l2MsUpaSoD3oLX6RseeXY0ce6eMtTfJC8ppIhKbjjTc0ew3T6vP8mLnWq990o1ubdf0UeSv\nTD/cwO4FpHwDqgt8C1wOx3AVD8IvROhdxjASjRfGjxHtwwF2evdag4LYTfM6vN7csyemw2AiXcBw\npGCTSyeB+BqWAjVa03X4hzBYWBZa0m+9mJ8NRGvI7aGJW/OwokwBI8GMz+W+NB3rZ9/ZhgxtXXzX\nO1eHkDUmtiGPzBNTejDN+FA20EUvixR0DmWdwQxlD2Otc51ywO97tMzdadSa3lrlTc0Ue4vy641K\nrxmEG17gyfWV9JS/m04rbn6WB7j+VFdzX3aq59Nea8y/dclqzWyoNn96F8ycPdNHr7XgOMBKmT5k\ndGGK9zsLZVIBIcX5OJMwnT6C1Puabt0ffZ+UUL7u61zrZMQv8hWCwwQnkpxeLOI1JkCSG+Mz6Rxc\nwXdCRS5xdtgIW+dxILAdDP/ndh40icY9llZMe8W2WEHRra1wbwgY87wRhMicSm4YM6j5TcMUY63h\ndySIuT3XmvcYjcb9rKg+mn64gX3Yibk+ys5UERmO3CNO9JpX4QAapuS1Ztswu1hrhE89m+e9N5+e\nw7AWyIOnWvPMFe4fLLoymL3WnHA3jkR8xrIrU2KztPi+UnOnz3XDA7jqknTHPz9hjHX5c6XrvE2L\nNNTHWkPXMEYbe1/yUKfWQ7ktRBey0wxgWxQVrGK74ErF3w0pphTDwGKZ6WSOGg/Jk7hkWBHBG+mE\n3kgo3fVM4yqg8Hwuo6GOq249wb2bTnKTpVRSaS+/J9luykR5cYP/S/dCei5IrkvCJasHaAAifqlH\nsG4wqIyQAa9p8tSVprm1nSl/cVdPejBeb9Hyjh1nOOovtSdc0Rv+265z/cwx9pGbZxw/feZUHp9X\njDPAwjDiXFUvsubbjxVvhpi4ZuTwvyQc7Ff9dWDXIaV9pc6LlFV4UxC5SVmo3MCRDwc8ze9RQJot\nRKbrlUaoxlrr1CoObDkxvARCRsK29FkN88MNbE9lWNLu08VdR3lgo5GAx5HG+M6x1vqze6YuxeNV\n60eV6sXqhH8xr+bMw41gTM02JnFZtzgEOOxwDjjwYcHJa81w/W4paJ3QFLyXPU+E7HDS/baeTwbp\nu7HqWyeEgEXMp247zmemu2EyHZsSrFYvk2lgNn45nDAdReX4N2KtJ3i2Sw5pKq/ryRnnsv4wSi2h\npqzyyeu71MFE0fs9t3Mq7/vUJ0m5ujqrtulLKodMecIPWkYU3yVDCl3MX5V3+fGSNUc9vCkD/F4o\ntQ8aa50+bNR7qZfdiMUrwBKPDJMer2o4vn0ZfVjiZ9wcP+1COtFQcV68KMVat+nDm0d/QsKZpDxB\nWMbpY8WNEz3WtOnj6raQkVIr8OH4bHnJ7bpISaF0I1JgSSG1Rm6gkYKnMdhvx1pjCAmlWGtYmwg/\ndvyb6esa5WekshzKkXsVjrLIFzTsWafZJ4JY+vIyexkm2gZ1NFJwo37XUHia8hjFN+Atkrz/U30K\neTsBxQbOxBh4+d0/xkl/ziOm+PZPNjB5gzumA0K3CXv7krLWhZzvVpw2jsYIsLvx2LiwkI8b/Fag\ncVN/frV9Dkq3S0/LYK7TMOaY03KZ/HuM5oR3p6/P03m95TJp870BOHtd8ysrlPNUR9/Hq/I5naQl\nSGGgkYLflWF7kFeuXQKWlYnym8avzz9J9+ieSIZDbSSadUu0gR29uailghr9VB6kRRhhp9mcUsE7\nhHxUXNq4TiOIm4fGvMjriuda71YH5SwAx0rvjcecuO/Pbc71Q8SFV/fbFcWAym71XSBPitPtXXnN\nHD5yvG1ca8MeJMk0aYF3Iow0ZYmIrL/QbrjvqxJjrUlsSOrSiR/iywD/lemHe7CFus3OVkeIm0Ys\noBGiq1hrhE+x1rRjrXkbYOH4PsuzNTm+7D0Q/NrZNBJnMg7PsuvXjvmmwAln4QEOdzj3vNa86aO+\n6NTURbqxSCpKo4Dru0G48/41Rg3v4At86w/vWGsInyDeQ6PxanimX5LP2E6mOkYA2zykw5yEY/rS\nQze1XKZuJeDF2T3FiYe2RL3WuiFqf20RAgzhoBTXDdbexap5tkV0qfvrEZZGqY5rWvNccJnie/md\nhFPY5Wu9nn9vL6m9lsuyHmMq+7281pgfL6Y+ZnfbdsUjDPofFMWuCeOpd1ww0gvCV9681vpiKqkN\nmu/gMrU5Xjkdx6MZ81jG3gdx1dDR+H3Ns3u4N026u9caxjZLMe+OJvXT/yX4YSo6LBd8IM84Jg6X\nhO9hJ+ITWxtJEp4hH8JEnmiDrN16uEN1LsTQGMYv/K1nz53n3W5gM5rIfxhGFeZFrLVJCjRvzN8b\nhG+nH25gT9POnTyXxadr1DZHWK+Lhj2vxgtTG2tNxot2niGPlZ43kql/EVzh7wkMmPblhBAxS8BO\nEYGF28da67hnE8Bp2bRwWqicno+mTaq67dkVtFMS+d5xkZjdzWRVGqYUJPwCJ37w7iPifwZE+VQo\nqib8LA4kq+3pfTUKHSgbWFcmME/rjq2vZxFaR8O6ahPnBzl24n0FWfvq45u56jzkEY+bGgdcAgzE\n3c9p/Q/b4kfzWdKfPNcySc9TSSwrfEVpuMG/qx//ZiQf4WrE6seKvSzVWAkwooicxryVFO/dh40d\njJ7AGOqbrxTUBd1KPODuHy3u7uvw2b3SvcJHTWmowgadxuyTyQxSfZhXlzTwWx8x5lARoSU3OZyE\nqO73Ka47rg9us5XuWcKelALavU6LNoyQwFTa2qeGxg1ooxEi/u3lPw4DxrSFl+gD3ZkNxy1deui5\nv0o/3MDuk05KP7LJ06R6j3xBI739aA0YSSz0KNZaf2Lb24JtuI7Bvg8/p7xAmKBNYCq1OES2GiLO\nzVhr5IW6+wr3zVR0s/Gc+RquzvU2lP2u8Kr/dS6FZIsFrw8ptkCtadf+7xHUvwIwh/LFtztpAk3y\npBeYgPamUcKYkQTPoxfxGcvCPCL+Z2KtA1++b3D1eLWyef3hPIRWkOoRrCfzCXqGrn+NcVRZvyzV\nEZIBvqCSnqeSysdk1jZXlwwpdInmovxJfrxEV28X80Cr+wAAIABJREFUa92UhQ77bFX86xNCMt+5\nfYlH53E/8ZguvqbxsYR46TTGLc02jP14vlV49FrjS0NXyeX9mysnLGzn1YV45HwbBoI4fI3j4SF4\n7+uN664xxIH2rt7ssEcVjVtAVHjhx1u4wdOPE7nQeKy1ea3BQ6VOrJXnUCd6sl1HhxmgNMGp3ZwX\n97fSH5aBDRtYjqcOirbxLiONrSt2uKQy0YeQB6KyUy44A76ei4zw8It8LR9yQe27fwFPq0CZNSeH\nEPtYoYfP38aXASm4QnyUwrOdFhFmIq2uXHZ89oS6NZuFfvfNyDzEW8GX+ziSjdLJXusLmlKkygIb\n/E4C2ttsmpCPNekSHq1x4nMgWCY40k6HpzZFxQWdDT/ZmGeOWtjkba6b3r0VESm5rX0qc26cnqPO\nJhL862legcf8d+2F2JoskQ89z4eyDhpoRevjvnzID417L7ng1ntbtvNQtvRI/6Fi4VsmcfMwI/Ir\n4XLBHT3abVtzfVew91L8HgVUQ763bUDafUIIrb0GIyFUX8dr/rbjTDvQwQWdg2yvDTq4JJw2L7TP\nclbH3crrSRlrK2CYKtAIUtuguifUEWhRtp9vMFmjljxuH1OYxi4joCGgsVYJbIUixL+5V3zyWi94\n1minWcoNyO2hj6YfbmAngTH52ptZ+qDR/qAtRO1JHpvG8jv+R5RGvdbMhD8mw0TuuSZ6BF8AeHgK\nf5zE2UmUrGnb8+ok4jLRlde64Lp+bXDJ2za0+yrNKsTVaOeBjiYc+J8Ut7lrXL95rXl7rOBPmSFE\nRHWsMqE80pjv1cE5L6EvK3U73U1YCdvZyl87hMpf84/PtW7qvsTvpKG29a6uzJS9bcAH3KxnPP9t\nr/XnbKJb6Wo1I7THrWXveK0xLwB4Qtfl37okPoe0F3X0cHuoSIadvdaNEXg8fSTBKBr7oR5pYIHm\n2RXnhymGhLDP1cX9NxvQi0XfKWq7/4JFYp2tZqVguy7ychP+xGtNWNSNG7ZdCPCfjFOvBdcOALUb\nmjuaMray0xCPlWegF89jrDVuK26UNfAnI910r8l/SqJ+uIGdTELbzLiMEApY9Fqv/yzPDq+ebj6E\ngdwPD/F8fBkwGbIdV4YdGh/OqWLdi7vWSudYa5RILSfDsdqEUxngPoq7TmX3hyAl8bbrfKU7hbvi\n6+IGZUDJaz22aerTU5yr5Mo3rozcKICVxptgVhjtV9Q7sdYBL7fxoMFuzmlRlo/SaYSu4q61Stzo\nYpwfEbWx1k/yBvhAOrGZpe7+EXsZG8ve9VqXdn1iebyV4uhtLbDu4vmgNIphBEaUbjIqdad+TWUj\nzZtKcYdveNv8ck91rLq7+9WE2qTrNwJbLNy5Mr/AkbZB31w8SH5D9qIMrHxn2rXhIaOw737m2OzA\nM8+5lDL7UPL9TTPwLyaK1tUojBBTrXQAx2/eV6y1eq0ZvNbceK31Afc8gfwEX/xmjzol3O+lH25g\ne6rGKYUR8s2LIRTAaU6x1qIfMrZGt+bZKqxHw0RjRm7k6W7+VsKljgsBl2qUss5rrXr39GuM5c81\n2WvdxnFHPgjtt2W6HAOd/igGvdbsvdTcxlxrC4WIvqwX2YAwSYPRc6VZDRXnY/uuxayQxTES/JT6\ngmvjppFs7OduoAKiMkek3ZZQBuagnRCSeOVGTZtWB2/a6us7maJD327si22a465reTGs6f1Y608p\n9Zzm1VrX23rOGF1J5RA0iCg+6MWhTV3+Ce6T/PHayynCJZzs4ZzY7R/FE474lLzWrN5j8DQzOYwo\nepo5wxKNAAzLBGHYtwg7pVru85hxsqpYumoZ7XOsNW4KSNvcn6yKQvtmEgLDNIA7VMiBLs+Gbsbx\nP4NS7COnLqddsPGqt8+56NFLxzx4oXYc553HrcTOm7Z8hGOsNb3EbF9V8ys/wYnwB2PiiDfhmtBW\nSe3JffhU+oMxsDuFgPpQGPMq4OTGrRAR+5+3SIhkh8dZXLQQeKfno/g41edSQbZ2imGf4JG2yT8Y\nl/JJZfJaL+cFm6FUlYEEHr1Z0ZSZcsQGs3/s15Thc1wgzyS/U1u+uoDdqHPiH1JJVJmA1zpUIrXS\n5Cl/q+ETr76DpUs17l2JHsCCUZvwOEHavqI263jfa9fVMJ6ko47L/DxL+fp/lN4tB3eX8Kk/6gB4\nSnfgeKusYs1lJ6/1eyFOQ7m8SXfIx6QKvoF1eJD4grYeN3doyAc39jtJ9JJ6p+G+DPu9BnReDnfa\n+ER6QghTjc/L43dDwrM6Kjw+mGS+6hnWlMI9Vl46HFLrMneMCk9fA6exyZsBtOGDKXqTodYtKCb9\ngvl7sdbhI8XE2zRv2WrryFTNg1uQxO3onpJ4K/1wA9sVWdzsxI3XXbjKccYY1qTYX8mYaHmt/2gr\nAoi1po1jtRy92VYN5GHaYR11cMQvfB6kaYvr4GZHmdcZ3jCvzrXuihgxsF5ukCQNQN7Mmg1vG7xd\nCrp3907DdYpuxruwea2D92WbDF82V3dirZ25dU2EBDaY6JGmCE/DecwjbRiiDQzH7hGFXndnYROg\nhdr2fYy1zmZnRvoe/KT/OnMIy7znUfqjxPWVc8BstkVYz90on/KljfyM7mmS9DSvbEnPlSLIoGip\nS8Yt2T2Vyz0ed5O0VxfOkGCCMIyfbmC0zrVeP+LcxVpTQz/BLuKuS/05Frv7GBPDWuCyTdDvEu4E\nAl7xx5NCCLzWamSHOE2qzwUnPkvghTwQ7/TMie+gdHBfbxFwX7o+oi8exUeg6JEuPhtPE6JpX8R8\nQ1vKT2nSNNtBptsAKq1dEW774VzrJta691pvCS1wMrjW349y3w30Wv//HuxbadoMJ6/wEuzpJA8S\n2h91r1hrm1ShR7HW3UeUno+x1m/FYN9dI2GcXII6H5wtBNegdHmutW2o3ihbAK3CwK2ZKViRhJ5t\n5XRH0vnmgoCFqYuru+8dwT6e2JNy74QQ/yjSh1FuzFfSFrf1YO14rq5iJA0SHvMAtQysOOjVjPsE\nnvt6gE/f9z7RifPwcijz/BwSYjqmpbuX79r1hO6TSVJOSlnG2HlJhkTLs8+P5TLAb/I95R+lQrj7\nGYwW7/vL7I9k2CEMDb8jTOENrCQ0pq5TMPilv1O4r/ZVuNepntnqtf5auDBU1bnAZVvAudYxvSNP\nE12GG0x2/UEXJnjKZ+9166UO+IsvZyWWQjfyThPR4xx3uxLi4lYscsK9myTuMZIyAith6wTLC2yJ\nEGvtXuttnxnLHs4gIOgQyeGpWZgY5pavlMuH0g83sPu05g0UfVg3HNaQvdwGrzVdeK037wCnFq4S\njvox5rmFU86XDvbgftOOEqRPCJfGa32KtSYish+gsSGZT8ql0rYzbV0sc8obLt7NWZzuFiaEe6Dd\nJTx/Wcvda+0/IiMWr60G+spyGGdV8gw91RexZdyjecJUfSFOiSqlEwaBUs80uAFBGjiWrU4z9uxI\n39V3agON8DuS0LGZ6OLoRgpvYQys0jpQj8T5ieN+N19gfJ/Hu0lSrq7yaRVX/O96rft66NK4fjdl\nw8oumeCDd1v2HWC3vdZPOzLhftgYuJN0JdjHj8FAJjeYKXutU3vzxtzc1zjxWB74fKRfVBbYeehR\nG+99AEpNZ68NB76Vzxoad4rMd+PDR45xnSXc1CYbY+lwT2kWrjnuWmxv1LKrWGvld461FsIzX4Mn\nuuyTFOcQ8gLt+aUKFtIPN7B7gUGvsKLxNmBWXt/C96TpD8aoPOp8Poi1Rngn45NXfcofujemGbVK\n0LIjq4lw59cYw5sllh9OBeH07BqZLmnHdBgfzjjlrpO8TwYR6b3WUMc0NbUZ24RDedpaxBY5q7c0\nG9+LI8ySqumE4zAil5tu1vqBGMpunxBCfXoKvzHPV0vgqT683pKioVjGk33eruThajmHcn6Px69M\nknI41tG4TmUP8r833bPUjDi6XnfZS/nbnrMtCtvxAUYEH0KmMI/yYeMAo/yxIxj2PISIUAd7cpEb\nRmYggbG97/Fca/EPL7d3Q8hf4TxcRaxNPleoDTcOr3EUa4dYXyNd51aqctpO90VyFJSL6sEmIbr3\na4yU2svhVuUv0mU+4+MjD/akl5niKR4bplWFWGt+M9a6ws0wpjzqDVwgg1vYr1MSY/rhBranMkZp\nFgSEFr3W9EdfVM61Zt/sVGky8J3gVh14yfHbC4TH9iGx37431yh0cXR83W4JvhlrbfSGm/F7Wu7K\nmeIYUCx6t/fXKsQ9jxXXNCQc2Sdx3uGYvgj3u44x6taMi3D7OO7SwDqMCXQmG4bRRgDJKoiweyqR\neq3N3aA8gU9Q4n2bal0n+FLi7WQ29s4059NonU4JuT5BhExvR7qLPFdeBVcOPL6hF06yc/qb01T2\nCa+1nMrlHo93krSXgFEKMGK3laSBEdFLxL3WATddU8MLXJ4ZQp8wCBoeeX5Uk2voRxdSEn6N8aBl\n2wQqZ753vJ4YjTdTFypykZcEF5x4e8NAOkm0WeNDO5q46y7Wu33e7ah1fCOlLST0gL0+/Qu3vIT4\n9fLtZePNsdYOx6FQI7vdG28o41tx1983vEL64QY2h1zYJNMsTLHWOrO6IDx22sMEIpwIz7XuYq3R\ne+7tqF71uFt7bJs280a3D6Ah1tqYR+2lhmGnANg6sp5zMIcfvVdpKWD76uNEi0kA96k6mHQzYugp\nrXgWpy14W63ID//fPITB2SsmC+a1trYjtfLzcVn18x4KiO+HccbZGz8wG8bC06A5inaKZWggtonz\ngzTwDvcMH+e9KXiqD+ct6RBrTVWebucPQvyU3zspj8+950HObJP7BYa18f8mjxv5mE7C2hlb675i\nrZlcr2U+UZlLvuQmjPQIwK7sLo96WV9uGhVx3DlcL2KqHx1Od47PHUyVDjxLKW/u1racHqygrcTF\nKvSVePURo+4NfZ1gf2ic9tg+rvlNe46lHsqeKskxSdiyzWzQkdlt1PyvjrU2eKs4Yqw1xmCPiubD\n6esa5WckNAJWfo61ph1rjcYUhFwbUSPiTQlRrAgFJ+YLvi40xQ3wQ74RiAoWgEmACsuOud4N5Eyd\nl73iEdBEXG5o+1aSe8Bv4L6bqorDDQDvWtf6NcYyX0dF3tWIz1lO8gaUcTjR8Q1Y7EuVA65NUwDn\nuh2fIcb4iWFc4Rcb203e/UkP1xJUr8on88+0yI8KXS0vedsYnTjkB7quMxOP4zWmWlj1hfdBpPsz\nftPfG/m2fNjzbo3PzTQOk0xwKbCXCP0mREJf5Kd2DGEVMqzhAh9g78BvXjV8pJftAON4j17rlKy7\naXPVffdCNfTsOl70mNcx1Y+oFrixCHD3W2tkahC0277zqnXU51gWTxTZbR3XeVqn4aPMwxWpSgrf\nnkET7ZQ2XuvGYq0Bz/QLbIMTPNZTdVKGt21t2y2nIf5o+uEebCFcdhqTpUVTrLWSedzqlnad3Es4\nGRxbssobT/SGpya3vXnU9ZS4PMUo3ghnin8voYSzVLCvoAZ3K8rrP6rrnCTc7qM3oDvzPScdZr/L\njsPXO+2/arjXGpdwUJzA0UfBcSRg7UkPPwqDfyFARR29+9fe6SscbsqEwhdI1g5YAGFOZHnSd36x\nSNuu8pAGZjKTYMaHAD7AjIe3wUa+WT93pMLJcDYjpFsFkx5+Vydj8ye1kGflTv52pQDqn6WUf8pr\njfm/2Tz61A1SNJiK1zpYCimByIZLMkz/ptbgjtc7NPEq/QTHg6R7LifSE0KIPNZNh6QbkzsrpsGJ\nSnwQ+k9bSNsLbZOl8dVblwpRPG4PvdbOI7YNZEX8w8cgEEUDHPiEerLR3ZS1z2P3yfaHIjjbK7yf\nl9pmyH8v1po0PISoesoVTj2860jA/YySeJR+pAd73OjM4POClWeir69dpkoCVKflOU6q5We4Tkhs\nE0N+avm5X2+lcKpHiqs2mMLnLdZVeKbXRkbcqvgHvls3+4t09Q5lysz3zqaR77HxuDkKfWmXsPaJ\nkRqDY3niM6YPrmKpjz13bgQMAFsuuCkK6BP8DuwEbwrtIy66aSik1MmFP3Ohx+e8vX0yb+nTdsEx\ndStJS7AsivsnvdZ1XUZb4PfY/1oZkjoyGeZe6+idLh8eat6V565ZjaAGZkYrwhTewIxPgmkHC58e\nZm1VfQx3OtyD1xrilfF92xwNBU4AZyvPa9TyGSfdBeoYeaT89cWwVfR5tr+ArzFYfxDWu1oaDBKQ\nLQEvM9xNG2PAI23exUYlAh3Het5KnUiGvGx7XIg01lqrZ9AqhbaHaweKp/wi36XAYzIcR4Py++lH\nerB9UKOPk4T2ZK0Z8xfubVDBRPqPwaSJhD+b4zF1E7yaZ533E3N5BqXBfS9J8BCjt3P1n4mh7dmE\nYKPygYp98RXLln8ed43VMcVec6kxElyPkI6mj+pqDZOfUa2x1kxsc99/iCj9B6sBV+LHsYVHD8dR\ne5Jvh8XuVdpsNMrgS3gMkHZv7safafyFxg42tWHoXAtugHfWTRxDLuOb2Udp/mw+VPQ7pFNV419E\nbP1X3fRufiyXAf4uvxv5mNIKkwirJ4RsPCNJ8I1rBpu44eZOyxieYfpQAmOokwHOgB8UANkX+gZL\n5QV21C6WtGsvbBcq21sCzX7LivqofAY+GfTdDRST+BW9zZ6XIgcACN8spTJ71vHocMFYKXN02h3E\nZQarJV3rbyietFixu5aHWGs/ZQROESGyeGghd1hGOBFL+tbJ8vFbppiY+t7hPMR+hG/o7ymJt9KP\nNLDjeuRYoOXMOyREPyljk701kbRleDpub092A8/hIblNfX4SbA65t+eXKZ1LLXa/d0JI+qAwe62b\nv69weu4TGFGo21u6G3wuUrQ3wXJkIt0qv1jlQNJRemsntK+NDT63o1d16bMX/XgSeNdTIeSWcXY0\nUjgajoZVvrJzbmFqUb6R+ySYT+FdSrgywK9YdEkSDkptZo/e+2n7+lT+907zKpNS/skTQkj6Kfw0\nvyepj7VOsch7XwjnWqt91dLHjxBjhTfbNfJ+A/7ogvjxJjRkiwOJkHvwpXl5ECI1qIyGmFoPc8Ih\nwCGD+x1f8kY9WHjkY/q6dP/FAldwDA9JhnfiL+m5zWc+l+2s6zKU3eZzSsAgbUZmQDPtE0Ik+F/c\nnylGy8Cng/se1HxEudvTtb4dUWuLhLZ3bez6920lA+lHGthB6IXMsCCh/fEeh5d4X3MwXSjfT388\nZjPuF/Cdhd2n27gd4lZwWVKuY61l59iFMpXZM/CJS7zBjSsyvka0Z+V0zzSXub4LScgN2HhSSIq1\nFjeytT+yOUw/EtPBlPfqFpttyhaD7WeG+Oh7DV77Fc6NMYExCDjdGWGcqCfd+6vh76GVNC6JBtoZ\n14r/exjTH/0LxjdT0FV7YXzEay0V/gl+3+JxeXlcc/k1xm1wUoaZ3nSYGeqH8BHNR36Zd4bRG7Dn\nKc6XnmvN9MhrrTj5fqeNheZBekR7XlntR41XHzGaMGncNjX4FwbzhdF+fsYO8PPxQ1olFq2FIS/g\ntSbCs7F7rzUdvNZZ33VntehTaib5zmy4gwL4vbzWmH6egW2GEYXRZyGSLwqx1r3XesGf/nhM8GDv\n1B+EN8Ov0m3cZo1ZXHW4E51+jZEztHmJyGqmcnHc8POj2Jv2F670uTPs1yJDzKIMcbCyIkccEiJO\nsdZa7ZYN2nPrXuvqcUYtgAt1i9TGzR7xyMONbzcY2PqaZajPR70gkG9HqZEV9E3mTJrVp2Ehk66/\ngBdZeoPP1bYdFfgmawzdq/F/mqcM48/we55kfPqo19r4Rfin+P2a5NKxYs6TEdXVP7XpCVzAjsKr\ngz/BvctDmjzcPdaa4cqpM/jQsOvoMizxh48pmXT+GeBXz5XPJZ0AXZPMa91pCt1n9vPKgcaR9Jz2\nOl97BLwAVyjRxg/y23lBPspiwu1S6uLa85aO13Otq0dYqPNO34H3Xuvr1uL2dXXG9e/ltcb0u3zk\nyMz/FDP/98z8PzLzv3bA+4eY+Y+Z+Z+bmYHSRo/0F9HyFgrpsXM2qUQt3LYShk+pcLNOcG+Cq6kq\nAFpW4b2w9DN7cxkYCz0iyOLFwiYRRVY/xiDFDX+eijXXwwpBaYQ37a7Vh+dAd4f2Xgpbo75V659A\nd/trnipc9oylP5vaDy1MdAfeOi94dJcbNXP+6WUeM/y1OB1qkxXYUDOMmrIn8FRniwvwkuYl1KLd\n+VM5Nc86Fgp8Oz80t236Xd4X/L6TkHfntc7j9SgvEf5tfr/L5R7ntYb267j4mg2apYMFOMAK/gF2\ngj/BHXl83ebt51p/xQkhTs9EbtBm+E2cd+4hvbdXnNjgbt0ftQgEJkjgtX7geZZYMdVwkUgbh2Do\ne6tDH4xTeks2yhBr7XxxX3SdCHveAFd58to4jn1oe22/aBnywHHDbgzwMf+B9MsNbGb+IqJ/h4j+\nSSL6s0T055n5Hxjw/g0i+s+PDGEAzCP95YMfJ5LSpILcCU4Oh8nxvMOjvHUCcNXcPjx/Evrb8zye\nEDJLjdyIr/aneuaANTvJfN24ci/E8XT/augK7sXV1eDH70H/VDT0B4FwzwQtUvZJwxXgQQ0P4F3a\n5P3VX4dERwvuXd6He/1HnVwGYwt7mCp7SLLXwQbQET7idrwHJoNsTPN+lZCGAZbLHue5wqe2vpv/\n7pXHgYjol5wQIhX+LX6/UxIRe6F2Y3sYz7fh8wklb/N+fMX6whjse/VaN+Ol8KMu5GB/5nqy3M3y\nz4F3t96e5sc1YvLrDVfPrZuJ4PrYey7uo8y0r4RrkpVHYpcl2jj8cbaiuT/MZJq+HveQ0nuEnmsd\nPnkzMRDIO210cGY4WFGM1XWBOdAvhPGcN5qmvRk+5j+Qfg8P9j9MRH9VRP5nEfljIvpLRPTPNHj/\nMhH9R0T014/cYJBkv5DHySMbyQ7OAIiT08P1qc5BhVMDeXfujrhhnS6Nwxdea7RYuFi3DW5qiQ97\ntnxOLc1loHE7LX+knZNu7uuuTLM3mSiqSaWBt+/9bF5ra2ZVkcZbN7+904hEHAI+2K7Y9o0D41H/\n3tGNB8DEb2FDzUM+Ga5HODfwBnbi8+i6vxXc4dfRfCT/YEE/4s19u99NeSw+7rXemas5eCt/wffx\npapvf6ezlq1aNjDqYDRVVSq9asuqky5gLbyZ+Q6XBtgJnpKtta3/XrqH2Fdqe9RsnATgzqFKcQ+L\nPUs4UJf3QZrxuFrRd3GGJOTnPJPaBcMuLkSS99FQTZyIyXRchdN+3OAey5LCv80nJd2TiEqstaEo\nDOBi/2l+gkeJiNLSw/VJ4FFipmNW2nvC+XT6PWKw/24i+l/h+X+jZXRbYua/i4j+WRH5x5g5lJUk\ntBY8u0CK0Hrt/tI8EX2xweVr071o5/kWXF60XkFkf9am9Wk7EtzaB3kZ8le7i4d6NPztdREFMQlZ\nkhp8mwyqTgbclAySFZ5UUxCp8gLBl56mmQASyqhTHaseN8uEyH8sJVUR8hoMzZSMW7xz6Qd+Jrem\niDePPcb2saPAtyIxDj0Y2f5V5v4wUmmXjL+Y6GsHdXu5toqhHZIGbDEUIofjxysBThV2B54n6Jtw\n7ZE5cTjaI/sb5mqjCNW+U5XADv2tfN4fv8HvKr1Lp4k3FZ7kkFf5t/LyAPcD+W+3da9V91j7y7Wq\n2vqhosPiG1AymuQmjIiqY2PAC524QTPVl2A4nn6utU4m1p1g5Xn/p/WG54YutGXifeKFz8or887r\nvoNBF4n925hwQb+swikGGvpitAzNbXCble02BfS/KN+s3wYNIQ9w7Xkr2R1rrfuS7t2SYqqN5R48\n+25pd4F1UAv+M/1oelf6fGzjOV/beK8NT9PfKh85/ttEhLHZY7/+2uuvbMOZ6U98/Un6O/62PxVi\ngsJXrVtp6suxENnbqX3ouPF5/5mQAM6L0c57fJXLkgzw3djdHmnyQUE0+dUG3Q0yjsJZG5mGLIoJ\n65B2i5UHXOOjz1nxrmcuH8LlVQS4uKq0vPPYGPZBaVqzOYC0phetHzImWkdtfe1SfWciYnrJOrKP\nhOjFFee127Dyq0VfJPTa4/RFRC9hYhb6kmUIszB9saz3Pd6/FstKR5uOE4+lIJwH0Rev9mW4Dpme\niGL+8F0PE23Yl5UxK57jM/H+M6bCmnKEMaVySngNTS7njoYK7zDlef4TTApvvbIsfy8FqeYo8W/x\noIHHRXPPZkKfbNkn2nfzASZn3Fs8pvwF73faH41plBhK9xnmhjjHvDSwDu8Ek2/QPoatn3qHc1xT\nX32PWSckredlzCw6hy8943AC/AXnbdmohtCx5N2GgLN5066LgdfS/Vq+4dDuwtu0EkG5P+mCNltU\nHW/5upXYF+m+3CbIi/uw2MGBWOu+yUctSZlwJz68Gs28Do0o8di6j+cFWuE8wCM+1L7hDPBQ73ak\nMhHpRo1wx73OxzZ6/m/89n/S33j99fCXjHfT72Fg/+9E9PfC89+zYZj+QSL6S7ystb+TiP5pZv5j\nEflPM7M//Ud/luyM6y8wwQa5CZthg6MyaGJTcBzRNrdDXpGxXs87HOsKP3hS4HDmhtY1xa22CYT4\nkixv3wyLIhs4+awUAtq4cAouN7jAh+XEdz9vw17oeiOeDBvzWDBdnPIR89iq7rQRkSveEuko82hw\nDO51lvONiJuPBvOcXsBMAIUue4+d9BGBDlOi0SfY+jZ6gAU4nWFtd4SIv+hlqy728pQfZQVxUSHf\noMO1fYl7IXeXMk15llRg9Jl+l/y3ecjn64kGMO+yNwxTuYlHB6NbbsJIQziaOuQmrGnzS3Q8yHTo\nW/exjG/Q8o36udZ36+IK2+rK76uNOhZBqAphX1EIEaFM39NJLiOioo2a+gudNHSY8keXmWdHp+3B\nTTAlqTWNCXErnQy4/U/iTMf3IVwLrVyA1wDHP/yKCP2Jrz9Ff4L/JNFvL+KX0P8k/+3N3tb0exjY\n/zUR/Rlm/vuI6P8goj9HRH8eEUTkT2uemf+2OJ1LAAAgAElEQVRDIvrLnXFd0jR7kK/7PwccGfKK\no8a352e4hHq5tGHx56FepnieN9bFkCcgepC6FSEZJTOVcSW1uHaTUOeI2zTC/vRkF7ah6fSjl41T\nEvI3GCr91oV/X7VU3oy8831QKRHmfhgvliAXdYTu8AWY8swDES17hxGDxcnkjdF5AxoNJ8K/euAG\ng5arAC2uX0y4jhCozShjcZ3OG0IHONPZcF7h8nXdN9RdEKs1duziRXFMnuTfpQs88vT+ju0wZ5QZ\nsbpWnhmmlpcGZvgPPNN/E+p9Fd7c8Jxhr8JrG6pWX8IJtADb7XAeCh94J5xQnxni17wLnemag7EK\nzzKVZz10wsWEBvRlWitc8NGuul84Luro/Sxa986/vC3mvW0uHuAzrox0POZr/YUXAZwkxs4rHVEL\nVyPb8wAnWeExt+bjnH65gS0ivzHzXyCi/4KWE/8/EJH/jpn/pVUs/14muc18Wg+Qrx7sLYTsINlw\n9CRrIZPGsMKPkSR4rEsgzwHuGymnegm8XLztvL0s1F5Qr/1Dg7JgYwxuaz3Iveccy6tlZlR536qF\nlPncwOVE11klQ0KUNi8+zhEH3nJry3d+z7f4kDB4sZF3S4dwEeDh+hJ5C57HrR2EA50/oBOeJcaM\nNPCVdBxjKEcXPpKuAtfQFtwSUUa8Rv1Z5xtqwvKnuX6Ce+JRynmme1JHXjn+sbfPC8rHt/My47zN\nW57h3ytXKYt7dn6er8Yb+gQmuRy9stkApmAUE5Yb/g3jusC219ro7xnTt3F2iIfdWz65/QOO8SLw\nNOexzXzSGDJBeyjx2j/57gulF6LbKdGXsIxrWpd/TgJUNY+k51CeaKXlU9sswolb3t8dXjzGB3xz\nCVl8LAWlZ78dsUFscPK/ZG98Id1T00+os7O3X2Mmd2h1cI/L9hBgYlpnfEsd2XfT7xKDLSL/GRH9\n/Qn27w64/8IVP5vKvKtc5Me/XDf5PY+HvFs0ZsQLrXizC3hsD5e2IZyE1keXYcqFHouACXe/8ntu\nEm6a4ZYg84VFKLkc8hwNgFIuiY4BrPoE0WGhh/Uc8hwx98JW49VjDN3otTh/6JcpDxJXDrp4zche\njfQfoWEwvhMd6VgwzDB01CwpcbD9+WTBix61BiUYOY8yShiTgiMXvNgAUzxG3rCgmL1HuAgw/h+9\nL1nUsSsZZnXsTWKvUab3jki6XFkSs6MKOTApuDLAr+pocIm8oIZajavwMl9gWTW8wyPn5U26Q32u\nqznC7bkxTq9gT73UXV6Gem7xRtx7vNXDS8arexnorjsvEtA+IQr9gOdXeh6NbUljMXjJPRTlmi4/\nL+MT2qyNoDuDsnV6V4YJcB0/G8FIW41gW2tDGzKtAC3l/IH2vjXRGdex5qYHowLJ8c8ZzoDv+ajR\nKu6uVyTAbYQE+gBw/m0J5yc815r+VvnI8VGy/jcylPNS8s0mvuEo43IBt6nj2J4O7m3gpj0KhwWi\ndW2vtRnn0OwnC4LI9phbuIU/E4Xg14RbF12S0HRW6B6elk9pT6Azc/ZWHxBy10ghoup9Fp+raqxj\nXgK8xd2x1cfY722MB6916R3bR5PY+hcOGW3zYX90FGDEKaYZYKTwDSPyDyKlgSmeQH1IKwgjpxH0\nRncfSFIqa0TY1rQOlhd9woNdqjnghrzcxOUKnwznLo+4WCG+CmI/ptX2ify3eMgNnLvltqebIg1l\nAmVu1GkeYJqXBnaieRTe0fOhD/F5ZVz1EBKFsjHU40HoReVD93AE20qpDQTwZMQDThez/TL44q3P\nYSHnRXbaWu6ko/c6a6+kYYTg4sRm0lxO+yhGWyh4raeWPdGdd/IRJgPuNIAyPGrnGzSA51hry7+E\n+GUDFvTqd9OPNLDdWKGDtbQ3FzVUUr6jtRNBGDbJBFd8905z8lRXuH2gRuRfXWN7RPPsJ5ug11r5\nWhueTH8yPI6kqGn2c/CCCfDwZw4D2dSZTINF3vC1/tYyQUskLEF5NhyhnfCYLZZbmlb776mEL+uq\nPq7aoa7AS4DHMp/qDvEBtTCxcTd+bXbG7+AoCw9jrTXEpn70uI30nVfZ0uujHuwGeFQ/V7g8093h\nm+0C1VlaKmFV+loMe8/vkf+d6/Vwy6+EA0Y2EYk9Z0NV71fG8kAjT/k0sA/xUQOaEk9q+9q0YYQd\ncEJ4xzf4GC+q4ScMBj5N8d6RN74oLLlMz0fdWcvkUOZCxuHxiieW2dpRPmEvrXyanQjaATyE7CWL\noWFVZ93Z/7qWdPkzr55OruGwlehfhD1/D84vGLm8nX4g/UgDu5W1kl8jVT3GewQb/LXXg8A2cMU3\nLyrDlA9wrxfXHDucHS56OkregfEu9EgAjja51IegFi6Mwl6F5MZldXSBm6wpG7PWyOFL71c24Ut+\nL9TsSe5PCOHq3UZ+2+ijkQett2cLHXHe8SNLVHk++bIZ41815rH81akxuqHoe3Dn3ZOgJK2xY5Yg\nld8djTADUmfj0Kyexw1+ebkfeUCdeO77etHAU2+vV+kn8gUmM+63eedyW4fVL1Y1TGeEgb4u5Tdh\nv9LofsA7x1pTqosCHx+7+xfPZcqreJa7O8/lR5z7vO2EECLyTdaNbHsWfN750LH4LKdykL1L3I43\nDck6h8ZyHvysHeB5t4UxRGIZKs0HiDwIxgzXo5G1XQxjywQ0OvZrElb5hq/2aV4inAAOY6s2NAd+\nKvcD3LzWPloWojJOwPP0Iw1sS0KXu9AzDzY1HmwOcMW/E2uNHuxjrLUQtEfxJBrvY8efJgaNk9ng\ncXpaOD0zxHjWsnWLzxzKE27xWrOufWiCOOxBuiEm1B0BZC3SOdM51eYJLYN6orO8NHApIyHARENF\nCGUEjHYNx6jmWE55Di/ShH6bTXrreJO3WB/x0pASv6+x9fASHWtO7N/J93PZSu/K8zO6RuJX32/S\nEYyBSuHREP9EXm7g3M3LZ/joB2v5+FLUnZLgaiRSNmRT+SPDuIV9wOh+12uNoTF6wfwF+jFeGdsA\n8AJrcCZe1ubu+VDfHTp4thCVJyrw6eZCRPWt+skm1cisTVbmNct3KM+0mifXpQh7lqaOxdZYHQo/\nKBIGOJ/gEnmzFg4x1RPcY623YFhZpzG/l362gX1jt6webB7w99SCjOY8yrkq5wle61U4F7h6rekL\n/6zrU95urk8T7mq315WkbFolPOAW2qwKGlxchUzlRcj8cc0GH5nfGaUOR61XrROeQyUSaQJseibg\nzVCH1OemHjXPlzmlOOuuUDUwa1gE8uxSV57akY/n03wJ8+lgBPAbsC0L3iKmEHO/Le/luXADc308\nCs+uqt9O1mNue98T0IwrPMDpnsFtVRRDXnVF9WIDOjbxl+Qf0cn3eRevdfsneY7PstZTZ/BShmm+\npaHG+FP8K6P6U3wcNsdax35QV0+4MmzAORrXNPBJ/RJ8ZpvP+oxjdYEjy2v90oUCnkykJ3x+qCiq\nYTsiRu817Tbd5puMCB/EC75IR8H7W2qXqUX3BuVqJHD11RZKg7vgfW/EnHrJXLBJjMb3glveBcNq\njzr2uztGTT/bwLa/wVMaLYdHr7WOfN4xZW/qnDzYEd891TLEYAt4rRk81VK91lrvF3tDdt3mLVce\nYk3Y6baF7EID1cAA9rhNWXYnXhrMyBPo4seSjUCzbgTebsEMS2nlt0NEyIbb51lFaMuP/UWhwP1e\nyyXG32u7ACfEVofntfE8+6S5+/wTe9nBUvmuO5Sjyx5pUKgzTAcS+WpHuYFpVVREbbPRyekUo1/4\njL19J39Xbm7hcg/P/cB85SeGkGd1PTsHfMa+TSv8Y/mLtfipvBpQSdOEBFtu4uFGHwUDsDGwn4Rx\nGP73jOVzvZVPOCEk8aTUlvys+tPyCG+fJ5zOiO6M5slA7+j4gq7iuQcf18zFfslE8oIOEaUOcx4A\nu6TAwkYd0y6Tlm+uA/lk2U7a6tRW8nPweeQxDErbkQj30e3x1eVBlH88JmwCwMuxuYGvajYvDbMk\n3bIcrnpo7eWSYq0XUfldil+QfraBneKiO7gMcMUXgMsAV3yXd0bZ9zU51Nt6rZnWz5Ay/mHbm6Zt\nYaB5Rw50q7UFFtZVXix1W2cZcLMRtjmsJ69TykLKBhj2aC+Y3FBbLXGcph5n5YGffK1SVb3xQzBV\nFIrjLUYKbwMe4SfbKo8hJEzx6D8qhhb2HvN+QgiFsBAUDu+X9/l9PdFJ1w2JSyjaknhCSTSWr+DG\nKb3JCPkpJvYM6Ogh1rZ8J9moSpSqImE8l1/xiKtt4uG7RYRxg+8SHsay5D6T/zS/K9411jr3slsH\n2XXQeWcdrzWc78BkwPuE0d3ALr3W4mOhl8qh2FieDdb+1BDv03yyyOIfTyQha5d/mEjhw8TXASbE\n9Np6VHjHV7OfEEJbL55irY/3sKrzPoNyNpfZs2x9X8Iw6nOW1czHL3bj/NReodZr7dto2h+ltuqU\nTqP0FHcq7/KqRz0vAe57QfZa63lSUU+ibqaA8bn0sw3sy12Nkge74jBR8lrnPBv+52Otl8ZxLzUY\nmHsnEV1k2h7L3F0SWwhvoTdL3SygvAr77TFsb5m2SHOsr4i27GXAGZbSZd86K5Bds8DYR48yCks0\nZ3wKQVgCDfYow3KDvU4hpuAW17+QWJsIxpHLvaqHob6yWEDwC+89LmXxVBjbfOW2EbUuA8ZXGU0c\nm8zYEn+x8NceFy/MA/ntPErKrTy/SUfzLERcn5cFc4yI4+OjHDlgEmD+orz8Wv76113sWZYcafva\nG9iYF8vfgE3e5Q4mA15ndD8wxCevNQU87zvSUtve7qVjgsHzaJin545PwoknfUC/L7zWasgu3L1G\ndFMVxSe7U3oePyVq0qHIGXDCEyhLuJKe/XbCzRUArgC2bBUN5Rw6vspM5bvQxBQWz2CYDn+6Csfh\nCbREQLsJQV68DmyPCMWPG7UNDteXD9Z6p1hrURut6+yFADxMP9vAHnZLGfJBcPdNAC4N3LYulGmA\n93Uxtedap1jrJRbTIXcMeSr5+zKAxow2fiJ23L528tWAZYL+YcDtnlvPt0LiDh082VszZodAVpC3\nNmywbi5pwbi1kCFpeNga7nAk4oQfitlwZnrhD7KQx1xng5G86gJVz7df2+vLCUayjxZP50/LLg9n\nXNM+Dk82/t7WBWiZPC9Ql/GheOY2R5j1CrzWoniiI+G0SwlDHDYnBZ7m827CcUWPeD/eXkmg0zwP\ncMjP5b5GbFPRviI+dy2LsDwOt9bI0/zTNfggX73WOa94vXEdnmXp1mzwKT3CLN/SvIt/z4COfBxW\nfo3R5C8Z0JKegZ8+Y1TEs/yBdq9D9SzLfr7DJ44BbS81O4/EO55rrXOP8w17fdC/8ZmUjwnc1bX1\nE8IsaacjLgmt/UM7pmVFY3mZZNxAB/1bQk3y6mKtObUP01Bm9TVjQtnwPeS1HcnT7PXA67BAm9mN\n30dH7mklL7GQToMJ0JSwTKqfA30o/WwD24JZyQeMaP/pfpuIuqAMnwh3vjU3OhkcZV7/5E9E78Za\nM+2FkmKt4yLnwWBLBvybwxQFGyU5p6CWYo2SW+B5risnsU1lyWIUpGGEQXoUi3wzBf02aZoL2uAF\nv0FntLDIl5S0i75sBsc7N3MLayQ3nhsYUdI2oMSffOxoctbsZiU0SPF8SS8RWYtByH+QRqv1ri5e\nUrop9AKMWMucx5aVIxgRlyus5KWHp9FreKzOOJ6uy2hULt0SttKQGPA0Tav0W/msJj6Yj17rTjPx\nxfOCZRugPEssi3Bu4Nko3nnDf8e4Phvp9dcYdVximyjUWfsZx+HCy/wU9tj7/C4dEX7AaErB7iCX\nV/fHqb7cuVD1qzDLp+WDQGb5nrQVERrx8nKnBglixk123PbbNFmb2/FxB3/P2WpX9nzrHKGHG50J\nqt9IOYADpYcLudeaBPGsOaHd2B6hX2Ni/EgD26byRgw2wsMvIjKIQ4O/7BXYwg9wm0CLpybfgJnb\nWGuc9NAnbNu4iT9ZKuLEnfGVUreFrQJxHiCJdTvLPBOdevZVulU5otKCTncyL/kp9GtSDEjCFFdT\nno0GlkNBylIFmK5WgQnEZ13arC+C6ovFQUF4qirbrPn+K9Ksb+/Du2FGOOm8BFMzfSsZTw9RbBwC\nvb77QzNZIef2TrhX+bncZct7BxvJ/t/xc4nyioOft8Nptb6Vb9bpJ/JTrHUUHW5oOw1W8VoPdoL1\n+QPs2x7tO15rIkrGPSU6M7DJ5754uHO77oZ6jAYxHZ7Z5rM8G4xmHPH2vgg/cD2MA9w7OOXnKjRB\nzuaUDV+4isweDGYCgzl4wGc6EVpufUp6BGjCLiXI4arPc7qyPnBrxTAMxvobrzavzjtMAHeAG/+X\nEL9ezag2o78VV2gnhcKPpR9pYAtmLnY1uZFf+Kq8yGT9BMcfgsFQXY21Xl5rXbzieJun08kmTQtn\nG3PhDOQwAneNbK/fHnNZ+5zochmj8GY6Aloog69+vUrtf21K6G8ZAy35/9h7f1Z9n+c/aObkCfgT\nNEUkggQsBEuxEEFs0tmqYCEYJGCfygdgZyGCEXsbCyvFRxBIKRJBjIgaxeZHsJTfmRTXzsxrXjN7\nXXvf57w/35w3WTjn3p2dmZ39NzvX3HPtrQJ7WPBdZStQGN9yU8eSIeRS4HMZN7bkrN8sgEwxp7b9\nxqG0o3Wu4wU/WB/+YzQe3lHWtOxmf1IOO0t3A1Os35mD61NFRmmmsIUF85r8Myk/mb42iX/7U73Y\nySHGZxyHK33HT6VP2+YEl/PTCFbcqybjEVdZcKbggUudNrk3XoPs9gPy6bUW6UffswF9V7b4Q8Nz\nY0Dbpv7t+GnEHXgP7Z3EWqfBDXUHISJJU8flvrzDqTLUX3QUqb/GCOVF+wl8tr/GuPp19W/NJsZa\n+17Ayd58GpdNJF96XPnSyRsD2KDNNVfJd89HsE2Yq4lPk+EzdYWYEKUOsMLxC4lvA0l45DSN6eLL\nApNCp7z6MbrOvLV2Mt/hpnJ5rVcDealA2lhuhIfcUWfD7V/T2fh++pEGdgzB7Wm5Dh1Y+1e+w51W\nRclTvYf7kTZ6rT9U9CPr0LDwFOWlhKZr3oQ/txvqLhn1cagby0CncsV66gPuSLs65LrCYZGU5mFa\n3GievJN407gwBmPMbUxtDjgxP85LgafBYjEgWabRMizxhUY35HkNOAreJsLGuZpekUgloQwAQ9kZ\nFl1FARZQB5igwAJKijQtHiGxR+FgFFCEa07KC42gkF08p/RxiLL8Ig82dnODO+X39RZjoV6Okkh9\nNFx6BB5K+VVH1zflwBv6+C15O8B5IV8NQBEp+avc+lIMlKTZ0pmrUjRAXzd8d97m7+Lzzg0hL98i\nEnIpfGK7s6F7hGMp07OnW4ZyjtldrDUf/KiSUHe2jVhVzkM6PG1NpN8acsfHzyE59lqLidhnruhU\n3xd92TGLl+IDgAm96Lg0Rml74P9K3lAu2H1PcMO81QcIUBKRX7/GOI6qe8jH+e19A/C3ph9pYKey\ntDSMyqmVh1b1Ws9wx78UkEJ+D29ea+f/oWJSZUoPp0LZaZN32/xHg/CUQIsolI3qGBdMAMXy7odE\nRGJR1zY1mwPBpwdFfEGwYktaT0RmQ3mSruYtRfMltOYijVejK/e4ng2dzuOqWHKrr4uU9li/nyQw\nzlvaNfQSXMscvMrHh+QyhpfX2vOi4j8SE2WRciVfGJfArEB97KH5zzcOibt1I3pfz3lQEVvcjLWu\npjWuLDYhdnHX025eTUSa9grmn+ojby/gntTHOkEjincL0ZIxYxs8OMrBhnG8d41lhH+FT4ftYq0T\nNvTBuE85Ho1+avvVkJATHCPepf9nxns8aPh6c4W8vtWy9YkTbAvN16lAGeFRXn/DIgEkHcuFLgSY\ncdGoDQ980RK5fosB7PnPNKKr4QgnNOnh++/4NnXcbvk7gC/x/QaTK2/PcF+/Buf0ghv0mWOtE8/L\nqQVwhL1rzUykMfvO9CMN7DhIDmKwqwc7Fe2E77Zu5vfwlCHr9eOjea2LvEO5Hra1re0GuN00nGJV\n1qNnZMErDZ4Om+U2lHG1rnPSxwhpxjn45lXOqusu71K1eTE2vi0eDCbj+6LL+x+wn3hDCP/6ogxw\nNjL4vcPm5eaxjfRNZvy4Xtz4PcR3K1VU/Cfm8c8N5IVxjQbcQiLDuOFNJ1L4Tb9q+Zx2a+Wpfr+u\nZoPbk/oBAYekAZfCR9mf3WkxxZjA3sW2X8m/S/fEIw2U6jOruGeG9Ct4owdb2MDbwL7D6B5gRzeE\nEJ2QPN7X9sJj8GMZ3/kDI3/7qQN8gg04Nv8ao/ddAp6fezhM/u7z5TQoN1jH97hgg9yEixQ6k/mG\nEGhvOkqbcW0btfwNxwPLhXbDMdwsdZUJea1X4TbWGnc8wrmd699sRX3TYKz0Iw1sw8zDaWebvOPE\nBjyIwZ681mIi9iHixx3e/BC/KLSMM9FL8Ygb0ouBmwohd3yalIcFoDk3shf3sDzY4GJTQKJcjve4\n2sGSDxh2RXA3SosYV11ReNDkNKeFHufl5fQwXjTuGUJ8Ms6EYyLptRbJ2MBM3eRNY7GES7Bldsvj\ngo7js+vGHVyobpizGZ6T7+zdM50bQ7ozvHWobIQq39T5Abbe/yGF2/OTMTzlcUp2uHfqqAzVYog7\nzSF4ZNZfNJteapxXQk3Za8Sc8k/1IgKG39d4Va91yllxJ6NZRKyvdRv7WXnawmse7MgDzAbYhCfy\nkof60WsNOEVm8/qUIeuxj4PB3XCE5O0e5PpjL0pwKTgB09WXdfZ9rlhr/zzjtWTXtUbohfH89pPX\nDZugb3zGwukmnI/bXf0aBPJsv8Br0ecEgRLz/aJJh3dIiwIn2B+hlkXSa4t7xc+8o1R35KhZyGy4\nzWvmw0aBWOsCf4y1FokQS8eL/xLrKWlsuJ7vRJ+epx9pYLf9NebXEMOewRhs/LiLtUY4tnvV63X9\nXhjBVelXHaCljJvrdDrfnnajgm4roxwqgGkZVzu8PcgImZhpgxW+U/+mGh7j6fB+NprSY80hIuyl\nZi+2EBwNapzXvJP6IrB4aVEXH4dLi6+WZNnUs/ezwi+ifg+2t0fwtYY9DOOCVQ/xJVP1Eue92gSL\nfP1Lgd1rnfdaiwAfjwUM2a4eYlsiietbLtpyZQ2wj8MNw8u1jbc+47Ke1qHehbzqsrauSdQHUI7+\nTnRNzFJG+LRXTvIGgLfoEGYM0wG39qYYz3AYdo00HflK8m882C/FTjv+YHS/4Ml+jLVeSqWXEybE\nO/uT4zHxx7bzVxinX19cRjL0LfADRwBHKk7U17H4BJh7rP0hIr3WVW6HI0+c7NtQEIYjDA8Se/rT\noMfymMBYNqvloIV1mnRXn6c9LKArMU1GcuAc6sIiwE3NrC+tfIjIMnYN8gQfw0pEzCzzr8Ra2yAP\n0xStc9vVL6cfaWCnsrQ0bmGmd7HWCHd8Cz6e1wJPr7VC3q9XWwvdhLzWFw9/ccA3dNyz7TQDvGxy\nfzpoNJPJtRso69cgVwQo4sLzRidcq0W3igpW0vetwT8YA4XxUVpHQ35ObL5c7ccmFzdxLiwtsGr2\n2Prvo1INIYl5Ti+LG93+hK1gfLt/Gk0vb3kHf2Xv7zAnLgraDtqNBTnAYg68ORjhYkVCG/i0oINB\nqCrosV9D99CP81E5vUVkMoyjXu/rOb8zuEVM9PqqK/pccfO/MB9gtD/cejngagXn7bwd4Dzk0Qt7\npRPjGvBojfU27g1sW/ybB9s8DzCRX2p0H/0aI4xXM6C35drOfVnS0GR46/cAM+yfDuU6Lp9bPJjj\n+F/3fNWRPO9vpEmVjMz6ruL1G8BibPNa3BvTzfAWN0DxSIQTrUwIBIPApKrzhTqF+vEFx9IWKJ3g\nAS4AQ/NgPASKlssjPO+7jhk3wEX4G7HWd3qx5G2a2e9NP9LAjrSJwf7O+65jmSnUf3xIXtcwKfls\n4OjwwZOe+oKpHJMnRnYxoBBomccTS9F/xhuG6NAlKlpF4phPMswG/XPB4umjthyFo93wtrrtbZVP\n6/CWdBytYGpXqIShq1wB3hpN83sQaPj8hrRjcwwHmSavNcRU6zLS0UvuY+E4PvT58mPy8xcEFcTA\n8mkM9p1yror8Oc8wFyrnMQ+SLMfxE7nA1PrtD/JxWszzTheR+HZAqP4p/wruE91ZOMgMj31lh3gP\n/NBAFMiPBvb0+a2x1iJC/MJghq/59x5uiTUaZWrX+w/OQsBXqVfmoWw7mBzAVllXP9ZRk59avNjX\nGeKKH+dby6dReQ+X88/HxFrhTmNYyrAGPG4IaXRSywu3mwFpfG+1/F1fXq0z+pOar55mNLI7XxPw\nRMsywSw7U3yetlaOyuW1tk8MDrhI1IKo+G+m83mNOetIl6bd1vYL0s82sDfr/D7uGjZvWfcJfz/W\n2sotE7K+mr/4+cF58cs5dV46LBCTOQb7PJUjJ7VWAnSDKwOuQR6sGiP83Z7lR8YmjtYmSvWLt4jc\n51liqo+xh/UD851wA/gyJt1AtHoFnxV45RNX7UlNF8oyTEftcWJkT/DVaFH602Zao6I0EA4ra0Jk\nWZJB7WEoVxlCQbT+QIyPIRrZthRgSIRLLjVyaZoX3nfEYD/V34ya+MNErjj+FkQLXc743fGddJzu\nVsCfMl9jtnXABc1jh3hYfoH/pS80YLfG9OSNfiUs5MlrDfUhW/FqO59a9jEtBjmXAUdIfgG++SBw\n5oFu5S1O8tp5ra+QkJRVxFbZchxMoC/5Kcaw1Bv8guXEQ5inwYIx/tOHMtLzDsQDb8/HDWvXh91r\nnXXMfzJwFf5/bxoMVtqEKE/LF5iNuH5DiP8mwlVX+5I7GmustJN1PGioXX9t+tkG9ubk/Op913EI\nev4k1tq5cay1yjPNSf/kbjncmd5oFElac6UBNPuxJTIn8AVHEXp4uQpNx8SBaYIPC8YiCF239Ct0\nw23CzpzgGEB1/b8UPBu+XoO0DmPjGV+DBFEAACAASURBVOFsZPFfh9vgtV2GqA4wEWmP8bEZQN7o\nKszhVmep0FOmVK0K4uA910se33+uJG2JqDg+ZmS8Z5NlLA5DqcaZ17l+yvPMBgvDYyBpBOhSJyW0\n7GarhwTqLt63SWeCBw9qnlkHzfmv4rrRce+11kY34o1e+Mkl8IDnRhXJbkvebjzLYCivfOA/GeFv\nxlqXtifYwAPlg77vyi//qVSP9DGNzF7rtkp5rUyHvG8aTQWx+GP57tOwjHyN2+plu6uPDsuh0S1h\nXLNu4VjrooahpugYkw4jOEsz6r+2s57wk2aMtZZ8+fAp1polcM0vIt1zbiboJa/y3f8oTtTtu/rl\n9PMMbIN9sYnBrt87JDyuWZN1+N3Ar4VgKxRkLWeTbaw1er3r7SFMI51ms1yLtQ/ZeYv0xJurFNoh\nPfGxuquBzpindlTvQgVMOmdtn/3Ova97TNP42AE760W817rEWEuuTZK1GEwL2U3LQtw+J3pOVTV3\nPNgjJENqF2rX9w7LAsHAXuM3hISHWrF3DqOy+B5DD2/yce5+BrrM8aAC8f53c/iO3kSlywfeXT5G\nRfHByHdrNXHV/7vOkTTL69sCvOfZ3EBKHIuKSz6e1/J2gDPkp5CQrl0mufo6Pr3vmnf0Hu/Czc/q\nAWZD+NljXb3NDDu9IaR7m7u8PZxEiqErIz8Z+AnJr03usfzFWGv0Wse/8FSu9QxlEbj3PTsI9N/w\nyelGceCaynRnnioNuNa8pL6pXNLm4HThT9gVMulGvc0x5jQQVZt1zka3hWgeQXjzB5yXoha/xngd\nPZZ1eCy5g2+ow0969Webivn1zmFxkH6egY2G3CYGu3hKAW4PcAM+piKy7rX2BuZDpXpHBA0s0BUj\nHGiOPp8UAyfXQrOlLaGCba5b3ZNY0Tj2JaeFzJpWUPBYEwccdBXxFxlaK2G5VkmtlasReBVV6k+b\nr77EI7VSWIjCPK3JctlW+gxF043HgJtJ/tz5kl8rHL9i8anG5LAdnKlGp+3EGAeI5wuLOsMV63x8\nJecIaa9hTc1XPA4K4vmBCjeURGhITkneuCJ1fLg8deEpj7r2KZ9b2GJAVHKd8BeUuV5yW0msHgnc\nx4eIm/Uy10y79jn/Di6GM1xJBxpYrxucWd8y3hsebHGdQUYvwLrR/eyhPom1fvZai4zx2MbySjfI\nuSx1Lu5keO0HY7LtamzLUE7ZPgXutSY5fY5wrmIeXV6r8kuRDfpV2k51NIaYeHn95SRA3pYMxrDF\n4y58pO1ODd7p2cXjGWlhJQPfsroXbvmlxsC3Kk/rk+3rHtJe76x6kNMM9LgBzM/yda818hZZp8TC\nqV5rG2WI60xXt8uP0mx6MffjYABeSD/PwDawSXCENvnyIyAm+ULjAPeFIBRr7XbDdH8iwmUZbXmT\nBG0Icb4opzUe+WlSHhaCGoTfJC3/uG3f2KtOe12h836jJArYsCaLcW3wQed9YJXhMNms+rprX0lt\nTE+JqGwifiGn3Xmtb+EXQJeRnfcA7iU5FnnJaQ1ZpXyNgjDnbgzjsehr8NFrXcouW/VSm2jGnqsk\nvocbBW6KmUuaopGHoTyMENn29imPqh4VOuys+L+0yZXX6ndGozwgcMiWGnoYwpYUoHhAf8mD/UL+\n2Ws9GM0HoR/cu6izQ7yB3+it3sLQGD2DPd4QYgL1CWODOA1uoH8hRGSPA4awCBnJXB6MaKly3XnA\nPxediK8R0EfFm10/c57r58QjP2det5+YRoXLepG0gW7qWhxkyqgieXsH4BSjOmrIZtgcGafX9I20\nWCgLgP+s3zpiculslM2A76ux1kXWHEPc2bVfrn8nPUidB3jwNq6bFsZ76ecZ2NrW5Ca/NjSuTTiN\ny170/Iq13nmtAx8UGZwlq9zbvXDnQ46Xe5vrTTq3HUDioskoj7sCd4dCP3WkrMY2ItENCIHcdjMx\nGvtwV3dXBvItG9vj+qfmnFaT5kJwc5IJK/w+vbK1uwxXHu/B9kvhSlw0wsrhADBxfBE0zE0c/RqM\nekPIkmAZ27r4pQG+6s0N9DQC47DRlF1X243eeRzRJw2OG+frCN7nc7Sc+Z3X2kpZ1wCEoQ282Ahu\n3u4Rs3DeLu+7HfIdeQw9uJK2cqdTP1M3NJPO7Did96RnASfsAA386pkmmOw82d/otSZeErSokXf8\nsE87fjLwk/hBl7i/euE//RCMiQz3Y8/3WosfHuR5xrJAv/jArmfK/acd4ons+O4S1+M61Dr45eCH\ntWiSb10L6Xqr32AFjqGsVYqEkd6gg/nu5LxL08i0UWibmhSBAegh1pr1apTNdbmV/lVnyu6avs1p\n6t5ze29sXkk/z8BeNsE1n2AglBH2kVPyVE+x1svrR7HWos7ejQloe1ka/rQ11gFclr3iL2GUFy+v\nFksON1472Ql/oGp1sUUvywatnBzUwifbrVz9p8L7EY+3fCRH5EPy+ViRajHqSvJJ/nyg9sOb8jEv\nPg9W5hTrRTxvObeyzGT3wJrfECJhu+KPoVy97SEjDJcG7zO7U5BVicxqIoxtrYanvgvHDucQxcCq\naHytJ4L79MJR8fvjYa2UUwM2Ei+ClzVhfzjepVk5z3nzUou1Rl/yBcVoxWvbJEfE5d07lT2zrWP5\n4OjVIpV8a34KCeFxH41eO8QjeNSFofmANxy1p8ayibxkdL/9a4wtLKTKMpcRn+kHr/cNv9ev6Ztg\nvYxy1B106VN2SBjCcyDWPKAuyfIJ3A7hxet2F/phkg8EkaBM+PaZ33CxARz/aTNEjWEZkuEO36eX\n1WahnDToBVdAufLLtnGAyddirVcZ6/xH3mgpNR6TJ3/qWovj/gXp5xnYsPd2MdhPsdYIT6+1SG5+\nzyOurrattlUOheHoi3Z8p0wmVCJaq9N5d1XLhBFACqNq3sk2wtHgjCe+ZFrxSAtYQZYuv4ukDdy7\nhpVvawvrxbZRrbehGgbh7oaQ8qIZbfjnsJGlDeLz3f4NfcxOzHX3+rPDZJnYGBriY6BphAcmPHDo\n2iW+9BX+HMNxTId6xXLiMq+pLAd57PKUj22Qp0mYBFlyuvRPJ617X6quSL7+8qYEHzbXrwotdCxx\ntldpZ8Pza3kOcZCW723f47ncrD+mB+iJ566fXa+6EYh5izzAbICJNKP7yWstxEsCT0iOTjt7rAeD\n+h3+aw4T9/VP9Fqb3f8aY/va2OWD8vtwmOR3Pw9TrLMYvI2GMbmMa66xLJUVa4iXNXPohza5J/4k\n+Czniwnbuc1DrHV+pZH7MXSj9xvCiNxuQZ1m8V+Ah9OsWSEaHiTUrYH34vy/kn6egW3yGIP9FGsd\n+BFrLeS1Filea+dhUm4PCVkWLd5MgvKKVh715N4dl53HPjGVC7XyZRXhgAl2LHVWaRgUCkGxD4UO\nvilIGDy4aEEtctlgaF76IvvUxudJV7QxH7mI96l6rSWd/sDDbuH3LzYmXKK9Kfz5cdqj82eYnYZg\nw8upOSCW67igwAYoi/2uSd4878p8n06xN2qkLBuXdx9r3Y+AUOOui6BFfhcft+iwm1O3TXWbcjvY\nifbd/KdxnQ64k84AYwhoeZ52RnmUreOVNuSmDbvoXvJWR103xL/utQb8wkviTyDfPdBcj2V9qMe+\nPnisdcnn3m5Foz77LqXvVS+4d7rPd5VtgoeaWO9eGHziuioeaSrjJ+OXRluqO3esM5HJa+37up3y\ntjGcYQzbYPyRCfWyVfisLy2NXCnHG8RaLwowhkXq6NbyMPKwgN2I39P0hNrh0dP9DennGdhoBPLJ\ns9IUa41wUxVdsdZ+9NVD0fMAt6R/pFmrrhrVmqvRwLbwhYiabzLEDeyWpo0G1aR94Xb81biPS9k5\nlpjNIK47A0FNm7iiawZ35x1ALZDbVJSv+DYE2ddA+I0h2xtCDMbiwWud5tEElxF3DglJb7AQJUxL\ng2lpuXqU+z3Y2ceymHzw20upaUzLGj/2Wrsf9XphceF4Hd4U4n1TLX0QwZtCYDzKms1t4yUDfifp\n81ZhVwOU9zKOvT/9hMEcpZyDK18N6XdjqyeMmWNiMx5z59p38mw8zhrm3jv9jPuG0TzQYhulDwvv\n2YMNddZhb8daL9xSFjbCJ9izYV76ZPLQBsLvjGsBmZUM1eq1Tl7QR0N5QIYjeJ30Mg6we2e4hOxT\nMioYIhv/LR2aHc9y2WtX3eW1JmkCn1buaqO+yGgABy4OczkCpvXFw8VDUU5ve+iTAu/Kg/LiPGB3\nIXwZMmGW+cIIu0vAkWnNRnL6ikf6FBS0PdL02S+zBTTbhfLF9PMMbBPwYPtIahm53X3XYhax1rH5\nY8JU5rhcgMtUJxsa6af1eABUOLaRhhHT3BkYRjnczMMqmm4IWXBWcBccvqRG1sMZb03Ua7A6fNBV\n3HTspqfkVDlhSUU7yUTwXms3DHHutg5a8E77Z6y7B/r+qSDHHd5z3zsK8OYFiU+NRHL9+IGFl/6i\nqreAKOA497wVBAxy9zKs5ex4FrBltFvFcRHrS47+LQC0ifjw95WfSo9xVJPrsaWa1r63NP57+3Cn\nte8hOGzrI0lSaWkhOfu4SeNQKRGD8b7jFpHqtZ74PRi8OaBDG3UN2oinxOeUrsv2iof69V9j3Bu3\nzfsMceTdgN6UQ9apTeZPMjA/87YFDGcdytVw/owyPmjgeZN6ZlJZOzU26a663r7vk3dI/ZSxPHqv\nYwClxFp7Z1B+XQCrHEREy7rGVnyNFFgp6wBLeYdj+Qg2HjiwnuKaPUn9kl5rG7zWtY15d688PDzc\nnfidXxf5iOYXpp9nYCsefqDA0TAbY61lea1jiRQVEIeiuDFtacgrLKL1H46/4cAF2WDm6wErreWe\n+layAV43A28MKJcXHK+y9y/bm9doqzEZbDO4Jg7no2sUsfgHtGjlcBa60eTDtmCmUtWvMQ8DWNc6\nsqD/DMOuel/Rw1zhVUY29BiOnTBZRuddqMj6zKd07ievmMmwuEma8gTH9qYINmyFJrz7k7dfc7RC\nBWstg8i1DcZp6a6uJr9ddVKq046py2/Jbdkvru9hHnBDiPq6T9rErUefr4pyEA9y7spPdUqIiPOU\nx6/Q0Vio6+x945ppq0FVj+C7Nk7ls6DbeKsR9mKs9dZrDbBot4zrjh/KLJW+9WnCP8W582AvmEoJ\nDSn3Wj/EWofxH/irDcs+x0urVsdCjOai4Ul8CpV9+zHeBI8Ug8Rri3VO3VDfEWstxq36uSVzmpwj\nwP8Y/kqCMJCQ16zEWutnN+1x92pZHwYPJdUVwBxwZyONy5WYSDN1mjTld4zLJv08A5tPQj+rLcd6\nF2sdG6uc5YPX2uQyPgMH6iaaEG6wgODzkeakz1uEmzojPCWwSKzY5uQOWStB2dtrYJtechKtMvo8\njH16EY7K9WoKfxWPlkvYjRZz7C+OoRe53/JS+e3hk5FoM+WZjbhtc4fRcWljDJNvou1ymeK1Fou7\nu3VxcKPtooEXGtXSiy3ILw3x8HqbEL/lnQbFWOpfLN95sCc1EkNy4LXGI0OhRhd91vmxwH5upOMW\n8vA1rQdNN+vnPt31+zSfXutqOlRcMkRsxns0pG3G4zZYb77s0bYL79Rb7Z+/ItZ674H+Ln6dvnm5\no9/VS13h0r3WhuMPh9vSp8e/vlizQxr0qOHnwPONzxIi4nXxp9uy/8w56rNchpqwAvfjVgucjskL\nhkoK2RC8tWGDLvDzr4OHtJmVZQcp5q9jNG4IEZEVfpl6voRw0O0heC4bwROPYr/bWS7xWXiM/SM9\n+3zIvp1+noGNowVvhqXBl57QXax1LI71mV7ralytrQPlDY3g/OyOuHWEjjQv9HmLEKchcYddBd+1\nW1gliRekOJbYRtFndcd3ny7LPWiKQtHrCyZf3fZSumuTvK/r8/J2owaxMAArXGKIM6b7+lRdB80O\nvtn+r/ctx+5T2bBELcX4iXE9NIKGCjogCwLWgCQO4gQ/2eCBjAW2S6frwOQzdn2lZi64r6+PN73W\nIsKe6BO6SUY8AvRlut7XnUEz5b/Fa+10qJaO6aY2tSwRpjuVFe2otJl0yL/rtU45i9faqLx4pSwv\neMVb2Midl1y3/D+9z2uLfuqSSVf47IKj1zofoHJ19bMv22C4DXjTmvD5GXH9IB0/pRlbLx22j3h5\nCLpxjdJddfP+dN4tcINU6Aar8nv0Xj+dKyf1PLO6ZF0z42shvNZDC4a4AmPQV03AAVcPaFi5Jc39\nZH715D1JP8/ArvZEHop+3rtS/1AR+YhxTntGLwUFk+hKyxUV8h5jrQuNVBqA980OB06hUZHGI9vt\nNIBfiKSuSKwjGybqwP4pNSrQ4SqqZ2zLH5auilhpQIF/lfFiW/tWW58Oz6qd0JRxj2Jwt+yX/xon\n3wRiUNaYg/pSXj6mpTmFRw5Ky5u4wtmU6mkH32KalB+bce+z/xhMCX3Blxc1DcvitcbyOtxwHHhc\nwhseM1HbSn6XgCHjGgtVf6yVGCE+zoN+rM+/VzzYInkInN0QsvYOyBJ0lny1/M+G+peodX0rghFL\n9+thv4bajtmW/Wt/Psqw3OkV8inoEd6wp0fD2Toey8K6ZyezrTbyEw3UF7zWpV4CJ8sL32p7IlLi\nnwO/8UvdXPgV+bm+93FbD33+BK+1//Iiwt1rnSEWcaiJCMLr4E9w28JhjH0cX4Dbq3AOR6kLBP7W\nwbDyiZ+TiGtPEb76F7vd5DoPjc6LxT9eQvRdayLxU+iFn7ehAS86w5Y3GG0Fx+M+jX2ufxedxZyG\nWfMXnzGZ/v6SmyAmubu9mWK6Eb+kcWzkscnTemO8u9R4/IL08wxsRRsPDkGHq3w51hq94XnIbmKt\nCZ4nfTehNP6zaeUQSvFdhww0d8cs5lOh5+pEiaSs2nIYLyuoKMKmGZTwaaWLSPWeytBlUlgvWJqu\n9INTfM3khrHAFx1oIHWv9TUiDE8JOWRI1vRs4QyUNDG/b1dzGzRMw9mRhfWgIWiASxhxHv5RbhHx\nKQIcHzW/+9oVJr6cmC9NXnKa4LyQslOabpNbw3KXOAa7Gsx1LFKqPAz7S4eoRzS2Qsby715WlJLz\nWMPpNccim1YOIgIx4bVvUzlVUcViDSESZyTAlHC5zJL11TfzuWBdhu+lY9mxbwawEhohZ17rYuAF\nXzbAdx5pkWcP9Ak/oh/LA/1Q3v0c+qcNXuulIGYvsoj/mJrQp+EhC/M0ebnv4d+YQAlcISJKDXTl\n+eS1nnQU3n9fOFspET+v2dDe8tvjTenOmnCE6PObsdbVM30fa51SoVyLBp84B3ymmVdM16u/Kv08\nA9skbTrfuLLG/QOGzQ/qsD1cKUiOe1EEMnzqLbwf2OvQDWUjUXY5cDngkd3htc8CYs5bLiXBA1+g\nJpixHvEaDJ6FpqMJoGrrW6rB4HVzOwPsXdXJvGLOrMxZD9WQwThegOHT77FGuLlnmNZQeMEBGEao\n7F6azLlS+tvBnYt7dFVMPvSKlwy4ER3GYasIP1C4RzrldtVWZc4y9NOI3nJYA9NjrP06P5Av1rjB\neKzpLF5hdUWvwuOEZfZg133m/YcyjKsU3K7GW11ROz6XqMT7gz4HoEjQ+TxhSymlEuzpKLUBBXfb\nqzeEBB6fdYR31TE/KIMSGfnfyWHv09mSKz83XmswhL0vBvQVBuXo286z7U6LwRA+Mb63cj3IUNrE\ntnFM8E9CWd/HWlvg+fimsHXcp2StRAfo0MbIe4AffU4CgddYTMKwRl10Jc3/jt9rAs47dWt8k3wF\nK3hV2onTI68NrBjKeI6qvBZrLfWc3cVa57EETrFsVkL3gSyyeLV27VEjVt6o9L85/TwD2+0nscxv\nYq0Xuuvia7kpllMpK9EI1jENnKh8IO+ei/LKrsfudbz71SK5YEhV4cFqBphSOkk1sUi5DRuE83Fp\n/AfpOmzHa8ADuBEN0rEuFtEImXD8NMLY2K3GWsWtbXYYG8vItxqtCEdtYTJP9QS3xvPqaxyEPJC+\nZg+81sHBjWWDPvt5YT4Gl6aMfjq9So4FhdjIOpjR8E4YjQd03tacFe28TbrxYOdYXbo5NYC3sUYy\n9nLqkJCg48EB6uu9xV3rwDN7BZLj19Aw90VnUd0NT9Y8YV/E3k9jDusTXyHvmY47e7QnCaT0D/G+\nxHOSk3hmf1/zWpdwA+QDMAnalGXrOTaU6c7bnTqutAH9r/VY1vt67DN6rU3COIcXmoKmHKLOg+B2\nBE+h0Hte26ufezj2Ccb3Dg6wMkCY7GoTdQjCCwzqphp+wRDDRhJWMZIX0e5U351KfCnxgasvx1oj\nPPAiP8Bdhx7Q1GS9XWS4SY9m1Tekn2dgm4SBe3mtVcx9Vde5sgxLNyYkN4+uDcwx1YUGy4vtjSe7\n8Agh+9QxfzFE2y2JYll0OJTNjY62Z33VTsvTiiFaKGgHx7aC3VAwytfQk8bQWteG6NlgOtswgLOM\nyf2Lh8k2n7LTgEsjq07aBD8LOblPzz1E3OHaux09ea25xe611uJBjYcB+hEZHziWAPmVmGuQ1ueK\nPfvOWaWOZJbRY8/8Km73YPv89TLuF43/2aYsnYNGLOLlSGUJ12OGDEmjijaIMmjhH+9iDi3JUcAv\n2fv6aN+09t1TpCx4tscjqWc8u8fjo7Th2TMey8xybL3Wwt5gCZgAzSVH9UBX2I0HGvjMZaIfy3f0\n9BDw0Cb+fTZ6W2WT2of+1+GpA4w+az94ncxwKbCqaydc2cBuk4mk91oLvK7ypR+GBi7DcsJGgeg8\naHyezotfXM/H9Bux1niCiEiPtYYYbGzLDvLJ4wFv6FbggTy/Kv08A9ttXZUx1joPPkevU4/HkRI8\nqeFgNbe5NIg9zldUyg/Z5E0SchloJhAmYrORvbyIcaG8H14WDLPdqEt4hoMs+XmlYZbgMVKoR1AB\nKIwcLsJiLCRRM9ZdXq3E0UbTOjA2nCgenXqWbS02GCbB3uVu/CFcgkrdo7oMcvewbuGDoYHGn1C7\nuBDQ0Jx4TL2ezJquK1S613rJsKa4xFFL9g29+qKpkGLnwMuTIZOy0tNYuEVm4Bc9WPyE+AnzoyN2\nl/xu8+K1hnI1gXPn1y20Wi0yXGuxLuP+4iJCsq+pq3TAu8aBMVzI6eXIijLWrSFb6qayLGOQBFg2\ngJd9JqQHTnlaxeM2eA2fe9CfeVqU37whRGT2WodeYyN8oh8MavtOfm7UE2wsX/2581pj2dvLwdTb\nT3uox8/JO56fXY4vfwp9xhm6dDutKLykIM+K69/14iDpkxhg1C4Os/CcR82ag3gJEdpFXhc/yzax\nDvgL1kulDxtirEuYmWUYJA4VOKiUbKNQROtbyqtskNcSEuJHRKUBeJ2FKFYabBdpWAsBvB7BvyT9\nPAPb1/76/lfNxK4ra0X9vms/oGCPqm/gj2thJk3CRWTzwqMVOBqfojA/QZOLQAoNLA7x/ahX259y\nudzwk2hK+x+4B1Pxi4pg4G0oOC97/RJfdPUR/1Yc1FVW4CWx8Cs/bMMqP5MrTp7lMmxTFy8Yt8I/\neTHMVMQ+1Lsi/uuC12YXuhGkdtP/skk3Mhk+4Q7wpWDcANdlgKuHQyxZJtkq3PLmj+VRx7L/SA3T\nq0nc+e4Gmq61m0MLDwMeD71wom+u9PGGEI951hwfv6YJbyMRc375wBLTHi/tpaEv9ALlET+BsRGk\nT34fYmtLN/O1lOjo850UtfmCIJp5urY+4EniMbf8NgAxO160YRu8URbHRFn8v8E81bO09/SCYRnx\nRKq+4fNoNIKHNvjGhlmWB/6s9zZ4I3+7cKoRzV5iOYhzTpgI0ZNne+aXNlDQNyM7+1r4mYD8OSal\nXPjJyO8Kpf04+DXG/o2djXMkIw8beLBX2w8EswX3AyLKFyeP+bblAMDPCS4D3g4uohJ3F0rum1XK\n/zjQQnvYEAYYxjDAs6mmtrFPPs6YG2rtnqLTGm60jLVGHms6/UYumMY51jpoMty0x2H3+GxZZ6Lz\nH+O9Ab629NKZE43F8i48kAb695X08wxsya0/pmmVFTo8fggOiwMXQMXLPB4ElUY3C2Apc0Uesjyg\nnSZmueo72t+wsad+Ezz6APAynv7kCOSewcUX/Fxhwy727Dp7qjnjCohk9R8xQeT2soIPRVEWKv7i\n3FMKEetZEYbaSdq1oiWXzNn4cYydsm2KWarX3Xnzg4CnTyODq3wl4skePjsso4fx+ExYKbuSlNwh\ncS0i8vO1jvSaa8H5uVJ02LUtkp9vEzfSr0P7E1cjjJNRGXexQF3HS+0hVHeK23Ztw2N5FDN2zrOW\n8eLGTlFnvR2ziUcGR18tLMGAa3e4v8Z7jeU0MNPIFknjOcoiZKD+Si/3vUE+y5j8Ri/1iUzBaK0N\nQ3iW7+DdQ539mTzHr8Bt5K8vwdGb3+PJod2d+j86Fp7Pni1VvNRCnOIAppPNz2xjAJxvgMyRm5W/\nVl4KiK5UEa6OrBUmFR6s/bBOBQ007tR5oLElxi2Ne8cVzvQLLipHNLNHHc7RN9OPNLBv081aR9Ng\nrl0bGxbCHD9r8F8b5OKRi9NgZYfXeuHPh5uFjqi8IKCF5323FpJlzTQ44QsdqApyEbyw8AOsDbFt\nh96aJS2l/2108TwYOv08w8koRjQ22OJtUp6IxaQ9dcvaoB7njV9TGdAp8WU4/6ANXjEohG8kZ8LX\nNzeW8ckwVPF3F8Oc5fSUG+DGuCwcEV2GM4bdCLSf8dz+S44XP4sHSoS1DqLrow9aSh8PETivH2Vt\n8HrQmzyuM3yY4y2WO3+K49YQO1+mVOIDeCB5cQLEPq24Ppo7niLYj79UBMdR4d1z7IkO5YQfHY/b\nQLxbWewVWc54lt8hWH1w2u8zsJ/5VS/2qRFObY78wJhs9LVs5n0BWY36cwAXaHP/c+YkwxY+8d21\nx3KdtTfJhT9zPibaO3QsVZjPleHOXGATcg5d/2ooyZUw/KOEkpgALEPXCh7SUhtOJwA3aP+Ceb0V\nuKzxn+BXGItl30Mu4CVIowuPy+XRAAAAIABJREFUacCgWDTXWGZ/Ko0CqqXDzx9MkAbhROPrqNB8\n+mvy76ffzsC2Z5SGF/nbXYY0Wmh8XVyn6cRbK43D/dGs8JBlUM+Hmn58yBSLXDc5Hb9QWY5fy/WP\ntLHw6hkq8TStzh1ofZEGPzbGtY6vL/gYh+wI1MS4Gk3s9dCyxokqXcbo9/YzjVkZPys+G+Fr50Zo\ngsCnUvkOfvWiC8hea5+9Bl/y2pKHBqqv6wnGyUTaE/zIiwem4q1hXoWI/k5gWRMLwN83huar4kzG\ndq56LWPB5hc22z3Y2YFK1yPkEaKAF+INeNwG02oBWpGkagUOfeGeLX60P3AEpp5PeHj43+LJBi+W\nxgOebPBAQbJOnPhhOTyvhLszPl3fOMzbGb3F4E1/NsKnNtgIv2tjz+/Ua+0/JITzafQ3wZ7hwxiO\n8Bd5uPzwOcGllOXMqDfYmTAus3DLABsGJGFJHzzhD++FThjwkk0b4vy0wEG9RPtNrTu/SkHtpny5\n0qjtoGONkQxmGtAORW7erZ6f4fHtHfcd+Rc62AU4V2KuEAZd7krKRD9rP99Nv4+BjQf6IXoYl8rL\nA/HIaxQ0FS6SU40yMI2s8hONLJlKTDh4/Xh5RIgKp44qoV11GC+T64VM4u1yO5IvXNy70SdcwAo4\nlos/xgQain4C4xgT103ef4zdmZL3e+z/LiVBP/IT4xVue94gXPlaqsrOXnSGm0p+wyHDmMAEe+vu\n8eWhyfJFtK+/cNLXOtX74WXRZnq/F666UkfPdogXuKoqcX+2Y0aISF3DSg9rOAzcQ5SShyzGeRhO\nzNuuTkWste/5OnI42sFTRV71WtepN/F7VPpjAUrCcD66ROIr/IG+lqseRfojvJ1MA/2d7K0dX2xQ\n6cev8y9lecXAnmBUntpobYp8KSxkMPS715rGx6gN+JzgMuDt4dD+u57lBr+X70hu4B3vmsQkQd5e\nhZPubbja4MUXggY8JofR4d6NcK19MYdW/gXm/D9X2yK1Dw/p9CxsfYLGWZ+GUDi+Und208ngHcc+\nePjhJO+W5tNeGoOn9PsY2CZhq9zPPEwV0/Cn1CntNDrysBVr7br9nAbgPv+moh+XGZF964ZUOPFA\n6hB9WjDaUR1uDC/N5QJsBr2JYDhMYROy2yiOcW6wFcNrvV7wGx8odsnujNXdIJ2nyQN9KZCZ9yz6\nqdeaVM1Loj9ukKEfIDRPKL584LiBt8OxZTQnjoplqIyk0e3Wdhqei97SW319fpBRWweFTVI0b7sH\nu84Z0rIpfkfLJrQSFspZjGB/aQhaTnkOvNbKUtZDo+m0ijniNbrCbzLgT/gDbzAUmO6Mfy0bjF+t\nyI9nbzIZtgUGxqtheckL/NKbfG9UczulLCL7B4FDr3UZZ2d6bqh+R4jGGXzi/6rBv+G/cPZG35B2\nuBPcpHuHvb0Gd9jeOC/GdYEBLyP+jifAm+UyEflMbcJGNzxh1j8ZYCxTo7GgxZAWvaHXHQ3DcyOd\n00BH8wHERD7zfZ7tnL+Yfh8De6Unx+ZVO3iZxfJgKjZFvdTLFg8+Rq92r1Wt4ntCkzewzWMxY60v\nGuflcGXHy77fA84jzKBtSWB8Q090sU5pmDIEwKCPkptcnJ85WrYWvHITBDvvuzNrh/2QNkb0/JkG\n3I7VHs4M5dHbnPDLEuzhKTv8CrfNIsdr9ZTIb8trGEq9CsRNJ74Qjlj6n1WSSZ0t2nXhkYZ6FTAq\nfWGa3MVa+y5UuPG6zJmO2VYe6yzzBhVMx3sEtsK+zvM66SIT9BjXGUA+g9daTdbP2VJ/9gYqdNVb\nJ9xca4hXy+Woqm207XXoNRcVI2Fmr3eX5fPgydsWv0u1HHiwJ0PYsJww7+N7xje2vzP4qyEa8iwc\nLKNxLVAvkno7wypSb9shPOnf9YBPfGlMHjzdrxjyxWtdF0PN2ytwLfDYrQgzmAWE4VpdMLE8I2PN\nO4z1ymp7+rasXisIdCZpXKPMVZnQIDntDJ++QyNpqB13GVmIpIDf6iDWWoEXardKcxprbcVrPffh\n/fT7GNi5Do8S6p07fcz78KLR8iJk4k0Hj4jHCjeaIdY6+MBbt2nAOkIux7s0jcXkP57xXqAljRW5\nojuqBqic1qYYuoTmnUqORfFWdkvu8NM2n4k3x12L5FU/8Cm4QXlG26qQVJ+dZoLHQ2D0u2pbIwsw\nlBms0UupWswBTp2tcZWFEyMP6zBWrFac0mbAyPgGmfLBEa7YE4vwKYXu+RV97rV2EWXV4cHBb817\nQrVdjwhUxbNB62OtFCqhhIdHhRKeMZ7H5AOdxn+kk8IPIYb9gHXB24gPjZ2uOjZ+rR9Dp8bviNdC\nQN7jjwbnNsFafzawXzdouwF9x29X/jr/TxwLKx9Urn1v/XsTLiDfOe6zkV7hMGZPsdYYnzyr6O9L\nhZ9u4Dt8oDDSQYA/vZbZDeR2NF+0zpc3+9E4zEh7w7SeUbiL551qVTaru/xOt3Wv9UQD3x+ZfcuL\njHfp9zGw11l3GjoQNlHQaOdh9QCvNOp2CNFofv3tBtpaY+WN10Yj4cy8lgccmJ5ddNHfkz7ewbyP\nAcsTOp+gPVm91AFYiFh5sC0irkFjsfNrmGwZDafitcZ2sT6Y3kw4GMUxvvYEvwD+65h+7/QdHG8C\nuYevvkB7+U4fLAp4efK6IcRE7AMGCgcA0uO62NCJwEPLhaPCYRt1PZRBFBgjnO3p6pPimRYehAG3\nTijvmVC+URbgkaVevmC3Srv0l8vdkEYM3eDF3B7QdVlZWh9j2aaBovUEJam4A96LBjG3WXDJWD+m\nozbZU7tNlrR7g1qKUSeAexLrLAvPYa/TgwGJ9EWevYyfnzBnZT9gGcbRKq/XPNAMz76/H2udDzRv\nyzd5rWH+hwWbcP6LAR/qBctXvTa42wFa4C2sQnqohw7tt1CPwgvshqEvYVy3VUBjsZVxGJ9J5kn+\n9mmjrPuYais8kjfuvD1NgYfXOs+JHJm2Sd5Ov4+B7UlbZkSYh3DVaRZx6Pue1F7nNNp5XeVOE218\naNA1g3TTm5DFBLx31yIxSbsFZVYnAPmi1Vh3BpwqYnrWJBapYl9h41w0oFgwo9e//lWwXWMh4LVW\nybywMQUMyObDdHD83ifmHZ/dCJ+M7REOjHJlwFiYd1bplNAkLQTvdw/ZXXm8fg/k824g/uoTBkV5\n6Enhtx4YVNKz7c8Vzu+ivfFa+1jYzjjt6e5AYSM5XxqFnWr8gFGX2ETXXlxcvNAT/kQnQctfwnq/\nB2Oh9XUyWr11oTod8aJsHS/Bz4Yw4lU18Qu91k3QX+Gxfp9fwQF9uPdap7G89VoL6sdpHGEsLNs9\n9x6nQf1+rDWNy9DeM7zyFy+bbLzW5TDMT84bw2fjerpBZOQDa15MqpG85ohjq4vsblzz/Dkv1oG0\n6RTpnY7wWA+OcNqkO5paZ03ubNs28fAbpeYxNEZorpwsNaODfdfYotfPtF/QZDIe929Iv4+B3UbF\nGnB76Plsr1O8HZzCcEuDz2lUANMlyGtvcEKTxg0RFfdCGa4M50ubZTpUJ4OzGL2sWd1YEeKv2Ocy\nLIVFv1kkjz40iFlsNhFc9uRvpbGim2zOl+TwFz6fY6cVGkwjsppY58Zdgbd2Na7yMzUR/ZiaSgYA\n4xhsWaJX4/XiP8dceznjqbsh7fw0WnR+QvzcS23Ar/ehju21SIzwwGstsrz5XuML2foB1NbmXGYt\n0a6igrde6jFmpdzfWq+bL8JvBPcBHpxGdAJtYGdMBOLO534gvPYHe8JHYlM1L+JV3PeM61N+n58V\n7zyRgf2WB5m8rAVGOLdtfI/XvMdWcznbZHh6nl3WWr6Dl3647FTuBjHSy7FH+61Yax84/OT8F5Jr\nrkcY6abY/TBXoBHa/ghNAnKjnZH6EOhMrlhrWhvKeYM/LvMfCDp56v2ve88t6xoPG3nqBI++zzQi\nduC1jlFrqT/mfy39Pga2r2r+JJQpzzR43tvIU69N3Wg6/OJxwQMvFJYuT62IRDjBkgkt2LYSeuem\nZVE22s4YFa6zykwrKj7mtTGU+gM5nV3u7slrfYXW8EsLb6YXjWxxgxBCNNLY7fhHLzQWcWaCyVgv\nXmsficITBhHaMRnWSpPF+3eHRxuBA7lFAqaSP1Nc77mWPiA2DFQsmISVG0IidMQfYiXGpVwnifU4\nZnXExvJtnYvd6tij7Mo5zWGLAasPyuCTB1wfT6QTasNoXZylaapPDNirbjbUXqIjSYqRN+qxzh/L\naYS+oR3y7JVnA/vM+A2aIlvFKWU0QqHPZoQD/O+81tO4RndprdSxB7m53UP4RF/G7AnXqO92B4e5\nmozshbsNS8BDC8fKCJf/HuH6QAPeaYAr0grCkM+bYSPrJcZX9F7HHBYUp9Bpexo80ZVqkFEeP3Dl\noICH2/W+DTStr+CYWF7r3vJB/76Yfh8D25PSJ1XZZingQRYHtS448ES6QrM+45gsPHxtpBFweW3r\nNCMPKUvneSlMODMMjBLd4Ok0PpdkHeb9tA4DXg7BMU59t4wVSwbFQ205lmWwLHn5cRvHrkl6b8FG\n1BG+whsGfOYjW/gqmHt0M7wCZzQUB/ByHmZrncD7AHUR0WxOsbc3CwWH9Kyc3nSfe4Wx97IuWfCu\nal/j1VO+wj4IF4evmE0qGQ6yBMw6S0WMQ7LpO+/6qphZ+dbVj7TaoKxFhNrIubujbd5u7snmhpAu\nw1TPR8+e8h3DuOFt+CWPA7wdP465a/I/JMuPP2VIx9aADlmoDRHpXuuUPROX65hnueKfe6DvPNPP\nnmUZ8BLe+T/KN3mt68Jan1rLpc5HoiZlvBv4tBp1qJnCIZrMSLtrYwoZcT5uXJuUPjaP89BuZXST\nbqq15Wfkrae5aZRstNU5zYbXipuS6g6ZctnCd3qxfz8DO1Jf8tth83WsfTnwcdzqdrHWA03wWrHW\nroTobEU7oOaz0YOTBBLzoGRTrtGAd7octEAHhlfBcHEnuuW1bvQ4Jo/5fjjz7DeYt6Xy0kuMWvCS\nD/5Co5GxHeEeC47hFTESJrPBHLKuxtJaHTrVBn/H7AHsnRpQAwYCtJAOHzY0rfPHhQrrrdf6g96F\nNGq6h2y1A0fHLJV9PrAuBza75v2oeEdx1zZ7u/vD/kArvgZng3KN3lgXOHSq73XajcFtFa/SdRls\nwrPexp0sWHZjamdYszxPyQSO6wcP9s57bCJbg7sb5oRz1G6HiSyvNYSN4L6tY03jydvUcUostMta\ny3dwsdrvP8JQD/iibV5rPCPbwhj0rAGc/7wePdEAP3rBUEB7AHw0mgfZ0liu+maUceUdXML3gPdb\nISKMB221nz2nPP8FDcnC8NIHW6vc8YoocEaYif5FDkKNebc69mWOEO/r6fcxsGHtem4+eK5psUaD\nU9ThYRCvGajvSuQ049zE4avJw3+NsX5LX9tkeIW9Mf/BwIKrAdxbwfWnCxHHIDYn6Cdf7IGF/TJ6\nmUADvGykDwFwsSGDLVobG9uwACcD1KR5n89SNRD5ZcVdmMj0qQ2e4SexTgqOkbza60Z5N114gt1X\n7HFGw1xTMza8e8M8Yq19ja1/fB2fyJpT5+XNQoNmWEpcNgWr0YwN1J3ZjXRD1M5fnW6/o/eG/rDZ\nhqTDlDccmznfGtSEJzRVqUlYvI0BjTpiaOuOZ95rfd/Zk219ZujKjWc55Ste1lJOXife7G6sAz6H\nl7RYa0/dc439HWlcdqv9ey1s4xQOY/royT6Hz17rZgxkvh7c+cl5kzQOnQ5hgH/BtPCxlUfj2/WZ\nUhsild6ATxqqWa9CeCbXrzFKle02L0Ne3kgTzztESDvdWjUQhojgXNvGa10N60lvX22QwID/nen3\nMbDXmRVeL7k3F1QkDTqnMbANwCiKjRF1enncyHizBRe3w3yeV6z1tQiGWGtXRGFpSq7YIV4WPWzU\n/QeYLyt8JMi6hCEU6NJyriNZGsGFOx2g14AZoQZ/6HbrxNRJTo7z0icbzl4mvCF1cTg0JD8rPH9M\nqPcRFjE2xDIQzLuiwC5CXoJkha/AHlHxtY5hG2m0Vn6WN3zIZcR6rN8VE523ibiHN9qUfKnXYf4K\n5CX9Byyxq2PxYqArcq0dzp9Gt9yLMDxP+W2d64UcWcJjD3Ti5FrmLyYrnkRZCt7uJUZOocMe8SoS\n724rdcOetY7XuVbaUmdKbWTbLE/BM+f5fPSfHotsELvc73idKy3hTu0E7QkutCn9Xuu78Q0dCvWl\nqtTX/rUxeIB3+gdcwzHbG+fex9e81tDXvuBqOl0w7yTXVQN8NPZ2306lQpCSo77xAzS3faf7dgm/\nR8M2m7E70RjT+JwY8cBvBKx9E9DrGE51n7aPtR7P8An3e9PvY2CvtFmrkKZDZcH9HE9rZHto4CEx\n0kDZjYA4aC3xDQxotKnxKaE4+ialIkf2V4cptAk9K++fAd0lG2wgFEVF8PaF6CvsLTZKCh7wmfbD\njY3bkttkYk+fr73EWL3QKm6U1xCTpO9e60SLhyzGEZP7lxBx8ciMd5Tc+EsmfcwxjEVbuQhQ4jmo\nszyIRUaXAX/qfLUX5YXp4TdRrvgidTh6XqXuaIExwP4zXgb1cC1S5xr2PYLG9e4XYVM3+C/BTkrs\nSa3d1c9LpOtBkWqoIV7F7d8mbD3f1MZ3e61F5Ogho+LuDF+X4wWjGej3uAvfVh3iHnit8Zcps69K\nZa+n8X3AF9kZt6dwkddjrfMB5tHIvvNa+wTEpw4w+BQdYJJ6GPNGhpwMsAUv3munLby00gq2oWP7\nR2Eni57HQjd5HpNJnsxb6ye3vQ3/WORxnIkVvKSDq4Ql16Yu13zwCH4WNFL4y/rBmAgybN2dnAzb\nI/Yb0w83sGFI4KP/vhziX1jFhtXp8Lvw62EqKz5U4EXIPCLrFOrltdZUKiySYYZ0A3aq6cTDZUC6\ndZQSdU7JDU0E7SjrteKZzqJOYxy9vwb5whANqzUhBvmWdlM9Gc3I9ChVJrxCZhGqUYqr0r8BmXd4\nEbL24yhZFw3EjbU8GsMywCYDeej+icedYq1LFfHVkDFZuXxsnhWzWlNZi9jgzfY5YR7a8ca2FJva\n88OHANI5EnREefsS47DXBpxdUmUJaw+QSzuLD7zXMz83yBDv2QhHT/JJYoPyER8+J0/rXE5YMaJF\n5F2P9qteaw4H6bB5LHbjjIUM4cjPCS4D3usGOcOleqeh/NKvMeJB1upegL2adrQo16au+Z1tOkc2\nRrJ7f0UyHGXV2SbP/X3paBnS42rzftpQF/mZ5uoPnQEDjZh7rZXw9nq3cmyH2QB7P/1wA7tYjmmY\n7QwYHuqggQO+fGq/ig9CQEQ7j2h/HZZln4FXuhiQQvLu8tzZg9HBfhaYZAZDgD2DYjmweLsVJDAT\n7s4Cy+i1nmw6yWkTq/mwv3bdZq/NDk0kQiHwhUR8QRFfSETvNs73481zQWcLnneDtxtC0KPbbg8x\nwIOBz1mgdL8mLjY5OjxOGK5Rfzhm4aos70KGdsRLnAvqd0bjj8mYWnid6kqYYq09q2VIasiIC+yh\nLrkwi1ENQ5TtvuPBdjwJuAVUBB8XOh62jFR+5uFG6GmEksH8pAn4Xu/sI6+iEw820IFye4lu0947\n91q/YoyLpN41oN2HiGjB9XVZygKGItEf4w5tz7/GePHosAnvAMdQpuewjdfgMH7fGWsdckvdM4af\ntCaG8Wvq0+lM4i88rV6/DP36whzggbc5zhrkt9p3lWXAJ7Q6x1pjUyain8Cj9mgsK1c0nXiYbFsg\nXjZVR12TzfU+0ehEY0RTwkEGTRBGQ0/s0UY+35l+uIHdE16x1+okh2+XZx6XgUBwUcFDElvQD137\n1KQcpeb6QIshEC9iLebV6Fw8cM0afbZ0t0D2dc2zXbBTC/T1Wn8mPbFN5EPbsodulbwI8B4mxxi+\nS2yQvvG5C+1o+DcilD6bSLsJwjXwNhyEGinFWQCH4h/DPDCk1K8+J373vEf/ASceSHyWYa7CrNT0\nWovA9K1vfnI9XYNcFK2PfUxMMsj2oDVaHx/Easq3Or3Di01cDxRRoisjUPEKR5Od19ppW9V0Y8tM\nDvXDHgRJax0bxhs8jusFSXbH3g7PDTROT1v9znv9pB5tyeb6/N7ABk+z7WmjvGhLOWgzbGSi3d9r\nraOt8BwyknVcvw3NAPnPf/wleUw8b8NAokx8V12Ltd4a1l+Acd6kGtK2+dvVjfA0rls73q9d25+5\nj3cvKYrREUH5bX/GMbgO+0YjWTf1L/Q1tuk2j0jQxQNJ4DzQCGhUM5Hh1xj7u2MVXmEd71ek38fA\ndiPtBgWHGfVOGL4DjxOagG+/3s/DluWbDPXR3moynaUw2BlWGjJYpBLWGEoWCxJoyiJdNC6rLcMh\n+Fry7BuD5Nr1Y9tJPDX6NNylVzZYw/W2otNpdJbr+YR+jdG1rOlmUdjNpO1hhgMu87oZyyvjxrdX\nungXzjKkFXy0lsveROJFxvBar65UU1PBEAaFWK4AMTKWnaYOQOXLj3Ja1kWu5f3LiiKg7BlPH67V\ns84P8eo+f1bvs3EtbV3c7guQHVPTaQEnQ9ye8doI2zNe4VUV0YA/p6fQkHv6pzAPGQ3k9H7vjOYc\ng73BDfhswHufjMbVqD+WfLGzBviliuex4KP8WW/Rj/y8h7/vAS/0k9e6LBg6pOvCbP1veHd1uwTj\nN626qYY9sqFPjKHeRspdOJk83hAiJuUhpHrd6xi2/CSLJBKfGY9jRTTXuVDPi8SZteFIs9aax1o7\n5qQ55jnqA8/f7P2K9MMNbDrgwr4xKcbLGnH8MrjSXLPoYR7JQ+jmkIvoWgCuXJbX2hUFerhW+9f+\n1FzsBb5ks2AxrOqapiozNyzr8V/ahCVdXqgsBgb/EA0pNGTIinwNmDX40OfS/qqru6/kb8dl2ieO\n+zCWu1RNpPzUxniFSoAQofvcax19MSCFcWVtXLzaBngonQ1903ksKnMmGurKws+67UuLEGgx3Wsd\nuGiMWpR9aFyTqh/GICY79KthueaGu2YVf8qf1aWeSXhtbMZDbYMdub8hZJydfmLvcR9IXapaTlhF\nZ4N4OoZPeHXDemckPy3hk7CQLQ9LWZ5DOcDgRgNxLC98Sz7NGxzl2lbxWpPwzrP1y6AeYKXf1sfq\nKyEiMuC9Dofx3sVay+C1XvUNRn3pMMTXXjfh8t8NvISGOEyYhr5DWnAlmRVpJGmRDI9FofKU53SK\n13Qi923Ey7MKaUod87C1E3A8Bxoxe4y1FpHBEfNPYrC/kKYDYcG1oCy8eaib8g8eWvetLh6u81RF\n1l3ORfGpOjIZjakggq9nFNYFwllYh1OnaywrsCGDIw2hxBERMHqGpWcuuhU4dFPYc+c88RYR543G\nk8JYKI1LyE/5lk6sDJfF24ZP/PEY/Nzj7+H5IzPstSZ1FkWAN423FtBJ/276Xem9j3d4vhi1aryi\nyzTlw0Gh+cFveq75dU1KoU9rYdRHFaiijkxDwiEizMM51UMhH7snPN/nKHvlAnjCt42gfsJFvE+v\nqPdT3LsQkVrm0QFd6GWYMG77JBxERIpByemkP1/yXq+2LzvmKcwj+7QPGxG5M9Atmr0PQxGpY1vL\nWK8DLOlmmg1PS5rvi8GWx7CS1++1XvI3GOJph93ib2BUzbIULWRrPG0DM4n9XmGOt7SNVboLTxtf\nzAvJtstzP9m7LVzmOoZ7Z6gvmbfeZpStPTjt6gq8xVpPE3bouX6An2vfs/TDDewrlXNLh7qHfBh+\nbvQp4vUDQmSKtU4MK5hCcD6eOy5P8fGhy7ufs6SjfDMMehsUce5sG9maXF7r4XBFm2vIi8hrXuvS\nPxS2GwUj2gD3PuTtIOBxPYCjeZV90y4zfuIYTHeiKzBrk48M5v4p1PbyCvMwX7er3u1kxxGNa/Gi\nLPjyYxqnGjB/zHLD/MOXR5lMNoTT66AEQxyjcShm3zAivGOhfcIbbxFZOZSdKdGLXWUhzIcbQp5S\n/lz9Dc5tXW0YR4tHqZ/L32dcp4H564zrRz5w/p94sKNc5M+6fZw2GOADv7tY6w6TMGI7LOmmb7zv\nDOytp3r1y+Cze52pr/A58ixl4rvqutd6MJojf2dw82HGo8IHIfFcfz1mWYtR6XVhDC4c16OFt/Nj\nHYJtCLZrhW9pg+jurtubzIEi95iYGfxZ4his6Kq9qzuEwzyEyngPWx6bKu619iarfdR1/j7Wuhvf\nJnf9/770WxjYs0LtB0gM/2CMo+IvNJo0sT/cWCxGFNDG7OVGLt7XuLoP5HBFzQaVkiLdnR6bFcNn\ncy7s3H24CVNE6zBAvjZN/lT0aCevglIex4691gL5GJZdn+8SG7Wbz+f7ru/gedPI/l5rHyyd5yhg\nULnd/fdqgWOwd0PiA57XU0odb2zOKSOGCQeP8S5cWx788u2Fq1Jez0OPOs5g3GrlO/FBQGJMHuzs\nBHLC8eFHaOR05S3wkhtu/vu0xdgY168cDqp19LIfk0Gd3Evd+FLjjkenf7rX2rYFBG96bWP2Nhnw\nayEdrbypswHXBlwywu/utUZ9e5V1HBsD/FLF80T8p/A9fBhwGou+5GeFv+7pFiy/GmtdBNYBNuHd\n0HKdUd4e4Ey7+hz/CTdqGiz56AovxvO48FvppZccsb1dnzg/paFuq4NsaYWhn03Xw8LCfj7HWgMv\nsBH2numKF4L+4vTDDew8XD17nf/XhMVPUIsPZR54YbjhFWpOg3AngVhrjNUO/muDhRHq68sN0Gw6\nF4OCEkSDk07D8v5X7VCmjSFaHgICNiFiuwa4U7OXUBgfaIhA8nJrd3U7vNukQ9E6/IzRRZjeSdvC\nTXztTMazAYwOBBXpYRrIwzp+6ehuZKaFsunjtF4CRv0eca/NhiEWBnJ6F0NevjVE88MglqjjrDZo\nfFu8dS/WQ2noauYrM/UGOHaScKt22dwQskk89Vu8yS1JNE/LfL6m76Lse3MwpMNAZB6T0U0GtznP\nvZQn+/z0vutHXqCviiGEc5lSAAAgAElEQVRsVIY2nz3bFArivAn305AnC6sNlmUaf9a5kx5ehf08\nJe9fE4Mt8hhrjfvLqkwd9lCH9du6AxhVpzrWDlt/sfu9vD7RI1+u3wM6MVk3hHSxUNtz/Undtj8b\nW6EgkqxFMGM8q+EigTOFfVgtR18dfhhrXWAXZF7l2xiEAdc5n2iks/TDDey+lC5bZxnAUqcFD4+s\ng1fUnGatQo0YbG0/1nBive1sGBFeLg7jRXWV7jZN0u54hQaANteSK+sQNTstySK0iRsOPL5BajCO\nlBeR8mAxPWR4Poytx87fbAinX21hOWOtr0/RJ3yQ2elHHOzAMFDo0ca0WzDftN8vUVKgjHhOqM+8\n1/nYRFl0vtd6TfLzDSHSwj34BpEL5lkdaaAmaVqtEe7Fn4dUCc9u8Ky1mt51L+cpNqc2pZv5xZtL\nWsLx27Y01+No8bFj34iXdznvJTxd2t9rYLPXefBYH9wiEnUHN4S88muMLlMtY2mmG39o5q4tHwvL\n/r3umYa+vhNrHXKkPB3GnRrqTvDvYEi//qbQi+YFFpH2S45CfZvCRlbdda91beud20JeujlkozuO\n8tgmdeeRPvoUG6nK9oVY693O33u0X4W/l364gQ2J9iXnGbfsZTgQmd5jrUUkvOOxKDSnz28icQXk\nSB53VT3Jl+FSQ0TAJC6nuq0bGR46FW0iy7rbw/ZznBgzKxsGwzeySRPx21I2ohjIgXmWD/tdx6Dm\njeG7dHb2igh7pu9YXDgYg71GqnqtPQWK5cByHRZovrJqqjhLbo7hn79zGTHUcoWG+JV63sOM800Y\nzgPajOVea1g0HLahPN+rHTYE6op6N4xkGDXl7OJfUDZGM3013/Fs5SHW9uVYa9vX++SN9b2BuxUz\n/5LjRTXry6pvdvhXddcHGS88GHw7Ie0O56b3A8PnI/IpJGQOETGiDYMTca3i4q8x8ljWcgpeTIii\ng0Wa86OMm/ZxjHI3sMPOsVzDCcuy8zGCF9oHo/ptr3WB9XF5jcegsxnvlbShq18Qp87gtqfQmNPw\njzaGkC88bcg73lS3SzG+VkCsEfO495h6kzRDUAuHphX3WjvnYirFTkJRLERp8IYrDVZl/7Xp9zGw\n14ilnQAHtU+G+oTWuh2Nf+1TdNToicg26jrUamx6HcibeVCcVNcdEwNwMkRppRnDZC1KaG/QDSmQ\n1WbqRoDhsZoXAXvU9vk1XNUBfLITaB7Cxo25vyYZ5zvmK/DWi3/usQX6Gn4MAxU4BjCtdThouH68\nczyghh3fpWmy19reahKaZBQDByKMsYRd3+TgYEFbpkCyFByOkWMHzlLJeApEs05ngJN05T5nk/Yc\nM22TqY7xal09NpJR/QqyBY/4zTGb1GTTEZoy3E6/Au5zugsRqeVovSDysXVHfxdrfdelLc7wAvPL\nPFolGMmrDS+LSDE4A5c92gde6/mGkMWDhGyx2I2m8pt4zjR7nqU/8l4oiAx4Bf7otVYWCCZQB5jn\ntcK4rsHqODVabKf9LX0w1CnGdBvh+JnZaCSOhUGylv+uuuM0jYFILp710bzm3MeGa9lvhx/FWs8T\nPeOe0v8x6Ycb2GApOMRnT8ng0GVIBGUaEnUt6OWpDYN3OihemMYu4h73OPX2+7tQVu00GAqDf37O\nO6wazfa21xrzQnKceq2NcbapKun+QzMuSP+ssVhZx57uSxYtfbrya+BHNjAY2CygjutjXDOHCLbH\nusopDIZ9iPgNIYlzf0OISvVaX2n0LKvmtykFx41ta8ZC5WN5BWLBqr28M8USo+5ejCGPB/DoPWKl\npuh3Bm0Oe2i7ds+2+F1CRqi0RwY2lY2gWMY+35ernG5M7dJ+ePa6ZSKaZvW8ray87AAwmi37szWY\n0cgUabRe3t9rrVTe1JOcV2Z6GKL5GZYVz3XlSfLD5wSXAc+g3ZfutX58UXEwhI9p34D5nJn0v4Xj\ncdTt5lKH8bde5nSJjF7jiNWWxMN84bHJOx/FPAgX2nGzl94ywJHfGoBu5E8rD1Y4xVozXdfpE7yM\n9gBDDqw5dobFkcFxnH64gQ3Hpiakf+XrdVqmiWOtVdGwXniwBtCzGgoN5s89d8WAXMqFXzYs1waD\noCEX8Chn6mbup7MN9HyFRccYhvgWfWQ7OPqoo41c8TZ1uyV8iteIOPm8wec+phq0FnzmDSEi8WMC\nxXiGxpu2WoQ7O/g2lAQX3aZ/p2kaxAKDwZliLgiE3/SIOMlSphj2JAI42YnXwz8u2nucmU+vm3hV\nb/TeaB+81mKye5FxKwsog5eN45vr+u77PhlY03G0j62uuBXv7l7r3gZW3BjXT3zeMuaz8rJPuoEd\nZa8P/CGMxKgsIvYJfSp7LGyRKso0BpYyTHKHIch9tU6Dc1Zlgnas9ufeMy3HYSHv3RBS+zfWNdiG\ndsvjBrZNtGdtU2NS8Rzn4IYQHqe7cBHMN5kMeNoAv6tjuTk/9G+b38Rar7ipVcxdh83PsITQ6Ssi\nPcQE4V1zvxbL/W764Qb2lUJx+aG7MaTCUHI8A9qP3CBoNLjFm8ovJyBuHPEV5ApXCZfvOpbFE63Q\nZcljX4Tz2OPBm2dYjyzIgI9F6rZVobIl73z4lTPDx2/Ic7vYV5v65vO3yd+mF/bEjtVkOl39USmG\nss9VhHIAg1hrK8PrELn/kpcc94g5jBfDfMFRIE7bcTNOOyOyTeZ7raWFhET4R5RhdBddD/8ABt5G\nyCsixjSOkwPU5lY5q6t3CIdoQKuc0ItdvNaHcfIdo+/bgv+4zuv8nhjoF99Kx6PVymWT46oiA9x4\nNHvarsgXjeuGtxnHc17ghYYQkbE8GeBU/uq91l+nSbk6zYanbzeKwfatjeX83BvTAV9j0++1Fjky\nrmVX9yKM6+5gSD/9CRik8HepLc2yES+4IWRniD6Vn3C/o64kmHCDPl3ecYu1Ub3mA3z9V/Eb2Sxf\nZFR6aBh1OGoeAVW/0feTNnrp/HyL4Db9Fgb2ZOfEIel2jNs7a6bi2371f5VHHuxCjsjEZVikqNzj\n9iN6v/xPcKtDFL+KNOi3I6OxAI2Iif8yJY8pyzHFSWNeRIrDDe+7Pr37GvP3CRCclo1b+Ly75zpC\nETymtuC45iDjGWWIRYXimdQpU6AF2Wnd7Ds+D4qtda3AwfuEQQ4OiyYh/jqe7Eks3zPeHcePOV9i\nXeVcEFy/pKzrxHFgjNiGnXrcDp5Co4LWBO863PEJ6Yq7K+y1LjZpu4uV2x4SdXA8LF5pM5reH1vd\nztARj8V722stIl82rkGml9oNhCcDeuUtxyPDRjr9K7HWboSU82XogD2UI3tT7vLUcvRdqL9Wy0ex\n1v659VqvPjcY4ukAQzy9qVv0I98DGOcR5nJZpVeXacHLijR5vCFETMpDyPYmEMo/8pQ5HzJLz/e6\nnT6smtgvcbjagsXsL7OGjJ9lEU+797VY61PN8RpuDNorJDfphxvY16FV9pbP6jJUDHDrHtMaaz3F\n0U5TY7LxwFY5vK4ovcGgLF2RF/BIMKW2LuMUNoKTLbmqCWdrHFLB7USL8pJrlxeRrQe7j7P08Zpw\nThLwYTIcDY5FjrXkTyplPfimG9aIidQnCarzsXW5yrxCXaN9teOtkyFyHVRvkwa53Wvtnx+xXjgc\nBPWpKHmAvamyIHPkMe4pe+kGKMY/e03XencHBCc+WFzO41hrjKe/4T9WU1jIqe4u/XkzPOSqry3i\nsVn3+bNx/SWvtYi8Y1w33HfDQwKBwj34JUc0Hr28aHc3hDwa1oGzM8af6ye+tx7qF3i+/pJjjttt\nrDXumXaovGlwc13pcO1vpx2M9LtkNYtGI4aiisDYWjWWQ71TPnhCXqwfO8jb27dNPuiG/FrMIx7C\nC97NX7uyr5RjkWSstQJuOfTKCq3wPHgCPmuQfxKD/QuS4rw5RPBICSNDHmKt4X+bNjrbyhTH6p6n\n8u6a86NptGqD3aDBTpsqu+5BT+Sk50Y+N8Yx24U7D7ZvshKioqBQFnzXXE9DjRPAZ3q1l2Drs8Ra\n8y0go0HNMAVtwwLjWjESValjqHV3va0rttVNB0IpuwnpLzhKGftqBn5AOMjFod8Q4uMKZmuh0UFJ\n1j108Z1oap/brzlSLxuNMu5crnWbWOt3vNYizTB+MoZHvC8Y1yIS32qI4LTxnp+OLcL53Lc26wwa\n2QOF92i8jzx4Bk/aybZafPXBDSHfd6/1Dc12/F6gidxwDoWhdR5TvYO/HmutA2xPWw24J9oDGNf5\n4WTS/xbOeN814f6pvNbYFz5OWn6lU12EaT6T5yv21GOtr0VyxWRH2ftheWyVfgOuYH/zBwBrPy14\nlH4ZxGDj2Wg3muZEgRymH25gyzUJZEi9H2sNCuoh1loEY6h9VsHDAEaFle/jQehiY5hIwztPxbZY\nTEI8TZzssa0HDq3dYjwSi9vig5vlYNxd3VO6w8WwCAV8hslQjg073mu9Fs7ty4gOUzLALfO+Jvnp\nptlxOvBlgW9HYgMHunESEhhVLfwDQjuA9sKxDQ3W53oPnE15NQdjMT+QNqOZx8oY9+JS12R9nYbL\nc0u1xrZoMfEd94Z1w5umm/b0XToNEUE4ltMLOrd2sodPfijmiM9Bj2/5WH48vrBIRrVI/TVGEan7\ngfdHqd/R4PhOdF7u/T4z7G/a9nOsxGC/YGSvsWgGHbZpVCcizfAeZCp7d4s38dAbvvewaWWxOi54\nxEsHPk1H/eI6Ti+aEZDmXYQag7VK8Vr/xR6vwy3gipVGsAfZdtphHIPtMXpqkZyln29g8/SBhVVe\nOFTJWz4cBMYTh07gS4h5cFPsqCtrMM7aj2so4mHjab9FN9z+4clv+Xpwl6GwSsD63R8q9p6OTlcf\nGkB/Dv3iUBCDvFCeoxTG/Ea+VqmvfXqURHv4QcOOjeYyDs6kjk2xFidab+wXvOToy9lNIRTzepS6\nOu0vMfLkujorN9ysRVl+eGXxSxyl9Ww5zlB/la2tH/7Z2tpl59AHQQlbb8bq/lAavNY6Uc28gE3i\nHLwIOR3eDWfHB9u6Z9HGjo8tHmvEvrvXmnF36duM6+/gY/nxFCLCBved1zr3gkBZS7nKpx0WZWVk\nUOs60gTdSAN0XC9vxmCj1xrbedEz3c+22ofjkBNu81UY8lx/ynIzzPHxKmeRl0I7RMA+oLwQnykf\nPF1u7IPjPtUR/MpfZwN66NODb0BHsdaf78ZazxpmxNVhHjb0Lsc57vemH25g+0pLy7jHb6rIh4Jx\nPU/jnDpchymv5gHCdIBVXKXa6Thl2NgHt2lo5dU3ekX0I0ytUY7Y2FrzIlLtRhCKQ0FEZPuiIl6v\nVq5aKwZaT/d2ps0DB9Q15tp1uVY611Qm0r5NQG1oQIvCPRnXpwb0m7B6oEI3UIG7cR03hFSG4w0h\neODx5FMbIrahSQlE+lQpLqLGM7t7Xp7MdB8BrCn3qcBa2BvX+3Xosvdfq3yHj+N9FUdBPwq1u3vQ\ndiPqtWNrwPkm4/rbeF0bf+kAeMkR+JcbRuThhhDWWZZ0tdzbR4Gz/L4Bzfs/5Z0eDFLOsxjsS7Zt\nrDW2w3VY32C1Dw1W8PuDx7e1z3mDcwpCQzC8QT6v4+A0zAPzF9/nvBD/Fvc85GMkMC89/1RXki8u\n7pMvjk8T+fwsR92FRjo4zvyyS2bcwNrj3ttUCT+B/Yr0ww1sMJDW5/WyYsLTa7coUFmWF61y8/lP\ncQauiuDPjvtXrvFC5cKrBuNaAB6qIi7jJVgLq7wJEeHDWIflkWEgpKA1F+mooGUok+ELXayr2MeL\n4NnXmvduVoM283fnJ8t6h5ix1qsjmvASDkJrpwoqPMQz8MHwNYbhy3Klbajfvkz5JI51WWJeZqHy\n/YRVBRPff0TGyoHdaYTuwjbikXT9h2eqSm0HAf1YzYgje8B8kKRxnSLvDeuTxA8KW7w/kJfSkysf\nY7xk3vJaD8CTcA4RIaN1g7PjZbfFTapeW4E1cPZrjJOxLbN+xb1GQsZKn+bGHmhWoYhgfZxu59p5\nvhNrjcxuvdaD0Qz967D8LN8qtYnVAQZ8h34G3chvThxeFXCPte6cx/Jp3UsG8KYP32E44hxv+a31\nF1fvrYNKmxS4KjFnFaYiYk+4CZ9cnazrUK6z9Aruc/rhBvaVxiHZea2L4ae8DjJWthmFdWOmUTkY\nQ4Ego7FaZJk6QXhT3Bx3WItMyGLFWtuD13oQYVf3IO5xHad362IOLMcgPK2a32kU47oZtVCHDZZX\nv8kwDgaInzziAa7g+7oYFEFM4sD3KG1UYSiuayyu0KlLsFgVYQ3gT58v8vK1hFA9vPhYaDZlWbIQ\nTXunk2FMM/T27gBKpW9jecNhxNqhqjx7rkXqMrvFm5DGdl/jg0ZXUS1hoO05ni7Fk3H4k/ADw3V/\nTd+d1zrxq3xZN9G8E2f9FN/9TrtjDPZqmz9dpr3X+s6whvrRiL6n1S/QHsG4Ds/V6c/x1r3W2uSd\n88VApbwQny/xZDkN6J7qRnrrY2VrtfgiMgPjuq3uhA/n5RZ3gPedf/roPvF8SseH7VH6+Qa2v6jn\nh5ZKnMxlTuFwrkOoAyzTGS7ATR5m9L69dxPbb7b+H8daG9l2WvvDfbNNXgzmwZlDnr3dmD/xZI0p\njNuwG1NW875ph9/da+31O2+yUD3LPoUJjHhfgFHyZe4HAHazmE3LkK/e5TRgq9faD1uDMtb7wW9E\n4w2JjD+FTpIr1PV2bKDBnaRQRpoZtw/lfsPOxrU1oFIvtvzaWNy1O/Hrkj+xwxARPMqQ7vPmhpC5\nZZSA8A738bGHe2x8OnZPmblagGvmoPyK11oIv+O8c2Xfu9f83c1Fl9/Nl+NYa2zvS+Ead3WLdst3\nA8N+nuDvYJDKaJpcsdYrn+EjkmeegWowOF4oLzCeRnnmOeWDp/Q89w+PNE53dU0D2dIjLuPnJ+Du\ndvI33nd9oOh2sd0T4WtG9/vpDzGwVfWvi8h/KtfvCv9XZvafUP2/KyJ/axX/PxH5m2b2Pz5zhoPO\nVPRjmRGuGKIBR9U0wpxsbWgteCLuZnJ4eqFrUD/HFwfPIJT0WMGKbutlMuReSCXWOm58eMFrDeMy\nxU/zOHAsNfZbyxhQv02aIe/5U89eS6596PM6KAbGgbcxnkPj7QxvEn6ar1vYE61Jc+kerAnD/RAp\nO3DF5+evMZZYOO2HejUGu0Hu3AVy9+EfF92RkU59mAzTNKtZls6kmuA2I+3JayJDhn8p8S7tvnJu\neDue3PYpL9R5ZKS9fTPHZNAdyBN4X/FKf6HtC7d6bEWq17puJZVpazWvNOMYHfmoo8FYoS0lxVRo\nODB3pWLNIwn5bGDnGJzdaw0ysE6NzycDWvpgAm0zbEt695B4SCjX+jOAldCYlGTM/6q6AA6y/KpU\nDPkF0JNY6xt40b5gCL0WV9211h73DPYr0i83sFX1Q0T+MxH5N0XkH4jI31XV/9bM/mdA+/si8q+b\n2T9cxvh/KSL/6gH33M9rpopiCo8crhKF/W8w0kuJlld6USkZWaO54Aq9ywPWZw0RIeMqumKpuKId\nk2wI+iWAm0MRchoZZ5N+88Kv8FpjXii/9WB/NZnGGMZLZmoi+sf/GmOEGQVAOq0QnbxaP9XVQ1vl\n2iEREmIf+/COXK7ckU3ISNJxKIcb451vLqxKQzwbX5/XPgp3ZRyirkyfDet+tvcxv7b0udF8sty3\nPDftP/IrOi/T3b3WjDtw7Tgbghm811G7ioozy/44vrE/6guO6MFv3uRJDjQkCyz5j7Ib8GwyLZ5G\nNKvAoY5tPBhmwJPlQFnuYq3b4TGdR4inAwzxdIDlJ6vi+7a+AOM6o/z6c68xy6WbvEjdpt8eLjLI\nqhv4bZ1I8Yg/0ou8FmuNN6sJ0g24JYcDpgMM8Tt8vm1qOi9vztAjLX2W/ggP9r8iIv+Lmf3vIiKq\n+l+LyL8lImFgm9nfAfy/IyJ/5ZS54q8x8tOv+JHelfEE3+GulgbcDv/elC2wPiD75MJb4TLt5pCB\nznXlk9f6+AYQka0Hm28ZQaP+ba91SVZyGWtNypy91nd1Lr/XCfOiAnzMeFObd7DK95l4biSvIZxD\nQno4SOU/v+ioA03SdRqR2ft8U36HppWmE3aivIMiu0ljHPKJzXTSnm1wnh8K5roq54nX+nZP8k0X\nr/J50/tc99ZXDOzhajrh9TbBsLwzyOUxZOSE7zuhKC/zxbG49Vp/wWi+pa0KU7lOGB/T5uB4pD08\nr01euiFEpBqspzeB3PEc+UvPbw33ocfnddDAaaz1AH8fl2Sg9HWr6+tWx0n6IwzsvyIi/weU/0+5\njO5d+g9E5L/b1qpIfO2/Nlk538OqqwZg+WqtnLXAQ4HHypf9ireHFN6letkZCvkOt7FuyEtfCvAb\nfPm+AeHsTIs/oo7Tu3Xn6XpSCK+1HHqtYw6t1gnRvhBLbU98D3g8wjZP2d4tv4jR3Cj0pVhCN9i4\ntnYY9zASPuTna/46DfM16QY4Lv5uWO5DRPblnu4xZsN43mB62KKIbN5sv5Nj4LvhcSKBAt7nxjD1\ndCsmhyc8pBHnFxrXJ7yuPfI991rXtvSIpsjIDypo04AcE03AmIYGoBnYyHMdbiZSvdbI9ztjrSe+\nW9o72FdoNzDvy7UwGooO5aluwpvqqhb9Gh6nu7rTFF7fNRb+fz6iVi1U+mqzgrc4wZmAq5nHDOET\n7Az31fH4HovE0z9WLzmq6r8hIv++iPxrWyRbk/8pIh+fYp/LgPiQC6Zy/arxZ9rgImvyF54WPBNR\n+PpZYf8q2MkTPeC5TT7CbbXlC/BDqoNVJS0RwpvozfEBVQXqROptcJAXi2eKyIvI6H2eeE78gycK\nA/m8Ho8EVuA50N7xxLx9OH8Y1Ki3ATYMWoERLWu1G9p8qKO61j4OuNzgbWj5Ac4u9aIfUhZWCbOQ\nHmZxiQAdh+56P4rB1+rLx1kZlSuXAVbLF1AR0XE0BqDwjHVRubc09SdSOwjumYx4g87m8XlgW0+v\nge6ejV7q8fMW6eFoyRYa3oZwBndJb9u1KXvf2zt+9ilxq1LAaI1Y/AN+7D0uOC/ETBccnWmArsK8\nrFSudDPNosOyn2OmzSPKss8Gqg6wic8XYFP9FGZ53MaG1kTw57PfDfPAvG7gX8rbnMcXKRmHX7JU\nrpvyn3bdce1JgQ71L56NDS/1sgx4MvDb5Q3Y3dKMvK2+1uRjMfSp4T0q/vv0RxjY/5eI/FUo/3ML\nVpKq/ssi8rdF5K+b2Z/vmP39z//JCeTP5J+Vf+ov/eVDMb5htNCgumnlyuRMGWOYpu4KsQb5Fg+j\napX9TQR0DG/rGO82/MOVMuVdwUwvQmLeefJGQZ4idcE/8SzGWQj0YvqOJfEWu90MndRbfvByEc03\n3VuaV4bCf5EhcCDW+9SuLiULfGPZK5RrvaChvxaINp5AMPIkmYTjvu0xxhh7XuXzyhcWiG0wBx6l\ndLOPKw+C2oB3I9znVxf6YZx5tnjG42knNJwveK8dqcW3F0LtjAzqRJruHR/iGg4Z6C/Vn7U7108P\nEiCjhz2hcSaUH2FfML4HWv0C7W27h3xLzPlNPmQd8mLdyP0OPsc8v1XuG531RproewtT4BrB4Rhr\nuKr5UFDw6OxTWS+b28BP5c8//x/588//99owO0PrMP0RBvbfFZG/pqr/vIj83yLyb4vIv4MIqvpX\nReS/EZF/z8z+1ztm/8LHv3SdrqoRCcBpMiVOf4FxT3/9twary+IOhvAKwxYYVxsuXpfzSrozF76r\nDsundWw+nNQh/P09MBBOnR1h1aKygme1YhJ+C7MbPNvTrqx+VDFZ7MmgZGP16WXChjOURYBvKSON\nbWgkBnR7nzbdVFJwZL3Y+fG8MHh9jZU1278FGHACd7PEpqS8njw3EOx018x3vvZtl17ZTn8s33ng\nj/gG0sCDGVCZo3Pmcp28coY8lum2J8P5VVjXE44ONF6uxnWUlrzjg569CBvrnozg/GR1+bZxbSLR\nw7HNDd9FFye7SaX/Qv70xcRvM7zv6k7atvxp9GjXiP8BLOH2DbjPPJ5xbQOb4X+mf1n+TP8Z8Tc1\n/jf7e/Ju+uUGtpn9har+RyLyP0he0/f3VPU/vKrtb4vIfywi/7SI/Od6XWvw/5vZXZz2fZsv4XaF\ne9HTZtYBzm0VvDtcHWAJ7/InPBXS3MtX+t4Il9Y3ybxQ3jZ5USle712e+XNbhf9tvzSdg7edvkOA\nI8mEp0ua99azKgXZzMjo0srv9gYS4G/SrTeT1JZDKItF/XCAdEatn+Mb3nWhNbmUxqs88CnsEqAL\nmlWp3p+l5XkohIe+lFcbk5WpIiYfF/AhJAJINhW9pvTjiS+tk337w4IPUu2gw6Q45wfpFm0U8QWD\n1w5wiGfTradtNSQfiY0uCNC8h8YbXV6k+ZqXW6n8Po1f3To9NDeZvhR/veq3tFKvrPxTtP857C03\nuDb5S+7K6y1vM/F5l2eh/UobHncO+jUZ4d+CG8Cs4hY3ZMHr9KFPgUcJTWG4AV8j+oVb8QY4jhfD\nRETtE/r6tfSHxGCb2X8vIv8iwf4LyP8NEfkbv1QGP2yqEOMhloOLyh4HHA1hu4HdwztsKUwy6kxE\nVD/qN8Wb+X8yJ0/q3sXb1bEd9E5dyXsQuSPf7oWnjeK7akBVkXZCNTy7oaX6aYDQHdbwiFYyX2/7\ngPXLRqViZpCVruuoRquml5lpRJIOt0+8VJl0bGjy90BkIgBLpEEhtMbjRZ1Cs3o9zj+k/VrPecEh\n3N2+0aH0IueNANO3Wtj+q6mE2wC7u3RfrR1nQzCDpxm+J644LxjyhHCtCvQQDzMVjDaGrBEdT83m\nZUVcyRXmmR67HdmblxlFhl+SBJ4Bs4qw9Vpj/sfA9AHvxnjHcRrmuuA95O+uunvrar0XeRYD/hQP\n+brXehqDu7+d/FG2W7lF0MyxVlfoRaqMO/qCR/RMPMHotpTvSP9YveT4XenW3iHoDlcIrsMhg8ei\n3cBE1sTrM+5kUkkrIIwAACAASURBVHy4MkHBNusA0V6qU5dx4XF7YFONLwGYFIdveU4gnsy/vLOH\neRiJyFs1Rmh//fpUBtGWTNIHNjp5TztOCtJ6fRuvBaAFzKxYibT5x/k8KR/RWKsXkTS8SxnrbUNz\n8ZxoLuBmZR94sLd7QnnkpHpWBj6V9MyoRJ5WyCr91O2Rn8w/1366RY7xDmOyv5vfMU8Tma5tHYkn\nA+NFnHFp3OL8Mb/W6DT0GB7ysToqMr8Lwz5s8fWBx42B/AXj+oq13hjXDrP38t9hbLPhvfNAj97o\nu7oxb5UG5bDMvwq7h9sXcQnGfXmg3/L4/LzV7++m39LAntMrXpAXfszTZHzv5ij0xOGmzYoxuRSB\nchzGveA3HrnzOsZ7p44Ngnfq7mi80D2ZX0yFn3UYGLsc+kJPAnMnDOpOaEWoPS9041pEbry2m0dM\nFVjA00D2uhzz9bDTrpDrFnmn8bINcmA7OVB7r/XGODvwYG8TKVsNge6TDrRbvMEQH9s9SFt+L6St\n1NMNGqf8Dgznb203ts7+Fw3uBdDW0EmoBq7tCefpJcfJ4D57ifGm3SXTRylvkg04t7A7A/iZ9t6w\nHwzg43Y3hr1t2oW0M3RPjd4wFof8t/L8anvotca6gvPKnx3hvRQ/LR3+cqy1OMyG9hcu3pZy6sV4\nIf2WBvYVl3qKvTGE6bYQ2+DbFlZ51DnTAVbh1X/mSh8XwusH6d26iTFzJMi/E3ftB91TvvEfZNsa\n2l7x9oYYCGPwbYAhHsddH9CabI3nqGuwaE4iphZgIiTb01hwX0hm7lIYjIrlTZsjjtUhUWzOqLxQ\nHGBY5r6RENN2OPBgj7to3F/2PLZbWkYZFru2zAvGNeqIPyB9xWhmvG/0hBt9u3XMiGFULs95Q/mC\n6Q0OhKjwWW5ZmnG00TgOv8RYcOLu032/mp5inBPYWHdjBL9qXN/VHbe5xuphngNm7+V/dbhIMRB3\ndUN7+1hrSeNyGu+7dIM3hWlUHW/93P5H7X1b6H3fVtdn/E74UJgcjQ50MdISyVKJvAQWaoHHCJQg\nKsFQCIQu9FZP0YtQQYGIXTCk6CGE9EEfCiuwQtIw8lLpIS8H89I5Yv0NCg4d/9/Rw1pzrjHGHGPO\nuS577b32nh/4fvdaY4x5XXPN+Vljjz2XvHe6+oiDfuWAyLMjM7HWN5g/L06w+0lmz7wayfryjEmz\nW06w3R9RECdn548NX2dIomoFaq/qVEgiTLzMX/IYjE17asvjlGea/3Qdl/1ZJ3lAPo64MWTbGzKu\nhX4kMur2JftpcsZlmuWazAumvGbpn5ycDKl098FW1ecipIFMXXPMe5EmWxhvM4zHmo1M5mvSwNqY\n+sq+0FVCIdjqwfbGU8dUYy+xa+NtK+Kk65rZ5hun9VbGjmrFtkVCXVaYb1cznXpvWe94mhv6fNZO\nrlnkELgkt7I8tufTjjT18A9y81m9fV/uC6++VtYiu3MZHhGSfRamBeqkeGnDoeWLTy8cpGizlCfy\nFRwD/cT2qHyO2C1Eeq29KUgvRZzT5B8Tql035kytLP2ltYyh7VIDZzlBpAeWciDyABY7xQxQ2C1t\n82yxyFh4rS3WTJQduDjBZniTtOIDicRBvDZa2AHzll4kzInneYEUr1HylJ54mScSOSZhSzORSGVl\n2ZyBsHWfsgtC1Ln4OvB76zhdqqbD0bt1WT4zcXmbFPyL4faPRs3AsFU2OkMas1gteqzT2h9gSr0c\nmFmWJggyHYDFa21elGOrqbCSVLokNw9owOs7kk9VThpLthcCns57QkY8siP6Ysk6alnXZGnHpZ+V\neT18Iy9Ti6aNZ9uq+jQu9sTAbMTK/bBV0hV59a5zkrT2pamRep9gt+KiYzIt6tbIs7TZEDLy1tgh\npAY2nwDuQo6VHTmyvvrlWGvb9p5zPub4ZuEivXb5mLVdbjfr8mWdeDl261mxU2WeYitkaNi+vS03\nTs99sRMXJ9g+/H7zJ3PPNvIIeV7n0FZOPiRlZlLFNBFQ+pVhnrhSzTxKWmSj8utBur+KokwVbHWi\ncJHVoSNOfRmCvM3pbGyu6oVUZrXRO+4i0+UATPgRh3aTjB1ZJa1odz4xmyM3+U2rubaujXMysuWc\n9fl8Mp2zMLY2UcjIUnE/rl7cOx4T9VjF3m36HIM19FLZeruxrKlDsss/6NxOdD303CU94Ryn5cPT\nfLoi0joV3i7MXxTCczYHy7lD/PP8R+Zc2kRvYwxIPiP/kLFZ7whsPntloU6T33IXiD3kupKWAc9r\nXdTB06s8luOc1jnOZNA5tvlszbPIp7eMaqy1Gaxef1p418lJ5O34sdRX3zjLcijm/9wX7PeXqLsX\na53lyZbhx1qXVdd86AA8JcH2EM+Z0QRdEuE4TwrsIs/KIidrINkjW5koJBgEtfFRcOkkMASPADfM\nA0AYLiLDPMBoh46YpjGm94Kw0KS+kSEZ3guDNt8QxY/zYCrHS/8k09xnbDqznhY9aXNb5i95t9zs\nof2cWUheK6MmDwKbRhSqsiBV3DJDQnv/CeKrOhJkWzZFdg6koj5Rgvb9yDFnswzyXeQ6IJXr6CGD\n7+G1zsXvJ/XHkustcOZ1teaTOYca16wUMOcV/Zyv5SVVPdJtFxBrAIi81qYeTXgEqyqrEeC9aalf\nJ4/f4h8xupFZkYz1sSXGLulzbHbHXTtlbNkhRJUHqEEUPpQd8sdLex155KX28ij6kjtjrYFTYq0j\nXJxgx4uW7cOFrJWpXdskZywLP+YJ2Cld7WXLi9JbCCb1El9csNg8MkjcDKJVmR2XkLms0W3Jw9pF\nOtkCqZP9ngj6xEVIZWD7vuBVW28Yr6FZxoVMPUatTLscs9tR0mtdhEfI01qnA5UY7CUvsuesz/OE\nnGUsq1GS5+JiynNWbc3Vnce8PpfZJI1zw0oTT55UnR7sKjawuGL+CfLofX4i/W8Tem+Rqt2GNaqw\nCxJ25ZfHz1ZyDd+B3SFr2wRvy+RJt1jpdN6PI2XeeXtY1nowZq91pSdancqs8ivSeMddMqrYbSTP\ntbSzTk69EdEu5jZHr/I1x0eQ7V4P9CZvuOu11jeuJdv6XJRt/qK2ew8SUV94eXg/isx55AycPISx\n89g8tS3a1zq6N3ontk5cnGDn5bnLtgznSP7SHjkHl9OTs7lOWk4eOe5dbbO9b1zLptDxIsyc3RwD\nmufb43xPJHIsjjHnY78dT1lTNtC3Su3Bx9Z/0zZ93rBpyNizE/2nVsZClo71RCf1y1f/2kTaqsUV\nJv+Ed/X7odDaYlOfoiJzzgEhy+dz5nLSVAyCijSTEcN1P8sB5MktOl80EysZa73XhV3gve7Pr+zD\nW6FehHq87EpcivxWdzXtDdjutW4gV0CTWW1j7k1l4xDDbFNLB9ej3461Dh4yVpMGKm2kbap/IYPu\nMytTJGkjae4tn8WKYdspCVlFn+uaZNxJZs2xJZu7w0VWl8emX7AMHpk+n2t7JZcVT38s5POPDpcd\nkaxdKVf1U3Ys2jvJ1e4mPOWj3/oo5G5c9tvSCWptEcd2PETEYwcuTrB99PdPNOE7k95O22mZfIeC\nR0UXf0nkFRo2stb2QieIYL6vzDEA5Vy3jnbuOPbmyPQDlEzqZ1Yvw1Y0MV+ITs4rnVQvuMPAs0gy\nXGs2M1qWpae0JI5N2hU/clSx1jK+n5esILKRFSGRVCH6dfS6kaF05e4ftlL2QSdIY+rXva91jVDX\nGNfeibKW3inXveudodeFfO1vQilXYj3B1+Zx+ma2PPUBYUXfrYWthDmPPdOxzRaPtyXWRRpGV6x1\nN/H2bFR5+8hx8SPDws4h58qu8gDAAXk39iG5rsl42/ER4SKKeFd02o4Nce4h1xXw2j/WdXZsdKx0\nh23KF46sGWuNcg1JGVliIjukeOfIyknPwVMSbA+9L35ZutTz2FRsGWYdWZaEfCkzOxUXUf2wUVmb\nY7fyBWrDolfnPfT16myty3RUPmSI1NnpKWzs88i6BaRnNgkylvejW4F62uqPHHn6l2OtZXYB0Xbr\nZMq2RXp9ZT3UsY2ZoG3dbT2A4tXqNk0pkxAuZydvt7J28EnFnhARWjL1CY2uvD+cqW4Twht4+7Bm\nqVi7rBz+FsZsnPz3B/ZFz48cPRk7h/O8zYGdXBC0TfQjxjmNU81whxCvriv0BQGVtj2yzfY7ybXz\n0Nb8EWNLn2RcIbMpH1mX4Lg7n0YZ673W8z9XnmSs+8TU2/4VRLhiu/xxVd4Xl70m1treNLbRpq2r\nZ7r1uDjB9idej0hGMhi59AyysZtUpG2NvOQ+Nta6s8It+QawTGrqxID2KIpjGeZhGXVy4GZSLPLh\n0hwAL+OeSBBqFpXzwkQ4y1mLtt8nHT9UJK8R3JfW64BqrDWgH6KBon0tfUEqSRu6+0qreCA5GS/k\nn+QFhVjgxMxt74DlaOmA0GttEYjLm9WRJ2VHiIh3j6vFycm6/ip0Vh/VKhb5pkYfS657ENaNy6vY\nnU/ldyKtTGQ4yLHLoKmTN26MbLnVyZwv+imr5X6281SOpRZ6fS76WU6Fc1+EQ7nVOTU9O8fdsgoB\nlvoj0orP7h1CHJvmeZJx//Eh4SI1XXDcs0OIlok6Grlr53RNr2ytvJhhSNRLVTaYdZmL3x45SffJ\nN+LiBNtbhb1Y65otOuVOrDWzWUNI2bqTgXTf2u05ch5pBpfM1jRlg4erxs2O0OXWz82SvDMZTFvv\niX6x5NRu02faYPNTE99a+ENiXmO5YseVtKzTSLt5NZU7hKiqm8tdkGkABSe3dVi7D7YV2HYxoF6O\nwjCea1b1ynNkmrXVOUx7TGFef4YVFfroVti6TV/llehUXDSbkfeA0VMHxs32td7D16v3VvSQEadr\n3qqc75DbYAMR6wsRMX1hb2wnn9YOISkcxE49IbbqpJ4dWUtvZPXQkIA8A6iS8p07hHTZJJklsym9\nc7yKSEd5ri6DtQ5YBk9KL9sXbcnndYKso/vHTbnnmY7knsc6koee7NTgaL2wTaw9uTtr7h5cnGB7\ncDwUpVNiVvV7WOJY63KRybHWskprL2brQoextg0I0sfwj3P2zjEYKoShO9Z6Fqh9rotqLbrJ1r83\nipav7QpGOePKNqarbdo9Fc6OLNmxm4ZzeaTINaSpM0EUVXTSWdgf0GovAOV+leLiB5bKZrnI4Y8Y\nlSzZzO31JrPIU5tsamS6bFh8/TfxVQ7z8zzXUbpugjj3xU1jreMmeaYCcZ3q00+FeFcKdgnlGcgV\ndAhePq8TYX0uz/zdRarkmqcZyH34DRD85r2dztrYCbxKlo3ezaNCmnvymOugCKPIp/rwsfY8yVgf\nW2Isj4+Iu7bnISn3Yq1ZnChZOudS7uh0/Vh82j9PjliOVO/S3pNFclL5Q8Raw0FjwuudDA/AExLs\nCCElmT6mdW7u+2iBIEem5e8AZ/WZ2VKeVFnIk71lbfbY1KdzkPRyeO8BUOoQ2FZ1xYt5SvInw9LN\nO1VMCsrygvuFfREovDQtmSTXtrG5IUY2VyG/jVE+mOjG6S8wRHaFTfCwmBGGiMyntQs9n6vFjMQH\ny3Muhqe9O/w7Ll20uI62gdHvVSqFdN0jHvcvR5zMM7Isz/w714JxytsYtzLWav/VOr4zC2F0U6+1\nLsopu36u0gXn+VCdlzdra4eQNDGsIddNfaRj51jJWuSYHJnRV8twiLWy873WEdkWNSrznM+r+iTj\n+LiXbDe93L12+Zh1mlx/1vUSnyom2U0LP63z1/wxomvHHWmXdnTFWrNpl6y7RdfkE2FX4oyLE2x/\nSl7Dn2Dki8xfaNPbHK0DTX0tRoDLCiIyuFK+ZiFiaa/qN+sClm3jrm2sNdl8ZDaZZPJMoFOs9WS8\nkOIlJpcVgSW9BbhoieqSVMfwXmg9XohOUR0lH7rM6PA6NHfkko/aIcTEddgfMdrBVPsRY/N85cRQ\nvLbHto8ReLx1cXaXED8khGxl65cIaDxAldkVFaug6LpKDmQDb4MS7KXxcHqsdeeQ6B05R73REQyk\nvZxP6gm4NbMie5299spJCHauKtM0Q0bSfFiW1O7MrfqifHO8R9ZMQ7EdT3qPSNfIdVXWYSPJc3QM\nbCPIRZ41nSyvJ9a61ucbP71x2Ctr23JTXroroPvCIvpKrRBzIL8NLk6wvSVybwy2v9+19l6Rknq/\naA5X2shb11tlL8+WWJJYlMe5+s4xgDBchJ362a318oQg6jDxC31buR6bYF0rurbnZnGfsFj3Pxu7\n4IeKkyxICxhyXZZbcE/TqGKXlVQUCX3QLjIOUXIMyViQrM1sRukkJ2PxUEVLPukCp+TODzfDi3kE\nuQ71zj25ERO5rlPAfoJ4h7cxbuiK0H7rDxctbrmvdRU1sjzpvR8xqjuHzdAT9wurc4hzMd9ZEsPq\nzKlTXN/uZ+tAZ30Fyq4qqxBkqV+bVvaVnTdtGw7WZxnHx5Zsy+NmuEhg1+O1VmUDaJFr9VsRWW61\n8abu7h835ftjrcsyVsda1zwdrvPnNrg4wfbQvwB072HNgP3h00QZRKx1YhteQTUi0CIRESoTZk9R\n3jjt1aXiC7tZmPuLoS7HYlthzsWLZypg9L9oxtSlLWPfjqGJt9AnYj3FWZeLxOrt97CUQZ6Nh0Zf\nNB9kuKwXwE78dToXV7W4Filz+fRQqWv08OlWHEUfFWj8yLGH3C0PEfvyCePOz8DK+SU0P4Jcc75D\n7tETMamSp5ts2vtae+Ega2OtpW5ruqo+IGzrdNSvS8cMZGrt1HU1efbyaeUh6hId57JE227ttS7a\nV9tiD4KMrrlupm5lXDTUeSTz/9iVqxfHFHnOumqs9QZ5S3cwnpBg+yTT+Okm2bzmleu4tiWjZUSx\n1kHhhXwrq24jLeOe0IZ2yKowFoIkjwHotzHOcsrZLgxQ9de0XUgZY80AKxcRLU5RRiavOkRkYXdu\nNza7ksvTgsyxLEY2sNQ7+cgfMnqXt7m9noctw+TNVFK5qKhow3RNTIcoG15+mKrSLHmufhtjxKxE\nenf/cYuWJ6LhKC7ve8fG8V73VE3bM06JtY4r0ETPMGuFhjTzEF7rE9e4Nuw8Y+9dFrp8LrGeXE/T\nyXZyfYjOI17yWLbbEjF1TPv0b2JlNXU9bIeQDpss4/7jLXHXri4fs7bL9WRdjqw/O687h1iHpUzZ\nsCljkS9MZ/mjogMCOYk3MWZY25YcZR6FCQfyyP58XJxgBxN+sIj791PglSl+oJfpRPGDtCLzHrnU\nRd652noWDB6XxwmCK3gRJLeyxxC8Qj6ISL4hQ2NmPi3qTWUT5rQkbKrtc2zcbll7IxUrPLsPHYuM\nHRnyQ8tCG5wFWvRbzhs6j9wu2zhz3hoSR6DrjYx5EFl7UcvaDxnt9XLus+p9Y4oKsXWbvqxwFvy+\nLJf0uPEOIT04YKFptaFaBON+O4Q4dVkvo4pN46UxdgjxMlv01IMqOi9tb76F3JK2blmDPDfDQfw6\n1jzWYZ/YPnD0dj1SZSYZ6+NcH+d45pPucZEPV8rwYq0B1AnynA4lPMLdPQ9w/1/di82BLQfpZ/nb\nCftaHzAn9uDiBNvHnrc2lvLlWY60UqeN3DI1L1vNlZOZcYDOAeLNeXt1QOIOS2Q6if/Jm1uEjMB2\nh+hp85r0ZOuVUNSn2heOUpSR9Uom7diRzYcsBM6TTVYLmXfOkT7JVpzHMdj+Obh8I2P9LY5szm2G\njqe2Oc5V8f1pkz7CHqdxh+e6DsZdvdYSAT/04NoFt1Bfhge9jfGWC6LKu+ys7HyYz/S5mNN40UPY\n5PPobYyttjn12ZPezcsjYdVQjzl1qANq5NqNHRbnNSKs8qnkIeGu3VG+rI8t2ZbHvXHX+dw9Zm2X\n6xbJk8z3XC+fZg6v2po2mD/K15sdvZZTliHLsyyXwcYupX1bKquXftFucdzjuLGe8BonOxgXJ9gR\nK4KSs5SrGF99pdikWDQ21rowWXRrL9qGNGvM5e6A8jjdsDLkY/HIQoVoFLyQhW3KxJBjVQen3kUe\n8O8Vl/OKE7Xbid8DS4EyU1l3JbN2hjznfhFea6G3/auqIbKWacL5w3R817wQ/Zo6GGikvtaA8EiT\nsJH5rngbY1DhqH01bJoLOxL5tI+LtP30kOcO20koj8SuPi7b0ZUd43G81i3YBtnxqgasf4tVw0hE\nXzTLPlq/1oZ7ZTF5VvqIwDn1apHgFpmukvIeG69+5piCY0ATaumZDe16dghRMpFezlFF2umf9xBD\nJn8/bQCz7Z93PbwHjqX9vMjYyN68sBKdj1vBLQvDpsVkGy5OsD2UMX40//dkELY2dIHlkQqiNaxO\nvQHEsrE5feHyi3RiYlIxA8uxOxEFyJEuTla2CBZVUcfQeYgW5AK8WOtFTuqGzGtRtjXea7bci9SR\nXO+I/QWv7AiVTSDjpl3htc4NEmuO6iCRdesJwrMxdWk2tbEP9tpzTa7hkGugcBVXngTcPojqIm0i\nluZdLwAM7g4RKWB+0NzzHLDMGO9OncC7sIfhblnPjvJa3wDsTBblbz3KOcWLP+9KF3mtgXZnOvoi\nnw15uLrimHx9nrytLB2TI1s+I5J82A4gO/KIyHMXkZ5t+uOuueyXfM5lfWV5HrmuwbtODXv3R42A\n6odFzss5Uj3FiZQ7lZi81iKPqJ5HyU/ExQl26H/qRhROQmSXh3Al94lwuhEEYdcMSurSDSOJ+vxP\neA5Vy4JGqjm/sjjW5hp7nGOt5+osBNo+iJg8GerNjb6tidWOMgvUufurCZyOsM8tjR855rCXtFza\ny2GeubpZWS2PDbCjViz9jnYS2zcylq9Cd37IWASMt8H5X5DU9p+XDo6N22fUDBEJZw9u2ZRp+NG8\n1gZbhlXPfte2kMf3WgdzuND5u4iY1cCkKdKJvnARXJCIgLbyWFtO0hXlFQsBVXTCxsvDfCoSKXDE\nDiE9BPy0bfocu7bXWpPUvh8jpmOdtsg3vH6Obq7j8in/Spn2RAeyVH82+b8x6C0YoNG4PUp+Ei5O\nsCP4pNnK87gWi2M+tRcmIkxr5UegsnrlYhm6DjN5Y+c43ZB2hxCAMo8qm7L0V0FIOa1HTn9b2LRr\nwHBeSONUs3YtJblmo5fPPqlRDqnr2SGkaxcR2/5eG4mVYb/2BSrujxiX0+VkzY8YUZpHZLpbn2xq\nY2atB9uM2V5y/ZBea4kNbHdtc1jsXvPIXRGSqoosO2HYqkhxlGy/Mda66SioYU9aaVOQsJasTsBr\nsdZNwsumDwP78KFEzmsNvbJhfZzr6hxn4iiPQx1rXa5DJEde3FxyzbN7ypEX7Svy7UgjUPQfm34P\n+kYTayl7WzKR664Ei4NofamtO5ED5pbczOC6BHu+4gQyizfPEQkk7OaBSJg9TZOcaL5wNHMnercM\npOLi0PqL7A2YiEyslQcDpMY5bLNstdUOITPxlDuQyHjktNVe5iQ89+2ccf4RJC96b6vE9GNImbZs\n21JbpU75Vm8WR6kaz45sFs2Tn7evNWOx9+LzpT7byCycSaV4mHHqVHSPdyHLrDH1Piv7aayL+0FO\n1ukbHLewVqU0qi+M2ZM2pY+waps+LsqpFktBX1wQ5e3W8WAslDd5YcxJC2BZ1vYfMYIBZvKHXas9\nFX3zW629emmjPsnXSX2kswTMlNV8+Fh7fmQeliAGxwC2e61z+azTQqYXFbTpRdpclkERuuH1O/xr\n4ZNiLmTaY73IyjzmtN2x1o5ujdyZz9tpjsd1CfaMsq/iqT6ynZZK8js+WuDXyo9GUEYuXhDjdC/a\nYwB6mz7oG11wsXyU7bXSXWTXhJOodlUMlHo+qXqwZYIib/b1LPoQ78pr6j0ZGxu5p7jVkyNT16zS\nFJXeK9d85WbCid1vZ7rirKOQkL0E+ZZYVe4ainijtzHeiqtX1prAvA93exvjwTANXv0jRmBXrPVe\nAr05fUH2KseFjGLbN0eWUnh1sfOitbH6wKaqh9NPdh5MMtbHOa1zrIikPM/HrHW5XNb5mTpFL4sp\nfqQIXd5SDhdp9bXy8y8JtO4HS4KjbyheLdY6wuUJNoCCOPn3cDn1TcnSvtbz6Lc/ZsxycZ50Ks5C\nVCQTFsPE7EbUSWde5JGhtgrraKQjjuZNT5dufu21nuqt9sgu0lORVtrKvve4KeZr4EUdFDxPytJJ\n7QaTfZuul7yezuVmSxvSnCAvWdCg8G2NVp9kJLJx+kA1BU5TzbCI4XdS348YSVfMHwSFjq3eqyfH\nuuJW8RDqef8+2IVhKuxGlPJWC8WK6nZVgTHHF1+QXLvsOR04pDEnCcg1w84WTr4x7kaura44Jl8v\n+yIgcC6RlrqoXoqgxXnI8xbpXpVfkhkyacm2PA492LUdQgT5XUOOi76z+TY+u22dv137XW+KtV5r\nf5D8YFyaYG/b73rRvdPK2SRgOS5plmQ6G82HAZm2dlUXoG/XJGEiiY27zulZ5jgvEJbn2+33zKcK\n7ZDlKVsqvbnQV0jVz9iSsZa9qeoTISdgR6aP1Q8ZqUzSgmsj8y8aANvQspNq557sXfkwo85F+dP5\nMo6LRWjDDxlTeneMRgPA6qxN7fYI9dQVj97fOsbN9rW+NUvtXEy6xjjbO/Jg3HzhM2sDa125e4hO\no761j37Q2ZqP3JqsS3uYztqwJ3MePCx583RwdF59uN2HZ+QhCbIl1TUvtT0/5G2MKi0r22ZaZVdL\ny6Z+Qi4bl/5YyFiEenCqI+swEmBlrLXR9cilbq/8Brg0wU77T3AhA7TXdLGYUrwrL/aei9wjXwov\nsVKubnalMGkYxTZ9DP0MIW/gJaRjSVTcE2ZLPZp/ILhUh0x38GI7a8rxnsohYYviqskmqpPajaKe\nOEw6cZy91nbfa5g+VJ2xyFo26sWgPTbJzpbVYjZuXwiheLhaZsFl4uX8n+B+pRCVIUzZs+mdVL08\noja3+qPDg92cY8+Itb71RN9R9WYVGPVdMa4Cr6EMqFVC3QvzncKl/epYa3Mbbk3r5rEybWjjtLOU\n6c+C8Mk6crlXWgAAIABJREFUWtkGm6N2ESlkkY3hlyHZtrqOHUI8Ilwn19q27OuO98RWrk9k78dg\nl7JQflqsdb0dh+W1EZcm2IDXV270T7Ztx1o7pKJqb+VB/kejMnZbxwn2R3U2LEK91pwBkPP686Sa\nc5ACuZd2aWtkzqvpPbics7W4VB509A8ZhR5Y+sYSPXOebbwHrSBN3JhKWzpQvGKWzHW1ewnmBwxZ\nif59rbOeKybRvdLS9eodMLBxmz6Ty63fxngGY53v5c148+/7w3HCvFkUYcet7ahEbNLpAS+MOZVc\n1/Qs8vEWC+9lMkrvl1GQxSP0tr5BHrv0ScbxsSTUu73WQEmuC9tlgJYk3AzeonxnUnZsi0/5J2Wp\nLfJaOSR6e6x1bRHpkZ9BvNbh8gTbIrpn1sVaS8wsk4VdlgNxrLXDsNywEQTlOnYtsC5ahmbYKmVy\nnYpQO4SY4ucMWJ2bT9Oe0pYq7fTy60O+BLK+CqwPRduYGjuEyAnZkkhxHjpnrY0ls6atLR7rJGlC\n143zGCkqG3lqVxBg12xthdebb8qoflcFfXELnLEmNK5BqGJAxhffvKr3WB/ZFCvHMlu7O5DrW+pr\nxMuTWRIY5N0TzpHTR/Vr2dg+reTRWy9FnsVxTuvpjNdaldP4ISJQplX524m1alv5XGNbu1Y2P9lO\nxn33tV4rPwkXJ9jxWxvTESOKtRbHRQYUyCN7R9crT7q1a7k3cGZi6+4QkuTmnp1uHFKkuNhSTvRq\nliUbxvQyGfjdwiL/RO7KS2G+nl3ZF2qbvCJz0o3NCyqD+KAdQoxNi0wr0i6Lq5B6aaO6x/bVu/pM\n4/+IEXA9tbcm1zfV1wdSfd49gVifUERGpSvC0TJ/E3JKUMipi6BTmLpJUUSUbYm13rqn9dnpXJs0\n0RQy6G/IHDLW7CNr485Fc1l7bMy5S8KjfFkfK+Itye3Rb2NU9en3bOf2mYYUfaP6finMu2b+lnw1\n+dZYaw7kkb2RS12vPMTxE9F1CXaO/fV7flpT3rl7FEuLrDODWzFTlVjKbeIoDVB6tXsuZsUuENvx\nPd/my80qSTgjs3FvDWZgCd1g6E9VohHbcnpQ50Nu+2Q5XfkykGOtjdcagPrxZy5M2IQ7hKS87VAk\n0yfwbXJRQR5BdXwb5ytu+6bGMHG1IKMTevZ0Nr13bXv10biojpnWwFiV2fE4fi6PsaYrGDh1670z\n+wGAvcb2jYxdO4Q06nwTktwqd2uZ1sZ+pmOHKOY8vPxbNiv1PeR9bxmKSIvjnDb/bXkb45xOncty\nzWSqPjm+LkC4pV+RtiffuX3L5/KndweZ/95SXzgzBssFzS7EwULn8a0sT+VEx9DnzTQWvbysH9cl\n2O4SIMke+X2V+5ACeWRfkx+5HHWyTAtJ4IqJhSG7Qy4Z+eeFaSwz8s4gJGaDJUv7lTEvtimtqab9\nqWRJknmW6YZ1P4bUjFK95sLcHUI8QunZVPQ9le16m2MDhbnN483oUiJ3dXLuAbeQoCx5umduEmkP\nnd7eikY3KnESTixqDRav9RPDIVXylfD5FtiyQ0igL0jsirSezr0+nWlDeYXArSLXXvt3Et8uG6+N\nW9OwPj5ihxBA2sLYlkTXi9eOwkw8kkwmbSFrfRq4bMuOi55xdqb8AXBhgh3xXhNr7T3JOF64yd0Y\nPP1YN7jaFNpJozY/FmlcOczolQKXGaUdcVT18q4g4jid56oRUMRaF8XRIhOfkwNek1P1rDKnLcvz\neRuJAzZpJdmyrWeTFoy6d46BZV9rKvJXl1dWTMxbnk1RJum6emRa5pH7zebBOlnBge1zo81DRnrk\nIScTpR7sfMCs6LmiW513ZNKZ1kUYLpPg3183x9kLgssUBXghlKfiURZGQxQ2/ZCxRUx6hmKHfnW9\nevTWRhHKOI+77RDSY7OlLkkmSW7+2/k2RlGWt1VeKU91MulVOSJt2dw4bWFnwNHfXN4bF5RIpa3J\nra5HLnWh3Lvgjn3qhJPmnksTbOljyEul13E1z1zU2bWLsCVNhA1pbDslTVD9QHa8z3016/QOIQAr\nqyW/6UDsZy0JfLbTd1Sqw2Ib/1hKdUGD83jdpSYmS5Ap2CHEy8ycp+cRz2YNmbbFAnBjoYu5KbCp\nEaHqIhLta90a6zYfeXoEub7BZEdA6MFmbXUu7lAkgLiPa8Tt1rgHwa7cl+HbGBv1vOvLYnamLx4A\nPEK9lsxaIhcQ5KqNHZeVMrttOkh4IpOSbG/dIcQL3dAknLW8sOXievR7tp3PHhvbZvNX7BriEViR\njwuGr3TtuaKryGvoSnPMwnRhgs35fxlrbd18QsdW4Mkj+x04mkg44y7Tp/mg2Neal0OdlSDWKZNk\ny4AMNq4SPJE2XQLvQTb0wqxd5dmQ21RvlWHpHi1CQoJzXmPjPZW0bMgkadh0obYf25p9rQE33KhI\n39A3Y38b7WtuLxfoGQC5HuwtnXoQTvScKDhNnr4Fuxfbx336IQIj/aTH1dWwlxzfXL8mD0uKTLoW\nSQ0dXCz0lTxC/SxrEfLWg1HvXtky1tiPtZ4PItLbIscACnJd2JoFvrguZf6t8rVNkD/LP16Opdfa\nwo4bqztCvgUPMMdcmGCndcMj0zOz9FhL5C5VsRU1+ZyJ2rpPpCGgLyA/uvor7DhZcLbW3ZFYLmsy\nKkg3C70sklWoCAtbFAszp/85f7Oln7DylrGpGxkwISilldnjPD0AiDeNLVeuzEuG0aiqsNbnSc6Q\n3eJ3GdLG5rFUWS0c1R85Imh6DWZ4d70evFaY93DhpfX0Homr6FUejs67fV2jSO/u4/ti5HouW62x\n9461foCFL+NtWkO2kOtIXyWKO8o4so6TzigrO4S0wjS6yHfDJpQdkabDJreBsS/W2iG07VhrzvKi\nL22+Rb24kNu0PpEv6+NxKeW1Zt/GT2vz5EAe2e+U78IxmV6OYC8DiqYtg4ixBP6m85nVuHISI81J\no+TiT4Kt3EljERGBmZD2XdCFThObnw7KKiSmTYvBIl8OtEzaUiHvy9foi3z98opGVG3KPF1Pqe1S\nr4vN9XA2FlE2JM57bJSdIdKRjaqSJayijmHZH5B94Qy42lCbdeFI7Egr69qdNum36AJ9fqPro5C5\nu7HZ6TkjTzGMiE6eVJn7FT2Vz6B3cz2iH8FWSen0EfZgR9qEIo89hH5r2rS7VUCwbrJDyIY8umy4\n3adxHjMHeKvsEBIS6+lfSWB9Yu0RaC+tT4qtLCbfRXsr9Vd5vs31eRP19jhQTW51PfKscxahlKZX\nnnRr5DfA5Qh2QVQPuaCRXLDWNWm8r16rFztg30WayY4I4HQTSLLJECEhvIzTRNwSOUxkj7D0Z7ad\nd6Wu2Krff6ayTV1SNaBsp3qFtqkiLqGmZWawaWEmEktMK+TW2sjiIj3gEF3HxhJmT2+LimzSYU0P\nzNO8XDQqtgUOJrmHpN2Rt/ox8D1xRz6bi1dzyR075d7XgzF5ahPx8fSt9Ft0N0pLDX1V590gHSS2\nmfcN8rj5Nn7M8H4UuHxyKRfH9XhrQc7d/P1yydGFW/956aM6mXoVdbJ7VUq5mkM4f1TTKIg0Xke6\nc3YlTTjH27qWRbk4eH66HsHei2ix27IIrs2rJl+TpsctN5Nhj9cHvL1uy0Day9vz9NL8n9PATnw4\n2y65K0KZbRcCzSpPID0w6P27ke+hYuJskFCPPBcEfWWerTx6ytibh9sXFo1x3vXG+r15dNxr+/KY\nO2HVNn03xF2rUdxN98XBC9i6stP80xrAdfXuuOsj8vAI5Zo8uJyLvTS795Y+gDzfvgx2Pb0hSS5s\nA6Kayw6IrslX5X1EvuKjuSd3OuZpFV/KTyRWHGe50QG+fEsaJd+ZBk59mnnJ9NvxnASbERDT+dPq\ntsqtbrPcuDLtNbVy+Yuc2qetf8UTDMYcd+3oZH7ZVp/DpmUnXyFfnPazx7UWJ+6tFLMtMau9t1Wd\nDzpv7V99iB5C5oyDah6cuozAtZW7tiJTbFL9LZyjo4a+J9/qC4q8ByCZbyq2yWJOQKOu5+EBKnHP\nKrAcio2KtOrp6Kmh35q/exvszf+tclvatK3znWkosrH6wGb3A0ImolzaFJ/sy/MxF7qQMDv5NHcd\nEfn3/rBSl8da5pUv1/EjSGwhT3V08g7lvfWR8t76SLnRpZDiHfPWcxLsaPa4uhzQAys2ypmURDgN\n5MoTiCS3Xlp30InQj2KvbTbkmnSekLYi/9lrXRD22QdFLPKWsHzbVtfj4xUbEufc0Hs2ZM6zTUW/\nxmb5kZbTFxYN4uqNrKjs3vRR2UV2K9M3zTrtb4Z7l/9I2LFI7S131WVo1PPKW/KVfeEYG1GPd9i1\ne3QbTuQ6Texc2qpPLuXiuP42xXb+a3b9cMlxJ7lXclv/HI9fIa45L0cXpVFyS2qdNKvI943q0/0K\n6jqek2AfBtpAjgNFLR9PJ+VdpNomNva8iNn5UaU+C9xucx6L99lLv6Rla5DJNZv6+GWzSYucbE1f\nOKjWP7Cx9UwJjLd5lU2g77bJYiGsTQwtb6oz3Nnoq6jcLrJstwqzvid9CfYu6WGT5Ca0+vpmiAq9\nY1/cpR8AsN2dP6HSF626Onpq6Lfk7dZwQ90WXdQXjTy8PI3stB8xHmWj+iJY54pPDuSOfj7VRJh1\n3VjalWm1LQvbsvxil4+iHO5MaznDiYT2Fh5oVdfONiSv9UF4PYK9xWt8VF6KTLfceSgH/AZ463wk\nAwA2TCh/YyTqnXdo8NIn2zltJtYmrUy/vPBmIt8pDxXDzfGzSMuD7cbzNtJUOymwKWKke2xsOXNf\nNWOtneq4dVyhZ8emSni9tB3l2FugOsqr7VlSbuqLW+L0stMdFmnuiLMrwHFf9KWPVdRhE+mL+vT0\nSyJCK8tadCv7wuR1BKF9mF1E1j5kKFLKy7Xg0i6tnCWB1WmLPOZ6VfO1cmXLStcdktLqiy3kFPDl\n3eR7Z5oqYTd5J51McwOHzHMSbEHMFmSWF7vp1sqzzmEKnifT6qryyqwp29f4ZHnOQBErHdnOn5Iw\nQ8RSK3myTaxYpUm2S1owzGvakx9WtFnk4V5OiRZZPsCGGzbsyNbaFFfcqWO7LyrjppbQeQip1reR\n1kvn1qyVtvM28NNXEt8SjXofjkZZRB1Gt8LZxXJjTCSjDaomaV6Z1tO7dd+ab1dfNPLz8pdEb2M6\neV7tw06b5sPLFg++Q1ZLucjb1XMhI5PWz3P6dwi5NnkQex0mIPPf641ukvRIXitXymvldtbnYK+1\nxHMS7KivLiE3N1zFpG4QFMostsSrZR77whZyvbAjdiqmp7SlXV2x1gCYg1cX2zo1fuQonylqNnIO\ntTa5ywIbkufyEorzlo2qkiFpU7d07GDcMoiGhaN3TY3QHYpBGWQOwmHcaEMaIrv74ha4Q5mtIpvT\nxa1wZsEeEduZl0VIJhvpm+SvkkfYnsb60NcPTiZW5OXl2AAribJXf0kit9r01N8Fl4fFJ/fpZbnK\nxiHMqV8yuVyyWP2GSJNHWH7LASDbc0vPciFnLG1w0rjy3voE5d44jPA5CfYWnEGmvYspmUIeSDdA\nurEq6kImb0bpeQYg71I/LcH1ZqMj/Sx419EZnLKS2OitZqvnynnDhjekUfUy8z1ZYYTWhNFJfsPS\n6s8ybpujfg0JfNjM6TuOd5G6yOtktnum55qDuHMH+QVRZ+KsfgDQ7Z3MWDkRBvqaf2Rt/lvJe6lf\n2xeN/Fvns6yHXPfm20Ocu2xW9AU7JxFx9T+5ooMgfKU+z+1WZvLv9WaXaeHGaTdxL4J9E1JudDf0\nWku8HsHe4vaKmECVTK8ov3CvHgf1pvdchXm/alOtLJnJscP1ZplIz9Cx1gzkl9VE6aNYa5ZksrN9\nS6VsJVXZ0RsQVd1apHuWSTN3qzlhw0IW1bEm6/LUyrJqxiu82+6IXJHezWdz3TibrOmLU/n1aWUt\nPXoPB30XziLXvIyL7iR7DW6gr5LTbh2vuj/C7CzR9QzZ6AOblud70+vXvbyLstc/ZLj5KbK6EGCP\n6EZhIgUBLvJd8g+92w65b4aDpOOtD1whad1AsLd4mbcQ9t40Jy4Mz0mwI5aW2dZKudX1yLPOYWmK\nfW1YjWT73E/Kd2C5TR/K9nppZ9vSiy300LpErqdBPMlX7WsN/7I1USGvqdjoGuRLEdgUZNouEqZs\na5P17NuoBwQ9B29bJLbGYAu9W7bXPw19zsd7UluR99a+qO4JfjTOmLP33COnsd6TYElWJyglruTb\nKnfJZ1vasj7b0uY8Nl7anjZs+oFij43XFwfYKE/tFliCmj/ZnOvP+jZ7bGzLvOPQEbMooINcy7Rb\nbpKczwpyW8hZ1M9Js4u818qVcqM7yWst8ZwEO+rDe8qjx/kt80EzjbMMJxFL4kFK7R+RSqvipUUe\nYXoGuve1bjXLBZc3TctbXCHckU1I0ms2znnuk0pdumKtHXDKL0JLVxtXK9NyRddVLi/qrX1x2lx6\n4px97vLwgJjXzq390DXd9hi1bDryOOptjtv7winAilrnHTan7ESyY0wUmQVktxbmsaRdbELSa+TF\nQ1bgDV/y1HmEhL0190aQ7T2bBKcF8gjPuSz3Tlu2PifB3oIu0kyB3Ji09sLOA+n28ENEJlIrK6Gc\njPPN6b2+XNsueagwj/mThPuWTdqUKYO6Yq1jODPryvPNr0o35Lr1mnNVVevV5dztTuF9mLzFlYmk\ng3yzZ7aStOc8Oj3mXg5uPVZg8mA/Ax09aqJ4gr7Y+nW3AIn/cTmNPB6BXL8d1Rf1csmRyfPQA89G\nv8Mm8k3lOhxyi/gEW5PXgDxnGau0pS3rNru2ZR7eln5NAm/rtwW3Jtg38Ygb3R281hLPS7BXeZlp\nQxrU3QeefO/XVxvQVeLMZkrPdEmuF9uZUYo0uqw5Q5mvJOFI3XdAn6wl2CttuGHD5ryqD/LZ44lK\n4CDvXEDU1QfquKJT6eDo5/vjiL5Q5dwKN81//0PG02BeNE/ri53k9wjPdKxbH2u9qpgKmT7U5ghy\nfcADlwuH+CpyzJFtHzk+NBwkHR/dFyGZ3UCwe73MRxP2B3CwXJtgRytQGnxFgGySB/ZW1yOXuqr8\nQHIt293zKQkusLzJMbJp7XcdvY0xn0/6aAI/nDg0yLL7qnQ25hUbMueKyMpFwLOxekAVdGRfTPWs\njLOW444aJrdO3zZZh3vtg30QundLaYDF/8vhJsS60hc3Js/Hvup8H3o82EWZAZnu8VTnMoM8qjbm\nfHesdQ0uAS7Js/z03sboeb+3ketlUQm91kcODFnu2R5nOHmsDTO5s9da4toEe4vHebU8cDd6wprX\n+tD5oEVFDNOT5DfryxyzLvI8A7ChJbBnZocQTe73xFr7YHB5M631aNsmVc5ZyoI82Jx7eaZuOXwa\n2Boi0kjqxqCbvEPyED2AAgDzffpiV763yfZWJJjE/8vgpl7rjlx7LoUlfQflU+pv5Kl1y7rdeRdx\nbtnwbeaK4iVn8Mlw/ceM6bNOxvNBtRwU3KEg13JcHM4v4BPg3aR5j7xGsrGQ6wfCtQk2gDrZlLr5\nmDw5sOw1B62z7kvpliSHdRCKrI9Hf8ZlDb1N+pZukfHaZTPE9nvJNo1ps0OI9Wgw9NZ9R4G8Vdic\n97wqfZONM+y6bHCcd7JA67krgLvdoEy6NW0tnTdWjsRjzbUN3LgvroQ7hNItZceqPd7natqq7kRy\nDZTLmftQ3LBx0tzsVegHQa1NBdGd/1lCbHShd/lm+d6qN7YQ7A2E+Uiy/kBea4knINgBtvT1Wg93\npOPi4GB05Dvff1XLdI9m24p32oSFWNIORDuEpGeOGy6aez3WHTbNHUI6bJa+uCE2kt3N3uuW59pd\noFe+MGYrbtHRh+c5Yq0zmB8jqqenDpZkHpCH1p1MrHO5O88d2SbirMjmnR4y8ifr88Im3mZPEuiC\nSAvyXaZnLU86Tmtp6yvFPeglv1K+JU1qZ03ekeYBiXXCtQl2tDKlcWd1LbnV9cil7ubEOmUvZqTa\np70PZ487OzZuXHXOb9GV+2rTRJicPj2NODQIdbr/ONBbkugRZW+HEJtfsfuhIdc3J5SqEpG+FHFD\nH3nk3ZI6LvhZ44Iegq21cc7y8OB9cWr1GoU5avuNXG9699q2btF7XqqADFNDn9BDptfld4fOiIiw\nS6JZ11no6i+IqZPr0GvtvVjhaNwqfGMPqfbkD+q1lrg2wV7rcW7KLTOr2Eck/ZQJoWeGnyqot+mb\n0qVdljVnlAR6inNYmmi32SNhywsBzcTz+FjrGFzeZOY0td8jih7plsOhRj6LH096ZeMEr7UqPyhp\ng/e6FfrhqqM0t4y1joo8cvI9stJ8stea8r/Hw1281rWvaxpJDyTfpe4BHoLsw4FXpU6SXO0X7tGf\neZdweciyD7iUK9vOvauFrn+HENEXZ/KLW4eIhPIOUv7gxDrh2gR7C7aQ71Yazv9OQqssysS3moMg\nxQuZLL960rYTm3ZrkMn1yX1R8WCzOc96rpzPMq7ZeHqgyOcUr7UsukGKq7hV2rlTzu6Lx5yDl7vs\n5XGHMIjmzLSSIB9FrulR+iIgy93ns2wPudbxxWetJT7BXj4Xgu0TaXbTkqMrX7XukOtse6e+CIl0\nJN9CyjfkdQGvtcTzEuwtZGFtGi4OTkKlPHk/upYEdsh3YZdIt8pvYpl3i7WOUCHYyXnHDT0gbOY2\nmWYvNhV9srnHFNB0VLZ0tTasSLtkcr/44vQseFhme5FiKg/IanXRj7Ye3THWursrOurX1YYm6b5T\nrDWcvthIllVeFQLuesTlueqLOw0QWXRAsD2dtzc22XTs9NNdY60jbCTFtTRPHmsd4doEO1q903i0\nOjlOaaVc6u5GrFOx4k71Pu192bLJtrTc6ZJcM1CLtQbO9U4WxVcIdo8nWs2dFe82N/SP0ReVMdlJ\nvoscdni279kXV4nBvjWmS/QgfVE+259dPJp9cRK5prdH6Iu68KxdRO7hwZdg56RvH+ooXno+Cck1\nB/nhvFjrCHeJwa4Q9It5rSWuTbAjl90qDzXV7SOSftd4uVrZ2qWs+eB0VjwTM+bXmuvQDxL/k9fb\nvhL93sM+10cJ153v36LvMXaCmG6HoBY1R4h5iCja6aWL5v87eq0lJg/2zlrsbcQdvdaqGsD9FygW\nhOKOkHNaiBYx3kuu70wmE9y+WEme95Nr9ufwkxG9nXEiwKzl0j4k3+zYLrrCm88pj7kzHoFfNMM9\nesl3JO8g3/eet3bi2gS7hlUkGz6Ztmk4/7szqrP39DH/Ak/v+lHS53yYvNPZlub73FkVeaLpD+Eg\n9G7CnYS7CJeoea1n3MtTKzERqYbRTfVTpzxKX9x3bn6Em2PC3ZeoByGUQMdV2Uuum+kfrS/YEwKw\nHtfShhyZPC/aWZBzwazvfbvItbEgxPM/2W5js2q/6zD9Hb3WCpZIYx/BDvOqpLmw11ri2gRbjkkr\nh6Pz5HYsV8f4vQf+jFaIiAn1sJ/drzoXeuMYx11irTeiuKRm3FgPCnt6J6No+N0L06WvXJeaFxv5\nslcyD9Lzg/bFuzuM0Ue9Le7xNDw7ox4JzXtkD8Fu6B7p/gCC+mwk0yrPYI5Yjh8k1tqDS46xioAv\npNmkLfJMdjOhfJS+6PZGC53njV5D0J/Iay1xbYK9GeQeRib3/brGwYr6lLftsssHG7v0X71hz5Dr\nR/BOFqh4pFnIiuct79qT02eO3aMRyoxapRq6UN3xjfojjot73LYPOy7OxgMSyi7sINA13WX6wpJl\nI8u6ComukfG77Gu9BqyPPQ90SL5dAs0dxBr3mawiHEWwXyjWOsK1CfaWMJBeuffk+jDYWqeFOpbe\n6cBrPdvWImjujgrBzo5Xx8YuEjIUhPI/iO4+fy/n1dgQg916U6PvkXr8vqB3J9VMxlueU+J6nLVw\n5QX0gRFu/F5JsoVcP1A4SAxTwx4yvcXmEn2BgmBPn6zOvf2rSzl0m6WO0zfA9Nj84iYx2AH5fjJi\nnXBtgl3DFpKdCdV88S+LhR2zEk0DeiGb8os6p70MpJfGPC6cm9OuGR5JbNk4acQzx+OiVUFHX4ia\njTzpVec7cc7aNRXyyOPitJnsKiSqhZ4Oa9lcpi+cSU7gmB1CttTrbHB56BDmSL8QadYyY6s9+A/c\nMZGXuUawt6R5Qq+1xLUJdsR40rhVYR5BWIga4w884CVkuyufbOWJXDOQtt3LD9HKmz0lmJ45HrtP\npqp6s745DMJGisNKOMglpoFoNYucdiu/1blSX9AtY7Af+7ZQmMb/jfviQv0R9kV060Rt8+R8jXsj\nRNCmhFrYSOm1vs5ckR1MljQrPlzbkg8Ncv0Yu6V0Qbanxxu9hlS/gNda4toEew2aRIJxmUWiWc+J\nJRcRDkjNnfTqOUSQ6+nwGp0xkQfHg23mS5dw20t+Va+1RK2yLe91o6GMx/daS9zag32VcXHTbrg6\nobRodVZN/wx90UOm2egdm4ePtTZw26qIslgsAgJd9Vp7i/GjokqwHSLdlBvdk3utJa5NsLeEgVjY\nr32eDCwPCLh0rHUEW+EWmRZEmhxZevi4Zl9Uaux58aXO9UpxVl+pLxg4Pgb7YqQhwX0I3QsWhOJC\nYKDeFx7BdHRafpVwEA82Vg7uebfn+tJ9MYO9z2UB6d/X2onBvhLcMBDrxUYgf12vtcS1CXYNNi5A\nyvPT5BVHfQ+yGxrlG1KcaGue/N3XHPrBTes1plN2Oa+1ROfDZZ/n+jFeGrMFxYK3F1eeK46+gBfu\ni2pXNLzTvvzqhNL5ys6g522Ood1lwMVhSaTnb3ZDL7dMe+nOEA8VKwi2SvO6XmuJaxPsaPVPY5sc\nWXlyPch2i8/Ep7OcaXpdNEPtc63exniRWOsq7MwehH8kM042+UQnveo0MLUruI414l3xWl26L46I\nwb7wbaFwBPuZnVFXHRNA4x4JSbQvu/L9AQTNtR5rY+g+uF58TExg9aHa3O3Jnv5dJtY6gvDMd4WI\neKSMA87UAAAJ5klEQVT6hb3WEtcm2GtwxVjrCF3rw8Kcool0mgeu3hnwY7AhOLQhkd6e/lefE4H4\nS5vSqI6n6Yu9Q/sJbg0Ax1zMJ+mLrq5otfUpCGXQButwCB6+F/2TDIyEqneaA/n0cblY6whrCfaI\ntQ5xUYJtGJTVvWCstYYg18JbrX/E+ByLBADdEEOeq9vvXTS+OMLktW3EYIdeuhfri2riJ5wkti50\nF421jjB5sPtisEvd5J182r5YQ64vHxpTQeCZLjzXSXf1WOsIq2Owh9fa4qIEW6D21ffTx1ovYHlQ\n7HctjehSO0G0wHBuZnIOny3W2kHTa/uEsdYRNnuwn3Wu2HJxn7AvtsZgP52nFqkvnK/yLByv9VV/\nsRNB/TLJEmn57afntX5G5IcKj2RXdMNrrXBtgp3G9rPGWkeQbCg58+fPVqz1s/XJFBZhV4Dpg+W5\nmT+fxVNrQbUY7IpH6hn7gtfEYKcF8zZVuSum5+p1fXHtH6w1sCYG+5n7wYO9D4y3lqzhkyCHSlrv\nNJ441jqC/Ia3td/18FpXcW2CneG5LPnZ5oAFK9aHp4q1jkDm+stFwiHXz+TBtwhfHGPt5s9nnhK7\nSeIT3xpAZ2x+wpP3xRo89UOGh9oD+LN6aj0IIv3UsdYRIoLtxmAPr3UN1ybYLxtrXT46s3TbPmus\ndQTbwKLBF97XeiWo8dp4GWv97OBWDPaL9MXkwW73xcsQStsXBbF8lY4AitHv9MWz3x8FQs/1k8Za\nF4g81hhe65W4KMEWBFP+6uSpB71E2VD1dRU/v6d2gXOTO2vGa/RF3YOd4gxfZUqsEsYXIlFND/YL\n9UULL+WptbCRdi/VF+we6ljrV5k5GwR7eK27cQrBJqIPA/gWTDznO5j5bzk23wrgqwH8XwDfwMw/\nWs00iod4BcivqPInq1jrVxr67719DB/8wIemExES8ipeawk3BtvGVb4I3nv7GD746z6khS8yRRSI\nxsUL9oeaLxJesB8mOMSSX2+uABjvvf/xaVy4ISG1LZieDGqnECykOskGse7GzQk2Eb0D8G0A/giA\nXwLww0T0Pcz8EWHz1QA+m5l/NxF9CYB/AOBL6xkDE6OkF/TA+Ivl08daB/jV9z+OT6ffLCSv5amV\nYDP5vZrXWuK9X/s4PijHxcvNEwJFWMTr9sV7n/w4PohlXLyWp9ZijIuE997/5Wm+8LzWL9UvAcEe\nXuvVOMOD/cUAfoqZfw4AiOg7AXwNgI8Im68B8E8AgJn/AxF9GhF9iJk/HubKxcELQXsdXtFTq8AA\n3l7UHWeQ578XiS+ugRigN36xxTGAHBcv3h1jXDgYfTH1wRvPHnzxY6aXgwwRwfBa78AZBPu3Avh5\ncf4LmEh3zeYXZ5lDsGev9UsO/AT9w5OXHvppAnh7A/DafTH9mA2DXGPuizcGfm2MCzkuXrkfgMQb\nGHj/bfTF/Kl2xXhVJK/12xte8EddGjYcZJDrzbjcjxz/9dt33bsKAw+Ij77/E/euwsADYoyLAQ9j\nXAx4+CiPcaHwos8YR+EMgv2LAD5TnP+2WWZtfnvDBsy9u/wODAwMDAwMDAwM3Adn7F72wwB+FxH9\nDiL6FAB/GsD3GpvvBfBnAYCIvhTAr1bjrwcGBgYGBgYGBgYeFDf3YDPz+0T0FwH8Syzb9P0kEX3T\npOZvZ+Z/TkR/jIh+GtM2fd9463oNDAwMDAwMDAwM3ALE49fDAwMDAwMDAwMDA4fhIV9wR0QfJqKP\nENF/I6K/Gth8KxH9FBH9KBF94dl1HDgfrXFBRF9HRD82//0AEf2+e9Rz4Fz0zBez3RcR0SeJ6E+c\nWb+B+6BzHflyIvoRIvovRPT9Z9dx4Hx0rCO/kYi+d+YW/5mIvuEO1Rw4EUT0HUT0cSL68YrNas75\ncARbvJjmqwB8HoA/Q0Sfa2zyi2kAfBOmF9MMPDF6xgWAnwXwh5n5CwB8M4B/eG4tB85G57hIdn8T\nwPedW8OBe6BzHfk0AH8XwB9n5t8L4E+eXtGBU9E5X/wFAP+Vmb8QwFcA+DtEdLkd1wZW4R9hGhMu\ntnLOhyPYEC+mYeZPAkgvppFQL6YB8GlEZN59O/BkaI4LZv4hZv7f8+kPYdpLfeC50TNfAMBfAvBd\nAH75zMoN3A094+LrAHw3M/8iADDzr5xcx4Hz0TMuGMCnzsefCuB/MvOvnVjHgZPBzD8A4L2KySbO\n+YgE23sxjSVK0YtpBp4XPeNC4s8B+Bc3rdHAI6A5LojotwD4Wmb++xiv1HgV9MwXnwPg04no+4no\nh4no60+r3cC90DMuvg3A7yGiXwLwYwD+8kl1G3hcbOKc42uPgacDEX0Fpp1ovuzedRl4CHwLABlr\nOUj2ADCtf78fwFcC+A0AfpCIfpCZf/q+1Rq4M74KwI8w81cS0WcD+FdE9PnM/H/uXbGBa+ERCfZh\nL6YZeCr0jAsQ0ecD+HYAH2bm2lc+A8+BnnHxBwB8JxERgN8E4KuJ6JPMbPfjH3ge9IyLXwDwK8z8\nCQCfIKJ/B+ALAAyC/bzoGRffCOBvAAAz/wwRfRTA5wL4j6fUcOARsYlzPmKIyHgxzYCH5rggos8E\n8N0Avp6Zf+YOdRw4H81xwcyfNf/9Tkxx2H9+kOunR8868j0AvoyIPkBEvx7AlwD4yZPrOXAuesbF\nzwH4owAwx9l+DqYf0A88Nwjxt5ubOOfDebDHi2kGPPSMCwB/DcCnA/h7s7fyk8z8xfer9cCt0Tku\nVJLTKzlwOjrXkY8Q0fcB+HEA7wP4dmb+iTtWe+DG6JwvvhnAPxZbtv0VZv5fd6rywAkgon8K4MsB\nfAYR/XcAfx3Ap2An5xwvmhkYGBgYGBgYGBg4EI8YIjIwMDAwMDAwMDBwWQyCPTAwMDAwMDAwMHAg\nBsEeGBgYGBgYGBgYOBCDYA8MDAwMDAwMDAwciEGwBwYGBgYGBgYGBg7EINgDAwMDAwMDAwMDB2IQ\n7IGBgYGBgYGBgYEDMQj2wMDAwMDAwMDAwIEYBHtgYGBgYGBgYGDgQDzcq9IHBgYGBvaDiD4A4E8B\n+CwAPw/giwH8bWb+6F0rNjAwMPACGB7sgYGBgefEFwD4LgA/C4AA/DMA/+OuNRoYGBh4EQyCPTAw\nMPCEYOb/xMz/D8AfBPBvmfnfMPMn7l2vgYGBgVfAINgDAwMDTwgi+iIi+gwAn8fMHyWiP3TvOg0M\nDAy8CkYM9sDAwMBz4sMAPgbg3xPR1wL4lTvXZ2BgYOBlQMx87zoMDAwMDAwMDAwMPA1GiMjAwMDA\nwMDAwMDAgRgEe2BgYGBgYGBgYOBADII9MDAwMDAwMDAwcCAGwR4YGBgYGBgYGBg4EINgDwwMDAwM\nDAwMDByIQbAHBgYGBgYGBgYGDsQg2AMDAwMDAwMDAwMH4v8DbnLj5YU/+DYAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x112bee518>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot result\n",
"fig=pyplot.figure(figsize=(12,8))\n",
"ax=fig.add_subplot(111)\n",
"ax.tripcolor(p[:,0], p[:,1], U[:,0], triangles=triangles, cmap=cm.viridis, shading='gouraud')\n",
"ax.set_xlabel(r\"$x$\");ax.set_ylabel(r\"$y$\");"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.5"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
huseinzol05/Deep-Learning-Tensorflow | Regression/elasticnet-regression-tensorflow.ipynb | 1 | 77311 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>time</th>\n",
" <th>temp</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.002732</td>\n",
" <td>0.1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.005464</td>\n",
" <td>-4.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.008197</td>\n",
" <td>-6.3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.010929</td>\n",
" <td>-9.6</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.013661</td>\n",
" <td>-9.9</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" time temp\n",
"0 0.002732 0.1\n",
"1 0.005464 -4.5\n",
"2 0.008197 -6.3\n",
"3 0.010929 -9.6\n",
"4 0.013661 -9.9"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import tensorflow as tf\n",
"import numpy as np\n",
"from matplotlib import animation\n",
"import matplotlib.pyplot as plt\n",
"from IPython.display import HTML\n",
"import seaborn as sns\n",
"import pandas as pd\n",
"from itertools import combinations_with_replacement\n",
"sns.set()\n",
"df = pd.read_csv('TempLinkoping2016.csv')\n",
"df.head()"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"X = df.iloc[:, 0:1].values\n",
"Y = df.iloc[:, 1:2].values"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"n_features = X.shape[1]\n",
"degree = 15\n",
"combs = [combinations_with_replacement(range(n_features), i) for i in range(0, degree + 1)]\n",
"flat_combs = [item for sublist in combs for item in sublist]\n",
"X_new = np.empty((X.shape[0], len(flat_combs)))\n",
"for i, index_combs in enumerate(flat_combs):\n",
" X_new[:, i] = np.prod(X[:, index_combs], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"class Elasticnet:\n",
" def __init__(self, learning_rate, alpha):\n",
" self.X = tf.placeholder(tf.float32, (None, X_new.shape[1]))\n",
" self.Y = tf.placeholder(tf.float32, (None, 1))\n",
" w = tf.Variable(tf.random_normal([X_new.shape[1], 1]))\n",
" b = tf.Variable(tf.random_normal([1]))\n",
" self.logits = tf.matmul(self.X, w) + b\n",
" l1_regularizer = tf.contrib.layers.l1_regularizer(scale=alpha, scope=None)\n",
" l2_regularizer = tf.contrib.layers.l2_regularizer(scale=alpha, scope=None)\n",
" weights = tf.trainable_variables()\n",
" regularization_penalty = 0.5* tf.contrib.layers.apply_regularization(l1_regularizer, weights) + 0.5 * tf.contrib.layers.apply_regularization(l2_regularizer, weights)\n",
" self.cost = tf.reduce_mean(tf.square(self.Y - self.logits)) + regularization_penalty\n",
" self.optimizer = tf.train.AdamOptimizer(learning_rate).minimize(self.cost)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"epoch 100, MSE: 13.565196\n",
"epoch 200, MSE: 12.895513\n",
"epoch 300, MSE: 12.673428\n",
"epoch 400, MSE: 12.584015\n",
"epoch 500, MSE: 12.555387\n",
"epoch 600, MSE: 12.546624\n",
"epoch 700, MSE: 12.543367\n",
"epoch 800, MSE: 12.541690\n",
"epoch 900, MSE: 12.540659\n",
"epoch 1000, MSE: 12.540012\n"
]
}
],
"source": [
"tf.reset_default_graph()\n",
"sess = tf.InteractiveSession()\n",
"model = Elasticnet(3, 0.0005)\n",
"sess.run(tf.global_variables_initializer())\n",
"for i in range(1000):\n",
" cost, _ = sess.run([model.cost, model.optimizer], feed_dict={model.X:X_new, model.Y:Y})\n",
" if (i+1) % 100 == 0:\n",
" print('epoch %d, MSE: %f'%(i+1, cost))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAD8CAYAAACSCdTiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4U1X6+D/Zk7bpXtaCSAsX2TcVBWQRxAUUvyoIboijjuM+rqOO4jLOuI/jbA7quCvOoOiPYWTYRBZR9gJCyiKyFVradE2z5/dHSEnSm5ukTUpLz+d55hnpvTnn3uTe97znXVU+nw+BQCAQnJ6oT/UFCAQCgSB5CCEvEAgEpzFCyAsEAsFpjBDyAoFAcBojhLxAIBCcxgghLxAIBKcx2uYOIElSN+B9oCPgA/5hsVhelyRpDnArUHbi1McsFsui5s4nEAgEgthRNTdOXpKkzkBni8WySZIkM7ARmApMA2otFsvLzb9MgUAgEDSFZmvyFoulBCg58d81kiTtBLo2d1yBQCAQNJ9ma/LBSJLUA/gW6A/8GpgFVAMbgAcsFotV6fNlZTUJuZisrBSsVlsihmoTtKf7bU/3CuJ+T3cSdb95eWZVpGMJE/KSJKUBK4HfWSyWzyVJ6ggcx2+nfxa/SWe20hhut8en1WoScj0CgUDQjkiukJckSQcsBBZbLJZXZY73ABZaLJb+SuMkSpPPyzNTVlaTiKHaBO3pftvTvYK439OdRN2vkibf7BBKSZJUwNvAzmABf8IhG+BKYHtz5xIIBAJBfDTb8QqMBG4AtkmStOXE3x4DZkiSNBi/uWY/cHsC5hIIBAJBHCQiumY18vYgERMvEAgEpxiR8SoQtCAOl4dSqw2Hy3OqL0XQTkiEuUYgEETB4/Uyb/keNheXUV7tIDNNz5Beucyc2BuNWuhaguQhni6BoAWYt3wPSzccorzaAUBlrZMVm4/wzLsb8Hi9p/jqBKczQsgLBEnG4fKwubhM9tjB0lo+Xrq7ha9I0J4QQl4gSDJVtY4GDV6OLcXHk2KjF/Z/AQibvEAQgsPloarWQUaaAYMuMdnXGWkGMtP0VNY6ZY9X1jmoqnXQISslIfMF2/8rqh1kpxsY0juP6eMLhf2/HSKEvEBAcgWjQadhSK9cVmw+Ins822wkI83QrDmCCdj/A5RXOxr+PXNC74TNI2gbiGVdICDUMerjpGCct3xPQsafObE33TqkyR4b0js3YbsGJfv/5iSZhQStGyHkBe2elhCMGrWaJ2cNZ9zQrmSlGVCpICfdyITh+UwfX9js8QNU1TqoiGD/t9bYqaqN7BsQnJ4Ic42g3ROLYEyEvVyjVnPDRRLTxhUm3O4fICPNQHa6QdbRm5Vgs5CgbSA0eUG7JyAY5UiGYDToNHTISkm4gA+MPaR3nuyxRJqFBG0HIeQF7Z6WEIwtGc44fXwhE4bnk5NuRJ0ks5Cg7SDMNQIBcPXYnlgOVHK4rBavD9Qq6JqXxtVjezZr3FMRzqhRq5k5oTdXjSlImllI0HYQmrxAAPz7m30cLPULeACvz5+N+u9v9jVr3GRH7SiRTLOQoO0ghLyg3ZOs6BoRzihoDQghL2j3JCvsUGnc8mo7FdX2Jo0bC6KkgSBAs23ykiR1A94HOuLvAvUPi8XyuiRJ2cA8oAf+zlDTLBaLtbnzCdofwaUGkkGywg6VxgX4f2v3c9PFfRJqThElDQThJMLx6gYesFgsmyRJMgMbJUlaAswCllkslj9IkvQo8CjwSALmE7QT5ATWyEFdmXJe90YCqzk1ZwLRNcGlAAI0J7pGq1FhNGgBeSG/bscxdh+sTKgQFiUNBOEkov1fCVBy4r9rJEnaCXQFrgDGnjjtPeAbhJAXxIGcwPpq1T5s9c4GgRVYCDZZSqmocZJt1jNU6hC30AyEF24uPo61xk6W2ciQ3rnNCjuct3wPh8vqFM9JpBCO5gO4akyBcMK2QxIaQilJUg9gCPA90PHEAgBwFL85RyCIiVgF1odLilkZVPirosbJ0g2H8Pp8XD9Rinm+RIcdKl2/HIkQwi2VuStoWyRMyEuSlAbMB+6zWCzVknTyBbNYLD5JknzRxsjKSkGrTYymkZdnTsg4bYXT7X5LjtdRURPZaelRq/jXyr0hAj6Y77Yf5Y6rB2PUx/+I5zrdWKsdmNMNTfo8KF+/HNYaOxq9jrzc1EbHYv1tzRkm8rJMlFrrGx3LzTRR0CNH9n7sJ+43qxn3m0hOt2c5Gsm+34T8opIk6fAL+I8sFsvnJ/58TJKkzhaLpUSSpM5AabRxrFZbIi6HvDwzZWU1CRmrLXA63q/H5SHbHNlp+Yd313NIwRRS7/Cwc3cp+R1if4ES6bSMdv3hZJmNeJyuRr9jvL/twIIcWd/CwIIcaqrqCR6pNfadPR2fZSUSdb9KC0Wzf0lJklTA28BOi8XyatChr4CbTvz3TcCXzZ1L0H4w6DQMLMiJeDyarRsAlSquOROZuBTt+sPRa9UJ6fUaT0kD0Xe2fZAITX4kcAOwTZKkLSf+9hjwB+AzSZJuAX4GpiVgLkE7YsLwbhEbbUSz/Rl0avIyTTHPlQynpdL1h1NSYePBv6xl1MDOzYq0idW3EK3v7Af/szBhaD6oVORlmoTDtg2TiOia1UAklenC5o4vaL9kpxvJiRBnrkJZ0J/Xv1Ncgqk5TstI4ZtK1y+H3elJWKRNoKRBJKL1nf12Swnfbik5MZaaUQM7c+2FvUSsfRvk1HtZBIIIKMWv53dI42BpreznunVI47qJsQtJj9fL4h8OoFKBT2bliJQQFc2Gr3T9SmyylHHBoC5x7UQiEWkBitZ3NnQML8s2HgbgujgilgStAyHkBa2a8Pj13EwTAwtyuHpsTz5bsZe1245id/pT9/U6Nef378h1E6W4NM55y/comlUiJUTFkngUfv2ZaQZsDnfDNctRUePgqbd/UEz+iobcAjSwIIcJw7uRnW6M2ndWjtXbSrh6bKEw3bQxVD451eUUUVZWk5CLER7604+ARlrQwx8lEvz3Mqutke041gxYh8vDE3PXyZou1CoYM6QrMyc0NlMofS4n3chzt54bMm/w9cxfuTcu7X7C8Py4zTcfLy2OOEfOiR3H5SPP4P431uCJw8f6zC3nkJ8n36s2EbSHZzmYBEbXRIwyEJq8oNUTLCCNem1IGKBBpwkJk4xmQgmMZTJoqXe4cbq9EW3xPh9MOrsbbo+P8ipbyIIRrw0/2EZ+9dierNtxlNp6d0z3v7qohKmje5JiiO11jZaIFdhx2OzuuAQ8IG/PErRqhJAXtFriqV0TIJIJxevzoVapGsofqFX+mvHZZj0GvUbWfJJlNrB4/UGK9hxvtGDEWtRMbkcxb9memAU8+B2ynywp5pbJfRXPC8yltHAFs+tna1yOYaNeQ57ImG1zCCEvaLXEUrsmGCUNNth2DzQ0B6moiex4TDXpWLHpcMj8wTZ3paJmWo2Kj5cWN9pRTB19Jpt3H1e+cRl2HbDicHlkTU/hi2Fmmg69Vo3DraymV9Y6OK9fJ9ZsPxrTNZw/IL6IJUHrQAh5wSlDyW7elLh1JROKkqMT/FpqqlGLtcZBltnIwIJsivaWK86vVNQs0o7CZnfHFNESjrXGETGMM3wua60rpjGzzEZmTOyNyahlc/FxKqrtpKfq6NM9E4NOS9HecirrnGSbDQyV8kSP2DaKEPKCFieW8gFNiVs3GbRkphmwNqHJh8Pp4ZeX9yM7w0hepomqWgffRIg8CZ4/kHgU7Px1e3wRF6hoJhKNGlk7eWaaQTaMM95CaMEM6Z1LikHL9PGFuDxe1m07SlWdi+93lmHUaxjRrwMTh3dviMYRtE2EkBe0OLGEHsbTyCN40Ygk4I0R7O4NqOD1fxeRnW5gUK9cvF5vTHHzHq+X+Sv3hixYUvesiAuUkomkc3YK0hmZsotLnd3F/JV7G2XDKi2GATJSdQzulcf2fRVUVNvJOFGjJqCZz1u+p1GhN7vTwzebS9BqNKIOfRtHCHlBi2JzuFi1VV5DDjbDxNLII2DuWbz+YIjtPJicdL8JxefzNST0yBEQ5uXVDpYrnAeQYtSi1fgj1j5euruR3X7t9qOyi4rO7aS71smNXZ302ltCye7D2Grr0alB4/NSjwZ+NDPWnM4hl5YSYxZ1hlRQqXC4vCzdcAi3x8PF55zRYOKK1n0KoMbm4qKzu6FWq9hSfJzKWgdFe8vRaPYwdfSZbLJErh24ubhM1KFv4wghL2gxPF4vv3tvIw6XvEMw3AwjZ/MeOagLl56b3+DULK92oI4QIZyZpufJWcMxp+jxeL2oVCo2WcqoqHE0RNc0hYOltXyybDcer5eVm0saHU+3VXHWgX10O7qXLtYSOlf6/5dTd6L75atwVYxz2bUGytLzOJDTjZ9zuvNz8Rm88m0vvF3zG0xc0bJq9ToNSzceknUi2+xuRedzhYIvQNA2EEJe0GJ8vKSYkorI5aSzzKF2Z7liW/ldMnn9k40hQi2SsK6uc1LvcGNO0TcaS6NW8cx7G6ixxeakDKchWsfno3v5AQYdKKLf4R/pdXQPHWpCbeReVJRnduBgv7PJ7dUdsrPxZmXjSs/kyx8OUevw4lWp0XpcmJx2jK56MuqryaktJ6e2go5Vx+hWcYiRu79rGLPUnMeOrn3Z9s0YZtx9Ax6PN3IxN5+Poj3yET0791eQbdZHFPTZZnlfgKDtIIS8oEVwuDxRQwf7dM+SNQsEJxLZne6YHY1yNWcMOg05GUbeXrSzyQI+xVHH2Ts3MOynTQw6WER23cn+9JWmDNafOYw9HQvZ26Enh7O7cjS9I6PO7s6Nk84iuNpOqdXG/Kp1UStq4vORXWfljOM/06NsP32P7KTv4Z2M27USdq3EN/dZfjl4OJlpfVl51hgq0rJDPu5weXG6Ijixa510zk4B5IX8kN55wlTTxhFCXtAiVNU6FEMHDVo1M2IoKmatju5oDKBUc2bd9mMxjREgvb6aEbvXcf6edQw8UITO609msqZksqLPGLZ2H8i2bv0pTe8gW8f+260lXD22V0jWaiz2dABUKirSsqlIy2ZzjyF8wZWofF66lR9i2P5NTCjZQretG5ntXc9Nqz9gyxmDWdpvPOsKz8Wt0ZFtNqBSEXGekgob+XmpHK+yN/gRjHoNIwd0EmGTpwFCyAtahIw0g2Lo4PkDO8eUtp+VHlkwqlX+8sPZCk24HS6PoqMxGK3HxfB9G7nwx+UM/2kjWq9fAO7t0JO1hSP4vuAcfs49I6bmJF4vfLjYwm2X92v4W1OrVAL4VGoO5HbnQG53vlRNJc1WzQV7vmPMtmUM27+JYfs3UZ6azcIhl1J/48040jIU56l3eHjhl+dRVesQNeRPMxLV/u8dYDJQarFY+p/42xzgViCwt37MYrEsSsR8graHkkDr1iGNmRN6xTSOUa+NOM6YwV2YdE53xaJkVbUORUcjQGfrES7b+l/G/fgN6XZ/pZyfOpzJij5jWNvrPI5lNK0nvVzW6vTxhTjcblZtiS3rVA6vD6pN6SwcMImFAyaRX3GIi4sWM3H7Um5a/SG+jfOx3XgzB7LGUOyUt69ba+zUO9xxtUsUtA0Spcm/C/wZeD/s769ZLJaXEzSHoI0THC0THK8db09RpUzTaONkpBnIStM1ygpV+bwM3b+ZyZv/w/D9mwCwpmTw5bDLWdp3HNYevamqa5oNP0BVnbNRpIpGrWb/Efm6+OFo1Co8MYQEHcrO562xt/DReTO4q2o9I1f8i9Q3/8rzurf5cshkvhg2lVpTqDAPd3oHCM5KBmKq7CloXSREyFsslm8lSeqRiLEEpy8atZqrxhRwwcDOzTIJxNriTg6DTsNZPXJYeyIZSe9yMGHHMi7ftJCulf7oFNuQs1lx/lTe0vbGrdH5P9hMAQ9+M1K4IK2xOTlcFlnIq1U0LGLRYv3DqTek8E7hJHo+8wi+d94h5bWXmPbDfC7ZupgPR87k64GT8Kr931u40zu8ybdRrwZUOJyeiA3OYy3vLGhZkm2Tv0uSpBuBDcADFovFGu0DgtOTWEoZxEu0FnfhBITQ1WML+HHbfsZvWMTUjV+RZavEqdGxtN94Vo28kpsem8G/3l2PO0YHb4D8vFRqbS4q6yJFqjR2BB8qrVWM17/32qH07mLGoNPg8Xqpd3gaFqhYqKi28+E3+9mpGUzt7L9z2ZZFXPv9Z9yx/B9M2vY/3hx/G3t69OeqsQUhnwvPSrY7T+Y2hGcoJ+O3FSSOZAr5vwHP4veFPQu8AsxW+kBWVgpabWI0gLy89mVbbO33O3fBNtlSBikmPbdOHRDXWPHeq8fj5Z3/t4PvtpdgP1LK9J1f8+b3X5JSX0udPoXPzrmKr4ZOoSolk8tH98SUalSMeNHrVDhdJyWzyaDlwrO78YvL++PyeDleWc+ClXvZsPMY1mp/N6sR/Tsze0o/NJpQoac36VGr/Y7ZcNRqGNanAwa9Bmu1g6wsE/deO4TNz/6PeodywbUARoPmZAkFnYEvzr6SFX3HMmvV+1z44wpemPcYiwZdzB91HgYPK2D2lH7U1rvYXBy9UmbR3nJuv8rEB4t2Juy3hdb/LCeaZN9v0oS8xWJpiFGTJGkusDDaZ6zWyIky8SC6y7QuHC4Pa7bKmxnWbD3CJed0i3l735R7/WiJhTXf7eHyzQu5csMXpDlsVJnS+fKiWSweMpnDbi1ZZiMTeucy5bzuuJ0ujHp1iPYaQK0Gk16L0+UiPUVL3x7ZXD9JIsWgo6KiDgCDCqaPLWDqyB4h5ovA8XC65sr3q+2Sk8pnS4tZs/Vwg4acYtTFLOBBvvZOZWoWf7z4Xv47cBL3LPkLl279mmE/beSNiXdxt6WUGpszpkqZxyvr2bm7NGG/LbT+ZznRJLAzVMRjSRPykiR1tlgsgZzvK4HtyZpL0LppSkXJROGotWH+51z+sXYeWbYqqo1m3r5gFv8ddDGq1FRe+OV51DvcIXZkt8cDyIdFer00OGCrbW7W/VhKWopetohXrOakx28cyu/e38ThMr/pRq2Crnlp9MpP56tV+xrOK692xNzgI+dEobTvFEw7li59uPe6V5mxbh5Xrf+c5+Y/xZf7JvPu6JtAq4s6R5bZgMcXOf4+2b+tIDYSFUL5CTAWyJUk6RDwFDBWkqTB+M01+4HbEzGXoO0RT0XJhOHzof73Z+Q8O4dbjh7GpjPy8YjpLBh2BfWGE0LH6aGqztmoZ2lVrQNHlPrzwUSqbx8req2Wp2efQ43NyaHSWvI7pKHXaXhi7romjacC7r16IHlZKVgOWBUXBrdWxwejrmdtrxE88N8/csXmhfQ7/CMvXvYgJVldFOdJMepYsTly7H3SfltBXCQqumaGzJ/fTsTYgtODPt2zZMvrRspKbQ6qTRtx3nMvXYqLcGm0fDl0Cp+dczXVKRmNT5axZ8SciXqCigRprOYUPWf18JckKLXaYs7sDSc73UheVgoGnYZBvXKjVtUE2NuxkPuve5nbl89l4o5l/PHDX/PGRXexWhoV8TPHKuoUI4MGFuaIKJtWgMh4FSSNSGF4TpcnJLY9UaiPHSX1d09j/PQjANYWjuCdC2ZxLLOT7PkGnVq2Z2m8maiZqYkv4hXvQhNM8MIZPRf3JA6dkT9Nuput3Qfyq6V/45H/vEzP0p/4cOTMhlDLYJxu5Zj9CcPy47lsQZIQQl6QNCKF4Z3fvxM3TJKiannR2gM2HPN5MP39L6S89hLquloOdDyTv4+ezbbuUSI7VMg24oCTCVeB0sRKDE7CbiRahnBZZb1sE5RuHdIart3h8rAljn6yXfNSOVxWx8qzxrCvQ0+e+PJ5rlk/n4KKn3nh4vuxGVJjHisn3Uh2ujHm8wXJQwh5QVJQaktnOVCp+FmluGuPxxvSIHtERTG3L/kbaYd/wmbO5NPL7uLLXuNkNc9G1+j0NupIFSCQcHXBoC489fYPEStFds5OibkkQ7xMH19IiknPmq1HQjJ7p44+k6fe/kFWyNvsbtweHxp1bF2jgpG6Z3LWGVlsLj7OYVU3nrv9Tzyy6BWGblvHy588wtNX/jbmkg7JMMMJmoYQ8oKk0JyIGqX2gCkmPUs3HMJcX81d377HRTuW4UXFtyOm8Neh06kzpsmOCURsFKLkOM3LNEU0mxh0ah6/aXjSEn40ajW3Th3AJed0C9nRKNnrg7/beE0+W3eX89yt54ZmEt83gbo5T9Dtzb/w8qePMmfqE+ztWKA4Tn5eqqhe2YoQ6WiCpBAQMHIER104XB5KrTYcLk/DvyPtAFZtPcJ3RUcY9+MK/vbuXVy0Yxk/5fbgoRkv8MrIWxQFPERuLhIQjHIEzCZyjB7UJabKmc0lEIoZWIRi/W6Vrl2OwPcQPJ9HpeKtMTfz4cW/JL2ukt9/9jhDf9qkOE69w4Pb08S2W4KEIzR5QVKI1qNVq1GFmF0CJplxQ7pG1FIzj5dw9//+zKCD27BrDbxzwSy+GjIZj0aLUucNg07N+f07UbS3vElhnEoF0VqKcP9EtP63ka49M82AzeGWNfXIfQ8Nu6q+F3NAl8EDi17jyQXP8col97Oqz2jZa01UtJEgMQghL0gaSsIxkknG4/GSFdaOTuXzcsnWr5m16n1MLjvrzxzO3y68jbL0DjFdR6pRy7TxvdBo1DEJxnCaUxCtuYT7ILLMevqckc30C2NbeOSuff7KvTF9D+G7qu96nceTV2fw5BfP8cB/X0PvcbKs34WNxjGb9JhaYIcjiA2VTy7v+RRRVlaTkIsRqdGti/BytWVWG6//u0hWq842G9Dr1BytqAegY9WxBu29xpDGP8b9gm/OGtOoUYdSY261Cp6/bQQ5GcYTDt34SxSfKhas2R+S9RrAqNcwamBnpo4+k1qbK66F56RjW/l7KLXa+M2bjdsTFhzbwzPznybdXsNfL7yd/w66pNEcOU0sUtban+VEk8CyBhGjZcVyK0g6gb6qwTHzkQiEK6p8Xi4uWszN376HyWXn+55n85cJd2AN618awOvztxB0uBvXm8kyGzEZtJRX2blqTMEp0cibgsPlYd32EtljdqcnYmSQ3DjB9xvrziSS43Zvx0Ieu+ZZnp3/FL9a9iZ6t4svh10eck54pUrBqUMIeUGLEG6eiYRaBTlVpdy7+A0GHdxGrSGVVy++lxVnjQWVCqNeI2tPzkk3MrAwhxWbGmd3mgwannl3fZsrg1tV66Cssl7xHKXIoGglgKPV1lGy/f+c14PfTHue5/79JL9Y+Q5AI0Ef7foELUPrfsoFpwVKETPhjNr5LW+8fx+DDm7j+55n86ub3mBF33GgUmHQqmUFPPjtyTMn9GLC8HyyzX6zkPrEBvZQWR3l1Q58nNQw5y3fk4hbSyoZaQbyMk2K5yhFBgUW1qbeu8frxevznchU9qMOMgoczu7Kb6Y9R3lqNr9Y+Q6TihbHdX2ClkEIeUHSiSUpJ8VRx0Nfv8ZDi15F7fPyx4vu5rkrHgsxz8iZYnLSjUwYnt+gnc6c0JtBvXKByDZ68GuYgbDN1opBp2FE/86K50SKDFJaWGO993nL97B84+GQksvh3+nRzM48cc0zVJoy+NXSvzP2x29iuj5ByyGEvCDpKMV1A/Q9/CN/+uA+LvhxJbs69ebe619jWf8LGzlXG42bqufJWcOZOeFkj1iHy0PRnuip/G1Fw5w9pR8Thudj1MubOyJFBsWSjKZEPLuvIzn5/PnWF7AZUrhv8Z84v3ht1OsTtBxCyAuSjkGnYWBhbqO/azxurlvzEc9/9gS5NeV8eu40Hp3+PNaO+eSkG1CrIDNNH3Hcqjonny3fgyeorVKsqfxtRcPUaPy7k5fvHMnI/p0avpfgHYwcsSZMRSKekgg+H1x+xxUsfPwvOHUGHlz0KheUble8PkHLIRyvgqTi8Xr5ZNlu1m47EvL3brVHueerV+lztJhj6R149ZL7+LFrX/9nnB6uHV9Itw5p5GaaeObd9REjctZsP4rJqG2I4Ig1lb+taZgpBi23TO4bc7PseBKm5IinJEJ2un/ROFbYnz/OnMMDHzzBXZ/9ji/69gCEkD/VCCEvSCoBu24woyyruft/fybFZWfFWWP4+/jbGlU4fPdrS0OHpEGFOSzfFLpIBBMcwRGtTHBOestnqyaSeJqXNydTN55yy0N657Jg1T7/udkSXHI/jyx8iYt/dzcLUtOZMmNsTNcrSA6J6gz1DjAZKLVYLP1P/C0bmAf0wN8ZaprFYrEmYj5B28Dh8rDJUtrwb53byS++eYdLi77GpjPy6qX3s6LPmIif9/rgYGktPp+P8/t3Ym2EVnbhBc+mjy/E6/OxpqgEh+ukKUevUzGgIKtNhE/KEasWH6C5mbpyJRFSjFrq6t1U1jnIDquKGWBt7/OZO+4Wbl/xFpc88ytc41ei6xh7DR1BYkmUJv8u8Gfg/aC/PQoss1gsf5Ak6dET/34kQfMJ2gBVtY6G8gRdrId5ZOFL9Czbz0+5PXhh8kMczu4a0zhHjtdx79UDI7ayC7cxa9Rq1CpViIAHcLp8fLO5BK1G06YSdKLFu0cjHu0/mOBFoqLaztKNhyjacxxrrYPMND0DC7KZPr6Q8ip7I/v9wiGTya05zlUbFmC7cTp1C/4DJuVw0GjEu8gJ/CSq/d+3kiT1CPvzFfj7vgK8B3yDEPLtiow0A9lmPf3WL+OuJX8hxWXn6wEXMXfsLTh1sTs9vT44Wm4jxaiTFfJyNVeCdxDhbC4ua1MJOkqll1tisTLoNKzYfDgk0ayy1smKzUfQaNRcNaZA1n7/3ugb6eKo4rzNK1Dfewc1b/4zasSUHM1d5No7yfyGOloslkBO9lEgtm4DgtMGg9vJr1e9xcOLXgHgpUt/zV8m/iouAQ/+BJwNxWUcLG3cTzS4E1KA4B2EHBU1jjYRPglgd7qbHe/eXKLF3AOyJY19KjUfT38Y54jzMC74nJRXXmjS/M1N6kok4aWxmztWyfG6pP+GLeJ4tVgsPkmSohYfy8pKQatNjHaVl2dOyDhthdZ2vx5LMdaLpzBofzH78vzmmSNZfvOMUa9BpfLXHY+F7h3N7PxZ3p3jcHnIzErFqD/5KJszTORlGimrtMt+Ji/TREGPnJDPtFb+OabgAAAgAElEQVRKjtdFbD9orbGj0evIy429LV+yruGuaUPYd6SafUeqQ47vr3Aw75e/54ajs0h98XlShw+Ga65RnC/4WbY73RTtLZc9r2hvObdfZWqR39Hj8fLO/9vBuu0llFXWk5dpYkT/zsye0g+NJj5dOZFjxUIyv51jkiR1tlgsJZIkdQYi759PYLXaEjKxqGQXP4m0d2q/XoThtlvItdc1Ms+M6NuBmy45K2K52zSTFpvdjddHQ3TNLZP78ORb62XnOl5Zz9795Y1szoMKcyNGhgwsyKGmqp628IRkZZjINsuHMmaZjXicrqQ/6x6XJ+o1lBxzRdwdLdtvZ+LbH9Hh8kmobrqJyqyOuAcNkT03/Fkutdoos8rX74n02yeDj5cWhzxPpdZ6vlq1D1u9M26TWSLHCqCk5CVTyH8F3AT84cT/f5nEuQRNJKH2Tq+XlJd+T+orL+DQ6P2FxfqOCzll9yG/pqcU3mezuzlUWkt+hzTMKXocLk/EmO1IiT2BCJu124421Lsx6jWMHNCpTYVPGvXaZsW7J4JYYu6jtSQszx+M6c23Sb/hWtJvnEHl/77B27FT1LmV4vVbKqEtmrkqHv9OIseKlUSFUH6C38maK0nSIeAp/ML9M0mSbgF+BqYlYi5BYkmUU09lrcD8q1sxLFtCWWZHnpv8CPs69Gx0XnDXoEjhfeYUPWf1OFmzpimJPRq1musnSlwztpAyqw1UKvIyTW3G2RpMa+hMFe0aYhHGzosuoe7JZ0l7+gnSb7yWygX/jRpxo9WoYna4J4vm9CtO5lixkqjomhkRDjVuGyNoNSRKq9BsKyLj5uvRHNhPzehx3NN/NrUm+e1jZqohRPuKNbwvIEyK9pZzvLI+ZkFn0GnI79C6/BXxcio7U8V6DbEuxPW/uhtN8S5Mn3yI+eH7qfnT3xQjbuYt3xOzwz1ZJHI3cSp2Jq3f8yRIGonQKgzzPsb80H2o7Hbqfv0wVfc9jP7tHyBCdMvgJmpfASFz+1Um9u4vb5ex0k2Nd2+pa4ik7V86ojs791c0mN9qX3wN7a4fMc77GNfQ4dhv/oXseEpKiM3uxu3xkQQ/ZSOaWyIiWWPFihDy7ZhmaRVOJ2m/fRTTP9/Cm55B9dz3cE66BAOQatLLhjCmmbTMnNCrWdds1GtPuaATyBOu7ZuMOl7+ZDPLNx4KcaQ/fuNQqt/5kKwJo0l74hHc/QdQN3g4ZVYbdW4vWp8Pg06TdNNGPMEGiTSZtbT5TQj5dkT4Q61S+SLG6CppFepjR0m/+Xp0G37AfVZfqv75Ed6eBQ1z2Owu2c8ZdJoW074Epw6DTkNGmoFn/rmekoqTEXOBMhW/e38TT88+h+p/vEvGNVegu34mc65/mWO6DOCkg/zKC3omxbTh8Xr5eOluthQfp7I2tmCDRJrMgsfS6HV4nK6k7kqFkG8HhEfQZJn19Dkjm5+P1VBb7250fppJG1Gr0G7eSPpNM9EcLcH+f1dT88obkHoyTltZ+3IkxbEkaD0EnrWNu45hrZVf7A+W1lJZ6yBz9BjWTL+TUZ+8wb1fvMgTVz+DV+1v77hs42FUKlXCTRser5dn3t0QYuePJ9ggkSYzg05DXm5q0kNghU7VDgjPGKyocbJ2+1EOl9XJnm+zu7HZGwt/w78+JfPyi1GXHqP2qeeo+dvbIQIeml/HXNC2CTxrkQR8gOc/2IDN4WJur4tZ0+s8BhzawaxV74Wcs7m4jKmjezJheD456caY6uhH4+MlxbKOXP98rb9bWFMQmvxpTjwdfgJ4fXCotPZkGKPHQ+qzT5Hy1z/hTc+g5t2PcF54kaxN81Q4lgStg3ieteNVDp7+5w9U1Lp4fdI9dC8/yJUbv6K4U29WS6MAf/mJWpszYWYSh8vD5t2Ru4ZVxGjnT0TiYGAMc0bzirbFghDyMdJWK+BVVNtjavwQjFoF+R3SAFBVVZJ++2z0y5fi6FGA9b1PQOrNvKXFEROopo8vxOP1+W2eQSVp21ISkiB+4ukmBVBW6T+3Xm/i+csf5ZWPHuSe//2Z/blncCinG1nmk+G2iTCTVNU6qKyNXNMoPLw3nEQkDgbG+HHbAeb89Q6+GjGFkpt+mdRia0LIRyGeH7Y1LgRLNxyM+zOdc1Mxp+jR7NlN+g3T0e7dQ1HhcH5/0X0YVpRjWrueQ0GmnmCb5vTxhcxbvke2JK2oGHh6E083qXAOZefz+qR7+M3CF3l04Us8MPNFDNoUtJr4q1YqXV+OwvUZ9OoTrSTl391EJA4Gxhj202Y6Vx0Da2XSK4pq5syZk5SBm4LN5pyTiHFSUw3YbJFX7Hj4dNlulm441FBMq97hYd+Rauodbgb0zAH8C8Gny3bz8ZJiFq79me92HOV4lZ2+PbJQN6G0arxEul+Hy8MnS3fHXAgsgEatIuWbpQy+bxaaoyXMHz6VP064E4fOSL3DQ7VN3t5aVeuktLKe5RsPN8xpd3rYf7Qm5PuKhMPloaLajlarRhshBCeRv21boC3dr1aj5niVvVGRslg5mNMNc3015/y0gey6CpZ2HRry3MTyfDTn+mrr3SzfdJiqOmejd9fh8vDxkmLZd6mq1smYwV2iXlPwGBdtW0LfI7v4ZMR0jmV2inmMSKSmGp6OdExo8grEmhF6qut9RyLe7TMAPh/jVsxj6qr38Wi1zL3yIRaeOTKmj1ZU29lSLG/zVMqgFfXCTx+mjy+k1u5i3fZjTfr8OxfcTJ+SYibsWM72rv3YnH4ZU0f3ZMGqfQl5PqaPL8Tj8bJyyxG8MnVx7U6P7LubiJj94DEGHtyOS61lVxcprjGagniDFIjlh422EJxKb71SpIscOreTX3/9R2aveg9rahaPTHs+ZgEPoNOpqIxQiTDwfcnRmuqFC5qHRq3G1AxTpVur44XJD1FrSOWO5W+Sts/Ch4t3Jez50KjVTDqnO74ohc/D391ERI0FxjA5bBSU7mV3p144dMa4xmgKQsgroPTDZqb5nTSxLASnikCkSyxk1lXyu3/9lnE7V7Krs8T9173M7k69UMdjbfIS94tgc7hYXVQi8wlYXVSCzdE4lFPQenG4PBHrv8fKsYyOvD7pbgxuJ48sfImirT/LntdUJSoW5Sf83VV6l2KNGguM0ffwj2h8Xoq69Y97jKYghLwCSj+szeFm/sq9pKXoWnVc+PTxhYwb0kVRWHc//jMvf/IQZ5VY+KbPBTx2zbNY0/zhk3Jb2kg4PT6k7lmyxyI9xB8v2d1QCjgcu9PDJ0uKY78AwSmnSSZCGdYVjuCLYZfTreIQdyz5G3Kqd1OVqFiUH7l3d/r4wmbH7E8fX8hkt3/R2tGtPx2yTM2K+48FYZOPQuDLX11UEiKMgm13rTkuPLA9/WbzEdnjw/Zt4OFFr5DirOeD82fy2bnXNKkPZwCdTs2E4fkx1eVwuDzs+rlCcbxdB6w4XJ5T/j0KYkMpwkatik9peG/UjZx1xMLYXd+yPb8fiwdOCjmenqrHZGiaCIv0XgeQe3cTUdpAo1Yz6OcifHo9M564gZ5ndaOmSr4pSqIQmnwUNGp/o+JUo/zDtLn4eMKz8uLF7nSH9J0M70Mpuz31+ZiyaSG//fJ5NB4PL1z2IJ+NmNYsAQ+wfW8FV40p4Llbz+X520bw3K3nMnNCb1kHWVWtA6tCL1Y4WQpB0DZQ0pI7x9mm0KPR8uJlD1JtNHPbirc4s3RfyPHKWifPvLuej5cWnwh9jE7g3XB7fMyc0JuX7xzJyP6dyEk3xPzuBmL24xXwDpeHiuL96LZtxTViJHldclukdWHSZ5AkaT9QA3gAt8ViGZ7sORNNNLt7IrPy4iEQlVK0t5wyaz1ZZj2pJj02u6tRFELwbkPjcXPbire4tOhrKlMzee6Kxzha0B/qmh+qFxwlEC1SIJa46tZg8hLER6Qqi2MGd+a3Edo4AqjVEC6ry9LzePXie5mz4DkeXfgS9133CvWGk89VrJFsShFct0zum9Qcl+C5B3+3CAlY120QvWNcmJpLS5lrxlkslsj5xK2cWEvyBqrvtZSgDw/drKhxhpT4DU9SArBs3c9t/36WwQe2Utq9F87P/s3NWR0xGbQ89c4PihmBsRCPUFYqgRCgNZi8BPERyazhcHnINsuXoQbQa9XYnY0F38aew/nX2Vdxzfr53LPkz7xw2UONdpxKIboOl4cPF1tYs/1ow9/CF4dk1uoPfk+H/bQJgE+0BfRZvod7ZwxLypzBCJt8DCgJI6l7JhC6WpdX+zM9h/TKZeZEeVNFc4mnTkjgBZjZU4P6wQfJObKf7wvO4Z1pj9J3n4vp441o1GqG9MplRQTbfazEK5QDi88mSxkVNY4Gu21OkKYlaJuEC06DTkOfM7JZGyRsg7E7vRj0GhwyNvJ/jb2eAcd2Map4Ldvy/8uiwZeGHJerOxN4JzdZSiMuLMnqqxrYGZgM2ob3VO31MOTnLRxLz+NQdj71xcexO5MfPdYSQt4H/E+SJB/wpsVi+UcLzJlwgregFdV2DHr/Q/Hd9qNYDlhJMepCqttV1jpZsfkIew5X8+Ss4QkX9PFEMVhr7LhWfEPOL2dhqq3i82FTeW/0DXgdao4EaTMzJ/bGcrCSI8dtUUb0c37/TlgOVDar8UGjRhMGLfUOd6sqDSFIHDMn9mJTcZmsszMzTU9VBJNhvUfF7yf9mtc//DW/+OYdijv1Zk+nk8+aXN2Z8J2uHIlOQgo3C2Wk6Rt2x1JJMWmOOlZJo0Clwlpjx1rtSLoQbgkhP8pisRyWJKkDsESSpF0Wi+VbuROzslLQahPzYuflJa6vp93pxlrtYNaU/lxR42D+8mK+2XS44Xh5tSOiXflgaS1frN7PHVcNStj1AJgzTORmGimrtEc99/J939LjT2/g8Xh5Y+Kd/G/AxJDja7aV8IupA0g16RnapyNHVv8UdcwOWSbuv86/1bRWO8g64di1Vjswpxua5FDKj/G8RP62bYHT7X4vOvcMvlq1r9Hfzx/YhQ07j1FqbRxtYtCpqTDn8Ool9zHn82d4dOGL3HfdKw29hM8b2Jn8LpkN59ud7pji9XMzTRT0yEmYA3Tugm0hC0uw+XPEnu8BWH+m/73JyTCS1cR3JR6SLuQtFsvhE/9fKknSF8A5gKyQt1pj0yCjkZdnTkgh/vDtXsCUEFeCEPBdUQlTzjsj4Zppr/xMyirlt74AKp+XG1d/yNXrP6fGkMbvr3iEbd0HNDqv3uHhjU83c/0kie+KYjPXDCzIaQj9Unm9vDl/V4uUJUjUb9tWOB3vd8p53bHVOxs5Zq8c1QOtRi27ADhcflv95h5D+HTENGaum8evv36dZ6c+RtcOZq4c1SPkeyq12iiTWSzCCTzHifiGHS4Pa7Yelj/o83H+nu+w6YxsOWMwADU2Fx8s2smU87o3+z1RUgSSKuQlSUoF1BaLpebEf18EPJPMORNJ+HYvEOMbT6wvQGVdcjoizZzYi42W0oYXIBi9y8H9X7/OqN1rOZTVhWemPkFJVpeIY+06YKWssl7RBKRSIVs2uLXW7hG0TpTizWdP6Yet3hkxfh1g3ohp9CmxcPZPG7jmh/kMeuvlRkIyWuRWtlnPUKlDQn0+SibUgtJ9dKo6xkppNC6tHvDn2ny1ah+2emdS35Nkx8l3BFZLkrQV+AH4j8Vi+TrJcyaEpjTbiER2ksIAUww6Rg9qLLjTbVU89+8nGbV7Ldvy+/HQtS8oCnjwC2aP1xsxezfbbODp2ec0intX+p42WcpOy047gsQgF2+u0fjzUpSSnLxqDa9c+mvKzLlct+ZjOm9ZJzu2UlarKs58kPDcEzmUyiWcv/s7ANb2Oq/RsWTXuEqqJm+xWPYBiTVGtxCJSs+G5IYBTh3dE7cP1m07gt3ppYv1ME9//gydqo6xos8Y/nTRXbi1upjG+nZrScQooqFSHvl5aY3+rvQ9VdQ4+HCxhVmX9hHVJAUx4fF4+WCxBWuN8rtXbUrn95Mf5qXPHiPnrl9gXbYab5euIeeER24Fk4j4+vBnWqtRkWLUNd49+Hycv/s7HFo9G88c2miOZFagBJHxGpF4KzjKkZNuSFrmq7/jfDFPvf09KzcdIsWg5WptCa999hs6VR3j03On8eol98Us4AGK9pTHnb0b7Xtas/2oqCYpiJl3/t+OiCGW4PeHqU48l2dMGU/tc39AXV5O+i03gjM0MidgFupfkB1xvGhadKQKqR8vKW6k2c9bvke2f2xB6V7yrYdZf+bwhqqTwSQ74U/EyUcglkQdJc7v34kbJklJ0+DD7eD91i9j5uLXUfl8/PGiu1nW/8K4x2xK9q5Bp2FgYS4rNkVwOJG8WGTB6YXD5WHddvmKpAE656byq6n9yU43YtBpcPp6Yd/wA8b5n5E653Hqnn+p0ZhFeyJH2ZRX26mottM5p3HJBSVT5MotR/hm85EGzX7q6DMjnnvhjuUALOs3XvZ4shP+hCavQKDqXFaaPuI52WYD44Z2baT53nxpn6T9cCEPn8/H1T/M5+FFr+DU6Jlz5ZMRBbxaBRcM7kxODFUzY6nPEdhNbN2t7Ls41SWXBW2DqloHZZXKETGHy+pYsfnwyedSpaLm5ddx9zmLlLfexDD/s5DzK6rtUbO4F68/IGtvVzJFen2Eafa7Zc/Vul2M2bUKa0omm3oMAUJ3I5eP7pn0hD+hySsQHAUQnhYdYKiUx8wJvXGMa7n+roGHT+Nxc8eyN5m0fQll5lzmXPlbDuSeEfFzXh9ceu4Z6LWahFTNjCXZBET9GUFsZKQZyMs0ycbJB9NoZ5iaSvU7H5J50VjM99+Fp2cB7iH+WPRYehyv3lrCqi0ljezt8fSs3fWzVfbcc/atJ91ew+fDpuJV+693YM8c/m9sAXmZJvK7ZCY9RFZo8jFg0GmYdWkfRVt1UyrTxeKxlyMjzUAXvZsnFzzHpO1L2NOhJw/OeFFRwIP/mjPSDAmpix1P9JGoPyOIBYNOw4j+naOeF74zdLg8lOR0peKvb4HDQfpNM1EfLYm5gUm4Vv7pst0N1xNr053KWgd9ZHopTNr2PwCW9RvX8Lete8t5/V9bmb9yLx5P8ouUCU0+RhJRSzpAc3uamsqO8txHj5J7cA/rzxzOi5c9gF1vivq5YGHb3HuJNfrIqNcwdXTPuMYWtF8CcfJyETEBAjvDxu9ROrfMuIfRH79O+qyZHPvnv5sUIbe6qIQxg7uSl2lqVM5EFaEmfpbZyIyJvTEZtQ0x/t3KDzL05y1s79ovRAELXlBSTHqmjuwR9zXGg2bOnDlJnSAebDbnnESMk8gO9+Ed4rUaNakmXZO7qgN8umw3Szccauj8Xu/wsO9IdUhnerm5ATTbisj8v8mkHTnA1onX8OdL76fGq3wt6Sl6zu/fkRkTeoV0oG/OvWi1ar7bcVS2e30wXq+P0QM7k2qKPcpHiUT+tm2B9na/aWlGCjqZGTOkK5U1DtlolZEDOjGkV57se7QmtQeDdbV0+n4lx4ssLMsfho/4YuI9Xh8rNh/mu+0lVNQ4mD6+kLFDujJqYGfcXh/7SxqbV0YO6MTQ3nkM6JnDuKH5VNbYGf/VXAqO7mHu2Fs4lCNftMNaY2f0oC7NkicAqamGpyMdE5p8BJqrbUciWuPvq8YUoNWoZCtazlL/TOZtN6Oy1VH79PN0+eWdPOP24lapefD1lbKZrwDVNidb9xxHo1EnrNSAQadhYEFO1KqVWebGhaMEgmgETKQmo1a2y1jE90il4rULbufpkgOctfZrrlbl+LudNYGKGidLNxzC6/Nx/USJDlkpzJzQC41a1XBNmWkG+pyRxdTRZwL+97vW5uTGczvS+c6VOLp2Y8Qjt/D95zuQS5Q/Xlmf1Bh5EEI+Ikqp+s0xc1RU2yM6cgK2xqUbDzUqcmR4759kLH8TlV5P9Vvv45xyBeB/GXIzTFEbOoU/sIlgwvBuUYV8n+5Zwh4vaBJKJtLyKltEU8yxei+/v/xRfjv3Pm5Y8xHlqdkNEWdqFYwa1JlxQ7rywkebZOvXh7N221GuGVuIQadpuKapo3vyyZJidh2w8t32o+z6uSKkYc8v1n/K5fZ6HLf9EunM3IgO3NxMU9KVIOF4lUFJ215dVMITc9fxmzfX8cTcdbKtx5Qcqkre/iyzMaT+NPiLjN307XvcufRv1BrS+PTRvzYI+ADWakdMDyv4H9hEpVBnpxvJNkcOLzXq1cyYKGrXCJqHXFCDUhJeRpqen0nlqf97kmqjmbuX/IWz9/k7UvlORJid0TGd8wdEd/KCv8ZMWVjxxAWr9rFm+9GGJKmKGicHS2spr3ZgtlUxcd0CKlKz+KD7GEUH7oj+nZOuBAkhL4OStm13ehplvwUyOgNx45EWgWje/oGFOdQ73A1z69xOHv7Py1y94QsOZXXhwRkvsNDdiZowG21WuiFi7Lvc9Yc/sE3FoNMwVOoQ8fiogV1IaWKjZYEgEh6vl/kr91Jnd8keH9LLrzkfyunGM1Mfx63R8sjCl5COWMhOPxnOO+PCXpzfv1NskwZtlaNFll29/nNMLjufnXM163+uxeHyRIxomz2lX+w33kSEkJchltjaYAKp0ZFSoAOLQLSIlAnD8slIM5CZpie9vtpfZKx4LTu6nsXD1/6Bo5mdqbY5eeqdH/h4aTE2h4vSEwI71lAvoNnNuoOZPr6Q8cO6YtSf1EaMeg0XDusqujoJkkLgPQvfvRr1GiYMz2fmxN4N74OlSx9emPwQWo+bp754lot0xxs0Z41azQ2TpKgKklGvIS/TH73m8fpr60RSArtYDzN5y38oNeexeMBFDSbYgJmnUYP7ZjpcY0GoWWHEGlsbTEW1ncNlNYomnqmjeyomV+SkGxtStceZbVz8p0foUlnCSmk0r0+6u6E8Kfht9Es3HGJ10REcTi95WSb698zmwmFd2bK7nIpqu6yTB0If2ESgUau5fqLENWML/TsElYq8TJOwwwuSgpIWnWLQctWYAjRqdUjo48aCs3lr6gPctuBlrn3pLqrO7Y57oL+meyzlS0YO6NTwPM9bvidybR2fjzuWvYnO4+atsbNxa3XkhCUCJrOXbCTapZBX6szelOqTPuDPn2+PmD5td3r4ZEkxt0zuG/GBCsSwq9etZcbTt2CqrWLeudfw0fkz8KnkV/uAJlNqrWf5xsNMGJ7Pc7eeS1Wtg69/OMA3Mk7R4Ac2kRh0GvI7nF4djAStD6X3s7L2ZN+Gxk7bMdRcWIj57l+ScfXlVH0yH/ews4HY+wxHM9OM2/kNgw8Usf7M4XxXOAJoHYmA7UrIxxIWqaRtG/WaiI0MotXH2HXA2mCbA2TDwgwL5pNy5+2o3G7ZNn3RCIRgdshK4bqJvdFq1P57rXGQbRaNsQVtn4w0A1lmvWxj7sy0xuG6wZqzY9oMAMz33EHm/02m+h/v4px0Scx9hpUWmPzyg9yx7E1sehN/H38rqFStJhHwtBTydqebUqut0Y8USwcjpe3b+QM6oVapFLPxImGtOallzJzQmynn9+BQaS35HdIwm3SY3vgjac89Rb3exO+v/A2bTxQzim8Ou4ImIxpjC9o+Bp2GVJO8kE816aI+445pM/BlZJJ+2yzSb5pB7e9ewD77NlCpQhYEc0rjqLFICqDJYePRhS9hctn5w+SHKM3oCIDzRMz8qQ4+SPrskiRdDLwOaIC3LBbLH5I1V0BTL9pbTpm1PkRTd3t8UZOQAg+IkrYNUFvvYt2OY3FdW6RU7NxULfeveZsBy7/A0aEzj0x6hJ/yejTp/uUSj06FDVAgSBYOlwdbhKgam92Fw+UJEfRyplnnpEuo/OI/ZFw/DfNvHkK37jtqX/0TPnO64txyCqDBZeepBc9yRvkBvhoymTW9RzYcay2F+ZLd41UD/AWYCBwC1kuS9JXFYvkxGfMpaeoThuVH3GqFd2ZR0oI/XlqsKOAjmXQCtrmPlxY3XJPJWc+dn7/EgP2b+KlDT+Zc8TiV6TlE9JpGIcUYXZMRCNoySiaT4N2yP5x5N1uKj1NZ29g06x46HOuSb0m/fTbGLz9Ht2UTNa++gWv0mIhzO1wexg3pisfro2hPOd6jR3l80UtIh3fyrTSKt8fcHHL+wILsVrGLTrYmfw6w50QbQCRJ+hS4Aki4kI9WLmDK+T0i2tojrbjhWnAslRcDJp1oqdg5Ncd5csFz9Czbz4YeQ3lx8kPU601NFvAAdfXORpqMQHA6oeQzC94tP/PuhpC6N3KmWW/XfCq/+A+pL/wO0xuvkXnVFOyXX4ntwUfx9Dmr4bONfHlmPVOrf+Syz19GV3qU+iv+j61XPUzWvsqGUgepJh1Fe8tDGosELAotLfiTLeS7AsFB54eAc5MxkfIKb6e23iXff5HYPeDRIm86Z6cwbVwBeq220S7A4/Xy3uJdlFc76FH2E0998Ry5teUsGngxb46/taHWdICAh18doeqd7H3WOpNeB0MgOJUo+cwC7/EHi3fJFjYDmVr0Oh11T8zBMfly0h59AONXX2D86gucoy7AMWUqrrPP5d/7XKzaeoy8mjImHdrBuB9X0PfILrxqDbVPPkv9nfdwrUrFlSdMQ4vXHwzplBZYYCwHKhvKHgQE/13T4ve9xUurcrxmZaWg1TZtdTNnmMjLkm84kJtpYs2OY7I/fM8u6dw1bUhMSQlKcwCUVNhY9P0hbp06AIDgunNzF2xj3fZjDP1pE48sfJEUl513Rt/EF8OnyiYneX3wzG0jWLf9KIvW7o96bQB5mSYKeuRg1LeqnzXh5OW1r1BNcb+h3DVtCCkmPeu2l3C8sp7cTBPDz+rIlNE90Zv0bFXIc7HW2NHodeTlhrX7mzgGJqyH//wHXnwR/apv0a/+FoA7TvwvmB96Duery27jicdvJi/ofct1utnx2VbZueV2FikmfYO8SBbJlgaHgW5B/84/8TdZrM1Mtx9YkCO7wvfrkcX3EXpHVtU6KTlWHfPWKdIcAWu+ixwAABa4SURBVNZsPcIl53Rr5PxZveUQk4oWc8eyN/GoNfxh8kMhTho5Vmw4yMwJvXA63Q01qqNdW01VPcntM3NqycszJ72TTmtC3K88U0f24JJzulFRbWfpxkN8v72E/67dT0aaXjGcOSPVgMfpijzHuWNg/hjUBw+gX74U1/oN7N5YjNbtotycw/7cM1hXOIKy9DzUKti7vzxk51xqtVEWpbNVMOu2lzSSF01BaWFMtpBfD/SSJOlM/ML9WmBmsiYLRL8U7S3neGV9gz183JCusolB0NjpGsscNrs7YtabXGPgqup6Ji96m2vWz6faaObZqY+zq0ufqHMV7Sln2rjChqp3v3tvAyUVjRdCrVrFmCFdRAy8oF1h0GlYsflwiGkkWr7K4BhNs/WdunL08msxXXM9f3t3vaIPIBDBYzJocbo8MbcMhNOg1LDFYnFLknQXsBh/COU7FotlR7LmC0TF3H6Vib37yxvs4Q6FLz7eMKdAvQvLAWvEH3LpxkPccNGJcr52O2c+cif91n/BkczOzLnySUqyYqt+Fxr3rsLpltfks9INXD02MXXiBYK2QjwtKAG6dUhj5oReiufYHO6GEsIB23kkX96gXjnMX7mXTZZSKmqcDf4zoz7297AlSg0n3XhrsVgWAYuSPU8wRr02ZGWMxVkTD9EaZhTtKccxzoOxupKMm2ag+2EdR3oP4qELH6DapByLG0zwAqTk9C2vim83IhCcDkQLhMhKM1BZ6yDjRNOdmRN7R1SEAhE0q4uOhBQ+K692UF7toFuHNGx2d0jEnM/nC5EpgQCJwOeNeg1Ol4css5EUo1bWJ9gSpYZPbw9dENESnOJFqWGGtcZO/Y5ddPrl9Wj37cU+9f9Q//GvDF9zkLXbjka1rQcIXoCUQsdaQhsQCFob0Qr+PTlruGx5AjnCc2zCKaus5/nbRuB0eRretSfmrlMcM8Wg5bEbhpGXaQrq9hYqf2ZP6UdFRV0Md9t02o2QT3Saf3a6kZwID9jZ1n30nD4bjbUC2z2/pu6xJxtVa/z8231s2RM5CsCgVYfUvVDajbSENiAQtDai7dDNKXrZ8gThxGL2sTs9zP9mL7dM7gv4HazRChlW1jrQa9UN76ac/GmJUsPtzogr12WmqePI1XAfWbyGRz94FHV1FTWv/Im6J+ZA0BYxUK3xF1P6otdF/vqdHi+1Yc1BTmXjAYGgNRLpnZg6+syI3dnCibXybKDIICh3pgog5+9LlPyJh3ajyYejVG44VkJMQNX1zCxayPSlb+NNTaPq7fdxjZ8Q8bMpBh0j+3eKaPLJlnlAIu1GWkIbEAhaI+HvRFqKngWr9vHU2z9ErDQbjpLZJ5jgsgmx1KFvDWWGoR0K+VjKDcdKwwM28gxSHnmA7KXv4+nchaqP/oWnf+MEh/CFZebE3uw5XC3rkOl3ZmbERUgUHRMI/AS/Ux2yUkJqQ4F8OYNwYhHY0LiU8fTxhVgOVMq+v906pLWakOZ2J+RjKTccD6raGvJunYVh2RLc/QZQ9dFneLt0BU4+gAHtQm5heXLWcD5eupvNljIq65yo8JevWV10lG+3Hg1pXCBCJAUCP3LKWr8zsyjaWyF7fqNyBmEE78rLq+2y59gcbuav3HuyyJnHp1AR043b46M1bLLblZCPVsRM6SGQQ11yhIyZ16DdsQ3n+AlUv/UevjRzowfQoFc3CssKXlgCMfUrNh1uqE8WCMdq7iIkEJyOyClr326N0JaP6EmPwWafQBbtd9tDI+HsTk/IuxitXlZrCWtuBetMyxHLjxIrmh3bybx4PNod26i/cTZVH36GL82fWhze0Du84XCAQANwh8tD0Z7jivMFzhUI2jvxJkFB7EmPBp2GzjmpTBtXSKpRXgcOvItKztfWUkse2pmQT9SPolu+lMwpk9CUHKH2t89Q+9JroPU/EPE8gIGFJRbvfryLkEBwutKUPswDC3Pi2qVXVNsjOmIDpUsiRdhB63G6QjsT8on4UYwfvEvGddegcjmpnvsu9XffF1JFMp4HMLCwNDUcSyBoj8TyvoQzYVh+9JOCWLrhoPLxjX6zTaQQztbidIV2ZpOH+DJfQ6JhNCpSf/8sKa+/gjc7m6r3PsV97ohGn1FqNBxO8MLSVsKxBIJTTazRMAFy0o1kpxtjHt/h8lCkUK4YTpYuMeg0rb6XcrsT8rFkvoY7TjuaVDy47M/krVuC+8yeVH0yH2/PAtnxDToNfc7IjlilEvw1NYb1yQtZWAL/HWgSrlKBz0dIdI1AIPATeB827CqNWnkyXlNNPObTgGO1NYc1tytzTTBKmWfBjtO0+mru/+ejSOuWcKT3ICoXLYso4APMnNgLo17+ocpM0zNn9tnMnBBaLEmjVjN9fCGDeuWSlWbA5/OfO7AgR4RPCgRhBJS1p2efg9mkUzw3XlPN6WY+PS0lh93pjjmlOZxgx2lnawkvffIofY/4G/U+dc2z2NMzo46RYtAxaqB8OeHhfTpErKcxb/keVmw6jPWEg7Wy1smKzUeYt3xP3PchELQHzCl6hveR97NB/KYaUPbdBWhL5tPTylwTMLMU7S2nzFrfpGzWwFatz5FdPPHl82TUV/Ovs6/ig1HXobJ7Y459jbfqZaJj+AWC9oJS5nhThXG4+TRQK74tmk9PKyGfiGzWjDQDkw7+wK2fv4TG6+GNCb/ifwMvAuTryUQi3qqXbSWxQiBobWjU6obM8S3Fx6msc5DdzFLi4e+vyaCNuWxxayNpQl6SpDnArUBAPX3sRAORpJAQTdjnI/Pvb3Dnv57HpjPy3BWPsbnHyW7qTW0w0iErBYfLQ6nVFvEhUSqS1JbsfwLBqUCjVnPDRRLTxhUmNMol2KEaS9ni1kiyNfnXLBbLy0meA0iAJuxykfbIrzF9+B6ezl344p6XOeDIRt3MBiMer/ekhlEbuSBaortXCQTtkdYc5XKqOG3MNc3RhFWVVtJvuRH9qpW4Bg6m+sN5XNSpM2OaWY7Y4/XyzLsbQmyFSiakRHevEggEApXP54t+VhM4Ya6ZBVQDG4AHLBaLVekzbrfHp9U2XWOdu2AbX63a1+jvl4/uya1TG5f+BWDvXrjsMrBY8Ey5nLI35pLZORujvvnr39/mb2XR2v2yxzpkmfjLw+Nl57E73VirHWSlGxJyHQKB4LRHFelAsySIJElLgU4yhx4H/gY8i79y7rPAK8BspfGsVltzLocp53XHVu+kaG85xyvrGzThKed1p6ysptH52u/XkTFrBurycjZedgN/HjKd8j9916wa8wEcLg9ri+QbgoC/Z+Te/eURt5ZaoKaqnsZX3Zi8PLPs/Z2OtKd7BXG/rZlENB5K1P3m5ZkjHmuWkLdYLJFbHwUhSdJcYGFz5oqFgEf89qtM7N1fHvLlh/8ghn/Pw3zfneDxsOyWx/hjxjlQ6wYSU963qtahmImXmWoQzlSBoA2SyMZDLUEyo2s6WyyWkhP/vBLYnqy5wjHqtWSkGRo17CivdpCZquNX27/gvC/ewpueQfmb7/KBxQgytvzmxKdnpBkiNvoGGCycqQJBmyTRjYeSTTINvi9KkjQYv7lmP3B7EudqwOP1MnfBNtZsPdyoYYfO7eSWf73Kebu+5Xh2J3xfLKC0Uw8q1q+THas58elK0TLdOqQxc0KvuMcUCASnlraYtJg0IW+xWG5I1thKhK+yAQGfbqvi8a9+T98ju9jZWeJ3V/yGoQc1TCtMXnx6eNZcRqqeob1zmTmxd6vc1gkEAmXaYtLiaSVpIq2y+eUHeeWTh+l7ZBcrpdE8fs2zVKX8//buPUaq8ozj+Bd2dRHZCsJ6ASQKLk9UvKBURWO9UcWmiEoVIRpNrca0NhptE42msViTWlPbxmhjbC21Daj1itHGugWjtWLBgtTbs6yXIkIDLCuIsLuwS/+YWRx2z86cZc7Mct75fRIS5pwzc553ZveZd99z3ucdyvLGzGpMvdWpsDGF69TEMWBA5tJ3ddUAqvaGRR9FZI+kZTWoXEHdnxf1LXvcqre57fl7GNK2lfmnzmTe5Mt3LfLx+ZeZVZly70/fuLmVmmwFyTfe+R++qmWPL6qkbexORPJL46TFoLqV3b9lz1vxN3769BxqdrTzy6k3Me+0Wbut4tRVi6brrpyfXXsKp004hNb2DlrbO9jJV4m5r5UgC43dab1WkXRKw2pQuYLqyXd9y/59ySqueu1RZix9ls2Darl7+m28N+roHsdHDcd8sCp6vlZfL6qkcexORArra/HB/hZUkgeYedZYpt1/K2OXNrB62Ch+c+VdjDzlWA7q3MnbK5tp2dK2a0GP7sMxSSZmFRwTCVta6uQEl+T32bCesW8upPW0M/ji1w9z46iDv5oQdU4Hf37JeT1nab7ccfIZZ45LLDGncexORMIT1Jg8QOchh8KaNXzx9POMOHxkj2SabzgGer/TZk8Sc9rG7kQkPMH15AE4+GCIqAcRZzgmyUqQaRu7E5HwhJnke1FonHy/mmqaN7Uy48xxiSbmtIzdiUh4KirJ5xsnHzyomjlzl6Si4JCISFwVleQhemGOwYOqYy/sISKSJhWX5KMW6J0zd0nksf9YsZaLzhjL4JqKe5tEJBAVOxbRNU6+rW1HrxdjW9s7mP9yY5kjExFJTtBJvm17B+tatuYtIXDAkBqG1fa+CvsHq1pUgkBEUivIcYiOjk7mNTR+tVDIkH2ZWB9d4re6agA1+1QD0as4NW9uY+PmVg4dvn8ZIhcRSVZRPXkzu9TM3jWzTjOb1G3fbWbWZGZuZucXF2bfPPL8uzQsXb3rVsnPt7SzaNka5sxdSkdn527HPr6wibUb868t2/BWz7txRETSoNjhmneAS4BXczea2dHA5cAxwFTgQTMryyygtu0dLH5nbeS+T9dtYV7Dyt2O7a1SZK4VTc0ashGRVCoqybv7++7uEbumA4+5e5u7fww0AScXc664Nm1pY13Ltl73L88p85tvBmyurtmwIiJpU6oLr6OAT3Mer85uK7l8K7fAVwuFxDm2i6pGikhaFbzwamYNwCERu2539+eSDGbYsMFUVxc/qnPqhEN58Z+fRO6rG7of4w4fzqB9M00//fhRLHjto7yvd/rxIxk9MpmlAEulrq62v0Mom0pqK6i9oSt1ewsmeXefsgev+xlwWM7j0dltebW05L8AGtd1Fx3Lf5o27DaLtctx44bzxaZtdJUvmzZ5DFu3tfdY+q99e8eu4mTTJo9hfUTBs71FXV3tXh1fkiqpraD2hi6p9ub7oijVLZQLgHlmdh8wEqgH/lWic/VQVTWQn1w9iXkNK1neuIHPv2zjwF6qSUZVigRUNVJEglBUkjezi4H7gTrgBTNb7u7nu/u7ZvYE8B6wA/iBu5f19pSqgQO58jzjsrOPjJWwu1eKVNVIEQlBUUne3Z8Bnull393A3cW8fhK6knfX7Ff1zkWkkgQ54zVXR2cnjy9sYlnjepURFpGKE3ySf3xh027141VGWEQqSdBd2XwzWpflTIoSEQlV0Ek+zpquIiIhCzrJ55vRqlmsIlIJgk7yXWu6Rpk4foTushGR4AV/4TVqTdeoSVEiIiEKPslHzWhVD15EKkXwSb5L9xmtIiKVIOgxeRGRSqckLyISMCV5EZGAKcmLiARMSV5EJGBK8rCrDLFq2YhIaCrmFsooKkMsIqErdmWoS4E7gaOAk919aXb74cD7gGcPXezu1xdzrlJQGWIRCV2xPfl3gEuAhyL2fejuJxT5+iVTqAzxjDPHaWasiKReUWMS7v6+u3vhI/c+KkMsIpWglGPyR5jZMmAzcIe7v1bCc/VZVxni5ohErzLEIhKKgknezBqAQyJ23e7uz/XytLXAGHdvNrOTgGfN7Bh335zvXMOGDaa6Opkhkrq62oLHnH78KBa89lHE9pGMHjk0kTjKJU57Q1FJbQW1N3Slbm/BJO/uU/r6ou7eBrRl//+WmX0IjAeW5nteS8vWvp4qUl1dLevXf1HwuGmTx7B1W3uPMsTTJo+J9fy9Rdz2hqCS2gpqb+iSam++L4qSDNeYWR2w0d07zGwsUA/07DL3M5UhFpHQFXXh1cwuNrPVwGTgBTN7KbvrG8AKM1sOPAlc7+4biwu1NNq2dyjBi0iwiurJu/szwDMR258CnirmtUuto7OTeQ0rWd64gc+3aCKUiISpIme8dnR2MmfuUj5dt2XXNk2EEpEQVUSXtXttmnkvN+6W4HMta9ygGjYiEoyge/JRtWmOGzecZSs39PqcjdmJUFoqUERCEHSSj6pNs2jZmrzPGbp/jSZCiUgwgh2uyVebZuCA3p93wvgRustGRIIRbJLPV5umc2f0cw47aAizp9SXMCoRkfIKdrgmX22aA2trOL5+BCuamtm4uZUDhuzLxPoRzP7meN0+KSJBCTbJ1+xTxcTxdbuNyXc50eqYPWU8bWdrIpSIhC3YJA8w85wjAXrUpunaXrNPle6iEZGgBZ3kVZtGRCpd0Em+i3rsIlKpdJVRRCRgSvIiIgFTkhcRCZiSvIhIwAbs3NnL9E8REUk99eRFRAKmJC8iEjAleRGRgCnJi4gETEleRCRgSvIiIgFLde0aM5sK/AaoAn7n7j/vtr8GeBQ4CWgGZrr7J+WOMwkx2noz8D1gB7Ae+K67/7fsgSakUHtzjpsBPAl83d2XljHERMVpr5ldBtwJ7ATedvfZZQ0yQTF+nscAfwSGZo+51d1fLHugCTCzR4BvA+vcfULE/gFk3otvAVuBq93930mdP7U9eTOrAh4ALgCOBmaZ2dHdDrsGaHH3I4FfAfeUN8pkxGzrMmCSux9HJun9orxRJidmezGzWuBG4M3yRpisOO01s3rgNuB0dz8GuKnsgSYk5ud7B/CEu08ELgceLG+UiZoLTM2z/wKgPvvvOuC3SZ48tUkeOBlocveP3L0deAyY3u2Y6WR6A5BJfOdmvzXTpmBb3X2Ru2/NPlwMjC5zjEmK89kC3EXmi7u1nMGVQJz2Xgs84O4tAO6+rswxJilOe3cCX8v+/wBgTRnjS5S7vwpszHPIdOBRd9/p7ouBoWZ2aFLnT3OSHwV8mvN4dXZb5DHuvgPYBAwvS3TJitPWXNcAfy1pRKVVsL1mdiJwmLu/UM7ASiTO5zseGG9mr5vZ4uxwR1rFae+dwBVmthp4EfhheULrF339/e6TNCd5iWBmVwCTgHv7O5ZSMbOBwH3ALf0dSxlVk/lz/ixgFvCwmQ3t14hKaxYw191Hkxmr/lP2c5c+SvOb9hlwWM7j0dltkceYWTWZP/uayxJdsuK0FTObAtwOXOjuPVcwT49C7a0FJgCvmNknwKnAAjObVK4AExbn810NLHD37e7+MdBIJumnUZz2XgM8AeDubwCDgBFlia78Yv1+76k0312zBKg3syPIvCGXA93vNlgAXAW8AXwHWOjuaazIVrCtZjYReAiYmvLxWijQXnffRM4vvJm9AvwoxXfXxPlZfpZM7/YPZjaCzPDNR2WNMjlx2rsKOBeYa2ZHkUny68saZfksAG4ws8eAU4BN7r42qRdPbU8+O8Z+A/AS8D6ZK/HvmtkcM7swe9jvgeFm1gTcDNzaP9EWJ2Zb7wWGAH8xs+VmtqCfwi1azPYGI2Z7XwKazew9YBHwY3dP41+lcdt7C3Ctmb0NzCdzW2EaO2iY2XwyHU0zs9Vmdo2ZXW9m12cPeZHMF3YT8DDw/STPr1LDIiIBS21PXkREClOSFxEJmJK8iEjAlORFRAKmJC8iEjAleRGRgCnJi4gETEleRCRg/wd2twNfoc7evwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7b6848f908>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"y_output = sess.run(model.logits, feed_dict={model.X:X_new})\n",
"plt.scatter(X[:,0],Y[:,0])\n",
"plt.plot(X,y_output, c='red')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlgAAAFACAYAAABgCwK3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl8E2X+x985mtI0lKNCaUsBV21+aN3FYxUEVBQqx3qjIHgi4rWKrgpaulq1qOAtrquIILoieK0Xh4CAIijrhYpiFAQspa1Qjh4pzTW/P9Jp03RmkjRpOm2f9+vVF6VJZp6ZJ/PMd77H52uQJAmBQCAQCAQCQewwtvYABAKBQCAQCNobwsASCAQCgUAgiDHCwBIIBAKBQCCIMcLAEggEAoFAIIgxwsASCAQCgUAgiDHCwBIIBAKBQCCIMeZoN2C327OAV4A0QALmOhyOp+12ewFwHbC37q15DodjWbT7EwgEAoFAINA7hmh1sOx2ezqQ7nA4vrHb7Z2Br4ELgEuBKofD8Vj0wxQIBAKBQCBoO0TtwXI4HCVASd3vlXa7fSuQGe12BQKBQCAQCNoqUXuwArHb7f2AT4Ec4B/A1UAF8BVwh8PhOKD1+b17K+MmK9+tm5UDB5zx2p0gDMSc6AsxH/pDzIm+EPOhP+I9Jz16dDaovRYzA8tut9uAT4CZDofjHbvdngbsw5+X9SD+MOIkrW14PF7JbDbFZDwCgUAgEAgELUzLGlh2uz0B+BD4yOFwPKHwej/gQ4fDkaO1nXh6sHr06MzevZXx2p0gDMSc6AsxH/pDzIm+EPOhP+I9J1oerKhlGux2uwF4CdgaaFzVJb/LXAhsiXZfAoFAIBAIBG2BqJPcgcHAFcAPdrt9c93f8oDL7Hb7APwhwp3A9THYl0AgEAgEAoHuiUUV4WcoxyCF5pVAIBAIBIIOiVByFwgEAoFAIIgxwsASCAQCgUAgiDHCwBIIBIIWwumEHTsMOIVUkkDQ4RAGlkAgEMQYjwfy8y0MHWpl0KBkBg+2cuutFioqWntkAoEgXggDSyAQCGJMQYGFuXMTKSoy4fMZKC42sXhxIgMGJJOfb8Hjae0RCgSCliYWMg0CgUAgqMPphOXLlZfWqiojc+cmAlBY6IrnsAQCQZwRHiyBQCCIIWVlBoqLtZfW5cvNIi9LIGjnCANLIBAIYkhamkRmpk/zPXv2GCkrU+2w0eqI5HyBIHqEgSUQCNosejQErFYYNUo7ySojw0daWtxar4ZNcHL+0KFWkTMmEDQTkYMlEAjaHB6PP5F8+XIzxcVGMjN9jBrloaDAhVkHq1pBgT+/atGiBKqqmj7HjhrlwWqN96hCIyfnyxQVmZg71wSInDGBIFKEB0sgELQ5gqv0/IZAIgUFltYeGgBms98g2by5mnHjXPTu7cVkksjK8jJlSm29AaYntJLzRc6YQBA5OnjWEwgEgvAJZQjk5bl04x1KSYE5c2pxOv3J72lpkm7GFoxWcr6cM3bkkfoLawoEekV4sAQCQZsiHENAb1itcOSR+jWuQDs5X685YwKBnhEGlkAgaFMIQ6Bl0ErO12vOmECgZ4SBJRAI2hTCEGg5CgpcTJlSS1aW/nPGBAK9I3KwBAJBm0O+4S9fbmbPHiMZGQ1VhK1JW8i10kJOzs/Lc7Xp4xAI9IAwsAQCQZvDbIa8PBcTJ7oB6Nu3dQ0BvctGRIqcMyYQCJpPG7z0BQJBR0aPxozQjxIIBMGIHCyBQNCm0JsGltCPEggESggDSyAQtBn0aMxoyUYUFxvZtUt/shECgaDlEQaWQCBoM+hRA0tLNsLng4kTk9pMPz899nYUCNoqwsASCARtBj1qYGk3dzawe7e+2vgoIZo8CwSxJ+qUULvdngW8AqQBEjDX4XA8bbfbuwNLgH7ATuBSh8NxINr9CQSClqEtSAzIxoycQB5Ia2pgFRS4cLv9YcrSUiPQ1JO2dKmZiRPdrV7xqIRI0hcIYk8sPFge4A6Hw3EsMBC42W63HwvcDXzscDiOAT6u+79AINAZ0Xov4h1W0psYplzVuHq1bFwpU1xsZNgw/XmH9JjXJhC0B6L2YDkcjhKgpO73SrvdvhXIBM4Hzqx720JgHTA92v0JBILYoua9SEqCGTPUP9dacgl6E8MMPn/qGPD59OcdEk2eBYKWwSBJsbtw7HZ7P+BTIAf43eFwdK37uwE4IP9fDY/HK5nNTV3/AoGgZXA64dhjYdeupq/16wc//oiq8XLbbfD0003/PnUqPPVUTIepW7TOXyhCnd944XTCccfBzp1NX9PLGAUCHaNaWROz50y73W4D3gZuczgcFXa7vf41h8Mh2e32kJbcgQPx80X36NGZvXsr47Y/QWjEnMSfHTsMFBUlo7RGFBXBli1Vit6L8nJYssQKNH0geuklH7fcUk1KSgsMWGdonT9/SqqM0vmV2LKlOiLvUEtdI7m5yl643NxaqqtdVFfHfJftArFm6Y94z0mPHp1VX4tJFaHdbk/Ab1y95nA43qn7c5ndbk+vez0d+CMW+xIIBLFDqyrPaoXU1MY3f48H8vIsnHRSsmq+UVWVkRkzwgmZxY7WkhfQOn9+o8qAzaZsQLVW1aMSestrEwjaA1EbWHXhv5eArQ6H44mAl94Hrqr7/SrgvWj3JRAIYouWxEBlJcye3VhaoKDAwrx5iTidypVyMhs2mOJi7LS2vIC2RIM2rVn1GIyc17Z+vZONG6tZv95JYWHzc+mEnpZAEBsP1mDgCuAsu92+ue5nNPAIMMJut/8KDK/7v0Ag0BnTprmw2ZS9MIFVZE6nX2ogHEpK4iP6qYe2OQUFLsaPr6VxSLABp9PAuHGuRt6hSZNqufpqt+4MELnJc3MNPyWD9+67LWzbJowtQccjpknu0bJ3b2XcBiNi5/pDzEnrsGOHgUGDkvH5mhpEJpPExo3+PKEdOwwMHJiMJIU2nLKyvKxf72xRD43TCUOHWikqapoHFo/9B49lyBAru3erjwWguNjAvHkJrF7tr7xMT/cxdKiHwkJXWDlrer9G8vPVKiolsrJavyl3rNH7fHREWiEHS3VBFEruAkEHJ1x19LQ0iYwMtXyjxsQj/KWntjlWK4werRwqlM+F1QoLFyawYEGDx6242MTixYkMGJCsK22s5qClpwWNvYuBIUQRThS0V4SBJRB0cLTyiAINJasVxozRsgDimxzdkm1zmnPTD5UormWAVFUZdd9OJxRaBm8gixYlMGSIlYEDkznuuGSOPTZZtOcRtEvaiaNWIBBEg2wELF9uZs8eIxkZPi66yMT06a4m7/P5YPHiBKqq/B4im01i7Fg3U6a4yciIj+in3NZn+HAPCxbErm1ONOKpoQRQwzFAli83k5fn0kXye6Stk2SDVylkG0hVlZGqKv/v1dUNXka9CbAKBNEicrAEukHMSesTeFPt21d9PpxO2LXLf3OMZ2+9YAMoI8NH164Shw4Z6g3DaPJ81HKIpkypjfqmr5UzJhOY86Zk4MTjGtEyMl0ubaNLPQcrfOKdPxcNYs3SHyIHSyAQ6JJwq8isVujfX6J///i2qQmuGty928SWLWZGjPBELS/Q0j35wpF0yMjwkZoqtar0hFplZm5uUsgxaVWkhku88+cEgpZCGFgCgaDFiGUCs5YBtGqVOeqehPFImp82zcUll7gwm5WNkFGjPMyerWzg5Oe3fH6W1jnessUcUg6jvNyA06l2niSs1tDGV8+e+hFgFQiiQRhYAoEg5pVczREAlcdQXq48luYaQOEeW0smzcvnY9gwK2++mYDH0/Q4cnI8TJvmUjVwFi60cPPNtKgnK9xEdZlgz57WOczM9DFunDvkNkeO1I8Aq0AQDcLAEgg6MC2lhB6JAKg8hiFDrJx6ajI5OTZOPbXpWCI1gCI9tnCrKZtD4PlQU8A/dMhAcbG6geP1GnjuOWJWaahkeGq3/mlKsGGrdQ7HjPEwc6a/0lItjJiT43+PQNAeEAaWQNCBaQkl9EhzmeQx+EU6DXi9/h5+wWOJ1ABqzrE1pydfKA+Ztj5UA3v2+JfjUAZOtPlgWoZnpK1/lAxbrXMoV1pu3lzNuHEuevf2YjRKpKf71e1XrqxpNyKkAoGoIhToBjEn8SWUEvrPP5uoro58PsJVhg81hsCxyFVlgRVuWlWD0aq8hyNREK6kg9b5UBrXQw9pV+IFn8NIUav0mzSpluuvd5OaKjF7duNz3KWLxJYtTS0frerKcM5hpFIQekOsWfpDT1WE4llBIGjjNPcmFSqnqaSEsNq3BKOlhxTs8Qgn50cOQx15pBRSayqc7QZuTw25mlIL2UMmo6bjFK4+lOyFKyhw4fH4c6783rzGRJMPpuVNW7jQwssvW+oNxbVrnZSX+8+xxaJu2KoReA7VZD3COc8CQVtFhAgFgjZKtPlToXKa0tMjH1OgAKgSwaG8cHJ+Ag0KORwH6nISTiccPoxqW59IDBS18F8kYVDtsFvTMKTZDI884uLKK5WNlxEjPJSVNa8gQcvw9HoNjUKps2db6s+xbNiuX++MSA7D44G8PAs5OcmccYb/Jycnmbw8odguaP8IA0sgaKNEmz8Vy6TuYGNv1SozOTmekLlM4eT8jBrlwWIJbUwGjmHYsGQOHlT23IdzbKGM10grGpXykiZNqtU0VuSEcPkzvXt7GTDAL0nR3IKESJLYlXK9wtVJkykosDBvXiJVVUb8yf0GqqqMzJvXttsCCQThIHKwBLpBzEn4RJtjJKOV05SerjwfSiHJUHk94eQyLVtmZvduIyYTeL2QldUwluBwnExgDtD06RYWLGj6HrPZh8fT0NZn/Hg3Dzyg7n1xOmH69ESWLGlqAMj7a+75VwvnaoV55deefTaBV1+NXmU+XLV1rVyvcPOrBg+2UlysHBrt3dvLZ5+1DcV2NcSapT/0lIMlPFgCQRtkzx4DRUXRi2JGEvpR8+pUVEQnACqP4bPPnGzaVM2WLVVs2tQwFqfT3yBYieXLzVRUwN13W3jlFWWPiF9zKrT3xOPxG2kDB1pZskR9f05n871/wR6gcMK8Fgu88EICixYpH1+gpykczS/Zm9a7txeQ6n6aEq30RVmZob4yUgmh2C5o74gkd4GgjeHxwOTJnVDTU2pOEnQ0Sd0VFUSVUK40htTUhvfn51vqQkzK258xQ9nbpEVwU2WPB3JzkxQr5QIpKjKyaZORU0/1MW2ai0OHDGzYYKKkJLzE72DUzqnHQ73n76GHLMyfr+5x2rPHSHGxgYULE8JqUi0btG43ih4/GS3pi+DxQtMGzWlpEhkZPlUPVrTirQKB3hEGlkDQxsjPt/DTT+qX7vDhsVfC1krqXr/eTEaGr07HqjHRVrw5HAbWrlU/1rQ0Hxs2aFfnKRFs+OXnW0IaV34MjBtnxWqVMBrB6TSQnu7jkktcFBa6Iqq6dB5y8/0HezmNEnryB0ewjx7s9f8s2Efp/AoOW6q52uXkRpxYcZJETaNtSBgwAeaRFm6o7MwVJFOFjaoiG5VzO/PdpiMYMjYVX880fD164uuZhjezN05DMqtXKx+vySRx5ZWuJoai1ndg6dLGBiv4DeYxYzz1Blgwo0cLxXZB+0YYWAJBGyK0aKXE5Mmh25FEilZSd2mpkbFj3SxZ0vRG2hwFdI8H7r3XwuLFCVRVaYeQTjjBy/LlyuE8LQINv/Jy+OCDSJbCxv32iotNLF5sIiWlqRfHcOggpm2/Yvr1F0y/bcf0+05MRUUYi3dzRGkJn/tUEs5lmzQcZ5gXqIQ0pde+q/sJwnVEL17dl802juZXjuEXstnMAHZwJJIEN9zgbuL50voOFBcbmT49kSefrG30uYICFz4fjeZSzoOLxNMnELRFhIElELQhysoMlJaq57Wkp/vIzIx92CWUttXMmbV06SJFpJOkhlx5Fgqbzccjj9Ty/fcmxXGZTBJ2u1fR2ydXJk6fbuHDD83s3RtdOqqFWn569Xukfv+j8/bvMf30I+Zff8G4b6/qZySDgVJTBru8vSkjjb30YB9HyD4sDtK1zm/l/6kmmcN0QqoLDZuNPi6+2MVl491MHGvCKlWTTDU2vw+LLhyiJ38w9JhihvUvwfhHGYbSUkzFu7HsK+UMSjmDTxuN6SBd+DHhBP7vxRw48S+4TzwZ35F/AoMhhJ6XgSVLLHTpIjUyMs1meOghF/n5LkUdLIGgPSMMLIGgDZGWJtG7t7poZUs1ypWTupXCPaNGeeq9N6EEQEPhdPrDTeEwYYKbtDT1cV11lT9sp1QlmZ/vCivnSokEXJzINwzkC07gW07gW/qzlYQaD+Q1fq9kteL509F4jz4a71HH4O13JL6sPngze+NLz+C+B2xhVfQpcfGFLqb/qxanE6oyrDhUcp0WVHpZNdPJnDkWlheb2eOWOLHHLv6c9CsJv+/gGH6lP1s5gW/pRRmDa9fBvHX1n/em9cI96DQ6DRzMNQPP5oGiP6OW/xec2yZjtUL//iLfStCxEDINAt0g5iQ81Mrsc3I8Me3lFjwf4bapiYYdOwwMHJiMJGmHBgOPNZxxBcsK3H23duJ4IEewl0F8zmA2cBob+Stf0onaRu/xYcCBnV+S/sLpU4/DMCAHb7YdX0YmGNW9Y4Fjb6gKDV1ZZ7P52Ly5uj7n69ZbLSxerHY8ElarhNPZdBwGg4R8C7DZJK4/73fyRn5J4o/fYf5uMwlffoGxvLzRZ3ab+/KhZyTLGcXHnE01tvrXom3j09YQa5b+0JNMgzCwBLpBzEl4BPfAS0vzGxThKGtHgtp8tGT/uFDaSTJKWlOB4wJtXalBg6yUlCjvozvlnMUaphy1in6/fcIx0i9N3vMT/fmcQXzFyXzLCfzA8ThJbpaB4fHAjBkWlixJUDSClAjWvqqogAEDklWrLcOliaaWJGH69RcSPt9AwuefkfDJOkzl++pfPkwiH3EOb3Mx73MenXt3bvPaVpEg1iz90e4MLLvdPh/4G/CHw+HIqftbAXAdICch5DkcjmVa2xEGVsdGzElktHSj3Naaj3CEMNUMmXAaMAd7yaxUM5T1nM3HnM3HDGAzxgBtqGqs/I9T2MhpbGAwXzCQA3RXHFckIq/hHq/Z7KNXL4mSEiNZWQZyc2sVvYbhCohqEWr8O7ZL/P00B+dIKxjFcgbyRf25cpHAlvSzObrgUmpHjoGkpLD32xwBVj0g1iz9oScDK1bPuy8DzwKvBP39SYfD8ViM9iEQCGh802mPoRi58uz11xOorvYLhAajJv8Qjk5TWprE4F6/ckLJCsawlDNZR2JAud5hEvk6cRDH3jIU7xln8M/3TmXpR0kUFxtJSqrbZ7WkOK5IqyZDV4WCJBl47TUnnTpBTo6N6mrlwgG5oOCDD8yUlMjiqpERSrcsLd1Aae8TKSz6K4X8k16UcCH/ZSxvcQafcGLJCrh+Bb6ULtSefxGHx0/Ac/IpYFAei5pBnJ/vorBQ21AWCPROzEKEdru9H/BhkAerKhIDS3iwOjZiTrQJxzsTS1p7PpxOuPPORN56S71lTfD71drX/Kl3DRtnf0znTz/CsvojzNt+rX/Nh4GvOLnOf3U2GxjMlVOMjbYfHH4sLjYwb14Cq1dHl4+2Y4eBQYOS8fnUjaFAr1I4c1JeDsOGWSktjVwfTM2DFXj8Dz2k7Cm744oi7uu/GMvrr5P4w7f1f/ccm0PNpOs4fNElYLM1+oxWPqFSAUKotkDx9ni19jUiaIqePFhIkhSTn+zs7H7Z2dlbAv5fkJ2dvTM7O/v77Ozs+dnZ2d1CbcPt9kgCgUCZqVMlCZr+TJ3a2iOLjupqSdq2zf9vMG63//j69ZMkk8n/79Sp/r8Hs22bJBmNDeelE07pPN6VFnKFdIAujU6ar2tX6evscdJtqa9IR/CHZDRKksEgSX37qm8/0rGH+/l+/ZTnVWt+1fYrn6/OnbW3Ge6+As+/0ej/95Zb/D/Bc1JT0/De4w0/SC+k3ClVJPVo2HhKiiTdeqvk3LJd2rZNkvbu9Z9vpXGYTMp/79cv9PdEHmck8ygQRIGqTdOSHqw0YB9+ybwHgXSHwzFJaxvCg9WxEXOiTqyaO0dCS8+HnNy9YoWZsjJtj1y4zYXPGezj+OKVjOUtxrAUG9X1rxd37U+3y8/BNeIcDh13KmXlCaSkSFRUGOr/bY1cHzUvjs3mY8IEd6Pz0a1bZ26+uVbVixlJHpbZ7KNTJ6ipMah64NS2N2VKbRNJDqX3WqjluWGvc2XV8yR8uQkAL0be5FLmH3EHq/adhHIoUzkEq5Z7pzXOSBphR4pYs/SHnjxYLRbNdjgcZfLvdrv9ReDDltqXQNDe0VLRjqTfn15Q6v2n1ddOs1diVRWJK5aS8sF7fF+6GguH61/6ipN4m4t5m4s53Pko1t7mZOZMCytuaGrUBfY/jCdy7pQsM9Grl4+hQz2KrXfuvBPVHLO8PFfIfK5A0tIkVq92qhqWWvlhst6VPCdqavguErl/2xUMX38xr/7jJ7LeeY4JLGI8ixm/bzErGcGD/JPPGNroc0YjKIncK+XehTNOPSbIC9o/0dX0amC329MD/nshsKWl9iUQtHdkFW0l2mLTXK3ef8uXm3E6Q2zA7caycjmdb5jEETlHk3LTdSQu/xCL9zAbGcQdPMaR/MZf+YpHuIdfyaa42Mjo0VYWLEikpMSEz2eoM1ASKSiIrFl0LJGbL69f72Tjxmo2bHDyzDNNjSunE959V3kby5eb2bVL3QhXorTUSEWF3zBXMkDCMeo9Hv9cnnWWtS6xXvm9u3YZmPvlyVzNQo5iO09wO1Ukk8sq1nM6H5HLKWyq/4zRqPx9Vioi2LPHEKAhpjxOgaA1iImBZbfbXwc+9/9q3223268FZtvt9h/sdvv3wDDg9ljsSyDoiMhK6ko0p99fPHE6/cncstEUqnJO9aYoSZg3fYFt2u2kHn8MXS4fR6d33sLgdOI+ZSCVD81m9xc/Mz5rPU9wBzs5stHHO3WS+OUX5cTvsIy6Fkb20qnNZVmZgaIi5df27PEv5WpGuBKhDPNwjHq5atOvKaZsyGRk+LchG2tF9OEOnqAPv1PAfRwihVxWsYmBLDeN4c98h8fT+NZks/mYMqVWsfXSvHkJmvtuaw8fgvZDTEKEDofjMoU/vxSLbQsEAj/BoaRo+v3FA7Wqx6uvdmv2U+zZs/FN0fTbNhKXLKLT229i+n1Xw/bt/0ftxZdy+MKx+Pr2AyAR9dY5gQ2ag2kLYda0NIk+fWDnzqavZWT46NtXUj12JUIZ5qHaI0FoiQn5vX37Nu1jeIDu3E8Bb2fczNq/zaLbq88zsmYZuSznZa4mn0JKyACgSxeJvLymuXnl5dpjGD5c3w8fgvaNUBQRCNoIcigp2n5/8UJNk8rjIXQ/RamaxMXv0mnRq1i+2Fj/mjc9g9oLx3L44kvx5hyvqK8UbIgmJUl1CufqBlawUadHrFY4/3x4+ummr8nGkpIRfs45fmPoo48iN8xlTbLFixOoqvKfP5tNwufzh+bUQ5IS6ek+zj23IXFezVg77W8pSIX38d1FN/PpyKe5ieeYxALGsYRHuYtHuYvSUmsjA1g23hs0v5THMHmyO+QxCgQthWiVI9ANYk6a0ppK1tHMR6iqx+HDPSxYEFz1JTHhTxt4cdBLdHrvbYxV/n1LViu1513I4Usvwz1oMJjC89A4nbBrl4GJE5PYvVv7M9dcU8usWfr0BAYSWEWopb+l1DaouZWSahV6kybVsmqVWXGO09O9rFnjJDW14W+hekbK3xlL0Q5mMZ2LeQeAInrzYOqTzPgqF2uyQXNMgbRUdW0gYs3SHx2iilAgEDSfeIuKhiISQ8/phK+/NmomSE+e7CYhwe9pce3ex422V5hsWkDmb1vhN//73CefwuGJV1J7/oVIts4Rj9lqhU6dGvKT1MjJ8TBzpv6NKwjfi2m1QlaWpPodChetfLlVq8x1hnJTAys1VaJLl8jG3hCSPJqxvM0Q1vMkt3MyXzO3/BJc1w6n8qFHqep1VNihST17eAXtnxarIhQIBM1HDq8VFbVctVtw8rkScpXY0KFWBg1KZuhQK/n5FjwK+faB7x071qrWHYWMDB+Z6V5mjfiIrcddxB5jb+6rnEbmwa3sNfbkUe7krF4/8PcTP6Vq3JXNMq5ktBK1jUaJK66oZeXKmjbXfiVUQjzE5jsUqpJw8mQ3OTlNvwxbtphV96M19oICF1Om1JKV5eVz0xDG9t7Ia0OewdelK5Y1q+l++kCqp8/ij93KBR/+0KRXNSFeIIgnwsASCHRGKF2faKvdIjGaIrlJB75Xkgx4vU0trK4c4LHMJ8gcfhJdLzmf5BXvY0Diuz5jOJ93yfDtZhqPsrY0JyYGpVb15dVXu3j88fbZ2y5W36FQlYTdu0scOqRsSTfnuxosWfHJZ7XkvnM1e9d/zcbsyzG4ajl2yUz+J/2VE/m6yeetVomVK50UFrbPeRW0LYSBJRDojHD0h6IhXKMpkpu01ntNJolTjf9jcfI1lJkyuPSLaZh/2443I5Pq6TMo3vgT50rv8T7n4yFBcz/NO94Gr4jJJJGV5W1xhe/WJlbfoVDyIBUVsf+uKoWj7302k8G/vMqZrGUbR/FnfmATp/IQ95AYICzrdBqZM6f1NM0EgkCEgSUQ6IyWFBWNxGgqKSHsm6fSDT0JJ9cwny+8f+UL36mMq34Zi/cwrjPP4tDC19n/1Q8475jOHjJa1KAM9oqsX9/+PRyx/A6pGagFBa6Y7kfNs1pR0fCd/YQz+TPf8zj/wIiPe3iEbzmBATQ0l9aDpplAAMLAEgh0R3NFRcPJqdLybBQVGSkubjBm0tPVhSuTkqRGrWUCb7R92cmj3EkxmcznWk7ma6oSu+O86VbKv/iWQ2+8i2vUGGQLJ14q9eHkLbU11OY8lsK0WgZqLPej5lnNz7c0+s7WYOVOHuc0NvIT/enPz2ziVO7gMQz4hHq7QDcIA0sg0CFaXoNgIsmp0jJmwFCniu1H6+ZZVWVk9uyGUIw1SeKm49fxFheznaO4k8fpxkG+4FSuZCEnHLGLvdMK8f3pqCbbassq9a1FOHMeyXcoHNQM1FjsR8uzun69uV4NPpBNDOQkvmYOf8eCm8e4i5XkckII8fJ8AAAgAElEQVTPIt1rmgk6BkIHS6AbxJw0JRx5BDVNILU8o7vvtjB/vrKGUKB2UI8endm+vZIBA5LrhDoV3rv6AN1WvUPS3H+T8P1mAFwksJjxPM1UvuEkwJ+HtXFjtapSeiiNJIEf+RrR0qZ65JHGcx4vLbVo9rNjh4FBg5Lx+Zp6nkwmibFj3SxZop5bNZqlLOAaerLX7y19eg47TzivxY9ZrFn6Q086WMKDJRDomGCvQSR9/ZRyUTweqKoCUDZ0gsMr5eUGxRYzPfiDa3bPJP20HFL+fj0J32/G2z2Vp1Jm0JddXMUr9cYVhA71dcQ8qeaiNecLF1qYPr2xJyteodFo9hMqTDxzZq2iHITMMsYw0PodP/Q+B1vtfnreMJGvTp3G2UNMqt5cgaClEQaWQNAGUAsJabUrUcpFKSiw8MYbiYTbHDf4xnc83zOPa/mdPtwv3YelvAxP/+OofOpf7N+8la3j/0kp6U22qxTqU8ofao95UrFGK4/O6zWwYEHs9NLCyeuLBaHCxGYzqnIQRqPExRfXsup7G8+OepdbeZpaLNzEv/nP7rNYNvePmOrHCQThIgwsgaANoJYAPG9eQtgJ4lqeDxnZEHI6Yfv2ur+NdDOcVaxkBN/zF65lPhZcbO77Nw6+/QEH1m3k8IQroFOnsPJxIskZEzRFO4/OT7SVdK0xRwUFLq65ppb09KbfHS2jEmDaNDdmMyxfkcAcbmUIn7GLPgxkE99wIpX/XScqCwVxRxhYAoHOCaddiRLBXiPtm5TEuHEu8vNd9TfW/sd4eOzE95jxzkBWkcsIVlOJjfm2W7h33BbSPl+Ee+gZjRouq4X6XK4GT0g8VOrbM1reHploK+niPUdyDt7q1WZKS4307OljxIiGtj4vvJCg2hkgM9P/IBH4/f6Kv3Ii37CCc+jBPl7dOxrjrMfAp22YCgSxRGQ4CAQ6J5x2JXJfvz17jPTq5WPoUA/TpjVOdpY9H0rNeTMzfcyaVUthoYX/zPVwLS/wD56g3/5dABxKSsN3y438lnstZx/dhXNDhPDkUJ/sCZH74aWn+zSVv/PyXCI8GAYFBS48Hn/OlZJifjTyFqHy+lpijmSDTqakxMT8+ab6HDy1ogxoeJAI/n7vJ5UxLOVeHuA+HiDr3w9Qu+MrKp97Mar2SwJBuAgPlkCgc0IlAGdmShQWuli71snYsW4MBnjjDQvDhjUO62h5PsaM8WDct5f+ix/kd/rwDFPpxy4cZDOZFzk5dTsVN/2DPn/uEpW2UXGxSbEiEWIjKtpRMJvhkUdcXHmlshRCNPIWLd1JIBgtg27pUjPLlql3CLjmmobws9L324eJAu5nzsh38XXtSuKKZXQdk4ux6PeYHoNAoITwYAkEOke+ccyd29TzFHgjnT3b0qiU3R/W8X9GlmuQb0aBcghXnubgnsNPkDT4NW6r9bcd2cggZjON9zkPCSOmEomyMnWZBSXCyfkKJJaioh2FmTNdjbyXgfIWzUXL09kSc6Rl0JWUqPsAJAluuMHdqNJU6fs9apSHsQVncaBoHV0uvxTz1h/pds4wDr28CM8pp8b0WASCQIQOlkA3iDlRxumE4mK/COjq1co6UU4nDB1qVbwpBmpbBW6zat239HvjSazL38NQtw6s7HQu9x+ezkYGN9pGerqXNWucpKaGP24tbSMl2nt/wFigdo3EWusqUm21aND67mZmejEYYPfu8L7XgdtUOh+GQwdJue5qLOvWIFksVD75LLWXjG/22MWapT+EDpZAIAhJYCXXkCHJrFhhZtgwD+vXN9WJCies43TCjt/Au+Yz0q86n+OuPoPkZe+C2UzNhCvY/9mXvH3lm02MK/B7EnJzI6sk0wpt2mw+eveOjcK4IPbyFrFWgdciVOh69OjIVf7lnCz5ey8jdenKoUVvUXPtFAwuFyk3T8H60AMi+V3QIogQoUCgU5QSf195xcQ335hYubKm0Xu1wjrp6T6e/7cZz4ermbLvEXqxAQBfso3DV19LzfU34euVXrfPhhBL420ZFEOOWmiFNidMcJOX54qLwrggcuRq0HjNkVpoL9CgCzcMGtgVoLjYSGZmUFcAs5mqhx/Dc4wd24xpJD/1GKadv1E55wVIVE+mFwgiRYQIBbpBzEkDWmETgGuuqWXWrMY3GKWwjgEfU7Pe4vKiWZzENwDspxtPM5XV/3cjb61JUlRLLy+H4cM7U1zc9DWt0EwwwS1wevXyMWiQhxtvdHPUUcKwipT2fo1ohTrDDYNGEt5MWLeGlElXYKyqxDX0DCpefg2pc0rY423v89EWaXchQrvdPt9ut/9ht9u3BPytu91uX2W323+t+7dbLPYlEHQEysoM7N6tfnmuWNFYSNLj8Uc5bDYfIGHCzbWJr1DU5TieLBrHSXxDKWncxWz6sosHuI+NP/dkxgxlXaOKCgMlJcr7jqSSTPaErF3r5KKL3Bw6ZOCttyycfXYyOTnJ5OUJgdFoiZfaejzQCnWGEwaNtHWU+8yzOPjecrw907Cs/4Su543CWFYaxREIBA3EKgfrZWBk0N/uBj52OBzHAB/X/V8gEIRBWppEr17qeSF//NHYyCkosDBvXiKuKjfX8SIO/o95tVeReehndtGHm3mWI9nBY9xFFQ0aQMGGWuD++/RR3ndzKslmz7bw5puWOokGA2CgqsrIvHlCYLS5dBRF/EgMyOZITHiP/zMHl63Gc9TRmH/8ga6jh2Pa9mu0w1akPRnDgtDExMByOByfAvuD/nw+sLDu94XABbHYl0DQEQil1h1o5DidsG5pLVN5iu0cxVyu5yh+4xeO4Y6uLzI07Wee42YOk9RkO8GGWuD+R49W3nekGktOp1/PSI1ly6Jr69JRae+K+M0xIENpxqk9GPj69OXgh6twn3QypqLf6fq3EZi/+l8sDgPoOMawoDEtWUWY5nA45CBDKZDWgvsSCNodhYUucnK0K6gMVZUYZz/BZ8VH8RS305tivud4xvM6/dnK05XXcsoQ5TwuUL7pyDeDpUsBJEwmCWh+JVlZmYE9e9SXGiEwGjmRhsLaIs0xIEM1jdZ6MJBSUzn41gfUDs/FuH8/XceeR8Ina6M9DKD9G8MCFSRJislPdnZ2v+zs7C0B/z8Y9PqBUNtwuz2SQCCQpOpqSdq2TZIOHZKkm26SpN69JclkkqR+/SRp6lRJcu+vkKSHH5ak1FRJ8msuSl9winQu70kGvPKfpH79/NsYMKD+bY1+pk5tuu+pU5Xfe9NNzT+WPn2UtwmS1Lev/z2C8Nm2TZKMRuXzaTL5X2/LVFf7vxdKx9evn/b3xe2WpFtukaTOnRs+07mz/29udxg7d7sl6aqr/B+0WCTpvfda7VjaGvK61VrH1Er7V7VpWlKmocxut6c7HI4Su92eDvwR6gMHDsTvsUtUf+gPMSdQUQEzZiSyYYOJPXsaSszXrXNRXm6gV3IF3V+fi/GoZ+DAAQDcfz2Vf/XI5/ZlY/DnNzWQm1tLba2LZctgxgwLK1aY+eOPhlL36dNd7N3b8H6nE955xwo09Xp98IGXadPCqx4MZuRI5cougHPOqaW62kV1deTb7WjI14jZDJmZylWmGRlezGZno3lta+zYYaCoKJng7zNAUZHEli3aXQVqay1UVjZ83yorYc4cqK0NUyh11tPYzIkkvTQX6aKLqHzuRWovHNvkbeGsWdEeS1sgpDRGXPdvIjPTG7f99+ih3teyJXf9PnAV8Ejdv++14L4EgjaNvEAsWpTQqFefrD2V6KrkocxnsT73DEbZsDplINV33YP79DMZ5zWwtcClqhVkNsOsWS7uu09b1yicJOHm3AwKClz4fLB4cQJVVf4bjc0mMX68WwiMNoNw2ye1VaJp1xOTZtVGI1UPPYqUbMP6zBN0vuFaDDU1HJ5wRSSHAcS/9VBrEKzZF6lmXlvfvxox0cGy2+2vA2cCRwBlwH3Au8AbQB9gF3Cpw+EIToRvhNDB6ti01pzEus1Ic1DT7ulMBX/nWe4yPk43n//ycZ8ykOppebiHngGGxk/F0R5LpC13mrP9Xbv8Y+7bV+hgRUrgNRKsMRbcPqmt09x2PVotmkwmiY0bI/MYWZ96jOSHHgCgauYsaq67sf61cNeseLYeijctvWboff9aOlgxuQwdDsdlKi+dHYvtCwQtQWu7tWWUnrhlw+oOHieV/eCDyr8MwvvPexQNKxlZK6i5tLRnxGqF/v3b/hO7Hoi32nq8CUfdXYlYe4yct92JZLViy78b24zpcLiWmltuC/vzgRp17dF721Je77ayfy3awXOOQNA89OJWDlwgOlPBLczhDh6nO/5Q4HqG8K8e9zLr3VOxJrd8tZ286K9cmUhRkRT2jU3QOkRrVOuV5hqQLfGQUDPlJiRrMrY7bsX24L3+v4VpZMkadYFUVRkwGmkXnsbWDoG29v61EM2eBR0SPZW5p6VJ2NMPksdMdtKPmeTTnQN8ylDO4mNO51O6XHh6XIwraLix/fgjbNzYtLG0QBBPmtPIuiWaVR++/CqqnnwWyWDA9uC9JD37dMjP6GmdaSmikcZoD/vXQiyZgg6JXtzKhqpKjnjxeb7c9yzJdR6rTxnKfdzPOs4kIQEmX+VqFe9Re/WMCNo/LRU+lZPcbbf/HdsD/4TOneCq61Xfr5d1pqVpbji3ZfZvIiPDqwuvuzCwBB2SlBSJtDQfJSWt5FauqSHp5ZewPvM4xvJyAL6yDuUup9+wkku63W7aTShBIIg3ag8J0RRbBBpZhrvuIqmqlpqbb1V8r57DV7GktfMBzWYovHs/T/04AeeE0VTdeIMu8hFFiFDQoZBVynNzrZSUKH/9W9St7HbTaeF8up86ANt9eRjLy3H/9VTKFn3ARd3XsI5hBOvltJdQgkDQ2ng8kJdnIScnmTPO8P80p+n4/guuYEfeswDY7s/H9PQcxffpNXzVUj0RmxPOjRWWtatJ2rCO1M0f68K4AuHBErRDtKQKghPbG5BatrLH6yXx7TdIfvRhTLt2AuA+/i8478nHdXYuu3YaKd6j3NKmPYUSBILWRC3hfN68RIzG0MUtcuXxsmVmdu++kcmGRF6UJtN95gxeX5fMmW9OauJtbu3wWfD4ZcHhsrLWq5xuCSyffer/ZfDg1h1IAG38lAoEDSjJLowY4WHyZDcZGX7jRC3hFAwtU9kjSViWfkDyrELMjp/94zwmm+rpM3D97Xx//I+OE0oQCFoDOST44YfqF/eHH4YWIQ1+QJsnXYsBL3O5nss23MbCy5IY/WZj1aLWDp/JeDyQm5vEli0N50AvgpyxIGHDev8vw4a17kACECFCQbtBqaHq/PmJnHaav3v93XdbVBNOZWIWjpMkEtasomvumXSZdDlmx894+/Sl4pl/c+CTL3Cdd2G9cQX6DSUIBG0ZOSVg6FArZ56ZHLLp+B13JKqGCsvL4YMPmhpoLzKF23kCgMs/uRGWvK34+dYMn4H/PAQaV4G09TQEQ1kZ5l8cSFYrnHJKaw+nHuHBErQLtMqhwW9sLV5saiT2p0QswnEJX2zE+tADWL7YCIA3rRfO2+/i8OVXgcWi+jk9hRIEgvaAekqAEgbeftvC1q1GVq+uqfdky57x9983U1qqbKA9xe3YqOJB7iX1tuuo7GrFdc6o2BxEDNBeH9t+GoJlo9975T5lIBaLBaht3QHVIQwsQbtAqxw6EqIJx5m/+5bkhx7AsvZjALxdu1F8+T/g5utISg392KqXUIJA0B4IZVSo8dNPZk4/PYkVK2pISQnfSCskn/TOldxU+Sgp117BodfexH2GPsJVZWUGVeMQoGfP2KYhxLv9mGGdP/+q+pTTUX+EjT8iRKgjWqqyoyOQmiphtYZeIJxOA+PGubDZfIqvRxKOk+fL/d3PpFxzOd1GnIFl7cf4bJ354KR8jk/ezpHPzWBI7hHk54dfpdTaoQSBoD2g/dAl1f0os22bmQEDkrn7bksERpqB78Y/QM2k6zC4XHS56jLMX3we6bBbhLQ0id69ldc8gOHDY5OGEBiSHTTIn5oRydrXrP3NSKDiDf9D7YSFY7jtNlpsf5EiDCwdEO8vZXtk9mwLVVWhv86ZmT5mzapl8+Zqxo1z0bt35ErP8nxNHFSK49Sb6DXiVBKXvo/UqROHrp/KlOEOzvv6QbYWd6vPBZs7N5GCAvVnK2FcCwSxRS4cUcZAsBxKMFVVRubPT6SoKNS64jfWbDYfPsnAwQce5fD4iRicTrpMGIv526+bMfrYopXjCRLr1pljcs9RyoMNtfZFu7/1L/5GpreIUtL4qOxEnn6aFttfpAgDSwfE4kvZkW/QkYQCZA9VSgrMmVPLZ58569vB5OW5+PVXA1u3ap/Hp+7ay4C5t7G25Fiu4FU8mPkXNzEsy8H/vfc4L73bS/FzSomkwrgWCFoGbaMifEzK6ikB+I21qioj8+YlUvBAJyqffJbDF1yEsaqSLuMvwvSLI+pxREtg+6DG3ruGe05+vqXZ95F4twWS9zeSFQB8xDlIdSaNXpL2hYHVykT7pRQ36NChAKOxsYcq0Bi1WiErS6KwMLT4oGHfPhLz8rh/0XHcyPMY8bGAq8nmF/7Ov/jk1z6UlppQezKWE0kDaeknvo5seAsEBQUuxo+vRT0cGDqtwOuNbJ/Ll5tx1pqo/NeL1I44B+OBA3S59AKMu4uA1rsm5RzPlSudpKcre/YWLrQ0+z4STlugWCLvL9DAasn9NQeR5N7KRNurKjgBsz3pmoSLloZUerqPxYtr6NtXwmJpqpM1apQHnw9N8cGZ0/aS9Nwckl54DmN1FQBvcAn3cT8/0z/scQYn0IcyrkNp8mihpAnWXgQFBYJwkY2KDz9MUKwe7t3bh80m8fPP6heFySTRqZNEdbX/8wYDSPWXcdNtNqzbCVS8uJCu4y4kYdPndLnkAqYNXstba3u16jVZUWGgrEz5nuP1+o+nOfeReGv5paVJHJ1eyRnFn+DDwCpGtOj+moPwYLUyWnkCob4kHaFTezhohQIqKw289lpCvXGl5C16/fUE5e1STb/Fj9PtpONJfmI2xuoqnMNyGZX2JeN4IyLjCpomkrbkE5/asebn6yM3QSCIF1r5maNHe1izpoZrrqnFalVeh71eI9XVRuRQoCQZGDvWpZo0npHhIyVF8nupsHLoP0vw9D8O8/ZfGf/KhRwocsYlP0kN7dy0xkRyH4m3lp/VCn8/fi2JuPiKk9lHjxbdX3MQBlYro/WlHDFC+0sSb5esnpHzC4KrA6uqjPWGhZoxKj+Zylio5e/MYTtHcU/FDEyHDuI6bQgHPlhJ9ZK36HP+8c0YocTkye5Gf4nGuNaiogIWLVI2GhcutDB9escKIQs6LloPoTabj2nT/N6jWbNcbNpUrWpkBbNpk5kRI5QvoupqyM1tSNmY8WhPdr/0X343HckpfMl/uRBLgE5TvB+GI8lNi/Q+EpjnFWnxUHOYlLEcgI0pufX7mzqVFttfpIhggQ6Qvwz+/lZGTCZ/3H/VKjNmM6ouZNFepQGzGfLyXCxbZqaqqunry5ebVd3iMiY8XMkr3Mf99OV3ADYnnEz6/HyMucPA4M+buOoqN7W18Pbbctgh9AKUnu6je/fG8yEvdLIrPpBonsDy89Wf2L1eAwsWJJKQ0HFCyIKOi9ZDaE2NgfJyAykp/uvS6TRw+HB4xsSePUYmT3bz7beJbN7c+LX9+03s3+//XQ61VVT04WvfR3zKUIbzMf/hcsazGB+mVhH5DBQ1Li42YjA0hAcDifQ+Em8tv8R1qwEYv+BMTutdTVqaRN++ndm7t+X2GQnCg6UD5C+l/4nIUPdFD+1CFu1VGlNWZlBthVFWZiQtTfnptHOyl0tZwo8cx3yupS+/8wM5XMB/ubTvRqoGnYXHa6gvJhg6NLnOuJLDBqEpKTGSm9s0cTTWT3xOJ6xfH/q5qSOFkAUdl0i8xJGEzjIy/A9MBw6EN471683UZP6JkazgEClcwlv8i5sBqVUehuV7zvr1Tj7/vJorr1Reb5p7H4mHlp9x5w7Mv23H16UrpkEn6VI7UBhYOsHphNWrI8+nirdLVs9oLZCZmT5Gjgw2RiX+xgf8mHgSSxiPnV/4laOZwGsMYDPvcQG/bkvgL39J5swzkxrlNIXW3AoWMlQ2mAMXOlkuorCw+UmvZWUGSkpCX9YdLYQs6JhE8hAaSehs1CgPFRUGiorCG0dpqZHBg718xwDO5QNq6MQNvMAD3MuIER7Kylqn0lc2hGbObHv3kcSPlgHgOmMYeq3cEQaWTmhuPlWsb9CtjVYJc6jy5lCLaeAiMtz4MV9ZBvEB55G1/3s86ZlM6/o8x/ITrzMBHw1hu+pqI7/8EtkJTU/30auXsrGnZDDH6okv3KfwjhZCFnRcInkInTZNvcuDLCY6ebL/s2lpEn36hDeGjAwfM2fWMmVKLTuzBnOZcTEeTPyTQjLefK5FJXbCkYVoS/cR+XjM778PgGvMua08InWEgaUTok14buvtVTweuO02FPW8ItH60lpMzWZ45MINOPoMZ5VvOCe5NuE74giqHnyYb5ds5vGKKXhQTg6PlDPO8PDHH/EvQAj3KbwjhpAFHZNIjIfycgNOp9q16fdcG43+bVqtcP754Y1h1CgPKSkN45i2/mzuzZgLwIOV/+Ay32sxrypsjkainu8jgcdzwcBKLF9+gduUiHPYOaE/3Eq0uH1qt9t3ApWAF/A4HI6TW3qfbZGWSnhuK/hlBYA6z5GcHLp/P3TuDAsWhKf1pZRkCbBvzY8c9fIDWFf7q058KV2o+ftUnJNvAJuNnk5UCwYiwWbzMWGCm2nTXGzYYG6VAoTgBFa5R2NNjYGMjAbtHYGgIyEbD1poFQ7JBGrUPfYY1NTUsny5ua6lTlPjLCen8fVmtcJLLyUwf88kajnA49zJy1zNAbqxjDFRa+DJjZaffz4h7HWzLRCo+XgD72JE4kNvLksfS9Xt8cTLgzXM4XAMEMaVNtHmUzmdsHVr6FYvekOrlPqttyy8/LLyE51Wbpqs0D5v2i42H3sdx18+COvq5Rw2J1N1653s/+p7nLfdCTZb/fujaathNEpcfLG/x2FhoYuUlNYrQAhOYN2yxf+jd9e/QNDahLMOBHqgw1FHP3TIgCtgCQ9c757gDh7mbsx4eZNLOI0NzfZwB3p4Bg5M5pVXIl839YBSSDP4HnExbwPwNhfr+njEMqsjQpW4yk8mwX/3eODeey0sXtygVmyzSYwf7+aBB/R/M9VudWMIUE1ujFZ5s3F3Edsve5T7HK9ixkstFv7NjTzsuYcLDnelsGtTo1U2ZBctSgircXQw06a5SUlpur3ly83s2WOMu/co+Ik9nmXgAkFbpaDAhcfj14wLV7pASx09eJ0qKzNQWtrw3jweogd7mcxLfMjfuKjbOtLS/tSMcTfu6qHW4qc1ZCHCQav7ROA9ojvlnMk63Jh5n/Oo1OnxQHw8WBKw0m63f22326fEYX9tnuA4eKhYekGBhXnzEgNkAwIaj+qkq7gWkZRHB6K00BnKykjOu4vuA09giONlAOZyHUezjdt5ij9IU33ikQ3czZuryc6OrAFZZmbTsbSlxFGBQODHbIZHHnFFJF0QSQ5taqpEcnLjCuMbeJ7/cgHdOMg7ztHY9u2KaMyRNLzXa4GLVl/WwPN7Pu9hxssazuIg3XR7PABIktSiP9nZ2Zl1//bMzs7+Ljs7+3S197rdHqkjUl0tSdu2+f8N/F1m6lRJ8ne/avwzdar/fVlZyq+DJPXt23hbekXtGLV+pk5t+Hx1Ubm0//q7JZ/VKkkg+QwG6TUmSEfzi+Jnf/5ZfSzV1f7z1tyxhIPSPAsEAv3gdvuv6379JMlk8v87dar/70qorWFXXRXeep5IjfQ/25n+/xx9tCSVlYU91m3bJMlobJm1Kh5orbn9+knSoUOSNGCA//8fMlqSQLqOFySQpJtuavW1VNX+MUhq8ZcWwG63FwBVDofjMaXX9+6tjNtgevTozN69lfHanSKBLtHdu431TzVOp6HePTptmothw6yKSZdZWV7mzath5MhkJEk5Zm80Snz+ebUu3aeBeDxQWNiZ55+X8PmUj8Vk8h9DYKjNUFXJpglzGfb1k6RIFQBs7nsuqc/lMfiGv6omq15zTS2zZik/oe7YYWDQoGTFcRgMEhdf7GbTJlOTsF84nqm21IRZD9eIoDFiTuKPWmoGNJ6P4GtbLi4Jdz1PTvbx/WclZF05hoQfvsN9/F849O5SpM4pTd6rNMahQ5W3q7Ru6m2t0VpzTSaJsWPdLFlioSsHKKUXZjykU4K3eyrJyTRaS//1r0QOHIjfNdKjR2fVhLkWNbDsdnsyYHQ4HJV1v68CHnA4HCuU3t/RDKz8/MYxcyXGj6/ljTcsKkaHRK9evrp4vvIc9+7t5bPPnG2iCrFHj85MmlTbqPIlkEmTarn+erd/oTPUkPTyS0gPP0Hnw/sAWMkI8inkS05hypRaPB6YP195W1lZXtavVz4vWouV/DlQX3S1UJvzKVNqdVcJo4drRNAYMSf6Qmk+nE6YPj2RJUuapmdorecmk8TGjdX8KbmMrufmYt7xG64hp3No0VvQqVPIsaitLY3WTZ3eB7TW3MxML5IEe/aYuIF/829uYhXDyWWV4ramToUZM/RhYLV0DlYa8Jndbv8O+B+wVM246miEGzNft86sWp0CBkpLTWi1axk9um1JPMyc6WLyZLlps18NXRb3Kyx0cWRvF93fnE/3gSdguy+Pzof3sYHTOJO1nMNKvuQUwH9uJ05001hNvYHiYvVKnXDUn5ujF6M153quhBEIBJGxcaOy53z9ejMZGdq5WlLPnhx64128PdOwfPYpKTdOVs9YD0CtCr2w0C+K2lpq8eGgteZarVJ9C7RrWADAAq5R3dZ776Gb44xriDAUHcmDpeUSbYyE1SrhdIZrC/tPYVuqIpQJnBOnE8WWi2wAACAASURBVHbt8p+bvn0lrIleEt95k+TZD2HatROAqqP/zPjtD7FUGk2wkWkySaxZU83llyepus2vvNLFzJnK5yfQ3d+cUKASWnNuNEqsXVtN//76uR5b+xoRNEXMib4Ing+nE77+2sgll1hDhruCCfZim37cQtfzR2GsOETN5VdR9fgzYAgt3yCHNFNSJPbvNzBvXgKrV7dMSoJW+DRSKipgxoxENmwwUVLiX3O7dJHYssU/0GP5kR/J4RAp9KKUwyQpbsdkgo0bq+KWFqPlwWojt972RziCdn4alIVtNh81NQZ69vTV9ZtTyhGC115zctppvjbluYIG/RP5Yu3f35/naFn6AcmzCjE7fgbgV/P/McNzP59VXkhlsgmqlEup+/aVVMVbvV4DCxYkkpCgLLrXEl3htebc54OJE5MYPVqfORICgUCd4Hxao8rzsNwyp0sXKaR8i/e4HA795w26Xno+Sf9ZiO+IHjjz7g05FovFL2SqJH4aK7HRWOaSBm8rPd3HJZe4+Mc/XJx/fsOiezUvA7CY8arGFUBWFrqpKhStclqJ5ghbduni98qsWeMkK0vZzdy7t6/NGVeyDMVxx9EgQzEjAePq1XQ950y6TLocs+Nn9tn6cDUL6O/5gTe5lJIydb0qOZRXUOBi0qTa+kTPYEKF5mLZOkJ7zg3s3h3bVhkCgSA+BEoMSJJBUT8LmrbMCSXf4hk4iIp5C5FMJpKfeoykF/4V0VjU0keiTUnQklSIdlvFxSYWL07kjDOS6xvXm/BwBa8CcnhQUpXSOf98dHP/EwZWKxIYMzca/blGVquce9SU0lIjnTpBamrrqYS3BPIFtnMn+HwG+hZtZOKLuaROuIiEzd/i7ZlG+QOPMbDrVhZyNV4Fx6vN5lNUvzeb4frr3SHFSuOFPOeZmV7U5lnkYwkEbQftfFqJwFxSn496/cJwH95cuaOofMpvWNn+eQ+Jb7zezLE0oJWDGopwc0nDaTKtta2amgbv20hW0IsyfsbOJk4lM9PHsmVOxZyzxxQ1CloHEYhoRZTCUDU1cNZZVkpKtHvYtbZKeKwIvMBO5GsKyWcU/jqIA8buMP12PNdfx46yZH67T90tbLNJLF3q9OdrqYgAtkZfQJnAXIXCQhcTJ7oZNiwZn4IjUq9KywKBoCmhOlHIVFUZmDcvEaMx8vBc7bgJVO3f7y/smXoTUrduuEaMbPK+PXsMdWFBbQwGeP75BNUcVC20jnfPHiPFxQYWLkwIK3yofe4aaJzcbiA3t8ETGJzGYTZrV+bHE+HB0gGBTzKpqXDuuaG9U+1FJbyszEDK7p95k7F8zcmMYgUVdKaA+ziK7fx6wW1gtZKSInHEEepq73v3+r17Sk+D4VQFthRqKvyZmVLIaiKBQKB/Iu1E0VwPdc2Nf8d56z8weL2kTL4K86Yvmrxn3rwEtKrKZeQcVDmkF463SSaUav28eQlhhw/DOXd92ckFvIsbM69yBSAxebK7/vVYpnHEGmFg6ZBImj7r+csVCuPOHRw76zq+k/7MWN6mhk7M5i7+xG/cTwG2zM6kpkrk51vIzbWyd6/61zWUURJtI+3moparcMEFSRw8qJ6n0RbnUyDoiESaTxtNWkL1jPuomXglhpoauky8BPP3m+tfczph1arInrCXLTNzxx0WBg1SbsOmhNbxjhjhYfXq8KVowjl3tzAHEz6WMI4SMsjK8tG9uxS2QdiaCJkGHRPLElg9YSzZg/WJR+n02kIMHg8eYwIv+K5jJjMoIaP+fVOm1AKEFGOV3xuO2z2e51RLPE8Jm83HhAlu3VQRtoVrpKMh5kRfyPMRLOvSq5ePQ4cMikU4WiLHYeHxkDLlGhI/fA9ft24cfHc53v7HhpD+kVD2bCn/PdR6qiZjc/XVboYMUVdk37ixaVeR4G0lJUn1560zFRSRRRcqOImv+IaTyMnxcOiQQTX8GO9rpNWU3CNFGFj6oSUMEUN5OdZnniBpwYsYDh9GMhqpvWQ8FbffzT/nZ7NyZSJFRVL9xarVVsJolDAY2m77ByUyM71s2KAf1X1xjegPMSf6QkkHS143H3oouq4Nmmuwy0XKpMtJXLkC3xE9OPj+Cv7odoxq/q7JJKlWNioRrhEYPMZwumCobVPeVmqqxOzZFpYtM3Px7md4in/wCadzRdaaRrpYgQSeU2FgqSAMrNanJXrlGSoOkfTcHJJeeA5jdRUAtedeQPX0GXiz7fXvS07uzJYtVfUXayhhzv/8x0lmpqSY2K4HIvVgqT3htRbiGtEfYk70hdZ8NFesOOw1+PBhulwxDssnazmQnMm5KWvZUHI0Sh6pnByPomGihrwWyQrwkTxox6odmLPSS68hA0gs2cUvs1/Hd+4YcnNDG2/CwFJBGFitT7QXR6MnGqmapJfmYn32SYwHDwJQOzwX5z3/xHP8X5p8NnhOKipgwIBkRTe7zeaja1d/CwU9N0y++26Laj/EYKIOHcQYcY3oDzEn+iKc+Yg0GhDRGux0cmDQWLJLPmMH/TidT9lNVt2LEllZ/rUxP99FYWGDsaclVg3Qq5eXUaM8zVKAj1UXDMsH79Hl2ivw9juS/Z9/w47fzZoNoeWHU2FgqdARDSw95VlF494NvKj27nZzZ5e53Fn7MF1qSgFwnTaE6nvuxXPqQNX9B89JOM2wA5k0qZZHHtGXTMW2bQZOOy2ZcCp79NbwWS/XiKABMSf6ItbzEeka7HTCyMFeFhSPZCCb+JWjOYNPKCGD9HQva9Y4SU1t/H65jY6aNwjg6KM9bNumHYoL51iafW+TJLqePZSELd9T+fCjHL72+rDPjZ4MLFFF2Eqole9rVW+0NKH0TbQqXwoKLLw018SIopf5WbLz4MGpdKkpZWePkzj4xrsc+u9STeMqGC0BOoNB2Q5fuNDC9Omtew6DyciQVFX3G5AYN87V5jTMBAJBbIl0DS4rM/BLSRdGsoJvOIFj2MYnnEFvivjjDyMVFY3fL1eda4lVm0wS27YpG16LFiVQURHesQRXuGtJQQS/Zln2IQlbvsfbK53DE6+q315bE9gWBlYrEW6rgUj0SaIlNdXfWFoJLRkEZ5UPy1tvspX+vMRk+vI7P5DDBfyX452bKD/xrLCalAaitdCoOV2DtV30QDhlyJmZPmbNqtVdeFMgEMSXUBpTwWuw/P5DdGUEqxoZWX/tuSNs6RqjUarrIkJdMrzyel1VZWTGjMiEPLWcCUqv/TPPhHX2QwA4p94BnTopjjmecjvNRRhYrYDT6dcfUULWConWw9Ucw2z2bEvI3n6NqGvE3GPEaczZfwXHsI1fOIbLWMRf+I73uICqalPEFyRoLzSmEDnjems1Iy8KNpvy8YwZo8+nL4FAED/kkNrw4eF7aQIf4PaTytl8zP/4K39iBx9UDsP2xw7V/QWKVa9dW0337uFl6GzYYIpofdVyJii95pq3mIStP+LtncXhy69SHXNbENgWBlac8Xj8ic+7d2u7gZvbTLO5hplWSM5m8zFtWsATgiSRsKauEfM1E7Fu/4ndpj5M4iWO5ScWcxlSwFcr0gsStD0//fsrN/mUiXd/wVDIi8LmzdWMG+eid++28fQlEAhanuA1e9UqMzk5nrC9NIFenUpTV67JXMH2tIEcUfU7XS8YjWn7r5r7t1r9TqI9e8IzB0pKwl9fte4rS5eamzgarFRTSD4A+++6DxKVH87bisC2Tu2+9ktBgYXFi9U9OhkZPlJSJM1mmnl5LtUvlmyYyfgNM7/LRys5USskV1NjoLzcnxiZ8PkGrA8/iOWLjQB4e6bhvP1O7vlmCv95M0Xx8/IFqVXy63TC9u1+Y0R+Ta3fYn6+i4ICCwsXWhS1XfTaaiYlBebMqdVVYYNAIGhdgtfs3btN7N7tL9q5/np3yHWiaU/bBJJ9b+O+bCwJmz6n699yObToLTwnnKS6Da1+rcFEsr7u2qV+X/FXMTYmn0IyKOFLTkY65RKODGsv+kV4sOJIOJ3OR43yUFGh/qUsLjby9ddG1UTBcLqcKxEq9p9V+hVdLr2AruePwvLFRnzdulF174Ps/993HL72egoeNqiGwHr08PHooxaGDNGOwWdn0+g1NXdwp07wyCMurrxS2WDUa8KjTFt5+hIIBC2L1pq9apU5ooewwHVFsnXm4OJ3qD17BMbycrpe+DcS1q3R/Gy47X7CWV/ldX3ChCTFhvYAvXr5GuX89uen/2/vzuOcru88jr8yF0wYQKE4cozg7sJnVWq19aKK61ZF0Varq63aelQRabWeVRSoO1XZKsWurkfFeletV2u1AtXa1daz9ShVqv12qWi5pYjgTIbJzOS3f/wSyGRyTo4Jk/fz8eDBJL9ffvkm3+T3++R7ffgO84kQ4JqdbqBxZPn0QvSWWrBKKH3mcI+vftVPkxIOk/LXRCAAJ54YTLouSbrjr1jhZzkfPz75L4/YFyzW2hUzkbf5SdVsRh77SwAiDYNp++Z5tM04F2/wtharIUPgxBM7uPvunq1za9dW8dhj244b36oGZGxxi504Es2dG6a2tmcLl7rcRGR7kM2swV4vPDxoEJvve4jBF3yLgY89zNCvncgnNy+g/bgTku6e2GMwcqS/1uCmTYGcz6+JrXLJDBvmsXq1f66voovbmU4tnSxgOjt/eR+Cwe3/PK51sHqht1086dbxSEyTku0aUPHrkmRaOfwb32jnuuuyyy81aNUyrh34n3wp9AhVeHj19bRNm0Ho3PPxhg1P+rhFi2rixpZl/vUxenQXgYDfJJ4ol0U31eVWHFpzqfyoTspLvvWRz9qDWYtEGNQ8h+BtNwPQcuXVtJ17fsqZ3cnS3+Ryfk1/HfIYMybClCmd/PrXNVv3uYT5zOdSVjOSAwa9xXN/GsCQ5CNOMtI6WNupfGf2pWuGTZxJljiFtro6eewZ3/UXDPrZzFN59tn03YQ1NfBf5yzjnUnf4J3AHhwbephAXS2hs2ew4Q9v0frd7/UIrvyy+sGgHyilnuKbaM2aqpQDK3MZqK4uNxHZHqW7Jgwd6lFXiBVnqqpo/d5cWr57FQANV32XwedOhy1bUpYp/nya6/k1XatcVRU88EAb55zTsXWfvXmTucwGYBp3sHrLcDZs2P67B0EBVk56O7Ov+zGyW8cjfvzRo4+GUq79lBiITJvWgZ8hPfO+8arWraXh8ksYdsDeNDzyEwDavn46H736R1rnzsNrbEz6uGzGlaXS2Bhhp52yX/NFRKS/aW4OM3FizyBr6dKawq3pFwjQ9u0L2XTnT/CCQQY+9jA7fHkqVWvXFOb4cdKN5x09OsLYsd7WfYawiUc5kQGE+REzWMxR/ercX9EBVi5rReUzgDxerut4BIOw++4RGhuzC0TSrRye7IMb2LCBQc1zGLbvntTf9WPo7KTly1/ho5dep+WHNxEZ05T0WDHpx5Wl98knAdauzWHdLRGRfiYchk2bkv/wzfbaku21LPylY9n41K/patqF2jffYIfD/42a137fi1Knls2K68EgHH3EFh7hK/wz7/Eme3MR/91tn/6g6AGWmR1pZs7MlpnZ5cV+vmx0dsKFF5JTV18+aWSSyabZNdYlOWVKMOmUVuj5Ycw2nUBg8yaC181l2L57Erz1fwhs2cKi+uP4DH9i9zceZNZduyV9PxK/yOl+raTmB3n+oqbd3zetDSUilSSfa0tvhq10Tfw0G59+nvCkA6let5YdjjmS4A3zoSv9+oK5yNhT43lc33YeR/AM/6gawVeqHmOnptp+d+4v6iB3M6sG/gocDqwEXgNOds69k2z/Ug1yzylbeVRJBiNmWc74LOnJMpSnzWa+pYX6u24nePMNVH38MQBLm6Zw+or/4k26r5MS/37EHzMxu3o2M0aydeqp7Vx/ff/5gm3PNKC6/KhOyksh6iOfa0tvrmVbhcMMmvs9gj+6yb950MF8cuOtRJp2yfk1QPLB8EkHyHseg668guCCW/EGDGDdg0/x9zEHZH5clippkPt+wDLn3HvOuTDwEHBskZ8zrd529QWD5JTCIF/pyjlyZIQnnghx1lkdhJN8h5J2Q876mMG338Tw/fak4Zpmqj7+mPDnD2Lto08z1VvUI7iC7u9H+nQH3X+tjB7dlXJNrEwyDcQXEelPepvEePNmP/lyMll1LdbV0fq9uXz80M+IfGoEdS/+jmGT96f+9ltzas1K14rWo6ems5OGi7/tB1e1tWy+5wGqJ++/dZ9cW+RKmau3VzzPK9q/CRMmnDBhwoQ74m6fOmHChJtT7d/R0ekV27JlnldV5Xl+yuDu/6qr/e2JOjo874ILPG/s2G37BQL+7Qsu8LeXspzgeaNH+9vHjctQhrY2z7vxRs/beedtD95/f8975hmvIxzxTjst9XPE3o/W1m2vPfHfuHH+ds/z/4/tf8EFqY+b7l+qOhAR6a9i15hx4/xzYMbzuud5p59ewPPo2rWed+KJ2w6w776e97vfZfXQVOf6Cy5I2PHDDz3vsMP8jQMHet4vf9nrY8W/X1ldB4srZQxUVguNbtxY/DC0pgZGj07eHDtqVBc1NSHWr+9+f2IzbCy4P/TQdmbPDrNxY2nLCbBqlf//++/DjTdCW1tCk3B7OwMfuI/gDfOpjs4U6fjM3oRmziJ86BQIBJhzXpj77kuXtsd/P5YuDbBixSCSLb+wYoXH0qWtWxfDGzIEWlth5kxoa9vWpRgIkDStTarnTKwDKT11R5Uf1Ul5KWR9zJ4NF13UvWts1arkXWWhEDz7bBBIfn0YOTLH82hVEG65k7ovHk/D5ZdQ/dprcPDBtE85ktaZc+j69J5JHxYKwc9/nrwcP/95Fxdd5Hdv1i1eSMNlF1G9bi2RT41g0z0P0rnf/hD33mV7LOh5TY6/Di5YMKDUXYQptxW7i3AVED8NbUz0vj6Ta3NsplQGxWqazCV1AcQ1CXd0MPAn9zBs0mcZfPklVK9dQ+cen2bTvT/l42eeJ3zYERDwm1QXLkwfX8e6RLds8WcgJlNf7zF8eM+hc/HdlK+80poyrU2i/jSDREQkF7Eutbq69F1l69YFUk58AjjwwK5enUfDU49m40uv0XrpFUQGNTDgmV8x7NCDGHrMkdQ9+Ti0t3fbP+0A/VUBWp9+haEnHMvQ00+met1awgd8no2/ecEPrhJkO9i/UDP6S6HYLVivAePNbFf8wOok4JQiP2dGzc1h6usH8POfd2VMAVDUVAZZlBO2pS7YaadI9EvVsyVo9YoIHbffz7D751H99/cB6PzX3Wi9dBbho7/kr/AWZ926QIbs6R6trQEmTw6yalVVt5xR8Vpaqpg3ry7lgMrYCSOW1ia22ntVFUQibP2/qSnC8cdXM3OmBriLSGVLnDiUmEIsXXLmhoYIc+e297g/W17DYEKXXkHbGdMI/s8PGfjAfdS9+rKfg3ZQAx2HfIHwYVPo3H0Pdh41ntGj67eWYwib2JO3OITnOaX6UXY7520AIkN3oHXmLLacOb3HtSgm3WuKX2Io0zV5zRp6vQp8oRU9VY6ZHQXcgN/ud5dzbm6qfUudKueDDz7JOFOhL2YPJivDunUBhgzxmDKle1mq6OIUHuRKrmI8ywDoHD+B0KVX0H7McSk/zKEQHHhgkFWrkjcxNzREossoZJbL+zBzZl3SfIVnntnOnXeWtmlX0lN3VPlRnZSXYtRHttecvGYQ5iDQ8gkDHv4pA+67l7p33+5Z3rqhfBIeQJAQg2npti0yfDhtp32Dthnn4e04rNvsQOjZ/ZnNa8r0/vzlL9W0tpbHLMKij8Fyzi0CFhX7eXojVRLhxH2SJUGG0nVnxZfz8MM7ueuuagJE+AqP0Ewz/4oD4L2a8QyZfxneV0+A6uSBU/wxjz46+evKVbYtef64gdJ3t4qIbC+y7TVJ7OEodLL7WDA0fPhg5i0/j8UtF1IVWMkpOzzF8Ts+z2cG/oWa95YR3LKJ2GUwRD3Layfwj3/Zj09ffhhdX/gCDBjgL/Mzxx+Tu3JlFYMGedHnCCQs+ZP5NWW+JlfT2lqQtyBvSvachbTrSpV4msCyv3pcf9DTNPM9JvJnAN5jV67iSn5a9TVeeKU96y7Lzk648so6HnqolpYWPwhvaPA46qgOHnusjkgku8VTs23BWr48wKRJg5Iet7raw7kAQ4bo13m5UGtJ+VGdlJe+bMGK37+Qye4T1zwMBr2kvRnTp7dzzVVbCGz6mEA4TKtXz9rQUBp3pkc5Uq/pmHC8uFaqdK8p3TV55MjyWQdLAVYOCv1BzonnUbd4IfXX/hd1f1kKwAfswtV8l3s5nU5qe91lGQrBBx/4n5GxY/0qSNd9mCjbJulya9qV9HQxLz+qk/JSrPooVfdfLs+dqKEhwpIlrRnHO6U778frzfUr2TW5khYa7VdyzSpeEJ5H3a9/xQ6H/xtDzziFur8sZeOg0czgR4zn/7iTaXTiLzbX2y7LYBB2281jt928rXmiJk/ONIPRY8yY3NLa9HZBPRGRSpIx1UyRpJuhl6ilpYrZszMHYtnmqy1Wyrm+VFbrYEkcz6P2+f9l0Ly51L7xOgBdOzUSuvAStpx0Bt61Q9h5cTWrV3sF73sHf6bKk0/WEgol/2JUVcEDD7Sx2265NTqm72MvTLodEZHtWWyZm1mzwiXtNck2GIp56aVqQqGeXYLx0s0OjBc/U7C/UIBVbjyP2ud+w6AffJ/aN14DIPKpEYTOv4i208+C+npqKP6Xb8gQOOmkDu66K3nQM3p0ZGt3Yi766sQhIrK9STcRqxhDVrINhmLWrMk8wSndoPR4/bEXQwFWLxX8w+151D73bDSw8lusIsOHE/rWBbSdeTYMGtTjIdnMgszHNdeE+cMfqlm6tOfHJN8vQ7HLLiLSHyUOQo+fhZfvpKtsg6GYbFudYj0XsXUQ4zU0eJx0UkfRuz/7ggKsHBX8w+151P3mGYLzr6X2zTeAuMDqG9OgoaGwLyBOpiCxpgaeeaaN2bPr+NWvavjww21depddFmb5crVAiYgUWrpzc6ZFSPOVbBjH0KFeXj+0Yz0XHR30WAexpSVAVRUln5FfCppFmKOCze7wPOqefdoPrP74JhDtCjz3AtrOOCtpi1Wh9CZI3LYmise8ed0fe/jhnUyb1sGoUfkFW5ohVV5UH+VHdVJeCl0fmc7NpVz4Oj7Iq6vruSxCruf9UpW9nGYRKsDKQUE+IJ5H3TO/Inj9tdQu+SMQDazOu5C2088seGCV7JdQPkFi6im8Hk1N+bXm6eJRXlQf5Ud1Ul4KXR/pzs2zZoV5440qTjwxmHItwZdfbi3q0ItQCFatCnDHHbU8+2xuvTiZ1kEsVNnLKcDqh41yxZNXXkLPo+7pxX6L1VtLAIiM2InQty+k7bQz00/D6IVUv4QuuyycNlHmrFnhtGmDUk/hDRS8qVpEpFKkO78++GDt1vFLgRSX81LMwgsG4d57a7t182V73s8212B/onWwchD7gCST8gPiedQteoodDjuYoaedRO1bS+jaqZGWq7/Phtfeom3GeQUPrmBbP/2KFdVEIrHgZwBz5tRllbE8mWyn8JZbRnMRkXKX7vza0lLFypXVQADPS36OLsUsvFDIH6iezMKF6c/7lbgOogKsHOT0AYlEqFv4S3b8wkEMPeMUat/+E12NO9My9zo+eu0t2s45tyiBFaT/JfTb39YwalSOQWJUugAzXm8WjBMRqWTZnl+TaWiIcNllxe016OyEyy+v6zELMGbVqipmzvTzDqbSVwuo9hV1EeYoYzLKSIS6RU8xaP611Lzjp7Tp2nkkofMvYsvXTof6+qKXMd0voTVrqpgwIfmXONOviGyn8PbX5l4RkWLJdYmEeG1tATZsCDBkSPHOu83NdTz0ULrFoAM8/HAdQ4d6KbsKK20dRAVYOUr5AYlEqPvlkwyafx017/pJmLtGjtoWWA0cWLIypl8sLsBf/1rNxImdbNoUyDkLe3yAuWJFFdCzpaq/NveKiBRT4g/4gQM9WlszdzQV+0dtLil0Mo3lhcpZB1EBVi9t/YB0dTHg8ccJ3jCfmnffAaBr1GhC51/MllNOTRpYFTtpdDa/hDZtCvDMMyE2b86tHPEBZvxsklwDNRER6S7+/PrBBwG+9rV6WlszP67YP2pzSaGTccJXBVGA1VsdHQz42SN+YPXe3wDoGj1mW2A1oGdTajFX4E3U3Bxm82Z46KE6krUyrV5dxebNvf8SBIMwfrzHddeFCYUqo7lXRKQUgkH/t/nq1emDmupqj9NOCxf9R20uKXQ0RGQbDXLPVXs7A++5k2EH7M2Q879JzXt/o2vsOD754U189PslbPnGtKTBFaSe2dfcXFfwYtbUwLXXhhkzpncD2rNV7NY4EZFKlM2gd8+DGTM6ir4KeroJXok0RGQbBVjZCoWov/1Whu27J4Mvu4jqFX+nc/wENt+8gI9eeZMtXz8d6lIHSun6sIu1rEEwCEcdVZxpsZ2d/qJ4kycHmTRpEJMnB5kzpy7tDBIREclONkHN6NGlay1KnAE4ZkwXEyd2VsyMwN6o+C7CTC0wgZZPGHjXHQRvu4mqf/wDgM7dJ9J68aWEjz4GqrOb8ZHXIqV5yDjrsdfHLW4+LBGRShc7Tz/4YC0tLT2vH6VsLUo1wUu9GKlVbKqcHXcczLnntqccDxX4eCP1P76N+h//iKqPPwagY+/PErroMsJTjoSq3Br/SplDKtXzF+pLUKzXojQg5UX1UX5UJ+WlVPWxeTPMnj2Al16qZs2a7j+U+2OS5HwoVU4Z+M53SNoC09C2nquH3cDAO2+nqsWvpI79J9F68WV0HPIFUuYpyCDdzL5S/Aop5LTYvmqNExGpREOGwE03tau1aDtTtADLzJqBs4H10btmOecWFev5chEKwS9+0f2+kazmO8xnxv0LCHr+gKjwwf9O6OJL6fj8QQV53mJ115VaJeaUEhHpa5WyflR/UewWrP92zs0v3pjyGQAAFQlJREFU8nPkbN26ACtW+H/vwgdcxjzO4k4G0g4ebDzoSJj1HTr32a+gz1tOq9jm80uor1vjREREyl1FdhE2NnqMbYpw/gcXcy63UIs/U+Mx/oM7Gy/ntvutqEFCX/0KCYXotjhoPmtx9ZfWOBERkWIodoB1npmdBrwOXOKc21jk58tKMAhfPXIT5y24mQAe9/M1vs8VvMMeTD+2nWCwfwUJ8QucJqa36e3sv3JqjRMRESk3ec0iNLNngZ2TbJoNvAr8A/CAq4GRzrkz0x2vs7PLq6nJPdFlb3R2wvVnvM1TzzfwytpdaWqCY4+F+fPpd7MyLrwQbrwx/T7jxsGf/4yCJBERkeylnPlWkmUazGwc8JRzbmK6/Uq5TENsKmexZmWUy2yPdEsqxKuu9nj55dY+HUCpKejlRfVRflQn5UX1UX7KaZmGoq3kbmYj424eBywt1nPlIzYeqlBBULmtcJ5tkk7N/hMRkWIIhWD58kBRMpaUs2J2hs0zs73wuwjfB84p4nMVTa4tUeW2wnm2STo1+09ERAopfvxvPpOqtldFe4nOuVOLdexiSAykevPByJRvcNascMmDmHRLKoBHU5Nm/4mISOGVW4NDqVVADJleqkAqEoE77uj5wejshGuvTf7BKNcVzpMtqXD44Z1Mm9bBqFGa/SciIoVVjg0OpVbxAVaqCLuhIZJ0/3vvrcPzYO7cni1Z5brCuZZUEBGRUirXBodSKtog9+1Bugi7pSX5xICurgB33z2A5ua6Htti3XHJlMMYp/gFTitxwKGIiJRGrMEhmUqZVFXRAVa2M+ySWby4JmmA0twcZvr0dpqauqiu9mhq6mL69Pat3XR9OZui3GY4iohI/1TuDQ6lUNFdhOm69BoavJStWJC6iTNVd1wsuOnL2RSVPuBQRERKp9JTqlV0C1a6CPukkzo488x2qquTN2NmauJMXF8rFtysWFFNJBKIBjfJuxqLIdOAQ3UXiohIIcUaHF54IcTLL7fywgshrrmmMpZogApvwYL0EXZNDXge3H33gB6PiwVmy5dnHjReDrMpNOBQRET6Qvz430pS8QFWphl2c+eGqa3tHoAdcYS/jMPkycGsuvvKIbgp1xmOIiIi/VFFdxHGS5UyJ1kTZ1WVv0ZWtt195TCbQgMORURESkcBVpbimzhzHctULsFNphmOIiIiUhgV30WYq95295XDbAotOCoiIlIaCrBy1NuxTOUU3FTqgEMREZFSURdhjvLt7ks11ktERET6D7Vg9UIu3X2hEH3eYiUiIiKlpQCrF7Lp7uvs9BcX7cuV20VERKRv6FKfh3RjmZSWRkREpHJpDFYRKC2NiIhIZVOAVQTplnJYsaKKVatSJ5EWERGR7Z8CrCJIt3I7BLjjjtqSlkdERERKSwFWnFDIT95ciC68/fbrSrnt2WfVTSgiItKfKcDCn/E3Z04dkycHmTRpEJMnB5kzp47O5MtdZXWcn/2sFkg+AD624ruIiIj0T5pFSOFm/CUeJ5X6eo/hw7WSuoiISH+VVwuWmZ1oZn82s4iZ7ZOw7QozW2ZmzsyOyK+YxZNuxt+DD9ayeXP+x0nU0lLFvHl12RZRREREtjP5dhEuBY4Hfhd/p5ntDpwE7AEcCdxqZj2T95WBdDP+WlqqmD07c4tUpuMko+UaRERE+q+8Aizn3LvOOZdk07HAQ865dufccmAZsF8+z1UsjY0eI0emmvEHL71UnVUglH7mYE8ahyUiItJ/FWuQ+2hgRdztldH7yk4wCJMnpx7NvmZNdoFQuiTQyYwaFaGxUeOwRERE+qOMg4bM7Flg5ySbZjvnnihkYXbcMUhNTel6EkeMGAzAggWwcCF88knPfZqaAkyc2JBVouZbboH6enjiCVixApqaYIcdYMmSnvsef3w1Y8cOzvMV9D+xOpHyoPooP6qT8qL6KD/lUicZAyzn3GG9OO4qoCnu9pjofWlt3Fi6QUkjRgxm/fptEdXJJyefAThlSjutrWFaW7M77uzZcNFFbE0CXVe3Lenz6tVVjBrlJ32eOTPM+vWFejX9Q2KdSN9SfZQf1Ul5UX2Un1LXSbpgrljLNDwJPGhmPwRGAeOBPxTpuQqiudlfjiExEIrdn4vEJNDXXBNm1qzw1qArm9YwERER2X7lFWCZ2XHATcAIYKGZLXHOHeGc+7OZPQK8A3QC5zrnUi9tXgZqaoobCCUGXSIiItJ/5RVgOeceBx5PsW0uMDef4/cFBUIiIiKSL6XKERERESkwBVhpFDL5s4iIiFQOBVhJFCr5s4iIiFQmJXtOolDJn0VERKQyqQUrQbqkzcofKCIiItlQgJUgXdJm5Q8UERGRbCjASpAuabPyB4qIiEg2FGAlSJe0eerUTq3CLiIiIhlpkHsShUybIyIiIpVHAVYSxU6bIyIiIv2bAqw0lDZHREREekNjsEREREQKTAGWiIiISIEpwBIREREpMAVYIiIiIgWmAEtERESkwBRgiYiIiBSYAiwRERGRAlOAJSIiIlJgCrAKKBSC5csDhEJ9XRIRERHpSwqwCqCzE+bMqWPy5CCTJg1i8uQgc+bU0Zk8Z7SIiIj0c0qVUwDNzXXcfvuArbdXrKjm9turAT+noYiIiFSWvAIsMzsRaAZ2A/Zzzr0evX8c8C7goru+6pybkc9zlatQCBYvTv42Ll5cw6xZYSWKFhERqTD5tmAtBY4HFiTZ9jfn3F55Hr/srVsXYNWq5D2tq1dXsW5dQAmjRUREKkxeY7Ccc+8651zmPfuvxkaP0aMjSbeNGhWhsVHBlYiISKUp5hisXc3sj8BmYI5z7oVMD9hxxyA1NdVFLFJ3I0YMLshxjj8ebrwx2f3VjB1bmOeoFIWqEykM1Uf5UZ2UF9VH+SmXOskYYJnZs8DOSTbNds49keJha4BdnHMbzOxzwC/MbA/n3OZ0z7VxY+nWNxgxYjDr139SkGPNnAltbXUsXlzD6tVVjBoVYerUTmbODLN+fUGeoiIUsk4kf6qP8qM6KS+qj/JT6jpJF8xlDLCcc4fl+oTOuXagPfr3G2b2N2AC8Hqux9oe1NT4swVnzQqzbl2AxkZPA9tFREQqWFG6CM1sBPCRc67LzP4JGA+8V4znKifBIBrQLiIiIvkNcjez48xsJTAJWGhmT0c3HQy8ZWZLgMeAGc65j/IrqoiIiMj2Ia8WLOfc48DjSe7/GfCzfI4tIiIisr1SqpwCUR5CERERiVGAlSflIRQREZFEykWYJ+UhFBERkURqwUohmy6/zZvhwQdrk25bvLhG3YUiIiIVSgFWgly6/ObMqaOlJX0eQhEREak86iJMkG2XXygEL7yQ+u0bOVJ5CEVERCqVWrDihEJ+114yiV1+69YFWLMm9dt34IFdWs1dRESkQinAirNuXYBVq7Lr8mts9Bg9OpJ034aGCHPntheljCIiIlL+FGDFSRc0jRrVvcsvGISpU5OvxXDKKR0MGVKUIoqIiMh2QAFWnHRB09SpnT26/Jqbw0yf3k5TUxfV1R5NTV1Mn95Oc7OWZxAREalkGuSeIBYcLV5cw+rVVYwaFWHq1M6kQVNNjT/wfdasMOvWBWhs9DTuSkRERBRgJepN0BQMwq67asagiIiI+BRgpaCgSURERHpLY7BERERECkwBloiIiEiBKcASERERKTAFWCIiIiIFpgBLREREpMAUYImIiIgUmAIsERERkQILeJ7WehIREREpJLVgiYiIiBSYAiwRERGRAlOAJSIiIlJgCrBERERECkwBloiIiEiBKcASERERKbCavi5AsZnZkcCNQDVwh3Pu2oTtA4D7gM8BG4CvOufeL3U5K0kWdXIxMA3oBNYDZzrnPih5QStEpvqI2+8/gMeAfZ1zr5ewiBUnmzoxs68AzYAH/Mk5d0pJC1lBsjhn7QLcC+wQ3edy59yikhe0QpjZXcAXgQ+dcxOTbA/g19dRQAg4wzn3ZmlL2c9bsMysGrgFmArsDpxsZrsn7HYWsNE59y/AfwPXlbaUlSXLOvkjsI9zbk/8C/q80paycmRZH5jZYOAC4PelLWHlyaZOzGw8cAVwoHNuD+DCkhe0QmT5HZkDPOKc2xs4Cbi1tKWsOPcAR6bZPhUYH/03HfhRCcrUQ78OsID9gGXOufecc2HgIeDYhH2Oxf/lAf7F/NBo9CvFkbFOnHPPOedC0ZuvAmNKXMZKks13BOBq/B8fW0pZuAqVTZ2cDdzinNsI4Jz7sMRlrCTZ1IcHDIn+PRRYXcLyVRzn3O+Aj9Lscixwn3POc869CuxgZiNLU7pt+nuANRpYEXd7ZfS+pPs45zqBTcDwkpSuMmVTJ/HOAhYXtUSVLWN9mNlngSbn3MJSFqyCZfMdmQBMMLOXzOzVaBeWFEc29dEMfN3MVgKLgG+XpmiSQq7XmaLo7wGWbMfM7OvAPsAP+roslcrMqoAfApf0dVmkmxr87o9DgJOBH5vZDn1aosp2MnCPc24M/rifn0S/O1LB+vsHYBXQFHd7TPS+pPuYWQ1+8+6GkpSuMmVTJ5jZYcBs4BjnXHuJylaJMtXHYGAi8LyZvQ8cADxpZvuUqoAVKJvvyErgSedch3NuOfBX/IBLCi+b+jgLeATAOfcKMBD4VElKJ8lkdZ0ptv4+i/A1YLyZ7Yr/5p4EJM60eRI4HXgFOAH4X+ecMmAXT8Y6MbO9gQXAkRpbUnRp68M5t4m4C4WZPQ98R7MIiyqb89Yv8FtN7jazT+F3Gb5X0lJWjmzq4+/AocA9ZrYbfoC1vqSllHhPAueZ2UPA/sAm59yaUheiX7dgRcdUnQc8DbyLP8vjz2Z2lZkdE93tTmC4mS0DLgYu75vSVoYs6+QHQAPwqJktMbMn+6i4/V6W9SEllGWdPA1sMLN3gOeAS51zankvgizr4xLgbDP7E/BT/GUB9EO9SMzsp/iNImZmK83sLDObYWYzorsswv/BsQz4MfCtvihnwPP0GRAREREppH7dgiUiIiLSFxRgiYiIiBSYAiwRERGRAlOAJSIiIlJgCrBERERECqy/r4MlIgVmZocA851zOS82amYH4K9xVg+8D3w9m7XOzMwDXnfO7Rt3XzPwn8CXnHNPmdlY/CS7TUAAaMefLr80uu+36J4j7i7n3P9keN698BP97g0scs6dELftSPz8jB5Qi7821Zxk0/Oj5X8biETvOtU597aZjcOfSr40bvdD45dcMLOBwBtAW+w9N7Oz8dOxBKLPP885d390207A3dH3oRZ/GYfznXOdZvZd/HWcuoAOYJZz7ul074GI9I4CLBEpiWjqkPvxg54XzWwOcC1wZpaHCJjZ7s65d6IJ2U+me2ByK7DYOXdz9PlG4wcRMfc5576TY7E/xF8fby/g8IRtLwKfdc51mVkt8BLwe/xFDpP5vHOuJcn9Hzvn9kpThrn4Sc8/E3ff/wGHOOc+MrMxwBIze9E59z4wC3jXOXd0tFwvAsfjrzT+B+B651zIzD4D/NbMRjrn2tI8v4j0ggIskX7CzPbHD1iGRO+60jm3MNpK8jpwL36QEAC+5Zx7Ifq404BL8VtC/gacE2tVMrMr8FetjgCtwEHRY9eY2QJgUvRxJznn3s1QxM8BW5xzL0Zv34bfipVtgHUvcAZwGX4OvqV0T8zeLR2Gcy7v1BjOudXA6ujq3Inb4oOlgUAd21qoCsLMJuOnwPkhcQGWc+75uL9Xmtka/Nf/Pn59DI4GtAOi5VoV3Te+teot/M/CcPzUOyJSQBqDJdIPRBP93gac4pz7HPBFYEFcAuDhwJ+cc3vidy391MwGmNlE/KBsSnTbUuCm6DFPB47Bb3n5DH5XXCyA2AO4LfqYR4A5cWVZYmajkhRzF+CD2A3n3D+AKjMbluXLfBT4splV4wda9yRsnwfcZ2a/NbPrzGzfhO2nRcsW+3dUtLzHmNkdWZahGzPbx8zewm/p+l9gYZrdn48+7/fNbEDc/UPM7HUze8PMLo22zmFmg4AbgG9mKMMhwA743YgAV+OnzlkDrAWeds69lOShpwF/c84puBIpAgVYIv3D54FdgcVmtgRYjN+S8S/R7WH87rlY60cbYMC/448tiuXpWgAcFv37i8CPnHOfRB8Xn4rFOef+GP37VeCf4zbsFW35KbQW/PQYx+G3pC2O3+icewAYhz9mahDwnJmdHLfLfdGyxf4tij7uSefctN4UyDn3ejTIbMJvoZucYtddouOnDgZ2B74bvX8NMCa6bSrwH/iJg8FPGXVLupY4M9sduA84Oa6b70T81qmRwGjgYDM7IeFx/4YfiMW/PyJSQAqwRPqHAPBWQgDRVMSkzFvi/u4iu+EGfwfGxm5EkxRHnHMf5fC89+C31P0imiOuG+fcBufcI8658yhhABFtjVuMH9wk274i+v9m4A7gwOjt9lh3bPT/B2Lb8IPIK83sfeAh4NPR1jIAzGw8fs61c+K6XcFvoXzAOReJJut+Aj+Qjj1uEn6w/WXnnMvvlYtIKgqwRPqHl4HxZhZ/Id031t2EPw7nlOj9k/Fn8f0Ff4bZUWa2c3S/s4FfR/9+CvimmQ2OPi5+vFNvvAHUm1lsHNcM/G6/WHl/Y2b7ZTjG88D3gZsTN5jZ0dEZd0S7EfcEludZ5pTMbEJ0nFOsO28q/kzBxP12NLP66N81wAnAkujtnaID0TGzIH6X7BIA59yezrlxzrlx+DP/3o62lmFm/4SffPh859zihKdcDhwZ3a8Ov0VyafT2vsDDwAnOuTcL9FaISBIa5C7SDzjnNprZMcAPzOwG/IDqPeBL0V02AHuZ2WX4rV0nO+fCwFIzuxz4dXQpgfeAc6KPuQ+/i+lVM+sAWszs4ExliXZRHpXYTeici5jZqfhjwwYSXaYh+phq/EHcaccDRZdAuD7F5kOA+dGy1uAP7L8ybvtpZnZY3O0nnXNXRt+3Y5J1E0YnCLwIBIGBZrYS+E/n3J3AscAZZtYJVAOP47dOkXDMf42+5thyDi+zrYvwIOAqM+uKbnuKJMFjEtfhj6u7ysyuit43MzqI/ULgNjN7O1qu54AfR/e5FT+4XmBmsWOd6pzrERiKSH4CntdjyRYR6Udiswidc5/q67KkYmafxZ/Z2KuxUCIi5UYtWCLS56LdVQquRKTfUAuWiIiISIFpkLuIiIhIgSnAEhERESkwBVgiIiIiBaYAS0RERKTAFGCJiIiIFJgCLBEREZEC+384YX1CV4zYEAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7b201b55c0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tf.reset_default_graph()\n",
"sess = tf.InteractiveSession()\n",
"model = Elasticnet(3, 0.0005)\n",
"sess.run(tf.global_variables_initializer())\n",
"\n",
"fig = plt.figure(figsize=(10,5))\n",
"ax = plt.axes()\n",
"ax.scatter(X[:,0],Y[:,0], c='b')\n",
"cost, y_output = sess.run([model.cost, model.logits], feed_dict={model.X:X_new, model.Y:Y})\n",
"ax.set_xlabel('epoch: %d, MSE: %f'%(0,cost))\n",
"line, = ax.plot(X,y_output, lw=2, c='r')\n",
"\n",
"def gradient_mean_square(epoch):\n",
" cost, y_output, _ = sess.run([model.cost, model.logits, model.optimizer], feed_dict={model.X:X_new, model.Y:Y})\n",
" line.set_data(X,y_output)\n",
" ax.set_xlabel('epoch: %d, MSE: %f'%(epoch,cost))\n",
" return line, ax\n",
"\n",
"anim = animation.FuncAnimation(fig, gradient_mean_square, frames=100, interval=200)\n",
"anim.save('animation-elasticnet-regression.gif', writer='imagemagick', fps=10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
arnoldlu/lisa | ipynb/sched_dvfs/smoke_test.ipynb | 5 | 1064204 | null | apache-2.0 |
ajhenrikson/phys202-2015-work | assignments/assignment03/NumpyEx03.ipynb | 1 | 67434 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"# Numpy Exercise 3"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"## Imports"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true,
"nbgrader": {}
},
"outputs": [],
"source": [
"import numpy as np\n",
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false,
"nbgrader": {}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Downloading: https://raw.githubusercontent.com/ellisonbg/misc/master/vizarray.py\n",
"Using existing version: github.ellisonbg.misc.vizarray\n"
]
}
],
"source": [
"import antipackage\n",
"import github.ellisonbg.misc.vizarray as va"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"## Geometric Brownian motion"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Here is a function that produces standard Brownian motion using NumPy. This is also known as a [Wiener Process](http://en.wikipedia.org/wiki/Wiener_process)."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"nbgrader": {}
},
"outputs": [],
"source": [
"def brownian(maxt, n):\n",
" \"\"\"Return one realization of a Brownian (Wiener) process with n steps and a max time of t.\"\"\"\n",
" t = np.linspace(0.0,maxt,n)\n",
" h = t[1]-t[0]\n",
" Z = np.random.normal(0.0,1.0,n-1)\n",
" dW = np.sqrt(h)*Z\n",
" W = np.zeros(n)\n",
" W[1:] = dW.cumsum()\n",
" return t, W"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Call the `brownian` function to simulate a Wiener process with `1000` steps and max time of `1.0`. Save the results as two arrays `t` and `W`."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"grade": false,
"grade_id": "numpyex03a",
"points": 2,
"solution": true
}
},
"outputs": [],
"source": [
"t,W=brownian(1,1000)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "b671a523fd8cb7621c2445244189d5a4",
"grade": true,
"grade_id": "numpyex03a",
"points": 2
}
},
"outputs": [],
"source": [
"assert isinstance(t, np.ndarray)\n",
"assert isinstance(W, np.ndarray)\n",
"assert t.dtype==np.dtype(float)\n",
"assert W.dtype==np.dtype(float)\n",
"assert len(t)==len(W)==1000"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Visualize the process using `plt.plot` with `t` on the x-axis and `W(t)` on the y-axis. Label your x and y axes."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"grade": false,
"grade_id": "numpyex03b",
"points": 2,
"solution": true
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f6b6a317690>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfwAAAFmCAYAAACIryg2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd8XNWZ//HPjHqvo2LJcvd1xTY2uGEwnYRAstl0NpCE\nJJCyCSTZNEI2yf42gd2wqaSQkJACKYQSCBA6uGBwwcY2xtdFtqzeex1p5vfHnRnNSKNmaUbS6Pt+\nvfxi5s6dmaNr4eeec57zHJvb7UZEREQim32yGyAiIiKhp4AvIiIyAyjgi4iIzAAK+CIiIjOAAr6I\niMgMoIAvIiIyA0RPxpcahvEDYD3gBj5vmuZev9dOA2eAPs+h60zTrAh3G0VERCJJ2AO+YRgXAQtN\n09xkGMYS4DfAJr9T3MBVpml2hLttIiIikWoyhvQvAR4BME3zKJBhGEbygHNsYW+ViIhIBJuMgJ8H\n1Pk9rwXyB5zzC8MwthuG8b3wNUtERCRyTYWkPRvWML7X7cCtwFZghWEY/zoZjRIREYkkk5G0V4HV\ny/eaBVR6n5im+UfvY8MwngRWAg8N9WFut9tts2kGQEREZpQxB77JCPjPAN8G7jEM41yg3DTNdgDD\nMNKAx7CS9jqBC4G/DfdhNpuN2trWEDd5ZnM4UnSNw0DXOfR0jUNP1zg8HI6UMb8n7AHfNM1dhmHs\nMwxjJ9bSu88YhnED0Gya5qOGYTwEvGIYRhuw3zTNIXv3IiIiMjq2CNge1627ydDSHXt46DqHnq5x\n6Okah4fDkTLmIf2pkLQnIiIiIaaALyIiMgMo4IuIiMwACvgiIiIzgAK+iIjIDKCALyIiMgMo4IuI\niMwACvgiIiIzgAK+iIjIDKCALyIiMgMo4IuIiMwACvgiIiIzgAK+iIjIDKCALyIiMgMo4IuIiMwA\nCvgiIiIzgAK+iIjIDKCALyIiMgMo4IuIiMwACvgiIiIzgAK+iIjIDKCALyIiMgMo4IuIiMwAER3w\nH91ezMfueIHHdpzC7XZPdnNEREQmTcQG/NaOHh7beRqAR3ecYs/RmhHfs/doDZX17fS5XCFunYiI\nSHhFT3YDQqWkujXg+aHies5fmjvk+XXNnfzs0cO+5/d+5WJsNlvI2iciIhJOEdvDr6jrAOCma5eT\nFB/NibLmYc/v6OoNeN7Z3TvEmSIiItNPxAb8qvp2AGZlJ1HgSKamsZMeZ9+Q5z+zpzTgeWuHc0zf\n53a7+clDB3nq1ZKxN1ZERCTEIjbgN7f3AJCREkeBIwk3UFnfEfTc3j4XrxyuCjg21oBf1dDB/uN1\nPPjSybNqr4iISChFRMB39rooqQqcs2/p6CHKbiMxPpr8zEQAqhuDB/z2rsHD960dPWNqw8nyljGd\nLyIiEk4REfB//8+jfPu+PZhnGn3HWjucJCfGYLfZyEqLB6C+uSvo+9v8gvuSonTr/Z1j6+GfKO/P\nEdASQBERmWoiIuDv9AzHH/NLzGvt6CE1MRaA7LQEACrq22lu6x70/ja/4H7ekhwAmoKcNxz/gF/f\n0kVzWzcut1vBX0REpoRpvyzPP6DWNXUC1hB/Z3cfKYkxAGR7evg7D1Wx81AVP7llC0nxMb73eefr\n37t1AYtnWz38ptbRB/yDJ+uoqGv3Pf/yz3cBkJORwIJZqXzimuVn86OJiIhMmGnfw69t7PQ93v1W\nDR1dTtq7rACenGAF9YS4aIpykn3nvXmqAZfL7Rvi987Xp6fEkZFi3Rw0BAn4vX0uXzKg7/ubOvnp\nw4eJjrLxtg1FAa/VNHay681qX3tEREQmy7QP+CfKmgCIjrLT7ezDPNPkW1Of6NeLv/aCeb7HxRUt\n/M8Dr/MfP3+FuuZOiiushLtZWUkkxkcTHxtFQ8vggP+rx49w60920NjaTX1zF3998QQHjtfR2+fi\nPVsX8p6LFhBlH1ysp6ymbUJ/ZhERkbGalCF9wzB+AKwH3MDnTdPc6/faZcB/A33Ak6Zp/r/hPuuM\np6Le5esKeeq1MxwrayLFM3efGNf/45272MEP//0CbvnJDsrr2n3z/RV17Rw+1UByQgyzc61RgLzM\nREpr2mhu6yYtOQ6wpg685XlLa1r54YMHA9qxpCgdm81Gn6t/iiEtKZbm9p6AHAEREZHJEPYevmEY\nFwELTdPcBNwI/HjAKT8C3g1sBq4wDGPpcJ9XUWv1ntd5ku2e3l3Ky2+UA5AYH3g/k5IYQ2yMPSDB\nbs9bNTS397DOcGD3lNLduCKPPpebX/z9Tco9c/Mtfuvyf/H3NwM+NzbaToEjKeDY5pV5vO/ihcDY\n1/SLiIhMtMkY0r8EeATANM2jQIZhGMkAhmHMBxpM0yw3TdMNPAlcOtyHVdS2E2W3UZTbP0e/85CV\ntT8w4NtsNhxpCXT39Ffce/VINQCLPMl6AMvmZgJgljbxowffAKC6oX8Nf1dPYMW+otwUouzWpfQm\nCm5dU+B7PNYlfiIiIhNtMgJ+HlDn97zWc8z7Wq3fazVA/nAfZp5pJD8ryRdw/cXHRA06lpYcG/Dc\nOwSfmRLnOzYrK5HcDGspX50nsW+ooj0A5yzI8j3+yofO5ZPXLGPBrDTf1EKbevgiIjLJpkLS3nBb\n0o1qu7plczMA+M+PnBdw3BVkDbw3CA+UmRrf/6U2G9+58Xxy0hOIsttwudxDluX9/HvO4e0b5/ie\nz8pOYsNy6/7Fu0qguX1sa/pFREQm2mQk7VXQ36MHmAVUeh6XD3it0HNsSJefX8T7LjdwZCbicKTw\nh29dRUVdG7sOVfL2LQuJiQ68p3F4yuwC3PGZC/jq3TsAWDQvi5jowBGBJfMy2ba/HFtMNBWegH/j\ntSs4UdpEeW0rOZmJXLZxHkPJykomPSWOY6XNZGUlYw+SwT9dOBwpk92EGUHXOfR0jUNP13hqmoyA\n/wzwbeAewzDOBcpN02wHME2zxDCMVMMw5mAF+quBDw33YZ97/xpqa1upre2vpe9IjuXajXNoamwf\ndH60X8zNSIjm0+9aQUNLF01BhuxTPT30t07WcrKsidyMBDYvy2HzshzfOf7fG8zSonR2vVnN4WPV\n5GclDXvuVOVwpIz4c8r46TqHnq5x6Okah8fZ3FSFPeCbprnLMIx9hmHsxFp69xnDMG4Amk3TfBT4\nFPAnz+l/Nk3zxER+f6xfLz4m2u7L7g/GO49fWd9Be1cvRbljv8Czsq0gX93QOW0DvoiITH+Tsg7f\nNM2vDTh0yO+17cCmUH33srkZpCbGcMNVS0Y815FuBfyTFdYyPm/W/VjkeaYQqhqGTvoDq3b/8/vK\n2Lq6wLfZj4iIyESZCkl7YVWUm8IPP7eFNYsdI55b6Flb/+qb1tK9lITgCX/D8d407DhUOWzFvXv/\ncYQndpXw878fHvN3iIiIjGTGBfyx8C/NC2fXw0/3VOqrqGvne/e/jss1eOVAW6eTIyXW1r6nK1vp\ndvYNOkeml5KqVp56rUS7JYrIlKGAP4Irzpvte3w2Ad+7NA+gs7uXr//qVV45XBlwzvGyJrxxweV2\n88dnTAWKae7b9+3hwRdP8vqxupFPFhEJAwX8EVy1vn8HPG9vfSwGLsWraezk1/94i94+l++Yd37/\n/KVWAuHOQ1WUVCvLNRLc/cghTlW28JOHDvKzRw/T53KN/CYRkRBQwB+Bf68+x5O1PxH8k/iqPGv8\nN63oL0Hg3fFPpp+BUzI/evAN9h+vY+/RGt/ftYhIuCngj8C/ZO/ZBvwPXLqIDctzcaT3Z9+3tPf4\nHtc2dWIDls7JJCHOWjbY0tGDeaYxYCRApoeSqsDRGf+Nlzq6dSMnIpNjUpblTTeLCtNobO0eVIlv\ntLx5AF09vTz8cjHP7Suj2S/gN7R0k5oUS0y0neuvXMIvH3uTex47AsCNVy9l88phtxOQKaa4omXI\n19o1ciMik0Q9/FH42r+t5c6bN477c+Jjo1k6x6r739xmBXy3201DazeZqVZ+gH+SH8CZ6qGX8snU\ndNJv+2WAT7xjGVd79lvo6NJGSiIyORTwR8lmm5g6+Kme3fq8G+q0djjp7XORmWIN9yclBA66NLVp\n452p6HBxPQ++dGLQagq3282Jiv6Af9X6IjauyGOOp0qjcjNEZLJoSD/M0pOsnrx3SL+h1dp+N8PT\nw89JD8wTKK9r50R5MwsL0sLYShnJ//31DQC2ri7wFVcC+NXjR2hu62HD8lw++rYlREVZ99QJ8db/\nagr4IjJZ1MMPs9QkTw/fM6Tf0GL14L09/MT4GH7xxYv4/qc3kZeZSEVdO9/9wz5OVw09LyyTp91v\niN7tdvPqEasq45aV+cRER2H3jAwleQL+VJrDD7Z9tIhELgX8MIuJtpMUH93fw2+xevjeOXyA2Jgo\nMlPjmZffv1lPY4uG9qcK/2qJLe39Ad8bzBcXprF0bmbAe9I8IzvHSpumxFp8t9vNt3+7h9t//VrA\nTYuIRC4F/EmQmhRLs2du/lhpEwCZqYM3zFlYmO573NN79kHiZEUzH7vjBW6/9zWcvSrbO17Vflsp\nD1xeCVCUN3hXxTRP7kZJdStPvXomxC0cWV1zF6U1bZTXtfPNe3fzf389oB6/SIRTwJ8E6clxtHf1\nUtfUyT6zlsS4aAqyB2+de8HK/kI8bZ1n1wvrcfbx37/fB0B5bTunKlXBbzx6nH3sPVrje97S0R/w\nvUV1cjMSB73P7pf0+fKBihC2cHTO+FVybGzt5nBxA02tGkUSiWQK+JMgL8sKCI9sL8YNXH7ebBLi\nBudPxkRH8cUPrAbg/mePcWLAci9/B47XBazt93rguWMBz3/+6GG2vTH6gLP3aA3P7Q7eI33qtRK+\n+4d9OMc4+nDfU0f52aPTb1fAt043cPNdL/PUa/3X428vneTR7cUAnPYU3PFm5A90zoIsADJSxl6i\neTycvX08vvNUwJLAYKWbK0fYwllEpjcF/ElQ6EgGYJdn290Fs1KHPDfZb8e+nYcq6Xb2cbqqJWA5\n2OHien780EHufuTQoPe/cbI+4Hlzew/3PXV0VO10u9387NHD/Ogv+wcF9d4+Fw++eJIT5c1853d7\neHhb8ag+s7K+nW1vVLD3aA01jdMrwDy28zQAXT19QY+X1rRiA2bnJAd9/2ffvRKAE+XNnKwY+uZt\nov19x2ke2X6KX//jLcD6uztWan2/N5kQrB0dRSRyKeBPguVzMwKezwoynO+V7tcbfPlABY9sK+Y7\n9+3lmT2lvuNvnbG21j1RNjiIJPndMGxdU+B73NUzcrZ4uV8AKK2xCgDtPVrDSwfKOerZzhesqYJ/\nvHJ6VDv8HT7V4Hv8yPZT02pXQP88ioEFktxut1UxMTmWuNjgFRmjo+y+m70jpxuDnjORtr1RgXmm\n0bf0s7iimQeeO8Yn//cljpU2kZYUy0fetpRCh/X7d+xMU8jbJCKTRwF/EuRkJHLXZzb7nqcPM8Sb\nlhTL7Tes8z33Bvrdb1X7jp0st5bsBRsq9k4d33j1Uq6/0mDr6lkA1DVZQaC6sYO7Hz4UkHzm9azf\nTcWZGmsI+GePHub3/zQ5WFw/6HzvEsPn95Xx0oFyq20Vzfz5+eO+5MTjpf1B5bUj1Ty3r2zIn32y\n9Tj7eHZvqS/R0Rs4wdpU6cNXLPY973b20djWPeKOip999woAqkM8fN7j7OO+p45y5wP7ifHUAmjp\ncPLc3v7r/Z6tC1hrOPjOjevJTovHLFXAF4lkKrwzSdI9Wdt2my0goSuYefmDh/wbPAlWnd29AUHU\n3wPPHqO8tp1CR5KvHn+2p0hMXXMXhTnJ3PfkUczSJuJio/j4O5YFvN9/nremsTNgOVplkOHf//j5\nKwHPt64u8CUMPrOnlP/8yHnsNWvJSImj0dP+181aLl83e9iff7L8+YUTvLS/nKr6Dq67fHHATZHd\nbuPicwsxS5vY/VYNNY2dOHtdZIwQ8LPS4omy20Ie8P036Rm4AdPH3r6UtYYjIG8kPyuJQ8X13PvE\nEVYvzGatkRPS9olI+KmHP0lsNhv/+6lN3PXZzSOfDNz24bW+x9FRdprbemho6eKB547hDcPNbT0B\nS6u8vWf/4Wfvdr+tnVbw6vH0Xus8S8oA3zB7U2u3b/e+msbOgB7um54h6fOW5BATHfzXaOAyL28C\n4fqlub5kxJ4pvEywqt66qSmrbaOlowf/H+fcRQ4AUhOtGzfvlMdICXlRdrt1wxPiksn+Ff28uSJe\nm1bmDUoSzfbs5LjzUBV3PzL9EipFZGTq4U+irLTBa++HssCvtO7Fawp4dm8pdz7wOrVN/UHY5XbT\n1d1LbEwU9z7xVv/3+K3x9wb/+uYuKuvbiYuxAro3Ea21o4e7/nyAM54AtqQonZLqNs5Ut1JWG9ir\nT4qP5uZ3LsfldvOJ/3lpUJv3H6sNeH68rJnoKDvv2boAu91GalIsHd2DA35XTy9/eu44CXHRvGfr\nAqKjJue+1Lt/gsvl9u1psGlFHgsL0tiyyhoxSfJcT+/1dqSPvIVyWlIsp6tacbvdE7ZHw0DDbcMb\nbETJe+Pi9fKBci5aXTDoPLB+z57dU8r5S3PDvuJARM6eAv408sN/vwCA1z2B1D/Ye3V091JZ38Fr\nR/p7de+/dJHvsTfgP7bztC+7HKCzp5eymja++ZvdAZ+XkRJHniOZl/aV8beXTga8Fhcbhc1mI2pA\nAFlSlM7RM01Be4pbzsnHbrfOT4iLptMTmNxuN4/vPE1ORgIHTtSx+60aX3vfsWnu0BclRMrr2nnL\nk5h4sqKFn3l+lgJHUkDyY1pSYKD0JsANJzUplj6Xm58/epjapi5uu37thN/UDFWzf8X8zKDHL1o9\ni7/vOOV7/rt/mly0ugCX281L+8tZOieD/CzrZztc3MBfXjjB4ztP89NbL5zQdotI6GhIfxpJTYol\nNSmW/KzBhV28pXk7u/sCenfv2DQ3YEh/YHa5V2Nrz6BgD7ByQRbneuZzBy7b6vZbnjbfs7Tw+iuN\nQb3WD166iPysRFbOz+Lf/BLdEuOi6ejqpbfPxdO7S3l0xynuefyIL9gDQZMJw+Hl/eUBz+uarZur\ngUl5uZmBfxeFQyzJ8+f0zKnvNWspqW6l3G/kpNvZh3mm0TdF4O+ZPaV849ev+a57S3vPkNXxOrqt\nNffZfqNI3//0Jm66dnnQ89OT4/jAJQsDjj31Wgm7j1Tzx2eO+W54oH+qpqO7NyCvQ0SmNvXwp6Gc\nIJXcCh3JNLR009nd6wuSGSlxXLwmcFh2qIA/MLELrMz+Dcvy6PJ7aVZ2EltXz+KB545z6dpC3/Fb\n3ruK4ooWzlmQFbAffEJcFOuX5XLp2kJstsBthhPjoujtc/HzRw+z/3hd0HbFxEzOPWnfEIF0YMDP\n8wv479m6YMQsfRg87F9S3cocTzneH//toG9k4Xs3bQio2vfn548DcLqqhdqmLn7z5FtcvKaA+bNS\nae/q5Yrz+pMfOz09/Nk5yVaCpiMpaPlmf5efN5u/vXyS3j7rZ3/wxf4RnfqW/tGkHmf/jd6BE3Wc\nu9gx4s88Hn0uFz/620GWzsmgoradqzfNDbjuIjI6CvjTkDfD39+iwjQOnqyno7vXV+71w1cYg+ZY\nk+JjiI6y+f5Rv2xdIbWNnQEFei5clc/1Vy3xzfXOcvT3WrPT4tm6poBFhekU5fYfT06I8VWS++Bl\niyhwJHPp2gJ6+9xBqwgCVDdaiYLeYJ+eHEtTW2CPfrK2kx2q5zrw2qcnxzIvP4Wunj4uXDVrVJ/9\n7gvn8+Lr/SMI3ox9t9vtC/YAh07Wk7vOCmz+hY/ufGC/b1ph91vVvOgZjfAP+K2eUsxb1xSwcn4W\naxZlj9gum83Gd25cz9fveXXQa95kTwgsPHSmujXkAb+yvoPDxQ0cLrZqOJypaePbHzs/pN8pEokU\n8KehgUPmF59b4Cuw49/DT00afGNgt9uYl5/K8bJm8jIT+dBli/nHK6d9Af/T71rBygVZAYldUfb+\nx3mZiURH2X090mAS42O4an0RADHD/IblZiT4hsovObeA9cty+d4fXw84p7lt+CH9Y6VNvH6slvdd\nsnDE5Y1j4d+L9TfwBspms3H7DeeN6bOT4mOs6QzP1It3n4SjA4rxlHhK9f7lheO8crgq4DXv9Ir/\nfUm3s4/mtm5+8tAhX9GkrNR4Vs7PGnXbgvWckxNiaGzt9iUZdvlNGTWEof7+wGmdphCvcBCJVJrD\nn6auu3wxm1fkce9XLubDVxjEe5bP/erxI74COMFGAgAu86x7X+7ZwnXDslzAykBftyTHl7kfTF6Q\n/IGz9bGr+9f9b/Rkv3/QL8EQrCFjb+1/t9vNU6+W8KvH36St00ljazd33P86z+wp5fQEbgrkcrsD\nEiLvvvVCfvS5C/ivj68nPnZi7pFvu34tV2+cA8D2g5V88e6dfPmn2wG46vwioqPs7DxcxeHiep7e\nXUprR+DmScWe0rydfsG3qa2bH/3tYECFxKwRhvGD+dZHzwvo0c+flUpvn9s3+tLldzPU0DI4cXSi\n1Q/4jtYOJw++eCLk3ysSadTDn6b8588BMlP6/2E/XdVCTLR9yAp+5y3JYc7NG0n3jABkpydw12c2\nB9RVH+ii1bN4+UAFS+dkDHnOWGWkxPFfH19PVX07C2ZZyw4vP2828wtSae1w8uO/HQSszXYWz07n\nWGkTD3pWCrR39XLQbxricHG9L3FwPDq7e/nSz14JCKTeKYmUxOA3UGcjPyuJf9kynyd2lQD4ChEB\nzM1P8eVU/N9f3wh434Wr8tn2RqVvSsbf134ZOBRvszFkmd/hFOWmcNHqAv7xymnf84Mn6/ni3Tv5\n7ic3BAzp1wVZKTLRgn3HzsNVvPfihUHOFpGhqIcfIRYVpvkq8tU2dZGTkTDsEHdOegKxfj35jJS4\ngOcDXXf5Yn747xcE3fp1PAqykwZVdVswK43VC7MDMuC/fs+rvHGiP7Hv4IBNgR7dcSpgq9qz9bt/\nHvUF+4vPLeAnt2wZ92cOxW4P/vczN0hlRa+xDM8PVRBpNPxv/mZlBf49eIf005JjqWnqpKW9h+0H\nKwJuWiaS/y6RN169lGVzM2hp75m0/A6R6UoBP0LYbDbevqHI97woZ+g59rMRHWUPmhMQSre+b1XA\n8/3H64iOGvom5s1TDbjdbp7dW0pl/dh3fuvtc7HHb6/7FfMyAzYfCrUFhWl88ppl5KQncOPVS0lO\nsOb6vZbPzWDF/CzysxKx2WDVguGD/1ArMkbDu/Tz0rWFzBswcvLSAWuKZcU8a0rof/60n98+eZRH\nthez+61qvvDTHewakHMwWq0dPTy6vdi3f4HL7eZkuVWw6aNvW8KmFXkUZFvJomfzdywyk2lIP4IU\n+mXT+2dsT1c5QarWFWQnB93LHaz8hWf3lPr2pf/NVy8Z9XeVVLUSFWXD7baK6ZyzIGtMvemz9aHL\nFvHAc9Zyu9WLHGxYngfA5pX5bF6ZT0eXk1NVrSwuTCPKbsdut3H7Detwu63d8AZufwz9hY/OX5J7\n1u06Z0E2//fZzcMuM1y1IJudh6p8CYSHius5XtZMU1sPLx8oZ+OKvDF/788fPczRM03YbDbeecE8\nWtp76Ol1sW5JDls8qyDm5ls3s8fKmpg3K3VCkzVFIpl6+BHEf323/5K5SJI2IBHxjps38lO/YXdv\nsAcGVQYcSnFFC9++bw/f/YO10c+Fq2bx0bcvDUtJ38vWzeaOmzdy4apZvP9yY9DrifExLJ+bSUx0\nlG8KID42moS4aN8NUWyMnf/+xHrfe67eOJfPv+cc/nXr/HG1zT/Ye6s8emWnxbNswDbPzW09viWG\n3mWBY1VcYe386F258Oj2Yt/3eS0psr73wRdP8oWf7KC8dnCRIhEZTAE/gtjtNr563bl866PnhaxG\ne7h99O1LmJPbPz2RnBDjK1/7pQ+sJic9gcQhht2ffLVkyOV1XjsPVfL/fr8X6F9fnj2GPQ4mQk56\nAh9525Ih6xUMZdXCbK7dPJfbPryO/KwkbnnvKs5d7GDx7DRWLcwmyj5x/3unJsUGlA2elZ1EYnzg\nlIO/xtZuTpQ3By3oNJweT72BKLuNHmcf296oBAj4noyUOBYVWkmeLR3OgGkYERmaAn6EWTw7naLc\niZ2/n0xbzpnFNz+yzvc8OSGGr1x3Lv/7qU0sm9tfF/5fLgzem60YYZ7Xf5MhgPjYKFaPokjNVGC3\n23jXlvnM9pTzPWdBFp9990pioseemT8a3/IrduO99gs9gXf1wv5rlpYUS1dPH9/9w76A+vz+qhqs\n/R7cfhUN/VdGNLR0cddfDvier1sSmNj54SsMvPe0nUE2YBKRwRTwZcrzH61Iio8mKT5m0E6D12ya\nGzASsNZT/e1wcQP7j9cOmcEfP2DZ2vxZqRO6/C6S2G02vvD+Vaw1HGw5x9ot8PorDT58xWLe51eH\n3/+Gc2DBILDqKfzowTf45WNvsv2g1YN39vbxh2dM3zl7zVqOl1nZ+d+4ft2ggkCFOcl895MbAGt3\nRREZWViT9gzDiAHuA4qAPuCjpmmeGnCOE9jhd+hS0zTHNi4oEWu4bV8/8rYl3PvEEc5d7GDFvCz2\nHavl4W3WHHByQgw//rw119/t7KO900lmajzJCTEB68r7gqxvl34r5mWxYl5/MmNmajwXn1sYMHVS\nlJvMoWIrmbC7p48+l4sou52Sqla6enpp63T6yiofK23iwlWzuPeJt3ybJq1d7GCfZ0fIVQuyhqyv\n4C2C1NmjHr7IaIQ7S/9DQINpmtcZhnE58D3gAwPOaTJN8+Iwt0umuEvXFvL8vrJhlxvOyUvhOzda\nyWudA24M2jqddDv7iIuJ4pd/f5MDJ+q45b3n+Er7vmvLPB7dfopLBhQ0ktHxr+Hgv7qio7uXo2ea\nWD43k2/ft2fQ+yrr2+ntc/mCfXSUnZveuZxP/u9LAMwaZrvhBM/ozN6jNZwoa/ZNL4hIcOEO+JcA\nv/M8fh74TZi/X6apD166iHWGg8Wz00d1frAEuKa2bjJT4jngKeDzwwcP+l67dvM8rjq/aNjiQzK8\nDctzcbncg1Y3PL37DMuCVGgscCRRWd8RsD3wp965POD9A3cW9OdfWOi7f9w3pmWYIjNRuOfw84Ba\nAM8wvduPeR4SAAAgAElEQVQwjIH/MscbhnG/YRg7DMO4NcztkynKbrdhFGWMa/VBa7uT6saOIV9X\nsB+fT16znJvfucJ3U3b1xjnkZyVyoqx50FTMNz+yjvzMRLp6+njztLUL3nWXL2bNgJ33HGlDB/yB\nvwveYj0iElzIeviGYdwIfHzA4fUDngf71/uLwB89j7cZhrHNNM19E90+iXwr5mVy+FSD73lzew/t\nXYG/ctlp8XzuX88Jd9MiWlZaPPf8x1ai7DbqmruorO/gWGlTwDlz81LJz0oCatlnWsP5s7IHD98P\ntR9EMGeq21hQoGF9kaGELOCbpnkvcK//McMwfgvkA4c8CXw20zR7B7zvHr/znwdWAsMGfIcjcpah\nTVXT8Rp/48YNbDtQTl+fi18+cohDpxtYNi+wet5/3byJwgkuQzwe0/E6D2fZ/GxeO1LN3mP9+yCc\na+TgcKRgzMvi8VdOc8qz0+GaZXm+FRI/+/IlmCWNrF46+mp97U7XqK5fpF3jqUjXeGoK9xz+M8B7\nPf+9BnjB/0XDMAzgTuDdWL3/TcCDI31obe3EbY0qgzkcKdP2Gq9bmMWbnl7+tv3lJHkSvT7xjmXk\nZSUSZ5s6vz/T+ToPZXa2NSS/65C1/O4dm+Zw7eZ51Na2Eu+3L0JuRgJd7d10tVsb8MTbYdW8jBGv\nxx03beCNk/X86bnjFJc2cs7c4XdzjMRrPNXoGofH2dxUhXsO/y9AlGEY24FPAV8DMAzjK4ZhbDBN\n0wSOAruxluY9aZrm3jC3USLMQr9h3ipP6dcFBam+3QUldIpyUljgWVY3OyeZd14wz5eU50jvr6Xg\nLR40VjkZiazxFP2paeocZ2tFIltYe/ieRL2PBTl+p9/jr4azTRL54mKjuGj1LF4+UEFpjVV3XcV1\nwsNut/HlD51LSXUrRTnJAeV+/Xfzy8saevndSDJS47ABDS2h2Z5XJFKo0p7MCGmerX3rmruIjrIP\nqrAnoRMTbWdhQdqgVRA2m42EOOtYyji28o2y20lKiKF1iGqKImJRwJcZwRvwAVISYyJmc6Hp7hvX\nr2Pj8lw2rxz7Vrr+UhJjaO04ux36RGYKBXyZEfy3ek3VcP6UkZ+VxCeuWT7kjoejlZIQQ3unE5dL\npZFFhqKALzOCf8W2jDGs7ZbpISUxFjfQ1qVevshQFPBlRvAP+IU5Z58gJlNTWrI1anPkdMMIZ4rM\nXAr4MiPE+SXpFTrObgmYTF1bVxcA8Oqb1ZPcEpGpK9yFd0Qmze03rONEeTPnDqjXLtNfYU4y2Wnx\nnChr9m3HKyKB9H+FzBjz8lO5fN3sQbu5SWRYWJhGR3cvN3//ZVxuJe+JDKR/+UQkIuRnJgLQ53Jz\noqx5klsjMvUo4ItIRFi/vH8t/6nKlklsicjUpIAvIhEhJz2B265fC0Bzm6ruiQykgC8iESPDU2Cp\nsU119UUGUsAXkYiR6imh3NSqgC8ykAK+iESM6Cg7qYkxNKmHLzKIAr6IRJT05Dia2npwa2meSAAF\nfBGJKOkpcXQ7++jq6ZvspohMKQr4IhJRvDsjalhfJJACvohElHTPRjqNStwTCaCALyIRJT1FPXyR\nYBTwRSSieIf01cMXCaSALyIRxVt8p6lV1fZE/Cngi0hEyUhRtT2RYBTwRSSiJCfGEGW3aUhfZAAF\nfBGJKHabzVN8RwFfxJ8CvohEnIyUOJrbeqhu6OCb9+7mZHnzZDdJZNIp4ItIxElPicPldvPErhLK\natv47z/sm+wmiUw6BXwRiTjeTP3qxo5JbonI1KGALyIRJz3FqrZ3vExD+SJeCvgiEnG8PXx/vX2u\ns/48t9tNW6dzPE0SmXQK+CIScbxr8QEWF6YB0NHde9af99qRaj7/o+2cqmwZd9tEJosCvohEHP+A\nn5eVCEBH19kH/IPF9biBQ8X1422ayKSJnuwGiIhMtJyMRG68eikLCtLYdqACGDrgn6ps4bEdp7Db\nbSQnxHD9VQZR9sC+0KkKq2df7PlvTVMnf3vpJFeeN5sFBWkh/ElEJo4CvohEpM0r8wFIiLf+mXvq\ntRJyHMkkx/QH887uXr73x9cD5vfzs5K4dG0BMdFRALR1Oqlu7ASsgO92u/ntE29hljax92gN3/ro\neRTlpoTrxxI5axrSF5GINjcvBbvNxj6zlh/+aT9ut9v32tGSxkHJfH998QT3P3vM93yvWeN73Nbp\n5EhJIy0d/RvzeHv9IlOdAr6IRLSV87P48ee3cM6CLIormqlt7vK95i2/+/F3LA14z56jtQCUVLXy\nl+dPEBtt5wOXLATg+b1l+N0zUOf3eSJTWdgDvmEYWw3DqDYM4+ohXr/OMIzdhmG8ahjGx8LdPhGJ\nPInx0cyflQpAdUN/MZ7GNqunnpkSz83vXO47Hh9rDec/vK2Ybmcf79m6gCvOLyI1KZZjpU1UN3SQ\nlRo36PNEprKwBnzDMBYAnwO2DfF6EnA7cCmwFbjVMIyMsDVQRCJWboaVre8foJs9Pfy05FhSEmN9\nx2NjrIBfUddOUnw0l62bDUBRTjId3b24gfXL8oiOsmkbXpk2wt3DLwf+FWgb4vX1wB7TNFtN0+wC\ndgKbw9U4EYlcuZkJAFQ3dPqONbdbPfz05DhSEmJ8x9s7nXQ7+2ho6WJ2TrLv+FXri3yPz1uSQ1JC\nDMUVLZyu0jy+TH1hDfimaXaZpuke5pRcoNbveQ2QH9pWichM4Ovh+9XX7+juxWazhvALHElcf5VB\nflYibZ1OTlW04AbyspJ85y+bm8l/fHANN127nDl5KTR7pgS+c9/egGRAkakoZMvyDMO4Efj4gMPf\nNE3z2TF8jG00JzkcWhITarrG4aHrHFrpKXHUtXT5rnOfy01CXDQ5Odb8/nsvT6Wpw8lj24rZfrgK\ngEVFGQF/L/6PF85O50RpEwDR8bFkpsaH60eZ0vR7PDWFLOCbpnkvcO8wpwS7Ha4A8vyeFwK7Rvqu\n2trWsTVOxsThSNE1DgNd59ArcCRz5FQ9JaUNJMbH0N7pJCbaHnDd0z1D+7sOVQKQEhc15N/Lp9+5\nnJ88dIhTlS28daKWxbPTQ/9DTHH6PQ6Ps7mpmqxleTaC9953A+cZhpFmGEYysAnYHtaWiUjEWrUw\nG7cbPvvD7bR3Oenu6SPek6DntWF5Lolx/X2hWdlJAz/GJz05jotWzwKUrS9TX7iz9P/FMIxDwLXA\n3YZh7PEc/4phGBtM0+wEvgo8DTwLfMs0Td0qisiEuHjdbKKjrH/2nnilhG5nH3GxgQE/PjaaW963\nyvd8pGH67DTr9foWrceXqS2spXVN03wEeCTI8Tv9Hj8EPBTOdonIzJCXlcTdt27hq798lRdeL6On\n10XcgB4+WNX55uWnsGxu5oif6b0haGjV8jyZ2lRLX0RmlJjoKC45t4CHXi4GGNTDB4iOsnP7DeeN\n6vMykq0CPI3q4csUp9K6IjLjzMtP9T0eOIc/VnGxUSTFR/Pm6caAJX8iU40CvojMOP672wUb0h+r\n5fOsof+7Hz407s8SCRUFfBGZcZL9qurFx41/ZvOma5ezakEWZbXtVNS1j/vzREJBAV9EZiRv0F9S\nNP618zabjTWLHQD84K8HcLn6y4y4XG66enrH/R0i46WALyIz0hfev4p/vWg+axY5JuTzDE/RnfqW\nbvaaNQD0uVz89x/28ZVf7MLZ2weA2+3mpf3lPPVqyYR8r8hoKeCLyIw0Ny+VqzfOxW4fVQXvEeVm\nJnLhKqsIz+HiBgDKato5VdlCa4eTcs9Q/2+fOsrvnzZ58KWTASMBIqGmgC8iMkE+eOkiAN+WuY1+\na/PPVFubhO44WOk71tbpDGPrZKZTwBcRmSDeJXpNnkDf1NYf8M0zjZysaA44v8WzPa9IOIwqPdUw\nDBvgneiqHWGLWxGRGSs9JY6GlsE9/MOnGnzTBwtmpXKyooWm9m5ee7maFfMyMYoyJqW9MnMM28M3\nDGO9YRiPAM3Am54/zYZhPGwYxvnhaKCIyHSSkRJHZ3cvXT29NHiq7xXlJtPa4WT/sTpiou1sWG5t\nCvq6WcsTu0q484H9uN3qR0loDRnwDcP4DvB94D6gwDRNh2maDmAW8DvgLsMwvh2WVoqITBOZKZ5S\nu63dVNS3Ex1l4/yluQB0dPcyKzuJdE853lcOV/ne19Sm4X0JreF6+PWmaW4xTfPv/jvWmabZBjxr\nmuYWoCHkLRQRmUYyUqzNdKobOymtaScvM5FVC7J8r19x3mzSkmIB6Ol1+Y5rPl9CbciAb5rmjwAM\nw/hnkJdf9j9HREQsGZ4e/sMvn6S3z8XSOZkUOJLZuDyXy9YWsnF5HqlJMYPe19qpgC+hNWTSnmEY\n1wHfBOYYhlHq91IMUBX8XSIiM5s34JfVWuvuL1lbAMAnrlnuOyfV08MHOHexg9eP1fLmqQZWzMtC\nJFSG6+HfDywD/gJcAGzx/DkfWBuW1omITDOO9ATf4+goO460hEHnxMf297XWGtYCqKd3l+L0G+IX\nmWjD9fB/DHzBNM0bhng9BrjLNM3PhapxIiLTTVZqPDbADeRlJgxZyW/zyjyio+y+JD+Airp25uSl\nBD1fZLyGW4e/DzhkGMY9wD8B77B+EXAl8AngztA2T0RkeomJtmOz2XC73eRlJg553o1XLwOs2vrz\n8lM5VdlCSXWrAr6EzHBZ+oeBy4E5wCNAtefPw55jV5qm+buQt1BEZJpJiIsCrF30RmKz2Xj/JQsB\nqG7sCGm7ZGYbrof/JyANeBb4f8AzpunZAkpERIb09o1zePDFk5yzYHRJeNlp1lK++uauUDZLZrgh\nA75pmosNwygCLgOuAu40DKMSeBr4p2ma28PURhGRaeWq84tYPjeT2TnJozo/PTmOKLuN2iYFfAmd\nYWvpm6Z5BviN5w+GYbwD+DLwVSAq5K0TEZmGbDYbRbmjn4u3221kpsbR0KqAL6EzbMA3DMOB1cO/\nDGtJXiXwPPD10DdNRGTmSE2K5VRFKy63G/so5v5Fxmq4ZXlvAMnAnz1/PmuaZme4GiYiMpOkJsbi\ncrs5dqaJJXO0c55MvOGy9H8JHATeB3wSuN4wjIVhaZWIyAzjrb73P3/az4my5klujUSi4Srt/cw0\nzX8BlmDtmpcF/MIwjMOGYfw2XA0UEZkJUhP7y+2apY2T2BKJVMP18AEwTbMPOAaYwBHABWwOcbtE\nRGaU3Mz+Ery1TSPPnja391DXrFlWGb3h5vAvxkrWuxxYjLVD3tPAD03TLA5P80REZob1y3I5cKKe\nvUdrqG/pHvH87/1hHzVNnfzsCxcG1OYXGcpwPfwfYC29+zKQY5rmOz3D/Ar2IiITLMpu59PvWkFc\nTBSt7cNvldvR1UuNZxRg//G6cDRPIsBwhXdWh7MhIiICqUkxtHQMH/C/8etXfY8r69tD3SSJECPO\n4YuISPikJsbS2uHE7Xb7jrV09NDnsrbOraxvp6mt/4agplHz+DI6CvgiIlNISmIsfS437V29AJTX\ntXPLj3fw1xdOAnDkdGAGf7UCvoySAr6IyBSSlWptpOPN1H/9WC0Az+61digvqWoNOL+msQNnryuM\nLZTpSgFfRGQKKXAkAbDrzSoAaj09+PhYa/uStk4nAD/49wtYvTCbzu4+bvr+S/x9xylcLneQTxSx\naC2HiMgUUujZYe+5vWWkJsay41AlAF09fXR299LW5cRmg5TEGHIy+tfu/33HKRJio7ji/KJJabdM\nfWEP+IZhbAX+AnzMNM0ngrzuBHb4HbrUNE2NV4nIjLBgVio2G7jd8PC2wFXQT75aQnunk6T4GOw2\nG4sK03hmT6nv9dPVrQM/TsQnrAHfMIwFwOeAbcOc1mSa5sVhapKIyJRis9m4dG0hz+0tG/RabVMn\n7V29JCXEALBmsYNLzy2kKC+Z3z55lKbWkQv2yMwV7jn8cuBfgbYwf6+IyLRhzO7fLS8hLpr//dQm\nAHa/VUNLew/J8VZfzW6zcd0Vi9lyzizSkmKpb+mi29nnW8In4i+sAd80zS7TNEfKKok3DON+wzB2\nGIZxa1gaJiIyhaw1HLxj0xwAbrjKID0lNuD1TE8mv7/8rERqm7r41F0v87NHDoelnTK9hGxI3zCM\nG4GPDzj8TdM0nx3hrV8E/uh5vM0wjG2mae4b7g0OR8pZtlJGS9c4PHSdQ2+6XONPvnsVH7xqmW/b\nXK/Vixz8+wfWkJESGPSve9tSbv/lLsAqtzuZP+d0ucYzTcgCvmma9wL3DnNK0J6+aZr3eB8bhvE8\nsBIYNuDX1ipRJZQcjhRd4zDQdQ696XiNazuseflFhWkcL2vmpmuW0dvlpLbLGXBeQUYCy+Zm+Arz\nVFY1Ex0V/pXX0/EaT0dnc1M1WcvybJ4/AQzDMIA7gXd7Xt8EPBjepomITD23vHcVfS43cZ71+EOd\n8/V7XqWuuYu65i7yMhPD2EKZ6sJ6+2cYxr8YhnEIuBa42zCMPZ7jXzEMY4NpmiZwFNiNtTTvSdM0\n94azjSIiU1FCXDTJnuz8oURH2blw1SwAfvDXA5TWKD9a+oW1h2+a5iPAI0GO3+n3+KvhbJOISCTx\nFuOpberin6+V8Ilrlk9yi2SqUGldEZEI4kjvr75XUd8xiS2RqUYBX0QkghQ6klk211rHX17b5qu9\nL6KALyISQWKi7XzpA2t4/yUL6e1z8+j24pHfJDOCAr6ISAS6eE0BKYkx7DlaM9lNkSlCAV9EJALF\nxkSRn5VEW4dTpXYFUMAXEYlYaUmxuIHWDs3jiwK+iEjESk20yvL+9YUTAPz+aZNf/+PIZDZJJpEC\nvohIhHL29QHw6pFqevtcvLS/nFcOV3GstGmSWyaTQQFfRCRCXb5utu/xK4erfI/vuP/1yWiOTDIF\nfBGRCFXgSPZts3vfU0cDXnO7R9qpXCKNAr6ISAQbuI2ulwryzDwK+CIiESw9Odb3ePXCbN8wf1WD\nyu7ONAr4IiIRLD05zvf4Y1cvxShKB6xEPplZFPBFRCJYRooV8FMTY0hOiOGcBVlkp8Xz0uvlHC1p\nnOTWSTgp4IuIRLD05Dhuu34t375xPQDRUXY++valuLF6+c3tPfzX7/bw+M5Tk9tQCbnoyW6AiIiE\n1oJZaQHPCx1JANQ2dXLrT3YAcKqylUvXziYxXmEhUqmHLyIywyTFxwDw1oAh/Yr69slojoSJAr6I\nyAxjt9sCni8qtEYA6pu7JqM5EiYK+CIiM9wF5+QDUN+igB/JFPBFRGawC87JZ15eKgA7DlbicqkC\nX6RSwBcRmYGuv9Jg4/JcPvq2JRQ4klg+L5Oqhg5efqNispsmIaKALyIyA21dU8AnrlmOzWbDZrNx\n5flWBb6HXz455Hu6enq544/7uOXH26luVKW+6UYBX0REWD43k6T4aNq7eul2Wtvq/vO1M9z/7DHf\nOY9uP8WxsmZaOpwBx2V6UMAXERFsNhurFmYD8KW7d/L07jP89cUTPL+vzHcDUNvU6TtfGf3Tjyos\niIgIAKlJ1kY77V29/OWFE77jh4sbKK9rw9nn8h3T7rrTjwK+iIgAkJYUG/T43Y8cGnSss7s31M2R\nCaaALyIiABRkJ414TlpSLDYbtHY4cbvd2Gy2Ed8jU4Pm8EVEBIDl8zK546YNfOVDa3zHUhJjBp0z\nNy+VPpebzu6+cDdRxkEBX0REACtxLycjkXn5qSwsSOOGqwxufd+qgHOWzc0gOcG6CWjt7JmMZspZ\nUsAXEZEAsTFRfP3Da7lodQFz81L5z4+c53tt4/I8X6+/td05WU2Us6CALyIiw8pIjQNgTl4KNpuN\njBTruWrvTy9K2hMRkWGlJsZyx80bSUu0sviz0uIBa3vdx185zfVXGiyenT6ZTZRRUA9fRERGlJOe\nQFxsFABZqVbA3/ZGBRV17dz7xJHJbJqMkgK+iIiMSW5GYsBzu5bmTQthHdI3DCMauBeY7/nuL5mm\nuXPAOdcBnwdcwD2maf4mnG0UEZHhxcVGcfXGOTyxq8Q6oIA/LYS7h/9vQLtpmluAG4H/83/RMIwk\n4HbgUmArcKthGBlhbqOIiIwg0zOsD9DS3j2JLZHRCnfAvx/4oudxHZA14PX1wB7TNFtN0+wCdgKb\nw9g+EREZhXjPfD5AZ3cfvX519mVqCuuQvmmaTsC7cPMWrBsAf7lArd/zGiA/DE0TEZExGDiK39bp\nJD05bnIaI6MSsoBvGMaNwMcHHP6maZrPGobxGWA1cM0IH6OJIRGRKWjtYgfrl+VSUddOaU0bbR0K\n+FNdyAK+aZr3YiXoBfDcCFwNvMs0zYGFmCuAPL/nhcCukb7L4UgZR0tlNHSNw0PXOfR0jSfON27c\nwANPH+VPz5hExUX7rq2u8dQU7iz9+cBNwEWmaQYrwrwb+LVhGGlAH7AJ+NxIn1tb2zqh7ZRADkeK\nrnEY6DqHnq7xxLO73QCUlDWRnxavaxwmZ3NTFe5KezdiJeo9aRgGgBu4EvgC8LJpmq8ahvFV4GnP\na98yTVO/OSIiU9TsnGQATlW2smF53ghny2QKd9LebcBtQV660++ch4CHwtYoERE5a/PyU4iy2yiu\naJ7spoxJTVMnvb0uZmUnTXZTwkaV9kRE5KzFREeRmRpH3TTbSOerv9jFN379Gs7embOcUAFfRETG\nJSMlnpa2nmm5Ft8sbZzsJoSNAr6IiIxLZkocbqC5LVgu9tTx/L4ydr1ZRbezf4FYaXXbJLYovLQ9\nroiIjEtGirX+vrF16pbYdbnd3P/sMQA+/a4VvuPVjZ2T1aSwUw9fRETGxRvwG1rHPo/f2+fiF38/\nzO+fNie6WT71zV184af9+7T97NHDvsc1jR0h+96pRgFfRETGJSPF2khnND38Q8X1PLbzFM1t1rmH\nTtaz+60aXtpfjrN3YC22ifHC/jJa2oNPN5wob2H/sVoe3laM21NTIFIp4IuIyLhkplo9/KMlIyfA\n3f/sMR7dfopv/XYPja3dAUPqN33/5ZBMC8RGRwU9vs5w0Nvn4icPH+Ifr5ympcMZ9LxIoYAvIiLj\nkukZ0n/jZD0VtVYS3NGSRr52z6s8+OIJ33nO3j5qPAG+ub2H7/95P3/1ex3gdGXLhLcvWO/++isN\nrtk8L+CYd9QhUingi4jIuKQlx7GwMA2Am+54nj6Xi2f3llLd0MFTr53xBdzKemu+fMs5+QHPAS5b\nVwhAQwh6+A1BagQU5aYwOyc5YIe2JgV8ERGR4d363lW+x02tPbhc/fPh3mF6bzDPy0wMeO/K+Vmc\nvzQXgPoQFPBpbO0mNtrOlz+4hq98aA2Xr5vN3HyrFv3XPryWpHhrwdoPHzzIibLpVTFwLBTwRURk\n3BLiorlqfRFgBdj2rl7fa97sfW9PPzUplqs3zgHg2x87n1vft4qsVCvxr765iz7XxBbwaWjtJjM1\nniVzMjCKMvjgZYuw26y+/cKCNG72W6b3t5dPTuh3TyVahy8iIhPCO5f/3T/uC+jFe3v43jnytORY\nNizP5fJ1s0lNivUdi7Lb2GvWsP+uWt5/ySIuXVs47jY5e/to63T6NvkJZk5u/85zyQkx4/7OqUo9\nfBERmRDe4A1Q1dA/P++fqAeQlhRHlN0ecL7dZiMlMQa3G3r7rCI5ZbXjr4LnnUbwriQIxj/I221D\nnjbtKeCLiMiEWLPIQVHe4H3avYG7ocXTw/cL9P6aBpTmfe1I9bjbVN1g3Ww40hKGPe+uz2wG4GBx\nPa4IXY+vgC8iIhMiJtrOHZ+5wPd8xfxMstPiKa5ooaWjh2OlTWSnxZOSGHzYfMMyK3HvtuvXEh1l\n49m9pb5RgbNVUdcOMOI2uBkpcTjS4+lxuth1uGpc3zlVKeCLiMiESUmM5V1b5nHV+UXcfO0KNq3I\no6unj6deLaGjuxdjdjo2W/Bx8xuuWsIdN29kwaw0LliZT4/Txcny8WXNn6lpBUYO+ACf8iTv3fvE\nW+P+3oHau5zccf/rvHGibkI/dywU8EVEZEJdu3ke77tkIYnx0SydkwHACU8AzUqLH/J9cbFR5KRb\nQ+9LPO8LtoZ+tPpcLg4XN5CWHEteVuKI58/NS/U9/u8/7Dvr7w3m0Ml6jpU28aO/HeTgyfoJ/ezR\nUsAXEZGQyfAstztZblXQS08eOnnOX6anPv94CvHsPVpLW6eTdUaObxneZPGfmjhdNfHVBEdDAV9E\nREImY0CAH3XA92TVv27WnvWcureIzqYVeWf1frfbTY+zb0JWC9T47RnQ3ROaTYJGooAvIiIhExMd\nGGbSkoNn6A+UnhxHbLSdmqZOfvWPI7R1jn1jm6Z275K8oacRhtPR3csDzx3jm/fuxjwz8sZAw/Hf\nhre9a3I26VHAFxGRkLrrM5v5+ofX8oFLFzE3yLK9YOx2W0Cinf+6/tFqbu+x1vePoZjOVz60xve4\nrdPJtjcqAWt6YDxqmjp90wr+VQjDSQFfRERCKiMljoUFaVxx3uwhM/SDKXD4Bfz6sQV8l9vNibJm\nEuOjsY+hmo5RlMEV580G4LEdp31FeSrqreV9HWfRO+/tc1HX3OWr399+FqMVE0EBX0REpqTZOf2j\nAbVNncOcOZh33j8xbuwV5L2b6ex6s8o3lXCyvJk/PXecz/5wO8fLmsb0efXNXbjdkO8pN3z0TJOv\n3HA4KeCLiMiUtOWcfLI9y/haOsZWgKe40sqEv3D1rDF/b2L84CmAnl5ry1+AkqrWUX+W2+3ma/e8\nCkBORgJZnmTEp3efGdX7j5Y04uydmCQ/BXwREZmSEuKi+c+PngdAc9vYAn5lXTs2OKsNeOJjo4Z9\nfSzV//zn6x3pCfzXx9cDYJaOPEqwz6zhf/60n/ueOjrq7xuOAr6IiExZiXHRREfZRgyyrx+r5eBJ\nq4qd2+2mrLad7PR44mKGD97BdHYHJtUNrNLX2NpNZX07n/ifF9l/bPhkPv/VBVlp8cTHRpOdFu/b\nOXA4JdXWSMKuN8e/pwAo4IuIyBRms9lIS4qlaZgA2e3s46cPH+KHDx4EoLa5i7ZOJ/PyU4d8z3BW\nLSC45O4AAA0sSURBVMwOeH7u4sDnh4rrue1Xr9HncnPP40eG/Bxnbx/1zValwOy0eBYVpgPW0sSW\ndienq1rodg49XB8d1R+ix7ssEBTwRURkipuVnUxja/eQZXZf3l/ue+zs7eNUhTV/f7YB35GewG++\neonveVFOSsAOf60d/b32bmcfL7xeFvRzvn3fXu76ywEgcGohPSkOl9vNd+7by6+HuWHwH2m484H9\n7DlaM/Yfxo8CvoiITGnL51p19Y8G6eVW1rfzlxdO+J7XNXdxqnJ8Ad/r9hvW8e4L57N6UTa3Xb/W\nt5vfQH985ljQ496d+oCAHQL9qw3uCzIlUNfcSUt7Dy0DpjGe3FXCJ//3RXa/dXZD/GNfryAiIhJG\nRbnW8rxyvwDqdbysGTfWWv/G1m5qmzo5U92KDZiTO7oiP0OZl5/qu2nITkvgk9cuZ/6sVB547vig\nc529roCqggPzANKS+oP8cBsIudxuvvzzXQHHNi7PY9ebVb45/V89foSrL1w45p9HPXwREZnS8j1J\nc8GK75TWWHXuvfXyS6paaW7vISkhhrgRsu3PxqVrC7n71gv5wKWL2LwijwtW5gOD6wQMfD47N9n3\nODczwfd44KY+3jl/f5+4ZlnAlMJIqwiGooAvIiJTWmpiDIlx0b7yus/vK+PBF0/gcrl9gdUb8E9V\nttLW6QwYQp9INpuNhLhorjhvNje+YxnZ6d5d/QID9St+G/7ERNtJTewP2HmZ/Vv1DrwpKa8dPIoB\nkJLoH/DPbnBeQ/oiIjKl2Ww2stPiqWrowO12c/+z1pz5U69ZxWui7DbyMhPJTI3jZEUzbZ3OgKAa\nSkmeIj0dA+rjHyquJz42is++eyWJ8YGhNi8zkWs3z+WxnacHbS50sqI54Hmu5+dITYoBz3R/R/fZ\n1eJXwBcRkSkvKy2eMzVtQXfNS06IwWazMS8/lX1mre9YOHjL8PoX2OnoclJZ38HSORksm5s56D02\nm413bZnPm6cbOF3ZSp/LRZTdCvxHzzRit9n4yS1bOHC8jsWzraV8/j38gfkBo6UhfRERmfKyPFvc\n/vbJwVXnvMF9yzn9ZXRDNaQ/UKKvh99/I1LpyTWYnZMc9D1eeZmJ9Lnc3PvEW4AVyE9XtjI3P4WE\nuGg2rsjzJfhlpvYn/RU6koJ+3kjC2sM3DCMauBeY7/nuL5mmuXPAOU5gh9+hS03TdIWvlSIiMtWs\nWpTNc/vKOHDCqqaXm5GAs89FQ0s33ry3cxZksWpBFm+crMeRnjDMp02cYD38Or9iO8NxpFltfPXN\nauw2G+cvzaXP5WZJUcagc6/eMIeSqlYuWl3AeUtyzqqt4R7S/zeg3TTNLYZhLAN+C6wfcE6TaZoX\nh7ldIiIyhS2fm8nbN8zhyVdLAGupXky0nVcOVwUM83/06qWU1rSxNEjQDAXv/Lx/D7+u2UokzB7h\npmPDijwe3XEKsJL8vBn7S+cMbntifAxf+sCacbU13EP69wNf9DyuA7LC/P0iIjJN+Q9ru4F/2TKf\n3IwErt4413c8NTGW5XMzsdttgz8gBLxJe/49/PoWqwxwdurwPfwcT0W/d14wD4Adhyqx22wsLEgL\nSVvD2sM3TdMJeG+DbsG6ARgo3jCM+4E5wEOmaf4gXO0TEZGpKzOlP4DWNnaSlRbP927aOIkt8u/h\n91Je105+ZqJvxGG0eQQ5Gf0jAY6MhJDUD4AQBnzDMG4EPj7g8DdN03zWMIzPAKuBa4K89YvAHz2P\ntxmGsc00zX2haqeIiEwP/pn377tk7JXmQiE6yk5cbBRvlTRy+69f4/J1s33D+96EvpF45/IBZmWF\nbjlhyAK+aZr3YiXoBfDcCFwNvMs0zUHbBJmmeY/fuc8DK4FhA77DMb7yiTIyXePw0HUOPV3j0AvV\nNc7KSub9Va1sWJHPQs9ytakgJTGW7h5r3v7ZvaUsKEwjPjaKWfmjG5qPTehfcnfO4pyQXb9wZ+nP\nB24CLjJNc9DmxoZhGMCdwLsBG7AJeHCkz62tbZ3gloo/hyNF1zgMdJ1DT9c49EJ9ja9cZ+06N5X+\nHuNjAofgT5Y1k54cO6Y2fviKxZilTWwwHKN639ncFIQ7S/9GrES9J63Yjhu4EvgC8LJpmq8ahnEU\n2I011/+YaZp7w9xGERGRUUuKHxxKm9oG9WmHdfG5hVx8buHIJ45DuJP2bgNuC/LSnX7nfDV8LRIR\nERmfgaVzpypV2hMRERkH/7K3Xv92xeJJaMnwFPBFRETGIdhGPZeEeHj+bCjgi4iIjEOBp7b9SKV0\nJ9v0mHgQERGZolbMy+Qjb1vCsjkZYLPW5k9FCvgiIiLjYLPZuHDV/2/v3kI1K+s4jn+3acnYKCPM\nNNrBTOnP2AEajTGdaZop1NIbxbuJKJRgMBAtSDJN8BAh41TQjeLUeGE3HURlSlFBVAoVL7ryT2VO\nsTuNzZAiOOTM9mIt7fUd93oP7r2W632+H9iw117PzP7z59nr9z7v4Vknjx7YsXfmwxBJkrSkDHxJ\nkgpg4EuSVAADX5KkAhj4kiQVwMCXJKkABr4kSQUw8CVJKoCBL0lSAQx8SZIKYOBLklQAA1+SpAIY\n+JIkFcDAlySpAAa+JEkFMPAlSSqAgS9JUgEMfEmSCmDgS5JUAANfkqQCGPiSJBXAwJckqQAGviRJ\nBTDwJUkqgIEvSVIBDHxJkgpg4EuSVAADX5KkAhj4kiQVwMCXJKkAR7f5yyJiDbAbeA/wbuDqzHxy\naMw24ErgMHB7Zu5qs0ZJkmZR2yv8bcDuzNwKfAe4cfBkRBwHXAd8HvgccFVErGq5RkmSZk6rK/zM\n3Dlw+CHgb0NDNgBPZeZLABHxBHAucH87FUqSNJtaDXyAiFgL3AccR7WSH/Q+YN/A8b+Bk1oqTZKk\nmbVsgR8RlwGXD/34e5n5IPDpiPgi8DPg/Ib/Zm6ZypMkqSjLFviZeSdw5+DPImJzRKzKzAOZ+ZuI\nuGvon/0dWDtw/AHgdyN+1dzq1SvffsFqZI/bYZ+Xnz1efvb4nantN+1dDHwFICI+Afx16PyTVKv/\nEyLivcA5wGPtlihJ0uxp+zX8G4HdEXExcCywHSAivg08mpm/j4hrgAeABeCG19/AJ0mSpje3sLDQ\ndQ2SJGmZudOeJEkFMPAlSSqAgS9JUgFa33jn7YiInVS78S0AV2bm0wPnvgDcDBwC9mTmTd1U2W8j\nerwFuIWqxwlcnpm+CWRCTT0eGPN94OzM3NJ2fbNgxDz+IPBz4Bjgmczc3k2V/Teiz1dQbad+CHg6\nM6/qpsp+i4hPAr8GbsvMnwydmyj3erPCj4jNwOmZeQ5wGfDjoSE/Ai6h2or3vIhY13KJvTdGj28H\nLs3MjcBK4IKWS+y9MXpMRJwBbKK6iGpCY/R4B3BrZm4ADtUPADShpj5HxAnAt4CNmbkJOCMiNnRT\naX9FxAqq+frAIkMmyr3eBD6wlepRDpn5LLCq/qw+EfERYH9mztcrzj0cuW2vRlu0x7UzM3O+/n4f\ncGLL9c2CUT0GuJXq5lLuNDmdpmvFUcBGqu29ycxvZObwPT00nqa5fLD+WhkRRwMrgP90UmW/HQQu\nAv41fGKa3OtT4K8FXhg43sf/d+Vbi3vwL4W36vEbfczMFwEi4iTgPKoJpsk09jgivgo8Auxtt6yZ\n0tTj1cBLwM6IeCwibmm7uBmyaJ8z8xXgBuDPwPPA45n5p5br673MPJSZBxc5PXHu9SnwhzWtflwZ\nLY05hp5Wjog1wL3A9sw80ElVs+WNHkfEicCXgR/iHF5Kg/N4Dng/VY83A5+KiC91VdiMGZzLxwPf\nBT4KnAqcW++uqqUz/JLfyGtGnwJ/eJ/9k4F/1N/Pc+Qe/PNoUk09fv2PeA9wbWY+1HJts6Kpx1vq\nc48DvwLWR8SOdsubCU09fgHYm5l/yczDwMPAx1qub1Y09Xkd8Fxm7s/M/1HN6bNarm/WvdW9Zxpz\nr0+B/yBwKUBErAfmM/NlgMzcCxwfEafUrxddWI/XZBbtcW0HsLO+46Gm0zSPf5mZH8/Mz1Ddd+KZ\nzPxmd6X2VlOPXwWei4jT67FnAs92UmX/NV0vngfWRcSx9fFZwB9br3B2HLF6nyb3erW1bv1Rpc9S\nfQThCmA98N/MvCciNgE/qIf+IjNv66jMXlusx1TvEj3Am+9eeHdm3tF6kT3XNI8HxnwY2JWZWzsp\nsudGXCtOo7o191HAH/xY3vRG9PnrwNeAV4EnMvOa7irtp4g4G7gDWEPVx/3AT6mePZk493oV+JIk\naTp9ekpfkiRNycCXJKkABr4kSQUw8CVJKoCBL0lSAQx8SZIKYOBLmkpEbOu6BknjM/AlTSwi3gVc\n33UdksZn4Euaxi7glIj4bdeFSBqPgS9pGtcD+zLzgq4LkTQeA1/SNLx9r9QzBr4kSQUw8CVN4zBw\nTNdFSBqfgS9pGvPAPyPiqYhY0XUxkkbz9riSJBXAFb4kSQUw8CVJKoCBL0lSAQx8SZIKYOBLklQA\nA1+SpAIY+JIkFcDAlySpAK8B2POxIZECUC0AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6b6a778410>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(t,W)\n",
"plt.xlabel(\"t\")\n",
"plt.ylabel(\"W(t)\")"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "1a35840ca7eaf864f9201ee4e0d947e0",
"grade": true,
"grade_id": "numpyex03b",
"points": 2
}
},
"outputs": [],
"source": [
"assert True # this is for grading"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Use `np.diff` to compute the changes at each step of the motion, `dW`, and then compute the mean and standard deviation of those differences."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"grade": false,
"grade_id": "numpyex03c",
"points": 2,
"solution": true
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-0.00243491486967\n",
"0.0317259798163\n"
]
}
],
"source": [
"dW=np.diff(W)\n",
"print dW.mean()\n",
"print dW.std()"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "b2236af662ecc138c4b78af673b476c1",
"grade": true,
"grade_id": "numpyex03c",
"points": 2
}
},
"outputs": [],
"source": [
"assert len(dW)==len(W)-1\n",
"assert dW.dtype==np.dtype(float)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Write a function that takes $W(t)$ and converts it to geometric Brownian motion using the equation:\n",
"\n",
"$$\n",
"X(t) = X_0 e^{((\\mu - \\sigma^2/2)t + \\sigma W(t))}\n",
"$$\n",
"\n",
"Use Numpy ufuncs and no loops in your function."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false,
"nbgrader": {
"checksum": "2b05883af2c87bc938fc4f7fe7e35f66",
"grade": false,
"grade_id": "numpyex03d",
"points": 2,
"solution": true
}
},
"outputs": [],
"source": [
"def geo_brownian(t, W, X0, mu, sigma):\n",
" \"Return X(t) for geometric brownian motion with drift mu, volatility sigma.\"\"\"\n",
" x=(X0)*np.exp((mu-(sigma**2)/2)*(t)+sigma*(W))\n",
" return x,t"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "401ffd490410ab0a18612d641e24c02f",
"grade": true,
"grade_id": "numpyex03d",
"points": 2
}
},
"outputs": [],
"source": [
"assert True # leave this for grading"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Use your function to simulate geometric brownian motion, $X(t)$ for $X_0=1.0$, $\\mu=0.5$ and $\\sigma=0.3$ with the Wiener process you computed above.\n",
"\n",
"Visualize the process using `plt.plot` with `t` on the x-axis and `X(t)` on the y-axis. Label your x and y axes."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"grade": false,
"grade_id": "numpyex03f",
"points": 2,
"solution": true
},
"scrolled": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f6b6a142b10>"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfYAAAFmCAYAAACfjbj/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XecXHW5P/DPmd5n22x2N5ts+kkPhDRIQkdAEAGRq6KC\nFBsq4r1evepVr14ULz9ERUVRsCAWBGlSpbckhPR60pPtfXd6n98fp8w5M2fqzuzO7D7v14sXuzNn\nZs5Oduc53+/3+T4Pk0gkQAghhJDJQTPRJ0AIIYSQ0qHATgghhEwiFNgJIYSQSYQCOyGEEDKJUGAn\nhBBCJhEK7IQQQsgkoiv3C7AsuxzA4wB+zHHcL1LuOw/ADwDEAHAAbuY4jvbfEUIIIUUq64idZVkL\ngLsBvJDhkPsBXMNx3AYAdgCXlPN8CCGEkMmu3FPxIQCXA+jNcP8ZHMd1Cl/3A6gr8/kQQgghk1pZ\nAzvHcTGO40JZ7ncDAMuyzQDeB+DZcp4PIYQQMtlNePIcy7KNAJ4C8DmO44Yn+nwIIYSQalb25Lls\nWJZ1gB+lf4PjuJeyHZtIJBIMw4zPiRFCCCGVoeDAN16BPdOJ3Q3gHo7jXsz5BAyD/n5Pac+KpHG5\n7PQ+lxm9x+VH73H50Xs8Plwue8GPKWtgZ1l2HYDfAGgEEGVZ9rMAfgfgGPhM+U8AmMey7M3CQ/7M\ncdxvynlOhBBCyGRW1sDOcdxmAMuyHGIq5+sTQgghU82EJ88RQgghpHQosBNCCCGTCAV2QgghZBKh\nwE4IIYRMIhTYCSGEkEmEAjshhBAyiVBgJ4QQQiYRCuyEEELIJEKBnRBScbbs70XXgG+iT4OQqjSh\nTWAIIUTuH28cxcBoEJv39QIAHvz6+RN8RoRUHwrshExyB08Oo2vQh3NPmw6NprI7JP7znZMTfQqE\nVD0K7IRMcg+9yKF70A9fIAKdToOL18yEhlogEzJpUWAnZJLrHvQDAB5/8zgAoNZmxLolTRN5Sqri\n8cREnwIhkwIlzxEyiSUS6cHS449MwJnkFgxH0257dUfnBJwJIdWNAjshk1gglB4sUaGz8H6Vc33o\nBQ7hSGwCzoaQ6kWBnZAxiMXjONQ+ojoyrgSjvnDabZUaKIMh9fPyBipzhoGQSkWBnZAxeOSVo7jz\n4e14a0+3dFu8goK8WyWwV+pUfCBlKp6dUQOgcs+XkEpFgZ2QMdhygN9v/d7BfiQSCTzx5jF84Z43\ncKLHPcFnxnOrBEWPPz3YV4KAbMSu02qwaFYtABqxE1IoCuyEjEFImNbec2wQ/3qvA0+9fQLBcAyd\n/ZVRNW3UGwKgXFYfHA1OzMnkIL/gaKm3wG4xpN1OCMmNAjshYyBfr35x6ynp60gsPhGnk8YtBMWP\nX8xi2Zx6aDUMeoYDE3xW6gbdyQuOi1bPgN2sB0BT8YQUigI7IWMgX04fcoekryPRiQnsA6MBxWuL\na+wLZ9bg9mtXYPGsOrh9YfiDKtnyKkKRGKLjdJEiziTcds1yrF/WjDqHib/dXZkzDIRUKgrshJTB\nRAT2IXcQ/3nfJtzzyE4AfJB/Yxef1FdrNyr+P+oLqT+JTDyewOfufh13PLStTGesNCQE8IVt/Nq6\nq4YP7H3DAVpnJ6QAFNgJKYOJCOy9whT7wVMj8AUj+M/7Nkn3mQx8kUmrmf//i1vbcxZ/EX+Gkz2e\ncpxuGk8gAqNBC6NeCwCwmfUwG7XYeWQAX/rpm9i0t2dczoOQakeBnZAiZQve4ej47xXXyhq8/Plf\nh6Svrz57jvS1zcSvW7++swsPvcBlfb5oPPnzjcd0fCAUhcWYrHLNMAya663S989uoQYxhOSDAjsh\nRUqdzrYYdfjohfMBTMyIXV4kZ5PQ9vTMJU24/KxZ0u0WU/7tIaKyn6FvHBLu/EFlYAeABa010tcO\nIUueEJIdBXZCijTiUW7D+vntZ2Pp7DoAExPYQxHla165cTZuvnyR4jarMGIXbd6fnN72BiKKErTR\nWPJCYf+JoVKeKoLhKO59bDeOdo0C4C9KAqEYzCmBffWiRunrGDWJISQvFNgJKdKINz0BTa/l/6TG\nM7C/vacbz20+mVYqtqnOAialPatBWL8W3f/UfgB8YP3ST9/Et367RbpPPhV/vLu06+yvbO/EjsMD\nuPNP2wHw2ffxRCJtRmF2swPf+uQq/nwqZAshIZWOAjshRRr2qAR23fgH9geeOYC/v3Y0bV0/dVob\nAKbVmVWfY8TLzz7Ifyb5VLxqM5kxCIX5cxVH4eJ6f0wleM9pccBk0CrOhxCSGQV2QookH7GLAV2v\n40fEEzEVH0hpopI6rQ0A02otmN3sSLu9vc+bdpt8Kt4fLO12MzGgiwl/Yk7AoY5R1eN1Wk3FFP0h\npNLln0lDCFEYFgL7169biVYXn72dHLGPf1Z86tKASSWwA8DS2XU43p2sZX/nn7ahsdYifZ9IJMAw\njGLq25+h81qxxOfWapVLBR+5YL7q8XqdhqbiCckTjdgJKdKIMG09p8UBi5CUptMyYACEJ2DEvvVA\nn+J7tal4APjA+lmK7w91jCq604nnLg+kgVCJR+zCbIBOo5EqzjXXW3De6dNVj9dpGcUMAiEkMwrs\nhBSpdziAOocROm3yz4hhGBj0Wqk5zHjqG1FuSTMZtKrH6bQatE2zZ3wecT09KstCL/WI3SdcKOi0\nDJ7dzO9Pz3S+AKDRaDDsCeFop/pUPSEkiQI7IUUYGAlg2BNCc50l7T6LSZd3LfZyyhYob7xsUdpt\n4qS4FNhlsw7BULSkfeaHhbr6ep0GHqFc7OVnzsp4fO+QHwDGrbwtIdWMAjshRfjzS4cBAK6a9Cxz\nq0mHgdEgdh4ZKPt5xFX2dq9bPA3rlzalbXWTm9Fog0Gv/POvEerI+8XALpv6TiA9M34sgV6cXRh0\nhxAM888r9l/PZSLyFwipJhTYCcniVK8HP//HnrQmJGIwumRdW9pjxDajP3t0d9nPTy1T/OPvY3HT\n5YtzPjacUtBGbBDjC/A/WyyuvH/EE8L+E0PoHPDhVK8Hn7v7dfz6qX0Fn3M4ElNsq9t7bAg6LSPV\niM9F3kWPEJKOAjshWfzk77uw/VA/Xtzarrg9EIrBoNegUWXEPp7Z22rb6szG/ALkhmXNiu/F2QeP\n0MNdfG6xy9rRLjf+31934rsPvov9J4YRicaxZX9vwee8++gggOQOAgCwmvVZZxjkqI0rIdlRYCck\nC3H0nVo4xReMpJVnFQXD4zdVLAbf6Q3JZin5BshPXMzi4jUzpO8bnHwAf+CZA3hzd5e011wM+K9u\n57vBxeIJ1X3vmSRSpuz3HOMD+zc+foY0S2DL8F6qocBOSHYU2AnJQlzD1miUwdIfjGZsqDKnJb0A\nTLmIU/FOW+ENUvQ6Dea0OKXv5fkCv3v2oHTRIO5xP9mbLCsrz07Ptua99WAfvviTN8GdGgbAL228\nubtbeF6z9B5azfkHdrWKf4SQJArshGQhjjXlLVHjiQQCoSisGfaJ33r1MgAAw6SPVktNDL5Oq7Go\nx8unw13CiF3U0c+PytWWG+Rb67JthXtzVxf8oSh+/zxfMva+J5Nr8majTnqDrQV0nUvNdyCEKFFg\nJyQPGtn0diAURQKQitKkclgMaKw1I5EAXni3XfWYUhG3pNktelx30QJ89aOnF/R4ozyw1yoD+Os7\nu/jba5QBP1X/cCDjqF2sQS82x0nNrE8tLZuJfKlBTO4jhKijwE5IHkKywOUV1t2t5syjTDFQvbj1\nVFnPSxyx63UaXHBGKxa15bdlTCTv9pap33mt3QRblqnyH/xpG37x+N602/3BKLoGfAD4nAQA0Asl\nZMX3R9wyl7rUkerrH1+Jr1y7QvFchBB1FNgJyUM4nEyeG/Xxo9AaW+bp789fxU/Htzbaynpe4gWH\nXlvcn7J8Kj61pavIbtGjzp7+s8qnz8VMdznu1LAUuN2+MBKJBHxC4Z4ffmYdgMw5DOmvpceS2XXQ\nahj4aCqekKzKHthZll3OsuxRlmVvVbnPxLLsH1mW3Vru8yCkUPJ93MFIcvpXbLbitGZOWGupt0Cn\n1Uij+3IJCIHSXMAatVxrow1XrJ+F7924BgDw39evSjtGXFpIlenCJhiOonfIj+M9fLKdVsMgFk/A\n7Y8gGI5h8axaNDj55xNzEDR5ZPIzDAOrWU9r7ITkUNbubizLWgDcDeCFDIf8H4B3AaTXtyRkgvUN\nJxPEQrItbKPe3CN2hmFgt5QmCI36wojHE+jo92LTvh7cfNliaYQrrllnaviSi4ZhcOXGOdL3qS1d\nDToNjAYtdMLI3mLUSZXpamwGdApT7QCfHa/XaXHPI7twWNZ+dX6rEwdPjUjT8vJp/UVtdXhrT7dq\nK1k1VpNO2oJICFFX7hF7CMDlADJVsfgvAE+X+RwIKUpnfzJo9Q0HcFIYgYpT8Y4sI3YAsJv1RQWh\njj4vfvinbRj2hDDkDuL2e9/C3X/biXse2YXN+3pxRNhqxp0aRruQuV5sYM/FbuGD8PzWGgDAxhXJ\nojapFza9woXQ4ZSe6mLQFgO7XbaW/4mLF+ALVy/D+SvVu7qlMhkmpsEOIdWkrIGd47gYx3EZN51y\nHOdDsvcEIRXFIxttn+rz4n9+vxX+YAR+IXkrW0IZwO/NDkViqtXhsvnF43twuGMUT7x5DMe6+L7p\nXbKRsYZh4A1E8KM/78BL73UAQMY99cX4zg2rpa/rhSnzc05rwVeuXYFrzp0r3VeTsu4uvxASTW+w\nShcAncJFiHixAAB6nRYrF7jyLqpj1GsRicZVa+QTQniUPEeIiq4BH9zCyFwuFIkjIEzLm3OMksX7\nxbry+ZJXrlOrYpdAAid63KqvVQptTXY4hOBrEKbgNQyDpXPqodUkPzJScwxOyQrYiP7t/HmwW/nn\n6lQZsRdKrCdPo3ZCMivrGnue8r70drky95AmpTPV3+eOPg++9dstqvfZHCaI4+/WFmfGvewAUOPg\n939bbCa46q2K+7K9x+Lebm8wCp0h/U/UZDFi264uxW2tLTVwqbSQLdZnrl6Ou/60DR88d17Gc53Z\nUiN9bdBrsfvYED5/rfLY6c1OKcFPLHgzs8VZ9O+Yw86/pzaHGXWO7Pvrp/rv8Xig97gyjVdgzzbP\nlvdUfH9/+oiAlJbLZZ/y7/P+I/2K72vtRqmMaU+vB6PC1x53AD5PlrrlQlZ9V48bWlmGvfgeJxIJ\nRGNx6HXKbWbi1P2OQ/3Svm+5vn4v3tjRobgt4AuiP1a6UeyiVid+8sUNcFgNGX8fYrKdAvNbndh3\nfAinOoYVx0SCYcSFLnIBoUKdJh4v+ncsIb2no4iFMucv0O9x+dF7PD6KuXgq61Q8y7LrWJbdA+Bz\nAL7BsuwelmW/wrLslcL9LwF4HsAS4b5PlfN8CMlH6hY1eZJYOBJDMBSF0aDNuUXLJIy29x4fxI8e\n3q7IkI/G4rjvib34ys/fxlBKUxN5d7iTvenNVjyBcNoUfSmn4kW5kgPle9vrHfzX4lZAkc2sh82i\nnNXItpsgF2kqfhwb7RBSbco6Yuc4bjOAZVnuv7Ccr09IMYZSmoxcd9EC/O8f3wMgBPZwDGZD7tao\nJuGYv796FADw2o5OXH7WLADAI68ewXscPzPw+s4uXHU2v+UsFo9LU/EAVIux/FGouy6Xzz7wUvnh\np9fhZK8H04Sp/7YmuxSsU987s1EHvS758zBM9v3/udAaOyG5VcIaOyEVJXXU2dJgwbXnzcMjrx5B\nKBpHIBzNmREPJAO7SB57xWx2INmG9FiXG69uV06xZ9sHbzRoJ2TkOq3OIgX1+796LhgGeHMX37Gt\nW5a9v2FZMxiGgV7HwKjnt6nZLYacVeayMRoosBOSC2XFE5IitVGJUa+VSq+KI/bUoK3GmHKMP5h8\n3lZXstSsuH7/6GtH8PbeHgDKpieZlGvveiF0Wg20Go209U3cw37mkibc8P6F0nE2oa6+vYD2rGqS\nU/GFbSEkZCqhwE5IikBKG1KGYWDQ838q/mAUkWg8rzXt1O1y8j7iGgYw6DWwW/TS9HXPkF+6f7or\nd2AvpNVpuYmtXfcdHwIAzJxmUywPmI18QM9npiMb8YIqdVaFEJJEgZ2QFGr7zsWR4sFTfNZ3pk5o\ncktm1ym+lxe88QQicFgMqLUbMTgaRDQWh07WyCWfEfuyufW4/Kw2fPuG9Pru481VYwbDQCo360rp\n4S7G+NRZjEItnlULrYbBO3u7x/Q8hExmFNgJAT+6FjuRpY7YAcAgbEl790AfgPyKrMxqcmCGrLub\nuC6cSCTgDURgt+jhsBoQjcXx6bteU4zw25qStdPPYF2qzx+JxHH12XMxqym/OuvlpNdppFG7VsOk\n1X4XR+pD7rGNtBucZjTVWdAzFMh9MCFTFAX2Ipzq9YA7NZz7QFIVeob8+PK9b+G3T+8HoByxnyfU\nMBen4kX5lnCVr8WHhUS3u/60DZFoHHaLQbHmHJaVnm2qt2DNokYY9BqcPr9Bul1sdwoA3grrS37t\n+fPQ4DThYxctQG1Kudn5rU4AgMU4thE7ANQ7TQiEolJpX0KIUuUs0lWR7/6O7zL74NfPn+AzIaVw\nopsvz7p5fy8+fcUSBMMxNNdbcOtVy9AkZH+nrqnnWyZWvqY86A5ix6F+vLmzEwDfHS2coY58jdWA\nWz6wGKFwDAOjyX3u02otWD63HruPDkrLA5Xi9PkunD5ffXbhsjNnIZ5I4OzlLWN+HZdQv753OIDZ\nzWNbsydkMqIR+xiIU7ekuqVuvwqGozAbdWhpsEr32VOKrOTbZvT6SxZiw/JmmI06+IJR3PuPPdJ9\nVrMe0Vj679Cla2fCoNdCq9HAYtKnlU69+fLFuHBVKz4sa8hS6fQ6Da4+ey4aatL7uheq3sm/H9//\nw3uKhERCCI8Ce4HkW6Go+tXkIO8sFonGEY0l0razydfUZ06zYfXCxrye22E14Mb3L0KdI73aWiKu\n3P6l1TD46AXz8eHz5imOS81+t5n1+NiFC7LWqZ/MGpzJCx0xC58QkjQlp+K7BnwIR/l2mmKf6XzJ\nRwihSKwspTzJ+JKP18UpdlNK8xX5tPdp8xrybjOq9njRtDozVi+cBo2GwQfWz4LNrFetIMcwDH74\n6XUwVNjU+0SRZ9z3jVASHSGppmRUknfu+q+PrywouA/Jmn6otdQk1UcepMV/02wlY61F7MUW25+K\nbrpsEc5c2gQNw+C6ixbkfPy0EnZuq3b1shH74GiWJjyETFFTfipeXhQkH8Oy7TqF9tkmlckv6xL2\ntV9tApA+YgeAJbNqAQDL59QX/BqRlCS59cuax7W++2RiM+tx/SUsAPobJETNlByxy8mLguRD3uRC\nXGPfe2wQw94QNpYg45eMr2A4it89ezDtdpPKtqzPfHApwpFYzj7gamjKuLQ2LG/GH57n0sr/EkIm\nSWAf8Ybw9Dsn0FRrwQVntGZtMhGPK7OQCx01Dcum4l/Z3onf/HO/VHRj9cJG1ZEeqVwj3rDq7Wq1\n4G1mPVBkSVSLSQ+Pn/Zdl4pWo4FRr1UtJkTIVDcppuIfeOYAXt3eib+8fBivpHTHSpXaFSpcYJeo\nvuHkyGvrwT5FJa1TKr2zSWWLxdW3LJY6KfKLVy9Dcz2/Tj5/RmEJm0SdyailETshKiZFYD/SOSp9\nzZ0ayXrsyR6P4vtC2j/GEwmczBK8O2UtK0l1yLRlUa8r7Z9GS4MV3795LT564Xx8+6Z1uR9AcrIY\ndQjQGjshaao+sCcSCcRiycSknuHsyXD/95cdiu8LCeztvV4EQlGsyrCHOUijh6qTKfmqHFO8GobB\nRatmSC1OydiYDDoasROiouoDeyAUQzSWwIq59WibZkffcKCginCFbFl7eRs/zb9hWRPmtKRXHivk\nIoFUhkz//i5n4QlyZHxZjFpEY4m0HQeETHVVn+nl8fPJT3arATqtBid7PfD6I3BYc3ffAvIPxpFo\nHJv396Kxxoylc+rx4tb2op+LVI7UEftXrl2BeCKBZUVsaSPjyyTkQQRCUeh1+f29EzIVVP2I3S0E\ndofFAKeN/+Me8eauH10vbFnKtyzssDeEaCyOea1OaBhGkf3+uSuXFvRcpHLIR+w3XLoQS+fUY/nc\nwivLkfEnJjjSOjshSpNgxM5vIXJY9DAKW5RGfepbmOTEz+18p+KH3fw2N7EdpVgitNZuxByhIQiN\n2KuP/N9/uss6gWdCCmU2JEfshJCkSRDY+SBus+hhFjplZRqxy9fepzdYMTAazPmhEE8ksGlvj9Re\nUwzs4uPMRp10QRGK0FpftfEHk//+MZVOa6RymYUiQrSXnRClqp+KF4OpyaCD08YHXXeGEXtEFnhv\n+cBi6LQM/CqBfWAkgHsf241Rbwib9vbggWcO4KEXOADJwC7WjK+zG6XRe4imBBVe3dGJ7/7u3Ype\nohh0JwsOlXqLGykvs5FG7ISoqfoRuzj9bdBrYDHyVcF8AfU/dPHYVawLFpMeFqNOMWIT3ffkPhzv\ndsNq0mNanbJ/tBjY6+wmnOr1Yk6LAzotAw3D0Ig9hXgxdLhzBEtnV14yWjyekAoOXbF+FmY12Sf4\njEghKLAToq7qhyhi5TiDTgurmf9D9wbVS3eKx4ojbLNJrzpiHxzlP+xj8Tgee/2Y4r5aYVbghvcv\nxIfPm4vLz5oFhmFgNGhojV0mKqst0D1YWKOd8fKd372L491uNNaaceXGOZQwV2UsFNgJUTUJAjsf\nQIx6LawmccSuHtiTo3s+sGcasfuE2/afHFbcrtUwsAvb6BwWAy5d2yY1kTEZ1J9rqpJPcXdXYEW+\nSDSGzn7+vOqLaOpCJp5JWmOnvztC5Ko/sEdlU/EmHRhkC+zJiwAAsJh0iMbiiESVI22xfvhoSoMQ\ng16bsWnMtFozhtxBaiMpkPfJfm1nF/YcG5zAs0knLw1Ma+vVKbndjWbKCJGr+k80+fS6hmFgMelw\ntMuN3z93IC3Ijvr4bHmbhR/ZW038B8Nwhg5fqcTj1bQ22pAA0NGffXTqDUTw7Qe2SFXsJit5YAeA\nex7ZNUFnok5eYIj6olcncSqeZsoIUaq6wD7qDSEh27YmjsLF6XWrWY9YPIE3dnXjXynV4fpH+GDT\nWMMnxM1pcQIADrcnG8fI14blDHoNvvSh5RnPq7mO79w1MJq97/aW/b3o6Pfh4X8dmtRr8vKp+GwS\nwnZCb4ZZlnLpG0qu+5+5tGlcX5uUhhTYaSqeEIWqCuy7jw7g9p+/jZdko91k8hz/o4hBGwDcvggG\nR4P4xeN7MDAaQL+QAe0Sjlkwgw/sr2zvwNEuvkNcpmn87920Fq2NtoznJpaw9fiyByjuVHLdPnVU\nW6kCoSg27+9RXFDl0iMEzpULXAD4/IRU3kAEN/3oVfzmn/tx72O7S3OyefIFo6hzGPF/nz0TqzM0\n9SGVzWKi5DlC1FRVYN+0rxcA8OK7yZF4OBIDg+Q6aZtsy9KIL4QfP7IT27h+vPhuu9T5rbGWD+zT\navlR9vFuD+744zYAyDhyNAkzApnYLXxgF0vcZtIjGynmGt1XigefOYD7n9qPf7xxDHszrJXH4wkc\n73bj3QP8v1FHvw8GvQafv2opFsyoQSyeSLswaO9LrnMf7hjFePKHIrAY9WioMec+mFQkvU7L16Kg\nqXhCFKoqsCfHfLKp+GgcBr1W2qp02rwGqSLVqDcsbbWymfVo7/Oi3mGSkm7E/0vPmkhkDOxidblM\nxBF7puI4AB/8eoeTwXzrwb6CRsETZeeRAQDAM5tO4seP7FK9eHn0taP4/h/ew6+e3Ic3dnWha8CH\n6Q02aBhGmk1J7cKl0yb/RdVG9OUSjycQCMWy5kyQ6mAxUutWQlJVVWBXC4HhSAwGffLHmDvdiV/c\nfg7sFr0iSA+6g3D7wpiRMp2+ZHad9HUwHJPqzLdN40f+t161FLdfu0LKpM/EISTkibXr1Xj8YUSi\ncanIzdt7evDajs6sz1sJNClBV7x42XVkAH99+TASiQSef/eUdP/Wg30AgHNOawGQnE0Ry/L+9eXD\n+Nqv3sGdD2+XHqPVZg/sh9pHcNvP3kTXGLfOvb2nG9sP9QNITuWS6pWpFgUhU1lVBXYxUIvb0QAh\nsOvSg67NrAzsvcIUuBhURTdftgitLj7YewIRjHj4zPnLz2rDb792Hs5gG/Nq4Wk26qBhGLj94Yyj\nfjHoi01jAICTJe5NpEQigXg8/dIpFI6ljbTFbYA/fXQ3XtzajmGPsjb/yR4PAICdWQMgGdgj0TgS\niQRe3NqO/pEg5JMVWk32X8Xf/nM/PP4Innr7eGE/mEwsHscDzxzAL5/YCwBS3QNSvSxGLU3FE5Ki\nqgL7qNDcZcQbltaqQ5G4YsQuspn18AXlI3b+samjNKfNiKXCqN3jD2NICFK1dlNB26AYhoHJoMWx\nLje+et878KtUvxMb1rQ0JLuI1diMacdNhL+8fBg3/9+raUsJXYPpI+SDp4bRIVsfTw384oVNnZ0v\n/CJeeEWiMbgzzGjkmooXkyRNOZZEskktNSwun5DqZTGq16IgZCqrqsAuDzqHhJFuOBqTtrrJ2cx6\nxYhQ3H6Vuq4OAHbZNLrYGS51ZJ8PcUowFI5h7/Eh6UJE5BECnjygjCVQldJL7/E7DY518u/r0c5R\nPPLKEXSrBPZnNp3Etx98V/perfWt02aQRup64cLL7YvgP37xturrqwV2cevh3uOD0gXBSJ41B1JF\nojH89eXDittOm9dQ1HORymGWtryVJrD3Dvtx452v4K3d3SV5PkImQtUE9lg8AU8gIiXQ9Qz5kUgk\nEI7EYVSpHGY1q0+zqgV2m3Cs1x+Rppkd1rFN0/7qyX24/edvK5LjxKl4u0WPmy9fxL9mIIIHnzmA\n/SeGxvR6pSL+/Hc8tA3Pv3sKOw4P5HyM2n78969tk74Wk+de2tauWEaRE0vzil7d0Ylb73kDr+/s\nxI//lixus/vooHRRV4in3zmBzft7Fbel5luQ6iPOwI14QvjP+97B02NYqgGATXt7AAAPPntgzOdG\nyESpmsDu9oWQSAALZvDrtj2DfmkK2KAy6rWoBPBMt4tb1TyBMIJCMl6uNd98yRugiFPUNrMebU38\nOvsr2ztLpW9QAAAgAElEQVTx1p5u/OrJfSV5vUPtI/je77emzRZkI+9T3zesbNiST8bx1oN90k4E\n0VnLkkVf9MJU/P4T/B7+L1y9LO055FUCQxF+dB2JxvGH57m0Y/ce57fc/fiRnfj9cwdznh/Azxak\nyrXTgVQ+8UL9WNcoBkaDePzNsQX21ERRfzCCHzy0Db95ev+kLihFJpeqCexiUluLywqjQYtBd1D6\nQzOqJM9lymJPDUBAssSs1x9BOBLLmQFfCPlebXHN32rSw5iSF5D6fTE6+r248+HtONHjUWSp59Iv\n24In/xpIBvZPf2AxPnPFEunCSu7lbR0IhGJY1FaLr37kNNz4/kWKxDRxSt4biMCg1+C0+elT4L5g\nFD8SsuQPnBhOW7eX8waiSCQS2HtsCG/s6srrZ6yUJQ9SWuKFuphDA/BLYcVKzcN4e08PjnSOYtO+\nnrSlHEIqVdUFdqfFAKfFgPY+L/4lrAurJc/JP8ivWD9L+lotYMjX2IPh0gZ2+Ug0IGTvWky6tNdQ\nWyIo1GOvHZW+DmcJjKl2y4rOiPX0k9/zU/PN9VasXTxNsRaeug+8ud6CRbPqsGF5s+L2oGzU73Ka\noWEY3HDpwrTnEXcI5CpH+9qOTtz9t53S9+L2umxK+W9KKof4dyOfaRrL9rdhT/J3Lx5PKLZhirs9\nCKl01RPYhallh9UgjXz/+c4JAMmpXjn5NKvdYsCVG2cDAOZNd6YdazeLgT3Mj9hLOLqTjx7EDxy1\nwC62nx0LsyzQvrmrC79/7mBeBXD6R5Kj9NSOdkPCSEh8T+QbBa46e47i2EwJh6OypEfxmLNXtOD7\nN6/FVWfPwcKZtdL9d/5pG3qHc/dvF6f1AeC+J/ZWTRU/UlriGnuf7Hc4PIYM+SHZ1s0Rb0jxd0kX\nh6RaVE9g9yQDe+poVG0dWP5H6LAacMX62Xjw6+fDqbK9zGzUQafl96CHIrGc5WMzWdTGB6gNy5Ij\nVnnGuLjf1mzQpbUKHWsTlFO9Hmzel0wOi8YSeGNXlyKoZiJ//9y+kGLNXSS+n+IWwFlNdkXCW6vL\nhjWLpqk+v3hRBfDZ8qLpDVZ84KxZioS6Qx2jeGUbX7RHPiNgMepwxy1r4apR753eN5w9sMvXR2ts\nBnzonDlZjibVQhyxyy9OI2O4SJbXZOgfCSiqLOYqokRIpaia0lvywJ46nT6ikigmn4oXq8JlwjAM\n6hwm9A4FEI0lVLfP5eMLVy9De58XC2bU4JzTW3DHH7chGFGO2M1GbVqCjnjfn/91CFdsmC1l6Rfi\nPa5f9XZvIJJzr3xA2CpkM+sx6g3Dq7LXXAzsaxZNw97jQ1i3pElaAnFaDfjeTWsyPn+D04yPXTgf\nf37pMM47vTXt/ovXzJDK1gLJZD6jQQufcDH01Y+ejuZ6K8wG9V/Z1CI5qcR98N+7cU3WZj6kuohr\n7AHZdrdQkSP2WDyu+CzZe3wIHtmFcbaqkoRUkrKP2FmWXc6y7FGWZW9Vue9ClmW3sCz7Dsuy38r2\nPPKp+I+/b4HiPrXKU/Lp9HwKkdRYDdJUebGJVmajTkouE0f9oZQRuzwr/9rz5mHDsmbMaeEz5F/a\n1oGHXkjPAs+HPPnu8rOSW83EDyO3L4yv/vId1fVoccQ+rdYMjz+MEz3u9Oc38M+/YXkz7rhlLS5a\n1Yo1i6bhQ+fMwTc/eUbO87vgjFb84vazpZ9Vjp1Zi1WsS3GbhmEUF3Di6F1tBwSgfnGXSCQw5A4i\nEo3htZ18kl0pchlI5bCoVA/MNmJPJBI4cGIIN975StqauVgNcensOhj1WmzZ34th4ffKaTOMe2th\nQopV1sDOsqwFwN0AXshwyE8BXA1gPYD3sSy7KNNz9Q75wTBArc2I81e24qbLFqGlwYqZ02y48bL0\nh5n0yQ/wfAK7POGmFGtpJmFkKU+e40fsyQ+iS9bOxI2XLcL81uS6v1rFunzIt+ddsX42PnrhfADJ\nKf4t+3sx6A7iPqGcqpw/FIVBp0Fbkx2JBPDWnp6sz99cbwXDMNAwDC47cxYanLk7pDEMU1BQNRq0\n0kUJA6DeyU/Bn3f6dMVxy+fy5X57hwO4/+l9eOTVI9J9L25tx3/88h088ExyTzJtcZtc5LtcxJmu\nTImjfcN+3PSjV3HXX/nEy7+8fFhx4S0WpVmzaBpaXVYMe0LoHwnAYdGjxmqk0rWkapR7xB4CcDmA\n3tQ7WJadA2CI47hOjuMSAJ4FcEGmJ+oe4DuziWvT65c1439vXovvfmoNZjenjwLl62H51AT/5CXJ\nLO1ip+LlxAAirrHHEwkEQ1HVxiPywGjKMNWci3ydXKfVwCHszfcKa4RqAa170Ict+3vRPehTzDa8\nJ4zqV8zNXSO/VFKnOY16DWZO46fMb7lisdS978wlTbhalrSnF9b539rdjc37evH8llOIxfkP9mc2\nnQQAvHugT/G8ZPKwyC6UFwo5LuEM+82fl7V7BviaDz98eJv0/e6jA9DrNFi7uBG1DhNi8QT6R4Ko\nd5pgMekQisSkaoiEVLKyfspxHBfjOC7T4mcTAPnCcB+A5gzHYsgdkvqo56OpzoIGpynvJCl5tnwp\n9jybUgJ7MBRFAuoFcuodprTHZXLvY7vxxJvH0m4XZxw2ClvNxL35YhlbtYS4b/5mC3791D6EI3GY\njTo01VkU95++gJ8eXz4OAd4TSA3sWtx2zQrccOlCrE1JypNvufvIBfPTEhE7+vgyuGrJTqkV7kh1\nM8lG7LOa+I6MaltaE4kEdh9Nr6J4qpevM7HvxBA6+n1gZ9RAr9OiTrbDo95hki7IxWZShFSyiVxw\nTI00WVNONRoG55wxAy6XPe8X+N23Ly7mvNDkshX0OpnodRpE4wm4XHbpA6Guxpz23GvMBuCx3QAA\nu92U8bX9wQh2HB7AjsMDuOXqFYr7xI+yGz6wFK46C1qEQhsarRYulx2MNvkB6HLZwZ1UlrCNxhNY\nMEdZOObi9XMwf1YdFs2qTwuepbZodp2iJavFrMeCOQ1p5wQA/3bJIgRjCVx5zlw01lrQ4DQratrH\nGEb1PfzsVcvQ2Jg+uzMRSvH7RZRmtvAX5wZhhk7+Hg97ghhyh7B2SRO27FMuNblcdpzYwhd0uvr8\n+XC57Fg0px4vbuVH+IvnNqC9l1+P/+8H3sWTd12hmgA7FdHvcWWayMDeBX7ULmoFkLE5+eM/+gAG\nB73o7y9/kQhNIlGS1zEbdXD7wujv96BD+GDI9Nznr5yOV7Z3wu0JZnztU73J21OPGR7lC2sEfEH0\nx2Lwe4PC7QH093vQN5isgNfb68bfXzqkePyZi6ch4A3CbNQiEIpBwzDwewJodpowMjy2Huj5uGbj\nHCyY7sTTb59AR78XWobJ+m9w1fpZQDSG/n4P7GYd5C07ege86OtzwyMrI9tYa8Ya1jUuvz+5uFz2\nijiPyeJjF86HQa9FKMAvOw0JdRDk77HYDdKoY3DbNcvx00d3S/f193vQK1xUmnX8793Stho4rAa4\nfWG0uazYfiC5mrh9Xzfamiig0e/x+Cjm4mm85iXTLm85jjsJwMGybBvLsjoAlwF4MdMTjOcVcqn6\ndFuMOikZLiArTqPmig38Xu9D7SMYylB5bWBU/faTPR7sPDIArSaZoCYmAIr7t+WJP9sP9WNLSkOU\nD26cDYZh0FDDL3dYzTppXXs8GA1arF7YKGXf6wrYM5yalBcMxxAMxxTLDzOn0QfxZHXhqhk4e0WL\nVKhqy4FeHOscVRwj/v2ZjTo011vSnkNsqSzmpmg1GvzvzWvx5Q+vwOxmh5QdD6RXZySk0pQ7K34d\ny7J7AHwOwDdYlt3DsuxXWJa9UjjkcwD+AuANAH/lOO5IpucaT6WqK2416eAP8nXNxcCaqTmNGIgH\nRoP4ndDYJHV7jbwIizxo/c/vtwLgO+CJwVjcFtbR58VDL3A43p3cwvbLlMz4j104Xyo847Dya4sT\ntS1MTIaLxnJXzBOlJgYGw9G0DOYZLuvYT45UNDEx8liXG9/9zSbF34gU2A26tATVeCIBtz8CnVaj\n+Nu3mfVSfsnHL0pusVVrKERIJSnrpzfHcZsBpLfySt7/JoCzynkOxShktJiN2aRDLM63lhX3WWcK\nmAbZGva+40M41D6COx/ejsvPasPVZ88FoGwoEwrHsgZfcR/9qT4vTskel+onX9wg1coHkrMVav3R\nx4P4+oXsGU69EAuEYlLZ4cZaMxqcJlxwRnphHDK5zGlx4uwVLTje7UZ7nxcnezzSjhmxgI3JqEu/\nEAxF4fGH4bDqM85SsTNr8aVrluNnj+6WRveEVCpKEZb5/JVLsXKBC3NV6skXQwxSvmAEb+3pAQNg\nXqv6c8s/UKwmHY518SPsf75zUrq9sz8ZoHO1U9XrNNmzEQUOq0Hx2uJ2HoNK/f3xkGzIk/+Hp9h2\nVyQfsa9bPA3/8ZHTVQuZkMlFr9PghksXSrUOemQtk5Mjdq3iIhrgOwu6/eG036NU4jS9mwI7qXAU\n2GVWLWzEF65eVrItUeK0uz8YRdegD9NdVjTX554S9gWjikIr4pSivO67GLhC4Zh0vvKKcwzDZKzS\nJlIrXSuuyZc7Cz4T8cPVV0AxkPeva8OqhY249aqlAIDuAZ/0eAroU49YkEoegAPh5Bp76qh8YCSA\ncCQuBe6MzytcdNJUPKl0FNjLyCoEzr6RAELhmGK/upp7vrhB9XafMC0dkLeAFb7+3I9fRzQWR73D\nhKs2KvfspzazkQfyy85sw3c/tTrttcTpfWce1frK4ewVLTDqtfj0FYvzfozZqMPnr1yKea18gZ19\nJ4bRMyRkOVOluSlHCuyyC+GgLHkOAH7+5Y1SO+eOfv53JVdPCfHv2VdkdUhCxgsF9jISW5QeFTJ0\n65zZA3umYDrqC+Nkj0fRQjIcjStasqplsctL4376isX4yAXzpO83rmhBncqFxq3XrMCqhY1p9fjH\nS73ThPv+/RysW9yU++AUFlmxEvHD2kS14acc1cAuFIoS19ctJr1U8KpDWOLKNRVvMmj5baBUWpZU\nOArsZSQG9ueE4hd1GfqVy525JL316fZD/VLmuygSiSsCfUil8YU8SWj1wkY01SWXATKdS0ONGZ+/\ncqlqe9tKp9dpMXc6nyw1KiQrlmqHA6ke4sh7VDYVHxFyR/SyZTbxAuBNoUa83Zq7C6TFpKMRO6l4\nFNjLqDYlOObTjOZ6Wc369Uv5Uevuo4Npx4WjMUWDmYtXz0g7pkE2Q6DVaKSSm8DkLa0qjvRHvEKN\n/BLU/SfVxWTgM9/lI3Zx+6R8x0udXTljlWuNHeDrUNCInVQ6mqcso4aawj845A1oWhr4EfaorDiG\nXqdBJBpHJBqXphc3LG/GuSldzwC+KMuOw8n62BoNg+/csBrjWHdm3Ikj9GEasU9pNTajorFQVKgf\nr5MlhTbXW7BmUaPUJChXDgzA71gZclOBGlLZJuewrUJYTXpFglo+I3YAuOUDi7FmUaPUbU0cfQLJ\ni4OwLLBnCl5LZtUBUI5a25rsk7oKm5gcFUpZUyVTS43dCLcvLOWhROPpU/EMw+AjF8yXvq/PkQMD\n8Gvz0Vgcwx4K7qRyUWAvM3kQtefIuhWduaQJn/3gUmmNPhZPJsmJFweRSHIqPlOr13mtTnzxQ8tw\n2zXLizr3apRatCd1ZwCZGmpsRsTiCWnbozRiT1mCkies1uaRAyMur337gS2Ix3NXR+wa8OHZzScV\nia6ElBtNxY+jXFm3qdRG+HUOI453K0fs2bZ0nT7fVdhJVjmzUfleFNvfnlS3GiFIu31h2Mx62Rq7\nMrAzDIMLVrbC7Q/nlXdy7fnzcKRzFD1DfnQO+DCj0Zb1+G/9dgsAgJ1Zg7ktpSl8RUguNGIfB//5\n0dPxyUvYghO5dFoNrClNY6YL6+75TMVPRWZZIGcA6PX0Kz4VNdbyjV7EdsliVrxauejr3rcAn7ty\naV7PazPrcfEaPlFV3n8B4Bs43fPILqnx06a9yfawsQJ6HxAyVvSpNw4WttXi3NPSk9vykbpGLCbU\nRaNxqUgNjUqTbLLlDpNRKzW3IVPLHKEs9L3/2IOB0YBq8lyxWoVR+v4TQ4rb73x4O/YcG8Te4/zt\nO48kE1fFi3BCxgMF9gonz+wFgKY6fiQSjsbgFe6zqpSGnaosRp3UwEbsVEemnrmyngxPvX0C0Xgc\nWg1Tkgu9ZuFv8N0Dfdh7nN+KKl9DF/9m5ZUi5VtTCSk3CuwVLiKMNM5c0oRv37BKmnZ/ZXunVDs+\n36S8qUAsIgIANRNUFpdMvFq7Cd+7cQ2sJh22cX0IhGKl6wEh6z/w4tZ2AMkeCwAw6A4CAAZGgtJt\ngVAU8XgCsXh6ISlCSo0Ce4UTO1HNa3ViVpMDelnXtYMnhwFQYE8lDp6cNgrsU1lrow0bV7QgEIqh\na8BXsnbMAPDlD/M7TUaFrahiW1gAGBgNwu0Po284IN0WCMXw/T++hx88tK1k50BIJhTYK9zXrluJ\nDcuasWEZX1FNHsQ7B3zCbRTA5MRZDbuZ3pepbsnsOunrUlZbXD63AfUOo5Qo55e1Ue4a8GHfsSHE\nEwmsmFsPABj1hXCyx4Pj3R5FwSlCyoECe4Wb3ezAjZctkkbqOq0GX7x6mXS/Qa+hsqkpPrhhNtqa\n7Fi9qHGiT4VMMHlZ5VKXUbaY9NI++YAssPcM+tEtZOPPE9b6T3R7pPuP93hASDlROnUVcgldqYBk\nMh1JWr+sGeuXNU/0aZAKIK8HX4qMeDmrSYf2cAyxeFxRPz6eSIA7xS+TiY2X5FvjgiFKpCPlRSP2\nKiT/sBLLxhJC0ul1GinXopRr7ABfMhoA/MGoNGJ3Cf0hDnfwrZpbGsRdLMmkOdr6RsqNAnsVkldX\nm9XsmMAzIaTyNQjNXbQlrmkg7r7wB6PSWnvbNHkHRQYNTnPa4yiwk3KjwF6FGNkHVEs9TcUTko3Y\nP0CsPlcq4ojdF4xKW0/nt9ZI96+Y1wC9TpO2tk972km5UWCvUs1CQBdLZxJC1HkC/GjaXuJCTuKI\n3ReMSB0YF7XVSvefv7IVABAVLijEJjM0YiflRoG9Sn3rk6vw4y+sh77ECUGETDZnL+cTKc8/o7Wk\nz2uVBXZxC1udw4hWF19ydlaTsj3ysjn81rcXt7Yrku0IKTXKiq9SZqMurUUpISTduadPx7I59Wio\nSV/vHguxlLM/GMWINwy9TgOzUYevX7cSgVA07e9z5rRkJ7j9J4awaiFtxyTlQZGBEDKpMQxT8qAO\nJKfiO/q8ONXnwawmh1TS2GJK/2gVOzMCyoI2hJQazeMSQkgRxOS5PceGkEgAazIURBK3wE132WAT\nRvkDowHVYwkpBQrshBBSBHFULjZ9EZPjUv339atxxy1rYTPr8e3rV/GPGQ2qHktIKdBUPCGEFMFq\nUmbZOzN0E7SZ9dJI3S4ck9qOmZBSohE7IYQUwWLSQatJ1pRw5NEm2KjXwqDXSFvwCCkHCuyEEFIE\nDcPAJuu2mE9gB/j99F5/uFynRQgFdkIIKZbTkqxDb8lz+6nNYqCpeFJWFNgJIaRI4pq5yaBTlHrO\n+hizHuFoHCGqQEfKhAI7IYQUySGM2GPxRN6PkQrb0F52UiYU2AkhpEh1Dn6LW6CAIC1WpKPATsqF\nAjshhBSpxqa+dz0bs4FvuxykwE7KhAI7IYQU6aylTVgyqxZf/vCKvB8jjti7Bn1IJHJP4feNBPDO\n3u68jiUEoAI1hBBSNLNRh3//yOkFPwYAfvfsQYQjcVyQo+vcvY/tRme/DxajHqfNbyj6XMnUQSN2\nQggZR2ajVvr6xa2nch7fM+gHAOw6OlC2cyKTCwV2QggZR2ZDcqI0n2z6xlq+M52X9r6TPOU1Fc+y\nLAPAJXzbz3EcLfYQQkgR5H3aY7HsH6WH2kfQLYzYfUEK7CQ/WQM7y7JrAXwdwAUAQsLNRpZlXwJw\nJ8dx75b5/AghZFKZOc2W97F3Prxd+nrUR2VoSX4yTsWzLPs9AP8PwO8BTOc4zsVxnAtAC4A/ALib\nZdn/GZezJISQScJi0uNrH+MT7kKR/KvPuSmwkzxlG7EPchy3MfVGjuO8LMv+i+O4J1mWvS3bk7Ms\new+AtQASAG7jOO492X0fBPBN8DMBf+U47hdF/QSEEFJl2Jm1WDCjBofaRxBPJKBRKUfrTekA5wtG\nEYnGoddRahTJLuNvCMdxPwUAlmWfV7n7dfkxaliWPQfAPI7jzgJwE4Cfye7TALgXwKUAzgZwBcuy\n04v5AQghpBolC9Woj9p7hvxpt3moKxzJQ7ap+OtYluUAnMuybLvsvx4A+kyPkzkfwOMAwHHcQQC1\nLMuKi0sNAEY4jhsUEvFeA3DhWH4QQgipJmYTP2EaDCcr0B3tHEX3oA8A0CsL7EY9fxFw11924MCJ\noXE8S1KNso3YHwawGMDfAGwAsFH4bw2AM/J47iYA8o2X/QCaZV/bWZadx7KsXnjeaQWfPSGEVClx\n25tYZz4eT+COh7bhm7/ZAgDwB/nbb71qKa5YPwsA0DscwF1/3YlnN58c/xMmVSPjGjvLsj8D8BWO\n467PcL8ewN0cx30pz9diwK+1g+O4BMuyN4FPzOsD0CPcn5XLZc/zpchY0PtcfvQel1+lv8f1tRYA\ngNFshMtlR59shO5y2aEVpuobXXbojcpJ0kdfO4rrP7B0/E42g0p/j6eqbMlz2wDsYVn2fgDPA2gX\nbp8J4GIAtwD4UZbHd4EftYtaAHSL33Ac9wqAVwCAZdnfADie62T7+z25DiFj5HLZ6X0uM3qPy68a\n3uNEjF9b7+p1o8Gmx8GTw9J9/f0eDI8EAABBfwjalDrxdQ7jhP981fAeTwbFXDxlm4r/A4D3AZgF\nfq28V/jvH8JtFwvHZPIigGsAgGXZlQA6OY7ziXeyLPssy7L1LMvWgt8n/1LBZ08IIVXKLvRyFxPi\n+oVADgCJRALBMB/4jXot5rU6pfua6y0IR+LjeKak2mSbir8LwDc5jrst5fZ5AB7kOK5d/ZE8juM2\nsSy7jWXZtwHEANzKsuz1AEY5jnsCwG/AB3+d8DqUEUIImTLq7HzL1yF3EIAysIejcWmPu8mghVGv\nxe3XrkAoHMNL2zrQM+hHPJ6ARpNzBZNMQdmm4k0A3mNZ9nqO43YAAMuyXwLwFQDfyOfJOY77r5Sb\n9sjuexxC1jwhhEw1tQ4TAGDLgT6cc/p0PLMpmRD31FvHEZKN2AFg2Zx64fheJABsPdgHhgHWLKK8\nY6KUMbBzHPdFlmU3APgjy7JPgs+M7wKwiuM4ajNECCFjII7YuwZ8+NvLhxX3PbflFJbP5QO50aBV\n3Oe08lP4v35qHwBg1cJG1QI3ZOrKWsKI47i3AHwLwL+DbwLzFQrqhBAydvJmMJv29abdL47YDXpl\nYE8doYvb4ggRZStQYxcy4v8LwAoA3wHwBsuynxivkyOEkMns01csVnz/7RtWAQAanCZ0Dvhg0GvS\nRuPzW52Ki4JRbwiEyGUbse8A0AFgPcdxhziOexR8+dePsCz79LicHSGETGK1NqPi+6Y6C1w1JgyM\nBuENRGAxpq+WMgyD2z+8Qvp+hJrDkBTZAvtHOI77HsdxUiFjjuN6OI67DMA/y39qhBAyuVlNysIz\nJoNOqkgHADe+f5Hq4+a1OvGJi1kAgNtLgZ0oZdvH/l6W+35dntMhhJCpo8VlRYOTz47XClvXPEJX\nt1ULG7FUyIRXU2Pjk+he29mJ9j5vmc+UVBPq/0cIIRNEwzD44WfW4f3r2vA/N64BAAx7+DXztmm2\nbA9FjTCNf7hjFPc8srO8J0qqCgV2QgiZQFqNBtecOxctDVYAwIVntAIA1ubYny5uewOAEZqOJzLZ\nCtQQQggZZx+5YD6u3DgHFlP2j2eHLLADQCQag16nzXA0mUpoxE4IIRVEo2FyBnUA0GmVH999w4EM\nR5KphgI7IYRUqf++fhUuWMlP3e84TLXDCI8COyGEVKnZzQ58cONsmAxaPLflJMKRWO4HkUmPAjsh\nhFQxm1mP0+Y1IBCKwU3FaggosBNCSNWzmflCN/4Q1Y0nFNgJIaTqicl2YkOYaCwOr1Dohkw9FNgJ\nIaTKWYTStD4hsN/3xF586advUnCfoiiwE0JIlRObxTy/5SSAZIb8W7u7J+ycyMShwE4IIVVObON6\ntMuNSDSZGf/Iq0cQi8cn6rTIBKHATgghk0jXgF/xvcdP0/FTDQV2QgipcivmJbvAPfraEcV9tAVu\n6qHATgghVU6n1eDzVy4FAOw7MQwAaHXxTWUosE89FNgJIWQSEPeyi84TSs2OUmCfciiwE0LIJJAa\n2BucJgBA77Bf7XAyiVFgJ4SQScAqC+xLZtdh3nQntBoGOw8PIB5PTOCZkfFGgZ0QQiYBq6zV661X\nLYXZqMMZrAsd/T68uqMTAPDMphP4e0pyHZl8KLATQsgkYNBrpa9NBj7If+zCBdBqGGze14OBkQAe\ne/0Yntt8CoOjwYk6TTIOKLATQsgk5bAaYDXp4AtG8fPH90i3Hzw1PIFnRcpNl/sQQggh1eDOz54J\nJuU2k1GH/pEAYrJ1drefMuUnMwrshBAySTTWmFVvF4O602rAqC9M1egmOZqKJ4SQSSwo69G+aFYt\nAMCTx972eDyBp946jv6RQNnOjZQHBXZCCJnEIrFkE5iFM/nAnqtoTTQWx83/9yqeeOs4/veP75X1\n/EjpUWAnhJBJLBxJBva2aXaYjTrsPT6EIXfmzPhjXW7pa5q2rz4U2AkhZBIT19en1ZrR1mTHRav4\nUrOv7+zK+JhwJJbxPlL5KLATQsgktqDVCQC4+py5AIB1S5oAAE+/c0LKjj/SMYqHXuCk3u0jXuVU\nPfV0ry6UFU8IIZPYFz60HAdODmMV6wLAj9xFQ+4gHBYDfvCnbQCAlQtcWDK7DiPekOI5guEYrCYa\nB1YL+pcihJBJzGbWY/XCRjAMv8OdYRhcuXE2AGDUG0YikdzfHghF8cauLvQNKzPhA8EoSPWgETsh\nhPX+2OcAABi1SURBVEwxVhPfMOanj+5W3P6rJ/chLgv0jTVm9I0EEAjTmns1oRE7IYRMMRaT+phO\nHtR1WgarFzUC4EfypHpQYCeEkCnGmiGwy9XYjLAY+eMosFcXCuyEEDLFWEz6nMfU2IwwiYE9XL2B\nfevBPvzk77um1BY+CuyEEDLF1DtMYADodckQcMHKVsUxC9tqYDbyrWCrOXnuvif2YvfRQbzH9U30\nqYwbCuyEEDLF1NqN+MGn1+Fnt22Ubvu3C+bhuosWSN+fPt8Fu9kAAPAEqr/6XEe/b6JPYdyUNSue\nZdl7AKwFkABwG8dx78nuuxXAdQBiAN7jOO72cp4LIYSQpGl1FgDAtefNg8mghU6rwQVntOLhfx0C\nALQ0WNE75AcAuH1hPLv5JNiZNZjb4pywcy6G3aKHxx/BsCeU++BJomwjdpZlzwEwj+O4swDcBOBn\nsvucAP4DwAaO4zYCWMyy7NpynQshhBB1l6ydiXNPn552u1GvhdPKj9gPnBzGo68dxR1/3Dbepzdm\nOi0f5iiwl8b5AB4HAI7jDgKoZVnWJtwXEv6zsyyrA2ABMFjGcyGEEJKHO25Zizs/sw4AYLPwSXbd\ng/6JPKWCbdnfi7+9chjxRAJBIfEvtZreZFbOqfgmAPLLu34AzQAOcxwXZFn2uwCOAggCeIjjuCNl\nPBdCCCF5aK63Sl9rNdWZhvXrp/YBAAw6LQIhPht+xBNCPJHAqDeMWrtxIk+v7MbzX40Bv9YOlmUd\nAL4FYAGA2QDWsyy7bBzPhRBCSB6WzalXfB+JVk9DmKffOSF9HY7G8esn9+Hff/E2TvV6Ju6kxkE5\nR+xd4EftohYA3cLXiwAc4zhuCABYln0LwCoAe7I9octlL8NpklT0PpcfvcflR+9xaXzogvnYcyy5\nUqoz6eGq5RPvKu09jscTuP+J9DCi0TCIxxPYepDf8jboi+CMCjv3UipnYH8RwP8AuJ9l2ZUAOjmO\nE/cbnACwiGVZE8dxQfBB/dlcT9jfP7mvsiqBy2Wn97nM6D0uP3qPSycSUm516+waBRONVeR73DPk\nxzNvH0+7/ZzTWvDq9k7pe7c7UPZzTyQSUuOdsSjm4qlsU/Ecx20CsI1l2bcB/ATArSzLXs+y7JUc\nx/UCuAvAqyzLvglgO8dxb5XrXAghhBRHLCsr8ldweVm10rdaDYPrLloAs+zn8JZxX348nsA37t+M\nb/12S1lfJ5uy7mPnOO6/Um7aI7vvfgD3l/P1CSGEjI01pfxssILLy3r86YH00nUzoWEYrJhbj837\newEAj71+DCvmNaDVZUs7fqzc/jB6hP3/f3qRw2c/uLTkr5FLdaY8EkIIGRepneAqecTuDYTTbhOD\n/ccuWoCVC1zS7d99cGtZzkG+re5wx2hZXiMXCuyEEEIy0mk1uPCMVrAzagBA2j5WibyB9IuO+a18\npTybWY8b379Qul3eoraURrzJi4uWBmuWI8unrFPxhBBCqt/HLlqAXUcGwLWPVHQLV3HEvn5pE646\new5GvGHMbk4mn+XT1W6sRmUj9olatqDATgghJCdzFfRm9wrT7peua0Odw4Q6h2ncz2FUNmIPhidm\ndoOm4gkhhORUI1Rr6x8JTPCZZCZ2oRNL4ar5wtV8LTSjQVuWcxjxyQJ7AcsWz20+Ce7UcEnOgQI7\nIYSQnBqcJpiNWrT3eSf6VDISR+xWU+bJ6JULXJjX6kQoHCtLBTpxKt5pNeQ9FT/sCeHvrx3Fj/68\noyTnQIGdEEJIThqGwfQGG3qHAojHi0s8O9Q+gue2nESiTIlr3kAEVpMuZ437JqFy3gvvnir5OYx4\nw9BpGdQ7TXnvICj1WjwFdkIIIXlxWA2IJxJFbXmLxuK48+Ht+PurR9E/GizD2fFT8TZz7gS5T71/\nIawmHTbt68U/ZfXkS2HUF4LTaoA3EEEiAby8rSPnY/zB5PvZ3uct+sJJRIGdEEJIXsQp7mIqqsnX\n5u99bHfJ26jGEwn4ApGs6+sihmEwXShO8483jpXsHBJC9zinzYgFwvbAf21tz/k4+YXSdx58F4++\nfhRHOkcx5C7uAogCOyGEkLyIo+FiArtbllTW2e/D81tKOw0+6g0jFk+gzp5fJrxem6zjXqo97XuP\nDyEWT8BpNeCGSxdiRqMN/aOBnM/vCyrfz+e3nMIPHtqGr973TlHnQYGdEEJIXqwFBPZ3D/Ti67/a\nhAefPYBQJAZ3SrnXsU43pxJHt/V5bnGTv7rXH4E3EMEDz+wvepQMAPc8sgsAYLfooWEYNDhNSCRy\nbxEMBNXvL/Z6gwI7IYSQvIgjdl8egX37oX70jQTw1u5u/O3lw3h200kAwFVnz+GfI0MwK9agEJDr\nHMa8jpcHzRFvCP985wTe3tODXz6xd8znIpaxzfdCSHwvLjuzbcyvDVCBGkIIIXkSG8LkM2IfEBLk\nbGY9XtvZJd3eNo2vBOf2p9d1H4teofFKg9Nc8GNHfWFohBarx7rcYz4XdmYtgOSF0Hd/txWXrpmJ\nKzbMVhz33sE+vLWnW8o3WLnAhc5+H3YeGRjT69OInRBCSF6cNgMAZXW1TAZHg2hwmjBvulO6zWrS\nYVaTHWajNq/nKMTxbn5P+qzm/PqXX7J2pvR1IBQFZK3T/cEIHnzmAI535x/kxaUFBsCFq1oBJAN7\nKBzDE2+l94n/5RN7sfvoIE718rUBau3GrHvw80WBnRBCSF5qhMA+4lNmtAfDURzuGJG+j8biGPWF\nFevd9Q4T7vniBjisBjgsBgx7gvjJ33fltR0sl3g8gSOdo6hzGFFjy28qftmcenxKaApzsscjzTAA\nwD1/34W39nTj0deO5n0O4l70FfMapNF/Plvv5BwWQ0nq2dNUPCGEkLw4rXzQ7B7wS7cdODGEu/66\nEwDw39evwuxmh7QGb7caMLfFgZ1HBrBmUSN0Wo3wPAb0Dgew++ggdh8dxKxmO+a2OFGso12j8AYi\nOJdtKehxFiMfRJ9LydA/2smP1LWyzPmsr985iueFYjdiTX2AD9SZqCXUaTRMSUbsFNgJIYTkRa/j\nA/PJXg92H+lHs9OE9n6fdH/fcACzmx3wCslgVpMOF62egWl1FiybUycd57AqA96r2zvHFNj7hvk9\n8rOaHQU9zmzMXi8+FksgHk/ggWf247T5Lqxe2Kh63B0PbZO+tsgCe7ZEvsEMRXosssA+3VVc21cK\n7IQQQvLW6rKho9+Lb973Du6+dT1CsnKoYlKdPyjWbOe3fZ02r0H5JExyJGzQa7DjcD+isbg0oi+U\nOENQ6NS3yZA9BHr8EfQM+bFpXy827evF6q+fn/M5zabkxUJqd7l4PAGNhv/ZOwf4C6KPXjAf7Mwa\nmIQLglahcA4AfP+mtfn9IClojZ0QQkjevvOpVdLX7X0eBGStScUiNOL2LatZPXCKgX/ZnHosmVWH\nQCiGN3d3F31O8hmCQphSOryJOQSiEW8IWw/2Sd/nkzFfKyuQk3o+8prwHf18wlxrow0zp9nRWMNn\n87Mza3D6/AZcvGZGnj9FOgrshBBC8qbVaHDtefMA8NvE5D3HPcIWNnEEbc2QCPZv588HO6MG11/C\n4n2r+QA2lnawvmD218skNbA311vhkJWk9QYieFKWzf6/f3wP0Vg863NOq01ut2MYBpcqsu+T75XY\nJa81ZbqdYRh88UPL8W/nzy/gJ1GiwE4IIaQgzfV8d7SOPh+CsiSwUWHE7s8xgp7RaMPXrluJOodJ\nmq6Wl5wtlHQhUfBUvDKw2y16zMmx1j/iUe4ICIWVPdenCZ3jRB8+bx7OWzkdgLImfEe/FzU2A+xZ\nEuyKRYGdEEJIQcTkt3+91y6tFQNA/wifENY/yo++89l6Jj5XsYE9Govj3QP8dHmhU/Fmow5nsC7F\n95efNSvrYwZTSs7uPjYIgF/fX7+sSTVhrlZ4H17Zzm/t8wYiGHKH0NpoSzu2FCiwE0IIKYhdNl2d\nnFK2oW/Yj3gigVO9XjBQJoJlYtRrYTRo0TcSwIETQwWfy+GOUelrgz57lnsqhmFw61XLcN7p/Ii6\n1WXDnBYHfnbbRtx61VLFsWsXTwMADKWM2A+38/v3b7tmOW66bDEYJn2LXFMdP4p/fWcX7vrLDnQK\n6+szyhTYKSueEEJIQeocJpyxsBHbZIllzfUWdPR70d7rRdeAD411FhgN+QVap9WAvuEA7vrrTnzp\nmuXpWfRZiNvGPnph8WvS171vAS47sw01dn5kbTPrsXKBC9++YRWcViO2H+pHvcOELft709rNdgul\nbFsaMm9NEwM7ABw4OYwmYSljRh4XPsWgETshhJCCaBgG373lTOl7rYbBKmGP92s7O+ENRFBjzX/t\n2FWTTDg7XmCtdnFqvKW+uD3fAP/z1DlMUsU4gB/Nz2pyoNZuxAVntEp73uUJcADQM+hDrd2oKEyT\narrLisvPapNmMF7d3smfc5aLgbGgwE4IIaQo554+HbV2I375lXOwqI1vfNIpFKwpZE+5PJM8Es2e\ndZ5KDOz1zvzatRZLDNzyZMF4PIEhTyjnazMMg6vPnotPXswqbi/XOdNUPCGEkKJ88mIWEIKVTstA\nq2FwpJNf87ZZCgjssqlqbzB35zi5vuEAGAD1ebZrLZZYQCZ1e18igbxnJ2rsyeNMBq2iSl0p0Yid\nEELImDEMg1g82eS8kBH7HFkp2NQ17FSxeFwxqu8Z9KGhxgS9rrDEuUKZhXyBQDh9e59YQz8X+S6B\neodJNdGuFCiwE0IIKTm/SpOTTNqakq1WfTl6vf/qiX34zP97DeFIDL5gBG5/BE115VmrlhPLz6rt\n23fa8huxy0vmzi6wrn0hKLATQggpCfl0+OK2uixHKum0Gtz5mXVgmGS9+Uy2HeoHwG876xnkM9LF\ngjnlpNdpoNMyqiV0U5vaZHPdRQvQ4DThotXFl4zNhdbYCSGElMQ3P7kKbl8YFpNO0Ys9H421/7+9\ne42Rs6rjOP7tXtrussu2pVt6I1puh4sQbGsKtAgUJUSIRuUdRiQYCQElRhPvRBOFEAJFE02EAL4R\nfYFCMFZEJEYgBEVeoJD+gyIVWmi30MK2tAvb1hczsx22u7OX9pnL6feTNJmZ52T2n7PT/c15nvOc\n082S+Ufxxtvjn4rfWrXs7I7BoZGJcwvrEOxQGrVXX2OfaIW9sVy0YikXrVh62GurZrBLkg6LOT2z\nJrXa3Hh6ujp5dWDXuDu9PfDXl0Yeb985xOvle8gXzatXsLe/bx/1yvX22QVNgpsuT8VLkppCZcJd\nZXe4aruHhvnbC1tGnu8YHBo5Fd53CF8mpqJrVgd73h3mmQ1b2bxt18jovWuC7V/rrbmqkSQdsSoL\n1bw6sJO+o95/jX5gx272A+m4OcQrO9iy/Z2R0XOtxWEOp66Z7ewe2svPHvwXABectRg4eDOZRnPE\nLklqCictnQMcWH+92tbtpevrZ55wDB3tM3hl666RYO+eVZ9gHX3KvTKRrl5fLCbLYJckNYXKbW+v\nlWe7V9tWXhP+2HndLD7mKDYN7GTnnmE62tsKv4e9YvTI/OnypQFH7JIkjaGvZyYd7W0MVM1+r6jc\nBtfb3cnSBT28O7yPja8P0j3FrVoPxXgj88ludlMvzXX+QJJ0xGqbMYP+ObNHgv3pF7bw2LOvsuaM\nRTz89P+AUrhWbwdbz9Pg402SaytoBbnpcsQuSWoa8/u62LVnmN1Dw/z8oed58dW3uPcPG9i3v7Rc\nbfesDpan/obUNtYp94V1utVuKgx2SVLTmFNenvWtXe/S3nbwSLhrVgcL5nTxqTXLAFjaX/xyshVj\n3a9+zSdPr9vPnyxPxUuSmkZlgZsdg0MsXdDDxtcH33e8cj374yuPY37fbD5S3ge+Hub2Hny//FSW\nk60XR+ySpKZRGbE//tzmkWvX1RumVF7rnt3B6jMWMbOzfhPXlsw/cHagsozsVHaxq5dCR+wppXXA\nKmA/cENEPFN+fTHwy6qmxwPfiIhfF1mPJKm5ze0trTH/1PNb6J7VQU9XJ2uXL+Hu37/d4Mrg2Hld\nI49vvuYcdu15j86O5hsfFxbsKaXzgRMj4tyU0inAPcC5ABGxGbiw3K4d+AvwUFG1SJJaw+nL5tLb\n3cngO+/xztAw8/tms/zkfu579EVOWtrX0Nra29r43pUrR75wNONoHYo9Fb8WeAAgIjYAc1NKPWO0\nuwq4PyIOXpFAknRE6exo5+pLTxt53tHeRtesDu748mq+8tkzG1hZybJFR3NsE86Er1ZksC8EtlU9\nHwAWjdHuauDuAuuQJLWQynV2YGQHt86OdtrGmCWvg9Xz4sAMStfaR6SUzgE2RMTOOtYhSWpifU04\n07yVFDl5bjOlUXvFYuC1UW0uA/402Tfs7+89DGVpIvZz8ezj4tnHxSuqj+cdc+Cq7S3Xr/F3OUVF\nBvsjwA+AO1NKy4FNEbFrVJuVwH2TfcOBgcGJG+mQ9Pf32s8Fs4+LZx8Xr+g+vuCsxczpmUV/z8wj\n+nc5nS81hQV7RDyVUvpHSulJYC9wXUrpSuCtiHiw3GwRsLWoGiRJrenzl5zS6BJaVqH3sUfEt0a9\n9M9Rxxs/xVGSpIw03531kiRp2gx2SZIyYrBLkpQRg12SpIwY7JIkZcRglyQpIwa7JEkZMdglScqI\nwS5JUkYMdkmSMmKwS5KUEYNdkqSMGOySJGXEYJckKSMGuyRJGTHYJUnKiMEuSVJGDHZJkjJisEuS\nlBGDXZKkjBjskiRlxGCXJCkjBrskSRkx2CVJyojBLklSRgx2SZIyYrBLkpQRg12SpIwY7JIkZcRg\nlyQpIwa7JEkZMdglScqIwS5JUkYMdkmSMmKwS5KUEYNdkqSMGOySJGXEYJckKSMGuyRJGTHYJUnK\niMEuSVJGDHZJkjLSUeSbp5TWAauA/cANEfFM1bHjgF8BncCzEXFtkbVIknQkKGzEnlI6HzgxIs4F\nrgZ+MqrJbcCtEbEK2FsOekmSdAiKPBW/FngAICI2AHNTSj0AKaU2YA3wu/Lx6yPilQJrkSTpiFBk\nsC8EtlU9HwAWlR/3A4PAupTS4ymlmwqsQ5KkI0Y9J8/NoHStvfJ4CXAHcD7w4ZTSJ+pYiyRJWSpy\n8txmSqP2isXAa+XH24CNEfFfgJTSn4HTgfU13m9Gf39vEXVqFPu5ePZx8ezj4tnHzanIEfsjwOUA\nKaXlwKaI2AUQEcPASymlE8ttVwAbCqxFkqQjwoz9+/dP3GqaUko3Ax8F9gLXAcuBtyLiwZTSCcAv\nKH25eM7b3SRJOnSFBrskSaovV56TJCkjBrskSRkx2CVJykiha8VP1wRrzH8M+BGlCXnrI+KHjamy\ntU3QxxcCN1Hq4wC+GBFOxpiiWn1c1eZm4OyIuLDe9eXCPSmKN0EfXwdcQenvxTMR8dXGVNnaUkpn\nUlqt9faI+OmoY1PKvaYbsU9ijfkfA58BVgMXp5ROrXOJLW8SfXwncHlErAF6gUvqXGLLm0Qfk1I6\nDTiPAws3aYrck6J4tfo4pdQHfB1YExHnAaellFY1ptLWlVLqpvRZ/eM4TaaUe00X7NReY/544M2I\n2FQeQa4HLmpYpa1r3D4uWxERm8qPB4B5da4vBxP1McCtwLcprcSo6XFPiuLV+iwPlf/1ppQ6gG7g\njYZU2dqGgMuALaMPTCf3mjHYx1pjfmHVsYGqY1s5sP68Jq/WOv5ExNsAKaVFwMXUXhFQY6vZxyml\nLwCPARvrW1Z23JOieOP2cUTsAb4P/Ad4GXgiIv5d5/paXkTsjYihcQ5POfeaMdhHqzWacaRzeFSv\n4w9ASmkB8BBwbURsb0hVeRnp45TSPOBzlPZK8DN8eLknRfGqP8tHA98FTgaWAatTSmc0sLYcjb5U\nN+HfjGYM9lprzG8adWxp+TVNTa0+rvxnXQ98JyIerXNtuajVxxeWjz0B/BZYnlK6rb7lZWNSe1JE\nxD6gsieFpqZWH58KvBQRb0bEe5Q+0yvrXF/uRvf/hLnXjMFea435jcDRKaUPlK/nXFpur6kZt4/L\nbgPWRYR9O321Pse/iYgPRcQ5wKcpzdb+WuNKbWnuSVG8Wn8vXgZOTSnNLj9fCbxY9wrzcdBofDq5\n15RLyk6wxvx5wC3lpvdHxO0NKrOljdfHlGZlbgeeqmp+X0TcVfciW1ytz3FVmw8C90TE2oYUmQH3\npCjeBH38JeAqYBh4MiK+2bhKW1NK6WzgLmABpX58E7iX0tmQKedeUwa7JEmanmY8FS9JkqbJYJck\nKSMGuyRJGTHYJUnKiMEuSVJGDHZJkjJisEuqKaV0RaNrkDR5BrukcaWU2oEbG12HpMkz2CXVcg/w\ngZTSw40uRNLkGOySarkRGIiISxpdiKTJMdgl1eK2slKLMdglScqIwS6pln1AZ6OLkDR5BrukWjYB\nr6eU/p5S6m50MZIm5ratkiRlxBG7JEkZMdglScqIwS5JUkYMdkmSMmKwS5KUEYNdkqSMGOySJGXE\nYJckKSP/B3B5skTUah1JAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6b6a778150>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x,t=geo_brownian(t,W, 1.0, .5, .3) #plotting with variables\n",
"plt.plot(t,x)\n",
"plt.xlabel(\"t\")\n",
"plt.ylabel(\"X(t)\")"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "00e3fda54f3eba73d67842cf7f02777a",
"grade": true,
"grade_id": "numpyex03e",
"points": 2
}
},
"outputs": [],
"source": [
"assert True # leave this for grading"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
davidjaimes/ncat | notebooks/Jupyter-tutorial.ipynb | 2 | 62328 | {
"cells": [
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAggAAABDCAYAAAD5/P3lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAH3AAAB9wBYvxo6AAAABl0RVh0U29mdHdhcmUAd3d3Lmlua3NjYXBlLm9yZ5vuPBoAACAASURB\nVHic7Z15uBxF1bjfugkJhCWBsCSAJGACNg4QCI3RT1lEAVE+UEBNOmwCDcjHT1wQgU+WD3dFxA1o\nCAikAZFFVlnCjizpsCUjHQjBIAkQlpCFJGS79fvjdGf69vTsc2fuza33eeaZmeqq6jM9vZw6dc4p\nBUwC+tE+fqW1fqmRDpRSHjCggS40sBxYDCxKvL8KzNBaL21EPoPB0DPIWVY/4NlE0ffzYfhgu+Qx\nGHoy/YFjaK+CcB3QkIIAHAWs3wRZsuhUSs0CXgQeBm7UWi/spn0Z+jA5yxpEfYruqnwYllRic5a1\nMaWv8U5gaT4M19Sx396IAnZLfB/SLkEMhp5O/3YL0AvoAHaKXl8HLlZK3QZcpbWe0lbJDOsaHuDU\n0e4u4JAy2wPk/C1JzrKWArOQ0fUtwH35MOysQxaDwbCO0NFuAXoh6wPjgQeUUvcqpUa0WyCDoQls\nCIwBjgfuAV7KWdY+7RWpmJxlXZezrEdylvXxdstiMKzrGAtCYxwI/EspdZbW+g/tFsbQ67kQuBHY\nFNgseh9FV6vCbUAeWBC9PgBeq2EfS6J2MQOBrRDTe5KdgAdzlvW1fBjeUUP/3UbOsoYBE6OvG7VT\nFoOhL9Af+BUwFLkZpV+DaY6V4UPkRpb1+ncT+m8nGwK/V0oN01qf025hDL2XfBi+DLycLMtZVo6u\nCsKfGnSq8/NheEpqHwOBEcDBwJnAsGhTP2ByzrJG5cPwnQb22Sy+0G4BDIa+RH+t9dmlNiqlFKIk\nJJWGi+jq5JPmq8BbJJQArfXqpkncczlbKbVQa/3rdgtiMNRCPgxXAK8Ar+Qs63LgXmDvaPPGwPeA\nH7VJvCRfbLcABkNfouwUg9ZaAwuj178BlFLvVejzgR4WFviM1npcuQpKqf6IyXIjxLS7GzAWuUnu\nXsO+fqWUellr3ZBJdq/jr9+BDn1uve07O9Rz0y6f8PtGZGgWe53oT6SBkZ/q1/nHZy47aloTRTKU\nIR+Gy3OWNR6Zxtg0Kv4KRkEwGPocxgcBiCwcsSI0F5iOhF+ilPok8C3gVGS+thK/VErdrbWuO2ys\ns/+aLZTuOKbe9krrIUCPUBB0B+PQ1P1bdKe6EzAKQgvJh+GbOct6gkJkxM45y+qXDIWMHBhjBWJe\nPgyDWvaRs6zPIVObAG/nw/DpEvUGAp8E9gGGJzbtl7Os7cvs4skqp0V0Yl8jgcOBjyMDhbmIZeWl\nfBg+UUVfReQsayhwELAnsAXi6/E28BxwTz4MP6iyn92RaSCA+/NhuCwqXx9R4MYhU0MfRTK/AjyW\nD8MFGd0ZDFVhFIQKaK3/BXxfKXUlklTq0xWafAI4Driyu2UzGLqRlygoCArYHJif2H4gcFb0+Z2c\nZW2bD8NV1XScs6yNgH8g/jsAPwCeTmzfFPgjYsnbiez71MUVdnMQcF8V4nyUs6whwB8QX4+0s2Ys\n0yPAt/NhGFbRZ/wbzgO+DaxXotqqnGX9GbigCkXhf5CBCsDngYdzljURGQhsWqLN+znL+iFwdT4M\ndYk6BkNJTJhjlWitQ2Bf4P4qqv848t8wGHor6Yd9+ruHJFkC2BI4rIa+D6egHKwmstYlGAxMQCwH\nrRjEPI5ER5S7ZvcFXsxZ1phKneUsawSi8HyH0soB0bbvAM9Ebaplt5xlnYkct1LKAYiFZhJwSQ19\nGwxrMRaEGtBar1RKfRX4JxIzXortou3PN1mE+YgJsSwaeoLHOQCqUy3QSr9eqZ6G/gq2aYVMhqrY\nOfF5FeJwvJZ8GM7JWdY/gC9HRS7wtyr7Pjrx+e6MqYC3KLbU7Qhck/h+FJIKvRRVjfSREXicU8EH\npgAvIIqLBZwGfC7avl5Uf29KkLOsTZCMq8npj9sQx89no37HIlaAODplNPBIzrJ2z4dhNVlaT0HC\nXwFmIkrAC4if2PaIz8/3KCgn385Z1pX5MJxeRd8Gw1qMglAjWutlSqnTgUcqVP0SzVYQtP5mcMXE\nSvvtUUy9YsK5QEWHy7EnTB6lOtSsFohkqEDOsgYAdqJoagkT9Z8pKAj75yzr4/kwnF2h748ho/GY\nq9J1oqiKLj4JOctKK8Yz8mH4Yrl9VcnHkXVYTsyHoZ8WJWdZNyPThbF5/3M5yzowH4alpi9+T0E5\nWA18Nx+Gf0zVeRG4KmdZ90R9bwCMRKwyX69C5h2j91uA4/JhuCSxbTYwJWdZtwNPIFbifsAFSISZ\nwVA1ZoqhDrTWjyIjjXIc3ApZDIZu4ELgY4nvt5Wody8wJ/qsgBOr6HsihfvOfCRrY7v5dYZyAECk\nGP0ISEZmZYZ55yxrB8SyEXNxhnKQ7Pt64H8TRUfmLGuXKmWeC4xPKQfJvp9CLCJlZTYYymEUhPq5\ntcL2XVsihcHQJHKWtU3Osi5GnAZj5iKWgiKitRouTxQdl7OscnPu0HV64dp8GLY7R8pyxEGxJPkw\nfBcZ9ceUSvN8IoV76upK/UZcgawcG3NKqYopfleFU+gDic/b5SzLWIwNNWFOmPqp5CG9sVJqPa11\nVZ7dBkOL2D1nWcmcBkOR8MFtgM/QdTXJZcCR+TBcXqa/SYj5egAFZ8VMX4ScZe2FRPnEXF2z9M3n\n3nwYVsrtAmK6/0z0uVR4ZXLtivvzYfhGpU7zYbgkZ1k3ACdHRQdWIQsUO3ZmkUzB3Q/xjaolLbeh\nj2MUhDrRWr+mlFpJ+eV5hyIxz4YWs98Fj/Rf8uZbozo0/ZYt7D8rf9ORK9stUw/hU9GrEnMAp1R+\ngph8GL4bzdNPiIpOorSzYtJ68FS1IYPdTLWp3hcnPm+Q3pizrA7E+TCmFn+aZN0dcpY1LB+G5e4b\ny6rM8bA49X39GmQyGMwUQ4NUGnkMrbDd0A3sdeLk4z6cN+89pTtDTWd+gyErF+7pTv5eu+XqJbyK\nTDHsmg/DJ6tsc2ni8+dzljUqXSGaevhmoqjIObFNVBzlV8kQug4W5tbQNl13WGatAv+poW+DoW6M\nBaExPgC2LrO9nHWhpSilDqI4NPMhrfXUJvS9M/DfqeJXtdY3N9p3rex50uQ9lFKT6BrTvoFCXbTX\nyZNfmnrZxHtbLVMP4xng74nvK5DzeD7wfIWRayb5MHwiZ1kzgF0oOCuemar2ZQoK8zLgr7Xup5t4\ns0n9DEl9b0RBSPeV5q0a+jYY6sYoCI1RacnZ91siRXUMAH6eKnsYicdulDOAY1NlpzWh35pRqG9R\nIuGN7uw4AfG878s8nw/DX3RDv5dScGY8NmdZP86HYXJaJzm9cHMp7/s2UHdK9BTpKaxBNbRN163k\nt9Rux05DH8FMMTTGZhW2v9sSKarjbopNk/sqpUY30qlSahCSGS/JCuD6RvqtF6UpMm/HaHTJbYaG\nmQzED/0umRVzlrUZhXwJ0HOmF5pJOlXyxzJrZbNt6rtZP8HQIzAKQp0opTZAlsItxTKtdTnv75YS\nLR7lpYqrjV0vx2EUH4fbtdZtucnpMqOrDjPy6jYii8DkRFHSYnAEhem22cBjrZKrVeTDcCldTf/p\nh345ksrEGprnF2EwNIRREOrnMxW2z2uJFLVxJcXmy2OVUo34ShydUda+EaIq7T2u0SZTY/eSdFY8\nMGdZm0efk86J6/LCQUnFp5pIkZjkcvQz8mH4YZPkMRgawigI9VNp7v7BlkhRA1rr+RQneNqC2hba\nWYtSajiS9z3JXLomaGktq/VllLIUdKqSWe0MjZMPwxlIel8Q/6Zv5CxrGIX8AJ10XU+hFtIRQ+UW\nKWoXyYyTu+Qsa79KDXKWNRpJyx5zZ9OlMhjqxCgIdaCU6g98o0K1npBCNotLM8rcOvuagCRgSXKN\n1rozq3IrCCZNfFkrfRjotWsCaJinUBODK51/tkuuPkTy/DoYOIDCfeb+fBjW4t2/lqhdcmRdbUri\nVnILXS2HZ1WRvfAcCk61K4A/dYdgBkM9GAWhPr5F6XSrIBf6Qy2SpSaidSReShV/XilV7veUIj29\noOkB2fGmXT7x7sCbOGpFf7VZx4A1m0/znG2nehMyc+0bms7NFJxzxwH7J7Y1OvWUPG9/mLOsLRvs\nr6lEaaOT0TtfBB5ITLWsJWdZg3KWdRNwTKL4wnwYzu9mMQ2GqjFhjjWilBqBpJYtx51a66UV6rST\nS+maJz52VvxRdvVilFK7UbzexGNa67Kr+bWS6X+ekPYs79HkLGt34JOI+Xyz6D2d1vfMnGUdini6\nL0C851/Oh2HD+SyaQT4MV+YsaxJyLm1Gwf9gAXBHg93/JNHHtsArOcuajCztPBDYCkkytBXg5sOw\n5QmF8mF4W86yLgK+HxXtC8zKWVaALMm8CslHsicS7RFzL8VhyAZDWzEKQg0opbYE7qd8prPVdF2h\nrSdyLfALYMNE2XFKqR/XsHbEURll62L4Wiv5PuBUqPPF6JXkLuCQbpGoPi4HfohYKGMHWD9axrlu\n8mF4Z7RuwfioaDBwaonqRemQW0U+DH+Qs6xFwHnIFNwQsv+3mMnA8dHiVwZDj8FMMVSJUuow4DkK\na7GX4gqt9cstEKlutNaL6boULMho5tBq2iul+lH8IFuCmJcNfZx8GM6hOCFVU5THfBhOQHxfylkH\n3gY+asb+6iUfhhcCewC3l5BlFbJk/P75MDwqlVTKYOgRKK1rizhSSk2h67ximo1abV5XSi2n9EIk\nz2itx5XYVqnfQcjI7DiqW2XtfeCTUbRA3ex50nWfUrqjeJEcrfcLrpj4SCN9xyilxgDPp4of0Fof\nUEXbg4B/pIqv1FrXnVNh7AmTR3V0qIwwRH1E4E28pd5+De0hZ1m/Bb4bfX0+H4Z7dMM+hgGjkDwC\nS5FpjFk9bR4/Z1mDkGmF4VHR20g4Y3oxJYOhR9EXphg6lFLlVjFbH0mZvDGwCTAayCFe0ntTOZ1y\nzDLgkEaVg1ahtX5BKfUU8OlE8ReUUjtorSstCduzch8YehSR5/6ERFG3nBvRuhE9frXUfBguA6pd\n+Mpg6DH0BQXBBro7o+Ea4Bta66e6eT/N5lK6KggKOAE4u1QDpdTGFOdNmNkLf7uh+zgYcRQEMa+3\nJe22wWBoDOOD0DhLgYla67vaLUgd3ETxglLHRXkeSnEExQ5gbQ9tNPQokis5TsqHoVlbwGDohRgF\noTECYHet9Y3tFqQetNYrKDb/DqN46eYk6emF1UhUhMFAzrImUEhDvgr4VRvFMRgMDWAUhPpYAvwf\n8Bmte31+/8uQBEdJMjMrKqW2o5A2N+YfWusePw9s6F5yltWRs6zxwKRE8RXtyEVgMBiaQ1/wQWgm\neWTe/jqtdU9Zz74htNavKaXuAw5KFB+glBqptZ6Tqj6RQlrYGDO90AfJWdY5wNeQFQwHIAmetk5U\neZFCsiCDwdALMQpCed5AphEC4NF12BHvUroqCAoJ7TwvVS+d++BdJEmPoe+xKRLnn0UeODwfhm3N\nRWAwGBqjLygIbwN/LbNdI1MGH6ReL/eWkMUmcDeSeGa7RNlRSqnzdZQoQym1C7Bzqt11NWReNKxb\nzEMU6GHAesBiYCaSLOviaF0Cg8HQi+kLCsLrWuvT2y1ET0ZrvUYp5SG57mO2Bz4LPB59/2ZRQ5P7\noM+SD8OLgYvbLYfBYOg+jJOiIeZKxOs8STJiIb28daC1/lf3imQwGAyGdmEUBAMA0XTKraniI5VS\nA6O0zOnloI31wGAwGNZhjIJgSHJp6vtgJBNlehW65cANLZHIYDAYDG3BKAiGtWitHwVeShV/muLF\nuW7VWi9qjVQGg8FgaAd9wUnRUBuXAn9IfN8f+FyqTo/OfbDnSX8brDpXnqEUe2ropzQvdtDx66ev\nGN9XolIMPQDb9T8LrBd4zsPtlsXQe7Bd/0BgQeA5QbtlMQqCIc21wC+ADaPv6WWu5wAPtVKgWtjt\n6Os2XG/9jhdQjIzTQ2rFF9bQecy4E2/I9UQlwXb9LYDDK1R7K/Cc21shj6FxbNcfDjwGKNv1Rwae\n83q7ZWo2tusPBb6ELGW9BbAICX99Gngs8Jx0hlZDBWzXHwvcC6ywXX9o4DlL2ymPURAMXdBaL1ZK\n+ZRItwz8Jc6N0BMZMFB9GxiZsWnzTjrPAH7QWomqYgTF/h9pngC6RUGwXf+XwC2B50ztjv57M7br\nXwJMCjxneo1NP0SWgAfJq7LOYLv+esAFwOkUL9wWM912/d0Dz+lsnWQ9A9v1BwEXAT8PPKfWVOML\nkPVt3kNWQm0rxgfBkEWph5UG/tJCOWqnQ40ttUkrvWcrRamWwHOmAZsguSfGAi9Hmy5AUhgPAz7f\nHfu2XX8k8ENgx+7ovzdju/4uwP9D/peaCDxnCbANsF3gOYubLVu7sF1/AHAHcBaiHDwI/C+ywNsE\n4KfA68BdfVE5iNgbOBmxqtRE4Dn/BoYDnwg8Z02zBasVY0EwFKG1fkEp9RTioJjkIa11zzaVarYq\nvVFt2TpBaiN6oCwB5tiu/2FUPCvwnLTTaLM5oJv77800dGwCz1kXHXkvRNKydwI/Cjzn1+kKtuuf\ni2TX7Ks0et681yxBGsUoCIZSBBQrCL0h98EbdW7rddiuPwoYFJu/bdffFNgL2BZ4DZgWKR5ZbRWS\n2+KIqGiE7fpjUtXmlrtZRdaHscBAYDowM/CckimWbdffFfgw8JzXou/9kfUccojV5MXAcz4s0XYw\nsCsymu8PzAVmBJ7zVqn9pdoPRVKF7wSsAN4EgqzRve36HcAoZDEqgO0zjs3rged8kGo3gOJ05ADT\ns0bTkan+k9HXGaVGjNFxykVf81nH2Hb9Ich/MRJJeT291H9fL7brj6CwANfPspQDgOi3rijRx/rI\nb8kB7wPPBZ4zL6Ne/JvfCDzn/WhufhvgvsBzVkR1dgN2AR4JPGduom38P7wXeM7c6FzfCfgU4iMR\nlFLebNfPIefXzMBzikz8tusPQyx676bljmTeCfhyVLST7frp//TV9Dluu/6GwOhUvTWB58zIkjFq\nsykyNfmfwHMW2K7fLzoWeyDTFPnAc14t1T7qYwNgT+Rc/wi5ZyT/N20UBEMRSqn+wNdTxQspTqTU\n41BaP6yVOipzGzzSYnG6m6uBz0YPv7OQm3dytc35tuuflHZutF3/BuArwEaJ4p/QNdU2wGnAH9M7\njRSTG5CbS5LQdv2joymTLKYBzwHjbNc/DomW2TCxfbXt+sMCz3k/sa8RwM+Qh/X6qf5W2q4/CTit\nzMN1OPB7CopQktW2658YeM5fEvXvRKZzBiXqZaWUPha4JlW2NfB8Rt0hiANfmjWIuf5jiLPfvVm/\nAfmvbgNmB54zKrkheuD+Bjg11Wap7fpnBJ5TybelFk4E+iE+Fb+ptbHt+scg//nGqfJbgeMDz1mY\nKN4UOZYX2q7fSWHhuNdt198ZOBc4MypbbLv+5wPPeTb6PiJqe5ft+ichx3WXRN8rbdc/OfCcrGis\nR4ChiHKSlSn2f4BzkOvitMRvCKJ9DEzU9TPafwGZlkkyBvExSrKUrtdnmoOBycA5tus/iCyat3li\nu7Zd/0rk2ihS1mzXPwT4E3LulaLTKAiGLL6EaMlJbtBat91pphIjFw289t9DVh4N7Jva9EKnWnpJ\nG0RqBXcjCa08YCqy/PJE4L8A33b9HQPPeTNR/0bgvujzGchoywPSq5U+nd6R7fp7IDfRjYDrEE99\nDeyHrPb5lO364xI36zTb2q4/AUnt/SSyLHQHMvJZklQOIhYChyCLid2FWBoGIQrDfwGnAP8Gskzd\nVvSbBgPvIMdpJjLHuxdikXgg1ewa4Jbo84+BHRAFI/3gT9/QQZa+/iIy9zwccVQrSeA5nbbrX4s8\ncI6htIIQK7xdFJLIAvEEYjmYBlyP/E4LeXj92Xb94YHnnFtOjhrYJ3q/vtbpE9v1fwqcjYxUL0GO\n51bI//g1YIzt+mNTSgJIivfNEIXgBOThfx0ySv8Nct7vgzgfj0+1HQf8E5iPKM/vI+vLHA9cZbs+\nJZSEevgDBZ++3yIKzgVI1FeSrCnD6ci0zebAJxCfjmoZjxzXPPBL5By0gW8jCt3sqHwtkYL1N0RB\n/R2ymOG2yHE5CLFAHAu8ahQEQxbfyijrDdML3HTTkWvUBRfsb88bPb6TzjEK+oHKL184YHL+Jmdl\nu+XrJsYBhwaec0dcYLu+hzw0dkcu/AvjbUmLgu36DqIgPB54zuQq9nURMgI8LjnyBibZrj8z2s/l\ntuvvVcJJbWvkXDoi8JzbKu0s8JxFtut/IqXgAPzOdv0/IiPnb5KhICAjpMGIEjAhPV1iu35HWsbA\nc25ObD8ZURAeqibENBqpTYnark8FBSHiakRBOMx2/cHpB29kSv4KooSlLRYnIcrBHcBXk7/Fdv0b\ngReAM23Xvz7wnJlVyFIJK3qfXUsj2/U/jiiiq4B9ktEytuv/Fhlpfx2xEnw31XxHYLfAc6bbrv8k\ncny/Bnwz8Jy/2q6/DTLd9F8Zu94ceXAeEHhOvM7MNbbrT0UU4vNs15+c2FY3gedcm/hNP0EUhDvL\nKMrJtkuIFPboWNWiIOSAO4HDE7/Dj67FSxEn21+m2pyOWDpuCDxn7fG2Xf8e4F1EIVsceE5oohgM\nXVBKjURuSEke11qXMhv3OPR553VO9Sb407yJZwTexO8FnnNV/qYj11XlAOCfSeUA1s4D/y36mp7f\nrAvb9fdGLDMzU8pBzMXIg2wsMhLKQiFhgxWVg5gM5SDm+uh9VHqD7fr7IlaNFcAJWb4UPcHLPvCc\n2YgVZn3gyIwq30AsQg8lQ+aiefUfR1/PzlB08sD9Udusfmsi2t+Q6GutjspnIE6L16dDaSN/irMR\np8dTbddPOxK/nwgxTZr8747e30SsEkNL7PvXGQrAVYgvwggK/gK9mXMyfuON0fvWkY9Dkp2i97uT\nhYHnLKNgURsDxknRUMz5FJ8XP22DHIbqSc9pxsSOW8ObtJ89ovdXbNcvpQC8j4zcdiTbnAoy4q2b\n6Ia3CYV5/Y0zqsXOf4/WEYveaq5GQuOOQaZekhydqJNkW2BLZF2UzhL/R+xE2XAIa+A52nb9lUho\nY63hd7GD5d1ZGwPPmW27/iuIUrkLXc/n9xP13rZd/yNgVezoF8n1NjAyyyKETGGl97fGdv1/IlaL\n3h7e+06WM2PgOQtt11+GTMcNo6vVJ1aWsyK+4nvFQjAKgiGBUmoshfnOmGe11vdl1Tf0GOaUKI9v\nlqrE9lqJb6b/Hb3KsU2Zba/VslPb9bdDfA0ORLz0N62iWWxVqMkc3iZuRuawP2u7/g6JKI9RSCTR\nYoodhOP/YgNKK2Ix2zZJzjnINMN2NbaL/4uiaIUE/0EUhB3pqiCkMwl2IscjXZZFJ/B2iW1xRtWR\nZWTqDcwps63U9f8Q0TSN7fp/iK0PtuvviPjmrCHyR1qrICilNkTmHjZDLsDke/JzOtwnzY1KqXcR\nR4cFiBab9XlRT87I19dQSo1GNPz0tJOxHvR8mhrOVobB0XuAOBiWo1zmwaqdXW3X3x+4BzGVv4SM\npN9AnPEg21McxMIArTs2dRN4zoe26/8NOA6xGJwfbYqV9b8GnrM81Sz+Lz5A0qOXo2y4Ww3MoT4F\nIY4+KTfNF58TaXN4VthstVNDitLKcdxvOjKmEj0tv0M953fs87E3Eul0B2JliBflOzfwnFcA+iul\n5iEmwQFNEBaK569L0amUWggcqrXO8gg2FKHG2CdW4Uem9XvBlUflu7RUaiByU3lPa92ZKN8cSav8\nfUQBTHKr1rrqueIsxp18/eg1azrLjSYB6NfRsY3G6Is9nDjDYxh4zundvbMotvtm5N50duA5P09t\nT0faJIkfirU+zNrF1YiC4FBQECZE73/JqB//F+u14r+ImIVEOB1iu/6ZNfhwzEamp7YuU2e7RN1m\noZBnW5YVIfZ1qNWfotw51yuIph++hET0bAkcikwpTAEuCjxnSly3PzIP0a8NcnYgD6SBlSoaIhQX\nV2UtVup24LBU6S7IyG+NUuodZP52awojrTSvIjeshlij9XdQKh2jXYRRDtpGfOCruQfEpmzbdn0V\ndP9iPLsgjnEryI67Lzd/PCt6/5Tt+v3LJXAqQ/z7ut2ZO/Ccx23XfxUYZbt+7D8xCngl8Jwsa80s\nZBS8ke36O7cg4ybA5UgegJ0QE/XN5auvZRaiIMQRF12wXX8TCv9ls6eERpOtIMR+EXNS5YsRh8dS\nTo/V+CzUck21i6uR5++4wHNeKFXJRDH0PfoR5fqmtHKwDDhCa73O5JA3lCSeF04v6Z3FPRTMzBO7\nS6AE8Q12PbomgYn5Xpm29yMPhu2RUK96iKMn9q6zfa38JXo/NHoly7oQeM5K4Iro60+jKINuJVJC\nYu/439uuX805A4VkWyfbrp+V/MdFnOmeCmpfFKsSRYMc2/U/DeyG3OfSjpOx5WmfVHmcuXFcFfus\n5ZpqObbrb45EtswqpxyAcVI0FDMbOFxrXeT9a+heopvnEArzolvashT0wmbEapdgGpIU5XDb9R9F\nYqrXQyyL8wPPeTeuGHjOMtv1T0VuqldH6W//jigNmyHOcAcBgwPPcZog20xkRLcJ8DPb9S9CRqM7\nI7kDvoDE1hfdxwLPWWy7/plI7oCLbNffHXm4zUQeRtsjGRP/EXhOKSfcABkpj49i5+9G/putgHmB\n5yxIN4iSF21C14V6Rtiu/yYSW15uHv4a4P8oKAedlPcvOAv4KmItfCTKKfAS8v8NR1ILHwnsl5GA\nqF7ORdYaGA48HGWyfBqYgViDRwCfQR72PkDgOU9E2TvHI4m0TgeeRczb30DyH2iKcyA0ymrgWNv1\nFyDK1NvIQ3tStN3LCH+9HUl29UPb9echFo8BUbtLEKfJtJ9EmgA59ifbrj8bCR3cGDlvZqdTLcPa\n9NCbUMhs2GFLKvPFSAKxZl7/CxEL8pgoA+QMxD+kE3HenAHcHnjOGmNB6Dt8iGjHWSFKK4HHkcQr\nOxvloLXYrr+77fqrEIejNyiE6P0WccZbabv+lFLtG+Ry5AY/BHkYfRDtR9M79QAAA3FJREFUcwYS\nNdCFwHPuQR6a7wHfAR5GMhk+i9xcT6G6KIOKBJ6zFBn9r0GUmBlIWN9ziHf/5yjO/phsfy2yqt4i\nxOJxF3INTI9k/Q7ZoV4xv0PC5LZCci4sQm6g08kYHdquvxy5lt4DwsSmF5EENCts1//Idv3M9LbR\negJTkEx4NvBA1joFifqLIjkeR6wcfwdeQfIFTEEcjHNU79RXkShvw95Ixs5+yOj/KuSh+ATiAHcq\nxb4fxwOXRfJMQc6zlxGF6B3g4MBznmmWnBFzEUfP0xDFcCGiAG+JHKushESXIdanjRBF4l3EInAj\n8vuOqWK/5yNRGaOQFNkfIhkOX6CQgwAA2/W3jkI3V0T7ejjatAFyXb2PXP/LbVnroWGi6bbzo697\nIlaWk5Br93wkk+jztusP7o94Lna7eaoMZU0cVXIAped7eqGZfP2ZqmPFl+ptrVf3n19UpvVMYLRS\nagBywxuEjLwWAe9qrTMXV2mUzs7OP/Xrp+6qt33Hmn5Zue3XNeZTOVoky5nqKiQkrNT883Qk3WvJ\nsMLAc1bbrv9Z5AH6KWRkOB+5wRWlWo7a3Ga7/mOIomAho/GFyI30YeDREru7ELlOq07TG3jONbbr\nT0Nu9KOQm+i/gFsDz3nTdv2fI2FbpdpfHnlpH4LcnHdAlIz5yLErqXgFnvOR7fo28lDYE7lu3kKO\nTdZ9K52xrhTl7knnUVB6SqVeTsr4apQU6lDEbG4hCsFbROsRBE1ebjrwnNB2/XGIGf5gRBkYhPyv\n7yDpjR9MtVkOnGK7/vWIgrFrVPcF4O8ZKbaXIuduWkH6KfL/JbkEsWClfWK2CDzHt10/jzhXjkGO\nyzNIZEiRD00ga3ocaLv+kUh2xo8hSuVURKmIUyiXVGYCWVzKQlJD7xrJNg85b9LX8RLgF6X6SpFU\n9Cpe28gaJgORqEEAbNffDLlvHIQoAndR8NEYilwjExD/nwuUiTQ0GAwGw7qC7fqjEUvKqsBzmhWd\nt05gu/5pyNoifw48J9N5PForxQeeNFMMBoPBYDD0DWL/llvK1In9jt4zCoLBYDAYDH2DePo5MwrJ\ndv0hFPwTnjBRDAaDwWAw9A3+hPgOHRPl25iK+FhsiuR4OARx0Lwf+J1REAwGg8Fg6AMEnvNklL78\nHMRRca/E5hVINNIVwI2B56z6/3ExLRI31pXNAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='IPy_header.png')"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlgAAACDCAYAAAEmB1WPAAAAGXRFWHRTb2Z0d2FyZQBBZG9iZSBJ\nbWFnZVJlYWR5ccllPAAANNxJREFUeNpi/P//P8MoIA4wEaOooKjkv4+P35ALVSdHZ6q6mSUvv8jg\nyqWL5/ft38v4rVX9wf9f/+X//2Jg+PXtP8NPIP79/b/ihCV3GUfTFQMDIywbfu9S////NwMDMLAY\n0AKL4c+P/wxKa+4x4onBBiBVDwpw9FhFFsMljiyGnhqIMZOQGTjMegCk5JGkHYHyB9DNRDYPnA1/\n9Kr/5yy7ychVfZORu/EWI0/7LUahibcZJWffYZSDpCrB2/5K/+mVbaCe+oielWCeBYopEAiMRigG\ngYNIGNkeeZB6qB6Q3H5opKO7aQE8G4IIjuKbeLMZMFV9AKVCOqR0Q6DjL0A9LgDzGCyGkdTdR3YP\nltTYABUHpXYHQqkMpAZqRj0QowdYPEwt02AqE2ABNRCFPrasDQUfUVLWUAKwMgSIP8BSHwHPUlRT\nItsx5AILCfBT0jwgNXAHXTakwKOCdGuUAmtDB0IKyagNE6Ex70Bu1gBlNXypAKn2/EBqQJOTIuHZ\nENbOAjUfkBU8ilH+D2pnqW68hy/ZfsDiqAVAB82HVskYZQ69Wt1I5jXCakkgeAhqOmCzC1/2ZII2\nHQ6A2lkg9td6tf9fKtX+v8tX/f88VeU/tOlAKH8HEJFdPiLxHfGod0Tm43G8IiHPockdQBJXQG7L\nIQUmulmNKDxQC37dhk3/m1va/4PYIPy5QrXhbZ5KAIxPCDs6OP0HYWLVU0M/pXaSg7HWhsAWfMNQ\n6CCTU6NRpW9IaQOPEoeT4vmBCih4NqQg+zjQMxvAsh+97YRhgABiHB38o3KjNCYmbkgO/FF98C8y\nKub/8mVLwPn/W5P6/3+//jP8+wFsqH77x/Dr+38Gmfl3GZcsWTQ6+Acr4L93q19g+MugDxr0Qw+s\nP98ZGBRW4B8pxTOgh3VADZtaaGMV1Nrfj9wLADVuSR1QJKaxiW+QEddgIqzpoM9Zgdpy50Ni3wlU\n+q+y/h4jjbMNKFDt0Tw8H0hPQO75EwkaoWNTDMiDfvgCF8uYGUaggssszlL8g3+ggLrlqyRA41Ru\njzYgx4g8ugAFhXj0B6IP/sEG9pAHALGlTqRAK8Bi7kZYT4LoUQe1zfc+0DiwFhLKOkD+BPTYRvL8\nBioMz/RjURsw6MazgI5KwJNFG5BTC61GS4kedRjk4AC+UQtSW/Pktv5pPfi3n4TY3oBFrADquQPU\nbEfhKJsIB9aPPnWiLAQW8A00Tv7+xJQhyAOLsKEfMpzST1Y25Ci6yQhsZ/0HtrNAk6uKXHU3H8Ak\nnyQqFwDbWf1/fv4HFfCkJl1w9U3CxAAjsYNxSAOLDISaFei1H9KEx39Ssyd60+H+lxq1/59K1P6/\nygIP/PXDmg5kFNgN6NUz0uCeIxFlyURKRhagegtxyWGpabEN/GEO/s2YNQelJ/+xWLWBngNxZAz8\nTRiI0QesBTxfD/GDf/QeX4J2ifIHokoGNx3SU5MZKSywN9JzhHRIDv4NwMDfhIG0HyAAO1ez0jAQ\nhMerF/UFpBZ/jtYnsN79BS+KYD14VjwpCvbiRRD0CdSbNy0+gPUJtEcVqp6EKP6AqGCTuFPTuq7Z\n7GazaW2agdIk3abZnW9nZ76ZrTbyDwveHgwDYjqnCWaYrAM/NT3j6aoQbyL7utL7jB7F40JPnngV\naV7b4eHR8Vj1sVTC6CcyCwoE/an3zb4UWHBmE3++7NObfyzaIEZ8d/PdYJZssD4BrBLA9kG0q04d\nhyXNsmUR6VPeLfoOcM9EdSn82Orbsy2YBTy1EFCQa129EFofrBpBYFkIMlMtLqoQVvDDAwvLZhwZ\nEg2ILJfDLi9+6AwRFy27ZDHfucWCDBUCTnLsvOTFK+CWGauyxUKKxinAzfgFRCdTH381ljwiAG3v\nPS6mI+DDdPDqvlha2y0oF7URADHBA4tfH8vH5EqRtzPyahM9r1sER9Pv36VZSxfalrGeXHG8kUHF\nMDjPslZBMk25HcTiaOBadwSlbOc0c+aHhqRBRftYsSgo1sUqpdmlmWmDpNJiHaO8BfJbuomtLm5U\nGIs24VnqOZ4VYM73G3AS3nhFhY2syPw/GuQs53o1C+Xlb3ll42tpiXVIKBbrciSZqdHzr4fsvGtp\nJxM5hqj0gsrzagMW7mEt56MVpTiZzGKpG+7sIc77nsItzlUU5OSUF5lrCSrXXFAFF08Rbp/JACNI\nZKcKbuQmgUoRy1SGYHRI79tVkV8pHQKsDNiw6/BYVYK0coxkaOnTLr9MckwTpMhjSWzsCcxjUe0R\niP0yipRRImcDtmii3bK0gAIYunh+iiKgTnn7m50N5dc6+TBeG26u8G2DgMyEXRGwsNw7jOWn1jmw\nWkVmTD9/VWBHSarO+2Hu2DYMA+6Ne1hbXca/dcAO16XT/zWxGhBQyGQ/BbVUDQcs+CbGToAt2Qp3\nsJGAbGMuD0QMUHYzTBwusCbGRjBsb6nXgEfUStnNBqiKfAnA3tW8NhFE8dniQWvBBDyIIG1TTI6m\nf0GjiCex1pMUoduDgic/EAQ/Gz8pCibgpQdpClJEUVP1JKLpXxA9Jm1jgqgY/EhBLWjtutNs4mSc\n2Z2Znd0k2300lDazs/tm3r735s17v/GLMX1y3BQK09nzY9Hyp0/Zr18+g4cPH/iJfu65D/FWTeGR\nFSDN+lPuGm3yhMb6cSEc0P6ANFgGA8u/YKgBxDffnsPfksV2Ydgnl3ysw0eOah8/vAdPn840mLCf\nVyLaavboHyNYuqz/VAVrNY4Fg6IwjrVtyscrbeKCoGVN4Tpc2yyNQ4Fi76A0DDNItWTv/cJxj09o\nbQJTXog/GXG1WlHwmORxSuBbOlp9O2fFyHe30FjVLZ3q332PCrL2vHZSKqBjAKmw5s2e5E13ZtiH\no/UHBa+bN8xAi8rLSEumhUDsXI9sfeHBX2QT+uZ/G9D9Gy/mlY2X8krXVf0znlcCt+YU3b9StkzM\nK1vvzMNOG4Kpc/tDmoc0lCbaBt8/ZNnQ1duoWB8pyfxk7PBkofm+EVeFCCzB6IbTOaXzjP45l7PM\nNtD9q7Hu6QVFN4N1BMb8vlA7ln+hsAYxPPkOKTQfEpyIEYY2kybfxQGpkL0KFToLCAjkBMEewHwz\nBf1w8ITf4xvRx9KFarUaY/0pe3nvuhkMGIIFH6rdHPrXyMBTMywMDCAFz6ygJO4FaYPOa85QHwii\nsyNfpRj9oxErU0dIs87QsiSQNmlav1BjJWQWU4SfFJTc3lAKtDlZFB1EGa6vsGoBUQQckVUkB88D\nDN0P0saqQxcqVTYzkWcF1atCRWtjaDFAMFUsdMvE1Mjky4nQxCjpn34xhTzaweDEBxgmPyZRW0Vt\nXq8yPG+KFsfySZxmGU0G6ugK1RoKUtbOig9UC5iF3BpfY9kjFtNiddwIWufXarlowuizvmA5769V\nWB11N46s4qS06IW+KbRHrDG7N4gPBh31Gqyxm6vnWZn+m6+xnCWmcnWT8IRlfMkmLXKGD9amYPFi\nONHOz3SI3nA8V9qlZ4o2a64gyrR0xPvc3pArmQ76BFmZoreC/aoMbWKMWonkxA9i90gKDkHM4kUs\n8vIlTbDWn8wFWCHMWQhu6USeFRIuPf9jk4m3479MMrR5xdMhARJpEvlO9EVkMW+LnHzJNYUwu2Hp\nRqQo2tHCgZBmZDf0OvzMJUyANIJQaYBt49dMI2mkAz1r5fuY0LD6RzKi6jPY80QtBDpA4Ktowbtt\nK/YPKlIXLO0fTCT8new8lzN9k96N9FVWfoNNtXyslRVQ2p4u9IhOJPKnKQQkR6CvYSPYJH8qY8O5\nDfKc9iqjJMyMfwkwkVxjRWtXDzfA7AYMFOTYj3j4mFmiH65yRYVKwIlXWBPW0FNxZfbv4EqOhUZ5\nzRovrqrdQ4wa4ljwQI+l8QipOtmK+vseFV5LFJwM40CphAEewo642ikqvMYAQ7PR7ZBAjQo+G/Qf\nUwRBKTHyBAXmIsXNiFpoYHhvy/mhg4KwFVPMbJtakJLY10xQfFb1LuE+PehK1cuV0XWNdXf6ngYB\nQcrlcvD6tcsV3b+qM/39bDiGLG1TWybmi8AnEXprV1u1lWA9f/ESVVv/7cB3Xc1ngIOQjG4izTWL\nCE57ysv8drTAgOPL5RNrQKg8X4u5Klh7du+qM6qbQbfOPFONAc9ig57wkECpBG2cBGuA6j7WoeGD\nTYMw8uKbTMH+mrIRZfdNoQDNeM08EM6iCToNt92SGstl6m+lpDaH85TiXjktjIf+CsDe1f00UkXx\n4Q2MCeXVmLTAkj7C/gVUY3xSgWxMjC+UB9doohSyJiRGgV1XMUv48N20GLLhwQgoT8ZI+Q/Yx67Q\ntInvtEL5eJDxnumdpq1z79w7c+eT80saoC13Zu4987vnnDkfoSy89tHDTzJXl43j7e2fahoCES9D\nDkhm8S6TThR3Qkt8+dWS3mhctP5+8OB97ebmpnpw8GsKlwoRYZLCcqwxswl5SOIyIRCIlob18ONP\n9fPzf7SL83OtcXHxQqTixeXjdI6Yk+sQFQhNpHX60/ibvKA59O2/OkT+NX+/bTaMhu+R19ZrP55k\nu8d8+mSpJzf/COJdJuhbU0S72sNlQiAQBmF9PjvfTU6W3bSuVtJFQjTjBim5V3Cn/54ZntZpCDQl\nsYHUzmltY211EpcFgUBYget0v3qWLhBymjZJqqVFmfkW8L/ONCzj7y7CIi/jvfrQz+VEUBNCI52z\njI9zMk+haDTQhoqxOMcosj6TfUrFGos3Dk3r3JU4jOMuerxrhXnuikZ3O69wXTmZueWcHytHB6LA\nK3bnouJpIy1oJNNjfkrVfMrKFSdq3trpfr2aPiZcNCpxTpApV6Qv7dXvjVhTrTY3AjcskE9KayZ6\nZzTNdtx+yE4ELry3Ww4i1iHFETBZIk0oHEuTvBmUjQWZle2pLSJ9bTnIt7Vcr1vEf/AAJHLGOXeV\n8rLLIZAeRWuR1Dzy0TrYSP53/W25bUJuIjcySjd326ZJHYR1vZbOEC3JKmd8v2+hJG2qJdb/EtYg\nKh8Mg1bTkcNlpFTr2ouR/XJgVS0QBmCjKTKiFt2g33yCJljwtUa+DzHr6wyh11UE9Nk81RsM80IJ\nbib1Ls0fNmleyYBROieyG4yK+bYmLEJWlTa23+z7ouRr6Gxq5xTMhJapcDI1BJMIaVKjUGAEynsj\nb3gOVi3VDEOohOOI7ISSfm5rLkIuBK2GmGSMU+kuJix58/DkfpPXP8lBWQNlcVjduaoSWqGJrIC2\n0+9wUzjiaO86Z65zloRFS2NVeudLqbDcOcQcrJgqPiGszMt3CWn9hqQVEMYlhZ95w9hoAGAujtnl\nmQAhcQQ9CX5IF+ma65zjhjL/hefzcbhWsEY9tC7ghI+arO2GBXX8clByjbxCa3YR7aoIZFV6ZwhN\nw2BRdyuo1BfCM6tmRQp72pxHXtEN5OrG94mssirJquv/wQ1UdWvGiW5oIpsM1IeMTLpx+qB8jJwR\nHFT5L6hZxauEIlowdkCFX0TAFBwI8bLkvSRYN+a1rPYtAqztjhDFoGIhLSgYo8YjPkYXNllTcE6m\n/KfP2hVrDqsBH18GyzJfxi4nCBmtSDWWWeaMaNlTID6qHVn5xUa7QzIktbF6yAsesZ7sJX3KX8wo\nkKslme+jhoUIEkVFZMrzbR7akNWG1yZwjFHx+4CoYSGChLKHKLzC9TZPtWZZ40V4XmNbtgY1rOCQ\nwSngpr44ueF4Tvg9CVNwJq7zioSFuBOEZdX4TAGUpqXYOOGhJWRCwBSsRqjkPqvgdn9cbxqIw4qM\n6uhXn1aFN1CR87HrHECbZGDVOFQ5mI1T+L6LOQeyYTVNPhMwBVMRkq+cw/mNLmH1zpeWIC1HZa9e\n1Xj53tAeRLr72P9XJepeCBXN6/O1Db2qm8BmnC23VSx4Tnh4+shqFxuA32pRwRgDXq9XmGA43SEl\nhxBWwSCtZvmYeu+jUqBPSE6mhgq6WdqGIKppOfCkiSc49DPhVr8uWwqrIhtHSbACydPKnMUcJ/yi\naq3O5Xzm3IROULnhPnCgvw56FJriKzrqYRHCShCCODPqW5lv663XTN9CyRPbvvrhcEq/1Yr6rZ5s\n1cYyz0HXtkb2y1mffTUs8+cNkQ7CLnc7CPprn2dIjxh1cGNKaww2ZFjnkM2W1qzvVWsbCwhtSROs\nweRhA1uRed/ysqWRXWJy2/wCccEawNyN0bXfk0gwlyn7A2tWsJJner4ZevwJL+VKdizLAn7Xq+ks\neTvfRVh2Bfyq5GeF/F3sKuCXoQX8xgUL+JmEVb+3638hP14iqRvCciBQtqaASRB+EBYlxoTGrkfl\n+jo8Wk8gIl5uYd2PeCtB0rLCkYNCjLDhTXt4OVJrppKwLOOwiDkIF1y4epYWKqpFYRYjc2uu7A//\nUg5rmWRXKrXpW3FRXC3Q+BrT/BAgdjv4Zp7QSPg8z2T36Twq1HTjafBWGHdwLCDprEtZY2mBmSBT\nlYT7El6tpDNE8zn0qETyUfL5aSYMjAT1lDTG4/a4NwNXuROG6JqYfrO70Nw9brDUsLaf70w2Go2x\ny8ZlZS73meFP6VsoFbW2ErSXj9MJanPLqp7go5l8PX8a1soL2FYsPgQcuXIxCAnC+v2PP3VCVB1f\n+ObpSh7e++7bJx0L/MrXpRpVO7MxEnDetSyjuERmHbmuDCSr6EI40t2iHVjchByC8Hi+jiUUl9Cv\noRlCwiKrKpJVvEzCGcZNu//D5tpxTIXcsgws7siRWkNwV9g5p++raKuGCBFhvf3WmwWtMwYoboIt\nG/nraXwOwrtNpg1HKvr6IcKpYSGamFLZlBOhHCKENRfy4nsIJCxHgNiSLBKUAdCui2E/SU5s1TL6\nGuMN4TgsBAKBCBr/CcDe1fy2cVzxkdCDZaQQiaKnNBFN2eJR9F9ACj0ETZ1KspsWRQ+i2msLKXFi\nw4YdUUngVo5dSyh6DSkYqdu6tsTESZBD4VXzB4g60hZpukjPFl1R1MXczqOHMknvzs7sznI/9H7A\nwh9LLmdn3vzm9+bjPSQsBAIRGPgygF9m9rdpbBpE2ADHcmBFExZ/whqv6lAprHPnL+7U6/Xhen2X\nNBoNst9ozBYKa3lsJkSAScp0gQC3ywRYYS1+dAWIqffMVw6bCBFwTGIVhNMlNDyT+Oabp9A9RCAQ\nviMss1DCO9hMCAQCcLAP68yZt9N37tzW7Dxk9/JYmuhkijRJkl4p/UU4mcf0qtK/53/4l+28xWPg\nrOJLAc6++uoeHqdAIBAtDPzu9/Ppp0+f3t/931Oyu7tL9vbq0W+//TdX1ex9lIjoTV2jJDVuFAur\ng7C6YmE1n8fCqtHvZl79tPzSRs1z5y8m6/X6Jpt03/r73/6axCZCBBkY4ka9wuqNfqgRk4y8e1cS\nGUpITifCYWJ97bvMKBDb6ms3y5n2jatLV0BNYSMiEAi+S8hD44+JGFVQj1z4/Zn//Hp0hiqvxdit\nchabA4FAWBEWpDc6iB9E3cEuddVYSqhMnGCGhUe/jC9QdzEav13BSfbguj/tTC9dit1J4g6EK+2U\nJt2Zx6v0Kvot/A5LepJmHl/LjrgbRxtXD/IUkoPUXwcx3PWXs+mIzWG9yI7zrB3fvStjzvToncq6\nh5WkceYc0l49y+T54E5nTG7PyxggI5tl2bJKhnqBjMy2khiwAItTbtanaNtBOXrfgVN/vDhdGwJF\nKfIyPEu0LbSTaPjvAv3NKUX1aFYvhu/FSKpoVFaY8zN0CfevJSK6rjydkyjWtk/HV47frXiVlj7l\n02cZIcb5DdlsMBGZ8vKSdXAASv0J/a50ai0IFUO/d4NTnpiqTDys06Q4ZdlxWn/9sA8bGXramGSL\nBRChNeawGML1IjL4DRqRFZHLPQejBMQ7n6bXBL2Off+TBwPD1x8OsH9PsPsbEs+c256OYyyjPkLU\nbYMRkxmzk2Qdw+w8nUpVpNLtzHPurQbE7duxSVadGGHtlHTBrmIG5bVU6kYKi0dWsLkze/RySYhM\nossPNTNj+i4zCsaa5bDv3MOpuHZivYJxqvzTCcD9VHlc6j59pkwMqwlOJ1SZ7WiS0wEzPm8jN5Ld\nbtLnqg4xPdKj1odFvtSlsPavJ8wmtKaHLpQGjl4sRY5eKilRPj/Kl7XXbpbTr39WBiUWZfMbL7mH\nDyfjEaQKX3SEJHHnbOeCRbYiYRUo+hyBDh/UNhIlq7ZX1L62BEkr4kKZ52UGmwOFtf+nRK+SgfyB\nyaHzJddX7WK3yvAbLdlZPhOH0XahR/Hh3izvsclR3YYRW6kxwuA2J/DsHMxfCE7Gg0tmlgszR5zn\nJOB9f5Zzr0qMU8EtWBCHFWRUjZV3FDOp4yxrL3DTHlk8X3VfvCHz4dYqISWr58zcXhGkiufIeyVP\ntxdsT8c1WrQUW51cGfu8P5PwKncmu73L2SJd/ITsdgJOeWsmkj0qQjKiae1F68TNelX97H7tdOdl\nuCaS8e3ps3hbmTZsrJbrkoMP2FvayAUd7BgdAIuUqAa8JivA8bVKmrmKRHCURriH3o6wBZ1NdHsC\nm6OKChKb046bd/DdGOf2ll8bh7nCZmQ1K5uMg34+ScyDEahc2ZwxGQQjZvNlg0xdDbdU1dlS1k8N\ncWK9snOiUIFRqFZ6K64hb/gCW8ygiWQn2BEgrQXBx01IdgJR8BZ40j5ukxxHDdkicN62EyeDgpXC\nthoEQWFVj7xLVdW7Jd/uMKfuIFQeTr77AHbIqoe0ZgXUgtVzNAdKiYdxi7L7UV1lOWV2SrKrLgwK\njtzjQUpUgSCCxBeVZOlUPI2U4SmiCgzTanTOOexMVkrJDsmt+LhNzFTprIK2ynDqSyVvCJd1MEi9\nJXGvgm6hd6gpVBnH3OxMxN7Z13XOb837sUF4pGHXFZSAso3dMmUdxH6IEERaoYFWLTqi6Dm2moJn\nWJFczcdtYtbRHyv8jQ2X3UIp9YqEhRAlGdUn+Quce6KKhkeia4rcwSkfN8ukw/oTgeayXUmVFQkL\n4RWynHspQWMvut0pgxgax2gTrwP4KuTM97DfIBy4BY4UG1U2Kh5luvMddtoLjuAjNlSgbxHmJK2o\nsBBBd1UznNtzAp07yXm2b91BxZEukLAQiD6CN/lutfwe1GggYUjQIq3ckbAQYUDaASGZuYOzPn/n\nQ7mRGgkLEQa3kDcxnLLpDuaxZv0HnHRHhAW8yfekCamZqa/HQa6IMOc7RIWFCIvKynBua5LuYDoA\nr3wos0shYSHCBLPJ92ED1cXLwFMNwLsWD2MDI2EhRKA8u4vFsrzdfV9pzu/1KrBljmsZBEWp2axb\nJCyEZwiyYfIOz2ZtdmKe6siJuIN+TzKhoG6RsBC2FIaKfTSpAFfBuB31IIBVgbqPhdy8xsP6YhBx\nNDAb0Eqn4kHbLMdzbeaD9CIsu0k/3EGnrlKG87vteau8yUemA2ZfK4fNLQSFtRwE0iq9FdcT9ypB\nm2jMc+7NOOz0Wp/f5YbCZ/ESfL6j4Pk1i/ZImZCdG7veN9xqEItzkvdJCAERR4GJNylp+dJ3h7yE\nD34Wh8Oci0GrXKvNh3ZdE6tU6i6qrHUFz8ha1JmK+RczdcFL1rkV0D5c89Gg1heF1R4FcvvXE1Vf\nkdVUK0dhK9da4otKNoQDxiOb33viUXknncy9se/yEk0oWaHjTb5zEii45UJpnLKoIGfeoJdyK2GE\np4TFVBZgZP9aQqeXp2pr+3Q8sj3dUlULAZ1b6ETBohMXJTp8xAehQzbtZFhmZLVpQTQq7W5FxhV3\nMckEjzAcp69j5ebtzJ+RsbGgKKxeUsg1Pknojav9Ja7K2/FY+Ux8p0dB1MY+rwT1RL1IiJJxlgRT\nxB174pPXgkzNwmqcuSabFh+bUFzvMosEsy62f1XVgMX5jZiAjel2BppONeiHOFsHZwmpylqnLiH4\n8eNdxLWUyBGdqgSdZIYuuJMKrPqr0Xm9qRtO6p4oVMJwKh1cbt6c03CHMYAiK3bI/RmLjmaWZUZl\nvfXaRUuNszIbpqpnq1TLRGyJveBSZE+zjNW9Hd5Lt2mc1eNqhxqDugNFOilxLjAqMKDBQJNjiixr\n9t6s7eACghvpVflepjzrOvx85GwpCS6h0dwFVMbelQQhTWq8OskevVyyrXr++5vRpN4kWf0ZmaR/\nWjVC4AH54SRGp0liHqu7i0TA4Nh2AyNSAINXpUx3mItl5MIAIaw5iB665WKgPKgDq3nCfky2g3q0\nWrWbIQ5WjoFEaBucFFCyhJFQm7xkkSUebsl5KVoDpKo3Ia2DEQEMtL44Rgh8il4t0tGpimhSw26S\nIiUi0mzqpPmMROiVpH9PNVv/xz4rhpOQ+ZmEByIjoEwnT3aQST9Id56NvCo3JRbcjOoJ7pgVkTpJ\nDCtRDo2WQ0jtOfwdCDut0s6MMOclYRnudAfSsvGsFFMGCx3XHLG3/H7y+FolVIc7BVO1i2Cxp5MV\n++ASdnZuVdtLJvoUgrjgk/aP9MvOmBu5QUII06M5Q++3SMuLvSnR43croTyJ3mFMduItQSLTAXpl\nDdw1M3fIjXfIsnewm69vlb2H1qdq1yxctX62v5N6k56GcIG4Vr2OtcUN4Dd0rpRsLLVWCnN9KMtW\n/HYlDHGqRYwpBn+ylT+r+Sort2nZpFPuuPwOEfYOeYG5FyDoeZd2klvhBs9V80JpsY2/moB7vaLg\n99KsnZLMVmQ8HiC7ZQXtZqbKq7IPGtB1sbngxh8SVfrREfJ8voroTb13Dou07sE81Ys5rOdX++9s\nDgu+q7PPwZ/0/4/FbpWrfiATzuT4Vj/mO3z67httww/Y+0Q48zmzGAY5eBAOkTx0odRSBXsfJ4BY\nRlTNY7z+WVnzmYGboYjmEjhUOcoDySoshJXL38zW63VCr+Xz5852uRZHLz0nrvriWIZJTNmVj5VX\nPy37NVJBhnNvHc0lUOoqzbHNd7CGgokul/DLr7/JU5Kaqe+2yKp9bX24+IGlK7R7aSxJ3cE0vSI9\nLqH2gz8/1AJi5EWzeYUwB/YPo0vI2/d2GNoy9ArrX/c3QDkZTZ6On33vfOb6tSWuhH7l4wfFELhN\n42gSoSBe3oLDBNZQcNG5rYFHSLlDYOQ8BVFDUwlMOxZ50xRerAwi3CGs2CGvC97RiQyaSrBdeoYo\n1lJ4CIsXm6cQckPn7lnyaP8QQr4NeWS14uWhXYQaHMxh/Xgitfzl198YbrK7fm1pKqRGDqrS6nDs\nLJpJ4NuwJhluBuF3wgL89CdvDPzjn3er5MU+q9qHix9EQmbgsOIJxit0Mh736/i6LTttldeGEayt\nEBIW4Bc/Px0LqXFLBx/D5W9ftmOaSCRYwDYMFw5TXkLZQ6A4QetDSK7yYRuGXWGFGGDoIgc/a+hC\nhILYUFmhwgo8YVnhJJJV4NVyAckKFVYoXAmT6JOrirO1BBnKwoC4DGgvo5XBKG5dCDeEw8uEAe3d\n7LjbORRt2TZciLWVRKJCwkIgEAhf4f8CtHc2vW0cZxwfGz7YycHMMYfWNP3Co5RPIKo9FG2TiGqB\nJi0SiDr0BX2JpLwZSJqKSoK0aZOYSttTDiKLtCj6Ekm226JFW62aD2DpKMemqOZQ9GQJaGKbdLyd\nZ/WsTDE0xZmd3Z1d/n/AaCmJS+7Ozjzzn2eemYHBAgAAkPYeGY1NFNrSUpfl5gEwyhFkwb15/twL\n2WarWW41WxPNZlO0Wk1xu9USrdu3V+Wx/Mc//t5BLgEAgBUiapjFE80kPSiCDdPDAQRWHMy98lpW\nCqpeqypR5V0ZGxsXn3zyyfilSxdQWQEAIB5hhWEYYCWHkQVd6blkZQeLX/rSw8PIMgAAAABAYPVG\nddsyzD0EAAAAAATWAdQU3rv15z9fcpBlAAAAAPDZi8H61re/W7h161al2bw11Lx1S1BQt0y1VrM5\nHcYc+I/mzmaEK4oyFQQFJrrihDeh0R9Ndz+d3Dsy0VH+uPu64+93f1+XyZHnOQ++c1UpRmr2pRdK\nL75UpnOqorc3a/7SpQvY1gAAAAAA+/CWafjBUzMNKa5O3PKElUx3BZZoUbrdmnv//X+Vdb/k41fz\nJKKmpdgZEyyE9okofm1YYO193t2j9/8d+boqj5XP1K41+rn+731/KiPzYphnETbeffdXDRQdAACI\nH80g9zks0wDC5shTU0+T+DloT7dZmfoujDd+nC+SgPE+1775HeSRmqL04ZOnfPFVk8fyid90F1y/\n/MU8efAcFBcAAAAA9MPht+ffIuGwdZDaP1BUvZ4v3/hJ3qUkf13sQ7TZBG3+vNn4+im38fipxuZj\nuQKKBgAAAAB08WKwfv72+ey3vv1dWmqgLNMY/29HJvJCVd5//19dY7Bu/DRf8t7jKs+6sxkShiub\nX8t5cVzy3kq5P9TXUFQACI8uK20PaXwM2SyHE63U3UDOggGtT9Se04Kr/uKrOm30elt9crAfmZev\nRc7XgjjAiUS74ipvlXPjZ3kyhBQAPrIvXqrj6HbGUrW9jjkG6+7f7ux/T/v7xKfPnzz1Xr06gAWK\nRPesxqmjYW76yBtLrth2XYOat6pbbMvvKHGHLgpP915nMYpGIkDZ9Bo1eY3DFtuDpbZOeCj3FTD/\n4mBV3lshxmdCdakkDl693hQ04lWW91y1pEyqlpe+nxcLqoqOnSKb2PdK7jff8ISVo9mzTAMLV7+S\nW6B4rdOL9RL6SCDFKIsQMnK9RB97qEhQTcVwP8dZyM7K6/AMLPVCwxJblA/ye2bky/Mapw/Jc0kI\nWjc7mRtyHXG1wz1+YOY5ZLnRH4vpEkhsLMjrWODf51lwxeXhWjOcv9QRWDLR+etLYElxtWZIWPku\n/DU+Nu6fu9IIM+f/883TlFlUIH1XaVCVP3F1PDfhumLyzNLgebRA+pGGco2FiKne5ZIQVoURkA24\nzvc4GUZPXH5mhQ31hMbpU/JcGpKxZgsuFsgLmqcXMbxk5BlUNctT2ExxmfWENNmPiO3VtqK9Gukh\nrByTtqqnwLr5Zn5aoxe2wwZ16b4XNmI3EA++c3WNBV3Xa/n3E6fIcPjjqio9goUPijmKPyucWUaM\nFhh4fOPU7u1YSMB1+z3xGRJFhg1/iQWmTk+4Sp4Ki4SJrgids2VIPqGiKkkjRyRMLscltALmsyNC\nGGLtKrBuvuUNBzb6UHJ+bEP12LmNRhIL8GffvbbNxmOfAdn8Wo4ajOkDegxegfpgLFeTIqsEcwAG\nmExbg9CP7ejFOn/GWhcRlw2psTkvr506k6bj2+iar2s2VtQpLFjQ+JSE3nDUMtaairXR3/Hbtn7F\nDtdfcjaUAny3L7SijE1b17ELPNyqsvdwMIElxRVl7mKPB1Y+9txGJe2F++TvPK9UiZO49pVcrxiS\niSuP5ijfsmcv1OEKB2lgVdXASmOl6vHe4jq1FMRTYzhgfkV+HgmDoolM5OGLUaEXtD1CEyHiFCnc\nAOl4Ind085AF7iGFa0zVQqMBvb/L1Gbp1ic+b5/DgQO9qxoiZISfzckIZvRua5btzQDi1R8d275H\nR3C/wJLiigrcbBdlWDr67MZAD4Odes8TTtOcxAfFXGeho+P1K4/kTp69WG8IAAaLfmdDkqgqmhw+\n4BiqKhtNEwGqY/JzqL4bGaILGPROgflLMQ636IZ5FFAltMSVI/Q8R5NhzerjWMBMgOHKTepk2DRU\n3CYa+xVTZZ0QgiNt4opOnmr7wOLRZzYcFPnunFmqe4XOE1tjufae++bGI7nR/MU68g6Au9QoJins\nL2EhkjUQu0IdpgYJNhO974BB745vayJuhKY1828mSfE3ljT4ukPrkXniuLMxzOJkUfH0FctE1mIU\neXuYxVWZxRW5Fx84+vRGRiYIhH7F1nK9cvZCnVzaD3EPfWXj4VwWOQOAVx8eiEJcdTYGvO7SQ9xh\n1BVZa9z4mbimkjh414yu18HrT0XZ4GeFnsetZnqyAMRVV6hMn4xjmJM9Wic1Tl0xVZdChoTVIRN5\ne1iKK6r0WSmoDslUlAkxRJpIkbV29mKdDNMD1OuUIiuDXAEDDBmqWGfCkSdFJqqHqwFElsnOpu4i\nomPsUYoKHUG3FbWQTgmqQdaUz5k4dyrg734oonIVFTvcGTQmWg9LQVWVCZXCIPmL9e38pXpWJohV\nMKhM2hREzLOZapqnD5kSNyw2RzVPP8/DjKESYGiwgGKvnNeq8YI0eSBrSZ0iYTiveNoIDzHahi9a\njbbZh1HEAQCGmbdlG42OBoE6krqerPMGhwodeZjRPN0JucGnxltnaHASez8q5zWVR9XlLwqW1Smd\njkfZskcRmmiFwAIAmO4JTtt6cezJ0o3JmjZ4HRSnpONRO84reoeFzhBOzUZBnQBUY9XmLZ08oFqO\nh3gBXlsI7VogsAAAJimn+BqNCkf2qK1rnDrB3g+j0B6IQn1oEHFXenlNZel4SupWwyZRo8hymKIV\nAgsAYFI0VBNwjbqz3I6H0POmz9PxqC3wcJ6pBp9iu6Y0rx+ooxqHtGrxfo5OgstNqDNej6CcAwAM\nsZqga6VhDZ01qYaFwTgoXumdGpvLmg2bKZGlMzQ4jrgrLTFLsXyqi4mOaK5YD3rXPyfMz4cHCwAw\niOgOCxhfeoWHKCY1Tj1hIh6LhwZVV76f5/WQgJ5IH3RGLLiG0DuEEFgAAAis+HvSJJR0gt4DxWNp\nDg2u2zyRIQEUkAWJ8nZDYAEAQJIJEPQeJB5LxwsFgQBAHyAGCwAA7IHES0OozzBzhGI8lubQ4LjF\nwdZpZkvozdazlSoEFgAApFfI6BDq0GKAoHcvHqvfJRM0hwbnEHcVG0sYlk0eGCIEgwb2hwRBBFYj\n7AsLEPSuEo/lKH72qk1bHyUcR+McBMZDYAFgPTBUA563mtPkia2oVtIOEPS+cNCWPjzzUGUIcodX\nwAdm0ClDI6a2agIQWACEhU0NRdoM5nGTi1+GiO5QSzXKiwwQ9F7tIa5IBE8kuM4kHo5hW42w3AII\nLACUjJSjeeqIRbdRTOGjKdl8cSwAZzVPr8RwySRuVFd6H+sxVKgaQzVj6f53SUenLM0mpAMDfIF1\n86083I4hsfFwDpUhXLY0G9nYRQBfw4kUPpNZy4cydIX5XByz5/g7CxqnLnQpc9OKZW45wLZCoPdz\nJaG7HmH5BXEILJkyUmRty4TYFFPC6pFcSYqrRv5SvYHcCJVqgjwR7Q1doVsDmCKs9HjIfHc0Re1W\nnAHeukHv7au8s+g9r3A6xV0lxcOqM9xmQ+dXp6NHs0XhUUyKwDr69AaJAKpIl1loFZAtelx5NFe5\n8kjO5QYcgjV8dKeMHzexxYhmI091bSXlz4UagW2bPFncKOkOD8delzWD3ic45kqnU5F2+2XDM9Wd\nLTrE9SsrgN0Ci35IkeXwg6aZJStSZLkyVW++ieHDg/hgLDcs05oUVySsaF0ZipfI5i/VsRhfNAaq\npnn6RNQiiz0oiwPyeMiWXI97OJa8hbxJ7pDmR5y0ZWFNDnpX9dZUNQLbJxO2ibOjKVIKFjxTskFz\nmvVrM66OIlAQWCyy6EGNtjdAZCClyHJvvpGvyASxxVwdl6KqmFuTiQz35TbjveWJq4sQVxESZGbN\nRBSeFjKC3MiPDODzWeA8jtRjQL17mUgkBPEWnrRNaPByCSpB70NCbdHSGjf6ScLRPG/Jkmda1hRZ\nvg1zIbTs5JDruvv+wEHvDU8h+/9qe4t8O4mI0rHnNpxByaRrX81lZB5Mu9SYu7vrx7gdeSN/Xz17\noV5I273LikuVX2fW1WiAmX7KXgoRfNiNAk6LphpUviYyemEEsoeet+xtC0MQzstUDssrxB6zilDf\naqYdsnHDtm4Jw0NDmyF8NG3inMihQRLxms+cxGrBhpmShuzYDtevigX3Q+EQ21G0A5r2ajXs9d0+\nJbDahFZVioeJLgKr7Rc2Rq7XkFSPndtoiBSw+ViuIO+p5NL9u3zPLt+u25EPu8fxM8v1VG4hEaDS\nRyaw2hpWU4HjW9xIL/UjuNgDRsakpFjJyRgOazSWSRZY+wwc2Y0gHhP2jJEXc8LQNc0lYcVyw+Xd\nL4vZpO4zyDMkzwe8fyVhwvU+Y9rLabjukS1b4nq2FkK+k9gvtKXODiVNEMlCYHUTWW96Mwsd32tz\nD4HV9Sjft+w9WFc4971op/D68MlTw/I6i/Iai/I4tCekXFfsE1b3FljrZ5bqqQ4GTYrAamtsLyck\na2v+vnE8fGiVCNA1WCxMg8aZUWPXrTEYFsE8Uz29N+zJ2E5Q3aS8njL0cQ8lfb0rmR8kJMYi/tpQ\n6iKLt0aI5b2z7Hcr91lhxgM/HvYelrYKrJ6bPR99ZoMqXObmG3md3tKYX9g/fjV/V4DtCphdA+p6\n4q3hFSRXrN3/8hUjxu2/3zlNwikjE3misvKYlccREk77RFOwBqAgxdUgTJctJOVCuYE4xDPGhiy9\nzG4N+apISXwWG9JDARu74xHmR+KEVVteT3OnImheTaZhMVFaViIiz2s7mZDuhcpjhoWWE7I9C9tW\nloUl8W5Rc6SfNx191guAr2oKrV4GdF9F+N9LZ/d7wzqSe2dXGHlCae91x9/dUPPLE1anF+tYh8Ru\nQzvMrmtH2LOYJ3l0S0kdgtFs7KhxIC/LhIWXOJeSzYtpaPp6wHyopqjcFUIYPu3FcMj3s+1/Bw+D\nlkU0Xi2jAo7iscL2YtmI0lY5JLSOPbdxSL4cF+rbNyQZ6uWePP1ePQNxlRhD2+Cx/weE/lIOQaH4\nBxoqPUSCo4e4chQ/t5CQZ0ABriQqyWaMCs2V902KKioP/DzKKSnnVKZmNE+vpSUfOvKkymVuMmX3\nVZEpY1F9Umk/B5IjOidJkUVKNHPjp96MQ+r9jKU0f2Zyf6gP+lYRWU1j4Nhw8dwAUY+2xB6Vaf49\nDM8WdTqovFQGxVOlWB6y3BPP8DOYFuF5GLfYNlUTtqaTDjqCe9WPAUxxmfOef1u9p2Ta+zMSd33i\nOpXl+yuK+Lz269xZXLLF/sdNzyB3FW68nqc4p4onttyOWXYdr/e+s+N/bpf36gwRtv9vf7B6RwzW\nnf3v4ddz2d9eK6No7FVcR8eIcC8rKfdY4EaKXPGZHvfrB183+LiWVkMSR9Bo24ykbJtoyHZpMPyg\n3G3/OfCzaAxg/dQJdI9kZpfl+Zbl+j7cp0B12o5rCZsMke2oUyp1tMFpLw8gnmIQWJ18/JoXr1WW\nguWE5QJrVf5e/uyvr6HQdK+cOgUk9NkZIH0CCyg/I+oIqq5RN/DiCoCoOBLWB9/3wm5g/J7getXb\n45BEF7kw4wrS2xs2+EztWgOP/0ADrttYQqwCEG7dJDumOnnAX3cNAGCDwFpcvlhstVqVZrN5otVs\niWarKego/ybk33b4f5WX537U02V63w+9ld8/1fB+NHvWd9FSop5V0CmjNOXdHzZwHnznKoSUPkXN\n85aQdQCEIqwybNtU42zguQIgYu45RPi3v/+zLMXTrBRPvpgSXQRW+3H1x6+9UkCWpsqQ60z/xjBR\nOp4/dYYwRGjXM6EOj84irhBXAMRA12Ua/rGySoGTqmP7I888ew5LGKQHXS9UGVkHgNnODi+eqyOu\nViGuALBIYAn9oaGhp6aexhh/8g26I/SmH9cwwwQA48KKPMk6oRNz8CgCEB/3isFqCM21NN6efwte\nrOQa9N29J/UmIWylfV0dACKqh1mx60EOEo86is4OAHYKrKLQ22hyHFmaSINOwqgi9Gd3YnYSAMHr\nYVmoh2Z0kti9FQEYCIH1+dERb6PJP/3lr/0uYkcz94pvvvE6KnUyDDkJaBJVJlbgX6e9/5CrACjX\nQ3+F8VlDHzmZpn0FAUilwPL58he/4G8vIN79zW/95RT83cOdc88/4yALre0JF/jXMLdymKH9sZDj\nACgJKurcmNzOpIbheQASJrDaeeIbj/trSwH7MW3AO1mmzYuRzQD0Jayoc3o5hI/GcCAAaRBYIFE4\nQn2V536Yl8Z8GtkLQP/IOrMmRVbNYJ2ExwoACCyQAoFFDcM0eskABGI6YJ2kiSRFzAwEAAILxC+w\ndI04TQ8vS0PeQDYCYAbqoHxu9PMz8uV5xfpYkudi6ykAEsg9t8oByYYXKOy2jg7N+CTx5O3VSMMX\nyC0AIquXVPd6xUfW0MEBAAILAACAmsAqyMOK2A1Qd2SqopMDQDr5Pz/JfMVm7fOCAAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Image(filename='jupyter-logo.png')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# iPython Notebook Tutorial "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### To have plots show up in this page you add:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Let's look at an example."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEDCAYAAAA2k7/eAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl0lOX5//H3ZRRkUalgXZBVAhjCGnYEAkEIoiKlrC0F\nrbT9HlS0XxX1SI3+6EFcqaK1LeBCS8CCbMqmaEAWDZE9C4LCFwgSRFBBCg3m/v2RIQQkMGQm88xk\nPq9z5pjnSeaea27hysX13M895pxDRETKv4u8DkBEREJDCV9EJEoo4YuIRAklfBGRKKGELyISJZTw\nRUSihBK+iEiUUMIXEYkSFwd7QDMzYBxwGZDhnHsr2K8hIiIXriwq/DuAmsB/gT1lML6IiJSCXwnf\nzKaaWZ6ZbT7jfLKZ5ZjZNjMb4zvdEFjlnHsQ+J8gxysiIqXkb4X/OpBc/ISZxQCTfOfjgCFmdiOF\nVf23vh8rCFKcIiISIL8SvnPuY+DQGafbAtudczudc/nADKAv8A7Qy8xeAtKCGKuIiAQgkIu2NYHd\nxY73AO2cc/8B7g4oKhERCbpAEn5A+yqbmfZlFhEpBeecleZ5gST8XKBWseNaXOCqnCeeeILExEQS\nExMDCCPypaSkkJKS4nUYYUFzcYrm4pRInosffviBzz//nK1bt572+Pzzz6lcuTINGzakYcOGNGrU\niIYNGxIbG8sNN9zApZdeeto4aWlppKWl8eSTT5Y6lkASfgYQa2Z1gb3AIGDIhQwQqf8DRUSKc86x\nd+9ecnJyfvI4cOAADRo0oFGjRjRu3JjevXtz//3307BhQ6pVq+b3a5wsjss84ZtZKtAVqG5mu4E/\nOedeN7N7gCVADDDFOZd9IS+ekpKiCl9EIkZ+fj7bt28nJyeH7OxssrOzixJ7lSpVaNy4cdGjT58+\nNGrUiNq1axMTExPwa5+s8ANhXn3EoZk5fbxiobS0NP3S89FcnKK5OCXUc3H06FG2bt1KdnY2WVlZ\nZGVlkZ2dzY4dO6hVqxY33ngjjRs3Lvpv48aN+dnPfhaS2Mys1D18TxO+evgi4qUjR46Qk5NDZmYm\nmZmZRYl97969NGjQgLi4OOLi4rjxxhu58cYbiY2N/UlvPVSK9/AjMuGrwheRUDh69CjZ2dlkZmay\nZcsWsrKyyMzMJC8vj4YNG9KkSRPi4uKK/lu/fn0uvjjoW40FRcRW+Er4IhJM+fn5bN26lS1btrBl\ny5aiBL9nz56ixB4fH1+U3OvXrx+U/nooBZLwPf0Vpou2IlIazjl2797N5s2bT3ts27aN2rVrEx8f\nT9OmTfnVr35FfHw8DRo0CNuK3V+6aCsi5d7hw4fZsmULmzdvZtOmTUWPSpUq0axZM5o2bVqU4OPi\n4qhUqZLXIZcptXREJOI559i5cycbN2487fHVV18RFxdHs2bNih5Nmzblqquu8jpkT6ilIyIR5fjx\n42RmZrJ+/Xo2bNjAhg0b2LRpE1WrVqVFixY0b96cQYMG8ec//5nY2NiIb8cEg1o6IhL2vv32WzZs\n2FCU3NevX8+2bdto0KABLVu2pHnz5kVJvkaNGl6HG/bU0hGRsLB//37Wr1/PunXrih55eXk0a9aM\nli1b0rJlS1q0aEF8fLxn69kjnVo6IhJyeXl5fPbZZ6c9jhw5QsuWLWnVqhV33HEHTz31FA0bNoy4\npY/hSC0dEQmJAwcOkJGRUfQ4mdwTEhJISEigdevWJCQkUK9ePcxKVXyKn9TSEZGgOXz4MJ999hlr\n165l7dq1ZGRk8M033xQl9pMPJXdvKOGLSKnk5+ezefNm0tPTix47d+6kefPmtGnThtatW9OmTRti\nY2O56CJ/PwJbypISvoic18m7Uz/55JOix8aNG6lXrx5t27alXbt2tG3blvj4eC655BKvw5US6KKt\niPzE0aNHWbt27WkJvqCggA4dOtCuXTvGjRtH69atufzyy70OVfygi7YiAhRW77t27WLNmjWsXr2a\n1atXk52dTXx8PB06dKB9+/a0b9+eOnXqqO8e4dTSEYky+fn5bNy4kZUrV7Jq1SpWr17Njz/+SIcO\nHejYsSMdO3YkISFBa93LISV8kXLu+++/55NPPilK8Onp6dSpU4ebbrqJTp060alTJ62aiRJK+CLl\nzNdff83KlStZsWIFH3/8MdnZ2bRq1YrOnTvTqVMnOnTowJVXXul1mOIBJXyRCJebm8vy5ctZsWIF\nK1asIDc3l44dO9K5c2e6dOlCmzZtqFixotdhShhQwheJMLm5uUWrLpYvX84333xDly5d6Nq1K126\ndKFZs2baIVLOSssyRcJcXl4eH330ER9++CEfffQRhw4domvXrnTt2pV7772X+Ph43dgk56RlmSJh\n6ttvv2X58uUsW7aMDz/8kD179tC1a1e6d+9Ot27dlOCl1NTSEfHY8ePHWb16NR988AEffPAB2dnZ\ndOjQge7du9O9e3datmypFo0EhRK+SIg559i0aRMffPAB77//PqtWrSIuLo6bb76ZHj160KFDB11k\nlTKhhC8SAgcOHOD9999n8eLFLF26lCpVqtCzZ0969OhBt27d+NnPfuZ1iBIFwirhm1ki8P+ALcAM\n59zyEn5OCV/C2okTJ/jkk09YvHgxS5Ys4fPPPycxMZFevXrRq1cvbrjhBq9DlCgUbqt0CoDDQEVg\nTxmML1Jmvv76axYvXszChQtZunQptWrVonfv3jz77LN07NiRChUqeB2iSKn5VeGb2VSgD7DfOde0\n2PlkYCIQA0x2zk0wX+luZj8HXnDO/bqEMVXhi+cKCgpYt24d7733HgsXLmTr1q0kJSVxyy23kJyc\nTM2aNb0OUeQ0Zd7SMbPOwBHgrZMJ38xigK1ADyAXWAsMcc5l+75fAfiXc25ACWMq4Ysnjh49yrJl\ny1iwYAHvvvsul19+Obfeeit9+vShU6dOquIlrJV5S8c597GZ1T3jdFtgu3Nupy+IGUBfM2sM9AKq\nAS+XJiiRYNu3bx8LFixgwYIFpKWlkZCQwG233cZDDz1EbGys1+GJhEQgPfyawO5ix3uAds65p4E5\nAUUlEgTbt29n7ty5zJkzh6ysLHr16sXgwYN54403tPGYRKVAEn7A/ZiUlJSir7XFggTKOceGDRuY\nM2cOc+bM4euvv6Zv376MHTuWbt26aV28RKRgbKlwkt/LMn0tnQXFevjtgRTnXLLv+FGgwDk3wc/x\n1MOXgDnnyMjIYNasWcyaNQszo1+/fvTr14/27dtr+wIpd7xalpkBxPp+EewFBgFDLmQAbZ4mpVFQ\nUEB6enpRkq9YsSIDBgxg9uzZNG/eXB8CIuVSMCp9vxK+maUCXYHqZrYb+JNz7nUzuwdYQuGyzCkn\nV+iIBJtzjs8++4wZM2bw9ttvU6VKFQYMGMCCBQuIj49Xkhfxg7ZWkLCWlZXFjBkzSE1NpaCggCFD\nhjB48GDi4+O9Dk3EE+F2p61IQHbt2sX06dNJTU3lwIEDDBo0iOnTp9O6dWtV8iIB0AegSFj4/vvv\nmTVrFtOmTWPTpk3079+fl156iZtuuomYmBivwxPxnD4ARSLaiRMnWLp0KdOmTWPhwoV069aNYcOG\n0adPHy699FKvwxMJSxHb0lGFH51ycnKYOnUq06ZNo06dOgwbNoyXX36ZGjVqeB2aSNhShS8R4/Dh\nw7z99ttMmTKFHTt28Jvf/Ia77rqLRo0aeR2aSEQJq/3w/X5hJfxyzznH6tWrmTx5MnPnziUxMZG7\n7rqL5ORkLrnkEq/DE4lIaulIWPnuu++YNm0ar732Gvn5+YwcOZKnn36aq6++2uvQRCKWWjoSVjIy\nMnjttdeYPXs2PXv25A9/+AOJiYlaSikSRBFb4Uvk+89//kNqaiqvvPIKBw8e5He/+x05OTmq5kXC\nkCp8KZXdu3fz17/+lcmTJ9OmTRtGjRpFr169tGZepIwFUuF7upVgSkpK0Lb9lLLnnGPlypUMHDiQ\n5s2b88MPP7By5Uree+89brnlFiV7kTKUlpZ22pbypaEKX84rPz+fmTNn8uKLL3L48GHuvfdehg8f\nzuWXX+51aCJRR8sypUwcPnyYyZMnM3HiROrXr8+DDz5I7969tce8iId00VaC6quvvuKll17iH//4\nB0lJScyePZvWrVt7HZaIBEg9fCmybds27r77buLi4jhy5Ajp6enMnDlTyV4kDKiHL0GRnZ3Nn//8\nZ5YsWcKoUaO45557tK+NSJiK2FU64q1NmzYxcOBAunbtSpMmTfjiiy9ISUlRshcpp5Two9C6devo\n168fPXv2pG3btnz55Zc8+uijWnUjUs4p4UeR7Oxs+vfvz2233UZiYiJffvklDz74IFWrVvU6NBEJ\nASX8KLBz505GjBhBly5daNeuHdu2bWP06NFUrlzZ69BEJISU8MuxvLw87rvvPhISEqhduzbbt2/n\n4YcfVqIXiVJallkOHTlyhLFjxxIXF0dMTAzZ2dk89dRTXHHFFV6HJiKlpGWZcpoff/yRN998k7Fj\nx5KUlMS4ceOoXbu212GJSBDpTlshLS2NBx54gMqVKzN37lzatGnjdUgiEmaU8CPcF198wUMPPcT6\n9euZMGECAwYM0AeOiMhZ6aJthPrhhx945JFHaNeuHW3atCE7O5uBAwcq2YtIicok4ZtZFTNba2Z9\nymL8aLdgwQKaNGnCnj172LJlC48++iiXXnqp12GJSJgrq5bOw8DMMho7au3atYvRo0eTmZnJlClT\nSEpK8jokEYkgflX4ZjbVzPLMbPMZ55PNLMfMtpnZGN+5m4Es4Ovghxud8vPzef7552nVqhUtW7Zk\n06ZNSvYicsH8rfBfB14G3jp5wsxigElADyAXWGtm84GuQBUgDviPmS3U+svSS09PZ+TIkVx99dWs\nWbOG2NhYr0MSkQjlV8J3zn1sZnXPON0W2O6c2wlgZjOAvs65x33Hw4GvlexL5/jx4zz11FNMnjyZ\nF198kSFDhuiCrIgEJJAefk1gd7HjPUC7kwfOuTcDGDuqbdiwgd/85jfUq1ePjRs3cs0113gdkoiU\nA4Ek/IAr9+K3CScmJpKYmBjokBEtPz+f8ePHM2nSJJ577jmGDRumql4kyqWlpQVtCxq/t1bwtXQW\nOOea+o7bAynOuWTf8aNAgXNugp/jqdtTTGZmJsOHD6dGjRpMnjyZ66+/3uuQRCQMefWJVxlArJnV\nNbMKwCBg/oUMoM3TwDnHSy+9RGJiIr///e9ZtGiRkr2I/ETINk8zs1QKV99UB/YDf3LOvW5mvYGJ\nQAwwxTk33u8XVoXPoUOH+O1vf8uuXbuYOXMmN9xwg9chiUiYK/PN05xzQ0o4vwhYVJoXhsIKP1p7\n9+np6QwaNIjbbruN1NRUKlas6HVIIhLGgtHL1/bIIeacY+LEiYwfP57XXnuNX/ziF16HJCIRJGK3\nR462Cv/gwYPceeedfPXVV3z66afUq1fP65BEJEKowo8gGzZsoF+/ftxxxx1MmDCBChUqeB2SiEQg\nVfhhbu7cuYwcOZJXXnmFgQMHeh2OiEQgVfhhzjnH008/zSuvvMLcuXNp3bq11yGJSISL2Aq/PDt2\n7BgjR44kKyuLTz/9lJo1a3odkohEOU8/8aq83niVl5dH9+7dOXbsGB9//LGSvYgELGQ3XpWF8trS\n2bRpE7fffjvDhw/niSee4KKL9CmSIhI8aumEieXLlzNgwAD+8pe/MGTIWe9VExHxjBJ+kCxatIjh\nw4czY8YMunfv7nU4IiI/oR5+EMyaNYsRI0Ywf/58JXsRKRPq4YeBN954g8cee4yFCxfSokULr8MR\nkXJOPXyPTJo0iWeeeYYPP/yQxo0bex2OiMg5KeGX0vjx45kyZQorVqygbt26XocjInJe2lqhFB5/\n/HHmzJnDihUruO6667wOR0SigLZW8MBzzz3H1KlTWbFiBTVq1PA6HBGJMurhh8ibb77Jyy+/zMqV\nK5XsRSTiqML307vvvsvdd99NWlqaLtCKiGdU4ZexlStXcuedd/Lee+8p2YtIxNJGL+exefNm+vfv\nz7/+9S/atm3rdTgiIqWmhH8OO3fupHfv3kycOJGePXt6HY6ISEC0tUIJ9u/fT8+ePRkzZow2QhMR\nz2lrhTKSn59Pt27dSExMZNy4cV6HIyJSJJCLtkr4Z/HAAw+wfft25s2bp/3sRSSsaJVOEL399tvM\nnz+fjIwMJXsRKVdU4ReTnZ1Nly5dWLp0KS1btvQ6HBGRnwikwlcJ63PkyBH69+/PhAkTlOxFpFwK\neoVvZo2B0UB1YIlzbkoJPxc2Fb5zjqFDh1KlShUmT57sdTgiIiUKqx6+cy4H+B8zuwiYAZw14YeT\nSZMmsXXrVlatWuV1KCIiZcavlo6ZTTWzPDPbfMb5ZDPLMbNtZjam2PnbgPcoTPhhbc2aNYwbN45Z\ns2ZRqVIlr8MRESkzfrV0zKwzcAR4yznX1HcuBtgK9ABygbXAEOdcdrHnzXPO9S1hTM9bOvv37ych\nIYG//vWv3HrrrZ7GIiLijzJv6TjnPjazumecbgtsd87t9AUxA+hrZj8HfgFcCnxUmqBCZdSoUQwd\nOlTJXkSiQiA9/JrA7mLHe4B2zrnlwHJ/Bih+m3CoP/lqwYIFbNy4kWnTpoXsNUVELlQwPunqJL9X\n6fgq/AXFWjr9gWTn3Ejf8a8pTPj3+jmeZy2dw4cP06RJE9544w26d+/uSQwiIqXh1Tr8XKBWseNa\nFFb5fvNq87SxY8eSlJSkZC8iESOkm6edpcK/mMKLtknAXiCdMy7anmc8Tyr89PR0br/9djIzM6le\nvXrIX19EJBBlXuGbWSqwGmhoZrvN7E7n3AngHmAJkAXM9DfZnxTqCj8/P5/f/e53PP/880r2IhJR\ntD3yBXr22Wf54IMPWLx4MWal+gUpIuKpsLrT9kKkpKSEbHXOl19+yYQJE0hPT1eyF5GIE4zVOlFR\n4TvnSE5OJikpiYcffjgkrykiUhYidrfMUPXwU1NT2bdvHw888ECZv5aISFlQD98PBw8epEmTJsyb\nN4+2bduW+euJiJSliK3wQ+H555/n1ltvVbIXkahXri/aHjp0iNdee42MjIwyGV9EJFR00fY8nnzy\nSXbu3Mnrr79epq8jIhIqgbR0ym3C//7776lfvz5r1qwhNja2zF5HRCSU1MM/i0mTJpGcnKxkLyLi\nUy57+EeOHGHixIksX+7XLs0iImFPPfwSPPvss2RkZDBz5swyGV9ExCvq4Rdz9OhR6tevz/vvv0/T\npk2DPr6IiJfUwy/m73//Ox07dlSyFxE5Q7mq8I8dO0b9+vV59913adWqVVDHFhEJBxFb4Qd7L50p\nU6aQkJCgZC8i5Y720inm+PHjNGjQgNmzZ2sbBREptyK2wg+mN998kyZNmijZi4iUoFxU+CdOnCA2\nNpZ//vOfdOrUKShjioiEo6iv8JctW0aNGjWU7EVEzqFcJPzU1FSGDh3qdRgiImEt4lfpHDt2jHnz\n5jFo0KDgBCUiEoa0Sgd45513ePnll/noo4+CEJWISHiL6h5+amoqQ4YM8ToMEZGwF9EV/vfff0+t\nWrX48ssvqV69epAiExEJX1Fb4c+bN4/OnTsr2YuI+CGiE77aOSIi/iuTlo6Z9QX6AJcDU5xz75/l\nZwJq6Rw4cIAbbriB3NxcqlatWvpgRUQiSCAtnTL5xCvn3DxgnplVA54DfpLwAzVr1iySk5OV7EVE\n/OR3S8fMpppZnpltPuN8spnlmNk2MxtzxtMeByYFI9AzqZ0jInJh/G7pmFln4AjwlnOuqe9cDLAV\n6AHkAmuBIUAO8DSw1Dm3rITxSt3S2bNnD82aNeOrr76iYsWKpRpDRCQShaSl45z72MzqnnG6LbDd\nObfTF8gMoC+FvwCSgMvNrIFz7m+lCa4kM2fOpF+/fkr2IiIXINAefk1gd7HjPUA759y9wMvne3Lx\n24QTExNJTEz060VTU1N5+umnLyROEZGIlJaWFrQPirqgVTq+Cn9BsZZOfyDZOTfSd/xrTiX8841V\nqpbOtm3b6Ny5M7m5ucTExFzw80VEIpmXN17lArWKHdeisMr3S2k2T0tNTWXgwIFK9iISVUK+edpZ\nKvyLKbxomwTsBdKBIc65bD/GuuAK3zlHXFwcU6dOpUOHDhf0XBGR8iAkFb6ZpQKrgYZmttvM7nTO\nnQDuAZYAWcBMf5L9SRda4W/cuJFjx47Rvn17v58jIlIeRN32yGPGjOGiiy5i/PjxZRSViEh4C7s7\nbf2VkpJyQatzZs2axTvvvFO2QYmIhKFgrNaJmAp///79NGrUiIMHD2JWql9uIiIRLyq2R/7ss89I\nSEhQshcRKaWI+UzbjIwMWrduXbYBiYiEqai6aNu3b1+GDRvGL3/5yzKMSkQkvEVFS0cVvohIYCKi\npbN3716OHz9OnTp1yj4oEZEwFDUtnfnz5/Pqq6+yePHiMo5KRCS8lfuWjto5IiKBi4iWjhK+iES7\nqGjpOOe4+uqrWbduHddff30IIhMRCV/luqWze/duYmJiqFmzptehiIhEtLBP+CfbObrDVkQkMBGT\n8EVEJDBhf9FWCV9EJAou2jrnqF69OllZWVxzzTUhikxEJHyV24u2O3bsoEqVKkr2IiJBENYJX+0c\nEZHgCeuEv3btWiV8EZEgCeuErwpfRCR4wnaVTkFBAevWrSMhISG0QYmIhKFyvUpn69atJCcns2PH\njhBGJSIS3srlKh21c0REgksJX0QkSijhi4hEibDs4f/4449Uq1aN3bt3U61atRBHJiISvsKqh29m\n9cxsspn9u7Rj5OTkcO211yrZi4gEUdATvnNuh3Pu7kDGUDtHRCT4/Er4ZjbVzPLMbPMZ55PNLMfM\ntpnZmGAFpTtsRUSCz98K/3UgufgJM4sBJvnOxwFDzOzGYASlCl9EJPj8SvjOuY+BQ2ecbgtsd87t\ndM7lAzOAvmZ2pZm9BrQoTdWfn5/P5s2badmy5YU+VUREzuHiAJ5bE9hd7HgP0M45dxD4Q2kHzczM\npE6dOlx22WUBhCYiImcKJOEHvJ6z+L4QiYmJJCYmqp0jIlJMWlraeT8Z0F+BJPxcoFax41oUVvkX\n5GSiP0kJX0TklJM5MhiJ3+8br8ysLrDAOdfUd3wxsBVIAvYC6cAQ51y2n+Od9carnj178sc//pHk\n5OSzPEtEJLqV+Y1XZpYKrAYamtluM7vTOXcCuAdYAmQBM/1N9iedbXtk5xwxMTEXMoyISLlXLrdH\nvvnmm3n44Ye5+eabPYhKRCS8hdXWChfiXB+AIiIip6jCFxGJMhFb4YuISOgEsiwzYCkpKT9ZlunV\nvzhEpGyYlaoYFU7PhyFdlhlsJbV0evTowSOPPEKPHj08iEpEgs3XgvA6jIhT0ryppSMiIuelVToi\nIhGgXK7SUUtHpHxRS6d0oqKloz8YIiJlIyxbOrqqLyKhNH36dFq3bs1ll13Gddddxy233MKqVau8\nDus05bKlk5SUxGOPPUZSUpIHUYlIsIV7S+eFF15gwoQJ/O1vf6NXr15UqFCBxYsXs2LFCiZMmOD3\nOCdOnODii4O30j0qWjoiIqHy3Xff8cQTT/Dqq69yxx13UKlSJWJiYujTpw8TJkxgxIgRjB07tujn\n09LSqFXr1K7wdevW5ZlnnqFZs2ZUrVqVZ555hgEDBpz2GqNHj2b06NFFr/fb3/6W6667juuvv56x\nY8dSUFAQmjeLEr6IRLE1a9Zw7Ngx+vXrd9bvm9l5W8wzZsxg0aJFfPfddwwePJiFCxdy5MgRAH78\n8Uf+/e9/86tf/QqAESNGUKFCBb744gvWr1/P0qVLmTx5cnDf1Dko4YtI1Prmm2+oUaMGF11Ucio8\nVzvKzLjvvvuoWbMmFStWpHbt2rRq1Yo5c+YA8OGHH1K5cmXatm1LXl4eixYt4sUXX6RSpUpcddVV\n3H///cyYMSPo76sk2lpBRDwXjIUapckd1atX58CBAxQUFJwz6Z9L8RYPwNChQ0lNTWXYsGFMnz69\nqLr/v//7P/Lz87n22muLfragoIDatWv79TrB2FrB84R/NlqlIxJdvCr0OnToQMWKFZkzZw79+/f/\nyferVKnC0aNHi4737dv3k585M1/98pe/5H//93/Jzc1l7ty5fPLJJ0DhL4aKFSvyzTfflOqXy8ni\n+Mknn7zg556klo6IRK0rrriCp556ilGjRjFv3jyOHj1Kfn4+ixYtYsyYMbRo0YKFCxdy6NAh9u3b\nx8SJE8875lVXXUViYiIjRoygfv36NGrUCIBrr7226CNcDx8+TEFBAV988QUrVqwo67dZRAlfRKLa\nH//4R1544QXGjRvHz3/+c2rXrs2rr75Kv379GDZsGM2bN6du3bokJyczePBgvzoQQ4cOZdmyZQwd\nOvS082+99Rb//e9/iYuL48orr2TAgAFn/VdDWQm7dfjdu3fn8ccfp3v37h5EJSLBFu7r8MOV1uGL\niEiphV3CVyUgIlI2tJeOiEgEKJd76XTr1o0//elPdOvWzYOoRCTY1MMvHfXwRUSk1JTwRUSihBK+\niEiUCPrWCmZWBXgVOA6kOeemX8jz1esTKX+0ECM8lMVeOr8A3nbOvWdmM4ALSvigPxwi5YmKuPDh\nV0vHzKaaWZ6ZbT7jfLKZ5ZjZNjMb4ztdE9jt+/rHIMZabgW6A155ork4RXNxiuYiOPzt4b8OJBc/\nYWYxwCTf+ThgiJndCOwBTu4XqmsEftAf5lM0F6doLk7RXASHXwnZOfcxcOiM022B7c65nc65fGAG\n0Bd4B+hvZq8C84MZrIiIlF4gPfzirRsorOzbOeeOAncFFJWIiASd33famlldYIFzrqnvuD+Q7Jwb\n6Tv+NYUJ/14/x9OVHBGRUijtnbaBVPi5nOrV4/t6j79PLm3AIiJSOoFcVM0AYs2srplVAAahnr2I\nSNjyd1lmKrAaaGhmu83sTufcCeAeYAmQBcx0zmWXXagiIhIIf1fpDHHOXeecq+icq+Wce913fpFz\nrpFzroFzbrw/Y5Wwdj8qmFktM/vIzDLNbIuZ3ec7f6WZvW9mn5vZUjOr5nWsoWJmMWa23swW+I6j\nci7MrJqtxPJIAAADAElEQVSZzTKzbDPLMrN2UTwXj/r+jmw2s+lmVjFa5uJs9zyd67375mqbL6f2\nPN/4IV0nf461+9EiH3jAOdcEaA+M8r3/R4D3nXMNgWW+42gxmsJ/IZ68iB+tc/EXYKFz7kagGZBD\nFM6Fb3HISKCVb4FIDDCY6JmLn9zzRAnv3cziKGylx/me86qZnTOnh/rGqJLW7kcF59w+59wG39dH\ngGwKl7feDrzp+7E3gTu8iTC0zOx64BZgMnDyIn7UzYWZXQF0ds5NBXDOnXDOfUcUzgXwPYWFUWUz\nuxioDOwlSuaihHueSnrvfYFU51y+c24nsJ3CHFuiUCf8s63drxniGMKCr5JpCXwKXO2cy/N9Kw+4\n2qOwQu1F4CGgoNi5aJyLesDXZva6ma0zs3/4NiGMurlwzh0Engd2UZjov3XOvU8UzkUxJb336zh9\nZeR582moE77W3gNmVhWYDYx2zh0u/j3fx4CV+3kys1uB/c659Zyq7k8TLXNB4fLoVsCrzrlWwA+c\n0bKIlrkwsxuA+4G6FCa0qr57fIpEy1ycjR/v/ZzzEuqEH9Da/fLAzC6hMNlPc87N9Z3OM7NrfN+/\nFtjvVXwh1BG43cx2AKlAdzObRnTOxR5gj3Nure94FoW/APZF4Vy0BlY7577xrQR8B+hAdM7FSSX9\nnTgzn17vO1eiUCf8qF67b4X7Pk8BspxzE4t9az4w3Pf1cGDumc8tb5xzj/lWfNWj8KLch865YUTn\nXOwDdptZQ9+pHkAmsIAomwsKL1a3N7NKvr8vPSi8qB+Nc3FSSX8n5gODzayCmdUDYoH0c47knAvp\nA+gNbKXwAsOjoX59Lx/ATRT2qzcA632PZOBK4APgc2ApUM3rWEM8L12B+b6vo3IugObAWmAjhVXt\nFVE8Fw9T+AtvM4UXKS+Jlrmg8F+7e4H/Uni9885zvXfgMV8uzQF6nW98v/fSERGRyKb96kVEooQS\nvohIlFDCFxGJEkr4IiJRQglfRCRKKOGLiEQJJXwRkSihhC8iEiX+P9jc6vPiOq8/AAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x106b0e490>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as pl\n",
"import numpy\n",
"\n",
"x = numpy.linspace(0, 100)\n",
"y = x**3\n",
"\n",
"pl.plot(x, y, label='Curve', color='black')\n",
"pl.yscale('log')\n",
"pl.legend(loc=4)\n",
"pl.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Let's define a functions."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"14.978661367769954"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def distance_modulus (distance):\n",
" return 2.5*numpy.log(distance)\n",
"\n",
"distance_modulus(400)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"261818300.82189918"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def distance (apparent, absolute):\n",
" log_distance = (apparent - absolute + 5)/5\n",
" return 10**(log_distance)\n",
"\n",
"distance(12.34, -24.75)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 2.51188643e+07, 2.89217448e+07, 3.33003639e+07,\n",
" 3.83418858e+07, 4.41466709e+07, 5.08302738e+07,\n",
" 5.85257434e+07, 6.73862717e+07, 7.75882432e+07,\n",
" 8.93347463e+07, 1.02859616e+08, 1.18432088e+08,\n",
" 1.36362162e+08, 1.57006766e+08, 1.80776868e+08,\n",
" 2.08145654e+08, 2.39657948e+08, 2.75941059e+08,\n",
" 3.17717266e+08, 3.65818198e+08, 4.21201390e+08,\n",
" 4.84969343e+08, 5.58391470e+08, 6.42929370e+08,\n",
" 7.40265918e+08, 8.52338773e+08, 9.81378942e+08,\n",
" 1.12995520e+09, 1.30102522e+09, 1.49799445e+09,\n",
" 1.72478392e+09, 1.98590827e+09, 2.28656564e+09,\n",
" 2.63274116e+09, 3.03132606e+09, 3.49025488e+09,\n",
" 4.01866341e+09, 4.62707056e+09, 5.32758776e+09,\n",
" 6.13416003e+09, 7.06284364e+09, 8.13212567e+09,\n",
" 9.36329209e+09, 1.07808514e+10, 1.24130227e+10,\n",
" 1.42922973e+10, 1.64560853e+10, 1.89474609e+10,\n",
" 2.18160194e+10, 2.51188643e+10])"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cepheid_apparent = numpy.linspace(11, 18)\n",
"cepheid_absolute = numpy.linspace(-21, -29)\n",
"\n",
"distance(cepheid_apparent, cepheid_absolute)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x10d190e50>"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAEPCAYAAACjjWTcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHgFJREFUeJzt3XuYFPWd7/H3VxBFJFw0CggqCl7CkUsUvERD7yKKLMec\nbOIaY4xIHjUhF2MSDV5OMj5mN2bZJJ7Dmg1nV03WRF1R48pmUEdix8sicpE7yEUQkIhXQLkNMN/z\nx69GmqFnpqcvU91dn9fz9DPVVdXV37LwM7/5VdWvzN0REZHqdkjcBYiISOkp7EVEEkBhLyKSAAp7\nEZEEUNiLiCSAwl5EJAHyDnszm2xmy81soZk9bmbdovmdzOx+M1tkZgvMbGTxyhURkXwU0rJ/Bhjk\n7kOAlcAt0fxrgQZ3HwyMBn5uZlZYmSIiUoi8w97d69y9IXo7G+gbTZ8OPBet8w6wBTirkCJFRKQw\nxeqznwDURtMLgUvNrIOZ9QfOZP8vAhERiUHHlhaaWR3QK8uiW919erTObUC9uz8YLbuP0LqfC7wB\n/Dewr2gVi4hIm1khY+OY2XhCH/0od9/VzDovAV9z9xVZlmlgHhGRNnL3Np8HbbFl3xIzGwPcBIzM\nDHoz6wwc4u7bzWw0sCdb0Deq1oHYampqqKmpibuMktH+VbZy2L/6etiwAd54A9atC6/M6bfegmOO\ngRNPDK8TTjhwul8/OPzw7Nsuh/0rlXyvd8k77IEpQCegLvryWe4+ETgWeMrMGoCNwFUFfIeIVKhd\nu2D9+ubD/J13oHfvAwM8ldo/3bcvdOoUX/3VJu+wd/eBzcxfB5yW73ZFpDLs2xfCfNUqeP31g0P9\nvfdCYGe2yi+6aP/0ccdBx0Kam9Im+k9dIqlUKu4SSkr7V9ly3b+9e0Nwr14dXqtW7f/5xhuhm2Xg\nQDjppBDg48btD/PevaFDh1LuRfOq/fjlo6ATtAV/uZlXa5+9SKXYuze0xjPDvHF6/Xo49tgQ6AMG\n7P85YEAI+M6d464+ecwsrxO0CnuRBNizp/lA37AhtMIbQzwz2Pv3b/4kqMRDYS+ScPX1Bwd6488N\nG0IfedPWeWOgH3ZY3NVLrhT2IgmxdSssXw7Llu1/vfYabNwYTog2bZ0PGBD60BXo1UFhL1Jl3nvv\n4FBftgy2bIHTT4dPfWr/z9NOC4GuSxWrn8JepAK5w9tvHxjmjQG/c2cI8qavfv3gED2JIrEU9iJl\nzB02bTq4lb5sWVg2aNDBod6nD2hwcGlKYS9SBhpDfdGig0O9c+cDu14aX8cco1CX3CnsRdrZvn3h\nxOiCBeH16qvhpxkMGXJga/300+Goo+KuWKqBwl6khLZvh8WLDwz1JUtCV8vQoTBsWPg5dGi4Zl0t\ndSkVhb1Ikbz99v5Abwz39etDC70x0IcNg8GDoWvXuKuVpFHYi7RRQwOsWXNwN8yuXQe21IcODZc2\nHnpo3BWLKOxFWuQe7i59+WWYPRvmzg0nUY866sDW+tCh4dJGdcNIuVLYi2TYtg3mzNkf7i+/HFrm\n55wTXsOHh5OoPXrEXalI2yjsJbH27QuXNmYG+7p1oaV+zjlw9tnhZ1899l6qgMJeEuOtt/aHemOX\nTO/eBwb7GWeoj12qk8JeqtLu3TB//oGt9m3bYMSI/V0yI0ZAz55xVyrSPhT2UhV274ZXXoF0Orxm\nzw4jN5577v6W+8CBGhtGkqvdw97MJgPjgHpgDXCNu281s8OB+4FBhMce/ru739XMNhT2CZct3E87\nLTx4OpWC88+H7t3jrVGknMQR9qOBme7eYGZ3Abj7JDMbD1zs7leYWWdgGTDS3ddn2YbCPmEU7iKF\nyTfs837guLvXZbydDXwhmv4L0MXMOgBdCC3/bfl+j1S23bvDJZCZ4X7qqSHYb7xR4S7SXvIO+yYm\nAA8BuPvTZnYVIfSPAL7r7luK9D1S5txh4UKorYU//enAcP/udxXuInFpMezNrA7olWXRre4+PVrn\nNqDe3R+M3n8F6Az0BnoCL5jZTHdfW9TKpWxs3QrPPhsC/qmn4IgjYOxYuOEGuOAChbtIOWgx7N19\ndEvLo/75scCojNnnAX9w933AO2b2EnAWkDXsa2pqPp5OpVKkUqkcypY4ucPSpSHca2th3jz4zGdC\nwE+aFK6WEZHiSKfTpNPpgrdTyAnaMcDPCSdf382Y/x1gqLtPMLMuwCvA5e6+JMs2dIK2Qnz0Ecyc\nGcJ9xgzo0CGE+9ixoYumS5e4KxRJhjiuxlkFdALej2bNcveJZnYYcC8wBDgEuM/df97MNhT2Zco9\nPJijsfU+e3a4xn3sWLjkknAFjQYLE2l/uqlKCtZ4cnXatPDauXN/6/2v/1pjt4uUg3a/9FKqg3sY\nx33aNHj0Udi7Fy67DH7/ezjrLLXeRaqFwj6B3MN4M40B7x4C/qGH4MwzFfAi1UhhnxDu4aqZxoA3\nCwH/yCNhKGAFvEh1U9hXucWL4YEHQsgfemgI+MceCw/uUMCLJIfCvgpt2RK6ZO67L4z9ftVV8MQT\n4QHZCniRZNLVOFWioSEMT3DffeFSyYsvhgkT4MILwzXxIlIddOllQq1dC7/5TXgddVQI+CuuCNMi\nUn106WWC7NgBjz8O998PixbBl78M//mfMHRo3JWJSLlS2FeQdetgypTQih8xAr7+dbj0UjjssLgr\nE5Fyp4e7lTl3ePFF+OIXw01OHTqEa+RnzAhX1ijoRSQXatmXqfr6cLnk3XeHIYRvuCG06I88Mu7K\nRKQS6QRtmXnvPZg6Fe65Jww2duONYWwaPWBbRCD/E7SKkDKxciVcfz0MGACrV4dumpkzYdw4Bb2I\nFE4xErPVq+Hqq8PDP3r3hhUrwrXygwfHXZmIVBP12cfk9dfhJz+BJ5+E73wnhH63bnFXJSLVSi37\ndrZuHVx7bbh0sl+/EPI/+pGCXkRKS2HfTtavD9fFn3kmHHts6KO/4w49jFtE2ofCvsS2bIHvfS8M\nI9yjR3jU309+Aj17xl2ZiCSJwr5E9u2Df/3XcPnkRx/B8uXw05/C0UfHXZmIJFHeJ2jNbDIwDqgH\n1gDXuPtWM7sS+EHGqoOBYe6+qKBKK8hLL8G3vw1HHBFGoPz0p+OuSESSLu+bqsxsNDDT3RvM7C4A\nd5/UZJ3/AfzB3Qc2s42quqlq40b44Q/h+efhH/8RvvQljR8vIsXV7jdVuXuduzdEb2cDfbOs9mXg\n4Xy/o1Ls3g1///dh1MmTTgrXyl9xhYJeRMpHsa6znwA8lGX+3wGXFuk7ytLcuTB+PJx8MsyZA/37\nx12RiMjBWgx7M6sDemVZdKu7T4/WuQ2od/cHm3z2bGCHuy9r6Ttqamo+nk6lUqRSqZwKj9vu3XDn\nneEk7N13q8tGREojnU6TTqcL3k5BA6GZ2XjgWmCUu+9qsuyXwGZ3v6uFz1dkn/38+aE1379/GLSs\nV7ZfhyIiJdDuT6oyszHATcDILEF/CHAZcH6+2y9H9fWhb/5f/gV+8Qu48kq15kWkMhTSZz8F6ATU\nWUi8We4+MVr2WWC9u68rrLzy8dproavmuONgwQLo0yfuikREcqfx7HPw2GNhqIM77wzDEKs1LyJx\n0QPHS2DPHpg0KTzce8aM8FhAEZFKpLBvxqZNcPnl0LUrzJunsWxEpLJpbJws0unQir/oIviv/1LQ\ni0jlU8u+ifvvD103DzwQwl5EpBoo7CPuYejh++4LY9ucemrcFYmIFI/CHti7F775zTDcwaxZuklK\nRKpP4sN+x45w/fzu3fDnP4cTsiIi1SbRJ2g/+ABGjQqPBpw+XUEvItUrsWG/dStcfDGcfTb89rfQ\nqVPcFYmIlE4i76D98EMYMyaMP//P/6w7YkWkcuR7B23iwn77dhg7Nlxt8+tfwyGJ/dtGRCqRwj4H\nO3fCuHFw/PFw770KehGpPAr7VuzbB3/7t9ClS7hhqkOHdvlaEZGi0kBorbj55tBXP22agl5EkicR\nYT91ahjjZtYsXXUjIslU9d04dXVw1VXwwgswcGBJv0pEpOTUjZPFihXh0YGPPqqgF5Fkq9rrUXbu\nhMsuC8+M/exn465GRCReVduN8/Wvw7Zt8Pvf66YpEake7d6NY2aTgXFAPbAGuMbdt0bLBgNTga5A\nAzDc3Xfn+11tNW0aPPsszJ+voBcRgQJa9mY2Gpjp7g1mdheAu08ys47APOAr7r7YzHoAW929Ics2\nit6yX7s2jHdTW6tnxopI9cm3ZZ93n72712UE+GygbzR9EbDI3RdH632QLehLYd++cEL2llsU9CIi\nmYp1gnYCUBtNnwK4mT1lZvPM7KYifUerfvUr6NgRbrihvb5RRKQytNhnb2Z1QLbnNt3q7tOjdW4D\n6t39wYxtng+cBewEZprZPHf/U7bvqKmp+Xg6lUqRSqXauAvB+vVwxx3w4osa80ZEqkc6nSadThe8\nnYKuxjGz8cC1wCh33xXNuxy4xN3HR+9vB3a5+z9l+XxR+uzdwwBn554Lt99e8OZERMpWu/fZm9kY\n4Cbgc41BH3kaOMPMOkcna0cCS/P9nlz8x3+Elv3NN5fyW0REKlchV+OsAjoB70ezZrn7xGjZlcAt\ngAN/dPdJzWyj4Jb9jh1wyinwyCNw3nkFbUpEpOwldojjO++EJUtC615EpNolMuzfegsGDYK5c6F/\n/yIWJiJSphIZ9tdfD127wj8ddOpXRKQ6JW7Uy+XL4Q9/gNdei7sSEZHyV7FXpP/DP4Sbp3r0iLsS\nEZHyV5HdOGvWhPFv1qyBbt1KUJiISJlq9+vs4/Szn8E3vqGgFxHJVcW17DdsgCFDYOVKOProEhUm\nIlKmEtOynzIFrr5aQS8i0hYV1bLfuROOPx5mzYIBA0pYmIhImUpEy/7hh2H4cAW9iEhbVUzYu8M9\n98A3vxl3JSIiladiwn7OHHj/fRgzJu5KREQqT8WE/W9+AxMmQIcOcVciIlJ5KuIEbX099OkTBjw7\n8cTS1yUiUq6q+gRtbW0Y3VJBLyKSn4oI+wcegKuuirsKEZHKVfbdONu2Qb9+8MYb0L17OxUmIlKm\nqrYbp7YWzj9fQS8iUoiyD/snnoDPfz7uKkREKlshDxyfDIwD6oE1wDXuvtXMTgSWAyuiVT9+EHmW\nbbTYjbN7N/TqFR5QcswxeZUpIlJV4ujGeQYY5O5DgJXALRnLVrv7sOiVNehzMXMmnHGGgl5EpFB5\nh72717l7Q/R2NtC3OCXtN2MG/M3fFHurIiLJU6w++wlAbcb7/mb2qpmlzez8fDf69NNw8cWFFyci\nknQtPnDczOqAXlkW3eru06N1bgPq3f3BaNkmoJ+7f2BmnwaeMLNB7v5htu+oqan5eDqVSpFKpQBY\nuzZcdjl4cNt2SESkmqTTadLpdMHbKeg6ezMbD1wLjHL3Xc2s8xzwfXefn2VZsydop06FF18MN1SJ\niEjQ7idozWwMcBPwucygN7OjzaxDNH0SMBB4va3bf/ZZGD063+pERCRTIZdergI6Ae9Hs2a5+0Qz\n+wJwB7AHaAB+5O5/bGYbWVv27uGSy1degRNOyKs8EZGqlG/LviyHS1i5Ei68ENavj6EoEZEyVlXD\nJbzwAlxwQdxViIhUD4W9iEgClGXYv/wynHde3FWIiFSPsuuz37oVjjsOtmyBji3eBSAikjxV02c/\nbx4MHaqgFxEpprIL+zlzYPjwuKsQEakuZRf2c+cq7EVEiq3swn7hwtCNIyIixVNWJ2i3b4dPfjIM\ngKY+exGRg1XFCdolS+C00xT0IiLFVlZhv2iRhjQWESmFsgr7pUth0KC4qxARqT5lFfYrVsDpp8dd\nhYhI9VHYi4gkQNlcjbNjBxx1FHz0EXToEFtJIiJlreKvxlm5Ek4+WUEvIlIKZRP2a9bAwIFxVyEi\nUp3KKuxPOinuKkREqlNZhf3JJ8ddhYhIdco77M1sspktN7OFZva4mXVrsvx4M/vIzL6fy/YU9iIi\npVNIy/4ZYJC7DwFWArc0Wf4L4I+5bmztWujfv4BqRESkWXmHvbvXuXtD9HY20LdxmZn9L+B1YFku\n22pogI0boV+/fKsREZGWFKvPfgJQC2BmRwI3AzW5fnjzZujeHTp3LlI1IiJygBbHlzSzOqBXlkW3\nuvv0aJ3bgHp3fzBaVgP80t13mFmrF/7X1NSwcWO4vj6dTpFKpdq0AyIi1SydTpNOpwveTkF30JrZ\neOBaYJS774rmPQ80dsh0BxqA/+3uv8ryeXd3pk2Dhx+Gxx7LuxQRkUTI9w7avEeON7MxwE3AyMag\nB3D3z2as82Pgw2xBn+nNN6Fv35bWEBGRQhTSZz8FOBKoM7NXzazFQG/Jm29Cnz4FVCIiIi3Ku2Xv\n7q0ObuDud+SyrU2b9NASEZFSKos7aDdtguOOi7sKEZHqVTZh37t33FWIiFSvsgj7zZvh2GPjrkJE\npHrFHva7doUHl/ToEXclIiLVK/awf+cdOOYYaP32KxERyVfsYb95cwh7EREpndjDvrFlLyIipRN7\n2L/7bnjQuIiIlE7sYf/ee3D00XFXISJS3WIP+3ffVdiLiJRaWYR9z55xVyEiUt1iD/sPPlDYi4iU\nmsJeRCQByiLsdfesiEhpKexFRBIg9rDfsiU8bFxEREqnoGfQFvzlZt6xo7N9O3TqFFsZIiIVI99n\n0Mbesu/YUUEvIlJqsYd9t25xVyAiUv3yDnszm2xmy81soZk9bmbdovkjogeQv2pmi8zs8pa284lP\n5FuBiIjkqpCW/TPAIHcfAqwEbonmLwbOdPdhwEXAPWbWobmNKOxFREov77B39zp3b4jezgb6RvN3\nZszvDGx1933Nbadr13wrEBGRXBWrz34CUNv4JurKWQosBb7X0gePPLJIFYiISLM6trTQzOqAXlkW\n3eru06N1bgPq3f3BxoXu/gowyMxOA54ys7S7b832HevW1VBTE6ZTqRSpVCqP3RARqU7pdJp0Ol3w\ndgq6zt7MxgPXAqPcfVcz68wEbnb3eVmW+XXXOVOn5l2CiEiitPt19mY2BrgJ+Fxm0JvZiWbWMZo+\nARgIrGpuO1265FuBiIjkqsVunFZMAToBdWYGMMvdJwLnA5PMbA+wB7jO3bc1txH12YuIlF7eYe/u\nA5uZ/zvgd7luRy17EZHSi/0OWoW9iEjpKexFRBIg9rA/4oi4KxARqX6xh33nznFXICJS/WIPe7Xs\nRURKL/awV8teRKT0FPYiIgkQe9gffnjcFYiIVL/Yw14texGR0os97NWyFxEpPYW9iEgCxB72hx0W\ndwUiItVPYS8ikgCxh32HZh9FLiIixRJ72IuISOkp7EVEEkBhLyKSAAp7EZEEKCjszWyymS03s4Vm\n9riZdYvmjzazuWa2KPr5V8UpV0RE8lFoy/4ZYJC7DwFWArdE898Bxrn7YOBq4IECv0dERApQUNi7\ne527N0RvZwN9o/kL3P2taP4yoLOZHVrId4mISP6K2Wc/AajNMv8LwDx331PE7xIRkTbo2NoKZlYH\n9Mqy6FZ3nx6tcxtQ7+4PNvnsIOAuYHQRahURkTy1Gvbu3mJQm9l4YCwwqsn8vsDjwFXuvra5z9fU\n1Hw8nUqlSKVSrZUkIpIY6XSadDpd8HbM3fP/sNkY4OfASHd/N2N+d+DPwI/d/YkWPu+FfL+ISNKY\nGe5ubf5cgWG/CugEvB/NmuXuE83sdmASsCpj9dGZvxCizyvsRUTaIJawL5TCXkSkbfINe91BKyKS\nAAp7EZEEUNiLiCSAwl5EJAEU9iIiCaCwFxFJAIW9iEgCKOxFRBJAYS8ikgAKexGRBFDYi4gkgMJe\nRCQBFPYiIgmgsBcRSQCFvYhIAijsRUQSQGEvIpIACnsRkQRQ2IuIJEBBYW9mk81suZktNLPHzaxb\nNL+nmT1nZh+a2ZTilCoiIvkqtGX/DDDI3YcAK4Fbovm7gNuBHxS4/YqVTqfjLqGktH+VTfuXPAWF\nvbvXuXtD9HY20Deav8PdXwJ2F1hfxar2f2zav8qm/UueYvbZTwBqm8zzIm5fRETy1LG1FcysDuiV\nZdGt7j49Wuc2oN7dHyxyfSIiUgTmXljj28zGA9cCo9x9V5NlVwNnufu3m/msWv4iIm3k7tbWz7Ta\nsm+JmY0BbgJGNg36xlVa+nw+BYuISNsV1LI3s1VAJ+D9aNYsd58YLVsHdI2WfwBc5O4rCqpWRETy\nUnA3joiIlL+S30FrZmPMbIWZrTKzHzazzv+Nli80s2GlrqmYWts/M0uZ2VYzezV63R5Hnfkws/vM\nbLOZLW5hnUo+di3uXyUfOwAz6xfd3LjUzJaY2XeaWa/ijmEu+1bJx8/MDjez2Wa2wMyWmdlPm1kv\n92Pn7iV7AR2A1cCJwKHAAuD0JuuMBWqj6bOBl0tZUwz7lwKejLvWPPfvAmAYsLiZ5RV77HLcv4o9\ndlH9vYCh0fSRwGvV8v9fjvtW6cfviOhnR+Bl4PxCjl2pW/YjgNXuvs7d9wAPA59rss6lwG8B3H02\n0N3Mji1xXcWSy/5BKyeqy5W7v0A439KcSj52uewfVOixA3D3t9x9QTT9EbAc6NNktYo8hjnuG1T2\n8dsRTXYiNCzfb7JKm45dqcP+OGBDxvuN0bzW1ulb4rqKJZf9c+C86M+sWjP7VLtVV3qVfOxyUTXH\nzsxOJPwVM7vJooo/hi3sW0UfPzM7xMwWAJuB59x9WZNV2nTsCrr0Mge5nv1t+tu3Us4a51LnfKCf\nu+8ws0uAJ4BTSltWu6rUY5eLqjh2ZnYk8ChwQ9QKPmiVJu8r5hi2sm8Vffw8DEUzNBpg8mkzS7l7\nuslqOR+7Urfs3wT6ZbzvR/jt09I6faN5laDV/XP3Dxv/HHP3GcChZtaz/UosqUo+dq2qhmNnZocC\njwG/c/cnsqxSscewtX2rhuMH4O5bgT8CZzVZ1KZjV+qwnwsMNLMTzawTcDnwZJN1ngS+CmBm5wBb\n3H1ziesqllb3z8yONTOLpkcQLndt2vdWqSr52LWq0o9dVPu9wDJ3v7uZ1SryGOayb5V8/MzsaDPr\nHk13BkYDrzZZrU3HrqTdOO6+18y+BTxNOMFwr7svN7Pro+VT3b3WzMaa2WpgO3BNKWsqplz2D/gi\n8A0z2wvsAL4UW8FtZGYPASOBo81sA/BjwlVHFX/soPX9o4KPXeQzwFeARWbWGBS3AsdDxR/DVveN\nyj5+vYHfmtkhhEb5A+4+s5Ds1E1VIiIJoMcSiogkgMJeRCQBFPYiIgmgsBcRSQCFvYhIkeUyiGDG\nup81s/lmtsfMvtBk2dVmtjJ6fbWQmhT2IiLFdz8wJsd13wCuBg54rGt0A9iPCGNwjQB+3HjtfT4U\n9lLxzGxfNITtkmhI2O9l3Exzppn9nxY+e4KZXdF+1UoSZBtkz8xONrMZZjbXzJ43s1Ojdd9w98VA\nQ5PNXAw84+5b3H0LUEfuv0AOUuqxcUTaww53HwZgZp8ktJA+AdS4+zxgXguf7Q98GXio5FVK0v0/\n4Hp3X21mZwO/Aka1sH4fDhx+JdtAizlTy16qiru/A1wHfAs+foDF9Gh6ZMaDLOZFg2jdBVwQzbsh\nauk/Hy2fZ2bnZmwnbWbTzGy5mf2u8TvNbLiZvRT9VTHbzLqYWQczm2xmr0SjLl7X/v81pFxE/9bO\nBaZFd/z+mjAmf7tRy16qjruvjcL2k00WfR+Y6O6zzOwIYDfwQ+AH7v4/Yf84JO6+28wGEv5KGB59\nfijwKeAvwEtmdh5hfKSHgb9z98ZfILuArxHGKhlhZocBL5rZM+6+rpT7LmXrEMK/h9aeBJY5pMGb\nhAewNOoH/KmQAkSS4iXgl2b2baCHu+/j4CFiOwH/ZmaLgEeA0zOWveLumzyMMbKA0AV0KvCXqLsI\nd/8o2u5FwFejVtzLQE9gQAn3TcqYu28D1prZFyEM5GZmg5usZhz47/Fp4CIz625mPQiDoT2dbw0K\ne6k6ZnYSsC/q0vmYu/+M0OLuTGiZn5rl4zcSwnswYUjZwzKW7c6Y3kf4y7ilwaW+5e7DotfJ7v5s\nHrsjFSgaZO+/gVPNbIOZXQNcCXzNwgNJlhCeNNXYDbiBMHDb1MbLNd39A+BOYA7wCnBHdKI2L+rG\nkaoSdd38GpiSZdnJ7r4UWGpmwwmt8o1A14zVPsH+k2JfJYxm2hwnPPu0t5md5e5zzawrYYTFp4GJ\nZvZcNDrqKcDGjEfNSRVz9+au8Loky7pzOHBc+sxl9xMu4yyYwl6qQeeou+RQYC/w7+7+i2iZs7/1\nfYOZ/RXhErclwIxo2b6otXU/4QqJx6IbWJ4CMp9+dFAr3t33mNnlwJSov38HcCHwb4QH0c+PLgN9\nG/h88XZZpG00xLGISAKoz15EJAEU9iIiCaCwFxFJAIW9iEgCKOxFRBJAYS8ikgAKexGRBFDYi4gk\nwP8HijnxelEcyKoAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10d190210>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cepheid_distances = distance(cepheid_apparent, cepheid_absolute)\n",
"\n",
"pl.plot(cepheid_distances, cepheid_absolute)\n",
"pl.gca().invert_yaxis()\n",
"pl.xlabel('Distance')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Let's define some classes."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# BIG"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###### small\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Hello everbody!Bye\n"
]
}
],
"source": [
"class A(object):\n",
" def __init__(self):\n",
" self.x = 'Hello'\n",
"\n",
" def method_a(self, y,z):\n",
" print self.x + ' ' + y + z\n",
" \n",
"a = A()\n",
"a.method_a('everbody!', 'Bye')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Type"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"ndksnvanskncklansvjkdsvkl\n"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1e+12\n",
"6.66666666667e+11\n"
]
}
],
"source": [
"class Galaxy:\n",
" def __init__(self, sfr, mass):\n",
" self.sfr = sfr\n",
" self.mass = mass\n",
"\n",
"gal1 = Galaxy(1.0, 1e12)\n",
"gal2 = Galaxy(3.0, 2e12)\n",
"\n",
"def some_operation(gal):\n",
" return gal.mass / gal.sfr\n",
"\n",
"print some_operation(gal1)\n",
"print some_operation(gal2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| unlicense |
BL-Labs/meetingsparser | refining add_meetingdays_to_csv.py.ipynb | 1 | 1448 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"refining add_meetingdays_to_csv.py\n",
"\n",
"currently, the code does 1 and 3 of the following:\n",
"\n",
"1 - a single match is found (ie one of the day matches) = daysfound.csv\n",
"2 - more than one match is found \n",
"3 - no matches are found = unmatched.csv\n",
"\n",
"\n",
"step 2 - \n",
"\n",
"- for each matching word, estimate the date it suggests\n",
"- compare all the dates\n",
"\n",
"step 3 - \n",
"This creates further decisions:\n",
"\n",
"- what to do if all the dates agree? (easy answer) = \n",
"keep as one item? \n",
"\n",
"- what to do if they are all different? (likely a tour) = \n",
"separate into another file called tours? or change the ItemType to 'Tour'?\n",
"\n",
"- what to do if they *mostly* agree? (tricky...) = \n",
"separate into another file for next round of deciding what to do with them."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
ritviksahajpal/open-geo-tutorial | Python/chapters/chapter_4_vector.ipynb | 1 | 26535 | {
"metadata": {
"name": "",
"signature": "sha256:683dcbf6525dd1cdbe96018dfbbf480acfcf12a98c5778118768bbb97a3793ac"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Chris Holden ([email protected]) - https://github.com/ceholden\n",
"\n",
"Chapter 4: Importing and using vector data -- the OGR library\n",
"=================================================="
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction\n",
"\n",
"The *OGR* library is a companion library to *GDAL* that handles vector data capabilities, including information queryies, file conversions, rasterization of polygon features, polygonization of raster features, and much more. It handles popular formats including the *ESRI Shapefile*, *Keyhole Markup Language*, *PostGIS*, and *SpatiaLite*. For more information on how *OGR* came about and how it relates to *GDAL*, see here: http://trac.osgeo.org/gdal/wiki/FAQGeneral#WhatisthisOGRstuff.\n",
"\n",
"The authors of *GDAL*/*OGR* provide a tutorial for the *OGR* library [here](http://www.gdal.org/ogr_apitut.html).\n",
"\n",
"> Note: As of 08/12/2014, the API used in this tutorial seems to be ahead of the current 1.11.0 release. Specifically, they demonstrate how to open a vector file using `gdal.OpenEx`, which is a change designed to unify the *GDAL* and *OGR* sections of the library.\n",
" \n",
"> A clone of the *GDAL 1.9* API tutorial can be found [here](http://www.compsci.wm.edu/SciClone/documentation/software/geo/gdal-1.9.0/html/ogr/ogr_apitut.html)\n",
"\n",
"In this chapter we will use an *ESRI Shapefile* that contains training data I collected in QGIS for the example image we've been working on.\n",
"\n",
"## Opening an *ESRI Shapefile*\n",
"\n",
"Just like *GDAL*, *OGR* abstracts the file formats so that we can use the same code for any format. It employs the same concept of a *dataset* object which we can gather information from:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Import Python 3 print function\n",
"from __future__ import print_function\n",
"\n",
"# Import OGR - \n",
"from osgeo import ogr\n",
"\n",
"# Open the dataset from the file\n",
"dataset = ogr.Open('../example/training_data.shp')\n",
"# Make sure the dataset exists -- it would be None if we couldn't open it\n",
"if not dataset:\n",
" print('Error: could not open dataset')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With our Shapefile read in, we can look at some of its properties:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"### Let's get the driver from this file\n",
"driver = dataset.GetDriver()\n",
"print('Dataset driver is: {n}\\n'.format(n=driver.name))\n",
"\n",
"### How many layers are contained in this Shapefile?\n",
"layer_count = dataset.GetLayerCount()\n",
"print('The shapefile has {n} layer(s)\\n'.format(n=layer_count))\n",
"\n",
"### What is the name of the 1 layer?\n",
"layer = dataset.GetLayerByIndex(0)\n",
"print('The layer is named: {n}\\n'.format(n=layer.GetName()))\n",
"\n",
"### What is the layer's geometry? is it a point? a polyline? a polygon?\n",
"# First read in the geometry - but this is the enumerated type's value\n",
"geometry = layer.GetGeomType()\n",
"\n",
"# So we need to translate it to the name of the enum\n",
"geometry_name = ogr.GeometryTypeToName(geometry)\n",
"print(\"The layer's geometry is: {geom}\\n\".format(geom=geometry_name))\n",
"\n",
"### What is the layer's projection?\n",
"# Get the spatial reference\n",
"spatial_ref = layer.GetSpatialRef()\n",
"\n",
"# Export this spatial reference to something we can read... like the Proj4\n",
"proj4 = spatial_ref.ExportToProj4()\n",
"print('Layer projection is: {proj4}\\n'.format(proj4=proj4))\n",
"\n",
"### How many features are in the layer?\n",
"feature_count = layer.GetFeatureCount()\n",
"print('Layer has {n} features\\n'.format(n=feature_count))\n",
"\n",
"### How many fields are in the shapefile, and what are their names?\n",
"# First we need to capture the layer definition\n",
"defn = layer.GetLayerDefn()\n",
"\n",
"# How many fields\n",
"field_count = defn.GetFieldCount()\n",
"print('Layer has {n} fields'.format(n=field_count))\n",
"\n",
"# What are their names?\n",
"print('Their names are: ')\n",
"for i in range(field_count):\n",
" field_defn = defn.GetFieldDefn(i)\n",
" print('\\t{name} - {datatype}'.format(name=field_defn.GetName(),\n",
" datatype=field_defn.GetTypeName()))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Dataset driver is: ESRI Shapefile\n",
"\n",
"The shapefile has 1 layer(s)\n",
"\n",
"The layer is named: training_data\n",
"\n",
"The layer's geometry is: Polygon\n",
"\n",
"Layer projection is: +proj=utm +zone=15 +datum=WGS84 +units=m +no_defs \n",
"\n",
"Layer has 30 features\n",
"\n",
"Layer has 2 fields\n",
"Their names are: \n",
"\tid - Integer\n",
"\tclass - String\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The shapefile is already projected in the same projection that our example raster image is in, so we won't be needing to reproject it. You *could*, however, do so using either the [ogr2ogr](http://www.gdal.org/ogr2ogr.html) command line application, or by [reprojecting the shapefile in Python](http://pcjericks.github.io/py-gdalogr-cookbook/projection.html#reproject-a-layer).\n",
"\n",
"## Tie-in with our Raster dataset\n",
"\n",
"The training data we just opened contains two fields:\n",
"+ an ID field (Integer datatype)\n",
"+ a class field (String datatype)\n",
"\n",
"Combined with the innate location information of polygons in a Shapefile, fields resemble all that we need to use for pairing labels (i.e., the integer ID and the string description) with the information in our raster.\n",
"\n",
"However, in order to pair up our vector data with our raster pixels, we will need a way of co-aligning the datasets in space. \n",
"\n",
"One (complicated) way of doing this would be to manually loop through each polygon in our vector layer and determine which pixels from our raster are contained within. This approach is exactly what GIS softwares (e.g., ENVI, ArcGIS, QGIS) do when doing pairing rasters with vectors, like when doing zonal statistics.\n",
"\n",
"Another less complicated way would be to use the concept of a Region of Interest (ROI) image where each non-zero pixel value in our ROI image corresponds to a raster representation of a polygon from our vector layer. In the example of our training data, most of the values would be 0 in the rasterized representation because our training data samples are small compared to the entire study area. Because we have assigned an integer ID field to each polygon, we could use these integers to store information about which polygons belong to which pixels. In this case, I have assigned values ranging from 1 - 5 for the classes:\n",
"\n",
"+ 1 - forest\n",
"+ 2 - water\n",
"+ 3 - herbaceous\n",
"+ 4 - barren\n",
"+ 5 - urban\n",
"\n",
"To accomplish this rasterization of a vector layer, we could use the GDAL command line utility [gdal_rasterize](http://www.gdal.org/gdal_rasterize.html), but we can stick to pure Python by using the GDAL function [gdal.RasterizeLayer](http://gdal.org/gdal__alg_8h.html#adfe5e5d287d6c184aab03acbfa567cb1)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Note\n",
"> I can't seem to get the pure Python code to work 100% of the time across Python installations (e.g., it works on my desktop and notebook, but not on Wakari) and every code example on the web leads me to believe I'm doing it correctly.\n",
">\n",
"> Since I can't figure out why this is occurring - because Python just crashes - I will first provide the `gdal_rasterize` command line that we can use to get the same results\n",
">\n",
"> In the following example, I write \"%%bash\" on the first line to indicate that I am using the Bash shell (you could use any shell you prefer). If you really need to execute everything from Python, then you could use the same `gdal_rasterize` command by invoking the shell via the [subprocess](https://docs.python.org/2/library/subprocess.html) module."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Command line version -- gdal_rasterize"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note:\n",
"> If you're running this notebook using Wakari, then the GDAL utilities won't be in your PATH. I have one block of code which will append the location GDAL utilities are installed within to your PATH. The code is\n",
"\n",
" # First I need to check if GDAL command line utilities are available\n",
" command -v \"gdalinfo\" > /dev/null || { \n",
" echo \"I require GDAL command line utilities. Adding Wakari location to PATH just incase we're on Wakari:\"\n",
" export PATH=/opt/anaconda/envs/np18py27-1.9/bin/:$PATH\n",
" }"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First thing we need to do is to figure out what the spatial extent and the pixel size of our output raster. To do this, I will use [gdalinfo](http://www.gdal.org/gdalinfo.html):"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"# Remember -- \"%bash\" as seen above just indicates to the IPython notebook that I'm now writing in Bash\n",
"\n",
"# First I need to check if GDAL command line utilities are available\n",
"command -v \"gdalinfo\" > /dev/null || { \n",
" echo \"I require GDAL command line utilities. Adding Wakari location to PATH just incase we're on Wakari:\"\n",
" export PATH=/opt/anaconda/envs/np18py27-1.9/bin/:$PATH\n",
"}\n",
"\n",
"# Print out metadata about raster -- we include \"-proj4\" to print out the Proj4 projection string\n",
"gdalinfo -proj4 ../example/LE70220491999322EDC01_stack.gtif"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Driver: GTiff/GeoTIFF\n",
"Files: ../example/LE70220491999322EDC01_stack.gtif\n",
" ../example/LE70220491999322EDC01_stack.gtif.aux.xml\n",
"Size is 250, 250\n",
"Coordinate System is:\n",
"PROJCS[\"WGS 84 / UTM zone 15N\",\n",
" GEOGCS[\"WGS 84\",\n",
" DATUM[\"WGS_1984\",\n",
" SPHEROID[\"WGS 84\",6378137,298.257223563,\n",
" AUTHORITY[\"EPSG\",\"7030\"]],\n",
" AUTHORITY[\"EPSG\",\"6326\"]],\n",
" PRIMEM[\"Greenwich\",0],\n",
" UNIT[\"degree\",0.0174532925199433],\n",
" AUTHORITY[\"EPSG\",\"4326\"]],\n",
" PROJECTION[\"Transverse_Mercator\"],\n",
" PARAMETER[\"latitude_of_origin\",0],\n",
" PARAMETER[\"central_meridian\",-93],\n",
" PARAMETER[\"scale_factor\",0.9996],\n",
" PARAMETER[\"false_easting\",500000],\n",
" PARAMETER[\"false_northing\",0],\n",
" UNIT[\"metre\",1,\n",
" AUTHORITY[\"EPSG\",\"9001\"]],\n",
" AUTHORITY[\"EPSG\",\"32615\"]]\n",
"PROJ.4 string is:\n",
"'+proj=utm +zone=15 +datum=WGS84 +units=m +no_defs '\n",
"Origin = (462405.000000000000000,1741815.000000000000000)\n",
"Pixel Size = (30.000000000000000,-30.000000000000000)\n",
"Metadata:\n",
" AREA_OR_POINT=Area\n",
" Band_1=band 1 reflectance\n",
" Band_2=band 2 reflectance\n",
" Band_3=band 3 reflectance\n",
" Band_4=band 4 reflectance\n",
" Band_5=band 5 reflectance\n",
" Band_6=band 7 reflectance\n",
" Band_7=band 6 temperature\n",
" Band_8=Band 8\n",
"Image Structure Metadata:\n",
" INTERLEAVE=PIXEL\n",
"Corner Coordinates:\n",
"Upper Left ( 462405.000, 1741815.000) ( 93d21' 3.44\"W, 15d45'16.33\"N)\n",
"Lower Left ( 462405.000, 1734315.000) ( 93d21' 3.02\"W, 15d41'12.23\"N)\n",
"Upper Right ( 469905.000, 1741815.000) ( 93d16'51.39\"W, 15d45'16.69\"N)\n",
"Lower Right ( 469905.000, 1734315.000) ( 93d16'51.06\"W, 15d41'12.60\"N)\n",
"Center ( 466155.000, 1738065.000) ( 93d18'57.23\"W, 15d43'14.47\"N)\n",
"Band 1 Block=250x2 Type=Int16, ColorInterp=Gray\n",
" Description = band 1 reflectance\n",
" Min=198.000 Max=1810.000 \n",
" Minimum=198.000, Maximum=1810.000, Mean=439.016, StdDev=139.717\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=1810\n",
" STATISTICS_MEAN=439.015984\n",
" STATISTICS_MINIMUM=198\n",
" STATISTICS_STDDEV=139.7168287663\n",
"Band 2 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 2 reflectance\n",
" Min=315.000 Max=2294.000 \n",
" Minimum=315.000, Maximum=2294.000, Mean=661.543, StdDev=180.790\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=2294\n",
" STATISTICS_MEAN=661.54288\n",
" STATISTICS_MINIMUM=315\n",
" STATISTICS_STDDEV=180.78985343571\n",
"Band 3 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 3 reflectance\n",
" Min=160.000 Max=2820.000 \n",
" Minimum=160.000, Maximum=2820.000, Mean=589.380, StdDev=270.708\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=2820\n",
" STATISTICS_MEAN=589.379808\n",
" STATISTICS_MINIMUM=160\n",
" STATISTICS_STDDEV=270.70755024913\n",
"Band 4 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 4 reflectance\n",
" Min=1105.000 Max=5138.000 \n",
" Minimum=1105.000, Maximum=5138.000, Mean=3442.298, StdDev=461.059\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=5138\n",
" STATISTICS_MEAN=3442.297712\n",
" STATISTICS_MINIMUM=1105\n",
" STATISTICS_STDDEV=461.05944906873\n",
"Band 5 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 5 reflectance\n",
" Min=353.000 Max=4548.000 \n",
" Minimum=353.000, Maximum=4548.000, Mean=2181.929, StdDev=427.101\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=4548\n",
" STATISTICS_MEAN=2181.928672\n",
" STATISTICS_MINIMUM=353\n",
" STATISTICS_STDDEV=427.10099628111\n",
"Band 6 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 7 reflectance\n",
" Min=145.000 Max=3705.000 \n",
" Minimum=145.000, Maximum=3705.000, Mean=1049.994, StdDev=375.115\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=3705\n",
" STATISTICS_MEAN=1049.99384\n",
" STATISTICS_MINIMUM=145\n",
" STATISTICS_STDDEV=375.11543521702\n",
"Band 7 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Description = band 6 temperature\n",
" Min=2335.000 Max=3546.000 \n",
" Minimum=2335.000, Maximum=3546.000, Mean=2678.677, StdDev=158.668\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=3546\n",
" STATISTICS_MEAN=2678.677184\n",
" STATISTICS_MINIMUM=2335\n",
" STATISTICS_STDDEV=158.66755034924\n",
"Band 8 Block=250x2 Type=Int16, ColorInterp=Undefined\n",
" Min=0.000 Max=0.000 \n",
" Minimum=0.000, Maximum=0.000, Mean=0.000, StdDev=0.000\n",
" NoData Value=-9999\n",
" Metadata:\n",
" STATISTICS_MAXIMUM=0\n",
" STATISTICS_MEAN=0\n",
" STATISTICS_MINIMUM=0\n",
" STATISTICS_STDDEV=0\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Wow - how informative!\n",
"\n",
"We will use the information about the Upper Left and Lower Right coordinates:\n",
"\n",
"> Upper Left ( 462405.000, 1741815.000) ( 93d21' 3.44\"W, 15d45'16.33\"N)\n",
"\n",
"> Lower Right ( 469905.000, 1734315.000) ( 93d16'51.06\"W, 15d41'12.60\"N)\n",
"\n",
"This tells us that our Upper Left X/Y and Lower Right X/Y are \"462405, 1741815, 469905, 1734315\". We can also see that our Landsat pixels are 30x30m.\n",
"\n",
"The projection is UTM15N, and the projection string is `'+proj=utm +zone=15 +datum=WGS84 +units=m +no_defs '`\n",
"\n",
"We will need this information for `gdal_rasterize`. We can print the usage of `gdal_rasterize` as follows:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"\n",
"# First I need to check if GDAL command line utilities are available\n",
"command -v \"gdalinfo\" > /dev/null || { \n",
" echo \"I require GDAL command line utilities. Adding Wakari location to PATH just incase we're on Wakari:\"\n",
" export PATH=/opt/anaconda/envs/np18py27-1.9/bin/:$PATH\n",
"}\n",
"\n",
"# Print out the usage\n",
"gdal_rasterize --help"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Usage: gdal_rasterize [-b band]* [-i] [-at]\n",
" [-burn value]* | [-a attribute_name] [-3d]\n",
" [-l layername]* [-where expression] [-sql select_statement]\n",
" [-of format] [-a_srs srs_def] [-co \"NAME=VALUE\"]*\n",
" [-a_nodata value] [-init value]*\n",
" [-te xmin ymin xmax ymax] [-tr xres yres] [-tap] [-ts width height]\n",
" [-ot {Byte/Int16/UInt16/UInt32/Int32/Float32/Float64/\n",
" CInt16/CInt32/CFloat32/CFloat64}] [-q]\n",
" <src_datasource> <dst_filename>\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Missing source or destination.\n",
"\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For better descriptions, see the documentation page [here](http://www.gdal.org/gdal_rasterize.html).\n",
"\n",
"Now let's run the command -- note that we need to rearrange the Upper Left and Lower Right X/Y pairs to be in the \"xmin ymin xmax ymax\":"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"\n",
"# First I need to check if GDAL command line utilities are available\n",
"command -v \"gdalinfo\" > /dev/null || { \n",
" echo \"I require GDAL command line utilities. Adding Wakari location to PATH just incase we're on Wakari:\"\n",
" export PATH=/opt/anaconda/envs/np18py27-1.9/bin/:$PATH\n",
"}\n",
"\n",
"# Explanation of switches:\n",
"# -a ==> write values from the\"id\" attribute of the shapefile\n",
"# -layer ==> the layer name of our shapefile\n",
"# -of ==> Output raster file format\n",
"# -a_srs ==> output spatial reference system string\n",
"# -a_nodata ==> NODATA value for output raster\n",
"# -te ==> target extent which matches the raster we want to create the ROI image for\n",
"# -tr ==> target resolution, 30 x 30m\n",
"# -ot Byte ==> Since we only have values 0 - 5, a Byte datatype is enough\n",
"\n",
"gdal_rasterize -a \"id\" \\\n",
" -l training_data \\\n",
" -of \"GTiff\" \\\n",
" -a_srs \"+proj=utm +zone=15 +datum=WGS84 +units=m +no_defs\" \\\n",
" -a_nodata 0 \\\n",
" -te 462405 1734315 469905 1741815 \\\n",
" -tr 30 30 \\\n",
" -ot Byte \\\n",
" ../example/training_data.shp ../example/training_data.gtif"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0...10...20...30...40...50...60...70...80...90...100 - done.\n"
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In a lot of ways the command line version is easier than programming it using the Python bindings to GDAL's API. Continue on for an example using this second method:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Pure Python version -- gdal.RasterizeLayer"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Import GDAL\n",
"from osgeo import gdal\n",
"\n",
"# First we will open our raster image, to understand how we will want to rasterize our vector\n",
"raster_ds = gdal.Open('../example/LE70220491999322EDC01_stack.gtif', gdal.GA_ReadOnly)\n",
"\n",
"# Fetch number of rows and columns\n",
"ncol = raster_ds.RasterXSize\n",
"nrow = raster_ds.RasterYSize\n",
"\n",
"# Fetch projection and extent\n",
"proj = raster_ds.GetProjectionRef()\n",
"ext = raster_ds.GetGeoTransform()\n",
"\n",
"raster_ds = None\n",
"\n",
"# Create the raster dataset\n",
"memory_driver = gdal.GetDriverByName('GTiff')\n",
"out_raster_ds = memory_driver.Create('../example/training_data.gtif', ncol, nrow, 1, gdal.GDT_Byte)\n",
"\n",
"# Set the ROI image's projection and extent to our input raster's projection and extent\n",
"out_raster_ds.SetProjection(proj)\n",
"out_raster_ds.SetGeoTransform(ext)\n",
"\n",
"# Fill our output band with the 0 blank, no class label, value\n",
"b = out_raster_ds.GetRasterBand(1)\n",
"b.Fill(0)\n",
"\n",
"# Rasterize the shapefile layer to our new dataset\n",
"status = gdal.RasterizeLayer(out_raster_ds, # output to our new dataset\n",
" [1], # output to our new dataset's first band\n",
" layer, # rasterize this layer\n",
" None, None, # don't worry about transformations since we're in same projection\n",
" [0], # burn value 0\n",
" ['ALL_TOUCHED=TRUE', # rasterize all pixels touched by polygons\n",
" 'ATTRIBUTE=id'] # put raster values according to the 'id' field values\n",
" )\n",
"\n",
"# Close dataset\n",
"out_raster_ds = None\n",
"\n",
"if status != 0:\n",
" print(\"I don't think it worked...\")\n",
"else:\n",
" print(\"Success\")"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Success\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we have **a** working method, we can check how many pixels of training data we collected:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Check rasterized layer"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Import NumPy for some statistics\n",
"import numpy as np\n",
"\n",
"roi_ds = gdal.Open('../example/training_data.gtif', gdal.GA_ReadOnly)\n",
"\n",
"roi = roi_ds.GetRasterBand(1).ReadAsArray()\n",
"\n",
"# How many pixels are in each class?\n",
"classes = np.unique(roi)\n",
"for c in classes:\n",
" print('Class {c} contains {n} pixels'.format(c=c,\n",
" n=(roi == c).sum()))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Class 0 contains 61782 pixels\n",
"Class 1 contains 270 pixels\n",
"Class 2 contains 129 pixels\n",
"Class 3 contains 145 pixels\n",
"Class 4 contains 106 pixels\n",
"Class 5 contains 68 pixels\n"
]
}
],
"prompt_number": 34
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Wrapup\n",
"\n",
"Now that we have our ROI image, we can proceed to use it for pairing our labeled polygons with the matching pixels in our Landsat image to train a classifier for image classification. We continue this step in the [next chapter](chapter_6_classification.ipynb)."
]
}
],
"metadata": {}
}
]
} | gpl-2.0 |
kgourgou/stochastic-simulations-class | ipython_notebooks/langevin.ipynb | 1 | 541386 | {
"cells": [
{
"cell_type": "raw",
"metadata": {},
"source": [
"<script>\n",
" function code_toggle() {\n",
" if (code_shown){\n",
" $('div.input').hide('500');\n",
" $('#toggleButton').val('Show Code')\n",
" } else {\n",
" $('div.input').show('500');\n",
" $('#toggleButton').val('Hide Code')\n",
" }\n",
" code_shown = !code_shown\n",
" }\n",
"\n",
" $( document ).ready(function(){\n",
" code_shown=false;\n",
" $('div.input').hide()\n",
" });\n",
"</script>\n",
"<form action=\"javascript:code_toggle()\"><input type=\"submit\" id=\"toggleButton\" value=\"Show Code\"></form>"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/kostis/anaconda/lib/python2.7/site-packages/matplotlib/__init__.py:872: UserWarning: axes.color_cycle is deprecated and replaced with axes.prop_cycle; please use the latter.\n",
" warnings.warn(self.msg_depr % (key, alt_key))\n"
]
}
],
"source": [
"# Importing some python libraries.\n",
"import numpy as np\n",
"from numpy.random import randn\n",
"import matplotlib.pyplot as pl\n",
"import seaborn as sns\n",
"%matplotlib inline\n",
"# Fixing figure sizes\n",
"from pylab import rcParams\n",
"rcParams['figure.figsize'] = 10,5\n",
"\n",
"import sympy as sp\n",
"\n",
"pale_red = sns.xkcd_rgb['pale red'] \n",
"denim_blue = sns.xkcd_rgb['denim blue']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Overdamped Langevin Equation\n",
"\n",
"The overdamped Langevin equation is defined as\n",
"\n",
"$$\n",
"dX_t=-\\nabla U(x)dt+\\sigma dB_t,\n",
"$$\n",
"for some potential $U$. $B_t$ represents Brownian motion and $\\sigma$ controls the \"strength\" of the random variations. \n",
"\n",
"In this example, we will work with a specific potential \n",
"\n",
"$$\n",
"U(x)=(b-a/2)(x^2-1)^2+a/2\\cdot (x+1).\n",
"$$\n",
"\n",
"This is a double-well potential, as can be seen in the following plot."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff75ac02290>"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlUAAAFMCAYAAADiN0l8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XecVNXdx/HPnbqVIi4i0mwcKSKgAiICItbEkhhLTNQY\nNSaP8YmJiTFNY0liYqIpTzTRGDUmxpZmVwzSUUABFfVaEGkKiMDW6ff54w66uzPbZmfv7M5+368X\nr2HPbb89O+U355x7juU4DiIiIiLSOb5CByAiIiJSDJRUiYiIiOSBkioRERGRPFBSJSIiIpIHSqpE\nRERE8kBJlYiIiEgeKKkSERERyQMlVSLSJmNMoNAxiIh0d0qqpN2MMXcbY1LGmIGFjqWnM8bcZYxJ\nGmOG5Xj87r9FTsd38FqfA77YieN/bIwZn8eQWrtWu+pVz+XiY4xZZ4xZW+g4pHfTt89eyhhzDXBN\nO3efZ9v2LMBJ/+vxjDE/AO61bXt9ga73O+BRYGuOp2zX38IYMxn4CTAO2BPYBqwB7rBt++/pfc4B\nrgZGAjFgBXCJbdtrjDGzgGm2bV+eY5wAPwMeNcZcYtv2u504T3tkrdcs9V80z2UvGGPKgKW2bR9S\n6Fha0a6/pzHmKOBmYBjwrG3bX+jSqFqOoyfUqXSQkqre6wHglWZl1wGjgIuAXY3Kt3kVlBeMMSOA\n64GFQJcnVdmuZ9v2S8BLXX1t27ZfAGYbY/4AXAzMtm37lWb73AfcZ4x5FTjFtu216bj7ADcC0zsZ\nQ9QY8z/AvcaYo2zb7rJkJlu9ev33LjbGmMOA24CxhY4lH2zbXphOrGqA5wsRQ7HVqXxCSVUvZdv2\nG8AbjcuMMZfhJlWP27adawtKTzAJb1spvL5eNkcD25onVLsZY0qANbsTqrTvA3+1bTvS2Yvbtv22\nMWY9cA7wt86er4O6Q/33OMaYg4Bf4rb6JQocTr5NxB3+ssDLixZ5nQpKqiQ3ljHme7gtH/sAm4Df\n2bZ9S+OdjDEDcLsYTwYGA9XAYuCntm0va+sixpi7gfOA8cAZwLnAIGAjcKtt2zc3238w8GPg+PR+\nNcALwM9s216U3uc5YAbuh+w8Y4wD7Gvb9vr2xtsorqG4Y40uBoYAHwL3AD/c3RrT0vVwWwXPA0Y0\n7oI0xhwOfBe3dagv8H76d/iRbdtvtlVnLdTjIOBA4MFWdjsSWNLomLL073VALtdswW+AP9NGUmWM\n2YSbAI5vVr4GN+n/lG3bTzYqPxu4D/dvcRyN6rWV+t+tXc/l3ij9xevT4I5Vw01O2629z+WOvJ7S\n+x8D/BQ4GKgHngG+1cFfbzqw07bt1R08rlM6W6fS/WmguuTieuAY3LEyXwdSwC/Tb3YAGGP64Tat\nfxH4O/Bl4CbgEGCBMWZmO66ze9zLTbgf+jcCXwO2p6/38RupMWYvYDluS8iDuF2YPwcMMNcYc1x6\n16uBh9L/vwY3WdvawXh3x/VT4LO44zMuA7YA30vXyW7Nr/c53O7UjDE9xphDgHnAYelznw/8CZgN\nPG+M2acddZbN0enH+W3s81yjnz8FvGvb9o4cr5nNcmAfY8yYNvZ7BhhrjOm7uyA9oHwUbqLcvDvy\naNzn4DNk1mtL9b9bm89l6bgOPpfb/XoyxhwKPA6MAG4Avo375ecZINSBEGfgdgeL5JVaqqSjLGAf\n27Zn7y4wxrwMLAXOBv6bLr4a943vCNu2VzTa917gNeAWYEI7rzcImGDbdip9jn8A64CrcN+AwW2h\nGgR83rbtj1tkjDH3A3b6emPS4ylmpTfPt217QXq/n3YwXgt3PMRk27YT6X2fBt4FTscdME0r18v2\nu47F/SZ/9e6WtfS+W4E/4H4w/bStCsviaNwPreda2ecQ27Z/2OjnY2nUctWcMWYibgLqAMNxWxcu\nAfrhtvhc3XxQum3bKWPMUuAE3MHyLZmD23IxDfcDFGAmEMdNkJonVTOA1bZtf9i8Xtuo//Y+l1uV\nPv/XgHeA/rhdSpfYtt2psWg9XEefy+16PQE/AILAmbZt7/6ScLcx5oe4rb/r2grMGOPH/ZJ2jzHm\npvS1xwGX27b9Wk6/rUiakirpKAf4bbOyl9OPgxuVnQm8DrzVuMUBaMD90Pm0MaavbduNB8S3dL07\ndydUALZtVxtj/gt81hgzxrbtNcBpwA4+aZXYve8GY8yzwKeMMfu2cvdZR+N1cLuJPh4Xke5u2grs\n3cbvlJVt23+jUdeYMaYC8APvpYtG5HJe3IRka7rrIYMxphyoa1Y8Abi9hf0PAM63bfsb6Z/vwm3l\nOx+39Xsh7mDxbF1oa3C7c1vzbPpxOp8kVUfj3lgxD/iiMabEtu1IumtzJG5LU0e197ncImPMhelr\nH5p+rg0G3sRN5Fs65k7cMT3tGedlpfe7fHdC2BPk8Fxu7+tpFrClUUK12x9wk6r2mAhU4HY3nm7b\ndtIY803gYWB08517w99L8kdJleTincY/2LbdkP7mXwof3zU2GPfNMFv30e43p2Fk3oGYTbZvj5vT\nj8ONMRuBvYDFLdxZZuN2Z43E/ebbRCfizTYnTgT3m3RO0nfJXYzbbVnSLIYOv17TH/IHAPe3sts0\nYFGzshHAzhb2vxz4TqOfy4GPbNt+3hgzBPgVcHcLx+4AprYWs23bW40xrwBHNSo+GngCN8ENpc8x\nF/dD1sHt/slFq8/l1qS7uG7DTTA3pI/fbIzZQSutgrZtX5hjrD1KDs/lVl9Pxpg9gD58kvh+LN1K\nub2doc0APgLOsm07mS5b517CjLJt+/Vm5+4Vfy/JDyVVkotYG9sr04+rgW/gfnvLZl07r1ebpaw6\n/RjG/dYJma0tuzWkH8tb2J5rvJ2+K64xY8z1uN0br+EOvH0HiOJ+e741x9O2dzzVX5uV9aXlpOrn\ntm03NPp5KnAXgG3bG4ErW7nWR+lzt2UOcFn6rsQ9cBPiK9OtFxtwPxjn4rbC1eHeUJCLtp7LrfkJ\n7hivxt3Nw3C7P+d14rw5M8aMo+WENpuVXZE05Phcbuv1VJZ+rG9he0ML5c3NABbath1tVDY0/djS\ne4RIuyipkq5Qk34M2badj8GgZVnKdn8wf8gnSVdFlv3gkzfKmha25zveDkuP8/hf3KTjqMYDxNOJ\nRa4OwW0ZaN4S1WQf27avalbm0MKNLLtbZdKxHYTbytfaeK3GUrjdQG2Zg/thPBV3rFyKTwYWL+KT\ncVUzcMdKeXp7erqL+HjgoUatHeAmqEk8vlV/N9u2X8btqiqYLnwu706aWjpHBS1/EWhsKu4g98aO\nwP27vZVbaCIuJVWSd+kxT5uAA40xe9q2/WHj7caYAbZtt7epHty7vuY2K9t9W/xm27Z3GWPeB0YZ\nY6wsXYC7x0m8ThZdEG8u9sRtMXsuyx13Mzpx3t0JadbpGIwxp5C9FWsnbgtRW2bjtkA0no6htbFr\nA2g6sWxLFuC2Ik3DbUVY06heFgI3G3dSzwP5ZBCzlw7ATQ6bTx45HViVfk6NsG17XfMDjTG3445Z\n68gYnSsKlfDnoEuey7ZtbzfG1AH7Nd+W7ubuRxtJlTFmT9ybCZY3KvPh3gH6TLYxnr3g7yV5pKRK\nusqDwDdxv7FevbvQGNMfWG2MWW3b9qfacR4LOM8Yc1uju//2wG0ReN+27d1jYh7CvQ37bNwpEXZf\n78D0vsvTXVPgfiOFpt948xVvNtmu19z29H5N1qwzxhwMfAH3jbrNcT5ZvJh+3BN3nqDG594P93b1\nbL/Xu2RJqtItDdcCf0nfIDAbeHn3BKHGGAv3NvdLW4hnAFnGtTWXHoS+GLcF4UDc8VS7LcSty2/S\nvvFU7an/jtr94dt4jrEw7ofz7pslrsB9TjZh2/ZX8hhHd9RVz2Vwk+0TjDGTbXe1gN0uaefxtbit\nnh80KjsDN9HKumxXL/h7SR4pqZKucgNwKvD99B1a83G7cS4BqoBft/M8Du74qWeNMQ/jtl5civum\nfEWj/a7HvQPwjvQA4jW4b+pfxb0Vv/HcUe/iJms/TM+Z9Hge482m+fWeaL6DbdsJY8w/gc8ZY/4K\nPIk7juiruB9ETwDHGGPOBx7pwLX/jvvBfr0x5uJGk5KeCHwF+IJt2/Esxy0iy51QwEm4SdOLxpgE\nbqtB49aBHwB/aSWekbTeFdnYHOCHuK1tH7em2e6ahB8BFwDr2zEpapv131HpGeJXkm41Sbd2/A63\nq3mtcSeS7erWTS/tvgmltNl4ugxd+FwGd+6544F/GmP+Dzc5OgKYzCd/59ZiixhjnsFt/X7buPNl\n/Ra3ZenF1o7tAu2uU+k5lFRJc201cbe0vcmki7Zt7zDuYr5X485Qfh7ugOKlwJcbz13TDlfjtgBc\ngTt+Zz3wddu2/9joetvT17sOdwLQvXA/7OcB19u2/Wqj8z2MO4XCbNw7k16wbfvNPMbbvI4yrtfC\ncV/FHax7HG7r0YvAabZtLzXGXIt7x93P+WRsUZvdEekPkZm4Sefi9J1pDu4cTGe2kFABPEX2RHI+\n7qD0Q9P/JgO3GmNuw014H2nWgvCxdCvWNNw5xdpjDu5cRg6ZY5QW485MfV+W43Kt/8bHt6er5wzg\n1+kP5gDuXY9zgQtx6+Z77ThHt2WMqQLuxR14vzvBXmfcNSL/ZKcX5G5BR5/LrWn8vrLAGHMabqvS\nj3Bfo8/izn32H9yW0LZ8BfiFMeZoYH/c1/fjbRyTF52sU+kBLMfJfUmsdFfAq8B1tm239u1UpMPS\n8x+dhzshZ5vL2kj+GGNCuEu2jLNt+/229m/nOQ/HXUsw68ynIiI9XWeXqfkRxdXELSKAbdsx4Pe4\nc1Lly2V0rhtVRKRbyzmpMu4MeQfxyYzHIlJcbgJONO66iJ1ijNkXdymQrLO0i4gUg860VP0Kdx6Z\nVgcGikjPZNt2He6M2H/qzHmMMQHcCR/PbTank4hIUckpqTLGnAsssW179zpOSqwk72zbvsC2bb/G\nUxVOetD5HcaYb3TiND/CnYW9PUsSiYj0WDkNVDfG3I87+WIKGIJ7l8cltm03n6DxY47jOJal3Euk\nt0mlUvh8nR2+KSLiuQ4nLZ26+w/AGHMN8G477v5ztm1raZUQ6QpVVZWozr2lOvee6tx7qnPvqc69\nV1VV2eGkSl8fRURERPKg05N/2rZ9bT4CEREREenJ1FIlIiIikgdKqkRERETyQEmViIiISB4oqRIR\nERHJAyVVIiIiInmgpEpEREQkD5RUiYiIiOSBkioRERGRPPAsqdr2l7tI1VR7dTkRERERT3mWVO14\n9F/U3f5rnFTKq0uKiIiIeMbT7r/EOzaJd2wvLykiIiLiCc/HVMVXrfD6kiIiIiJdzvukavVyHMfx\n+rIiIiIiXcrzpCr10XaSG9Z5fVkRERGRLlWQKRXiK5cX4rIiIiIiXaYgSVVslZIqERERKS4FSapS\nWzaTfH9TIS4tIiIi0iUKNqN6bLXuAhQREZHiUbCkSlMriIiISDEpWFKVXL+W1EcfFuryIiIiInnl\nWVIVGj4ioyym1ioREREpEp4lVRWTpmSUxTWuSkRERIqEZ0lV5eQjMsoSb79BqqbaqxBEREREuox3\n3X/DRuCr2qtpoeMQf/klr0IQERER6TKeJVWWZRE85LCMck0EKiIiIsXA07v/QuMPzyhL2K/iNNR7\nGYaIiIhI3nmaVPlH7I/Vt1/TwkSC+JrVXoYhIiIikneeJlWWz0donLoARUREpPh4PvlncEJmF2B8\nzSqceMzrUERERETyxvOkKnDgQVhl5U0Lo1Hir7/qdSgiIiIieeN5UmX5AwQPnphRHlcXoIiIiPRg\ngVwOMsaUAncDewFh4Abbth9v7/HB8YcRe2Fhk7L4Ky/hJJNYfn8uIYmIiIgUVK4tVScDy23bngmc\nBdzckYODo8ZBKNykzKmrJfH2GzmGIyIiIlJYObVU2bb9YKMfhwEbOnK8FQoRHDOO+MqmXX7xVcsJ\nmjG5hCQiIiJSUJ0aU2WMWQz8Fbi8o8dmmwg0tnoFTirVmZBERERECqJTSZVt20cCpwJ/6+ixwbET\noNn4KWfnDpLvre1MSCIiIiIFYTmO0+GDjDETga22bW9M/7wGmGHb9oetHJZxoY0/+TH1q5ouqNz/\n1NOp+uL5HY5JREREJI+sjh6Q05gqYDowHPimMWYvoLyNhAqAbdtqmhaMngDNkqpdSxbhHPcZLKvD\nv4s0U1VVmVnn0qVU595TnXtPde491bn3qqoqO3xMrt1/fwAGGmMWAI8C/5PLSYLjDoVmyVNq2xZS\n72/MMSwRERGRwsj17r8I8IXOXtzXpy+B/UeSeNtuUh5btYLSwUM7e3oRERERz3g+o3pzwSx3AWp2\ndREREelpCp9UHXJYRlly43skP9xagGhEREREclPwpMo/oAr/0BEZ5fHVK7wPRkRERCRHBU+qIHsX\nYExdgCIiItKDdIukKjQ+Sxfg2rdI7dpZgGhEREREOq5bJFW+Qfvg22vvpoWOoy5AERER6TG6RVJl\nWVbWtQCjzy8oQDQiIiIiHdctkiqA4MTJGWXJde+Q3KyJQEVERKT76zZJVWDoCPxDhmeUR5fO8z4Y\nERERkQ7qNkkVQGjqzIyy2AuLcBIJ74MRERER6YDulVRNOhICwSZlTm0N8VdeauEIERERke6hWyVV\nvrJyglmmV4gumed5LCIiIiId0a2SKoBwli7AxGsvk9qx3ftgRERERNqp2yVVgZGj8Q2oalroOJpe\nQURERLq1bpdUWT4foSNmZJTHlszHSaUKEJGIiIhI27pdUgUQnjIdLKtJWWr7NhJvvV6giERERERa\n1y2TKt8eAwiMOjijPLZknuexiIiIiLRHt0yqIPuA9djK5aTq67wPRkRERKQN3TapCh48Eau8omlh\nIk5s+ZLCBCQiIiLSim6bVFnBIKHJ0zLK1QUoIiIi3VG3TaogexdgcsM6EhvWeR6LiIiISGu6dVLl\nHzwU/4j9M8pjS+YXIBoRERGRlnXrpApaGLC+fDFOPOZ9MCIiIiIt6PZJVejQKRAMNSlz6uuIr1pR\noIhEREREMnX7pMoqLSM0cXJGuRZZFhERke6k2ydVAKGpmcvWJOw1JLdvK0A0IiIiIpl6RFIVOOAg\nfAMHZZTHlmrAuoiIiHQPPSKpsiyLcJZFlqNLF2iRZREREekWekRSBRCachT4mobr7NhO4o1XCxSR\niIiIyCd6TFLl69uf4JjxGeUasC4iIiLdQY9JqiD7gPX46hWkamsKEI2IiIjIJzqVVBljfmGMWWKM\necEY85l8BdWS4NjxWH36Ni1MJoktW9TVlxYRERFpVc5JlTFmJjDatu2pwInAr/MVVEssf4DQpMxF\nlqNL5uE4TldfXkRERKRFnWmpmg+ckf7/TqDMGGN1PqTWZVu2JrV5I8n31nb1pUVERERalHNSZdu2\nY9t2Q/rHi4AnbNvu8uYi/6DB+PcfmVGuAesiIiJSSJ0eqG6MORW4APh658Npn6yLLC9brAHrIiIi\nUjBWZ8YiGWOOB64Fjrdte1cbu+etFSvV0MA7X/kSTqShSfkenzubPc86J1+XERERkd6rw0Oack6q\njDF9gIXAMbZtf9iOQ5xt2/LXklT/8F+Jzn2ySZlVWkbfG36DVVqWt+v0ZFVVleSzzqVtqnPvqc69\npzr3nurce1VVlR1OqjrT/XcWMAB40BjznDFmrjFmSCfO1yEls08Cv79JmdNQT3Thf70KQURERORj\ngVwPtG37DuCOPMbSIb5+exCaMp3Y4uealEfmPkl45vFYoVCBIhMREZHeqEfNqN5cybGfBqtp65xT\nvYvo0vkFikhERER6qx6dVPkHDiJ46JSM8uicx3CSiQJEJCIiIr1Vj06qAEqOOyWjLPXRh8SWLy1A\nNCIiItJb9fikKjBkGMGDJ2aUR55+BCeVKkBEIiIi0hv1+KQKoOSELK1VWzYTX/1iAaIRERGR3qgo\nkqrAvgcSMGMyyiNP/0cLLYuIiIgniiKpAig5PrO1Krn+XRKvv1KAaERERKS3KZqkKmDG4B+xf0Z5\n5Kn/FCAaERER6W2KJqmyLCtra1Xi7TdIvG0XICIRERHpTYomqQIIHjwR396ZK+U0PP1IAaIRERGR\n3qSokirL58veWrVmFYkN67wPSERERHqNokqqAEKHTsE3oCqjPKLWKhEREelCRZdUWX4/JcednFEe\nX7mM5Jb3CxCRiIiI9AZFl1QBhKYchdW3X9NCxyHyzKOFCUhERESKXlEmVVYwRMkxJ2WUx15YROqj\nDwsQkYiIiBS7okyqAMLTjsEqK29amEoSefbxwgQkIiIiRa1okyqrpITw0cdnlEcXP0eqZlcBIhIR\nEZFiVrRJFUB45vEQDjctjMeJzn2qMAGJiIhI0SrqpMpXXkH4qNkZ5ZH5c0jV1RYgIhERESlWRZ1U\nAZQccyIEAk0LIw1EHnmoMAGJiIhIUSr6pMrXtz+hI2ZklEcX/ZfEe2sLEJGIiIgUo6JPqgBKT/wM\nhEuaFjoO9fffhZNKFSYoERERKSq9Iqny9etP6adPzyhPvreW2JJ5nscjIiIixadXJFUA4ZnH4Rs8\nJKO84T8PkKqtKUBEIiIiUkx6TVJl+QOUnfWljHKnrpaG/9zvfUAiIiJSVHpNUgUQPHAUoUnTMspj\ni+eRePetAkQkIiIixaJXJVUApZ/5PJSUZpTX33+3Bq2LiIhIznpdUuXr24/Sk8/IKE9uWEd04bMF\niEhERESKQa9LqgDC02fjHzI8ozzyyEOkqrUuoIiIiHRcr0yqLL+fsrMvyCh3Gupp+PffCxCRiIiI\n9HSBtncpToH9DiR0xAxiS+c3KY89v5Dw1KMJHGAKFJlI9+fEoqSqd+HU7CJVU41TvYtUzS6chgbw\n+bAsCywLLJ/76Pvk54+3+XxYFX3w9d8DX7898PXrj9V8kl4RkR6kU0mVMWYs8G/gZtu2b81PSN4p\nPe1s4qtX4NTXNSmvv/8uKr/3Eyy/v0CRiRSOk0qR2r6N5Kb1JDdvJLVrxydJU02120UejXTJta2y\ncnz99sDanWj13wNf/wHu/wdU4dtzIJavVzawi0gPkHNSZYwpA34L9NjR3b7KPpSecib199/VpDy5\neQPR+c9QMuvEAkUm4o1UfR3JzRvcBGpT+nHzBohGCxKPU19Hsr4ONm/Iut0qLcM/fD8C+x6Af8T+\nBEYcAFWVHkcpIpJdZ1qqIsCJwFV5iqUgQtNmEV0yn+T6posrNzz2MKFDp+Dr279AkYnkl9NQT/yt\n10mue4fkxvUkN68n9dH2QofVIU5DPYk3XiXxxqsfl9UP3AuG7UdgxP4Ehu+Pf9gIrGCogFGKSG+V\nc1Jl23YKiBrTs8ceWT4fZWd/iZqbrgHH+WRDJELDP++j/IJLCxecSCc4sRiJtW+SsNcQt9eQfG9t\n0+d4kYhv3QJbtxBfsdQt8PnxDxlG4KCxhA45DP/w/dRlKCKesJxOvskaY64BtrVjTFW3fjffcvut\n7JrzVEb5kGtuoGzsuAJEJNIxTjJJ5J23qH/lZepffZmI/TpOPN41F/P58PftR6BvX/exXz/8ffvh\nr6hwY0k54KTAcT75f8rBSZeRcnASCRI7d5DY/qH7b8dH0AUT8Ab2GEDFpClUTJpC6eixGispIu1l\ndfgAL5Oqbdu678LFqdoaqq/9Nk5dbZNy36DB9PnBz7D8Pe9GyaqqSrpznRcjr+s89dGHxFavIPHG\nGuJvvQ6RhvycuKQE/z7DCAwehm+vQfgq+2L16fvxo1VWnvfWHyeVcgfE7/yI1I6PSO3cnn78iNRH\nH5LctL7TY72s8gqCB08kOP5wgqPGqpswR3pv8Z7q3HtVVZUdTqrylSl0+MLdja+iktLTPk/93+5o\nUp76YDORJ/6VdRZ2kUJIfriV+MplxFYuI7nunc6dzLLwDRyEf59h+PcZmn4chm+PPd2pDzxk+XxY\n/frj69cfRuyfsd1JJkm+v4nkurdJrHvHHRv2/sYOdWk6dbXEnl9A7PkFEA4THDOe0PjDCY45BKu0\nLJ+/joj0Qjm3VBljJgK/AoYDcWAT8Fnbtne2cEi3bqkC95tyza+uJfnu2xnbyr96BaFxEwsQVe70\nzcZ7XVXnyW1b3ETqpRdIrn835/P49hxIwIwmsO+BbgK19z5YoXAeI/WWE2mgonoL21e9QuJdN9ly\ndu3o+ImCQUKHHkF45nEEhu2b/0CLjN5bvKc6914uLVWd7v7rgG6fVAEkNqyj5sYfZn77LSmlz1U3\n4B84qDCB5UAvQu/ls86TWz8g9tILxFcuI7lhXU7nsPr0JTByNEEzlsBBY/APqMpLbN1J8zpPfbSd\n+Guria1aTsJeA8lkh87n3/cAwjOOIzRhElYwmO9wi4LeW7ynOveekqo8aXjsH0Se+GdGuW/vfejz\nneuwSnrGrM96EXqvs3We2rWD2AuLiC1f4o4h6qiSUoIjRxEwYwiasfj23sfzbjyvtVbnqfo64q+u\nIr56OfE1L0Os/WOyrIo+hKcdTXjaMfj2GJCvcIuC3lu8pzr3npKqPHFSKer+8Cvir67K2BacOJny\nCy/rER9UehF6L5c6d5IJ4q+sIrZkHvHXVnf4Djj/4KEEJxxOcMx4/ENH9Lq729pb504sSvy1V4iv\nXkH85RdxGurbdwGfj+AhhxKefiyBkaN7xGu/q+m9xXuqc+8VcqB6UbF8Psq+9D/U/PxHpLZtabIt\n/tILRIfvR8mxny5QdFIsku9vIrp0PrEXFuLUVHfoWP+Q4QQnTCI0cRL+vQZ3UYTFxQqFCY0/jND4\nw3CSCRJvvk5s1XLiLz6fsVRVE6kU8ZXLia9cjm/vfSiZcRyhSdN6TIu1iHhHLVWtSG7eQPUvrsns\nMrAsKi67iuBBYwsTWDvpm4332qpzJ9JA7MXn3Vn8332rQ+f2Dx1BaOJkghMm9aixfV2ts89zJxYl\ntnwp0fnPkNz4XruOsSoqKTn+FMJHzcYK9b5pGfTe4j3VuffU/dcFYiuWUvfn/8sot8orqLzqhm49\n8FcvQu9lq3PHcUiufZPo4nnEXnqhQ+N6/MP3+ySR2nNgvsMtCvl6nrt/p7eIzH+G+EvLINX2AHer\nb39KTzzsTP5FAAAgAElEQVSN0NSZWIHe0/Cv9xbvqc69p6Sqi9T/429E//tERrl/6Agqr7im235T\n1YvQe43r3IlGiC1fQnT+nA4NOrf6DyB8xHRCU6YrkWqHrniep3btJLr4OaIL/9uuKRp8A6ooOekz\nbrdgLxjTpvcW76nOvaekqos4ySS1v7uRxJuvZWwLTZlO2blf6ZaDV/Ui9F5VVSUfvPY20QXPElsy\nr/2DoQMBguMOJTx1JoGDxmqtug7oyue5k0wQX/0i0flzSLz1epv7+/bam9JPnU5w4uSi/hvqvcV7\nqnPvKanqQqmaaqpv/CHOju0Z28rOvoDw9NkFiKp1ehF6x0mlSLz+Cs7SudStfLHds3z79xlGaOoM\nQocfia+isoujLE5ePc+Tm9YTmfM4seWL2/z7+vcZRsnJnyN48MRu+YWrs/Te4j3VuXccx8HZtYO9\nDhyupKorJd5bS82vroNEs0Vq/X4qL/8hgf1HFiawFuhF2PWchnqiSxcQXTCH1NYP2nWMVVpG6LCp\nhI6c6U6BUIQful7y+nmefH8jDY/9g/jKZW3u6x+xP6WnnNntb2rpKL23eE917o1UbQ21t95Ect07\njHzoESVVXS26dD71996eUW717Uefq27A17d/AaLKTi/CrpN8fxPRec8QXbaw3Yv8+vcfSfio2YTG\nH95tx+H1RIV6nifWv0vDow+TWJM5n11zwUMOo+yMc/HtsacHkXU9vbd4T3Xujbp7/kDshYUAOSVV\nved2lTwJHzGDxLp3iC38b5NyZ9dOav/0Wyq/8YNedRdQb+I4DonXXyEy90kSr73cvoOCQUKHTXXX\nlBs6okvjE28Fhu1L5aXfIfHOmzQ8+lDWMZe7xVevYNfrr1B60mcIzzpR7xEi3VCqvo7Yi0s7dQ69\nsnNQdsZ5JDe+l7HwcvKdN6m/70+UffErRT1Itbdx4jFiy5YQmfskqfc3tusY34AqwtNnEzpihsZK\nFbnA/iOpvPwHxN94lYZHHiS57p3sO8aiNPz7fqLPL6DsrC8RNGO8DVREWhV/8XlIJDp1DiVVObAC\nASouvpzqG3+AU72rybbY8wtxohHKv3SpFmPt4VLVu4gueJbogmdxats343nZuPFYU2cRHDtBiXUv\nEzxoLAEzhvirK4k8+hDJjdmn0Uh9sJna3/yU0OFHUvrZc/D17edxpCKSTfT5hZ0+h5KqHPn69af8\nov+l9tc/zZgkML5yObX1N1FxyTexSkoLFKHkKrl5A5H/Pune5dWeby3hEsJTphOecSyDDjYa99CL\nWZZF6OCJBMeMJ7ZiKQ3/vA+nemfWfWPLFxN75SVKTzmT8PTZSsJFCii59YMOr3KRjZKqTggecBCl\nZ3yRhgfuydiWsNdQ8+ufUnHpd/BV9ilAdNIR7pQILxP575Mk3ni1Xcf49hxI+OjjCU+ZjlVa1sUR\nSk9i+XyEJx1J6OAJNDz6MNH5z2SfhiHSQMOD9xBbOp+ysy8gsO8B3gcrIh8PTu8sJVWdVDLjOEim\naHj43oxtyfVrqbn5Oiovu6po7vopNk4sSuz5hUSee5rUls3tOiZwgCE86ySC4yaqdUFaZZWWUXbm\neYSOmE79/XdljMPcLblhHTW//DGhI4+m9NSz8JVXeBypSO/lpFJKqrqTklknYJVXUH/vHyGVarIt\nteV9qn95LZWXXYV/730KFKE0l9r5EdH5c4gumotTV9v2AT4/oUMnE551IoHh+3V9gFJUAuklrWJL\n59Pw7/uzP+cch9iiucRffonycy8mOGa894GK9EKJt98g9VGzib1znD9QSVWehCdPw1dWTu2ffgPx\nppODOjs/oubm66i49EoCI/YvUIQC7gSu0blPEXvx+fYtmFtWTnjaLMIzjsXXf4AHEUqxsnw+wkce\nTfCQw2j4z/3EFs/Lup9TvZPa399EaNosyj77BaySEm8DFellYlkGqAdGj8vpXEqq8ih48AQqL/se\ntbf9MmPNN6eulprf/ISKr3yT4KiDCxRh7+SkUu76bXOfJPGO3a5jfAMHET76BMJTjsIK60NN8sdX\nUUn5Fy4mfMRM6u//c4t3CcYWzSVhr6H8vK92u9UaRIqFE40Qy7I6QnjyUTmdTzOqd4HExvXU/t/P\ns9/14/dTfsGlhCZO7vI4evsMvO4SMvOJPvc0qe3b2nVMYORowrNOJDh2fE7jpXp7nRdCT65zJ5kk\nOn8ODY89BJFI9p0si5LjTqbkU6d3m0lDe3Kd91Sq864RfWER9ffc1rSwpJR+N97KwH0GaEb17iAw\nZBiV376G2t/+jNSHW5tuTCapu/N3OLU13XIR5mKQ2Pge0QXPElu2GGLtWEImEHBnPT/6eM16Lp6y\n/H5KZp1AaOIk6u69ncTrr2Tu5DhEnn6E+JpVlJ//Nfz7DPM+UJEilW2AeujQyTkvJaakqov49xxI\n5RXXUPv7n2c27zsO9fffRWrXDkpO+gyWX3+GznLiceKrlhFZ8CzJd95s1zFWRR/C048hfNRsTcAo\nBeXrtwcVX/8u0QXP0vDP+yAey9gnuXE91T//EaUnn0H4mJN056lIJ6V2bCdhr8koD0+envM59Wne\nhXx9+1Fx+Q+pu+1XWcfyRJ78N7FVKyg/58sE9jcFiLDnS330IdGFc4kueQ6npn2znvsGD6Hk6BMJ\nTZqKFdTCxtI9WJZFyYxjCR40lrp7bsu+3E0iQcO//k78lZcoO++r+Pcc6H2gIkUitmxxxvxxvj0H\n4u/EGEaNqfKAE4tS96ffEX91ZYv7hI6cSelpn8/r/DTF2gfvpFIk3niV6II5xF9ZmX1SxSwCY8ZT\ncsyJBMwYrBxvl21LsdZ5d1aMde4kk0SeeZTI4/9s+S7VcAllnzuX0NQZXfZ8bkkx1nl3pzrPL8dx\nqL7+SlIfNJ2fsORTn6X0U6cDUFVVqTFV3ZEVClN+yeXU33sHsWWLsu4TWzyP+OqXKD39HEKTpnn+\nJtkTpHZ+RGzZYqKLnyO1bUv7DiopITzZXULGP2hw1wYokieW30/piacRHHMIdffcRur9TZk7RSPU\n/+0O4varlJ9zoZbEEumA5HtrMxIqgFCOd/3tpqTKI5Y/QNl5l+DbYwCRpx/J2rri1FZTf88fiD2/\nkLKzv4R/LyUBTiRCbNVyYi8sJPHma+1ulfIPHkp4xrGEDj9S8/xIjxUYti99rrqBhkceJDr3qazP\n//iKpVRvWEfFxd/AP3hoAaIU6XliL2Q2cAQOMJ3uUlf3XwEkNqyj/r47Sb63tuWdAgFKjjuFkuNP\nznncT09tLt7dvRd7YRGx1SvadwcfgN9PcMIkSqYfi3//kQVp7eupdd6T9ZY6j7/5GvV/+SOpjz7M\nvkMwRNnnLyA8JfdBtu3VW+q8O1Gd54+TSLDre5dmrGxQ9oWLCR858+Ofc+n+U1JVIE4q5d7p88gD\nLc9PgzsJZdnnv0zQjOnwNXraizCx8T03kVqxBGdXljm+WmD1H+DOej51ZsHv4utpdV4MelOdOw31\n1D90L7HnF7S4T+iIGZSddT5WKNxlcfSmOu8uVOf5E1u1grrbb2laGAzS78ZbsUrLPi7SmKoexPL5\nKJl5HKHxh1P/8L3EX3oh636prR9Q+5ufEpwwifC0We4g6yK5ldpxHFKbNxBfs5rY8iUkN2WfWbol\ngYPGEp5xLMGxE7D8/i6KUqT7sErLKD/vEgIHjaX+73dCNLMVN7Z0Psn31lJ+8f9qCIFIFtnmpgoe\ncliThCpXSqoKzNevPxUX/S/xV1dR/8DdLc78HV+5jPjKZVh9+xM6fCrhydN65CSATkM98TdeJb5m\nNfHXVuPs3NGh4317DiQ0aRqhSUfiHzioi6IU6d7Ck44kMHQEtX/6Lan3N2ZsT27eQPWNP6L8CxcR\nOuyIAkQo0j2lamuy3omf67I0zan7rxtxYlEiT/yLyLNPtGuxX/+Q4YQmTyN02NSs3V7dobnYcRyS\nm9aTWLOa+JrVJNa+1a7frTGrtIzgoVPcRHK/woyVaq/uUOe9TW+ucycaof7+u7N+894tPH02pad/\nESsYzNt1e3OdF4rqPD8i856h4cF7mpRZffvR9ye/y+gF8rT7zxhzMzAFSAGX27a9ItdzicsKhSk9\n7WxCk46k7r47Sa59q9X9kxvfo2HjezT88z4Cow4mPHma24TZhWMp2uKkUqQ+3Epy/bvEX3/FbY3q\nwPioj/n9BMeMJzT5KHcdvjx+IIgUCytcQtl5lxA44CDqH7wb4vGMfaILniWx7h3KL/pfTRYqvV7s\n+SzL0hx+ZN6G1eSUVBljpgMH2LY91RhzEPBnYGpeIhL8g4dS+a2riS2ZR8MjD+LUtvHtxHFIvPYy\niddehnAJwbHj8e89hOoDRpAo6Yd/4KC8z2HjOA7Orp0kN29o9G8jyfc3ZV1io738+x7gdu8dOgVf\nRWUeIxYpTpZlET5yJv7h+1L3p9+S2vpBxj7J9e9S87MfUHb+1wiNm1iAKEUKL/n+RpLrM++6D0/J\nT9cf5N5SdQzwbwDbtt8wxvQzxlTYtl3bxnHSTpbPR3jaLEKTpxF/ZSWxZYuIv7q67a6zaIT4i88T\nBxq/tVp9++EfuDe+gYPcx73Sj/364ySTEI/jJOIQj+EkEu7P8Rgk4jjxOMTjpOrrSH2wieSmDSTf\n35hxO2pO/H4C+xuCYw4hOO5Q/Hvt3flzivRCgSHD6fPd66n725+y3vjiNNRT98ebSX76c5SccGq3\n7kYX6QrRLHNT+YeOyOv8brkmVYOAxt19H6bL3u50RNKEFQwRmjiZ0MTJpGqqib34PLFli7KvC9YK\nZ9dOErt2wluvd1Gk7efbYwCB0Ye4iZQZo5mgRfLEKi2j/MLLiB5wEA3/+Cskm30Jcxwijz5EctN6\nys/9ClZYE+NK7+CkUllXNOnsDOrN5evuv3Z95amqUndOp1RVwn6nwxmnE9u0keoF86heOI/Etq2F\njqxVViBA6agxlE2YSPn4QwkNGVrU35L1PPee6ryZM04nMmEcm2/+edb3h/hLL9CwfSuDr/w+wYF7\n5XQJ1bn3VOe5q1u9kp3N7zb3+9n7hGMJ9M1fveaaVG3GbZnabTDwflsH6c6FPAr1hdmnUjHrZBJv\n28SWLSL20gsQaSh0ZFilZfj3GYp/yHACBx1McORorJISkkA1wIfF20usO3S8pzpvQd9BlH/3Buru\nupXEmlUZm6Pvvcu6736L8ou+QXDkqA6dWnXuPdV559Q980xGWXD0IeyI+aGFes0lic01qXoG+DFw\nhzFmIrDJtu26HM8lnWD5fARHjiI4chRlZ55PYu2bJLdsJrXlA/w7txHZtInUh1vbvWZehwSD+Aft\ng3/wUPffPkPxDx6C1bd/UbdEifQUvrJyKr52BZFHH3LXHG3Gqa2h9rc/o/SMcwlPn63XrRQlJ9JA\nbFXmBAWhPA5Q3y2npMq27aXGmBeNMYuBJHBpfsOSXFihEMGDxhI8aCzwyTcbJ5FwpznY+j6pLR+4\nj1s/ILn1A5z6WqxAEIIhd9qCQNB9DAbT5Y0eg0F8e1R9nDz5qgYVzezuIsXK8vkoPfUs/PsMo+7e\n2zPvzk0laXjgbpKb1lN25vlYAc0JLcUltnJZxhqyVlk5wbET8n6tnF89tm1/P5+BSNexAgH8gwbj\nH6QlK0R6q9BhR+AbOIjaP96Cs2N7xvbYorkk399IxcWX4+vTtwARinSNrHNTHXpEl8x/qGYGEZFe\nIjBsX/pcdT2B/U3W7cl33qT65z8isf5djyMT6RrJLZtJZLnrvSu6/kBJlYhIr+Kr7EvFN75PaNqs\nrNudHdup+dW1xJYv8TgykfyLPPt4Rplv4N74R+zfJddTUiUi0stYgQDl51xI2dkXgM+fuUM8Tt1d\nv6fhsX/g4fqwInmV2rWDWJYJP8NHHdNlN2UoqRIR6aXC02dT8Y3vYbWwJFTkiX9Sd9fv3dUVRHqY\nyHNPQyLRpMwqKyd85NFddk0lVSIivVjwwFFUfvd6/EOGZd0eX7GUmt/8lFRNtceRieTOaagnuuDZ\njPLw9NlYJV23koCSKhGRXs4/oIrKK64hOHFy1u3JtW9R84ur3QXTRXqA6KK5mZNhB4KEjz6+S6+r\npEpERLDCJZR/+euUnHha1u2p7duo+eWPib/xqseRiXSME48TmftkRnnoiOn4Krt2uhAlVSIiAqQn\nCj35DMrOuwT8mQPYnYZ6av/vF+x89ukCRCfSPrHli3F27WxaaFmUHHNSl19bSZWIiDQRnjKdisu+\nh1VekbkxlWTrH39P/T/vw0mlvA9OpBVOKkVkzmMZ5cEJk/APHJTliPxSUiUiIhmCI0dR+Z1r8bXw\nQRR99nHq7vgNTjTicWQiLYu/8hKpLe9nlJcc+2lPrq+kSkREsvIPHETld64lcOCorNvjq1dQc8sN\npHbu8DgykUyO4xB5JrOVKmDGEBi+nycxKKkSEZEW+corqLjsqhaX9Uiuf5fqX1xNYuN7Hkcm0lTy\nnTdJvvtWRrlXrVSgpEpERNpgBQKUnXsJJaecmXW7s/Mjam6+jvhrL3scmcgnso2l8g8ZRmDUwZ7F\noKRKRETaZFkWpSecSvmFl2EFQ5k7RCLU3noT0SXzvA5NhOTmjcRfeSmjvOTYT3fZkjTZKKkSEZF2\nCx06hSE/vgGrsk/mxlSK+r/eQcMjD2rNQPFU1oWT99iT4MQpnsahpEpERDqkdORBVF55Hb6998m6\nPfLUf6i/+zaceNzjyKQ3Su3YTmz54ozy8DEnYWWZb60rKakSEZEO2720TUt3BsaWL6b2/35Oqr7O\n48ikt4nMfQqSySZlVnkF4akzPI9FSZWIiOTEV1ZOxde/S2jSkVm3J956nZpf/pjk9m0eRya9Raq+\nzl3nr5nwjOOwwl23cHJLlFSJiEjOrGCQsvO/1vKagR9spuama0i8t9bjyKQ3iC54FppPQBsMEZ55\nXEHiUVIlIiKdYlmWu2bgFy8GX5Y1A6t3UXPLDcSy3J0lkisnHiM6L3MdyvDUmfgqKgsQkZIqERHJ\nk/DUmVT8z7ehJEu3SyxK3R9uJjJ/jveBSVGKvbAIp3pX00Kfj/Dsrl84uSVKqkREJG+Co8dR+a1r\nsPr1z9zoODQ8cLcWY5ZOa3Hh5ImT8Q+oKkBELiVVIiKSV4Ehw+hz5XX4hwzLuj367OPU3fk7nFjM\n48ikWMRXryC1bUtGuZdL0mSjpEpERPLO128PKr/5IwKjx2XdHl+5jJrf/pRUbY3HkUlP5y6c/GhG\neWDUwQSGjvA+oEaUVImISJewSsuo+NoVhI6cmXV7cu1b1Nx0DcmtH3gbmPRoCXsNySx3k5Ycd3IB\nomlKSZWIiHQZyx+g7JyLWlyMObVtizvlwju2x5FJT+QkE9Q/fG9GuX/YvgRGji5ARE0pqRIRkS71\n8WLMF/wPBAIZ2526Wmp+8zNiL71QgOikJ4nOn0Nq88aMcq8XTm6JkioREfFE6PAjqbjsKqyy8syN\niTh1f/otkTmPaTFmySq1awcNj/0jo9w/fD+CEyYVIKJMSqpERMQzwQNHUfntH+Nr4bb3hn/9nfr7\n78JptpabSMO//g6RhqaFlkXZWV/C8nWPdKZ7RCEiIr2Gf9BgKr9zLf4R+2fdHlv4X2r/cDNOJJJ1\nu/Q+8bdeJ7ZscUZ56MijCbTwPCoEJVUiIuI5X5++VF7+A4LjDs26PbFmFTW3XE9q5w6PI5Puxkkm\naXjgnoxyq7yC0hZugCiUnJMqY8wMY8wWY0zh5oMXEZEeywqFKf/K5YSPPiHr9uSGdVTfdA2Jjes9\njky6k+j8OSQ3b8goLz31rIKt8deSnJIqY8x+wDeBRfkNR0REehPL56PsjHMp/dy5kOXuLWfHdmp+\ndS3xV1YWIDoptNSunTQ89nBGuX/4foSmzvQ+oDbk2lK1GfgMUJ3HWEREpJcqmXUC5RdfDsFQ5sZo\nhNo//IrI3Cd1Z2Av0xMGpzeWU0S2bUds29YzW0RE8iY0/jAqv/lDrMo+mRsdh4aH/0r93/+Mk0x4\nH5x4Lv72G8SWZXaIdbfB6Y1lzsLWjDHmQuAiwAGs9OM1tm3P6ejFqqq6V99nb6A6957q3Huqc+91\nWZ1XjSc+7JdsuvF6Yhszx9HEFs0lsGs7e3/ru/grKromhm6qNz3PnWSS9x7+S0a5r6KSoV/+Mv7K\n7lkXVmeaUo0xdwEP2bb9RDt2d7Zt08KZXqqqqkR17i3VufdU597zos6dhnpq7/wdiddezrrdt9fe\nVHzt2/gHDurSOLqL3vY8j8x9ioYsy9GUnXMh4WmzPImhqqqyw1O056NDsvDzwouISFFxF2P+NuEZ\nx2XdntryPjU3XUP8rdc9jky6WouD04d1z8HpjeV6999JxpjngOOBnxpjnspvWCIi0ttZfj9lZ51P\n6ZnnZ78zsK6W2t/+jOjS+QWITrpKi4PTz+6eg9Mba3NMVTbp7r72dPmJiIh0SsnM4/BX7UXtnb/L\n/LBNJqm/93aSW96n9JQzu/2HrrSuxcHpU2d228HpjenZJyIi3V5wzCH0aWXNwOgzj1J3x29wolra\npqdykkka7r87o9wqr6D01LO8DygHSqpERKRH8A8eQuWV1+Lf78Cs2+OrV1Dzy2tJfrjV48gkH6IL\nWpg5/ZQzu93M6S1RUiUiIj2Gr7Ivld/4PqFJR2bdnty0npobf0h8zWqPI5POSFXvouHRFganH3l0\nASLKjZIqERHpUaxgiLLzv0bJyZ/Lut2pr6P21ptoeOo/moG9B3Ach/r77+qxg9Mb6zmRioiIpFmW\nRemJn6H8wssgGMzcwXGIPPIgdbf/Gqeh3vsApd0iT/2b+KrlGeU9ZXB6Y0qqRESkxwodOoXKVgaw\nx1evoPoX15D8YLPHkUl7xFavIJKl268nDU5vTEmViIj0aIGhI6j87vUEDhqbdXtqy2aqf/EjYqtW\neByZtCa5eSN1d9+WdVvZ2Rf0mMHpjSmpEhGRHs9XUUnF179LyXEnZ98hEqHu9ltoeORBnFTK2+Ak\nQ6qulto/3gxZpsAoOf4UQodOKUBUnaekSkREioLl81F62tmUX/wNCIez7hN56j/U3noTqfo6j6OT\n3Zxkkro7f0dq25aMbcGx4yk5+YwCRJUfSqpERKSohCZMos+V1+FrYbHlxGsvU3PjD0lsXO9xZALQ\n8K/7SLzxaka5b6/BlF9waY+626+5nhu5iIhIC/x7D6HPd68nePDErNtTH26l5qaricx/RtMueCi6\ndD7RuZnLBbsLaF+BVVpWgKjyR0mViIgUJau0jPJLvknJp0/PuiAz8TgND9xD3W2/JFWzy/sAe5nE\nu29R//c/Z26wLMovvAx/Cy2LPYmSKhERKVqWz0fpSZ+l4qstt4LEX11F9U++p1nYu1Bq5w5qb/81\nJBIZ20o/83mCo8cVIKr8U1IlIiJFL3jwBCq/ez2+wUOybneqd1H7+19Q/+BfcOIxj6Mrbk48Ru3t\nt+Ds2pmxLTRpGuFjTipAVF1DSZWIiPQK/oGD6HPldYSPmt3iPtF5T1P98x9lXdhXOs5xHOr/difJ\nde9kbPMP34+ycy7EytY120MpqRIRkV7DCoUp+/wFlH/1CqwWJpdMbd5I9Y0/IvLc0xrE3knRuU8S\nW7Yoo9zq24+KS76JFQoVIKquo6RKRER6ndC4ifT5wc8IjDo4+w6JOA0P/cWd06pag9hzEX/tZRr+\neV/mhkCAiq9cjq/fHt4H1cWUVImISK/k69ufikuvpPRzX4RAIOs+iTWrqb7hKuKvrPQ4up4ttnIZ\ntX+8BbK09JV9/ssE9j2wAFF1PSVVIiLSa1k+HyWzTqTyyuvw7b1P1n2c2mpqb/sltX/+P1I7d3gc\nYc/iOA4NT/6Lujt+A1kG/IdnnUD4iBkFiMwbSqpERKTXCwwZTp/v3kB4xrEt7hNfsZRd136byH+f\nwElmTg3Q2znxGPV330rk0Yezbg8cNJbSz5zjcVTeUlIlIiICWKEQZWd9ifKvXYFV0Sf7TtEIDf/4\nG9U/+wHxt173NsBuLLVrJzW33EBs+ZKs2/1DhlN+4WVYfr/HkXlLSZWIiEgjoYPTg9hbmZAytXkj\ntbfcQN3dt5LKMv9Sb5LYsI7qX1ydddoEgOC4Q6n81tX4yis8jsx72UfmiYiI9GK+vv2ouPRKYkvn\n0/Dv+3Fqa7LuF1u2mNjLL1F68ucITz+26FtimoutWkHd3bdCLJp1e8lxJ1Nyypk9epHkjlBSJSIi\nkoVlWYSnziR4yGFEHnmI6KL/Zr2bjUgDDQ/dS2zJfMrO/hKB/Y33wXrMcRyizzxKwyMPZq+TQICy\ncy4iPOUo74MroN6ROoqIiOTIV15B2ecvoPLK6/CP2L/F/ZKb1lPzq+uo+8sfSH203cMIveXE49Tf\n8wca/vNA1oTKquhD5Te+3+sSKlBLlYiISLsEhu9H5bd/TGzJPBr+8wBOXW3W/WLPLyS2bAmhw44g\nPPtTBIYM8zbQLpSq2UXtH28hufatrNt9g4dQ8bVv4x9Q5XFk3YOSKhERkXayfD7C02YRHH84Df95\ngNiSedm7v1JJYssWEVu2iMDocZQc+2kCI0f32HXunFiM6OK5RJ5+FKc6+8D84NgJlH/5UqySUo+j\n6z6UVImIiHSQr6KS8i9cRHjqTOofuJvk+ndb3Dfx2svUvvYy/mH7UnLspwmOP7zHDGh3ohGii+YS\nmfMYTivL9YRnf4rS087uNQPSW6KkSkREJEeBfQ+g8srriC2a63YJNtS3uG9y/bvU3fk7fAOqCM8+\nifARM7BCYQ+jbT8n0kB0wbNEnn0Cp7a65R39fso+/2XCU2d6Flt3pqRKRESkEyyfj/D02QQnTia6\nYA7Rec+0OAUDQGr7NhoeuIfIY/8gPOM4wlNn4NtjTw8jbpnTUE9k3jNE5z7Z4pix3azyCsq/cjnB\nA0d5FF33ZznZ+oLbYIzxA3cC+wN+4Nu2bWefRvUTzrZtLT/JJP+qqipRnXtLde491bn3VOetc2JR\nYnRTURUAAAjVSURBVM8vJPLs46Q+3NquY3yDBhMcfQjB0eMIHHgQVjDUZHtX13mqvo7oc08RnftU\nq61tuwUnHE7pZ79Q1APSq6oqOzwALteWqnOBWtu2jzLGjAbuAibneC4REZGiYYXChKfPJjRtFvFV\ny4nMeYzke2tbPSb1wWaiH2wmOvdJCIYIjBxFcPQ4gqMPwTdwUN5jdFIpUh9uJbn+XRLr3ia6ZD5E\nGlo/yLIIHjqF0hNOxT94aN5jKga5JlX3Avel/78N2CM/4YiIiBQHy+cjNHEywQmTSLz1OpE5j5NY\ns6rtA+MxEmtWk1izmgbuxTegCmfioST2G4V/n2FYZeVYJaXtHhTuJBMk399McsO7JDe8R3LDOhKb\n3oNIpJ2/iEXo8KmUnHAa/kGD23dML5VTUmXbdhJIpn+8nE8SLBEREWnEsiyCI0cTHDma5Kb1RJ59\nwl14OJVs+2DcMVi75jwFPNV0Q0kpvrJyrLIyrNJyN9kqLUs/lpLaucNNojZvgES844H7fIQmTaPk\nhFPxd0FrWTFqM6kyxlwIXAQ4gJV+vMa27TnGmEuBCcDJXRqliIhIEfDvM4zy879K6clnEF38HPE1\nq1qdjqFVkQZSkQb4KL8x4vMTOuIoSo4/Ff+eA/N88uKW00B1+DjZOh041bbt9qTAuV1IRESkiCV2\n7aR+9UrqVr1E/epVJFuZD6orWYEAfWYdyx6nnU6wSskUbkNSxw7I8e6//YD7gem2bbezU1Z3/3lN\nd+h4T3XuPdW591TnXcdJpUhufI/4mtUkXnuZxLtvQSrVNRcrKSEwZDj+ofviHzqc4Khx+Pr265pr\n9UBe3v13Ie7g9CeMMbu7BI+zbTuR4/lERER6PcvnIzBsXwLD9oUTTyNVX0fCXoN/7evU2TZOfS2p\n+vq279Rrft6KPviHjUgnUSPwDx2Bb8+BvX4G9HzLufsvB2qp8pi+TXpPde491bn3VOfea17nTjKJ\nE2nAaajHqa9z/338/3qchjoIhvAPGUZg6Aisvv177LqDheJlS5WIiIgUiOX3Y5VXQHlFoUORRtTu\nJyIiIpIHSqpERERE8kBJlYiIiEgeKKkSERERyQMlVSIiIiJ5oKRKREREJA+UVImIiIjkgZIqERER\nkTxQUiUiIiKSB0qqRERERPJASZWIiIhIHiipEhEREckDJVUiIiIieaCkSkRERCQPlFSJiIiI5IGS\nKhEREZE8UFIlIiIikgdKqkRERETyQEmViIiISB4oqRIRERHJAyVVIiIiInmgpEpEREQkD5RUiYiI\niOSBkioRERGRPFBSJSIiIpIHSqpERERE8kBJlYiIiEgeKKkSERERyQMlVSIiIiJ5oKRKREREJA8C\nuRxkjKkC7gFKgCDwLdu2l+czMBEREZGeJNeWqi8Cf7FtexbwA+CG/IUkIiIi0vPk1FJl2/YtjX4c\nBmzITzgiIiIiPVNOSRWAMWYv4FGgApiVt4hEREREeqA2kypjzIXARYADWOnHa2zbngNMMsacgDu+\n6viuDFRERESkO7Mcx+nwQcaY6cDLtm3vTP+8zbbtqnwHJyL/3969hMZVhmEc/1eqiKi49AKKoj4u\n7KYUlSgEjIUqIhgUxArWpYiXUtRVV6IEwYpdiKgNChVESjUuYtGK1gpSFV2o4LuqCknAekO8RFqj\ni/ONnRknc/3ODDnz/FYnPV/Iy9snk/fMOXOOmZmtFf1eqD4N3A0gaQPwXbaKzMzMzNagfq+pegx4\nWdI0cBpwb76SzMzMzNaevk7/mZmZmVkj31HdzMzMLAMPVWZmZmYZeKgyMzMzy6Dvm392ImkSeA24\nJyLmW+w/Dhzm5L2vpiLCF3gNoIuebwUeBP4GXoiI2SGXWCmS1gMvARcBJyj6/k3TGuc8E0m7gGuA\nFeChiPi0bt8NwOMU/w9vRYQfnZVBh54fpfjk9wpFtrdGxNJICq0QSVcCbwC7IuLZpn3OeQk69Lyn\nnJcyVEm6BNgOfNhm2c/p2YGWQaeeSzoD2AlsoviF/ETS/tq9xqwvd1Lk+C5Jm4EZ4I6mNc55Bune\neJdGxISkK4BZYKJuyTPAZmAJOCRpX0R8PYJSK6OLnv8DbImIP0dSYAWl1+ndwMFVljjnmXXR855y\nXtbpv0XgVuDXNmvWlfSzx1Wnnl8NfBwRv0XEMsXwde2wiquoKeD1tH2Q1v10zvOYojiSJP0ROUfS\nmQCSLgZ+jIjF9C7gfFpvg1m158k6nO/cloEbKYamBs55aVbtedJTzksZqiJiuYtTHKdL2ivpsKTt\nZdQxTrro+bnAsbqvjwHnlVtV5f3X09T7lXRKsJ5znkdzfn9I/9Zq3/c42zm063nNcynbTwyvrOqK\niJWI+GuV3c55CTr0vKbrnA98+q/DswHb2QHsTdsfSDoUEZ8NWs84GKDn9XyE2YOmnkPRv6ualrU6\nSHHOy9Euv852OZr7uhM4APwEzEmajoj9wy9rbDnnw9FTzgceqiJiD7Cnj+97vrYt6V1gA+A/Nl3o\ns+eLNB7VXAB8lK2oimvVc0mzFEePX9TeoYqIE03f55znsUjjuyTnc/Lt+lbZXhxSXVXWrudERO1g\nAUnzFNn2UFUe53wEes35MG6p8L9pWtLlkl5J2+sprkX5agi1jItWRzBHgE2Szk7XRUxQfCrN+vcO\ncHvavgV4r36nc57V28BtAJI2AgsR8TtARHwLnCXpwtTnm9N6G8yqPU+vIwcknZrWTgJfjqbMymp4\nHXfOh6Kh5/3kvJTH1Ei6CXgYEMU54KWI2CLpUeD9iDgiaQa4nuLj/XMRMZO9kDHSZc+ngUcoPhq6\nOyJeHV3Fa5+kU4AXgcsoLnbcFhELznk50vUMkxS9vA/YCPwSEXOSrgOepDg9uy8inh5dpdXRoef3\nA9uAP4DPI+KBkRVaEWl4fYriNi3HgQXgTeCoc16OLnreU8797D8zMzOzDHxHdTMzM7MMPFSZmZmZ\nZeChyszMzCwDD1VmZmZmGXioMjMzM8vAQ5WZmZlZBh6qzMzMzDLwUGVmZmaWwb8i9zvPy1EV9QAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75d0cb390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"a = -1;\n",
"b = 1;\n",
"\n",
"def U(x,a=-1,b=1):\n",
" return (b-a/2)*(x**2-1)**2+a/2*(x+1)\n",
"\n",
"x = np.linspace(-1.5,1.5)\n",
"pl.plot(x,U(x),color=pale_red,linewidth=5)\n",
"pl.title('The potential $U(x)$ with $a=-1$ and $b=1$',fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Deterministic System\n",
"\n",
"Let's write the equation down, given the specific potential. First, if $\\sigma=0$,then the equation is an ODE\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\\frac{dX_t}{dt}&=4c(1-x^2)x-a/2,\\\\c&=(b-a/2).\n",
"\\end{align}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Defining the derivative of the potential\n",
"def Uprime(x,t,a=-1,b=1):\n",
" return 4*(b-a/2.0)*x*(1-x**2)-a/2.0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"By numerically solving $U'(x)=0$, we can find that there are three equilibrium points for the system. Approximately, those are \n",
"\n",
"$$\n",
"\\begin{align}\n",
"x_1&=-0.955393,\\\\\n",
"x_2&=-0.083924,\\\\\n",
"x_3&=1.03932.\n",
"\\end{align}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "AttributeError",
"evalue": "__exit__",
"output_type": "error",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[1;31mAttributeError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-5-bde72c621a56>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[0;32m 5\u001b[0m \u001b[0mxinit\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0marray\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;33m[\u001b[0m\u001b[1;36m2.0\u001b[0m\u001b[1;33m,\u001b[0m\u001b[1;36m1.0\u001b[0m\u001b[1;33m,\u001b[0m\u001b[1;33m-\u001b[0m\u001b[1;36m0.08\u001b[0m\u001b[1;33m,\u001b[0m\u001b[1;33m-\u001b[0m\u001b[1;36m0.9\u001b[0m\u001b[1;33m,\u001b[0m\u001b[1;33m-\u001b[0m\u001b[1;36m2\u001b[0m\u001b[1;33m]\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 6\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m----> 7\u001b[1;33m \u001b[1;32mwith\u001b[0m \u001b[0msns\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mcubehelix_palette\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;36m3\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[0;32m 8\u001b[0m \u001b[1;32mfor\u001b[0m \u001b[0mi\u001b[0m \u001b[1;32min\u001b[0m \u001b[0mxrange\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;36m5\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 9\u001b[0m \u001b[0msol\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0modeint\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mUprime\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mxinit\u001b[0m\u001b[1;33m[\u001b[0m\u001b[0mi\u001b[0m\u001b[1;33m]\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mt\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;31mAttributeError\u001b[0m: __exit__"
]
}
],
"source": [
"from scipy.integrate import odeint # importing a solver\n",
"\n",
"t = np.linspace(0,10,100)\n",
"\n",
"xinit = np.array([2.0,1.0,-0.08,-0.9,-2])\n",
"\n",
"with sns.cubehelix_palette(3):\n",
" for i in xrange(5):\n",
" sol = odeint(Uprime, xinit[i], t)\n",
" pl.plot(t,sol,alpha=0.8,linewidth=10)\n",
" \n",
"pl.title('Five different solutions of the ODE system',fontsize=20)\n",
"pl.xlabel('t',fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we can see, out of the three equilibrium solutions of the system, the two are stable and the one in the middle is unstable. We will use this information for comparisons with the stochastic system.\n",
"\n",
"# Stochastic System\n",
"\n",
"Let us now assume that $\\sigma>0$. In that case, we have an SDE, which we can solve with Euler-Maruyama. The scheme shall be : \n",
"\n",
"$$\n",
"X_{n+1}=X_{n}+f(X_n)\\Delta t+\\sigma \\sqrt{\\Delta t}\\cdot z,\n",
"$$\n",
"\n",
"where $z$ is a standard normal distribution."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def EM(xinit,sigma,T,Dt=0.1,a=-1,b=1):\n",
" '''\n",
" Returns the solution of the Langevin equation with \n",
" potential U. \n",
" \n",
" Arguments\n",
" =========\n",
" xinit : real, initial condition.\n",
" sigma : real, standard deviation parameter, used in generating brownian motion.\n",
" Dt : real, stepsize of the Euler-Maruyama.\n",
" T : real, final time to reach.\n",
" \n",
" '''\n",
" \n",
" n = int(T/Dt) # number of steps to reach T\n",
" X = np.zeros(n)\n",
" z = sigma*randn(n)\n",
" \n",
" X[0] = xinit # Initial condition\n",
" \n",
" # EM method \n",
" for i in xrange(1,n):\n",
" X[i] = X[i-1] + Dt* Uprime(X[i-1],a,b) + np.sqrt(Dt)*z[i-1]\n",
" \n",
" return X\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can reproduce the picture from the deterministic case, but this time with the extra stochastic part. When $\\sigma$ is small, we see a similar picture with previously as the deterministic dynamics overpower the stochasticity."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff75a797610>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAFkCAYAAAD13eXtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8JPdd5/9X9a2WWsdImns8M76+jh3bsePYjuPcIXfI\nHdgEyELCLizLbrIXsBBuwsKPwAaWLAsBAuSA3E6wnTh3bMeJ79v+2h7PfWh0X60+q35/fLs1Lalb\n6m51z6hn3s/HQyNNd3XVt46u+tT3+6nv1wuCABERERFpn9CZLoCIiIjI2U4Bl4iIiEibKeASERER\naTMFXCIiIiJtpoBLREREpM0UcImIiIi0mQIuERERkTZTwCUiIiLSZgq45Iwzxvy9MaZojDnvTJel\nGZ1WfmPMe40xx40xOWPMf2vws58wxvjGmM3tKp+s1GnHmIisFDnTBZCNwRjzW8Bv1Tn5d621r2jh\n4v8C+CpwsoXzXMEY8+vAP1lrD7V41qel/K1gjBkA/goYB/4dcP8a0y/fZkHp57QwxrwX+HvgV621\nf3y6lrsBteUYM8aEgJ8FfhK4ENiK279HgDuBj1hrH62Yvrw/KuWACeBh4GbgE9ba2SrLqvbZagJg\nwFo70/AKbRDGGAN8GDhQemkI+O/W2qb3nzEmCdxlrb1y/SWUM0EBl5T9C/DIstd+F3gO8H5guuL1\n0VYu2Fp7P2tc+NfLGLMH+D3gdqClAdfpKH8LXQzEgU9aaz+x2oTt3GYNOufHH2vHMWaM8YAvAW8C\nvgn8KTAC9APXAe8GftIY81pr7feWffyTwJdLf8eAHcArgf8N/Jox5j3W2u/UWHTlZ2uZb3B1Ngxj\nTC9ue/4Pa+1nSq/9GvAtY8xV1tpCE/O8Bvi/wHNbWlg5rRRwCQDW2ieBJytfM8b8Mi7gunk9d2Yb\nxLXowg3QVfqdrmPajbLNvDNdgLPUa3HB1mettT+57L2/NsZ8GrgN+EPghmXvP2qt/eKy1z5ijHkB\ncBPwVWPMjdbaB6sst9pnzya/AkRxN7FlfwX8DvA+4P/VOyNjzCXAn+BqNhsO1GRjUcAlTTPGfAL4\nGeAK4P8DbgTeZa29tXTi/RXgJUAfcBz4EfAha+1TNeazp9x0ZYwZxDVxvgnYDszgmjg+bK29e9nn\nN+NqYl4HbME1h/w/4M+stXljzHeAl+KCh+8aYwJgb8WytgO/DbwG16QyWyrrH1pr71hrfYGfWF7+\nRtbBGBMBfhn4aWAv7nt5CPhcadrcavuh3nVYth1+2xjz28BvW2t/t8r8qm6zikm80l37z+NqN44C\nf2Gt/bNl86l7P7ZCvcddxb7cBfxUaT12AmPAPwC/Ya0NKqZ/Na7G93Lctv1saTlPAXlr7fmNrrcx\n5nZcILPDWnti2ed3AIeB71trX7b8O9Jo+Wu4HLd/v1btTWvtt4wxb6WB2k1r7T3GmHcAdwAfxR1D\n55p3AD+y1vrlF6y1k8aYJ4F30kDAVboRfiO4PD7cTZB0KCXNy3qU83k+jAty3g88Zoy5EvgucE3p\nvfcCHwdeBfywdDGpNh8AjDH9wA9xF5LPAD+HC3CuBL5vjHlZxbQDwL3AW3F5Lj8HfBv4X8CnSpP9\nJi54AXcRfCelXBhjzBbgHlzzyWdL6/BHgAG+XbrQ1lrf9wGPLS9/o+tQKvdHgMeBDwC/gLs4fwj4\nNGtoYB1+s7T+Xmm6d5R+V7N8m72DpU3Jv4drQvpD4D8CPvAnxphXNrkN1q3B465yX74N15z2y7gm\ntV8rrVN5vtcD/wrsAf4A+A3gIty266lSjnrXu7xv31Zldd5ZKt8/LStvw+VfxXHcsfB2Y0ys2gTW\n2q/UqKWqyVr7A+D7wI3GmN2NfLbTGWN6cMdGtSD1GPD801si2UhUwyXr5QFRa+3Pl18wxrwYV6vw\nm8tqiE7iqtbfi7tQ1PKbuIvbC62191Z8/p9wQcmfAVeVXv4QroblZdba20uvfaqUYPqTxpjrrLW3\nG2PKSf7fs9Z+v2JZv42rEfo31trF4MMY88+ALS3rsjXWd73r8G9wzSw/VfH5TxljngGuNcZ0WWsX\nqi2kkXUobYfyTdbjqzXr1NpmpXX1cLUyr6pY1sPAXbjk6281sQ1a4bk0dtx5pc9cV86rMcZ8HdgP\nvB0XCAP8TyCMq70tHzsfN8Z8DVeLNrmsHPWu9+dwtUBvBz62bB7vBLLA51dZ33rLX8sXcc1crwce\nMcb8A27f3ddMntEy3wFeDFwPHFz2XsIY07fKZzPW2myzCzbGXI67IXg5kFr2dgC81Vr7lWbnv4Zy\ngFkt4X8e6DXGRK21+TYtXzYwBVyyXgHwhcoXrLWf4lTtUvmuL8ypE++eNeb5LuAJ4OllJ+YF3J3z\nG40xfdbaaVxz3pGKYKvsv+ESeJ9idW/BXTA/V/mitfawMeabwBuMMXuttftLb61Y3xasQwHYYYzZ\nba1dvDg18FReo+uwXgHw58tee7j0e3vFa41sg3Vr4rgLcM2gi8FFqbnuJLCtYrqXAceXBeoAfwy8\nmpXqXe+x0v55lTFmyFo7Vir3Dlyg8sU1tk295a/KWjtvjLkBF5i9FRek/D6wYIy5C/gK8A9N7p9y\n7Vm17kN+C3eTUE2ACwJXNHPXwxjzetz34BO4APui0rz+Hhe85oEfVPnc3wJXU1/Oolea7gNVjone\n0u9qaQDlBwH6afGDR9IZFHBJK6y4kBtj/gMur8QAiYq3AlY57kpP+GzHXTCW1xyUPw9wnjHmSGm6\n5U9QYa09jjvp11S6GG4B7qyR72KBN+Ce7Ktcx1UDl0bWAfdk6O/ggsMnjTG34p5w+rq1dt9qy1nn\nOqzXkrJZaxdKtV9dpXI1ug1aoonj7tkqr2VwSc8YYzbhmg0fqDLdD6ssv9H1/gwuef0tuOZPcLVb\n4J7mW8uq5V9LKXfsnaUcwDcCL8Llv70ceAXwO8aYd1lrv1HP/CpEcetarabsb1i9qfxAg8sCwBhz\nES5R/T9baz9e8fqlwCXW2m/X+qy19n3NLLOKYul3te9ieZ+EW7Qs6TAKuKQVlvS5Y4z5PeDXcc0n\n/wV3cc4Cl7Ky6WS5chPAQ8B/pvYTagcqpl0zqbyGcv5NrUfQy8143cteX9HH0DKNrAPW2r8wxjxe\nmvY1wJtxSel3Ar9Y2Q9SFc2uw3qttc0b2gat0ORxl1ljtsnS7xVPdVpr08aY4rKXG13vL+GSqN/O\n0oBrCrhljbLB2uWvi7X2GPDXpZ9yP1L/Dvgg8GljzIUN1nSVH7A4VuW9Z6vUDLXCH+Ka5j++7PWT\nuG4uTofVaq7K38G1zh9yllLAJS1ljAkD/wnXEeKLrbWTFe8lan7wlPLJKFalmXD5sjK4O8n+Jos7\nV/q9IvG5pNkTZN3rUGat/Raun5447smud+OeWvyWMeaiVTqBbNc6rFfD22A9WnDc1VLOJVoxD2NM\nFytrKxpab2vtnDHmX4EfL9VW9uCaE//6TOb5WGst8F+NMcPAe3ABy20NzOK1uO9m2/c9LNb0/jju\nwYHlLub09SM3Qqnj1irvdQNT1tqO7WNM1kdPKUqrDeHu8h+qvOiVrPmIeCmwOApcZIwZWv5+6XH7\n8rR5XLPhRcZ1rVA53S7jhrB5zirLmi59/jnGdQK53KWl30+sVe5m16HKZ7PW2tustf8W18w4xCrb\nrV3rsF7r2QZNWtdxt4oxXNBV7Wm7Fy5/ocn1/jSuuekNuKdBob7mxKYZY2LGmN82xnxkjUnLzdDJ\nVadaOu+34o67L1prJ5otY4MMLvi9Z1lZkrim0VX7/TLG/LUx5h5jzN11/JSne/Hy+Vhr07jm511V\nFnMh0NATn3J2UcAlrTaOy2NYMuZb6cmh9+Du/rqqfK7SZ3EXoP+0bB4DwEPGmJsrXr4J96TYO1jq\nV4G/A8oXuHLTz/Kais/hasiWdPxYygd5OXCPtfbIGuVteh2MMVcbY6wx5v1V5lGuLVnria12rUOt\nbVavRvbjerXiuFuhlBf3I2C3cb19l+frAf+jxscaXe9bcE+1vR6Xy3XQWntno2VtRKlvtzcCHzDG\n/Jtq0xjXv917cM2WddVUlYKQj+NqGn9lveU0xkSMs7wrmeXKQfbcstf/A65Z8xOrfdha+++stS+w\n1l5bx095ulrb5GaWNWEaYy7ABWGfW/b6heusgZUOoiZFaSlrbcEY80XgHcaYTwK34qr0fwF38r4F\neKVx46rdZK2dqjKb38flMf1PY8xWXFL8VuDfA8O4mp+y38U1JfxNKe/kGVzS7/uBz1d0D7Afl0/z\nG8aYy3C95z+FezLrLaXPX4nrV+u8Unnz1NefUTX1rsNDuDyr/1Na/r24ROPnlZb9KO4R+9W0ax2W\nb7N6cooqNbIf13K5MebtNd570Fq7r4HjrtEuAf4Ed0x9yRjz57iL+ztwzUfVguGG1ttamyuV/c24\np9z+qMHyNeu9wDeAfyptl3/F5SClcDVU7wY2AT9vrR1f9tnK/eHhHtz4MVxHryeAt63yVOxq+7Ls\nwdJDIztwtbNfwwWkVVlrnzbG/ADXN9xTAMaYl+ICrtfbOjoPbqH/C/yyccMblZ+a/WXc97Iymf/F\nuH7jbsN12ryW8gMpa3UTIxuUAi5ZSzNDu/wC7q741bhmkvuAt1hr7zLG/A7w33EXldtxycFLWNcr\n83W4/ozehOtRex7Xz9PPVfaxZK0dKU37e7gk30Fck86v4jqDLPs87nH9V+GaH34EPGWtHS99/ndx\nF5gtpTJ9F/i9NRLWKy3ZTvWug7W2WDrx/jouaHovrnbkIO5x/Q+vlcvTxDrUOwB1tW22miXzbWQ/\n1jHfd5d+qvkgrpuKX6T+466eZZbX41+NMT+D61D0d3FNuJ/CdW3wE5yqCSxP38x6fwb4t6XlfqrK\n+0vK1Ej5a7HWPmaMeS4uGHgdbt16cEHkIVwz3MdqHD/L98cMbmiwXy99plbO4Vr7sqy8T8uf8VeZ\ntuxtwJ+XnkqM4m5crrPWntYuGKy1J4zr3PYPjDFX44LoAeC1y/o3G8El9D9Ta16lHLp/wgWe5fSA\nA8aYR4GP29JYjdIZvCBofqg0Y8wf44Y3CQP/y1r7pYr3XoXrlbkA3Gqt/f11llXOUsYNWfEzVAy3\nI7LRGdfP1wxuGJcV+VzSGsaY9+E6Nv7pM10WkfVoOoerFMFfaq29AXd3tLx54KO4zvRuBF5t3CCc\nItWUn7CrZ0BlkdPKGPMuY8zXjTE3LnvrZ0q/T8uTeOew17AsGV6kE62nSfF7nGpimAKSxhjPWhsY\nY/YC46W+XTDG3IJrW39yXaWVs0op5+pluCagY+WetkU2GIvrEPRzxpiP4gaVvgqXGzdKY7lo0gDj\nukl5GNdTvEhHazrgKj29U07cez9wS0VP11tZ2gHcSeD8ZpclZ61XAv8Hl3P1789wWUSqstY+VMqz\n+xAu32kI91Tk54DfKt9YSutZN6ai0lHkrLDupHljzJuBn6X6mGJltXpblnOYtfZjrN3zvMgZZ619\nAJeULSLSlHUFXMaY1+Ce3HmNtbayJ+tjLB08dQfVh3hYNLv/6RXZ+9079xCK1jUkmIiIiMjp1FBl\nUtNPKRo3SOvtwCur5d4YYx7BPZp9DDc6+7uttTUff53d/3SQyy0d59Tv3QyRWFPlk9NreDjF6KiG\nCOtE2nedTfuvc2nfdbbh4VRDAdd6arh+Atfn0WdLvS4HwLeBR6y1N+H6xPnn0uufWS3Yqimop+sV\nERERkY1tPUnzfwP8zSrv3wHc0Oz8AVhHH2EiIiIiG8XGHktRNVwiIiJyFlDAJSIiItJmGzrg8nwF\nXCIiItL5NnTApRouERERORts8IBLSfMiIiLS+TZ4wKUaLhEREel8CrhERERE2kwBl4iIiEibbfCA\nSzlcIiIi0vk2dMClbiFERETkbLChAy4IVMslIiIiHW+DB1woj0tEREQ6ngIuERERkTbb+AGX8rhE\nRESkw238gEs1XCIiItLhOiDgUtK8iIiIdLYOCLhUwyUiIiKdbcMHXJ4CLhEREelwGz7gUg2XiIiI\ndLoOCLiUwyUiIiKdrQMCLtVwiYiISGfb+AGX+uESERGRDrfxAy7VcImIiEiH64CASzlcIiIi0tk6\nIOBSDZeIiIh0tg0fcHmBr1ouERER6WiR9XzYGPNc4MvAn1prP7bsvf3AIcAHAuA91trjTS0oCMDz\n1lNUERERkTOm6YDLGJME/hz4Zo1JAuC11tqFZpdxak4+HVAZJyIiIlLVeqKYDPA6oFatlVf6WT/l\ncYmIiEgHazrgstb61trsGpP9lTHmdmPMh5tdDqCAS0RERDpaO9vpPgT8F+ClwOXGmLc1PSclzYuI\niEgHW1fS/GqstZ8s/22MuQW4HPjiap+JxaoXJ9EbJ5pKtbR80nrDw9pHnUr7rrNp/3Uu7btzR6sC\nriW5WsaYXuCzwJustXlcLdfn1ppJLleo+npmah4ySprfyIaHU4yOzp7pYkgTtO86m/Zf59K+62yN\nBsvreUrxauAjwG4gb4x5O/AVYL+19iZjzM3AD40xaeABa+0Xml2W5/uoUVFEREQ6VdMBl7X2fuDl\nq7z/F8BfNDv/JZQ0LyIiIh2sM9rplDQvIiIiHaxDAi7VcImIiEjnUsAlIiIi0mYKuERERETarEMC\nLuVwiYiISOfqiIDL830FXSIiItKxOiLgQr1wiYiISAfrkIAL5XGJiIhIx1LAJSIiItJmnRNw+Qq4\nREREpDN1TsClGi4RERHpUB0UcClxXkRERDpTBwVcquESERGRztQxAZengEtEREQ6VMcEXKrhEhER\nkU7VQQGXcrhERESkM3VOwKVuIURERKRDdU7ApSZFERER6VAKuERERETarIMCLuVwiYiISGfqoIBL\nNVwiIiLSmTom4PICX7VcIiIi0pE6JuACFHCJiIhIR+qwgEvNiiIiItJ5FHCJiIiItFnkTBegbPzg\nGEHII9GTIJqM4XneyokUcImIiEgHWlfAZYx5LvBl4E+ttR9b9t6rgD8ACsCt1trfX21eB+7dj++7\nHK1Q2CPekyDekyCRSpDa3EtXf1IBl4iIiHSkpgMuY0wS+HPgmzUm+SjwY8Bx4HvGmM9ba5+sZ95+\nMWBheoGF6QUATjx5nEQqwYDZQ//Fe4nEo80WW0REROS0W08NVwZ4HfCry98wxuwFxq21x0r/vwV4\nJVBXwFV1YbMZjj/wDCceO0zfrs1sumgnyeH+6k2Pck4KggC/UCQUCeu4EBFZQxAEFHN5/IJPUCzi\nF93vwA+IdncRTcZ1Lm2hpgMua60PZI0x1d7eCoxW/P8kcH6zy1oUQFAoMrX/OFP7j9M11Mf2awzJ\nof51z1o6V3psmomnDzN7fJxCOksoGqZrUy+p7UOkdgwR7+vZMCeNIAg2TFlE5MwqBzyFTI5CJkcx\nm8eLhOkaSBFJxNq23PT4NCcfeZb06BTFbL7mdJGuONuefzF9u7fqvNUCpytpvkV7amk/XAtj0+y7\n7R62XHEBw5fuxQvVtxgXxfuuJqTOz5xJgR8wPzoJAYTjURL9GyeAaEYxX8DzPEKRcNPz8AtFpg+O\nMP7UIRbGZ5a+ly8yPzLJ/MgkJx54mmh3gtSOIXp3bqZn2+Bp33azx8YYe+Ig6bEp/KJPcqiP/j3b\nGDh/+7q2gYhsHIVsjvx8xv2kM+TTWfLpDIVMDr9UaxT4AQQBftHHLxQJBz7ZhdzKmYU8+nZtYcuV\nFxDv7W5pOcefPsLxe58kKK6dE11YyHL4jkeYPTbOzusvxQt1VscGG027Aq5jwLaK/+8ovbaq0BrB\njxcOEY6vLPLkEwfwp+e4+FVXE+/pWny9mC+wMDlHemKW9OQs6YkZ0pNzZGbSuODNI5qIEu2KE+2K\nEe2KE+/ponfbIJv2bD3jwZhf9Dn20D6OP7qf7NzC4uu92zax94WXkdq66QyWzsnOLTBx4AT2oaeI\nJRMkB1Js2ruV6LK7s0Imx8iThzj51BHmx2aAgHhPF/27NjO4dyv9O4frCj7yC1mOPriPE48fpJB1\nJ6pYlWNi6cILzB08wdzBEyQHUux90XMZOG9z1UmL+QKZmTRdfd0tCYaOPPAMx+56DIBIyINQmML0\nHGMPPc3M04fZcdWFbL10N+HoynUIAndyDnwfAt/93/fxIhG8cKSlgePwcKpl82pGEAQUF9IUsxmC\nYoFQNEYk2U0o2r67/LPJmd5/56r58RnGnjnK2L5jLEzNNfTZEO4qVOv8tXBijIMnx9l22V52XXMx\n0a74uss7+tQRxh58imgkBJH6g6f00ZNMPBjh4lc9n1BYQVezvGCdvbcbY34LGLPW/uWy1x8B3oAL\ntH4AvNta+0yt+Xz3Tz4dlJ9SrCkUgnDtE3A4HqV/7zayM2myM/PkK4KURsX7e9j5wstIDvY1PY/1\nWJiY4chdj5GZnK0+Qchj+zWXMHjxrtNbsJJCNsfIw/uYePoI+AGxeIRctgC4wLhn2yADe7cT600y\n8fQRJp89RlAo1pyfFwmT2jZI787NpHYOV30wYurACY7d88SqVeD1Grp0D1uuvJBQOEQQBKdqoUan\n3J2f55Ho72Hggh0MnL+NcKzxBzUmnz3GkR88uuZ04XiEYbOTvh2biMVDeH4BigU3nFUtnkcQ7SKI\nJyESh3LwFQTgFyGfwSvm3ZO94ShBNAGR6t+d4eEUo6M1jrN2K+bxsmnIzldZXw+/qxcSPafWr0m5\nuQWyM/N44RCJ/h4i8bMnkCvvv/K5vJNrvztBdjbN9METTB04QbbBIGu5yvPmakLRCMOX7iGxKVWq\nKfPBD8DziHTFiJXzrVapgZobmeDAt++vq2arltTOYc678YoNVzNfzOVZmJwlFA4R60mu2RzrbmZZ\nd6XK8HCqoRk0HXAZY64GPgLsBvLAUeArwH5r7U3GmBuBP8YF8Z+31v7ZavOrK+DyQjUvGm0R8th8\n+flsvmxvS6tSA99n/uQU8yMTBEHgatb6eoj3JAh7OUYfPcioPepGMvJw/yz+XlqOQXMe255/8brK\nV8jmCIXDdX2J/KLPxNOHGXl4H37u1Imi3hNHPbxImMGLd7H58vMJRyMEQcDIw/sYfeTZlsy/rGuo\nj6Hn7Gb8yUOkR6dWLU//7i1sumgnXYN9dV3Q0uMzPPuNe1YJMgMoFlxAVPEd9DyIJKLEumJEE1ES\nvV30DKdI9nfXPDkEoTDEutx88lkXsFWbLhIjiPe4aSvWoVUBVxC4JpNV74BLAaGfSVOYniLIZgj8\nAL90EVlsdqn8SDRBkEgRjkWI9/YQTa59p+8XfdKjk8wcHWP26Bi5mflTb3oeyaE+encO07trc8ub\nbFyhS4EvAYQizQeMQUDpylBzklguy757nmLm6KhLdk7G6dmyidTOYXq2bGr9xTEoHbvFHJ5fJAhF\nIBqH0Ma6CK9HEATk01my03Nkp+fJzsyTmZ4nOz3Xkhu+slaeNwl5RJMJYt0JYqkkyaF+encNE4nH\nyEzNse+2u5ecs2sLTp2Tqhx3PdsG2f3S59V9XPlFn/mTE8wcOsnCxAz5hSyJvh56tg+y6YIdTd3M\nAos3yuP2MHPHx5ecR6M9XSQHe+ka7CMxkKKwkHX7cMrtz9zcAgQB8f4e+s5z5/ZmahBPW8DVavUF\nXJ67mz9dAh/8IslNPex6wYXEU8nSidMj8ELu78UTaUVQFApDOFr1JJudTXP4jodX5B1RrtXwPNbc\nJ6FQ6STuvgw92wY578VXuAO3mIdCDq+YdxfiSALCK0/42Zl5Jp4+wvThk4s1gYmBFMOX7aVv95aq\nQcXM0VGO3/fU0otXSUtPHCWRZJytV17EzNFRZg6NtHTetVVu+5XbINabJN7bTby3m1hPF7FUF/FU\nN9HuxOI2K2RyPHPrD8nPZ6ovorSvGxGOhkkNp0ht7iW1uZdoV/M3HoEXgng3QbwbwpF1BVyBHzB3\nYpyJZ44yPzJBMZsnFIvQtamX5FCfO+n1J/EKOdInx0mfnGR+fI6FqfTax3mlitrtaE8XyaF+ujf3\nuyeVQx75+Qy5+Qz5+QWy0/PMnZjAz9e3jWO93fTuHCa1Y4jkUP/SgHGxjEHp0CgFP1U7Zg4I8lnm\njxxn4ukjzI5MEYqEiSai9GwdpOe8bSS3bl77QuX7kJvHy6ZdLSWlfRYKL/lZmM9z4tGDZEenan73\nyjXHqR3DJPq7CcdjRBKxFU/yBsUiQXaeYGHBJXHnfQr5gELBp5DzKeYKBMU8XiHvaiVxtSReKERX\nbxfdQynCA0MQ7153beR6ZabnGX/qENnpeYKiT6QrTqynywUjPV3uuxryFmuKAj8gKPrkZtNkpubI\nTM2SmWptYFVLO86blbxwiMRAioWx6bUnDnx3bvKX1YB5Iff980KL15yuoT76dm0mlkoSSyWJJhN4\nXvnrEoAfsDAxw/Thk8wcPllzW4aiETZdtJNBcx6x7kRd61TM5Zl89hjj9jC52XRdn1mLFw7Rt3sr\nQ5ecR9em3ro/17EB14OfvjVIT6fJzmVXPxFH69sp6xL4p2ofSkKRENsv28mm3fUlXQdeiCCRWtIc\nkpmeZ/8376GwPEmymC/dDTeoIvCK98TZc+35JBIryxZE4gRdKYJQzN0RPFW6I6ghtXOYnddftlgt\nm51Nc/zeJ5k9OlbzM+0+cbTdaicbz6v4Xbl9T/0d7eliYO82+s/fztEfPs78yET1ZRTzLRmEPdmf\nZHDvMAM7N9VVLV7MF5kZmWbmxDSZ2QU8zyPeHScxtImtl+whE4rWvMNbfLIyCKCQxctnyc8vMHlg\nhIkDo+QWcos3IqUPlGru/Jas66I1UgrWLyAUCZEa6iG1uYe+4Z6aff4F5ZuqcIQgFMXzCxRmpzn6\nwAGmj9euLQ3HIvRsH6Jn+xZC8TheyMMLh/BCIUJeQCIeECW36nYrZPOcePI4EwfHCAKIxGIUgsZq\nuL1I2N2g+UX8bBY/v77jMhwJsfXSHWwyu6F7oOmgKzM1x/TBE8ydmCAUjRDr6SK1Y4ierYNr5g75\nhSInHnya8ScPNbXsM2FjnDdLNZb1XIMWz4Heqf8vzqZUGxsES4+lZRUEVYU8+ndvZejSPXQNVM9H\nLGRznHwtWHziAAAgAElEQVTkWSb3HcXPN3G9rFNyuJ94f89i/Qm472i8t5ueLQNLasQ7NuCa3f90\nkMsV8H2ffDpHenKeiUMTzI0tu/NuZ8BVJdBarm9bP7uu3k24zurUIBIj6B4gm87z7DfuoZDOVr4L\nhXzLetD3PI/U5hT9OzfRu7WPUDhELp1jYSpNeirN1PFp8ll/9QO/JJKMs/P6y0iPTTP62P5T7f6L\nF9Gg4rf7Tvmr5QaEQuCF3e+mH1otNdP4xYoqb899mZtuzghKAe8698GqJ5UWLaOKRE+Crc/ZRu+2\nlX3SFXIFZkammT42xezJmRVNdWXhSJiiFyHSFScUjS7pj8cvFMH3CXm+29Qhb/G4OiPnjpamFQSn\ngsPSgwlLFuVBV383A7s2MbBr06rf+amjkxx9+DCFuppsli1kMVB1y+/d0svWS3fQ1du1ZFK/6DO6\n7ySjT5+gWKi4GQx5bpSOcMQdg/Uo1d43daO3isE9Q2y/xkDPpoaCrtx8hpGHnmFq//GqgV8oGnFP\nGu/aTGr70IqHTOZHpzhy16PkZlpT49EewbJzJ0QiYQrlfXnqCs+pGtWKvz3cObSVNYhN1LY3LRRx\nx+ga+vduY9s1Zkme5dzIBIfveITCQrb6h/zC0mbQNjZvdw320r9nG317trL9vKEODbgOPBPkqlQ7\nZucyjB8cZ/LQuDuZ1RNw+UUIiksvcJU1FYsX/eBUAFE+6dYh2Z9kz3UXEE3U1/acS+d45of7yWcq\nTm4trO2oJhQO4YU8itXuBLxQqZmxzrviOk7Oiyf9eizZDzWaZyotBlmrJ5G7ZtwG7vTbcbIJhVw5\nysdXvXeO61Su8Spk82RmM2RmFsjMZOoKikIhDz9g6fYLStu8DUFiS5SbN0KVeY3LjqPK7/ayC12j\nwpEQA7sGGdw7RCLlAqEgCMhn8hx/9AhTx2rXajXDC3lsu3QHQ+cP43ke8+NzHH7wINm5lRecJd+9\ntW5A6ripXK+BnQPsuPYSvN6hNb/bxVyB0cf3M/bkoVUfqqlUbibrGkiRGEiRm1tg7ImDbTuXNq18\nDVqlpreh82ZZZfNys/zi0iDldKnzPB1LdbHn5VcT7+1m5ugoh77/UPVk/1rncM8rXePamFfoebzi\nA2/rzIBr7tCzQbZW9Iq7uxuxxzl5oEpbdLn5ospdarvEkjHOf+GFxHtWDwBz6Rz77nyKXDpXkfsR\nbIwLmReCcLj2QRkUobhGoFPS1IljSVkqq6or8mUaPT6XBDw1BMXSRaeNx34ofFoCrVZYsu9CEbd9\nNsh5YSPq6uvCL/rkF3L4xfZup9Rwilh3nPEDtZvzq373VgRepy/4B1dLd971l7DgJ5g9Ps78yCS5\nuYVS/4chvHDY1ZTOZyhmqvRDVY9qzdZLbqjPkAaCmXWfN0MRdw6va32rtBBUiMTCRGJRMnM1ck9b\nqY7a2HA8yuAl5zH66P7qwVYxt/Z1tNz03yav+ODbOzPgmj9yIMjMr92Nw8x8mMM/fIJCOnPqC3eG\nRGJh9lx3Ad2behZfC4KA/EKO7FyW7HyWsX0nyc7XDiQ3hPLJGUpfxHLNQP3HxrpPHC2Q7E8yuGcI\nQiFmxheYHZ3Fz1ccH2fqrm6D2wj7Tpq35v4Lhc7IDV4o7LnFLiZdr1XbEFSvEfKW/VFPbmD5Bm7x\nJnflE96rl2F5C0nl/ELL5lUqi+83fH4JhTwCIBKLEIlHyMxmajb9r6q8jUPLg69y683qtdWx7hgX\nvdgQiUcZ3XeSY48eabwMjfI8l5NZsxa08mnJZU3vjbQOeV4pDaH1QXjnBlzHDgeZ2fr6NClkCxx+\n4AAzIzNrT1xD+SmV9QqFPeLdCYrFIn7Bp5gvtmS+neZMXrR7t/Sy+eJtJAeSS/KYfN9ndN8oI/ZE\nqfPQc2+/1EMBV2frqP23GPxAKSmJJakdp6UMoWXX3gYCuTVn7ZHsT5Y60o4R64oS7YoRjrpRTTzP\nc79DnnvCsztOsWK4r1w6y4knjjN5pMpDN3UXohQc1hlkR2JhLnyxWdJaM35glKMPHz49uyQcXdo8\nulqztxdqvpKlnEbTSNrJGjo24EqfOBosTNcfQAVBwPj+UY4/fmzVZO1wNEwilSCeSpBIdS3+HU1E\nCYoBhVyeQrbA9PEpRp8Z2bDXZK/UFLlRyxcKeYRjEfKZ1R+lDoVDDOzaRO+WXubG5pg+MUVuvskm\nBWCL2coWs23VJ0fnJ+Y4dN8B16x7hnkebDHbmJ+YZ/ZkAzcMK54Gap2OumDLCtp/Z5bnQc9wiv4d\nm+jb1ld11IhaYrEIuSoPWqSn0hx/7OjKh8ZaLBT2OP+Gi5a00pRNHh7n8AMHT881p/zQUbUnxduh\nssZyRa1g/To24Fo4eTxITzaeeFrIFRg/MEZmOo3vB66zyMUAK0EkHq275+WNdGGulOxPsvN555Ff\nyHPwvv34hQ2Q/1Uh2Z9k91W7iaYSpCfnmTw8wfSxSQq5U/kisWSMob3DDJw3SCR26oQUBAGZmQWO\nP36soQAkFPbY+bzdDOysb3ijYr7A4QcOrfrIPkA0EWX4wi3kF3JMHh5fsg6tsP2yHQxfuAWAhek0\n08enmJ+YJ7+QI5/1SxfOipNBNfU+YRYK1dU0vCEu2JVPFhXb0/9RKOT6uNsgp7yW2RD77xwTTUTp\n6usitaWP/u39NbsPWUutgAvcuTE9Mc/kkQl3TQoC1wWMd6qmzC8UyaVz5BZyDV8XPA92X7OXvu0D\nNaeZOjbJ4fsOdMzx1XTLVbWnzIOglM/qn3pKtNw0XTo/d2zAlRk7GcyP1+4b6nQp5osce/QIE4dO\nX1nCkTDhWJj8Qm7JxSDak2Toou0Mnb8Zr5jDC3wWphc4cPe+DREURhNRtj5nOwO7NhGPR5ecOMrd\ne2TnsyRSCaJdsVUD3yAImDkxzbFHj6y5btFElD3Xnk9yoLEewoMgYOLAGMcfP0Zx2RNRkViYzRdt\nZXDPMKHSGGN+0Wf62CSThyeYH59b90mnf8cA5z1/z4rtEERiBMl+gnCUYi5PPp0lN5Nm7sQ4s8fG\naneg6gp5qinEo3qOyRoB2hm5YHuuSSXW200oFnNjQ5b6o/L8Al4+Qzk3xvPcvliYSjccAMeSMXq3\n9JHa0kvPUIpivsjsyDTTJ6aZG51pe9L76VDef6Gwx+DezVD6Lm343NEOEEvGSKQSJHq7iPe4m/h4\nT4JwtDVPv60WcDUiCAKKuSLZ+SyzI9OngrQaPA+2P3cnQ+dXH1O2UmZmgWOPHWWuYvioZkRiEfq2\n9RH4AZNHJ1uaepMaTjG4d5jeLX3kFly3UgtTaRamF/CLRdfvYHn/lVq4Jo9MMnFwbOmT/OVgqs7m\n5Vf8j/d0ZsCVnRgL5kZHz3QxFk0emXDVqaXxqk5VO5a2V7Xt1kQOQDga5vwbLiLZn8Qv+GTnMxQL\nAfQO0jW86dSQPYEPmXm8zCzFTJYTTxxj4tD4uu/W491xwrEI6cmVvcfX4nkwdP5mtphtiyeeVp04\n/KLP6DMjnHz6RNWLYbI/ye5rzye2jp7Wi/kCEwfHyc5nCfyAnuEUvVv7Vu1nyfd98gt5cvPuYYhc\nOktmJlP3Sairr4sLbzSLwRxAEAoTdPVCrDyCwUpBEJCdmWf22BhTzx6vPbZmPWokm7Yi4PI8SG3p\nY3D3EF7IIz05z/zEPOnJeXdC80KEohGSw/0ktwzSvWWQrsHe2s0vuQVC8xNLyhoEAdm5DOmJZfOG\n0iD0MWLJU7kzib4ksWTtQN8v+MyNzTAzMsPMyDT5hRbWrJUSmFPbh4hFYebYOPnlHR7XNZ9w6c6b\nU7WVyxK6QyGPvh0DbL1kO7Gk+16Ut9XsyAwL0wvks3mK2QKFXIFCNl/1vOGV+lgLxWJE4lHCsTCR\naMj9xCJu3FEvDJEo2YUCE88cPX19ODUp2Z9k4LxB8gs5VxOUzlHMFUoVFeWaotDiuseSMbp6u0j0\nufSTRpoHm9Gq8+ZylbVjU0cnlwQV0USUXVftJrW5do/qQSzpOu4u5t3NTz6Dn3NdzlSeA7Nz7rd7\nirCcm1c+nXlue/Yn6dvWT89QarGT5vxCjrFnRxk7MLquFpuu3i7Oe/4eEsv6rKtXsVBk6vAEY8+O\nNvV0ZscGXLmpiWB25HQN31Kf2fF5Dtx7sLEnqRvoNT4cCbH3hRfRvelUTU0QjhL0DNbuIK4i8MrN\nLTB1ZILJIxOn+ucp98/ihWo+led5HqktvQztHaZn2PXqe/LpEUaePLZmANe9qZsdV+yiqy+55PWV\nJw6PwPNWH4B5Fbl0lolD40wfmyLwAyLxCIN7hunfOdD2wXmDeLc72QQ+FPJ4xVxFEuepLiu8wKeQ\nyTF5eILxg2NV+0iCUr9t155fMRyPR5DoIehKNZTAGQQB0wdPMPLQvqaHtIiluujfnCTRHXX9dU2n\nyc5myDZSY1rxtFa8J0H/rkEGdm0ilohAeeibSJQgHCMIRynkXTNetCve2GCxhSze3GTNsSFbyTVt\nZ5g9Oc30yBzpqfQquR1BRfBTcUyUO6YMhQnHo2y75hL692x1w3UVC2RGR5k/Okp2Zp6gUCTwXROy\nC/yWBdLhyOq5JaXE4mRfgj3X7CXaXf+QZ0EQUMwXKeaLriPbSAgiEUJdKYJEz8r+ncrjQi7eeDpj\nTx7k+N2Pt6UJuBzAL0ynmwqEPc9ji9nK5ou2rnuA4nZqV8BVyfd9FxjNZ4kl4yR6EzXPoa62vW/l\nEHpBUOrzqqJGPfBL53d30Qi8iqGnAC89tTg0VS2Z2QX2/7C5FpvkQJK911+4JEWlWeXeBdJTaYq5\n0hiopa91UPSZOTHN3PjKh/o6N+CanQ5mjx0708UAIAhF3DhziW4yM2kOfPv+1Zt1Vsxg7cdWQ5EQ\n57/wwqVdSkQTBD2b6rsIB74bMzGfJQDSM1mmj0wwdWhkWW/2EO2KkEzFSPYl6OpPkuzvrlolPj8x\nz6H79lc9+COxCNsu28HArk3uCxVLEpT78AqF2DTUx8RkuuIppNJxWCy4AZULGfe7Bd14BOGoGyw3\nm27J/BbnW2raq7snc9/HW5jBy84t3lFOHBpnoTREVSKVILWll80XbV0cliSIJV2tVh09LtdcbNFn\n8tljnHxk34p9vULII9HfQ+/OzfSdt5l4Xw8eAd7cRKnZzp3007MZCtk8bijQ0lAz4dKwM3gUCRGE\n4hTDMQJCbtD17q621wAQ+JDLuLIWc3gtqlFZMhaq5/I3gkjMDewdCrMwOcvEU4eZOnC84WFEUjuG\n2XHdpasPsl0OYkpd28weHeXIPU9RyOTr+v57kTBbrjifofM30+1lqKdLnarFWByCrLupp7cm9x3j\nyA8ehkLrUhx6t/Sy7bIdJFJdBEHAwpTLdZwdmSEzu7DmTWFXbxe7rt694qbwzPPckFCh8GL/h6lU\nnNmZhSVBjJu0nBpQOj7zmTWDl/UIwlF3HCwb2H59Mw3c+TEzx2LLUBX5TJ4Dd+8jPVn/TWTPYA97\nrr+g7hFfWiGXzjF1dIKpI5MszLjvW8cGXPn52WDmSOv6/ggiMYgmCKIJdyAXc3iFnAtSFmugPIJw\nabiBcNRdyMsdslUcdPl0lgPfvZ/MRCPNObU7GgxHQuy57gJ6hlztUhCOESS6V21aqnupfkBmeo7c\nbJpwPEqiv8cNkRAEkEvjZeZW/eL6RZ/Jw+NMHJqgmC8QjoTp31ka2qQrQRBPQbxrxcm5rgGQg8Cd\nmEuDa+MX3O86jsEgFIFovDTgcnTxsWdvYRovW39zaK15B12p5rd/Ie/u5gqngp/F8QfL/4/GCbr6\nWjgsjRs7bvLZY0wfGiGfzuCF3Hhfib5u4n09JPq7iaW6q49BFwSuzNn51RN3I3FX6xFNtO5EvB6+\nX/FdzlfU4Loap8oAPPBKneBGyt/t6Knvdp3r4gbKPc7E04fJTlc5zkIe0WSCaDJBor+HvvO20LO1\nvgc5litkchz90ePMHD656nTdWwbYcf1lxFMuoBga6mHs6Ahedt5tl7p4ria3K7XuYVCmD41w+PYH\nCXLryxnr3tTN1ku2L9a6V+MXfTIzCyzMLJCZXnA3N6VctVhXjME9Q/Tv3LTmuIunUxCOEXT1QHRl\nMFP3wPGlc6eXncfLLbBaAFM/jyCWIIj3uPNSu77fhRze/OTq152Cz6H7Vx+HtCy1uZc9Lzh/SXoG\nlK75gd+ym7LVZOezZGcX2PvSF3ZmwFXMLARTBw80/fkgHIVIbDHQWvUkUm4OaOTEmy9w6PaHmTtW\nu8fnGgtb7NnXC4Xo3tLP9qsvJt5XqroPhZq6s2xaELi7pcxsfSdnzzt10Y3Ea26vuk8c1crjl3t+\nLwWny+/u1tpGhTxeZgYvdyrRuq5FR2KlYKIFd3VBAPkFF9BWbNfywOGrbbszphSEd/lplo7y4BHE\nk6UTcft6aW6LJR1mtm57B0FAdnqezNQcnucR7Y4TTSaIJBpsJq1jOZP7jnH8fou/LAgOxSJsvepi\nNl24Y0kwv+S7t3hRTte8kQmiXQTJ3pb2wD03MsGROx8hPze/YsSPSCxMarN7cKF7oJsgCPCLPn4x\ncLk/nktOj61WI1iN5xGEY+6874Vc0/+SG+ozq57vflPnTb/oavdzC26dGy2XF4J4d/Xm43apuMGr\nPUnA8cePMvpM7RuOvm19nPf8vSsCapei0QcEePNT7vg/DQbNczoz4AqCIJh42taddB6Ewu6gicRK\n0Xn7g5bA9xl/6ggjDz+z4mRYyQuHiPV0EUslifd2l34nSfSnmn58uC3yWXdglu88Sgm6i9Xe5cFG\n67hwNR1wtZJfdHk/+axbtxq5P0E04arP23VXV873Wu94Z6fJ0GA3YyfGXX5GOHzavk9SWzFfYHLf\nMTKTbtDx7s0D9O3ZWrUJt+p3L/DdRTm/4GoCS71tB/Ee1xzfpjJP7T/O/MkpPA9iXRFSwymSvTFC\nxTz13AwFXsjVZEdirhfyJflypZrMUo7g8paIRX6hVIteGmfPdy0NdQdi5ZvMaKK0rbxTtfKFnEsk\nX2z68wgWUyg8d3MYiRPEEivzoKpY93nTLyw2uXv5LNW2cRBy3+lycNrW2qy15BZcbdcqqSCTRyY4\n/tjRJX06eiGPLWYbmy/csuQGJwhFXM5ZbFnSfDbtWj/aHHx3bMAFBGMHD5fae1fheQSJUnLnGboo\n+EWf3FyafDpDKBwmFCn/RNzvaLjtid0bzYYIuJYr54/5efB9VwsaS7R1bK1OtCH3ndStI/bfspy1\nci1Y+cJbDgpqBlEtKYNfSvquGEtwsTkaFgc8LqcsrLU+sO6ytnTf+b674SzmXRAYjpS26Qa76fOL\nLoe0ULsJulgoMj8+TybnEe3vJzk0QDQRrkjTKQW3q6U6lFNYihXBd2Ww3AKNBlxtznhtTNDV5+4k\najR1BbGkqwpfY9DLdguFQyT6ekj0reydVzaQUn7ehrmlEDlXlYOZZU7rd9MLQSQEtOCGayPeUIdC\nEOsioLkuEk6bUJggNUSQmSO0MMPKo8Aj1N1Lz9BOepYHi43cLHueq6GMxpcsIfCLrmkzO3/am583\nVMCF5xGkhgmy826DlDdGrMslS7cw4VhERETOAM+DrhR+POlatcoPT0XjBLHkup7iXlO5/8NEiiCX\ndvnMNRLtF5u4Sw/fecX8umrKNlbABW5HJHpckyGcSm4XERGRs0co7HKwzgTPc3ngsSRBvtz1TKlb\nlnDEBVnLHnhYrCkLAoIm6mc3XsC1nIItERERaQf3hAfB8sT7tT7TxIDXehRJREREpM0UcImIiIi0\nmQIuERERkTZTwCUiIiLSZgq4RERERNpMAZeIiIhImzXdLYQx5k+B6wEf+IC19t6K9/YDh0rvBcB7\nrLXH11lWERERkY7UVMBljHkJcKG19gZjzCXA3wE3VEwSAK+11i60oIwiIiIiHa3ZJsVXAl8GsNY+\nCfQbYyoHFmyuVzARERGRs1CzAddWYLTi/2Ol1yr9lTHmdmPMh5tchoiIiMhZoVVD+yyvzfoQ8DVg\nArjJGPM2a+0X15rJ8HCqRcWRM0H7r3Np33U27b/OpX137mg24DrG0hqt7cBiUry19pPlv40xtwCX\nA2sGXKOjs00WR8604eGU9l+H0r7rbNp/nUv7rrM1Giw326R4G/AOAGPM1cBRa+186f+9xpivGWOi\npWlfCjza5HJEREREOl5TNVzW2ruMMfcZY+4EisAvGWPeC0xZa28yxtwM/NAYkwYesNZ+oYVlFhER\nEekoXhAEZ7oMZYGqVjuXqsY7l/ZdZ9P+61zad51teDjVUG8M6mleREREpM0UcImIiIi0mQIuERER\nkTZTwCUiIiLSZgq4RERERNpMAZeIiIhImyngEhEREWkzBVwiIiIibaaAS0RERKTNFHCJiIiItJkC\nLhEREZE2U8AlIiIi0mYKuERERETaTAGXiIiISJsp4BIRERFpMwVcIiIiIm2mgEtERESkzRRwiYiI\niLSZAi4RERGRNlPAJSIiItJmCrhERERE2kwBl4iIiEibKeASERERaTMFXCIiIiJtpoBLREREpM0U\ncImIiIi0WaTZDxpj/hS4HvCBD1hr761471XAHwAF4FZr7e+vt6AiIiIinaqpGi5jzEuAC621NwDv\nB/582SQfBd4K3Ai82hhzybpKKSIiItLBmm1SfCXwZQBr7ZNAvzGmB8AYsxcYt9Yes9YGwC2l6UVE\nRETOSc0GXFuB0Yr/j5Veq/beSWBbk8sRERER6XhN53At4zX53qJsJsvwcKpFxZEzQfuvc2nfdTbt\nv86lfXfuaDbgOsapGi2A7cDxivcqa7R2lF5b1X/9D7/FpsFBrnrBFVz7ohcQi0WbLJqcCcPDKUZH\nZ890MaQJ2nedTfuvc2nfdbZGg+VmmxRvA94BYIy5GjhqrZ0HsNYeBFLGmPOMMRHgjaXp13Ti+Ai3\nfuUbfPQP/5JHHnyMIAiaLJ6IiIjIxtFUDZe19i5jzH3GmDuBIvBLxpj3AlPW2puAXwT+GQiAz1hr\nn2lk/lNT0/zzP3yevRfs5vVveS3bd25d+0MiIiIiG5S3UWqR/uPP/WqQyxVWvO7hcc0Lr+bHXv8K\nunuSZ6BkUg9VjXcu7bvOpv3XubTvOtvwcKquHPWyDd/TfEDAPXfdx0f/6GM8+8yBM10cERERkYZt\n+ICrbH5unr//2D9xx3fvUm6XiIiIdJSOCbgA/MDn1ptu41/+8QvksrkzXRwRERGRunRUwFX2yIOP\n8X//998yNjp+posiIiIisqaODLgATp44ycc+8jfcetNtjJ4cO9PFEREREampVT3NnxHZbJY7vnsX\nd3z3LvZesJtrrr+ay658DtGoOk0VERGRjWPDBFyDgwMcPz669oQ17N93kP37DnLzl77Oy1/9Eq67\n8RrC4XALSygiIiLSnA3TpPgbf/BfeNXrXr7u2ql0Os3NX/4aX/zMV/Q0o4iIiGwIGybgisaivPzV\nL+GD//OX2HvB7nXP78H7Huau79/dgpKJiIiIrM+GCbjK+vr7+Nlf+GlueOn1657XbTd/i4nxyRaU\nSkRERKR5Gy7gAghHwrzhLa/hJ3767UQjzTcx5vN5bvrsv6ppUURERM6oDRlwlV1x9XP5hQ++j8Gh\nTU3P45mnnuWBex5qYalEREREGrOhAy6Ardu38IsffD9XXPXcpudx85e+zuzMXAtLJSIiIlK/DR9w\nAXQlu/iJn3k7v/Cf38dV11zZcDNjJpPhq1+4pU2lExEREVndhumHqx679uxk156dvOGtr+HB+x7h\n7jvv5eRIfX13PfbwEzz20BNcduVz2lxKERERkaU6ooZrua5kFy988bX8+w/8HL19vXV/7qtfuIWF\n9EIbSyYiIiKyUkcGXGWJRII3v+P1dU8/OzvHLTfd1sYSiYiIiKzU0QEXwCXPNQ0l1N9/94Mc2Hew\njSUSERERWarjAy6AN7zttSSTybqn/+oXbqVYLLaxRCIiIiKnnBUBV09PN29462vqnv7E8RF+dOe9\nbSyRiIiIyClnRcAFcOXzL+fiSy6se/pv3fpd5mbVN5eIiIi031kTcHmex5vf9UZisVhd02cyGb7+\n1W+1uVQiIiIiZ1HABdA/0MePvf4VdU9//z0PcnD/4TaWSEREROQsC7gArrvxGrZu21L39F/9wi34\nvt/GEomIiMi57qwLuMLhMG9822vrnv740RPc/YP72lgiEREROdeddQEXwN4L93Dl8y+ve/pv3Pxt\n5ubm21giEREROZc1NZaiMSYCfALYDRSAn7XWHlg2TR64HfCAAHiltTZYT2Eb8do3/RhPPvoU2Wx2\nzWkzmQw3f/FrvOun34bneaehdCIiInIuabaG693ApLX2xcCHgf9VZZpJa+0rrLUvL/0+bcEWQG9f\nile+9mV1T//wA4/ywD0Pta9AIiIics5qNuB6JfCl0t/fBF5UZZozXlV0/Y0vYPPWzXVP/9Uv3Mr4\n2EQbSyQiIiLnomYDrq3AKECp5sovNTNWShhjPmmMud0Y88H1FLJZ4UiYH3/76+qePpfL8S//+AWK\nBQ37IyIiIq2zZg6XMeZ9wPtxeVjgaq6uXTZZtcDtvwKfLP39fWPM96y196+2rOHh1FrFadjw8OU8\n9tDzue/u+poLR0dO8qM7f8ib31H/k47itGP/yemhfdfZtP86l/bducMLgsZTq4wxfwd8xlr7jVLN\n1n5r7a5Vpv8j4HFr7T+sMttgdHS24bLUY2Z6lv/9h39ZVwI9gIfHz/7iT3HBxee3pTxno+HhFO3a\nf9Je2nedTfuvc2nfdbbh4VRDqVPNNil+A3hn6e8fB75T+aYx5mJjzKdKf0dwOV6PNbmsdevtS/Hj\n73h93dMHBHzuU19mfi7dxlKJiIjIuaLZgOtfgIgx5nbgF4FfAzDG/Iox5jpr7VPAYWPM3biuIf7V\nWntvS0rcpOddcwXPe/4VdU8/OzPL5z/1JeVziYiIyLo11aTYJm1rUizLZDL85Z/8NRPjk3V/5tLn\nXmp/6rAAACAASURBVMJPvvcdhCPhNpas86lqvHNp33U27b/OpX3X2U5Xk2JHSiQSvOun3kYoVH/w\n9PijT/LpT3yWQqHQxpKJiIjI2eycCrgAdu3Zyate97KGPvPkY0/x6b/7LPl8vj2FEhERkbPaORdw\nAbz4FTew98I9DX3GPvE0n1LQJSIiIk04JwOuUCjEO9/zFpLJZEOfe/rJZ/jkx/9ZQZeIiIg05JwM\nuAD6+vt460++qeHPPfPUs9z02ZvbUCIRERE5W52zARfApZdfwut+/Mca/twD9z7E44882YYSiYiI\nyNnonA64AG58+Q287s2vbvhzN332ZtLz6hhVRERE1nbOB1wAN77shbzhrY2NnTg3N8fNX/p6m0ok\nIiIiZxMFXCU3vOQ63vT2+of/AXjwvod58rGn2lQiEREROVso4Kpw/Y0v4M3vfGNDn7npczezsJBp\nU4lERETkbKCAa5lrb3h+QzVdM9Mz3HrTbW0skYiIiHQ6BVxVXPeia7j4kgvrnv6+Hz3A00/ua2OJ\nREREpJMp4KrC8zze8hNvJB6P1/2ZL//LV8lmsm0slYiIiHQqBVw19PX38bo3199H19TUNN/++vfa\nWCIRERHpVBs24AqCgGIuTzF35obRueb6q7nw4vPrnv5Hd9yrvrlERERkhQ0XcBWyeU488DSPf/bb\nPP7Z7/D457/L/m/dx9zIxGkvi2tafBOxWKyu6fOFPD+68942l0pEREQ6zYYKuIq5As/edjejj+3H\nzxfdi37A3PFxDnz7fqb2Hz/tZRrY1M9r3vSquqe/6/a7Nbi1iIiILLGhAq5j9zxBdnq+6ntB0efw\nXY8yPzp1mkvlnlrce8Huuqadn5vnofseaXOJREREpJNsmIBr5sA+pvcfhsCvPZEfcOj2hylkcqev\nYLimxTe/8414eHVNf8d37iIIgjaXSkRERDrFhgm45kamCPIFKOTAL9ScrpDOcPjORwj80xvQDG8Z\n4jnPNXVNO3pyDPv4020ukYiIiHSKDRNw5TMVeU/FAvjFmtPOHR/n5KPPnoZSLXXjK26oe9o7vvOD\nNpZEREREOsmGCbgKuWW1WsX8qs2LJx95ltnjY20u1VLn7dnJrt0765p2/76DHDl0tM0lEhERkU6w\nYQKuYr5KjVYxD9RoOgwCDt/5KLn50zdwtOd5vPjljdRy3dXG0oiIiEin2DAB14oaLoAggELtLhaK\nmRyH73gYv7hKon2LPedyw6bBgbqmffTBx5kYn2xziURERGSj29gBF7hmxWLtoCs9OnVag65QKMSL\nXvbCuqYNCPjB937U5hKJiIjIRtd0wGWMeakxZsQY8/oa77/HGHO3MeYuY8zPrTW/Yq52kjx+cdUk\n+pnDJzl0+0OnLei6+trnkUwm65r2vh89wOjI6c01ExERkY0l0syHjDHnAx8E7qjxfhL4EHANUADu\nMcZ80Vpbs9fSmjVcZcU8eB541WPE2SOjHPr+Q5z34isIRcJ1rUezYrEo1914Dd+57ftrTpvL5fjb\nj/0j7/uln2F481BbyyWdJZfN8cSjlpMjY+RyOfyiT7FYxPd9/KJPKBxi0+AAl191GYNDm850cUVE\nZB2aCriAY8Bbgb+r8f51wN3W2jkAY8wdwIuAm2vNsLhWwAUu6IrEoEYHpLNHRzn4/YfY/ZIr2x50\nXX/jC7j92z+gUFi73LMzs/ztX/4jP//L/3bVC2dQLDI/OU5+IQ2hMP3Dw3jRuAs05awRBAF333kv\n37z1u6TTaw92/s1bvsPlV13Gy1/9EjZvHV5z+vGxCR598HHGTo4zMz3D9l3bueyKS9h53o6Gy1oo\nFPCLPtFYFK+Vx6FfcN2/eCEIR3WMy1kvN58hPTpJenSazNQsxXyB8a0DRIYG6N21ubXfL9mQmgq4\nrLUZAGNqdgS6FRit+P8osG21eRbydQRcQeA6Ro3Ea04yd2yMg997kN0vfV5bg66eVA9XXXMF9/zw\n/rqmLwdd7/+l97JpyCXdB0HA2Og4+585yMLEGJt7o4QrvnNThw/Q09fL4I4dhBLdEE3owtSs4P9v\n786DLMvuws5/z13f/nKvfemq7r7dra0FaiS0tboRCJCwGJAHPBrssVEMxNgRA2N7zMTYMGEiJjyO\nMTBM4BkPCIeBMJsCs4odJBBaW1LTre7W7a7q2quycn/73c/8cd97mVm5Z1V2Zlb/PhEZlZX58r3z\n3r3vvt/5nXN+R+dfWQq6P0StM1Bm/oFv2a9JM+bnFvgvv/57XLpwedt/o9E899Wv8fxXX9gw8Gos\nNXn+2Rd47itf48a1m6t+d+HlV/mrP/8M3mMP8x0f/tYtM61aa1587ut87q+/wKWLVwAYHRvlG77p\nLbzzybdTKBTu/IP8tczSfhbaBGOdTLTWEIeooIlKlneL0IYJbpkgNunMLhF3Awr1CuWpUazC9jaO\n3y2tNTrT/eT57mZYpHGCTjMMy9zzjp64x7TOO/JpnH9vWnmnfoORlJ2IuyHN6zN0Zhbpzi4Rr7Oi\nfq7TI3rxKvWzRzn5jjccqvPn5vVpPvfXX+DqpWvEcUKlUmZ0fITRsf7X+CiTRyYYHRvZ+E4Gr38S\n5dcOw7wnr7/WmiSIiLsBaI1VcLHLhX0ParcMuDzP+0HgY+T1GVT/35/wff9Pd/A4Wz7LTedwraQ1\npBGYG1+I27fmufTnX+bMk4/f+wu21hD1UGnEtz75OO3Zaa5PL9DaRnmKxlKDn/k3P4dt25imQZpm\nxFHEO976IA+eObLm9nEcszg3T7vRZPLIBNV6rX8yKkChyU8sZZpgWPnFwjDzf+/ihA0abZYu3SIN\nY0zHpn72KMXR6q7vb99kKSrs5McrS/JjtwHtlNClev767UVTkpTP/dln+cxffhblKM6cmGB8pMLY\nSAXXsUjSjJu3F7lw5Ta9DbauWhl4TR5ZDprSNGNhbgG9UQmVPv/Fl3nl6xd5x3ue4Olvey/FUnHN\nbRbmFvmdT/wBF/yLq36+uLDIn//Rp3jxq8/zwQ+9jwfOHEP1A1eVZdxZvkWbFthFEmXTXeigsgTH\njHFdteqip7WmdWuB2Qtfpz3f7p+7/WNgKGonpxh76CSVo2Or/i5LUsJmh7gbotMs30pL6zyA0hqF\nwnRtrIKN6TpYroNhm4TNDt25Br25Bt35BsFSGzINSuHWyxTHapTGaxTHaxRGqpt+ALanF5h76Qrt\n6Xl0mg3vI//7OsXxOoWRCoZ5YNYm7VwSocJ2no1Ege2inVJ+nPaS1v2OUZZnQwfnmc5AGWi7sOJa\nuIv7jkNU3KN1Y4aFV6dpzbTQmaZQKzB6aoKxB49huEW07e4oAEjCiMbVGRqXb9GZnu937HT/E1Ch\nDYNeLyLoBSRJSqlcoFgs0rg8TZaknHnvW3Yd+L+WvvrMc/zWr/4u2Yq51Y2lBjeu31xz26kjk3zg\nu97PI294ePmHOoOwiwrbqHRtskWbNlgO2nLz1y5NUYO53Fma/8ww0W6FJFU0r8/SmVkk7vSIu8Hw\nurBScbzGkccfonps/F69DDum7mbPP8/z/iPwm77vf/KOnz8J/JDv+/9N//+/CHziztut9Kn/8z/v\nqCGGaWE47qahXKFe5g0ffAfFkcq27jONE9IoGe6DmG8fpMnSjLgXETbbdG5PE3cCkjABBc12izCL\nmWl3ePnKNLd2sLl2uejyniceYXykvK3bF0slRkarhGFEGORv2jRNAUWh6DI5NUF9JA+MlGli2DaG\nU8B0XAzXxbCdTSN8rTWX/uYFbj53cc3vJh88wfkn34Ll2mv+Rmf5hXHlh94g66G1zn/X/0JrdJah\nTAPDdrDKFdQGF7M4Trj48iWCXkitXuHUmRPYzvYyUWkY0Ju5hd7GkO+AYdkUj57AsO9NtktrTfPm\nPK98/mu8+sxLGFpj2yaGoXBqLsWjZezy6g5BmmkuXr3Nixdu0OmG96Qd6ymXS3zgQ0/x8KPnOXJ0\nEmUo/uKPP8Mf/u6fE8drVwUfmxrhkXPHOT6V91ZL5RLHTxyhUCzkvckkJU3yD2XLNolaIdMvT7N0\nYzEPxfrvKbtgU5moUp2ookzFzCu36TV7qx5LGSaG46z64CnUy0ycO0bYDujMNegttXexX+mgv7jN\nWxuKyuQIY2ePMn7uGKFOuXTxKq42iK4t0Lm9dckXwzQYOTnJ0Tc+QOXoKFcuX2duZp4kTlGGwjQN\nlDIwDIVbcHng/Glq9fU7N3Gc8Mznv8qXPvcsjaUmxWKBR9/4MO988onNswi7oLOUcH6WuN1a9/dm\nsYRdrYPjEgYR7YUGS9dnaE/PEzY7GChGjo1z9NEz1I5PYlhbD0lncUTcaZN2O6RRODxntNbMX5lj\n8foiQauHXbApjZQZOTXJxMMP4NSqW963zjKSboek0yIJegTNLtf/9hqN6fWv107J4fgbTjJ2agxl\nGJiFIlaxjFkskUQpYatHEkbEQUQSxiRBRHs2fw2yJCWLwvx615ckKUmckCQJSZoShDG9ICKKElCK\nyalxJo/kr9eDTz2+5XU6iyOyOEKnKYbjYrqvXfbma3/7Ev/hZ39px++/D3zoKb7zu54iaTWJW41V\nr892ZZmm1+0RhhFZltGaaXLjuZu02wFpf96rW3AplYoUiu66r8mJxx/kzNsf3bIjlAQRSzfmaE0v\nELS6+XFNUtIkJeyGdJptnv4n37OjF/1eBFyf8H3/D+74eQF4jnzSfAY8Azzh+/76717gr376N3Sy\nzoV+U6aVZ3Y2u4lrc/q9b6FyZCzvrQVtSEKUztCmTWY4zF1ZYOHCDaJWb+M70um6NcG01nQ7PbTO\nMByTxITbS03ml9qE8XLwlgGRTmmmMRmaY1MjPPlNj+I697anWK5WOH7iCKa5Ts9cqbznYNr9f63l\njIJS3Hzm68x//eqG9+2Ubc5+04MUKs4woFL93QAcx8ovHv3XJO5GdJe6JGGMXXAojZWxC2sDGW1Y\n6PJIPlza1253+PSffYZnPvcVomg522NbNg+cPcUDo+OMFsuUaxUK9TLVExOUp8aW30BpjGrODtu2\nE9ow0dWJfJgRSMIeCzdukHTbZFmG6bhUjxyjMrrxXLw0ilm8dIuFl6+xcH2aLAo37IjbFYfCkTJ2\n1VmT+Xn12izP+9dotLae57UTrmOTZhlJkvdOCwUH07TodFY/jm2ZPHjmCI+cP06tsjYbBmCYJlma\nDtuctGN6tzuknRjTMrFMMz8Xd/BhoPtBeZRmRFFCL4iI4wTDNLFti1K5RKlUfE0+YDTQbrWZn11g\nqdsh0im1fna9XC5RG6lRrVUx1mmLJl8002l36bQ7zLSaXAmbRFucl1NHp3j3+76Zx7/xTZj9DNvX\nX3iZT/72HzM/t4BlGlTLRTpBSBQlFIsuDz/6EG9/4hsYH6mjDJV3aEwDZZoow8By7e0PV8UhqrOY\nZ4XX0esFzN2YpTHdoDnfImlHmHq9Y6GwbYvKaJXR0+OMnDlCYaSaZ6gMM88aGUY+vBz1UOuU/4mD\nmCtfepXOQmfdtihDUZqoUTl5jOqpoxRG7wi+kggVdiHqonRGmqTMvDzN7MWZbe3HWxopMfXQUeIg\nojPfprPQIQ6T5WHzOzuLaTxcUZ9lGXEUkyTJhsGJBjqdgGY7wHZsjp04wqknHuPoWx6844Y6/9yK\nAoh7ebZn5a8NC12sgVPc02knM9Oz/L8/83HCcGedwZFaibc8cprH3/wQR45NDfMkaZbRbXfpdnt5\nR9RxKFfKWHecq2EYsTC3SLPRHL6W4UKP9pUmoEkzzcJSmzBaPoeUMigWXQqlIrZtrxrhUJUC+sQo\nvTii18kfv9vponoxNctlslRhpFjCvCPbmGYZC7PzhL28vf/tT//I3gdc/VIQ/xzwyOdn3fJ9/9s9\nz/sXwKd83/+C53nfA/zP5LHGz/q+/2ub3ednfu63ddTtbbqdz7qM/nDaJieZMuDkW04zdmx1piuP\njq8RdsL+/Zjrp44HE3w3kGUZvW5v3TdVmmYkaUaWZRiGwjBNCpMlasdrGPb6EXaeIcovJrthOzYn\nTh2nUNh4rtsqSrF0u82VL1wE02RN2jBLh7XQTMvg9DeepXZ0uUettUbHKYu3lujMt2nPtYh7ay+e\nxVqRymSVymSV8ngFZSh0mq/IS+wK3Ri+9KW/5bN/86V1syzjpssJuzz8cLMsa/lDb6RK9cQktRMT\n1Coay7xjiGvwVLfxcsSp5uLNRYKlBUpWfnzvdGOuRVcVeMg7z9nzZ7Bti+7sEouv3qRxZZo0Sug0\nljYtZ7KSVbRxRgsYjonpmBiuiTIVKMWVG3M88/yru854KeDIZJ2zJyc5fWycYn+YvRtE3J5rML/U\n5sb0As1Wj7GRCsemRjg2NcLUeG3NBWc9WZoRNyOC2Q5JZ+1xUyhMKw+8zH4gsPJI5BmyhDRJSdN0\n3fdRHKcE/YupUgrTUDiuk385DqZl9+eNrT3CvV5Au9Wm1wswjbwHXK1Vcd3Npxt0uz1mb8/R623S\nESOvzVetVXELLmmS5NmMJCEKozXncaY100mP2aS3Za5tZHSEdz35Di74F/FfeoVapcg3vPEBTh8f\nB61JewnNuTZLMy16Sz2SOKVULlEsFkjihDjJ55YpBZZpUBotc/JND3D2jWcwVD8L3V+0kCqTG9Nz\ndBYWmKw62LaF67q4BQfDMIjDhNkrM8xdm6Ez3yHb7hQQ8uNVKLiYlkWxXmT05BgjJ0ext5juEbR6\nXPr8RaLu+kPs6zwQxdEKU4+epHZsDJUlwyAuyzKWri8y/dLN1fv2bmKwYnjVgVKDfxSGmWcm88+M\nfva0f+5GYbSqs7hxk1Wesco0i80OvSBmbGKUN377N3Pk0bMQB6ioC3FAGickcUycJMRRni1Da0zL\nxHEcbMfGKlUxqmN7MuTb6wX8Pz/1C8zPzQPgOhbeueNMjFYxTcVio8P16QVuzy0HRaWiw1sfO8v5\nM0eG78xavcbU0UkWF5ZYXFgiW/GeHwTLpXKRSrWK49osLjTotNqr2hLMdelca3FnxrrVCWi2exiG\ngTnMICt0pomShHTFMGOsM27HPQqmxXipRM12MA0DpfLP7SyD+midSq2KQhOHId12G3PF5/Lf+ckf\neu0yXPfSZ/797+go7E+e26BN5fEKI8dHuPH89bW/HEy4GwRMgwBsxUbY1akq9aMjlMYqzF64zeL1\nhXXux1i+cCvVnz+wdRC4WdC1HmUoCpMlCpNlsiQjaUfE7YikE5PF+ZwYwzIwbBNlGRi2gWEZw0m+\nOtWQ9Sf8WgZW0cIdLw2DOKUMjh6foj5S27ItcRDx8l++RDK4iA7mgUG/x7b2+Y+fzecQha2AoNUj\nSzKyYY9RE8f5ENPg9TAMo/+VB51KDZJkGZnOh20brQ4Li206WUzbShk9VmdyvIbjWIS3O6TzeY8+\nWmeY0LJs6iNVxuplTAPckSL2iAtFY9jDNAwDp/8hYhkmBgqlDJSd3yaOYqIoH6rdjis35vjcl15m\nzCpwemSckXKZSrWCoSBoNdG7yLCtpMz8uNp1F7Pm8Kx/lZcuLs+RcJTBpFVkoliiZFpkBkQqo0dK\nh5RUaU4eH+fsiYlhkLUew1BkmR5O0hxIo5Q0SNBxBobCsPLMiTIN0JqoGRI3Q5J2vKPhBaVUfi6Y\nxrAUxt0yTAPbsjBtG6M/h7HT7TE/t0i3u37A5BZc6vUatZEalmkOA78oilmYX6TTXj+rci/0spR2\nFlMvFRirlinaNpZlEiYJC90uN+YbBFlCoPPX5vyxSd547gQqzkiDJL9O9D88Bh/aaZrRC2MMpbAt\nE8sy1+2HOlWXY284ydTpKaIootVs02621xwHnWaECwFJIyLuROt2PHbCcWwcN19lrhRUJmuMnhqj\nfmxkmJ3WQBxFLNxY4Oaz10jjNJ+bqFlxLcmvIdYmmdNivcgR7xiFaoGFK/MsXJvPp4FsQ5qmhGG4\nrbqORj+AXzmisN1gC5aP3UAviGi0epSKLmPnx6lOVjBtAxTbf48pgyu3m4TYHD02ycRojbIyIUrR\nWvWHMwN6nR7dXgCGonpkjMnTR5gYq2HrwQpilc9hs4tkwC///K/y8tcvAPDwA8d425sewF4naxpE\nMdduzhMnKd4DxzA3GLrTmSZc7BEthSSdGKXALNo4Iy7uaCG/zqwjmO3Sud7c3mtxhyzTRHFC1F+k\n5zo2jmNt2hG3LAvTNInCaM082UMecCV5hitZ/2StHa3zwNvPM3dplhvPXXuNW7i1nQZd95oyFNVz\nI9jV5czWyGidyaOTG2YqtNZc+vxFWjO7O4EHBh/aWZYR9IJdX5zj/jCXbZnYFYfSiSrBTJdwcflD\nU2tNFKeEUUwUJcOh27F6mVJxdVZPGQq77uLUXbI4I+3GJN2EdMXF17AMnNEC7ngRq7j1/C2dZkRL\nIeFCj9Z8h/n+fCKFolopUK+UtpzAvlPKULhjRdpmyrMvXGHKLjLuFCgWnHWHswBMx8SuuSirf+y1\nHnbClakwXROzYGGX7OECjCxMiZaC/CK4TpbyMDD7wVOWZcRJShDE9MJoeJFdS2FZ5rZKvKx5LMOg\n4NoYhkGWZYRxMhyq3YhjWRSLDqWCs+GHUZpmNFpdekFMvVaiUto4W33nh/Z2uaNFiscrmM7qD800\nSAjmuoQLwZqJx3fLNE3cgoux4npkWiblqSqZkRHGEVEQ0b3R2vI5KZVnTm3L6g+95lmmfNpothyg\nqbzzPPh3Y5oojLcdLK3kFlxs2yZJkm132AbPYTvP03D679WqgzNS2HB0ZEBrTdyMCBd6xI0wvz4p\nlb82OsvfE0FEEMUooFR0qdaKVI5WKR+tUawUsB0b27YwLZsv/+0rfOYLX8M0Dd71jd5wLueGj59m\nZGl/9a9lrJ4ukWYE8z2CmS7Zensos3y9c8eLWCV7+JyCmS7dmxvOTHrNHf6ACzacLzV2epxTbz0D\nwPzlOW48d3WzhWf7Yt+DLqWoPjiKXXFW/axcKVOrVylXyyRxflEIegHzl+dYupRn+sxBlsDaeTra\nMBRx/34Pyjm1G1bZoTBexBktrBrSzecnRYTzAVEjWDX/I4wS4iSlVNw4+DnIBhd0YFUger/JtCYM\nY3r9Cct3c57alkmtUlw3c5immjCKCKKEOE6xLQOrHxg4trlhkLWewQflZnYbcEH+wWYWbZSphkP8\ncWvnAccOHzXPUhkGylD3JMupBiu3t8gqK/LnqZTKh7gtE9Mw8nMjCO+qHY7jEMc7z/bu9NgppbCq\nDu5oAbvuYpgGOtP5KEOUEjdDwoVgw2BmJa3Xi0EVTt3BHStC/5zQqSaJUrJMY5n5ccsHgfI/Hjx2\nGiZkYUqWLB8HZfQDRjcfrYmW1q4g3IzpmP3nly9iO0h2GnDt8dreXVImmKzZQ3FlT2z87ATKVFz/\n6tUD9QFvGAbFYoHePgUeWmvalxvUvTEMu/8hmqTMXrjNjcZVQOeTaEsWyjRW9RaSLCOJEwzDwLZt\nLNva9sTkOI4JuuE9z+y81pJORLsToa41h3OolAE61asuIiu5jnXXix8Gr/kgt60zveOL9924nwOt\nAUMpigWHYsFB18v9Xn5IL9z+6+zYFrVKkYK7cSbUNBWlorsm27obe70wQGeapLPXAdaaRx1mw+/Z\nPertfRhr9LCzlKYpRHkQNvjd3dhNZmw38uxVPpyfBz5q15nI9U8vTdQIiRrrzxndad5bZ5o0SEiD\n3V1jtl0y6hA4mAEX5POIBsUU+0x7dXPHTo1jF2yufOkS6Tai+deKYZr9oCu863k8u5HFKa1LS9Qe\nHCNqhHSuNde8IePWxhOwsywjDEOiKMKyrLxHSL9Hs+LfvFOp8gm6cXzog62VtNbo5LV5PrZj4zhr\nS3bYjk0cxbsOvEzTJEuz++q43CsKKBZsigUbrSGM4nxLJZ1/QAxes8EEfaUMLNPAtg9PYUqxPa/l\n+8OwjA07brsxKF0kDoeDG3BBf2m+Hk7atta52FUnazz4nod3tprlNWCYJqVykSiKSJN0096cUgam\naQxXcqVpxvTMIkmSUHRtipvM9dhI0olp+PO77lVAvye1zVId+13Bd7u0hjhJsMy8HtZ+Wm/C7UpK\n5Svxth945atyLMsaZiezLCMKo13NT1puh7Flx0GTr1bc7nmapppOL6BcdNf8zd0Mke2GUmyasRL3\nv0xr0iTbk4DaKuUrkJ2ai+Hm99+50lw1L/V+YTt2njXdxfUm6V8/7tVVeTBn7SAFpAc74IK8oryO\nQGeYGwzbFKpFHnyPx+Uvvkp3ce9WFu2UUgrXdcEFBittNrjd8n8MDNfmxJkySwtLzM0usNTqYhrG\ncImr6v+N6o+hm6aBZZpYlrEqkLibYOt+NbfYIoxiLMtkaqy2b0GXMk2K5XJe3FPrTctHDAIvx7VX\nrARdK38u6o6fGRSKBdI0JQqjHc1RMUyDgptPcI7imDhczmKmaUa7GxKEUb6EesWy7kEnoeA6K4Ys\n8gnNWaZptnt0+sPPrXZApVygVilglx0KU2WcukvcCgnmesTNiI0umMpQmAVrOP9skHEFQOdDwDoZ\n/DuYRJ0vFrDKNlYp/zKLFmmYkHYTkm7c/0o2fNw17TANiv1aakkvIe3GRI1wW3NoDpPtzCe715I0\nI+3P8UozvelCg93cdxBE9MI4X4CjM1zD7E8RsCm49rqr8LbDLFi4owWckQLKMbk+vcARw8Xtv37l\n0/Xh6vT7RbFYGM7/3clKzW4vpNUJhgumHNvKvxxruNgrSdP+eZBRKrqbTuGwqy6VMzWUZZB0YtqX\nl/or//ffwZw0v5404tzbz1Gd2rjMQZZmXP3KZRo3t1/tfT2WY+bL3/vDZ6h8JY3l2liulX85Fom2\n6TV79OaWSMN78MYZbM+zQpKmNJeatJptMp3ldYRcF6fgYtsWs7fn1hShU/1l4fmJmxeL3O2FYzsy\nvXpl0OCUGmyzorUeDtUM5rfsh8VGl86KFUSWaTI5Vr1nF/DN2BUHd6JIHKaEiwnlUuWO0EhDi4uO\n1gAAG7tJREFUmuZlSPZQlmXDjGuW5TXQ7lxyrpTq1/WxWF0vK6PTCVhYbNENVp9zhpGXIUjihEwv\nlyuwXIu0bJJVTObnWvQaPcpYlA0bSykyoJVFtI2UM+emOHf6COUVK/LSKF81mXTi/H3omJhFC6to\n57XKthkA5DseaDDUtv4mi7O87MVSQNxaf4L9sLTLVBnDWn0OZWlG72abYK7HnYGbYRirspoayLJ0\nW2UIho/dfw7Lq8/29jrebPdotnu4jk2l5K5aLKBQ+etqKlJLsRh0IcwoaRPb2tkiAWBYhb0XxMNz\naaVixWVsrIqKdlHYWGu6vYhOLxyuWm2mMTfivKjtuFngqF3C6r+++SpUh2LBxnXt4bvBsIx8sYGV\n1+NSloEyFYZtrDo3b84s8flnX6HVDlBK8da3PsJT734rY1WXudvzXP78ReLXfA7dvTeoh7dSHMUb\nFkjVGtqdgHY3IN3FXL5apcTYaF5weGVHy6kXKJ+pE8fLr2kWp7QvN4h3EdwqpTBLNk7NyY+3kS+6\nwMjf/+/9e997H6xS3MCD3/pWSmUDFQcb1urSWjP7ym1uvzK9+Vi5YaypL2XaJkcfPZ5PyN/soqwU\nWWkU3NLwMeNWm3B2nqjZJkvi/MOzH2yErYDGraX1m6z6hfM2Krq6hUxrbt+8TaOxeVmHQRA2qM8z\n+NfaRbCRZZqlZpcgXL4gGkoNsxwDidaEOqWoLFYmkspFl9H69rYzsiwLx83nN6VJmvd0Vtb32uac\niHY3ZKm5NvtpmgaTY7UtXwfDyLOLO5kTZZgGzlgBd7yEVbRYaHQ58vCjnDn/AI0r08y9dIVgcZ0l\nziuqVb829LCUgYIVS+z7hhtS53WP8nILSR5A96vJD1cr6XzrjXYQcKW1yKX5mR0n9OvVEg+fP8m5\n00eYmqjjujaWZRH0AtrtLvFrNDl5IC/sGpJ2ElzLwbIsjJJJ6pIv7tlE0onoXG9DlOWvlbXxQpS0\nXwNssyykQuXL9Z38wz+OE+JkuSaX6Vp5GZCs39lJsruaM5SmGfNL7TUlNQxlUK4WmTx7lNOPnaN6\n8gjuSA2U4m8+9Tn++Pf/ApVl1E2HcbvIqONiWSaGUpiDenz9fyHvWIZRQhBEa64jK3WyhEthE20o\nHjl7jDOjI9idlDTc/P0SRgmdXrhqdWovS7kVd2hmq6dNGCimrAKjpovb31s1yFJ6pBRqBUamqtRH\ny4zUyxQ3GIru9EK+9NyrXLkxN/zZxOQ4P/yjH6NYcPPK+t0l4m6Pv/2jZ4k62ytqPKi11gsi4iSl\nXi1S3qcO7IBlWRSKhXV/F8cx4R2ds043pNnurQm0HMfZMitmWRajYyOMjI1gKpY3HQfqx0Y4/baz\nGEa+T3HQC+j1grwOY5rRuLJA80Zj1f3lc5Hzr0ENOOUa2GUHu+ZgVZx1twDSWnN7vsn3/vd///4N\nuLzvfg9OpZgHSnEPFXVR8QYrKYKY+cuzNG4tETRX1EUZFvXsv05ZnlUYPTHCsTecXHf7mZW0YaIr\n4/mGppveUC9P+s9SgkaLmRev0bg6Oxj72Pzvd0ADS4sNZqZndtzTNQ2DSrlApVRYs2LFdC3q3hhR\nMxpOvO8FEYuN7pqep6EUYZbSyRLaaUw7i4dFGxVQNmyqhk3VtCkok4Jj5xWKrXyJsdasmtg/CLSM\ndeuH5UUeK6fqZKV8vlrUyGtHrbfaLghj5tYLbFa8BuMjFZw70tRmf1saZTv5CsL+m3swxJGkyZqs\nhFIKu5YvqbZrbv7cgCu3lnjbU+9jbHL1lkBhq0t3domo0yNu94j6X3G7u+pics8Yy4ET/c2ADaVX\nP49hJ2Cwdcn2ztXC2HK1/+J4HaUUC/OLXL54hauXrnHl8nVmpmfWb5YyOHP+NI889hDeGx5mcqq/\nObfOIA4hS/LNi5Wi2epw/dotLl+8yvzMHEcn6xyZrOPam8+QGNQV6nZ2NnfGME3GxkcZGx9ZdT5m\nWtNpdeh0uqRJgmGYw6DKsk0sM59LZ5om86/OcPvlLTqBfRsN/655Txh5DbWRqQq4BtrNCySbhoFl\n92soGSYzl2a5/rVrdFrdfM/LLB+a0VrnnbD+EM4gGzWYR9psd2m2V5e46WQJpSOjvOGbH+fRJ960\n4X5016/e4Dd++beYn8tLztjKYNR0GV8RxOzUUhpxJWqtCeBdx+JEucqodrAxhlMtFHmAEvefM+RJ\nzqU0ZD4N6Gwjm5wnTwwef9ubcVyHm9dvcfXycg1Ix7aoV4vUqyXKJRetNQtLHW7cXlz1urmuyw//\nyA8ydXRy+c6zlApdmjNzXPj8BRavz2841zeMEtqdgCTT2LaFtXIVeZpScEyMnRRHvUcM06BU3Hw7\noSRJCIOQbi+k0eqRrDqvFfV6lbHJMdx+WY1Ws02r2V61w0OhUGBkrE6tXltbeidLGDlW4/RbzwxL\n+ehBEmNwrqUxKkvpLnWZfWWa9lwLrfMkS2mkRGm0TGG8hlWv8tWvvsDMzVtUSgXKJZdKKd8vNghj\nZhdaXLs1z/xSlw995Dt5+lvfcf8GXI/910+vnceVpcv7cGVpfoHuBztK59syBN2I5myHxu023fnW\nqg+x4kSdI28+T/XISL5X1XBH8iyvBzbINBgm2i5CobyrTNRAsNRm5vlXaV6fWR1glFzKU2NUjoxS\nPjqGXXRJgoi4F5J0Q+JeSJak+XYSlkmWZdz6sp9fQQb3HYTMTM/S7e587z1DGVQrBSoldxjx1x4a\nwyrnAWivG/LCly8TNAIMpUh1RpClBDolyFIyWw23XrnTqTMnOffgWWamZ5m5Pcfi/CJaZ4zWa3zL\ne97IRD813LnVon2jmQc5gzfV4EN/EMBqjWEqzrztAWpHR/IPhmaL5lKTbqdL2kuIFgOiRohK87/X\npo3jusMUdxhGREFI3J/YaVsWtmNTKjg4toVlGnk1fNNafsPCuvXhBkN0yjUwqjbu6OqihHOLLZqJ\nxdMf/NZ+le3tCZsd5v2rLL5yhWyL4WrLtRg/N4VVKtG6vURnprF61a5S/ddx/Q86x7WIwnhFUZ4V\n1xBDUZ4cxbBN0jAmjWLSOCFLUqyCg1srUzsxSfXEBHZp/V7uSr1uj2tXbnD18jUaS00KxQKnTp/g\noUfOUyytv1/jZtqtNs8/+yLPfeVrtJcWOTZZ5/iRUY5OjAyzJ4VigbGJUarVKkrlve7GUn7O3Nmj\nNlYEK7ZjUy6XKFdKGwT+O5PGKY2bi0TdPMtiOnlgZro2ZqmEThOiZoewHRC2Q3rNHmEn7yy65QLF\nagG3UsCpFLGnjuCOjmCXXCYnKszdmsv3JNRZfq0yrXzRUX/bsySIuPrFF7j6FZ/GHc/bsiwq1QrV\nWmXVHpUaSOKEMI7QtSLu8TEefPPD1Efq23q+YRDyu5/4JM9++blVPy8pizHLZcR0h0N36ymXSxSK\nhbxkyrFRSueOMn3zNs999QWa62T0FTBquhyximuCuiBLmU8CFtKQdAc519GxUb7vB76HU2dPAvm5\n8yu/8GtcePnVbd8HwEf/0ffx2JseWfPziYkKczdmUN0lkl5Ic6ZJ0OwRdULCbkjYiUl1f+6uscWE\n8ixBJ/HydIF+YJ1v85TiFG2KY8V8M+5+cK2jjN5Cl6y//dwgHojjdMsFBIZpUCwW8+tkf+/ZYZJh\n8Dmc35A41czMzNPr9kiSZLhn4uj4CI5tUzk+gVMpsnT5FtnKPXnjZFgrbV1KMfHoGY6+5cH80tU/\n/9cNALM031szjZc7s6aNthyw3P4OM7mXv36B3/7136ex1FhzN8dPHuP7/8FHGJ8YY3Kyep8GXIbi\njX/v/Xc9aTMJIsJWl6QXUhit4lZLd3V/u5XGCd3ZJZRhYJdcnGppx89t/uVr3PziS6t+poEwDGk1\nWrSa7R3XhjGUolwqUD5epXKiShjGXLo+y8uXpjep1L168+qV3viWx/jIR787zxAN2tgfajUGE8bD\nTp6tTGOCTszNF27Qut1cHez0ma7N2Xc/Rrle6L95lreCyrKMKIqHBQ27jYiluZDOXIMsSbGLLsWx\nGsXxGsWxGlbBZenKNAuvXCdY2Gal/RU7IViuxeipMUZPjlOsF0nTlE67S7vd5frMEr3E4Kz3IKfO\nntrefa8jjROWLlxl/sVXCZurA+livcS4d4r6+VMY7nIvU2cZ3fkmwUKTuBfm55WxOnUetboES23C\nRhvLUKx87ynToHJsnPqpI1RPTmDtIFDcT4sLS7zw3EtM37hNt93m4YfO8PD544zXS2s2+4XBNjL5\n5sJ5HTQrD7R38di63wnb7obpWhlgu3knziksdyqiLqrXXLe9ANouoMujq94bk5NVZme3V327t9hi\n5vmLLFy6RRhGeWBp2+s+Z7tSZPzhU4yeP35X58Dli1d49pnnuH7tJnMz86tWPheVScEwcZSJrQzG\na3WOTI4zUq1SqJRwayWOvPk8xbHlubtZlnH51as89+Xnef7ZFwmC1ZXdHcdhsl5nrFhGK2iGAYud\nNp322sz8Zh7/xjfzXR/5DgqF1R2JnQZdT33be3n/dzy17u+Gx25w7PuBgLYcsItopYhaXRpXb7N0\neZpwqb3u/ayVLxBRpkHt1BTVU1MYtSKuCQVTo+JguDl5HMQsXJ1n/socYTchSlKiKCFNEywFtqnI\ndDasX6aUwrItbNtB2faGHTnTtUnjZFVSAPLM8KDqf/30FJNveGB4fNM4oXHlNgsXrtObWxvsqMFc\n6oJDaXKE+pmjlCc3r3q/W1EY8fyzL/LsM88RxzHFYoG3veMbePRN3rADdt8GXGbB4bGPvO+1a9Ah\noLXmxhdeZPHCjfV/D4RBQLMffK280DmOQ6FYoFAsYJoGjcXmMDO2lEZcjna2fcJ6Add7nnonH/iu\nHQTJK8oeN2/MsvDyNVq35iHTKNNg7KGTTL3p3OqLv9Z5byUJUUmcB0RK9T/INk91r9Sdb7J48Tqd\n24uEjY1Xuhq2RfXoKKPHytTGiqur0Vsu2i31H/feTsTXWUa02KA3twhoipNjOCP1fJXj3dyv1tQK\nFjdenSYNY6yiS2mivqbm3aHWP0dU1Muz4fdwYYJWBrpQzTPfqPxcjENUEi739FU+jUGbdp4JGGRO\nNzo3dZZ3QsJe3qEAtGnnj7POOb2TgGsgSzPibkAWJ8OMZRbl3ytD4dYrlMbrq87ve0FrTbPRZG52\ngbmZeeZnF4iiiInJMR569EGOHJ3a0f2lacrtW7OEQUCpUqJWr1HcYD6R1ppOp8v1y9e5eOEyl165\nzK2b02tuVx+p820ffJrH3/bmDR83imJ++ed/lVcvXNq0fd5jD/MDH/v+Da+BOz12vcUWjcvTNK7e\nJmqt7oCZBQer/+WUC5QmR6mdmlw/WB5cN9P+dnqmjTZsWrfmaVyZJmx2+llYG9MysFSKYWhMS6Ex\n0IaNNp3hfrgrEwdOtYRTKWLaFjrLiLshYatL1OoStXvoLMMpF6mdmsqnCG0g7obE3R4oA6tgY7kO\nxh4u/tqN+zbgcmplvL/zrtewRYdDlma8+qdfWrc3cKc4SdDAxMOnyIKY3nyDNFwOwuIs5VavzZcu\nvrLt+lsDKwMu0zT54Hd/gLe/+4kd3cd60ijOM7/O9qve360szdBpvmpMZ1l/X7AM07Gx+0Ouyxes\nOA+urP7wzSG0mw/sQ2tV8NXdMJO05d2YNtot5wtn7nFwvfqBMvp7qGx4k9fV8bvHOu0uly9eYXFh\nkThOmJya4NE3eRvWxlspCiN+5eO/zsVX1s90nTpzkn/wQx/dMACEuzt2WZIS90IMMx+W3mg+ndg7\n923AVZoc4fwHvuk1bNHhEXcDLvzh50l6mw8fOrUyp9/zZoqjVSDv8UXtHkmQD8sVx2oYVr4r+rWr\nN5i+cZswDPOVUFE8LL4ZhiFhEBL0Qnq9gDAIMQwoFIucPH2Cb/mO9zE+MbZpW8TB8br9wB7UPxsu\nTtCgdX/uZ35d1MpYu4hg5WTcA+B1e/wOgCzL+OynP8+f/eGnhp1Ux3F46xNv4Tu/+9uwttiXVo7d\n4bbTgOvQdMlNRypBb8QuFTjz5ONc/suvrspYrTRy7jjHn3hk1VCRUgq3Wlozj81xHc4/9ADnH3pg\n222QC4c4dJTKh/fuqH13MLqg4jAwDIN3P/VOvvm9b2dhfpGgG3D85LF+aRUhVjtEAdehaeq+KE3k\nGcAbX3yJzu3FYQ+9MFpl6k3nqJ8+ss8tFEKI+5NpmsulTITYwKGJYkzZ62xLbq3Mufe/jbgXEncD\nTMfGqRRfs7lPQgghhFifBFz3IbvoYu9z9WEhhBBCLDs0yxpkDpcQQgghDqtDE3BZEnAJIYQQ4pA6\nNAGXDCkKIYQQ4rCSgEsIIYQQYo8dnoBLhhSFEEIIcUhJwCWEEEIIsccOR8CllBQ+FUIIIcShdSgC\nrtdy42IhhBBCiHtt12kjz/OeBH4D+Ie+739ynd/HwF8Dinx7sm/xfX9X25TJcKIQQgghDrNdBVye\n550DfhT4zCY3W/R9/+ldteoOskJRCCGEEIfZbocUbwL/FdDc5Db3bAxQMlxCCCGEOMx2leHyfT8A\n8Dxvs5sVPM/7FeAM8Fu+7//0bh4LJOASQgghxOG2ZcDled4PAh8jn4c1mI/1E77v/+kWf/pPgV/p\nf/9Xnud92vf9r+yqkTKkKIQQQohDbMuAy/f9jwMf3+kd+77//w2+9zzvz4E3AZsGXI67fnNGJqpM\nTlZ32gTxGpNjdHjJsTvc5PgdXnLsXj/uRXGrNXO1PM97mDwL9lHP8yzgXcBvbnVHUZis+/NumDA7\n27rbdoo9NDlZlWN0SMmxO9zk+B1ecuwOt50Gy7uaNO953nd6nveXwAeA/93zvD/q//xfeJ73dt/3\nXwaueZ73RfLSEL/v+/4zu3kskDlcQgghhDjcdjtp/pPAmtpbvu//Hyu+/7G7aNcqUhZCCCGEEIfZ\nIak0LwGXEEIIIQ6vQxFwySpFIYQQQhxmhyLgkgyXEEIIIQ6zQxJw3YvFlEIIIYQQ++PAB1yGY6GM\nA99MIYQQQogNHfhIRoYThRBCCHHYScAlhBBCCLHHDnzAJSsUhRBCCHHYHfiASybMCyGEEOKwO/gB\nl+vsdxOEEEIIIe7KwQ+4JMMlhBBCiEPu4AdcModLCCGEEIfcgQ+4LEeGFIUQQghxuB34gEuGFIUQ\nQghx2B38gEuGFIUQQghxyEnAJYQQQgixxw5+wCWV5oUQQghxyEnAJYQQQgixxw50wGXYJoZ5oJso\nhBBCCLGlAx3NSHZLCCGEEPcDCbiEEEIIIfbYwQ64ZIWiEEIIIe4DBzvgkgyXEEIIIe4DBzvgkgyX\nEEIIIe4DBzrgsiTDJYQQQoj7wIEOuGQfRSGEEELcD3YV0XieZwIfB84DJvDPfN//7B23+SjwPwIp\n8PO+7//iTh9HhhSFEEIIcT/YbYbrB4C27/vvAT4G/PTKX3qeVwL+FfA08BTwo57njez0QWTSvBBC\nCCHuB7sNuH4Z+J/6388CY3f8/u3AF33fb/u+HwCfAd610weRDJcQQggh7ge7GlL0fT8lHyoE+BHg\nP99xk6PkgdjALHBsp48jGS4hhBBC3A+2DLg8z/tB8mFDDaj+vz/h+/6fep73j4G3At+1xd2o3TRO\nAi4hhBBC3A+2DLh83/84+QT5VfqB2AeBD/czXivdZHVG6wTwuc0e593/w4d3FZSJg2NysrrfTRC7\nJMfucJPjd3jJsXv9UFrrHf+R53nngF8D3tufo3Xn7wvAc8DbgAx4BnjC9/3W3TVXCCGEEOLw2W2h\nqx8knyj/Sc/zBsOM3wb8U+BTvu9/wfO8HwP+hDzg+t8k2BJCCCHE69WuMlxCCCGEEGL7DnSleSGE\nEEKI+4EEXEIIIYQQe0wCLiGEEEKIPXYgdof2PO+ngHeQT7D/Ed/3n9nnJolt8jzv3wLvJt9T89/4\nvv9f9rlJYof6q4q/Bvxr3/d/ab/bI7avv2ftPwdi4Md93//DfW6S2AbP88rALwGjgEP+3vuT/W2V\n2IrneW8Efhv4Kd/3/73neSfJd94xgFvAD/i+H2/09/ue4fI8773Ag77vv5O8wOrP7nOTxDZ5nvc+\n4LH+sfsO4Gf2t0Vil/4VML/fjRA743neGPDjwDuBDwEf3t8WiR3474Cv+77/NPB3gf9rf5sjttLf\nI/pngT9b8eN/Dfzfvu8/CVwE/tFm97HvARfwLeQRI77vfx0Y8Tyvsr9NEtv0afKLBcASUOqXCRGH\nhOd5HvAI8Af73RaxY+8H/tT3/a7v+7d93//h/W6Q2LY5YLz//Rirt8ITB1NAnli4teJn7wN+r//9\n75G/Jzd0EAKuO/ddnOv/TBxwvu9r3/d7/f9+DPik7/tSZ+Rw+XfkG9FLoHz4nAXKnuf9jud5n/Y8\n7+n9bpDYHt/3fx0443neK8CngH+2vy0SW/F9P/N9P7zjx+UVQ4gzbLFn9EEIuO4kF/5DxvO8DwP/\nEPgn+90WsX2e5/0A8Fnf96/0fyTvvcNFkWdHvpv8/fcf97c5Yrv6c++u+L7/EPkoz8/tc5PE3dvy\n+nkQAq6brM5oHWd1yk4cYJ7nfQD4X4Bvl90EDp0PAh/2PO9z5BnKfylZkkPlNnnArH3ffxVoeZ43\nsd+NEtvyLuCPAXzffw44LtMxDqWW53lu//sT5PHMhg5CwPUnwEcAPM/7BuCG7/ud/W2S2A7P82rA\nvwU+5Pt+Y7/bI3bG9/3v933/7b7vfzPwC8BP+r7/F/vdLrFtfwI87Xme8jxvnHx4Y26/GyW25QL5\nynw8zzsDtGQ6xqH0Z8D39r//XuCPNrvxvpeF8H3/c57nfdnzvL8BUuAf73ebxLZ9H/nEz99Ysafm\n3/d9//r+NkuI+5/v+zc9z/sE8Hny954M6R8e/wH4Rc/zPkVeUueH9rc5Yiv9hNC/A84Ased5HwE+\nCvwnz/N+CLgC/KfN7kP2UhRCCCGE2GMHYUhRCCGEEOK+JgGXEEIIIcQek4BLCCGEEGKPScAlhBBC\nCLHHJOASQgghhNhjEnAJIYQQQuwxCbiEEEIIIfaYBFxCiPua53n/q+d5p/e7HUKI1zcJuIQQ9y3P\n884CPwmc3d+WCCFe7yTgEkLcz76JfNsbIYTYV7K1jxDivuR53l8CT5IHXIO9Ph/wff/qvjZMCPG6\nJBkuIcT96seB3+x//xPA3wVm9q85QojXM2u/GyCEEHvB9/2/9jzv6f5/P+37/l/ta4OEEK9rkuES\nQgghhNhjEnAJIYQQQuwxCbiEEEIIIfaYBFxCCCGEEHtMAi4hhBBCiD0mAZcQ4n6W9v8t7GsrhBCv\nexJwCSHuZ5fIi57+S8/zftTzvIf3u0FCiNcnCbiEEPezTwC/B3wj8GPAxP42RwjxeiVb+wghhBBC\n7DHJcAkhhBBC7DEJuIQQQggh9pgEXEIIIYQQe0wCLiGEEEKIPSYBlxBCCCHEHpOASwghhBBij0nA\nJYQQQgixxyTgEkIIIYTYYxJwCSGEEELsMQm4hBBCCCH22P8PHzS7fhphKlUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75ab6b450>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"with sns.cubehelix_palette(3):\n",
" for i in xrange(5):\n",
" path = EM(xinit[i],sigma=0.1,T=10)\n",
" pl.plot(t,path,alpha=0.7,linewidth=10)\n",
"\n",
"pl.title('Trajectories of the Langevin SDE, $\\sigma=0.1$',fontsize=20)\n",
"pl.xlabel('t',fontsize=20)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff75ab4f810>"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAFkCAYAAAD13eXtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXeUJFlemPtFpM+sLF9d7e303O6e6XG7M2uBRbt4kIBd\nEAJJPAlkz0MOOYRbQAIhCUmADg8B74AeZhGLQCBYBNplzezs+J7pnmlz23d1d3V5k95ExH1/3Miq\nzIzILN9dXXO/c3prNjLMjYgb9/7uz1pKKQwGg8FgMBgMW4f9oBtgMBgMBoPBsNMxApfBYDAYDAbD\nFmMELoPBYDAYDIYtxghcBoPBYDAYDFuMEbgMBoPBYDAYthgjcBkMBoPBYDBsMUbgMhgMBoPBYNhi\njMBlMBgMBoPBsMUYgcvwwBFC/KoQwhVCHHzQbVkPD1v7hRDfLYS4J4SoCSH+6RqP/TUhhCeE2LVV\n7TMEedj6mMFgCBJ90A0wbA+EED8K/Ogqd/+clPIvbOLlfx74X8DUJp4zgBDiB4Ffl1KObfKp70v7\nNwMhxADwi8As8LeBMyvs3/7MlP/vviCE+G7gV4F/KaX8d/frutuQLeljQggb+BvAdwCPALvR7/cO\n8ALwM1LKt5v2b7yPZmrAHHAO+GPg16SU+ZBrhR0bhgIGpJS5Nd/QNkEIIYCfBG76m4aBfyal3PD7\nE0J8PxCVUv70Rs9luL8YgcvQ4L8Db7Vt+3HgJPC9wGLT9unNvLCU8gwrTPwbRQhxGPgJ4HlgUwWu\n+9H+TeRRIAH8hpTy17rtuJXPbI284+uPbUUfE0JYwO8D3wR8GviPwCTQD7wH+E7gO4QQXyul/Hzb\n4b8B/E//v+PAPuDDwH8GfkAI8V1Sys92uHTzsZ0orvF2tg1CiF708/znUspP+Nt+APiMEOJpKaWz\ngXMfAn4MeCcvPh5ajMBlAEBKeQm41LxNCPF9aIHrjzdjZfaAeQ4zcQOk/L+lVey7XZ6Z9aAbsEP5\nWrSw9TtSyu9o++2XhBC/BfwZ8FPA+9t+f1tK+Xtt235GCPEs8AfA/xJCfFBK+WbIdcOO3Un8CyCG\nXsQ2+EW0oPQ9wH/dwLn/FcvfsOEhwwhchnUjhPg14K8DTwD/Hvgg8O1Syj/xB95/AXw50AfcA14G\nflhKebnDeQ43TFdCiCG0ifObgL1ADm3i+Ekp5Sttx+9Ca2K+DhhFm0P+K/CfpJR1IcRnga9ACw+f\nE0Io4EjTtfYCHwe+Bm1Syftt/Skp5RdXul/gL7e3fy33IISIAt8H/DXgCPq7HAM+6e9b6/YeVnsP\nbc/h40KIjwMfl1L+eMj5Qp9Z0y6Wv2r/W2jtxl3g56WU/6ntPKt+j5vBavtd07s8APxV/z72AzPA\nfwN+SEqpmvb/arTG9zT62f6Of53LQF1KeXSt9y2EeB4tyOyTUk60Hb8PuA18QUr5ofZvZK3t78Bp\n9Pv932E/Sik/I4T4Ftag3ZRSviqE+BjwReBn0X3oncbHgJellF5jg5RyXghxCfg21ilw+e/iz9Hv\n2vAQYpzmDRuh4c/zk2gh53uB80KIJ4HPAe/2f/tu4FeAjwAv+ZNJ2HkAEEL0Ay+hJ5JPAH8TLeA8\nCXxBCPGhpn0HgNeAb0H7ufxN9KD0b4Hf9Hf7EbTwAnoS/DZ8XxghxCjwKtp88jv+Pfw0IIA/9yfa\nTvf7PcD59vav9R78dv8McAH4R8DfRU/OPwz8Fiuwhnv4Ef/+LX+/j/l/w2h/Zh+j1ZT8E2gT0k8B\n/zfgAf9BCPHhdT6DDbPGftf8Lr8VbU77PrRJ7Qf8e2qc973AHwGHgX8D/BBwHP3sekLasdr7brzb\nbw25nW/z2/frbe1dc/u7cA/dFz4qhIiH7SCl/MMOWqqOSCm/BHwB+KBvAnvHIIToQfeNMCF1HHjX\nOs+bAb5OSvnfV9zZsG0xGi7DRrGAmJRyadUlhPgytFbhR9o0RFNo1fp3oyeKTvwIenJ7n5Tytabj\nfx0tlPwn4Gl/8w+jNSwfklI+72/7TSFEGu1/8h4p5fNCiIaT/+ellF9outbH0RqhvyKlXBI+hBC/\nDUj/Wo+tcL8bvYe/gjaz/NWm439TCHEVeE4IkZJSlsMuspZ78J9DY5F1oZtZp9Mz8+/VQmtlPtJ0\nrXPAi2jn68+s4xlsBo+ztn5n+ce8p+FXI4T4U+AG8FG0IAzajBNBa28bfedXhBD/G61Fm29rx2rv\n+5NoLdBHgV9oO8e3AVXgd7vc72rb34nfQ5u5vh54Swjx39Dv7vWN+Bn5fBb4MuC9wK2235JCiL4u\nx1aklNX1XlgIcRq9IPhKINv2swK+RUr5h+s9/wo0BMwwh/8i0CuEiEkp62s87w+gFzeGhxgjcBk2\nigL+R/MGKeVvsqxdaqz6IiwPvIdXOOe3AxeBK20Dcxm9cv5GIUSflHIRbc670yRsNfinaAfey3Tn\nm9ET5iebN0opbwshPg18gxDiiJTyhv9T4H434R4cYJ8Q4pCUcmlyWkNU3lrvYaMo4Ofatp3z/+5t\n2raWZ7Bh1tHvFNoMuiRc+Oa6KWBP034fAu61CeqgHZe/miCrve8Z//18RAgxLKWc8du9Dy2o/N4K\nz2a17Q9FSlkUQrwfLZh9C1pI+ddAWQjxIvCHwH9b5/tpaM/C0of8KHqREIZCC4EBM/dqEEJ8Pfo7\n+DW0gH3cP9evooXXOvClkOP+X+AZVuezaPn7/aOQPtHr/w1zA2gEAvSzhsAjX3Ob38Tv1/CAMAKX\nYTMIDARCiL+P9jUQQLLpJ0WXfudH+OxFTxjtmoPG8QAHhRB3/P3aI6iQUt5DD/od8SfDUeCFDv4u\nEvgGdGRf8z12HfjWcg/oyNAfQwuHl4QQf4KOcPpTKeW1btfZ4D1slJa2SSnLvvYr5bdrrc9gU1hH\nv7sesq2CdnpGCDGINhu+EbLfSyHXX+t9fwLtvP7NaPMnaO0W6Gi+leja/pXwfce+zfcB/EbgA2j/\nt68E/gLwY0KIb5dS/p/VnK+JGPpewzRlv0x3U/nNNV4LACHEcbSj+j+UUv5K0/ZTwAkp5Z93OlZK\n+T3ruWYIrv837FtsvJPIak8mdCTpP0a7CRgecozAZdgMWnLuCCF+AvhBtPnkn6An5ypwiqDppJ2G\nCeAs8A/pHKF2s2nfFZ3KO9Dwv+kUgt4w42XatgdyDLWxlntASvnzQogL/r5fA/wltFP6C8Dfa86D\nFMJ672GjrPTM1/QMNoN19rvKCqdN+38DUZ1SypIQwm3bvNb7/n20E/VHaRW4FoBPrdA2WLn9q0JK\nOQ78kv+vkUfqb6Mn+98SQjyyRk1XI8BiPOS36yGaoc3gp9Cm+V9p2z6FTnNxP+imuWp8gyuNH838\nHeBXN8HEa9gGGIHLsKkIISLAP0AnQvwyKeV802/Jjgcu0xiM4iFmwvZrVdAryf51Nrfg/w04Pvus\nZ4Bs3n/Fe2ggpfwMOk9PAh3Z9Z3oqMXPCCGOd0kCuVX3sFHW/Aw2wib0u040fIkC5xBCpAhqK9Z0\n31LKghDij4C/6Gsre9DmxF9ah5/PpiGllMD3CyFGgO9CCyx/toZTfC3629zydw9Lmt6/iA4caOdR\n7l8euUn8xK0hv2WABSnlqnKM+cEwp6SUv7iJ7TM8QIzAZdhshtGr/M82T3o+K4aISylzQoi7wPFm\nv5YGQoghKeWsv29dCHHP3zfavAoUQhxAm0RekVJe7HCtRf/4k0IIK8Qkd8r/G3r8ZtxDyLFV9MT2\nZ0KIWXTU4legs4zft3vYKBt5ButkQ/2uCzNooSss2u597RvWed+/hdZwfQMw4m9bjTlx3fhRif8K\nyEopv7/Lrg0zdLrLPu3n/hZ0v/tdKeXc+lu5JgRa+H21rS1p9Djwz7oeLMQvoQMZ1uLD9f3tQrWv\n9XwDna6jnUeAtUR8fkQ3TTQHtzSiSb9DCPEU8P9JKVdKImvYJhiBy7DZzKL9GFpqvvmRQ9+FHqhW\nStz3O2hTxj9AR3w1zjEAnBVCnJVSfoO/+Q/QaRQ+Bvx20zn+pb+9Mdk2TD/tmopPolfF34H2p2lc\n6zjaj+VVKeWdFdq77nsQQjzjX/ffh5hCGtqSlSK2tuoeOj2z1bKW97hRNqPfBZBSKiHEy8CXCSHe\n3Yg69H1r/nmHw9Z6359CR7V9PTri9paU8oW1tnUtSClrQohvBJ4WQrwm/YzozQid3+670GbLVWmq\nhI5Q/hW0pvFfbLSdQueoOwYUpJR3u+zaELILbdv/Ptqs+WvdriOl/NvrbWMIf4xOBbKEEOIYWgj7\nqbbtj6CDfgKm4fYgEH//Q2gh+BNSyp/YxDYb7gNG4DJsKlJKx1+RfUwI8RvAn6BV+n8XPXh/Cviw\n0HXV/kBKuRBymn+N9mP6V0KI3Win+N1of4YRtIN5gx9HmxJ+2fc7uYp2+v1e9Aq7kR7gBnpl+kNC\niMfQ2fMvoyOzvtk//kl0Xq2DfnvrrC6fURirvYezaD+r/+Jf/zW0o/FT/rXfRofYd2Or7qH9ma3G\np6iZtbzHlTgthPhoh9/elFJeW0O/W2tKgP+A7lO/L4T4OfTk/jG0+ShMGF7TffvCz+/5x/Sic6jd\nD74b+D/Ar/vP5Y/QPkhZtIbqO4FB4G+FaOWa34eFDtz4KnSi1wngW7tE1XV7lw3e9ING9qG1s/8b\nLZCGIqW8IoT4Ejo33GUAIcRXoAWur5erSB68ifw/wPcJXd6oITB9H/q7bHbm/zJ03rg/QydtXg3x\ntr+GhwgjcBlWYj2lXf4uelX81WgzyevAN0spXxRC/Bhavf/T6FVzQOCSOivze9DagW9CZ9QuovM8\n/c3mHEtSykl/359AO/kOobOe/0t0MsgGv4sO1/8I2vzwMnBZSjnrH//j6Alm1G/T54CfWMFhvZmW\n57Tae5BSuv7A+4Nooem70dFMt9Dh+j+5ki/POu5htQWow55ZN1rOu5b3uIrzfqf/L4x/jE5T8fdY\nfb9bzTUb9/FHQoi/js6F9OPo6NffRKc2+MssawIb+6/nvj8B/F/+dX8z5PeWNq2l/Z2QUp4XQjyO\nFga+Dn1vPWghcgydp+sXOvSf9veRQ5cG+0H/mE4+hyu9ywaNd9o4xuuyb4NvBX7Oj0qMoRcu75FS\nbmrt15WQUk4Indz23/ga7F60T9fXtjm/T6Id+q+udE4hRBatzX8U35wpdJ68n5Zbl1PMsMlYSq2/\nVJoQ4t+hy5tEgH8rpfz9pt8+gs7K7AB/IqX81xtsq2GHIoT4VfSktFRux2DY7gid5yuHLuMS8Ocy\nbA5CiO9BJzb+aw+6LQbDRlh3aR9fgj8lpXw/enXUbh74WXQyvQ8CXy2EOLHeaxl2PI0Iu9UUVDYY\n7itCiG8XQvypEOKDbT/9df/vfYnEewfzNbQ5wxsMDyMbMSl+nmUTwwKQbkRJCSGOALN+bheEEJ9C\n29Yvbai1hh2F73P1IbQJaLw9ostg2CZIdELQTwohfhZdVPpptG/cNGvzRTOsAT9Nyjl0pniD4aFm\n3QKXH37eSKr4vcCnmkLSd9OaAG4KOLreaxl2LB8G/gva5+rvPOC2GAyhSCnP+n52P4z2dxpGR0V+\nEvjRxsLSsPn4aVKMO4phR7Bhp3khxF8C/gbhNcUadMq2bHgHI6X8BVbOPG8wPHCklG+gnbINBoNh\nXWxI4BJCfA06cudrpJTNmazHaS2euo/wEg9LzF84qwDi/QNk9h7stqvBYDAYDAbDg2ZNyqR1RykK\nXaT1eeDDYb43Qoi30KHZ4+jq7N8ppewY/jp/4azyPA+V6EH1715XmwwPjpGRLNPT97t6jGEzMO/u\n4ca8v4cX8+4ebkZGsmsSuDai4frL6JxHv+NnXVbAnwNvSSn/AJ0T57f97Z/oJmy1oFaTbsVgMBgM\nBoPh4WEjTvO/DPxyl9+/CLx/ree1lLeuTJsGg8FgMBgM25V15+HaMoyGy2AwGAwGww7DCFwGg8Fg\nMBgMW8z2E7g8Y1A0GAwGg8Gws9h+ApfyYAP1HQ0Gg8FgMBi2G9tP4EKxikL3BoPBYDAYDA8N21Dg\nAjzjx2UwGAwGg2HnsD0FLuM4bzAYDAaDYQdhBC6DwWAwGAyGLcYIXAaDwWAwGAxbzDYVuIzTvMFg\nMBgMhp3D9hS4jNO8wWAwGAyGHcS2FLgsY1I0GAwGg8Gwg9iWApfx4TIYDAaDwbCTMAKXwWAwGAwG\nwxZjBC6DwWAwGAyGLWZ7ClymgLXBYDAYDIYdxPYUuIyGy2AwGAwGww7CCFwGg8FgMBgMW8y2FLhM\nWgiDwWAwGAw7iW0pcBkNl8FgMBgMhp3E9hS4TKZ5g8FgMBgMO4jtKXAZDZfBYDAYDIYdxDYVuJQp\nYG0wGAwGg2HHsD0FLozAZTAYDAaDYeewTQUujFnRYDAYDAbDjsEIXAaDwWAwGAxbTHQjBwshHgf+\nJ/AfpZS/0PbbDWAM8AAFfJeU8t6qT24ELoPBYDAYDDuEdQtcQog08HPApzvsooCvlVKW13UBI3AZ\nDAaDwWDYIWzEpFgBvg7opLWy/H/rw+TiMhgMBoPBsENYt8AlpfSklNUVdvtFIcTzQoifXOv5TXkf\ng8FgMBgMO4WtdJr/YeCfAF8BnBZCfOuajjZpIQwGg8FgMOwQNuQ03w0p5W80/lsI8SngNPB73Y6x\n7WX5L5WJkRzOblXzDFvAyIh5Xw8r5t093Jj39/Bi3t07h80SuFp8tYQQvcDvAN8kpayjtVyfXOkk\nXpPfViFfJq/ym9Q8w1YzMpJletq8r4cR8+4ebsz7e3gx7+7hZq3C8kaiFJ8BfgY4BNSFEB8F/hC4\nIaX8AyHEHwMvCSFKwBtSyv+xpgsYp3mDwWAwGAw7hHULXFLKM8BXdvn954GfX+/5TVoIg8FgMBgM\nOwWTad5gMBgMBoNhi9m2ApdJC2EwGAwGg2GnsG0FLpMWwmAwGAwGw05h+wpcxmneYDAYDAbDDmH7\nClzGpGgwGAwGg2GHYAQug8FgMBgMhi1mewtcxo/LYDAYDAbDDmDbCFyWHdIUo+UyGAwGg8GwA9jm\nApfRcBkMBoPBYHj42T4CVyQS3Gg0XAaDwWAwGHYA20fgMiZFg8FgMBgMO5R111LcbCw7RMNlcnEZ\nDAaD4Z2A52JVCgCoZAbsbTM9GzaJ7fNGjYbLYDAYDO9EPA977g64dQCs8iLewP7wedHw0LJt3maY\nhsvUUzQYDAbDTscqLSwJWwA4Nb3NsKPYPgJXxGi4DAaDwfDOw6oWgtsqOROpv8PYPgJXmA+XEbgM\n2wSvWsWtVFBmADQ8YJRSuMUSyvi47gycmv7XjutArXT/22PYMraND1e407yZ3B5mvGoNt1gi2tuD\nFd02XW1NKKUoXblO+fotUB6x4SGyTz2OHYs96KYZ3oG45TKLL5/BK5exIhGyTz8BI9kH3SzDBrCq\nxc6/lXOoROY+tsawlWybWdCkhdhZVCemyJ99GzwPKxIhffwYycMHsCzrQTdtTZQuX9XClk99Zpbi\neUn2qccfYKsM70SUUuTffBuvXNb/33XJv/EWztE9D7hlho0QZk5c/q2Ech2I3Kep2vN0e2oVsCOo\nVC9EzeJyszACl2HTUZ5H8YIE1wMUynUpXrpMdWKSntOniPY8HCu28o2xFmGrQfXeBIl9u4mPDD+A\nVm1PlOdRvn4TJ5cnNjhA8tDDJ1xvd+pz8zgLiy3blOswf+EqHDj4gFpl2AherQb1apc9FFYlj8oM\nbF0jlIJ6FauS02kpmuZdq7yASvej0gMmYnIT2D5P0GSa3zE4i3m8SgU8V/9zXVAKZ2GRhS++TOna\njW3vf1K5e4/ipcsdfy+clyjHvY8t2r4opcifOUfpynVqk9MUL17WAvcOwy2VKF27QWXszgPpv+Vr\nN0O3z8vreNUQHyDDtqeWX1xxH6u8Rc7zysMqLmDP3caev+Nfp61fK4VVnMeeHYNy3jjxb5BtI3CF\nabi2Q1oIr1anNjWNV+m2CjE0U5+d9ZPWNj5OtfwhK4/S5WssvPgqzmLuQTWxK7XpGQpvXei6j1cu\nU7p6PfQ3pRRuqfyOcbCv3L5LbXqmddvYHWozcw+oRZtPbWqG+edfonT5GoXzl1h86XWU49y369cX\nc9Rnw5+ncl3KN4KaWMP2p74KgQu3DvXy5l5YKez5cazCTLjDfjueg52bxJ6/C/XK5rblHcQ2Eri2\nX6b52uwcc3/+PLnXzzL3uS9Sm5p+oO15WKhPT7EsbPko1bI6cnN5Fr70Crk3zuEUOjuN3m/qC4vk\n3nhrVSu58o2xFqFRKUX51m3m/vx55j//AvOf/xJucWdHGbmlMqVLV0J/K7x98b4KJVuFs5gj/+Zb\nLeORs7hI/tyF+yZUd9JuLf1+6zZeNbgoVK5LdXyC2tTMttcqv+NwHZxSyNgXiQc2WeXNXZxaxfn1\nCU71CvbcXahsnzH7YWJ7C1wPUMOlPI/C2fNNmhlF/ux5vHq9+4HvcJTr4Cx0GBxC3mdtYoqF518i\nf+48bunBCidusUTutTe1CbSN2PBQiA+DIv/2RZTn4ZYr5F59g+IFiarpFaNXLpN/860dq+lSSlF4\n6wIq5HmBvv/i5Wv3uVWbi1suk3v9bOg91ianVhSENgOnUKQ2OdV9J8+j1OZv6CzmmP/8l8iffZvc\n62+SO3PWCF3biNDoxEgcr2cwfF9vk1wYnBpWab5Lw2xUogc6+mAq7MLs5rTlHcY2Eri2l9N8bWom\nsGJUjkPl5u0H1KKHA3dyAuW2vjc7GiG923f6DH2niurde8x/4UUK5y/h1R+MVqRw/hIqRKCODQ7Q\n+8wTpB85EvjNzeXJnz3PwhdfCjX5OLk89bkug9tDTOXWnRXvrXLrNvX5hzNjtlevk3v1zVDNUYPS\nlWtUJ7dW812+fnNV+1XG7iy5PtTnF1l85UxL2+vTs/dFQDSskhCBSyUzkAipo6jU5mi5lMLKz4Rr\n8OMpvN5RvJHDqP7deIMHteAVhltrzYxvWBXbR+AKzTT/4DQDldt3Q7eXb47h7QAzyZagFPXpycDm\nWDZFz4EhBk7uI5qMBayNzcdXxu6Qe+2N+64VciuVUIEpks2SfeZJrEiE1JFDRLLBAag2MdnVdLYT\nhXS3WKIow02J7XTTgm1XlOeRP3MOt7iy6aRw9jxOvnNo/0Zwy2Wq4xOB7amjh4OBRp5H6fpNarNz\n5F49E9onS9dubisT/lZRm54hd+Yc+XMXtuzdbAjPxaoF/bJUIgOWhUoGc6tZm+G0XilghSRTVekB\nvIF9kMqC5c/F0ZgWvAb2hhfSrhlfrrWybQQu/ZLbVJjKeyBCl1sqU58JV5kqx6Eyduc+t+ghoVqk\nthgc3GLZlP6bSTJwcj89x/ZjJxIdT+MsLOLcZ61IbXImsM1OJuh79insmB5sLNum5/GTaz/31PQD\nN5duJkop8ucuhPpYxnePBra5xRKlqzfuR9M2hYapNFR7ZwWHTOU65M6c3RJ3A51wt3UMtGIx0seO\nkDq0P7B/Zewuudfe7CzgKk/71u1QMzdo39vc62epTU5RvTvO4itncCvbSzjQ5sS2dxCJQVSPiyrV\nGzzIrW3MYd1zsQvBcY5IDNXTJe1EPI1KBhea1mY78r8D2JDAJYR4XAhxVQjx90N++4gQ4mUhxAtC\niB9a6VyWZYUOZg/CrNhJu9WgfGPMpARoQymFlZ+lXmgfECzivanl/2dbpAfiDHzwOTInjmN1yNhe\nvRfUlG0lYQERiX17A4JhrL+P5KEDaz5/+dbOENKVUpRv3MJZCArEyYP7yT71ONG+4GRRvnFr20al\ntlO+ej1Uq2RFovS//9nQ/GteqUz+zbc3VZDxqjUqd8YD21OHD2JFtcbVatdyKW/FYCNnfoHqCmPc\nw4pSiuLFyy1CqqrVttyU6pYrFC9doXD+EvUV+rlbqZC/cJl5eZeFq/co3JmlPLVItejq6GbHRUWi\nqHg6cOxGzIpWYTbUD8zNDIbPvU2oeCqwLUxDZ+jOuhOfCiHSwM8Bn+6wy88CXwXcAz4vhPhdKeWl\nrie1LWjvD8oDQhzqtwjleVRDBrmWfWo1Krfvkjpikg02cIp56gu5QDkmO5kgkkrQsppTHnYlR+rI\nIRIH9lGSVwNaw9rEFOqUuC/JMz3HoT4b1GbEd4UnNk0/eoza5FRoqpDEnlHsVCrgd1O9M076+FHs\nh6zEkVetUZ9fwFnMLf0LM1XZqRQZ8QiWZdFz+hQLL7zSulhSivxbF+h//3Ph/prbBCdfCNfGWRbZ\nZ04T7c3S8+RjLL74aiACtT4zS/naDdKPHN2UtpRvjgWEJysSIelrtux4nOShA1Rvrj0lRFFeJb5r\nBDvZWdP8MFKbmMINMSFWbo+TOnqYSCq56dd0SyUWXnxtKVimMnaH1LEjpB85EujrtekZ8mfPoyoV\nQFG3rGXh0J4Dy081Y1lYto1teVgRGytiE8skSe/1IDsMYUFm3aiVA8JaZa5A4c4cnjdGct9eMo91\nGW9jSbQFqmkcd+u63uP9yoK/A9jIyFcBvg4tULUghDgCzEopx6WUCvgU8OFuJ7vxh5+mPBWSk+Q+\nR9XUJqd19t8VKN+49dD5pWwllZkp6vm2FY9lER0ahHR/YH+rnAOnjh2Nkn70WGCF5dVqoULQVlCf\nmQ1oUu1EIlRTA2BHo/ScPtXSZisWI/vUabJPnSZ15FAgolE5DtU7gU8FnDpWaUE70G4zM0/p6g3m\nPvs8+TfOUb5+k/rsXEdftezpU0v1MqPZnvAAg3yByq3u/mxKqQcaCdzJXaDn8ZPEh4cAsGMx7dcX\nIjyXr2+Oj6dXq4e2JXlwf0sdz9SRQ13rekb7+nS9xTaU41C42Dmx78NIo+5p+I/eqoMP1nRN1yX3\nxltLwlaD8rUbLL58Brdc8S/vUZRXtbm3ViNgTrSs1qhApSt0uDUHp1Slni9Tmphn/sJt3Nk1Bml4\nHna+9Zh6sULu+iReXWtEK7fvdPc1tSMQDaar2KycXG6x9I7IXbhugUtK6UkpO4Xv7Aaa3/AU0LXg\nVy1XIH9jgupCm0PnfTYphpkTwyZer1oNVffvCDwPKz+DPXcHKze1cjhyvYJTKlILCFw2saFBVKY/\nRGWtsIrhhpKxAAAgAElEQVTaSd2OxYiPDAVOW5u4P2bF2lTQryE+MtxVuxYfHqLvve8ideQQaXGc\ngS97H4k92n/JjsdI7gt298qt260DSr2CPTemn/XCPazc9LYRumpTM5SuXFtVe5KHDhAbavUBSR0N\nDzAoXbvZUaCqzcwx/9kvMvfpzzP3+RcoXb2OW75/ZgvluB0d1JP797Zsi/ZkyD4ZrKepXIfq3RDB\neg14jqMDR9oFN9sOaNXteIyBE+EatdhAP73PPU1i9y4S+/YGfq9NTO6o3ILV8YmuQQ6V2+NLAtBm\nUbx4BTeXD/3NWVhg4YsvUbl9l8VXziwLfKHfVKexpnW7W6mz8Prb1Dr4GC+dv17FKs5jzY9jz9xo\nSW6qlKIwNqvH5KbTl9vHp/bTboFZUXkeuTNnmf/Cl5j//AsUzr69o1OX3C/d/qrtQsXxudaXfh8F\nLrdYCo1USz/6SKgzcPn6rR3ZOazCjNa61CtY5ZzOLux2XrVbxXmU67X6b/krtvjQoC6CmgnRclUK\nS3XEGsJKM9WJqS1/vsrzwgWu0ZXrJMb6+8icOE766CHsROvqL8zPyy2VqE/7A6VS2G0CllXJQeXB\nR1R5dYfC+Yur2jeS7SEjHglst2yb7OlTge2qXqd8Yyyw3S2VyZ85u5TGwCuVKV25zvznXmDx5dep\n3L235X6T1bBo00hERwSGEN81THL/vsD2yq07616pK9cl//rZUH+35P6gTyHAwMlj2PHW/hcbHqL3\n2aeXTNiZE8ex4kENReG83BFR18rzOmu3lnfaVC1XdXyCyu3uvpnKcSi8fbE1CCisb3Ra3IVsV45D\n7tU3KIdoi63SIvbMLey521iFWR2R2Ha96nyRerESOLdXLncNVlKxoDl2o47z5Ztj1JrSqlTvTWpT\n+g5lq4yv47RqtPb527piWRZOqYZbrBLv1Q6D2WySeF8wRHYrmL49hm23dsJYNsPeEwep7e7n5h+3\nJR+sVYnn5+l/5PB9ad/9wHPqLM4UWk1inkOsOEnPwWMB80W9mKcwXabaELb8j9iyI8QyKUYP7cKy\nLNRQmtzVQmBwT1kV0iPDuP1JShcutZppXYeMVyUzumtL7hWgNDnDvOtgNb13KxJhjziEHd2A7+BI\nFuf6KKWJ1j7j3Rtn5LEj1POLFLx6wPQYrcyT3bcL+z77RYyMLH9jk6+chVot8C00sKNRkkP9pEaH\nGRBHiSRCTA0AI1mYOkTueusAWhu7zf6nTxBN6wFcKcWdz5zDUl7Le2jgLixQWligcukyQ0+eYPBk\nUMDbDG69Phm4576jBxjd2zmCq/dpwc3x1qFNlUu63+4eWdP1ledx9/Ov4C4sBNphx2Lsf/ZxYpmg\nlgFg3wefZur1t3ArVXr2jTL63mewo63fauo9T3LvhddaD6xV4c5tRp4Nmh0fJhYu34BqpWOfbVAf\nv0d/l+e4WqqLecYuyhWv147yFMoCsEj0pkkM9uDVXSKpLE6xTL1Qwq1WmxaaFkopVJsJ0lKK8qXL\nJLw6u959Gsu2qS0uUGws6Dr4SSrXo3hnFisSCdXgW7MzjIhw32TPSbGYn2rfyMBAal2+qW61xsLN\n4JxbvX6TvY8fI5YJBg3cb5RSVGYXqBeKpEaGlvqNUiq8SsAKbNao3vLEpJS3hBBZIcRBtKD1jcB3\nrnQSpfT/FO7N09+jB+PcYhFV23qneeV5zMkbqDan78ju3czMFACb6PBwQAU/+cYlatmBbe0IDNpM\nUbkxhlupEMlkiA8NEOnNBj46q7SI5Qa1Sl65zPy1y3j9e7WTpF/U1CrOA4parmklZVkowOrr85+d\nvznRh1VrfX7l+TmKkV6wLCKDg4GM2pMXb5CNbmxw7Ebx8hhe2zuPDw8wO7/xNA72nj14461m0cL4\nFPeujRN3FkP9E71ajbmbt1C9WydktjMykmV6WptF6nPzLF4Kagqifb0kD+4n2tdLpCejhWhgLlcF\nOicGtfYfwLt+u/VePYfbL79Fz+MnAO03VRhfIZM62q9p8tW3KDkWid2b+3ycXJ7SVNBM4w2PLD2b\ncGwi/f2BFBITb0p637V6B22lFIWzb4dH59o22ScfZ6HkQCnffiDZSIXqwhR9x5afydytMVR2pEWL\noTK9RAYHAylv5i5ew+0fJNbft+r2bieU6zL/xsXAdxwb6MfJF1q1lp7LnVffpuexE+u/nuOy8OIr\nuLWgaTx56EDHgJrG9QEy+wZJ7+4nEongJnpQvbuIAY2RTnkequ6gHAdvcZbChcu4leXrKeWhLIu5\nS9fJTy/o6ODc+Io+z8V7c7g1F2w7VAu7eOMOkSNHQv0TAWw7Gqi9OHtvGkLSRqxE8dIVnLCi657D\n2BfP0PvMk2s+52bh1etU705QGbuzbKa2bHqfeYL4yCDWwgRWrcTQ40+v6bwbiVJ8BvgZ4BBQF0J8\nFPhD4IaU8g+Avwf8Nto78BNSyqurPXdtoYhTrhFNxe+bSbE2MRXMMm7ZJJt8H9KPHAkIXJ6fmLDd\nx2M74VWrLL70eksuqBJgRaPEBgeIDQ0SHxkikkljVbpMLk4Ne34cr28Xdn6mxWGylmtSLfuDfGyw\nVTOgklkdmtz8Tj0XamVIpEnsGQ0IXLWJKdRjJ7ZEoFVKUQ0pmRIfXZtmohOxkSEi6XQgB1flxk3i\nuzsLkVY5pxMfhvhMbCXKdSm8FTQlWpEI2adOE0mvvT2RVJLUwf0BM0Hljh/la1sUO9Ri7ETxgiQ2\nNNDVWbyd2tQMlbE7Op3CI0eJ9mRa2xPiuxnpzXYMnGgmeWh/QOCqTc3glsqremZerUZJXgsXtiyL\n3qefIDYULPeC8rByU5RrJdqdsK1yDqIJVHpZiLIsi57HTjD//IuBiblw/hL973t22y8cw6iM3Q2t\nBpA5+SjVyWnK11qjTjcSsaiUonD+Im5I8tjEnlEyJx8l/chRCm9dCPrHKbBjEXqPjhLPLveLsJxb\nlm1jJeKQiBNJJRigQu7qPb2wbZxMKbAs6rNz5F56hf6jw0s5AwPYURyiFCfzHbVf4NfenJjqOJ+p\nWAqrTeCy6pXQPF3dcMuVUJNog9rkNLWpmY6R4luFk8tTGbtDZXwiWOJNeRTlFRKJY6HJY1fDugUu\nKeUZ4Cu7/P5F4P3rPX95coHs4V2BgUH50RurVWEq1w2UmvFPhHIc/bvjhL78xO6RFt+caF8vsZGh\nZT8cn9LlayR27+q4KniQePU6i6++GZp4UzkOtalpalPTFC9Ccv8esiPx7qkY3Br2XKvfgud6OKUm\nk6LvIN/uSI1to+JprGqrn5JVLaASaZ3fKBJp6ejKcajPzoXmPtoobrGEVwr6IGzWtSzLInn4AMUL\nsmV7dXwCb/hgV5OlnZvGGzrQpZ6Zj+toX41qEaJxvN5dEI2jlKI+O4dXqRIbGlzV5FK6eiO0n6Qf\nPbYuYatB6tgRKnfGWzUNSlG8fFWv4kOifZMH91OfmQttj1etUpLXljRkK1Gfmyd35uySBrY2NUPf\ne99NtFebUTs5yycP7FtVWpJGeoVWrYaicvsOGXG8te2OQ21iCieXxy0UcfOFrlHR2ScfD590nDr2\n4gQ41Y4TqJWfQUVj0JTPKZJOkT5+jFJblQA3l6dy67aOsH2IUI5DKcQvKz66i2hfL3Y6pYNVWvqe\n9uVaj5arMnY3tK9EMmkyj5/EsiyseIzsM09QGbujFxP+HBYf6KH3wAB2bPm7jyQSONEVUnPYEaxM\nL33HoTA2TXk6t3QfWBFQ4OSKzF+q0v/oXiIJfyESjaOSWZ3PKxqnePb8qoJgqnfGAwKXV3coXb6K\nMz9PPGWT2Tu4ZP63auWOxUM6UbpyfUVtXOGCZGBoIJhrbgvwqjUtJE+HJIZtws0X8HJzROLrm+u3\nl4TQlOajPJsns28Qq0kbUpuaofD2RbxqlehAP73PPBFwFm3g1evk33xbO8Gv04E1eSCYyTl97CiL\nbQKXV61Sun6LzKPH1nWdraLhgOvmu5lElqncvkvMGiI1sjbTQr1Q0Y/YsvQAANjJJHYqOEmrZE9Q\n4KoUUVmFFY0QHxkORCdW702uWwhSnodbKoNSS6awBmERWtH+voAD/EZI7NtD6fK15QFfKZTnUp5c\nJLMvRGvRwK3pYISQQrbL+zh+QIOvma1XsOfHcQf3Uzgvl6LlrGiU3nc/RWwgGLjQwMnlKd8I5nOK\nrjPRazN2PEbq6CFKbYWsaxPhZsTEvr30PHZC+0ksLFKUVwPOvJXbd0js3U1ssPM9NShebo22VK5L\n7vU36X/fc9jJBNV7EwFneSsSIbFn96ruz7Jtkgf3B+6vcnuc9CNHlyaM2tQM+XPnQ+t1htHz+MnQ\nYBKqJezFSVArBREo7MVJvMH9Oou5T+rwAarj9wL5qopXrhPfvYtIyHe73VBK4eYLlG+OBVIyAKSP\n68hNOxYjdfhAILfaerRc1XuTgcWTvohN9uknWpQAlmWROnSAxOguajOz2MkECS+H1fbO4n2DVNXK\nQr1K9WJX8vQcGiGSilO4PavnSoVvMVC4lTrzl+7Sf3wP0XQSr2/3UiqH+vwi1XtBQTE2NBgIFKvP\nL+AWS0R8HyrleeRePaMDORQ4Cw7KcbVCBLSJ0XNXnRvMyRdWFcnrlcuUr98kfXxr59X6wiL5N851\nNgM3UAo8D6dYIRJfuwkVtlFpH20eaOp4nqI8lVsyP1UnJnX5DF917MwvhJo/GhTOXfDzK61P2Ipk\nMkRDBvPYQF+oyal845ae2LcJyvPIv/HW2goHK0Xh9ixutclXIJldEqI6Uc+VtSnCjiy9wtjQQLh2\nIJEOpohQLvgq2rAJpjY5vapoRbdYonzjFoW3L7L4yhnmPvcCs3/6WRaef5GFL77EwhdfwmkK4Q4r\n57NZ5sQGdjRKonm16PfH0uTCcpHuSMxPLLiM57g4MxOoeodBoF3YWj6Q2o1rLQOachzyb7yFF+Yv\ngd9X3roQ/FYsXcpoM5LPpg4d7FrOqYGdSJA5qbVClmURG+gn++TjoavcwtsXV+wX9Q5lorxKldyZ\nsyjXDTUnJvbs7myeCSG5f1+gX6t6fclMWLkzrq+3SmErc+I4yQPBCEgqReyFe6sQtnw8F3thosWM\n37FEletSPC9XHWGplMIL8WPaKpTnUZueoXD+EvOfe4GFF14OnbgTe3cTbUpJkjx8MGh9UB6519+k\nNj27qvttJCwN5M8Ceh470XK9ZuxkguT+vcSzyYCwBRbx/i4ldZqJJSESw7Is0qP99D2yW2uY2srf\neTWHeTlOrW6jIjG8eh23VKJ4MSgoWrEY2adPE8lkAr9Vmp5r6fK15ahZC7AsyjN5nHJjPFFrysel\nFyZtJvBolGjIgrB0/VYgwfBmUrkzzuLLr69C2GJJsA1WU1k9kY9//OPrPngz8Wr1j5emWgUkt1wj\ntWeY6qIum9E+IbjFEvHRkcBAXl9YDKjM10r62JGOGoFoXy+Vsbu0dBql8Kq18BXpfUbXgrsY8IcC\nIBLRubGqtdbnqdTSx+uUaiSHtEO96tuDSmawKiG1vwAiMQoTeXCcltOlDh9cMtm0YFng1AJ+AGBB\nsodIKqkT8DWfzPOI9feGDgwNqpNTLL58hvrMLE4uj1cuB7QWqlanOj5BpKcHOxYLHYQyp0RHrel6\niWTSur80D45KoZQi0ZdB9Qyh0n26OC1QmckzL+9SmVykdvce8dFR7HiTv1InYQstqOXkmB4bmh2m\nXRcnXyCxd3dAgCpduU7xdjCIOP3IkU3rz5ZtQyRCfQWVffap04F+Y8eiWJFIwNlb1etaKGs3XTdR\nvHgl1N8GtGa6PreAsxBMuJx5/CSRNWRht6IR3FIpoDVyKxVU3Qnta51IP3KU9LFg4lgtPI0H/Fp1\nAIOF17tLWwTaU7h4ru4rfmFkgEgyiVerBdJPuKUS0WwP0Z7uK3gnl2fxpdcoXb5KdXKK+MjQmnzq\n1oqTL7D44qtUxu50rHYALPm8NX8vViQCnkt9rlXwVrUa1fEJnPlFIpk0kWS4tqs+N0/u9bOh/sSJ\n/XvJHF+5soBVmMNyW8c8lciQGdlFqbRyom38jPSNvFfRZJx4b4rqfCFomvOgMr1I+doNytdvUrl1\nu6OPW3xwAOW6AS2XV66QPHyA+sxsUKvnB7cpzyMx4PcTO6oX0ytQn1+gFOLOnXn0GKkjh6jcHqd9\nXnWLpdBxayMoz6N4QXbNNWhFo8T6+/DKFb3AWdrPIjWi/e7Su/b82Fquu200XP0njgbzgjgu+Su3\nyb/5VseHUroajKgqb7BQbqQnQ/JAZyf4SDodWtanNjF537Kjd0IpRfHSFarjISpby6b36Sfoe/Zp\nBj/yFfS991niu0YaBy7tVs+XtXYxloSo1r54A3sCmi6V7MHJ7sbJBye0UCffpuMCTasWtRNwJBKq\nZepWW9EtliicPb+qAAvluuTPnCV/9u3Ab5F0ekmNvplE0imSB/c1wnCXtpencrg1D5XKagfnTD+1\nfJnczamlEklupUrh9dd0sIFT6ypsARTvzuHV3dBnUZ+Z1cWQfZRSFC9fY+58MON4pKeH1LHDG7vx\nNpL79xJJd36+iX17OzrJJg8dINoXNHWXrt3E6SBQueVy+KKjiTDtV7Q3S2wVzvJhbQy0IZendHmF\neCHLJpLtIbFnlOwzTy6ZwwK75WdCkxDbsTjewD5IZbUZKRIUfKxKQefWayL96LFQrWPxwuWu2f4b\nJlnPT0rr5gvkXj+7ZTnzlOOSP3MObxUFqJP794Z+w6FaLp/67ByLL75K7o1z1KZnW+7dWcxpYSvk\n3mIjQ6vzA/NcrFqwj4YWqO6CSmZptgLFepIMnNiH3e5PZPm+OV00d5Fsz5IGNbl3T3DurVSojk/o\nIvXt+PtWZgtLkZPWKjRcem4Kfgt2MqkjoHsyofNqfWZ2xe8YpcCpd80X2cCrVll85UzHqhJWLEbP\nYycY/MoP0nP6pH73zfNjqaKzGYTkJVuJbSNwxdIpEiF5a6ozC107Tm1yusVM5CzmQh3frGi09V8s\nhp1KEsn2EO3vIzY8RHz3KOlHj9H33DMrOsCnjh0OHawKFy8/0PIE5Ws3qHRIHJd98rGljO6WbRMb\n6KPniVN+PbXWNhfvzOJ4Tc8glsQb2o9K9aISPXh9u1G9o/4Kua1+YirV3Tcing6aKZUHVa06Dksy\nW5ucCXWuXiqtscYyS2EJbuOjI3o4c511m6I7kT58ICTZvqIwmV8yRbmxDLnrU4Fr13MlnIlx7Nkx\n7NmxjsJWvVBpcqhVoZNE6co16nMLugzK5WuBCC6NRc/pk5sesWbZti7jFEKzKTH0WMvSTvLtq1zl\nadNiyPsqt2tKV0moKW8VxPp6Q4XC0H0HB8g+dZr+D76Xoa/+EAMffC/Zp06T6GTSrpbCI4jjKbJH\njkPMH4vsiBa6QooRW4W5FtOPHYuROfVoYD+vWg34ozVTGbsbMMG4+cKWVd4oyiuhwRPtxEaGyZwI\n70N2LOaX4+qsJalNTJF77Q3mPv155r/wIvlz51l8NSTjP34W/6efWNU3YlXywX5oR1uCGVZFJBrI\n9h5NxRk4sY9I0heym4KWutFz8tEljZGdTCyVrWqmcO5CqH/cktCnFMUJX8FQr67oBF+bmgktep8+\nvuznmD52BDtE01i8eKWzQO+5WAv3sGdvYc/c0guTDijHZfHlMx0TvEZ7e+n/wHtIHtyPFY1iWy52\ntK3PeAqnUsfrW7v2f1s5zacO7V9XWYzStZv0Pn1a/3eIdstOJRn48vdv6gTSqAFYeKt1BeDm8zrK\nY52D9kYo3xzrmG0589iJUPOQHYvRc/IRcq+dbdmuPEXuyhh9Q6PLqtxIrCU/lJMvULgQ1I50M/EA\nOk9XMhMopmpVC6hkD/GRIaxotGWgU65DbXo2kH+peOnKykEBtr2qmpzxgSz27G1wa3ri6t+zrlVM\nGBG3RHq0n+J4s6BnUZ2aJ5XLE8n2kD93Ec8Jb2dxYoH+bCpci2dHUFaE/K02AUMth443b8u/+Rbx\n3bs61jVMHT20ZTmZ4rt19Fi7Kavn8ZMrmqSivVlSRw4FsoU78wtUxu6SOrQc5OLV61RDzKSxwYFA\nCodmrEiE+N7VOcuHkTy0n8K5kJqwTcR3j5J98rHVj0cqWAsPACuC1zsajNiOJfB6R7RjfeuJsHNT\n2onen5Tjo7t0oErbIrUydofE3j3EBlr7gXLc0KhA8KO194xuqmmxkc4jFMsiNjhAfGSY+K7hFbXT\nid27sJ97Rud/Csnk34xbLHYsExTt7SX7rqdWFz2n1JKrQMvmZHblCOSw06V6AykJIokYAyf2sXDl\nHk7ZWbGuS2Lf3oAFIrFvT4iiosNixffjQikqM3kyewZ0ZGS90tGsqBd4Qe1WpCdDoqkMmhWNkDn1\nKPkz51r28yoVKrfvkmrXIiuFlZtqeiYKq7SgBdNE0AWldPV6x/ea2LeHnsdOLL/XSoFIbopYJtlW\nctCi5sRJhWiSV2LbaLhAd+RGhvlOhGmVahOTOPkCTi4fGnmWPnp4S/LLJPbtIdobVAsXL1+77wV4\nK3fGKXYoRps+fozUwWDEZYNEJkZqV9sEa4GzkOuoLatNz7D40mtLZoVm2vNvhaESYWbFkq7jaNuh\nZsXCWxeoNkW2Ve9Nhg7GdjpF9ukn6P/Aexj6qg8x+Be+fMUoRysaIU5RC1vg+8vcW7mO5GrwXKxy\njtTu/paQcL0ahaK8Svn6Le2j1GGFWlso4pRCHDvtCF7/XkqLDk7AF0TpXHbtzalWOwpbyYP7O2qh\nNgPLsuh54jGspkk5/ciRVefbST9yBDskRUXx4uWWCaNyexzVbl7wo8k6leoB7XC9nqzZS8fvGQ0t\nodMgeegA2aceX9N4ZBXmQ7WaKjukkxCHXiiLSod8h07NT1bsn9uyyDRPMk0U3roQ0ByXx2530Hpo\nn7qwBe968ao1HczRjm3T88RjDH74y+l77hlSRw6u2hUgNjhA3/ue1c7iXczbnYj0ZOh99qnVB1Q4\nVf2vDZVaZ/WURCY0GtCORek/dThoHbBt7GSSSG+W2PAQmRPHQ9OpxEdHWr7JMOx4vMnys6zlKk1o\nbVG3Mj/O/EKoL2VGPBLwzYrvGiEWMl6Xr90M9EertKDdUdrbWpwPaBWdXD68bJBlkTkl6Dl9qknY\nyvsLFkW0p23RbVvUC+sLkNs2TvPAx0ulCnYtT3W2aUXQnNdpcIC+97yL6vhE4MGrukN9bj7wUu1k\nkp4nTm2qw91y0ywi2QzVdlW664IiVE27FVTvTVIIs7WjfRfSjx7rfP9+Tb9YT4LqXGE5Z5kd0Un1\n5hbAtnQpCH8iqdy6ra/XpDWyLEsrU6LR1lVCJyJRreFq+SgUKhaHaALLsoNhzJ5HbWISr1bDTiXJ\nv34uqPGxbPqefZr48CB2IqETCEZs4ntGdUjvfIj2QSmS/SmSA5nAdmBVzqDdsApzWPWyjiqybGqL\nJcBaiur0SuVW3z+/DmX7UlV5atlJFZaELddVflBJq69BNJ1g4OReaoV612iyxrtLHjpA5pTY/G+l\nTdNmx+MkD+wnNtBH6tiRVadfAG2WjGR7QjThiurEFLGBPuxkQhfBbau9mDywj8SeUWJDA7j5cA1G\nz+MnfRN7E04Nq5zHLs5i5Wd0YtpIbCnkvqV9loVynFCTRVo8Qvp4l28xjHoVOxfivxJPoXqG9WSR\nSYQ7XsdT2snaa0t5Ua+iEuklYc2ORbFsm/pMq5ld1evgqaVxzKs72p+2i7bYWcwR3z264cATpRSF\nN98O1V5nTj5K6sC+dednsiyLaE8PyYP7iCQTOLn8qlwS7FSK/ve8a1XRtkvXKs5jtQtcsSQqo4Xh\nju+uc+P1Ai7EZ0r17yZx4ADJQ/pf5tFjZI4fI3XkIKmD+0nu20NsoD+8pI9l4VWqXTV/2WeeJJJM\nLGuI/bHGKddIDvdiR+yOfmnlqzdbXH9Ap5xJhwhc+v1kAtHDynWx4/Fl7XutpOvRhuE5Ov+Yr4VS\nSvmpH9qem23T9+wzeqHUKEtXzvnnXR5LKzN+2y1b55N0XFJHDpLJJB5Op3kALJt4b4poqqlD+/cc\nGxyg911P6Zw+Icn5qvcmQ/P6pI4e2tLsybGB/lBTXfnm7Y7OvJtJt3DlxL69umhttwG+rgdkO2KT\nPbKraaL3j/E8SvIqCy+8zNxnvsDiS6/7mrTg9axolN53Pbk6k4JloUJUvpZfvDk2PEikJzwqsTJ2\nh4UvvhzUYACZk8dDs4NblkVGHKfnicdaE0X6vk6J/vBrWaXFQCmLNeHWscrLQl5qpFer333tVlND\n2hus22lH9F/LojJXWE7Z4QtbxBIUL1zWE4ZlL5spLIvsoREs26bv8ODKPolHDpFp8uvYFDwXKzeF\nPX0De+YGVlOxbjsWJb5rpGM4fTfiQ4OtqTaWrueRe/0sJXk1NMw7dVg75FqWRfaJxwLRkLGhweW+\nU69g5WewZ7TfnFWY0RURlAduXa9+nXAhNnX4QOukbFn0nD6lNe1reb5KYeenCOsbXlvZnlAsC683\nbL9g4fTkoQOh2vryjTHq/iKlcuv2ymktlOqoaV8L1dt3Q31xY8NDJLto69dCI3/awFe8n57Tp0js\n29NRU2YnEvQ993RQGO+G8kL97tbqLB9+fNs7jaeWfMLseIxIKrlmgTTZZNprJ3X0MPHhQZKHD2BF\noq3X93wtl1MNdXnQ2euDQU/Jg/s7fg/R3izxkPJd5eu39FjnOksaqE40a3Krd8aXo5GV0koR1yGz\nu494rK4X/25dl7bLtX5zsXRieRHsK3+8SgV3FUEc7WwvDVexhl1aIJKMUZlbDq+ODQ/R+66nsPzM\n3NHeHh0+usKqxE4kyD5xasvLVUT7+rRpq01b45bKmxbO6tUd3GJRm04XctTn5qlNzejBLaSTL/mJ\nrHDt5hVYJBHDczxtmgoryup5HSOFEr1Zss8+s6pSKMsXtwIDkuU5qFSfLn49OKBzcK3SIT6+excZ\n0UJ4cLkAACAASURBVF3AjPZmiQ3renKq7oDnEe9Pk9nbIW8YaHNOsmddPhdWfqZlhWtZFnYsRnWh\n3NXXInnogM7r5nlNH7oF0STxPXu0L100RvXeZJvjuwUKUrt6l8zEdsQmmoxTnSuEXnPosUeJHT2y\necKWUlApYC/e81fi+ruwnKp2Fl6LX5xSflqDmu7nvlAZHx7EmVsI9kc/WWo78V0jLf4flm0T3z2K\nV6uhXJf48JDOORaJYOWnsfPTuu0d8135Eadhi4ZIhPioXrxEs1l6Hj+5rsS9Vnkx3P+nZ7Cldl1X\nLYkdBRVi7vFcwFoqH2VZFtGBvmBYPtoclBjdpSN727RbVjweGIe9UlnX3FxnxK9bLJF741zAJGTF\nYlro2eSKHpZtE+3NkhjdRerQAZKHDxAbHCSSTi85lGefeGztpYAqhUCSZyxbf7v+t7ZmDRcsWR8a\nKSKIxPD6d6868WgnrERcj7dtJuNofx/ZJ/RcYkUiWoO7sEBzP3HLNVLDWb2wiyVbxsra1HQgO78V\niZA93X1ujvRkAi4juspMjIRV6hg8tHQNt45KpPEcbznStDGeAJFknN4ju7DcGla1qIWtkJI9lm1R\nzVXwHNUyfsb6++gdHVyThmtbOc03VvXx3hSDjx2gulAkEo8SE6dbpHUrEiF15FBrri3V+J/GCl9L\n5fejLEAklSR99HAgRUUjnDUREnXXDaWUNjPN6xxB9YXFQH6fbsRGhlYlbKGUn19rmZ79g9SKddzy\nCongmq83NMjBr3ofc4urP0YfmNITgtda8sWqFlGpXqLZHvo/+N7wumRt2KnUqpN0xvr7GHjfu3Fu\nXcWyFbFsqutxVq2EqhbXXqC1Xg1d4cb37yMyV8HNhTv7R/v7yJw4jh2P6zwxSw2xKE/Okjp5EtuO\nULl9l8Lbl9oaa2En4oEs9om+JOndfZQmFlsGjdTRwww/faqlyHhXGgOW5/jfa7RVs+bUtJDZodaY\nVZzX/ithkVRKQa2shQOnjuXW9aDatKBQyR5U76gesN/9FLlXzqzoAA2Ehpvb8RjZJx5r3VgpBII5\nOmGV86h0f6hpMZJO0XMyGAG4alxHRxW2E42H+2Z1QWUGtJ9Lm2nLKs5rLbMf4RjN9pA+fiQQoegW\nSyy89GowWs+y6HvuGT9FRKvgW7x4mdjw4JoXu0vCVsgiq+f0qTWZ89aLHYsRHxlaiugOoDw/s3q0\n8yLMqel6s+2HJnu61jJcLSozoM/lOvr9rSIycSUsyyJ97Ig2Gze2RaM68XBTm1OHD+pSeJ5OBAqg\nPI/SxCI9sShWtYiXHV5aWFXvBjPcx0dHlhQonYhme4jvHg1UHilfu0b6sf1YkVVEiBYXKN6a1X13\nKXmpJntoeKk8UTdUIkN0eBdOm/BXD1nYrcT2ErjA7zgu0VR8yeHXCwntTh3cR/n6Td/PwAtoeexY\nlHSyijV9ExVLorLDnR1MN4HU0UNU7t4LOJEXL14hPjy8YucCP5LjynUqt+92dExdiegawpWplQIr\neCsSJfvup8i/8XbHhJHNJA/uJ3PyUSLxOLBGgasRrVhq67iVAvhqd7tDXbLW89j0Pn169dFRbp1I\nfoJIf0gJk2jcVzm3rp7swgxeWJb8Tiilc2e1Y0cgM0hGWORefSPwsxWLkX3qtDZ3HNqv+3jz5ON5\nlG/dxrLtVmGsicwpgZ10AqbQzN5+sCxKUzmsSIT08WMkD3aoF+g/Az1R17A8Rw/uXkjKDMvWk08k\noiOVuqVi8BxfUAlGQVqF2UCuqMA+lQLYUVR2GDsapffdT7P4yutdFyTRvt7QLNYBlMIOE3I6H6CF\nlnWEh6+E9m9s7+s6uemaNa2WPk7XQG3Vwi9HLepzpo4c0ql22oTYdoEKdM6raLaHjDjeMkmDTqC6\nltqMynUpXbup88SFaOyT+/d1TplxP6kWtTnWc7RmqXckmN6hEXAToh3VubQ2iUgsNOfaRkjsGUU5\nDpU749jxOGnxSKCOqp2I64L012+2dKfy9CLpPf3YVLDn7qJSWdx4L7Xp4DiY6GK+BPT4WZynZyTF\n3HjTc1TguQ7lqUXSe5oWHnZUJ49uG3Pr01NU707q/t2UvDQ5lF0xQA90cJfqGyVWsgLatjBN+kps\nLx8u6LDyDX6AVjSqV60qKGwBpHf36zHEc7CqBZ0scjMizjpgRSJkQla0XqVCKTTXUZDytRuUr91Y\nv7DV16tNr6vU6oVFd6hEhmhPlv4Pvpf+D7yHzInjxIaHgquyRmTHYyc2ZLINjVaslVveVaMuWf/7\nng3NNt/Jb6sTVn42vC9E43j9e/XqrB3XafEJWJFaOVTLozKDYNvEhgZDk8M2my7sWCzUX6V87WZH\nYSs+Mkx87x6d0sJuXWBYlkXP3n52PXucwa/8AKlDbT4USpfosAqz2LO3fd+lWa2lq5V9bVOIMKU8\nbfKrlbsLW412hEQQUS2uKGwtHV9aAL/v2vEYfc8+09V8lTpyaFWaT+3H0SHvUCzZ2edwIz5+ndoS\n1ndSvetPUxLTiXUDOFWs4rKQadm2n69qhW/askn52fDju3eFRiaXrlzXtQ5XcAmoTk4z//yL2jQe\nMpbb6VTXHG33jWpRl0lqaOTdOvb8vdb+rJTeJyyqNJ7etDQzW0nywD763/csve96kmgHP9rUkYN6\ngdVSzcKjeLfRlxRWOUftysXAWGsnEl0TY6M8rIV7WMU5ojFIDvYsB974El5pYgGvEeCFpfNCpvtb\nxjzlKfK3ZmiuogJgRSP0HFg5oE0ls3oxZVlEQ9LkOIurq1HczEMrcIFeYYWpBO1YZCn1/hJuHWtx\nclUTwnqJ7xoOD2e9MbaiA71XdyjfCE/BsBqivVl6372GcOWmMhEtm32zmWVZS3mP+p59mqGv+hB9\nzz1D+pGjpI4epv8D7wnmRFkPsWSI5lGFCoPR3iz9H3iO5KED2tcmEiH96LG1OdHWSkG/CvD9IPbq\ntsTT4ZNraUE7SitPT7K+3R8/S/5y8xV2mHYrEltymLV8R+rlAt8WmZMikB4hdfhgyDcR3odjw0M6\n5YBl6fsZ2Bvu11GvElmcxCouYBVmKY3f9hMHjmHP3dETSKjgsUl4TqvZzuuQZ6oLdm5qKau0nYjT\n+9wzocXS7VRydfUxPa9F8FgilsIbPoQ3uB/VOxryPFX4cRvBc3UiyfYrpVehpeuCygyGR1YW57GK\ny8Juw7TYjeSBvUsLA8uy/MVmW1St61K8eJn5L3xJa+197bRSSofo37rN4itnyJ85G6pB0ye3tUlr\nk/22WqiW9AJj+mbHbP5Ui9iLEwS/Pa3JthYnloJECEuPEIktTd47Afv/Z++8w9u4rrT/3kHv7EWi\neoFc5Kq49x7HcZJ1sknW63TvZuPsxs7uOtX50p3uJBsnjp04dtxLLMuSZVm990I1kqDYewOJXmfm\nfn8MCAKYAQiCAIt0f8/jx+JgMHOBGdw595T36HSS1iRRJc1PwUFPUq/BsNMtU2rPmNdMKYi7P2nB\nYZxTLPveRF5AcEDyMFFLGaCV8sYSFxWB3hEIoVgLO3Hs/OaaUuk5yaljhlpxzBAePQcBNRYl5dpx\nBr08nJ1FZ5NUZlxIkRIiz+tN88FUER+MlbYEq1rCWFmkGN8lkQDgc0oXqAAQQmA+bzlGnMPJoS8q\nwl/fCOuqS9LeaOGu7vT9wWKMKrgTrQacRgOi1YLTaKAyGaApK52Yp0ngFVZhRMqrUvpsGbwyk4IQ\nUJ1Z7t1ICCsm7a5SwXy+XVKUJiSHqi8FFWJOLbVGGTX8CAE1l0r3S4qQKDfcKbsfCSAlw+otUn4S\nH1XU3hHNpUkTh8qgR/GN10DweMHpdYr5KZxeB93cKrn0SAq6OVWSjkziPaDWQiyqBjci77+HaDCe\nSB0OciCFaMui0kC0lIEEvTIjlwRckvFJCIjfmbklR0xkMYnYw40WSW1JVHo9bFdcJmnDJfSNMy5b\nkp0aeMCl+KAVE7WuOA7UWCQLW5CQH9QUBtR5yi+KBCF7sKs0UputyRAPLab0gQWkKkwyZtSlCy0C\nADhO1utRbbVAP2+OYiNwMRSG71Q9Ai1tUJtMiI64xp3rAOkhZ1l5fsFEeAFI0gKuXsQLOwIukJAX\norlsrFBm1NjKsFgnYT/IUIdykQWJiShPMql9pmFYvADhrh7pI9OxRtre9kEUn18DIcyPGV+iGK+2\n1qUTFqYUxN0nW2yr9VroS8wIOZM9SoE+F/Tz5oIkPCeowQriH0HE5YW/dzQikVBxaNZDXya1SBJt\nFdLiWm+W9hDFuOh1aqiWEAJ1kRWR/oktDFOZcQaXYkKhksElREGCLhirihDxBBH1Sg8Prc0EQ1Up\n4lVEKZCAS0o8nWRpbjpUJqOkhp0SRsyUQE9FUVGQTWU2QVtRBnVRETRFNnC6/DVVVhSp0+jyktA5\nUahebnCRSBBUFNJOUrmEMUnQoxj+Ec0KApJqrfRwTQ0jplvVUDFWVeZG6kofgLSCUvKaETJuONS4\neGFGg8uwaIGins3oecWi6lhOSZ6MKqKSwgmUKud0gYAabVI1HeFAObXcqyhEQUJeULUWJKDwUNca\nIJpKpImPU0khhpQwG4kEgIArrmmkMhpQdO0VCDS1QgyFoauuTD+5J42FVwxnUr1ZFgKiRpvk1UzS\ntqIgvhHQotwV6hNRDCdOtA1MOjR6UJPCfQ3EWqJI1240tOjac1B23+jn1yjKIxiXL0HUOZK2DY8Y\nCCISyEIwknAwLF4A45ICFz3xEXAuBWkBUQDn6QcNeQG9GcQ7mNHYiqNY0UogFlUqehZnOyq9HsZl\ni6XcWkKkeYFKVe7BfveYpiMAQArrqcwWqJSkYNIYW6MY5xRLygUJDaSpQOHrdMJcUj024xIOPGeA\np6VJIdc0JpUz6glL/U1xHMClD/mqi4rOQoNLqQeYKMpMJ+KT4uaE41BknwPeHwYIB27+MlC1Ruqt\nFgkmrV7i7/UOgqq1BYunG5csRLinV6FyRzmBPtzbr6gbZL3s4oI0UwYQW0Unk9qna8pQ66QHa5LH\njYKEfIrJ1TkhCspVXxp92upDaiyWyvLF8VfjKe+Unz7FuzURVCYjtFUVijpzRvsyGBePk5isNUC0\nVYFz904wpD6au2SUfi8qyQ2fZASP5kfEE+rFWJg4YYWo0YHqTLLJlPhHYkaiPAlftFYkHYNaK0CG\nu+Qinr5h6b6N/ZY5nS67hsIp45AL6BJQk0KeB+EkgyXFU0rCPtBoeKynYa5QKnVcSN08SfHdpGOZ\nSuLdD1Ih3kHps8eqhI3LFyPgGGvJQrTatPcbp9XCdtXl8DeckckAZIumtATmC1YUbt4bJUNi+ygk\nEpAKi5SQzVfKUKWk+rMI/YJ5CHX3jQnUEg7gAH/PCIgqte8phaFILxXgJM4Po2FERWOLgFrLwZUZ\noHOJUsVjwmHDvf0Ap5J6vxICKorwNHZCjCrndauNutiiY+KRmtQ2V7kwO3O4UsrtCSHQmPVQV1SC\nqBOaeOqMoGaFSTOe2DjRB2l2SAn0dtl2MRSCPyXZmVKKYGu7bF9tZXnhJp10+VvTZXDFwooy0qx2\ncjqFb1hxchUtZekNIY6TQkqThOpMcb2jXDEuXZzsfYy1yBnX2BpFZ4RorYSi9y0JAqo1glrKY7lL\ncyUPks4kGcapHkcSU8zX6KR99BbFyqlRL1QSQlTR40hHPVuJqNSSESbfWxJAzLUgho8oGh7UYEsb\nwqMGq6wgAUB+crmEqIKBnz7UnxOEgFrK01bMEc+gZITyERgWzodpxXJJv668DLZVl2SUZuB0Olgu\nvhBF114JbUX2VYWcXg/LJSth/cClhTe2MiS2Z4XGALFknhQmzFBcQE3FBYukzBQIx8lbBRGAUgIx\nmvKbJAS6YiO4kV6pGbvfBeLuk4pzlPJqY1W51GAFVBoYly1WjMCEu3viDewDjc1S9WDKnK6xGCSp\nHMJJ82AOi1+1NY2czUSOMal3F4J0+jyJu/ickK2KOZViUik12qRKnFQ9JJEH5+6TEovzoGGSipRA\nX4poSklsqK0DmiJbXJ0+6hxRLGnPtpw6J5QmdUKmtYJGkodIDnOQSFBSk5+snEc0nOahmkXVl84M\nagzLQ04qtZQIS1SxXK904TqibPRPELXFDNsVlyPU3gGASOKME81t0ZshxlsqiVIIgFPBaDPB449K\nhpNaW5hck1iVX7qQQdJ+6byaOqPkdUy5TyBEpXwuW+WEf8uS11PuYVM0EFNeJymJ/iTsB42GJvU7\nUvJuQavPf6ifkHgjerlWXCwR3OcEODWMJQYYq86T2hmBji2ERts1afSye0ZttcB6+cWIutwINDYj\n6kw2RolKBXWRDZqSYmiKi6AuthVcoHp0zMQzqJzYTrjxw+6xED04DtCZIJbUxLoOJEcoqM6ckxdl\nNqIpskE/vyZZNoEAgArAmBSD1mKASqsGhAg4V+ac1FHPFhJ6TqqMRpjOXw7/6QbZ3uGuHojB0Nh9\nRrh4VSOnUcO6WGrdI1rLc86FJCoV1FZzVrp/6ZglBlfCjyAcSFNuX6z8oCDShSNCVNIISiQaAvG7\npFyTPCMl0NsxMrRf9iP2nayDymyC2mJW9G6pi2zQZKMblOvYlLxbGkNBDM+sSRdWDPsnF1akFJxv\nCMoP1SyueyyBnhqskkdUpZb+S/iuqCiChGOCmSn3GDXa8pa/oSm2QVO8cpIH0YOmGAS6EgsgTLzE\neaLEBTjTMn7LGmoukfIPU75nEvYDrj4pjyrb+zgSUlxZp51LEvcxWCXDL8VLTvwjUiJ/rhQyfyuV\nuNFF4y21ZIi8ZJCFvOl9o4STjBAFL66myAbbFZchOuJCdMgJotFAXVwEtcU8NQZW6lADLpCQwgOT\nqCCWzJWkHrxDyt4vjV6qZE4tTCmZG+ux6QVAY+K8OeilzWKMy5cg0j+YVLCSanTpSrMXjqbWckXv\noGF+DSCI8DfI20clGfUEUrcUCliXVEKlVUte60nqoKmLbJMyuGZeSDFT0nzGcvsMD2XCQbRVKYcB\nZA2U84fKZIRx+WLZdioI8B49gejwCKJD8s9TUO8WoJyXMF3hxFHShBWVXc0TIOxXzlczFWfvOSNE\nMpp0Run/qQ90TmraKpbUQCyZB2osBtWZQC1lefFunTVo9BmNB2oqGj8HipBYSEC5Cplz9WZsrjx2\nsjRzSUxAcVwIUVR8J2G/fGGXLVRULGYpmMEFxIyuSuWQfrZQcdywrqa4CMZlS2BYOB8am3VajC2E\n/cpixImJ7ToTxNJ5MQ9nYh+XBM+W7O1Sux6xfCHE8oWgtgkY/WcJnEajqEMpteXlQDgOuuLs7jE6\nGkZMg2HRfBjtWeiyEQ7GpQuhqayGaKvMizrBZB0hM+6uoIqq17EJNORLU25fMv5qQqWW+k2lrtNE\nPn1iZB4wLFqgqAMkBAJwKyiNc0ZDdrpBuUIpSESh0/x0G1xAXAMsiUgo91y7TAb6JDWN0qLRgVpK\nQYuqpXOcQ6vcbEgbqlNpMofxElFrYvlcCt9tJCiFK8bL6YoGFcNKo5WV2TCaW5LKhARyE1ESjuXU\nha9wIwTUVjk5FXSRT2PMzBDSScJAIbGdcKDmUoil80EtZRBtlZJszHihdk6luKg/V9BWVUCj1A6J\nEGgrK8bpgUniHsRs8t6MixfAuHxp5vGUl8GwfLlkaOkteZmLlQRQJ8KMM7gUJztR6l2l+PDU6IFs\nV2exiivZKRUaxOYLSeDyAkWFdKWVuGFhdqrYOcOH5cnjhMufhtBkUGsVHmDKIqhZEQ0qhgYyJsoz\nCovWoOhNlVrWTGA60pslHR0loysakrTH0hldlILzKRhFau3EjA5CFI3EXL1caQtZpuJejRldYkmN\nFGrXTPy8JOhR9CbPCKIhZfV3Y1H6B7w6tjDL08P6bIcQAvP5KxS9gLr5NZKHUK0FIAkzU71ZMmyL\n50IsXyS1mJpANa5xyUIYly1RfI0zGGDOpp/wBFEpCaBOgFlhcBEqxtqxyD0dWXm3ElD6cZGIv6Bt\nfziNGpbLLgIZJ4RFNBroayaR/5EF0zqpjwchil6utPkl4x1O8bMaz+oy7dmAaK1IbsFhLsstpK23\nQEyn3s2H0xtdabxbomlicwkAyUDLk5eroPpb2aLRg5pLIJbEHoLFc6RqO60R0BikCtbRTgwKczWX\nrWbVFKM4h2gMLOSfZ1RGA0wp4T51kU0SzNYaIJbOh1ixGGLZAlBblbRg0RpyLgoxLl0kVXAnwk2w\nt+4EUU9CHmLm+T+VVrl8BERhxSiV209wQtIapck+0XijVBJhLFSYCYDabIL54gvgPXo87T6GWMua\nSSGKkhdLFKQHQWpOjNIKNJ8l55OE6szyh1U0NJawPgGUDK64ejRj+lBpIJYtkK6rSjO5KlS9GSIh\nykrgfBjE3R9XoweQwbulUxSmHZeYl4t4kjXSJlyxqCiRQSa04s87hJOUuGNzrMyMCrhllZrgI1IX\ngWzDw1MBpYq5oGKs0wEjvxgWzgPRqBEZGITKYIBh0fzknL08f+eGpYugMpsQbO8EUathWr5EknAo\nEJqiIkVNxGyYeQZXtkrzhMstCS7mRZEpmwcLa3ABgK6yHPySRTIVegAAx02sJyAgPWCiYSnRlg+D\nRMMpbnMCai4Zm/woVTZcZ0D+Vhy1FlBpU3r55VCtmK4f3Uz6rOcyhOSvUENniqnp98nmChIJAP6R\nsUrktN4teb+2bKF6S6z/ZHLIiviGQYvnjG0QeKmaLeyXckotZXEjT1EOQlMgiY48QQ1WqYIxtWLU\nPyIl4U+2FVG+iATknk7C5WZgM7JCP7ca+rmFjdaMQgiRukpUy7u4FALd3CoEzjSP25RdiZwNLrvd\n/hsAVwEQATzscDgOJ7zWCqAj9hoFcL/D4ejN6sDZJqxayhRd+Vm912CV6yrxYekBPVml6HEwLlsM\n3uOR6XPp586ZWOseUZBW9RlzJiQ9HRqrvkE0JDdeR7WXZgqESJpc/uTV/oRV56MhyNbkKk3O9wxj\nhqM1pm1hRPwjkhSG1pBf71b8BGm8XJHAmJcrEoxV8sU860IUnKtXkhwxFqXp/DDDQ99EkvHghruQ\n9FujotTNI9GzOI0ohROpzjgtbcwYsx+po8IqBJrbJv7eXE5ot9tvALDU4XBcA+BLAH6fsgsFcJfD\n4bjZ4XDckrWxBWRlcFGdaXIVNWna+sgFAPMPIQSWiy+EyjI2fk6vg3HZogzvSkGISg1os0xQ5dwD\nkjhkWv2t6Z8UE1EsUY8GJ1StqJwPw7xbZzWxFkbyRHoKztMvVTnn2bsVP0O6XC7fMIh/JJZPJr9/\nic8J4hmYGflbuaDRKS6ESCQATFbSJR9QUbHoZlLPD8Y5j9pqgfXSiWsi5mri3wrgbQBwOBwNAIrs\ndnviU5JAsXwoCwjJPPlxKtBxxBGzQekHR0LeKUn45DQaFF29CuaLLoD5wvNQdO1V2Vc+8BHJ2BLk\nLVHSQgVw7n7FSX3a9beUUGsVvW7EPzy+EvTovrPRY8CYPDqjcv5QrCGxjMl6t0ZJV7EYCSh3xkjc\nJ+SV39eEm9bODxNBsRUTIMkwFLAYKSvCfoXvVsUKZxjTQq4GVxWAxGzJodi2RJ6y2+277Hb7Tyd8\n9AxeLtFSPvlWL4hpPqWeRxTk/fuEaEz/awIGThYQlUqKc8+bC06bZZgrGgI30j1+M2WikPcRDSmW\nqs9Ir086EdSgB5yzMzaJZjCMBV75es3Ez8rIO/GquizIh3crft40Xq6cjjVTKoezgeOkfLRU0jTI\nnkoUw4l60+z5bhlnFflKmk+9ex8DsAHAMIA1drv9nxwOx1vjHaS8XPI6ud0aiBH5A1VrK4Ypj4l4\nft6NiDs5l0tHgzCXV0PkeYQGehF2jbUL0Fis0JdVQm2Y+tVR1OeF39kHCirLPSAqFfRlFVDrjVDp\nDaCg8LY0Qoxmbs7KqdWwVpXkTatk9PrlA8GigafFJX+BSp4KjdkCQ9VcqLRyz2DEPQJ/ynek0uth\nrSxsUcRsJp/XbiYglhik3wCffnGi0ulhqanKq1ZPWDsHgZ7OjPuotFoIkcwLOGNZCXTF2V+T6b9+\nFvgRQsTjTtqqEoOwls+flhGJPA/PUAg0ZS4wV1VCY5qEsn6emf5rx5gqcjW4epDs0ZoDIJ6n5XA4\nXhz9t91uXw9gJYBxDa7BQSmHiuOpXBRUpUZAbUVgMI95VlQPLuU8YY8HobZ2EL9bJhAadrsQdruk\nHDJTScET7MdO7FcuewcATg3RUoWoqAMCFAjEwoamcin0mCGUIXA6DA3lJ8+ivNwSv375gmiMaVv7\nhD1uhL0eUIu85xbxDIOkXFcB2ryP72yhENduRmAql3Kn0vwGeK0V4Tzd/3GoGhxRKffigyS0yZtL\ngZAPnHcgrafWE+aALK/JjLl+Kis4MbkoQQwEMNjrnJbCHBJwg6RWknFquPwiEJgB3xdm0LVj5MRE\njeVcQ4obAXwcAOx2+2UAuh0Ohz/2t9Vut2+w2+2jvvUbAZyayMGpgiEjiSXmuURaa1AIT1IQ37Bc\njT0BEvaDG+4EcfWB+EdAAm4p7BgOSGG7bHq5ZYsoSknvShOzSiM1XFUy/DT68UX9ZniIjdoqpX51\n6TwQlIJ4BqXvPXFbOnFXxrmF1pC+MX2+crdSSZPLNdrPlY52OTBYYo2QFeY0lVLHhVmAWqNcjDTR\n5PmY3A34yKRyapXDiUyHjzF95OThcjgc++x2+xG73b4HgADgIbvd/lkALofDscZut78LYL/dbg8A\nOOZwOP4xkeNTU7H00BSiAAiopbQwSY6EjGno5PL2sC9eiZP0EyZkrNx7skMMeZSNP7VOapWQIZ+N\nGm1ANJi2Nc6MN0KIdO2pwSLpFyn2vJT6JYqjOS8Cr+BdIDNK3JUxdVBjERANyX4D+czdkp1Tb5HO\nOZq/pNFJDbdTvTxaA8SSGkk/LKFHrDiTREMnCNWZZFp/JOSXIgJZHYCCuHrjv3WqM8WaQU/wuHzc\nfQAAIABJREFUWglR5V6ZrDqRMY0QOnPaMNAk1yql0iTEqfOSJJ8WPgrO2V6QQ4tFcyanFE0pOGeH\n3IDQGKRG3Nl4/ERB0slJPcao2neeKLhrnFIptOobUpSHEG1VgN4shRFS1a81eqlPF0ORsz6skaJZ\nRw22MU9ToaBUKm4RRcnQynQuKkrGGR+V9KEm6HmbUddPiIIbks+nYun8rMKKxD8ia4JNzWWgpokt\nXpWOA7UWYsm8GeXhmlHXjjFhysstE7qZZp7S/CiETE1ZtFojhdYUNa0IqMECaioBCftBAiMT0oLi\nPAMQS+flHgqNBJSbL1vLsz8mp4Joq5Tlc826lR4hUhsXnVGq1ExRkef8wxB1JuVV7Uz35DEKC6eS\nFj8xj/mUKKATEhPazWZfruBdLqYMVSysmOrlCvslAeZMUFEuSA2ABEakPM0JCJWycCJjJsKkdgGI\nRgUXvkYPsWQuqLUCUKlBjTaIpQskDTAuSztV5KWm2znCKUw+VGuceAKqRi+FHzk1AKm10URXjDMG\nwkE0KeSm8RGQkJfpbzGUISSm7zYLc6NmGVTBQ5dNA3oS9CjrdokCSFChYjkd0XBSiHZsXLNskck4\n65i5Hq6pRGcEtVaABN2gRCV5f5RWQ4SAGm3SaivsBxEiUsiAioAogvCpvQylHCyqN008QTcaVm73\nketKWGeEWL5QCnXM9lWe1iDlZKV4s4jXKc93m0UCkgzG2QDVm+XhPD6WBJ9usUhFEH96o4r4XaAG\n2/iefSEqhY9T0eiZsc2YdpjBFYMarDJ5gbTEwlup2W9UiErCnCnKxpxnEGKpfkKhRRJ0yzeqtZOv\nLJztxhYg9XAzl0ihxUQUiguoRn92fGYGY7ag0kiV0ylh/0xhRRL0ZhZ0jhlk1JKh8lqISjIgCmkY\nsy6FgnFWwkKK+USlkZJxUxF5eSI3EPeMyfcXFPs6UoONGQ+jaA3ZhQpZ/haDMeUodopIF1akVMqP\nHQcSdKfPoc1gbIFTM4OLMSNgHq48Q/UWKdyYUoZOQj5A45JCXNGQVDrNR2PvMUuGWswDRoJuuf4M\nUYEa2KSRCDWXgAwrSUUk7MMMLgZjyqG6dGHFqCy0R0JeZUOKkOR5kIog/hFQa3nyfhmNLVUsf5X5\nFhjTD7sL8w0hseba8vAh8Q6BeAZiJeARSFWDFCTkjfUIDMRWe/L+Y9Rgzdhj8pxEo1dcScchKkng\nksFgTC1qjeJvTyaCSqmiDiLVmSSPfur7Q54xw4pSIBIcx9iaM3UdQRiMcWAerkKgUkO0loFz92f/\nHpEH5+qRQmCyXAYCaswyv+wcg5pLYt5EuZ4c1bL8LQZjupCS51PyuEK+ZCX+kE8558pUDKg00uI0\nMSeWUslzptEnLFwV4FQQi+ewBRdjRsFcJoVCZ87sfUmHUmWi3jQ7W31MBWqtpK+jBJODYDCmDcX5\nbzSsCEjCzkreLa1RqirkVIpV2STkA/EOjWNszWXGFmPGwQyuQkEIqLUsL/0flVzrjDGktiFyTxbL\n32IwppF0YUXfkJRe4e4DBLnRlNj/khptiukZaeHUMWNr6ptlMxjjwQyuQsKppRyCUe8U4UC1RlBT\nMcSiaoil88evtNPomI7UeKg1MiFXqmNeQQZjulHyPktdO1yKPV7j3q1ROFX2Is0qTSyMyIwtxsyE\n5XAVGo1O6llIRQBEllNEi6qBoFvKS1DoaykailgeUhZQU4lUVBAJSmFGE/veGIzpRrFaMdP+Co27\nqdEGEnCn1+nSGCAarIDexAqLGDMaZnBNFekmAkJAjUWgWqOUZJ/YkkKtkxTvGeNDiDRZK0zYDAZj\nmhgNKyq02pGhMSh78wkH0VoOztWHeHEMJ3UEoQYr82gxZg3M4JopqLUQS2okDa5wQBJRNRUzLw2D\nwZjViKYScO7ezDupNBBtFennO50JYuk8kEgQVKWWCmLY3MiYZTCDayYR83Yh136JDAaDMdPQmyBy\nc6ScLQpJhJSoAI4DJSpAFdPLG8+AUmvTtgZiMGYDzOBiMBgMRmHRGrNrxcVgnMWwDEMGg8FgMBiM\nAsMMLgaDwWAwGIwCwwwuBoPBYDAYjALDDC4Gg8FgMBiMAsMMLgaDwWAwGIwCwwwuBoPBYDAYjALD\nDC4Gg8FgMBiMAsMMLgaDwWAwGIwCwwwuBoPBYDAYjALDDC4Gg8FgMBiMApNzax+73f4bAFcBEAE8\n7HA4Die8dhuAnwDgAbzncDh+PNmBMhgMBoPBYMxWcvJw2e32GwAsdTgc1wD4EoDfp+zyOwAfA3Ad\ngDvsdvuKSY2SwWAwGAwGYxaTa0jxVgBvA4DD4WgAUGS3280AYLfbFwFwOhyOHofDQQGsj+3PYDAY\nDAaDcU6Sq8FVBWAw4e+h2Dal1wYAVOd4HgaDwWAwGIxZT845XCmQHF9LorzckvF1kRfg7R+BEOVh\nrSqBWq/N9tCMKWC868eYubBrN7th12/2wq7duUOuBlcPxjxaADAHQG/Ca4kerbmxbeMyOOiN/1uI\n8vD1OuEfGJH+6x9BcNgDKlIAgNakx3mfuBmm8qIcPwIjn5SXW5KuH2P2wK7d7IZdv9kLu3azm4ka\ny7kaXBsBfB/AM3a7/TIA3Q6Hww8ADoej3W63W+x2+3xIhtY9AP4lm4OGXF6MtPRipKUHno5+iIKY\ndt+IP4SOnbU4776bcvwIDAaDwWAwGFNDTgaXw+HYZ7fbj9jt9j0ABAAP2e32zwJwORyONQD+A8Cr\nACiAVxwOR9N4x9z2q9fhGXBNaByutj4IUR4qTb4iowwGg8FgMBj5J2dLxeFwfDtl08mE13YDuGYi\nx/MNuSc8BipSeLsHUbSQ5eQzGAwGg8GYucx6pXl3e/90D4HBYDAYDAYjIzM6Fqcx6GCdXwlzVTFM\n5cXwD7nQvr02aR93BzO4GAwGg8FgzGxmnMFlri5F8aJqFC2eA3NlCQg3piqhL7HIDC5f/zD4UIRJ\nRDAYDAaDwZixzBiD68rP3wVer4fGqE+7j95mht5mQsjtH9tIAU/XAEqW1kzBKBkMBoPBYDAmzozJ\n4aqwz8tobI1inV8p28byuBgMBoPBYMxkZozBlS22BQoGF8vjYjAYDAaDMYOZfQbXPLnBFRhyI+IP\nTcNoGAwGg8FgMMZn1hlcWrMBxlKbbLunk3m5GAwGg8FgzExmncEFANb5FbJtLI+LwWAwGAzGTGVW\nGly2BVWybSyPi8FgMBgMxkxlxshCTATbPLmHK+TyIezxQ2c1xbe52nrhauuDsawIZectAKealfYl\ng8FgMBiMWc6sNLjUei1MlcXw948kbXd39KPiwsUAgJ5DDWjbfiz+mqezH0s/eNWUjpPBYDAYDAYD\nmKUhRQCwKelxxcKKIy09ScYWAAycaoWne3BKxsZgMBgMBoORyOw1uJTyuNr7ERzx4sy6vYrv6dxz\nstDDYjAYDAaDwZAxaw0u69zypD6LABDxBVH3+jbw4ajie9zt/fB0DkzF8BgMBoPBYDDizFqDS6VV\nw1xdKtse9vgV9h6jcy/zcjEYDAaDwZhaZq3BBQBFCmHF8XB3DDAJCQaDwWAwGFPKrDa4lBpZJ8Kp\nVdBZjLLtnXtOglJaqGExGAwGg8FgJDGrDS5LdSk4tSrt60vuvALzb7xYtt3TNci8XAwGg8FgMKaM\nWW1wcWoVLHPLFF+rvtyO8vMXosw+H4YSq+x15uViMBgMBoMxVcxqgwsAihfPkW2zzqvAghsvAQAQ\njsO8ay+U7ePtHoK7va/g42MwGAwGg8GY9QZX5cVLoS+2xP82ltmw/MPXJrXxKV0+H8Yym+y9nbuZ\nl4vBYDAYDEbhmZWtfRJRadS45HMfhLOxE4QQlCyrkeV1EY5g3jUXwvHOnqTt3l4nXK29il4yBoPB\nYDAYjHwx6z1cgJTLVX7+QqlBdZok+pJl8xS9XN0H6go9PAaDwWAwGOc4Z4XBlQ2EI5h33UWy7Z6u\nQXh7hqZhRAwGg8FgMM4VzhmDCwBKls5V9HL1HGqYhtEwGAwGg8E4V8gph8tut6sBPAdgAQAewOcd\nDkdbyj5RALsAEAAUwK0Oh2NaM9QJIZjzgRVoeu9A0nbnmU4ER7wwJCTfMxgMBoPBYOSLXJPm/wXA\niMPh+Fe73X47gJ8B+FTKPiMOh+OWSY2uAJSdtxAdO48j4g+NbaRA7xEHFt+2avoGxmAwGAwG46wl\n15DirQBWx/69GcC1CvuQHI9dUDgVh+pVdtn2gZMtiAbC0zAiBoPBYDAYZzu5GlxVAAYBIBYmFGNh\nxkT0drv9Rbvdvstutz8ymUHmm8qLlkKlTR6uyAvoO9Y4TSNiMBgMBoNxNjNuSNFut38RwJcg5WEB\nkufqipTdlAy3/wbwYuzfO+12+w6Hw3E007nKy6cuh2rRVeejZffJpG2DJ5tx8YeugEoz6+XJpoWp\nvH6M/MKu3eyGXb/ZC7t25w4kF6V1u93+LIBXHA7Hpphnq9XhcMzLsP/PAdQ5HI7nMxyWDg56JzyW\nXAl7/Dj6zFpQMfnzL759FaouWTZl4zhbKC+3YCqvHyN/sGs3u2HXb/bCrt3sprzcMqHUqVxDipsA\nfCL273sBbEt80W63L7fb7S/F/q2GlON1OsdzFQSd1YSyFQtk23sONciMMAaDwWAwGIzJkKvB9RoA\ntd1u3wXgPwB8CwDsdvs37Hb7lQ6HoxFAp91uPwhJGmKdw+E4nJcR55E5H1gh2xZy+TDc3D0No2Ew\nGAwGg3G2klNIsUBMaUhxlNOvb4W7vT9pm9ZiRNmK+bDWVMAytwwag27KxzXbYK7x2Qu7drMbdv1m\nL+zazW4mGlI857PD537gPJnBFfEG0HOoIa5AbyyzoWhRNaovWw6d1TQdw2QwGAwGgzGLOecNLtvC\nKhjLixAYdKXdJzDkRmDIjd7DDpTa52HOB86DuapkCkfJYDAYDAZjNnNO9VJUghCCedeuzGpfSimG\nGjpw4oX3cerVLRhu6oYoiAUeIYPBYDAYjNnOOe/hAoDSZTVYfPsqdO+vQ9gbyOo9ns4BeDoHQDgC\nY1kRTJXFMFUWw1xZAmN5EdPyyoB32ANRFGEttYGQGdmQgMFgMBiMvMKsghhVlyxD5cVLEXb74eka\nhKdrAN6uQQRHMic0UpHCPzAC/8AIENNRVeu1WHjLZai4YNEUjHz2QCnF9le34MT2WlAAi1Yuxj1f\n/ghUatV0D43BYDAYjILCDK4ECCHQF5mhLzKj4kLJWIr4gug/0Yy+Y41Z91rkQxE0bzgAS3UpDCXW\nQg55VtFyvBnHt9fG/2492YK6faex8vqLpnFUDAaDwWAUnnM+h2s8tGYD5l1zIS7/949gyZ1XZG1A\nUZGi94ijwKObXdRuPSLb1nqieRpGwmAwGAzG1MI8XFnCqVWovGgJKi5cDFdrL/pPNMHbM5TR6zVw\nqhXzrruI6XgBcPYModPRKdve29IDSinL5WIwGAzGWQ0zuCYI4QiKl8xB8ZI5oJQi6g/B1z8Mf/8I\neg7VQ4jw8X1FXkD/iWbUXHn+NI54ZpAYSkwk6AvCNTCC4koms8FgMBiM/CCKIhoPNaCzoQOVi6qx\n8rqVINz0BvWYwTUJCCHQmg0oMc9FyZK54EMRWRix72gj5qxaAU517kZvw8Ew6venb6XZ09zDDC4G\ng8Fg5I0j7x/Enrd3AwBO7z2FkT4nbvznW6Z1TOeuFVAAqi9bDqRExiK+IJyOjukZ0Ayhfn8douFo\n2td7m1jvSgaDwWDkh2g4ggPv7k/aVrvlKJw9Q9M0IglmcOURfZEZJUtrZNt7Dzswg3pWTimUUhzf\ndjTjPj2sWTiDwYghiiKaG1vQfKb1nJ03E/F6fDiw5zAG+ganeyizhrbTbeCjfNI2CuDQhgPTM6AY\nLKSYZ+asWoHhM11J23z9w/B2D8FaUz5No5o+Ohs6MNI/knGf4b5hhPxB6E2GKRoVg8GYifA8j599\n7zc4cfQUAOCyKy/B/37va1Cpzk2tvpamNjz29R8hGpEiBA/+5+dw+4emNyw2G2g62qi43XGoAVd9\n+FoUlRdN8YgkmIcrz1jmlsGskI/Uc7hhGkYz/Rzfdiyr/Xqaewo8ktmDyAsYrGtD+45auDv6x38D\ng3GWsHfHgbixBQBHD9Ri6/s7p3FE0welFE/+6um4sQUAz/35JXjcmcW4z2UopRB4Hq0nW5RfFymO\nvH9wikc1BjO48gwhBNWr7LLtw01dCLnOrR+Kx+lGi4LOlqXEItvWy8KKcVq3HMGZd/eh+2A9Tr+2\ndVbkAAq8gIPr92HdU2tQu+0YRJH1GGVMnFO1dbJtG9dtOSdDi431TehsS46WRCNRHNhzeJpGNDOh\nIkXbtqPY95vXcOgPb6F23T5EQpG0+5/eewpehQ4yPM/jxNFT6OnqLdj9xgyuAlBqnw+tOSU8RoHe\nI8puzrOVEzuOy25cS7EFV9x9tWzfXubhAgAEhz3oTzFSW7YcgcgL0zSi8aGU4t2n38HeNXvQdOwM\ntr+6BQfW7Z3uYc0qerr6sG/XQXg9vukeyrTS2twu29be0oEmh7LH4mxmy3vbFbfv3bFfcfu5ylBD\nO3oOO0AFEXwoglNbjoJmWPCJgogjGw8lbfN6fPjaFx/Fj7/9Czz8pW/gpb++VpCxMoOrAHAqDlWX\nLZdtHzjZAj6D5X02wUd5nNp9QrZ95Q0XY+4yeWFBX1sfhBlsVEwVw01dsm1Rfwj9J2euIn/dvtNo\nOZ48vsPvH0LQl10j+HOddW9twMNfehRP/OQP+I8HHkZ7q1wg+FyA53l0dSh7ujet3zrFo5le/L4A\n9u5UNqxOn6jHsDNzXuy5xFDDmJEuihROtw9iSsJ8Kqd2nUDA44///erzb2Kwf6yC8Z031+NkbXop\no1xhBleBqLxoCbiUpsxClMdAmtjybMbZM4Qtr27Fpuc3YP3Ta/H27/+B137+MkL+UNJ+nIrDhdet\nhD8UQBjRJO8XH+Ux2DUw1UOfEjzDHtRuO4Z3n34H655ag86G9CHC4TPKD5yeg/UQhZkXpvO7fdj5\n+jbZdoEXcGr3yWkY0exi2DmCl54dW01HwhE89cRfpnFE00dXe3faRdfeHQfgVzDgKaWoPXwCWzZs\nn/VGSDQSheNgPRyHGrBzyx5E0knpUODA7kPKr51jUJHC0zVWvenxB8ELIkRehFSXCKi1ami0mqT3\n8VEex7ZIreYEXsC+XfK8rrdfW5f38bIqxQKhMehQceEi9NU2JW3vqz2D6lX2KW9lw0d5tBxvgnvQ\nhSWXLkNJVWlejtvb0oN/PPE6RF6AKGaOey+5dCmefvI57N1xACF/EBadCZctOh+qmPpvT1M3qhZW\n52Vc0wkVRfR39KP1RDOajzdjqCu5nLvleDM+/Z1/RXlNRdL2iD8IbxqdmLAngKG6NlSsXJy0PRqO\nYM/bu9F2qhWiIIBTqaBSx/5TcTBYjLBfcR7sH1iR3w8ZY/urWxEOKre3OrGjFpffvgrcLK4wC/gD\nqDvpwMna0zhVW4fOti5Yi6z4zIOfxg23Xjvp4x/cc1hmZDQ3tqK9tRMLFs2b9PFnE0rhxFEi4Qh2\nbd2Du+69Pb5NFEX88dfPYOeWPQAAvUGHH/3me3n73vy+AJrPtMBqs2LBonkFnbN9Lh/e+u0bGO51\nglKKox31oKAgqcKOMfZs348PfuSOgo0nH0QjUahUXEF//wGnG0KCYTrkkkLylFJQgYKoCBZduBiW\nUiuObkrOfTu+vRaX33kFmpta4VMI5Z88dhqtTW1YtHRh3sbLDK4CUn25XWZwhVy+KZeIoJRi49/e\nQ2NMBX/f2r341DfvR8X8ykkdVxRFbHlxI/gID47LPBlRSnGsuR4nYm5aTq3CiN+DtsFuLKmUJsje\nltmdx0UpReNhB/at2Q3XoCvtfqIo4uimw7jz83cnbR8ZJ4+t+0Adyi9YGG9PwUd5vPPkasUelYm0\nnGhGyB/CxTddkuUnyY6mY2dwJk35NQB4h71oOdGCpZcuy+t5C00oFMKGNZtwaP9RNDe2yjyLHpcH\nf/jln+Fxe3HPP901qXPt36XsqdixeTc+8+CnJ3Xs2UZbS+bikE3rt+HOD98WN3w2rtsSN7YAIBQM\n4y9/eB4/+vV3cx4DpRR1JxuwdcMO7N99KF4hePuHbsGXvvrZghhdAi9g/dNrMdzrBAB4gn443S7o\nDDqZZ2aUxvomDA4MobyiLO/jmQzeYQ8aDtajfn8dhnudMFlNuPWBO7D4oiUFOZ+ncywqQinFsHss\nTCjyAlQqDksvW465y2pwfNuxpMVNJBTB8a1HUd/dmvb4a954Fw9/66G8jXfGhBTrDzYgGj678psM\nJVbYFsiNmsHT6S9wIeiob48bW4CUNLhDIQw0Uer2nsZQ9/jKvZRSdPoH48YWgLiuTqezD0IswbGn\nqXvWViP1tfXi9V+8gvf+si6jsTVKy/FmmWdDKX8rkeCIF85GaR+BF/Dun98Z19gaZecb2zDc58xq\n32wIBULY9vLmcfdLJ3p7/MhJPP37v+Hd1RsUQ0XThXNoGI9+5TG8/Lc3cKa+OWMY9+9Pv4zVr67N\n+VyuETfqTinLxezaugc8nzkP5WyjvTmzwdXZ1oXGemkB29PVixf/+qpsH8fpRjQ2NMm2A4AQ4dG+\n8zhOvrgRLZsOITjsib827BzB26+txde++Ch+8Ojj2LV1b5Icw6Z3t2L3tn25fKxx2bN6Z5L4c/ew\nJAUzXk7rvp3TJ2+QSCQURt3eU/jHb17Hs996GntW74obj36PH+ufXgtPwnedTzwJaSgefwiRhO9M\n5AWo1BwWrVwEc5EZF1y7Uvb+o5uP4ODu9FWf+3YdRH9v/lJdZozB9fIvXsUrj78E31kinRAMhnD6\nRD1q+zqx5tABvLx7J3bVnwYvCBhq6IAwTlJfKj6vD51tXTklltdulT/0us90wZvmR0Apxe5te/GX\nJ5/Hjs27FSf+SCiCfWt2Z3X+vuAwOgaTvTecWrr1InwUfS4p5OZ3+9OOaboZGRhBp6MDg10D8Lm8\nEGLfic/lw8bn3sOrj780IQ9dOBhGV+OYsSREeLjb+sZ9X9f+0xAFARufey+t1owSAi/g/b+9B1HI\nT2HCrje3w5+QdJqOTkenrJ3G4f3H8JPv/BKb12/D839+Gf/3iz/NCBmJYecIvv/oT9HXk7322SvP\nvYHXX3grp4XCwT2HR9NMZLhHPKg9fO7kwFFKx/VwAVLyPM/z+L9fPJU2x2ndPzYobm/bfgzdB+rg\n7XWir7YJtc+uR9OGA1j7+rt46LNfx8t/eyPjtf/bUy/C7XJn94Gy5NTe0zi6+Uj8b14Q0OeSfi+J\nxv7c+XNk750J1Yondx7HM48+hY3Pb0Cno0PxduajPPa+vSvv56Y0OX/L6fbJXp+zaA60eh0AYNWd\nHwCX0rx6aHgYPZ296c8hUqx7S/l+yoUZFVIc7nXi3afewcf/55NQqad/aNFoFLu27EVDXSOWrViK\nW++6UXbBEmlubMHm97ajsb4JXR3doCIFBUXUHwIo0OUcQjASwR0XX4qR5m6UrViQ1Th2b9+Hp574\nKyLhCCrnVOCxn34DFVXlEKI8/H3DoACsNeWK7m7XoAttaR7MjkMNWHXnFbLtzz/9Mtavfh8AsHHt\nFry/djO+9s2voLJ6LOfoyMZDig/cGz95M2xlRdDoNNDqtNi9ez/2vnhC9r0REKhUKgiCgPahXswp\nrgAhBD3NPbCW2rL6XqaCaDiCrS9tRv0BuT6QRqeBKIhZGcEanUbWT7L52BksOH8hAMDV1ivzphAV\nB5qyzT8wgveeWoMzJyZefNHf1odD7x3AlfdcM+H3JtLR0I7Te07Jti9auRiuQRdG+oaTth/fdgy3\n3C/l3lBKZZ6JoweP4/SJeqy85IJJjWuU4aEReL0+VFVXQBebbMd9j3MEP3j0cfT3pF/NCpGoJM9B\nCFQ6TfyefvOltxGNRPEvX/jnCYWc9o+T+Lxj8y6suurSrI83mxnoH0TAP76nc9/OgzBbzGhuTB8l\nOLDnEPp7B5Lmq2ggjIEUuRVKKRz7T+DZrZtA1CqoNOqM18/n8eHZP76AR7791Sw+0fgM9zqx+o9r\nkrb1u4fAi9J8IooiKKUwGPX4z0e/jG9+9XtJ+7acaUNfTz+q5kwuNSRXhroGsfWlTenWDEk0HKjH\npbdcjsqFVXk7f8jlk56tkK6l0yV/HpUVj2k+WkttWHHleajbNxZpGfAMIxqOQK1Vp322b9u4Ax+/\n/6OwFVknPebpt2pS6G3txY7XtsUn6Oni+JGT+OuTf4+veLZv3IW25nY8+J+fU9z/VG0dfvLdX8oe\nvgQEnFoFMSptr21vxWWLl6DoVGtWBlcwEMRf/u95RGLh1v6eAfzpV0/jgbvuxGBdWzxh0FxdihUf\nvV6m/3Vi+7G0PwjHwXqZwbVr6964sTVKk6MF//vQd/Fv//V5XHfT1fC5vDIdEwBYdtlyXHrL5fG/\nt63fjleefwOE4xQnMk7NQRAE+EIBDPvcKLUUobe5GyuuOG/c76UQCBEe7o4+RHxBmCqKIahVWPun\nNWkbnmZqyA0ANcvnYdnly7HooiXoa+nB+meSq16aas/gpk/fCo7jFMOJ5ecvRHDIDW/MPU8pRVuv\nEz1DbmiMOiR2SicAbvvMnaheMgciL4KP8tjw7LtwDSSHNw+8ux+LLloiy99zD7kw0DGAyoVVsJak\nn1ii4Qi2vLBRtl2r1+KW+29Hc20Ttr+6Jem1uv2nce3HrofOqEfLmVbFFeWuLXvzYnCte2sDXnr2\nNQi8AIPRgOtvvQa3331LxkRq14gbP/zmz9DbrexhLKsoxZJ5NbD5BLQPDuBkRzv4YBgagy6eT7fm\njXfRUHcGHEfg9/nh9fgR8AdQVGLDB++9A3d/NDnB2e3yoO5k5u4Th/cfg9fjg8VqnuC3UHj8Hj+2\nvLgRA+39mLdiPm7+9K1xT0IutCWEE4UoDyESRYXNBm8ohBAfBSEcCEcgCgLeXb0hbTIMSSkFAAAg\nAElEQVQ5IHkl3l39Pr7wlQfi24abuhS9kGd6e6SFcYSHGOWh0qjBZTC89u08iOtuPoIPXH254uvZ\n4PcFsO6t97BjzQ4YiBbVRWVQq6RHcddwsodNFEVce9PVWLx0IRYuWYC2lMKCPTv2475PfyTnsUyG\nxsMNWRlbo+x8czs+/t+fzFseXGI40RcII5wSNSIE0IcjoJTGz/mBD16J+gN1oLECrwG35LAIB8Iw\npGpnxoiEo9jwziZ88jP3TXrMqu9///uTPkg+2Pb69u+P/h762/thKbFMOqk7FwYHhvDUE3/BK8+9\nCZ832WJuOdOKFRcuR2VVSnVZOIKfPPZLxUoHAABBknBlIBzGQpMNlRcthSpNUuQoJ46exvaNO0FB\nIUYFCJEoejt7MV9tgo4bs5cjviCcjR0oWjQn9jCWHo7vP/teWg9MwBPA8lV2GCxGAEBnezd+/v0n\nICiEnfgojwO7D2OwfwgjzYOyyju1Ro0P/fu98X6IO1dvxu9/9RSEqACR5yWjK/Zw0hv1UmNRiniD\n0agQRXVxOURewEU35i+52+f14fUX3sKWDduhVqswd16yaz7iC2KooQOde06iZeMhDNa1Y6SlBw27\nT2L7ur0IeIMTPmdJVQnu/MLduOYj16FqYTV0Bh0sJRYc2XQ4adKPhqNYcP5CmGxmtGw8JBM3nXft\nSlhrKjDU0C7lwfWPoKt/BKCSxAZJWJHdev/tuPD6i2AwG2G0mmAutqByYRXq9iZ7oiil6G7qxgXX\nrgSn4jDUPYgtL27C+8+/jzNHHDi25QhKqktQOkc5GffQhgNorpXnyNz4zzdj/ooFKKkuwfHttUn3\nnCiIMFqNqF48B2teX6coYtnX248PfvQOqCfh2R7sH8IvfvBE/Nx8lEdzYys2vbsVtUdOQKVSoXpu\nVdI53C43fviNx9GtYASazEb8v59/Cw88+GkYO1woUuuwpKoawUgEfSMjoKIoPZxj+zsHnRgacMLt\n8iAUDEHgBfi9ftQePoGKqnIsXDw/fuw92/fh8L7MTd2pSFFaVoxlKzInHJtMOgQCk89/Hejox8bn\nNqB221GAUlQuUPZGiIKAN3/9GrobuxAJRTDUNQiP04NlCtqD2bJ3x37UnWyAKAgQQtJCZln1HFTa\nitDjdIKKIqggStXQUR7gSMZoQ0dbF+645xZodVrp753HEXLJ5+f9ZxwY8Y1tl87BY+nC+fj4/R+D\nw9GclMsFAPUnHbjlzhuhHWfuVoJSil/+8Hd47+2NGHa7MOQdQaezT/JqUaB1MFkWRsWp8OVHvoiS\n0mL4/QGcPJasDeVxe3HnPbdOeBz5YO+aPfApKLYXlRdh7rIajPQne7q9wx5UzKtESZW89V0u9B5p\nRCCWL9sz5II3RYaoyGJAudmI0uXzoDXpAQAGswHRUAS9LT0IRkI40ycZ+pRSEE6Kulx9wxXoak++\nDh2tnbjzw7dBo0men0wm3Q8mMuacc7jsdvuNdru93263353m9fvtdvtBu92+z263f2Gix9/68uak\nRMJCE41GsfrVtXjkwW/iQIYkur8++XdZTtPbr6/DQG/6Tu6cSgUkVPE5errR73JhsL5t3HGdPlEP\nURAQ9YcghKPxENOJdvl7w54ATr28KS4t0HCgPm3Jfnwsh+oBSDlnv/7x7+OetHRs2bAdz7/0GrzB\nZGP0yg9egaKKYgCAf9iNZ/70wphMBAX4cASiIOCWu27EQ19/EACSdMqGvC74QgEMdQ8hEso85myJ\nhCP4wTcexztvrse+nQfxyx/8Dof3S70dR1p6cPLFjTj8p7fR/P5BjDT3QBQkF35HnxN1rb0I+ULj\nCuglojPqcNOnbsX9j30WCy9YlPSaVq+Lhw8TaTrWCG/3oEwQl1OrYFtQieIlc6AtMqOxvR8dCaE6\nITI2ruvvuwErb7hYduzqxXOw6i55yHi414mtL23C+mfW4qUfPo/T+5PDpZtf2IhwICR7Hx/lFXtj\nzl1Wg5XXXxT/nOddLfdUndhei2gkgj3blfNOQsEwDu3NbICMx5EDx9IuLs7UN+OPv34GD3z0QXz6\nQ5/Hv37kS/jcfV/GQ5/9b3R1yHPvjCYjHvvZN7H8vKUIDLkRGJJydzhCcNvKi7FqyVJQgUKIZPZy\njvLiX19NCpkpVScqhT+3b8p/7osS/e19eP2Xr6C9rg39bX3Y8tImRR01QRBwcNMhtJ5pw7DPDafX\nhQgfReOhBriHxi8WSceoJETioqPSWoRLFiyU70wBIRSNf/d33Xs79Ibk7y4SjmDju5JYajQYVuxJ\nKooiOp1y7/Unr74OHznvElianLjriitkquUjwy7FhP1sOHH0FA7vPRpfaAIALwpoHejGkVZ52kJx\nkQ2Ll0lzyTU3XCl7vbOtS9b+ZyqIhiPoV8g5/eh/3ofP/uiLuPvfPoziymLZ67v+sSNvAtejHq50\n4cRSm+QZdqboHl5177Wwldkw4E42CCOhCOYvrMFn/+1+qFI0NP2+ALa+v2PSY87J4LLb7YsBPAJA\nMWvabrcbATwG4BYANwN4xG63Z92eO8pHcbS5Dv/2wH/hS598qCCKr4n4fQF895Ef4pXn3hjX4Ojp\n7E1Kouvt7sPq15QrlSqqynHNjVfCVmyVXcDdDXUYPDV+teLxA7XSwzjFd3uqsyNe3ZcIH4pI/ffO\ndKI2i8bRjoMNEEURT//u2YzJg4B0Y4f9IfhDARxqPgVfSHqA6I163HTfDfH91j+7Gt5ASj4GBRaX\nlONT992DVVdfhorqcnCEJMlJdAxJPaz6WsdPHs+GtW+9h/aW5Cq+t15ZA0/3IOr/sSMeqhtFEETU\nt/aio29MQJEPR+MPAbVGjZLqUhgtRpCEcWv1Wlx886X4/I+/hEtuvlR2rUdZquABaDp2Bs4z8gmz\naGEVVBo1nN1DqHV0YDBldS7GVvtX3H0VLr9DblSNctU916BMQYKkbt9pNB52KIYEIqEITu48Ltve\ncKAeQV+yx4/jONz2wB1J3raLb5LnHbkGXXj/rc0ZG+/u2JxdEUY6ao9kl2QuCAIi4QgC/oDi791o\nMuKxxx/F4pj+zlB9chiHEIKbL1iJK5cthxjhsypEcI944hWNPq9PsWfg57/8r7JtrU3tScrzfl8A\nL/7lVfzPf3wbT/z0DxgemrzYp3fYg3eeXA0+kry42PXmdgQ8fmx9fwe+/fAP8IV//go+/aHP40c/\n/CX2NtbicMtpHGmtw+6Go+hzOxXvmWxpjyXMJ+YsVthsKLVYUVOq7G0VIjyqSorxwJc+hVvuukn2\n+ntrNiIajUrhxBSNQK3ZACwoQ4TnQUHBCyJ4QYBapYqfj1KKGqpDjaUIfCiSZHhteW97Ts+l1a+u\nVVxQEkjzSCo1pVXxcFhFVTmWnSf3du7deSD+72HnCI4dOg5H3ZlxCzmCwx40v38Q9W/txMDpVtl3\nlIme5h5ZoYul2IIFFywEIQQqtQrX3Xej7H2ugZFJ3SejhL0BhGMSEIFQBKGY8a3SjnmgSm0mAIDT\n0ZH0XWi0Gtxy/+0Y8CQbXJRS2NQmlJQV4/qb5Xmu7761YdKVw7l6uHoAfAxAupKyKwEcdDgcPofD\nEYJkmGVUCbz05rEwUsdQL/rdToiUor9nAI8/9uuCtrt45831aG1KL7qXypsvvY3BgSFQSvHXJ/8u\ns9hVahV+8ccf4w/P/RoPf+sh3PcvH5Wpzjf39aGpsRX+gfQT5lBnH1ocrYqVTP5QCC39yoaJyAs4\n+OImDLbLX0+NnrsGXXjz+dWKnoc586px9Q3Sw5yCIuIPSYndVGrD4Yjpl1x5z9Xx+LenexA7dh2Q\nHWtuSSnuuXQVHKt3ITTsxd0fuRMAkkTxekYGEeGj6BlHHiEbpDJvuVJwU2MLHGmkCpq7BzHskSfu\nRoNhRAiPCz90GT729U/g3371FfzXk4/gy098FZ//yYP48hNfxc2fujUeTk3H4osWJxlqgNTgu/O4\nPERXsqwGp/eewqs/ewk+b0D2PgCoKrZg1W2r4PcF0FjfBNeIvIJKpVbhrs/fDU41sZ/6sS3Jq3BK\naVyZOZHlq+workwOEZRUlWD+efL8xI1rMstInKw9nbNaOM/zOH28Pqf3JmIwGvCdn/wvliyXBGYp\npXA2yOcGQghuOO8CXH/e+RAjfFZViutWb0BfTz8O7TsqC9uXlBXjpjuux5Lli2Tv2xHzcnV39uDb\nD38f77y5Hh2tXdi38yC++/UfYtiZu2cpEopgzZOr4XfLPQThYBjP/+YFPPXEX9HU0Ayfx4dILCcm\nEV4UcKK9Ee+/vTlevTsRfF4fhgYkwc/Rhz4hQJlVKp65ZKH8OwEAFcfhtqXno23zEdz14dtk97h7\nxINdW/fCqSCdUmqfjxG1AI1BJymTiyJEkcKg0sMfGDOICCG486JLoQJBNBgGn/D5//y7ZxEKyT3B\n6WhrbsfxIycVFzk6o16muaUiHKzEkBTSVPJy7di8G0///m/42hcfxZfv/xoef+zXeOzrP8ITP/1D\n2vuSD0VQ98Z29J9oxkhzN5rW78fp17YgqBAiBKTfga9/GEMN7Yj4guhyyCtKa5Yni8MuvmgJapbL\ncyf3r9ur6EGfCIn5W4OxMROOgIulC9hMemhj4b/giBdBZ/LcWDy3FL6oQrqIh0fLiWbc+wl54G5o\nwIm9O+TPtomQk8HlcDhCDocj0wxTBSAxxjYIIKOE+Icf/FA8Z2vAMzbpCrwAz7AHP/nGz+EaTJ6M\nw8EwHIfq8atHf4NP3Hw/PnnrA3j6p8/ApxCrT0ckEsXmNH26bMVWfOpzH5c97CLhCJ7/88vYt+sg\nThyVV2t9+L4PJuVr3HrXjSivKgdJmRB2O+owkMbLFQ2EsOmZ9OXmhCNoiXhx0QN3Qh+z5BPpGXRJ\n3pmEh+acJXNRY5+ftJ874MWrL7wpe79Wp8V/f+c/8fC3HsKXH/ki1IQDn2JYOr0uCGoxnnNFRYoD\nb25Gl4Kb/vrzzodapYIQjqLu9W246opLYTQZk7xBIhXR6exDTx4aWb/y3BsIK6wkqUhx/LB8hRUM\nRTAwLJ9sKKVoc/Vg7+kjePK3z+Df7/8vPPnrp9HU2Aq9UQ9bmS1jLkkiBrMRNcuSJyAqUvSk5MMJ\nVMTR/XXY9PyGmNFDoErJHagus2FBRRF2vrAWjzz4DXz3kR/iK595JEkIcpSymnJc85HrshrjKH6P\nH/UJocbOhg7F4oFLb1NOHr7klsuS/o4KPFra2zPKP1CR5qx11HCqUXa99UY9FizOXnVcb9DhOz/5\n36ScKV+vEyEFYwSQHsZXL1+Bz914Cz5x2y145DtfxWM/+wZ+/ocf4se//R7UKddM4AX8/ZlXFNuy\nXHmdVLJ+4+3Xy17buXUv9u06iG997fvo7UpeRA0NOPG9//nZuJ55JURRxHt/WSfLx0xk16598QUl\npRTRkHIIlYLi6JnTePmpiTf9jYcTE4zQErMFGpUKxjIbPvTFf4KlyCKbP288/0KUWawYPN0K1wEH\nrrxmlezY77z+Lkba5J77Uvs8nD5RD54XJAOIEIAANr0ZXSmLYKvRiBvPvwCggBgVEA2EIESi6O8Z\nwOsvrI7vF/AG4B5KLxvxzpvrkxYxo2g0aqhjifpcgsFSWVQKNadKuj5XX3+lbNU8NODE5vXbZEUf\n+3cdQu1heT9bAOg/0YRwSpW5p2sQx/+2Ht2H6uPePD4cQe+xRhx/7j2c+Pv7aFy7F0f+vAatCnmc\nNSuSny2EENzwiZtki/yQP4Tdb+1Ec20Tjm05gu2vbcW6p9Zgx+tb0xYopeKNfSeCKKLPKfl9pLxW\nAsJxKC1KLjRJNbqPHDgGrV6bZCAatXqY9UZse3kzKirKsOrq5DkMkHouTkY3cNwnhd1u/2IsD2tv\nwv8nWkI4blmCRqvBPV++F3qTHlEh+UctiiK6OnvwrS8+htW/fxOHNhzAW799A3/+7yfx+x/9EVt3\n7YY/FIQ34Mfba9/Dzx56HFte3AiXgveIj0Qx2DmArsZOuAZd2Lt9H7wpye6EI7j7Y3fit8/8Av/0\nqXuT2kmMcnDPYfz5t8/KtpdVlMqqRjQaDT6u4OVqGxjA0R0HZXIAQpRHw1s70dQmX0UQFQe1UQeN\nUY+GllaE1cCF998OU8VYvDwcicYVd/nwWM/CS265FCuuHKsAjAo8TrQ3IhyKyFZd//61L2DewhoQ\nQnDLnTfin66+HlqVPEm0e6AbNDYhD9a1Yc8heRizzGrFvISwQDQQQuvafbjp1mvjAqijdDn70NPc\nPSldpubGFuzYpByeEnkBzb3JE7BKp4FHo4bGoIXWpE9aKav1FL0ep+TVC4YRjUSxY9NufOfhH+Cb\n//X/sG3jzgk97JakqK6LvJCkHyOKFGd6h9FwKLmCjdOowKk4qDiC5fMrsaSmHBGex/P/WAvngBQa\n5aM8nv3jCwgG5Cu3y25fhTlL5Fo+AGC2mVA+r0K2/cjGQ/HrcHSzPK9xzpK5aROrF164CLayMXmP\nfpfksY6M07x9x+bdCAVCE87zOK4QTrzk8ovwiyd/jB8/8T3cdPv1sNosCu+UqJxTge8+/g0sP29p\n0vbUcKISZRYraqDHsvJKrLzkAixauhDLVyzFvR+Xr5IP7zuKYwoPwauv+wAA4LqbrpKFpD0uD574\nyR8QSuMVqD/ViD/86s8T/s3senN7Ri23cDQCV8CLcDAsebhDEdAMdWkUwOuvvo331sirWDMxWqGY\nGk4EgKJF1ai+aCk+8x//Co1BBy5mxC6pqsJli8cM4+GmbpxvKZONr7O9Cy19yYaI1myAsbwY9aca\nxwwgAoAQVJSUws8L4HTJxvIlCxejprQ0/kGFCI9oIIR3Xn4HR9btwqa/rcfT//Mk/vadZ7D2j2/L\nwsxDg07s2b5fdl8vq5qPD957B4wmqXBp9BnBEYIFZdLvtb99LP+spKwY51+YfZuug3vlXmkqUvQf\nb4Y7EMD7tcfw9sEDaO2XziEKItq31+LkS5vQ/P5BHP7T22jdfCSewwgAfFRAX0sPUkMvNctrZOeq\nmF+JFVedL9t+ctcJrP3T29jx+jbUbj2KpmNncGzLUbz569cUn9upeDolg2tg2As+dt/8f+reOz6O\nu87/f07ZLq1677JkSZZkS7blHnfHdhKn95BGDaEcLXTuEuC4g4OjHBAgJCQBAiHFJs3p7r032ZJl\nSVa3etu+O/P7Y1arHc3KTvje7/vj9348/HjIq9Xu7M7M5/MuryKE9xLZIpM6NeFq1Cdch/YdRRAE\n3Rg3zZmMIAiMDY2x9+97uOG2aw3v2987wFO/fvaKxzddXJES1NDQ8CTw5Id83S70Ha0c4Iql64zy\nXO76yu28fuv2mL+/2NfFsYMnaA8vghd62g2sDoAzbRdI2hFP/d7TVC2pJDkzid62Pnrbexm8NKTr\nGu0/fxK3x40oiYiiiCSLrLt2JY98+6HIcx7+wn0c2nvYgJfweb0GS5svfuNT5OYZMQc337mBV198\nnZYGfUdr24kT3Dg4TNosbQSjKipH//IerkuDtA3061JVQRAw2y26rPzg7v3c94k7yPjsDRz+83v0\nne+gZ2BUdyuowRCJmcksWjeXgC/A9r++RygYor23G0/AF35fJbLQb7plPTffsT7y9+7BMUYvjVKQ\nlElj32QSKIgCzT1dHHvpXdIeuonm7Uc409GmP2ZRZNHsSqQp1Wlg3M1Mhx2zxYTHJUTOiS8YoP1S\nF71N7VQvrTJ8j1cKVVX53jeen9ZqKBgM0dLXC6iRzlRObQlHX9oZ6SKZ7Rb8Li/5mcnsb66PfB5V\nVQn5ApjDLNDWplZ++7Mnee6p57n7wVu46Y5rDSyWqbFwbQ07/zbZUQ2GFNx+Ba8/gM1ioqm9lxGP\nNwZ7VSC7JIdcuxVz+Hi2nTnFmFdLriSThCiKeD0e2lpaWLbSOHq46yu389S/PR2pwh1OO8tuXEbd\n1fNp3HOK5376EqIkIZq062C0f5j+lk4y8tJpq281fKcrb1lGWtr0ScyS6xbx1rPa5tsdFrcNBoKR\na23hsnkc2D25IYSCIRpONfLjh3+E0+bAZDFhc1ixxdmxxVlJzkhm8XWLyIzh3lB/qt5wfMtXLyA9\n3Ul6ei1Ll2u4MlVVCQZDBINBgoEggUAQQYDEpAQDXV1VFI5d6DC8bunqWlr2nCY4RRbk4ntHEH0+\nUouzSMxL5+OfuYtd7+9hoE+PFQF0XfOU1CSWrpiLKIqkpcWzfPUidry7d9rvNVYc3HOYv//tFT75\nuXuv/GTgwJsHObHtmOGzCQJMLI99Y9pxK4pCwOsnGB5tmSQZs2xCVVXcfn0SGAqFeOrXf8RsFrnz\nvps+0LH0dncjioKWcIUPJyMxEVEUKKguIi0tnrvuv568/AwO7juK1aeS45UjHqwTkRCAGVlZtF6a\nTFCCQYXDF85TmjW5HeXVljA6MoDX49GB9GVJIiEuHkEQKL/xKmSfn/PbjuEb8yAicM3ceTz5/rs6\n7GwwGOT3v/kTRQlacSrKEs0nztO47zRX3TTZVX7xzy8Z2I5m2UTNrAoe+c8v4HZ5eG3z27z+t7e5\n1HaJoowcEhxa0jDWO6C7z9ZvWsG5Mw18kDh59BSpqXG6a7u3sZ3RviGe3b6NEbdWmNd3tHPb4iWU\n5eQA4O4dwh1OfKZeI8NjXo0QpagRAeuE1ARmlOfGlHzY9LGNNB8/T8B/5XGzz+3l6FsHuONLt037\nHL/Li3doFEGA7iiihmSSEASB6mVzsE6Rw/EOjmJTQ8SlJ+L1+jh9/AyiKGCxmgkFQwQDQTISkyOf\n9dSO41x950rmL5rD0YP6AmnP9n2sWreYVVd/uKkB/O/ocMXa2Q4AT5SVlTkBBVgC/MuVXqivbwxz\nkhPJIhOaphI+dfE8i2fOoXuoL0LpnBq+oJ+znS1U5ZVyYtf0QNoR9xjDLm2MFKkOfRC85Ke7a0g3\nErj7wdv5xQ9/c9njn7uwhtKKcvr6Ys/Bb777Rn763V/obvKO/n5e/+PrLLl2BQGXl7HOPvrPteHx\n++gbiWpPCyBbzagquoTx1Zff4epN65EkiaJrl+B7ZTc9UwT+Qv4A5QtnMTiktULzZxXSdOw8nYOT\nc/CA149ot1JcWsht996m+wxN7x9lcMRFpjOZ1qFu/MEwQFEUQYVXXn8fuypx6MxZAlMqOIczjlu/\neD9NL+/CPwVwzZifWSUzOHjkhG5c2dLXxRtPv0Vace60APTpYu+OA5w6FhvLoyoKSkjBG/LTOThI\nTrJWsV7sGcbn0V9vtsQ44pNsNF+aoosTDBHwBXQjvpHhMR7/6dP8/cW3ePChjzBnntFCYjIEMgoy\n6W7pjhwPaDiEUEild2gMk91iMAKftbiSVXetYay9l3Obd9F8qUfHVA24fch2CwIC29/dT1mlsapE\nlLn9a3fTcrIZs9VM/qxCBFXlxF+30V1/kTiLieExD2JAQraYQBB4/287SC/IMBxPQmoCqUU5017r\nAIU1M7G8uJOBwSGGXJNwT29Y8+b62zbR3zekWegoCp4xNyrQOXCJuOwifB4/Po+f4X7tb5tPt3J8\n10lu/fIdOpPz4aERzp8zjuaLSksue3wAowPjDF0aIjXXi8OpH80PX+zBM6IfHwiiQEJFEfkmE01b\n9XgOn9vHube1BFKUROJzUlm3aCF/3vL6ZbWH5i6cy8DA5Hhn4bKFbHvbOBoGbXSnBEOoIQVBFBFN\nEpIooigqf3n6ZZyJiayJASCPjov1rbz6+zcMIGkBuOZT13P4rYP0tPZwaXiSVDKh6l6cnktJpjY6\nks0yJ9oa6ezVd5D8Xj+//fmzDAyMcvtHbr7ssQCcPdNEKBTSHU+6MxFVhVCcI3IOy6srKa/WGLDd\nxxppedfYvalMzqSpvRNBElEUhVAwyMW+ProGB8lM1KYAtrwMtu84hN8X0BWmSXZnZH09eeAsy29b\nxeyCbLqPnKPz4DkS7XEsKi1jz7nJ9UVF5WJ/L045nhRHgqYhFgiy4+VdlCysRDbJuMbdvPLimwbd\nvryUTGqWz6G/X+twr96whuLcYrb8z0sAkXuu9VyH7jquqpmDzW77QKOtvksDHDl0VqdDd+LNw7x1\n5GQk2dLeS+H1I0fITUnFZjaC96NjeEx736A/iBxOerNm5EQ+hzEE5qyex97X9tAxcAmPz4PDaicj\nIQWLyfheJ3efZvaqeTHJPgCD5ztQFJXBURfu8IhbEIXIuateNY+u7ccYn0KKatx3lrwlVRzcewRv\nFHvfbDUjqQIJtviodU7l6K7T3P/QvZw++W1Dd/nH33+czNxcKmIwzy8X/yhL8ZqysrJtwHrgB2Vl\nZW+GH/9aWVnZwjBQ/uvA2+F/jzY0NHwgz56xkTHMFjNWu9XQFQEtmTp84TQN3a2XfZ2uoT76xy7f\nmmwfMILKnTYHgUGPASC8dOViKudML8hpMptYtWwpr/x6M+8/9y5jMcCHS1YsNOhAAWzdtouGv++m\n5b0j9IcprO39UbPscLKVnJpswJP19w5EtFlESSSYEEcgaBwtZKRMilmWL6hgxD2Gxz950QUDIQRB\n4Avf+IxOX0ZVVc7sOoGqgiiI5CWmR45pAm9wpqONjpZOjrXoxxOiLLFqwwoSM1KYdftqZJvx5pqT\nkaNt7lEx7nVz+PSpD81m8fv8Brq2qqr4vD68bq9uwWvp1RIpa3I89YeMCVrVVbPptCkxy4mpelkT\n0dXezb9/67/40WM/M/hvBX0Bek810/zuYeyKQsDlIRAFzu3sHaajdyiCQZgIURRZd996rn5gIyaL\nmeSSXJwVeWw9rgf+q4oaEcE9evDEtNg/W5ydWUuqKJk7E2/fMCee3krbqQu8duQQO86foP5SKy6P\nm6DPD6pKT2sPp3YZR2BzVtVeEbtmsVlYcsMyuoemYNRCIY3uXlLIijXLUFHxurxaZ0VV6R7sI+D1\nTbZaor9Hf5BXf7VFZwEVa5yYW5BDSmpsvZ+h3iEObd3Pc//+LE998wk2//xFno8c314AACAASURB\nVPz6b9n/2l7dWC7WODGpOBvZaiatsoiUGIDgiVBCCiNtvaSNKaTb4y4Lql8UHidOxJy51SQm690W\nVFWToAi4vBQmprB21mxCvkDknE/E7//nmcuy53xuL28/vTUmI23ZLcspmTuT1fesIxgKMjhu5ESl\nOye/07oNC/n05z9GZkKK7jlBvwZjePFPWyIyLNOF3x+gs60bZcqale5MIC4z2bA2TERW7UxKr1sM\nAoy5vXT0DtHU3otrLIgYUHGNuvCMeQgEQgQVhaPhtcnssBKflUr9ybMGPFVS3OQa2RrG1kpmmdzF\nVcz95Cay55excGYZTtskOSYUJhE1DXSiqJOfYWxghHNhd4p3t27D7fLoiBKSIJKXksnsZfriLD1G\n93awe0DXHYt3xvGFb3yG9Kw0JFkivyiXjTes4yv/+i+UzTIaxR87eDzyc8/5dna8fYi2wSm4PQHG\nvR7eOXrSUDRPjZFw4awEQ5F7NOcy9wLAvKvnc66rmcauFtr7ezjX2cyOs4c5dOE07QM9+AL6gnff\nq7ELDpgEzHdFedZOwEDyyvJJzU0jpcx4PP1nL6IqCof26fd2URSprK4wFEVdTZ1kZKbzsYfvM7yW\n2+XmVz/+3WU/c6z4R0HzbzQ0NKxqaGjIbmhomNPQ0LAh/PgPGxoaDoR/frmhoWFRQ0PDkoaGhg8s\nWjI2qiUqsknWRBzj7ZgtZh2YcNw32SkRBAGT2YTVbsVsMekUiOs7mgmGYrcxNQ8/I0AvL0zDPbT1\nAO6xyQpCEAQ++vB9BswRaFVOZXEp+17cRfOJC5zccZyXfvK8gYkhSRJ3ffwOwybePTTEhSmMw4v9\nkzeEbDEhShJ1S+ZSM2+24f3fe3P75Gc+UG/AiqUlxjFU3xrpphRVF9M7JRlVUSksyDPYRIz3DOhA\n3VnOVGRJ0m22iqKy5dB+BqMEBBFAsshcHRbls6c4mXXrSsOxp8hWZpYWGzpZrX2dvPKnV6+oIxYd\nr760lf7eyapGRcUz7iHJEk8wEMTv80fGARPft8diNjC0BEGgYmkVu3cfQp5C1S7LziEj3nnZDfTw\nvqN88ZNf5y9Pv4hrdJyuw+c4+sQrNL15gJ5j57EriiGXmMAhiFOurzX3Xm0wXd1Wfxq33/i9KGGR\n2aGBIdouo82jKgrte09z+vn38I252XLoAPUd7bh8XvrGhzja0cDQ+FhYjkTVbc4hJURzbzu/ffxJ\nvvqxr9Fw6vKjjVlLq+hzGQufBNFO0B9gyYqFBH3BcKKjgqrdm/0jQ5H3nxquURd//9VmvOMexi8N\ncuzAccNzaqZ0GT3jbg68vo8/fe8ZnvnOk+zZspvetsmkWAkp7H91Ly//998YHx7TsHVRuA9VVRke\nc3Oxd4gjbx9kfGiM4qvrIoKK04UgCKyuqJpWr8uZEE951UxCgSBjXf2MdfXjHRxl8eL5YdaeQtAX\nCAO1gyydWcFNCxZTU1jEsvIKlEBIJ1cQCoX4yff+h66O2BIvu1/eGZORWLWsmrnrtMQvPT8DW16C\nAQ9lNVmIt2ldQEeCg7lr51G1tIq5pZVkJ012I1QmBY3/8vQLl8WWdbR1at2tKPxWnNWK3WLBeQXh\n67SKQoYtZk40dtDaNUDPwCijLh/ZzrTwdaMdvxJSONOuTQ2SZ+ahKAr1p84Z8FTJjskkd7BnUAeA\nN9ksFK6ay8KHbuSmTVeDIKCoSqQj4vF76RyZ3E+UoMLB1/cR8Pt5Y/NbhuQuOzmdzNwMMqYkWPZ4\nO/FJ+jG9qqoGYsOcedX88g8/4S+v/YEfP/4DHvz0vSxYMo+6JUYSy9FDWuHa3tDG3378V8Y9XoY9\nUQ2BMH4NQaDxUgenmjoIRieHZpnMGk2kOxhSGI8qFCewarHYiNHR3NhK3+igltQIk2875nNxvreN\nnWcPc7j5DCNubQ+5cLyJ3hjaaaDht1weH8NRotQTReoEiSdWMeQZHKVp76mYRcCi5UZpnQny1vI1\nSyNs/eiIJe1ypfinMa+eiNEpAHZRFDFbzdidDmwOGyazCUmWMFvM2OJsOJwOLDYLpRUzMFst2J32\nCPvAG/DFHDvGJ8UzhscA/zRJMpmJGv7K7/Vz4DU9jiKvIIdrb1qve0xRVUyqhNWl/yqH+4Y58o4R\naLzoqjpyc42Ezf3nG3Sb+IQgn2SWI1TXWbMrWL3BqG1yeN8xhodG6O/so6e1R6dFApCVmohvxMXg\n+fAGIgr0u41U8gxniuGx5r1nGIu6wWRRIi8pA9OU9+ge0m+qokmmqqaSvIKcyGNxmSkkxKjg1s6d\ni9Vm3LiONJ5h2wvvGR6PFYP9QwY9tKA/SIojgbLsQm3tVbWKVFEVLg0PM+710BJDXLektpRTp+px\nu9yIkhTpKkqSyNVzarhvxWq+/PDHWL5m6bR0kEAgyIt/fJlP3vJpXn7yRXxRKsg2ixlHDM0d0IvB\nLrpuMZVL9Di2w/uPsuv9vVoiGOO9g74AKqquqo0O/7iH+he2077nFKjQ3Hsp0u3TPqNAIBTkeGcj\nPSMDk0mPqjI0Osy+c8dpvtTBpUv9NDY0851/ecygyhwdFxpbCKhT7a4g2eLkyNuHaD/TRqIlLvwe\nk8+5NDaIElK0TlsMoHZvaw/PfeO3HHt6Kwff328wg48e644OjvLHR59m3yt7LsvIA+g438GfvvsM\np949rHWQQgrd/cMca2jj9IUuzh5pZNdLO3nqm0/w1jNv4qydiTXp8tY7WUnJVOXkxUzSFyydz/CF\nLg7+4kVO/fkdTv35HU488ya5wwpyQCHg9qEEgphlmZsXLmZpeUWk+Fw8s5zKvHxCAf3363a5+e3P\nnzK8X2dTR8xuZV5ZHqvuWqur8MdCbkPFn56QHHls8fVLMVnMmK0WZi2upDK3hLzkyXt7opvc3toR\nU+R1IlqbJhiK0YB5TbIx4QoJV1dTJ42nmw1yEBlxyciipLts/IEgJy+2klqWT2vzRcamGB3LohRJ\nJiPHFoNBbnE6uPFz91A5r5KQQjhZ0X53MQpuATDYNcDLz2xhaHBYp3EmAAWpWZTVlcccNcdyWIkG\nzoNWNDWfvMCJ7cdoPd0S8bWtrTMKIJ8708jBt/az+efaOtTvGo5dMArgDQVo6u+hsXOAuJw0iq+u\nY95DN1K8ro6UsjxGXfp9UwmEcKY4dQSZWPHac68gqGCSJMyyjFmWMUkSogpy2PptcHyEwxdO4wnj\nAve9YuxyBX0BXL1Duu4WaGSyxPQkiqo0CRFrQhzxOXos9cW+Xh577CcGRxiL1cKK9UY81nDvEJ5x\n7T74xOceICllkpjm9/pjeglfKf7pEq6xGMKIScnaDSjJEhabBZvDps1dw92AZasW84OfPUpVzSwN\nWG4xY3fasdgs9IwNkFaRydp7r+aOr93Np3/2OR74948zEBjD4XTgcDqwxdmQTTI5yelI4uSGd3Ln\nCQZ79HPgW+65kfwijY0RCoXwu7zMTMuPOV459u4Rw0kRRZG7P2rscnUNDkaSLJfPS//oqIbPiBrv\nVc4uZ97CGhKS9F53oVCIHe/ujti4CKIYWYQcNjPx4Sq869A5VFXl+OGTBKdsgpIgIowGdV05JaTE\nNG2uLisjLgZNOxKCJmOwftNaw68yqo3CfXHjQe687xYDjT4QCvLHZ//G8AcQd3z2ied0bEEVlaAv\nwMysAmxmKw7zZEIXDCkoqsqF0WH6uwYMr1W7dh5vvjKpGTWRBFXk5GEza4D5eJ/CZx/5FD/8n+9S\nVqkXNFWCIYJuzRnA5fHy7qkTPPn+O5zt7EAJL3QpiUYpD1EWI9/prMWVBpPpsdFxfvtzjRkriGJs\nW6gwdX2iqo0Ov8vLqT+/HVHdVlSVnfV6WRNREEHQqur6nhZa+7vxuT00tDdzuKUet9+LFDXW9vsD\n/Pd3/ntaVuHO93YjyZLOTicpLgGr2cLhtw7x/p/fITMhVZ9TCTDqH6e2PJe5pXksXVmLIyJ9oo3W\ngl4//YNjHG+6iNvn05KjcNJlMpuoqCqLvNzuF3foutVXCq/Lyzt/eY8zzV0cqm/lQkc/bm9Auw7C\nG6SqqjQdO88bT2/ldEcfpooC8pbPIaUsP2KtFR3LyiowxeiOz58/h8bX9hpGfA6rlQdXrWFpeQXL\nymfxsVXrKMnUF2qCILB+Ti15KcZC6eypBp1mUCgY5N0YHpgmi4l1D2zUdZi9Xi+njtdjmaLenhEe\nJyZnpTAryk1g9vIaDWieU0yiXevOKIoSGaG98OfNMe3CABrqz2tEiqgEID0hAUEUDBvm1Nj/2l5A\nQLKYic5bJFEkM17/naiqypGWZuyZyZw5ec44TnQ4DclP6+nYDE5BEKjIKQbUSGcIQSAYCtEyONlZ\nDAWCvPrSm2GNr+iEMgW7xUbZNJ6xscaKvVGaiqqq8uZTb/DKrzaz7S/vseV/XuKJRx7nia8+zuG/\n78NqtuDz+vC4PLhGXYwPj/PyU1vCjHXoHY9KVgQMn/viYDfDXi8tg6OkVRZFxrppswoj48SJUEIK\nWUWXVXxibHSMgwenHy0rwZBWRKiaJE7HgLY+tZxqprtZLxE03tWPzx+IaG+BdvyCKFK7Zq4OjlGw\nXJMrCikKO8+e4fl9uxn3eHQuHaAVZ/FJTlKyjfdRd7N2PuPi4/jsI5/UXi8snPyPxD9dwhVLiXrB\n0vmsWBebEbBg6Xw+8+VPIskSn/qXj0a8swS0UaPFZuHAyRPMrCsnqzgbi83CsUMnIqMnQdD8kyw2\nC8XZRo2k3S/t1D1ms1l59EffZM3q5WQ5UphfXEmiI7bZb8Af4OAbRkHRxWuXUDijQNtcRQFBEhFk\nkeN9neQursSXnYBstyBbJrsguQU5JCQmIMsyK9ctN7zmu29s07mgT3S5MqKMiMd7Bhlt72Xne3uR\nZEl3o6UlJCOoAns2T1qJDF3o4lIMiu78dQtZd81qrcsSgw0oWWSSU5OpW2TUMUkuzUWagstQgiGW\nVFUyb5FRoXzINcpP/+1/DI9Hx4HdhwyCdEF/kJzkDBxWO6gqSfaoNr0KwVCIk03GBTWrKIsxnzui\nfA0ghDejuUXFkcdG23sJev0UlRTy3R9/i89/7SGSkhMjycDUDXTY5eLVwwf5485tdA8NRmwnNLE+\nEdliipzv/IoC1nzkasNC+NSvn2VkaBJXI5lkRFliQckUqYlAkMb6JsbH9cl+287j+KKEXc92tNM3\nqr2eIImR8xLN/moe6GRfy2kuDvagqiqiKBiMg5tb2vjb00YtN78/wJ7weTFH4feyE7XxUzAQJOAP\nkGRxRMx7J95fUVWaerqxWkwEOvpYsLQa2SQT9AZ0C+a5zs7ImHgi6ZpVXR5ZB3rbLtF45IMxuiKh\nasD0oVF3ZNQLGEb1EzHYPcieV/fyxt+2IWSnMv/hm8iYrS8s4qw2Vlbqx5xllTNxjgV147Spf7O0\nrIIlZeXE22KL6sqSxPW1daSmJGlN3KjE5dnfPYfHoxVQh7YeYKjHyJZccuMyg1n5icOnCPgDyCY5\nkoiZJVNknVt283Ld6Ds1N43sGdkIgsCMzMk1dKLL1dnWFVMw8sjbh9i9dTdel5dAMBgpRjISEonP\nTjVoz0VHd3MXbWGMnSBqSVd05CSkGYraYZeL40dOcuroaUOBEI3fmoj2hraYulmtp1vob7pETlRH\nbyJx6R7rp324l3O9FznQVs/g8JABFlGQlk1GQUbECm1qxEy4osZrF+tbaThkND53jbhoPdWCNSAR\n8AYIBUOR66F/bBglECQQCkbGiYIgYLGYsTpsuq/KFwzQ3t9Dy6lm3nn2zchrOHPTGY9BZnPaLm9a\n/tYLbxK4gkVaBDKkolOAn9rlGu3oo2dglOjlVZBELDaLrgjQjjcNOSeJv+7dxf7GhkhRpwSDkTG8\nKIlcd/MGQJO5mRrRItzVNZVcd/MGgyPDh4l/uoRrAsMVHfEJcTz40EfIyNZrBdXWzeEL33g4sihk\nZKVz14NGOmlP1yX+7ZF/Z+/OA4SCIbb+/R3Dc+YtqmX59cZxXfPJC7RHqeoGfH4Ovrofz4VhSjLy\ncdouP044tfOEwWNMEARuf/A2JItJ+2eWkcwmmjo6GbWLdIwMGjpmlbMnq6E1McaKnW1ddEUx6gRJ\nk7hIm4IHuLD7BIf3H0VA0HWUssKb4MmdJ7hY3wrAuZ3H8E0ZV0gmiYqlVVx380Zkk2wYbYmyhCTL\nrLtmVUyGoShLpFUUGh7vP9PKF7/1WZKTjYvQoaPHee+1bYbHQUvQn/jlM7rHVFQIqszI0BZ/JaSQ\nYpvS8lahs/eSDugKE90t/fUhiiI5aakRlhNoyfhQuPoSBIFlq5bww589yvzCGdNKUgD0ucZ44dhB\n0lZXk1aYicluRbaG9YUEgdTcNK791PWG7+7U8TMx3QBq62azYlYVCXa77tiCgQAnj0x2r7zD4/SF\nzytoCefuc1r3UjabkG0WpPD5lERRd06jxyQxgfIqvPjnzZw/N8mO9Xl9/NdjP2N8dDwiwGsyyUiC\nSHrCJPBaDSkQUsmISwq/vhBJ+N4/c4rOQa0wcjW2U5KVbCAsDLpHCSlKZLMO+QIUpE7iifZsie1F\nmFGQwbKbruKB732Mm794W1QHjZhWPYLAFdX6PeMe3njiVd555k1SKgsNv69Kz+bBB+5g0VV1XH/r\nNXz28x+lb5ouSqwQZYmsuTOJz5qsxFVVxecLMjM5B/fIuAYWH/cQDAQZGhzm5b+8wmD3AAe3GhOe\nzMLMmDZMB/ZMQiEsNosmV5GQhCAIzFlZQ1F1seFvJsSPkx0JWnETNqaf6Oy88KfNOgHV/a/uYeeL\n2xlzu5jA7gVDIRRVJT0hAWfe5ceJB17TqwyJskR8YhwVRVnMLc+ntjSfZLs+iVIUlRee3RwTe5OT\nmYV1Ch4v6A/SOcV2y+/18d6ftU7hjMw8bXRJOHmxmREQuNDfQc/oAN6AT+vaRK2hSQ4nifZ4ZtZN\nr6WVEWOkONA9ECEjHHg1tmSIqigEPd6oEf3kmL5/dIhQMBQZJwqigCyL2t4jS1imfPbWvk4CoSDn\nDpyNjKH9Xh+uGMK34lT2efQxqSpvv2aEhcyfUcL9K1azoHRyOiCJmiaJy+vBFcZpt529SEcUlnK4\nrYeeKeKyoiRSddVsTFOS7guNzfz6pc2RNWTyoDRiR3xCPF9/7EuUhycUWcVGQlv3FBHuO+6/lTjL\n5R1FLhf/dAlXrA6X0xmP3WHn+//9HZatWkxJWTF3PXAbX/7O53WjCoANm9bG9Ju60NjCz37wKz77\n4JcNjusA6zetZe7aecQlGhOoXS9uR1UUui508ufvPcvJHbHxMQ6nph0UHRNg3OgIBYOMXugHn4Jn\n3IN73IN7zI17zM1Pvvlz3vv7Ntxjbl0VVhXFkMzMzqCqRk/7D/oDdA1FM+MEiiqLME3ZuA/uO0Ig\n3A41WUyah5dkIiV+MiF555k3cQ2N0XTSuBnkleXjcGp+UyvXXYUoipjsVkxWM7LNjGQ1I8kSazau\njPkdAaTHWLDHuvqRgypffewL2lhrSjz+37+no82IFXryV88wOqxnUwX9QUoz8zGFuyZKIEiCzaHX\n7RE0S5IJkCZAfHI8qYXp7I+hBL5y+WLDY4NTFuORs22sqKjk46uvZlauvlsqyiKmcNdSUVV+85tn\nmbVcT4CIS4zjxs/dbBjlALyxxTgOsjvsfObrn8aZm0Zxhl6AVAkEORalqN95oF7XdTtxsYURjxvZ\nZkYOXwcAZdUzJ5OuKTFVCTs6QoEQP/veL7RRhsfLf/zrTzh28DgBt2YArgRCoChkJqYgR7ojakTb\nKSM+OdJtnjiYQDDIC/v2RBZMp9lEYVSyEVRCjHpdkc16AuTtHPLRdfgcHY3tXDzTajjWlXeu4a5v\n3sv8DQtJTE8iv7xAMxwP4z+UQIyES9LGidkzsnXJWayo33eGl3+9hVAMQH2R1cmXvvU5PvLxO3E1\ndho6oaIkYk9NwJoYhznOhmw1Y09LJG9JFfMeuoGiNfPImFOCzx+grWeQI2cvcvJ8J4EhH6nxWtIa\nCoXwur24x9xs+eurvPz4SwZxZc0Dc70hgQ4Ggxw9eEL3PFucjVsevIl7/+0BVt65JtJ5DXr9DLd0\n07HvNEp7L4RZlAUJGZEN3zOusfN6ui6xa9teVFVl3yt72P/aPjx+L0El6rsO4yxNgkxCvlGIdyJ6\nWrtpPWPEVy27fRVZOanYrWZSEuKYkRa1gYaxVvUnzzE+pu/8yqLE/OVzY5rLTx0r7tmym7GwI4VF\nNlMcLurMVjOS2RSTWR89Ly9Iy0YAyi6TcNmdDsM+pCoqfR19XKxvpbslBiFCVbXOugpJtrDuVpj1\ni6riD/oZ93noHR9GFAUNPyWKiJLE3IU1EWWAiQiEglzs05KNHc+/T39HH51NnQiy/vNZzTLqmHta\ni7oTB07Q22+EbaxeexVZKcmsnFVFVpJ23WqFnpZ0XRrsi3xv+17ZQygYou1oI2ePN+GfUnSJJoma\nVcbC4Xe/+ANulydmpzQvMYVvPfJZauZPrsHZJcYOV09rj24fdg+PU55ZhBRjj/og8b+hw/W/GlNV\n3wGcCVqlkpCYwOe/9unL/r0kSXz6ix/nkYe/HRNXEkuEMCM7nTlzqxBFkaU3XcVbf9iq+31vWy9/\n/+VmLta3TstOyyjMZNOnb+D0rpPsn1J9ndtfz7yr60jNScPn9vLq43+no7GdwvQc6jv0mlm9IwOR\n29Pr8mJz2hFFgVmz9fP+1RtWRCo1JSzmeGl4gPLsosh4pnbjIgb3ntZZONS3txMKBJEtZo2QYLOQ\nYU/SJTnjw+Ns/e0r9E+RthAEmLNmkgVzw23Xag7qigaSn2DsLFw6P4K7ixWOjCTsqQk69WKA3lMX\nmL2ylvUbVrF1q74qcns8fP0z/8ojj34hAojet+sg+3Ye1D1PRSXFkRDp2KGqKCGFpHgHKY6EKHam\ntmn0jw2RFB6V1Kyey7a3dxmuG2dCPCs3reb8Zn23ZKilS8MfyBJBX4CesCdiosPBdfPqqJtRyp7W\n87T29Ro2tsH+Ibbt3cPGu9dy4WgjzpQEFt+wFEeCMeHv7xvgaAwQ/AMP3UNyShLK3DKKj57WyXIo\nQYWj+4+jKAr+MQ+9URuHLxBgb+M5bSQZNRqqqZvN1x79Is/89jlef/lNvOMe3fUuSdro88ZbrqXr\nxHn2ntEXLp3t3fz+l8/Q3dnDudMNBtN1SRRZUFTCqCuAZDahhJTIOC3B6qAoI4OOgX4ksyaqqfiD\n+INBXti/h9sXLyM7KZmc9EQ8Pj+XBscY9oxNMulUTeQyKc5BSlw8Le8f5Xz/CKqihEkP2vlOSE2g\n+ioj09ceb2fV9cvY7fZSP0V9XRQFKhZUsPCGZaTmphEKhrhwvImT24/REcN4HGB0YJTDvUOkx9ux\nW8wEQiECwRDn23pp7OgjMS0RobXbkNhm11WQH+P4IufO7eXgnpOcrb+oFzdWoTQjn4Hx4Ui3T1EU\nXGMudu7fT22hnvY+7+r5MXWOTh/XyCLRYXPYWHPDamRZxjMwylBzJ0PN3Yx19OmxV4lxdPQOk2iL\nJ8kez5B7DFXRikqLzcKLz21BHAly9B2Nlj/mdUeSrIlwmG2cae6m9jK6ZVO7W6Cd11lLqxkryKD+\nhe0IgsDcGUWc7myJiDsDMbFkSQ4nZXUVjPSNGEZ1radbWHG79nNHYzsntumxSPmpmfR5hiLEENls\n0hh+upMDCFr3Ly0+iZzSXOISpxcMBm2sONWi7tLFSzTEwNSaLCZ8Y+5I8i6JEom2eIbck4WogMB4\ncBxXwB0peCZU+2++83oSkxJ4/80dWGyWyAj0Yn8XeSmZWDDzxhOvkluWhyBq9jkT75UQ9tDtO9Oq\nczuZiFefe8XAeSnMzGTR3RvwDI7S+MpuSrOyI6QrWRQIhlR6RwYpSM5EspjobGzn55/4UcxRniDA\nzPnlxE8Zi/f3DUT8kUWzrK3pioogwNKyChaVljF8rAmlZmYEKpCQlogtzoYnqmMXCobobbsU6X61\nnm4h3uZgQUk1Lb0f3vP3n67DNd1I8cNEbn4O93/qng/8/A2b1kY2xPIFFaTHqK5az7RMm2yVL6zg\nti/fQVxiPLVr50eMnCdCBfb+fTfjw+O88JPnIy3S7MQ0LLLZ8NzJn1UCXj8FRXnEO/XfwYIl8yN2\nEBNdgpCqRKQuJpzbs+dPgodHPW7aBvpQgqFIq99kNlFTYxTqbK1vJTSl+rbYLDprmszsDBZfZaTL\nxrJCig5BEGJ2ufrC0hWf+tonyE41noPhwRF+8O0f8/qWtxgZHuXJKaNEAFmUKU3Lj2wuEyOoouxU\naooLJ1lF4fW8f1Qb95qtZioWzuLt142+mqs3rCClKNugCaQEQgyHway9p5sNmkiZKcn84Hc/4F9/\n+HVy8o3t6qMHjtPW18XNX7ydtfetj5lsAbz/5g5DJyQlLZmrVmug+uTSXEoK8gzV9dDAEC1NrYbu\n1uELTXj8/siCC9r3cfeDtyNJEh99+F4++pl7scXbkGTNUshsNVNcXswPH/8+H3n4Hu7/lwfISJyS\nVCsq77+xLWayJQgCG2vnUVGQg1WSCHr9uu9rRl4aN9YtJD05CdEkI5tNEcV7f0DrdHUPDWk4odx0\nEuJtDPtdEQ880MYXSTZNKXxo1E1vZz8Bt4+Ay0vQ60cJBKlZVo13aAzv8Bj+cQ9Bn9alOf2Xdznz\nt/dJEkXmzMwjPSmeZKedouwUltaVc82nb4gkKJIsMXN+Gbd+5U4+8p37mTFHbwcU+cyiSFffMOfb\ne2ntGqCzd5hLg6OcP9LAoa37Od7Qjj8K2yKZTWRF3a+xYvvz79N0rMnQaQCwiiYK04xVev/YMH1R\nMjCJaYksvNbYsYVJKxiVCaHgEOVFhbRvP87R373K8T+8wcUdJxht7zWsh9lpiZjCx1WYHAZSh5/i\n8/i4eP4irz7/RuT5Yx4jyyvObCOkqmz5xUsMxeia9LZdimlHVLdRs0RK64v6XgAAIABJREFULMwi\nM7xGpSbGUZg60fmdPoHLTEsnqyiLgspCw7OGLg0x3DdMwOfnnWfeNPyt2WzmoS99PPJ/ySwbOunx\nVjvFqTnUFJYhCAIzpwHLR0esseLx94/E7G4tWb+ABeUF1MzMpSQvjZy0REoyM5ElEZOssQJNskTr\nYBTTUdDGsClpyZSUFXPrPTciyRImsylioh1SlEhSMdgzyMkdWuczumPkCrh5cf9efvarpwxs1MH+\nIY6fME6TVq9dhiiJONISmX3veh3WVwwzFkd9LjweL0FvQDMNnwY3JUgSc9caPTSjPY4FBGSzCZvF\nzJ1LlrOkrEJz5RgepysK3ykIQmwcVxSTfYK5Gm9zMLvg8vdqrPinS7hijRTjnZevBmLFhk1r+eqj\nX7iiea3ZYtaB0AVR5KpbVn6g95BkiZV3rGb9g9cghy9Si81C3UajrUrziQv85Qd/1NHSRVGkMM24\nEUdHwB+gqLDAeNxmU2TDjb4YO8NjxVlLKhFFkfTq4kiicLajI1JRBt0+Ah4fqcmJ3Pm5O3Sj0GgF\n9OgonVdmYBJ+9OH7yMqZHGfdcPt1kZn45SJtVqFBxDXg8jLc0o3ZYubTX/w4NpN+tKYoCl6Pl2d+\n82e+9tnvGK4VFZWZGfkR9WJVUQgFgqQkOIizW6jIzQ1Xd1H0d68LX8BP5dJq9u87zNCAfpEXRIF1\n165GlESSYtyMg+c7UEIK3YeNINb0yiLMDiuza6v45ve/giPObnjOc394gcazRiPYiQgGg7y3dbvh\n8bUbV0VYuqIkkldXQX6qvmOhBIIc2H6A3lOTXVSXz8vBC+eRwma5E3HVqiU6w/Vrb9rAt//ja1TN\nq6SovIi7PnY7P/r195kxU0uU0ysKuOv6jYYkLxQIGpItURS4fv4CKnPzEQWB0oIMRCYB3tlpCWQk\nO7FbLHzru1+OSIlIFnMksfAFAvxt326aeroxxVu55at3M+wLb9hRSZdFtHJpYJSLUSrTqqol3hZB\nwH2qmRNPb+XoE69x+PEtHPzFS9S/uJ3RqPsyzmZhZkEGs4qzyUlPImv2DB37KTpSc9O47tM3sO7+\nDQY4AYKgT2qjzksoEMLjC3CqqRNfOOnKmjcT02UAyCP9I5w7oIn0inKM1w2GKErLxhpDvbuxqzVC\nLljzkasj61V0jPUOs/utXQTcXgLjmjBv0OMnI2Si57jR7HhqmE0ys4qyMcsSCda4SQzVBL4upNB8\nqYOQEor4NGpMv8nXiLPYECQR16iLl37yPMNT6P8HXjd2t5zJTiqi/PoKV9Zq64sgsLi8XCump8+3\nmLe4BkEUscfbySg0eoO2nm5h98s7YxpTL75hKVetW8q9n7gLq82CIAoU5GWTn5xBVdYMlhXOZl5u\nOQUJ6ciiNsYrnXvl9TE9hkfpcK9RyiclMxl/k2Y/FWe3kpmSQFFOKgvKSiLJy0REJ8himDS1KGya\nnpqWEmGVm23mSAOibaCHc50tOqyrKEsoqsKF/k7eOn2U5ks9tPb08OPv/oy/PP1C5H22/uVVTRg2\nKhxWC2vu2Bj5v2Q2sfT+a0lPn4QKSJI2Dh1wj2iuCjFEekG77bNLc8iMwZKMTrgmjrmuupK8VD3z\ntW3nCQ7/ejP1L2yjdfsx4mwWna4dTOK4Av6ADk/2j8Q/30hxGgzXPxLzF81l3sJazpw4y2ub39TG\nMlPO3er1KwwbYV55PkXVxZc1ds0syuLqBzaSnGlUs569ooZj7x4xqM3HEhzMS82ibagHn1/TG5pq\noQLgH4gNSly1fjlvbHlLRzkecY8z7nVTsVjTb5LMJjJqSuk8UE99h16TTA0pFNkTubBlN+Vl+Rw7\nUB8WWzQegyAKzF5jFNVzJsTzk9/+gP5LPQiimYys6bEX0WGyW0kuyWGgUd+W7T3dTHJJDnNXzmXd\nsuW8u2eXzq8t4NPYU1N9LQFmFBaSqGiA0ZA/GJEJyAufo3ibjYyEBPrcLh2tt22oh/H9u2moP294\nzfkLa0lL127S5NJcHfAcYKipk4GCDB37byKy5k/iNNLSU/nMVz7Fjx79qe45oVCIn/3Hr/jRr79P\nXJwRG3TkwHGGBvULrSiJrFqvZ6pmzC6hJDMrYkILgAp7tu6kcMnkc/c1niMQCmKyTOI1ZJPM7fcZ\nLVhq5s/WYRyiQxAEFt62jlPH63nvZJQExZRLRxQFbqxbpJM0iLNZmFdRwPCYG6vFRHwYO5JYmElB\nTRn/9sOv89hX/4OOti5kq1nDpgQVfIEAm48cwHH+DOUdTYTEqIUxvLEk2eI5365X+Z+IgqyUy1rs\nxAp7WiI5C2PYJEWFIAhULqkipySHt556Q9eFEGXZQEOPbgx5fAFOne+kprKA7PmXNyU+/v6RyGYm\nSuEkIpyvJMTbyEh2kr+4itC7EtsP6hMTt9/Lxb5OrrtxA3nl+YbXDnh8vPubFwxFjCSKFKdfHsAe\nHfEOKzVleZxt6aYwOYtB92hkpAbgCfh47/QkgF8SRURR0NTNVYiz2CPkhPHhcf702NPMWlJJ7dr5\nhPxBLhw3Fid1GxfqSCaiLFF67WKK19WhhELsfKCBpjajawBo+K0l6yflVwqriuhp1YtQH3v3cMxk\nK3tGNrXhNXHTLRvZeMM6BASCbi+bv/s0bd2T8BVV1YqRwupiwwQkVsRiKhpDJTspznB9AZQvmUPy\nof0MjhjdAmBynLh4+WRz4KY7ruO9rdvxeX1YHdaI1VbbQDcj7jFmF8zEZrbi9ns52XWeUa8bc9T3\nrgRCbP7rqwwODPHJzz/Ie2/vnPq2LKydg2OKrJEoSVx1zUo2P/d3FH8QURARBJV+1whZztjSIKIk\nYnZYWXPvesPvFEWJSYxYdsNqgkdaDGuU3+XF7+phuLUHX7jQmCCygZZwqapKR0P7tPI3HzT+qTpc\niqIwNmbEcH3YkWJ0CIJAVc0svv7Yl/j573/E+k1rtVGcoHkf3vPR22P+3VW3rjB0YEA70Utvuorb\nH7kzZrIF2ga26PqlVzw22Sxz8+dv5c6P3YY93o493qFzLwdtnQoMeGKCRItmFJAQZ0xGx0UfiWmT\n456suTMZcI9HJACiY1ZuHr5RF1aXhwS7ddpqwpnsjAkqBJBlmeqaig+cbE1EepWR3DB0oRO/y4sg\nitz68K0sLptDcpyeYehz+wzjDEecnVxbKmowpKlyh5OtlAQHcVFdg7KiAszWsHWULCHLEj3jAzGT\nLYD1109qiSUWZhmYagGPj5YpNlAASTOysafoF5b5i2ojFOTo6O8d4Nc/eSLmyPqdGCPOusVzSU7R\n4yVMdgvzlxlb6539/bh9GiajfaCf460thu7WppvXk5H54c4dgC0pnk13XEdBWmzPM1mSuHXhEmpr\nqyhYWaN7T5MskZYUH0m2BEGgMAx8TUhM4F9/+A2y87I0eRerBZM9/M9qwe8PcPLo6Yicy0QkOuKw\nWmN3iOLtFpKcxg7jdGFNcDBj/QJm37v+sl2n6EhMT+K2R+5k8aYlkbVDk/24vB+o1x/gbHsvninO\nFNHhc3s5vTvKwkgQkGSJ9OR46qoKqZqRQ1pSPFa/n6/89MvMrq00MF0vDnRTsSK2IXzXwbOcuWAs\nMAvT07GYYtvrAFicdtIqiyhaM4/qe9Yx9xObsFrNVJfkUpqdRcqEenuMa9sUHr8JCJhkCVEUcJis\num5iMBDk5I4TPPudJ9n8c6P0SHxSPLOWVBoeB228Z7JZuOWeG6Y9/rSkFHKiOteFVUaoQ6xkSzbJ\nrHtgow6bKcthxp/TQfXSagPBJBQIkj/NGjo1HDGA81MjPs6ONUaylTQjm+J1dSy7ZgWiWTZ09wRJ\nRBTFyDhxIhISE9h0q9Z9msD3TsSIZ5z950/S1NPG/vMnGfW6DYpASkiDqux4Zzdf+dQ3GRya8r0J\ncM2d18b8LHWL5yKbTUgWLRGUZZEhzxihKFKFWZZwOqwUzSqg7vol3P+9j5MRoxPY1tJuKBxMZhM1\nS+eRWWO0PoqOOLsFQYCQf1KuxTXqYnRgZFpdtg8T/1QJl9vlNmz4VrsV02Vu+A8TWTmZfOwz9/GH\nFx/nmZd/x9cf+xKWaRbo5MwUA84hNTeNu795L3UbFhosWKZGxcIKkqZJyABscTZu/dIdFFYVsfGG\ndVjDF7fJYtLJCsTbHJgkmd0v7TBYZAR8AVLMRv2Yjv5LBIOTN6I5zkaPTTXceNnJySSFHekFQaAk\nLx15Gup75bLqD90duFIkFGYarFFURaXr0Fl8Y25SclJZfvNK5hZVkJcyeWMpioI/Sg9GVVXmlJTj\n6R+LiPtNRN6Uc7A47PAum2RsDhtWhy2mXRNAflEu1TWTi7lklkkoNLavgx6jNs103Yq7P3q7bpGb\niMP7jvLGlrd0j/V0XTK0xgHWXbM65mtXrVlActyURVrVfCNPtLbw/N5dKKqqG3NZbRbu+egtMV/v\ng0TekipuXH6VYVM2yTK3LlrC7HnVzLp9FTl1FVTcutKgwTYRGXNmYE+dLBISkxL41//8Olm52nnX\nwLrGa9NkNkXG3CnxSUgWMya7RXNoiLqWCz9gd8uW4qT02sXUfOw6MmbPuKIUxNQQJYmF1y3hzq/f\nQ8XCWRRUFlI6dybZaQkUZCZTnJNqvMcE8Hj8vPiT53UekdFxevdJg/mxyWahKDsVa9R4cLilh5DX\nz2e+9hBxzjhscTbMFhNmqxmz3cIfn/yrIbEPeHx0H23kfLeeAg8wM0sPeRAEAWduGgUr5lDz4Ebm\nfvJ6Sq9ZpMlVZKdiTYwjY04JoihQmp/OVRWzIp246DBbTDqGuYBAZmISjjhbpFsZHSrEVPaev2EB\nUozxanRcdd1y0pONopagiUlHX1cZBRkfqAO19KarSJpGRwugeEUNWWn6QtEiy3jOtDIci2UYI2Ip\nzgMaESgQJN1mNlzTZoeVkg2LEASBeYtqkc0mTDaLlvSHk/8Ju7KJcWJ03HLnDREbm+h7CzTmYnNv\nh8YsFWJIxERBVdqa9dMUgNK8XGbMjY1fKy2fgTPRiWTSpJIEBGRJJCnZQm1ZHouri1m+rJqZ19by\n2pE9/Or3f+BXP/sdXq+xSDkRY80sr5yJ2Wwib2k15vjpCy9RFCMFerR7RVdTl9F54DL2btOF9Oij\nj37oP/p/KR5ta+0xaCAlpyRxzY3GtuH/SQiCgOkyonoTkVOaS3JmCg6nnZpVtay8Y/UVq47Ie4gi\ncQmOmKKLzhQnt375DtJyta6C2WJmfNxFY30TAppq7oTgXmZiGqnxibjH3MQnO3U34bmDZ+k800Zb\nf3dkPRMQEE0ixSVFEaNsj9vDU797Dn8oGKYLa/osC0tnkpU0mZDIkojZJDEwZfQpyhIbP3W9jjY8\nNRwOC273h1PfFUSBgNvHWKfe03Ksq5/uww10H2nAosDQ0BjxJgcWs5mBMW28poQUJFnSGIjmOBL9\nVsOinpLgICfc6TPZrcxYN5+SxbN5Y8vbMQUNoyMnP5svfvOzJCTqE1o1GGKwaXorG4C4jGTyr5od\nc4MXRZGq2lnseGc3gYB+Az157DR5Bbnk5mtV8JbnXzN03jKy07n/k3fHfG2zw0bjgdO09+htQDoG\n+znX2akZkJtlXefjxjs3sXz1og997iKfRxJJSE3C1ueiufcSgWCQVKeTG+cvpGp+NeU3LY+05q2J\ncaSU5jLc0q3hvMIhW82U3bDMQN+22W0sXDqfU8frGZlaLUeFZJIIBUKUZORjNVs0+QpJQjTJSCaZ\n3Jm5zFszD1ESkS1mJKspzNDUuiuCJBCfk0bhqlqKVs/DkZ4Us7v9YSIuMY6S2lIqFs6ibGEFas8g\ndlEk3mElMd5O//B4hE2o2XdJ+Nw+mk80UTJ3pq5zFwqG2Pr713VFBkD18hriRQElENSt/Rang5yK\nIlzjLpoampHCnRdBEOjp6iUnL5v8wtzI8zv2neHA/qOcvNiqe31BFLhl/VpSirJJLs0js7aUGVfX\nkVlbijMnDZPdGvM6dKQn0X2sEVSV9MQELg0PMzAe7jgIgpb8WS2EAgGiFSxXVlWz8vqV9HQNGJLL\nWOFIcHD1AxuvmBQLgoDf4+f4MaPJ+b2fvIvcohzdc/s7+uifsiZFR05JDqvvXnvZBN5ks2D2+Rnp\nGcQXCBJns1Can47FJNN/7iK25HjsqYmXXTeHe4cmMUNhMd6QP0DQF8BmlinKTjUcQ/nNy7GHbXaS\nU5N57WVN6V6UpYhQ8sTf3P+pe0hJ0xekoiiyaFkdjngHp4/VI0oioSnXV+Qzmk1h5t+U70FVded1\nIu6860ZK5sQGmouiSGd7F60XLmr3pSighBQsJhOV+flkVBfBzEz++78ejxh593T14nZ5mLtAb2f0\nwp8209ujt/Bad+1qyitnIplkkktyNOJYIEQohpCrxxdgzOVFVdTI9+X3+OiNQBXCkBWvn3X3rnss\n5geaJv6pMFyjMebNU9l5/zdDEATK6sovq5lyuZhRW0peWb5OODU1J5UbP3+rIXG79qYNvLHlbULB\nkKbwLEmEQiGSoxSQ972ym5nzyzBbzSiKwpndJzHLJtKdyfSMaCBh2SwjIPD+WztYsGQewWCQn/7g\nlwwNDiOgWe5IJhkBWLRkPv5uPRYqLSmewVEX/cOuyDikYkkVCanTyzz8n0R6dTGdB8/G/F3IF8DV\nM0BBYhzHeofIjkvGUWzlxMVGAqEgHpcHh8VGkdPYVgatuyVKItl15WQvmBUhD8yZVzWtv1tWTia3\n3H0DS1csiincmjQjO2bFHh3ZC2J7pE1ERmY6n/7ix/jJ9/UK+qqi8vP//DX2732Ziqoytr9jFO1c\nu3FVbPHRcCxet4Q9x/S2Pp4JvJqgZxjl5Gez6ZZrpv8gHzCSSnKYs3QumYlJePx+7BYLqaW5zNy0\n1DBOsyU7mX3vetp2naC/oQ1rQhwzNizENE0yn5ySxH/+4jH27T7IkQPHOX74JK4pOkoCAsUzC0l3\nphiSEgSBlfesizl6+L8VgiCQWVtKc9hbNc5uoaokh9NNnQQVRXdORvpHeOWXL3PbI3dF4AVNRxsN\nEgECMHftPIbrW+mZUtT11bfizEtnzcI6dmzdwfDIqJaEhkfJf/jNn5gzv5q4OAcBj48zOw7z5vGj\nutcQTRJzFsxh0cev/9Cf1xxnI2P2DHqOacXCproFePftpmtoEJPdiiiKWGQZp92Ew2LFabNRlp1D\ncUYmeTUzuGdpFYfePMiZPaeM5zMq5m9YYCDxTBc33nc9Lzy3GZdnEg/rsNmYt8yo31RYXcy5adYk\n2Syz7v4N05IoomPGujrcvcN4p5w7VVFpfHUvQa+ftHVGN46JSC/I1Ig//gBKUD/dyM9MNqwxuYsq\ndf6TZrOJqppZHI1h7p6SlkxpuRHSAdr1eu2N6yktm8FPf/BLesPSHtEhSiKyWcZutrBp3gJ6R4d5\n5+TxaZs+8XY7K24yWr1FR93ieWx7S8N9iWGvxXbXCFX3Xg02M488/G3DBGz7O7u48/5bIzhsvz/A\nuTONhteeM3dylG5NjGfGeq2LpwRDeAZHcfcN07pd0w102q1MlNRKIIRkEXV7uJb4BomPYeF1pfin\n6nCdOdlosIAoKM6PsPH+/xaCIFBSW4rP7dWAtUurWfuRq7HHaGna7DZcY66IWrcoiZhUiZnZhRGN\nrIAvwEj/ME3HzvP+n96J0KYlSaI7LAcxoQx9qaeX1RtW8MzvnouZXMxbVMvtn7+X1IoC7KkJOPPS\nyJg9g5wFs6jZuBiTw4rJYqZicSXLbll+xbb9P9LhAq0SHL7Yg/8yXncmWUISRQaHXVglM/np2dhM\nFtKdycxIykYWjIlRbnois5ZqHZaUmXm6jT8pJYltUwCdWbmZPPjQR/j45+6naEbBtEmNZJIZaeud\nlrFlcdopXld3xQ5Jbn4OY6PjNDXocQGqonJgz2Hcbo9BoFeSJT77yKemxSkBZBRk88pfjewg0He3\nSitm8I3vfYV4Z9w/fO4mQhAEkktyMFktOBLiyF0wi/xl1dOO3UVZImlGDjkLZpExp8QwVjY8XxTJ\nL8xj0bI6Nt2ykdq6OSSlJOL1eAn4AxQU5/PZrz5EcWUxjVN0lErnzowAm/+/DFuyk55j5yO4ELNJ\nJslpZ8QXNOTu7lE3g90DzJynsdnefuZNA+FmxpwS5qysxeSw0XuiSbfR+cc9XDrexEhzN/EmC2fb\n21FDSlgzTsTv8zM2Os78RXNp3nGMJ/72MuPRoxkBZKuFux68jfzCy7O8pwt7WiI9RxtB1bB8cwqK\nqC0qZt26FayoqqYmJYvaomKq8vIpzcomKS4OySxTuGoeZpuFwsoiZq+Ygy3OxlDPoCHxik+K5+r7\nN1wR2jERkiSRlZXB/l0HUVQVWZL4xOcepKzayBh0JDg4+nbsgmz5rStj4rxivqdJJqU8n5HWHgIx\n8HlDzV2IgvD/tHfn4XFWV57Hv6UqSSWVqrTvuyX7yrYs25Kx5d2Wt2AWQ3BICMGNG0IyJgkQZyAL\nkHRI0pM8QzLT/SRPd6ZJTximJwndyWQINE3IQhKWAAlgY+KLbQw2Nl6xJFvyIkuaP6okVKoqqSRb\n1KLf5x+XSlWvr/W6Xp333nPPIb0wdEa1v7+fjr3vsP3pV0P7bGakhcxuecsKqL+0NeQ4XV3dvPR8\n8A0YQNu6ZRE3xAzIL8xj+eol7N93gCOHjgxWzHc4HLgz3CxeuZAtn9iEq/00RVk+inzZ7Dp0MGwu\natvSVlrDNIgeqqAwn1/87PHBWmmOQH/KOa1zeeiBH7N395sh7+k93xuUi/ba9p2DQdsAX7aXj938\nkbA3wY6UFNI8GXiKcuk730vn/iO4nCkcCOyO7e8P3BANth7q53yg2n5JfjYLrl4yphmuuAq4/vz8\nq7z4XHBhuWnT65m/ODQZOFE4XU5qm+poXNpEpaka8Y5s1pyZtJ/o4PjR49TUVbGgaQ49ncF9uI4f\nPM7xg8eClsQy0twcPHGEPvoHc9L6+/vZ9tKrvPKn0PXstPRUbv/CFrJzsknNSCerJB9feSGZBTmk\nezNxpadS2VDFjIUzqWyoHjXYgvEHXOBfgjj6auQ6Z+CfFejsOs2Zsz04+vrJ8WbjcabhGBZXOFMc\n1FeX8IHbNlI2ryGoH+WAgqJ8yqvK6Gw/SU1dFRuv38DNn/orakYItIY6f+Yc7cN2Mg2oXNSIL0xB\nyXBmzZ3Jnl17OXQweAmw93xv2FIRi5a3snz1yBctl8vFjhe2c2jYlLr/l6g/52PF2qVsvfvTeAK7\nIi804AL/xdFbXkD+1Eo8hTkXPd9vwECyb+PsGaxZ38ZV117Oqg+sICc3m7ySPDKzPYMFiouri1l/\nyxVhSyC831KcTv8F/e33dlBm5WSxcNM6dr+8O2SJ+8Thd+k9fx6ny8kLj4e25Vm9aS2+PB9pHjcd\nbxzgbIT2KvleL0c623n3lH+Wpa/Xv7z05p63MA31PPS9h9h3NPj/Skqqk4XLW/nwpmvGfR5d6an0\ndJ3h1JD+jWkuF70d3fScjDDWaZUUDNlB6Up1UVZXzuwVc8kvK6Cr/RTdnV0UVBSy/pYr8OaG72Eb\nSXVdFes2rMFMn8qNWz7G3AWzw74uNS2VN3fsDZlVrJhawcrrVo3pZ+JMS6WgoZqTB4+F3cn87t53\nOPTKbvp6esnMz8aZ6uLcqdPs+sUzHH1lN4ePdw6W8xhQX1lI5pCbrox8Hw0fXEaqO/Ra5/N5w3ap\nCLecGE56ehqLV7SS7naz6/U3SHGm4Mvx8vHbNnPdjR8ip6yQkuZpuLOz8PQ6KMv0sevQwaAepE5n\nCrfd/Wl8+SOvkjhdTvbs2svB/cE5bju2/YU3doVuGhtw/Nhx1lzWhsPh4MlHfxOShtHSOjdoN2Yk\nmfk+3vnz6zgdDo68e3Lw3+AI9DsGf17XQMmkmrJ8mtYvSOAlxTBFT33Z4ysJkYgGGnDf8pnNOBwO\n2o+c4MGv/HPYmlhDORwOynKLeLszeDv8vr2hlXAdKQ5u/8Kt475znQhZxXk033IlR197k+6j7XQf\n7+D08c6gvnkOh4OplcW8ZPfR29dPT/fZkOPkZ3uory6m+YZ1eMvCbycesGjZAhZF8SEMJ29qBW8O\nqzgN4ExPpWhW+Gn6cFwuF1u/9Gm+9sVvRdwlOdTay8Inyw/XunoRL7/yWlBSpzPQiHjTxz/q374+\nQQFRrDUtm03D/Aa6O7vJnsDAbzwqF82k91wPx1/fT0ZuFrWrWsgsyOHqz2zk4f/6o5Cg68X/eIHX\nXwzNAS2uKQkq0Fgxt56Od54Ped2A1bPm8NbRo5w7fx76+jl/+iyujHS+ec/9IcuzOKCsqpwtn735\ngn925Qumc3jb7og7n4fKzM+mJkxfR/BfFwdSO/r6+qK6KYokLz+XpatH30E+Z+VcHh+S3J7mTmN1\nlEuJw7ncaUzfuILXH3maE3tCNyb0dJ1h/9PbOfDcDvIGchwDOWzF+T72DQlas7MyyPN5/GV1plaQ\nP60SX2VRxDy2opJCpk2vD7qBK68qi7icGE5KSgpXf+QKVqxdysH971BTVx1USsmZ6qK4qY6iWVOo\n2XeY4vpKHvrpIxzp6CDV5eLDV6+nYlpoLclwLlnYzAvPBO/6PnYktDXQUPv2vs2unXuYNr2ebS+F\nTjA0NYffmTtcaqabwhk1HNn+Bj6PmzMDBcXPnScl1Ul/X/9gCY5UlzNo93u04irgCltlfpw1uBLZ\nwIUupyiX2Svm8lKYsgPDzZxuOPxy+H5WQ/31lk3Ma42cNxAraVkZlA+pwNzf18/ZzlMcfe0t9j/t\nT3Z1p6dSW17A7v3Bd+TpqS7qKgrJz8mi4YPLRg22LpQ7OwtPYQ5dw4oylsyuD6lGP5p0dzqf/+pW\nvnLn13nrjchF9SqqyqIqKAuwYNl8Hvyn/+OvoxNI/PTlZXPHlz5F09zoLj6JLM2dTtoIy66x4khJ\nobatmdq24M9fcU0J6zZfyqPffyTkPZ3HQ/NaW9bMCwqGyufU89qya8AIAAAQ/ElEQVTjL0QMbLwZ\nGSybPpMnt/uXlvr7/H33evpCb+TcGW7u/JvbB7tYXIh0n4eiWXUcfiVyYV+A0hZD1dKmsD3vhruQ\nYGsszPzpdHV28dozr5Lp9bD82pVBpXbGypnqwmxYyp7H/xhSy29AX28fx3YG7+6rLM7FmeLgxMlu\nvF4PzW3NlDZNwVuaH3Xwd8ttm7n/a3/PO28foqi0kFu33jKuYDo3L2fElm0Oh4Oc6hKW3bSBeR9s\nY99f9pBbXEBxXUXE9wzXsmBuUOugaD3x6K8oKStm757QemvRBlwAZfMMR7a/gdfj5kigjmZ/fz99\n5/voG7LzP9ebOa6fYVwFXGGrzF9ADa5ksOCyVv7y3A7OdIXmAKSm+Zf+psyuY3rrDA5/sYPXtoVW\nPB+w4drLWXf5qokc7kXjSHHgzvFSuagRT1EOu37xLL095ynO83G+t48DR04ADoryvFQV5+F0plD3\ngQXkhun4PhFKWqax5/H3ZhVc7jRKW8be6gH8NcS+9PU7uWfrfRw+GL5o5+r1bVF/wHPzcvjE7Tfx\nwHd/yJnTZzEzpnLr526hpCz6Apby/praYlh45bs8+/+eHvF13jwv9XODawll5GQxZc0l7P3VnwZn\nhdOyMsjI85GR5+XYzn3Mqallx9v7BnvW9YebNXfALZ/ZfFFnvytaZ3Bk+56wv0DTsjKoX99KTgw3\nNETicDhoWXMJLWsuuWjHTHGmUH9pK6mZbg6G6UwRaRzlRbnMCeygdYVZNhxNVU0l3/6Hv6Wrq5tM\nT0ZQOY6JkpnrpWHRnDG/z+vLYvpMw2vbI/98auqqeXNYYPXs757HTJ8aspmptKKEgsLwJUHCySzI\nIbu6mK7TwSsovWd7glJexlLTb6i4CrjCVZmfjDNcQ7k9GVy55Wqe+J//TvvRdnJL8qhtrKWmcQrl\nU8uD8qva1i2PGHAtWbmQ627c+H4N+6LKq6+g8fo17Py3pzh7spuKotzBcg8DQUj18jkUNda+b2Mq\napzCuc5ujrz6Buk+D1XLZpMWRf2eSHJys7nnG3dxz2fvC6ksn5aeyrIolkGGWr56CQuWzKO763RI\nkVSJT/PXt3Li0LsRd8iBv8F6uETx4qY68k0lPd1nSfNk4Ex777pQ2FjLjh//mnVzmnnwqV+H7WYB\nsGR+C22XR7dsHa10n4fi2fWDOxYHxzSjhtpV4wsgEpkjxV/gN99UcvDFnbTvPsBIW55TM93UrbuE\nvProZ4nCcbqcCZOeM29hc8SAa+r0Ou7++p1s2XQHXafey4nrOdfD//7BT0JeP54Z/bJ5DbS/eQiX\nM2Uwj2tosOUAcryZEXdWjySuAq7OztAq89kJ8p9kIpXVl/NX990E/f0jTiMvWDyPB777IKe7g5NS\nG+fMYMvWj79v0/ETwVOYw6wb1mF//ntOHjgWNNtTNq8haDny/eBwOKhcPIvKxaGNv8erqKSQu//2\nLu793NeCcmvWrG8L2/ZnNG63G7d77BcFiQ2Hw8HqTevoONoetklxmjuNxhH+v7nS08JuEvGWFmA2\nLKX/p09xSd1U/rgrdNt8aV4un/zif7qwf0AENSub6es5z/Fdb5OR46Vs/vSg5PjJyFtWgLlyCR4X\n7HjyJQ5v2xPUzB2goKGK2tXzou50kCwuWdjMg9//l5DnMz2Z3HbXFjIyM1ixZimP/iy4UHR3V+im\nhKbm8F0IRpJTU0pmvg9vppsTYXbPZ2Wmk+pyUr0s/KaLkcTVb+CwOVwKuAD/xXi0Nft0dzpXfii4\nrlJlTQVb7/7M+zKNPNHSPG5mXttGaYsZLI5XuaiR6uVjn7qOV5XV5Xzt2/fQ1NxIYXEB665YzXWb\nw7efkuTjSnVx+Zar8OaFXvcal8wifRx31QC5taXUX9rKIjOdHE9w8O5OS+OmG64lKz87wrsvzMBS\n2vxPX0PTpnWTPtgaKjPXS82Kucz75AZqV7WQU1tKTm0pDVctZdoViyddsAVQXFpEbX1okv2WrR+n\nqMS/A3z1+pWjHifFmcKMWWO/EXekOChtMXgjlKvJ9XnIKsmjcObYV1Ti6rfwyY4wfRQn+ZLiWF11\n7eVkZGTw8p+2UVFVzsaPbrgoCbDxIsXlpLatmeplswPtXuJnF9rFUl5Zxt3fuDPWw5AY8fg8bLj1\ngzx8/484G9iNm5WTxbxAscbxKpxRw9TuM1zT3cW//fFZ2ru68GZkcNX8VhrXLhz9ABconnaMxhtn\nWiqlzdMobY5uY0yy2/zJj/HVL3xzcOfuR27cyPxF79XTK68sY0ZTw4g5y/XTpgTtphyLwpm15OZ6\ng3aIDsj1ZVK7qmVcv3viJuDq6TkfOiXoYNw/sMnK6XSy/qq1rL9qbayHMqFGawgsksgKKgr52L03\nsuMP2wCYuXgWmb6xLysPVzavgfNnzpGX5aXr7Fk86elUL5uNO/vCjy1ysTQ0Gr734HfY8cpfKKso\noba+JuQ1a9a3jRhwNbWMf0e2M9VF3cKZbN+5b7AFF/gbaNfOaxj3Tvi4Cbg620O3P2d5syI2FhYR\nSWbeXC+tV4xts0Q0qpY0kV1VzMkDR8kqySe7Jv52CYrk5GazeEVrxO/PX9yCL9sbtroBQNOcsedv\nDVW1YAYVjz0XNMtVU1FIzQWksMRNDldHmIArUXZViIgkkuyqYioWNpJTW6qlPklIqamprFy7LOz3\n3Jlu6sdQ3DWctKwMlly7kum1pVSX5DFrajmLr19zQbvR42aGq6NdJSFEREQkOqsuXcHPH3405PkZ\nsxouykax8vnT8VUUcurQu/jKC8kqGb0d0kjGPSJjzHLgJ8Bma+1jYb7fA/wef9mKfmCVtTZiwZGO\njjAzXL7JXfRUREREwispK6apuZFtfw5u6TN7DNXlR+JwOPCVF+Irj64/7mjGFXAZY6YAdwB/GOFl\nJ6y1UVfR6zgRGnCpJISIiIhEsvGjG9j+8o7BbgYer4elqy5+7uPFMN4ZroPA1cAPRnjNmBIDwuVw\naUlRREREImloNNz1lTt44tFf43anc811G8ZVKPr9MK6Ay1p7BsCYEXvHuY0xDwHVwE+ttd8Z6cXh\ncriUNC8iIiIjaZ4/h+b58V8Ae9SAyxhzE3Az/jysgXysL1trfznKW7cCDwUe/84Y85S19s+RXqxd\niiIiIpKsRg24rLUPAA+M9cDW2u8PPDbG/AqYBUQMuDo7TpIyrHJrRWURhYUKuhKFzlXi0rlLbDp/\niUvnbvK4GGUhQnK1jDHT8M+CXW+McQGLgYdHOkj7iY6QLvZ9/U6OHg1f1EziS2GhV+cqQencJTad\nv8Slc5fYxhosj6vwqTFmvTHmN8A64BvGmMcDz99ljFlgrX0d2G+MeR5/aYhfWGtfHOmYYXO4chT5\ni4iISOIbb9L8Y0BI7S1r7TeHPP78WI4ZNodLuxRFREQkCcRNa5+ecz1BXztdTtwZ7hiNRkREROTi\niZuAazifz6seXyIiIpIU4jbg8marrY+IiIgkh7gNuHzZvlgPQUREROSiiNuAy6vG1SIiIpIk4jbg\n0gyXiIiIJIu4DbiUwyUiIiLJIm4DLtXgEhERkWQRvwGXlhRFREQkScRtwKUlRREREUkW8RtwaUlR\nREREkkTcBlzK4RIREZFkEbcBl5YURUREJFnEZcDlznSTmpoa62GIiIiIXBRxGXBpOVFERESSSVwG\nXGrrIyIiIskkPgOubM1wiYiISPKIy4DLp4BLREREkkh8BlzK4RIREZEkEpcBl4qeioiISDKJz4BL\nNbhEREQkicRnwKUZLhEREUkicRlwZStpXkRERJJIXAZcKgshIiIiySQ+Ay4tKYqIiEgSib+AywGe\nrMxYj0JERETkonGN503GGCfwAFAHOIHPWWufGfaa64HbgF7gf1hrfxDNsb3eLJxO53iGJSIiIhKX\nxjvDdQNwylq7FLgZ+M7QbxpjMoF7gDZgJXCHMSYnmgMrf0tERESSzXgDrv8FfDbw+CiQN+z7C4Dn\nrbWnrLVngD8Ai6M5sPK3REREJNmMa0nRWtuLf6kQ4HbgX4a9pAR/IDbgKFAazbF9PhU9FRERkeQy\nasBljLkJ/7JhP+AI/Plla+0vjTG3AnOBK0Y5jCPaAWlJUURERJLNqAGXtfYB/AnyQQKB2GXAhsCM\n11AHCZ7RKgeeHenv+dULP406KJP4VFioYDlR6dwlNp2/xKVzN3k4+vv7x/wmY8wU4EfAskCO1vDv\nu4FtwDygD3gRuMRae/LChisiIiKSeMaVwwXchD9R/jFjzMAy41pgK/Bba+0fjTGfB57AH3B9RcGW\niIiITFbjmuESERERkejFX6V5ERERkSSjgEtERERkgingEhEREZlg402av6iMMd8GWvEn2N9urX0x\nxkOSKBljvgUswd9T879Ya38W4yHJGAV2Fb8KfNVa+2CsxyPRC/Ss/c9AD3CvtfbfYzwkiYIxxgM8\nCOQCafg/e0/EdlQyGmNMI/B/gW9ba79njKnA33knBXgHuMFa2xPp/TGf4TLGLAPqrbWL8BdY/bsY\nD0miZIxZAcwInLtLgf8W2xHJON0DHI/1IGRsjDF5wL3AIuByYENsRyRjcCOw01rbBnwI+O+xHY6M\nJtAj+u+AJ4c8/VXg7621y4E9wF+PdIyYB1zAKvwRI9banUCOMUb9fRLDU/gvFgDtQGagTIgkCGOM\nARqAR2M9Fhmz1cAvrbXd1trD1tpPxnpAErVjQH7gcR7BrfAkPp3BP7HwzpDnVgCPBB4/gv8zGVE8\nBFzD+y4eCzwncc5a22+tPR348mbgMWut6owklvvxN6JXoJx4agCPMebnxpinjDFtsR6QRMda+2Og\n2hizC/gt8LnYjkhGY63ts9aeHfa0Z8gS4hFG6RkdDwHXcLrwJxhjzAZgM/CpWI9FomeMuQF4xlr7\nVuApffYSiwP/7MhV+D9//xzb4Ui0Arl3b1lrp+Jf5flujIckF27U62c8BFwHCZ7RKiN4yk7imDFm\nHfAF4APqJpBwLgM2GGOexT9DebdmSRLKYfwBc7+19g3gpDGmINaDkqgsBv4DwFq7DShTOkZCOmmM\nSQ88Lscfz0QUDwHXE8BGAGNMM3DAWtsV2yFJNIwxPuBbwOXW2o5Yj0fGxlr7EWvtAmvtQuCfgPus\ntb+O9bgkak8AbcYYhzEmH//yxrFYD0qishv/znyMMdXASaVjJKQngWsCj68BHh/pxTEvC2GtfdYY\n8ydjzNNAL3BrrMckUfsw/sTPnwzpqbnJWvt2bIclkvystQeNMf8KPIf/s6cl/cTxj8APjDG/xV9S\n5xOxHY6MJjAhdD9QDfQYYzYC1wM/NMZ8AngL+OFIx1AvRREREZEJFg9LiiIiIiJJTQGXiIiIyART\nwCUiIiIywRRwiYiIiEwwBVwiIiIiE0wBl4iIiMgEU8AlIiIiMsEUcIlIUjPGfMkYUxXrcYjI5KaA\nS0SSljGmBrgPqIntSERkslPAJSLJbD7+tjciIjGl1j4ikpSMMb8BluMPuAZ6fdZaa/fFdGAiMilp\nhktEktW9wMOBx18GPgQcid1wRGQyc8V6ACIiE8Fa+3tjTFvgy6estb+L6YBEZFLTDJeIiIjIBFPA\nJSIiIjLBFHCJiIiITDAFXCIiIiITTAGXiIiIyARTwCUiyaw38Kc7pqMQkUlPAZeIJLO9+Iue3m2M\nucMYMy3WAxKRyUkBl4gks38FHgFagM8DBbEdjohMVmrtIyIiIjLBNMMlIiIiMsEUcImIiIhMMAVc\nIiIiIhNMAZeIiIjIBFPAJSIiIjLBFHCJiIiITDAFXCIiIiITTAGXiIiIyARTwCUiIiIywRRwiYiI\niEyw/w80hiotN+GzQQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75a81f950>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"with sns.cubehelix_palette(5):\n",
" for i in xrange(5):\n",
" path = EM(xinit[i],sigma=0.4,T=10)\n",
" pl.plot(t,path,alpha=0.9,linewidth=5)\n",
"\n",
"pl.title('Trajectories of the Langevin SDE, $\\sigma=0.4$',fontsize=20)\n",
"pl.xlabel('t',fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Changing the $\\sigma$ from $0.1$ to $0.4$ provides random \"kicks\" that are hard enough for the solutions to jump from one equilibrium to the other."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff75a64f2d0>"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAFkCAYAAAD13eXtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXeYJNd5n/tWdZqePLM7s7vYAGARDgASQiBA0iCYAIpJ\nDKJIBYu2KMuUbNlXtnztey0rZ/n6WrJE+tHVpXRl6UoUZVKiGESQYiaRM7BYAHt2sTnM7OSZ7ulc\ndfxHdc90d53u6Z7YM/u9z7PP7p5Kp7p6t37zfd/5fY4xBkEQBEEQBGHjcLd6AoIgCIIgCDsdEVyC\nIAiCIAgbjAguQRAEQRCEDUYElyAIgiAIwgYjgksQBEEQBGGDEcElCIIgCIKwwYjgEgRBEARB2GBE\ncAmCIAiCIGwwIriEbYNS6n8opTyl1KGtnstq2G7zV0p9RCk1ppQqKKX+Q5vH/plSyldKjW7U/IQw\n2+07JghXEtGtnoCwvVBK/QrwKy3u/m2t9X3rePmPA18EJtbxnCGUUr8A/IXW+tw6n3pT5r8eKKWG\ngD8CpoGfAp5ZYf/6z8yUf20KSqmPAP8D+Dmt9X/ZrOt2IBvyHVNKucA/A34EuB7YS/B8LwAPA7+r\ntT5atX/leVRTAGaAI8CXgD/TWqcs17Ida8MAQ1rrhbZvqMNQSnUDj2qtb9vquQgbhwguoV3+J/BC\n3divAzcDHwXmq8Yn1/PCWutnWOHFv1aUUtcAvwE8CKyr4NqM+a8jNwIJ4C+11n/WbMeN/Mza5Irv\nU7YR3zGllAP8HfBe4OvA7wGXgUHgdcCPAj+ilHqn1vo7dYf/JfC58p/jwH7gfuD3gf+klPqw1vpb\nDS5dfWwjFtu8nY5DKXUX8P8Ar97quQgbiwguoS201seAY9VjSqmfIRBcX9Jad3z0ZgVei7y4AZLl\n3zMt7Nspn5mz1RPYobyTQGx9Wmv9I3XbPqGU+ivgq8DvAPfUbT+qtf5s3djvKqXuBj4PfFEpda/W\n+jnLdW3H7hiUUjcB/5UgGlna4ukIm4AILmHDUUr9GfBjwPcA/zdwL/BDWusvl//j/Y/Am4ABYAx4\nHPglrfXxBue5ppK6UkrtIkhxvhe4ClggSHH8ttb6ibrjRwkiMe8C9hCkQ/5f4L9prYtKqW8BbyYQ\nD99WShng2qprXQX8KvAOgpRKqjzX39FaP7TS/QI/XD//du5BKRUFfgb4p8C1BP9+zwGfKe9baPYc\nWr2Hus/hV5VSvwr8qtb61y3ns35mVbs4Sqn/BPwkQXTjIvBxrfV/qztPy89xPWj1e1f1LA8C/6R8\nHweAKeDPgV/UWpuq/d9OEPG9leCz/XT5OseBotb6cLv3rZR6kEDI7Ndaj9cdvx84D3xXa/2W+n8j\n7c6/AbcSPN+v2DZqrb+hlPoAbUQ3tdZPKqU+BDwE/AHBd+iKovzD63sgqL0j+MFF2MFI0bywGVTq\neX6bQOR8FHhRKXUb8G3grvK2jwB/ArwNeKz8MrGdBwCl1CDwGMGL5FPATxAInNuA7yql3lK17xDw\nFPABgjqXnwC+Cfxn4JPl3X6ZQLxA8BL8Qcq1MEqpPcCTBOmTT5fv4f8CFPDN8ou20f3+c+DF+vm3\new/lef8u8BLws8C/JHg5/xLwV6xAG/fwy+X7d8r7faj8u436z+xD1KaSf4MghfQ7wP8G+MB/VUrd\nv8rPYM20+b2rfpY/QJBO+xmClNp/Kt9T5byvB/4euAb4LeAXgRsIPrteyzxave/Ks/0By+38YHl+\nf1E337bn34Qxgu/CB5VScdsOWusvNIhSNURr/QjwXeBepdTV7RwrCNsRiXAJm4UDxLTWP1kZUEq9\nkSCq8Mt1EaIJgoLtjxC8KBrxywQvt3+ktX6q6vi/IBAl/w24ozz8SwQRlrdorR8sj32yXKz6I0qp\n12mtH1RKVYr8v6O1/m7VtX6VICL0j7XWS+JDKfXXgC5f61Ur3O9a7+EfE6RZ/knV8Z9USr0CvFYp\nldRaZ20Xaeceyp9D5Yexl5qldRp9ZuV7dQiiMm+rutYR4FGC4utvrOIzWA9eTXvfO6d8zOu01qXy\nvv8AnAY+SCCEAX4eiBBEbyvfnT9RSn2FIIo2WzePVu/7MwRRoA8Cf1h3jh8E8sDfNLnfVuffiM8C\nvwa8G3hBKfXnBM/u6cr51sC3gDcCrwfO1m3rUkoNNDk2p7XOr/bCSqlbCX4geCvQV7fZAB/QWn9h\ntecXhHpEcAmbhQH+tnpAa/1JlqNLKKV6CV5Ylf94r1nhnD8EvAycqPuPOUvwk/N7lFIDWut5gnTe\nhSqxVeE/EBTwHqc530/wwvxM9aDW+rxS6uvA9ymlrtVany5vCt3vOtxDCdivlLpaa730cmpjVV67\n97BWDPCxurEj5d+vqhpr5zNYM6v43hmCNOiSuCin6yaAfVX7vQUYqxPqAP8FeDthWr3vqfLzeZtS\narfWeqo87/0EQuWzK3w2rc7fitZ6USl1D4Ew+wCBSPlNIKuUehT4AvDnq3w+leiZzT7kVwh+SLBh\nCERgKM3dCkqpdxP8O/gzAoF9Q/lc/4NAvBaBRyzH/X/AnbRWs+iU9/tZy3dCuAIRwSVsJqEXuVLq\nXxHUlSigq2qTocn3UynVT/DS3kc4clA5HuCQUupCeb/6FVRorccI/tNvSPlluAd4uEG9iwa+j2Bl\nX/U9NhUu7dwDwcrQXyMQh8eUUl8mWDH2D1rrk82us8Z7WCs1c9NaZ8vRr2R5Xu1+BuvCKr53pyxj\nOSBWPt8wQdrwWct+j1mu3+59f4qgeP37CdKfEES3IFjNtxJN578S5dqxHyzXAL4HeANB/dtbgfuA\nX1NK/ZDW+mutnK+KGMG92iJlf0zzVPmZNq8FgFLqBoLV1v9Wa/0nVeO3ADdprb/Z6Fit9T9fzTUF\nAURwCZtLjeeOUuo3gF8gSJ/87wQv5zxwC+HUST2VFMDzwL+l8Qq1M1X7rlhU3oBK/U2jJeiVNF5P\n3XjIY6iOdu4BrfXHlVIvlfd9B/B+gqL0h4GfrvZBsrDae1grK33mbX0G68Eqv3e5FU7bXf49tKpT\na51RSnl1w+3e998RLPD4ILWCaw54YIW5wcrzbwmt9SXgE+VfqEA9/xTw74C/Ukpd32akq7LA4pJl\n26kNigz9DkFq/k/qxicIbC4EYUMQwSVsCUqpCPBvCIwQ36i1nq3a1tXwwGUqYiZuSRPWXytH8FP0\n4Cqnmy7/Hip8LlMRKSsJrHpavocKWutvAN9QSiUIVnb9KMGqxW8opW5oYgK5UfewVtr+DNbCOnzv\nGlGpJQqdQymVJEhZVtPWfWut00qpvwfeV45W9hKkEz+htS6uftprQ2utgX+vlBoBPkwgWL7axine\nSfBvc8OfPSxFet9HsHCgnhvZWh85YYcjqxSFrWI3wU/5z1e/9MqsuES8LCwuAjcopXbXby8vt6/s\nWyRIG95Qtlao3u+gClrY3NzkWvPl429WgQlkPbeUf395pXmv9h4sx+a11l/VWv84QZpxN00+t426\nh7Wyls9glazpe9eEKQLRZVtt94/qB1Z5339FkIL7PoLVoNBaOnHVKKXiSqlfVUr97gq7VtLQ3U33\nqj33Bwi+d5/VWs+sdo5togjE75N1c+kmSI029f1SSn1CKfWkUuqJFn5V9nvjxt2OsJ0QwSVsFdOA\nR1CjskR55dCHCX7qTVqOq+bTBC+gf1N3jiHgeaXUl6qGP0+wUuxD1PJzwJ8ClRdcJfVTH6n4DEGE\nrMb4sVwP8lbgSa31hRXmu+p7UErdqZTSSqmPWs5RiZastGJro+6h0WfWKu08x7WyHt+7EOW6uMeB\nq1XgHF45rwP8nw0Oa/e+HyDw6Xo3QS3XWa31w+3OtR3K3m7vAX5WKfWPbfuowN/uwwRpy5YiVWUR\n8icEkcb/uNZ5KqWiKqDeSqaeishO143/K4K05p81O1hr/VNa67u11q9t4Vdlv02J3gmdj6QUhS1B\na11SSn0W+JBS6i+BLxOE9P8lwX/eDwD3q6Cv2ue11nOW0/wmQR3Tzyul9hIUxe8F/gUwQhD5qfDr\nBKmEPy7XnbxCUPT7UeBvquwBThPU0/yiUupVBO75xwlWZn1/+fjbCHy1DpXnW6Q1PyMbrd7D8wR1\nVv+9fP2nCAqNby9f+yjBEvtmbNQ91H9mrdQUVdPOc1yJW5VSH2yw7Tmt9ck2vnftWgL8V4Lv1N8p\npT5G8HL/EIHnlU0Mt3XfWutCee7vB/oJPNQ2g48AXwP+ovy5/D2B11ofQYTqR4Fh4Ce11tN1x1Y/\nD4dg4cb3Ehi9jgM/0GRVbLNnWeG58qKR/QTR2a8QCFIrWusTSqlHCLzhjgMopd5MILjerVswD94g\nKotIVrJ2EbYxIriE9WI1rV3+JcFPxW8nSJM8DXy/1vpRpdSvAf8HwUvlQYLi4Bq01rNKqdcR+Bm9\nl8BRe5HA5+knqj2WtNaXy/v+BkGR7y6ClM7PEZhBVvgbguX6byNIPzwOHNdaT5eP/3WCF8ye8py+\nDfzGCgXr1dR8Tq3eg9baK0cFfoFANH2EIDpylmC5/m+vVMuzintotQG17TNrRs1523mOLZz3R8u/\nbPw7ApuKn6b1710r16zcx98rpX6MwFD01wlSuJ8ksDb4YZYjgZX9V3PfnwJ+vHzdT1q218ypnfk3\nQmv9olLq1QR1T+8iuLdeAhF5jiAN94cNvj/1z2OBoDXYL5SPaVRzuNKzrFB5ppVj/JXuh8AA9mPl\nVYkxgh9cXqe1XtferytRrnv7CwKxWEnpn1FKHQX+RGv9qc2cj7DxOMasvgWaUuq/ELQtiQD/WWv9\nd1Xb3kbgtlwCvqy1/s01zlW4wlFB+4sfo6rdjiB0Oirw+VoAHtdah+q5hPVBKfXPCYyN/+lWz0UQ\nbKy6hksFbSdu0VrfQ/BTT33Y/w8ITPLuBd6ugkadgrAWKivsWmmoLAibilLqh5RS/6CUurdu04+V\nf5dano3lHdQVwwtCJ7GWlOJ3WE4dzAHdSilHa22UUtcC02XPFpRSDxDkzI+tabbCFUm55uotBCmg\nSxWnbUHoMDSBIehnlFJ/QNBU+g6C2rhJ2qtFE9qgbJNyhMApXhA6klULrvKqnEpx30eBB6ocrPdS\n28B2Aji82msJVzz3A/+doObqX2zxXATBitb6+XKd3S8R1DvtJlgV+RngVyo/gArrjw56KkrZitDR\nrLloXin1fuCfYe8VVqGRi7IgrIjW+g9Z2XleELYcrfWzBEXZgiAINaxJcCml3kGwIucdWutqh+pL\n1DZF3Y+9dcMSqdMnDECsr5+u3XvWMi1BEARBEISNpq1g0qpXKaqg+eqDwP22mhql1AsES64vEXRd\n/1Gt9SuNzpc6fcIUCiVMPInpXW9zaWGjGRnpY3Jys7vCCOuBPLvtjTy/7Ys8u+3NyEhfW4JrLRGu\nHybwMvp02U3ZAN8EXtBaf57A6+avy+Ofaia2aliDTYUgCIIgCEInspai+T8G/rjJ9oeAe9o+sWnF\nt04QBEEQBGH70Hm9FCXCJQiCIAjCDkMElyAIgiAIwgbTgYJLUoqCIAiCIOwsOk5wORLhEgRBEARh\nh9FxgguMpBUFQRAEQdhRdKDgQgSXIAiCIAg7ig4VXFLHJQiCIAjCzqEzBRcS4RIEQRAEYefQmYJL\nUoqCIAiCIOwgOlRwSUpREARBEISdQ4cKLolwCYIgCIKwc+hQwSURLkEQBEEQdg4dKrgkwiUIgiAI\nws5BBJcgCIIgCMIG05GCy5GUoiAIgiAIO4iOFFziwyUIgiAIwk6iMwWXRLgEQRAEQdhBdKjgkgiX\nIAiCIAg7BxFcgiAIgiAIG0yHCi5JKQqCIAiCsHPoUMElES5BEARBEHYOIrgEQRAEQRA2mA4VXJJS\nFARBEARh59CRgsuRCJcgCIIgCDuIjhRcYCStKAiCIAjCjqFDBRciuARBEARB2DFE13KwUurVwOeA\n39Na/2HdttPAOcAn6NXzYa31WMsnNz6drAcFQRAEQRBaZdWCSynVDXwM+HqDXQzwTq11dlUXkAjX\ntsYYQ3F6Bi+TJdrXR2xoYKunJAiCIAhbxlpCSDngXUCjqJVT/rU6ZKXitiZ37gKZE6fIXxxj8dhx\n8uMTWz0lQRAEQdgyVi24tNa+1jq/wm5/pJR6UCn12+1fQSJcm4ExhvmpeRbn0+t3Ts+jUCew8mPj\n63Z+QRAEQdhurKmGawV+CfgKMAN8Xin1A1rrz7Z8tES4NhyvVOK7f/MdJs4EYujGu2/ijvtfs+bz\n+rk8xvetY44rdXmCIAjClceGCS6t9V9W/qyUegC4FWgquOLx5el09SeJ9fVt1PQE4IWHjjI3NkU8\nEXzuZ468wu33vorRAyOrOt/ISPC8FktZ8vHwV2uoL06sO7n6CQsbRuXZCdsTeX7bF3l2Vw7rJbhq\narWUUv3Ap4H3aq2LwJuBz6x0kkKhtPTn3Nwi5FZfAiaszMvPnKCQL9WOPf0KTqKr7XONjPQxOZkC\nIDc2U/MsK0xdmiE60L+6yQobRvWzE7Yf8vy2L/LstjftiuW1rFK8E/hd4GqgqJT6IPAF4LTW+vNK\nqS8BjymlMsCzWuu/bef8jvGlimsD8T2P6YtTofG5ybk1n9vL5uzXzBfWfG5BEARB2I6sWnBprZ8B\n3tpk+8eBj6/2/GILsbHMXp7FK3mh8fl1EFx+roHgKojgEgRBEK5MOreCWQTXhjJxzm7TkJpZsAqx\nVjHG4EuESxAEQRBq6GDBJasUN5LJC3bBZXzDwvT8qs9rCsXQCsUKEuESBEEQrlQ6V3BJBdeGYYxh\n6sJkw+3zk6sXXF6DdCKAya9k2yYIgiAIO5POFVySUtww5ifnKOYaR5vmJmZXfW4/27iTk58vYOS5\nCoIgCFcgHSy4JKW4UTSLbgHMT62+cN7PNo5iGd8Hb/X1YYIgCIKwXelgwSWRkI2iUf1WhbmJ1Qsu\nr0mEC6RwXhAEQbgy6WDBJRGujcAYw+T55hGuXDpLvkmkqhmNLCGWtkvhvCAIgnAF0sGCSyJcG8Hi\n/CLZVGbF/Vbjx2U8b8UIlkS4BEEQhCuRjhVcjjEiujaAldKJFVaTVvRzK0fFRHAJgiAIVyKdI7ic\n+r6JIrY2gqnzYcEViYUbDsxPtr9SsVFLn2qMpBQFQRCEK5COEVyOY5mK1HGtO7b6rWtedU1obDU9\nFVeq3wKJcAmCIAhXJh0juHDrI1xISnGdyWVypGYWQuPX3XFDaGxhar5tz6xmHlxL+xTE/FQQBEG4\n8ugYweW4EuHaaCYt6cSBkUEGR4eIdcVrxkuFEum5dFvn91pY2egXimJ+KgiCIFxxdI7gsqYU5cW8\nntgMT0cOjuA4DgO7B0Lb2lmpGDSttkW4nPodMcViy+cVBEEQhJ1AxwgubBEuKZxfV2wRrt0HRgEY\nHB0MbWtHcHn5QqhpteO6RLq7QvtKHZcgCIJwpdExgktSihtLsVBk9nJ45eHIgREABnaHBVc7PRVL\ni+Holpvswk0kQuMiuARBEIQrjbAfwBbhhGwhkJTiOjJ9cSr0eXYP9NDd3wPA4OhQ6Jj5yfmWz19c\nDJupul1dONHwV0ysIQRBEIQrjY6JcFlTiiK41g1bOnHk4OjSn/stNVyp2RSlYqml89sEV6Q7iZuI\nh8YlwiUIgiBcaXSM4LIVzTuSUlw3bA7zIweWBVe8K74U7VrCGBamWotyWVOKXV24cYvgkgiXIAiC\ncIXRMYJLIlwbh+95zFyaDo2PHByp+fuApXC+VQNUa4Qr2SURLkEQBEGggwSXFM1vHGdePINX8mrG\nEt1d9A3314wNjqxupaLxfasHl9uVsAsuMT8VBEEQrjA6qGheIlwbgVcqcfShI6Hx0UOjoYUKAxbB\n1UqEy8/mQgYebjyOE4lYemSCKZYwvm8X2YIgCIKwA+mcN56kFDeE408dJ7sQTvfdeNdNoTGrF9fE\nyoLL1rTaTQb+W47r4sZioe1SxyUIgiBcSXSM4LJHOySluBby2TwvP/ZiaHz/jQfYfWAkNN431Icb\nqX0O+UyOnKUgvhpb0+pIctnw1LGkFY3UcQmCIAhXEJ0juMSHa915+bGXKObqhI3jcOubbrfu70Yi\n9O3qD42vlFb0m0S4ADE/FQRBEK54OkZwSUpxfcksLHLiaR0aP3zbdda+iRVWY4BqTSl2VQkusYYQ\nBEEQrnDWVDSvlHo18Dng97TWf1i37W3AbwEl4Mta699sdi5Zpbi+vPDgEfy6lYmRaIRXveHWpse1\n2+Kn0rQ6Eq19fpFkcunPdmsIWakoCIIgXDmsOsKllOoGPgZ8vcEufwB8ALgXeLtSKlylXYWsUlw/\n5iZmOXP0dGj8xrtvoruvu+mx7TaxNsWitWm1E18ulLdHuIpN59HwesZQSi+SH5+gMDGJ8byVDxIE\nQRCELWYtEa4c8C7g5+o3KKWuBaa11pfKf38AuB841uhkYw8/A1GfRFUNkWN8jDFWawGhMUe++3xI\nrMaTCW563S0rHmuzhpifnCObzpDsDYu1RvVb1TV59qL51iJcxvfx0ouUUmlKCym8hVSNwHMvjtN3\n683Wno2CIAiC0Cms+i2ltfaBvFLKtnkvMFn19wngcLPzFTNZiuk0biJGrDdZtcUAIrhaZeLcZcZe\nuRgav+WeVxPvCgufepK9SRI9XeQXl4WU7/m8/NhL3Pm2u0L7r1S/BY1SigWMMfbFEuXtS1GsUuN+\njn4uR+7SOMlDBxruIwiCIAhbzWYVzbekmIwDhdlU3aCkFdvh5cdeCo11D/Rw/R03tHS84zgc/p7r\nQuMnn3uFTCrs52WLcFVbQgA40WhIWBnft6YDS+lFFo+fZOHZI+QvjTUVWxUKY5fxW2yyLQiCIAhb\nwUblYS4B+6r+vr881pSI6+Jl8sRikaUXdM9wN25s5ciMAL7vszAxQzxR+1jf+N7Xs3dfOFXYiDe8\n+27OHT1Fsa7O6vzRk9z7vntqxi6f9jDx4Hrx8u/D+4bpGemr2a800EMxUyvOhnpjxPt6AchOzTJ/\n8iyF2QUcIB6LtDxfgER6jsEbr23rGGGZkbrnJWwv5PltX+TZXTmsl+CqCV9orc8qpfqUUocIhNZ7\ngB9d6SSeb3C8EtmFDNFk4N2Um0pBVARXKyxMz5NJ14qaWFecgatGmZxMNTjKzqFbr+PlR47WjB15\n6CgHX3WY7v4eIChgT03MYHyfeDxKoRBEmVIFyNRdL+87lAq1UaipsVliOUNhaobMiZNtzM6BumZC\nU8fPku8dxI1JLVe7jIz0tf39EDoHeX7bF3l225t2xfKq305KqTuB3wWuBopKqQ8CXwBOa60/D/w0\n8NcEb8ZPaa1fWfGk5fdoKZ1dElySUmyd2cth+4bB0aFV9SxUd9/Eiac0paooV1DL9SKveftrg79n\nsuEVipFIjelphcD8tPY/Fj9fwHgeuTPnms7FcRyiQwNE+/uJ9vfhRKOknj0SLKgoY3yf/JjUcgmC\nIAidyVqK5p8B3tpk+0PAPY222wkUVzGdpauyWm4LBZfxfXLnL+Kl0kT6+kjs34vbwavhZsdnQmND\ne8JGpq2QSCa48S7FS3VRrlPPn+Sm17+Knv4eSunF0HGR3h5rIXyjwvnchTH8ot0iwolFSewZJb53\nNNSPMb5nhPz4RM1YYXyCxL69EuUSBEEQOo7OcZqvorSYq4qcbJ35afbkGfKXximl0uQvjZE7c37L\n5tIKsxaD0qE9w6s+n3rtTcQStULH9/ylVKOXTgNQyBeZuDzH/Nwi0XJNVj2OxYvLS6XIj42Hxt2u\nLrqvu4b+O2+j6+B+a/PrxFX7QnYhxvOs5xMEQRCErabDQgHlF6gJRFesr3vLIlylVJrC1HTNWGFy\niuQ1BzvS88kYY49w7V1dhAsg3pXghrtu4qWHX6gZP/3CKW587c2MvXyWc69cYuLyHA7g+4Yb8w6v\nPbg/dC5bhKuUSofGHMeh95Ybrf0X68+XkCiXIAiCsE3orAhXVcCimM4Gf9iC9j7GGHLnLli32dJo\nnUBmYXGpUbUxBr9YxHUd+obDzajbQd19E7E6/y7f8/nyJ77Ikw++yOWxWYy/LIpPvXyey2ctUStL\nhMtG/Kq9K4qtCo2iXAWJcgmCIAgdRmcJripKZcHlbEGEqzS/QGnBvnLE61DBVSmY90slSvMLeOlF\nkqZIcWJqTeeNd8W58a5wVybf5o8VcXEcB/1kuKGALcIV2icWo2v/vhX3qz5nfHQkNJ4fnxBfLkEQ\nBKGj6DDBtRyt8HLF4KW5yYIriG6Fndor2NJgncCS4Mrllj6zgYFusmfO4eXC5qTtcONdKhTlshmS\nupEgjTf2ykUWZhZqtjmRCE6kubdW16EDK+4TOmZ/gyjX+OW2ziMIgiAIG0nHCK54X09orJjObXpK\nsTQzh7fYOIrlpRdr7Ag6hdnLMxjAlJbd2/sHghq4/PkVPWebEu+Ko+6ujXJVX6eCE10WSyeeai/K\nFenpITayq+25NYxyjV0OWVYIgiAIwlbRMYKra9dgKFJRSmc3NcJljCF33l67tbRPqYSfa63x8mYy\nd3kWPK/m8xoYCJpNF6am8TLhtjztcONdit7hwOTNAMYr4UZcrjqwi0PXjAY7VS0mOP3CafLZ2s+p\nWW1W8pqDDfsqrkSjKFenpn8FQRCEK4+OWcrVtTu8mq64GDbW3EiKU9PWZsz1eOl0qF/gVpLL5Mim\nMhhv+bNyHIe+/u7lfc5dpOem1vop2ogl4rz1R+5HP3WMfDpDdybFvquGicUiFIslxsdm8avSgV6x\nxKnnX+Hm179qeU4NCudju4aJ9q++vYWbiBMbGqQ4U2uLUUql13ReQRAEQVgvOibClRgaAKd2Oqbo\nWZsjbwQVk9NWKKU6K3JSsYOobgbd258kEln+PIuzc2uuP+vu7+GO+17DnffcwqGrR4iV+x3GYlGu\nu+VQqEP58ac0ftWcbClFx3VJXr12d3ib/5fXofV2giAIwpVHxwguNxKxvjSLm5QWKkxM4ucLofHE\nvr2hsYrhZ6cwVzY8rRZclXRiNblzF9al/syzCM5Xve7mUFovl85y7thy2x5btCnRhg1EMyKWc5cW\nUh1ZbydVj18yAAAgAElEQVQIgiBceXSM4AKIDtpemhsvuIznkbswFhqPDQ2SuGpPaNxbzNaIm5Uo\nFYqk51L4G5QetUW4bIKrtJCiNL8QGm8XW6Rs+NAeDtwYjlQdf/LYkuiJ9PaQ2Lf8ecaGh0i0YQPR\njEhPd6hnpPE8/Ex2Xc4vCIIgCGuhY2q4AKIDA9SXo5fKdVyracDcKoWJKYyln1/Xwf248ThuPI5f\nqI5+GbzFTNP6oMzCIpdeuciFExeYPHcZ3/PpGezljR96MwO7B9d1/rOXZzEYqBJ0/RbBBUEtV3Sg\nf9UF6sb3rQX4icF+1N03c0HXtj+aHZ9h8vwEo4f24DgOyWsOkdh/Ffh+S95creI4DpG+3pCgLKXS\nRHrsn4UgCIIgbBYdJbgiPT04URdTWhYOxvcppdLEBtbmmN6M+mJrCAq5Ky/qSF8v/nRt2xxbQXY+\nm+fksye4eOICM2O1bYEAFufSPPGlx3jbj71j1YInNPd8gfRsqqZgHqB/oIdKM/BqvMVFSjOzxHat\nrseit5gJrRx1YzEiiTi79u9meN+u0L0ff+oYo4f2VO2/MV+7aH9fSHB5qRTsHd2Q6wmCIAhCq3SU\n4HJcl1hvksLcchrRMVCam98wweWXSpQWwimyasfzaG8PxTrBVW85kJpN8Y2//Cr5xeZF/jNj00xf\nmmL3/rB31GqoGJ5SlU7s7ukiFosQGxrALxQCkVRF9sx5inPz4ATO8LhO4IM1NLCi8aitED3S14vj\nODiOw41338RjX3i4ZvvFExdJzaboG9rYFYO2GkDbsxUEQRCEzaajarhwHKK9ltqjufkNu2Rw7rqI\nTSKO251c+nukN2zK6qXSNQXZJ57WK4qtCq88e6KtORpjmBmb5tyxs2TTteLJWjA/WI7MdSfpOhiu\nq/ILBQoTUxQuT5Afv0z+0jiZEydZfPnEikXmtl6S1Z/PQXWQZH/dMzSGE0/r5je5DkR6e0KF+36h\ngJ/vPN80QRAE4cqiswQXWAWXt5jBL4RrrNaD0mxYzMWGBmtSftYXebGIqZqTLYXYiPPHzoVMQW0Y\n3+fcy2f52p9/ha/9+Vd49HMP8cAnvsjk+YmlfSoRLlvBvNvdTXSwv2UvqlIqRXGq+X3YVmhWR5bc\nSIQb7lShfc69fHbDVww6kYi1XqtT2zEJgiAIVw4dJ7jcRBw3EQuN16f01gNjTJBaqyM6VFvU7rgu\nke7mL/LF+XDkp3/3ADff82riyVrbA7/kcfqFUw3n5ZVKvPLsCR7447/n0c8/tLQKEaBUKPHoFx6m\nkAuK+Jda+njVLX2CiFOkO4njOHQd3N/wWvUUp8P1bEvzLhQs1hlOSORcd/t1uJHar1Z+MTBn3Wjs\naUV7I3JBEARB2Cw6TnDhOMTrU1IYCpOtR5BaxUulQ02YHde1RoSsxprlaI/veeQs6cS3//g7+Z43\n3ca1tx4ObTv5XDh9Z4zh5HMn+OIffp6n/+EJ0rN2oZBNZXjum0/jlUosTM0HRex+VUufwW4cx8Et\nu+FH+/voOnCV9Vz1FOfmrY2pg/u1pBN7kqG6r3hXgsHRcOeA2YnGYm69iPaFn50YoAqCIAhbTWcK\nrsE6cWOC1XWttN1ph6IlnRgd7LdaUEQszbUrAmRxIbxyr6s3SaTcW/C6268PHZueSXH57HjN2IsP\nH+WprzxBPrPyfZ4+copjj7+M8U1NdKsrGSeRiOGWo1tL4wf303fHrXTfcJju664lefgaktdejVO/\nYtAY6+cCdod9W30bwNAei+Aa33jBFem3CONMFr+BiBQEQRCEzaADBZdLpCtOJFnt0RSImeLk1Lpe\nqjQ7FxqLDdk9sqyF84sZjO+TsZiz9vQv79833M+ea8KO9SeriufHTl3ixYdfaGneFY4+eKQ8kep0\nYrlgPpkM7R/p6iK+exfx0d0k9oyQ2DtKbDhsD1GcsadvrfVbvWGBAzC4J3ze2cvrnxaux43FcLvC\nfS4lyiUIgiBsJR0ouIKoTCjKBRSmpten8NoY/EwGLxt2IY8ODlgPcROJUDQoMAHNWuu3uuvSotfd\nEW4cffHEBbLpDIsLizz2xUdCUbIKew/vQ7325sa3Yy2YDwsuG/Fd4UhUaXY+5KRvjLGnFC2pVmgQ\n4doEwQUQtUS5xB5CEARB2Eo6yocLWGpgHR/oITs+EwS3yjrEzxfwLIajbZHP4GZmKUzNQ6kAkdiS\nyIv09ODG7e7njuMQ7e2lWBcV81Jpa4Sre6D2pb//hgN09SbJpZdFnvENJ545wcSZcQqWVYv7bzzA\nq95wK0N7hjHGMDcxy+Uz46H9qk1PBwYrBfOtuatH+vtwYlFMcTnlZsppxfju5ShVJZpXjRON4nbZ\n+yAOjg7iuA6mqrYsu5Ahl8nR1R2OQK0n0b4+ChO10VAvJYXzgiAIwtbRsREuNxYl2lOJ0iy/tAsr\n2BY0xfdxM7NBnVIqg+P74C0Ljdhw85Y71rRietEa4eoZqN3XdV1rLdfLjxxl+lI4Vbrn2n284fvf\nyFA5Nec4Dne/+/VE47UrOMMrFJc9uFrBcRxiw+FoVP2q0PzFcK/JSG9PQ8f8SDRK/65wtHDu8tbU\ncZXSiyHBKAiCIAibRecJLpZf4La0YnFqZvUvzlIBjAnaBZUjTY7vgQnO1yidWMFqOZC2R7iqa7gq\nHP6e63DclVv6JPu7ef177wkV7/f093D7fXfU7uz7S6nIWDxKMhnHiUZx4mFrjUbYBFdpbjmtWEql\n7e2Phpp/XluVVnQTCdxY3f03SIkKgiAIwmbQcYLLOMtTig90g1vbD9B4nrXYvSX8IJpVTGdrzeU9\nL+gHuEKTY1uEy8/lWbTYN9TXcAVjPVx1fXNPLMd1uef99zZMux2+7fqaAvz6+i3HcZb8t1ol2t+H\nEw3XpxXn5jHGkDt3IXSMG48TH23enmhor6VwfnzjBZfjOEQsaWcxQBUEQRC2io4TXNWO7o7rEu/v\nqe+8s+q0olMRXAuZunGP6GDfiiLFiURCqTpjDItzNsFlt0u4/o4bm17j9vvuaNpn0XEc7n7X64jG\nA4G0lnTi0jld15pOLU7PUppfsBqHJg5cZbXPqMbqxbUJKUUQA1RBEAShs1h10bxS6veA1wM+8LNa\n66eqtp0GzpW3GeDDWutwEZANp/YlHh/sIb9Qu5qwODuPXyzh1ntIrYRXCgrC0+HVifFka+eK9Pbi\nZZaPz+WKePkikeSy+WesK068y158v+eavfQO9VlNTQ/edIgbXhNui1NPz0Avt993J0995YkawXXV\n/iCi1OoKxWpiw8OhQvPS7Bx+LuwJ5nZ1ER/dveI5bSnF9GyKYr5ALGH/fNYL28KKSv/LdqJ/giAI\ngrAerCrCpZR6E3C91voe4KPAx+p2McA7tdZv1Vrf17LYglDPwmhvEjda62SOMatr9eOX8LIFTLHW\n8gDXIZZwwFu5X2O0zgA1m8lj/Nrz2dKJFRzHsRbP9w33c/e7XteyGDh82/Xcft+dxCIusViUV916\niMGhIKpj8+BaiehAX8gx3vg+3mK4HU/Xwf0tzTOWiNM7HBY+mxHlcrvDDvjG8/AzYbEtCIIgCBvN\nalOK9wOfA9BaHwMGlVLVORyH6ur3dqh7kTuOQ3wo/NJeqclyCGNwPI+ipZ9ftKcLx3VxsgsrT6/O\nNiKbLYT8s2wF89Vcf8cN9O9eLjiPdye45/vvbSvq4zgON77mRt7+jtt4+7vv4Nrrluu6WrWEqDmf\n61qL5+uJ9HQTs3h3NWJoi9KKjuNYa+5KYg8hCIIgbAGrFVx7gcmqv0+Vx6r5I6XUg0qp327rzE54\nSjHLasVSKo1nSXc1xPcAYxVc8b5AoDiFLJSaR7nqV79lM/maPoYA3QPNBVc0HuO+D38vt9//Gm57\n6x2848ffZa13WolKq6PqaJObiOPURwRbpBUh1XXoQFspOWvh/KYZoFoK5+dFcAmCIAibz3oZn9a/\ngX8J+AowA3xeKfUDWuvPrnSSkZE+vEKBTK72hZzojuIP91NM14qlZD7DwMHmK+UqlLIZ5ieL+Pli\nyJqhe1cfkXIRejSSJzkSFglL5+mLkz+2/LEVCiVcB+KJ5bF9B3czMtLcnLWUjTB851VgfGJ9PcR6\n2zdzTecXKcRrH2Fy9+CK126E2dXDhXPn8EuedXvX8ACj1zdOJ9qum7/5IMcePVo7tpBe9RzbIRfZ\nw+XLl2vG3Owiu4a6w2nqK5zNeB7CxiHPb/siz+7KYbWC6xK1Ea2rgKU6La31X1b+rJR6ALgVWFFw\nTU6mwC/hFmobDZuSwevtpzBTm/KbOnWRfP9QSxEXPz1H+tRYjfM5DkQSMTwcvPI1C4U50l4covb0\nnvE8ClXzS6WyeJ5PPl9aUp0l3OBeGuGVcBYmcMr+X9mFNH7fCMTsru2NyI5N18wluKVI82uvgN/d\n23AVaHz3KFNTdmuFkZE++3VjcQr52jmOn59i7NIs0XYXPbSJ8R2KPpi6xtVjJ84T371rQ6+9nWj4\n7IRtgTy/7Ys8u+1Nu2J5tSnFrwIfAlBK3Qlc1Fovlv/er5T6ilKqknt7M3DUfprWpuQY3/qC9HO5\nloqgjTFkT54NFcsbN0LM4obuZBv/A3AikRo7hFylhquqjmulGi4nl1oSW9Vj7eJZ7r1dS4h6GqUV\nY0ODVquFlUh0d5GsX0RgDPOTq/RSa4OGdhdTm5PSFARBEIQKqxJcWutHgaeVUg8Dvw/8a6XUR5RS\n79daLwBfAh5TSj0ITGit/7blk9uiVcbgxmNE+8JqstDCasX8+YsULc2Lo329xPcfCE+hmG26YrFi\nEmqMIZMpLM2xQn1bnxqMD4WwUHKK+XKdWet4mXA92loFV3RwwOqv1XWouWFrMyrtiarZLD8um1Av\nzs3j10W9BEEQBGEjWXVOR2v983VDL1Rt+zjw8VWd2HGCX3Ur/8AQ2zUUWmVWnJ5talNQnJ0nd3Es\ndD4n6tJ9/WGcrh5MPh20+Kk5MB80trZNMRqFQoFi0cMr1zsZY3CASDRCollz5kI2FN2q3B+FDHS1\nFqL0i8WahtPBxBzcrrU1hnZcl65DB8ieObc0lti/b1UrHysM7Rnm0olat/rNKpyP9PfhxmL4xSoB\nbQylmdkVnfIFQRAEYb3Y2CKaVWJwcOrt5U0guKqFACynFW1tefx8gcwrp8pO9bW1Wz0HR3GTyUDc\nJXo4+tSzPP7EUaKxKG9982s4eENv/QyWDy/XHmUz+aqLGYgEDvPNasqcfON+fk4+g0n02qN8dVjT\nicmuFd3fWyG+dxS3K0FpfoFIb29bNhA2hvZarCE2ocUPlJtz7xomP15bPF+YmrEKrtL8At5ihkhP\nN9GB/k2ZoyAIgrDz6UjBheMuNZRewvdw43Gi/X2hFi2FqRmSdYLL+D6Z4yfLBdMGp0o9dY0OEuvr\nxi9bUJw+O8Zf/fVXlrafOzfGz/zsR+jvDtf/wHJKMZstVF8QaG56SqmAUyo03Ox4RYxXbFiwX41v\nMSRdSxSqZh6OQ2xokNiQ/f7bxZZSnJ+cw/c83MjGrxaM7Q4LrtL8An6hiFvV5Dt/aZzs2fNLf09e\nfZDEVfVuJ4IgCILQPp3XSxGsER4nPQ1ekdiu8Mu7OD2DqUsZ5i5copSu1G0tb4v2JukaGcS40aXr\nPPP0SzXHZrN5HnvkmcbTi1oiXOXrN6vfahbdWtqnEBZSNmweZKtp6bMZJHuToTSr7/nMT69sNLse\nRHp7cBPhFaDV3QpK6UWyZ2vTnrmLY6HvlSAIgiCshs4UXNFw7ZTjezipKasJqp/P17Sg8XI58pfG\nl3covzSdWISegyNBys9djqyMX67tIQjw1JNHKRbs0ahKD8elgnlYejF3DzRYyWf81sRUPmOpXwvj\n5/KhsUhXe7YSm4XjOFufVtwdFuoV+wvj+2RPnqa+S7oplTANvgOCIAiC0A4dKbhMVz/GDaeaHN8j\nkp0jamnZUh2tyJ29UCtajAEHeg+OLhteRpZXGk6MTWLqomqZTI6jz9rdLKwpxbK/V0NLCIuQMo4b\nbmVkfCiu7KDfqKl0p2JLK85NbM5KRYC4RXB56UX8XJ78xTFrTRzYha0gCIIgtEtHCi4iUUzfbrvo\nMj7xZLjGq5JWLM0vUJype5EbQ9fIANGeZUFi3EA0zUzPUiwVsbV+fOLhJ63Tq7TOqU4pLkW4bDVc\nxtjTifEkJhZOAzr55pEw4/v4+XDkxe3QCBc0sIbYpAgXBPVtNsuM7LkLwSrWBtg+Z0EQBEFol84U\nXACRGKZvxCq64v1JnFIRvNJSFsjPF/DSizVFzxXcqEvXSF0BeDnCNTFebglpqRs7d+Yily6Mh8ad\ncsozm62u4QoEoLWGyyviWHy9TKIHkwgLNKeYa+rJZYu6uPE4ziYUoK+WwT3hlOLcxCzGt1lkbAyN\n6v+apXD9vES4BEEQhLXTuYILypGukaVoVAU3GiHak8DxSlAqG4YayLxyqqaWq0LXnqGwXUL5nOOX\nyqvXLE2zMb41yuXEopRKXm3LGmPAcUj22iJW4eiWiZbbB0UTFlFprOaoFezpxM6NbgH0DvYS66pd\nfVkqlEjN2VsFbQS2Oq6VkJSiIAiCsB50tuCCqvRireiKl4vTHWPK0a68tc1PpKebxEB9FGm5aP7y\n2ER5yO5w/9zTL5DN1gocJxqprd8CjG9I9iXDNge+vVjeJHqWrxu3RLkqIs33IJcKei/OjeEszuFn\nw/fZ6YLLcRwGR7eucB4g0tVFxFL/1wyJcAmCIAjrQecLLghEV/8IJrIsumL93TVlV45vAo+rUrFm\nsVny4L6QEalxI0sC63KTlCIYisUizz75fM2oG43VWkIAGGMvmC80KJaPL0fCrGlFr4iTmsKdG8fN\nzOOUCsFKzXwaPxW2U+jkgvkKQ5a04mYKLrC3+mmGRLgEQRCE9WB7CC4AN4LpG8WUo0FuNELUlr7z\nPTBB/VNs1zDRHos3VVm4eSWPqYnpypHhcxkDBp54+KlaP6aISzZbV5NlDN19TSJV1SS6a1OYkViQ\nYqw/tpij3qoAwM+EzxnZFoLLYoA6Nb+pc2jmmp/YFzY59YvFTa0zEwRBEHYm20dwAbgupncYv38U\nE+si3shk1PdwHIfk1QeCwvrQeYK039TkNH6lON0B4zjEYnXm+8YwOTHFqVfOLA05jkM2Hz5vd70A\n9EoNi+VDY5a0YiP8fD4UNev0lCLAwMhAaGx+cm5T51DpVlBPJJmk69B+3HhY+EpaURAEQVgr20tw\nVYjGMX27iVx1ECy9Ax3jE9+3FzeRwPHDwqiSmlyq31o60OHqQ/s4fHh/1WAQ3Xji4aeqTmDIZXIh\n0ZPsqRM9pfCL2kTj9qbY8W5sUbbQ8b6PX/Soj3xtB8HVv6sfx629x2wqQ2GT03ahdj2OQ/L6a3Fc\n1+pI7+fEGkIQBEFYG9tTcJVxk71Ed49g6nSKE43QNVq2gbAIrsoKxZDgwmXPnmFe99pXLw+VRdVL\nR46xMJ8KPLVSk2QzWcDU+IElu2tf1o7NwDTaQBi5Lia+cmsev1C2wqgSe51uCVEhEo3SOxSOLs1P\nbnJacWiQ5LVXE0kGRfS9N9+4ZKbrdkmESxAEQVh/trXgAojvGQGnVmwk9wzh+uVUnmfxs2okuByH\nPaPD3HLTtfT1ldN+ZWHjG5+nHn0GSnmcUoFcdQ1XxfQ0Ga8dK1oiXLHGkSjTPYCJVM7hYGJJ/N5d\nmK7ldkFeoXzdKqG3HaJbFQbr/dDY/LQiQGLvKH2330rfrbcQHehfGrdHuERwCYIgCGtj2wuu2PAQ\niav2gOuA69A1Okh8sDfwsTLGmlKkHA26PG4RXHt2EYlEuOs1NwdjVZGkpx5/Fgo5fM8nm6uuzQr2\n6aqOjnjFoE1P3fkbRrggWBjQP4I/sBd/aB+mb1fgRu8upyD9Qik0r+2wQrHCgEVwzW2B4GqEVXBJ\nhEsQBEFYI9GVd+l8koevpXsgDg7LFhDGx9j8r9wIOC6FfIGZ6boWQOUIF8Br73oV3/7u0zWrE+fn\n5rl88RL98VjIRSIejxJxquqqrPVbiQb2E7VzIFL3WKr+7uUrEa5qwbV9Ilw2wbUVEa5G2D5LEVyC\nIAjCWtn2ES4gsFhIJEN+W07O4mJeMTyt+G9VMbRriHh5ldrAQC/XXnPVkjUEAAZOHj/FYiobEk7J\nZAxTXI6mObZ0YrPoVjOqBJdfTilWz2s7WEJUsAquqfla240txB7hkqJ5QRAEYW3sDMEF1oJzmyVD\n44J52LNvFFNVfH7DdQfLJy+LAeNz8tRFu+DqimKKy9EnxxLhokn9VlPcSGCWCvj5cCrTTW6fCFfv\nQA+RaG3NXTFXIJtq3rB7s3DisdCzNaUSpmRJTQuCIAhCi+wYwUWsxShPxRKivn4L2Ltvz5IgA7ju\nugPlP5VrsYzP6dMXWZjLhF7K3ck4frEcCSkV7O7yNjuIVonEqiwhKicN5rWdargc120Y5eoEHMfB\nTdhWKkqUSxAEQVg9O0dwuZGWUnaVnowTDSJc1em7q/aNkEwmlsWT71MoFDl79lKoFKs7GYd8YAPR\nMLq1Uv1WMyLR5YL5pZsxgSWExYusk7EZoM5NdFAdl6xUFARBENaZ7fWmXgETbyHSsxThCtdwje4d\nqVkR6Louh689EAguw9KqwzPnxiw1XHH8QjkKsp71W5XjI9FlS4ilQbOtCuYrDOy2Rbg6SHBJ4bwg\nCIKwzuwowUVsZeNQ3AiZxQyphVTtsBthZHT3kmVEheuvqwiuZYuH85cuhwr0k8lY0Di7VAiaaIfm\ntsa0XyRWV78F4OMmt086scLAaIevVBRrCEEQBGGd2VmCKxLFNKmTMo4LjmstmN89MhwUc9dZMlx/\n3UGqHeUNMDUzR6muR2MyGcd4BtJz1LfdMW5kaXXkqnGjeLaUokUcdDq2CNfC9AJ+hzSJlpWKgiAI\nwnqzswQXQLP2OG4UHMeaTtyzbzT4gxOpSRcOD/czNNAL5SbXvufj+4aZhdTSftGISyxWFlR5y2q7\ntdZvAbiRUA2XYyBiKfDudLp6uojXraz0Sx7p2VSDIzYXa0oxZ2nTJAiCIAgtsuMEl2mWuqs4zDcq\nmAdwnKXC+uCvDtdfdzDwvQK8UiC8phfmlxpnJ5PxpRSj8cJRGhNdh7Sf44QjXIAb7/weivU4jtPR\njvONVil2ileYIAiCsP1YteBSSv2eUuoRpdRDSqm76ra9TSn1uFLqYaXUL659mm0QidUIphpW8OBa\nPkd9WvHA0p9LpUBQTS/M45TThMmqHoq+rXfjav23qjC+j18Kizk3uj0186C1jqtDrCGi0dDKT+P7\nNca2giAIgtAOq3pbK6XeBFyvtb4H+Cjwsbpd/gD4AHAv8Hal1E1rmmU7OA40WK1oIlGMMSsLrjrB\ndt3hKsFVjjKlszlyxSLg0NOzLKhMnSgykdja67cop7Tq0pJuLIJb369xmzCwO2wN0SmF847jyEpF\nQRAEYV1ZbXjkfuBzAFrrY8CgUqoXQCl1LTCttb6ktTbAA+X9Nw3TaLWiG2VhfoFcXT1OLBpjaHg5\n4mLqIlw9PUn27dsNQLEqyjGbXgDHob9/WeCZ+gjXOkS3APxsPiy4EjHwLW7624CO76koKxU3lkIW\nZ3EGJzNfswJYEARhp7JawbUXqK48nyqP2bZNAPtWeZ3VEY0vtcKpIRLl8pjFf2vfCG51CsmSkry+\n3OanEuHCcZhOLQDQ21ctuOoiXGv036rg2SJc8Rh42zPNZYtwpefSlOq9xrYIMT/dQAoZ3PQ0Tj6D\nk0vhpKa3ekaCIAgbToNip7ZptgSv5eV5IyN96zCVgELCIz8ztfT3aHcPyT2DHHk2RTxee9uHrz9Y\nc23jdZPOz9bsc/NN1/Dgw8/ieT6OE6SdZtMLOA4MDffhVPoawvL5HYfefbuWar3WwvTlMfxEjFJV\nf8hET4JE1KF3V/e6XGOttPv8hvcMkp6rbTAeMR4jI8PrOa1VsbA4yOxMrRDojjnsWsfvaCexnv/2\nViIzNo9X82/Qo3sgTiS+/SxOOoXNfH7C+iLP7sphtYLrEssRLYCrgLGqbdURrf3lsRWZnFxHWwAT\ngWgvTjEHkRg5p4f0ZIoT+hyFutV+vX39tdc2BqfoLznLQ9Dmxyt6QZcfB4wx5AoFSnjgRjFls9Ni\nvrh0fhONk5ten6bM6al5SgWv7HgfiDvfdSkUSkxdnoPo1tpDjIz0tf38En09zFyuTSOe1hdxEltv\n5lrMe6HvycLUPP56fkc7hNU8u7XgpBZr/m0B5CZmIdGzaXPYSWz28xPWD3l225t2xfJqU4pfBT4E\noJS6E7iotV4E0FqfBfqUUoeUUlHgPeX9NxfHga5eTN9uTPcAlFOM42OXQ7uOVhfMV46tq+OKx2Ps\nHh6q7LD0+2IxB46LKQ+ZUlUN1zqlE6EqnVWVVozEyyavXmek4dplsIPruMT8dIMwfkhsATjbNDUu\nCILQKqsSXFrrR4GnlVIPA78P/Gul1EeUUu8v7/LTwF8D3wE+pbV+ZaVznn38ZQrp7Gqm0zK+7zM5\nPhUa37N3NLyzpY5r90Cl7mhZ9Mxl0sFfnSCl51fVcFU8wQqLWVJjU5Ryq3thG89b7tNYEVwOuOW0\nzHZ9WXVy4bx9laJ4ca2ZRt/VbfpDgyAIQqusuoZLa/3zdUMvVG17CLinnfOdf/o4JR9ueM89xHs2\nJqU0Mz1LsVT7H3symaR/wBIWjIQ/mt5Ed/CHiuZxAj8uz/OJRKIY4y0VzZtYEqJx5s6MceHRFzGe\njxuLcPVb7qB3T3s1SjXF2o4LeLixyLJX1HYVXDZriKkO8eKKRHCiUUyp+rM1mEIBZ5u0UzLGhHp+\nbjm+xacORHAJgrDj6SjXTL9YYvKl0xt2/qmJ8Gqo0b0j1peSzTw14rlEo9XjQan8pYnpQH1FE/hE\n8Ht3YXqH8X3Dpaf0kgjzix6Xnni57ShJTVuZ8lzdeFXPyG1qDdG/qz9kMJpLZ8lnOqONznZeqVic\nnbyrbmYAACAASURBVCP19PPMPfoki8dP1qa6t5IGPxw4vif2EIIg7Gg6SnABLJyf2LC0zcz0bGhs\n1+4G0aa6CFcuWyCfLbJrcGh50HWIRl1OnL0Q/N1xMKacSnQcMpNzeHVpxPz8ItmZhbbm7dW85MOC\ny/E82IapLjcSoX9Xf2i8U6Jc29X81JQ8Mq+cxi8GQrw4PUN+PFy7uBU4fpNorES5BEHYwXSc4Cpl\n8mQ26IU7OxOuDxraFa4jAkKCa346WElSLbhisSiO4/DMi6+QWlyuP6tEE1Jj4XoxgLkz423Nuz7C\nZRyIJKoiXBho9iLrYAZGwmnFuYkOqePaphGu0sJCXSoUipYfNraERilF2LapcUEQhFboOMEFMH9u\nY34an5u2Ca4hy54EKw8jy6JmbiYNjsPort245RWP0XgUXJdCqcRDTy+VsC297NKX7IaO82fHMb49\nImV8H28xQymVxstk8PN5/Gxdis1xlwrml9imL6uB3ZbC+akOEVxdtibW20BwpRdDY142i/E7IGXX\n5HvqSIRLEIQdzHoZn64rC+cn2Hfnjete8GtLKQ43ElwQ2EmkZ3CMz/xMGiJRuqIRDu27ijOXLhCL\nx5Zqqp4/doq7b1XsHhrAFIsUjUNu1u6vUsrkWZyYpXdvbTrTz+dJv3S8NqJlxVm2hKiMeEUMDVoa\ndTAD1ibWHSK4rBGuzreG8CyCC2PwszkiPd2bP6GqOTgS4RIE4QqlIyNcxXS27TqnlTDG2FOKww1S\nigCxLszAHvy+EebSZsn64fCBQ0QjUaKJ2JIo9I3h248/H1yr5JEea96uZO5sOK2YO3exBbEFuDs8\nwjU5R2bBIho2me1Yw2WMwVu0m+16mfUx4V01vgc0qTWUCJcgCDuYjhRcAAvnJtb1fJnFLPm6l2Us\nGqOvv7f5gW4EE40zP7UsAOOxGIcPHAwiXO5yFO742YucH5vElEqkLtnrtyosnLtc69nl+xRnW4vs\nuIl4aHXfdhVcPQM9QWq2ilKhxAOf+CIvPHhkS3srunFLSrFY7IzUXANMvhCq36rgLW6sz92KrFBn\n6PgedPBnKwiCsBY6VnDNn7+8rqsVZ2fC6cShXYMtpS0zC4uhF/91V1/N8O6hUEPpbz72LF6hQHq8\neYTLyxdr9vHSixivtaX7seFwGtTxi9typaLjOAyOhu/HK3m89PALfOkTX+TUkZNbYjjquK5ddHVw\n4bytfqvClke4WvmhQKJcgrBjyc6mWDg/QSl/Zf4776AarlrhUljIkJtLkxxan8aetvqt+nRiajZF\nPBEj0V1rvDo/GV41ObxnF9ffdAuf+dNP14xfnJjmuceP0Jt3KRSLnLx4kePnzjOTSjHY28u+XbvY\nt3sXe3ftYu70OP37RwAozoWv4UQiOJEIxvcxnofjOESHBuk6eBCTnqhtkWIM+B75oseXv/A1Tp04\nze7R3XzfB97R2PqiQ7ju9huYujBp3ZZLZ3nygcc4feQkb/zQm4lb0nwbiduVWHb5L+Pn80S6O7Ne\nzltsLri20gy1af1WBa8Ise1hLCsIQutMHD3N5edfAWNw41Guvf8uui22QDuZjhFc/fuGmDpTm0Zc\nOD+xboJrtskKRd/z+O7ffIfLp8fAcbjpdbdw21tuX9rPtmquf/cAt9/1PXz3gW9x6cz5mm1f+8bD\nDCf7OHXxIqVy1MpxXabm5piam+OFkyfBcdj92CB3T13i3vveABbB1XX1QRJ7AkFWifAsvSwjUSjV\nFXD7Jb7+5W/z5KNPAzA9NcPC3AL/6t//JG59CrKDuObV12KM4blvPUMhY48eTV2Y5NEvPMKbfvAt\nmyoYgsL52sUPnVzHZS2YL2OKJUyxiGOJ2m0KLViXBIs/BEHYSSycn+DycyeW/u4XSlx+7gTX3v+a\nLZzV5tMxb+Fdh68Kja2nPcSsLcJV9uA69sSxQGwBGMOxx15k7NSl5XlYVs0NjAziui7f+443hbZN\nT81y/Ny5JbEFEO/rhmrRYwxTM7N868vf4fd/67+zMDkTOk9sMPCoKuQLfOur3+VvPvk5jjxzNBBf\nFid8U8jxzBPP14yNXRrnxLGToX07jWtvPcz3/dT7UK+9GTdi/1qOn7rEBX3eum2jcBO2lGJnrlRs\nVjBfYUvruFpKKW7PWkRhc+jk+knBTmExx4XHXgyNL07M4ndKB4xNomME1+7D+0Jj+bk0+XVardZo\nhaIxhlPPh3tr6ydeXvrznEVwDZYbL99w8/Vcs3/P0rjxDV4x/CWKJuPEkuFUSSmTJ5NK8eRRXTMe\nSSaXXvZ//f//Ld/4yrd57ukj/M+/+FuefvxZTDQWOtfY2bPk6j27gCceeSo01onEu+Lcft+dvPOj\n7+GAOmjd59lvPE1xEwvpbSsVvewWF583wM/lV6wD3LI6LmOau8xX8LZnLaKwsfjFIumXNPOPP83C\ns0fIj10W8bUNML7hwiMv4Flqtoznk21gnbRT6RjBlejrJmlr87JOUa5GHlzTF6dYnEuHtl0+M87c\n5By+55GaDltUVBzSI7EY971uOf1oU+xONIIbjdgFV76AXyhyYby2hilajm5NT82gXzpes+07X38I\nE+2ivu7tzMnzYMLX1y+eYN6SsmyEMYbjL7/C1770TV564dimF6z3DfXxhg+8ide/7w2hbdlUhhcf\nesFy1MYQ6Q77Vnmp9JYU8a9Es3Ti0j4rRMA2DOOHhZTjUP8ddowvPRWFELmz5ynNB/8P+7k82TPn\nSD0jwqvTmXzxNIuXG3e5yHSI5+Jm0TGCC6D/0J7Q2Pw62EP4vs/cbFg0De0a5MzRUw2PO/G0JjWb\nrrFvAEh0d9HVExRNO9Eoe0eGefX1VwPglXyqvYZi0Rh3veY2furf/AQ//BM/xC3XX0d/T8/SdmMM\nxUye8clZ/Cr3+ehQILjOnQ6n0GamZ5meXcDEa4v7T52+CJYIh8Hw1GPPNrzPeh7+zmP8+Sc+ybe/\n/iCf/NP/ybe++t2Wj11PDt18Nfuu3x8aP/7UMeYmNqdVjdudxIlEasaM5+FnOi/K1axgvoK/VREu\nS8G8caOYiKWMVFYqCnXYFhX5xWIgvJ59gfz49hJeXqFEbi7dsOPITmBxco7LLzQvZxHBtYUMWARX\nbmaBQnptL7f5uQX8uv/wu7u7iUVjnDt2ruFxZ4+eZtISYavu/+fEghfG977hNezZNYhX8sDA6PAw\nb77jDj78ju/l/T/yXq6+9iB33P09vO+D7+KH7r+PeKycEjTgFYoUSiWmyv+pOK5LtC/wBzt/9qJ1\nbieOncQklj3EfN/nzNmxIEJg+Uf81GPP4rVgO7Ewn+LrX/pWzdjD334suK9NxnEc7nzbXUSidYLH\nNzz91Sc3JcrkOA6R3p7QeCkVjopuNS1FuLL5rXkx2Wqz3AhEwqlxqeMSqjGlEqbY+DvhFwpkT58j\nfeRF/Hxn1ldWM3dmnJc/+x1O/P0jPP1X31jz+60T8QpFzj90xPouqmZxcq4jswUbRUcJrkRfN12W\nVYnTx8+TnVkgV67pKrVZtGy1hNg1yKWTFyk2OZdX8njhoSOh8YGRZTsJx3VxXJdkV4J/8u77eP/d\nd/PDb7iH9937Bm48dJB4Ik7PnmWfqcFr9uI4DiOD5XMYH6/kY3yfsYnAlys60L9kbHrujL1I/MSx\nkxCNL/V7HBufJlfxh7LUyizML3D85XCtWj0PfusRiqXaCEMul7N+hptB72Avt9zz6tD41IVJTr/Q\nODq5nkT7w99JL7VFtQd+yR4talAw/7/Ye69gSbL0POw76cq762+7e2+7293jZ2cHs36BWQOAAUAk\ng0YSRUmUIhRSKBih0AP1qAc9iKGQHhgKBgUGQIgAISwELhbQLna52N3ZMTszPa6nzXT39d6WN+nN\n0UNmVaU5Wdf0bUfu99J9s7KysrIyz/nO/3//90cMckFhP4boHFO/xQuBfqW9fX8Z4folfLAP6Xtn\nqxq0TfYC9UmBUm1i493boN4CVmvJ2PLphf99gG1a2Hz/Lkz54K4ptmb8e0k44/DE2EJ0kT83FulB\nWLm7isrd1cC29GgR577yAsT0wZ49TEuIoRLWPls58L0sm4JwOxoiCKCGAbWlYSjrRZ0oBQhBerQI\nXuxf5tRwAVIuhdFSEVvlci+kbJs2tvereOHKBQhFV8tm6Ab2ttkp1ZXFVdi2Az6ZBZHrWFnpDzTE\nsUGpGJbH4INffISrz87Gftd2q4MPf/Ex87X9vTJGx0di3/swMfvqVazeWUE71O7p5hs3cPrSGSQY\n2riTRDfa6Mcjj3BRCqI0QHQ3ikUTGdB0sWe86zCaUxNBAJ/NwAqlYxxFAXxRO+o4IErTtRkRRNBk\nPlhRexJgEC7KCW6UK4xfEq5fwoejGA2b1TrozBRjofH4YZsWNn5xJxL16exUYXRUSNkn09vvMHBs\nB+3tCpqrO2htVXqE0o/UiJsZUivB8UgpN5DIPZwer6ZholNvI1fKQZAY0fRHjCfurmSlFVlQyg3s\n+nw9BoFlCZHPZ7GztM3Y+2D4U4pAP62otvpMvRsmzU4OB/clBIWpCYwWS67Sy9vPthxsdyNcnmB+\na2MbToyA2DAMrK6sA1IalHCufssPxgS3cH+JWa3Zxds/i0a3uijvDW5V9DDBCzw+9+3PR7Ybqo5b\nb3768D8/m0GYvTq68WjTF5beI1sAQHQZRO0TULsTjW7xmTSzWXXYGkKvVUC0Noilg2gdEOUh6CpY\n6WxOiE8p/geUZvglBoPleyeWisyOG9S2YbWezMq33RvzMFhV95SivnK8uehxw9IMbF6/i3v/9udY\nf/NTNNf2mGSLkwSc+/LzgWxPFwrD5/IkUNks4wf/4i/x43/1Q/zlP/8e9hj9ix81njjClSxkkShE\nNTMsHNQ+pwsWyTA7ekQMn8ymcPrymQOPVxgJES5BgGM70Dq+EKq3ismdikaFcqdHMVoqBlY6juVg\nv9qALfDgk64YfnN98EO4OLcMEAJHTGF1bSf4omNDFIOTGQXFR+99wjxWp93BB7+It4/Y32M7wT8q\njE9N4Ny16cj25U8XH7qAnvA8k7g8yigXMaOTDtHagLedJZjnsxl2laVfOE8pTDk4QRFDYaYtHwjM\nlCLvRrgIq1LxPyx/noeKp5y8Olo0NSXkc8jMXoQ4HO2iYTLauD1utLbKqM1vxr5eX9p+6rRMtmlh\n4a/eQ31hE44xWHd5+tVrkLIpZELZIQBQGJ1cTgI3fvoxdMW9d0zNwPUfvAfnkO3zHhaeOMIFAOPP\nXzzUfpaiwz6EJxNLfySXo6ugqWvTmH316sBjpQsZiCEzTCII0DpasOKEOhBSCSSL0XRUqpRDNpNG\nxnccSikc20FV63+fjbX4BxQAFu67mqydWqev3/KQkAR87WuvRt7z8fUbTAH8oOgWAOzvPl7CBQAv\n/trLEBPRiMigwgdLM7B3cxGb7392YEPxQWClFe1HmVaMIUBErgGOw+yhKGTS4DPRNIUtK/3BnTrs\nhtHmwfqLMNRaC/Xl7ah3HnXYbX04ASCEqeP6pXD+BEApiNoCaeyANHYB4zH30jwmWClFzluUsqJc\nZu3JEmKbqo7N96LGn4F9OirkR1R5fVJobezDiukM0gMhGH/hIorTEwBcKVAYWqNzqHn8KDA0A7Wd\nYEBGbSnYPmZW66TwRBKuwtQ4zn7leeTPjiE9WkRqOI9kKQciRPUehzFGDWu4LMOC0YpOKFPPzmDk\n9ChKE/G9BwuMG4YIApRmSPhHKbKTw8w2NJzAI1nKYSQXFGM7toPdVsd7O8X66mDCtbO1i067g+Xl\nTdCQFmZm6hRefekiuND2druD+58Ffb06HRnX3xlsjlrZqz72QSyVTeHal56LbI/rw0gdB2tvfor9\n28uoL25h9WefoLUx2GZk7u4CfvLDN3D/zlzg+/JMHdcjTF3EpJaJYwOdGhyGYJ7PZsElkxE9C7Vt\n0G5/yDgid0TCVZ1bx+IPr2Pz3TtY+MF7wevMtITwRbZYhGsA+X/YMOtNtG/eQevjm9A2th77fX9s\nGIpLuKgD4ljgOrWnksiyCZer2xRLhcgYS03z0S6GBoBSiq3378I+RKFX/TGTgaNCa8ZfYz4hYujy\nWVz49Vcx9tz53nYhKUHKh6LulEKpnmyUqxVzPJbJ+aPEE0m4AKA4NYGpr72IC99+FRd/4zVc+htf\nQJZBhLTmYMJl6AY6neCNoXZUJBNBoXVhrIjSWAmEEFx+5Urs8cKCeQDgRCGYToRrXZA7NRzZt4tU\nPs0kXDsVd5XTarbQPoQWYWFuGSuLqxHx8czMaeSSAq49E40Whp3n3zkgugUApmUO1H89Kpy6EG0B\nVduuMEPFra1KxOeluhBPYt998zr+9b/8Y7zx47fwh7/3J/jTP/xuz0pDyDMiXLJyoLP7iWFAis9p\nN0FDEykRBRBJBCEEXIoV5fIWCHETsKkfOhXl2A72bi319qe2E9RXMi0h+oUkLC8u4jwewuXoBpT5\nRdiKCscwoG1uw6wcTrrwRMGLbkVwjMjl4wR1nEjzeKBPuAjP9zSvfjwpacXawibaW9EFoZBORra1\nNvZgD7C/eNJgtKPVhdlTI5j+tZdx5W99DadfvYr0cPS3ST+CtGKzwj7ezvIOlBPqXnMcPLGEi4Vk\nITrp6QcQrno9RBIoANOJNHOefmam9/+zV84hGVMxEhbMA4ADAkMNDQqUIjMWHymTEjxG80FnfccB\ntjZdLdZB0a0u5u8uYHVpHSAcKOl/p/MzLjH5lZej5HFxfhnX3/kQrWYbnY6M99/58FCf9SSkFXND\neUihqkTbstHYj5LB+mK0RFwfsCp7963rgb9v3biDP/3DP4dt2eAkyWtkHcQj03ENIFy2qrtWCr4o\nmJDJ9Fb+zLRiV8cVF+GiDmAdrjpMb8mR1h16U4bRLQuPsYTo///JSSka++VItadRfgoJl6Ew07iH\naq/0BIEZ3ZKkQNSWnVasP/bIpN6SsfPJfGQ7n5Rw4VufBycFFxqOaZ9o/+CHDYNRqDP6zDSy4yVo\nK2toXv8Y7U9vR4oYWGnFkzZAbcUQLlD6yOyEWHiqCFciHxXTH5RSrFeCKx1DMyCS0IqakIAgmxd4\nXHzpEvN4RcbNordVv7k8AEBICAMtK0RiYySXC9S+OQ5FZb8KRVawsRolC2Pjo5Ftt298BlVR3SI6\nzxFdSoiYnHD3vXB2BMPDJdi6BXm/gc5OFWqtje995/v4p//z/4H/83/7v2CawclSFETMXo1+/8r+\n46tU7IIQgpHT0UKEciitaCoaU7NlKjqz/ZLjOKgzVsV3bn6GP/2j78K27Men46LUJUAxsFTDvf8s\ns3cf+s1amcJ5LwU5aAJmCfVZ0BmtsQBAKbvXkzArFH0RWVaE6zH0VKSUMsmV3ZEf++R9JFAKosZE\nx5+ylCJLMB/ubyqUimBVET+2NlYe9u+sMCv2zrz2DKRsqqdr8uNpSStSSpn+WVI2DX17F0a5Auo4\nsFUNyvxSYBGTYQQtlErzRF33mwMI3PLNpcfWleDpIlyM6sWDIly1UBpMbStIJYPh3PGpcaRDPiAX\nXroELqQZ4wUeuaFov0e1GX2wk7loyLgLatmAoSOVSaLga/MDQuAYFjY3tpmC+S99/QsQhb5DvVbv\noLW5j85OFXpDBggPSghmpk6B57nuIfHy556FWm3CMUxQ24GlaJD3atBbCtqN6MD8+S99DucvTUe2\n7z0BES4AGDkTJZ6VUNi+vrzNnrBjBgp9gMXDnZt38Z0//LcAI1L0SCJcB/QWtFWXGBFKAS8Vx/vu\nK6Y1RNf8dFA14iHTT3FaDrk76LE8uPwki/CB6Ky7Az35SskDYLc7TAuCJ7WVUywMJZ5IP+Jr+qAY\npN/q/S0KEApRc+LHmVaklKKzE13wDV06g7w3fpXOR+URyn4devvJL26wDTNSmUh4DmI6ASOUgndM\nM9AFI1HIMqJ71kBN2FERl1IEAKUlY3f18VhEPF2EixHhMjoqM2LRhV93RB1Xv5UOEa6pZ2fCb0My\nncS1LzwT2Hbh5UuRNjMAoDJW+MlMfHTLarUASpHMJPtpRa+Pr22YWFvewM5m9IY4f3Ea0xenAAqo\n9TbMrg6HUhgdBaaqA4RgZibYf3CmNAwx1A8QlMJoyejs1WAqei8yIgoivvKrX8TYxFjk8x+nF5cf\nTMK1We5FISilqC/FO04bjAHNYEy0fnx26x6++//9DHbISuSRNLJmrMYox7u9CB0nIMgltg1QCj7b\nJ1l8OkoUHU1z9WcDJmBim4eKiGhxEa79eMLl13CBEGaU61EboBoDIrgPlVhbBkhrH1x9C6RTCxBs\ny7SOdn9R6tqFxIA8ZR5nLJd5LhldzLLSitZjJFymrLmRZx8Iz2Hi5cu9v1PDBaQZnVXqy09+lIu1\naBUzKVDLZpJk/zZCSIyO62TSioZmQDvAvX751uAejw8Lx3Kan52dFQD8AYApABaA/3Jubm41tI8J\n4G24VIICeH1ubu6BnnReEiCkk7AU38qbUuhtBSnGjQsEU4qmbsBxHKQS/QeWFwWcvXyW+d5rX3wW\nmWIWlY19lCaHcf75C5F9qEOh1qODcSItRbb1zsNz/k5kExjN57GwswNCOBC4hOvGhzcjIvZMNoPS\ncBEXZ8/j9vufBq+BB6OtQhzO9PRbgEs+tM0KXn/lFbx98yY6oebF1Lah1VowEyKSxRxe+cqvIF/I\nMfsulvcqoJQyKy8fBgxZw/aH96C3FORPj2D8xUvgeA5DE0PgeC7go6Z1VMhNGdliFvJenSno7IK1\ngtQPUUV0794itN09/O1vfrl3DajjwJYVCIx+i8eFLStQV9bhaBq4ZAJCJgmRtyCkE33tCieApgtw\ndjci6WxO4MBJ/fuPCAK4hBQxarVlBbxj9VLRTJgawEdTqX7E6eK0Rge2bkCMMz31gxddp3sfiG2C\n4tG4b1Pbhlmtxb5utzsAYxHy4B9MQTq1XkSKGIob6U4XcfvtW5i7fhcA8MyXnsPVLzxz8LNnqC6p\niv9A1+MsLKt4QsGKOIYjXAAgDhWhrqwFttmqBltRmQuOB4Gtqu5xM+meZ2IYLDPP1FA+0HWEEIKx\n2bNo7AaJYWN5G+PPX3hk4+xxwE4npph+gABgh1LD6dECOiHJh1JuYDhmLj4KYvVbPmwvbEJTNCQZ\nxQsPE8d96v4TAPW5ubl/MDs7+00A/yuAvx/apz43N/drD3R2DCQLGXRCZENvyfGEyxfhsk134E8n\n+w/g+NR4rOU/IQTTz8wEBPVhaM1OxECV4zmIIjt4SCnttVpJZhIY6Ua4OPfhsg0LzXoz0pbnzLnT\nIIRgmEgwY9i7Y5rgCd/TbwFAa7cJQ1ZxZmwUf+8br6Ncr2Ntdw9ru7to+GwNbN2E01Lxpa+43l3F\nUgGiKAb0XZqmodVso1CMplVPGo5lY+UnH/WiUZWWDBCCyZcvgxcElCaGUN0KPrCVzTKyxSxqDLG8\nH6wIl36Y9iEEWNzcxa25ZbxwpU++7XbnxAgXpRTKwhJs1b3HHdOE1WxCt0yAIxBSCfApCRATQMqA\nE7YjAcBLfK+1VG9bOs0gXDKQGLwGIqYGmgwSLl3VsbWwiWQ6ibFzY/HkllIo5ToK6eBnUMJFWgdR\nXgzf8o9Ub2TW6gN1HQ8twmWbkfQf0RWUKxruvXunt+32WzeRzKaYi74eDohu9T/TihLeJxQsDReL\n5HCSBCGbhRWqSDdr9QDhkpsdVLYqKI2XkGdU0B0Efa8MdXkVgNunNH35AsQSI1rDmPTTI9HPG5s9\ni/m3bwdMsE1ZQ2e3htxkfJX74waLcCVy6UDq0I9w1CvD0ELLJxThah7Cud6xHazeWcGVA3w3TxrH\nfepeB/B/e///CYDfZ+zzUOh5opBBJ2RoFqfjopQGTE8tyx3Y/BqubAxROyyUcsOd2AjpheoT2QRA\nKahtg4SiB46m9yY+KS1hKJ8Dz3FwfBETx7LBicH3nZs+g+rCJsz1CjKpFGSVPckNp7M9/RYAVFfK\nvfPiCMH40BDGh4bw6rWraHY6WNvdw369DlEQ8PzFC7DKLWB0yG2wPT6C7c2gg315r/JICFf57mqE\nGFXn1jFydQpiKoGR06NRwrVVxplLZ9DaGFzpw4xwMTRcqVQKmqqB+kJIRBBw836QcFntDhKTh2tJ\ndRDsdqdHtnropoAcCkvWYMkaKM8DfNudZEPHEJKCGy0S+5EAPpOGGarYdQnX4D6UxNJBqQN4GqtO\no40f/8GPek3fx8+OYWhA1FPeq6EwE3rGWOlD1jZLjxDHh4VB6UTAjbQ4hhGIHJ4ImKSSYvtuNOVx\nYO9QUz1c4++nRMdFHYfZPotVLQwA4nCJQbgaSJ45BduycOutm5j/cM59ZjiCz//ma5h59jzzWHHn\no61tBP/e2GYTLgZ5SDEIl5RJIjc5ErGOqC9tP3WES8qmBhCu4JiWGi4E5kzANX81Ff1Q/ZEHgaXf\nEiQRVshcdfnTRcx+/sojjSQeV8M1AaAMAF6a0PHSjH4kZ2dn/2h2dvbt2dnZ/+FBTtIPZqViDOGS\nZQWGz8PFNi1wHAfJ1/Imw7CaOArk/YY74fl+tGTGJXSsChV/I2FCCDL5FIYL+cCkyXLdLUopbH9w\nD4QQnB6Napi6GE6moXkRB62tol1uRzQbp169itzpURSyWTx/8QK+8flX8LWXXkQpl0N9ud9iglUV\n+Sha/BiyhnKoWTng+jvV5t0BL04431jdAbUHi8wPG+GaPn8O/9Hf+63ANsIL2NqrQPXtb7faJ6bj\nMhuscDjr2N4dQwhoKFokpBJuasoHpo7rMFVclPbaBwHA/ffv9sgWAGzOrWN7gIN/t1IxAFbDaj5K\nZIhjPxLfKEfXD9V/72FUpMYRpA7D867XO7R7XUwdcGz33htUmRj5zKejUtExjMjYRUSBaYANAMJQ\nlPjYsozq+i5+/Ac/wvwH9/tecQ7FrZ9/eqTn1m53Ir57ga4N3fO2bKj16G/B0i0BfvE8dfWOfez1\nsAAAIABJREFUjoXW+i7sR9mr9YhgjaFiNsnseAG4gYaAkbQoIFmKzr0n0VeRRbiuvnYtsq1da8Wa\nZj8sHBjhmp2d/a8A/Nfoj/oEQLhnDIu4/Y8A/sj7/1uzs7Nvzs3NsRv5eRgdPTjaJBljqNwMNq3m\nTIP53k6rDslfDUEpsuk0Esk+4TozPXqoz43DakeGlBDgCByo5fVPLKUhSQJK+QSkkGHm/toqbN85\nZQopTIwMo+rXVtlO4LwtzYSwU4couQPNzJlJLGy6VYyhRQKmJiZQX6th6uUp7G7UwHmpSl7iQQhB\nqpDB7BevghCC6soO7v3wg8D5UVVDmlBkR/O4ePks7t6+G3hdldux1+tBrqMfczfmIPJsIbW8vovh\nrz+PzAsz+PAH7wbPrdlBe3UHUuKA29qyMFxKB6pQk0k+eK8AGBrO4zd+66v44BfXUfYai0PkoSoE\nG7tlPHt52tuTYigrMc0Mj4rdRQ00XMFj2JEm5oLIgwjufpQDbMOrVCRAqpABR0xkhzM9zZeZEWCu\nBjUuMHSIXiQ1/N39EJNActj9bduVRuD6WjLF9k4Vo2NFZBnedWazA0HgAr53UjGLBCOyrEKGpQQH\nbJ43kR59CNopH5qLNWgDvn8XKVgondA93oW614blRD9b62gQeIATgq9t3FnG1csljIz1o8yd9SrS\nggCHp5FnRsjmYHWCk7+Q4pE64e/xMKBWLOih3yVRzA8YZ3Kg6wUYbfcechyKhbktLP38HvhkIjIu\nOKaJlEiQO2SWo1GvwGDcJ0P5BASfrqy1U4MUylBImSROT7MXyudfmkHl5jy0RrM/mJs29JVlTDx3\nAWI2B05gy14eF9YsK3I9R8fzaOxvAzHP0nAxCd4XIW7NTGBHDkbKeF1/4HnEaCuRc3vuV2bRLtex\nHSpI2FvaxLWX3WyFaVrY3txFKp3E2HjUeugkcOAoMzc393sAfs+/bXZ29vfhRrludyNbc3NzVuh9\nv+vb/6cAngMwkHCVGf0NwzBtwNCDKzRzv4n9vRYIFwwNLi9uwfCVruqagUyuGHi/QblDfS7zXBQd\n7Yrr5uxQd9UEQsBJAgzDQmWnBlHvsyHqOGjtVgNaESEpYrhUAvVNhoaqQ/TOmzoUkmqBWhSGlxId\nL5RAKXX1PJLQ80ESBRH5dAbl1QqGZkZQXinD8bQBjm4ChMPwuUlUKt5KPZuFkM9Gwt9LH83j1CtX\nkEhlA9cPAFaWNpnXa3Q0d+zr6IdcbmDrs7XY1w3dwvwH8xi+dAZSOoWObyVpmxY2F7ZQDPWvJAIf\niTZurewH+lzu7zci39W0KMrlNs7NTGNr05emJBzuL2/g8nS/0fne6g6k0Qd7SB3TQpsREZIyKTht\nOfAdTMvpV/91IxwUkEbysBwKaAYq2/tAIuPtQmFaTlCnZJvQOhpSuVTvu1NejERd9FoDbTsJ27ZR\n3q4G/HIMzYBtO7h3dx3PPTcTMRSGbaC530ZmqB+Z1mQLsBj3ii2CCzfBNVqQkWKbo54AKKVoL0eb\n7/LpdLDJN4D6dgXW8MmSP9KSIxouSilaDRmW6QDhILml491/9ym+9Xde611rSRKgMUwoqSBBM4XI\nNdVtGR3yCNtSHRP6bi3yTMIhA8cZK5WBUW2i09Hw6SfLaNQ6IKIAgbCjYivz25hk2DOw0N7ch81o\n0lzergU8+srzW5E5KjmeiR03qzUFqZEclFDP3/pmBdmxLLC3ByokQBNpQEo/khT7IDi2g1atHdCd\nAUCr3on+Xj7sb1YD18lJJiPXaW95F9lL5459brqqo1ENdlggHAcTHCYuncXqvWDf3fsfzePya89C\n03X869/9Y+xs74KA4Gvf+DK++TcOlqAflRweN6X41wD+jvf/3wbwhv/F2dnZy7Ozs//G+78A4EsA\nBnfvPCSEpBTx8KCWDUOO5pQDTaup60getoTIMry9DgvZNzkST+MipSRwnobKqASrnqxWOyLMTRYz\nGBsO5uod0+pNanpLwUguqJlKSBJOnzmFVCkHMZ3sCZAnhofAcRwoBVbeW4Rj+T6LUnAij9L5ycCx\niozBprG6C8d2MMpg+fsP0RqCUoqdj+4fuF/l3hoopZG0oilraIcmntRIgSlWDeu4WCnFhLdqvXw1\n1B5JELC8sRMIkZ+EqNpqRluxcMkkMlMTKFw5i/yl00ifHkZqooTk2VNInj2N5JlTSJw5heTkGDJT\nY0j52l8RvR8tIoRE/bgojfR4o4kMwvJL4tiAbaHJMCfsFqKomo71dUafSgootdC1YaUUAUBIgDLE\n3P7vcdKw2x1mGXtqJjro27JysoaJXo/DMEzdgmlYrj0EDRJkUIp6pY2FOxuR90UOn8qztXGO/VRY\nQxzG9LRrqUEaOyBKE2KpCFXR8d7b99Dw7js6wFqjVWW0P2KAWlasPomGJCCHFcz7kR+Nptfkmu/5\ntXRwch1EOV7KrVtNfRKtyExFi5AtPimBMn4vP8K/J8txXq21Bto8hUEphdbooLa4hZ1P5rHy3p3I\nb50byoHjeZy5fIbZpWT97iquv/MhdrZdKyYKijd/8g72dt3xzLFtqB31RGQjxxXNfwfAN2dnZ98G\noAH4LwBgdnb2nwD4+dzc3PXZ2dmN2dnZD+Cu0f5ibm5ucHfkQ4IQgmQhGpXRWzISIfNSf9Nq2/sR\n/YJ5KZ2IrVA8DPwPFpFEwDCQzPZ/ULNWh2Oa4DzNmMXQ5ySHhzA2qUESJRimT29mmOB4HqasYvxi\n0GMmPVrEK998DT/78VsghEDKJGG0FZzuRlgIgS6HJhHqoDhzCnzo+xbOjWPno/sB3ZOtGejsVDE0\nOQSe5wMWEXJHRqcjI3uCNghd1Je3oR5iADRaMtpbFYycHsWq16aBUgpT1dDmg2uIoYtnoFabkHeD\n5DesQWCJ5hMJN/w9c3EKoiD2rDo4gYciK9gp13BqzCXLJ6HvsZrR+0Ms5t2JmRDwSQl80j0npzAR\nnEwtA1wrSHiIZYDaZi86xGfSQWJIKSxZBfzOz7wIKkgg4bY+phZpn0S9wpAudvdqKJWyKPh1kdSB\nXOtgFL6igrgKOUJAkxkQJXgdqCZD7jjgBAHJYjbSjPtBYJSjCwihkAefy4KTpGAfP0phd2QI+RNK\nx8VoqTr+qk/HBnjOJV6ODcu2sbi5gffu3MLLX7iCv/k7v4pRxsRFBQkQvLEopDsg1PEKIQbYgTwB\nOND0lFKQTrXfwkhrg0sVMLewCz3UaoqaJgij4KF9yKbJgzR+/nuEUsrUIbHIhe9NSBekiDxEl3WY\nmgnRJ4EhuuwuioTDF29YHRnyvXlQywLheWRmL0IoHL/w6aiC+S7Cv6eYSUJIJ2Ap/e3UdqDW28wq\nxi6UShOtzX2o1RaUajMQnd7bq0PeryMzPtRbNuY9sssLAqaemcbCR3OB4+2s7GBtJxj5oqC4f2ce\nvEXw7l+8A7WtID9SwJf+1leRZ5ifHxbHIlxzc3MOgH/E2P5Pff//n459VgcgUchECVdTBk4HIx7+\nCFeXcKV9HlzZBxTMK/u+CJcoAhwJEC5QCrNcReKU28KBRbiEYh6ZMRVjpSI29/sTpq2bME0NoBRj\npT7hIgKPs19+HqcIxQfvfoJOpwMpm4JoA7NTU95OrJAzxfBs1ONESIjInxlFcy1Y2Vdf3kb+zChG\nRod7TL+L8m4Z2YvHI1y2aaGxvA3bspEq5ZAeLYIXBdiGhb1PFyL7J4dy4CUxQpgq91Yx8lLfRNBU\ndVCHQvZWIoQQcCKPwtQ4swghTLgMVoTLq4YSRRHnL89g7q7bF62rnVpa3+4TLkWFY1kRzU0XjuOg\nulVBq9qCZZiwTDeKYZsmbMtBbiiHYUuBFJoDhUIexGGI28NRIl5kpgOJroCm3QFHyOegB35LGrUY\n4XlQMRkhXMTU0NgPpjxYjXaXVnbw/LPnIfj0cXJV9vm3kfgIFwBIGUBt9cXNlGLl3QV06hrA8cid\nGcW5r7zQiyI/CFzvLUYKd3TYJbi5LJyQN5fV7pwg4WIL5uVWmHAJvX2Xt7awuuNWDr//7h1ohol/\n/N/93dARCGi62BsHKCdExfmONfh3eALAjnD5MhSWHukXqVar2NllkChKMT49gb2Qw3irdrgIl9Uc\nRLj619ZU9ACBAFzD0zjbIgCAbUIQOCRzKait4POo1GUUJoPkgyhN0NzIoVKLrs3MMqgnR6G2DXV1\nHbkXnj3wvXE4PuEK/p5dA9RWqH+kUm7EEq6dT+ax8tFd1GMIcKuuwDYtWKoO0YtmFXzRxalrUcJV\n36uhXoveM0vzK5BX6lC9uaJVaeLDv3ofr/+Dbw38noPwdJixhHDYnop+Dy7LjFpCpB8gnRiuRCFw\nvWCS2WDKUt8rQ5ocBzWMaLk/AKFYQHpEx2iIcJmyBuo4EAUBxVz/YR29Ng3Jq4L8x//kv8XH12+A\n4wjGkYC21bXLiE5G2eEss/k34KYVw4SrvVWGpRsYHR+NEq79KmYuTjOPNQiO7WDpR9eDVaUcQWoo\nD07gI87MADD5uVlQ24kQLnmvjnFQiEkJSr3dczu3HQeyrCGbTaEwNQFeFCDloq1tIilFRoRLSvRX\nkZevXuwRLnAEhOOwtL6Nr7zyXG8fu90BxygRdxwHb//Zm9gd4CBNbRtOp4PTZ4Zx/uIkcvkUQAiE\nXAZoB+9tSrjeYOtYNkxVh2NakKQkxPDEqstAKg8QAt6/qvU0X45uuY2nu2SI8ICUBNTgAEQsA429\n4G/gmIyelIRgdX0PF8+f6qXDLMOCIetIZJOuncWgiYLjQKV0L41Y36ihU2m77+F4tDfLqM6tY9TX\n+/S4MGuNSIqF8HzPtVzIZSNmqCdZqRhXoSi3QgTbMsARN4uzVek/i6piYH5pF3q6BJqg/YiZmAxG\nPzkhSu5s+7GP/pRSWM0WHFWDUCoE/LUopWxLCH+EixEhnL+xFLm/REnAF7/9MgqXZvDDf/n9wGuH\nTSlarfj9qC/CxYpuJUu5SJu44MHd96eHMn3C5XnVyXU1SrgsHdTUAOlgQ1e71Y4QHVtRQS07ttrz\nILCaVouSAGoP9jJkdQ1IjxQihEuNIcF6W8Fff++v8dG9e7Gf0e6oGMkU8Ew21SNceR/hKo4VQTgu\nIA1QmjIatUbEyGppfhmpsfMBXWpls4xmpYFCTMXpQXg6Cdcheiratu0aiHb/NqMpxQexhFCqzUge\nO1HMQwhXmGka21sJbr87ThSRHi1grBhMG3ZviNFiEZw3gIiZZGCiyWTT+OrrXwLgtvpZ3HrPfYEx\noY1Mj7gTYLhnHYDc5DD4pBTQ81DbQXNtD2MTI8DN4P77x+yp2Nrcj1p4OBRqjDNwYWoc2fEhUEqR\nKGQi763eX0dKFFANPaCdjopsNoXSBbfFUTjVDBwypZj0Ea4rQR0XEQTslGuQVQ2ZlHtPWc0205Nn\nb3V3INkCXI2I41BsrFewsV7B2HgRl148j4Lvp9RlHbW1CtSOAdNeg6loLlnqnhPPYer5SRQm+wMM\noU5vcOYEAXw2461EfcL3tgI+nwHlPDLECW5UxKcvotRBYy/UI82ykEoloKr9gZQXBdRbMqrVFoZ9\nQnm52kEimzyU4SZNZHqEq73f6p5A7/4t313F0KUzAdfuo4JSCmMvqjkTh0s97zye0azc8lo5nYh3\nD4MwUF4IphTdk8Xsi9OYu70G3R+tJQTNcgPVagNDo+NAnDqC54EQ3yKOxTQbeZTQ1jah73gRp1Ug\ne222l+qihhnRyxG+X5kLIBLdMjQTS59tRMa/8xcmMFRII+Wlo/3H1WUNhqZDYrjXd+EYZr/3KPN1\nP+E6un6LeIQrM5RBddVLcXMcwAmQOw47cq22QMXkgVGuOH85alvHJ1wMo2OeR7TAIwSmVnKY0Zu4\nxo5ebc+v4eP7gzW+tu1gt1nD6WYTqaIbqPCTI14QUBgpBKL1umFAV3QkQu341LaKRqqFoUJwTF+5\nvYIXf/WlgecRh6eql2IXrAiX1gz2tGs2WoFSetuyIAkiBN/K70EE8yxju8zEMDPdYOyVY9OJgPt9\nxmPKUMd8PcImGA21u0iVcsie8h3D9yBKKQn5iUKsZoRwHIozk5Ht9eVtjE1ES5nLx/Ti0hjeNHEg\nPIcJL2VICMHI1enIPs3VXRBGsUS7rSA7Odwb6KRsKjIwmbIWEGcOEs0DwNBICaNj/etLBB4UwPJG\n3xg2TudRCxn1suCE0nP7ew2899Zd/Pw7b0BXDRiqgcW35rC/sIf2bhNavR0gW4BLktc+WYPWDoXu\nfaJzsegN/jRIuAD0U0yEBExTAUBpazDDiwaH4srs2YDRLicK4CURW9uVwGf0BMCHcTgXJFeDBEBp\n+Ei2RwBtzUBtIdrc/SgwK1VmoYO/0pRPpyJ6MWpZzInjWGBEuGiqCLkdXZwNjRVw+rKvQtI7L8u0\ncOPtm5H9A8dkXfPH7MVFLQv6biiysdrX0cS19AkQ3dB3WLizDsu0e107AIDnOUzNjLmmtTyPLMP7\n6aAo16DoFhBMKbLmhYMIF7z0fWbId27ewlitt2FL0XmK2CZgDPbRo5YV28A7PN4cBayUIoeDi0mo\nZcGxgp/LSrUaLZlZDXr/1n22cN37vR1Ke6832m1QuF1fcqHfvDQRDG5oug6TseA2dAPVZvT3XPts\nBc4xi2eeSsIlZVIRdu4YFixfhKYeMg60TDsQ3QKATPEBIlysB2u0CIlhFmrW6swKtO7kRwjByJlx\nZFLRSExXv5UeLaIwNTHwnEauTvX/8A1MwzMjrmUGq4mwB1bnerXSRCEdPafjVioancObWI5cm3aJ\nkofi9ERPMO5HjuH9pJgWznzx2d7gzAk8073YP3DojAE+EXK0vnz1Uu//3UKIpfV+5MqW5Z5Wwg85\nxpi3Cwow30dEEftre7h1fQHNrTqs7iA0YFFLwWHjxlpgYCKm1vvte2JZv8Nz26vA8S1GaChdUa+2\nvSba/fclRQGJhITp6f59yYkChIQIRdFg+iYiuepVjLGq5ljfI5GFpVswZN9A6Pv88t3VI1Uz+eGY\nJtTVaJUfl0y6ui3bxvKtJcx9eB8Gg6zY7ROwVHCcSIQGcIlupxMd/DO5FBI5CVJCjCwebr57Gxqj\nt2oPzErFx0u4bFWLVEraigrbM+M9UL8FBL6DbdmYv+0SNv/lOTs1CkkSeunJPCOiciDhYozdflDD\ncFOgtsNcVMYZnrpfwezdB2Ja6gvkPcJFbQdqy+gtQPwgPq0jC0alFltVyxpvDgt/StFxHNTqbeyt\n78I8BIkLL1Z4SWRKPtR69Jovza9EtiVLOeQmR0B4Drav8Mu0TDimhWzJrVD0ozQRdAVQdQ2GztD5\nagaqjShh1TpqRAt4WDyVhItwhJkm8uu46iExrG1ZEcKVZkTKDgNKKbPvU2asCHGoFAh7A256kKUV\n4X2VfumRImZOBQmVJEqY9CwjJl+ZPTCNkZ0YQnKou2LwyAZPMHTOXbUPcphOlXJIMlYbXEsHCc3w\nrWYL2gElwCyYjGgUC2I2FdHocAKPkdloqX4mkwpcFyGVgJBLwwgJ5Q/ScRkDqhS7CNhDeDqu5Y3d\nntcZAFitaNREYegLz12bxvNffxEvf+vzmH3hfM+ANHB8ngdAsbmyH4paDbgPCAeloaC8FKpY1N3v\nymczveN24dgObEUPiqiFhJti9NCotLs7u/84DpIJd3IYGS4glUq4HnQC36uEbfsJrVdxxZz8WZBS\nkBuM+8X7/AeJcmmrG8wJJzXtFpW88f/8FB/+1fu4+cYN/OxHN9AJLRROpK8iK7rFC6AAZBbhyqdQ\nrtRRGMlHCFer08HtNz+N/6wnMcIVMzkbnmaOpfcJtPShNJDyXpnbhqa4163b+YMQgvMX3TGV2jao\nbSM3FI02tQ8Qzh9IuBwHsG1o9Vaky4WQSkDMxBsi23r/3iKEID2Uicg+5EoTNBU9b+LYgB5/Lw5q\nV3VcwmXpZq8qkFKK+/fXMT+/gRvvz+GdN+8GfLgiNjRgE+kUo+pPC6UVbcvG+mZUlnHh6kWMT46B\nF8VAT2PTtmAbZkAw30VpPBThMhgRLgpYholmpw2L8ays3Iq23joMnkrCBRys4/JbQvQ9uIKr9mzx\neIRLb8kRo0RO5Hsl69LIwT2whEI+kK5Ijxbx4qVLOOW17UlIEr764guQRBHF86eQPkSjVUIIzn7p\nOfAJESAcCAHOvDgFoeu6e8AgWzwfTSt2NvYxNFKKbC/vHj3KxfJKm379czjzhWdRPH8KqeE8ClPj\nmHn9c0x9ztDlM5HIJs9zyHgO71I2jdRQHoQQVEJ9Fg/ScbE1XMEI1/SFc5B8peVEEKAZBrZ9Axsr\n/SAzCNeVX7mKq689g0svX8aVa2fx+rdewDPPTyHt6QiI4DVzpoCmGGj7U2v+CZcQkHDFHsdj7952\nr8UTAMB0U6i7NxexdmcL63e20fERGrOjBggWCOmZpgJAoxoiXKaNjBc1JIQgl0uDF3gQ729eFNAJ\n6eSUWufwTZMJgdph3K++qFD5sxUYzVYgpXMQzEYTRiWa4hWHhyCWithZ3g60+3AALM4HB/oTEc6z\nBPO8AF3VYdvB/pGCyCORFFGuNCCmU5GFoqZpWL61jNpuTOqa4xHxVqOOFzF8PHBM9m9mVqputIhB\nuHi/hxJ1ApWsc5+u+vZ0r9/k6SGkfZFtRzeOHOGyNY0p3g/DMUwoZbZ+a9BC2Q4RkMxQNkKolXID\nEBOgYjSaT9Q283e0ZcXtlRoDVtu5w8CfFSiXm2i1lV7FsNzRMH9/C4DXTDwXXcAzdVxDjK4TIRK8\nMb8SWeQLkoh/9N//Q/zqt78KThICES7DsmAbFgqMasfiWClwjVVdh23ZQcKmm67tDaWoM+x6tha3\nmJXtB+HpJVwHVCoGm1Z7gnmfJUQikwQfU8J/EJT9aHQrNVzoESjpEG0BhFAD6NRwHqlkEr/5hdfw\nD3/zN/CffuubmDk1CU7kMfHipZijRJEsZHHlb34VM6+/hGu//jxKZ/pGmAcSrunJgP4BcLVOxUw0\n9XrUtKJjO5FyaQDIjJVQunAKZ7/4LC7+xms495UXmOQIAISExEx95vJpJIs5JAuZ3rRS2QxGeFgR\nrgDhYtpCBCNcgiDgwqWZ3t/EI4WLvrRiWMdFKYUSrjoDkPEtGKxmE4LAY+b8OL7++vPIFdLgeoTT\n0ySU/QOQ+y1nvvEKnv2PX8fMN14JDtIc7wrwb6z3UotGo42lH11H5bNVOI47oOyv1VyDTbiEK0yG\naKJ/zXoRLkoBasMxLaR9rYxy2VRAX8hLItqhyJBck49kRSC3GANa9/MtC+peBTtvfID2jVtMEhV5\nq21DXV6NbCeCgNS0Gz3dXdmJvFbebwVStLaqPZAGBoipUORFyF61rf+3yOTcKO5+vQMQgvxwPlA5\npWhueu7GTz5ma1wICZLpLh5jWpHGEC5HNzwzWkZKMcGuUNxaLaPV8D1jlIJwHC5cDGYMHINNuNoD\nCNcgO4jwsZn+Wwfot2wtuAjNDGV6+rwulHLDnfzT0XMn1AHRoud4UDP2Y0W4TB1GrdKrPq54HmZ+\nQrm5UYFl2eCzmahJLY4inA/+JnM3XSsHCkA3LGi6ifHRUYiiiHQmDT5EuLoRrjzj+guiEIh8aV6U\n0fSlFf0ZD5aOy7FsbNxfj2w/CE8v4ToowuXTcNkMS4gH8eBiphN9TJpPpwPpQhZ64uXue0QByVIO\nhBAkRBG8l3cefeb8kbuncwKP7ORIpGKSOObAnL+YSjA71CctinBJ01GF86x0opBOHNlPaey58xB9\nui1OEnDp6y/1rDK6qGweHOHqphQppTGEK3rdL1/z6bh8flxd2LISmIy1kDgfcFdmokfmHNPs6VYA\ngOMIisWMLy1NAVA06v4Il/tPaigHwnHIjBYxfMWfbiUAIVDqMsqLe6hvVDH/5j2otSY2t8r49O4a\n7iztotpUoDTdwcZW9UBq1PuCoGIKpmGh3fRNaI4Nx7ID0YNsLuUjiW7vTlkJHrNTVw7dloRS6lYr\nMUxOHd1wKy0dB429FmzLgrq6fqALvLaxzYxWpKbOgPPSoGFtBiEEhmmjExKy250HjHIxKxRFdHqE\ni++R00w+BYNPou5FOTmeQ9YXFVB1tzFwZbOMNUbTdwBPnI4rLqUIuNojtump7xn3nfu9T0LaHkox\ndmoYhVAGw9EN5Bjpq06jDSfGgf2gdGLvIw2TWaGYGkS4qAPHCH7PZCEF4uubSClFeaeK9//iHcx9\nsgSLj6Ynid4JRH6p4xy4ADkq4SJqC1y7DKtWAywDhqqi7QU4/I+0ZdrY2qx6hCt6riwizZKy6C0l\n4PO3eH8RACDLGhRFg6rqMGQTe6u7yOYy4CURthMkXI5lx87z/rSi5ul3/YTL1AYTLgBYubXM3D4I\nTy/hYlYqujcApRTVct8/h2V6mjlmOhGIF8wHzo8hnu+CTyWDqzUPo9emAn8nSzmMXInqlg4FwvA7\n6pbWD0BxJhpBSprUXXH43nrUCBcrnShlDvaRCUNMJXD+m69g8nOzGH/pEmZ/+8s49/yFyH6NcgOG\n76EZFOEyDRM0xCgFQQDPqAidvRbVce1VG2j7vp9fVM3Sb2UKmd6q0GpEB/TSWKmfbvZ6dMpyUMPF\nSUKga8DECxch5X3fkXCotzv4+O3bWPpgCY7loFyuY3OzDNO0oBsWVrZrqHeJHAWsdvRcaTLTTyd2\n4TiQBL63KACAZEJCykeEeVGA41AoPssIrakyzVJZMDqqW4Xpi8wQjsAxLbdE31s42IaFdrkDalpw\nGNYrXVgduW9B4IOQz0H0KhPVjooWY9IkAo9KKF3E0uodGpTGphQD9wsvAmICmYlJ7LetwD2aLWR7\nXTIcx+51Qbj5xg1YrBQrK8J1Am1ejou4lCLgpRXDmleOc7t5dP/2CGt5p47KbnQ8vvTCTGQbNQxI\nSQnJUKENdSja9ejvSSllSgRY2iSj1YEph+4/jgyWglhR8k8EKSCy39+vY35hE4ufzONqxb0/AAAg\nAElEQVTTn36M6z+/yxzX/VEus9Y4kFANIrys8ySqex0Mr4NJtdp0uxUgqihdXd4Dn0kzI1wsbZ6Q\nkAKLaPcEac9b0XEcrK1uwrKdgDB/uFjC+99/F5IguhFA39tNy3KlDTHznV84r/YIV//38Ivo23In\n0AWmi+r20WU1TzfhCt14lqLBNizIsgLF13jWMi1whEPSdwOk88eLcFmaEfFwAiGR0LE4PNTz8wlD\nKLIfwsLUBM586TnkTo9i+Mo5zHzjlcGGeYNASEw5+GC9S/7MaKRXZTGXg6XqkCsNUNurEjtihItV\noSgxKgwPAymTwsjVKYw9MwMh6U70kYpTSlHZ6p/jIGuIQW19wigUCxif6JfndyNRAXsIXxqCpd9K\nh9KJYQyd87XBgVv9JPvTsYREyCon8DjzhWd73/GjuQX82Vvv4Afvf4g/e+sXaLQ72PTr2ggBdSg2\nt9zUOyUx6RMhgXotnBKlSAohTRAhGPVV0XI8AcdzgbQipeRQrZsAQO22XOkJiCkkkUMqEX0eGntN\nOI4Ta9dAKWWnEglB6vx0j/zuhwwYe/sJAsrl4Hk/UISLOq6GKvgpru9SI3xcgkwhi0o4RUSCDtrd\nSUPrqLj7/t3oRzIiXKw+jodFs9HEn/7Rd/G//y//DN/9k7+EOYBAsRCXUgTA7PfHJSTUdqq4+fMb\n+MX33saP//hn+PPffwM/+e4HkX2Lw1lMTEWbjA+uVIw+h46iRogJ4TiIw0ORfWWW4WlxsOEpYRAu\nCBLSXqstSim2vGe2awGzfm8DDIUCYPbvfVa7qjAO3VORUhDZ51nlFSZUa203+O7YIKHFarulolaX\nwSUkhOkYNU3mZ7OE892xYnN1E5qi9aRBAMBzHArFArSOisWP5mEZViC1aTk2EgkReoynV9cawrL7\nixVDc/+lDo0sWmrNJrKDugUcEk8t4eJ4LjBhW5btrtxbcsSY0zZtZFIpcL7qj+MK5uX9aJlospiN\n9CgkPA9xJPpgAvGEixCC0swkpn/1JZx65QqExPH7PAJgpxEO0HFxQlQzVsy6ZMYxTMjlOhzTRr3a\niFQCDgIrpTioeueoGDsXHWDLG30d1yBriK4lBHUotHoH8l4dZlMJ2Iz44U8rdnVcSzE6LoVhCZHx\nIlGUUmaEa3j6dJ8cUgrHptB1C2ZvwCFu0/LwcUeLGLlyDk1Zxo2FfhVNR1Xxzq17MPT+b98dnPbK\nLbdXJuFgNZtRDRAhaDSCRMaxKZKhqkoi8Bib8WlmqANe4oMVfoSgsRrUSMWhn55x06O2ZkIgFMXx\n7qDn01QZFtqVDtO7CQDMSi2Qtu0icfY0+FT/OsaVehNBQLXSDnjv2B35+I2sYyoUQUg/pehDppjF\nPmOBk0gnkPSIt+pL1cx9cA+dRmiiOcFKRUop/vw738fNj2+jVq3j4+s38L3vfP/gN/qPcUSCtrPX\nwk/+8Me4//5dbN5fR223Do3RmQIArrw0Az5c9Yu+QelhdVysdCKfyzKzE2o4Cgz0iFMsGISLChIy\nYy4ZkGUNhkf4/O3JNtajcxCxLXes0A2m52MYgyKMAehyQG9oyDo0zUSn26uXAoTQgFSF8DyWbi6B\ncJxHukKfzRTOx+u45m7eB0B7mSoAKGZyPU/N5U8XYeuWa33kAy9yUGIWeCVPOK/5qkRty4JjO4HM\nSBcdQ8XFl/zzIj3W8/PUEi7A1XFRSrGysoOPPp7DJzcWcOMnH6EcJlyWhUzIT+q4LvMdhollXGNS\naSyaViQcd3K92A4CHyVsh1nVDl06gwnfzSUKArLe9aOWDaXcgKWbqOwfLFTuIq7/1klhNBAVchGO\nWMRZQ3T1W1qjA1NW4ZgWqGpg8/3PmJ8167OH6Oq4VjZ3e6JNW+nruJgRLi8d7ihqdOAjBMnhYmBS\n6JaaK74ol5hlk9XxFy5iq9mAn5BQSrG64ysioLS38LQsBzvbDQAEjm4wB8NGLfgdevotn24kWchg\nxN/LlLrVdW05SLjqS9uxg6Af3dUtBYWtGnBMC4mUiERKRKaQimgKm7tNWDEpRdYExKdTSEz27xlK\nKfbWYrx1OA6246Duuw7UcZgk7lBgDdTes8q6XzKFDMoxKfz8SMGdOHxaIMeycffd0L17ghquaqWG\nBU9T08WnH99CpXz48eCoRQdL81tB/WmMFjWdTWLq4gQ4ga39A8C0hmD1VGQZGQuFfE/v54d6RP8t\nUBptEA8AQsLNlhCCuu+YjmX3CP/WwhajCMJNU7OiW6xm74eqUnRscL4WX47jwFQNVPxRI0rBccT9\nfO83IQKPzfkNKG0lRjjPsoaIzoldT7OFu26PXcsnii+F3N9NxYh8T44n/Uh5CIIkIjeU6+m3esfR\nzb7foQ8tTcbUM9N9UmcZx3p+nnrC1WzK2POiTpRSLN5awuLdoEeGZdrIpsKE6+gRLkop2gzClWUI\nzQFAyGYi0SxxdIT5ADwMHNdhmhCC0WdmcPbLz/csB7pRLsCdbJRKA5uLa4c+l4i+AYB4DA1XHMbO\nRiNc9d1aIC8fZw2h6wYc04blM48UeQHtzTIzynVu+iySXUGop+PSTRNbvknR9gZrVoSrS7hYK2gh\nnwPhebd02WMV3XJlWdF7ka84/Rsn8GhwFlxG5e6rGzYUXQOfEXwrf9IjXetrtT4BC5ETSima1VZA\nA+RYDjIpKUC4EoUshiaHfdozB0JSgmnZ0HuGrQSgFDsfxThGd49vO1BrLZfUtDo9d+pExl0tl8Zz\nCDMuy7CglNmu2qy2WsmzpwPPYafRYf5WgHcleSGq46qzxbQHgVWhSHlXh8KMiBaysZpJQeSRZ0wc\nm/MbQSE4Yywgjj2wiCYOC/fZHkTX3/nwUO+njnMk0TalFK1AU+f4c37+tUvgeI4pWesalB4mwuXq\ntxiEK5+LRG2oQ4MWLB4GVija0QImSjiAd7WZiUIGtRCJ67qvV7crUNQoYaKmzqxOFEejVfOHuf5E\naQTO0VRNOA5104m9nYhPquGSLsILoA7F0qeLTOE8S8fF9OJqdmBqBtaWN+BQGogwj5SCVkWSIEbs\nNwjvzjumyo58D00M9VLxve+om96xg8fSTR2aYWDi/Cl33DvGcwM85YQrmc+iGVoROqaFlbnV3t/U\noXBsG9m0j2ARcizTU6OtuOXzfnAE2fGoT1UX6YszkMZGwGcySEyOIzV15sife2wcI6XoR3F6wvXE\nSogohT1VKMXq7YVDH4spmj/BCFemkI00I6cODfhxxQnnDU2PEELR017Ie9FJnBd4XLjss4foRrm2\n+hGS7mAdF7EAYgiX5wRfmhjqPdROIMLV76vJgq7p2Nrdcyt/CHF7BpomeEmAapvgfSv/XlpxvwnD\ndJjn1Km33RWfbwbjAEiSEPBCShazEETBq/7xVrocQSKbQKf3zLifp5QbaKzEpxa1Rge2bsBqtz29\nBwEvcBA8sphIiciNRFfE7Z1aZJvr6cTqYxq8F/bjolvd7ywKqIR0XOYhUjdMxAjm1Y4a8AICADEp\ngRd5VAdEjwrDBeih9JSpGdjzN6Q/QWuIOML18fVPmdW+YRxJsA3A0K1g21p/+oq4Ua3xM0P4wjee\nw8zsKW87jbZlchxQy0YuxosrYP3RkWPNqokYjHAZqgFq2QEayCelweNbjH6rS15IqEcpgEArr621\nKLGym03YmoZas42mrwAmcSoa/aeWNXDRA1MDMYJjtiHrUHQLqmGjaxLY5Thne/ZDtMcqlj5diFwr\ngB3hEpJSdExzKJbvLkBTVNhW/7kQOB6FfJDMSqLoqQ/6RIl6/41rhl0aHwqkFAFXOC+CRz5khSQm\nJCwvrGDmufMAPX6xyVNNuBKFdKSdgGPZ2Nvup0+6eV9/25xUNsWsQDsIrOhWeqQQ0W/5wYki0hdm\nkHv+GlLT52KF9A8FcULZI7DzzFgJF779KkbGolG8wwrnHcuOenARtg7pQTDGTCv274U4awhV0WAq\nYcLlXrvOfnQSB4CLs/3KyK6Oa3XTT7jch3yQBxdLc9RNN/uJS1crJKtGb+EVtsHoYnlxFbZtQ8y4\nFh9cSnKb/hKCptzxbDi8398bnGzLwbYnnrearYA2qd7VLBKut38y4VtNehN20itaGD49Eri/pJQE\nzbIjBQu7NxaYFYuUUjTnV1xzUd8sm0hLvc9MTQ5heHay/z08yJVWpMcZtazoxEkIiBSMUhzUqoOI\nIhp1OTDe2LJyKFPM4AnFaD94EXKTod8qZFCr1l2dXdy5cQR8MvqsR3yCTkDHZVkWVhZXma/puo5P\nPhzc1xGI0Q8NsAtRVD1InihFrpjGb/9nX8Xf/W++id/5z7+GX/udz2N6tl9hzTlOoKqx91bDQDqX\njhgrW4YJzbcojI0+EzeiTXzv17t6Jt+9d5DhaZxgvosWIyMQ0HEtRQs82jv7+H9/+Cb+xZ98H//8\nj/8SP33vBoRCHnwyyc6qxN1TlILI0eitrpqo1r3xzBsPCAGGShlcmZ3st1KjDkAd6LKGne3onBlX\n3MKKct375C6oZQcE88VMNqJv7hlS+76n7RWmqIzKY8Bd1IYjXLqqg3cIhovBlKWYELE0v4JT50+5\ni81j4ukmXPlMhHAZuoFOp9MjWrbprpAzqf5q4zjpRADoMG6euHTiEwHCsVe1RxxkE/kMrn39c5Ht\nlQo7hRNGmMwAgHgMD66DwCJcZZ+OKy7CVVvfjQigJW9lxopwAcDF2fO9/3d1XNv7VWjeBGwrKrS2\nHPBzAdxij67QOdzIFXAdmgGPcFGgW6UIAJpmuC7kiE/Hzt3tRx0pIZB9qZiWLIPjuf5E0OVMtoPN\nTffepo7jelx5aPhNfjkBAEXCv1jx0ooJTxM5cmY0SOgJgSNFLUosVcf+7aCPDbVtKPNLaK9sRb5X\nIpMAOILM2VEkRwoonipFJjRTM6GFqsVYVhFcMhlcCVOKPUaFon+SIhwHcByq5aaXUvA+86hpRceO\nVigSAnA85AY7nXgYraTDRyf3rYXNYFrxBHRcaysbMIx4kvn+2x8wIyeUUtiGCdu0mIJ5IZdlRkMA\nQFWMkB8bRa6YQSafGjCG0IAvXBeOboB45rFhtCp9ksXqJtDrQ4r+cwr4q9v6vyvLzDMAhn6LCn29\nU5WhPbLNflSqvFmB7htbKKX47l/+DIvrbuSYArh+6z7q3jkR1rWISSsStcXU+uomh6o/9UrdLhen\nT5WQTIqYnCi4EhQCL4JHsXQ32rP0KIRr/vY8ALeasItS1u0m4vdU647X3eea5zlo3n0aK5wfL0VS\n8Y7tIJlIYtinERMTIghHsLSwAo44mLoUnWcOi6eacPGSiDBHVwwN1KEwvAoW27LcCkXfA3scwuXY\nDmRGtINlFPpEgbWqPUYaYXLqdGRbvdkMVI7EgSWYP8kKxS5YlYq13WqviXKcNUR1Jdqjq5tS1Bsd\npo5raLiEoWEvlezpuCiAte3+xN3ZiUYA03nXg4tSykytdAdGKZlAJpeEt1gE4PIYRTNAeA4Co5E3\npRTz9/piZqWlBNyXW7IMXuRwvlcyTwCOwHFcY9Vu6s+fKmv4q3I5Ho5NkQp9NieQXgXoyKlghAtw\ntWfZyWjFbnVuPdAdQllYhlmr90rP/UgVc8idn4TkRdKEhIhUPnoPNUNVkEwDzVRQyNsoN2CEIrC8\nwONcwBePgnBAdbcOYpmA7Z7jkQmXbcG27AApobzbkJoZ4SpmIlXXLFBCI10iDFUPRHhZms5B/VVZ\niEsndlEpV3v7UEqhVJvY+WQec997G3f/9A3c/c7PsPjvPsLe0j7qOw0oDQWWYYGTJEgMuwUA0Cwn\nqKihFJncweMHk3AZXeE8g3D5Uk+2Eh2z+Fw/zeQnXKZHuAIR2UGSFdtiNy73DE91RUN9vx5t2UVp\nLypMKbC11ifib/z8I8wvbyIc9V3bdu+dcH9fIEY4bxkgGsOTTEhgf7sO3Rdlo9QBz/OYOO3+btNT\nIX2yZaC6V0MztJBwDINZ4ZsMCect28bO7j4oEJhnhkvu5732W1/sWTVI3rXritp5jutFr9Qqo/oa\nbprQijAIIJVIoJgv9FwNJE+z1261UdnewaVnz4E/ZrDgqSZcABA2x1Z0t82F4eW/Lc8Swo/jVCgq\nlQYcM/jj8AkRKUbFyxMFVlrxAC8uFnKlQqA1EuCmCiP+QAwYjPD4cUxPD0KsjsvrjRdnDSEz/KdE\n3wDFsgIBgAuX+1Eu4qtW7KLl6zdJKUWt2UBbk2GaJnOwIzwfGLBKY4XIwCTLOsRMkpmu2N8to+mR\nJdfMsR0gmKquY/TsECYni0in3UGEEAJQwHEoNtfdAdxvVdEIfXfbpkingoQrmeufTzqfQTobvMaO\nQyFNjkT6YFLbwfZHc67OStdh1huwLScSFSSigKFfeRFCiCjlRqLPcWsj2NIp3KsOQETIu89IJ46c\nGcWpi75Fhm2BEziUvRZHxHF7EdrN1qE9jfSWjOWffYI7P7iJuz+6jdauR2y7FYoswpXPxlYo+kE4\ngvxEdCzamPOlFVlyhsjEPxiLBxAuAHjrx29j98YC5v7iHSz98Doqd1cDGkm9o0Kuy6hv1bG7uIf1\nWxvY/mwdhNF7DwBUPXSOlCKTC5mXMsjkoErFQV5cjmX1iFkfBHy6/5n+dGWPcPkilwMJF9MOQux5\nzm0vbQMUTKmKP624ueLeF3Pza/jJzz7oLXSoQ0G9ibHlEUcm4Qov+AwVXLuMaFECAc0Usb0c0l06\nFCOjeSTSaVCOYGgog+Ko77pSCmKbuHd/C7VqO0B6DmMNsV+rw3bcHofdd4q8gFw2CzEhojQxhFd+\n/VUAvggXF41w2brJXPQ7jgMbDOInJSDwPIre/Sj6FpjLc4soDGXxxW89j+Lw0XnEU024KKWwQ8xV\nMTSvVUs/whWpUAybZB4CLDuI7MRQxPvjSQNlWEMcxz+EcARDDHK5u3Gwr1Kk0ACIOgufBGwLY6dK\ngYEPCOq4WGlFkxFal3ztNeLSipcYOi4/4er4qmc/uXcHH9y5ibevX8fv/rN/hQ5DcB0eFEsjuYiI\nWla0WLLqTycqLYXZrmTodB7JXAqj3QnHK2aktoPNjYr7TMmux5Su6lBDGjTHRpRwZYN/D48zyu6b\nCkavTUe2d7YraG+We2lMQ9ED4z2XTCA9OQYpn42Yd6ZHMmgpMhRfWkCttWH6olVxKUU/WHYQ49MT\nGD837vNDc0B4Dh3FgNr1f6JupOqg9i+UUtSXtrH4w/d795JlWNi4sepGu7zv1WGkFLMxHlwcQyqQ\nHYte9835jb6u7QE1XO1WBzvbg7VuWqODW+98jIXrt5nPPYDI8wkAnUob1aUdpo2ApofOkToRwgUx\n+j4W4aLdCNeASkWHFd1KJQKLoW6Ey7Gdno1Ab3FESGw/WOBg/dbWwoa3qT8GZb1n3i+c3/3/yXvz\nIMvO87zv953l7mvv3dOzLz3YAYIASIHgAoCiJcWKFKliJVbKlTibE1e5nErF+SOqcioV2YlUjiqO\nnTgy5cSSLFISKVIkBQrgCoDYgcEAg5npWXt677693H0525c/znLPuef0DADKDmi9VSxibt/lLN/5\nvud73ud93pUdtrf2+MM/fg5pO0gJzUaH2nad2naDbs+g5XVESARc/r2XEvotlPZuor5XZgo4KGyF\njZOl23Js/siEO4eoKYSqsPDQiMO/47Bba/LSC5f43nPvcPniKq1WL1E4r2fTaKEN8dqOO+6tkGC+\nkiugpnW3IloIpo/OcPz+k6T04fUTQqBpWiRdmGQP0W51Ylo+TdXQvGs1VnEzGLqvF5Nw/arbRmr+\nxDQ/8yuPx77zTvETDbgML70Sju5gEDjFOrbjWkLkoruND5NSbCXqt+7cpPr/9/gL9N+ZSKD8N1dv\nPwHDX1xbn9uG2UdpbjE9mYl5pIR1XInWEAmpPT3ExrS3koXzJ04fQ3jJDl/Htd9sBxVC7bq7q1vf\n3qK2736Hqqmsr2zwR7//tRjNPaqzqE6WYoCr2x0cmI694nkjBewWRBiubD5Ns9shU8oyPlbw/uT+\n3XEc+j2DXY/BkaZJI6GFVSaTiqTn3e9NRfKek9PDxazeavHG5Ut8+cvfYA8z8djX31zE2HcXu0CA\njOsurmazw/L6kMalVtvnd776HF999TW+9OKP+NKLL/Kd8+/w1tWrvP3863TaLlBM2kmHzU4d244Y\n5PoxfXSGdC4z7LkmJSBQNIWdHY+J8s75dmlF27BY+dEFVl++4DLkoXtuGTad3fZtGa5cORfXcEmY\nn5mMiLQB9FwqVgxkdAfU/A1HYhHN+y9xv7YYZ7empicZ9wye7YEZgKz3btyMvTc4/NG0BO6GrrG8\nleji3hsFXDCSUhTIJMA1ujb0BvzRn3yb3/gff4tn//x7Mf2On1K0u/FCF2XEx9H34grYLYbnlSpk\nbt8h5Db6Lcu02PSYpDDDdfjwFLqmYRtWsB8xLIt//sWv0+sNcByHZrNHv+cfj6Td7FHb8FOK8eOR\npltAJbp1lG6ysFyqOjJbYv3qWiDN8M9VURRm5z1JjRCoY+Mcv+sQqfRID1+/WrA74NqVdX743Xf5\n4VeeZ5Cg7Q2zXOteP8iwfquSL6JqCmOTxYCdfejph5k/Naz+zxVzaJpCL8RSJum4GvuNIZjyfz9k\najteriCEQA/ug2Tx8k32999ft4yk+MgArpsXbmK/D28Qy7JotztIKel3+qgjQktfwwVuxYFt2ZEK\nRfjggMvqG/QTSks/0oJ5Pw7a1X4IH5HxBOf87fX4YjUa/7pNTwFErwVSMj3nHWNo5763uRu0argj\nw+WBiTDDdZCOK5vLMnd41vucCHbAPsvV6w6QpsXK5oZ7vR0HTThgG1y/epOXzkVbsCijDNd4Pg64\negZqNq7f6vX63Lrh7ozb9XYiu1Us51hf3yFTzJDSNcqe470QAscT46+uuLtYxzBj6UTAdZgfSWdm\nihmwfB2LzcSMKzg1TJPXL11kp15nZXmN3/udL7OTio87s91j9c0r3jM9XIz8XXnW60cXFhU/+51X\n2a03UXX3mncHBss7O7x19Rr/6ve/yj/4td/kj3//a/Rb8XRxmEXZ29iLGR3qmVQAtKaPzRCm3ISm\nhtKKru+QuZ+sEenuNLj2zMtRXdkIu9Ord0HVcRyH3mjLMNxKq0EIGEjLRnS7TOkKZqOF3eoEJqKt\ndofZk/FeqEFaUSiu1xMu69bu9Nx+eHdIK24vb/HWd97g+WdejI3HM3ed4rHHHwGIPCNXVlYYJJj6\nJl0D/9jsgYkoFCP6KJFK0Q/fH++z+VDfUKmqiSbPykj7qWd/9AYXL9+gXm9w48YtLt6I2tr0ml1M\nw0zWb+Wi85Vf5WqEAJd/bH460bFt3nzudb7xf36N7/7es+xt7LpMaZKkw2O4tpY2A72SknK7D2iq\nQiGjUankXWsL22VWL964wfKyO9d0Wz36/fj13lxx/56s4TIR7V3EINl/TqopZHGCXqfHez96d+SP\nkmolH6nY08fHUMqTnLkv2hNYKCK23myv1Hjz2bhvmw+4DMui5m1kwhW646USwjaZrOoo9U3ot9F1\njaf+2lNMH51h+uiMawYMkQrEJIarXo8DrkxINlMuFMkX80NLLulg246bvv2Q8ZEBXM/9q+/y57/z\nTKKtvh+LF6/yv/79/41/8Gu/yf/1W19kZ2sHJdTCwXYc+qZbHSGlu1t2bDvqMi8EudvQvUmRlE5M\nl/MHluZ/pEJRGTVxE2El9geIqYSG3O+nifW/7rY+rlbAHTf5Una4+/XOUTqSmqfjSmK4woArlc+g\n6FpEwwUH67iS04ruAtvrGTSaDeqtRjDhqJqCcBykZfL86++wHHKAjzBc0tVK6SO6GyklAyO+QN64\nchPHsbFNm7bHbg2rEQXZfBo9pbG2vk2m5C4ew7SiCBbSjfV9LMtGGib7I6lUx5GkVTXQmviRrWSH\nrtmORXXC3YWu7+xgeyyM4zhYpsVzP3iRbiqehu/sNNlb3YsK5r1zz014x+mxGFJKrl5fRihKxFfM\nv272wMRxHM699jZvvLMY+bNb0j+cZJPSiVNHpgPwPH1sJvKsKKrKzm57CLCkgzTNSGUnwN7VVa4/\n+xpG6/aGnd1GD4RCt9mNMT/pXIa9vXjV5XipQMUTcDuWxWC/id1ss7u+yfyZw7HfWF1cGaa7VI3a\nzj6/9Y//gF//h7/Db/yj32XtVrySzI/NpQ1++OXvceX1y1w8d5Hd9d3IaZw+e4qPPfYgqVQqMOYE\nd2N8dXkFhCA/M8bcY3dz1y99hrv/2pMcuvsw40fG0TOhZtSeNKO736bwwD1kjx0he/wo6TOnvEpz\n/xJKVE0hHfosipa4sVTV4UIvpeTK0pp7HaT7e7vNBtbIJr+110xOKY4ALh8URhmuKOB667k3uPbm\nFbqNDjurNV76+ovYvTiolooW+NytXV0dXhNcLVIpo+N0e5R1BWk7Lmu6ucHa9haDnsGgb9KoJ3Q9\nELBb20dKGdvMISWyXUeYyd0ZpJ7BzFR490fv8a1/9o1IlsA7WaZHUth6tQLpHHf91L2cuf/I8Nn0\nnegjH7dZubzM/kj2wAdcW7t7SOmmSf3Cn7Smk/d0nK5sQaJ064jOPtlcBj3tetapHgi0LCtgx3p7\nrZgetrHfQFEV1NC1CTNciqLw4EP3DT/gff7t81fY3Hr/XRXC8ZEBXOAO9osvJ7dTsSyLP/nSn9Lx\n2mmsLq/xnW//ACFEUI3SM0KDRzr02j0yaVcA50eumEP5gF5YH8Rd/iMXQiQ2rv0wOq6puXgV4E5t\n9/au4ZaNNdrzbMSDS0rJD557gX/6j36bP/zdr1J7H0L8SMhoL68pr2om/Jqv40p5O2PDMFnf2GVr\naw8jtBPX8xnUlP6+AdfJBHuIpbUtt2Fyd8Cqz255EaR8HBvpOHz9Oy/R9Qo8RIhV8zUSo3opgE7C\ngrB4yd2tN/eGBo6zE1OAcMvgvd6h9XoLS3X/Xq241DsM0yG2ZXPxwjIri8vujqwgLvoAACAASURB\nVDwUjmmSy2UigCtdSLs6CF+XYlsoqsLYVJm2n5rxgJ/RN7Asix9ceBcjBGKkx/41tpqhRVu4RQSq\nQqbiiakVFaloNFsdjIEJQng2F9FrIaXE6htI2+bi9Wg3BCUbLTg4SL/lx+T8pNe6xD8sgWE5tFre\nXOOdR9h1vl9vs/bapXhFT8Imp9fo37ZCMSKYly7AGq+WKRWiGwfHttm5vkSp34rZTgy6/WDDIYXK\nl/7wWWqeK3+93uLrX3km9tvgguQ3n30dx3ZottsYlok5MBh4Gjld0zl64jDZbIaHHnkg5qv23s2b\nnPjCI5x4+uOMn55Hy6RQdY10VqM8VSJfDWUafMC100DRNNKz06Rnpuh2RtNvrmA+UjTi9aEcFc4L\nVQkkJ4Y5XHz951FPaXRHtESNWgO723Nbxl3f5IUfvMcrLy1SH3GST0op4kgk7mZ8d32H629H2x91\n6m12bsUrooONhOOwfm3EEkVKKp5erZjPoAqJ0R9wdfmm95OS3S3XEV4oInJdhBAMen1a9VaU4ZK4\n5rsH2Hs4qTzXb9T51m9/k4s/ehfbtKKMueOgKgqTIa2mms0GPSaVQpmHn7iLX/yPP8djT93LzOEJ\nRrdYfruyCy9GmTO/xU+g34qkE11z5UIpSyY0Lwqji9Kqkfc28Uqo+MhPG0vLpj/SxaHupQbDwD8z\nUhj26c9/ilwu514zfwMvJc8+90rSpbtjfKQAF8DNd68nWg2sr27QGvFGuXL5GrZjB8K3sHhWOhIp\nHQrZEf3WB2xaLaWkvfkTDLjgL0zHVZmoxoDIoD+gkdCA2Y+kCsVRD64f/eBlnvuz77G2ss75t97l\nS//PH78vu4kgRlIiU3NxwFVbcXdoqXyWdqfPO+/eYHl5i5tLm2xs7eE4EjWTQtFU1LSOPqKnOkg4\nf+TYPLpfIeNdm97AYH17l06nz8beDuHdXVBOLCUCSavd4ZvffwUp5QjD5Z5TJkTZtwZdrm2t8r3v\nvxQBpb4dhNE3ImmpmfEJCrkcuXIhcGkH2Krto2d0FEVhrFrwANHQ72t5qcYrf/4GzRHDQNu03B6K\noUk95z9PluGekzeuJmcqtEZ28371YbPV4s3tleCqJFX5CVVB4BqqRvQwejoACwKXsYo1KpZueks6\nDrv7zYBlg6hg3jJMdtfi4H766NBnR9U0JmejnSQUTWXHSyv6u15zf3it2pt7iSn7JHBo9k2svkEn\nscl5PiKY93fo45US5WJ8Hmu0OghjQDWrxqrsfBPU6zfX2NiInvPaygbdhL6QSxdu0vbauOzUh+Pf\n8HRxx08dDcb+ww/dG9OUNXtdVjajkoNwW590PqS78kB8d0Q3GAOit6tQTJjn/M14tx9eG9zj1FIa\n3X4USDW391ygfmGF995dplHvsFNr8tI3XolmX7xFPQK4vI1fqpDjjT9PTjvtrMb93nz92e76bkTX\nJKVE0wQlr2+qogjKhSz7+/shVt61mEHCXYeOkEmlhtONZz9z68qtIeCSgG0gHCeWHgboqzm++7XX\nePUbP6LXaA+fUSu6QZoeL5EOgR6tGjIKVXWkqqOnNE6cPcSTv/AITz91D8ePhzIkjlt5uH51lb3Q\n+qpl02jZFOteZ4VIw+psAUXXGJ+O96gUtkVBF4GZq5IazsV+9HYbbnPqTp/uboOd9S2QQ9sHiDJc\nAHPHZvns558AJCL0TF9eXOLW8p31y6PxkQNcRnfA6pU4xb21EdcKmQOD/UZj+FCFGC5/x174MZtW\n9+vtmEu6UJWgo/tPRCT57/TbMOh8oNRiKp+hXIheP+k4iVVUfiSnE4cTpmGY/OC5FyN/39zY4sYB\nbtaJMQIepw7592Z4bq5Wx2TQH3Dt+lrEuXhgmLTaXVTvwdPScYarv9/CSnAV1zSN4yc9zYIQwU7u\nyo1VNut7Ef2BGjId9Z9dgeTarVVeO385ugt1HBzLIZvSMW2LK5urnLt1jfX9HS5cuMQ/+Y3/m0sX\n3HTZxtoWrUaLZqjXnyIUxipVxqoVimNFZGilj6YVi8ExOWFGJmFcqAgXiIYYrmzF04FJx901e8zp\n2HSZ9gjgCi9Yt1bXud73LCwOsMgAyI70o5Namu0Q2ygUt+3P3FiVTy6cIaWp4DNclo3lONRDi7Ya\n0m/VVmuxRSdTyMY8mqbno9pFJazj8hZZu9sNOgdYCUL9TLXI6SfvIzNaXScU2rU6752/xI3VZRrt\noeYsXylGbFd8YDpRLVEqxAFXq9PDcSSzc1XXBT/E3K5eWUFKyY9+9HbsczgOexvr7nww6IDRwzZN\nLrz4TvCWnfow9ePfx9Nnh03cc0JjfirKgKu6zuX3oindcA+/jA+4lOFzM2h0ItYHsU4NSR5cPtBK\ntIZwx1EvfE8CwKXHAFdja48b1ze5eX24mApVpd/uRdYlIQToOuZgRDflOKwubVBP3KBJ9hLaT/nF\nIKPrnjQtJqfKqKEilUoxR683MqdKGC+WmBsbJxOky4fP+62ry65o3mO2hHf+Mjz2hcApjLN47hYb\nF29gt9pYzRZOr4fEzVQAaJrK4ekKs5Ml9LB+qzrynKaH665QFLLFDGcXZiLMlH8fwiyXEAKyaXab\n7twQblhdyRdQNYXxBPsTcCs5hW2CYwUFB71QU/f11y/z3pe+y+KfPM/1Z17l1ttX6NTqaKGNbiYE\nuNK5DLlSnkcff5hygs3Ht7/zauJx3C4+NOBaWFj4zMLCwtbCwsLPHvD3v76wsPDawsLCywsLC//J\nB/nu62/He/RtJZhI2rbDTn0/yNlGAJe3ov24gvkk/VZushIrJ/0oR1JKUdgmSmcfpb6BaO+Beece\naFomHeupKG2H2ubBKcA7CebPv/lOfAJhWHH3vmKE4coXPR1X2FzScdi6tcWLX3kecyTVYzs2jgP1\n3Qa2aSNUhUKCMeJBLFeQVhQEovvryxus7kTHrKop3HX2ONlc9NgEku+/+javvvEOuzt73o7VZtAd\nsLq3w+s3F9ls+CXbAtMwMU2T3//il3n5hde4evkavVYPIwQIq6Uymqpy/yfud9nEEEhaX98h45mG\nFvIZsl4pdhh8JFWSpXVtmLLwzjNXCT1flhEALjWjhkxX3c+YhhmI8wHeuHCRPSXeegeGVVW58ZHJ\nVU9RC3U4EEKgqgpzY2PcNT/PWMFrbO04wcK9HdJBKaEKxUivQS+mj81E01VSMjs3sqNWBHv13tBu\nQUZZLmt0EQbGTh0inRFky6OAS/CtP3mGZ575Dldu3eSVd86x6Y2bQiUf0Uj6wHSiUiala2TTqUiq\nxpGSdrfH9EwFRREu6PIATr/d48o7V1hM8NES0qGxvurOB519lPYu13/0Bj3PlNayLOqtIYttDkyQ\ncPrsUL/Y22ty9mhULK2mNJaXViOvhb2fVF1Fz+iIsCbQM0v1I55qjTNcPtBKmud8jW+vPwjSQtJ0\nx6mmx1OKW0sbXLwQBT4++B9N99lO/DmxpOTiK9FimCAch92taIGFkk67qXIpWbs2cq0si0Pz4xHr\noXIxg2Gaw+lDCCSQ95jbtG+PEBrD6zfXXPbcMSOGq8PnTuDkxyGVZePSTffE/EPuD5CGiXQcZmfG\nuP+eY0yPuZs0v72O0LSIKSwAqei6q6Y0NEVw+sxs5PclsHb5FuvnLjFY38SxLHZ6bVdjBsHGOJtK\nk8u6xtUTCbYzQJBSFLYV6Me6vR7OYIBjGDiGGbn27V7PfS00JrO6HmQXxuZc6wld1/n8U5+I/d7S\nvymGa2Fh4QTwd4EXD/h7Dvg14Engc8DfXVhYiPOAB0RteZvGSDojieFybIfa/l5iShGPZv1xGa4k\nwPWRd5cfDTWuAwpCyiAHLjr7iakQP/RsOhDrBh+3HWrr6/S2N9zPj2jDki0hMt5PS15+Ppl6fz8G\ni36MujYLIdy04si5vPqtl9nb2I2loGzHQdEUbMtmZ62GbdpU5uIFAgfpuE6FDFD9iW55fXvI8HiH\noWoqTz71CX75F5+MHZt0bL79Z9/jH/3P/5jf/J/+d772R3/GP/viV3nl0mVsZzgxCuFplEwLieSb\nX32G7z/7PM296PMyOTZGearCw5/2WjKFFrXV9e2AaRGKyulTh9A0NSoqHUkPOY5DOVzoINz0WCYE\nIIQ5CO5FvdEapjFDqMAMs4QCnn/nHfpOAtgPBPMjk6uiUQtXHCnucUxNuqxmtVAIrq1fNVcLA65Q\nSjGpYfX00ZnoC45FdbIYFWkDUgg2fOPSIK3oVVUlFP6ouoJw7IAR9KNWb/LmG++EHMQlF65doW8M\nELpKJyzGt20UIaiU3GewVMih5LKkyoUAFDTbHXRdY2Kq7DJvoSbM3/nG92IFD37shcaPaVhceuNa\n8CzvNupR00rHIZfLRfqr9nabzI5YOii6xvZmjV7IC80xomDUb9kUjm4tDLhGUq1SkosALjFsrJ4E\nuLxKxW5/ANJxGUnHRtgWmipjDJfRM4bPppTuZ7BBOmwtbUQq6S0zzgKvb+zGjHuHx+4w6Ju0QgJ3\nLeOOh+ZuM0jfBm+3LKZnq6RCrJCqKO7php9PKUlpOgI4c2ImuCx+1DZ3sDptxMjGxk8TOvkqpNzn\nopVQzTdVzXLf3cc4enQGNcR86579g15J6BupqJGqYl/zdvhQZbjB6/exGg3sVpt3v/8mvVsrtM+/\nx/rOjne5ZDDuKrmCK4hXFaoTw82wDI3nQkjXqGoC6Ui6dVeTZ3e6WM0WVr2B1WrRbzbp9/sue2eY\nqJqKkA5pVbgV17bB2MxwPD9430kmJ0eyWgc8S7eLD8twrQO/CBwk3nkMeG1xcbG9uLjYxwVmH8gl\n7Mb5KMOxtZkAuCybTq/rCuMUEaEPwZ28fhyGy7HsxEX2J0q/BaDpSP3OVYFi0EnuYu9/TSZFpRhl\nfqTjsL284j7Qgw6ivRMBE7czPb1xbSnxvgJsb9Wo7yd7w8QioazdF863u21ev/AOL557g8tXr+FI\nxxXs+2k06WoJ/AXLtmx213fQEyjkgxiu6dkpCl6q1d+NhlOJ/tWYnZ5g9vQCCx97kEfvOxP7HuH1\n6Kvv13n91fOsrm0jBNE2Et73h1MZe5t7Mc3bRGWMh556mLn5WdcrLDQ5NOotHB9zCiiV8tx/eo4z\nR6e4576jHD0+xfhEkUyIiZw7Os3UVGjPJBTSxUzE98mteHLPdmt7l9RIybWu6bEq5H5/wCvXrsRM\nKoWqoqS0RBuPWshTx7/eh+bcZ7JayPt7LdfuQUpqITDhA65Bt8/+llvBZdnDVjth/RbgtmERgun5\n6DMvNJXFxU2X5ZJu5Zvluc4npZ511V2oIoBLUTh35Qq2YUXun2VbXLpxLVoEhMsIjJWLwXgoF/II\nVUVNp9CKBRRNo+H5j82GdIxWu4NhDHjnnFuQJEcXR2Av5C20eP4W/Z4RMHc7+/E02Mzk5DA97jj0\n9ltk0umI5EBNaUgkKyGWa7SPYqaQji1cYR1XNwy4fEuIUEpRKiGbkiTphHet+r0+ImgG71UMI+kb\nrnVQb69Jd7eB5RWw+EUr4KW5LANrYEZMlM2RauFWp09t5zatnrx5amdr+B7VW5/WR9ktx6FSzpLO\n6BHABaAoMsqsSUjrOnffNceR+QlvfAzvcb/fY/PydZq7nUgV8G69yR987QX+5f/7NS5dWMQ0THqj\n3lhCcN898+jSDsAJuKlaX4erVZMZp3Ba0QdcipCcPuNal0jLDgpLalsN9vfaOIbBypKrN4w0rM4V\nUXWV6mQpov+VhXFk2p2rc6FCLIGrke2NFgZIibRsWs2WaxZrWdiGha4pZFLpIXB0HCbHvfnPtlBx\n+MLnR1iuf1OAa3Fxsb+4uHg7I6cZIJxPqQGzB7w3MW6+eyPYTbRb7ehOzws/ZbFT32MgbeRI6amu\nqoHlvx8fxGW+s70fzXMDWjZFpprcguKjHLIwjpMrJ1cshuKgMmFwF7eJUZQvJVuhEllhWxD6jtu1\n9XnlAHbLj6vvN62YBLjmqjhS8sZ777Lb2Kfd7XB1+Sarm5uoukZ+skK6mCNdyaOmtaiY2YE3fnie\nwcjC2a+3ExdTIQQnFzyHZaGAjAIuH4A++NDdbkVSpshnH3mQ2ckRXzMROhc5FLGHAZc/IfhMkWVY\ntOvRnXE2neH0/aeZPjpDKqUzNTPpph5CJ7nTagbGp0IRKIpCPp3i6LFJ7nvgGJ/45Bl+/r/+RX7p\nv/n3+eX/9le46/5TUcNTocTaKIWLAza3dmMGiKcOH2WiEh0/0rbZ2N1HqaaHqRPF1bqV5qdiO+de\nr0+zPWQI/Mqs2bkqCEE1n3ePQ7oLq2M7QUpRaFqg99y6tUW70+bl82/xnVde5MVzb2BrbmuicPie\nSafumY++rgo6PYOV1X1PTOtquax6E2vUDwlQFQ9wlXLBWNtrdbi1uYlj2VHrA2Brd4c3Xjs3fMHb\n7U9UhxueUjEfbBQQoBbytD2mbHqmMryejsPyrVsYg4ELeBOAyZ7nMzjoG1x+e8l9Ubq/WavvRdrF\nAJTzw3m03+gE6c6pqnt/haIE1eDLS8MUnWOOMlyZWLeObqj3XacZnvc9mUiY4QrPZwkWOKqmuGnK\nsJlp2HzWsWht72P2Blh9g0G774HfUMrff/5sMwKMIpYQUrK8sR/tJRiOEDO06zOjQqB6VXEbI21z\nfHYLIJ2LAi4pZKzqb352jOPHJynmMugpNTKfddttLnz/IrXVOqtXazR3O5iWze9+83neOb/I4qWr\n/N4Xv8S7b1yIVdbmcikc2/FSi0ZI/zbcsWnlA9rb6Vn8++HLfoSE+fkquXzcqPbK5TVanR612g5C\nUSIViuVcAVVT410sVA2ZqyAVlUI+tJmxHVIZDSOpGl9Ax08lS8CxyaTdFL0fY5MlZqYy7lrmWd7c\ndfY4hw+7GzIplNGh9r7ijoBrYWHhb3o6rJdC///5D/g7dzy0UYdks2+w7FXWJKUTgaBUtba/R98z\nXgxXl+VSUVZHKArZD2C4mdzOZzyxj91HPoSATBFZmsYpTSHT+QgdG8Qd+iyOjY/FnMY7nR7t8CIY\n0oMdpOHa290PRN8HxZ0a5QaRALjypSwD24i5SW/uuvsAVdd44j98ms/9jb8S8WEB0DyR7JXrG5jh\nUncp6Wwn72D9tKLwPGfsUaCuqdz/yEPu1zgOiqrx7z39OJPh3aEQgX4AhqJWH3BNlat86v6HmZ+e\nZdAzaGzX2V7eitlyTI2P89BTDwf/PnR4zivpG47bja1dUjmPXRAiYM7CRo7SMNFSOqqmRnQ1fmQS\n2qP4sbW15zJcod8s5vOcmT9OdWwIuvyFerfTZurEFIqmIlSV7ESZ6QdOxr53Z2snurNUBNVSgbSm\nki2mvZQi+AumbdrUm20M04oYnm7e3ODSjes0O65GqNPrcnVtKX4i3oQ9PT/OzOEwy+W6zl+5uune\naz+tWK9jx0C5RPesOBTNZQYB3r5+A3BTdHKkSEFR1YiO0U8LjofGS3W8Ep1ZBfTzeZRMhlRKY8Lr\na+dIycr2JtKyaG/vYXd7WKaDY0ukUJCKyl6zixQKl95awgz5abXbLTrNFvbAwB4YOKaFQJCWw41s\n2FRyeszdRLimne5ryzcPZrhSWT3WZNoxLAaNNkbfiKbnpERRXE+50IUKnX/cAkfRNbAt+qF7EgaO\nwnHo+WlFDzibnrO97pv8hgxb16/cCp638LFt77XoDQyUkbUhMKINAy6P4ZKa2y7INMyg32twjJbF\ntFeNlxoBXD3DcD360jqKqpLNpvj4g8fdTUohR2rEz6/b7dFo9YJ1a2etzuWlddq9QWTueO3F12NS\nh3w+g+UxeXZIHqJ5AEorFRKbhAOgKEhvDVZCbLeC5PTCodjba9sNLly+CZaNlksHLX3y6SzZXAZF\nEyOASwznr1SOfKgYy7FtFFWglzPMLswyd3aWI/cd5vjHjlGZLtMeqVoVEh545AwLDxzl/sdO8eQv\nPIIQAtHeQxheP0oh+Cuf/2Rwbh8m7qj8Xlxc/CLwxQ/4vetEGa1DwMu3+8DJ+09w5a2oWH5jcZlH\nP/cAF861Io624D407rMg2G81KGVzCCCd0oNFMpdKR3bZxWqR6QMEd0mxUm/Fdunzdx1mcvInj+GK\nxzi2MaC7thx5VSiS/EThQFBZmypTLRXZa3otYGw3Dba9vc+JE+5DpOgO+ckitmmhSgc1cg0Fs0cm\n+PofP4OeUhN+YRirt1aoVrNBb6ukcB2zBcj4e7KllDtGQjto0zJJpTXuf+J+Hv3cA6ytbDB7bJqt\n5W0XwEuJrinoGpgKXLu+xn33HQ9AptLtJt7/x37qfr7xlW9h2RpOT0bE4QCHp2c4cfdxqhMF7IFB\nL60xPlHhP/ulz7O6vcvSRo3NQZ/llS0UXcV2rGBhmCiXqE6UqBZKFMsFHpoe4/ryMpdvXo96RHnx\nxOc/yYkzQ8fxu+49wYXzF5AKOF7afWt7j1PHT+Psu/9WNQ1pWUjTDp61SjFFuuye681OL/YsTB6b\nIaXHwa5l2eztNUil9Qj9P1Ytk9JUPv7Ivfzw++50YA4GSCGo7dd57MGzlCcKFI8cYvyeU4lj8Ppi\nl1Rax3YsbxETTI6X3ebN1TyD9oBiNkPHMEC4Ok8hBM12h+nTR5iYLCKlZGt5nf1WPXL9ekaPXFYl\nH9KCdIx9HG+afPiJszzzpZcQiuLq3XSdfrfPreVdTp+ZRUlpKJ0OKkTGvGNZZAvpYAwVx4vs1Orc\n3Nhwv8t2U5LhY0ln9MicZ1kWjhDMTFaD1+cOz5LyNiX+a6ZlcPSJj7H5ytscOTrJbq1JrV6nb5qA\ncFlb2wbbwQGEYZIqF+kaFo7QuPbecnAcUko2llfRFAXTA3yOZTMxNobdG1ApZ9BTOo33jGBsHJ6d\nQryrkM6mg2Pa3txkbCyHqqrsbKjIkbm8OjtGtxndmOmmgV7MRMacY9jk8znSocU7XS2SKg+fx57T\nwuoOWTGpKbRwIvYAgWcVIByJYRkUs1mXxUPgWA65bIpPfOIkP3zxauS+9BttlEGPicPTXLVsFEVg\nWjbrtQYg0DQlOObJQ5P89K8+xe//wz/AHlhI6X5Pc7+NEFAc9zoyNFroukLAf0gQjsbYuDsPa+Wc\n+xx5jGPPGKAKmDo+C45Df69OpZxHKIJiIUc6o9PuGQjhgvmB6dDtDrCl9H5BsLqyg6IIdE0JANPe\n9g4lPSq1LldyCA/o4n0WIJ1NkUppVI/OULrNemjlBL3tDXRNpZfRsQ0LIRyOH5/ixrUNOu1oBuSt\nd67hOJJcJcvuFghHMFGtUpqsIG2D2cPjwbgSmkZhyttUWBmqNwvBcVq2gwAMy6Q87ss93Oe2NFGk\naww8Paz7u7ZhMX9kik88eW/SWYD3mwsLR7nr7DGu3toasssfIP4iSu2SVuZXgd9eWFgo4dbm/xTw\nd273JXc9ehcXXr4UeW3l6hpX31vmyuItjJH2G7ZpB2XsjmOxur0dVCz5kVZ0BgMrOEA1naJWawWp\nmtFeW+FwLJv6ZlxEbmWz1GrxdiE/kSElykh/N7DobdWTvbuAgRSUcnl2g+bLEsey2a7tMz/v6V8M\ni+5WnX6rhzHSB00vZNnY2Of7z70cu6ejYRhtzr25yLETRw5+k2OjJFSFAYiU4k2iw/PrDwaMH57m\nxMcWqNVabGzsI4VgbHacndVtHNtBRWD2+iCgUe9w8b1bnD49jxCCzesbFBeOJfyaQqVaZau5inRk\nxPsJCVOlcd7+youoAqrHZsiYZtCHcX5ynCOHZyifnqfXG3Bjq82Ni5e5/uZVZspVTs/P8db5JRwJ\nlgPSsDkycwhN1blwdREntHvOZDI89tOPR8ZooVRxr7V0j1M4NreWN/nMQ49gbm+QSis4Xgqu2+oF\nOqPdzX10A8zugPb+SLWYIrAyWejFGb/NzZ1Af6GlXN1WOpUCR2AMLBxDBPfeGriVQysbteA1Q08P\n+xV60fMY1KtXloNzET4gHa8gHUk6r+M4kko+T6vfd1O7ltuOY21rl3lbUKu1aOw0WLq+ErHBEEKg\naBqXLi5x9Ljn1i4lSruLz5aVqgXmjk2yurzvsqre5H716ibzh8fQ0bA7AwZ9IwIWVcXxduvufUoV\n0py7cjOYh2zLdoFhRKunRJ4Pe2DiSEm5UAhez5RKGIZFKqUFr62vbrPfNtFOHGfSa4a9tL0ZnINj\nS/p9c6ivk9Cvt9BK8MNvvzXUJUlJd7/DXrNJJqVh2U7g0l7Uswz6JlfevcXUkWm2b20Hz3k+lUFX\nVWTo+A3D4sI7N5ibn6G93461UlKKeYyROXXj2gZiYmT+sGwy+XTkuvTbJhjDz4q+gxidVxQRmAv7\n4ViOV2Uq6Qz6VPMlj1GWqKrCfXfNkc+lmZgusdcIgwLJxZfOc/qTH6PXGeA4kvXthsdoCxzHcY9Z\nCO5+4gG6Awc9k8ZoR8fz5uoek8VpJstw6a1rkfOUjsNsJY8ZSjOrKQ2zZ9A3TWxv3PbaPRRFoKka\nuqYiHUkunULTVVRNxTJtpHQ1gZbt0OwMqOTTSARbW25LK8WwEN5jsLvd4PChUmTsptMp+t1B1DLG\nu6aGYdFV0gxutx5KiTAdhHTIzIzRWdtBmja2lCw8cpZzr15xKwU9rdXKRo2+aaA3e64+UVWZnp3B\nlpJsRkdP68H9l45CL/Tber6I46Xefea83e4G7y8+eB9CVbGvXKc96HvLnvdcWDa6VO+4JgE8/eRj\nXPkX34wwwe83PmyV4s8uLCx8H/gC8OsLCwvf9l7/ewsLC495Qvn/HnjW+9/fX1xcvC1KmTo8SXkq\nXsh4/e1rbG8mWUJEd9Z9c4BQFRRFBCg3l0oHfcbArVBsrmyz+PUXeO9L3+XWD9+OeL6EY9DqxsCW\nns+gZ+O555/YEAKZVMF4G+F8UqWi40i2ayPCWnOQnE7MZzj3xjv0R8qxdU0f+lmF4uqlO+i4btMH\nTkmJuAu5Inj0Zx4LtBYDj1rWdI2J6TKKIlC9nYtPrO3tt7h1y03d9feTdO6AHwAAIABJREFUdVwA\nJ08fB7yJPDR0yrk8aUuAYWIPTLbfu0l7t+3ZSLi/5etdstk0d5+e5+d+5qd48oH7uevoYTRVdQ1H\niW4S5ian+Pg99wXeMel0mr/xt3+VwogOaWZuxhPOExRQ1DsmdsjLyWcBjd7wefD1Nr2EPqKZSgEl\nHRe0A2yFCk1SGXd8hQ2IdWe4k/eNCmt7DUxvklRDWgwpJa9+8yX+9P/4E/70n3yN8y++7X4ulEry\nq4c0XaBndKr5QuT6O5ZNba8eCOa3ljbYb0XPSc+k3HYvtZCMwIlqeQDu+8TC8LeF2z+z2enxw5cv\n0ul2sS075ium6dFBaKqSK2tDiwHH00cdmT2Eqvhjb6Slk20jgPEQmzM2OyLwB+peX0c1l6Ny/11o\nOZVGJ7rY9/smqRBrLKXEaHe46BcqSUm33sXsGTjCRlEUtNC4KwVGnTs4lk0/pCEUQjBVrQaaHT98\nHddoShFI9DTs1BoJZrAJlhAjG8NkawgtynB552j2DLcLieJXJbrp+9OHJxDesjF3LN5dY/36OoPd\nXVAUTMum5m1G/J6BEjj5wEnGvOKq8Zn4uraz1XT1R1KycSPqPi9Ni6mRTIyv4wpX4tsDE2ybQj4T\npLhURaFYzA+raj2gZFgm7U4/SI82uj0MzxzYj36vhzmiecoX0kFKMRxaSkNJpyM2K4khBKTce6YX\nc5QXDlO5+yjlu45y5ulPUJ4eH3aKGQzomwNABulagWCs5Fbcjk2PVEMq0WckPz7hXr+QnKPb67sS\njnQKJZNGSemkJscZOBbhZ1tKiWZ7zO4dxPAz83P89f/0VzhyLN5G607xoRiuxcXFPwP+LOH1/yX0\n318Fvvp+v1MIwakHT8caWi5duMHmRrx8O8kl19eBaZqLVHOpjJvW8m5oJptm5aV3cbydQ3Nlm51K\ngekHTsW+a9CMi/TTCZVrP/GhpWLd64VtIEleTLVsmmoh7sW1tR0FXMIaYCYI5rVchldeeCH2+v0P\n38vho4e4OdKK5erl63z+5548+PhvA7h6/QHlsQKNutuqQ0+nGJsZw7Rt/Gki3BhY11XGpspopjuO\nhKKgaCqOZbPpaZLmZsfpbtcpHY5PxKdOHuLl74A9kk6cLY9HK/Ycyf56nfxYHkWogI0IVekJs4/Z\nMyJ4P59N0+lbsTTbWLnCU598nOmFQzzwqQcpVeL0vi+cDypCfdF2eCH2Jhkj1IZJepuRpMav2fGy\nq9FQ9Vgz3nCfMR9wFfPDZ6dX71IsFWnuN4Ipz5GS2l6dQ3PTQWNgcPsALl246R2QZPnGCulSlmwx\nixQCISVT065uSEjIFjNUR0xBbcuhtldH9RaHzaVN9pvRc8p4G6nadghwJegZy5NVjt17gqW3L2MM\nBlxaXWK9toMQ8NqVKzxw5iSnxg+R071NibTRUtFNzRsXrgw9vHDTPpqicGr+CIVslos3rkV9/qQL\nuMqFXESjWpoaj6XbB4MB/f6AbDaDViqynxLuYiwJNEopRePkkVku3RiK2dv7Ldr5DmPZDL161xP+\nS2xpu+JuReBfjYzQcWy3mrdfb8WE1nOz0zR2o3P28s0VPvGpR2KieYD89FjsNaPZwRipck1ymY8V\nACSZn+papJExuCyS2TMRAvKFFKdOHqLfbDFWyKJrgm6rT7PTZXV/n/VajcnqsMvG7lad5so6Asn2\nfju4l/5mSFUE9376geC3JqZKRIUbsFtrgxA0dhrRSkxA2lagv/PDr1SMAi4DTU1TyGVxuRN3LiyX\nC+w0OnRa/UCjNbBMmt0B/sPf6vVwbInZHZD2xOKWYdMdDEiFWowVijn29+NdCDRdRa9W3peeWaZy\nQYNsIQSoAmG5PY/vfeJ+Xvra8wDstcOcjFv4Ui4W3THuWEyMOsyPAK5UvoSqa5Em6pZtYwwGFGen\ng2PVq2V6VnwcKl3L1TansojWbdrL6SnOnD3FmbNx3HCn+Eg5zR+951ggxvOj2WzRGNlha5qWDLi8\nyUhTNTRFJaVpEYbLbnUDsBV8/2qyS3oi4PqApqk/CSE1Pf7iHRiu8qgXlyPZ3n5/DNfG/l6iM/0n\nn3g04lztx9rqOu2ECtUgbgO4Gs02+WKW6SNTTB2ZZnJ+EnXE22jgP5zexJTO6Jy8a1iRFh6Py8tb\n7Ow2aG8luEUDJw6No+lqZDHVNZXxQimiO0E6WIZFq9YCoSAFI3oAidGN3oNqNR+zTlBUhTOPnOWv\n/le/yBP/zhOJYMuPQ4fnYq/V9upBWiywszCHFXN+CXh3N85w5XxjWC3OkPpVq1IIdJ/hyg2fnfp2\nndm56Zjh6UZtDzUX7ZMXNoN0HIde3+0N5x00AFPTQzF7rpByhfOhsC2b7b0GSiaNbdls3FinOZLi\nSXsl5WGGaxRIAqBq3PP4vazt7PDC+bdZ3/XOVUK71ePNi1f58vd/wNuXr7K316TZaEfAdLvT4/Vz\nixGhse1I5qoTKBIOz8xRKZYiRUQ+CzEREswLTUNJpShX4prUuleV2Wy0WN3aQtE0hKYidA2haRye\nnUcTIYbLduh1DTqNJt16103zOg75vO6tzzLoR5vSdDRVwez02V3fpbMTB+NHEyQAt266TvfSjKdh\ntHw2cW6tR1qq+RWKB1hC+HEQw+U95359nzkYmmA2Ox3Gx4tMVwvo3r3abbT4p19+hudfe5uLyzf5\nwbk3uXxrif5ggJSwfmMTa9BnO+Sd5T9DJ+4+SiZkUTA+GT+3Hc8AdeXKiB0EUCllY63Fch4LGLY5\ncAwL6dgu4AqJuMvVoW+cf46GZdLtm1iWjWFZwfcY7V5Qzes4Nt3BcJMsFEHl9FFsK2GtTWkH2kHE\nQku592r0TI0eh88e4e7H70fRNfba0XlGSoexSsX/R4wplCL6nUJRyBeLsXml2+2gl4cAVuh6MuDq\n25hKFvQMMnPwXBr2F/ug8ZECXHo6xZG7j0Vea3e7MWp59tAM1YRSVN+iX9NVsp6nht8MVwJGwk59\n0OzEuoiD22JiNP6tZLgSUorCNmPpVD+0bIpKweu/J30NnUOj0cYIpWeFY2EmAKXzF+OVicdPHmX2\n0AyVapmp6bjh6O1MUEdNT8PR8FyqFUW4wMmbm6OAy98xDs935tA4D/2U65M1apJ6/fo6G5dvxZ3Y\nLYOMKvnMpx8ONBYAp+cOoyAiAmh/EqxvNlxwJtQYmDJGGn6XS3mOnj7sdbdXOXrvcX72P/+rPPTU\nw6TfR5p77nDclWV9bXM4pkMTtl+pKE13UUpKKWa9CsWkySdguIRA1Vw9STEEuKTjUCmVYqm3zdpe\nJJ0IRHoddvs9JBLLMOl3++ClT/Kh5zKT16jk85FqMelI2p0e3d6A3fUd9uv1iO5NURR0DxBHGa44\nONisNfiD3/0KN7bXMa0o49jtGuzuNKntNnj21df50rPf5eW3LnHuzRtYHtB46eXzmLaMAC4BHBqb\n9ATFgntPLZAKVVQOKxSHi4aazyGEoJKw6Pn+dS+/8BqOdMiEDGtTeopDc3PYyvD7XX2TpNVsY/dd\nF3lFCMJ7MVURgCCXcj9ndvr02z3qq3Em4PjZEygjaZn6fp3GbtzHTng9CXOT8bRbK1wRHHhwhRiu\nBDbLr1qTngat3+xh4XmtAb4zu9kPVWL2+tgBkHGfzfNLtzz9ryCdz2I7kqWNDX749jneuX6NK5eX\n2dzcj7DZiidpOXVvSBrh2IxVs4HzuR+Dvkmn0Wb1ahRwYdtMTkQXe6EoFE+46asIw+Wlrwv5bAR4\nlqslVFVB09VgGh94fnKt7oBWqLOHdCRGq+uOT0mECczl0mj5HDJhU6WndbTS+ywe86oIYy8bbuXk\n/Z9+gC/8B5/DVu2ortqRjJe9Ss20zvjUSFV0DMRBrpCPMa69/gAtNxzvrb1dhCYic0RK09BQaHtj\nTmZLiecNBK2YPkx85PrTnHzwFDdCXdZbnQ7mwMA27WDxm5mdQhlIbl5dinxWS+nQH6AogrznMO+Y\nlisV6RskcDlI28Fo92Jg6i9NSlFRkUJxe+H5IaWbTkl60LIZNFWlmM3S6rjXSHqTznZtj/lDQ12J\nMXINm50ON5ZWRqoW4ZNPPBb896mzJ2MM2NXL13nw4/cnH/8BTbgNw6TXi4MpgE7IwiJIKYYAZiaT\nYuHBY3TafRbPL0fApZSS1ZubLGzvUZgZMiui74K7p598lJ3LmyxeXaNaKFAplOh3BqRHSrXBZZMa\nW02qM6VYxYs5wnAJRXD3I2eZfvCUq9G5TeVmUhxKAlwr62ROn3WdwEOTj9EzyBYzOIaJ2e3HnNOF\nqpD2OzaMjJHBwKAeaHrc70xl0sHz6EdGSwf6LT82d6KAq9/p0d4fMgjtkJdSu94mk5tgcrIamCqC\nq2HJFTOUcjnqneH4cxzJ5sYWnfUG+80ogEzn0sM0684ejuO4FYV21Gfp+z98k+++eB5HQmGsSLfZ\njgHvoRBX0B70OL98nXfXbvLyzYtMTFfpdvug6KgpDcuTic6Ux9BVLXCbLxbyPP34Z/nut3/gfqcH\nTE8dGZbSqzkXeFTGyqxEs/DU9xt0O11eecH1ucsWc/Q8tvnw7ByqojLoOC74sB26HQPHkfQGfe98\nJFNjBba7LkBKpTWMgY2qisBqxzZNbNNi+9YGpXR0DJRnxpk5NM366tBbyjJtXn72ZU4XMoxPDPt3\nCs8nMTdRZn+kdU5rv0XKn3P9Vm0HeXD5IQSWo7D04mU6e14aK6e4H1c8MOa4VWl+kYIjHTrtNrkQ\ngNus1wNrl2whR6fZDaoE12s1VtY3mCpWODkxi+qBS0URHD46GWk4jzlA8dzRdzbrwTGCYHt5m/UE\n/63JEf2WWiyQHq+ipbVYNxXHdigGKUUQmkLZY7rTGZ2+VwU48BidVqePrYTGNRKj3UORro9cN2Qe\nni9ksB33HgldD/R3iqaQPTx3sOdYQshUDtGPyriFbbibTyEY6BqKrjAx4RaCdLsDLNOmXHKNTh/8\n1JlIz0P3QOKAK6vpSERgcgvQlw6K1UfaaYTRpbG+4hq3akqQ8SqkM0jbobVao3J0xh0n+TFobkfW\nRqln+LCWEPARY7gAxmbGqUwPRZRtr8TXDLEnU7NTTFTjeX81pbmmicD8rMuU+BULpXwmRtP60a9H\n0wtSSgajTVP5txRwCZEIrEigXAG0jOutVAn1VJRSIiXUatGKNbMdvYZXV1ajlVhApVLm7L1D1/Wk\nvPjVxesxr6kgDmC4GuEebCMeR+EU5bD/4PD70ykdIQQfe/wsh09OBz3D/Gg1O9SXQhoVxw68WgCq\nhRLHp2eoeFo36cjI2Asv0o2tBrYto42rIZZSBIGez6Ko6gcGWxASzoeiXm/gpId6NT9Mj12ThkEv\nIZ2YqRaHO1FFjaQLIlo+byGamBoPUlJ+qBYx6r+218AJ6Z121qLsSSfUDNvoDTAGBpMzk+6YCpXu\nZ4tpxhJ0XFsb22ze3KDeijLd6VD6x7IsGvWmW10VYrjeenuR73z31aCjiqqp5Es58IsRRsPzQnWv\ng6DV7NJqdbCkBOE2dgb32TlUdfWAjsfGZ4s5PvP0p3js8UfczzsOH7/3DEfnhrpB1QOwlQNSii89\n/yqGx9qksxkURUERCkdm3NRyWtMxUej1DNcHzJb0PV2NAKbHizS6XdJZHT2toWqKC2Y9hgvpslz7\nCd0XsuOliKDY7JvUlrd45Xuv8cqPLvPeO0NFkw+WcxNRhsu2HQbt3vCplBIhBNlCiPlLYriA/eW9\nAGwBbK/tRvzlbK96LxytbicAdT3DoN3v49gSB0Eq61l6BJsSt8hhq7HPpY3lYG5SNZWTp2dxvOsu\npeTVF1/lX/zLb3BpeWnIHnnPxeVXL8Y6ROiqoFyObk60cgklpZMp5uiOiP8d23ENP4VbEKSmdcpe\n66dgzhECw3JtQVrdAc1wwZKn7et7GZ0woMvnM9iWOx7UQh4lm0GkdDITVdKHPpCPuVsgMCpGlzLY\nMC+tb7mPkRCk0jqVaoEH7z3JU7/8GX72v/h5TpyNSyKSAFcm7JvmxQCBMHsojU1Er0lzvwGKEjJv\nhbyn72wubwzXGlVzney935Gqjsy9f1uppPjIAS6AakhE2fIAlxXK/U/PTlHOF4KKHj9UVQ10XMcO\nzXDq5CEmxsscPTnHkel4JYwf/ZEGqWa3H0t3KLqGlj2AYvxJjwTAJexkHZdQFK/Fz2ilosN2bTj5\n2paNFTaXk5IbG+sxK45HH/94UBUIcOzkEfQRXVmn3YnslqM/fADgaoYB18EMV78fZ7hS3o5dKIJH\nP3d3rDK11zfYvbGO440Rl90K7aiCSr+hn1E6nJoMAUDHdqhvNRCZqBjY7MUBVyp/5/ZMB0UqpTM9\nGxf67/meReGUonf8jmkmGp5mw4anQkQo9q2wvs2b+OaPxSfL7k7L25kPQ0rJdqgNz6gZZJjhApfl\nmphxxbDhqriDdFyrS2vsbe7FGa6R+1vb3olVKJ5/50qsJU6hWkRRBLNj4zx6+iwz1bHQxmCIuARg\n+JohT3fizlOCubFJ0h74cmwbx3GoTldRVZWf/+Wf5X/49b/H3/mPfoGffvzhqNWExwRWxuILwNZm\nLdKjVCiQyWeZn5l17TmATCqN0Tfp9Y2A1bJsG9O2GSu75pkDYaPpbspP1VU0VSEfAC6J0enRbkV1\nmqliFi2dCllrQH3bbaHU8CpDl5a2A/8ln+FKl/OuWaoXhtdoeKjBleRCXmbuRUj2QWrtRZn1gWlh\nmY5raCqlV3UXnRNsXQYLcK0xHB+2YYPwWVD/eR5+br/bZqtVRygK84fHyeXSgfbxuW9+l6996Vtc\nfPsK167d5K3Ll10JgXcOrZHNjAQmxvIxIbqfusuMl6MMF67Nx/A5UlDSKUoeMRCudB2YJggYWDY9\n4lkB0xsHvcHQDLVQzGB55yIANZNBy+dJj1c/ELvlfoEANUkv7H7/zevLsU3nySOzVAtp8sVcsnRk\nZP2XjkPWRW2Ru9uX0c/W6y23YDvEzOY9x3+j2Y1mt/Q0sjyDU5lFlqaSz+EDxEcScBXH3AHmOE6w\nq7VHAJfRMxgfaROihEzcxkolJibKnDp1iBLE3NHDMRhhuJLTibmfTIf59xEy8UG4TU/FbMqrVAyV\n1dqSWsgawuz6TWDd9+w1WzS63Rgb8ODH74v8W9d1jp9KsIdI0nFJeaCGqx4uVZcyMr92khiu0Cya\nDqWo0pkU1Zl4NU5zr0VrfccFT4OQ0aKUnkA3NDmPAq6RNFRzu4kp7sBwCYH+YwAugLn5+K50x1tc\nBAQs0aA7CNqW9Gpxn63cyCIf1jpshTVQ3jU7eupobILu1FuMV0Y0GarKxtqQOdxZiwKuMMMF0G/3\nyBddZkSJ3DONsQR9ybV3r9LpdjFD7K2mazGd3s72biyduL5ec/UunR5mdwASJqcn+Vv/5S/xsYUF\nSrkc9x45xoOHT1JIj1TSeRlpY2AOga0CWlpnphRl6h3TYvrY8D6lNZVsjJkXQTl+OUHDdfXytZjt\nSqGS58ShIevk9geU2E6UcR2YBjPjZbLFNC3PgV3Net5OqhLq3uGmoDrdfsSjKeuNjSMe4Op3+0F2\notlpu/50UrKz4447f74WQkRYLt8ZPrDtcZw7Vyh6YXTMyGLc947P7JsYfXN4vKHHsGcNyBe9SlUf\nkAsC1/lDR+aG1XsjG7gbtQ1Mx+LkGfe+ScNg8eJVvvenz+IMTHAcNEXQbLXY3t0NQPdodDptbmyu\n8YPXzgftq4SqonpsbX6qmgC4PA0XgNdXsxRKw/qbWZ/hUhRBvdsNmUF78gbHQUqJ5ViBNUShUsCK\nbfz48PNQQoGWsE0cx+HGtSXEyDg/emgas96IZSgAr7VOdE62mi2ymRSRrhpC0Buxfqr72t6UGvSd\nLHiWMdI0aY3MO24njoQCjQ8RH0nA5fc77PZ7Adq2vFxrvpCnUMjT7/aZrI4ALlVB1TVUVfVKZd0Y\n7Yc4GqMpxUHjL0k60Y9EhstMHOjg6rhGKxVHGa4AMHg5mBvra4HXlB9Hjh1OrLJKqlZMBFwJYMtt\nVaLRGAXNoUkyUcMVTimOaFImZ6toIyxIu9Nz04qDbiTHbwxMV0grhuyWEAI1BDhG06PSkeze2Il8\nJs5w/RgTnRfzR+JM0+bWdsAKC4/yl45k64ZrAttNqELLjo+AmdD4CVtC+KBzdn6GyojHnrRtiplo\n6kSoKqsrrieRbVnsbw4BvJSSTi9e9Vpf30dqqYAdqde7vPHmEnv1PgPDtTbwj2Xt1hr15sHpRD92\nt3cjFYrNZodWs0O71mJQb9PfazKot/nb/93f4pEnHubf/dVP8elPneGznz7L04/exd/8wmf52PET\nFDM5975797Xft4L/1jSNLzz1aRxzhGkxLKaPzQT/drrxc1azmQDAJonmk+KxTz8aA2e5TNbtrhBa\nR1RdkMulIK+4Y1dTA3uUcilPJmxxISWO47i6NC989rNcKVEqFWmFqvgcx6HpMar7e553VajXbW5i\neHyGZ2ZsG1bwnEcA1wGMiXQcjE7P/ZueAT3DwBqeoxU2GGWYCmx2euRK7ljwAZcQwvW6kvDkz32O\nzzzyCRaOHos9v7Zjs9HZpeC1jWvs1/nDf/4HQWoRXH8vRRWsbW5h9/sj/JpryPzqO29z8eYtXjp3\nkd/5yrddsXdpqHfLzozHmjE7jiTvgQWEghibojQxhVQ1bKkELJdhmUgkQlGo7TXQfZ8uby/q2E5w\nXn7qszhWwhxtZg3ouQ8nGk/0fLRNNtY26ff7EYYrpWnMTo5jt9rI0AbJMSw6qzXaS5sY27XIvbDq\njSA16N9woSmR8QnQaLS8v+kBM+4DLqSkuXRANiV8LlLSSdiM3ik+cqJ5cFvwAIEoG4YM18zstOvm\n2zOYqER3h6qqQgoqhYNb0yTFoNXFsZ0g3fWXxRIiCEVFKhpiVIBumW6z5ZFwGa7o9ZC2w+5eA9u2\nUVV1WGUnHaRUuLG2HqvEu++hexIP5/RdJ+Fr0deWb67Q6/XJho32DqKZFTXCcHlvBtzJp90aAuzB\nwADpsWBejAKusckiei4dmXzarR6ttRpOezyioey2+m6qw9sgSEeS0rWA5HY11XE92v7SJlMnxsmk\n3UVh1NlZ0TXU1I9HZ88fjfcvW11ZZ/Lxx1g+d91luLxLanQNtq5vYzsKSmhRFJoa33yoejB+/JSi\nVIbNXWdmpzFr3SiAsm0yI9dZqCrrK+5kt7+5H7F+6RsD7JH7rakqW1c36D9xD0JTuXJ1kytXNt1r\n7IBh2tiOJJdx7Q06zQ7rerQvazph8dip7UYqFNfWa+4GwtXCA675p93pI8sV9EE/0N3seRV+9xye\np5AqAIL8RAEHSXGywid/+Uksy2ZyepxrL7zL8ltLkd/WVSWY/wDsTnzzp4Z6xpUrpTvOdYpQ+OzT\nT3Dz3DWuvXkleD2jp9zNqBD+wCSdVilNldjuuPdK9dPrqmB6coy8mqLhCfCldPU9/x97bxpr2XVe\nia29zzzceXjzWMOrYs0simRRpChSs2Vbatvw0O50nNjoNhJ00k434gRBkABBEvSfAEmAdNBBdyNo\nR0jbTttW25ZtDaZESZRIcZ7qVbGmV/WGeuOdx3POzo8z3DPse9+rgWSJ1AIk1rv33HPPPcPe317f\n+tbXaLSDYMMPuAghyGezuBjTHFWbDeTMFHZ3OAFXqFKxGwRcfW7AxSS3Mm93ew9/+zffQ7VSw8mz\nD+H0iaXEAtsNvAmiaUQSXE9REbFXa0D19GHbtXogbGeOA7tnYfHoPNo3qxCYjd3tPazvRvWFtW4T\nF6+u4Mj8NP7kL59DfbcSz1pCkkRs1WvoNhpQbAc0VCBy9dYKGBtU6bU6Xbx1+To+tTRYfNqakgjU\nJCoAod8rpNKgigzVMNHaaUCUBHR7fbdK37IgiCJq9Rby+cGCmXnFAP7OW90ucuk09GwKu1vJ+0/i\nLFIOhCGZlCuX3J6iRBBAvArT2YkSBMFtxWNVaxAE13esfnUdzHLAKEX/ynXI9Qa0xXkQQmBVatD9\n+YEQMOaaWDdC9kSMithr9lzxOwEEVQHafRihquDGumvoS0U+E9mp1HHzh2+js1vD/EN3Zn76QDJc\npsdw1UM9sfyy1bGJErqtLsAYNFWFobk3LfUGeEEUkMsMb6rLhcMiQdbHpkIxDJ4f1xAdl6QpUCQJ\nWmi167tl73ian17L10Y52K5WUWs2I5V4BAQnzzzE3X+xVEA2F2VEHObg6qVr0Q2HBVyCiFp9OMPV\nCk1iri1EdBhTYiL5UtmEoEiRtFij2YbT76N2K9rgvFlvR6qnfP1WkLZhDKqhRLVshIAxYOOSm05L\nCuYBydDuOaU9PjGWMMpsNppIH52EnNIDhstHu9ZOBIdaPpXUbxACZmRRb3XRbLZdrRN1z6EgCCgU\n88hPFiMfYZYNwYnuh4gCNje20Ov1k+nEVguKpkSO0dB0OLaD1390Cd/95ltY9oMtuNYwhqyi37fQ\n7PRh2w5s28ZOdbAqJYRwLTXiKcX1jW3Xmyx0+ouZDDp7DUCQQAqTILIExljQASOlK8FtRQUKSRTR\nafSRzWYwOT0OSZJQq8cmMwaYmhK5zjaH4aKhik9RFJHOjC7PP/vIaeSLOcwdnw9/FcTw4+O1RbNg\nIzuRw1al7vp2+T5tAsXkeN51NQ924v7Aht/UmBBo+cHYa9VjhTcMqHhjeqvZQafTi9hj6IVMwAD6\nAZdj2WBe8KuHPbhUA71eH//3v/h/8MpLr+HK5av4sz/6c/zkBy8nfn/H66vJBSEQJAF7dbe/YRcW\nerbfDs79f+o4KJWLmDw8BYDgUHkCUugZF0UBkiTir5//Cb79wqtYWffv3eizI0kCGHOwWdmD0+vB\nrjfg9ProtttY3ViHHOstu7lTgRiayxqNFmgs/a0rSjBeEEpBvEVZOpOCY9kRHVfP6qNrW7Bt22X3\nvHNiBwGbW/zU6nVgGAoERXbT5zHcfcDl6hbDIMzB1cveuE4QpBU3yOYIAAAgAElEQVTnQtXuVrUG\nu9dH/doGWOAJ5nXG2NxG+8p1ON0u7HYbeihwAqEgsoJGuwemGHBSJbDMGKr1dnAYove8BQwXXEeD\nxmayGIQ5DFvvXMd73/gxOhyrnIPggQy4JEWGoqtBhaIPy7IxNjHmevB4KHnVisEERoCx8aQ4OLJ/\nTmqmGxLOf+wYLoDrOUKG6Ljc9Bpz/bj8z9sOGKHY9GjWIGhgDFe8NibhlOL84bmhEwUhBEeOHUq8\nvvxutLk5P+ASwaiUZLiGpRQ7vURQocSYpEzecAfVEBtiWTY67Tb2bkVNUBstOyJA9xmu4DsYg6xJ\nyIRLv4lbP1i9uYOtK1vcdKJsaonX7hSCKGBiajzx+q3VDcw+dRqEs6KLe9RphSEpLEnFRgtgkuKK\n6L2JulQuQhAFFEIBF2PMbbrb7CMdWuUTQYDDHGysbSQCrka7BUVXYYQquPzF1rU3r2N3NyoLIJTA\n8LRUVt8erHLDprSqzNV2VvaqsEIGkKtrm3Bi5o+FTAY9PxiiAoRsDjZIcJkVWYSiiG7z9KByimBz\n5Xawj10/JeE4YH0LzOpDc2x0Q/eu3eIwXDGLjVw+6WEVnAcQfOqzn3SPeaoI3Vs4Wp0e5HCATQBV\nVdAXAUGk2G21IYQWHoRSlPIZFMdCi1k/4PLOrZLWg/T09q0t0G5MksAYqs1GkAba221EGC5BFoNx\ntuvrbhgLjHjNtHs9mSABgoyf/OgVl40M4bWfvJk4B51eL1Gh60NSRMBxYFk2Gu0OKr1B8Oh/JKcb\noJRi4tAUGAEEUBwqD9hiVZFABIJmp4ufvOUxiCwZ40ne87W+57HAloVupYZbN1dg9XuQY+PObr0B\nGpLG1GuNRMskXVHQ9cZaqg0WZaZpuC1tQv2Fu3Yf7b5neNqzgxZ4cRPxVrcLw1RBZfm+phRBSMJo\n27ZtXH/v+mAT0Q+4BuOUtVdB49oGWNi0PGxjs7WNhufvaIQyIEQUAElCo+eAGTlAUtDrW2iGFtxU\nkiDKQoQ8gOOgHksrdustXP3WS9h45dK+EqVReCADLgAwc2aiKsnuWRgbL6EbuglmxydBCQ3oP0EQ\ncOZhXsdvF3opi/RssgeZr+Oye31Y8aieEsgmv9XNRwbcnop8awhJc1fv4UpFx3F1S5te5O/7SDHG\ncNUPuEIpxdPnhl8jADh6PKnjeuPltwJTRwAgjKPh8hiuSJWieyDBP9vtdlCO3evyGK7ouaCUIl/O\nJKoVG/U2mtv1oO8XADTbToQBYswNuPzAhTEGQRKRGRu4iZOQpcHaO6vYuZZ04peMew+4AGCGk1a8\ncfUmtHwa46cWkh9w4gzXcPb49sZ2ZKICEFRGpnKpwHXet4OwbQd5z16EhFKQqytr2I4ZajZbLcia\nDCMzkAuYejhYS6ojguotMtDNhbsAqJqCsYkyx1qBYWd7sMK9dXMT8XukkMlExglqGHAcAeEfn9YH\nWivfCsAPuDrNNqrbVTfRZQ+q5lKajMprb4PZtlulx9Nwxe6FvNe8u9fooFttBmbPgJu2L5XdYJcQ\ngpnjc2BwF5iqNLjPBUqhGCrsXAqp0ydQYSTCtBFCMDaWx9h0MfIb4TB0Oj30LSsSjL/zwltIG+Yg\noPUaRfctK3Az391pRIodAMDw0oo+wwXG0PeqZnUvpcgUA7bt4Pt/+0Li3OzuJLtACBl9aHpI0uSA\nfa7Umtht+V0MBr8xrxrotzpIF9IoTRbBGFBKZVAw05AlEaIocNjnwf1CRAFUliBJ7v1RadbR9vyu\nGGO4tbMFQqj3/gB7zXZkv7VqHUKsTZSuyMHiVggxT4YyGKt8Vrvv2GgFAVc/uDftUO9XxhjavS4M\nQwUkCVb7PjJcQCKtePPWbfRDujQqSdAUGWOFwSLC7vQCy5QBoufb8arNwwyXH7w1G63g+a9WYppU\n6poHxxdeO+9ex+U//S7e+7Pv4cqfPYeL/+83UV+5nUjp3ike2IBLMTW0OtHBxrIslMdLgZkbAOia\nhk+cPI35uRmcPHMCv/uPfxulmeQq3kfh6AzUjJl43Q+4eP5bsqkl7Aw+cuBVkDgWl0USdQVgDFkj\n6h4OQrDplTr7KcXNShVNb9LwU4qUUJw4fXzk4Rw6spCwh+hbfXzzL74zeMHmpxTbPSsQ3Qa/hUUb\nSvurHFfDNTrgAoDCWAZUlgYDN2NoNN2O85VVz51YENFq9iKeUMxhbqqAeRJdx4EgCa4Z4pQ3qIQH\nayK4ja0jB08g3QeGCwCmZzkB1zXX7Tq3OIlUzOU6znDphREB19pm4jU/4CKEDFiu0HXzBb/hdPPV\ny9cjiyoAaHU7kGQZgiRA886Fz3ABAOhg0vPPZlpPnjMWcgZXdBVzi7MolguxjRi2dtxr2mp1UNmr\nITLAE4JCOhVZ/QuG7qYTQz5AKV0eBNNeRd1tz7/t9rV12I1mpIBdU2RIkoD2bh2dlVtw2oNeeMFX\ni2KEFQJchssV8tfRq7fQ2qzA9sThn/7cU5Ft5x6aQ7/ZgWPZUEP6TEWRoWZMVGsNOLKEnd1kscT4\nRAGZvAlNG3w/C7Fc/r2xd3sX61fWQCl1vei8YMv/qX4z7d3deuK3mBMFOI6Dft8Knsu+32rIVN1z\nq+h4/ZU3k5MngHqlnjhnFmFuKjz0nOmKd22YE7Cee7UGbu9VY55bQDmXQ311G4QQnHrsOIqFFDRV\nxuPHjyObMdy5YUi6/+nHz2B8ZgyCIkHQFYhSlOXaqdfQ6nbcThSxfbT7lmtK7KFWrUFQYwGX7DJc\njDFQbXC/a6Hz6jNrfcdG2wt2e10ruDcjDBcbMFyMJQvOqCxG+3zeIeIV8e9evB4dfynB/NxULIDl\nhDlDUsSSJAaN2X3tqePY6HjnscK5r4tTSQLGarVRv3kbtZUNVFc2YXe6cNptOJzCnTvBAxtFWEhO\nppqiQlGVxGCcS2fw+c89g9/4rV/B5PTE0FW4oMpIz45BzSbTg34rn4+lfgsACOXbQ3D6yUlBSnFw\nXhzbVaBubldg9aygw/zVtXW4/DoJgtbFowsw9mEMFVXBhacfQ9B013vmXnv5DdxaWfW/NPlBKqBW\nbSQ8k1yE04pNt/iixwu4kuehUEq53i3awIeo4TXnrnhpRaaYaNaabvoiVHGo+ClF73/+oJsqppAq\npaLaKZ59Cbk3D64weML5leursG0bVJZQmMlD1qOVaMGhySLk1PDrFjTHDiHs/eUHXGHDU4W45zqc\nzrx26XpiPz1m+SQRDM9JO8xwgVCAUui6jCcuHMGZ0zNIBwuC6ODNHBa085mdn0axlAy4trfdgGtt\nfSuRTsyZJkRRjOhbBEMP9ZwjAKEwdcU1ZRXl4H6obVfR3Kli5Uevg/X7kYVc2nSvcafZRXdjE93V\nZLVUvNckAIh9J9KwF3A1qSdOH094r2VKWUjeNRUFASIVQAmBltIgqjIcx8aVS9dcTWboe1IpA6lc\nGoQw5MNVqt6+6rVWIJh/54W3g7f9RVn4d1Zarm9drdZOGH+mpkqwg2dgYN9AHHcfTNbBQPD8d36Y\nODeAa/PSjTXI7vQtUEmEaiqggvubxvI5yJocYU4296rY3K1CkGjkHJdzWdS8FDdlwOGFMZw9NYcT\nR6fx+PFjQxfj89Nj+OIvPYOHzx1zP+uZlwIEG3s7YIzh5rb7zMix7hvU65W5HbJZcVOKUuTYNEV2\nG3F3+kFzdgBQaFRjBgA9xwpsJRzHCR7tMOvLAFi2BUEkkbZFPuIs/zC02x28t3wVO9sxxjEkXbFt\nB6++vox4NfyhuJwkseigUCaHkyq6prjOEKExxTe7DuaOEIozE9ExbwSc7sAdv3g8aV+0Hx7YgKvV\nS+aODc8cssMR8oX7halZM8Iy+MgfngIVKJR0kuHqNdpwLPvjG3ABfHsIjo5LVGUADLlQStFnQra3\n9gKGxmEMV9fdFb27CnS3PXWWX50YAWP41BOnYcgEpN8FrG7w4P3V17/p6YA4bX2o4JX9cgKumI6r\ny/HgkmMDmo9CyXNv1lX4E0Gr1XXL4istdJtdQNHR8hlSP+DyNVzuHwBjge8TIQTF2QLMsbAGhyRb\nllDxvqUU84Uc9JgGqNfrYXNjC0SWQAWKscVyMImEGS4tP7wijjGG2+v7BVwFN00W8sWhjncuQgzX\nxuoGrFBQ1uv3wUJfKyki9JQOTYkGofNHJ/H0U0vI5w3MzhTw2COHBt5J4WN1nKCdz9ziLAoJhssJ\nAq7VtS3XOiF0PxW8FGSY4aKKkqgslUQRZjYVpBMBN9i88b2XcNtLmYYn65Q3hrUqLbTrHfS2o/ok\nAIlekwBgbccrcgG728dTTz+eeL1baWBhdizQCxmqCsPU3DHT+4kX377k/jt03OVSzmO2HZQnQ9Xh\n3rOztr6D7/7p9/HG917HreWb3ntOsChLZfQg2Kk2mwHhtbMe/Y1UoFB8C5HQ6SR927UuUAy88+bF\nRPsv9+sYmG2jGWKFQAm6/Z4rKBcoVFOFntFw/ORCgpl699otMMYinSUMTYeuqqjf2sKlP/8h9q5u\nhL8SSzNTmJ8ZT5Awpq7iN3/rFyHKEs6e9jtpEMi6BiKKaPV62KxXsV2vAYRCTemgqgJB0yCapuu9\nRRDRqNWrdYAgIpz3U4e9di+i91JCUzshbnDds/qRedXyU9ksVMHpXc+e0w+smMI4SDpxY+02/rd/\n9s/xr//Pf4P/5X/83/HcN58fvBka2y6/t4JGvRXxSRQEAacfPRfZX5gFJgKBOT8ObW4G2kKySTrg\n6riIJEamAF+3e+29G4nt5w/PIztVTLzOBWMQRYqFz57HxPmlg30mhAc24IqbHAKA6gUEnWaS1gsH\nXFQUkiwXIcgfngbgijMTKRqvvcHHpmk1Bwc1QCWUQpRF6IoSqdZxHKBvWXjrTbfM9/buXrCiEuSB\nxu7E6WOjD8RxQBo7MNDFZ55x25sQxoJS/WtXbuDiW8vR/o8+qODqvHiBQaxSscfx4JI57BYAGIYM\nzVTdZsxecMAY0PSC/731Blr1dsC+BtodxgJtBvMqOcNGm4QQTJ47DL0c8pSjomvHIUrufwmFfJ8C\nLkII14/r1spqQMFLqoTSfDE4fv/sZGaGF6NU9qpBKxkfsixHfKLyEwVXaxG6Dr2OhbShRQKuXruH\nenOQVm22Xf1WGIceOoTJw9NuanY8jyd/+Wmcf/ZcpCprejqPhelkM3TmMCi6inQmjWwuw00pbnsp\nxfX1bZfhCt1OhbT7m+xuf9BtgHACZQD5kK6J2TasegPXL6+h4xVGUNGd9AkhbmWjh+0b2xHmwUdc\nMN/aqcJwaKLCdGasDJPj+lO7tQVdV3Du7GGcPXMYh+anoOhqRIy9/I5XnBIOuMp5UEUCIUB5IhvS\nKXqsraagtl3Fuz98a3B97T6yZgqCQKHpSrDwaHY6bhBEaKJ9EwCI2aipMuDaZVRuN8AECd/91vcT\nnwEQXItmSIoi6Ip7X3qFKf65ngiu+eDC1r15RVSV4PeVQ9XS3Uoj4dlICMFXv/Jp6CHmR6AUv/Yf\nfAVZz8g1m01hYWHKZao9Y04iCnh37RaoJELWVchpE4KmgqoyiCQEhxVmuGo1N7AOp/Q0z/m/1+qB\nhnRbshNjQSUBrV4XvZCBeN9rcZQO++Ex9xy1+xZfv7UP097r9vC1f/2HqIXc+r/5l9/BxppXLBLK\npLz8ysXQ97r3+tJDR5GZKA/G77BpNSUw58YhaipAKJTxMWiLSZZJUxWQeLeSehOWZWHl2s3E9guH\n51E8dQiZsfS+0qFUKYXpE1Mwx5KtBQ+CBzbgqtaTqzaJiGCMJVKKQNLAcOz0oUjfvvLpxUill8qp\nOuxWGx/LCsUA3J6KyZQbGIOkiCCERNKKPhvyR1//Dl6/cg1X1gYpET/IOLx0CBpHWxP+PlLbBOm7\n1/jRRx5C0Ru4iGMHD99fff2bQQl+8P2eG3C1UotMFqEDDP7ZqDe9CkVEPLh8byhe8FkYzwJgkNTB\ngFf39IR7axVcCTVdB3XXZYosDrrSOyzCcPkQFBnznz4LJRtmXglcR2oCItD72lZqihNw3byx6vrg\neIGPkTNQmi96OheG7OIkct6ChYfba7cTr41NlCOMmCQJ0OXkdcmXSgEj7dgM/V4ftUYs4IppV8an\nxvD0rz6DX/4vfhWf/60vYerINKhhJlLJRw5NwoilCwgASRAwMzcNQkggKgfgVZc52NqquA7z61uh\nsnkXxZDIPsxyORwH8YKXfmPwLB4Yw+5OqAsCAFmVYKZNiCHBb7/TR2U9qTehsWdn+90V6KqKR44N\nVtumruOpM6eTjtkAardcFpIQAlWVkTaMxL0VTJahZ2isnAchBKIqIZ3WkSmkgvGVikJyPLX7AGOQ\nJQnTM2WQ0MIDAK5tbgCEYPtWkhXttjpu9WAIiiJh+/ourl6+hlXPHDcOvxFxmOFy/O8kCPRiqiIj\nH1RIE697pPeXJIJqWqCVKuc4LeFi99jEzBh+9/f/IR559CzOPnwS/+Cf/kMcC1gtF+fOHIVvQaGn\n3HPl+8qlRugi4ylFYOCNBrhaNADodqzgWXNsB1JsyBZFAT2vvY+Pft+CJivRCj0wCJRiz++oEMN+\nKcV//+++kUwjAtEgWZDQbLZxcTlk8+ONwecfPQMiCJDy/nn3fggBzLkxiIYajPMAoIyVoR+aj3yX\naRqgMR1uo9HErZW1SJcJwDVSL40VoUyMYeKR45h/eAFzZ+cw+8ghzHziKKYeOYrCbAH56Tymjk+i\nNFeE02xGTG3vBA+k8SngUqmU0sgqz1BUtOstdJrJgEuNBVypySKOfPkCmpsVKBkjqH7xoWRN1GOr\nq/ZeHb1Gkj1T0h/xCkUfggTEDAIJc8AcO7p6Z27Q0a4CY7kstqruxMAcBjiuSe2LF5cju/Z1S8PM\nTsEY0G2BtiqR7xcEAV/8/BP4g6/9pbedAxCK7c1tvPjS27jw+OnBPrx2HrVKbV+Gq9loDlKKISiy\n5LaNkJSEfq1QzuDWpVW3gXejAzCg2ewChKBb7+C9q4MVGyEUzGHIhyci5iT0IYA7yAuyhIVnH8aV\nv34R/dj9LRnqfW0rNTOXDJxWV9a8Y5ECjVWqmIJZMGGePA6J0yonjNsbycl9PKYf6q3fRjaroxEu\nTCEE6XwRq9495Fd8VhuDoMQiTmLl6QdJYasRMWUCogxmdUG8Sz09Nw7l1WUIAkW3Z4FQCkWR0Nmr\nQdioYu0nF5GZH4coiLBsC36uq9PpYq9Sx/Z2xTMHHXx/IRMOuLoBA55ozgsgl9FAKIHT6YJZvBQ4\nhVLMoZQ1IRg6rFotqAytbFRh5AwoQcBIIIQCrn6rg+rKBmRJwNmjR3BoegrNdhulXA4Cpaiv7UQM\nnXvNNjq70YVs2tAh1odMon7FKQNKJXcCFHUZ/W4bZx5ewKsvX4HVt0EVJdpFgtmBvlJRJTx24SS+\n992XIwHX6s425iensbO6DeZEK3tbexXIuhxUJwKALItoV1p44d9/m3+sgJf6jTJcLORtJega0AJ0\nQ0O2mIOkKrDhstGEEBCBuOwyccd8u9OLMFyR8+KNJYQQyIaM8XQRv/qf/P3BNrXo83DyxGF8/a9/\njL7tIFvOQtEUWJaFVNbg6zY9bG+6c5TjOGj4AVco6NE9VqvbsdFrtCGbGnqNFlRRisyfkiyhazsI\nF3YzxiCJEhQWDU4EgaLSaA2xhBjOcL352tt45cXX+O+9+jae/eLTKJWLYKKE19+4HF3IMAemmcER\nrzpdm5sB6/VgVWugsgB9qjTISsXOl1wugWoaere3AEqRP7IAxOQNzUYT10L2Ez4WDs0Fti364hz0\nxbmgO4h/juqvvgkn1lKpv707Ukc2DA8kw9VstNCoNyLUKSEEhqajvleP+HD5UDhUp5I2kD88lQi2\nAHArFeu3thJVGYIqR5pcfqTB8UkBkDRAdexA53D60AJMTQMBgWPbg95n4d1SCkIJJFHE8ZNHE++D\nMZDWHmhrD7yKlOPH5l1KHgixVAzf+tuX0A7T3l7AVR0WcMVE891ONyHYlBXZdd7nMVzlFOC4btB+\nAFlvdgAiYK/SQCucbqDuTFXMhhlAFlhBhEG9qhpJVzH/7PmI/xEAZOfu/MEeBR7DdXt9E71uL1Gm\nTwiJOFkPA0+/VQ4FXMyy0F2/jWwuyoRQWYYcsiTpeQFXLRRw2ZyK/uJYUnNBFQXyeNkNughABIqZ\npVkIsuj2AdRkaMqAcSyn0ti5uIKrf/UixLblpg5DhRhvvvWeJ+oOicd1PWg2DcQYLo5uUKIM+fE8\n7HZyzIJAIaZMUEHAsWfOgQg0mjJkDNsr20HVnaApkcBkZ/lmxLYjpesYLxSCNlJO30IzZOBYv5UM\niovjpUQHiAAEYN4UMVbOe8egAoxhbDyLZz57GidOzSGbCbNuLGIns3RmDk8/fR6yKHj2Cf5PY7iy\nfgv9bh+VcPsoxtDcrUCQhAgTrKgKtvYquPhGdCEXht/oOsxwWWEtLyUQTB3ZuRlkHj6D4uyUm8ZT\nZNcwVBjofqgowJwo4KGnHo42a/dPjAezlHKrGuPp31hBj6rKOHZyKfi4ltaQyqcizO1RTkuzna1d\nt41MowXHG6sEWYSgyJBFEaIguKycqqDqWY50q013vgyZeQqS6Jn8xhZ7DoEWe+YpIdirN/gM15CU\nYrVSxZ/+2z/nvgcADAzf+9YP/IPBy6++G9uA4ewjpwK5BlVkGCeOIXPuONJHZ6ISIJocEMSUCf3w\nAvTFOZicdlfNRour31o4PJ94LW6HIseLagCuvvIgeCADLr/aSQyLAzUdlFI09uro8hiuO6ziUrMc\n4Xzc+RkfH/1WAK5wPu4YbUPSBqLbr37yAiaKBTDbCbrLhyHIAgiAo8cWoarJ60Q6dZBu8twH7xOC\nn/vCE+4f/sDGGNqtDr77fMhZOgi4quCJ5sPiTFc0z/HgkiV3lcvxJSvktUDA6Ttk93oWepaDzc29\nSMUVIRTFQmogmAdchoszuYWbtqoZA4e+8CjMySLktIHCsVmUTnD8se4Bpmkgl4+mShgYVm+uJQIu\nAGB9vh9bGPsJ5rsbm2C2jVwu9NwRAqoqYB07iHt7np9Oo90OhPNdjo6wFNddedAX52GeOA796BGk\nlmYxOT0GxYhdS8YgiiLy6cFEaggiOns1kFBLnzfevMw1PA0jEnD5bXJCoIQhZ8jJCRmuHsvXQ04u\nzaJ8YgFUkkBDqcVuo4vapht8hh3m7b6F3fducc9BGOEgq8YJuKaO7lNpRSlMU4fuMRu+cB5w03wL\nh8bwxBNH8aXf+TJOPnUa6fTg2CfnSzh+bgGmoeHC+ZMgxC3b97G+u4Nao46d8HFZPa/whEQqxxRN\nxWuXL8NqdyOL4rChqa/hanXCAVfyJ+meHrLAmUjDmJgex9TDSzj8pcdx7Jc+hclHj8OcLAapVNVU\nMXHCXQgSJ0IdRf/2cPaRMyO/7zNf+nRifOxbfVQrNdRrUWZSMjWY6RTEbAaC18quesMV9PvWRro6\nCFKoKEDWlMSwqEoKtFj7NkqAvWqdy3DFe8oCLvv2R3/wJ4mG6XG89vKb2NutYH1jF+vr0ewSYQ4e\nfjR6fgghoARJdp8TcIVhmMk5u1apDdFv7V9pKBWT94ndbHG7QOyHBzKl6A/eYYbLLwHf29hNOOMK\nogDxDr1BlLQRoYaHbvdx0W95YIKcDFXiE16I4QLc0uSff+IxvLG9iZde9Z2eB6lJ/9qcOsVhtwCg\nx79xmSAFTYSnpso4e2YJr72+7F4y77r94Iev48Jjp5HJmGBUAGMM1b2auzonNCms91KSjUYTPa+P\nYhiqKru9EAUxcX+IIkW2YGJvux64N4MAO3t1VCuN6GBECcbLWaA5OHfMYRAETiAYYxWVtIGFZx/m\nn6v7hJm5KeztRttX3FpZw/hisjfYfnoF27KxtZkUP/sBF7NsdNfcySCVdj3tHNsBlWWXsek76FRb\nUNJqwHABDPVmA2nTRKfXhRhz2C6PJcXwPsRMGsikgX4XcmMbpbECHNtBp971dIYM5Uw6YnaYMU1c\nX1uDk1ICB+719e1EEFXMDg+4rG4fRBAiqUMqCshInMITSQqYzdLsGKggoHRyEdWV2+gArvO8F3Du\nru1Bz+rQQhNJ5dq621h5H9RWtzDxyFKC7fIxsbQASgU4PIsVACAE5VBBBxUFUElMxI+6RHHi0aM4\neSyLVqMDx2FIeV0BmKzh0fOn8eMX30BD7qIXsmJYvn4NJ29t4fDD7tjA2g20vQW1pEro1F0vsp16\nDdc3NgDG0Gt2ApnHJ544jxd/+BOAhUXzoWtCkuO7X6WbL3D0WSGEU++SrqJwdAaFozOwmzWgug1B\nFkPGruGAy/MdC4ERiiPHDsMwDTQbSZ3wzNw0pmenUCjlExq17c0dWLF0tKQpMJyo4Wp7p4Zeox3o\nkMOu61QUoMgiSKTmDzBUBbLgVmazUJq01emiUW1AjqXveCnF57/zQ1y7kmSP4nAcG89/54duj0RC\nItrZqakyxkqc68G5L9k+AZfJCbjeu3Q1qd8y9JHjiA9BUyEYBuxm9Lr1tneAudFdbeJ4MBmudZ/h\nGgyyKd1dGW+vJQd25S40LlQUIKf2r/z62Oi3fPAMUO2ocJ449qDbvAdBEPD46VN45uzZRL8+QRYg\nyxKOHeGU8TKWbJoNgCkGWNrteu/jC5973L0nQgOabTt47Q2vnQYV0W61Bw/WiLRiYAsRTynKUiDK\n5KUVi+NZ76v8R4fg1q0tMAwGfAAwMgYy8fuLOcFkHgavpc77DZ4B6q2V1QjD1bdsvPrOe/jed3+E\nvd1KYnsfa7fWEwUMpmkGA19343YQPFBK3bSix275UCBic2UzYlr57tX38Prli4nFVCabcVO/+0FS\n4JhFjI8VIKkyzFIKes6ApEoYz2cjg3nW0AAw2P3ovRgPLBIMV3OQdrG7vUihDuC2ycnlzYQGLeyZ\nNOaljKlAMfXYQyDw7B98HYntYHtlB9Trq8cYw/bFlcTPTVeGn3MAACAASURBVM+UE3Y4/UYbnUoD\n9bXthFxCMlSYpQxy+SHtmtyjQrkUrcjiFXD0tnfh1KoAYzBS2iDYogKYnoVEBTz58EOQwxW6AHYq\ne3jndU/7yBhau3uDIkfGsNOp4fWbV/CNF34UjEH9pqufTGfS+NRn3LZFju0E7zc9c0oqi24fxRh8\nhitfHB1w8Z4RABAkOdkWKhwYDPEHFERhaIeNC089CgDJilm4euZaNcpwUUlAmpM6q97YGARcIbaM\nSgIkz/YlDF3VQAmJdB0gXhuqajXaL5CIQqK10K2VVXzrG88ljiOdSeMJji3JT370Cl596Y1EUdP5\nh49xK+J5zDA4xSlh8BiueAU14KYTDxo38NKK/a07Tys+kAHXpifAjQZc7gNc3UpW7txpOjH4HEfH\nFcfHLqVIxaT4N2TJAADgBFygBK2tChbGxvHVp55CxuuzSAgBFQVcePw0ZIlzuzl2gmVkhILpWc9A\nZjApZzImnnj8tPeZwfY3bnjVkFTwXME9eA+TFmae/EHZ13Dx2vr4KyhOwJX3eiAGEyshgfjTsexg\nb4tnDgc94IKvtp0EU0MEIdkM+gMAzwD15o3VoPlt37LxtT//Nr7x/Ev4znM/xv/6P/8f3OojALhx\nLTn5+y2EmG2jux6tYFxYHAeVo83A06YZiJ591JoNVFuNRBpkWDqRC0nB0XNuYQUBIMoitIyOz/3q\np5AuGUHAnfFW7uFrxgjxDH0HKMYDLk8v5Fg2nL4dbTHkmf0KAkU+PxhrqCJHbDDG5gcaPaOcQ/7o\nDIggQEynQFUFVFXQh4hLf/EjbL1zHbWbm+hxqqnLpw/B4LAE9dUtbjoxNVUCIWRkL0YQEui3fIiq\nlGCGe5tbqL1zGZW3b6BycQX16xvo11tgasrVRFoWzh47hFI4uCMAwPDG22+jWW0AVhetWhONVgsX\nb1zHc6+8jHfXVtDoRlNVzLbRb3fx5KcvIJNNuwxdiAHq9fvoWxaUlI42Jy2me15mheLo0n5eGywA\nfJF7WI0+xB8QAM4+cirxlmmaOHnmIQBImvDCZbjiKUUAKM4kHdIrN24PYbhcfZoc6YNIglY4QcBF\nCOAwMMZQizE6kh4lNmzLxh/+m3+XYEcJCH7lN7+KZ7/wdCJFats22u12ZDEsigLOnDoSZDMi4LRv\n2z+leDCShKffGgapkEd8ILqbSsUHMuDa3XGp77Bo0vD1C5wUYNwS4qBQODquxDYft4CLEL49RFg4\n79juoBv9YLCCzqVT+OqnnsT5o4exdGgWP/9zT+Kzz34iGrQF++U8ZH46DwCTotf25InFBGV/4+aG\ny4xQAbVwuw9vH+PjxcFA4U2wnU4HrWYrMXEEGi6A29C76JmUUoFEeiACLvPgV1wtnj2SCLh4lhDx\n1iYfFCanx0FjgXW1UkXDK0L4/stvYvW2t4JzHPStPp77m+fjuwEwaA0Uxtyiy2Z2NzYT1XkTk3k8\n9pWnIgFXxuRXQSpq8hqUDpAGCOPcY4/g5Hl3ohMEis9+5jHMzI4jM5Fx7z+7j4w3vkSumSBFWEtN\nVaHHNTaesNjy03shtlIQBxWpxZKnFyMENLQPxVCRKUaDuPGzhyF6fRgFTYOgaSCUwulZ2HjlElae\nfyPxG82JArRcCqnpZDFBdWUTdU5mIO15lOVGpdYIUIoVKIi6AoDDPHhjM+vbsOptNG7cRr/hpgSd\nfh+CKOLZT5yKaHMBhlqzgW9+/Tv47l89h3/+f/1/+P4br+P6+jr6lmt1IHG88USL4RMXHgalFOm0\nGblOgJtWVNIG2hydzUEYLlVVE787AGfCJwdguABgamYyYfz8xa98Liim4X3n9tZOYAkRxth8MiDs\n7NYC93zfKDzc5UMNCec1WXFF6oQEOi7BG9Nsy3YNakOIN62++PYl7iLsyWefwKEjC9A0FY8/+YnE\n++4xDZ7948fdbblzwYhzOQy8lCIPC4cO7hRPZQlidrh9x0HxwGm4+v1+EM0LguDllpFwlQ4jbglx\nUOzHcBHh/hlO/lRBlIF+dGVIrB6Y4t3Ijg1RESMSJ0JppJpNlmU8fOQwJh6aRPmIt4J3rKAtQgDe\najDMLInRh3xivAhJFGCFUj/tVgfbO1UU8tNuhWIA96HOZVO4rSlotToIjPQIsLdTAYlNHLIijWS4\nUlkdsiKi17VARTHRmsSxbMwen4OeMUOtXkI/JxZwUfHDeQQlScLYZBnrq1Hn7LXb25B3Kvjx6wOL\nC+YFqZeXr0RKpt33GJfhml2YcSsT1zYS78mlAg4dXoBZyOIHf/I99Lt9ZFIpiIIQcZgHEDS8DmOO\nozMbBUEU8Ov/8d9F88urEPrtQACu53TvfrChyjIUSUK3b7kxOKVgjESc9gvp5IBrd3pwLBu2ZzES\nTimGK1ILXsBFlWil4fj8eCKtIcgSph49jhvPvcr/QZxFZ+GYG+Cmp0rYePlS5L3Obi2xPZVEGJ55\n435aprHJKJMiqIqrVQs76zMW0eS4rwGtazdhGoZ7zITi2MIUJgpZ3NzYgVcGCRDgW3/9HGQJqGzF\nj5W4rEzoOVMVBU+fPAXWswBFRjqbxsb1aMuWVtsNuPyeqWH4DFc+n/M0TcnzOTUzOTzdRCji9jnu\nfeTqQ3mCeX9MIYTgl379FzG3OIvba7fx2CfPYmJ6cD8XOALtrdvbiebKAJAfL0Jxqgmrj+B3egwX\nFQdGqnJorvQtJSgl0DyGi3pN5O1un8twhXHzRnKhNTU9ic996Zng7wtPP4YffPdH6McLb0Ln9vw5\nt68usfvR+WFI8cF+AZcgClBVdaSI3zB0lMfvbOEmFwuwOP077wQPHMNV2QszFG5aUZVl7g3n465T\nipyeimEoaSPBYnwcwGN2Ivl1xwalNJrPTwxO7t9GIRTUMpZYsRAO6xXWbYHSyPEIgoCZqaRQ8cbN\nTQSmp+FjIm4q0vACZ+L3NITHpCZE88pg9RX4koV3SVDwWC7CKdRwLBuHzh4BgIRhprvLOMP14a15\neBqV1bXb+Mb3XoQTmjyZ4wap9VodW7ejTMnuzl5CBCyKIianx9G8fJXjPUWgTE8AcFNpz/69z0NP\nGxAFEccWDkWqzgAkDE8PH13EQyf36VQwBEZ5ElooaFJMNXI9Ml5g4Fh2gt0CkoJ5H/12N2C4CMig\nSXuoIjWTMSDK0QpEABibn+DuMz1dwvQTJ4Nq2FHQsiZSXp9KJW0cqNAnNVkIWI9RAZdhGtBTUfaR\nUAJtsoTIs8EJAhkhYJaF1qUr/gdBCMHTj5xMpInb9Sb2NmvJ3RACxdBAJRHFbBafOncWv/G5z2Ky\nVETNs0FIZ9IchqsNOa27LHYMuudlJogCMhwdFDAinegdE1e47Y9t+wi9ZUXGhacexVd/7Rdw+txD\nke2KpWSas7pXxd5OsuAhlUkhM8Iyxtdw0VDgL4pCsBDwXeoJpUFKkXr6LX7AFb13Nzneexc+9Whk\noWGaBh594hHO0REwQpDJmDh8yCtOiEtXOOlERoY3Cg+Dp+MKY97337oDSPnsPcs/HjiGa28nKs4V\nJBEaHS2QvduAS04ZrsjUSQ4WwMdQMO+DY4lA7L672icIKv8kVYLVdR+Q+EQJeC2WsrFz6FhRE1Ue\njUxjt6WoRAK+2dkJXLsereS5cXMDDwOxgMt9QDMZE6ahYWvLG7SYA0DALsdLRVbVwQNNCJggJrQF\nhXIG67f2IgOZD1WVMTY/Dsd2EvofEE7A9SExXIBbGfXSCy9HXnvh+y+hvckRg3orzyuXr6GYy6Bf\nqYDKMq5zvG0mpydgrd/mrgblUh5CKKWWLWXx2b//eTz/x98FAJRyBdSbDTiMIVPK4vznP+GmpJiD\nXC6LyZmJwKvnjkEImJEHapsgzAEhBHpOR92zXciYBjYrFdiWO/EkAq4MX+vUb3Vgh5tHCwJg25GJ\nh1KC6WNzWL05CFipKGB8YfiEmVuchDlRwOYbV7D73urQiurJ04uRySM1XeK2KAsjPT1YtIxKrY2N\nl91q4djrStaEWBpHf3cPdqcDp1EHazquF5Z/mN4xBeXzBGCU4NTRWRSez2DXb9/EWPJZ8bbXDA1P\nPPMYjoxNgG5E2a/qzU2UTiwgnU0FLvM+mh7D1eK0gQtPxoViHpW9ZEEIT+MYAaXJrKrjBup3kwbz\nISsyMtmMZ23jgoFxe0emMynoRRm3X73M3Zef/o4E7cTtbNBuWAHDRSIMlyflcBxOSjE6z/LMjnms\n0ZPPXMCPvv9itLCGACAE584uRckUuz8o3OIJ5g94Hg1Tx84Ir6w70W/58B3w79aDC7iHgGtpaelp\nAH8I4D9aXl7+S877fQDPY8C9fmZ5eXm0BwOQiORFSYAmjQ6o7lbD5TayNtCtJPPjwMdQv+WDUi/Q\niLETdi8SDLnWEO2ASYpDy6eTzKRtAX6mLr6i8RFL5TFJAekMaPO52eQktXLTTV1V45M8EZBJDxgu\nd4duwNXtdJMTiRpLIYty0nF+PANQgRtwjU8UQAhBv9NJVIwJopBYVX2oDNdc0gC13+97k0l0sGPM\nAYGAK+9exkOqFDBXl194BcyyI5WW06UCuqvriIMIAtSZ5ESmmTqe/bufxQtf/wHW3luFIudBBYqn\nfuXTGF/gM0B3DUEEM/MgdTfw0XNGEHBlDa/liuVAAiJCbAAoZPgajn6zEzH8paIAuxdNKVJFwZkv\nXUD1j55DY68OQinOfPoctH0EvpKmYOqxh5A/OoONVy6hEWv2LGoKyksz2K0MAov0VAnbb18fvlNK\nYE4OtEKjNFzlsSK3RyScPqiqBG7bpLkH0m3C6VuovbcKZkXd+QMQClWVcPrwIp57PaRFiwWTWdPE\nsRNL+I1/9JtI59Lo1pq49PUfRLZpb1fRa3aQMo2gCtZHs9OBkhrCcIXGgnwxhyuceGUkwwXwJ/4R\nDFdiETkCxVIhOY5xkEqbEEURWiGN9k4ybSxQClVRIrpCwGWN2402dE+mQwUKRZJBCIFAabDe7HS7\n6PX7kP0eqyFio9ftJQJVAsLVV6YzKTzy+MP48Q9eir5BKM6djTaAJnYPDN4zcQ+B6346rsW7CLgA\n15PrAw+4lpaWFgH8HgB+F1EXe8vLy8/e6b7j5eeiJELjmGWGcbcMF+AaTf4s4OJAkBPBELF6YKE7\nZlCpyKdmeQ7/xLEGWTzmJH2yCEk+VKKCsGBsdiYZcG1u7aHVbMU0XO7+wilF/3sR8vIKQ9Gi9xJv\ndZ+fKACEJgIuQgjyXiGG1e667X1C78fZLeDDZbhK5SJkWUZ8qU4oibtluCywALz3xkXYJ44EK+GV\nlXVY9Ybn2K2A2TbKQ1h3/chipMFuGKIs4clffhob19bRrDRQmh1LiMnvGyQVjpYBbVehh5zvM4YO\nEBpYQ4QZLlmSkNJ1UFkMRMk++u1u4HIOwK30bHciKUVtfgZSPo0v/vaXUdncg2pqMO5gfNFyKcw/\n+zDqa9u4/fp76OzWIac0zHzyVMSvEAD0YhaCIg316TLKuaiPnqZC0zS3eiyG8ngJoDyrmJge01uU\nUEmEPlVE88YmP/VDKAAbhxYmcWtnF+/duhU8hyldx0ShiPFCAYeWpvHJ3/g5CN5kr6QNKFkzMVbX\nbm4G7EwYbdsCI0CH4/CvaYOxgFepmM1lYab2KajiBlzOXeuOwiiWC7hy+erIbXRdD+x3MnPj3IAL\ncNOK7ZjZsl+IMkgpElBCoIiy+1yHrlut2UQx647j4T6KPHYrV8hC5hgnA8BTzz6Bl154JVLRuLA4\nh1KcXQ17Zd3DeTRSw5+tu9Fv+RCzaRBJBOtziIKDfP6uPgWsAfg7AP7ViG3uSvy0txuN7AVJHCmY\nB+6e4QK8SsUbyca7wMfP9DQMJsogvdjq0IoyXEHANeRK62XOyjkcxHHSiYyKyYGaEDBRCRpa67qK\nUik3SBF6B7Fy7SYn4KLIZFKRgIsw5vk98QKuGMMlqYgLZOVMDmY+hVrMoiSXSwE9V/jZb3WTDBcn\n4KIfUpUi4Apkp2encGsl5sDsTYphMMcBcRy0Gk1sbO9islxAu9PFtne+7XbHNet0bExxbBvUmSlI\nvL504a8lBBOLSdbtfYFqgtk96LnB/ZjxtEpO3wJzWCTgKmQyIITAHMujdjPqqu/6QoV86giFYBqQ\n0wbElAl5rBw04xVEAYXJIdVv+4AQgvRUCempEuyeBSolGVPAnUBTUyVUrvKbPIfTiT7yhRxWbw0L\nuCgYFZKBhG256R/GIml3OW3AyqfQqXPK5j3WqziWwaGpaZSyOTQ7HaQNHabmMhtTCyU88fOPJ56N\nzEwZm4mA6zZULTmNdW0L7XYnIYhXVTXCPPIm3tn54U3afTAiJIY94thu39nEtgfTHfngWUPEkUoP\nAsLM7Bg2XrnE3c7QNHRpNDgQRNFlxuRoGtFQFFjEQnhArzVbg4ArNM/y9Ftj48NNQHP5LH7p138B\nf/y1P3W/y9Dxd37jFwDE5gCv6TkIuafAdZSG6270Wz4IIZALBXQ3+DHDfrgrBdjy8nLnAOlBdWlp\n6Q+WlpaeX1pa+r2D7jvufi1KYqIUO/FF98RwDV/JyKmPqYYL4FtDWL3IqkMcxXARAn2M43MTCbj2\nTyf6YLFqxQTLRQjeeWs5YcCpqArUVDrKcAEey5W8hWU9tp0gwjGyA5sKWQdUE2OzYyBCtBH1WDkH\np2/DavdgdXogsZQKrxvCh5lSBIZoVfwBWFUw7ZepMxZU4t1Ycweb1ZiA3rEs5FMm9Fj7DymfgzJ1\nn1OD9wpPz0UzBSgpHRBEpNOD62z3+rGAy00nGuPJe7rf6gxsITxQUYR59BDMk8e5pon3CkEWR04a\nvuXDQd8bllYs+5Mo77n0gyyOl546WYQQX7wA7nknBKWJHAghyJgmJovFINiaOTSGJ79wFlRPjsvp\n2aTvVHOzArGbnJhb/R7aHP2WHhsHDi8tJooGPvnppGFnAryJP9S0OwJeSnYEeOancaQyg0IG2dSg\nDWGDU2kzWfhFCPLZVCD38Js3p/3rFdq86unsiEAjPV43Nzi9U/dhjc594gz+6//hn+J3/tP/EP/l\nf/97KJTLiUCUMOfAxQejMMqLa/4O7CB4kMfLdx2w7RtwLS0t/fbS0tILS0tLPwz993MH2Pc/AfAP\nAHwBwG8uLS0dqFdJQjQvCgMPLh4I4Xr1HBS8noqAm6+OU/UfKwgS92Eg1sBZe8BwJW8+NZeKiKOD\nfThWMDhzje6GDU6xfl9JHRfBO29cRByZbBoQZZgHDLgUlXOvKQac7CSc3CSYmQcIwbHHH4JmakFa\nsVjMIO0VWXTrTfTbB2O4PsyUIgBMzyQZJb8S57OfPI+lBbdkndkOmBdwXV91A65bG0lvp+nYoCvo\nGvTDC3c9QL2vIATQUtAmxgDqNgI2vUnHake7KxQzGVBZhJZL+oX1W11YnSSbk/Sq++BgThQSrveA\n+1zKZjIQ4gnnDdMYTFyc5zJ4fjnPMZEU6EcPDU0rZoopjM9EA4u5IxN44vOn3WeKo9tVs2ZyEcwY\nehvJCr5Ov4d6PSkV0WILKkEQ8Lv/+Hfw5Kcv4Pxj5/C7//lvD3WYj2CYhosXcO3jjB7HQRiudDp6\nHw5rcJ/lmdpSgrGY3INSgpzpz4VRhgtImp7yGK6DpOlM08DC4Xk3HTqkm0fg+fg+abjuVr/lQ9BU\n6EcPud0g7hD7jvbLy8v/EsC/vNMdLy8v/wv/30tLS98GcArAK6M+k0rJsKwe5JDdgCAImJwdQ32I\n14hmaiiP3b3WgxVMrOhyoj9jdjyHUolvxvhxQcuuwe7EVonEBrzro5kqKCVBFYysDK7b+OI4SuUM\nGt3dhDWAnlUhyDJadhU2i96CaiENyUied8YYmv1qII49cngm0iZHUETYdj9y7wDAxFQJuXIe2awZ\nbatDmJcpjE4IE9MlyNr+jGmplMLf+/1fww+/9m20NivIZIxgQNIFt2murEjotgb7V3U5cXzF8Syk\nOKv2AeLs+SX88dcQOS7bsbFYnsTZ44u4vb2Hv/3xa0EBBSEEq7e3QQWC9e0dr4x8gPnpsWBfVBIx\nfuHsh/r7DgLr8ARaa+4EUsik0ex03DY9oYKPiXIBufEcxmeKuKVEr6Hg2BAJjdz/AFCezMEofDBj\nCG+s2lkYx14s/Tn10Cx32/mFCfwodm/OL04F2/bqDrrbUT2UqAnQSil093ro9aKfldIm1EIZOutj\nbzmqR2KUQdFkPPML5/HWT66gXmlheqGMhWNToJRANExoZf6Y3joxi1uvvpd4XddUtLuDoFdRZXRa\n9cTzVionx/VSKYX53/ll7vcNg9NX0OxGAz0iUsimhG4/fi4MqCPug/jxFAoGdF2BZXECDg9TM6XI\n59LaIey8dSWx3eTMGC5uRj3KHDDMz4whRUxsb7qyCFmRMJPN4+rOOqjgWkMAQKPTgqyIyBRTke+r\nVvYS5/b4iYU7njM7tI1+LSrNoOhCL5bR6u7AoXF9YhqCzNeBhjEzW04cH+CmMk+ePnTvC8BSClji\ntKrbB/djeZ048qWlpaMA/rvl5eXfXFpaEgF8EsAf7bejy8s3I41NASCXT0E2dPTWk6sYANAyAra2\n+MHYgaEq6MUCOluS7n2/P+UgPYD0RogDRQrHYXAsB7II9LqDbR1Nw9ZWHaTHQGIBV2erAsgaSL2V\nyNN36n2gxT/vxKYgPZdhS6dNKKritu4ggN2zuZlNSVKxW+tDVhQ4EfuPJLsligKq9R7Q2L8psI/S\n7AS26h30e4PfsXlzB+29OvqWE/lOBiTu771qB6R5dwLM+wOK8YkyVm4M9D4CFfC5J86j37eRS6eg\nyFJkMuv1LVy5sY7VnSqoocNutoIeiOPFfPAbjUOLqDQtoPlgP0d9SQ7uXVPTwRwnUjQgCAJ0SYUt\nSqi2+uj1oim0XtfiiumrjT5azvv/20ulFHesUiZL6L03uK5EoBCKOe62+VI5cW9OTE0Ntu33QWPv\nd+0GGqQOUq+DxETEnZaDulMHM9JwNB1WqC8fEUU4kpsSPfmJw8HrfoDRkSkaQ8Zeks1Exhkfmqyg\nFRLIWwxYfud64jcB92G+ANy+qPF992x07EZizOy0+qgPuQ+GXTszleZaQQQgyflJTJtobUUzRFop\nlTgHzHKQNg2cP3EYa6u76PdsaJRifWXTtUp0WNDieq/WQK9roQ8afF+n08HtjWilHgEBFdU7P7c9\ncM6jhdbqbdBWJ5GF6Ox1ALp/S51uj3GuPXDk2BS2t/lFcneDOw0w70rDtbS09HNLS0t/Czdd+D8t\nLS39lff67y8tLT22vLx8CcDNpaWlF+FaQ/z58vLyT/bbL69Bbi6fhTmiBc/dusxH9sHRcX2sKxQ9\ncA1QQxD9FT1ntaCXPcqalyK0LcBxOKJIMrJ8momDa00IwZyn42Lg21IAQCaXdvVkHJfwOGRFviNx\nK8DX+XXrLVidA6QUCXE9mz5k/NKvf9mrVnRNS3/l138R2fSgF+bcZFI78+IbF+EIIogkuj3/JBG6\nqiDvaUu0hTlIQ4xCHzQoGTOwtchwUhGFtGtvoqR1UIFymzfHgy0AEc3Lh4H0TBljZw9D1BXIKR0z\nnzzl6tU4KJWLePozTwZ/z8xNR9uycFI/xPYCT540wPNSIoRAP3IoKJigkgT98OLw1BAh3HSiD62Q\njtgT+IjofL1WNuucLgdxDdddg9Bkz1kMORd3UKHoo1geXVgRFs37yB+Jif0JwcSRpF6JUIJcxtVw\nTc8UsXBoDGZGh6m5acPwqNXudNC3rIhgfosjJcgX85DupgBIUrnzDGlVOZIPcuDx2RxSpXiv+q17\nxV0xXJ7vVsJ7a3l5+Z+F/v1f3el+4/otwC01NbPDo8h7qVD0kV2cROXawDeIiAIyHIHmxw77BFyU\nUoiKCMuJuYOn9KCEmAkip5rHAnM4FYpeX6+h4Oi4Li5fH/mZtCd21tMZr03U8FoPRd2fqk58hmOO\n26u30G93XTPYkJ1FXDRPxdHC5w8KD51awj/5b/8zrN1cR2msiGzaRPWlQVuZ+akxXLwWrWS8unob\noq8joQSCYWDxyDz0+VkI6RTEA/YzexBABQotn0Zrcw/j+aR+ZqLoubh7g7ikKbBa3cR2kX3KYuDk\n/mGBEILyyUWUTy4eaPvP//xn8MjjD6PT6WJiaix6b3IrFRlg9VxdZhyhhRaVRBjHjgTPHiEEqNtA\nPylqZ5LK9+8K/ab0TBk7F6PtpMyQQN9vZbO5nmSI9LvQ3QwFFSLtzACAWJyA6w41XMD+wvm4hgsA\nsgsT6Fab2Lm04prqnjsKdYLXoJsGCyMfkiJCoBQpXUMj1pS52mxiVh9tCTF2lzYLIARMy4DUo/tM\n2AXBE8wfcLzUdI3btule9Vv3igdKFR6vUATccuVUfnjAdS8Vij7M8TwmHz2OnWX3Rh07ewTiPQjx\nPzKgAr8cPARRlWG1og+HUQ4JMnmMlW3xKxQ5fj/J4xGDAX521q98G/4QZr3WHUTWoOsqmpzKJR/y\nEI+oURjGcPmNvMMB14PU1icO0zRw9Lib3mGMgVAa9BGcn04KcqmiRE87AeaPHQ6MMH/aoBczaG3u\noZBJ49j8HC5edx30M6aJU4fcgEX2gmtJV4f6HvkQlZ/O8WOU6zzPRZ3wgiYqcoOmSA9OSeZ/Vt4/\nIOIFXGGGyy9k6XOCH/1+6gmpwGG0OAu6u2Cx9xPOpzLJOZEQgvFzRzB29nBwrhljSKVTQX9iAJA1\nGZkYA+QXQKV1IxFwbVcqEYbr9l1UKI6EpIDJetKGKI47YAoFQcDM/DRWrg8WivlCDmMTw60rPgg8\nOCM+hjBc+6UU70PARQhB4egMCkfvrCnuxwKiDPSGBymSpqDTir4f8d/iulRb3B6K+5ZPE+KyXJ6G\nY3qqDEGgsEYEXBm/w7soQze0kQHX3TBcoiqDSkKktQgLiV39wEUQhUR59oddoTgMhBAQSQLruixO\nLm0ibehBxRIBQDkGh3OLdy4ifVCgh8rqnzpzBsfmaNra9QAAFSlJREFU5tDt9TFRyLuthAgJ0nG8\nlFYcH8kFmyAmbJO4Y4N4gNQSjz33n+99YJRyEFQ50k4pwnCNWMjo+zj73xFGMHHR7e4/w5UaYcwa\nDmwJIbjw1KP4m7/4dvDahScfhajIEfNOKlAIkoBiNoO1SpT4WN3ajvRR5Hpw3WMgw7S0G4CPyEDc\naWr2C7/wWXztX/1bNJstaJqGX/yVL3/oGYUHasTnargKWRgZI8IUhHE/Uoo/w3C4BqjDg5T0VB71\nnUEVDJVFpKdCqx0qIm4cShwbzEoKH7klwvFtZB2k6/b4kiQRk5MlrKwn7xsfQcBFCMyUia3N3aHb\nKvv4vfFACIGc0tEZUkXr67gEmWMJ8SGanu4HKktwvICLEIL5qTG8cema+7csJ/VpgoBJDhP20wI9\n5mNUykbL5iVDDZiTeE85Hj5s/db7AUaTXRe47PcBnmMIcqJ9GJONAwUxhBJkZsrYvXwreI3HcPFw\n31OK++BO0mBhjGK4DNOImLfuh0995pPIF3O4dWMVE1PjOHP+FBqvvxV0VPAhqRKmSkW8cf165PW1\nrW2I2uiA654YLsBtuaWmQNojmOM7DLjmF2fxe//NP8LeTgW5QhbaAarP3298uCKDEBhj2OV0RM/m\nsqCC4AZdHNwP0fzPMAKcRtZh5ObHUTg+B1GRA2FuZHVPiKvNiiHs5zX4rgPE/5ICR8+CeenF6UOL\nicnfh6ZprhDeg8HRPYQh30XABWCoEBlAYH76IHpwjUI8GJybGmgaKSddNjUzeXei2QcEkq6OZK7C\n1zi82h+GjyzDdQAcZOHkG88yUQYjFEzWwfT9C1t8xE1QDe2AAdd9TCkeyITzLgTzgGvcqQ/xn+Tp\nt0aBEIJTZ0/gS1/5PM4+ctplsDljj6RIGMvnE83hO/0etry5ud3uoFaNBkWU0AOZte4HppojzymL\n9+U9ADRNxeT0+AMRbAEPUMDVbLTQi+WOJVEKqjGGpRXvR0rxZxgBUcIojRSVJEyeX8Ljv/0lLH3l\nySi7FWx0wMDioI7MqgmWnQDLjmP+6JGhmwXslgc9NXqgivdRPChGdiTwGS7OJDAq9fFhg8rRgGHe\nC7iIIEQaVfuYW/jpT8drheFVleGq5YMwXD+tGq6ROEggdSfbiTJYugwWGAoffDoyyrkIi2gcmOG6\nzxqu+7HNEAwLYngVincKfsAlQpAkTBSi30sEiiuXXC81HruVL+aCvo73dlAUTBtR2XwP5/JBwQMT\ncO1sc9itfCbIuZoch2cAUH4WcL2/IBRshCbjQKu8AwRSw4S2+2FmRN+zTC768JqZ0TYFiT6KB4Qy\nolGqz3CJHBO+B5rhimm0UoaOQibFZbeAn279lo94WjEMOR1muD6eKUW/UnEUGKEfyMRIBYpUaHEn\nSxIkUXQXBEMYb+CDTykeeLHJwbC0Ik8wf6fgBlyqBEIppkrRRTOl4YArKZi/r0J0WRtuR3QXWrgH\nDQ9QwJXU1uRCbQmGBVzqAej9n+EeMWrFeiAdwwEGnTvsN+YjnUkhO6Qpcjo2MBmmwfHOccEIuSvR\nPBCdjBPwGS5eSvFBZrg46cH5mckE8+VjVOD704JRAVfY/kPUDpBS/CgyXMD+z6nAaT7/PiFu3aOr\n2kh2S5Kk+5v2PkCK66C9/3gYxnDFx7W7AS/gElXXh3CqFPUAI4KAG1dvot/vvz/6rciXETB9SJP7\nB8Cz8F7x4ARcW0mGK9xQNcUJuCRFgvAAswQfFcQbR0dwnxiuuw24AGBukZ/OysYYLsM0RgySBOrd\nBlyc3nSD3bqTj/hTpuESOGmLI6eWuNnlYqkwsnfZTwu0fHqoHjDMYg4zPw1D+BD7KL6v2C9deNB0\n4n2AOVGAGrIMMrXROjzjfrJbwMEYl3sJuIYxXCMqFA8KnixAMTUQAPl0GmrIIoeKFH2rj5VrN9//\ngAtwU81KdDxhonxPbOGDggcn4OIwXPnCaIZLG6Wd+RnuH0YZoN6vlOI9DNRz8/yAK67hMkx9eNqS\nkLvy4QJ8awj+b/T78fEYLh6L9KBAUFWoM4MmvmI6haUL50E4EdfsR0C/BbjaH15zaiIKiYl8v7Ti\nR1I0D7dSceT7H2DARQWK+U+fQ2Fp9v9v795j5DrLO45/zzlzn9n71bu21xu7fm3HMiQkThycS93Q\nUgoxioOaFKWiBTVVgwS0QUpVCBX8UyFBW6pWqgqpoFLVSyRaRaQ0oDZpCyk1FCVqIa+Jg4JwQm6U\naG3ixOud/nFm1jsz58zMzsyZc2b29/knu2fG49fKztlnnvd5n4fRnXMsHris6YGGfC/rt8DPxrS6\n/0WR4Rpv/3BBmKDseqpycMRxHBanL2W5qkPQnzr1/ZCmp73vbVUujPtF9F6KciZPudR9UX4SJCZk\nDKzh2rBVNDo1ysT8JP/3o0uB2Y59g183MhBcj7LjNnT/LTtue3VXjhfa1uPS39H5j2LYL/z6G1Ox\n1OTYueOQ7XAb6FJriIAjzetbioNVwwWQ275AZm6W8uoqXuVAwfziHM+dqR2ZsrQ8PO/D/PRYQ1PT\n7EihoX9Pq23FLbul2E4Prh5KF3IsXL0PgFMrL/Pd00+HPrfnGS6oZLnCG0N3E3BNTk8EdkvvRdF8\nUGmAm/VHQF04d57FmRlOn/Hb/biVrbz/ffw7NQ1UAVzXa9mktSPNthYHWGIyXD8OCLgmNmS4HMfh\nunceZWHPImMz45jD+9l/7YF+LnHrcpzgLFe7NxPHaV3H1cUn47lts2QDslOBW4oOIXVcnddwQXhr\niOp4Hy8d0Hk7wTVcVW46tR5sAbzxqkM1j2cyGfZdHn5SdNAUAk4qBs1VbdX8dCiL5iFRW4r1WmV+\nelowX9W0jsvp6CBQVTqdZmqmdjSPg8PEZJNpAG1KjY023H/SM1PrdXHrdVyus/6zHLQLNT0zuame\nYFtdYu74gQHXZG2EWxof4frbburTiqRGKgMXztde28ynNy8VPNiV6smmzm9Mruty6MqDnHzsW+vX\n5rfNMTlVe2MqFCvztQJmoOG4HWe4oHnhvJdO4db9+xzXXd9uHCRHjh7mhR+9yLdPPkGxmOcdJ95G\nqQc1JUkxumOWVD7L6quX+sRN7F5oeF6zLUUn5TUt3h5ogTMVfZ2eNO6VsRbF5D0d61PVtG9UZ01P\nN7rm6NV86YtfXv/+wKF9fmlElxzXpXRwP+d/cIby6irZuVnS42NMlEqc/8kKzulnGR8f4zWPpqc+\ne16/NeQSE3BdWK3tepvL5chH8QaRjpRT2cbqnc18mm2W4erBp+K3vO0Yr/70PKe++z1mZqe59Y5b\nGraBHMehUCpwbuUc5bWL61ukZdcDN5oMFwTX8wxCdiuIl/K49fZbuPX2W+JeSiS8dIrlm9/E84+f\nZu3CKhN7FhlZmG54XrOAK5VNxz5CJFJuqmGmItD37cR6o+PN2770vIYLmn/o7EF7jCPXHyZfyHPa\nPs3UzCTXH7uu69es8nI5int311xzUx6Lhw+wePgAT6df5xtfO9n0NRRwbU5i7/oTk+PDfdMaNOks\n5Ux+fcxP2U01nCRppuw1jgVZ18UJxapiqcAd77mtjecVOXf2nH8Splz2T91Vfs4y3WS4mgVcASfa\nnJh/OUm43FiJpRve0PQ5zYqzvWGt36ry0hA4KSLugKtFhiuCLcWy64Xf13oQcDmOwxVXHeKKuq38\nfthjLlPA1WOJDbjq628kfuXiJOXsa37xeyq7uW3AJkFVP082lUpFXoCaQKsqqA6sXU0zXAEF1oOa\n4RJfqwzXMCt7qcAgo5/v4yDFYgHP87h4MbiIPZKi+YgzXHFa3rMrsGh/oyhOKA6zxBaRTEx3Xxgo\nPeY4kM5BJr/5mqumW4r9Cz6afcrtZkvRy6ZxA7rJA2QCfjm7CT+hKM2lm5xSHNaWEOvCAquYAy7H\ncRhpMmcwki3FJr242mr4nGD5fI7tS4uhj3uex9T0ZOjj0ii5Adfk8B0J3dJcN7TLe1+bJYYUnDo4\npLvIOjmOE5rlSgdcdxMyTFU646Y8vJDAKuz60Ah4v/ZrpE8r9b33NlKGa/N2770s9LGpmSmdUNyk\nxAZckwq4hk9AJqvtXl49UgyZe5jNZbuuGQyr48rNTNU0OXVcl0wUvWukr8LquIZ9SxHXpZypyxZl\nC30b6dNMs7E3kbSFcBwCxy/AUARce/Yuhz42O6f6rc1KbM5zYkpbikPHS8Pq63XX+jd7DcI/5Xaz\nnbj+GmEZrmKO/PbLee2552GtTGZ+BreLejFJhnQhx/kfrzRcH/qieaBcmPA/KF1c9Q+g5Luf79cL\nzTJckbSFqHSbd9ZWGx8bgoBr564dpNNpLlxobOkzt00B12YlN+BShmvolN2AYts+1m8BoT2juunB\nVRWW4Urls7jpNPmdgz/gWS4JK5wf+gwX+FmuYvI+FI+OBQdcnud1dQq5KdeDuoCr296CSeGlPJZ3\nL3HqyacaHlPB/OYl8ieiWCxE9+aQ+GQaf0GV0/3ttVYIKZztSYYrpPlpswJrGVyhW4rDXsOVYGGt\nIQrFxvFMPRMUWA1Bdqtqj9kdeF0tITYvkQHXuLJbw8lLs1aYqNRtOZRzI/6pxz7qd4bLy6aHt+v4\nFheW4doKW4pJFZbhiqRgvioouBqigGt3QB2X53lMqpPApiUy4OrFrChJqFyR8sQCaxOLlAtjfS+0\nDRuLkelBTVUqm2Fke+2nvvHlbV2/riRT6JZibgtsKSZUWA1XJC0hKspDHnDNbZtl2+J8zbX9Bw2e\nNzz/xn5JZMClyFmiki/kcQNOReZ6sKUIsP3ay5nYvUB+apSp/UvMv3F4BjtLrcAtRdfByyjgisvI\nSMkfGF8nkoL5qoAsfbnPmfsoOY7DiTuOs21hHgeHpeWdvPWWt8S9rIGUyKJ5FcxLVBzHoVAscPbs\n2ZrrvaoZTOUybD9ysCevJcmWLuZxMynWXr9UMJ0dibBWSFryUh6lkSIrK7Xv70haQqz/pWnWCuO4\nr74C5XIspRJR27Y4z933/AaAfr67kMgMlwIuiVLQtmIvarhka3E9l2mzs+ba9P6lmFYjVUF1XJHW\ncAHkSqxNLMZWKtEPjuMo2OpSRxkuY4wHfA7YDXjAPdbar9c9593AB4CLwF9Ya+9v9/XHJzVHUaJT\nLDU2P+3FKUXZemYP7SY/Ocr5V85RmBmjNKdRJ3EbHRvhzA9rr0VZw1VDAYk00WmG607grLX2euB9\nwB9ufNAYUwA+ChwDfhb4kDGmrbSVg6MMl0QqKMOlNiTSCcdxGN0xy+zBZQVbCTG3MNdwTV3RJQk6\nDbj+CvjtytcvAvV3mmuA/7LWnrXWngf+A3hzOy88MjZCSoN9JUKLOxYartWfwhGRwXT1kSvJ5S7V\nUM1vmwtsbSDSbx1FNtbai/hbhQAfBP667inz+IFY1YtAW+fjld2SqF1x+A2cfOy/efmllwHYu28P\nS8s7Yl6ViPTC+MQYH7j3t/j2ycdJZ9Jcde2VamEgidAy4DLGvBd/27CMP6WzDHzMWvsVY8zdwBXA\nO1q8TNsb2wq4JGqlUpH3f/gu7HdOkclk2Lt/j4pBRYbI6NgIN958NO5liNRwyuVyR3+wEoidAI5b\nay/UPXYjcJe19lcq398PPGCtfajL9YqIiIgMnI4CLmPMZcDfADdUarTqH88BTwBXAWvAN4GrrbUr\n3S1XREREZPB0Wp3+XvxC+YeMMdVtxp8Hfgd4xFr7DWPMvcDD+AHX7yvYEhERka2q4y1FEREREWlP\nIjvNi4iIiAwTBVwiIiIiEVPAJSIiIhKxRLR0N8Z8GrgWv8D+g9bab8a8JGmTMeaTwFH8mZp/YK39\nYsxLkk2qnCr+H+Dj1tovxL0eaV9lZu2HgQvAfdbaf4p5SdIGY0wR+AIwAWTw33sPx7sqacUYcxD4\nB+DT1to/M8Zsx5+84wLPAXfWt8naKPYMlzHmBmCPtfY6/Aarn4l5SdImY8xNwIHK/7tfBP4o3hVJ\nhz4KvBz3ImRzjDGTwH3AdcDbgePxrkg24T3Ak9baY8C7gD+OdznSSmVG9GeAr264/HHgT6y1NwKn\ngV9v9hqxB1zAz+FHjFhrnwTGjTGleJckbXoU/2YB8BOgUGkTIgPCGGOAfcCX4l6LbNrNwFestT+1\n1j5vrf3NuBckbXsJmKp8PUntKDxJpvP4iYXnNly7CXiw8vWD+O/JUEkIuOrnLr5UuSYJZ60tW2tf\nrXz7PuAha636jAyWT+EPolegPHh2AUVjzD8aYx41xhyLe0HSHmvt3wJLxpjvAY8A98S7ImnFWrtm\nrX2t7nJxwxbiC7SYGZ2EgKuebvwDxhhzHPg14P1xr0XaZ4y5E/i6tfaZyiW99waLg58deSf+++8v\n412OtKtSe/eMtfZn8Hd5/jTmJUn3Wt4/kxBwPUttRmuB2pSdJJgx5heA3wXeqmkCA+eXgOPGmMfw\nM5QfUZZkoDyPHzCXrbVPAyvGmOm4FyVteTPwzwDW2ieABZVjDKQVY0y28vUifjwTKgkB18PAbQDG\nmCuBM9bac/EuSdphjBkFPgm83Vr7Stzrkc2x1t5urb3GWnsE+CzwCWvtv8S9Lmnbw8AxY4xjjJnC\n3954Ke5FSVuewj+ZjzFmCVhROcZA+ipwovL1CeDLzZ4ce1sIa+1jxphvGWO+BlwE7o57TdK2X8Yv\n/Py7DTM1f9Va+8N4lyUy/Ky1zxpjHgD+E/+9py39wfHnwP3GmEfwW+rcFe9ypJVKQuhTwBJwwRhz\nG/Bu4PPGmLuAZ4DPN3sNzVIUERERiVgSthRFREREhpoCLhEREZGIKeASERERiZgCLhEREZGIKeAS\nERERiZgCLhEREZGIKeASERERiZgCLhEZasaY3zPG7Ix7HSKytSngEpGhZYzZBXwC2BXvSkRkq1PA\nJSLD7DD+2BsRkVhptI+IDCVjzL8CN+IHXNVZn8vW2h/EujAR2ZKU4RKRYXUf8PeVrz8GvAt4Ib7l\niMhWlop7ASIiUbDW/rsx5ljl20ettf8W64JEZEtThktEREQkYgq4RERERCKmgEtEREQkYgq4RERE\nRCKmgEtEREQkYgq4RGSYXaz8NxfrKkRky1PAJSLD7Pv4TU8/Yoz5kDFmb9wLEpGtSQGXiAyzB4AH\ngTcB9wLT8S5HRLYqjfYRERERiZgyXCIiIiIRU8AlIiIiEjEFXCIiIiIRU8AlIiIiEjEFXCIiIiIR\nU8AlIiIiEjEFXCIiIiIRU8AlIiIiEjEFXCIiIiIRU8AlIiIiErH/B8DOHMOV9Hg5AAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75d0c1fd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"with sns.cubehelix_palette(5):\n",
" for i in xrange(5):\n",
" path = EM(xinit[i],sigma=1,T=10)\n",
" pl.plot(t,path,alpha=0.7,linewidth=5)\n",
"\n",
"pl.title('Trajectories of the Langevin SDE, $\\sigma=1$',fontsize=20)\n",
"pl.xlabel('t',fontsize=20)\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With $\\sigma=1$, the trajectories can now move freely between the equilibrium points. We can still see some kind of attraction though to the area around them."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"Let us attempt to set $\\sigma$ to a larger number and see what happens."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff758d2d250>"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlQAAAFkCAYAAADmCqUZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXecJFd173/VPR0m57izQdJKV9IqrBKSsFBAAhFFkAi2\nAWGC4dkGG4f3wDaY9Ai2AYP9sI0wCBQASSCUVmElrcIq7mpzqtkws5PzdI5Vdd8fVT1TXfdW6J6s\nvd/PR5/VVFdV3wp977nn/M65EqUUAoFAIBAIBILy8S13AwQCgUAgEAhWO8KgEggEAoFAIJgnwqAS\nCAQCgUAgmCfCoBIIBAKBQCCYJ8KgEggEAoFAIJgnwqASCAQCgUAgmCfCoBIIBAKBQCCYJ8KgEggE\nAoFAIJgnwqASrAgIIT8nhKiEkHXL3ZZyWG3tJ4TcSggZIYTkCCF/W+KxtxNCNEJI22K1T8Cy2t4x\ngeBUo2K5GyBYORBC/gnAP3nc/RlZlt+8gF//7wAeAjC+gOdkIIT8A4A7ZFnuX+BTL0n7FwJCSCOA\n/wIwBeBPAexy2d96z6jx35JACLkVwM8BfFGW5X9equ9dgSzKO0YI8QH4EwAfBrARQAf05zsI4AUA\n35Nl+YBp/8LzMJMDMA1gH4BHANwuy3Kc8128Y3lQAI2yLMdKvqAVBiGkCsBLsixfuNxtESwuwqAS\nmPkNgP2WbV8HcA6ATwGImrZPLOQXy7K8Cy4D+3whhGwA8A0AzwNYUINqKdq/gJwFIATgTlmWb3fa\ncTHvWYmc8mtkLcY7RgiRANwP4N0AngTwfQBjABoAXA7gjwB8mBDyNlmWn7UcfieA3xv/HwSwBsD1\nAP4NwJcIIX8sy/I2m682H2tHssTLWXEQQi4F8J8AzlvutggWH2FQCWaRZfkIgCPmbYSQz0E3qB6R\nZXnFe19ceAPEwAwAlca/KQ/7rpR7Ji13A16nvA26MXWPLMsftnz2E0LI3QCeAPBtAG+0fH5AluXf\nWbZ9jxByGYAHADxECLlKluU9nO/lHfu6gRByNoB/he5NVJa5OYIlQhhUgnlBCLkdwMcAXADgXwBc\nBeCDsiw/anSs/wfA1QDqAYwAeAXAl2VZ7rE5z4ZCaIkQ0gw9BPluAF0AYtBDEN+SZflVy/Ft0D0p\nbwfQDj1c8d8AfiDLcp4Qsg3ANdCNg2cIIRTAaabv6gLwVQA3Qg95xI22fluW5e1u1wvgQ9b2l3IN\nhJAKAJ8D8FEAp0H/bfYDuNfYN+f0HLxeg+U+fJUQ8lUAX5Vl+euc83HvmWkXiRDyJQCfhu6dGALw\n77Is/8ByHs/PcSHw+t6ZnuVaAB8xrqMbwCSAXwD4R1mWqWn/t0L32J4P/d7eY3xPD4C8LMunl3rd\nhJDnoRsqa2RZHrUcvwbAAIDnZFm+1vobKbX9NpwP/fk+xvtQluWnCCHvQwneSVmWdxBCbgGwHcAP\nob9DpxTG5PRdgK59gz4xEbzOEaJ0wXwp6Gm+Bd2I+RSAg4SQCwE8A+BS47NbAfwUwA0AXjYGC955\nAACEkAYAL0MfKH4F4BPQDZgLATxHCLnWtG8jgJ0A3gddZ/IJAE8D+A6Au4zdvgLdOAH0Qe4DMLQo\nhJB2ADughzfuMa7huwAIgKeNgdTuej8J4KC1/aVeg9Hu7wE4BOCvAHwW+uD7ZQB3w4USruErxvVL\nxn63GP/ysN6zW1Ac6v0G9BDPtwH8BQANwL8SQq4v8x7MmxLfO/OzfD/0cNfnoIe8vmRcU+G8VwB4\nGMAGAP8XwD8COBP6vavhtMPrdRee7fs5l/MBo313WNpbcvsdGIH+LtxMCAnydpBl+UEbL5Mtsiy/\nCOA5AFcRQtaXcqxAsFoRHirBQiABCMiy/OnCBkLIm6B7Bb5i8fCMQxdE3wp9ILDjK9AHrytlWd5p\nOv4O6EbHDwBcZGz+MnQPybWyLD9vbLvLEIN+mBByuSzLzxNCCiL6Z2VZfs70XV+F7tH5Q1mWZ40L\nQsivAcjGd21yud75XsMfQg+DfMR0/F2EkGMA3kAIqZRlOc37klKuwbgPhYnUIaewi909M65Vgu5V\nucH0XfsAvARd3PxUGfdgITgPpb13knHM5bIsK8a+jwPoBXAzdEMXAP4egB+697Xw7vyUEPIYdC/Y\njKUdXq/7XuhenJsB/Nhyjg8AyAK4z+F6vbbfjt8B+BqAdwDYTwj5BfRn91rhfPNgG4A3AbgCwEnL\nZ2FCSL3DsRlZlrPlfjEh5HzoBv91AGotH1MA75Nl+cFyzy8Q8BAGlWAhoAB+a94gy/JdmPMOgRBS\nA31AKnSsG1zO+UEAhwEctXS8aegz33cRQuplWY5CD7cNmoypAn8LXSDbA2feC31AvNe8UZblAULI\nkwDeSQg5TZblXuMj5noX4BoUAGsIIetlWZ4dfErIaiv1GuYLBfAjy7Z9xr9dpm2l3IN5U8Z7R6GH\nKWeNByOcNg6g07TftQBGLIY4APwzgLeCxet1TxrP5wZCSIssy5NGu9dAN0R+53JvvLafiyzLSULI\nG6EbXu+DboR8E0CaEPISgAcB/KLM51PwfvHKa/wT9EkADwrdyGPC0F4ghLwD+u/gdugG9JnGuX4O\n3TjNA3iRc9z/ALgY3jSDkrHfX3HeCcEpijCoBAsFM1ATQv4Muq6DAAibPqJwePcIIXXQB+VOsDP/\nwvEAsI4QMmjsZ81AgizLI9A7dVuMwa4dwAs2ehMZwDuhZ8aZr9HRMCnlGqBnVn4NuvF3hBDyKPSM\nq8dlWT7u9D3zvIb5UtQ2WZbThveq0mhXqfdgQSjjvTvB2ZYBEDDO1wQ9rLebs9/LnO8v9bp/BV0c\n/l7o4UlA904BejacG47td8PQbn3A0OC9C8AfQNefXQfgzQC+Rgj5oCzLW72cz0QA+rXyPF23wTmU\n3VfidwEACCFnQs9W/ktZln9q2n4ugLNlWX7a7lhZlj9ZzncKBAWEQSVYKIpqzhBCvgHgH6CHN/4a\n+uCbBXAu2NCGlYKLfi+Av4R9hlefaV9X0bYNBf2LXYp2IcxWbdnO1NixUMo1QJblfyeEHDL2vRHA\ne6CLvl8A8L/MdYA4lHsN88Xtnpd0DxaCMt+7jMtpq4x/maxIWZZThBDVsrnU674fegLFzSg2qCIA\ntri0DXBvvydkWR4G8BPjPxDdOv5TAF8AcDchZGOJnqpCAsMw57MTi+TZ+Tb00PlPLdvHoZeBEAgW\nDWFQCRYcQogfwOehF/p7kyzLM6bPwrYHzlEwVoKcMJ71uzLQZ8ENZTY3YfzLCIsNCkaImwFlxfM1\nFJBl+SkATxFCQtAzo/4IetbfU4SQMx2KHC7WNcyXku/BfFiA986OgpaHOQchpBJ6SNFMSdcty3KC\nEPIwgJsMb2MN9HDfT2RZzpff7Pkhy7IM4G8IIa0A/hi6QfJECad4G/Tf5qI/e2DWU3sTdGG+lbOw\nvHXUBKcAIstPsBi0QJ+l7zUPagauKdSG4TAE4ExCSIv1cyMdvbBvHnpY70yj9IB5v7VEX2LlHIfv\nihrHn0P0IodWzjX+PezW7nKvgXNsVpblJ2RZ/jj0MGALHO7bYl3DfJnPPSiTeb13DkxCN6p42WpX\nWjeUed13Qw+RvRN6NiXgLdxXNoSQICHkq4SQ77nsWggTVznuVXzu90F/734ny/J0uW0sEQLduN1h\naUsV9NClY90rQshPCCE7CCGvevivsN+bFu9yBKsNYVAJFoMpACp0jcgsRubNH0OftVZyjjNzD/QB\n5vOWczQC2EsIecS0+QHomVa3oJgvAvgZgMIAVgjNWD0N90L3cBUVNjT0GNcB2CHL8qBLe8u+BkLI\nxYQQmRDyKc45Ct4Ot4ynxboGu3vmlVKe43xZiPeOwdClvQJgPdErXxfOKwH43zaHlXrdW6DXqXoH\ndC3VSVmWXyi1raVg1DZ7F4C/IoT8IW8fotd3+2PoYUVPnibDyPgpdE/h/5lvOwkhFUTHWmrFSsGI\nTli2/xn0sOPtTgfLsvynsixfJsvyGzz8V9hvSbxvgtWBCPkJFhxZlhVCyO8A3EIIuRPAo9Bd7p+F\n3jlvAXA90df1ekCW5QjnNN+EriP6e0JIB3TReQeAzwBohe65KfB16K7+2wzdxzHootpPAbjPlD7f\nC13P8o+EkE3Qq7/3QM9seq9x/IXQ60qtM9qbh7d6Pjy8XsNe6Dqn/zC+fyd0Ie9m47sPQE9Bd2Kx\nrsF6z7xoesyU8hzdOJ8QcrPNZ3tkWT5ewntXasr8v0J/p+4nhPwI+uB9C/SaTzxjt6TrlmU5Z7T9\nPQDqoNcQWwpuBbAVwB3GfXkYeq2xWugepj8C0ATg07IsT1mONT8PCXpixFugFzIdBfB+h6xSp2dZ\nYI+RlLEGunf1MegGJxdZlo8SQl6EXhutBwAIIddAN6jeIXsojrtIFJI03EqfCFY5wqASeKGcpUc+\nC31W+1boYYzXALxXluWXCCFfA/B30AeN56GLb4uQZXmGEHI59Ho+74ZeEToJvc7RJ8w1hmRZHjP2\n/QZ0EW0z9JDLF6EXOyxwH/R09hughwdeAdAjy/KUcfzXoQ8g7UabngHwDRdBuJmi++T1GmRZVo1Z\n/T9AN4puhe7dOAk9nf1bblqaMq7B6wLHvHvmRNF5S3mOHs77R8Z/PL4AvYzD/4L3987Ldxau42FC\nyMegF8z8OvQQ613QU/8/hDlPXmH/cq77VwA+bnzvXZzPi9pUSvvtkGX5ICHkPOi6o7dDv7Ya6EZi\nP/Qw2Y9t3h/r84hBX7rqH4xj7DR/bs+yQOGZFo7R3K4HeoHTHxlZfQHoE5PLZVle0LVH3TB0Z3dA\nNwYLIfc+QsgBAD+VZflXS9kewdIgUVr6WGkIMW+H3mmHAHxTluWFdN0LTjGIvjzDx2BaDkYgWOkQ\nvc5VDMArsiwzeirBwkAI+ST0wr0fXe62CAR2lKuhejd0Tca10Gdn33feXSBwpZCh5mXBXoFgSSGE\nfJAQ8jgh5CrLRx8z/hVamsXlRljE5gLBSqOskJ9sWtoCuk5jYGGaIzjVMDRP10IP0QwXKkULBCsM\nGXrBy3sJIT+E3uddBF2bNoHStGCCEjDKiOyDXulcIFixzEtDRfSig2tgrKotEJTB9QD+A7rm6TPL\n3BaBgIssy3sNnduXoeuNWqBnFd4L4J+MopiCRUDW1/T75nK3QyBwoywNlRkjo+iXsixfuDBNEggE\nAoFAIFhdlCtKvxjAeKGuDSHkIIBrnMI1lFIqSXYrMAgEAoFAIBAsDemxYaTHih3LoeZWVK8pqt9b\nktFSbsjvauhVg79ACGkHUO2mfZEkCRMTS73yhWAhaG2tFc9uFSOe3+pGPL/Vi3h2KxcpnmKy8tKp\nHFKm59XaWotSKDfL778AtBFCngPwEPTCaQKBQCAQCAQrH826pjkA6qXUmT3lZvlloFceFggEAoFA\nIFhVSByDSgItq4p1AbGWn0AgEAgEglMLrodqfkl6wqASCAQCgUBwaqEp7DZhUAkEAoFAIBB4hNJF\n0VAJg0ogEAgEAsGpA9X49RCEh0ogEAgEAoHAIzzvFADMS5IuDCqBQCAQCASnEnYGlfBQCQQCgUAg\nEHhEGFQCgUAgEAgE80PiZfgBQpQuEAgEAoFA4BnhoRIIBAKBQCCYJ06i9HkYVcKgEggEAoFAcOpg\nY1BxSymUgDCoBAKBQCAQnDLw1vGbZR46qrIWRxYIBCsPSim2PfEcjhzswZnkDNzwjusgSfOdcwkE\nAsHrDEeDqvyQnzCoBILXCXf/7B787D/vmP174OQQPvFnH13GFgkELEoiCWUmAn91FQJNjcvdHMGp\niF2WH4D5FPcUIT+B4HUApRS/v+fhom0P/+5RaNr80oAFgoUkOzaO6aefR2znHsw8+yKSPceXu0mC\nU5FF8lAJg0ogeB2QTCQxPTVTtC0aiSGTzixTiwQCltTRXkCdG8xSPcdBVYfBTSBYaKgGyclomoeG\nShhUAsHrAKsxVSCVSi9xSwQCe9RYvOhvms9Dy2SXqTWCUxIn7xQgPFQCwanO1CTfoEqnhIdKsHKg\nnMGMKk56FoFggREGlUAgcGJ6cpq7PZ0WHirByoFq7GAlDCrBkuIaYhYGlUCwrFBVRX4mAnWZQmxT\ndgZVUhhUghUEJ0lCU4SGSrB02K7jV0CUTRAIlg8lkUT0pR1QE0lAklBzwSZUnb5+SdswbRfyE6J0\nwQqBUv6yHsJDJVhSXEJ+EtXK9lEJD5VAME9SR4/rxhQAUIrkwcNLPkjYhfxSydSStkMgsMWmhIfI\n8hMsKUJDJRCsXPIWY4YqKhRLNtNiYytKFx4qwQqB2hlUwkMlWEqEQSUQrFy0LJv2reVXhocqI7L8\nBCsFW4NKeKgES4fjOn4AhChdIFgmqKqCcoynpZ5123moUikR8hOsDKgqPFSCFYCrh0osjiwQLAs8\n7xSgFyxcKrKZLJIFDZcFUYdKsFyMjY7j9795GH6/D+/78E2oD4e4+wkPlWBJed1l+akKpNg4JFUB\nDVeDVjcBkrQsTREI5oNdleelnHXbeacAIC0qpQuWgZnpCD75wT+fff+2/P4J/OyX3+fuS1XhoRIs\nIa8rDZWqwDd1Er5MHFI+DV98ElLSfkAQCFYytgbVEmqo7PRTgDCoBMvDYw8+WfTuRSMxPP/sK9x9\nhYdKsGRQCsk1pLdaDCpK4YsMQ7LMSKR0bEmbIRAsFHYhv6UUpdsV9QRElp9geeg91stsGx0e4+4r\nNFSCJcNVkI7VsziyFBuHlOPMmNWl05sIBAvJSgj52RX1BICUqJQuWAaGh0aZbfF4gruv8FAJlgxP\nBtUq8FBlpyfhS0W4n0lU83ahAsEKw1aUvpQaqiknD5UwqARLz8gga1Al4/yMU6GhEiwZi2xQzUuU\nTgj5ZwBXAfAD+I4sy/fb7ZscOul8MlUBfP75NGdpoFQI6O2gGqTEFKRMAvBVQKtrAwL8zJ7XCytD\nQ2XvoSqnDlVsYBzx0SnUr21DTUfzfJomOAVJJVOIzESZ7fGE8FAJlhfXdfwASJSWraIq26AihFwL\n4FxZlt9ICGkCsBuArUHlavVpCoAVPPjms/BFxwAlAwSroNV3AH5RdcKMlIzAlyh4S3LwzQxDa90A\nTVWRPtYLNZlCsL0V4e6uZW3nQqLaaqiWLoztJEpPlSBKV/MKeh7cjrG9xwEAkk/COR+4Dm2bTpt3\nGwWnDsMc7xQAJBM2HiqhoZo/haKpkiQm/E54ioQtj4fqWQCFtI0IgCpCiCTLclmtkVRlHpexyFAK\nX2QEkmIMntkkpPgEaEPn8rZrhWFNLpDUHJDPILZzP3JjEwCATP8gqKKgcsO65WjigrMSNFSOonSP\nHqpcIo0Dv3oSsYHx2W1Uo+h/ft+qMKiO95zAsZ5enHHmadhITl/u5pzSjHD0UwCQsFlXUnio5oeU\nnIEUn4BEKbRwLWhDByCJmt1cFlmUXrZBZRhOhenvpwBsKdeYArCyhen59JwxZSBlEstiAI72jmDr\nLx9DMpLEuX9wHq5635vg86+QUCnnGaqx6KwxVSBzcvB1YVBRSleEhsop5Jf2UCk9MTqN/Xc9gWyU\nLQ6aGl/5JU2efHQb/vmr/wZVVeHz+fCFv/8LvOO9b13uZp2yDA+OcLcnhIdq4VFykGLjmBqLIZdT\n0NGlQQpWgVY3LHfLFp1ju3rwxC8eQyaZwcU3XIJrPngdJJ+LIbmSNVQAQAh5D4A/AeCpB6M+P2hl\nHXzW2lMrWJgopdmFbnUhvQa4PcAFRFUU/Oa7dyM+rXuCnrtnG2KTUbzzMzdBWm43r6Zx63vkp9kB\nWX2dLIdCFQWwW05jiTRUiqJw9SoF8nkF+Zz9ZGXySD8O3/cMVJt9NEWFmlfgD6zc8Pavfn4vVFXv\nKDVNwy9vuxtvu+kG+JbwtymYw86gStp4qEApqKa5D4YCBikTxxP378LLzxwBAKxZ34w//Nw7EX6d\nG1SpWBL3fe83UIx+dvvvnkNLdyvOu+oC5wNXskFFCLkRwJcA3CjLMmt1cKjbsBFUVZCwGFShCora\n1tr5NGdRoFRDZJzvjWpqCMEfCi9ZW47slGeNqQJ7nt6Fjeefhje99w8W9btbXZ6NmkkjyikzQzmz\nUppXXM+3GshGYpi0+YwqClpaahbd0B0dGXfdJ53OcO93z5O7cOB3z7lKBuqrAqhsqCm3iYsKpRR9\nJ/qLtk2MTcIvKWhpff0I6lfT72VyfIK7PZ9XkMsrCHKM86b6MCpslqZZ7SzmszsuH5o1pgBg6OQU\n9r10BO+8ZDN3/0wsiQMPvoTo0CRaNq7BeTdduaInS3a8+tqRWWOqwJGXDuC69zmPg7EY4DbV9fsl\nNJf5zOYjSq8D8M8Arpdl2X6KbCD5/FDq2hFJA8jlYQ1S5dIZTEx4ssmWlkwCfhvv2fREFAgtXaiy\n98ggd/vv/uN+VDbWYf25Gxble1tba92fTTbJPFMAyMywRVupqmJ8NAJppYQqyyTnEGoDgPGRGfgC\ngUVtw1F5wHWfZCKFbK542/jBXhz67XOevmN0cAo1+ZWpcMzZeNYOHjiBc88PLnFrFgdPv78VxMne\nIdvPkpks16CaHIvCX1W5mM1aFhb12VGKY/vYAqonj47Yfuf+u7ZiStYnINN9o0glM9j49isWp32L\nyMljw8y23oMnMT4WdfR0+rJZuE1xVUWZvX+lGsPz8bF+CEAzgHsIIdsIIU8TQrrtdm7YtBmoNBrn\n5wwyKzTk51TF3UsK5kIyPTLF3a6pGn77/XsQneTX+VoKJI5+ilIKJcHPMtMcwlCrBTv9VIGl0IY4\n6acK8Ip7ju0+6vk7lJTzdS4nduFMu6rcgsVFURSMjdp7TZMrIInjdYOSRWSKNZzSyQxXWJ2JJmeN\nqQJj+08sWvMWk5kxNhEnm8pgctguZmCwUkN+sizfBuA2r/sXhT58flCgyFJcDk2SK5oGKcuvnQJg\nyY3AmVGH9PhYEvf+y69x69c/gUCovJl577E+PPPkdtTV1+Ld7387gqWch3MvlHQOVOO/nDSfBypL\nCJdmU/DFxgFNAQ3Xgta1Lnsmi5ZxzqCjeQXgTLpPHOvD/b9+ED6fDx/4yPvQvW5N2W1wyvArkEql\nUddYvC3BEZs3ndkNNa8g2lecpZVPr1yDKpfLcbePjfDDToLFZXx0ApqNrhAAUlZXqYHI9CsdKZdG\nZJodn9LJnN4fVxT33/Eh9jeRT6RXvEaSR2SMP5Ec7BlAa3cb/yBKV65BNS8kCfBVGLWnTGgK4Fs5\nbnopm4DkdHNL9FDl01n0bduNbDSBpjO70XkJKUljM82xys2M9o7g4f96EO/9/M0la3cO7T+Cv/7T\nLyJvxKWfe+oF/Ntt3/V+Ho6HKp+0H4g1m4GQv7OqrwFp/BikVASaPwBa0+T9HIuAXcmEAjxh+tjo\nOP7i1r9B1vBuPf34s7jzgZ+ivqG+rDY41aAqYK3/o2TzyEYsHbEEbPrQm9Hz8Iuwxu+VTAnPaomx\n81CNjQgP1XJgJ0gvYOuhWqERipWMlE1hZpJjUKWyen9sMahig3zPYS6RRmXj6tHoAcCMjUE11DOI\ni958Cf8gqjHhPqtjR9+4CpaeYeAVxVxhpRNcF20usRM4+OunMPTyQUwePomeB1/A0KuHPR+raZqt\nVV70HS/sx8sPvVBSuwDgod8+OmtMAcCBPYdw+IDs+XheyM/JoKIlhPykTHzWmJrdtgIW1HYL+Wmc\nMMbvf/PwrDEF6OG4Lb/f6niefDaHbDoLyvmhT3kI+aUtxT1TnNBwuKEW/mAAgUpWGJxfySE/mwKq\nYx7E+oKFh7fkjBn7kJ/wUJUEpUAujZlpTqmTZA5Q2ElQfJAfDsvZLAm0Usmms0jF2OsGgEEnTSnP\nO8WxQyTQso2qZTOoKEdHJa2kWYqmAln+QytQioYqNRVFpLd49ja255jn42NTMaiWTqciGOC6ap/5\n9dNIWD0QLgz0sYL3Y3IJ8XXOs8snnDxUJRhUnLIVULLzKsC2ELh6qDgG1a5X9jDbDu49ZHuOA9v3\n4Yef/T7+5dZv4dffvhNpi7dpZsrdoLJ6qFLjrEFV3aqnWVdwDCplBYf8bDVUwqBaFniLIptJ2Xg7\nhYaqRJQcssk0Min2fmqqhpxFN0k1DXEbfVF2lRlUTo6FyaEJpG10u9yIkq8ClCtTX2UGFddDVYKB\nQilFdngUqRN9UEtYXsMrUibumg1QiocqydGsZG2sbB48/VTbuja88zM3cZqlomfnEWa7E9OcgXmw\n3z5bpwhKmXtBKXX0bFCvS7NoCpBjf/ASAOSXd6B3FaVbrjEaieJYD2ukHtp/hOt9SkQS2PKTh5Ax\nOsfje47h1S2vFO3jVUNlJjnBPuuqNnuDamVrqPjv0fjIOPeeChYXt5BfQnioFgQpl8IMRz9VIB0v\n/iw5EbGtNbfaPFQzLsWGh4/xs+G5Hiqfn79Uz2rzUMHHC/l5N1BiO/cg+sprSOw9iKknn0E+urAh\nIE8hJU3xfOPTk+z5Spn58zL8GjuacMHVF+LCay9iPnMSsFuhlNoYVGxqKhdN1d2kJpR0DrARpAPe\nNVRSJmFr2Eq5hTekS6FUDdXuHfu4+0UjMQwNsPf62K4e5Cwz+hN7i72angwqy2w1yfNQtemqdV7I\nbzV6qDKZLKKR5Q8Ln2q4GVQpkeW3MOTSiEzZT8gzlsl6fNA+SWOpDSqqKMgMjSC2ez+iO3cj65AV\nysNtbBvs4Yf9rLIRQC80zjOoohMR7Hz81ZLaBSyXKB3gxy7VvCdHW346guygaQBSNSQP96DhiksX\npm1qHvAwWEuU6mEnyb2eUmqKLdVVShVq3kvU1KGLstedux57n9ntur8dyUSSOzAN9Q8jORHBgV88\nisjwFOrXt4PcdBWCNZbUNZ5+yiHcB3j3UHHDfbNf4m2dusVAX3bG2Si0aqh2vcqG+woc2neEyfbr\n5aQ0RyfmjKF8NuepbIK1QnVqgjWoqhxCfivaQ+XwHo2NjKOhsTyxv6B0KKUYGXJOBrAXpQsPlWco\nhZRLY2bK3kNl1RjFHAyqpQj5adkcsqNjyA6PITc+MbeYM4DswDDqr7gUoc52T+eKuHiobHVUHjxU\nlFK8tO3yVw1EAAAgAElEQVQInnxoD6hG8faPXO+pTbOnK2nvBYSnofLqocoOs3H63PhEyT/KfDaH\nlx96Ac/e8zSmR+c8QFKaDfdRf2BebU5zDCrA++x/mmMgNXbolaAb29lsN7ssCO65bXQ4I0OjOHT/\nc5g8PgwlncXUkX6c2LqD3ZGnn3IQpAMeNVQ24b4CkmFQLUdoh+byrt5Jq4dq16t7bfc9uK84QYFq\nGtegSkQSUPIKNEXFjtu3QNPcdWRpk4dKzeWRibBGakFDtdo8VDkHo1bUolpaIjNRJgHCivBQLQBq\nHpKmcEsmFMgkUkX9k5NBlYstnkGl5fKI7dyDyS1bEd+1D7nRsSJjqkC6r59zNB9eDSozQ8eG+P2i\nnUFlmEGZVA73/M/z2PrAbttyP26sKA+VVw1VdoQjfFQ15CanEWpv9XQOqmm4/cv/gzGj5s7LD72I\nT3zrT9G6to0b7qOVdZCyKdYboykA3JdMSE3xww9KJodQXbXr8byXqOChamxvZD6bGZsGpdRT2QM7\nL4eqqhiQe9FUPbfsyOQR9sXnZ/g5e4+8GFRO4T4AgJLDL//7Tjxw36Ooa6jDJ//8Y7jq2itdz7sQ\nuOmngOJBYnhwFCMOgt1D+4s1b+MD47aZLNGJCIaf3oWBw96SBswaqtRklNFbhhtq4A/qk4VVJ0p3\n8VAJlg63cB/gpKESBpVXClIHXsmEAulkVjcg/BVQc3muhrdA1mbR6oUgeegIMgPuWlzVbp1HDm7O\nglw6i8nBCbSts3i8HDxUo4MzuOfnzzveUy8sn0Hlq2CLe2qqEUKzd5wp8QTUBH+gyY1N2BtU2SSk\nbBJQFUhUxfGDA7PGFADks3nsefBJ3Pj+S/ia/8o6fWVvS/8tqYprmFLJ5JC3yTzwEk6hmuYY8qtp\nrEVFMADFZKTkMjmkYklU17uvwTY5zq/ADgBTyUSRQaWks9BUDT6/6RnxBOlJ53AYzbtrqBzDfQCe\ne3E/fnHbrwHos+Nvfum7+H+/+D7OOOt013OXi6Io2LfrAPoPH0P6WC+o6en7JAlnrmlHd2sTJEkq\nCmvu3mEf7gOA3mMnkUykUF1TBQDoc6hg3PvSASR6BpDIegt5JuJzvxdex1rVNmeQc8smrGSDysEw\nFwbV0jLsUjIBcMryWxkhv3wqi6FXD4GqGjovJQh76D+XHMNrH+GUTCiQSmX1ftlfoWf3OXjTF0tD\nRTXNkzEFuBdJnt1PVYtkD3YM9gwwBhVfQ1WBPS8exZbfvAhVmX/W+PIZVJKkW4emi8zF0oj37YQk\n+VB15ukINLOhrKxDwb7c2DiAc9mvSk7DFyt2eY73s53txGiUb0wFwnqRNJ6Q3oNXjaefKuBl9h+f\niTMLQYaqwqis1QdfSZLQ2N6IiYHia5oenfZkUA2csMmKADCdZC12JZNDsHquyrnVQ6Wkcq7hMFcP\nleoc7gOAhx9/qejvfF7BXT+7B1/5zhedz10mqqLii5/7iq24vMAtV1+Gm990adGs2yncB+hG6OED\nMi69Qk8w4IX7CowfH0YVwDWoAn4/8pbQd8y0oDZXkN46tzJ9RTigz3JMj0/N5lkjeoXgZFCNiuKe\nS4qTB7ZAysazuxI8VGpewc7/vB/ZqG6oDL58EBd89EbUWz0dy4yUS4Nq1NGg0qul5wGEEbOpP1VA\nSecWpVq6Eol6NpRpXgFVVEgVznrk2FTMsRJ/gcGeAVx8g0VTrbET/8fvfBo7nnjNUxu9sLw9pEmT\npKRzmDo0hNzoBLIjY4i8+CqUODuY5xw6SSWeQM+D2/Hs136O7d++EyO7egAAUpKdlfPiz4kY34tE\nw4U1CDkP24OGKj3pZFC5e2qmR/jeKXM4bz46qqE++1kE16CyGoFa8aDmpp8C3At7SlnncF82m8fe\ng6zR8dxTL3Brai0EL2/f4WpMAcB9z+3AybFJaIYRrGkadu9wNqiAubCfqig4eeik7X4xI3wc58zq\nWhsbmG2xmbn3jytIb5s7RvL5UMFZckhxyWhcLuzKJgBi+ZmlxkvIz06Urq0AUfrYvuOzxhSgTyT2\n373VcUK85Kh5SGoeiXgaSt7+nqVTWUhGvxwfcvfULoaXKjfBRj4qGurR8KYr4QuznnDVg5eKN6bx\nFkPmCtMtHqqTx8dtjalQZRC3/M2HXNtjZXkNKpPHJzVerDGiiopUz/GibVomi/y0vZEQnU5jeKcM\nqmpQ0ln0PLgdybFpbsFQXqw0HmMfKJX8erjP0t4CXop72umnAG/hFLNgvkBjR5Plb46OymOm37jD\nwDPFMaiYNlvuryeDSlFAHQTVvHAfDVbN/v/eg8eRy7H3nlKKX//iPtfvLwercNyJB1/aPTvrPnG0\nz1MK/yHj/ENHh5B3EFsnjE6f56Hq5GTKJGPOIb/qtuJ3ZzXpqJxDfmNLnrCQjSURGxiHyll26PWO\nW5V0QA/5aZxnshI8VLF+drKupLLYd8fjyNkVi1xipKxu+Mw4lEwATOv5wVmQXiAXX/jry3NKuoTX\nrkGwpQk+zjqubmVoAL6W+PQLWInH9MgUUlYj0WK09x3lG5rtXQ345Nc+irMvZ6NdbiyrQUVNwnTe\nIJwZGIKanhs0sqPOLvyZKWt1WDrrpbLCc5emk1koJhclDYShNXbNCugpd7kcDx6qeYb8eIYRY1Bx\nPVTeDCq7LD8AmE6x90lJmQZyqjGxaTdB+uyhdoOOTbhPq20BNbxyO3bZL4uzdcs2xxXvy6W/12FZ\nAwsvHTqO0THd1c4rl9DG0fod2i9D0zT07j/OfGYmbXQ8PIOqez270HKhbIKaU7gZflUtxV6t1bT8\njJMoPZVMF+nHFpuR12S8/IN7sOu2h/Dqj+7TEwBOIbx4qCiANGeysBI0VDHO4sEAkJmOY/9dW6Fy\nJnBLjiFIjziUTACAVDILSc0jG08Ved3sWOjSCVTTkJ9ix59Aq56Z7gvzDCr3cYNXJb3jtE60dLP9\n6dBRU6RC05haiRNj7O/z3M1r8ckvvBXN7ayn3wvLHPIzDBVK+V4NSpE+0Tf7p5N+SsmrSCfZznX8\nQC8zS9UouGsgAUA01Am14yyoHWdBa1kPhOa8IvzMRPeOwKlj9bLwLF+Q3lz0N8+g8rL2H9U0xDmh\n1QLRdAqKxbIv8lBZBekaX5Au+dgAnl1xT164j/oDQCCs/wdgx26+oQzo2Yn33nG/7eflcpJjUF1+\n9ul48+ZzUGOZcVFK8eBzeomJXZxw37tveTuqqovreSUTSfT3DqB3f69jO7KGq59nUJ12NjtbS6ez\noJqG1FSEyfALNdSgIlRcDoTroSp1gWQlry/d5GV193ngVDYBWLrSCfl0FscefQXU0Hdko0kcf+wV\nl6NeP2QyGWZi5vP50NDEDky80gnL7aFSsjluOLxAfGgCh+7b5uhVXwpmM/wcSiYAQDqle6icCnqa\nyS3wxEOZiTJljKRAABV1unzGzwn5eTGoeE6CxvYmdJ+1ltleVOCT0w9NjrJRgze8iSAQrFiFldKB\nWQ2VmsnPdkRW0r0noSkKqKIgN84R1xkei3iUP4POxVOIjBTfuEQiC9Um/pyIJPRz8soN2FV3d7j5\nlFKk5xvycyiZUMDqsQK8eahmxiPIchbSLPp+i5eqyKtmFaSnWUG6r8KHikpWl2NX3JMb7gvXAJIE\nGghjfDKCvn7n8MIjv38cM9Pu2SBeyWayXNHtZ951HT79zmvxrisuZD57ds9hjI6MYf+uA8xnl155\nMc7eRJjte1/bXzyz4rUlr4BSigRH4LuBY1DlFAWpqZirIL1AoGp+mX5Scga+iRPwTw/CN9HrqUhu\nuTh5qAA97LcURE+OMkt7TB8bXNEZkgsJL9zX2t6CRk5hVV7phOX2UCWGp1yXb5s60o+jW15eviWN\nVAWSqvfVkUm3kF8WUPP8cB9naFtoD1VukpWpBFrmdL9cD5WXaA3HSdDQ3sg3qGR7g0pTNUyOs+Ny\na4ch7ylzndgVEfJz0tzQvILMyQHdmLLMDqRgEKE1nQCAWMTeuh07WvxSOcWfEzMOqfqSbzbkNLsJ\n1PHm5xJp2zWUAPeQH6XUU8ivvqWeEeclo0lkXc4/fHwQeZewpVWYnjcJ6a36NN6zDFSHIVWwrxo3\n088m3FdIDKCBSuzcbR/uK5DL5vDbXz3gup9XBvuHmI60ua4GlYaA+y0Xb5r9/wJ5VcW3//FfkbEM\nILX1tdh41uk494Kzme/Zuf0111kwhW5U8UTp1mrrAJBT8ogPT/IXRW5jtXfz0lCpeUix8dk+W9JU\n+GaGS1qnsxScROnA0gnToydZw41qFNMuxvHrBV7JhK7uDtTUsVnGvNIJtIRlxxaD2JBzJlyB4VcP\nY/BFdoK0JJgmJq4eqnQOVMkjxhGk13W3sadeYA0Vz6AKts5FVcoRpVNKuQaVnYdq+NjQXLKDpf+Z\nnkww2YJVNSFU1YQLX+bYFjtWhCjdTcScOtaLzDAbnw91tiPU3gpV1ZBM2HtZxk9MFt08p/izs0El\nlbwGoZuOwm0Gm5iJI58tHjSC4SCq64uLgfor/KhvZWeDbl6qE4edw0sAx6Aya6hUa4YfJ5W/JgQf\nJx2WckJ+vGKes+E+AAiEufqp6uoqZtuD9zyChE3NslI5eYIN961pmTNGqsIhvPWyC5h9DuxlhewX\nX3YhfD4fNl1wDvPZkcPHmG084tksFMusKxAMoKGxHhWWbFQKYLp/lL8oMs9DNQ8NlZRiS49ImgJf\nZLTsTsoJNw/VUpVOiJzke0wnj9hna76e4HlvO9d0oKaGLVrMrZauasu6mHV8mDW8G0/v4npzTmzd\ngfT00q8TKZkmmm4aKlC98necYyi2nLOe2baQHipdP8X2NcEWs0FVuig9k0wjmyoeX/wVftQ21aK5\nqxnh6uJz5rM5jBulhKw634lRdlxu7TCPn6vRoPLgoQIALZVGlrN4bKizHcH2ViSiWcfrz2cUTA/O\nzc6d1kCKOxlUpjYXN9DeoHISpAPuZRP4S840cSugc4Xpo846qv6j7iX/rZl+ioOGireGX6A6BB/P\nQ8UZDGkyiuceP4Cf/3ArHr7nVaST2dlwHwCokLBzz1HmuL/8u08hYKmjkkym8OC9j9hfWAmc7HM2\nqKRgEO+8+jIEeKU1LFx0mR4ePOc8NuQ3PTPDeAz9HGN0hlNZuNlwqYc5GTTTA2N8DxXHoKoIc8om\nePFQUQopxX/fpWySW75kvuSybh6qxS/uqeYUJIb5Ho7po4PQSghnaaqGoR2H0bdtNxIlrMe53PAE\n6V3dnaipZQ2qlVgtnWd4rL/2Ipxx4+XMdqpR9D69aymaVUTBoFIVFdGIuwE0PRqDavl9+EMB3VC0\nsJBlE/IzESajTgoG4Df0UwBssvycPVS8sayhrRE+nw+Sz4c1Z3Yznw8VdFRWg4ojSG9tNxlUq9JD\nJfmgST5PafYMfj+CbS3whUJIpNw7rLFjczMQp1W6EzPOlj/llU6Yh4fKrb6PU4V0K3ZL0DgxfJI1\nVK1Mp6whv7k2m4t6Uo0in2INRN2g4nmo2MHw6ftfxrYt+9B/YgKvvXAM993+wlwdMAA9R44jblkq\nIRwO4pqrLsLbbnoLc77f3v0AMh6r8Dpx8gRreJoNKl84hMamBlxzIRvGs3LJ5ZsBALV1NVh/+jrm\n82i2+P0861L2nNEU2wE2Ge2pqqpkPpsaHEOaM1kw16AqUFGuhiqbdCwjIsUnFlxP5aqhGl58gyo2\nOG679peazSPS5579VuDAXVtx9KEX0bdtF1777wcQ6XMvRbASGOZ4qLq6O/khP5tEguXSUeWSaWSs\nvw1JQm1XM9a+8Tx0vYH1JI/vO474iP0KEwsO1QBD6xqdSXlyoEwMshOo2q4WBGtZb/6CGlS8cF9L\nc5ETgC9KdxkLOSVfGkxjHl+YboTcLQbVJNdDVTf3x6o0qACoOc1WkO5EqK0Fkt8PNa8gPuP+Mkz0\nTkM1frAzk/ZeqLI8VA4GlZMgHdAHKidXt52HikeppROS0QSiUXfXtTXkZydK5wrSA374ghV8DZVl\nMIxPRfDKM8Vr2p3oGcXMzNwgvOMldmZ40fkbEYCCD370Zqaad2Qmikd/v9XmyrzDy/DrNhtUoRCk\nigq864rNjusndnS1o3NNx+zf557PGkuxzNz9blvfjq6N7IwymmENk2ZjZYGqGrbDzKQyzLMJ1Vdz\ni3iWu0Cyz8Y7VUAC4IsML2jmn1MdKgCLUj7DCk8/ZYa3/iWPxOgUpo/Naa6oqmF4h/faZ8sJz0PV\n2d2BmlrWoEravEvL5aHieaeqWxtm17c8/S2XIVDNelR6n9y56G2bJZ+bjT46RVjMzHCy2Oq62/RV\nLixZ10omt2BlIXgFPQMtxWOTFAwyiV9UUWaLIfPgaolNBtUaJ2E6E/LjCdLNHqpVKEoHgHyK7RAD\njXWoqK/j7D1HsFMflGaOD0OzrMHj80vw+YsflppXMXlSt3AjU/ZGU4JTp6f45KWF/Fyr7GrUUbTu\npWTC3PbSqqWP9o0ip7gvUpzIZpE1GT+zehpKi4xJrn6qOgRJkuDjhMKsovQdW16GyjGuzVlvr728\nm/n8sosJpFwaXd0dePNbr2E+v+fO30GdRyVmRVEw1M968qweKl+gAu2Ndbjy3DNsz3XxGy4sMrg2\ncYTp0cych2rdOevRPzKMoeg40vm5gSjB8bo1Gu2prGY9VDmO0V/dyno0gTJF6aoCZN07ekldWD2V\nm4cqHksguYiLvwJA1CXjdOpIvyd9EM/jsRpqWamqyvUEdq3pQC3PoLJbfmaZqqXzDKraNS2z/18R\nCmD9NZuZfaaPDpbkfZwPkjJ3z5yWnDET5Rhedd2tkHw+BGs4fcQC/E6oqnKLbwdbW4r+liSp5FpU\nEY6HyuxEWLNxDWOkzYxNIxlNFGmoNM0uw2+1h/xgMwjXVqPqTOcFbkMdeqbC5OE+5rPa+hBq69mH\nNXZ0AqqiIhYpP+TH81DZhfw0VUPGg3jRabDyUiXdabtTtfSx3hHuQMtth6l0wmx7NbWoWJqdfgqA\nqyg9m8rgtaf4uoQhw22bSCRx6MAR5vPLLiJ66FFT8Ycfv4X5fHx0Aq9sL382OTQwwhhk9dWVRbWn\n/IaHCgBuuvJi23MV9FMFzuUI0+PZJDRKEc+mcPcDv8dPbvsleqYGsGPwEGKGsZXIsfe6udkwqCo5\nnSVn9s8L9wF2CyQ7a/2kNCtGp74KfR1M677ZxILpqdzqUAGL66XSVA2xAedMwmwsiYSH8FB6ku0r\ncsmVUaHbicnxKSiW96u2vhY1tTWo5mio7JafWT4PFfv8ai2FIrsuPRvhBtY4PLF159KI6U0GFW+V\nDx6JKPvuFK4rxAn7ZWPzN6jyM1FAZbPx/RzDmpfp5xT249egmpsUhqrCaFvLZjAOygNFTo/IdJJZ\ntidcFUR1rbmvWq0GFSdds6ImjNCaTq5wDdDdh75QUK8lIbPu9Nr6MOob2WOn+qcxNRpzvFepWBKq\nww+bp6Gy81BlIglbbYUZu8HKrmSCnYaqgZMCH5uM2l7PaN8ocqq7hwooFqYrmZye2m+5bl4m2JxB\n5Vw2YfdTryFrk0k2eFR32+5+dS+T6trR1oTuLmP2k89gwxnrceWb3sCc48H7yhen8yqkm71TAOAL\nByEZovj17c3YfAarjQJYg2rt+jWotehMVKqhZ7Ifrw0dwdDQSNH2wxN90ChFmmNQNRlu9coq9t3n\nGVS8kglAGR4qGzE6raqH1tAFKrHPXopPeFplwA03DxWwuMU9E6NTjh7mApOH3bP9eN7sfDKzrNlv\nXuAK0o2wNs9DxSubACyPhopSihgnoaBuTbFB5avwY8P1lzD7xQbGMcVbN26BkfJmDxVrUNU2sxGd\nvOV+huqrZw0pro5qATxUfP0UP4nKX6Iw3a5kgpluwob9BuT+opAfN8Ovvb64javRQ0UphcKp0Bqo\nDkPy+VB1xmnc40LGemXR/jEolkFYkoCauhCqa4OoCBR7RTSV4uRhdxft0Sdfw84f34+9tz+KuPXH\nVoKGyi3Dr4DdYJWMJpGzdD4VwQBqGmu5+wfDQdRYZlGUUkQ42V0AMNY3iizHoKrieBUYHVUmx5RM\nULPsfSgInHkaqkJhT1VR8MojL3PbWGhnPpfn6qcuu5jM/hCknP5jvOkD72T22/HSLgxxMkW94CZI\nB+Y0VAXe88aLmGPOPPsMNFoqR/t8Pm6230h8EpRj+afyGQzFxpHhhGqbHUTpPE8kr2QCYOehytpP\nDnKpouQEQJ+z0Mp6oCIAraGDOUQCIGVcwuseyHvQfSymMJ2nn+KtCuBFR8XrL6iqlV6lfomxy/AD\nwM3y45ZNwPJ4qLLRJPKWdfokv4872Wg//3RUcxJ/Tjy5Y/ErqJs9VJxQXhcnc0+xTD5rTUbiYnmo\nuPqpVr5Ehe+h4htUSl6ZXRTeTIPFy772bLYkxMARq0HlUNDTQFqNGio1mWJmJZJPQkVIb1Z4w9qi\nQapAyNBP8cJ9NXUh+HwSJElCbT37wIaOuxdwO/rUa0iMTmPmxDD237UVijn11M5DxbFoveof7Awq\nO++Uk+i5gStMZy37XCaHqZEproeqIczOKtlaVNmiUCfVNGic6vP+oH6/MnkFE9E4NFPHU/BQHdh+\nAHGH0Kimahg5PoydL3MMqovOwvhwBJHpJKS83jFeesVFRcLvAg/99lHb73CCJ0hf02z1UIXhM5Vt\nOHtdF67bXBzO+9RffJx7fl49Kif6ZkaQyrMdz5yHylvIj1cyAdBn4z5LCQpQe60ft1RCqAqoMJa0\nCddCq2RrpC2Ehypns3yRmcUM+UU5C+p2crIyk2PT3CzLAlSzX1Ehs8BVrBcauxpUAN+gsi+bsPQe\nKl64r6ajmStRkHw+nHbDpcz21HgEY/uc19+cF6pSpAHiFabuPIM1qPIWg6rOFMacb6afmkwhNzFZ\nZATb6qda7AwqduKu2oyF0YkIM8bWNNYiYEmqWXs2GxkYOTEMxSQN4Gf4Wfqn1eihUiLshQWqQ7Mv\njy8QQLVleY7w+rXwV1eBUsp1o9c2zD0kbthv3N3IyZl+2Ll4ClM9ptmlz8eEMCSAm7nk1UOVt5mB\nlpLhN/u5x9IJ4/1jAKVcUXo9z6Cylk5IZYo8VDzvlC8UhOST8OiTr+LDn/kWPv8fd+Lv/+c+TET1\ngYXm89BUFS89uN3xmgBgz0t7mZpCPp8PR14awn9+dwt++LUH8PhvtgOUwufz4aZb3sGc47EHtyLr\nYUVzK9yQX6vVoApBqiheE++Tb78af/2pD+Ijn/ow/vuuH+HSK1ivFQBsurA0g0rRVK4h3OxkUFmM\nl1BdNbfeVAE7LxWDqnA9TVqlxVgLsOcDnf8A6pblB8w/5Kdkc7qWiVIgn4WUmIZvehDS2HFEe1mv\nZ/v5Z6Cmkx1EpjjyhALZWMK2XlV2gatYLzR2VdIBeK6UDixPtXRehXSzIN1K81lrUbeundne+/Su\nkuqNlYTJO5XN5PVlZUz4/D60rWMnkFYPldnrVm7Ij1KK5OEeTG19BpHtr2DysaeQ7tOTLvIzEe5q\nJjz9FFDaAsncJWc4XsT6lnom/KmpGob65zxn7kU9gVWpoVJm+AaV2eNTdfoG1F12EcLr16J283mo\nvWATACA+PMmuoi1JqK2b67grqwMIWtaQy+TcX/qc5YfBuPU9FvfkeajCdexLZA1bFpjhCNLt9FNO\nn/M8XWN9I1A1DarFtSmBb1AxxT0TiSIPA8+g8leF8cCjL+K7P/wNkkbywcnxKfxmm7FoLKU4ulPG\npIcFPHneqe72Foz0z/3QXtl2GKPHdQH7je++AYFgsYETjyWwbevzrt9lRlVV9J9klw/ptqQB+0Kh\nWQ1VAb/Ph6su2oQ/+exHsJHYJ1mcveks288kScIGTq0qKz6fD/WNekfC01BlLR4qu3BfAa86Kikd\n44jR/YD1HeLoqKydbznkPGioxkfLW36GUorjj7+K7f/3Drz43btx5O5HII33whefgJRNIjMdZ/SP\nUoUftWta0MKZKTvpqFIcQXqBhV5nbaFxDPnVcLL8VriHqs4iSDcjSRJOfwvrpcpGEhjeySbMLARF\nGX68zL2WemblDEBf+spMIVoAlBfyo5Qisf8QkkeOzo7PNK8gvns/oi/uQIYjqQi2NttGVPycPsZO\nlB5xEaQXkCQJawn72+s/oT9nqlFMjLlk+AGr00OV53ioKqrDjMcn3N2FuosvQOVp6yEZrlhe51TX\n2Qi/SasjSRIaO4r1RhmHOhcFGIPKWlzP4/IzPBd+XRvbwdgV9yzLQ+WxdIKdID3gDyBcEYRkGSYz\n+TxSJiG0EosV6WasFXkB4Mldh/CDH/+W2b6zpxeK8WN/+aEXmM9rOEbnseMnmG11AfZe9u3Xl26p\nb6jDdW+9mvm81MrpYyMTTCZZdTiIenNpAkmCFAxww9NedCGVVZVoqGR1cR1d7fjBbd/Bv/7XtxAK\ncTw8JhqbGuA3SlPwsvysnWu1TYZfAU8eKkohpVh9Hq2sZ2vM+DghlBXuoRp86SAGXtg/dx55DCd3\nzxnXkRG2/6pb0wpfhR/NHC1H5OSobYFUJ2/2SvZQUUptPFS6QVVVXQmfZY3RnKIwgmlg6TVUVKOs\nRhbFWiMeDes70MRbO26RDCrk5/qfGU7JhIa2RlTWsr95q4fKZ+qfSg35UUoR33MA6eN93M9z4xPI\n9LEeWGv9qaL2zNNDxTOoAGAdZzIzYBhU0UiK0V0Gw0HU1lvu32rTUFFKoUQ5HqoaoyN3yT7jGVQt\nZ7ILw9Y3Fb84GQ8iVqtBlRyfKVq/jvJKJ1g8VGouj2yMffnrWlkjwC7Lr5QaVAW8Fvcc6+UbVEF/\nAJIkoZITojHrqHQPlamop8VD9fTuQ/ivux/itjGbV3BiZAJjk3EM9LDen3fccllRgU6NapiIsQN3\nSGFDVhGTV+89nLCffOgojhzs4baLx8leniC9WMfmC+m1tqweKgCOheoKUE3DaY1dqDAZHV21Lbjt\n7nw+T/AAACAASURBVB/h/M2b0NjUgBuuucrxHE0mkTy3DpXVQ2WT4VeAVy2d8VDl0owYHdCz+xh8\ni+Sh8mBQRSMxpNOlVcuPD0/ixBM7mO19uwaQMcqDREbYCVP9ej0cVNPRhJA1zV6jmO7hZ4Q56S2z\niZVrUMWicSQt62UGggE0t+r9kCRJnksnLLWHKjUV5S7NUtXMeX8tnG6jpXLSyZWL5FIyobGtEZWc\nYr6KZjWojP5FUxEKs79HO08opRTxXfu4BpMbdvopwG6BZH6ha37JBL6xxhWm905C0zR+uK+7hfWi\nrTYPlZpMgVoGG8knoSJshGmclnOZiiI1wQ6wLZvYsEqFT0OoWh94FVVjXjIeVoMKsIT9PHioeItn\nhmtDCFV5WyeNUrqAGqqZoiwUTVUx3j/GNahChg6Il+lnDvvlk+kioaRZsLxtz2HctuVZx3Ye7BvC\n3sPszLatsx5nX9CNjjVzHpRYNgXNMmOorAyjNsR2ItOmmQzZdBbOOmcjs89D921xbJsZboZfsyVT\nz9Ai+QIBZl8vs24lr6AhXIPLuzfh/I6NuGLteTi36wxUmRaWveaKy7jPpECTaSZYyUlHtob87ATp\nBQKV7Htq9a5IaU5WWrAKqOBosyTOGocLYFDxPFS8hbJLWdNPyeZx6N5t3MwtTdFw7OU+AHYGla5l\nkSQJLZzQg122n1MB4JUsSu85zK6r2dnVXuSV4pZO4BT3XGoPFbf+VGcLN0vTSk1HE2q7WK3VlI3B\nXDaUFmmoeCUTGtoaEK4KMUaBqlFoJsPAV+EHMnH4xo4jnB5jrlPN5pnEE6ppiO3cg0w/O/F1wxcK\n2eqnAEAKBNiJlqpy3wOuhsrGQ9W6rg0hi4c9m8ljfDjKNahaeB7J1WZQ8QTp/eNx/OzfnsDP/m0r\nju1mf6gFIr1szL6uuxWVbU1MqAGKikojhOQl3AfwDaqi1eQ9aKh4moiqhkpUhNhjeQZVOp5iV9YO\nVKCuiV8yoUBlbRXzMunL88zNnKaGp6DkFa4gvdoIF/E9VKbinhaPlJpVQCnFU7sP4bZHnnFsIwDs\nPT6AvkH2R/LG68+FJEno3jDXWSWz7IDSWsfPdpwxJR1IksQVpz/9xHOIRb3NJPv72I5kTSurnwLA\nD/l5eOfyxiw5WBFAS1U9KgMhRv9VWeHHmc1smKFAs9lDxRGlWxdcLktDZS1Rwsk05HqnAL6HaiFC\nfhwNVfd61lM9VkLY7+gjLzkuGTV2dAJjxyeRjlmuX5JQbyos2MKZKdstluz0fStZQ7Vn535mG7Fo\nAvmlE1iv/FJXSnerkO5GM6fmkVPiQVmoeUimwZ2noWpoa4Tk8yHMqX5uDvv5/BJ8kVFIoJAkCcFK\ndgJoDi9TTUPs1V3IDvLLzYTXd3O9TAUCNvWnCujV0jk6Kos3WS/9416DqoDP5+PWo+o/Mc43qLia\nuWUwqAgh5xFCjhFC/qzUY62C9MnpJB7degiDfVMY6J3Avf/xECYG+bNK3oKhjRu7Ifl88HEGk7Dh\noeIZVE2cbBy+h2ruO70skJyaZD1oVQ2VCITZl5inq+B6p9r1H44Tum7MWUc1ahikWY4XsKZa7/xc\nPVQmgyoSTeCBbTvwt//9a/x0y7OeXsXjw2NQLR6AuoYqnHexPgiZDaoEZ0Fdv022fGQ6AdX0nK+7\n8WqmQ89lc3j8oSc9tNKrh8rBoPIw6+bVUgoEi88l5VU0VdWhxcZgMXuoeHWozB6qYF0VVyNlpoLT\n0THvKef9oUHWOwRgUTxUlFJupfTudWwK+ZhHYfrY3mMY22M/mStw6Gk2bFzT3liUOVm/oQN+Syal\nmstjxjIh1BQVGYclr1ayhmrva6xBtfnSC4r+9lo6YUV4qBwE6VaaOR7ISO9IcZmd+ZIvvk+8kgkF\nT00lx6Ayayf9+WRRfaVC5MZMzlQXMt3Xj+wIfyJSvels1F18IZquvwbhdd3cfYLt7vfSz9VRFV9z\nMpqYnXQWCISCXCF+AV75hP4TE3xBOu+ZL7WHihBSBeBHALyNTBasgvRDx4qNJ1XRsPOxV5njKKXc\n9ZMaDFe7n+PuD1XpRkyWY1DxLNm8qjFx3PjI1FwtCw/FPXkzzqr6SgR4HirObK0c/VQBro7KdL6x\nE7rXhRfyq63TPWBcD5WpdEIuncOe/cfxjX+5Ex/4+Ndxx+PbMTzFLyB69ZXno9GiJ1E0DbFscedw\n+TUEfkM7tdbFoKoOsp0HoAtNo+NzOqpwOIwb330Ds99Dv93iWmWbUor+Pl7JBBsPFUdDRRXFtdK1\nwglbVYSKDe98NIlghR8bm9cyCQPAXMkEwL1sglu4DwACPA2V+T3VVKb4HQUAjvgcACBJjKEtgZYt\n/gTALHcCAH6/H52GINqMF2F6aiqGnode9PTd1vVDgblwXwGf34fmM9nBJmIptZCedl69YaVqqFLJ\nFGROyG/zJecX/c1bIJlX3HMpNVSaoiLO6WPrSvBQ1XQ0M+JuqmqYOTE07/YVMOunKKU2IT+joC9H\naG72UPmzxWNSkCM/MXtD0yf4Wak1F5yL6rP09Up9wQDqLrkQ9VdeViQyr2isR3gt6ym2wlsNRbUI\n02dG+YJ0J+8XT0fVf2ICk5yini3d7HI1yyFKzwB4OwBPq0OeeGArchO6i9UqSKeUYmCYHYwPvXQQ\nquVHlokkkLOkd0o+CXWGq72CY1AFDSOGJ0hv6WpBJS/jwfrj1ihiA4bR52H5GZ4mopSQH28NP7eS\nCQUaO5xrUY0ZHTq3qGeD7gGxq5ZOKUVWyeOnjz6Jv/r7H+Op53ZzM3YKXHX1ZfjK//4oNp/Papki\n6eJZ+elkbkCqb6pGdX21XveEY1DV2BhUADBjqYz97pvZsN/QwAhueetH8J1/+j5efPYVrqdjcnwK\nKctaauFQEM2W2jqzHipJms1CNeM28+bpgKwhv/RMHKGAH5WBENY2sHVwLjJ5BbghP1MbmjbyZ5Rm\nXMsm8DSO/gAbci8gSXxjax5eKrv71t7BdpBuGipNUXH43m3c4qXnXLsRtS32s+ECBUG6mSaOQTXb\njxi4FQBeqSG//XsOMUtBtXe2oaOr+D7wPFR8UfrSeaiS4zOMAReoDiNUb6/5sSL5JDSfxT7fhVyK\nxmxQJeMZ5C1lfwKh4Kwh5Rby80vFz4rvodL7Oy2XhxrnLHGz+XzuCiahjjY0v/Va1F9+CeqvuBSN\nV7/RNZoCeFvPb4Yb7nNOquk6rbMosQkA4tE0shbnRSAUQH1LPWeyh7K8VGUbVLIsa7Ise66SmB6b\nQmT7K0geOQo1kSzSlkxFUkim2Y4sHU+h11KBluedql3TOltjg+ehCgT0y+SF/BraGlHLWcrFUZju\n5w0M6lxtDkqR5nSSVfU2BlVhbTwT5QjSZ/dzqJZONRWjJ/UOnWtQNeoGVdBfAb+ldlBeVTEai+KO\nl7fj0IC7SPHq6/8A//jNv0ZFhR8XcQyqGVNByIqAH22mWiCSJKH7zG5klBxTK8sv+RDmCZ8L57Wk\nQq9dvwaXXM4W1UzEk9j6yNP48t98A+9/yx/j21/+XlHVZ26GX1szfBajwTwzK0dHZXVnA/oPffZ4\nTUMmEkfIOPdpjZ1oq9Y7FL/fj09/7uNYu2GuY+fWoTIMoMYzutB5KbvUDfP9vLIJKTeDijPRMMOt\nRVW+V4LnYQwEA+joKt2g6ntmNzeFvn1jKzrPbseZf+C8WDsA1HezHuQ6zmKt8aHJIkPErQBwNpH2\ntCboUuMl3AfwPVRJnoZqCT1UXP1UFyfby4Xms9jQ0nTPwMI9r6I1/HglExpm28wP+RnvmcQuicQ3\nqHTjXYmwDg5/TTUqT7OviSf5/Qh1dSDU2e7JmAK8lU7gRWvsBOkFgsiia63zPoAuSJf8foDj9V9S\ng6pckod7EHmxOJTXP2zfoezfvq/ob6YmFICGDXOeDV8Va1AVnAZ2BlVNI/uD5wrTC98t+UAtmhC9\ndpZ+/nwqy4TxfH4J4Rp9WRx/gDXIlEzx4DAzstAGlX6+2PAY0im9bTxReoMR8rMrnXDHK89jhFPC\nwMymDWvwd5/+EL7ynS8iEK4GBXDxhaxBFcskoRoDamd3U9GMgkoS1py1luudqg5WOnZ8PGP0pg+w\nXioz6VQaTz66DX/9mS8hYczMuEvOtLGDps9UI6ocHZXC8ZxWmDRU2VgKVNUQNkKKPsmHTe2n46r1\nF+J/f/7P8eFbbyk6lleHSpWAy7/wQVzwsbehImRvjM5+v4uHStI45RJ4nlszPA/VPEJ+OY4hGgwG\nGA8J4GxQaYqKoVcPM9vDtSGcfc0Zui6xqx5t59h79irrwghxRL6VTXUIWAxcTVGRMHmgUw6CdEAP\nY9vVqltO9uzcx2y70BLuA+wMKo6HagkrpcdKLOhpR8PpXYxXOpdIIz7ivsSZK1QrKk3DLZlgMiyc\nQn4+v4/pM3kZ5wVvaH6a7eMDje5SgVLxexCllyJILyBl4lh7OieUZ2FWkM4dT0o3qFx6wMVBSxUP\nkrxwX4GjO2XU1QRnM9d2DLAd47oLTkNrq24IZHwKYhbpFc2rCFYFkOWsNbfx3LU40NGEE3uLPWE8\ngyo+NIGmhkr4AxWIzgShZoqvo7EuhIqqakzGWIFpZV3l7AwhEK6AamlLXWUFaoxrSCXSGOV44jZu\nWofmVucsPwDwn8vqwiJjM2htrcVjP9aXeaGUchfM7WxrQkFuWxUIM/ola/r9bPurwrjmwrNx3eZz\n0NnUgOYLzkZbm165OxoJY01nC1oa6zA5Mzd4UFBEM0k0VdVhzfriH0hFMIRNl52FxP/zrp8qEJ2M\nzL4PBd5z8w3Y8sv78Mo+2fHY8dEJ3P2zX+MfvvkFjI+wxnt3C9uptHQ2ItSgf1+8MoS0pS5PfXUQ\nVQ7PbayS/RlW11TOXsP4jP77CFkM8YC/Amo6y1xrUxPbsWYyWXRv7GCKLNpR7Wc7EzWbm/2u1GgM\n1hy/qtpqx+uMxYNQLJmB9bUhBOvc32kemRSnNEk4hHM3nQZJkoq0a9NTM6itDSLM6cCjQ5NQLRMg\nySfhvLecXWTYbn7vlXjq+P1QOQZwQ2cd6qr8CHGycFvO6MLI/uLCtNp0FK2bda/XgSg7UFqpCflR\n5+G3v1Qk4kkcPcKuX/fmt1zBvI+dXewkhLtAsqoyxy4Wuzl1jbrPXVfW97ef1Y3RQ8V6o8zgGM4w\nnm+516SkkjC/4TMc/VTn+rbZ87d0sH1TQZRuDX8BfA0Vzej9Seo1jlZrbbun8acUErkmWH/FPlUp\numcJjgd3w1ldtveVqipmRpNYd3orXnqanSiZWU+60dpai5kJP6hFF9nM6UfdWCiDqjQ/qYlMNo8x\njuVdIJfJ4cXHXsN5V52PTDSJpDWUJklAfR0mJnQjhjNxhppV4KusKKrJAehhlWRWRQVHGMczqDRF\nxYk9vWjY0AEfZaXBM1NRIKlh5DhrDFU1zBkBFaEKIF7coYwNTyNteL32P7+P0SbUNtVB9VXMXqcT\nGnzwV/iL9GfpRBpb7ngSO585CEBfD45aLPBwZbhI8MzzUFkJBivwmZvfgjesX4sKUyg0K/ln2yr5\ngvBJGWw+7ww8+fzuouNn0jE0VdWha11xp6vAj8rmRiTzpemnAGBqNMrcp9z4JD7/ruvw2pkb8OKh\nY9h97CQ3SQEA7rnzAVx9/ZsgH2ars3fWsz/iSEqBL69/n8IJa01PRpH029/LqXHWMNAgzV7DaK8+\niQhxRO9jg5PcdyIcDiFjGbQG+idQxQmJ87CWxQCAXDIz90zjSca9ncpqSDq8n5JCmWNikQRotjxH\n+egoJyzh9yMSzaC5tQmT48U6xEP7TxSFRguM97Ai4oauetS3Fz/rXLASa6+6AH1Ps8sgNXTWIR6J\nI6ayzznc3gRYDKqhw/1oMMLgUY5H1crYwCSyftYDtly8sn1H0ULnANC5ph2BUDXnfWTfW56HSssr\nGB+PlRx2KxU1pyA6zGpUtRpe292pPa2LMaj6dx9H2+XnobW1tqxzAvqi4+ZfRoST4ReqnWuzxul7\nCh4q8wois8dyQn6J6TjGx2NIcrJi85l42ddih5JlPdTZeLLoeyY44VlfuNK2LVIqCh+lWHuae4JB\nVaNuO/goa8RMTcbRyqkC4MR8svwuJoRsA3ArgM8TQp4mhJTsExxwCPcVOGCE/cylCwrUdDYXpSr7\nAhWQOCENXnS+prYKkiSh1mPIz9wGp9IJaZsaVAWsKfFAcY0f+ZVDzOfkDWd77mh8Ph83xvz4z+cK\nWvL0U03NjfCbYv9OhSQBoLamEt//5mdx7eZziowpAPCbhdHGeTaffwZzjoKOas364heX/n/23jtO\nkrO8Fj6VOvd0mjyzszObZqN2VzkSJCEhCSEhhMjByOCA8QXbcB2v47X9+TrzOQE2GEwQIBEESCJJ\nAiFppdXmNLO7k/NMT0/nUOn+UR2q6n2qw+wgo+/3Pf/sbHV3dXWF9z3vec5zHkGCy+NCgUDIZkAl\nEiAjsZKGZmPSSvFV8ByHq3Zuwf+47zZ88qO/gI+984143V03w2W7X3Rdx9/++f+LCcoyIWq7xQXe\nkubj16OhapDyq5jE2hkqoNyFnQgPIUxvxS1ccImM5kJT1Kolhd0mBDCuWd0g3dIvQUNVR8xPCtMX\n6LRfbpkdg/xh6/nTOR7gRWy6YR88dgd0Doj0hR27O1A6qoowXc4XIWcbX5dSE+95OeMYoZ/afzmb\n7gNAO6UTRSAAAPXSrDSaiexygtHHuEN+uIgOA80E1YYmM7dCdsogQykBxRyb/lbslglUhZ+pupdy\nSzel/Ozh9rPgv5TOGabb9meL5yCJmnGsGxhOonTdpEfO2Hv2wuhf6BSVZu3+gAftXW2O7wNMpp7U\n3Poyi9KPjIyMvHZkZGTLyMjI8MjIyM0jIyOOubuB228iy8qn5uvrcQBg7PgF5FJZ0n8qTFTWCISO\nqkiYxnnLbtCBCHvSS4oKN+FzUTX4JAS4WqmEyR8fx8yh08xrFobKw35WzhgPi1ws4cKxC8zrO6/e\nzWyrF2SO2XR/OAEq3jSg1WOoQh4v/uLj78feXUNkHz/zNdDL+7n8ANsEOF3MQfQIiMRsk5QgoVQs\nIZ1nHyZzym/HlcPw2KhrVdWQXrauQO2+Zy5JxOWDffit3/og3v8r72a+4+LoONI2809JEtFpu1cq\nbWcqsR5RulJiBymzKL1QNmV1E/tOr6YYpgCgvajsFYv1guO4+jqqdYnSN1hDRZw3l8u4Fyhh+sKc\nA6AiPOP8EdsYIroBjoMgidj55ldbGs327+2Bt81DtuEByqX4NnBaTGZRTGXrGnqaoxnQ9XJGs4J0\nAAi2NWebALw8Oqos4bodaKDJqRfeSBB+opVT/Hzjwh0uvQJheRzC6jT45QkLYOFsHlS0qWdtgUdV\nq8sEoKosfCQPu2hSizKKiyw75fK7wfEcaeZ7KcGJIlvkpWnQywUniqwwwEYQBXIhbXxWBUx2PANb\nnHVxgiSazt/GaKheNlF6cHMfoq+9CWK4NiFpmo4ZosEob18ZqxrOPn+GZKjCg6znjEAg9QJRVeIu\nX0gnUXr3ge3M9tTUkpGOszFU8akEXvjMkxj/wWFoBOPgC9XYHsqLSi27kI8dv8j4EnmDPgzscq6u\noKJRWSmln4rEwoBp8ndiqDqDbXjf9a9GdzQMXddJTQlvFkaLHugAerqjCBMpJ87PMeybLkiYHJ9m\nPJzcggTJNHHvuGoXoh0sIE7M1QYFXddJZ37AaOp539veiG07Gldx9fV1Q7CxLPYVlpMXVb2gjT1r\ngKrSH0wUeIi279dUDRmifxhV6ZfPt+Zn5NggWdfp3HojQPUyMlSdPc1X+lG2BT47QyXVQHt4czeu\n+MBd2PXa7Th4917sqFQAEkUeACC4JHLCTk4v1W05Yw65BTD8s45MhtZPUYJ0oHnbBODlqfTLEvop\n/yUAKmCdrumqAi5TW/hxqgx+baEGIEwMVbEgI5lg7TMsgIqyTSgvtvhyyk/neGhBA2RwHEfqqHKE\noF4KlMeTDWaoOI6jhenl+6NRBTSzv0LGAo3qAapYbwx8BcyRDFXri72XtcpP8PsQedX11dLLpXgG\nRbuvhkvElTeyQObk08fI/n0V7xelJOPC0fN47NPfxkOf/zEe/eFZzJu0KZkc+wBL5Rs3QNgmyKqG\n2M4BSzoRMJyOMwvxaoPkQrqA44+dwbHvnEZ+jaZ4Ja+Ets7ad1CASs4aD8s5otpoxxXDtQvfZDSq\nghDc7A0UjUUA0w0sCSI6/FZgNhCN4b3X3oQ2jxdyUYFWUhkgz0kSeDOw4HlAdIHjOPSEiYmlQOTC\nRQljFyaYzWZ2ihd4bLt8O92/0DQoaIUiNKJ3GACUFlcgiAI++rsfaphS3dTXzWwT3HZAxT7s9vSj\nPahBQ3SxDBXglPZjJ2Wq0q+Qa2116chQ6ZqlHQYA6OBoBsocpG3CJfhQUbYJ5fPf3cMy19OTLGOg\nazoJqPwR2/kTrefC1xlF784uRPtrZevQ2NV0JZzSfpS9Ck94mf08pfxOHj3NsKK9/T3o7KYnr2Zt\nE4CXx4sqQzBU/gYL0EZB2SckLs5ZujYwoRQZXoST8+DyKQNsmRYbs5NxZnEZ7orAZQIj3qCzD1WF\nodJ9YcA0hlKVfvklFnBWABWn1Kk2VWVw6Ti45AK45CK41BK41DK49IoBHEt58vmgrBPUsjyBBFSu\nOtICm1n0QJ1KP0sPP2psWkfK72Wv8uMEAcED++DdtgXHv8SarG8d7saBa7bghR9bWzvMnJ9B99be\nauk4AIjhAE4+ewoXjoxi/OQYc/K/+9QI3nT7HkRDPmTS7IAkqhpUWUGgjV1BlRQV7nAAoYEupuFl\ncmIBbR3bkFxI4fhjZyAXnB8aye/BvtfvsVCupBdVrgBVUXH+JbYKbec1uxz37xT1LBYEgcfmLZ04\nOW0VykZjESjxPHiOqwr4d3UMwiu5EYj50Ofy48qBoapeSikoDuk+9sHWJQ84pYSgiz3Xs8sEcyBI\nGCcAlVk/1T/QAY/PQ4JHs3WCknBOK8srceiahp17h3H3/XfiW1/9juN7NxEThp2hWo+GinJKr+js\nlGLJku5xSyKytnOeXFnDJlgHdC+hB8nlNoiholJbguhs6lkJwjaB09V1ds1ytk0AgIEhVnx+5sQ5\n6LpuAc7FVBaa7foIksCs3HV7+pvjofOCZdLjAOPcEB5poYEuzNkWS6mpRbjteiwYvnp2Nv7nKeVH\npfuc2CnA2Sndfi2AlwdQ0QzVpQGqtk0dEL1ui7WIJitYHp2BQFitAHBkQLj0sqHZM8XMBMsa9W+3\nsmKUhkpWVei6Dl4wOhXo/gggiNB5EZymkML04loanogV5LiCDRgqVQG/Mml5HqjQgu3QA9bzQbml\nV7yomukiYQ7OdnzhmB+BsB8ZguywtJz579ZQXWqIAT/GR9jqmu17etHdFyHFZCtlh3RZUXFhYRVP\nHzqL737yUYweHiGRrKrqePr5cWiajpS9kSkAjySikEhDLZaYVAoAlEoK004CAJJTi1i5uIAjj55y\nBlM8h75r9+DqX78f4W7rgOLklj55agwF28Dp8rgwtK9xOsoe9VJ+r7v3oKOpp5wtQDKBP4HnsTXa\nhw+87X5cO7TNIj6XizKd7iMAFSQ35JICSWMf4JmFFSRNAk6d4wCOx9j5Cea9ZoZqaMAAUhGiEiOx\nVANR9jZH5tBVFfKqsWJ98EPvMVg6h+htZ1/jbUwQraGq3+KmHq1dSFh1EyRDRbAcXmKQyrcIqESq\n/Uy+5OyS3iDs3m0ANp6hKgOq4V3bIdquRXxlFfOz1hY0FOvtixA+ZyKhJ6R+cwvC9PR8nNTzUI7r\npZ+jlF+z/lOVcLkkuGzMrabrKBCTJdU4eiOjlMkz4JQTePgIO5RWguN50jV97uR49W8lmUJubLLa\nMcTO8lb3pangU9b7lARUtu+T3BIEG7up68a55kUeuretlpYvyzmolJ9iyxrxLrGmGVRKJNDg8smG\nYAowNGP2Z6SeWzqZ1q8DqOxjE8dx2ET0XARsLWde6YAqubKGpSm2v9b23b3gOA77rhhkXltKZTGX\nSOOlsXksrGUa9kgDgOXVLI6dmUMmy1KVbklALp5EYTUNF0GzZxJphAZZQLV6fganHnqS7OcFGD29\nrvzle7H9zmsheVyMToRqkKwUZZw7dIrZvu3gdkv6p9kId9K9jnbu68fVN+3AKqG7CZbBgUhUhCjE\nqS5xPsgCu/p0YqjmZxJwCS74CLH7sZMmTUa5hQnJULlrq7BN7UZrmkgPyxwllpLVB8JJP1X9HWUR\nZiDgx4d+64OO7+sLsyBfCFgZt/VoqGhjT+Oa5xNW0TIlTKcq/UhR+kYwVLmiQ4VfE2Q3paG6BFF6\nPQ2V2+PGjt2smeypY9aCEVKQHrb1Z+NFkl2jqhqdhOmecACSTeOiqxotYxhgAdXPC0OVSWdwYYS1\nE7H377OHn9D0/Xe0n6EArK89TFbBtRpU2m/+5JjRrmt+EatPPoPM8VNYe+YQMmdH6977ZnCi6zoJ\nqPps1YUcxzkK03mBh+6vMfl6GVBRDJW9lZgrYDIuBgCVZam4UnP3JweAs/nH0Q2S15Hy0zRwuvXY\ndQCbdrF9/QArQ6UTonS2+2jj+G8DVBeOsE01u/sjCIaMG2LvFexJyBVljC0mqkK7ZuPwSZYJkwQe\nAs8jH08hn3AGVMGemFUPhPIqimgt4PK5sOu+m3Dg/XciUEm5qTJzqey6LAAoFWSMHmY72A9f3Xq6\nDzDsBLZfYW0xEor68cZ3XAuO47BKdLf3u4wHRyL0WipxzuWiApUof6aqLCF6MDtpCDDDXhaYHD1p\nqmwUJCRW17Aatw5+HFAFYx0xP3wuHlouj2gv6zeyupKGrpSg63pdhgowPKoq8epbb8RV11/BvIfn\neXT63dBUDavLWcQXs1AUjWl1RAGqhhqqOquwwqr1OnmI/ZMMFQGoWtZQEStHpVCkBemNXNKB/TUZ\nEgAAIABJREFUDRell+poqABg7362MvbUcaslSVP6KadqV4qhIoTpYxcm8Dd/9gk8fu4kVrP1TTwF\nl0QKpEupLOI//DESTz+LUryxb9XPKk4cOc0sZPs29aCjq77nj59gTCnrBJ2oxt7IyPwM0n2ViGzr\nY6o5c6tpZJcSyI5csDAeudGL0IgqVSriS+lqd4tKSG4JXQSTSQrTVQ2812e5jyspbApQKbJ1rK8K\n0ishE8fdQvUfl09azgXJUNXTUDkxVA5SBKpRMi/wVlkMqaH6ORelm+PCERY8bN/dW/072h5kvIka\nhTfgxa5rdzfWcgDwlCnMfDyFQiINiTA+SyfS4EWBpOvtEWz34+q3HEDX7k1WZohYzdtbUQDAynIa\nmaS1ikMQBWw7yAr0m43Xvfd2DOwehCiJ6B+M4T0fuhneMsVLMVT+ciUTdS4oXy4lV2Rc7wGaoQLP\nY3baAEgRD1sEcPREDVDpDvopn8sLvnzjHyzfK0oqDX84yAj95ZKKTDwBrVCA7uR5U/kda0lo5fdw\nHIdf//ivMN5U+w7uAQoljI3EsTCTxuJcGhfPLkO1PUIbpaGqMVTW69SsF5WHqvLbkJRfcd0pP1K0\nfikpP+K6mq/bvgN7mNdPHbfqmCgPKqbCj0r3AYDYOOW3tLCMX3vvb+Kxb34Pz544iU/99ElkHQok\nAMAba4PLz147pShDSaYgryaw9syhpifjjY5jL7HpPie7BHNQgCpPeE79zBkqoo1JYIMAleR1IzzA\nZjRmnj0FJWmzx9A0lFabq/Ck2Kn2iI+xggFo6wRF1cB77IuEMkNFpfxkO0NlvXZ2nRI0FZxmvW46\nAC3YAS0QYxsPqzJQqs11lIZKLbOXtL7UiaGix6WuzV0I22wtBvdusaZHX8kpP7kkY/zUOLN9+54+\ny//3XTnYcF8urxvXvfEGvPdPH8RHP/1xvPk33opr77qu4ecqK/38qsFQUamUzJqxmgwTOipzRPvD\nuPyefcbNac/hEhdZJCa7+WXWj2bosq1wE+9tNiJdUbznj34Bv/3vH8GDH70d0XYDyCiKijWi3YW7\nfDtQKT+ZAAVyvgiVmKRJDRWAuakKQ8UCqsnpRcQr6S1BwviFSeY9/e0RbB2I4rabtmOw33hAlKTh\nrBztYI3e1uaWyUGHioquAQB6+7vxe//7Y3CXK/gisTDe/+BbkUrkUSrWBhtV0bFg8wyjqvzWpaFy\n0QwV5ZaeXE4yrMHPLOWX3+iUn7qugQtwYqhqx7Fn/07m9cmxKSTXas9aUx5UDgxVMym/rz/0KIom\nAFVSFJyed/Yn8rWHwIsCBILFVisSA01DsUGz559VHH+JlSXU009Vwk/cSzliTLHbJpw/dxH/9Def\nxOc+9SWsLLPu5q1GlnClv1TLBHPEdrJpv4Wj51EgJCdyojkPsmkCUHVFfEgfO8k893SDZJVd6JWF\n6a5GDBUHSHYDUHulH8VOiS7ogSj0YDvgZguRuFxtXK7XILkVhopKt+u8CF4QcOcH74a/7CsZ6Yri\nlne9zvbhjQFU/y29/CZPTzDI0xf0oXewA+Ya/D0HBvDEI0cctVKXveYAbn7HrQiErRP0q992M849\newJrRO+jSlQBVTwFTVZIViZTnswokWglurd3YNdrt1dz8JymWBE5cZEFr02joetYIo51+Gp2Qmg1\nSsUS5s6NYlPUA1f5NycIMBUKt0Et6zSolF+xKMM+JCoOgIpiqHLpHBJl0OgSRPhdXqbx8QsvncMd\nt14NXZQwdp4F3JcPD+CW6626GKXcNzHSFcbijHXATSzEESEmJipKSyvw9NcY0htfcx2+8Oi/Y25m\nHlu2DYJPZzByiLW0SM1YTfDW0xyZ8qEqrqVRSGYZDZUk8BAkwdILUi6WUMjmLVU+lG1CK07pgINt\nQq5OlV+j4Hjo4CzaBA4wBq51tBuhzpvLtHoNhUMYGNqEKVuT69MnzuL6V10DOV9EKWO9BznOaHRs\nDkeGqglROlURVy/t540ZCwOX34O8zVpAUTSIZYZSa9FTbCMilUzj4iirn2oOUBEMFcF6m5+V8QsT\n+MgvfrzaQulHjz+NT3zmr0mj0GZC1zTDJd1+bBvEUAFA98HtmHz6mKXaDwAWZtKYWUthfimNcMiD\naw4MQEykgN7Gv2VmnAVUne0BqOkM1EwWoqmK0jHlR0haIHng9rH3kRlQiT43ONsCm1NKljnObkAK\n1DRaAKB5QxBsdgZcIQNdUwBerOuWTlrKtJTyM9675bKt+NAn/gdyqRwCkSBhDPoKZqguHGXTfVsO\nbANvo9ADbV7svIp11w54XHjn77wTb/zVNzFgCjBW97c/8Kq6x1ABVMWU0R+QZqiMybqtvxMCcREH\nrt6G3bfssAoa7ReVWM2LPo9lAskWZRRktjphx5WXBqhOnziLt7/hF/DgL/4h3vyeP8KpswZIWSVW\nRtFYBMVyFaVEMFRFIr0i5wpMyoYTBZKlmb9o1bFRab+vfesnBngWJIxfZBmqgU52JVmh0imbiNWF\nVVKQ7iI8ikpLywxwj0TD2HPZLnh9XqjZLAp59lraV7zrE6WzA8H44y/g+b/5MuOkzXEcQjGWjbN7\nUZHGnhtmm7DOlB/gzFKtI+r5UFVi3wFCR3XM0FFR+ilvyGt5nsfOL+Lzf/5FfPYPPo2zz9s6IAgS\nm87Q1Ooz4WSAmSw4XwdfuaWGRNheqKYiGM3BGPNnGSePsvqp/oE+tHc0lmb4iUkzS6QtzQzVZ/71\nvyz9KKcnZ/DV//p6K4dsiXwiDc2WzhI8LrgJ25z1huR1Y/OrDzDbj47O4cyFJSRSeYxPJ/DjQ2NQ\n0jmmqlG3LSyKBRlLRM/KrnYDRMkr1kWkz0mUTgAqXXKTbumapkMtp2Pt6T4AbKUfyVCZrrcnAN1W\n1MFBr4rTeVFkF6K6Dr1YrFt4wkSDccnlcSPcGaFd1skF3StAQ6XrOilI3375DrKS5rrX7Ee4rCnw\nuSRs747imv1bMXSQBVrmGNgzhL07nJklc+pELZQcNVSA0dds6NYrqyCWE3hsu+MabL35AFNJZzc+\nI6t+RJdFmB5Psw64m3Zthv8SH/R/+utPYq2c8kpn8vhff/GfyBeKpH4qEougWO6ZRKX8CoQxqlIo\nMQMs7yVKzgHMXrACqs4Auyq8OD6HF4+OQAVPAqpNhJ+LmslCV1WHSr81yETKz7dtC/MAafkC1Ixz\n7y01k0ORsMgoprKQTeeGZqjUuhWp1KBh7xZQCdHrQohoc2HXUVGi9JY1VA7Gnvbql4rNRVOxgTqq\nUgMNFeAgTK8CKqI60qSfSq5m8aV/ewqTpycwMzKNh//uq5g1txPhOJqZKz/zJ46cItsCpeqwS96Y\nUbBB6qgsgGrjqv6aqZYGaP1UM+wUQAOqHME+VFrPrCzH8dxPXmBef+TL30KyQZGJU5AtZxyqoS8l\n+q7eZen3uJYtYDllHePnltJIZ4oo2fwRdX/M4kE1OxlnjJPbAm54y5XiJVsa1NMCQ6VLHnAc56Cj\nMu41KeBmKuA46BbioBFDBY4zLBtsYRanUyyVvjgFmTCAbSnl1wxzDmyYsefLDqiSK0ms2YSBHM9j\ny/5t5GBbWEli76ZOXD+8CZdv6UFXOIDwENtuxh6Cz4er9vejLUDT9R5bg2K6yq9GzfdfsxtX/PK9\n2PXmV+PqX78f/dftZc3+AKBUtF4Ih55n5tV/PMMOsDvXWd1XiVw2h5EzVuC6mkjj4W/9BPEU+30G\nQ2UACirll8/kSZZOU219lqgKPwDzNkDV5vajP8aySl96+CnMzS0zk6Xf40YsFiEFjEoqg0gPUem3\nlIJuXwXzPKRoGFKUBSWlJbaHVSUKq0kLQ2AOs1Egx3HgqMGrjjCdGjR4h0HeE2lDiGgMmlq1Mlk0\noGptEnZkqEyh6zoKWRUaUfVKxsvMUO0lhOkjZ86jWCjSTZFN+qljL45ZBbq6jhcfP2T9QJ20H5Xu\nA4BUgV1AVcIXqzBUhFDXdP+pG8RQjV+YwIff/1u466b78T9/7Q8s+jJzZDJZfP+7TzLbD1zZHKDy\nEal3ssqvzNg8/s3vGy2+bJHP5dfNUpGGnnUMkNcbvCgYC3AYz8c4IYQHgLVUHiX7WCxK0Ntqi8Pp\nCXZM6myvgTV5ZdUCiJ3c0p1SfgAcdFTGdZBCQVpDWBGmaxppo2D/jO5jfb44pVRlt3ji/tCyGcg5\n9llxrvK7BOb8lSpKTxE0e9fmLngDXoYWBIDklCG+NE8wVP8+ewh+HyRRwKuuGWJeE3kebtsNRgKq\ntQx00woz2BND1/5t8FZa1YgEetdV64V10JuI5cbM+ZJMrtTWa5dQidnpeXL7lx5+EhPT7EMaiYZR\nyjin/PKpHDnBqrZBj/Sg0nXM2VJ+HMfh9Vex1UFHT5zHE49+n9m+qTMKVzQMsY1NFSqpFKKEuefq\ncppZfYuhNnA8DxdR5m22T7AH5RdUCXspdqs6qlKenRydGKrIUA+CUfYcpG3idSrllyMGp3ohEn5p\nalGugqdSXsbhR47j2f98Fs/8+eewcpZlFZkgnvH1MlTNpAN6+roQa7dOmoqiYOTs+YYM1eR5Vvh9\n8eh5aKbS/nrC9GOHaUCVK5UgE/YAroC3yly7iJSfhaGqUynYSvz9X/wzzp4cQSFfwOHnj+L3f+NP\nSFbtkS9+k2kWzgs8Dl61v6nv8buJlJ+DD5WqqvjON55w3NfXH/p2lXlvJdbbcqZULOGT//gZvPe+\nX8LHP/QHZEsse3Tu3YJATwyLySzT2aASa6kCSmkroNLBQfeFobV1QhfdmJlkj7nLBKi0YhFqurbw\n9zm4pfNEdXBFmO7EUHEiDz4UJjWE1UwM0T5HFyT2ORdd0F3sPc3lkoCmQuDYe06TVSgEm0um/HS9\nroaqYbxSAVWlcs4cbWWamxpsc3E2PVVPJF4JjufBez3o7WzD5Xt7La/1RoMMzSvwPATbJKZrGrKp\nOpMQx9HovZJT1jRwNi8LHQB4serxE0+zN0zPlh6ShWglZqfnyO3ZXAHffPQpZntbwF+llqmUXy6d\nI6sTFRtrQ1X4JVeSyCat6TSB5/Cq/TvQG2NXLg99/hFm20BnDFI0AjHEUsdKMo22aBvjElwsKija\nhMtSuCz67WRThPJy3AKgK6HrOnIJZyFxhtFREZV+dQAVJbx0+dxMyi3Y145NN+xDMMqeA3uDZKrK\nr1UfKo7nSc80pWj8louHJpBaMs6LJqs4/ZUfIb9av3LJ3lIDQFMOy1SUCEDlsg22HMdhr4OOivSg\nKgMqRVHJ6qp8Jo/pEZPI3YGhSqcypIC7EilCR+U1aeNIhkq2aqiaTdU5xcpynPHlOnPiHB775vcs\n25JrKXz1Cywr9Lo7b0Yk2pzDOMVQ5YiFhK6oOPz8USwt1GGL8wU89LmHm/pec9Apv8YM1cNf+hYe\n+tzDmJmaxUuHjuKPPv7n5L1nDo7n0HfTZZiosxBbSxcgZ4pWJq78fOj+CNTYAGYm2MrGrphVyF4y\n6agcbROIRR4AQHLT5p6yZuinPAGylVJifgXjp8YgZ6g+rA5VsV52TuMKKfCJOQgiC2jUkgKFSG2T\nDJWmsMCO42lGnIyNaY78slf5ZQlDyaqw3AaoNFWDnLfRiRwHDyFEp0LweaDlC7hyXz9iYR9WEjnE\nemPIT9E3uUsUkLdNwJm1NAJEv61K6JIHnE2Ux8kF6N5g3Z5nUtnjZ5VK9x0YbPDLGsfsFA2oAHpl\nH/B4AdRJ+aVzNGOh2FN+7EQ+Z0v3AUAsYjCIb7j2AD75nacsr1FU/0BnDGIkzKbwYDBUHM8j0tGG\nlXnroJnKFOExPYBiGVCJ4RA4SbJYGlTa0LjarWyXli+gmHceQO2phFbbzyhEOnDHHdei/8qdUEsy\nCskseIGHJxwAx/MIEs280wk7Q3XpVX6AoaNS7NVmRQWiW8TSRSvg0FUNYz84jD0P3Oy8Q4qhWqdb\nerOC1b0HduPpHzxj2Xby6Gn0RlnDP1855TczscL48VTi/Esj2Lx70PgPxVApMk6cOFUX8KTyOcT8\n1nHF114DyhSgsixeNA26LINzNVfFSsXiHG298KlPfBY3vOY6hCPGs/KVzz+CnK31jSiKeM8H3t70\nd/nd7HFmCE2frir49jfYHq/2+OZXvoO3vOtNdVtFmUMtKcgTvk/NMFTf+84PLf+fnZrDscMncDVh\nAGyOU0dGq82JqUiW031yugB3xZ3ftNCPz8dRsJ93gUfU5uQvL8eBLYMAHKr8NIeUH4z5i2KoSgXF\nMPR0eRmh/As/HsHjXz8CXdPhD3rx3l+7GR3dNbBESmEA6N4g9NSShWTgdB0o5WqtbUyhlRTIBItJ\nVvldSroPDgu9V4JTOsVQ+SuAxTbYFrOE6DTgbbpNgGDS2wxtiuKqy/qxfWevowiRTPutEgjcHBI7\n8FUBFmU0xhsXWfS4IKsqUsQqbXhHBCi2lp6xx4wDQ+UUARMlz/Mcy9bpOnTT+Ymnczg6Po/vPH0O\nx87MVQcOClDZK/wAoKO8yrpx7w6E/bTuyhwDnVFIkZAjQwUAEUKsnbKJPqXyJMFxHFydRNpvkV0Z\nq9ksikSFXyWySwkLs0W6pTtoqORckdQftW8z+nQJLgn+jjC8USNVCQABClA1oaGyT4rNBKmjKshI\nLaWZnl8AsHxqnLGSsAQl/lwnQ0UCKoIdpBiq0yfOQrdNdi6fVDWInTjPtsWqxPmXalXKuoO5JyXg\nNkcjhspFXD87G3yplX6LDl5W6VQGn/rHzwAAVlcS+PqXH2Xec+e9t6G7t3GmoBI+AuhmCUAVj6/h\n+WdYMbo9isViSyxVdjnBiLvdIT/JwJojl81heoL1DTv83JG6n4vPreDFxw7Vfc9aeWwqmnVUprnJ\nUgBRjo6Yn5EDlEw6KkpD5VTlBxiAyh9lx99MqggxFDTmZBNDlc8W8YNHj0Evj1nZdB6PP/wSs08y\nOJ4UpwMA7yK6c8gqaY0iEYsIsvirBUD1yk35EamTCgOk2+i5Yo4AVASl6RQCkaKSBI5k9wAaUKUJ\nRs0c5M0jFwBdr1t1IHrdWCP6c4WjfnR2h8CvzTk2Wm0Yuo7ZSWfzQCp8tpuPSvtp5ZsuX5JxdnYF\n2aKMVLaIF47P4GvfPYnp+TUm5afrOmaIgaEzalQwSqKAO65u7LQ8uHkTeJfL6J1nu0/0UglaoYhI\nD0vfJzOmSYfnIZg8W0hAReiolHSWrPCrhCarllQX6ZbukPKLj7HAl+c4S5WQPSgNlT3lR9omrMO7\niKr0k4sKVqdpoS0AXHziBWd2ZgMZKtLY0zZxp+dWEOFcDMDMZnJYtqUrfKaV/wShn6pEfG4Fq/Pl\nNItDyu+4g36qEkniWvjMKT+iXN1eFHGpgGph3hk0Pv7oD3Dy2Gl88bNfsRiTAkYl5TsffGtL30Uy\nVFl20fijF44zDHVHVzvue/sbmfd+62vfRXyluTY8VLqvGUPPC6Nj5L384nMvEe+uxfc/9wTJtJsj\nl5dRklWrjsq04JgZnWY+Y0/3Acb4V9FROflQFSankD5+GukTZ5A5eRbpk2eQOnwMay+dhpbMMHhC\nUTQUtPK9zYtVlmry4hJk20Jq7PwC0uYuH06tmgDoPlrKIlCL0JICmWCJyZTfpVT4Aa9gQEWYSgZa\nYKjcLQAqSvOjybKj70ijSj/6S1wMJcrpmnGB69CQktdNpvu27+kzKsU0FXxirrXJRi6CS6+AX57A\n7BTLCtULj405IPv5lZHoUpK1F0hlinjsqVF8/Z++geRKEvlMHi8+9jw+9bF/wTQhVu6I1a7BLZfv\nho+YuCvRGW5DoGyLwPG8xciuEoYwndVFmRmqiiC9EhSgMrehqUR+ebVhFVtmoTZgk15UDgxVYpwF\nVHYtmD18bX7L7wCAQrZgacXidrvB294jl2QoLbb2kIj2MwagctaGJCcXEB9hJwMAG9rPTybSvy7T\n6vXcN36Cl/71mzj9he+jr43V+kyvWvUpFf2UXFLIdh/mGH1pxPiDF5nClFQyjYuEMa3lPUV2MeU1\n6SYbidIBQL1E6wQnhqoS/+dP/gHffvgxZvsb77+zKe8pc5AMlc2mRNM0/PBFFojeec9teMcvPACP\nrbS+VCzhS5/9alPfT1X4NdNy5vxZ1kcMAKYmZhzP38Vj58nWalSspfKQM4UaW2pmqEaJhWg7vdCq\ndHoQRBECsRjOzi4gPzaB/MVx5C6MIX9hHIXpWZSWVqAVZPgCLOBdnUnWjqmsi5oaI9hnHTh9dMr4\nkxfq9/WUPKTInSdSfmpJoRmqn0HK7xULqLJEyq+awrABqhKV8muFoaJ6BOVLFmrdsm+HBsl1g+Oc\n0351HKV5t4REhh0Qd+ypCeg5uQAuudT4wuo6+MQshJUJ8Jk4sqkk2VrGKURRhGBviEm1nymDiiTh\nSVWJc4fO4l8/+gn8wy/9NZ74zGNYmmJXwS6XiFCwds78HjfufO2Vjvsc6IxBitQmRLLSL5lGhKj0\nS5kYqkq6rxKCz2cwXrYo2czyqNWtPTILtc9wRBrIiaFanVhgtjmWBZeD53kEIuzAmjaBf47j4KXc\nqVttkEwA3XyqgORS/edi7HsvkCt0nbBG4dbrQ1VHlJ6aXsKCaVLrDbLP/FTCZopYboo8M7HCVK/a\nY/RwGVARXlQnTjuL0SuR563790bb4IvV0iHUeddUvZpqAX52Kb9KzE7NMS2nPF4P3v6+t7T0Pbqu\nw+uSmMRAPl+EYqp2PHZxGvGUddzieR533HMbItEw7nngDcy+v/3I41iuU51bifUyVKNnLzi+9iKR\n9lMVFd/7z8eZ7R6XiBCxOEmmCoAOlCpzQXlhW8wVsDTNXp8uB0Alm5g6F7Ggkx0sXyoRDLHHFr9Y\nqxTXy2k/ElABOH20vGgW3Q27HlAslUCk/DRZZdgwgNZJ0tmgFgAVBYVeCc2RKYBS1VDZBlsq5dcK\nQ0X2wyqU4CVSJkB9QKVrGs4fGcUzj/wY0+emLO9xSvvRPc+Mi7yyvAbFNpEIAo/B7VZdAp9PWvoe\nUcFlV8EVagPRzBzR+6kjgnYHIBmJhSHbWCcq5aeoKlRNQ5rQfZlDLsqk0LoSm4c6GR3bG2+5BqID\nM2Pop0yAKkQBqhTplm5hqMLs73d1sCyVvGodfHONdHSwDthmhkrTdBQLClSCTVFLClLEtXLVYesq\nQQnT7c/WhjRIJp6h5YsrjB7FHrmVJBaIjgi0D9XGi9JXL1hX9wMRFmxP2wBVxYNqvI5+qvrZc1PI\nVxhm28BtbvTtFFlNQbDPYFRdbT4M33OjlXXUVAgCOzGZRc6Xau7ZCFBR8ea331MVqzcdmgae4+Al\n0n4503Pxo6NnmNevueFKdJQtTt76nvvgsS0S5JKM//r0lxseQobwgmpGkD56zvlaUjqqM8+dRnyW\nfaYP7OxBgHiWKjqqqh9VeVycvTDLLKTNhp72KC3Hq6lJauwuOhRYVCLQxo456dkVFCum06ILcknB\n/DSdYp2ZiGMtnnHWT5lC97ZBt7FYuj9MVkfLxWYZqnW2w6oECQJ/zhkqTdOY8nkACJSbFrIpP3bi\ndrU1D6h4UQBnd0DXdXgI4R7goKFKpLG6sIrP//Fn8dBffgFPffmH+M//9e84/tSx2pvWwVDNENqZ\n9miQTPdwqUVLd27r79HAZa2Dxewcu4oYHOrDuz/wDnIX0VgEBRtzSKX8SrKKVK64jtvM9F09MVz3\nGtYMMNbmx603X0V+ZqCr3SJGF9oIYXoqjVB7mGmjkC8qKFVM6ghAJRFVQnK8dj51XUd+zdlBvRJm\nL6qKhiqVKGD05BIunl3Bqe+8VBucypGaWSKZEJe3ceUWWelnF6YT/fw2okFyZrW5gomJHx2BYreE\n2EBRej2GKmljRvvCUQbEJ/M5JPO131JJ+dXTT1VC1zRcPGYY59qF6UdPNgZUKyurOPiLb8ANv/Mu\nXPvRtzJmxUoyBUFiz5XdOmG9oes6FufrFA8QEQj68cC739T6d5VZNcotPV++hvFUBkeIhuhvePMd\n1b9D4RDe9La7mfd8+5HH8fwzLzp+fymTh2zv2Sjw8LXXt3zI5/KkIL0SR144xqTQz1dSwaboag9g\n5/YOeAlmJbFm3H9Vx/Ty8zFL6Kec0n2AUUWslvuaSoSHnUz0TTSHyy3C7WEByGpZ/6qLbsxOxutK\nH04fm6qrn6oGL0CL9kF3+aCLLmiBGPRQN+mW/v+n/OpELpVjBH4evxdi5UbjOEv54qVqqACdLLGk\nykQBGlAtTy/hUx/7Z0zZdEBPf+VH1d/iKEyvc5EnCY1JezgIPcRWznAA+LUFciXP5VKMjw/FUPVt\n3YLX33s7+gZ6mdfCkRDTJJZqxSPLMtaIlFEs4nNcOVWif3gT7v7Ve/GBv/pl0oRTUzS87YHXk58d\n3LoZnAngkQxVOgOe5xBuZ8FWKl0ABKsgvRIUoFLWktDLqQi9WKprmVCJ4lqm6iLOSSJURcPcVLI6\nABUzBZx9+GnLZ9YmFqARD63o1KvKFGSln92LitDhFFplqIg0BRUDN7GFBaVMHjPPnrJufBlsE3RN\nYyoNXaKI7jYWUE8nDCDMizzcATdKRQWzU6z3z9aD25lt1bSfaeBeS2YwPsmmcQXbAiWfyyObNcxy\nqaplJZGESDyDygb181tLJBmxucfjxj1vucvxMw+86z4EiGeoYZSZeB/Zz8+4hk8eO8vMDZ1dHbjq\nusst297yzjeR9/Vf/uHfOnpXUek+X3uoYbW4kyC9ut9sDmdOnqv+X9d1TJ5mtXNX7O2DyyWSXTsS\nSeN5LKULxlhRntipQh5Luo849tJyHKWVOESKBQ6FEbhsNwJ7d8G/Zyf8e3YieHAfQtdcgcirrkfs\nxoPoHGbnnngF2Ikux3RfJU4fmWyKoQIASB5osU3QOoagB9sBjiO7YJQIQMWMj5pK+D1y9FjjFK9E\nQJUhPahsD6jpJFxqlR90HQIx0buIfC1AAyq5KJPGi6mVJFZmyzeYIDE+FpyuO/Y8W12QOoMOAAAg\nAElEQVRYxeoCS52GfG7DJZcyQFNlhomCroPLsvuZWWQFw32beiGKIh781fcwr23dwvrxeIhBq1iQ\nSf3Uvh1deOCufTh44x4LC+Dxe3H1ndfil/7mQ3jfn/4i9r/mICS3CzxB7WqKioEtA7jB5rw80BnD\n5h1Wt3ve7Wb9dzQNaiZLWydkiowgvbovrxe8x/Yg6zrkhHEO5XSarPCTiHRaZeDmRBGpZIFZza2N\nzVkm+uTEArnia6ShAhwq/exu6ZSGqkUvKoqhYoLnMHDTfnTsZbsSTP30hJWZ20hRukPrmcxiAirx\nzNZL+/nDRg/K6fFlRvsVjLXhmruuYz578dgFqIpqAVTHTrEi5oGhTeju7WS2LxEWHZWQ15IQCECl\nblA/Pyrd19Xbhff/6rsRIcx2Q+E2stKumahYiviJlFe+WIKmaXjy2FnmtTvuvY0BoqFwG95N+F+l\nk2n82e/+FVl0Ye9kAFy6fqoSh587Wv17ZWaZNDDu7jSeVXMhTvW4syVjDNB1yOWMjK5ppCDdXOHn\n6WW7hZRW4siNXKArtMMh+LYOwbd9C/w7tsK/Yyu8gwNw93ZDikUgdPQidgXrep+4MGs0cBakhoBq\nfiaB1aX6xr71QrCPwwDpBceMj3X8HpsOElD9nGuoKEG6vw6gokTpLTFUuk72nxN5kNYJAs83NZlV\nYvxEefB0EKYzwUsAx5EVIAGPC0K5ia4e6iSRPpdZtbJehQwpxpshwFp/mZl61S034I57bqtuH9q6\nGa+9/hrm/f4Q+/An5paRIfrO9Xa1we0S8bp33Ipf+YcP4/UP3oUHPv52fOTffhO3ve8OdGyyTiYc\nwcDoigZd8uIDb7wZVw8PweOSsK23Ex++91a4bH33OI6jWaqUkzC9AClM0/scx9VN+2XnVpiFiugS\nyH6SlUoiThKRStCT3dRPjgMwAGRqZmndDBXlls6YexKguFUvKkocbY+2/k6IHhe23HolONtgrpUU\nTD9j8mSimiPr2rpWg04MVWqa1kBtogBVudKvYplA6acG9wxh8+7NjLatmCtg6tykRfx67CQLqA5c\neRk6u9kK1OVFZzG1spYkNYUbxVCRgKq7A4FgAL/8kQeZ1975/reS3mZNRRVQUQ2SS3ju7EWspq1A\nxBCjv47c3f3vuJc01Tx94iz+458/z2zPUvopYuFlj/NNACqzfcLEKbYYoasjWAU40ZiPYY80XUc6\nW9FRGf+Shp6i1dDTs7mf+a7S4jJKSyu0hqqB7hUA2jZ1MZpJtSRXmXSqc4A9Tj93uuF7nILyGLQX\nRQAUoLrEdB8AGgq1Pia9rE7plKknU61UBlSqrDLGgRzPkcyAc+iku7deyMMdCqBIHU84gEQTVV0A\nMHb8Iq6+01i56pIbnJPOqRJl/dR5AlBFA17oqgZNViC4JGihbvArExbcx+kauEzcSAvqOniCndJd\nPszMsCmHvk0GoOI4Dr/5+x/Gm952NzKpDHbu2YH4KZam9hMppbkpdhD2SCL85RSq4PMi6vMi2l2/\npJonjNk0DShlSnAXCvjo/dbUnxhhwZDY1mY4BJtCSaYQJoT3yXSRBGCVkGIRFGetvQ/luHFuzdV7\nlfCG/Ah0R7Fso/crLWhUWUM2TTQMBbBydhLZ5TUouSI0hW4qLAmcATDqrLCaSflRGqpWvaiaYaii\nW/uM74u2ofeqXZh93jqorpybwrY7rjX+w3HQOc5wSC4HBxigigJbdaLkYJuwRNynALApyt6Xi+kk\nCnIJ/nKF3+QFFlBt3j0IQRSxdf9WnH3eKpw+f3gEQ7sHqv8/RgjSD1yxDwWCGXRKUWmyAjWTJdtx\nmAGVrqpQSzJkRYXb63Y0LAaMdNShbz+L0z89BW/Qh5yfXflXjDpvef1rMDc9jy/8x1eg6RrueOPr\nSO1Ss6HXAVSZYhGP/fQos/3aG69CB2FrAhhg63/+8W/gl97561hZsj6fD33uYey/fC+uubGmx1yv\nZcLoOdoywfKesxcw9sh30LF1EOMnWUDV21UDCf6gG163xBT1rMSzCAW9KKXy8AGYIdipjmjN0JP3\nuCHFouAEoSpNAFAFriKhoSrUqcyuBC/wiG7vx5Ltd8RHp1ASeZQKjaUPZ549hZve/OqG76NCillZ\nQ03ToarEgtNWxVjP77HpeEWm/IgKP3vKr9Ig2SndZxcd1w2HlJ+azcFHrPDBcQjGaCdXKibPTNSq\n2ZqpbhAkFPNFTJ6eYF6Llg3Zqq12JDdZXsrl1oxO36U80/IGANY0F9PEVJJEywqZ4zhs3T6E/Vfs\ng9vjRoHw2vJQHcSJCPs90FTdMQdOBVXNoeoCsudYoCkE/KS1AQWQCjNzEBdY/61UpgCpTjGD/UEG\njEo/XdfJpsi+9hCZMqikFlYn61eJTT9zAmtlnY1K0MoulMBl6q8GmxKlU1V+PwOGKrKtr/r35lez\naYNCIg3F7O1FAad1WCfQLsoSI0ivRMDtQdTH3kuHxi/CF/GhWJAxO8VOvpvLqcztV+5kXjv/0ih0\n8NA5DquJNCYIdmz/FfvQSTTjdkr5KUmjqpdiqMwpv7VUHp/+7X/FX7/vL/AvH/kEFgkLjko888iP\n8YPPfw/zY3MYO34Bzz3xHPOezm6DSeY4Du/54Dvw6NNfwdd/8EX8xu99mPE0aynqaKh+fPQsppfZ\nc/6Wd9UXv4cjIfz+n3+c1EH95R/+XZX90zUd2SX2GW6U8svnC6Qgvb2TBeXHTo8ie2EckwRD1dtZ\ne055nkNbG7vIWV4x2Dk5nYOuaZg+x4rzzfopwecDx/OQ2tnfoOs6REI7VCBMpKmIDQ8w2+Ij04yG\nGAA6e9j5aXl6ibTKaSbEUBCc6Z6nCnYkt8QuHDaCoeLYRjMtII1qvMwaqjqmnpWoAKpL9KACAOga\nRDdhGJbNwUMAKnfIj4Fdg8z2tvYQ3v5772ZcaOWiXHWzbUqMJ4gYP3HR0q0eMLRb/jKNqZhofD3Q\nzpqGAuBTyzQ7Jboxu8Cyaz193YwWwRwFQtvmIbp/UxHyuaGqGnivp+4K2Rw8kdJSkimLl0ol/Du3\nk/sViUo/LZdHG1FwkMoUSQuN2r6CFtE7YBhxqukM8gTY9HdFEehmV7jZxQR0TccKscI0x+LxC1gq\nD74UQyVKApvetYWTW7pZRLsR/fwaMVSix4W2vhpYcPm98BDHZhEGk9YJreuoKA2VXiiRzHMlhtpZ\nLdOzY6PIyAVMjS1bfJ4AINQRruryth1k78XE4ipW5lYAQcJxQj81tHUzwpEQnfJboEGzslYBVM6i\ndF3X8dTzY1ieMfaxOh/HF//350md6vzYHH7ytacs29JZ9hzZdV4ut2t9InRbVBkqwjbh3ARb7bxn\n1zZcdvnehvvdd2AP3v8r72a2p5Ip/Nnv/hVURUU+kWbaPgkeF9yEpMEcF0fGoNlAfndvF1518w3M\ne49fnMbqWg5FG4MjSQI6bbqpGMGMra4Zixxd0yGvrpFMlwVQlVt1Se0suNN12jYhT5hIUxHd1s+w\nNYVEGhMn2Ht7z+Wb0T/IHsMZeyFKk8HxPKRoDSRSfRApDypaQ9Vqyg+taa4c4udAQ2UbfDlnQNVa\nhR+MtJiLFafpigJPiN2XNxLE1Xdcg77tRn6aF3hcfuuV+KW//lVs3b8Ng3u3MJ+p6qgIYXouU7AO\n0IJo6QNWiWjAWx2oFTM1K4jQA+wNyxUz4IpsKb8eiGJmep7ZXkn3OYXdMgEA/EQHcirCPg9URSN7\n+DkFpaGiGAoh4Ie7nz52sY0e6INEJU02V4JecgYSHM9DjLJpRTmeQD7Nfi7Q3wF3KMCANE1WkJpd\nxtpE/RWarunIltODlIZKcongAHAFZ/8rj9/LtGuQi7JFK0ECqhar/HhRAE8YBVYisqWXEfsHiJRv\nxqzr2wCGSlVUZsLjeR4ZwgPI3x2tdke4ZnAreNt4oGgaPvvw90n91OY9g9W/fUEf+oc3Me85f3gE\nECTSLmH/FYZFSEcXC6icGCq5DKhIUXrZNiGeyGEpbh0DsskMvvGJR6BpGjRFhVIsQZEVfOufvs4I\n7QsymwLq6mHB5kZEvZQfFQ+86fam9/3W97wZVxF6qlPHz+BHTzxNp/s6Iw0Xf+eJdN/2HUPYRcxB\nJ8anMbPAegX29kUZZq93ex/zvnS21s9zeXQCqRXrvjgO6OmsLSD5MqCyN3EHjLGFAlSFJgGV5HMj\nZNO86rrOeC8CwMCWDuw5yBY0nX62fmPwut/fXgOc9s4AAN0YeUNSfgBt6dJi/PdrqBwYqtKlVvjB\n6BbNcRxErwTFtj8/AaiCve3wtfnxvj99EInFBLxBL7yB2vu27N+KszZ9yPiJMbz27agJ00s5FHIl\nfOnTT2Pq4jJcbhEHr92K62/eBV9YxAXC7DBi6ixv766t+yPQs2vgqEbL5vcJInRPELNEU2TKKsEc\nFKDyeEW4JKHq4USFzy1BEgWoqg7B14I/GJHyo8K/a4fjwMcJAoSAH2qGNSR1u0QUbemgXDKNQNh5\nwpBiUUaTlZ+dR4mo8Av2d4HjOAS6Ikja0nuTTx5tKffuxFABBqDS/bTWg+M4BKNBrNn0fpnVdNXQ\nk6rya9WHCjBYqqKDUas53VeJQFcEK2cmLNssE9sGMFS0fopO94UHu+EO+jH2/RcRCwRxzdA2PDd2\n3vKenzx/ClKePV+De6yVi9uvGGYml9GXRnHDa3c4CtIBkCm/ZaeUX6LMUBE+VJVJ5ryDQHji5Bge\n/8QjCCQz0BQVSzDSMObQdR0FhT1/3T3NNztuKeqk/Owx1N2Og3t3NL1rnufx23/8G/jgOz6MuC11\n+JMnn8V2H7tQWq+hZ58kYEckCEkULL5OqWwepwhfwd4uNiXWt3cL8PAzlm25oox8tgR/0I3x4+w9\n1BkLwCXVFiEVhkoMt4ETRUsXBl3XyS4XuXRz3nEAEBveZHmOirKKvC1lyAs8+gZiiHUE8cQ3jlj0\n24mFVSyMz6NnS/15hwqz/KJ5hmojROnA+pJ81vi5S/npdVJ+62GoAEAkjBK9AQmRrbXJQPJ70Hv1\nLgAGYxHtiVnAFAAMXbaV2c/c2Fz1Zq2k/b77tRcxddEYLEtFBYeeHsE//sm38LVPfJMpq+U5DmET\noFLytt/N8YZPR6Of6o8CHIeZSVZD1F+HodIUFSXiYRMlAR4iXWqOcHniVhUNEsHwOAUnCEyKzR5C\nMAB3H1tJZzlGoioEALyEQV2uQZNrKcoOspkpoi2MS6gWRlA6DLtDNwCEo15H7Z9KMlTlc1PK122Q\nTeqoTDpFn599XlptPQPU11FFCUDlJxzrzQyVTmg8Wm0/Q5l6GvopVpAeGuhCz5XDVabtpm3DCLhZ\n8PT8mVMMY2hmqABgx5XDzOdmR6dx/sIspmbY766kriiGankxzrBsFUE64MBQKRo0TceFSeemwEd+\nehKrySxS+SJGCWZB0VRGuye5JISjLTqgNxmtMFT33HB5y2xlOBLCR37nQ8z2mam5demnALrCb6g9\nApckYhexQB2ZZQFVT5RliNsHe5nMkqxqSKwaC53Ji8SCuNs6zlUWrxzPMxXKmgND1WzKD2B1VCmi\nQrB3UwSSS0Qw5MPmrexCdb1pPykSri64FMKMVLJbHuk6QJEN62Ko/j8IqConk9RQteCSDqAKqCRC\nV6Oms7js3bdh9wM3Y8c9N+LqD78ZXmKCMke4I8yaUuo6JspVcrrkQWIlg1NH2EFMVTWMHGbZqZDP\nDcG0YleIm1f3tkGv18Gb46GXvataZagKRM8/UeLB8xx8DXQGld5UutsDdz87sdYLMu1ninrsVCXc\nvd3MNrEtiEAHC45yqfpu5xQgLBCGnh7TPRgggAMVkXYvIjE6JUpW+ZUnfiPt56wHaiRMpxiqQotV\nfoCzjsoX8cNjT9nDIeW3uFpLf2+AW7qjBxVRldm2qQuS143usjmnW5Rwy849zPtycgGzyRooCndF\nELK5acd62xGxTci6ruOLX/gOs7+tW/oQKhdP+AM++G3FFYqiILFqnfCVZO36Ua1nNE3H9HwS+QYV\nVyNzKxidY88FAJKd6uruvDTheb1QnX2ozNHXHsFVw1sc+17Wiz2X7WK2zU3PoUA8994GhUeFQgGT\n46zx8lBZB7d/C5v2Xc5Y03QevwfRNuvzx4kCRJ8HQeKZWV7JQNN0zBGpwz4b0yWYFkouW5NqXQdp\n7FnKFw3PtCbC1xGGxzQvU4Bq05YaiNq7gWk/ThCqPVdJhsrO2qoywyvpvNB0+k7XNBRm5pCfnGHG\n4lIThs72WPcTNDw8/LfDw8PPDg8PPzM8POzc2bYcxXwRJduF4QWBEXpXRelEmedGMlRqOg2O59G5\ndwi9Vww3bcewhWCpxo6XVzMuD5576lxLN1LULnSn/EI4DlrQOV2l+yMAz0PXdcxOtQioCNF1ZRUQ\nICpazBEqnzOpt6euzoaKemk/sS1IgiV7uPt64BveBs7lAu/zIrB3FyKvvREBwpgwl8rUTcXxksQw\nXsU8O7D7orWBJtDESldy8fD4JMQ6/SRLRWqoTPQ+l3dm1hpZJ1BVfq36UAHObumRQZZ1AQBPKMD4\nv2klpVb8sAFu6SXCuFPkecA2KLpDfnjKC4P+62ogal/vJvRH2Os3nphDSTH2bU/3AUaqNdpj/VxR\nkfHTZw8z7739tVeAy9RADZn2s1knVATple+iWKrz4439gGRVQ8EhTVtQXj79FIDqeNiIobrn+oPg\nOW5dgCoUbkPQVvkrywqW4yyobFRocXF0nGEO20NBBMvP0/6tbCVcqpCBYloUDGzvq9ocVIL3+cBx\nHDoG2HO9li5gaSWDos0qSBR5q7Cd5y0tWty9PZYUuqaVZS4EqGqWpeI4DrHhAciqgh+NnMajp17A\niYULyJl0qANbas/+rgObmLEttZLELOH23kxU0n6Uhorp4HEJ6T5d05B4+lmkXjyK9JHjWDlyEZqi\nopgr4fDXT+Annz3U8rGvC1ANDw+/CsC2kZGR6wH8IoB/bPSZNNFg1h/2s+7VG1nlB2dApaQy60LQ\nVNpv/KTRoiCXLeHYISMHrmoa0sUcisRq0BwRG6CiGCoAgNsH3c0KsXVw0Ms6gbVEEtmsNX3ncrsc\n/VwAusJPcgngRLEuQxXwuKrUskKYfTaKegxVM+wUYDz4gd3D6LjrdYjd9lr4tm8Bx/PwtbHHncsU\n66bPADbtRzmkmw0BfZ2Rhmn3trIDt+QS0LGTHYjraagAgJOd036N3NK9hK6t1So/AJAcegtGh2jQ\ny/EcbStRSfuZVo+aquEn3zuNz/+fR/DEf3wX2QZMYiUohoonLkZooKYL8sVCiA0ZzwLHcXj9btbi\nQdU1XFw10uabCUAFgLm/ZpKLTHoi4PfiDbddYwCqcgEJVem3aANU8pqVobBX+qmahsk5No1FgWt7\n9GztheiSaIaqx3Zsug4U0uDyqXW3BqpGuaq5noaqIxTEdbu3GV/dJJNij35i4bhIWDI0sgKh0n1b\numtjaF9XDB22xaYOIGFa/PQPsXq0CrPUMcC+li8pmJgmKrQ7gxBMKTzB57WMjYLfh+DBfQbIEgS4\nytYXdNqveR2VHPLgP559Gj+9OIpMKY94LokTixeqC8BNQ7Xz4Q94MER0SRgnKgObiSqgIhgqTlUt\nC2NKkN5suq84t2BZwGhFGdn5NUwcmUZyYX2O7+tlqG4B8A0AGBkZOQcgPDw8XLe+NkUAKibdBwC8\nAF3XHVzS66egmCgPBIJHYiv9ZBlasXWn4cE9gwwITC6vYXU+jpe+fxhySUVOLuDF2TM4PHsWz02f\nwmKept5jXRF4bMxOPXCitXUwXhm6L1S9gSh2qrevuy6VTwnSXS4BvNcDXx0Aa9V9tX4eKXNPwNBF\nudYhjjUPMj4iNdwUoLLpEagefn5Tyld0S/BG6qcP2sK189S7nx10KB8qyWUzrnNI+zVySyd9qNYh\nSheJiZDjOYQHnVlEKh1aBVQmhurpJ07hR985jolzs3jx8UP4xj98ramFDuWSzhGfMwMqaCp2XD9Y\ntVLpCYVxw17WW2ohE8diZhUDREUfYL2/FE3FbIoVl9975/Xw+TzlPpzzgKqggxSmW9kmxQao7AzV\nSjrH+PN4/F68908fJBcS1f1IAu75tfuwdf9WFOQGgnRdBx+fgpCYA782D355Yt3tgQBzc2TnlN/d\n1x2EWNZVroehAoBN/ey4sbRKAKoGqUfK0HPIBDilSARX38AmZVayNaDb38fe/xXtU6yXvQ/yJRlz\ni+wkXi/dVwnvQD9it9+Mjrtvh2do0DhGSpieag5QHfrpYfzOH/wlltLW48nLRazl02jvaoM/UBtb\ndEEiPdrW60dVGYcpQJVaSGHhSK1/IsVQ6U0yVKVldl7OxzNIzLALlmZjvYCqG4B5FFkpb3OM1Cp7\nswSIXDI4HoqiWQzsAKM7OMU01Y3yAFup9LOHmnLWpziF2+ep2iqY4/xLIzj8uEERTq0tIl8uS9Z1\nHRfjs7jqtn0MQLn+Drbli1zP0VZ0QYv0QucF6AB0dwB6W+1Bn9mgCj/JJUDweesDKtNkXfeYHYIy\n9wSaZ6fqBTWxZDMFejVjCjOgUlUNssw+0AHboE0JsKv7cwnw+GrgyBPwINRpvedpDZXNEyuVgJJK\nM0CDYiXM5rm+OrYJuqoiffwUlh99AivfexLFBdpdHKBX9KHuNgh1jFypdGil0s9sL3LskNVzZ/zk\nGOYusoUV9qAYKo5wVW4zASqumIWvzYPr33kldt+yAwfesAe/9bvvgo/4HWeWxvH7H/8znD7O9pgz\nPxdzqWVW4C2JuO/um2rfq6ng1+ZJhspsnaAphveZOewM1XKSnRR3Xbsbkc4I7vnwfcxrlbjqNQfR\n3teBHVftJBkqi/FvPmUxDSb7iLYQFVG6SxRJ5iQc8OHV+2tif7tPX1OhKtjUzj73K0mbJokDRMIP\nyxxUD7+hbjOgCuOq61irhoVMHMlCBl6vhJCfHd+EciuoWB8LqLIFGaspdrHTbxekE4AKMATqHMcZ\nffcASIQpbMUz0Sk0TcN/ffrL+L2P/DEyaZopXs2nsGmrdarXfWF0EYurxQYGx05RkV9QKT+e43D+\nsRegVqq4L8GDSkmwwEktyChkWs+4VGKjbBMazoAUoGrvjqCjg50UZkfZE+kN+9HZ2byLOQCsrXDV\nhZXoczHWCR6thBjx/Y1i33W7MDNiFZ7/5OGnq7qvpI1RKJZkeHt8+KOH/gCnnj2Nlbk49t2wBy4d\neNLWygKKQp6TWgSh9/cAmsZUyiVWWG3Fjp1DdfenEpoaySXAHwmiU6RXvBwHBM3gVm50zGxokQAK\nNvNdb0cUffu2XjKg6u5ntV+5TBE+FwdfnePU9QCSfi+UbJ5M97ncAnq39oA3nfeuLd2MRUAl2sJW\ns1N5cgrtUTfS8YzhLg9AJ/pFmRmq7MIaUhMrAM7CHQlh8O6bq4yRvpUdxLLJTPVayEV24C4Wi+jo\nCCJ+ahT5MeMC6IqC9OFj6H7bXRAJcKHv2YzxH1g1Qh1DUUQ7whCIajkA4Hf2Y/RR67b8UgIdHUHI\nGR3pNaPZdmqNBQijz5/GgetYkbE5Jr3s0CXahiHR48LQ3oEqo5yZXEIJgOQW0bPDSI24Y524/VXX\n4etPPMns78ypEfz6gx/DzbffiP/x8Q9iaJshvu3qM+4vTdcwnWSB6J2vvx5RG9jlSjls6mTvvWRi\nrXq9cgvLsD/BLp8bWDPATVFWsEZUaV73ugPo6Aii49aDePEL38cFm2N6m9eNvXsH0dERxLW3XY7C\n77ETRnskWD2O9Pg87NOUWMog1D64rmczviAhg3KK3uPBmk2W8IZrD8Al1q6nyOktjyfFRByb+ljA\nGrcZmEpeNzq7nOeRQqGIKUqQbmKoYoM9uO3K3fh//sjLML7nlidw2bY+6GusuDzaE0OwIwivNMh+\nL6F38/ndiISsi6K2zija65yb0qwxLrd53Vi1aabGj53HvR+4k/xcOpXB7//mX+HJ7z1Dvl6JRD6F\nnqF+uCIxaMUipLYwPB2d8Hewi+rEwiraAi64m2mwbgtlUzeUF9giLp7noJYUyPNL6L5yGKn0POxn\nri0ShKtOqzHAWLwspdismaZqUOtYBTWK9QKqOVgZqV4ArKOkKU49/iKzTfC4sbzM/qgcgRBFr4d8\nb73gVbU6xEpeF+xD0dp8HFp3a/sEgK5tbCrALKJXiDLO5547iVfddScGLtuOgcuMaqMM0dakkM63\n/DsrcX5kgtkWjkQxNToHV4A1ggSANHEMkktAiROhcvSNFfRYKxPz6VzLx6wE2BJt945tWFlpnTVk\n9k0Qr7lMEbl0Flmx/nEK4bABqAhBusfvRnzVBgDqpKHbIlawkV9ehdsrYvPWKNZWc0ZFzqIA2BaD\nFQ2VnCuWwZQRxUQSEz98HqGrLwcAlHT2dyZXUlhaTILjeeTy7PXLlK9V4py1D6Emy5g7dRHeQVbn\nhXAbOre2Y+micSyh7iD69/RgNVkEOJr1U1xuY5llwovZeArz03GIggYBwAqR4gCAl354BDc9cHPd\nJtHLy+yEJdhS28G+dqxUzC91HXwqyaz8croLm8OdCLp8SDv04vzRE8/gqR88i3vuvwsP/tp7oZaN\nSRfTqyjZVsgcx+G+97wNOl8CZ0uThV0seJ6Zmq8+O7lJwqYj4AVg/NZlImUTDLgRaAtU99EXa0Mi\nnkQ8bUymHknEjt4Y4lNL1feUNPaazY4sGK9rKvh0ijlPWqmIlbllwNV6g+SsiXnZtbkXz52pMUDh\nkB+3HNxteX8pX2p5POEyGQz0sWLvVRugEtyuuvs+c/IcVBtD1t4WQJuJ7c0JbggFDW9/7/34j3+x\nNmPOyUWcW5jG7SnWXiOjcCgsG0yz1+9GPluf2e/rizIAtqDzdY8/ETd+byzoxYRtbJ84M4mx0Tmm\nOrhYKOKjH/xtjJyxerNRkSnlsTgyhfw9rwY8QBFAptw6J9QRRtL0nbqu4+zRMeqqFKYAACAASURB\nVDKj0ygUX4BkqIQyu33+mdPwbO4Fny8w92oyqwAl9hyVMnkUkhn4YiFoWbpIicpKtBLrTfl9D8D9\nADA8PHw5gNmRkZG6alK7ASEABO2NkctBlSu6A81V4VnCdMLISj8CoTYTvVt74XaoCtR1HTKR133p\nMFtGSlWbkFV+TQaloUq9MIpDf/cVHPqHrzImlE4eVFIDDZVZP7XeY5baowjs3QXe7QbvcSN4YC9c\nnXTVWKvhd0z5NaZyK2k/iqHyhtn9OlX6ufweeAgWBQC8fgk9m0LoHQiRhYeVKsssUUJdnJ2HUr5v\n3V43XLZ7SFNV5MorU5+fbo6saZqlPL8SlKYAADio2Pu6YVx9/wFc8abLcMW9l4ETxbqlyU76suxi\novq5+BINqArZAkYOjzjuG6B9qOyVTRb9VCkHzpaa0zkecPmwupTEZT3bEfY4r2o1VcPXH3oUH3z7\nhzEzPwdd1zGVZFMaN918PfqHBqCFexjusYuw8zA3SFaS7HjkCtXGyCVCsL99MFbVguqaBjVXxM7e\nduwb6MSuvnYcGOyGRxKRLU902UwOJVu6lAMwf85Is3KFjGO6oZ5zf90wVcy985brqumzzvYw/vhj\n74HHBpzXpaHSFPT1sIxsspC3jMeNBOlkus/ETvEedzXV/aYH7kbQzY6Rh0bP4xzRsaLSTYLjOMS6\nGvv29XWw86NTyq8SlZSf1yXB62LHn/Mvsc/VoZ8ebgpMVfdx7gJpoNu1mUr7OfeXrBeuWJQ0la5U\nTq6en4acdSjYIVJ+y2cm8PzffwVH/u1beOETD2NtlO1NCADKJbBTwDoB1cjIyHMAXhoeHv4pgL8H\nwLqq2aJEVG4wbWfKUchSgKp12tACqAgvKiXN6lKaCV4QMEhUNQCGyJjaY3wlgSlbs01KHKkUSkw/\nsWZC13VSQxXUy87zqRxGv/1Ty+8tJLOwH6woGh5UgtdLirsBq34KMMxIWz1mjuPg274F7Xfeitjr\nb4F3iPUyWW84itKVxr4ilQqTAmWZ0M4CBE84yFgEAEBssLOp9IhC6EVElwuarCLvsBLNjtQGfcqL\nqlLpJ0kSRNE6qGqqhkJizdqlvhzycpx+HlTFcGbvCCDc3Wb8riZ0CqTB52K8KkpfcQBUAHDiqaN1\n902J0u39Ki36KULYr7v9AMchvpyESxBxoGc79nVvg79OX865mXn8xZ/+Hf4vde8dJ8lZnos+Fbo6\nh+nJs5M2zmat0ionBIhoY8CAZcBgG/va/nGcr4/tc+zre47v4Vzf45+NwQbb4oAzNiKDBUJCq7Ds\naqXNaXYn557p6Znp3F3p/lFV3VX1vdVhJZD1/n76wVb3dFdXffV9z/e8z/u8F1KTKBLNyd//4fcY\n/8cfNsx2bdHVybKyG5nNmh5MybLXw2+abRbKVRQJq4jdo101QCWXKoBulM3HQwF0RkM1zVJpPQtN\n1ZAitHJ+UUJqehlb6a2GoIkr5drqAmCFbgNUnbEI/p+fey/++f/7DfzLY7+Pg0Tv1Buq8tNU+P0+\nErRmCnUg2kyQTlX4jdr0U2JHHQgtTSxiX/coOBcE1QF89hvfR9k2Rjm/ZGxCzOjsaw6oBjrZeYxv\n0pFCs4HRzgj73vFTV5lj84QZNADcf89dGIyxrN/U+irmnj/PHO8dZYsCGjXsbhR8wI9SmQBU5pyq\nazrWLk3D3dJY5zhmo1dY28TlLz0DzdRdVXNFzJ+iAeRrxVBhfHz898bHx+8ZHx+/f3x8/EKz91OA\niqzyg0fbmXYBla47Lrbgpyr9FGjlG2OEKD8qACQ7ZcXpk2cd/+ZFweg16DgpHUqlfVFcZn0DZVdJ\nvE8QHI7QhdSGQ4RONZH1+Y1FiQ8GEE5EGFDg80uIu+0UbvCcrbB/R7VQwoV/fBLP/vcv4OXPfA25\nZZo1aRQkoCpWoKtK02olMRYFeJ5kqCK9RF9FnkOUqNrp3NnY5d0KhRBSC+EICmlv36zKwhIU002b\nsk5oVumXW6YF6FqlwoiigRsvTfas9ON46PBmqABg6twkqbu0oilDxXGIDZoLoa7TlZKBCIq5Iorm\nfMNxHLpCcRwdOoCPvfUBdHpUcOq6jvUiyx4eue0w9h6ot03Ro13QzRSZqmqABnS4NpG6riO9agBZ\nlWCoAmZvM4qd6ukMIx4N1OawagOfIV3VUN7MIUXc+4BozK2Xnz0LVLwrwThNMdz72w3C+TwaCYHn\neXCESF1vMId6npv5N810VF4WIFZQLWfslgk+G6CauTiFsBTE9iRb+LOysYUvPlP3MXK35upqoOMC\ngHjUj0jYueZxktTU70+zMSydUZahnrkw5ej3CQB54pl//4ffg7H+USRD7HlOp1eRvjKLwqoz69Qz\nzDJUN1rpB6D2XNpDsPldrZ4jQBHvXOc1VcPVx48xID2/TpMpSvU1YKhuJGSiBDLsAagqRG7Z72Eu\n6B3Oi2VU+tEGnzcSlB8VAMgNeu69fJLddfuIkvQb8XWi0n3JEAuIsra+XqQHlanfEYJBBEIB7Dyy\ny/H6rW++DVKYXaRvxDqBiunvvYz18TloVQW5pTSuPP6MY4fbSgiiyKZkdaBUrDa1TuB4HlsFtsoU\nHBAiHMABYPjew4DtQe8+uB0Rt6O++xxjxsJKtVcQ/RKKy41Ld4smS0Wae9rd0olKv/yqN0itrhKm\nkcSYbqX5KFnpt5IxJjyOx+oyC0pqn6/ruPDsOc/XSYbKBqgifcl6NZdSYXphGlWyYawRE35HLIg3\n3LIfn/qDj+PnfuXDkJpUhVnx3kd/3HmA46DEevHdr5/Ff//Nf8Gf/P7jCPjYz1pdWYNaKDKsISeK\n8Cfj0HWd1E/tHjUWeq1sbKTkvPG/2VIJ3754Fo+feRFTa/Xnvbi2idQS+3sDonFOp795HJl575Y2\nAMCV2/fnIZ9f81aRLZlUrf3MgXl/B5sAKsoCxIpKuYKZKbbLhdMywQ6oDB3icLwXMT8rB3ji1AVc\nNtkfd6qus6dxmx+3XQL1GVRotvkkEpAguar9VEXF5FknaMwR1e59A71Yur6ARCDKMHD5SgWruSzD\nUlEM1eps6oayQMX0Fin9sTc235xPI7e8hXImD82ar12M/Nxz55BbYuc0XaeNQ18zhqrdaIuhyhOA\nKnxjlgn2INN+N2CdAADJviQSRJPNRgzVudMXoLj0AVRO/0bAyQIFqMLsQ+4EVDRDxUk+cOaD+K5f\nfS/uevud2LZ7EPe++37c/5MPveraL3ukXdWTxdVNZBebO0O7g9J/tZL2q2QLWJ5gfYXCYQk+j8qR\n5O5B3PKxd2L0Dbdg70/cj33vedBB77sjMDyI6GHDtZtiqNStIjQCMNijPL8ItVAkU37pi9dRnJyG\nrmkkoMoS1aBWVNcoQEUtiM0BFZnyW92ArunQAGSaCI/PP3PWczKmbBNEm79VvEm6D1II4AWkpth0\nR0fCuGY+TcejH30f/vqf/gL7DrEiY3uEpSD27WPfM31pHj946jKgG/oMpcDOg2uzM6SeU4xFIUWC\n2CpWmPmT4zjsHDGub42hKpSQK5fw2PFn8PLcNC4vL+KfTr2A+Q0DQBfXNhkjUQA1kLeZL2P8+BTz\nuuN7S407DpBBjB9ro8dxHAmq2tZRmczzMAGoMoX6tRUD3qnqyevT0Fwb/2Q0jLgNyIhmW5RyoYQV\nM53FcRz2dY86FnsrPvON76MqKzX9lBXNGCp3/z6gfUDFcRzTiQMArrnSfnliDRTAo5grQuB5JILs\nOj2VXsXq+UnHpryjpwM+1+ajUqpgkyh8ahapcxOkR5/bfX7mxRlsXFtB+sI81KoCna/f39zyOmaP\nnXV/RC1kgo16TTRUr0b4QwG6czSASoHVJkihNrtHk4CKAC83yFABwI5DLEtF+V1ZUSyUMH7JSVNS\nrNmNgBOqh18yzD4IW00YKkkSIATrD2EgFMAHfut9+OgffwwPfuBhSAGJBlQ34EXlDk1RIRNpiw2i\n4XCzoNJ+rQjTr3/7hGNSsqK7P9JwQott68bogzej7+bd4AUevAeg4gN+RA7th68rCS4YYEwaAaC6\nzC56TOg6CtcmyZRfNpVG/vxl5C9eIfv5FdLeE5yczrCMgrlYyYUKqvmyAXKo9jGuCCToFjSljSw2\nMyXSg8se60tpz/YVVSLFbE/5xYbq2g9SPxUwno1VQuORNEvVVVObNDSyDX/+t/8vPvbxj9T6LLpj\nON6LElHgUWtLZYZfZJ/3tfk5KGsscyTGoxADEjKEtclQfxwB89pagKqSK+Ib508jX6nPnzqA5ycM\nIXJhbQsrDRgqHcDcTJoBFfbgdLVhWpAKiqGyM+dk2q8dHZWu18ZoM4bKJ9Cfq2kaPv+Zf2SO77Cx\nU0IkXGuZtbm26VhjQlIA+/pYHejaVg4vjk8xc0dHZ8SzYToA9BHWCG5QRv4O13WjANXEmWuOvn45\nIuVXydXHXEeQBXdT6VXomo55WxNkjufRQ7TVWW3Tj0rXdaTOT5Lzg7uSN7thnKdakVFMbdW0nZqi\n4uqXn4XeYCw7AJX5ua8bhsodXuyUruuOm2lFoAFQocMlVtN1VDm2d9qNmHtasf/ug8yx/rHGJaIv\nv+hEzBQ4UUqvXsrPHfmVdagm++HVx49vYNgIeADTBiBQ13Wkzk1g5pkzDTVRFWJBAoDMRHOjR3fc\nSPuZ9NU50lMq0RlEtK+D8f1qFJxHmih68yHwks9oR9PPag54noOWZ/Uy/g7295Rn5xEiNFIFkyov\nTc223SBZVxQoG85UnK4q2Lhu7ALXLy4gc3mxpW4kHMd5pv3mr7UmVj3/DL3DpBgq+2RbY6hUGRzR\nu85q45Qm2E/L+0crV2oMmSAI+MDPvBd/9fd/ht17nRupqD+EnkiSdKK269kAGlCtpjehbLJV0GLc\nKACoEgvLyEA9JWQBqiefeg6TaVYjNZVeRbFaQTG92VBDBQDruRJKWQOQ6bxAtrtqN+1Hp/yaAao2\nGCqtbo8zNEADKus++iCTc8DX/+1bpCRjn80Y2Z7uo/riHRoewdgQ+0xPLK4yGipB4JDsotfASECC\nQLBd7TJUgFFAJLo2AeVCGXNX6lVuOYIdLWbqa0OSAFRzmTRkVcXyy+Oo2gD/q1HptzWXQnkjR/Y5\ndbOA5ZJSs7iRC5WatnPmmTM1I2GvkKv1cWkVRb1uGaqIh2WCUqoyqFIQ+Vbb89TDdjNm51P46K/8\nCd7zC/8Nv/M3X8Rsqr6o32ilHwCMHtyOO95+V804cP9dB5AkTCXtcdoFqF61lB/JUBEeSZqOnLmI\neLqkBxvvhNpJ+em6jitfegZXHj+GmadP4+XPfA3r46xOATAqEanILqy1zdrRDFUFnEfKT6nIuP6t\n48xxQeTROxBFaM8u4q+8QwiHIESc1z8wPAh/Xz0VJfSwuznKSdoX9iOxs4ddeHQdQoZls4oWINd1\n+AnH5FK1MWB3p/0qK+sor9fHSjVXRnHJ21ndHmTabyWD2UvseBWIHful4xdJvRStoTJ+a6AjioC5\nYSPZKdEPiD5DEE4A/JqZoqoyTMn2XaP41Of/Fx44eic6Q3EMxXtxuG8XeI5DkRCO512AKkAAqtnZ\nVShEqy0xZixklFwiZKtW0yoVzE3P4d++/V3mfYCxiRxPLRspPxJQ1T9ro1BC3vRa0/0RaMRiypXz\n7fX3IwChg6GiUn7tuKXb9HE93R0Mi1iWZZTMdjs+vwDOVVAwNzOPv/7k55mPNRzc6y1VxGQdUJUJ\nQBUKB/GW2w8zxxfSGRYM6To6PYyqE6EAikSle2uAyglEeZ7D0A5WND9+qt4BgNJQbaXq1ygiBeFz\nLcCKpmE+sw5NVvHyZ76G1LkJ6JqOnhFCR9VmpV/KZHVVYtwEiUzVlsVSVVXogg/Z+VXMPcdWIbrD\nzlAFhreBDwehvF4ZqnDcQ5BOWN5LYYnxkGkaNpD055/9CmbmDdpxYW0Df/WNp2sgiqr003UdSr4A\njdgFu+NNP/MW/Ke/+g38+t/8Nt796+8jB6c9Lp+/6nDXpcBJu5VtmqZhifA9oVJ+gJH20xSVZIRa\nYqiIc6YqBgFg6dQVrF6w6TJ0J03s+Ayvxri6js0pdgFuFJQXVTFf9mSoZr5/GpUt9vtHju5B50P3\nIDjSnjkdx3GI33U7pN5u8OEQgjtHEb35kOM9OpEWdLcaAYBwfwK8KCDcxwpVpQJ73Ys2MWeA2OmW\nm+iz7IBK13UUFljQVl1rrRUJVemXXVxDaoFlhgY6oswOtFIsY/xFttSb1lAZ1657/2jtWKN0X34z\nj7KLDRZ4DjGb5x3V71MURRy99WYc7tuFXZ2DkMw0AwmoXM8FxVBNTixhZoa9xlbhQqXKsjV+W3si\nRVXxiT/4U8gNWJ1LSwsoF0vY3GALAeznpGo6Zq4bc6UejAKBsKNVEABjLi631sQaAJl24XjOKHHH\nq8BQ2XSrgsCTflRW2k/0i+CKmzVAqCgKPvEHf4oKcZ9/8R0PIWwTsTdjqILxMLZ1sbraxbUNdk7V\nNXR5AapwgDS3vhGGCgBG9rJG1NdOjdfWQKrKb3OxvgZxHEeyVFNpY5xUtgq48vgxvPzZryFEpMRT\nbVT6qbKCNVPsTzFU8Ti7Nm1tGDIETVZQLSm48pVnW9L5yRYbJfAQY1EI8caFAq3Ef7iUH2U06Q9L\n7TfnNC9oVVZw5rxTxzCbSmPKplNRbJSnJivYOHYcmSefQfpbT6I46XSUpiLaEa0BxCxR+mwPVVVx\n/nQdUFDVYGsXp8gHwyvW1zLMhCCJIsISXdGSXVg1wItr0AmWB1WTXD1V5bdw8jIDBIvrW5j8zovM\ne/MeVKwnoEL7aT8vhgqqzPzu3HIaCycuMe/v2DmAoUfuhtTl3a+vUYiRMBJ3H0XXmx9C9PABpqm2\nXGLHupuh4iURgaQxtsL9CWY3HyJS4aWyXNMf+IiNCLVAO84rs1ljZuR0BgqhaZQ3tlpidqmU38bE\nYp1Fs783IKGLuG/nj7GpmCrhyWQBqi4LUGkqQLifW4BqbZ5laxLxoEP46mWrEqSKHoi5i2Wo2PtV\nVqp45sS0QzPCh0PgfSIUWUGFAMA+m4btqy+cxjjhn2SPmfU1LG2y2rmgz8+A2JnJ1ZrpKTi+dr3s\nwbeT9qM2wxwHmH5fVPP2djRUbkd60johb4AGn18Ep6mGpxaAf3jsi6Sp5ZtuPYAjO21dA3hj0bWC\nAlShZBz9yTij89ksFJFzEwUeDBXPcYgF/Syg4jjwTTIHgAegGhsG75pXsutbWJlehqIoKLo0ehzH\nQXMJtrvj7HPsTi/nl9ex9NTLzPs2UhuotmhPtH5tvlblTmmo4kl27ZGrKkpFGenlHE5++msopYm2\nP4Rbu8VQ+eJxY24OeXe9aDVew5QfXTFFsSb+kN/wlGqLpTLeu7q2QU78J67UO4rbvXfyF6/Umybq\nOvLnL5Ou0l6RbeG9dh1V59gw4y2ilKueaTEqyHQfYZlQO8e5VVI/JUl1D6pGkdzDtifRFRWX//X7\nNT8qTdVw9cvPOnxRrFCKlXpzS1s0BlQLbaVmaQ2V2abAtqPVNQ3Xvv4Ck5bgRQF73nnPK+4r2CgU\nYpIRXBNfaFt3DUTxooCQi6USBB5+l5eZrhugCgD8hM0sk/Jz/0ZNQ3XdAL3FCbrqS1eUlp6LcG8H\n2emTMqkMSj70uj3OAEydn0J23TlJ0hoqAf5YGDFzQeUqBeardV4ETM0QBaiSrt5pFEMFAGHK68yV\nsq6WK6i6LFACkp8ZU4qmIlcsI5uvA1efuXi7NVgA4BP4WjHDxGIKX3meXcTcoQM4Mc0Ch3iAXaQX\nFzMGiLJMFAMEk1Iu0NWf1Hd7MVSiMc9wwius8nNZYjTyohL9xrPCFTdw5cJV/OPnvsi8d9tALx59\nw12OY2I85tBQUim/SFcHREFAX5JlOmanbfO56ZHYN8iyWbGgHzzPoVpRHeknIRRsaS6i5ttgJIQR\nG2trxfipq2QT5ECAHaP79+9h3reayyJXdm62RIF3sKcAAF3H6lxrEoGUrYhDJcZXwO9DpIMds3MT\nG1iZz0IlilWiA13Y/Y67meMWoLLMWgkXhbbjPx5DRehoapYJ7bBU5uK7skqnJk5cmawt0BZDpVUq\nKM+xVUXFKdqmnopmDBUAnH6x7q8j+n2OFIUVK+ca7zjtQQrSKf2UGXKxjA0ihWa1PGmmoQp1xjBw\n+17meGl9C9e/eRy6rmP+hQsOiwZ3VIjUqJcoHTBo5SKx8/A8Ry9ROgDYKv1S5ydrmjJ7jDx4M4LJ\n9ppxtxsKIQ53pPwEHsGRbY7Xw/0dtYqU2jGCpSqYDFBAYlNMjpQfx8E/wApJ5bU0lHwBVcJZu/ae\ndGPRJwAIkg9B1wKjqBrjS8cBCEgiYkE/Au60ga7j63/5VUdKjTT2FHh07R+ps3he6T5zsaAAlbsZ\nrRdDRY4v14YgT2xaoh0xdPcSTauVKgo2I0Mhboy93Drhnu4TIVdVlKsyPv31p5jUCMdx2NnF6vOu\nrbJals4IOw/nChVs5Gz3xx+C7qrq5KC31IpG13Vv2wSfAWxfcZWf2pyhsnr6+UxAVc5l8T/+4H8x\nFY28wOPXfv59TDscX4dzDJMpv0QEQjRCpv1mp+wNl4371T/YgZFdzvs0ZOvGULTp6vgW0n0AzVDx\nooAxYr6+9tJVUqIiEV5puw7swvZdo8zx6XX2GQoTBTmtCNOrhTIy1+rXiUr5dT1wF7bddzNz3Kti\nmBMF7H33/QjEwwy7r6k6VFWDz9TGVXIsE99uvHYaKi9TT6+UH3BDgCrlAajSWzlMmCXElnVCaWqW\nfPgr84st6amA1gDV9MQMMun6efUeYQXPmWvzjuqJRtHQMoHnDJbAFasXWebBAlR8A/M7K3a+5Q6E\niXRO6twkpr57CjPfP93w78ub7M6o4iFKt6Id+wTSLd00jLU7f68RVX2hngSGiArOVztkwsDVnvIL\nDg+CCzoXbsEnINTvvO5hwl/N0lG5FwbACajEWBRSL7sAVdfWUWqS7pbXmwMqAIj0OcdfyQWGinIZ\n6/ImFjbWwXEcegiWaubCFB773b/GsrkRqJTYyU/g+frmRNfBVdgxZk9fUeXcybhz3HgxVBSgKrjG\nL8UuRToi6O1nwU5ZqSJvA1RWeilLACpJFCBXNXzl+ZexkmE3GffuHMNDYwfI83ZHRyiMCNGO5fpF\nGwDgOOhEn8NGgEouVjDxxEkc/5N/xuXnryOTdj3bHAddEKHzApMKB9p0S3cxVINkpZ9xrqLJ5v7N\nF76NRUJ3+sGffT+2Ew759pYzAM1QBSMhSF1JDFKAysVQAQao/OD/8RDe/K6bsWd3H46M9iFuq9q1\np/3cVYJe4QWodt/GAqrV2RSWZoniEIJS7t+5DbfdyQKZjZjIyFbCRCuuVqwT1i5PO1qYUSAp1NeF\n7oM7mRQmFWLIj0OPvhHhng5wPA8/8czKVbWmjWvUaaDVeO0AVZRmUCgNlRR6JQyV96T/g8tG2k/N\n5qGrqicTpasqynOtaXiolF+SEOCfeanOUnVs74fkAgC6pjvF3A1iemKG/U7TMiEx3Efmj8tUKkES\nwPv9LdkDCD4R+9/3ENs6B8D8Cxca+n8AQGWLYKgapPyA9nRU5IJnMVS2Sj8q9bnzzUfBE9Vxr3Yo\nFRYUOADVjtHaLt4e0cE4fN31SSzaxfYFszRKAR+hsbKl28REDFI3y5gom1sozTYGsNV0pqU0rBt4\nl2zp3vXiFk7OX8K5+Ul84cRzeG5iHD3xMGmSuLW2ic//18dw5umXUdggmJtQsG6XUC15NEM2GChd\n15FeIBiqRKsMFbvAuX2o3IJ0AIgkoujxYKjyNkZCtBgqov2OXxQgV1U8e55tdNsfT+C+XWPoi8U9\ni1LskQiF0EFoIt3mjxSgQqXAzMmaqmHhxCWc/PN/xcLxi5DzJcgVBSvzWZSKtt52PAdwAiD4PFJ+\n7Wiomqf8MsUCeB8PjuewuZXH1/6dregd278bj/7s+xjbEMApSAeAErHZDYQDCIwOY7Cb3Wg6GCrb\nuBR9Au56aB8efMtNDLC1M1StCNIBOPylrOB9AuJdcfQT1X7XThNNyBX2mR7YOUACqguXx3Hzx96J\n4ftvqh0LEwA91QKgys7Xdc2arjNiBY7nwQsCxICE5J7GRUJ9N+/G0Y+/F8ld9fdJEaLDh86DNzXD\nlF1Tu/GaASrRIx3ciKFyiw8bhdXHz4uhAoCTVyaNG6coKFybhN6gnLw0Pdt08ZBlmRT4Hd3DNlK2\n9/XjeB69h1mWKnW2tbTfxDUWePXGDIq6c++ww+SwUbRS4WePcHcCe4jcdCtRdlXU6ZpOgml7bM4s\nQ5Vb27mSGpeC6StkY6ioqlKKefthRCMNVWj3DrOvoMhUWfEch8QdN6PzzQ+h85E3ILmbNRS0vKjC\nREXmjM0tW4zHIYSCEKgUcZPSdb1aJXv/uSPiatlTNBkqXddxPT3veM0wodSxk2BVAaMK6Fuf+TqW\npomq1pG+GttBeU/BH6o1Tt1KbzHCdp/II+Ji+9oBVGzKj2aoevrYBb+syMib5ricINQWUApQST4B\nxXIFmwXn88IBeNdNt0HgeXAch5t3N7f6iAdCpPnj/Pic05pCChr6M9f3wWwQres60lfncOpTX8bE\nt0+QXnq5TdsGguMAnocu+F6FKj/nOI3Hwoi4LEtUTUNBNa7v946dZgx1/X4/fvf//k1wpTLbAsgn\nMhYoZMovEoQvEcfYA3cxr83YN+vEOpIYYDdF5aJSS0m6U45e4bZNAFDbHO65jXXyn7w4yRwTOOdm\nMhQNId6dwKEjBxgz7o31TcxMzaLDBtZIhmou1bSFmH3+p9gpn99X03b13rSb/IxALIgjH30b9v7E\n/UzxlORnN/+aUP/M1zWg0j361XlW+QGvasoPADK5Aq4tGLnd4jXnwJIVFVXb4FRz+aaakRzBuoQD\nfhzazpatnn7xnAOg9RFpv9xSmmlAyfyG9AY21p3VOzzHoTti7Cg7x4YRmdpBggAAIABJREFUH2K9\nQaiQ/AKENgAVAPQd2Y3eI/TgrgXBNrgZKrlYbspqabKKrRZLcH1+CT63S7eqoVKSayk/VVaguB3e\nOQ6StcBYDsw36FPWLKiUX6AjhvgdtyJ8YG/tfCCyoIhTq4bXVShIuqVbepydAyyYnl1dx3LGGDO+\nhMGESD2N/dM8f0MLaT+vlN9mOY+SC/gomorFzQx6ExEcGOz2dCYvFNnJr3O7bQdO2GPotuvopZ9y\ni3G9Un7BCMFQ5UvQbIsxDaii6CZSrHaGSohFa+dBM1Sig2W0Iuz3oytSHwu3HWqeto6HQogEJKa6\nVJFVzNnT4RwH3c/+Zk6uoLyVx/kvPIGL//QkSuveOkd7w3GONwAVROkVV/lZKb/yRgFr52axenoG\nfUkWoGyY9/I7T73EvPau978DQ6ODkDNsJaTYkWDGhRegAoAdR29mUlLra5m6PQFRXBWIheAnZDDF\nggyppwu+rtaeTzrlZzxDY0f3Ma+tzLPaJp9LL9e/axs4joM/4Mfhm9kx9dKJM450WsAnMp5y1RZa\n0NhTbpR+yg7muvaOID5Q3/hynNHNYt9DB5HYTjemFwkmVEX9tzbS8LYarwmgkkQBZWKi8GIp/DeU\n8jMGrZco3YofXDZZIBM9FytV/Nnj38GH/+df41c++Xd47sK12ntL043F6VS6Lxr0Y99wP1O9tZpa\nc/TfC/d0IDLApgJWmrBU18fZHUZPNAaB5xHqiiPUGYMUCSLgUVVpD58k1OjPdmL32+9CqIveQXEC\nj9GHWKrYbSraLN1nxcYrTvuVAcVYuKyxli9XMbO6iYX1LISg35gMq0Xwa9MQUhPg12drf/Oqha5D\nJipSgj2d8A/0OSZwnRCJcnJ9oY8Qmg9LQ9UdjzraZ1hx8orBalqpJR+R9mPOrYsdQ9UWhOn+eASi\nLQ1QqhgL4EqO9ltb2DA+syMSxJGd/egdZUXz1ITbYe92T2lwhPqETDZFjrOAwYuhEkQBgTD7rBRt\nu1w65RchRemGhsr4LuueAN4aqqJMgHHXOBkZ3Ya+zsYLcTxggEgq7Xf99DXnAQLYlzMbOPO33ySL\nXNzhAFQcbCm/V8BQ6Ro4XYNaVbB5fQVKSYYmq+gm5rH1UgmTM8u4TvRvfOSdbwQAyBvsou9O9wFA\nOc+m6y1AJUk+bBtk02uz0yYbS23QOA4JwhRTTXQhfvfRlquNvTRUANA91IOkS++kEGuq6AJUAzvr\nv4VK+z31xDMQw/WxwXEcQjego7JrhqkKP/sGmeM5jL3lNgztSKB/OIZdB7rR3RcBiOfCCkFnx5Rs\nK+1rliFpJV4zQFUkJgq5WHaI0gBAlAQIVhlmi2W6RuhQVBVrDXZMAPDilSlo5ufquo6/+vrTOHnV\nWGzypQoe+/dj2MwbF7qytAKVEMNaQQnSI8EAgn4Je3awVgNu13SKpUqdn2hIlU42SveN1b+zWdqv\n5kHVJkMFGJWK+9/3BlJ3NPrgzejay/52t4kmKUgn5pDMqyBM53QN0FRUsgVkSxWcm1nBQiaLmbVN\nnJtchF4pgs8s1JgsTq6Az7ZW9ttyaArZ5kCk+ltSDJWN2aEYKrvP0x2uVikA8OLVSQiRcK2Js9Rk\nB+zvCCNI9BeTW9BRcRxXS6Pquo6SLEPRVKwW6M3OwmYdpPnB4cd/9m246UHnRK4Ru3y/DbRxFENl\nA1SrLVgmAAZD5fX7mumoKFF6tCOKXiLlV1ENhkrXdYi2Jty5DPsZfp+AMrFwhFyAyhcO4qjLTNYe\nEX8AoqmXpHu+XXf8dt3nnBvkioLzXz5FGuJSUa2otVSOLvAG6yX6SKf06loa+SvXUF1LN2arTEBQ\nzuQda0d3jB2r64U8njh2jjm+d2wEI6OG1kZpAVApssJshjieh2RLr4/sYLMSM1OmMJ305eIRJ9q2\nFNbzbVm3NAJUHMfhpgePOF5TNBZkiC5X9IGd9UrjWwlANXltGk8+8YyjL227lX66pkG2+d15pfwc\n5xkOIRoPoKMzBJ+JEVSPDZAmyxCI31o1N55KucpY+TTqtegVrwmg8gk8SQ1TlJsUtt0Y4oJ4hq4j\nvb5VA0tesVko4qpZ7fHdly7ipWvOyqaKrOD8VH1nUZ6dd39ELWiGypiEDu8eZV576YTTsLDn4A7m\nJlazRWwQehErJq+xlVh9MWMC6LQBmXgTQFWr8GvBPI6KSF8Su995twMEJbb3Y+jew/ATovxytuCY\nrCktU8fObcyxQmqjZTaroTBdlVHJFrG8kXOIHze3Cpg58RI49yJaad13p6VQZciEHsw9aQCATgjT\n7TuxKME+Fsp1QHHHvh3M69MraaRtgI73Sw5mxB3h/oQh6nRbVpXL0Ij0mzssx/SyrEDXgdX8BgmK\nAGBx0+kdl51exjt+6cdx+1vvqB2jQI7PLsCnHPFtgCpNuL+7BenmF0H3cJYnzWNtY7PdlJ+iaihX\nlFrLGU3TSFAmiQKKhN7TbZEhRYK474E7yXMHgLj5rAs+AQmCodpMbSBjN+u1jUNVUXHu25dRyNDP\nYny0Dz6iz2TVZKk4S48lSCRDpZXKKF69js3nT2Ltm9/BxgsnIRNicYuJrLpK3rtj7FhObWzge0+z\nRsNveehWQDa0UwrR10506ZfKhCA9GA44gM/IdnYTOVsDVDRDRQGq7MJqWybPjQAVABy6/yaHBEMm\ndJJMys/GUO3YNYqx/azE47FP/x1Um0aJ0lE1EqbLxYrjurgZ6KoqY6OYdTj9U9XoXil6ZXOrtsbZ\nw1pLGroLtBGvHUNFeAo1TPcB7bWf0fWG+il7/ODyBGZW0viHp9jKDwAOV/XS9KwnY7RFMVTmpHJw\nlAUHp0+eQcnGeEmRIJK72Z1NI3E6lfLri8UhhvwOENWMoZJqHlTtM1RW9N+8Bzf9zFux7c4D2PXW\nO3Dog28GL/AQAxIEF/OiK6pjR0LtcqMDXaRAPDPZWtovRLlZW1S9IqOSLaBAaFFmrrIA1hDgvnLR\nYu3z1FfGUEGt1na64XiY2cVWKgoUU5PW2xHHKJFmevGKc+xIPXTaTwz7IUUD4AQePmLhraabt0rq\nOWiAOqvCbyXHen/Vzl2RsZavP0vr1xfAcRwG99SfDSrlJ1m7Yk1jClh0oNY4VdM0rBGAKhkPkno/\nT+sEolLZbu5J+VBFOqKIxiIIuJ4zTddRkivIFyo1hqqwVWDmGoHnIPB8SwyVFA5i18E96IvR6fiE\nacnRs6sLPkFAjChgcKT9eAE6L0LTdFz87ji2VtgNpC8cwIGfehhHPvo2RAZY1tNK+9UqiXkBnIdO\nrha6Dnk1jc0XTkJzp8k11Wh8n3U+m91RdpNxfXYWGy6bCZ8o4A333wyusAFlc4sBO3wwACHgvFeU\nfirgYvhGiYzEnJnyI9cxjkOoK86AUE1RkVvyflbc0QxQxTrj2HG4vsEiGSpb8UG0M4ZIon4tOY7D\nL//Gx5i/2drM4vuX6x1AKIaqUcrPbVlg7+OXKWZxcv4Snjz1Aj70rp/HyRcMDRwJqMo0oyxvbMHn\nY+FOJVc0tLXEJt0fbm4f5I7XDFBVc0UorsWsKUpsU5RO6acCxE04eXUKn/zKd2sLkDumbVVRWrmC\nyjI9MLKbdMoPAHZ0diDmYgDK5QpefMEpkKQ8qdYuzzDXCgCKhSLZw68nGkfn7iGHv0u4N8k4stvj\nlTJUVnTsGMDut92JwbsOQjC/j+M4+AlvobJNmE6C6VgYyV0sEG1VR0X187MYKk6VUd4qoEw4ts9M\n0PeXq756gAqqDJn4bncVDYDaQuY4F6Cm6+IFgfR1s/f0o1iq4y9fcH63h44q0l8X5UoxovVDCzqq\n+Egvdr/9Lsg8h2K1jC3CI8oei7a0Xym9hc2ZFcQ668CAYrdqDJUXO2X+ho2VDFMt6pcEBAM+R3uR\n2nfdQKWfUpUZJoPjuBr4HSEKVVby6yjKak1E7GXqCYBkqIIuiwxfJIhQdwL7++kSc4uhSo6NQoqG\n0EGUlU+ccbqr66KEq8cmkJ5l77kg+XD4Q4+ge9+o8Vt72ErNsqWjsgAVx8EXi0AIEOPeFbosozzv\nfPY5TYFaURiHcMoygiKG7jp6ALFoCFwl37J+qpEg3YrGKT/2RHTOqMyMEzqqrRYsBwCj6IZpRM1z\njED+8AP1tJ1MaahstjkDRJbg4JH9ePitDzLHXzh3Hqs5Y8xSGqqNVAYVjyb3bkBl3zBNrM/XtF7F\nQgl//om/hKZphlzBbfGjadAJz0glswFe4CG47QVM3XZDQ/E24rVJ+ZmIueTaLdA/ygaA2urnRzNU\nD7/1QWbRyhXLWCYM8qyYTaUdIjkvcbqXKB0AeE3F3fcfZV5/9qkXHP/u3DPkEPACRn/B9JUZ5m+n\nJ1grh45QGAGfz1HGChgOwDHCn8WKdkw9byQCRNrPzkpRDJU/FkYHAagyk4tNS3ABjwXPYqjUKnJr\nGyTTsTSfQaXMPpSvLqBS6s05beEjfL2MFwgdlU2YTqX9mumorl2bxspSfbKWOjtqmior7L0EAUCK\nsoC7VYPPbXfsR2TPEJbzzRktS5huxdnPfQtX/+E7tX/TVUDmuTdJ99EtZ0LgJR9THg8YaU0qyPFl\nFToQgvRwPFyraHvgjfcyr6/k1lGoKIBujIushwcVAJKhCrpTfuEAxICEI7to+wSLoYrv3oFgMoYO\nQmQ/d3nWsQhOnZzG8lV2gecEHgd/6o2I2gprKEBVKVkMVX2ccT4Jyb0DCHZFwRPNwe1RXXUxi6rC\nsFMAIHA8YkRbHXfcc9sB6LoOTtehZtnrTaXBaVNP53cNjQwy1YtrqTQK+aJ3b0Og7qNmi60WXMYB\n2jJBIBqwjx3dC7+5LlGidJ9t82YXpNvjYx//CMmyfufyeUMHKPBsxwMY9glUVPPOtd/SUJWVKgqy\n8/lLLa/i+tVJcBwHwYOlcoeVLva52+LA2NjTDNXrBFBJJqospZ0DmO7j90oYKnaiH905gjvuua31\nz4Gho1qyOZvLa+tQCP8dL1G6FffefSvz+onnT6FiGwCCT0T3QZZNoKr9qHSfJUinFr5GaT+fxIMP\nBkjX4lcj/AmCobItOuS9j4UQH+4F73oIlGKFacRMRaP2M5wiYyNFp4R1TcfcJCFCl0uvmoUCp8pQ\nqsTukKDKAWfJfy2aCdNtVVX9nQkME9YIzz5dB/ScKCJy0FZazXGI7xl06PqkKMtiqIViw2INe6wt\nppHyqO6zh12YboXIcbWMHMVQSeZGiRak1yd30jIhEQQfDIL3t67LaNR+hqzws4HeN77tITZNq8q4\nMrdUM54lPahMQEVV+QXdKT9zkR8Y7se2BAtukuEwAokwpGgIwc4Ywn5f7fOt0FQV06bB8NqVGcye\nYPsBAsC+9zyADtfiSwKqsgLwnMNbTRd8EAM+JHb1oufW7ei6aRjRvdvJlkjVdMbpE6WpqBL+Qaqq\nobOJsalPEHH8G+P4wl88ha2NAtQcO39TALtEVPi5U36SX0L/IHv+czPzHhoq43rEiYrWrfkUU6xF\nRbN0nxU+yYf99xj2BwpRDWuv8usnGCoA6O7pwgd/7v3M8Zn1NVxdMSo+23FMr7quqWo+39kyzWS/\neLxx2s/x70q1tikidVRbhde/hgoAii5hOumSHnZpqFpd0DxSfr19PXjwTfe1cbZGTK04d0YUS0UB\nqqgNUB0a24GIS3dRLpVx6oSzTQtV7bc5vVRrPGwFVeFn6SUoQWhjQNWeqWe7QTNUNkBF7RBiYQg+\nEYlR1leklbRfM1H6FiH4tWJ6YhW6a8HjdN0BYuyxNLGI5770DM49c8bhReQZ7TJUYjPrBBZQlV1p\nwjv2skD92e85GdLg9mEk3/QgYrfehM43PQh/3DkmeFFwVKFZ0SpLNX71OiouwMMT1TTpfA4lF2jg\nOA5+c8dNaqgshuaGGKoghGCQnKC9KodoQGUyVJQg3ZaW7exKYs8Qu1idnZiuAUIq5WfNnSUirWEH\nVBzPQTR/SzAewj07naaO8WAII8kuhE2riGAy5mmfMGHqqOaeO8+8BgB77tuJngOseXGom02XyVXV\nAAd24bNtbHMcB19QQqg/idjRW8C5U+CqCjlTn9c5TWEE6QCgKXpTQNUbSYLnOMxOruLfv/QSVKK4\nggJU5Ty7TrkZKoAWps9MzjZkqCJ9nUz3CaVURWGtuR64VUAFoFY1S6X8fEJzhgoA3vPouzAwyM7N\nT165AFlVPBzTabZNdqXHLYYq6yENOHXcWDP5ALHBczHKaqH+GRSgKm96MVSvIw0VAKbSryWU2CpL\npWtkyq9voAd33ncUfg8mAKAFhdPLTmFgZYkdGFTKz85Q8bKMu4mqG3faLzbUA8ktqNZZawGqwq83\nagAqkRCYxoa8U36SJDRtivxKgtZQmXqTShWqSyPGCXwNFFI6qrUrzRtWN0r56XIV+Qbl3jNTGUAi\njAyJtN/k2Ql8/r/+LY796/fxjb/8Kr76F19uem6eGipiVwd4VPopjVN+Jc0JVO7Yx6b9rlwcR8rV\nAFmMhBEYHjTcuqkJt5MtFJBbEKaXCyVMr7C2F3fetp9sF7K4SWggzTSCTixKxXMXsfmDU9g4cxXr\nVxaxftn4b+PaMio2+wHKMqEjHoQQCrTFUJFu/BZD5VHhZ4Wu67hzjL0f0yvLyG8a8yKZ8jN/f4nS\nUNlSfr5wsMYs+kMSxnr78e4jt2NXdy9uGhzGR+68HzzPIyCo0DUNoU4jtUXZJ0yeuY5qoYTcIivk\nH711CEMH+0kQK/p95HNfrag1RgZw2llYwalVcBxHtkWqpupzsVoqQyXS86qqNW290x+pM7bjlxaR\n22DXH6qDAClKJ9KllI5qdtqDoTKXYl7gER9kN76NGs1b0Q6g2rZ7EIneDpLpFcx7k+zvJH+XFZLk\nwy//JiFQL5dwfPI6qaNKzayQonEm5ac3BlRXLo4ju5VriaFSbR0FaIYqT9r2vG4YKp+ZJy+6Un7N\nqvwAtAyodE3FKoHqe/t7EAwGcMd9t5N/98a3PoQP/8KjzPGpZeeA1kplJmed3WwMqLRiidRO/ODZ\nk6ja2CcvEbdcrCNvRVEwRfTw64sbu0JfiB1oUjiIYCerCRBEQ7j4w2SoKOsEi6GiBrMUDdUWBKry\nMb+UJitF7UGWtZsMlVySHT3l3LEyu4qSQjweBKA69cRJR9f6y8cvYr1RZY5mmBG2XOVnvMD2ttLU\n2vMQIVJ+pWr9nBRFRX8ygcFuNg3z/NM/oL/T1JY4DoH1rNJ1HZW15oBq9toc0gVW+Pu2Nx3F/jG2\nfY48lMC2O/cjsb2/Vl3o9wnQqT5fAJTlFKorq6hmcqhulVDNGv+VMwVsnr6M6loaqqI4rQDM6Iib\nKb8WNRkAEKSqSM2xnPMw9ax9ZqmMo3tGGRNFVdPwzNNGtXGjlJ+bvQOcDJVkA0Z+yXiODgwM4qdu\nvxs/dvhWxMzNUzDAQ17P1OaFRDjA2L/lNnKY+MEluC96MB7AjtvNzafsAToJw99yWTFc0q0gAJVl\nh0A27rbpqGSiEAgAVFVHZ8TbzDgiBRGxO7/rwMyic73g/X6ykKcVUTrQwDrBwzbBCiqTkG9B4tAO\noOI4DruPsq1oRF6opaL7G7BTVtx57+04SkhZjk9dg0pUEC5eX8Df/V//GzOXnGQAVeWn6TpyFdps\nU9M0vHzyDL0BahNQlTfzqBIMVSDyOmCorLJfwGCoLLSqqRrZ7flGGapMZguya4CFw0FEosak9vAj\nDzB/s214AL/6n38Je/axKbfZ1XXGvVXNO28CBaiiNqZILRZxy9EjCLsaXRYLJbx00ulJRaXs7IBq\nfmbB2WsLQEiSEPUb5e1umwIrqIfVV7NM+OExVIEGDBVZjGBbrEJdcaajOQCsXmA1ZPYgUzJmP79K\noYJyg76Auq5jdpLdkXPVIjMhUuBp1t62wx3mbp5O+XkAKo4n037WQhYl3NLnJxbx7WPX8E9fO4vP\n/dvL+NsvnkJvhGWXjn3vefo7qWeNE+DrMj6jUlXw5PPX8di/voR/+ufjmDpzjX2/Lb737e/DDYWC\nkoQ7b9uHA3tHmfdPLy5j99vuwpGPvg33/M5P4+7/81GM3rGfTPeJotDUALE4MY31pXUH+AWAUNCH\ngN8HIdQeoCLHV65Bys/GUClbWSRiAfJ+PPGEcT9IU08LUJFVfnaGqj5/SDwtkxB9PHySgMriMoJJ\nY/wIPI84MfdcO3mZOdY51FG75pxCa+ioDZyhozKNGBUFa0sZXDozh2PfuYDnnryE1NKmAah0HVIP\nC6iUrWztnlQ9WGZV1dARIvpTmnFo317m2PS8M20tEO2FgNYBFZXpmJma8zT2tIKa6/IrzVPq7QAq\nABg6OMoccwrSaf2UPSwbBdElflc0DccmLjMtaABg/sos/uGPPo+//6PPY/6qUfno1lBpuo5iteTp\nVQcAp35wmkz5uYtI7Os0JUovZXIOl3YrJDeZ00L8yAGVXfSolKs1kCAXWMGvL+BjSj6tCphmkVph\nEX2vrQXH3Q/ciVuO1jtkJ5IJ/OEn/jNC4RD6BnoRdelEqrKCxbRzB2NHvrquI0eYU0Zsk5NaKkGS\nfLjr/juY97nTfjSgqk/sEx7pPkOD4PdcXChAJZk5+x8qQxULM6aQcr4ETVHp/LULgPUcYtMjqfNT\nDV26/UE/eFdZrSKrkKsKKoUqaZlgj5nxReiuk+Y0lUlvlAhR7MI1bwNYa/dNGXuKXhoq0MJ0yzGd\nEqXnMjksLG0iX7R1rZfZz7h0/grWVglGjQJUPA/e74cQjeDMpSVMz29A03Rk8xV89S8eR7noLU4/\n/gJrqnh4z06IooADe1mG6urFcYcxrxQJom9smBakN1g4rKiuppGaYW1GOkyH9HZF6XTKrwhd10lR\nuj0tq2Rz4Hke27vYqq7LV6YxNz1Pt50xGTqSoZJohopTqqROLRSWwHEcyksr4H1iTWZA2ScsE2Li\n5FBdI8V5MVQuQKXrOqbn1vFvn/om/urX/gKf+OAf47O//Rl86fPP45lvX8DT3zyHv/3T72Di8iKg\nqRCCAQhRlt2urq4BmkZW+MEnQlN1hKUAOKLdgiAI+OlfZrMQS6kcypX6M0k2DAdt7BnSckZ3hY0l\ncFspcLk0hntjzDy8urKGImWEa3ufF6BqVtmsEfNJI0ClE6t/M8sEKoZGB/Hun/ox5vh4ahkVzbsy\nevbSNL7wB4/hy3/2byhlnc+Lpume6T4rTh1/GSA2oAxDVbQzVOyPLq1vMeyrLyBCaFJxSsWPHFD5\nXAucVelHuqQTD7bdsC+1sorxy9ehEsg8lSIAla3lA8/z+B+f/CP8/h//Nn7jv3wcn/3HP8fOPYZo\nl+M47NnLslTTy07Gwo58C4UiVJcY2e8TIdmQu2o+iPc/fA/z2cePnYRsE5pSKTu7EeYEZehppvtE\n4m+t6N4/CsGV244ljOss3EAfv1aDFwVIxI6vki3QgMqVTuk5tIMBZKX1LU8qPLe8jpUz1xEkxlAh\nX8HWeh5Kkwlq9tIsbVdgS/tpqkpOsAvj3oCK08x2B+0wVABt8GkBqhZ6NQJAyBdAnNi5P/80YWpL\nbV5MZkHqSmJ6wbnBKObLuHz8Ivs3MAooVlZZHcj9dx4GAIwO9yHk0v0VCsW6u7QZ8e44zVC5/Wio\n0DSkrs4why1AZWio2F2pXpXJxYxuwK2iUiwjT7BLboYKALZ1JhGW2Ofu21/5DhQXAy2IPESeR1VV\nmGsg8rxjbpVM7Yuu61BLFfgDLFAPRYzfqleqkNPrNZaKYqi2ckXH5oXjOXQM2NJ5HoAq6BqXSxs5\nnJtYwdWXrmN9KU1eV0VW8ZW/P47smsHK0Gm/NLRKmW1uDiAwOmp8jqohSDy/R+++FXtv2evwNQOM\nazVnS/tRgnSA7uMX8nPgKgXw5Rz44ib4/DpC5Qz6+1hwNG/r4Vr7bhtDFUhESOscql2b4z0UQ0Uw\nMlbkiEp1y9ST43n0bWcrDr3iQz//AXR2sWzrxZUZdG1r3Nbq8vGLmF1wbuhUTWsKqDLrG5hdZIF+\no5SfIPKUdy8TN6KfAl5jhgqoV/qR+iliMbR2zV/8u8fxwR/7efzyh38dH3v048i42KPUamNABQCi\nKOINjzyAt7/rEXR1O2/6HkLA6670swOqRqaeVujVKnRFxe133YKgC7wU8gWcfrHeZ4piqBSbHwzZ\nw88UpPsaME1SOIgD738DAkEffJKAnv4IognTK+uHyFABHsL0zbyHZYLzvYF4GPFh9gFPnWeBZerc\nBF7+7Ncw/tXngDK7ky/my0inGk9OgFGRUqgST58NUJUKNCOTWV6vCZSZsFJ+pG2CN6CihOkWMxCM\nhhy9xLyC4zj0d7AL1LNPPMVqO0iGykzVBMPI5dnF7PwzZ5ljAPDUE8eYY1F/CIcOGdVhgsBj7x42\nRXL5wlXHvxPdCdrU0wYmosOd6Njb7/DPsiJFtHFKmpVufMCwDeEkdjL1Yqm8dFR5aj7oMM5H1/Wa\niWQk7EdfhF1wnnriGYZ9jUSM9iZkhR/RdgYwFxdNQzjm+k0cELEdqywu19JzIb8PvGvVUVTNkSKP\n90YdbCqnKWRrsGDCeX1WCOaOilKxiq98+mvQVJVM+1VX05DX2TleCPggdHXVzjlCgNU3v+NhcByH\nvXfsY16bWmgOqEhRepBegEeJjMDMDFGhbLveHMchQgCxPJF1sQed8vNmvHNZ9l5YbWe6h7rha1C4\n5Y5QOIRf/LWfZY5vFAvQO3i85zfej+4GVeabrk2pznOelgn2ePnMJeaYVqnPybqiOgAWx3Gkjsod\nN1LhB/wHAFRWpR/FUlBeStBUZNIb+Nxf/n0tHTA7NYe/f+xfHG9bIVN+jduv2GPPPrZfUSOGqlmF\nX+1vSiVIfgl33UeYfNq0LCRDZaZTdF0nU351y4TGgyEx0osdezux+0A3uvoiBi3NcWS649UML3NP\nL8sEd/QeZkHu6oUpxy63vFXA+NdfqDkGuxlRwPCi2ki3NrHPTrJK9nN/AAAgAElEQVSpMM7WgqZE\nNXU2Y+HaggFKZGefqnrKrw3bBIDWUClVQzzOcTh032Hvv7VFTGCv7YVLU1hfdoINjmAPdHPCXSfA\nFGCkOt2aMl3X8dzTLzDv7Yt0oqunzmBQab/L522AStcQRY5smm0xVJxPRLgvgUAijFAvq99ZXWa1\nKMlEsAamgNa8bayg3Pjzm3kUiHFhidKVzWyt/2EkJKEvmmR+UiaziUzJOafETHDSTD8F1DVUVsl4\nsjuMUMT06eKA3oEoJFvvtcpSCkEzbcxzHCJEyXvWxgYlRwhXfYKl4gUBkt+4N5qmNywEccf8+AKe\ne/xZSF1Jp4gdBsAtzbAVo754pFZyL6sqtsV7HNe2t6sb95iV1nvv2M/8/eLyFqrmcymE29BQeTAa\nI0NsSndmlmWo7BoqAIj0s2xPM2F6uxqqPAGorCKJ/h3NBenueMMjD2DPdvYZ/vq/P4XkaBd+4U9+\nCT/xq+9F5wA7dmTFOdfIusYYelJx6sWzTLsoXVFrBWP2dJ8VvhZc+V83DJXPlZcsrmehVKpYOM4i\nTT8lCtRUXL5wBYqrwu7Ec059Roow9WwPUBHC9JRTmK4U7ICK8qAiPG3MG0yl/V44dqL2u0gNlcmG\nrKbWkHN9n8gLtaqWZoBKI0wY+WCgqaj3lYZX+xmyyo/Qp3QfGGWbR+eK2JypW1hMPXnKoSVwjzcA\nKBQq2NpqzfV89jrR10+p1tibIuFJY8XCpQnwq5MQ0jPg16ZrzBZXY6hat00AAAg+whtLqwG0N3/k\nrbjvvQ9ix007sffoPtz77vvxrv/0HoRd1z0k+NHf55zUdF3H5XMu4bGHKB0AVhe9RbLnnnEWWExd\nn8bSAmszMtzTj5CNhaaE6XaGiitlIVYLCEXZ8W25Uvu7ErUxIsWC4Gz3v1yRUSi6va1Ml3Tb89ae\nMJ0dp2vzqwzbF4yGaq7VlcX6ghoJ+yEJPnSG2Gq4FZcBarzTuI/NKvyAOkOlmmkdUeQxsiuJXQe6\nceCuEXT2OTc3WqUCyaYvofr65Wxsb8cOli2mdFS6ptXSjV5FIJGOKLbvG0SYMI19/vFjmBufrxVC\n2KO6xo5BKRGDbDL5VUVFIhDBLQN7MRzvxY7kNvzkO98BwQQZg2NDzLOhajrmlgz2kHTN1zSUCQ1U\n0IuhIlj1WcqLyfVckzqqVxlQUSk/y4Pq0H03Ma81C47j8JEPvpdZR6qyjM/+2efA8TwO3HMIj/6X\nDzN/627SvF5k11Oqbdyl81dQIiQA1vPqLhwDPDJf7ve8XgCV5GIMiulNXPvGcZSIEuHoNhbJcpqG\npUV2QK6urGHVlpKjXNJ7+1oHVL39PawwXXEK0/VKFZpJv7fKUFk709vvvoUZILlsHmdfMszzGlX5\nTY6z7FRPNFaj6cUmqTvSwO6HWOFnRYDoN1fxsv0ndv6+UADJXWxfMqvab2suhVVXClAkOtnnEUGW\nMAPcRpQJz1yagU4xQyY4ashQXZ2p2Q5wqgw+Mw9UCoCqQNf19mwTAGPSbaCjEkQBD7zvITz6+x/G\ne3/rA3jwAw/j4L2H0efqD8ZxHHaPsILT+RmX7stDlA4AK0TqzIoLx845xOTPEvqsRCCCgRGnKSBl\nnTA3s1DbrHCmpiJElDPzJg8R7HI2cg101MdcOsPeq0QsCFHkHeNfeIVu6VR7DYud0nUd5cX6tYua\nE3dflF1A08VNyDYn63giDCnoa4mhqgOq+sLEcRwkSUCwM0Km0fhq/ZmIEgAhawIVMehHdICYSynT\nW1VtCKiG943g1z77W/jg7/wk3vuRe5jFWNd1fPWTj0MLt6YR9CVjUMyWS1Zv1lggjJ2dgxhJ9CHZ\nVbcN4XkeY0fZtN/0fAa85CPTZZVimREw+wM+cD4Jasc2aC5gPEq0kqEZqhYA1UqmYRFO24AqS5AA\n8Sge+dm3YeTAqOffNYpd+3bh9hHWQPjY957HyycNOUCIyDwpqub4bet5dj09csthhhTRVA2XiH62\nVqWfXT9lhVufS8XrNuVXXN1kFkEACPclkdxNVBloKlYIIRoAXDR32LquI5ViAVXfADu4vYLjOIwR\nLNUUk/YzblgzD6ra+00wEwgEcMe9rBeWVe3nIxyLrSq/iQYO6QANxuxBMlRN/ubVCAoklTI5xiUX\n8B70PUTab+3SDFRZwcS/n2BeI1N+uRIKBG1vuQc7Pnt+FVR2yxKmN2KolubWodpK9DldB59ZAFSZ\nBFOCKDD9v9zRqNLPK3oIQ9cYAaDn3GLZBqL05SliUTAjt5HDtO2Zfo4AVN3hDob6j0VDGNrGLtRX\nLo4b/8dsyRKMULtHDpxPZFrjBJL1MZcmjBu7OoxxZi/IaIuhIsZpiqiIswTpysZmbVMFABGTTe4M\nxR0l64BROr5aqG/gYokgAlG/R4WfqzGyKUqnduhCKAj/Ntbhmtuqe4RRDFWxIkNRNaPFjJ8oGCJS\nNLpWB1SlKqv9SprAQRd8GN3Vi/vefIB5Ty6TxZPfOtUQTACGAFuIRKCU6wyVO/yu6YBK+80vbUET\nONIvqkToPYMhCXooDgQi0P3OTeMwYdK5ksqg5B5PrpRfqCsBzrVWyoUyqTW2on1AxTJUj3zorbj9\nLXfccLbCHwvjgd37EJbY8fOpP/kMZFmGzy9BdPl76TDYQSsoQLV7zw7cftctzPGz11mT5xpDRQCq\nQKI5OP+RM1RjY2MPjI2NpcbGxt7Wzt+FKV2U+6QkEQfe9wbwImX4VsXKDO2SffGsAaiyW1mUXW1a\n/JIP8Q6WVm8UuwlAxeiozLTfVoY1LIyQKb/6ZEqZfD7//R9AVdSGGiqywi9WL2G2/62u69CqVcdk\npJb+4zBUuaU0W7IaDnhOBF17hxmzPaVcxdUvP4vcIqt38lEM1UYOpQo7uQ8f3E4KJ2cnCB1V1XhQ\nKcuE2nnJKlIus0DO/K9tdsoKyjHdo8LKiu5BFlBJPDthuKuPOA9ReqVYJs0x7XHu+0bab3Z6nqnU\nA4DucALdgz2MLQWpo7LSfmaqNED4w3AA/H294HQnC+KPh2oNn9MbLLjo6jAAl70go71+fkTKrwFD\nVV5wXuOIOXHzHE96Uq0X6+a10XgIgWigadsZoL6pohYUIRKGv7+X0SVBkSGZGzmfKJDNbXPlCpI7\nt3kwpVXWY0lV4Q+aDBWR4u7oM3+zCSYfeOQghney43Xi3BQuTzcec1I0AE4Qa8U7skrYa7gsT0b2\nj8LvYuMUVcNSKmv07nRFeZM1Ew6GJOhBU6/nuqbBgB99vSzbNLfgqnh1ARhe4MleiI16mLZrm0Bp\nqKKxxu7yzcIfCyPg8+HhvSwwnptZwJf+8asAaN8ui1HUdR0ZAlCN7duNo3ezfXjPXplkwHZDQEWY\nzTK/4wZMPYEbBFRjY2M7APw6AA9HQDoGx4bQSbSYcMeed9yNUFfc2e/JDE5TsbzMll8DwKVzVwAA\nKRfoAYDeno62G/+S1gkelX5b6yygijZI+QFG+a7fNXlvbWZx7vQFow+Xa5OglKvQVI1uOeNgqMxO\n4tkcMt87hvS3nkTme8dQNb2GvDRUP+ygNFTuljMAzWRZIUg+dO1jF921S+w1AYyFwR2bqQw52Xb0\ndpBU98w1go2Ry4CukTtWe8xP047ppCC9kX7KjBtjqFiQyFfZZ2FuLuWcmDxE6RQD447xU1dRypcY\nfzUAiPnDCPqD2HvXAWYBogDVpZcvAJpq6MUABILsQq/rgL+/h3F2B89DMlP96wRD1Zk0GargDTJU\nxFitlNj3RjuihqHsojM9IfmEWiFCd4RdQMtKfWMYS4QQiPhRqrKfbwdUounfp+s6FLI/XQS8zwep\nh5VUSMH6GKTSfrlSFR07twGCCN3FqHGAAapsoatqTfxOCdKTFqAy3dJ5gce7P3Q3ggRoPvHSDEpE\nm5nauUeD0HkRStmZ8rOHr+qc+wRRwI7dLFs3OZ0GR1SZlTMsoAmEg/WCEY6dbygd1YwbdHPs8xht\nU5hO2yY0qPIjNFSRVwioxKAEXhRweNswBjvY83/s03+Hp554hqyOtWxssuUSKq5xxIHDzr07cPPt\nhxkT0fXNLOZderp6yo+9h8Ee9rzcEfgRM1RLAH4CQPPaczMe/sBD+Knf/SBCnY3RYe+RXeg7YlbY\nEQBI0zQsE+k8AJiamEE+X8AK0WevrycJsjyoQYztZyv9ZlJphzC9Bqg2WEAVS7BVRvaqg2AoSNr2\nn3juFHiBrzU3tcfmagYrS+yC1hOtf5dlm5A7d6l2fmq+gM3jL6I4NfOaMVS+kDfzZI9mOe7eQ2yO\n3vM7CYZqZYa9fsGgBEEUMUo0eZ25PFerbrOCAwC5XHPG9or5aRbcA7QgvZGpZy18xINuVvp5BQWo\nStkqAq6y6GKpjPW07dnyEKWvTHun+6xQFRWXXriAJ7/xFPNadziBu3/8HiS6EzVmwgpKmH710jXk\nxq/X/k14VELXAClJzC2iD4Ft/ajKKrYI3VyXWTnHN0v5taGhoiLSEYW8nmGAGcfziJtNhAOEVq/q\nAFRWyq+xbYI1jgzLBOe44AQOXMj4zVTaz2dzVafSfgVVrTPNDWw8aqEq4HkOkl8gzztp2QPwfM2L\nKd4Rxo89yvY8VVWN8T6zhxQLAoII2dRQUSk/n1qF6tpQ7iAqFqcmV6EVXGyUpqJMzPMBOwghSIAR\nSkc151qjiBQbbZ3gXQzyaqT8Yq8QUHEcB38sDI7j8NYDNzErrq7r+MQf/ilSORYYWsJ0qodn1B9C\nKGz8d/AIm6Y9O+lkwbVyBbqmkXrhEMEY2oMXOIj+FuZi6m9v5I/Gx8fL4+PjjRParvixX3wn/KEA\n2YrAimBXHLvffnf9AMczVU2ZjRzpMA0YYOvKhaueDFVLjl626OnrRizuPF9ZUbFg6xGomICF8qFK\nEIZ0WrkC3VbRcM9DdzHvefH4ywDoar1rl9j2Hp3hiMNAVAz5oSsq27BW15E/dwlymn0ofxQMldGj\nsPkDSzFZ9ujYNdjQvNQelIbK3bIHAKJR4zuHCfZrfSmNbIkd7ly11DJDpfuc17ettjP24EUPcOed\neuzsTzLsbDFfwTaifHnenp7zEKUvT7EiUIkwEDz2tWNYXGTfu3NkFPe8+34AYAT/I0O9CLnGYqkq\nY/zZF1FcM/ZvnMI+/5oO8CDOV/BB6u1GJsuCqVjEX+sS4GCoWugPZgWloaIi0hFFZYG4bj3dNUAl\nET3tZE2FpmvgeA7haMBgqJpU+YlmZSOpnwpI4EyW09/HLvR2QoOqUs7myzWbErJht0tHZc11Pr+A\nCjHmO/psrJxQ//K9hwZx852sXnKdSNsCRjN1MSQBvFDTULkrxwAg6PdBXnOyxgOdIaYauFJRMH15\n3sG4caUsSoSRaNBevESQAKNEyn12vr6pM8tWmPe0W+n3atgmvFKGCqhnGPpiCdw+yt5DTdXw7OkX\nsebq62kxioub7PoU84drDD5FQpxzASq1XDEyMa6NJif5IAYDjk4CzPmHvTuNNIumMGxsbOznAPw8\njPvOmf/7h+Pj40+2+2Xd3VGUd/Rh5mn2NV4UcO8vvgOJQScdt7URgFquLxZLTczNpq9Pksi7rzeJ\n7u7WKkXscfCmMRx/9pTzO1bWMGKiXL1YRHd3FPk8+529Q70QVRWKqx1HPCjAbz6Eb3nH/fiff/in\njlTL/OwCKqU8QvEwSi533JlL4+xvs+mnAKB/qBO6XAXNjYBkM3qGuklGzIobuXZURLvjNe8xr+jo\n62j6fcO37sHUcxfI13hRQCAWQjGTI20TyO/sjhvf2R3FwI5+LLlAQ2pxC/EdznPyQ4ZMGIfaI7tZ\nRK6gYPjOAyguzaGybtwVSkMVDPtbus7ZXBiKS2Mgbi0jtmMMQoCeKLoGOrG24BwRPckEJl1sUzq1\nUjuHzAqbMunsiZMaoVsODODEWWeV4PjEBPO+iBTEz/3ehzCwzXjOi2oY5XJ9MyIIPMZ2DuHMxeuO\nv7u+kMLwZCd4gYdGpIl1FfBBYSBVIBJCuC+BPDHVdZqCdE4U0LMtWZtElagE95SuV6vkvdHLzSUM\nADA40o3q+fPM8e5929E7kcbk2QnwHAefIDoq+wCgqiro6YiA5/kGovQ6oBI4HV1dEWyspeDmU0S/\nD119HeBMUL4ZDECxMTZ2b6qw3weB5xxiYVlWoJVK6BvtQ9UnI593XimJUxCzXaeVSR55AArYsRQM\n+bFtqA7qc/kg5Fz9t+05uA1nTjj1opksDWyliOEj1tUTB6+q0HTdcd5W+CURfD5bu5eaomK1UsHw\ntgQmZ52/5cq5eYwdWUJ0dBd4fwDZjTkSUCV7Eo6xkUk5Be1Uym9qZgWapoHneXA8j+4elmjoiPpx\nxlpxzShv5BAP+yARRURzxFwXT4Q855Q8kfLbvr0fYY8ehq1GrCeOTbPF0xv3HsRGsYDrq05GTtN1\nXEpN4WDfTnSZlZFyDVCxDFUsEEb/tg4IgoA3v/0+/PUn/7fj9fH5FZQqVQRN1p1XZEREHW60EIhH\n0d0dRaQrjgxRmATcuCAdaAFQjY+PPwbgsRv+BlusreWgEC7EALDzLUch+wNYW3MyPZwUBW8DVF7p\nPitOHj+LEDHYenqSzGe3EqM7tzOAamp5FQ/eZDTXVCtVpBYz2NpiB6c/HAUqZcAFqNILaUi1eUPA\nnn27MH7ZuYA88c1j2EGkdy6eOsccs+unAGCzIENOecIpNgQemWwFXI4GB93d0Ru6dlS0Uk2oCGLT\n74vtHgY8ANW2Ow+gmi+hmMlBbFE3F0nGat85uHeEAVRXz89jzw4n1VzN55Al7D7cMTOfR2hXHvB1\ngIvq4HNpkqECL7R0nTlOYqhlXVGwOXEVWnKIScV0d0eR6OlgAFUiwu5Gr16aMM5B1yC4BMY6gJWl\nTVJDtWdHFyZm1x2VdO4dKAAc2DeGru2Dtd/JVViafPdgLwuoFlfw8C37sXFthfGgAwwzyqXZFHrj\nzk8rVYHiWg6pDXbyrAnSAwGkbUavuq4bbLZtUdRkBanlDaaUvtyiT2VpIwfOra3ieVQicUdLJr/g\nYwBVRakiljCAciAaaGqbIPBAaj6N0jKr3xNCEtLrNlY1EAAcgKrOaHCmweeWC0ScP3nV6HOn6HDz\nH3KxiLXVbC0bUC56V9wF/ZJjvHOqcyz0b2M1ZelMAZqmM70JpVgAOi8inc6juFWETHxfwC+C5zlk\nF1KQzO9VTOuA7UNJBlBdvbAApVTC5vUr0COd4MsllArstdddzy3P8eBsFbIjVKXfaga/998+h9//\nzZ9GJBbxfO6DSXYDOntxDontbLq2+P+z995xkpzVvffvqdA5zExPTw6ba3OSdldaZQkhCQQCmZxt\nBNgXDJjr8PrFYL/gdLEvGONr42t4MeAAtq8xxpbJBmQBklBO29pdabV5J+fpXPePDlNVz6nQ090z\n07PP9/PRRzvV3dM13RXO8zvn/A4xEmc+nSd/dzaTRcbSuCXJEuYX8lhYrPNa7zceixJec+Aw/vWF\nZ/D0c+YFlg4dT108iT09m5EIxZEvFFEoFnFhmr9utIWimCjbnrR1JNHZlcCYYRpKoVjEU6fO4ZBW\nKtnIzi9g4jwvvhTLMYYcdlKolh9QNcI2oSZtLNzdgXC3+UTp3DGMvkO8HwgA6KE2FNt6UQzGUYx2\n4vycc6bx2FMpnCek9Z4u57ypHZTBJ+WYPkt0E7R3J8j5eNa87uFr+M6FB3/8MzLld5oYqWO0TFAC\nPkiyVE1FekEOBJtu6lkh4JLOA5yL0ivEh7rJ1KAaCWL4hn0Il9MojDGyjspKom/p+Bgm6qhOp86Q\npppuKT8AOHuq/J0xBj2SQKF9ANkiL8U7uqQb0EPtXEEwUGrYkCbOcGkXAKQ7cdjHB7dnXiyPxaDm\nHEoyLp0e4UeihH0I+FVs27Sk1qTzWXIW11t/+c3mv4Xo5N3Sw+/rxcmlmwqVypGYhOkRfmWrl9No\no5d4VbRimSBZzlHGmOfC9EA44KnZRbHW4wDwdychqSrinUsKM5X2yxZypaJ2AIqPrkWypvzy0zMo\nEKq5EjKrD1Y3cJ9lLAdVR1WdU2lrNGvYv/J3lSYWED5rMZxkmTHaHkLQ4gdUyBcwRQxE9kWD1fql\nXDpDNp0Eyymj4vxC9RpcSYsO9sYhW64Ti/MZvPj8KJhehDRbuuanF/mAKmA1irSk5EOhAHr7+fTq\nT3/2LN7zoU/heWJgdwXKMd2u06+WlB9VkB6LRRtyH7BevxVZxj2vfiUOHOInOejQ8dSlkxhfmEau\nUMDI7AzyllIDVVIQMyz+GGOuaT89m0Oe+Bsrx7tTWclyPaiA5Xf5vUzTtP8EcBuA39c07ZteX8sY\nw87X3Yz2zX0IJmLoP7ITO15zo/0XyRj0YAx6Ww/0SAIXiPooI+l0Bqee5wfTdne7V/ZT2Dmm5w0X\n9fTUNGfTwBhDtDMBOcTLp1Y7fOrgeOyhJ8wFDQDyhQIuEEWRRoWqUltEtYvasRIeVBU81VARrehW\nmMTQvY//bja95Eoofh9CXQYbCQ+DcxOGVeTQDn6m3NTIFHTFMpuxqGORWBVaOfucZURGIIxcoI17\nnifbBACQJBQTg/ZB1TgfVHX08QsKRedff7piOmi5qJ144Tw+9j++hE98/E8wZVnBVpSeLcMdVeVg\njFCnupKd2LHfsnCSzatBXdcRJ1TsOYO6Q6kPEmOYHiVSyYqKfC6PsXP8dSNR3m+qIcNrYTpjzLWO\nyh/0ozjCq0X+gZKRbMzQxu0nAsxsPodoIla9UafJGqql18lqOaAirgGSJYCyLvgkWYJq6O6j6qjO\nVY5nO6NZQ2G6Xj6O5onUuJ8xZI2zMGVL1yBj6Bnkg+txSz0ckxjUSKDa4JBfzJJBd8AwIDpbri+t\ndIGpiozBXr6p4eQxc7CzuEB89tYUGdGxd+ddL+G2AcD5C+N474c+he9/i591CQBRG4NPikINtgnW\nSRsAEInWXz8F0AtifTGLj3/yo9h7cDf3WFHX8eTFkzg1PoLzNgXpPksDzaGr+XvmU5ZRRLkJQ61z\noYD7n3oOn/vKN3D/D35KWvhU97+ZKT+KVCp1L4B7l/um4WQb9r39jmW9lupwc0NRZCRcugvt6OpJ\nIt4Ww7TBuDNXKODc2CSGu0sn++RF3sYhHPBDDYeQJxSqokWh0nZuRSweM7mtp9MZPHfsGIyZ9XNT\nk9yU+Yg/gIjBZK/S4UcVpAY3DSN9+hx0S8pEiTWmPsoLbgXngDeFCgCGr9+PieNnq4WavVdo1Q7R\nikIFlMfPOJc6Iblhqc4hGAlB9fuQMwTJhXwBizkJxj1LL2Y5tYZJDLqlduPiqQvIZbKmYaM5og7I\nU1F6BcWHYmIQ0sQZMEuKiOlFSONnUEwMAuVieEqhKiwWwRgz/Q2joxP42XcfwvipC9g0GML2vYOY\nmp7D+3/jz7BgCGoOD+xEuDx4tqL0BPwqhvvb8MKZSZMhZYVbX3Ez/3dIMnQmVS0RCpk8IkRR+Kwh\nLUUFVIxJmBoj0q+yitFTl1C0KBahoIpQ2SKAUpFrKkyPhTBPpPwrhKNB6FZVSZbhL9s5xA0BFaVQ\nZQo5RDvbAVnB/Owcdw1QZbk6yxBYUqistZsAf65TCz5/yFftlKOsE8bOjWJxbhHBSBC6GuAMPVk+\nAx3l9yl/7jOzRDG3T8XCyCR85fSVLvO3o56BdrxwzDxMeFo3f0bh3tK4oaIsQy/qyKez3Gw4YEmh\nAoDc6DiCQwPIG4x5h/riOGXpIrTO/KRSfpynEtHp9/o3vhzpXBFf/qu/5x5LZ7L4vQ//EZ579gTe\n84FfMIkLZKdfLQqVjW0CpVDV60FVgbrGZ2bmEQwG8Huf+ij+n1/+bTz9xLOmx3Xo+MmpZ9ER5vch\nFghzQ+MPHNoHSZJMExkuTc5gdGoGyXJ3fd7gGfbVHzyIf/tpyan9G/f+AO/6+TeCr2wr7/8qp/xW\nlAvE2Bk3upJtkIiD3AuMMVKlMjqmT57hp4dHQwEwWfaU8pNlGVdexbt0P/XMMdPPPzvNO6T3xs1K\nh1pVqIiAauMw2m84alqlMlVBcAOvyDQLakCyEdmnQvbgx1R6roIr3nMXDrzzThz65Z/DtldeU53j\nFmiLQCp3nlHjZ4z4FBmRTvPnGKFMSC1TJxbm+ZtEvC1UHWJboVgo4vxJc/E31WnoyTbB/AIUO4aq\naS0jTC9Cml46VxKEQjU1toBeQrn9x898FQ99+2F89fP34cH7nsM3v/eQKZgCgPMzS4pLp8GNXNuY\nRDafw3Sav2BTRrZgrOpBBAD5hQw5YWB+MVMN/PJkyo9hxtIBpjMJYBLp6l5R1QC6w7WR1gnBAP+9\n+nu6qoaj0Y5YtXDCLuUX6+oAJBUzlFO3pdZSUWRkR8e4tC2TJTBL0wJVS2Kso1JlGUHiuDx/oqwG\nuFgnVDoCZwglN+BTMG9M0xJ/O1VHNT61iPieLQj3taFtaw8iA0vmoIVsDtD1mhUqAIgRM96mxi0B\nFdXlZwmorF24ACDpOt7xnjfj45/4dYRtMgL/+Ddfw9f/8d9N26hOv4XRSTJ4qinl16QOP4BeEFfm\ntYbCIfz+n/4ONm3ewD1HBzA+T6QiDR1+FaKxCLZu5zsInzpluBeXrxdTcwv493IwVeFv/+Hr5DEC\nrELKb7XIZnOmQjSv9CRrt0wwspUw+DQFVBf5dEI0wo+0qED5QFFpv2cMgdpsehHHLvI3hl295tl2\nasgPvVAgzTvlcAhKLIrEzdchun83Iru3o+Om69aUQuWLhWrK4zOJIT7cjXCyzfQ6JkkIlYMkt5Rf\nsFx3ZiTSzl9c5uay0OM9VXdvKqAKhf0Y3MirQWefM6eh85RC5TGQNKGopfQfFVTlMtXUXTgegc+S\nvsnnCmRANW8wP/zuvz6GR4nRULPZpRu7MTgZ6I0jLfHHXt9ALzZt5WvTALN1Qm4hC5+qmGxAgFLR\naaZ8c6bqYyTGMDVhuRjLCsAYLp3iF2EVVQ0AFCLVUYtCFW6UrvgAACAASURBVHZJUQeJq6zRA0pW\nZETbS6tqKuWXyecQTbRDlxU6oLKkSBVVgk4E7HJA5QIgiVCoVMV8/lFpvzPlOirKaNaUbi4WUCwW\nMUucKwHVGlBZRu8Uipg6wav/l168CH8ihthQJ4KJyNJ5L8nVwchONVRAKUtQmF8wKflRwh17ymIG\nS6X8AlaFikj5Vc7Do9dcgb/81AfJzj8A+O69/2n62RcJwmdJKetF3fy5Vd6ihoCKdElvUMpPDQXA\nLNfTQjqLfFnxj0TC+Mjv/jriAW/vF/OHSfX+4JH93LYnXzjLbXvk+CnrMA4szC/g2Yu8EAJcRgrV\npQt8QWw8FibdsI2UPKiW/6dqO50d0+cIab1ycFIBVXFxyculwhWEQnVhchpTi6UT+uHTL3BSfzQY\nwM5e87xDJRigayeCJcUMAJiiILhxGKGtm7mi1GYjqwo5p7CCl8GVXgklKwGV83cfITxJKIVqbmoO\neiiOYucQdNlHy/9hPwY38q301ULeMpSxZ00pPyNyOaiiVNiyjw5jjFSpEnE+Fb5guCFmMzk88RQf\nUM1lFqDrOiJtkWrqDAAkiWFR54+/624+ah8oK0aFqnzRJW7icl8MkiojR3b5SZiyDj8u12dRg5wr\nqpra0Q6lna9nq8UtnXJ9NhKyKFRMWUr3Vaik/WyL0hMxQFIwM0sozxaFSraxClECKqcCyYQ6F42Y\n95cqTD9XWSCofugAcvMZpCfmUMjmwYp5oFj6jvSijtn5LOfUosoSFFnC/Iih1o5JpmP49BPnkRlb\nqA59r5CeT2N6lGpAUJY8qKguP8v3kB0ZNS08w0Eft+5emEsjrZSCXV3X6Roq6/WMOg8rHbN6EQN9\nSfz5H78fN127j3vac8+ewKJlMRzp8eaYXq9C1aiUH5MYeR3PGAbJJ7oT2NezBe1B58V8UPVDlRVy\nsXnFYT6gevrUWe4++fDxU+TvfvwcPxILuIwCKsoBfbA/CW3roOPrero66lOoiJTfaUNh+iyhBsXK\nqg9TFDBrka2uV63xK3Qk2snU4smRS8gXCnjk9CnusaPbtkK2dBipIT9t6Bf2Vpe0EjgVpnupsfJK\npY7KLeCOtvMndYQYoDk3WS7kVAModg5jPscfU04KlXExQKb8lqNQVZDVar2UEWYwJkz08vsVDfIX\nPmNANZ9LYzHD30QKehGLuQx6N/eZX5vOIHWGV1Kvv/kot21p340KVaa8X/zfspDPI7lvCIwYSyIx\nhrmZRZO/ly6rKBaLpM3DwMEdiOzZibZr6UGwtc3zcz5mQwHz9+rr7a4ubipUCtP9djVU7VFAVjDr\nkvKTJMZZClSQgz7uZs9kGVLA/Fn7/Aq0O69CoD0KXzSEnS/h1fNzJ86V6leYhLkL0xh78gwmn7uI\n0cdPIzubXipML9AO9ZVhzvMjk+ZFcrmwXNd1nHv6AhhjCAf4z+TUU8TNUFKQL9d+uSlUALB4yrzI\nkSSGCLHYm1yUUOgcRsYX52rxZFXhm0mogKqsUFVGI4WCfnz019+KpGWuXKFQwLGnzF6DVNqP6vSr\nt8uvUQEVYJf2W7ovBcMByJKMvT1bqj5UFDF/eeFDLDZ37d3BFavPLKRxxpDFyuRypGoFAKfGRjFh\nSTGqIT+XraiFlgqoLpzjL4y93Qns2UmnEip0d7Wj1rEzRrq6k2izDFbOFZYc0+eJ2V0xww3ZSx0V\nQKf9ToxexLMXz2PeMr9LliQc2cLnkNVQgKyfkus0a2skTtYJ/mjjAiqvClUbMSwzTChU81OGk0+S\nsJDnb+zBsA9dAwmuHmpxdsE0UDhPBFRebRPssLqOl9+o+k+q0y9ADEleMKT8qFqoCrPZBfRs7DPd\nkI+fu2QazQQAye5OaLu2ITsyhqn7H8DUjx+s1rAY91svFlEoz2oLE6rI7OwCJEWGTnyfUlmBnjbW\nUSkKxs+PcZ91IBxE79GDCG3ZyAU21d9Xg0LllvIzKngA7VBeVaiIlF+ukC81D8gKpsmAauk1imp/\nrCvEdQigr08dw1246ldeh6O/9kbsufMo/Ja6n+xiBqNnRlBMZzB3ZqmeTi8UMXd+slqorus6ZoiA\nKuCrdORlzGpLOaCcujCDdLmQPeLnj9HHv/csRk9ZggpJrs7xc6uhAsxFyxWs9Y9AqcMXagAL4B8L\nRgjLGYeUn3F4NGMMe3fyY7SefPRp089eO/3qTfk1qssPsC9Mr+6XLMMfCkBiEnZ1byYHgwOGgIpY\nbPr8PuzZzw9hNgZQT75wllQrKzx29kXzfnvoMHeixQIqXqHq7e7wFFBZ/VJqwa4w/WR5SDOlUMUN\naQTvARXvR/XC+CgeeIF3nD68fRMihI+QGvKbOleq+9AyClXjAr9wl7caqg6ikyZCqFazlvFCC4TT\nbjASBOscQN+WAe4xYx1V3V1+FERAxQoGhYro9GM5/hKwkMtUZXOngGous4DeTb2m4/s4seg5cGgf\nCrNzmLr/AWRHxpC9NIqp+x9cSk2Xb6J5g8cPpVBV0l3U6KlKWmhqYumircsqLhJjcno29brW6dWi\nUAXdFCpLp5wS512xKwGVxCSohMIxMTEJSDYKldEl3WEygBSh91MiCtOLBmsXJkno39rPPefsc2dK\ngbGlqzU/nykpVLoOvVjE9Bw1zHkpuDn34FLHV6XT78KxpeMoHCCGNC+k8cR/PIsXHz27pHBJCvKV\nGiqqy49QuqzEO/jvZqpcr5S2Od+tUKl3Vk35mT+rvbuIgOoxc0BFKVTzFye4buIicV7Idl1+TUz5\nATYK1bR5oR+Mlj47iTHsSG5Ab9R8fZKZhK7ywHA79f7gYT5t+pQhoHrkuVOO+/nE2dOmTkFfnQv6\nlgqoKMuE3p4OcqCqkXpTfgCwjRiUXDH4nKMCqsRSQGU1DgR46wQA2L57GyKWLzRXKODCDO/pc9uV\nu1GgpqkHaYVKsbmYrgYrpVAF2mNgsuSqUCUG+ECDqqEyKVQAaeoZ7OkH/GEMbOPT0MY6qjw5HLm+\ngMpNoaJqqOan0ohZi16hI50v3ZisnlNGZrML6NnUZzq+qYBq557tSL9okd2LRSyeKqdtytYJOUN9\nCtXpV1FnsoSxJSurAsaACrKKi4RpYs8Gu4bpJewUKmsNJ1CyTXDCqFAxWYZMnIsxF3PP8dEJwK4o\n3Wjq6aRQEc74AG2dYF3w9RNlFeeeO8vPC0VJKSkpVDpQdFaoAGDkiZPVVC9kBflcASMnl1SvCBFQ\nzZcXJCd+egqnHjlbWjBLUtXugVKoIh7Mndu6+Hq66dHS9XeRCKi4gnSAnOdHKVQAsIcwEX7miWOm\naQCBtijX+VzI5rA4abYJqa2Gij+vow1sTqKUHmMNFQCEDFkTxhi0ziHctHUXuruSiPnD2NOzpXou\n2C02qcL0Y2cuIJcvjR96+MSLxKuWmM2kcXJsqfFBKFTdCcRjYQwP8jI6UMqLJxPxugMqbQcfUD1f\nVqjIgKpzScL0qlDJsowDu7a57stwbxe2DfSgkOcv7krIjwKpUK2dlJ+TQuWr84A2IskSQom4Yw2V\nIkmllnQLZFH6pIeAqrwyG9T4G9D5k0tdJaRCVU8NFUAqVMjnqkEApcRNTc5jsJ8fjbGQTSOdyyBT\n4PezwnwujUhbpGqMWdR1nCQWPTv3aMgR6ZVsZTwSYyUDzgVvClXWQaEypfxklSxI79nYx23jfp+i\ngFmPG10nu+fCNdRQKfEYqY6ZvKiI73FibBJgEmaIcztkUKgUG4WKyRIYUS8HeLs+DRDHc0mh4lNP\nelGHnssAhTx0XXesoQJKgcDFR8tD32UVIyfHUDAoTCGfyhVsZPOF6jibFx87i2L5VpZPZ1As8nP8\nGGOIDboH0m3UOVJWqKiAKkiNMGH2NVRWhWrDYHd1MHuFdDqDE8eWGkGYxDz5UbVSDRXAB6OMMezo\nGcB73/XzuKJ/u6lg3e7auGXbJkTj5kAwk8vj+LlLOHn+Embm7YfGV3j0zKnqvztc6rHdaKmAilKo\n+sodELt3bCBf09kRh6LIqKeGCgC2EZ1+p0cmkM3nyZRfmymgcndLr7Bvk/sXeuvRQ2CMmS46FRS/\niiJhy7CWUn6OCpVHU0+vhLraHH2oAj6FTDOStgkWhWqBCKgqrtndxKwto5M3VUNVr0IFSSl5Lxlg\n0FEs19/5fApfI6IDXR10p9+UQ7oPKDl4j42MVxWqC+NTnCN2IBjA8MYh5Kf5gCo/PYNCuTlDl31L\nKgXsaqhKxzWVzqnUUE2Nly7aOpOgMwkXX+AXYT0b3W+sgPe0n5NCJcsSVNVgutnGp5QAi1s6pVCN\nTQCMYWaWUElMY2foG6gSUOmAGzbXJ0uncP/WAW5ROnFhHPNjfLcdAOi5Ilh2AYV8AbNEN2zAkoo6\n99CzpUBMUkzpPqC0KI4R52PlWCtkC1iYKn0v+cUMqU6FYiH4krwSbaWDWFxMVRUq/nznxs4Arl1+\npqdKEnbv4RfrT3BpP+dOP72oQycyFlb7guprm+hDBXgLqPyEaWxRlsnB8XYBlSRJOHiIT/s9feos\nHibSfdZaaAA4PnIRc5k0+g5tR2LbIGexUAstE1DNzc5xeV9FkZEo3wzs6qh6Kj47ddgmAEBnMoFE\np/mgLhSLODMyYRqLUSFm+OK8pvz0QgG7XEbkBFUfjhzYDV3Xkaf8eHRilRII8KvtVcRvY/vPJAaf\nw9DK5RBOtkFizHZIctCnkHnzUCzMKQnp+UVTIESuWMt1AZG2CNctkp5fRLZSNEuoLHUrVAB50yxk\nygF/IYdEFy/rU3VUmWIWWdlenapwIvV8VeE4QaT7tJ1bgUwGOvH3AgaVSvG5KlTTtShUsoqpkUlk\nLJYmqt+HDqImhcJrYTo3esRAKKiajiOqfgoozQT0lVNbVGH6eFkJIhUq42Bkm5Sf7BRQEeq19foU\nCAWQHODtQEbG6ZmhxXwByCxgdjbNpUmD4QC3yElPzGLixFksTi9i6gLveN+3ma9JnDN0n86Mlu4N\n+XSW7PALxcLwJdz9CNuH+EzHVNnaIT1PKG21pPx0nVOoAGDP3u3cticffcb0M1VHNXdhSR0sUma3\nimxbK0gqVCtYlA6UFnhWdFmyadixvzYeJOwTnnzhLGmX8LZ3v4m7jxd1HbNaEttecU1Z0Vu++NIy\nARXV4dfT1V4daLl7Bx1QdSfLTrsNGPpIO6aP0LYJBhmSmhVWWOQvNLmJSbSFgtjQbb+SOjA4DFnx\no1jUYQ2lJUUGiEn0a6nDDwB84SC5cvJFQ1Wn80YRKn//qk0qJBj0kwWPkiQhTFwU5gyFlQsz9gqV\nJEl0YftE6WZBGXvW7JROQNVRVQOqYh6JJFF0e4n/O/JSAfMFd7n8+LET1YCKrp/SkJ8mRsKUqQRU\nxQJQNKxMqRqqmfLnnSNWsJK1hkpRSXWqe0M3JA/DjAHvCpWsyAjYeKuFLR1+CuH7BZRTUg7WCROV\ngIo45gKGm41dyk8O+GwXlZRTfDGTgW65Sfdv5YOakXFaxSzmC2DZBUxN8cdQR08H2rfwRe7nHngG\nF588xW0PtQcxsHOY2z6fXjqHZi6VjrGcg0LFFAUq4TlWQQoGEUvEIVsWn5mFNNLzi56L0sGkqvlv\ndRNgG1Dt3ccHVE899oypWJpK+c1eXFKoakn36bredIXKFwkClmt5fiFjmjeoKvz1rshYzeUQVEB1\n4tylahe+kWtuvAovfcUt3PZv3/v9pftxHbHCqgRU2UwW//4v38Jffvr/x8MPPOb+Ath3+FXo702g\nnfAOKlkmoDEBFVGYfvL8KGmbEDesRCWfCmbttigWudVudrR0guzfTI+CYQCuGN6Eog463dcCHlRA\n2fiNkIQbne4D3Dv9og7pRyfrBF3XyRSA0eQxluCDl+mxUuqL8qGqu8sPIFWIYjmgYjYKlU8nbuCz\nM7g4Sg9hNXIi9TykoL1CtXPPDuQniaHFZbIjY9CLRVO6DyiNbrJS7fKzGY4MALPTiyjkC6UOvxd4\nP6weIhVrRy3WCXZeVCFjQTVjUBxuWk7mnhWFapY4v0MG93O7gEoJB22vgUySyKDKmvbrI4KgkTEb\nhSpXACsWMD3DByHt3e3oP7KT2z5x4izO/+wYt71P60bPMJ+KmzOkl2fLAVV+kZ7jV6lzU5P26qQc\nCYFJEuJJPuiaGpmiFWkqoAJolUovcCk/ANiqbYLfErzPTM/gtGHYbzjZVl1spstNGbm5xdKoHdQW\nUKXTGU4hV1UFAeJ4Xy5MkuAnFvLGwnTqmlyAXrNHX99AD3r7zcoilbbTdm5FZzKBO155K/fY6VNn\n8cwT5WOv1QKqT/7eZ/DJ3/0M/uHL/4zfeN9H8L1v/sD1NVT9VE/30snBGCPrqPqqLrP1B1QaoVA9\n/eI5znfH71M5wzFKpbLK6tnRUmfLvi10QLWtuxdtwRDyuQIIVRtqwGfjQbW2AiqAnulXb4cFRbAj\nBkjMto6qzWFoNqUwVcw9s4sZzuRP9aumoChG/O6Z8fJKuhm2CXBRqAp5dHbzQV5A8YFZzg+ntJqR\nE6nnIakK0kUdp4kAbPvubcgR9VPV/c3lkJ+cQt5SPBomLu6VdBe1b5XUhq7rmJlaLHf4EfVTG+oL\nqKgpBIB9HZWxw0+JRmx9rwAgXu70o1J+E2OTpREuRN1ewIMPleTSlOKp04+wAhmdmCM7Hys3+Cky\noOpAYusAAtYFiw7krGk1BvRsS6JnkA+E0rl8texhbnQaxXwB+bSdQlW6Bvo67QOqSic01ek3NTJp\n0+Vn87namHsy4rNSfCp27NG47UY/KkmRMavn8dkffQ9/9J1/w5//8DsYm5tFrpzSpiwT7AYj26lT\ntYz88gLd6bd0f6Ji/3xRt7k2OruXUyqVlaPXHwEA9A/2Yd/B3dzj937926V/1FEetOIB1ZlTZ/Ed\nw7wiXdfxmT/6S8wROV0jpEJlkUHvvO0q088+n4JrjpQ/uAYcLJRj+tg00X5KzQZzKUwv5nLVlfzW\n/m7Se+XQcMnIM7eQga7yj8s+xcaDam2l/ADA37YyCpWkyAh1xGytE9q7+eGrFSJE0FcpTKcK0q21\nNJRCNTte+o5p24T6U37ONVR0yo8xZlI57EiG27llycilUUxPTePU+BR3Y+3pSaK9o400UDSSuTSK\nvKW+guzyK69us8QKVjJcBKcm56HLKi6RHX7eAypK2a0seqyEbMbPmAKqNvvgHXB2Sx8fncDc7Dz3\nGfsVxTQtQbVRTJSoc0u8l06/5GCSS71ksgXMED5TlfTtzAxfDtHR2wEmSeg7tMNxnwAgMdgOf9iP\ngF9GOzV3slxHpRd1zF2cKClUVA1VfGnUkN29oPJ9kwrVKK1Q2aV66U6/IqlQgUnYc4AwqDQUphcK\nBfzd/fdhdK60IBufn8PfP/Tj6gKv7g6/BtZPVXA19ySCy2yuQNdQudSXHiAK061cfcOR6r/vuOul\n3OM/+M59WJhfaC2F6uEHHuW2zU7P4u//+p8cX3eB9KAy1xoduWI7PvDr78HwcB92aEP4xO+8G/HK\nTboBAVVHoh1d3XxhppUYIeu7XbByYxPV/LosSXi5xV9jYyKJDYnS35tfyJDDcBVFWvMeVBVCnfxF\nK+igFtX1Xl3tpHWCxBhiXQ4BFdnpV7qALRLdVpWC9ApUQFVVqJZx0fCE7OPkbj2fL62OCznEO0Kk\n+WOIMIm10hGMIUSMtzl+7HmcMAwLr6Bt3YDi4iJpNWAke2kU+VnzwoTq8pubX0S+UHA09gSAqfE5\nnD5xkevKlGQZyUH387cC1RVWmJsnVSr7lJ/ZMsEJp5Tf5MQUponUqdGDKtKbgI/oYmKyBBZwbvag\nFKyipRNZkmX0buItJ0bG+Bt0sZx2m6YCqvJCuOfgNtdmmd7t5VROIUd2ZxrrqGbPjSKXzpAp4Yqb\nPVNkqB10HZVcVaj4a8LUyKT3GirAIeVHJKMYox2/DQrV97/1I1yaMtcETS0u4B+/8nUADXBJb2D9\nVAU3c0+JiC1z2dyyLGXcAqqu7k5s2rKh+vN1txxF2HLMpxfT+OF3/6u1FKqHH3yc3P7PX/lXjF6i\nV38AcOEsoVARs8le+eqX4guf+x38xR9/APv3GEezNEbO1Ig6KisxojXaLaCq1E9VeMXV+/HWu2/D\nzp1bcWh4E15z8HBVks0tpFEkJGWJ0d2Da1Gh6tm/BZKhnVz2q+jaw7sGN4Jwso1UqEqWCfbBpt2A\nZMDZMqECnfKrKFRNsE0ASgsH4oaMfBYo5iFJEjo6ebWCCpSsxAMRRPz8sXQidRLHz/BqkLZxEPkp\n+4L06q5NTSNvUXplSUKYqKOanefrPwCzQvWT/zyGL3/8b7jndA11QSYKYe2Q/D5ycHLmEh882qf8\nDJYGNpYJFSpO9rIkQbGc38Vi0VRTU/395bSkGgpg822HoRJBmxJQAULRNuLVK4+soyIK04u5AoqF\nIqledZSv275wAN0O57ziV9A5XFalCnl0E+laY6ff5AsXgKJu0+W3dC6rNmm/akBFKFTTI1NYJDyN\n7AIq0i3dTqGChJ17NK4reOTiKC5dHEE+n8cX//Jvyff5+te/hfNnL9YUUM002dSzAtU9bVSoGGHQ\nm8lkl1Vf2tYex6ZNdKkMABy9wTyzMxAI4Obbb+Ce9+MfPgDdt/xO8xUNqAr5Ah7/2RPkY9lMFn9t\nc9AUi0VcukAoVH18oSL0IhhRkmb151kulB+VlTixSqSsE/KTU9DL9VfWVIIiy3jDW+/G//jU7+D2\nXftMXjO5hTSKOh8gshzf4ScF/GA13ERWCn8sjCv/26vRd3gH+o/sxKH3vhoqoUo0glCyDT7i4hJU\nFcc0Y5gckFy6eZCmnp4Cqhnoul2dQIO+J4X/HFk+C5RNOju7+JuuW0CVSLThtjfdhn2H9nKPHT92\nEs89f4bbvmWghzT0JLHUITJZWlKXDcwsZJElhjUbFarRi9NkXQ/VpeaGj1Cks2RAZaNQBb0rVL2b\n+6oKEKVSnTrJuz73DnbiyOsP4PD770b7pj7yPZSgzzSAmsKLFxVg0+k3wavixXwBUxN8ijLgVxAw\nKLl9h+3Tfj1bk1U1lRVyZLrW6Hs29XypCYFSqIwBr8+mML0SVJIK1ehUbQqV3Tw/G4UqGApiq8bP\nZn3y0afxrW98lyx5AYBcPo+/+ORf1a1QNSflxx9TWeN1k1gYpRczyzY9Pkhcmypcc+PV3LaX3HET\nt+2RBx9DRo1B90eW5Ue1ogFV6tnjmLcp6gSAb//b98iLxvjYBLcqDUfC9EHgcNA2gm2EY7qVGBFQ\nUSvA/PQMph98BIXFNArEqkFNJqASq/TcQsY6PgsA7UG11jr8jIQScWy78yi2vvxqBIjgpVGEu9rQ\nHg5yRdXJWNixEJ5K+c3XoFBFbVJ+BUphkWVILjMHvaITRc3IpasFsR1Ep1/YJeW3b992XP/am3D7\nG27jHnvoJ49gynL8qrKMoc52sn6KEcNuraghHzcSBwCm59IoEEXH1qJ6K/6gH1feftj1fbnXdfEB\nVW50rLoQquBWQyWFQ5BU55sCYwxv/ujbcfRV13JeOQBw6vnT3LZ4WxiRjjBUX+nY8Xd3mpRfAAh0\nxegiaQPeFSo+oBqfXODGYBXzBYyP8te0WMQPZkiHxfqTiPbTadhezbBgLuTJlN9CJleykAEMg5Ht\nu/yAUh2VtetaaYtXGwaoGqrJixNVD7kKjDH47RaBpLlnAQBVQ1U6dqk6qkcefBxf/txX6Pco8+Mf\nPYCfPcRnfpgs4cK5i5izdIY2e45fBbeUX3Exy521hVyBvLZ6CqiuOkhuDwX82EsUoe/YoyFmWYCk\n0xk89ujTKHb0o9jjPrXEyooGVI+4WCQUi0V87s++yG0nC9L7ugGZX9EzvdjkgMqDQkVI+0osSipF\n2QuXMHXfT7jtcjQCORCA4vdxfh6FbA65NB/Fy0Raa615UK0GwUTJLX/HQGfJyFORMdQZRyIadFSo\nqJTfbLWGilKozDelSDzMBUmZhbTJy6pCQ+qnKlAKVWbpPSmFKuiiUO0pe+Vs1vgUzTzRyr+xNwkp\nmyUVqtAW99SuEvIjRqQMxib5m4HEmGOHUu+mPrzjd+9BcoBQtN32o6MNzBII6YUCcuPmjkZKoZIk\nBn9ZdaRScRSBUAA3v+lWaPv5rq8XiMVmrHJ+F0tBOkMBiZ39CCQi8LeF0K71wt/R5nr9k4IB7jl6\nNoti3hz8xxIxhCzu4MWijvFJ8/lQzBUwQQRU8RgfuPUf4VWqcEcI0aTh/CvkEYlHELG8XgewYEkR\nkV1+htQ+k2VEdhm8n2QJ4R1LN89wPMydj3liERSIBE3BoQmyy8/u3lT6HVRA9e1/+55jKUyFv/7S\nPyBv+LvPTI7jk1/5Kt5y1z24+5Y34Wtf+Ub1MaoBbMVqqMopv2KhiPxihuy+npvgjxsvDTt7rthD\n/r6Du7dBIe69sizj0FE+CHvgvx4q/WMZMcPKBlQPuntO/eS+B/HEo0+Ztl0k/G16+3schlBSYl1j\nAqpYPFp6b8fnEJ1UsozoQVqSpKR1X1epzoBJjEyFLUzwtSmywv+Na1mhWilkVUGwPYr2cBBXbOrD\n4S39GOqMQ1JkUgGsQA9InodeLHpSqJgkIdrBq0ETF/iBsg1L94FWqJhhJh/lRaVIMtldVqESUEUi\nYfQNuHfKbenvRmFuHro1PSdJCG4cAlwGVishH2JR/uY7Rhz3duqUJMu44fU3l4KpwdqDKaCkQlTO\nRSPWtB9VQxUKLLmku6X7rHR08mmnM0QNVSXoZIVyQJVZgBL0oX1rDzq29yHQHgYoxdKCnReVtSaT\nMYZuogZvZMJ8ky7mC5gc8xZQde3ehGif+TPedHjYFCQzvQCk59DTz6tHRj8qco6fJCFo6cYLbhxG\nxy3XI3b4IBK33AB/z9LxwRgjVSorth1+pTfltxVpH6pqQLWf9+aiUtdxosHg4qVR/PSFE0jncrj3\nqcfw1z/5Ec6OlI7RQqGAv/jU56rCxMxKpfwI1TY7FBOOtgAAIABJREFUv4hCLo9cuR6N8qKi/mYv\nljKhUBDbhvgavyMOqcCrrjnEbXvg/ofIffDCigVUCwuLePoJ3rSNkhr/959+wfQHUQpVT3+3Q2tq\n8xQqwL0wPRan01eB/l5ED7q3dwLmDiPqpr9IRPFU99Za9KBaDUKEt4w/GnJUNnwBf3UcSIVioYDF\nuUWbLj/+AkJ1+lEBlZNxXc0QCpWRBKFQAUDET9eDRCNBDG9ecqreQqhUVrb1d5PnoRKLQlJVRz8g\noJLyIxQqIqCiVp/dwz145x+8G9f93A2c83WtUHVU1sL05EASfst52m1QWNwK0q1QKb98nldJopVj\nrpAHdB1skf98vBbZkmm/eavylENnjD++OINPHRgf4fclRgRUkiJj95tvxdB1e5HctRG73nALkpv5\nETDS3Dh6BgjrBENARapT0RCpJCmxKAL9vWTTDlWYbsW2fgo2RekOXX4AEG+LY2ij+yzX1115NYY7\n+CD/v06m8Bc/+i4ePv0C91ihUMBP7nsQgE0NVRMUKkmRS47pRnRg5MnnkS0HVE5zVo14VfBffoM5\nrd/VFsPR647YPBu48uqD3OSEC+cukQ0gXlixgOqRB5/gLgidXQn80ofexT332SdTuO/7P67+TFom\n2ClULgdtI3BL+9kFVAAQHB5A9IB9xFxBNVxQqYBKJ4oQ6ZSfCKiAUqefFS++V6S559Scq0t6Baow\nffw8L+E3xCW9giRDpxYbZUJhP4Jh/qbY00UHObt3bIRkUDm2EMWzVrb08zdEYMmLiQpSTM8L+REj\nVJ8JIqAKR0PVwFeSZVz3mhvwC3/wLnRv8DYE2Q1qXwszsygYRk6pfh9uftNLqp1a4ZAPB3YuWQzY\njZyxI5F0nulZIR41pPxyaZMSCZS0ej3gLZjzYu6ZG59EV4I/b0Ym+bTvBGGn0GbTVeuPhrDp1kPY\n9fqbkdy5gS7nyGfQO8Ard8ZOP7rDr/ayB6ow3YpTQEXemwoFTkvVAdO9ibJPMLKztx89sThu37WP\nWwzmCgXMZXibigqPljvsKR+qZqT8AKCNaCQ4fd/jVcd0rwGVYmNSauXodYfw3rtuwd5Ng7h29zb8\n5hvvRKTXXp2OxaPYScxSrKb9amTFAqqf/tfD3LaDh/fjJXfciI0Gf4gKn/tfX6wGYKRC1ddtI6va\nm6c1CmoEjRHKNsFIcMMgovv32D6utLeZCljVkLfuN2rsxFq0TFgNwsQF0m5Is+l1NtYJXlJ+gHeF\nqqEBFeCa5ukk0n5bNvMeQwCwd9dGkxq8dbtzQNURDSNhc4FWy+eGr9v+Iif7FUiyRCpU42P8fK5g\nOIj3/tkH8eaPvh2/8le/ihted3NN9ghuyIEAmbKzpv2ueOkhvOvjv4BXvmQHXvuyPehoK3sf+X2k\n67oTlEJFYVSoWJpXreELkcEJBXWtKFi8qHJjE0gm+O92ZiaNtKE7q1jUl+YqGmhr93Y9onz2AKCH\nCKjm07lqRoP0oHKwRrHDU8rPKaAisyfEgHDLfYmqo6ogSQw3bC3Vm3VFYzg8XJvNzOMPP4lCvrBi\nChUADBzli8EXx2dw/oFnAcDWcNmI4lPta9UshDZvxPWH9uI333gn3nvXLdhwcA8Ul3TmVdfyab+f\nrvWA6oH76YBKlmW865ffwT127vR5fPZPPg+AHjvT299NFv4xvbk1VID7DcVJoaoQ3DiEyD765LG2\n9TrV+RiRZPPfKPn9kNagZcJqkNg+DMVSi9a9111pidoEVJ5Tfp28MjFxYYLb1hCXdAO6S9pv83bz\nylGSJRy8glZe9+zcaDrX3FJ+duoUsKRQKZGwbbCvlBcQMaKhojLTzojP50M4FsbG3Zs4t/pG4SO6\n/bIjvH1CRGXoSUbhM3TaqfFYzWM9qBoqikonJCvk6HRf0Hv3LGXtwo3HGhuHT5XRTqTuRseXAqi5\nhWy1+66C3yfbd8VZsQkC2xMRBCwDp4u6jvlyMEcrVLUHVPUrVJQPFR/sWTMnex0CqltuvwmdkaXv\n8/qtOxAmBnjbMT+/gOPHTtBdfk2ooQJKXZztxEJt4kQppeZFoaqlYUeJhNFxy/WIH7kCbdddjdgB\ne+GiwhEioHrqsWe47kgvrFhAlXrmBLft4OFSPdHho1dg/5V8GuxrX/kG/v1r38TYCL+i7+ntpr2l\nVqCGKhIJY4AofqtAFaVThDZtQGSvpRBRkhAYNufRvQRUssx3Ool03xKKX8W+t9+O9i39iA12Yfvd\n16PDgy8RqVBNztooVPwFNtbBHwtTI7zK0tAuP8BVoTp83TZs2FWqi1J8Kl76mquwe9cG7nk+n4Jt\nWwZN509Hot1RQdlqF1AxBsVgIGiX9lNDpfQdlfIbJ+YFNlzdIyD9qEZGOfuEPDG3sNZ0H+Bdoaqq\neLk0d8PWwaAHvAdUtHXC0nGu5/NVG4wklfYzBFQzs3zqKR4NeFYaSHNalArGBzbw9UMz5QH19By/\n5aT8vBSl15jyo7Dcw7p7u8hpHLIs423vfhNkw3UioKq4ReMVIADY2tWDrRuHue2PPPQ4ZiljTw8i\nwHIZut5+zp7d0HrTc2o8vyVVhb+vBz6P59DGzcPo6jF/5oVCAQ//lJ/q4vreNb+iQWzYNFS9aDDG\n8J4P/gLnFAsAf/IHf85tSyQ7SsOHSa+P5gdUAKDZGHxKkoRwDavk0OaNiF91JdREB9TODrRdfSU3\nKsZLyo8sSBfpPhPRvk7se9vtOPiuV6Bn/1ZPqgHV6Td5aYLzkpIVGSrhr0QpVFQHSUNc0o3v4aJQ\nBcN+vPnDb8P7P/vf8YHPfgiHXrIfiY4Y9u02q3a33ngFVL+fO3+2OKi0dgGVEouahgPbBVRKJaAi\nUn6Uj53q4u/UCNREOzcmRc/lkZ+cMm2jnOFrLUgHgGAoiJDTDbtMtKySkEeyP+zqP2WENvc0jMea\nmKxeW7uItJ/RMX1imldwY5GA50BDl+wV28FN/HEzs1AOqPLOHlRe8RJQOSpUTILuJStCXIP2HORV\nqjvuuhV9Az3c4npv/yBeevuN1Z8j/gBec+AwXn/FVbhyHx9sPfrQ4ys2y69C24YexGy6bButUC0H\nxhiZ9qsU8dfCqgVUBy2z6rZt34Jf/MA7uecVi/wJUrUtqNGNtpHYGXxGYxGua8ANf2832q+/Gu3X\nXU2mFlSn9twyosOvOVBF6aNnRrhtIZuOQaqGiqLRKT9qSLIRHQxMlhHriJXSZOUUy2/+yhtw1ZU7\n0N3VjttvOYR3v/3l5E15q03aT5YkbOyxCZQsyq2vM0HeYKspPxuzTCsroVAxSYJKzPYzdvvpuo78\nNBFQ1WiZUKEj4b7Cjjos3mpJ9wE2XlS5HIrlESFZQ7qVLEwfLzmjZ7N5PP4sP4ooFvXXoFDZnw9D\nG4mAylGhqv06GAgH4XNJTzoGVIC3YJa4h73mTa8yXUs6Eu14yz1vAMBnKxhjePc9b8Zv/dI9eOuR\na/H+m27Djt5+MMawaydvTPn4w0+haEmL+vy+kkDRJBhjGL6e7m5fCwEVQKf9HvoxX6bkxqoV2Bw8\nzMuAd7/xlUg9exzf+48fOL62t6+8ArYzT2tyDRVgP4LGa7qvFryl/ERA1QwohWr0NB9QUfVTQCnQ\nkhUZBaJY1kjDgwJZhQ6Ho15WzDfPsiLQ09WBP/zte0xPpToG7eoIh7sT8Nl05CiWCQJMURDo70X6\nzLml3YpGIAf9AHTPAZVvBQIqAPB3J5G1jMDKjowCO0smnIX5hdIgagNMlpd9HiaSHTh7+pzt45Fw\nkDzvAUBnDHqgNtWBMQYpFETRapWwsAgWlZE+e766raOt9N5Gh/RMNo/ZuQyefO4SFgnj4aHeNs6k\n2BYHT7S+4QQkWTIFBtl8AelcnnZJX0ZROmMMbV1tGHmRr9+t4B5QSaQxuuWNuE3bdmzB73/6d/CN\nf7oXsbYYXv+2u5Ese6FRi+v8Qga9iQRYwhxoDg31o62jDVMTSyoqNWWgmepUhY5tgwh3d2D+kjll\n77Uovdnsv3IPfH6faazVFDGM3I1VUagkWcLeA7wcyRjDhz78PmzZ5lz0WlWobGwT3FpTG8FWbTOt\nSDQhF+0poCJNPUXKr14ixEiczCI/8NUuoGKSRI6gsdLwgIox5/ltlhuWXVcVAHLhYmed4FSQrhK1\nRJHdO0odf4xBjkURu3I/mFpSBsKhgG3AYPq9KxRQUepxfnIaxUzpeLBTp2otSK/gVkdF1ZhV0APR\nZXU223lRLZ46bQq0JElCJ9Gx98yJETxznA9CNgy0o6sz4l2hkmTbWWpqtI2c6zezkLGZ47e8gNbN\ni8qxyw+gO/2459Cfx+GjV+Djn/wIfu2jH8DQhqWaWnoUWZqc5SerCg4QtclWmmWZYMROpVorClUg\nEPD0WbmxKgHVjl2abZ1RIBDA//fHH3YskusxpPyseWry0tXgYAoo1ThQJmzNCag81FBRCpVwSa8b\nqiidgipIr0B5UVlpykXDIe2nW1MqDikWnbgJdvd2ka3WmoMxIZX6kgJ+tB09hORddyBxy/VQ2+LV\n4I4x5kmlWokaKqC0QKHUpuxIyVeMDKiWUT9Vwa3Tj+qCrODVe8oKVUeVn53DwjG+qah3kA8wnzh2\nkau4UGQJRw8OlX7wXKzNbFWqYjCGQW2I2z67mGmYDxXg3unnSaFyo8Z7E3UvyC1kbIcjHzjsbiTd\nLMsEK8ldGxC0LC6bUZS+XKi0X60sK6DSNE3WNO2vNU27T9O0H2uadrSW11vrp6z09HXjI7//G7a1\nSL3GVbCng7Y5cSNl8OnmQbUcvClU5r9R8vsheTRDE9gTitEuy1bsFCqA7vSz0vAaKgC6Ux1VDQEV\n2QLOGPZYVGZJlrB7B61cydEIV9Rt/X1VDPvtVCNUYaUuuABdSL9w4nnMPfscMhd4ZWa59VOAu7kn\nVbQPlF26/csLIiiFauH4yaoKZ2ToED8qheKKPf2IlI1kPStUAHlM6kwCAmEMbucDqunFDFlDtZyU\nH+DuReXY5QfaLZ17To2lKD4i5ZebX7QNqA4e8hBQrUDKDyh990PXmfdnrShUAO1HVSvLjTTeCmAu\nlUpdB+AeAJ+q5cUHPUTNVxzZT/pTAUD/oMHXwous2uD6qQo79/AOq70OKY/lIvtVMJfaA6upp0j3\nNQZJkjxdkB0Dqk4PKb8VVqggWd6PSfY3AJvtb33XGxAx3NRf95a7keyjj3+1rQbrAMN+e1GofL7m\nFdRy70UEVPmpGSwcO44C0Y6u1PJ3W3BN+dmooqV03/KuedR1QycGA/v7ezG019ngGADa40Hs0ZaO\niVoCKqrTTw/GACZhgFCoFjI5co5fwKOPnxV3hcrl99aR8rODTvnZK1S9/T2u96SVSPlV6N672TSh\nQmIMssu9baUCqu7eLmzYxB9XtbDcgOrLAD5U/vcoAG+GDwACwQB27OYnqVO89i2vxk0vvd607cg1\nV5ovNE2QVb1y68tuQkdi6aQLBAO45fabGv4+jDFXlcqqUImC9MZBFaZboVzSK3hJ+TWj8NJJoeJS\nfkC1MJ3D5sawbfsWfOEfP4vf+v1fx59+/o/wrl9+B+QgfZOvJbDQ1aVjPe6h/mWlitIB+85EEsZc\nXZqd6HANqGwUqhq7+4xQ5p4cjCG8U0M82ea62Lj2yg3mTEMtCpWlqF4HoIdKqlGkLYL2bvfbTtij\nwkzhVEPlC/jc3fibkD0hA6r5NIpE0CuVFeEDLirVSqX8gNI+DV5rNttUXD6nlVSgr7rusPuTHFhW\nniGVShUAVELiDwL4O6+v3Xdwt+eaB8YYfvNj/x2bt23C4w8/gf7BPrzjF99iftIqBlTBUBCf/dtP\n4//83ddRKBRw5913oG+gMfPDrKihALJzvLdLBdniki43yTH6csRLQOWoUHmpoWrGRcMx5Ue8n6wA\neT6145S66OhsNy16qJQRUKNSo/hQDMYhLU57q6FawQsuk2X4upLIXrTv/qqgxGMm361aSbjUUEWJ\nz0aXFUD1NgyZgqqhshIYHqx65fVtGcDxh1Pk87Zt7ESvZcRRTQpVIIpiOA02PwVIEvRoElCXaogG\ntw9h8hJv9GpkuQXpgLMXlWtBOuDRNqHGGioq5beQJr3t5HLJx4FD+3Dvv3zb9ndGY80z9aToPajh\n/IPPYmGs1EWnyBIyDl3QK6VQAcCRa6/EV774T8t+vWtApWnaO1FK61W6sHUAv51Kpb6jadp7ARwA\n8Aqvb0jZJTghKzLe+I7X4I3veA35uM5kDwm95gRUQEmWf/f7f75pv79CrQpVPakGgRkvhenOCpWX\nGqomXDQkGbok0yMvqPoUWaHPlBpugnYKR621RHq8G4VgFJGE8xBlYGUVKgCI7NyGyYlJ6Nms4/NC\nmzfU9T6JTnpYdYU4FVAFYnUtIKWAv9zub9PvL0kIb19K9fVt6ScDKr9PxpH9RINCLWoRY9BjXaVA\nqvyzkQFtEE/88DHHXxFaZv0UAPhDAQQjQSwSC1nXgnTAm/pUc1E6HVBR9bKeFaoVqqGqIPsU7H3b\nbTh93xPITM8jns5i/hQ/r7eCsoIB1a49OxCNRcjxPF5wDahSqdTnAXzeur0caL0cwF1lxcoTt77s\nWiSTjYuI5zMBZKihoAZUn4JYA99zNYh0RDB1yv5xX8hfHQod7Eqgf9emZbdrUzTyO2s1uvudb2wA\n0DeYsP2Mgj7376EzGWvKZzwzHUR+wXJxkCR0dsW542NRn8PiAu+90p6IQQl6UzyzfmD6x+ZtvrYY\nuvu8zaYzE0PvsP2IpwptbZGVPT6TUXQN3on5CyPIL2ZQzOVQzOZQzOVRyOZKVhnDfYgO0cOmvdLZ\nGUEgGEB6kR/jAgBRIuXX1tfj+buyYzoaRnaavqYm9mxDz9BSkLvzyq344Ve/zz3v8L5BBAP8jTAc\nDTTsu9p39Q7c+7+/4ficjmS8rvdL9CZw9vhZbnus3f2Yy84UMOdiZRSOBhGsYf+yIf4zzS1mECAa\nPjq7Yogko0gmo9i6fROOH3ue/J19/Z0rf31PRjG4tXR+nP7Yl3DeIaBq71jZ8/vlr7oVX/nS15b1\n2mWl/DRN2wTgPQCuT6VSvIObDTfeeh3i7Z0YHXUOgGqBZQquhWC5vN7Q91wNCi7yceetNyJ78RKY\nIiMw2I+xseVF2BTJZLTlP796YB6KntN52H5Guq5DURXkiTqHCvPpXFM+Y6bL3PmhM4U8PtgifS5N\nTqeBOc9rJqiJduTGl+YV+oYGl/23yS4jdAAgmyuuzvEZjgPlmIYBkMv/AUAaQLoB+9SRaMf5s7zr\nOADEOsw1RLoviMm5AjBX3/vqfj8A/ncwVQEbMH+X0e5OhONhzE8vzfHrSoSxfTOtLC6k8w37rqRg\n0FZBqiD7fHW9X8SmQ9fT781m4Zb0m5/PYo74rO3Qi3rJHNVQfF/I5JCR+M9gaiaNxfLv3ntgj21A\npTNlVa/vkksJUGaFz+/Xv/11OHn8RTz0k0dqfu1yi9LfiVIh+r2apv2npmnf1zTNMTj72B/9Bv7f\nj//qMt/OgVWsoVpJnLyoJJ8CJRxEaPMGBIcHl12EKaChzD2tOHndMMZczT2bVidA1VHZWCSQheqA\nx07aJeJXXYngxiH4ujoR2bcLwY3L75zxUjC7kjVUK42TdUKkdxC6LwSdSdB9IRTjvNnlcrCrowpt\n3QzJsrjwBXy44547qzWEHfEgbr3Wfk5mI69NTJIwsM3e9wyoL+UH2BemNy7lV9vnwSQGlRiJk1/k\n08+SQbVy8qNa6ZSfFaf6U2Bla6iAkpfkH37mY/i3+2qvpVpuUfqHAXy4lte86nUva06UuYq2CSuJ\nUw0VdYIJGodbUbokS/C7fAexRByTF+0LaJsVFBg75py2ASAL1XWwmhckks+H6P497k/0gBdft5W0\nTVhpnKwTYh3tKCYaE0QZoRoLJL/ftiZs+5Gd2LRvM8YfeQrSxQuOpQZu9i+1MrB9CMcfec728eWa\nelawK0z3FFA1oSgdKBWm5+bpNLDp7Q0B1d4Du7lxPRWi8dUNqJxMkYHVWzAFg7XbbbS+lOFhxaOv\nB4XKYUCyF+NPwfKJtDtfcIIRejCyEbfC9GYYewIAfEEokaX31iW52nrOISsl40Qjqm9VFV4vkwfW\ns0Ll5JberO4sX08Xty28YyuYg02AL+BHLMHX5XE0WD2nDD6NhOsMFuI2XlTeuvy83Jtq/zy8Xu+N\nAVU4EsL2XfywZACIrLJCFXDpSF9phaoeWj6goga3cqyHgEooVKuGm0IVdFlhAe4BVdOCAsYQ3bgV\nhbY+FOPdKCY3AIrNezEJemRJEdEBFMPuBfnNxFNAtY4nAtgpVJIk2Y7vqhc1HkNkz46Ss70sIbRl\nEwIb3NO2kt9dKWx0OULfpj7IDg78q6pQMck9pbeMexPlls79WlniPms71/SV9KGiCLl8livZ5Vcv\nrX8lEjVUUDzM+hMsH9Xvgz/oJ4ciA86WCRXcvKiaOVGdMQYEo7bDZo3okQQKahCskC2lBu3SgytE\nzIMK4/NwI29V7AKqSDRiO5qrEYS2bEJw80agWPTspWWtr6Kf1Nh9Vnwqejf34WzqDPl4uA4fKgCI\nd9IBldvYmQpMlqHnbSwogGWNRfOiUElEkHng0D78zee/atoWCPhXbBamHa41VC2kQLe8QuXtBF0P\nAZVI+a0mTl5UbhcEAIh1OgdUa0rW9odKacFVDqYAwB/ww+93XjCs9g2hmdi5pTdjCLsVxlhNxqRe\numGb0TBDDUquUI+xJ1Aquqfc4D0pVAAkNzf15dRQLTOg2rl3B9razdchzSYNuJK4Kfxr6troQusH\nVE2Yl7QWcVKoRMqv+Til/bwpVG4pv9YXi5tFzKXLcqWNPVcSO7f01S4kpvCS8mu0QgWAnOsHlJpF\nAh7SY250DvA1ZU4u6kZcA9LlKFQe/iYqoPL5VLz3V99dVXyi8Sje8Ytvrvn9G01wHdVQtf5V/DJJ\n+ck+FUyWoBNdGk7BlqAxRNrtb+r11lBJsgypjhEl651YPIrRS2O2j69nhSqRpGvYYjU6z68EXlJ+\nzVCoBjTaOiEUCzfE3PjQ7Yfx4tMvVH/evH+L6+DkCszOiqT6hJVTqADg5ttuwN6Du3H2xXPYsHmY\nU6xWg0DID8YYOT4HaK2UX+sHVEyCDgbmVCGyDgKqyoDk7OwC95giUn5Nx0mhclthAaWaC9WvIpfh\nfXCFOuWMWzfbeq6hikTD8Pl9yGbMPkOxVS4kpmBebnxNCKjCsTASfZ0YP28OuustSK+w/chOvPmj\nb8exnz6DeGcch19+tefXNkWh8rCAtguoAKAzmUCnTaC+GjBJQiASxCJxbwOEQrXySBJAzSur0voB\nFQDbgErUUDUfx5Sfhws3YwyxRJy76AOtdcFYDdzqhdZzlx9jDJ3JDpw/ax7NsRYVKsYYmE+FnrUf\nntEs0+EBbZA7t+otSDeycfcmbNy9qebXuQdUy/OhcsO1dmuNEVwnAVXrFxcB7nVU60ChAuxXJiLl\n13zCDnU8XhQqALZu6c3s8FsPuAZU6/zz6+ru5LatxRoqwD3t16yAanD7MLfNbTrBSiC5pfyWsdiv\nJ+W3VrGrQ2WS1FLlEOsjoHI7SddLQGWzMhFF6c3HydzTa2rBro6qlVZgq0H0Mg+oOrv49MxaVKgA\nD4XpTQqodly1kzPx3HVNY9z668FJoVrOFAJgfQZUdl2Tql9tSB3cSnF5BFTrKOVXy3ZB43CuofLW\nQm3nRdU0l/R1gptCtZ5HzwDAnv07uG3aji2rsCfuuFknMLk5txx/0I83/dZboR3egY17N+PuD74W\nm/et/mfkWJS+zEBBVhVILtcMSW2xgMpGoWq1xdK6uJLrTHYMmZZj778WoZQoJjHIQuFoOk5dfnUr\nVC120Vhp3NSY9f75vfr1L8PXvnovTj1/GgBw463XrQn/IArXTr8mmpF2D/fgtb/6hqb9/uXgWENV\nx31JDQWQyc7ZPt5yCpVNp3SrqffrIqC6nFN+StDfUpJoqxKKBMEkCXrRbFvBGEPAo0Jor1C11kVj\npXFVqNaxbQIAtLXH8Rd/82k89rMnEAwFsHvfzjV7zrul/Bo9HHmt0wyFCgB8oQAyU+sooHJI+bUS\n6yOgumyK0vkbt0j3rQxMkhCJhzE7OWvaHiwHWl6wV6jWx2nYLNzGz6x3hQoomTIePnrFau+GK6up\nUK1FHAuq61SoHN+35QIqWuVvtXKI9XF0X8Y1VKLDb+Wg0n5exs5UsAuoWmn452rg5JSuqsqaVWsu\nR1xrqC6zgKpZCpWbdULL2Saskxqq9XF0XyYKVXyoi6uX6thKuwQLGg81z6+WgMofCsAX4G84rXbR\nWGmcaqjEZ7e2kFwWB5dfQNUshcp5Id1yCtU6qaFaH0f3ZVJDJftUbH/19VDKJ1Ny10b0H+Y7gATN\nger0C3kYO1OhYu5pRQQFzkSj9h2W63nsTCsiUn5mmCRBt7v/1KNQrbOUX8gm5ddq18bW0gVt0KXL\nQ6ECgOTODejcPgRdLw3/FKwcVEDl1dSzQqwzhrFzo6ZtrVYnsNLIioxwJIz5uXnusfU8dqYVcUv5\nradrsWeYDOh5bnM93efuKb/WCqjsFKpWK4dYH3dk1wNzffyZFUrusevrb2oFOgeS3LaOvtpmYkU7\n+PRVq8naq4Fdp59QqNYWjl1+knR51rvZqXJCoaqyXrr81sdd+TJSqASrh3Z4hyllFwgHsOf6fTX9\nju7hbm5be8/aGVS6VrENqFosJbDeYYpie7293Oqnqtjdn5rZ5ddixp6q3weFmMnZauf3+sg1uB2Y\nIqASNADVp+Ldf/xL+Nm3HkIhX8CBl1yBGKE4ObHn+v24/2v3YX66lL5q62rHtiu1ZuzuusIuoPK1\n2AV3vcMYg+T3oZjO8A9ergGVXdNUU7v8WiugAkoNPrMTM6ZtraZQrY+A6jIpShesPoFwENfeff2y\nXx+MBPGeT74Pj33/EciyhH03H4RfzGJ0RSg8Jqy+AAAMH0lEQVRUrQPz+QAioLpcFSpdkmjjniYq\nVHKL2SYApToqEVCtBZgEHQwMut0TVnR3BAInQtEQjt517WrvRkthZ50gaqjWHpLPhwL5wGV6HbZN\n+dWhUAV9pdfr9D2vJRUqosGn1RZM62fJYLP60QGhUAkELY5I+bUOdoXpl6tCZatE1XFfYpJEznat\n0IoBFWVBI7r8Vosm5KkFAsHaIGozfkZ1a9MXrDiSTZDraHK5nmlCUTrgbO7ZigFVcrCL29bZz3dW\nr2XWT0Blu/pZP3+iQHC5Yjd+RihUaw9bLyqR8rNQ3+fhVJjeigHVvpsOIhwPV3/u3zqAoe1Dq7hH\ntbM+aqiApuSpBQLB2sDeh2r9XMLWCyLlZ8bOwLMeY0/AuTC91WwTACDeGcd7Pvk+PHP/k1ADPuy+\ndk/LHTPr5mqkM7tOChFQCQStjm1RulCo1hy242da7ObYMJq02F9vChVQati58vYjq70by2b9HOFN\ncKMVCARrA7saKp+ooVpz2KX8Wk1taBhNq6FyCqjWjVbSUqyfI9yuKF1YJggELY9dDZVQqNYetuNn\nLteAqgldfoBbQNWaClWrs36OcKFQCQTrlnA4RM6vFD5Uaw+7lJ9QqCzUq1Ctw5Rfq7MsXVDTtCSA\nLwIIAFABfCiVSj3UyB2rGVvbhMv0JBYI1hGMMcRiUUxNTpu2+1rMp+ZyQNRQWWAMOmNgVhNOoVCt\nO5Z7hL8FwJdSqdTNAD4M4Hcbt0vLRChUAsG6hur0EwrV2oMpMkB4Tl22ChUAyObjVAcc7BS8YetD\nxQBGqLmC5rMshSqVSn3K8OMQgDON2Z3lozfJ60MgEKwNqE4/UUO1NpF8PhQXF03b2OXqQwVAD8bA\nZseWNvgjdQdUPpuUn6TIYEJIWBWW3QqgaVo3gG8AiAC4uWF7tFxsvT7EgSUQrAcohconFKo1ieRX\nuYCq3gCildHDHSgyGcguAIoKPZKo+3fapfxEum/1cA2oNE17J4B7UFIpWfn/v51Kpb4D4LCmabej\nVE91WzN31BVh7CkQrGs6u/ibULw9vgp7InCDqqO6nBUqMAY93AaE2xr2K2WfCkmVUcyZR1ELy4TV\nw/WTT6VSnwfweeM2TdOu1zStLZVKTaVSqW9qmvZlL2+WTNKtz42gmMthapTfHgz6EG7i+14uNPO7\nEzSf9fD9/dwbXoZ//ad7qz+HwkHc8YrrEQrzU+rXG632/WViYWRHxkzbwtFgy/0djaCZf7M/EsLi\n5Kxpm+pXL8vPeS2w3FD2bgAHAHxa07Q9AE57edHo6Kz7k5aLXgSlUS2m81ho5vteBiST0eZ+d4Km\nsl6+v4ENG/Dx//kR/PNXvo5gMIh3vu/tmF8oYH6h9f82J1rx+8vqvBq1sJhrub+jXpr93ckBXgnU\nGbvsPudmUWtgutyA6uMAvqhp2t0AfAB+aZm/p3EwCToYGBrbmioQCNYOR284gqM3tO5oissFtaMd\niydPmbYp7Y1LdwlKUHVUooZq9Vhul984gDsbvC/1I0lA0ZxPFj5UAoFAsLL4e7uhJhPIjY4DAHw9\n3fAl6y/EFpihzD1FQLV6rK/qNSYDKFg3rsaeCAQCwWULk2W0XXME+YlJgElQ2uOilb8JCIVqbbG+\nAipJIuIpcRILBALBSsMYg5roWO3dWNdQ5p4ioFo91lc+jLJOEAGVQCAQCNYhZMpPXV86SSuxrgIq\nnaqXEgGVQCAQCNYhoQTvwxZoi6zCngiAdRZQQeWjdZ3YJhAIBAJBq9O2oRfh7vbqz5JPQc/+rau4\nR5c360ob1EMx6IvTYPksAKAYiAKKzQBJgUAgEAhaGCYxHHzXK3DugWdRyObQvW8zQp3CnmK1WFcB\nFSQFxc5hILMISAxQgyLlJxAIBIJ1i+xTMXTd3tXeDQHWW0AFlHynAuHV3guBQCAQCASXEeurhkog\nEAgEAoFgFRABlUAgEAgEAkGdiIBKIBAIBAKBoE5EQCUQCAQCgUBQJyKgEggEAoFAIKgTEVAJBAKB\nQCAQ1IkIqAQCgUAgEAjqRARUAoFAIBAIBHUiAiqBQCAQCASCOhEBlUAgEAgEAkGdiIBKIBAIBAKB\noE5EQCUQCAQCgUBQJyKgEggEAoFAIKgTEVAJBAKBQCAQ1IkIqAQCgUAgEAjqRARUAoFAIBAIBHUi\nAiqBQCAQCASCOhEBlUAgEAgEAkGdiIBKIBAIBAKBoE5EQCUQCAQCgUBQJyKgEggEAoFAIKgTEVAJ\nBAKBQCAQ1IkIqAQCgUAgEAjqRKnnxZqmdQN4FsCrUqnUjxqzSwKBQCAQCAStRb0K1ScAnGzEjggE\nAoFAIBC0KssOqDRNuwnADIAnG7c7AoFAIBAIBK3HsgIqTdNUAB8F8GEArKF7JBAIBAKBQNBiuNZQ\naZr2TgD3ANBRCp50AN8E8FepVGpG0zRABFUCgUAgEAguY5iu6zW/SNO0/0JJ3WIANgMYAfDaVCr1\nbGN3TyAQCAQCgWDts6yAyoimaV8A8AXR5ScQCAQCgeBypRE+VPVFZAKBQCAQCAQtTt0KlUAgEAgE\nAsHljnBKFwgEAoFAIKgTEVAJBAKBQCAQ1IkIqAQCgUAgEAjqpK5Zfl7QNO2TAK4CUATwwVQq9bNm\nv6egcWia9gkA1wKQAfxhKpX62irvkqAGNE0LAHgKwMdSqdSXVnt/BN7RNO3NAH4NQA7AR1Op1H+s\n8i4JPKJpWhjAlwC0A/ChdP59e3X3SuCGpmm7AfwLgE+mUqk/1zRtAMCXURKfLgB4ayqVytm9vqkK\nlaZp1wPYkkqljqJkDvqnzXw/QWPRNO1GADvL398dAP5kdfdIsAw+AmB8tXdCUBuapnWgNI3iKIA7\nAdy1unskqJF3ADiWSqVuBvBaAJ9e3d0RuKFpWgilGOW7hs0fA/CZVCp1A0pzi3/B6Xc0O+V3C0rR\nHlKp1DEAbZqmRZr8noLG8UOULgYAMAUgpGmacMVvEbTSGIPtAP59tfdFUDMvAfCdVCq1kEqlLqVS\nqV9c7R0S1MQYgET53x0ARldxXwTeSKMkHFwwbLsRwDfK//4GSuelLc0OqHpgPpDGytsELUAqldJT\nqdRi+cd7ANybSqWEz0br8D8BfAhiNFQrsgFAWNO0r2ua9kNN025e7R0SeCeVSn0VwLCmaccB/ADA\nr67uHgncSKVSxVQqlbFsDhtSfCMAep1+x0oXpYsLewuiadpdAH4ewPtWe18E3tA07a0AfpxKpV4s\nbxLnXmvBUFI2XoXSufeF1d0dQS2U699eTKVSW1HK1PyvVd4lQf24XkObHVCdh1mR6oNZThOscTRN\nuw3AbwK4PZVKza72/gg883IAd2ma9hOU1MXfEipHS3EJpYBYT6VSzwOY1TStc7V3SuCZawB8CwBS\nqdQTAPpEuURLMqtpmr/8736UYhpbmh1QfRvAawBA07SDAM6lUqn5Jr+noEFomhYD8AkAd6ZSqenV\n3h+Bd1Kp1BtSqdSRVCp1NYDPAfh4KpX6/mrvl8Az3wZws6ZpTNO0BEqph7HV3imBZ06g1N0OTdOG\nAcyKcomW5LsAfq78758D8E2nJzfVNiGVSv1E07SHNU27H0ABwHub+X6ChvN6lAor/6G8utIBvC2V\nSp1d3d0SCNY3qVTqvKZp/wTgpyiddyLd3lr8JfB/27tD3CijMArDR1SwgOp2avotgKS2CWugigWM\nrmsCAVHNFkhGg2MBULqKqwiV3ULTBDGDhZBP3Pz5n8fMjJkc+eaKe/Opqr5nf+XMdu4c/uVw6PMx\nyWmSp6p6neRNkl1VbZP8SrL72394yw8AoMlN6QAATYIKAKBJUAEANAkqAIAmQQUA0CSoAACaBBUA\nQJOgAharqt5W1cnsHQCCClikqtokuU2ymbsEQFABy3WR/bMsANN5egZYnKr6luQy+6D6887k2Rjj\nYeowYLWcUAFL9D7J58P3D0mukjzOmwOs3dHsAQD/a4xxX1WvDj/vxhg/pg4CVs8JFQBAk6ACAGgS\nVAAATYIKAKBJUAEANAkqYKmeD58vpq4AiKAClutn9pd6vquq66o6nz0IWC9BBSzVlyRfk7xMcpPk\neO4cYM08PQMA0OSECgCgSVABADQJKgCAJkEFANAkqAAAmgQVAECToAIAaBJUAABNggoAoElQAQA0\n/QY2okiwETQYkAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75a600c50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"with sns.cubehelix_palette(5):\n",
" for i in xrange(5):\n",
" path = EM(xinit[i],sigma=2.4,T=10)\n",
" pl.plot(t,path,linewidth=5)\n",
"\n",
"pl.title('Trajectories of the Langevin SDE, $\\sigma=1$',fontsize=20)\n",
"pl.xlabel('t',fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now the kicks are strong enough that the attractiveness (or repulsiveness) of the stationary points looks completely irrelevant. The dynamics are all about the stochastic part.\n",
"\n",
"## Changing the properties of the potential\n",
"\n",
"We now fix $\\sigma=1$ and look at the paths for $a\\in [0,b]$. We will start from $X_0=1.3$.\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff758c5c510>"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAFkCAYAAAD13eXtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4G1XWxt+RZMuW3G3Zjlscp0x6J40aILQQeg1l6Sxl\nAwu7wO6yBZayC0tZ4KNs6L2TngAJkN57ncRx71221ct8f6jeOyNZkuXK/T0PT5iqsWRrzpzznvdw\noiiCwWAwGAwGg9FzKPr6AhgMBoPBYDAGOyzgYjAYDAaDwehhWMDFYDAYDAaD0cOwgIvBYDAYDAaj\nh2EBF4PBYDAYDEYPwwIuBoPBYDAYjB6GBVwMBoPBYDAYPQwLuBgMBoPBYDB6GBZwMRgMLzzPv8fz\nvIPn+YIu9nuf53knz/OZvXVtDAaDMZBR9fUFMBiM7sHz/EYApwIYJwjCUZntrwK4D8DfBUH4p8z2\n8wCsAfAlgOcALAfQQO3zFwAfCYJQ4V4luv8b8PA8zwN4BkCZe1UGgD8KgtAQ8KDeOdezAJYCOAbA\nAqAIwAIAHwqCUBPu+dzn1ADYKgjCpEiOZzAYkcMyXAzGwGclXMHP+QG2n+fefl4X21cKgrBHEIRv\nBUEwezbyPF8I4J8ACqN1wf0FnueTAKwF8LUgCA8LgvAwXAHOOp7nw3ogjea53DwKYAuAFgAGAPsA\nKLsRbE0HsB7A+EiOZzAY3YMFXAzGwGcVAA4yARfP80MBjARwGMAMnucTZY4/H66Aa02A88/AIMlm\nyfAogBgAX/itexMAD+D2PjwXAFQA+B+AJQD+A2CKIAhPh3sSnudH8zy/AsC9AOwRXAeDwYgCrKTI\nYAxwBEE4wPN8NYAzeJ5XC4Jg8dvsCaZeBvA2gLPhKlMBAHiezwYwDsAOQRAaeZ5/H8DNAAoFQajg\nef5nAGe6z/ELz/MigGF+5+d4nv8TgDsB5AKoBvCqIAgv9dCPG22uArBdEASnZ4UgCK08zx8DcDWA\nt/roXABQIgjCb8M8RoIgCMcAXAy4NHpwBdAMBqOXYRkuBmNwsBpAHIAzqPXnw6XH+gQuHRCdBZvn\n/neV+19am/U3AF+5///vcAUVjX7b/wngHADPArgfgBPAf3iePyfSH6S34Hk+Aa7sX4XM5hoA0/ri\nXAwGY3DCMlwMxuBgFYA74AqofgQAnucVAOYCWCUIgoXn+W3wBVgePBmwVZBBEISNPM+f7V5cLwjC\nBve5AVcZM1cQhHM9+/M8fwDAVgDXAVgXyoW7z38PgJMAUgFsAHC3IAh08Bhthrr/bZfZZgCQxPN8\njCAItl4+lwc1z/OPAtDBFcgOB/CYIAgnwjgHg8HoJ7CAi8EYHKwFYIUrgPqDe90MACnubZ59nuR5\nvkgQhBL3unMANAqCsCuC1xQBvEKtO+D+NyeUE/A8fztc2bFpgiBU8jyfA+A4ACHIMe8AmIrQdGWc\ne78HPcGiH0nuf60yxxnc/6aAzOgFIprn8pAJ4GNBEKoBgOf5GwBs5Hl+YiRdjwwGo29hAReDMQgQ\nBKGT5/lNAObyPJ/j7mS7AK5gwxNw/QhXCfB8AG/wPD8RQBaAD7rx0iep6zC5s1/xXR3I8/wkAG8A\n+I0gCJXu42t4nm8F8HOg4wRBiESALofD/a9c4Bbj/lfZB+fyMEoQBP/zfQaXiP7PAB4M81wMBqOP\nYRouBmPw4CkLenRa5wI4LghClXt5F4A2+OwhPHYQq7vxmnIZnVB5GkAHXP5fAAC34WougF+6cd5Q\nCZZt0rr/7eiDcwEAqGALbjF+I4BLwzkPg8HoH7CAi8EYPHjsIc51i7hnAvjBs9F9w/4JPmH9PLgy\nM9/38nWC5/lkuALD7wVBcPhtmuu+Jrr81xPUwxVwpsps0wJoEwTBILOtp88Fnuc38Dwv9x4o4cpK\nMhiMAQYrKTIYgwRBEI7xPF8Kl43DHLhuzrRwfS2Ay3men+beZ6sgCPrevVIAwAi4rm8btf4MAPsE\nQWjneb5QEIQy+kCe5/8HYArC03A9LAjCRv8NgiAYeZ7fCyA/wPXtC+H8UT+Xm8kA5MTxGfC52DMY\njAEEC7gYjMHFarg6/m6Cy+SS1kL9CFcQch9cmRfZ7kQKTwYqLkrXCACeIM9ro8DzvBouEb/HhuJh\nAL+jDxQE4a4oXsdKALf5r+B5fjhcgdOz1PpRAMopn7NIzzUCQJW/oz/FGgCEBxfP81MAqAF8FOZ1\nMRiMfgArKTIYgwtPWfEauMxMCd2QIAgn4cqQLEQQOwiKUvc5H+d5/vfueYHdQhCEYgB74ZoP6LGw\neBWuILCE5/l0AM3dfZ0QeAOA1t0B6OF3cDnzv+1ZwfP8WXCN6fk4Cuc6Ha4uzO+CnOs5AC/zPB/r\nt+5BAJsBPB/mdfkT7z6uy6YGBoMRXViGi8EYXPwEwAxXJuTHAPv8CJdnV5UgCAdlttOluq/hCuDO\nhWtMzfYuriHUwdZXwxVU5ML1XfSC+/pvh8so9E8hnKNbCIJQ5w5anuZ5fipc9g6pAC4QBMF/DE49\nXIL1gAamYZ6rAUBxkHPt4nn+LQAf8zxvdJ/rIIA7KS+vLq+L53kdXFmxXABj3avLeJ4/BOBtQRA+\nC3Qsg8GIHpwoRj4ijef55wCcBpcW41+CIHznt+1cuLqQ7ABWC4LwVDevlcFgMPoUnuf/JgjCk319\nHTT99boYDIaPiEuK7ie5sYIgzAFwIVyz2vz5L4DL4QrIzuN5fnSkr8VgMBj9BHVfX0AA+ut1MRgM\nN93RcK2HqyQAuLx9NDzPcwDA8/wwAM2CINS4vWRWwSWGZTAYjAGJ+yFzd19fB01/vS4Gg0ESsYbL\nHUiZ3It3wDWvzVOfzAZpBNgAtziWwWAwBho8zysBzBME4S99fS3+9NfrYjAYUrotmud5/lIAt8Ln\nXi0H193XYTAYjL7Cbc7a74Ka/npdDAZDSrcCLp7nz4erk+h8qv28BsAQv+Vc97qAiKIochyLyxgM\nBoPBYAwIwgpaIu5S5Hk+CcBGAOcIgtAks/0ggPlwBVpbACx0e+8EQmxsDGvUGKMfodMlgn1+AxP2\n2Q1s2Oc3cGGf3cBGp0sMK+DqTobrWgDpAL50i+VFuDx0DgqCsBQut+vP3es/6yLYYjAYDAaDwRi0\ndEc0vxjA4iDbN8E1q43BYDAYDAbjVw0b7cNgMBgMBoPRw7CAi8FgMBgMBqOHYQEXg8FgMBgMRg/D\nAi4Gg8FgMBiMHoYFXAwGg8FgMBg9DAu4GAwGg8FgMHoYFnAxGAwGg8Fg9DAs4GIwGAwGg8HoYVjA\nxWAwGAwGg9HDdGt49aDC6QBn0gOcEmJ8EsAGaTMYDAaDwYgSLOByo2ipAmczAwCcdgvEpMw+viIG\ng8FgMBiDBVZSBACHzRtsAQBnau/Di2EwGAwGgzHYYAEXADjsxCLndACis48uhsFgMBgMxmCDBVwA\n4HRI11FBGIPBYDAYDEaksIALAOeUCa4ctt6/EAaDwWAwGIMSFnABstksjmW4GAwGg8FgRAkWcAEB\nSoosw8VgMBgMBiM6sIALgUqKLMPFYDAYDAYjOrCACwAc0gwXxzJcDAaDwWAwogQLuACAZbgYDAaD\nwWD0ICzgAuQDLqcNEMXevxYGg8FgMBiDDhZwOZ3gZAIrThSZ+SmDwWAwGIyo0K1ZijzPjwewBMCL\ngiC8Tm0rBVABwAlABHCDIAi13Xm9HkEuu+XBYQMUyt67FgaDwWAwGIOSiAMunuc1AF4BsDbALiKA\nCwRBMEX6Gr2CnCWEB4cdiOm9S/k101pSg5qdx6DRpWDoGZOgULFAl8FgMBiDh+5kuMwALgTwWIDt\nnPu//k2QDBfnsIGpuHoeS4cRBz/+AU67K/hVKBUYeubkPr4qBoPBYDCiR8QaLkEQnIIgWLrY7U2e\n5zfyPP9MpK/T03AylhBemDVEr9B6stobbAFAS3F1H15N/0AURbQ0t/b1ZTAYDAYjSvSkaP6vAB4C\ncCaACTzPX9GDrxU5QTVczBqiN+isayGWLe2GPrqS/kFjfRMWLrgNV59/E/7xx2cgsm5ZBoPBGPB0\nSzQfDEEQPvb8P8/zqwBMAPBtsGN0usSeupyAGCwtCJSmi1U4kdQH1zRQifTzO9LSTixbO4zIyEgA\nx/X/inRP8J8nX0JDXSMAYOPPW3BSEDD79FN69DX74m+PET3Y5zdwYZ/dr4doBVzEnZHn+SQAXwJY\nIAiCDa4s11ddnaSxsSNKlxM6CoMpoNDMZrb0yTUNRHS6xIjfq9bKBmLZaXegpqwRsQnx0bi0AYXF\nbMHPP24m1u3YegAjRo/usdfszmfH6HvY5zdwYZ/dwCbcYLk7XYpTAbwAYCgAG8/zVwJYBqBUEISl\nPM+vBLCN53kjgL2CIHwTzvm/+WwplnyxAgXD8vDwXxYhLSM10ksNTrCSotPuMj/9lWZaegNrpwk2\ng1my3tJu+FUGXDu27IbZRL4fleVM08ZgMBgDnYgDLkEQ9gCYG2T7qwBejeTcP61Zj9dfWAwAqKmq\nxZcffYPf/v6OiK6zS4LYQnCAK+hSMm+InoLWb3mw6A1IzMkI61w/rFiH71esw9gJo3HrPTdCoRh4\nvr7r126SrKssq+qDK2EwGAxGNOkxDVekNNY34b//IjxUIRw82jMvJoqSDJeojCEHVztsLOCKFFF0\nBbQKZcAsYcCAK0zhfGlxGZ574mWIooh9uw5Ao9Xg+luuCvuS+xKL2YKtG3dI1leWV0EUxV+tpo3B\nYDAiQV9Rj+bjlUgtykFqUU5fX07/Gu3jdDrx/BMvobOTvNm26/U9M9dQFImxPiI4QKUmduFYp2L4\niE5whlYoGkqgbDgJRUtlwM/PUC8fcJn14QVcO7bsJrr5lny5HA57EMuPfohcOREAOjsMaGvV98EV\nMRgMxsBEX9mAfe+tQsWG/dj/wRq0lkY26EZ0inDY7FHpFu9XAdeyL1dg9479kvV6vQGwd2X5FQG0\nfkuphEhns5gXV+iIIjhDGxQNpVC0N4Bzv7+c1QTOJB8wdAYIuMLNcFVQZbemhmZs37IrrHP0NXLl\nRA+V5aysyGAwGKFSunYXRId7HrIoonz9vrDPYWk3YM/i5dj4zw8Ic+5I6TclxdLicvzv1fdkt+nb\nDYCpA4iJi+6L0gGXQgUoqbekhzJctdV1eOXfb6CutgFZQzKRmzcEOflDkJufg9y8IcgtyBk4GiRR\nhKWlCYrGarIc6wdnMUDUpBDrnA4njI1tsvtbwsxwVZRVStat+u57zDljZsBjzGYzOHBQx6kD7tNb\nBConeqgsr8bEKeN78YoYDAZjYKKvqEcbldFqK6mBobENWl1KgKNInHYHDn++Dh3VLouelhNVaDpa\njswJRRFfV78JuP70u3/AYpG/WTudThibG6FJ0kX3RWmXeYVKkuHqifE+oijib394CiUnygAAFaWV\n2EntM7SoAE+9+Ffk5A2J8qtHGVGEorUaBosh+Bwni0nS8WlsavM9gdC7h5HhEkVRVli+ffMuNNY3\nQZclFd9//sHXeOf/PoRGG4/Hn3kEp8yeFvLr9QQ7t8qXEz1UsU5FBoPBCIlA2ayaHUcxcv7skM5R\nvGY72qsaiXUdtc3dCrj6TQrlyJESYlmhIG/f7a2tUS/vcbRgXqHslQzX3p37vcFWIMpLKvDxO19E\n/bWjjt0CziINjkRwLk2cG050SMrChvrAo2ss7QaIztBC3bZWPTraOyXrnU4n1iz/UbL+8P6jWPzq\n+3A6nejsMODFp1+D0ykf+PUW69eS3lvpujRiWS6Dx2AwGAySjtomtJyQl2DU7TsBe4DEDrHf/mLU\n7JA265nbuueZ1m8CLn9Onz0Rw0cOI9bp2w3gzNKbaregLSGUKmlHYg9ouJZ9tSqk/Q7tOxz11442\nnJXMyogAnJoUODOHAWoNta+JWO6saw54XtHhhM0YOOPjTzDbhFVLfoDDL5PpcDjwynNvEvs01DXi\n4N6+e6/lyonX3nwlscy8uBgMBqNrytdLdeAeHBYb6g8UBz2+s64Fx5fJ62nNrd2LQfpdwJWcqMWD\njy9CShpZZ+2RgIvOXimUgEJJlBA50QlEMfvRWN+EzRu2Eevu/N0tuOP+W3DRZecRrf81VXUwGU30\nKfoXNvL6xIQMiMlZgDIGYiwVcFmMxLKhLvhw5lDLirRg3p+Gukbs3u5LL6/67nsUCycl+61d/XNI\nr9UT7Ny2h/ic0zPScP6Cc4l9aqvrYLOxBg4Gg8EIhKGhFU1Hyoh1SfmZxHLN9qMBOw5tJgsOfb4W\nTpu8OH7QZbguGDUBLQerkJhEWubr2w2A1RjUqDRcOOpcokLl0hj1YJZrxXdr4PTTLRUWFeDam6/E\n9bdchYcfX4TcfJ9XiCiKKCkui9pr9wScjcpwxfoaG0QqwwWrkbCHoDsU1claYtmsDy3Arigly21K\npZJYXvndGgCAvq0d77zxkew51q/dDKvFGtLrRZsNVHfi6WfPQUKCligrOh1O1FbX9falMRgMxoCh\nfAOZ3UoYko6xV88ltMOGhlboy6XfpaJTxLFvN8DcEjioshnMcFgjlxn1q4DrrFFjMSprCCo27Iej\nkbQRaO8wuhRBVJakW8jYQrj+7Rkdl81mw6rvvifWXXL1fCKrVTSykNhecrw0Kq/dIzidgJ0KUvw7\nSVVqiJzvV4wTnV4dl9VghrXD91lySoXEmM7SHtpnXUFZJlxy9UXE8tYNO9Dc1IL33vgIHXr5PyZD\npwHbN/e+jYTVYpWUE8889zQAQP7QPGJ9ZRkrKzIYDIYcxuZ2NBwkteBDz5yMuJQEZIwuINZXy+iz\nytfvQ7NQQawbMp1HXEoCsa47Wa5+E3D98fwFOH0E71vRQQqs9e7yEmeJYllRzhYCkHYqOqOT4dr0\n81a0NPvKaPGaeMy7iJyORGvXTp7om4CrZtcxHPj4B1RtOxzY8M1uJjoTRWWMqyzrgeOAAGVF2vBU\nq0tBXAqZ1bSEmOGiNVwXXjIPQ4t8f2AOhwOvv7AYK75dQ+yXlk7O51y3+peQXi+a7Ny6B0aDr5yY\nlp6KcZPGAADyh+YS+zIvLgaD8WvGaXegYtMBCEs3ombXMVj8HtorNu4nKigaXQoyRg8FAOTMGEOc\np+lImfdY0elE8eptKPt5D7FPYm4GRl40G3Gp5H3J3BZ5DNJvbCEueuwGbHx9qXeQsSY2lth+Yl85\n9qYdQmx8LNRDcpA9dRTiU8Ob1E0girK2EAB6LMO17GtSLD9v/tnQaMmApGgUGXB11c3YE9TtPYHj\ny1xdcy3HK6GKVyN70gjJfhLBvIxPmqjWEEFyU0013vviY7RU1mOKNgO6xCQAgDY7TVJSDCXDZTab\nUV/b4LsmjkNeQS7mX3Y+Xn9xsXf9Lz9uJI7LLcjBHx5fhN/f9Zh33bZNO9DR3onEJPKJpidZv05a\nTvSURPMLqQzXIBLOi6KI0pPlyB6SKfkbYDAYDDnKN+xH+S97AQC1u48D3GYk5eqQOiIP9ftOEPsO\nPXMyOLfbQWpRDuIzkmFqclXORKeI2l3HkDdnPI5+9Quaj5OyFJVGjXHXngOFSinNcLUOggxXetEQ\nTL3rEmgyXWL5eCrgam83oqWyDXXHG1C+fh92v7kUNlM33OdFJzg/ebzIcb46bw9ouEqLy3BgzyFi\n3aVXXSTZbzgdcBWX9aplgdVgQvGa7cS6yo0H5LNclH4LsTIBF5XheuGFD7F66Q/Yvmc/vty9zXve\nhKw0qJOogEvfCc7YBk5fB1jlmweqymuIa8vOyYI6To1zL5qLmNjAMzDve/guTJgyjvA5s9ns2LBO\nvjulo70TJ0+Uor6uAWZzaN2TXWG1WLF1A/lee8qJgFxJcXBkuJxOJx773d9w53X346rzbsLxo8G7\nhhgMBkMURdTuEaiVQHtVI8p/2UvYCMWnJUE3zncv5TgOuVSWq2aXgL3vrJQEW4oYFcZdc7Y30Ipm\nhqvfBFwAEJ+aiKl3LEDaiDxoYkj3b6ONDK7sJguajpZH/mK0+N4jmAcgKqTmp92Fzm5NmjoehcOH\nSvbLzNIhIdEXeJiMJtTV1Hf79UPl5JrtsFOBrKGhVeLaC8gI5uUmAahiXf5mAIxGM3buPebd1GI0\noNXoKhXLZrha26HQ10Nh1EPRXCEb+NL+VAXurFByShLOOHuO7M8454yZmHnqdHAch3MvPIvYJldW\nXL92E6658Gbcdf3vsPDi2zD/tKtw4alX4Lr5t+DuhYvw0jOvSeZ/hsLhg8ck5cTxk8d6l6UlxcGR\n4dq5dQ92bXM9pVosFrz6/JtdHMFgMH7tdNY2wxqirrfg9IlQKMnwJnvySChifdUra4cRhjpS2hKb\nqMGU2+cTemI6w2UaDBkuD6q4WIy/YR6GnzqRWG+0SjvIDA3BbQWCImcJ4SHKJUVDpxE/riJtBy69\n5mLZfTmOk+q4ekk431Jcjfr9UssEAKjaRvlUOR3SQFQu4OI4IDYeAHD0RAWclJlpU6frl9eV4SKz\nYZZOszd7xQGyBqt01se/DDf/8gsk+8fExuCeh+70Lp9DBVz79xxCfZ2vRHn4wFE8+9f/SDoYrRYr\nGuubUHy8BCu+XYM3X3pH8lpdUU8F0pOmTSA6LDOzdUSWrl3fDn1be9iv09/YvX0vsXzkwLF+343L\nYDD6lqZjpKBdGaCCoU7WIktGAqOKi5WVxnhIGJKOaXdfgsQccjIJrS0eNBkuDwqlAmPmzSDW2Tgn\nCqflE+uMDfJz+EKBdpn36rcA+YCrG5PC167+mfBZSktPxalnzQq4P63j6g3hvMNqx/HlmwNubxYq\nyMieym4p4+IBTv7XyVNWPHxMmpFsMnQgJiEesQnxUKljoYzzlZJFpwiryS+os8tluMiAq8Av4Jo4\ndTzyCsgs0bU3X4mcvGzvcl5BLkaPG0Xs89OaDQBcHl5//+PTsNm6DrgjMU5taiCNX+kRREqlEnn5\nZOfmYBjxs3en1JhwxTer++BKGAzGQIHuIBxx0SzMevg6jLx4NlKH54JTKhCbqMGYK86EQqWUPQct\nnveQMWYoptw+XyJrAeRKioMow+UhOTmJWO4wmJBZlE6sMzQGz3DVVNXis/e/wr5dB6QbaQ8uf+8m\nhZK0M4AYsf+XKIpY+tVKYt38Ky6AShW4X6EvMlzl6/eSYkAO5C+fCFRvP+LbTAnmVfHkL6rDZkfd\n3hM4+f0O6BtdaeAjMgFXc2cnErLc3YKiiDgtqd2zdPqVN2VKinTnnn+Gi+M43LXoVu/yqNHDcf0t\nV0nOce6FZKfoutU/w2Qy468PP4XWZjKoT89IQ0yM9LNrrG8K3M0ZgKZGMuDKyEyX7CMVzg9sHVdr\nS5tsI8jaVa73nMGgaahrxJcff4v7fvMQLphzOR644xG0teq7PpAxaDDrDeis9fu+5ID0UfmIS9Yi\nd8ZYTPrNBTjjb7dg9sPXIWVY4PnDCVlpEvuh/FMnYNy15wTOmCXGg/MrT9qNFtgj9GzsN12KNLHq\nWMRr4r2ZIafTCTGGA8f5kk0WvQF2ixUqdazkeH2bHnctXAST0QSO4/D0y3/HzFOn+3aQlBSpt0IZ\nQ87+c9iIzJfNZgPHcUEDJ1EU8fUnS1Be4ovMFUoF5l9+ftCfffgocjhmSQ9nuDrrW1C5+SCxLnfG\nWCQMSYewxNfdV7vnOArnToVKHSPRbyk1WsAJ2M1W1Ow8isqth2HrdH12lVsOYtx5Y3H4WJnktZsM\nHUjITgdEEVxbLeK0MTD4/V2ZOy1IynQ9YdCDxB0Oh0TXNHQYmQU9ddZ4fPDGo6ita8ak8UWIa6+G\naIoHYuMhxsYDKjXOOu90vP7SYq8hbenJcjx6318ljvQLb70Gt993M0RRhMlowtUX3OwdOG2xWNCu\nb0dySnKAd1kKneHK0MkEXLRwfoBnuPbvPii73mAw4pcfNuDCS8/r5Sti9EeaGpuxfu0m/PLjRhw5\ncIzYdmjfEXz72TLcdu9NfXR1jN6Gzm4l5WUiNiGeWMdxHAifogCMvvJMHF+2GdZOI/Jmj0fWxOFB\n9+cUCsQlJ8DU4pNzmNs6kZCVFuQoefptwAW4hM/+pbh2gwnxyfEwtvnWGRv1SMrTSY7dsG6L91hR\nFPHZ+1+RAZecaN4fpYoKuHwB2vbNu/Di06+itbkNp8yZipvuuF5SlmppbsV/nvyvxEzz1DNnQZdJ\nlo5ohg7Lh0Kh8HYn1tXUo7PTgIQEabqzu4hOEceXbiI6PGKTNBh2zjRwSgVKftjpnWnoMFtRv7/Y\n1e1BjfSxOziUrN2F6p1H4TBT0b8IbFy2Ex2d0k7Dps4OaDKToWirAWfuhJrOcBn8zkWZrDbUNRLa\nqqTkJEnAo+hswdC8TAzNc493cNjBOToAsyubJypVSE0Zgukzp2DHlt3e4w4fII3x5pw5C7fecyMA\n1x+2RqtBZraOcLlvqGsKL+AKJcM1yLy49uwIPOdsxbdrWMDFwLKvV+G1598iZqDSHNp/JOA2xuCj\nmdJv0Uam4aBO1GDCDfPCOiYuhQq4WjsiCrj6bUkRAJKSqfE+Biu0qaSwOlBZsbqyhlg+uPcwGuoa\nvcu0hkukxsFIzE/d5axd2/bi7394Ck0NzXA4HNi2cSfu+81D+NOiv+PoIVfL6rZNO3HndfdLgi2F\nUiEZSiyHOk6NPOpG21NZrppdR9Fe1UisG3nRbKjiYqGMUWHIdJ7YVr3tMES71TsWSXSKKNlVge+f\n+gwVG/dLgy03FQ1NsuvNNhucVr13TmZcAtmdau70nc8119L3JRxMvwXA5YRvCz6LknPYoWhvlIjn\n/Rk2ohB//ufDUCjIP5dMSnPl//sVCo10hiuUgGuAW0PI6bc8HDt8HMVCScDt3cVkMsNqZfMo+zNN\njc14/cXFQYMtACgtLg+7hM8YmNgtVrSWkvfzdD7ygCsS4lJpt/nIhPP9OuBKTiF1XHqLUxJwGesD\nBVxSG4Nf1vqZX4aS4fLHaceBvYfwt4efkhVR79iyG/ff8jDuXrgIf3nwCYnGQKONx1+e+iPGjOcl\nx8pB67h6wgDVaXeg9CfSXTdjzFDoxhZ6l3NOGQMofHlaY5MercddWiyL0Yq9Kw6hdGeF7LBPzk+4\nWNXWLNm3yfupAAAgAElEQVTuobnNF6ioqYDLYqRukH46rmAdigAAmymUDDNgM+PUM2chLl7aZZmc\nkoSnXvwr4jXxkm2Z2WRmtbE+9IDLZrOhrcWnD+M4DukZ0iemPOpnqqmqg8MevXmivUl9bQNqqnx/\nlyqVirDBAIAV3/aMeP6Td77AgjOuxpXzFuKjtz9jg8D7KV9+9C1sMkHxmAm8pGOX1lcyBietxdUQ\n/eYPx6UlQqNL6dVrkHQqRmgN0a8DriQq4GozOaFJpzJc9fKZkxoqwwUAP3+/wbcQzBYCkJifHj9y\nAn958AlYLMHNVouPS5/Qx08ai/99+irOmnd60GP9kRig9kCGy9DYBrvR9/MoY2Mw4qLZxD5xyVoi\nAAOA6h0CWmv02PHVPrRWS8WrKo0ahWdPxZw/XO9tz61qbZHs56Gy2i/gorpEzJ3k+835lRUlGa5h\nZHDCUXM3nfFJcKQXwJmoo5oigPhYpaRzVKVS4R/P/xnZOVmy163LIgOuhgC/i3K0NJEPCqlpKbJ6\nwIQELTGCyG63o7ZmYA6xprNbYybwuGrhZcS6dWt+IWQE0WDdml/w7hsfQRRFGA0mvP/mJ7hr4SIc\n3Bd+Zymj52hr1WPFN+T4rUuvno9Pl7+L1957AUUjColtzErk10ETpd/K4AuI+cO9QbTMT7sVcPE8\nP57n+WKe5++V2XYuz/PbeZ7fzPP845GcX5Lhau+Adgh58zM2tEksG5xOJ2qqpTel40eLUVVR7do/\nmC0EXNoeDyVltXjkT68QJpUAcPWNl2P8JPIJnTilUoFbfnsDXnzrWQzJzQ64nxxFvdCpaGwknxCT\nC7MRlyzVieXNGkcsN5fUY++yg7AayfJhjDYOIy6cidkPXYvCs6YgRqPGqEtOhTItAY2dgZ8IKqpc\nvldiTBxi8gqJbRYq4PLPcElNT0nBPGelTPLUWpdYPiENUJGZNDhsuOLaBUTZ8IHH7sXEKeMDXjed\n4QqnpCgRzMuUEz0MFgPUPVTANfWUSZh9xgwioDQaTPjp+/VRe82ykgq8+PRrkvUVpZV48I5H8cJT\nr6A9wEBzRu/y9adLiAfadF0afvvg7cga4tJf0kbRZSe7YXzNGBA4HU6JE3z6aKlheE8TrfE+EQdc\nPM9rALwCYG2AXf4L4HIApwE4j+f50eG+Bq3hatd3IC4/n+hEMHeYYW8nswXNjS0So0oPP/+wwT3W\nx4fIcQClz4Hbbb6yuhEP//UttHeQppu333czfvvg7Xj57X/jP288jYlTyRtzTt4QvPLO87jpjuuh\nDOAJEgw6w1VaXN6lriFc6IBLGyBNm5SfiQTKDI6WT+hG5mL6vZcjb/Z4or1WGaMCN5YMGGgqqhog\nqrVwpuVDTQXZ/uanAAgvLrqkSGi4nA6JV5j/mCFRRWn07FaMHs/j+defwtU3Xo5nX3kCF10WXMBN\na7gaw8hwSQTzMh2KHvIknYoDT8cliiL27STtWSafMhEqlUoilKeHjEeKyWjCE48+6+0klWPVkh9w\n69X3YMO6wB50jJ6nXd+BpV+uINZde9OViPXrQB9GBVylLMM16GmvbCCqMKr4WCQXyFccehI6w2Xq\ngwyXGcCFACRiKZ7nhwFoFgShRhAEEcAqAOeE+wJ0x1d7WzuU6jjEJ5NlRXNVNREB0IJ5f376fgNE\n2kCT1m8BgFIFfYcRDz/+Jlopo7OFt16DhbdeA8ClvZlyyiS89L9/4cW3nsXl1y3AXYtuxVuf/Ddk\nvZYc6RlpRIbPYrGgRkaX1h0MVMAVqC7OcRzyZgXO5BWcPhFnPHAl1InyQ4hPlpJPorkpqcRyeXUj\nnKm5gEIBlToGKtr81E/H5Wle0Le1Ezq5mBiV90kYAGAl9VuiKpbU5akoKxF3qXLy9In47YO3Y8ac\naQF/Xg99leEaiOanFWVVaG7ylZXj4tTev4+LLjuPKBEcP1rc7fmKoijihadeJbpIAZebP01bSxue\nfOxf2L5pZ7dekxE5S75YTlQQUlKTcRFlnzOMKimWsgzXoIe2g0gbmS8Z2dMbxGrjCU2yw2yNaJZz\nxFcuCIJTEIRAr5gNwP/u0wAgsBtZACQlRfdYE00mKS42NrQSw42rqwIHJhWllSihdVZyARfH4Zvl\nm9DQRAYll1+3IKD/y6RpE3D/H+7GtTdfCY1WPvgIhugUUb3zKPa+uxInVm6VfMFE23HeSI1GCpTh\nAoDM8UWI0ZKicpVahYmXTEHRvFOC/hEcOUj66EzMLSCCofr6Zpj9SgmSmYoGf3sOV2BEBx15BbnE\nWBy6nEgP0RaVZMAVybxM2t6jqak5ZEF7OBkuuhmA1q4NBPbu2EcsT5g6HjExrixjdk4Wps+eSmwP\nRTy/a9tePPfEy/jgrU8k2Y5lX69yZbP9OO/ic/DCm8/gxbeelXS0iqKI/3vhf0xM3wcYOo349vNl\nxLqrbrgM8VQTy7ARdEmxIupZf0b/QqLf6oYdRHfgFJy0rBiB43xvhYoRKdwkthDugEubTTnOtxqh\n8HPL7CoT9NOPG8kVSmnJz+FwYPWP24l1F8w/C/c+dGePCPbMegP2f7gGJ5Zvgb6sDjU7jkJHubdH\nU8fltDsIXxEgcIYLABQqJUbO9w2DTspKxIyrJyN9VH7AYwCXnu7oQXLCe2G6Dika8merKvdlJYMK\n591jlsqpzEUBZXhKC+bpgAtUSZH2+AoFdZwaKam+LKzT4SSyOMGgM1zpg1zDtZea9jBlOjkr9eIr\nyLmX69ash6Ez8KDa8tJK/PmBf+D75Wvx4eLPcMd19+O2a+7Fh4s/w4Z1m/H6C4uJ/YeNKMQDj90D\njuMwadoEvPXpq7jltzcQmr3qylqJaJvR8yz7eiU62n0lmsSkBFxy1XzJfmnpqUhKJrP+ddQ8Usbg\nwdjUBlOTr4rBKTikjcgLckTPItVxhV9W7Cnj0xqQGa1c97qg6HRkgFVIWfQbOw3Q6RJhHD4EFRt8\nAtzOViM4ixGpCUqo4jVobiRLO8PSdSht9q1b/9M23H3tmd7AKU4bDy312ht/3oZGv+xWnDoWjz52\nO9KzQje2DJWqPSew+5O1sBnJhGGagszCVJVXSt6jSGmvbSbMTuNTEjAkP/BNHwB0cydCl+KEsaUN\niRlacByHhIxUxLoDY7lrOyGUwGDw3TiTU5Kw4KHrsPPJeuza43Mdb21uhE43CQCQkpWClhO+LI7F\n5HuK5QCkJceiqcE3YBoARo8t8r6+025HWy35Xqbn6KDwC7JEhwatTb6SBOewIyNDCy7APMhADMnN\nIkqbNosxpM9I30ZmTkeMzAt4XGrqcMTExnjb5dta2qCOlT6QdIdo/V7J4XA4JA7zZ583h3jNBZef\njf97/i1vp6fZZMahvftx8RXyOrrP398iyW6Ul1Tgg7c+keyrTdDgv4ufQn4+WQJ+6E93obO9HV9/\nuty77uN3Psd1Ny+I6nvbG/Tk59eTGI0mfPPpEmLdjbdfjcJh8jodfkwRdm7zZUubG+oxeWrk0o3+\nwED97HoaYd9xYlk3Kr/Le1RPkjokDa3Fvoddlcxs366IVsBFpHwEQSjneT6R5/kCuAKtiwEs7Ook\njY1kis4hkpmn5uY2NDZ2wBFHppoNLa4beltlJcTUHJQWk9mPWUUjUdnaDLvbub22thFHhHKMG10I\nADBZnDBSr/35B0uJ5bmnTwLMRjQ2tANRynDZzVYUr96Gur0nZLcnOcmf/+jhE5L3KFIaBTJLEpeW\n1PW5RRFKpQNJOl+krzeJgLUDOl2i7PGb1+8mlkePGwV1XjaGjR1BBFyHDxbjlDkzAQDOWDLQ9Dc/\nBYCWhlYIR8mxO+mZmb7XN3fA/50TVWo0t5rhkh36UCiUXgNXQERTXatU29UFaZR3lnCsDLlDu+6i\nqa0mA0ZVrCbo+5+TN4QYEbVvj9AtjaA/gT67aCEcOSHJYKRnZkle85wLz8Jn73/tXV67ZhNmnk7a\nlHhYv25ryK//8OOLoE1Mkf0Zr735GqxcstZrRdHWqser/3mPmMHZ3+npz68n+ebTpWht8T2waLTx\nOO/i8wL+PLkFeUTAtW/PMUycNqXHr7OnGMifXU9TvpsMuJKKcvr2vYojO9ubKpswKsCugehOl+JU\nnud/BvAbAIt4nv+J5/kHeZ6/1L3LPQA+B7AewGeCIIStgk2iBli369vhdDqhyUimOhUtcNgc4Mwd\nEG0WiWg+OykZIzNJW4Z16/f6FiiT05bmVmzZQJYT5583E5y5E5yJLMNFirFJj11vLAkYbAFAhiaB\n0CU11jdFrYVdIpjPDMFIzm5xDfJ2IyqU8vo3Pw5Tc9DGTXRNa6ctHPw7DmkNl9lABlycwxbU9FRS\nTlQH0NMFEM6HQ2YWbX7adaeiKIpopJz3g4nmgYHtOE/7b02eNlHi2g8As06bQSzv3LZHVqPT2tIm\nEdUH0hBeef2lOPPc0wJeW1pGKq6jpj98+/mygKUqz7itvsRut+PgvsNBS64DAavFii8+/IZYd+nV\n84NmF2ldK7OGGJxYDWboK8iH0t52l6eJhhdXd0TzewRBmCsIQpEgCLwgCGcLgvCyIAhL3ds3CYIw\nRxCEUwVBeCmS14iNjSEcvp0OJwydRihjVJIf3tDm6kprqyqDya8NPFapgjZWjXE5ZO3354374HC7\n14qU6emPK38ivugL8jK92TCuvT6iG7M/oiji8Jc/Sbw8OKWCCDZUSiVysjOJfaJlgCq1hEgNsKff\n9VE2C4iJ6zLbRw+eHTvR5Q5Ci5b9NVlxSWStnPbishgNqKV81vyHPHclmPeuj4JwPpJOxXZ9B+Gm\nHRcfB20XTRYDWcdFB1xTZkyS3W/MeB6Jfp99h74Dxw4fl+y3a9teYnnUmBH4+vuP8Ps/34+pMyZ5\ng7kzzjkVdy66pcvru+rGy5Cu82UqbVYb3n39Q2IfQ6cRrz3/Fi47+3rcfs29fRbwWi1W3L1wER68\n41Fcc+HNA+r3gOaHlT8Rmke1Wo2rbrg86DG0cJ5ZQwxOWk+SzgParDTEp/Zt6TUabvP92mkekHYq\ntuvdwvlMMkDwlBVrS8iAJFWrhSYjBSN12Yj1c/Ju1Xdi5053MOCXpRFFEauX/kicY/55s7x6L04U\noWirlRpRhUHryWoY6khxtUaXgml3X4Ih08gy0ZB0smQVrU5FqSUEqU0rO1mOrz7+jrzh0b5WMdJR\nOP606zsIzyiFQuEd8k133lVVVHuDXDVl+2HpJF9327eb4PTTn2Vm63wdTQ474UYvAkCsdCwPgKgI\n53X0PMUQMlxyHYpdNWIMVC8uq9WGg3vJQcNTT5EPuJQqJabPIrsVd1DzSAFg51ayTH3K7GlITknG\nxVdcgOdffxrfrv0Un654F3/712PeTshgxMXF4bZ7bybWrVuz3vu7v/mXbbjtmnvw3RfLYeg0oKyk\nAk/95fmgs/zKSirwwB2P4O4bHsDu7fsC7hcua1f/gjJ3adlsMuPLj77p4oj+y44t5Gd78ZUXEE0o\nchQWkQFXVWVNQM9FxsBFX04+UKeN7DuxvAdaNG/qx12KERPIGoK2MDC0ugKuqhoyw5Cm0WLERbNQ\ndNYUjM4iRfjffLneJRz3C7gO7T9C3MxUKhXOvYT0g+FsZnCdgWcDdkXVVnKkSOqIXEz77aVIyE5H\n4hCytKSLJz/kkih0KopOJ4xN1KxHvwxXZVkV7r35Ibz58ju47zcP4fkn/4vOjk5JhqurgOsoZQcx\nbMRQb8YyOSWJ+HK1WW2or3V9dnSXoqXD5BX4d7YYcWgXmfXIy8/x/r/EXT5GLR3b5Ln+aGS46PE+\nIWS46A5FXVbXQlA6IzhQSorHDgkS93B6MLs/M0+dTizTA+CdTid2bSXnf9KeaYlJCcjKzgyrm3je\nRXMlZsP/98L/8I9HnsHf3MPq/SkWTmLrhh2y57JabXj890/g0L4jKBZO4snHno1a+Y9uPjhx7GSA\nPfs/5SWk1vbs887o8hhtgobw23M6nAPSJoURHLqcmDK0981OaWK0cVDE+GIFp1U6U7kr+n3ARc9T\n9HlxyWe4ykupyDghESmF2Rh27nScdvpMYtvB0nKUHq0mbCFWLfmB2GfOmTORklsAUU0GPlxnM0Df\n3EPA2NRGdOABQOFZU6B0f5C0o3sqRwYF0chwmds6Ifr5RcVo4hDr57G19KuVxE1yzbIfcfu192H7\nVrI0hC4CrkD6LQ9SfynXF7AyNgaqeMr81OQKhir2VaHZQD5ZpPvbZ4RYTgQQlQxXJAOsw/Hg8pBP\nZbiqK2sGxBBruXE+wQKh6bOnEttPHDtJlJ2OHy32fgcAgDZBG5XmAaVSid8+eDux7siBY9j405aA\nx3y4+FPZLNfSL1egttqnAevsMGDdml+6fY0AJPMfy0oqYLeH/8Xf19hsNtRUk/Y9+YXBLWY8sLLi\n4MZutsLQQFaAkvL7PuDiOKkXV7j0/4ArkBcXleHq1FshAiijAq7cghzXeBmOw4LfLYTWr8PRbLfh\n8f98gNZW1zk7Ow1Y/+Mm4viLLjsP4Dg4k7MIrRcHuEqLzvBuelXbyPJKYq4OSfm+JzZ1ogYxCb4S\nWKaW/PnLSiq6faM1NAR2mBdFUdIwALiyMo89sRjPvfIFOjpNEDllwMyRhyMHjxLLYyeQ053orI3/\nbEQ1peMyG6wwd1pQd6IRTZ2kWFFjEb03Ps5CzrsMGnBRGS44bGGXitMyUgnBtr6tHRZzcAfi5jBc\n5j0kJiUQMwdtNjtqghj89hd2byf1VpMDlBM9pKalYNSYEcS6nVt8JUS6nDht5uSIRmfJMXXGZEmG\nzR9amH/i2Els3Uhmudr1Hfj4nc8lxy77elXQEmQo1Nc1oL6WfPK3WW2oKB14GZ7qylo4Hb4GhIzM\ndGgTQjOLpkf8yA2xtlqsWL92E3Zv39ft953Ru7RXNsCvNwsaXQpiNOrAB/QitHY8XPp9wBVIw6XJ\nSCE7FfWdsMenoaaOvJkNL8r0DqqOVcdi3rzTie01TS14+O4/oaWpFT+vWU9kdjKzdZg6Y7JrQamC\nM4UsSXIOOxTNleCMekDsunvJZrJIuhLzZo+TPPH7lxW1ajVS/IJOm9XWbf2ORDDv16FYUlwm+VL3\nZ9WPO3Dr/c9j/7HyoIJ5h92BY4fJn9UjmPcQtFMxyfXlW9bciHXHDuPlt5fgsb8txnubf4FQT3ah\nJkGJjuoml37LQeu3gnyJKxQQ/crJHEAMxw4FpVIpyVB1peOKJMMFSIf3yt1o+hPCkROSpolA+i1/\ngpUVd24hy4mnzO56BFM43LXoVtkOSn7sSLzx4cs4fe4cYv1Hiz8jbuifvPsFOqm5q4ArC0O/F+Fy\ncO9h2fXHj5XIru/P0COX6O+CYHTVqSiKIv72h6fw5GP/wiP3PY7Xnn8r4utk9D76CrJDuC9mJwZi\n0Ge4kmlrCHeGSxmrIrsGRKCj3YmGNlKbNHp8PhQt1d6g645FN6JIR3b+lZdW4qG7/4Ql1PDUCxac\nS9gyQK2FU0uWMjm7BQp9HRT1J8Hp6yXCcn9qdx+H0+ZL/8cmaqAbN0yyXwKl48rRkWWr7t5oJYL5\ntARvOW3rejK7la5Lk9yAmpr1+Mvf34TRELikWnqy3OttBLhmo+XkkQGrpKRY6m8NkYDDtVX4aPsm\nbCk5jp+37sW+E6WobG2BjbIKyEhIRO2e4zL6rTjpUHKaaJQVJdYQwcuK4cxR9Id+su/vLfGfvvcl\nsTxhyjhJCVYOOuDavX0f7HY7Oto7cfQQObXgFGokUHcpHD4UV1x/iXc5Lj4O9z50J1597z8YwRfh\npjuvI/Y/frQY29wzGGuq6iQDmP1Z9vWqbl1bwIDr6MDTcUkDrtBF0fSDBz1T8cCeQ9jpp/Nb8uUK\nrPyOTRAYKPTvgOtXluEi9BtUWfH4+j0w+81CUymVyCvMBGczQ9FYBs7UDk1cDBZdtwBFGWTQVVle\n5e3+AVz12gsumSe5HjExA6JKmt7kRCcUxjYom8qhaKoAKBdap8OJ6u3kF2bujDGy/kG0cD6DKit2\nVzBtbCRnKCbGmqFoLAVn1EtKJL+5ayFeffd5DC0ggyWDwYS9O8lxLf7Q8xPHThgtyeRJS4p+zQoJ\ncVh3TP4G40+qRgttrBoNB0/C0Ulqu4KWEz379IE1RLQyXP15eG9ZSQU2/Uyak3oGvnfFqLEjiYYK\nQ6cBRw4cw54d+wgfrGEjCiVdotHg7gduw2NPPIS7Ft2K9756A1cuvNT74DV8VBFOm0uasXqyXO/8\n3wew+T1QxVFGievXboSeeiAMhwMBM1wDMOCisvT0aK5gFBTmSfwJ/Y115QLbV597UxKsM/ofTocT\n7dXk92dSPwq44lMHeYaLFs37G3/SwvkTu8gvpMyUJO8fJud0QNFWC669EbmjsnDttFkYoQv8QU6f\nNYXohvHCKeBMywt6M+dsJij0pJas+Vg5LHpfqUGhUmLI9NH0oQCkwvlkjjQX7U5XjiiKMDZSHYop\n8eAAtFSclPgezTp9BkaP5/G/Vx/B6bMnENv27Ajc7k57L9HlRADIGpKJWLUv4GnXt3tvSDsPH4Xe\nFLwpIVmjwYXjXCJsh8WGpmNUaSGQ4ak/fWANEc4cRX+KZIb39lc+e+8rYnnUmBEhZ6MUCoVk3+2b\nd0ksIqKd3fJ//Xnzz8a1N18pm5G76Y7riWXhyAl8+L9P8Qs1o3XRY/diSK7PcNlms+P75esiuiZ9\nm16SFfJwYjCUFMMIuGJiYiS+dGUlrr/9lqZW2UYHm82OfzzyDFqaWyXbGP0HQ30L0f0Xo41DfFr/\nGX006DVcgboUAVJ7BADNlJg6J1caMHFOO9LyUqGOi8XVU2diFOVA7+HCS+VnuAFw6bnS8+HQFcKp\nTZUYpwJuewK/8iJtBZE1aTjRGehFFBGnUUIV5wtE0uLIwKE7Gi5LuwEOP9NNZawSaq3rtbZtI1vO\nR48bhfSMNEAUEasQceG5pxDbA/kLOewOybYpMtodhUIh+eIsL62Ew+7A8jXkjWlU1hBcOWUGbpp5\nGu6ZOw+fvfcE/v2nhzDcL2iuPezTdgX13/JDkuGKQqdisAyX1WIlfocVCgXS0ro2nQWAoUWk03J1\nZU2XAv2+oKaqDj/9sJ5Yt/DWa8KyaZhB67g27STKRIDUDqK3GMEX4dSzZhHrPlz8GbXPcMy7aK5k\nKPfyb1ZH5FZ/cN+RgNtqq+uJDE9/x+l0SrL0Q8PQcAEy2d5iV8C1eukPstMJANeDzj//9O8B2dX5\na0GunBjO90ZP86suKWqokmKrkRSrDh3Lw5mQAZEc9QilSoH0oalQKZW4aupM8JQ/V3JKEuacSVpI\nyKJSQ0zKhDNzOBwpOdKbd6ertbWjpknyi5Q7a5z0fKIIRXMlVC2VSEjzBQvpVEmxqrwm4hEjEsF8\nisb7C72ZKnnOOcP9Hjhs4CBi8vjhhJ6rsrxKNrg4cugYDJ2+zyI5JUnSeeaBtjuoLKvCT9+vR52f\nDkrBcTh/7ESMHZKLwnQdps7ikZ2ZjBzKJLa1Rg9TuzvIjY0HQhlETY/3iYIXVzANV1Mj2e6cmp4S\ncpddvCYeQ3J9AabT2T89iL748GuiA61gWL4kQOmK6bOmEr9rpSfLCXuIuPg4jJs0tvsXGyF0lovm\n7gdc4vsLLpmHGD/vnpqq2qCZ4UAc2HMo6PaBZI3Q2NAEs9+DgjZBi9T0EEaL+VFECedLi8vgcDiw\n4ltSq0XLFg7sOYS3/vtueBfM6DX6s34LAFTxsVCquzZTDkS/D7hoW4j2IBquFiP5lJdfmAcxMR3O\njKESk87MIlcZSKlQ4MopMzC1aDg4jgPHcXjoL/eH5FDtheOA+EQ4k8gbL2fuAOxWqdFpUQ4SskgH\neQCAxQDO5hKaJ+l83lKa2Fho430BmMViCWlmnxy0JYTWHdiZzBbs3k+WE2d7gk6768tRo4nDWGqe\nldzNY8dmsnV/+uypsp1fADCUKiWUlVTgk3dJsfXE3AKkxLuyfJyCQ/7EHHBOB7QZyUjKI9/z2mOu\nP1gxljRPDQhdUozAGiKcDFdTIzVDMUT9lgfaabu/CecbG5rw/fK1xLqFt1wd8PMPRFJyYlB/rSnT\nJyI2NvIvvu4ycvRwzDlTPoicMWeat7s5JTUZZ5xzKrE9EvH8ISrDlUjZpkRr5FdvIC0n5oWdxaA7\nFUtPlmP7pl1o8HvYUavVePntf2PKKROJfb/9bBl+XPVzeBfN6HFEUZQEXP1JvwV034trAARclIar\nvcOb3VHGxhA/fKuBzHDleBzIY9RwphfAmajzZrvSC3z+SUqFAvNHT8Rbi5/Hkp8/x2lU63fIqLUQ\n/TImHABzTTUaDpEai9zZMtktAJzV19WXmOH7uTiOgy6FHHnh71kVDpIMV6orkNm97wSsfrXz7Jws\nb1ecf5lt+hRyPrpcwCU3eiUQdKfimmU/EiVTjuNw6nDfa2aP0iEuwS1GdliRPZW8nhqhAaJThBhP\n/t4EhOu+NYSchiuQ90+kHYoe5G40PYnJZA5rYPrXnywhhOPZOVmYe37XDuJyBPPEOqWPyon+3Hyn\nNMulUChw16JbiXULrrqIWN66cUdYD0xGgxEnBFIYf/6Cc4nl/m4R4g/tGxZuORGQKymWYdnXK4l1\nc88/A8kpyXj8mUclD0UvPf0aaqpInS2jb7HoO2Ft9+l2FSqlpIGsP9AdHVe/D7hiY2Og0UoHWHvw\nF87TGa6cPD99FsdBTEiDU1cIZ3wylNoEpA4n9VtcUycSEkLMjMjBcRC1vsxVw8km7PpoA0S/8kp8\nWhLSR8p/wXiyWwCQqCOj6DRKAB5pKclIOfh6Aq4tO8gs3OwzZvieOm2+9P+0SWSAs3vHfqK82dLU\nSowb4TguqLiZTvkbDaRx6YScPKRpfe/F0Ml++ztsyBxfBIVfSc7SaUFLvUmauQpGN4XzScmJREea\n2WQOqKmhOxR1meF12dHWED1ZStq9fR+uu+g3uPyc67H41fe7NJDUt+mx4pvVxLrrbr4SKpUqwBHB\noUderG8AACAASURBVHVc/kTbfysSRo4e7iu7u7ngknMlQfH4SWOJz83pcGLVku9Dfp0jB48RJdr8\noXk+f0A3JSfKQr/wPqacynDRD12hkJ2Tibh4X9Wis8Mg0fhdevV8AK4s4z+e+zNi/DKiFosFa5aR\nM3MZfQs9zicxN4P4bu8vDOoMFyCn4/J12XnKihabDUar70apUqkk2hrXhliIKdlwphdAN57UFTUe\nKeu2K7EYnwSbAzjy8wkc/OEY7BZSoJk7exw4hUz6XBQBq09kr0mOh0Ll+3hS1aQAPBJrCFEUpR5c\nGUmwO0Rs2UGWLPxvJP4ZrjGjCqDR+K6lraWNyLLs2kZ+6Y0aMyLoQNq8gtyA5QRXdstXVsoYnuUN\nEF3XZYNKHYPM4WTQUiN0PV7Hn+4K5zmOgy5EHVd3M1yFvdSp2Naqxz///G+viefnH3wt6cKj+fbz\n5YQ2Jz0jTZKJCYcRfJGraYMiryCXfJjqQ377+9u930+5BTmSIdiA6/eDznKtXPJ9yOJt2n9rwpSx\nKBpZSKwrLS6LWNfZ29BNP+F0KHpQKBSShw9/+LEjCd0oP3Ykbqc+m+LjA6+7czDT3/VbHrojnB8Q\nARddViSE8+5OxRZKMJ+dk9WlGDmdLyCCH1OTXlJyC5f2qkbs/HKvV0tEvN6ofOQEsIKAzQzOb54B\np+CQmO7LtqUnkB9yJBkuW0sL7GZfuUyhUiA2Jx/HSmrRpvdlZLQJGkycOt61IIpExkelUmLStPHE\nef3Ht+zYQpUTuyj9qOPUyM6Rsd8AMHPaJGR4fm4Fh6FzqPfOYQOsRuSMJo9vPF4DmzGM7r1oCOep\nkkV9AB1XMyWaD1fDlT80l/AgaqhvRGenIcgRkfHmS2+jgyolvvb8W8Tfnj+GTiOWfLGcWHfVjZcR\nth/hwnGc7O/PKXN6xg4iEnLzc/DJsnfw2vsvYPGnryI1TV78fe6Fc4mMTHNjC7asl47QkoMOuCZO\nGY8MXToS/fStZrMFtdUDo0RGa7hoHWeo0GVFfy6hAlxA2ind3/SPv3b6u37LQ1w3vLgGRsAVxItL\n6y4p0h2Kuflk56EcMfFqpBTlEOsaj5RFeJVA1fYj2PPOCpjayGvhFByGnzUe4xfOkzU6BchyoocE\nPx1Xhpb8kEPKcIlOV/BgMwMWA0wV5BeMJlULLj4Rm3eSMw9nzJjgKwO5OxS9p1QoMXXmFGL/PTtc\nnlsOhwO7qNl5obTu052KgOtme9vvb0Ph3KlI5wsw7pqzkUgNMOXsVnBGPVKGJCE+yXczEx0ONBwK\n3QxSpEqKkVhD0DquQBqd7ma4YmJikEdbaUQ5y7Vr215ZUXFbqx5vvvyOZL0oivjvv18nRtokJidi\nwRUXdvta5H5/+kM50Z94TTzGjOehjgs8702boME5F5xFrHvjpbe71MdZrTYcoQw7J0xxjQMbPpKc\nUjEQyor6tna0tfoqFDExKmTnRHZjpYdYe0hMSsBZ550uWV9QmEd8/9bXNhDyFEbfYTdbYagnPdKS\n+8HAajkGfYaLHu9DZLgyUgCOQ4uB0m+FEHABgG5sIbHcFGHAZdYbULxqG+AkS5KalHiccsUkDB2X\nEWz0ICGY9+DfqZii0ULp1+nV0tyKzg55nRDX0QxFfTGUdSegbCiBsqkcypYqGJvI7IQmKx3gOGzZ\nSpqUzpnhJ+q3U5kiVSymUQHXgd2HYLVYIRw5QWRFEpMSMHocqfmSQ66kcPrZczCcL0Lh3CmYcMM8\n1+eklGqtOHMnOI7DECrL1VYWxtO+3BDrMMnKDrGkGKHLvD+hDO+NFLPZjJef/b+A239YsQ67tpFB\n9Tuvf4h1q38h1l1x3SWI13Ttg9YV02ZNITRgarVakmEdKFx6zXxiuaGuEc8/8XJQGcPxIydg8/PN\n02VleA2Z6bLiQOhUpB8U8wrIjG040NYQHs67+BzExUk9DmPVscjLJx+wWZYrNJx2Byo27sf+D9ag\natthiFEuX7dXNRDd4f1pYDXNr07D5W8NoVLHIHvKSGmGK4/8wwpExuihxBDmzroWmFrkyybBaC2u\nktgJ5I4bghlXTUaiLgGc0w7OFOC8lH7Lg3+nolKhQBpVVqwsr5aey2qCorMJnFNq/mdoJZ/mtFnp\nqK6sQXmZ7zwKhQIzJ4/w/iycjcz2iCo1CgrzkK7zaWssFgv27zmMnVQ5cdrMKSF9mcrNUbvx9mul\nO9JaK6fdm31LGULqxExNYYxQkbWGCO8LRdKpKFNSFEURzXTAFWaGC+jZmYofLf6cKE1xHCeZuPDS\nM6/BZHL9vi7/ZrXEVT6vIBdXLbw0KteTkKDFb+5e6F2+7d6bZG+mA4HhI4fhSup92bJhO775dGnA\nYw7uo8uJvmH3dMAxEDoVy8sid5inCVRSXHCltJzoobe7fAcDNqMF+z9Yg5Ifd6H1ZDWKV23D/g+/\nh9UgTRJECi2Y76/6LcBVGYuRMy0PgQERcNFeXLSOZNSCU2HRkjfNUDNcsQnxSB5Kfrh7312JHa98\n7f1v1xtLUL5+X9An0daSGmI5/7SJGHXBNChjfAEHZ2iR93hy2ME5pQJabZqG0JilxVOO8zJlRc4S\nWM9DB1waXQq2biBnJ04aX4QkrRpwuK9HJsPFcZwky7V1466w9Vsexk8eRwjnTz1rFoaPKpLuqFDI\nuvoDgDaFzKYYm9shOkNsgJCzhrCHl+XKzCaDErnxPvq2dsIyQavVRJQFooXz0bppnDxegi8//pZY\nd9m1F+Ovzz5KfD51NfV4742PsH3TTrzy7zeI/VNSk/HsK09Aow1hrFKILLz1Gny89G18uvxdXHXD\nZVE7b19w5+9ukWR9F7/6Po4FmPNHG55OmOzLPhcNwJJid0b60KSmpSCF0sxNnTFZMr3CHzk7CUZg\nTC3t2PP2cujLyYpBW0kNdr+xFO2VDQGODA/6/P054AKAPDnj8hAYEAGXJMOlJwMuhVKBhhZSjJyT\nF1rABUjLitZ2I4xNeu9/nbXNKF23Gw0H5btaRFFEa2ktsS6DL4CoTYX/LZ+zWwGLVDMgp98CXD9X\nQprvxpVBC+dlRvxwNjJAEjkFRFUsxNh4GNrILJpGl4ItG0jhrrec6B5LROuZPIO76bb0H1evh3Dk\nBLEu1Fl3Q4fl464HbkW6Lg1TZ0zGw48vCrwzXVZ0ExMfQzgAO212WDrCEJN3JZy3WwGrKaApamYI\nGS5a1xXqDEUaqTVEebe7ax0OB1546lXCfkCXlYHb7rkJY8bzuOK6S4j9v/t8OZ587F9EZ5xarcbT\nL/2tRzoIh+Rmy882HWDExMTg8WcegdbPfsZut+Off35OYiXicDhweD+pr5ww1VdOHVqUTxjK1lTV\nwmSMXtahJ6AfEuWy2+HAUxMs5MTy/tDzSFmGKzDtVY3Ys3h5wGqBpd2Ave+uRPWOo936/unvA6vl\nGHrmZEy5/eKwjxsQAVeweYqAS3fi3/2lUCgCdr7JkTGmEEEFVm7q9p6QXW9oaIWt0/dFp4yNQWKe\nzmVBEUcGSZxJ5peX0m+JfiNp/IXz9IgfWeE8lZFypufDqRsGiyYLVoNvG6dUwAynpGQxZ4ZrXApn\nM0s6FAEAMa6AaxoVcJWXVBJ/dCNGybf0B+KaG6/Al6s/xPOvPyUJsP0RAwRciI136fn8MDWFXhoO\nJpznDK1QNJZC2VwBrq2WPhQAoMsmA66mhmbJTLdo6LcAVweuWu3TN7Tr29Ha3L3u2qVfrZQEzIse\nucebqbr1nhuJgMfpdBIWEAqFAo8/8whGB3GHZ7gYkpuNR/7+ALGurqYezz9J6rlKi8thMPge0JKS\nk4iOvri4OORSmqT+HkDQhs0FEZie+nPD7ddC6/4dPfWsWV2OZJOUFKPwsDIYaTpajn3vrYTNQD6k\n02NtRIcTJ1ZswbFvN6C9uhEOa/hzKvv7wOpA0JWxUBgQAVeweYoAUEs5BmcN0YU1micuWYuic6eD\nC9BB6KGtrBZ2s7SDrY0qJyYPzfJ2w4haMgjgzJ0Apa+iBfNivE+PlOgnnM9IIMV6EmsIpwOcOzMj\niqIru+bO3NB2F/FpSfjp+/VERmPY0GzkDnEFDpzNLNuhCHdJLy0jNagPzimn9lAnGZ2JciPGJ0OT\nQeq4jOEEIRLhvPtzNnVA0d7gncapcI9roomLiyPsSxwOB1qaya6b7nYoei9VqUThcHLEUndutA31\nTXj39Y+IdaefPYe4ecVr4vH7P98X8Bz3//Hu0OaPMgAAp82dg8uvW0Cs2/zLNrzy7zewYd1mnDxe\nIjHyHD95rMSzTiqcLyOWqyqq8dwTL+P1FxYT/oV9gcVsQV2NrwTFcVzQ8l8ojJs4Bp+ufA8ffPsW\nnnj+L11qRuUeVui/0187tXuO49Dna+G0kfepzAlFmP2H65E3R9q0Ur+/GHveWoaNT3+I7a98jcNf\nrEPZL3vRWd8i2Zemvw+sjiaRWUAD4Hn+RQCzADgBPCgIwi6/baUAKtzbRAA3CIIgnxoIgWC2EABQ\nXUWeOidEwbw/BadPxJDpPKwdZMnv0GdrYWp2BXiiw4mW4ipkjif1Ra0l5Oun+ltNxMRDVMZ4AyEO\nIjhThy8QczolWSlRmwIYXV8CSUEyXDWVtbDb7b4uLpsFTocTwoaTqDvRAGWMCpqsYmh0KXBYyCBB\no0vG6m9Jvc75Z/s5e9vMhMM8AEBFdo1MnTk54I1+Rk+17stkuERwEOMTpQFXGMJ5aYbLBtFqhEIu\no2WzyAZ+mdk6otzdWN9EOMl312Xen8LhQ4mMVNnJckybOTnIEYFZ8sUqohSl1Wpw/x/vlux3yuxp\nmHfRXIllxLU3X+l19WaEzl2LbsPh/Udx/Gixd92yr1cFnLU4cYpUN1I0ohDr127yLvt3Kra16vHA\nHY+ircX14NHS3IrHn3kkWpcfNpXl1UQ2KTsnM6iVRqgkJGhDnhDieVjx/9spLS4PKxs/mLEaTK5u\neyrpV3D6JAw7Zxo4BYcRF8xEUn4mhO82wmGlpBeiCFOTHqYmPRoPl6Hs5z2YsHAe0qkZvP4MFMPT\naBBRhovn+TMAjBAEYQ6AOwC8Qu0iArhAEIS5giCc3Z1gCwjepQi4Ag9/QvHgkiMmXg1tZirxX8Zo\nMovTdIz0PHI6nGj7f/beO8yNs1z/v99Rb6vtvbvIvbe4xE5sJzakkEAgQICQBqElnJNDPXDCj3w5\n9E7gQOiEFCCNJKQSx0nce13Zu+vtvWm16tLM7w+tpHnfGdXV2rve+VxXrnhGM6NZtXnmee7nflqY\ngGuWKOAiRDLXjyorBjwQx/KCShsuRY6LuM0i81O9RgOz6O4sGAyiu1P0YQ14cebf59DV0As+JCDg\nDcDR2oPuQw0S/Vmv14XW5tjfwqk4bL96TewcBR7ER2tKBCbIYMuKEUwmIxYsiWPwOkHYwAgABL0Z\n4FQwFGQecEkyXAEfuKEuKsMXgbCNBOMk03FlK8MFIKsZrrd30Tq+j9z9wbjlznv/425qgsNV11yJ\nuz7zsYyfeyaj1Wrwtf/9UrQklozFcgEXK5wXicAf/sGvo8EWALzz5j6EgtLu5YsFW06U89+7GCjC\n+fg4WnroIIojmHvDBtRvX0U1cBUvrMOKT9wAY5G80W8UAWjfcyr+w9NgYHU2ybSkuBXAMwBgt9sb\nAOTabDZxvYuM/5cV2C7FUYeTEut2ttMlvXQE88lgI/Ohc+1UGc7ZNYCQL/YB1Rj1MBXTd0uSgCvg\njZalCGMHIWjH20014f+rNCoY82KdbPF0XIIg4PwrR9DbmNpQ3H0nae3Wuo1rkM9kXIiXMWVkMlxL\nViySnZO3Ys2yjOfnJYUNjBB7fdkMVyQzmRJqDd3gIIRAhDgXpzjGqNIh1nTAJbGEyFDDBWRvpuKo\nw4kTR+mxTlu2S00jI1hzc/DzP/4Ad3zqo/jCg5/HVx56gBJuK6RHeWUpvvCNz8c1RI5gMpswxzZL\nsl6upCgIAva9fRCvv/Qm9Zjf50fLhckZBZUKrARiIh2KE2EybVWmO84u+vpRsWZ+3OkopqJcrLjn\nBszeuRaF82ugj6O7cnYOxPXt8jlc02JgdbbI9KpYCuCQaHlgfF2jaN2vbDZbHYC37Hb7VzJ8HgDh\nzh6jyRAdbMzzPMacrmgg1tXBZrjSLynGw1pdDLVRh+D4qJig1w9Ha0+0bMjqt3Lry6SzEse7BMVa\nLeIZhWAplHYoasPBlaDRRTNM1hIL3MPh7QrNFrQOxb4UbS3tWL95Ldp2H0fnsdR+OAJCCHsP0uaV\nO2/YDkGjp8+REZMKGjrYMRgNWLBknqR1fdL0WwDAqagSraBSA7pwFtBQQAe23hEnQoEgVJoUPuaE\nA1TqmB1Gok2Dfpm8l3S8z+RmuJiLRnMbeJ5PO/g5vP8odfNSN7tWEjiyFBTm48N3vD+t51GIz8Yt\nV+A3j/0ch/cfRVd7Nzrbu9DZ3o2e7l7wIR6cisM9n/u47KiykrJimMzGqGO6a8yFlqZW/OR/H5Z9\nrvNnGyUO9dnkQmMLfvbdX8Hr9eET992BpSsXRx/LpiXERFC8uOLj7KQDrpzKxM1nap0GlVcsQuUV\nYV1X0OeHq28Epx59FQF3OJkQ8gfg6huGuVT6e+dop7NbU3VgdbbIVhqCzWZ9DcBLAIYAPGuz2W62\n2+1PSXdLHWtuTjTgAsJix0jA1cmUFFP14EoFwnEomFuN3mOxmv+gvS0acLH+W3n18sGeYMhhAi4H\nBHOBtENREwu4ItSuqEJv4wD4II8CZsRPa1Mbug414MLrtAeW1qjFwlu3IuALwt03AvfACFz9IxB4\nARcEF6XZyS/Iw9oNq4BAEhsFtVRvsXLNMknANWn6LQAgBLy1FNxoX/jfOSXRDlOVRg2d1QSfY/zv\nEMI+MuaSFPUZKq1swCXozHR5NegPd3Aywk52WDprAyHbpRjwgXhHAbUu3NGaoli0sKgAlhxz1ErA\n6/Git7sPZRXpWTKwwuxUrTwUskttfTVq6+lseiAQQH/vAExmI6y58gPgCSGYO28Wjh46GV330Fe+\nK8muRjjf0IQdN2zP3omLEAQB33nwRzjfEB6r9ZX7v4HfPflwtLuVzXDVTLBDMVPYkUAtTW0IhUIZ\nO95fLgiCIMlwWSrS05mqdVpYq4qRU1WMQXssmzra3i8bcI0yhqc5U3ScT7bINODqQjijFaEcQDTq\nsdvtf4n822azvQhgMYCkAVdRUfxW0ILCPEqvxCGIoiILerr6JJmExUtnQ58FMWYE3xobFXANn2tH\n4Ue2gQ+EJMZvs1bNgVnm7xBCRgyP9kcdzEkoCAvnhVvkaE5UKhSWFYAQgpBfC8dwOJgzWg1YedNS\nnHjZLvHish88iXOErqOrtSqseM9SVK2Wb9G/4wN0S/qNt+xAaVkuQj49HHFsD4hag6ISab1+286N\n+P2vom835syrx4JFk3cHHcYCQP6LmVtegF5HLHDUBAIJP1diXD4TfEN004TaZIGlbg5Gzp6AMB6M\nEQjIt2qh0tFuw3MZvd/QwFD0ub1eH+WzpFarMGtWCZyNZyEEw8c1lmugL0zdzmTOvHocOXBC9Hx9\nWLJsTsr78zyPw/vogOuad21K+fVSmHzKy5PfLMyZV08FXC3N8cuGFxovTNr7e97eHA22gPBNwMM/\n+D/84g/fAc/zEunH8lXzkJt38T9rhYVm5OZZozMdfT4f/N6xCXuCZcpU+b6N9Y1QXfgagxbVcyuk\nFZsUKJtXSQVcvv4h2b/zGBPgVS+qmTKvx2SQacD1CoAHAfzGZrOtANBpt9tdAGCz2XIAPAngervd\nHgCwGcDf4h1ITH9//EGuRhPdhdLS0oPy6hr89Y/PUJ0vc+fPhtPph9OZ/gDieKiK8kHUKgjjglPX\n4ChaTrfBP+YBLxKh6nLNcAscPHH+DqIzhW0FxnF1d1CpQV6tx8DA+EVZEMARDmQ8IMspNGHZ7ddi\n9NfPAQdj+/SOjEDg+WgbLafisGTnAhiL82Vfz872Lhzad4xad+W2K8PbMs8phuc0sscrKa/AlVs3\nYPfr74DjOHz83o8mfB8nG3UOnQHsae6BrjK1uyYS4ihRo6DWwmcugW/QBU6lARFlv4b6hgE9/Vwa\nPS1+7ursjb4W7MUmvyAfI1294IKxY7p6u+Dk9SlnuSqrK6mA69jhBixcuiSlfYFwtmNA5F9nMBpQ\nWVt7Sd8/hfSZO1+q7YpQUJRPeRQ2nG5ET/eIbHlyojz7t1ck697etR9P/OV5zFs4F35Rp3RunhWB\nIHfJPms19dUYORwLUg8fOA2DST6LOJkUFVmmzPet91QLtWwqK8TAoPy83mSo8ujXsq+xS/J3Bn0B\njDCGp4J16rweqZBucJiR2tVut+8FcNhms70D4McAPm2z2T5ms9lutNvtowBeALDPZrO9BaDPbrf/\nI5PnEZNjlXYq8jyPl557jVp/7fXbJvpUEtQ6DfLq6DLlYEObRL+VV1+e0D9EMNIfQjawiZQTww+S\nqHA+gtGkxpb7PgCNSJDuDQTg9o//kBFg0XYb8sqtVElSDPt6LVq6IGY+KPOc0XOL439FCMHXv/0l\nPPHCb/DkS38KlyYvIYaJWEPocyCM//2CWgc+rzLqO8b+/XKdioWFBZSGamRoJHqRkbrM54c92cTH\nDAUlJeZESHRcaWpRDu6ly9DLVy9Ny79OYWowd178gOsr33yAGn/j8/kk3YLZ4s3X35Fd/4vv/xon\nj9GNGZdKvxVB0nSi6Lgk+i1Leea2NZaKIurG0TPgQMBN/2Y6O/sB0fg1Q4EVWtPEB95PZTLWcMkI\n4U+KHvsZgJ9lemw5pON9nDh68AR6umJlRq1Oi607tmTzaaMUzqvB0PmYBiFsD0FLp+Ppt6JojRA4\ntezcRAAQtPSHTdDoQPyiElfAB11ODqrrq9B0Lua3M+hywqTTYf7m2SiqC9fJBbU0cAqFQnj5eTrg\n2nEDHaCGhfPS8UOIE8AB4aBr/qK5U+LOxMgI5z0DaZifchz4guqwMS2nojNNrH5NplNRpVahoCif\nCq76+wZQUVUuo9/KB2ReZ+IZhaBLzSZgohcNdvblmhRnXypMLWbb5Ev4777pWixbtQRz582i3utz\nDU0S4fhEaWluo2xmxDhGRvHw939NrbtU5bsIco7zMx1JwJWmfkuMWqeBqSQPrp5YdnW0ow8Fc2OB\nNivHsVZP/9FdyZg2/dxybvP/epZOYW+6ej0sTEkpWxTY6DsyZ2c/nF30RTRpwCXjyRVBAKTZJeYi\nH8mqsOMwBt0uzNk4C+XzRbI6mQDp0L6jVHlBb9Bj87aN9HmkmeGaakjd5tOwhgDCQZZKLSnrSTNc\n8iVrVjgf0R2yHYpFeTmyvinE64zq/JLBZrjaWzoQDKY2WmNszIXTJ+g5fUrANT0xW0woq6DL5gWF\n+bjncx8HEJZZiDnf0Ih04HkeJ46ckpTFxexmsltiN3cA1IgiYOIjfSZKtmxVLhcEnsdYN/0bNZEM\nFwBYq+gAig2wJP5bVUrANWVg3eY72jrx9ht7qHXvuvGaSXt+XY5JGvGLtGOm4jxozcnTofECLqh1\nANPSLwl+xgdKs+MwtPPKUb04VvIUCJF1ZGcD1C3bN0Vn5UWJE3DJdShORXQ5ZnCamD4l6PHBz8wD\nywhJhssnO8iatVT4xhe/hd//6i9oZVriC/PknbGJwEtKjfHIsVpQUBQTVQeDQXS0dqa075H9xyg/\nueq6qstiOPRMZemKxdTyfV/6FMyW8M3nHDbgOtuEVBkbc+H+u76Iz9/zJdz+3k/ijVd2y263W+R2\nDwCf/PydCbNo1XWXNsPF3qx0tHdRGrOZhnvAQRmeaox66HMnlrxgAyhxwCXwgkyG6/LuUASmU8DF\nmJ/ueXM/AoHY3Xx5ZRnl+TIZsK7zYnKTZbciaHSyWSS2nAgg7N8lyoMQPgSEgqhi0vGd7cxFVq2T\nZGhGhh3Yu/sAtW6nXHu4Sg2B0IJa8QzFqQ7hCAz5jAFqOo7z8eBU1FBxIgiATGm4htGmuF0e/OWR\nx/HK869T64us8YNz4kk9K5dpWVEpJ15efPQTH8LSFYtQVFKIT95/JzZsWRd9bA6j8Wq0N0kGq8vh\n8Xjx1fu+Ec2E8jyPn3z7YYw56RuCtpZ26nPHqThs3rYBD/z3Z+P6wl1qDZfJbKSHsYd46WzaGYTE\nDqK8cMLzDFkPr9HO/qgBqnuA7ohU67UwFiZxrb8MmDYBF1tS5Bnn2p03bp/0gZcF8+LPg0paThQh\nm+WSC7gIkZYGA15JOr6dyWrIBXSv/2sXVW6qqqnEwqXz5Z9TyzznNMluRTAW0q+vezALARch0vmJ\nAekd8c73XJPSpIMi0RgicSAHAPC5UjJgBeTGlCQPuARBkAjmV0+md5rCpFNSWowf/vrbePyFP+CW\n226iHisuKaJ+P71en+Q3g8XvD+B/Hvh/OHWcFrs7R8fw+B//Tq3b/RpdTly2cgmsuVbMW2TDTR+g\nB3QDgF6vm9Ac0Wwh+e7MYOF8NvVbEQwFOVAbY9eOkC8AV39YU+toZ/23ijOyn5huTNuASwyn4nDN\ndVsn/RxMxXnyaVaOILc2dcNJwZAjcSqXzXABkm5DEvShsoYO7np6+uETz7+S0W+9s2svtbzjhm1x\nA1Q2YIvX8ThVmdBMxQQIcTR1YoqKC/Hrx36Guz97u6SzVkyhOOAy5FAaMYLUs1zsLL3jR07G2TLG\nhaZWSlOmN+ixZMWilJ5PYfpBCJHquM7G13GFgiE89JXv4PD+o7KP/+Ox59DfF7tAv/k6XU4U60I/\nfu9tklJ1VW3llBgHVT9b0XFFmKjhqRyEEGmWazzQGp2B+i1gWgVc8T1S1q5fNaG5dKlCCEGBTFkx\np7wQan0aonJOBcEU094IerOs5goAwHQbkoAXer2eTofzAjq7Y18YNjAIhUKwMz+wV26lxfJiBIM1\nGhAKSKA7m6JIZypmJ+CSZLjiCOcNBj1u/dj78Ohzj+DOT39U0siRazWjRDT0VdBbIBgYy5AUyF5A\nRwAAIABJREFUA65lq+gy+pmTDZKSD8tBSTlxObRaxQ7icmbOPDrgOhdHOM/zPL77jR/jnV374h7L\n7/PjT7/+K4Bwdr35fEv0MY7jsPGqK6LLBqMB93/509T+y1cvTff0JwVliHUYPpR9wXyEnEq6iSgS\ncDnaZp5+C5hGAZfFGl/A9673XHvRzqNQpqyYsn5LhGApRCivAnxuGfjc+CUoSXYpEOlUpHVcbR3h\nD3C425Hep+1CO7yemHA8N88q6WqiUGvBF9aCtxSBL6yJL6SfohgnLcOV3IuLOg+TER/6+Pvx6HO/\nw8c/eRvKKkqQl2/F/Z+8GZrx+Y4CUQFagyTrSYK+6HudiJLSYmokDB/icXj/sQR7SPVbGzevTfo8\nCtMbaaeiVDgvCAJ+9t1f4bV/vUGtr66txMc/eRu17qXnXkNbS7ukO3HpykXIZUwv16xfiS88+HnY\nFszBtp1X4YO33zKRPyVrsKL+lqZLN9g7E0aGHbjQ2EIZf2eCu3+YMvDWWozQ5cg39aSLlRnVM9rR\nD7/LS98EcyTs2zUDyNYsxUlHo9HAZDJK2oujcwAvEtaaUqj1Wkrwl45+KwohgN4sOwSZQqODgNiw\nShIKAHwIVbWV1By8SMAFtTY8iFlEw+lz1LJt4dzkejeNbtqVEiOw5qeeodGwG/9EyxhyXlwyMxVZ\nTGYjbrvrVtx2163ASA9UntiPjaA3xawotEbKm4t4HBA0yVPtazasosa5HHjnkMTuI4Lb5cYpxoRy\n41VKwHW5IxXON0uGnf/t0afx3N9fpLYrLS/Bd3/xEPIKcvHqi2+goy2s/eJ5Hr/9xZ/Q00mXhjbH\nyZxfe91WXHsRZB/pUF1bCZVKFW0g6Ovtx5hzLNrdOZV5Z9c+/O/XfwCP24N1m1bjoR9+PWMN82To\nt6hjEUQtK939Ixg6T3dsm0vyodbNjAz7tMlwAVJrCAC49vqtkzKmIh6cikPFuoXRZVNpPqw16Q0M\nTgvCSUtZPjeqa+JkuGQE7mzANW/h3Oye4xRDY9BBY4pl5YQQD+9IZiMqKFTqsOXGOETgwyapqSII\n4Hz0gHBBH+u+lUwi8IzKWk+wsB2GB/YcljSVRDh68ATVPFFZXYHK6gxuGBSmFSVlxbCIOr09bk80\neAIA15gbf3nkCWqfgsJ8fO/hh1BUUgi1Wo07P/1R6vG339iLxnPN0WWO47Dx6vWT9BdkH41Gg0rG\nYmc6ZLlOnziLh776XXjc4akU+946iDMnGzI+3mgWHeZZ1HotTMV51LqOPaeo5ZlSTgSmW8Bllc4t\nmqzJ94mo2bwM89+7GfXbV2PJR64Fp5rcl5EVsXOjvahihPPRDJdMVsp+5jy1bFuQ+oDj6YrEADUb\nZUVC5P245JAzLw14qSkDAiGAyFVe0JnpgI4PybrRsyxatgAGY6zpYmhwmJpEIObAnkPU8ur1K5Ie\nX2H6QwjBXFbHJdJ1Pv/Uv+Aai90MmMwmfPcX36Q6bjddvT7hzdqSFYuQlz+9WvunmwFqZ3sXvvYf\n35R4hiVqgkiGnCVENmEF8WMi93m5xy9nplXAxXYqLl2xCJXVFXG2njw4FYeSpbNRvWkJdJbUxrBM\nBMGYS+t7+BBq8uisV1t7H4LBkCQ483l9lKgVAOYtvPwDrsnrVEziOM+HwA20gus5D26wjZqNKDE0\n1Zno8i/HURkvACDu5Oet0WiwYg0tRGZ1WkDEDuIItW7N+ks7+1Lh4sEOuY4EXH6fH39/9Bnqsfd9\n+D0SUTkhBHd/9va4x79y64bsnOhFpJ7RcTVPYWsIx8govnzfg3CMSBtqmjMcTcQHQ3D10gFQNkuK\ngNSPi0XJcE1RWLO8nRdRLH9J0RogmPOpVQVGDnkig0+vz48z9lZJBqbxXDNlclhWUZqw4/Ny4VJ1\nKpKxQZCAN2zt4PeAG2wDGekBQkFJwMUGV4C0I5T4xoA45UExbODEZrIA4OjB4+jtjnUHaXVaLFXs\nIGYMbKdiRDj/6ov/xtDgcHS93qDHjbe8W/YYy1YtkTXJJYRg01XTp5wYYaID4C8Wfp8fX3/gIXS2\nyY9Xam6Uz2gnY6x3CIJo4oQu15z1AdKJMljaHCN01uwI9KcD0yrguukD10e78zZv24irr73yEp/R\nxUMwF1LZK0IIVi6h71gPHW8Mi69FSATzM6CcCExSSRFJvLh4XpKRIgA4jwNc/wWQUCw4EwAIOpkf\nmvEB59H9BSEcdCWBvQieOdkA5yi935N/fopaXrthFXT66dkYoZA+bMDVaG9CMBjEE3/6B7X+3Tdd\nm9D38K7PfEwi0F6yfCHyC/Pi7DF1kQ6xnnjXX7bheR7fefBHkmYXMS1NbXF1m4mQCOazXE4Ewl3j\n8WyTrFUlk25YPpWYVgFXaXkJHnn8F3j2jcfx9W9/CSrV9Bg3kxUIAZ9bRml8Vi+3UZscOnaO3Qv2\nGSaYjzBZAVeiDBfxjIaF9DJI1muN8uOSCIFgYDJfvuQ6ruLSIhl7iJhxZdP5C5JyIutIrnB5U1ZR\nQnnCuV0ePPHHf6CzvTu6Tq1W45YPJ/5czJpbj607tlDrtlwzPW9+S8uLoTfEbmSdo2PRgfNThd89\n/CfsevUtat3SFYtgtsRu2DxuD3q6+thdkzLZ+i0gPG4tXllxJum3gGkWcAGASq2aFm27k4JaC8ES\n+4CuWkYHTw32FklWo4ERzM9bNDMCLn2uBRCNivA73Qj6Agn2SBGVRjrfkg8CggDiHqY2FRLcucmV\nE6OPMZkv4nel1q24gS0rxnRcf/vL09RjC5fMx8IlMqOdFC5bCCESe4g//eYxannbzi2SAexy3Psf\nd0W9vVavX4l3veea7J3oRYTjOMlrwvqQXUoaTp/DY3+gRylV11biG9//b9nsXLo4O/up5ZxJ8sOK\nF1hZa2aOfguYhgHXTEcwWqMX5IL8HNTXxrqIeF7A0YPHo8ujDidV8+dUHGbb6B+XyxVOrYIhjw5q\nsqLjkpupGPQDfg8loBeAqHksOytRwPh0gXhoDXRQFwoCoeTBIhtwHRy3h+jvHcC/X3qTeuz9H705\n6fEULj/YsqLYIoQQgvd/9L0pHSc3z4pf/vnHeG7Xk/j2T78BtXraWDpKuPrazdTyy/98LaPy3GTw\n8j9fo5Zz83PxrZ88CEuOWSL4TzfgCvmDcPWNUOvM5ZMzsSWnShrIcRoVzKWTPyFmKqEEXNMNQsBb\nSyGMl6PYLNehfbEy0rmzdHartr4aBsP0co2fCBfNcT7gB8dkt6A3hzOS5nzwRXXgRWJ4wVwg0drR\nB+Qkw8xJCmXFRUvny9pDPPX4c1TjREV1Oa7YtCbp8RQuP1jHeTEbtqxDDdOYlAyTefK7tCebq6+9\nElpd7Dvd09WLY4dOXMIzChMKhiRO/p//8qdQVhH2fWQzXM1pBlxjPYNU5tyQnwONYXI0nTmVxQCT\n8LeUF026pdJUY2b9tZcLKjV4a/hLt2o5HXAd3n80KvpsODUz9VsRWMf5ydJxEZ8LYDoQeaNIQKxS\nQ8gtQ6hkNkJF9RAsyUs2go6+kBG/K86WMTQaDVauXUate+OV3XjhqZeodbd86D0zS/+oEIUtn4m5\n9WPvu4hnMnUwW8zYxBi2/uvZVy/R2cQ4dvgkRoZjv1kmswlrNqyOLk80wzUZA6vjodZrYSyiPdqs\n1TNLvwUoAdf0RW8Gby7EkgX10bl8QPjurKsjLIJlDU9nWsA1WdYQkk5F3xh18yaotZIMFYCwSF6d\n2ggLQct0MPrcGbnO/+3Rp6lxWNbcHFwzxUasKFw8yivLYDJLu2OXrVqC+YtsMnvMDHbeSGvQ3npj\nj0QPe7F58zVaKL/xqiuoIfOspUVHW5fEEDURrH5rMgTzYvJn0Z6ZebMuvofmpUYJuKYxgqUAmup5\nWLx8IbX+0L5wluvsaTu13rZghgVck1RSlGi4GARjXtL5iknR6CjtFxF4IOBNsEMY1o+LD9FalPe8\n/zrFCmIGIyecB4AP3j4zs1sRlq5YFC3VAUDAH8DrL+3KyrEz0YMFg0Hs/vceah07H9VkNqK0PCY6\n53keLRdSH000mTMU5ajZvBw51SXgNCpUrFuY2QziaY4ScE13VBqsWkePZzm07yj6ewcwPBgTROp0\nOtTOqmb3vqyRDLEeHM2Ox45aG3fouEA4iXlpRjBjfwCApDDmp6ikUDKuJIJWp8WN75c3tFSYObA6\nrtm2WVi5dvklOpupAcdx2HH9NmpdNsqKj/zij7hu0y345G33ob93IPkO4xw5cBxOhzO6bLFaJHIB\nQG40UWrGrUGfH25xxp8A5rLJFbBrjDqsuOs6bPzKRzHnXesm9bmmKkrAdRnA/lgeO3Qcp0+cpdbN\nmTdrWncSZYLWbIBKNIU+5A/A70wetCSFEEAln+USjFaAy87Xii0rpiKcB6TdihF2XL9tRkwZUEjM\n1h1bomaThBDcce9tM8p8Mh7XXr8NnOi722hvirrxZ8KJI6fw2O//Bp/Ph/MNTfjuN36c8r6s79am\nq66Q/f2un1NHLaeq4xrrHoT4rtFYYIValzhzny1mmlBeTMZ/uc1m+6HNZttjs9nettlsq5jHttls\ntv02m+0dm8323xM/TYVE1M+pRa5oaKzb5cEzTzxPbWObAfMTWQghk1dW1MQLuLI3vJcVzsPvkR+K\nzRBv9Mr7PvyebJ2awjRmtq0e33v4Idx06/X45g+/hrUbVyffaQZQVFKIVevom9d/PftKxsd75YV/\nU8tHDhzD8cMnk+7n9wfw9ht7qXVbtssby9bNpjNc7NzceDi7BqnlyS4nKoTJKOCy2WxXAphtt9vX\nA7gLwE+ZTX4C4CYAGwFcY7PZ5k3oLBUSwnGcJN186jg9BmLeDNNvRdDn015c3pHsCGFZ4Twwblia\nRN+VFmotBFUsQ0cgUMOw47Fo2QIYmXloG7dcgYqqmaeZUJBn+eql+MwDn1DsQRh23LCdWn79pV1p\nCdEj+H1+iaUDAPz+V39JKms4vP8oXGOxruTcPCuWrVwsu22m5qdsh6K5TAm4LgaZZri2AngGAOx2\newOAXJvNZgYAm81WB2DQbrd32e12AcCL49srTCKrkmgwZorDPAtrfuoddsbZMk1kAis+i9mtCIKW\n0XH5kttDqNVqrL+S1kgoRqcKCslZv3ktNUdyzOmSZJtS4cCeQ1TQFOHk0dM4vP9Ywn13vcKUE69e\nD5Va3salqrqC6lIfGhymrCTicTFG+ihIyTTgKgUg7ikdGF8n91gfgDIoTCorZASVESxWC9WBM5PQ\nswHXSHYCLkFDZ7gElQaQG0Y9UVjhfIo6rrs/dzuWr16CopJCfPqBe7BgsZJkVlBIhkajwbZ3XUWt\n+9dz6ZcVX/vXrriP/f6Xf46b5fL7/Nizex+1bsv2TXGPpVKrUFNHN0Mly3IFvX7aIuciCOYVwmRL\nvZZIcamoMS8ChUUFcbvT5i2YM2NFsfpcZrzPcJa8ddQ68IawPkwAwFtLJm4FIYOgM1IdkSToA0LB\nuNtHKCwqwPd/+S08/sIfcPOtN2T9vBQULld2MmXFIweO4+Sx0/B4ktuyAMDYmAv73j4Y9/GG0+fi\nPn5gzyG4XTHZQH5BnsT2h6VuTi21nMxxXiKYL8yFWpeaP6DCxMi0ba0LsYwWAJQD6BY9Js5oVYyv\nS0pRUfyBvgrJ2XTVWlxokrYFr1i96KK8tlPx/TMIpRAP6fA7xrJ3nkUWhHxecGoNCOPczodC4LLk\n5u4YNSLkiWW2cvQCdLnZfa2n4nunkDrK+5c9iooWY9Gy+Th1LNbpff9dXwQA5OVbUVZRiqqaclx/\n87W4cusVkv3feeMtBPyx2acVVWWYM68eu16Nabr+8shjuO49V40/X+y928tkt3ZcfxVKSxNLFRYv\nteFVkUC/u70z4edh+DhtiF1YV6p8fi4SmQZcrwB4EMBvbDbbCgCddrvdBQB2u73VZrNZbDZbNcKB\n1nUAPpTKQfv7s6SvmaEsWCp/J1RVVzvpr21RkWVKvn98COEc6/gdndfhQk/XMFSabFpkxH5cQ/4A\nTv71NThae1A4vwYL3rcFZII2EYTTg0Ms4HL2D2I0kL070qn63imkhvL+ZZ/t79pKBVwRhoccGB5y\n4MxJO155YRf+34//B2sZG5Zn/vYytbxl+5XYvH0jFXA1nD6Pp598Be+9dUf0vfN4vNQ2ALBm49qk\n721xGS0XOXPqfMJ9us93UsuafKvy+cmQdAPVjK4Edrt9L4DDNpvtHQA/BvBpm832MZvNduP4JvcC\neBzAmwAes9vtjZk8j0J6LF6+EBqt9EJsWzDzLCEicGoVdDm0tsrnmLyRHZ37z2KkuQtCiEf/qQvo\nPnIu+U5JkJ2rmA0DVwUFEYIgYPBcO7qPnEPQF0i+w2XMVddcicLixLomQRDwo2/9HGMicfzgwJBk\n8PXWnVswa06dRIv1x/97lBoqf+CdQ/B6fdHlwuICLFwyP+m5sl5crc1t1HFZLrbDvEKMjG/z7Xb7\nV5hVJ0WPvQ1gPRQuKnq9HouXLcCRA8ej64pLi5BfkJdgr8sffa4FPkfsR9EzPAZjYfY7CgFgpLWH\nWu490YTyVRMUrGsNEEDCthAASCgIhALZtaBQmPG0v3MSza+EtUVdB89ixd3XTzg7O10xmY343sMP\n4enH/4nW5jb09vSjr7dfMiqrv3cAv/7J7/AfX/0sgHCHoXiUz+y59aipqwIAfPSeD2H36+9EH29p\nbsPPvvcIPN4AGu3NaDhFj2LbvG0jZcQaj/yCPORYczDqGAUAeL0+dHf2oLJaOqtQVjBfqgjmLxYz\ny3p8BrBy7XIq4JppA6vl0OdZ4BAFQlmzhpBhrIc2FHS09sA36pJk2dKCcOFh2KLRPsTnDg/JVlDI\nEn0nYq7qzs4BjLb3w1pTkmCPy5vq2irc96VPRZdDwRAGBgbx5J+ewjNPxoylX3j6ZWzetgkr1y6T\nzF/cunNL9N81dVXYumMzXn3xjei63/3yr3Gf/6pr5M1OAcA/5kHTKwfgGRxFxZr5qJtdQ5mqXmhs\nlQ24xrrp3ydFMH9xmZm3L5cx116/jfKRuenW6y/h2UwNDHlmanmyAq6A2wv/KGPbIAD9py9M+Niy\nZUUFhSwS8Pio5eHmzjhbzkxUahVKSovxifvuQFVNJfXYDx76Kc41NMJ+JiZIJ4RIgqaP3P3BlEbb\n1NRXx71Z9jndOPb7F9F7rBGj7X04+483Ucj8PsSzhlD8ty4tSsB1mZGXn4uf/+GH+PQD9+AXf/wh\nlixfdKlP6ZLDWkNky4uLZaxnSHZ936lsBFxMhsw7RmW8FBQmSihA240MNaXUXD7j0Oq0+K+v30dZ\n7fR29+HLn3uQ2m7JikUoKqEDmoqqcontBHvsFWuW4b+/9QVZKx+f043jv38R7v4Rar3BSbvhxxvx\nIw24lHLixUQpKV6GlFeWKt5LIvRMhitrXlwM8QKu0fY+eEecksAvLdQ6CJwahA9fFAkAbrgLfGEt\noFK+xgoTh2cCrtGOPgS9fqj1SumaZeHS+bj5gzfgH399NrpuZIgOgrbu2Cy776f+8274vH6cPW1H\neUUJauprMNs2C7Pn1qG6tiquq3w02JKZB1tsyaGWm5taZI/BzlA0Kxmui4ryS61w2TNZbvMsrH5L\nTN+pC6jeuCTzgxMC3loM1XAs60D4ELjhTvAF1ZNiuqowcxB4AXyA6WzjBYy09qDQVi2/0wznjk99\nBHt3H0BXR7fkMY1GjSu3bpTdT6/X48vf/E8AqVt6RMqIHjbYGre8KTLTAVdXeze8Xi/0en10nVQw\nTxTB/EVGKSkqXPboLEYQkW4i6PYhmMFA2mTEy3ABQN/J5ok/gd4C3pRPrSIBL8ho78SPrTCjYcuJ\nEYabFB1XPPR6PR742udkH1uzYRUsOWbZx9IlXrBVMLcKq+69CTqrCVq1GnnGmOxAEAScP0F3PTol\ngnmrIpi/yCgBl8JlD+E46K2scD67ZUU+GJLoKsRDrca6B+EeHJ3w8wiWQomAnnM7QNwjcfZQmK4Q\nzyi4vmZwfRcmXa/HlhMjDE+ijksQBAw3daHtrRNwD0zPz+/SlYtx4y3vlqzfumNLxscUBAGuvmG0\n7zmF4396Cft/9KRssLXw1q0wl+Zjxd3Xw1ScJykr7nnyVWpm45gimL/kKAGXwoyA1XFlu1PRPeCA\nIPLo0eYYkVtDz2zvP5WFLBch4HPLw8OyxasdfYDfE2cnhWmFIIA4B8CNdIOEAiAhP7jhLkDgk++b\nIfEyXO7+EfhGJ6cjdrChDcf/+C80v3oQRx95Ad6RyTMknkzu/uztKC2P2Wfk5udi3cbVaR/H53Tj\n3PN7sO+HT+Dgz59C00v7MdzYCT5Il3oLbNVYeOtWcONaL12OCcvufDeqK8up7Vpb2mmrDzbgUgxP\nLzpKwKUwI2B1XJ4sB1ysfstcko+ixbQDdFbKigDAqcDnlUMQ6bYIhPBFmU8+2FphCiPwICPd4Mbo\nzxPhQyCeyfOPC/njO8sPN09OlqvrUEP03wG3F21vn0iw9dTFYDTgOz///7Bq3XIsWrYA//OdL0Gn\n16V1DIEXcPLRV9F14Cxl0sxSYKvGwg9cHQ22ImgMOqy9eSu1rtc5iqZXDkblE5KAq0wJuC42SsCl\nMCOYbGsIVr9lLi1A0YJagIsFRa6+Ybj6hrPzhBo9BCs9Q43wQRDX9CzNKAAIBcENtoPzyn82iWt4\n0kY6SQTzItItKwq8IMnKSLYRBEkA0HPkHPxj0zNLW1ldge/8/Jv4ySPfzciKp/9Mi6TkJ0ZnNaH2\nqhWywVaE2bZ6anlgbBR+pxutu46NC+ZFkgZCYC7Lh8LFRelSVJgRGNhOxSxruCQBV1k+tCYD8urK\nKeFx38lm1G1dmZXnFAw54ANecK5YEEd8LggW5c512hH0gxvqAAnFzzSRoC9cNmY0fNkgWYZLEARZ\nXyi5bc/8fRf4YAizd6xF2Yo45p0OFwIuL7WOD4bQsfc06revkt3nckXgBbTuOkqt49Qq5NaWIX9O\nBfJmV8JYaE36+pdVloJTcdHxQ2M+H/zBIDr2noI+n/79MxZaoZKZu6swuSgZLoUZgcQaIoslRUEQ\n4JJkuMJ3j8WL6bvOvlMXKCHrhJ/bxMzJDPgmVeujMAkEfeAGWiXBlqDSQtAaqHXi4FqCIGScAYsn\nmgcAv9MtbQiRe3qeR8NTuxEY8yDk9aPxxX1xu4HZ7FaEzgNnEPRmv4N4KtN/toXOfBNg5b3vwZKP\nXovKKxbBVJSbUrCrVqtRUlpErRvxuCHwAhpf3EetV/RblwYl4FKYEUjMT0ecWQt8/E43Au7Y3Tqn\nUcGQH+4YKpxfQ1lSeAYdCe0j0kalgcDFEtUEQjjoUpg2ENcwCBMkC1oj+MJq8GbmwugbA4IyAUnA\nC26gBVzPeRDnQNqBVzzRfIRU7CFGWnoogX3IH8Boe7/sts5O+fUhXwBdB88mfa7LBbnsVvHiWTAV\n5WZ0vLIKulFn2B1+PwRm6LbSoXhpUAIuhRmBxqgHp4kFJrw/SAVJE4ENoEzF+SBc+KulMeiQP5ue\nu5Y18fw4bBaEBLLzdylcHEiIDnZ4vQV8fiXAqQCtAYI6JsAmgMQChA8EwA11ggT94eaJsUHAl15n\nYcjPBFxMRiUVHVefTBeuo03eI87ZGV+v1L73dNIA8HKh81gjXL10dqtm87KMj1dWQes6IwEXiyKY\nvzQoAZfCjIAQImMNIdVx8SEeY71DSUW/YuT0W2KKF7Hdik1pHT8pGj29rNhDTC94+rMgGHNjAQ8h\nkrIxcTti+wgCxlqboiOfInBjg2lludiSorWqmFoeaemJaoNk9w+G0H+6RbJeLuCSE8wTUXNJYMyD\nnmPn2d0uOwRewJkX91PrihfVZ5zdAsJj3cSMeGQCLkUwf8lQAi6FGYMhSadi0OvHwZ8/hUO/eBp7\nvvdXdOw7nfAiE0FiCVFK/5gVzKumOot8Dhfa3zmZ7unHRclwxfCNunDsdy9i7/cfx9mndsfVCk0p\nWM0dR3ehCQYLBNE6IvAgnnDHGRntQ9AtvXEgAW9aZqlshstSWQSN2SB6PIDRjr64+w83dSLokZay\nRzv6JN8h77CT0mmpdBpUrFtIbdP+9smUvnvTmYGGVjjEmT4C1GxZPqFjshkuj0aq/TIWKYL5S4US\ncCnMGJIJ5zv2nY7OGgt6wqLfQw8/jaHGjoTHlQjmS+j5ZGqdFiXL5lDrWt88Bs/QxJ3nAQAaHcS5\nDBIKAKGZUZJhaXr5AEZauuEbdaH32Hkc/tWzOPLI8+g71Tx1L+BMhgsc87NMuHDWS7zKNQziHgGX\nYMIA6+WVCLaEp9JqkFdPG2kmKivKlROBcOmevSEZZfRblvJCVK1fRGkdvcNO9J+5kNK5T0cEXkAL\nq92aYHYLCHcqihnxeaEx0RlwRb916VACLoUZg9T8lM4MDNrbJPu4+0dw4k8v4+Sjr8I96JA8HvIH\nJSN7TKV5ku3qt62E2hjT4vDBEM4/vzc7wn3CScuK0zXLJQjhcw94w+Lw4HjwyIeSlshCgSAGGqTv\n4WhbL848+Qb2/egJtL55bOp1wfFMIEikPkuCMVcSVBMHXa4TmMwY8XsAX2pZLrakqNKokD+rgloX\nTzgf8gcxcFb6ukdwtNLnyeq3LOWF0OWYULpsNrW+7a0TWe3onUoM2FvpG7UJarcilFfSovne7l7U\nMTYbhfNrJvw8CpmhBFwKM4ZE4318TndCIe+gvQ0Hf/4UOpkOKlcfbUapz7dArdNK9tcY9Zh17Rpq\n3VBjB/pPZ+cuXmACLjIddVxBP7i+JqgGWsP/9V+Aqr8Zqr4mqHobwfU1Ad74/mnDzV2J7Q1G3bjw\n+mHs/8nfwuXibOroMkXgw52lkUVAIlgHAKjUEAz0rDzxVgII+PxK6ZzNFLNcrA8Xp9Ugl8lwjXb2\nywarg+fbE/p4sTou6YiZsJVB1YYl1B/l6hnC0PnE2eXpiCAIaH2Dzm4VLayDqVh6o5Z5KeOHAAAg\nAElEQVQuZrMJFmvsxjIQCEJdno+5N2xA/twqzH7XOhTOUwKuS4VifKowY5CYn4o0XIPn2qnHVDpN\n+CIiusEWQjzOP78HlvJC5IxfJKT6LbqcKKZ02Rz0HD0PR0tPdF3jv/Yjf3Yl1HppkJYWWgMgKi+R\ngAcTzQ0IPI/uo+cx1j0IPhiK/RcIQgjxsFQWoebKpVnTg3CjfSBseU0E4UPgRrrBF9cBnPSna7Ch\nlVrWmPQSc00ACLi8aHxxHzr2nUb9tlUoWliXks/RpMBmtziVfMCFcc81j3wZWsgtBTR68OYCqERZ\nLeJ3h7VcWlEgxvMgYwNhk1ydCYKlCCHGaV6lUUNvNcFYaIU7MjiZFzDS0oPCedXUtmzXrbW6hAqy\nHG29UeNUgecx1kV/ZyKeUMZCK4oW1FE3IW1vnUDB3CrZv3m6MtjQRjfaEKB2gtotMeUVpbA7Yr9t\n3Z09WLpqMcpXzcvacyhkhpLhUpgxSMf7jEHgw2EJW06sWr8YK+65ATlMtxYEhEuB4/tJOhRL4nf/\nEEIw9/oNlFbF7wxnXSYKm+FCwDvhMTDNrx3GuWffRteBs+g5cg59J5owcKYFQ+c7MNzchbbdx9H8\n2sTPHUC4fJiClQEReBCnNGsj8AIG7HTQPP/mzVj9mZtRvnoeOK00QPMOOXHmyTdw5NfPxbUvyBSB\nFzDS2oPB8x2JtWNsgEkS/CRr9BA0BslqfWFJLPulNULQJshyBXzgBlvBuYZBgv7w/z0O8AE6Q6Ua\nt1DJY8qK7Pck6PVLblbqt6+mXu/AmCeaTXYPjlLZMLVRB31uLPNcvWkJdSxHa0/2xmFNETr3n6GW\ns5XdisAK57s7e+JsefkjCAJ6unrBszc2lwgl4FKYMaj1WqgNMR2VEOLhc7oRCgQl+pSCeVXIqSjC\n8ruuw9wbNlCPOTv70XP0HAC5GYqJ261NRbmo2rCYWtd54IxESJw2Kg3TySYAwYkZoKYiWu49dj4r\nYnTiHqFLZISDMG7qKjBBCHGPSMw/Rzv6EBDN4VPpNMitK4OpOA9zr9+AK/7zVtRsWS4beDk7B3Ds\ndy9M/D0Q0frmURz77Qs4+eeX0fD07vgbJulQZOHN9IVZ0BphKKtktqGzrMTnBvweELcD3GArCPPa\nEc+opEsx8jrlzaLLit2H7ZRAfqChFYKoNKvPsyCnuhg5lfSNSkTHxRqeWsoLqeyipbwQubW0Dqnr\nkB2XC96RMQxfoJsPaq5cmtXnYIXzXR0zM+DyeLy49yP348M33Ik73/8pjDoSTxc5feIsvvnl7+CX\nP3oE/b2T092cUcBls9nUNpvtLzab7S2bzfaGzWarldkmYLPZ/j3++L9tNtslytkrKMSQ61Qcae6i\nhvfqckzR0iAhBOWr5qFwQS21X/OrhxBw++DqZUxPkwRcQFgcS802E4Bzz70zscCFEIlwnvgzF87z\nIR7ekeTzJoNe/8StF3g+7C0lQsgpBl9cD75kFviSWRBUsbIlAcA56Qs3m3nJn1NJWXFoDDrUXb0C\na++7BeWr51FDxYFwRqrvRNPE/o5xAh4fWt86EV3uO9EET7xRUsk6FFn0FvCWQghqLXhDDvi8cmk5\nVGeUjgQa7gTn6AkH4ix+j0SDFc1w1VdQ9hAAcPap3dGMYN8JupxYvLgehBBYq0uo9Y628EVfTjDP\nUrbaRi33Hj9/2Rih9hw7T8kU8mpKEsoQMqGccZufqRmuZ598Hucbwt/ptpYO/PmRx+JuOzw0gq/e\n/w3sevUt/P3RZ3DH++/Fs397IeuZsUwzXB8CMGy32zcB+BaAb8tsM2y326+22+1Xjf//8mw3UZhW\nGFjh/IhTUooqsFVJLmKzd6yhLuABtxdnn3oTIV/sQqXSa6nySDxUGjXmXreeWjfWPSgpNaQLe5FF\nIHPhvG/UBfCxr6zaoMW8927Gwg9cLbULaEw+9iURxDtKjbYROBUEgyggJZxkIDfxjlE+U2x3Yjxh\nsM5ixNzrN2DNZ25G/hw6M5St0lXfyWYq6wPE7/BjNWuCTIcii2AuAF9UByG3LG5GTJLlSqSNA8Az\nMw8jAZdKq8aC922hjEmFYAin/voaRtv7MNRM/12R2aGSgCuS4ZII5qUBV9H8WqqjN+jxo/9MS9zz\nny4IgiAxdK29YkHWn0ea4erO+nNMB955k54f+eqLb8Afp7njpedeg3M0doPpdnnw0+/8Evff9UW0\nNMfvwE2XTAOurQCeHv/3awA2yGyjZLQUphysjssz5MTgOfoLVWCjRcGR/aqZ1P8Qo10xl+SnLL7O\nn10pGWx94fVDEouJdGD1PRPJcHmH6IyMsTAXpUtno2hhHYqXzKIeS+ZTlhBBAGEGMgsGq0TLJOgt\nEp0aN9oPCALcgw5quDLhiCSYYjEW5mLWjrXUOldf8gHNqdBzVOqSPhQvKJWUFGN/94C9DXu+9xj2\n/uBxDDcnH61DoTVKdX2RpwSRPBby0wGXuPSaV1+OuTdupB4PuL04+vsXqaDcWJwb1TDmVBVR4n/3\ngAM+pxtj3bT+LtJ8Qj23WoVSxreu+1CD7N8ynXC09VLfK6LiUL3KlmCPzChXNFwYHhrB2ZN0Kdrp\ncOKdXXsl2/I8jxeefkn2OKdPnMUnPvQ5/PH/Ho0brKVDpgFXKYB+ABjPXPE2m40VR+hFZcfPT+Qk\nFRSyBWsNMdDQCv9oLFPCadTIrStjdwMAVG1YLClJikmm32KZtWMtVKLuRD4Qgv2Zt6KC/LTR6Bmv\nJr+0ZJUinmE68BP/3ayQerSzHwEZl/GU8HsoTZEAQDDJmD8SAt5CX5xJwAt4xyQeUNbaMmhEWr14\nGPJzJA0MAffEdG+uvmHZwcwjzV3yJWOJaD6csRJ4Aeef3wO/0w2fw4VTj78Ov0zHZVwIkWS5AEBQ\nacJDsXNojZXUh4v+OS9bPlfiE8Vm8UoWxwJxtU4r+T50H7JTVhxaswFaCy3wj1DOBCKO1l64+rMT\nEF8q2EC8cF4NtCb5oHgiFBYXQK2OvX+OkVG4xlKfOnA5sP+dQ7Iebi8+84pk3ZEDxxMGpcFgEH/6\nzWO4787/gts1sdcxacBls9nutNlse202257x//YC2JbCcf4TwD0ArgXwYZvNtmJCZ6qgkAXYDBfr\nEp83q1xysYmg0qgx+13r4h473YBLZzFiNpNlcbT2oIvx+koZjgPUTKCRoQEq68IvttTQW00wFouC\nIl7AyIXMyhacmynj6c2AKo7NhM4IQUcHzJyzX2IHwdoWxH1uFQdjoZVaN9Gyolx2C0igdYsjmg+4\nvfA5Yl2bIa8frYwzeVJ0Jgj62Osl6M3gC2vCWj+NnmqykNhCyFh91F69QpLdFMNmbK01dFmR9bBj\nBfNijIW5sNYymZppnOUK+QPoP0U3oZQunxNn64mhUqlQUk4H1DMty7XvrQOy648cOCZ5LZ5/6l/U\n8pr1K3HFJtozEQDOnW3E7n/vmdB5JfXhstvtvwXwW/E6m832O4SzXCcjmS273R5k9vu1aPvXASwG\ncCTRcxUVxc8eKEx9psP7pwuVItEUw7pVcxP+HUVFCzF4vBHdp6QdfFXzq5CX5mtQeM0KjJxrQ++Z\nWNDQ/NohzFk3DyYmGEgFl88C31AsS2PW8DCkcE7s39zopvVfxTVF1DYVi+tw/vVYAODp7EPRZrr7\nMhkhvx+OblqYn1NeDo05/vmGLDVwnDsdXQ6MueFop2f8zV2/AKaC1N6H/KpiuHpjQRbn8WT8OeZD\nPPadjC+893f3o2gFHbCMeQfgF7lhmHOM0BdYMOKV6u+6DjZg8Y5VsMgE9vHOWSg0I+gaA1GpoDIY\nqQBnzJcL/3C4xBcK0oFfSVmurDdcwV07sfsnT2GAGfOTV1OCahud+fQuqkXnvpguUdxFCgClcysS\nvtbzrlqG/b+PlXr6TjRhzQevintDNJVp3X+WakzQW02Yuy7sizUZv5u1dZXobIu9Ry6nY1r8PmcD\nv8+Pw/vj35zsfm03PvPAnQCAgb5B7N1NDxD/5P0fw8o1S/Dqi7vwv//zUwz2x27Ke7u6J/Q6ZvrJ\nfRXALeP/vwHAG+IHbTbbXAD/Y7fbPzwekG0A8LdkB+3vT9y2qTB1KSqyTIv3L8Qn1lhpyoqS/h1V\nW1eh52wrBHGJiCPwabQZvQZ1O9dhoKkrKsAP+QLY8/uXsfRjO9I25CQhNZVudo84MMYl/oGQe+8c\n3XSmJ6DWUNsYmDvorpMXUNU3mtb5Emc/da6CWosRNwBP4teQGHOjMwQHWocovzFTaT7cPIE7xfdB\nbaUzZj1N3ciZX5fSviyD59rhHY1fcmg/cQFFa+ghzZzbR4ldna4AnLwTg63SsqTA8zj4xC4s/tB2\nan3y7x4BwAMututUBxXCYm6eCbiGHB4Qp3x51XbLVXD95p/wiPSG+fNrJedAcnPYXSm43JyE562t\nLIHaoIsOxfa7vDi7+xRKEmTZpirn3jxBLRctrsfgkGvSfjcLiunye8OZZixdlT1z1anMoX1H4HbF\nbxh66okX8L7b3guVSoVHf/8MgqIyd3VdFarr6jAwMIbla1bh7s9+HN/++g+ijzc3tlHvV7rBV6Ya\nricAqG0221sA7gXwZQCw2WxftNlsa+12+zkA7Tab7QCAtwA8b7fbD2X4XAoKWUOlUcfVjVgqiqCL\n85gYY0GOxEvLWGjN+M5bbzVLxv6MNHeh+3D6/kMSobTfk5EBKmtjoM+jL57WmlIQUdemd2QsvWHc\ngowVhDEvrss6tZ25AML4dgMttAg73bElrOHkREqKbDkxbzajdevok47GEeRtIXxO+cBtsKEtfQF9\nPLSm8EggJtji1CqQBPYUGqMei2+7NlqOzakqDlttMOhyTAk1j8mGKKs0asl8xa5pWFb0DDslJffS\n5XMn9TnLKuhy7kwqKe7dTZcTt2zfBL0h9rs40DeIQ3uPgOd5vPjMy9S2191E3+RmuwEhoyuE3W7n\nAdwhs/47on9/aQLnpaAwaehzzfDLXNAKbKmPEKm5cikG7e1RH66KNfMndE5lK23oP3WBupg2vXwA\n+bMrU7KaiKLWQiBc1GaBCDwQCgDq1EcHBTy+aFYBCHdTsYGoSqtGbk0JhkWlpaHGThgLUiuDEo+T\nsioQCCeZFRgXlRqCKR/8SB8G22khdar6rQimEmnAFRlDkw4Btw8DjJasdvNy+ByuWAclL2D4QheK\n5tfGNpIb7QPAlyBT1vTyAaz8xI2UVUNGcBygMyLkoV9DOXNYFmNBDlZ9+mYEXB5oLca4r5e1ukSi\nBwQAndUErVnqms9SttKGjr2xErKjpQfugREYC2UaK6YovccaqWVLZRFMRZN7/uwQ65kScAmCgL2M\nfuvqazdDb9Djpedeja578dlXwKk49HTFJkxotBpsf/fV1L5yrv2Z/D5EUJzmFWYc8e6607lYq7Qa\nLL/z3Zj33s1YevtOlK+eWMBFCMHcGzdSF7uQLwD7s2/LdtskOJCMAWp6flziGZNA+PWSu7jnzaKt\nF9Lx4yJu+iIvGKzJTT/F2+tMGOoYobIzOqsJ5rL0TCT1uRZwmlimLuj2yc5fTEbfySaqxGzIz0FO\ndbGko1PyGsUZ7SN3QxBhrHsQvccb4z6eDoLOLDtHMRU4FQddjinhxYcVzkewyNhByGEqzpN4ek0n\n53mBl3pvTZZYXgwbKFxst/mxMRc627vg9WZuTZMJLU2t6O2OaTo1Wg1WrF2Gd914DbXd3t0H8Ojv\nnqTWbdm2ETlW+tqQV5ALvT7WiOR2eTDqyNy6Z/qpDxUUJgg7xBoIX6xNCeYgyqHWa1G6dHbyDVPE\nkGfBrGtW4/zzMa+Y4aZODDd1In92Yl8pMYLWEB5aHCHgAZC6AJ/14JJ7vQAgf04FmkVd1iMXusEH\nQ5RBrCw+d9jSQXzOclYQiVBpMHCB7jAtsFWnr3njCIxFudRAZVfvcErZFzFsObF0+RwQQpA/uwKd\n+2IZmiHWADVOl6JvlJ4rqTEbKNF58+uHULSwDqoUslGJEPQmhIKZBVypwAZLEZKVE8WUrbJRsy57\njp1H/bZVyT9nUwBHaw+V4SNqFYoX1SfYIzuUldOve293H0LBEFRZfs18Xh9ef+lN2M+cQ19PP/p7\nB9DX0w/XuH1Cbp4VX/vfL2LZqiVJjpQd2OzWitVLYTDosWDJPFTXVaHtQtg7MRQK4eTR09S21928\nU3I8QgjKKkpxoSmWve7q6IE1N/2GJkDJcCnMQOQyXAVzpe7yl4LyVfMls+S6D59L6xisjitdA1Sp\nfks+4DIV51F6uJA/gFGmY1B6cgI4J72NoDOlVfIEwuad/a10wFU4N/WgNHwQHtxQJ8wW+iLk6k9P\nxzXWO0RbPhCgZFx7lFtbSnl9eYecMa2bINAO+0A0w8VquObsXEd7ho260b4nUb9tiqg0CAl0gKVS\nZ++yYCzMpeaXRpBzmI9H0cI6qmMy6Pah/2xLNk5v0ulmAvGi+TUpecRNFKPJiNz82E1MKBRCf192\n5wOeOdmAez70OfzgoZ/i+adewoE9h3GhqTUabAHAyLADX73/Gzh57HSCI2UPNuCK2DsQQiRZLjG1\n9dVYuFS+SiEpK04gW6gEXAozDjlNlJy7/KWAcAS1V9OWdQMNrfAn6LqRwI74CfqkWqEEJPLgEkMI\nkZTM4jqqR/bxOkECdPebnEFnMhzt/Qh4RGOVtCrkVuUl2EPuXMZAfGMw59H6NLFNRCpIxPL15dCP\ndz+qtBpJliea5WIF84SLNg2wJcWc6hJUrqM7HNvePhFXXJ8OQUIHu0nmZ6cF4aRzFYH0MlwqjToa\nwEZgPa2mIkFfQDIAnnXQn0xY4Xy2Rvz4/QH85md/wH13fgEdbcllBF6vD1+570E0nJrcUrCcu/w6\nkZ/W9ndfTRnCirnu5p1xb7jldFyZogRcCjMOQz4tzua08d3lLwXWmhIYROJzIcSj93gag5U5FQRV\n7CJKgLQMUD1MSZEatM2Qz3TiSUpmYgQehBk6zest0gAxBTr20XfMhdV5ULHluWQEw4GfKZ8JuNLo\nVORDPHqZoddsB1pcHVccwTwfDNE6MkKgNRtQfeVSasYg7w9SPleZEiK0yalKBWmpcwJYq2kLEX2+\nJe0sDxuoDDV1TvmB1o7WHvD+2Dlqc4zIm1WeYI/sMhnC+XNnG3Hvbffh8T/+PeFgZw1Tlna7PPji\nZ78eHSY9GRzYc5jSu862zUJRSSywz82zYsMWqXG1TqfD9ndfFfe4Ej2cEnApKKSOPtdMtexXrV88\npcwUCSEoW8HMkjtiT0s8L2joCxoJpj6yRprhit89yA6yHuseiJuNI65hkFDsAiQAkqHUqeAedGCA\nKSmVzSsJd2Omw/gFwywTcKX6Wg81dlDaKpVOI7GmYIPS4ciYn3iCeWYMi9ZsAKfioDHoULuF9lKa\n0BzLcVhvOpWKA3zZGwWTP6eKmqybzwSgqWAuK6DK17w/CEfL1O68cw/Qtif5sysT2m1km2wK5wVB\nwKO/fQKfuf0/ZYc577zxGjz43a/g4T/9CH97+c948Z2ncMe9H6G2GXO68IVPfw0XGlsyPo9EsAam\n6zatljnP7ZJ1W67ZBLMlfid4eaWS4VJQmBCLPrgN8266Eos/vF0yI24qULJsDiDqDHT3jcDZITXD\njAvrxxVILeASeF6mSzH+j5HWbKA7AwVQVhFRQkGQMVpzJZjy0tZuAUD7OychHhppLjQhvzI3g4Ar\nHPDozDqoRJ2KIV9AIlqPB9vyX7y4XiJkN5cWQGOMvR8hXyA8bzGuYJ4JuESBBjs+Z6xnML0ZizKw\nmSKVhgPxsSapMggCEAom9Xkzl+ajfttqaEx65NWXo/aq9Ke8EUIkti2DzPD4qYZnkA642DFSk002\nS2FvvvY2fvfLPyMUom8SCosL8O2ffQMPfO1z2HT1etgWzEF+QR44jsOH7/wAbrvzA9T2o45RPPCp\n/0ZbS3bfO78/gEP7aHd5ufE8K9YsQ3Ep3SF73c07Eh67jA24FA2XgkJ6qDRqlC6fgwJbNTjV1Psa\n6CxGFMylLzDdR1IXz2ea4fKNuqjh2RqTHmpd4qBIksGRKSuSsUFaIE44CBlot3xON3qYIKdmWSUI\nIdQQ7FSIepURIpPlSj4oOej1Y8BO3+2XLpVqdAhHJKWkocZOyocMQMz0lAm4dDmxc9OaDLRZqwD0\np2HHIYdkcLVaBeJ1JQ6k+BC4gRao+prADbWHA68EVG9agvVf+BCW3r4z7Q7QCAVMU8SAvS09y5SL\njHuQtg9I1aMuW2SamSFuB7i+ZnCDbcD4d+r4YWmDxjXXbcVvn/gFVl+xMu6xbv/kbbjltpuodSND\nI/jCp7+GUUf2HPZPHDkJj2gcWX5BHubOl3aQq1Qq3P+lT0GlCt/cvPumHZi/yCbZTkxpGa2F6+8b\ngN+f5s3dOFPvSqOgoAAAKFtBa4H6TjVT89gSIhli7UvJcV6i30rgFB4hj7GsGGrspC+EQb/Ud8tc\nkJE6u3P/GQgiGwO9RYfiWeNlyQwzXICMjisF4Xz/mRb6XPIsyGH0ShFY1/nhpk6Jhksg4dfD76Sz\na6zpbG49rc3pt08sWxDyy2S4+OC4nYg8xDkQDXCJ3xMOuvjEQdeEuoB5HgWWIHVz5BsZm/Cw8cmE\nzXAZClI09s0S0pJiCqL5UBDE0QsSCoD4PSDOcGfj8BD9/b3ncx/HFx/8fMJSHBB+zz9x3x248ZZ3\nU+v7ewfw2B+STvtLGdZdft2m1eDilG/XblyNp157FH9+5jf4j69+JunnUqvTorA4dnMoCALl9ZUO\nSsCloDBFyZ9TRWUDQr4A+k6n2J2lUkMQBTQEQvRuNRGpdiiKsVYVU4atfqc76sAPANxoPzUvUFBp\n0vfdAhD0+dF14Cy1rmppBbjx0ivhQ2l1YyYMuFK4kLPmoyVLZsX98WZ1S6Md/Qh4mIAmToaLHUXF\nNnj0nZuYjosNuCL+VsQdx+BR4EE89GMk6Ac32CHVpWUJ4hmBmgshr5LOEg1OMNicLEL+IHwOUeBM\npM06k01BYT60ouz0mNMF52iSUnHQF/6tGCdimjwyTAePctmjeBBC8Jn/+gR2MrYMzzz5PPp7J25V\nIQgC9r19kFp3xaa1CfcxW8ySpoJEZKsBQQm4FBSmKJyKC2u5RPSk48mlTr+smKoHlxhOrUIe4x12\n7p97wsJwn1uiBxIshVGBeDp0Hz5HzSJUG3QoX8h4b4XSKCuKSpzmfBP1kDtJwOUbdWGkhc4YFCcY\nqqzLMcFYLAoyBQEjLcxdckTD5WRLivS55daWUSJ0R2f8RoVUkJQUx/VsxOuU71b0uqjycAQS9IEb\n6kgv6E0R4g1/hgpraHPiQbtUwD0VYOeK6nMtF92oleM4lJanN1ORBOksMeGDAB+Cgwm4rHnplUc5\njsNn/useFBTF3j+/z48//vqvaR1HDvuZ85IRPcvXLJ3wccVkSw+nBFwKClOYspV0WdHR1gv3QHJ9\nESDVcaUinJdkuFK8Ky9aVEctj7b3ofmVA+DG6DtYQaOHoE8exLHwwRA69pyi1lWsXQCVnmkOSLWs\nKAhJM1xiLRtL74lmWrhfXph0Ph6b5RpiA65IlyKr4WIyXBqDDuZSWv82MoGOPYloftz4lAh8NNAR\nw3kcknURSMALbrgjq7YSCAXDQ9ghDbhGO/om3DQwGbgvcTkxQtplRbkblqAfw0zAlZtmwAUAer0e\nH737Q9S6l//52oQF9K++8G9qefW6FTAY9HG2zoxsDQNXAi4FhSmMscAKaw1zd5WqeD6TDFcGGi4A\nKFkyWzJ+qGPvafSeoTMQfE5R1NwzHfpONVOdg5xGhYq18yEwXY7sHXpcBIEqc2oNGmj0sbIoHwxJ\nujWp8zkhLScmQ2Kh0ccELnEyXNocOuACpGXFkQuZm1pKNFwip3m2dIhQEPDRGjPJe+D3gBvqzFrQ\nRbxj0fdKb9bBXCjK+AnA0PmLW1bkQ3y4uSSBJtJziQXzEdIVzhOZGxbe64GTEbhbrZkFkDtv2I7K\n6tiNB8/z+N0v/pzRsQAgEAjg3y+/Sa27JoMu2GRkpIeTQQm4FBSmOGyWq+dYY7hclwR2xE9GGS65\ngEsQwhddkSaMcATz37cZOitd/mrY1QjXcDiAENQ6QCsNHpIhCALa3j5BrStdPhdakwFQ0aadKZcU\nGZd3QghMrON8nLKiq28YYz0iiwtCJHYNcrCzOt3D9EVbICoIggCfRDRPv6YAkMcGXM0yVhwpEq+k\nCCD8Pos6EIlnlNbjqbXgC6plxkm5w5quNDtH5SBe+jMpLStevIDL53Tj0MNPY+/3H8fRR56Pa74q\nEcxfZEuICGkHCjI3LI4h2s7FYrVkPJNRpVbhjk/R/lxvvbEHZzN0oT/wzkGq29FiNuCKZXUpNQil\ng1JSVFCYIRQtqINKFwssAmMeDJ5LQbui1kKcxwnrMeJ3kgW9fgTcsfIMUXGUJQGA8CzE4Q6ohjqg\n6r8AeGI/dhqjHgtv3UrN/AsFQjj5cgOCgRAEXfrBFgAMne+AW2zTQAiq1i8Kn46aDrhSznAx4m6B\nqGBidFyunkHIwbr+59WXS8p+cuhyTOBEwUzQF0TAK3o/OA4hX4ByJ+fUKqgNUlsOa00p7dM24Mh4\nzA/b+crpYplRAlGWSxBAmHKiYLACnAp8fmU4oBZBAh5wAy3hDtVML4B8CPDTfxcbcA01doAPTo5Y\nn6XnyDm4+8OfxdH2PvSdbJbdjjU9NU6RkmLSQEEmw8UGXHkZlBPFXLl1A2wLaG3qb372h/QtPgQB\nrz37ErXq6k3LoVOrshLoi5GK5nszsiRRAi4FhSmOSqtG8WK6ZJWSeJ4QqbFogiyXxPA01yx1xg74\nQEQu5Jyzn7qY5lQUYc67rqB2cQ270bCrEXwm2S1eQOubx6h1RQtrY9oySYYr1YCLyRCqtTAV0RcS\nV7fUaFbgBfSy5cSlycuJQDgLaMinn8M9IgomOJW0nGgxynY+qvVayTzCTMuKfJJxn4MAACAASURB\nVIAOVjgTHRwQjyP8Hgd9lNeZAEAw5ETPPRx0MeVFQQDn6AU33JnUq0sOcTkxQk6xGRpD7H0P+QJw\ntPbiYsDqJx1t8s/LlhQNl6ykKA0U4sKHZJshRgbpgCtdwTwLIQR3feZj1Lrjh0/+/+2deZArV33v\nv6db+zKjWTR398y9177H1zYG2xgDNthcY8xmHCAkLI8UBPIgIQlhScjLSiV5VEi9hCRUHpWAkyIh\nqfcS4iy8EHYwEIwXvIANt21z9332Tbv6vD9aS59zurWNNJqRfp8ql6+klnRG6m59+7d8f3j4u49I\n9wkhUMj7C6fVc6dw//2PS/e97IjjCcbaGGXWCqmxUURcdWHZTBbLSz5dvA0gwUUQ2wA1rbjw47Mt\nphXVqIO/4Gqlfosp3kysXKzNJKyt9bkcO66VU2wXn5nFucdONl2vypn7n8DKabm4/LJbrq3fMBVB\nWS62Fk1RB0cbBuK7ZAfqaiTDzfKpC1K7vxE0MXl4WtvOD9VtPLPk+jyZoTncaxFGF1pa8XhnacVy\nUelMS4y4+wEckVXMg2WUmrNwHDBdrvpmAPb4PoiwngJl+XUYSkS0FbyK9hljmJyWB5WrEd/c0hpO\nfP1RnLn/ia5Gvwpr8v6/ela3NShm8lqkODKqfyabwS6lS/HShVkUiz4XJT4XK0sLGy+YV7n+ec/B\nDTfJY6o+9fFP4+gTFj779/+KD//aR/BTL/8ZvOLm1+Fdb/5lXLygNJhkV3HfF7+Gouu73bNrElfx\nyrHYZcHFGOtKWpEEF0FsA5K7JxGM16+wRNlGbqmF8SuqAWqDwvmW6rc8BJv6o8gYA3/pNZp7+4+/\n9BByyy2sucLahXkc+8rD0n3jV+yVIzuGofiNoaUoF1NNRw0TsT2ygFlfWIddlK+w1UHVk1dON3Xi\nd6MKrnW34DJMFDwiXH6ohfOLHUa4tKL5SNgRUy5YdkkroLejHj+8ZgD22B7YozsglMgcEzbMpXN6\nIb4ftq0X6FfiXWpa0e06f/H7P8ZDf3EvTnz9ETzznw/A+vdvy69ZyHZc0K92RK7PLmp1XFr91vhI\nazMUizkY86dhzJ/ummAIR8KSFYNt27h0wWdEmE86flkpmO+G4AKgRbmeeeoY3vO2D+ATH/sUvvW1\n72BhfrF2/x/8xh+hXBVXxRyM5fP40tfkc8OdR55biwZ3O8IFdKdwngQXQWwDGGPaj7V6YveirQiX\n5sGl1514ncjUomYACNgFPOvOwzBDdTFkl8o4/pXvNV0z4FgV/PCz34BwRfEC0RAOveYWfeNO0ora\n4GgTwZEkQrG6eBK2QO58/SrWLpUx+4RsPNtKd6IbtXi6GuESjAGMeYz18Y+MjF62Q6qXyy2stiVo\nq+hF8wFNTBmZZW00EyI+a2MMIpaCPTkDEdTH+LD11mxNkF+XTDiFGai95/i+MTBXDVtuYRWr5+bw\no3u/iR999hso5+v7wMXHnnGaHMpFZxzR/CkYl475CoxGFJUIF2whN1BAt4RoaYZiuQhj/jRYIeM0\nHCx1VpTNMkswLjwF4+KPa2K11ciMV4ciACwq+9RGU4pVDh2+HLfd8aKWtv3h94/i/3z6s0C5BGPh\nLM6encWTR+WI+R23uboTi7nuWpPAo+Ozg5mKJLgIYpugpaPmmgsuqF5cpYJvyi23oHpwKREuYXtG\nyFipIN8vBFDIIJaK4ooXyP5cFx9/BqvnmrtLH//Kw3KhPIBDd93imZrpyBpCGxztnArVOq6My1Bx\n/unTkvFqMBbRxho1wzelyKqDqxuP9XFjhoIY2SOnQTup41IjNEbQETaigTmtiI40N68NhGBP7IOd\nlGvNUMy2ZI6qCnkRSda6IQNBE2N75M/y0Xv+Axcfe9rztU7e9yiMpfM1UcHsMthqG8Pg4QjwQka/\n4FD3Z71+q0nBvBDO2lz7JCvl2695s8tgy5fAhACzHWGCQsYjMuMjFPxSisvyPrnRonk3b//5/9by\nLNtP/9U/4OmHHgCzS/jy1+Xo1rOuuxo7XV5ZDGipK7sdKKVIEEOEWnjbSoQLRgDCqNfZNBrx09Rl\nvpjXCphrr+tOKxaztR+P3Vfu0Lr/nvnCAw07fBaeOYsz9z8p3bfjOZdjSjFXrdGJNYQ2ONoRPHHF\nUHTt0iJgl2CXba1RIX3N/rYHn6t+TNmVnFOLVxF8WkqxQQ0X4JFWPNaB4FJTiqEAwIx6QbwHItbi\njy5jEIkJCNd35PwYNnHGF7Y+oSCSkOwn1LSiaFCrNfvkCaxfkIURy6221c1WzOYADzPcNUVwaRGu\nJgXzbH2hNkJHosWB8zUKWXksDwSMhbPYrdQmPn30GfWZzvY+gmu5RxEuANh72R788q/9fC0VOD4x\nhhfffjN+4f0/h//1if8ppS/L5TI+8of3IJvL44tfkyPld7zqCKBak3Q5rdgNwRVovglBEFuBjiJc\ngBPlyru8lIo5LdUobFvrUlRruBqlI1l21RlIDUhdjMxguPy2w3j83voV6fKJC5g7ehLpwzPa6xQz\neRz9l29K90VSCa3zUcLUrSGals1rKUVH8MR2ytGY5fMrOP7lB3H++yc1MbTj2a3Pk6sSiIQQSkRr\nxdfCFsit5hGNOqJUSyl6eHC5SR3YLXVxLh0/ByFEy4OihRCeKUWgEsXK6Ok/EQjptYHN3icUkywl\nWD7jWVxfI58Bc3uUGSYQjErNDpPT43jq2962DLGK67+78eHE987gmjt4fQ0A2PoixOgO9emeqAXz\nVdTC+eyc6jLvL1BKmbXagGgVVsw3/oy07T3S/cLG1Yowffj+R733ER/xqaYUU+Ptz0FtxF2vfwWO\n3HkrstksJibHpXW9/zd/Cb/zwT+o3T515hI+9OFP4cKleho3GAri1pfeAoGccuHXXcG1WxNc7XfG\ndhzh4pzfyjm/yDl/pc/jb+GcP8g5v59z/rOdvg9BEA7qiVu9kvZD9UfyunLOr2bkeqlYGIGIainh\nfwJjpXytJoYphc7jh2Y0F/pjX3pI6x4TQuCpz31bFjaM4crX3aqvxf081fqilaJ5oRfNA0B8Su5+\nWzy7jJP/9SNNbEXGkxjZK0cOWkWt41pfytRSiur7NOpSBICRvWlpRl9+eV1rfmiEagnBAma9wDsY\ngVC7QFHx3mp3WoDiwcYKjT3D9HRiwnlPI+DUcgGIjkS0kUwAsPvGK3HDu+7G/ttvkO6/+MxszYS3\n9j6Z5ZZTd8U17/1/fXap5mUmhEBGmaPoW8Nll7F26rhv1LhdweAZJQPw7MPTCIXqFyWXLs7i1All\n4LkQvp/Dkiq4Ut33FIsnYphMT2gi8Obbnq8Nvf7+k7LIvvnW5yORiOvmu10WXDt275DWN3up/cHb\nHQkuzvkBAO8D8G2fx2MAfhvAEQAvAfA+znl3ZTFBDBnRsaRkdllYyaCUb6FeqYXCea1+y9MSQj6B\naV1ouVUncqRuF47h4MufJ/1IZ+dXcO7ho7Xb+dUMfviPX8fskyek5172omuRmpGvLDW8UorNrCG0\nlGK1hquF0xQD9h+5oeUokopXHZcwDAjbRn6t9S5FwIlGTRzofMyPNkcx6Ep6MAYRk39cJe+tNhCq\nB1sxp38HtY2F1vkqzd8M1H9YZ67fV787GsLVb7wdh+66GWYogMkrpxGflPfjE4+clmrTGATYeuNB\n5VV8B4SLeuF8YTUjGdea4aDUXeyGrVyCXWgQNW4npSiEb5o2HA7iOdfIzR0PfUdpXrFLcoMCM2od\noZrg2kiEq2ov0kZ92i+8583YraT63dzxqiPOP9TJGqVCVweph0JBpKfqEfDNND49B+C1APz6e28C\n8KBlWWuWZeXgCLObO3wvgiDguI5HU/IPSHahhU7FFiJcTeu3PArmRUyOBrHcKlDIaKNfYAYRnxrT\nvMROfP1RFDN5nHv4KB78+D9j9km5AzCxexIzt8lePZ4YpiT+mDKY2hOPLkXASfmp44lqbxMKYNcN\nHDe8+yfa7k50o9b0ZJayADMdywFXjVAgGpIFkA9TfJ90ux17CFvxZDJD8vuJ6Ij02YpIUvbeahUz\nIEUiGVAbSK1RyOgdkS7B5o5k7Lwijevf+ALw174Iz/vlNyB91Uz9PQpr2H+dPL/ywtOzWC8pkZDM\nUvP9Bf4pRaBeOJ/xMDz1EuYsuwJDs9lQhGyp0HqnXSkvp2CZCRFO1G7feD2XNldNRrWosBkEAiGU\nSmWsuv5uxhhGRtsfPg8AyK/DmDsBY/kCjLmTrdXPCRuJ0gp+4/1vgmHon2NqPIXnPr9yjjBMKSLr\n1Ap2u46rtfSzHx0JLsuycpZlNZJ3OwG4W0BmAezy2ZYgiBbRbAVaqePSRvyUtStM3YNLP/lLQsoI\nQMTlK11WzMHIyD8iIlQXL/uP3ADTldooZfN48M8/i6f+/b9QzsknXzMcxOHX3yqly3xhzNsAtRFa\nl2L9fdTarORkHIde9my88FffBH73LUju8r/abgXPTkXD0NOJTeq3qqiCa+n4+ZavvtWCeUMVeGYQ\ndmo3RDAKO5Jsud7JCzXK5ZdW1KNbCSk6qtYfpqZi2HXdIYTckaRyCcbyRUwdmERszGVNIYCTDx2X\nvduE7YiuJjQUXJU6LrWRxXOkT6kAtizX/4hACGJ0Ry1dClQEQ4tF/aygCItQBPbYLoiQ87c/TxFc\njz/yBPK5+gWU1tkbCEIEQlhWumaTI0mYZmdzFI3Vudo5hNklGIvnmgpKtjoHVi7imsP78eafvF17\n/PY7b0UgUP/MRGhzC+fbpemlCuf8HQDeCSeazCr//13Lsr7cxvt0FnsnCEIiNjECt+tPdq4FE0nG\ngGBIbpMu5aVIhRbhGlcL5pUTVzACmEGIYER6TOssc9XuhBJRXPaia3H8q/V0RtGjzT6xexJX/sSL\nWkvvVTGDUgSOlQq1HxsNrwiYy5hy5iXXI5YIoDg/h/F9YxhJJyBCUdhtGJw2Ijop/12O4DKRX5G/\ny2YdilXGp3fACAZqxe+F1Qwyc8stfX4NU4pVIgnYkYR+f5uIcEwqwmf5jN7cIISnHYSENpS9kkKu\nijIhYCxfcC4sDIb91+/Dk1+td5heePwZzDx3BvGAK3KzvggRH2todVH0SynCFeFqVjAvBIylC3IE\nDwx2arfz3oEIUK4fQ6yY14fQey5OXpsIRQFmwB7bA2P+FC7bO4UdU2O4WBnIXsgX8P1Hn8CNL6jU\nuSkXKMIMAszwSCd22KFYzGnnEFbKgy1fhBjd6V0TWMxJ6d63vellePCxp/HUU47/FmMMd96liLBg\nBHBHDrshuIRwhCEzei+4LMu6B8A9bb7uOcgRrT0A7m/2pHS6w1AlsSWg76/3rOzfIVkm2GvrLX3u\na7kkCot1QZIIAVHX80qr8pXsrpkd0uuun5mHO6EYS40gmk4iKyaQvXDW+00Zw+SeKTBXNGH8NS/A\nhUee0gQe4ES1nvWaF+Ly257dmjO3i0wxjpxL7MUjhvT3uRHlMhbdHd2MIT0l/5BM3vk8LB/9QX2T\nQhYT41EYnaTTFOzxOB4yGEQlfVjIFhEJBxBSrvZH06MtH1PpK/bg4g/rRpDZk+cxc9W+Bs+osCgL\nhEgs3LPj2C5FsbRYHz/ESnlMjEVguAaQF5YWsOYWw4aByT07tP1hcTEIUUmHMgiMJQMIRB2BWlhd\nxtqF+v684/I0Tjx2HuvzlX3OFrjw5FkcvG6yVuPD7DKSRh6RySnf9R8t+EdNM3NLGEuGUVailDv3\ny8dR9tJ5ZBVxFN+9D5FJpzYoU04id6m+H0eDNuItfB9L8yfg3ntG0+MIJpznFeMmVo9ZeN51HJ/7\n4ndr2zzx2BN45WtuAwCs5ebgjqUlUkkww8TSiiy40lPjHe0f6vmjipFdQWx8DJEJuQHFLhaxevwU\n3JdFoWgUH//rj+K3fvWjOHn8DN7+7jfi+Tc/W3peKcawslIfAxQo55HawP5cLuSxdvLHKGczCCSS\n4G2M8fKiG7YQXtGrBwB8knM+AsAG8EIA7232QrOz7c3ZIrYO6XSSvr9NoByS0ymLZ+db+txZ2ZDq\nB9aXlrHGnJRVOp3EqmIymjNM6XWN1VXpQF8rMKzNrgLlEPwSDCIYwdy8njaaPnI9jv7zfdJ9E4f2\n4YpXvxCRVAJz8+vac5rBCkL++1bWsGb4fC7lorRmwQzPz9AIhKRhzfNnLwHR7oiRaCqGzEL977x4\nagHz52THchEKtfTdptNJjByUBdeJB49i8rmHmz53flaOqpUZ6+lxbATCUjH4/LlZ6TM15s9L+5kd\nSXruD4YRBkNdAC1dmoeIlZ0I0twp+UcpHMO+Fz8HR//lW7W7Tn73R9h19RHEAvW1rF88j1U74tuB\nuaY0ltTyPXD+f/wHJ7F0fl7apOj+Dos5GHPnpLUFkyNYtSNYrW5TYNK+mVtZRSbY5PuwSzBdxfcC\nwNK6qM+tFDYMAM+74UpJcH3zq/fj7T/vjNcx1uTay9WsDRgMS8r4sHgi0f7+YZdhLM77prnWz57E\nak4AoWgtwsmWL2qdxMVEGoFIAn/48d+v3aetpfK3Vt/LLhYwe2Gxs7pDYTv7UmV/La2tIhnYmHVp\np12Kr+Scfx3AnQA+wjn/QuX+D3HOb6oUyv86gC9V/vuwZVn0a0wQG0Sr/5lfbqleRy2cd//olXIF\nFF0z4pjB5JEyQjhpGzfVNEcgpNsyVJ/m4yG041kHsfvGKwGDITKWxFU/fQTXvOUORFKdp63acpv3\nMT3VXlOdJ5hvXwj6EUvJ6cLMwhrybcxRVEkfnpGEwtqFBa2A2wstpRgK+mzZHUQje4hiXrM2UBsz\naverExQqqSOWXdG6++zRKUxde7nUCCJsgRPfOy3XNpaLnmOqqqhdiiN75WjYyplZ5FRLiGpKUdhO\nKlHpBIzvnZEFnvZ35Zt33Kr1W4GwlCJ3UpVhXHft5TBc9586cQYXz1eiQV5F82ZIc5nvxBKCZVc0\nTzWpyQVw6rmKeRhL5zTXfcAR3mglrV35WyU6TCuy5UvavrQ7tbGygo4iXJZlfR7A5z3u/6jr3/cC\nuLfzpREEoRJKxmCGgjXfn3K+iMJatuEIGAA+I36cuoR15Yc5nErIDuqlvPxDYQSkK0YRSYKtyVf2\ngIcVQAVmMBy662YcfPlNMAJmx/YKEu24zaut4qyB4HLVkLD8uiNuu7DeWEquL8ssrOljfVqs4QKc\n+rjU9E4snah3KM4+eRzTL352g2dBsjAAADPYWUF0q4hQTPlM63VcLLOobBvV99vqY5rnUh5C2GBr\nsjeSHUkCwQgMANO3PgfWv9ajXBceexrT1+1GPOQyBV6bd2rGlO9YCCFdlABOVHbldD19NfvD47U0\nMQAEE9Gafxxbndd+vMXoDhjBEOBOtplBCMZqAoUJG7BL+v7t/ttVkepRuyhCUSTieVxzeEbysXro\n/kfw6te+DMyufwYCcI5vZmBRMeIdHW3zokgIrSFBxFIQgTDMJVd62S7BnDvh/RLBaFvNGiIUkT5r\nVsw5jRdtwDJLMLJ6Q1IqGUU0GkE225mIo9E+BLGNYIxps9lUZ2tPDNO3A2pNLfTVHOY9CuZdaEXN\nqLTyNyn2NYOB7ogt58WkAmxml/09eIR/wbxEKKp0d5baGgXTiNio/NlkF1ZRWOk8wgUA6WtmpNuq\nzYYX+hzF3ka4nM+0DisXnI5Zuwym2iT4RLcAeBTO58HWF8HKsnAQrjmOO559OaLj9WNH2ALHHzol\nr6dUAPL6APBSriAZAxuhAEan5QLq1TPybMZY9b0KGbB1OV1sR5LefmaMeURoGvtxMdV/y6tZpPJ5\n3XidYg9x/yO6J5YRqDUPLClR11S7gquYldLyApWxUNEk7HiD7xeVZoJkGvbEPt8otCcbNUAt5sCW\nL3k+xBjDrh3jno+1AgkugthmeKUVW0JNK1ZO5OuK4IqolhCqkakadQiEpFl5QCU61C0x1QqMeUS5\nvNOKzPZ2mdc3NHSH9G6kFYXQBFdmfkVLKUpp3RaYPDwjVdSunZ9HdqFxWtFzjmIvMUz9B7GQAcsu\nK2mnQOMUkhmQrR0gwFblKKuIpQBXqtkwDcy8RPZ1u/iD41hbl/dTY3VeS+OplhCheBSJXRMN+++j\nk6OAXU0lutZlBBpGbNpyTBfC4/jUL3Rq9hA3yILrkQcfQymn1Fm6mhiWlIuAsRGfzl8fWEY5N4UT\nteNUJNO+ncQiGIE9OQ2RGG/7PKL9/cVc87RsFbsMY/Gskvplklnung3YwpDgIohthjbip8WZippQ\nqoTd1ZRidEz+oVOd6bUTGmP61XobM+C6RqtpRZ85il70po5LIK6mFOeWUcq6PmeDyb5SLRBOxjB6\nmRx1UZ37VTTj0xaMVjeKlmrOr4Ot62mnpj+0qjBRndIT+g/j1LMO1OYsOhsKHH/opBLlymtRrqIq\nuBJRBMJBxCb9rTdiEyNgq5e0odB2amfjiI06GaKR47xqeGqY3ulHMwjBDFxxYI8UpVpfz+DoD45K\nm7ovnjRbiHairnYJLCvXxNlu7z7m2GEIw1WeAMBOTsKeuMw3ndyUQFj3HbRbcLYXAsbSOSlKCgBi\ndKdjGVKBIlwEMUSoEa5sC8XRACACet0LoLtjSy7zQugpDa8r6MQ4RCjmnDD90iU9RgT0IdbeG/qb\nnmqbqsKxkN34uBC7jFA0iEDY9UNTll8zlIi2bY0BAOlr9ku3m6UV9ZTiJgguNWqYXZFESS3t1Ox1\nGqSsRXzMszONGQb2H7leum/2R6ewsiJHQNQol1owH0o4gjm5Wx527iaaisFQIjx2LNX0YkSbDNFo\naLzq1h+MegtVxoBQBIZh4LnXyRMfHvzuY/K2bsGlDLRPJfRaUGPhDIz5U05K2PWZscyKLILNoDQx\nwHmvAOyJfbCjI85/kzOOUN5IdJwx/RylNhZ4PW11DiwvR/TsWMqZthAfq0W5Go0ZagYJLoLYZmgp\nxRYjXNoVYyEDlApahCviHh/UpGC+BjOcE+fOQxBjuzc3nVilVbf5FrsUAWjpUgbhfG4boSLY1CiX\nm1Zd5lXSh6elNNfquTlPz7Mqm55SBPTaOOXhVscHaRHb6v2GCRH3j0JMHp5x0oEujj94QrrtRLnq\n0Uw1pRiMVwTXHn/BFU/I+5UwgxAjLQw8D4SVOreiv8jXCuYbiNBg1XX+Sun+hx78vryhJLjkc8NY\nMlIXVcKGsXAGLL8OVsjCWDoPY/5ULYXnVSzveV4IhCBSuyBSuzqPaim05TgvBNjyRRhKnZ0IRiBG\nKp2ohlmLcu0iwUUQw4O78BcAcosrsMstRF3MoD5rbHXeQ3DVUw56wXyTE2I/hFYFtY6MdSGlCPQg\nrVgp2lc7Fd2006EoPy+O0X1yfVCjtKLditN8t2EG0EgYNCmmruET4RKJSf9GCDhdsmqUa/7ps1ha\nVKJ9a3M1caHVcFUjXLt8BBcDohGlVjAx0XRfc97Y0C8efNKK2kB5v+kKqAuuG5UI11NPn8KiK5JV\njRQXi0WsuQyRGWMYiUdqxw9bW9DSpayYgzF30hFiUtTSo+ygl7RaB2fbMBbPwVDFoWHCVi4cnSgX\noxoughgmApGQ1MEmbKHNQvSEMacI1UV5aR4l1xxDI2gi6K4dala/tZVQUorwSSmqHj++RfPVx7st\nuCrRikaCq90ORTftpBW1lOJmRLjgbxkiguGm3a01jID23Qkz2FI6cvzQPozsk320jqlRrmI9yqWO\n9QklnDUmdnkXdUdG4wi4fNIF0JY1gRq98xQM5ZKWim342VVE7lgqiUMH90oPPfxYffRRVewtK9Gt\nkWQMpmk4nbqlvKcVDOBcyKlzMkUk0Zn5aIe0VDhfLsFYOK2PI2PMEVtqLZxhQsTGsCM91nF3NQku\ngtiGqNYQrXYqiuiIFAnKrcqCKpJKSicT7Qp6Kwsur5SiV3dSgzmKnoRimkHmRuwhmN1ChGsDgmvy\n8Ix0e/XsLHJL3oJcSyluRoQLeh1X7f7YWOtRUsY0CwQ7mW7p+Ywx7L/9Bum+xWMXsDArf6/GmlPL\nVViTj4NQJaVohoKeMyujKSUlHIq1aW3g3eAiodpBBCONI2iGWTv2b1SGWT/0iAXAiURV17msjH0a\nqxTbs1IexvJFufOyybhkddB9z6k0CVSpDSjPZ5yLyELWqTtTz29GwCnY97sgiI8hEAqCX77X8/Fm\nkOAiiG2IVjjfah0XY1L3Vm5VPuFIbu8tFsxvGQxDsQqAdx1Xi8an7tdVf9g3FOUS1QiXv6hq1xLC\nTWQ0rkVv/NKKuvFpj324qgQj2o+0YCZEm6OT7MSkE9VCpSC9jSjS2IHdSO3fJd137EE5GsiKOSCf\n8a3hApxh6yqxEVn8t2u8qU2G8Cic1wxPg80tG2r2EKrgetSCbdtOVKciWJcW5QhX1fSUrS/q753a\nifL4Xs+pEyIQcor5NxOPwnlj5RLMhdMw507AnD+lpUNFIAx78rLG5zgzABFL4Rd/7m5cttd/7qYf\nJLgIYhsSU60hWvXighzl0iNcrh8GrWDe3NS0QEe04sWlGZ82jzxoacWVWbC1hdb9fdxUI1yjEV8f\np1CHNVxV0le3llbsV0rRqeOSf4RFbLS1Gic3wTDs9H7YO69wvK3aTPXsPyJHuZZPzSKTk9dgrM35\ndikC3oXz8aQquNqcwekV4VL2NaZ23jWoi6u/rrPN1VfOIBatv8fi0hpOnbkke3AtynVNtQiXKlRC\nMefvC8dhT87AHpmSokutRh27TaMGAm3bcMwxWG3g6F/bNj6Oqw8fwN9+4kNtr4kEF0FsQ6KddioC\nUi1XVotw1X8YtKvqrRzdqqAXziv+O0K0n1KEh+CCgLE6C2PhtG+tmC+VCJthGogmvT/TjaQUASB9\n9Yx0e+XMLHLLuoN6uQ8+XFXcTuPC1QXWNoy1L9QqjE7vwMheuXNwNaOIg0LW04eripc1hDtdLIKR\n9i9UjACEK/LKhJAvHrwMTxsUzKvbBAImDvPLpMdOnLooe3ApKcXUqB51kvXJBwAAG5dJREFUFWCw\n3UKXMYj4GOypAyiP7UZ5cqatqGM3EdFU01QnANjRUdhje1tP+ZoBiNH2o1sACS6C2JaoES7Viyu3\ntIbv/eW/4Vsf+Tuc+tbj2vNFdBTCDCC3okS4qh5cQkht8cAWr9+q0izCJYRee9LKj3Uw7KSsFFgh\nC2PuhOOo3Wq0yxVh86vj2khKEQAiowlNSHilFe2iLD43xRaiSiSB8sQ+2CNTTt1Mn6Kn8Z1yI0lm\nMSsJ7HKxDLtU/5xYwIQZru9niZ3jgCH/sEuCq93oFlBJiTUonC/mdLsWo4XPz2UKOqOY5J44fUG2\nhFiQBZfXHEWRmJDc/GsYJhBJds3moSMCQdjpGdiJSdixUYhIwpnLaIYcY1zDhD2S7igyKmIplKcO\ntL0kElwEsQ2JjCXBXCf5wmqm1m0ohMAP/+nrWD07h3KugGNfeVhPOTIGEZ/Qa7hGomDZFRizx2Hk\n5EJrP9+jLYX6o61FuNqPbtWeOjIFO7VLSpcATkGusXwBbPlCS6LLPVrIS3AZwYD0g94palpx7kcn\ntG2qQ9Dd772phGJOZMvrR3uT0C9elmC7ZjAWMvJnFIpHpMYSMxjAuKuIOpaKIpKsHyvt1m/Vnqce\nb0V5ILO8qEhrosFV27RfEVwnT12UzIOXl7yL5mvrM0MQiQ6jkptFIASRnIAY3Ql7bA/syctgTzkp\naHvH5Y5fW6fpzhbSjyokuAhiG2KYhjbzsDo3b/bJE1g57Rq+KoCVU/owVjuaRFap4YqV52Esndfr\nNIDNL3ztAD2lqES41IL5djrHKiOM7PSMp62BkV3RBjB7L7JxhCs8EuvKUO/Jw9PS7fVLi9o2ag3X\nZqYUtwqeRsLBSO07LmTlzkV3OrEKv/sW7L7xSuy8ZhrPfsVVte9PBMKdi0m1cL7aqZjPaJYMrRTM\n17at1DZNK35tx09dlCNcWkpRFlxOKpEkRDvQp0UQ2xSvHwq7VMaxLz+kbev1Y1vKFVF2pZSMgIFQ\nWBcgAsxxXN7qBfOAR4RLFVztmZ56v0cQ9vhepzhYqRFR3bU9sRsLro14cLmJpBLS1XspW5BSY0II\n3fh0M1OKW4SoMg+xWg9pV+ocC1k1wuUhkpMxHLrrZlz10iuVdGLn9UteES62vuh4Ryn7sZ/Nhvfr\nOuubuUwWXGfOzaIk6vuLmlJ0Cy47OqINdieaQ4KLILYpXoLr7AM/9DRB9RJcuSW5iDqalFMlApWC\n0vT+zguaNxuthqskp/k66FD0pFocPCkXHrNiTitm1nBF2bzG+2y0fqu2FsOQTWwBFNbra7NLZbhn\nyLCA2dH8xu1OJJUAM+t/d3E9h2I276Q7A2EtpRj0iHABcIR0XjX87KB+q4o64scuwVi5pJWB27HR\n9hpaKhGuZCKGCdfUilKpjLNn65HwJSWlODrunG+kkTdEWwzf0UUQA4Jqfrpy+hJO3veY57aZWT3y\nogozd92JHUk6Qiu1U3dw38owA8Jt3Aq5K5HZ7bnMN8WVeqq9R6ZJx6hL9IViIS2qtNEORTdq+quw\nVhcEuunpBj+LbYphGtq4rOzccq2bV0spxrxrGVl+XR/WvJHaNMa0tKKKnZiAGNnRcBsNl0O/GuU6\neexU7d9a0fzBq1FO73caHDZ63AwpJLgIYpuiRrgWf3xWGtPjJre0hlK+qN3nJjIahR1Jojw57Qyg\n7mMhc8cwpke5bJew6EZKUUHtXmTZlZq5qYYQTot/bWOmWXx0K6UI6Okvt4GnPkdxGwnrLqNFiytN\nJiKSRCEn7zPhkHdjBFObTCLJDftP+Q7oZgbKY3sgkpPtvwdjtXrMmX1Kp2JFcBWLRayv1buUDcNA\ncnTEOSf0cV7qdocEF0FsU6ITzWfGucnMyVEuVXCFd+1xhNZ2sH9oRCNrCFUIdeNKPZKQHe6FDZb1\nmW3pIfgSO+VhuLGJ7g35DSVlweX2k9JMT4ewYL6KeizVfO0YQ165hgmZJf17FLZuo9IN/ymPCJcw\nQ7Anpzfkb1UtnPeLcKkF8yOjSRhDmG7uNvQJEsQ2JZSI+toHhEfjGLt8j3Rf5pIiuNSUYmoD9SZb\nCKEUzkvmpx2Ynjal0r0o3eWXVvQQfHuffxUCFdfv5J40xjqc0+aFnlJsEOEawoL5Kp6dihUKWflz\nCkcD+vebX5cil8IIdOXCRUSTUopchBNO3eAGo8/Vwnm1U7EquJaVsT6psfYu7ghvhvcII4htDmMM\nsYlRrJ6b0x47cMeNWL+0iMVnztbuUwvntZTiWH8cobtOowiXFmHqTi2KiKWA9frny4pZxzdJTQl5\nCL7E1ARueu8bkFteQ3xqDIbZvevgRilF1YNrGC0hqjSaTaqN9YmFwNYX640k+XUYq/IxKCKJ7qTe\nzCDs8cvAciuOSOrW6wYjENDNT0+fPItyqaxFuEZJcHUFinARxDZGrf8BnNluU9ccQHxK7ixcdxXO\nCyF0wZUaEMFlqBGuurBgostF81UCIW20Cst6RLl8BmcHY2Ekd010VWwBej2YLLgopVhFi3AtrEBU\nvqvimtx1GooGwewS2NJ5GLPHYS6eBSvJeccNdSeqhCpdgdGN14TVMAwgGMFIMobxsfpaS6USzp45\np89RHNenLBDt0/ERxjm/FcA/Ani7ZVmf93i8COBbcMazCgC3W5bVwaRXgiD8UF2yAeDgnTeBGQyx\ntOIv5IpwFTN5KcJhhAIIxrZ57VYF1fwUvU4pVt83lgIr1AUNyyxXiprr78EUW4quCT4fGnUpUkqx\nTjAWQSAWRinjmIuKUhm55XWE4lHpOGEGQyDsfE7qJIYqwgxqg7m3InZyEsbiOcxcthMLrvKCk8dO\naynF0VT36gqHmY6OMM75AQDvA/DtBpstWpZ1pKNVEQTREuq8vMnD00jNOGmC2OSoc0VcqS2pdioG\nwkHkltT6rURX3M23BA1Tit4Rpm4gIgkIZtSiaEzYYLk1ub6rB12SjWhUw6W5zA+x4AKci5eVTN2H\nymsgfCgabHiciFAU9kj7s/n6QjgOe+ogpvkhPPL407W7Txw7ibzSKUA1XN2h06P9HIDXAmg0x2Ib\n7HEEsb0Zu3wPdjznCoAxJPemceium2uPmcEAouNyaqPaqainEwejYB4AYAYUw8hyvVi9W8anXjAD\nIib/MGnO873okmxAQ8FFKUUJvY5rSfq8AGhGskDVIHgE5clpx6NqO8wcrWIYmD4gj4ByIlyKyzyl\nFLtCR0eYZVk5AOCcN9oswjn/DIBpAPdalvWxTt6LIAh/GGM4/LoXg999i2f9TyydQna+fl2UubSE\nkT1p5BYHtH4LcKILRkD23yqXnMhXD1OKACCio3LxfCELlAr1rrIev79KIBIGMxiE7UjQcr6IcqEE\nMxTw8OEiweUmM7esXYiERhIQRgDMLkEYJkQs5TRMbIexVz5MH5SnJZw4dgq79sjF9JRS7A5N9xLO\n+TsAvBOOkK/WY/2uZVlfbvLUDwD4TOXf3+Sc32dZ1iMbWSxBEN74FVvHp8Ywf7TuHr0+64gBPaU4\nQBEuwPkBVAWXEZDC7gKs+ym9YBgiGHW6FCuwzFJ9FEoPU5peMIMhmIiisFKv3SqsZxENJXWn+dDw\nGp8CegNKZm4ZiV2yR1owEYc9tR8oFZ0JDAMwvHl6vyy4zpw8g3BYtp2govnu0FRwWZZ1D4B72n1h\ny7L+qvpvzvlXATwLQEPBlU4P2El/yKDvb+uRPbgLp775eO12aWkN6XQSVkbuvNoxnR6o728tE0Vh\nuf43jsRMBBNRLF2sb2MEApjowd+cD+zA+ukTtdtmbgWj09MwAgGsZi7BpcWQTMUR7oLYbfTdxVMJ\nSXDFAwwT6STOB2WxkEzFBmofaJdwaQ+edN3OL64iqKSAU1MjSE91t56p3595Op3ERHoc87MLAIBi\nsYQfP31c2mb/gV19X+cg0I04qFarxTk/BCcK9hbOeQDAzQD+qdkLzc76uDMTW550Oknf3xakFJFr\nThbPzGJ2dhXLiidX3jAH6vtjJblAdXVpFSIHuONJNlhv/mYRhOEqnhflMhaOH4NI7YKRzUsnzJW1\nAlDc2BqaHXtMiVZcPDMHO5nA2rI8aDlXtAdqH2gXGwZgMKCSfs0urWHutOyvVWLdPU62ynlz3/Te\nmuACgKLi0WYjuCXWudVoV4R2FA/lnL+Sc/51AHcC+Ajn/AuV+z/EOb/JsqynAJzmnD8Ixxri/1mW\n9XAn70UQROfUOhUr5JbWUC4UB7toHvDoVPQYx9KrdBAzIOLj0l1GdsUZ/bLJXYqAvxeXanw67EXz\nRsBEVDkOlk9dkG6rTQiDwsyBy3wfM0wDyZEBqvHsI50WzX8egOa9ZVnWR13//vUNrIsgiC5Q7VR0\nF84vnbwI21W/Y4aDCMa2UWdVC6heXKxchOhlh6L6/olxiNyKZIhpLF/c9C5FQBcJ1XmKmi3EkAsu\nwKnjyi7Uj5XcghzVCQ6o4JpuILhGRkdojmKXoE+RIAYc1QB13jol3Y6PjwyOB1cVtWusXAKze+Qy\n7wVjsEd3yvYU5aJjUeFmE37I/KwhbK1ongSX2qmoMowRrjHy4OoaJLgIYsBRR/wsPH1GfnxiAFu+\n1ZSiXdz8dF4o6lgGNKLHXYqAv+BSI1zDnlIEWhBc8cEUXNMH9vk+RnMUuwcJLoIYcFTBlVuU0ySx\nQRRczIBwRe2YELLjPLAp6TyRTEMY3kJGMGNTHMlbFVyUUvQelVWDsYFLvVcZTY36mpuSy3z3IMFF\nEAOOmlJUiU8OouBiWpSLFfPyNptRl2IYsEd3eD+2SR5OracUh9uHC/AeBl8lGI+ADXAt0/R+7ygX\nCa7uMbh7D0EQAPRORZX4+AAKLkCv4yopgmsT0nkAgEgCdsSjC3QTImwAEEqoXYoZCCEopehBKBGF\nGfYWnoOaTqziV8dFKcXuQYKLIAYcr5mKbgayhguAMJQIl9jEonl1LSNTTgrRzSZFS8xwEEag/rfa\nxTLKhSINr/aAMeZbxxVK6HMUBwm/TkUqmu8eJLgIYgholFYcyBouQC+cV9nM9JAZqI/3qSACm1MP\nxBjT7AwKa1k9pUgRLgD+hfOD2qFYhSJcvYcEF0EMAWrhfBUzFEQoPqBX7s0GCm9WSrGCiI7ATkxA\nMAMiGNHMUXuJVse1mqGUog9Rn8L54ICnFP0iXKlxElzdgo4wghgC/ARXJJUYPA+uCqr5qcZmF0Az\nBpGchEhObu77QhdcueV1QNRdwphp+A5AHzZik97R4EGPcKXGRpEaG8XS4rJ2P9Ed6AgjiCHAL6UY\nSQ3wyI5mEa5NrOHqN5rgcrmpA5ROdDOsKUXAu1MxNdbES45oGRJcBDEE+HUqRsYGbIaiGzMgOb27\nEWAABjOy54XaqZhVvNgMKpivEZ0Y8dw1Br1LEQCmD05Ltw3TQCIZ79NqBg8SXAQxBPh1Kg50hIsZ\n/lEsY3NMR7cKaoedOiPQDJIHVxUzGEB4VD8uggPepQjoEa7RFM1R7Cb0SRLEkOCVVhxowQX4dypu\ncsF8v2kW4TKDw/V5NMPLcX4YIlxqp+KYj/s80RkkuAhiSPAqnB/olCIaFM4P2VW7V5eiG4Nc5iW8\n6rgGvUsRAK669jDSO+pNHS988U19XM3gQYl7ghgSPAVXarAFl2/h/BAVzAPNC76paF4mlpYFVyAW\nHoouzlAoiD/95EfxuX/+T6SnJnDX61/Z7yUNFHSUEcSQoKYUzXAQgWioT6vZJHwiXJrr+4DTLDpD\nLvMysQn5WBmGdGKVnbt34Od+6W39XsZAMlxnHYIYYuJTYwiP1juOxg7sHlgPriqCIlwAgEA42HA4\nNZmeyozsSyMQrU8CGDu4u4+rIQYFOsoIYkgwTAPXvOmlOPGNRxEIh3Dgjuf2e0m9x7eGa7gEF+B0\n2ZUXip6PUYRLxgwFce3P3Ikz33kC4ZE4pm+7rt9LIgYAOsoIYohI7p7Es958R7+XsXn4RbiGLKUI\nOJ2Kqh1EFarh0hnZk8ZVb3hJv5dBDBDDd9YhCGJ4YGbF5FRhCCNcjQrnKaVIEL2HBBdBEIMLY55p\nRTFkthBAY8FFES6C6D3Dd9YhCGK48EorDpnxKdBEcFENF0H0nI6OMs65CeAeAAcBmAA+aFnWd5Rt\n3gLgvQDKAD5pWdZfb3CtBEEQbSPMoJ5UpJSiBBmfEkTv6TTC9VYAa5ZlvQjAOwF8zP0g5zwG4LcB\nHAHwEgDv45zTjACCIDYfrwgXpRQlKKVIEL2n07PO3wF4f+XfswDGlcdvAvCgZVlrlmXlAHwbwM0d\nvhdBEETneFlDDGVKMeb7GAkugug9HR1llmWV4aQKAeBXAPyDsslOOEKsyiyAXZ28F0EQxEZQzU8F\n4BTTDxmNU4okuAii1zQ9yjjn74CTNhQAWOX/v2tZ1pc55+8BcB2Au5q8zPCd3QiC2BqoES7DHErB\nFYxHfB+jCBdB9J6mR5llWffAKZCXqAixVwG4uxLxcnMOckRrD4D7m71XOj3gg3QHHPr+ti+D/N0J\nIbCyegHlXBYAEEmNIT5gf2+r318wGkYxm9fun9wxitSAfSbbhUE+9giZTrsUDwB4F4AXW5blNSvi\nAQCf5JyPALABvBBOx2JDZme9XZCJrU86naTvb5syFN/dyG4wcxEwDGRCY8gM0N/bzvcXiEc8Bdfy\nWgHFAfpMtgtDcewNMO2K5U7jyO+AUyj/ec55Nc34MgAfAPANy7Ie4Jz/OoAvwRFcH7Ysi/YqgiD6\ngxmAGEn3exV9J5SIIju3rN1vBoeviYAgNptOi+Z/E8Bvejz0Udc29wK4t8N1EQRBEF3Gr3DeJB8u\ngug5w2dGQxAEMaT4CS6apUgQvYcEF0EQxJDg5cXFTAOGST8FBNFr6CgjCIIYErwiXGQJQRCbAwku\ngiCIIcFLcFE6kSA2BxJcBEEQQ4JnhItc5gliUyDBRRAEMSRQSpEg+gcJLoIgiCEhGKeUIkH0CxJc\nBEEQQ4JhGgjG5JmKlFIkiM2BBBdBEMQQoaYVyfSUIDYHElwEQRBDRFARXJRSJIjNgQQXQRDEEKFF\nuEhwEcSmQIKLIAhiiFAFF0W4CGJzIMFFEAQxRMQmRqXbkdF4n1ZCEMMFCS6CIIghIn3NfsSnxgAA\n0YlRTF17sM8rIojhgGLJBEEQQ0QwGsYN774buaU1hEfjVMNFEJsEHWkEQRBDhhEwEZscbb4hQRBd\ng1KKBEEQBEEQPYYEF0EQBEEQRI8hwUUQBEEQBNFjSHARBEEQBEH0GBJcBEEQBEEQPYYEF0EQBEEQ\nRI/pyBaCc24CuAfAQQAmgA9alvUdZZsigG8BYAAEgNstyxIbWy5BEARBEMT2o1MfrrcCWLMs60Wc\n86sA/A2Am5RtFi3LOrKh1REEQRAEQQwAnQquvwPwD5V/zwIY99iGdfjaBEEQBEEQA0VHgsuyrDKA\ncuXmr6AuvtxEOOefATAN4F7Lsj7W2RIJgiAIgiC2N00FF+f8HQDeCacOq1qP9buWZX2Zc/4eANcB\nuMvjqR8A8JnKv7/JOb/PsqxHurNsgiAIgiCI7QMTorM69ooQez2Auy3LKjbZ9qMAfmhZ1qc7ejOC\nIAiCIIhtTEe2EJzzAwDeBeB1XmKLc36Ic/73lX8HANwM4MmNLJQgCIIgCGK70mnR/DvgFMp/nnNe\nTTO+DE4a8RuWZT3AOT/NOX8QTq3Xv1mW9XBXVkwQBEEQBLHN6DilSBAEQRAEQbQGOc0TBEEQBEH0\nGBJcBEEQBEEQPYYEF0EQBEEQRI/ptGi+q3DO/wTA8wHYAH6FCuy3D5zzPwJwC5yZmn9oWda/9HlJ\nRJtwziMAngDwe5Zl/W2/10O0Duf8LQB+FUARwO9YlvWffV4S0QKc8ziAvwUwBiAE59j7Un9XRTSD\nc34NgH8F8CeWZf1vzvleOJN3DADnAby1kU1W3yNcnPMXA7jcsqwXwjFY/fM+L4loEc75bQCuqnx3\nrwDwp/1dEdEhvw1gvt+LINqDcz4O4HcAvBDAqwHc3d8VEW3wNgBHK/OG3wDgz/q7HKIZnPMYHH3y\nFdfdvwfg45Zl3QrgxwB+ttFr9F1wAbgdjmKEZVlHAaQ454n+LolokfvgnCwAYAlArGITQmwTOOcc\nwJUA/qPfayHa5qUAvmxZVsayrIuWZb273wsiWmYOwETl3+NwZhITW5scnMDCedd9twH4XOXfn4Nz\nTPqyFQTXTsg721zlPmKLY1mWsCwrW7n5TgCftyyLfEa2F38M4P2gYfPbkRkAcc75v3HO7+OcH+n3\ngojWsCzr/wKY5pw/DeAbAD7Y3xURzbAsy7YsK6/cHXelEC8B2NXoNbaC4FKhE/82g3N+N4C3A/jF\nfq+FaB3O+VsBfMeyrJOVu+jY214wONGRn4Bz/P1Nf5dDtEql9u6kZVlXwMny/EWfl0RsnKbnz60g\nuM5BjmjthhyyI7YwnPM7AfwPAC+3LGu13+sh2uJVAO7mnN8PJ0L5WxQl2VZchCOYhWVZxwCscs4n\n+70ooiVuBvBFALAs6/sAdlM5xrZklXMervx7Dxw948tWEFxfAvCTAMA5vx7AWcuy1vu7JKIVOOcj\nAP4IwKsty1ru93qI9rAs642WZd1kWdYLAHwKwO9blvW1fq+LaJkvATjCOWec8wk46Y25fi+KaIln\n4HTmg3M+DWCVyjG2JV8B8PrKv18P4AuNNu67LYRlWfdzzr/HOf8vOHMX39PvNREt89NwCj//0TVT\n82csyzrT32URxOBjWdY5zvlnAXwXzrFHKf3tw18C+GvO+TfgWOq8q7/LIZpRCQj9MYBpAEXO+U8C\neAuAT3PO3wXgJIBPN3oNmqVIEARBEATRY7ZCSpEgCIIgCGKgIcFFEARBEATRY0hwEQRBEARB9BgS\nXARBEARBED2GBBdBEARBEESPIcFFEARBEATRY0hwEQRBEARB9BgSXARBEARBED2m707zBEEQvYRz\nfgDAtwA837Ks0/1eD0EQwwlFuAiCGHReA2AMzrBngiCIvkCCiyCIQecWAA9YllXo90IIghheSHAR\nBDHo3ALgm/1eBEEQww0NryYIYuDgnP8UgLfDSSU+D8C3AawB+JxlWZ/o59oIghhOSHARBDGwcM7/\nO4A/AzBKKUWCIPoJpRQJghhkXgLgIRJbBEH0GxJcBEEMMrcBuK/fiyAIgiDBRRDEQMI5vwrADpDg\nIghiC0CCiyCIQeUIgCKA7wAA53yUc763v0siCGJYIcFFEMSgcguAxyzLylRuvxeOACMIgth0SHAR\nBDGomABOAADn/LkAMpZlkds8QRB9gWwhCIIYSDjn1wL4CwD3A7hoWdYf93lJBEEMMSS4CIIgCIIg\negylFAmCIAiCIHoMCS6CIAiCIIgeQ4KLIAiCIAiix5DgIgiCIAiC6DEkuAiCIAiCIHoMCS6CIAiC\nIIgeQ4KLIAiCIAiix5DgIgiCIAiC6DEkuAiCIAiCIHoMCS6CIAiCIIge8/8BQvcRE3rcXR0AAAAA\nSUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75a6d5350>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"b = 1\n",
"arange = np.linspace(0,b,3)\n",
"\n",
"\n",
"with sns.cubehelix_palette(3):\n",
" for aval in arange: \n",
" path = EM(1.3,sigma=1, T=10, a=aval)\n",
" pl.plot(t,path,linewidth=4)\n",
" \n",
"pl.title('With $a=0,0.5,1$',fontsize=20)\n",
"pl.xlabel('$t$',fontsize=20)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7ff758be2290>"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAl4AAAFkCAYAAADxKDXQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd8JGd9+PHPbFHvXafrbe58d/b5XM6+s33uxtiOIbhh\nemyKIRACJLQEQvtBnEAoCRAwodkQG0wJ2Ma9nPudrxeNyqn3vkXbZ35/zGq1q1VfabWSvu/XS6/V\nPDPzzGhOt/ruU76PYhgGQgghhBBi/lkW+gaEEEIIIZYLCbyEEEIIIZJEAi8hhBBCiCSRwEsIIYQQ\nIkkk8BJCCCGESBIJvIQQQgghkkQCLyGEEEKIJJHASwghhBAiSSTwEkJEqKr6U1VVQ6qqrp7iuJ+p\nqqqrqlqWrHsTQoilwLbQNyCESIyqqvuBvcA2TdNOj7P/e8BHgC9qmvaVcfZfC/wFeAi4F/gT0D3m\nmM8Dv9Q0rTlcZIS/Fj1VVVXg/wGN4aIS4B80Teue8KTk1PV14I9ANeAD1gM3Ab/QNK19pvWF68wC\nXtE07ZzZnC+ESJy0eAmx+D2CGQRdN8H+a8P7r51i/yOaph3SNO13mqZ5R3aqqroW+Aqwdq5uOFWo\nqpoHPAX8VtO0T2qa9knMQOdpVVVn9MF0LusK+zTwMtAPuIEjgDWBoOt84Hlg+2zOF0LMDQm8hFj8\nHgUUxgm8VFVdA2wCTgIXqqqaO87512EGXn+ZoP4LWSKtW+P4NGAHHowq+yGgAnctYF0AzcCPgD8A\n/w6cq2na12ZaiaqqW1RV/TPwYSA4i/sQQswh6WoUYpHTNO2YqqptwGWqqqZrmuaL2j0SVH0buA+4\nErP7CgBVVSuAbcDrmqb1qKr6M+DdwFpN05pVVX0W2Beu4zlVVQ1gXVT9iqqqnwXeD1QBbcD3NE37\nj3n6cefaLcBrmqbpIwWapg2oqloN3Ar89wLVBXBG07QPzfCcOJqmVQM3gjmGDzOQFkIsEGnxEmJp\neAzIAC4bU34d5nitBzDHCY1tFbsm/Ppo+HXs2K0vAL8Jf/9FzOCiJ2r/V4CrgK8DfwvowL+rqnrV\nbH+QZFFVNQezNbB5nN3twHkLUZcQYmmTFi8hloZHgbsxA6snAVRVtQBXAI9qmuZTVfVVRgOtESMt\nYo8yDk3T9quqemV483lN014I1w1m92aVpmlXjxyvquox4BXgDuDp6dx4uP57gHqgEHgB+KCmaWOD\nyLm2JvzqGGefG8hTVdWuaVogyXWNSFdV9dNAKWZAuwH4jKZptTOoQwiRYiTwEmJpeArwYwZSnwqX\nXQgUhPeNHPNlVVXXa5p2Jlx2FdCjadrBWVzTAL47puxY+HXFdCpQVfUuzNay8zRNa1FVdQVQA2iT\nnPMTYBfTG3emhI/7+EjQGCUv/Oof5zx3+LWA2Ba+icxlXSPKgPs1TWsDUFX1HcB+VVXPns0sSSFE\napDAS4glQNM0l6qqLwJXqKq6Ijzz7U2YQcdI4PUkZtfgdcAPVFU9GygHfp7ApevH3Icn3BqWOdWJ\nqqqeA/wAeI+maS3h89tVVR0Anp3oPE3TZjNQfTyh8Ot4AZw9/GpdgLpGbNY0Lbq+X2MOtv8c8PEZ\n1iWESBEyxkuIpWOku3BkHNfVQI2maa3h7YPAIKNpJUbSSDyWwDXHa+GZrq8BTsz8YQCEE7dWAc8l\nUO90Tdb6lB1+dS5AXQCMCboID9rvAW6eST1CiNQigZcQS8dIWomrw4O9dwNPjOwM/+F+htEB+Ndg\nttQ8nuT7RFXVfMwA8XFN00JRu64I39PYbsH50IUZeBaOsy8bGNQ0zT3OvvmuC1VVX1BVdbxnYMVs\npRRCLFLS1SjEEqFpWrWqqg2Y6R/2YP6RHjvA/Sngraqqnhc+5hVN04aSe6cAbMS8v1fHlF8GHNE0\nzaGq6lpN0xrHnqiq6o+Ac5nZGK9Papq2P3qHpmnDqqoeBlZNcH9HplH/nNcVthMYbxB9CaNZ8YUQ\ni5AEXkIsLY9hzhB8F2ayzLFjpZ7EDEY+gtkSM+5sxjFGWqQy5ugeAUaCvUj6BVVV0zEH+4+kr/gk\n8NGxJ2qa9oE5vI9HgL+JLlBVdQNmAPX1MeWbgaYxedJmW9dGoDV6hYAx/gLE5PBSVfVcIB345Qzv\nSwiRQqSrUYilZaS78TbMpKgx44o0TavHbDG5k0nSSIzREK7zn1RV/fvweoQJ0TStDjiMuf7gSOqL\n72EGg2dUVS0G+hK9zjT8AMgOzxgc8VHMTP/3jRSoqno55vI/989BXZdiztr8/SR13Qt8W1XVtKiy\njwMvAf82w/uKlhk+b8rJD0KI+SEtXkIsLc8AXsyWkScnOOZJzJxfrZqmHR9n/9guvN9iBnJXYy5/\n89oU9zDdBbRvxQwuqjDfi74Zvv+7MBOOfnYadSRE07TOcPDyNVVVd2GmhSgE3qRpWvTyOl2YA9sn\nTIQ6w7q6gbpJ6jqoqup/A/erqjocrus48P4xucCmvC9VVUsxW8mqgLPCxY2qqp4A7tM07dcTnSuE\nmHuKYcx+CTZVVe8FLsEcq/ENTdN+H7WvAbMbQcd8E36Hpmkdid2uEEIsHFVVv6Bp2pcX+j7GStX7\nEkLEm3WLV/iT3Vmapu1RVbUIs9sguuncwPyk50nsFoUQImWkL/QNTCBV70sIMUYiY7yex+wqADM3\nUJaqqkrUfiX8JYQQi174w+YbC30fY6XqfQkhxjfrFq9wcr+R1qy7MdeDG9tv+UNVVdcB+zVN+9xs\nryWEEAtJVVUrcI2maZ9f6HuJlqr3JYSYWEJjvABUVb0Z+AxwbfQMKlVV34k5Jbof+CPwU03TfpfQ\nxYQQQgghFrFEB9dfB3wJuG6yJIyqqt4DlGma9qWJjjEMw1AU6ZkUQgghxKIwq6AlkcH1eZi5Zq4a\nG3SF9z0E3BSe+ryP0aSI41IUhZ6eGS1lJhJUWporzzzJ5Jknnzzz5JNnnnzyzJOvtDR3Vuclksfr\ndqAYeCg8qN7AzMFzXNO0P6qq+gjwajgHzWFN0x5O4FpCCCGEEIteIoPrfwz8eJL938PMRC2EEEII\nIZAlg4QQQgghkkYCLyGEEEKIJJHASwghhBAiSSTwEkIIIYRIEgm8hBBCCCGSRAIvIYQQQogkkcBL\nCCGEECJJJPASQgghhEgSCbyEEEIIIZJEAi8hhBBCiCSRwEsIIYQQIkkk8BJCCCGESBIJvIQQQggh\nkkQCLyGEEEKIJJHASwghhBAiSSTwEkIIIYRIEgm8hBBCCCGSRAIvIYQQQogkkcBLCCGEECJJJPAS\nQgghhEgSCbyEEEIIIZJEAi8hhBBCiCSRwEsIIYQQIkkk8BJCCCGESBIJvIQQQgghkkQCLyGEEEKI\nJJHASwghhBAiSSTwEkIIIYRIEgm8hBBCCCGSRAIvIYQQQogkkcBLCCGEECJJJPASQgghhEgSCbyE\nEEIIIZJEAi8hhBBCiCSRwEsIIYQQIkkk8BJCCCGESBIJvIQQQgghkkQCLyGEEEKIafL7A/zuf/9v\n1ufbErm4qqr3ApcAVuAbmqb9Pmrf1cDXgCDwmKZpX03kWkIIIYQQC+1fv/gtnntyPx/86Dtmdf6s\nW7xUVb0cOEvTtD3A9cC3xxzyHeCtmIHZtaqqbpnttYQQQgghFtqJI6d47sn9CdWRSFfj88Ct4e8H\ngSxVVRUAVVXXAX2aprVrmmYAjwJXJXSnQgghhBAL6Kc/vD/hOmbd1RgOqDzhzbuBR8NlABVAT9Th\n3cD62V5LCCGEEGIhHT54jCMHjyVcT0JjvABUVb0ZeB9w7SSHKdOpq7Q0N9HbETMkzzz55Jknnzzz\n5JNnnnzyzOePYRg8cN+v56SuRAfXXwd8FrhO0zRn1K52oDJquypcNqmeHudUh4g5VFqaK888yeSZ\nJ5888+STZ5588szn14FX3uDwweNzUlcig+vzgHuBGzVNG4rep2laE5CrqupqVVVtwI3AEwndqRBC\nCCFEkhmGwU9/EDu2a/fe82ddXyItXrcDxcBD4UH1BvAMcFzTtD8C9wD/Gy7/taZpdQlcSwghhBAi\n6V7Z/zraqdqYsvd+6J2zri+RwfU/Bn48yf4XgT2zrV8IIYQQYiHpus7Pf/hATNneyy9i89aNs65T\nMtcLIYQQQozjxWdfoa7mTEzZez44u8SpIyTwEkIIIYQYIxQK8fP/jm3tuvyaS9mwaV1C9UrgJYQQ\nQggxxvNPvkjjmebItsVi4d0fuDPheiXwEkIIIYSIEgqG+PmPfhVTduV1+1izblXCdUvgJYQQQggR\n5am/PEdrc1tk22K18K733zEndUvgJYQQQggRFgwG+eWPY7PUX/vmK1m5umpO6pfASwghhBAi7PE/\nPUVHW2dk22q18s6756a1CyTwEkIIIYQAwO8PcP99D8aUXX/zNVRWVczZNSTwEkIIIYQAHv3D43R3\n9US27XYb7/ib2+f0GhJ4CSGEEGLZ83l9/Op/Hoopu/Gvr6esonROryOBlxBCCCGWvT89/Bh9vf2R\n7bT0NN7+vlvn/DoSeAkhhBBiWfN4vPz657+NKbv51hsoLima82tJ4CWEEEKIZe0PD/6Zwf7ByHZG\nZgZ3vOeWcY/1Odyc/t0Ls76WbdZnCiGEEEIsci6Xmwd/+XBM2VvvuImCwvxxjz/1m+cYauocd990\nSIuXEEIIIZatn/3wfpxDzsh2dnYWt73zr8c91tXZn1DQBRJ4CSGEEGKZqqmu448PPRJTdss730pe\nfu64x3ceqU34mhJ4CSGEEGLZ0XWd73z9++i6HimrrCrn9neN39qlh3S6jtYlfF0JvIQQQgix7Dzy\n+8epPlkTU/bRf/gQ6Rnp4x7fX9dKwO1N+LoSeAkhhBBiWRnoH+Qn//XzmLJLr9jD7ksumPCczsOJ\ndzOCBF5CCCGEWGZ+9N2f4nS4ItsZmRl8+JPvn/D4wLCXPq15Tq4tgZcQQgghlo1jh07wxJ+fjil7\nzwfunHRpoO7jZzBCo2PBMovyZn19CbyEEEIIsSwEg0G+843vx5St27CGv377X0163tjZjOU7N876\nHiTwEkIIIcSy8PCv/kjjmdguw7/77Iex2SbOJ+/uHsDZ1jtaoEDFzk2zvgcJvIQQQgix5HV1dvOL\nH/0qpuy6m65mx85tk543trWrYG0lGQU5s74PCbyEEEIIseR9/5s/xuv1RbZz83L4wMfeN+k5hq7T\ndbQ+pqzi3Nm3doEEXkIIIYRY4l598QAvPvtKTNndf/veCddjHNFf347fORzZtqbZKT1rbUL3IoGX\nEEIIIZYsr9fL9+79YUzZ1h0qb37LtVOe2zWmm7F021qsafaE7kcCLyGEEEIsWb/6n9/Q2d4V2bZY\nLHz8Mx/BYpk8BAp4fPScboopS2RQfeT6CdcghBBCCJGCmhtbePAXD8eUveX2G9morp/y3J6TDRjB\nUGQ7ozCX/DUVCd+TBF5CCCGEWHIMw+C7//oDgsFgpKy4pIj3fvCd0zp/7BJB5edsRLEoCd+XBF5C\nCCGEWHKeefx5Dh84FlN2zyfuJjsna8pzh3uHcLR0x5RVJJA0NZoEXkIIIYRYUlwuNz/4j/tiys7b\nfS6XX3PptM4fm7srf01FQssERZPASwghhBBLyve/+WMG+gYj23a7jY/+44dQlKm7Cg1dp+tIXUxZ\norm7oqVM4GUYxkLfghBCCCEWuScfeYbH//RUTNkd772VVWuqpnX+QEMHPoc7sm2x2yjdtjb2oARi\nlpQJvIaqj4PXudC3IYQQQohFqqWxlW+PWQR79dqVvP09t0y7jrjcXWetxZaeNlrg92DpbZz1PaZM\n4KUH/FgGO0HXF/pWhBBCCLHI+Lw+vvzZb+D1eCNlaelp/NPXP016Rvq06gh6/fScaowpi8ndZRhY\nhjpRgv5Z32fKBF4AiqGD3z31gUIIIYQQUX747Z9wprYxpuwjn/wAGzatm3YdPaca0QOjubvS87Mp\nWFc5ekDQn1DQBWBL5GRVVbcDfwC+pWna98fsawCaAR0wgHdomtYxVZ2K142RkZvIbQkhhBBiGXn+\nqRf5v98+GlN2+TWXcsNbr5tRPVPl7lJ8iTcOzTrwUlU1C/gu8NQEhxjAmzRN88ykXsXnNgfaT2Pm\ngRBCCCGWt/bWTr75le/GlK1YWcknPv/Rac1iHOHpdzDU1BlTNnY2o+Jzzf5GwxLpavQC1wMTtWIp\n4a8ZUfQgBH0J3JYQQgghloNAIMBXP/evuN3DkTKbzcY/f/3T00qUGq1zTAqJvFVlZBXnjxboIfDP\nqC1pXLMOvDRN0zVNmypC+qGqqvtVVf1/M6lb8co4LyGEEEJM7r7//DnaqdjuwQ9+/G/YvHVmWeYN\n3YibzRjf2uWeeWvSOOZzcP0/A58A9gE7VFX96+meOBdNeUIIIYRYul5+4TV++8AfYsr27LuIt95+\n04zrGmrqxDs4GntYbFbKto9ZSHsOxndBgoPrJ6Np2v0j36uq+iiwA/jddM5VAl6KCzOw2OzzdXsi\nrLRUJjIkmzzz5JNnnnzyzJNvOT3zzvZu/v3L34kpq6wq51+/+3nyC2a+tE/jY6/EbFft3EjlquLI\ntmEYDHYPMxep3ucq8IppfVNVNQ94CLhJ07QAZqvXbyarwJqRScg72nfa39aFkZU/yRkiUaWlufT0\nSNLaZJJnnnzyzJNPnnnyLadnHgqG+MSHvsjQoCNSZrFa+OxXPoU/oMz4OYT8AVreiO1mLNy6NrYe\nvwdrKBjZNJTZdxgmMqtxF/BNYA0QUFX1bcD/AQ2apv1RVdVHgFdVVR0GDmua9vBk9dnzCmICL3xu\nkMBLCCGEEFF+9t8PcOLoqZiyuz78bradvXVW9XUerSPkD0S203KzKNywIuaYsWkkjPTsWV0LEgi8\nNE07BFwxyf7vAd+bbn323Hy83aMTJCWthBBCCCGiHXz1EL/+WWwH2gV7zuO2d017GHkMQ9dpfflE\nTFnFzk0oltgWLcU7Zux5AoFXymSut2VlY1iskW0zi33i0zaFEEIIsfj19fbz9S98y2yUCSsuLeIz\nX/oEFsvswpne6mY8faNdlorVQtXuMS1noSBKVJorg8RavFIm8FIUJe4HmYsMsUIIIYRY3Pw+P1/9\n3L0M9g9GyiwWC5//6j9QUDj7YUktLx2P2S4/ewPpeWNjkTGtXfYMsM5+iHzKBF5AXNOdpJUQQggh\nlrdQKMTX/unfOHYotkvwXXffwTnn7Zh1vUPNXThaumPKVu7ZHnfc2NyiibR2QYoFXkZ6dsxUTSXo\nh2BgwuOFEEIIsXQZhsG3v/5fvPhsbLqHneefzTvuuj2hulvGjO0q2riSnPKiMTegg39M4JWRk9B1\nUyrwwmKFtMyYImn1EkIIIZann3z/Fzz6hydiylavW8UXvvEZrFbrBGdNbbjPQe/pxpiyVXvHaT3z\ne1CixpQZFivY0md9XUi1wIv4JjwZ5yWEEEIsP7994A/8+qexMxjLyku59z+/MqskqdFaXz5OdBdb\nTkURBesr446L72bMSTjbQgoGXmOa8HzDZlOfEEIIIZaFJx95hh/8x30xZXn5efzrf32Z0vKShOr2\nuz10Ho5NmLpq7w6UcQKqsb1uRkZi47sgBQMvbGkYUbMFFAwz+BJCCCHEkvfqiwe498vfjinLyMzg\n69/9F1avXZVw/e2vV6MHQ5Ht9PxsSseuywgQ9KOERseZGwBpSzHwUpS4Vi/pbhRCCCGWvhNHTvHl\nT38DPTTa02Wz2fjyv/8TW7ZtTrj+UCBI2+uxWe9XXrQNizU+HIpLmpqWBbPMFxYt9QIvxhnn5XWB\nMRdLUwohhBAiFZ2pa+Tzf/8lfL7RZKWKovC5r36K83bvnJNrdB2tI+D2Rrat6XYqz1PHPTZumaAE\nZzOOSMnAi/QsjKh1txU9CEH/At6QEEIIIeZLR1snn/nbL+ByxgY7f/fpe9h39SVzcg1DN2h5KTaF\nxIrzt2DLSIs/WA+BP3aYU6L5u0akZuClWCA9K7ZI0koIIYQQS05/3wCf/tt/pq+3P6b8vR96Bzfd\n8uY5u06f1oynbyiyrVgUqi7aNv7BvmGih9obVjvYxgnQZiE1Ay/iZzeOndIphBBCiMXN7Rrmsx/7\nF9paOmLK33Lbjbzzrjvm9Fpjlwcq27GBjPzxW7HiZzPOTTcjpHLgNXbKZsBjNv0JIYQQYtHzDHv4\n509+hTqtPqb8yuv28ZFPfWDc9A6zNdTSzVBzV0zZqr3xywMBYBjx47vmqJsRUjjwwmrHiGrWU5DZ\njUIIIcRS0NvTx8ff/xmOvhHbCnXBxbv4x3/5OJY5mD0YrfXl2OsUbqgip6J4/IMDPpSohh5DsZgz\nGudI6gZejJNMdezUTiGEEEIsKvU1Z/jb934yrqVr63aVL977Oex2+5xez9PvoOdUU0zZuMsDhcWN\nKU/PSjhbfbTUDrwyxi4fNCxpJYQQQohF6vWX3+Dv7v40PV29MeUb1Q187dtfJDMzY86v2frKyZjY\nIbu8iMINKyY8Pr6bce7GdwHYpj5kAdkzMRQLSnjJIMUIQcAbt5C2EEIIIVLbnx5+jO/e+4OY5KgA\nF116Af/0tX8kM2vu/7YHhr10HKqJKVu1d/vE48dCQZSAN6ZoLsd3QaoHXoqCkZ6N4nWOFnldGBJ4\nCSGEEIuCruv8+Hs/46Ff/i5u31tuu5EPf/L9WK3Webl22+un0QPByHZaXhZl4y0PFBbX2mVPB+vc\nhkqpHXgBZORAdODlc2NQuoA3JIQQQojp8Hl9fP0L32T/My/HlCuKwj2fuJu3vf3mebt2KBCk7bVx\nlgeyTRzkxaWRmONuRlgEgZeRno0BkURmStAHoQBY53bwnRBCCCHmzkD/IP/8ia9w+oQWU56Rkc7n\nvvoP7L38onm9ftex+rjlgVacv2XiEwwDfPOTrT5aSg+uB8BiBXvsYDtJpiqEEEKkrqaGFj76vk/G\nBV2FxQV860ffmPegy9ANWsckTK08Tx1/eaAR/uHImHIAY5z4Yy6kfuBFfMZYWT5ICCGESE1HDh7j\nY3/zKTraYhOWrl2/mv/62bdQz9o07/fQV9PCcG/s8kArL55geaCRY8ZLmjqHaSRGpHxXI4R/eGfU\n1FP/MBi6uaajEEIIIRZcKBTi4V//kZ/85y8IBoMx+3ZduJMv3vtZcnLmvutuLEPXaXzmjZiy0u3r\nyciffLzW2N60+RjfBYsk8MKWjmGxoejmP6RiGODzwNhlhYQQQgiRdM2NLdz7pW9z+rgWt+/6m6/l\n45/9MDZbckKOziN1uDpjF9yecHmgEUE/Ssgf2TTATJw6DxZH4KUoGBnZKMNRzYY+V/x6jkIIIYRI\nmlAwxEP3/56f/+gBAv5A3P67PvJu3v7eW+d03cXJBH0BGp46GFNWtmM9uZUlk54XtyRhWpY5xnwe\nLI7Ai3CTX0zg5cYwjHnpfxVCCCHE5Brrm7j3S99GO1Ubty8nN5tPfP6j7Lv6kqTeU8uLx/C7PJFt\ni83K+msumPI8xTs2jcT8NewsmsCLtCwMFBSzARAlFICgH+zpC3xjQgghxPIRDAZ58OcP88v7fk0g\nEIzbv+ey3Xz8cx+huKQoqfflHXLRMmYm48o928komGKslq6D3xNTNJ89aosn8LJYzP7WqOZAxesy\ns8oKIYQQYt7V1zbwb1/6NrXV9XH7cvNz+eg/fJArr9uXtK7FaGeePIgeDEW27TmZrL707KlP9Lkj\njToAhtUO1knSTiRo8QRemE1/0f2wiseBkVMk3Y1CCCHEPAoGg/zqp7/hgZ88GDdjEeDSK/bwsc/c\nQ1Fx4QLcHThae+g+FhsMrrvqPGzpUwdQFo8jZtvIyJnXuGJxBV6ZuRiO7tEs9iE/BH3zkuBMCCGE\nEHDqeDXf+fr3qas5E7cvvyCPj336HvZdfcmCtHIBGIZB3V9eiynLLi+i8txp5AvTgzB2maCMvLm8\nvTiLKvDCYoP0nJiHpHgcGBJ4CSGEEHPq2OET3H/fg7zx2uFx919+zaV89B8/REFhfpLvLFbPyUYc\nzbHJWje+aTeKZepcn4rHSXS4aFjT5n3s+OIKvAA9Mw/r2MArt1S6G4UQQogEGYbB4QNHuf++/+Xo\noRPjHlNQVMDfffoeLrtqb5LvLl4oEOTME6/HlBWrqyncsGJa5ytjuxkz8+Y9nlh0gRcZ2RiKJbKe\nkqKHzEUtJaeXEEIIMSuGYfD6Swe5/38e5NSx6gmPu+pN+/jIpz5AfsHCtnKNaHv1FN7BqMYYi8KG\n66ZOHwGYSVMD3pgiI3N+uxlhMQZeigUjIxfFE5XTyzMkyVSFECnL5/XhcDhxDJlfzpFXhxOv10co\nGCQYDBEMBgkGRr8PjZQFQ4SCQXTDwG6zYU+zY7fbzdc0O3a7bXTbbseeZiPNbicrO4vc/Fxyc3PI\nycshNy+H3Lxc0tLsC/1IRIrQdZ2XX3iNB37yIDWn6yY87uxd23nX3Xew68KdSby7yfldHppeOBJT\ntuLCrWSVFEzr/LjWrrRMsM3//42UCbwMw5j6oJFjM/PAMyaLva6bKSeEECJJfF4fnR3ddLZ10tHW\nSUd7F92dPeEAyxEOslz4fL6FvtUY6enp5ORlk5ubEwnM8vJzKS4tpqikkJLSIopKiiguLaKouBC7\nXQK1pSYUCvHC0y/xwP88RENd44TH7bpwJ++6+w7O3jXFkjsLoPHZQ4R8o9nybZlprL383OmdbBjj\ndzMmQcoEXn/6xx+x/vrdlO/YMPXBaZlxazcqXidGVmo0fQohlgbDMOjr7aelqY3Otk4627voaO+i\no62TzrYu+vsGFvoWZ8Xn8+Hr8dHX0z/1wUBefh7FpUUUlxRSXFpMcUkRZeUllFWWUbGinPLKUjIy\nZJJTqjMMg/qaBp578gWee3I/HW1dEx67+5ILeOddt3PWji1JvMPpc3X1034wdl3INfvOxZ41zd/D\ngNdMxB5moGBk5M7lLU4oZQIvn8tD9e/3U7huBWk5mZMfrCgYmXko7tE3DcXjkMBLCDFroVCItpZ2\n6qrPUFdzhvqaM9RpZxgcGJr65CXObL1zTNoykl+QR3llGeWVZaxbv5LcggLKK8qoWFFG+YpycnJk\nOMhCMAxyU6hYAAAgAElEQVSDhvomnn9yP88+uZ+25vZJj7/kiot5x123s3nLxiTd4ezUP/46RPWU\nZRbnUXXh1mmfP7a1i4zseVubcayEAi9VVbcDfwC+pWna98fsuxr4GhAEHtM07atT1WcEQ3QcqmHN\nZedMeW0jMw+iAi/8wxAKgjVlYkkhRIryer001DVRp52hTqunvqaBM7WN89YlaLVayc3PJW/kK898\nzc3PJTMzA5vdjs1mxWazYQ2/2mxWrDYbdvvo9xZFIRAMEvAHzK+A+eoPBAj4gwQDZpk/vN/tcuNw\nuHA5XDgdLpwOJ06nCz2kz/nPODToYGjQQc3pOvY/E78/Nz+XFVUVVFZVUFlVTmVVBStWVlJZVUFp\nWQlWW3L+6C0XTQ0tPPfECzz31Is0N7RMeqyiKFx+zaXc+Te3sX7j2uTcYAL6alsZqGuLKdtw7YVY\npvs7ZBgoHmdMkZ6kbkZIIPBSVTUL+C7w1ASHfAe4BugAnldV9beapk08VSKs42A1qy/ZMXX+DXs6\nhi0dJWi+USpEZbIXQogow+5hjh85xZEDxzhy4Ch1tQ3oeuLBh6IolJQUUV5eSsWKcipXVlC5soLi\nsmLy8vPIzcshLz+PrOzMBUsuOZZhGHiGPTidLpxDrvCrk6GBIXp7++nv7aevp5++3gH6e/sZ6B+c\n0RjciTiHnGhDznEXVLZarZRXlsUEZdFfuXlTrLUnMAyDpoYW9j/9Es89uZ+G+qYpz7HbbVx+7WW8\n4323sWrtyiTcZeL0kE79mGSpBWsrKd6yevqV+NwoxujSQoZigXlcFHusRJqHvMD1wGfG7lBVdR3Q\np2lae3j7UeAqYMrAyzvoor+ujeLNq6a8ASMzD8XZE9mWwEuIZcIwwNAhFIBQwByrEQqhB0N4nR4G\nugY4dkTj+KlaquubaO7sRp9l8GCzWCnLzaMwK5uCrCwKMrMoyMqmIDOL/MwsrNEfEjv90NmML7sb\nV1EeoaI8fEV5ZBbnkVlkftmzFnZ9WUVRyMrOIis7i/KKsimPDwVDDAwMhoOxfvp7B+jp7qWro5vu\njm66Onvo6eolFApNWdeE1wiFaG/toL21Y9z9ObnZscHYSJBbVUFZRemyHPw/0D+IdqqW6pM1VJ+s\noeZULUODjinPs9lsnH/xuVx+zWXsuWw32TlZSbjbudPxhsZwz+BogQIbrr9wRh9s4gfV54KSvMl5\nsw68NE3TAZ+qquPtrgB6ora7gfXTrbvt9dPTDrwMZ8/oEkJBHwR88551VgiRBHrIzLMTDq4IBaO+\nDxD0+BnqcuLodtLd2s+pmmZq2zto6uulwzG7VpqstDQq8gooz8unIi+firwCirJzsMywtSrg9hJw\ne3G0dMfts2WmRYKwzKI8skoLyFtVRkZBTsq0ikWz2qyUlBZTUlo84TGhUIi+nn66OrvpbO/G5Rii\nob6Frg5zu6uji0Agfn2/6XI53dRW14+7MLOiKBQVF1JWUTruV3lFKXn5eSn5bKfL4/FSW11H9cka\ntJNmsNXZPvHA+LGsVivn7d7J5ddext59u8nJXZwtiAGPj8ZnDsWUVezcRG5lyfQr0UMo3jFLBCWx\nmxGSN7h+Rr/x/bUtZFl0sounHizvGM4j6BqNXrMVL1mlM/hHWOZKS5Mzi0OMkmc+vpDfT9DtJOh2\nEnC70H2jiQ31kI6rz81QtxNHl5OhLic93YPUdHVQ09XBmb4eQjPsOizMyg4HWAXhICufnPSMef8D\nHfT4cbb14mzrjSlPz82ieF0FxesrKVpXQdHqcmwZUy/wmyoqKgrYtmP8z9e6rtPd1Utrcwdtze20\nNrfT2txhvrZ0THt25XhGZp729fZz+oQ27jEZGelUVJVTXlFKcUkhRSWFFBUXRH1fGPk+IyP5H9yH\n3cN0dfbS3dlLV2c33ZHve2htbqe+pnHGXeNWq5Xde3dx7Q1XcNWbLiW/ILnBxXw4+vARAsOj7wvW\ndDvn37aPzILpB5K+/l7cjH4os9jTKFxRltTAfL4Cr3agMmq7Klw2oYJVpQy2hBvJDDjx+CHWX3P+\nlBdSrFlYGA28PH29uK3zn/J/KSgtzaWnxzn1gWLOyDMPMwyzi9A/DH4Pin8YJTTaIhL0BelrHWSo\n04Gj24mzx4UeMuhzOdG6OtC6O2gdmNkf6+LsHNYWl7JxRQXq2pUUF+ZhsVmwWC1Yw68Wm/llHfk+\n/IoBoUCIoD9I0B8yvwIhQkEIBnSC4X0hb4Cg14ehz7y1zeccpv3YGdqPhRciVhRyygvJW1VG3soy\n8laVkVm8OFpuxvs9t9oyWbN+PWvWxwdnnmEPHe1dtLd20NnWFcmJ1hHOjxbwB+LOmQmv10djfTON\n9c1THpuZlUlhUQH5hXlkZmaSkZlBRkY6GZnppGekm9vpUd+HXw3DiCTADYwkwg0ECQQCMWWBQAC3\n001vTx893X30dvfhdrkT+vlGZGdnsXWHyqVX7uWSKy6OrKHoD7Do33ccLd3UjGntWrV3B66AgWsG\nP5ulrzumJSiYnktvr2vC4ycz2w/RcxV4xbwTaJrWpKpqrqqqqzEDrhuBOyerYMNlZ/PGA09HtjsO\naay94twpZykYGbkYji6UcLeCogfB74H0xdVvLcSSF/Sj+NyjwZYeOybI6/TS09hPb2M/A+1DGLqB\nYRi0Dw1Q3dlBTXcHva7pv8GWFxWyZcMazj1HZdv2zVSuqSAjN9N8TzEAPRjbjWkkNtjeUCyQlolu\ny8DjU/A4vHj6HXj6HOZrvwNvvxM9OM2xUIaBq7MfV2c/7QfM4bG2zHQK16+gePMqijatnDr1ziKR\nmZXJ+o1rx51Rp+s6/X0DZhDW2hkXlPX3DszJ4P8RnmEPnmHPhOPNUoXNZmPD5nWo2zazZdtm9lyy\nk+y8QixLMJF40Ovn1G+fg6gPNOl52azas2NmFYUCZgaEKMnuZoTEZjXuAr4JrAECqqq+Dfg/oEHT\ntD8C9wD/i/kW92tN0yZeiwBYfcEWjvz2hUgW2oDbS8+pRsrPniKhqsWCkZ6D4h19Q1Y8DgwJvIRY\neKEgiteJ4nHEr4lmGDh73fQ29NHT1I+r1x0pbxno40R7K1pXBy6fd7ya45SVl3DhnvPZecHZnLNr\nB0UlhUB860v0n+iYP9d6KGqwfnB00H4wYAaNTP7HXTF08Lmx+tzkANl5aRjlZRgZGyPLkBi6gc/p\nHg3G+hw42npwtvWiT2MMVNDjo+dkAz0nGwDIrSqhaNMqitVV5FaWoFhSvzVspiwWS2SM2Y6d2+L2\nBwIBerv76O7siXx1dfbQ3RX+vqMbr2d6v0OpbOXqKraEg6wt2zezYdM60tJHu6KXcmt6zZ9fxjsQ\n+7NtumkP1rSZhTCKxxHTSmTYM8CW/O58ZS4/KSTIePlnT9D22qlIQf6acs6968apz/S6sQ60jlak\nWNDLNyR1lsJitJT/o6aqZfHMdR3F5zJnDvncMW90ekhnoG2InsY+ehv78bn9kX2Dw26OtbVwrK2Z\ngeHpdb1s2rKBvZdfxJ59F7F+49pxu+Hm5JkbOvi9KOFuUQKeSCv7tE63Z5qTgTJzx03SqId03N0D\nOFq6cbR242jpwdM3s8St9uwMMwjbvJLCDVXYMxduklEq/Z4bhoHL6aaro5u+3n4GB4YY7B9koH+Q\nwf5BBgeGGOgbZGBgkMH+oYRmZ86W1WqlpMwMLkvLSyguLaKkrJjSshJKyopZs241efmTd2ul0jOf\nS51H66h++PmYsqrdZ7HphotnVpFhYOltRAmOvufoeWUY2YWzvrfS0txZfdJJqWyjKy7YEhN4DTV1\n4erqJ6d8ihQR6VkYFmuk60IxdPC6IVMGMQuRFIZhBlkehxl0RQUlhmEw2OGg/XQXPQ19hAKjf9h8\nwQCnO9o41tZCU3/veDXHsFqtnHPedvbuu4iL9+2eVjqEOaFYzPeZ9CwMis2fNzASiHnAPzxpV6US\n8KAEPBiOLkjPNoOwjJzIh0OL1UJuZTG5lcWR7NuBYS+O1p7RYKy1J2ZdurECbi9dR2rpOlILFoX8\nVeWUbFlN6fb1ZOQv36zxiqKEFwfPYaM6+eR6wzBwOlwMDgwyNOjA5/Xh9XjxeHyR731eHx6vN3bb\n48NiUbCNJLy128OvtnCZHZt9JBmujYyMdIpLiykpN4OtgsL8JdlFmChPv4PaP70cU5ZdXsj6ay+Y\neWVBX0zQZUDSlggaK6UCr+yyQvLXVjDU2Bkpaz9QzeYb90x+YmQJodF10yweB7oEXkLML7/HDLa8\nzrgxW75hP51aN+2nuxge8kTKdcOgsbeHo23NVHe2E9Qnb2HIzMrkwj3nsWffbnbvvSA1kmkqirlm\nbFqm2QFpGGZ3pH8YxeeOa+mLnAbmPp8bQzHXhjMy8yAtK25CkD0rg+LNqyKpdQxdx9nWS19NC321\nrbjaJwlUdYOhpk6Gmjqpf+J1CtZUUnb2ekrPWrfgecRSmaIokdUFxMLSQzqnfvMcoaiJFRablbNu\nvQKrfeahS9wSQenZC7bSTUoFXgBVF26NCby6jtax/poLsKVPniDPXEIoasFanwv0IFhS7kcUYnEz\nDPC5sLj648dt6Qb9rYO0ne6kt7E/ZnZfn9vFkZYmjrc34/ROPubGbrdx8WW7ueaGKzl/97kxY1lS\nkqKYq2nY082ui0nGtkVOMQzzj4HHgWFLw8gumjSRo2KxmDMcV5Wx7qrz8DmH6a9tpb+2hf66tolb\nwwwYbOxgsLGD2kdeoWjjSsrOXk+Juhpr2vJLPCoWh8ZnDuFs64kp2/Cm3WSXzaJrcOT/WnTRAgyq\nH5FyUUnJljXYczIJuMxPyCFfgO5j9ay4YIoV0m3pGLa0SFOiuYSQM6H+WyFEFEM3AwnXAErIH7PL\n4/TSUd1Fe3U3PtfoeoeGYVDf08WBpjPU9Uyd8HHrDpXrbriKfddcurhbHaw2jOxC8/0n6Defm8cZ\n99xGKEE/ylAnhrPXPC8rf8oFe9Nzs6jctZnKXZvRQzpDzV3017TQV9MSm9k7ihHS6dOa6dOasaTZ\nKNmyhvKzN1C4oQqLVbq6RGoYONNO84tHY8pKtq6ZOg6YiH84pkXeUCxmV/8CSbnAy2KzUrlrM80v\njD70tgOnqTxfnTx/zUh3o3O0+V3xOCTwEiJReghleBDFPRD75qUb9DT20Xaqk/6W2D/0vkCAo23N\nHGisp3+KgfJl5aVc/eYruPaGKxfNenEzYkvDyC3ByCk2x5l4HObXOF2sih5EcfZguPowsgrM969p\ndIdYrBYK11VSuK6SDdddiGfASe/pJrqP18clah2h+4N0H6un+1g9tqx0yrato2LXZvKqShP+kYWY\nLb/by+mHn4+ZcpyWm4V68yWzzmEX19oVNb5yIaRc4AWw4vwtNO8/ZnZpAO7Ofhwt3eSvLp/0PCMj\nD6IDr4AXgv4FmS4qxKIXCpjB1vBgzGB5PaTToXXTdKQVz1BsN1qvy8nBpjMcbW3GH5o4PUJGRjqX\nXrWXa2+4kp3nn708BhYrCtgzMOwZGLml5qfw4SGzS3LsoYaO4u7HcPebA/Gzi2a0FFpmYS6r9mxn\n1Z7tDPcN0X3sDF3H6/H0jj9TMjjso/1ANe0HqsmpLGbF+Vso27F+UWXOF4ufYRhof9yP3xmVa0uB\nrW/bhz0rY3aV6npMuilY2G5GSNHAK6Mgh2J1FX3Vo1mG2w+cnjLwwmbHSMs0ZxmFKR4HRq4sISTE\ntAV8KO7+uJw3QX+QtpOdNB9rxz8cNTvIMKjr6eJAYz31vfFrE0ZTz9rEX916A/uu2ktm1tJI/jkr\nimLObkzPxggGws97KC5FhTlkIjwOLD0bPacI7JkzWpkjqziftVecy5rLd+Lq7IsEYX7H8LjHuzr6\nqPnTS9Q9/hrlO9ZTef4WcleULIqM+WJxaz9QHfN3H2D1JedQuH7FrOuMm2VtsZmTWRZQSgZeACsu\n2BrzD9B9ooENb7qItOzJo14jMy8+8MopliWEhJhK0I/F2RO3gKx/2E/L8Q5aT7QT9I92j/mDQQ63\nNHKw6cyk3Yk2m419V+/lLbffxNbtUwwZWI5sdoz8cozcktEWxvG6IcPJWY20TPTcMkibWQuAoijk\nVpaQW1nC+msuYKipk67j9fScbCDoiR97pvuDdLxRQ8cbNeRUFFF5wRbKd2yQVjAxL9zdA9T/5bWY\nstyqUtZeuSuheuMH1ecueDyQsoFX0YYqMgpzI9lqjZBO5+EaVl9y9qTnGRm5GEPdkSzTSigAAS+k\nLeNP10JMRg+hOPtQhgdiWrg8Di/NR9toP92FHhrNUeUN+DnQdIbXGurxBMYfLA5QWFzATX99PTe+\n7XqKS6bIxSfAYg2PBStCGXaYrWCh+JmKit+Dta8JPSPX7LK0zXxmomJRKFhXScG6Sja9+WL6alvo\nOKjRX9fKeAn6XZ391P7pZer/8jplO9az4vwt5FZJK5iYG6FAkFO/eTZmOS1rup2zbr08sUkfoSD4\nYj8ULnQ3I6Rw4KVYFFacv4UzTx6IlLUfqGbVnh2TL4thsUJGNkR9alc8DgwJvISIZego7kEUV19M\n8k9Xn5umI6101fYQ3fPl9vl4rbGOg01n8AUnHr+1dbvKW++4icuu2ovdLukKZkyxYGQXmDMbvS4s\n7vi0HQAWrxPD6zJnQeYUTTkLciIWm5XSrWsp3boW76CTjkO1dBzSxu2K1ANBOg/V0HmohpzKYlZe\ntI2yHeunXFNXiMmceeIA7q6BmLJNN+4hsyixIGns+EnDlg72WY4Vm0MpG3gBVOzaTMOzhzDCUbB3\nwEl/fRvFmyaf+aRn5mGNCbycGHllC968KERKMAzzDcnZG9OiMjzoof71JrrrY2fBOTweXmmo5VBz\n44TJTm02G1dceylvuf0mtmzbPK+3v2woCmTmomfkgN+DxdVnLlcUfQiGOQh/eAgjtxgjqyCh97mM\nglzWXbmLNft20l/bSvvBavprW2Gc5ZFcHX1U//4F6p94nRXnb2HFhVtJz5U1csXM9GrNMSvWAJSf\ns4GKczYmXLfiiZ1MkgqtXZDigVdadgZl29bSdbQ+UtZ+4PSUgRfpORiKJfIpXjFCZnPjAubtECIl\n+IexOHpiWlB8w34aDjbTfrorJuFpv9vFy2dqOdrahD7BuoTZ2VncfNuNvPWOmygqltQt80JRID0L\nPT0LfG7z3y/oiz3ECKE4ujHcA+h5pZCek1AAZrFaKNmympItq/EOuug4VDNhK1jA7aXp+SM0v3iM\n0m3rWHnxNkpLF3EONpE0ngEn2u/3x5RlFOay6YYpVquZjoAPJRCVU5Dw+K4UkNKBF5iD7KMDrz6t\nBe+gi4yCSYIoRcHIzEUZHo12LZ4h85OjEMtR0G/+wfa5ooqCNB9po/loG6HgaFdjt9PBS/U1nGxv\nGW+4DwD5BXm87c63cPNtN5CTs3zXAUy69Gz0kixzxqmzF0WP7fJVQgGsA+0Y9kwzAJuDIRYZBTnj\ntIK1xI0FM0J6JC9Y0/pKys5TKT1rnSRmFePyDrk5+rPHCAyPfghULApn3XL5nEzgiFsiKC0LrKkx\n9CHlA6+8VWVklxfh7uo3CwyD9oPVrL/6/EnPMzLzICrwwuuCYGBWA1GFWLT0kPkHengwMtZBD+m0\nneqk4WALAe9oV2Ofy8lztac51dE2YXXFpUXc/q638ea3Xkdm5sKPlViWFAUjKx8jI9ecBenui09D\nEfBg7Ws2B+Dnlc3JmnTRrWCefgdtr52i41DNuEsV9Z3poO9MB/V5r1N1wVYqz1dJy5ZxtsLkd3k4\n+vPHIpPnRqy9Yhd5q+Zg4XtdRxmOTeqcKt2MsAgCL0VRqLpwKzV/eilS1nGohrWXnzv5gE57ZvwS\nQu4BjPw5+EcVYjHwOrEMdUdaRQzDoLu+l/rXmvA4Rj9lDnmG2V9XzZHWZowJuhQrqyq44z23cO2N\nV5Em6/ulBoslPK4rH8XVayZjHXuI14nhc2PklpqD9edonGtmUR4br7+ItVfuovNIHW2vnsTT54g7\nzu8YpuHpN2h6/gjlOzeyas92skoK5uQexOIUGPZy9OePxSXzLTt7A6svPWdOrmHmxBttxTeXCEqN\nbkZYBIEXmP8g9U+8HvlkFXB56K1uomz7+olPUhSM7CKUodEFtxXPIEZu8axn/wixKISCWBxdMfm4\n+lsHqXu1EWfPaJnb5+Oleo2DzQ2EdH28mlizfjV3vu9WrrjmMqwycy01WW0Y+RUYWYVmHrYx0+cV\nQ0dxdGF4HOj55TPKgD8VW3oaK3efRdUFW+mva6X1lZMM1Me3mOrBEB0HNToOahRvXsWqvTvIX1sh\n6SiWmaDXz7FfPB43g7HkrLVseetlk2csmC7DQHHH1m9kFUAKrY6xKAIvW7qd8nM20v766UhZ++vV\nkwdemAPpDGdPJBmhYhgow4NmQlUhlhrDMFs9nD2RT3vDgx5qXjpDX/PoG5EvEODVhjpebaibcFmf\njZvX867338GefRctj+V8lgJ7OnrRyokH4Ac8WHobMXKKzfQTc7hWnWJRKN68iuLNq3D3DNJ/tJaG\nV06hB+J/v/rCC3nnrChh1Z7tlG6TcWDLQcgf4Nj9T+Bsj501XbRpJWfdkmC+rmheV8xsbQMl5dZs\nXhSBF8CKC7bEBF6DjR24uwfILpvkgSoWjOzC2IWz3QPmP8ICLpApxJwL+LAMdaEEzFUbQoEQjYda\naDrSFpmpGAyFONh0hpfO1DDsHz/x6crVVbzvnndy2VV7JeBarEYG4A8PhoPw0e5jBVBcfRgeJ3pB\n+bwsnZJdWsDat19Jxd6z6XijhrbXTuIbil/ZwNXey+nfPseZJw+w8qJtVJ6nSlb8JSoUCHL8V0/h\naO6KKS9YV8m2O66auzxwhoHF3R9blJk3J2Mc51Jq3c0kcsqLyF9TzlDT6D9c0wtHOeuWyyc9z8gq\nwHCNDj5V9JCZUDVLxhmIJcDQUVz9ZhJUzHFcPQ191L7UgNdltnjous7RtmZeqK3G4fWMW01peQnv\nev/bedONV0uX4lKgmJ/yjYwcMyAf2/0Y8mPta0HPyjez38/D8At7ZjqrL9nByou30XOqgdaXTsS1\ndgD4htzUP/46jc8dpvI8lZUXbZt81rpYVPRgiJMPPsPgmfaY8rxVZWy/8xqs9jkMQ/yeuGTDqdba\nBYso8AKo2r0tJvDqPl7PmsvOmbzVy2LFyCqI6fNV3AMYmXM30FSIBeEfxjLYhRIyW6+GBz3UvHiG\nvhbzd90wDGq7O3mq+gR9bte4VeTl53Hn+27l5ltvIC1dWhuWHKsdvbDKTJjr6I5bA9IyPIThdaHn\nlZt5DufhPdFitVC+YwNl29cz1NRJy8sn6NOa49JRhHwBWl8+QeurJynbto6Ve7aTV1U65/cjkkcP\n6Zx++Dn6a1piynMqi9nxzmuxpc/tRJ241q707Dkd0zhXFlXgVXrWWrLLCnF3h4MoAxqfPcy226+c\n9DwjqxDDPboOnRL0S0JVsXjpIRRnD5ZwupRQIETj4VaaDrdGuhW7nQ6ePH2cM73d41aRmZXJre94\nC7e8461k50i28SVNUTAy8zDSs1EcPVjGZPNW9BDWwXaM9Bz0/LJ5y3WkKAoFayspWFvJcO8gLS+f\npOtIbcz6fADoBt3Hz9B9/Az5aypYtXc7xZtXz83Aa5E0hm6g/WE/PScbY8qzygo4+91vwp45xwFR\nwBfXsqtnp+YasYsq8FIsCmuv3MXJ/306UtZzsgFXZx85FZMMmLfZzZw33tGcIRZ3vyRUFYuPbxjL\nUAdKKIhhGPQ29lPz0hm8TrNb0e3z8VzNKQ63NI6b/NSeZuevbnkzd77vNgoK85N772JhWawYBRWE\nMvOwDHXGLcCt+FxYeoYx8svnPedRVkkB6l/tZd1Vu2h/vZq2108RcMevRznU1MlQUyeZxXmsvHg7\nFTs3YU1bVH+2liXDMKj588t0Ha2LKc8szuOc91xPWvbc5wCMm8loz5iTBMLzYdH9BpdsXUNOZTGu\njr5IWcMzh9hx5zWTnmfkFEFU4KX4PeD3pOw/jBAxDB3F2Yfi7kcBhofC3Yrh2YrBUIjXm+p5sU4b\ndwFrRVG47qarec8H7qSsQrpvlrX0LPTStTFjA0coho4y2IHuc5uJV+c59U5adiZrrziXVZfsoOtY\nPa0vn2C4ZzDuOE+fg9o/v0zDM29QdcFWWRcyhRmGQf1fXqPjYHVMeXpBDue89/r5+XcLBeMy1ZuT\n6FKzlXTRBV6KYrZ6nXjgyUhZX3UzjraeyccD2DMw0rJiFplV3AMYEniJVBfwYRnsQAn60EM6jUfa\naHyjGT1kYBgG1Z3tPK2dZGA4fuYYwLkXnM09f383GzZPnn5FLCOKBSO3BCMj12z9GjMg2eJxYPiH\n0fMrIX3+Axyr3caK81Qqz91Mf10rLS8dZ7ChI+644LAvsi5k+dkbWLlnOznlqdmdtByF/EFqH32F\nzkM1MeVpuVnsfO/1ZOTPTy+TMjyAEtXGb1jtKZUwdaxFF3gBFG9eRe7KUpytPZGyxqcPcfa7r5v0\nPD2nCGt/VODldWIE/WCTQcUiBRmG+Ybi6EXBwNHj4vSzNbj6zN/hjqEBnjh9nOb+vnFPr1q9gg/9\n3V1cfNmFkqhSjM+ejl682lx6yNkb88dLCQWx9LeYsyNzS5KSgic6H5izo4/Wl0/Qfbw+ZvF2MNeF\n7DxcS+fhWgo3rKDqom0Ub1ol48AWkLt7gJMPPcNwd2yLpT07g3Peez2ZRfPUfa3rKO4xywOlcGsX\nLNLAS1EU1l25i2O/eDxS1l/XylBzF/mryyc+MS1rgmWEJjlHiIUQCmAZ7ETxDxMKhmg40EzT0TYw\nwOXz8kz1SY62NY97ak5uNu+6++3cfNsN2O2yvI+YgqJg5BRhpGeFW1ZHc7xF3iN9w+gFlUmdIZZb\nWczWt+1j/TXn0/rqKToOVhP0xuefG6hvZ6C+nYzCXKou3ErFrs1zP3BbTMgwDDoP11L7yMvogdiJ\nEuJe0QwAACAASURBVLaMNM55z5vILp2/9E3jLg+UmdrjV5WJ1mZbAEZPj3Pqo0YONgyO/OQRhqIS\nshWsq2Tn+9486XnK8BCWqGWEDEVBL9uwLJcRKi3NZSbPXCRuOs9c8ThQhrpQDJ2B9iFOP1eLZ8iL\nruscaDrD87Wnxx3HZbFa+Ku3vZl3f+BO8gtSZ0HYhSa/5zNg6CjOXixjBipDOAN4bsm0WhPm45kH\nfQE6D9fQ+srJuMWVo1nsNip2bqRq91mTpxpaYhbi9zzoC1A7ziB6gMzifLbdceX8dgUbBpaehpiJ\nInpOsdlCmwSlpbmzalZblC1eEB7rddV5HP3po5GywYYOBho6KFxXOeF5RmYehrM3snCwYhgo7vAa\njkIsJD2EMtSFxesk6A9S92ojbSfNDwlN/b385eRRup3xCxED7N57Ph/8+F2sWbcqmXcslhrFgpFX\nRig922xx1UcDfAUDxdmD4XOjF1TMW9qJidjS7ay8aBtVF26l93QTLS+fwNESny5FDwRpP1BN+4Fq\nCtZVUnXRWZSoq1FkJYY55ers4+SDz+LpG4rbV37OBjbduHfO83SNpXid8csDLYLk6Is28AIoXFdJ\nwbrKmEGYjU+/QcFdN0w8piWc0Vlxjo4PU4YHMHJkGSGxgHzDZjePHqS3qZ/q5+vwuf04vV6erj7B\n8faWcU9bs3419/z9XVxw8XlJvmGxpKVnmzMfwx8Eoin+YSw9jUlJOzEexWKhdNs6Sretw9HWQ9ur\np+g+cQYjFL/Q+2BDB4MNHaQX5FB1wVYqz1OxZ0k3ZCIMw6D9YDV1j72GMSYHm8VuY9ONF1Oxc9P8\njys1DJRFsDzQeBZtV+OIoeYuDt/355iys999HUUbV058kh7C0n0mpl9Yzy9fFJHyXJIumOSLe+aG\nYU7pd/UR8ASofekMnbU9kW7F52pP4x+nWzE7O4v33vNObr7lBlniZwrye56Y6K7vsfTMfIz8srgP\nrcl+5n6Xh/aDZiuX3zk84XEWm5WSs9ZSuWszBWsrl9Rg/GQ886DXj/Z/L9JzoiFuX1ZZAdtuuzJ5\n3bu+Yaz9sR9IQ6XrkjpZbtl1NY7IX11O0aaV9Ne2Rsoanj5E4YaqiSNuixUjKz92GSGXLCMkkiwU\nxDLYjuL30FXXg7b/DAFvgKb+Xh47cZQe1/jditfccCUf+Oj7KCpZPuNXxMIxMvMw0jIjkz2iWTxD\nGAEPesGKBV2aJS0nk7WXn8vqS8+h93Qjba+eihn/O0IPhug+Vk/3sXoyCnKoOHcTFeduIqMgdVMP\npApHWw+nHnp23PF1ledtZuP1Fyc1uW388kA5iyZDwaIPvADWXrkrJvBytvXQV9NCibp6wnOM7DHL\nCIVkGSGRRD43lsEOgsNeqvfX013Xi9Pr5anqE5yYoFtx/aa1fOzT97Bj57Yk36xY9qx29KKV46ed\nCPqx9DaNdj0u4IdXi9VC2fb1lG1fj7Ojj7bXTtF9rD5+WSLAO+ii8dnDND53mMJ1K6jYtZmSrWvm\ndtHmJSDg+f/t3Xl8HGX9wPHPzG42yWZzn03SHL2mHIW2nHK0QikgIJe38lNQEblBQBFEQDxAfijq\nT0UUvBAVBAQFuW/kLrT0mtIrTZu0ue9rd+f5/TGbNpvdpMk2mexuvu+XlXRmdzp9OrP7nef5Pt+n\nn+2vr2HbKysjhnNdnhTmnX40xQfNdvikoiwP5EucB9GkuMKyygrJn19B8/o90+u3Pr+C/HkzR+71\ncqWg0rPCqt3qXbKMkJhcSil7vbzuFppqWlj34of0dfXvdVjxvAv/h9M/eYoMK4qpM7TsRGtdWFKz\nhkJr34k10IPKio/yPJkz8pl/5rHMPvEw6t/dQN3b6+hri7JYvILWzXW0bq7DleaheMEsShbPI7O0\nYFrXvxvo6mX766vZ8dY6gv3+iP2+kjz2/8zxePOdL90QkduVkgYpiVMMPSkCL4Dq4w8JC7y66ptp\nWldD4f5VI75HZeTCkMBL88syQmISBf10bjKx2towX9tC3fpd1LW18vjq99jZETkzCODE05Zx/qXn\nkpefOE9zIsmlpGEVVKF17EIftkyLXfG+j0DWnCk6uUgp3jQqjj2ImUcvoG1rPfUrNtC0dmvUXrBg\n38DuGZHeohyKF8ymYL9KvIU50yYI62vvpva1VdS/a0bU5RpUevh+zD7p8KnpHYyyPJCVkZdQaUIJ\nn1w/1Jq/P0/jmj1Jf96iHA676KxRpxHrzbVheQsqzYeVW7ZP55EoJOnYQX1d6G31tG1vYe0LH9LW\n0sWLG9byds3mqC+XYcWJI9f5JFFqT+L98CXZNQ0rswjljc+8WX9vP42rt1C/YgOdOxr3+vr0/CwK\n5ldSML+SrJmFcVmaYl+v896WDra9soqd738YdYYogDvdg3H6MRQeUB3zn7OvBkcMBilXClZh9ZRc\nZ9M2uX6oquMW0bh2C4OfAT0NbTSs3jLq+PPwZYTo6wJZRkhMFBWqfdTexIdv1LBt1Q7W7azjqbWr\n6Orvi3i5zFYUCUPTUN5sVEqaPUlkSMV7lELv2GUPPWYXx12B6pT0VEoPm0/pYfPpbmilfsUGdq3c\niL878p4Ee5Hu2tc+oPa1D0jJSKNgfgX58yvJnVWa8Dlh3Q2t1Ly8koYPNsMIHTEp3jTKjzqQssP3\nw502hd+NloXWk1jLA0UTNz1eSinV1BRl/H2c1v7jRRpWbdr9+/T8bA675Gx01whPKEqhN9WgBfp3\nb7K8OdNiGSHpCZhkgQH0tno6tjey9vkN1NU18Z81K9nYGDnbCuC4E5dw0TfOl9mKE0yucwcoC629\nAb03cshcuVKwckshJW0KTmzsrKBFy4Za6t/bQPOGWrD2/t2oe9zkzSmnYH4FeXNn4smYur/jeK5z\nKxCko7aB7W+soWldzYiv82R5qTh6ATMOme/ojMWRaN0t6B17eiiV5sIqnjVlNTgd7/EyDOMnwJGA\nBVxhmuY7Q/ZtAbaF9ingC6ZpRi41P8Sh85Zz6TUXcOpZJ8d6SoDd69WwevPum6a3uZ2GVZsoWTQ3\n+hsGC6oOWUZI62lH+fITohCbiFN9ndBcx+a3a9j0bg1vbN7Iyx+uJ2BF5kzMKCvh8msvlCKoInFp\nOiqnBCvVi9a+E00NXWzbb896zCqyayXGae+E7tIp2K+Sgv0qGejqpWldDU3ramjdUjfi0Js1EKBp\n7Vaa1m4FID0vi8zyQrLKC8kqL8JXkoceBz3XVtCiq76Zti11tG6up33bLix/5ESeQWm5mVQcexAl\nC+fGxfkDdnDfFb6UlcrIScjC5zFFFoZhLAHmmKZ5lGEY84F7gaOGvEQBJ5um2TvWY/oH/Pz0h79k\nZlU5By06MJbTAsCbn03JwXPY+d6Hu7dtffE9ig6aPWKvV8QyQii0jgZUbmnM5yGmqdDQYk/tdtY8\nt4F1H27j8Q/ej1qTy+128+n/OZtzvvIZUtOkmrZIfCo9C5WShqdzJ8G+PR//GqB1NGAN9KKySyAO\nc6SG8vjSdw9FBvoGaNm4naZ1NTRvqI06w29Qb0sHvS0du0ddNJeOb0b+7kAsq7yQtNzMSU/UV5ai\nu6GF1s125f62rfWjnvcgb2EOFUsOpujAWSOPEk0RraslbAmrRFkeKJpYu3SWAf8EME1zvWEYOYZh\n+EzTHBwr1EK/xkUpxY9v+il33/8LvBneGE8NKj+6iF0rN6JCvV59rZ3sfG8DpYfOj/6G0DRprWPP\nul96XyfB/h5Ijf08xDQTDKC17mD7O5tY/coGnl27mhW1W6O+dMGiA7ji2xdTNWvkWnNCJCS3h6w5\n+9G8eTP6sHwcva8T5e8PDT0mxsOGO82zuzaYFQjStrWepvXbaFpXM2qVfAAVtOjc3kjn9kZ2sBaw\n86V8M/JJzfLi8aWTkpGOx5eOJyOdFF+avS09bcSq+kopLH8Af+8Agb5+Ar39BHoH6N6o0byznc4d\nDbRuqSfQ0x/1/dH4ZuRTuXQhBfMr47Oaf2AArWtYCYmMnIQdlYr1rEuAd4b8vim0begS5XcZhlEN\nvGKa5nVjPXD9jl3cdec9fOP6S2M8NUjPzWTGIQZ1b6/fvW3Ls+9SsF8lnozopSKUNwfV0x6W66V3\nNGAVVMZt17iII/09DGzfwtpn1vLau2t5as0qugciP/iyc7I4/9JzOenjJ6DH+VO/ELHSdB2VXUzQ\n40Vv3xm23JAWHEBvrkFll0zJWo/7Qne7yJtTTt6ccuae8hE665toWldDy4fb6drVMqa8MH9PH62b\nduzlD9LweNNI8aWT4k3D8gcI9Pbj7xsg0Ns/4tDneHgyveRUz6D44DnkzRllpZc4oHc0hs2cVbrL\nTgdKUBMVLg7/F7sBeBJoAR41DONs0zQfHuvBHn/kKY5aeiRHHnNYzCdUsWQh9e99uHsRT39PHxuf\neIP9P3Vc9DdoGlZ2Ea7mPVXDtUA/Wk+bPWtCiGhCC7U2vLeON/+zin+/9y4fjpA8f+Jpy7jue5cR\ntOIkZ0KIyZaeiZWSit66I2zWo6YUWlu9PfSYVZiQeTqarpFVVkhWWSGzTjiU4ICfzrpmOrY30rmj\ngY7tjfS3d+/9QNFYioGuXga6xpyts1cp3jRyqmeQUz2D3FkzSM/Pjutga7e+brT+8Il3KrMw7mbK\njkesgVcddg/XoFJgd/K8aZr3Df5sGMYTwAJg1MCrenYFWzbtKYD6kx/8goef/j25eTGO4RZm0nXK\nEax+7L+7NzV8sJk5R+1P2cKRivtl0hXsZqBtT5emq6uZ7PIZ6O6U2M4jzhUWyhplsbICAdo2buCD\nx9/lX8+8yQsb1uIPRibPV86ayQ0/+AaHH7V4Cs5SgFznU2Fom6viHLp3bGOgtTnsNXpPGy41gK9y\nNi5PYgw9jqakLA8O2zORq7eti5atO2nespOWrTtprdlFYAy5VhMhJd1D4dxyioyZFM4rJ7u0ID6H\nEUehLIv2DVsZ2r/n8maQWxHfPXR7E1M5CcMwPgLcZJrmSYZhLAbuNE1zSWhfFvAA8HHTNP2GYfwN\neNA0zYdGO+bqlevUOWddhDWkC3XJsqP57q3XxtzAVtBixd2P0VW/52b3+NI57JJPkOId4SYPBtAb\nt4R1jVvp2aickuivT2AyzX4fDPTRvmYNzz3wXx5+603q29siXuJ2u/j8eZ/mc+d9Go/HDtylzZ0n\nbe68qG2uFFpvO1p7Q0TBVaXpWDkzkn6tXGVZdDe20dvSgb+rz+7V6rZ7tvyDP3f3EewbGPU4mksn\nJT0Vd3oq7jQP7vRUfDkZBHWd1CwfOdUlZM7Ij8tCr+OhdTWjdzbt/r0CO/0nTkqTxFpOIuY6XoZh\n/BBYCgSBi4HFQJtpmo8ahnEpcC7QA7xnmuZlYzik+t/v38WffvvXsI3fvuUqTvjYCMODY9C1s5l3\n73p0d6I9QPHCuex39pIR36N1taB3hlczDuZXJN1SQvKFFAOlUB3NrH/yDf7y0HO8sWUj0e6hAw/e\nnyuvvyQieV7a3HnS5s4btc39fRFrPQ6yMvJQmQXTPq826A/g7+5joLsXf08/rhQ37nSPHWylpaKn\nuCI6JJLuOg/6Q50gez5fLW+2PSs2TjgeeE0CVV/fyqXnXc2GdXty9DN8Gdzz919SWFwQ84G3PL+C\nmhffC9u24JwTyZ83c4QzUehNW8NyElRKKlZ+ciXaJ92NOtksi+5NH/Lo7x7nof++QVtv5IymjAwv\nX7v8y5xy5olRk+elzZ0nbe68vba5FURv2xmRuwOgPF679ytBZ6xNlWS7zrXWOvS+PX8fpelYRbPi\nKrcr1sArrvoh3W43137vKlI8e/Kpuru6+fHNd2JZsc/iqFxyMBlF4QnyGx57jcBI3bmahpVVFL7J\n348WpSqzmB7UQB/rHn2a71x9J/c893zUoOvY447i9w/dxWlnnywzFoUYje7Cyi3Fyiwcvsoj2kAP\netNW6B+9VINIYv3dYUEXJH5C/VBx9+1QWT2T8y85N2zbirfe57F/PBHzMXW3C+OsY8N6q/o7utn0\n9Nsjvyk1AystPCFX62iEKJXHRXLr21nPPdfdyTU//g2rdtRG7M/Pz+WWO27gptuvI78gbwrOUIgE\nFKqfaOXPRA37QtWsIHpLLVpX84jrB4okpRT6kJqaAMqdai+4niTiLvACOOuzH+fgQxaEbbv7Z7+n\ntmYvtU9GkVVWyMyjwyvi17+zntbNdSO+R2UVooYEa5qy0IYk+okkpyxW/usZLjn3Ov764qv0+sNz\nUjTgjE+ewh8e/g1HLT1ias5RiETn8WIVVKE84cWqNUDvbEJvrZMH3mlE624NX3AdsLKLkyrNJy4D\nL13X+dZNV+IdUuy0v7+f2278CcFA7Ddg1XGLSc8Pj5rNR18deXqvKyWiSJvW0wb+6CvYi+TR09LG\nnVd8n2tu+QVbmhoj9leUl/J/f7iDy669aJ9WWRBCAC43Vl45VkZkj7HW34XeVCOfu9NBMGD3cg5h\npWcl3cS2uAy8AIpnFHHx1ReEbVu32uRvf/xHzMd0pbiZf+axYeVe+1o72fLcOyO+R2Xkolx7cs40\nQG/fJd3fSezNfz/HVz95Mf967S2Cw3IL3S4XX/rKZ/ntP37F/AONKTpDIZKQpqGyCgnmlqGGFVS1\nF9rehtbdJp+9SUzrbAwr5aQ03c7tSjJxG3gBnHTaMo5aemTYtj/efT8frt8U8zGzK4spO+KAsG07\n3lxLW83O6G/Q9CiJ9n1ovZGLHovE1tHazi1f/w7X3fRTdnVETqQ4YN5s7n3w13zxwnNwu2XGlRCT\nIs1nDz0Oq9WkodA7dqG174R9mGwl4tRAD/qw71WVWZCUs1vjOvDSNI1vXH8JObl7hgeDwSC3fvcO\nBvpHLzA3mlknHEJa7pDEeQXmP18l6A9Ef0OaD5UaXthP65RE+2Ty7ENP8qUzzufFd96P2JeRmsoV\nV57Pz/5yJ2UVpVNwdkJMM+4UrPyZWN7IlUv03g705hrwj30RaBHnlEJvH55Q70FF+fdPBnEdeAHk\n5uVw5fWXhG3bunkbv7/rvhHesXcuTwrGGceEbettbmfrCytGfI+VVYgaMkapWUG0zuYRXy8SQ+PO\nRq459xp+9KP/o6Mncvr6Rw4+kD/+87d8/AtnJPQSFUIkHM1eaNvKmRE2yQlAC9gLbcvIQ3LQetrQ\nAuGBtJWVXAn1Q8V94AVwzEc/wkkfPyFs24P3PcJ/X34z5mPmziplxqHzw7bVvraajh2RidQAuD0o\nX3jip9bTKk9dCSoYCPL3ex7gS2d9jRWr10Xsz/P5uPH6S/n+PbeSWyglIoSYKio9C6ugEuX2hG3X\nlEJvq0dr3wVKhh4TVjAQUS3ASsuE1OSdtJQQgRfARVedT1HJniQ7pRQ/uO7HrF+zIeZjzj7xMFKz\nM/ZsUIr1j7yMNcLMSeXLi0y075BE+0SzbrXJ1z51EXf/+k/0DysRoWsaJx6+mD88fBdLzjppis5Q\nCBHGba8cYqVnRezSe9rQm7ZBIPb0EzF1tM6mYQn1GmpYXnWySZjAy+fL4Js3XRlWEbyvr5/rr7iZ\nuu31MR3TneZh3unhQ449DW3UvBSZ5wOEEu3DZ1hoA71S0T5BdHV189Nbfs6l517F1trImnDluXnc\n+p1L+NYvbyYjLzlzC4RIWLqOyi7Byi4OS/sA0AL99jJvPfJZnFD6eyK+P5UvORPqh0qYwAtg0aEH\ncek3vx62ra21nWsvu5H2tthuuPy55ZQsmhu2rebllTSZ26K/IdWHSs0I26S1N8BAb0x/vph8Sime\nf+olvnj6V/n3o09HLFGS6nbziaOP5Nd/vp1DzjgpafMKhEh4moby5mAVVISNPkBo6LF9J1pbvcx6\nTASBAXux9CGblMuDysgd8S3JIqECL4DTP3kKnzv3k2Hbdmyr4zvfuIX+vtjyrWaffAQe35ACbUqx\n9oEXoud7hdZxDEu0R6G37oDgCIVYxZTZvm0H11x4PT+4/nbaOyIXkD2wbCb/e91FXHjHN/GWFE/B\nGQohxi0lDaugMmJZNwjNemzaKgVX45llobfuQFPhaT1WdtG0ePBNuMAL4MsXfZFlJy8N27Z21Xp+\neMP/EgyOv8RDSnoqxllLwv7BLX+AD+57mt6WKLNm3B5UTknYJs0K2ktbSJJnXBgY8POnu+/nq5++\nmPfeWRWxP9ebwddOXs5t/3ct+398OdqwxF0hRJzTXaicGdGHHncXXG2VHNx4oxR6e33kskC+fBg2\nmpSsEjLw0nWdq797BQsPPShs+6svvM6vf/I7VAw3Wv7ccuae+pGwbf7uPlb9+Wn8PZFPTio9K2J5\nC83fF5phIzf6VFrx1vt89TMX8ce778cfCK/NpmsaS+bN5/Zvnc+nv/NV0mZWTosnLCGS0u6hxyiz\nHrEXW9Zbd0jNxTiidTWj9XWFbVNpvojl+ZJZQgZeAB5PCjfffh1VsyrCtj/y93/x4F8eiemYZYfv\nx8xjwoO53uZ2PvjLM1GLq6rMgoh8L723w37KEo5r2NnILd++jWsu+g47aiMnXFTlF3D1mafzrVvO\np/pjH0VLmx5PV0IkvZRUe+jRmx2xS+vvRm/cCv2RdfqEw/o60YetxajcqVjZM6bVA3DCBl4Avkwf\nP/r5zeQPq7P0mzvv5cVnXonpmLNOOJSig2aHbeuobWDdQy+hhidsappd3M817EmrsxH6umP688X4\nDfQPcN/v/sa5n7gg6r97hieVsxYeyo2XncNJl51N2qx5oCf3rBkhph3NnvUYzCmNXOvRCqC31Nr1\nomREYmr4+9Hbwh+Ile7Cyi0DPaFDkXFL+L9tUUkhP/r5zXgzwlcvv/W7d7BqxepxH0/TNeafeSw5\nVTPCtjet3cqmp96KfIPuwsoLX9RVA/S2OqkrM8mUUrz24huc96kL+f1d99EfZRmpxTOruObsM/jK\n1Z+gYvkxkJk/rZ6shJh20jPtoceItR5B72pGb66Vz2anWYFQMv2eoFcBVk4puFNGfl+SSvjAC2D2\n3Gpuvv16XC7X7m1+f4AbrrqFmi214z6e7nZxwOeW4S0Kr+W0/fU11P43SjDn9mDlloaVKdCUhd4i\nuQWTZdvWWr592Y189+rvs7NuV8T+kqwczjt6KZd+5QyOOfd40uftD560KEcSQiQdtwcrvyIiDxdA\n8/eiN26VxHunKIXeWo82bNa/yipK6ur0o0mKwAtg8eELuea7l4dt6+rs5tuX3UhzU8u4j5eSnspB\n55yEJzP8wtj01Js0rNkS+YbUDFTmsOKqwQG7a1Vu7gnT3dXDXXfew1c/cwlvvx65tqbX4+HUAxdy\nxRmnctb5y6g8/nC0/DLQXVGOJoRIWpqGyiokmFeOGnb/7068b9kOASkDNJm0jga0gfD8OsubPS3q\ndY0kaQIvgOWnHs+XL/yfsG276hu47vKb6ekef2JlWo6PBeeciCt1SFeognUPvURbzc6I16uM3Igl\nLbT+7oh1qMT4WZbFU/9+ji994ms8eN8jEWVDNE3jsMpZXHr8SXzms8dz2OeOJGP+AShvtgwtCjGd\npWZgFVRFTIQC0AZ60Ju2oPW0yQPyJNB62tB72sK2KU86Kmt610xMqsAL4PNf/jSnnnVy2LaN5iau\n+vp1NDU2j/CukWXOyOeAzyxD0/d8eatAkNX3P0tPU/gFhaahsosjcgv07ha03ij1wMSYrF9tctlX\nruHHN/2U1ua2iP2VeQWcf/RxnHPKR/noF4+k/JiDobAK3KnOn6wQIv643Fi5ZVjZJZGJ90qht++y\ne7+kCPbEGeixyysNoVxuO69rmj8MJ13gpWkal3/rQo445rCw7RvWbeSSc69io7l53MfMm1PGvDPC\n13QM9Paz6k9P0d85rCdN07FyyyK7ttt2woBUUh6P7dt2cPO3fsTF517Fug/MiP1Zael8YtHhfOW4\n41j2ySNY8PFFeKoNux7MNL+xhRDDaBrKm41VWIXyROYWaQM9du5XT7v0fu2roD9yOSBNs2cwJvk6\njGORdIEXgMvt4oYffhNj//A1GBt3NXH5V7/Jf19+c9zHnLFoHlXHLQ7b1tfWxQd/eQZ/77ClikJP\nV9GXFYqsBybCtTS38rNbf8WXP3URLz/3WsR+l65z7ByDC5ecwPJlh3Dk5w6l8GADVVgFKZJAL4QY\nhSsFK68cK6sYNewBTVMWevtO+azeF6GJZZo1fDmgGfL5HKLFUuV9kqjGxsi19PZFT3cP37/+dt58\n9e2w7ZqmccHlX+aTXzgTbRw9I0opzEdfZeeKDWHb0/IyOfBzJ+ArHlbJvqcdvT08F0y5PXbUHwdL\n1BQWZjLRbb4verp7eOC+R3jwvkfo643eO2gUz2D5fgsoLytk/tLZZM8sxMpJnBs63tp8OpA2d17C\ntHlgwF5Ye6A3YpfSdFRWESo9KyF60OOiza2A3dM1rD0tX17E5LNkUFiYGdOFkdSBF0AwGOSuO+/h\n4b8+FrHv1LNO5rJvfR23e+xdn1bQYvVfnqFl4/aw7XqKm/lnHUvRgbPCtmsdDejDKtkrTcfKLZ3y\ndani4kYF/H4/jz/8JH/+3d9oa22P+poZWTksm38As4qKqT50JhULy9GyClCZ+aAlTsdtvLT5dCJt\n7ryEanOl0Hra0Doa0Yj8PlQp6fbizXH+cDflbe7vt2t1DS8bkeqzv+8SIHgdLwm89uKxfzzBL26/\nCysYXn1+8eELufG2a/Fl+sZ8rEC/n1V/epKO2oaIfTOPXkD1CYeiu0LBgLKHGLX+8Er2CruOifLm\nTNkFOdU3qmVZvPTsq9z7qz9Ttz1yiR+wF7M+bt7+7D+jjPyZucw7ZhbeghysnBLwpEd9Tzyb6jaf\njqTNnZeQbR6wy/9o/ihr8wIqPRuVWRC3OUpT2uZ9nXbbDYsnVKieWrKW85HAawzefv1dbrn2NrqH\nlZaoqCrnB3feSGn5jBHeGckKBPnw8f9S/+6GiH05s0rZ/1PH4ckIPSEpC61tJ3pf5N/P8mbbBeLN\nqAAAFYJJREFUU2unIPiaqhtVKcWKt1byu//7AxvWbYz6Gq/Hw5I581lcUU1mXgZzj6omryIXfHn2\nh18C9XINlZBfSAlO2tx5CdvmSqF1t6J1NkXv/dJ0lC/frkEVZz04U9LmSqF1t6BHKZmkPOl2T1cS\nL88mgdcYbd1Uw/VXfi+i2nlWdhbfu+N6Fiw8YFzHq3tnPR8+/jpqWE9aao6PAz+7jMzSAntD6AK1\nb+hwypNuT7F1+EnK6RtVKcXrr7zF/b9/IOosRYAUl4sjq+fykeo5+DLTmXVYJaX7FaOlebGyihKy\nl2uohP1CSmDS5s5L+DYPDKB3NESMVAxSLo89/DjF6SJDOd7mcdqh4CQJvMahtaWN7179fdauWh+2\nPSXFzVU3XM7yU44b1/HaaxtY87fnGBhWWkJ3u5h3+tGULBwyu7KvC72tLrJL1pViJ92nOFd7yqkb\nNRgI8tKzr3L/Hx5ky8atUV+jaRqLZ1axZO58MtPTmXlQKVWLZ+JOT0VlFiZMguveJPwXUgKSNnde\n0rR5fzd6ewNaMPrajio1w34gnG6TpYJ+O4XGHz6jf3cKzTSpSi+B1zgN9A9w+/d+xvNPvRSx7xOf\nP4NzL/gC3oyxryPV39nD2r8/T/u2yHUDy47Yn9knH7En72ukJERNs2fopWWO7y8To8m+UQcG/Dzz\n+HP87Y8PjZjDBbBfSSnHzduffF8mRbMLmHNkFWlZ6aiMXLsmVxKtXJ80X0gJRNrceUnV5oPDj13N\naMqK3A2ojLwp/6xyrM0Heu3vr2HlIuJl0piTJPCK5Q9Uij//9q/88e77I/blF+ZxweVf5viTlo65\n5IQVCLLpqbfY8ebaiH3ZlcUc8JlleHzpgy+OOu0WwPIVoHx5k97DM1k3am9vH48//CQP3PcwzY0j\nr5M5t6iEY+cYlOXkkVWUydyjq8kpybJnwWQVxsVT5ERLqi+kBCFt7rykbPNgwE4V6W2PSBcBULrL\nflj05kxJMrkTba71tKO174rIf4unMklOksBrHzz35IvcfvOd+P2RBfMWLDqAS6+5gNnzZkV5Z3Q7\n3/+QDY+9hhUIfyLwZHqZe9pHKJhfaQdzSqF17ELviSyhYKVlonJKJjWJfKJv1M6OLv75wL94+K//\noqM9+hJJGrD/jHKOmj2Pkqxs0nypzD6yiuI5BeBOjbu8iYmWlF9IcU7a3HlJ3eb+PvT2XVFnP4I9\ncqHSc+zhNndK1NdMhkltc6XQOpvQuyMfpFVqhj1Sk6QzF0cjgdc+WrNyHbdcdxuNuyJnZ+i6zmmf\n+Bjnff0csrLHNgzYWdfE6r8+S397ZHJmRkkeVUsXUrBfFZqu2d3YHQ2RSfcuD8qXN2n5TRN1o25Y\nv5EnHnmKZ//zIr09kT14ALqmcXB5BR+ZNY/8DB/p2WlULiynZF4ReooblZmP8sbfTKGJltRfSHFK\n2tx5Sd/mSqH1ddq1v6zoFe4VoNIyURl54Jn8GmCT0uZK2XluXc1RA00rY3CWeXJ/bo9EAq8J0Nvb\nx/33PsCD9z0ctfcrKzuLr1z8RT52xnJcrr1H9wPdfax98AXaNtdF3e8tyqFq6SIKD6hC8/faQ4/R\ncghcKaEu7OwJ7QHblxu1q6ub5598iccfeYqN5qYRX+fWXRxSUcWR1XPJSk8nq8hH5cJyCqvzQbfX\nTlO++K2NM9GS/gspDkmbO2/atLlloXU32w/Po3yXKk86Vkae3Zs/SUHKhLb5YGDZ1YIW6I/cjYbK\nLra/k6YxCbwm0I7aOn55x28jlhoaNG+/OVxyzQUccNB+ez2WFbTY8uw71L72wYiv8RbmULl0IUXz\ny3C116MFRphBM8E5BOO9UZVSrFm5jsf/+RQvPfMq/f2RN+SgVHcKh1XO4vCq2WSkppI3M4fKReXk\nlmaD7kJ5c1AZOeByris+HkybL6Q4Im3uvGnX5lbQrn7f3RqRdD6UPYqRGxrFmNg0kglpc2Wh9XbY\nAdewyV+7X6K77HyuBC/tMxEk8JoEr7/yFr+647cjzshbfurxfO3S88gr2PvU2a5dLdS89D6Na7YQ\npS4fAOn52VQeu4DiKh+u/q6oCZwQKuKXkWMPze1DT9FYb9S21naeefx5nnj0abZtqR31tRmeVI6o\nns0hFbNI86RQPLuQykVlZBb4ULp7T8/dNMwHgGn4hRQHpM2dN23bXFlovZ12zcYRHqAh9BCdlolK\nzQCPd0JmQ+5Tm1vWkMBx5MXBVWoGVnbxtHtgHokEXpNkoH+AB//yT+6/9+/09UX28KSkuDnimMNY\nfspxHH70YXg8o1+Q3Q2t1Ly8koYPNtvj51Gk5WVSecyBFFdn4x7ojlpBGULdvd5sewZkDDfCaDdq\nb08vK95ayfNPvcSrL7xOIDDyzQgwp7CYRTOrmFtUQkqKm9L9iqk4uIz0rDSUO9XOVUvLnLa5AIOm\n7RfSFJI2d960b3OloL8HvbsFbaBn9JeigScdlZqBSssAlyemz8mY2twK2sFWd2vUNBf7/EK5ar68\nuF+v0mmOB16GYfwEOBKwgCtM03xnyL4TgB8AAeA/pml+fwyHjMvAa1DDzkZ+87N7efGZV0Z8TWaW\nj48uP5blpxzP/gfNH7UMRU9TGzUvr2TXyk0jBmCaSyezNJ/skixyClLJKc7Ekx4ZYCmANB8qxQ5y\ncKfaPWF7uXmH3qhKKWprtvPmq+/wxitvs3rlGgKBkbvMAbLS0lk4s5KF5ZVkp3vJyPNSPKeQsv1L\n8KSn2E9HGXl2l/Q0D7gGTfsvpCkgbe48afMh/H320F1f54ijGEMpl/3ZOd7esL22uVJgBSHQbxc+\nDfTb5zTC98/u9Sl9edOuTMRYORp4GYaxBLjaNM3TDcOYD9xrmuZRQ/avAZYD9cBLwNdM01wf/Wi7\nxXXgNei9d1bxy9t/w5ZNNaO+bkZZCSecchwnfOyjlFeUjfi6nuYOtr38PjtXbgRr7/8W3px0OxAr\nySS7JAtvTnrUAE9pOrg9qBQ7EFPuVLsq/pAhvgyvm/889Byvv/gGK977gKaWtr3++bqmMa9oBosq\nqphVUIQv10vxnAKKZhfiy/PavXDpoZk8DlbhTxTyheQ8aXPnSZtHEfTbPUs97SP2Lg23uzcsJRU0\nl50fq9v/DfulaeFtbll2YBXoB3+/PewZ6B81/2zon6m8OShfrgwp7oXTgdfNQI1pmveGfr8WONw0\nzS7DMKqBP5qmuSS071qg0zTNX+7lsAkReIG9BM6/HnqCh//2GDtqR67IPmi/BQbLTzmejy4/huyc\n6LNAels62PbKSna+9yFqDAHYoJQ0N9klWaRlpqJpWqhjSbP/FwrINM3+v2AwyM7WDtZ8WMPK9ZvY\nWFdPwBrbB0CeN4NFM6s4qLyCwsIcO9iaYwdbuNyhJzQfpHqnbf7WWMgXkvOkzZ0nbT4KZUF/D1p/\nt/1rhCT2cR1S03GlpBBUmj18GMMx7dzh0OStaTLLfF/FGnjF2rolwDtDft8U2rYx9N/GIfsagLFX\nH00ALreLMz/zcc749GmsX7OBZx5/nheefmXEoqHrPjBZ94HJz2/7NYXFBVRWz6SieiaV1RVUVJdT\nWV1Bdl4WxhnHUrl0IbWvraZpfU3UGmDD+fsCNG0NL2rnDwZo6uqiqatz96/Grg5ae7qxxhFo53oz\nmFtUwvziUuZVllI8p5DiOYX4CjLQPF5UWgZWaoY9tClDiUIIsXeabqeGpPlQStk9Yf3daH1dMNA7\nYk7vqIdUFtZA/5iGMoeb6or709FEhbWj/XuP+VooLHRmjcKJVFR0KEuOOxT/wJW8+tJb/Pvhp3jp\nudcZ6I8+o6VxVxONu5p45433wrbn5ucwe24V1XMqmD2nioqTD8Lf00/bjkbadjTTVtdEZ2MbSiks\npbCUhVIKpRRBS9Ha201TZweNXZ209Y6ezDkSl65TmVfAnKJiFsyupLp6Br78DHLLcsguzcWTlU1K\nZjYpvix0tzwRxSoRr/NEJ23uPGnz8cgHQFlB/F2d+Dvb8Xe2Yw2MPDMyJpqGKy199y93mhd3hg8t\nidbDTQSxfnvWYfdsDSrFzuca3DdjyL6y0La9SvSu6QMXHsSBCw/ikmu6eOm513j2iRdYtWL1mN7b\n2tzGO83v884b70/yWYbLSfeyf9VMFh0wl8WL51MwsxBvQTauVM/u/AGVkkbQnUqvptHrB1qjV6cX\neydDMM6TNneetPm+cIEnD/Jy7d6wgV47KT70SxvyMyq0bdgRFNj5WSl2fu/uHF9XCsGhoxN9QN/e\nR1ZEdLE+XMQaeD0N3AT81jCMxcAO0zS7AUzTrDEMI9MwjArsgOs04PMx/jkJyZfp49QzT+LUM09i\nZ90unvvPi7z47Cts3bwNKzi2nKrJkpuVSVlJEQsXHcjHzl5GUVUlepQq/HFTZEQIIaYjTbMnSA2b\nURjx2awUKIu87DRamjt2v28y1/kV+2Zfykn8EFgKBIGLgcVAm2majxqGcQzwY+xr5B+maf50DIdM\nmOT6WPn9fnZsq6NmSy01W2rZtqWWmi3bqK3ZgX9g3xMsB2maRklpcSiPLPRrVgUzq8rx+fYsQC1P\npc6TNneetLnzpM2dJ23uPCmgmsCCwSA763ZRs7k2FJRto6mhCU3Tcbl0dN3+5XK79vzs0tFdLly6\nju7Syc3LpXKWnbBfXllKWtreC93Jjeo8aXPnSZs7T9rcedLmznN6VqOYQC6Xi7KZpZTNLOWopUdM\n9ekIIYQQYpLIILAQQgghhEMk8BJCCCGEcIgEXkIIIYQQDpHASwghhBDCIRJ4CSGEEEI4RAIvIYQQ\nQgiHSOAlhBBCCOEQCbyEEEIIIRwigZcQQgghhEMk8BJCCCGEcIgEXkIIIYQQDpHASwghhBDCIRJ4\nCSGEEEI4RAIvIYQQQgiHSOAlhBBCCOEQCbyEEEIIIRwigZcQQgghhEMk8BJCCCGEcIgEXkIIIYQQ\nDpHASwghhBDCIRJ4CSGEEEI4RAIvIYQQQgiHSOAlhBBCCOEQCbyEEEIIIRwigZcQQgghhEMk8BJC\nCCGEcIgEXkIIIYQQDpHASwghhBDCIRJ4CSGEEEI4RAIvIYQQQgiHSOAlhBBCCOEQCbyEEEIIIRwi\ngZcQQgghhEMk8BJCCCGEcIgEXkIIIYQQDpHASwghhBDCIe5Y3mQYhhv4A1AJBIDzTNPcOuw1fuAV\nQAMUsMw0TbUvJyuEEEIIkchiCryAzwOtpmmeYxjGcuBW4LPDXtNqmubx+3R2QgghhBBJJNahxmXA\nI6GfnwWOjvIaLcZjCyGEEEIkpVgDrxKgESA0fGiFhh+HSjMM4z7DMF4xDOPKfTlJIYQQQohksNeh\nRsMwvgJ8FTtPC+yerMOHvSxaAHcVcF/o55cNw3jJNM0VsZ6oEEIIIUSi05Qaf767YRj3An81TfOZ\nUE/XFtM0Z47y+tuAtaZp/jH2UxVCCCGESGyxDjU+A3wq9PPpwAtDdxqGMc8wjL+EfnZj54CtifUk\nhRBCCCGSQayzGv8OLDcM4xWgDzgXwDCMbwEvmqb5pmEYtYZhvAUEgUdN03xnIk5YCCGEECJRxTTU\nKIQQQgghxk8q1wshhBBCOEQCLyGEEEIIh0jgJYQQQgjhkFiT6yeEYRhLgQew13p8Isp+We9xgo2h\nzb8AXI49KeK3pmne6/ApJhVZ19Q5hmH8BDgSsIArhk7oMQzjBOAH2P8G/zFN8/tTc5bJZS9tvgXY\nFtqngC+Yplk/JSeaZAzDOBD4J/AT0zR/NWyfXOuTYC9tPq5rfcoCL8MwZgFXAq+O8jJZ73EC7a3N\nDcPwAjcAh2LftG8bhvGwaZptzp1l0pF1TR1gGMYSYI5pmkcZhjEfuBc4ashLfgYsB+qBlwzD+Idp\nmuun4FSTxhjaXAEnm6bZOyUnmKRCn9M/x16uLxq51ifYGNp8XNf6VA411gFnAR2jvEbWe5xYe2vz\nI4C3TNPsMk2zDztAi7YOpxg7WdfUGcuwn0YJfcnkGIbhAzAMoxpoNk2zLtST+ETo9WLfjNjmIRpy\nbU+GPuBj2IFVGLnWJ82IbR4yrmt9ygIv0zT7xjCcIus9TqAxtPnuNThDGoEZk3tWSU/WNXXG8Gu3\nKbQt2r4G5LqeCKO1+aC7Qtf1D507reRmmqZlmmb/CLvlWp8Ee2nzQWO+1h0Zahy23uNgHsuNpmk+\ns5e3ynqPMdqHNh9KnlbHQdY1jSujXbtyXU+O4e16A/Ak0AI8ahjG2aZpPuz8aU1rcq07Y1zXuiOB\nl2ma9wD3xPC+uwd/NgzjOWABIF9IYxBjm9cR/nRUBrw+YSeV5KK1eWhd0xLgg8GeLtM0A8PeJ9f5\nvqsjvLellD3DAtGu6zqHziuZjdbmmKY5+DCBYRhPYF/XEnhNLrnWp8B4r/V4KScREZXLeo+TLtqT\n0JvAoYZhZIVyNY7Cnm0nYifrmjrjaeCTAIZhLAZ2mKbZDWCaZg2QaRhGRaiNTwu9XuybEds89Bny\npGEYKaHXLgVWT81pJrWwz3G51h0R1uaxXOtTtmSQYRinANcABvaYdL1pmicPW+/xVuB49qz3eOuU\nnGySGGObnw18E3ta7M9N0/zb1J1x4jMMQwd+B8wltK6paZo75DqfeKHciqXY7XgxsBhoM03zUcMw\njgF+jD0M/A/TNH86dWeaPPbS5pdir+PbA7xnmuZlU3aiSSQU5N6BXaLGD+wAHgO2yLU+OcbQ5uO6\n1mWtRiGEEEIIh8TLUKMQQgghRNKTwEsIIYQQwiESeAkhhBBCOEQCLyGEEEIIh0jgJYQQQgjhEAm8\nhBBCCCEcIoGXEEIIIYRDJPASQgghhHCIBF5CCCGEEA6RwEsIIYQQwiESeAkhhBBCOEQCLyGEEEII\nh7in+gSEEGKiGYaxGDgHUEAlcD5wAZADlAHfNU1zy9SdoRBiupLASwiRVAzDmAN8yTTNy0O//z3w\nBvAl7F7+V4AVwE+n7CSFENOWDDUKIZLNFcC1Q36fAbSYpvkGsA24A/jDFJyXEEJIj5cQIuncZppm\n75DfHwX8HsA0ze3AN6fkrIQQAunxEkIkGdM0awd/NgxjPlAKvDB1ZySEEHtI4CWESGYnAP3Afwc3\nGIZRPXWnI4SY7iTwEkIkDcMw0gzDuM0wjANCm04AVpmm2RfarwFXT9kJCiGmPcnxEkIkk1OwA6t3\nDcMIALOAtiH7rwf+NBUnJoQQAJpSaqrPQQghJoRhGPnAbUBzaNNNwK+APmAAeMw0zeem5uyEEEIC\nLyGEEEIIx0iOlxBCCCGEQyTwEkIIIYRwiAReQgghhBAOkcBLCCGEEMIhEngJIYQQQjhEAi8hhBBC\nCIdI4CWEEEII4RAJvIQQQgghHCKBlxBCCCGEQyTwEkIIIYRwyP8DISSI3m8k1zkAAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff758c1fe50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"b = 1\n",
"arange = np.linspace(0,b,3)\n",
"\n",
"\n",
"with sns.cubehelix_palette(3):\n",
" for aval in arange: \n",
" pl.plot(x,U(x,a=aval),linewidth=4)\n",
" \n",
"pl.title('With $a=0,0.5,1$',fontsize=20)\n",
"pl.xlabel('$x$',fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Above we have the potentials corresponding to the paths. To make things more concrete, here is the path superimposed on the potential."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def plotOnPoten(a,T=2):\n",
" x = np.linspace(-2,2)\n",
" pl.plot(x,U(x,a=0.5),linewidth=1,color='black')\n",
" path = EM(1.3,sigma=1, T=T, a=aval)\n",
"\n",
" pl.plot(path,U(path,a=0.5),linewidth=4,alpha=0.7,color=pale_red)\n",
" pl.title('For $a='+str(a)+'$.',fontsize=20)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlUAAAFKCAYAAAA0bqphAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4XOWd9//3maLepZFsudfjbmwwNtiAKcaYlkDo6ZuE\nhPQny7O72WdTN788eXaX3WQ3ZQMhfUPikEBCsenG2BRjG3f7uMs2Luq9TDu/P0aSJTSypJmRjkb6\nvK5Ll2TpzDlfbkYzH93ne+5j2LaNiIiIiMTH5XQBIiIiIiOBQpWIiIhIAihUiYiIiCSAQpWIiIhI\nAihUiYiIiCSAQpWIiIhIAihUiYiIiCSAx+kCRGR4M03zo8Av+tjMBj5uWdavh6CkYcM0zQzgDcuy\nFjpdi4g4T6FKRPrrt8CTF/j520NVyHBgmuYlwE+AeU7XIiLDg0KViPTXHsuy/ux0EU4zTXMW8G9A\nORB0uBwRGUYUqkQk4UzTLAW+CawGxgANwFvA/7Usa1OX7X4JfARYAPwrsAK4y7KsdUNccr9ZlnUA\nuBnANM1fAJc6W5GIDBdqVBeRhDJNs4TIqcD7gLXAJ4H/B5jAy6ZpXt9lc7v947vAqfZt9w5pwSIi\nCaKZKhFJtG8SmZ2617KstR3fNE3z94AF/Acwt8v2BuC1LOtT/T2AaZrXAA8AR4B8YCPwacuyroy7\nehGRGClUiUh/pZmmmXuBn9dblmUD7wdqgD92/aFlWSdN03wRuMk0zSmWZR1r/5EN/Km/RZim+Qng\n/wIXt++zFDhIJLD19phHgcXtx+qL0b7dly3L2tjfukREFKpEpL++QWQWKhobWGSaZhlQAmxuD1jv\nZQE3ATOBY12+fyzKtj2YprmQyBV3H7Us6ySAZVmnTdOsAV7p7XGWZX2iP/sXEYmHQpWI9NcjwO8u\n8PPDRE7FATT1sk1L++fM93y/oZ81/H/t23Y9rTgRGAds6Oc+REQGhUKViPTX0b5Oh5mm6W3/MquX\nTTrCVH9DVNd95xK5mvCPlmWFuvzoaiBEpK9KRMQxClUikjCWZdWZpnkGmG2aphHlFOCc9s/7Y9j9\ndMANvPme718J7LAsq940zcmWZR1/7wNN03wYWMTAeqr+1rKs12KoU0RGKYUqEUm0PwJfAO4BHuv4\npmmaM4jMKr1tWdapGPZb1/75RJd9pgLXcr4p/m/bj92NZVn3x3C8uJim6QGmAY2WZb071McXkaGn\nUCUiifbPRK4AfKS9sXwvMBH4DBAAPh/LTi3LOmya5jvAVADTNF3AfxE5pXjUNM1CoCr+8gckvb2W\ndMuyWt7zs3FEZuTWAzcOcV0i4gCFKhHpj/6cNgPAsqwq0zSXAt8msgBoCVBLpJH8ny3L2hNHHXcC\n3zdNcxyR16+HgJeBTwAXA1+NY9/9YpqmD/gNkdDUcTrzuGmae4CfWZb1WJfNOxY3FZFRwLDtgf++\nm6aZCfyayJU+KcC3Lct6PsG1iYiIiCSNWG9T8zHggGVZ1xD5y/EHCatIREREJAnFGqoqgcL2rwuA\nisSUIyIiIpKcYjr9B2Ca5joilzjnATdZlrUlkYWJiIiIJJOYZqpM0/wgUGZZ1gwilzP/KKFViYiI\niCSZWK/+Ww48B2BZ1i7TNEt7Weivk23btmEYMR5OREREZEgNOLTEGqoOA8uAJ0zTnAQ0XChQARiG\nQUXFgO9MMaL5fNkakyg0LtFpXKLTuPSkMYlO4xKdxiU6ny97wI+JNVT9FPi5aZobiNw24tMx7kdE\nRERkRIgpVFmW1QTcneBaRERERJJWrEsqiIiIiEgXClUiIiIiCaBQJSIiIpIAClUiIiIiCaBQJSIi\nIpIAClUiIiIiCaBQJSIiIpIAClUiIiIiCaBQJSIiIpIAClUiIiIiCaBQJSIiItJFdXVVTI9TqBIR\nERFpZ9s2q1dfHdNjFapERERE2h07dpTW1taYHqtQJSIiItJu48YNXHWVZqpERERE4rJx4wauvHJl\nTI9VqBIREREBQqEQmza9qlAlIiIiEo/du3dSXFzCmDFjY3q8QpWIiIgI8Z36A4UqEREREQBefXUD\nV14ZW5M6KFSJiIiI0NLSwrZtb3P55ctj3odClYiIiIx6W7a8yZw5c8nJyY15HwpVIiIiMurF208F\n4In1gaZp/g3wYcAGDOBiy7Jy4qpGRERExAEbN27g29/+blz7iDlUWZb1c+DnAKZpXgncGVclIiIi\nIg6orq7iyJHDXHzxkrj2E3Ooeo+vA/claF8iIiIiQ2bz5tdYunQZKSkpce0n7p4q0zQvAU5YllUe\n775EREREhlq8Syl0SESj+ieBXyZgPyIiIiJDbuPGV+JuUgcwbNuOawemaR4A5lmWFexj0/gOJCIi\nIpJgx44dY9myZZw5cwaXq9tckzHQfcXVU2Wa5ligoR+BCoCKioZ4Djfi+HzZGpMoNC7RaVyi07j0\npDGJTuMS3WgflyeffIYVK66kqqqp2/d9vuwB7yve039jAfVSiYiISFKKnPqLv58K4gxVlmVttyzr\npoRUIiIiIjKEwuEwr732akL6qUArqouIiMgotW/fXnJz8xg/fkJC9qdQJSIiIqNSIm5N05VClYiI\niIxKieynAoUqERERGYXa2trYsuUtVqy4ImH7VKgSERGRUWfbtreZMWMGeXn5CdunQpWIiIiMOok+\n9QcKVSIiIjIKRe73tzKh+1SoEhERkVGlvr6OAwf2s2TJ0oTuV6FKRERERpXNmzdxySVLSEtLS+h+\nFapERERkVBmMfioYwlBl2/ZQHUpERESkVxs3buCqq1YmfL9DFqpeeumloTqUiIiISFSnT79LVVUl\n8+YtSPi+hyxUrV+/fqgOJSIiIhLVxo0bWLHiKlyuxEegIQtVzz///FAdSkRERCSqRN/vr6shC1Wn\nTp3i3LmzQ3U4ERERkW5s2x4Zoeqaa65hw4aXh+pwIiIiIt1Y1gHS0tKZPHnKoOx/yELV9ddfr1Al\nIiIijtm48ZVBueqvw5CGqldffYVwODxUhxQRERHpNJin/mAIQ9XkyZPJzc1l7949Q3VIEREREQAC\ngQBvvPE6K1ZcNWjHGNIV1VeuVF+ViIiIDL3t27cxefIUCgsLB+0YQxyqrlWoEhERkSEXuTXNykE9\nxpCGquXLV7B9+1aam5uH8rAiIiIyyg12PxXEGapM0/ygaZo7TNN82zTNNX1tn5WVzYIFC3nzzc3x\nHFZERESk3xobG9i9exdLl142qMeJOVSZplkAfB24HLgZeF9/Hrdy5TW88opOAYqIiMjQePXVDVx8\n8RIyMjIG9TieOB57HfCCZVnNQDPwmf48aOXKa/jSlz4bx2FFRERE+m/9+me48cabBv048Zz+mwxk\nmqb5F9M0XzVN85r+PGjBgos4d+4sp0+/G8ehRURERPoWDAZ54YX1rF5946AfK55QZQAFwPuBjwO/\n6M+D3G43V155Na+++kochxYRERHp25YtbzJ+/ETGj58w6MeK5/TfOeB1y7Js4Khpmg2maRZZllXZ\n2wN8vmwAbrnlRl588UW++MUH4jj8yNAxJtKdxiU6jUt0GpeeNCbRaVyiG8njsmHD83zgA7cNyX+j\nYdt2TA80TbOUyOzUDURmrLZalnWhOxTaFRUNAJw6dZJVq65k794juFxDuqrDsOLzZdMxJnKexiU6\njUt0GpeeNCbRaVyiG8njYts2S5Ys5Fe/+h1z584b0GN9vmxjoMeLOdFYlnUaeBx4E3gG+Hx/Hzt+\n/AQKCgrZvXtnrIcXERERuaB9+/YCNnPmzB2S48Vz+g/Lsh4BHonlsR23rFm4cFE8JYiIiIhEtW7d\n06xZcxOGMeBJp5g4du5N9wEUERGRwbR+/bPccMPgL6XQwbFQddllK9ix4x0aGxudKkFERERGqFOn\nTnLq1IlBX0W9K8dCVVZWFosWLeaNNzY5VYKIiIiMUM899yyrVt2AxxNXp9OAOHrpnU4BioiIyGB4\n9tlnhvTUHyhUiYiIyAhTW1vDO+9sY+XKft3sJWEcDVXz5i2gurqKU6dOOlmGiIiIjCAvvvg8y5ev\nIDMzc0iP62iocrlcXHWVblkjIiIiibN+/bOsWXPzkB/X8eXMV668VqcARUREJCFaW1vZsOFlVq26\nYciP7Xiouuqqq9m48RVCoZDTpYiIiEiS27TpVWbPnoPP5xvyYzseqsaOLaWkZAy7du1wuhQRERFJ\ncuvWDe2Cn105HqoArrpKVwGKiIhIfMLhMM899yxr1tzoyPGHRai6+mqFKhEREYnP9u1byc/PZ+rU\n6Y4cf1iEqmXLlrNr104aGxucLkVERESS1Lp1zzhy1V+HYRGqMjIyWLz4EjZtes3pUkRERCRJrV//\nDDfc4MypPxgmoQo6Vld/yekyREREJAkdPnyIhoYGLrposWM1DLNQpb4qERERGbh1655h9eobcbmc\nizbDJlTNnTuPhoYGysqOO12KiIiIJJl1655mzRpnllLoMGxClW5ZIyIiIrE4d+4chw4dZMWKKx2t\nY9iEKtApQBERERm4559fx9VXX0NKSoqjdQyrUHXVVVezadOrBINBp0sRERGRJBE59efcUgodhlWo\nKikZQ2npeHbs2O50KSIiIpIEGhsbePPNN7j22lVOlzK8QhVETgG+8oqWVhAREZG+vfLKS1xyyRJy\ncnKdLiX2UGWa5lWmaZabpvmyaZqvmKb5g0QUtGrVap57bl0idiUiIiIj3Lp1zzh2A+X38sT5+A2W\nZd2VkEraLVt2OadPn6Ks7DiTJk1O5K5FRERkBAkEArz44nP80z990+lSgPhP/xkJqaILt9vNDTfc\nxLPPPp3oXYuIiMgI8uabrzN58hRKS8c5XQoQf6iaY5rmk6ZpbjRN87qEVATcdNMtPPPMXxO1OxER\nERmBhstVfx3iCVWHgG9alvV+4GPAo6Zpxns6EYArrljJwYMHOHfubCJ2JyIiIiOMbdvDqp8KwLBt\nOyE7Mk3zLeAuy7LKetlkQAf60Ic+xPLly3nggQfiL05ERERGlHfeeYc777yTQ4cOYRgJ70aCGFqc\nYp5ZMk3zPmCsZVkPmaY5BigG3r3QYyoqGvq9/+uuu5Gf//wR7rjjQ7GWOOz5fNkDGpPRQuMSncYl\nOo1LTxqT6DQu0SXruPz2t79n1ao1VFY2Dsr+fb7sAT8mntN/fwWuMk1zI/AE8BnLshK2FPrVV1/L\njh3bqa6uStQuRUREZASwbZs///mP3HbbB5wupZuYZ6osy2oEbk1gLd1kZGRw5ZUref759dxzzwcH\n6zAiIiKSZN5+ewter5eLLlrsdCndDLsV1bu6+eZbefrpvzhdhoiIiAwja9c+xl133TtYvVQxG9ah\natWq1bz++mYaG5PvXK+IiIgkXmtrK0899QQf+EBC1x5PiGEdqnJyclm6dBkvvPCc06WIiIjIMPDC\nC+uZN28B48dPcLqUHoZ1qAK4+eb38cwzTzldhoiIiAwDa9c+xp133uN0GVEN+1C1evWNbNjwMi0t\nLU6XIiIiIg6qqKjgjTde5+abB+06ubgM+1BVVFTEggUL2bDhZadLEREREQc9+eTjXH/9DWRlDXwN\nqaEw7EMV6F6AIiIiAmvX/p677rrX6TJ6lRSh6sYbb+GFF9bj9/udLkVEREQccODAfs6dO8sVV1zl\ndCm9SopQNXZsKVOnTmfz5tecLkVEREQc8Mc//p477rgbt9vtdCm9SopQBXDTTbfqKkAREZFRKBQK\n8fjjfxi2V/11SKJQdQvr1j1NKBRyuhQREREZQps2bcTnK2b27DlOl3JBSROqpkyZSnFxCW+//ZbT\npYiIiMgQWrv2Me6+e/g2qHdImlAFkdkq3QtQRERk9GhsbOS559bx/vff4XQpfUqqUNWxurpt206X\nIiIiIkPgmWf+ymWXXY7P53O6lD4lVagyzVmkpaWxc+c7TpciIiIiQ2C4r03VVVKFKsMwuOmmW3n6\naS0EKiIiMtK9++4p9uzZyapVNzhdSr8kVagCuPnmW3n66b/oFKCIiMgI96c/reWWW24jLS3N6VL6\nJelC1cKFi/D7/Rw4sN/pUkRERGSQ2LbN2rWPJc2pP0jCUBU5Bah7AYqIiIxkO3e+g9/vZ8mSS50u\npd+SLlSBVlcXEREZ6TpmqQzDcLqUfkvKULVkyVLKy89x7NhRp0sRERGRBPP7/TzxxOPcccfdTpcy\nIEkZqtxuN2vW3KzZKhERkRHopZdeYMYMk8mTpzhdyoDEFapM00wzTfOwaZofSVRB/RXpq9Lq6iIi\nIiNNsjWod4h3puprQFUiChmo5cuv4MiRw5w+/a4ThxcREZFBUFNTzcaNG7j11vc7XcqAxRyqTNM0\ngVnAM4krp/9SUlK4/vo1rFv3tBOHFxERkUHw5JN/5tprryMnJ9fpUgYsnpmqh4CvAI615Wt1dRER\nkZElWU/9QYyhyjTNDwOvW5ZV1v4tR4LVypXXsGfPbs6cOe3E4UVERCSBjhw5xMmTJ1i58lqnS4mJ\nEcvtXkzT/D0wBQgD44FW4NOWZb18gYcNyn1l7r//fqZMmcJXv/rVwdi9iIiIDJGvfe1rNDc389BD\nDzldCsQwYRRTqOrKNM1vAMcsy/p1H5vaFRUNcR0rmq1bt/C5z93Pm2++k1QLhAH4fNkMxpgkO41L\ndBqX6DQuPWlMotO4RDdcxiUUCnHppQv51a8eY968+U6Xg8+XPeBQkZTrVHV18cVL8Hq9vPXWG06X\nIiIiIjF6/vn1+Hy+YRGoYuWJdweWZX0rEYXEyjAM7r33w/zud79h2bLLnSxFREREYvTTn/6IT3/6\nc06XEZekn6kCuPPOe3j22adpbHR++lJEREQGZvfunRw/foybb36f06XEZUSEquLiYpYvv4K//OUJ\np0sRERGRAfrpT3/M3/zN/Xi9XqdLicuICFUA990XOQUoIiIiyePcubM8//w6PvKRjzldStxGTKi6\n9tpVlJUd59Chg06XIiIiIv30i1/8jNtuu4O8vHynS4nbiAlVHo+Hu+66l8ce+63TpYiIiEg/tLS0\n8Otf/4JPfeoBp0tJiBETqgDuvfdDrF37GIFAwOlSREREpA9/+tNaFi1azPTpM5wuJSFGVKiaMWMm\nkyZN5uWXX3S6FBEREbkA27Z5+OEfJ/0yCl2NqFAFalgXERFJBq+++gqG4eKKK65yupSEGXGh6n3v\nu43XX99EeXm506WIiIhILyKzVJ9NulvMXciIC1VZWdmsWXMTjz/+B6dLERERkSgOHTrIjh3vcPvt\ndzpdSkKNuFAFkVOAjz32G+K9WbSIiIgk3sMP/4SPfvRvSEtLc7qUhBqRoWrp0svw+/1s377V6VJE\nRESki5qaap588k987GOfdLqUhBuRocowDDWsi4iIDEO/+c0vueGGGykpKXG6lIQbkaEK4K677uWv\nf32SpqYmp0sRERERIBAI8OijD4+oZRS6GrGhauzYUpYsuZSnn/6L06WIiIgI8NRTTzJt2nTmzZvv\ndCmDYsSGKoB77/2wblsjIiIyDNi2zU9/+iPuv/+zTpcyaEZ0qFq9eg0HDx7g6NEjTpciIiIyqm3Z\n8hY1NTVcf/0NTpcyaEZ0qEpJSeEDH7iLP/zhf5wuRUREZFR7+OEfc//9D+ByjdzoMXL/y9rde++H\n+f3vf0coFHK6FBERkVHpxIkyNm/eyD33fMjpUgbViA9Vc+bMpaSkhFdffdnpUkREREaln/3sp9xz\nz4fIyspyupRBNeJDFURmq373OzWsi4iIDLXGxgb+8If/4ROfuN/pUgbdqAhVt99+Bxs2vExVVZXT\npYiIiIwqjz32W664YiUTJkx0upRBF1OoMk0z3TTNP5imucE0zTdM07wp0YUlUm5uHqtWrebPf17r\ndCkiIiKjRigU4pFH/ptPf3rkLqPQVawzVbcAb1uWtRK4G/j3hFU0SO6778P8z//oJssiIiJDZd26\nZygoKOCSSy51upQh4YnlQZZldZ3ymQicTEw5g2f58itobGxg164dLFy4yOlyRERERrRQKMT3vvfP\nfPOb38EwDKfLGRJx9VSZprkZ+C3w5cSUM3hcLhcf+cjHefjhnzhdioiIyIi3du1jFBQUcu211ztd\nypCJK1RZlrUceB+QFKtrfvSjf8MLL6zn1KlhP7EmIiKStFpbW/mXf/kuX/vat0bNLBWAEUuPkWma\ni4Fyy7JOtf97L3CVZVmVF3jYsGhmevDBBwmFQvzHf/yH06WIiIiMSA899BCvvfYaTz75pNOlxGPA\naTDWUPVlYJJlWf/LNM0S4C3Lsib38TC7oqJhwMdKtNOn32Xlyst4660d5OcXOFqLz5fNcBiT4Ubj\nEp3GJTqNS08ak+g0LtElelzq6+tYtmwRTzzxLKY5K2H7HWo+X/aAQ1Wsp//+Gyg2TXMj8BSQNNdK\nlpaO44YbbuKXv3zU6VJERERGnB/+8AesWnVDUgeqWMV69V8r8MEE1zJkPve5L3H77Tfzmc98nvT0\ndKfLERERGRHOnTvLr371KC+/vNnpUhwxKlZUfy/TnMXixRfzhz/8zulSRERERoyHHvp/3HPPhxg3\nbrzTpThiVIYqgM997sv8+Mf/SSgUcroUERGRpHf06BH++tcn+NKXvuJ0KY4ZtaFq6dJlFBX5eOaZ\nvzpdioiISNL73vf+mU9/+nMUFBQ6XYpjRm2oMgyDL3zhf/Ff//V93bpGREQkDjt3vsMbb7zO/fcn\nzXVrg2LUhiqA1avX0NzcxKZNG50uRUREJGl95zvf5Ctf+TsyMzOdLsVRozpUuVwuPve5L/HDH37f\n6VJERESS0saNGzhxoowPfeijTpfiuFEdqgA+8IG72L9/H7t373K6FBERkaRi2zbf+c43+OpXv4bX\n63W6HMeN+lCVmprKpz71AD/60Q+cLkVERCSpPPXUk4RCYW699TanSxkWRn2oAvjoRz/OK6+8yIkT\nZU6XIiIikhQCgQDf/e63+ad/+iYul+IEKFQBkJOTywc/+FH++79/6HQpIiIiSeGxx37LuHHjWbny\nGqdLGTYUqtrdf/8DPP74H6iqqnK6FBERkWGtubmZf/u37/FP//RNDGPA9x0esRSq2o0ZM5abbrqV\nn//8YadLERERGdZ+9rP/ZsmSpSxadLHTpQwrClVdfPazX+QXv3iE5uZmp0sREREZlmpqqvnJT/6L\nf/zHrzldyrCjUNXFjBkzWbJkGY899lunSxERERmWfvCDf+fGG29l2rQZTpcy7ChUvcfnP/8lfvKT\n/yIYDDpdioiIyLCye/cu1q79HX/3d191upRhSaHqPZYsWUpp6TieeupJp0sREREZNgKBAF/84gN8\n/ev/TEnJGKfLGZYUqqL4/Oe/pBsti4iIdPGDHzzEmDFjuPvu+5wuZdhSqIriuutWEwj4efXVV5wu\nRURExHF79+7h0Ud/ykMP/aeWULgAj9MFDEcdN1r+/vf/jauuulpPIBERGXXCtdUErL0Ejh3hnb/8\nme995X9TWjrO6bKGNc1U9eKOO+6murqK9eufdboUERGRIWG3NOPftZ3mx39L8+9+TmDbWxzd9hYT\nMtO5LiPF6fKGPc1U9cLj8fCtb32Xf/iHv+Xaa1eRkqInk4iIjDx2IEDwsEXg4F5CJ45DONz5s8bG\nRsrKjrNs2eUQCmHbts7eXIBC1QVcffW1TJs2nUcffZgHHvi80+WIiIgkhG3bhM+cImDt48ypo7Q1\nNPXYJmzb7Nm7i+nTZ5Kelk7K4qUKVH2IK1SZpvkvwArADXzPsqwnElLVMPKtb32XW29dzZ133kNR\nUZHT5YiIiMSso08qeHA/dkM9AK7U6FGg7PgxPB4v48dPwDN7Hp65C4ey1KQUc0+VaZorgTmWZV0O\nrAG+n6iihpMZM2Zy22138K//+l2nSxERERmwaH1SHYGqN01NTRwvO8bcOfNwl44n9cpVmqXqh3hm\nql4F3mr/uhbIME3TsCxrxC3u9OCD/8CKFUv42Mc+yezZc5wuR0RE5ILsYJDQ8SNR+6SiMdIzMDKz\nCFeWYxM57Tdt2gwyiktIX30rhts9NIUnuZhDVXt4amn/5yeBZ0dioAIoKCjky19+kG984x/5wx+e\nUFoXEZFhp2ufVPCIBX7/hR/g8eCZMp3CpUuoC3pofuJ3AJSVHcflcjNh6lTSbrwNIz1jCKofGeJu\nVDdN833Ax4Hr4y9n+Pr4xz/FL3/5KC+99DzXXbfa6XJERESA6H1SvTIM3KUT8Jhz8EydgZGSSkqW\nh5aHfwptbTQ1N3Hs2FGWLr2M9Otuxl3oG5r/iBHCiOdWLKZprga+Bay2LKuuj82Tfhbr6aef5sEH\nH2T37t14vV6nyxERkVEq1NREy/69NO/ZTeDs6T639xQWkTFvARlz5+POyen8vh0KUfXH39N2/Ci2\nbfP6669TWlrKwo99guzLlg/mf0IyGPBpqZhDlWmaOcBrwLWWZVX24yF2RUVDTMcaLmzb5q673s/q\n1Wv45Cc/E/f+fL5skn1MBoPGJTqNS3Qal540JtEl+7jE0iflmTkbz8w5uIqKo7autG16GcPahb8t\nSNmJ45w7d47L7vsYadfdOOpbXXy+7AEPQDyn/+4GCoG1pmkaRGaiPmJZ1qk49jmsGYbBt7/1Xf7l\n/g/zgamTyb3kMlw5uU6XJSIiI1S3PqmjB6Gt7cIPaO+T8phzcY+fhOHq/SL/wL5dBHZtJyXVQ1Nz\nE0ePHuGSG24m7erVoz5QxSqeRvVHgEcSWEtSmNZUxwOLFnLkL39k1tGDpN3wfjzjJzpdloiIjCDx\n9kn1JXT6JG0bXwQiwW3f3j2Mm2FScs/HMDxaFzxWGrkBCp09zfRpM9j8+mtMmDARnvkTadfeiGe6\n6XRpIiKSxOyWZgKHDhA8uI9w+dk+t3flF0aC1Mw5uLKy+32ccF0tLev/0nn60LIsAsD8L/49rozM\nWMsXFKoGzDN5GiknjzNl8lQs6wCLF11M6wtPk9rSjHf+IqfLExGRJHK+T2ofoRPH+tcnNWNWJEj5\nSgZ8ms72t9G67globQXg9Ol3OX36NEse/BrekrEx/3dIhELVAHnmLiRwcC8TwmFOnjpBZVUlRYVF\ntL32EuHjibPWAAAgAElEQVTmJlIuXa5z0SIi0quY+6RmzsE9YfIF+6QueNxwmNYXnyFcXQVATW0N\n1sEDXPaZz1G4aElM+5TuFKoGyHC5SLt6DeHf/4KZM2dhWQcouGw5LsMgsO1NAtveJPPjn9ViaSIi\n0s1g90n1xf/Wa4SOHwWgpaWFnTvfYcrVq5h11z1UVjbGvX9RqIqJq6AQIzOL4mI4caKMd989yYQu\nzepNv/gx7qkz8M5bhHvcBM1ciYiMUkPVJ9WXwIE9BN55G4BgKMj2d7ZRPGsucz/5Bb1HJZBCVYwy\n7v4oTT//EaY5i23btjJmzFi8nvMLgoaOHiJ09BBGbi7eWfPxzJqHKzPLwYpFRGQoDHWfVF9CZ96l\n7dUXIrVhs2vXDtIKCrn4wa9haCHrhFKoipGRlk7ajbfBs09QXFzM0aNHMGfO6rGdXVeH/61N+Lds\nxj1pKt7Z83FPnKKbU4qIjCBO9Un1JdxQT+v6v0AoBIBlHcAfCnPF338Td3ZOH4+WgVKoioNn8jQ8\ncxcw3d/G669vYty48WT1Nhtl24SOHyF0/AhGRiaeWXMJLl8GpAxpzSIikjiRPql9BA/uc6RP6kLs\ngJ/WdU9gtzQDcOrdk1RWVrD0wa+ROm7CoB57tFKoilPqFdcROnqYGTNmsmvXTpYuvQx3H39x2M1N\nBLZv4dze7YQKx+CZPR/PNFMLromIJAG7pZnA4fY+qXPO9UldiG3btL60jnBlBQDV1VUcOnSIRR/+\nBPm60m/Q6F08TobLRfr772bcY7+gsrKSQ4csZpmz+/340OlThE6fom3Ty3hnzMYzZwHuouJBrFhE\nRAZquPVJ9cW/ZTOho4cAaGpuYtfuncy45nrG3Xz7kNYx2ihUJYArv5DUy69iTsDPG2+8TlGRj6LC\nooHtpK2NwJ4dBPbswFVcEmlunzELIzVtcIoWEZELiqtPavwkx3pnA4f2E9j2ZuTrYIB33tlG6Zz5\nmJ/4rK70G2QKVQniXXAxaUcPMa+hgT17dnHZsuWkpETvl3LlF0JqKtSUR/15uPwcbeXnaHt9A55p\nJt7Z83GNHadfBhGRITCgPinAPW4CHnPukPRJ9SVUfpa2V54DIGyH2blzBzm+Ei76yj9ieNXDO9gU\nqhLEcLlIu+YGCivLGTu2lD17d7No0cVEi0Hhmiq8F11C8e23c+71Nwlae7FbWnpuGAwStPYStPZi\n5OXjnT0fjzlX92YSEUmwmPukZszGNUyuogs3NtC67kkIBrGBAwf2YxsGl/zvr+HKznW6vFFBoSqB\nXHkFpFy6nOkBP1veepOTJ08wccLEqNsGdmyl0RUiZelKUpZeQej4YQL7dxM6WQa23WN7u7YG/xsb\n8b+1CffkaZGlGQbxMlwRkZEu2fqkLsQOBGhd/xfspsjK6MePHaWmpoZlf/uPpIyL/j4kiadQlWDe\nBRcTPHqI+QsWsmXLmxQUFPS6zELz3t2EKmtJW30Lnmkmnmkm4YZ6ggf2EDiwJ/q0czh8fmHRrCw8\n5rzI6cEc/RUiItKXSJ/Uu5HbxSRRn9SF2LZN2yvrCZefxQYOHbKoKC9n4X0fI3fRpU6XN6oYdpRZ\nkUFiV1Q0DNWxHBWuraZ57a85VXaMEydO9LrMQkqqB39bEFfJGNJvvL3b/QLtcJjQqTKC+3cTPH6k\nc+G23rgnTMIzax6eKTOSfmkGny+b0fJcGQiNS3Qal540Jj2Fa6tJP3OU6q3bk65Pqi/+rW/g37KZ\nsG2zb98empoaWXTzbeTffl+/zmbo+RKdz5c94KnI5H73HaYipwFXMC4Y7NcyC+FzZ2l+4jHSb7mj\n87y34XLhmTgFz8QpkXP91j6C+3cTrqmKuo/QyTJCJ8toS0vDO3MOntnzcRf6BuW/T0QkGby3TyqY\n6sFuC/a6/XDsk+pL8MjByPIJ4RC7du0kHA5zybWrybn1TrWHOEChapB4FywmePRgv5dZsGtraPnz\nY6Td/IEeYchIzyDlokvwLryY8NnTBPbvJnjkAASivDi0thLYtZ3Aru24SsZGmtunz8Lo5UpEEZGR\nZCT1SfUlVFlO68vPti+bsJ20tDQWXrqMrFvvGvazayOVTv8Noo7TgFXl56Ius9Bx+q+b1FTS19yG\nu3T8Bfdt+9sIHrYI7N/V95UqXi+e6Sbe2QtwlYwd9i8amoqOTuMSncalp9E2Jp19Ugf3ETxi9don\n1fma6/FEbjPWcd+9YdgndSG2bROuqqD1qcdprath27atFBQUYM6eQ8Ytd+IeYGP6aHu+9JdO/w0z\nrrwCUpauoHDzhj6XWejU1kbLU38k7fqb8UyZ0etmRkoq3jkL8M5ZQKiqguD+3QQO7oPW1p4bBwIE\n9+8huH9PZHp7zny8M+d06+ESEUk2A11PKnXiJIzx0yN9UkmysLLd0ky4upJwdRWh6krCNVWEqyuh\ntZWm5ia2b9/KuHHjmTJlGmlXXDfgQCWJpVA1yLzzFxM8cpDpdrjPZRY6hUK0rv8rqVdeh3fuwj6P\n4S704V5xDSnLriR47BDB/bsJnToRddtwTRX+zRvwv/la5IqW2fMjV7QM89krERGIbz2poqnjhu2M\njN3WSrg6EpjCNVWEqyoJV1d23gz5veob6tm+fRvTp09n/LgJeBcs7tf7hQwuhapBFlkUdA3Na391\nfpmF/AKysqIvs9DJtml79QXslma8Fy/rV+gxPB68M2bjnTGbcF0tgQO7CR7Y27luSTehEMHDFsHD\nFkZ2TqT3ata8IbvZp4hIf42kPinb7ydcU3k+QLV/jvo63Yvq6ip27trBnDnzKCkuwT1hEimXrxy8\noqXf4gpVpmnOA54E/t2yrB8npqSRx5WXT+rVq+Hl9cyYMZNdu3eydOll/Xqsf8tm7OYmUlZcM6Ar\nOVy5eaQuvYKUJcsJnTgWWVi07AiEoyws2lCPf8tm/G+/jnvC5MjCopOnJV2fgYiMHP3tk+o0zPqk\n7EAgMuNU0xGeIgGqP6cpL+Rc+Tn27dvD/EUXUzxjFu6JU0i5aImu9BsmYg5VpmlmAP8JvJi4ckYu\n74zZuH1jmLT1dSr/+DsOHNjHoosu6tdjA3t2YLc0k3rdjRjugf0vM1yuyAvN5GmEm5vOLyxaW9Nz\nY9smdOIYoRPHIn/pmXMiC4vmFw7omCIisYrpvnsz5zjWJ2WHgoRrayKn62q6hKf6uqh3xxgwtxtX\nfiFGQSEbd+3i0ede5Bvf/xGTLr1sWM3ASUQ8M1WtwBrgHxJUy4jnyssn/bqbmLd/N1u3buGAdYCp\nU6b367HBIwcJHjlIyqXLcRUV48rJxcjOGdANMl0ZmaQsXop30aWRO6/v303wyEEI9lyawW5pJrBj\nK4EdW3GNKcU7ZwGeaTN1Q05xnG3bkdM/oSCEQvjPNRE4cgK7tga7pRm7rRU74MfweMGbgpGaGrm8\n3OuNvMkFg9jhcGQmw5uCkZKC4W3f1psCXi9G+/fxpoDbrTevQWa3NEeuZj64t199UkZ+AV5z7pCu\nJ2WHQth1tYSrKyMN4+0fdn1t1DMAA+Z248rLx5VfiKugqPPDyMmlsqqKv//7r3Dw4AF+/T+PM3Xq\ntPiPJ4Mi5lBlWVYYaDNNM4HljA4et4fFiy/h7bffwuVyM3nSlH4/1r9lc7d/GxkZGDl57SErF1du\n+9c5eRgZmVGnhA3DwF06AXfpBOwV1xA8dIDA/t2EK85FPWb47Gnazp6mbdPLeGbMiizNMMz6FGRk\nsG2b0Kky/G++ht3SjMtXjOHxEjpzCrsxes9JINrSJInkMnoErnB5zzd+95RpeCZNw1U8JjKzoNPn\nF2QHg4TK2vukyoZPn5QdDmPX13bpeWpvHK+t6fPOFv3iMjByz4cnd0d4ys2L+px56qkn+Yd/eJC7\n776PH//4EdLSkuOqxdFKjeoOSFl2Bbz5GsuWLWPz5s14vV7G9bEuVW/s5mbs5mbCZ0/3/KHbjZGd\ncz5wdYSv3Dxc2TkYqWkYqWl4512Ed95FhCrORZZmOLQ/ev+C309w7y6Ce3fhKvThmT0f78zZGGnp\nMdUuo48dDGI3NhBurMduqCd0+iRBa1+v2/vramlta6WttRV/wE8wGOzxYdth2tr8hELnvxcKhdrP\nvETpIez81vmfuV1u3B43Ho8Ht9uDx+OOfHa7cXs87d+P/Nzj8ZKamtr54fF4MYDQsSOEjh3p9b/F\nNaY0csXtpGkYefmjsgdmOPVJ2baN3VDfPThVVRKurY46ez9ghoGRk4uroH3mKb8IV2ERrrz8Pts4\nbNumurqar371b9m9exe//OX/sGTJ0vhrkkEX9+Kfpml+A6joR6P6kK0ymgwCVZWUP/ITGhsbeeON\nN5g/fz5jxowZ0hpcaWm48/Lx5OXjzs3Dk5eHOy8fd2Ym/jOnad6zC//J6EszdDDcbtLM2WQuvIiU\niZM1eyUAhBobCZw7i//0u7QeOUTg7Jke2wSDQVpbWmlpbaG1tZWWlsjnrl+HgiHS0tNIS0trDzCR\ngOP1ePB4vV3+7cXj9XT+29Pl/pcXek4aGNjYhMPhqIEtFAr1+F4gEKCtrY3W1lba2toIh8OkpqaS\nlppGaloqaamppKaldX7OzMggPSMDVy8hypWWTtqMmaTNNEkpGYsrO3vE/R4Fqqpo2buL5j27CdXX\n9bl96sRJpM+dT7o5G1ecMzO2bRNuaCBQUU6gsoJgZTmBikqCVRXYgUBc++7gzsnF6/PhKSrGW1SE\np8iHp8iHy+vt1+PDfj+thw/Ssn8fbceOcPr0Gb7+7HPMvulmvvOd75Cerj9cHTLgX8REhapKy7J+\n1Memo25F9b4UFWRw6oknqX7jNbZt38rCBRdRUDBMmsINAyMrG+xwr6ddejwkNxfvrPalGTL7WDLi\nArS6b3TDcVzs1hYCu7cT2L+71+eJ3++nqamRxqZGmpqaaGxspKmpkUAgQFpaJDBFAknPr73elD5f\n1aLemWAIhUIh2vxttLV1fLTS1ubH39ZKa1sbLS3NtLa2kpqaSkZGJunp6WRkZJKRkUFGRgbp6el4\nos1cuAw8s+dHTikWFWNkZvU7bA2H58pQ90nZto3d3NR91qljoUy/H4j/uWJkZrX3OhWe/5xfFNNt\nwOxgkNCJYwQPHyBYdgQCkcC+/8A+6urqmLPoYiY++PUhCdjD4fkyHA3piuqmaS4GHgImAQHTND8A\n3G5ZVm2s+xxtDLebtKuuxzd2AgtDIXbufIfFiy8hNyfX6dKgfWp8QA+pq8P/1ib8b23CPXlaZGmG\niVPUWzJC2OEwoWOHaX1lfeebVFdtfj8NDfWRANUYCVBNTY3Ytk1mZhZZWVlkZmZSWFhEZmYkXBgD\n/0Owd4Zx4Q/bjtSd4Ftzud1uMtIzyLjAHQrCdpjW1laam5vbP5qora2hubmZlpZmPB5Pe8jKJCsr\nm6ysLLKzs7HbT7f3kJJC2jVrcJdOwBhGPTZD1SfVdZXxcE1VZ+N41DtKxMBIz4iEpsKi843j+YVx\nj7UdChE6eZzgEYvgscPdfo8qKsrZt38vJSVjuPyy5XiGyx/YMiC695+Duv51EKos5/DPfsihd7ay\n5JKlZGZmJuQYRk4urrwCXPkFEAoRrq8jXF8bCUyJaLrsJ+/FS/FMmIKRk9vnX9z6qym6oR6XcFMj\ngV3bCLzzdo+fBUNB6uvrqauro76ulrr6OoLBINnZOZ3hqSNIpaSkJjI69eD0TFW8bGza2tpobm5u\nn8lroLGxkcbGBrAhMysyjllZ2WRnZZGZlUVKlKtwXWNKI0u3TJhM8fQJVFb2fzHJuOofxD6pga4y\n3pcez5W0tM7A5O4yA5XIW3jZ4TChd09EZqSOHe4R/ALBANaB/dTU1jB37nwK8gsw8vJJu3YN7pLS\nhNVxIXrNjS6WmSqFKge994lst7aw7fvfo3znNpYsWUp6ghvAXYVFuCdOwTNxCq4xpdgtLdjtIStc\nX4fdUEe4LhK4BrK6byyMvPzzjfM5kSb6yOdciscV6Rc8isF+4bMDfoLWPtpee6nbbE4oHKaxsSES\noOrrqKurpaWlhezsHHJzc8nJySU3N5eMjIzEzjz1U7KHqt7YgN/f1hmwIp8jH263i6ysbHKyc8jO\nySYnO5eMzPPj33VMPDNm45k5G3fp+IQuiRKurYkEqYP7Imsy9cFdOh6POTfqelJRVxmvqex360Gf\nUlJwFRSRM3Eczd7M88sVZGQOyum1SNA8FblrxZGDUUNg2A5z5sxpDh8+THFxMTMuWkz6rHl4ps8a\n8qurFaqiU6hKMtGeyHY4zPrvfQtj7w4uXbKUlBjO1fdLSgru8ZPwTJyCe+KUHrensYPBnoGrvha7\nvp5wfS0kqMEzmrTcbPypmVECVx5GVvaovGoKEv/CZ9t2ZLmMNzcSPvNu5/eDoSC1tbVUV1dTU1NF\nQ0MDGRkZ5ObmdQaorKwsXMbA/z8YGZkYmVlghyOpIRzGxo6EuKgf4cip6Av8PMXrwd82eM/H4cYG\n2lpbaWisp76+gYaGeurr6wkE/JGglZNDfn4eGRlZZGZm4Y62rEpOLp72W1oZ+QUDOu0W6ZPaR/hc\nz4sPehwnvwDvzDl4Zs7GlZ2LHQy+Z4XxxKwy3snriVxlV/CetZ7aZ8cHMzzYtk3o6CH8W18nXFXZ\n63bBUJBTp05SVnYcIyOTKStXMXPVjbjGlDp2gYJCVXQKVUnmQk/kR7/xVcYePcDlly6N3sSaYK5C\nH+5J7bNYJaUXnpK3bWhtOR+46rsHrnhfIC848+AyMLJyOtfi6hq8XDm5kJo24q6c6hDvC1+4oZ7A\nvl0Edm/v1svRM0Q1kpuTQ35BAfn5BeTm5uEZQF+ckZePd+YcXGPG4S4ZM+gLxvp82ZSX118wlEUN\nZrQvImrTGfLsju2h/WfRAh7d9ttzmy776eXDtrse9z0/C4Ww62oIV1YQrqnq9zgEggEaGhqor6+n\nqamB2to6WlqaycjIJCcnp/0jl+zsbNyu6P8/3eMm4pk5u9tsUix9Uu6p0yOnrlzuQV1lvFt4yi+M\ntBcMYmtBtz82qysJlh3t9gfJhbT52zhxooxTp05SUFDIpJkm4778f4bFH4kKVdEpVCWZCz2Rbdvm\n23/7RRZUn+GaSy6N+tfmoElJwTNhMu6OWawBXslnh0LYjfWEqyrxv7OlX3/Rdjt8PKdzUlK6BS5X\ndvu6XDm5GFk5GJ7kXZptoC98diBA24bnCB460O37UUNUbg75+QUU5BeQm5fX65tuD4YRObU0Zhyu\nMaWRWYEhDrWj5Q2h64re4ZpKgieO9/q71fE7FAqHaGxooL6hgfr6uvbA1UhGRgY5Obn9CloD4vFg\nZGZhN9QlZpVxlyuyyniXWSdXQWFkceMYXhP7eq7Yth1Zlb++jnBdTWQttYpzhMqO9hkme9PU3ETZ\n8eOcPXeGMWPGMnnyFDLSM0i5dDkpl/TvHrCDbbT8Dg2UQlWS6euJHAqF+MJn/obLw35uuegi3A5d\nRecqKo70Yk1qn8WK4cUsXF1F4MBugtZe7JaWC247mD0yRlZW98DV5fTiYPVXJEp/3hBCZUdpffaJ\n7t/HpqGhgcrKCqoqK6lvqG8/RVRAQUEhubm5/X5DdZWMxT123PkQlZGYCyriMdrfEOxQiHBtdXsj\ndwWhsqN4Gmp6/R3q6JGrr69/T9B6z4xWVvbQveYYRuSPn/bg1Ncq47Hy+bIpPxsJS+H6ukhIra8j\nXF9D+NxZ7OamhB2rvr6OY8ePUV1dxYTxE5gwcTKp7e0cKZevxDvvomHzR95o/x3qjUJVkunPE9nv\n9/PFL36G4rPv8oUrVyS8eX3AUlO7z2IN8E3VDoUIHT9MYP9uQifLop4KiHqFTm5epIG+ObarfvrF\n42mf2WoPWtk53Rronb7vYbTnS7imiubHftFjW3/AT1VVVSRIVVXi8XgoKvJRVFhEfn5B/94s09Ii\nAaqkFPfYcbh8Y4bNm0BXekPoqSM8hGtrIjNbleUEDx3Abow+TueDVl1n2GpqaiI9PZ2cnByys3Pb\nP2fj9fRvQcuouq4ynn9+5smVV5Cw55Zt29DWSrimmnBlOaHKcsJVFYSrKkjxGIN6UUMoFKKquooT\nJ8poampiwpQpTFq+koyZs/FMmJzQqwoTSb9D0SlUJZn+PpFt2+YnP/khL//6Uf7t/bdSlDM0NxDt\nD5evBPfEyXgmTsVVMnZAs1jhhjqCB/YSOLCnWx9WtJkqIysLjzkP74xZkcd29nHVtfd1Rf7iTMjt\nJXphpGecD1gdM1zZubhyczEyB7+B3ufLpvxkBW0bXyB42Or2Mxuburq6zhDV2NhEQUEBRYVFFBYV\nXXANpQ5GfgHuMaW4x47HPaYUIzd/WM/cddAbQk8XbC0IBiMzW9VVhCvOEti5Lep2YTtMY2Mj9fX1\nnc3wDQ0NpKamkJ3dPqOVnUN2Tg6pKanxF+12R/q4XAa23x91LbR4DcYseHNLM5WVFVRUVFBbW0NO\ndg4lEycx/f98d/AuNEow/Q5Fp1CVZAb6RH711Vf4+pc/y0O33Ig5ZuzgXbzudkeusvN4Iwvq9fc5\nkpaGZ/wk3JOm4p4wud+zWHY4TOhUGcH9uwkeP9LnX5PuCZMiK01Pmd7tHlrd+iE6A1eX4NXUmPCF\nHzu5XOfvs9h+arHbVYsxLhpoB4OEzpyi9anHe7whBIIBKisrqagop6qyktS0VIoKfRQWFZGXl99n\nH56rNBKe3GPGRUKU07OgMdIbQk+xjEln2KqqIHTiOMFD+3tug01TU1OXkBX5bBhGZC2tzKzOxUt7\nW0/LSYkIVWE7TE1NDRUV5VRWVhIMBigq8uEr8lFQWIjX48U77yJSr7wuQVUPPv0ORadQlWRieSKX\nlR3nW5/+GPdPncjsOfMGt4E9LQ3PpKkYWTnYDXUETxwb0IrFruIx59fFKh7Tr5kcu6WZ9DNHqX7r\n7b6vfEpLi1yuPXs+7kJf3/sOBc/3UnRdLqL968H4y7hTaur5Hq7cvO79XNk5nX0jtm0TrqogaO0j\nsHNrt12kpHqora2noqKciopy6urqyM8vwOcrxufzkZZ64eDmnjwV97iJuMeU4ioqGTEr3esNoadE\njokd8BM6e5rggb29BK2O9bS6r6XVdT2tyIKw7avqZ2TiTen79kODIZZQZQNtba2ds1HV1dVkZWV2\nBqnsnJxu67OlXnMDHnNuUszydtDvUHQKVUkm1idy3R9/w56XnqOlpZmLFi4mbQhuU+EuHY9nzgJc\nWdkET50gdOIY4YpzA5vFau/F8kyccsHego5L5MNnTxPYv5vgkQMQuPALoatkLN7Z8/FMnxXbfbg6\n+jC6Bq6GuvOzXA31MV/9E4+O03odQaqtzY/P56O4uJiCgqILLnXgnjQFz/RZuMeOjwS3JHqRHwi9\nIfQ0FGMSqiynbeOLhM+ejvrzjvW0Gpu6h62W5mZC4RDp6emRj7R00tIzuv17sELXhUJVIBjovIVQ\nc1MzTc1Nka+bmzEMg8LCokhfYlFRtxk4z+z5kdnzcROHbc9UX/Q7FJ1CVZKJ9Yncsu4JgseOcPz4\nUcrKyli48CLy8/IHocKejPR0POZcvHMWYqSmEjxxLHJT0JPH+z+LZRi4fCV4JrU3u/u6z2L1WGne\n3xZZcHD/rr5vzOr14plu4p29INLjlaAgYYfD2E0NhOu6LoRa1xnCYr1tRjSRZtdKysvLqaioICUl\nheLiYkpLx5KRkdXrquXucRPwLrwE99hxPVasHsn0htCTU2NiB4O0bX45+v0KuwiGgrS0tNDS0kJr\n++eW1vP/7ghdaWlpeDxePB5P+4cXr/f81+e/H/mILD0WJhQOEQ6Hu3xE/u1yGbS1BQiHw/j9bZ0h\nqqmpmVAoRGZmRpebXUc+Z2Zmdt7Y28jOwVXkw1VYjLt4TJ+32UkW+h2KTqEqycT6RA43NtD61OOE\na6qorKpk9+5dTJs2nQkTJg7plLp73ES8cxfinjIdDINw+dn2kHWUcPm5/u8oLa1zZXfPhMkUTyzp\ndVxCVRUE9+8mcHBfnyHOlV+IZ858vDPnDPpfkLbf32Vmq7b7gqj9WMDRH/BTUVFBefk5qquryMnJ\npbi4GJ+vuLPJ/L1/ZbuKS0i5dAXu8ZOGxQKCTtEbQk/DbUzsYJDgEYu2l9b1a/uO0NXW2kogGCQY\nDBIMBAiGIp87vxcMEgwGOr82DAOXy9X+4cbtcmG4XLjdke95PB4gso3X6yUzM7MzPKWmpnW+froK\nCnEV+iIfRcXdVmUfiYbb82W4UKhKMvE8ke1QiMDOrfi3vkFTfR07drxDXl4es2bNGdqFQtu5x00k\n5bIrO+9ZFW5uInTyOKGyowRPlQ1oFitr8kT8ReNwT5ra6z2w7GCQ4LFDBPfvJnTqRB/FufFMmR6Z\nph8/adBfGG3bJlxxjsDOrT0W3uyquaW5fTbqHPX1DRQWFkaCVFExXm/Py9bTC/OwL7kS95TpozpE\nvZfeEHpKpjHpnAWuqoy0FdTVEq4sT+jsb4eUVA9+w4MrryCycGr7+5974hQ8081IgErg8g7JIpme\nL0NJoSrJJOKJHK6vo23ji7QdO8SePbtpa2tl/vyF/bqEfqgY2TnYAX+/g9V7Z2SMzCzck6dFmuYz\nsyJX2rnd4HKDy4Xd1EDw4P7I7FVbW5+1eGfPxzNrXo/7HcYjVFlOYNubBI8c7HUbG2hoqKf83DnK\nK8ppa2uluLiEYl8xBYWFURfgTL16deQqx7R0vfD1QuPS00gbE9u2IRTC9reB34/tbyNcV9N+4+Uq\nXNm5eKZOB7cnsi5XVSXh6gpchT48U6Zjh8LYtdXkj/PRkF2C4fHQ8d43UmefBmKkPV8SRaEqySTq\niRy5kedBWp57irKyYxw7dpTS0nFMnTotvoX6HDKYK6pH4x43EbwecLm7hDUjslyDywXuSHgzXO7O\nr8PVlQQP7O1z32E7THV1dWejuWEYkSBVXEJeXl6P/ijPrLl4F14S9XYveuGLTuPSk8YkOo1LdBqX\n6CaZdMsAAAzYSURBVGIJVaNrjnOEMgwDzzSTjDtymfz4bxk7tpTDhw+xadNrTJs6jfETJuAydLqo\nN6F3+zh9OECBQICKyorI+lFVlWRmZuHz+Vi86BIys7J69L2lrXk/7vETHV+xXURE4qNQNYK4i8eQ\nfueH4Y+/Ye6ceUyc2MDBgwc4cbKMmTNNfL6S/jeyp6RAKBT5kD41NTdRUVHR3h9VT0FBIcW+YmbN\nmt1ztem0NDJu/2DkvmY69SAiMmIoVI0wbl8JmZ/5Cm0vPUv2oQNcvHgJlVUVWJZFWVkZpjmLnOx+\n3ObG7ydlxdV45yzsPN3l3/oGoaOHBv8/IgmEbZu6utrO03qBQACfr5jJk6ZE7Y9KWXI53kWXjroG\nWBGR0UQ9VQ4a7PPYtm0TPHSAthefIWzbvPvuKY4cOURRYRHTZ8zscwXurlxjSkm5dAWu7GwCO7cR\n2LNj0Ooe6p6q/mptbaWyqoLKykqqq6tIT0+nqMhHsa+YnNzcHv1RGfd+HFd+YcKOr76H6DQuPWlM\notO4RKdxiU49VdKNYRh4Z87GO3M2wWOHmbDuScaOHcuxY0d54/XNTJgwkclTpuBx9/00CJ89Tetf\n1w5uvdk5uMdNJGf8GGpPnY2s81RXG7lnnwNC4TA1NdVUVVZSWVWB3++nsLCIYl8xs2fP6XFaz1VY\nRPodHx4RiwGKiMjAKVSNEp4p08m8/8v439zIDLeH8eMncOjQQTZu3EBxcQljx5ZSUFDQ62rdQ8Fu\nqCd4YA9NFacwJs0kdeHFGKlp2G2t2LXVnZdPhyrOYdfVJv74QHNzE5WVFVRVVlJTW0NWVjZFRUXM\nm7eAnPfc4wsg/Y4P4S4ek/BaREQk+ShUjSKGx0PqimvwzJoHa3/NgvkLaW1r5eyZMxw8aOH3tzGm\nZCxjx44lOyfXsXgVamwksH0Lge1bBvU4YdumoaGe2toaamoiH26Xi8KiIsaNG8/8BQt7LEnhmTaT\n1GtvVG+UiIj0EPM7g2ma/w4sA8LAly3L2pqwqmRQuYuKyfzMV2h58veknT3N5MlTmDx5Co1NjZw9\nc5qdu3ZgGC7Gjh3LmDFjyczIdLrkhAiGQtTV1XaGqLq6WtLS0snPz6e4uATTnEV6Wnq3x7jHTyT1\nqlW4cofm3ooiIpK8YgpVpmleCUy3LOty0zRnAT8HLk9oZTKoDJeLjNvvA8AOBQnu34Px9utkZWYx\nbfpM6upqOXPmNFu2vEV6enpnwOqxPMAwFbbDNDU10djYQH19PTU1NTQ2NpCdnUN+fj4TJ04iP++i\nnreDSUsj/eY7er09joiISG9inam6FngSwLKsA6Zp5pmmmWVZljMdxRIX4/9v7+5j3arrOI6/2972\nsnt778iegbC5TfcVMhWXBcyYTJkMVHRx8SmiCQSMfywq+BhNCP4hZiERI38YIzJMQGOUgPOPQQYo\nY+CCT4vBpy8umRJ3L2MPbrS7G+1t6x/nXG5v1/uw3tP2tufzSpp71vNr9+033/Z8e87p76R6SK+9\ngvTaKwAoj5ym91//4MLnn8HsMk6cOM7w8BAHDx4kk0kzMDBINptlIDtAdmCAvr6+tp2LVa5UOHNm\nhHwuRz6fJ386Tz6f48zIGebNmxfEOTjImjXG/Pnz614KpueytfRu2qLr6YmIyKw02lQtA6oP9x0L\n7zs464ik7ZJ9/WTesZ6eS1fy+r6nWZRIsGjhoqCBGRkhl3+NfC7H0PAQuZdyFAoFstn+8WYr/JuZ\n5QzhFSoUCkWKxQKFQoFioUAhXA72QuUZGTlNb28v2ewA2WyWJUuWsGrVavr6+uteWDq1cjW9GzeT\nyA5oT5SIiEQqqrNttXXqQskFC5m39eNUKhXKr75C+fhRMsP/pd//DksvemPcaGmUXC5HPp8jl8tx\n5Mgr5HJ5KpUyyWSSVCo18W8yRbLmvkQiQbFYDJqnsSaqWCTdkyadyZAJb+l0mkwmw8KFi1ix4k30\n9/dPOSVE5sqrg0k3Nc2BiIg0WaNN1RDBnqkxFwPD0z1o8eKBBv+77tUxOVkyCKyZcFelVOL0Xw5w\nas/j9PVdwNKli6tWQqlcolQKbuVyuf5yqUypXKJSqbzROFXfZro3qXfVagaveS/ppcu6eg9Ux9RL\niykv51JO6lNe6lNeotFoU7UH+BZwv5mtAw67++npHqQZWyfqillsLzUytxoAlWIBkikSqRSjLx9i\ndP+zcPwoqWSSVBLSM6y2sRnVi4Xx6w4msgOk376O5IJFpC5Zfs6epwpwCuBY957W1xX10gTKy7mU\nk/qUl/qUl/oaaTQbaqrcfb+Z/cnMngdKwPZGnke6S6LqHKqe5SvpWb6yoefRG1xERDpRw+dUufs3\nowxEREREpJPpN+QiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUi\nIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIB\nNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIiIhIBNVUiIiIiEVBTJSIi\nIhKBhpsqM9tkZkfM7ANRBiQiIiLSiRpqqsxsFXAH8Fy04YiIiIh0pkb3VA0BHwFeizAWERERkY7V\n08iD3P0sgJlFG42IiIhIh5q2qTKzW4HbgAqQCP/e5e5PNjk2ERERkY6RqFQqDT/YzB4Efunuu6ML\nSURERKTzRDGlQiKC5xARERHpaA3tqQqnUfgqYMBRYNjdb4g4NhEREZGOMavDfyIiIiIS0IzqIiIi\nIhFQUyUiIiISATVVIiIiIhFoaPLP6ZhZCngAWA2kgK+4++9qxtwEfBEoAfe7+85mxDLXmNkm4BfA\nLfWmojCzIrCP8TnBNrt715/4NoO8xK5ezKwH+AmwAhglyM2/a8bEpl7M7F7gXUAZuN3d/1i17n3A\n3QR5etzdv92eKFtvmrwcAl4O11WAm9x9uC2BtpiZrQV+Bdzr7j+oWRfnepkqL7GsFzO7B9hI0K/s\ncPfHqtadV600pakCPgPk3f3dZnY58CBwVVWQfcCdwPow0D+Y2aPufrJJ8cwJM7xm4v/c/doWhTQn\nTJeXuNYL8CmCevi0mV0H7AA+WTMmFvViZtcAb3b3DWb2VmAnsKFqyPeB64BhYK+ZPeLu/2xDqC01\ng7xUgBvc/UxbAmyT8DPjPuCpSYbEtV6my0vs6sXM3gNcHr6HFgAHgMeqhpxXrTTr8N9DwJfC5aPA\ngpr1VwG/d/d8eMmb54CrmxTLXDKTaybGcd6v6fIS13rZzPib+ynqv+a41Mtmgm/XhB9oF5pZFsDM\nVgLH3X0o3Eu3OxwfB5PmJZQgPjVS7SzwfoIN4QQxr5dJ8xKKY73sBT4WLp8E+swsAY3VSlOaKncv\nuXsh/OftwM9qhiwjaLbGHAUuakYsc4m7n53BoZkLzOxhM9tnZne0JLA2m0FeYlkvVL3uMD/l8JBg\ntbjUS20NHAvvq7fuVeJRHzB1Xsb8MKyP77QurPZy97K7vz7J6tjWyzR5GROrenH3StWeuduA3VXb\no/OulVkf/pvq2oBmth14J/ChaZ6m6zrjWVwz8cvAw+Hys2a2193/3LxIWyuia0l2e71A8BqvrBlW\n70tQV9fLFKaqga6rj/NQ+9rvBJ4ATgC7zGybuz/a+rDmtDjXS63Y1ouZbQVuAbZMMWzaWpl1U+Xu\nDxCclD5BuJH4ILDV3Us1q4eY2O1dAuyfbSxzyWR5mcHjfjS2bGZPA28DumYj2WBeYlkvZraT4JvS\ni2N7qNx9tOZxXV0vVYaYuAfmYsYPYdSrj6EWxdVuU+UFdx9ruDGz3QT1EYuN5BTiXC9Timu9mNn1\nwDeA6909V7XqvGulKYf/whOPPwdsc/dinSEvAOvNbDA8/r+B4BdMcXJOx2tma8zsp+FyD8E5NH9r\ndWBtVu+bQFzr5UnGj/V/GPht9cqY1cse4KMAZrYOOOzupwHc/T/AgJktD/NwYzg+DibNS/h+ecLM\n0uHYTcBf2xNmW034TIl5vVSbkJe41ouZDQL3ADe6+6nqdY3USlMuU2NmdwOfIPhp5tghni0Ehyqe\ncfcXzGwb8DWCn27e5+4/jzyQOWayayaa2dcZz8sO4FqCqQN2ufuO9kXcGjPMSxzrJQn8GHgLwQmm\nN7v74bjWS3iOxyaC17odWAecdPddZraR4IOxAjzi7t9rX6StNU1ePg/cDIwAB9z9C20LtIXCBvO7\nBNORFIHDwK+BQ3GulxnkJXb1YmafBe4CXmK8X/kN8GIjtaJr/4mIiIhEQDOqi4iIiERATZWIiIhI\nBNRUiYiIiERATZWIiIhIBNRUiYiIiERATZWIiIhIBNRUiYiIiERATZWIiIhIBP4PHGIgfndNEgwA\nAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ff75a5944d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plotOnPoten(1,T=10)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
prabhamatta/Analyzing-Open-Data | notebooks/Day_13_C_Baby_Names_MF_assignment.ipynb | 1 | 1330809 | null | apache-2.0 |
ashwindeo/dataschoolers | 2_ProcessBookHiLoGradRate.ipynb | 1 | 9431081 | null | apache-2.0 |
modin-project/modin | examples/tutorial/jupyter/execution/omnisci_on_native/local/exercise_1.ipynb | 1 | 7111 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"<center><h2>Scale your pandas workflows by changing one line of code</h2>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Exercise 1: How to use Modin\n",
"\n",
"**GOAL**: Learn how to import Modin to accelerate and scale pandas workflows."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Modin is a drop-in replacement for pandas that distributes the computation \n",
"across all of the cores in your machine or in a cluster.\n",
"In practical terms, this means that you can continue using the same pandas scripts\n",
"as before and expect the behavior and results to be the same. The only thing that needs\n",
"to change is the import statement. Normally, you would change:\n",
"\n",
"```python\n",
"import pandas as pd\n",
"```\n",
"\n",
"to:\n",
"\n",
"```python\n",
"import modin.pandas as pd\n",
"```\n",
"\n",
"Changing this line of code will allow you to use all of the cores in your machine to do computation on your data. One of the major performance bottlenecks of pandas is that it only uses a single core for any given computation. Modin exposes an API that is identical to pandas, allowing you to continue interacting with your data as you would with pandas. There are no additional commands required to use Modin locally. Partitioning, scheduling, data transfer, and other related concerns are all handled by Modin under the hood."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<p style=\"text-align:left;\">\n",
" <h1>pandas on a multicore laptop\n",
" <span style=\"float:right;\">\n",
" Modin on a multicore laptop\n",
" </span>\n",
"\n",
"<div>\n",
"<img align=\"left\" src=\"../../../img/pandas_multicore.png\"><img src=\"../../../img/modin_multicore.png\">\n",
"</div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Concept for exercise: Dataframe constructor\n",
"\n",
"Often when playing around in pandas, it is useful to create a DataFrame with the constructor. That is where we will start.\n",
"\n",
"```python\n",
"import numpy as np\n",
"import pandas as pd\n",
"\n",
"frame_data = np.random.randint(0, 100, size=(2**10, 2**5))\n",
"df = pd.DataFrame(frame_data)\n",
"```\n",
"\n",
"When creating a dataframe from a non-distributed object, it will take extra time to partition the data for Modin. When this is happening, you will see this message:\n",
"\n",
"```\n",
"UserWarning: Distributing <class 'numpy.ndarray'> object. This may take some time.\n",
"```\n",
"\n",
"Modin uses Ray as an execution engine by default. Since this notebook is related to OmniSci, let's run examples on the OmniSci engine. For reaching this, we need to activate OmniSci either via Modin config or Modin environment variable. See more in [OmniSci usage](https://github.com/modin-project/modin/blob/master/docs/development/using_omnisci.rst) section.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import modin.config as cfg\n",
"cfg.StorageFormat.put('omnisci')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Note: Importing notebooks dependencies. Do not change this code!\n",
"import numpy as np\n",
"import pandas\n",
"import sys\n",
"import modin"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"pandas.__version__"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"modin.__version__"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Implement your answer here. You are also free to play with the size\n",
"# and shape of the DataFrame, but beware of exceeding your memory!\n",
"\n",
"import pandas as pd\n",
"\n",
"frame_data = np.random.randint(0, 100, size=(2**10, 2**5))\n",
"df = pd.DataFrame(frame_data)\n",
"\n",
"# ***** Do not change the code below! It verifies that \n",
"# ***** the exercise has been done correctly. *****\n",
"\n",
"try:\n",
" assert df is not None\n",
" assert frame_data is not None\n",
" assert isinstance(frame_data, np.ndarray)\n",
"except:\n",
" raise AssertionError(\"Don't change too much of the original code!\")\n",
"assert \"modin.pandas\" in sys.modules, \"Not quite correct. Remember the single line of code change (See above)\"\n",
"\n",
"import modin.pandas\n",
"assert pd == modin.pandas, \"Remember the single line of code change (See above)\"\n",
"assert hasattr(df, \"_query_compiler\"), \"Make sure that `df` is a modin.pandas DataFrame.\"\n",
"\n",
"print(\"Success! You only need to change one line of code!\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we have created a toy example for playing around with the DataFrame, let's print it out in different ways."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Concept for Exercise: Data Interaction and Printing\n",
"\n",
"When interacting with data, it is very imporant to look at different parts of the data (e.g. `df.head()`). Here we will show that you can print the modin.pandas DataFrame in the same ways you would pandas."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# When working with non-string column labels it could happen that some backend logic would try to insert a column \n",
"# with a string name to the frame, so we do add_prefix()\n",
"df = df.add_prefix(\"col\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Print the first 10 lines.\n",
"df.head(10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df.count()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Please move on to [Exercise 2](./exercise_2.ipynb) when you are ready**"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.10"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
idc9/law-net | explore/Iain/pref_attach/PageRank_DAG.ipynb | 1 | 124425 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Investigate PageRank in a DAG"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The autoreload extension is already loaded. To reload it, use:\n",
" %reload_ext autoreload\n"
]
}
],
"source": [
"import igraph as ig\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy import stats\n",
"from math import *\n",
"\n",
"%load_ext autoreload\n",
"%autoreload 2\n",
"%matplotlib inline\n"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"N = int(1e5)\n",
"M = 1\n",
"\n",
"\n",
"# uniform attachment\n",
"ua = ig.Graph.Growing_Random(n=N, m=M,\n",
" directed=True, citation=True)\n",
"\n",
"# preferential attachment\n",
"pa = ig.Graph.Barabasi(n=N, m=M,\n",
" directed=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Time vs indegree"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x114866590>"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABJ0AAAJoCAYAAADMP5DXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xt4ZWd9H/rvT5INGHuE7RnJ4CE2JMb2OBhMKWD5ggwE\nGpKQtCehnDQnTWjIU5KUpG2aQNpzbJpeIG0OuTWnbUooUDhcQtMGmh4wzogapiEJmGAHbAzBlzFY\nnhlfawKMRu/5Y28pGlmjkT1L2nv2fD7Po4e93/WutX7a4mF+fPe71qrWWgAAAACgS2ODLgAAAACA\n0SN0AgAAAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOid0AgAAAKBzQicYYVX1/1TVP17x/rVVdXdV\nPVhVpw+ytq1UVedU1WJV+d88AKATVfWMqrqhqh6oqp8agnreUFX/foNz31ZV/3Sza3q0qupvV9X1\ng64D6I7/AwYjrLX22tbaP0+SqppI8stJXtJa29Zau2+w1R1ureanqr5cVS/q6BSto+Mck6raXVWv\nHnQdAMAx+7kkf9Bam2yt/cZWnriqXlhVd64ca639y9baj2/BuQ/rzzbhy71h6dkWq+rpg64DjndC\nJzhxnJXkcUk+/1h2rqrqthwAgOFUVeMbmHZOkj/bxOOve4gMSTiTv6xl1HrFYfl84bgmdIIht/pb\nlpUrgpa+5aqqf1BV81V1V1X9yOq5VXVekpv7w/dV1Uf722eq6o+q6r6q+mRVXbpi391V9c+q6uNV\n9XCSp/XHfrGqPlFVD1XVf62qM6rqP/WXln+yqr5lnd/lfVX11f755qrqwv74a5L8rSQ/17/0779W\n1TuSfEuSD/bHfvYIx9i14viPr6pfrqrb+tv/R1U9bmlzkh+qqtur6p6q+oUV+13dP+47++f606o6\nr6pe3/9cb6+ql6yYv62q/kNVfaX/+f/iUii3tCy8qv5VVd1bVV+qqpf1t/2zJFck+Y3+eX5to/89\nAACOTX+Fzuur6s+q6kBVvbWqTu5vW+qpfq6qvprkt/vj392/hO6+fk/07f3x65JcleTf9P9N/7aq\nOrmq/nW/b/hqVf3mUh/yKI7/zFX1/sN+X3JfVb2nf45Tkvx+kqf0+7EHq+qsfj/zzhX7H7FnOsrn\n9PSquq6q9vd7pv9UVdv625b6sw+t6M8+1t/1/v7Y89c7Rv84O6vqA/1t+1b1RLWqj/prKzY8ql60\nqi6oqo/0/96fr6ofWLHtbVX1G1W19Lv8z6p6Wn/bx9LrHT/b3/YDAR4ToRMMv6N9y3JWktOSPCXJ\nj6XX/EwedoDWbk1yUf/tZGvtJdW7p9OHkvxKkjOTvCXJf6vD7/X0Q/1jnpbkjv7Y30wvIHpKkm9L\nsifJW5Ocnl6wdfU6tf5+km9NMpXk00ne3a/vt5K8K8kv9S/9+97W2g/3z/nd/bF/fYRjvGvF8X85\nySVJXpDkjPSWvS+u2H5ZkvOSvCTJ/1VV56/Y9t1J3p7kSUk+k+TD6TUbT0nyi0lW3iPh7Um+meTp\n/fN9R/9zWvK89FaUnZnkX6XfWLbW/kmS65P8VP93et06nxUA0L0fTO/f7W9Ncn6Sf7Ji21np9QHf\nkuTHq+qS9Hqc16TXV/y79L4MO6m19uL0/k3/yf6/6V9M8ub0eqOL+/95dpL/61Ee//eq6qQV+/xA\nkpcmeVr/uD/SWvtaku9M8pXW2mn989/dn7+yb1yvZ1pPJfkX/XovTLIzyTVJsqI/+64V/dmV/f22\n9cc+ud4xqncZ3oeSfLn/WZyd5D0rzv/8HN5HvXVVfRvqRfvh3EeS/Kck25O8KslvVtUFq451dXp/\nly8l+ef93/OF/e3P7P9O79/gZwesInSC4Xe0pcrfTPKLrbVDrbX/nuR/pddEHe1435XkC621d7fW\nFltr70nvH+rvWTH3P7bWbu5vX+iPva21dltr7aEk/z3Jl1pru1tri0nen14Is6bW2n9srX2ttXYw\nyT9N8qyqOu0ov99hv/+RjtFfafSjSV7XWru79fxhf17Sa8Kuaa19s7X22SR/muRZKw59fWvtoyt+\nj+1J3tRaO5ReI3RO9VY4TafX6P391trXW2v70wvu/vcVx7q9tfbbrbWWXkD15KqaOsrvCQBsvl9v\nrX2ltXZ/egHDyn+/DyW5urV2sLX2jfTCoH/bWvuTfl/xziTfSO/LrbW8Jr3+4IHW2sNJ3tTB8X+1\ntTbfr/eDSZ690V/0MfZdaa19qbV2XWttobV2IL0vJl+4atpa/eny2FGO8fwkT07yc/1e6puttT0r\njnPbUfqojfai353ky621d/Q/3z9N8oH0grwlv9ta+1R/33flkZ/vqF0yCFtuYtAFAMfsQP8fyiVf\nS3LqBvZ7SpLbV43dnt63TUvuzCPNr3j9F2u8X/Pc/W+1/kWS708v0Gn9n+1JHtpAvUc7xuPTu2fV\nn69ziJW1rv6cVv8e+/vNztL76s8/O8lJSb5a/Svq+j93rNh/6dvGtNb+oj/v1CT3bODXBAA2z94V\nr29Prx9asm/Fl1VJ755NP1xVf6//vtLrAVbu09tQtSPJKUk+VX95G8yxHB5aPJbjr+5dnnzkX+2w\neh5z39UPeH41vVsCnJpkPMm9GznvBo+xM70v6BaPsPvR+qiN9qLnJHlBVS2dt/p1vGOtc2XjPTTw\nKFjpBMPva+k1MUvO6ui4X0ly7qqxb0ly14r3Xd5A8QfTW0X1otbak/rnXgpsjnSu1WPrHWN/kq+n\nt4x8M93ZP8+ZrbUzWmunt9ae1Fq7eIP7uyklAAzOU1e8Pie9fmjJ6n+j70zyz/v/3i/9m39qa+29\naxx3f3o920Ur5j+ptbbylgfHcvzVjtZP/K2s33et51+kd3uCi/r7/tCq/Vafe61a1jvGnUm+pbp7\n2t2R3JlkbtXnu6219lObfF5gBaETDL8bkvxgVY31b6S4ennzo7GyYfj9JOdV1auqaryq/mZ619x/\n8BiOv57T0lsyfl9VPTHJv8zhTcp8evdIWunuVWNHPEZ/VdLbkvzfVfXk/uf1ghX3RehkeXTr3TPh\nI0nesnRZX/9mmVcebd++tX5PAGBr/GRVnV1VZyT5hRx+L6HVfivJ362q5yVJVT2xql7e70EO0+9D\nfivJr/RXPaV/npd2cfw1zCc5c+XNuVc5Nev3Xes5Lb3bNTxUVWcn+Uertq/uz/alFzCt/OJvvWP8\nUZKvJnlTVZ1SVY+rqpkN1vZofCjJM6rqh6pqoqpOqqrnrrqn53pW/57AYyB0guH3M0lekeS+9O4L\n8LtHmb9eQ7G8rbV2b3rXuv9set/O/Wx6N4W8b53jHMsqnXekdwnaXUluSu+mjyu9NclF/SeV/Of+\n2JuS/J/9sX+Q3nX96x3jZ5PcmOSPkxzo77/0v3Mb+VZuPSvn/3CSk5N8Lr2l4u/P+ivQVu77q0l+\noP8UlV95lDUAAMfm3el9efTFJLemf+PotbTWPpXefZd+o3+J1heS/O2VU1bt8vP94/5hVd3fP88z\nOjz+yn1vSfL/Jvnzfp+0ug85Wt+1njcm+StJlu4j9YFV2w/rz1prf5He5/iJ/tjz1jtG/7K670nv\n4S53pLci6ZXr1NOO8HpdrbX/ld5N2F+V3oq2r/Rrf9x6+61wTZJ39H+n79/oeYHD1V/esmQTDl71\n1vT+T+380qUnVfWsJP82vfuvHEzyE621P9m0IgAAgBNeVX05yd9prf3BoGsBOFFs9kqntyV52aqx\nX0rvqQ2XpPd4yn+1yTUAAAAAsMU2NXRqrX08vUuCVlpMsnRDvSfl8JsWAwAAbAYP8wDYYpt6eV2S\nVNU5ST644vK6C5J8OH/59ISZ1tpaj2UHAAAA4Dg1iBuJvzbJT7fWviXJ30/y2wOoAQAAAIBNNIiV\nTve31p60YvsDrbXJI+xrCSwAjLjWWg26Bg6nBwOA0bcVPdhWrHRauoxuyV1V9cIkqaoXp/do0CO6\n8sors7i4mNaanyH4ufrqqwdegx9/l+Phx99kOH/8XYbvh+GlBxuuH//7NZw//i7D9+NvMnw//ibD\n+bNVJjbz4FX17iSzSc6sqjvSe1rda5L8WlWNJ/l6kh9f7xhzc3Op8gUoAMBW0oMBAMdqU0On1toP\nHmHTczd6DM0OAMDW04MBAMdqEDcS5zg2Ozs76BJYg7/L8PE3GU7+LsDxyv9+DSd/l+HjbzJ8/E1O\nbJt+I/FjUVVtmOsDAI5NVaW5kfjQ0YMBwGjbqh7MSicAAAAAOid0AgAAAKBzQicAAAAAOid0AgAA\nAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOid0\nAgAAAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOid0AgA4TlXVZFW9v6o+X1V/VlXPr6rTq+ojVXVL\nVX24qiZXzH9DVd3an//SQdYOAIw+oRMAwPHrV5P8fmvtwiTPSnJzktcn+Whr7fwkf5DkDUlSVbuS\nvDLJhUm+M8lvVlUNpGoA4IQgdAIAOA5V1bYkV7TW3pYkrbWF1toDSb43ydv7096e5Pv6r1+R5D39\nebcluTXJ87a2agDgRCJ0AgA4Pj0tyf6qeltVfbqq/n1VnZJkurU2nySttbuTTPXnn53kzhX739Uf\nAwDYFEInAIDj00SS5yT5N6215yR5OL1L69qqeavfAwBsiYlBFwAAwGOyN8mdrbU/6b//QHqh03xV\nTbfW5qvqrCT39LffleSpK/bf2R9b0zXXXLP8enZ2NrOzs91VDgBsqbm5uczNzW35eau14f3yq6ra\nMNcHABybqkprzc2sH6Oq+liS17TWvlBVVyc5pb/p3tbam6vq55Oc3lp7ff9G4u9K8vz0Lqu7Nsl5\nazVbejAAGG1b1YNZ6QQAcPx6XZJ3VdVJSf48yY8mGU/yvqp6dZLb03tiXVprn6uq9yX5XJKDSX5C\nsgQAbKahX+m0uLgYT/MFgNFkpdNwstIJAEbbVvVgQ38j8dnZ2SwuLg66DAAAAAAehaFf6TQxMZG9\ne/dmenp60OUAAB2z0mk4WekEAKPNSqe+mZmZTE1NDboMAAAAAB6FoV/p5J5OADC6rHQaTlY6AcBo\ns9KpT+AEAAAAcPwZ+tAJAAAAgOOP0AkAAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkAAACA\nzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkA\nAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic0AkAAACAzgmdAAAAAOic\n0AkAAACAzm1q6FRVb62q+ar67Krxv1dVn6+qG6vqTZtZAwAAAABbb2KTj/+2JL+e5B1LA1U1m+R7\nkjyztbZQVds3uQYAAAAAttimrnRqrX08yX2rhl+b5E2ttYX+nP2bWQMAAAAAW28Q93R6RpIrq+oP\nq2p3VT13ADUAAAAAsIk2+/K6I53z9NbaC6rqryZ5X5KnD6AOAAAAADbJIEKnO5P85yRprf1xVS1W\n1ZmttQNrTb7mmmuWX8/OzmZ2dnYragQANsHc3Fzm5uYGXQYb0FpLVQ26DADgOFattc09QdW5ST7Y\nWntm//2PJzm7tXZ1VT0jybWttXOOsG/b7PoAgMGpqrTWJBtDpqralVdemd27d2dsbBB3YwAANtNW\n9WCb2kVU1buT7EnyjKq6o6p+NMlvJ3l6Vd2Y5N1JfngzawAA4NHbs2dP9u3bN+gyAIDj2KavdDoW\nVjoBwGiz0mk4La10mpubc4kdAIygrerBhE4AwMAInYZTVbXFxUWBEwCMqJG4vA4AgOOTwAkAOFZC\nJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAA\noHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QC\nAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6J3QCAAAAoHNCJwAAAAA6\nN/Sh0969e9NaG3QZAAAAADwKQx86PfWpT82VV16ZxcXFQZcCAAAAwAbVMK8iqqqWJGNjY/nKV76S\n6enpQZcEAHSoqtJaq0HXweGqqg1zjwgAHJut6sGGfqVTklx22WWZmpoadBkAAAAAbNDEoAs4mjvv\nvDNnn312qnwJCgAAAHC8GPrL64a5PgDg2Li8bjjpwQBgtLm8DgAAAIDjltAJAAAAgM4JnQAAAADo\nnNAJAAAAgM4JnQAAAADonNAJAAAAgM4JnQAAAADonNAJAAAAgM4JnQAAAADonNAJAAAAgM4JnQAA\nAADonNAJAAAAgM4JnQAAAADonNAJAOA4VVW3VdWfVtUNVfVH/bHTq+ojVXVLVX24qiZXzH9DVd1a\nVZ+vqpcOrnIA4EQgdAIAOH4tJpltrV3SWntef+z1ST7aWjs/yR8keUOSVNWuJK9McmGS70zym1VV\nA6gZADhBCJ0AAI5flUf2c9+b5O39129P8n39169I8p7W2kJr7bYktyZ5XgAANonQCQDg+NWSXFtV\nf1xVP9Yfm26tzSdJa+3uJFP98bOT3Lli37v6YwAAm2Ji0AUAAPCYXdZa+2pV7Ujykaq6Jb0gaqXV\n7zfkmmuuWX49Ozub2dnZx1ojADBgc3NzmZub2/LzVmuPqQ/ZElXVhrk+AODYVFVaa+4r1IGqujrJ\n/0ryY+nd52m+qs5Ksru1dmFVvT5Ja629uT///0tydWvtk2scSw8GACNsq3owl9cBAByHquqUqjq1\n//qJSV6a5MYkv5fkR/rT/naS/9p//XtJXlVVJ1fV05J8W5I/2tKiAYATisvrAACOT9NJfreqWno9\n3btaax+pqj9J8r6qenWS29N7Yl1aa5+rqvcl+VySg0l+wnImAGAzubwOABgYl9cNJz0YAIy2kbi8\nrqreWlXzVfXZNbb9w6parKozNrMGAAAAALbeZt/T6W1JXrZ6sKp2JvmO9JZ8AwAAADBiNjV0aq19\nPMl9a2x6S5J/tJnnBgAAAGBwtvzpdVX1iiR3ttZu3Mj8xcXFTa4IAAAAgK5taehUVU9I8gtJrl45\nvN4+Z5xxRhYWFja1LgAAAAC6NbHF5/vWJOcm+dOqqiQ7k3yqqp7XWrtnrR0eeOCBvO51r8vU1FRm\nZ2czOzu7ddUCAJ2am5vL3NzcoMsAAGAL1GY/Dreqzk3ywdbaM9fY9uUkz2mtrXXfp1RVm5yczL33\n3puxsS2/EhAA2GRb9bheHp2qapvdIwIAg7NVPdimJjlV9e4ke5I8o6ruqKofXTWl5SiX1wmcAAAA\nAI4/m77S6Vj4lg0ARpuVTsNJDwYAo20kVjoBAAAAcGISOgEAAADQOaETAAAAAJ0TOgEAAADQOaET\nAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQ\nOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEA\nAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0b+tDpuuuuy8GDBzM/P5/W\n2qDLAQAAAGADapiDnKpaLm5iYiIzMzPZvXt3xsaGPisDADagqtJaq0HXweGqqg1zjwgAHJut6sGO\nm9Ap6QVPe/fuzfT09KBKAgA6JHQaTkInABhtW9WDHTdLhpZWOk1NTQ26FAAAAACOYuhDp49+9KP5\n5je/mb1792Zubi5VvgwFAAAAGHZDf3ndMNcHABwbl9cNJz0YAIw2l9cBAAAAcNwSOgEAAADQOaET\nAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQ\nOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEA\nAADQOaETAAAAAJ0TOgEAAADQOaETAAAAAJ0TOgEAAADQuU0NnarqrVU1X1WfXTH2S1X1+ar6TFV9\noKq2bWYNAAAAAGy9zV7p9LYkL1s19pEkF7XWnp3k1iRv2OQaAAAAANhimxo6tdY+nuS+VWMfba0t\n9t/+YZKdm1kDAAAAAFtv0Pd0enWS/77ehBtvvDGLi4uHjS0uLmZ+fj6ttcNer+Vo2wEAAADo3sBC\np6r6x0kOttbevd68iy++OGeccUYWFhaS9EKkq666Kjt37swLX/jC5dezs7NrhlPrbQcAAABgc9Rm\nrwCqqnOSfLC1dvGKsR9J8pokL2qtfWOdfZeLe+1rX5tXvvKVufDCC7Nz584sLCxkfHw8VZWFhYVM\nTExk7969mZ6eXt5/fn5+ee5a2wGArTU3N5e5ubnl92984xvTWqvBVcRaqqpZJQ4Ao6uqtqQH24rQ\n6dz0Qqdn9t//tSS/nOTK1tqBo+zbkmRycjL33ntvxsbG0lrL7Oxs9uzZk0svvTRVlT179mRmZiZz\nc3Op+svPbOXctbYDAIO1VQ0Pj47QCQBG20iETlX17iSzSc5MMp/k6iS/kOTkJEuB0x+21n7iCPu3\nz372s7nooosyNvaXVwIuLi5m3759mZqaSmtt+fVagdLKuQInABguQqfhJHQCgNE2EqHTsdLwAMBo\nEzoNJz0YAIy2rerBBv30OgAAAABGkNAJAAAAgM4JnQAAAADonNAJAAAAgM4JnQAAAADonNAJAAAA\ngM4JnQAAAADonNAJAAAAgM4JnQAAjmNVNVZVn66q3+u/P72qPlJVt1TVh6tqcsXcN1TVrVX1+ap6\n6eCqBgBOBEInAIDj208n+dyK969P8tHW2vlJ/iDJG5KkqnYleWWSC5N8Z5LfrKra4loBgBOI0AkA\n4DhVVTuTvDzJf1gx/L1J3t5//fYk39d//Yok72mtLbTWbktya5LnbVGpAMAJSOgEAHD8ekuSf5Sk\nrRibbq3NJ0lr7e4kU/3xs5PcuWLeXf0xAIBNIXQCADgOVdV3JZlvrX0myXqXybV1tgEAbJqJQRcA\nAMBjclmSV1TVy5M8IclpVfXOJHdX1XRrbb6qzkpyT3/+XUmeumL/nf2xNV1zzTXLr2dnZzM7O9tt\n9QDAlpmbm8vc3NyWn7daG94vv6qqDXN9AMCxqaq01tzM+hhV1QuT/MPW2iuq6peSHGitvbmqfj7J\n6a211/dvJP6uJM9P77K6a5Oct1azpQcDgNG2VT2YlU4AAKPlTUneV1WvTnJ7ek+sS2vtc1X1vvSe\ndHcwyU9IlgCAzWSlEwAwMFY6DSc9GACMtq3qwdxIHAAAAIDOCZ0AAAAA6JzQCQAAAIDOCZ0AAAAA\n6JzQCQAAAIDOCZ0AAAAA6JzQCQAAAIDOCZ0AAAAA6NzQh06//uu/nve+9725/fbbc+ONN2ZhYSHz\n8/NprS3PWVxcfMTYeuPHuh8AAAAA6xv60Ol1r3tdXvWqV+Xcc8/NxRdfnMc//vHZuXNnZmdns7i4\nmMXFxVx11VWHjSU54viSx7ofAAAAAEdXw7yap6qOWNzExET27t2bJNm5c2cWFhaWx6anpzM/P7/m\n+JIjbT/afgBAd6oqrbUadB0crqraMPeIAMCx2aoebOhXOq02Pj6eiYmJzMzMZGpqKlNTU5mZmTls\nLMkRx5c81v0AAAAAOLqhX+n0a7/2a5mamsoLXvCCPPjgg7nwwgtz4MCBTE1NpaoXyi0uLmbfvn2H\nja03frTtR9sPAOiGlU7DyUonABhtW9WDDX3oNMz1AQDHRug0nPRgADDaXF4HAAAAwHFL6AQAAABA\n54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQA\nAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO\n6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA5zY1dKqqt1bVfFV9dsXY6VX1kaq6\npao+XFWTm1kDAAAAAFtvs1c6vS3Jy1aNvT7JR1tr5yf5gyRv2OQaAAAAANhimxo6tdY+nuS+VcPf\nm+Tt/ddvT/J9m1kDAAAAAFtvYgDnnGqtzSdJa+3uqppab/J3fdd35S1veUsOHDiQ3bt35+lPf3ou\nvfTS3H///dm+fXuqKmNjY9mxY0f279+fqampVNW6BSwsLOTmm2/OBRdckAMHDmxoHwAAAAA2rlpr\nm3uCqnOSfLC1dnH//b2ttTNWbD/QWjvzCPtuuLjJyck8/PDDmZmZye7duzM2tvYiroWFhWzfvj0P\nPPBAxsfHU1VH3QcA2BxVldaab36GTFW1ze4RAYDB2aoebBArneararq1Nl9VZyW5p4uDPvDAA0mS\nPXv2ZN++fZmenl5z3s0337w899ChQxvaBwDoxtzcXObm5gZdBgAAW2ArVjqdm95Kp2f23785yb2t\ntTdX1c8nOb219voj7PuYVjrNzc0d8XK5xcXFnHHGGY9Y6bTePgDA5rDSaThZ6QQAo22rerBNDZ2q\n6t1JZpOcmWQ+ydVJ/kuS9yd5apLbk7yytXb/EfZvL3/5y93TCQBGlNBpOAmdAGC0jUTodKw0PAAw\n2oROw0kPBgCjbat6MHfOBgAAAKBzQicAAAAAOid0AgAAAKBzQicAAAAAOrfh0KmqTtnMQgAATmR6\nLQBg1Bw1dKqqmar6XJKb+++fVVW/uemVAQCcAPRaAMCo2shKp7ckeVmSA0nSWvvTJFduZlEAACcQ\nvRYAMJI2dHlda+3OVUOHNqEWAIATkl4LABhFExuYc2dVzSRpVXVSkp9O8vnNLQsA4ISh1wIARtJG\nVjr93SQ/meTsJHcleXb/PQAAx24oe63W2qBLAACOczXMDUVVtWGuDwA4NlWV1loNug4OV1Xtyiuv\nzO7duzNZp/ZMAAAgAElEQVQ2tuGHHQMAx4mt6sE28vS6Z1TVdVV1U//9xVX1Tza7MACAE8Gw9lp7\n9uzJvn37Bl0GAHAc28hXV7+V5A1JDiZJa+2zSV61mUUBAJxAhrLXmpmZydTU1KDLAACOYxsJnU5p\nrf3RqrGFzSgGAOAENJS91tzcXKpc+QgAPHYbCZ32V9W3JmlJUlXfn+Srm1oVAMCJYyh7LYETAHCs\njnoj8ap6epJ/n2QmyX1Jvpzkb7XWbt/04txIHABGmhuJD7bXWqcmPRgAjLCt6sEmjlLEWJLnttZe\nUlVPTDLWWntos4sCADgR6LUAgFG2kZVOf9Jae+4W1bP63L5lA4ARZqXTYHutI9GDAcBo26oebCOh\n05uS7E/y3iQPL4231u7d3NI0PAAw6oROg+211qlJDwYAI2yYQqcvrzHcWmtP35ySDju3hgcARpjQ\nabC91pHowQBgtA1N6DRIGh4AGG1Cp+GkBwOA0TYUNxLvF/I31hh+IMmNrbV7ui8JAODEodcCAEbV\nRi6v+29JLk2yuz80m+RTSZ6W5J+21t65acX5lg0ARpqVToPttdapSQ8GACNsaFY69edc2FqbT5Kq\nmk7yjiTPT/I/kmx5IwQAMEL0WgDASBrbwJynLjVBfff0x+5NcnBzygIAOGHotQCAkbSRlU5zVfWh\nJO/vv//+/tgTk9y/aZX1zczM5NRTT83Y2Fh+5md+Jr/zO7+Tb/u2b8tf/+t/PR/72MdyySWXZHx8\nPGNjYznzzDNz//335/zzz8/NN9+cHTt2ZGpqKvfcc09aaxkbG8v09HSqKouLi9m3b1+mpqbSWsv8\n/Hyqas3tVZWFhYXcfPPN2bVrV8bGelnd6jlH82jnAwAnhIH2WgAAm2Uj93SqJH8jyeX9oU8k+cBW\nXOhfVcd8jtNOOy0PPfTQ0vFyxRVX5LrrrsuLX/zi7NmzJ5deemmS5Prrr19z+8zMTK699tpMTU3l\ngQceyOTkZPbv35+xsbFcddVVy3N27969HEatZXFx8VHNB4ATgXs6DbbXWqcm93QCgBG2VT3YUUOn\nfjHnJDmvtfbRqjolyXhr7aFNL66D0Gm1iYmJ3HDDDbnkkkuysLCQ8fHxJMmhQ4fW3D4xMZFrr702\nV1111fIxbrzxxuzYsSM7d+5cnrN3795MT08f8bzz8/OPaj4AnAiETj2D6rXWqUfoBAAjbKt6sKMu\ntamq1yT5nST/rj90dpL/splFdWnbtm3Lr6sqMzMz2bVrV2ZmZjIxMZGZmZnMzMysu/2KK67I5ORk\nkmRycjK7du3K1NTUYXOmpqbWrePRzgcATgzHe68FAHAkG7m87jNJnpfkk621S/pjN7bWnrnpxVW1\nSy+91D2dAGBEWek02F5rnZqsdAKAETY0l9dV1Sdba8+vqhtaa5dU1USST7fWLt704jQ8ADDShE6D\n7bXWqUkPBgAjbGgur0vysar6hSRPqKrvSO/JKh/c3LIAAE4Yei0AYCRtZKXTWJK/k+SlSSrJh5P8\nh616ep1v2QBgdFnpNNhea52a9GAAMMKG5vK6QdLwAMBoEzoNJz0YAIy2rerBJtYp4MYkR+w2Bnmf\nAQCA451eCwAYdUcMnZJ8d/8/f7L/n+/s/+cPZZ0GCQCADTmmXquqHpfkfyQ5Ob2e7ndaa2+sqtOT\nvDfJOUluS/LK1toD/X3ekOTVSRaS/HRr7SPd/CoAAI+0kXs63bD0+N4VY59urT1nUyuLpd0AMOpc\nXndsvVZVndJa+1pVjSf5RJLXJfnfkhxorf1SVf18ktNba6+vql1J3pXkrybZmeSjSc5bq9nSgwHA\naBump9dVVV224s3MBvcDAODoHnOv1Vr7Wv/l49Jb7dSSfG+St/fH357k+/qvX5HkPa21hdbabUlu\nTfK8Y64eAOAI1ru8bsnfSfLbVTXZf39/esuyAQA4do+51+o/+e5TSb41yb9prf1xVU231uaTpLV2\nd1VN9aefneR/rtj9rv4YAMCmOGro1Fr7VJJnLTVCS/cEAADg2B1Lr9VaW0xySVVtS/K7VXVRHnk/\nKNfJAQADsZGVTkmETQAAm+lYeq3W2oNVNZfkryWZX1rtVFVnJbmnP+2uJE9dsdvO/tiarrnmmuXX\ns7OzmZ2dfazlAQADNjc3l7m5uS0/71FvJD5IbmIJAKPNjcQfu6ranuRga+2BqnpCkg8neVOSFya5\nt7X25iPcSPz56V1Wd23cSBwATkhb1YNteKUTAABD5clJ3t6/r9NYkve21n6/qv4wyfuq6tVJbk/y\nyiRprX2uqt6X5HNJDib5CckSALCZNrTSqf8UlXOzIqRqrb1j88paPq9eCABGmJVOPYPqtdapRw8G\nACNsaFY6VdU703siymeSHOoPtyQDa4QAAEaFXgsAGFUbubzuuUl2+boLAGBT6LUAgJE0toE5NyU5\na7MLAQA4Qem1AICRtJGVTtuTfK6q/ijJN5YGW2uv2LSqAABOHHotAGAkbSR0umaziwAAOIFdM+gC\nAAA2w4aeXjconpwCAKPN0+uGkx4MAEbbwJ9eV1Ufb61dXlUPpfcEleVNSVprbdtmFwcAMKr0WgDA\nqLPSCQAYGCudhpMeDABG21b1YBt5eh0AAAAAPCoDC52q6u9X1U1V9dmqeldVnTyoWgAAAADo1kBC\np6p6SpK/l+Q5rbWL07u31KsGUQsAAAAA3TvijcS3wHiSJ1bVYpJTknxlgLUAAAAA0KGBhE6tta9U\n1S8nuSPJ15J8pLX20bXmPulJT8r4+HjOP//8XHzxxZmcnMxJJ52UO+64I1//+tdz0UUX5eyzz85t\nt92Wpz3taTlw4EBmZ2czNjaW++67L0960pNy//3354wzzkhrLQcOHEhV5cwzz8xJJ52UXbt2ZX5+\nPvv378/27dtTVfnmN7+ZT3/603n5y1+eL37xi7nggguyb9++LN1Qc2xsLDt27Mj+/fszNTWVqsri\n4mL27duXM844I7fccksuuOCCHDhwINu3bz9s3pEs7b963tL49u3bc88996S1lrGxsUxPT6e1tuY+\nj8aRznu0bQAAAADrGcjT66rqSUk+kOQHkjyQ5HeSvL+19u5V8za9uP4d29edMzY2lsXFxcPGJicn\n8/DDD2dmZibXXXddXvziF+fjH/94qiqHDh3K+Ph4kuTUU09dnrd79+6MjT3yisbFxcVcddVV2bNn\nz2HzlsY/8YlP5IlPfGIefPDB5Zovv/zyVNUj9nk0jnTeo20DgK54et1w8vQ6ABhtW9WDDSp0+v4k\nL2utvab//v9I8vzW2k+tmjf03c7ExERuuOGGXHLJJVlYWFh33t69ezM9Pf2IbfPz89m5c2cWFhYO\nm7dyfLXx8fFU1SP2eTSOdN6jbQOAx2pubi5zc3PL79/4xjcKnYaQ0AkARttWhU6DWrpyR5IXVNXj\nq3fd1ouTfH4QhWzksrG1VvhMTk5mYmIiMzMz2bVrV2ZmZjI2Nra8wml8fDzj4+OHzZuamlrz+FNT\nU5mZmXnEvKXx8fHxbNu27bCaZ2Zm1tzn0TjSeY+2DQAeq9nZ2VxzzTXLPwAAjK6BrHRKkqq6Or0n\n1h1MckOSH2utHVw1p01OTrqnk3s6ATCiXF43nKx0AoDRNtKX122UhgcARpvQaThVVVtcXPSlEwCM\nqFG/vA4AgCE2Ozv7iAepAAA8GlY6AQADY6XTcKqq5kEiADC6rHQCAGBgPEgEADhWVjoBAANjpdNw\nck8nABhtVjoBAAAAcNwSOgEA8AhuJA4AHCuX1wEAA+PyuuHkRuIAMNpcXgcAwMC4kTgAcKysdAIA\nBsZKp+HkRuIAMNqsdAIAYGAETgDAsRI6AQAAANA5oRMAAAAAnRM6AQAAANA5oRMAAAAAnRM6AQAA\nANA5oRMAAAAAnRM6AQAAANA5oRMAAAAAnRM6AQAAANA5oRMAAAAAnRM6AQAAANA5oRMAAAAAnRM6\nAQAAANA5oRMAAAAAnRM6AQAAANC5iUEXcDRVtfx6x44deeYzn5n7778/Z599dvbv359zzjkn8/Pz\nOeuss/Lwww/nO77jO/KZz3wm27dvz/XXX58zzzwzr3jFK/L1r389T3ziE3PXXXdl+/btedGLXpQP\nfehDueOOO3LxxRfn/vvvz7333psLL7ww5513Xvbt25dbbrkl9913X57//OdnbGwsDz74YM4999x8\n6UtfykknnZTLLrssZ511Vvbu3ZtPfvKTOffcc/PQQw/lvPPOy3333Zft27enqjI2NpYdO3bknnvu\nSWstCwsL+cIXvpAdO3bk/PPPz549e/L0pz89X/jCFzIxMZHLLrsst956ay644ILs27cvVbW8f1Vl\nenr6sM9lLYuLi5mfn09rLWNjY5menk5rLfv27cvU1NTy/ouLi0cc2759e/bv37+8bfXcpXMs1dRa\nW36/Y8eOw/Y9mrXq4Oh8bgAAAAyraq0NuoYjqqrhLa7vlFNOyde+9rWjztu2bVsefPDBR3XssbGx\nLC4uHrZ/VeWKK67I7t27Mza29kK1xcXFzM7O5vrrr0/SC+4uv/zyVFX27NmTmZmZ7N69O0ly1VVX\nrTn2iU98IqeeemoefvjhzMzM5LrrrsuLX/zi5bnXXXddXvSiF+X6669fPn6S5XNOTk4u77terUv1\nrq5jvfn0+NyAUVBVaa1JzYdMVbVh7hEBgGOzVT2Y0Ok4NDExkb1792Z6enrN7fPz8zn77LNz6NCh\n5bHx8fFUVRYWFpb3T5KdO3cecWzl+W644YZccskly3NvuOGGPPvZz14+x/j4eJIcds6N1LpU7+o6\n1ptPj88NGAVCp+EkdAKA0bZVPZhlEcfolFNO2dC8bdu2Pepjr1y1srR/VWVmZiZTU1NH3G9qaioz\nMzPL75f2mZmZycTExPL+S/PWGhsfH8/k5OTytl27dh02d+n96uMvWbnverWurHej8+nxuQEAADDM\njquVTu7p5J5OHM7nBhzvrHQaTlY6AcBoc3ldNDwAMOqETsNJDwYAo83ldQAAAAAct4ROAAAAAHRO\n6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAA\nAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54RO\nAAAAAHRO6AQAAABA54ROAAAAAHRO6AQAAABA54ROAAAAAHRuYKFTVU1W1fur6vNV9WdV9fxB1QIA\nAABAtyYGeO5fTfL7rbUfqKqJJKcMsBYAAAAAOlStta0/adW2JDe01r71KPPaIOoDALZGVaW1VoOu\ng8PpwQBgtG1VDzaolU5PS7K/qt6W5FlJ/iTJT7fW/mL1xKq1P4MnP/nJeeihhzI+Pp4HHnggT3nK\nU/KNb3wj5557br7+9a/n/vvvz+Me97icd955ufHGG/Pc5z433/zmNzM1NZWdO3fmpptuyi233JKq\nysknn5yTTz45z3nOc/K4xz0ul112WT7xiU/kCU94Qh7/+MdnYWEhN910Uy666KLceuutOfnkk3Po\n0KHMzs5m7969Of/883PGGWdkfn4+X/ziFzMxMZGDBw9m27ZtufTSS3PttdfmrLPOylOf+tTcdNNN\nOfXUUzM+Pp6pqak873nPy+c///n8+Z//ec4888ycf/75mZyczHXXXZdLLrkk4+PjGRsby5lnnpn9\n+/dnqQFcXFzMAw88kHPOOSdzc3N5yUtekn379uW2227Lc5/73HzpS1/K6aefnkOHDuXWW2/NSSed\nlMsuuyxPecpTUlVZXFzM/Px8WmsZGxvLjh07sn///mzfvj1333137r333lx44YU5cOBAtm/fnnvu\nuWf53Evz77777tx999158MEHc+WVV2Z8fHz577O4uJh9+/ZlamoqrbXMz8/n4MGD+eIXv5gLLrgg\nT37yk9Nae8ScleeYnp5+xN9/qe6qyvT0dA4dOpSbb745u3btytjYka8WXVnPkf47tdY+Kz+jtepZ\naWFhYbmWJEc93+rPaOX8x1LvVh17UI7XugEAAE5YrbUt/0nyV5IcTPLc/vtfSfLGNeY1P93+XH75\n5e3gwYPtiiuuOGx8cnKyjY+Pt9NOO215bHx8vI2Pj7dt27Y94jgr5y3N/cY3vtFaa+3QoUPtyiuv\nbBMTE+2KK654xLmW6lhvTlW1K6+8sh06dKgtOXTo0PK8qmqXX355m5ycXK7/4MGDbS0r61l9zCNZ\nea4j1bPSwYMHl2vZtm1bu+KKK9Y93+rPaGV9Bw8efNT1btWxB+Wx/A2B40OvFdn6XsTPUXu19f5s\nAMBxbqt6sEFdXjed5H+21p7ef395kp9vrX3PqnnWdXdsfHw8n/nMZ/LsZz87hw4d6vTYu3fvzuzs\nbObn57Nz584sLCwsr35afa6xsbGMjY2tO2diYiJ79+7N9PR0kmR+fj5nn3328ryxsbEsLi4uz7/x\nxhvz7d/+7Y+oa2U9q495JKvPtVY9K91000155jOfufx+fHw8hw4dOuI+qz+jqlqu74Ybbsgll1zy\nqOrdqmMPymP5GwLDaW5uLnNzc8vv3/jGN6a5vG7ouLwOAEbbVl1eN5Cn17XW5pPcWVXP6A+9OMnn\nBlHLiWZmZia7du3KzMzMYeOTk5MZHx/Paaedtjw2Pj6e8fHxbNu27RHHWTlvae4VV1yRJJma+v/Z\nu/Pgts4z3/O/FwcUJe4UQYCSqM3WSom2ZFmUCJISJbuduDPj3LQzWSp3epmeSWrqdiV9e6qzdE1V\nOzVVU5OuupPJdHXf1O1OZjqeLE7c3YlvHGexlkQiJVsyRS3WbssWwU3gvkiieIB3/iCABklQlkSK\nAOHvp+qUcA7Oec+Dc0j75YPnfY9fwWBQXq9XwWBw2rnicdxtH2OMgsGg/H5/Ylu83eT3i4uLE/HH\nh7VNNTWe5DZnknyumeJJVlVVlYilqKhIdXV1dz1fqmsUfx2/P/cT73y1nS4Pcg8BZKbGxka98MIL\niQUAAADZKy2VTpJkjHlc0j9KypH0rqQ/sdYOTtlnxuCY04k5nZjT6e6xM6cTgIWAicQzE5VOAABk\nt/nqg6Ut6XQv6PAAAJDdSDplJvpgAABkt6weXgcAAIDZMcZUGmMOGmPeNsacNcZ8Mba91Bjza2PM\nJWPMr4wxxUnHfM0Yc8UYc8EY80z6ogcAAB8GVDoBAIC0odLpwRljKiRVWGtbjTEFkt6S9HFJfyKp\n11r7N8aYr0gqtdZ+1RhTJen7knZKqpT0uqT1qTpb9MEAAMhuVDoBAABgRtbaLmtta+z1iKQLmkgm\nfVzSP8V2+ydJ/y72+jlJP7LWutba9yRdkVQzr0EDAIAPFZJOAAAAC5wxZo2kbZKOSwrEnhQsa22X\npPgjP1dIaks6rD22DQAA4KHwpjsAAAAAPLjY0LqXJX3JWjuS4um/DzRO7oUXXki8bmxsVGNj44OG\nCAAA0uzw4cM6fPjwvJ+XOZ0AAEDaMKfT7BhjvJJ+Luk1a+23YtsuSGq01nbH5n06ZK3dbIz5qiRr\nrf1GbL9fSvpra+0bKdqlDwYAQBZjTicAAAB8kO9KOh9POMW8IumPY6//SNLPkrZ/xhizyBizVtI6\nSW/OV6AAAODDh0onAACQNlQ6PThjTJ2k30k6q4khdFbSX2kikfRjSSslvS/pU9bagdgxX5P0p5LG\nNTEc79cztE0fDACALDZffTCSTgAAIG1IOmUmY4yNRqMyhlsDAEA2YngdAAAA0qaxsVHRaDTdYQAA\ngAWMSicAAJA2VDplJmOM9Xq9CoVCCgQC6Q4HAADMMSqdAAAAkDbBYFB+vz/dYQAAgAWMSicAAJA2\nVDplJuZ0AgAgu1HpBAAAgLQh4QQAAGaLpBMAAAAAAADmHEknAAAAAAAAzDmSTgAAAAAAAJhzJJ0A\nAAAAAAAw50g6AQAAAAAAYM6RdAIAAAAAAMCcI+kEAAAAAACAOUfSCQAAAAAAAHOOpBMAAAAAAADm\nHEknAAAAAAAAzDmSTgAAAAAAAJhz3nQH8EGMMXPW1qJFi1RSUqKhoSHdvn1bhYWFKiwslNfr1eLF\ni9Xd3a2NGzfqzTfflOM4CgQCGhsbU21trfr6+tTf36/CwkJFIhG98847qqmp0TvvvKMnn3xS7e3t\nun37trZu3aqzZ89q/fr16uzslMfjUUdHh7Zs2SKfz6exsTEFAgH97ne/0759+3Tx4kX19fXJ5/Np\n9erVunHjhm7fvq01a9bIGKPh4WGNjIzI6/Vq8+bNGhwclM/n08jIiJqamlRTUyNJCofD6urqkrVW\nf/Znf6ZDhw5p6dKlGhkZkTFGPp9Pmzdv1s9+9jOtWbNGpaWlGhwclLVWXq9Xq1ev1tDQkMrLy7V2\n7Vq9/vrrqqio0MWLF1VdXS3HcRSNRjU0NKRHHnlEnZ2dOnnypGpra7Vs2TKVlJTojTfeUGlpqXw+\nn4wxcl1X77zzjgoKCtTW1qZ169Zpw4YNunz5skZGRnTs2DF9/etfV29vr95++2319fWprKxMFRUV\n2rhxo5qbm7VhwwZJUm9vr0pKSnTt2jXt2rVLTU1NKi0tlbVWw8PDCgaDunDhglzXVX9/v/x+vzZv\n3qyLFy+quLhYV65cUXl5uaqrq+W6rpqbm9XQ0JD4XG1tbTpx4oR27dolY4z6+/u1ZcsWeTweRaNR\ndXd3KxKJKBwOyxijQCAgn8+nCxcuqKysTI7jqKysTJcuXdKGDRt08eJFlZeXq6KiIvEzHI1GFQ6H\n5fP51NPTo6VLl046PhAIJK7b+fPnE9vLy8vV09Mjv98va63C4fCMrwsKCvTDH/5QH/3oR1VWVqbX\nXntNzz33nDwez7R943HE//X7/TLGKBqNqrOzM/FecmzxaxG/BskxJP+uxj9rcpup1qeee6qpx93N\n/ew7W/N5rvtxL3FlauwAAAAAspC1NmMXSZaFZS6X/Px86ziOlWQdx7G3bt2ywWAw5b7FxcV2bGzM\nNjQ0pHzf4/FMWo+3m7w0NDTYSCRiI5GI3bNnj3UcxxYXF1uPxzPpeGOM3bNnjx0bG7NFRUXT4vB6\nvbahocHu2bNnxtd3+9z19fWT9o3HEf/X6/XaPXv22PHxcVtfXz/p2Hhs4+PjiWthjJkUw549e2wk\nErHW2sRnTW4z1frUc8ePj5vaztT3H3Tf2ZrPc92Pe4krU2PHh5skazOgz8EyvQ8GAACy13z1wczE\nuTKTMSZzg0NW+Od//mc9//zzM75/6NAhPf3004pEIg/UvuM4am9vlyRVVlbKdd0Z9/V6vfrNb36j\nffv2zdhWvBJqptd3iyMSidx1X6/Xq1OnTunxxx9XNBpN+d62bdsS1yK5La/Xq1AopEAgoO7u7sRn\njR+3ffv2lOvJ7cePj5vaztT3k93PvrM1n+ea67gyNXZ8uBljZK2l7C7DGGNsJvcRAQDA7MxXH4w5\nnfChkp+fL8dxJE0kTZ577jkFg8GU+xYXF6uhoWHG9z2eyb8+8XaT1dXVye/3y+/3KxgMynEcFRcX\ny+PxTDreGKNgMKiGhgYVFRVNi8Pr9SoYDCoYDM74+m6m7huPI/5v/L2qqqppbcVjS34vvi25Xb/f\nL0mJzzq1zanrU88dPz5uajtT33/QfWdrPs91P+4lrkyNHQAAAEB2+lBVOjGnE3M6MacTczrNhUyd\nF4k5nbAQUemUmYwxNhqN8t8JAACy1Hz1wTI+6ZTJ8QEAgNkh6ZSZYvP56dChQ9MqewEAwMJH0kkk\nnQAAyHYknTKTMcYy9xsAANmLOZ0AAACQNsz9BgAAZotKJwAAkDZUOmUm5nQCACC7UekEAACAtCHh\nBAAAZoukEwAAAAAAAOYcSScAAAAAAADMOZJOAAAAAAAAmHMknQAAAAAAADDnSDoBAAAAAABgzpF0\nAgAAAAAAwJwj6QQAAAAAAIA5R9IJAAAAAAAAc46kEwAAAAAAAOYcSScAAABMY61NdwgAAGCBI+kE\nAACAaRobGxWNRtMdBgAAWMBMJn+LZYyxmRwfAACYHWOMrLUm3XFgMmOM9Xq9CoVCCgQC6Q4HAADM\nsfnqg1HpBAAAgGmCwaD8fn+6wwAAAAsYlU4AACBtqHTKTMYYG4lE5PHw/SQAANmISicAAACkzb59\n+5jTCQAAzAqVTgAAIG2odMpMzOkEAEB2o9IJAAAAaVNbW8ucTgAAYFaodAIAAGlDpVNmMsbYoqIi\n9fb2yuv1pjscAAAwxz4UlU7GGI8xpsUY80o64wAAAMBkQ0NDunjxYrrDAAAAC1i6h9d9SdL5NMcA\nAACAKYqLi1VVVZXuMAAAwAKWtqSTMaZS0u9L+sd0xQAAAIDU+vr65PGk+/tJAACwkKVzkP43Jf2l\npOK77WRMZk/zkJubq2g0Ktd1lTz/lNfrVSAQUHt7e2I9Go3K4/GouLhYvb29kqSSkhK5rqu8vDwN\nDAzI6/Vq69atamtr061bt3T79m1FIhGVl5fLcRwNDw+rpKREXq9Xixcv1pUrV1RUVKQVK1ZocHBQ\nlZWVOnXqlIwxys/PV3l5uTZt2qQzZ87IdV0NDw9r+fLl8vv9MsYoJydH77//vsbHx7VkyRIVFxer\nra1NTzzxhN577z01NDTo1q1bGh8f1+XLlzU+Pq7+/n7V1NRo5cqVun79ukZGRjQ+Pq7Ozk5t2LBB\nw8PD2rJli86cOaPPfvazevXVV1VUVKRwOKxbt26poKBAK1eu1JUrV7R69WoFAgG99dZb2rhxo3Jz\nc9XX1ydJWrp0qXp6etTX16eamhotXrxYK1eu1LvvvqtwOKwLFy7os5/9rC5duqS8vDz19/fr/fff\n182bN7Vs2TI9/fTTam9v12uvvaa8vDz93u/9ngYGBvTee+/JdV25rqvPfe5zampqks/n09NPP63j\nx4+rp6dH/f39cl1Xy5cv1+9+9zvl5ORo0aJFamhoUE5OjqLRqHp6ejQwMKCPfOQjunr1qtra2lRU\nVKV6wBsAACAASURBVKTCwkKFw2Ht2bNH4XBYb7/9tqqrq2WM0Y0bN9TT06OPf/zjeuutt1RaWiqf\nzyfHcVReXi5jjO7cuaPjx4+rsLBQ3d3dev/99/W5z31Ora2tWrduncrLy3Xjxg0NDQ0pGAzq0qVL\nKi8vV0lJiV599VXt2rVLjuMoGo2qu7tbPT09ysnJUW1trY4cOSKv16uGhgb19fXJ7/fLWqtr167p\n5Zdf1mOPPaaKigpVVFTI5/PpwoULKi0t1cDAgDZv3pxoz+/3y+/3J17Hf09d19X58+dVXl6uiooK\nWWsVDocT52lvb9eVK1e0YcMGeTweeTweBQIBRSIRnTt3Th6PR1u3bpXrumpubtauXbt07NgxrVu3\nTr29vXIcR1u3bpUkdXZ2TovF5/Ppxo0bstZOavvixYuqqqpK/PEUj7OsrCxx7ePHx9u01qqzs1N9\nfX3asmWLJCU+ywf9d2lq+4FAQNZadXd3yxijQCAwqY1oNKpwOJyIP9U+rutO+xypjk+O/17jndrO\n/RzzMNvJtHMBHzYknAAAwGylZSJxY8zHJD1rrf0zY0yjpP/FWvvfptiPWcSBh8Tr9aq2tlbj4+M6\nfvz4tPc9Ho+i0WhiPTbRXGK9qKhIN2/eVDAY1KFDhxSNRlVWVqahoSFJUn19vTwej5qbm1VbW6to\nNKqmpqZJ5zDGqK6uTqdPn9bw8LAkKT8/P5FsTaWwsFCPPfbYpLaKioo0Ojqq/Pz8xPnjbZ89e1aD\ng4MqLi5WT0+PJE2KU5oYQjIyMqKCggKNjo6qtrZW1lodPXo00f7jjz+uY8eOJT7vTH+Mua47qX1j\njOrr6yVJR44ckTFGDQ0NiTai0aj27dunpqamRPxT93FdVz6fb9LniE/sm3x8cvzGGDU3N39gvHHx\ndu7nmIfZTqadCw8PE4lnJh7mAgBAdpuvPli6kk7/u6R/L8mVtERSoaR/sdb+4ZT96O0AD5HjODMm\nd+6V1+tVKBRSOBxWdXV1Ynu8ksl13UTlVar/3kxNbt2LqQmwmUxt++zZs5I0Kc5UHMeRtXbSsfFr\nFf+8gUAg5bHnzp2b1r7jOJKUuNbJbXR3d6uyslKu6046JnmfqW2ePXs2UfGV6njHcWSMkeu6Hxhv\nXHI793rMw2wn086FuXP48GEdPnw4sf71r3+dpFMGIukEAEB2y+qn11lr/8pau8pa+4ikz0g6ODXh\nBODh8nq9CgaD2r17d8r3p1aMTB26VFxcnGjD7/erqqpKRUVFiffr6uoUDAYT+wSDwWnnMMYoGAyq\nsLAwsa2goCCRpEmlqKhIdXV102JxHGfS+eNtFxcXJ/apqqqaFmfy8cmfKTne+DmTP+9MprYfjyPe\nXnw93obf71cwGJwU/9R9qqqqpn2OuOTjp8Z/L/FObed+jnmY7WTauTB3Ghsb9cILLyQWAAAAZK+0\nVDpNCsCYvZoYXvdcivcy/is25nRiTifmdGJOp6mY04k5nXDvGF6Xmah0AgAgu2X18Lp7RYcHAIDs\nRtIpM9EHAwAgu2X18DoAAABkNpJOAABgtkg6AQAAYJrGxsb7ftADAABAMobXAQCAtGF4XWYyxlie\nCgkAQPZieB0AAADShqdCAgCA2aLSCQAApA2VTpnJGGOj0ShPhQQAIEtR6QQAAIC0IeEEAABmi6QT\nAAAAAAAA5hxJJwAAAEzDk+sAAMBskXQCAADANEuXLpXruukOAwAALGAknQAAADDN4OCgLl68mO4w\nAADAAsbT6wAAQNrw9LrMZIyxxcXF6uvrk8fDd5QAAGSb+eqDkXQCAABpQ9IpMxljbCQSIeEEAECW\nmq8+GD0JAAAATGMMuUAAADA7JJ0AAAAwTWNjI0+wAwAAs8LwOgAAkDYMr8tMxhjr9XoVCoUUCATS\nHQ4AAJhjDK8DAABA2gSDQfn9/nSHAQAAFjAqnQAAQNpQ6ZSZjDE2Go0yrxMAAFmKSicAAACkDQkn\nAAAwWySdAAAAAAAAMOdIOgEAAGAapjgAAACzRdIJAAAA0zQ2NioajaY7DAAAsIAxkTgAAEgbJhLP\nTMYY6/V6FQqFFAgE0h0OAACYY0wkDgAAgLQJBoPy+/3pDgMAACxgVDoBAIC0odIpMxljbDQa5Ql2\nAABkKSqdAAAAkDY3btxgMnEAADArGV/ptHfvXv32t79NdyhIYcmSJbp169YH7peTk6Px8XHl5uZq\nbGxs0nsFBQUaHR2d1Kk1xmjx4sXyer3y+/0aGRmR4zgaHh7W8PCwJGnlypUaHx/XwMCAbt++rZyc\nHBUVFamkpESjo6PKyclRb2+vbt68mTjPnTt3FIlEZK2VtVYej0cFBQW6efOmiouLlZubq7KyMr3/\n/vsqKipSeXm5KioqdP78eY2PjysnJ0fLli1TZ2enjDHauHGj8vPzdeLECZWUlMhaq0gkovLycuXn\n5+vq1auqqKjQ5cuXtX79enk8Hr3zzjtav369HnnkEV2+fFljY2NatGiR7ty5o9LSUv3FX/yFfvrT\nnyoUCmnHjh168803NTY2ps7OTg0NDWnVqlXq6+vTokWLtHjxYu3bt0+nTp1STU2NXNdVTk6Obt68\nqYsXL2rFihUaGRlROBzW0NCQfD6fduzYobKyMi1ZskRnzpzR7du3df36dT3//PMKhUJqa2tTeXm5\nIpGILl68KL/frz179sgYo66uLj366KM6cuSI8vPztW7dOoXDYW3cuFEXLlyQz+fTuXPnlJeXp9LS\nUrW3t2vp0qVatGiRzp07p8cff1yDg4PKycmR4zhavHixuru79fnPf14nTpxQX1+fjDEqKirS6Oio\nfD6ffvnLXyonJ0cDAwPaunWr3n77ba1atUpLlixRfn6+nn/+eb3zzjuSpOLiYl29elXWWkWjUQ0M\nDCRej4yMqLi4WMuWLdOzzz6rX/ziF1q1apUuXbqk7u5u7dmzR/39/ers7NS7776r1atX67333lNF\nRYUeffRReTwe3b59W6dPn9af//mf67XXXlNpaan8fr98Pp/6+vpUUFCg3/zmN1q1apWi0ajee+89\nlZWVaf369YpGo7p27ZrWrl2r4eFhbdy4UR6PR67rqrW1VSdOnFBtba0CgYCstRocHNTmzZu1bNky\nWWvV3d096XckGo2qs7NTV69eVUlJiXJyclRVVaVAIKCenh75fD5dv35dv/rVr7RmzRqVl5cn9gmH\nw4mf/9LSUh07dkwNDQ1yHCfRvuu6On/+fOJ3IF7pEI1GE7FEo1GFw2E5jqOtW7dKkrq7u2WMUXl5\nuW7cuCFjjMrKynTp0iVt2rRJvb29KikpSZzTWqvz58+rtLRUAwMD2rx5s8LhcOK4CxcuqKysTI7j\nKBAIfGDFRfy69PX1afPmzert7ZXf7095XDz+md7/oPOEw2H5fD51dXWpr69PW7ZskaTE+bds2SKP\nJ3O+15nN533YqHTKTPE5nYLBoA4dOpRRP88AAGD25qsPlvFJp3THAADpUl9fL2OMjhw5ck/7xxN2\nubm5iYRrMo/Hk/JJVI7j6ObNm1q0aJFc11VZWZmGhoYkSQ0NDTp8+LCkiSdZpYqlsLBQjz/+uI4e\nPZqII3684ziKRCJyHEfRaDSRPDPGqKCgIJFInhpf8mtjjBoaGu76h280GtXevXsTMTiOI2NMyj+Y\no9Go9u3bp+bm5vv+gzp+bFNTk/Ly8hLxFxUVqbq6Wk1NTZImkqA9PT3yer331O7DNJvPOx9IOs2O\nMeY7kv4bSd3W2sdi20olvSRptaT3JH3KWjsYe+9rkv4HSa6kL1lrfz1Du1aSmEwcAIDsRNJJJJ0A\nfLh5PB4ZYxSJRB76uQ4dOqTGxkadO3dO1dXVie2O46i9vV2StGLFihljmSmhNVc+6A/f7u5uLV++\nfFoMqY7r7u5WZWWlXNe97z+ok4+dKvY/7sT62bNnE1Vg6TSbzzsfSDrNjjGmXtKIpO8lJZ2+IanX\nWvs3xpivSCq11n7VGFMl6fuSdkqqlPS6pPWpJtBMrnQ6fPhwxlXIAQCA2WFOJwD4kAsGgwoGg/e8\nf1FRkRzHUV5eXsr3Z6pucRxHDQ0NkqSqqioVFRUl3qurq5Pf75ff758xlqKiItXV1U1aT247/m/y\nH63GGBUWFs4YX/LreMXS3Z6iNTU+x3EU/4N56nHxfWd6/27ixzqOMyn+qdeguLhYVVVV99zuwzSb\nz4vMZ609Kql/yuaPS/qn2Ot/kvTvYq+fk/Qja61rrX1P0hVJNTO1HQqFSDgBAIBZyfhKJ+Z0ylzM\n6cScTszpxJxOzOnEnE6zRaXT7BljVkv6r0mVTn3W2qVJ7/dZa5caY/5W0jFr7Q9i2/9R0i+stf+S\nok2eIAwAQBZjeJ3o8AAAkO1IOs3ePSSdeq21ZfebdIpEIhmVPAUAAHNnvvpg6Z/hFAAAAHOp2xgT\nsNZ2G2MqJN2IbW+XtDJpv8rYtpTy8vL05S9/WR6PR42NjWpsbHx4EQMAgIfq8OHDiQcEzScqnQAA\nQNpQ6TR7xpg1mqh0qo6tf0NSn7X2GzNMJL5L0gpJv9FdJhKXMmdCfAAAMLcYXieSTgAAZDuSTrNj\njPmBpEZJZZK6Jf21pJ9K+okmqprel/Qpa+1AbP+vSfpTSeOSvmSt/fUM7dri4mL19fUxxA4AgCxE\n0kkknQAAyHYknTKTMca6rjvpIQMAACB7zFcfjK+uAAAAMM3+/fsVjUbTHQYAAFjAqHQCAABpQ6VT\nZjLGWK/Xq1AopEAgkO5wAADAHKPSCQAAAGlTW1srv9+f7jAAAMACRtIJAAAA08S+AU13GAAAYAFj\neB0AAEgbhtdlJmOMNcaovb1dy5YtS3c4AABgjjG8DgAAAGljrVUkEkl3GAAAYAEj6QQAAICUwuFw\nukMAAAALGEknAAAApOTx0FUEAAAPjp4EAAAAUvriF7+oaDSa7jAAAMACxUTiAAAgbZhIPDMZY6wk\neb1ehUIhBQKBdIcEAADmEBOJAwAAIK2qqqpUXl6e7jAAAMACRdIJAAAAKZ0/f1779u1jiB0AAHgg\nDK8DAABpw/C6zBQfXicxxA4AgGzE8DoAAACkXW1trfx+f7rDAAAACxCVTgAAIG2odMpMyZVOZ86c\nUXV1dTrDAQAAc2y++mAknQAAQNqQdMpM8aRTYWGh+vv75ThOukMCAABziOF1AAAASJsdO3bo1q1b\n2r9/PxOJAwCAB0KlEwAASBsqnTKTMcZ6vV65rstE4gAAZKGsrnQyxlQaYw4aY942xpw1xnwxHXEA\nAAAgtWAwKK/Xq2AwyETiAADggaSl0skYUyGpwlrbaowpkPSWpI9bay9O2Y9KJwAAshiVTpnJGGM7\nOjpkjFEgEJAx3CIAALJJVlc6WWu7rLWtsdcjki5IWpGOWAAAADDdqlWr9OlPf1p8AQgAAB5U2ud0\nMsaskXRY0tZYAir5Pfu3f/u3+ulPf6qbN2/q2LFjWrJkiW7dupWGSIGFLT8/X6Ojow+t/fjcH1Ot\nXbtW165dS3mM4ziKRCIqKChQbm6uBgYGFIlEtHjxYhlj5PV6devWrUS7q1evliS1tbVJUmJi27y8\nPDmOo5ycHA0MDMgYo7q6OrW1tcl1XfX398taq/Hxcbmuq/LycvX19am4uFi5ubny+XwKhUIqKCjQ\nihUr1NnZqRs3big/P1+O4+jmzZtyXVc+n08rVqxQV1eX+vv7VV5eLq/Xq5KSEg0PD6u6ulrhcFgn\nT57U7t27dfDgQS1btkyLFi1KxH/r1i2NjY3p9u3bun79utauXauCggK1tLQoPz9fK1eu1IYNG9Te\n3q6hoSGFw2Ht2LFD4XBY3d3d2rRpk1auXKmenh797ne/U3l5uZ5++mm1trZqYGBAo6Oj6u3tVUlJ\nidavX6/6+nqdOnVKGzdu1LFjx7Rp0ya5rqudO3fq3Llz6urqUkFBgZYvX65jx47p1q1bKikp0R//\n8R+rqalJ/f396unpkbVWn/zkJ9XV1aXR0VG9/vrr+tjHPqaioiL19PSop6dHLS0tWrZsmR5//HE9\n9dRTeuWVV1RcXCzXdVVaWqre3l6NjIzI5/OpoKBAfX198ng86ujo0KpVq1RUVKTe3l6dP39ezz77\nrLq6uuS6rsLhsAYHB/X5z39ep0+fVjgc1nvvvafPf/7zamtr061bt3T+/Hk1NDSos7NTa9askeu6\nOnfunNasWaNHHnlEV65cUW9vr8bHx/Xcc8/pwIEDWrJkicLhsOrr69XZ2alnn31WR48e1Z07d9TR\n0aFnnnlGvb296uvrU1FRkUKhkD7ykY/olVdekdfrVV1dnZYvX66xsTG98sor2rBhgx577DF5PJ7E\nz2c4HFZJSYmOHDmi8vJybdmyReFwWMYYlZeXq6enRz6fTzdu3JC1Vq7r6urVq9qwYYO8Xq/Ky8t1\n48YNRSIR9fb2yufzyXEclZaWqqmpSevWrVNvb6+stfJ6vdq6deu08/v9fhljZlz3+XyJOFL9u3Tp\nUl26dElVVVWJtucSlU6ZKf70Osdx1N7eznxOAABkmfnqg6U16RQbWndY0v9mrf1Zivf5ag0AkLF2\n796t48ePJ9bjiTOPx6N9+/bpyJEjk6pEPB5PIllaXFyskZER5efna2hoKGX7RUVFM7430/7J529u\nblYwGNSBAwf01FNPTVtvampSQUGBRkZGUv47PDwsY4wikYiKi4vV09Mjr9f7gFcrNZJOmSneByss\nLFR/f78cx0l3SAAAYA5lfdLJGOOV9HNJr1lrvzXDPiSdAAALytmzZ1VeXq7KysqU1X/zfX6v16tT\np05p+/btKdfvt+2tW7fOKr7Dhw/r8OHDifWvf/3rJJ0yUHKlUygUUkVFRbpDAgAAc+jDkHT6nqQe\na+1f3GUfkk4AgIxVW1urY8eOJdaLiorU398vY4waGxvnvdKpuLhYfX19ifPHK5sOHTo0qfIpvn6/\nlU7xIZFziUqnzBTvgxlj1NDQoEOHDj2U4ZUAACA9sjrpZIypk/Q7SWcl2djyV9baX07ZjzmdgDnC\nnE7M6cScTszpxJxOuFfJX/w5jqO2tjZ5PJ7Ezw8AAFjYsjrpdK+MMTaT4wMAALND0ikzJSedCgoK\ntH37dh07dixRKUfVEwAACxtJJ5F0AgAg25F0ykxTK52MMYk5wUKhEE+zAwBggZuvPhhfUwEAAGBG\nO3fuVDAYlNfrVTAYlN/vT3dIAABggZjb5x4DAAAga+zatUtNTU2SNGlOsLipc4UBAAAko9IJAAAA\nKf3kJz+Rx+ORx+NRIBCYlnDat2+fKisr1djYmHi4AwAAQBxzOgEAgLRhTqfMFJ/TKf4Ez/hTOJN1\nd3ersrKSuZ4AAFiAmNMJAAAAaRWJRPTzn/9cqb4E9Pv9zPUEAADuikonAACQNlQ6Zabkp9d5vV7V\n1tbqpZdeUkVFBXM6AQCQBearD0bSCQAApA1Jp8yUnHSKi1c0HTp0SB4PxfIAACxkJJ1E0gkAgGxH\n0ikzJSedHMdRNBqVtZa5mwAAyBLM6QQAAIC0e/LJJ1VfX58YZmetTTnHEwAAwFQknQAAADCjkydP\n6kc/+pGuX78uY4xWrlypxsZGRaPRdIcGAAAyHEknAAAAzCgSiegzn/mMwuGwmpub5bqumpubFQ6H\n0x0aAADIcMzpBAAA0oY5nTJTqonEHcdRQUGBRkdHFQwGdfjwYZ5YBwDAAsVE4iLpBABAtiPplJlS\nJZ2kicRTa2urtmzZImutwuGw/H4/yScAABYYJhIHAABARigsLJTX61VdXV0i4bRv3z5VVlYyvxMA\nAJgRSScAAADMKC8vT8PDw3JdN/HkOuZ3AgAA94KkEwAAAGZ08+bNxOtjx44lhtQFg0F5vV4Fg0H5\n/f40RggAADIVczoBAIC0YU6nzDTTnE4NDQ367W9/K2OMotEoczoBALBAMZG4SDoBAJDtSDplppme\nXhcKhVRRUZGOkAAAwBxiInEAAABkjGAwqEAgkO4wAADAAkLSCQAAAB9ofHxcVKADAID7wfA6AACQ\nNgyvy0yphtd5vV6FQiGqnQAAyAIMrwMAAEDGWLJkiSKRCNVOAADgnpF0AgAAwAcaHh7W6tWr1djY\nqGg0mu5wAADAAsDwOgAAkDYMr8tMqYbXxXm9Xl2/fl0ej0d+v1/GcPsAAFho5qsPlvFJp46ODo2P\nj+vkyZP6+c9/rpycHHV0dOjtt99WX1+fVq9eLY/Ho2vXrmlwcFCLFi3SnTt3VFxcLI/Ho6GhIUUi\nkUnt5ubmanx8nG/pAADzyhij3Nxcua4r13UT23NycjQ+Pq7FixfLGKP8/HyVlpYqEolo8eLFWrJk\nic6ePatFixapuLhYq1atUk9Pj1asWCGfz6eWlhbl5uaqoKBAknTnzh21t7crLy9PruvK5/PJ6/Vq\n1apVGh8f18WLFzUyMqJHH31UwWBQOTk5amlp0dDQkNasWaOenh4NDg4qNzdXubm5euaZZ3T79m0V\nFhYqEokoHA5rZGREy5cv15NPPqkXX3xRv//7v6+TJ0/qE5/4hNrb2/Xoo4/KdV2dPn1ajz32mK5f\nv67169crEAjIWqv+/n5t2bJFjuOQdMpAMyWdvF6vdu/eLdd1deLECe3cuVNHjx6V4zjzHSIAAJgF\nkk66+7dsAABgYSsuLtbg4CBJpwyUqg+2a9cuvfzyy/r4xz+ulpaWxPba2lodPXpUHs/0WRui0ajC\n4fAHVkTd634AAGBuMJE4AADIaoODg+kOAffh9u3bev755yclnCTpxIkTCofDk7ZFo1F1dnZq3759\nqqysvOs8UNFo9J72AwAACw+VTgAAIC2odMpc99oH83q9CgaDOnz4cKJCKZ5EampqUjQalbVWXq9X\noVBIgUBgWhvd3d2qrKyU67p33Q8AAMyd+ap08j7sE8wWczoBALIFczqlntMJC1NBQYGOHj2q6upq\nWWt148YN+f1+hcNhNTc3J/pf8cSU3+9P2Y7f71cwGFRzc/Nd9wMAAAtPxlc6ZXJ8AABgdnh6XWaa\nqdIpPz9ft2/fnpRQqq2tlTEmkTQ6ePCg9u/fr+bmZu3evVt///d/ry1btqSc8ymOOZ0AAJhfzOkE\nAACAjPHNb35Tq1evnlRB7rqumpub1dzcLNd11dTUpAsXLujgwYO6fv26PB6PnnjiCe3bt++uFeYe\nj0eBQICEEwAAWYZKJwAAkDZUOmWm+5lXs6ioSI8//riOHj2qvLw83b59W8FgUC+99JJWrVrFXE0A\nAGQgKp0AAACQ8YaGhvS9731PS5Ys0ejoqCKRiI4cOSJrrYLB4AfO6RQXjUbV3d0tvnAEACB7kHQC\nAADArDz33HO6efPmpG0ej0eHDh1SKBSa9HS7VOJPvKusrFRjYyMPewEAIEuQdAIAAMCsnD17dtL6\nrl275Pf7ExOEf1D1Und3d2JeqObmZoXD4YcZLgAAmCcknQAAADCn3njjDTU0NGjp0qWqrq7W0qVL\n5bpuyiF00WhUn/70p+W6rowxqq2tVSQSUVdXV2K/5OPmahgew/kAAHj4SDoBAABgzjU3N2t4eFiS\nNDg4qPPnz6ccQhcOh3Xs2DFJE5Oa3rlzRytWrNDy5cu1d+9etbe3J47bu3fvfQ/DmynRxXA+AAAe\nPp5eBwAA0oan12Wm+3l63b0oKCjQ5cuXUz7NzlqrxsZGNTc368knn9SJEycUiUQSx3o8HllrZa2V\n4zgyxtzzE/Fc19WePXv05ptvaufOnTp69Kgcx1F3d7cqKyt5sh4A4EOLp9cBAAAgK2zbtk1+vz/l\n0+yMMYkJx5uamhQMBicdG41GZa1NHJfchs/nm3GIXDQaVUNDg44dO6ZIJKLjx4+roaFB0Wg0EYvj\nOHryySdVXl4+L9cBAIAPGyqdAABA2lDplJnmutJJkkKhUKJqyePxqLy8XD09PfL7/TLGJCYd9/l8\n6urq0uXLl7V///7E8a2trQoEAonjfD6f9u/fr+bmZgWDQR06dEgez799n9rd3a0VK1ZMqppKrmqa\nqQoKAIAPg/nqg5F0AgAAaUPSKTM9jKTT5s2bdfnyZeXn52tkZET5+fkaHR3Vtm3b1NTUpP379+vE\niROqra2VMUZNTU2JfXbv3q1IJKKTJ08qGAzqwIEDunjxorZv3y7XdeU4jkKhkCoqKhLniw/bO3r0\nqPLz83Xr1i0Fg0EdPnxY1lqdP39e27ZtSySlamtrdfTo0UmJq9mKJ9LiiTUAADIFw+sAAACQNS5c\nuKBIJKKhoSFFo1ENDw8rGo2qpaVFeXl5OnbsmFzX1ZEjR9TU1KRIJKLh4WGdPHlS4+PjOn78uFzX\n1dGjR7V7925t27ZNeXl5kqRIJKJPfepTcl1XnZ2d6urqkiQdOHBAp06d0rZt2xSNRjU2NibXdbVv\n375Jx0vSiRMnFA6H7/oZotFoov0P+mI0ebLyvXv3qrOzU5FIJOWk5jxFDwCQrah0AgAAaUOlU2Z6\nGJVOD2rJkiW6detWYj0vL083b95MuW9NTY3efPNNSVJ9fb08Hk8igRX3xBNP6MyZM3JdVx6PR9u3\nb9fp06cVDAZ18ODBSUP+kkWjUTU2NurIkSOSpIaGBh0+fHjGyqjkycolyXEcFRQUaHR0NDEcUJL2\n7dun5uZm1dbW6qWXXlJFRQVVUQCAh47hdSLpBABAtiPplJkyKek0G47jTEo4pdp+4sQJrVixQn6/\nX/v371dTU1NijidrrS5evKiqqiqFw2EtX75c0Wg00U5HR4eWLVuW8tzx4X1NTU2JydDjvF6vrl+/\nrt7e3sQQwfj2VPNTfVgxPBEAHh6G1wEAAACzkCrhNHX7zp07tWnTJnV1dSWqoo4fP66dO3eqrKxM\n1dXVWrp0qUpKSrRt27ZJ7dwtEWKM0YEDB/TWW2+ppqZGjuOoqKhIjuNo165d+oM/+ANt27ZN+fn5\niQST67pqbm6eNsxvrobgTW0nk4f2JQ9PbGxsnJTsAwAsHCSdAAAAkDUWLVp01/effPJJFRYWaAdz\nYwAAE3NJREFUTto2NDSkpqYmLVmyJLHt1KlTGhoakiQNDg6qrq5Ora2tKigokOM4amhoUHl5+YxJ\nm2g0qv3792vbtm164403JiW6zpw5o+PHjyfmrYons4wxCgaD8vv9iYTQ+Pi46urqtGLFCu3du/eB\nky9Tkzjxua0yNakTDofV3Nw8YyIOALAwMLwOAACkDcPrMlO2DK+byfbt23Xq1Kl73j8/Pz8xCbkk\ntba2qqqqSnv37k08ce/FF1/UO++8o3Xr1mlwcFA+n0+VlZUfmMyprq7W+fPnFYlE5PF41N7eLr/f\nr3379qmpqUmLFy/W6OhoYv+7Dem7m+Q5prxer06dOpUY2uf1ehUKhRQIBO7axlwOd/ugtpKHJ+7c\nuVNHjhxRb28vQ+0AYI4wvA4AAAB4CO4n4SRNJEDiCSdJ2rZtm+rr6yc9cW/NmjV66qmntHr1aj32\n2GNav369Fi9ePKmd+DA6j8cjj8ej/Px8nT17NlEFVVhYqPLy8kSVTyQSmZRwkqY/QS/VELlU2/x+\nv4LBYGLeqKqqqsR6bW2tIpHItKfyJbcTr5RasWKFgsHgjEMXZzr/1Pc/qMoqPjwxPjn80qVLJz0J\ncKbPfq8yeWghAGQTkk4AAADAXaR6Wl78KXkzGR0dnXZcPLkSjUa1du3aaQmlwcFBHTp0SB0dHdqx\nY0fKdjdv3qzly5dr+fLl2rNnj+rq6iYNmWtra1NNTc2kbd3d3ZKkAwcO6NSpU4mJyn/1q1/pxRdf\n1MjIiFasWKHly5cnkkBTk0xT57xqaGiYlCyKJ3EikcgHJpTudehcb2+v3nzzTUWjUQ0PDycSfKtW\nrdLevXtTnudekklzNV8UiSsA+GAMrwMAAGnD8LrMlO3D67LV5s2bdeHChUnbdu7cqZMnT6qmpkZD\nQ0O6cOGCtm7dqp/85CfavHlzyna+/e1va82aNXr22WcTCZX169crNzdX586dkzTxu9vS0qKKigqV\nlpZq9+7dam1t1caNG3X16tVEJdSBAwcSiZ0zZ84oHA4rGo3qq1/9qs6fP69gMKiDBw/qxo0bikQi\n6u/v18aNG3X58mVt3rxZ9fX1On78eMo4408hdBxHLS0tKikp0Sc+8QmdPn1atbW1+ru/+7vEkweN\nMSovL1dPT4/Gxsb0yCOPJI597733NDAwoE2bNiWG8FlrZxz+F682++QnP6mTJ0+qtrZWL730kvx+\nv3p6ehLHTE1KeTweBQKBaW1PHWp4t6GHyW3G25vNcMN7GTIZ38fn8+nGjRsyxkw6L08ZnHtcU8yH\neeuDWWszdpkIDwAAZKvY/+vT3udgmd4HY2GZqyU3N9fm5eWlfG9wcNA+8cQTKd/Lycmx//qv/2o3\nb95sJdlHH33UxhKiDxxHqu2O41hJ1uPxWMdxbH19vQ0Gg1aS3bFjh21pabEdHR3WdV0bCoXsrl27\nprXh8XhsUVGR9Xq9ds+ePXZsbMzW1NRM2+/JJ5+0u3btso7j2IaGBjs+Pm737NljvV6vbWhosKFQ\nKLG+Z88eG4lErLXWRiIR29HRYevr6ye1t2vXLuu6bmKfrq4uG41GJ627rjvp32g0asfGxuyBAwds\nfX19Ipb4uZKNj4/b2tpa6ziOLSoqspKsMSYRW/z9qfHGzRRTfD2Ve9nnXo+beg3utc0HjeFB20x+\nLxKJpPwZAOaaND99sLR3au4a3MRFAAAAWWq+Ojws998HY2FhmbzMlLRKtaxdu/ae9vv2t79tvV7v\njO+fPn3aXrt2zVZXV8+YcNu2bZu9du2a3bFjh3Ucx+7evdsODQ3Zqqoq6ziOLS4utsaYROJv06ZN\niURb8hIKhWwoFLKtra02FArZtra2GROCjuPY9vb2SYk1x3FsR0eH7ejosJ2dndZ1XdvQ0GA9Ho/d\ntWuXvX379qQE1djYmD179qwdHx9PJIZCoZDdvXv3pCRce3t7Yom3m5yg6erqsnfu3LG7d+9OfH7X\ndRPJG4/HY/Pz860xxtbU1FjXde34+Lg9ffq07ejomJYEehhJn5najCcTk98LhUKJnwmv12u7urqm\nJaXuNSF2t0TcXCbU7kW6zouZSfPTB0tnZ+ajki5KuizpKzPsMycXEwAAZKb56vCw3H8fjIWF5cO1\nbN269b72T5VYW7NmTeL1unXrJr03NbkWT4J5PB7r8XhmrIabuuTl5VljjN2+fXui8mvx4sWT9tm2\nbZt9//33rcfjmXb8jh07bEFBQWI9nhA7ceKE/fGPf2xPnTqViNXj8djW1tZJya54cuzMmTOJaq9T\np07ZEydO2Ndff922tbXZtrY229LSYk+fPp1ILCV//paWFtvW1mZramqsMSaRUPR4PJMSfTU1Nfat\nt96yu3fvtsYYu3Xr1kQib/v27TYUCk1LKF2/ft0eOnTI3rlzZ1qi626VafdaFXa36rXx8XH71ltv\n2YMHD06qwOvo6LANDQ2TKvzuN4kWb6ezs/OhVMp9GEnz0wdLV2fHI+mqpNWSciS1StqUYr85upyY\nK4cOHUp3CEiB+5J5uCeZifuSeearw8Ny/30wFhYWFpZ/W+LVYYsWLUps83g8d61UkyaGI95r5duD\nLOvXr7dNTU32u9/9rl25cuWM+7366qu2urp60rZvfOMbtrm52f7oRz9KDBuNf75NmzbZlpYWOzw8\nbP/hH/7BXrlyxX7/+99PVN1t2bLFnjx5MjEUdevWrXbJkiWT2v/Wt75lt2/fPi2WzZs3W8dxbE1N\nzaThpvHKs3glWrzirqWlZVJV3caNG+27775rW1tb7fXr1xMJwJkqysbGxhKJuOSEobX3lsxK3idV\nUu6DhpHOplLtXhJtD0qanz5YWiYSN8bslvTX1tpnY+tfjX3gb0zZz6YjPszshRde0AsvvJDuMDAF\n9yXzcE8yE/cl8zCR+Py6nz5YOuIDAOBBbdu2Ta2trYn11atXy+fz6a233kq5/86dO3XhwgWNjIxI\nkvLy8hQMBnXr1i3t3r1b0WhULS0tam1t1eDgoKSJBwJEo1EVFhaqvr5elZWV+vGPf6zBwUEVFhbq\nC1/4gn7wgx+oo6ND+fn5+tjHPqZXX31Vo6OjKigoUEFBgbq6uuTz+fTlL39Zw8PDGhgY0IYNG1Rd\nXa1f/OIXCofDeuKJJ/Sd73wn8XlWr16tH/7whxoYGFBvb6+8Xq/WrVsnSeru7lZ7e7s++tGPSpLe\nffdd1dXVqaurS1euXNGmTZu0bNmyaZP/V1RUzEsfLF1Jp+clfcRa+/nY+r+XVGOt/eKU/WxXV5eW\nLl2qS5cuadOmTYmnT5SVlenEiRP6xS9+obVr16qzs1M+n0/PPPOMWlpa9PLLLys/P1/vvvuuvvCF\nL6ilpUVXr17VnTt39MQTTygSiejs2bPatGmTcnNz1d/fr0WLFunMmTN6//33VVZWpqVLl2rp0qV6\n9dVXtWzZMj3zzDO6du2aOjo6tGnTJr3++uvKzc3VrVu3ZIyR1+uVx+PR4sWLdefOHZWVlWlkZERl\nZWU6duyYPB6PioqKND4+nvihGxkZUWVlpdrb22WtVW5ursbGxhLXIP5DDQBAtiLpNH/upw+WjvgA\nAMD8IelkjPV4PDLGKBKJkIABACALkXSaPySdAABA3Hz0wbwP+wQzaJe0Kmm9MrZtmuQkEwknAACA\nWbnnPhgAAMBspavSyZF0SdJTkjolvSnps9baC/MeDAAAwIcEfTAAADCf0lLpZK2NGGP+TNKvNfEU\nle/Q2QEAAHi46IMBAID5lJZKJwAAAAAAAGQ3T7oDSMUY81FjzEVjzGVjzFfSHU+2McZUGmMOGmPe\nNsacNcZ8Mba91Bjza2PMJWPMr4wxxUnHfM0Yc8UYc8EY80zS9ieMMWdi9+r/Stq+yBjzo9gxx4wx\nq4QPZIzxGGNajDGvxNa5J2lmjCk2xvwkdp3fNsbs4r6klzHmPxpjzsWu5/dj15B7Ms+MMd8xxnQb\nY84kbZuX+2CM+aPY/peMMX84H5/3w4I+2MNFHyxz0QfLPPTBMg99sMyw4Ppg1tqMWjSRCLsqabWk\nHEmtkjalO65sWiRVSNoWe12gibkdNkn6hqQvx7Z/RdL/EXtdJemUJoZjrondn3iV3BuSdsZe/0IT\nT8SRpP9Z0t/HXn9a0o/S/bkXwiLpP0r6/yS9ElvnnqT/nvy/kv4k9torqZj7ktb7sVzSu5IWxdZf\nkvRH3JO03It6SdsknUna9tDvg6RSSe/EfhdL4q/TfT2yYRF9sPm4xvTBMnQRfbCMW0QfLKMW0QfL\nmEULrA+W9guW4gLulvRa0vpXJX0l3XFl8yLpp5KelnRRUiC2rULSxVT3QNJrknbF9jmftP0zkv5z\n7PUvJe2KvXYkhdP9OTN90cQThH4jqVH/1uHhnqT3nhRJeifFdu5L+u7Jcknvx/6n55X0Cv/9Suv9\nWK3JHZ6HeR9uTN0ntv6fJX063dciGxbRB0vHNacPlgGL6INl3CL6YBm3iD5YRi1aQH2wTBxet0JS\nW9J6KLYND4ExZo0msqTHNfFD2i1J1touSf7YblPvSXts2wpN3J+45HuVOMZaG5E0YIxZ+lA+RPb4\npqS/lGSTtnFP0mutpB5jzP8TK7n/L8aYPHFf0sZa2yHpP0m6ronrO2itfV3ck0zhf4j3YTB2H2Zq\nC7NHH2we0QfLKPTBMg99sAxDHyzjZWwfLBOTTpgnxpgCSS9L+pK1dkST/0erFOuzOt0ctpV1jDEf\nk9RtrW3V3a8V92R+eSU9IenvrLVPSBrVxLcF/K6kiTGmRNLHNfHtznJJ+caYz4l7kqm4D0AK9MEy\nB32wjEUfLMPQB1twMuY+ZGLSqV1S8oRhlbFtmEPGGK8mOjsvWmt/FtvcbYwJxN6vkHQjtr1d0sqk\nw+P3ZKbtk44xxjiSiqy1fQ/ho2SLOknPGWPelfRDSfuNMS9K6uKepFVIUpu19mRs/Z810QHidyV9\nnpb0rrW2L/bNy79KCop7kinm4z7QT3h4uLbzgD5YxqEPlpnog2Ue+mCZLWP7YJmYdDohaZ0xZrUx\nZpEmxg2+kuaYstF3NTGG81tJ216R9Mex138k6WdJ2z8Tm8V+raR1kt6Mle0NGmNqjDFG0h9OOeaP\nYq//O0kHH9onyQLW2r+y1q6y1j6iiZ/5g9ba/17SfxX3JG1iJaptxpgNsU1PSXpb/K6k03VJu40x\ni2PX8ilJ58U9SRejyd9+zcd9+JWk3zMTTzUqlfR7sW2YPfpg84M+WAahD5aZ6INlJPpgmWXh9MHm\nc7Kre10kfVQTT/O4Iumr6Y4n2xZNfKMT0cRTaU5Jaold86WSXo9d+19LKkk65muamOn+gqRnkrbv\nkHQ2dq++lbQ9V9KPY9uPS1qT7s+9UBZJe/Vvk1hyT9J/Px7XxB9irZL+RRNPa+C+pPee/HXs+p6R\n9E+aeMoW92T+78MPJHVIGtNER/RPNDG56EO/D5roVF2RdFnSH6b7WmTTIvpgD/v60gfL4EX0wTJq\nEX2wjFtEHywjFi2wPlj8UXkAAAAAAADAnMnE4XUAAAAAAABY4Eg6AQAAAAAAYM6RdAIAAAAAAMCc\nI+kEAAAAAACAOUfSCQAAAAAAAHOOpBMAAAAAAADmHEknAPPKGLPaGHM23XEAAAB8mNAHA5AOJJ0A\npINNdwAAAAAfQvTBAMwrkk4A7kvsW7Lzxpj/Yow5Z4z5pTEmN/be48aYY8aYVmPMPxtjimPbd8S2\nnZL0H5La8hhj/sYY80bs/f9phnP+qzHmhDHmrDHmf0za/qfGmEvGmOOxeP7v2HafMeblWLtvGGOC\nD/WiAAAAPGT0wQAsRCSdADyIdZL+1lq7VdKgpOdj278n6S+ttdsknZP017Ht35X0H6y126e086eS\nBqy1uyTVSPq8MWZ1ivP9ibV2p6Sdkr5kjCk1xiyT9L/GjquTtClp/29J+j9j7X5S0j/O7uMC+P/b\nu58XnaI4juPvTzMLv5pnrSxmo1jIcpSiJFlOyY7CSlPiT7DyHygLlOxYyM6PhR+RIkpSbEY2FhYz\nUdQkvhZzRo9hMj2ezFy9X6tzv91z7z27T+eee48kaVUwg0nqlNGVfgBJnfSmqhb+CfAUGE8yBvSq\n6kGrXwKutDdtvap62OqXgf2tvQ/YluRgOx4DNgNvF93vVJLJ1t7UztkI3K2qDwBJrrY6wF5ga5K0\n4w1J1lXV578btiRJ0ooyg0nqFCedJA1irq/9FVjT2vnNuX+qn6iq20vdKMluYA8wUVVzSe4s834T\nVfVlqetKkiR1kBlMUqf4eZ2kQfwSNKrqIzCTZGcrHQbutbdgs33f9B/q63YTmEoyCpBkc5K1iy7d\nA2Zb2NkC7Gj1J8CuJL3W/0Bfn1vAyR8Pm2wfaJSSJEmrixlMUqe40knSIJba+eQIcK6FlmngaKsf\nAy4m+cZ8GFlwHhgHnrVl2O+BSX52Azie5CXwGngEUFXvkpwBHgMzwCvm/20A82HnbJLnwAhwH5ga\naKSSJEmrhxlMUqekyl0zJXVTkvVV9SnJCHANuFBV11f6uSRJkv5nZjBJy+XndZK67HTbAvgFMG3Y\nkSRJ+ifMYJKWxZVOkiRJkiRJGjpXOkmSJEmSJGnonHSSJEmSJEnS0DnpJEmSJEmSpKFz0kmSJEmS\nJElD56STJEmSJEmShs5JJ0mSJEmSJA3ddxHaQZ+5FTdfAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x114fa4b50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=[20, 10])\n",
"\n",
"plt.subplot(1, 2, 1)\n",
"indegrees_u = ua.indegree()\n",
"plt.scatter(range(N), indegrees_u,\n",
" marker='.',\n",
" color='black')\n",
"plt.xlabel('node age')\n",
"plt.ylabel('in degree')\n",
"\n",
"plt.xlim([0, N])\n",
"plt.ylim([0, max(indegrees_u)])\n",
"plt.title('uniform attachment')\n",
"\n",
"\n",
"plt.subplot(1, 2, 2)\n",
"indegrees_p = pa.indegree()\n",
"plt.scatter(range(N), indegrees_p,\n",
" marker='.',\n",
" color='black')\n",
"plt.xlabel('node age')\n",
"plt.ylabel('in degree')\n",
"\n",
"plt.xlim([0, N])\n",
"plt.ylim([0, max(indegrees_p)])\n",
"plt.title('preferential attachment')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# time vs. page rank"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x11251ff50>"
]
},
"execution_count": 57,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABKUAAAJoCAYAAAC3G1IbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xt43Hd55/3PPTM5WQcTx5qREyUpFGhiO4ktW7Y0imzJ\nhbJPaWmvQOLA9oLSXXrBQ9k+3R52absND5Qu28MWCuHZ0qXsQgMNLSmlLKVNHSnYGseHGDuGxE6B\nJI7sWCcbnxMy8/s+f8xPykjWYSTN/A4z79d16Yo085vf3JK4rJv7e3/vrznnBAAAAAAAAAQpEXYA\nAAAAAAAAqD8UpQAAAAAAABA4ilIAAAAAAAAIHEUpAAAAAAAABI6iFAAAAAAAAAJHUQoAAAAAAACB\noygF1Dkz+//M7HdKvn6fmZ00s7Nmdm2YsQXJzG42M8/M+HcRAAAsmZm93sy+bWZnzOxXIhDPB83s\nM2Ve+zkz+3C1Y1ooM3uXme0MOw4AlcP/+QLqnHPufc65j0qSmaUk/YmkNzjnmp1zp8ONbqqZEiQz\ne8bMtlXoLVyF7rMkZtZvZr8UdhwAAGBJfkvSI8655c65TwX5xma21cyeL33MOfdfnXO/HMB7T8nN\nqrDwF5V8zTOz14QdBxB3FKUAlGqVdJWkpxbzYjOzyoYDAAAQPWaWLOOymyV9t4r3n/MWikjxRq/E\nUmt5YlR+vkCsUZQCasD0lZrSjqKJlTIz+49mNmxmx83sF6dfa2avk3TEf/i0mf2L/3zWzPaa2Wkz\n22NmXSWv7Tez3zezXWZ2QdKr/cc+YmaDZnbOzP7ezFaY2V/57et7zOymOb6XL5vZC/77DZjZrf7j\n75H0byX9lr+18O/N7POSbpL0D/5jvzHLPVaX3P9qM/sTM3vWf/5bZnbVxNOSfsHMnjOzETP77ZLX\n3eff9wv+ex0ys9eZ2X/2f67PmdkbSq5vNrP/aWYn/J//RyaKdhOt52b2R2Z2ysy+b2Zv8p/7fUk9\nkj7lv8+flfu/AwAAsHh+h89/NrPvmtm4mX3WzK70n5vIp37LzF6Q9Jf+4z/jb9E77edDa/3Hd0jq\nk3S///f8tWZ2pZn9sZ8zvGBmn57IQRZw/9umxfvrfk5y2sz+2n+PZZK+Iel6Pxc7a2atfi7zhZLX\nz5ovzfNzeo2Z7TCzMT9f+isza/afm8jNvl6Smz3qv/SH/mOb57qHf582M/uK/9zotHzIpuVQ/6bk\niQXloWZ2i5n9s//7fsrM7i557nNm9ikzm/hedpvZq/3nHlUxb3zCf+5uAVgUilJAbZhvpaZVUpOk\n6yX9exUTpOVTbuDcv0pa43+53Dn3BivOlPq6pI9Luk7Sn0r6PzZ11tQv+PdsknTMf2y7igWk6yW9\nVlJO0mclXati4eu+OWL9hqQfl5SWdEDSF/34/kLSA5L+0N9a+HPOuXf67/kz/mN/PMs9Hii5/59I\nWi+pU9IKFVvrvZLnuyW9TtIbJP2emf1EyXM/I+l/S3qVpIOS/knFhOR6SR+RVDqn4X9L+pGk1/jv\n90b/5zRhk4odaddJ+iP5yadz7ncl7ZT0K/739B/m+FkBAIDKeoeKf7N/XNJPSPrdkudaVcwBbpL0\ny2a2XsX85j0q5hR/ruJC2RXOuZ9U8e/5+/2/59+T9N9UzItu9/97g6TfW+D9v2ZmV5S85m5JPyXp\n1f59f9E5d1HS/yXphHOuyX//k/71pTnjXPnSXEzSH/jx3iqpTdKHJKkkN3tzSW62xX9ds//Ynrnu\nYcVtfl+X9Iz/s7hB0l+XvP9mTc2hPjstvrLyUL9498+S/krSSkn3Svq0md0y7V73qfh7+b6kj/rf\n51b/+dv87+lvyvzZAZiGohRQG+Zrh/6RpI845wrOuX+UdF7FRGu++71Z0tPOuS865zzn3F+r+Mf8\nZ0uu/V/OuSP+83n/sc855551zp2T9I+Svu+c63fOeZL+RsUizYycc//LOXfROfeypA9LusPMmub5\n/qZ8/7Pdw+9Uerek/+CcO+mKHvOvk4qJ2oeccz9yzj0h6ZCkO0puvdM59y8l38dKSR9zzhVUTJZu\ntmKHVEbFZPDXnHMvOufGVCzsvb3kXs855/7SOedULGCtMrP0PN8nAACork865044536oYgGi9G93\nQdJ9zrmXnXMvqVgs+h/Ouf1+TvEFSS+puPA1k/eomBuccc5dkPSxCtz/E865YT/ef5C0rtxvdJE5\nl5xz33fO7XDO5Z1z4youWm6ddtlMuenkY/PcY7OkVZJ+y8+jfuScy5Xc59l5cqhy89CfkfSMc+7z\n/s/3kKSvqFjom/B3zrnH/dc+oMt/vrW2JREIXCrsAAAEYtz/YzrhoqTGMl53vaTnpj32nIorVhOe\n1+WGSz6/NMPXM763vzL2B5LepmLBx/kfKyWdKyPe+e5xtYozs34wxy1KY53+c5r+fYz5CdHE1+Zf\nf4OkKyS9YP6OPf/jWMnrJ1Ys5Zy75F/XKGmkjG8TAABUx1DJ58+pmAtNGC1ZyJKKM6PeaWYf8L82\nFf/+l76m+IRZi6Rlkh63V0ZwJjS1qLGY+0/PW1bN/q1NiWfROZdfAPqEiuMGGiUlJZ0q533LvEeb\niot33iwvny+HKjcPvVlSp5lNvK/5cXx+pvdS+fkzgAWgUwqoDRdVTHQmtFbovick/di0x26SdLzk\n60oOeXyHil1Y25xzr/Lfe6KgM9t7TX9srnuMSXpRxVb1anref5/rnHMrnHPXOude5Zy7vczXMzgT\nAIBw3Fjy+c0q5kITpv99fl7SR/2/9RN/7xudcw/OcN8xFfO1NSXXv8o5VzpOYSn3n26+XOLfau6c\nay5/oOLogzX+a39h2uumv/dMscx1j+cl3WSVO61vNs9LGpj28212zv1Kld8XQAmKUkBt+Lakd5hZ\nwh/2OL2FeiFKk4pvSHqdmd1rZkkz267ivv9/WML959KkYlv6aTNrkPRfNTWRGVZxRlOpk9Mem/Ue\nflfT5yT9dzNb5f+8OktmM1SkBdsV5zb8s6Q/ndg26A/03DLfa30zfZ8AAKD63m9mN5jZCkm/ramz\njKb7C0nvNbNNkmRmDWb2037+MYWfg/yFpI/7XVPy3+enKnH/GQxLuq50ePg0jZo755pLk4qjIM6Z\n2Q2SfnPa89Nzs1EVC1Cli4Jz3WOvpBckfczMlpnZVWaWLTO2hfi6pNeb2S+YWcrMrjCzjdPmic5l\n+vcJYBEoSgG14f+R9BZJp1WcTfB381w/V9Ix+Zxz7pSK++1/Q8UVvt9QcXDl6Tnus5Qun8+ruMXt\nuKTvqDiYstRnJa3xT1t5yH/sY5L+i//Yf1RxtsBc9/gNSYcl7ZM07r9+4t/Cclb25lJ6/TslXSnp\nSRXb0f9Gc3ewlb72E5Lu9k+C+fgCYwAAAIv3RRUXlr4n6V/lD7aeiXPucRXnPn3K3wL2tKR3lV4y\n7SX/yb/vY2b2Q/99Xl/B+5e+9qikL0n6gZ8jTc9B5su55vL/StogaWKO1VemPT8lN3POXVLx5zjo\nP7Zprnv42/Z+VsWDZ46p2NF0zxzxuFk+n5Nz7ryKQ+LvVbEj7oQf+1Vzva7EhyR93v+e3lbu+wKY\nyl4ZhxIdZvaHKv5D9JKKpxy82zl3NtyoAAAAahf5F+qdmT0j6d855x4JOxYAqBdR7ZT6ZxX3F69T\ncYXigyHHAwAAUOvIvwAAQKAiWZQqOXJdkh5T8QQGAAAAVAn5F8BBIwAQtFTYAZThlzT3gEEAAABU\nFvkX6o5zjqHVABCw0IpSZvawpEzpQyquTvyOc+4f/Gt+R9LLzrkvhhAiAABATSH/AgAAURLJQeeS\nZGa/qOJpE9uccy/Nck00gwcAABXlnLOwY6gH5eRf/nXkYAAA1Lgg8q9IzpQys38j6TclvWWuhEiS\nnHN8ROzjvvvuCz0GPvidxOGD30v0PvidRPMDwVhI/iWRg0Xxg3/DovfB7yR6H/xOovnB7yV6H0GJ\nZFFK0iclNUp62MwOmNmnww4IAACgxpF/AQCAQEVy0Llz7nVhxwAAAFBPyL8AAEDQotophRjr7e0N\nOwRMw+8kmvi9RA+/EwBxxr9h0cPvJHr4nUQTv5f6FdlB5+UwMxfn+AEAwPzMTI5B55FCDgYAQG0L\nKv+iUwoAAAAAAACBoygFAAAAAACAwFGUAgAAAAAAQOAoSgEAAAAAACBwFKUAAAAAAAAQOIpSAAAA\nAAAACBxFKQAAAAAAAASOohQAAAAAAAACR1EKAAAAAAAAgaMoBQAAAAAAgMBRlAIAAAAAAEDgKEoB\nAAAAAAAgcBSlAAAAAAAAEDiKUgAAAAAAAAgcRSkAAAAAAAAEjqIUAAAAAAAAAkdRCgAAAAAAAIGj\nKAUAAAAAAIDAUZQCAAAAAABA4ChKAQAAAAAAIHAUpQAAALBgzrmwQwAAADFHUQoAAAALtnXrVnme\nF3YYAAAgxizOq1xm5uIcPwAAmJ+ZyTlnYceBV5iZk6QTJ05o1apVYYcDAAAqLKj8i04pAAAALJiZ\nyYxaIQAAWDyKUgAAAFiwnp4eZTKZsMMAAAAxxvY9AAAQaWzfix4zc57n0SkFAECNYvseAAAAIouC\nFAAAWCqKUgAAAAAAAAgcRSkAAAAAAAAEjqIUAAAAAAAAAkdRCgAAAAAAAIGjKAUAAAAAAIDAUZQC\nAAAAAABA4ChKAQAAAAAAIHAUpQAAAAAAABA4ilIAAAAAAAAIHEUpAAAAAAAABI6iFAAAAAAAAAJH\nUQoAAAAAAACBoygFAAAAAACAwFGUAgAAAAAAQOAoSgEAAAAAACBwFKUAAAAAAAAQOIpSAAAAAAAA\nCBxFKQAAAAAAAASOohQAAAAAAAACF/uilHMu7BAAAAAAAACwQLEvSvX29srzvLDDAAAAAAAAwAJY\nnDuNzMylUikNDQ0pk8mEHQ4AAKgCM5NzzsKOA68wMxfnHBIAAMwtqPwr9p1S2WxW6XQ67DAAAAAA\nAACwALHvlPI8T2YsngIAUKvolIoeOqUAAKhtdEqViYIUAAAAAABA/MS+KAUAAAAAAID4oSgFAAAA\nAACAwFGUAgAAAAAAQOAoSgEAAAAAACBwFKUAAAAAAAAQOIpSAAAAAAAACBxFKQAAAAAAAASOohQA\nAAAAAAACR1EKAAAAAAAAgaMoBQAAAAAAgMBRlAIAAAAAAEDgKEoBAAAAAAAgcBSlAAAAAAAAEDiK\nUgAAAFgw51zYIQAAgJijKAUAAIAF6+3tled5YYcBAABizOK8ymVmLs7xAwCA+ZmZnHMWdhx4hZk5\nM9Px48e1atWqsMMBAAAVFlT+RacUAAAAFsw5JzNqhQAAYPEoSgEAAGDBenp6lMlkwg4DAADEGNv3\nAABApLF9L3rMzHmeR6cUAAA1iu17AAAAiCwKUgAAYKkoSgEAAAAAACBwFKUAAAAAAAAQOIpSAAAA\nAAAACBxFKQAAAAAAAASOohQAAAAWjBOQAQDAUlGUAgAAwIL19vbK87ywwwAAADFmcV7lMjMX5/gB\nAMD8zEzOOQs7DrzCzFwqldLQ0JAymUzY4QAAgAoLKv+iUwoAAAALls1mlU6nww4DAADEGJ1SAAAg\n0uiUih4zc57nyYxfCwAAtYhOKQAAAEQWBSkAALBUkS5Kmdmvm5lnZivCjgUAAKAekH8BAICgRLYo\nZWZtkt4o6bmwYwEAAKgH5F8AACBIkS1KSfpTSb8ZdhAAAAB1hPwLAAAEJpJFKTN7i6TnnXOHw44F\nAACgHpB/AQCAoKXCemMze1hSpvQhSU7S70r6bRVbx0ufAwAAwBKQfwEAgCgJrSjlnHvjTI+b2VpJ\nPybpkBWPdWmT9LiZbXLOjUy//kMf+tDk5729vert7a1GuAAAICADAwMaGBgIO4yaVKn8SyIHAwCg\nloSVf5lzLvA3XQgze0ZSu3Pu9AzPuajHDwAAlsbM5JyjaydAc+Vf/vPkYAAA1LCg8q9IzpSaxon2\ncQAAgCCRfwEAgKqLfKfUXFilAwCg9tEpFT3kYAAA1DY6pQAAAAAAAFCzKEoBAAAAAAAgcBSlAAAA\nAAAAEDiKUgAAAAAAAAgcRSkAAAAAAAAEjqIUAAAAAAAAAkdRCgAAAAAAAIGjKAUAAAAAAIDAUZQC\nAAAAAABA4ChKAQAAAAAAIHAUpQAAAAAAABC42BelnHNhhwAAAAAAAIAFin1Rqre3V57nhR0GAABA\nXWFhEAAALFXsi1K5XE6jo6NhhwEAAFBXWBgEAABLFfuiVDabVTqdDjsMAACAusLCIAAAWCqLc+u1\nmTnP82RmYYcCAACqxMzknOOPfYSYmduyZYsGBgbIwwAAqEFB5V+xL0rFOX4AADA/ilLRY2auUCgo\nkYh90z0AAJhBUPkXmQQAAAAWrK+vj5lSAABgSeiUAgAAkUanVPSYmUulUhoaGlImkwk7HAAAUGF0\nSgEAACCyOGwGAAAsFZ1SAAAg0uiUih4OmwEAoLbRKQUAAIDIoiAFAACWiqIUAAAAAAAAAhf7ohTb\n9wAAAIJHDgYAAJYq9kWprVu3chwxAABAwHp7e8nBAADAksR+0LkknThxQqtWrQo7HAAAUAUMOo8e\nM3OpVEpDQ0PKZDJhhwMAACqMQedlMjMGbQIAAAQsm80qnU6HHQYAAIix2HdKbdmyRQMDAxSmAACo\nUXRKRY+ZOc/zyL8AAKhRQeVfsS9KkRABAFDbKEpFj5m5OOeQAABgbmzfKxMFKQAAAAAAgPiJfVEK\nAAAAAAAA8UNRCgAAAAAAAIGjKAUAAAAAAIDAUZQCAAAAAABA4GJflPI8L+wQAAAAAAAAsECxL0pd\ne+21yufzYYcBAAAAAACABYh9Uers2bN68sknww4DAAAAAAAACxD7opQktbS0hB0CAAAAAAAAFiD2\nRaktW7aotbU17DAAAAAAAACwAOacCzuGRTMzVygUlEjEvrYGAABmYWZyzlnYceAVZubinEMCAIC5\nBZV/xb6a09fXxwl8AAAAAAAAMRP7TqlUKqWhoSFlMpmwwwEAAFVAp1T00CkFAEBto1OqTNlsVul0\nOuwwAAAAAAAAsACx75TyPE9mLJ4CAFCr6JSKHjqlAACobXRKlYmCFAAAQPAoSgEAgKWKfVGKhAgA\nACB4vb29HDYDAACWJPZFKRIiAACA4OVyOY2OjoYdBgAAiLHYF6VIiAAAAILX1dXFYTMAAGBJYl+U\n4vQ9AACA4PkDUMMOAwAAxBin7wEAgEjj9L3oMTOXSqU0NDSkTCYTdjgAAKDCOH0PAAAAkUW3OgAA\nWKrYF6UYdA4AABC8gYEButUBAMCSxH77Hq3jAADUNrbvRY+ZuTjnkAAAYG5s3ysTreMAAAAAAADx\nE/tOqUKhoEQi9rU1AAAwCzqloodOKQAAahudUmXq6+tjphQAAAAAAEDMxL5TiplSAADUNjqloodO\nKQAAahudUmViphQAAAAAAED8xL5TyvM8jiMGAKCG0SkVPXRKAQBQ2+iUKhMFKQAAAAAAgPiJfVEK\nAAAAAAAA8UNRCgAAAAAAAIGjKAUAAAAAAIDAUZQCAAAAAABA4ChKAQAAYME8zws7BAAAEHMUpQAA\nALBgK1asUD6fDzsMAAAQYxSlAAAAsGBnzpzRkSNHwg4DAADEmDnnwo5h0czMxTl+AAAwPzOTc87C\njgOvMDOXTCb14osvKpVKhR0OAACosKDyLzqlAAAAsGDOOY2Pj4cdBgAAiLHYF6UGBgZUKBTCDgMA\nAKCumJlWrFgRdhgAACDGYr99T5KSyaQuXryoK6+8MuyQAABAhbF9L3omcrDDhw9r7dq1YYcDAAAq\njO17C1AoFJTL5cIOAwAAoG40Nzdr9erVYYcBAABirCaKUslkUj09PWGHAQAAUDduu+22sEMAAAAx\nF/uilJmpq6tLZnT1AwAABGVwcFAvvPBC2GEAAIAYi31RyjmnXbt2aXh4OOxQAAAA6sqpU6fCDgEA\nAMRY7ItSUrFbik4pAACA4DQ3N2vNmjVhhwEAAGIsFXYAS5VKpZTNZpXJZMIOBQAAoG6sW7cu7BAA\nAEDMmXMu7BgWzczcyZMnlU6n6ZQCAKBGBXUkMcpnZi6VSmloaIiFQQAAalBQ+VfsO6VIhAAAAIKX\nzWaVTqfDDgMAAMRY7Dul4hw/AACYH51S0WNmrlAoKJGoifGkAABgmqDyr9hnEhSlAAAAgtfX1yfP\n88IOAwAAxFjsi1K9vb0kRAAAAAHbtWuXRkZGwg4DAADEWOyLUrlcTqOjo2GHAQAAUFc8z9M999zD\n4iAAAFi02BelGLIJAAAQjt27d7M4CAAAFi2yRSkz+4CZPWVmh83sY7Nd55xjrhQAAEAFlJt/Tejq\n6mJxEAAALFoq7ABmYma9kn5W0m3OubyZrZzt2okVukwmE1h8AAAAtWYh+deET3ziEzLjYEQAALA4\nUe2Uep+kjznn8pLknBub7cKNGzeqpaUlsMAAAABqVNn514RkMln1oAAAQO2KalHq9ZK2mNljZtZv\nZhtnu3D//v0cSQwAALB0ZedfkpRIJLR69eqAQgMAALUotO17ZvawpNI9dybJSfpdFeO61jnXaWYd\nkr4s6TUz3Sefz0+ewMcWPgAAgNlVKv+SinM9x8fHyb8AAMCihVaUcs69cbbnzOy9kh7yr9tnZp6Z\nXeecG5/hWl1//fX69Kc/rb6+PvX29lYvaAAAUHUDAwMaGBgIO4yaVKn8S5KuvPJK3X///UokEurt\n7SUHAwAgxsLKvyyKJ9eZ2S9LusE5d5+ZvV7Sw865m2e4ziWTSWWzWQ0MDCiRiOpuRAAAsFhmJucc\n07SrrNz8y7/WJZNJDQ0NqbW1NdhAAQBA1QWVf0W1ivM5Sa8xs8OSvijpnbNdWCgUJk/gAwAAwKKV\nnX9Jkud52r59O3M9AQDAokWyU6pcZuYkqaurS4ODgxxJDABADaJTKnomcrBUKqWhoSHmSgEAUGPq\nvVOqbO3t7dq5cycFKQAAgAClUills1ml0+mwQwEAADEV+06piYSov7+fmVIAANQgOqWix8zcyZMn\nlU6nWRgEAKAG0SlVpnw+r1wux0wpAAAAAACAGIl9UUqSOjo6aB0HAAAIUFtbm3p7exl0DgAAFi32\n2/fa29u1d+9eJZPJsMMBAABVwPa96GHQOQAAtY3te2V64okntG3bNlbpAAAAAsSgcwAAsFSx75SS\nWKUDAKCW0SkVPQw6BwCgttEpVSZW6QAAAILX0tJCQQoAACxJKuwAlmpoaIhVOgAAgICtWLFCY2Nj\nSqVin04CAICQxL5TKpPJUJACAAAI2JkzZ3TkyJGwwwAAADEW+6LUyZMnFee5WAAAAHGUTCZ1yy23\nhB0GAACIsdgXpVatWqWtW7dy+h4AAECACoWCRkZGwg4DAADEWOyLUpK0c+dODQ8Phx0GAABAXbnr\nrrtYGAQAAItWE0UpScyVAgAACNiePXtYGAQAAItWE0WpO++8U5lMJuwwAAAA6g4LgwAAYLFqoihl\nZgw7BwAACFhzc7NaWlrCDgMAAMRUTRSldu/erdHR0bDDAAAAqCsXL17U2NhY2GEAAICYqomi1MaN\nG5VOp8MOAwAAoK5cc801WrlyZdhhAACAmIp9Uaqzs1ODg4PMMwAAAAgYnVIAAGApLM6zmMzMFQoF\nJRKxr60BAIBZ+LMjWX2KEDNzkrR8+XKNj48rmUyGHRIAAKigoPKv2Fdz+vr65Hle2GEAAADUnXPn\nztEpBQAAFi32nVJmpuPHj2vVqlVhhwMAAKqATqnooVMKAIDaRqdUmeJcVAMAAIizs2fPamRkJOww\nAABATMW+KCVJd999N1v4AAAAAuac47AZAACwaLHfvjfx+bPPPqubb745zHAAAEAVsH0veiZysMbG\nRv3whz9k+x4AADWG7XsLtG/fvrBDAAAAqCvnz5/XyZMnww4DAADEVM0UpTo6OsIOAQAAoO6cOnUq\n7BAAAEBM1UxR6uzZs2GHAAAAUFeam5u1Zs2asMMAAAAxVRNFqeXLl5MQAQAABOiJJ57Q6dOnlUjU\nRDoJAABCEPssor29XWNjYyREAAAAAUqn05y8BwAAliT2lZxDhw5pbGws7DAAAADqSltbm3p7e+V5\nXtihAACAmIp9UapQKGj79u0kRAAAAAHK5/PatWuXRkdHww4FAADElDnnwo5h0czM+f/V8ePHtWrV\nqrBDAgAAFWZmcs6xTyxCJnKwZDKpS5cu6Yorrgg7JAAAUEFB5V+x75SSJOccMw0AAAACVigUdOjQ\nobDDAAAAMVUTRalkMqnrrrsu7DAAAADqzrPPPht2CAAAIKZqoihVKBR05MiRsMMAAACoO29+85vD\nDgEAAMRUTRSlJOn9738/w84BAAAC1tPTQw4GAAAWpSYGnUvFLXzHjx9XJpMJMyQAAFBhDDqPntIc\nTJJOnDjBgTMAANQQBp0vUDabVTqdDjsMAACAusOBMwAAYDFqolMqkUjo+PHjam1tDTskAABQYXRK\nRU9pp9Qtt9yi7373u0okamatEwCAuken1AI457RixYqwwwAAAKg73/ve99TX18dcKQAAsGA1U5Tq\n7OwkGQIAAAhYPp9XLpfT6Oho2KEAAICYqYmilCQdOnSIZAgAACBgqVSK2Z4AAGBRUmEHUCmNjY1a\nuXJl2GEAAADUlYcfflhbt25l2DkAAFiwmhh0LhVX6YaGhpTJZMIMCQAAVBiDzqOn9LCZl156SalU\nzaxzAgAAMeh8wTZu3EjbOAAAQIA8z9PJkyfDDgMAAMRUzRSlvvzlL9M2DgAAELCf//mf57AZAACw\nKDVTlBobGws7BAAAgLrDYTMAAGCxaqYolc/nww4BAACg7jQ0NHDYDAAAWJSaKUq9613vUqFQCDsM\nAACAunL+/Hk61gEAwKLUTFHqqaeeUk9PDzMNAAAAAtDU1KRUKqXu7m4OmwEAAItizrmwY1i0ieOI\nJ6RSKQ0NDSmTyYQVEgAAqLCgjiRG+czMmZnWr1+vPXv2KJVKhR0SAACooKDyr5rplJKkbDbLSh0A\nAEAAnHM6cOAAneoAAGDRaqZTKplMamhoSK2trWGGBAAAKoxOqegpzcHoVAcAoPbQKbVA2WyWZAgA\nACBgnZ0abP+0AAAgAElEQVSddKoDAIBFqZmi1J/92Z/JjEVUAACAIOXzecW58x4AAIRn3qKUmX14\n2tdJM3ugeiEtznvf+17mGQAAgJoRlxzsscce08mTJ8MOAwAAxFA5nVI3mtkHJcnMrpL0kKR/rWpU\ni7Bnzx4NDw+HHQYAAEClxCIHk6S3vvWtLA4CAIAFm3fQuRX3xD0g6bCkPknfcM59PIDY5lU6ZFOS\nXnjhBQadAwBQY+p10HmccjCGnQMAUFuCyr9mLUqZWXvJl1dI+nNJg5I+K0nOuQPVDm4+pQnRVVdd\npQsXLiiZTIYZEgAAqLB6K0rFLQeTpA0bNmjfvn3M9wQAoEZEoSjVP8frnHNuW3VCKh/HEQMAUPvq\nsCgVqxysoaFBZ86cYWEQAIAaElT+lZrtCedcX7XfvJI4jhgAANSCuOVgR48epSAFAAAWZdai1AR/\nsOZbJf1Y6fXOuQ/P9powvP/976dlHAAA1Iy45GDveMc71N/fr0SinPNzAAAAXlFO9vD3kn5OUl7S\nhZKPSPnoRz+qfD6v4eFhzTe8HQAAIAZikYPt2rVLIyMjYYcBAABiqJzT977jnFsbUDwLMn3IZmdn\np/bv369sNsuKHQAANaLeZkpNiFMO1tPTo4GBAXIvAABqRFD5VzmZQ87Mbqt2IJWwf/9+5fN55XI5\njY6Ohh0OAADAUsQmB9u9eze5FwAAWLB5Z0pJulPSL5rZM5JekmQqnvxye1UjW4Rly5bp7Nmzamho\n0MqVK8MOBwAAYClik4PdcccdHDgDAAAWrJztezfP9Lhz7rmqRLQA01vHE4mEPM9TMpnU8ePHlclk\nwgoNAABUSB1v34tNDvbiiy/qqquuCiscAABQYZHZvuece85Pfi5JciUfkdPR0aFUKqXu7m5W6wAA\nQKzFKQc7evQoh80AAIAFm7coZWZvMbN/lfSMpEclPSvpH6sc16I453Ts2DENDAzIrO4WVAEAQA2J\nUw727ne/W21tbert7ZXneWGHAwAAYqKcQecfkdQp6Wnn3Ksl/aSkx6oa1SLt379fZjZZkPI8j1U7\nAAAQV7HJwQ4cOKB8Pq/BwUEGngMAgLKVU5R62Tk3LilhZgnnXL+kjVWOa1E8z9P27dvleZ48z1Nf\nXx+rdgAAIK5ik4NNuOaaazhsBgAAlK2c0/d+aGaNkr4l6QEzG5F0obphLd7g4KBGRkZkZsrlcsrn\n88rlchodHWXwOQAAiJNY5WBSceD52NgYORcAAChLOZ1SPyfpoqRfk/RNSd+X9LPVDGopCoWC7rnn\nHq1cuVLZbFapVErZbJbB5wAAIG5ilYNJ0saNG9XS0hJ2GAAAICZsofOWzCwh6e3OuQeqE9KCYpkx\n+FQqpaGhIbW0tGh0dFTpdJrB5wAAxFRQRxJHXVxysGw2q/7+fiUS5ax9AgCAKAoq/5o1WzCzZjP7\noJl9ysx+yop+RdIPJN1T7cCWYuPGjUqn00okEspkMhSkAABAbMQtB1u2bNnk56VjEwAAAOYza6eU\nmf29pNOSdqt42ktakkn6VefcwcAinMNMq3TLli3TmTNnlEqVMy4LAABEXb11SsUlB7v66qv14osv\nXvbchg0btHfvXjqlAACIsaDyr7mKUoedc7f5nyclvSDpJufc5dlHSGZrHR8aGtINN9wQdDgAAKAK\n6rAoFdscLJFIKJFIsIUPAICYC337nqSXJz5xzhUkDUUpGZrL0aNHtdBZWQAAABER2xzM87wpW/g8\nz9Pw8DB5GQAAmNFcRak7zOys/3FO0u0Tn5vZ2aACXIw3velN6u3tled5YYcCAACwULHNwZYvXz45\n7HzlypXq6+tTW1sbeRkAAJjRgk/fi5LZWselV07gy2QyQYYEAAAqrN6278XBTDlYIpHQsWPHlEql\nlE6nNTIyora2NuXzefIyAABiJgrb90qDudPM3u1/vtLMXl3dsJZmYoUunU6HHQoAAMCixSkH8zxP\nb3/723Xdddfp5MmT8jxP2WyWvAwAAMxq3qKUmd0n6T9J+qD/0JWS/qqaQS1WMplUT0+Pnn/+eQ0M\nDMiMRVUAABBPccrBJgwODmrz5s26/vrrdcMNN8g5p2PHjpGXAQCAGc27fc/MDkpaL+mAc269/9gT\nzrnbA4hvTjO1jjc1NenUqVNKpVJhhAQAACqsXrfvxS0Hk6TGxkadP39+8mu27QEAEE9R2r73I1es\nXDlJMrOG6oYkmdkdZrbbzL5tZnvNbGO5rz137py+9rWvMUwTAADEXaA52FLyL6k4U+rSpUtTHmPb\nHgAAmEs5Rakvm9mfS3qVmb1H0r9I+ovqhqU/lHSfvyp4n6Q/WsiL3/rWt2rFihXK5/NVCQ4AACAA\nQedgS8q/7rjjDnV3dyuZTGrz5s06ceIE2/YAAMCc5t3j5pz7YzN7o6Szkn5C0u855x6uclyepOX+\n56+SdHyhNzhz5oyOHDmitWvXVjQwAACAIISQgy06/0okEjp8+LC6urr0/PPPq7W1VWYmz/M0MjKi\ndDpNcQoAAFxm3plSYTCzWyT9kyTzP7LOuednuG7W4Jubm3X69GklEmUdMAgAACKqXmdKBa3c/Mu/\ndsYcrHSGlOd56uvrUy6XUzabVX9/P3kZAAAxEVT+NW+nlJmdkz/LoMQZSfsl/bpz7geLeWMze1hS\n6dRL89/ndyS9QdKvOue+amZvk/SXkt64kPvfeuutiwkLAAAgEqqRg1U7/+ro6FA6nZbneXryySeV\ny+WUz+eVy+U0OjrKwHMAADBFOUfUfVzSkKQvqpi43CvpxyUdUDFZ6V3MGzvnZk1yzOwLzrlf9a/7\nWzP77ELv//jjj5P8AAAQQwMDAxoYGAg7jCioeA5WrfwrkUho06ZN2rVrl5xz6uvr0+DgoBobG3Xh\nwgUGngMAEHFh5V/zbt8zs0POuTumPXbQObdupucqEpTZdyX93865R83sJyV9zDnXMcN1c27fO3Xq\nlJLJpDzP0+joKPMMAACIoXrdvhd0DlZu/uVfOyUHe/DBB3XXXXdpfHxczjndeOONyufzSiaTOnjw\noNasWUMOBgBAjASVf5Wzsf+imd1jZgn/4x5JL/rPVWsg1Xsk/YmZfVvS70v65YXe4Pz58xobG5uc\nZ9DW1qbe3l55nlfxYAEAAKog6Bxs0fnX9u3btWLFCrW1temee+5RNptVKpVSd3c3BSkAADCrcjql\nXiPpE5K6VEyAHpP0ayqeyLLBOber2kHOEduswXd2diqXy2lkZERtbW3K5/NThm8CAIB4qONOqVjm\nYMlkUseOHVMymaRLHQCAmAoq/4rk6Xvlmi0hWrZsmZ5++mldf/31kqTe3t7Jk18GBgZIjgAAiJF6\nLUpF2VxFKUnq6enRwMAAp+0BABBTkSlKmdnVkv6dpDWSrp543Dn3S9UNbX5zJUSpVGry+GFJzJQC\nACCm6rUoFaccbO3atfrOd74z+XUymdTQ0JBaW1sDjw0AACxdlGZKfUFSq6Q3SXpUUpukc9UMqhJK\njx9OJBLKZDIUpAAAQJzEJge76qqrpnxdKBS0fft2ZnkCAIA5ldMp9W3n3Hoze8I5d7uZXSFpp3Ou\nM5gQ54xtzuA3bNigffv2UYwCACDG6rhTKrY5mCRmeQIAEGNR6pR62f/vD81sraTlktLVC6lynHOs\n0AEAgLiKVQ62adMmJRIJNTc3K5lMauPGjWppaQk7LAAAEGHlFKU+Y2bXSvovkr4m6UlJ/62qUVXI\ngQMH1N3drRdeeEFxHugOAADqUqxysCeffFLHjh3T2NiYNm3apP3796uvr48FQgAAMKuaPH1vumQy\nOXnyHqfAAAAQL/W6fS/KZsvBDh8+rJaWFrW1tSmfz1+2hc/zPA6fAQAgBkLfvmdmm83skJmdN7Pd\nZra62sFUS6FQ0M6dOzU8PBx2KAAAAHOKaw7W0NCgFStWqKWlRdlsdvIk5HS6uOPQ8zz19fWpra1N\nvb29dFABAIDZO6XMbL+kD0r6lqS3SPr3zrk3BRjbvMrtlPKv1YkTJziaGACAmKm3Tqk452Bmpp6e\nHu3YsUPj4+NTOqKGh4dn7aACAADREnqnlKSEc+5h59xLzrm/kRTLSZUT2/WampoYtgkAAOIgtjmY\nc06Dg4M6cuTIZVv00un0jB1UAACgfqXmeO5VZnbXbF875x6qXliVcfvtt+uJJ56QJF24cEFjY2Os\nyAEAgKiLdQ5WKBS0bt06bdiwQZ/5zGd02223SZJGR0f1yCOPaGxsjJlSAABA0tzb9z43x+ucc+6X\nqhNS+Rayfa+rq0uDg4MkQAAAxEwdbt+rqRysqalJ69at0+7du5XNZtXf38/BMwAARFxQ+VddnL7X\n1NSkU6dOKZWaqzEMAABEUb0VpeJgIUUpqXgScqFQYJYUAAAxEYWZUjXjwoULOnLkiAqFgoaHhxXn\nQhwAAEDcdHR0MEsKAABcpm46pS5evKjGxkZduHCB1nEAAGKETqnoKScHu/XWW/X000+ru7ubWVIA\nAMQM2/fKUE5CtGzZMl28eHHKY7SOAwAQHxSlome+HGxiu15TU5PGx8d1xRVXBBUaAACogKDyr3mH\nLE07/WXCGUmHnXMjlQ+pskoLUhMJ0tVXX618Pi/nHKt1AAAgkuKcgxUKBUnSuXPn9NRTTymTydAl\nBQAALjNvp5SZ/R9JXZL6/Yd6JT0u6dWSPuyc+0I1A5xLOZ1Szc3NunDhgu644w4dPHhQnudNPtfT\n06OBgQG28QEAEGH12ikV9xxMkhoaGtTe3s7JewAAxExktu+Z2T9Jeqdzbtj/OiPp85LeLulbzrm1\n1Q5yjtjmTYgaGxt15MgRrVq1St3d3XrsscemPH/ixAmtWrWqajECAIClqeOiVKxzsJJr5ZxjfAIA\nADESpdP3bpxIhnwj/mOnJL1cnbAq5/z583r66aflnNNXvvIVtbe3Tz5nZpNt5J7ncTIfAACIkljn\nYBMmClKcvAcAAKYrpyg1YGZfN7N3mdm7JH3Nf6xB0g+rG15lbNu2TStWrNBNN92kVCqlzZs3K5VK\nqaenR5lMRp7nqa+vT21tbert7Z2yxQ8AACAksc/BzEw9PT167rnn9OCDD4YdDgAAiJhytu+ZpLsk\n3ek/NCjpKy4CLUULaR0v1dnZqYceekitra0yMw0PD6utrU35fJ7WcgAAIqaOt+/FOgfbsWOHVq9e\nrZaWFm3btk2Dg4Pq6OjQrl27lEwmgwgTAAAsUmRmSvnBZCRtkuQk7Y3KiS+LLUpNFJ5aWlo0Ojqq\nlpYW9fX1KZfLKZvNamBggNNhAACIiHotSknxzsE2b96swcFBjYyM6MYbb5w8ka+rq0u7du1i4DkA\nABEWmZlSZnaPpL2S3ibpHkl7zOxt1Q6smjZu3KhCoTC5Za+vr087duzQ0NAQBSkAABAJcc/B9uzZ\no+7ubm3fvn2yICVJ+/bt0+joaIiRAQCAqChn+94hSW+cWJkzsxZJ/+KcuyOA+Oa0mE6pdevW6eqr\nr9a+ffvkeR6nwQAAEHH12ilVKzlYMpmcUpTasmULi4AAAERcUPlXqoxrEtNaxcdV3oD0SPre976n\n8+fPT37NaTAAACCiaiIHW716tQ4fPiypWKB68MEHKUgBAABJ5RWlvmlm/yTpS/7X2yV9o3ohVVdp\nQWrz5s366le/qkwmQ3IEAACipiZysImClJmpq6tLo6OjSqfTzJQCAABlDzp/q6Ru/8udzrm/q2pU\nZVrsoPMJJ06c0KpVqyoVDgAAqIJ63b4n1V4O1tjYqPPnz2v58uUaGxtTIpGYLFJNXyD0PG/W5wAA\nQHVF6vS9qFpsQpRMJpXNZvXoo4+S5AAAEHH1XJSKqsXkYMuWLdPFixcnvz506JA+8IEPTJ5+3N/f\nP9k95XnelJORS58DAADVF3pRyszOqXj88GVPSXLOueZqBlaOxSREmzZt0le/+lW1trbKOccKHAAA\nEVdvRalazMHMTGYmz/MkSU1NTTp69Khuuukm5fP5yw6dGR4eVltb24zPAQCA6gsq/5p1yck51+Sc\na57hoykKydBiPf7447rrrruUz+fV19entrY29fb2TiZJAAAAYarFHKyjo0N33nmnEomE2tvbdfr0\nabW2tiqbzc546Ew6nZ71OQAAUDvqcvueJG3YsEGHDh1iBQ4AgIirt06pOCgnB2toaNCFCxckST09\nPXrggQd06tQprVy5UslkUplMZs6udWZKAQAQntC378XBUopSZqaGhgadP39ezc3NOnXqlJLJZCXD\nAwAAFUBRKnrKzcGSyaQKhcJMr1dPTw+zogAAiKjQt+/VOueczp8/L0k6e/asRkZG5rze8zwNDw8r\nzkU8AACAIDnnZlz0c84pl8tpdHQ0hKgAAEBU1FVRKpFIzNj+PTF8czYTJ8AwfwoAAKB8nufpiiuu\nUEdHx2XPbdy4kVlRAADUuboqSnmepy9/+ctTHksmk+rp6ZmcJzVTR9To6KhyuZzy+TyregAAAAvw\n4osvat++fVMe27Rpkx566CFJdKMDAFDP6qooJUl33333ZFdUY2Ojnn32WX3pS1/S8PCwCoXCjB1R\nnAADAABQGYlEQolEQjfddJO2bt1KNzoAAHWsbgedT9i0aZP27t0rM9PmzZu1f//+GU/k4wQYAADC\nwaDz6CknB0skEnLOycwmi03T862J0QqFQoHTkAEAiBAGnQdk7969kooDN/ft26eOjo4ZO6ISiYQy\nmQwFKQAAgDJ4nifn3JTup2uuuUaPPvqostmsEomEli1bpkKhIDOjGx0AgDpU951SpTo7O/Wtb31L\nR48e1erVqzmiGACACKBTKnqWkoMdPnxYt9xyizo7O/X4449LKs74HBoaUmtra8ViBAAAi0enVACS\nyaSampqUSCS0efNmPfroo9q6davWr1+vvr4+5hoAAABUUFNTk6699lo99dRTOnjw4OTjmzZtmnPb\nHsPQAQCoTXVblFq3bp3279+vdevWKZFI6Morr9TWrVu1e/du5fN5DQ4O6sknnyT5AQAAqJDXvva1\namtr0+23367GxkaZmW677TYNDAxoZGRkxrzL8zyGoQMAUKPYvudLJpOSpEKhIKm4knfp0iVls1nt\n2LFD4+PjDDkHACAEbN+LnsXkYMuWLdPFixenPNbQ0KALFy4omUxOzpXq7++fMkJheHhYbW1tyufz\nbPMDACAgbN8LWDabVXd3t5LJpNrb23Xp0qXJjqktW7bMuzpHWzkAAMDsXv/611/22IULFyQVFwXz\n+bxyuZxGR0enXJNOp9XV1SWpmG9t376dbikAAGoEnVLF++jgwYO69dZbdfToUd16663atm2bcrmc\nNm7cOHls8WxHFU+0ledyuRlX+AAAwOLRKRU9lT5sJpFIKJFIKJvNamBg4LLO9BdeeEE33XTTlHys\npaVFo6OjdLIDAFAFdEoFyDmnO+64Qy0tLVq/fr22bdumHTt2aGhoSIODg+rq6lIymVRXV9eMRxWP\njo4ql8vNusIHAACA2Xmep3w+L8/z5Jy7rAO9tbVV2WxWqVRK2WxWK1euLGvOFJ3sAABEG0WpEmfO\nnJncsjcyMiKpWLAys8mPmZKadDo9JVGaqXAFAABQb77xjW9M+TqRSKixsXHW63fv3q3h4eHLCk5m\npv7+fg0NDWlgYEBjY2OzLghOFKIKhULZA9IpXgEAEA6KUiUaGhokFecarF69Wm1tbbrzzjvn7YKa\nnijRQg4AACD99E//tBoaGpRIJNTd3a0DBw7o/Pnzs17f0dEhSTPmXolEQplMRmY264Jg6Ul95eRw\n01/D6X4AAASLmVIlJk6AKZVMJrVp0ybt27dv1jkHAACgepgpFT0LzcHa29v12GOP6ciRI7r99tsv\ne3716tW66qqr9MQTT6irq0tmpsHBQXV0dCiXy804q9PzvMtmSk0/qa80h3vkkUc0NjZ22Qyq0tfM\nNj8UAIB6w0ypgNxyyy2TiU5pQaqpqUmpVErd3d3auXMnXVAAAACLdODAAXV2dmrdunVatmzZlOca\nGhr05JNP6tvf/rYKhYJ27dqll156SZ7nae/everr65uxe6m0c2pCaQdVaQ73yCOPaNu2bTN2QzGG\nAQCA8NApNYP29nbt2bNH4+Pjk6tpE6txK1eunHGVDQAAVAedUtGz1Bzstttu0+HDh2d9PplMqlAo\nSNKCu5fm66Ca6X4zvQYAgHpGp1SIrrjiiimrbxOzBm644QZdd911zBwAAABYgkQiofb2diWTSTU1\nNU15rrm5WV1dXZKKCfFc3UszDSifr4NqpvvN9BoAAFB9dErNYPoKWunq2mzXlIuVOAAAFoZOqeip\nZA7W3Nysc+fOTRaWksmknnvuOY2Pj6ulpUWtra1TcqbS7vVt27Ypl8spm82qv79/xtlT019HDgYA\nwPzolApRV1eX0un05OpbS0uLOjs7Z7ym1HzHCXO6CwAAwFRnz56dzJ1SqZS6urr0tre9TRs2bNC9\n9947Ja9azOl6ExbTDTVfbgcAAJaGotQMPvnJT+rEiRPq7u6eLCB96EMfmnLN/fffP7m1b3h4WIVC\nYd6C0+jo6IKSJwAAgHqyd+9eXbx4UY899pjy+bwGBwc1MjIy+XxpLrVv3z51dHRUbUA5i4kAAFQf\n2/d811xzjS5duqRly5Zp7dq12rt372XXTAzdXL58uU6dOiVJ6uvrUy6X08aNG7V///7JI4gPHjyo\nNWvWTFmNc86pt7d3ss2c0/wAAJgf2/eip5I5WGNjoy5duqSuri69/PLL2rNnz5Tnt2zZMrk1b3ou\n9cgjj1TtAJr5hqMDAFDLgsq/KEot0De/+U2tWrVKa9eu1ejo6GSykkwmtWnTJu3du1eNjY26cOHC\njPMNmGcAAMDCUJSKnkrmYIlEQh0dHfrbv/1b3XjjjZc9n0wmdeDAAa1cuVKJREItLS2BnITMYiIA\noJ5RlCpDGEWpxsZGnT9/XsuXL9fo6Kje8IY3TFmte+qpp7R+/XpW1QAAqBCKUtFTiRwskUhM2RJ3\n4MABtbe3X3bdRO7lv696enq0Y8cOjY+PV70wxWIiAKBeMei8TPfff3+g7zeRFJ05c0ZHjx5Vf3+/\nhoaGNDAwoGQyqTVr1sx55DAAAEA9myjuXH311VMef9/73jf5eXNzs5LJpNrb23Xp0qXJx51zGhwc\n1JYtW6bMeiodSF7J4eSLGY4OAADKR6dUGdavX6+DBw+qoaFhsig1MVdqpqOHWVUDAKBy6JSKnkrn\nYJs3b9b+/ftVKBSUSCT0zDPP6Ac/+IHuvPNObdu2TTt37py8trOzc3KOZyqV0rFjx3Tvvfcql8up\nq6tLZjbZxT5fRxU5GwAAM/v/2Xuz4Lau7O73f86hBhIAWdUSJXXLUn/lbtsaOYADABKgBrc79T18\ndZPueOiuVOUt1dXpfrsvN095Sd2qVOUhSWeo5CWV9HVLintIJ9VJ2xIpWxwkDgJByrKcTtmWCICD\nKLttkpII4Jx9H+i9vc8+52AkAZBcv6pVJoEzbMAi8edaa/8XdUrVCU1NTfjlL3+JRCKBp0+fAtio\nmr333nsOryhelaOqGkEQBEEQRPH86Ec/gt/vBwD4fD6cPXsWFy5cwMGDB3H16lUkk0mEQiEYhiG6\n0fl/eRKKTzfmX7t1VMnQdD2CIAiCqD3UKZUHPpFP0zREo1Fb5U02u+Sihj+nmpsTBEEQBFE+1ClV\nf2yFBvv8/7PDa2pmZgaHDh2yTcJ78OABdF0XNgnckFzulJInI3Ofz9bWVtEZtbS0RNP1CIIgCMID\nMjovgq1KSum6jvb2dsTjcdtjc3NzMAxDtHjzlm/GGI4dO+YqlDarW4raywmCIIjdCiWl6o+t0mAN\nDQ0IhUIYHR0VnlCxWAxDQ0O4ePGiZ3FwcXERmqbh8OHDYIzh4cOHaG1ttRUNBwcHbddQv6fpegRB\nEATxBZSUKoKtqtJpmobGxkasra3ZnovFYrh+/ToAYHFx0dW/QPUy2IyuKerEIgiCIHYzlJSqP7Yq\nKRUKhfDGG2/g2LFj4jHexXTgwAHcu3cPp06dEjqokEaSi3punVFy5xQlpAiCIAjiCygpVQTVMjrn\n6LqOyclJfP/738fExAQsywJjDIZhYHJyEowx/Pa3v8U3v/nNTW0FX1xcpPZygiAIYtdCSan6Q9Zg\nhmHANM1Nu/avf/1r/M7v/I74PhQK4caNGzh37hwmJiZsySdZIxmGgWQyiSNHjrhelzEmtvlRZxRB\nEARB5IeSUkVQ7aSUG4ZhwOfz4bPPPrM9pmnapgkeElEEQRDEboaSUvVHNTVYNBpFLpfDzZs3AcBW\noGOM4dy5c7hx4wY0TRNb/eROKt4JxRizbfMrVkuRhQJBEASxG6GkVBHUOikVDofxD//wD+jo6HBM\nbBkaGkJ/fz/ef/99W5t5uZAgIgiCIHYrlJSqP2rRrc61ViAQwCeffALDMGBZFmZmZtDV1QXLsmAY\nBlKpFA4fPmzb2leuvQJZKBAEQRC7FUpKFUEtk1I+nw+//e1vYRgGIpEIbt26ZXu+t7cX9+7dw2ef\nfYZAIIBHjx7BMIyKEkuUmCIIgiB2I5SUqj+qrcHa2towMzMDYCNBlU6n0draivPnz+PGjRviuJaW\nFqG51K19mqa5WiHk01dkoUAQBEHsVqqlv6jUUyZra2u4c+cOLMvCG2+8AZ/PZ3t+fHxcbOlbWVlB\nOBzGhQsX8Mwzz+D8+fOOzqpC8EpduecTBEEQBEFsV2ZnZ2EYBoCNwuCBAwfw8OFDjI6O2o5bW1vD\n8vIyAODgwYNCn/l8PkQiETQ0NKCvrw+HDh0CkF9fce/Qvr4+x3kEQRAEQWwO1CmVh3379mF9fd3z\neV3XEQgEsLKyUjBJJFfoZCPOYrufqFJHEARB7FaoU6r+KEaD7dmzB9ls1vP5/fv34+nTp2XdPxQK\n4Wc/+xleffVVDA8Pi8djsRjefvttaJqGxcVFHD16FKZpwjAMzM3NQdd1obksy8Ldu3fR2dnp0Ffq\n1tUs3yQAACAASURBVL/Lly/jyJEj1KlOEARB7BqoU6oOKJRosiwLn376qetxhmGgv78fXV1doroW\niUTEea+++ipyuVzR3U+HDh2iSh1BEARBENuGQjqqUELqxIkTtu+bmprE17du3cLx48eRyWTQ0NAA\nYKNYePnyZWFo3trair6+PhiGgb6+Phw5ckSYo8/Pz+PChQvo6OiAz+dz6CvehZXL5TA2NgZd1ykh\nRRAEQRBbAHVKVUggEMDa2hoYY+DvZSAQwHvvvQfDMNDa2orl5WUcOnQICwsLOH78uOiWunr1Kl56\n6aWixhgD5ClFEARB7E6oU6r+qIYGm5ycxLlz57C2tgZgIyn1+PFjx3GhUAi3bt2CpmmIRqPC0JwX\nA8fGxoRJOQBcuHABIyMjYnueYRiYnp7G6dOnhb6iyccEQRDEboeMzougHpJSAHDmzBncuXNHfP/g\nwQP8wR/8gaPlGwDOnz+PkZER+P1+rK6uwufzCe+pcDiM4eFh4ZlAEARBEAQlpeqRetFgADA1NYWe\nnh5YlgVd16HrOnK5nO1rwzBw+/ZtaJqGYDCIXC4HAGhoaEAkEsGVK1dw+PBhW+KJioEEQRDEboa2\n720j5IQUAHz88cei5fvGjRs4fvw4zp8/D9M0cenSJcTjcaytrcE0TayurorRwjdv3kQsFiMTc4Ig\nCIIgCAU5MSQPmDl37pzQTn6/H+FwGMAXRuXARudTe3s72traxHa9WCyG+/fvQ9M0HDt2zGalQAkp\ngiAIgqgOlJTaApaWloQgAoBcLofh4WGEw2EcP34cf/zHfyz8ofr7+9HT0yOOHR8fx9LSUi2WTRAE\nQRAEUbfI3f18Sx8ArK6uiq8fP36Mv/mbvxE+U6ZpArD7W62uriIej2NoaMhWSBwdHcXDhw+Ry+UQ\njUZp4jFBEARBVAFKSm0B3/zmNzEyMmJ7rLGxEVNTU0L0/PVf/zXm5uYwNDSEvXv3iuO4CToJIIIg\nCIIgdiPldiZpmoa+vj6cOXMGfX19YkqypmmiKx0A+vr6cPLkSVy8eNFmdB6JRGCaJmKxGMbGxmyJ\nKoIgCIIgtgbylKoSuq6LRBP3OOjr68OlS5eE+TlHHklMEARBELsd8pSqP6qtwZ599ll88MEHeY+Z\nnp5GW1sbNE1DLpfDwMAAbt26hcbGRtFZpWka5ubm8OjRI3R1ddn8pn74wx9iZGREdFcBQCQSwcjI\nCG3hIwiCIHYd5Cm1DfnJT36CQCDg+lxHR4f42rIs4TfFGBPjiltaWhwjiWUsy8Li4iK2cyKRIAiC\nIAiCU2yyp1BCCgAOHToExhjm5+fx3nvvYWJiApZl2bb6McZw6tQptLe3I5fLQdM09Pf34+DBgxgd\nHRUJKV3XxQAadY211GOkBQmCIIidBiWlNpHvfOc7WFlZwYkTJ2wT9Hp7e7Fnzx7H8YwxPHz4EIOD\ng0ilUnj06BGSyaTr2GHLsnDhwgUcPXoUfX19No8EEicEQRAEQWxHNku/aJqGV155BX19ffjKV76C\ntrY2NDU1wTAMR8GQTz3m5/34xz/Gt7/9bdG13tzcDE3TXLUb12O18Juq5b0JgiAIYqug7XtbTCgU\ngqZpuHnzpucxsVgM169fF1v83Ka9LC4u4ujRoyIZFYlE8M477+DFF1/E6Ogo+vr6MDQ0ZPNMIAiC\nIIidAG3fqz/qQYM1NTXhxIkTuH37tucxU1NTOH/+PFZWVsRjsqUCAAQCAfE8958yTdPVTmFxcRHP\nPPMMcrncptstFJr4t5X3JgiCIAgV2r63Q/j7v/973Lp1K+8xN27cwOLiomsFjHdCtba2Oqb0DQ8P\ni4kxIyMjNLWPIAiCIIgdh9cWv8ePH+dNSAEbXVFyQko1PQdge97n88E0TWGartopHDp0CJFIBIZh\nIBKJuNotFIvc7V5MF9ShQ4fE9GYvqweCIAiC2G5s+6SUrus4ffp0rZfhyfe+9z10dnYWPG55eRlL\nS0sYGRkRSabFxUUhUC5cuIB33nlHCCG/349vfOMbaGpqArAx8vj3fu/3bOacBEEQBEEQ251yuvp1\nXUcsFkMkErElofr7+9HX1+eZ6OL+U7qu4yc/+QmWlpZs95e//ryCXPLaAOdWvMXFRVFo9Jr4p2ka\nhoaGPK0eCIIgCGI7su2TUr29vXj33XdrvQxPJiYmXLfUTU5OIhgMQtd1NDc3IxgM4uWXX4bf7wcA\n+P1+MMZsAuXjjz/GO++8g6tXr2JtbQ2maWJ1dVVc/+bNm4jFYuQxQBAEQRDEjqHU5Iuu62CMYXV1\nFefOnbPpokuXLuHSpUueHVaMMdGJ9J3vfMfRubS4uIjh4WGYpik63cvh4cOHNo3HO7MMw0B3dzda\nW1s9X9vhw4cpIUUQBEHsGMhTqkZEo1FomoaRkREwxsAYg67r0DQNpmnCMAzE43H84Ac/EJ5Rg4OD\nuHjxIkZGRuD3+7G2toZIJIJsNis8q8hjgCAIgthpkKdU/VGvGmz//v3IZDKeBbrm5masra3B5/PZ\nDM854XAYP//5zwEAx44ds/k3tba24t1330VbW5s4fn5+HkeOHLFdo5A3FLCR/Dp//rzQeNevX4dp\nmhgYGMDExAR5hRIEQRA1Z8d7Smma9vuapt3RNM3UNC2oPPf/aJr2G03T3tM07Zu1WmOl5KtijY6O\nYmxsDJZliYRUU1OT2H7n9/sRDAbBGMNHH32Ey5cvi6oa75CKx+N4++23MTw8jEgkQh4DBEEQBEEU\nZLM1mNuUumrwv/7X/3I8lslk8to6fPbZZzBN0zUhFQwGMTw8jCNHjuDw4cPCv4kXAPv7+9HZ2Ynm\n5mYYhoFYLIbW1lbbFORiJ+S5bcV79OgRJiYm8m7hIwiCIIidRi3LL7MAfg/A2/KDmqadBPAKgJMA\n/jeAv9W2aY9yY2Oj53OWZaGxsRGGYaC5uRmWZWF1dVU8v7q6KrylXn75ZRw7dkyMOjYMAz09PTh1\n6hQYY1heXsaNGzccHgOygabb/b2eIwiCIAhiR7OpGiybzW7FGgvy0UcfOR5rb2/Hvn37Sr5WW1sb\nZmZmcPHiReRyOSwtLWFwcBAPHjwAsNE1dfPmTZimibW1NUxPT2NoaAgXL17E0aNH0dfXB9M0Hdvy\n8iWW1K14xRiZk34jCIIgdho1S0oxxt5njP0GgCp2/i8AlxhjOcbYRwB+A6C32uvbDB4/fpz3+ZWV\nFZw8edK1WscNzJuammxVs7/8y79ET08PJicncf78eVGNu3jxIlpbW4WwyeVyiEajrpW6Yqt4BEEQ\nBEHsPHayBovH45icnLQ9durUKddj/X4/DMNAIBDAzMyMKAYODAwIbQVsdLfL9Pb24uTJk3jvvfcw\nMjIC0zSFr+eXvvQl+Hw+ABuT/A4ePJh3vXKSSdM0XLt2DfF4HENDQ46Oe9JvBEEQxE6kHjeqHwUw\nJ32f+vyxHcmdO3ccjwWDQZHQ4h1TnO7ubty8eVMIJ7kat7i4iMXFRZimiVgshrGxMddKXSlVPIIg\nCIIgdg07UoPdvXvX9fHV1VWcPn1aTNwDNjyp5GIgNyDnhMNhvPPOO7h48SI6OjpEERHYGG7z/vvv\ni8731dVVLC8ve65LTTLlcjm8+OKL6OzsxIULFxxJJ9JvBEEQxE5kS5NSmqa9pWnajBSzn//3/2zl\nfbc7v/jFL8QUPhnTNIXnFLBR4YtEIjAMA11dXXjttdfwzDPPIBqNYnx8XBzX09ODQ4cOIZfL4c6d\nOzh48GDB9nCCIAiCILYvpMG8kTuQ7ty5g46ODvH9kydP0NPTI7ykAGBoaAjpdBrz8/MYHh7GvXv3\nhMfn2toaurq6hKY6deoU+vv70dDQgP7+/rwaS00y8et6JZ2K2d5HEARBENuNhq28OGPspTJOSwE4\nJn3/zOeP7WiamppEd9Tv/u7v2qp2Xjx+/Bg/+clP8PLLL2N8fFyYpo+Pj8Pn82FlZQWBQADvvPMO\nTNPEwYMH8emnn6KlpQVLS0t49OgRNE1DLpfD+++/j1OnTtGUF4IgCKLmXL9+HdevX6/1MrY1pMG8\n+eijj/Dqq6/i5s2bsCwL+/fvh2EYME1TGJB//PHHePXVV/HMM88gEongypUraG1txcWLFzE8PCwS\nWz6fD6Ojo0JT8fMLTd8Dvkgy8Ql8p06dsn2vJp1KuTZBEARBlEqt9JdWa6NETdOGAPzfjLGpz78/\nBeD/AxDCRsv4WwCeYy4L1TSN9fT0YGJioppL3hI+H7eY9/HGxkY8efJEPB6LxXD58mUxshgADMNA\ne3u78EbgY4wfPnyIs2fPiusmEgn88Ic/FMLKNE20tLRgeXkZDQ1bmqskCIIgiJKo1kji3UalGqya\na90sAoEA7t27B8uycOzYMddjZmdnceDAAXzlK18Rj6n6SiYYDMLn82FsbAx9fX0YGhoSRT7LsvIm\nkdTnCx1PEARBENWiWvqrZm0xmqb9rqZpcwDCAP5D07T/BADG2F0AVwDcBfArAN93E0OcS5cuVWO5\nW47XS+zt7YWu69B1XSSk+PF/9Vd/hUOHDon2cmCj42p6elpM9uvu7kZraytOnTqF5uZmAEBzczNa\nW1sxOjoKy7LElsBPP/0U9+7d28JXSRAEQRBErdksDbYdWVlZwVe/+lV8+9vftj0eCAQAbGikAwcO\nOM4zTRO3b9/G/v37oeu6zUvq9u3buHHjBnK5HIaHh/Huu++CMZbXmJwbnGuaZpvAp07kIwiCIIid\nTi2n7/2CMXaMMdbIGPsyY+x/S8/9v4yxrzPGTjLG3sx3Hbn7Zyfyh3/4h7hy5YrrhJXu7m6cP38e\nmUxGPLaysgLLsrCysoLGxkZMTk4Ks8z29nYYhoGOjg7RMq7rOgzDAAC0tLS4Tqih8cMEQRAEsXPY\nLA1WD+zdu7fgMY2Njbbvc7mczXsTAF544QX8+te/xsmTJ3Hs2DG88sorCIVCjmutrq6CMWYrFMpw\nvXXu3DncuXMHIyMjYjgN94ja7Cl6bjqNtBtBEASxXaj59r1K2K6t4+Xgtb2PJ5R4t5PsTSUfc/Xq\nVbz00ku2LX0HDhzAvXv38Pzzz+O///u/XT2luHDi/gZySzpBEARBVAPavld/1IsG6+zsRDwez3vM\n66+/ju9+97slX/v+/fvCt9Pv9+PJkyfCv1PFTX/pum6zSHj06BEMw8Di4iKeeeYZmyY7fPhwyesD\n3HUaANJuBEEQRMXs+O17m4XblLrtQjHVPY4qgMLhsJgM09PTA13XEQgE8OTJE/j9fhiGgZaWFhiG\nAb/fj2984xvw+XxiYsvBgwfF2OGXXnrJ0+S82PHDVJEjCIIgCKIanD59Wnwdj8cdnVAy+/btwx/9\n0R+J70vZFvfcc89hamoKwMZwmQ8++ADRaNRxXDAYxPr6uuNx2SJhbW0Ny8vLIqklT9E7ePBgSRqK\nay7TNHH37l2HTitWuxEEQRBEPbDtk1LbefuevO2uFPx+P/72b/8WH330EXRdx8TEBDo6OrCysgLG\nGFZXV3Hq1CksLS1henoaa2trME0Tq6urmJqawuXLl22CZXh4GIuLi7Z7cMHT2tpacPzwZrWhU2KL\nIAiCIIhCvPvuu7bvvbbSARtaa3V1VXzvlpTy0pKZTEYklSzLwgcffIDLly/bBsIMDg5ifHwc/f39\n0HXdUSxtbm62JZ8uXLiAY8eOgTGGBw8eYHBwEBcvXixaQ3HNdfToURw4cAAdHR1oamqy6TRu0ZBP\nuxEEQRBEvUDb9+qc//zP/8Sf/MmfuLam884odQoMJxgMYmxsDK2trfjss8/g8/kQDAYxOjqK7u5u\nNDQ0YGRkBABsk/fUVvBr167h0aNHnpNgvNrQS5kgQ9sECYIgCC9o+179Uc8a7Otf/zo0TcNvfvMb\nz2N0XbclgEKhEN544w3cu3cPL730kuN4wzCwvr4OXddx/vx5jIyMwO/3Y21tTWile/fuoaOjQySy\ndF1HT08PJicn0dfXh8uXL+P48eM2vWRZluOxfFv5ZM2lrq+vrw/Xr18Xr62cKX40/Y8gCILg0Pa9\nIjl58mStl7BlBAIB/Nmf/ZmnVwI3Nffi9u3bCIfD+OyzzwBstI7fuHEDpmni1q1b4nHAPnlPbft+\n9OgRWltbsbS05Ohi4q3pPMnFK3Kldk9RqzlBEARBEJvB//zP/+RNSLkxMTGBhw8f4sCBA45upxMn\nTuDJkycwDAOapmFoaAi3b9/G2tqaMDG/d+8eTp06hb6+PgAbQr63txdTU1MwTRNjY2PQNM2xbe/V\nV19FLpcTzxXqauJdULJNA/etGhsbE/qpnCl+m23AThAEQRDFsO07pdra2jAzM1PrpWwZXgbnm3Vt\nn8+H1dVVNDc345NPPoGu62CM4fz586JribeWq11MlmXh/PnzuHHjBoANn6vh4eGyTDzVe16/fp0q\ndARBEAQA6pSqR+q5U6oY3IzJZTo7O/Hzn/8cr732muh08tI/vHOdd0wtLi7i448/xokTJ9Da2opP\nP/1UGJ1rmiY6kZaWloRW0nUd09PTOHPmTFHd5Q8fPsTBgwfx8OFDvPLKK0I/vf3222Xrp800YK8W\n1NlFEASxdVCnVJHs5IQU4DQ4rwRN0xCNRhEOh2EYBgKBgPBZaGtrsx03NDSEZDKJ69evY3l5WXQx\njYyM4O7du2CMie4mzuTkJJaXlwGgZD8D9Z4kLAiCIAiC2Cry+VABQCKRwIcffoiJiQnkcjm88847\nuH79Oubn57GwsIDh4WFx7MrKiuj0XlxcxMsvv4xgMIiBgQGhs1ZXV7G8vGzrYJK7ngKBAILBoK1D\nSfXa5N9rmobDhw/DMAyRjOFhmqYwQS/Vp3O7eVFRZxdBEMTOYNt3StV6DduJzs5O/Md//AcOHz6M\nd999F8FgUPgeuFXEuPgBgNdee83hnzA4OIgLFy7gxo0b0DQNsVhMJJRU4URJJoIgCKJcqFOq/qgH\nDdbQ0ODpq1mIUCiE8fFxz6SNYRhgjImQOXPmDO7cueM4JxwOAwBu3rwprtHb24uJiQnPLnDLsnD3\n7l3hRWUYBlKpFFpbW0UHeSQSwaVLl/Dd735XfH/58mUcOXLE1m2laRqCwSCmp6dtei2fT6faabSd\nOo+2Y2cXQRDEdqJa+ouSUlVk3759riODy2XPnj3IZrMlncNNN/fs2WOr8oXDYYyMjAjRIrem8w6r\nH/3oR+jq6rJ9+B84cAB3795Fa2srjhw5IgQNNy2XhVO9ixuCIAiiPqGkVP2x3TTYVhMKhfDzn/8c\nx44dEwW/cDiMf/3Xf8Unn3yC06dPA4Brwc40TRw4cEBs83v48CHee+89tLe3i+sbhgHLskSCrKGh\nQSSrXnvtNbGVUCVfsqaUITP1mKwi6weCIIithbbv7UA225S91IQUsCEqbt26JRJSmqahq6sLk5OT\nOH/+PObn5x1b8xhjGBsbc7R1Hzx4EC+++CKCwSC+9a1vibbpxcVFsd3vxo0bOH78uGdbtdqaThAE\nQRDE9sDn81X9nnv37q3KfVSz80L84z/+I44cOYL+/n7ouo6Ojg4wxnDs2DG0t7fj3Llz6Ovrw1e+\n8hV85StfEbrIsiy89957WFtbA7CxzW9gYAAdHR2265umCcaYMDbnGuurX/0qMpkMDMOwHR8IBDy3\n4XHttbS0VNSQmXrdJkfWDwRBEDsEuTV5uwUARlF+NDQ0sFAoxBoaGmyPDQwMsFwux2KxmHg8HA4z\n0zSZaZpsYWGBWZbFFhYWmGEY4phIJMKy2aztvM8rqayhoYEtLCwwGdM02cDAgLinaZqMIAiCIFQ2\n5ErtdQfF7tBgfr/fpmUKRUtLC8tms2xhYYFlMhkWDoeL0mDpdJoNDAwwXddZIBAQukw+TtM08Vws\nFhPnGIYhNJau6ywYDNo0G1+PZVmMMSb0Wy6XE9orFovZdJh6LP9+YWFBaEU3PceR7yGfTxAEQWxP\nqqW/qFNqF6DrOnp7e22PhUIh3L9/H3v37rX5MeRyOQwPD+Phw4e4fv06kskkwuEwJicnceHCBQCw\nGXT29PSIc8fHxzE8PIyxsTFx31Ao5FmpW1xcxI0bN0S1j/tXeUFdVQRBEARBFENTU1PZ5z5+/Ng2\nyKUQV69eRSwWwzPPPIOBgQFMTEwUPKe7uxsAMDIyAsuysLKyglOnTuGNN96wdfwEg0E8fvwY3d3d\nGBoawpe//GXRHRSLxYRJeiKRQCgUQiqVwujoKBoaGoRekzudotGo6I4aGxvDpUuXbJ1GaldULpcD\nY6ygATo/7+jRozhw4EDddVURBEEQ9cu295Ty+/1isgnhjc/ng67rWFlZQVNTE95//300NDTg2LFj\nIiklv5ehUAgjIyNYWlrC8ePHPU0ks9ksIpGIMNVcXV11mKEvLy/j0KFDYIzZ/AgWFhbw5S9/WVxr\nZmbGcxRyKb4HbtSjFwJBEARRHOQpVX/sZE+pcDgMxhhu3bolHvv832DBc3VdR3t7O+LxuOvz7e3t\naGhoQCKRQDgcRiKRwMrKiu3ee/bswdjYGLq6ujA1NeWqwXihbnl5GZ2dnTBNE7quI5VK4ciRI7Z7\nyobguq6js7MTiUTC1YdJPlY2ai/kESqfx6mW+ThpPIIgiK2BPKWKZLclpLq6ujyTMX6/H319fa7P\nra2tCdHz+PFjHDt2DK+88goikYg4Rn4vb926hf7+frz66qtCYHR1daG1tVUcY1kWvvGNb2B6ehrt\n7e1YW1uDaZpYXV1FPB7H9evXYRgGDh8+DMaYw4+gtbUVzc3NADYMPOVRyGpXFPe4KuR74Ea9eiEQ\nBEEQBFFfnD17FkNDQw6tUGwR1+fzIZFIeD5vGIZINI2Ojjp07MTEBC5fvowHDx6IbnZN04SX5+Li\nIkzTxIULF3D8+HF8//vfF95elmXhlVdecayde4Lyrqrp6Wl0d3djcHDQkcSR/UN7enowMTEhuqp0\nXfdM+sj3aGlpydtVtZmQxiMIgtgBVGOP4FYF6sB3oNrB/QO8njt79mxJ17p27ZrNU0oOwzBsnlEA\nbN5PsseAYRgsEol4+hKkUinb2uPxOJuZmXFcX/ZYkL2mLMty9T1QUX0Q1HWqXghuxxMEQRD1Bark\naUBBGqyQ1soXwWDQpql0XWe6rovvQ6GQQ/cEAgHH99yTiV9L13U2PT0tdFA4HLbpL/mauq6zZDLp\n0DbZbJYNDQ0V1EPcU9QwDBaNRlksFiuovdyuUS1tVazfFUEQBFE61dJfNRc1FS2+DoTLTgi/3+/6\neDQadZh1GobBZmdnmWVZLJfLsZaWFgZsmHxmMhmHqSYXUKpxJ4+WlhZmGAZraWkRomd+ft5VYBRK\nIHkZp3sltMhonSAIYntQLVFEQRqskkgmkzYT8VQqxe7fv8+uXbvGUqkUy2azDl2laRpra2sT33Pd\nY1kWi8ViwuhcNTbnialYLOYwZTcMw6ZtuN5R9ZabHlITXuFwmBmGwWKxWF3qpGKLlgRBEETpVEt/\nbXtPqVqvYaeiaRpSqRQOHjyIL33pS6K9vLm5GY8fP0ZfXx8uXbqEY8eOwTRNGIaBVCpl8w1YXFzE\n0aNHhc9BT08PxsfHIf+bMwwD09PTeO655zA2NoZYLAZd13H+/HnhH1XsmF/Zz0D2MeBbATVNE6af\n+Y4nCIIg6gvylKo/SIM5aWlpwdLSEh49egTGGF577TXcuHEDANDT0wNd120+VZxoNIpcLofJyUmh\nexhjOH/+vDhfRtM0RKNR4fFkmib+7d/+Db//+79vO45rG8uycPToUaG/pqen0dbW5qqHZB+p7u5u\nTE5Oisenp6dx+vTpuvNtIk8pgiCIrYE8pQhPSjH4LhcuptLptM3v4PHjx8IHQdM09Pf3o6GhAf39\n/Th06JDNC+rgwYPw+/0ANvyu9u7dC13XhY8UP/+FF17A4cOHceHCBRw4cACmaYrJMl4JKbdJfLIP\nAvcx4F4Dx48fxyuvvIKFhQVxzsGDB9HT01M13wOCIAiCIHYun376Ke7du4fXXnsNx44dsyWUJiYm\nXBNSAHDz5k387Gc/E7qHMYa7d+9iZGTE9XjGGEZHR6HrOkzTxMDAAF555RUYhgFgo+AnaxvVpP17\n3/ue+N6yLDD2xXS9/v5+3LhxA8lkEiMjI8Inyu/3o7Ozsy59m3RdR2trK5aWlrCZxXaa+kwQBFEl\nqtGOtVUBqVV57969NW/brlb86le/Kus8XdeZpmmssbGxqOPdjuW+BYFAgE1PT7NsNivazLPZLItE\nIqLdO5VK2VrA5a8TiQSbn59nlmWx2dlZ2z1mZ2fzthHy+7htu1O3+MleA/i8LX5gYIBls1nRyh4O\nh1kul8t7T4IgCKJ2oErt4xTlaTAKCG2UTqcdvlFewf2gwuGw0DLyVjsvewV+r0wmY9sOyLcCqtrG\nsiybjQLfIihv24vFYiydTju2v5mmyRKJRF37Nm2FHQNZPBAEQVRPf9H2vV1CU1MTnjx5gsbGRjx+\n/DjvsXy6yv79+7G2tpb32JaWFiwvL0PXdfT39+PmzZviuVAohH379mF0dFRM+RsbG3NsybMsC1/6\n0pfw6aefoqWlBR9//LFnN5hlWbb7uI1Illu4Gdtofx8ZGRHVQF3Xce3aNbz00ku0dY8gCGIbQNv3\n6o+dpsH279+Pp0+flnxeW1sb7ty5g46ODoyPjwMAent7cfv27aLO9/v9WFtbw5kzZzA1NYWlpSU8\n88wz4vmzZ89idnbWcV5DQwOmpqYQDAZhmiaAjSnJiURCbLdLJpM4cuQIAMA0TcRiMUxMTAgdxu+V\nTwtZloVz585heHgYwIbue/TokejKKoWt2manbj/cjG2GZPFAEARB2/eITYQnohhjRSek2tvbCx4L\nfNGqvri4KMQY59atW3j99deRTCYxNDQEYEOQPH36FPPz87zSCl3Xsby8jNnZWc+EVC6Xw507d7C4\nuIiJiQnxeE9Pj9h25zYWWNM0sRUwGo3ajvP5fLR1jyAIgiB2OT6fr6yEVHNzM95991309vbig1Ec\nOAAAIABJREFU5s2bWFpawrlz5xwJqcnJSXR2dorv5WTJ6uoqGGOYnZ3F/v378a1vfct27j/90z8h\nGAza1moYBsLhMH7wgx+IhFQwGMTNmzdFEdCyLLz66qvI5XJYXFwEAPz0pz/F/fv3cfnyZQBf2B4Y\nhoHu7m60trY6XuPDhw8xNjZmW+/y8nLJ75WbRivmnGK2z8mvQ95myF97OQV4N0sIgiAIYouoRjvW\nVgVQ/theivyh6zoLBoNFtZ4/efKEdXd3uz5///59trCwwObn5x3t7NFolCWTSTY/Py/GB7uNEc5m\ns2LKX3NzsxhVLLe7M8ZYOp3O216uttTLkwSrQaHpgQRBEIQ7qFL7OEVpGmynRKVakmsSt8f7+/uL\n0lNua9F1XXytbuXr7e112BPEYjHbNj1d11lXV5eYuif/NxQKsVQqxTKZjKclAmMbW/+i0ahYW7kT\n7mQ7hWK2AJa6fc40TTY7O2uzisj3uoqBdBtBELudaumvmouaihZfB0Jmp4bP52MffvhhUceePn3a\n8zld14VQchNsPGSxpAoI1XMqkUg4RIJpmmIkspdo4uOVixFWmy1EyJuAIAiifKoliih2nwbz+XwV\nnc8TPG7PXb582TUhlS8JVsl6uEdVKdcKhUJ5k0Wyx1UlHpyWZdl0UCF9VWoSS71HOByuax8sgiCI\n7UC19Bd5Su1yXnjhBbz//vuuz3V2diIejzseNwwDPp8Pa2traGxstE3n80LXdXz00Ud44YUX8OTJ\nk4LHc0+AkydPYmlpCSdPnsSnn36KQCCATz75xOZlYFkW7t69i87OTlcfBRneCq5pGlpbW7G8vOzw\nNuAt5qOjo+jr68PQ0JDrlsJSvBFK9Sag8cYEQRBfQJ5S9QdpsC9w86PSdR3d3d0Oa4NyaWpqKmir\nEA6HsWfPHoyOjqK9vR3T09NimxzXTU1NTVhZWbGdFwgEsLKy4uoXNT8/j+PHj2+KfpGfY4zl1TmM\nbXiCci3mNY3Z6/4HDhzAwMCAzUOL9BRBEERpkKcUURW8ElIAMD09jWAw6PgQv3XrFr7+9a/Dsqyi\nElLAhkj49re/bUtI7d+/33Fcc3Oz8ATo6OjAgQMHcOzYMTz//PPo6urCkydPcPHiRSGyeAKpo6ND\neET19/fnFUx8dPDFixddvQ0ePnyI0dFR5HI5jI6O4uHDh+Je3JugVG+EUrwJyvFd2ExoBDJBEARB\nFI+ckNI0DbquIxgMOhJSwWDQc5BLIQolpLq6uvD2228jk8mAMYbGxkb09vaK5y3LwptvvimKeG7X\n/uyzz7C0tGQ7h/tSaZpWkn45d+4cUqkUFhYWhJ7QdR2HDx8GY6ygzpE9QUtJKHGN9+KLL2J8fBzd\n3d0YHBx0FB9lPUeahyAIosZUox1rqwLY2FOPOmj/3snR0dHBmpubGQC2f//+vCOKK43p6WmbJ4Bb\nyG3Yso9UIY8oeQud3NatnufWYq5uvyvkX+V1/2K2BJbTsr5Z0DZDgiDqEVSpfZyiNA22G6MS/6nJ\nyUnW2dm5qevRdZ2Fw2GWzWYd2whv377NwuEwMwyDBQIBsf5oNMpCoRAzDINFo1HhGQWABQIBlslk\nGGMbeoRvB9Q0jc3MzOTVMLJ+kd8vVU9stc7Jd31Z58RiMdI8BEEQeaiW/qq5qKlo8QDLZDKssbGx\n5iKFovJoampiuVxOJIVkESWLm2AwyHK5nMNHKhaLsfn5eVfBlM1m2dDQkMMA08vHSk4gqeaZDQ0N\nbH5+viRvhFIo1XdhM6llQowgCMKLaokiitI02HaP/fv328zEvYa2yLFnz56y7lVMQU/X9ZKTXolE\nglmWxRYWFmyvhWudaDTKpqamHPe5du2aGDYzPT1te76trY3lcjmWy+XEoBnDMAombzKZjGOojZue\n2Gqdk+/6ss7hr4k0D0EQhDvV0l81FzUVLR5gs7OzNIGvDsLv9zNN01hTU1NZ52uaxnRdZ7FYjJmm\nKZJC2WxWJI9kQdfS0sKSyaQQE7xSyAVINpsVSSV5ep8sqnK5nGNSi9wxZZomS6fTIkEmJ69yuRxL\np9OeSbBKqdXEl1omxAiCILyoliiiKE2DUWxuhEIhFovFWENDA4tEIgWPj8Viong2Pz9v63iSQ+3O\n4okjron6+/sdpujhcNgxtRjIn7xRB9NwfeemJ9Tin9vXXse7fa/i9bysc6LRqE07kuYhCIKwUy39\nVXNRU9HiP/9A5VvLKKoXZ86ccYiUfMer1Tse+/btY//+7/9ue+zBgweMsS+SQnNzc2xoaMiRfJyZ\nmXHdjqcmqBKJhO28oaEhx1Y9NemUzWbF4/y+PGmVy+VKbvfeTmOFt9NaCYLYHVRLFFGUpsEoNjcM\nw2CpVIql02nPiX48zp49y54+fSqKZw0NDay3t9e1U0mO/fv3uz6uaZpj58Hc3Bzr6uqyPRaJRPIm\ngngRsLm5WXRiFUpIeW2n4wVGVXdxjVbutju16FjMVEHSRgRB7Eaqpb9qLmoqWrz0QaomSeQP+FqL\njJ0efr+fRaNRpuu6Y7sdD13X2VtvveWanFIF0tDQkG1rnvz/Wb4n38LHO6rke/Nj+X35cy0tLQ7x\n4rY9T/W1kqtopW5xI58mgiCIyqiWKKIoXYNRbI6O4l8PDAywZDJZ1HmGYdiKZ3Lk61zn98t3PrDR\nLcW1na7rwj5BRk3WZLNZNjs766p13JJBqVTKdTsdt1lQC4+qRit12x1fr3zfQtcgHUcQxG6lWvqr\n5qKmosXXgZCgKCx+eMit4V7Ha5rGUqkUm5+fL5hQlIVBOp12PK/rui0JFgwG2fr6uuu2O7ljKhwO\ns0wmI8SQ6lVV6hY31RQ9nU5XrdpGlT2CIHYCQHVEEUVpGozsEyqPtrY2x/uoekAVE2rRb2JiQugu\ntfgXDAaZYRgsFouxVCol9I98zNmzZ20d6F1dXQU7mPIla3hiR71POBy2dUrx7YvqQBquyfh9yrEa\nkNfAd1l4bS+UUX2o8g3VKQfSagRB1CvV0l81FzUVLR7UCVWNePbZZ8s+182EXtd1Nj4+7nj89OnT\nLBQKiX3+hSYrGobBEokES6VSLB6P257r7Oxkg4ODjvuGw2GbCJGNzWUvhpaWFkdLt9puXoynlJsZ\neyEBt1nihCp7BEHsFIDqiCKK0jTY6OhozTXKTgy3CX1+v99V8/Jpej09PUVdWy4Q8g4h7kk1MDAg\nOqNkWwOvBBHXbPzx+fl5xtgXOiaTyYiuKbfJfHwNvFiXy+VYLBYTBu2yhsnlciV5SqmYpskSiYRj\nDfK6vfCyetgMXUVajSCIeqZa+qvmoqaixQMiyUBRf+HlWwBsVOnk7/Nt/fOKfF5i3LhTbonnlUH5\nGN6u7Ta1Rj5GFQ35/AxkoaRW12ZmZvK2i2+mONnNk/So6kgQOwugOqKIojQNRlEdDaVpGpuenvbU\nvJOTk2XdIxQKieIaL7bJOoV3BcnaJJ9vlayP+AAbYEOvZTIZmy0DT3yFw2GhdRYWFmwm7JvRWc5f\nl2oJISeX3K7vZqxeybZBL9LptOiU0zSNpdPpiq/pBukigiDKoVr6q+aipqLFAyyTyZQ98Y2ivNi7\nd++mXMfL/LxQdHZ2skQi4SmK5DZ4XddZR0eHo4KotmtnMhlb9bC5uTmvj5SXMOHTAuXKnppk8mo5\nL0fw5BMZbtsMN7MLq17FDVUdCWLnAVRHFFGUpsEoStdPxXY0yeHz+ZhhGKyvr4+dPXvW8byXr2ox\nekrTNNbT0yM6lOQJgLJOMU2TJZNJW7HPTX/F43FXfTY4OGjzcVK3BJqmyXK5nDBKb2lp8exUL0Z/\nqP5V8lq4obzXdbx0xFZMKJ6fn7etrVDXVjmQLiIIolyqpb9qLmoqWjzg2eFCsXMjlUqxXC7nWjHU\nNE0Yc/LH3P59DA4O2rbuqVNuJiYm2MzMjKcQkX0JeJXPNE3bmuQuK96WLv9XFnqycCqmepdOp4UP\nRLFbATdLlNS7uNnNHWIEsVMBqiOKKErTYBTbM9wm7ckRCoVYOp12aJDZ2dmC1/aaGqgmvOQtgZqm\nsUQiwebn5x2f3/mm83npD1mjqX5d3EpBtl9QE11qx5asIza7KGdZlm3LYiFbiHKoVBfVcyGSIIit\nBaiO/qq5qKlo8QCzLMvmBURRWui6vi2MSuUqYH9/PwuHw8wwDNbT02PrlOPeClwUaZrm6k3FRQn3\nhfJKbMZiMVvySv5QXl9ft1X51Gk54XDYJnjchJSbcMpnoqlOJeTnFCMy1K2E5Vbj6j3psxWVTIIg\nagtQHVFEUZoGo9h+wSfpFToukUg4urmTyWRBzVjo+XA4zNLptMPLE7DrO54YkxNV8nQ+OWmlenyq\n/lU8oZVKpRwFPTc7Bq+OrXy4JW7K6eraioJfJbqo3guRBEFsLUB19FfNRU1Fi994k1gikaj5h/x2\njhMnTtR8DYWio6Oj6GNlHwNN0zyrdgBEZSpfYvP27dtiIiA37eQJKfk66r9D2RdA7ujTdZ0lk0k2\nOztrm8wHwFMwcGHjNpWwWJHBq3H8fSlGXLh5KnAz1HpO+lBVjyB2FkB1RBFFaRqMYnvFiRMnXM3G\n3UJOQnhNzpNtD9RzY7EYm5ubc2gwuZjlpt91XbdtEYxGo6K7Su2U4sbogF3XyEkY3hXFu9TVbiw3\n24RSi29uiRu1o75QYmurC37l6qJ6L0QSBLG1ANXRXzUXNRUtfuNNYtlstuYf9BS1iXzt58DGtJpi\nBBjvpsrnlQB8Me3RrcoYi8VYNBpluq6zaDRq++DPZDI2McdN3Zubm21iiye/1EobFzahUEgk0Nxa\n0AshJ8FkceFV4fOqJvIuM0r6EARRDYDqiCKK0jQYxfYLdahMPh3Fu6q9JudpmmbzuFJ1ibwNjodc\nzMpmswV1F7CxJVDXdRYKhdjTp09tE/28BtjIHVSyv6fbFkDVjkGeticbsXvhlrhR1xaJRPJep167\nvMtdFxUHCWJnAFRHf9Vc1FS0+I03iS0sLNT8Q56i9Hj99dcrOv/kyZO25JCXsGpra2O6rgtx4Pf7\n2dTUlOd1b9++7ZgOWEzIpp08acMrczMzM57nJRIJ4TXl1iKtCptwOMySyWRZvgNe5ude9/WqJlay\n/Y8gCKJUgOqIIorSNNh22P6/3cOrm32z/VR9Ph8bHx93PB4Oh0VRyjAM1tvbK7w71a2AqjawLMvm\ntSk/z7UHH0gjWy2oiSq1qOfWKQVsFAfdbBNk/6qGhgbHVL9sNiu2DXLbBnVwTakJJfW1u91XpRxD\n92pQ6lpoyx9B7ByA6uivmouaiha/8SaxXC5nG51LsbPCTZD5/X5mGAZrbm4Wj+Wbwuj3+1l/fz/T\ndZ319fXZ2slPnz5tO3Z6epqtr6+XtGUQcApETdNEp1Y0GnVUJ/mas9ksY8y90sa3y6mizstzyot8\nQserNdvN3L3U7X8EQRCbAVAdUURRmgbz2r5FUVkcP37cc8IwsKGL8j3P4y/+4i9Kuu+VK1dcH+/q\n6mJPnz5lkUhEJKbU4p1bJ002m2XT09MiKSQ/r/pcyl8/ePDANhnQbbAN1ys8oZSvsMY7nry6fdLp\ntO3aPHlU6TRkPpSnFJN2fq1Kkjq1TmjRlj+C2DkA1dFfNRc1FS0eYKZpkqfUDg6fz8c+/PBDx+PF\niLFyz1H9DICNJMzg4GDZVeGGhgY2NzdnE3E8iRUIBFgmk2G5XM5WlZM7p6LRqKjiydP5stlsQWPN\nQuJGvW++a3lt/yuXWgsngiC2B0B1RBFFaRqMOqVqF4U6pXiHuFtBrJzrBYNBTx2laRqbm5tzJKS4\nWXhzczNLJpO251XfJ/lrdaCLlwbiWwQLFdb4NeVOKJlUKmW7H+9El88pxqzcTY/xa4RCoaL1U76k\nTiHdVA9dSvW6FZEgiNIBqqO/ai5qKlo8YPvgotiZ4TY9j0chTykePp+P9fX1lb2GQCDA1tfXbb4G\nbutymwgIbFQZLcti2WzW1Xg9GAwK4cINMVVRkk6nbVvodF13VAdVbwRuzK5eJ51O26bQqEacXqJn\nM4WGOuaZPKoIgvACqI4ooihNg1HUf2ialjd5eOLEiU3ZCnj16lWbrcDs7KzteW5VoG6Z45oqk8mw\nhYUFlkqlHMkvwzBYPB5nMzMzbH19XXhKMZZfl2SzWcdQGbckj9sWwFKSO156Rr6vbPFQSD95vaZi\ndFO9dClR0ZEgdgZAdfRXzUVNRYtHeR0zFLsz3Lb3lSLE1GSS27aFnp4ex3F8i142m2VDQ0Ou/2Zl\nwahpmvCMkkVJJpNhMzMzjgoi4G2sGQgEbJXFaDTqWJ96jUJCbLOEhtvIZtoSSBCEG0B1RBFFaRqM\nov5js72neLjZZvCupng8zpLJpK1TStYV6gRjYMMIPJvNuhab5W4vuVOK64V8w1p4lxIfKqMmhNRt\nfqlUynVKn1tyR56MrOoZteOrpaWl6El8Xq/Ja2KzrJtKNWknCILIB1Ad/VVzUVPR4kGdUhSVh5eJ\nqBrFCjv5OF3XRTKIizP1ecCZMJMN05PJJJubmxPnqxMF8xlryvfhvg5ua5a3DKqG5l7+VZUmp2Th\npCbGCIIgZIDqiCKK0jSYHPv27av55/l2D3mSXS1is/1Z+/v7WTweZ4lEwja9WE1IARuf/4lEougt\noVzXeA19cRsS49ZZ5LbNz80DSj3PLekl6xnZJ4trQf54qb6g/H75ipL8mIWFBZbJZIo2aZevv5s7\nm3b76ycIL4Dq6K+ai5qKFo8NT6l8k9QoKCqJrfLLaGtrc3RM+f1+puu6owOLt7fLj8lJq1QqZRNl\nuVzOtRuK+zGoj/PxzdzDSp5UyEWVKmo2y7OAG7mT9wBBEPkAqiOKKErTYBRbG16JvhdeeKHmaysm\ndF1nkUiEaZomdEVjY6NNizQ1NYnPf9Vw3C3cPD/Vicde0++8up1isZiYAihfe25uzjNR4Zb0mpub\nczU251+rnlhunejpdNo10SZ3dKn2Dep2Q3XaYDEm7bX2oaolu/31E0Q+gOror5qLmooWj42kVD7P\nIQqKSiNfh1RbW1vR1yk0pUjXdfbTn/7UcT+5KwrYaGOfmppiiURCjGmWP0iz2axjKg6wkWDik3NC\noZDYIug2CUcNVdTIYswwjLK6m+SqFPd92EwhkE/clXMcQRC1A6iOKKIoTYNR1CZK0R6FolhvznLC\nrRjmdVwul2O5XM7TmP25555jnZ2dntdwS/i4DZBRk0xqckldl5cusSzLVgCUNRZ/PbK+UDvRucen\nrIN4Eo1POJaH2RQyble3IXoNsHGjXnyoasVuf/0EkQ+gOvqr5qKmosUDbGFhgaa/UGxZaJqWN+mZ\n7zlN02xVN1VMGYbhmCjjNimHP97b28umpqZYc3Oz7f7yB2kymXS0xQcCAZsgc0vAmKbJUqmUYy1c\n4PFuKrkbi28nbGlpKcofQUY169zsCpXc5s7Fndt1iz2OIIjaAlRHFFGUpsEotn+cPn16U6/X0dHB\nxsfH2aVLl9jk5KRrkUwNnggoplOqmJATC7zoxf2q1Al8anLJ6zoq6nY6t+l6ageOPFVZ7aRS7RXU\nxBIfZuPld6Wao7sl4LzY7dPydvvrJ4h8ANXRXzUXNRUtHsj7YUJBsRnBO4sePHjgaBvP10Xllizl\nCafm5mbRap5Op9nMzIytS0k+V57Y4iXuePu6KmrOnj0rJtp4TZNRhRWf2rewsCDWl2+in2EYbH5+\nvqRfcGpFz6tyWC5q5dNNWJqmyWZnZwseRxBE7QGqI4ooStNgFNsndF139dDUNC1vB1Kp0d3d7dA/\nhbqleHFrfn7edu6VK1fy+mxpmsZ6enpEkUy2HMjlciyZTIqtbOrfCslkUugc1Z+WF/NUiwS5w1vV\nGaFQyJEUUjujeKJKTSwZhuF4j/Jtwcs3nc/N8N1LU8nPbbWnUr17NtX7+tzYjmsmth9AdfRXzUVN\nRYvfeJNYJpPZdHNGip0XlUyg0XWdDQ0NVTzFZm5uTlTsZLEUjUY9W9abmpqEWNE0zbXVXtM0Nj09\n7eoZJXf/uLUoq8JK13WWTqfFLyOviX68Y6ucDiOvNvRoNLopXVOWZTk6oLym8qivgz7cCaL+AKoj\niihK02AU2ycCgQDr7+/3fL6np4e9+eabZSWonn322aKPddMw3AaAf3bLHlR+v99REAQ2LBF4sUxO\n7iQSCZZKpQoOQuLnyedz8/RUKmW7Bi/8qUkn1bMqmUyy2dlZtr6+LrbyNTc3C30jd5zLw154Qot3\nxScSCYdZuZvReqGERD6vJK/n1ERVsfYGhZJf5Nm0udB7SlQLoDr6q+aipqLFY2P7XiqVqvmHPcXu\nCHVKXikRi8XEh3y5UyP5ZBe3dTQ3NwuzTvlxucLmVl2TEzg8WlpaWDabFee4dSPKhuhqBbCYxA4/\nVm5nL9Wcs9D1ZTGlVjhVEbvZnlJUwSKIzQOojiiiKE2DUWyvKGR3wbeMlWKkXoqFhle3dyQSsekj\n9ZpvvfUWi8fjQouohWi+dS4ajbJQKFSwgMjN1flrdjMnV/2wdF0X19V1XUy5kzvguQZz66qX7RD4\nFMBsNiuSV729vez27ds2Q3T++PT0tG37npeuUBNKbp1aHLcipWqtUKy9QaEECXk2bT70nhLVAqiO\n/qq5qKlo8Z//INL2PYp6ieeee87xWEdHB5uamhLm5Mlksijjz3whVxHluHbtmmObIU+GcdwqX6Zp\nssHBQdu1ZmdnxXPT09O25+TKnptXQilVGzdzTi4S8wmgUhI++XwdSumOKva+VMEiiM0FqI4ooihN\ng1Hsjtgs36lf/epXjqEvgUBAFMHcBq7IW/KePHniOjSGJ7tKNW3XNE0ksriu4ffXNM1z66BhGMLm\noBw9J08bdOtwdzuHJ73yTe6TO694B7ps/i5rF7ciparHirU3UM9TLR3Is2mDzSxW0ntKVAugOvqr\n5qKmosVLHw6qlw4FRb1EKT5UhY5paWlxrcIBXwgI+TkuDtTqmVfLNvdlCAQCYnIMr1pyjwVuzq5W\n/Mqt2qjTcdSWdbWlXE0oydNpvPCqCFaS2MqXaKIKFkFsLkB1RBFF6RqMYndEpfYFcsiJF3mCr7yl\nrbm52ZGgeeONN0q6T6Hudl3Xbd1buq6zcDhs6wSXu6rkmJ2dtSUGvLY98k4qrtH4a2poaGDz8/Ou\nf7/wZJL6nqvd6TJeCTLDMMRaVVQdJL+eaDRqG6yjFjhl3CwT3JJmteoer4fO9a0oVtbD6yJ2PkB1\n9FfNRU1Fi8cX1YZcLufo9KCgqPcoRuR1dnayeDzO0uk0y2QyRU2y4eH3+1kmk7G1YycSCU9j8fX1\ndWGqHo1G2Ztvvmm73tmzZ1kymXRNuMhiMhwOF5UsUit73MdBrbjJH+aqf4RbAkulmIpSoQ93ucOt\nUKKJKlgEsbkA1RFFFKVpMB7/8i//UvPPU4rNiVInWlfq6drZ2ckSiQQzTZNls1kWj8fZ1atXXRNB\ncrJI/rrc16lu0QM2ki/q3xNdXV22+7W0tNgKZul0mkWjUcc9ent7beudmZkRW/xCoRAzTdOh60Kh\nEEsmk2xubo5NT0+LxJDf78879diyLEeCqxwNIhuxy2svNNAmnU7btJlXIqza1EvnOhUrie0KUB39\nVXNRU9HiAdsfkR999FHNP8wpKIoJtaMpX6ysrIjtdnNzcyXfa3p62ibueKeVbCzOE0lyQsgrwuGw\nZ8JF9keQW8a9RIDaqq++L7ziJosdXsl0S1DlE0GVmHBms9miK4bF3I8giNIAqiOKKErTYDxK3TZF\nsf3CK1lVahJLDvnfTVNTk+fAF7f7tLW1sfHx8bzG7PnW3Nvby7LZrMPDyjAMNjc3Z9MioVCI3b9/\nn92+fVsUCWWvSnmSnhw82cSN0lOplEheyebpuq6z9vZ2FgwGbQNYAAijdDmBJneXyfDOc17oSyaT\nbH5+nuVyOVc9ks/IvNTiWi6Xc52CWG4SqFgj93I65Su5XrnHU7GS2K4A1dFfNRc1FS1+401ijG38\n0ZhvbCwFRbmh6zrr7e1l3d3dm3bNy5cvOx7zEk98hLPb2OZiqoQ9PT2sq6vL9djGxkbb48Fg0NVk\nVA7eXeUmZNz8IPKJALm7yuuevMVdnYKTTqdtnVbFJMG8KCRaZmdnbWuamZkp6foEQVQGUB1RRFGa\nBitUxKDY+VGo43uzEpZdXV0Vnf/hhx+y119/3fbYBx984JoIc9s6KCeEZCNw2dZA7qby+Xy2Ypqb\nAXsp3V6apolO9nxJDbU46KWP1KE7sVjMc8udV1JLxm37YLkdQcV0N8n6LxwOOzrHOMUmg0rtqCqn\nA6uei5X1vDaitgDV0V81FzUVLX7jTWKmaZKnFMWWxOnTp1lPT0/F1ylmm15vby/r7e3Ne0ylFUm3\ndajXDIVCjtfMjUV555KXqblcpfMy15ThokjXdVtlUA5+vtv2OV7lm5mZKVgJy/eBq4oWVYDJflty\n2z5RHiR+iFIBqiOKKErTYAMDAzX/nKao76hEt2xmfPjhhw6PKV7024zXxRNPjx8/dmz3y+dt5dY1\nL19bvU84HGaZTIal02mWSqUcE4a9urYAuz5aWFhwaMJ0Ou343Vts8kUuMhaj//JRTHeTmgSLRCIV\nDccpdXvdTtqOVy9bHIn6BKiO/qq5qKlo8RtvUtnTLygo3GLPnj2bdq0TJ06I6pZaoXMLTdPY6dOn\n2S9/+UvX50vxkyolZMGkihTZ24F7Iqi+T/F4nE1PT9uqVnwyTT7/Jlk8GYbBrl69aru37Cmldkql\nUinHpBkvEZTvA1etBHol3LLZLJudnd20D+vdmpgh8UOUA1AdUURRmgZLJpNb9rlEsTNi7969NV8D\nAHblypWSzymnyysej1fcQZivkKkOd5K3AfIOLjk55JUksizLMb3czTdK/hvLzVtK3gIo66hi9Y2b\nFiqmu0n10JITQ+Xoq1K31232drxaasKdlGAjNh+gOvqr5qKmosVvvEksl8u5dllsRocp1OBJAAAg\nAElEQVQLBUW9RDAYZJlMZsu3qap/YCQSCds0HNXvwG08s2EYLJVKObqN5KSPmkzirfD8Grwri0/2\n46JI0zTXNnjukxWLxRwm6/L5sheDW4JEHW3s5lNVSDzk82nwum+lbJckF4kfohyA6ogiitI02GZO\nZKOg2Mp46623bN8XmsyXL/L9uy/U8Z4v2trahB7ySvZy3yn5Mb6lELAPsCmUJMrlcsKrSvbKlPWE\n+jeWvM1PLRiWqmeKKRjm0zTq9OZ8E6aLXc9WeUoVuk4ti3Xkd0XkA6iO/qq5qKlo8RtvkmsLKlD5\nRBAKinqKd955h4XD4S1thdd1nT1+/FgIEC50otEou3r1akn35hU63jUlT8+TBVU4HBYJHNXfinsE\nyAaahQzi1Yl82WyWpVIp16k16rQYXumTzTpVvwJZPMRiMWEkKos52cjUTWCk02nxXmqa5toyzynW\n7HO7dB+R+CHKAaiOKKIoTYNRUFQablvotkq/c/2QLyFVrM7RNG1Ti98tLS22glo2mxV+V83NzezB\ngwdCP8lJIrVTKhqNspmZmaJ1gKoxVD2RTqdt2kzdAuj1XDGUooWKXf92LHzVw5q3S2GTqD5AdfRX\nzUVNRYvfeJOYZVm2DgsKip0emqaxM2fObMm1h4aGPEcxl3tNXv3j12lraxPP8Q9gr1Zs0zTZ7Oys\n7Xyv+7hN5OMeV1z4yNd168xSBRgPOXmmvj9y8imdTjvWpAqM+fl52zFeo5aLTTYVK2jqRXTUyzqI\n7QNQHVFEUZoGk2Mzh4Hs1vjnf/7nqt/zT//0Tyu+hlvH9FaEqnuef/558TX3zVSn5rmZi8vfnzhx\nwtaJPTU1JZJBbgkques6mUzaOqOK8QXt7OxkDx48sHVCaZrGUqmUo8t6fX2dDQ0NiU4nWdskEgmH\np1QymbQV4LLZrON3aaHPX1VPpFIpmzZTtwCqnVL5LBvU51QtVE5SSqWYwle9aZBCvqYy9bZ2YucD\nVEd/1VzUVLT4jTdJ/BKPx+NV/zCnoKhFhMNhdv/+/aKP9zIRV6OpqUl0NXklfwzDYP39/WLSTLEt\n8H6/n+m6zgKBgPgv70JSjdLlD2bVOFOeeBOLxVg0GhVrmpmZsXlCyQkqADaR4jUpcH5+XtxTncoj\n+zWo7w9PBqkiKxwOu45ajsVijpZ5lWKTTcWKsO3STUUQKkB1RBFFaRpM/j1YyXYoivqOfL5hmzVd\nb7OC/5vcu3cve/311/N2V/NjGxsbmaZpzOfzMV3XPbul5H/jTU1NLBgMikQYn9Tc39/veT+5+3p9\nfd3m6dTf32/7vru7W1y/t7dXdEqpW9V4gsI0TTY0NGS7H++Yko+RdUA2m7UlwUzTFEkobrHA9Q63\nSIhGoyydTovESSaTYYlEgqXTaZv2cLNsUKfkWZZVsLNcpZA9gnxvN+uFdDpt8yAt5n7VSAKp75fX\nlkbScUS1Aaqjv2ouaipaPGD7AY1Go66jXSkodlqEw2HW2dlZ1LH5BJZbNDU1sdXVVTY9Pc1CoRDT\nNM32h0coFGKZTEYIiVJCFnSapgnBFQqFbNvj+Aez3CEl+zupH948yaVuqeOjkfnjsvCSk0+qCSi/\n/vr6upiiw9fd0NDAksmkw2iUnytPoOEJNzcR5Wawrh5Tyla3Uquf26GlnSA4QHVEEUVpGoyCYrdE\nsd1gxSbpwuFwWf5Tvb29LJVKCf3DB+TwrjBZr0SjUcdWPFlTcR2jaRqLRqO29fBEm5t+1DRNFBa5\n16iXzUEoFHK1bOBaRV2Tm48nJ5+HVTFen2pBsRj7BLck0FYmqvJptWrqOOrIIjhAdfRXzUVNRYsH\nbD+gpf7xTUGxG2Lv3r0V/VycPn3akZSZnZ0tajtfKS39oVBIJJPcOqTUpIxpmiyRSLhutTMMg/X2\n9tqqfXNzc45r9/b2sunpaYcxOr++XCHk1+bJLXUiodxurVYm1cmBXJDxe8geEaUKrULwqYFq9Y2E\nBrGdAKojiihK02AUFLsl8k35LkdjGYZRti0C7wQv5r5yEoMX49z8PfOFrutFHcsLcbJXlNf1eBJL\nLuTxBJdspi7j5WFVTAeRW3c84G2foJ5Tyr0qIV8xslqenNSRRcgA1dFfNRc1FS0eENt9VOM/CgqK\nrYlQKMSePn3qEBybZUyqaZpt252maSyRSNg+fLPZrK1TqdRrq+KKf+jKCSAvAcNfP+/KbGlpsRm5\nqx/gqogC4Fq1VJ/fjApYNpu1+Uusr69T5YvYlgDVEUUUpWkwCordEl1dXXmfL2X7Kt/dUcnfLYZh\nuJrEnz171qbPeKcStwqQC1XF+vFeu3bNVau4vS43GwMeahJO7iZPJBK259w6mLw8rIrpIPJKfuXT\nQ25JoFK7lcopLOY7pxodTNRZT8gA1dFfNRc1FS0eEL9ggsFgUb8wKSgoKgtu1FnJNYrpoJKPaW5u\nFoadpmnafBfk6OnpKbiFVzVaB74YoSxvu1tfXxcJb9WTQvbXMAyDxeNxkXhSP8D5yGX5/ePHyVsI\n1U6pzRAcs7OztnXPzs6K97Bek1P1vDaidgDVEUUUpWkw8pGikONrX/tazddQbpw5c4Z1dnYK36S+\nvj7xHDcNv3btmuf5pXRLBYNBlkqlXLuP5C10HR0dYlue+rMWCoUcWkreUqd6cHIPKXl68EcffZTX\nL4y/LlkfyRpL1UY8yZTL5VyfUxNPsl5KpVK2e+YbAFOu1YFqm1CMzlA1Sam2Ctux44imJBMyQHX0\nV81FTUWLxxdtqdyXptYfahQUuyEKia99+/ZVdH23rbhDQ0PMsizHdDs5uEeV/JgqjFpaWmxb8ngS\naH5+3iYQuZ9CKBRiDx48sF1DPi4UCtmqnaFQyLb1jgs5vj1R/aCXRVIh885SMU3T1inFK5KFRFKt\nEkPbVcARWw9QHVFEUZ4Gq+R3fa0/z3ZabIf3tJbm6F/72tdYT0+P7THVH6m/v198rjc1NbH19XWW\nzWZZPB53Lar5/X5xvM/nY7du3cq7BnUrXX9/P7t27ZoYgBIKhVgqlRIaIZ1O2wzUA4GAY7jTiRMn\nbLppenraZjXArReK+Znlw2zyaZWZmRlbR3tXV5etC1z+d3j27FkxXVA1NldtDgC4djAV4xlVLd1S\n7L3ydRzVewGu3tdHVA+gOvqr5qKmosV//ouL/3JTDQP37NlT8w9eCopK4tlnn7V9X0jobFYU2orX\n09NT0KDT5/OxyclJhwAqtrLe3t7ueCwcDrNkMmkTXvmup2maLYGkaZo4l49U5kkgy7I8E9tzc3OO\naTS8o0oVhoZhiISKlx9BvkpdMUKgFLGwvr7Orl27JoxRVfN4tRpZKDFUK4NPYncDVEcUUZSmweSk\n++3bt0v+bCnW04aiuKi0i7kW4VXk2ixLAPVexRSw1cTe7du3bcUnddtcKV1ScqJH/nyWE0jqZ3M6\nnbb9rBiGwdLptK1ryW1rnNskN/4zm++1c70TDodZJpNx/cyXu2lkywU54eZWAHSb+FepLqlXvDqO\ntuvrIXYnQHX0V81FTUWLB2yeLNuhOkRBUUmoHTuFIhgMsr/7u79zVAXzBe8QyjdGudi4ffs2i8Vi\njp/NQCAgJuap7eCFQu5Myvczn89nzqslWW4flyMcDrtO+EulUq5TCHlCpVRBUmwXU7FiRq0+trS0\n5DVVZ6xwZa9WBp/E7gaojiiiKE2D8UmkPDEViURsv4NPnjzJdF0vaegFUHm3bTlRSoLs9OnTW7KG\nL3/5ywWPybdFrlY62O3/1y9+8Qv2/PPPFzy3u7vb8e9jKxJS+d4jvn6uSfr6+mwa6Pjx445z5ILY\nqVOn8t7z7Nmz4jrDw8PsypUr7O7du7bXGYlEbFvpgsEge+utt9jc3JzD+6mnp4fF43H24Ycfsra2\nNqFL5GIh//zOZrMskUgIzTI3N8fi8bhrco5Py5P/rpJ/vtXurbm5OTYzM8MymYyYdDwwMMAymQyL\nx+NscHDQ9nOl6zqbn58X56dSKdsEZX4feTpfNptlQ0ND4jqGYTgKVvKWPrnrvJTin2maLJlMspmZ\nGdvwG+7BVa7ecbvXZvlSqY+rQ3YqKSDWslOKurTqC6A6+qvmoqaixQO2P2Ki0Sht4aPYsdHW1sam\npqZKPm9ycrLoKt6JEyccnU2FxFa+mJiYEAkxVXQODg6KD/779+8Xfc1CE2v4ljuvyXwAWDwet1Xp\nuLhKJBKifV4WSOp7wn215M4r2aB9YGBAiCE3USRXPWWBpY5GdvNUKEbM8A90dUui/B55eWDJv1P5\npEG+dvnexYxuLta7wUtIkTAhOEB1RBFFaRpM/f1CHlMUpUa9Tc3e7MFJm5EoLOY96u/vtxX4YrFY\nQTPz7u5u8TOs6zq7f/++zUvLLbhPlfwYL3iFw2H29OlT2/unFjij0ajnmrhO5AWz9fV1YUEg3yuX\ny4nPBrX4Jt9bnt6cr/gnbyvk/wb435WyBQL3Nq2UzfClUh9X/cIqKSDWspOLusjqD6A6+qvmoqai\nxW+8SeKPSp5tJ1FEsVOjGuKt1Ip2JRGNRtmDBw8KGm2Oj4+L5FBfX19RP+Nu1Vcesgmo2unU1NTE\n3nzzTWEOyj/cC3VexWIx0YLv1jLPyWaztmqmrutsfX2dra+v294Hty4mxhjLZDI27wa3ypksTOTX\nxwWaKljckkGq8Xsmk3EYs+fb4sePcxOFXusttWuM2D0A1RFFFKVpMAoKivqMP//zP2f/9V//lTcp\npmrKwcHBgjrTMAzPgp+u6+zNN990fVz+uphEna7r7MqVK47HVSsEr+KbuuZkMslmZ2cdxb9EIsFm\nZmZc16S+F7xjqphimVqYy2QybHZ2VhRj+ff5fD0zmQwbGhpyLVaqBUp1C2S+4mW+Diu3a6fT6YoL\nhF7dafm6yAoVP4nqAFRHf9Vc1FS0+I03iTFm/0dMQUGx88Lv99s6k6oVhmGwVCrFFhYWWCqVchUu\n3KCUd2ndv3/f0YnEEz3yJD4enZ2drtslVTGxvr4uKqFNTU3s6dOnjg8P+XehlzeEaqrulgBaWFiw\nCT1562I8Hrd1iKmjm91+H3sJG6/OL/KXImSA6ogiitI0GAUFxfYOrml8Pp9ngVDWJ6FQyNW2IF/I\nus1N63CtkU/f8UQL70T3Kr55rV/WTqFQyFFodLOR0DRNHMM7peRindyxJaMW5uTudJ7U8yrY8XNV\nT1QesViMmabp6LZSC5JenVj5Oqz4ddSO+UoLhF7daW7X5fcupqhJVAegOvqr5qKmosUD4o+nbDZL\nW/coKCg2PeSOJcuyHAbvvOVdfYx/zVvo85mLugkxNx8qVTD6fD6WTCZtgsOyLFsrO7+2nBxzS0Cp\nCSDLslwTaA0NDWxmZsb2mLrN0E1UeAkbrzb2SvylaNvfzgOojiiiKE2DUVBQ7Iwo1L2kaRoLBAJM\n07SaeJd1dHQIr6lkMmlL8qjeVcVEMBh0DMJxmwo5NTUlOppUw/lIJOLaKV7slEPAWXRTC4L5jlf9\nroqxP1D1XiKRsGnQVCplu1Y+A/5icdOYhfxL5feQCpO1BaiO/qq5qKlo8fhi8stm7v+moKCoTpQz\nKUgWQ+3t7VURR9z3SfUu4JHP9HZmZqaoTk75dfT39wuzTd7RND8/7/pa5Wl/HLk9HbAnuNxao9VE\nFRcxuVyORSIR14oV995yG93MmLN1XR1NXcxo5HKSS7Ttb2cCVEcUUZSmwSgoKLZnlGJ1UkyHeiVa\njHt45ruPbNwu/83X3Nxc9JZAOXi3E399Xl1ivBPcTf95DYPhmon/V31dqqZSC4tqQZC/Nl4k9epw\nLwa14JdOp233CofDtmvJhU4vW4lS78knXucrPNLgm/oBqI7+qrmoqWjxn/9CKPYXUC2muVBQUHwR\n8mSm5ubmkqcJnj17lj19+pTF43ExTUauKLW1teX1xJLbs0+fPl10d2UgEBA+AMX8zuECoqWlxdEK\nHY1GxTS/M2fO2NZ/5swZNjExIZ6XX0soFBLCQBVffGscT2Cpbdzc60oWAqooUsc0c7wMy0tNGBUr\nMMpNRPFz3Kpv1Dm1/QGqI4ooStNg3d3dNf9coaColyhlMMyPf/xjduLEibLuU0wCJp9W8fl87OnT\np7bkR77BMNyeQN1619TUxObm5tj8/Dybm5srultJTgCFw2GWzWaFZ6Wu647tfrJumJ2dLfheqB1Q\nqtbjyRV1Up+6hS8UCrn6LPH3V9UybkW/XC7HZmdnbYkl/riXLuEFQV3XWTAYZJlMxqHPKrE4kDWR\nZVm298ftWnKhs9yupWI9pQqdQ1QfoDr6q+aipqLFw71TKhgMOn5Jqb/k3IIM0ikotiZOnDjBnj59\nymKxmKhIZbNZNjc3V9J1ChmPu3kVFIpif+5DoZBtG56b/wCw8bvm8ePHLJFI2MYayx+u/z97dxrc\n1nXej/97L8ANJAiSWLiIpCiKpEhRJEVSlEiQlGUtjtc4aWs7bfp3mxdpksl0OpN0OtM2yTSTyTLz\nS9xJpxNP2qQvWideYjtKbCe2rNVaLYr7vksEwH3fQGI7/xf2vQFAUCIlGaLk72fmjETg7gCBh+ec\n+zxut1udgbTedtY7BqXDqrS0NCAZe/BIltKJFirpeqip0Upi809yhtFGApDNHkPwOsHne7Ok83T/\nAMITFLFtLgZzu91rOqaCq4DdjZadnS2io6Pv+XeZ0srKyu7q8ZSUlNyV7URERIjIyMiwXYcdO3aI\nzMzMu77dvXv3CkmStkxcvpECMDU1NWsquAEfDcBVV1evWV6Z4eO/bb1ev+Yx4E8Vcw8cOCCGh4eF\ny+USLS0t6ozlioqKgL97lBhL6eRROjaGhoYCCqUog1EOhyOgAnHwcSqxhjKoJklSQGeR/+Bb8G37\ndrs9IO1BcGdQqE4Kl8ulxlChBsSUinh6vV79v5Jzqra2dk08o+zP4XAEDNIFUwrJKLOo/G+LUzrN\nlH2E2sbdTEdwq3hpI9vcaKeO0gl2t2ctsVPpwQCEJ/6650HNHR08oN5P63a7hd1uFw0NDaKhoWFN\n3peNtoKCgnv+5cfGtpG22ffqRkbWLBZLwM+3O4oXGxsrJEkSRUVFoqCgQMiyLHbv3h2QzPK9994T\nL7744m1t/3amid/uZ4J/O3nypBgYGBA///nP1x0RVBKjh+oIUT6vhoaGAtbPz8/fcAJ35dw1Go2a\nONzhcARsT6koY7PZxKlTp0KOcPl8PlFTUyNkWRbV1dWiqakpIEF6S0vLbY9e3W4gcrORv+DcCcp+\nQuUduNnMqY1WkWEwtbUA4QmK2DYXgwXPHmhoaFA73pubm0VjY+O6MzaUP4LvRX6a223/7//9P2G3\n2zdU8UtpP/nJT8TS0pJ44403Ql4L5bO8sbEx5LX48Y9/vO53jc1mE/X19eLEiROiqalJ2O32Wx5P\nqNvNf/azn206J8/p06eFx+MRzc3N677GoQaJS0tLhSzLasdT8DpDQ0Pq96dSdVd57vXXXw9YR5Ik\nUVdXJ06dOiUcDkdAkZH1vj/tdruw2+3i1KlTN33v2Ww2MTw8LFpaWtRjkCRJ/OY3v1lzvhqNJmA5\n5bXxz0W0kfe5RqMJqLbm/3io2TW3yvtzq6pqofJMut1ucfr06TX7V9YZHh5eN9/PzWZWh+qEul1K\nPBCcqkBJKaAMvt3Od3ioynT+nVH+g40bWf9Wj9+Jm21zs4N8dzuuYyqFBwcQnvjrngc1d3Tw+NNM\nqf3799+VPzrZ2NgerKbT6YQsy8JqtYqKioqw7FOpeAf8KR+V2+1WR/TuRtPr9cJmswmbzbZmavp6\nM8YMBoPweDzC6/UKu92uzjRbL1hWZof5U2Z5+Qew6wVw/oFIqKA0OMhZbzTO/9opFXCCczf4rxM8\nNX2zVWRuFUyxwyr8gPAERWybi8FulW/E4/Gov7uh8qKsV1Bhs5/xd/szfL1bgoJnYAbnspEkaU0s\nquSk8b8W/k3Jy+f/vH+FrlAz/f2vob+RkZFbDnAEn5syI0Q5n410Tim3tN8sr6syI0f5WelkWu+7\nSjmn4A4W/+8b/7w+oa6B/2wd/2MKlb9HWTbUa+2fK3G9Kmehci2uN5skuACJckzB11pJnB1q+zeb\n9bvRmSyhlluvo0p5L8bHx286H1C4+L/ewUVd7pb7tRLwvT7ue71/unvCFX9JH+3r/vRxuUx4vd57\nfShEROtyOp3o6+tDUVHRPT0OWZZRX1+Pr33ta7h69Sp8Pt8t16msrMTFixchyzJ8Ph+qq6tx5coV\ndXv79+/HtWvXYLVacerUKXR0dGDv3r3KH61obGyExWLBF77wBZw/fx6SJKG2thanTp3CkSNHcPHi\nRVRUVODChQvQaDTw+XwYGxuDJEkwm82YnJzE+Pg4iouL1WNqbGzE7Owsjh07Bo/HA0mScPr0aRw8\neBA+nw8HDx5EXV0drFYrzpw5A5/Ph66uLhiNRmRmZsLj8UCr1cJutyM5OXnNOY+NjSE9PT3kcj6f\nDw8//DAuXbqkbl+W5bvx8tBNSJIEIYR0r4+D/kSSJDE6Ogqn04mdO3eqnyeNjY0wmUyYmJjAyMgI\nnnjiCXWd7373u4iIiMC+fftQU1ODc+fOYWxsDN/73vfQ398PrVYLj8ejLp+eng673Y7IyEi4XK6Q\nx/GLX/wCP/7xj9HV1RXwuLKu2WzG4uIinE6n/7Grn1EWiwURERFwOBxITEzE008/jZKSEsTHx+N7\n3/serl+/juTkZIyNjanr//CHP0R3dzcAoLCwELOzs+jv70dlZSVSUlLw9a9/HVNTU0hPT8f3v/99\n+Hw+tLa24oUXXlhz/P/8z/+MAwcOoKWlBd/5znfUx7/85S/jl7/8pXpdv/Wtb2FsbAwHDx7EW2+9\nhZiYGOTk5KC1tRUmkwkZGRmw2Ww4fvw4hoeH1e1kZmZCo9FgcHAQCQkJMBqN6O/vBwBkZGTg61//\nOg4cOID33nsPPp8PGo0G+fn5+NGPfoTOzk51O9HR0VhZWUFWVha+/e1vY3BwEN///vcR6u+InJwc\n/M///A/++q//GkNDQ0hNTcWxY8fgcrnwyiuvBCz7gx/8AIWFhRgfH8czzzyDl156Cf/5n/+J7u5u\n7NmzB88//zzsdjvKysqg1+tx7do1JCUlYXZ2Fg6HA1lZWcjMzMTy8jJycnKQn5+PiYkJTE5Owul0\noq6uDhaLBfHx8RgZGUFWVhaysrJQX18Pl8uF+fl5fPGLX8SVK1cwMDAAt9uNvLw8xMTEoKqqCkII\ntLW1YWBgAHq9Hqurq+prUFtbi5mZGczMzCA5ORmVlZX47W9/i8XFRVRUVCApKQkffvghDAYDJEmC\nz+fD7OwsEhMTIYTA1NQUfvjDH6KzsxOZmZl47bXXEBUVBYPBoB738ePHkZ2djeTkZHzxi19U/+b5\n13/9V+Tn58NgMGBkZARHjx5FX18ffD4fZFlGTEwMTpw4gaqqKhiNRvT19UGj0SAnJ0f9zpJlGQkJ\nCXj66afR1taGoqIivPDCCzhw4ADeeustGI1GFBYWwmg04tSpU7Db7XjkkUcwNzcHnU6HN998E8XF\nxUhKSkJfXx8iIiJQXV2NlJQUjI6Oqs3hcODo0aMYGBhAbGwsOjo68IUvfAEXL14EABiNRvX6TExM\nYGZmBomJiYiIiEB+fj58Ph/6+vqQl5cHWZbhcrnQ0NCAxx9/HD09PTCZTHjuuedw+fJl9Xt5fHxc\nfW/Ksgyj0YjOzk6YzWYkJSXh8uXLqK2tVeOOkZERTE9Po7CwUL0+Pp8P4+PjePbZZ3Hp0iVUVVXh\n5ZdfxsTEBDQaDfbs2QMAmJiYQFJSErq7u7F79271MZPJhMnJSVgsFvX8RkZG1MdMJhM6OzthNBqh\n0WjUmMdkMmF8fFyNg5T/G41GdHd3Iz8/H1NTU+p2PR4P2traIMsy8vPz0dXVBZPJpF7j/fv3q3Gc\nwuPxoKOjA2azGSkpKZCkjX+9+sdpycnJIdf1er2ora1VY7GzZ8+qyyn7Vs47OTkZQghMTEzAYrEE\n/N9/28r7I/jx4GMLde3XW+5m26KPhC3+CkfP1yfV8PEID+7yCBkbGxvb3WzFxcXC7XZvKC/FJ5lD\n43byvPiPcIUqVayMTioj2htNwNra2hqytHKoUeKampqQOSSCZyjU1tYGfCcE58oKnil1O7katuLo\n36dh5hYQnpE6ts3FYBu97ZiNje3T024nv+edNL1er86M0+v1Abm9lLbe7Een0xmwfKjZ2PHx8SFz\ngOr1ejUJvH8OMSXXV3AxmeDjCj4mZfZccHVB/+NV/lW2u7q6um5s5//5rNzWKIRYU8HQ/7lbCTVb\nMdRscuXaVVZWBsy4D963Ervdakb7Rm4HvNksxlDL8dbCjQHCE3/d86Dmjg4eEB6PJ+CPkIqKinXL\negIQGRkZ9/zDmo2N7cFuOTk5AT8rt/A5nc57dkynTp3a8LL+CXw1Go1wuVxCiPVvd9BoNKKsrCzg\nVo31OqeUAGR4eHhNB9Lo6GjICodarVbY7XbR2toqmpubA57z349yy4vyc3l5+ZqqMevllAqVRyLU\nclvltgXFpyW4AsITFLFtLgZjY2Nj22ptM3nqfvOb36x5rKWlZU115/VaqGWCH9NoNKKpqemu58/T\narXizJkzG74mSq6x4AqGSoy6Xhyk5AgLriSoHMPNqvUpOc6UbbW0tIS8Xv7Lhxr428iAYKj40T/H\nWqjltsrgYrCtNNgIhCf+uudBzR0d/EcXKSBXicfjWXPfNhsbGxuwsVH9uLi4NXkv/Ft8fLwYHBzc\n1AyB/fv3q18wwc/FxMSEXCf4cavVKvbv3y8kSRLl5eXqSGRMTEzAqGRRUZFaoU8JjAwGgxgaGgrY\nnk6nW1NRR6nuE9yx39raqn45BVeh8V83uOJO8GhpU1OTsNlsorKyMmDdULkqlNHC4M6f4FwX/lWN\nZFlWRy31ev26s6Nulsh0owlB72bS1jtxPwRXdwMQnqCIbXMxGBsbG9v93ELNYP1/+e0AACAASURB\nVK+urg6ZJ+1OZoaG2t7ttuD8djerBu1/7Ep843a7A56rra1dk7PMP2ecMoNLyXEXvG5wBcXgGWE1\nNTUBMeNmZkptpoJhqJxyoWZzbbXBxWBbbbARCE/8dc+Dmjs6+I8uUoBQvaRsbGz3T/skKzFtZNuS\nJK37GSLLslp5ZrP7rq6uFqdOndpwQYa6urqAnysrK9Xyzf4zjDQajRgaGhJlZWVq5RmlMo3/yFOo\najr+s4b8q/j4Xye9Xr/uNOlQVX9aW1vV5Kn+o4XKFO5Qt9cFjwYpnT7KFPjgqeX+lfiCZ041Nzev\nqQwUfJ7BX/ab7djZSgHDVg+u7hYgPEER2+ZiMDY2NrYHra3X+eQf04RaZqOdVq+++uqmq13672No\naCigGrHb7Rb19fXi9OnTYmVlRTQ3N4vh4WHhcrnE6dOn18Q3/jGPJEnizJkza2aV+8dR67X1ZiGF\nminmv2273S6am5vF0NCQaGlpWVMtMdQsoY0OBirrOhyOm8Z1W2kmUrCtNtgIhCf+uudBzR0d/EcX\nKYASoAf/4txOLpVPa/skc9qwbc12p5Ur/X+/Dhw4oM5W2UgnUGxs7IZyLd2N3CU3u7XXvymjQaHu\n31e+MIOrJG30M0apzhR8beLi4tSZS7W1tWtma/kHE8G5mPw7hpTl/EeMQlVwCh7dCv4MlWVZlJWV\nram+t97y641qKTkFlAAg+NjXCwg2+qXs/1oYDAbh9Xo3nRNqsx07Wy1g2MrB1d0ChCcoYttcDMbG\nxsZ2P7dQMWhVVdVN16mpqVkzG0iSpIDZ4TeLDUPlidpojKvX6wNmmAfn4gzO4RQqvvGP84JzYa1X\nZVKW5ZDVMkOlOPC/Y0mSpIC8oP5VoDda5fh2BgLv5wG7rXbsQHjir3se1NzRwX90kdbwer1rZgnU\n19eLV155JeCXXq/XC1mW19wm8+qrr4q6urqAPxqzs7NFbm6ukCRJFBQU3PJDQ5blNXllbtXMZvOm\nP0w3myMrIiLips/n5uaKF198MeRz3/nOdz7RL4b09PRPdPvKuWdnZ4vIyMgNr/eNb3zjtvdpMpnu\n6Jizs7PXfa/k5+ffdN3HHntMdHZ2il/96le33M+LL74oTpw4cduzDH/9618HdDb893//t6ivrw+5\nPf/fq29961vinXfe2VDn1e9///s1j/n/Pu/evTvkegcOHBCyLIu9e/eKixcviu3btwc8v3379pDB\nwMmTJ0VPT4/40Y9+JP7whz+Ia9euifr6elFXVydOnjwp+vv7xcsvvyzeffddcfXqVfHyyy+vGR1a\nr4P3rbfeEq+//rqoqakRkiSJ0tJS4XA4hMvlEs3NzaK5uXnNNSkuLhanTp0STqdTlJWVCVmWxYED\nB4TX6xUej0dUVVWpAYnb7Rajo6NiZWVFvPLKKyGTkzc0NIirV6+K119/XTidzjWjbsrPG+nwCJV3\nYHh4WNhsNnUUTAihzpRSOrxcLlfArdejo6PC5XKJ1tZW9VZsjUYjampq1GWU5ZXl3G63sNvtAfvx\nP6bg41aOQen8U0bdNtOxs5GAQRnV878GXq835LFuBVu9YwsIT1DEtrkYjI2N7e62//3f/71n+5Zl\nWbz//vvi5MmT6y4T6u+I2xk0VPZ1O7PjT5w4EfDzO++8E5ALM1S7du2acDgc4tq1awEdQf6DsrIs\nC61We8sBTOU7PPg6KeciSZKw2+1idHRUNDU13fI6lJWVidXVVTU+qK+vD1hm+/btIa/TzQYrbxUP\neb3eNfmompubQ+aUcrlcawrZhJol5b/t4eFh4XA4xMjIiBgZGQkY5A2erRU8uBfcCRU8i2ujA4Fb\nPa65ma107EB44q97Gcz8BYA2AF4AZX6PHwVwDUAzgDoAD99kG+teQJfLdcupkTU1NeL69eshPyA+\niQ/7+6Gxkg7bg9aqqqo2NBPrXjX/+/X9R8828jmk3KqnjHjp9fqAUa1Q+wLW/z03GAxidXX1llVQ\nQgmuVKNsUxlNc7vda/L9+S8XPDstuIJN8HZDzWLbSC4o/2Pwz1m12U6imwUMwftR9uWf/0qp8LMV\nbKXbEdcDhCco+rQ03KUYTGmVlZWitLQ04D1/q89dvV7PWeyf8hbO7+bNxrfKjO9QzwU/vtG/G271\nd0l5ebnweDwBeRP37t0btmvkP5MmVH7e4uLikOttdBa6/2sRPBtnvc+CUPHE8PBwwDIbSfatdKD4\nDyopg2ShXt/gnJj+OTr9K8L5v1ahBqtCzaxXYhrlPRmqU8b/eijVjYPfP8psc5/PF7JwzK2Emmke\nSnBqnM3O4LnZbK2NzGj3z2O6FWYOfdoA4Ym/7mVAtAtALoDTCAyISgCkfPz/QgD2m2xDCPGne2nf\nffdd8f7774v+/n7xk5/8ZENfDq+88krYPuzZ2NjY7nb7l3/5lw0HxBtZ7kc/+lFA4OO/znvvvSeO\nHz8uvvOd74jBwUHhcDjU5j/6GNwkSRK//vWvN93hv5mcC7Isq4nUm5qahN1uXzML6saNGyGPQcmp\noMwwC1WZz3/UT9lm8CwvZb3h4eGQxx78R5GSQP5WHVx38lzwsYWy1W5HDAUIT1D0aWm4SzGY/+25\nbrdb/UMuLi5OuFwu4XA4AmYiKLdyKDMN3G63aGxsFE1NTQGdtjdLI/BJpRjIycm5aQfAzWaa385g\nplK0Ivh8JEkSJSUla/4o9m9FRUUb3o8ys1bpACopKRH79u1Tn4+Ojhbl5eUB6+zevVtcv35dXLt2\nTZw4cUI0NDSs6UAKdXyhZqvs3btXDAwMiD179qjrKTN93W63sNls63Zq3KrTUrnjYd++faKkpERI\nkiQqKyvFH/7wB5GXlycAiIKCAmG328Xq6qp6LSoqKkRjY6Ow2WyioqJC3V5xcbH4zW9+I9xut1rU\nw/82reBZzUpOHCXfo/L9Mzg4KIqLi9XiIcr3kcvlEi0tLepAkv81jYuLU2+78p+t7Ha7A5azWq3q\ntpXzV87nxo0bory8XE0orcwU379/f8B5KANAcXFxQpIkUVFRIYaHh9fMpHE4HGohE2UWdnDCbmVw\nrKqqSmi1WmG1WgPeBzqdTgwNDQXEC/55gZTvKrfbHdCxcuDAATE8PKzOkPZfT+k0U3JOejyegOOK\nj49XO5aUZYLPTak2539d/Ae5lNfY/7Xzn1Gu2MjMcmUZJcbweDy37GhxuVzqa6kkNFfW8f/cVSgz\n5jfbceN//Ovx70Dyn2G+GevN1tpoleOtNHPo0wYIT/wlfbSve0eSpDMAvimEaFjn+UkAqUIId4jn\nhNvtRmJiIhYXFz/pQyUiovuIJEmoqamBJEk4f/48bvV9p9FoIEkSrFYrzpw5A1mW4fP5cOjQIZw/\nfz5gmwDUxwwGA5aWlmC1WnHq1CkcPnxYfU4RHx+P4uJiXLhwQV1nenoaAPDwww/j0qVLAfsFAJ/P\nd0fPXbx4EXFxceqx+S/jTwiBQ4cOqds6e/YsJEm6rWv+SZEkCUKIrXVQD4A7jcFGR0dhsVjU94vH\n40FXVxd2794d8H4cGxuDEAKyLCM5OTnk+0tZTpIkmM1mjI+Pr/mdlWU54Dmfz4epqSkkJSVhenoa\nJpNpzbaV7c7OziI3NxcTExOYn59HTU0NRkdH0dvbi/z8fKSmpkIIgZGREUxOTgZsS9nv6OgoJicn\nkZSUhMnJSUiShOTkZJhMJnR3dyMrKwsvvfQSsrOzA66Bsv7w8DD6+/tRXV2N6elpWCwWeL1etLS0\nYG5uDjU1NQGPd3V1IT8/H1NTU0hISMDly5dRW1sLSZLgcDjQ3d0Ns9mMwsJCTExMqNc4MTExYNmJ\niQmYTCZMTk7CYrGo5zk9PY3CwkIAuOVr5PF40NLSgpmZGRQUFCA5ORmjo6MYHx9Xr4PFYgl43fy3\n5fP51hyHsg/luYSEBFy8eBF5eXnQarXqa+31ejE1NRXyNfE/p4mJCXW7yjZD7Sf4MeV9F+q8b/X8\nekLtK/g5k8mE0dFR9XUI9fmsXPuOjg6YzWakpKSo53qzaxl8Tfxf84KCAvV6Bq9/q/NQjsVoNEKj\n0ax5fZX3bltbG2RZxp49e9Y9r1D72ui1Xu+4zGYzLBaL+ju8kfMLvi43W/5uutl7ZL3nN/K++iSO\n/5Pc9lbYH60vXPHXlu6UkiTpLwD8nRDikXXWFa2trSgqKvqkD5OIiO5DSkeTx+PZ1DpNTU0oLCzE\n+Pg4tm3bBq/Xqz4vyzIkSQp4DAC0Wi0aGxtRWloKj8cDWZZx9epVLCwsqH8c+v8hKMsyxsbGkJ6e\nDo/HE7BfSZICntNqtbDb7UhOTgaADT/nf04Oh0NdJthWDwDZKfXJuNMY7F7HkERERPTJCVf8tbGu\n69skSdL7kiS1+LXWj/99agPrFgL4IYC/u9lyu3fvRmxs7N06ZCIius+s14kiSRKqqqqwb9++gGUk\nSUJ8fPya5TUaDTQaDeLi4rB3715YrVYkJiaioqIiYLm4uDhUVlaqPxsMBmi1WlRWVsLn88FqtUKr\n1aK6uhrf+MY3cOzYMRw+fBgAsG3bNhQVFakjxxaLBVarVd1vaWkpDh06BJ/Ppz6n1WphtVphsVjU\nfW7kOVmWodFo1GM2mUzrXsObzWCh+1M4YjAiIiKiO6X9JDcuhDh2O+tJkpQO4E0A/58Q4vrNlv3u\nd7+LpKQkLC0trXnu8uXL6Ovrw1e+8hUsLy9Dp9PB6XTe8hYOIqKtSLk14l4oKSlRp+SH2759+/BP\n//RP+Ku/+it19s+rr76KyspKzM3NISkpCZmZmfD5fOo6kiRhYGAAf/M3f4O6ujocOHAAp0+fxocf\nfoja2loIIXD27FkcO/anr6n+/n4sLCxg79698Hq9uHLlCkwmE5aWlhAbG6t+zywtLcHr9UKj0aCi\nogIffPABxsfHUVhYiJKSEsTHx+P69evQaDTIyMiAx+PBpUuXMDExsWamkiRJOHPmDDo6OtQZVv7L\nnjlzJuQMJmW9mz2nbFM55snJyXVnSm01Z8+exdmzZ+/1YdzXwhGD/du//Zv6/0OHDuHQoUO3s0si\nIiLaAu5V/LVVbt/7RyFE/cc/GwCcA/BvQojjt1hXjI6Orrm1AgCqqqpw8eJFtLe3B9zeV1xcjJaW\nlrt+HkREnzQlx9G9oMy4Cf6s3YzS0lI0NjZuej2tVgubzYbnnnsuZN4jIQQeeuihNXmc3njjDTz3\n3HMhb3EDgNbWVhQXF6s/t7S0YM+ePbBarbhy5cq6x1NeXo7m5uaA7U5MTAR817S2tqKwsHDDuZo+\nibxO90OuqI3i7XufjDuNwV599VWkpaXh5MmTWF1dRVxcHPbs2QObzQa9Xo+RkRE0Nzdj586dmJmZ\nAQCYTCY1v82VK1fg8/lw9OhR9PT0IDIyEp/73OfwyiuvIDs7GzqdDjabDampqbhy5Qo8Hg8yMzPV\nvEl9fX2Ijo5GTEwMVlZW0NHRgZKSEoyPj0On0+HGjRuQZRlerxePPfYYzp8/r3Yy5+fno7W1FXFx\ncSgrKwMAjI6OYmxsDCaTCfn5+Xj77bdhNpvR1taG3NxcREZGYnFxEbGxsdi9ezfGx8cxNDSE8fFx\nJCYmYnZ2FlFRUSguLobP58Po6CiGhoaQm5uL2NhYxMfHo7OzE16vFwaDATabDfPz80hMTMT09DRy\ncnKwtLQESZKQk5ODgYEBREVFYWJiAklJSRgaGkJmZia8Xi9mZmag0+kwPz+v/nvo0CF0dHQgKioK\n+/fvx/T0NCRJQl1dHQwGA1wuF7xeL5xOJ8xms5qXaGxsDNnZ2Zibm8PMzAw0Gg3y8vIwMjKC+fl5\n5OTkIDExEefPn4dOp4PH44HJZIJWq8W2bdswPDyMqakpTE1NIT8/HzqdDn19fUhPT0diYiL0ej16\nenpw8OBBNDQ0YGRkBNHR0TCbzdDr9bDb7dDpdJienoZOp0NKSgq6u7uRmJiI3bt34+LFi4iJicHS\n0hI0Gg0sFgsKCgpw48YNTE1NITk5GQkJCRgaGsLk5CTS09MxOTmJ0tJSXL16FYmJicjPz0dvby9W\nV1cRERGBmZkZjI+Pw+fzISMjA3q9HisrK/B6vTAajVhYWIBOp4PdbkdaWhri4+MxNTWFHTt24MSJ\nE0hOTkZBQQGampowPz8Pj8eDiooK9Pb2IjExEcXFxRgcHITFYoHNZkNmZiYGBwdht9tx6NAhJCUl\n4dy5cygpKUFSUpL6nRMVFYX+/n7U1NRgfn4eSUlJam4op9OJyspKnDhxAllZWVhYWEB2djYGBweR\nk5ODlZUVJCUloaWlBampqeqt69evX4der8fq6ip0Oh2Sk5ORk5ODpqYmOJ1O5ObmoqWlBUajEfn5\n+VheXkZjYyPi4+PhdDoRERGB8vJydcAjOzsbLS0t2LFjBzIyMtDf34/CwkI0NjZiYWEBRUVFMBgM\niIqKwvz8PE6fPo3s7Gysrq7CbDYjPT0dVqsVy8vLePPNNxEbG4uenh7s27cPDocDGRkZmJ2dRVlZ\nGRobG5GWlgaXy6XmEXv77bfx7LPPqnmxWlpasLi4iLy8PFRWVuL3v/89MjMzIUkSpqamMDAwgMOH\nD2N5eRlerxcrKyvIy8tDfX09tFotvF4vMjMz0draisXFReTk5KCoqAj9/f2YnZ3FkSNHcPnyZeza\ntQvd3d0oKiqC2+3G1atXIUkS+vr6sHPnTjz22GNoamqCLMvYvn075ufnYTAYMDc3B4PBgKmpKczO\nzkIIgcjISOTn5+ONN97A8vIyHnroIcTFxeH8+fPIzs5GZmYmmpqa4PV68eijj2JoaAgJCQmIiIhA\nTk4Oenp64PF4MDk5ieXlZZSWlmJ+fh5xcXFoaWlRf29KSkoC8otNTU0B+FNOttzcXAwMDCA7O1v9\n9/r166iqqkJrays6OzvV95mSP296ehoJCQno7OzE7Ows8vLy1PxvynOzs7NISkqCRqOB2WyGRqOB\nwWDA7373O5jNZhw8eFD9/Dx37hzKy8tRU1OD8+fPw+fzQavVIicnB9evX0d1dTVGR0fX5OPzz5OW\nm5uLS5cuqfnojEYjWltbMTMzg9zcXMzMzMBkMgXkQQvmny/NP3edsnyonInBbpZDMThNwmZzhq3n\ndvPebVTY4q9wZFMP1QB8DoANgBPACIA/fvz4vwJYANAAoPHjf03rbCNk2VL/igTB5S5dLldAdQel\nRUVFbbpyChvbg9w0Gk3ISjqbqYh2Jy06OnrTJZzD0TZ7THer5LkkSaK2tlbU1tYKSZKEXq8XWq1W\nVFdXi/fff1/djyRJQpZlYbVaxYEDB0Juy2q1ipiYmIDHgitf2Ww2YbfbRWVlpVpxRakYpFRP2r9/\nv/r5K0mSsFqtAVWo/M+9srJSeDyegEo38fHxQqPRiP3794vm5maxuroqmpubhcPhCNjuRqqveL1e\nYbPZ1PenRqMRbrf7ptVt1iuHrFSx8S/drPyrnEeoyjChtrWZijGfRHWZB6ViDRCe6i+floa7FIOx\nsbGxsbGFsykxqX88udGmxJShqigGV5b0X351dTUgxnO73WviFK/XG9An4b8vr9cbEDcGx6ehlrlZ\nRcRQ+1zv3O4UEJ74657PlLoTSpLNW1V2Ce7Z9F8eCKyK0tvbi7y8vIAeUI/Hg76+PmRlZeHatWvI\ny8vDnj17MDY2plZ3EEKo1V127doFAGoP/urqKs6ePYtnnnkGf/zjH5GZmQmbzYb9+/erPcmzs7Mo\nKCjA2NiYWmlkYmICc3NzyMnJgVarhcFgQH19PSoqKjA5OYnh4WG0trYiMzMTiYmJWFhYUJeNjY3F\n66+/ju3btyM7Oxv9/f2IiIhARUUF+vv7YTQa1V7Y+fl5/PKXv8Tf/u3f4ve//z22bdsWUDVneXkZ\nRUVFaGlpUUfESkpKYLfbUVZWhg8//BBarRalpaU4c+YMSktL1WovU1NT0Gq1yMvLg9FoRH19Pd57\n7z088cQTiIyMhFarRXp6Ol566SV1NCE1NRUffvghvvrVrwIAPvjgA5SWlmLnzp04ceIEjEYj9u/f\nj97eXiwuLuKDDz5AXl4eDh06hFdeeQW7d+/GmTNn8NRTT8FsNmNgYAAJCQlwu93o6uqC1WpFc3Mz\nLBYLPvOZz+AXv/gFbDYbDh06BLfbjSeffBJdXV0APsoVc+7cOQwMDOCpp55CWlqa2lve09MDjUaD\nV199FV/60pdgsVhw8eJFzM7OIjExEXFxcWhoaMDs7CwqKiqQn58Pl8uFs2fPwmKx4Pr16ygoKEBh\nYSF2796NtrY2jIyMwGazobS0FIuLi9i1axc8Hg9Onz6N9vZ2PPfcc0hOTkZ3dzc8Hg8WFxdRXV2N\nhIQE/N///R8yMzOh1WqRnJyMXbt24cKFC4iJicH58+dRWFiIhYUF6PV63LhxA0ajETt27FBH8qxW\nKy5evIjExERERERgz5498Pl86u1aRqMRs7OzKCwshMvlwttvv62+F5VRi4KCAnR0dMDlcmFwcBA7\nd+4EAMzMzCA+Ph59fX0QQgS8J3p7e2E2m9Xj9d+/x+PBhQsXkJeXB5/Ph4GBARw4cADnz5+HLMvI\nz88HAExMTKgVm1ZXV3Hy5EmUl5cjKSkJly9fhlarRVVVlTrbR5ZldcTGaDRi165d6iiK/+ubmJio\njmbMzMzAYrGgqKhIPf+qqipYLBa0t7fD5XKhv78fJpNJHXnKz89HcnIyJicnERcXh5dffhmPPPII\ntFotPB4PBgYGUF1djcnJSfV3XjmP4JEO5bNNiNBVd5TPOaVSkzKKNDY2FlC5SBkl8nq9aGpqwo0b\nN/D0009DluU1SbiVz4DgSj7BVZz8R2jcbjcuXLignrt/ZSblWvpX2FqvMs7tjvy4XC5cunQJtbW1\n0Gg0txx1Wm/kK7hSVPD1DrXdjYyi0e3hTKmt5+MOeiIiorBS4rvb6ceQZRkOhwMpKSlqLDc6Ooq9\ne/euu69XX30Vf/EXf6E+dubMGVRXV6O7u1uN+UZGRpCRkRFwR4FGo4HdbocQQn1OkiScPn0ax44d\nC5hxD2BNARtlRut6MezY2FjAHWOh7gq4U5+a6nt3gpVfiIiIHnzslNp62ClFREThptVqUVFRgcuX\nL9/2Nmpra3H69GkcOXIEFy9ehE6nw8LCQshl9Xp9wHMajeajmT0fV2E2GAwYHx/H0aNH16SRkCQJ\nNTU1EELgwoULAc8ZDAYsLS2p6RUABKRcOH36NA4fPqz+fObMmTUDnkL8KX2FJEmora2966ka2Cm1\nAeyUIiIievCxU2rrYacUERGFk81mQ0REBC5evIg///M/39A6P/vZz7Br1y488sgjATOKGhsb1QIz\nCkmS8Nprr+GZZ55RH/PP5ypJEjQaTcA6wEczp5SZT7Is4/3338dnPvMZeDyedXOyajQaNDU1obCw\nMGROqfHx8TUzp0LNgHpQckrx/gIiIiIiIiKiMLjTjoONpgiIj4+/5TKxsbGb3r/S0bLZ89Dr9QHb\nCF7f/3kg8DwPHjyIbdu2ITk5GZ/97GfXLLfeNfnyl7+Mhx9+GFarVT1mq9WK3bt3w2q1qknYtVot\namtr8fnPfx4GgwHAR9evurpaXa+mpgZWqxWyLKvXwGAwoLa2FlarFVqtFjU1NTh06JD6s9VqVfet\nkCQJ1dXVAR1SynkoHUtKahVlGxaLJeT5ybKM1NRUpKSk3LfFbIAHYKaUkodFyW3icDjQ3t6OyclJ\nREdH48knn0RHRwempqaQkJCAxcVFHDx4EJIkqcvOzs6qVUeUKhdTU1PQaDTIysrCu+++C7fbjdnZ\nWbjdbqSmpmL79u0YGBjAzMwM3G43jEYjlpeXkZiYiMzMTHR0dKCxsREmkwmpqano6urC5z//edhs\nNiwsLECSJJw/fx5jY2M4cuQINBoNFhYWsLCwAI/Ho+b3iYqKQnJyslqKPDY2FvPz8xgcHMTS0hJ2\n7dqF/v5+PPHEE5ibm0NDQwOWl5cRExMDjUaDrq4utbJMW1sbSkpKYLPZ1GoUVqsVly9fRmlpKVZW\nVlBRUYHBwUFMTEwgNzcXV65cgUajUSsR6HQ6xMXFoampCXFxcZienkZZWRncbjcGBwdhNBrh8/ng\ndDphMpnQ2NiI/Px8dHZ2wmAwIDk5Gfn5+bhx4wYKCwtx/vx5DA0NQafTwWQywWKxQKfTITIyEkND\nQ7BYLJibm0NfXx/0ej3Ky8tx/vx5VFZWYmRkBD6fD263G7GxsRgbG0Nqaqr6Omk0GiwuLmL79u1q\ntRXlfWAymVBfXw9ZlqHT6bCysgIhBKqqqnDhwgVotVokJSVhbGwM1dXVOHv2LFJTU7G0tITZ2Vn1\nHJQ8RF6vF/Hx8Xj00UfR2dmploNXKvkkJiaq17asrAwLCwvo7u7G6Ogo8vPzMTIygqSkJNTU1ODc\nuXNYXl7Gnj171GpFLpcL169fh1arhc/nw+rqKmJiYrBjxw54vV5s374dN27cwOjoKDIzM9HX14fM\nzExs27YNDQ0NiIyMVK+HkndpZmYGIyMj2LNnD1ZXV7F3714MDw9DCAGPx4OxsTFoNBq4XC4kJycj\nMjISPp8Pubm5ap6mY8eOobe3F21tbdizZw+6u7sRHx+PhIQE3LhxA5GRkYiOjlarvjgcDlRUVKCu\nrg6ZmZnYvn27uk8hBFZXV+H1erG4uIht27ZhdHQUBw8eRGxsLOx2OzIyMvD2228jOzsbqamp6Ozs\nhMViwdLSEpaWlpCdnQ0AmJ+fx/DwMHbu3Ine3l4YjUbMzc0hMjISpaWluHTpEtLS0rB//340Nzdj\neXkZaWlp6OnpUX+fBwcHYTabYTabsXPnTly7dg0WiwWzs7NISEjAxMQEZmZmsGvXLiwvL8PpdCI2\nNhYJCQlob29Xr3lqairm5uaQmZmpftkqv89vv/02KisrUVRUhJdeegmPP/44ZFnGjRs3kJCQgOvX\nr2NxcRGf+9zn8Oqrr0KSJGRnZyMvLw/Dw8Pqvqqrq5GcnIyrV69Cp9Mh1IpTYAAAIABJREFULS1N\nfR8qv9fp6eno7OzE0NAQJEmCwWDAysoKnn/+eZw9exa7du1Sz8HtdqO2thbd3d3o6emB1+uFy+XC\n4cOH8e///u84ePCgWnnotddeQ09PDwoKCrB//34YDAY0NjZiaWkJDocDzzzzDBYWFjA+Po6BgQFM\nTEwgLy8PX/rSl9DX1we73Y6Ojg5UV1ejs7MTOp0OTqcTGRkZAIDp6WksLCyon60DAwNq7re3334b\n5eXlOH78OHQ6HbZt24adO3fC4/Ggra0NWVlZyMnJwcTEBHp7e+F0OlFWVobc3FxcvXpVnZKdk5MD\nn8+H/v5+xMXFwWazIT09Xa261NPTg6NHj6K4uBgjIyPo7OxUc5r5fD4152BDQwMqKirUc921axeK\ni4vh8Xhw9uxZaLVaPPTQQ2ogo4yIJSUlobOzc92KL8F5EH0+n5o3LCUlBV6vFx0dHWoFL4vFApPJ\nhO7ubuTn52NsbAyjo6OYn5/HwYMH1+z/ZpVfgkfg/HOIKTnBTCbTmtxhn8D3PWdKbTGSJInm5mYY\njUa1ElV6ejqam5uRm5uL8vJyvPDCC8jPz0dubq76Gfz6669DkiQcOXIECwsL8Pl8mJ+fh9FoxPbt\n29He3o7a2lr87ne/Q1ZWFk6dOoUDBw5gbm4O8/Pz+OY3v4m6ujpYLBb8x3/8B7KysjAwMIDi4mKk\np6ejoaFB/U7cuXMn5ubmMDk5iYGBARw9ehQulwvnzp1DVlYWqqursbKygj/84Q+IiYlBUlISpqen\n1QpdaWlpaGtrQ15eHtxuN2pqatDU1IT4+Hg4HA6YTCakpKSgs7MTBQUFGBwchM/ng0ajQUZGBurr\n69W4RMmruH37dmi1WjQ3NyMuLg7Hjh3D9PQ0urq6kJSUhPHxcciyjPT0dIyOjqK6uhpOpxN//OMf\nERkZCYPBgLa2Nhw9ehTPPvssfvrTn2JxcRE7d+6E2WzG8ePH8Q//8A8YGhrCzMwMSkpKcOnSJZw5\ncwYxMTHIy8vDvn37cODAAayuruKdd96B1+vF8vIyTCYT4uPjMTs7i8nJSTidThQUFGB2dlbNw2I2\nm9U/ADs7O/HYY4/BZrOhv78fVqsV9fX1EEIgLS0N7e3t2Lt3r5orMjExES+//DIiIiJgMBhQWVmJ\nwcFBtdLdysqKWnlNlmUMDw8jMzMT8fHxWFpagsFgUCu1jY2NISUlBWazGfPz81hdXVVjifn5eUxN\nTanxX3JyMtrb27Fjxw5cv34dhw8fxujoKC5cuICqqiq1glxDQwP+8i//Un1v1dbWYmxsDDk5Obhw\n4QJMJhP27t2L8fFxpKWlYXx8HD09PdizZw/MZrP6vtixYwdefPFFFBYW4otf/CLeeOMNaDQalJeX\nY8eOHfjVr36lVimbmZlBbGwskpKS8NnPfhZvvvkmNBqN+r3S3t6OvLw8JCYmwu12Y2hoCHq9Hvv2\n7UNXVxfS09MBQI19lQqGXV1d+PKXvwyHw4G4uDj09vZicnISUVFRSExMhEajwenTp/HEE09Ap9Mh\nKytL/Z48dOgQPvjgAxw+fBgDAwPQ6/Vqflav14uBgQE1P+X58+dhNBqRk5ODzMxMXLp0CQcPHsTc\n3JxaxXFubk6tlvjrX/8aQgjodDrMzc2hoqICy8vLyM7OxsTEBPr7+yFJElJSUvDUU0+ho6MDIyMj\nGBwchF6vx9LSErKysgBArd4WGRmJgwcPYmRkBE899RTGxsbQ3t6O6elptQro0aNH0dfXp+Zjraqq\ngiRJsNlsOHfuHIqKigLyjirfxx6PB/39/UhKSlLzciYmJqK7uxsAEBMTg3fffRfp6ek4duwYGhoa\nkJ2dDa1Wi8TERPT39yMvLw8ulwunT5/GI488gsjISBiNRrS3twP4KGfr9PS0+vfEwMAASkpK8NOf\n/hTPP/88pqam0NPTA0mSYDQakZKSgsLCQkxMTKzJGWowGPDWW28hJycHqamp6owb/7/3lZymVVVV\n6O3txe7du+FyuXD8+PGb5lnV6/UYGhpSO0j8YwwlFvDP65qSkqLmIlXiA4vFgtHRUUxPT6OgoED9\nu+zixYsBuUiVPNFGoxGdnZ0wm81rOl2Uz+4nn3wSMzMzaixlNpuRkJCAP/7xj/jsZz8LrVYLIPSM\nouD8ocF5Wnfv3g0Aa+IgJXbzzyl1s+p6Suzkn896I/HS7VTju9t4+94GfJxlHpcuXUJVVRV8Ph8u\nXrx4y/VkWUZlZSUuXboUhqMkIqJPq9jYWLUTEvhoZHB5eRlarRYPP/ywmmNAmRquUHIDnDp1CocP\nH16Tp0BRXV2N1tZWzM/PBzyu0WjUhJr+3/PB+/fPVQAg4DH/fSsjhADUYzEYDFhcXFQHS5RjDpX3\n4E6xU2rrYQoFIiKiBxs7pTZAkiShVLEKDryJiIi2ol/96lcQQuD5559f0xkV7Oc//zm+9rWv3XK5\nzXj//feRkpKi5lKQZRlNTU0wm83IyMhQv1P/67/+C1/96lfVPAiyLKuJPddzq7wHtzvix06prYed\nUkRERA82dkptgCRJora2dt0RZCIiIgqkVI4BEJC8s6amRr21fL3YwL8KzXozpUJVfvH5fGtmZm1m\nNhU7pbYedkoRERE92NgptQGSJInh4WFkZGTcdOSWiIjo0+q1117Ds88+e8vltFothoaGcPny5XWr\n2mg0GjQ0NMBisWwqp9TY2NiGqsish51SWw87pYiIiB5srL63QSkpKWsy2sfFxd2joyEiIrp9SqLV\nYLGxsQEzi/y/5zQazZrKM/5VYf7sz/5MzQelPKfRaAKq8ijVaFJSUvD0008HbEtJ0K9UiykqKkJK\nSoqa6FZJ6H+zyi8brSJDRERERJ8u9/1MKSFEQGUiWZZhNpsxPDyM9vZ2zM/Po6KiAt3d3WqVvamp\nKUxNTakVX/R6PZxOJ0pKSmC327Fv3z709vbC5XKhp6cHMzMzOHDgALRarbp9pVLA9PQ03G43ZmZm\n1Ip8ERER+Pu//3u88MILWFhYUCvT1NXVITc3F0lJSbh+/TocDgcSExMRGxsLvV6PmJgYDA8Po7q6\nGg0NDdDpdEhPT4fNZsPS0hJSUlJw4cIFmM1mtVKZ2WyGyWRCV1cXoqKi4PP5MD09DZ/Ph8LCQrjd\nbuTm5qKnpwdOpxOtra3Q6/WIjIyEx+NBQkIC2trasGPHDvh8PszOzmJ+fh7R0dHw+XyorKxETEwM\nBgcHUVhYiMbGRpSVlaGnpweyLKOvrw+yLCM2NhZerxcmkwnLy8tYWFiAVqvF9u3bERERgd7eXpjN\nZrjdbthsNiQmJsLr9cLpdKK8vBzvv/8+dDod8vLyEBUVhZmZGfVcxsfHodfrkZWVha6uLrhcLqSn\npyMqKgrK65+RkYGZmRn09PQgNzdXPba0tDRIkgRJkjAyMoKCggJcuXIFTqdTreoQHx+PuLg4uN1u\nTE1NIS8vD5OTk4iMjIQsyzAYDHC73XA4HNi+fTuWl5extLSExMREZGdno6enBy6XC7GxsRgeHoZG\no1GvocvlgslkwtzcHFZWVrBt2zYMDw8jKysL9fX10Gg02LNnj5oIWZZlREZGYnBwEElJSdDpdGrl\nOOCjPyZNJhMGBgYwOTmJiIgIpKWlqdchJSUFLS0tWFpaCqiIERUVhZiYGBQXF8Nut8NgMCAmJgat\nra1IS0vDysoKhoaGsG3bNqysrGDXrl1oa2tDbGwsIiMjIYSA0+nE6uoqsrOzMTg4iKKiInR3d8Pl\ncqkVBc+dO4eEhAQkJydjcXERQgiUlZVBCKG+btPT04iOjsbJkydx5MgRRERE4OLFi6itrcXQ0BD2\n7NmD5uZmtdrf4uKiWoUxMjISdXV12LVrl1pRJD4+Hk6nE16vF+np6Whvb0dcXByGh4fx+OOPw2w2\no7e3F3V1dcjOzsbMzAzS09MxMTGBqakpZGVlqdVLYmNjsby8jOTkZJhMJvV90dbWhoiICLjdbiQk\nJKiVcoaGhrC8vIzV1VVERkairKwMTU1NKC8vh8PhgMViwXvvvYekpCS1wpJSZSk2NhaFhYVYWVmB\nwWBAYWEh2trasLi4iOzsbGRmZmJ+fh5OpxPt7e2YmZnB3r17sbS0hLq6OhQWFkKn06GnpwcWiwXt\n7e147LHHEB8fj9/+9rf4yle+gpMnT2JpaQlpaWlobm7G448/jqWlJczNzeHcuXM4evQoTCYThoaG\nsLi4iJSUFERERMDhcCA5ORlGo1GtGjU8PIxt27ZhdnYWEREREEJgbm4O5eXliI2NxQcffICEhATE\nxMRg//79OH78OKKjoxEREYGqqirIsozZ2VkYDAbMzMxAq9UiMzMT7e3tOHbsmFrJtLe3F5IkQa/X\no7+/H0tLS8jIyMDy8jIuXbqEv/u7v8Pq6ip27NiBS5cuYX5+HpmZmZicnITdbkdCQoJahXF6elr9\nvdLr9ejs7ERvby8OHjyI3Nxc2Gw27N27F++99x4iIiJw5MgRXLhwAQMDA3jssccwOzuLiYkJrKys\n4OjRo+jo6EBXVxeeeeYZSJKEnp4eGAwGjI+Pw2azoaSkRK1KlJ2djYWFBeTm5sLhcKjVfaKiopCT\nk4OOjg7Y7XY8+uijamUY5TNJqWgzMjKC7u5umM1mFBUVwePx4MKFC2qFmuAKNv6VZ5Tqe/5VYUZG\nRgKWV2Y4Kd+d/rOcXC5XwL7uRnU95pR6sHCmFBER0YONt+9tAAMiIiKiBx87pbYexmBEREQPNt6+\nR0REREREREREDyx2ShERERERERERUdixU4qIiIiIiIiIiMKOnVJERERERERERBR22nt9AERERER0\n/7lx4wbeeecdHD9+HAkJCWhtbYVOp0NmZiaEEFhYWMDAwADGxsag1+uxtLSEmJgYHD16FCdPnkR0\ndDScTqdaQTchIQFDQ0Pw+Xzw+XzQarVwOp2Ijo7GwsICfD4foqOjsbq6Cp/Pp1bqnJ+fBwDExsbC\n5XLB7Xbf1vloNBp4vd67eYmIiG4qMjISLpdrzeMfJ5gOuY5Op8Py8vJNtytJEiwWC7Kzs3H58uWA\nfen1emi1WsTHx+PGjRuIj49HbGwsRkZGAraRkpKiVrj3ZzQasbCwgJiYGCQmJsLhcMDr9cJgMMDl\nciEyMhJLS0uQJAmrq6vqMRsMBvh8PkRFRSE+Pl49h6mpKciyjLm5OeTk5MDhcKjfF+Xl5YiIiEB/\nfz9mZ2fhdDoRERGBqKgopKWlYXl5GRqNBkajETExMRgYGEBsbCzGxsYQGRmJhIQEREdHw2AwwGAw\nYHp6Gh6PBykpKQAAr9cLm82GyclJZGdnIyIiAiMjI2p159nZWVgsFqSnp0On02FychJarRYDAwMo\nKyuDLMvqNnQ6nVqJXpZlmEwm3LhxA3FxccjOzkZjYyP27duHgYEBpKamwmazwefzwe12Y3BwEIcP\nH0ZHRweKi4sBAFarFb/4xS/w2GOPYXp6Gn19fXjkkUfQ0tICh8OB0tJSlJaWoqmpCfHx8RBCYHl5\nGaWlpZidnYXb7Ybdbkd5eTkkScLExASWlpbw+OOP48qVK8jLy1Ovv8lkgkajUassKxWTw4XV94iI\niGhLY/W9rUeSJAZgREREDwhJklBbW4tTp07hyJEjuHTpEjweT1jiL3ZKERER0ZbGTqmth51SRERE\nDxatVovGxkaUlpbC4/EAQFjiL+aUIiIiIiIiIiL6lJIkCVarFbt374bVaoVWG75MT5wpRURERFsa\nZ0ptPZIkievXrzOnFBHRHWBOKeaU2so5pVJSUnj73q2wU4qIiOjBx06prYcxGBER0YMtXPHXA1N9\nT+nNS0pKQmNjI+rr67F9+3Z4PB709PTg4Ycfxg9+8ANYrVZER0dj586diI2NxbvvvgudToempiYA\nwK5duzA7O4uYmBhMTU3h6tWr+NznPofl5WV8+OGHSElJQVJSEoaGhrCysoKIiAhMT08jMTERExMT\n2LFjB95//30kJCRAq9UiKioK8/PzkCQJUVFRSEpKQlxcHBYXFzE4OIi5uTmkpqYiLS0NXV1dSEhI\ngMPhgMViQV5eHhobG9We1snJSfh8PiwtLUGWP7rzUumd9Q8MY2JiIMsylpaWEBERoSQoU5+PjIyE\nx+OBz+dTf/b5fOp9o+vZSK88ERFtnjIiKssytFot9Ho9PB4P5ubmAp6PioqCx+OB2WzG3r170dnZ\nqY5q9ff3w+12IyEhAampqRgbG8OuXbtgMBgwMDCA1dVVREZGorCwEJcuXYLL5VK/c5R1JEmCRqNR\nR/bKy8vR39+PJ554AnNzc6irq8PY2BjKysrQ0NCgfj89+eSTyMjIQF1dHSRJQmpqKs6cOYOHHnpI\nfVyWZZSXl6OnpwclJSVISUlBXFwc3nzzTezZswcREREwGo3QaDQwm82QJAmyLCM5OfkevzpERERE\n9El5IGZK+Xw+PPzww7hw4YLa0UJERET3N6USzAcffMCZUlsMZ0oRERE92MI1U+qB6JQaGxtDenr6\nLWf6EBER0f1Fq9WGrSQxbRw7pYiIiB5s4eqUeiCq71ksFlitVvWWNiIiIrr/KZVgiIiIiOjB9EDM\nlAKYU4o5pYiI7l/MKXXznFKyLHOm1BbDmVJEREQPNt6+twEMiIiIiB58rL639TAGIyIierDx9j0i\nIiIiIiIiInpgsVOKiIiIiIiIiIjCjp1SREREREREREQUduyUIiIiIiIiIiKisGOnFBERERERERER\nhR07pYiIiIiIiIiIKOzYKUVERERERERERGHHTikiIiIiIiIiIgo7dkoREREREREREVHYsVOKiIiI\niIiIiIjCjp1SREREREREREQUduyUIiIiIiIiIiKisGOnFBERERERERERhR07pYiIiIiIiIiIKOzY\nKUVERERERERERGHHTikiIiIiIiIiIgo77b0+ACIiIiK6//zjP/4jrl27htXVVdhsNqyurmJycvJe\nHxYRERHdRyQhxL0+htsmSZK4n4+fiIiIbk2SJAghpHt9HPQnkiQxACMiInrAhSP+4u17RERERERE\nREQUduyUIiIiIiIiIiKisGNOKSIiIiLatG9+85vMKUVERER3hDmliIiIaEtjTqmthzEYERHRgy1c\n8dd9P1NqbGwMSUlJ6O7uRn5+PiYmJiBJEoxGI1pbW2Gz2VBXV4eMjAz09fXh29/+Nk6fPo0zZ84g\nKioKp06dwuOPPw6fz4e2tjYUFRVhfn4eFosFjY2NmJ+fx6OPPgqfz4eBgQFcv34dQgi0tLSgqKgI\nkZGRGBgYwNLSEqxWK9xuN1JTU3H+/HnIsozJyUnMz89DCIGEhAR4vV5otVp4PB7ExMQgJSUFKysr\naG5uhsvlgtFohNPpxPLyMjIzMzExMQGn06meb0pKCkZHRwF89CbR6/WYn5+/V5efiIiIiIiIiOi2\n3PczpWRZhiRJ8Hq9kGUZPp/vXh8WERER3WWcKbW1cKYUERHRg40zpTbIvxOKHVJERERERERERPeH\n+776nizL0Gg06v+JiIiIiIiIiGjru+9nSg0PDzOnFHNKEREREREREdF95r7PKXU/Hz8RERHdGqvv\nbT2MwYiIiB5s4Yq/eL8bERERERERERGFHTuliIiIiIiIiIgo7NgpRUREREREREREYcdOKSIiIiIi\nIiIiCjt2ShERERERERERUdixU4qIiIiIiIiIiMKOnVJERERERERERBR27JQiIiIiIiIiIqKwY6cU\nERERERERERGFHTuliIiIiIiIiIgo7NgpRUREREREREREYcdOKSIiIiIiIiIiCjt2ShERERERERER\nUdixU4qIiIiIiIiIiMKOnVJERERERERERBR27JQiIiIiIiIiIqKwY6cUERERERERERGFHTuliIiI\niIiIiIgo7NgpRUREREREREREYcdOKSIiIiIiIiIiCjt2ShERERERERER/f/t3XusHGUdxvHvAxUU\nCKXEcBNpNWDQaEAIlIgRo4gkJopBAokCImq8RPESxVtE/zFqgorGSwziBS+IIFIMV4NoNIBoQUqR\ngtZwjaBBq0JCTP35x76F7fEUK+3OzO75fpI3mXl3Z3fm/fWc8/Td2Rl1zkkpSZIkSZIkdc5JKUmS\nJEmSJHXOSSlJkiRJkiR1zkkpSZIkSZIkdc5JKUmSJEmSJHXOSSlJkiRJkiR1zkkpSZIkSZIkdc5J\nKUmSJEmSJHWut0mpJK9JckuS9UkOmufxfZL8I8l7+tg/SZKkWWQGkyRJQ9HnmVKrgFcDP9vE42cC\nl3a3O9parrnmmr53QXNYk2GyLsNjTbRAmMFmlL/DhseaDI81GSbrsnD1NilVVWuq6g4gcx9L8ipg\nLbC68x3TFvMXyvBYk2GyLsNjTbQQmMFml7/DhseaDI81GSbrsnAN7ppSSXYE3g98nHnCkiRJkrY+\nM5gkSeraokm+eJKrgN3Hu4ACPlxVl2xis48Bn62qh5Ns2EaSJEmbyQwmSZKmQaqq3x1Ifgq8t6pW\ntvWfA3u3h5cA64GPVtWX5tm2352XJEmdqConSLYyM5gkSXo8XeSviZ4p9X949ECr6kWPdiZnAP+Y\nLwy15xpQJUmSnjgzmCRJ6k1v15RKckySu4HDgB8nuayvfZEkSVoozGCSJGkoev/6niRJkiRJkhae\nwd19b3MlOTrJbUluT3J63/sza5LsneTqJKuTrEryzta/JMmVSdYkuSLJ4rFtPpjkjiS/S3LUWP9B\nSW5utfrcWP92Sc5r21ybZJ9uj3I6JdkmycokK9q6NelZksVJftDGeXWS5dalX0neneSWNp7faWNo\nTTqW5GtJ7k9y81hfJ3VIcnJ7/pokJ3VxvAuB+WuyzF/DZf4aHvPXMJnB+jd1+auqpq4xmkz7PbAU\neBJwE7B/3/s1Sw3YAziwLe8ErAH2Bz4FvL/1nw58si0/B7iR0XXKlrX6bDgT73rgkLZ8KfDytvxW\n4Ett+XjgvL6Pexoa8G7g28CKtm5N+q/JN4BT2vIiYLF16bUeewFrge3a+veBk61JL7V4IXAgcPNY\n38TrwOgi3X9oP4u7bFjuezymvWH+6mKMzV8DbZi/Btcwfw2uYQYbRGPK8lfvA/YEB/kw4LKx9Q8A\np/e9X7PcgB8BRwK3Abu3vj2A2+arAXAZsLw959ax/hOAL7fly4HlbXlb4M99H+fQG6O7Il0FvJjH\nQpE16bcmOwN/mKffuvRXk72AO9sfxkXACn9/9VqPpWwciiZZhwfmPqetfxk4vu+xmPaG+auPMTd/\nDaBh/hpcw/w1yIYZbDCNKcpf0/r1vacBd4+t39P6NAFJljGaab2O0T/k+wGq6k/Abu1pc2tyb+t7\nGqP6bDBeq0e3qar1wN+S7DqRg5gdnwXeB9RYnzXp1zOAvyT5ejut/6tJdsC69Kaq7gPOBO5iNL7r\nquonWJOh2G2CdVjX6rCp19KWMX91yPw1KOav4TF/DZAZbNAGm7+mdVJKHUmyE3ABcFpV/ZON/xgz\nz/oWvd1WfK2Zk+QVwP1VdROPP1bWpFuLgIOAL1bVQcBDjD5x8GelJ0l2AV7F6BOivYAdk7wWazJU\n1kGaw/w1HOavwTJ/DZAZbKoMpgbTOil1LzB+QbO9W5+2oiSLGAWic6vq4tZ9f5Ld2+N7AA+0/nuB\np49tvqEmm+rfaJsk2wI7V9WDEziUWXE48Moka4HvAS9Jci7wJ2vSq3uAu6vq1239QkYhyZ+V/hwJ\nrK2qB9unNxcBL8CaDEUXdTAnTIbj2gHz1+CYv4bJ/DVMZrDhGmz+mtZJqRuAfZMsTbIdo+8uruh5\nn2bROYy+R3rWWN8K4PVt+WTg4rH+E9qV+J8B7Av8qp0auC7JoUkCnDRnm5Pb8nHA1RM7khlQVR+q\nqn2q6pmM/s1fXVUnApdgTXrTToO9O8mzWtdLgdX4s9Knu4DDkjy5jeVLgVuxJn0JG3+C1kUdrgBe\nltGdmZYAL2t92jLmr26YvwbE/DVM5q/BMoMNx/Tkry4vtrU1G3A0ozuS3AF8oO/9mbXG6FOh9Yzu\nrHMjsLKN+a7AT9rYXwnsMrbNBxldrf93wFFj/QcDq1qtzhrr3x44v/VfByzr+7inpQFH8NiFNq1J\n//U4gNF/1m4CfsjojhPWpd+anNHG92bgm4zuFGZNuq/Dd4H7gEcYBdVTGF38dOJ1YBS87gBuB07q\neyxmpWH+mvT4mr8G3DB/Daph/hpkwwzWe2PK8teGW/1JkiRJkiRJnZnWr+9JkiRJkiRpijkpJUmS\nJEmSpM45KSVJkiRJkqTOOSklSZIkSZKkzjkpJUmSJEmSpM45KSVJkiRJkqTOOSklaXCSLE2yqu/9\nkCRJWijMX5L64KSUpKGqvndAkiRpgTF/SeqUk1KStrr2SdutSb6a5JYklyfZvj12QJJrk9yU5MIk\ni1v/wa3vRuDtY6+1TZJPJ7m+Pf6mTbznRUluSLIqyRvH+k9NsibJdW1/Pt/6n5rkgva61yd5wUQH\nRZIkaYLMX5KmkZNSkiZlX+ALVfVcYB1wbOv/FvC+qjoQuAU4o/WfA7y9qp4/53VOBf5WVcuBQ4E3\nJ1k6z/udUlWHAIcApyVZkmRP4CNtu8OB/ceefxbwmfa6rwHO3rLDlSRJ6p35S9JUWdT3DkiaWX+s\nqg3XJfgNsCzJzsDiqvpF6/8mcH77tG5xVf2y9Z8LHN2WjwKel+S4tr4zsB9w55z3e1eSY9ry3u05\newLXVNU6gCQ/aP0ARwLPTpK2vlOSHarq4S07bEmSpN6YvyRNFSelJE3KI2PL64Ent+XM89z/1f+O\nqrpqU2+U5AjgJcDyqnokyU838/2WV9W/NvW6kiRJU8b8JWmq+PU9SZPyX2Gkqv4OPJjk8NZ1IvCz\n9knaX8euK/C6sc2uAN6WZBFAkv2SPGXOSy8G/toC0f7AYa3/BuBFSRa37Y8d2+ZK4LRHdzY54Akd\npSRJ0nCYvyRNFc+UkjQpm7p7y+uBr7RgsxY4pfW/ATgnyb8ZBZaq/+wRAAAAxklEQVQNzgaWASvb\nqd4PAMewscuBtyRZDawBrgWoqvuSfAL4FfAgcBuj6yvAKBB9MclvgW2BnwNve0JHKkmSNAzmL0lT\nJVXe9VPS7EqyY1U9lGRb4CLga1V1cd/7JUmSNKvMX5I2l1/fkzTrPtZuc7wKWGsgkiRJmjjzl6TN\n4plSkiRJkiRJ6pxnSkmSJEmSJKlzTkpJkiRJkiSpc05KSZIkSZIkqXNOSkmSJEmSJKlzTkpJkiRJ\nkiSpc05KSZIkSZIkqXP/AdMCmE/P5fkFAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x115de8590>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=[20, 10])\n",
"\n",
"# uniforma ttachment\n",
"plt.subplot(1, 2, 1)\n",
"pageranks_u = ua.pagerank()\n",
"plt.scatter(range(N), [log(v) for v in pageranks_u],\n",
" marker='.',\n",
" color='black')\n",
"plt.xlabel('node age')\n",
"plt.ylabel('log PageRank')\n",
"\n",
"plt.xlim([0, N])\n",
"# plt.ylim([0, max(pageranks_u)])\n",
"# plt.ylim([0, .0003])\n",
"plt.title('uniform attachment')\n",
"\n",
"# preferential attachment\n",
"plt.subplot(1, 2, 2)\n",
"pageranks_p = pa.pagerank()\n",
"plt.scatter(range(N), [log(v) for v in pageranks_p],\n",
" marker='.',\n",
" color='black')\n",
"\n",
"plt.xlabel('node age')\n",
"plt.ylabel('log PageRank')\n",
"\n",
"plt.xlim([0, N])\n",
"# plt.ylim([0, max(pageranks_p)])\n",
"# plt.ylim([0, .0003])\n",
"plt.title('preferential attachment')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
abhipr1/DATA_SCIENCE_INTENSIVE | Week_1/DATA_WRANGLING/WORKING_WITH_DATA_IN_FILES/data_wrangling_xml/data_wrangling_xml/.ipynb_checkpoints/sliderule_dsi_xml_exercise-checkpoint.ipynb | 1 | 32308 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# XML example and exercise\n",
"****\n",
"+ study examples of accessing nodes in XML tree structure \n",
"+ work on exercise to be completed and submitted\n",
"****\n",
"+ reference: https://docs.python.org/2.7/library/xml.etree.elementtree.html\n",
"+ data source: http://www.dbis.informatik.uni-goettingen.de/Mondial\n",
"****"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from xml.etree import ElementTree as ET"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## XML example\n",
"\n",
"+ for details about tree traversal and iterators, see https://docs.python.org/2.7/library/xml.etree.elementtree.html"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"document_tree = ET.parse( './data/mondial_database_less.xml' )"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Albania\n",
"Greece\n",
"Macedonia\n",
"Serbia\n",
"Montenegro\n",
"Kosovo\n",
"Andorra\n"
]
}
],
"source": [
"# print names of all countries\n",
"for child in document_tree.getroot():\n",
" print (child.find('name').text)"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"* Albania:Tirana, Shkodër, Durrës, Vlorë, Elbasan, Korçë\n",
"* Greece:Komotini, Kavala, Athina, Peiraias, Peristeri, Acharnes, Patra, Kozani, Kerkyra, Ioannina, Thessaloniki, Iraklio, Chania, Ermoupoli, Rhodes, Tripoli, Lamia, Chalkida, Larissa, Volos, Mytilini, Karyes\n",
"* Macedonia:Skopje, Kumanovo\n",
"* Serbia:Beograd, Novi Sad, Niš\n",
"* Montenegro:Podgorica\n",
"* Kosovo:Prishtine\n",
"* Andorra:Andorra la Vella\n"
]
}
],
"source": [
"# print names of all countries and their cities\n",
"for element in document_tree.iterfind('country'):\n",
" print ('* ' + element.find('name').text + ':', end=''),\n",
" capitals_string = ''\n",
" for subelement in element.getiterator('city'):\n",
" capitals_string += subelement.find('name').text + ', '\n",
" print (capitals_string[:-2])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"****\n",
"## XML exercise\n",
"\n",
"Using data in 'data/mondial_database.xml', the examples above, and refering to https://docs.python.org/2.7/library/xml.etree.elementtree.html, find\n",
"\n",
"1. 10 countries with the lowest infant mortality rates\n",
"2. 10 cities with the largest population\n",
"3. 10 ethnic groups with the largest overall populations (sum of best/latest estimates over all countries)\n",
"4. name and country of a) longest river, b) largest lake and c) airport at highest elevation"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"document = ET.parse( './data/mondial_database.xml' )"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# print child and attributes\n",
"#for child in document.getroot():\n",
"# print (child.tag, child.attrib)"
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd"
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Create a list of country and their Infant Mortality Rate \n",
"country_imr=[]\n",
"for country in document.getroot().findall('country'):\n",
" name = country.find('name').text\n",
" infant_mortality_rate = country.find('infant_mortality')\n",
" if infant_mortality_rate is not None:\n",
" infant_mortality_rate=infant_mortality_rate.text\n",
" else :\n",
" infant_mortality_rate = -1\n",
" country_imr.append((name, (float)(infant_mortality_rate)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 10 countries with the lowest infant mortality rates"
]
},
{
"cell_type": "code",
"execution_count": 88,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Country</th>\n",
" </tr>\n",
" <tr>\n",
" <th>Infant_Mortality_Rate</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>1.81</th>\n",
" <td>Monaco</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.13</th>\n",
" <td>Japan</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.48</th>\n",
" <td>Bermuda</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.48</th>\n",
" <td>Norway</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.53</th>\n",
" <td>Singapore</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.60</th>\n",
" <td>Sweden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.63</th>\n",
" <td>Czech Republic</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2.73</th>\n",
" <td>Hong Kong</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3.13</th>\n",
" <td>Macao</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3.15</th>\n",
" <td>Iceland</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Country\n",
"Infant_Mortality_Rate \n",
"1.81 Monaco\n",
"2.13 Japan\n",
"2.48 Bermuda\n",
"2.48 Norway\n",
"2.53 Singapore\n",
"2.60 Sweden\n",
"2.63 Czech Republic\n",
"2.73 Hong Kong\n",
"3.13 Macao\n",
"3.15 Iceland"
]
},
"execution_count": 88,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = pd.DataFrame(country_imr, columns=['Country', 'Infant_Mortality_Rate'])\n",
"df_unknown_removed = df[df.Infant_Mortality_Rate != -1] \n",
"df_unknown_removed.set_index('Infant_Mortality_Rate').sort().head(10)"
]
},
{
"cell_type": "code",
"execution_count": 149,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"city_population=[]\n",
"for country in document.iterfind('country'):\n",
" for state in country.iterfind('province'):\n",
" for city in state.iterfind('city'):\n",
" try:\n",
" city_population.append((city.find('name').text, float(city.find('population').text)))\n",
" except:\n",
" next\n",
" for city in country.iterfind('city'):\n",
" try:\n",
" city_population.append((city.find('name').text, float(city.find('population').text)))\n",
" except:\n",
" next"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 10 cities with the largest population"
]
},
{
"cell_type": "code",
"execution_count": 165,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>City</th>\n",
" <th>Population</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>1763</th>\n",
" <td>Seoul</td>\n",
" <td>10229262</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1421</th>\n",
" <td>Mumbai</td>\n",
" <td>9925891</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2594</th>\n",
" <td>São Paulo</td>\n",
" <td>9412894</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1629</th>\n",
" <td>Jakarta</td>\n",
" <td>8259266</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1251</th>\n",
" <td>Shanghai</td>\n",
" <td>8205598</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1942</th>\n",
" <td>Ciudad de México</td>\n",
" <td>8092449</td>\n",
" </tr>\n",
" <tr>\n",
" <th>443</th>\n",
" <td>Moskva</td>\n",
" <td>8010954</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1725</th>\n",
" <td>Tokyo</td>\n",
" <td>7843000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1250</th>\n",
" <td>Beijing</td>\n",
" <td>7362426</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1467</th>\n",
" <td>Delhi</td>\n",
" <td>7206704</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" City Population\n",
"1763 Seoul 10229262\n",
"1421 Mumbai 9925891\n",
"2594 São Paulo 9412894\n",
"1629 Jakarta 8259266\n",
"1251 Shanghai 8205598\n",
"1942 Ciudad de México 8092449\n",
"443 Moskva 8010954\n",
"1725 Tokyo 7843000\n",
"1250 Beijing 7362426\n",
"1467 Delhi 7206704"
]
},
"execution_count": 165,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = pd.DataFrame(city_population, columns=['City', 'Population'])\n",
"#df.info()\n",
"df.sort_index(by='Population', ascending=False).head(10)"
]
},
{
"cell_type": "code",
"execution_count": 229,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"ethnic_population={}\n",
"country_population={}\n",
"for country in document.iterfind('country'):\n",
" try:\n",
" country_population[country.find('name').text]= float(country.find('population').text)\n",
" except:\n",
" next\n",
" for state in country.iterfind('province' or 'state'):\n",
" try:\n",
" country_population[country.find('name').text] += float(state.find('population').text)\n",
" except:\n",
" next\n",
" for city in state.iterfind('city'):\n",
" try:\n",
" country_population[country.find('name').text] += float(city.find('population').text)\n",
" except:\n",
" next\n",
"\n",
"for country in document.iterfind('country'):\n",
" for ethnicgroup in country.iterfind('ethnicgroup'):\n",
" try:\n",
" if ethnicgroup.text in ethnic_population:\n",
" ethnic_population[ethnicgroup.text] += country_population[country.find('name').text]*float(ethnicgroup.get('percentage'))/100\n",
" else:\n",
" ethnic_population[ethnicgroup.text] = country_population[country.find('name').text]*float(ethnicgroup.get('percentage'))/100\n",
" except:\n",
" next"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 10 ethnic groups with the largest overall populations (sum of best/latest estimates over all countries)"
]
},
{
"cell_type": "code",
"execution_count": 241,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ethnic_Groups</th>\n",
" <th>Population</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>Han Chinese</td>\n",
" <td>1.593119e+09</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>Indo-Aryan</td>\n",
" <td>7.776357e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>European</td>\n",
" <td>6.668512e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>African</td>\n",
" <td>2.896678e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Russian</td>\n",
" <td>2.705583e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>Dravidian</td>\n",
" <td>2.700124e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>Japanese</td>\n",
" <td>2.506371e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>German</td>\n",
" <td>1.706358e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>Mestizo</td>\n",
" <td>1.666139e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>Javanese</td>\n",
" <td>1.413179e+08</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Ethnic_Groups Population\n",
"0 Han Chinese 1.593119e+09\n",
"1 Indo-Aryan 7.776357e+08\n",
"2 European 6.668512e+08\n",
"3 African 2.896678e+08\n",
"4 Russian 2.705583e+08\n",
"5 Dravidian 2.700124e+08\n",
"6 Japanese 2.506371e+08\n",
"7 German 1.706358e+08\n",
"8 Mestizo 1.666139e+08\n",
"9 Javanese 1.413179e+08"
]
},
"execution_count": 241,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.DataFrame(sorted(ethnic_population.items(), key=lambda x:x[1], reverse=True)[:10], columns=['Ethnic_Groups', 'Population'])"
]
},
{
"cell_type": "code",
"execution_count": 243,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[{'country': 'N', 'length': '604', 'name': 'Glomma'},\n",
" {'country': 'N', 'length': '322', 'name': 'Lagen'},\n",
" {'country': 'S', 'length': '93', 'name': 'Goetaaelv'},\n",
" {'country': 'S', 'length': '460', 'name': 'Klaraelv'},\n",
" {'country': 'S', 'length': '470', 'name': 'Umeaelv'},\n",
" {'country': 'S', 'length': '520', 'name': 'Dalaelv'},\n",
" {'country': 'S', 'length': '320', 'name': 'Vaesterdalaelv'},\n",
" {'country': 'S', 'length': '241', 'name': 'Oesterdalaelv'},\n",
" {'country': 'SF', 'length': '145', 'name': 'Paatsjoki'},\n",
" {'country': 'SF', 'length': '300', 'name': 'Ounasjoki'},\n",
" {'country': 'SF', 'length': '550', 'name': 'Kemijoki'},\n",
" {'country': 'SF', 'length': '107', 'name': 'Oulujoki'},\n",
" {'country': 'SF', 'length': '203', 'name': 'Kymijoki'},\n",
" {'country': 'SF', 'length': '121', 'name': 'Kokemaeenjoki'},\n",
" {'country': 'SF', 'length': '162', 'name': 'Vuoksi'},\n",
" {'country': 'GB', 'length': '346', 'name': 'Thames'},\n",
" {'country': 'NL', 'length': '925', 'name': 'Maas'},\n",
" {'country': 'F', 'length': '1013', 'name': 'Loire'},\n",
" {'country': 'F', 'length': '647', 'name': 'Garonne'},\n",
" {'country': 'F', 'length': '812', 'name': 'Rhone'},\n",
" {'country': 'F', 'length': '480', 'name': 'Saone'},\n",
" {'country': 'F', 'length': '453', 'name': 'Doubs'},\n",
" {'country': 'F', 'length': '290', 'name': 'Isere'},\n",
" {'country': 'F', 'length': '776', 'name': 'Seine'},\n",
" {'country': 'F', 'length': '514', 'name': 'Marne'},\n",
" {'country': 'E', 'length': '1007', 'name': 'Tajo'},\n",
" {'country': 'E', 'length': '897', 'name': 'Douro'},\n",
" {'country': 'E', 'length': '742', 'name': 'Guadiana'},\n",
" {'country': 'E', 'length': '657', 'name': 'Guadalquivir'},\n",
" {'country': 'E', 'length': '925', 'name': 'Ebro'},\n",
" {'country': 'I', 'length': '652', 'name': 'Po'},\n",
" {'country': 'I', 'length': '248', 'name': 'Ticino'},\n",
" {'country': 'I', 'length': '313', 'name': 'Adda'},\n",
" {'country': 'I', 'length': '75', 'name': 'Mincio'},\n",
" {'country': 'I', 'length': '415', 'name': 'Etsch'},\n",
" {'country': 'I', 'length': '405', 'name': 'Tiber'},\n",
" {'country': 'I', 'length': '240', 'name': 'Arno'},\n",
" {'country': 'D', 'length': '2845', 'name': 'Donau'},\n",
" {'country': 'D', 'length': '45.9', 'name': 'Breg'},\n",
" {'country': 'D', 'length': '43', 'name': 'Brigach'},\n",
" {'country': 'D', 'length': '147', 'name': 'Iller'},\n",
" {'country': 'D', 'length': '264', 'name': 'Lech'},\n",
" {'country': 'D', 'length': '295', 'name': 'Isar'},\n",
" {'country': 'D', 'length': '168', 'name': 'Ammer'},\n",
" {'country': 'D', 'length': '35', 'name': 'Würm'},\n",
" {'country': 'D', 'length': '517', 'name': 'Inn'},\n",
" {'country': 'D', 'length': '150', 'name': 'Alz'},\n",
" {'country': 'D', 'length': '225', 'name': 'Salzach'},\n",
" {'country': 'A', 'length': '254', 'name': 'Enns'},\n",
" {'country': 'A', 'length': '358', 'name': 'March'},\n",
" {'country': 'A', 'length': '250', 'name': 'Raab'},\n",
" {'country': 'SK', 'length': '403', 'name': 'Waag'},\n",
" {'country': 'I', 'length': '749', 'name': 'Drau'},\n",
" {'country': 'A', 'length': '453', 'name': 'Mur'},\n",
" {'country': 'H', 'length': '1308', 'name': 'Theiss'},\n",
" {'country': 'BIH', 'length': '945', 'name': 'Save'},\n",
" {'country': 'BIH', 'length': '346', 'name': 'Drina'},\n",
" {'country': 'BIH', 'length': '140', 'name': 'Tara'},\n",
" {'country': 'BIH', 'length': '120', 'name': 'Piva'},\n",
" {'country': 'RO', 'length': '615', 'name': 'Olt'},\n",
" {'country': 'RO', 'length': '953', 'name': 'Pruth'},\n",
" {'country': 'UA', 'length': '1352', 'name': 'Dnjestr'},\n",
" {'country': 'D', 'length': '440', 'name': 'Weser'},\n",
" {'country': 'D', 'length': '211', 'name': 'Aller'},\n",
" {'country': 'D', 'length': '281', 'name': 'Leine'},\n",
" {'country': 'D', 'length': '292', 'name': 'Werra'},\n",
" {'country': 'D', 'length': '221', 'name': 'Fulda'},\n",
" {'country': 'D', 'length': '1091', 'name': 'Elbe'},\n",
" {'country': 'CZ', 'length': '440', 'name': 'Moldau'},\n",
" {'country': 'D', 'length': '1324', 'name': 'Rhein'},\n",
" {'country': 'D', 'length': '524', 'name': 'Main'},\n",
" {'country': 'D', 'length': '544', 'name': 'Mosel'},\n",
" {'country': 'D', 'length': '227', 'name': 'Saar'},\n",
" {'country': 'D', 'length': '367', 'name': 'Neckar'},\n",
" {'country': 'CH', 'length': '288', 'name': 'Aare'},\n",
" {'country': 'CH', 'length': '164', 'name': 'Reuss'},\n",
" {'country': 'CH', 'length': '36.3', 'name': 'Limmat'},\n",
" {'country': 'D', 'length': '866', 'name': 'Oder'},\n",
" {'country': 'PL', 'length': '1047', 'name': 'Weichsel'},\n",
" {'country': 'PL', 'length': '448', 'name': 'Narew'},\n",
" {'country': 'PL', 'length': '772', 'name': 'Western Bug'},\n",
" {'country': 'IL', 'length': '251', 'name': 'Jordan'},\n",
" {'country': 'TR', 'length': '1364', 'name': 'Kura'},\n",
" {'country': 'IRQ', 'length': '193', 'name': 'Schatt al Arab'},\n",
" {'country': 'TR', 'length': '1900', 'name': 'Tigris'},\n",
" {'country': 'IRQ', 'length': '2736', 'name': 'Euphrat'},\n",
" {'country': 'TR', 'length': '720', 'name': 'Murat'},\n",
" {'country': 'TR', 'length': '720', 'name': 'Karasu'},\n",
" {'country': 'IR', 'length': '950', 'name': 'Karun'},\n",
" {'country': 'R', 'length': '740', 'name': 'Northern Dwina'},\n",
" {'country': 'R', 'length': '558', 'name': 'Suchona'},\n",
" {'country': 'R', 'length': '1809', 'name': 'Petschora'},\n",
" {'country': 'R', 'length': '74', 'name': 'Newa'},\n",
" {'country': 'R', 'length': '224', 'name': 'Swir'},\n",
" {'country': 'R', 'length': '78', 'name': 'Narva'},\n",
" {'country': 'R', 'length': '1020', 'name': 'Western Dwina'},\n",
" {'country': 'UA', 'length': '1352', 'name': 'Dnister'},\n",
" {'country': 'UA', 'length': '2201', 'name': 'Dnepr'},\n",
" {'country': 'UA', 'length': '775', 'name': 'Prypjat'},\n",
" {'country': 'R', 'length': '1870', 'name': 'Don'},\n",
" {'country': 'R', 'length': '3531', 'name': 'Volga'},\n",
" {'country': 'R', 'length': '1480', 'name': 'Oka'},\n",
" {'country': 'R', 'length': '1805', 'name': 'Kama'},\n",
" {'country': 'R', 'length': '2428', 'name': 'Ural'},\n",
" {'country': 'R', 'length': '3650', 'name': 'Ob'},\n",
" {'country': 'R', 'length': '4248', 'name': 'Irtysch'},\n",
" {'country': 'R', 'length': '1591', 'name': 'Tobol'},\n",
" {'country': 'R', 'length': '2450', 'name': 'Ischim'},\n",
" {'country': 'R', 'length': '688', 'name': 'Katun'},\n",
" {'country': 'R', 'length': '4092', 'name': 'Jenissej'},\n",
" {'country': 'R', 'length': '1779', 'name': 'Angara'},\n",
" {'country': 'R', 'length': '992', 'name': 'Selenge'},\n",
" {'country': 'R', 'length': '1636', 'name': 'Chatanga'},\n",
" {'country': 'R', 'length': '4400', 'name': 'Lena'},\n",
" {'country': 'R', 'length': '2824', 'name': 'Amur'},\n",
" {'country': 'R', 'length': '560', 'name': 'Schilka'},\n",
" {'country': 'R', 'length': '1620', 'name': 'Argun'},\n",
" {'country': 'R', 'length': '2129', 'name': 'Kolyma'},\n",
" {'country': 'KAZ', 'length': '2129', 'name': 'Syrdarja'},\n",
" {'country': 'UZB', 'length': '807', 'name': 'Naryn'},\n",
" {'country': 'TAD', 'length': '1415', 'name': 'Amudarja'},\n",
" {'country': 'TAD', 'length': '1141', 'name': 'Pjandsh'},\n",
" {'country': 'TAD', 'length': '133', 'name': 'Bartang'},\n",
" {'country': 'TAD', 'length': '395', 'name': 'Murgab'},\n",
" {'country': 'CN', 'length': '1001', 'name': 'Ili'},\n",
" {'country': 'CN', 'length': '3260', 'name': 'Tarim-Yarkend'},\n",
" {'country': 'CN', 'length': '4845', 'name': 'Hwangho'},\n",
" {'country': 'CN', 'length': '6380', 'name': 'Jangtse'},\n",
" {'country': 'CN', 'length': '4350', 'name': 'Mekong'},\n",
" {'country': 'CN', 'length': '2980', 'name': 'Saluen'},\n",
" {'country': 'CN', 'length': '2170', 'name': 'Irawaddy'},\n",
" {'country': 'IND', 'length': '2511', 'name': 'Ganges'},\n",
" {'country': 'CN', 'length': '2896', 'name': 'Brahmaputra'},\n",
" {'country': 'CN', 'length': '3180', 'name': 'Indus'},\n",
" {'country': 'RI', 'length': '150', 'name': 'Asahan'},\n",
" {'country': 'CDN', 'length': '3185', 'name': 'Yukon River'},\n",
" {'country': 'CDN', 'length': '1903', 'name': 'Mackenzie River'},\n",
" {'country': 'CDN', 'length': '664', 'name': 'Nelson River'},\n",
" {'country': 'CDN', 'length': '1392', 'name': 'Saskatchewan River'},\n",
" {'country': 'CDN', 'length': '1197', 'name': 'Saint Lawrence River'},\n",
" {'country': 'CDN', 'length': '58', 'name': 'Niagara River'},\n",
" {'country': 'CDN', 'length': '200', 'name': 'Detroit River'},\n",
" {'country': 'CDN', 'length': '120', 'name': 'Saint Marys River'},\n",
" {'country': 'USA', 'length': '0.1', 'name': 'Straits of Mackinac'},\n",
" {'country': 'CDN', 'length': '560', 'name': 'Manicouagan'},\n",
" {'country': 'CDN', 'length': '124', 'name': 'Riviere Richelieu'},\n",
" {'country': 'USA', 'length': '177', 'name': 'Merrimack River'},\n",
" {'country': 'USA', 'length': '655', 'name': 'Connecticut River'},\n",
" {'country': 'USA', 'length': '493', 'name': 'Hudson River'},\n",
" {'country': 'USA', 'length': '3778', 'name': 'Mississippi'},\n",
" {'country': 'USA', 'length': '4130', 'name': 'Missouri'},\n",
" {'country': 'USA', 'length': '2334', 'name': 'Arkansas'},\n",
" {'country': 'USA', 'length': '1579', 'name': 'Ohio River'},\n",
" {'country': 'USA', 'length': '523', 'name': 'Allegheny River'},\n",
" {'country': 'USA', 'length': '1049', 'name': 'Tennessee'},\n",
" {'country': 'CDN', 'length': '1953', 'name': 'Columbia River'},\n",
" {'country': 'USA', 'length': '225', 'name': 'Truckee River'},\n",
" {'country': 'MEX', 'length': '2330', 'name': 'Colorado'},\n",
" {'country': 'MEX', 'length': '3034', 'name': 'Rio Grande'},\n",
" {'country': 'MEX', 'length': '965', 'name': 'Rio Lerma'},\n",
" {'country': 'CR', 'length': '199', 'name': 'Rio San Juan'},\n",
" {'country': 'BOL', 'length': '383', 'name': 'Rio Desaguadero'},\n",
" {'country': 'CO', 'length': '1538', 'name': 'Rio Magdalena'},\n",
" {'country': 'YV', 'length': '2140', 'name': 'Orinoco'},\n",
" {'country': 'CO', 'length': '6448', 'name': 'Amazonas'},\n",
" {'country': 'CO', 'length': '2253', 'name': 'Rio Negro'},\n",
" {'country': 'BR', 'length': '1450', 'name': 'Rio Madeira'},\n",
" {'country': 'BOL', 'length': '1931', 'name': 'Rio Mamore'},\n",
" {'country': 'BR', 'length': '2640', 'name': 'Tocantins'},\n",
" {'country': 'BR', 'length': '2830', 'name': 'Rio Sao Francisco'},\n",
" {'country': 'RA', 'length': '3998', 'name': 'Parana'},\n",
" {'country': 'RA', 'length': '2549', 'name': 'Paraguay'},\n",
" {'country': 'RA', 'length': '1790', 'name': 'Uruguay'},\n",
" {'country': 'SN', 'length': '1120', 'name': 'Gambia'},\n",
" {'country': 'SN', 'length': '1430', 'name': 'Senegal'},\n",
" {'country': 'GH', 'length': '1500', 'name': 'Volta'},\n",
" {'country': 'RMM', 'length': '4184', 'name': 'Niger'},\n",
" {'country': 'CI', 'length': '430', 'name': 'Bani'},\n",
" {'country': 'CAM', 'length': '1400', 'name': 'Benue'},\n",
" {'country': 'CAM', 'length': '1400', 'name': 'Schari'},\n",
" {'country': 'ETH', 'length': '1120', 'name': 'Atbara'},\n",
" {'country': 'ETH', 'length': '1783', 'name': 'Blue Nile'},\n",
" {'country': 'ETH', 'length': '320', 'name': 'Pibor'},\n",
" {'country': 'ETH', 'length': '306', 'name': 'Baro'},\n",
" {'country': 'ZRE', 'length': '230', 'name': 'Semliki'},\n",
" {'country': 'EAT', 'length': '275', 'name': 'Akagera'},\n",
" {'country': 'ETH', 'length': '1658', 'name': 'Jubba'},\n",
" {'country': 'ETH', 'length': '1820', 'name': 'Shabelle'},\n",
" {'country': 'CAM', 'length': '918', 'name': 'Sanaga'},\n",
" {'country': 'ZRE', 'length': '4374', 'name': 'Zaire'},\n",
" {'country': 'CAM', 'length': '530', 'name': 'Sanga'},\n",
" {'country': 'ZRE', 'length': '1120', 'name': 'Ubangi'},\n",
" {'country': 'ZRE', 'length': '280', 'name': 'Bomu'},\n",
" {'country': 'ZRE', 'length': '1130', 'name': 'Uelle'},\n",
" {'country': 'ZRE', 'length': '100', 'name': 'Kwa'},\n",
" {'country': 'ZRE', 'length': '200', 'name': 'Fimi'},\n",
" {'country': 'ZRE', 'length': '900', 'name': 'Lukenie'},\n",
" {'country': 'ANG', 'length': '1983', 'name': 'Kasai'},\n",
" {'country': 'ANG', 'length': '1100', 'name': 'Cuango'},\n",
" {'country': 'ANG', 'length': '970', 'name': 'Cuilo'},\n",
" {'country': 'ZRE', 'length': '130', 'name': 'Ruki'},\n",
" {'country': 'ZRE', 'length': '830', 'name': 'Busira'},\n",
" {'country': 'ZRE', 'length': '1300', 'name': 'Tshuapa'},\n",
" {'country': 'ZRE', 'length': '970', 'name': 'Lulua'},\n",
" {'country': 'ZRE', 'length': '1450', 'name': 'Lomami'},\n",
" {'country': 'ZRE', 'length': '1287', 'name': 'Aruwimi'},\n",
" {'country': 'ZRE', 'length': '350', 'name': 'Lukuga'},\n",
" {'country': 'ZRE', 'length': '104', 'name': 'Ruzizi'},\n",
" {'country': 'ZRE', 'length': '350', 'name': 'Luvua'},\n",
" {'country': 'ZRE', 'length': '300', 'name': 'Luapula'},\n",
" {'country': 'ANG', 'length': '2574', 'name': 'Zambezi'},\n",
" {'country': 'MOC', 'length': '402', 'name': 'Chire'},\n",
" {'country': 'ANG', 'length': '1700', 'name': 'Okavango'},\n",
" {'country': 'RSA', 'length': '1750', 'name': 'Limpopo'},\n",
" {'country': 'RSA', 'length': '2160', 'name': 'Oranje'},\n",
" {'country': 'RSA', 'length': '1251', 'name': 'Vaal'},\n",
" {'country': 'AUS', 'length': '2589', 'name': 'Murray River'},\n",
" {'country': 'AUS', 'length': '2739', 'name': 'Darling River'},\n",
" {'country': 'AUS', 'length': '1579', 'name': 'Murrumbidgee River'},\n",
" {'country': 'AUS', 'length': '83', 'name': 'Eucumbene River'},\n",
" {'country': 'AUS', 'length': '403', 'name': 'Snowy River'}]"
]
},
"execution_count": 243,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"rivers_list=[]\n",
"rivers_df = pd.DataFrame()\n",
"for rivers in document.iterfind('river'):\n",
" try:\n",
" rivers_list.append({'name':rivers.find('name').text, 'length':rivers.find('length').text, 'country':rivers.find('located').attrib['country']})\n",
" except:\n",
" next\n",
"rivers_list"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
4dsolutions/Python5 | About_Decorators.ipynb | 1 | 5011 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Decorators\n",
"\n",
"\n",
"\n",
"\n",
"I use UFO as a decorator not because I want or need people to believe in UFOs, but because the science fiction idea of being abducted is you stay the same but for something lasting the UFO did to you.\n",
"\n",
"In the case of decorator syntax that's useful because to \"decorate\" (\"abduct\") is to \n",
"\n",
" * feed a function to a callable (the decorator), and \n",
" * keep that function's name for whatever gets returned\n",
" \n",
"Since function type objects are just objects with a ```__dict__```, we're free to apply arbitrary attributes to them. Lets have the UFO decorator decorate any function with a new attribute named 'abducted'."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"def UFO(f):\n",
" setattr(f, 'abducted', True) # f.abducted = True same thing\n",
" return f\n",
"\n",
"@UFO\n",
"def addS(s):\n",
" return s + \"S\"\n",
"\n",
"@UFO\n",
"def addX(s):\n",
" return s + \"X\""
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"hasattr(addX, 'abducted')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The value of abducted for addS is: True\n"
]
}
],
"source": [
"if hasattr(addS, 'abducted'):\n",
" print(\"The value of abducted for addS is:\", addS.abducted)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the example below, the Composer class \"decorates\" the two following functions, meaning the Composer instances become the new proxies for the functions they swallowed. The original functions are still on tap, through ```__call__```. \n",
"\n",
"Furthermore, when two such Composer types are multiplied, their internal functions get composed together, into a new internalized function."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"class Composer:\n",
" \n",
" def __init__(self, f):\n",
" self.func = f\n",
" \n",
" def __call__(self, s):\n",
" return self.func(s)\n",
" \n",
" def __mul__(self, other):\n",
" def new(s):\n",
" return self(other(s))\n",
" return Composer(new)\n",
"\n",
"@Composer\n",
"def F(x):\n",
" return x * x\n",
"\n",
"@Composer\n",
"def G(x):\n",
" return x + 2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below is simple composition of functions. This is valid Python even if the Composer decorator is left out, i.e. function type objects would normally have no problem composing with one another in this way. \n",
"\n",
"To compose F and G means going F(G(x)) for some x."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"184884260614963204"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"F(G(F(F(F(G(10))))))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Thanks to Compose, the \"class decorator\" (a decorator that happens to be a class), our F and G are actually Compose type objects, so have this additional ability to compose into other Compose type objects. We don't need an argument until we call the final H."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"184884260614963204"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"H = F*G*F*F*F*G # the functions themselves may be multiplied\n",
"H(10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
rhlobo/playground | ipy-notebooks/regex - Parsing multiple groups.ipynb | 1 | 5571 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"import re"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s ='\\n#here's a title\\n\\nhello world!!!\\n\\nPosted on 11-09-2014 02:32:30'"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "SyntaxError",
"evalue": "invalid syntax (<ipython-input-8-53c97802230d>, line 1)",
"output_type": "pyerr",
"traceback": [
"\u001b[0;36m File \u001b[0;32m\"<ipython-input-8-53c97802230d>\"\u001b[0;36m, line \u001b[0;32m1\u001b[0m\n\u001b[0;31m s ='\\n#here's a title\\n\\nhello world!!!\\n\\nPosted on 11-09-2014 02:32:30'\u001b[0m\n\u001b[0m ^\u001b[0m\n\u001b[0;31mSyntaxError\u001b[0m\u001b[0;31m:\u001b[0m invalid syntax\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s ='\\n#heres a title\\n\\nhello world!!!\\n\\nPosted on 11-09-2014 02:32:30\\n'"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# this grabs the title\n",
"re.findall(r'#.+\\n',s)[0][1:-1]"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
"'heres a title'"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#this grabs the date\n",
"re.findall(r'Posted on .+\\n',s)[0][10:-1]"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "IndexError",
"evalue": "list index out of range",
"output_type": "pyerr",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[0;31mIndexError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-9-3630455036d1>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;31m#this grabs the date\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0mre\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfindall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34mr'Posted on .+\\n'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0ms\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m10\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m-\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mIndexError\u001b[0m: list index out of range"
]
}
],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#this grabs the date\n",
"re.findall(r'Posted on [\\d\\-\\s:]+',s)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 14,
"text": [
"['Posted on 11-09-2014 02:32:30']"
]
}
],
"prompt_number": 14
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"re.findall(r'^[#\\W+]',s)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 15,
"text": [
"['\\n']"
]
}
],
"prompt_number": 15
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"re.findall(r'^[\\W+]',s)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 17,
"text": [
"['\\n']"
]
}
],
"prompt_number": 17
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# result = re.findall(r'#.+\\n(.*?)\\n+Posted on .*?\\n', s, re.MULTILINE | re.DOTALL)\n",
"result = re.search(r'#([^\\n]+)\\n+(.*)\\n+(Posted on [^\\n]*)', s, re.MULTILINE | re.DOTALL)\n",
"result"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 45,
"text": [
"<_sre.SRE_Match at 0x7f0eea6eb588>"
]
}
],
"prompt_number": 45
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"regex = re.compile(r'#([^\\n]+)\\n+(.*)\\n+(Posted on [^\\n]*)', re.MULTILINE | re.DOTALL)\n",
"result = regex.search(s)\n",
"result"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 47,
"text": [
"'heres a title'"
]
}
],
"prompt_number": 47
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
sebastiandres/mat281 | laboratorios/lab01-PythonNumerico/PythonNumerico.ipynb | 2 | 43643 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"<header class=\"w3-container w3-teal\">\n",
"<img src=\"images/utfsm.png\" alt=\"\" height=\"100px\" align=\"left\"/>\n",
"<img src=\"images/mat.png\" alt=\"\" height=\"100px\" align=\"right\"/>\n",
"</header>\n",
"<br/><br/><br/><br/><br/>\n",
"# MAT281\n",
"## Aplicaciones de la Matemática en la Ingeniería\n",
"### Laboratorio 1: Python Numérico\n",
"\n",
"## INSTRUCCIONES\n",
"* Anoten su nombre y rol en la celda siguiente.\n",
"* Desarrollen los problemas de manera secuencial.\n",
"* Guarden constantemente con ***Ctr-S*** para evitar sorpresas.\n",
"* Reemplacen en las celdas de código donde diga #FIX_ME por el código correspondiente.\n",
"* Ejecuten cada celda de código utilizando ***Ctr-Enter***\n",
"* Pueden utilizar tabulación para obtener ayuda de ipython notebook."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"#Configuracion para recargar módulos y librerías cada vez \n",
"%reload_ext autoreload\n",
"%autoreload 2\n",
" \n",
"%matplotlib inline\n",
" \n",
"from mat281_code.lab import *\n",
"from IPython.core.display import HTML\n",
"from matplotlib import pyplot as plt\n",
"\n",
"HTML(open(\"style/mat281.css\", \"r\").read())\n",
"\n",
"alumno_1 = (r\"Sebastián Flores\", \"2004001-7\") # FIX ME\n",
"alumno_2 = (r\"María José Vargas\", \"2004007-8\") # FIX ME\n",
"\n",
"HTML(greetings(alumno_1, alumno_2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Contenido\n",
"1. Overview de Numpy y Scipy\n",
"2. Librería Numpy\n",
" * Arreglos vs Matrices\n",
" * Axis\n",
" * Funciones basicas.\n",
" * Input y Output\n",
"3. Tips"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 1. Overview de numpy y scipy\n",
"\n",
"¿Cual es la diferencia entre numpy y scipy?\n",
"\n",
"*In an ideal world, NumPy would contain nothing but the array data type and the most basic operations: indexing, sorting, reshaping, basic elementwise functions, et cetera. All numerical code would reside in SciPy. However, one of NumPy’s important goals is compatibility, so NumPy tries to retain all features supported by either of its predecessors. Thus NumPy contains some linear algebra functions, even though these more properly belong in SciPy. In any case, SciPy contains more fully-featured versions of the linear algebra modules, as well as many other numerical algorithms. If you are doing scientific computing with python, you should probably install both NumPy and SciPy. Most new features belong in SciPy rather than NumPy.*\n",
"[Link stackoverflow](http://stackoverflow.com/questions/10766082/why-do-numpy-and-scipy-have-a-lot-of-the-same-functions-which-should-i-prefer/10767644#10767644)\n",
"\n",
"Por ser python un lenguaje open-source, existen miles de paquetes disponibles creados por individuos o comunidades. Éstos pueden estar disponibles en un repositorio como github o bitbucket, o bien estar disponibles en el repositorio oficial de python: [pypi](https://pypi.python.org/pypi). En un inicio, cuando no existía una librerías de cálculo científico oficial, varios candidatos proponían soluciones:\n",
"* **numpy**: tenía una excelente representación de vectores, matrices y arreglos, implementados en C y llamados fácilmente desde python\n",
"* **scipy**: proponía linkear a librerías ya elaboradas de calculo científico de alto rendimiento en C o fortran, permitiendo ejecutar rápidamente desde python.\n",
"\n",
"Ambos projectos fueron creciendo en complejidad y alcance, y en vez de competir, decidieron dividir tareas y unificar fuerzas para proponer una plataforma de cálculo científico que reemplazara completamente otros programas.\n",
"\n",
"* **numpy**: Corresponde a lo relacionado con la estructura de los datos (arrays densos y sparse, matrices, constructores especiales, lectura de datos regulares, etc.), pero no las operaciones en sí. Por razones históricas y de compatibilidad, tiene algunos algoritmos, pero en realidad resulta más consistente utilizar los algoritmos de scipy.\n",
"* **scipy**: Corresponde a la implementación numérica de diversos algoritmos de corte científicos: algebra lineal, estadística, ecuaciones diferenciales ordinarias, interpolacion, integracion, optimización, análisis de señales, entre otros.\n",
"\n",
"#### OBSERVACIÓN IMPORTANTE:\n",
"Las matrices y arrays de numpy deben contener variables con el mismo tipo de datos: sólo enteros, sólo flotantes, sólo complejos, sólo booleanos o sólo strings. La uniformicidad de los datos es lo que permite acelerar los cálculos con implementaciones en C a bajo nivel."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2. Librería Numpy\n",
"Siempre importaremos la librería numpy de la siguiente forma:\n",
"\n",
" import numpy as np\n",
" \n",
"Todas las funciones y módulos de numpy quedan a nuestro alcance a 3 carácteres de distancia:\n",
"\n",
" np.array([1,4,9,16])\n",
" np.linspace(0.,1.,100)\n",
" \n",
"Evite a todo costo utilizar lo siguiente:\n",
"\n",
" from numpy import *"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"print np.version.version # Si alguna vez tienen problemas, verifiquen su version de numpy"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Importante\n",
"**Ipython notebook** es interactivo y permite la utilización de tabulación para ofrecer sugerencias o enseñar ayuda (no solo para numpy, sino que para cualquier código en python).\n",
"\n",
"Pruebe los siguientes ejemplos:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Presionar tabulacción con el cursor despues de np.arr\n",
"np.arr"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Presionar Ctr-Enter para obtener la documentacion de la funcion np.array usando \"?\"\n",
"np.array?"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Presionar Ctr-Enter\n",
"%who"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x = 10\n",
"%who"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Librería Numpy\n",
"## 2.1 Array vs Matrix\n",
"\n",
"Por defecto, la gran mayoria de las funciones de numpy y de scipy asumen que se les pasará un objeto de tipo **array**. \n",
"\n",
"Veremos las diferencias entre los objetos array y matrix, pero recuerden utilizar array mientras sea posible."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Matrix\n",
"\n",
"Una matrix de numpy se comporta exactamente como esperaríamos de una matriz:\n",
"\n",
"### Pros:\n",
"* Multiplicación utiliza el signo * como es esperable.\n",
"* Resulta natural si lo único que haremos es algebra lineal.\n",
"\n",
"### Contras:\n",
"* Todas las matrices deben estar completamente alineadas para poder operar correctamente.\n",
"* Operaciones elementwise son mas dificiles de definir/acceder.\n",
"* Están exclusivamente definidas en 2D: un vector fila o un vector columna siguen siendo 2D."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Operaciones con np.matrix\n",
"A = np.matrix([[1,2],[3,4]])\n",
"B = np.matrix([[1, 1],[0,1]], dtype=float)\n",
"x = np.matrix([[1],[2]])\n",
"print \"A =\\n\", A\n",
"print \"B =\\n\", B\n",
"print \"x =\\n\", x\n",
"\n",
"print \"A+B =\\n\", A+B\n",
"print \"A*B =\\n\", A*B\n",
"print \"A*x =\\n\", A*x\n",
"print \"A*A = A^2 =\\n\", A**2\n",
"print \"x.T*A =\\n\", x.T * A"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.1 Array vs Matrix\n",
"## Array\n",
"\n",
"Un array de numpy es simplemente un \"contenedor\" multidimensional.\n",
"\n",
"### Pros:\n",
"* Es multidimensional: 1D, 2D, 3D, ...\n",
"* Resulta consistente: todas las operaciones son element-wise a menos que se utilice una función específica.\n",
"\n",
"### Contras:\n",
"* Multiplicación maticial utiliza la función **dot()**"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Operaciones con np.matrix\n",
"A = np.array([[1,2],[3,4]])\n",
"B = np.array([[1, 1],[0,1]], dtype=float)\n",
"x = np.array([1,2]) # No hay necesidad de definir como fila o columna!\n",
"print \"A =\\n\", A\n",
"print \"B =\\n\", B\n",
"print \"x =\\n\", x\n",
"\n",
"print \"A+B =\\n\", A+B\n",
"print \"AoB = (multiplicacion elementwise) \\n\", A*B\n",
"print \"A*B = (multiplicacion matricial, v1) \\n\", np.dot(A,B)\n",
"print \"A*B = (multiplicacion matricial, v2) \\n\", A.dot(B)\n",
"print \"A*A = A^2 = (potencia matricial)\\n\", np.linalg.matrix_power(A,2)\n",
"print \"AoA = (potencia elementwise)\\n\", A**2\n",
"print \"A*x =\\n\", np.dot(A,x)\n",
"print \"x.T*A =\\n\", np.dot(x,A) # No es necesario transponer."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Desafío 1: matrix vs array\n",
"Sean\n",
"$$ \n",
"A = \\begin{pmatrix} 1 & 0 & 1 \\\\ 0 & 1 & 1\\end{pmatrix}\n",
"$$\n",
"y \n",
"$$ \n",
"B = \\begin{pmatrix} 1 & 0 & 1 \\\\ 0 & 1 & 1 \\\\ 0 & 0 & 1\\end{pmatrix}\n",
"$$\n",
"\n",
"1. Cree las matrices utilizando np.matrix y multipliquelas en el sentido matricial. Imprima el resultado.\n",
"2. Cree las matrices utilizando np.array y multipliquelas en el sentido matricial. Imprima el resultado."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# 1: Utilizando matrix\n",
"A = np.matrix([]) # FIX ME\n",
"B = np.matrix([]) # FIX ME\n",
"print \"np.matrix, AxB=\\n\", #FIX ME\n",
"\n",
"# 2: Utilizando arrays\n",
"A = np.array([]) # FIX ME\n",
"B = np.array([]) # FIX ME\n",
"print \"np.matrix, AxB=\\n\", #FIX ME"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2.2 Indexación y Slicing\n",
"Los arrays se indexan de la forma \"tradicional\".\n",
"\n",
"* Para un array ***unidimensional***: sólo tiene una indexacion. ¡No es ni fila ni columna!\n",
"* Para un array ***bidimensional***: primera componente son las filas, segunda componente son las columnas. Notación respeta por tanto la convención tradicional de matrices.\n",
"* Para un array ***tridimensional***: primera componente son las filas, segunda componente son las columnas, tercera componente la siguiente dimension.\n",
"\n",
"<img src=\"images/anatomyarray.png\" alt=\"\" height=\"100px\" align=\"left\"/>\n",
"\n",
"Respecto a los índices de los elementos, éstos comienzan en cero, como en C. Además, es posible utilizar índices negativos, que como convención asignan -1 al último elemento, al -2 el penúltimo elemento, y así sucesivamente.\n",
"\n",
"Por ejemplo, si a = [2,3,5,7,11,13,17,19], entonces a[0] es el valor 2 y a[1] es el valor 3, mientras que a[-1] es el valor 19 y a[-2] es el valor 17.\n",
"\n",
"Ademas, en python existe la \"slicing notation\":\n",
"* **a[start:end]** : items desde índice **start** hasta **end-1**\n",
"* **a[start:]** : items desde índice start hasta el final del array\n",
"* **a[:end]** : items desde el inicio hasta el índice end-1\n",
"* **a[:]** : todos los items del array (una copia nueva)\n",
"* **a[start:end:step]** : items desde start hasta pasar end (sin incluir) con paso step"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x = np.arange(9) # \"Vector\" con valores del 0 al 8 \n",
"print \"x = \", x\n",
"print \"x[:] = \", x[:]\n",
"print \"x[5:] = \", x[5:]\n",
"print \"x[:8] = \", x[:8]\n",
"print \"x[:-1] = \", x[:-1]\n",
"print \"x[1:-1] = \", x[1:-1]\n",
"print \"x[1:-1:2] = \", x[1:-1:2]\n",
"\n",
"A = x.reshape(3,3) # Arreglo con valores del 0 al 8, en 3 filas y 3 columnas.\n",
"print \"\\n\"\n",
"print \"A = \\n\", A\n",
"print \"primera fila de A\\n\", A[0,:]\n",
"print \"ultima columna de A\\n\", A[:,-1]\n",
"print \"submatriz de A\\n\", A[:2,:2]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Observación\n",
"1. Cabe destacar que al tomar slices (subsecciones) de un arreglo obtenemos siempre un arreglo con menores dimensiones que el original.\n",
"2. Esta notación es extremadamente conveniente, puesto que nos permite manipular el array sin necesitar conocer el tamaño del array y escribir de manera compacta las fórmulas numéricas.\n",
"\n",
"Por ejemplo, implementar una derivada numérica es tan simple como sigue. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def f(x):\n",
" return 1 + x**2\n",
"\n",
"x = np.array([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]) # O utilizar np.linspace!\n",
"y = f(x) # Tan facil como llamar f sobre x\n",
"dydx = ( y[1:] - y[:-1] ) / ( x[1:] - x[:-1] )\n",
"x_aux = 0.5*(x[1:] + x[:-1])\n",
"# To plot\n",
"fig = plt.figure(figsize=(12,8))\n",
"plt.plot(x, y, '-s', label=\"f\")\n",
"plt.plot(x_aux, dydx, '-s', label=\"df/dx\")\n",
"plt.legend(loc=\"upper left\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Desafío 2: Derivación numérica\n",
"Implemente el cálculo de la segunda derivada, que puede obtenerse por diferencias finitas centradas mediante\n",
"$$ \\frac{d f(x_i)}{dx} = \\frac{1}{\\Delta x^2} \\Big( f(x_{i+1}) -2 f(x_{i}) + f(x_{i-1}) \\Big)$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def g(x):\n",
" return 1 + x**2 + np.sin(x)\n",
"\n",
"x = np.linspace(0,1,10)\n",
"y = g(x) \n",
"d2ydx2 = 0 * x # FIX ME\n",
"x_aux = 0*d2ydx2 # FIX ME\n",
"# To plot\n",
"fig = plt.figure(figsize=(12,8))\n",
"plt.plot(x, y, label=\"f\")\n",
"plt.plot(x_aux, d2ydx2, label=\"d2f/dx2\")\n",
"plt.legend(loc=\"upper left\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"#### 2. Librería Numpy\n",
"## 2.2 Funciones Básicas\n",
"\n",
"Algunas funciones básicas que es conveniente conocer son las siguientes:\n",
"* **shape**: Entrega las dimensiones del arreglo. Siempre es una tupla.\n",
"* **len**: Entrega el número de elementos de la primera dimensión del arreglo. Siempre es un entero.\n",
"* **ones**: Crea un arreglo con las dimensiones provistas e inicializado con valores 1. Por defecto array 1D.\n",
"* **zeros**: Crea un arreglo con las dimensiones provistas e inicializado con valores 1. Por defecto array 1D.\n",
"* **eye**: Crea un arreglo con las dimensiones provistas e inicializado con 1 en la diagonal. Por defecto array 2D."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# arrays 1d\n",
"A = np.ones(3)\n",
"print \"A = \\n\", A\n",
"print \"A.shape =\", A.shape\n",
"print \"len(A) =\", len(A)\n",
"B = np.zeros(3)\n",
"print \"B = \\n\", B\n",
"print \"B.shape =\", B.shape\n",
"print \"len(B) =\", len(B)\n",
"C = np.eye(1,3)\n",
"print \"C = \\n\", C\n",
"print \"C.shape =\", C.shape\n",
"print \"len(C) =\", len(C)\n",
"# Si queremos forzar la misma forma que A y B\n",
"C = np.eye(1,3).flatten() # o np.eye(1,3)[0,:] \n",
"print \"C = \\n\", C\n",
"print \"C.shape =\", C.shape\n",
"print \"len(C) =\", len(C)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# square arrays\n",
"A = np.ones((3,3))\n",
"print \"A = \\n\", A\n",
"print \"A.shape =\", A.shape\n",
"print \"len(A) =\", len(A)\n",
"B = np.zeros((3,3))\n",
"print \"B = \\n\", B\n",
"print \"B.shape =\", B.shape\n",
"print \"len(B) =\", len(B)\n",
"C = np.eye(3) # Or np.eye(3,3)\n",
"print \"C = \\n\", C\n",
"print \"C.shape =\", C.shape\n",
"print \"len(C) =\", len(C)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# fat 2d array\n",
"A = np.ones((2,5))\n",
"print \"A = \\n\", A\n",
"print \"A.shape =\", A.shape\n",
"print \"len(A) =\", len(A)\n",
"B = np.zeros((2,5))\n",
"print \"B = \\n\", B\n",
"print \"B.shape =\", B.shape\n",
"print \"len(B) =\", len(B)\n",
"C = np.eye(2,5)\n",
"print \"C = \\n\", C\n",
"print \"C.shape =\", C.shape\n",
"print \"len(C) =\", len(C)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Librería Numpy\n",
"## 2.2 Funciones Básicas\n",
"\n",
"Algunas funciones básicas que es conveniente conocer son las siguientes:\n",
"* **reshape**: Convierte arreglo a nueva forma. Numero de elementos debe ser el mismo.\n",
"* **linspace**: Regresa un arreglo con valores linealmente espaciados.\n",
"* **diag(x)**: Si x es 1D, regresa array 2D con valores en diagonal. Si x es 2D, regresa valores en la diagonal.\n",
"* **sum**: Suma los valores del arreglo. Puede hacerse en general o a lo largo de un axis.\n",
"* **mean**: Calcula el promedio de los valores del arreglo. Puede hacerse en general o a lo largo de un axis.\n",
"* **std**: Calcula la desviación estándar de los valores del arreglo. Puede hacerse en general o a lo largo de un axis."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x = np.linspace(0., 1., 6)\n",
"A = x.reshape(3,2)\n",
"print \"x = \\n\", x\n",
"print \"A = \\n\", A\n",
"\n",
"print \"np.diag(x) = \\n\", np.diag(x)\n",
"print \"np.diag(B) = \\n\", np.diag(A)\n",
"\n",
"print \"\"\n",
"print \"A.sum() = \", A.sum()\n",
"print \"A.sum(axis=0) = \", A.sum(axis=0)\n",
"print \"A.sum(axis=1) = \", A.sum(axis=1)\n",
"\n",
"print \"\"\n",
"print \"A.mean() = \", A.mean()\n",
"print \"A.mean(axis=0) = \", A.mean(axis=0)\n",
"print \"A.mean(axis=1) = \", A.mean(axis=1)\n",
"\n",
"print \"\"\n",
"print \"A.std() = \", A.std()\n",
"print \"A.std(axis=0) = \", A.std(axis=0)\n",
"print \"A.std(axis=1) = \", A.std(axis=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Desafío 3\n",
"\n",
"Complete el siguiente código:\n",
"* Se le provee un array A cuadrado\n",
"* Calcule un array B como la multiplicación element-wise de A por sí misma.\n",
"* Calcule un array C como la multiplicación matricial de A y B.\n",
"* Imprima la matriz C resultante.\n",
"* Calcule la suma, promedio y desviación estándar de los valores en la diagonal de C.\n",
"* Imprima los valores anteriormente calculados."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"A = np.outer(np.arange(3),np.arange(3))\n",
"print A\n",
"# FIX ME\n",
"# FIX ME\n",
"# FIX ME\n",
"# FIX ME\n",
"# FIX ME"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Desafío 4\n",
"Implemente la regla de [integración trapezoidal](https://en.wikipedia.org/wiki/Trapezoidal_rule)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def mi_funcion(x):\n",
" f = 1 + x + x**3 + x**5 + np.sin(x)\n",
" return f\n",
"\n",
"N = 5\n",
"x = np.linspace(-1,1,N)\n",
"y = mi_funcion(x)\n",
"# FIX ME\n",
"I = 0 # FIX ME\n",
"# FIX ME\n",
"print \"Area bajo la curva: %.3f\" %I\n",
"\n",
"# Ilustración gráfica\n",
"x_aux = np.linspace(x.min(),x.max(),N**2)\n",
"fig = plt.figure(figsize=(12,8))\n",
"fig.gca().fill_between(x, 0, y, alpha=0.25)\n",
"plt.plot(x_aux, mi_funcion(x_aux), 'k')\n",
"plt.plot(x, y, 'r.-')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Librería Numpy\n",
"## 2.5 Inputs y Outputs\n",
"\n",
"Numpy permite leer datos en formato array con la función **loadtxt**. Existen variados argumentos opcionales, pero los mas importantes son:\n",
"* **skiprows**: permite saltarse lineas en la lectura.\n",
"* **dtype**: declarar que tipo de dato tendra el array resultante"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Ejemplo de lectura de datos\n",
"data = np.loadtxt(\"data/cherry.txt\")\n",
"print data.shape\n",
"print data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Ejemplo de lectura de datos, saltandose 11 lineas y truncando a enteros\n",
"data_int = np.loadtxt(\"data/cherry.txt\", skiprows=11).astype(int)\n",
"print data_int.shape\n",
"print data_int"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Librería Numpy\n",
"## 2.5 Inputs y Outputs\n",
"\n",
"Numpy permite guardar datos de manera sencilla con la función **savetxt**: siempre debemos dar el nombre del archivo y el array a guardar. \n",
"\n",
"Existen variados argumentos opcionales, pero los mas importantes son:\n",
"* **header**: Línea a escribir como encabezado de los datos\n",
"* **fmt**: Formato con el cual se guardan los datos (%d para enteros, %.5f para flotantes con 5 decimales, %.3E para notación científica con 3 decimales, etc.)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Guardando el archivo con un header en español\n",
"encabezado = \"Diametro Altura Volumen (Valores truncados a numeros enteros)\"\n",
"np.savetxt(\"data/cherry_int.txt\", data_int, fmt=\"%d\", header=encabezado)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Revisemos si el archivo quedó bien escrito. Cambiaremos de **python** a **bash** para utilizar los comandos del terminal:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%bash \n",
"cat data/cherry_int.txt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Desafío 5\n",
"\n",
"* Lea el archivo data/cherry.txt\n",
"* Escale la matriz para tener todas las unidades en metros o metros cubicos.\n",
"* Guarde la matriz en un nuevo archivo data/cherry_mks.txt, con un encabezado apropiado y 2 decimales de precisión para el flotante (pero no en notación científica)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Leer datos\n",
"#FIX_ME#\n",
"\n",
"# Convertir a mks\n",
"#FIX_ME#\n",
"\n",
"# Guardar en nuevo archivo\n",
"#FIX_ME#"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Librería Numpy\n",
"## 2.6 Selecciones de datos\n",
"\n",
"Existen 2 formas de seleccionar datos en un array A:\n",
"* Utilizar máscaras de datos, que corresponden a un array con las mismas dimensiones del array A, pero de tipo booleano. Todos aquellos elementos True del array de la mascara serán seleccionados.\n",
"* Utilizar un array con valores enteros. Los valores del array indican los valores que desean conservarse. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.6 Máscaras\n",
"Observe que el array regresado siempre es unidimensional puesto que no es posible garantizar que se mantenga la dimensión original del array."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x = np.linspace(0,42,10)\n",
"print \"x = \", x\n",
"print \"x.shape = \", x.shape\n",
"\n",
"print \"\\n\"\n",
"mask_x_1 = x>10\n",
"print \"mask_x_1 = \", mask_x_1\n",
"print \"x[mask_x_1] = \", x[mask_x_1]\n",
"print \"x[mask_x_1].shape = \", x[mask_x_1].shape\n",
"\n",
"print \"\\n\"\n",
"mask_x_2 = x > x.mean()\n",
"print \"mask_x_2 = \", mask_x_2\n",
"print \"x[mask_x_2] = \", x[mask_x_2]\n",
"print \"x[mask_x_2].shape = \", x[mask_x_2].shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"A = np.linspace(10,20,12).reshape(3,4)\n",
"print \"\\n\"\n",
"print \"A = \", A\n",
"print \"A.shape = \", A.shape\n",
"\n",
"print \"\\n\"\n",
"mask_A_1 = A>13\n",
"print \"mask_A_1 = \", mask_A_1\n",
"print \"A[mask_A_1] = \", A[mask_A_1]\n",
"print \"A[mask_A_1].shape = \", A[mask_A_1].shape\n",
"\n",
"print \"\\n\"\n",
"mask_A_2 = A > 0.5*(A.min()+A.max())\n",
"print \"mask_A_2 = \", mask_A_2\n",
"print \"A[mask_A_2] = \", A[mask_A_2]\n",
"print \"A[mask_A_2].shape = \", A[mask_A_2].shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"T = np.linspace(-100,100,24).reshape(2,3,4)\n",
"print \"\\n\"\n",
"print \"T = \", T\n",
"print \"T.shape = \", T.shape\n",
"\n",
"print \"\\n\"\n",
"mask_T_1 = T>=0\n",
"print \"mask_T_1 = \", mask_T_1\n",
"print \"T[mask_T_1] = \", T[mask_T_1]\n",
"print \"T[mask_T_1].shape = \", T[mask_T_1].shape\n",
"\n",
"print \"\\n\"\n",
"mask_T_2 = 1 - T + 2*T**2 < 0.1*T**3\n",
"print \"mask_T_2 = \", mask_T_2\n",
"print \"T[mask_T_2] = \", T[mask_T_2]\n",
"print \"T[mask_T_2].shape = \", T[mask_T_2].shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.6 Índices\n",
"Observe que es posible repetir índices, por lo que el array obtenido puede tener más elementos que el array original.\n",
"\n",
"En un arreglo 2d, es necesario pasar 2 arrays, el primero para las filas y el segundo para las columnas."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x = np.linspace(10,20,11)\n",
"print \"x = \", x\n",
"print \"x.shape = \", x.shape\n",
"\n",
"print \"\\n\"\n",
"ind_x_1 = np.array([1,2,3,5,7])\n",
"print \"ind_x_1 = \", ind_x_1\n",
"print \"x[ind_x_1] = \", x[ind_x_1]\n",
"print \"x[ind_x_1].shape = \", x[ind_x_1].shape\n",
"\n",
"print \"\\n\"\n",
"ind_x_2 = np.array([0,0,1,2,3,4,5,6,7,-3,-2,-1,-1])\n",
"print \"ind_x_2 = \", ind_x_2\n",
"print \"x[ind_x_2] = \", x[ind_x_2]\n",
"print \"x[ind_x_2].shape = \", x[ind_x_2].shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"A = np.linspace(-90,90,10).reshape(2,5)\n",
"print \"A = \", A\n",
"print \"A.shape = \", A.shape\n",
"\n",
"print \"\\n\"\n",
"ind_row_A_1 = np.array([0,0,0,1,1])\n",
"ind_col_A_1 = np.array([0,2,4,1,3])\n",
"print \"ind_row_A_1 = \", ind_row_A_1\n",
"print \"ind_col_A_1 = \", ind_col_A_1\n",
"print \"A[ind_row_A_1,ind_col_A_1] = \", A[ind_row_A_1,ind_col_A_1]\n",
"print \"A[ind_row_A_1,ind_col_A_1].shape = \", A[ind_row_A_1,ind_col_A_1].shape\n",
"\n",
"print \"\\n\"\n",
"ind_row_A_2 = 1\n",
"ind_col_A_2 = np.array([0,1,3])\n",
"print \"ind_row_A_2 = \", ind_row_A_2\n",
"print \"ind_col_A_2 = \", ind_col_A_2\n",
"print \"A[ind_row_A_2,ind_col_A_2] = \", A[ind_row_A_2,ind_col_A_2]\n",
"print \"A[ind_row_A_2,ind_col_A_2].shape = \", A[ind_row_A_2,ind_col_A_2].shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Desafío 6\n",
"\n",
"<img src=\"images/generador_eolico.jpg\" alt=\"\" width=\"280px\" align=\"right\"/>\n",
"La potencia de un aerogenerador, para $k$ una constante relacionada con la geometría y la eficiencia, $\\rho$ la densidad del are, $r$ el radio del aerogenerador en metros y $v$ la velocidad el viento en metros por segundo, está dada por: \n",
"$$ P = \\begin{cases} k \\ \\rho \\ r^2 \\ v^3, 3 \\leq v \\leq 25\\\\ 0,\\ eoc\\end{cases}$$\n",
"Típicamente se considera una valor de $k=0.8$ y una densidad del aire de $\\rho = 1.2$ [$kg/m^3$].\n",
"\n",
"Calcule el número de aerogeneradores activos, la potencia promedio y la potencia total generada por los 11 generadores del parque Eólico Canela 1.\n",
"\n",
"Los valores de radio del aerogenerador (en metros) y la velocidad del viento (en kilometros por hora) se indican a continuación en arreglos en el código numérico."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"k = 0.8\n",
"rho = 1.2 # \n",
"r_m = np.array([ 25., 25., 25., 25., 25., 25., 20., 20., 20., 20., 20.])\n",
"v_kmh = np.array([10.4, 12.6, 9.7, 7.2, 12.3, 10.8, 12.9, 13.0, 8.6, 12.6, 11.2]) # En kilometros por hora\n",
"P = 0 \n",
"n_activos = 0\n",
"P_mean = 0.0\n",
"P_total = 0.0\n",
"print \"Existen %d aerogeneradores activos del total de %d\" %(n_activos, r.shape[0])\n",
"print \"La potencia promedio de los aeorgeneradores es {0:.2f} \".format(P_mean) \n",
"print \"La potencia promedio de los aeorgeneradores es \" + str(P_total) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tips\n",
"* La práctica y la necesidad hace al maestro.\n",
"\n",
"* Preguntar: en línea y en persona, pero tratar de solucionar los problemas antes.\n",
"\n",
"## Enlaces útiles:\n",
"* http://www.labri.fr/perso/nrougier/teaching/numpy.100/ : Lista con 100 recetas prácticas.s\n",
"* http://sebastianraschka.com/Articles/2014_matlab_vs_numpy.html : Desde el lado oscuro a numpy.\n",
"* http://pages.physics.cornell.edu/~myers/teaching/ComputationalMethods/python/arrays.html : Otros consejos."
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| cc0-1.0 |
melissawm/lpwithnotebooks | exemplo/IDEB.ipynb | 1 | 78027 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Exemplo: Análise do IDEB"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Neste notebook, vamos analisar dados relativos ao IDEB calculado por município no Brasil. Os dados estão no arquivo"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"arquivo = \"IDEB por Município Rede Federal Séries Finais (5ª a 8ª).xml\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"obtido no site <a href=\"http://dados.gov.br\">dados.gov.br</a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Como nosso arquivo é um .xml, vamos usar o módulo xml.etree.ElementTree para parsear o conteúdo do arquivo. Vamos abreviar o nome desse módulo por ET."
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import xml.etree.ElementTree as ET"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### O módulo ElementTree (ET)\n",
"\n",
"Um arquivo XML é um conjunto hierárquico de dados, e portanto a maneira mais natural de representar esses dados é através de uma árvore. Para isso, o módulo ET tem duas classes: a classe ElementTree representa o documento XML inteiro como uma árvore, e a classe Element representa um nó desta árvore. Todas as interações que ocorrem com o documento completo (por exemplo, leitura e escrita no arquivo) são feitas através da classe ElementTree; por outro lado, as interações com um elemento isolado do XML e seus subelementos são feitas através da classe Element.\n",
"\n",
"O método ET.parse retorna uma ElementTree."
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"tree = ET.parse(arquivo)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Para vermos o elemento raiz da árvore, usamos"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"root = tree.getroot()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"O objeto root, que é um Element, tem as propriedades *tag* e *attrib*, que é um dicionário de seus atributos."
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"action": "hide",
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/plain": [
"'result'"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"root.tag"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"action": "hide",
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/plain": [
"{}"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"root.attrib"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Para acessarmos cada um dos nós do elemento raiz, iteramos nestes nós (que são, também, Elements):"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"url {}\n",
"id {}\n",
"nome {}\n",
"nome_estendido {}\n",
"descricao {}\n",
"inicio {}\n",
"final {}\n",
"formatacao {}\n",
"data_atualizacao {}\n",
"aditividade {}\n",
"url_origem {}\n",
"tempo_aditividade {}\n",
"portal_dados_abertos {}\n",
"disponibilizacao {}\n",
"estado {}\n",
"fonte_gestora {}\n",
"fonte_provedora {}\n",
"grupo_informacao {}\n",
"base_territorial {}\n",
"periodicidade {}\n",
"multiplicador {}\n",
"produto {}\n",
"publicacao {}\n",
"unidade_medida {}\n",
"orgao_primeiro_escalao {}\n",
"valores {}\n"
]
}
],
"source": [
"for child in root:\n",
" print(child.tag, child.attrib)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Selecionando os dados"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Agora que temos uma ideia melhor dos dados a serem tratados, vamos construir um DataFrame do pandas com o que nos interessa. Primeiramente, observamos que somente o último nó nos interessa, já que todos os outros compõem o cabeçalho do arquivo XML. Assim, vamos explorar o nó *valores*:"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"valoresIDEB = root.find('valores')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Observe que temos mais uma camada de dados:"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/plain": [
"<Element 'valores' at 0x7f66cce61958>"
]
},
"execution_count": 59,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"valoresIDEB"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/plain": [
"<Element 'entry' at 0x7f66cce619a8>"
]
},
"execution_count": 60,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"valoresIDEB[0]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Assim, podemos por exemplo explorar os nós *netos* da árvore:"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n",
"valor {}\n",
"municipio_ibge {}\n",
"ano {}\n"
]
}
],
"source": [
"for child in valoresIDEB:\n",
" for grandchild in child:\n",
" print(grandchild.tag, grandchild.attrib)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vamos transformar agora os dados em um DataFrame."
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {},
"outputs": [],
"source": [
"data = []\n",
"for child in valoresIDEB:\n",
" data.append([float(child[0].text), child[1].text, child[2].text])"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/plain": [
"[[4.7, '120040', '2009'],\n",
" [6.0, '130260', '2009'],\n",
" [5.9, '140010', '2009'],\n",
" [5.5, '150140', '2009'],\n",
" [4.0, '211130', '2009'],\n",
" [6.3, '220190', '2009'],\n",
" [6.9, '230440', '2009'],\n",
" [7.1, '261160', '2009'],\n",
" [6.5, '280670', '2009'],\n",
" [7.1, '292740', '2009'],\n",
" [6.0, '310620', '2009'],\n",
" [6.3, '313670', '2009'],\n",
" [6.4, '317020', '2009'],\n",
" [5.7, '330455', '2009'],\n",
" [6.9, '410690', '2009'],\n",
" [5.7, '420540', '2009'],\n",
" [5.8, '431490', '2009'],\n",
" [7.3, '431690', '2009'],\n",
" [7.1, '500270', '2009'],\n",
" [5.3, '520870', '2009'],\n",
" [4.4, '120040', '2007'],\n",
" [5.3, '140010', '2007'],\n",
" [5.2, '150140', '2007'],\n",
" [3.4, '211130', '2007'],\n",
" [4.3, '220190', '2007'],\n",
" [6.8, '230440', '2007'],\n",
" [7.5, '261160', '2007'],\n",
" [5.4, '280670', '2007'],\n",
" [7.2, '292740', '2007'],\n",
" [5.5, '310620', '2007'],\n",
" [7.0, '313670', '2007'],\n",
" [6.0, '317020', '2007'],\n",
" [6.1, '330455', '2007'],\n",
" [5.8, '420540', '2007'],\n",
" [6.2, '431490', '2007'],\n",
" [6.5, '431690', '2007'],\n",
" [6.5, '500270', '2007'],\n",
" [5.5, '520870', '2007'],\n",
" [6.7, '530010', '2007']]"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Como a biblioteca <a href=\"http://pandas.pydata.org/\">Pandas</a> está na moda ;) vamos utilizá-la para tratar e armazenar os dados. Mas vamos chamar a biblioteca pandas com um nome mais curto, pd."
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Inicialmente, criamos um DataFrame, ou seja, uma tabela, com os dados que já temos."
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {},
"outputs": [],
"source": [
"tabelaInicial = pd.DataFrame(data, columns = [\"Valor\", \"Municipio\", \"Ano\"])"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Valor</th>\n",
" <th>Municipio</th>\n",
" <th>Ano</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>4.7</td>\n",
" <td>120040</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6.0</td>\n",
" <td>130260</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>5.9</td>\n",
" <td>140010</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>5.5</td>\n",
" <td>150140</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4.0</td>\n",
" <td>211130</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>6.3</td>\n",
" <td>220190</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>6.9</td>\n",
" <td>230440</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>7.1</td>\n",
" <td>261160</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>6.5</td>\n",
" <td>280670</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>7.1</td>\n",
" <td>292740</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>6.0</td>\n",
" <td>310620</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>6.3</td>\n",
" <td>313670</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>6.4</td>\n",
" <td>317020</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>5.7</td>\n",
" <td>330455</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6.9</td>\n",
" <td>410690</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>5.7</td>\n",
" <td>420540</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>5.8</td>\n",
" <td>431490</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>7.3</td>\n",
" <td>431690</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>7.1</td>\n",
" <td>500270</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5.3</td>\n",
" <td>520870</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>4.4</td>\n",
" <td>120040</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>5.3</td>\n",
" <td>140010</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>5.2</td>\n",
" <td>150140</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>3.4</td>\n",
" <td>211130</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>4.3</td>\n",
" <td>220190</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>6.8</td>\n",
" <td>230440</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>7.5</td>\n",
" <td>261160</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>5.4</td>\n",
" <td>280670</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>7.2</td>\n",
" <td>292740</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>5.5</td>\n",
" <td>310620</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>7.0</td>\n",
" <td>313670</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>6.0</td>\n",
" <td>317020</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>6.1</td>\n",
" <td>330455</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>5.8</td>\n",
" <td>420540</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>6.2</td>\n",
" <td>431490</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>6.5</td>\n",
" <td>431690</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>36</th>\n",
" <td>6.5</td>\n",
" <td>500270</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>37</th>\n",
" <td>5.5</td>\n",
" <td>520870</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>38</th>\n",
" <td>6.7</td>\n",
" <td>530010</td>\n",
" <td>2007</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Valor Municipio Ano\n",
"0 4.7 120040 2009\n",
"1 6.0 130260 2009\n",
"2 5.9 140010 2009\n",
"3 5.5 150140 2009\n",
"4 4.0 211130 2009\n",
"5 6.3 220190 2009\n",
"6 6.9 230440 2009\n",
"7 7.1 261160 2009\n",
"8 6.5 280670 2009\n",
"9 7.1 292740 2009\n",
"10 6.0 310620 2009\n",
"11 6.3 313670 2009\n",
"12 6.4 317020 2009\n",
"13 5.7 330455 2009\n",
"14 6.9 410690 2009\n",
"15 5.7 420540 2009\n",
"16 5.8 431490 2009\n",
"17 7.3 431690 2009\n",
"18 7.1 500270 2009\n",
"19 5.3 520870 2009\n",
"20 4.4 120040 2007\n",
"21 5.3 140010 2007\n",
"22 5.2 150140 2007\n",
"23 3.4 211130 2007\n",
"24 4.3 220190 2007\n",
"25 6.8 230440 2007\n",
"26 7.5 261160 2007\n",
"27 5.4 280670 2007\n",
"28 7.2 292740 2007\n",
"29 5.5 310620 2007\n",
"30 7.0 313670 2007\n",
"31 6.0 317020 2007\n",
"32 6.1 330455 2007\n",
"33 5.8 420540 2007\n",
"34 6.2 431490 2007\n",
"35 6.5 431690 2007\n",
"36 6.5 500270 2007\n",
"37 5.5 520870 2007\n",
"38 6.7 530010 2007"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tabelaInicial"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Observe que nesta tabela temos dados de 2007 e 2009. Não vamos usar os dados relativos a 2007 por simplicidade."
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {},
"outputs": [],
"source": [
"tabelaInicial = tabelaInicial.loc[0:19]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Obtendo códigos IBGE para os municípios\n",
"\n",
"Na tabelaInicial, os municípios não estão identificados por nome, e sim pelo seu código IBGE. Para lermos o arquivo excel em que temos a tabela dos municípios brasileiros (atualizada em 2014) e seus respectivos códigos de 7 dígitos - os códigos incluem um dígito verificador ao final - usamos o módulo xlrd, que não estará instalado junto com o pandas por definição (você deve instalá-lo manualmente) se quiser executar o comando abaixo. Veja <a href=\"https://pypi.python.org/pypi/xlrd\">aqui</a>, por exemplo."
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {},
"outputs": [],
"source": [
"dadosMunicipioIBGE = pd.read_excel(\"DTB_2014_Municipio.xls\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Podemos olhar o tipo de tabela que temos usando o método *head* do pandas."
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"tags": [
"codecomment"
]
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>UF</th>\n",
" <th>Nome_UF</th>\n",
" <th>Mesorregião Geográfica</th>\n",
" <th>Nome_Mesorregião</th>\n",
" <th>Microrregião Geográfica</th>\n",
" <th>Nome_Microrregião</th>\n",
" <th>Município</th>\n",
" <th>Cod Municipio Completo</th>\n",
" <th>Nome_Município</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>11</td>\n",
" <td>Rondônia</td>\n",
" <td>2</td>\n",
" <td>Leste Rondoniense</td>\n",
" <td>6</td>\n",
" <td>Cacoal</td>\n",
" <td>15</td>\n",
" <td>1100015</td>\n",
" <td>Alta Floresta D'Oeste</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>11</td>\n",
" <td>Rondônia</td>\n",
" <td>2</td>\n",
" <td>Leste Rondoniense</td>\n",
" <td>3</td>\n",
" <td>Ariquemes</td>\n",
" <td>23</td>\n",
" <td>1100023</td>\n",
" <td>Ariquemes</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>11</td>\n",
" <td>Rondônia</td>\n",
" <td>2</td>\n",
" <td>Leste Rondoniense</td>\n",
" <td>8</td>\n",
" <td>Colorado do Oeste</td>\n",
" <td>31</td>\n",
" <td>1100031</td>\n",
" <td>Cabixi</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>11</td>\n",
" <td>Rondônia</td>\n",
" <td>2</td>\n",
" <td>Leste Rondoniense</td>\n",
" <td>6</td>\n",
" <td>Cacoal</td>\n",
" <td>49</td>\n",
" <td>1100049</td>\n",
" <td>Cacoal</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>11</td>\n",
" <td>Rondônia</td>\n",
" <td>2</td>\n",
" <td>Leste Rondoniense</td>\n",
" <td>8</td>\n",
" <td>Colorado do Oeste</td>\n",
" <td>56</td>\n",
" <td>1100056</td>\n",
" <td>Cerejeiras</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" UF Nome_UF Mesorregião Geográfica Nome_Mesorregião \\\n",
"0 11 Rondônia 2 Leste Rondoniense \n",
"1 11 Rondônia 2 Leste Rondoniense \n",
"2 11 Rondônia 2 Leste Rondoniense \n",
"3 11 Rondônia 2 Leste Rondoniense \n",
"4 11 Rondônia 2 Leste Rondoniense \n",
"\n",
" Microrregião Geográfica Nome_Microrregião Município \\\n",
"0 6 Cacoal 15 \n",
"1 3 Ariquemes 23 \n",
"2 8 Colorado do Oeste 31 \n",
"3 6 Cacoal 49 \n",
"4 8 Colorado do Oeste 56 \n",
"\n",
" Cod Municipio Completo Nome_Município \n",
"0 1100015 Alta Floresta D'Oeste \n",
"1 1100023 Ariquemes \n",
"2 1100031 Cabixi \n",
"3 1100049 Cacoal \n",
"4 1100056 Cerejeiras "
]
},
"execution_count": 69,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dadosMunicipioIBGE.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Como não são todos os dados que nos interessam, vamos selecionar apenas as colunas \"Nome_UF\" (pois pode ser interessante referenciarmos o estado da federação mais tarde), \"Cod Municipio Completo\" e \"Nome_Município\"."
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {},
"outputs": [],
"source": [
"dadosMunicipioIBGE = dadosMunicipioIBGE[[\"Nome_UF\", \"Cod Municipio Completo\", \"Nome_Município\"]]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Em seguida, precisamos selecionar na tabela completa dadosMunicipioIBGE os dados dos municípios presentes na tabelaInicial contendo os valores calculados do IDEB. Para isso, vamos extrair dos dois DataFrames as colunas correspondentes aos codigos de município (lembrando que nos dadosMunicipioIBGE os códigos contém um dígito verificador que não será utilizado):"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {},
"outputs": [],
"source": [
"listaMunicipiosInicial = tabelaInicial[\"Municipio\"]\n",
"listaMunicipios = dadosMunicipioIBGE[\"Cod Municipio Completo\"].map(lambda x: str(x)[0:6])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Observe que usamos acima o método map para transformar os dados numéricos em string, e depois extrair o último dígito.\n",
"\n",
"Agora, ambos *listaMunicípiosInicial* e *listaMunicipios* são objetos Series do pandas. Para obtermos os índices dos municípios para os quais temos informação do IDEB, vamos primeiro identificar quais códigos **não** constam da listaMunicipiosInicial: "
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"indicesMunicipios = listaMunicipios[~listaMunicipios.isin(listaMunicipiosInicial)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"E agora vamos extrair as linhas correspondentes na tabela dadosMunicipioIBGE."
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {},
"outputs": [],
"source": [
"new = dadosMunicipioIBGE.drop(indicesMunicipios.index).reset_index(drop=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Por fim, vamos criar uma nova tabela (DataFrame) juntando nome e valor do IDEB calculado na tabelaInicial."
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"dadosFinais = pd.concat([new, tabelaInicial], axis=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A tabela final é"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Nome_UF</th>\n",
" <th>Cod Municipio Completo</th>\n",
" <th>Nome_Município</th>\n",
" <th>Valor</th>\n",
" <th>Municipio</th>\n",
" <th>Ano</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>Acre</td>\n",
" <td>1200401</td>\n",
" <td>Rio Branco</td>\n",
" <td>4.7</td>\n",
" <td>120040</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>Amazonas</td>\n",
" <td>1302603</td>\n",
" <td>Manaus</td>\n",
" <td>6.0</td>\n",
" <td>130260</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Roraima</td>\n",
" <td>1400100</td>\n",
" <td>Boa Vista</td>\n",
" <td>5.9</td>\n",
" <td>140010</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Pará</td>\n",
" <td>1501402</td>\n",
" <td>Belém</td>\n",
" <td>5.5</td>\n",
" <td>150140</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Maranhão</td>\n",
" <td>2111300</td>\n",
" <td>São Luís</td>\n",
" <td>4.0</td>\n",
" <td>211130</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>Piauí</td>\n",
" <td>2201903</td>\n",
" <td>Bom Jesus</td>\n",
" <td>6.3</td>\n",
" <td>220190</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>Ceará</td>\n",
" <td>2304400</td>\n",
" <td>Fortaleza</td>\n",
" <td>6.9</td>\n",
" <td>230440</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>Pernambuco</td>\n",
" <td>2611606</td>\n",
" <td>Recife</td>\n",
" <td>7.1</td>\n",
" <td>261160</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>Sergipe</td>\n",
" <td>2806701</td>\n",
" <td>São Cristóvão</td>\n",
" <td>6.5</td>\n",
" <td>280670</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>Bahia</td>\n",
" <td>2927408</td>\n",
" <td>Salvador</td>\n",
" <td>7.1</td>\n",
" <td>292740</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>Minas Gerais</td>\n",
" <td>3106200</td>\n",
" <td>Belo Horizonte</td>\n",
" <td>6.0</td>\n",
" <td>310620</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>Minas Gerais</td>\n",
" <td>3136702</td>\n",
" <td>Juiz de Fora</td>\n",
" <td>6.3</td>\n",
" <td>313670</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>Minas Gerais</td>\n",
" <td>3170206</td>\n",
" <td>Uberlândia</td>\n",
" <td>6.4</td>\n",
" <td>317020</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>Rio de Janeiro</td>\n",
" <td>3304557</td>\n",
" <td>Rio de Janeiro</td>\n",
" <td>5.7</td>\n",
" <td>330455</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>Paraná</td>\n",
" <td>4106902</td>\n",
" <td>Curitiba</td>\n",
" <td>6.9</td>\n",
" <td>410690</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>Santa Catarina</td>\n",
" <td>4205407</td>\n",
" <td>Florianópolis</td>\n",
" <td>5.7</td>\n",
" <td>420540</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>Rio Grande do Sul</td>\n",
" <td>4314902</td>\n",
" <td>Porto Alegre</td>\n",
" <td>5.8</td>\n",
" <td>431490</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>Rio Grande do Sul</td>\n",
" <td>4316907</td>\n",
" <td>Santa Maria</td>\n",
" <td>7.3</td>\n",
" <td>431690</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>Mato Grosso do Sul</td>\n",
" <td>5002704</td>\n",
" <td>Campo Grande</td>\n",
" <td>7.1</td>\n",
" <td>500270</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>Goiás</td>\n",
" <td>5208707</td>\n",
" <td>Goiânia</td>\n",
" <td>5.3</td>\n",
" <td>520870</td>\n",
" <td>2009</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Nome_UF Cod Municipio Completo Nome_Município Valor \\\n",
"0 Acre 1200401 Rio Branco 4.7 \n",
"1 Amazonas 1302603 Manaus 6.0 \n",
"2 Roraima 1400100 Boa Vista 5.9 \n",
"3 Pará 1501402 Belém 5.5 \n",
"4 Maranhão 2111300 São Luís 4.0 \n",
"5 Piauí 2201903 Bom Jesus 6.3 \n",
"6 Ceará 2304400 Fortaleza 6.9 \n",
"7 Pernambuco 2611606 Recife 7.1 \n",
"8 Sergipe 2806701 São Cristóvão 6.5 \n",
"9 Bahia 2927408 Salvador 7.1 \n",
"10 Minas Gerais 3106200 Belo Horizonte 6.0 \n",
"11 Minas Gerais 3136702 Juiz de Fora 6.3 \n",
"12 Minas Gerais 3170206 Uberlândia 6.4 \n",
"13 Rio de Janeiro 3304557 Rio de Janeiro 5.7 \n",
"14 Paraná 4106902 Curitiba 6.9 \n",
"15 Santa Catarina 4205407 Florianópolis 5.7 \n",
"16 Rio Grande do Sul 4314902 Porto Alegre 5.8 \n",
"17 Rio Grande do Sul 4316907 Santa Maria 7.3 \n",
"18 Mato Grosso do Sul 5002704 Campo Grande 7.1 \n",
"19 Goiás 5208707 Goiânia 5.3 \n",
"\n",
" Municipio Ano \n",
"0 120040 2009 \n",
"1 130260 2009 \n",
"2 140010 2009 \n",
"3 150140 2009 \n",
"4 211130 2009 \n",
"5 220190 2009 \n",
"6 230440 2009 \n",
"7 261160 2009 \n",
"8 280670 2009 \n",
"9 292740 2009 \n",
"10 310620 2009 \n",
"11 313670 2009 \n",
"12 317020 2009 \n",
"13 330455 2009 \n",
"14 410690 2009 \n",
"15 420540 2009 \n",
"16 431490 2009 \n",
"17 431690 2009 \n",
"18 500270 2009 \n",
"19 520870 2009 "
]
},
"execution_count": 75,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dadosFinais"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Para terminar: um gráfico\n",
"\n",
"Para usarmos gráficos em notebooks, devemos incluir no notebook o comando\n",
"\n",
"% matplotlib inline\n",
"\n",
"ou \n",
"\n",
"% matplotlib notebook\n",
"\n",
"Como isso é geralmente feito usando a primeira célula do notebook, mas no nosso caso não gostaríamos de sacrificar a legibilidade do documento, usamos uma nbextension chamada init_cell para que este comando seja executado na inicialização do notebook ([Detalhes](#sobre_inicializacao))\n",
"\n",
"Primeiramente, vamos importar a biblioteca matplotlib."
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Em seguida, vamos substituir os índices da tabela dadosFinais pelos nomes dos municípios listados, já que gostaríamos de fazer um gráfico do valor do IDEB por município."
]
},
{
"cell_type": "code",
"execution_count": 92,
"metadata": {},
"outputs": [
{
"ename": "KeyError",
"evalue": "'Nome_Município'",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mKeyError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/indexes/base.py\u001b[0m in \u001b[0;36mget_loc\u001b[0;34m(self, key, method, tolerance)\u001b[0m\n\u001b[1;32m 2133\u001b[0m \u001b[0;32mtry\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 2134\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_engine\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_loc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2135\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0mKeyError\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32mpandas/index.pyx\u001b[0m in \u001b[0;36mpandas.index.IndexEngine.get_loc (pandas/index.c:4433)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/index.pyx\u001b[0m in \u001b[0;36mpandas.index.IndexEngine.get_loc (pandas/index.c:4279)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/src/hashtable_class_helper.pxi\u001b[0m in \u001b[0;36mpandas.hashtable.PyObjectHashTable.get_item (pandas/hashtable.c:13742)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/src/hashtable_class_helper.pxi\u001b[0m in \u001b[0;36mpandas.hashtable.PyObjectHashTable.get_item (pandas/hashtable.c:13696)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;31mKeyError\u001b[0m: 'Nome_Município'",
"\nDuring handling of the above exception, another exception occurred:\n",
"\u001b[0;31mKeyError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-92-9b6c50c0a7c0>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mdadosFinais\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mset_index\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m\"Nome_Município\"\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0minplace\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/core/frame.py\u001b[0m in \u001b[0;36mset_index\u001b[0;34m(self, keys, drop, append, inplace, verify_integrity)\u001b[0m\n\u001b[1;32m 2915\u001b[0m \u001b[0mnames\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mappend\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;32mNone\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2916\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 2917\u001b[0;31m \u001b[0mlevel\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mframe\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mcol\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_values\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2918\u001b[0m \u001b[0mnames\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mappend\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mcol\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2919\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mdrop\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/core/frame.py\u001b[0m in \u001b[0;36m__getitem__\u001b[0;34m(self, key)\u001b[0m\n\u001b[1;32m 2057\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_getitem_multilevel\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2058\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 2059\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_getitem_column\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2060\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2061\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0m_getitem_column\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/core/frame.py\u001b[0m in \u001b[0;36m_getitem_column\u001b[0;34m(self, key)\u001b[0m\n\u001b[1;32m 2064\u001b[0m \u001b[0;31m# get column\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2065\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcolumns\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mis_unique\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 2066\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_get_item_cache\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2067\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2068\u001b[0m \u001b[0;31m# duplicate columns & possible reduce dimensionality\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/core/generic.py\u001b[0m in \u001b[0;36m_get_item_cache\u001b[0;34m(self, item)\u001b[0m\n\u001b[1;32m 1384\u001b[0m \u001b[0mres\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcache\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1385\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mres\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0;32mNone\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1386\u001b[0;31m \u001b[0mvalues\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_data\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1387\u001b[0m \u001b[0mres\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_box_item_values\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mvalues\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1388\u001b[0m \u001b[0mcache\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mres\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/core/internals.py\u001b[0m in \u001b[0;36mget\u001b[0;34m(self, item, fastpath)\u001b[0m\n\u001b[1;32m 3541\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3542\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0misnull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 3543\u001b[0;31m \u001b[0mloc\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mitems\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_loc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mitem\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 3544\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3545\u001b[0m \u001b[0mindexer\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0marange\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mlen\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mitems\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0misnull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mitems\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/miniconda3/lib/python3.6/site-packages/pandas/indexes/base.py\u001b[0m in \u001b[0;36mget_loc\u001b[0;34m(self, key, method, tolerance)\u001b[0m\n\u001b[1;32m 2134\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_engine\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_loc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2135\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0mKeyError\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 2136\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_engine\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_loc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_maybe_cast_indexer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2137\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2138\u001b[0m \u001b[0mindexer\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_indexer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mkey\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mmethod\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mmethod\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtolerance\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mtolerance\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32mpandas/index.pyx\u001b[0m in \u001b[0;36mpandas.index.IndexEngine.get_loc (pandas/index.c:4433)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/index.pyx\u001b[0m in \u001b[0;36mpandas.index.IndexEngine.get_loc (pandas/index.c:4279)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/src/hashtable_class_helper.pxi\u001b[0m in \u001b[0;36mpandas.hashtable.PyObjectHashTable.get_item (pandas/hashtable.c:13742)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;32mpandas/src/hashtable_class_helper.pxi\u001b[0m in \u001b[0;36mpandas.hashtable.PyObjectHashTable.get_item (pandas/hashtable.c:13696)\u001b[0;34m()\u001b[0m\n",
"\u001b[0;31mKeyError\u001b[0m: 'Nome_Município'"
]
}
],
"source": [
"dadosFinais.set_index([\"Nome_Município\"], inplace=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finalmente, como nos interessa um gráfico do IDEB por município, só vamos utilizar os dados da coluna \"Valor\" na tabela dadosFinais (observe que o resultado desta operação é uma Series)"
]
},
{
"cell_type": "code",
"execution_count": 82,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"Nome_Município\n",
"Rio Branco 4.7\n",
"Manaus 6.0\n",
"Boa Vista 5.9\n",
"Belém 5.5\n",
"São Luís 4.0\n",
"Bom Jesus 6.3\n",
"Fortaleza 6.9\n",
"Recife 7.1\n",
"São Cristóvão 6.5\n",
"Salvador 7.1\n",
"Belo Horizonte 6.0\n",
"Juiz de Fora 6.3\n",
"Uberlândia 6.4\n",
"Rio de Janeiro 5.7\n",
"Curitiba 6.9\n",
"Florianópolis 5.7\n",
"Porto Alegre 5.8\n",
"Santa Maria 7.3\n",
"Campo Grande 7.1\n",
"Goiânia 5.3\n",
"Name: Valor, dtype: float64"
]
},
"execution_count": 82,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dadosFinais[\"Valor\"]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Estamos prontos para fazer nosso gráfico."
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f66d061e6a0>"
]
},
"execution_count": 91,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAcEAAAEICAYAAAAnXE+UAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xe4XFW9xvHvS0AIhgQpciOC8WKQGiIEBKQFEBsoIIqA\nkNgCSpHrBUS9UkQFQQXpBBUCRqQGQxGihEAoQkJ6qEqR3gmEUMN7/1hrcnYmM2dmzjlzSs7v8zzn\nycwua689B86atfde75JtQgghhN5oma6uQAghhNBVohEMIYTQa0UjGEIIodeKRjCEEEKvFY1gCCGE\nXisawRBCCL1WNIIhLGUkbSvpgTq3/aKkuyS9r8Z2+0ma0I46nSjp8LbuX0f5O0h6olnl52MMkmRJ\nyzbzOB1J0hBJd3R1PbqzaARDtyLpUUk759cjJS2UND//PCLpAknrFrYv/WGaX/azd15/oaS387LX\nJN0jafsuPL9Jub6blC0fl5fv0N5j2J5s++N11GVV4JfAV2y/XaPMsbZ3aUt9JK0OHACcl9/vIOm9\nwu/qCUmXSdq8LeX3BJJG5P/2Xs3ne3KxMZW0Sv5v4HVJj0nat2z/ffPy1yVdLWmVwrr1JU2UNE/S\nvyTtUVpnexbwiqTdOuVEe6BoBEN3d6ftfsAAYGfgDeAeSRuVbbey7X6Fn0sL607OZfQHzgGuktSn\n2RVv5RgPkhqF0narAlsBzze7TmU2BEbZ/k+TjzMSuN72G4VlT+XfyUrAlsD9wGRJOzW5Ll1lReBw\nYDXgk8BOwBGF9WcBbwNrAPsB50jaECD/ex6wf16/ADg7r1sW+CtwLbAKMAr4U/GLIjAWOLBZJ9bT\nRSMYegTbC23/2/b3gFuA49pQhoE/k/5YrFFpG0nHSbpC0qW55zit2GvL37onSXpF0lxJXyysu1DS\nOZKul/Q6MLxKVcYCexcayX2AcaQ/gsWyfl54v9jlvtxjPkLSrNwDuFTSClW2XUvSVZKel/SipDPz\nqv8GTi5sZ0mHSXpY0guSTpG0TF43UtJthW23ljQlH3uKpK2rnCvA50i/syU4ecL2McDvgV8VjvE7\nSY/n3tM9krYtrOubP6OXJd0LLNaLrPF7+ryke/Pv90lJxcaoWEYfSb/On8XDwBfK1g+Q9AdJT+dy\nfl7ti4/tc3IP/W3bT5L+G/hULuf9wJeBn9qeb/s2YDyp0YPUKF5j+1bb84GfAntKWglYD/gQcGr+\nf2QicHthX4BJwE6Slq9Ut94uGsHQE10FbFtzqzL5D9QBwCPAs61s+iXgclJj+WfgaknLSVoOuAaY\nAHwQOBQYK6l46XFf4BekHs5tVPYUcC9Qurx4AHBRo+cDfBX4LPBRYAipx7WYfM7XAo8Bg4A1gb+0\nUuYewDBgU9Ln8M0KZa4CXAecDqwK/Ba4LvdoK9kYqOce5VXAprlRAJgCDKXl93B5qaEHjgXWyT+f\nAUYU6lfr9/QH4EDbKwEbAROr1Oc7wK7AJ0ifyV5l6y8E3gU+lrfZBfh2HecJsB0wN79eF3jX9oOF\n9TNJPXXyvzNLK2z/m/SFqdjbKxLpvErbPwm8A9S8RN4bRSMYeqKnSH8Yi17I3/pLP+sX1h0h6RVg\nPnAa6Rv3wlbKv8f2FbbfIf2BX4F0yW5LoB9wUv5GP5HUwOxT2Pevtm+3/Z7tN1s5xkXAAZLWI13K\nvbOO8y53uu2nbL9E+qM/tMI2W5B6Ckfaft32m7mnUc2vbL+UL5GexuLnVvIF4CHbF9t+1/YlpMuZ\n1e47rQy8Vsf5PEX6A74ygO0/2X4xH+M3wPK0/CH/KvCLXNfHSQ1ySa3f0zvABpL6237Z9rQq9fkq\ncJrtx/NnfGJphaQ1gM8Dh+fP9TngVOBrtU5S0jdJjeqv86J+wKtlm80jfZEqrZ9XZf0DwHPAkfmL\n2i7A9qTLr0WvkT/XsLhoBENPtCbwUtmy1WyvXPi5r7Du17ZXJv1hGAacIulzrZT/eOmF7feAJ0gN\nyYeAx/OyksdyfZbYt4argB2BQ4CL69yn3DOF1wtIfyzLrQU8ZvvdOsss1v8x0jmX+1BeR9m2a1bY\nFuBlWv6gt2ZNwMArAPly7335kusrpPvCqxXqUF7XYv1a+z19mdSAPSbpFklbValPa8f4CLAc8HTp\nixfpvt0HWztBSbuTGtPP2X4hL55Pul9d1J+WLw5V1+cvaruTvpg8A/wvcBnpv9milcifa1hcNIKh\nJ9oDmNzoTvn+0xzSPZMvtLLpWqUX+Z7Yh0m9lKeAtUr3ybK1gSeLh6mzLguAvwHfpXIj+DqLf5v/\nr3rKreBxYG3V/1j/WoXXa5POudxTpEaAsm2frLAtwCyqX7or2gOYZvv1fP/vKFJv7AP5S8w8Uk8R\n4OkKdS3Wr+rvyfYU218iNVhXkxqNSlo7xuPAWyz+5au/7Q2pQtJngfOB3WzPLqx6EFhW0uDCsk1o\nuVw6N78vlfPfpF7xg/l8Ztne3vaqtj9Dutd7d2H7NYH3Ud8l6V4nGsHQI+SHFD4q6QxgB+D4Npaz\nHrANLX9gKtlM0p654Tic9Mfun8BdpB7XUfnS0w6kS4Ct3WNrzY+B7W0/WmHdDODzSo/O/1euR1vc\nTfpjfpKk90taQdKnWtn+SEkfkLQW8H3g0grbXA+sq/TY/rJKw1E2IF1yrOR60iW6JShZU9KxpPtp\nP86rViLdb3ue1EAcw+K9ocuAH+W6fph036+k6u9J0vuUxjwOyL2oV4Fij7HoMuAwSR+W9AHg6NIK\n20+T7jn+RlJ/SctIWkdVht9I2pH0MMyXbd9dXGf7ddKVgZ/l39GnSPdjS1+OxgK7KY3/fD/wM+Aq\n26/lsofk3+uK+SGfgaT7lSXbAxNtv1XlPHu1aARDd7eVpPmkP1aTSH8INy/7Jg1pLFRxnOAPCuuO\nysteJ/3huoA8Zq2KvwJ7ky7j7Q/safudPJZuN9LTji+QHlM/wPb9bTmxfD+v2v25i0kPQzya61yp\nMarnGAtJdf4Y8B/SZbK9W9nlr8A9pEb4OtJDJOVlvkh6YOR/gRdJPbZdC5f3yl1EatD7FpZ9KP9e\n55MegNkY2MF2aUD+jcANpN7OY8CbLH5p8vi8/BHS57OoN13H72l/4FFJrwIHkZ6+rOT8XI+ZwDRS\nQ1V0AKmHdS/pv5UrSA1QJT8lXc69vvDf6N8K678H9CXd37sE+K7tufl85uZ6js3rV8rbl+xP+qLz\nHGnoxafLGrz9gHOr1KvXU0yqG0ILSccBH7P99a6uS2eTZGCw7X81oexfAs/ZPq2jyw7VSRoCnGe7\n2n3PXq/HxP+EEHou2z+uvVXoaDkxJhrAVsTl0BBCCL1WXA4NIYTQa0VPMIQQQq8V9wS7udVWW82D\nBg3q6mqEEEKPcs8997xge/Va20Uj2M0NGjSIqVOndnU1QgihR5FUnmpUUVwObYM8wPfIQphvCCGE\nHqhX9gRz+O2ppKDdl0mJ7CfbHldl+2GkwbaH5UXfICX3HwH8vNI+ZftfD+xru+HsvtlPzmPQ0dc1\nulsIoRM8elJr6XuhJ+h1PUFJIuUF3mr7v21vRkp+/3C1fWxPLTSAAK/nee0eyuW1yvbn29IAhhBC\naK5e1wiSkvvftr0oRsj2Y7bPyPl7F0iaLWm6pOGwaJLSa/PrLYDDJU0nZSuum5ePVJq49AZJD0kq\nTlb6qKTV8uurlSYInStpVOeddgghhHK98XLohqQcwEoOJk02sHEOWp4gqTz9/n5gW9vvStoZ+CVp\nahZI87l9ghS4/ICkM/JcZ0XftP1SzlGcIunKnMW4SG4cRwH06V/z4aYQQght1BsbwcVIOos0q8Db\npHDhMwBs35+fLipvBAcAY/K0JybNKVZyk+15udx7SdPNlDeCh0naI79eCxhMCiFexPZoYDTA8gMH\nR5pBCCE0SW+8HDoX2LT0xvbBpOT1ertcJwA3296IlFRffEK0mNy+kLIvGXlKl52BrWxvAkwv2z+E\nEEIn6o09wYnALyV91/Y5eVlp8tLJpGlHJubLoGuTJqIsBtAOoGXy0JENHnsA8LLtBfly65a1dth4\nzQFMjSfQQgihKXpdT9ApLHV3YHtJj0i6GxgD/JA079gykmaT5m8bWWEiypOBE/ODMY1+ibiBNEHo\nfcBJpIlaQwghdJEI0O7mhg0b5kiMCSGExki6x/awWtv1up5gCCGEUBKNYAghhF6r6Q/GSPov4DRg\nc+AV4FngcNsPNvvYNerVUHRaO481CLg2P1HakIhNCyEsjbpL5FxTe4I5UmwcMMn2Ojmi7EfAGs08\nbp31qis6TVJvfII2hBB6hWZfDh0OvFMWUTbT9mRJ/STdJGlajin7EqRek6T7JV0o6UFJYyXtLOn2\nHEe2Rd7uOEkXS7ozL/9OXi5Jp0iak8vdu0K9qkan5TJGShovaSJwU4263ifp/ByDNiEnwSBpM0kz\nJc0kJdGQl/fJ9ZsiaZakAzv4Mw8hhFCnZjeCGwH3VFn3JrCH7U1JjeVvCmHUHwN+A6yXf/Ylpboc\nAfy4UMYQUoO2FXCMpA8Be5LiyzYhDUw/RdLAsmO3Fp1Wsimwl+3ta9R1MHCW7Q1Jl3tLEWoXAIfm\nQfFF3wLm2d6cdIn4O5I+WtxA0ihJUyVNXbhgXo1qhhBCaKuufDBGpEHrs4B/AGvScpn0Eduzbb9H\nSni5KY/vmw0MKpTxV9tv2H4BuBnYgtRYXmJ7oe1ngVtIjU31ikhn5V7blMLiv9t+qc66zsiv7wEG\nSVoZWNn2rXn5xYVydwEOkDQDuAtYldSQLmJ7tO1htof1WXFAa1UPIYTQDs2+3zUX2KvKuv1IUWWb\n2X5H0qO0RIgVB6i/V3j/HovXuXyQY72DHufS0mPD9sF5lofigLzX21DXhUDfGscWqYd4Yz0VjcSY\nEEJonmb3BCcCyxenDJI0RNK2pAix53KjMpwUNt2oL+Xpj1YFdgCmkKLP9s733lYHtgPurlCvFSR9\nt7BsRaprqK557sBXJG2TF+1XWH0j8F1JywFIWlfS+1s9yxBCCE3R1J6gbecZE06T9EPSvbVHgcOB\nscA1OaJsKmmKokbNIl0GXQ04wfZTksaR7hHOJPUMj7L9TIV67Q6cKuko4HlSz++HVY7Tlrp+A/ij\nJAMTCst/T7qkOy3fV3yeFOMWQgihk/XY2DRJxwHzbf+6q+vSTBGbFkIIjYvYtBBCCKGGbt0ISvpJ\nHn83S9IMSZ8srbN9XL29QElDJX2+wWMPkmRJPy8sW03SO5LObLCsYZJOb2SfEEIIzddt01AkbQXs\nCmxq+6389Ob72ljcUGAYcH2D+z0CfAH4v/z+K6QnS+smaVnbU1n8ydO6RWxaCKE36qxYte7cExwI\nvFCaz8/2C7afApB0TE5cmSNpdGnguqRJkn4l6e6cNrOtpPcBPyM9MTpD0t6StshJM9Ml3SHp41Xq\nsAC4T1LpuvLewGWllZJ2k3RXLucfSnmkxTSb24GLJe0g6dq8rt5jhxBCaLLu3AhOANbKjdnZkrYv\nrDvT9uY5kLovqcdYsqztLUhPoB5r+23gGOBS20NtX0p6unNb25/I637ZSj3+AnxN0lqkcYBPFdbd\nBmyZy/kLcFRh3QbAzrb3KSuvkWOHEEJoom57OdT2fEmbAduSosoulXS07QuB4Xlow4rAKqRLlNfk\nXa/K/97D4ukyRQOAMZIGk4ZRLNdKVW4ATiDNfnFp2boP53oNJF2qfaSwbrztN9py7DyuchRAn/6r\nt1K1EEII7dGde4Lk6LNJto8FDgG+LGkF4GxSrufGwPm0pLdAS4LLQqo38icAN+ee5G5l+5fX4W1S\ng/q/wBVlq88g9Uo3Bg4sK+d1Kqt57IhNCyGEztFte4L5Xtl7th/Ki4YCj9HSaLwgqR8plq28cSr3\nGrBS4f0A4Mn8emQd1fkNcIvtl1pys5coZ0Qd5TR87IhNCyGE5unOPcF+pMuG9+bg6g2A43Ik2fnA\nHFIE2ZRWyii5Gdig9GAMcDJwoqTp1PFFwPZc22MqrDoOuFzSPcAL9ZxUo8cOIYTQPD02Maa3iMSY\nEEJoXCTGhBBCCDVEIxhCCKHX6paNoKSF+f7dHEmXS2ptmqNK+/+49lYV9xuao9I+W7Z8flvKCyGE\n0L11y3uCkubb7pdfjwXusf3bOvYTadLaV0v7N3jcXwFbAw/bHlFYPr8t5VUof1nb7zayz/IDB3vg\niNPae+gQQg/SWZFhS7Ol6Z7gZOBjAJJ+kHuHcyQdnpcNkvSApItIT4z+Aeibe5Jjq+1XLjegXyEN\nW/h0Ho9Yabsjc2TbLEnHF5b/NNfjNkmXSDoiL58k6TRJU4HvS1pd0pW5jCmSPtVBn1MIIYQGdetH\n9CUtC3wOuCGnx3wD+CSpt3eXpFuAl4HBwAjb/8z7fcX20Py64n62p5cdbmvgEdv/ljSJFJx9ZVl9\ndsnH2iKXNV7SdsAbwJeBTUgJMNNIA+xL3lf6RiLpz8Cptm+TtDZpmMf6ZceJxJgQQugE3bUR7Ctp\nRn49mdS7+y4wzvbrAJKuIkWqjQceKzWAFWxTZb/yRnAfUv4n+d8DKGsEgV3yT2nffqRGcSXgr7bf\nBN6UdE3ZfsW4tZ1JYxZL7/tL6md70X1H26OB0ZAuh1Y5rxBCCO3UXRvBN0o9uZKypJZy1SLK6iKp\nD6kn9yVJPyH18laVtJLt14qbAifaPq9s/4qXWKvUbxlS6Pab7alzCCGE9uuujWAlk4ELJZ1Eaoz2\nAPavsu07kpaz/U6d++0EzLL9mdICSWPythcVtrsROEHS2BzwvSbwDnA7cJ6kE0mf6a7knlwFE4BD\ngVPycYbanlFl24hNCyGEJuoxjaDtaZIuBO7Oi35ve7qkQRU2Hw3MkjTN9n6V9ivbfh9gXNmyK0mX\nYBc1grYnSFofuDP3TOcDX7c9RdJ4YBZptonZwLwqp3IYcFaOglsWuBU4qLVzDyGE0BzdcohET1S6\nr5fHNN4KjLI9rb3lRmxaCCE0rt4hEj2mJ9gDjJa0AWmWizEd0QCGEEJormgEWyHpk0Bf25NqbWt7\n3+bXKIQQQkfqVoPlC3FppZ9BknaQdG2D5QyTdHo767IR6V7dne0o40JJe+XXv889xRBCCN1Ed+sJ\nVhoaMaiRAnI02VSgXTfSbM8hDbLvELa/3Zb9Zj85j0FHX9dR1QghdDMRkda1ulVPsBZJq0i6OkeW\n/VPSkLz8OEkXS7oduLjYe5S0haQ7JU2XdIfSjPVIGinpKkk3SHpI0smF4+wjaXaOWftVYfl8SadK\nmivpJkmr5+VDc31mSRon6QMV6j4p91D75B7inHyM/2nyxxZCCKGK7tYIljI/Z0gqH7IAcDww3fYQ\n4McsPoZvA2Bn2/uU7XM/sK3tTwDHAL8srBsK7A1sDOwtaS1JHwJ+BeyY128uafe8/fuBqbY3BG4B\njs3LLwJ+mOs1u7C8kqHAmrY3sr0xcEH5BpJGSZoqaerCBdVGWoQQQmivbn85tMw2pGQXbE+UtKqk\n/nndeNtvVNhnADBG0mDApGzPkptszwOQdC/wEWBVYJLt5/PyscB2wNXAe7REoP0JuErSAGBl27fk\n5WOAy1s5h4eB/5Z0BnAdafD8YiI2LYQQOkd36wm2R7XotBOAm21vBOxGGsJQ8lbh9UIa/1LQcANl\n+2VS0PYk0oM3v2+0jBBCCB2ju/UEa5kM7EeKLtsBeMH2qzVyRQcAT+bXI+s4xt3A6ZJWI81QsQ9w\nRl63DLAXKWB7X+A22/MkvSxpW9uTSZFst1QoF4Bc7tu2r5T0AKlHWVXEpoUQQvP0tEbwOOCPOXJs\nATCi9c0BOJl0OfT/SJcfW2X7aUlHAzeTskavs/3XvPp1YItc1nOk+4nkepyb02IepvWnStcELpBU\n6oX/qI5zCCGE0AQRm9YAddAM842I2LQQQmhcvbFpS9M9wRBCCKEh0Qg2oLN7gSGEEJqrp90TbDdJ\n/wWcBmwOvEKa+uhw2w/Wuf/PgFtt/yNPpjva9oK87nrSAzMrA9fmJ1LbJRJjQgg9TU9KwelVPUGl\nx0jHkcYBrmN7M9KDKWvUuX8f28fY/kdedDiwYmm97c/bfqWj6x1CCKE5elUjCAwH3rF9bmmB7ZlA\nn2JIt6QzJY3Mrx+V9CtJ04CvlEKxJR0GfAi4WdLNhW1Xy8UsK2mspPskXZGfHEXSMZKm5Ni00aox\nviOEEELz9LZGcCPgnjbs96LtTW3/pbTA9unAU8Bw28Mr7PNx4Gzb6wOvAt/Ly8+0vXm+VNoX2LV8\nx4hNCyGEztHbGsG2urT2Jkt43Pbt+fWfSJFvAMMl3SVpNimfdMPyHW2Ptj3M9rA+Kw5oW41DCCHU\n1NsawbnAZhWWv8vin8UKZeurRbK1pnwApiWtAJwN7JXDs8+vcKwQQgidpLc9HToR+KWkUTmkmjwd\nk4ANJC1PukS5E3BbHeW9BqwEvFBh3dqStrJ9JzlijZYG7wVJ/UgRbFe0doCITQshhObpVT1Bp3ic\nPYCdJf1b0lzgROAZ4DJgTv53ep1FjgZuKD0YU+YB4GBJ9wEfAM7JT46en49zIzClPecTQgihfSI2\nrZuL2LQQQmhcxKaFEEIINUQjGEIIodfqkgdjJC0EZufjPwLsb/sVSR8CTre9VxvLvZAUV9bqwyaF\n7Y8D5tv+dVuO10q5d9jeuiPKiti0EJZuPSlibGnUVT3BN2wPzQPGXwIOBrD9VFsbwO6kUgMoqbc9\niRtCCN1ed7gceidpolkkDZI0J79eQdIFkmZLmi5piVQWJWdKekDSP4APFtZtJukWSfdIulHSwNYq\nIek7Oc5spqQrCzFnF0o6XdIdkh6WtFdhnyPzPrMkHV9YPj//u4OkyZLGA/fmZT/IkWlzcgB3CCGE\nLtJQIyhpE0mH5J9N2ntwSX1IY/LGV1h9MGlUw8bAPqTZ4csHlu9BiifbADgA2DqXuxxwBmlQ+mbA\nH4Ff1KjOVTnObBPgPuBbhXUDSYkvuwIn5WPsAgwGtgCGAptJ2q5CuZsC37e9rqTNSLPOfxLYEviO\npE+U7xCxaSGE0DnqbgQlfR8YS+ptfRD4k6RD23jcvpJmkMbnrQH8vcI225DixrB9P/AYsG7ZNtsB\nl9heaPsp0mB4SA3jRsDf83H+D/hwjTptlHtts4H9WDzO7Grb79m+l5YZJ3bJP9OBacB6pEax3N22\nHymc0zjbr9ueD1wFbFu+Q8SmhRBC52jkPtW3gE/afh1A0q9IlzLPaMNx37A9NF9yvJHU6zu9DeVU\nI2Cu7a0a2OdCYHfbM/MMEjsU1r1VVnbp3xNtn1ej3LZEroUQQugEjTSCAhYW3i+kpUFoE9sL8pRE\nV0s6u2z1ZFKPbKKkdYG1SSksRbcCB0oaQ+qdDgf+nLdbvRRbli+Prmt7bivVWQl4Om+7H/Bkjerf\nCJwgaazt+ZLWJE3T9Fwr+0wGLpR0Eumz2wPYv7WDRGxaCCE0TyON4AXAXZLG5fe7A39obwVsT5c0\ni3Tfb3Jh1dnAOfny5LvASNtvle0+jjQTw73Af0g9U2y/nR9gOV3SANJ5nkYK0C5alpZe3k+Bu4Dn\n878r1aj3BEnrA3fmKQHnA18HqjaCtqflYRx350W/t11vRFsIIYQO1lBsmqRNaZkSaHJP/wOeG/Tz\nbV/f1XWpJmLTQgihcfXGptXsCUrqb/tVSasAj+af0rpVbL/Unop2ldzDfBCY0NV1CSGE0DXquRz6\nZ9LQgHtIc+QV7wMa+O8m1Kvp8tCLmiQdRBo+0dq9vhBCCD1Qj5tFQtIgUjTaRoVlx5Huye0KHGG7\nTdcPy8uWtCNpLsC3bX+vwbJ2yHXZVdIXgQ1sn9RonZYfONgDR5zW6G4hhFDT0hzZ1mGXQ8sK3ZN0\nT9Cke4JXt7F+3U6VWLMPAAcBX5C0gu0321K27fFUDgQIIYTQhRoZLH82qUGYTZoU9iBJZzWrYu2w\nv6QZOZZsCwBJ75f0R0l35wi2L+XlIyWNlzQRuKlYSO4VHk56kvNYUvJLKQptkqQrJN0vaazy46GS\nPpuXTQP2LJQ1UtKZ+fVuku7K9fiHpDUIIYTQJRrpCe4IrJ9nZyePzWtt3F1XWTEPxN+OFJe2EfAT\nYKLtb0paGbg7Z41CatyG2H4pN3wlzwGftv2mpMHAJUCpa/0JUqLMU8DtwKckTSXNGr8j8C/g0ir1\nuw3Y0rYlfRs4Cvjf4gaSRgGjAPr0X72NH0MIIYRaGmkE/0UasP5Yfr9WXtbZqt3ELC2/BMD2rZL6\n50ZvF+CLko7I26xAOheAv1d5wnU54ExJQ0nBAMXItrttPwGQY9kGke5JPmL7obz8T+SGrMyHgUuV\nAr3fR5pKavETsUcDoyHdE6xyviGEENqpkUZwJeA+SXeTGpwtgKl5hgRsf7EJ9avkRdK9uqJVaGlM\nyhuN0hOtX7a9WOKMpE9SPdbsf4BngU1Il42L9wOLg/YX0tjneAbwW9vj88MzxzWwbwghhA7U6h9v\nSXLL46PHdEJ9asoRZU9L2tH2xDx+8bPA70gzNOwN3CxpG2Ce7XmSbgQOlXRovgz5iToG+g8AnrD9\nnqQRQJ8a298PDJK0ju1/kxJwqpVbimQbUet8IzYthBCap1YP5jBJT9u+zPYtnVKj+hwAnCXpt/n9\n8bb/nZ9PeVPSdNLlzG/m9SeQYtNmSVqG1GvctcYxzgaulHQAcAM1grDzvcNRwHWSFpAi4CpFrx0H\nXC7pZdKsFx+tUY8QQghN0uo4wTxs4Gekp0HPY/FLjSLN99e/qTXs5SI2LYQQGtch4wRtvwv8OI+R\n+3OH1S6EEELoBuoaJ5gv9W0padHlPUkr5QdLQgghhB6p7ti0fJ9t08I4wWWAqbY3bWL9Sseeb7tf\nK+t/T3ri8t4Gyx1EWQRbHfssJAUGlOxu+9FGjtuIiE0LIXSUpTkmrVwzYtOKT4qSn5psKHatWWx/\nuxMP94btoY3uJGnZfHk5hBBCN1F3bBrwsKTDJC2Xf74PPNysipXLcWXXFt6fKWlkfj1J0jBJX8yR\naTMkPSBpiYHokjaTNFPSTODgwvI+kk6RNEXSLEkHNlC3FSRdIGl2jkMbnpcvFssmqZ+kmyRNy9t+\nqR0fSQgVw0wUAAAgAElEQVQhhHZqpBE8CNiaNMbtCeCTVE5E6TK2x9semntqM4FfV9jsAuBQ25uU\nLf8WaVzh5sDmwHckVRq+0LfQ0I7Lyw5Oh/fGpPGBYyStkNdtCuxle3vSgPs98iXk4cBvSrmjRZJG\nSZoqaerCBfMa+gxCCCHUr+7LmXk+va81sS4dRtJRpMuWZ5UtXxlY2fatedHFwOfy612AIZL2yu8H\nAINZMtas0uXQbUhJMNi+X9JjtMSsFWPZBPwy55q+B6wJrAE8UywsYtNCCKFz1DOz/FG2T5Z0BhVy\nO20f1pSaLeldFu+5rlBpI0k7A18BtmuwfJF6iDe2rXpVFQfZ7wesDmxm+x1Jj1LlPEoiMSaEEJqn\nnsuh9+V/p5Jmly//6SyPARtIWj736HYq30DSR4CzgK/YfqN8ve1XgFdypBqkRqnkRuC7kpbLZa0r\n6f111m1yqSxJ65LCuR+osN0A4LncAA4HPlJn+SGEEJqgZk/Q9jX53zHNr86S8hOob9l+XNJlpPSa\nR4BK2Z8jgVWBq/Ottqdsf75sm28Af5RkYEJh+e9Js0FMy/fpngd2r7OaZwPnSJpN6rGOtP1Whdt9\nY4Fr8nZTSXmjIYQQukgj4wTXBY4gNRSLGk/bOzalZi3H3QQ43/YWzTxOdxWxaSGE0LhmjBO8HDiX\n1GNa2NaKNULSQcBhpBneQwghhA7VSCP4ru1z2nKQQsqKSA3oIbbvqLFPKSXm3DqPsViqTB5DOMz2\nIQ3U84vABrZPqnefGuWtDOxr++yOKC+EEELHaqQRvEbS94BxFCaVrTIre7lFwwokfQY4Edi+kYo2\nW050GQ+M78BiVwa+R7pn2Cazn5zHoKOv67gahRCWCr0pAq2ZGhksPwI4EriDlidD23Kzqj/wcumN\npCMLKS3Hl2+s5BRJc3LKyt6NHlDSIEkT8zFukrR2Xn6hpHMl3QWcnBNezszrZhR+3pC0vaRVJF2d\ny/mnpCF52+Mk/TEn1zwsqTRs5CRgnVzGKfWcbwghhM7TyGD59kz+2lfSDNKYuIHAjgCSdiENSN+C\ndKl0vKTtCoPZAfYEhgKbAKsBUyTdavvpKscoWYWWXt0ZwBjbYyR9Ezidlic/PwxsbXthvoRaOt9S\nz3U34ChS4/9bYLrt3SXtCFyU6wawHikFZiXgAUnnAEcDGxXKqud8QwghdJK6G0GlGdaXYPuiOnYv\nXg7dCrhI0kaklJZdaBnu0I/USBQbhW2AS2wvBJ6VdAsp1qz8suViSS6le4L57VakxhRSSszJhf0u\nz2UvQdJg4BRgeB7btw3w5XzeEyWtKqk0qfB1tt8C3pL0HCkJplw954vSDPWjAPr0X71S1UIIIXSA\nRu4Jbl54vQJpsPo0Um+obrbvlLQaKTlFwIm2z2ukjA72eqWFkvoBlwHfqdDrrOStwuuFVP5s6zrf\niE0LIYTO0cjl0EOL7/OTj39p9ICS1gP6AC+SUlpOkDTW9nxJawLv5JzSksnAgZLGkC5xbke6N9mI\nO0i5pxeTkl0m17HPH4ELbBe3LSXDnCBpB+AF269WGBRf8hrp8mhJPee7mIhNCyGE5mnPfICvA/Xe\nJyzerxMwIl+CnCBpfeDO3JDMB74OFBuFcaTLmTNJ2aVH2V4scLoOhwIXSDqSlATzjdY2zvFrewHr\n5nuIAN8GjiOlzcwCFpAeFqrK9ouSbpc0B/ib7SPrON8QQgidpJHEmGtoCdBeBtgAuMz20U2qWyAS\nY0IIoS2akRhTnJvvXeAx2080XLMQQgihm2jknuAtzaxICCGE0NlqDpaX9JqkVws/rxX/7YxKtpWk\nn0iamwemz5D0yVa2vVAtE+q255g7SLq2veWEEEJovnp6gjcB/wVcBfzF9n+aW6WOkccj7gpsmqc1\nWg14XxdXawk5ru3dausjNi2EsDTqLrFvNXuCtncHPkN6qvJ8SbdI+p6kVZpeu/YZSBrC8BaA7Rds\nPyXpmBxbNkfSaJWNb5D0WUmXF94v6tlJOkfS1Ny7PL5sn/slTaNlUD41YtYulnQ7adhGCCGELlBX\ndqjtebYvAD4HnAf8jDSBbXc2AVhL0oOSzpZUCuw+0/bmtjcC+pJ6i0X/AD6pllnl96ZlPORP8tNG\nQ4DtJQ2RtAJwPrAbsBmp11xyPClmbQjwYxYPFtgA2Nn2Ph1ytiGEEBpWVyMoaWtJZ5ASYrYG9rD9\n26bWrJ1szyc1SqNIvdhLc5TacEl3Kc3uviOwYdl+7wI3ALspzWr/BeCvefVXc29vet5vA1Jm6CO2\nH3Iab/KnQnHbkHt6ticCxZi18bbfqFR3SaNyj3PqwgXz2vU5hBBCqK7mPUFJjwKvkHpDo0jDI5C0\nKYDtaU2sX7vkAfmTgEm50TuQ1IsbZvtxSceRIuDK/QU4BHgJmGr7NUkfBY4ANrf9sqQLq+xbr4px\nbbneEZsWQgidoJ4HYx4lDZL/DCn8uXgPzeQZIbobSR8H3rP9UF40FHiA1Ai+kLNB9wKuqLD7LaTY\ntO/Qcim0P6nhmidpDdKl4UnA/cAgSevY/jdQvLzZaMzaEiI2LYQQmqdmI2h7h3oKkvRp239vd406\nTj/gjJxx+i7wL1JP9hVgDvAMMKXSjnlapWtJ9z1H5GUzJU0nNXqPA7fn5W/mWR+uk7SA1PCV8kKP\no4GYtRBCCJ2r7ti0mgVJ02xv2iGFhUUiNi2EEBpXb2xaIzPL1zxmB5YVQgghNF1HNoK94gEOSe+X\n9F1JHfnZhRBC6AJd9oe8WqSZpA0lTZZ0jaTD2lDuAXkg/GxJ0yUdUWW7gyQd0Eo5O0jaumzZssCZ\nwG2236tRjzUk3SzpBkknNHoeIYQQmq898wmWe7TeDVuLNLM9F9i2LRWQ9DngcGCXnA6zPLBEQ5ej\nys6tUdwOpPn+7igtyGMIW52LsLDts8DwOqteVcSmhRA6S3eJMutMdfcEJa0o6aeSzs/vB0talLZi\ne8/qey+hYqRZLrdirJmkoTl6bJakcZI+UKHcHwFHlMqy/ZbtUn0nSTpN0lTg+zm67Ii87jBJ9+ay\n/yJpEHAQ8D+5l7qtpEGSJuZtbpK0tqQBkh4rXRrNl0ofl7ScpO/k85gp6UpJK+Ztliingc8thBBC\nB2rkcugFwFukWd4BngR+3sbjVos0g+qxZhcBP8wRZLOBYyuUuxFwTyvHfZ/tYbZ/U7b8aOATueyD\nbD8KnAucanuo7cnAGcCYvM1Y4HTb84AZQKn+uwI32n4HuCqfxybAfcC38jZLlFNeyUiMCSGEztFI\nI7iO7ZOBdwBsL6CNT4S2EmkGFWLNJA0AVi7MaTgG2K4Nh760yvJZwFhJXycn4lSwFfDn/PpiUiRa\nqcy98+uvFY6xUb63OZs0YH7DGuUsYnt0bqyH9VlxQO2zCiGE0CaNNIJvS+pLfgpU0jqknmGb2F5o\ne5LtY0kRZV9WCqM+G9jL9sakYOpGosnmkhrXaqpFlX0BOAvYFJiSH4Cp13jgs0qzamwGTMzLLwQO\nyedxPO2LWAshhNAEjfyxP5YULL2WpLHAp2jjTBJVIs0eo6WhWCzWzPY8SS9L2jZfmtyfFG1W7kTg\nFElfsP2MpPcBB9j+fSt1WQZYy/bNkm4j9eb6Aa+RotJK7sjrLib17CZD6tVKmgL8Drg255VCSo15\nWtJyefsnWyunmohNCyGE5qm7EbT9d6UZFLYkXQb9vu0X2njcipFmtl/JD95UijUbAZybHzB5mApP\nadq+Pud6/iM/UGNSBmhr+gB/ypdcRbrX94qka4ArJH0JODT/XCDpSNIl3OLxLwUuJz1RWvJT4K68\n7V20RKm1Vk4IIYRO1FBsmtKksIMoNJ62r+r4aoWSiE0LIYTG1RubVndPUNIfSTMwzAVKA8UNRCMY\nQgihR2rknuCWtjdoWk1CCCGETtbI06F3SlqqG0FJC/Pg+Dk5tm3lNpazKJJN0nq5zOn5idoQQgjd\nRN33BPOA9vGkB1beIj1E4jzoe6kgab7tfvn1GOBB279oZ5lHA8vablOwwPIDB3vgiNPaU4UQQuh2\nmh3R1uH3BIE/kIYmzKblnuDS7E7SPVAA8tOcXwWWB8bl8Y3kHt8RpPujs2zvL+k4Uu7ovaQs04WS\ndrI9PA/IP4yUlXoX8L3CsIoQQgidqJFG8Hnb45tWk25EUh9gJ1LDj6RdgMHAFqQe8HhJ2wEvAv8H\nbG37hTxgfpE8ZONcYL7tX0tan5Qu8ynb70g6mzRW8KKy448ipenQp//qTTzTEELo3RppBKdL+jNw\nDYWkmKVsiERfSTOANUl5n3/Py3fJP9Pz+36kRnET4PLSeEnbL9UofydSqsyUnAveF3iufCPbo4HR\nkC6HtuN8QgghtKKRRrAvqfHbpbBsaRsi8YbtoXlA/o3AwaSAawEn2j6vuLGkQxssX6Tw7B91SG1D\nCCG0SyOJMb0m2cT2AqUJfa/OlyxvBE6QNDbHpK1JChKfCIyT9FvbL0papUZv8Cbgr5JOtf1cvny6\nku3Hqu0QsWkhhNA8jcwn+OE8j99z+edKSR9uZuW6ku3ppNkl9rE9gTTzw515VogrSI3XXOAXwC2S\nZgK/rVHmvaR7iBMkzSJdbh3YxNMIIYTQikaGSPyd1BBcnBd9HdjP9qebVLdAxKaFEEJb1DtEopHB\n8qvbvsD2u/nnQiAeXQwhhNBjNdIIvijp65L65J+vk4YIhBBCCD1SI0+HfhM4AziV9FToHXTDaYAk\nLSQN6C/Z3fajde47iDTm7891bHet7Y3aVMkGzH5yHoOOvq7ZhwkhhA7T7DSYjtTI06GPAV9sYl06\nyhu2hza6U55NfhCwL+neZwghhKVczUZQ0jGtrLbtEzqwPk0haQXgHGAYaRLfH+SZ5EcCe5IGv/ch\nRaKtnwfMjwHGkR4Een8u6hDbd5SV3Qc4iTSh7vLAWbbPk/QzWr40rA5MsP0NSVcDawErAL/LA+ND\nCCF0gXp6gq9XWPZ+4FvAqkB3awRLqS8Aj9jegzTo3bY3lrQeaYjCunmbTYEhtl+StANwhO1dAfKg\n+U/bflPSYOASUkNa9C1gnu3NJS0P3C5pgu1jgGPyTBSTgTPz9t/Mx+pLSo650vZi91YjNi2EEDpH\nzUbQ9m9KryWtBHyfdC/wL8Bvqu3XhSpdDt2GdD8T2/dLegwoNYJ/b2WA+3LAmZKGAgsL+xTtAgyR\ntFd+P4AUqfaIUjban4Df2r4nrz9M0h759Vp528UawYhNCyGEzlHXPcGcbPIDUtjzGGBT2y83s2Kd\nqFJPt+R/gGdJGaHLAG9W2EbAobZvrLDuOOAJ2xcA5J7mzsBWOZVmEumyaAghhC5Qzz3BU0j3zUYD\nG9ue3/RadbzJpAZ8Yr4MujbwAOlSaNFrwEqF9wNIjdh7kkaQ7huWuxH4rqSJeWaIdYEngR1JDd7w\nsvJezg3gesCWtSoesWkhhNA89YwT/F/gQ6S4r6ckvZp/XpP0anOr12HOBpbJkWeXAiNtv1Vhu1mk\nuf9mSvqfvN+IHIm2HpV7jb8nzRs4TdIc4DzSl4sfkGajuDvPLP8z4AZgWUn3kR6m+WeHnmUIIYSG\n1B2bFrpGxKaFEELjmhGbFkIIISxVohEMIYTQazUSm9btFCLSRBrCsMRg9g44xkhgmO1DOrLcekVs\nWgiho/SkOLPO0qMbQQpjAiV9BjgR2L5rqxRCCKGnWJouh/YHXgZQcoqkOZJmS9o7L99B0i2S/irp\nYUknSdpP0t15u3VaO4Ck1fNkwlPyz6fy8u3zE6AzJE2XtFI+1rWFfc/MvUryce+VNEvSr5v1gYQQ\nQmhdT+8JliLSViDN0L5jXr4nMJQ0yH01UjzZrXndJsD6wEvAw8DvbW8h6fvAocDhrRzvd8Cptm+T\ntDZpjOD6wBHAwbZvl9SPyoPqAZC0KrAHsJ5t51i18m0iNi2EEDpBT+8JvmF7qO31gM8CF+Wosm2A\nS2wvtP0scAuwed5niu2n8zjBfwMT8vLZpFkkWrMzKUZtBjAe6J8bvduB30o6DFjZ9rutlDGP1Ej+\nQdKewILyDWyPtj3M9rA+Kw6o+SGEEEJom57eCC5i+05Sr69W16k4SP69wvv3qN0zXgbYMje8Q22v\naXu+7ZOAbwN9SQHa65Fmqyh+vivker4LbAFcAexKGkAfQgihC/T0y6GL5IanDymMejJwoKQxwCrA\ndsCRpNSX9phAumR6Sj7mUNszJK1jezYwW9Lm+Tj3ABvkmSX6AjsBt+We44q2r5d0O+mSbFURmxZC\nCM3T0xvB4rRJAkbYXihpHLAVMBMwcJTtZ3JD2ahlaektHgacJWlWXn4rcBBwuKThpN7kXOBvtt+S\ndBkwB3gEmJ7LWAn4a57jUKR4tRBCCF0gYtNqkHQq8JDts7vi+BGbFkIIjas3Nq2n9wSbStLfgPeR\npkQKIYSwlIlGsBW2P9eR5UnaHXjQ9r0dWW4IIYS26RWNoKSfAPuSotXeAw60fZekDYFzgVdIM8yf\n3kCZxwHzbdc12F3SEOAAYK9a2xZFbFroqSKiK/QES30jKGkr0lCETfPDKquRLnFiey6wbSdVZT3g\nG7bf66TjhRBCqGGpGSfYioHAC6VJdG2/YPspAEnH5PizOZJG54H2SBoq6Z851mycpA/UcyBJg/LE\nuqX3R+QeI8DngU/n5RGbFkII3UBvaAQnAGtJelDS2ZKKAdtn2t7c9kaksXy75uUXAT+0PYSUJHNs\nR1WmEJu2YS7/5xW2GSVpqqSpCxfM66hDhxBCKLPUN4K25wObkbI4nwcuLQVZA8Ml3SVpNil3dENJ\nA0jRZ7fkbcaQBtt3lIhNCyGEbmKpbwQBcoboJNvHAocAX86D1c8G9rK9MXA+OdqsHSpGpZXVJWLT\nQgihm+gND8Z8HHjP9kN50VDgMVoaqBdylNlewBW250l6WdK2ticD+5MCuOvxLPDBfMlzPhUauYhN\nCyGE7mOpbwSBfsAZecqid4F/AaNsvyLpfFKs2TPAlMI+I4BzJa1IaqS+UaXs/5O0aOol2x+W9DPg\nbuBJ4P4K+0RsWgghdBMRm9bNRWxaCCE0rt7YtF5xTzCEEEKoJBrBJpD0hZwQE0IIoRvrDfcE6yZp\nIWlcoEgRa4fYvqPGPvNt9yu8/yywPfDDjqhTxKaF0LNFfFz3Fo3g4t6wPRRA0meAE0kNWt1s30AM\newghhB4hLodW1x94ufRG0pE5Ym2WpOMr7VBpmxyldr+kC3NqzVhJO0u6XdJDkrbopPMJIYRQJnqC\niyvNVL8CKXN0RwBJuwCDSYPcBYyXtJ3tW0s7VtsG+A/wMeArwDdJQzH2BbYBvgj8GNi9WAlJo0gJ\nN/Tpv3qzzjWEEHq9aAQXV7wcuhVwkaSNgF3yz/S8XT9Sg3drYd9q2/wHeMT27FzuXOAm285xbYPK\nK2F7NDAaYPmBg2MMSwghNEk0glXYvjNPu7Q6qWd3ou3zWtml4jaSBgFvFRa9V3j/HjV+B5EYE0II\nzRP3BKuQtB7QB3gRuBH4Zo48Q9Kakj5Ytks924QQQuhGoie4uNI9QUg9uxG2FwITJK0P3JmnHJwP\nfB14rrSj7WrbLOzE+ocQQmhAxKZ1cxGbFkIIjYvYtBBCCKGGpaoRlLRQ0gxJMyVNk7R1B5R5gaQD\ny5btLulv+XWtRJkft7cOIYQQmmOpuhxajDDLiS8/tt1Q4kuFMncBfmR7eGHZX4DrbV/USJ3aYvmB\ngz1wxGlt3T2EsBSI6LXGxeXQQuKLklMkzZE0W9LeeXk/STflXuNsSV+qUM5NwHqSBuZ93g/sDFyd\n38/P/w6UdGvuic6RtK2kk8gP20gam7e7WtI9kubmQfEhhBC6yNL2dGjFxBdgT9KM8psAqwFTJN0K\nPA/sYfvVPCbwn5LGu9A9tr1Q0pXAV4HfAbsBk2y/WnbsfYEbbf9CUh/S7PGTJR1SGoCffdP2S5L6\n5npcafvFjv4gQggh1La09QTfsD3U9nrAZ0mJLyJFlF1ie6HtZ4FbgM1JwyB+KWkW8A9gTWCNCuVe\nAnwtv/5afl9uCvANSccBG9t+rUodD5M0E/gnsBYpVWYxkkZJmipp6sIF8+o68RBCCI1b2hrBRWzf\nSer1tRa+uV9ev1nurT1L6kWWuwMYKGkTYGtgibmNco7odsCTwIWSDijfRtIOpEupW9nehBSxtsTx\nbI+2Pcz2sD4rDmj1PEMIIbTd0nY5dJGyxJfJwIGSxgCrkBqrI4G9gedsvyNpOPCRSmXlnM9LgTHA\n32y/WeF4HwGesH2+pOWBTYGLgHckLWf7HWAA8LLtBbl+W9Y6j4hNCyGE5lnaGsGKiS+SxgFbATMB\nA0fZfiY/rHJNDrKeCtzfStmXAEcBR1dZvwNwpKR3SGkxpZ7gaGCWpGmkWSQOknQf8ADpkmgIIYQu\nslQNkVgaRWJMCCE0LoZIhBBCCDVEIxhCCKHX6nWNoCRL+lPh/bKSnpd0bVfWK4QQQudb2h6Mqcfr\nwEaS+tp+A/g0aVhDtzT7yXkMOnqJERkhhF4uotQ6Rq/rCWbXA6X/gvahMPhd0haS7pQ0XdIdkj6e\nl4+UdJWkGyQ9JOnkwj7n5MHtcyUdX1j+aE6iQdIwSZPy6+1zlNqMfJyVmn/KIYQQyvXWRvAvwNck\nrQAMAe4qrLsf2Nb2J4BjgF8W1g0ljS3cGNhb0lp5+U/yU0hDgO0lDalx/COAg/MA/W2BN4orIzEm\nhBA6R69sBG3PAgaReoHXl60eAFwuaQ5wKrBhYd1NtuflwfL30jK4/qt5HOD0vP0GNapwO/BbSYcB\nK9t+t6x+kRgTQgidoFc2gtl44NcsmQN6AnCz7Y1IYdnFWLO3Cq8XAstK+iipZ7eT7SGkSLXSPu/S\n8hkvKsf2ScC3gb7A7Tk9JoQQQifrjQ/GlPwReMX27JzpWTKAlgdlRtZRTn/SwzbzJK0BfA6YlNc9\nCmwG/A34cmkHSevYng3MlrQ5sB5V0moiNi2EEJqn1/YEbT9h+/QKq04GTpQ0nTq+JNieSboMej/w\nZ9KlzpLjgd9JmkrqOZYcnuccnAW8Q2okQwghdLKITevmIjYthBAaF7FpIYQQQg3RCIYQQui1emQj\nKGlhHmg+R9I1klbOyz8k6YoGyhkk6Y1c1szi4PgQQghLvx55T1DSfNv98usxwIO2f9GGcgYB1+bh\nEEg6ENja9oiy7ZYtH8vXWZYfONgDR5zWFYcOoceKSLHQm+4J3gmsCYt6dnPy6xUkXSBpdo4mG15H\nWf2Bl/P+IyWNlzQRuElSP0k3SZqWy/xS4Zj3STo/x6ZNkNQ3r/uYpH/kXuY0SesoOSX3YmdL2rsZ\nH0oIIYTaevQ4QUl9gJ2AP1RYfTBg2xvnwegTJK2b016K1smz0a8ErAh8srBuU2CI7ZckLQvsYfvV\nnAf6T0nj83aDgX1sf0fSZaQxgX8CxgIn2R6XI9qWAfYkxa9tAqwGTJF0q+2nC+c1ChgF0Kf/6m39\neEIIIdTQU3uCfXPD9QywBvD3CttsQ2qIsH0/8BiwboXt/m17qO11gMOB0YV1f7f9Un4t4Jd5bN8/\nSL3PNfK6R2zPyK/vAQblUOw1bY/LdXjT9oJcr0tsL7T9LHALsHmxQhGbFkIInaOnNoJv5PDpj5Aa\np4M7qNzxwHaF968XXu8HrA5slo/9LC1RaEvEqXVQfUIIITRRj/5jbXtBDqG+WtLZZasnkxquiZLW\nBdYGHqhR5DbAv6usGwA8Z/udfH/xI1W2K9XtNUlPSNrd9tWSlgf65HodmB/oWYXU6B5ZrZyITQsh\nhObp0Y0ggO3p+RLlPqQGpuRs4BxJs0lB1iNtv1WhiNI9QQFvk4KtKxkLXJPLm0qVrM8y+wPnSfoZ\nKR7tK8A4YCtgJmDgKNvP1FFWCCGEDtYjh0j0JhGbFkIIjat3iEQ0gt2cpNeofRm3O1kNeKGrK9GA\nqG/z9KS6QtS3mbqirh+xXfPx+h5/ObQXeKCebzPdhaSpUd/m6Un17Ul1hahvM3XnuvbUp0NDCCGE\ndotGMIQQQq8VjWD3N7r2Jt1K1Le5elJ9e1JdIerbTN22rvFgTAghhF4reoIhhBB6rWgEQwgh9FrR\nCHZjkj4r6QFJ/5J0dFfXpzWS/ijpudJUVt2ZpLUk3Szp3jz91fe7uk6tydOC3Z2n5Jor6fiurlM9\nJPXJ05hd29V1qUXSo3lqsxmSunU6haSVJV0h6f48jdtWXV2naiR9PH+mpZ9X/7+9+3mxKYzjOP7+\nCMUIC9JkFAvZIo0FSUQmwpKysbJAZKHY+A9kZzND5FcYdmJDYUGaSQklidxJKIlZST4W51HT5J4Z\nUc8zzvdVt3vP7S4+3W73+9zvec79SjqYO9dIcU6wUGlM1AtgA9ACHlGNa3qWNVgbktYAw8DZX0OK\nSyWpE+i0PZimfQwA2wt+bwV02B6WNAW4Dxyw/SBztFqSDgErgJm2t+TOU0fSa2CF7eIvPk//O3zP\ndq+kqcB0259z5xpL+k4bAlbafpM7zy/xS7Bc3cBL269sfwMuAdsyZ2rL9l3g05gvLIDtd7YH0+Ov\nwHPSYOYSuTKcDqekW9GrV0ldwGagN3eW/4mkWVR/ut8HYPvbRCiAyXqq0XXFFECIIliy+cDbEcct\nCv6inqgkLQSWAQ/zJqmXWouPgQ9Ucy6LzgucAA4DP3IHGSdTDd4eSEOtS7UI+AicTq3mXkkduUON\n0w7gYu4Qo0URDI0laQbQDxy0/SV3njppCPNSoAvollRsy1nSFqqxYwO5s/yB1baXAz3A3tTeL9Fk\nYDlw0vYyqpmnRe8XAEht263AldxZRosiWK4hYMGI4670XPgH0rm1fuC87Wu584xXan3dATblzlJj\nFbA1nWe7BKyTdC5vpHq2h9L9B6pxZ915E7XVAlojOgFXqYpi6XqAQdvvcwcZLYpguR4BiyUtSquo\nHVST78NfShtN+oDnto/nzjMWSXMlzU6Pp1FtlhrPPMssbB+x3WV7IdXn9rbtXZljtSWpI22QIrUW\nN7oMLdgAAAC7SURBVAJF7nJOs0ffSlqSnloPFLmha5SdFNgKhZgiUSzb3yXtA25RTaQ/Zftp5lht\nSboIrAXmSGoBx2z35U3V1iqqgcdP0nk2gKO2b2TMVKcTOJN2100CLtsu/rKDCWQecL1aGzEZuGD7\nZt5ItfYD59Pi+BWwO3OeWmlhsQHYkzvL78QlEiGEEBor2qEhhBAaK4pgCCGExooiGEIIobGiCIYQ\nQmisKIIhhBAaK4pgCCGExooiGEIIobF+Aj3cWIwbyiIDAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f66cc64ae80>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"dadosFinais[\"Valor\"].plot(kind='barh')\n",
"plt.title(\"IDEB por Município (Dados de 2009)\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Comentários sobre a geração dos documentos e do script \n",
"\n",
"Para converter este notebook para um script Python, use o comando"
]
},
{
"cell_type": "raw",
"metadata": {
"tags": [
"codecomment",
"verbatim"
]
},
"source": [
"jupyter-nbconvert --to python 'Exemplo1.ipynb' --template=removeextracode.tpl"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"O arquivo removeextracode.tpl tem o seguinte conteúdo:"
]
},
{
"cell_type": "raw",
"metadata": {
"tags": [
"codecomment",
"verbatim"
]
},
"source": [
"{% extends 'python.tpl'%}\n",
"\n",
"{% block input %}\n",
"{% if 'codecomment' in cell['metadata'].get('tags', []) %}\n",
" {{ cell.source | comment_lines }}\n",
"{% else %}\n",
" {{ cell.source | ipython2python }}\n",
"{% endif %}\n",
"{% endblock input %}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Célula de Inicialização <a id='sobre_inicializacao'></a>\n",
"\n",
"Através da extensão \"init_cell\" do nbextensions, é possível alterar a ordem de inicialização das células do notebook. Se olharmos os metadados da célula abaixo, veremos que ela está marcada pra ser executada antes de todas as outras células, obtendo-se assim o resultado desejado (esta célula permite que os gráficos da matploblib sejam renderizados dentro do notebook)."
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {
"init_cell": true,
"tags": [
"codecomment"
]
},
"outputs": [],
"source": [
"%matplotlib inline"
]
}
],
"metadata": {
"celltoolbar": "Tags",
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
},
"latex_metadata": {
"affiliation": "Universidade Federal de Santa Catarina, Florianópolis",
"author": "Melissa Weber Mendonça",
"title": "Exemplo: TDC Floripa 2017"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
jadijadi/persianlettercount | persian_letter_count.ipynb | 1 | 162551 | {
"metadata": {
"name": "",
"signature": "sha256:6fdfe924b976dfe69ed19141a307fbb6fcd0a099b51f5bcfc56731b03e5a22e4"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Distribution of persian letters\n",
"This code will use the dump of Persian wikipedia to find some stats about the persian letters distribution and frequency. It is done by www.Jadi.net and published under GPLv3 Licence\n",
"\n",
"## extracting a huge farsi file from wikipedia\n",
"First of all, this part reads the wikipedia dump and spits only the TEXT of articles. This will use a random number generator to keep only the 10% of articles.\n"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import xml.etree.ElementTree as etree\n",
"import re\n",
"import random\n",
"\n",
"inFile = '/home/jadi/w/wikipedia/fawiki-20150807-pages-articles.xml'\n",
"\n",
"random.seed()\n",
"counter = 0\n",
"\n",
"for event, elem in etree.iterparse(inFile, events=('start', 'end', 'start-ns', 'end-ns')):\n",
" if random.random() < 0.9: #only work on 10% of articles\n",
" try:\n",
" elem.clear()\n",
" except:\n",
" pass\n",
" continue\n",
"\n",
" thisTxt = None\n",
" try:\n",
" if elem.tag.endswith('/}text'):\n",
" thisTxt = elem.text\n",
" elem.clear()\n",
" except:\n",
" continue\n",
" \n",
" if not thisTxt:\n",
" elem.clear()\n",
" continue\n",
" \n",
"print thisTxt[1:10000]\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "ParseError",
"evalue": "no element found: line 100001, column 0",
"output_type": "pyerr",
"traceback": [
"\u001b[0;36m File \u001b[0;32m\"<string>\"\u001b[0;36m, line \u001b[0;32munknown\u001b[0m\n\u001b[0;31mParseError\u001b[0m\u001b[0;31m:\u001b[0m no element found: line 100001, column 0\n"
]
}
],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Removing tags\n",
"Will read the output text file from the previous step, will remove whatever between tags because tags are repeatative wikipeida syntax. We will also replace some arabic chars with persian equvalents"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import re\n",
"\n",
"inputText = '/home/jadi/w/wikipedia/wiki_fa.txt'\n",
"f = open(inputText, 'r')\n",
"alltext = f.read()\n",
"text = alltext\n",
"text=re.sub(\"\\n\", \" \", text)\n",
"text=re.sub(\"\\[+\", \"[\", text)\n",
"text=re.sub(\"\\]+\", \"]\", text)\n",
"text=re.sub(\"\\{+\", \"{\", text)\n",
"text=re.sub(\"\\}+\", \"}\", text)\n",
"text=re.sub(\"{.*?}\", \" \", text)\n",
"text=re.sub(\"\\<.*?\\>\", \" \", text)\n",
"text=re.sub(\"\\[.*?\\]\", \" \", text)\n",
"text=re.sub(\"\\s+\", \" \", text)\n",
"\n",
"# changing some arabic chars to correct persian ones\n",
"text=re.sub(u\"\u064a\", u\"\u06cc\", text)\n",
"text=re.sub(u\"\u0643\", u\"\u06a9\", text)\n",
"\n",
"\n",
"print text[1:10000]"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"/ / ''' ''' – ''' ''' – ''' ''' – ''' ''' /\u0647\u0641\u062a\u0647 /\u0647\u0641\u062a\u0647 } \u0646\u06af\u0627\u0631\u0647\u200c\u0647\u0627\u06cc \u0628\u0631\u06af\u0632\u06cc\u062f\u0647\u0654 \u0631\u0648\u0632\u0647\u0627\u06cc \u0627\u062e\u06cc\u0631: – – ''' ''' – ''' ''' __NOTOC__ __NOEDITSECTION__ \u0639\u0645\u0644\u06cc \u06a9\u0647 \u0634\u0645\u0627 \u062f\u0631\u062e\u0648\u0627\u0633\u062a \u06a9\u0631\u062f\u0647\u200c\u0627\u06cc\u062f \u0641\u0642\u0637 \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u062f \u062a\u0648\u0633\u0637 \u06a9\u0627\u0631\u0628\u0631\u0627\u0646 \u0628\u0627 \u0648\u0636\u0639\u06cc\u062a \u00ab\u062a\u0648\u0633\u0639\u0647\u200c\u062f\u0647\u0646\u062f\u0647\u00bb \u0627\u0646\u062c\u0627\u0645 \u0634\u0648\u062f. \u0628\u0647 $1 \u0645\u0631\u0627\u062c\u0639\u0647 \u06a9\u0646\u06cc\u062f. \u0634\u0631\u0645\u0646\u062f\u0647! \u0648\u06cc\u06a9\u06cc \u0645\u0634\u06a9\u0644\u0627\u062a \u0641\u0646\u06cc \u062f\u0627\u0631\u062f\u060c \u0648 \u0646\u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u062f \u0628\u0627 \u06a9\u0627\u0631\u06af\u0632\u0627\u0631 \u067e\u0627\u06cc\u06af\u0627\u0647 \u062f\u0627\u062f\u0647 \u062a\u0645\u0627\u0633 \u0628\u06af\u06cc\u0631\u062f. \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0627\u0633\u062a \u06a9\u0647 \u0628\u0627 \u0647\u0645\u06a9\u0627\u0631\u06cc \u062e\u0648\u0627\u0646\u0646\u062f\u06af\u0627\u0646\u0634 \u0646\u0648\u0634\u062a\u0647 \u0645\u06cc\u200c\u0634\u0648\u062f. \u0627\u06cc\u0646 \u0648\u0628\u200c\u06af\u0627\u0647 \u0627\u0633\u062a\u060c \u06cc\u0639\u0646\u06cc \u0647\u0631 \u06a9\u0633\u06cc\u060c \u0627\u0632 \u062c\u0645\u0644\u0647 ''\u062e\u0648\u062f \u0634\u0645\u0627'' \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u06cc\u062f \u0628\u0627 \u06a9\u0644\u06cc\u06a9 \u06a9\u0631\u062f\u0646 \u0631\u0648\u06cc \u067e\u06cc\u0648\u0646\u062f '''\u0648\u06cc\u0631\u0627\u06cc\u0634''' \u06a9\u0647 \u062f\u0631 \u0647\u0645\u0647\u0654 \u0645\u0642\u0627\u0644\u0627\u062a \u0645\u06cc\u200c\u0622\u06cc\u062f\u060c \u0622\u0646 \u0631\u0627 \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06a9\u0646\u06cc\u062f. == \u06af\u0634\u062a \u0648 \u06af\u0630\u0627\u0631 \u062f\u0631 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 == \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0632\u06cc\u0627\u062f\u06cc \u062f\u0631\u0628\u0627\u0631\u0647\u0654 \u0627\u0646\u0648\u0627\u0639 \u0648 \u0627\u0642\u0633\u0627\u0645 \u0645\u0648\u0636\u0648\u0639\u0627\u062a \u062f\u0627\u0631\u062f. \u0628\u0631\u0627\u06cc \u0622\u0632\u0645\u0627\u06cc\u0634 \u0628\u0647 \u0628\u0631\u0648\u06cc\u062f\u060c \u0645\u0648\u0636\u0648\u0639\u06cc \u06a9\u0647 \u0628\u0631\u0627\u06cc\u062a\u0627\u0646 \u062c\u0630\u0627\u0628 \u0627\u0633\u062a \u0631\u0627 \u0627\u0646\u062a\u062e\u0627\u0628 \u0648 \u0634\u0631\u0648\u0639 \u0628\u0647 \u06a9\u0646\u062f\u0648\u06a9\u0627\u0648 \u06a9\u0646\u06cc\u062f. \u062f\u0631 \u0628\u0627\u0644\u0627\u06cc \u0647\u0631 \u0635\u0641\u062d\u0647 \u0646\u06cc\u0632 \u0642\u0633\u0645\u062a\u06cc \u0628\u0631\u0627\u06cc \u062c\u0633\u062a\u062c\u0648 \u0648\u062c\u0648\u062f \u062f\u0627\u0631\u062f \u062a\u0627 \u0628\u062a\u0648\u0627\u0646\u06cc\u062f \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0631\u0627 \u0628\u0647 \u0633\u0631\u0639\u062a \u067e\u06cc\u062f\u0627 \u06a9\u0646\u06cc\u062f. \u0627\u06af\u0631 \u0686\u06cc\u0632\u06cc \u0631\u0627 \u062e\u0648\u0627\u0646\u062f\u06cc\u062f \u0648 \u0628\u0647\u200c\u0648\u0627\u0642\u0639 \u0628\u0631\u0627\u06cc\u062a\u0627\u0646 \u062c\u0627\u0644\u0628 \u0628\u0648\u062f\u060c \u06cc\u0627\u062f\u062f\u0627\u0634\u062a\u06cc \u062f\u0631 \u0642\u0633\u0645\u062a \u0645\u0642\u0627\u0644\u0647 \u0628\u0646\u0648\u06cc\u0633\u06cc\u062f. \u0628\u0631\u0627\u06cc \u0627\u06cc\u0646 \u06a9\u0627\u0631 \u0627\u0648\u0644 \u067e\u06cc\u0648\u0646\u062f '''\u0628\u062d\u062b ''' \u0631\u0627 \u0627\u0646\u062a\u062e\u0627\u0628 \u06a9\u0646\u06cc\u062f (\u062f\u0631 \u0646\u0648\u0627\u0631 \u0628\u0627\u0644\u0627\u06cc \u0635\u0641\u062d\u0647 \u0628\u0647 \u062f\u0646\u0628\u0627\u0644 \u0622\u0646 \u0628\u06af\u0631\u062f\u06cc\u062f) \u062a\u0627 \u0628\u0647 \u0635\u0641\u062d\u0647\u0654 \u0628\u062d\u062b \u0628\u0631\u0648\u06cc\u062f. \u0633\u067e\u0633 '''\u0648\u06cc\u0631\u0627\u06cc\u0634''' \u0631\u0627 \u062f\u0631 \u0635\u0641\u062d\u0647\u0654 \u0628\u062d\u062b \u0627\u0646\u062a\u062e\u0627\u0628 \u06a9\u0646\u06cc\u062f. \u0622\u06af\u0627\u0647\u06cc \u0627\u0632 \u0646\u0638\u0631 \u0634\u0645\u0627 \u0645\u0627\u06cc\u0647\u0654 \u062e\u0648\u0634\u062d\u0627\u0644\u06cc \u0645\u0627\u0633\u062a. \u0627\u06af\u0631 \u0645\u0627 \u0628\u0647 \u0645\u0648\u0636\u0648\u0639\u06cc \u0646\u067e\u0631\u062f\u0627\u062e\u062a\u0647\u200c\u0627\u06cc\u0645 \u06cc\u0627 \u0628\u0631\u0627\u06cc \u067e\u06cc\u062f\u0627 \u06a9\u0631\u062f\u0646 \u0686\u06cc\u0632\u06cc \u062f\u0631\u062f\u0633\u0631 \u062f\u0627\u0631\u06cc\u062f\u060c \u0627\u0632 \u0628\u067e\u0631\u0633\u06cc\u062f \u06cc\u0627 \u0645\u0648\u0636\u0648\u0639 \u0631\u0627 \u0628\u0647 \u0641\u0647\u0631\u0633\u062a \u0627\u0636\u0627\u0641\u0647 \u06a9\u0646\u06cc\u062f. ''\u0631\u062c\u0648\u0639 \u0634\u0648\u062f \u0628\u0647'': == \u0648\u06cc\u0631\u0627\u06cc\u0634 == \u0647\u0631 \u06a9\u0633\u06cc \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u062f \u0635\u0641\u062d\u0627\u062a \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0631\u0627 \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06a9\u0646\u062f. (\u062d\u062a\u06cc \u0627\u06cc\u0646 \u0635\u0641\u062d\u0647 \u0631\u0627!) \u06a9\u0627\u0641\u06cc \u0627\u0633\u062a \u067e\u06cc\u0648\u0646\u062f '''\u0648\u06cc\u0631\u0627\u06cc\u0634''' \u0631\u0627 \u062f\u0631 \u0628\u0627\u0644\u0627 \u06cc\u0627 \u067e\u0627\u06cc\u06cc\u0646 \u0635\u0641\u062d\u0647\u200c\u0627\u06cc \u06a9\u0647 \u0641\u06a9\u0631 \u0645\u06cc\u200c\u06a9\u0646\u06cc\u062f \u0646\u06cc\u0627\u0632\u0645\u0646\u062f \u0648\u06cc\u0631\u0627\u06cc\u0634 \u0627\u0633\u062a \u0627\u0646\u062a\u062e\u0627\u0628 \u06a9\u0646\u06cc\u062f. \u0635\u0644\u0627\u062d\u06cc\u062a \u062e\u0627\u0635\u06cc \u0644\u0627\u0632\u0645 \u0646\u06cc\u0633\u062a\u060c \u062d\u062a\u06cc \u0644\u0627\u0632\u0645 \u0646\u06cc\u0633\u062a \u0628\u0647 \u0633\u06cc\u0633\u062a\u0645 \u0634\u0648\u06cc\u062f. \u0628\u0631\u0627\u06cc \u062a\u0645\u0631\u06cc\u0646 \u0627\u06cc\u0646 \u06a9\u0627\u0631\u060c \u0628\u062f\u0648\u0646 \u0631\u06cc\u0633\u06a9 \u062e\u0631\u0627\u0628 \u06a9\u0631\u062f\u0646 \u06cc\u06a9 \u0645\u0642\u0627\u0644\u0647\u0654 \u0648\u0627\u0642\u0639\u06cc \u0633\u0631\u06cc \u0628\u0647 \u0628\u0632\u0646\u06cc\u062f. \u062c\u0627\u06cc\u06cc \u06a9\u0647 \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u06cc\u062f \u0647\u0631 \u0686\u0642\u062f\u0631 \u062f\u0644\u062a\u0627\u0646 \u0645\u06cc\u200c\u062e\u0648\u0627\u0647\u062f \u062a\u0645\u0631\u06cc\u0646 \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06a9\u0646\u06cc\u062f. \u0628\u0631\u0627\u06cc \u062a\u0645\u0631\u06cc\u0646 \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06cc\u06a9 \u0635\u0641\u062d\u0647\u0654 \u0645\u0648\u062c\u0648\u062f \u0645\u062b\u0644 \u0647\u0645\u06cc\u0646 \u0635\u0641\u062d\u0647\u060c \u0622\u0646 \u0631\u0627 \u062f\u0631 \u00ab\u0635\u0641\u062d\u0647 \u062a\u0645\u0631\u06cc\u0646\u00bb \u06a9\u067e\u06cc \u06a9\u0646\u06cc\u062f. \u0627\u06af\u0631 \u0645\u06cc\u200c\u062e\u0648\u0627\u0647\u06cc\u062f \u0628\u06cc\u0634\u062a\u0631 \u0628\u062f\u0627\u0646\u06cc\u062f\u060c \u0648 \u0631\u0627 \u0628\u0628\u06cc\u0646\u06cc\u062f \u062a\u0627 \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0636\u0631\u0648\u0631\u06cc \u0628\u0631\u0627\u06cc \u0627\u0639\u0636\u0627\u06cc \u0627\u06cc\u0646 \u067e\u0631\u0648\u0698\u0647 \u0631\u0627 \u06cc\u0627\u062f \u0628\u06af\u06cc\u0631\u06cc\u062f. \u06cc\u06a9 \u0631\u0627\u0647 \u0633\u0627\u062f\u0647 \u0628\u0631\u0627\u06cc \u06a9\u0645\u06a9\u060c \u0627\u0633\u062a\u0641\u0627\u062f\u0647 \u0627\u0632 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0627\u0633\u062a\u060c \u062f\u0631\u0633\u062a \u0645\u0627\u0646\u0646\u062f \u0647\u0631 \u062f\u0627\u0646\u0634\u0646\u0627\u0645\u0647\u0654 \u062f\u06cc\u06af\u0631\u061b \u0628\u0627 \u0627\u06cc\u0646 \u062a\u0641\u0627\u0648\u062a \u06a9\u0647 \u0647\u0631 \u0648\u0642\u062a \u0628\u0647 \u0627\u06cc\u0631\u0627\u062f\u06cc \u0628\u0631\u062e\u0648\u0631\u062f\u06cc\u062f -\u0645\u062b\u0644\u0627\u064b \u0628\u0647 \u06cc\u06a9 \u063a\u0644\u0637 \u0627\u0645\u0644\u0627\u06cc\u06cc \u06cc\u0627 \u06cc\u06a9 \u062c\u0645\u0644\u0647\u0654 \u0646\u0627\u0645\u0641\u0647\u0648\u0645- \u067e\u06cc\u0648\u0646\u062f \u00ab\u0648\u06cc\u0631\u0627\u06cc\u0634 \u0627\u06cc\u0646 \u0635\u0641\u062d\u0647\u00bb \u0631\u0627 \u0627\u0646\u062a\u062e\u0627\u0628 \u06a9\u0646\u06cc\u062f \u0648 \u062f\u0631\u0633\u062a\u0634 \u06a9\u0646\u06cc\u062f. . \u0647\u0631\u06af\u0648\u0646\u0647 \u0628\u0647\u0628\u0648\u062f\u06cc \u0631\u0627 \u0627\u0639\u0645\u0627\u0644 \u06a9\u0646\u06cc\u062f. \u0632\u06cc\u0627\u062f \u0646\u06af\u0631\u0627\u0646 \u0627\u0634\u062a\u0628\u0627\u0647 \u06a9\u0631\u062f\u0646 \u0646\u0628\u0627\u0634\u06cc\u062f. \u0627\u0634\u062a\u0628\u0627\u0647\u0627\u062a \u06a9\u0648\u0686\u06a9 \u0631\u0627 \u0647\u0645\u06cc\u0634\u0647 \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u06cc\u062f \u0628\u0639\u062f\u062a\u0631 \u0627\u0635\u0644\u0627\u062d \u06a9\u0646\u06cc\u062f \u06cc\u0627 \u062f\u06cc\u06af\u0631\u0627\u0646 \u0627\u0635\u0644\u0627\u062d \u06a9\u0646\u0646\u062f. \u0634\u0627\u06cc\u062f \u0627\u06cc\u0646 \u0645\u0633\u0623\u0644\u0647 \u06a9\u0645\u06cc \u062a\u0631\u0633\u0646\u0627\u06a9 \u0628\u0647 \u0646\u0638\u0631 \u0628\u0631\u0633\u062f. \u0628\u0631\u0627\u06cc \u062a\u0648\u0636\u06cc\u062d \u062f\u0644\u06cc\u0644 \u0639\u0645\u0644\u06cc \u0628\u0648\u062f\u0646 \u0627\u06cc\u0646 \u0633\u06cc\u0633\u062a\u0645\u060c \u0631\u0627 \u0628\u0628\u06cc\u0646\u06cc\u062f. \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0628\u0627 \u0648\u062c\u0648\u062f\u0650 \u062f\u0627\u0634\u062a\u0646 \u062a\u0639\u062f\u0627\u062f \u0632\u06cc\u0627\u062f\u06cc \u0645\u0642\u0627\u0644\u0647\u060c \u0647\u0645\u0686\u0646\u0627\u0646 \u0628\u0647 \u062e\u0627\u0637\u0631 \u0627\u0636\u0627\u0641\u0647 \u0634\u062f\u0646 \u0645\u0642\u0627\u0644\u0627\u062a \u062c\u062f\u06cc\u062f\u06cc \u06a9\u0647 \u06a9\u0633\u0627\u0646\u06cc \u0645\u062b\u0644 \u0634\u0645\u0627 \u0645\u06cc\u200c\u0646\u0648\u06cc\u0633\u0646\u062f\u060c \u062f\u0631 \u062d\u0627\u0644 \u0631\u0634\u062f \u0627\u0633\u062a. \u0634\u0645\u0627 \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u06cc\u062f \u06cc\u0627 \u06cc\u06a9\u06cc \u0627\u0632 \u0645\u0642\u0627\u0644\u0627\u062a \u0645\u0648\u062c\u0648\u062f \u0631\u0627 \u0627\u0646\u062a\u062e\u0627\u0628 \u06a9\u0631\u062f\u0647\u060c \u0628\u062e\u0634\u06cc \u062c\u062f\u06cc\u062f\u06cc \u0628\u0647 \u0622\u0646 \u0627\u0636\u0627\u0641\u0647 \u06a9\u0646\u06cc\u062f. \u0628\u0647\u062a\u0631 \u0627\u0633\u062a \u0646\u06af\u0627\u0647\u06cc \u0628\u0647 \u200c\u0647\u0627\u06cc \u0645\u0627 \u0628\u06cc\u0627\u0646\u062f\u0627\u0632\u06cc\u062f. \u0628\u0647 \u062e\u0635\u0648\u0635 \u0633\u06cc\u0627\u0633\u062a \u06a9\u0647 \u0628\u0647 \u0627\u06cc\u0646 \u0645\u0639\u0646\u0627\u0633\u062a \u06a9\u0647 \u0645\u0642\u0627\u0644\u0627\u062a \u0646\u0628\u0627\u06cc\u062f \u062c\u0627\u0646\u0628\u062f\u0627\u0631\u0627\u0646\u0647 \u0628\u0627\u0634\u0646\u062f \u0648 \u0628\u0627\u06cc\u062f \u062f\u06cc\u062f\u06af\u0627\u0647\u200c\u0647\u0627\u06cc \u0645\u062e\u062a\u0644\u0641 \u062f\u0631\u0628\u0627\u0631\u0647\u0654 \u0645\u0648\u0636\u0648\u0639 \u0631\u0627 \u0645\u0646\u0635\u0641\u0627\u0646\u0647 \u0648 \u062f\u0644\u0633\u0648\u0632\u0627\u0646\u0647 \u0628\u06cc\u0627\u0646 \u06a9\u0646\u0646\u062f. \u0627\u06af\u0631 \u0645\u062a\u0648\u062c\u0647 \u0634\u062f\u06cc\u062f \u06a9\u0647 \u062a\u063a\u06cc\u06cc\u0631\u0627\u062a \u0634\u0645\u0627 \u0631\u0627 \u0627\u0635\u0644\u0627\u062d \u06cc\u0627 \u062d\u0630\u0641 \u0645\u06cc\u200c\u06a9\u0646\u0646\u062f\u060c \u0628\u0631\u0627\u06cc \u067e\u06cc\u062f\u0627 \u06a9\u0631\u062f\u0646 \u0639\u0644\u062a \u062a\u0627\u0631\u06cc\u062e\u0686\u0647\u0654 \u0635\u0641\u062d\u0647\u060c \u0635\u0641\u062d\u0647\u0654 \u0628\u062d\u062b \u062e\u0648\u062f\u062a\u0627\u0646 \u0648 \u0635\u0641\u062d\u0647\u0654 \u0628\u062d\u062b \u0645\u0642\u0627\u0644\u0647 \u0631\u0627 \u0628\u0628\u06cc\u0646\u06cc\u062f. \u062a\u0645\u0627\u0645 \u0645\u0634\u0627\u0631\u06a9\u062a\u200c\u0647\u0627 \u062f\u0631 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u062a\u062d\u062a (GFDL) \u0645\u0646\u062a\u0634\u0631 \u0645\u06cc\u200c\u0634\u0648\u0646\u062f. \u0627\u06cc\u0646 \u0627\u062c\u0627\u0632\u0647\u200c\u0646\u0627\u0645\u0647 \u0642\u0627\u0628\u0644\u06cc\u062a \u062a\u0648\u0632\u06cc\u0639 \u0622\u0632\u0627\u062f \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 \u0631\u0627 \u0628\u0631\u0627\u06cc \u0647\u0645\u06cc\u0634\u0647 \u062a\u0636\u0645\u06cc\u0646 \u0645\u06cc\u200c\u06a9\u0646\u062f (\u0628\u0631\u0627\u06cc \u0627\u0637\u0644\u0627\u0639 \u0628\u06cc\u0634\u062a\u0631 \u0631\u0627 \u0628\u0628\u0646\u06cc\u062f). == \u0628\u0647 \u0645\u0627 \u0628\u067e\u06cc\u0648\u0646\u062f\u06cc\u062f == \u0647\u0645\u0647 \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u0646\u062f \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06a9\u0646\u0646\u062f \u0627\u0645\u0627 \u0627\u06af\u0631 \u0645\u06cc\u200c\u062e\u0648\u0627\u0647\u06cc\u062f \u062f\u0627\u0626\u0645 \u0648\u06cc\u0631\u0627\u06cc\u0634 \u06a9\u0646\u06cc\u062f\u060c \u062f\u0631\u0633\u062a \u06a9\u0631\u062f\u0646 \u062d\u0633\u0627\u0628 \u062f\u0627\u0631\u062f. \u0627\u06af\u0631 \u0645\u06cc\u200c\u062e\u0648\u0627\u0647\u06cc\u062f \u0639\u0636\u0648 \u0634\u0648\u06cc\u062f \u0628\u0631\u0627\u06cc \u062e\u0648\u062f\u062a\u0627\u0646 . == \u0645\u0631\u0627\u062c\u0639\u0627\u062a == === \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0639\u0645\u0648\u0645\u06cc \u0648 \u0631\u0627\u0647\u0646\u0645\u0627\u0647\u0627 === * * - \u0631\u0627\u0647\u0646\u0645\u0627\u06cc \u0648\u06cc\u0631\u0627\u06cc\u0634\u060c \u0634\u0631\u0648\u0639 \u0645\u0642\u0627\u0644\u0647\u0654 \u062c\u062f\u06cc\u062f \u0648 \u0686\u06cc\u0632\u0647\u0627\u06cc \u0628\u0633\u06cc\u0627\u0631 \u062f\u06cc\u06af\u0631 * - \u067e\u0631\u0633\u0634\u200c\u0647\u0627\u06cc \u0631\u0627\u06cc\u062c \u062f\u0631 \u0645\u0648\u0631\u062f \u067e\u0627\u06cc\u06af\u0627\u0647 * - \u0648\u0627\u0698\u0647\u200c\u0646\u0627\u0645\u0647\u0654 \u0627\u0635\u0637\u0644\u0627\u062d\u0627\u062a \u0645\u062a\u062f\u0627\u0648\u0644 \u062f\u0631 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 * * === \u0634\u0647\u0631\u0648\u0646\u062f\u06cc \u062f\u0631 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 === ==== \u06af\u0648\u0634\u0647\u0654 \u0622\u0645\u0648\u0632\u0634\u06cc ==== * * * * * ==== \u06a9\u0646\u062f\u0648\u06a9\u0627\u0648\u0647\u0627\u06cc \u0639\u0645\u06cc\u0642\u200c\u062a\u0631 ==== * * === \u062c\u0627\u0645\u0639\u0647\u0654 \u0648\u06cc\u06a9\u06cc\u200c\u067e\u062f\u06cc\u0627 === * * - \u0641\u0647\u0631\u0633\u062a\u200c\u0647\u0627\u06cc \u0645\u062e\u062a\u0644\u0641 \u0627\u0632 \u0645\u0634\u0627\u0631\u06a9\u062a\u200c\u06a9\u0646\u0646\u062f\u06af\u0627\u0646. \u0627\u06af\u0631 \u062f\u0648\u0633\u062a \u062f\u0627\u0631\u06cc\u062f \u0645\u06cc\u200c\u062a\u0648\u0627\u0646\u06cc\u062f \u0646\u0627\u0645\u062a\u0627\u0646 \u0631\u0627 \u0627\u0636\u0627\u0641\u0647 \u06a9\u0646\u06cc\u062f. ''\u0627\u06cc\u0646 \u0646\u0648\u0634\u062a\u0627\u0631 \u0628\u0647 \u0648\u0627\u0698\u0647 \u00ab\u0627\u0637\u0651\u0644\u0627\u0639\u0627\u062a\u00bb \u0628\u0647 \u0645\u0641\u0647\u0648\u0645\u06cc \u06a9\u0647 \u062f\u0631 \u0637\u0648\u0644 (\u0622\u06af\u0627\u0647\u06cc) \u0648 (\u062f\u0627\u0646\u0634) \u0628\u0647 \u06a9\u0627\u0631 \u0645\u06cc\u200c\u0631\u0648\u062f\u060c \u0645\u06cc\u200c\u067e\u0631\u062f\u0627\u0632\u062f. \u0628\u0631\u0627\u06cc \u062f\u06cc\u06af\u0631 \u06a9\u0627\u0631\u0628\u0631\u062f\u0647\u0627 \u0631\u0627 \u0628\u0628\u06cc\u0646\u06cc\u062f. '' '''\u0627\u0637\u0651\u0644\u0627\u0639''' \u06cc\u0627 '''\u0622\u06af\u0627\u0647\u0634''' \u062f\u0631 \u06a9\u0648\u062a\u0627\u0647\u200c\u062a\u0631\u06cc\u0646 \u062a\u0639\u0631\u06cc\u0641\u060c \u00ab\u062f\u0627\u062f\u0647\u200c\u0647\u0627\u06cc \u067e\u0631\u062f\u0627\u0632\u0634 \u0646\u0634\u062f\u0647\u00bb \u0627\u0633\u062a. \u062f\u0627\u062f\u0647\u200c\u0647\u0627 \u0645\u0648\u0627\u062f \u062e\u0627\u0645 \u0628\u0627\u0644\u0642\u0648\u0647 \u0645\u0639\u0646\u06cc\u200c\u062f\u0627\u0631\u06cc \u0647\u0633\u062a\u0646\u062f \u06a9\u0647 \u0645\u0627 \u0622\u0646\u200c\u0647\u0627 \u0631\u0627 \u062f\u0631 \u0631\u0627\u0633\u062a\u0627\u06cc \u0634\u0646\u0627\u062e\u062a \u0648 \u0641\u0647\u0645 \u0647\u0631 \u0645\u0641\u0647\u0648\u0645 \u0645\u0627\u062f\u06cc \u06cc\u0627 \u063a\u06cc\u0631 \u0645\u0627\u062f\u06cc\u060c \u0628\u0647 \u0648\u0627\u0633\u0637\u0647 \u0631\u0648\u0634\u200c\u0647\u0627\u06cc \u067e\u0698\u0648\u0647\u0634\u06cc\u060c \u0648 \u0628\u0627 \u0627\u0633\u062a\u0641\u0627\u062f\u0647 \u0627\u0632 \u0627\u0628\u0632\u0627\u0631\u0647\u0627\u06cc \u0634\u0646\u0627\u062e\u062a\u06cc \u0628\u0647 \u062f\u0633\u062a \u0645\u06cc\u200c\u0622\u0648\u0631\u06cc\u0645. \u062f\u0627\u062f\u0647 \u06cc\u06a9 \u0634\u0631\u062d \u0645\u0642\u062f\u0645\u0627\u062a\u06cc \u0627\u0632 \u06cc\u06a9 \u067e\u062f\u06cc\u062f\u0647\u060c \u0627\u062a\u0641\u0627\u0642\u060c \u0641\u0639\u0627\u0644\u06cc\u062a \u0648 \u06cc\u0627 \u062a\u0639\u0627\u0645\u0644\u0627\u062a \u0627\u0633\u062a \u06a9\u0647 \u062b\u0628\u062a \u0634\u062f\u0647 \u0627\u0633\u062a\u060c \u062f\u0633\u062a\u0647\u200c\u0628\u0646\u062f\u06cc \u0634\u062f\u0647 \u0648 \u0630\u062e\u06cc\u0631\u0647 \u0634\u062f\u0647 \u0627\u0633\u062a\u061b \u0627\u0645\u0627 \u0633\u0627\u0632\u0645\u0627\u0646\u062f\u0647\u06cc \u0646\u0634\u062f\u0647 \u0648 \u0628\u0631\u0627\u06cc \u06cc\u06a9 \u0645\u0646\u0638\u0648\u0631 \u0645\u0634\u062e\u0635 \u0622\u0645\u0627\u062f\u0647 \u0646\u0634\u062f\u0647 \u0627\u0633\u062a. \u062f\u0627\u062f\u0647\u200c\u0647\u0627 \u0639\u0646\u0627\u0635\u0631 \u0627\u0635\u0644\u06cc \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0647\u0633\u062a\u0646\u062f. \u062f\u0627\u062f\u0647\u200c\u0647\u0627 \u062f\u0631 \u0635\u0648\u0631\u062a\u06cc \u0628\u0647 \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u062a\u0628\u062f\u06cc\u0644 \u0645\u06cc\u200c\u0634\u0648\u0646\u062f \u06a9\u0647 \u0627\u0641\u0631\u0627\u062f \u0628\u062e\u0648\u0627\u0647\u0646\u062f \u0628\u0631\u0627\u06cc \u062f\u0631\u06a9 \u0628\u06cc\u0634\u062a\u0631 \u0627\u0632 \u0622\u0646\u0647\u0627 \u0627\u0633\u062a\u0641\u0627\u062f\u0647 \u06a9\u0646\u0646\u062f. \u0627\u0637\u0644\u0627\u0639\u0627\u062a\u060c \u062f\u0627\u062f\u0647\u200c\u0647\u0627\u06cc \u062e\u0644\u0627\u0635\u0647\u200c\u0627\u06cc \u0647\u0633\u062a\u0646\u062f \u06a9\u0647 \u06af\u0631\u0648\u0647\u200c\u0628\u0646\u062f\u06cc\u060c \u0630\u062e\u06cc\u0631\u0647\u060c \u067e\u0627\u0644\u0627\u06cc\u0634 \u0648 \u0633\u0627\u0632\u0645\u0627\u0646\u062f\u0647\u06cc \u0634\u062f\u0647\u200c\u0627\u0646\u062f \u062a\u0627 \u0628\u062a\u0648\u0627\u0646\u0646\u062f \u0645\u0639\u0646\u06cc\u200c\u062f\u0627\u0631 \u0634\u0648\u0646\u062f. \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0632\u0645\u0627\u0646\u06cc \u0627\u0631\u0632\u0634 \u067e\u06cc\u062f\u0627 \u0645\u06cc\u200c\u06a9\u0646\u0646\u062f \u06a9\u0647 \u0628\u0631\u0627\u06cc \u06cc\u06a9 \u0628\u064f\u0639\u062f \u062e\u0627\u0635\u060c \u06cc\u06a9 \u0641\u0631\u062f \u062e\u0627\u0635\u060c \u06cc\u06a9 \u0647\u062f\u0641 \u062e\u0627\u0635 \u0648 \u062f\u0631 \u0632\u0645\u0627\u0646 \u062e\u0627\u0635 \u06af\u0631\u062f\u0622\u0648\u0631\u06cc \u0648 \u0622\u0645\u0627\u062f\u0647 \u0634\u0648\u0646\u062f\u060c \u0644\u0630\u0627 \u0627\u0637\u0644\u0627\u0639\u0627\u062a\u06cc \u06a9\u0647 \u0628\u0631\u0627\u06cc \u06cc\u06a9 \u0645\u062f\u06cc\u0631\u060c \u062c\u0646\u0628\u0647 \u0627\u0637\u0644\u0627\u0639\u0627\u062a\u06cc \u062f\u0627\u0631\u062f\u060c \u0628\u0631\u0627\u06cc \u0645\u062f\u06cc\u0631 \u062f\u06cc\u06af\u0631 \u0645\u0645\u06a9\u0646 \u0627\u0633\u062a \u0627\u0635\u0644\u0627\u064b \u0627\u0631\u0632\u0634\u06cc \u0646\u062f\u0627\u0634\u062a\u0647 \u0628\u0627\u0634\u062f. \u0628\u062f\u06cc\u0646 \u062a\u0631\u062a\u06cc\u0628\u060c \u0627\u0637\u0644\u0627\u0639\u0627\u062a\u060c \u0622\u06af\u0627\u0647\u06cc\u200c\u0647\u0627\u06cc \u0628\u0647 \u062f\u0633\u062a \u0622\u0645\u062f\u0647 \u0627\u0632 \u0639\u0646\u0635\u0631\u0647\u0627 \u0648 \u0631\u0648\u06cc\u062f\u0627\u062f\u0647\u0627\u06cc \u062c\u0647\u0627\u0646 \u0647\u0633\u062a\u06cc \u0627\u0633\u062a. \u0628\u0647 \u0632\u0628\u0627\u0646 \u0645\u062d\u062f\u0648\u062f \u062a\u06a9\u0646\u06cc\u06a9\u06cc\u060c \u0645\u062c\u0645\u0648\u0639\u0647\u200c\u0627\u06cc \u0627\u0632 \u0646\u0645\u0627\u062f\u0647\u0627\u06cc \u0632\u0628\u0627\u0646\u06cc \u0645\u0639\u0646\u06cc\u200c\u062f\u0627\u0631 \u0648 \u067e\u06cc\u0648\u0633\u062a\u0647 \u062f\u0631\u0628\u0627\u0631\u0647\u0654 \u0645\u0648\u062c\u0648\u062f\u0627\u062a \u0627\u0633\u062a. \u062f\u0631 \u0632\u0628\u0627\u0646 \u0627\u0646\u06af\u0644\u06cc\u0633\u06cc\u060c \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0627\u0632 \u0646\u0638\u0645\u06cc \u0633\u0627\u062e\u062a\u0627\u0631\u06cc \u0648 \u0630\u0627\u062a\u06cc \u062e\u0628\u0631 \u0645\u06cc\u200c\u062f\u0647\u062f. \u0627\u0632 \u0645\u0646\u0638\u0631 \u060c \u0627\u0637\u0651\u0644\u0627\u0639\u0627\u062a \u0645\u0641\u0647\u0648\u0645\u06cc \u0686\u0646\u062f\u0634\u06a9\u0644\u06cc \u0648 \u0686\u0646\u062f\u0645\u0639\u0646\u0627\u06cc\u06cc \u0627\u0633\u062a. == \u062c\u0633\u062a\u0627\u0631\u0647\u0627\u06cc \u0648\u0627\u0628\u0633\u062a\u0647 == === \u0645\u0641\u0627\u0647\u06cc\u0645 \u062f\u0631 \u0637\u0648\u0644 \u0627\u0637\u0644\u0627\u0639\u0627\u062a === * * \u0631\u0627\u0628\u0637\u0647 \u0639\u0644\u0645 \u0648 \u062f\u0627\u0646\u0634 \u0628\u0627 \u067e\u06cc\u0634\u0631\u0641\u062a \u0628\u0634\u0631 === \u0645\u0641\u0627\u0647\u06cc\u0645 \u062f\u0631 \u0639\u0631\u0636 \u0627\u0637\u0644\u0627\u0639\u0627\u062a === * * * * * * * * * * * * \u0627\u0647\u062f\u0627\u0641 \u0639\u0644\u0645 \u0627\u0637\u0644\u0627\u0639\u0627\u062a \u0648 \u062f\u0627\u0646\u0634\u200c\u0634\u0646\u0627\u0633\u06cc \u0631\u0627\u0647\u0628\u0631\u062f\u0647\u0627\u06cc \u0627\u0637\u0644\u0627\u0639\u0627\u062a == \u0645\u0646\u0627\u0628\u0639 == * Earl Morrogh, Information Architecture, An Emerging 21st Century Profession, Pearson Education, Inc. , 2003. ISBN 0-13-096746-7 * Alan Liu (2004). ''The Laws of Cool: Knowledge Work and the Culture of Information'', University of Chicago Press * Bekenstein, Jacob D. (2003, August). Information in the . ''Scientific American''. * (2011). The Information: A History, a Theory, a Flood. Pantheon, New York, NY. * Shu-Kun Lin (2008). 'Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship', ''Entropy'', 10 (1), 1-5. Available online at . * Luciano Floridi, (2005). 'Is Information Meaningful Data?', ''Philosophy and Phenomenological Research'', 70 (2), pp. 351 \u2013 370. Available online at * Luciano Floridi, (2005). 'Semantic Conceptions of Information', ''The Stanford Encyclopedia of Philosophy'' (Winter 2005 Edition), Edward N. Zalta (ed.). Available online at * Sandro Nielsen: 'The Effect of Lexicographical Information Costs on Dictionary Making and Use', ''Lexikos'' 18/2008, 170-189. * Stewart, Thomas, (2001). Wealth of Knowledge. Doubleday, New York, NY, 379 p. * Young, Paul. The Nature of Information (1987). Greenwood Publishing Group, Westport, Ct. ISBN 0-275-92698-2. == \u067e\u06cc\u0648\u0646\u062f \u0628\u0647 \u0628\u06cc\u0631\u0648\u0646 == * * Review by Luciano Floridi for the Stanford Encyclopedia of Philosophy * * This essay is continually revised in the light of ongoing research. *\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## now lets keep ONLY persian chars\n",
"````\n",
"$ sed 's/[^\u0622\u0626\u0627\u0628\u067e\u062a\u062b\u062c\u0686\u062d\u062e\u062f\u0630\u0631\u0632\u0698\u0633\u0634\u0635\u0636\u0637\u0638\u0639\u063a\u0641\u0642\u06a9\u06af\u0644\u0645\u0646\u0648\u0647\u06cc\u200c ]*//g' wiki_fa_only_text.txt > wiki_only_farsi_chars.txt\n",
"````"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Doing stats\n"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f = open('/home/jadi/w/wikipedia/wiki_only_farsi_chars.txt', 'r')\n",
"alltext = f.read()\n",
"alltext = alltext.decode(\"utf-8\")"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Alphabet distribution"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### most frequest letters"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"allchars = {}\n",
"for i in range(0, len(alltext)):\n",
" allchars[alltext[i]] = allchars.get(alltext[i], 0) + 1\n",
"\n",
"allwordsnum = allchars[' ']\n",
"totalcharsnum = len(alltext) - allchars[' ']\n",
"del allchars[' ']\n",
"del allchars['\\n']\n",
"\n",
"import numpy as np\n",
"from matplotlib import pyplot as plt\n",
"\n",
"letters = u'\u0622\u0627\u0628\u067e\u062a\u062b\u062c\u0686\u062d\u062e\u062f\u0630\u0631\u0632\u0698\u0633\u0634\u0635\u0636\u0637\u0638\u0639\u063a\u0641\u0642\u06a9\u06af\u0644\u0645\u0646\u0648\u0647\u06cc'\n",
"lettervals = []\n",
"letterlist = []\n",
"for letter in list(letters):\n",
" print letter, allchars[letter]\n",
" lettervals.append(allchars[letter]*1.0/totalcharsnum*100)\n",
"\n",
"width = 1/1.5\n",
"plt.figure(figsize=(20,10))\n",
"plt.bar( range(len(lettervals)), lettervals, width)\n",
"plt.xticks([x+0.3 for x in range(len(lettervals))], list(letters), fontsize=18 )\n",
"plt.title(u'Percentage of persian letters\\n10% of wikipedia articles are tested', fontsize=34)\n",
"plt.ylabel('Percent', fontsize=20)\n",
"plt.xlabel('Letter', fontsize=20)\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\u0622 193306\n",
"\u0627 3908207\n",
"\u0628 1191550\n",
"\u067e 210176\n",
"\u062a 1510602\n",
"\u062b 59821\n",
"\u062c 287223\n",
"\u0686 92149\n",
"\u062d 211581\n",
"\u062e 291213\n",
"\u062f 1861543\n",
"\u0630 50086\n",
"\u0631 2525170\n",
"\u0632 551658\n",
"\u0698 34366\n",
"\u0633 1129394\n",
"\u0634 692128\n",
"\u0635 140904\n",
"\u0636 57585\n",
"\u0637 142536\n",
"\u0638 38914\n",
"\u0639 392996\n",
"\u063a 174189\n",
"\u0641 372662\n",
"\u0642 287271\n",
"\u06a9 728996\n",
"\u06af 348562\n",
"\u0644 729613\n",
"\u0645 1541968\n",
"\u0646 1831045\n",
"\u0648 1606199\n",
"\u0647 1638034\n",
"\u06cc 2915877\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAABJEAAAKvCAYAAADa7l5VAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYZFWd//HPh4Eh55wHFREBUaKBMJIEA4gBxUDaNYu6\nKrK4/mAwZ1dWXNYVBsSwIooCKhKGQXIQFSQqMEiQIDkzTH9/f5xTU6drqure6q7u6pl+v57nPn27\n6txzz7333Oq+3zrBESEAAAAAAACgm8UGXQAAAAAAAABMfASRAAAAAAAAUIkgEgAAAAAAACoRRAIA\nAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAdGH7Bba/bfsa24/YHiqWfQZdvkVZea4HXZbx\nZHtGcexHDbo8AAA0LD7oAgAAurN9oqQDuiR5RtJDkm6SdImkkyLi5nEoGrDIs72XpFMlLd3m7cgL\nxt5kPs+T+dgBABMMLZEAYOG3pKS1JO0s6QhJN9j+H9vLDLZYKNk+qGhZcP6gy4Nq+R46Wc0A0sOS\nfiHpu5K+I+lYSbcOpnSTjgddgMnA9vTic+q2HrabU2y381iWEQAwWLREAoCFy91KD7GlZSRtIml7\npc91S3qPpI1svzYinhvfIqIGWhYsHN4gaZW8fp+kF0fEgwMsz2TF/TIYvZz3KH5yvQBgEUYQCQAW\nLjdHxEfavWF7I6VWE6/ML+0m6cOS/nOcygYsarYq1n9FAGn8RQSt5hcObvkJAFhE8YcZABYREXGb\npL0kzSle/sRgSgMsElYp1v8xsFIA44dWRACArggiAcAiJCIek/Tt4qV1bb9oUOVBR3xbv3BYoljn\n4RqTQT8+m/h8A4BFGEEkAFj0XNry+0btEjnZ1/ZM2zfZfsj2M7bvsn2W7UPrDM5te3YxoOqB+bUV\n8/azbd9pe25+f4MOeWxt+6u2r7D9j1yOx23fbPtU2x+0vVqNsixh+922/8/2LbYftf2U7dttn2b7\nYNuVXbnbDRJre2Xbn7R9ue37bT+d051se7sueZ2Ypyc/oXh555Zp4rtOY257E9sftf0z29fnaebn\n2n4wTzt/nO0dq46rTb6r56nEr87X/4l8zk+0vUOH89H2Grbk25e6NVK2d7B9rO2/5HPU2Pcs25+y\nvUqXbedPra7hsyIe1eZ6jWjqdQ+fvn1mfm2K7Xfm8/P3XL/usv1r228fwT6Wtf0B27+yfVu+tk/Y\nvtX2T2y/uWY+5fFukF97nu3P5XpznzsMwmx7pXytf2v7DttP2n4u35c352M7yvY2dfZfUc4VbO9n\n+7u2L8nletbpc2SO0/3/PttL1Tzuvn0GjBfbG9j+jO3f57rzTL73/pLvh26fUzPyOZ5VvDytTZ2f\nXxdsz39fUvm5cH6HbbreL7Z3s/3fubwP5Ot3j9PfkX/vdt8WeZzYuj/bS9k+JN9bc/J5aTsAuO29\nbJ9k+zqnz9nncr29y/bFtr9j+81m4goAk1lEsLCwsLBM4EXSiZKG8jKrRvqNi/RDkt7eJs3Wkv7c\nkq7dco+k11Tsb3ZOO0/pofuVkm5vk9c8SRu0bLumpNNrlGNI0jOSlu1Sjj2UZsqqyudvkraqOKbb\nijLvJOlVku7okuc8SZ/pkNfMmsc3JGlem+1P6WH7MyStWLNe7S3pgYr8vq00fuKcTtdwLOvWCO6V\nlST9ssa+H5L0rx3yOKrutZJ05AjLOaPI5wSl2RV/X7G/CyStWjP/d0m6t8YxXC1po4q8yuPdUGnQ\n/ifb5HVry3avlXR/D3X3eVX771LGfSU9XXM/d0vascY57NtnQB/qSNd6JmmKpC/XPAc/lrT0KOr9\n/M8BSdN63KbtcUh6nqrr/5CkRyQdWHEuTizPm6QXSbqmQ3l2KrZbXc2/ZXWWz/Xzs4uFhYVlYVoY\nWBsAFj0rt/z+SPmL7b0knarmtOXPSrpSKbjyjNLDwY6SlpW0hqQzbe8XEadV7NdKAaxjJK0g6TGl\nB4O7cpleOSyxvYmkcyStV7z8sKSLlMafWVzS+kqDG6+Sf5/Sdsf2IZK+p2YL2yckXa5m8OP5Sg+B\nU5UfWGzvFhGXdTmWxs8tlB7QllV6KL4o/1xT0i6Sls/pPmv7hoj4eUte50p6XOlhZtf8WrtZ9jrZ\nIP98TtJNkm6W9KCkuUrn9aVKs/NJ0usknW37VdFlVj7br1WqA43/A4YkXSHp+vza1pI2k3So0oNp\nra5cY1i36ux7FUkXStq0ePnu/NqjSi3ydlbqoraipO/ZXiMivtiS1RWSvpPXd1O6bo3Xr2iTdrSm\nSjpNaXbFeZIuVrrGyyudq3Vyuh0lnWd7h4h4vFNmufVF2eLjYUmXSbpT6f7YNO9rMaW6c7ntl0fE\nrRXltKS3Svpq/v3uXNaHchmnFWXYSimY16hfc5XqwV+VAlDLKt3bL5G0qkbfVXBNpfMYSp8d1+fy\nPaFUF5+vdMxTlQJ259jeMSKu7JJnPz8DxoztJSX9SimILqVzcKfS+b5f0nJK93OjHr9dqYXR9Ih4\ntsjqCknHSlpX0hvza49JOqnDrh/LP4/NPw9QOg9Sqs93tdlmgfvF9taSzlKqB1K6B/4o6QalurK2\nUt1fOec/0/aKEXFMh3KVVst5b6D0OXaR0t+E5STNb/1me4qkMyVtW2x7i1KQ9QGlz4xVlT4TNxYz\n0AGY7AYdxWJhYWFh6b6o95ZIH9fwb1s3Kd57gVJQqfH+dySt1iaPlZSCMo10D0tav8P+Zhfpns0/\nv6uWVkNKD1lT8vpySg8Jje0elfS+xvst2y2mFHw5TdLybd5/pdJDamP/MzqkW1vpYauxz9slLdfh\nmOYU6Z7K+X6ytXxKDxbl8d/c5boc2Mt1LLb7otLD+wpd0mwl6Q9F/od3SbuqhrdSuV7Slm3S7aH0\nEDpPzRYOHVsijUXd6vE++UWR5zOSPtShDpzdcn/s2iXPshXZiFoddch3RpFv49xeLemFbe6ZjykF\nEBvpj+2S735FuseUgoBTO1yri4u0V0lyhzzL1hfP5vK+r026qcX6acU2F0hap0uZt1UKRKxXsf9u\nLZHeIOkISS/okmYlpZkqG/ldV3GN5hRp+/IZMIo60rHuKX3WNtLdKmmvDul2VwrsNNJ+s0O6ncv8\neihveb52qrnNqpL+Xmx3itp8vigFAj+b79dGPdy6Q54nttTXIUk/l7R6m7RL5J/7FNs8Kum1Xcq8\njqSPSDq4H9eZhYWFZWFcBl4AFhYWFpbui3oIIim1ACr/mf97y/u/rvNgUqT/QZH+mA5pygeoIUnH\n18j36CL9k5K2HeG5saS/FHkdUJF+MaUxPxrpP94h3ZyWY3p/lzzXVGpp1Ejb9lgkHVT3Oo7wXKyk\n1ApjSKnbTaegwBeKcvxT0tpd8ny5hgcwugWR+l63ejj2HVquV8cHPKXWKJcVaf/YJe2JvRxTD+Wd\n0VLeO9Wlq5rSLIvlNVigC5qkZdTsPjZX0vSKMiyrFEBs5PumDumGWpZ31zi+fxZlff4oz1VlEKnH\n/I4r8ty9S7q+fwaMoo506ga2bZHmDklrVeT5YqWAWCN4ucC9L2l6kedYB5GOLbap83fjs0X60zuk\nKe/ZIaWgcdvPwmKbrxfp6abGwsLCUrEwsDYALCJsbyTpNxo+wOk3i/c3k7RX/vWvkj5XI9vD1Wy2\n/07bVbPuPK30bX23ck5VaiHR8IXo3q2km72UHoykFJj5QbfEETEk6dPFS++usY9rI+K4LnneqxRA\naRjIALsR8bBSFyIpfVv+4tY0+fodUrz0pYjoOHV9pO5+J1fte5zqVjcfKNYvjoiZnRJG6sLzweKl\nLW2/ahT77ocjI+KBLu9/S6mLm5QCp//aJs1BanYJOikiZnfbYUQ8ofRQ3lDnXrgyIirrg1Iwu+H+\nGunHU1k39uiYariJ+hlwWLF+RETc0y1xRFyvZve0qUot1wbC9qpqfhY9otS6p8oX1eye/TrbrV23\nW4Wkj0VEVdeziVxfAWDCYUwkAFi4vND2f2n4FMpLS3qhUquRcsygWWqO7SKl8XIaflrjH2tFxD9s\n36Q0nsZKSmNC/KXLJmdHxEMV2b485yWlFhPHdklb5fXF+o9rbnO5UuunZSRtbnv5iHisS/pTauR5\ntVKXMykNPjwmbE9Tan2wsdK4PstoeF3YupFU0sskXdeSxaZKrSak9ID1wxq7PVmpK14341G3utml\nWD++xr6vtn21UjfAxvYXj3Dfo/W0pP/rliAihmz/UM2gz6vbJBvJvTCrWK8zu99PauY7R6nLnJWC\nA5+vud2o2V5O6TNmc6UxcZbX8M/F5Yv1l9bMdsJ8BjTkcXz2zL/OVRqLrI5Zkt6b13dUGjx/EHaV\ntGRePyMHNbuKiKdtX6p03FYa5+7MLptcmwNnVeYU6wfbPiG6jDsGAJMdQSQAWLisI+lDFWlC6dv2\nj8TwwZXL1havtP0d1bNi/mmlwXC7Pej/oUZ+ryjW/5Rb0IxUeUyvzwP61tEIciymNLD3DV3SXlsj\nvweL9RU7phoh27soPYi/vIfNVm3z2suK9TtyC4oqdVqJjUfdasv2OhoeGLuo5qYXqhlE2rpbwjH2\nl4h4ska6S4v1dsGP8hocaPtNNfIsA5Ar2146Ip7qkr7O/S2lYNP/y+uftb27pB9JOicibquZR09s\nr6nUVXN/NQd2r7JazXQD/wxo4yVKY8tJaQywr9VszVdOZLB+30tVX1lfN2nz5UgnzyvWq8pft77+\nTKmL9RRJW0q60faJSq3L/hDDByAHgEmPIBIALHxaW3k8ozQ48c2SLlHqynJTm+3WKdZ30fDWG3VV\ndR+4r0Yeaxbrt4ygDKXymN7YMVVnVvUxPVLxvpRaAjQsMYJydGT7cElfanm5U0uf8iFs+Tbvr16s\n31Fn/xHxmO1H1P3BeDzqViert/w+p+Z2Zbq6wYSx8Pea6e4s1pe0vVyjtYTtZTX8etfpmtaqcS90\nCiKF6t3fUup2tIOaLaZ2zIts36PU6ut8Sad1605Zl+3NlVrYtF7Hqvuk3T3SzkA/Azoo77nlVP3l\nQjur9KksI1GWf1sNnxmtrn78PVJE/NX2oUotdxfLZft0Xp62fZXSAPG/js4zegLApMGYSACwcJkd\nEVNalmUiYp2ImB4Rn+4QQJKaXcgaYgRL1ZcP3VoxNJQPbqPtMlAe00iOp84xVXbNGiu2X63hAaTL\nJL1faXrqNSQtXdYFpW/TG9r9jV+uWK/T+qWhqqvJeNStTsr69FxL67tuymOqG0wYC5XdeDqkK8s8\n2vPf2KYf97ci4hml8YY+qDR4d3kPrSXpzUoP7HfY/j/b69bJt508xtov1Awg3a/UImlXSRspzcBY\n3iNlS5a6/wcP7DOgi37cc1M0OBPl71HaeRrz6hWSTleaTKBhKaWA6H9IusT2dbZf3yYLAJg0aIkE\nAJNHGbA5OCJO6phybD1arC/XMVU9j6vZQmaXiLhglPlNNIcX68dHxHsq0ld1oynrwDI9lGPZHvId\n77pVjme1uO3FawaSymPqNibWWKs6t53SlWUuz39Iel5E3D6qUo1SRMxTmgntONvPl7ST0sP4DmqO\nl7SY0uDOr7b9yogYScvEN+X8pNRaa9uKbprj0dVsPJTX/PaI2GhgJRmZsvxHR8TRHVOOkzzBwxtt\nr6BUT3fMP7dRc/ymTSWdbvtjEXHMYEoKAINFSyQAmDzKmXvWHlgphpfjBR1T9Z7XII+p7/LAuY3u\nQPMkHVFjs6oBfcuZhzbomGp4OZZX9YP3IK9D62xK02puVz50D3JGprqDMJfX65ly4N+IeESpW6uU\ngjMT6l6IiFsiYmZE/EtEbKLUGuhoNVvDrS7pP0eY/W7F+rdqjPM15oNej5Pynlvd9sL2P/2E/eyO\niEcj4jcRcURE7Kg0vtzbNXzMtq/k8dgAYNJZ2P7gAABGrhzLoc5MTGNl2ADBNaZp7maiHFMdvXaJ\nWVXNsVXui4h/dktse3Glb827+WOxvp7ttWqUo8505QO7DhFxt5oPpI0Zm+ooz1XdAXjHwuZ5TKMq\n5aDqf2rz/kJzL0TE7bnlyXuLl3e3PZKxhMoH+ToDs08fwT4moj8pzewnpVaF/RocfqRd93rdbmGq\nr09GxCmSdpbUCFIuKek1gysVAAwOQSQAmDzKqZD3sD3aVkAjdbmkB/L64krjpozUGcX6O2xP5K4q\nTxfrdR6Wy4eyOl3P3qoFB5ludYOaD0GW9K4a+dYZpHnQdaucqv6QqsS2X6rmzGySdF7fS1Tfkkqt\nHDrKrdLKazWrTbLyXnhf3maiO71YX0IjG+i5vE+6do/NreoOHME+Jpw87tS5xUsf7lPWvX5OjXS7\n36k5GPmmefy3CS0iHlKavKJhjUGVBQAGiSASAEwSEfEHSefkX6dI+nHNFhCS5k+h3Y9yzJVUjiXx\nGdt1Wru0c5qkG/P6ipJ+0MvDs+3xfAgoWxKt1zFV0wNqzgq1YreHrDww8beqMoyIkDSzeOmIbl0y\nbL9cNYJIE6BufbdY39H2AV32taSk/y5e+lNEXNop/Tj5rO1uM8R9TNLGeX1I0vFt0nxPzWnmn6fh\n91hXtqdU7L8221Nt1x3rbFqxPk/N4HIv/lasd5yh0bYlHavBzkjWb+Wg+++y/ba6G9pewfbSbd4q\nr8HquYVjHT19vkXEPZJOLF46vpfP4379Pcp5rdpD8rJbad3ZCgFgkUIQCQAml0PVDExsI+kK27t3\nSmx7FdsH275YIx+zpJ1vKM3aJKWWGOfZfl+7B5b8gLub7dPygKfz5aDIe9X8RvsNkn7fLShlex3b\nH7Z9raR/68fB1HRtsb6h7W26JY6IIQ1v4TPT9ita09neQdKFSt+K15nt7htqPvCtrHTut2yT72uK\n/T9bI9+B1a2IuEQpoNjwv7bfnwMH5T7XlvQrSdvnl4YkfWI0++6DZ5XGhDnH9gvLN2wvZvtjkr5a\nvPy9iLitNZM8RlI5zfsHbJ9ue9NOO7b9fNuHKwVi3jyagyisI+lO299qV1+Lfb9Q0g+Ll87pYWa9\nUtma6V22P9X6OZIDZD9Sas012hkhJ4wc/Pyf/Ksl/cj2VzoFBJ1sb/tbkv4uaf02yW5V8xxNVZfA\nXItrivW31NzmM7kcUgooXm37La33bYPt5WzvZ/u3Gn6/j9bPbP/G9ttya7V2+17G9jfU7Db4nKSz\n+lgGAFhoMDsbAEwiEXGz7TcrTYm9gtJMM7+zfbekK5UGGJ6i9G39pkqtHxr/0PdttqeIeNL2m5S6\nY6ynNPPUf0v6Ug4q3JPLsb7SP+2t00GXeV1k+2BJJyg99LxC0mW2b5N0tVLrjKlKYwxtruGtH87Q\nOImI+2xfqOb4HxfY/p3SQ9RzzWRxWLHZ5yXtq9SdbQNJF9u+QtLNStdlS6VjkqSrlLpllTO6tSvH\nA7YPUaoDi0vaROnh7XKlVl1TlM75i5W6Cn1VqbtVY0DioQ75Drpu/Ws+lhcrdaf5rlIrtwuVZjKb\npjSmSaOrTUj6fxFxfh/2PRqnSnq+UmDrOtsXKQV1llOqK2VLsWslfapTRhHxU9sbKrVQsaTXS3q9\n7RuUHvIfkbS0UrfHl7Tk3c9p7FeQ9FFJH7X9iKQ/K82c9phSXd5UqY41rv/jkj45kh1FxHm2z5O0\na87vy5I+ZPsPSq1qNlSaGW6qUsDufUoBpUXFoZLWkrSP0pfDh0n6WD7+W5TO7QqS1lX6vGh0+W17\nvSNiyPZparZA/HH+vPibmsHkkPSFiHi42PRUSR/I66/LQfpL1JxFMCSdHRGNFouKiPttv0EpGLO2\nUn08RdIDti9T6nobSp//myjVm0ZL03JMpdFaTNKeeZmX75cbJTWOb31Jr5RUBpg+FxH/6GMZAGCh\nQRAJACaZiJhle1tJ/6v0cCWlf9736bLZ4+rz4MM56LCdUvBnz/zySpJe12GTp5S6vLTL68e2/6b0\nrXyjVc1GGj4DV6sHNLx10Hg4VNJspeNcWu2/5Z8fRIqIm2y/RdJP1XyA2U7DB7sOpTFy3qma40tF\nxJm236p07ldWevh+uYYP3hySvqPUWqDsHvZol3wHVrci4qHcKuskpRZpjX236+LziKTDIuL7o91v\nHzyrFCj8mdKg4DvnpdVFkvYtZ2VrJyK+mh/g/0upW5uUHr47tkiSdJekv1aUs23rkDbmKs0UNzVv\ns6KadaGdGyW9KyJuGMX+364UEG7U3/W1YCub+5XGQyr3U/eYJqzcemtf24dJ+rTS+V5CC97PwzZT\nCio+3OH9I5RmhlxP6VlhzzZp/qvcPiLOt32ipIPyS5vlpfS4mt1eG9tda3srScdJ2lvpmqyqzn8H\npFS/+hlEKj/TpigF5jfvkPZJSTMi4ut93D8ALFQIIgHAxBctP0efYcRfJU3P3U3erNTiYX2lViLz\nJD2k9C32n5Rat5wTEU/1u3x5XIzX5rF33qY0c9I6SkGWZ5Qebq9RevD4WUQ80SWvKyS9LHfDeoPS\nA/naSkGSZ5VaJP1VKWBxrqTzu3SfiR6Pp9Y5iIhrbG+h1O1oF6UWKCuoy9/jiDjL9ouVxsXZS80W\nQfcoXZ8fRcQvJcl27WsREb+y/aJclr2VWuosIelupRYE34+Ii3PXksYMekMR0TGIlPPtZ93qSW4Z\nsY/tV0l6h1J9WkuppdsDkm6S9FtJx0fEg53yKbNs+TkmIuIe29OVAoHvVAr4rK50rv4o6YcR8ZMe\n8vtt7i62r1KdebmkNZXq2tNK3RlvlnSF0vm/qCrLHvZ9l+1VlIIQOyi1OHqBUnfLJZUewu/Kx/VL\nSadFRNvgcN3959Z1OykFid6h1MpqeaXjnJP3c2JE/NP2tCLPbvmOyWfAWOUXEV+zfZxSl71dlYLp\nqynV/ceV7usbJV0s6axuQbuIuDt3cf2AUgBpEzWDU93KcIjtM5Xq8EuVrnk5KUCn1k/3KgXCNlcK\nCO6s9HnUGKvoEUm3Kf0tOD+X/5E2WZX76KXO7u002P6rlVoEvkjpM2t5paDoA0rBx3MlnZz/bgHA\npOU0nAQAAMCCbG+iZuuN6yOi0zf0qMn2DElH5l9PjIjKGeUAAAAmAgbWBgAA3exfrF8+sFIAAABg\n4AgiAQCAtnKXqI8XLy1KAxIDAACgRwSRAACYZGxvbfsHtrfv8L5t7yvpQqVZwiTpyoiYNW6FBAAA\nwITDwNoAAEw+SygNwPsu2/dKulppoO55SgM6NwZibnhIzSm/AQAAMEkRRAIAYPIpZ9VYU2kGr06u\nk/TWiLh5bIsEAACAiY4gEgAAk88VknaS9FpJ20laW2k68JUkPSHpXqVBtE+PiF8MqpCLsH5PBw8A\nADAuHMH/LwAAAAAAAOiOgbUBAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkA\nMG5sL2X7w7Zn2b7P9lzbQ3k5bdDlq2J7elHe87ukm1Ok27kP+23kNTTavBZGtmdXnU/bBxVpZo53\nGScD29OKc3zbOO1zUtd9YFBa/o5tMOjyAJg4CCIBWKg5eaHt/W1/Iz9sPlo+eIzmnx/ba9j+pO2L\nbd9t+xnbd9g+1/b7bS/XQ14r2/6i7ettP2X7kZzve21P6SGfo/JxPWt7s5Ed2fizvaKkSyUdI2m6\n0pTy5XEvbNOFditvOYV7P49rYTtH/dLr+Zys52k8jfc55poC4ytafgKAJGnxQRcAAEbK9jaSzpW0\nQpdkI/7nx/ZbJB0naZWWt9bNyy6SDrd9QERcWJHXxpLOk7Re8fKSkl6Rl7fY3icinqqRzxH5129F\nxHV1j2cC+JKkLfN6SPq9pL9Kejq/9udBFGqMuOVnv/OdbMbqfE5atk+UdED+9eiIOLrXLPpbIkCy\nPUPSkfnXkyLi4AEWZ9QW8uPhHgfQFkEkAAuz5dQ9gDRiOYB0SvHSU0pBoHskbaTUkmaKpA0lnWX7\n1RFxRYe8lpD0czUDSLfnvJaT9Nr8czdJX5f0oYqifVfS1JzHjB4Pa2ByS6t3Fy8dGBE/HFR5RmGQ\n38zybXB3fGs+cr2es363sAPaWdTq2KJ2PAAmKYJIABYFD0m6WtJVeVla0g9GmpntDSWdXLx0gaT9\nIuL+Is3zJf1S0mZ5f6fZ3jginmyT5ZslbZ7XfyvpjRExt9jXJZLWlvQe21+MiLs6lOudknZV+kf0\nI1WtliaYF0paNq8/s5AGkBQRF2gAXcEjgu7nFSLiJEknDboci7KImCOGQgAAYFLjHwEAC7M/Sdo4\nIlaNiN0j4oiI+LmkO0eZ7+eUuppJ0m2SXlcGkCQpIm6RtKekR/JLa0v6RIf89s4/50n6aCOAlPO5\nXdJn86+L5zwXYHslSd/Iv54eEWfUPpqJoewSeO/ASgEAAABgxAgiAVhoRcTDOZjTN7ZXlbR/8dKR\nHVoXKbcY+mbx0gdttxtDYNP88+8R8bc27/+uTdpWX5K0hqTHJR3aIc1EtkSxzixLwMTC2CeYiBa1\nermoHQ+ASYogEgAMt7eaM4Y9JulnFenLqcTXlLRDmzTL55/3dMijfH351jdtby/pvfnXoyNitC2t\nasuz0x1h+4JidroHbF9j+5hctk7bzp8OXNKs4q1ymvARTxdu+4xi+3d2Sbd7y76+0yXtirafy+me\nzONZle9PL/I5v9cyd9jnq/NMfY18T7W9ZEuaymnObZ9YpDsqv7aM7fcV1+9p23+3/TPbe42grKva\n/oTts3M+T+XZEG+yfYLt3XvMbxnbH8uzFP4z53er7VN6LZ/tg4rjn1mRdhPbH83n4fp8/ufafjDX\n7eNs79jL/nso51K232D7m/m6/CNfl6ds32n7t/kcr1gzv9nFcR+YX1vR9qH5vTvzsQ3Z3tB52m41\nB9WWpKO84D25QB0v7+m696ztJWy/w/bJuZ48VJzrK20fa/t1tvvyP6mTfW3PLPb3jO27bJ+Vz8sy\nNfNa2vYhtn+Z6+Xj+fPh8fz7OU4zbu5st/0CYSRlf5XTDJy/tX2b7SecZuK81/Yltr9s+3k185vR\nek/YXsz2frZPs32L0+fc/LrTJo8NbH/G9u/zOXwmn9O/5Gu33WiPO+9ndq6XRxYvH9ihXnate/0s\ns+2X5HtCX6TMAAAgAElEQVT1cqfPqLk5v/tt/8H2D5xmWF1zYTienN8qOb+rcj5P2L453zOv7CUv\nAJNURLCwsLAsUovSoNdDeZknaYMetj252PasmtvcXGwzo837f8zv3dph+42K7b/e8t7iSt32hvLP\nxcbxPB6qFEgbqlj+T9JybbafVmPbxtL23FSU79+K7Y/vku5LLfu6vkvafYp051TUrVld8plTpNup\nS7r9lGana9TVYzukm1+fu+R1YpHuSKVxqK6tOO+nSlqq5vn+uKRHa1zLcyStViO/rSTdWqNuLStp\ndtX5lHRQkeaELvs9pYd6eYakFft4T21f8xwOSXpY0ptr5Nk4N/OUAkOvVBp4vzW/eUoTAdzWw/HP\natnXtOK9yntW0l497O/HI637RdqtlWZ5rNrXPZJeU5HXthp+H1ctu46ybiyh1BW7zr7mSvqCJFfk\nOaO8JyStozTGX7s8D2jZdoqkL6v5+dT12klaepTHf34P57rT39K+lTnn9V89lOnCiXw8RZ57KHUp\n75bXfyr97zFHzc+O2v9HsbCwLPoLA2sDwHCbFetX19zmakkvaLN9w/VKU9uvb/sFsWCXtt1a0pY+\nKuklSv/IvT8ihmqWaVRsf0nS4cVLzyg9fNwuaSVJOym1vJJSIGRj2ztHxOPFNo9IOlZpIPD1JL0x\nv/6YFhwA+YERFHNWsf7qLul2afn9RbbXioh2LcPKfPrS0qgT2x+R9C2lLg4h6aiI+Hyfsl9JaRD3\njTT82q2idIyNMareJOlXtvfqVLdyC4vjlYI0DfdJukzpYXyqUv1+WX5vV0mX2t4uIh7qkOfmks7N\n5ZTS8V+nFHB9Lue3lVLdarzfLxvkn89JukkpCPyg0oP5ypJeKmmTnOZ1ks62/aqIeK4P+15ZaTbG\nUKrz10m6Q6mb6lSlIM32SoGzFSSdYvvNEfHLGnlb0saSjsnbPibp95LuyvtttDA4SdKqStfpRfm1\nK/LS6q89HV1ZGPvDkr6tZheeUDrXf1QKkK2g1H13C6UH1qVGuq+8v72UgqJL55eelXSlpL8p3QMb\nSNpR6dyuIelM2/tFxGlt8lpPKRjamP1zKJf7BqXzurRSQGYLpfHw+jFb3ZScZ0h6Uulvwa1Kn6OW\ntJZSYGutnPYIScsoBdPrWErS6Ur31XOSLlW6vlOV/sbM59QS8ldKAQflMt2pdD7vV6rDW6tZf96u\n1MJ0ekQ828Mxl06T9BdJ2ykdpyTdqPQ50WqBvxdjUOavavhsqf9U+sz7h1J9WDHn9WKlc9h6/Sfa\n8cj2Lkp1YGqR55VKn0NLSNom5/cRpfuH2eQAtDfoKBYLCwtLvxeNriXSE8W27625zVeLba5p8/7+\nxftnSlqieG89pYfIIaUHnXWK99ZXsyXQ/4zj+dtbw7+V/JWk1VvSLCbpk0oPI410J3XJc+ciXc+t\njrrke3+R70Zt3l+hKOM9Rdp3dMjvmiLNyyvq1ohbIil9u9x4/1lJ/1JxnPPrc5c0JxbpGt9cnyNp\n7ZZ0UyV9peUaH9Yl308V6e6T9A61aRGn9EBzQ5H2Fx3yW1zN1nlDSt+K79Em3auKe6P8Jn60LZG+\nKOmtklbokmYrSX8o8ju8T/V1O6UWJFt0SbO0pE8rBbWGch1fpkv62S11aUjSdyUt25LOkqYUv88s\ntjuyZvmnFdt0vI+VHnznFWkvl7RNh7SrSHq/pK+Mou6/QCnY0kj7HbVpDacUtPxeke5hSeu3Sfet\nIs1fJG3SZd+bK93PbY+vh7qxRL4m0yUt3iGNlQK/5efeAp9TRfoZberGBZKmtUm7ZLH+3fI6S9qr\nQ/67KwUpG2m/2Yd75Kg693Gb7fpWZqUg69wizb+X905L2uWUPk++NFGPJ6dbUcNbuv21XZ1V+vv/\ncL5/n2nce6IlEgsLS7EMvAAsLCws/V40wiCS0je15YP1PjW3+3ixzZ1t3l9C6Zu+RprbJH1f0k80\n/MHnuy3bnaZm8GOlcTp31vDueeeqSxc6SR9rOWcvrXFN+hlEOrXId4FAjKQ3FPXg39R8sP1+m7Sr\nFXk90u6hQaMMIikFUE4q3ntC0htqHGevQaQhpUDNkl3Sl101HlX7LonrFg8Sj0ratKKca2l4sG6r\nNmkOLN5/VtK2XfJ7kYYHdkcdROqhbq2kZquDO1TRdajfi9KDa+N43tMl3eyW89Oxa2eX+tK3IJJS\nK5lbinQXqmaXyVHU/V/3ciySflCkP6bN+1cV74+qm9oY1Y1XFOX7UZd0M1rqxrVV10Kp1Uwj/R2S\n1qpI/2JJT6kZ7F271+PpUuZa93G/yyzp9WX9XdiPJ6cpg1kPS9qwS37TNTwITBCJhYVl2MLA2gDQ\ntFzL70/V3K5Mt8DA2BExV9KbJd2dX9pQ0iGS3laknyXpE41tbL9BaXweKbUSebg1X9sr2V6h9fVR\n2k3NrnlDkj4Q3bvQfVtpDJKGD3VKOEZmFevturSVr52qZllbu7i1pr0oIuaNsmzD2F5WaYydd+eX\nHpS0W0Sc0c/9FD4REc90ef8IpYcJKdX9/duk+aiaM+t9NSJu6LbDSF0E/7N46d1tkr23WD8xIq7s\nkt+NSnVs3OV7rtGNbB2lB7XxNLNY36NjquGeVmohOEhvUupGKaXWHO+KiKfHame2N1Mae0lKrSs+\nV2Ozw9XsqvPONoNiNz5XQ6nVz4QSEZcqdcWUUkuUuj5V41ocVqwfEe27/ZZluV7N7slT1eyCOp76\nXeby7+ogrn9fjyfX7/cUL301Im7vkt9sST/tpcAAJhfGRAKApqVbfq87tkP5oN6ah6T0MGx7S6Wu\nQXsrjc8xV2ncix9I+t9G0CIHGxoziM2OiJMb+eQZYGYoNZ9fJb92t9KA4F+I4WMSjcSuxfpFEdF1\nTJSICNvHK43DIrUPzoylqiBSozy3RMQdtmcpjXmzoe1pETGnw/Z9HQ/J9upKXRkbY2PcoTSw7439\n3E/hjoiY1S1BRDxu+xdKAU0pHf//tiR7fSO50sCtdZT7HTbDWa7b5Yx+rWNjtTNTqVVO39mepnRN\nNlbq7rGMhk/DvXUjqdKYT9f1cd9TJb1caVydtZQCyp3+L3tpzWzPjg7jUI2jcla907s9rPbJ64r1\nn0ZE5TguEfEP2zcptXRbSWksu78USeYoBdMt6cMaHvgcF/nvxcuUvnRYQdKSLUkaX0Csanu9qJ61\n8yFJZ1Xsc4qkPfOvc5UC73XMUvMc7ahxDPyOUZnnFOu72t60KoDeL2N0PJsoBcKl9Fle93P37TX3\nDWCSIYgEAE2tLY+mtk21oPKf+46tlyLiAaVvwA/vlCaboTQe0rOSPth40fbzlYIb6zWyzD/XyXnu\naXuXUT5EblWsX1RzmwuL9Wm2V4yIR0ZRhtpycO4epYfwtW2/qBGYsb2qmgPGzip+flzp4XAXpRmL\nGsoAWNcATI+ep9R9sdHC6zpJe0bEXX3cR6vLa6a7VM0g0svKN2yvouagrZb08QUbbLRVTk2/fst7\nW0rzW0HPVRrUtauI+KvtB9UcDHzU8gCzn1cK4tS1ap/2vYLS7HmHqDmweJXVaqb7w4gK1V+vKNb7\neR918qpi/ZW2v9Mx5XCNemqleloGkX6i5oQH/2p7G6UH77Ml3VgnUDUSthdTCgQcpmZrrsrNlOpm\nVRDpTzXK/RI1W+Q+I+lrbVpptbNesd56z4+1sSjz5UrdzjdSCtZdZftHSi0TL4yIx0ZX5K7G4njK\nv+t31fzbU/dvCIBJiCASADS1tuJp26qojTLdqP65tL2F0jhDkvT1lpYqP1b6R/HZnOaHSoGuQ5XG\nO9hSqQXTO0dRhNWL9Tk1t2lNt7rSmELj5Xw1u2LtojQDjjS8ZVHjYfZCpfEdpqgIItleW9ILc5qH\nlcYT6pfvqfn39jKlAVLH+vz8vWa68sFz9Zb31m75/YPqXWvgp9zH/VF/Jqe/t8lrRGwfLulLLS93\nerguH94W6Ko6gn2vqzSG0fN73H/dfd83gmL125rF+i3jsL91ivVdNLLWkCuXv0TEzBxobHyWvlTN\n1mAP2r5EaYDq0yLi1hHsbwG2l1BqdfKGlrf6VTfr1I3yXC6nkXVP7luwt6a+lzki5tl+h6TfKNWN\npSX9a17C9rVKf0vOlvS7Hj7H6hiLa1B+7tb62xARj9p+RMO/FAAASWJMJABoyGNFPFm8tGantC3W\nKtYfHOn+87eNxykFOG5VMbZHfqBpdIX6akQcFxGPR8SDEXG0muMXvM123W+w2ykfRp6ouU2ZzurD\nw3aPytYOu7RZj0aa/A1yo/XLqztsd0GfWxqUDxjrqk8tWiqM5Nq1XrfWVjLR4yIt+H/GSOqXNPy+\nHDHbr9bwANJlSjODbaM07fvSETGlsUg6ukjbj/+ZfqRmAOkxpfGjXqvUSm15pVm5yv3PL3rN/OuO\n4zaWyms82u61dYy2nobafKkaEe9WCk5fqeGBnFWUunl+TdLfbJ9le9M+HMdn1AwgDSl9pu+v1NVu\nZaVB8su6cUGxbZ26Wadu9ONcTtH4GpMyR8TlSq2C/lvpS5FGHXB+/UNKM5feZfsTNVsLDep4Rvq5\n20taAJMILZEAYLib1OzWUzcYs0GxPpoxbt6j1BUkJH24ZVDkxjgjofRPbatjlQbqXkxpEN7/GWEZ\nypZUy9bcpkwXGmVrrBEoxy+aXqw3AkPXRcQ/i9dnKXVjWqvo/lYGkfo5HlIoXdejlFo6rS/pgtzt\nsOt4U6M0kmvXet3KAMBQRPTjf4aR1K9e03ZTdiU9PiLe0zFl0rdv4W2/XNJO+dfHJG3fbUysMRg0\nf7w8qmbLntbJCsZCWU8Pjog6473UEhE/lfTT3IJsZ0k7KHWf20zNwM0ekq60vVtEXDaS/eTxsf6t\neOmgiPhhxWZj0UKkPJe3R8RovpAYL2NW5tzt60O2PyZpO6WxhnZQ+jvdqOOrKgUUX6k0gcZojcXx\nDPpzF8AihpZIADBcOXDuVh1TDbd1sT6igXdtryHpy/nXn0dE6wCoG+efT0TEP9pkcXOx/sI279dV\ndnmYVnOb1n9yx3U2m9ydpNFEfxXbW7Z0T2sdl6Xxu9VsjdT4GW3Sj4Yl3aUU3GoEDNaVNNv2Jn3c\nT6sNa6YrA6D/bHnv3mLdttfS6JX1aw3brYMFd7JBdZLu8oC1jes8T2l2uip1z2MduxXrJ9YYVL2f\n+x5P5UxSL+iYamz219oFsy8i4q6I+HFEfDAitlS6hz8u6YGcZBmlbqsjtZ2aAbdrawSQpD7cE22U\n53L1PEbTRDfmZY6IuRFxcUR8OSJer9Q97NVKs2027Gu7H0GksTie8nO3Vr2xvaLoygagg4XhjwMA\njKcygPDy/A1xR7bX0/DxTc4b4X6/odSM/VGladVbNb4R7NS8vPz2cjTf/l9drL+qY6rhdijWbxuv\nQbVbtHZp6zZI9sVqzqi3m+0N1AyY/TMi/qI+y1M0T1czyLi2UiCpH91g2qk7YHSZrrz2jTI3Ztay\nWmZaG6E/KwVwpNQaetsuadOOU7Bt5ap0NawqaYm8fl9L67R2+11cw+v2aJVjndSpY9P7uO92xmRw\naKXB2hvGY7bGsvVPP+popYi4NyL+U9I+xcubjaIrcU91I4+dNxZjD/1J0tN5fRkN/4JkvPRaL8e9\nzBExFBEXRMQ+SuMiNezdLnmP2Y/F8ZSf7evl/1uq9DLpAIBJhiASAAx3upoPuctLemtF+oOL9Xsj\nou6MZvPlcVoaA7ge2aGl0aP55+odAlvrt0k7EmUQbKc8I1xHeRyIQ4qXRhpEG62yC9ouGt7iZHaZ\nMHcTbDzo7qzhLUSGpe2niLgvl+ua/NKaSoGkzcdgd+va3rVbAtvLS3pT8VK7FljlN+0jGeB1mIh4\nUsNn/TmwxmYHVyept/tifZka6d+qBQcb79f+uwZ6c6up9/dx3+08Xawv0TFV735drO9te1of827n\nzGJ9D9vj0fpJkhQRl0hqzIZppXG1RpRVsV7nS4APj3A/3QuRPhvPHev9VOipXk6AMpf1r931H/jx\nRMRNSi1iG8bzcxfAIoggEgAUIuJBpVnQGo623faBM4+T8fHipe/2ur8cEGqMcXS1pP/qkPT6/HMx\nSa9r8/7ebdL2LCLOVbNrnCX9d0Vz+kPVnLUolMZmGoQyALKTpEYA5Y8R0S6o1ki/ioa3/OrneEgL\nyK1fdlFz9rfVJc2y/ZIx2N03bC/V5f0vqtld4TGlac0XyEPS3Ly+k+1P1d257aVyl4hW/1usH2R7\nuy55vEjtW+aNxANqzhq4Yg7edtrvupK+1af9NvytWH9jRdoZksaqlVrDA8V6nZYJdf1KzWNdXNIP\nbded6bJnEfEHSefkX6dI+rHt2mO52F5gAgXbq9XcdhU1gz6hkc+OV9aNnTvcN4197q40S9hYKQee\nf5ftt9Xd0PYKfbjWZQvBuvWyr2XO17WuacV6u+s/8OPJvl+sf6pbcDd/Nu5Xd58AJh+CSAAmg15n\nTTlSzW8PnyfpDNvDWiTkFjq/VfMh/B9KD9y9+nelsXvmSXp/l1nByhYhn7M9v3tP7kLxyfzrXEmt\n4yn16rBifTdJP29z/FNsf1zDH7RPjohrNAB5ANTGQNXLqzmeTKfxjcrXt2hk0yV93+RA5a6Srsov\nraYUSHpZ56169qzSDEJn5vGh5rM91fZXNLxl0RciYoGukhFxu9L90PBl2yfkLoBt2d7C9uckzVH7\nLhE/UrM11pRcxj3a5PMqpeDAkho+w92IRMSQhrcamGn7FW32u4PS9N1rqL+zi52pZouTHW1/qzVA\nbXtZ29+U9B993nc7fy7W9+jXQN75PH9AaYYxKQ04fIHtbdqlt72K7Q/Y/uoodnuomgHCbSRdkYMt\nbeV9Hmz7YqUZ8lrdYfv7tnfNrcLa5bGOpFPUbF1yY0TcNsLy/0nSHXl9BaXP3LJ1qZwcohSks8Zo\n5qyIuFTNiRks6Ue2v9IpsJbLtb3tbymNTbd+u3Q9KP+GbN96HsapzB+xfY3tD+eAcqc83qVU9xrO\nbJN0IhyPlOr53Xl9eUnntrsnbe8t6TSlz6q5re8DgMTsbAAWcra/r/TQUCq7A1jSb2yX/wyFpOMi\nou0MZhFxu+0DlKZYbgy+fLvtc5W+adxAqTVJIxD/pKR9c1edXsr+AjUH9/2fiLiqU9qIuML27yS9\nRtKLJd1k+7eSpiq1TGoc8/c6dIerLSLOyEGGxkxW+0ja0/ZspQedFZS6gZXf4F+tPnR3GqXz1RyA\nvKFTUOgKpYf0sq78IyJu7pC+ryLiYdu7SfqdpO2VWkSda/s13epBD76rdN12kXSb7fOVrt3KSvW5\n/Kb9PElf71LWr+QHnw/mlw6SdIDta5RavT2mdB7XkrSlUlBs/uZt8nvO9ruVpihfKac/y/ZflOpR\nKAX2GgPbn6JU13aueezdfF7Svkrd2TaQdLHtK5Ra3zmXv9G98Cqlc3N4m3x6FhF/tT1Tze6fH5W0\nv+0rlQbTXUtpHKRllc7BwZJ+1o99d3CWUiBiWaUxum60fY5SC6VGAOhvEXFcrxlHxHm2Pyrp20qf\nk43Azk1KrfAeVXqQfZFSsHOKpF+O9EAi4manQY1/ofT5tKmk39m+W9KVSoP9T1Gq95sqfU40vly4\nfcEctaTSdTpE0lO2/5TTPSJpKaUBw7dX8//ouRpFt6OICNv/IekH+aVdlK7HpUrB2OWVxudaW80W\nn5urP/dEO4cq1cd9lK7fYZI+ZvsPkm5R+uxcQWmA8S3V/DKlH+NsXaV0rjdUOtd/zn/77lGzq/kD\nEfGllu36XebNJR0j6RjbcyRdq3RvPKv0mbV9zqvhvIhod79OiOOJiEdsH6jU3XSq0hdkV+TPv+uU\ngqHbStok5/E1pRlfF9YB/gGMpYhgYWFhWWgXpTFshkawHFkj77coNUXvls+tknYcYdnPznncLWmF\nGunXUPpHtlNZzpG0VB/P7UeUAgTdjn+eUrBt2Yq8phfb3DZGdWG/lrI9LWnpLul/05L+5Br7KI9j\nVpd0c4p0O3VJt7yki4q0DylN/d6abn45u+R1Ylm/lVq4XVdx/X5et84ojaNxd837a55SYGazLvlt\nLem2OnVLw+/ztudTKbjVSHNCl/3uqRQM6Lbfc5TutxnlOe1DHV1SqSVJt3P3qKQDerju5bk5oMfy\nHCzpuS5lOb8l/bTivcr7WNLrlR6g69SXH3TIo/IcFGk3Vm9/Ex6V9Ik2+Tyay1Qnjzsk7THaupH3\n+5mK/c5Tav25eM17oqy/He+JLuU5TOkzqe49/0dJa/ThPOyh9OVMp311rHv9KLNSN/W6dWiepJPU\n5XN00MfTkt+eSl+GdcvjGKWg65zi9Q36UcdZWFgWjYWWSAAWdqExmmUoIk61fYHSw+kblaayX1kp\nsHSTpFOVAg89dyuwvb9SV7GQ9PFoP25Pa3nus729pH9TCpg8L29/vdI32MdF6krSFxFxjO3/k/Qv\nSv94vkBphqsnlAbpnC3phxFxRZ3sip9jNSvU+S15XxERT3VJP0vpuBrb1BkPKVp+dktXeZwR8Zjt\n1ygFtHZQ+mb5d7b3itSlod2+a4nUOmNbpfr7NqXrt4pS/b1M0syI+E0P+Z2U68PblB6KtlEa02l5\npQekeyXdmPM+O9JYNd3y+4PtFysNIP0WpaDXskpdQ6+WdFJEnClJtuuc91rXJiLOyvv9mKS91Pym\n/R6lbkU/iohf9rDf2iINmruP7bcoXZetlT5THlIKRvxa6WH/jnKzqmxHWsaImGn7Wknvk/QKpTFb\nllWzlWWnPOvW7zNtny1pf0mvVWpdtoZSi4xHlVpUXC7pjEjjsXXMqvpoUmsvSdNzN8U3K83Wtr5S\nvZ+ndJ5vUbrO50k6p8NnxKpK9+NOSq0zNlZqFbKMmnX9z0rdl34aEU+3yaNnEfF522cptULZKe/z\nKaXg7e+V7tkrpf7eE13K8zXbx0l6l1IX3EZLw2WVWsLcrXTPXyzprIi4YST7abPfs526935Q6RpO\nU2rt2Oha2PF4+lHmiPim7Z9J2l3pvtgil2GlnOQRpe7Tlyj9DezajXvQx9OS31lOY819SM3/a6bm\nfC6RdHxEXCjNr2Nj9fcawELMEYP7bLB9glI3jPsiYouW9z6h1JRytUjjRwAAgA5snyjpgPzrjIj4\n7ACLAwAAgEXQoAfWnqn0LfAweeyF3dW+nzoAAAAAAADG2UCDSLm55ENt3vqmpNrTCAMAAAAAAGBs\nDbol0gJs7yPpzqr+xQAAAAAAABg/E2pgbdvLSPq0Ule2+S8PqDgAAAAAAADIBjqwtiTZnqY0K8cW\ntreQdK7SzBdSmiXkLknbRcR9LdsxWwAAAAAAAECfRUTbBj0TqjtbRFwbEWtGxEYRsZGkOyVt1RpA\nKtJXLkcddVStdGO1TOb9T+ZjZ//sfzLvfzIf+yD3f9BBB8m2bOvoo4+edMfP/tn/ZD529s/+2f/g\n9j+Zj539L7pLNwMNItn+iaRLJL3Q9h22D25JQmsjAABqmDlzpoaGhnTkkUfqyCOPHHRxAAAAsAga\n6JhIEbF/xfvPG6+yAAAAAAAAoLMpM2bMGHQZRuToo4+eUbfs06ZNG9OysP+JuW/2z/7Z/+D2P5mP\nnf2zf/Y/uP1P5mNn/+yf/Q9u/5P52Nn/ounoo4/WjBkzjm733sAH1h4p2zHIsttjM2ncwno9AAAA\nAADAws+2osPA2gPtzrbw63fAZ2wCUwAAAAAAAKM1oWZnAwAAAAAAwMREEAkAAAAAAACVCCIBAAAA\nAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAA\nAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAA\nAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQA\nAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIB\nAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJI\nAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkg\nEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQi\niAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACV\nCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABA\nJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAA\nUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAA\nAFQaeBDJ9gm277V9bfHa12zfYPvPtn9he8VBlhEAAAAAAGCyG3gQSdJMSXu2vHa2pM0iYktJN0s6\nYtxLBQAAAAAAgPkGHkSKiAslPdTy2jkRMZR/vVzSeuNeMAAAAAAAAMw38CBSDYdI+s2gCwEAAAAA\nADCZTeggku3/kPRsRPx40GUBAAAAAACYzBYfdAE6sX2QpNdK2rVTmhkzZsxfnz59uqZPnz7WxQIA\nAAAAAFhkzJ49W7Nnz66V1hExtqWpUwh7mqQzImKL/Puekr4haeeI+GeHbWKQZbctqd/7tybC9QAA\nAAAAAJOTbUWE27436KCF7Z9I2lnSapLulXSU0mxsUyU9mJNdGhEfbNmOIBIAAAAAAEAfTegg0kgR\nRHtUdYkAACAASURBVAIAAAAAAOivbkGkCT2wNgAAAAAAACYGgkgAAAAAAACoRBAJAAAAAAAAlQgi\nAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWC\nSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJ\nIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABU\nIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAA\nlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAA\nQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAA\nAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAA\nAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAA\nAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAA\nAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVFp80AUAAAAAAAAo2R6T\nfCNiTPKdLAgiAQAAAACACajfAZ+xCUxNJnRnAwAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIB\nAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqDTSIZPsE2/favrZ4\nbRXb59i+2fbZtlcaZBkBAAAAAAAw+JZIMyXt2fLav0s6JyJeKOm8/DsAAAAAAAAGaKBBpIi4UNJD\nLS/vLemkvH6SpDeOa6EAAAAAAACwgEG3RGpnzYi4N6/fK2nNQRYGAAAAAAAA0uKDLkA3ERG2o9P7\nM2bMmL8+ffp0TZ8+fRxKBQAAAAAAsGiYPXu2Zs+eXSutIzrGaMaF7WmSzoiILfLvN0qaHhH32F5b\n0vkR8aI228Ugy25bUr/3bw36egAAAAAAMGg8cw+ObUWE2703EbuznS7pwLx+oKRfDrAsAAAAAAAA\n0IBbItn+iaSdJa2mNP7RkZJ+JekUSRtImiNpv4h4uM22tEQCAAAAAGARxDP34HRriTTw7mwjRRAJ\nAAAAAIBFE8/cg7OwdWcDAAAAAADABEMQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAA\nAACASgSRAAAAAAAAUIkgEgAAAAD8//buPMySs64X+PdHhiQsBgKEHRNAuIDs+yJhBIOIyHoRA7Lo\nBR9AkVUW0TBsIi5sinoR2RQEgWsEBIRAJoAIsoRF9kgiYV8TCCYQMu/9o6pJ2+nu6p4559SZqc/n\nec7T06dq6vfW6dPVdb71vm8BMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAh\nEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAg\nIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADA\nICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAA\nwCAhEgAAAACDdozdAADYqqqay3Zba3PZLgAAHEiESADsZ2Yd+MwnmAIAgAON4WwAAAAADBIiAQAA\nADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEA\nAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIB\nAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIi\nAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg5Y2RKqqJ1XV\nJ6rq41X1qqo6ZOw2AQAAAEzVUoZIVXVUkockuXFr7XpJDkryK2O2CQAAAGDKdozdgA18N8m5SS5a\nVecluWiSL43bJAAAAIDpWsqeSK21byf50yRfSPLlJGe01k4Yt1UAAAAA07WUPZGq6upJHpXkqCRn\nJnltVd2vtfbK1evt2rXrx//euXNndu7cubhGAgAAAOzndu/end27d29p3Wqtzbc1e6Gq7pPkmNba\ng/vv75/klq2131y1Thuz7VWVZNb1K8v48wBYFo69AADT4LxvPFWV1lqtt2wph7Ml+XSSW1bVRap7\n5/xckk+O3CYAAACAyVrKEKm19tEkr0jywSQf659+0XgtAgAAAJi2pRzOthWGswFMj2MvAMA0OO8b\nz0yGs1XVnqo6bmCdJ1fVedttIAAAAADLbdbD2ap/AAAAAHAAmXWIdHiSc2a8TQAAAABGtmOzhVV1\n9Mo/+69HrXputYOSHJnkvkk+M7vmAQAAALAMNp1Yu6r2bHN7e5I8sLX2yn1q1RaYWBtgehx7AQCm\nwXnfeDabWHvTnkhJnrbq38clOal/rHVekm8leWdr7dN71UoAAAAAltamPZH+x4pVpyV5bmvt+XNt\n0RbpiQQwPY69AADT4LxvPPvSE+nHWmtHzaxFAAAAAOxXZn13NgAAAAAOQFvuiZQkVXXNJI9McrMk\nh6e7K9sFtNautu9NAwAAAGBZbDlEqqpbJXlHkkPTTaT9tSQ/WmdVAwwBAAAADjDb6Yn0rCQHJ3lo\nkpe01tYLkAAAAAA4AG3n7mzfT/Km1tp95tukrXF3NoDpcewFAJgG533j2ezubNuZWPvcJP81myYB\nAAAAsD/ZToj0r0luNK+GAAAAALC8thMiPTnJravqAfNqDAAAAADLaTsTa98tyTuTvKyqHpzkg0nO\nWG/F1trTZtA2AAAAAJbEdibW3rPVjbbWttPDaa+YWBtgehx7AQCmwXnfeDabWHs7PZFuP6P2AAAA\nALCf2XJPpGWjJxLA9Dj2AgBMg/O+8WzWE2nuw84AAAAA2P9tZzhbkqSqbpDkvkmuneRirbU79M8f\nleTmSU5orX17hm0EAAAAYGTbCpGq6ulJfjfJSrem1f3ADkry6iSPSvKCmbQOAAAAgKWw5eFsVfUr\nSZ6c5G1JbpTkWTk/TEpr7T+TfDDJL824jQAAAACMbDtzIv12kv9McvfW2keTnLvOOp9Kco1ZNAwA\nAACA5bGdEOl6Sd7aWvvBJut8Ocnl961JAAAAACyb7YRIlWTPwDqXS3LO3jcHAAAAgGW0nRDplCS3\n3mhhVV0oyW2SfGJfGwUAAADActlOiPSaJDepqsdtsPx3082H9Kp9bhUAAAAAS6Vaa1tbseqiSd6T\n5IZJPtA/fbMkz0lydJKbJnlfktu11tabdHumqqptte1zqp9k1vUrY+4TwLJz7AUAmAbnfeOpqrTW\nat1l23kBq+qSSZ6X5FfzP3sx7UnyyiS/1Vr73j60dTttESIBTIxjLwDANDjvG8/MQqRVG7x0ul5I\nl05yZpL3t9a+sU+t3H4bhEgAE+PYCwAwDc77xjPzEGkZCJEApsexFwBgGpz3jWezEGnLE2tX1WWr\n6uiqOmyD5Yf1y4/Y24YCAAAAsJy2c3e2Jyd5Y5IfbbB8T7/8SfvaKAAAAACWy3ZCpGOSnNBa++/1\nFrbWzkrytiR3nEXDAAAAAFge2wmRrpLklIF1Tk3yk3vfHAAAAACW0XZCpJbk4IF1Dk5y0N43BwAA\nAIBltJ0Q6bNJfn6jhdVNnX7HDPdWAgAAAGA/s50Q6bVJrlVVL6yqi6xeUFUXTfLCJNdK8poZtg8A\nAACAJVCtta2t2AVF701y/SRfTvKuJF9KcqUkRye5YpKPJbn1RpNvz1JVta22fU71043wm+lWM+Y+\nASw7x14AgGlw3jeeqkprrdZdtp0XsKoOT9fj6D5JVm+wJfn7JL/VWjtjH9q6nbYIkQAmxrEXAGAa\nnPeNZ2Yh0qoNXjbJzZJcMsl3kvx7a+2b+9TK7bdBiAQwMY69AADT4LxvPDMJkarq1CRvbq395iwb\nt7eESADT49gLADANzvvGs1mItJ2JtY9IcuZsmgQAAADA/mQ7IdInklx9Xg0BAAAAYHltJ0R6fpK7\nVtUN5tUYAAAAAJbTjm2s+6Ukb0/ynqp6UZJ/T/LVrDNIsbX2rtk0DwAAAIBlsJ2JtfdscZuttXbQ\n3jdpa0ysDTA9jr0AANPgvG88m02svZ2eSE/b4np+IgAAAAAHmC33RFo2eiIBU9Qde2Zvfzn2OPYC\nAEyD877xzKonEgBLYfZ/TAEAAIZsO0SqqoOT3CHJtZNcrLX29P75iyT5iSTfaq2dN9NWAgAAADCq\nbQ1nq6pfSPI3SS7fP/XjSbSr6lZJ/jXJr7bWXjXrhq7TFsPZgMmZ+rFn6vsPADAVzvvGs9lwtgtt\nYyM3TfKPSfYkeXSSv8+qMRCttX9LcmqSu+9TawEAAABYOtsZzvb7Sc5OcrPW2leqatc663wgyY1m\n0TAAAAAYy9RvaALr2XJPpCS3SXJ8a+0rm6xzepIr7luTAAAAYBm0GT9g/7adEOniSb4xsM5Ft7lN\nAAAAAPYD2wl8vpzkpwfWuUGSz+99cwAAAABYRtsJkd6c5E5Vddv1FvZ3brt1kjfNomEAAAAALI/a\n6qReVXXlJB9JN2Ttz5IcleTeSe6a5Ogkv5nkzCQ3aK0NDXvbZ1XVxpyQzO0GgTFM/dgz9f0HABbH\nece4vP7jqaq01tadWX7LIVK/oRsn+YckV1tn8X8muWdr7eN71cptEiIBUzT1Y8/U9x8AWBznHePy\n+o9nZiFSv7EdSX4xya2SXDpd76N/S/JPrbUf7WNbt9MOIRIwOVM/9kx9/wGAxXHeMS6v/3j2OUSq\nqiOT3CzJniQfaK2dPtsmbp8QCZiiqR97pr7/AMDiOO8Yl9d/PJuFSDu28J//NMmjkqxsYE9VPa+1\n9rgZthEAAACAJbbp3dmq6tgkj+6//XSSz/T/59FVdd85tw0AAACAJbFpiJTkwUnOS3JMa+06rbVr\nJ7ljuj5l/2fejQMAAABgOQyFSNdPN2H2O1eeaK2dkOT4JDeYZ8MAAAAAWB5DIdLhST61zvOf6ZcB\nAAAAMAFDIdKFkpy7zvPn5vyJtgEAAAA4wA2FSBuZ+z3xquqSVfW6qvpUVX2yqm4575oAAAAArK9a\n2zgPqqo9WT8wWumFtO5/bq0dtM8Nq3p5kpNaay+pqh1JLtZaO3PV8rZZ2+etqjL7LK0y5j4By2/q\nx56p7z8AsDjOO8bl9R9PVaW1tu7os62ESNvWWtvbHk4rdS+R5OTW2tU2WUeIBEzO1I89U99/AGBx\nnHeMy+s/ns1CpB2b/cd9DYP2wVWTfKOqXpruLnAfSvLI1tp/j9QeAAAAgEkbKyQasiPJjZP8RWvt\nxkm+n+SJ4zYJAAAAYLo27Yk0oi8m+WJr7QP996/LOiHSrl27fvzvnTt3ZufOnYtoGwAAAMABYffu\n3dm9e/eW1t10TqQxVdW7kjy4tfbZqtqV5CKttSesWm5OJGBypn7smfr+AwCL47xjXF7/8ez1nEgj\ne0SSV1bVwUn+M8mvjdweAAAAgMla2p5IQ/REAqZo6seeqe8/ALA4zjvG5fUfz2Y9kZZ1Ym0AAAAA\nlogQCQAAAIBBQiQAAAAABi3zxNoAAADACLo5iWbPnET7NyESAAAAsI7ZT2zN/s1wNgAAAAAGCZEA\nAAAAGCREAgAAAGCQOZEAAABgyZjYmmUkRAIAAIClZGJrlovhbAAAAAAMEiIBAAAAMEiIBAAAAMAg\nIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwKAdYzcAAAAA1qqquWy3tTaX7cIUCJEAAABYUrMO\nfOYTTMFUGM4GAAAAwCAhEgAAAACDDGdjv2R8NAAAACyWEIn9mPHRAAAAsCiGswEAAAAwSIgEAAAA\nwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAA\nAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQA\nAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgE\nAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiI\nBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBI\niAQAAADAICESAAAAAIN2jN0A9k5VzWW7rbW5bBcAAADYvwmR9muzDnzmE0wBAAAA+z/D2QAAAAAY\nJEQCAAAAYJAQCQAAAIBBSx0iVdVBVXVyVb1x7LYAAAAATNlSh0hJHpnkk5n9DNIAAAAAbMPShkhV\ndeUkd07y4rhtGAAAAMColjZESvLcJL+TZM/YDQEAAACYuh1jN2A9VXWXJF9vrZ1cVTs3Wm/Xrl0/\n/vfOnTuzc+eGqwIA+6Bqfp2CWzNqHQBgLLt3787u3bu3tG4t44lbVf1Bkvsn+VGSQ5McluT1rbUH\nrFqnjdn27mR61vVryyfSY9cf29T3n+ma+nt/6vs/pvm89onXH4CNjP13X/1p15+yqkprbd0riEsZ\nIq1WVbdL8rjW2i+teV6INOFfqKnvP9M19ff+1Pd/TEIkABZt7L/76k+7/pRtFiIt85xIq/kpAwAA\nAIxo6XsibURPpGmnslPff6Zr6u/9qe//mPREAmDRxv67r/6060/ZgdATCQAAAIARCZEAAAAAGCRE\nAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgk\nRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAY\nJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAA\nGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAA\nABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAA\nAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEA\nAAAAGCREAgAAAGCQEAkAAACAQTvGbgAAAMAyqqq5bbu1Nrdtz8q89n9/2HdgfUIkAACADc0j8Jhf\nODV7s97//WnfgbUMZwMAAABgkBAJAAAAgEFCJAAAAAAGmRMJAFh6U5/cFgBgGQiRAID9xNQntwUA\nGJfhbAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAA\nAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOWNkSqqqtU1YlV9Ymq+o+q+u2x2wQAAAAw\nVTvGbsAmzk3y6NbaR6rq4kk+VFVvb619auyGAQAAAEzN0vZEaq19tbX2kf7fZyX5VJIrjtsqAAAA\ngGla2hBptao6KsmNkrx/3JYAAAAATNMyD2dLkvRD2V6X5JF9j6Qf27Vr14//vXPnzuzcuXOhbQMA\nAADYn+3evTu7d+/e0rrVWptva/ZBVV04yZuSvKW19rw1y9qYba+qJLOuX9nqPo1df2xT33+ma+rv\n/anv/5jm89onW339x64PTNPUjz1j/91VX33nfeOoqrTWar1lS9sTqbp3zN8k+eTaAAkAxtD9aZo9\nJzMAAOwPlnlOpNsk+dUkP1tVJ/ePO43dKACmrs34AQAA+4el7YnUWntPljvkAgAAAJgMIQ0AAAAA\ng4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAA\nAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAA\nAACDhEgAAAAADBIiAQAAADBox9gNAACAZVZVc9lua20u2wWAeREiAQDAoFkHPvMJpgBgngxnAwAA\nAGCQnkgAAMCGDOcDYIUQCQAAGGA4HwCGswEAAACwBXoiAQAALCFDCYFlI0QCAABYWoYSAsvDcDYA\nAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGDQjrEbAGxPVc1t\n2621uW37QDGv199rDwAX5LwHYLkIkWC/NI+TnvmdpB14Zv36e+0BYGPOewCWheFsAAAAAAwSIgEA\nAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAM2jF2\nA9g/VdVctttam8t2OXDM672XeP8BAABsRojEPpj1B+75hQMcaOYR9nj/AQAAbGa/DpHm0SNBTwQA\nAACAC9qvQyQ9YQAAAAAWw8TaAAAAAAzaz3siAQDAgc0NTQBYFkIkAABYeqZxAGB8hrMBAAAAMEiI\nBAAAAMAgIRIAAAAAg8yJBAAwYOoTG099/wGAjhAJAGBLpj6x8dT3HwAwnA0AAACAQUIkAAAAAAYJ\nkQAAAAAYJEQCAAAAYJAQCQAAAIBB7s4GbMu8bvOcuNUzAADAMhMiAXthHmGPWz0DAAAsM8PZAAAA\nABgkRAIAAABgkOFssBfmNS+QOYEAAABYVkIk2GuzDnzMCQTA+ly8AACWgRAJgC3zQRbG5OIFADAu\nIRIA2+SDLLBYAmwAWA5LO7F2Vd2pqj5dVZ+rqieM3R4AGFtVzeUB+4c24wcAsF1LGSJV1UFJ/jzJ\nnZJcJ8mxVXXtvdva7pm1S/39qbb66qs/zdpTqD/0wfjELawzzw/Su+ewTfXVX/ba6quv/nTrj1lb\n/fHrT89ShkhJbp7klNbaaa21c5O8Osnd9m5Tu2fXKvX3o9rqq6/+NGurr776060/Zm311Vd/uvXH\nrK3++PWnZ1lDpCslOX3V91/snwMAAABgBMsaIhmoDgAAALBEahnvSlFVt0yyq7V2p/77JyXZ01p7\n9qp1lq/hAAAAAPu51tq6d19Z1hBpR5LPJLlDki8n+fckx7bWPrXF/39EkpcleU+S5yf5YZK7JLlT\na+2h82gzAAAAwIFsKYeztdZ+lOS3kvxLkk8mec1WA6Tek5O8Lsllk5yabn6l+yR5zoybCgAAsHSq\n6uiqemVVmVsWmJml7Im0r6rqIq21s8duBwAAwKJU1SWSPCDJQ5P8VJJ/TPLg1tpZozYMOGAsZU+k\nfbUSIFXVT1fV66rqdmO0Y+z6AADzUlW/XFWvrarLTLE+bEVV3aiqLr6AOjetqhcn+VKSRyf52yRX\nSfKH8669TluuVFWfrqrfXHRtYP4OyBBplSOS3DPJkROtDwAwL9dJcq8kF51ofVhXVR1aVQ+oqvcl\n+VCSS8253mOTvC/dZ497J/npdPPKviHJh+ddfx0XTnLNJJdecF1gAXaM3QAAAODAUlWXTXJoa+0L\nC6x5RLpQ8ZtJrtJa+/Siavf1r5ZuGNmvpwtuPpPkkUm+MufSJyW5arrPdg9L1wtpkfWBCREiATAz\n/d01fyrJ51trPxy7PQAHsqo6Psl3Wmu/NnZb1vGkJDdIcvsF1nxskqOTPDvdXEALGXVRVYcleXGS\n/51kT5I3Jnlha+2ERdRP8tmR6wMTIkSCOaiqayQ5p7V2+thtYfGq6ppJvtpa++7YbRnBldPdVfOG\nST42clsmbeWKfGvtv8Zuy6JV1U8l+UZr7cyx2wJz9rB0ocHSaa09eoSaT1z17SKn7XhSugDnxUme\nPsL539j1gQk50OdEgrG8IN0fdKbpQ0nuPnYjxtBaO621dqHWmgBpfI9N8tqxGzGSdye5z9iNGENV\n3bmqrjd2O8ZQVcdW1T+NVPtSVXXHqrr3Iuu21r6S5Nwxam+mqm5VVcdX1YeqamHnQ1V1yap6TlV9\nuKr+oaouv6DS1+q//v5IAc7Y9Serqq7R90SDyRAiwXw8MMnvjd0IxtFa+4nW2ivGqN1P5vnqqjqx\nqo4asf7uqrrqousvk6q6zBg/g772FdKF2cdU1dXHaMNYqupa6YZU/ktVTXFS1ycn+cWxGzGSU5Ps\nXmTBqjqkql6Q5GtJ3prk/06h9maq6vpJTkxy1yQ3SvLMqtq1oPJvTvKodMPo/neSN1ZVLaDuXyZp\nSV7dD+tetLHrT9m/Z6IXDpkuB5mJ6f+QXizJ2a2188ZuzzxU1clJjk9yVJJLttbuMVb9qlpY/f7D\n6vWSXD7JYUnOSfK9JJ9P8tHW2vfUP3Drr2itnVNVj07ygSRvqaobttZ+sIjam9Q/Z1H1l8xvJblb\nug9Ri/YHSS6Z5IQkT0x3m+fRVdWVkrwjyZ+11l44pzKfTHKPJLvSzYnytDnV2ZKq2plujpZzkvxb\na+3d86zXWrvNmPX7mrdIcof+2w8leVtrrc27bmvtfUnet+D6f5nkAekCnNcnWeTw0TFrb+ZXdYfB\nGgAAFJ9JREFUkhycboLpf0o36fMTq+pZ8/x71A8lv2W64969khyXrkfmL6QLl+amtfa2qjouydOT\n/FWSB8+z3rLVH1NVHZzkqUnumOTTSZ7ZWvvkouq31g5f0567pzvmPvVAH1JdVTdN8svpJrI/vrX2\n2ZHacaEkt053AelbSd7ZWvv+GG2ZjNbaAftIsjPdOPEHHKj1k9w2yXOTXGmL61+pb9NjR3pNKsnF\nkxw0o+3dPN0fzCuseu4n091S9PKrn++XXSXJj5I86kCov2q7f93/XDd6fGDOP1f1R6y/QZvuPPLv\n+kr9x41R32OUn/lxSY5d89xvJHn8qu+P6t8Xx43UxsOT/HmSX1hAraPS9YpZezx43YL2de710wV1\ne5L8ZP/9tZK8Z52a705yyBz2cez6hyc5L8mzF/Ez3aD2nyy69hba9uf9636F/vu/6r+/ypzr3rSv\n86T++5v13z9jgfv+6r7mY0Z67Uetv6odCzvWJ3ldX+u8/uv3k9xsxH3/+UX+DJIcme5ufB9M8oeZ\n0WesLdS9TpKzVx1nf5Tkz5JceMGv9zXTXTxafcz/ZpJbj/UemMLDcLb93xOS3Ku19qUtrr8y+eJF\nZlG8qm5bVc/try5vxRWTfDddV+NZ+L0kv966OQGSJK21L7TWvtVa++rq53s/TDeM8+IHSP0V/5rk\n2CTXTfLbSb6U5Nwk/5zkdzP/K/H/luRXR6x/Urorn1OtfwGttTcn+VS62wwv3Kr6o90xqKpuXlUv\nrqrrjNWGibldkt9f89yD0/1OzF1V/VJV3WrNc7epqruseuoSSR6e7sPlPNty83Q9YG6S5PHpLixc\nKt2kt/fse8ocUPWr6g59zZumO+ZdLl2vzGckuU3mPNxjVf2bpAuXFlH/Yukuju3p23CFqnpoVf1d\nVZ00h3rr1W597cvPu3ZV3aOq3lhVVx5YdaX+31bV49INK2tJ/nse7VrlE+l6ITyyn4fpmf3zl5nF\nxled815hk9V+LcmHkzxr1n97xq6/jPpj/j3T9cS7WJJj0n3Gefwcax5eVTetqp/YYJW3pwtX5n5X\nwqq6VJL3Jblfkhun2++/mnfd3sOSHJKuQ8PV+roPT/LSBdVf8YwkV0/3Pjgk3etwbpI/WXA7pmXs\nFGuej0yjJ9KHk7x/G+v/cd+mu8yo/puSfGEb61+hr/97M6p/8jb3/w/6+nc9EOqvs/2n9Ns/PsmV\n51FD/eWtv0573pDkv0esf/zI9Y/MuL1ebpeuV8QtR6p/x77+TWe4zWM32p90c/HsSXK1/vtK94Hu\n7CSH9s/dsF/n0XPY391JPrPOc99e9f1R+/KeSNfT9DIbLPtckpenG9Z6ZpL/THLdNevcq69/7wXU\nP2XW9depuavf3t3SBQRfyZqrvzm/d8jvzOFnvrb+l9e+P+dZv9/+Si+I7+T8q+BnJnn7POqNWTvd\nMLFTtrjuM9LN1fT1JO9PN43CLNvy6+nuAHrZNc/frn/+u+luLHB2kufNqOabkvzXFta7Sf+zeOaM\n93nU+tts63WyqlfYHOvcv6/zi6ue+2aS986x5h/1Na+6yTqfTPLxBbzO/6dvyx+kC0tPTHfB+ogF\n1H5zklPXPPdnfXu2NEJmRu14eZIfpOv5fLH+uYOy4B5RU3voibT/+2iSG1fV/TdaoZ/o9ueq6nXp\nxoa/o7X2phnVv2K6k8atekz/9SMzqv+xdPt/341W6Pf/9lX16nRzg7yrtfaGA6T+6jq/kC7E+MvW\n2t1ba1+cdQ31l7f+Ou25Xrog+3Mj1v/Zser3Tk93MnPFkep/Nt0Y/TuPVP9zff2fn8XGqup2SV6Z\n8+8CtF69JDmun3/vTumG3ByS5Hf6ZXdcs+5223BMVV13g8UnJLlGVf3UqueumuSwqrpo//3KleOz\n96L2dZKclu7GCes5Jcm9051Y/3eS27fW/qP/v4dU1YOSvChdl/8PLqD+HWZZf8DfpJtz6edaa+/t\na+6oqnsm+X/peqG8b8Y119Zfec3ft+D6f5QuvDos3fw/xyS5VGvtmDnV26j2G9L9fs2z9uFJztjK\niq2132utXS7JLdLNz/b2Gbfl2CTfb619fU3dk1pr12+tHZbkEemOP1+eUc0rJvnqFtY7t/964RnV\nXZb6P9b3Sjtlbe/PVVb+7m7p/bIX9S9cVS9Jd0xLkkf1PfH+KF2vy0/No27v6unee6duss456S6k\nzNvKfEwfba19M11voB3pLiYswiH9fEQrVv62HjKPYlV1cN/r8uBVT+9K1wvxr5J8tar+b5LLtdbO\nXW8bzMjYKdY8H5lGT6SrpDtx3JNuAt9XJnlezp9k8RPpEuk96U6wnp/kIjOs/9J0f6zuv8k6hyb5\nuZx/xWxmV8jS9TT4/Bb3/+wkL0yfUh8I9de05eR0EwruWMT7e7P66SbUvFb/7/+V5OKLrD/2/o9R\nv2/D2/vfyTf077sfJbnHAuu/Zcz667TnkP537/kj1a/+Nfirkeof3O//rK7Cv7D/uf7EBsvvkfN7\nQ3wt3Un0KekuduxJFxydmy5c2/acDekmzN2T5Dc2WH73fvnL+9f+Z1e1Z1e/zqP77++5F/WfnW7O\njctvsPzVq+q9P8nLkvxDuivDZ/XPn5Xkvnv5+o9af1Wdx/bbflm6C0IrNU/un3tNukBvpXfMDzLD\nuUE2qf/hVfXfMa/6a9pyvXQ9Xr6Y5HbzqLFMtZP8Rf+aPj4DV/nTzVPyzP7ncHZmPEdNv90XDKzz\nhL69M6md5CXpjukP3GD5Ef0x5uv97+pM52QZu/6aWn+X5KxNlv9J/9rvnFP9lWP5u5O8It2NTFaO\nBSdlgx6bM6r9piSnb7L8Iv17/g3zasOqWj/V1zor3Y0k/jkzHHEyUPtxfa1/STd1wxv77981x5rP\nTncesrYH4oWS3CXdBYXvJflCksPm/RpM+TF6A+a6c12Ic17GDZHmXj/dldXH9AfNb/S/XN9Ld8Xy\nhHTB0X3TXZ2ade1RQ6y+DYelO6ncbP/vl+TSc3r9R62/6ufwP4ZoZFWQM8/333r1c/6QlSPTfWjc\n9ge2fd3/RT7Grr+qHW9KN6HkGUneluSYBdc/fsz667RnJUR4yEj1L97XH2Xi23Rd22c2qWy6E8XT\nNln+iL7eq/u/B+9NNxfNtZO8qz8unpjk6ntZ//n98eTwDZYfk/M/RHy9X/f0dLdfXh1ifSHJwXtR\n/5+TfHGT5W/s3/sfXNWOHyX5drpeMLuyQQC0P9RfVectOX8S27WPlZor7Xh2NhnysT/WX9OWN6QL\nS68zrxrLVDtdSLES3H2tf0++NN0538vSnfed1L/nVt6DH8zsA6RDh45t6S5gfTczvLFFkiv3x5E9\n6e6E95p04frfppsb8kf9stOS3G8Or/+o9de05bX9z/kCFwSS3KD/HfxK5jSkqH/vnZf+oka6i0bX\nSnKNee53X+uv+9+9QzdY/rD+5/Cgebelr3d0f1w8c9Xv3dwnlU43ZOxP+5/zWenuyvvojV6XGdV8\nf5IPD6zzqOzlxSKPrT+qf7Fhr/UTyz0k3ZwE10k3cekP0s2FcUq6IOn9Sd7aWvv2WO08kPWTqL4v\nyYNbay/pn7thuiuzR7XWvjBC/Up3Endqm/Mt5terv0hj1+eC+q7Ou9PNDXH1NsLwwqr6xXQf7B/Y\nWvvbEerfM10P0Pu01l47g+19JN0cV7feYPl7kvyv1toR+1prg+2/Ncm1W2tHbrD8Qemu1L8+3cSa\n30zypHSh0V+nmxvn5CQPbXtx++eqOjnJOa21dYdvVNXnk3yvtXaD7W57f6jPBVXVV5J8qLV2l8GV\nD5DaVXVokgckuU+6v/GXTnfR6ux0H2K/lm4+mI8mOaG1dvIc2lDpLljsbq1dYLhwP5z6jekmV79V\na21WUyisPee9drqhemclOTVdgPbmdNNGzOUD1tj1V7Xj4enuwvfKdL1Qvpau99n90k2ufNF0c68d\nP6f6u5PctrV20Dy2P1D77umGyT4v3R1o96xa9nP9sm8luda8z3/Xads/phtCf3hrbd4T2S9c/3M/\nMt153Z51ll8jXcB+jSTX35u/9WzNjrEbwHxU1U+mm8TwG/Ou1Vr7XpLn9I+VD9TfSHelaEdr7ePz\nbgNZmRPgmitP9CdNi5r37AL10528fTLJz6TrkbDo+os0dn1WqarLpLsye8t0Q7nGCJAukm5i2bOT\nvHWE+hdL8tR0Hy5mNRfJmekmdl6v3gPTzb/0nBnVWs/l0935cCP3Ttfj9T7rnFz+7Azqn5Xu5hAX\n0AeGRyV5wQzqLGt9LmhPujBjMrVba+ekm4fmRUPrzrENrar+Nckdq+oXWmtvSbo71KW7O9nvpgu2\n7jfLAKmv/T/OeRdt7PqrvCjd+d39+sdqH0vyyNbavO9QOIrW2vFV9Q/perz8SlX9R7qeV9dKd5fe\nb6a7c/aiA6TfSRcuvuxADJB6r0zX8/EtVfWidOcEV043rO/oJHdI99nn8QKk+dIT6QBVVScmObm1\n9pjBlWdf++R0w1qOSnLJ1to9Ft2GKaqqj6YbVnWTtvlkf5OtX1U1x6uDo9afsqo6KN3kkj+d5JfS\n3Vb+sHRzNjxovatVc27PZZP8fbrg4hmtteMWXP8K6YY5/Ey6O2H+wYy2e1y6IVHPSfcB4gvpwuL7\np5tU/r/S3QluXhOpnpTkKq21q62z7Nh0J5cvaq09dE71n5Huw+kfp5t34QtJLptuuPhx6T7U37C1\ndsqBWJ8Lqqq3pOvhdv3W2ro3GamqC83jGDRm7WVQVbdI1/PmwunmhTo43fEo6S5kPqC19i8jNW8y\nqupm6e6Id7l0fwNOWsTF475HytGttVFuEtX3hjs2Xa+wG6brmPG5dD3Bntta+9YC6h+a7uLKDdKd\n99w53eiPn2mtnTnP+mOqqiemuxvsxdYs+nq6YX3Pn3V4zAUJkZi5qjo83bxAByVJa+2747ZoGqrq\nZ9LNQ/P9dF1sT0iX0B+SrlvnPZKc0Vp7woLrH9rXv1eS77TWfmfDjcynftINs7xnurtpPPZArD9l\nVXVCktuveuq9Sf6wze4ulEP1V0Ks66YLsR6Sbj6kF7fWfmNB9S/V179bupPJiyT5i9baI2ZY57B0\n7+ubrrP45HSTqM9t6GxVPSVdWPWn6YanrYQov5buhPKr6ULcufTArapLJnlnug8Ma52e7gYT75pH\n7WWozwVV1a3TDZv9RpLn9v/+arqJ3X863d+9M+bxd2/M2suiqm6T7g51N0o3jcKn0w1j+8vW2nfG\nbBvz1V8sP3qM4WzLYJ3znnPTXTh7VN9b7YDW/z28RbopVM5I8rkxLmBPmRCJuejnrji1tfawsdsy\nJf0VoT9Kd1VorW+lu0PN3OZmUX/c+lNVVY9IdzXu0+nmyDh9wfV3p+tGveLdSZ7VWlvIMLZ+LqKV\neYpauqvzz2ytvWMOtS6ULqi6Vbq5UM5K8p4kr593j4c+xHpHunmu1vp4uhDr83Nuw0FJ7prz9//7\n6Sa0fX1r7YfzrL0M9bmgqrptugm8b7nO4m+m+1D3qgOtNoypqq6b7u5b854uYSlV1SOTXDXdXFSf\nTndHtLn2foLVhEjMRVVdKckPFzEnExdUVZdKd2XuUunu1vGlJB9d1Phs9cetz2L1J3OXTXcid+Ki\n52Cqqseke699qq//5UXWX6Q+xLprutBsJURZCbHOG7NtTFtVHZHk+unel+emG2L10QWFi6PVBmB6\nhEgAAAAADBplMjIAAAAA9i9CJAAAAAAGCZEAAAAAGCREAgAmpar2VNVc7ibXb/vEDZYd1S9/6Txq\nAwDMmxAJAJiied5ZZKNtt4HlAABLTYgEALAYteYrAMB+RYgEALCJqjq2qk6sqjOq6uyq+mRVPbmq\nDl61zoNWDZHbuTJkrn88pap2Jfl8v/yBa5Y/cE29n6+qN1fVN6vqnKo6par+qKousU7bTquqU6vq\nJ6rqOf33P6yqp8zr9QAApmvH2A0AAFhWVfWSJA9KcnqS1yY5I8mtkjw9yR2q6pjW2nlJTk7y1CRP\nSXJakpet2szudL2PLpHkkUk+kuT4VctPXlXvKf02vpXkjUm+nuQGSR6X5M5VdavW2vdW/d+W5OAk\nJya5ZJK3Jvluzg+sAABmplozLB8AmI6+x1BrrR00sN6Dkrwkyf9Lcr/W2g9WLVsJex7VWnvBmm3v\nbq3dfp3tHZnk1CQva639+jrLfzbJO5K8N8mdW2vfXbXsgUlemuR5rbXHrHr+tCQ/meSEJHdrrZ09\n+AIAAOwlw9kAANb3yCTnJvn11QFS7xnpegvdbxvbG5oL6bf7rw9ZHSAlSWvt5Uk+ukG9luSxAiQA\nYN4MZwMAWKOqLppuGNk3kjymat3854dJrj3DsrdKF1r9cq1f8OAkR1TV4a2176x6/pzW2sdn2A4A\ngHUJkQAALujw/usRSY7bZL1Zzgtw6SQHpRsmt1m9iydZHSJ9fYZtAADYkBAJAOCCzuy/fri1dtNF\n1mytXWab/88ElwDAQpgTCQBgjdbaWUk+keS6VXX40Pqr/2u63kTrOa//utHyf0tyqaq6zjbqAQAs\njBAJAGB9z0k3D9FLquoSaxdW1eFVdaM1T38ryVU22N7KELQjN1j+3P7rX1fVFdapd7GqusVwswEA\n5qNa0wMaAJiOqtrT//MVG6zSkjy8tXZ2Vf15kocn+XaSf0lyepJLJblqktsmeUlr7eGrtv2qJL+S\n5E1JTk43UfZJrbV398vfm+QWSf4+yefS9U76p5WJsavq8UmeleTsJG9Oclq6OZCOTHJ0kne31u68\nqt5pSfa01q62968IAMDWCJEAgEnpQ6SWZO0d0Faea0kOb619t1//F5M8NMnNk1wyXW+jLyR5W5K/\na619dtW2j0jyvCR3SHKZfntPba09rV9+9XQ9jm6d8yfv/rXW2itWbeM2SX47yc/02zgjyZeSvDPJ\nq1prH1617qlJmhAJAFgEIRIAAAAAg8yJBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAA\nwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIP+P01m1EpnCBpyAAAAAElFTkSu\nQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7f1d661d6c90>"
]
}
],
"prompt_number": 14
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Most frequent initial letters, first letter of words"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"allwords = alltext.split()\n",
"\n",
"initialchars = {}\n",
"for word in allwords:\n",
" initialchars[word[0]] = initialchars.get(word[0], 0) + 1\n",
"\n",
"import numpy as np\n",
"from matplotlib import pyplot as plt\n",
"\n",
"letters = u'\u0622\u0627\u0628\u067e\u062a\u062b\u062c\u0686\u062d\u062e\u062f\u0630\u0631\u0632\u0698\u0633\u0634\u0635\u0636\u0637\u0638\u0639\u063a\u0641\u0642\u06a9\u06af\u0644\u0645\u0646\u0648\u0647\u06cc'\n",
"lettervals = []\n",
"letterlist = []\n",
"print 'Initial letters'\n",
"for letter in list(letters):\n",
" print letter, allchars[letter]\n",
" lettervals.append(initialchars[letter]*1.0/allwordsnum*100)\n",
"\n",
"width = 1/1.5\n",
"plt.figure(figsize=(20,10))\n",
"plt.bar( range(len(lettervals)), lettervals, width)\n",
"plt.xticks([x+0.3 for x in range(len(lettervals))], list(letters) , fontsize=18)\n",
"plt.title(u'Percentage of persian initial letters\\n10% of wikipedia articles are tested', fontsize=34)\n",
"plt.ylabel('Percent', fontsize=20)\n",
"plt.xlabel('Initial Letter', fontsize=20)\n",
"plt.show()\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Initial letters\n",
"\u0622 193306\n",
"\u0627 3908207\n",
"\u0628 1191550\n",
"\u067e 210176\n",
"\u062a 1510602\n",
"\u062b 59821\n",
"\u062c 287223\n",
"\u0686 92149\n",
"\u062d 211581\n",
"\u062e 291213\n",
"\u062f 1861543\n",
"\u0630 50086\n",
"\u0631 2525170\n",
"\u0632 551658\n",
"\u0698 34366\n",
"\u0633 1129394\n",
"\u0634 692128\n",
"\u0635 140904\n",
"\u0636 57585\n",
"\u0637 142536\n",
"\u0638 38914\n",
"\u0639 392996\n",
"\u063a 174189\n",
"\u0641 372662\n",
"\u0642 287271\n",
"\u06a9 728996\n",
"\u06af 348562\n",
"\u0644 729613\n",
"\u0645 1541968\n",
"\u0646 1831045\n",
"\u0648 1606199\n",
"\u0647 1638034\n",
"\u06cc 2915877\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAABJEAAAKvCAYAAADa7l5VAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYZFWd//HPh4EhDzlKGERABEQBAZEwkhQVEDMG0poV\nM7Ls+oPBHNa4gqxpAMWIYmBXBBwGEZAgkpMCgwgCSs4MM9/fH+cUdbqmqu6t6uqunun363nu07er\nzj333Fh1v3WCI0IAAAAAAABAN0sMuwAAAAAAAACY+AgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAA\nAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAA2X7Wba/avtK2w/YXlBM+w+7fIuzcl8PuyzjyfbM\nYtuPWVzWbfvEIu+DB5l3xXoPKdY7awD5TS/yu2UQZQQADMeSwy4AAAya7RMlHdQlyROS7pN0g6QL\nJJ0UETeOQ9GAxZ7tfSSdKmnZNm9HnjD2JvN+Hua2j9W6h3ntDHq9k/ncBIBFHjWRAExGS0taW9Ju\nko6SdJ3t/7G93HCLhVLLL+HnDLs8qJavoe+pGUC6X9LPJR0v6euSjpN083BKN+l42AVAU0tNnH5q\niXE8+2R7brHvd6u5zMxB1sQCgMUJNZEALO7uUHqILS0naTNJOyjdBy3pbZI2sv2yiHhqfIuIGvjl\netGwr6RV8/zdkp4TEfcOsTyT1WS8XqLl70Redy9lHOZ2LS7KfdjPfmTfA0CBIBKAxd2NEfG+dm/Y\n3kip1sRO+aU9Jb1X0lfGqWzA4mabYv6XBJDGX0RMylrmEXGspGMXt3VHxKGSDh2LvCcRt/wFAIzC\npPyiAQCSFBG3SNpH0tzi5Q8PpzTAYmHVYv4fQysFMPFQmwUAsFggiARgUouIhyR9tXjpGbafPazy\noCN+QV40LFXM89AMNHEPmxj6OQ4cOwAoEEQCAOnClv83apfIyQG2Z9m+wfZ9tp+wfbvtM2wfXqdz\nbttzWodstr1SXn6O7b/bnpff36BDHtva/rzti23/I5fjYds32j7V9rttr16jLEvZfovtH9m+yfaD\nth+zfavt02wfaruy6XO7jkttr2L7I7Yvsv1P24/ndN+zvX2XvE7MHc9+t3h5t5Zh4rt2UGt7M9vv\nt/1T29fmYebn2b43Dzt/gu1dqrarTb5r5A5XL8vH/5G8z0+0vXOH/dH2GLbkO5Bzq1+2d7Z9nO2r\n8z5qrHu27Y/aXrXLsk93QKuRoyIe0+Z49TX8ebtObm1Psf2mvH/+ls+v223/r+039LGO5W2/y/Yv\nbd+Sj+0jtm+2/UPbr66ZT7m9G+TXnmn7E/m8udsdhjm3vXI+1r+xfZvtR20/la/LG/O2HWN7uzrr\nryjnNNuvs3287QtyuZ50uo/Mdbr+32F7mZrbPbB7QD9azpG255k7dG5texPbX7R9Td7XD+X5L9l+\nxmjW7TxAgEZ2KO8210bbjp+d74cuPi86lMG2X5TPj98U5/CTtu/Kx/iztp9ZtT0ThUfx+VQea0nl\nPficDvv9mLzcnLzM0cUyB3dYZqFruKUMG9j+mO3fO92bnnC6t1/tdL+tvAZsz2i3Pts72f6m7ets\n3+8OHYDb3tj2J22fl6/xJ/I5ca/tK/K+fZ/tDavKAgBPiwgmJiamxWqSdKKkBXmaXSP9JkX6BZLe\n0CbNtpKuaEnXbrpT0ksq1jcnp52v9NC9k6Rb2+Q1X9IGLcuuJelXNcqxQNITkpbvUo69lR5sqvL5\nq6RtKrbplqLMu0p6kaTbuuQ5X9LHOuQ1q+b2LZA0v83yP+lh+V9LWqnmebWfpHsq8vuqUn+Dczsd\nw7E8t/q4VlaW9Isa675P0ls75HFM3WMl6eg+yzmzyOe7SqMr/r5ifedKWq1m/m+WdFeNbbhM0kYV\neZXbu6FSp/2Ptsnr5pblXibpnz2cu8+sWn+XMh4g6fGa67lD0i419uHA7gEDOEfanmeSprfuH0nv\nkPRYl3I+JGnvftct6ZAejul8Sbu2LH9i8d5BHda/lKS/11zHPEmfkuSKbSrL/d0BHJ9y399cI/2o\nPp9a1lf73iTpnB6Wa7sdkqZI+qzqXWM/kLRsl/0wo1yf0ufL8R3y+m7Lsv8p6cma23LboK5FJiam\nxX+iY20AkFZp+f+B8h/b+0g6Vc1hy5+UdInSl9cnlH7l3EXS8pLWlHS67ddFxGkV67VSAOtrkqYp\nPaz8XtLtuUw7jUhsbybpLEnrFS/fL+kPSv3PLClpfaXOjVfN/09pu2L7MEnfVLNG6iOSLlIz+LGx\n0kPgVEnPlPR723tGxB+7bEvj71ZKX6CXV3oo/kP+u5ak3SWtmNN93PZ1EfGzlrzOlvSwpGdL2iO/\n1m6UvU42yH+fknSDpBsl3av08LSKpOcpjc4nSS+XdKbtF0WXUflsv0zpHGh8bi6QdLGka/Nr20ra\nQtLhSg8OtZpyjeG5VWfdq0o6T9Lmxct35NceVKqRt5vSA+pKkr5pe82I+HRLVhdL+nqe31PpuDVe\nv7hN2tGaKuk0pdEV50s6X+kYr6i0r9bN6XaR9DvbO0fEw50yyzUQytoj90v6o9JD+RJK+2eHPP88\nSRfZ3jEibq4opyW9VtLn8/935LLel8s4vSjDNkrBvMb5NU/pPPiLUgBqeaVr+7mSVtPomwqupbQf\nQ+necW0u3yNK5+LGSts8VSlgd5btXSLiki55DvIeMC5sHyLpG0r74S9K+/xhpfvyrkr3z+Ul/cz2\nFhHxtz5Wc62k45S2+aDi9a+3T67bOxW3yzqmKJ1ToXS+XKsUcHggL7e2pBfkv1MkHaU0SukHa23B\nOBvQ59MDSvtdSvt9xTx/mtrv44uL96+WtL3SPpOk65U+l1rd06bsS0v6pVIQTErH5O9K59Y/Ja2g\n9HnRuE++QdJ02zMi4sk26xiRvdLAH+/M+V4j6XKlz4qNle6HjXIcLukTxbIPKt3XblO6v0xTOs+3\nUDoXaH4MoL5hR7GYmJiYBj2p95pIHyrSz5e0WfHes5S+jDbe/7qk1dvksbLSl95Guvslrd9hfXOK\ndI1fCY9XS60hpS+MU/L8CpKuK5Z7UOkX9Clt8l9CKfhymqQV27y/k9KXyMb6Z3ZIt47Sl+HGOm+V\ntEKHbZpbpHss5/uR1vIpPQCX239jl+NycC/HsVju00oP79O6pNlG0p+K/I/sknY1jaylcq2krduk\n21vpIWG+mr9Ad6yJNBbnVo/Xyc+LPJ+Q9J4O58CZLdfHHl3yLGuR9VXrqEO+M4t8G/v2Mkmbtrlm\nPqAUQGykP65Lvq8r0j2kFASc2uFYnV+kvVQdanIUaRrX1+OS3tEm3dRi/rRimXMlrdulzC9Qejhe\nr2L93Woi7asUSHhWlzQrKz2wNvK7puIYzS3SDuQeMIpzpE5NpEY575b0sjZpn6sUbGik/dYo171h\nnWPTZrkTi+W61USapVRrZckOaSzpVRpZ223HLus9pEg3bjWRNPafT7vWLO8x/Wy/RtYSulnSPh3S\n7dVyfn2pQ7oZRZrGfrmt3XYo31OUAoXlcf5vdajtJGlppVqQ3xjtMWZiYpo809ALwMTExDToST0E\nkZR+jSu/YP6t5f3/rXo4aEl/cpH+ax3SzCnSLJD0nRr5Hlukf1TSC/rcN1b6lbXrQ0mRfglJs4v0\nH+qQbm7LNr2zS55rKf3a30jbdls08iGmdhCph32xslItjMaX8k5BgU8V5fiXpHW65LmjRgYwugWR\nBn5u9bDtO7ccr0O7pJ2q9At2I+2fu6Q9sZdt6qG8M1vK+3d1aaqmNMpieQwWaoKm9Ot740FrnqQZ\nFWVYXimA2Mj3VR3SLWiZ3lJj+/5VlHXjUe6rngMVFfmdUOS5V5d0A78HjOIcqRtEelRtAsJF+n2L\ntA+oTdC+z3UPNIjU4356YZHfKV3SHVKkG5cgksbn86luEGlmr9uvFOBtLHObpLUr0j9HzaaUj6vN\nZ4tGBpEW5Otm04p8tyzS3zraY8fExMTUOtGxNoBJy/ZGkv5PIzvd/FLx/haS9sn//kUjq4Z3cqSa\n1cLfZLtqVJfHlX6t71bOqUo1JBo+Fd2blXSzj9IXVykFZk7uljgiFkj6j+Klt9RYx1URcUKXPO9S\nCqA0DLSD3boi4n6lJkRSagrynNY0+fgdVrz0mYjoOHR9pOYU36ta9zidW928q5g/PyJmdUoYqYnF\nu4uXtrb9olGsexCOjoiFmpIUvqzUxE1KD6ZvbZPmEKVaMZJ0UkTM6bbCiHhE0seLl+pcC5dEROX5\noBTMbvhnjfTjqTw39u6YaqRF4h4g6dsRcUWX909XqoUopdqgi/zInRFxoVIzXynVhplIxuPzaSwd\nUcwfFRF3dkscEddKOin/O1WpZmSV4yLixoo05f3kXzXyBICe0CcSgMXdprb/WyP7k1hW0qZKtUbK\nPoNma2Q/FS8v5n8cEZV9BkTEP2zfoPSwsbJSfwNXd1nkzIi4ryLbHXNeUqoxcVyXtFVeUcz/oOYy\nFyn9Yr+cpC1trxgRD3VJ/5MaeV6m1ORMSs08xoTt6Uq/Dm+i1K/Pchp5LmzbSCrp+Up9TJQ2V6o1\nIaUAzvdrrPZ7Sk3xuhmPc6ub3Yv579RY92W2L1NqBthY/vw+1z1aj0v6UbcEEbHA9vfVDPq8uE2y\nfq6F2cV8ndH9flgz37lKTeYs6X2SPllzuVGzvYLSPWZLSasr9R1T3hdXLOafVzPbCXMPqPDjbm9G\nRNi+XNJLlI7Nhlr4HjHh2N5a6X62oVJAYemWJI1juprt9SLi7+NZvi7G4/NpTNieIuml+d95Sn3d\n1TFb0tvz/C5KgzN0U+eeMreYf67t3SLi3JrlAYBKBJEALO7WlfSeijSh9Gv7+2Jk58plbYudbHfq\nCLXVSvmvlTrD7fag/6ca+b2wmL8816DpV7lNr8gd+tbRCHIsodSx93Vd0l5VI797i/mVOqbqk+3d\nlR7Ed+xhsdXavPb8Yv62XIOiSp1aYuNxbrVle12NDIz9oeai56kZRNq2W8IxdnVEPFoj3YXFfLvg\nR3kMDrb9qhp5lgHIVWwvGxGPdUlf5/qW0oPh/8vzH7e9l6RTJJ0VEbfUzKMnttdSaqp5oJodu1dZ\nvWa6od8DaggtGuWsxfYSSsGII5Q6xa+1mNJ9b6IEkcbj82msPFeptpqU+pj7Qs3aouVAGetXpH1S\nNc7ZiLjD9nlKQakpSh3jnyrpZ5LmVNTiBIBKBJEATAattTyeUOqc+EZJFyg1ZblhoaWaozxJqebF\n7m3SVGkd+a3V3TXyWKuYv6mPMpTKbXplH8tb1dv0QMX7UvqltmGpPsrRke0jJX2m5eVONX3KL/kr\ntnl/jWL+tjrrj4iHbD+g7g+c43FudbJGy/9zay5XpqsbTBgLdUfIKh+Ml7a9QuRR2mwvr5HHu59m\nMI1roVMQKVTv+pZSZ/A7q1ljapc8yfadSrW+zpF0WrfmlHXZ3lKpBkTrcay6TtpdI+0M9R5QV0Q8\nWCPZ0MtZxfZSSjVf9m15q9/73rCMx+fTWCnLvoKqf7xqZ9WK9++LiPkVaRoOU7rG11d63ntDnmT7\nRqUfBc6WdHpuqgsAtdEnEoDF3ZyImNIyLRcR60bEjIj4jw4BJKnZhKwh+piqgvXdajE0lF/yOw5V\nXlO5Tf1sT51tqmyaNVZsv1gjA0h/VBoOeTtJayqNUPP0uaDUYXlDu8/EFYr5OrVfGqq+lI/HudVJ\neT491VL7rptym4b54Fn3gac1XVnm0e7/xjKDuL4VEU8o9Tf0bqXOu8traG1Jr1Zqanub7R/Zfkad\nfNvJfaz9XM0A0j+VaiTtoVSDZYWWa+SZxeJ1vzcO7R4wSX1MzQDSAqVmegcqNXldRdLSLce0bNo0\nkZ4FxuPzaawM4p4+Rd3Vup9IUkTcpFQD87NKwezymtxU0r8p1YD8h+1P225t8ggAHVETCQA6KwM2\nh0bESR1Tjq3y1/IVOqaq52E1a8jsvhj2k3BkMf+diHhbRfqq5inlObBcD+VYvod8x/vcKvsLWdL2\nkjUDSeU2jXufI4WqfdspXVnmcv+HpGdGxK2jKtUo5RoGJ0g6wfbGknZVqp20s5r9JS2h1Pnui23v\nlB8Ue/WqnJ+Uamu9oKKZ5oRtwoWng4IfLF46JCKq+m6bqMd0Uf58Ku8pt0ZE3SaFYyb3t/gftj+m\n1DR7FzXvKWvmZCtI+ndJu9nePQe0AaCrifTrAwBMNOXIKusMrRQjy/Gsjql6z2uY2zRwuWPTRnOg\n+ZKOqrFYVYe+5UhZG3RMNbIcK6r6IW2Yx6F19K/pNZcrH4qGOYJY3U6Yy+P1RKMpmyRFxANKzVql\nFJyZUNdCRNwUEbMi4t8iYjOl2kDHqlkbbg1JX+kz+z2L+S/X6OdrWJ1eo57t1fxx4aoaASSp5r1s\nCBblz6ey7GvkPqomhIhYEBF/ioivRMRrImJtpfOm/PHihZLeO5wSAljUTJgbHABMQH8s5uuMxDRW\nRnQQbHs0fT5MlG2qo9cmMaup2WfJ3RHRdWhj20sq/SLbzZ+L+fVsr12jHHWGKx/acYiIO9R84LFG\ndmbbTbmv6nYYPRa2zH0aVSk7Vb+8zfuLzLUQEbdGxLFqjuIkSXvlvnB6VfbdUqdj9hl9rAMLG6sm\nfj0dT9tbqbrvnWEZq2uyn33f6zKXK40cKaVaq8McfKBSRFwaEYdK+nbx8n7DKg+ARQtBJADo7PRi\nfm/bo60F1K+LJDVGU1lSqd+Ufv26mH+j7YnarEFqfiGX6nVoW37pr9P07LVauJPpVtdJatTUsKQ3\n18i3TifNwz63yqHqD6tKbPt5ao7MJkm/G3iJ6ltauYPYTnKttPJYzW6TrLwW3pGXmeh+Vcwvpf6C\nAeV10rV5bK5Vd3Af68DCyvuZBni+1T6e2USubTJWn0+9fpb0vExuBnZ28dJE3s+l8p6yZsdUAFAg\niAQAHUTEnySdlf+dIukHNWtASHp6CO1BlGOepK8VL33Mdp3aLu2cJun6PL+SpJN7eZixPZ5fMsua\nROt1TNV0j5qjQq2UO9luK3dM/OWqDCMiJM0qXjrK9rqd0tveUTWCSBPg3Dq+mN/F9kFd1rW0pG8U\nL10eERd2Sj9OPm672whxH5C0SZ5fIOk7bdJ8U83h25+pkddYV7anVKy/NttTbdft62x6MT9fzeBy\nL/5azHccASsPT36cJm6tlUXN/UrnYkOde1od5fHcrVvgxfZekt46oPWOhbH6fOr1s6TfZcpBHd5s\n+/U1l5PtabaXrZu+Iq+V8/Vbx/Rivu5okgAmOYJIANDd4WoGJraTdHH+It6W7VVtH2r7fPXfZ0k7\nX1QatUlKNTF+Z/sduUlWaxmm2N7T9mm2p5Xv5aDI29UctnpfSb/vFpSyva7t99q+SiM7cB1rVxXz\nG9rerlviiFigkTV8Ztl+YWs62zsrDW+8puqNdvdFNR8oVlHa91u3yfclxfqfrJHv0M6tiLhA6YGt\n4Vu239n64GF7HUm/lLRDfmmBpA+PZt0D8KRSfyln2d60fMP2ErY/IOnzxcvfjIhbWjPJfSSVw3C/\ny/avbG/eacW2N7Z9pNKD+6tHsxGFdSX93faX252vxbo3lVT2d3NWDyPrlcqaB2+2/dHW+0gOkJ2i\nVJtrtCNCQk/XVGmMBGqlmpCDcLmk2/L8NEk/s71+mcDJYUrXslV/hMNxNYafT1cW86+pWZxymR1a\n92k7Obj+P42iSTrF9uc6BZzzcdnB9pcl/U1S5TpqeqWkm2wf2a2Wq+2XSvp48dLpndICQInR2QCg\ni4i40farlYbEniZpc0m/tX2HpEuUOhieovRr/eZKtR8aD+IDG+0pIh61/Sql6vLrKY089Q1Jn8lB\nhTtzOdZX6ouhdbjhMq8/2D5U0nclTVXqUPOPtm+RdJlS7YypSn0MbamRv1T+WuMkIu62fZ6afWOc\na/u3Sl+2n2omiyOKxT4p6QCl5mwbSDrf9sWSblQ6LlsrbZMkXarULKsc0a1dOe7JD2A/V/rc3EzS\nZbYvUvrVfIrSPn+OUtOSzys1t2p0SLxgoUw1Ic6tt+ZteY5Sc43jlWq5nac0ktl0Sbup2ZQjJP2/\niDhnAOsejVMlbawU2LrG9h+UgjorKJ0rZU2xqyR9tFNGEfFj2xsq1SCwpFdIeoXt65QeIh+QtKxS\ns8fntuQ9yD5upkl6v6T3235A0hVKI6c9pHQub650jjWO/8OSPtLPiiLid7Z/J2mPnN9nJb3H9p+U\najZtqDQy3FSlgN07lAJKGL1TJf2/PP852y9T+nGg0XQqJH0jIm6um2FEhO3/lHRyfml3SdfbvlDS\nXEkrKvVntk7O/zile+Buo9uUsTFGn0+nSnpXnn95DjhdoOaIjSHpzIg4q1jmUqX77IaSlpF0Rf78\nuVOpFqAk3RMRZe0jKf04sLak/ZV+rD9C0gfy9XWT0rU7TdIzlD6PGjXHBt1n1nSl+9pn8mfKFUqf\nKY8p/RiyrdJ9tOEa9VAbE8DkRhAJACpExGzbL5D0LaWHKyk9TO7fZbGHNeDOh3PQYXulL9cvzS+v\nLOnlHRZ5TM0vu615/cD2X5V+NW3UqtlII0fganWPRtYOGg+HS5qjtJ3Lqn3zm6eDSBFxg+3XSPqx\n0sOTlDq6Ln/JDqU+ct6kmv1LRcTptl+rtO9XUXr43lEjO28OSV+X9DFJZfOwB7vkO7RzKyLuy7Wy\nTlL6xb+x7nZNMB6QdEREfLvNe+PtSaVA4U+VOgXfTe0fiP8g6YByVLZ2IuLz+aHyv5WatUkpaNOx\nRpKk2yX9paKcdZuTzFMaKW5qXmYlNc+Fdq6X9OaIuG4U63+D0gN34/xdXwvXgvinUn9I5XrqbtOi\nYBjb8gWle9hWef0ztHDH5b+WVDuIJEkR8X3b05VG8LPSvXL31mRKQYIjNLLvnmHouu8H/fkUEefY\nPlHSIfmlLfJUeljNJsaN4Nw7JP1CKYi0sha+N96qkU3YlGsHHmD7CEn/oXQ9L6WFPy9GLKYUtL6/\n49Yldc/Zh3KejfTramQAvHXdZ0g6KNeWA4BKBJEALI6i5e/oM4z4i6QZubnJq5VqPKyvVEtkvqT7\nlH5lvFypdstZEfHYoMsXEXdKeplT3zuvV3oAWVfpC+4TSg+3Vyp9Gf5pRHRsthARF0t6fm6Gta/S\nA/k6SkGSJ5V+8f2LUsDibEnndGk+Ez1uT619EBFXOo0m9B6lh6KNlX7F7fj5FRFn2H6OUr84+6hZ\nI+hOpeNzSkT8QpJs1z4WEfFL28/OZdlP6ZfepSTdofSr9rcj4vzcJKwxgt6CiOgYRMr5DvLc6klE\n3C9pf9svkvRGpfNpbaWabvcoNb/5jaTvRMS9nfIps2z5OyYi4k7bM5QCgW9SCvisobSv/izp+xHx\nwx7y+01uLnaA0jmzo6S1lM61x5WaM94o6WKl/f+Hqix7WPfttleV9GKlGiPbSnqWUnPLpSU9qnRd\n/1npgfa0iGgbHK67/ly7blelINEblWpZrai0nXPzek6MiH/l4EQjz275jsk9YIzyG3Q5697PHra9\ng1KTrX2VagGuonScR5v3J22foRR431XpOn5M6f70e0mzIuISqfZ9b6yu5VrnyYA/nxQRh9k+Xel+\n8Tyl66scgGGhMkXEmbafr/Rjwy5K9/wVlGqItl2mWPYLtk9QahK6h1IwbHWle+vDSsfleknnSzqj\nS1C4PA61jkVE/Cw3Rd5L0k5K1/dGSp8pU5R+2LhFadCOH0XE+XXyBYAGp+bHAABgEGxvpmbtjWsj\nYstu6VHN9kxJR+d/T4yIyhHlAAAAMHh0rA0AwGAdWMxfNLRSAAAAAANGEAkAgAHJTaI+VLxEh8QA\nAABYbBBEAgCggu1tbZ+c+zNp975tHyDpPKU+MyTpkoiYPW6FBAAAAMYYHWsDAFBtKaUOUt9s+y6l\noaYbQz2voWZHzA33SXrLeBcSAAAAGEsEkQAAqFaOQrGW0ghenVwj6bURcePYFgkAAAAYXwSRAACo\ndrHSsNkvk7S90lDTq0taWdIjku5S6kT7VxHx82EVcjE2VsONAwAAoAeO4PsYAAAAAAAAuqNjbQAA\nAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgCMG9vL2H6v7dm277Y9z/aCPJ02\n7PJVsT2jKO85XdLNLdLtNoD1NvJaMNq8FkW251TtT9uHFGlmjXcZJwPb04t9fMs4rXNSn/vAsLR8\njm0w7PIAmDgIIgFYpDnZ1PaBtr+YHzYfLB88RvPlx/aatj9i+3zbd9h+wvZtts+2/U7bK/SQ1yq2\nP237WtuP2X4g5/t221N6yOeYvF1P2t6ivy0bf7ZXknShpK9JmiFpdUnldi9qw4V2K285JP0gt2tR\n20eD0uv+nKz7aTyN9z7mmALjK1r+AoAkaclhFwAA+mV7O0lnS5rWJVnfX35sv0bSCZJWbXnrGXna\nXdKRtg+KiPMq8tpE0u8krVe8vLSkF+bpNbb3j4jHauRzVP73yxFxTd3tmQA+I2nrPB+Sfi/pL5Ie\nz69dMYxCjRG3/B10vpPNWO3PScv2iZIOyv8eGxHH9prFYEsESLZnSjo6/3tSRBw6xOKM2iK+PVzj\nANoiiARgUbaCugeQ+pYDSD8pXnpMKQh0p6SNlGrSTJG0oaQzbL84Ii7ukNdSkn6mZgDp1pzXCpJe\nlv/uKem/JL2nomjHS5qa85jZ42YNTa5p9ZbipYMj4vvDKs8oDPOXWX4N7o5fzfvX6z4bdA07oJ3F\n7Rxb3LYHwCRFEAnA4uA+SZdJujRPy0o6ud/MbG8o6XvFS+dKel1E/LNIs7GkX0jaIq/vNNubRMSj\nbbJ8taQt8/xvJL0yIuYV67pA0jqS3mb70xFxe4dyvUnSHkpfRN9XVWtpgtlU0vJ5/olFNICkiDhX\nQ2gKHhE0P68QESdJOmnY5VicRcRc0RUCAACTGl8EACzKLpe0SUSsFhF7RcRREfEzSX8fZb6fUGpq\nJkm3SHp5GUCSpIi4SdJLJT2QX1pH0oc75Ldf/jtf0vsbAaScz62SPp7/XTLnuRDbK0v6Yv73VxHx\n69pbMzEVUliMAAAgAElEQVSUTQLvGlopAAAAAPSNIBKARVZE3J+DOQNjezVJBxYvHd2hdpFyjaEv\nFS+923a7PgQ2z3//FhF/bfP+b9ukbfUZSWtKeljS4R3STGRLFfOMsgRMLPR9golocTsvF7ftATBJ\nEUQCgJH2U3PEsIck/bQifTmU+FqSdm6TZsX8984OeZSvr9j6pu0dJL09/3tsRIy2plVteXS6o2yf\nW4xOd4/tK21/LZet07JPDwcuaXbxVjlMeN/Dhdv+dbH8m7qk26tlXV/vknYl20/ldI/m/qzK92cU\n+ZzTa5k7rPPFeaS+Rr6n2l66JU3lMOe2TyzSHZNfW872O4rj97jtv9n+qe19+ijrarY/bPvMnM9j\neTTEG2x/1/ZePea3nO0P5FEK/5Xzu9n2T3otn+1Diu2fVZF2M9vvz/vh2rz/59m+N5/bJ9jepZf1\n91DOZWzva/tL+bj8Ix+Xx2z/3fZv8j5eqWZ+c4rtPji/tpLtw/N7f8/btsD2hs7DdqvZqbYkHeOF\nr8mFzvHymq57zdpeyvYbbX8vnyf3Ffv6EtvH2X657YF8J3VygO1ZxfqesH277TPyflmuZl7L2j7M\n9i/yeflwvj88nP8/y2nEzd3stj8g9FP2FzmNwPkb27fYfsRpJM67bF9g+7O2n1kzv5mt14TtJWy/\nzvZptm9yus89fe60yWMD2x+z/fu8D5/I+/TqfOy2H+125/XMyefl0cXLB3c4L7uee4Mss+3n5mv1\nIqd71Lyc3z9t/8n2yU4jrK61KGxPzm/VnN+lOZ9HbN+Yr5mdeskLwCQVEUxMTEyL1aTU6fWCPM2X\ntEEPy36vWPaMmsvcWCwzs837f87v3dxh+Y2K5f+r5b0llZrtLch/lxjH/Xi4UiBtQcX0I0krtFl+\neo1lG1PbfVNRvg8Wy3+nS7rPtKzr2i5p9y/SnVVxbs3uks/cIt2uXdK9Tml0usa5elyHdE+fz13y\nOrFId7RSP1RXVez3UyUtU3N/f0jSgzWO5VmSVq+R3zaSbq5xbi0vaU7V/pR0SJHmu13W+5Mezstf\nS1ppgNfUDjX34QJJ90t6dY08G/tmvlJgaCeljvdb85uvNBDALT1s/+yWdU0v3qu8ZiXt08P6ftDv\nuV+k3VZplMeqdd0p6SUVeb1AI6/jqmmPUZ4bSyk1xa6zrnmSPiXJFXnOLK8JSesq9fHXLs+DWpad\nIumzat6fuh47ScuOcvvP6WFfd/osHViZc17/3UOZzpvI21PkubdSk/JueX1F6bvHXDXvHbW/RzEx\nMS3+Ex1rA8BIWxTzl9Vc5jJJz2qzfMO1SkPbr2/7WbFwk7Y9W9KW3i/puUpf5N4ZEQtqlmlUbH9G\n0pHFS08oPXzcKmllSbsq1bySUiBkE9u7RcTDxTIPSDpOqSPw9SS9Mr/+kBbuAPmePoo5u5h/cZd0\nu7f8/2zba0dEu5phZT4DqWnUie33SfqyUhOHkHRMRHxyQNmvrNSJ+0YaeexWVdrGRh9Vr5L0S9v7\ndDq3cg2L7ygFaRrulvRHpYfxqUrn9/Pze3tIutD29hFxX4c8t5R0di6nlLb/GqWA61M5v22Uzq3G\n+4OyQf77lKQblILA9yo9mK8i6XmSNstpXi7pTNsvioinBrDuVZRGYwylc/4aSbcpNVOdqhSk2UEp\ncDZN0k9svzoiflEjb0vaRNLX8rIPSfq9pNvzehs1DE6StJrScXp2fu3iPLX6S09bVxbGfq+kr6rZ\nhCeU9vWflQJk05Sa726l9MC6TL/ryuvbRykoumx+6UlJl0j6q9I1sIGkXZT27ZqSTrf9uog4rU1e\n6ykFQxujfy7I5b5Oab8uqxSQ2UqpP7xBjFY3JecZkh5V+iy4Wek+aklrKwW21s5pj5K0nFIwvY5l\nJP1K6bp6StKFSsd3qtJnzNOcakL+UingoFymvyvtz38qncPbqnn+vEGphumMiHiyh20unSbpaknb\nK22nJF2vdJ9otdDnxRiU+fMaOVrqv5Tuef9QOh9Wynk9R2kfth7/ibY9sr270jkwtcjzEqX70FKS\ntsv5vU/p+mE0OQDtDTuKxcTExDToSaOrifRIsezbay7z+WKZK9u8f2Dx/umSlireW0/pIXKB0oPO\nusV766tZE+h/xnH/7aeRv0r+UtIaLWmWkPQRpYeRRrqTuuS5W5Gu51pHXfL9Z5HvRm3en1aU8c4i\n7Rs75HdlkWbHinOr75pISr8uN95/UtK/VWzn0+dzlzQnFukav1yfJWmdlnRTJX2u5Rgf0SXfjxbp\n7pb0RrWpEaf0QHNdkfbnHfJbUs3aeQuUfhXfu026FxXXRvlL/GhrIn1a0mslTeuSZhtJfyryO3JA\n5+v2SjVItuqSZllJ/6EU1FqQz/HluqSf03IuLZB0vKTlW9JZ0pTi/1nFckfXLP/0YpmO17HSg+/8\nIu1FkrbrkHZVSe+U9LlRnPvPUgq2NNJ+XW1qwykFLb9ZpLtf0vpt0n25SHO1pM26rHtLpeu57fb1\ncG4slY/JDElLdkhjpcBved9b6D5VpJ/Z5tw4V9L0NmmXLuaPL4+zpH065L+XUpCykfZLA7hGjqlz\nHbdZbmBlVgqyzivS/Ht57bSkXUHpfvKZibo9Od1KGlnT7S/tzlmlz//78/X7ROPaEzWRmJiYimno\nBWBiYmIa9KQ+g0hKv9SWD9b711zuQ8Uyf2/z/lJKv/Q10twi6duSfqiRDz7Htyx3mprBj5XHad9Z\nI5vnna0uTegkfaBlnz2vxjEZZBDp1CLfhQIxkvYtzoMPqvlg++02aVcv8nqg3UODRhlEUgqgnFS8\n94ikfWtsZ69BpAVKgZqlu6Qvm2o8qPZNEp9RPEg8KGnzinKurZHBum3apDm4eP9JSS/okt+zNTKw\nO+ogUg/n1spq1jq4TRVNhwY9KT24NrbnbV3SzWnZPx2bdnY5XwYWRFKqJXNTke481WwyOYpz/397\n2RZJJxfpv9bm/UuL90fVTG2Mzo0XFuU7pUu6mS3nxlVVx0Kp1kwj/W2S1q5I/xxJj6kZ7F2n1+3p\nUuZa1/GgyyzpFeX5u6hvT05TBrPul7Rhl/xmaGQQmCASExPTiImOtQGgaYWW/x+ruVyZbqGOsSNi\nnqRXS7ojv7ShpMMkvb5IP1vShxvL2N5XqX8eKdUSub81X9sr257W+voo7alm07wFkt4V3ZvQfVWp\nD5KG93RKOEZmF/PtmrSVr52qZllbm7i1pv1DRMwfZdlGsL28Uh87b8kv3Stpz4j49SDXU/hwRDzR\n5f2jlB4mpHTuH9gmzfvVHFnv8xFxXbcVRmoi+JXipbe0Sfb2Yv7EiLikS37XK51j4y5fc41mZOsq\nPaiNp1nF/N4dU430uFINwWF6lVIzSinV5nhzRDw+ViuzvYVS30tSql3xiRqLHalmU503tekUu3Ff\nDaVaPxNKRFyo1BRTSjVR6vpojWNxRDF/VLRv9luW5Vo1mydPVbMJ6ngadJnLz9VhHP+Bbk8+v99W\nvPT5iLi1S35zJP24lwIDmFzoEwkAmpZt+b9u3w7lg3prHpLSw7DtrZWaBu2n1D/HPKV+L06W9K1G\n0CIHGxojiM2JiO818skjwMxUqj6/an7tDqUOwT8VI/sk6scexfwfIqJrnygREba/o9QPi9Q+ODOW\nqoJIjfLcFBG32Z6t1OfNhranR8TcDssPtD8k22soNWVs9I1xm1LHvtcPcj2F2yJidrcEEfGw7Z8r\nBTSltP3fakn2ikZypY5b6yjXO2KEs3xulyP6tfaN1c4spVo5A2d7utIx2USpucdyGjkM97aNpEp9\nPl0zwHVPlbSjUr86aysFlDt9L3tezWzPjA79UI2jclS9X3V7WB2QlxfzP46Iyn5cIuIftm9Qqum2\nslJfdlcXSeYqBdMt6b0aGfgcF/nz4vlKPzpMk7R0S5LGDxCr2V4vqkftvE/SGRXrnCLppfnfeUqB\n9zpmq7mPdtE4Bn7HqMxzi/k9bG9eFUAflDHans2UAuFSupfXve++oea6AUwyBJEAoKm15tHUtqkW\nVn6571h7KSLuUfoF/MhOabKZSv0hPSnp3Y0XbW+sFNxYr5Fl/rtuzvOltncf5UPkNsX8H2ouc14x\nP932ShHxwCjKUFsOzt2p9BC+ju1nNwIztldTs8PY2cXfDyk9HO6uNGJRQxkA6xqA6dEzlZovNmp4\nXSPppRFx+wDX0eqimukuVDOI9PzyDdurqtlpqyV9aOEKG22VQ9Ov3/Le1tLTtaDnKXXq2lVE/MX2\nvWp2Bj5quYPZTyoFcepabUDrnqY0et5hanYsXmX1mun+1FehBuuFxfwgr6NOXlTM72T76x1TjtQ4\nT610npZBpB+qOeDBW21vp/Tgfaak6+sEqvphewmlQMARatbmqlxM6dysCiJdXqPcz1WzRu4Tkr7Q\nppZWO+sV863X/FgbizJfpNTsfCOlYN2ltk9Rqpl4XkQ8NLoidzUW21N+rt9e87On7mcIgEmIIBIA\nNLXW4mlbq6iNMt2ovlza3kqpnyFJ+q+Wmio/UPqi+GRO832lQNfhSv0dbK1Ug+lNoyjCGsX83JrL\ntKZbQ6lPofFyjppNsXZXGgFHGlmzqPEwe55S/w5TVASRbK8jadOc5n6l/oQG5Ztqft7+UamD1LHe\nP3+rma588Fyj5b11Wv5/t3rXGvgp1/HPqD+S09/a5NUX20dK+kzLy50ersuHt4Waqvax7mco9WG0\ncY/rr7vuu/so1qCtVczfNA7rW7eY31391YZcpfwnImblQGPjXvo8NWuD3Wv7AqUOqk+LiJv7WN9C\nbC+lVOtk35a3BnVu1jk3yn25gvprnjywYG9NAy9zRMy3/UZJ/6d0biwr6a15CttXKX2WnCnptz3c\nx+oYi2NQ3ndrfTZExIO2H9DIHwUAQJLoEwkAGnJfEY8WL63VKW2LtYv5e/tdf/618QSlAMfNKvr2\nyA80jaZQn4+IEyLi4Yi4NyKOVbP/gtfbrvsLdjvlw8gjNZcp01kDeNjuUVnbYfc289FIk39BbtR+\neXGH5c4dcE2D8gHjGRpQjZYK/Ry71uPWWksmepykhb9n9HN+SSOvy77ZfrFGBpD+qDQy2HZKw74v\nGxFTGpOkY4u0g/jOdIqaAaSHlPqPeplSLbUVlUblKtf/dNFr5l+3H7exVB7j0TavrWO052mozY+q\nEfEWpeD0JRoZyFlVqZnnFyT91fYZtjcfwHZ8TM0A0gKle/qBSk3tVlHqJL88N84tlq1zbtY5Nwax\nL6dofI1JmSPiIqVaQd9Q+lGkcQ44v/4epZFLb7f94Zq1hYa1Pf3ed3tJC2ASoSYSAIx0g5rNeuoG\nYzYo5kfTx83blJqChKT3tnSK3OhnJJS+1LY6Tqmj7iWUOuH9nz7LUNakWr7mMmW60ChrY/Wh7L9o\nRjHfCAxdExH/Kl6frdSMae2i+VsZRBpkf0ihdFyPUarptL6kc3Ozw679TY1SP8eu9biVAYAFETGI\n7wz9nF+9pu2mbEr6nYh4W8eUycB+hbe9o6Rd878PSdqhW59YY9Bp/nh5UM2aPa2DFYyF8jw9NCLq\n9PdSS0T8WNKPcw2y3STtrNR8bgs1Azd7S7rE9p4R8cd+1pP7x/pg8dIhEfH9isXGooZIuS9vjYjR\n/CAxXsaszLnZ13tsf0DS9kp9De2s9DndOMdXUwoo7qQ0gMZojcX2DPu+C2AxQ00kABip7Dh3m46p\nRtq2mO+r413ba0r6bP73ZxHR2gHqJvnvIxHxjzZZ3FjMb9rm/brKJg/Tay7T+iV3XEezyc1JGlX0\nV7W9dUvztNZ+WRr/W83aSI2/0Sb9aFjS7UrBrUbA4BmS5tjebIDrabVhzXRlAPRfLe/dVczb9toa\nvfL8WtN2a2fBnWxQnaS73GFt4zjPVxqdrkrd/VjHnsX8iTU6VR/kusdTOZLUszqmGpv1tTbBHIiI\nuD0ifhAR746IrZWu4Q9JuicnWU6p2Wq/tlcz4HZVjQCSNIBroo1yX66R+2ia6Ma8zBExLyLOj4jP\nRsQrlJqHvVhptM2GA2wPIog0FttT3ndrnTe2VxJN2QB0sCh8OADAeCoDCDvmX4g7sr2eRvZv8rs+\n1/tFpWrsDyoNq96q8Ytgp+rl5a+Xo/n1/7Ji/kUdU420czF/y3h1qt2itUlbt06yz1dzRL09bW+g\nZsDsXxFxtQYsD9E8Q80g4zpKgaRBNINpp26H0WW68tg3ytwYWctqGWmtT1coBXCkVBv6BV3SphWn\nYNsqVelqWE3SUnn+7pbaae3Wu6RGntujVfZ1UuccmzHAdbczJp1DK3XW3jAeozWWtX8GcY5Wioi7\nIuIrkvYvXt5iFE2Jezo3ct95Y9H30OWSHs/zy2nkDyTjpdfzctzLHBELIuLciNhfqV+khv3aJe8x\n+7HYnvLevl7+3lKll0EHAEwyBJEAYKRfqfmQu6Kk11akP7SYvysi6o5o9rTcT0ujA9ejO9Q0ejD/\nXaNDYGv9Nmn7UQbBds0jwnWU+4E4rHip3yDaaJVN0HbXyBonc8qEuZlg40F3N42sITIi7SBFxN25\nXFfml9ZSCiRtOQare4btPbolsL2ipFcVL7WrgVX+0t5PB68jRMSjGjnqz8E1Fju0Okm91Rfzy9VI\n/1ot3Nn4oNbfNdCba029c4DrbufxYn6pjql697/F/H62pw8w73ZOL+b3tj0etZ8kSRFxgaTGaJhW\n6lerr6yK+To/Ary3z/V0L0S6N5491uup0NN5OQHKXJ5/7Y7/0LcnIm5QqhHbMJ73XQCLIYJIAFCI\niHuVRkFrONZ22wfO3E/Gh4qXju91fTkg1Ojj6DJJ/90h6bX57xKSXt7m/f3apO1ZRJytZtM4S/pG\nRXX6w9UctSiU+mYahjIAsqukRgDlzxHRLqjWSL+qRtb8GmR/SAvJtV92V3P0tzUkzbb93DFY3Rdt\nL9Pl/U+r2VzhIaVhzRfKQ9K8PL+r7Y/WXbntZXKTiFbfKuYPsb19lzyerfY18/pxj5qjBq6Ug7ed\n1vsMSV8e0Hob/lrMv7Ii7UxJY1VLreGeYr5OzYS6fqnmti4p6fu264502bOI+JOks/K/UyT9wHbt\nvlxsLzSAgu3Vay67qppBn1D/o+OV58ZuHa6bxjr3UholbKyUHc+/2fbr6y5oe9oAjnVZQ7DueTnQ\nMufjWtf0Yr7d8R/69mTfLuY/2i24m++Nr6u7TgCTD0EkAJNBr6OmHK3mr4fPlPRr2yNqJOQaOr9R\n8yH8H0oP3L36d6W+e+ZLemeXUcHKGiGfsP10857chOIj+d95klr7U+rVEcX8npJ+1mb7p9j+kEY+\naH8vIq7UEOQOUBsdVa+oZn8ynfo3Kl/fqpFNl/QDkwOVe0i6NL+0ulIg6fmdl+rZk0ojCJ2e+4d6\nmu2ptj+nkTWLPhURCzWVjIhbla6Hhs/a/m5uAtiW7a1sf0LSXLVvEnGKmrWxpuQy7t0mnxcpBQeW\n1sgR7voSEQs0stbALNsvbLPenZWG715Tgx1d7HQ1a5zsYvvLrQFq28vb/pKk/xzwutu5opjfe1Ad\neef9/C6lEcak1OHwuba3a5fe9qq232X786NY7eFqBgi3k3RxDra0ldd5qO3zlUbIa3Wb7W/b3iPX\nCmuXx7qSfqJm7ZLrI+KWPst/uaTb8vw0pXtuWbtUTg5TCtJZYzRyVkRcqObADJZ0iu3PdQqs5XLt\nYPvLSn3Trd8uXQ/Kz5AdWvfDOJX5fbavtP3eHFDulMeblc69htPbJJ0I2yOl8/yOPL+ipLPbXZO2\n95N0mtK9al7r+wAgMTobgEWc7W8rPTSUyuYAlvR/tssvQyHphIhoO4JZRNxq+yClIZYbnS/favts\npV8aN1CqTdIIxD8q6YDcVKeXsj9Lzc59/yciLu2UNiIutv1bSS+R9BxJN9j+jaSpSjWTGtv8zQ7N\n4WqLiF/nIENjJKv9Jb3U9hylB51pSs3Ayl/wL9MAmjuN0jlqdkDe0CkodLHSQ3p5rvwjIm7skH6g\nIuJ+23tK+q2kHZRqRJ1t+yXdzoMeHK903HaXdIvtc5SO3SpK53P5S/vvJP1Xl7J+Lj/4vDu/dIik\ng2xfqVTr7SGl/bi2pK2VgmJPL94mv6dsv0VpiPKVc/ozbF+tdB6FUmCv0bH9T5TOtd1qbns3n5R0\ngFJztg0knW/7YqXad87lbzQvvFRp3xzZJp+eRcRfbM9Ss/nn+yUdaPsSpc5011bqB2l5pX1wqKSf\nDmLdHZyhFIhYXqmPruttn6VUQ6kRAPprRJzQa8YR8Tvb75f0VaX7ZCOwc4NSLbwHlR5kn60U7Jwi\n6Rf9bkhE3OjUqfHPle5Pm0v6re07JF2i1Nn/FKXzfnOl+0Tjx4VbF85RSysdp8MkPWb78pzuAUnL\nKHUYvoOa36PnaRTNjiIibP+npJPzS7srHY8LlYKxKyr1z7WOmjU+t9Rgrol2Dlc6H/dXOn5HSPqA\n7T9Juknp3jlNqYPxrdX8MWUQ/WxdqrSvN1Ta11fkz7471Wxqfk9EfKZluUGXeUtJX5P0NdtzJV2l\ndG08qXTP2iHn1fC7iGh3vU6I7YmIB2wfrNTcdKrSD2QX5/vfNUrB0BdI2izn8QWlEV8X1Q7+AYyl\niGBiYmJaZCelPmwW9DEdXSPv1yhVRe+Wz82Sdumz7GfmPO6QNK1G+jWVvsh2KstZkpYZ4L59n1KA\noNv2z1cKti1fkdeMYplbxuhceF1L2R6XtGyX9P/Xkv57NdZRbsfsLunmFul27ZJuRUl/KNLepzT0\ne2u6p8vZJa8Ty/NbqYbbNRXH72d1zxmlfjTuqHl9zVcKzGzRJb9tJd1S59zSyOu87f5UCm410ny3\ny3pfqhQM6Lbes5Sut5nlPh3AObq0Uk2SbvvuQUkH9XDcy31zUI/lOVTSU13Kck5L+unFe5XXsaRX\nKD1A1zlfTu6QR+U+KNJuot4+Ex6U9OE2+TyYy1Qnj9sk7T3acyOv92MV652vVPtzyZrXRHn+drwm\nupTnCKV7Ut1r/s+S1hzAfthb6ceZTuvqeO4NosxKzdTrnkPzJZ2kLvfRYW9PS34vVfoxrFseX1MK\nus4tXt9gEOc4ExPT4jFREwnAoi40RqMMRcSpts9Vejh9pdJQ9qsoBZZukHSqUuCh52YFtg9UaioW\nkj4U7fvtaS3P3bZ3kPRBpYDJM/Py1yr9gn1CpKYkAxERX7P9I0n/pvTF81lKI1w9otRJ5xxJ34+I\ni+tkV/wdq1GhzmnJ++KIeKxL+tlK29VYpk5/SNHyt1u6yu2MiIdsv0QpoLWz0i/Lv7W9T6QmDe3W\nXUuk2hkvUDp/X690/FZVOn//KGlWRPxfD/mdlM+H1ys9FG2n1KfTikoPSHdJuj7nfWakvmq65fcn\n289R6kD6NUpBr+WVmoZeJumkiDhdkmzX2e+1jk1EnJHX+wFJ+6j5S/udSs2KTomIX/Sw3toidZq7\nv+3XKB2XbZXuKfcpBSP+V+lh/7Zysaps+y1jRMyyfZWkd0h6oVKfLcurWcuyU551z+/TbZ8p6UBJ\nL1OqXbamUo2MB5VqVFwk6deR+mPrmFX11qTaXpJm5GaKr1YarW19pfN+vtJ+vknpOP9O0lkd7hGr\nKV2PuyrVzthEqVbIcmqe61coNV/6cUQ83iaPnkXEJ22foVQLZde8zseUgre/V7pmL5EGe010Kc8X\nbJ8g6c1KTXAbNQ2XV6oJc4fSNX++pDMi4rp+1tNmvWc6Ne99t9IxnK5U27HRtLDj9gyizBHxJds/\nlbSX0nWxVS7DyjnJA0rNpy9Q+gzs2ox72NvTkt8ZTn3NvUfN7zVTcz4XSPpORJwnPX2OjdXnNYBF\nmCOGd2+w/V2lZhh3R8RW+bVVlX553FApAv66iLh/aIUEAGARYPtESQflf2dGxMeHWBwAAAAshobd\nsfYspV+BS/+u9MvQpkq/Ev37uJcKAAAAAAAAIww1iJSrS97X8vJ+Sm2Llf9WDYMLAAAAAACAMTbs\nmkjtrBURd+X5uzRy9B8AAAAAAAAMwUQMIj0tUodNdOgGAAAAAAAwZBNxdLa7bK8dEXfaXkdpGMqF\nFKNSAACAkY61feywCwEAAIBFU0S43esTsSbSryQdnOcPlvSLTgkjonI65phjaqUbq2mY65/M2876\nWf9kXv9k3vbJvP5DDjlEtmVbxx577KTbftY//PVP5m1n/ayf9Q9v/ZN521n/8Ne/uE7dDDWIZPuH\nki6QtJnt22wfKumzkvayfaOk3fP/AACgi1mzZmnBggU6+uijdfTRRw+7OAAAAFgMDbU5W0Qc2OGt\nPce1IAAAAAAAAOhqysyZM4ddhr4ce+yxM+uWffr06WNalom8/sm87ayf9U/m9U/mbWf9rJ/1D2/9\nk3nbWT/rZ/3DW/9k3nbWP/z1L46OPfZYzZw5s23/mq5q7zZR2Y5FtewAAAAAAAATkW3FItSxNgAA\nAAAAACYYgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEA\nAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEk\nAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQ\nCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoR\nRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBK\nBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACg\nEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAA\nqKg0cd8AACAASURBVEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUWnLYBVhU2R6TfCNiTPIF\nAAAAAAAYDYJIozLogM/YBKYAAAAAAABGi+ZsAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQA\nAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJ\nAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFE\nAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoE\nkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKAS\nQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACo\nRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAA\nKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAA\ngEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAA\nAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUGnCBpFsH2X7GttX2f6B7aWHXSYAAAAAAIDJ\nakIGkWxPl/Q2SdtExFaSpkh6wzDLBAAAAAAAMJktOewCdPCgpHmSlrM9X9Jykm4fbpEAAAAAAAAm\nrwlZEyki7pX0RUl/k3SHpPsj4uzhlgoAAAAAAGDympA1kWxvLOkDkqZLekDST22/KSJOKdPNnDnz\n6fkZM2ZoxowZ41dIAAAAAACARdycOXM0Z86cWmkdEWNbmj7Yfr2kvSLirfn/t0jaMSLeU6SJYZbd\ntqRBr9+aiMcDAAAAAABMDrYVEW733oRszibpekk72l7WKVqzp6Rrh1wmAAAAAACASWtCBpEi4gpJ\nJ0u6VNKV+eVvDq9EAAAAAAAAk9uEbM5WB83ZAAAAAAAABmtRbM4GAAAAAACACYQgEgAAAAAAACoR\nRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBK\nBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACg\nEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAA\nqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUGnJYRcA/bE9\nJvlGxJjkCwAAAAAAFm0EkRZpgw74jE1gCgAAAAAALPpozgYAAAAAAIBKBJEAAAAAAABQiSASAAAA\nAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAA\nAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEA\nAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAA8P/bu/MwWc66XuDfHzkkYTESIGGXgIKA\n7ARlkXBYRTYB5WJEFr3ogwKyK4iGsKl4lVWuXkTAJYqCGgEBIcBhNcgSFtlkCSSyE0kgkECS894/\nqoZMJjOnZs7p6uqZ/nyeZ55zpqumfm/3dPdUf+tdBgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAA\nAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYNCuqRsAAAAAa1XV\nKMdtrY1yXFgGQiQAAAAW1KwDn3GCKVgWhrMBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEA\nAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIB\nAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIi\nAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwS\nIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAM\nEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAzaNXUDANi8qhrluK21UY4LAADsHEIkgG1n1oHP\nOMEUAACwsxjOBgAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwaGFDpKq6XFW9qqo+XlUfq6pbTd0m\nAAAAgGW1yKuzPT/J61prP1dVu5JcZuoGAQAAACyram3WS0UfuKr6wSSntNauvY992pRtr6qMscz2\nZu/T1PWBaXjtAwDLwnkPTKOq0lqr9bYt6nC2ayX5WlW9rKo+UFV/XlWXnrpRAAAAAMtqUYez7Upy\n8ySPbK29t6qel+RJSY5bvdPxxx///f/v3r07u3fvnmMTAQAAALa3PXv2ZM+ePZvad1GHs105yb+3\n1q7Vf/+TSZ7UWrvnqn0MZ9O1E5aO1z4AsCyc98A0tt1wttbal5OcXlXX7W+6c5KPTtgkAAAAgKW2\nqMPZkuRRSU6oqoOTfCbJL03cHgAAAICltZDD2TbDcDZdO2EZee0DAMvCeQ9MY9sNZwMAAABgsQiR\nAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJ\nkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEGbDpGqam9V\nHTewz1Oq6oIDbxYAAAAAi2TWPZGq/wIAAABgB5l1iHR4knNnfEwAAAAAJrZrXxur6piV//b/HrXq\nttUOSnLNJL+Q5JOzax4AAAAAi6BaaxtvrNq7xePtTfKQ1toJB9SqTaiqtq+2z6F+klnXr2z2Pk1d\nH5iG1z4AsCyc98A0qiqttXWnKtpnT6QkT1/1/+OSvK3/WuuCJGckeUtr7RP71UoAAAAAFtY+eyJd\nZMeqzyV5bmvt+aO2aJP0RJLKwzLy2gcAloXzHpjGgfRE+r7W2lEzaxEAAAAA28qsV2cDAAAAYAfa\ndE+kJKmq6yZ5dJJbJjk83apsF9Nau/aBNw0AAACARbHpEKmqbp3kzUkOTTeR9leSnL/OrgaYAgAA\nAOwwW+mJ9PtJDk7y8CQvba2tFyABAAAAsANtZXW2byd5bWvtAeM2aXOszmalAlhGXvsAwLJw3gPT\n2NfqbFuZWPu8JJ+fTZMAAAAA2E62EiK9K8nNxmoIAAAAAItrKyHSU5LcpqoePFZjAAAAAFhMW5lY\n+2eSvCXJy6vqYUnel+TM9XZsrT19Bm0DAAAAYEFsZWLtvZs9aGttKz2c9ouJtU0yB8vIax8AWBbO\ne2Aa+5pYeys9ke44o/YAAAAAsM1suifSotETSSoPy8hrHwBYFs57YBr76ok0+rAzAAAAALa/rQxn\nS5JU1U2S/EKS6ye5TGvtTv3tRyX58SQntdb+Z4ZtBAAAAGBiWwqRquoZSX47yUq3ptX9AA9K8ook\nj0nygpm0DgAAAICFsOnhbFX180mekuSNSW6W5PdzYZiU1tpnkrwvyb1m3EYAAAAAJraVOZF+I8ln\nktyntfahJOets8/Hk1xnFg0DAAAAYHFsJUS6UZI3tNa+u499vpjkygfWJAAAAAAWzVZCpEqyd2Cf\nKyU5d/+bAwAAAMAi2kqI9Okkt9loY1VdIsltk3z0QBsFAAAAwGLZSoj090luUVVP2GD7b6ebD+lv\nD7hVAAAAACyUaq1tbseqSyd5Z5KbJnlvf/MtkzwnyTFJjk5ycpLbt9bWm3R7pqqqbbbtI9VPMuv6\nlS38PiatD0zDax8AWBbOe2AaVZXWWq27bSsvoKq6XJLnJfnFXLQX094kJyR5ZGvtWwfQ1q20RYjk\nDRWWjtc+ALAsnPfANGYWIq064BXS9UK6QpKzkryntfa1A2rl1tsgRPKGCkvHax8AWBbOe2AaMw+R\nFoEQyRsqLCOvfQBgWTjvgWnsK0Ta9MTaVXVkVR1TVYdtsP2wfvsR+9tQAAAAABbTVlZne0qS1yQ5\nf4Pte/vtTz7QRgEAAACwWLYSIt0lyUmtte+st7G1dnaSNya56ywaBgAAAMDi2EqIdI0knx7Y59Qk\nP7T/zQEAAABgEW0lRGpJDh7Y5+AkB+1/cwAAAABYRFsJkf4ryU9ttLG6qfPvmuHeSgAAAABsM1sJ\nkV6Z5HpV9aKqutTqDVV16SQvSnK9JH8/w/YBAAAAsACqtba5Hbug6N1Jbpzki0nenuQLSa6W5Jgk\nV03y4SS32Wjy7VmqqrbZto9UP90Iv5keNVv4fUxaH5iG1z4AsCyc98A0qiqttVp321ZeQFV1eLoe\nRw9IsvqALcnfJXlka+3MA2jrVtoiRPKGCkvHax8AWBbOe2AaMwuRVh3wyCS3THK5JN9I8h+tta8f\nUCu33gYhkjdUWDpe+wDAsnDeA9OYSYhUVacmeV1r7RGzbNz+EiJ5Q4Vl5LUPACwL5z0wjX2FSFuZ\nWPuIJGfNpkkAAAAAbCdbCZE+muSHx2oIAAAAAItrKyHS85Pcu6puMlZjAAAAAFhMu7aw7xeSvCnJ\nO6vqxUn+I8mXs84g1dba22fTPAAAAAAWwVYm1t67yWO21tpB+9+kzTGxtknmYBl57QMAy8J5D0xj\nXxNrb6Un0tM3uZ9XJAAAAMAOs+meSItGTySpPCwjr30AYFk474Fp7Ksn0lYm1gYAAABgSW1lOFuS\npKoOTnKnJNdPcpnW2jP62y+V5AeSnNFau2CmrQQAAABgUlsazlZVP53kL5Jcub/p+5NoV9Wtk7wr\nyS+21v521g1dpy2Gs+naCUvHax8AWBbOe2AaMxnOVlVHJ/nnJHuTPDbJ3yX5/kFba/+e5NQk9zmg\n1gIAAACwcLYyJ9LvJjknyS1ba89P8ql19nlvkpvMomEAAAAALI6thEi3TXJia+1L+9jn9CRXPbAm\nAQAAALBothIiXTbJ1wb2ufQWjwkAAADANrCVwOeLSX5sYJ+bJPns/jcHAAAAgEW0lRDpdUnuVlW3\nW29jv3LbbZK8dhYNAwAAAGBx1BaWlL96kg+mG7L2wiRHJbl/knsnOSbJI5KcleQmrbWhYW8HrKra\nlEszTr3c5NT1gWl47QMAy8J5D0yjqtJaq3W3beUFVFU3T/IPSa69zubPJLlfa+0j+9XKLRIieUOF\nZeS1DwAsC+c9MI2ZhUj9wXYluUeSWye5QrreR/+e5F9aa+cfYFu30g4hkjdUWDpe+wDAsnDeA9M4\n4BCpqq6Z5JZJ9iZ5b2vt9Nk2ceuESN5QYRl57QMAy8J5D0xjXyHSrk388B8neUySlQPsrarntdae\nMMM2AgAAAL0uRJs9IRoHYp89karq2CQnpIt/P5kuSPrR/vsHtdb+dh6N3KBteiJJ5WHpeO0DAMti\n2c97lv3+M5199US6xMDPPizJBUnu0lq7QWvt+knumu6Z/L9n20wAAAAAFtVQiHTjdBNmv2Xlhtba\nSUlOTHKTMRsGAAAAwOIYCpEOT/LxdW7/ZL8NAAAAgCUwFCJdIsl569x+Xi6caBsAAACAHW4oRNqI\nmbgAAAAAlsjQ6mx7s35gtNILad0fbq0ddOBN2zers5mpH5aR1z4AsCyW/bxn2e8/09nX6my7NvPz\n+7kNAAAAgB1inyFSa21/h7sBAAAAsIMIiQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAA\nABgkRAIAAABgkBAJAAAAgEFCJAAAAAAG7Zq6AbA/qmqU47bWRjkuAAAAbHdCJLaxWQc+4wRTAAAA\nsBMYzgYAAADAICESAAAAAIMWOkSqqoOq6pSqes3UbQEAAABYZgsdIiV5dJKPZfaT3wAAAACwBQsb\nIlXV1ZPcPclLYsZjAAAAgEktbIiU5LlJnphk79QNAQAAAFh2CxkiVdU9k3y1tXZK9EICAAAAmNyu\nqRuwgdskuXdV3T3JoUkOq6q/aq09ePVOxx9//Pf/v3v37uzevXuebQQAAADY1vbs2ZM9e/Zsat9q\nbbHnrK6q2yd5QmvtXmtub1O2vaoy+/m+K5u9T1PXn9qy33+Wl+c+ALAslv28Z9nvP9OpqrTW1h0V\ntpDD2dbhWQ4AAAAwoYXvibQRPZGWO5Ve9vvP8vLcBwCWxbKf9yz7/Wc6O6EnEgAAAAATEiIBAAAA\nMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwaNfUDQAAAFhE3RLrs2eJdWC7EiIBAABsaNaB\nzzjBFMA8GM4GAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAM\nEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAA\nDBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAA\nAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAA\nAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgA\nAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RI\nAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOE\nSAAAAAAMEiIBAAAAMEiIBAAAAMCgXVM3AAAAABZNVY1y3NbaKMeFeRAiAQAAwLpmHfiME0zBvBjO\nBgAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwyMTaAMCgsVaoSaxSAwCwXQiRAIBNGiPssUoNAMB2\nYTgbAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg6zOBgAsvKrxVnFrbYxV5wAAdh4h\nEgCwTYwR9owXTgEA7DSGswEAAAAwSIgEAAAAwCDD2QDYNsaaF8ecOAAAMEyIBMA2M+vAx5w4AACw\nGYazAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAA\nAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAA\nAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAgxYyRKqqa1TVW6vqo1X1n1X1G1O3CQAAAGCZ7Zq6ARs4\nL8ljW2sfrKrLJnl/Vb2ptfbxqRsGAAAAsIwWsidSa+3LrbUP9v8/O8nHk1x12lYBAAAALK+FDJFW\nq6qjktwsyXumbQkAAADA8lrU4WxJkn4o26uSPLrvkXQRxx9//Pf/v3v37uzevXtubQMAAADY7vbs\n2ZM9e/Zsat9qrY3bmv1UVZdM8tokr2+tPW+d7W3KtldVklnXr2z2Pk1df2rLfv9ZXsv+3F/2+z+l\ncR77ZLOP/9T1geXk7860pn78l70+y6uq0lqr9bYt5HC26l4tf5HkY+sFSAAAAADM10KGSElum+QX\nk9yhqk7pv+42daMAAAAAltVCzonUWntnFjfgAgAAAFg6ghoAAAAABgmRAAAAABgkRAIAAABgkBAJ\nAAAAgEELObH2ZlXVzI/ZWpv5MQEAAAC2u20dIiWzDnxmH0oBAAAA7ASGswEAAAAwSIgEAAAAwCAh\nEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAg\nIRIAAAAAg4RIAAAAAAzaNXUDAAAAgMVSVaMct7U2ynGZDyES+8UbCgAAwE43689n43yOZH6ESBwA\nbygAAACwLMyJBAAAAMAgPZFgmxlrKGFiOCEAAAAbEyLBtjRG2GM4IQAAABsznA0AAACAQUIkAAAA\nAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAA\nAAAGCZEAAAAAGLRr6gYAAACLqapGO3ZrbbRjAzAOIRLAFox1Mu1EGoDFNcbfqPHCKWD7E2AvLiES\nwJbN+g+PE2kAALgoAfYiMicSAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAA\nAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAA\nAAAM2jV1AwBgu6iqUY7bWhvluAAAMEtCJADYklkHPuMEUwA7wVjhfbI9AnwXL4BFI0QCAIB98EF+\namM8TtspwHfxAlgcQiQAABjkgzwAmFgbAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACA\nQUIkAAAAAAbtmroBAFtRNc6SyK3NeulmAACAnUWIBGxDsw58xgmmAAAAdhLD2QAAAAAYJEQCAAAA\nYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAA\nAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYNCuqRsAbC9VNdqxW2ujHRsAAIADI0QC9sMY\nYc944RQAAAAHznA2AAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBJtYGABgw1sqUVqUEALYTIRIA\nwKbMOvDZPqtSCtEAgESIBADApixviAYAdMyJBAAAAMAgPZEAAAC4GENZgbWESAAAAGzAUFbgQoaz\nAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAza\nNXUDAACAjVXVKMdtrY1yXAB2LiESAGwDY32ITHyQhO1h1q/T8d5TANi5hEiwH1wRBKYxxnuED5IA\nAGyOEAn2myuCAAAALI+FnVi7qu5WVZ+oqk9V1W9N3R4AAACAZbaQIVJVHZTkT5LcLckNkhxbVdff\nv6PtmVm7tl/9KWurr776y1k72bNn2vpT33/11R9DVY3yNVt7Zny8LVb33qO++ktaf8ra6qu/fBYy\nREry40k+3Vr7XGvtvCSvSPIz+3eoPbNr1barP2Vt9dVXfyfW3syH0jvc4Q5L/UFWffXH0zbx9dRN\n7jfG/Fp7RjjmFqoLkdRXf0nrT1lbffWXz6KGSFdLcvqq7/+7vw2Ayc3yQ6zJ5IFhmwmjn/a0p00c\nYAPAzreoIZJPFQAArCLABoCp1SIuKV5Vt0pyfGvtbv33T06yt7X27FX7LF7DAQAAALa51tq6XXYX\nNUTaleSTSe6U5ItJ/iPJsa21j2/iZ49I8vIk70zy/CTfS3LPJHdrrT18rDYDAAAA7GQLOZyttXZ+\nkkcm+bckH0vy95sJkHpPSfKqJEcmOTXd3EoPSPKcEZoKAACwcKrqmKo6oarMLQvMzEL2RDoQVXWp\n1to5U7cDAABgnqrqB5M8OMnDk/xIkn9O8rDW2tmTNgzYMRayJ9KBWAmQqurHqupVVXX7qdqyCG0A\nABhDVf2vqnplVV1xGevDZlTVzarqsnOoc3RVvSTJF5I8NslfJ7lGkj8Yu/aadlytqj5RVY+YZ11g\nfnZciLTKEUnul+SaS94GAIAx3CDJzya59JLWh3VV1aFV9eCqOjnJ+5NcfuR6j09ycrrPHvdP8mPp\n5pV9dZIPjF1/jUsmuW6SK8yxJjBHu6ZuAAAAsLNU1ZFJDm2tnTbHmkekCxW/nuQarbVPzKt2X//a\n6YaR/XK64OaTSR6d5Esjl35bkmul+2z3a+l6Ic2zPrBEhEgAzES/suaPJPlsa+17U7cHYKerqhOT\nfKO19ktTt2UdT05ykyR3nGPNxyc5Jsmz080FNJdRF1V1WJKXJPm5JHuTvCbJi1prJ82jfpL/mrg+\nsESESDCCqrpOknNba6dP3Rbmr6qum+TLrbVvTt2WObt6uhU1b5rkwxO3ZemtXJFvrX1+6rbMW1X9\nSJKvtdbOmrotMLJfSxcaLJzW2mMnqPmkVd/Oc9qOJ6cLcF6S5BkTnP9NXR9YIjt5TiSY0gvS/UFn\nOb0/yX2mbsS8tdY+11q7RGtNgLQYHp/klVM3YiLvSPKAqRsxhaq6e1XdaOp2TKGqjq2qf5mg7uWr\n6q5Vdf95126tfSnJeVPV30hV3bqqTqyq91fV3M6HqupyVfWcqvpAVf1DVV15TqWv1//7uxMFOFPX\nX1pVdZ2+JxosDSESjOMhSX5n6kYwjdbaD7TW/mqK2v1knq+oqrdW1VET1d5TVdeaZ+1FVFVXnPfv\nYFXtq6QLs+9SVT88RRumUlXXSzes8t+qahkndn1KkntM3YiJnJpkz7yKVdUhVfWCJF9J8oYk/29e\ntReh/kaq6sZJ3prk3kluluRZVXX8nMq/Lslj0g2j+7kkr6mqmkPdP03SkryiH9o9b1PXX2b/kSW8\ncMhy8yazZPo/pJdJck5r7YKp2zOGqjolyYlJjkpyudbafaeqX1Vzq99/WL1RkisnOSzJuUm+x6BU\nlwAAF0lJREFUleSzST7UWvuW+ju3/orW2rlV9dgk703y+qq6aWvtuxPWPncetRfUI5P8TLoPUfP2\ne0kul+SkJE9Kt8zz5KrqaknenOSFrbUXjVTmY0num+T4dHOiPH2kOptSVbvTzdFybpJ/b629Y8x6\nrbXbTlm/r/kTSe7Uf/v+JG9srbWx67bWTk5y8hzr/2mSB6cLb/4xybyHjk5dfyM/n+TgdBNM/0u6\nSZ+fVFW/P+bfo34o+a3Sve/9bJLj0vXI/Ol04dJoWmtvrKrjkjwjyZ8lediY9Rat/pSq6uAkT0ty\n1ySfSPKs1trH5lW/tXb4mvbcJ9177tN2+pDqqjo6yf9KN5H9ia21/5qoHZdIcpt0F5DOSPKW1tq3\np2jL0mit7civJLvTjRF/8E5uQ5LbJXlukqttcv+r9W16/ESPSSW5bJKDZnS8H0/3B/Mqq277oXTL\nil559e39tmskOT/JY3ZC/VXH/fP+97rR13tH/r2qP2H9Ddp096le66tqP2HetX1N95XuA9uxa277\n1SS/uer7o/rnxnETtfHwJH+S5KfnUOuodL1i1r4fvGpO93X0+umCur1Jfqj//npJ3rlOzXckOWSE\n+zhZ/f65dEGSZ8/j97mP+n80Rf2Btv1J/7hfpf/+z/rvrzFy3aP7Ok/uv79l//0z53jfX9HXfNxE\nj/2k9fs2zPV9Psmr+noX9P9+O8ktJ7z/PzXP30GSa6Zbje99Sf4gM/qMtYm6N0hyzqr32fOTvDDJ\nJef8eF833cWj1e/5X09ym6meA8vwZTjb9vdbSX62tfaFTe6/MvnipWZRvKpuV1XP7a8ub8ZVk3wz\nXVfjWfidJL/cujkBkiSttdNaa2e01r68+vbe99IN47zsDqm/4l1Jjk1ywyS/keQLSc5L8q9Jfjvj\nX4n/9yS/OGH9t6W78rms9S+mtfa6JB9Pt8zwVLUnXS2oqn68ql5SVTeYsh1L5PZJfnfNbQ9L95oY\nXVXdq6puvea221bVPVfd9INJfj3dh8sx2/Lj6XrA3CLJb6a7sHD5dJPe3q/vKbOj6lfVnfqaR6d7\nz7tSul6Zz0xy24w83GNV/VukC5fGrn+ZdBfG9vb1r1JVD6+qv6mqt8241r7qt77+lceuX1X3rarX\nVNXVB3Zdqf/XVfWEdMPKWpLvjNGuVT6arhfCo/t5mJ7V337FWRx81TnvVfax2y8l+UCS35/1356p\n6y+i/j3/ful64l0myV3Sfcb5zRFrHl5VR1fVD2ywy5vShSujr0pYVZdPcnKSBya5ebr7/Wdj1+39\nWpJD0nVouHZf99eTvGxO9Vc8M8kPp3seHJLucTgvyR/NuR3LZeoUa6yvLE9PpA8kec8W9v8/fZvu\nOaP6r01y2hb2v0pf/3dmVP+ULd7/3+vr33sn1F/n+E/tj39ikquPUUP9xa2/TnteneQ7E9U+cara\nq9pwzUzb6+X26XpF3Gqi+nft6x89w2Meu9H9STcXz94k1+6/r3Qf6M5Jcmh/2037fR47wv3dk+ST\n69z2P6u+P+pAnhPpeppecYNtn0ryl+mGtZ6V5DNJbrhmn5/t699/DvU/Pev669Q8vj/ez6QLCL6U\nNVd/c2HvkCeO8DtfW/+La5+fI9df6QHxjVx4BfysJG+ada1FqJ9umNinN7nvM9PN1fTVJO9JN43C\nLNvyy+lWAT1yze2372//ZrqFBc5J8rwZ1Xxtks9vYr9b9L+LZ834Pk9afwvtvEFW9QgbudaD+lr3\nWHXb15O8e8Saf9jXvNY+9vlYko/M4f7/774tv5cuLH1rugvWR8yh9uuSnLrmthf27dnUCJkZteMv\nk3w3Xc/ny/S3HZQ594hati89kba/DyW5eVU9aKMd+slu71xVr0o3NvzNrbXXzqj+VdOdNG7W4/p/\nPzij+h9Od/9/YaMd+vt/x6p6Rbq5Qd7eWnv1Dqm/us5Ppwsx/rS1dp/W2n/Puob6i1t/nfbcKF2Q\n/amJat9hitprnJ7uZOaqE9X/r3Rj9O8+Uf1P9fV/ahYHq6rbJzkhF64CtF69JDmun3/vbumG3ByS\n5In9truu2XerbbhLVd1wg80nJblOVf3IqtuuleSwqrp0//3KleNz9qP2DZJ8Lt3CCev5dJL7pzux\n/k6SO7bW/rP/2UOq6qFJXpyuy//75lD/TrOsP+Av0s25dOfW2rv7mruq6n5J/ildL5STZ1xzbf2V\nx/zkOdb/w3TB1WHp5v65S5LLt9buMkKtofqvTvf6GrP+4UnO3MyOrbXfaa1dKclPpJuf7U0zbsux\nSb7dWvvqmrpva63duLV2WJJHpXv/+eKMal41yZc3sd95/b+XnFHdRamf5Ps90j69tufnKit/czf1\nXNnPNlyyql6a7j0tSR7T98T7w3S9Lj8+Vu10vV6+3Vo7dR/7nJvuQsrYVuZj+lBr7evpegPtSncx\nYR4O6ecjWrHyt/WQMYpV1cF9r8uDV918fLpeiH+W5MtV9f+SXKm1dt56x2BGpk6xxvrK8vREuka6\nE8e96SbwPSHJ83LhJIsfTZdI7013gvX8JJeaYf2Xpftj9aB97HNokjvnwitmM7tClq6nwWc3ef/P\nSfKi9Cn1Tqi/pi2npJtQcNc8nt/7qp9uQs3r9f//0SSXnWf9qe//FPX7Nrypf02+un/enZ/kvnOq\n/fqpau+jTYf0r73nT1S/+sfhzyaqf3B//2d1Ff5F/e/2BzbYft9c2BviK+lOoj+d7mLH3nTB0Xnp\nwrUtz9mQbsLcvUl+dYPt9+m3/2X/2N9hVXuO7/d5bP/9/faj/rPTzblx5Q22v2JVvfckeXmSf0h3\nZfjs/vazk/zCfj7+k9ZfVefx/bFfnu6C0ErNU/rb/j5doLfSO+a7meHcIPuo/4FV9d88Vv1V7bhR\nut4u/53k9rM+/iLWT/J/+8f0NzNwlT/dPCXP6n8P52TGc9T0x33BwD6/1bd3JrWTvDTde/pDNth+\nRP8e89X+tTrTOVmmrr+qzt8kOXsf2/+of9x3j1G/r7HyXv6OJH+VbiGTlfeCt2WDHpszqv3aJKfv\nY/ul+uf8q8dqw6paP9LXOjvdQhL/mhmOOBmo/YS+1r+lm7rhNf33bx+x5rPTnYes7YF4iST3THdB\n4VtJTkty2NiPwTJ/Td6A0e5YF+BckOlDpNHbkO7K6uP6N82v9S+ub6W7YnlSuuDoF9JdnZp17UlD\nrL4Nh6U7qdzX/X9gkiuM9PhPWn/V7+EiQzSyKsgZ8/m3Xv1cOGTlmuk+NG75A9uB3v95fk1df1U7\nXptuQskzk7wxyV3mWPvEqWrvo00rIcKvTFT/sn39SSa+Tde1fWaTyqY7UfzcPrY/qq/3iv7vwbvT\nzUVz/SRv798X35rkh/ez/vP795PDN9h+l1z4IeKr/b6np1t+eXWIdVqSg/ej/r8m+e99bH9N//x/\n36p2nJ/kf9L1gjk+GwRA26H+qjqvz4WT2K79Wqm50o5nZx9DPrZj/VXteHW6oPQGYxx/EeunCylW\ngruv9M/Jl6U753t5uvO+t/XPuZXn4Psy+wDp0KH3tnQXsL6ZGS5skeTq/fvI3nQr4f19unD9r9PN\nDXl+v+1zSR44wuM/af1V7Xhl/zu+2MWAJDfpX39fyojDifrn3gXpL2qku2h0vSTXGavmqtp/3r/2\nDt1g+6/1v4eHjt2Wvt4x/fviWated6NPKp1uyNgf97/rs9OtzPvYjR6XGdV8T5IPDOzzmOznxSJf\nm/+q/sGG/dZPLPcr6eYkuEG6iUu/m24ujE+nC5Lek+QNrbX/maqdO1k/ierJSR7WWntpf9tN012Z\nPaq1dtoE9SvdSdypbeQl5terP09T1+fi+q7Oe9LNDfHDbYLhhVV1j3Qf7B/SWvvrCerfL10P0Ae0\n1l45g+N9MN08V7fZYPs7k/xoa+2IA621wfHfkOT6rbVrbrD9oemu1P9juok1v57kyelCoz9PNzfO\nKUke3vZj+eeqOiXJua21dYdwVNVnk3yrtXaTrR57O9TnoqrqS0ne31q75+DOO6h+VR2a5MFJHpDu\nb/wV0l20Oifdh9ivpJsP5kNJTmqtnTJCGyrdRYs9rbWLDRfuh1S/Jt3k6rdurc1qCoW157zXTzdU\n7+wkp6YL0F6XbtqIUT5gTV2/b8Ovp1uB74R0PVC+kq7n2QPTTax86XTzrp04Yhv2JLlda+2gsWrs\no/Z90g2TfV66VWj3rtp2537bGUmuN/b57zpt++d0Q+gPb62NPZH93PW/92umO6/bu87266QL2K+T\n5Mb787eezdk1dQMYR1X9ULpJDL82dq3W2reSPKf/WvlA/bV0V4p2tdY+MnYbyMqcANdduaE/aZrX\nvGcXq5/u5O1jSX4yXY+Eedefp6nrs0pVXTHdldlbpRvKNUWAdKl0E8uek+QNE9S/TJKnpftwMau5\nSM5KN7HzevUekm7+pefMqNZ6rpxu5cON3D9dj9cHrHNyeYcZ1D873eIQF9MHhkclecEM6ixqfS5q\nb7ogY6nqt9bOTTcPzYuH9h2xDa2q3pXkrlX106211yfdCnXpVif77XTB1gNnGSD1tS9yzjtvU9fv\nvTjdud0D+6/VPpzk0a21eaxQOInW2olV9Q/perz8fFX9Z7reV9dLt0rv19OtnD3vAOmJ6cLFl+/E\nAKl3Qrqej6+vqhenOye4erphfcckuVO6zz6/KUAal55IO1RVvTXJKa21xw3uPPvap6Qb2nJUksu1\n1u477zYso6r6ULphVbdo+57sb2nrV1WNeHVw0vrLrKoOSje55I8luVe6ZeUPSzdvw0PXu1o1cnuO\nTPJ36YKLZ7bWjptz/aukG+bwk+lWwvy9GR33uHRDop6T7kPEaenC4gelm1T+8+lWghtlMtXqli2/\nRmvt2utsOzbdyeWLW2sPH6n+M9N9OP0/6eZdOC3JkemGix+X7kP9TVtrn96J9bmoqnp9ut5tN26t\nrbvASFVdYqz3n6nrT62qfiJdz5tLppsX6uB070dJdyHzwa21f5uoeUuhqm6ZbjW8K6V7/3/bvC4c\n9z1SjmmtTbJIVN8b7th0vcJumq5jxqfS9QR7bmvtjDnUPzTdxZWbpDvvuXu60R8/2Vo7a8z6U6qq\nJ6VbDfYyazZ9Nd2wvufPOjzm4oRIzFxVHZ5uXqCDkqS19s1pW7Qcquon081F8+10XWxPSpfQH5Ku\nW+d9k5zZWvutOdc/tK//s0m+0Vp74oYHGad+0g2zvF+61TQevxPrL7OqOinJHVfd9O4kf9Bmtwrl\nUP2VEOuG6UKsX0k3H9JLWmu/Oqf6l+/r/0y6k8lLJfm/rbVHzbDOYeme10evs/mUdBOpjzZ0tqqe\nmi6s+uN0w9NWQpRfSndC+eV0Ie4oPXCr6nJJ3pLuA8Nap6dbYOLtY9RehPpcVFXdJt2Q2a8leW7/\n/y+nm9T9x9L9zTtzxL95k9ZfBFV123Qr1N0s3TQKn0g3jO1PW2vfmLJtjKu/WH7MFMPZFsE65z3n\npbtw9pi+t9qO1v89/Il0U6icmeRTU1zAXmZCJEbRz11xamvt16ZuyzLprwr9YborQ2udkW6FmtHm\nZlF/2vrLqqoele5q3CfSzZFx+pzr70nXjXrFO5L8fmttLsPY+rmIVuYpaumuzj+rtfbmEWpdIl1Q\ndet0c6GcneSdSf5x7B4PfYj15nTzXK31kXQh1mdHbsNBSe6dC+//t9NNaPuPrbXvjVl7EepzUVV1\nu3STd99qnc1fT/eB7m93an2YSlXdMN3qW2NPl7CQqurRSa6Vbj6qT6RbEW3U3k+wmhCJUVTV1ZJ8\nbx5zMnFxVXX5dFfmLp9utY4vJPnQvMZnqz9tfearP5k7Mt2J3FvnPQdTVT0u3XPt4339L86z/jz1\nIda904VmKyHKSoh1wZRtY3lV1RFJbpzuOXleuuFVH5pXsDd1fQCWixAJAAAAgEGTTEYGAAAAwPYi\nRAIAAABgkBAJANjWquqhVbW3qh6yxZ/b26/ycyC1j+qP87IDOQ4AwHYgRAIAJtGHL7NY1a2t+lp9\n/M9V1dCyv7OaHHJTx1kVOs18OeKhQKuqdvfbnzrr2gDActg1dQMAgKU2ixDnn9Mtdf/lLR7/ekm+\nM4P6+2OMlU3amn/nWRsAWAJCJABgW2utfTPJN/fj5/5rhOZMqdb8O7QfAMCWGM4GACyM1UOy+v+/\noqq+XlXnVNV7q+oe6/zMReZEWhm2leSHkqwcb+/aoV7rzYlUVVetquOq6l1V9eWq+m5VfaGqTqiq\n6499/9eqql1V9etVdXJVfbOqvl1VH6iqR1RVrdrv+CSf7b99yJr7/JCqenmSt/Tbn7pm+zFrah5b\nVW+tqjP7x/1jVfWUqjp4nfbt7fe9UlW9pH+szt/q/FQAwPagJxIAsIiumeQ9ST6T5C+TXCHJA5L8\nS1XdubW2Z52fWRmmdWqSpyV5TP/9c1ft88ENfmbFMUl+K13g8oEkZye5bpKfS3Lvqrpta+3D+3OH\ntqqqLpnkNUnumuQTSf4myblJ7pjkhUl+IsmD+93fmuQHkzw63X08cdWhPpjkzHT39SFJ9vRfKz6/\nquZLkzw0yelJXtn/3K2TPCPJnarqLq21C9Y09fJJTk7yrSSvSrI36w8tBAC2OSESALCIdid5amvt\nGSs3VNXfJnlDkifmoiHIRbTWPp/kaVX1S0n2ttaevoW6b05yZGvt26tvrKobJ3lXkj9IcvctHO9A\nPCVdgPTCJI9prbW+LZdI8uIkv1xVr2qtvbq19raq+lz6EGmd+/yhqjorfYi03mNSVQ9NFyD9U5IH\ntta+u2rbU5M8NckjkrxgzY/eKMlfJfnl1tosJkoHABaU4WwAwCL6XJJnrr6htfbGdD1kbjlW0dba\n19YGSP3tH07X2+cOVXXQWPVX9EHRo5J8KcljVwKkvi17kzwhXc+iB67+sQMs++gk56ULg767Ztsz\nk5yxpt6K7yZ5ggAJAHY+PZEAgEX0wdXBySqnpxvGNZp+3qWHJzk63TC61edLLckVk3xlzDakG0J3\neJJPJTlu1fRHq52bZCbzNFXVpZPcJMnXkjxug3rf26De51prX59FOwCAxSZEAgAW0Zkb3H5+RuxJ\nXVWPTjeH0v8keVOS05J8J114dN90QcshY9Vf5Qr9v9dJctwG+7Qkl5lRvcP7f4/YR72VmmuZ/wgA\nloQQCQAg3UpoSY5PN4Ts5q21r6zZfts5Nues/t9/aq393BzrfaC1dvQWf3a9YAkA2IHMiQQA7FQX\nJNnK/EVXTLfC2bvXCZAum+TmmV9g8vH0K6P14dZmrKyattF93nB7a+3sJB9NcsOqOnztdgCARIgE\nAOxcZyQ5sqoO3eT+X003dO3oqvr+MLGqumSS5+fCIWaja61dkG5VtqskecF696GqrlJVq+co+kb/\n7zU3OOwZA9ufk+TgJC+tqh9cp97hVXWzzbQfANiZDGcDALabza5CdlK6ybHfUFXvSLeK2Adba69d\nb+fW2t6qekGSJyX5SFW9Ol2ocockl0u/OtuBNr53RFW9fINt326tPSLJM9LNwfTwJPeqqrcm+UKS\nI9PNlXSbJL+drtdSWmtnV9XJSW5XVX+TblLuC5L8S2vtI0k+0f/8z1fVeenme2pJ/qq1dlpr7WVV\ndYskv57kM1X1b+kmMr98kmsluV2Sl/bbAYAlJEQCALaTlosPKVvvtqRblv5ySe6V5LbpemD/ZZJ1\nQ6Te76ZboexhSX413ZCyNyX5nSRP36DO/rh0kgevua2lC8jOTPKI1tr5Se5TVb+Y5KFJ7pHksul6\nTJ3at+mENcd4ULqJwe+W5Nj+ttOSfKQPye6b5A+S3D/JD/Tb397vk9baI6vq9emCqzune/zO6Lf/\nYZK/OdA7DgBsX7X+6rkAAAAAcCFzIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBI\niAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMCg/w+V2OIqhyY47QAAAABJRU5ErkJg\ngg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f1d3caab890>"
]
}
],
"prompt_number": 15
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### most frequent final letters (last letter of words)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"allwords = alltext.split()\n",
"\n",
"finalchars = {}\n",
"for word in allwords:\n",
" finalchars[word[-1]] = finalchars.get(word[-1], 0) + 1\n",
"\n",
"# lets repeat for final letters\n",
"import numpy as np\n",
"from matplotlib import pyplot as plt\n",
"\n",
"letters = u'\u0622\u0627\u0628\u067e\u062a\u062b\u062c\u0686\u062d\u062e\u062f\u0630\u0631\u0632\u0698\u0633\u0634\u0635\u0636\u0637\u0638\u0639\u063a\u0641\u0642\u06a9\u06af\u0644\u0645\u0646\u0648\u0647\u06cc'\n",
"lettervals = []\n",
"letterlist = []\n",
"print 'Final letters'\n",
"for letter in list(letters):\n",
" print letter, allchars[letter]\n",
" lettervals.append(finalchars[letter]*1.0/allwordsnum*100)\n",
"\n",
"width = 1/1.5\n",
"plt.figure(figsize=(20,10))\n",
"plt.bar( range(len(lettervals)), lettervals, width)\n",
"plt.xticks([x+0.3 for x in range(len(lettervals))], list(letters), fontsize=18 )\n",
"plt.title(u'Percentage of persian final letters\\n10% of wikipedia articles are tested', fontsize=34)\n",
"plt.ylabel('Percent', fontsize=20)\n",
"plt.xlabel('Final Letter', fontsize=20)\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Final letters\n",
"\u0622 193306\n",
"\u0627 3908207\n",
"\u0628 1191550\n",
"\u067e 210176\n",
"\u062a 1510602\n",
"\u062b 59821\n",
"\u062c 287223\n",
"\u0686 92149\n",
"\u062d 211581\n",
"\u062e 291213\n",
"\u062f 1861543\n",
"\u0630 50086\n",
"\u0631 2525170\n",
"\u0632 551658\n",
"\u0698 34366\n",
"\u0633 1129394\n",
"\u0634 692128\n",
"\u0635 140904\n",
"\u0636 57585\n",
"\u0637 142536\n",
"\u0638 38914\n",
"\u0639 392996\n",
"\u063a 174189\n",
"\u0641 372662\n",
"\u0642 287271\n",
"\u06a9 728996\n",
"\u06af 348562\n",
"\u0644 729613\n",
"\u0645 1541968\n",
"\u0646 1831045\n",
"\u0648 1606199\n",
"\u0647 1638034\n",
"\u06cc 2915877\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAABJEAAAKvCAYAAADa7l5VAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYZFWd//HPh4EhDzmnQZIoiAIKImGIigqsCcVAcM2K\nAQPrrj8YTLjsKiurLuuKQzCLooKKhGEQAQmikhREGCRIkJwZZr6/P84p6nRNVd1b1dVdPdPv1/Pc\np29XnXvuubHqfusER4QAAAAAAACAbpYYdgEAAAAAAAAw8RFEAgAAAAAAQCWCSAAAAAAAAKhEEAkA\nAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAhsL2pra/bPtq2w/ZXlBMBwy7fIuzcl8PuyzD\nYHsJ2wfb/oXtO20/VeyT3xfpTi5eP2SYZR4E23OL7dlwAPktVvsHAFBtyWEXAACGxfbJkg7ukuQp\nSQ9IukHSJZJOiYgbx6FowGLP9r6STpe0bJu3I08Ye5NuP9teStJZkvbukKTdPllczslo+TvIfBeH\n/QMAqEAQCQA6W1rS2nnaTdK/2P6GpI9ExONDLRmeZftQSd/M/14YEbsPsTiowfZykk5TM4D0oKTZ\nku6S1KgZc/MQijYZedgFGIKPaGQA6XJJ10t6NP9/e5tlFpf9NFbbMa77p9/7fkvNu+kR8bdBlw0A\nFncEkQAguVPSj1teW07SFpJ2ULpfWtI7JW1s+5UR8cz4FhE18Ev4omE/Savm+XskPS8i7h9ieSar\nyXq9HFbMHxURn+2Sdqxq7mBw+jk2HE8A6BNBJABIboyID7Z7w/bGSrUmdsov7SXpA5L+a5zKBixu\nti3mf0oAafxFxKTsFzPXgtsi/xuSTuqWPiIO08igEwAAk9qk/AIBAL2IiFsk7StpbvHyR4dTGmCx\nsGox//ehlQKT0SrlPxHB+QcAQA8IIgFADRHxiKQvFy+tZ/u5wyoPOlpc+i1Z3C1VzNOsBONpqeok\nWMT0e9/n8wIA+kAQCQDqu7Tl/43bJXLyGtuzbN9g+4E8fPQdts+2fXhuUtGV7TmtQyfbXikvP8f2\n7bbndRuq2fZ2to+zfbntv+dyPGr7Rtun236f7dVrlGUp22+z/T3bf7X9sO0nbN9q+wzbh9mubCLd\nMrz0bvm1VWx/zPZltu+1/WROd5rtl3TJ6+TcSeo3i5d3axkmvusw5ra3sP0h2z+0fX0eZn6e7fvz\nsPMn2t6larva5LuG7Zm2r8rH/7G8z0+2vXOH/VE53Pagzq1+2d7Z9ldtX5v3UWPds21/wvaqXZad\nWRyLclTEo9scr6P7LN/MIo9Z+bUptt+S98/f8vl1h+2f235TH+tY3vZ7bf/U9i352D5m+2bb37X9\nupr5lNu7YX7tObY/k8+be/J7t7RZduV8rH9p+zbbj9t+Jl+XN+ZtO9r29nXWX1HOabYPtP0125fk\ncj3tdB+Z63T9v9v2MjW3e2D3gF4U23rzyJe73ytcYwh72zOKNLcUr29r+3/ztfqY0/3lKtuftr1K\nu7za5L2G7UNsn2T7Stv3Od2jHrZ9k9M9+c22p/SzX4bB9pa2P2f7t06fS0/n7fq97f90lx9o3Md9\nvzw+ZVaSbumwXNvjnPOyh/z57nRPO9D293MZHrY9P59jf8vLf9H2vk4jEQLAYEUEExMT06ScJJ2s\nNBLUAkmza6TfrEi/QNKb2qTZTtIfW9K1m+6S9PKK9c3JaecrPXTvJOnWNnnNl7Rhy7JrSfpZjXIs\nkPSUpOW7lGMfpQevqnxukrRtxTbdUpR5V0kvk3RblzznS/pUh7xm1dy+BZLmt1n+Bz0sf6aklWqe\nV/tLuq8ivy8r9Us4t9MxHMtzq49rZWVJP6mx7gckvaNDHkfXPVZKnR33U86ZRT7fVBpZ8dcV67tQ\n0mo183+rpLtrbMNVkjauyKvc3o2UOu1/vE1eN7cs90pJ9/Zw7j6nav1dyvgaSU/WXM+dknapsQ8H\ndg/o8dzo616h5ufEfEkHd8h7Ruvxyufi/C7ruVvSiyrKfLikZ2qW+89KHdRX7Ye5xfZ0vefU3K8n\nF2Vou3+KtMsp9UHVbb8syNt8vKQl2uTR832/5fjUuf90Os5D/3yXtImkq3vYnn8e7TFmYmJiap3o\nWBsA6mv95fih8h/b+0o6Xc1hy5+WdIVScOUpSRtK2kXS8pLWlHSW7QMj4oyK9VopgHWCpGmSHlF6\nML4jl2mnEYntLSSdK2n94uUHJf1Gqf+ZJSVtoNS58ar5/7a/Ytt+u6Svq1lz9TFJl6n5ILKJ0kPg\nVEnPkfRr23tFxG+7bEvj79aSvqC0P+7N5btXKQC2h6QVc7pP2/5TRPyoJa/zlIbkfq6kPfNr7UbZ\n62TD/PcZSTdIulHS/ZLmKe3XF6rZAe+rJJ1j+2XRZVQ+269UOgcan68L1Bw+fEmlh5DnKz0cPqma\nTbnG8Nyqs+5VJV0kacvi5Tvzaw8r1cjbTamZ0EqSvm57zYj4fEtWl0v6Sp7fS+m4NV6/vE3a0Zoq\n6Qyl0RXnS7pY6RivqLSv1s3pdpF0vu2dI+LRdhlJklPtqLKG1IOSfqs0HPwSSvtnhzz/QkmX2d4x\nIm6uKKclvUHScfn/O3NZH8hlnF6UYVulYF7j/JqndB78RSkAtbzStf0CSatp9E0F11Laj6F077g+\nl+8xpXNxE6VtnqoUsDvX9i4RcUWXPAd5D+jFV/N2TNPImnBfaZ+8Y7kr09meKemovL6rlQIPTyld\n+y/N6daQdKbtLSM1l25nPaXzKZQCDH9SCj49obTPnqt0T5kiaXNJv7H9ooi4tWZZx02+j5yjZqf6\noXT/ukrpXF9Zad9spLTNH1I6l1/fklU/9/3blY6/JL2/eP0Upc/TVn9qU/6hf77bXkHS+Wp+doXS\nNXmN0j5cOq97a6X9GKK5MICxMOwoFhMTE9OwJvVeE+kIjfx1cIvivU2VgkqN978iafU2eaysFJRp\npHtQ0gYd1jenSPd0/vs1tdQaUvoSOiXPr6D0Bbix3MOS3t14v2W5JZS+hJ8hacU27++k9JDaWP/M\nDunWkfTTYp23SlqhwzbNLdI9kfP9WGv5lB6Ay+2/sctxOaSX41gs93mlh/dpXdJsK+l3Rf5Hdkm7\nmkbWUrle0jZt0u2j9KA8X81aHh1rBYzFudXjdfLjIs+nJL2/wzlwTsv1sWeXPMvaBH3VOuqQ78wi\n38a+vUrS5m2umQ9rZC2Pr3bJ98Ai3SNKQcCpHY7VxUXaKyW5Q55lbYGnc3nf3Sbd1GL+jGKZCyWt\n26XML1Z6cF6/Yv3daiLtJ+mTkjbtkmZlpZEqG/ldV3GM5hZpB3IP6PEc2ajOthfpTy7S16mJ9GQ+\n/2+StGObtLtr5PX8b13WfZjSSKBtj2Fx7X2nyO+XNff/uNVEytfbWUW6P0h6aYe0b1K6dzXSfrBD\nun7v+21r+FQsM1E+3z9ULHO7pB26lHkTSf8m6VWDuG6YmJiYymnoBWBiYmIa1qQegkhKvxDOLdL/\nreX9nxfvVT4USzq1SH9ChzTll8wFkk6qke8xRfrHJb24z31jSddWPRwU6ZeQNLtIf0SHdHNbtuk9\nXfJcS+kX50battsi6dB+HiZ62BcrK9XCWKDU7KZTUOBzRTn+IWmdLnnuqJEBjG5BpIGfWz1s+84t\nx+uwLmmnKtXMaaT9fZe0J/eyTT2Ud2ZLeW9Xl6ZqSqMslsdgoSZoSk1wGs3H5kmaUVGG5ZUCiI18\nX9sh3YKW6W01tu8fRVk3GeW+qh1IqZnfiUWee3dJN/B7QI/lnN7Ltqv3INKCfL50C/AdXqTtGnTr\nYbvOLvLcvEu6xv4fzyDSG8r7gjr8yFCk37NIf7ekZdqkObRIM9ZBpIny+X56kZ5makxMTEOb6Fgb\nACrY3ljSL9SsQi5JXyref76kffO/f5H0mRrZHqlmNfO32K5qKvGk0q/13co5VenhpOFz0b1ZSTf7\nSnpenp8dEad2SxwRCyT9a/HS22qs45qIOLFLnncrfXlvGEgHu72KiAeVmhBJqXnR81rT5OP39uKl\nY6PL0OGRmvudVrXucTq3unlvMX9xRMzqlDAinpb0vuKlbWy/bBTrHoSjIuK+Lu8fr9TETUqB03e0\nSXOoUq0YSTolIuZ0W2FEPCbp08VLda6FKyKi8nxQCmY33Fsj/Xgqz419ai6zSNwD+nBsRNzZ5f2T\nlYIYkrSF7eUHsM5y/+89gPwG6eP5b0g6PLo0G5WkiDhfqWajlJr9vXwMy9bVRPl8zyby9Q9gEqFP\nJABINrf93xrZ78WySv1M7KiRfQbN1sh+NF5VzH8/Iir7IIiIv9u+Qalfh5WV+sq4tssi50TEAxXZ\n7pjzklKNia92SVvl1cX8d2ouc5lS7aflJG1le8Xo3NeHlDq2rnKV0q/YUmqGMiZsT1dq/rOZUr8+\ny2nkubBdI6mkF0m6riWLLZVqTUjp4eFbNVZ7mlKTjG7G49zqZo9i/qQa677K9lVq9nuyh1LzrmF4\nUtL3uiWIiAW2v6Vm0Gf3Nsn6uRZmF/N1Rvf7bs185yo1rbGkD0r6bM3lRi33x7KjpK0kra7UX1F5\nX1yxmH9hzWwnzD1ggELS97smiHjE9k1Kfa5Zabuu77ZM7lNoB6XreVWlpsvlj8HrFfN19/+Ys72W\npMYogXdExG9qLjpbzWDkLkpNpodhony+S+n6b3iv7Z9HxPxOiQFgrBBEAoBkXY3scLOdUPq194Mx\nsnPlsrbFTrbrdtS6Uv5rpQ5Eu33J/F2N/F5azP8h16DpV7lNr84d+tbR+IK9hFLH3gt1UFq4pkZ+\n9xfzK3VM1Sfbeyg9iO/Yw2KrtXntRcX8bbkGRZU6tcTG49xqy/a6GhkYq/vwd5GaQaTtuiUcY9dG\nxOM10l1azLd7+C6PwSG2X1sjzzIAuYrtZSPiiS7p61zfUgo2/b88/2nbe0v6tqRzI+KWmnn0JAcB\nPifpIDU7Fa6yes10Q78HjIGHIuKOGuka22V12S7bmyh1Pr6/Uuf1ddTd/+OhHPhhiTY/1nRS1vjc\nYLBF6slE+XyX0vXfqC35ckl/sj1LqSnj1QSUAIwXgkgA0NT6C+NTSh1j3ijpEqWmLDe0WW7dYn4P\njay9UVfryG+t7qmRx1rF/F/7KEOp3KZ/6mN5q3qbHqp4X0o1qhrqPkDVYvtISce2vNzpV+byoWfF\nNu+vUczfVmf9uTbCQ+r+YDwe51Yna7T8P7fmcmW6YT7M/q1mutuL+aVtr9BobpObGZXHu07TtFaN\na6FTEClU7/qWUmfwO6tZY2qXPMn2XUq1vi6QdEa35pR12d5KqUZI63Gsuk7aXSPtDPUeMEbqbJNU\nY7ts767UIXUZvOtWE6bX/T8e1m2Zr/qxpp1VB1SWfkyUz3dFxAW2j1Xq7F5KtRI/l6dHbF+m1OH+\nzyKiToAWAPpCn0gAkMyJiCkt03IRsW5EzIiIf+0QQJKaTcgaoo+pKqjfrRZDQ/ng0LXPiRrKbepn\ne+psU2WzgLGSH87KANJvJb1HqdnFmpKWLc8FpQ7LG9p9dq5QzNep/dLwWMX743FudVKeT8+01L7r\nptymYT7MVu3bTunKMo92/zeWGcT1rYh4SqmJz/uUmj+V19Dakl6n1NT2Ntvfs73ewrnUk/tY+7Ga\nAaR7lR5W95S0sVLnyOU18pxi8brfL4d2DxhDA9km26tp5JDytyr1O7erUs2W5Vv2fxncmEjf7wdx\nD5ui4Zkon+9p5RH/plQL6QKNPNdWlLSXUp9Nf7R9qe2d2mQBAKNGTSQAGL0yYHNYRJwypHI8XMyv\n0DFVPY+qWUNmj4i4cJT5TTRHFvMnRcQ7K9JXNaMpz4HleihHVYe6wzy3yv6slrS9ZM1AUrlN3frE\nGmt1OytuTVeWudz/Iek5EXHrqEo1SrnJyomSTsxNnXZVqp20s5r9JS0h6UBJu9veKSL6qZn42pyf\nlGprvbiimeai0NRsUfJONWuw/EHSrhUdUk/U/V+W+cKIaNfv2EQ2UT7fnxUR50o61/bqGnn9v1DN\nZ7sdJF1o+40R8ePhlBTA4moi/VIBAIuqu4r5dYZWipHl2LRjqt7zGuY2DZztKWo2B5qvZtOAbqo6\n9C1HytmwY6qR5VhR1Q9+wzwOraP/TK+53MZd8hhPdTthLo/XU+WDekQ8pNSsVUrBmQl1LUTEXyNi\nVkT8c0RsoVQb6Bg1a8OtIem/+sx+r2L++Br9fC0KnV4vSsr9/5mqEc00cff/ov5ZMmHLHxH/iIgf\nR8QREfESpVq071CzKe8UpWDz0kMrJIDFEkEkABi93xbzdUZiGisjOgi23W9fONLE2aY6em0+spqa\nfZDcExH/6JbY9pJKv/J28/tifn3ba9coR53hyod2HPIQ5Y0HKGtkB7PdlPuqboexY2GrmkOnl52q\n/6HN+4vMtRARt0bEMZLeVby8t+1++hIq+4Kp0zH7jD7Wgc4a+z+0aO//8vrZzPaaA8p3vJpCLkrX\n/4MR8U2lH0kawe/VNbJzcwAYNYJIADB6ZxXz+9gebS2gfl0m6b48v6RSvyn9OrOYf7PtidpUQkpD\nuTfUeVguHz7qND17gxbuZLrVnyQ1ampY0ltr5Funk+Zhn1vlUPVvr0ps+4VqjswmSecPvET1LS3p\nTd0S5Fpp5bGa3SZZeS28Oy8z0f2smF9K/XVMXF4nXZvH5lp1h/SxDnTW2P9W9f7fSNJ+Y16iPuTm\nn40gmNVfx9rt9Hrfb3iqmK+z3LDvwT3LIzVeX7w0qMAdAEgiiAQAoxYRv5N0bv53iqTv1KwBIenZ\nIbQHUY55kk4oXvqU7Tq1Xdo5Q9Kf8/xKkk7t5eF5gL8211HWJFq/Rvr71BxBaaXcyXZbuWPi46sy\njIiQNKt46ZO21+2U3vaOqhFEmgDn1teK+V1sH9xlXUtL+p/ipT9ExKWd0o+TT+d+Qzr5sKTN8vwC\nSSe1SfN1NYdjf45GXmNd2Z5Ssf7abE+1Xbevs+nF/Hw1g8u9uKmY7zhCo21L+qqGO4LW4qju/p8q\n6Zua2P2cloMYHGm7do0e22vmc6xVr/f91uVcZ7kJcA8u86p1L8m1Z8vPn7qjPwJALQSRAGAwDlcz\nMLG9pMtt790pse1VbR9m+2L132dJO19U8xfIpSWdb/vd+Utlaxmm2N7L9hm2p5Xv5aDIu9Qchno/\nSb/uFpSyva7tD9i+RtJHBrExNZVDGW9ke/tuiSNigUb+ujzL9ktb09neWdJFSr/i1hnt7otqPqCs\norTvt2mT78uL9T9dI9+hnVsRcYlSQLHh/2y/p/WhzvY6kn6q1JmrlAIyHx3NugfgaaU+TM61vXn5\nhu0lbH9Y0nHFy1/Pv+CPkPuiKWtPvNf2z2xv2WnFtjexfaRSIOB1o9mIwrqSbrd9fLvztVj35pK+\nVbx0bg8j65XK2kxvtf2J1vtIfqj9tlJtrtGOCImRyv1/pO2FanrlGkg/V2q+NJH3//ck/TLPT5V0\nju0jOwVF82fTHra/IWmu2tcY6um+X7i6mH9DzWUmyuf7pba/b3u/Tv0c5Wbsp0hqBK8ekHTxAMsA\nABP6VwsAWGRExI22X6c0JPY0SVtK+pXtOyVdodTB8BSlX+u3VKr90HgQH9hoTxHxuO3XSjpP6VfW\n5ZVqhxybv9DelcuxgaTttPDwxWVev7F9mNKv3FMlvVTSb23fIukqpdoZU5X6GNpKI2s/nKlxEhH3\n2L5Izf4qLrT9K6XORZ9pJouPF4t9VtJrlJqzbSjpYtuXS7pR6bhso7RNknSlUrOsckS3duW4z/bb\nlc6BJSVtIekq25cp1eqaorTPn6fUVOU4peZWjQ5xF3TId9jn1jvytjxP6WHua0q13C5SGslsuqTd\n1HzQC0n/LyIuGMC6R+N0SZsoBbaus/0bpaDOCkrnSvlL/TWSPtEpo4j4fn5gP1Zp375a0qtt/0np\nofQhpaHY15D0gpa8B9l3yzRJH5L0IdsPSfqj0shpjyidy1sqnWON4/+opI/1s6KION/2+ZL2zPl9\nQdL7bf9OqWbTRkojQ01VCti9WymghME4VdIRSsd0qlKw+1+V+u16VGnwhJcp/SD8oKSPS/q/4RS1\nu4gI22+SdLbS58jSStfSUfm++zelYe6nKd1PXqBmU+O210+f930p3Rf2zfPvy8Gnq9TsjD4kfS/X\nQGpkMux7cMNSSoGvN0h6Ov9gc5PS/WdJpX23k6Rlim35SETU+bECAGojiAQAAxIRs22/WOmL/K75\n5XUlHdBlsUc14M6H8xfelygFf16RX15Z0qs6LPKEUpOXdnl9x/ZNkv5XKbAipdG3Nm6XPrtPI38l\nHg+HS5qjtJ3Lqn3zj2cfJiLiBtuvl/R9SSvml1+ikZ1dh1IfOW9Rzf6lIuIs229Q2verKD1I7KiR\nnTeHpK9I+pSksnnYw13yHdq5FREP5FpZp6jZ78q6kt7YJvlDkj4eEd8Y7XoH4GmlQOEPlR62d8tT\nq99Iek3V6FcRcVx+aPtvpWZtUnpg7FgjSdIdkv5SUc52TXXamafUn8vUvMxKap4L7fxZ0lsj4k+j\nWP+blALCjfN3gzyV7lXqD6lcT91tGraxKOdA8oyIebZfLekXSkFcKQUnNmtJerPScarb1LFhXI9R\nRDxie4ZSAP9wpUDHsmp/TT67mKRL1OHzST3e97NTJB2k5uh3rfd9KfXhNOLeOUE+38vPiKlKAePt\nOqS9X9KHI+JbHd4HgL4RRAIwmUXL39FnGPEXSTNyc5PXKf1KuoHSL5TzlaqW/1Xp1+TzlZqaPDHo\n8kXEXZJemfveeaPSyD3rKn3Zfkrp4fZqpb4efhgRj3XJ63JJL8rNsPZTeiBfRylI8rTSl9W/KH1Z\nPk/SBV2az0SP21NrH0TE1ba3Vmp2tIdSDZRp6vI5FxFn236eUr84+6pZI+gupePz7Yj4iSTZrn0s\nIuKntp+by7K/0q/DS0m6U+mB6BsRcXFuEtYYQW9BRHQMIuV8B3lu9SQiHpR0gO2XSXqz0vm0tlJN\nt/sk3aDUXOWkiLi/Uz5lli1/x0RE3JUfXN+Spy2Vags9oDSi3rci4rs95PfL3FzsNUrnzI5KzUam\nKXX0+w+l2myXK+3/31Rl2cO677C9qlLTpZ2VHh43VWpuubRSTYo78nb9RNIZEdHp4bvW+nPtul2V\ngkRvVqohsqLSds7N6zk5Iv5he3qRZ7d8x+Qe0Ie6+dVZf5lmYPlGxC22t1Oq5fV6pfN3WaU+bm5S\nCpCeFhGP2W4EY6rW3+v+r9LLvXGeUtO8Lyr1Cbe7pOcr1WZdWqlG3e1KTbJ/LemXuWPuTvn1c99f\nYPsVSuf06yRtrTSC2TJlsg7LDvvz/YVKNSt3Uwp8bS5pPaX78FNKAd1rlWp8fSfftwFg4Jy6vQAA\nAOPJ9hZq1t64PiK26pYe1WzPlHRU/vfkiKgcUQ4AAAD10bE2AADDcVAxf9nQSgEAAADURBAJAIBx\nlptEHVG8RIfEAAAAmPAIIgEAMCC2t7N9qu0dOrxv26+RdJGaHeFeERGzx62QAAAAQJ/oWBsAgMFZ\nStJbJb3V9t1KQ0ffpdTp6hpqdsTc8IBSB7MAAADAhEcQCQCAwSlHq1hLaQSvTq6T9IaIuHFsiwQA\nAAAMBkEkAAAG53JJu0p6pdIQzOsoDR+9sqTHJN2t1In2zyLix8Mq5GJsrIaDBwAAgCRH8D0LAAAA\nAAAA3dGxNgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQDGje1lbH/A9mzb\n99ieZ3tBns4Ydvmq2J5RlPeCLunmFul2G8B6G3ktGG1eiyLbc6r2p+1DizSzxruMk4Ht6cU+vmWc\n1jmpz31gWFo+xzYcdnkATBwEkQAs0pxsbvsg21/MD5sPlw8eo/nyY3tN2x+zfbHtO20/Zfs22+fZ\nfo/tFXrIaxXbn7d9ve0nbD+U832X7Sk95HN03q6nbT+/vy0bf7ZXknSppBMkzZC0uqRyuxe14UK7\nlbccan6Q27Wo7aNB6XV/Ttb9NJ7Gex9zTIHxFS1/AUCStOSwCwAA/bK9vaTzJE3rkqzvLz+2Xy/p\nREmrtry1Xp72kHSk7YMj4qKKvDaTdL6k9YuXl5b00jy93vYBEfFEjXw+mf89PiKuq7s9E8CxkrbJ\n8yHp15L+IunJ/Nofh1GoMeKWv4POd7IZq/05adk+WdLB+d9jIuKYXrMYbIkAyfZMSUflf0+JiMOG\nWJxRW8S3h2scQFsEkQAsylZQ9wBS33IA6QfFS08oBYHukrSxUk2aKZI2knS27d0j4vIOeS0l6Udq\nBpBuzXmtIOmV+e9ekv5T0vsrivY1SVNzHjN73KyhyTWt3la8dEhEfGtY5RmFYf4yy6/B3fGref96\n3WeDrmEHtLO4nWOL2/YAmKQIIgFYHDwg6SpJV+ZpWUmn9puZ7Y0knVa8dKGkAyPi3iLNJpJ+Iun5\neX1n2N4sIh5vk+XrJG2V538p6Z8iYl6xrkskrSPpnbY/HxF3dCjXWyTtqfRF9INVtZYmmM0lLZ/n\nn1pEA0iKiAs1hKbgEUHz8woRcYqkU4ZdjsVZRMwVXSEAADCp8UUAwKLsD5I2i4jVImLviPhkRPxI\n0u2jzPczSk3NJOkWSa8qA0iSFBF/lfQKSQ/ll9aR9NEO+e2f/86X9KFGACnnc6ukT+d/l8x5LsT2\nypK+mP/9WUScWXtrJoaySeDdQysFAAAAgL4RRAKwyIqIB3MwZ2BsrybpoOKlozrULlKuMfSl4qX3\n2W7Xh8CW+e/fIuKmNu//qk3aVsdKWlPSo5IO75BmIluqmGeUJWBioe8TTESL23m5uG0PgEmKIBIA\njLS/miOGPSLphxXpy6HE15K0c5s0K+a/d3XIo3x9xdY3be8g6V3532MiYrQ1rWrLo9N90vaFxeh0\n99m+2vYJuWydln12OHBJs4u3ymHC+x4u3PaZxfJv6ZJu75Z1faVL2pVsP5PTPZ77syrfn1Hkc0Gv\nZe6wzt3zSH2NfE+3vXRLmsphzm2fXKQ7Or+2nO13F8fvSdt/s/1D2/v2UdbVbH/U9jk5nyfyaIg3\n2P6m7b2tMBIbAAAgAElEQVR7zG852x/OoxT+I+d3s+0f9Fo+24cW2z+rIu0Wtj+U98P1ef/Ps31/\nPrdPtL1LL+vvoZzL2N7P9pfycfl7Pi5P2L7d9i/zPl6pZn5ziu0+JL+2ku3D83u3521bYHsj52G7\n1exUW5KO9sLX5ELneHlN171mbS9l+822T8vnyQPFvr7C9ldtv8r2QL6TOnmN7VnF+p6yfYfts/N+\nWa5mXsvafrvtn+Tz8tF8f3g0/3+u04ibu9ltf0Dop+wvcxqB85e2b7H9mNNInHfbvsT2F2w/p2Z+\nM1uvCdtL2D7Q9hm2/+p0n3v23GmTx4a2P2X713kfPpX36bX52L1ktNud1zMnn5dHFS8f0uG87Hru\nDbLMtl+Qr9XLnO5R83J+99r+ne1TnUZYXWtR2J6c36o5vytzPo/ZvjFfMzv1kheASSoimJiYmBar\nSanT6wV5mi9pwx6WPa1Y9uyay9xYLDOzzfu/z+/d3GH5jYvl/7PlvSWVmu0tyH+XGMf9eLhSIG1B\nxfQ9SSu0WX56jWUbU9t9U1G+jxTLn9Ql3bEt67q+S9oDinTnVpxbs7vkM7dIt2uXdAcqjU7XOFe/\n2iHds+dzl7xOLtIdpdQP1TUV+/10ScvU3N9HSHq4xrE8V9LqNfLbVtLNNc6t5SXNqdqfkg4t0nyz\ny3p/0MN5eaaklQZ4Te1Qcx8ukPSgpNfVyLOxb+YrBYZ2Uup4vzW/+UoDAdzSw/bPblnX9OK9ymtW\n0r49rO87/Z77RdrtlEZ5rFrXXZJeXpHXizXyOq6a9hzlubGUUlPsOuuaJ+lzklyR58zympC0rlIf\nf+3yPLhl2SmSvqDm/anrsZO07Ci3/4Ie9nWnz9KBlTnn9d89lOmiibw9RZ77KDUp75bXfyl995ir\n5r2j9vcoJiamxX+iY20AGOn5xfxVNZe5StKmbZZvuF5paPsNbG8aCzdp26slbelDkl6g9EXuPRGx\noGaZRsX2sZKOLF56Sunh41ZJK0vaVanmlZQCIZvZ3i0iHi2WeUjSV5U6Al9f0j/l1x/Rwh0g39dH\nMWcX87t3SbdHy//Ptb12RLSrGVbmM5CaRp3Y/qCk45WaOISkoyPiswPKfmWlTtw31shjt6rSNjb6\nqHqtpJ/a3rfTuZVrWJykFKRpuEfSb5Uexqcqnd8vyu/tKelS2y+JiAc65LmVpPNyOaW0/dcpBVyf\nyfltq3RuNd4flA3z32ck3aAUBL5f6cF8FUkvlLRFTvMqSefYfllEPDOAda+iNBpjKJ3z10m6TamZ\n6lSlIM0OSoGzaZJ+YPt1EfGTGnlb0maSTsjLPiLp15LuyOtt1DA4RdJqSsfpufm1y/PU6i89bV1Z\nGPsDkr6sZhOeUNrXv1cKkE1Tar67tdID6zL9riuvb1+loOiy+aWnJV0h6Sala2BDSbso7ds1JZ1l\n+8CIOKNNXusrBUMbo38uyOX+k9J+XVYpILO1Un94gxitbkrOMyQ9rvRZcLPSfdSS1lYKbK2d035S\n0nJKwfQ6lpH0M6Xr6hlJlyod36lKnzHPcqoJ+VOlgINymW5X2p/3Kp3D26l5/rxJqYbpjIh4uodt\nLp0h6VpJL1HaTkn6s9J9otVCnxdjUObjNHK01H8o3fP+rnQ+rJTzep7SPmw9/hNte2R7D6VzYGqR\n5xVK96GlJG2f8/ug0vXDaHIA2ht2FIuJiYlp0JNGVxPpsWLZd9Vc5rhimavbvH9Q8f5ZkpYq3ltf\n6SFygdKDzrrFexuoWRPof8dx/+2vkb9K/lTSGi1plpD0MaWHkUa6U7rkuVuRrudaR13yvbfId+M2\n708rynhXkfbNHfK7ukizY8W51XdNJKVflxvvPy3pnyu289nzuUuak4t0jV+uz5W0Tku6qZL+veUY\nf7xLvp8o0t0j6c1qUyNO6YHmT0XaH3fIb0k1a+ctUPpVfJ826V5WXBvlL/GjrYn0eUlvkDStS5pt\nJf2uyO/IAZ2vL1GqQbJ1lzTLSvpXpaDWgnyOL9cl/ZyWc2mBpK9JWr4lnSVNKf6fVSx3VM3yTy+W\n6XgdKz34zi/SXiZp+w5pV5X0Hkn/Popzf1OlYEsj7VfUpjacUtDy60W6ByVt0Cbd8UWaayVt0WXd\nWyldz223r4dzY6l8TGZIWrJDGisFfsv73kL3qSL9zDbnxoWSprdJu3Qx/7XyOEvat0P+eysFKRtp\nvzSAa+ToOtdxm+UGVmalIOu8Is2/lNdOS9oVlO4nx07U7cnpVtLImm5/aXfOKn3+P5iv36ca156o\nicTExFRMQy8AExMT06An9RlEUvqltnywPqDmckcUy9ze5v2llH7pa6S5RdI3JH1XIx98vtay3Blq\nBj9WHqd9Z41snneeujShk/Thln32whrHZJBBpNOLfBcKxEjarzgPPqLmg+032qRdvcjroXYPDRpl\nEEkpgHJK8d5jkvarsZ29BpEWKAVqlu6Svmyq8bDaN0lcr3iQeFjSlhXlXFsjg3XbtklzSPH+05Je\n3CW/52pkYHfUQaQezq2V1ax1cJsqmg4NelJ6cG1szzu7pJvTsn86Nu3scr4MLIikVEvmr0W6i1Sz\nyeQozv2f97Itkk4t0p/Q5v0ri/dH1UxtjM6Nlxbl+3aXdDNbzo1rqo6FUq2ZRvrbJK1dkf55kp5Q\nM9i7Tq/b06XMta7jQZdZ0qvL83dR356cpgxmPShpoy75zdDIIDBBJCYmphETHWsDQNMKLf8/UXO5\nMt1CHWNHxDxJr5N0Z35pI0lvl/TGIv1sSR9tLGN7P6X+eaRUS+TB1nxtr2x7Wuvro7SXmk3zFkh6\nb3RvQvdlpT5IGt7fKeEYmV3Mt2vSVr52upplbW3i1pr2NxExf5RlG8H28kp97Lwtv3S/pL0i4sxB\nrqfw0Yh4qsv7n1R6mJDSuX9QmzQfUnNkveMi4k/dVhipieB/FS+9rU2ydxXzJ0fEFV3y+7PSOTbu\n8jXXaEa2rtKD2niaVczv0zHVSE8q1RAcptcqNaOUUm2Ot0bEk2O1MtvPV+p7SUq1Kz5TY7Ej1Wyq\n85Y2nWI37quhVOtnQomIS5WaYkqpJkpdn6hxLD5ezH8y2jf7LctyvZrNk6eq2QR1PA26zOXn6jCO\n/0C3J5/f7yxeOi4ibu2S3xxJ3++lwAAmF/pEAoCmZVv+r9u3Q/mg3pqHpPQwbHsbpaZB+yv1zzFP\nqd+LUyX9XyNokYMNjRHE5kTEaY188ggwM5Wqz6+aX7tTqUPwz8XIPon6sWcx/5uI6NonSkSE7ZOU\n+mGR2gdnxlJVEKlRnr9GxG22Zyv1ebOR7ekRMbfD8gPtD8n2GkpNGRt9Y9ym1LHvnwe5nsJtETG7\nW4KIeNT2j5UCmlLa/v9rSfbqRnKljlvrKNc7YoSzfG6XI/q19o3VziylWjkDZ3u60jHZTKm5x3Ia\nOQz3do2kSn0+XTfAdU+VtKNSvzprKwWUO30ve2HNbM+JDv1QjaNyVL2fdXtYHZBXFfPfj4jKflwi\n4u+2b1Cq6bayUl921xZJ5ioF0y3pAxoZ+BwX+fPiRUo/OkyTtHRLksYPEKvZXj+qR+18QNLZFeuc\nIukV+d95SoH3OmaruY920TgGfseozHOL+T1tb1kVQB+UMdqeLZQC4VK6l9e9776p5roBTDIEkQCg\nqbXm0dS2qRZWfrnvWHspIu5T+gX8yE5psplK/SE9Lel9jRdtb6IU3Fi/kWX+u27O8xW29xjlQ+S2\nxfxvai5zUTE/3fZKEfHQKMpQWw7O3aX0EL6O7ec2AjO2V1Ozw9jZxd8jlB4O91AasaihDIB1DcD0\n6DlKzRcbNbyuk/SKiLhjgOtodVnNdJeqGUR6UfmG7VXV7LTVko5YuMJGW+XQ9Bu0vLeN9Gwt6HlK\nnbp2FRF/sX2/mp2Bj1ruYPazSkGculYb0LqnKY2e93Y1OxavsnrNdL/rq1CD9dJifpDXUScvK+Z3\nsv2VjilHapynVjpPyyDSd9Uc8OAdtrdXevA+R9Kf6wSq+mF7CaVAwMfVrM1VuZjSuVkVRPpDjXK/\nQM0auU9J+o82tbTaWb+Yb73mx9pYlPkypWbnGysF6660/W2lmokXRcQjoytyV2OxPeXn+h01P3vq\nfoYAmIQIIgFAU2stnra1itoo043qy6XtrZX6GZKk/2ypqfIdpS+KT+c031IKdB2u1N/BNko1mN4y\niiKsUczPrblMa7o1lPoUGi8XqNkUaw+lEXCkkTWLGg+zFyn17zBFRRDJ9jqSNs9pHlTqT2hQvq7m\n5+1vlTpIHev987ea6coHzzVa3lun5f/3qXetgZ9yHfdG/ZGc/tYmr77YPlLSsS0vd3q4Lh/eFmqq\n2se611Pqw2iTHtdfd9339FGsQVurmP/rOKxv3WJ+D/VXG3KV8p+ImJUDjY176QvVrA12v+1LlDqo\nPiMibu5jfQuxvZRSrZP9Wt4a1LlZ59wo9+UK6q958sCCvTUNvMwRMd/2myX9QuncWFbSO/IUtq9R\n+iw5R9KveriP1TEWx6C879b6bIiIh20/pJE/CgCAJNEnEgA05L4iHi9eWqtT2hZrF/P397v+/Gvj\niUoBjptV9O2RH2gaTaGOi4gTI+LRiLg/Io5Rs/+CN9qu+wt2O+XDyGM1lynTWQN42O5RWdthjzbz\n0UiTf0Fu1H7ZvcNyFw64pkH5gLGeBlSjpUI/x671uLXWkokeJ2nh7xn9nF/SyOuyb7Z318gA0m+V\nRgbbXmnY92UjYkpjknRMkXYQ35m+rWYA6RGl/qNeqVRLbUWlUbnK9T9b9Jr51+3HbSyVx3i0zWvr\nGO15Gmrzo2pEvE0pOH2FRgZyVlVq5vkfkm6yfbbtLQewHZ9SM4C0QOmefpBSU7tVlDrJL8+NC4tl\n65ybdc6NQezLKRpfY1LmiLhMqVbQ/yj9KNI4B5xff7/SyKV32P5ozdpCw9qefu+7vaQFMIlQEwkA\nRrpBzWY9dYMxGxbzo+nj5p1KTUFC0gdaOkVu9DMSSl9qW31VqaPuJZQ64f3fPstQ1qRavuYyZbrQ\nKGtj9aHsv2hGMd8IDF0XEf8oXp+t1Ixp7aL5WxlEGmR/SKF0XI9Wqum0gaQLc7PDrv1NjVI/x671\nuJUBgAURMYjvDP2cX72m7aZsSnpSRLyzY8pkYL/C295R0q7530ck7dCtT6wx6DR/vDysZs2e1sEK\nxkJ5nh4WEXX6e6klIr4v6fu5BtluknZWaj73fDUDN/tIusL2XhHx237Wk/vH+kjx0qER8a2Kxcai\nhki5L2+NiNH8IDFexqzMudnX+21/WNJLlPoa2lnpc7pxjq+mFFDcSWkAjdEai+0Z9n0XwGKGmkgA\nMFLZce62HVONtF0x31fHu7bXlPSF/O+PIqK1A9TN8t/HIuLvbbK4sZjfvM37dZVNHqbXXKb1S+64\njmaTm5M0quivanubluZprf2yNP63mrWRGn+jTfrRsKQ7lIJbjYDBepLm2N5igOtptVHNdGUA9B8t\n791dzNv22hq98vxa03ZrZ8GdbFidpLvcYW3jOM9XGp2uSt39WMdexfzJNTpVH+S6x1M5ktSmHVON\nzfpam2AORETcERHfiYj3RcQ2StfwEZLuy0mWU2q22q+XqBlwu6ZGAEkawDXRRrkv18h9NE10Y17m\niJgXERdHxBci4tVKzcN2Vxpts+E1tgcRRBqL7Snvu7XOG9sriaZsADpYFD4cAGA8lQGEHfMvxB3Z\nXl8j+zc5v8/1flGpGvvDSsOqt2r8Itipenn56+Vofv2/qph/WcdUI+1czN8yXp1qt2ht0tatk+yL\n1RxRby/bG6oZMPtHRFyrActDNM9QM8i4jlIgaRDNYNqp22F0ma489o0yN0bWslpGWuvTH5UCOFKq\nDf3iLmnTilOwbZWqdDWsJmmpPH9PS+20dutdUiPP7dEq+zqpc47NGOC62xmTzqGVOmtvGI/RGsva\nP4M4RytFxN0R8V+SDihefv4omhL3dG7kvvPGou+hP0h6Ms8vp5E/kIyXXs/LcS9zRCyIiAsj4gCl\nfpEa9m+XvMfsx2J7ynv7+vl7S5VeBh0AMMkQRAKAkX6m5kPuipLeUJH+sGL+7oioO6LZs3I/LY0O\nXI/qUNPo4fx3jQ6BrQ3apO1HGQTbNY8I11HuB+LtxUv9BtFGq2yCtodG1jiZUybMzQQbD7q7aWQN\nkRFpByki7snlujq/tJZSIGmrMVjderb37JbA9oqSXlu81K4GVvlLez8dvI4QEY9r5Kg/h9RY7LDq\nJPVWX8wvVyP9G7RwZ+ODWn/XQG+uNfWeAa67nSeL+aU6purdz4v5/W1PH2De7ZxVzO9jezxqP0mS\nIuISSY3RMK3Ur1ZfWRXzdX4E+ECf6+leiHRvPG+s11Ohp/NyApS5PP/aHf+hb09E3KBUI7ZhPO+7\nABZDBJEAoBAR9yuNgtZwjO22D5y5n4wjipe+1uv6ckCo0cfRVZL+u0PS6/PfJSS9qs37+7dJ27OI\nOE/NpnGW9D8V1ekPV3PUolDqm2kYygDIrpIaAZTfR0S7oFoj/aoaWfNrkP0hLSTXftlDzdHf1pA0\n2/YLxmB1X7S9TJf3P69mc4VHlIY1XygPSfPy/K62P1F35baXyU0iWv1fMX+o7Zd0yeO5al8zrx/3\nqTlq4Eo5eNtpvetJOn5A6224qZj/p4q0MyWNVS21hvuK+To1E+r6qZrbuqSkb9muO9JlzyLid5LO\nzf9OkfQd27X7crG90AAKtlevueyqagZ9Qv2PjleeG7t1uG4a69xbaZSwsVJ2PP9W22+su6DtaQM4\n1mUNwbrn5UDLnI9rXdOL+XbHf+jbk32jmP9Et+BuvjceWHedACYfgkgAJoNeR005Ss1fD58j6Uzb\nI2ok5Bo6v1TzIfzvSg/cvfoXpb575kt6T5dRwcoaIZ+x/WzzntyE4mP533mSWvtT6tXHi/m9JP2o\nzfZPsX2ERj5onxYRV2sIcgeojY6qV1SzP5lO/RuVr2/dyKZL+oHJgco9JV2ZX1pdKZD0os5L9exp\npRGEzsr9Qz3L9lTb/66RNYs+FxELNZWMiFuVroeGL9j+Zm4C2JbtrW1/RtJctW8S8W01a2NNyWXc\np00+L1MKDiytkSPc9SUiFmhkrYFZtl/aZr07Kw3fvaYGO7rYWWrWONnF9vGtAWrby9v+kqR/G/C6\n2/ljMb/PoDryzvv5vUojjEmpw+ELbW/fLr3tVW2/1/Zxo1jt4WoGCLeXdHkOtrSV13mY7YuVRshr\ndZvtb9jeM9cKa5fHupJ+oGbtkj9HxC19lv8Pkm7L89OU7rll7VI5ebtSkM4ao5GzIuJSNQdmsKRv\n2/73ToG1XK4dbB+v1DfdBu3S9aD8DNmhdT+MU5k/aPtq2x/IAeVOebxV6dxrOKtN0omwPVI6z+/M\n8ytKOq/dNWl7f0lnKN2r5rW+DwASo7MBWMTZ/obSQ0OpbA5gSb+wXX4ZCkknRkTbEcwi4lbbBysN\nsdzofPlW2+cp/dK4oVJtkkYg/nFJr8lNdXop+6Zqdu77vxFxZae0EXG57V9Jermk50m6wfYvJU1V\nqpnU2Oavd2gOV1tEnJmDDI2RrA6Q9Arbc5QedKYpNQMrf8G/SgNo7jRKF6jZAXlDp6DQ5UoP6eW5\n8veIuLFD+oGKiAdt7yXpV5J2UKoRdZ7tl3c7D3rwNaXjtoekW2xfoHTsVlE6n8tf2s+X9J9dyvrv\n+cHnffmlQyUdbPtqpVpvjyjtx7UlbaMUFHt28Tb5PWP7bUpDlK+c059t+1ql8yiUAnuNju1/oHSu\n7VZz27v5rKTXKDVn21DSxbYvV6p951z+RvPCK5X2zZFt8ulZRPzF9iw1m39+SNJBtq9Q6kx3baV+\nkJZX2geHSfrhINbdwdlKgYjllfro+rPtc5VqKDUCQDdFxIm9ZhwR59v+kKQvK90nG4GdG5Rq4T2s\n9CD7XKVg5xRJP+l3QyLiRqdOjX+sdH/aUtKvbN8p6Qqlzv6nKJ33WyrdJxo/Lty6cI5aWuk4vV3S\nE7b/kNM9JGkZpQ7Dd1Dze/Q8jaLZUUSE7X+TdGp+aQ+l43GpUjB2RaX+udZRs8bnVhrMNdHO4Urn\n4wFKx+/jkj5s+3eS/qp075ym1MH4Nmr+mDKIfrauVNrXGynt6z/mz7671Gxqfl9EHNuy3KDLvJWk\nEySdYHuupGuUro2nle5ZO+S8Gs6PiHbX64TYnoh4yPYhSs1Npyr9QHZ5vv9dpxQMfbGkLXIe/6E0\n4uui2sE/gLEUEUxMTEyL7KTUh82CPqajauT9eqWq6N3yuVnSLn2W/Zycx52SptVIv6bSF9lOZTlX\n0jID3LcfVAoQdNv++UrBtuUr8ppRLHPLGJ0LB7aU7UlJy3ZJ/4uW9KfVWEe5HbO7pJtbpNu1S7oV\nJf2mSPuA0tDvremeLWeXvE4uz2+lGm7XVRy/H9U9Z5T60biz5vU1Xykw8/wu+W0n6ZY655ZGXudt\n96dScKuR5ptd1vsKpWBAt/Weq3S9zSz36QDO0aWVapJ023cPSzq4h+Ne7puDeyzPYZKe6VKWC1rS\nTy/eq7yOJb1a6QG6zvlyaoc8KvdBkXYz9faZ8LCkj7bJ5+Fcpjp53CZpn9GeG3m9n6pY73yl2p9L\n1rwmyvO34zXRpTwfV7on1b3mfy9pzQHsh32UfpzptK6O594gyqzUTL3uOTRf0inqch8d9va05PcK\npR/DuuVxglLQdW7x+oaDOMeZmJgWj4maSAAWdaExGmUoIk63faHSw+k/KQ1lv4pSYOkGSacrBR56\nblZg+yClpmIh6Yho329Pa3nusb2DpI8oBUyek5e/XukX7BMjNSUZiIg4wfb3JP2z0hfPTZVGuHpM\nqZPOOZK+FRGX18mu+DtWo0Jd0JL35RHxRJf0s5W2q7FMnf6QouVvt3SV2xkRj9h+uVJAa2elX5Z/\nZXvfSE0a2q27lki1M16sdP6+Uen4rap0/v5W0qyI+EUP+Z2Sz4c3Kj0Uba/Up9OKSg9Id0v6c877\nnEh91XTL73e2n6fUgfTrlYJeyys1Db1K0ikRcZYk2a6z32sdm4g4O6/3w5L2VfOX9ruUmhV9OyJ+\n0sN6a4vUae4Btl+vdFy2U7qnPKAUjPi50sP+beViVdn2W8aImGX7GknvlvRSpT5bllezlmWnPOue\n32fZPkfSQZJeqVS7bE2lGhkPK9WouEzSmZH6Y+uYVfXWpNpekmbkZoqvUxqtbQOl836+0n7+q9Jx\nPl/SuR3uEaspXY+7KtXO2EypVshyap7rf1RqvvT9iHiyTR49i4jP2j5bqRbKrnmdTygFb3+tdM1e\nIQ32muhSnv+wfaKktyo1wW3UNFxeqSbMnUrX/MWSzo6IP/WznjbrPcepee/7lI7hdKXajo2mhR23\nZxBljogv2f6hpL2VroutcxlWzkkeUmo+fYnSZ2DXZtzD3p6W/M526mvu/Wp+r5ma87lE0kkRcZH0\n7Dk2Vp/XABZhjhjevcH2N5WaYdwTEVvn11ZV+uVxI6UI+IER8eDQCgkAwCLA9smSDs7/zoyITw+x\nOAAAAFgMDbtj7VlKvwKX/kXpl6HNlX4l+pdxLxUAAAAAAABGGGoQKVeXfKDl5f2V2hYr/60aBhcA\nAAAAAABjbNg1kdpZKyLuzvN3a+ToPwAAAAAAABiCiRhEelakDpvo0A0AAAAAAGDIJuLobHfbXjsi\n7rK9jtIwlAspRqUAAAAjHWP7mGEXAgAAAIumiHC71ydiTaSfSTokzx8i6SedEkZE5XT00UfXSjdW\n0zDXP5m3nfWz/sm8/sm87ZN5/Yceeqhsy7aOOeaYSbf9rH/465/M2876WT/rH976J/O2s/7hr39x\nnboZahDJ9nclXSJpC9u32T5M0hck7W37Rkl75P8BAEAXs2bN0oIFC3TUUUfpqKOOGnZxAAAAsBga\nanO2iDiow1t7jWtBAAAAAAAA0NVE7BNpoGbMmDFp1z+Zt531s/7JvP7JvO2sn/Wz/uGtfzJvO+tn\n/ax/eOufzNs+1uu323aJs5BjjumtG8aq5lK9GPb+n4w8yAM4nmzHolp2AAAAAAAmshREGvQztwca\nRMLYsK1YhDrWBgAAAAAAwARDEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoE\nkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKAS\nQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACo\nRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFRactgFAAAAAAAAaLA9ZnlHxJjlPRkQRAIAAAAA\nABPMWAR7xi44NVnQnA0AAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAA\nAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAA\nAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAA\nAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAA\nAAAAQCWCSAAAAAAAAKi05LALAABAXbbHJN+IGJN8AQAAgMUJQSQAwCJm0AGfsQlMAQAAAIsbmrMB\nAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJI\nAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkg\nEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQi\niHFmO8sAACAASURBVAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAA\nAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAA\nAAAqEUQCAAAAAABAJYJIAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAA\nAACASgSRAAAAAAAAUIkgEgAAAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAA\nAAAAoBJBJAAAAAAAAFQiiAQAAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAA\nAAAAAKhEEAkAAAAAAACVCCIBAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIA\nAAAAAAAqTdggku1P2r7O9jW2v2N76WGXCQAAAAAAYLKakEEk29MlvVPSthGxtaQpkt40zDIBAAAA\nAABMZksOuwAdPCxpnqTlbM+XtJykO4ZbJAAAAAAAgMlrQtZEioj7JX1R0t8k3SnpwYg4b7ilAgAA\nAAAAmLwmZE0k25tI+rCk6ZIekvRD22+JiG+X6WbOnPns/IwZMzRjxozxKyQAAAAAAMAibs6cOZoz\nZ06ttI6IsS1NH2y/UdLeEfGO/P/bJO0YEe8v0sRELDsAYOzYljToe7/F5wkAAMBIw/zeNTbrrr/+\nyc62IsLt3puQzdkk/VnSjraXdTp79pJ0/ZDLBAAAAAAAMGlNyCBSRPxR0qmSrpR0dX7568MrEQAA\nAAAAwOQ2IZuz1UFzNgCYfGjOBgAAMD5ozjZ5LYrN2QAAAAAAADCBEEQCAAAAAABAJYJIAAAAAAAA\nqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAAAAAA\nACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQAAAAA\nAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIBAAAA\nAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJIAAAA\nAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkgEgAA\nAAAAACoRRAIAAAAAAEAlgkgAAAAAAACoRBAJAAAAAAAAlQgiAQAAAAAAoBJBJAAAAAAAAFQiiAQA\nAAAAAIBKBJEAAAAAAABQiSASAAAAAAAAKhFEAgAAAAAAQCWCSAAAAAAAAKhEEAkAAAAAAACVCCIB\nAAAAAACgEkEkAAAAAAAAVCKIBAAAAAAAgEoEkQAAAAAAAFCJIBIAAAAAAAAqEUQCAAAAAABAJYJI\nAAAAAAAAqEQQCQAAAAAAAJUIIgEAAAAAAKASQSQAAAAAAABUIogEAAAAAACASgSRAAAAAAAAUIkg\nEgAAAAAAACoRRAIAAAAA4P+3d+dhllx13cC/PzIkgWAkYJA9AQHZA0KQNQxLEBBZ5UVAARV9QUVW\nEURDgiDiAgTFBVFQXwQVNSyyBhgWWWQJiGwSCIJA2CSRQCIhc94/qpp0Jt1d3TP33rrd9fk8z316\n+lZ1/U7drrld91vnnAIGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAA\nYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABg0K6xGwAAAADLpqrmst3W2ly2C4sgRAIAAIA1\nzTrwmU8wBYtiOBsAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAA\nADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMGjX2A0AYPOqai7bba3NZbsAAMDOIUQC2HZm\nHfjMJ5gCAAB2FsPZAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkA\nAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJ\nAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYtbYhUVZetqpdX1ceq6qNV\ndcux2wQAAAAwVbvGbsAGTk7ymtbaj1fVriSHjd0gAAAAgKmq1trYbbiYqvreJKe11q65wTptGdsO\nME9VlWTW732V7fJ+OvX9BwAWZ+rnHWPu/3xqb77+1FVVWmu11rJlHc52jSRfqaoXVdUHqurPqurS\nYzcKAAAAYKqWdTjbriQ/lOSXWmvvrarnJnlSkhNWr3TiiSd+99+7d+/O7t27F9hEAAAAgO1tz549\n2bNnz6bWXdbhbFdM8q7W2jX672+b5EmttXusWsdwNmBydKue9v4DAIsz9fMOw9mma9sNZ2utnZnk\nc1V1nf6pOyf5yIhNAgAAAJi0ZR3OliSPSvKSqjo4yaeS/PTI7QEAAACYrKUczrYZhrMBU6Rb9bT3\nHwBYnKmfdxjONl3bbjgbAAAAAMtFiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAg\nIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADA\nICESAAAAAIOESAAAAAAM2nSIVFV7q+qEgXWeUlUXHHizAAAAAFgms+6JVP0DAAAAgB1k1iHSEUnO\nm/E2AQAAABjZro0WVtVxK//svx696rnVDkpyVJIHJfnE7JoHAAAAwDKo1tr6C6v2bnF7e5M8tLX2\nkgNq1SZUVduo7QA7UVUlmfV7X2W7vJ9Off8BgMWZ+nnHmPs/n9qbrz91VZXW2ppTFW3YEynJ01b9\n+4Qkb+0f+7ogydeSvLm19vH9aiUAAAAAS2vDnkgXWbHqM0me01o7ea4t2iQ9kYApckVs2vsPACzO\n1M879ESargPpifRdrbWjZ9YiAAAAALaVWd+dDQAAAIAdaNM9kZKkqq6T5NFJjk1yRLq7sl1Ma+2a\nB940AAAAAJbFpkOkqrpVkjclOTTdRNpfSvKdNVY1wBAAAABgh9lKT6RnJjk4ySOS/EVrba0ACQAA\nAIAdaCt3Z/tmkle31h4w3yZtjruzAVPkLiHT3n8AYHGmft7h7mzTtdHd2bYysfb5Sf5zNk0CAAAA\nYDvZSoj0L0luOq+GAAAAALC8thIiPSXJravqIfNqDGxWVc3lAQAAAKxtKxNr3yvJm5O8uKoenuR9\nSc5aa8XW2tNm0DYYMPvxuQAAAMDatjKx9t7NbrS1tpUeTvvFxNrTNvVJ7piuqR/7U99/AGBxpn7e\nYWLt6dpoYu2t9ES644zaAwAAAMA2s+meSMtGT6Rpm/pVAaZr6sf+1PcfAFicqZ936Ik0XRv1RJr7\nsDMAAAAAtr+tDGdLklTVMUkelOR6SQ5rrd2pf/7oJLdIcmpr7b9n2EYAAAAARralEKmqfjPJr+XC\n21it7gd2UJKXJXlMkufNpHUAAAAALIVND2erqp9I8pQkb0hy0yTPzKp7orfWPpXkfUl+bMZtBAAA\nAGBkW5kT6ZeTfCrJvVtrH0py/hrrfCzJtWfRMAAAAACWx1ZCpBsleV1r7X83WOcLSa54YE0CAAAA\nYNlsJUSqJHsH1vn+JOftf3MAAAAAWEZbCZFOT3Lr9RZW1SWS3CbJRw60UQAAAAAsl62ESH+b5GZV\n9YR1lv9auvmQ/uaAWwUAAADAUqnW2uZWrLp0knckuUmS9/ZPH5vk2UmOS3LzJO9OcvvW2lqTbs9U\nVbXNtp2dp6qSzPr3X3FMseymfuxPff8BgMWZ+nnHmPs/n9qbrz91VZXWWq25bCsvYFVdNslzk/xk\nLtqLaW+SlyT5pdbaNw6grVtpixBpwqb+hs50Tf3Yn/r+AwCLM/XzDiHSdM0sRFq1wcun64V0+SRn\nJ3lPa+0rB9TKrbdBiDRhU39DZ7qmfuxPff8BgMWZ+nmHEGm6Zh4iLQMh0rRN/Q2d6Zr6sT/1/QcA\nFmfq5x1CpOnaKETa9MTaVXWFqjquqg5fZ/nh/fIj97ehAAAAACynrdyd7SlJXpXkO+ss39svf/KB\nNgoAAACA5bKVEOn4JKe21r611sLW2jlJ3pDkLrNoGAAAAADLYysh0tWSnD6wzhlJrr7/zQEAAABg\nGW0lRGpJDh5Y5+AkB+1/cwAAAABYRlsJkf4jyY+st7C66dPvkuHeSgAAAABsM1sJkf4+yXWr6vlV\ndanVC6rq0kmen+S6Sf52hu0DAAAAYAlUa21zK3ZB0TuT3DjJF5K8Lcnnk1wlyXFJrpzk35Lcer3J\nt2epqtpm287O03V8m/Xvv+KYYtlN/dif+v4DAIsz9fOOMfd/PrU3X3/qqiqttVpz2VZewKo6Il2P\nowckWb3BluSlSX6ptXbWAbR1K20RIk3Y1N/Qma6pH/tT338AYHGmft4hRJqumYVIqzZ4hSTHJrls\nkq8n+dfW2lcPqJVbb4MQacKm/obOdE392J/6/gMAizP18w4h0nTNJESqqjOSvKa19ouzbNz+EiJN\n29Tf0JmuqR/7U99/AGBxpn7eIUSaro1CpK1MrH1kkrNn0yQAAAAAtpOthEgfSfID82oIAAAAAMtr\nKyHSyUnuWVXHzKsxAAAAACynXVtY9/NJ3pjkHVX1giT/muTMrDFQsbX2ttk0DwAAAIBlsJWJtfdu\ncputtXbQ/jdpc0ysPW1Tn+SO6Zr6sT/1/QcAFmfq5x0m1p6ujSbW3kpPpKdtcj2/EQAAAIAdZtM9\nkZaNnkjTNvWrAkzX1I/9qe8/ALA4Uz/v0BNpujbqibSVibUBAAAAmKitDGdLklTVwUnulOR6SQ5r\nrf1m//ylknxPkq+11i6YaSsBAAAAGNWWhrNV1d2S/HmSK/ZPfXcS7aq6VZJ/SfKTrbW/mXVD12iL\n4WwTNvWupUzX1I/9qe8/ALA4Uz/vMJxtumYynK2qbp7kn5LsTfLYJC9N8t2NttbeleSMJPc+oNYC\nAAAAsHS2MifSbyQ5N8mxrbWTk3xyjXXem+SYWTQMAAAAgOWxlRDpNklOaa19cYN1PpfkygfWJAAA\nAACWzVZCpMsk+crAOpfe4jYBAAAA2Aa2Evh8IckNBtY5Jsmn9785AAAAACyjrYRIr0ly16q63VoL\n+zu33TrJq2fRMAAAAACWR2329nZVddUkH0w3ZO0Pkhyd5P5J7pnkuCS/mOTsJMe01oaGvR2wqmpu\nzTddU7/dJtM19WN/6vsPACzO1M87xtz/+dTefP2pq6q01mrNZVt5Aavqh5L8XZJrrrH4U0nu21r7\n8H61couESNM29Td0pmvqx/7U9x8AWJypn3cIkaZrZiFSv7FdSX40ya2SXD5d76N3JXlFa+07B9jW\nrbRDiDRhU39DZ7qmfuxPff8BgMWZ+nmHEGm6DjhEqqqjkhybZG+S97bWPjfbJm6dEGnapv6GznRN\n/dif+v4DAIsz9fMOIdJ0bRQi7drED/9+ksckWdnA3qp6bmvtCTNsIwAAAABLbMO7s1XVA5M8tv/2\n40k+0f/MY6vqQXNuGwAAAABLYsMQKcnDk1yQ5PjW2vVba9dLcpd0/cp+dt6NAwAAAGA5DIVIN043\nYfabV55orZ2a5JQkx8yzYQAAAAAsj6EQ6YgkH1vj+U/0ywAAAACYgKEQ6RJJzl/j+fNz4UTbAAAA\nAOxwQyHSetwTDwAAAGBCqrX186Cq2pu1A6OVXkhr/nBr7aADb9rGqqpt1HZ2tqrK7LPMimOKZTf1\nY3/q+w8ALM7UzzvG3P/51N58/amrqrTW1hx9tmszP7+fywAAAADYITYMkVpr+zvcDQAAAIAdREgE\nAAAAwKDNDGdjDd0YzdkzPhMAAABYRkKkAzL7ScYAAAAAlpHhbAAAAAAMEiIBAAAAMEiIBAAAAMAg\nIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADFrqEKmqDqqq06rqVWO3\nBQAAAGDKljpESvLoJB9N0sZuCAAAAMCULW2IVFVXTXL3JC9MUiM3BwAAAGDSljZESvKcJL+SZO/Y\nDQEAAACYuqUMkarqHkm+3Fo7LXohAQAAAIxu19gNWMetk9yzqu6e5NAkh1fVX7XWHrJ6pRNPPPG7\n/969e3d27969yDYCAAAAbGt79uzJnj17NrVutbbcc1ZX1e2TPKG19mP7PN/GbHtVZfbzfVeW/fex\nLLz+TNXUj/2p7z8AsDhTP+8Yc//nU3vz9aeuqtJaW3NU2FIOZ1uD3zIAAADAiJa+J9J69ESaNq8/\nUzX1Y3/q+w8ALM7Uzzv0RJqundATCQAAAIARCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAbt\nGrsBAAAAwEV1dyibPXcn40AIkQAAAGApzTrwmU8wxXQYzgYAAADAICESAAAAAIOESAAAAAAMEiIB\nAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIi\nAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwS\nIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAM\nEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAA\nDBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAA\nAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAA\nAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RIAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgA\nAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMCgXWM3AAC2i6qa\ny3Zba3PZLgAAzJIQCQC2ZNaBz3yCKQAAmDXD2QAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmR\nAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJ\nkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAG\nCZEAAAAAGCREAgAAAGDQrrEbAAAAwPKpqrlst7U2l+0C8ydEAgAAYB2zDnzmE0wBi2E4GwAAAACD\nhEgAAAAADBIiAQAAADBIiAQAAADAIBNrAwAAsHTcHQ6Wz1L2RKqqq1XVW6rqI1X171X1y2O3CQAA\ngEVrM34AB2JZeyKdn+SxrbUPVtVlkry/qt7YWvvY2A0DAAAAmKKl7InUWjuztfbB/t/nJPlYkiuP\n2yoAAACA6VrKEGm1qjo6yU2TvGfclgAAAABM17IOZ0uS9EPZXp7k0X2PpIs48cQTv/vv3bt3Z/fu\n3QtrGwAAAMB2t2fPnuzZs2dT69ayzkxfVZdM8uokr22tPXeN5W3Mtnd3Cph1/XKngE3y+jNVUz/2\nx97/sesDwCKN/XdP/enWn0/tzdefuqpKa23N2yMu5XC26o6YP0/y0bUCJAAAAAAWaylDpCS3SfKT\nSe5QVaf1j7uO3SgAAACAqVrKOZFaa+/I8gZcAAAAAJMjqAEAAABgkBAJAAAAgEFCJAAAAAAGCZEA\nAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmR\nAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJ\nkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAG\nCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAA\nBgmRAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGCREAgAAAGCQEAkAAACAQUIkAAAA\nAAYJkQAAAAAYJEQCAAAAYNCusRsAAADLrKrmst3W2ly2y+z43QNclBAJAAAGzfpD/3zCCebB7x5g\nheFsAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAoF1jNwAA\nYEhVzW3brbW5bRsAYCcRIgEAg5YjxJlH2DO//QIA2GmESADAJglxAACmzJxIAAAAAAwSIgEAAAAw\nSIgEAAAAwCAhEgAAAACDhEgAAAAADHJ3tm1qXrda3vxtlgEAAIApESJta7MOfNxmGQAAAFib4WwA\nAAAADBIiAQAAADBIiAQAAADAICESAAAAAIOESAAAAAAMEiIBAAAAMEiIBAAAAMAgIRIAAAAAg4RI\nAAAAAAwSIgEAAAAwSIgEAAAAwCAhEgAAAACDhEgAAAAADBIiAQAAADBIiAQAAADAICESAAAAAIN2\njd0AAABgOVXV3LbdWpvbtgGYDyESAACwgXmEPfMLpwCYH8PZAAAAABgkRAIAAABgkOFsAADAUjIn\nE8ByESIBAABLzJxMAMvCcDYAAAAABgmRAAAAABhkOBsAABua17w05qQBgO1FiAQAwCbMOvAxJw0M\nEeACy0aIBAAAsLQEuMDyMCcSAAAAAIOESAAAAAAMMpwN2FbGnhtg7PoAAABjESIB29DYcwOMXR8A\nAGDxDGcDAAAAYJCeSLDNzGs4VWJIFQAAAOsTIsG2NI+wx5AqAAAA1idEAgAYYFJ9AAAhEgDAJplU\nHwCYNhNrAwAAADBITyTYD4Y1AAAAMDVL2xOpqu5aVR+vqk9W1a+O3R4uqqrm8the2owfAAAAsLyW\nMkSqqoOS/GGSuya5fpIHVtX19mdbe/bsmWHL9qsFO7j2UCjylk2sM88QZc8ctqn+pqtP+v/e2PXH\nrO13P3Z9r/+064/7+x+z9tj7nth/9dWfYm311Z+epQyRktwiyemttc+01s5P8rIk99qfDU37D+qY\ntdXfqfU326vsDne4w8g90fbMeHvbqf6Ytaf+vjt+fa//zqw/r/fe2doz4+1tsfoOPvb93VVf/WWt\nrb7607OsIdJVknxu1ff/1T8HLIXN9Cx76ibXM5wPYHNm/d67fWwmEDnppJMmPoze310A5m9ZJ9be\n1F+2zf7xP+mkkzZf2MTGAOuax/tu4r13M7bygdfrz840dJye2D82a7uFSAAwvlrGE8equmWSE1tr\nd+2/f3KSva21Z61aZ/kaDgAAALDNtdbWvNqyrCHSriSfSHKnJF9I8q9JHtha+9gmfvbIJC9O8o4k\nJyf5dpJ7JLlra+0R82ozAAAAwE62lHMitda+k+SXkrw+yUeT/O1mAqTeU5K8PMkVkpyRbm6lByR5\n9hyaCgAAsHSq6riqeklVmVsWmJml7Il0IKrqUq21c8duBwAAwCJV1fcmeUiSRyS5VpJ/SvLw1to5\nozYM2DGWsifSgVgJkKrqBlX18qq6/VhtWYY2AADMQ1X9n6r6+6r6vinWh82oqptW1WUWUOfmVfXC\nJJ9P8tgkf53kakl+e96192nHVarq41X1i4usCyzOjguRVjkyyX2THDXxNgAAzMP1k9wvyaUnWh/W\nVFWHVtVDqurdSd6f5HJzrvf4JO9O99nj/klukG5e2Vcm+cC86+/jkkmuk+TyC6wJLNCusRsAAADs\nLFV1hSSHttY+u8CaR6YLFb+a5GqttY8vqnZf/5rphpH9TLrg5hNJHp3ki3Mu/dYk10j32e6R6Xoh\nLbI+MCFCJABmor+z5rWSfLq19u2x2wOw01XVKUm+3lr76bHbsoYnJzkmyR0XWPPxSY5L8qx0cwEt\nZNRFVR2e5IVJfjzJ3iSvSvL81tqpi6if5D9Grg9MiBAJ5qCqrp3kvNba58ZuC4tXVddJcmZr7X/G\nbsuCXTXdHTVvkuTfRm7L5K1ckW+t/efYbVm0qrpWkq+01s4euy0wZ49MFxosndbaY0eo+aRV3y5y\n2o4npwtwXpjkN0c4/xu7PjAhO3lOJBjT89L9QWea3p/k3mM3YtFaa59prV2itSZAWg6PT/L3Yzdi\nJG9P8oCxGzGGqrp7Vd1o7HaMoaoeWFWvGKHu5arqLlV1/0XXbq19Mcn5Y9VfT1XdqqpOqar3V9XC\nzoeq6rJV9eyq+kBV/V1VXXFBpa/bf/2NkQKcsetPVlVdu++JBpMhRIL5eGiSXx+7EYyjtfY9rbW/\nGqN2P5nny6rqLVV19Ei191TVNRZZexlV1fct+newqvaV0oXZx1fVD4zRhrFU1XXTDat8fVVNcWLX\npyT50bEbMZIzkuxZVLGqOqSqnpfkS0lel+RPF1V7Geqvp6punOQtSe6Z5KZJnlFVJy6o/GuSPCbd\nMLofT/KqqqoF1P3jJC3Jy/qh3Ys2dv0p+9dM8MIh0+ZNZmL6P6SHJTm3tXbB2O2Zh6o6LckpSY5O\nctnW2n3Gql9VC6vff1i9UZIrJjk8yXlJvpHk00k+1Fr7hvo7t/6K1tp5VfXYJO9N8tqquklr7X9H\nrH3eImovqV9Kcq90H6IW7beSXDbJqUmelO42z6OrqqskeVOSP2itPX9OZT6a5D5JTkw3J8rTAqrF\nRwAAFmRJREFU5lRnU6pqd7o5Ws5L8q7W2tvnWa+1dpsx6/c1fzjJnfpv35/kDa21Nu+6rbV3J3n3\nAuv/cZKHpAtv/iHJooeOjl1/PT+R5OB0E0y/It2kz0+qqmfO8+9RP5T8lune9+6X5IR0PTLvli5c\nmpvW2huq6oQkv5nkT5I8fJ71lq3+mKrq4CQnJblLko8neUZr7aOLqt9aO2Kf9tw73XvuSTt9SHVV\n3TzJ/0k3kf0prbX/GKkdl0hy63QXkL6W5M2ttW+O0ZbJaK3tyEeS3enGiD9kJ7chye2SPCfJVTa5\n/lX6Nj1+pNekklwmyUEz2t4t0v3BvNKq566e7raiV1z9fL/sakm+k+QxO6H+qu3+Wf97Xe/x3jn/\nXtUfsf46bbr7WP/XV9V+wqJre4z3SPeB7YH7PPfzSZ646vuj+2PjhJHaeESSP0xytwXUOjpdr5h9\n3w9evqB9nXv9dEHd3iRX77+/bpJ3rFHz7UkOmcM+jla/P5YuSPKsRfw+N6j/e2PUH2jbH/av+5X6\n7/+k//5qc657877Ok/vvj+2/f/oC9/1lfc3HjfTaj1q/b8NC3+eTvLyvd0H/9ZtJjh1x/39kkb+D\nJEeluxvf+5L8dmb0GWsTda+f5NxV77PfSfIHSS654Nf7OukuHq1+z/9qkluPdQxM4WE42/b3q0nu\n11r7/CbXX5l88VKzKF5Vt6uq5/RXlzfjykn+J11X41n49SQ/07o5AZIkrbXPtta+1lo7c/XzvW+n\nG8Z5mR1Sf8W/JHlgkhsm+eUkn09yfpJ/TvJrmf+V+Hcl+ckR67813ZXPqda/mNbaa5J8LN1thseq\nPerdgqrqFlX1wqq6/pjtmJDbJ/mNfZ57eLr/E3NXVT9WVbfa57nbVNU9Vj31vUl+Id2Hy3m25Rbp\nesDcLMkT011YuFy6SW/v2/eU2VH1q+pOfc2bp3vP+/50vTKfnuQ2mfNwj1X1b5YuXJp3/cPSXRjb\n29e/UlU9oqr+X1W9dca1Nqrf+vpXnHf9qrpPVb2qqq46sOpK/b+uqiekG1bWknxrHu1a5SPpeiE8\nup+H6Rn98983i42vOue90gar/XSSDyR55qz/9oxdfxn17/n3TdcT77Akx6f7jPPEOdY8oqpuXlXf\ns84qb0wXrsz9roRVdbkk707y4CQ/lG6//2TedXuPTHJIug4N1+zr/kKSFy2o/oqnJ/mBdMfBIele\nh/OT/N6C2zEtY6dY83pkOj2RPpDkPVtY/3f7Nt1jRvVfneSzW1j/Sn39X59R/dO2uP+/1de/506o\nv8b2n9pv/5QkV51HDfWXt/4a7Xllkm+NVPuUsWqvasNRGbfXy+3T9Yq45Uj179LXv/kMt/nA9fYn\n3Vw8e5Ncs/++0n2gOzfJof1zN+nXeewc9ndPkk+s8dx/r/r+6AM5JtL1NP2+dZZ9MslfphvWenaS\nTyW54T7r3K+vf/8F1D991vXXqHliv717pQsIvph9rv7mwt4hvzKH3/m+9b+w7/E55/orPSC+nguv\ngJ+d5I2zrrUM9dMNEzt9k+s+Pd1cTV9O8p500yjMsi0/k+4uoFfY5/nb98//T7obC5yb5Lkzqvnq\nJP+5ifVu1v8unjHjfR61/hbaef2s6hE251o/1df60VXPfTXJO+dY83f6mtfYYJ2PJvnwAvb/Z/u2\n/Fa6sPQt6S5YH7mA2q9JcsY+z/1B355NjZCZUTv+Msn/puv5fFj/3EFZcI+oqT30RNr+PpTkh6rq\np9ZboZ/s9s5V9fJ0Y8Pf1Fp79YzqXzndSeNmPa7/+sEZ1f+3dPv/oPVW6Pf/jlX1snRzg7yttfbK\nHVJ/dZ27pQsx/ri1du/W2n/Nuob6y1t/jfbcKF2Q/cmRat9hjNr7+Fy6k5krj1T/P9KN0b/7SPU/\n2df/kVlsrKpun+QlufAuQGvVS5IT+vn37ppuyM0hSX6lX3aXfdbdahuOr6obrrP41CTXrqprrXru\nGkkOr6pL99+vXDk+dz9qXz/JZ9LdOGEtpye5f7oT628luWNr7d/7nz2kqh6W5AXpuvy/bwH17zTL\n+gP+PN2cS3durb2zr7mrqu6b5B/T9UJ594xr7lt/5TV/9wLr/0664OrwdHP/HJ/kcq214+dQa6j+\nK9P9/5pn/SOSnLWZFVtrv95a+/4kP5xufrY3zrgtD0zyzdbal/ep+9bW2o1ba4cneVS6958vzKjm\nlZOcuYn1zu+/XnJGdZelfpLv9kg7fd+en6us/M3d1LGyn224ZFX9Rbr3tCR5TN8T73fS9br82Lxq\np+v18s3W2hkbrHNeugsp87YyH9OHWmtfTdcbaFe6iwmLcEg/H9GKlb+th8yjWFUd3Pe6PHjV0yem\n64X4J0nOrKo/TfL9rbXz19oGMzJ2ijWvR6bTE+lq6U4c96abwPclSZ6bCydZ/Ei6RHpvuhOsk5Nc\naob1X5Tuj9VPbbDOoUnunAuvmM3sClm6ngaf3uT+n5vk+elT6p1Qf5+2nJZuQsFdizi+N6qfbkLN\n6/b//sEkl1lk/bH3f4z6fRve2P+ffGV/3H0nyX0WVPu1Y9XeoE2H9P/3Th6pfvWvw5+MVP/gfv9n\ndRX++f3v9nvWWX6fXNgb4kvpTqJPT3exY2+64Oj8dOHaludsSDdh7t4kP7/O8nv3y/+yf+3vsKo9\nJ/brPLb//r77Uf9Z6ebcuOI6y1+2qt57krw4yd+luzJ8Tv/8OUketJ+v/6j1V9V5fL/tF6e7ILRS\n87T+ub9NF+it9I7538xwbpAN6n9gVf03zav+qnbcKF1vl/9KcvtZb38Z6yf5o/41fWIGrvKnm6fk\nGf3v4dzMeI6afrvPG1jnV/v2zqR2kr9I957+0HWWH9m/x3y5/7860zlZxq6/qs7/S3LOBst/r3/d\nd8+jfl9j5b387Un+Kt2NTFbeC96adXpszqj2q5N8boPll+qP+VfOqw2ral2rr3VOuhtJ/HNmOOJk\noPYT+lqvTzd1w6v67982x5rPSncesm8PxEskuUe6CwrfSPLZJIfP+zWY8mP0Bsxtx7oA54KMHyLN\nvQ3prqw+rn/T/Er/n+sb6a5YnpouOHpQuqtTs649aojVt+HwdCeVG+3/g5Ncfk6v/6j1V/0eLjJE\nI6uCnHkef2vVz4VDVo5K96Fxyx/YDnT/F/kYu/6qdrw63YSSZyV5Q5LjF1j7lLFqb9CmlRDh50aq\nf5m+/igT36br2j6zSWXTnSh+ZoPlj+rrvaz/e/DOdHPRXC/J2/r3xbck+YH9rH9y/35yxDrLj8+F\nHyK+3K/7uXS3X14dYn02ycH7Uf+fk/zXBstf1R//71vVju8k+e90vWBOzDoB0Haov6rOa3PhJLb7\nPlZqrrTjWdlgyMd2rL+qHa9MF5Refx7bX8b66UKKleDuS/0x+aJ053wvTnfe99b+mFs5Bt+X2QdI\nhw69t6W7gPU/meGNLZJctX8f2ZvuTnh/my5c/+t0c0N+p1/2mSQPnsPrP2r9Ve34+/53fLGLAUmO\n6f//fTFzHE7UH3sXpL+oke6i0XWTXHteNVfV/rP+/96h6yx/ZP97eNi829LXO65/Xzx71f+7uU8q\nnW7I2O/3v+tz0t2Z97HrvS4zqvmeJB8YWOcx2c+LRR6bf1T/YsN+6yeW+7l0cxJcP93Epf+bbi6M\n09MFSe9J8rrW2n+P1c6drJ9E9d1JHt5a+4v+uZukuzJ7dGvtsyPUr3QncWe0Od9ifq36izR2fS6u\n7+q8J93cED/QRhheWFU/mu6D/UNba389Qv37pusB+oDW2t/PYHsfTDfP1a3XWf6OJD/YWjvyQGut\ns/3XJblea+2odZY/LN2V+n9IN7HmV5M8OV1o9Gfp5sY5Lckj2n7c/rmqTktyXmttzSEcVfXpJN9o\nrR2z1W1vh/pcVFV9Mcn7W2v3GFx5B9WvqkOTPCTJA9L9jb98uotW56b7EPuldPPBfCjJqa210+bQ\nhkp30WJPa+1iw4X7IdWvSje5+q1aa7OaQmHfc97rpRuqd06SM9IFaK9JN23EXD5gjV2/b8MvpLsD\n30vS9UD5UrqeZw9ON7HypdPNu3bKHNuwJ8ntWmsHzavGBrXvnW6Y7HPT3YV276pld+6XfS3Jded9\n/rtG2/4p3RD6I1pr857IfuH63/tR6c7r9q6x/NrpAvZrJ7nx/vytZ3N2jd0A5qOqrp5uEsOvzLtW\na+0bSZ7dP1Y+UH8l3ZWiXa21D8+7DWRlToDrrDzRnzQtat6zi9VPd/L20SS3TdcjYdH1F2ns+qxS\nVd+X7srsLdMN5RojQLpUuollz03yuhHqH5bkpHQfLmY1F8nZ6SZ2XqveQ9PNv/TsGdVayxXT3flw\nPfdP1+P1AWucXN5hBvXPSXdziIvpA8OjkzxvBnWWtT4XtTddkDGp+q2189LNQ/OCoXXn2IZWVf+S\n5C5VdbfW2muT7g516e5O9mvpgq0HzzJA6mtf5Jx30cau33tBunO7B/eP1f4tyaNba4u4Q+EoWmun\nVNXfpevx8hNV9e/pel9dN91der+a7s7Ziw6QfiVduPjinRgg9V6Srufja6vqBenOCa6abljfcUnu\nlO6zzxMFSPOlJ9IOVVVvSXJaa+1xgyvPvvZp6Ya2HJ3ksq21+yy6DVNUVR9KN6zqZm3jyf4mW7+q\nao5XB0etP2VVdVC6ySVvkOTH0t1W/vB08zY8bK2rVXNuzxWSvDRdcPH01toJC65/pXTDHG6b7k6Y\nvzWj7Z6QbkjUs9N9iPhsurD4p9JNKv+f6e4EN5fJVKu7bfnVWmvXXGPZA9OdXL6gtfaIOdV/eroP\np7+bbt6Fzya5Qrrh4iek+1B/k9ba6TuxPhdVVa9N17vtxq21NW8wUlWXmNf7z9j1x1ZVP5yu580l\n080LdXC696Oku5D5kNba60dq3iRU1bHp7ob3/ene/9+6qAvHfY+U41pro9wkqu8N98B0vcJukq5j\nxifT9QR7Tmvtawuof2i6iyvHpDvvuXu60R+3ba2dPc/6Y6qqJ6W7G+xh+yz6crphfSfPOjzm4oRI\nzFxVHZFuXqCDkqS19j/jtmgaquq26eai+Wa6LranpkvoD0nXrfM+Sc5qrf3qgusf2te/X5Kvt9Z+\nZd2NzKd+0g2zvG+6u2k8fifWn7KqOjXJHVc99c4kv91mdxfKoforIdYN04VYP5duPqQXttZ+fkH1\nL9fXv1e6k8lLJfmj1tqjZljn8HTH9c3XWHxauonU5zZ0tqqemi6s+v10w9NWQpSfTndCeWa6EHcu\nPXCr6rJJ3pzuA8O+PpfuBhNvm0ftZajPRVXVrdMNmf1Kkuf0/z4z3aTuN0j3N++sOf7NG7X+Mqiq\n26S7Q91N002j8PF0w9j+uLX29THbxnz1F8uPG2M42zJY47zn/HQXzh7T91bb0fq/hz+cbgqVs5J8\ncowL2FMmRGIu+rkrzmitPXLstkxJf1Xod9JdGdrX19LdoWZuc7OoP279qaqqR6W7GvfxdHNkfG7B\n9fek60a94u1JntlaW8gwtn4uopV5ilq6q/PPaK29aQ61LpEuqLpVurlQzknyjiT/MO8eD32I9aZ0\n81zt68PpQqxPz7kNByW5Zy7c/2+mm9D2H1pr355n7WWoz0VV1e3STd59yzUWfzXdB7q/2an1YSxV\ndcN0d9+a93QJS6mqHp3kGunmo/p4ujuizbX3E6wmRGIuquoqSb69iDmZuLiquly6K3OXS3e3js8n\n+dCixmerP259Fqs/mbtCuhO5tyx6Dqaqely6Y+1jff0vLLL+IvUh1j3ThWYrIcpKiHXBmG1juqrq\nyCQ3TndMnp9ueNWHFhXsjV0fgGkRIgEAAAAwaJTJyAAAAADYXoRIAAAAAAwSIgEA20pVHV1Ve6vq\nRSPUPrGvfdzw2gAAO4sQCQBYGn1As9HjIenuQpdVX5fWqtDpqXPc9pqBVlW9uF9+9VnXBgCmadfY\nDQAA2EdLctI6yz6Y7o6H101y9sJadODGCryWPmgDALYPIRIAsHRaa08bWOU/FtKQ7aEGlm20HABg\n0wxnAwC2lfXmRFo1fOuoqvq/VfXhqjq3qs6sqj+tqsPX2NYdquoFVfXRqjq7qr7V/9wJVXXI4vbq\nu+25alX9YVV9uqrOq6qvVtUrqurm+6z3mSQn9N++ZfWQv3753iQP6ZefsWr5Gfts53JV9cyq+li/\n72dV1alVdfwabXtYv42HVtVdq2pP/5rtnfkLAQAsJT2RAIDtar2hWr+b5C5JXpnkdUnumOTnklwr\nyZ32WfeJSX4wyTuTvCrJoUlum+TEJLur6s6ttYWEJFX1Q0nekOSIvt0vT3JkknsneUdV3ae19tp+\n9ef0z98+yYuTfGafzZ3ULz8myXOTnNU/v/I1VXVUkj1JjkrytiSvSXKZJPdI8rqq+r+ttReu0dQf\nT3LXfv0/6n8eAJgAIRIAsGyqn4h632FYZ7TW/nITP3+LJDdsrf1Xv7GDkrw5yR2q6tjW2ntXrfsL\nrbUz9t1AVT0tya+nC0z+bn92Yiuqaldf59JJdrfW3r5q2a8leW+SP6+qo1tr326tnVxVR6QPkVpr\nb1u9vdbaSVV1jfQhUmvts2uU/cskV0vyE6217+5jVX1vunDpeVX1ytbal/f5ubsluXtr7Q0HuNsA\nwDZjOBsAsIyemm641urHQzf5s09bCZCSpLV2QZKVoW/Hrl5xrQCp99z+61022+AD9KNJrpnkD1YH\nSEnSWvtiut5VV8zFe1Ltl6o6JslxSf5hdYDU1zs7XU+sQ5Pcb40ff4UACQCmSU8kAGDZtNbaQQfw\n8+9b47mVUOmI1U9W1WFJHp3kPkmuk2441+oeUFc5gHZsxa36r0dX1YlrLL92//V6SV67xvL9rXfZ\ndeoduarevv51BvUBgG1IiAQA7DRnrfHcd/qv3w2nquqS6Ya5HZvkw0lemuQrSc5PFyQ9NcmiJte+\nfP/1/hus05IcNuN6x/ePrdQ7c0ZtAAC2GSESADBV90oXIL2otfazqxdU1ZXShUiLcnb/9Z6ttVcv\nsN4vt9b+cIs/u96E5gDADmdOJABgqq7Vf/3HNZbdfpENSfKu/utxW/iZC/qv6w3922j5/tQDACZO\niAQATNXKpNp3WP1kVV0zybMW3JZXJPlUkl+sqruttUJV3aqqLrXqqa/1X49aZ5vrLm+tvT/J25Pc\nt6p+ep16N6qqI9daBgBMk+FsAMBUvSrJ6UkeV1U3SvLBJFdPd6e0Vyf5iRnWuk8fTq3l9a21l1bV\nfZO8Psk/V9U7k3woybeSXC3dsLtrpLtD27n9z705yd4kz+zb//Ukaa09vV9+apInJPmzqvrHJN9I\n8vXW2vP75Q/qt/HnVfXL6SbMPivJVZPcOMkNktwy3TxRAABCJABgx2jZwnw9rbVvVdUdk/x2kt1J\nbpeuN9DTkjwna4dIW6qxat0bJzlmn+er//rfSV7aWvtwVR2T5HFJ7pHkYelCoi8keX+S38iFvYvS\nWvt4VT00XVD0yCSH9tt7er/8DVX1+CQ/l+4OdAcn+UyS5/fLP19VN0vyqCT3SxcqHZTki0k+muTk\nJP9+APsOAOww1ZpzAQAAAAA2Zk4kAAAAAAYJkQAAAAAYJEQCAAAAYJAQCQAAAIBBQiQAAAAABgmR\nAAAAABgkRAIAAABgkBAJAAAAgEFCJAAAAAAGCZEAAAAAGPT/AZ4Ymg/2dW9RAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7f1d66148d90>"
]
}
],
"prompt_number": 16
}
],
"metadata": {}
}
]
} | gpl-2.0 |
ethen8181/machine-learning | networkx/max_influence/max_influence.ipynb | 1 | 162670 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"toc": true
},
"source": [
"<h1>Table of Contents<span class=\"tocSkip\"></span></h1>\n",
"<div class=\"toc\"><ul class=\"toc-item\"><li><span><a href=\"#Submodular-Optimization-&-Influence-Maximization\" data-toc-modified-id=\"Submodular-Optimization-&-Influence-Maximization-1\"><span class=\"toc-item-num\">1 </span>Submodular Optimization & Influence Maximization</a></span><ul class=\"toc-item\"><li><span><a href=\"#Influence-Maximization-(IM)\" data-toc-modified-id=\"Influence-Maximization-(IM)-1.1\"><span class=\"toc-item-num\">1.1 </span>Influence Maximization (IM)</a></span></li><li><span><a href=\"#Getting-Started\" data-toc-modified-id=\"Getting-Started-1.2\"><span class=\"toc-item-num\">1.2 </span>Getting Started</a></span></li><li><span><a href=\"#Spread-Process---Independent-Cascade-(IC)\" data-toc-modified-id=\"Spread-Process---Independent-Cascade-(IC)-1.3\"><span class=\"toc-item-num\">1.3 </span>Spread Process - Independent Cascade (IC)</a></span></li><li><span><a href=\"#Greedy-Algorithm\" data-toc-modified-id=\"Greedy-Algorithm-1.4\"><span class=\"toc-item-num\">1.4 </span>Greedy Algorithm</a></span></li><li><span><a href=\"#Submodular-Optimization\" data-toc-modified-id=\"Submodular-Optimization-1.5\"><span class=\"toc-item-num\">1.5 </span>Submodular Optimization</a></span></li><li><span><a href=\"#Cost-Effective-Lazy-Forward-(CELF)-Algorithm\" data-toc-modified-id=\"Cost-Effective-Lazy-Forward-(CELF)-Algorithm-1.6\"><span class=\"toc-item-num\">1.6 </span>Cost Effective Lazy Forward (CELF) Algorithm</a></span></li><li><span><a href=\"#Larger-Network\" data-toc-modified-id=\"Larger-Network-1.7\"><span class=\"toc-item-num\">1.7 </span>Larger Network</a></span></li><li><span><a href=\"#Conclusion\" data-toc-modified-id=\"Conclusion-1.8\"><span class=\"toc-item-num\">1.8 </span>Conclusion</a></span></li></ul></li><li><span><a href=\"#Reference\" data-toc-modified-id=\"Reference-2\"><span class=\"toc-item-num\">2 </span>Reference</a></span></li></ul></div>"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<style>\n",
"@import url('http://fonts.googleapis.com/css?family=Source+Code+Pro');\n",
"@import url('http://fonts.googleapis.com/css?family=Vollkorn');\n",
"@import url('http://fonts.googleapis.com/css?family=Arimo');\n",
"@import url('http://fonts.googleapis.com/css?family=Fira_sans');\n",
" \n",
" div.cell {\n",
" width: 1000px;\n",
" margin-left: 0% !important;\n",
" margin-right: auto;\n",
" }\n",
" div.text_cell code {\n",
" background: transparent;\n",
" color: #000000;\n",
" font-weight: 600;\n",
" font-size: 12pt;\n",
" font-style: bold;\n",
" font-family: 'Source Code Pro', Consolas, monocco, monospace;\n",
" }\n",
" h1 {\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
"\t}\n",
"\t\n",
" div.input_area {\n",
" background: #F6F6F9;\n",
" border: 1px solid #586e75;\n",
" }\n",
"\n",
" .text_cell_render h1 {\n",
" font-weight: 200;\n",
" font-size: 30pt;\n",
" line-height: 100%;\n",
" color:#c76c0c;\n",
" margin-bottom: 0.5em;\n",
" margin-top: 1em;\n",
" display: block;\n",
" white-space: wrap;\n",
" text-align: left;\n",
" } \n",
" h2 {\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
" text-align: left;\n",
" }\n",
" .text_cell_render h2 {\n",
" font-weight: 200;\n",
" font-size: 16pt;\n",
" font-style: italic;\n",
" line-height: 100%;\n",
" color:#c76c0c;\n",
" margin-bottom: 0.5em;\n",
" margin-top: 1.5em;\n",
" display: block;\n",
" white-space: wrap;\n",
" text-align: left;\n",
" } \n",
" h3 {\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
" }\n",
" .text_cell_render h3 {\n",
" font-weight: 200;\n",
" font-size: 14pt;\n",
" line-height: 100%;\n",
" color:#d77c0c;\n",
" margin-bottom: 0.5em;\n",
" margin-top: 2em;\n",
" display: block;\n",
" white-space: wrap;\n",
" text-align: left;\n",
" }\n",
" h4 {\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
" }\n",
" .text_cell_render h4 {\n",
" font-weight: 100;\n",
" font-size: 14pt;\n",
" color:#d77c0c;\n",
" margin-bottom: 0.5em;\n",
" margin-top: 0.5em;\n",
" display: block;\n",
" white-space: nowrap;\n",
" }\n",
" h5 {\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
" }\n",
" .text_cell_render h5 {\n",
" font-weight: 200;\n",
" font-style: normal;\n",
" color: #1d3b84;\n",
" font-size: 16pt;\n",
" margin-bottom: 0em;\n",
" margin-top: 0.5em;\n",
" display: block;\n",
" white-space: nowrap;\n",
" }\n",
" div.text_cell_render{\n",
" font-family: 'Fira sans', verdana,arial,sans-serif;\n",
" line-height: 125%;\n",
" font-size: 115%;\n",
" text-align:justify;\n",
" text-justify:inter-word;\n",
" }\n",
" div.output_wrapper{\n",
" margin-top:0.2em;\n",
" margin-bottom:0.2em;\n",
" }\n",
"\n",
" code{\n",
" font-size: 70%;\n",
" }\n",
" .rendered_html code{\n",
" background-color: transparent;\n",
" }\n",
" ul{\n",
" margin: 2em;\n",
" }\n",
" ul li{\n",
" padding-left: 0.5em; \n",
" margin-bottom: 0.5em; \n",
" margin-top: 0.5em; \n",
" }\n",
" ul li li{\n",
" padding-left: 0.2em; \n",
" margin-bottom: 0.2em; \n",
" margin-top: 0.2em; \n",
" }\n",
" ol{\n",
" margin: 2em;\n",
" }\n",
" ol li{\n",
" padding-left: 0.5em; \n",
" margin-bottom: 0.5em; \n",
" margin-top: 0.5em; \n",
" }\n",
" ul li{\n",
" padding-left: 0.5em; \n",
" margin-bottom: 0.5em; \n",
" margin-top: 0.2em; \n",
" }\n",
" a:link{\n",
" font-weight: bold;\n",
" color:#447adb;\n",
" }\n",
" a:visited{\n",
" font-weight: bold;\n",
" color: #1d3b84;\n",
" }\n",
" a:hover{\n",
" font-weight: bold;\n",
" color: #1d3b84;\n",
" }\n",
" a:focus{\n",
" font-weight: bold;\n",
" color:#447adb;\n",
" }\n",
" a:active{\n",
" font-weight: bold;\n",
" color:#447adb;\n",
" }\n",
" .rendered_html :link {\n",
" text-decoration: underline; \n",
" }\n",
" .rendered_html :hover {\n",
" text-decoration: none; \n",
" }\n",
" .rendered_html :visited {\n",
" text-decoration: none;\n",
" }\n",
" .rendered_html :focus {\n",
" text-decoration: none;\n",
" }\n",
" .rendered_html :active {\n",
" text-decoration: none;\n",
" }\n",
" .warning{\n",
" color: rgb( 240, 20, 20 )\n",
" } \n",
" hr {\n",
" color: #f3f3f3;\n",
" background-color: #f3f3f3;\n",
" height: 1px;\n",
" }\n",
" blockquote{\n",
" display:block;\n",
" background: #fcfcfc;\n",
" border-left: 5px solid #c76c0c;\n",
" font-family: 'Open sans',verdana,arial,sans-serif;\n",
" width:680px;\n",
" padding: 10px 10px 10px 10px;\n",
" text-align:justify;\n",
" text-justify:inter-word;\n",
" }\n",
" blockquote p {\n",
" margin-bottom: 0;\n",
" line-height: 125%;\n",
" font-size: 100%;\n",
" }\n",
"</style>\n",
"<script>\n",
" MathJax.Hub.Config({\n",
" TeX: {\n",
" extensions: [\"AMSmath.js\"]\n",
" },\n",
" tex2jax: {\n",
" inlineMath: [ ['$','$'], [\"\\\\(\",\"\\\\)\"] ],\n",
" displayMath: [ ['$$','$$'], [\"\\\\[\",\"\\\\]\"] ]\n",
" },\n",
" displayAlign: 'center', // Change this to 'center' to center equations.\n",
" \"HTML-CSS\": {\n",
" scale:100,\n",
" availableFonts: [],\n",
" preferredFont:null,\n",
" webFont: \"TeX\",\n",
" styles: {'.MathJax_Display': {\"margin\": 4}}\n",
" }\n",
" });\n",
"</script>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# code for loading the format for the notebook\n",
"import os\n",
"\n",
"# path : store the current path to convert back to it later\n",
"path = os.getcwd()\n",
"os.chdir(os.path.join('..', '..', 'notebook_format'))\n",
"\n",
"from formats import load_style\n",
"load_style(plot_style=False)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ethen 2018-10-25 17:38:52 \n",
"\n",
"CPython 3.6.4\n",
"IPython 6.4.0\n",
"\n",
"igraph 0.7.1\n",
"numpy 1.14.1\n",
"matplotlib 2.2.2\n"
]
}
],
"source": [
"os.chdir(path)\n",
"\n",
"# 1. magic for inline plot\n",
"# 2. magic to print version\n",
"# 3. magic so that the notebook will reload external python modules\n",
"# 4. magic to enable retina (high resolution) plots\n",
"# https://gist.github.com/minrk/3301035\n",
"%matplotlib inline\n",
"%load_ext watermark\n",
"%load_ext autoreload\n",
"%autoreload 2\n",
"%config InlineBackend.figure_format='retina'\n",
"\n",
"import time\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from igraph import Graph # pip install python-igraph\n",
"\n",
"%watermark -a 'Ethen' -d -t -v -p igraph,numpy,matplotlib"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Submodular Optimization & Influence Maximization"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The content and example in this documentation is build on top of the wonderful blog post at the following link. [Blog: Influence Maximization in Python - Greedy vs CELF](https://hautahi.com/im_greedycelf). "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Influence Maximization (IM)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Influence Maximization (IM)** is a field of network analysis with a lot of applications - from viral marketing to disease modeling and public health interventions. IM is the task of finding a small subset of nodes in a network such that the resulting \"influence\" propagating from that subset reaches the largest number of nodes in the network. \"Influence\" represents anything that can be passed across connected peers within a network, such as information, behavior, disease or product adoption. To make it even more concrete, IM can be used to answer the question:\n",
"\n",
"> If we can try to convince a subset of individuals to adopt a new product or innovation, and the goal is to trigger a large cascade of further adoptions, which set of individuals should we target?\n",
"\n",
"[Kempe et al. (2003)](https://www.cs.cornell.edu/home/kleinber/kdd03-inf.pdf) were the first to formalize IM as the following combinatorial optimization problem: Given a network with $n$ nodes and given a \"spreading\" or propagation process on that network, choose a \"seed set\" $S$ of size $k<n$ to maximize the number of nodes in the network that are ultimately influenced.\n",
"\n",
"Solving this problem turns out to be extremely computationally burdensome. For example, in a relatively small network of 1,000 nodes, there are ${n\\choose k} \\approx 8$ trillion different possible candidates of size $k=5$ seed sets, which is impossible to solve directly even on state-of-the-art high performance computing resources. Consequently, over the last 15 years, researchers has been actively trying to find approximate solutions to the problem that can be solved quickly. This notebook walks through:\n",
"\n",
"- How to implement two of the earliest and most fundamental approximation algorithms in Python - the Greedy and the CELF algorithms - and compares their performance.\n",
"- We will also spend some time discussing the field of submodular optimization, as it turns out, the combinatorial optimization problem we described above is submodular."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Getting Started"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We begin by loading a few modules. There are many popular network modeling packages, but we'll use the [`igraph`](http://igraph.org/python/) package. Don't worry if you're not acquainted with the library, we will explain the syntax, and if you like, you can even swap it out with a different graph library that you prefer.\n",
"\n",
"We'll first test these algorithms to see if they can produce the correct solution for a simple example for which we know the two nodes which are the most influential. Below we create a 10-node/20-edge directed `igraph` network object. This artificially created network is designed to ensure that nodes `0` and `1` are the most influential. We do this by creating 8 links outgoing from each of these nodes compared to only 1 outgoing links for the other 8 nodes. We also ensure nodes `0` and `1` are not neighbors so that having one in the seed set does not make the other redundant."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"vertices count: 10\n",
"edges count: 20\n",
"neighbors: [6]\n"
]
},
{
"data": {
"text/plain": [
"[[2, 3, 4, 5, 6, 7, 8, 9],\n",
" [2, 3, 4, 5, 6, 7, 8, 9],\n",
" [6],\n",
" [7],\n",
" [8],\n",
" [9],\n",
" [],\n",
" [],\n",
" [],\n",
" []]"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"source = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 3, 4, 5]\n",
"target = [2, 3, 4, 5, 6, 7, 8, 9, 2, 3, 4, 5, 6, 7, 8, 9, 6, 7, 8, 9]\n",
"\n",
"# create a directed graph\n",
"graph = Graph(directed=True)\n",
"\n",
"# add the nodes/vertices (the two are used interchangeably) and edges\n",
"# 1. the .add_vertices method adds the number of vertices\n",
"# to the graph and igraph uses integer vertex id starting from zero\n",
"# 2. to add edges, we call the .add_edges method, where edges\n",
"# are specified by a tuple of integers. \n",
"graph.add_vertices(10)\n",
"graph.add_edges(zip(source, target))\n",
"print('vertices count:', graph.vcount())\n",
"print('edges count:', graph.ecount())\n",
"\n",
"# a graph api should allow us to retrieve the neighbors of a node\n",
"print('neighbors: ', graph.neighbors(2, mode='out'))\n",
"\n",
"# or create an adjacency list of the graph,\n",
"# as we can see node 0 and 1 are the most influential\n",
"# as the two nodes are connected to a lot of other nodes\n",
"graph.get_adjlist()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Spread Process - Independent Cascade (IC)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"IM algorithms solve the optimization problem for a given spread or propagation process. We therefore first need to specify a function that simulates the spread from a given seed set across the network. We'll simulate the influence spread using the popular **Independent Cascade (IC)** model, although there are many others we could have chosen.\n",
"\n",
"Independent Cascade starts by having an initial set of seed nodes, $A_0$, that start the diffusion process, and the process unfolds in discrete steps according to the following randomized rule: \n",
"\n",
"When node $v$ first becomes active in step $t$, it is given a single chance to activate each currently inactive\n",
"neighbor $w$; this process succeeds with a probability $p_{v,w}$, a parameter of the system — independently of the history thus far. If $v$ succeeds, then $w$ will become active in step $t + 1$; but whether or not $v$ succeeds in this current step $t$, it cannot make any further attempts to activate $w$ in subsequent rounds. This process runs until no more activations are possible. Here, we assume that the nodes are progressive, meaning the node will only go from inactive to active, but not the other way around."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2.74"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def compute_independent_cascade(graph, seed_nodes, prob, n_iters=1000):\n",
" total_spead = 0\n",
"\n",
" # simulate the spread process over multiple runs\n",
" for i in range(n_iters):\n",
" np.random.seed(i)\n",
" active = seed_nodes[:]\n",
" new_active = seed_nodes[:]\n",
" \n",
" # for each newly activated nodes, find its neighbors that becomes activated\n",
" while new_active:\n",
" activated_nodes = []\n",
" for node in new_active:\n",
" neighbors = graph.neighbors(node, mode='out')\n",
" success = np.random.uniform(0, 1, len(neighbors)) < prob\n",
" activated_nodes += list(np.extract(success, neighbors))\n",
"\n",
" # ensure the newly activated nodes doesn't already exist\n",
" # in the final list of activated nodes before adding them\n",
" # to the final list\n",
" new_active = list(set(activated_nodes) - set(active))\n",
" active += new_active\n",
"\n",
" total_spead += len(active)\n",
"\n",
" return total_spead / n_iters\n",
"\n",
"\n",
"# assuming we start with 1 seed node\n",
"seed_nodes = [0]\n",
"compute_independent_cascade(graph, seed_nodes, prob=0.2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We calculate the expected spread of a given seed set by taking the average over a large number of Monte Carlo simulations. The outer loop in the function iterates over each of these simulations and calculates the spread for each iteration, at the end, the mean of each iteration will be our unbiased estimation for the expected spread of the seed nodes we've provided. The actual number of simulation required is up to debate, through experiment I found 1,000 to work well enough, whereas 100 was too low. On the other hand, the paper even set the simulation number up to 10,000.\n",
"\n",
"Within each Monte Carlo iteration, we simulate the spread of influence throughout the network over time, where a different \"time period\" occurs within each of the `while` loop iterations, which checks whether any new nodes were activated in the previous time step. If no new nodes were activated (when `new_active` is an empty list and therefore evaluates to `False`) then the independent cascade process terminates, and the function moves onto the next simulation after recording the total spread for this simulation. The term total spread here refers to the number of nodes ultimately activated (some algorithms are framed in terms of the \"additional spread\" in which case we would subtract the size of the seed set so the code would be amended to `len(active) - len(seed_nodes)`. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Greedy Algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With our spread function in hand, we can now turn to the IM algorithms themselves. We begin with the **Greedy algorithm**. The method is referred to as greedy as it adds the node that currently provides the best spread to our solution set without considering if it is actually the optimal solution in the long run, to elaborate the process is:\n",
"\n",
"- We start with an empty seed set/nodes.\n",
"- For all the nodes that are not in the seed set/nodes, we find the node with the largest spread and adds it to the seed\n",
"- We repeat step 2 until $k$ seed nodes are found.\n",
"\n",
"This algorithm only needs to calculate the spread of $\\sum_{i=0}^k (n-i)\\approx kn$ nodes, which is just 5,000 in the case of our 1,000 node and $k=5$ network (a lot less that 8 trillion!). Of course, this computational improvement comes at the cost of the resulting seed set only being an approximate solution to the IM problem because it only considers the incremental spread of the $k$ nodes individually rather than combined. Fortunately, this seemingly naive greedy algorithm is theoretically guaranteed to choose a seed set whose spread will be at least 63% of the spread of the optimal seed set. The proof of the guarantee relies heavily on the \"submodular\" property of spread functions, which will be explained in more detail in later section.\n",
"\n",
"The following `greedy()` function implements the algorithm. It produces the optimal set of `k` seed nodes for the graph `graph`. Apart from returning the optimal seed set, it also records average spread of that seed set along with a list showing the cumulative time taken to complete each iteration, we will use these information to compare with a different algorithm, CELF, in later section."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def greedy(graph, k, prob=0.2, n_iters=1000):\n",
" \"\"\"\n",
" Find k nodes with the largest spread (determined by IC) from a igraph graph\n",
" using the Greedy Algorithm.\n",
" \"\"\"\n",
"\n",
" # we will be storing elapsed time and spreads along the way, in a setting where\n",
" # we only care about the final solution, we don't need to record these\n",
" # additional information\n",
" elapsed = []\n",
" spreads = []\n",
" solution = []\n",
" start_time = time.time()\n",
"\n",
" for _ in range(k):\n",
" best_node = -1\n",
" best_spread = -np.inf\n",
"\n",
" # loop over nodes that are not yet in our final solution\n",
" # to find biggest marginal gain\n",
" nodes = set(range(graph.vcount())) - set(solution)\n",
" for node in nodes:\n",
" spread = compute_independent_cascade(graph, solution + [node], prob, n_iters)\n",
" if spread > best_spread:\n",
" best_spread = spread\n",
" best_node = node\n",
"\n",
" solution.append(best_node)\n",
" spreads.append(best_spread)\n",
"\n",
" elapse = round(time.time() - start_time, 3)\n",
" elapsed.append(elapse)\n",
"\n",
" return solution, spreads, elapsed"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"solution: [0, 1]\n",
"spreads: [2.74, 5.098]\n",
"elapsed: [0.263, 0.755]\n"
]
}
],
"source": [
"# the result tells us greedy algorithm was able to find the two most influential\n",
"# node, node 0 and node 1\n",
"k = 2\n",
"prob = 0.2\n",
"n_iters = 1000\n",
"greedy_solution, greedy_spreads, greedy_elapsed = greedy(graph, k, prob, n_iters)\n",
"print('solution: ', greedy_solution)\n",
"print('spreads: ', greedy_spreads)\n",
"print('elapsed: ', greedy_elapsed)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Submodular Optimization"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we have a brief understanding of the IM problem and taken a first stab at solving this problem, let's take a step back and formally discuss submodular optimization. **A function $f$ is said to be submodular if it satisfies the diminishing return property**. More formally, if we were given a ground set $V$, a function $f:2^V \\rightarrow \\mathbb{R}$ (the function's space is 2 power $V$, as the function can either contain or not contain each element in the set $V$). The submodular property is defined as:\n",
"\n",
"\\begin{align}\n",
"f(A \\cup \\{i\\}) - f(A) \\geq f(B \\cup \\{i\\}) - f(B)\n",
"\\end{align}\n",
"\n",
"For any $A \\subseteq B \\subseteq V$ and $i \\in V \\setminus B$. Hence by adding any element $i$ to $A$, which is a subset of $B$ yields as least as much value (or more) if we were to add $i$ to $B$. In other words, the marginal gain of adding $i$ to $A$ should be greater or equal to the marginal gain of adding $i$ to $B$ if $A$ is a subset of $B$.\n",
"\n",
"The next property is known as monotone. We say that a submodular function is monotone if for any $A \\subseteq B\n",
"\\subseteq V$, we have $f(A) \\leq f(B)$. This means that adding more elements to a set cannot decrease its value.\n",
"\n",
"For example: Let $f(X)=max(X)$. We have the set $X= \\{1,2,3,4,5\\}$, and we choose $A=\\{1,2\\}$ and $B=\\{1,2,5\\}$. Given those information, we can see $f(A)=2$ and $f(B)=5$ and the marginal gain of items 3,4 is :\n",
"\n",
"\\begin{align}\n",
"f(3 \\, | \\, A) = 1 \\\\ \\nonumber\n",
"f(4 \\, | \\, B) = 0 \\\\ \\nonumber\n",
"f(3 \\, | \\, A) = 2 \\\\ \\nonumber\n",
"f(4 \\, | \\, B) = 0\n",
"\\end{align}\n",
"\n",
"Here we use the shorthand $f(i \\, | \\, A)$, to denote $f(A \\cup \\{i\\}) - f(A)$.\n",
"\n",
"Note that $f(i \\, | \\, A) \\ge f(i \\, | \\, B)$ for any choice of $i$, $A$ and $B$. This is because $f$ is submodular and monotone. To recap, submodular functions has the diminishing return property saying adding an element to a larger set results in smaller marginal increase in the value of $f$ (compared to adding the element to a smaller set). And monotone ensures that adding additional element to the solution set does not decrease the function's value.\n",
"\n",
"Since the functions we're dealing with functions that are monotone, the set with maximum value is always including everything from the ground set $V$. But what we're actually interested in is when we impose a cardinality constraint - that is, finding the set of size at most k that maximizes the utility. Formally:\n",
"\n",
"\\begin{align}\n",
"A^* = \\underset{A: |A| \\leq k}{\\text{argmax}} \\,\\, f(A)\n",
"\\end{align}\n",
"\n",
"For instance, in our IM problem, we are interested in finding the subset $k$ nodes that generates the largest influence. The greedy algorithm we showed above is one approach of solving this combinatorial problem.\n",
"\n",
"- Given a ground set $V$, if we're interested in populating a solution set of size $k$.\n",
"- The algorithm starts with the empty set $A_0$\n",
"- Then repeats the following step for $i = 0, ... , (k-1)$:\n",
"\n",
"\\begin{align}\n",
"A_{i+1} = A_{i} \\cup \\{ \\underset{v \\in V \\setminus A_i}{\\text{argmax}} \\,\\, f(A_i \\cup \\{v\\}) \\}\n",
"\\end{align}\n",
"\n",
"From a theoretical standpoint, this procedure guarantees a solution that has a score of 0.63 of the optimal set."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([2.74 , 2.358])"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# if we check the solutions from the greedy algorithm we've\n",
"# implemented above, we can see that our solution is in fact\n",
"# submodular, as the spread we get is in diminshing order\n",
"np.diff(np.hstack([np.array([0]), greedy_spreads]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Cost Effective Lazy Forward (CELF) Algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**CELF Algorithm** was developed by [Leskovec et al. (2007)](https://www.cs.cmu.edu/~jure/pubs/detect-kdd07.pdf). In other places, this is referred to as the **Lazy Greedy Algorithm**. Although the Greedy algorithm is much quicker than solving the full problem, it is still very slow when used on realistically sized networks. CELF was one of the first significant subsequent improvements.\n",
"\n",
"CELF exploits the sub-modularity property of the spread function, which implies that the marginal spread of a given node in one iteration of the Greedy algorithm cannot be any larger than its marginal spread in the previous iteration. This helps us to choose the nodes for which we evaluate the spread function in a more sophisticated manner, rather than simply evaluating the spread for all nodes. More specifically, in the first round, we calculate the spread for all nodes (like Greedy) and store them in a list/heap, which is then sorted. Naturally, the top node is added to the seed set in the first iteration, and then removed from the list/heap. In the next iteration, only the spread for the top node is calculated. If, after resorting, that node remains at the top of the list/heap, then it must have the highest marginal gain of all nodes. Why? Because we know that if we calculated the marginal gain for all other nodes, they'd be lower than the value currently in the list (due to submodularity) and therefore the \"top node\" would remain on top. This process continues, finding the node that remains on top after calculating its marginal spread, and then adding it to the seed set. By avoiding calculating the spread for many nodes, CELF turns out to be much faster than Greedy, which we'll show below.\n",
"\n",
"The `celf()` function below that implements the algorithm, is split into two components. The first component, like the Greedy algorithm, iterates over each node in the graph and selects the node with the highest spread into the seed set. However, it also stores the spreads of each node for use in the second component.\n",
"\n",
"The second component iterates to find the remaining $k-1$ seed nodes. Within each iteration, the algorithm evaluates the marginal spread of the top node. If, after resorting, the top node stays in place then that node is selected as the next seed node. If not, then the marginal spread of the new top node is evaluated and so on.\n",
"\n",
"Like `greedy()`, the function returns the optimal seed set, the resulting spread and the time taken to compute each iteration. In addition, it also returns the list `lookups`, which keeps track of how many spread calculations were performed at each iteration. We didn't bother doing this for `greedy()` because we know the number of spread calculations in iteration $i$ is $N-i-1$."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"import heapq\n",
"\n",
"\n",
"def celf(graph, k, prob, n_iters=1000):\n",
" \"\"\"\n",
" Find k nodes with the largest spread (determined by IC) from a igraph graph\n",
" using the Cost Effective Lazy Forward Algorithm, a.k.a Lazy Greedy Algorithm.\n",
" \"\"\"\n",
" start_time = time.time()\n",
"\n",
" # find the first node with greedy algorithm:\n",
" # python's heap is a min-heap, thus\n",
" # we negate the spread to get the node\n",
" # with the maximum spread when popping from the heap\n",
" gains = []\n",
" for node in range(graph.vcount()):\n",
" spread = compute_independent_cascade(graph, [node], prob, n_iters)\n",
" heapq.heappush(gains, (-spread, node))\n",
"\n",
" # we pop the heap to get the node with the best spread,\n",
" # when storing the spread to negate it again to store the actual spread\n",
" spread, node = heapq.heappop(gains)\n",
" solution = [node]\n",
" spread = -spread\n",
" spreads = [spread]\n",
"\n",
" # record the number of times the spread is computed\n",
" lookups = [graph.vcount()]\n",
" elapsed = [round(time.time() - start_time, 3)]\n",
"\n",
" for _ in range(k - 1):\n",
" node_lookup = 0\n",
" matched = False\n",
"\n",
" while not matched:\n",
" node_lookup += 1\n",
"\n",
" # here we need to compute the marginal gain of adding the current node\n",
" # to the solution, instead of just the gain, i.e. we need to subtract\n",
" # the spread without adding the current node\n",
" _, current_node = heapq.heappop(gains)\n",
" spread_gain = compute_independent_cascade(\n",
" graph, solution + [current_node], prob, n_iters) - spread\n",
"\n",
" # check if the previous top node stayed on the top after pushing\n",
" # the marginal gain to the heap\n",
" heapq.heappush(gains, (-spread_gain, current_node))\n",
" matched = gains[0][1] == current_node\n",
"\n",
" # spread stores the cumulative spread\n",
" spread_gain, node = heapq.heappop(gains)\n",
" spread -= spread_gain\n",
" solution.append(node)\n",
" spreads.append(spread)\n",
" lookups.append(node_lookup)\n",
"\n",
" elapse = round(time.time() - start_time, 3)\n",
" elapsed.append(elapse)\n",
"\n",
" return solution, spreads, elapsed, lookups"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"solution: [0, 1]\n",
"spreads: [2.74, 5.098]\n",
"elapsed: [0.257, 0.327]\n",
"lookups: [10, 1]\n"
]
}
],
"source": [
"k = 2\n",
"prob = 0.2\n",
"n_iters = 1000\n",
"\n",
"celf_solution, celf_spreads, celf_elapsed, celf_lookups = celf(graph, k, prob, n_iters)\n",
"print('solution: ', celf_solution)\n",
"print('spreads: ', celf_spreads)\n",
"print('elapsed: ', celf_elapsed)\n",
"print('lookups: ', celf_lookups)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Larger Network"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we know both algorithms at least work correctly for a simple network for which we know the answer, we move on to a more generic graph to compare the performance and efficiency of each method. Any `igraph` network object will work, but for the purposes of this post we will use a random Erdos-Renyi graph with 100 nodes and 300 edges. The exact type of graph doesn't matter as the main points hold for any graph. Rather than explicitly defining the nodes and edges like we did above, here we make use of the `.Erdos_Renyi()` method to automatically create the graph."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"np.random.seed(1234)\n",
"graph = Graph.Erdos_Renyi(n=100, m=300, directed=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Given the graph, we again compare both optimizers with the same parameter. Again for the `n_iters` parameter, it is not uncommon to see it set to a much higher number in literatures, such as 10,000 to get a more accurate estimate of spread, we chose a lower number here so we don't have to wait as long for the results"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"celf output: [95, 6, 61, 42, 29, 97, 52, 12, 98, 58]\n",
"greedy output: [95, 6, 61, 42, 29, 97, 52, 12, 98, 58]\n"
]
}
],
"source": [
"k = 10\n",
"prob = 0.1\n",
"n_iters = 1500\n",
"celf_solution, celf_spreads, celf_elapsed, celf_lookups = celf(graph, k, prob, n_iters)\n",
"greedy_solution, greedy_spreads, greedy_elapsed = greedy(graph, k, prob, n_iters)\n",
"\n",
"# print resulting solution\n",
"print('celf output: ' + str(celf_solution))\n",
"print('greedy output: ' + str(greedy_solution))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Thankfully, both optimization method yields the same solution set.\n",
"\n",
"In the next few code chunk, we will use some of the information we've stored while performing the optimizing to perform a more thorough comparison. First, by plotting the resulting expected spread from both optimization method. We can see both methods yield the same expected spread."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABFkAAAMRCAYAAAA3MWmxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAWJQAAFiUBSVIk8AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzs3XmYpFV99//3qep1umdn9q1n3wEHNI8oIiTiA4isCU+iRAQFg4mY/IgmaqJGTTTuikuMYQmgkscNkYBC4mBifFxmFIbZmZmerWffumem17rP74+qnunp6e7p6uma3t6v6+qruuq+z13fqmrQ+nDO+YYYI5IkSZIkSTo7qb4uQJIkSZIkaTAwZJEkSZIkSeoFhiySJEmSJEm9wJBFkiRJkiSpFxiySJIkSZIk9QJDFkmSJEmSpF5gyCJJkiRJktQLDFkkSZIkSZJ6gSGLJEmSJElSLzBkkSRJkiRJ6gWGLJIkSZIkSb3AkEWSJEmSJKkXGLJIkiRJkiT1AkMWSZKkXhRCeDCEEEMIsa9rUX5CCLe1fnYhhNf2dT2SpIGnqK8LkCRpMAohVAFbejB0ZoyxuleL0YAVQjgPeAvwv4ElwGggALXAdmAN8EvgmRjj2r6qU5IkZRmySJKkASU3w+AnubtvjTE+2HfVFE4I4Q+AfwJGdXD4vNzPy4A35c6fFGPcfe4qlCRJ7RmySJJUeL8G3trNc3cWshANDCGE64Bvkl3aHYFvA48DLwFNwBiyM1teC1wJDOuTQiVJ0ikMWSRJKrxjMcYX+7oIDQwhhBRwH9mAJQHeGGN8soNT/wP4fAihErgVqD93VUqSpI4YskiSJPUvrwCm5n7/ficBywkxxqPAVwpelSRJOiO7C0mS1E+FEKaFEA7kOp3sCSFM7OLc29t0RXms3bGqNsc+lHvs8hDCd0IIO0IIDSGEnSGEb4YQfqebtaVCCLeEEL4dQtgaQqgPIdSGEF4MIXwhhDCnm9epDCHcE0L4UQihJoTQGEI4HkJYH0J4NITwf0IIpW1fByf3YwF4oM1ra/1ZXuCarw4hPJH7TBpCCNW5jkIv6874bqhq8/vGs7lQ+245Iev2EMJzIYS9ufdgYwjh8yGEKV1cp6O/oVeFEB4OIWzJvQ8xhHDa/jEhhPNCCH8TQvhZ7jmbcrf/GUL4sxBC+Rlew/wQwl+FEP69zefW+jf7gxDCm0II6W6+H4tCCPfnrtMQQtiVu+713RkvSdKZhBjtLihJUm9r113ouRjja3t4neuA7+fuPgO8Prb7H+8QwgJgBdl9OaqBC2OMRzqp5cNAC/B3ZLvUtJcAfx1j/McuapoBfBdY1kXpLcCfxxjv6+I6VwH/SnYD167cEGP8fuh+x6bT3u/eqDmEEMjOGLmrk/HNwJ1k90l5C0CMsaP3uEshhBtytQI8EWN8Y77XaHOt24AHcnevBN4NXN3J6bVk3+v/7OA6VZz6N5TJ3bZ/faNjjIfbjPsj4KvA8C7K3ARcF2Nc3cHzXgj8pouxrX4GXB9j3N/ZCbn34mtAcSenfA34OSffr8tjjMu78dySJJ3gciFJkvqxGOPjIYT7gD8FXge8B/hE6/HcLI9vkQ1YWoA/bBuwdOBq4OVkvzD/I7ASKAV+D/j/gArgEyGEmhjjI+0HhxAmk/0iOolsqPAw2fCnmuwX7ouBe4DZwBdDCHUxxoc6uM4bge9xct+RfyMbLGzJPTaLbFhxU5thO4Glufrvzz32AbIbwrZ1rBA1Ax/hZMCyl+zn8D+5a7waeC/ZbkBrOhibj5Vtfr82hHB7jPH+Ts/uvo+Rfe+eA75MNtw4D/hD4I+BEcATIYSXxRg3dHGd64ELgHXA54DfAmnglWQ35QUghPBWTn5OO4EvAauAmtzzXg38Cdn3/ZkQwrIOuiMVAY3A02T3oFkDHCTbcWkW2VDrFcCrgEeB13dUcAjhylwtIVfjfcAPgTpgMdm//TuBC7t43ZIknZEzWSRJKoB2/+W/u92FamOM2zq4Vinw/8h+AWwBXh1j/EXu2H3AO3On/nWM8eNnqAXgBeA17cOY3KyB/wIqyX6RrYox1rU750dkZ0RsB14XY1zfwfNVAD8i+8X3EDCj7XVCCOeR/YI/guxmrdfHGH/c0RuSW0pS0XaGQsizhXMv1bwAeJFsmLANuCTGuLPdNWaQDV0mtz7Wk5ksuWt9j2yY0eolsqHAL8iGMBvbz2jq5Dq3cXJmBsCDwO0dzIZ6G/DPubvPxhhf1+54Faf+DT0HXBVj7HCz3RDCLGA1UEY21Hp7jLGxg/NeSTY8KQf+Jcb4tnbHRwHFMcZ9XbzGvwP+Jnf3tTHG59odLyL7/s0gG7K9Psb4k3bnlAL/DlzR5mFnskiS8uaeLJIkFd7FZP8L/pl+vtDR4NyX01vIztAoAr4VQhiZW0rUGrA8S5sZLmfwto5mu8QYfwv8fe7uGOBNbY+HEF5BNqwA+JOOworcdY4B78jdHQ3c3O6UPyMbsAC8r7OAJXet+q6WgJxJL9b8DrIBC8A97QOW3DW2Avf2tNZ2bie7BKbVHLJLfb4JrAcO5vYjeXMuIOiOvcCfdhTOxBi/DrR+Dr+XC5U6k5ANarrqZnQv2YBlO3BnRwFL7nl/TnZWDcCb2+/PEmM83FXAkvNhoPWcGzs4/gayAQvAl9sHLLnnaSQbhDaf4bkkSeqSIYskSQNAbvlGa6BSBXyDk0sx9gK3dmdmA/BijPFXXRz/F6D1Ole2O9b6BfYI2f/q31W9LwIHcndf1e5w6x4jtWSX1xRSb9XcugxlL/CDLi7zbeBwF8e7JcZ4CLiM7N4u/6+DU0YB15KdJbI+N7vnTP4tFyZ15uttfm//2bf1PzHGzWd4rhtyt9+LMTac4dzludtS4KKuTgwhFIcQpoYQFoYQloQQlgALyS5HAuho8+G2S4i+3sFxAHKzyJ45Q62SJHXJPVkkSSq8Hm9821aM8aEQwuvIzjBp3bw0Am/pYC+LzvzyDM+xN4RQDcwEzm93+BW525FAkt0Htlsmtf6SW7rRet1fnGE2RG/ojZpLgfm5u7+OMSadDYoxNocQfgNc3oNa218rQ3Zj4H8NIYwHLiE7K+qi3O+ts4FmAD8OIbyu/VKZdrr87MkuRWrV/rNv6/muLhJCmA60dsJ6VwjhXWd43rYmtX8ghFBGdu+WPyK7F0xnG9dCx5sot76Wo2SXMHXlF3S+MbAkSWfkTBZJkgaWu8l+WWz1lRjj03mM35PHOWPbPT4+j+dpa1ib38dy8v9/1PTwevnojZpHc7KLTj7vX6+JMe6NMX4/xviBGONVwDjgzW2eqxj4aug6RTpTXW2Pt//s2zp0huv09D2HU993QgjTyG6s+xmyAVNXAQtk93Zpr/W17OvGbK9e/+wkSUOLM1kkSRpY7iS7MW2ry0II5edgRgic/P8NO4H/nce4rpaoFNpArPmMYoxNwKMhhHVkOycVAwvIztrocqZJL8ic4Xjb/3/5ZbJtr7trR7v7/8rJWUQ/ILtE7gWyYUhD66yiEMJPgUvpuC25JEnnjCGLJEkDRAjhYk5uTFtLdrnIYuCznNy09Uwm5HHOgXaP7yP7hXcksLqbe8C0d4Dsxqkp2nThKaDeqPkQ2WVZgfzev4KLMa4IIfySk3vIzKPzkOVMdbU93v6zz8cpG9Xm9rrJWwhhHtk23gDfjDH+URenj+7iWOtrGRdCCGf4Gzhnn50kaXByuZAkSQNACGE42c4yxWTbHr+Kk91g7gohdNRVpSOv6Opgbu+PqtzdF9odXpG7rQSWdfP5ThFjbOFkCPA77bvJdPcyeZzbGzU3ku3oA3BxCKHT//8UQiim481XC6nt7I+u3psuP3vgd9r83v6zz8cWsi3AITu7pKeWtvn9W52dFEKoJDuLpzOtr6WSbCjZld85w3FJkrpkyCJJ0sDwFbJtfAH+PDc74I85uYfE13Mbjp7JkhDCy7s4fgcnl1y0b6383Ta//2U3nqszj+duR5Bd/pSvtkujztS+uLdq/lHudjwnuyN15GaynX967Az7qnR0btvwaFMXp/9BCKGii+Nva/N7j7vs5JbwtH7GS0MI+SzTaqvtjOthnZ4Fb6fr2dk/avP72zo7KffPz+u6V5okSR0zZJEkqZ8LIbyFbEchgO/EGP8JIMa4h2yL30h2ucSjIYR0Ny75zyGEkR08z4XA+3J3DwGPtj0eY/wp8J+5u7eEED5whrpLQgh3hBDaL8G4j5Ntjv8h1zGps2uUhxDad4xpu2HuvK5q6MWav8rJvUg+H0I4balT7kv6p7q6fjddFUL49hnCsFZ/B8zN/b6Z7CaxnRkPfLGjECeE8DZOtm1+Nsa4Np+CO/D3QGPu94dCCGdqzTwthHBHu4c3tPn9LZ3U/Urgo2eo5YfA1tzvd4cQTuv8FEIoAR7gzBvrSpLUpdCzpcmSJKkrIYQqsssmAH4NvLWbQ3fEGFsDCEIIc4GVZJc6bAMuaHs8d84ngXtzd/8uxvjBLmr5FfBysl/I/zF37VLg93LXaJ3pcGuM8ZEOXtcksm1up+UeWgE8SPbL/VFgONng4xLgemAMMDfG+FK767wR+B7Z/+CTAI+RnXVSTXYmTRXZ/Tj+AHh7jPH77cZvyZ1zBPiLXB2tX+qPxxi3FaDmjwLvz93dA3yC7KazAK8G3kt2ds4a4EKAGGPeG7GGEN4APJG7u55sSPArssuCjpLdX+YCst2FWpcAZYBrY4xPtbvWbWTDA8i2cH4F8BzwJbKzXs4D/pBsWBeA48DLYowb2l2nipN/Qx+OMX6oG6/jzWQ3rg1AM9nlbj8k+xknuec+H3g92c/6/8UYX91mfAB+k3utAM+SDbuqyX5G1wJ3kf0bOET2M9waY6zqoJYrgadztTQBX8zVUkd2CdH/l6ul9T0CuDzGuPxMr1OSpLYMWSRJKoB2X0rz8dYY44O5a5SQ/RK/jOyX6MtijD/r4LmKgZ+RDU8Ssl8Of9pJLR8m+4X3I3TciSUB/jrG+I+dFZibxfEoJzcl7Uoj2cBiewfXuYbsl/AxZ7jGDR2ELLdxMjxo77kY4ym19UbNub1YvkLnS5yayC5duYJsaNHTkOVVZAOByjOdm7MXuKv9e5S71m2cfJ+uBO4BrunkOrVk3+v/bH+gJyFLbtwbgX8hG6icyb/HGE+pLYSwBPhJF+P3ATcAHwMuo5OQJXettwL/ROezVb5KNoxrfb8MWSRJeXO5kCRJ/dcnOLnfxoc7ClgAYozNZGcj1JH93/ZHQwidBhcxxo8Bv0t25kgN2XBgF/BvwCVdBSy58TUxxsvJ7l9xP7CO7Bf0DNlZBavIBhpvBSZ2FLDkrvMkMAt4D9nZFfuAFrKzKdYDDwM3AU92MPZBsi2ZHyfbnrmp0DXHGJMY411kQ4ongf1kA5ltZMOi34kx/mtXdXRH7nMeB1xN9m/gWbLLXY7n6q0lu5TmO2T3GJnTUcDSgWaysz/uAH7apv7NZGd2LOooYDnL1/IDsjOO/gz4d7KfVSPZz2sP8N/Ap8n+PV7bwfgXyc5k+QLwUm5c6+f1D8D5nf1z0cG1HiC7KfFDZGcFtdbwFNlw6U96+DIlSTrBmSySJA1yPZ2FoIGv3UwWZ2ZIklRgzmSRJEmSJEnqBYYskiRJkiRJvcCQRZIkSZIkqRcYskiSJEmSJPUCQxZJkiRJkqReMCi6C4UQhgOXAy8HLs7djs0dXhhjXHeG8cuAdwGvASYDkWyLwZ8CX4gx/rZApUuSJEmSpEFisIQs1wPf6+RwlyFLCOFu4AtAOvdQQ+62LHebAe6OMX6tN2qVJEmSJEmD02BaLrQX+Hfgw8Cd3RkQQljEyYDlGWAxMCz3cz6wPHfsvhDC7N4vWZIkSZIkDRZFfV1AL3kixvj91jshhKpujruFbIhSC9wYYzza5tiqEMJ1wA5gOHAt8LleqVaSJEmSJA06g2ImS4wx08OhE3K3G9sFLK3XrQU25u5W9PA5JEmSJEnSEDBYZrL0VHXudm4IobJ90BJCGAHMzd1deTZPFELYAoxo85ySJEmSJKl/qAJqY4wzz+YiQz1keQT4W7Lhx3dDCO8G1uaOLSa7X8tw4McxxqfO8rlGlJeXj1m4cOGYs7yOJEmSJEnqRWvXrqW+vv6srzOkQ5YY444Qwo3AN4HXAas5tbvQHuBjwN/1wtNVL1y4cMyKFSt64VKSJEmSJKm3XHTRRaxcubL6bK8zKPZkORsxxqfJBiybcg+VcbJ9cxkwimy3IUmSJEmSpE4N+ZAlhPBh4FdAI/AGYFzu5w3ATuCdwM9CCKP7rEhJkiRJktTvDemQJYTwJrJ7suwFXhNjfDLGuD/38yTwmtyxRcBf9WGpkiRJkiSpnxvSIQtwT+72X2OMB9ofzD32cO7udeesKkmSJEmSNOAM9ZBlYe52SxfnbM7dVhW2FEmSJEmSNJAN9ZAlyd1O7+KcGbnbugLXIkmSJEmSBrChHrI8n7v9wxBCZfuDucf+T+7uL85ZVZIkSZIkacAZNCFLCOG81h+gbSegUW2PhRDavuav5G6nA0+HEJaFENK5n2XA05yc5fKFwr8KSZIkSZI0UBX1dQG9aF8nj/+83f2ZQDVAjPGbIYTfIbsB7quAFWRbOQOU5m4j8Dcxxh/3arWSJEmSJGlQGUwhS4/EGN8dQvgBcCfwSmBC7lA18DPgSzHG9kHNOdPQ0EBtbS11dXU0NzcTY+yrUqTThBAoLi5m+PDhjBgxgrKysr4uSZIkSZL6zKAJWWKM4SzG/ifwn71YTq84evQoO3bsMFhRvxVjpKmpiQMHDnDw4EGmTp1KZeVp2xtJkiRJ0pAwaEKWwaahoeFEwDJixAhGjx5NWVkZqdSg2UZHg0CSJDQ0NHDo0CFqa2vZsWMHM2fOpLS09MyDJUmSJGmQMWTpp2pra08ELJMnTyaEHk/UkQomlUoxbNgwysvLgezf7ZEjRxg/fnwfVyZJkiRJ557TIvqpuro6AEaPHm3Aon4vhMDo0dmmXq1/u5IkSZI01Biy9FPNzc0AbiSqAaP1b7X1b1eSJEmShhpDln6qdbNb92DRQNE648qNmiVJkiQNVX6Dl9QrXNYmSZIkaagzZJEkSZIkSeoFhiySJEmSJEm9wJBFkiRJkiSpFxiySINYCIEQAtXV1X1diiRJkiQNekV9XYBUaA0NDTz88MM8/fTTrFy5kn379tHc3Mzo0aNZtGgRr3rVq/j93/99zj///L4uVZIkSZI0gDmTRYPaE088wcyZM7nzzjv57ne/S3V1NZlMhoqKCvbt28dPfvITPvrRj3LBBRfw+te/nv379/d1yZIkSZI0oNXXHeNAzd6+LqNPGLJo0PqXf/kXrr/+enbv3s38+fO5//77qampob6+noMHD9LU1MSKFSv4yEc+wuTJk/nxj3/Mjh07+rpsSZIkSRqQWppb2LB6M8vX72dlzTGaG5v6uqRzzuVCGpRWrlzJ3XffTZIkXHfddXzrW9+irKzslHPS6TTLli1j2bJlvOc97+EjH/kIxcXFfVSxJEmSJA1MSZKwZ+su1uxvpD5dAinIkGbj+m0sOn9OX5d3TjmTRYPSBz7wAZqampgxYwaPPPLIaQFLeyUlJXzkIx9h8eLFJx5bvnw5IQSqqqoAeOqpp7jqqqsYP348qVSKz33uc6dco6mpifvuu49LL72UMWPGUFpayowZM7j99ttZu3Ztl8+/b98+/vqv/5qlS5dSWVlJRUUFS5Ys4f3vfz8HDx7sdFySJHzxi1/kggsuoLy8nHHjxnHttdfy85//vMPzY4zMmTOHEAL33XdflzVddtllhBB43/ve1+V5kiRJkoau2gOH+MXKTaw4FLMBSxtbmks4euhIH1XWN5zJMgC1PPm9vi6hoIquueGsxm/fvp2nnnoKgHvuuYfKysqzrunTn/409957LyEERo4cSSp1aj65a9currrqKp5//nkAUqkUFRUVbNu2jQceeIBvfvObPProo9x4442nXfu///u/ue66606EKSUlJaRSKVavXs3q1at5+OGHeeaZZ5g/f/4p41paWrj55pt5/PHHASgqKqKlpYUf/vCHPP300zz22GOnPVcIgdtvv533v//9PPDAA/zpn/5ph69306ZN/Nd//RcAb33rW/N8tyRJkiQNdk0NDWxYv4OtLSXEVHmH58SQYs3mvbziopHnuLq+40wWDTrPPffcid+vueaas77enj17eO9738vdd9/Nrl27OHToEEePHuXmm28GoLm5meuuu47nn3+e3/3d3+V//ud/aGhooLa2lpqaGt797nfT0NDArbfeyqZNm0659tatW7n22ms5ePAgf/Inf8LGjRupr6/n2LFjrFq1iiuvvJLt27dz4403kslkThn7iU98gscff5xUKsUnP/lJjhw5wqFDh9i8eTO/93u/x+23397h67nttttIp9OsXLmSF154ocNzHnjgAWKMXHrppcydO/es30NJkiRJg0OSJFRvqGb5i7uozpQRQ9exwt5Qzp5tu85RdX3PkEWDTuvSnLKysl4JCBoaGviDP/gDvvSlLzFhwoQT1546dSoADz30EL/61a+49NJLeeqpp3jlK195Ym+XSZMm8dnPfpa77rqL48eP89nPfvaUa7///e/n8OHD/NVf/RVf/vKXmTNnDqlUilQqxZIlS3jiiSc4//zzWbNmDd/73skZTMeOHeMTn/gEAH/zN3/Dvffey7BhwwCYOXMm3//+95kyZUqHr2fy5MknwqcHHnjgtONJkvDQQw8BdBrUSJIkSRp6DtTs5b9XbObFo0U0pbq/n+WaPcdP+4/Gg5Uhiwad1mU3o0aNIoTQ4Tkf+9jHmDhx4mk/99xzT4fn/+Vf/mWnz9caSNxzzz2dbpz7pje9CYBnnnnmxGPHjx/n//7f/0sqleIv/uIvOhxXUlJyYsZM27E//vGPqauro7S0lD//8z8/bVxpaSn33ntvpzW/7W1vA+CRRx6hubn5lGPPPPMMO3bsYPjw4fz+7/9+p9eQJEmSNDQcrz3KipUb+fnuJmrTXe932ZEI1Nce7f3C+iH3ZNGQVFdXx549e057/MiR0zdlKi8v54ILLujwOi0tLfzyl78E4K677uKd73xnh+e1prbbt28/8diKFStoamoihMDSpUs7rbW+vv60sStXrgTgwgsvZOTIjtc3XnbZZZ1e8+qrr2by5MnU1NTwxBNPnLJXzP333w/ALbfcQkVFRafXkCRJkjS4tTS3sHn9NjY1psmEjvdd6Uo6yTB3WIaZ86pIF6ULUGH/40wWDTpjxowB4PDhw8QYOzzn4x//ODHGEz+tM006Mnbs2NM2um118OBBmpqyvd8PHDjAnj17OvzZv38/cDIwgexmuZDt+NPZuD179lBbWwtkZ7602rdvH5Bd+tOZzpYLQbZ99W233QacumTo4MGDJzbSdamQJEmSNDQlSULNlp0899ttbGgqIRPyD0imhHpeO38ccxbNGjIBCxiyaBBauHAhkN1LZePGjWd9vXS6838hJEly4vff/OY3pwQ3nf20Hzty5MhujVu+fPlZv5a27rjjDkIIPP300+zevRuAb3zjGzQ2NrJw4UJe+cpX9urzSZIkSer/avdnWzKv7KAlc3eMTBq4ZFIpL3vZXMqHDytAhf2bIYsGnbbLZJ588smCPtfYsWNPhDDbtm3La2zrJrq1tbUdLlPqyrhx4wCoqanp9JyujgHMmjWLK664gpaWFh5++GHg5FIh2zZLkiRJQ0tTQwOrnn+J/9p6lAOdtGTuSmnSzPnDE161bBZjJo0rQIUDg3uyDEBF19zQ1yX0a9OmTeOqq67iqaee4vOf/zxvf/vbqaysLMhzFRcXc/HFF/OLX/yCp556ije+8Y3dHnvxxRdTVFRES0sLTz/9NLfccku3xy5btgyA3/72t9TW1jJixIjTzmnbyrozb3vb2/iP//gPHnjgAa688kp+85vfUFRUxB//8R93uxZJkiRJA1eSJGx7aRvra6E5VQYd9w7pVIgJVcVNzJ03jZKy0sIUOYA4k0WD0kc/+lFKSkrYunUrb37zm2loaCjYc7XubfLggw/y/PPPd3nuoUOHTvw+fPhwbrrpJgD+9m//lrq6uk7HtbS0cPToyd24r7zySkaMGEFjYyOf//znTzu/qamJT3/602es/YYbbmDs2LGsXbv2xKa911xzzYlZNpIkSZIGr7YtmZtT+c/BGBfrec3MESw+f44BS44hiwalZcuW8eUvf5lUKsXjjz/OhRdeyP33339is1nIbji7adMmPvnJT/KjH/2ox891xx138L/+1/+ioaGBK664gn/+538+sVktwO7du3n00Ue57LLLTgtEPv7xjzNmzBg2bNjAJZdcwtNPP32ipXKMkY0bN/KZz3yGBQsW8Otf//rEuIqKCt7znvcA8OEPf5jPfOYzJzbVra6u5oYbbjilG1FnSktLufXWWwH42c9+BrjhrSRJkjTYnW1L5mGZRi4em+J3LprL8DGjClDhwBU6676i3hVCWLFs2bJlK1as6Nb5a9euBU5u4qqeeeKJJ7jzzjtPbOwKUFZWRmVlJXV1dTQ2Np54/KqrruKzn/0s8+fPB2D58uVcfvnlzJgxg+rq6i6fZ+/evdx4440ngopUKsWoUaNobGzk2LFjJ8770Ic+xAc/+MFTxv7qV7/i+uuvP7GHSnFxMSNGjKCuru5E56LWetruN9PS0sLNN998ohtQUVERlZWVHD58mKKiIh577LETM2W2bNlCVVVVh7WvXr2aJUuWADBx4kS2b99OUVHPVhL6dytJkiT1X9mWzFvZ1FjUo45B2ZbMCTPnTR90HYMuuugiVq5cuTLGeNHZXMc9WTSoXXvttWzevJlHHnmEp556ipUrV7Jv3z5qa2sZM2YM8+fP51WvehVvetObWLRoUY+fZ/z48Tz33HM89thjPProo6xYsYKDBw9SUlLCggULeMUrXsEb3vCGDvdsefnLX866dev4yle+wuOPP87atWs5fPgww4cP5/zzz+eSSy7hpptu4jWvec0p44qKivjOd77Dl7/8Zb7+9a+zYcMG0uk011xzDe973/u45JJLulX74sWLmTdvHhs2bODWW2/tccC+/o11AAAgAElEQVQiSZIkqX9KkoTdW3exdn8j9enSvPddgWxL5gULplBeOfQ6BuXDmSzniDNZ1F9t376dqqoqkiRh7dq1LFiwoMfX8u9WkiRJ6l9q9x9idfX+HnUMgmxL5iVTRzF64nm9XFn/4kwWSb3ia1/7GkmScOmll55VwCJJkiSp/2hqaGD9+u1saykj9rAl8/yRaabOnkUq5Xau3WXIIg1hv/nNb05sxvvud7+7j6uRJEmSdLaSJGHbxu2sr4s0p8p71JJ5ZnETc+dPo7jUjkH5MmSRhqBXv/rVbN68md27dxNj5DWveQ033HBDX5clSZIk6SwcqNnLiztrqUuX9aiX8LhYz+JZ46kcPbL3ixsiDFmkIWjHjh3s2rWLCRMm8IY3vIFPfOIThNCD3a8kSZIk9bnjtXWsfWk3uyiHHrRkrsg0smjCMCZMn1uA6oYWQxZpCDpTS2pJkiRJ/V9Lcwub1m9lU2MxSch/35WiJMOcYQkz51UNupbMfcWQRZIkSZKkASRJEnZV17DuQFPPWjLHyNRUAwsWTqGswpbMvcmQRZIkSZKkAeLIvoOs3nqAg6lySJfkPX5UpoHF00cxesK0AlQnQxZJkiRJkvq5xuMNbNiwna2ZMuhhS+YFI9NMsSVzQRmySJIkSZLUTyVJwtaN29hQhy2ZBwBDFkmSJEmS+qH9O/eyuqbnLZnHx3oW2ZL5nDJkkSRJkiSpHzleW8eal3az25bMA44hiyRJkiRJ/UBvtGSeOyyhan4V6bQtmfuCIYskSZIkSX2otSXz2oNNNKTOpiXzVMoq8g9n1HsMWSRJkiRJ6iOntGRO9aAlc1LPkumjGTXelsz9gSGLJEmSJEnnWOPxBtZv2MG2TGnPWzKPKmLKrNm2ZO5HDFkkSZIkSTpHMpkM2zZuZ8NRaE6V9agl86ziJubMn05xaf4zX1RYhiySJEmSJJ0D+3buYU1NnS2ZBzHnFGnQO378OF/5yle49tprmT59OsOGDaOiooKZM2dy880388gjj1BfX3/KmKqqKkII3fr57W9/e8rY1772tYQQuO2227pd44MPPtit57r++ut74y2RJEmSdA4dO1LHr1ds5Bd7mrMBS54qMo28fFyaV1w014Cln3Mmiwa1J554gjvvvJPdu3efeKyiooJUKkV1dTXV1dV85zvf4b3vfS8PP/wwV1xxxSnjKyoqqKys7PI5iouLe7XmCRMmdHps9OjRvfpckiRJkgqnpbmZl9ZtY3PTWbRkrkiommdL5oHCkEWD1oMPPsgdd9xBkiTMnz+fD3zgA1x11VWMHTsWgCNHjvDss89y3333sXz5cn7605+eFrLce++9fOhDHzqndbcNhCRJkiQNPL3RknlaqoH5tmQecAxZNCg9//zzvOMd7yBJEq6++mq+/e1vU15+6r+cRo4cyU033cRNN93EY489xo4dO/qoWkmSJEmDxZF9B3lx6wEOnVVL5jG2ZB6gDFk0KH3gAx+gsbGRKVOm8I1vfOO0gKW9W265hRjjOapOkiRJ0mDTeLw+15K5zJbMQ5ghywD0w5WDe8bFG5ZNPavxO3fu5MknnwTgXe96FyNHdm9jqBDyncMnSZIkaajLZDJs3biNjUcDzanyvJcGpWLCzJJm5sybZkvmQcCQRYPO8uXLT8xKeeMb39jH1UiSJEkarPbt2MPqXUc5mi7tUe/eCbGeRbMnUDFqRO8Xpz5hyKJBZ+3atQCUlpYyf/78s7rWpz71Kb761a92enzJkiU8++yzZ/Uc7U2cOLHDx0eOHMn69et79bkkSZIk5e/Y4VrWbNrDnlAO6dK8x1dmGlk0qYLxU+cWoDr1JUMWDToHDhwAsu2Oz3YJ0LFjxzh27FinxzsLRM7Gnj17Ony8oaGh159LkiRJUvedfUvmFuZVwAxbMg9ahixSFz74wQ+e8xbObsArSZIk9S9JklCzpYZ1h86iJXO6gfnzbck82BmyaNAZO3YsAIcOHSLG6Ia2kiRJknrs8N4DrN52sMctmUcn9Sy2JfOQYciiQWfhwoUANDY2sn79ehYsWNDHFUmSJEkaaBqP17Nuww6297Alc1nSzILRxUyeaUvmoWRQhCwhhOHA5cDLgYtzt2NzhxfGGNd14xrlwF3AzcB8YDiwB1gDPBtj/HQBSlcBXHbZZYQQiDHygx/8wJBFkiRJUrdlMhm2btjGhmOBlrNpyTx/GsUltmQeagZFyAL8LvC9ng4OISwCngBm5R5qBo4D03M/rwP6TcjyhmVT+7qEfm3q1KlcffXVPPnkk3zxi1/kHe94ByNGnLklmkuLJEmSpKFt7449rLEls87CYJqztBf4d+DDwJ3dHRRCmAb8hGzA8jPgNUBZjHEUUJm7/8Ver1YF9dGPfpTS0lJ27NjBH/3RH52xM8+//du/8ZnPfOYcVSdJkiSpPzl2uJZfrdjIL/c2ZwOWPFVmGnnF+CJeftFcA5YhbrCELE/EGCfEGK+JMX4IeCaPsV8FxgPLgStijP8VY0wAYozHcvf/vNcrVkFdeOGFfOlLXyKEwJNPPsnLXvYyHnnkEQ4ePHjinCNHjvDd736Xyy+/nFtuuYW6urperaGxsZH9+/d3+ZMkSa8+pyRJkqTua25qYu2qTTy36TB7etiSeVF5M5cuq2L81IkFqFADzaBYLhRjzPRkXAjhAuDq3N27Y4xNvVeV+todd9zB2LFjueuuu1i3bh233norAJWVlYQQTglVZsyYwRVXXHHaNT71qU/x1a9+tcvn+fznP88tt9xy2uPf+ta3+Na3vtXl2C1btlBVVdWNVyNJkiSpt5xsydx8Vi2ZFyyYSukwWzLrpEERspyFN+VufxtjXNunlaggrr/+el73utfx0EMP8eSTT/LCCy+wf/9+QghUVVVx8cUXc+ONN3LjjTdSWnr6tMBjx45x7NixLp+jvr6+UOVLkiRJ6mWntmQuznu8LZnVlaEesrwyd/ubEMIo4APATcBk4BDwP8BnYoz/3Uf1qRdUVFRw9913c/fdd3d7THV1dY+fb/ny5XmPue2227jtttt6/JySJEmSunb2LZmbWDC6xJbM6tJQD1nmtvn918Bssp2FjgETgBuA60MIf2kLZ0mSJEkaeLItmbez4Rg9bsk8q6SZOQumU1Sc/8wXDS1DPWQZlbt9C5AB3gncH2NsCCFUAfcB1wCfDCH8Osb4XJ9UKUmSJEnK294du1mz65gtmXXODPWQJdXm9u9jjF9uPRBjrA4h3AxsAKYB7wUMWSRJkiSpnzt2uJY1m/ZkOwb1sCXzokmVjJ86tQDVaTAb6iHLUWB07vfPtz+Ym9HyFeDvgdeGENI97WQkSZIkSSqs5qYmXlq/nS1NxSQ9aMlcnLQwtxJmzK0inU4XoEINdkM9ZKkhG7IcjDHu7+Sc9bnbcmAssPdcFCZJkiRJ6p4kSajZvJO1h1to7GFL5unpBubbkllnaaiHLC8Ci/M4PxaqEEmSJElS/nqjJfOSGWMZOc6WzDp7Qz1keRa4BRgTQjivk9ksC3K3dcCBc1aZJEmSJKlTDcfqWb9hB9uTnrdkXji6hEm2ZFYvGup/Sd8juy8LwLvbHwwhlAHvyN39UYwxOVeFSZIkSZJOl8lk2LR2C8vX7mV7LIeQ39qgVEyYU9zIay+YxpTZUw1Y1KsGzUyWEMJ5be6ObvP7qHbHDraGJTHGAyGEfwA+BrwnhFDDyRbOM8i2cJ4GNAEfLewrkAa2GF1NJ0mSpMI6uGsvq3bUUpcu69GUgYnUs3DORCpGDu/94iQGUcgC7Ovk8Z+3uz8TqG5z/x+AhcCbgS8BnwshtO061AS8Jcb4fO+VemYhBGKMZDIZd7XWgJAk2YleIc//kiBJkiSdSePxBtat356duZIuy3t8ZaaRxZMrGTfFlswqrMEUsvRIzP7n91tDCD8E7gQuBCqBbcB/AJ+KMa4513WVlZVRX19PbW0to0ePPvMAqY/V1tYC2b9dSZIkqTckScKOTTtYeyShuQf7rhQnLcyrhOm2ZNY5MmhClhjjWf3n8xjjY8BjvVTOWRs9ejT19fXs2bOHlpYWhg8fTklJCSEEZwqoX4gxEmOkqamJuro69u/P7httKChJkqTeULv/EKuq9+e6BuW5NsiWzOojgyZkGWxGjBhBQ0MDBw8eZP/+/Se+wEr92ZgxYxgxYkRflyFJkqQBrLmxiQ3rt1HdXELsweyVMUk9i23JrD5iyNJPhRCYMGECFRUV1NbWcvz4cVpaWtxcVP1KCIGioiKGDRvGiBEjqKys7OuSJEmSNEAlScLurbtYc6CRhlQZ5DmBvyxpYuGYEiZV2ZJZfceQpZ+rrKz0i6skSZKkQe3Y4Vpe3LSHfaEcUiV5jU3FhFklzcxZMJ2i4uICVSh1jyGLJEmSJKlPZFoybFq/lZcaikhC/kuDzkvqWTJ7PJWjRxagOil/hiySJEmSpHNu3449vLjrKMfSpXkvDSpNmlk0ptilQep3DFkkSZIkSedM/dHjrN2wkxrKIV2a19gQIzOKGpm/eBrFpfmNlc4FQxZJkiRJUsElSUL1hm1sOBpo6UHXoFGZBpZWjbFrkPo1QxZJkiRJUkEd2rOfVdsOU5sugzxX9xQnLSwYEZg2Z5ZLg9TvGbJIkiRJkgqiqaGBdet2sC1TCumyvMdPCfUsXDiVsor8Z75IfcGQRZIkSZLUq5IkYefmnaw93EJTqizvjW0rM40snTKcsZOnFqZAqUAMWSRJkiRJvabu4GFe3LyPA6lySBXnNTadZJg7LGHm/CrS6XSBKpQKx5BFkiRJknTWWpqb2bh2K5ubS4g92Nh2Qqxn8byJDBsxvADVSeeGIYskSZIk6azs3lrD6r0N1KfzXxpUnmli8fgyJs6YW5jipHPIkEWSJEmS1CPHa+tYvXE3e0I5pEvyGhtiwqySZuYunU5RcX7LiqT+ypBFkiRJkpSXTCbDlvVb2Xg8TaYHS4PGJPUsnTWO4WNGFaA6qe8YskiSJEmSuu1AzV5W7azjaLoUUvmNLUmaWTiqiCmzZpNK5TlYGgAMWSRJkiRJZ9RwrJ61G3awM5ZDujS/wTEyPd3IgkVTKSkrK0yBUj9gyCJJkiRJ6lSSJGx7aRvra6G5B0uDRmQaWDp9FKMnTCtAdVL/YsgiSZIkSerQkX0HWVV9kMPpsryXBhUlGeZXRmbMm+XSIA0ZhiySJEmSpFM0Nzayft12traUEtP5L++ZTD0LF0yhvHJYAaqT+i9DFkmSJEkSkF0atKu6hjUHm2lMlUHIb3xFppElkyoZN3VqYQqU+jlDFkmSJEkSRw8d4cVNe9mfKodUcV5jUzFhTlkLs+dXkS5KF6hCqf8zZJEkSZKkIayluYVN67eyqbGYpAcb246L9SyZPYGKUSMKUJ00sBiySJIkSdIQtWf7blbvPsbxdGneS4PKkiYWjS1l4ozZbmwr5RiySJIkSdIQU193jNUba9hNOaRL8xobYkJVcRPz5k+nuLSkQBVKA5MhiyRJkiQNEZlMhuoN29hwLEWmB0uDRif1LK06jxHnjS5AddLAZ8giSZIkSUPAwV37WLXjCHXpMshzdU9x0sLCkSmmznZpkNQVQxZJkiRJGsQajzewbsN2tmfKIF2W9/hpoZ4Fi6ZSOiz/mS/SUGPIIkmSJEmDUJIk7Ni0g3VHMjSlyvPe2HZ4poGlU0cyZtLUwhQoDUKGLJIkSZI0yNTuP8Sq6v0cSpVDnst70kmGeRUJVfNmkk6nC1ShNDgZskiSJEnSINHc1MSGdduobi4h9mBj24nUs3j+JMqHVxagOmnwM2SRJEmSpEFg15adrD7QSEOqLO+lQcMyTSyeUM6E6XMLU5w0RBiySJIkSdIAduxwLas37WFvKIdUSV5jQ0yYXdLMnKUzKCr266F0tvynSJIkSZIGoExLhk3rt/JSQxFJyH9p0NiknqWzx1M5emQBqpOGJkMWSZIkSRpg9u3cw4s1RzmWLs17aVBp0syi0cVMmjmbVJ6b4krqmiGLJEmSJA0QDceOs2b9Tmooh3RpfoNjZEZRI/MXTaOkLM+xkrrFkEWSJEmS+rkkSdi6cRvr66ClB12DRiYNLJ0+mlHjpxWgOkmtDFkkSZIkqR87vPcAq7Ye4ki6DPJc3VOctDB/BEyfM8ulQdI5YMgiSZIkSf1QU0Mj69dtY2umDNJleY+fEupZuHAqZRX5z3yR1DOGLJIkSZLUjyRJQs3mnaw93EJjqjzvjW0rM40snTKcsZOnFqZASZ0yZJEkSZKkfqLu4GFe3LyPA6lySBXnNTYdM8wtzzBzfhXpdLpAFUrqiiGLJEmSJPWxluYWNq7byuamYmIPNradEOtZPHciw0YML0B1krrLkEWSJEmS+tDurTWs3ttAfbo076VB5ZkmFo0rY1LV3MIUJykvhiySJEmS1AeO19axeuNu9oRySJfkNTbEhFnFTcxdOoOi4vyWFUkqHEMWSZIkSTqHMpkMW9ZvY+PxFJkeLA0ak9SzZOZ5jBg7ugDVSTobhiySJEmSdI4cqNnLqp11HE2XQiq/sSVJMwtHpZkyazapVJ6DJZ0ThiySJEmSVGCNx+tZu34HO2I5pEvzGxwj09MNLFg0jZKyssIUKKlXGLJIkiRJUoEkScL2l7azrjbS3IOlQSMyDSydNorRE6cVoDpJvc2QRZIkSZIK4Mi+g6zaeoDDqfK8lwYVJRnmVSZUzZvl0iBpADFkkSRJkqRe1NzYyPp129naUkrsweyVSdSzaMEUyiuHFaA6SYVkyCJJkiRJvSBJEnZV17DmYDONqTII+Y0flmlkyaQKxk+dW5gCJRWcIYskSZIknaWjh47w4qa97E+VQ6o4r7GpmDCntJlZ82dQVOxXNGkg859gSZIkSeqhluYWNq3fyqbGYpIeLA0al9SzZM4EKkaNKEB1ks41QxZJkiRJ6oG9O3bz4q5jHE+X5r00qCxpZtGYYiZWzXZjW2kQMWSRJEmSpDzU1x1nzcad7KIc0qV5jQ0xUlXUyLzF0ykuLSlQhZL6iiGLJEmSJHVDkiRUr9/KhmMpWnqwNGhUUs/SGWMZOW5aAaqT1B8YskiSJEnSGRzavY9V249Qmy6DPFf3FCctLBiZYtpslwZJg50hiyRJkiR1oqmhgbXrtrM9UwbpsrzHTw31LFw0ldJh+c98kTTwDIqQJYQwHLgceDlwce52bO7wwhjjujyv9zngntzd52KMr+2lUiVJkiQNAEmSULOlhjWHmmlKlee9se3wTANLpoxg7OSphSlQUr80KEIW4HeB7/XGhUIIFwF/2hvXkiRJkjTwHDtSx4sbd7MvVQ6p4rzGppMM84YlVM2fSTqdLlCFkvqrwRKyAOwFfg38CtgJfC3fC4QQUsA/ARFYAVzUmwVKkiRJ6r8ymQxb1m9jY32KTA82tp0Y61k0bxLDRlQWoDpJA8FgCVmeiDF+v/VOCKGqh9f5M7LBymeBMRiySJIkSUPC4b0HeGHroezGtnkuDSrPNLFkQjkTps8tTHGSBoxBEbLEGDNne40QwlTgI0AN8EHgi2d7TUmSJEn9W3NjE+vXbaO6pTTvjW1DTJhd0sycpTMoKh4UX60knSX/TXDSF4DhwNtjjHUh5BlfS5IkSRpQdm+t4cV9DTSk8p+9MjapZ8mscQwfM6owxUkakAxZgBDCtcANwLMxxsf6uh5JkiRJhVN/9DhrNuxkF+WQKslrbEnSzKLRxUyeOZtUKlWgCiUNVEM+ZAkhVAD3AU3AO/u4HEmSJEkFkiQJ217axrpaaOnBxrbTUvUsXDSNkrL8lhVJGjqGfMgC/B0wHfhYjHFDXxcjSZIkqffVHjjEqi37OZQqhzwnoFRkGjl/ynDGTp5amOIkDRpDOmQJIVwI3ANUAx/r22okSZIk9baW5hZeWreVTU3FxDxnr4SYMKe0mdnz3dhWUvcM2X9ThBBSwNeANPCuGGN9H5ckSZIkqRft37mXVTV1HEuX5r2x7eiknvPd2FZSnoZsyAK8BXg58GPgJyGEynbHW9+bdJtj9b3RLlqSJElS4TQ1NLBm7XZ2xHJIl+Y1tjhpYcGIwLQ5bmwrKX9DOWSZkbu9Eqjr4rxXtzl+ObC8gDVJkiRJ6qEkSajZUsOaQ8009WBj20nUs3jhFMoqhhWgOklDwVAOWSRJkiQNEscO1/LiS3vYlyqHVHFeY8szTSyZUM6E6XMLVJ2koWLIzn+LMX4oxhg6+wEeyp36XJvHl/dhyZIkSZLayWQyvLRmCz/ddCgbsOQhxMjMogZec8FUJkyfVKAKJQ0lg2YmSwjhvDZ3R7f5fVS7YwdjjMk5KkuSJElSgRzeu58Xth6mNl2W98a2IzINnD9jNKPGTytMcZKGpEETsgD7Onn85+3uzyTbslmSJEnSANTc2MT6dduobimFdFleY9NJhnkVCTPnz3JjW0m9bjCFLJIkSZIGud1ba3hxXwMNqfxnr4yL9SydN5FhI4YXpjhJQ96gCVly+6j05vVuA27rzWtKkiRJ6pn6o8dZvWEnuymHVEleY0uTZhaNKWZSlW2ZJRXWoAlZJEmSJA0+SZKw7aVtrKsNtPSgLfO0VD0LF02jpCy/ZUWS1BOGLJIkSZL6pdoDh1i1ZT+HUuV590WtyDRy/pThjJ08tTDFSVIHDFkkSZIk9SstzS28tG4rm5qKiXm3ZU6YU9rM7PkzKCr2646kc8t/60iSJEnqN/bv3MuqmjqOpUvz3th2dFLP+bPGMXzMqMIUJ0lnYMgiSZIkqc81Hm9g7frt7IjlkC7Na2xx0sKCEYFpc9zYVlLfMmSRJEmS1GeSJKFm807WHG6hqQcb206insULp1JWkf9YSepthiySJEmS+sSxw7WsemkP+1PlkCrOa2x5poklE8qZMH1ugaqTpPwZskiSJEk6pzKZDFvWb2NjfYpM3hvbRqqKG5m3ZDrFJSUFqlCSesaQRZIkSdI5c2jPflZtO0xtuizvjW1HZBo4f8ZoRo2fVpjiJOksGbJIkiRJKrjmxibWr9tGdUsppMvyGptOMsyrSJg5f5Yb20rq1wxZJEmSJBXUruoaVu9voCGV/+yVcbGepfMmMmzE8MIUJ0m9yJBFkiRJUkHU1x1n9cad7KYcUvntn1KaNLNoTDGTqmzLLGngMGSRJEmS1KuSJGHbxu2sq4OWHrRlnpaqZ+GiaZSU5besSJL6miGLJEmSpF5Tu/8QL1Tv53CqHPKcgFKZaWTplOGMnTy1MMVJUoEZskiSJEk6ay3NLWxct5XNTcXEPGevpGLCnNIWZi+oIl2ULlCFklR4hiySJEmSzsq+nXtYVXOU4+nSvDe2HZPUs3TWOIaPGVWY4iTpHDJkkSRJktQjjccbWLt+OztiOaRL8xpbnLSwcGSKqbPd2FbS4GHIIkmSJCkvSZKwc/NO1h5uoakHG9tOpp5FC6dSVpH/WEnqzwxZJEmSJHXbscO1rHppD/tT5ZAqzmtseaaJJRPKmTB9boGqk6S+ZcgiSZIk6YwymQxb1m9lQ30RSZ6zV0KMVBU3Mn/pDIqK8wtmJGkgMWSRJEmS1KVDu/fzwvbD1KXL8t7YdmSmgaUzRjNq/LTCFCdJ/YghiyRJkqQONTc2sm7ddra2lEK6LK+x6STD/IpI1fxZbmwracgwZJEkSZJ0ml3VNaze30BDKv/ZK+NjPUvmTWTYiOGFKU6S+ilDFkmSJEkn1NcdZ/WGnewO5ZAqyWtsadLM4jHFTKyyLbOkocmQRZIkSRJJkrB143bW10FLvm2ZY2R6uoEFi6ZTUlZamAIlaQAwZJEkSZKGuNr9h3ihej+HU+WQ5wSUykwjS6cMZ+xkN7aVJEMWSZIkaYhqaW5h47qtbG4qJuY5eyUVE+aUtjB7QRXponSBKpSkgcWQRZIkSRqC9u3Yw6pdRzmeLs17Y9sxST3nzx5P5eiRhSlOkgYoQxZJkiRpCGk8Xs+a9TvY+f+zd99hluZlnf/f33Mqdo7T0znUdA4zDkFEgsCCBAEJKuqqgGBY9we6uArrCgq7ICJpWUHJgtkVWQF1FXaFAQHBYaa7p3Oo6u7qnNOpdJ7798c5DTVNh3qqntOV3q/rqquqzvN9zve+5o+pc336fr53tEM53/kpzdkA62eWWNLhwbaSdCOGLJIkSdIkkGUZ3Qe62Xl+gL68B9sCi6iwYf0S2qbmv1eSJgtDFkmSJGmCu3L+Itv2neB0qR1Kzbnuba/2senuKSxYurpB1UnSxGHIIkmSJE1Q1WqVA7u72FtpIsvZvZIiWNncy5rNy2lqzhfMSNJkZcgiSZIkTUDnjp9m6+HzXCq35T7YdmbWw5blc5g537HMkpSHIYskSZI0gfT39rJr12G6Blqh3Jbr3nJWZe3UjBVrV3mwrSQNgyGLJEmSNEEc6zzKI6d76Snl7165KypsWnM3U2ZMb0xxkjQJGLJIkiRJ41zl0hW27znKiZT/YNvWrJ+Nc5q5e4VjmSVppAxZJEmSpHEqyzK69h5i96XEQN6xzBEsK/ewbsMyWtpaG1OgJE0yhiySJEnSOHTx9Dm2dp7mfKkdcjagTKv2smXJdOYs9GBbSSqSIYskSZI0jgz0D7B3VxcH+pqJnN0rpci4p22AjrUrKDeVG1ShJE1ehiySJEnSOHHqyAm2HbvM1XJr7oNt52YVNnfcxbTZMxtTnCTJkEWSJEka63qvVtix+wjd0Q7lfOenNGcDrJ9ZYkmHB9tKUqMZskiSJEljVJZldB84wo7zGf15D7YFFlFhw/oltE3Nf68kKT9DFkmSJGkMunzuAtv2n+RMqR1ydqC0V/vYdPcUFixd3aDqJEk3YsgiSZIkjSHVapUDu7vYW2kiy9m9kiJY2dzLms3LaWpublCFkqSbMWSRJEmSxohzx0+x9fAFLpXbch9sOzPrYcvyOcyc71hmSRothiySJEnSKOvv7WXXrsN0DbRCuS3XveWsytppGSvWrG2lH5kAACAASURBVPJgW0kaZYYskiRJ0ig61nmUR0730FPK372yICpsXLOQKTOmNaY4SVIuhiySJEnSKKhcvsoje7o5TjuUWnLd25r1s3FuC4tWerCtJI0lhiySJEnSHZRlGYf3HWbnxWAg71jmCJaVe1m3YSktba2NKVCSNGyGLJIkSdIdcunsebYeOMW5UjvkPD5lWrWXLUtmMGehB9tK0lhlyCJJkiQ1WHWgyv5dXezrzT+WuRQZ97QN0LFuBeVyuUEVSpKKYMgiSZIkNdDZY6fYeuQil8utuQ+2nZtV2NxxF9Nmz2xMcZKkQhmySJIkSQ3Q39vLrp2H6Kq2QTnf+SnN2QDrZ5ZY0tHhWGZJGkcMWSRJkqSC1cYy99JTas/dvbKQChvXL6Ftas5DcSVJo86QRZIkSSpI5VJ9LHNqh1Jzrnvbsj42zW/j7uWOZZak8cqQRZIkSRqhLMs4tO8Quy6mYY1lXtHUy9pNy2huaWlMgZKkO8KQRZIkSRqBkYxlnlHtYcvyWcy6y7HMkjQRGLJIkiRJw1AdqLJvVyf7epuJYYxlXtM+wMq1Kx3LLEkTiCGLJEmSlNOZoyfZ1n3JscySpEeZECFLSmk68DTgccBj69/n1i+vj4hdN7mvDXge8Bzg8cAqoBk4AXwV+EBE/HNDi5ckSdK40dfTy65dhzg0zLHMG2aWWOxYZkmasIYVsqSUDhS0f0RERwHv8wzgb4Zx32eAfzfo916gH1ha//rRlNJ7I+KXR16iJEmSxrOjB7t55EwfvcMYy7yIChscyyxJE95wO1lW3OZ6cPM/PYOvxTD3v5GTwDeBbwDdwAeHcE8zsBf4EPCZax0vKaUO4G3AjwCvTSntiYj3F1irJEmSxonKpSts33OUE8MYy9xe7WPTgnYWLHMssyRNBsMNWZ52k9c7gHcCbcBfAF+kFngALAKeCvwY0AO8DiiqI+YzEfHpa7+klFYM8b7/Anw9IqqDX4yI/SmlH6P2yNHTgV8FDFkkSZImkSzLOLT3MLsuMayxzCube1njWGZJmlSGFbJExBevfy2ltBj4S+AU8JyI2H+DWz+eUnoL8PfAW4HHDGf/G9RTvf2qG973L7e4FimlT1ALWVamlOZExNnh1ihJkqTx4+KZc2w7eHoEY5lnO5ZZkiahIg++fRMwD3jxTQIWACLiQErplcAD9Xt+vsAainZm0M/O1pMkSZrgBvoH2L+7awRjmauOZZakSazIkOXZwOWI+MrtFkbEV1JKl6lN9RnLnlr/fgI4PZqFSJIkqbHOHD3J1u5LXBnGWOZ5WYXN9yxg6qwZjSlOkjQuFBmyzAeyoSxMKSVqnSHzC9y/UPXHn36h/uvHI6LIQ3olSZI0RvT19LJz1yEOZ+3DG8s8q8ziVY5lliQVG7IcA5anlJ4XEZ+7zdrnAu1AZ4H7Fyal1AT8CTANOERt0pAkSZImmEeNZc5pMRU2bFhC6xTHMkuSaoqM2z9FrbHyoymlp9xsUUrpScBHqY1v/usC9y/S+6g9KtQH/EREXBjleiRJklSgyqXLfOPf9vLguaB3GGOZHze/ie+5f7UBiyTpUYrsZHkz8EJqY5z/X0rpa9RGOB+tX18EPAX4PmphzF7gLQXuX4iU0lupPSZUBX5yKGfMSJIkaXzIsoyuvYfYfSnlHsucIljR3Mvazctpas4XzEiSJofCQpaIuJhSejLwCeDfUQtTnnDdsmtHiP0T8DMRcbGo/YuQUvoN4A3UumxeHRH/a5RLkiRJUkEunj7H1s7TnHcssySpQYrsZCEijgPPqj8S9FLgfr5zuO0p4EHgr8Zid0hK6VeA/1b/9bUR8bHRrEeSJEnFGOgfYN+uLvb35R/LXI4qa9ozVjiWWZI0BIWGLNdExJeBLzfivRshpfSLwLvqv74+It43mvVIkiSpGI5lliTdSQ0JWcaTlNLPAL9f//XNEfH20axHkiRJI9fX08POXYeHNZa5Jetnw6wmFjmWWZKU04QJWVJK8wb9OnvQz7Ouu3Y2IrL6PS8BPkLt3zXeERFvanylkiRJapQsyzjWeZQdZ/uHN5Y5OZZZkjR8DQlZ6gfgfj+1iUJTuXlzZkTEzxa07ambvP7V635fCXTWf34HcO3h2p9OKf30Ld7/xRHxL8MvT5IkSY109eJltu89xsnUDjnHMk+p9rFp4RTuWrK6QdVJkiaDQkOWlNIm4E+Bjddfqn+P614LoKiQZTgG938uuM3alkYWIkmSpOHJsozOPYfYfTlRHcZY5pXNvazZvIKm5gnT5C1JGiWF/SVJKS0EvkBtmtAOamOaXwtcBt5DLcR4OtABnAb+EBgoav+IyHmUGUTEiqL2lyRJ0p138fQ5th48w/lyW+6xzDOrPWxZMYeZ8x3LLEkqRpFx/a9SC1j+AXhhRPSnlF4LXI6IN15blFL6OeB/Uhvv/EMF7i9JkqRJYqB/gL27ujjQ10yU23LdW86qrJmasXLtKg+2lSQVqsiQ5dnUHv/5jYjov9miiPhgSmkm8DvAL1ELXCRJkqQhOd19km1HhzeWeX5WYdPqu5k6c3pjipMkTWpFRvfLgSrw0KDXArjRzLw/qF+71UGzkiRJ0rf19fTw0Lf28rUTfbWAJYeWrJ/7ZsLj7u8wYJEkNUyRnSwZcCEiBh9uexmYkVIqR0T12osRcSmldBFYU+D+kiRJmoCujWV+5Gw/fcMYy7wkVVi/YSmtU/I9ViRJUl5FhizdwKqUUikisvprncAmYAvwrWsL648LzQJ6CtxfkiRJE8zVi5fYtvc4p4Y1lrmXzQunMX/JkgZVJ0nSoxX5uNBuaqHN+kGvPUDtSdlfvW7tW+rfdxS4vyRJkiaILMs4sPMgX9xzthaw5JAio6Oph6fct5z5SxY0qEJJkr5bkZ0s/wi8gNrEoEfqr70PeDXwspTSFmArtc6WTdTOZPlAgftLkiRpArhw6ixbu85yoTSMscxZD1uWz2Hm/DmNKU6SpFsoMmT5C2AlcOXaCxGxO6X0M8AHgY31L6gFLO+OiI8UuL8kSZLGsYH+Afbu7ORAfwtRyj+Wee3UYIVjmSVJo6iwkCUizgD/+Qav/3lK6fPAc4AlwAXg8xGxp6i9JUmSNL6d6j7BtqOXuVpuyz+WOSpsXnM3U2Y4NUiSNLqK7GS5qYg4DXzyTuwlSZKk8aP3ag87dx/mSLTDMMYyb5zdzMKVHXavSJLGhDsSskiSJEmDZVnG0YNH2XFu+GOZN2xaSkubY5klSWNH4SFLSikBLwKeCSwF2iPiGYOuTwUeA0REPFD0/pIkSRrbRjyWedE05i92LLMkaewpNGRJKa0GPgVs4DtP08Z1y3qAjwCrUkpPjYgvF1mDJEmSxqYsyzi4u4s9V0pUc3avpMhY1dLP6s3LaWq2GVuSNDYV9vBqSmk28HlqE4S2AW8ELl6/LiKq1EY3J+AlRe0vSZKksevCqbN85cED7Kw0Uy2Vc907M+vhycuns35zhwGLJGlMK/Kv1OuoPR70f4DnR8RASumXgBsd8/63wO8BTyxwf0mSJI0xA/0D7NnZycHhjmWelrFijWOZJUnjQ5EhywupPRr0uogYuNXCiNiXUuoD7ilwf0mSJI0hJ4+cYPux4Y1lvisqbHIssyRpnCkyZFkJ9ETEjiGuvwTMLHB/SZIkjQG9Vyvs2H2E7mGMZW7N+tkwp5mFKxzLLEkaf4oMWQIY0gO2KaUmYAY3OLNFkiRJ41OWZRw90M2O8wPDGsu8tFRh/QbHMkuSxq8iQ5aDwMaU0qqIOHCbtc8AmoGdBe4vSZKkUXLlwiW27z3OqVL+scxTq71sXjSdeY5lliSNc0WGLJ8DNgG/Avx/N1uUUpoKvINa58v/LnB/SZIk3WFZlnFwVxd7KsMby9zR0s89jmWWJE0QRf41eyfwc8B/SCldAN49+GJKaTrwbODNwFqgm9ooZ0mSJI1D50+eYWvXOS4O42DbWVmFLSvmMWPe7MYUJ0nSKCgsZImI0ymlFwKfAd4A/Dr1P7cppbPUzmBJ9a+zwA9HxJWi9pckSdKdMdDfz+6dXXT2txLl/GOZ100Llq/xYFtJ0sRTaF9mRHw5pXQv8FbgpUBL/dKs+vcB4K+B10dEV5F7S5IkqfFOHjnO9mNXRzCWeSFTZkxrTHGSJI2ywh9+jYhDwL9PKb0aeAywECgBJ4BvRsTloveUJElSYz16LHPL7W8YpDXrZ+OcZhatWt2g6iRJGhsKC1lSSlvqPx6IiMsRUQG+XNT7S5Ik6c7LsozuA93sOF+l37HMkiTdUpGdLA8BGXA3YLeKJEnSOHfl/EW27TvB6VI7lPJ9bJxa7WXL4unMXeRYZknS5FFkyHIByCLidIHvKUmSpDusWq1ycPch9g5zLPM9rf10rHUssyRp8inyL98e4HtSSm0R0VPg+0qSJOkOGfFY5pXzmDHXscySpMmpyJDlk8DjgJ8GPljg+0qSJKnBRjKWuSmrsnY6LF/tWGZJ0uRWZMjy+8AzgPeklKrAxyIiK/D9JUmS1AAnDh9n+/GrVIbRvbIgKmxau5D26Y5lliSpyJDlI8B5YIBaJ8vbUkrfBE4B1ZvcExHxswXWIEmSpCHqvVrhkV1HOMowxzLPbWHRSscyS5J0TZEhy8uB4Dv//jEPePZt7gnAkEWSJOkOqo1lPsKO89mwxjIvK1VYt2EZLW2tDahOkqTxq8iQ5bcLfC9JkiQ1wJXzF9m67wRnSu2Q8/yUadVeNjuWWZKkmyosZIkIQxZJkqQxqlqtcmB3F3srTWSOZZYkqSH8KylJkjTBnTt+mq2Hz3NpGAfbzs4qbFk1n+lzZjWmOEmSJhBDFkmSpAmqv7eXXbsO0zXQCsMYy7xuRrDsHscyS5I0VIWHLCmlMvBjwEuB+4H59UungAeBvwT+KiJuNnFIkiRJI3S86yjbT/XQU8rfvXJ3VNi4djHt06c0pjhJkiaoQkOWlNJa4K+AjXz3n/Nl9a8XAm9IKf1oROwucn9JkqTJrnL5Ko/s6eY47VDKP5Z507xWFq5wLLMkScNRWMiSUrob+BK1zpU+4H8BXwS660sWAU+l1uGyGfjnlNL3RMTxomqQJEmarLIs49C+Q+y6CAN5xzJHsLzcw1rHMkuSNCJFj3CeDxwAnhsRe26w5sMppTcDfwesAt4E/GKBNUiSJE06l86eZ+uBU5wrtUPO41OmVXvZsmQGcxYubUxxkiRNIkWGLM8FAnjFTQIWACJib0rpldS6XH4IQxZJkqRhGegfYP/uLvb1NhM5u1dKkXFP2wAd61ZQLpcbVKEkSZNLkSHLPOBKRDxwu4UR8UBK6XL9HkmSJOV05uhJtnZf4kq5NffBtnOzCps77mLa7JmNKU6SpEmqyJDlKLAgx/py/R5JkiQNUV9PDzt3HeZw1g7lfOenNGcDrJ9ZYkmHY5klSWqEIkOWvwVek1J6TkT8/a0WppSeA7QDny5wf0mSpAkryzKOdR5lx9l+evMebAssosKG9Utom5r/XkmSNDRFH3z7fOCjKaUXR8RXb7QopfQE4KPAPuAtBe4vSZI0IV29eInte49zMrVDqTnXve3VPjYtaGfBMscyS5LUaEWGLC8A3g/8JvBASukB4J/57hHOTwUuAr8LvCCl736IOCI+UWBdkiRJ41KWZXTu7mL3lRLVnN0rKYIVzb2s2bSM5paWBlUoSZIGKzJk+Ti16ULXUpOnAk+5bs21a7OA37vFexmySJKkSe3CqbNs7TrLhVJb7rHMM6o9bFk+m1l3OZZZkqQ7qciQ5UvUQhZJkiQN00D/AHt2dnKwv4UoteW6txxV1rRnrFi70rHMkiSNgsJCloj4gaLeS5IkaTI6eeQ4249d5Wq5LfdY5vlZhU33LGDqrBmNKU6SJN1WkZ0skiRJGobeqxV27D5Cd7RDOd/5KS1ZPxtmN7NopWOZJUkabYYskiRJoyTLMroPHGHH+Yz+YYxlXpIqrN+wlNYp+R4rkiRJjdHwkCWldB/wM8AaoA94CPhwRHTf8kZJkqQJ7Mr5i2zbd4LTpXbI2YEypdrL5kXTmL94SYOqkyRJwzHskCWltBJ4J9AP/FRE9N1gzWvqawZ/cngB8LqU0osj4vPD3V+SJGk8qlarHNzdxZ5KE1nuscwZq1r6Wb15OU3NNiRLkjTWjOSv87OAHwb++iYByxOAd1M7ti2AvcAV4F5gGvAXKaU1EXFmBDVIkiSNG+eOn2br4fNcGsbBtrOyCltWzGPGvNmNKU6SJI3YSEKWp1ILT/7yJtffQO3jwxXguRHxAEBKaSPwT8AC4FXA20dQgyRJ0pjX39vH7l2H6BxohXK+81OasiprpwfLV3uwrSRJY91I/lJvqH//4vUXUkrtwLOphTDvuBawAETEI8BbqAUwzx7B/pIkSWPe8a6jfHHbETqrbZDyta8siApPXTuXlWtXGLBIkjQOjKST5W7gSkScvMG17wWaqYUsf36D638B/D6wfgT7S5IkjVmVy1d5ZE83x2mHUr6xzK1ZPxvntrBo5eoGVSdJkhphJCHLHGqPAt3I4+rfj0XEnusvRsTZlNJVYNYI9pckSRpzsizj8L7D7LwYDOQdyxzBsnIv6zYspaWttTEFSpKkhhlJyHIJmJVSmhIRV6+79r317w/e4v4BoDyC/b8tpTQdeBq1cOex9e9z65fXR8Su29xfonY+zCuoddeUgX3AnwLvvdHBvpIkSde7dPY8Ww+c4lypPfdD2dOqvWxZMp05C5c2pjhJktRwIwlZdgFPAJ5P7fEfAFJKLcDTqT0q9OUb3ZhSmgbMAI6MYP/BngH8zXBuTCk1A58Gnlt/qQ+oAvfVv34kpfT0iLhcRKGSJGniqQ5U2berk329zUTO7pVSZNzTNkDH2hWUmwr59ydJkjRKRnKC2t9RO7z2t1NKCwe9/ka+8xjQp29y77VOl1t2mOR0sl7TbwM/l+O+/0YtYOkBXg5MAaZSC4/OUuuK+cMC65QkSRPImaMneeBbneztayVSvo9Wc7IKT1k1kzUbVxmwSJI0AYykk+X9wGuA1cD+lNJDwEJgGbUuls/d6DyWupfU13x1BPsP9pmI+Hagk1JaMZSbUkp3A6+t//rrEfFHgy5/NqX0SmpB0Y+nlN4eEVsLqleSJI1zfT097Nx1mMNZO5TznZ/SnA2wbmaJpR2OZZYkaSIZdsgSEedSSi8A/haYT+3RoWt2c5NukpTSDODH67/+w3D3v66W6jBvfQnQClwAPniD9/3fKaU9wBrgJwBDFkmSJrksyzjWeZQdZ/vpzXuwLbCQChvXL6Ftav57JUnS2DaSThYi4usppTXAy4DN9Ze/CfxZRPTe5LY1wIeB/ogoqpNluJ5W//6liOi5yZp/pFbz0+9MSZIkaay6evES2/ce52Rqh1Jzrnvbq31sWtDOgmWOZZYkaaIaUcgCEBEXyHFmSUR8k1oQMxZsqH9/5BZrdtS/r08ppYiIBtckSZLGmCzL6NzTxe7LJarDGMu8sqmXNZuW0dzS0pgCJUnSmDDikGWcu3Zg79FbrLl2bVr961JDK5IkSWPKhVNn2dp1lgulttwjA2ZUe9iyfDaz7nIssyRJk8FkD1mm1r9XbrHm6qCfDVkkSZokBvoH2LOzk4P9LUSpLde95aiyuj1j5dqVlMtODZIkabKY7CGLJEnSdzl55Djbj13harkNUr5752UVNt+zgKmzZjSmOEmSNGZN9pDlCjALuNXD1VMG/Xy5seVIkqTR1Hu1wo7dR+iO/GOZW7J+NsxuZtFKxzJLkjRZTfaQ5Si1kGXRLdZcu3Y5InxUSJKkCSjLMroPdLPjfJX+YYxlXpIqrN+wlNYp+R4rkiRJE8tkD1l2UJswtPEWa65NINrZ+HIkSdKdduX8RbbtO8HpUjuU8n00mlLtZfPCacxfsqRB1UmSpPFksocs/w94KfDklFJbRPTcYM0z69+/cOfKkiRJjVatVjm4u4s9lSaynN0rKTJWtfSzevNympon+8cpSZJ0zWR/YPhTQC+1R4Zedf3FlNLzgbVAAH92Z0uTJEmNcu7Eab784EF29bSQpXwfh2ZVe3jy8ums39xhwCJJkh5lwnwySCnNG/Tr7EE/z7ru2tmIyAAi4nhK6b3ArwG/m1K6APxpRFRTSs8FPla/588iYmsj65ckSY3X39vH7l2H6BxohXLOscxZlXXTg+WrV3mwrSRJuqEJE7IAp27y+lev+30l0Dno9/8KbAKeC3wC+FBKqcp3pgp9A/iF4sqUJEmj4XjXUbaf6qGnlH8s84KosGntQtqnT2tMcZIkaUIYVshSDyGKEBExqkFPRPTXHwt6NfByagfdloGHqD0i9J6I6Bu9CiVJ0khULl9lx55ujtEOpZZc97Zm/Wyc28KilasbVJ0kSZpIhhtw5Pz3n4a/DxEx7PeqPz70h/UvSZI0AWRZxuF9h9l5MRjIO5Y5gmXlHtZtWEZLW2tjCpQkSRPOcEOWlTd5/fuADwB99e9fBLrr1xYBT6X26E0r8IvA14a5vyRJ0k1dOnuerQdOca7UnvuY/2nVXjYvns7cRUsbU5wkSZqwhhWyRETX9a+llNYDHwR2As+OiHPXLdkD/HNK6X8A/wB8CHjccPaXJEm6kepAlX27OtnX20zk7F4pRcY9rQN0rFtBuancoAolSdJEVuR5KG8EpgI/e4OA5dsi4lxK6VXAw/V7frLAGiRJ0iR15uhJtnVf4nK5NfcDyXOyCptXzWf6nFmNKU6SJE0KRYYsTwUuRsT22y2MiG31cclPK3B/SZI0CfX19LJr1yEOZe1Qznd+SnM2wLqZJZZ2dDiWWZIkjViRIctsgJRSOSJuOX0opdQEtFE7m0WSJCm3LMs43nmUR87205v3YFtgIRU2rl9C29T890qSJN1IkSFLJ7AG+Angk7dZ++PUApbdBe4vSZImiasXL7N97zFOpnYoNee6ty3rY9P8Nu5e7lhmSZJUrCJDlj8Ffhv4QEqJiLhh0JJS+klqk4cC+OMC95ckSRNclmV07uli9+US1WGMZV7Z1MuaTctobmlpTIGSJGlSKzJk+V3gecDjgY+nlN4KPAAcrV9fBDwJWEztOLqvAe8ocH9JkjSBXTh1lq1dZ7lQass9lnlGtYcty2cx6y7HMkuSpMYpLGSJiN6U0jOA9wCvoBamvIxaxwp855z/DPgI8CsR0VfU/pIkaWIa6B9g785ODvS3EKW2XPeWo8rq9oyVa1dSLjuWWZIkNVaRnSxExBXg1SmltwAvBu4H5tcvnwIeBD4VEYeK3FeSJE1MJ4+cYPuxy1wtt+Ueyzwvq7D5ngVMnTWjMcVJkiRdp9CQ5Zp6iPKeRry3JEma+HqvVtix+wjdkX8sc0vWz4ZZTSxa5VhmSZJ0ZzUkZJEkSRqOLMvoPtDNjvNV+ocxlnlJqrB+w1Jap+R7rEiSJKkIDQlZUkr3A88ElgJTIuKVg661AHcDERGHG7G/JEkaf66cv8i2fSc4XWqHUr6PKFOqvWxeOI35S5Y0qDpJkqTbKzRkSSnNBz4BPOvaS9QOvn3loGUlapOF7kopPTYiHiqyBkmSNL5Uq1UO7j7EnkqZLGf3SoqMVS39rN68nKZmG3QlSdLoKuxB5ZTSFODzwA8Cx4GPAVeuXxcRPcAf1Pf+kaL2lyRJ48/5k6f5yoMH2dXTTJbyfSyZmfXw5OXTWb+5w4BFkiSNCUV+IvmPwGbgG8APRsT5lNLzgCk3WPsp4LeApxS4vyRJGif6e/vYvesQnQOtUM45ljmrsm5asHzNKg+2lSRJY0qRIcuPUns06DURcf42a3cA/cDaAveXJEnjwPGuo2w/1UNPKf9Y5gVRYdPahbRPn9aY4iRJkkagyJBlDbXg5F9vtzAispTSRWBWgftLkqQxrOfKVR7Z3c0x2qHUkuve1qyfjXNbWLRydYOqkyRJGrkiQ5Yy0B8RcbuFKaUETOMGZ7ZIkqSJJcsyDu87zM6LwUDescwRLCv3sG7DMlraWhtToCRJUkGKDFkOA6tTSgsj4tht1j4RaAW2F7i/JEkaYyqXLrN19zFOldpzH7c/rdrL5sXTmbtoaWOKkyRJKliRIcs/AauBXwDedLNFKaUy8FZq57f8XYH7S5KkMSLLMrr3H+GRC1nu7pUUGatb++lYt4JyU7lBFUqSJBWvyCP5fw/oBV6fUnpVSt89hzGl9DhqY56fDFwA3lfg/pIkaQzouXKVb35rPw9fKjFQyvfvObOzCk9ZOYM1mzoMWCRJ0rhTWCdLRHSllP498GfAHwJvp3buCimlB4GlwBxqcwR6gR+PiNNF7S9JkkZf9/4jbD83QH/O7pXmbIB1MxJL7+lwLLMkSRq3inxciIj4VErpScC7qZ27cs19g37+GrUxz98scm9JkjR6eq9W2LbrCMdph5zdKwupsHH9YtqmTmlQdZIkSXdGoSELQER8A3hSSmkVtaBlIbXHkk4AX42I3UXvKUmSRs+xg91sO9NHX87ulbasj03z27h7uWOZJUnSxFB4yHJNRBwADjTq/SVJ0ujq6+lh+47DHKUdSs257l1e7mHdxmU0t7Y0qDpJkqQ7r7CQJaX0RuByRLxriOtfA8yKiDcXVYMkSbozjncdZdupXnpzdq+0V/u4d9E05i1e0qDKJEmSRk+RnSy/BRwHhhSyAL8CLAMMWSRJGif6enrZsfMQRyJ/98rSUoUNG5fbvSJJkiashj0uJEmSJpaTR46z9fhVenKfvdLP5gXtLFjq2SuSJGliG82QZR5wdRT3lyRJQ9Df28fOnV0cytqhlK8LZXGqsHHTMlraWhtUnSRJ0thxx0OWlNJM4BXAVODhO72/JEkaujNHT/JQ92Uq5XzdK61ZP5vmtbJwhd0rkiRp8hh2yJJSehPwxuteXpBSqg7xLQL4k+HuL0mSGmegf4BdOzrpHGiFcr7ulYVU2LRhCa1T8gUzkiRJ491IO1nSoJ/jRtdY3AAAIABJREFUut9v5SjwYeCdI9xfkiQV7OyxUzx85CJXym1D/8sOtGT9bJzTzOJVdq9IkqTJaSQhy3uAj9d/TsAB4BTw+FvckwEXI+LCCPaVJEkNMNA/wJ6dnRzob4VyvjNUFkSFzeuX0DbV7hVJkjR5DTtkqQcl3w5LUkpfAk5HRFcRhUmSpDvn/MnTPNR1gcs5u1easwE2ziqzaFUHpVKpcQVKkiSNA4UdfBsRP1DUe0mSpDujOlBl785O9ve1EDm7V+ZHhS1rF9M+fUqDqpMkSRpfCgtZUkplYDEwEBFHb7N2UX3vIxGRFVWDJEkaugunzvJQ51ku5exeacqqbJiZWNJh94okSdJgRX4y+jHgIPDmIax9Z33tSwrcX5IkDUG1WmXPIwf48qHLtYAlh3lZhaesmcOy1csMWCRJkq5TdMgC8JEhrP0Dav9m9rIC95ckSbdx8cw5/uVbB9nT20KkoX8MKGdVNk2t8vj7O5gyY3oDK5QkSRq/CntcCNgEDAD/OoS1X6mv3VLg/pIk6SayLOPAri72VMpkpXzdK3OyCvfes4Cps2Y0qDpJkqSJociQZRG18czV2y2MiIGU0oX6PZIkqYEun7vAQ/tPcr7UnuvslVJkrJtSZcVaz16RJEkaiiJDlqvAjJRSU0QM3GphSqkZmFG/R5IkNUCWZXTu6WL3lRLVUnuue2dlFe7ruItps2c2qDpJkqSJp8iQZRfwBODZwGdvs/bZQDOwp8D9JUlS3ZXzF3l43wnODqN7ZU17lVXr7F6RJEnKq8iQ5W+A7wPenVL6ZkQcv9GilNJC4D1AAJ8ucH9Jkia9LMs4tO8QOy+m3N0rM6s93LtyLjPmzW5QdZIkSRNbkSHL+4FfAlYBD6eU3gH8PXCofn058FzgdcB84DDwvgL3lyRpUrt68TJb9xzjdKk91/zAFBmrWwfoWL+ScrncuAIlSZImuMJCloi4mlJ6HvAPwBLg7fWv6yWgG3heRFwuan9JkiarLMs4sv8IOy4EAzm7V6ZXe7hvxRxmzp/ToOokSZImjyI7WYiIHSmle4E3AD8FLLhuyXHgk8DbI+JskXtLkjQZVS5fZdvubk6mvN0rwaqWPtZsWUm5ye4VSZKkIhQasgBExDng14BfSykt5ztBy4mI6Cp6P0mSJqsj+4/wyLkB+nN2r0yr9nLvspnMXrC0QZVJkiRNToWHLIPVQxWDFUmSCtRzpcL23Uc4TjuUcvwpj2Blcy9rN6+gqbmhHwEkSZImpYZ9wkopJWAuMCUiDt1uvSRJur2jB7vZfqaPvpzdK1Oqvdy3ZDpzFtq9IkmS1CiFhywppe+jdibL04Ap1EY1Nw26Pgt4Z/3110TE1aJrkCRpounr6WH7jsMcpR1KzbnuXV7uYf3m5TQ157tPkiRJ+RQasqSUfgl4D3DTE/Qi4nxKaR7wQ8AXqR2EK0mSbuJ411G2neqlN2f3Snu1j3sXTWPe4iUNqkySJEmD5ZhDcGsppccD7wUy4PXAMuDETZZ/jNoo5+cWtb8kSRNNX08vD31rL988k9Gbs3tlaanCU7YsYd7iuxpUnSRJkq5XZCfLf6IWnPxWRPwuQO1Ylhv6Yv37/QXuL0nShHHyyHG2Hr9KT87ulbasj80LprBg6eoGVSZJkqSbKTJkeXL9+/tvtzAizqWULgH2L0uSNEh/bx87d3ZxKGuHUkuue5ekChs2LaOlrbVB1UmSJOlWigxZ5gEXI+LCENdXgXyfHiVJmsBOd5/k4aOXqZTzda+0Zv1snt/K3cvtXpEkSRpNRYYsF4A5KaWWiOi71cL6wbczge4C95ckaVwa6O9n144uOgdaoZzv3x8WUWHjhqW0TmlrUHWSJEkaqiJDloeBp1N7bOgLt1n7cmrnt3y9wP0lSRp3zh47yUNHLnG13Fb7yzhELVk/m+a2sGil3SuSJEljRWHThYBPUPt4+LaU0rSbLUopPQt4MxDARwvcf0RSSqWU0itSSp9PKZ1KKfWnlM6nlL6eUvqNlNL00a5RkjRxDPQP8MjWffzL0V6ulvOdoXJ3VHjK+rtZtHJxg6qTJEnScBTZyfLHwE8DzwC+nlL6MNAKkFJ6PrAceA7wg9TCnb+JiL8vcP9hSylNAT5DrRPnmgvADODx9a9Xp5SeHhEHRqFESdIEcv7kaR7qusDlnN0rzdkAG2c3sWhlB6VSkf9OIkmSpCIUFrJERKSUXgR8Engh8HuDLn+6/v3aR8lPUQtkxorfpBawBPBfgA9ExIWUUgvwYuAD1EKiD/PoIEaSpCGrDlTZs7OTA30tRM7ulbuiwuZ1i2mfNqVB1UmSJGmkiuxkISIuAy9KKT2D2rkr3wcspNa5cgL4KvDxiPg/Re5bgJ+of/9YRPzOtRfrB/j+eUqpDfgY8LSU0uyIODcaRUqSxq8Lp87yUOdZLuXsXmnKqmyYmVjSYfeKJEnSWFdoyHJNRHyB2x9+O5YsqH//1k2u/9ugn6cAhiySpCGpVqvs39nF3t4mopxvAtC8rMKWNQuZMuOmR51JkiRpDGlIyDIOdQJrge+5yfXH1L+fiAjHTkuShuTimXM8fOAMF3J2r5SzKutnBMvusXtFkiRpPGloyJJSWgHMr/96KiI6G7nfCHyI2hkyr0gp7eXRZ7K8CHg3tfNafnUUa5QkjRNZlnFgVxd7KmWynN0rc7IK996zgKmzZjSoOkmSJDVK4SFLSmkl8AbgJcCs666dB/4KeHtEHCx67xF4D7AS+CXgbdTGUF8AplM7T+ZrwH+PiM+OXomSpPHg8rkLPLT/JOdL7bm6V0qRsW5KlRVr7V6RJEkarwoNWVJKP0LtgNh2bvzRcjbwauCnUkovj4i/KnL/4YqIakrpl4EDwNup/XeZOWjJdL7TkSNJ0nfJsozO3YfYdbVEVmrPde+srMJ9HXcxbfbM2y+WJEnSmFXYP5WllB4H/Cm1g2H3AD9H7ZyTafWvNfXXdlELYf4kpfSYG7/bnZVSuhv4CvBO4E+Ae6nVvJpaV84q4KMppbeNWpGSpDHryvmLfO3B/eyoNJGlof9pLUXGurZ+nnh/hwGLJEnSBFBkJ8t/BcrAPwIvjIje667vA/allD4B/C3wLOA3gR8usIbh+gTweOAjEfGqQa/vA34npdRdX/NrKaU/johHRqNISdLYkmUZh/YeZuclqObsXplZ7eHeVXOZMXd2g6qTJEnSnVbkQ9/fT+1w2F+8QcDybRHRB/yH+q9PKnD/YUkpbQCeWf/13TdaExGfBM5Q++/1/DtUmiRpDLt68RL/+uB+tl8pUy2Vh3xfiow1rX088f6VBiySJEkTTJGdLG3AhaEcaBsRB+qH4LYWuP9wrR/0861qPwDMBVY0tBpJ0piWZRlH9h9hx4VgIGf3yvRqD/etmMPM+XMaVJ0kSZJGU5Ehy35gXUqp9VadLAAppTZgKrCjwP2HKxv08zJqZ8bcyPL690uNLUeSNFZVLl1l655uTqX2XL2gKYKOlj5Wb1lJuWnoXS+SJEkaX4p8XOjjQDPw80NY+3P1tR8vcP/henjQz6++0YKU0vOBu+q/fr3hFUmSxpQsyziy7zBf2n2yFrDkMK3ay/cvbWfd5g4DFkmSpAmuyE6W91A7Y+X3UkpTgPdGRGXwgnoHy2uBtwCfAv5HgfsPS/3RpX+kdhDvL6eU+oB3R8TJlNI04KXUpg4BdFI7tFeSNEn0XKmwbdcRTqR2KOX4sxnBquZe1mxeQVNzkX9uJUmSNFYV+anvI8BF4Arw34HfSCl9E+iuX18EPJbaY0IXqD1285GU0vXvExHxswXWNRQvB75A7XyW1wOvTyldAqYPWnMCeHH94F5J0iTQfeAIj5ztpy/n2StTqr3ct2QGcxYubVBlkiRJGouKDFleTm260LXUZCrw1JusnQX8zE2uBXBHQ5aIOJZSegy1x5heDGwCZlILjfYBnwPeFxGn7mRdkqTR0Xu1h+27DnOMdig1D/3GCFY09bJu83KamnPcJ0mSpAmhyJDltwt8rzuu/mjTe+tfkqRJ6njXUbad6qU3Z/dKe7WPexdNY95iu1ckSZImq8JClogY1yGLJGly6+vp5ZGdh+iOnN0rwLJShfUbl9Pc2tKg6iRJkjQeeBKfJGnSO3H4GNtO9NCTs3ulLetjy91TuGvJ6gZVJkmSpPGksJAlpTQjIi7mvOexEfHNomqQJCmP/t5eduw8xOEsf/fKklRhw6ZltLS1Nqg6SZIkjTelAt9ra0rpZgfdPkpKqZRSehPwlQL3lyRpyE51n+BLW7trAUsOrVk/j51b4r7vWW3AIkmSpEcp8nGhZcAXUkrvAn4jIvpvtCildA/wSeDxBe4tSdKQDPT3s3NHF13VNijnO0NlERU2bVpKS1tbg6qTJEnSeFZkJ8uH6u/3OuAbKaVN1y9IKf0C8C3ge4HzwE8WuL8kSbd05uhJvvTQoVrAkkNL1s/9sxP337/agEWSJEk3VVjIEhE/D7wAOAlsoRa0vA4gpbQgpfQ54PeBqcDngc0R8edF7S9J0s0M9A/wyNZ9fPVYL1fL+R7xuZsKT1l/N4tWLm5QdZIkSZooCp0uFBGfTSltptbV8kLgd1NKLwZWA/OACvDrEfE/i9xXkqSbOXfiNA8fusDlchukod/XnA2wcXYTSzqcHCRJkqShKXyEc0ScBl6UUvpl4F3AE6h9rN0F/HBE7Cl6T0mSrlcdqLJnZycH+lqInN0rd0WFzesW0z5tSoOqkyRJ0kRUeMgCkFJ6MvBaIPjOvxt2AC9NKb0tIqIR+0qSBHDh1Fke6jzLpZzdK01ZlQ0zE0s6OiiVijy2TJIkSZNBoZ8gU0pNKaXfAf4vsBzYD/wg8JdAM/AW4IGU0soi95UkCaBarbJ7+36+fOhyLWDJYV5W4Slr5rJs9TIDFkmSJA1LYZ8iU0obgH8F/jNQBj4I3BcR/xQRLwN+CrgAPBF4OKX0qqL2liTpwqmzfOXBg+ztayXS0P+8lbMqm6YN8Pj7O5gyY1oDK5QkSdJEV+TjQv8GtFKbLvSqiPjs4IsR8ScppS8CfwQ8DfjDlNLzI+KFBdYgSZpkqtUq+3Z2sq+3mcjZvTInq3DvPQuYOmtGg6qTJEnSZFJkyNIKfIZawHLqRgsi4gjwjJTSfwLeCvxQgftLkiaZC6fO8nDnWS7mPHulHFXWTg1WrPHsFUmSJBWnyJDl5yPiQ0NZGBHvSin9I/DJAveXJE0SI+lemZ1VuLfjLqbNntmg6iRJkjRZFRayDDVgGbR+e0rp8UXtL0maHIbbvVKKjDXtVVats3tFkiRJjdGQEc5DFRH9o7m/JGn8GEn3ysysh/tWzWP6nFkNqk6SJEkaQciSUnoNcCUiPnKDa9OAUkRcvMX97wZmRMTPDrcGSdLkMNzulRQZa9oHWLV2JeVyuXEFSpIkSYysk+U9wDHgu0IWYC8w/zbv/zLgLsCQRZJ0QyPqXqn2cO/KucyYN7tB1UmSJEmPNtLHhW7174k5/q1RkqRHs3tFkiRJ482onskiSdL1qtUq+3d2stfuFUmSJI0zhiySpDHD7hVJkiSNZ4YskqRRZ/eKJEmSJgJDFknSqBpR90rbAKvW2b0iSZKkscGQRZI0KuxekSRJ0kRjyCJJuuPsXpEkSdJENNKQZU5K6f/e6HWAm1x71BpJ0uRR617pYm9vk90rkiRJmnBGGrK0AD9wi+u3ugYQI9xfkjRO2L0iSZKkiW4kIcsfFVaFJGnCsntFkiRJk8WwQ5aIeEWRhUiSJh67VyRJkjSZePCtJKlwdq9IkiRpMjJkkSQV6uLpczx08IzdK5IkSZp0DFkkSYUYSffKjGoP99m9IkmSpHHOkEWSNGIj6V5Z3TZAh90rkiRJmgAMWSRJw2b3iiRJkvQdhiySpGGxe0WSJEl6NEMWSVIudq9IkiRJN2bIIkkaMrtXJEmSpJszZJEk3Va1WmX/ri729ti9IkmSJN2MIYsk6ZbsXpEkSZKGxpBFknRDdq9IkiRJ+RiySJK+i90rkiRJUn6GLJKkb7N7RZIkSRo+QxZJEmD3iiRJkjRShiySNMnZvSJJkiQVw5BFkiYxu1ckSZKk4hiySNIkZPeKJEmSVDxDFkmaZOxekSRJkhrDkEWSJgm7VyRJkqTGMmSRpEnA7hVJkiSp8QxZJGkCs3tFkiRJunMMWSRpgrp4+hwPHzzDBbtXJEmSpDvCkEWSJhi7VyRJkqTRYcgiSRPIiLpXWgfoWG/3iiRJkjRchiySNAHYvSJJkiSNPkMWSRrn7F6RJEmSxgZDFkkap+xekSRJksYWQxZJGofsXpEkSZLGHkOW66SU1gL/EXgWsAQYAI4CXwX+KCK+OIrlSZrkqtUqB3Z1scfuFUmSJGnMMWQZJKX0GuAdQEv9pcv1n9fVvzLAkEXSqLB7RZIkSRrbDFnqUko/D7yXWpDyduD9EXGofu1u4JlA8+hVKGmyGmn3yr0r5jBz/pwGVSdJkiTpGkMWIKW0AnhX/ddfiIgPDb4eEceBT97hsiTJ7hVJkiRpHDFkqXktMAX4+vUBiySNBrtXJEmSpPHHkKXmJ+rf/2xUq5Ak6t0rnWe4ULJ7RZIkSRpPJn3IklLqAO6q//qtlNITgN8Ankitu6UL+Azwjog4OTpVSpoMqtUqB3Z3safSRJTsXpEkSZLGm0kfsgCrB/38A8AbgTJwCQhgbf3rJ1NKz4yIR+54hZImPLtXJEmSpPGvNNoFjAGzBv38JmAP8ISImAFMA54LnAQWAn+dUjKYklSYarXK3h0HeKDrUi1gyWFGtYcnLZvGmk2rDFgkSZKkMcDA4NFBUwAviojdABGRAX+fUnol8FlqHS0vBv7yjlcpacIZWfdKv90rkiRJ0hhjyAKXB/38D9cClsEi4nMppT3AGuAZGLJIGgHPXpEkSZImJkMWODro5+8KWK67tgZY2thyJE1kF8+c4+GDdq9IkiRJE5EhC+wAMoZ+Pk00sBZJE9S17pW9lSYyu1ckSZKkCWnShywRcTWl9FXg+6mduXIz1651NrwoSROK3SuSJEnS5DDpQ5a6T1ALWZ6dUlp7/bksKaXnUXtUCODv7nRxksYnu1ckSZKkycURzjUfpfbYUBn4VErp8QAppVJK6dnAR+rrvoYhi6QhuHjmHP/yrYPs7mkhS0P/X22KjDUtvXz//SsNWCRJkqRxxk4WICIGUkrP5/9v787D5LrvOt+/v1W9at8sa7UkS7Ik29qcBIY97CFghhAYYNgcBsKScJP7sM6FGRLgXpjAvZAbmCFANpaEbUIygWTCFodclsAQybbcki1bUmux9n0p9VLnd/84p6Oy6G5XSVVd1d3v1/PUc2o5v1PfKnW3uj79O98fPA48CHw6Iq6Shy5zit0GgG9KKdmTRdKEnL0iSZIkzV6GLIWU0qGI2A78GPAaYAN5Q9zPAH8MvCOldL2NJUrqcHfTe2VT7wib7L0iSZIkTWuGLDVSSpeBny4uklSXLMt4/sARZ69IkiRJs5whiyTdBWevSJIkSRpjyCJJdyDLMg4fGOSZStnZK5IkSZIAQxZJatj1S1d44rnTXCj1O3tFkiRJ0mcZskhSnbIs49jzxxm4nKiW+hsa6+wVSZIkaeYzZJGkOty8foMnD5zgTPRDqf5xzl6RJEmSZg9DFkl6CS8cOs5TF0YZcfaKJEmSpEkYskjSBIZv3mTfwDFeoB9K9f+4dPaKJEmSNDsZskjSOM4cP8WTpyrcbHD2yvzqTXY5e0WSJEmalQxZJKnG6MgI+weOMFjth1J3/QNTYmPPMA/s2EC5y9krkiRJ0mxkyCJJhQsnz7L3+BVulBubvTKnOsSuNfNZsnJtiyqTJEmSNB0Yskia9aqjVZ7df4Tnh3ug3NvQ2PtKN9n28H109/S0qDpJkiRJ04Uhi6RZ7cq5i+w9fJ4r5T6I+sf1ZiPsuLePe9dual1xkiRJkqYVQxZJs1KWZRw6MMizlTJZua+hsauo8PDDa+npa2ycJEmSpJnNkEXSrHP90hX2Pneai6X+hmavdGejPLyki9X3b25dcZIkSZKmLUMWSbNGlmUce+4YA1eg2uDSzPekCju2rqZ/3pwWVSdJkiRpujNkkTQrVK7d4MlnTnA2+qFU/7hyVuXBBbB200ZKpQYGSpIkSZp1DFkkzXgnDh1n34VRRhqcvbI4q7Br073MXbSgRZVJkiRJmkkMWSTNWMM3b7Jv4Bgv0A+l+n/cRcrY0l/l/q3OXpEkSZJUP0MWSTPS6WMnefL0TYYanL2yoHqTXRuWsmDZ4hZVJkmSJGmmMmSRNKOMDA+zf2CQo1k/lLrrHhcpcX/PMA/s2EC5q9zCCiVJkiTNVIYskmaMCyfPsPf4VW6UG5u9Mqc6xK41C1iycm2LKpMkSZI0GxiySJr2qqNVnh04zPMjvVDubWjsunKFbdvX09Vd/6wXSZIkSRqPIYukae3y2QvsPXKBq+U+iPrH9WUj7FjRz/I1m1tXnCRJkqRZxZBF0rSUZRmHDhzhmUoXqdzX0NhVVHj44bX09DU2TpIkSZImY8giadq5fukKe587zcVSf0OzV7qzUbYv6WLV/c5ekSRJktR8hiySpo0syzj63FH2XwmqDS7NvDxV2LFtNX1z57SoOkmSJEmznSGLpGmhcvUGTz5zgrOlfijVP66cVXlwYbB240ZKpQYGSpIkSVKDDFkkdbwTzx9n38VRRhqcvbI4q7Br073MXbSgRZVJkiRJ0i2GLJI61tCNm+w7cIyT9EOp/h9XpZSxZU6VDVucvSJJkiRp6hiySOpIp4+e5MkzNxlqcPbKgupNdm1YyoJli1tUmSRJkiSNz5BFUkcZGR5mYGCQY1k/lLrrHhcpsbFnmM07N1Aul1tYoSRJkiSNz5BFUsc4/8IZnjhxjRvlxmavzK0OsWvtQhavWNuiyiRJkiTppRmySGq70ZFRnt1/hEMjvVDuaWjsuvJNtm1fT1e3P84kSZIktZefSiS11eWzF9h75AJXy30Q9Y/ry4bZsWIuy9esaV1xkiRJktQAQxZJbZFlGc8fOMKzlS5Sua+hsaujwkMP30dPX2+LqpMkSZKkxhmySJpy1y5eZu/zZ7hU6m9o9kpPNsLDS3tYtWFz64qTJEmSpDtkyCJpymRZxuDBYxy4BtUGl2a+N1XYvm0NfXMbGydJkiRJU8WQRdKUqFy9xhPPnORcg7NXurIqDy4M1mzcSKlUal2BkiRJknSXDFkktdzx54/z9MVRRhqcvbI0q7DzgRXMWTC/RZVJkiRJUvMYskhqmaEbFfYdOM5J+qFU/4+bUsrYOidj/RZnr0iSJEmaPgxZJLXEqcEXeOrsEEMNzl5ZUL3J7o3LmL9kUYsqkyRJkqTWMGSR1FQjQ8MM7B/kWNYPpe66x0XK2NQ7wqZtGyiXyy2sUJIkSZJaw5BFUtOcf+EMe09co1JubPbK3OoQu9ctZNHyZS2qTJIkSZJaz5BF0l0bHRnlmf1HODzSC+We+gemxPquIbZuX09Xtz+OJEmSJE1vfqqRdFcunTnP3sFLXCv3NbQ0c182zM6Vc7ln9drWFSdJkiRJU8iQRdIdqVarPH9gkIM3u0jl3obGrokKDz58Hz19jY2TJEmSpE5myCKpYdcuXmbP82e5XGps9kpPNsL2Zb2sXL+5dcVJkiRJUpsYskiqW5ZlDD57lAPXg2qpr6Gx96YK27etoW9uY01xJUmSJGm6MGSRVJcbV67x5LMnOVfqb2j2SldW5aFFwer7N1IqlVpXoCRJkiS1mSGLpEllWcaJQyd4+lKV0VJjs1CWZhV2PrCCOQvmt6g6SZIkSeochiySJjR0o8JT+49zKvqhVP+Pi1LK2Dq3yvoHnL0iSZIkafYwZJE0rlODL/DU2SGGGpy9sjC7ya77lzF/yaIWVSZJkiRJncmQRdKLjAwN8fTAUY6nfih11z0uUsbm3lE2bttAuVxuYYWSJEmS1JkMWSR91rkTZ3jihWtUyo3NXplXHWLXukUsWr60RZVJkiRJUuczZJHE6Mgoz+w/wuGRXij31D8wJTZ0D7Fl+3q6uv1xIkmSJGl281ORNMtdOnOevYOXuFbua2hp5v7qMDtXzWPZ6rWtK06SJEmSphFDFmmWqlarPL//CAeHuknl3obGrokKD+24j+7exsZJkiRJ0kxmyCLNQlcvXGLvoXNcLjU2e6UnG2H7sl5Wrt/cuuIkSZIkaZoyZJFmkSzLOPLsIAeul8lKfQ2NXZEqbH9wDb1zGmuKK0mSJEmzRandBXSiiJgXEcciIhWXx9pdk3S3bly5yqc/8zwDN7rJov5v/a5slJ0LEo/s3mjAIkmSJEmTcCbL+H4eWNPuIqRmyLKME88f5+nLidFSYyHJ0qzCzgdWMmfBvBZVJ0mSJEkzhyHLbSLiEeCNwKeBz21zOdJduXm9wlMHjnM6+huat1ZKGdvmZqx7YCOlkhPeJEmSJKkehiw1IqIEvLO4+YPAZ9pYjnRXTh55gafODTHc4OyVhdlNdm+8h3mLF7aoMkmSJEmamQxZXuyHgZcDv5ZS2hPRwLIrUocYvjnEwP6jHE/9UOque1ykjM19o2zcuoFyudzCCiVJkiRpZjJkKUTEauDngNPAT7e5HOmOnDtxhr0nr3Gzwdkr86pD7Fq3iEXLl7aoMkmSJEma+QxZbnkHMB/4oZTS5XYXIzVidGSUAwNHODLaC6We+gemxIbuIbZsX09Xtz8OJEmSJOlu+KkKiIhHgdcAj6eUfq/d9UiNuHTmHHsGL3O93AcNnOHWXx1m1+p5LF21tnXFSZIkSdIsMutDloiYC/waMAK8oc3lSHWrVqs8t/8Izw11k8q9DY1dW6rw4EP30d3b2DhJkiRJ0sRmfcgC/CxwH/C2lNJAu4uR6nH1wiX2Pn+Oyw3OXunNRth+Ty8r1m1uXXGSJEmSNEvN6pAlInYBbwKOkYctUkfLsowjzxwMqnkEAAAgAElEQVTlwI0SWbmvobErqLD9wTX0zmmsKa4kSZIkqT6zOmQB3g6UgZ8CIiLmTbBfb/FYllK6MWXVSTVuXLnKE8+e4nypv6HZK93ZKA8t7mLNRmevSJIkSVIrzfaQZV2x/Z2X2O83issgsL6VBUnjOXHoOPsujDLS4NLMy7IKO7espH/+RPmhJEmSJKlZZnvIInW0keFhBp4e5Fjqh1L9367lVGXrPFi3eSOlUqmFFUqSJEmSxszqkCWltH6yxyMiFVdfl1J6b8sLkmpcOnOePYOXuF5ubPbKoqzCro3Lmbd4YYsqkyRJkiSNZ1aHLFInyrKMwwcGOVApN7Q0c6SMB/pH2bjV2SuSJEmS1A6GLFIHqVy7wRMHTnCuwea286s32bV+CQvvWdK64iRJkiRJkzJkkTrEqcEXePLsEMONNLdNifu7h3hg+3q6uv12liRJkqR28lPZJFJKDcwlkO7M6Mgo+weOMFjtg1J33eP6smF2r5rH0lVrW1idJEmSJKlehixSG105d5E9h89ztdzX0LiVVNj+8Fp6+hobJ0mSJElqHUMWqQ2yLOPowWMMXAuyBgKWclbloYXBmo02t5UkSZKkTmPIIk2xoRsVntx/nNPRWHPbBdWbPLLpHpdmliRJkqQOZcgiTaGzx0+z99QNhhppbgts6LrJ1h0bKHeVW1SZJEmSJOluGbJIU6BarfLM04c5NNLbUHPb3myEnSv6Wb5mUwurkyRJkiQ1gyGL1GLXLl5mz/NnuVzqa+j0oOWpwo5ta+ib29isF0mSJElSexiySC107OBR9l1OVEv1N7ctpYxtczPWPWBzW0mSJEmaTgxZpBYYvjnEvoGjvEA/NJCTzKsO8ciGJSxYtrh1xUmSJEmSWsKQRWqyCyfPsuf4VSrlxk7zWVeqsG37Brq6/baUJEmSpOnIT3NSk2RZxnMDhzk41EMq99Q9rjsbZceyHlau39zC6iRJkiRJrWbIIjXBjStX2fPsKS6W+htqbrs0q7Bryyr6589tXXGSJEmSpClhyCLdpROHjrPvwigjpfpPD4qUsaV/lPu32txWkiRJkmYKQxbpDo0MDzPw9CDHUj+U6v9WmlMdYvd9C1l877IWVidJkiRJmmqGLNIduHTmPHsGL3G9wea2a6LCQzvW0d1bf88WSZIkSdL0YMgiNSDLMg4fGORApUwq99Y9riursn1xmdUbbW4rSZIkSTOVIYtUp8q1Gzxx4ATnGmxuuyirsHvzCuYunN+64iRJkiRJbWfIItXh1OALPHl2iOEGmtuSEpt7h9m07X7K5XLripMkSZIkdQRDFmkSoyOj7B84wmC1D0rddY/ry4bZvWoeS1etbWF1kiRJkqROYsgiTeDKuYvsOXyeq+W+hsatpML2h9fS09fYOEmSJEnS9GbIIt0myzKOHjzGwLUgayBgKWdVHloYrNm4kVKp1MIKJUmSJEmdyJBFqjF0o8KT+49zOhprbrugepNHNt3DvMULW1ecJEmSJKmjGbJIhbPHT7P31A2GGmluC2zousnWHRsod9ncVpIkSZJmM0MWzXrVapVnnj7MoZHehprb9mYj7FzRz/I1m1pYnSRJkiRpujBk0ax27eJl9jx/lsulvoZOD1qeKux8cA29cxqb9SJJkiRJmrkMWTRrHTt4lH2XE9VS/c1tSylj29yMdQ/Y3FaSJEmS9GKGLJp1hm8OsW/gKC/QDw3kJPOqQzyyYQkLli1uXXGSJEmSpGnLkEWzyoWTZ9lz/CqVcmOn+awrVdi2fQNd3X7LSJIkSZLG5ydGzQpZlvHcwGEODvWQyj11j+vORtmxrIeV6ze3sDpJkiRJ0kxgyKIZ78aVq+x59hQXS/0NNbddmlXYtWUV/fPntq44SZIkSdKMYciiGe3EoePsuzDKSKn+04MiZWzpr3L/VpvbSpIkSZLqZ8iiGWlkeJiBpwc5lvqhVP+X+ZzqEI+sW8ii5ctaWJ0kSZIkaSYyZNGMc+nMefYMXuJ6g81t10SFh3aso7u3/p4tkiRJkiSNMWTRjJFlGYcPDHKgUiaVe+se15VV2b64zOqNNreVJEmSJN05QxbNCJVrN3jiwAnONdjcdlFWYffmFcxdOL91xUmSJEmSZgVDFk17pwZf4MmzQww30NyWlNjcO8ymbfdTLpdbV5wkSZIkadYwZNG0NToyyv6BIwxW+6DUXfe4vmyY3avmsXTV2hZWJ0mSJEmabQxZNC1dOXeRPYfPc7Xc19C4lVTY/vBaevoaGydJkiRJ0ksxZNG0kmUZRw8eY+BakDUQsJSzKg8tDNZs3EipVGphhZIkSZKk2cqQRdPG0I0KT+4/zulorLntgupNHtl0D/MWL2xdcZIkSZKkWc+QRdPC2eOn2XvqBkONNLcFNnTdZOuODZS7bG4rSZIkSWotQxZ1tGq1yjNPH+bQSG9DzW17sxF2ruhn+ZpNLaxOkiRJkqRbDFnUsa5dvMye589yudTX0OlBy1OFnQ+uoXdOY7NeJEmSJEm6G4Ys6kjHDh5l3+VEtVR/c9tSytg2N2PdAza3lSRJkiRNPUMWdZThm0PsGzjKC/RDAznJvOoQj2xYwoJli1tXnCRJkiRJkzBkUce4cPIMe45fo1Ju7DSfdaUK27ZvoKvbL2dJkiRJUvv4qVRtl2UZzw0c5uBQD6ncU/e47myUHct6WLl+cwurkyRJkiSpPoYsaqsbV66y59lTXCz1N9TcdmlWYdeW1fTPn9O64iRJkiRJaoAhi9rmxKHjPHVhlNFS/acHRcrY0l/l/q02t5UkSZIkdRZDFk25keFhBp4e5Fjqh1L9X4JzqkM8sm4hi5Yva2F1kiRJkiTdGUMWTalLZ86zZ/AS1xtsbrsmKjy0Yx3dvfX3bJEkSZIkaSoZsmhKZFnG4QODHKiUSeXeusd1ZVW2Ly6zeqPNbSVJkiRJnc2QRS1XuXaDJw6c4FyDzW0XZRV2b17B3IXzW1ecJEmSJElNYsiiljo1+AJPnh1iuIHmtqTE5t5hNm27n3K53LriJEmSJElqIkMWtcToyCj7B44wWO2DUnfd4/qyYXavmsfSVWtbWJ0kSZIkSc1nyKKmu3LuInsOn+dqua+hcSupsP3htfT0NTZOkiRJkqROYMiipsmyjKMHjzFwLcgaCFjKWZWHFgZrNm6kVCq1sEJJkiRJklrHkEVNMXSjwpP7j3M6Gmtuu6B6k0c23cO8xQtbV5wkSZIkSVPAkEV37ezx0+w9dYOhBpvb3t89xJYdGyh32dxWkiRJkjT9GbIAEXEf8I3AlwM7gXuBYeAQ8DHg7Smlk+2rsDNVq1Weefowh0Z6G2pu25uNsHNFP8vX2NxWkiRJkjRzzPqQJSLWAkd48UkuV4C5wI7i8vqIeG1K6RNTX2FnunbxMnueO8vlcl9DpwctTxV2PriG3jkNzHqRJEmSJGkasMsojJ2r8ufANwNLUkoLgTnAq4HDwGLgQxGxoj0ldo4syzh28Cifev5SHrDUqZQyHpozyst3bzRgkSRJkiTNSLN+JgtwEdidUnqi9s6U0jDwsYh4NbAHWAB8P/DWqS+xMwzfHOKpgaOcpL+heG5edYhHNixhwbLFrStOkiRJkqQ2m/UhS0rpMvDEJI8fiIh/BF4JvGyq6uo0F06eYc/xa1TKjc1CWVeqsG37Brq6Z/2XmiRJkiRphvOTb33OF9tZtwxOlmU8N3CYg0M9pHJP3eO6s1F2LOth5frNLaxOkiRJkqTOYcjyEiKiC/iC4ua+dtYy1W5cucqeZ09xsdTfUHPbpVmFXVtW0z9/TuuKkyRJkiSpwxiyvLQ3ACuADHhfm2uZMicOHeepC6OMluo/PShSxpb+Kvdv3UipZE9lSZIkSdLsYsgyiYjYAfxCcfPXUkoD7axnKowMDzPw9CDHUj+U6v/ymFMd4pF1C1m0fFkLq5MkSZIkqXMZskwgIlYCHwL6gX8BfqK9FbXepTPn2TN4iesNNrddExUe2rGO7t76e7ZIkiRJkjTTGLKMIyKWAH8BbAAOAl+bUrrZ3qpa79y5K1wv99a9f1dWZfviMqs32txWkiRJkiQbZ9wmIhYCHwceBo4CX5FSOt3eqqbG/VvXsSyr1LXvoqzCF21ewuqNa1pclSRJkiRJ04MhS42ImAt8FHg5cIo8YDna3qqmTqlUYufW1fRkIxPvlBKbe4b4vN33M3fh/KkrTpIkSZKkDmfIUoiIfuAjwOcD58kDloPtrWrq9c+bw457xj9lqC8b5vNW9rLl4Y2Uy+UprkySJEmSpM5myAJERA/wQeBLgUvAV6WUnm5vVe2zYt0q1pVffNrQSip88cOrWLpqeZuqkiRJkiSps836kCUiysD7gVcBV4GvSSl9pr1Vtd+2BzcwrzpEOauyY37G7l0b6enra3dZkiRJkiR1LFcXgi8AXltc7wY+FBET7XsspfSKKamqzbq6u3jZxqVEBPMWL2x3OZIkSZIkdTxDlhfP5ukrLhOZ8cs415q/ZFG7S5AkSZIkadqY9SFLSulxYMKpK5IkSZIkSfWY9T1ZJEmSJEmSmsGQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkpogUkrtrmFWiIjz/f39S7Zt29buUiRJkiRJUo39+/dTqVQupJSW3s1xDFmmSEQcBhYAR9pciiRJkiRJerH1wJWU0oa7OYghiyRJkiRJUhPYk0WSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFmkDhcR90XEmyPiIxFxNCKGIuJqRDwREb8YESvbXaPUqSJiXkQci4hUXB5rd01SJ4mILRHxjoh4JiKuR8TliNgfEe+OiC9pd31Su0VEKSJeFxF/FRFnI2IkIi5FxKcj4qciYn67a5RaLSLmR8TXR8TPRcTHIuJcze9WW+sYX4qI10fEPxTfP1cjYk9E/FhE9EzFa5hKkVJqdw2SJhARa4FBIGruvgLMBcrF7YvAa1NKn5ji8qSOFxG/Cryp5q7XpZTe26ZypI4SEf8b8EvA2C+414AuoK+4/a6U0ve2ozapE0TEHOAjwJfV3H0ZWMCt380GgS9LKR2a4vKkKRMR3wD86QQPb0spHZhkbDfwIeDVxV3DQBXoL27/M/n30LUmldt2zmSROttYkPLnwDcDS1JKC4E55D+oDgOLgQ9FxIr2lCh1poh4BHgj8Ol21yJ1moj4fuDt5KHKfwHWpZTmp5T6gZXAdwF/38YSpU7wn8gDlgT8R2BRSmkReRD5bcAlYB3w222rUJo6Z4CPAm8FXt/AuJ8n/9xyE3iM/HPMXOBR4ALwCuCdzSy03ZzJInWwiFgIrE8pPTHB41uBPeT/2b8lpfTWqaxP6lQRUSIPV3aT/+f9meIhZ7Jo1ouI9cDT5L/ovj6l9FttLUjqUBExCNwHvDul9B/Gefwx4D3FzSUppYtTWJ40ZSKinFKq1txeT/7HXphkJkvxR+AjQC/wppTS/3vb4/+WfJZLAnallJ5sevFt4EwWqYOllC5PFLAUjx8A/rG4+bKpqUqaFn4YeDnw31JKe9pdjNRh3kQesHzagEWa1L3FdqL/R/6l5vqcFtcitU1twNKg15IHLJeB3xznuB8GniU//e7f33GBHcaQRZr+zhfb8qR7SbNERKwGfg44Dfx0m8uROtHYL7IfaGsVUuc7Umx3T/D42B+4TqeUTrS+HGna+dJi+7cppZsT7PMXxfbLJnh82jFkkaaxiOgCvqC4ua+dtUgd5B3AfOBHU0qX212M1EkiYiOwvLi5JyL+TbF63fmIqETEgYj4pYhYPtlxpFlibKbX6yLiJ4vTuImInoj4FuBXyE9z+NF2FSh1uAeL7dOT7DNQbLdFREyy37RhyCJNb28AVgAZ8L421yK1XUQ8CrwGeDyl9HvtrkfqQJtrrr8S+P+ArwO6yT8sbiH/wLg3Ih6a8uqkzvKrwK+Tn8rwC8CliLgEVIA/AA4AX+//N9KEVhbbFybZZ+yxecVl2jNkkaapiNhB/h8+wK+llAYm21+a6SJiLvBrwAh5ACnpX1tUc/1nyM+F/zcppQXkv9y+mnwFiZXAfy9mTEqzUtGH4s3AjwCjxd0LufUZaj5wTxtKk6aLucW2Msk+N2quG7JIao+IWEneibufvOnaT7S3Iqkj/Cz5KhC/YugoTaj2d78EvCal9GmAlFKWUvoY8D3F41uAb5zi+qSOUayM8nfA/w38PrCT/EPgZvIlne8H3h0RvzDhQSTNOoYs0jQTEUvIG0RtAA4CXztJIylpVoiIXeQrphwjD1skje9azfX/mVJ65vYdUkp/Tj7DBeDLp6QqqTP9DvA5wLtSSo+llJ5MKV1PKT2XUvpF4PuL/X7c0+ukcV0vtv2T7FO7Mte1CfeaRgxZpGmkaLj2ceBh4CjwFSml0+2tSuoIbydfYeungIiIebWXmv16i/tcalOzVe158f8qYBnnsbUtrEXqWBHxIPCVxc1fGW+flNLvkq/yWAIenaLSpOlk7P+cVZPsM/bYtZTS1RbXMyUMWaRpoug38VHg5cAp8oDlaHurkjrGumL7O8DVcS5jfqO47elEmq0GyJul1yu1qhCpw22ruX54kv0OFdv1rStFmrbGft+abKbX2ApE+1tcy5QxZJGmgYjoBz4CfD75X0y+IqV0sL1VSZKmm5TSDeAfiptbJtl17LEjLS1I6ly1YeR9k+w3FvLPiL/AS032iWL7RRHRN8E+YzPG/noK6pkShixSh4uIHuCDwJcCl4CvSilNtta8NOuklNanlGKiS82uryvuW9+uWqUO8DvF9lUR8a+Cloj4WuCB4uZHp6wqqbM8UXP9+8bbISIeBZYXNz/d8oqk6eeDwBD5ynbfe/uDxffQFvJZkx+Y2tJax5BF6mARUQbeD7yK/C8kX5NS+kx7q5IkTXPvJp/CXQY+GBGfAxARpYh4FfCuYr9/xJBFs1RK6RD5QgMAb46IX4iI5QBFb6/HgPcWjx8B/sdU1yhNpYhYNnYBFtc8tKj2sYj4bMaQUjpF3jcP4G0R8Z3F5xsi4tXAe4rHPpBSenIqXsdUiJQ81VbqVBHxxcAni5s3gcuT7H4spfSK1lclTT8RMfaf3etSSu9tZy1SJ4iI+4HHudXY9ip56DLWFHqAfObkiamvTuoMEbGS/BSG2v4sV4H5NbdPk/8RbM9U1iZNtZrfpV7KhpTSkZpx3cCHgFcXdw0BVW79f/PPwJfPlKa34EwWqdPVfo/2AfdOcrlnyquTJE1LxV/ptwP/J3mg0kU+XfszwH8EPseARbNdSukk8DLgzcDfAhfIPxheIf9e+TlguwGLNLGU0gj56ls/QD5Dcoj8/5u9wE8AXziTAhZwJoskSZIkSVJTOJNFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkiRJkiSpCQxZJEmSJEmSmsCQRZIkSZIkqQkMWSRJkiRJkprAkEWSJEmSJKkJDFkkSZIkSZKawJBFkqRZKiIei4gUEY+3u5ZWiohXRMRHIuJcRGTFa35Lu+tql4h4S/EevLfdtUiSNNN0tbsASZJ0dyKiC/gO4FuBncBS4DpwCjgEfAr4m5TSP7WtyDaJiM3A48AcIAPOFdtrDRxjDfAG4KuATUB/cZxTwJPF8T+eUjrZxNI7VkS8HPhB4AuBNeR/tDsNvAD8E/n78ZcppetNer71wGPApZTSrzbjmJIktYohiyRJ01hE3AN8FHh5zd03gQC2AFuBVwOXgUW3Db8MPAMcbX2lbfN68oDlU8DXp5QuNTI4Ih4Ffh+YX3P3JfL3ciWwG/hu4O3Am5tRcCeLiJ8Ffpr86wvywOoSsApYB3we8CbgNcCHmvS064GfAQYBQxZJUkfzdCFJkqa33yMPWK4CPw6sTCn1p5QWAQuBrwT+K/kH4RdJKf1pSmlrSum7prLgKfZQsf2jOwhY7gf+iDxg+Rfg64A5KaXFKaU55B/+vwf4S/KwYUaLiG8D/hN5wPJH5F93vSmlpeSze7aTfw3ua1uRkiS1mTNZJEmapiJiK/kpLADfk1L6k9rHU0pXgb8C/ioifmSq6+sQ/cW27tODarwe6CM/LeiVKaUXHSOlNAi8B3hPRPTdVZXTw5uK7Z+nlL6l9oGUUpU8XNkH/NIseT8kSfpXnMkiSdL0tb3m+p9NtmNK6ebt903U+DYiHi/uf6nLW8Y5Zk9EvDEiPhURFyJiKCIGI+LdEbHtDl8nEVGKiP8QEZ8sjnszIg5HxG9GxKZx9j8SEQl4ZXHXe2rqPlLn0469v5+8PWC53Xjvb00tDxev/3BR96WI+LuI+IGI6J7suBHxaER8OCJORcRwRJwpmvh+9UuM2xIRHyj2r0TEgYj4mYjonWzcSxh7Pyb9WoOXfD/qfk3Fv9UnipvrxvkafOwOXockSS3jTBZJkmaG1cDzTTrWBfJGphO5d7w7I2Il8DHy5ruQn0JzHbgPeB3wbRHx7SmlDzZSTETMAf6UW7N2RoAb5KfrfB/wnRHxrSmlD9cMO0s+C2UJ0A1cASo1jzVidYP7f1ZEvJG8X8vYH7auAfOAzy8u3xIRX5tSunHbuG7yWTLfXnP3FeAe8tOWvi4i3pZS+olxnvOLyf8d5tSM2wC8Bfhq8sa0d+OO3o87fE1ngQXAYvKvp9v/7SpIktRBnMkiSdL09S8113+9aIJ711JK35hSWjHehfyDOuRBx1+PjSk+QH+YPGD5a/IAoS+ltIC8KeqvkocevxsRGxss6f8hD1iGgB8A5hc9Z7aQBwZ9wPsj4oGa1/CKot6/L+56U83reEWdz/u/iu0XRsQbIqLcSNER8Q3AO8iDph8H7kkpzScPP14FHCSfafMr4wx/G3kY8Rzw74B5KaWF5IHDD1H04Cn6pNQ+52Lgj4vn+Aywqxg3j7xB785i/J0Yez9+OCK+6A7GN/yain+rbyxuHhvna/IP7/C1SJLUEpFSancNkiTpDkXE+4CxxrXD5Kvo/CPwz8Dfp5QmnLVRnGrxHvLTYV5Zx3N9EXmA0g38UErpv9U89r3AbxXP/+UppZFxxv8G8P3Ar6eU3ljn61tPPkOnBPxASumdtz0+h3wZ5Y3A797exLc4FepLgNellN5bz3PWjL23OPby4q7TwN+QL1P8T8C/pJSGJhhbLupeB7wqpfTxcfbZWBy/B7hvbAnoYtnpZ8iXiX5ZSunYOGO/FfgA8HRK6eGa+/8T8LPAeWBrSuncbeO+A/jd4ub7UkqPvfQ78dmxXwF8nFt/pDsAfJL8a+3TRS3j/mJ5l6/pleSnDA2mlNbXW68kSe3gTBZJkqa37yOf6TFM/mH9y4GfIl8+90xE/FNEfHtExCTHeEkRcR/w38kDlnfWBiyF7y62bx8vYCn8frH9ygae+jXkv6+cAn779geL02zeVtz8xkZnm0wmpXSaPKAZmw1zL/Bt5DNP/g64GBHvj4gHxxn+SvKAZd94AUtx/OfJA7EubvWOgTw0C+APxwsjCn9CPrPnoeI0rTHfVGx/6/aApfD75EshNyyl9FfAN9SM30oemv028BRwMiJ+KSKWjjP8bl6TJEnThiGLJEnTWEppOKX0I8Ba8lNpPkB+GsrYjIJXkC/z/IcRcUf/7xezRT5E3jvjU8AP3/Z4F/A5xc13Fg1N/9UFGOvFsraBp3+k2H6qWMFmPH9TbOeSn0LUNCmlAymlLyB/H99Kvlzz+eLhfvLQ5TMR8U23Df38Yrt5ovejeE/G9ls7ztjvnmTccfLA67NjI6KHW0tWf3KC15OAv23wbagd/xFgE/C15L1m/pG8Pw7kIdSPAk9EvvJVrTt6TZIkTTc2vpUkaQZIKZ0B3llcxk51eRT4z+QfWL+ZfPbF2+/g8O8BdpPPYHjtODNVlpDPogEYbxbD7fpfepfPGuszc2KSfY6Ps39TpZT+F7d6khARu8ln77wB6AXeFxF/N3bKDzA2E6OXCRoF32ZOzfWxsfOLS71jlwBjM3lemGT/yd7Ll5RSGgU+WlzGwp0vJl/i+evIG+O+PyJeVnP60J2+JkmSphVnskiSNAOllE6nlH6bfCbI2EpB39PocSLi/yBvUnod+LcT9Hip/X1id0opXurSaB3kzW07RkppT0rpzeSrJkEeCnxrzS5j78mH63k/UkpvGWfs/17n2Mdb+mJfQjGb6q9SSo8C7yru3g3sqtltWr0mSZLulCGLJEkzWNGXY2xp4wcm2/d2EfF1wM+Rn3r0WErpiQl2PQ+Mncpz353UOYmxUGey464ZZ/+p8n5uLSNc+/6OBVt38n7c6dgL3Pp3WDXJfpM9drfeVXO9We+HJEnThiGLJEkz3/ViO1zvgIjYRt4ktQT8fErpTybatzh9aOxUmq+50yIn8Jli+7lFb5jxfFmxvU6+gs2USSll3ApZat/ffyi2OyJidYOHHRv7qgZrGQaeLm5+8Xj7FA2Qx32sSa7XXB/v/WjoNRWyYntXzZslSZoKhiySJE1TEbGhWAZ4sn3mkK8IA7C3zuMuIp/9soC84e3P1DHsvcX2sYjY+RLHX1xPHYUPkn/IXgq8fpxjzQF+bGzfSZrjNiwivjAiJj1NKSJeRd4LBV78/v41cIy8R3ZHWtgAAAPuSURBVMovvcQxbn8/fod89tC2iPj+Bsf+cbH9vohYcvv+5Kc0rZ/smJM811fUsUrVv6+5Xvt+3M1rulJsF9ZVqCRJbWTIIknS9PUQ8ExEfDAi/l3tsrcRMTciHiVfDWhDcXe9TW//ANgM7AO+s6Z56WTeRb7STB/wNxHxfRGxoKaeFcVS0p8kb5Bal5TSIPCbxc1fjIjXR0RvccwHgD8nX+3mBvDz9R63Tm8GjkTELxeBy2cb9kbEyoj4SeCPirteIF+CeKzuEeCN5MHCt0XEhyJiV8347oh4eUS8DThc+6QppQHyZaIB/mtE/EJErKkZOz8ivioifo9bocqYXwfOAMuAj0fEjprn+w7gt4DLd/h+/AHwVET8WERsH1utKiLKEfFgRPwG8OPFvh9JKX32dd3lazoIjAALI+K1d1i7JElTIur7vUmSJHWaiPhq4H/edneF/DSN2r/6V4H/nFL6v24b/xj5ykGfTCm9sub+sV8OrnJred7x/HJK6Zdrxi0nn3nyBcVdGXCJfIWduTXj3pJSeutkr+22OseWkP7K4q4R8tNSFhW3h4BvSSl9eJyxjwNfArwupfTeep+zGPsBXtzMNpEHFP3kr2nMCeDRlNKecY7xOuA3uLX6UqW4LOTWSkDc3gw4IsrAO4AfrLn7SlHDAm6dOvN4SulLbxv7JcDHuLWK02Xy8KuX/LSdTwI/CbwvpfTYRK9/nNdyElhRc1e1OPaLXgv5KlZfn1K60MTX9D7gu2pez6Xi+o9OdiqbJElTzSWcJUmaplJKH4+ILeRLNX8h8DD58rnzyD+EHgL+FvjtlNLTEx5oYi+13O682+o5U3zA/xbg24GXkZ9KMwwcAP4J+DPgfzRSRErpRkR8DfAY+bLJO8hX8xkE/hJ4W0rpYCPHrNN3Au8Gvgr4XPJGrkvIw6OT5DN9/gx4d0rp2gS1vyciPkE+e+crgXXkgcJ5YAD4BPkMkdvHVYEfiojfB34A+CJuBRxHgSeAv5hg7CeLJabfSt6vZj5wBPgA8F/IA5Y7sQV4NfClwMvJZ0gtJA+5TpH3z/kj4E/Gm/10N6+p2P8E8Bry053WFffPG2dfSZLaxpkskiRJkiRJTWBPFkmSJEmSpCYwZJEkSZIkSWoCQxZJkiRJkqQmMGSRJEmSJElqAkMWSZIkSZKkJjBkkSRJkiRJagJDFkmSJEmSpCYwZJEkSZIkSWoCQxZJkiRJkqQmMGSRJEmSJElqAkMWSZIkSZKkJjBkkSRJkiRJagJDFkmSJEmSpCYwZJEkSZIkSWoCQxZJkiRJkqQmMGSRJEmSJElqAkMWSZIkSZKkJjBkkSRJkiRJaoL/H2ozHr4/BZf/AAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 648x432 with 1 Axes>"
]
},
"metadata": {
"image/png": {
"height": 392,
"width": 556
}
},
"output_type": "display_data"
}
],
"source": [
"# change default style figure and font size\n",
"plt.rcParams['figure.figsize'] = 8, 6\n",
"plt.rcParams['font.size'] = 12\n",
"\n",
"lw = 4\n",
"fig = plt.figure(figsize=(9,6))\n",
"ax = fig.add_subplot(111)\n",
"ax.plot(range(1, len(greedy_spreads) + 1), greedy_spreads, label=\"Greedy\", color=\"#FBB4AE\", lw=lw)\n",
"ax.plot(range(1, len(celf_spreads) + 1), celf_spreads, label=\"CELF\", color=\"#B3CDE3\", lw=lw)\n",
"ax.legend(loc=2)\n",
"plt.ylabel('Expected Spread')\n",
"plt.title('Expected Spread')\n",
"plt.xlabel('Size of Seed Set')\n",
"plt.tick_params(bottom=False, left=False)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We now compare the speed of each algorithm. The plot below shows that the computation time of Greedy is larger than CELF for all seed set sizes greater than 1 and the difference in computational times grows exponentially with the size of the seed set. This is because Greedy must compute the spread of $N-i-1$ nodes in iteration $i$ whereas CELF generally performs far fewer spread computations after the first iteration."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABGgAAAMRCAYAAACwAIC3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAWJQAAFiUBSVIk8AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzs3Xl8XXWd//H35yRt2ibd91Joy9ZWWlq6sooiooAgFJRxwUFAwGVEHX7qII446IyMiiK4DCqUERBQccFaBBzLUkpbulNaqKUrpWvaJk2zNPd8fn+ck/Q2zU1Om3tzs7yej8d93OV8vud87s0Nmne/53vM3QUAAAAAAID8CfLdAAAAAAAAQGdHQAMAAAAAAJBnBDQAAAAAAAB5RkADAAAAAACQZwQ0AAAAAAAAeUZAAwAAAAAAkGcENAAAAAAAAHlGQAMAAAAAAJBnBDQAAAAAAAB5RkADAAAAAACQZwQ0AAAAAAAAeUZAAwAAAAAAkGcENAAAAAAAAHlGQAMAANDGmdkcM3MzW5/vXtoSMxsZfy5uZrfnux8AAFqCgAYAgDwyszPN7Dtm9rKZvWVmVWa2z8w2mtksM/s3MxuV7z6BbDCz29MClZbc3pXv9wIAQLYR0AAAkAdmNs7M/k/SXElfkTRd0jBJRZKKJR0r6SJJ/ylprZn91sxOyFe/HZmZvSvtD/9rOuoxAQBA21aY7wYAAOhszOwSSY9IKolfWi/pMUkvSdoWvzZU0tmSLpN0gqQrJL0q6fZWbBVthLu/K989ZMlPJP02w7Zhkv4aP35F0ieb2M86SXL39ZIsW80BAJBPBDQAALQiM5si6TeKZsq4pH+X9N/uXtNI+R/M7MuSPibpztbrEsgNd98uaXtj28xsX9rTCnd/tXW6AgCgbSCgAQCglZhZF0mPKwpnJOlf3P3HTY1x91DSr8zsGUmn5bhFAAAA5Alr0AAA0Ho+Ialuwd9nmwtn0rn7VnefnWm7mX3AzB6PFxeuMrM9ZrbczL5nZiOa2nfDKwSZWX8z+7aZrYwXLN5uZs+Y2QUNxvUws5vNbKGZ7Y5r55vZNWaW8bSTRo431Mz+28xWxfvYY2ZzzewmMytoYj8z69Zxaeb9NXqln7rXJf09rfyBRhakndNgf4Vm9n4zuzte3HmnmR0wszIze83M/sfMTm2ql6M4ZqKrOJlZTzP7spm9aGY7zKzGzLbGP7+b4pAw8edkZhPN7EEz22Bm1fF34U9mdm5TfbSWTD/bprZbtDD3o2a2Kf5dWWtmPzGz4Q3GjjGzn5nZGjOrjN/742Y2LmFvJWb2JTP7m5m9HX9+u8zsJTO71cz6ZOMzAAB0HMygAQCg9Vyf9vh72dihmZVIelTSxQ02FUkaH98+Z2afdfdfJtjfOEmzJaX/sVos6XxJ55vZ5939nviP2T9LmtBgF9Pi22RJ/5LgeJMk/UXS4AabzoxvHzezi919b3P7akXfk3RzI6/3lDQ2vn3KzG5z9/9srabM7HRJf9Dhn+Xg+Ha+pC/En+faBPu7QdK9ktJDnYGSLpH0ATP7jLv/LCvNtxIz+5Kk7+rQf6Q8XtKnJV1mZu9y9zfM7MOSZkrqnlbXTdKHFL3397n7C00c5z2K1pka1GBTP0lnxLcvmNmV7v58C98WAKCDYAYNAACtIA5SpsRP90v6Wxb2aZKe0MFw5jVFIdA0Se+S9B1JVYrCml+Y2Uea2WUPRX/g95T0DUnnxPu6RVJ5XPMDMxsb142RdJek9yh6b5+StDWu+5yZnZ/geL9T9EfrD+P9TJV0jaTlcc1ZyryobEu9pSjAujbttdt0MNiquzVcrLZQ0mZF4cXVcY+TFQUX35S0S9HCtd9u5DM/2mM2yczGSHpWB8OZRyR9IO7rCklPxa+PlvScmfVvZpcXSPqppDcU/Vynx+/zW5Jq4vd3t5mdfCR95tn7FYVrSxT93KYoCq1+HW8fKuk+M5sm6WFFP6ubFL33cyT9KK7rLunBTLORzOy9ij7vQZJKFX1ml8fHO0/StyWVKQq7ZpnZKVl9lwCA9svduXHjxo0bN245vin6F3OPby9laZ/Xpe1zjqRujdRMl1QR1+yR1LuRmjlp+ymVNKaRmkvTarZLqpZ0TiN1EyWl4rrfZ+g7/XgHJJ3fSE1XRSFWXd3HGqmZWbe9mc9pZNp+bm9k+7vStl+T4HM/XlJBE9v7KAqYXNJaSUEWjln3ma3PsP2FtP3dlKHmu2k1M5v5nFxRyFDUSN0n0mruyuLvSPrx5xzFmMZ+tg3f058kdWmk7ncNvt8LJPVspO6utLoPNrK9VzzeFQVmh+0jrjspvS5bnyE3bty4cWvfN2bQAADQOgakPd6WserI1J1mUyPpanevaljg7vMl1Z1m01vNz8z4d3df3ch+/iRpY/x0oKQfeSOneLj7Uklz46fvbPYdSPe5+7ON7Kcm7vVA/FKzp0u1Fnd/091TTWzfo2hWjBSFOQ1PA8uq+DSxs+OnT3nm047+TdKq+PFHzazh6TfpqiT9s7tXN7LtIR2cKdUm1qJJqErSde5+oJFt6etBDZR0rbuXN1J3b9rjxt77TfH4/ZI+kmEfcvc1kv4jfvoeMxvVWB0AoHMhoAEAoHX0Snu8L2NVQmY2RNGpMJI02903NVH+P5LC+PEFTdS5Dp7u0ZhlaY+bqlsa3/czs95N1EnS/Rmbcd8o6Zn46bQE+8oLM+tlZqPM7BQzGxev41ObVpLrq2+l/0z/J1ORu9dK+kX8tIuiWTyZPOvujQaJHl1ZbFH89PjkbebdM+6+I8O2pWmPV3iGS3y7+5s6eLpfY6HKjPj+2SaOVWdO2uOzmqkFAHQCBDQAALSO9H9JL8nC/sanPZ7XVKG775S0Jn7a6NWFYjvdfVcT2/ekPT5slk2Gul4Zq6KZP8ua2C5J8+N706HvOa/M7GQz+6mZbZS0V9Kbkl6VtCK+zUorH9DILrIp8XdB0ktpj5v6LjT185WiU+Gkpn++bU3S72xz772u9pD3btEVxybHTy9t5Mpch9wUfU/qDE3yBgAAHRtXcQIAoHXsTHvc8Co7RyN9kdetGasOrRndYFxD+5vZR90sHLl7U7Vh2uOMl8mWtCue1dGU9FkczS1s2yrM7GOSHtChVzdqSvfmS1qk7nMJFa1r0pT070pTn2dFM/up+xm3p3/sy/iddffQDl4ZPunvQcPvdl8d/f+37nGU4wAAHQgBDQAArWOFotNeCiVNNLPCBOEE2hgzO0nRaVldFIUYdylaTPcfkvbWrdliZscrWiBYimb/oONL///Vf5D09SMY21ywBgDoBAhoAABoBe5ebmaLFF1Vqbuiy/s+1fSoJqWfijQkQX1dTVOnMLW2/gmCqvTZRg17r1+o18yCeG2UxhQfbYON+KSiK0xJ0gx3fzpDXd8sHrM5dZ9LoOjSzk0tQp3+XWlL34WOYJeidZxMUtdM69gAAJBJe5qWCgBAe/eLtMf/2sJ9LU97fHpThWY2QNFlfaXm13xpTV3V/BWOpsf3DdfskA5d16epQGRsM8fwZranq1vvpbSJcEaSpmTxmM1J/F2QdGba47b0XWj34qtD1f0sTjezpKfAAQAgiYAGAIDW9L+S1sePzzezzyYdaGaDzezCuufxFXbq/hi80MyGNzH8Uzr4v/lNhQr5cG2mDWZ2nKT3xk8XuPveBiVvpj2e2sQxPt5MD5Vpj4uaqa2bfdzNzBr9/1Hx6zdm8ZjNSf+Z3pCpKF7E9rr4aY0OvYoQsuOJ+L6fDn7WAAAkQkADAEArcfcaSR+WVB2/dI+Zfa2pf2k3s8DMPippiQ7OJqlzd3xfJOlBMzvsD30zmyLpa/HTPZJmHv07yIkbzOz8hi+aWVcduhDvPY2MnZP2+F8bC0zM7BpJH2ymhy1pj09upvaN+L6Hop9lY76r5i+tfSTHbJK7L5H0Qvz0IjO7PkPptyW9I378SILLQOPI/UgHTx27y8ze11SxmQ0ws3/JfVsAgPaANWgAAGhF7r7QzD4k6RFFl9v+lqTrzexRSXN1cLHQoYpOR7lMmf+Af0DSPymaZXKepEVmdpeimTU9JL1P0hd18CpCn25kFko+7VC00O4sM/uxpD8pOm3pFElf0sHTn55194cbDnb35Wb2vKR3KlrTZ5aZ3SPpbUnHSLpK0scUfa5nZWrC3Teb2XpJIyVdZ2YrJS3SwSBtv7tvjB//r6R/UbTOyP1mdpqkZyTtVnSVrBvjfl6UdHaWjpnEp+LxxZJ+bmbnSvq1oqs2jYi3183AekvSLUewbyTk7nvi3++/Kvq9m21mf1A0s2aNoplL/SSNU/Q7+35FvweNBZAAgE6GgAYAgFbm7k+a2RmK/ih7l6I/0r/a1BBJjykKZNL342Y2Q9Kjki5WFGz8spHx1ZI+6+6Ptrj57NovaYak2YqCpC82UvOSpCub2Me1kp6XNEzRH7vvb7D9r/F+X2uml28q+nx76/DP8DlFPye5+yIzu1XSfyn6A/zL8S3ds5JulrQyG8dMwt1fj2ci/UHRwsofV+Ondr0u6WJ3Z4HgHHH3v6cFZCMkXR7fMmlLoSkAII84xQkAgDxw91fd/d2KZnb8t6T5imZ+1CgKLjZJ+oui4Gaku3/E3Tc0sp997v4BSZdK+q2kzYoCmTJFi+reJWm0uzcW3ORdfHrOREnfk7Ra0XsvkzRP0mckvbOpWT/uvlbSJEk/VHSp62pFs1nmSrpe0ayRykzj0/YzU1G480dFM0xqmqj9jqIZO3+WtFPSAUUzVZ5VdJWnC+L3kbVjJuHuLytaDPqrioKtXXFv2+PePi3p1PgzQw65+zxFP4trFM2e2aDoO3FA0XdmgaQfK/q9nZifLgEAbY25Z/MiAgAAAE0zszmSzpW0wd1H5rcbAACAtoEZNAAAAAAAAHlGQAMAAAAAAJBnBDQAAAAAAAB5RkADAAAAAACQZwQ0AAAAAAAAecZVnAAAAAAAAPKMGTQAAAAAAAB5RkADAAAAAACQZwQ0AAAAAAAAeUZAAwAAAAAAkGeF+W4AyZjZOkm9JK3PcysAAAAAAOCgkZLK3H1US3ZCQNN+9OrevXu/sWPH9st3IwAAAAAAILJq1SpVVla2eD8ENO3H+rFjx/ZbtGhRvvsAAAAAAACxyZMna/Hixetbuh/WoAEAAAAAAMgzAhoAAAAAAIA8I6ABAAAAAADIMwIaAAAAAACAPCOgAQAAAAAAyDMCGgAAAAAAgDwjoAEAAAAAAMgzAhoAAAAAAIA8I6ABAAAAAADIs8J8N4DccXeVlZVp9+7dqqqqkrvnuyXgEGambt26qW/fvurVq5fMLN8tAQAAAEBeENB0YNu3b1dpaWm+2wAycndVVlaqsrJSVVVVGjx4cL5bAgAAAIC86BABjZn1lPRuSVMlTYnv+8ebx7r76gzjZkr654SHmenun2wwfo6kc5sZ92N3/1zCY2TNvn37VFpaKjPT4MGD1atXLxUUFLR2G0CTUqmUysrKtG3bNpWWlqq4uFglJSX5bgsAAAAAWl2HCGgkvUfS749i3F5J25rY3kVSv/jx4ibqyiRVNrGt1ZWVRYft37+/+vbtm48WgGYVFBSob9++qq2t1c6dO1VWVkZAAwAAAKBT6igBjSRtl/SKpIWS3pJ0X3MD3P1mSTdn2m5mX5R0l6QaSY80saub3X3mkTSba/v375ck9ezZM8+dAM3r2bOndu7cWf+9BQAAAIDOpqMENE+6+x/qnpjZyCztt+70p1nuvitL+2wVtbW1kqSuXbvmuROgeXXf07rvLQAAAAB0Nh3iMtvunsr2Ps1sgqQJ8dOZ2d5/rtVdsSkIOsSPGB1c3dWbuNIYAAAAgM6Kv94zq5s9s0PS7Hw2AnR0XF4bAAAAQGdHQNMIMyuU9LH46SPufqCZIbeY2RYzqzGzHWb2NzP7tJl1y3GrAAAAAACgAyCgadyFkgbFj2cmqD9F0dWeKiQNkHSepJ9IWmBmx+WiQQAAAAAA0HEQ0DSu7vSm5e6+tIm6OZI+IWmopO7u3lfSYEm3SqqWNF7SX8yMlXoBAAAAAEBGBDQNmFk/SZfETx9sqtbdb3f3X7n7Vo9XN3X37e7+X5KuiMtOkXRNrvoFcsnMZGZav359vlsBAAAAgA6NgOZw/ySpq6RaSQ8d7U7cfZak5+OnlzRVi7atqqpKP//5z3XFFVdo1KhRKikpUVFRkYYMGaLzzjtPX//617V8+fJ8twkAAAAAaMcIaA5Xd3rTU+6+vYX7mh/fH9/C/SBPnnzySY0aNUo33HCDnnjiCa1fv16pVErFxcXasWOH/v73v+tb3/qWJkyYoPe9733auXNnvlsGAAAAgHbJ91co3LAu323kDQFNGjMbK2la/LTJ05vQ8f3yl7/UZZddpq1bt2r06NG6//77tWXLFlVWVqq0tFQ1NTVatGiR7rjjDg0bNkxPP/20Nm/enO+2AQAAAKDd8cr9Sr38osJXlyr8x+v5bicvCvPdQBtTN3umVNKfsrC/6fF9540A26nFixfrM5/5jMIw1Ac/+EE9+uij6tbt0KumFxQUaNKkSZo0aZK+/OUv64477lCXLl3y1DEAAAAAtE9eWanUyy9KlfslSeHrr0nuCk4ak+fOWhczaGJmFkj6ePz0UXevaabemtn+fknvjJ/OanmHaE233XabampqNGLECD300EOHhTMNde3aVXfccYdOOeWU+tfmzJkjM9PIkSMlSbNnz9aFF16oQYMGKQgC/fCHPzxkHzU1Nbr33nt1zjnnqF+/fioqKtKIESN07bXXatWqVU0ef8eOHfq3f/s3jR8/XiUlJSouLta4ceP0ta99TaWlpRnHhWGoe+65RxMmTFD37t01cOBAXXLJJZo3b16j9e6uE088UWame++9t8mezj33XJmZbr311ibrAAAAAHReXlWp1MsvSPsrDnk9fGOVUm+sUnw9nk6hw8ygMbMBaU/7pj3u02BbqbuHjezifEnHxI+TnN70VTM7SdKvJb3s7uVxHwMlfVLS7XHd65LuT7C/VlE76/f5biGnCi++vMX72LRpk2bPni1Juvnmm1VSUtLifX7/+9/XLbfcIjNT7969FQSHZqNvv/22LrzwQi1btkySFASBiouLtXHjRj3wwAP69a9/rYcfflgzZsw4bN8vvviiPvjBD9YHMV27dlUQBFq5cqVWrlypX/3qV3rmmWc0evToQ8bV1tbqyiuv1B//+EdJUmFhoWpra/XnP/9ZTz31lB577LHDjmVmuvbaa/W1r31NDzzwgD73uc81+n7Xrl2rF154QZL0yU9+8gg/LQAAAACdgVdVRTNnGoQz9dvXrFboruDksWpmjkSH0JFm0OxIuy1Oe31eg23HZRhfd3rTKndfkOB4RYqCmKcl7TWzPWa2W9J2SXdK6i5phaT3u3v1Eb4X5NFzzz1X//jiiy9u8f62bdumr3zlK/rMZz6jt99+W7t379a+fft05ZVXSpIOHDigD37wg1q2bJne85736KWXXlJVVZXKysq0ZcsWfeELX1BVVZWuvvpqrV279pB9b9iwQZdccolKS0v16U9/WmvWrFFlZaUqKiq0YsUKXXDBBdq0aZNmzJihVCp1yNg777xTf/zjHxUEgb773e9q79692r17t958802df/75uvbaaxt9P9dcc40KCgq0ePHijFeveuCBB+TuOuecc3TSSSe1+DMEAAAA0LF4dZVS81+UKvY1XfeP16NTnjqBjhTQHDUz6yWpbupF0sWBfyPp25L+LmmTotlIPSS9LWm2pOskTXX39VltFjlXdzpRt27dshIuVFVV6cMf/rB+/OMfa/DgwfX7Hj58uCTpwQcf1MKFC3XOOedo9uzZOuOMM+rXshk6dKh+8IMf6MYbb9T+/fv1gx/84JB9f+1rX9OePXv01a9+VT/5yU904oknKggCBUGgcePG6cknn9Spp56q1157Tb///cHZUxUVFbrzzjslSV//+td1yy23qEePHpKkUaNG6Q9/+IOOOeYYNWbYsGH1wdUDDzxw2PYwDPXgg9GvUaaQBwAAAEDn5dXV0cyZfeWJ6q1X7xx31DZ0mIDG3S3hbX0jY8vcvUe8/c6Ex1vp7re5+3nuPsLdS9y9yN2HuftF7n4/M2fap7pThfr06ZNxGt23v/1tDRky5LDbzTff3Gj9//t//y/j8erCjJtvvjnjIsMf+9jHJEnPPPNM/Wv79+/Xb37zGwVBoC996UuNjuvatWv9TJ30sU8//bTKy8tVVFSkL37xi4eNKyoq0i233JKx5+uvv16S9NBDD+nAgQOHbHvmmWe0efNm9ezZUx/60Icy7gMAAABA5+M11dHMmYThTDBxioJhw3PcVdvQYdagAVpTeXm5tm3bdtjre/fuPey17t27a8KECY3up7a2VgsWRGfU3XjjjfrsZz/baF3d6UmbNm2qf23RokWqqamRmWn8+PEZe62srDxs7OLF0VmAEydOVO/ejafR5557bsZ9XnTRRRo2bJi2bNmiJ5988pC1ce6/P1py6aqrrlJxcXHGfQAAAADoXLymRqn5c6XyskT1wYTJCo45NsddtR0dZgYNkC39+vWTJO3ZsyfjiuHf+c535O71t7oZLo3p37//YYsC1yktLVVNTXTBsF27dmnbtm2N3nbu3CnpYNgiRQsLS9GVlTKN27Ztm8rKov/47d+/v37sjh07JEWnK2WS6RQnKbrE+DXXXCPp0NOcSktL6xcd5vQmAAAAAHX8QBzOlB3+j9qNCU6dpGB4piVkOyYCGqCBsWPHSorWjlmzZk2L91dQUJBxWxgevKDYkiVLDgl9Mt0aju3du3eicXPmzGnxe0l33XXXycz01FNPaevWrZKkRx55RNXV1Ro7dqzOOOOMrB4PAAAAQPvkBw4oNf8lqWxPovpg/GkKjh2R467aHgIaoIH0U3tmzZqV02P179+/PsDZuHHjEY2tW3C4rKys0VOrmjJw4EBJ0pYtWzLWNLVNko4//nidd955qq2t1a9+9StJB09v4tLaAAAAAKQ4nFkwV9q7O1F9MG6iguNG5rapNoo1aDqZwosvb76okzv22GN14YUXavbs2br77rv1qU99SiUlJTk5VpcuXTRlyhTNnz9fs2fP1qWXXpp47JQpU1RYWKja2lo99dRTuuqqqxKPnTRpkiRp6dKlKisrU69evQ6rSb/ceCbXX3+9/va3v+mBBx7QBRdcoCVLlqiwsFCf+MQnEvcCAAAAoGPy2gNKLXxJ2pMwnDllgoIRo3LcVdvFDBqgEd/61rfUtWtXbdiwQR//+MdVVVWVs2PVreUyc+ZMLVu2rMna3bsP/oetZ8+euuKKKyRJ//7v/67y8syroNfW1mrfvn31zy+44AL16tVL1dXVuvvuuw+rr6mp0fe///1me7/88svVv39/rVq1qn6B44svvrh+dg8AAACAzslra5VaOE/aXZqoPnjHeAUjj89xV20bAQ3QiEmTJuknP/mJgiDQH//4R02cOFH3339//cK8UrQ479q1a/Xd735Xf/3rX4/6WNddd51OP/10VVVV6bzzztPPf/7z+oV9JWnr1q16+OGHde655x4WpnznO99Rv3799MYbb+jMM8/UU089VX/Za3fXmjVrdNddd2nMmDF65ZVX6scVFxfry1/+siTpm9/8pu666676BYjXr1+vyy+//JCrPmVSVFSkq6++WpI0d+5cSSwODAAAAHR2nqpVuHCeVLorUX0wdpyCUSfmuKu2zzJdpQZti5ktmjRp0qRFixYlql+1apWkgwve4ug8+eSTuuGGG+oXwZWkbt26qaSkROXl5aqurq5//cILL9QPfvADjR49WpI0Z84cvfvd79aIESO0fv36Jo+zfft2zZgxoz7kCIJAffr0UXV1tSoqKurrbr/9dn3jG984ZOzChQt12WWX1a8Z06VLF/Xq1Uvl5eX1V4iq6yd9fZ3a2lpdeeWV9VddKiwsVElJifbs2aPCwkI99thj9TN01q1bp5EjRzba+8qVKzVu3DhJ0pAhQ7Rp0yYVFh752ZN8ZwEAAID2z1MphQvnyXftSFQfjDlFwQkn57ir3Jo8ebIWL1682N0nt2Q/zKABmnDJJZfozTff1H333afLL79cI0aMUBAEKisrU9++fXXuuefq1ltv1cqVK/WXv/ylPpw5UoMGDdJzzz2nhx9+WBdddJEGDhxYf8rSmDFj9IlPfEKPP/64vvrVrx42durUqVq9erXuvPNOnXnmmfUhS48ePTRlyhR9/vOf13PPPXdIOCNFgczvfvc7/ehHP9Kpp56qwsJCFRQU6OKLL9Zzzz2nGTNmJOr9lFNO0cknR/9Bvfrqq48qnAEAAADQ/nkqpfCVl5OHM6Pf0e7DmWxiBk07wQwatFWbNm3SyJEjFYahVq1apTFjxhzVfvjOAgAAAO2Xp1IKF82X79iWqD44eayCk47ub4e2hhk0ANqE++67T2EY6pxzzjnqcAYAAABA++VhqHDxgsThjJ04usOEM9lEQAPgqC1ZsqR+4eIvfOELee4GAAAAQGurD2e2b22+WJKdcLKCk5k13xgWiwBwxM4++2y9+eab2rp1q9xd73znO3X55Zfnuy0AAAAArcjDUOGShfJtbzdfLMmOP0nB6HfIzHLcWfvEDBoAR2zz5s16++23NWjQIF133XV64okn+I8sAAAA0Il4GCpc+op865ZE9TbqBAVjTuHvhiYwgwbAEWvusuEAAAAAOi53V7hskfzttxLV28gTFIwdTzjTDGbQAAAAAACAROrDmS2bE9XbiFEK3kE4kwQBDQAAAAAAaJa7K1y+WP7WpkT1dtxIBadMIJxJiIAGAAAAAAA0yd0Vrlgi37wxUb0dO0LBuImEM0eAgAYAAAAAAGTk7gpfXSrftCFRvQ0/TsH40whnjhABDQAAAAAAaJS7K1y5XL5xfaJ6O+ZYBadOIpw5CgQ0AAAAAADgMO6u8LUV8g1vJqq3YcMVTJhMOHOUCGgAAAAAAMAh3F3hqhXy9WsT1dvQYwhnWoiABgAAAAAA1HN3hatXytclDGeGDFMwcYosIGJoCT49AAAAAAAgKQ5nXn9N/uaaRPU2eKiC06YSzmQBnyAAAAAAAJAkhWtWy9e+kajWBg3P+BIYAAAgAElEQVRRMGka4UyW8CkCAAAAAIAonFmzOlGtDRxMOJNlfJIAAAAAAHRy4T9eV/jGqkS1NmCQgsnTZQUFOe6qcyGgAZqxf/9+/fSnP9Ull1yi4447Tj169FBxcbFGjRqlK6+8Ug899JAqKysPGTNy5EiZWaLb0qVLDxn7rne9S2ama665JnGPM2fOTHSsyy67LBsfCQAAAIAOJFz7hsLXX0tUa/0HKphyOuFMDhTmuwGgLXvyySd1ww03aOvWrfWvFRcXKwgCrV+/XuvXr9fvfvc7feUrX9GvfvUrnXfeeYeMLy4uVklJSZPH6NKlS1Z7Hjx4cMZtffv2zeqxAAAAALRv4ZtrFK5emajW+g1QMJVwJlcIaIAMZs6cqeuuu05hGGr06NG67bbbdOGFF6p///6SpL179+rZZ5/Vvffeqzlz5uj5558/LKC55ZZbdPvtt7dq3+lhEgAAAABkEq5bq3DVq8mK+/VXMPUMWQExQq7wyQKNWLZsmW666SaFYaiLLrpIv/3tb9W9e/dDanr37q0rrrhCV1xxhR577DFt3rw5T90CAAAAwJEJ17+p8LXlyYr79lPB1DNkhUQIucSnCzTitttuU3V1tY455hg98sgjh4UzDV111VVy91bqDgAAAACOXrhhncKVy5IV9+mrgqlnygqzuzQDDkdA08n8eXHHnuXxgUnDW7yPt956S7NmzZIkff7zn1fv3r0TjTOzFh8bAAAAAHIp3Lhe4atLmy+UpN59VTDtLFmW181E47iKE9DAnDlz6mfDXHrppXnuBgAAAACyI9y0QeGKJcmKe/VRwfQzCWdaETNogAZWrVolSSoqKtLo0aNbtK/vfe97+tnPfpZx+7hx4/Tss8+26BgNDRkypNHXe/furddffz2rxwIAAADQPoSbNypcvjhZca/eKph+lqxL19w2hUMQ0AAN7Nq1S1J0SeqWnrZUUVGhioqKjNszhSktsW3btkZfr6qqyvqxAAAAALR94VubFC5blKy4Z68onOlKONPaOMUJyKFvfOMbcveMt6VLE577eQQyHWvPnj1ZPxYAAACAti3cslnh0leSFZf0VMH0s2Vdi3LbFBpFQAM00L9/f0nS7t27uTITAAAAgHYrfPut5OFMcYkKTj9bVkQ4ky8ENEADY8eOlSRVV1ezZgsAAACAdincukXhkoVSkn90Li5RwennyIq65b4xZERAAzRw7rnn1q8986c//SnP3QAAAADAkQm3va1w8YJk4UyP4mjmTDfCmXxjkeBO5gOThue7hTZv+PDhuuiiizRr1izdc889uummm9SrV69mx7l7ixcVBgAAAICWCLdvPcJw5hxZt+65bwzNYgYN0IhvfetbKioq0ubNm/XRj3602SsgPf7447rrrrtaqTsAAAAAOFy4Y5vCRfOlMGy+uHuPaOZMd8KZtoKABmjExIkT9eMf/1hmplmzZum0007TQw89pNLS0vqavXv36oknntC73/1uXXXVVSovL89qD9XV1dq5c2eTtzDJf3gBAAAAdHjhzu0KX3k5YTjTPQ5neuS+MSTGKU5ABtddd5369++vG2+8UatXr9bVV18tSSopKZGZHRLIjBgxQuedd95h+/je976nn/3sZ00e5+6779ZVV1112OuPPvqoHn300SbHrlu3TiNHjkzwbgAAAAB0VOGuHQoXJgxnunWPLqXdozj3jeGIENAATbjsssv03ve+Vw8++KBmzZql5cuXa+fOnTIzjRw5UlOmTNGMGTM0Y8YMFTVyObqKigpVVFQ0eYzKyspctQ8AAACgg/PSnQoXzpPCVPPFRd2imTPFJblvDEfMPMnCQcg7M1s0adKkSYsWLUpUv2rVKkkHLxkNtHV8ZwEAAIAj46W7lFowV0olCWeKogWBS3rmvrFOZvLkyVq8ePFid5/ckv2wBg0AAAAAAO2M7y5VauFLycKZrkXRaU2EM20aAQ0AAAAAAO2I79kdzZyprW2+uGvX6LSmnr1y3xhahIAGAAAAAIB2wvfuVmp+wnCmS9do5gzhTLtAQAMAAAAAQDvge/fE4cyB5ou7dFHB9LNkvXrnvjFkBQENAAAAAABtnJftjcKZAwnCmcIu0cyZ3n1y3xiyhoAGAAAAAIA2zMvLlJr/onSgpvniwsJo5gzhTLtDQAMAAAAAQBvl5WVKvfyiVJMwnJl2lqxP39w3hqwjoAEAAAAAoA3yfeXRzJma6uaLCwpVMPVMWd9+uW8MOUFAAyDv3D3fLQAAAABtilfsi2bOVCcJZwpUMO0MWb/+uW8MOUNA00GZmSQpDMM8dwI0ry6gqfveAgAAAJ1ZFM68IFVXNV8cFEQzZ/oNyH1jyCkCmg6qqKhIklRRUZHnToDm1X1P6763AAAAQGfl+yuimTNVScKZQMHUM2T9CWc6AgKaDqpnz56SpK1bt6q8vFxhGHIaCdoUd1cYhiovL9fWrVslHfzeAgAAAJ2R798fhzOVzRcHgYIpZygYMDD3jaFVFOa7AeRGv379VFFRof3792vz5s35bgdoVo8ePdSvHwuaAQAAoHPyyv3RaU2V+5svDgIFk09XMHBQ7htDqyGg6aCCINCxxx6r0tJSlZeXq7q6mhk0aHPMTEVFRerZs6f69eunIGBSHwAAADofr6qMZs4kCWfMFEyarmDQ4Nw3hlZFQNOBBUGgAQMGaMAAzkcEAAAAgLbIq6qimTP7E6wfaqZg8nQFg4fkvjG0Ov65GgAAAACAPKgPZ5Jc3MVMwaRpCgYPzX1jyAsCGgAAAAAAWplXVys1/0WpYl/zxWYKTpuqYMiw3DeGvCGgAQAAAACgFXlNHM7sK09UH0ycomDoMTnuCvlGQAMAAAAAQCuJwpm5UnlZovpg4hQFw4bnuCu0BQQ0AAAAAAC0Aj9QE4UzZXsT1QcTJik45tgcd4W2goAGAAAAAIAcO+Jw5tTTFAwfkeOu0JYQ0AAAAAAAkEN+4IBSC16S9u5JVB+Mn6jg2JG5bQptDgENAAAAAAA54rVxOLNnd6L6YNwEBceNynFXaIs6REBjZj3N7FIzu8PMZpvZTjPz+DammbGe4HZlM/uYYmaPmtkWM6sys41m9gszOzG77xQAAAAA0F54ba1SC+ZJe0oT1QfvOFXBiONz3BXaqsJ8N5Al75H0+xbuY6ekVIZtVZkGmdk/S/qFos/SJZVJOlbSdZL+ycwudff/a2FvAAAAAIB2xGtrlVr4krR7V6L6YOx4BaNOyHFXaMs6SkAjSdslvSJpoaS3JN13hOOnuvv6IxlgZqdK+rmiz/FhSV909x1mNiJ+/b2SfmdmJ7v7jiPsBwAAAADQDnmqVuEr86TShOHMmHEKjucEjM6uowQ0T7r7H+qemNnIVjruf0jqoigY+md3T0mSu28wsxmSXlM0m+arkv61lXoCAAAAAOSJp1IKX3lZvmtnovpg9DsUnHBSjrtCe9Ah1qCpC0Zak5n1kXRR/PSuhj24+z5JP4uffsTMrDX7AwAAAAC0Lk+lFC6aL9+Z7ASK4OSxCk4cneOu0F50iIAmT85WNHtGkp7OUPPX+H6opLE57wgAAAAAkBeeSilcPF++Y1uiejtpjIKTmrymDToZApqDHjez3WZWbWabzex3ZnZxE/XviO+3unumEwtfa6QeAAAAANCBeBgqXLJAvj1hOHPiaMIZHIaA5qCpkgokHZB0jKQZkv5sZo+bWddG6ofG91sy7dDdKyXtaVAPAAAAAOggPAwVLl4g37Y1Ub2dcJKCk8eKVTDQEAGN9KCk90vq6+693L1E0elID8TbPyTp3kbGFcf3lc3sf398X9LSRgEAAAAAbUc0c2ahfNvbiept1IkKRp9COINGdfqAxt2vcfe/uvuetNdWu/u1kr4bv3S9mbFyEwAAAABAUhzOLFsk35rxpIpD2MgTFIwdRziDjDp9QNOMbyqaIWOSPtBgW0V8372ZffSI7/dlsS8AAAAAQJ64u8Jli+VbNieqtxHHK3jHeMIZNImApgnuXiHp1fjp8Q0218WkwzKNN7PukvrET5PNeQMAAAAAtFlROLNIvmVTono7bpSCU04lnEGzCGiOXt0VmoaYWf8MNelXbnotQw0AAAAAoB1wd4XLl8jfShjOHDtCwbgJhDNIhICmCWZWLGlc/HRdg80vKrrikySdn2EXF8T3WyStym53AAAAAIDW4u4KVyyVb96QqN6GH6dg/GmEM0isUwc01vxvytcVrTHjkv6SvsHd96a99iUzO+SzjMOdm+Knv3Z3b3nHAAAAAIDW5u4KX10m37Q+Ub0dc6yCUycRzuCIdJiAxswG1N0k9U3b1Cd9W4Mg5XEz+7aZTTGzrmn7Gm1mP5f0lfilB929sVOUvqFoFs00STPjY8vMjpP0hKTjJO2RdGfW3igAAAAAoNW4u8KVy+UbG55U0TgbNlzBhMmEMzhihfluIIt2ZHh9XoPnoyStjx8PlHSlpFslpcxsr6QiScVp9b/VwZkwh3D3ZWb2KUm/kHS1pI+bWZmk3nFJhaQr3D1TbwAAAACANsrdFb62Qr7hzUT1NvQYwhkctQ4zg+Yo/aekeyQtlLRdUTATKFpv5teS3ufuH3L36kw7cPcHJZ0h6XFJ2xSdErVJ0v2SJrr7/+X0HQAAAAAAss7dFa56Vb5+baJ6GzJMwcQpsqCz/5mNo9VhZtC4+xFHlO7+tKSns3DsVyRd1dL9AAAAAADyz90Vvr5Svu4fiept8FAFp00lnEGL8O0BAAAAACDm7grfWCVfuyZRvQ0aomDSNMIZtBjfIAAAAAAAYr5mtfwfryeqtYGDCWeQNXyLAAAAAACQFK5ZrXDN6kS1NnCQgsnTZQUFOe4KnQUBDQAAAACg0wv/8brCN1YlqrUBAxVMPp1wBllFQAMAAAAA6NTCtWsUvv5aolrrP0DBFMIZZB8BDQAAAACg0wrX/UPh6leTFffrr2DKGbKCDnNBZLQhBDQAAAAAgE4pXL9W4WsrkhX37aeCqWfKCglnkBsENAAAAACATifc8KbClcuTFffpp4JphDPILQIaAAAAAECnEm5cp/DVZcmK+/SNw5kuuW0KnR4BDQAAAACg0wg3rVe4Ymmy4t59onCmC+EMco/5WQAAAACATiHcuC55ONOrtwqmnSXr0jW3TQExAhoAAAAAQIcXrn1D4eqVyYp79lLB9LNkXQln0HoIaAAAAAAAHZa7K3x9pXztmmQDevZSwfSzZV2LctsY0AABDQAAAACgQ3J3ha8ulW9cn2xASc8onCkinEHrI6ABAAAAAHQ4HoYKl74if/utZAOKSwhnkFcENAAAAACADsVTtQoXLZDv2JZsQHGxCk4/W9atW24bA5pAQAMAAAAA6DD8wAGlXpknle5KNqBnr+hqTYQzyDMCGgAAAABAh+DV1UotmCuV7U02oE8/FUw7g0tpo00goAEAAAAAtHteuV+p+XOlin2J6m3AIAWTp8sK+bMYbQPfRAAAAABAu+b7yqOZM5WVieptyDAFE6fICgpy3BmQHAENAAAAAKDd8r17lFrwklRTnajeho9QMH6iLAhy3BlwZAhoAAAAAADtkpfuUmrhPKn2QKJ6G3WigrHjZGY57gw4cgQ0AAAAAIB2J9y+TeGi+VKYSlQfnDxWduJowhm0WQQ0AAAAAIB2JdyyWeHSVyT3RPXBKacqGHlCjrsCWoaABgAAAADQboQb1ylcsTRZsZmCUycpGH5cbpsCsoCABgAAAADQLoRr31C4emWy4iBQcNpUBUOG5bYpIEsIaAAAAAAAbZq7K3z9NfnaN5INKChUMOV0BQMG5rYxIIsIaAAAAAAAbZa7K3x1mXzjumQDunRRwbQzZX365bYxIMsIaAAAAAAAbZKHocJli+RbNicbUNRNBdPPkvXsldvGgBwgoAEAAAAAtDmeSilcvEC+fWuyAT2Ko3CmR3FuGwNyhIAGAAAAANCm+IEDSr3yslS6M9mAnr1UMO0sWbduuW0MyCECGgAAAABAm+E11UoteEnauyfZgD59VTD1TFnXrrltDMgxAhoAAAAAQJvglZVKLZgr7StPVG/9ByqYcrqskD9t0f7xLQYAAAAA5J1X7FNq/lypcn+iehs8VMFpU2UFBTnuDGgdWQ9ozKy/pGmShkoaIKm7pF2SdkpaLWmZu3u2jwsAAAAAaJ+8bG80c6a6OlG9DT9OwfjTZEGQ486A1pOVgMbMTpX0SUkXSBrTTHm5mb0k6VFJv3H3ymz0AAAAAABof7x0l1IL50m1BxLV28gTFLxjvMwst40BraxFAY2ZfUTSlyRNqnspvi9XNGNmt6QqSX3j20BJvSS9X9L7JP3IzB6R9F/uvqklvQAAAAAA2pdwxzaFi+ZLqVSi+uCkMbKTxhDOoEM6qoDGzC6S9G1JpyoKZd6S9FtJcyW94u7rM4zrrijMmSrpA5LOlXSTpGvM7KeS/tPddx1NTwAAAACA9iN8+y2FSxZKCVfACN4xXsGoE3PcFZA/RzuD5s+SUpIelvQLSS8kWVcmPp1pbnz7oZkNknSVpC/Et72S/uMoewIAAAAAtAPhpvUKly9JXB9MmKRg+IgcdgTk39EGND+X9B13X9eSg7v7dkn3mNmPJX1UEosHAwAAAEAHFr65RuGqV5MVB4GC06YqGDIst00BbcBRBTTufmM2m3D3UNJD2dwnAAAAAKDtcHeFb6yS/+P1ZAMKChRMOV3BgEG5bQxoI7J+mW0AAAAAANK5u8KVy+Ub3kw2oEsXFUw9U9a3X24bA9qQVg1o4kWCu7r73tY8LgAAAAAgPzwMFS5fLH8r4YV7i4pUMO0sWa/euW0MaGOCbO3IzI41sxvM7NJGto03s/mKLr9dambzzOyUbB0bAAAAAND2eCqlcPH85OFM9x4qOOOdhDPolLIW0Ei6XtJPJU1Of9HMekt6VtKU+Hgmabqkv5nZgCweHwAAAADQRnjtAYULX5Jv25psQElPFZz5TllxSW4bA9qobAY058f3jzV4/VOSBkraKOn9ks6VtCJ+7QtZPD4AAAAAoA3wmmqlXn5RvmtnsgG9+6rgjHNk3brntjGgDctmQHOsostkr2nw+uXx619x96fd/QVFoY1JujiLxwcAAAAA5JlXVSo17wVp755E9dZ/gApOP0vWtSjHnQFtWzYXCR4oaY+7H6h7wcy6SZoq6YCkJ+ted/cFZnZA0glZPD4AAAAAII+8Yp9S8+dKlfsT1dvgoQpOmyorKMhxZ0Dbl82AJiWpV4PXTo+PMc/dKxtsK5dUnMXjAwAAAADyxMv2KrVgrlRdnajejjlWwamTZEE2T+wA2q9s/iask1RgZmemvXalotObnk8vNLMuknpL2pbF4wMAAAAA8sB3lyr18gvJw5kRxyuYMJlwBkiTzRk0T0k6RdIDZnabpKGKruwkSb9vUDtBUoGihYMBAAAAAO1UuHO7wldellKpRPV24mgFJ4+VmeW4M6B9yWZA89+SPibpJEmPxq+ZpD+6+4IGtXULBz8vAAAAAEC7FG7donDJQikME9UHY8crOP7EHHcFtE9ZC2jcfYeZnS7pdknTJZVJ+oukO9Pr4tObPhRv/2u2jg8AAAAAaD3hpg0Kly9OXB+cepqCY0fmriGgncvmDBq5+0ZJ1zZTc0DSydk8LgAAAACg9YTr/qHwtRXJis0UnDZVwdBjctsU0M5lNaABAAAAAHRc7q5wzWr5mtXJBhQUKJg8XcHAwbltDOgACGgAAAAAAM1yd4WvrZCvX5tsQGEXFUw9Q9avf24bAzqIowpozOz+LB3f3f26LO0LAAAAAJADHoYKVyyRb054Id6iIhVMO0vWq3duGwM6kKOdQXONoqswNXZdNE973HB7w20uiYAGAAAAANooT6UULlko3/Z2sgHde6hg+lmy4pLcNgZ0MEcb0Hwzw+tdJX1GUm9JGxRdRvuteNswSe+UNFLSHkk/k1R9lMcHAAAAAOSY1x5Q+Mp8+a4dyQYUl6hg+tmy7t1z2xjQAR1VQOPuhwU0ZtZV0t/jfV7t7g83NtbMPiLpPknnSHrP0RwfAAAAAJBbXlOj1MKXpD27kw3o3UcF086UdS3KbWNABxVkcV9flXS6pE9nCmckyd1/LenTks6S9OUsHh8AAAAAkAVeVanUvOeThzP9BkQzZwhngKOWzYDmI5JqJP06Qe2jik5v+mgWjw8AAAAAaCHfX6HUvBekfeWJ6m3QkGjmTJcuOe4M6NiyeZntEZKq3D3VXKG715pZVTwGAAAAANAGeHmZUvPnStVViept2HAFEybLgmz+2z/QOWXzt6hcUi8zG9dcoZmNV7SQcLJIFgAAAACQU76nNDqtKWk4M2KUgolTCGeALMnmb9L/Kbp09v1m1jdTkZn1kfRLRZfY/r8sHh8AAAAAcBTCnTuUenmudOBAono74WQFp0yQmeW4M6DzyOYpTt+QdImkyZJeN7P7FF1me0u8ve4y25+SNFDS/ngMAAAAACBPwq1bFC5ZKIVhovpgzDgFJ5yU466AzidrAY27v2FmF0n6jaIA5t/iW0MmabukD7v7mmwdHwAAAABwZMLNGxUuXyy5J6oPxp+m4LiRuW0K6KSyerKguz8vabSimTErJIWKAhmLH6+Q9HVJY+JaAAAAAEAehOvWKly2KFk4Y6Zg0jTCGSCHsnmKkyTJ3fdIukPSHWbWRVK/eFOpuyc7oREAAAAAkBPuLv/H6wrfWJVsQFCgYPJ0BYMG57YxoJPL6XLb7n7A3bfFt5yFM2bW08wuNbM7zGy2me00M49vY5oY183MrjCzX5jZcjPbZ2bVZrbRzB4zs3c1c9w5acfJdLs3628YAAAAAI6CuytctSJ5OFPYRQXTzyScAVpB1mfQ5Ml7JP3+KMY9Ken8tOfVkg5IOja+fdjM7nb3LzSznzJJlU1sAwAAAIC88jBUuGKJfPPGZAO6dlXBtLNkvfvktjEAknIQ0JhZIOlMSeMk9ZXUpal6d/+PLB16u6RXJC2U9Jak+xKM6SJpjaSfS3rS3VdLkpmdIOm/JH1I0s1m9oa7/6SJ/dzs7jNb0DsAAAAA5IynUgqXviLfuqX5Yknq1l0F08+SlfTMbWMA6mU1oDGzyyXdI2loknJJLikbAc2T7v6HtD5GJhx3q6T57p5Kf9Hd15rZVZL6SzpP0i2SmgpoAAAAAKBN8tpahYvmy3duTzaguCQKZ7r3yG1jAA6RtYDGzM5XdIntQFKNpAWKZrJUZesYmTQMWI5g3EtNbHMz+19FAc0oM+vn7qVH2yMAAAAAtDY/UKPUgpekPbuTDejVRwXTzpQVFeW2MQCHyeYMmlsVhTPPSfqou7+dxX3ny660xwV56wIAAAAAjpBXVSm1YK5UnnBZzH79VTDlDFmXJlepAJAj2byK02RFpyxd00HCGUk6N77fJmlnE3W3mNkWM6sxsx1m9jcz+7SZdWuFHgEAAADgEL6/Qql5zycOZ2zg4GjmDOEMkDfZDGhMUpm7b8jiPvPGzI6RdFP8dKa7exPlp0jqJ6lC0gBFp0X9RNICMzsup40CAAAAQBovL1Pqpeel/RWJ6m3YcAVTTpcVdJSL/ALtUzYDmlWSijvCrBEzK5T0sKQSSRsVXdGpMXMkfULRosjd3b2vpMGKTveqljRe0l/MrGuuewYAAMD/Z+/Ow+1KqwL/f9c+mafKWHOlKqkhqcxzVTEPSiM4AdKKaAMN2IP+2tZuxV//bEHoBhW1pX2kHRhEUVpRgRahW35gUVZRUypTJam5UmOqMs/jzdmr/9gnEkKSe869++RO38/znOfcs/e79rsuz1P3XlbW+76Scv8+mnf/I5xobyvQmH0dxbJVRFHn/zWU1Bd1/lf4cao9bX6yxmcOlN+lWt50kmo/nQPnGpSZH8jMP83MF0932GTmzsz8CPCW1rCFwDsvQs6SJEmSRrByzy6a99wJPSfbGh/X30SxaBkR0eXMJLWjtgJNZn4G+CTwOxHxY3U992KLiA9TLW1qAm/PzLv68pzM/DvgjtbHH6gpPUmSJEn6LuWOFyjv+xY0T7U1vpi/kMb8hRZnpEGkzmO2P9X68gTwZxHxEWAtcOgCYZmZ764rh/6KiP8P+H+pNjt+b2b+VT8feS/wCmBuf3OTJEmSpHMpn3uGctM6uOC2md9WLFpGce2cLmclqVN17gL1TqrCxukS7LWt14UkMCgKNBHxc8B/aX382cz89EDmI0mSJEm9KZ96knLLxvYGR1AsW0Vx5dXdTUpSn9RZoPnVGp91UUXEvwF+u/XxlzLzd2t69C2t9201PU+SJEmSyEzy8UcpH93aXkBRUKy8heLSy7ubmKQ+q61Ak5lDskATEe8Afq/18YOZ+ettxsWFjt6OiNdTLW8C+Lv+ZSlJkiRJlcykfGgzue3x9gJGjaKx+jZi+szuJiapX4bNQfcRceZPm2lnfD31rHt7M7NsxbyFamPjAD6ame/vYMpfiogbgc8B92TmodYzZwHvAj7QGvcI8KlzPkGSJEmSOpCZlA+uJ599ur2AMWNorHkpccnU7iYmqd+GTYEG2HWe63ef9XkO8FTr648CjdbX/yIi/sUFnv/mzPzWGZ/HUhVi3gVkRByk2lPnzJ98DwI/mJknek9fkiRJks4vm03KDWvJF7e3FzBuPI1bXkpMmtzdxCTVovYCTUSMBt4O/HNgBTCjdWsPsA74C+DPM7On7rn74Mxjxi/rZeyYsz5/nup/v5cA11N9n6OBF4ANwF8Bf2ZxRpIkSVJ/5alTlA/cS+7e2V7AxIk01ryMmDChu4lJqk2tBZqIuB74ArCQb5/mdNqlwOuBfwb8fES8OTOfqGvuzDx7vnZiruvHfFuAX+5rvCRJkiS1I3tO0rz/bti3t72AKZdUy5rGju1uYpJqVVuBJiKmAF8HZgM9VB0k3wCeaw25GngN8CPAYuBrEbH09N4tkiRJkqTvlCeO07zvW3DwQHsB06ZXGwKPPnuxUA4AACAASURBVHsBgKTBrs4Omp+nKs48DbwxM8913tsnI+LDVKcaXduKGZKnP0mSJElSN+XRozTvvROOHmlrfMy6jGLlGqIxnLYalUaOovchbXsT1Sa5//I8xRngn5YGvZtqCdSba5xfkiRJkoaFPHSQ5t3fbL84c8VVFKtutTgjDWF1/tc7Fziamf/Q28DM/HpEHG3FSJIkSZJa8sC+alnTyZNtjY9rrqVYvJyIjrfllDSIWF6VJEmSpEEi9+ymufZuOHWqrfEx90aK+QstzkjDQJ1LnJ4AJkTEa3obGBGvBSYAT9Y4vyRJkiQNWeWOF2ned1fbxZli3gKLM9IwUmeB5otU+8p8KiJuPt+giFgKfJJqv5q/qXF+SZIkSRqSyuefpXzgHijLtsYXi5ZS3DDP4ow0jNS5xOm3gHdSneS0PiK+BPwD8DwwrnX91cD3URVyngJ+u8b5JUmSJGnIKZ/eRrl5Q3uDIyiWrqS46pruJiXpoqutQJOZhyLie4C/BhYDP9J6nel0eXcT8JbMPFTX/JIkSZI01JSPP0L5yHkPwf1ORUGxYg3FZVd0NylJA6LWTYIz8/GIWAX8KFVxZgUwq3V7F7AO+CvgLzKzp865JUmSJGmoyEzKh7eQTz7WXsCoUTRW3UbMmNndxCQNmNpPcWoVXj7bekmSJEmSzpCZlJs3kM881V7A6DE01ryEmDqtq3lJGlgesy1JkiRJF0mWJeWGteQLz7cXMG4cjTUvJSZP6W5ikgZcbQWaiGgAVwGnMnN7L2OvbM39XGa2t025JEmSJA1h2TxF+cB95K4d7QVMmEjjlpcSEyZ2NzFJg0Kdx2z/KLAN+GAbY3+rNfYtNc4vSZIkSYNS9pykee9d7RdnJk+hcdsrLM5II0jdBRqAT7Yx9vepTnT6sRrnlyRJkqRBJ0+coHnPnbBvb3sBU6fTuO3lxLhx3U1M0qBS5x40i4BTwH1tjL2rNXZJjfNLkiRJ0qCSx47SvPcuOHK4rfEx81KKlbcQo9wuVBpp6vyv/krgYGY2exuYmaci4kArRpIkSZKGnTx8qCrOHD/W1vi4/EqKZauIRqPLmUkajOos0BwFpkTEqMw8daGBETEamNKKkSRJkqRhpdyzi/KBe6Gnp63xcfW1FIuXEUWdu1BIGkrq/K//YaqCz+vbGPt6YDTwaI3zS5IkSdKAK599mvLeu9ovzsy5gWLJcosz0ghX50+AL1Bt/PvfIuLy8w2KiCuA3wES+GKN80uSJEnSgMlMmg9vody0DjLbiiluupni5kVERJezkzTY1Vmg+TjwNDAX2BgR/zEiFkbE5NZrUUT8IrABmAM8B/xujfNLkiRJ0oDIZpNy/f3kE+0vEigWLqG4cb7FGUlAjXvQZObRiHgj8L+Bq4Ffb73OFsDzwBszs72tzCVJkiRpkMoTx2muvQf272svIIJiyQqKq2d3NzFJQ0qtixwzcyuwFPhNYCdVMebM1w7go8DSzNxc59ySJEmSdLHloYM07/pm+8WZoqBYscbijKTvUucpTgBk5j7gF4FfjIhrgctat3Zk5tN1zydJkiRJA6HctYNy3X1w6oKH2H7bmLE0Vt1KTJve3cQkDUm1F2jO1CrIWJSRJEmSNKyUT2+j3LKx7c2AmTSZxurbiAkTu5uYpCGrawWaqHa6mgFMyMxnujWPJEmSJF0smUn50IPktifajomZl1KsWEOMHt3FzCQNdbXuQQMQEbdFxP8CDlLtOfPkWfenRsQnI+ITETGh7vklSZIkqRvy1CnKB+7prDgzew7F6tsszkjqVa0dNBHx08DvAI3zjcnM/RExE/h+4JvAn9aZgyRJkiTVLY8fo3n/3XDwQNsxxc2LiTnXe4y2pLbU1kETEWuAjwEl8EvAbKoOmnP5NNWpTm+oa35JkiRJ6oY8sJ/mnbe3X5xpNChW3Uox9waLM5LaVmcHzc9TFV0+kJm/AVzoh9E3W+8rapxfkiRJkmpV7niBcv390Gy2FzB2XLUZ8CVTu5uYpGGnzgLNy1vvH+9tYGbui4hDwNU1zi9JkiRJtchM8qknKLc+2H7QlEuq4sy48d1LTNKwVWeBZiZwMDPbXZTZBMbUOL8kSZIk9VuWJeXWTeTT29qOiUsvp1i+mhjVtYNyJQ1zdf70OABMj4gxmXnyQgNbmwRfAjxf4/ySJEmS1C/Z00O5/j5y1862Y2LO9dWGwO43I6kf6jxmeyPVHjQv720g8M7W2HtrnF+SJEmS+iyPHqV59x3tF2ciKBYtpbFgicUZSf1WZ4HmT6iKLh+JiEnnGxQRrwM+CCTwqRrnlyRJkqQ+yf17aX7rdjh0sL2AUaMoVt1Gce3cbqYlaQSpc4nTZ4F/AbwWuDciPgGMBYiIHwCuBb4P+GdUhaEvZOZXa5xfkiRJkjpWvvA85Ya1UJbtBYwfT2P1S4jJU7qbmKQRpbYCTWZmRLwJ+FPgh4DfPOP2F1vvp/v+/oaqmCNJkiRJAyIzyScepXxka/tBU6fRWHkrMW5c9xKTNCLVusV4Zh4G3hQRr6XaZ+Y24AqqjpkdwN3AH2fm/6lzXkmSJEnqRJYl5YMbyOeebjsmLr+SYtlKouFJTZLq15WfLJn5deDr3Xi2JEmSJPVH9pykfOBecs/utmPi+pso5i1wM2BJXWPpV5IkSdKIkUcO07z/bjhyuL2ACIrFyymuuba7iUka8S5KgSYipgE3ACeBRzLz+MWYV5IkSZJOy727aa69F3pOthcwajTFylsoZs7qbmKSRD8KNBExCljQ+rg1M0+dY8ws4PepNg0+3Qt4LCL+CHhfZrb5k1GSJEmS+q58/lnKTevaP6lpwkQaq28jJk3ubmKS1NKfDprXAl8BnsrM68++GRETgNuB+Xy7OAMwAfh3wNXAW/sxvyRJkiRdUGZSPvYw+djD7QdNm0Fj1S3EmLHdS0ySzlL0I/ZVVIWXPz7P/X8P3Nz6+mvAj1N10vxlK+7NEfG9/ZhfkiRJks4rm03KDWs7Ks7EVdfQuOWlFmckXXT96aC5DUjg785z/z2t+9/KzH92xvW/jYgG8Bbg7VTFG0mSJEmqTZ44QfOBe2Df3rZjiptuJm6Y50lNkgZEfzporgaawMazb0TE9cB1rY+/do7Y09fW9GN+SZIkSfouefgQzW99s/3iTFFQLFtFceN8izOSBkx/OmguBw5kZvMc925tvZ8Evn6O+xupumuu6sf8kiRJkvQdyt27KB+4F071tBcwZgyNlbcS02d0NzFJ6kV/CjQFMOU891a33rec60jtzDwVEfsuEC9JkiRJHSmffYrywQ2Q2V7AxEnVSU0TJ3U3MUlqQ3+WOL0AjIqIm85x72VUHTL3XiB+MnCkH/NLkiRJEplJ8+HNlJvWt12ciRmzaLz0lRZnJA0a/SnQ3NN6/3/OvBgRi4AVrY/nWt5ERNwIjAae7sf8kiRJkka4bJ6iXHcf+cRjbcfENddSrHkJMXpMFzOTpM70Z4nTJ4G3Af82Ikqq05yuAv5z6/4uzn/C0/e03tf3Y35JkiRJI1geP05z7T1wYF/bMcX8hcTcG90MWNKg0+cCTWZ+IyI+DbwL+JnWCyColjf9UmaeOE/4T7bG3N7X+SVJkiSNXHnwAM21d8OxY+0FFA2KZSsprvCcEkmDU386aADeCzxOVZy5onXtaeBXM/OPzxUQEa+gOuXpFPDlfs4vSZIkaYQpd+6gXH8fnDrVXsDYsTRW3UZMndbdxCSpH/pVoMnMEvgI8JGImNm6truXsLupNgguM7PNcrckSZIkQfnUk5RbNrYfMHlKdVLT+AndS0qSatDfDpp/0kZh5vS4HqCnrnklSZIkDX+ZSbn1QfKpJ9qOiVmXUSxfTYwe3cXMJKketRVoJEmSJKkb8tQpyvX3kztfbDsmrp1LsWAxUfTn4FpJunj69NMqIubWnUhEFBExu+7nSpIkSRq68tgxmnff0VFxpliwhMaipRZnJA0pff2J9XBEfCYi5vU3gYgYHRE/BTwGvLO/z5MkSZI0POSBfTTvuh0OHmgvoNGgWHUrxZzru5qXJHVDX5c43Ud1VPbbI+Ifgf8J/FVm7mknOCICeBXwY8CbgenAEaCD3b4kSZIkDVfli9spN6yFZrO9gHHjq82Ap1zS3cQkqUv6VKDJzJdFxA8CHwZeCbwC+L2IeAx4ANgE7Ab2ASeBqcA0YA6wClgOTASCasPg3wM+lJm7+vXdSJIkSRrSMpPc9jjlQ5vbD5oylcbqW4lx47uXmCR1WZ83Cc7M/xURfwu8HngP8P3AvNbrbRcIjdb7k8CngE9n5gt9zUOSJEnS8JBlSbllI/nMU23HxGVXUCxbRYzy/BNJQ1u/foplZgJfBb4aEdOBVwMvBdYAVwAzgbHAXqqOmkeAu4A7M3Ntf+aWJEmSNHxkTw/luvvI3Tvbjom5N1DMX0S1g4IkDW21lZkzcy/w162XJEmSJLUljx6hef/dcPhQewERFIuWUsye093EJOkisg9QkiRJ0oDJfXtprr0HTp5oL2DUKIoVt1DMurS7iUnSRWaBRpIkSdKAKLc/R7nxASjL9gLGT6hOapo8pbuJSdIAsEAjSZIk6aLKTPKJRykf2dp+0NRpNFbdRowd273EJGkAWaCRJEmSdNFkWVI+uJ587pm2Y+KKqyiWriQajS5mJkkDywKNJEmSpIsiT56k+cC9sHd32zFxwzyKm272pCZJw14x0AnUISImR8QPRsSHIuKrEbE7IrL1mt9GfBERPxURd0fE/og4FBHrI+IXImJMG/GrIuJ/RsT2iDgeEc9ExCci4oZ6vkNJkiRpaMsjh2l+6/b2izMRFEtX0Ji3wOKMpBFhuHTQvBb4Ql8CI2I08EXgDa1LJ4EmsKz1emtEvCYzD58n/h3AJ6j+t0zgIHAN8G7gxyLiBzPzG33JTZIkSRoOcu/u6qSmnp72AkaPprHyVmLGzO4mJkmDyLDooGnZCXwF+FXgpzqI+y9UxZnjwDuBCcBE4AeAvcBq4A/OFRgRS4A/oirO/BlwWWZOBa4DvtZ6zl9HxKyOvxtJkiRpGCife4bmPXe2X5yZOJHGS19lcUbSiDNcCjR/m5mXZeYbM/MDVMWRXkXE5cDPtj6+LzM/k5nNrHwZ+Jete29rFWPO9kFgNLAWeEdm7gLIzKeBNwPPAlOBX+rrNyZJkiQNRZlJ85Gt1THame0FTZ9B4yWvJCZO6m5ykjQIda1AE5WZETG7W3OclpnNPoa+BRgLHAD+8BzP/RLwKBDAj595LyKm8u1lUb99dg6tJVG/3/r4tnDhrCRJkkaIbDYpN6wlH3+k7Zi46hoaa15KjPEYbUkjU+0Fmoi4LSL+F9VeLDuAJ8+6PzUiPtnaRHdC3fN36NWt9zsy8/h5xvx96/01Z11/GVX3zJljzvZ/Wu9XADf3KUNJkiRpCMkTJ2jecye5/bm2Y4qbFniMtqQRr9YCTUT8NHAH8P1U+69E6/VPMnM/MBN4F1UHy0Ba0HrfcoExW1vvN5/VBXM69sXM3NNL7JnjJUmSpGEpDx2kedftsH9vewFFQbF8NcWN8zypSdKIV1uBJiLWAB8DSqo9V2ZTddCcy6epCjdvOM/9i+WK1vv2C4w5fW9S69V2bGYeA/afNV6SJEkadsrdO2l+6w44drS9gDFjaNz6Moorr+5uYpI0RNR5zPbPUxVdPpCZvwFcqAr+zdb7ihrn74uJrfdjFxhz5m+YScChDmJPx0/lO4s7kiRJ0rBRPrONcvPG9jcDnjSZxurbiAkTex8rSSNEnQWal7feP97bwMzcFxGHAMvlkiRJ0hCVmZQPbyGffKztmJh5KcWK1cToMV3MTJKGnjoLNDOBg5l5oM3xTWCgfyofoepuGX+BMWduZHz4rFh6iT0z/vAFR0mSJElDSJ46VZ3UtOOFtmNi9nUUC5cSRdcOk5WkIavOAs0BYHpEjMnMkxcaGBEzgUuA52ucvy+2UxVorrzAmNP3DmfmoTOubz/r/neJiPGt5wO0/5tLkiRJGsTy+DGaa++BA/t7H9xS3LyImHODmwFL0nnUWbreSLUHzct7Gwi8szX23hrn74vTpywtvMCY06cvPXSe2MsjYkYvsWeOlyRJkoasPHiA5l3fbL8402hQrLyFYu6NFmck6QLqLND8CVXR5SMRcd4NcSPidcAHgQQ+VeP8ffEPrfeXR8S484z53tb718+6fifQ0/r6e84T+7rW+3a+u8AjSZIkDSnlzherk5qO93ZORsvYcTRueznF5RdqWJckQb0Fms9SFTFWAfdGxM8BYwEi4gci4mci4u+ArwDjgC9m5ldrnL8v/gY4QbUM6T1n34yIHwDmURWTPnfmvdZeO19pffz5iCjOip0I/OvWx89ltrulvSRJkjT4lNueoLz/bmieai9gyiU0Xvoq4pJp3U1MkoaJ2go0rQLEm4AvATcDv0m1zwzAF4GPAd/XmvNvgJ+sa26o9rU5/QLO/C0w9cx7ZxZSMvPFVl4AvxERPxkRjdbz3gB8unXvc5m56RzTvp+qi2YN8MetuYmI2a3vcTawH/j1+r5TSZIk6eLJsqS5eSPl1nP9OXxucellNG57OTG+t/M0JEmn1blJMJl5GHhTRLyWap+Z24ArqIoyO4C7gT/OzP9T57wtu85z/e6zPs8Bnjrj8y8Di4A3UC3T+qOIaPLt05fu59udMN8hMzdGxHuBT1AVnH4iIg7y7cLUEeAtmXm+3CRJkqRBK0/1UK67n9y1o+2YuO56igWL3W9GkjpUa4HmtMz8Ot+9Z8uglJk9raVM76UqKi0AGsAGqmVNv3OhU6ky8zMRsQX4BeAVwHTgWeBrwEcy8/HufgeSJElS/fLYUZr33w2HDrYdUyxcSnHd3C5mJUnDV1cKNAMhM/tcos/MEviD1qsv8WuBH+3r/JIkSdJgkvv30Vx7N5w40V5AYxTFitUUl17e3cQkaRgbNgUaSZIkSf1Xvridcv1aKJvtBYwbT2P1bcSUS3ofK0k6r9oLNBExDXgj1b4u04DRFxiemfnuunOQJEmS1JnMJJ98jPLhLe0HXTKNxqpbiXHjupeYJI0QtRZoIuI/AB+kOkYboLdlRwlYoJEkSZIGUJYl5eaN5LNPtR0Tl19JsWwl0bApX5LqUNtP04h4D/DR1sfHgX+gOrmpzd5ISZIkSRdb9pykXHcfubv9g0fj+hsp5i30pCZJqlGd5e6fpeqI+X3gZzIza3y2JEmSpJrl0SPVSU2HD7UXEEGxaBnF7Ou6mpckjUR1FmhuoCrQvM/ijCRJkjS45d49NB+4B06ebC9g1GiKlWsoZl7a3cQkaYSqs0CzG5iYmYdrfKYkSZKkmpXbn6Pc+ACUZXsBEyZWJzVNmtzdxCRpBCtqfNY3gEsi4toanylJkiSpJplJ+djDlOvvb784M206jZe80uKMJHVZnQWaDwEHgI9FRJ3PlSRJktRP2WxSbnyA8tGH2o6JK6+mccvLiLFju5iZJAlqXOKUmY9HxBuAzwFbIuI3gc3AC73EPVNXDpIkSZK+W548QfOBe2HvnrZj4sb5FDfO96QmSbpI6tyDBuAx4H8D/wr4wzbGZxdykCRJktSShw9VJzUdPdJeQFFQLFlBcdU13U1MkvQdaiuORMRVwDeBOacvtRNW1/ySJEmSvlPu2V2d1NTT017A6DE0Vt1CTJ/Z3cQkSd+lzu6V/wrMBV4EfhH4/4Gdmdnm7mOSJEmS6lI+9zTlpvWQ2V7AxEnVSU0TJ3U3MUnSOdVZoHkd1ZKlt2bmXTU+V5IkSVKbMpPy0YfIxx9pOyZmzKRYeQsxekwXM5MkXUidBZrJwBGLM5IkSdLAOH1SU77wfNsxcfVsisXLicKDWCVpINVZoHkcmB8RozLzVI3PlSRJktSLPHGc5tp7YP++tmOKeQuI62/ypCZJGgTqLJN/AhgL/EiNz5QkSZLUi9y3h+adt7dfnCkKihVrKG6YZ3FGkgaJ2jpoMvP3IuJlwB+0umg+W9ezJUmSJH23zCSffIzyka3tbwY8diyNVbcSU6d3NzlJUkfqPGb7U8AxoAQ+ExH/FdgKvHCBsMzMd9eVgyRJkjRS5MkTlBseIHftaD9o0mQaq19CTJjQvcQkSX1S5x4076Q6xel0j+Q1rdeFJGCBRpIkSepA7t1Nc/39cPx42zEx61KK5WuI0aO7mJkkqa/qLND8ao3PkiRJknSWzCSfeJTy0YfaX9IExOw5FAuXeFKTJA1ide5BY4FGkiRJ6pI8cYJy41py186O4ooFi4nrrnczYEka5OrsoJEkSZLUBbmntaTpRPtLmhg9mmLpKorLLu9eYpKk2ligkSRJkgapzCQff6Ra0tSJqdNoLF/jZsCSNIT0qUATEbNbX/Zk5gtnXetIZj7TlzhJkiRpOMsTxynXryX37OooLubeSDFvgfvNSNIQ09cOmm2t94eBhWdd60T2IwdJkiRpWCp376LccD+cONF+0OgxFEtXuqRJkoaovhZHTu8wVpzjWl+eI0mSJI14mUn52MPkYw93FjhterWkafz47iQmSeq6PhVoMvO7+iXPdU2SJElSe/L4ccoN95N7dncUF9ffRHHTzS5pkqQhzuVFkiRJ0gArd+2k3LAWTnawpGnMGIplqyhmXda9xCRJF02fCzQR8Q1gT2a+tcZ8JEmSpBEjy7Ja0vT4I50FTp9BY/lqYpxLmiRpuOhPB82rgBdrykOSJEkaUfL4MZrr74e9ezqKixvmUdw43yVNkjTMuMRJkiRJusjKnTsoN66FkyfbDxozlmL5KoqZl3YvMUnSgLFAI0mSJF0kWZaUjz5EPvFoR3ExYybFstXEuHFdykySNNAs0EiSJEkXQR47Wi1p2re3o7i4cX61pCmiS5lJkgYDCzSSJElSl5U7XqyWNPX0tB80dizFstUUM2d1LzFJ0qDR3wLNJRHxqX7EZ2a+u585SJIkSYNSliXlI1vIJx/vKC5mzqJYtooY65ImSRop+lugGQe8o4+xASRggUaSJEnDTh49SnP9fbB/X0dxxU03EzfMc0mTJI0w/S3Q9AB315GIJEmSNFyUL26n3LSuwyVN42gsX03MmNm9xCRJg1Z/CzR7M/PVtWQiSZIkDXFZlpQPbya3PdFRXMy6lGLpKmLs2C5lJkka7NwkWJIkSapBHj1Cc939cKCDJU0R1ZKm629ySZMkjXAWaCRJkqR+Kl94nnLTejjVwZKmceNpLF9FTHdJkyTJAo0kSZLUZ9lsUj60mXz6yY7i4tLLKJauJMa4pEmSVLFAI0mSJPVBHjlMc/39cGB/+0ERFPMWEnNvcEmTJOk7WKCRJEmSOlQtaVoHp061HzR+fHVK07QZ3UtMkjRk9blAk5lFnYlIkiRJg102m5RbHySf2dZRXFx2OcWSlcSYMV3KTJI01NlBI0mSJLUhjxymue4+OHig/aAIivmLiDnXu6RJknRBFmgkSZKkXpTPP0v54AZodrKkaQKNFauJqdO7l5gkadiwQCNJkiSdRzablFs2kc8+1VFcXHYFxdIVxGiXNEmS2mOBRpIkSTqHPHyoWtJ06GD7QUVRLWm6bq5LmiRJHbFAI0mSJJ2lfO4Zys0boNlsP2jCxGpJ0yXTupeYJGnYskAjSZIktWTzFOXmjeRzz3QUF1dcRbF4OTF6dJcykyQNdxZoJEmSJCAPHayWNB0+1H5QUVAsWEzMnuOSJklSv1igkSRJ0ohXPvs05eaNUHawpGniRBrL1xCXTO1eYpKkEaMrBZqIuBpYBEwDLtjnmZl/0o0cJEmSpN7kqVOUmzeQzz/bUVxceTXF4mXEKJc0SZLqUWuBJiJuAT4GrO4gzAKNJEmSLro8dJDmA/fCkcPtBxUFxcIlxDXXuaRJklSr2go0EbES+AYwDgjgOeB54Hhdc0iSJEn9lZnks09TbtkIZdl+4MRJNFasIaZc0r3kJEkjVp0dNB8AxgMPAu/KzHU1PluSJEnqtzzVQ/ngRnJ7h0uarrqGYtEyYpRbOEqSuqPO3zAvARJ4e2ZurvG5kiRJUr/lwQPVKU0dLWlqUCxaQlx9rUuaJEldVWeBZhxw2OKMJEmSBpPMJJ95inLrps6WNE2aXC1pmjyle8lJktRSZ4HmcWBeRIzKzFM1PleSJEnqk+zpoXxwPfnC8x3FxdWzKRYudUmTJOmiKWp81qeBMcAP1fhMSZIkqU/ywH6ad/5DZ8WZRoNi6QoaS1danJEkXVR1/tb578Drgd+PiO2ZeXeNz5YkSZLakpnk09soH3rQJU2SpCGjzgLNLwP3AWuAOyPiH4H7gUMXCsrMD9aYgyRJkkaw7Omh3LSOfHF7R3FxzbUUC5cQDbtmJEkDo+5jthM4vb39K4CXX2B8tMZboJEkSVK/5f591SlNx462H9RoUCxeTnHVNd1LTJKkNtRZoPkTqoKLJEmSdNFkJvnUE5QPbYbs4M/RyVOqJU2TJncvOUmS2lRbgSYz31nXsyRJkqR2ZM9Jyo3ryB0vdBQXs6+jWLCEaDS6lJkkSZ1xka0kSZKGpNy3l+b6+ztb0jRqVLWk6cqru5eYJEl9YIFGkiRJQ0pmktsep3x4S2dLmqZcUi1pmjipe8lJktRHXSnQRMSrgH8OrABmtS7vAtYBf5mZt3djXkmSJA1vefIk5cYHyJ0vdhQX186luHmRS5okSYNWrQWaiJgJ/BnwPacvnXF7DrAa+FcR8TXgJzJzd53z90VEdLKx8asy85tnxF4HbGsjbnVmru0wNUmSJJ0h9+6pljQdP9Z+0KhRFEtWUFxxVfcSkySpBrUVaCJiDPA1YAlVYeZu4BvAc60hVwOvAW4Dvhf4+4i4NTNP1pVDH+3o5f4UYDxwEtjcx+f0dJqUJEmSKplJPvkY5SNbO1vSdMlUGstXu6RJkjQk1NlB8zPAUmAv8LbM/No5xvzniHgd8LnW2J8G/luNOXQsMy+/0P2I2ECV65czII5ssgAAIABJREFUc09fnyNJkqTO5ckTlBseIHf19m9q3ymuu55i/kKXNEmShoyixmf9KJDAT52nOANAZv498FNUXTY/VuP8tYuIZVTFGYDPDGQukiRJI03u3U3zH7/RWXFm1GiKlbfQWOgR2pKkoaXODpp5wHHgC22M/UJr7Pwa5++Gd7TedwJfGchEJEmSRorMJJ94lPLRhzpb0jR1WrWkacLE7iUnSVKX1FmgGQ30ZPb+WzQzy4joqXn+WkXEKODHWx//PDNPDWQ+kiRJI0GeOEG5YS25e2dHcTHnhmpJU1Fng7gkSRdPnb/BngEmR8SK3gZGxEpgcitmsPo+4NLW170ub4qIuyPiYEQci4htEfHZiHhZd1OUJEkaPso9u6olTZ0UZ0aPplh1K40Fiy3OSJKGtDp/i32Fal+ZT0bErPMNiojLgE9S7VfzdzXOX7d3tt43ZuaGNsbfCpStr68D3g78Y0T8TkTEeaMkSZJGuMykfOxhynvuhBPH2w+cOp3Gy19DcdkV3UtOkqSLpM4lRr9OtWfLEuDhiPgj4HbgeWAcMBt4NVXhYwLVaU+/UeP8tYmI6cD3tz5eqHvmOPBx4H8C6zPzcKsYsxz4APADwM9S7WHz4a4lLEmSNETl8ePVkqY9uzqKi7k3UsxbYNeMJGnYqK1Ak5k7I+INwBeBy4FfaL3OFsALwA9nZmeLiy+etwFjgFPAn51vUGa+SHVU+JnXElgH/GBE/CXwVuA/RcTHM3N/91KWJEkaWsrduyg33A8nTrQfNHoMxbKVFJde3r3EJEkaALX+k0Nm3gcsAN4PPEi1jClar2xd+xVgYWbeX+fcNTt9etNX+1lEel/rfSLw2v6lJEmSNDxkJs1HH6K8987OijPTZlRLmizOSJKGodpPUWp1iXwI+FBEjAamt27tzcyeuuerW0TcDKxufex1c+ALycxtEbELmAXM7W9ukiRJQ10eP065/n5y7+6O4uL6myhuutklTZKkYaurx1y3CjI7ujlHF7yz9b4X+NsBzEOSJGlYKXftpNywFk520DUzZgzFslUUsy7rXmKSJA0CXS3QDDUR0QB+ovXxc5l5sp/Pm0PVPQOwrT/PkiRJGqqyLCkfe5h8/JHOAqfPoLF8NTFufHcSkyRpEOlTgSYiXtH68mhmrj3rWkcy846+xHXJ9wBXtr7udXlTRERrU+DzOX1y0zHgG/3MTZIkacjJ48dorr8f9u7pKC5umEdx43yXNEmSRoy+dtDcTrXp7yNUmwKfea0T2Y8cuuH05sBb29zE+PaI+N9US6Eeysxm65jtZVSbIf9wa9yvZ+be+tOVJEkavMqdOyg3roWTHTQljxlLsXwVxcxLu5eYJEmDUF+LI89QFVe2n+PakBQRU/h2QaXdzYGvpeqS+TDQExEHgQnAmX24vwt8sK48JUmSBrssS8pHt5JPPNZRXMyYSbFsNTFuXJcykyRp8OpTgSYzr2vn2hDzz6kKKyXw2TZjfgH4XmANcDnViVUnqTqL7gL+MDPvrT9VSZKkwSmPHa2WNO3rrHm4uHE+ceN8qmZkSZJGnsG0vGhAZeYngE90GPN54PPdyUiSJGloKXe8QLnxAejpaT9o7FiKZaspZs7qfawkScNYbQWa1ibBJzPznjbHrwHGDbJNgiVJktShLEvKh7eQ2x7vKC5mXkqxbCUx1iVNkiTV2UFzO/ACcFWb4/8CuKbmHCRJknQR5dGjNNffB/v3dRRX3LSAuOEmlzRJktRSd3Gk09+w/kaWJEkaosoXt1NuXAenOlnSNI7G8tXEjJndS0ySpCFoILtXJlNtqCtJkqQhJJtNyke2kNue6CguZl1GsXQlMXZslzKTJGnoGpACTWv/menAkwMxvyRJkvom9+2lufEBOHK4/aAIinkLiLk3uqRJkqTz6HOBJiLeAbzjrMvTI+IbFwoDpgILgAS+2tf5JUmSdPFks0n56Fbyyc42Ambc+GpJ0/QZ3UlMkqRhoj8dNNcBrzrr2phzXDufO4Bf6cf8kiRJughy7x6am9Z11jUDxKWtJU1jXNIkSVJv+lOg+SLwVOvrAD4FHAD+/QViSuAgsCUzO/znF0mSJF1M2TxF+chDHR+fXS1pWkjMvcElTZIktanPBZrM3AhsPP05Ij4FHMvMz9SRmCRJkgZO7t3d6po50lng+PE0lq8hpk3vTmKSJA1TtW0SnJlFXc+SJEnSwMhTpygf2Uo+1dkJTQBx2eUUS1YSY8Z0ITNJkoa3gTxmW5IkSYNI7ml1zRztsGum0aCYv4i4do5LmiRJ6qOuFWgi4nLgSmAi1R4155SZd3QrB0mSJPWu6prZQj71ZMexMWMmxZIVxISJXchMkqSRo9YCTUQUwM8B/5bqlKfeZN05SJIkqX3lnl2Um9b3oWtmFMXNi4jZ19k1I0lSDWorjrSKM18C3kDVMbMfmEp1ctN2YCYwrjX8CLC7rrklSZLUmTx1ivLhzeTT2zqOjZmzKBavICZM6EJmkiSNTHVu7Psu4I3Ai8DLM/P01v07M3M2MAl4FXAn0ADen5lzapxfkiRJbSh376J5x9c7L86MGkWxeBnFmpdanJEkqWZ1Li/6CaolS7+QmXedfTMzS+COiHg18GXgExHxaGbeU2MOkiRJOo881UP50Bbymb50zVxKsWQ5Md7CjCRJ3VBngWZx6/0LZ11vnPkhM5sR8XPAVuA/Aj9SYw6SJEk6h3L3TspN6+DYsc4CR42iWLCYuPpa95qRJKmL6izQTAL2Z+aZv/WPA5PPHpiZD0fEQeAlNc4vSZKks2RPD+VDm8lnn+o4NmZdRrF4OTF+fP2JSZKk71BngWYHMP2sa7uAqyPiyszcfvpia0Ph8Xx702BJkiTVrNy1ozqh6XinXTOjW10zs+2akSTpIqlzk+BngAkRcekZ19a13n/4rLHfD4ymKupIkiSpRtnTQ3PTOsr7vtVxcSYuvYzGK19LcY1LmiRJupjq7KC5i2rJ0iuBz7eu/TnwQ8CvR8REYAPVXjX/mWpD4b+tcX5JkqQRr9z5IuWD6+H48c4CR42mWLiEuOoaCzOSJA2AOgs0fwG8m6og83mAzPx8RLyNqoPm184YG8DjwK/UOL8kSdKIlT0nKbc+SD73TMexcdnlFIuWE+NcfS5J0kCprUCTmeuBWee49Vbgp6hOa7oaOAB8DfjNzNxX1/ySJEkjVbnjBcoHN8CJDrtmRo+mWLiUuPJqu2YkSRpgdXbQnFNmNoH/0XpJkiSpJnnyJOXWTeTzz3YcG5ddQbFomV0zkiQNEl0v0EiSJKl+VdfMejhxorPA0WMoFi0lrrjKrhlJkgaR2go0EVECL2TmVW2O3wZck5kWiSRJktqUJ09QbnmQ3N6HrpnLr6yKM2PtmpEkabCpuzjS6T/D+M82kiRJbSpf3E65eUPnXTNjxlR7zdg1I0nSoDWQ3StjgeYAzi9JkjQkVF0zm8jtz3UcG1dcVRVnxo7tQmaSJKkuA1KgiYjLgUuBnQMxvyRJ0lBRvvB81TVz8mRngWPGUCxaRnFFW6vPJUnSAOtzgSYiXgG86qzLkyLiVy4UBkwFXt/6+q6+zi9JkjSc5YkTlFs2ki8833FsXHk1xcIlxBi7ZiRJGir600HzauD9QJ5xbWLr2oWcXvi8F/jVfswvSZI07GQm+cLzlFs2dt41M3Zs1TVz+ZXdSU6SJHVNfwo0G4DPnPH5HcBx4C8vEFMCB4EtwBcyc08/5pckSRpW8sRxys0byRe3dxwbV15DsXCxXTOSJA1RfS7QZOaXgC+d/hwR7wAOZOa76khMkiRppMhMcvtzlFs2QY9dM5IkjUR1bhL8aqDDvygkSZJGtjx+nHLzBnLHCx3HxlXXUCxYQowZ04XMJEnSxVRbgSYzv1nXsyRJkoa7b3fNbISens6Cx46jWLyM4rIrupOcJEm66AbkmG1JkqSRLI8fo3xwA7nzxY5j4+rZFAsWE6PtmpEkaTiprUATEc0+hGVmWiSSJEkjQmaSzz9b7TVzqsOumXHjKBYvp7j08u4kJ0mSBlSdxZHofUgtMZIkSUNO1TWznty5o+PYuOZaipsXE6NHdyEzSZI0GNRZoJnTy/1LgNXAvweuAN4FbKpxfkmSpEEnM8nnnqHc+mAfumbGUyxZTjHrsu4kJ0mSBo06Nwl+uo1hmyLiT4GvAp8EVtY1vyRJ0mCTx45We83s6kPXzOzrKOYvsmtGkqQR4qLv/5KZJyPi3wEPAu8H3nOxc5AkSeqmzCSffZryoQfh1KnOgsePp1i8gmLWpd1JTpIkDUoDskFvZm6JiIPA6wdifkmSpG7JY0cpN60nd+/sODZmz6G4eSExyq4ZSZJGmgEp0ETEGGACMHYg5pckSapb1TXzFOVDm/vQNTOBYskKipmzupOcJEka9AbqiOsfb8397ADNL0mSVJs8eqQ6oWn3ro5j49q5FPMXEqMG6s8ySZI0GNT2l0BEzO5lyDjgauCHgPcCCXy+rvklSZIutswkn9lG+dAWaPaha2bpCooZds1IkqR6O2i2dTA2gHuBD9U4vyRJ0kWTR49QblpH7tndcWxcN5dinl0zkiTp2+r8qyB6ud8E9lOd3vSXwCcys8N/apIkSRpYmUk+vY3y4c3QbHYWPGEijSUriBkzu5OcJEkasmor0GRmUdezJEmSBqM8cpjmpvWwtw9dM3Oup5i3gGjYNSNJkr6bfyFIkiT1IjPJp56kfGRL510zEyfSWLKSmD6jO8lJkqRhwQKNJEnSBVRdM+tg756OY2PODRTzbrZrRpIk9aorfy1ExDjgdcAK4PTRBLuAdcDfZ+bxbswrSZJUl8wktz1B+chWKDvtmplU7TVj14wkSWpTrQWaiCiAXwTeB0w5z7CDEfFrwEczs6xzfkmSpDrk4UNV18y+vR3HxtwbKW66mWg0upCZJEkarmor0EREAJ8HfpjqRKfjwHrg+daQK6k6ai4BPgysAd5S1/ySJEn9VXXNPN7qmunw35EmTa66ZqZN705ykiRpWKuzg+bfAm8CSuCDwG9n5qEzB0TEJODngPcDPxwR/yYz/0eNOUiSJPVJHj5Ec+MDsH9fx7Fx/U0UN863a0aSJPVZnQWa9wAJvC8zf+tcAzLzMPChiDgKfBR4L2CBRpIkDZgsy6pr5tGH+tY1s3QFMdWuGUmS1D91FmhuAk4BH29j7MeBjwDzapxfkiSpI3noYLXXTKddMxHVXjN2zUiSpJrUWaA5AjQy81hvAzPzWEQcpiroSJIkXVRZluSTj1E+9nDnXTOTp1RdM5dM605ykiRpRKqzQHMf8H0RMTszn7nQwIi4FpgKfLnG+SVJknqVhw5We80c2N9ZYES118wN8+yakSRJtauzQPMR4HXAxyPiTZnZc65BETEK+D2q7plfq3F+SZKk88qyJJ94jPKxhyCzs+DJU2gsXUlcMrU7yUmSpBGvtgJNZt4VET8GfBJYGxG/BXyT7zxm+5XAfwBmAz+amd+qa35JkqTzyYMHqq6Zgwc6C4wgbphXdc0URXeSkyRJosYCTUQ0z/i4CPh0LyF/FRHnup6ZWWdnjyRJGqGqrplHq71mOu2amXIJjSUr7JqRJEkXRZ2FkHNWWwbwOZIkaQTLA/urE5r60DVT3DifuP4mu2YkSdJFU2eBZk6Nz5IkSeqTLEvKxx8hH3+kD10zU6sTmqZc0p3kJEmSzqPOPWierutZkiRJfZEH9ld7zRw62FlgBMVNNxNzb7RrRpIkDQj3epEkSUNeNptV18wTj3beNXPJ1OqEpslTupOcJElSGyzQSJKkIS3376v2mum0a6Yoqr1m7JqRJEmDQO0FmohYALyZ6iSnacDoCwzPzHxt3TlIkqThL5tNysceJp98rPOumanTqhOa7JqRJEmDRJ3HbBfAx4B/Q3USUzunMXX415QkSRLk/r00N66Dw4c6CyyKaq+ZOTfYNSNJkgaVOjtofgH46dbX3wC+DuwAmjXO0RUR8U7g070MO5KZk84TXwDvAd4F3Aw0gMeBPwc+lpkn68tWkqSRK5tNykcfqrpmOjV1WrXXzKTJ9ScmSZLUT3UWaN5D1RHzy5n5kRqfezH1AHvPc+/IuS5GxGjgi8AbWpdOUhWllrVeb42I12Tm4ZpzlSRpRMl9e6sTmo50+Cu1KCjmLai6ZqKdBl9JkqSLr84CzdVUhYn/VuMzL7ZvZearOoz5L1TFmePAvwY+C5TAG4HPAKuBPwDeXl+akiSNHFXXzFbyycc7D542vdprxq4ZSZI0yNW5+PpF4GhmHq/xmYNaRFwO/Gzr4/sy8zOZ2czKl4F/2br3tohYMjBZSpI0NGUm5fbnaN7+tc6LM0WDYsFiGre9wuKMJEkaEuos0HwZmBwRi2p85mD3FmAscAD4w7NvZuaXgEepNkz+8YubmiRJQ1fu30fz7jso198Px491Fjx9Bo1XvIbCJU2SJGkIqXOJ038Ffhj4/Yj4vszs8FiFIenVrfc7LtA59PfATcBrLk5KkiQNXXn8GOXDW8jnn+08uNGgmLeQuG6uhRlJkjTk1FagycwXI+I1wJ8C2yLifwCbgRd6ibujrhxqsDAitgBzgVPA08DXgP+emdvOMX5B633LBZ65tfV+c0REZnq0uCRJZ8lmk3zyMconHoVmHw6AnD6TxpLlxMRzHrgoSZI06NXZQQPVKU7PA2uA/9Tm+Lpz6I+ZwAxgHzAFWNh6/auIeE9m/vlZ469ovW+/wDNP35vUeo2EziJJktqSmeQLz1M+tLnzpUxQdc3MX0RcO8euGUmSNKTVVhyJiPnAHVQFDoATwG6qk50Gu+3A+4G/Bh7LzJMRMRZ4LfBRqk6Zz0TEc2d1/ExsvV/oL8qjZ3xtgUaSpJbcv4/m1k2wb2+f4mPGTIolK4gJE3sfLEmSNMjV2b3yYaoOlEeA9wJ3DZXlPJn591R7xZx57QTwlYi4C1gL3AD8GvCSi5+hJEnDR7/2mQEYNZpi/gJitl0zkiRp+KizQPMyqiVLP5KZF9qTZUjJzAMR8WHgU8CtETEzM3e3bh8BpgLjL/CICWd8fbhLaUqSNOj1e58ZIGbPobjpZmLs2JqzkyTp/7Z353GS3XW9/1+f6u7p2Sczk2X2TBJCCDuy6FVkkUUEggKuF5fAZbuiF+5PxF1BvaLgvYCAssjmQhAUQQREWVUUkEWQQCDJZDJbJsvsS09Pd9fn98f3VHd1T3VPT1d1Vy+v5+NROXXqnPM936pMMtXv/n4/X6m7OhnQ9AMnFlM40+Tz1TaAKyhTt6BMjboI2DLFtY1jJ5fIylaSJI3Tdp0ZIC6+hNp9H0isWdvh3kmSJM0PnQxobgQeGhHLp1hyerH5BqU+zf2mOKex0tM3Z787kiTNL+3WmWHVKmrXPoC4dJPTmSRJ0qJW62Bbrwf6gOd2sM354jubnu9uev6pavu9EbF8kmufUG0/0elOSZI0X+WZAUb+84uMfPbTMwtnevuoXfsAeh71eGqXbTackSRJi17HRtBk5g0R8SDgDyPiIuA1mXmqU+3PloiIqYoZR8Ra4Jer3S9k5t1Nh98P/D/KNKfnAm+YcO11wDWU2jw3dLLfkiTNR9aZkSRJmplOLrP9yerpAPAK4NciYjdwxxSXZWY+rlN9mKHLI+I9wFuBf8rMPQARsQz4Psoy2/cG6sCvNF+YmQcj4nXAy4BXRcQx4N2ZORIRTwbeUZ16Q2Z+bW7ejiRJc886M5IkSe3pZA2ax0zY76eMHrlmimvmyzLc31k9iIgzlNWZ1lKmbAGcBl6YmZ9sce2vA/cHngz8GfDWiBhhbPWm/wBeOHtdlySpu6wzI0mS1L5OBjTP7mBbc+lO4H9Rlgl/EHAJsI4S0txMqR3zJ5l5e6uLM3Oomsr0POB6SlHgHuA/KdOaXpuZZ2f5PUiSNOfyzAD1m24k9++dWQO9fdSuvg+x80qi1smyeJIkSQtPJ2vQvKtTbc2lzBygFDh+fRtt1IE3Vw9JkhY168xIkiR1XidH0EiSpEXMOjOSJEmzZ1YDmohYAVxc7d5TjVaRJEkLjHVmJEmSZlfHA5qI2ECp6fKjlNWPGt/CMiK+DfwV8EeZeaTT95YkSZ3VmToz1xA7r7LOjCRJ0hQ6GtBExCOADwCXMRbMjB4G7gP8JvD8iHh6Zn6hk/eXJEmdYZ0ZSZKkudWxgCYiLgM+CqwHjgBvAj4J7KtO2QY8DngBsBn4cETcPzPv7FQfJElSezpSZ2bjJdTu+wBi7boO906SJGnx6uQImpdRwpmvAU/MzLsmHP8W8ImIeB3wj8D9gV8EXtrBPkiSpBmyzowkSVL3dDKgeQqQwHNahDOjMvPOiHgO8B/AUzGgkSSpq6wzI0mS1H2dDGh2ACcy88vnOzEzvxQRJ6prJElSF1hnRpIkaf7oZEBzFlgWEZGZOdWJEVED+qprJEnSHLLOjCRJ0vzTyYDmJuDhwNOB95/n3KcDy4H/6uD9JUnSeVhnRpIkaX7qZEDzXuARwFsi4nhmfrzVSRHxNOAtlHo17+ng/SVJ0iSsMyNJkjS/dTKgeQPwk8CDgY9FxBeBTwH7KaNldgCPBu4HBPAV4I0dvL8kSZrAOjOSJEkLQ8cCmsw8GxFPBP4c+H7KdKeHTTitMRb6H4Cfzkxr0EiSNAtG68zc9HUYsM6MJEnSfNfJETRk5j3AD0TEI4EfBr4DuKQ6fDfwZeCvM/NfO3lfSZI0xjozkiRJC09HA5qGKoAxhJEkaQ5ZZ0aSJGnhmpWARpIkzR3rzEiSJC18bQU0EfEY4FHAicx8zTSv+f+A1cAnneokSdLMWWdGkiRp8ZhxQBMRy4G/ADYDP34Bl+4F/gr4mYi4T2YOzbQPkiQtVdaZkSRJWlzaGUHzTGAL8KnMfN90L8rM90XEz1JG3jwdeG8bfZAkaUmxzowkSdLi1E5A80NAAm+YwbWvBx5NCXkMaCRJOg/rzEiSJC1u7QQ0D622H5/BtY1rHtbG/SVJWvSsMyNJkrQ0tBPQXEopDnziQi/MzOMRcQK4rI37S5K0qFlnRpIkaeloJ6AJoJ3J61E9JElSE+vMSJIkLT3tBDT3ANsiYn1mHrmQCyNiPWWp7Rl+85QkafGxzowkSdLS1U5A81VgG/Ak4IYLvPbJ1fZrbdxfkqRFwTozkiRJaieg+SjwVODXI+L9mTk4nYsioh/4NcoKUB9u4/6SJC141pmRJEkStBfQvBP4DeA+wPsi4lnnKxgcEauBd1fX3Am8q437S5K0YFlnRpIkSc1mHNBk5kBEvAD4W+ApwI0R8TrgQ5n57eZzI+LewNOAn6dMi6oDL8jMmY3jliRpgbLOjCRJklppZwQNmfmhiHgu8CeU4OVVwKsiYhBoFA5eDzS+QQYwCLwoM/+unXtLkrSQWGdGkiRJU2kroAHIzHdGxJeB/0Mp/hvAcmDzxFMpNWd+PTO/2u59JUlaKKwzI0mSpPNpO6AByMyvAddFxBbgMcC1wMbq8CHgm8BnMnN/J+4nSdJCYJ0ZSZIkTVdHApqGzDxAKQIsSdKSZZ0ZSZIkXaiOBjSSJC1l1pmRJEnSTBnQSJLUAdaZkSRJUjsMaCRJaoN1ZiRJktQJBjSSJM2AdWYkSZLUSQY0kiRdAOvMSJIkaTYY0EiSNE3WmZEkSdJsMaCRJOk88swA9W99g9y3Z2YNWGdGkiRJ52FAI0nSJEqdmVuo3/ot68xIkiRpVhnQSJI0gXVmJEmSNNcMaCRJapKHDzFy09etMyNJkqQ5ZUAjSVryMpO86yD1W2+GI4dm1oh1ZiRJktQGAxpJ0pKVIyPk/r3Ud90Mp07OuB3rzEiSJKldBjSSpCUnh86St99GffetMDg443asMyNJkqROMaCRJC0ZOXCa+m23kHtuh5HhmTdknRlJkiR1mAGNJGnRy+PHqO+6mTywDzJn3pB1ZiRJkjRLDGgkSYtSZpKH7iZ33UzefVfb7VlnRpIkSbPJgEaStKhkvU4ePFBWZDp+tO324uJLqV17f+vMSJIkaVYZ0EiSFoUcHib33k79tltg4HTb7cXmrdSuvJq4aH0HeidJkiRNzYBGkrSg5eAg9d23krfvgqGh9hqr1Yjtl1O74l7EqtWd6aAkSZI0DQY0kqQFKU+dLIV/9+2Ber29xvqWETuvpHb5ldaYkSRJUlcY0EiSFpQ8crgEMwcPtN/YylVltMz2HUSPfyVKkiSpe/w2Kkma9zKTvOsg9V03w+FD7Te47qJSX2bTFpfLliRJ0rxgQCNJmrdyZIQ8sJf6rlvg5Im224tLLiOuuprYcDER0YEeSpIkSZ1hQCNJmndy6Cy5Zzf1226FwTPtNRZBbN1eRsysWduZDkqSJEkdZkAjSZo3cmCA+m23kHt3w/Bwe4319hI7dlLbeS9ixYqO9E+SJEmaLQY0kqSuy+PHSuHfA/sgs73G+pdTu+IqYscVRF9fZzooSZIkzTIDGklSV2QmeegectfN5N13tt/g6jVlGtOWbURPT/vtSZIkSXPIgEaSNKeyXicPHigrMh072n6DGzZSu/LexKWXWfhXkiRJC5YBjSRpTuTwMLnv9rIi08DpttuLTVvKiJn1GzrQO0mSJKm7DGgkSbMqBwep376L3L0Lhs6211itRmy7nNqV9yJWre5MByVJkqR5wIBGkjQr8tRJ6rtuIffdDvV6e4319RE7r6J2+ZVEf39H+idJkiTNJwY0kqSOyqOHqd96M3nwQPuNrVhZRstsu5zo9a8sSZIkLV5+25UktS0zybvupL7r23D4UPsNrruo1JfZtIWo1dpvT5IkSZrnDGgkSTOWIyPkgX1lRaaTJ9puLy65jLjyamLjxa7IJEmSpCXFgEaSdMFyaIjccxv1226FwTPtNRZBbNlWRsysXdeZDkqSJEkLjAGNJGnacmCA+u5byD27YXi4vcZ6eokdO6ldcRWxYmVH+idJkiQtVAY0kqTzyhPHqe+kaZZJAAAgAElEQVS6mdy/FzLba6y/n9rOq4jLryD6lnWmg5IkSdICZ0ADRMQO4BnA44AHAZcBZ4FdwEeB12XmHS2u2wncNo1bPDwzv9ip/krSXMhM8vA95K03k3ff2X6Dq1ZTu+pqYst2oqen/fYkSZKkRWTJBzQRsR3YDTRXozwOrAIeWD2eHxHPzMxPTdHUVD+9DLXbT0maK5lJHjxA/dZvw7Gj7Te4YWOpL3PpJgv/SpIkSZNY8gEN0Pg17oeBdwKfyMwjEbGMMqLmjcAVwAci4prMPNiqkczcNBedlaTZkiPD5N491G+7BU6faru92LSlBDPrN3Sgd5IkSdLiZkADR4CHZOZXm1/MzLPARyPiycBXgLXAC4BXzH0XJWn25NlBcvcu6rfvgrNn22usViO27aB2xb2I1Ws600FJkiRpCVjyAU1mHgO+OsXxmyLic8BjgIfOVb8kabblqZPUb7uF3LsH6iPtNdbXR1x+JbWdVxL9yzvTQUmSJGkJWfIBzTQdqrZWtZS04OXRI2VFpjv2t9/YipVltMz2y4le/0qRJEmSZspv0+cREb3A91S7X5/ivH8H7gf0AQeBzwJvysx/nfVOStJ5ZCZ5951lRabD97Tf4Np11K66N7FpC1Grtd+eJEmStMQZ0Jzfi4BNQB141xTnfRdwrHq+s3o8KyJeB/zvzMxZ7KMktZT1OnlgL/Vdt8CJ4223F5dcSlx5NbHxEldkkiRJkjrIgGYKEfFA4JXV7hsy8xsTTjkD/DHwHuArmXkyyk8sDwFeDlwHvBi4C/i9Oem0JAE5NETu2U199y1w5kx7jUUQW7aVFZnWrutMByVJkiSNY0AziYjYDHwAWAF8CfiliedUS26/aMJrCXwZeFpEvBf4EeBXI+KPM/PorHdc0pKWZwao33Yruec2GB5ur7GeXmLH5aXGzIqVnemgJEmSpJYMaFqIiA3APwJXADcDT8nMmfwK+pcoAc0q4HHA33Ssk5LUJE8cL4V/9++FdmdU9vdT23kVcfkVRN+yznRQkiRJ0pQMaCaIiHXAx4D7A3uAx2fmnTNpKzNvi4i7gUuAKzvXS0kqhX85fIj6rm+Td83of1PjrVpdpjFt3U70uGidJEmSNJcMaJpExCrgI8DDKCsxPT4z93S3V5I0XmaSBw9Q33UzHD3SfoPrN5QVmS7dZOFfSZIkqUsMaCoRsQL4EPDdwCFKOHNzm21eQRk9A3Bbez2UtNTlyAi57/ayItPpU223F5dtLiNmNmzsQO8kSZIktcOABoiIZcD7gccCR4EnZuaN07guzrN8dmPlpgHgk213VNKSlGcHydtvo777Vjh7tr3GajVi245S+Hf1ms50UJIkSVLblnxAExE9wLuBJwEngB/IzC9P8/JPR8Q/UEbefDMzR6plth8M/CbwQ9V5f5CZhzvcdUmLXJ4+RX3XLeTe26E+0l5jfX3E5VdS23kl0b+8Mx2UJEmS1DFLPqABvgd4ZvW8D/jAFDUY9mbmw5v2L6eMkvk9YCgijgMrKUtzN7we+O2O9ljSopZHj5QVme7Y335jK1aU0TLbdxK9/i9fkiRJmq/8tg61pufLq8dkJi61/YvAE4BHAJuADcBZ4FvAZ4G3ZObnO9dVSYtVZpJ330Xu+jZ56J72G1y7rtSX2byVqNXOf74kSZKkrlryAU1mfhqY0bIlmfk+4H0d7ZCkJSXrdfLAvrIi04njbbcXF19KXHk1cfElrsgkSZIkLSBLPqCRpG7I48eo79tDHtgLg4PtNRZBbN5G7cp7Eesu6kwHJUmSJM0pAxpJmiN5ZoDcv4/6/j0dGS1DTw+xYye1nfciVq5svz1JkiRJXWNAI0mzKIeHyYMHyP17yXvu6kyj/f3Udl5F7LiCWLasM21KkiRJ6ioDGknqsMwk77mb3L+HPHgARtpcIrth1eoyjWnrDqKnpzNtSpIkSZoXDGgkqUPy+DHq+/eS+/fC4MRF39qwfkNZkemyzRb+lSRJkhYpAxpJakOeOUMe2Et9/144fqyjbcdlm0sws2FjR9uVJEmSNP8Y0EjSBcqRYfLgHaWuzN13drbxWo3Yur0EM6vXdLZtSZIkSfOWAY0kTUNmkofuKXVl7jgAI8OdvcGKlcS2HdR2XEEsX97ZtiVJkiTNewY0kjSFPHF8rK7MmYHONt7bR2zeQm3bDli/0foykiRJ0hJmQCNJE+TgYKkrs28vHD/a2cYjiEsuI7ZuL0V/XY1JkiRJEgY0kgRAjoyQd95B7ttD3nMXZHb2BusuorZ1B7FlG9Hf39m2JUmSJC14BjSSlqzMJA/fQ+7bSx7cD8MdriuzfEUp+LtthwV/JUmSJE3JgEbSkpMnT1Dft4c8sBcGOl1XppfYtJXYtp3YcLF1ZSRJkiRNiwGNpCWh1JXZR33/Xjh2pLONRxAXX0ps20Fctono8X+tkiRJki6MP0VIWrRyZIS862CpK3P3nZ2vK7P2Imrbtld1ZVwaW5IkSdLMGdBIWlQyE44cor5vL3nHfhge6uwNlq8gtm4rBX/XrO1s25IkSZKWLAMaSYtCnjpZ6srs3wsDpzvbeE8vsXlLWRp74yXWlZEkSZLUcQY0khasPDtIHthPff8eONrhujJAXHIpsXUHcdlmotf/XUqSJEmaPf7EIWlBGa0rs38vedfBWagrs47a1u3Elu3EcuvKSJIkSZobBjSS5r1SV+Yw9f17yTv2wVCH68r0Lye2bi/BzNp1nW1bkiRJkqbBgEbSvJWnTpZQZv9eOH2qs4339BCbtpQpTBdbV0aSJElSdxnQSJpX8uxZ8o6qrsyRwx1vPy6+pIQym7ZYV0aSJEmahzKTwaE6w/U6q5f3dbs7c8afTiR1Xdbr4+vK1OudvcGatWX60tbtxPIVnW1bkiRJ0owMj9Q5OTjMqTPDnDwzxKnG88FhRurJxtX9/Ld7X9Ltbs4ZAxpJXZGZcPQI9f17yAP7YehsZ2/Q309sKXVlWLvOKUySJElSF9QzOT04PC58KdshBoem/sXsycEO156c5wxoJM2pPH2K3L+3TGE61eG6MrUeYtPmsboytVpn25ckSZJ0jszk7HDr0TCnzg7PeOHVwaE6wyN1enuWxvd6AxpJsy6HGnVl9sLhQx1vPzZeUqYvbd5C9C6dOaqSJEnSXBqp1yeMghnm1JkhTg4OMzwywxTmPE4NDrNu5bJZaXu+MaCRNCuyXifvvrPUlbnzjs7XlVm9ZqyuzIqVnW1bkiRJWqIyk4GzI+PClzIqZpgzQyNz3p+TZwxoJOmCZSYcO1rVldkHZztcV2ZZP7FlG7VtO6wrI0mSJLXh7HB9fABTBTKnBoepz85gmBk5NTjc7S7MGQMaSW3L06fJA3up79sDp052tvFajbhsM7FtB3HxpdaVkSRJkqZppF4K9I6OhjlTivWePDPM0EiHR7jPkpNnlk6hYAMaSTOSQ0Pkwf3U9+2Fw/d0vP3YcDGxbTuxaSvRZ10ZSZIkqZXM5MzQyDkrJJ06M8zps3M/JalTImDVsl6W9/V0uytzxoBG0rRlvU7ecxe5b8/s1JVZtZrath3Elu3ESuvKSJIkSQ1DI/VxKyQ1RsOcGhxmZD7NSbpA/X01Vvf3sWp5L6v7e6ttHyv6e6gtsZIGBjSSppSZcPwY9X2NujKDnb3BsmWlrszWHbDuIuvKSJIkacmqZzUlqWkq0qlqNMzg8MKYktRKTy3Gwpflfazq72X18l5W9fcumSW0p8OARlJLOXCa3L+3LI198kRnG2/Uldm6nbjkMuvKSJIkacnITAaH6+OmIjUCmdODwyzUsTABrOhvHgUzNhqmv6/mL2KnwYBG0qgcHiLvOFCWxj50d+dvsGFjWRp781aib2kslSdJkqSlaXikPm4qUmNq0qkzwwwv4ClJy3pro6NfmkfDrFzWS61mCNMOAxppiSt1Ze4m9+8hD94B9Q4XElu1itrWHWW0zMpVnW1bkiRJ6qLM5PTZkXHhS6NQ75mhhVugtxYxOgqmEcasWt7H6v5e+nod/T5bDGikJWi0rsz+veSBvTDY4boyfX1jdWUuWu9wRkmSJC1YmcnZ4fq4mjDNU5IW8GAYVizrqQKYvqZRMWXlJL/Dzz0DGmkJyYEB8kBVV+bE8c42XqsRl24qI2Uu3WRdGUmSJC0oI/U8ZypSI5AZGlm4KUxfT21c+NIYDbOqv5cepyTNKwY00iKVmXD6FHn4UHkcuQdOner8jdZvKFOYNm8llllXRpIkSfNDZlLPUgtmaKTOcD0ZHqkzPJKjrzVPSxo4u5CnJMHK0QK940fDLOvt6Xb3NE0GNNIikZlw4jh5+J7RUIbBM7Nzs5WrSrHfrduJVatn5x6SJElakuqZoyHKuFClXj/n9aHR/caxxnllf+GOe2lteV9P0yiYskLSquW9rFzmlKTFwIBGWqByZASOHR0LZI4chuGh2bthXx+xeRu1rdth/Qb/ApAkSdKozGSknpMGKkOTBCytzqvnYotVLkxvLcaFL43lqlf199LbYxmBxcyARlogcniIPHK4Gh1zDxw9AvX67N40YnxdmR6HR0qSJC0m9fq5wcnQFCNWpgpeNH1BNSWpxWiY/t6avwxdogxopHkqBwfHT1c6fnTubn7R+lJXZstWYln/3N1XkiRJ59UYrTI0aXgyPkg5J3BpClgW8gpEC0F/b63laJiV/b3UDGE0gQGNNA9kJgycHh0dk4cPwamTc9uJFSuJrdupbdthXRlJkqRZMFK/0Loqk5+n+aOnFueskNQIYvqckqQLYEAjdcFYQd9D5JFqytKZWSroO5XePmLzVmrbtsP6jQ6llCRpgctMMiFpbKGU85h8n6bzq93yXaU6N8sJo9c2yq6OXZ9N7VZ9GG23qa2p2pvYtzbam+y9texr8/tu571Ooy/1HLuXFqaVy3rGhS+NQGZ5nwV61RkGNNIcyHodjh1pWvL6EAzNYkHfqfQvJzZsLMtiW1dGkqRZVc+kXi/TUUbqpfjp6PN6MpKTPJ9wfr3Ouceb2m5uV9LMLeuttRwNs7K/l56aIYxmlwGNNAtyeLgq6HsPHD5EHj0C9ZHudGbVKmL9xSWU2bARVq4y4ZckLUmZrYKPsWDk3PCDaYUqUwUwxiVSdwXQ21Ojtyfo7anRV4ux/VqtBDKjo2H6WNbrlCR1jwGN1AF5dnBsdMzhe+D4Mbo2hnXtOmJDFcis30gsX96dfkiSNIXM8WHG+MCDc0aInBN+TDHapOVxp5dIC0pvLejpCfpqY+FKb0+N3gkBy2TBS+P1WuAvJ7VgGNBIM5CnT5divkeqFZZOnuhOR2o1uGh9CWI2XEys30D09XWnL5KkRSUzWxcorScjE4qXTjbVptW0ndHgxLBEWnRqwZQhSm8t6OsZvz/ZeYYqWooMaKTzyEw4eWL8CktnBrrTmd7eKoyppiutW28NGUnSqBKMnLsiTNm2em0sfBkZyXHHrGUiLR3THY0y1Xk9tZo1WqQ2GdBIE5SCvkerYr5VINO1gr79Y6NjNmws05f8bYIkLRqNmihTjVQZGmkKXSZuJ7zmFB5p6ahF0NdqJEqLkSl9PUHPxOClOq/H0SrSvGFAoyUvh4fJo4dLEHP4EHn0MIx0qaDvylWjo2Niw8UW9JWkeaieJRgZqVfhyaSjUlqPWJk4UkXS0lEK1jbCkUZQ0hiVUgUpo9OAGgFL6/orNb8jSouOAY2WnHEFfY8cgmNHu1vQt2nKUixf0Z1+SNIiVorR0mKEysTRKPUymuU855ipaL4LoFZNNQmg/BwfRJR9AqLV/oRjVNdG9WSsrVJ0NTjPscb+Oe1FdZ8WfWt1fTT3bazg69g1U7235n62et8T22vRt2l8DtN5bxFhwVpJUzKg0aKXA6fHr7DUrYK+EaWg7+gKSxuIvmXd6YskzbKsgu9MSMrqOc3PS8jReF7OrWe5IM95npBQB+rTHKkycWqQmYq6qaeaRlKLalsLepqfV/u10fOarmlxvLmtc57XHFkhSQuVAY0WldGCvkcOjYYyDJzuTmd6eksI05iudJEFfaWFLqvAoIQNjefnhg/jnzddc77jjbbOd69Jn5+vL1Pc90LuxVhoMtW50nw0Mcwowce5IUrLIGWKUOWcAKY6Ho6YkCRNkwGNFrSs1+H4sdHVlfLIITh7tjudWbZsbHTMho2wZh1Rq3WnL9IS1FwXpGyrlWnqOX6/UXx13Hmtr5sYmkjqrMZIkfOPKJkiNLmA404vkSTNZwY0WlByZJg8cgSOVEteH+liQd8VK0dHx8SGjbBqtV/6pGmYuGrNaEAyMjFQqTedN1XwUqa0uHqN1Hk9taYCpbWgp6cUL+2pjV8p5kKn8BiWSJJ0LgMazWs5dHZ8/ZhuFvRds3YskFm/kVhhQV8tbqWwao4fZdKo7zEhXGk8nyx4aYQowyM5Wm9EUuc1VojpqdWaVoZpDlPOfa2neWWYxjnVcwMUSZLmjgGN5pU8MzAaxuThQ3DieHc6EgHrLmoq6LuRWGZBX81f9cmm6YxO5xm/33h+vvMkzb5acM7yuY0QZSxoOffYOdtq2V1DFUmSFiYDGnVNZsKpk+MDma4V9O2pCvpeDOs3EuvXEz3+56EL06hVUm8qslrPCa9X+/UJ548FLOOn7Zw77adFHRWn90hzrjHd59wRKq1Ho/TUytSgc0as9LjijiRJKvwJVHMm63U4caxpytIhODvYnc4sW1ZGxTRWWFprQd/Z1rzKTCO0mG54kePOn845Y6vMnPP6DAOU6bQvaf6KoGnESeuRKn3THLHS49QfSZI0Cwxo1FEnBoYYqX6VnyMjcOIEefwoefwYefw41EtB33JGH/T1jbs+oUygL/+YdNWUJCbsj17S/GTs+mX9pYbM6jXE6jXk8hVExNjxY4OjZ59zz6Tl6wkt6+Gcc15OPJ7NO9O8rkXfznvtJH1rWgq3VVAyWYAyus8krzcdb/W6pKUpovxfORrLDdNYdniS582vRVTXjj2vRUxrxMrEkSo9NQMVSZI0vxnQqGNy6CxfuvkuTg5PPLISelfChs3d6NaYBE4AJwaAge72RdKCNTEwGP88LjyQGPe8VZtTtD/ZuZOGH3PUr6bnkiRJmh4DGnVM/dabYWAZ9Lm6kaTuGFcXpHreUxsbWdFTq40uG3zueeOnsPTUaqPLABs4SJIkabYZ0KhjYsNGONalVZckLSglAIlx01Ba7vfUJnn93OClEaZIkiRJC5EBjTom1m+E2wxopMWkFowWTW0dqNSqkSjnCVQmnGeQIkmSJI1nQKOOib4+6OnpdjekJau3eZpO0xSeiSNOeiY7rzloqfZd/leSJEmaGwY06qjo6Zl86SVpCWgUVm1MtxlXw6SxP3p87FhZmaZp9EnTqjQ9zavRTFJXxek9kiRJ0sJmQKPO6umFc1Zxkop2wovRLee+Pq4tJnm9+Xwmef2cPpzbTuN4q9fBkESSJEnSzBjQqKNWr1xGHDoy7rXo6YXe8oieHohadaCsijLu3HOeNHZj3EmtfgSOc66L1ue1eDFaHDynb5P83B0TOnT+62Lsn1Nc13ghJhw973Xj7tv6/RheSJIkSdL8YkDTIRGxCfgV4KnAVuAY8AXgtZn5iW72bS499F6XMnJ6P7FqVVnVad16olbrdrckSZIkSZrXDGg6ICIeCHwS2Fi9dBy4mBLWPCUifjUzf79b/ZtrPQ98SLe7IEmSJEnSguLQhjZFxArg7yjhzFeA+2fmOmA98H8pM0t+LyKe2L1eSpIkSZKk+cyApn0vAC4HTgLXZeaNAJl5PDNfCnyAEtK8sntdlCRJkiRJ85kBTfueVW3fnZn7Wxx/dbX9joi4Zo76JEmSJEmSFhADmjZExBrgodXuxyY57XOUgsEAj5v1TkmSJEmSpAXHgKY91zK2evGNrU7IzDrwrWr3vnPRKUmSJEmStLAY0LRnc9PzA1Oc1zi2eYpzJEmSJEnSEmVA055VTc8HpjjvdLVdPYt9kSRJkiRJC5QBjSRJkiRJUpcZ0LTnVNPzFVOct7LanpzFvkiSJEmSpAXKgKY9zXVntkxxXuPYHbPYF0mSJEmStEAZ0LTnJiCr5/drdUJE1IBrqt1vzEWnJEmSJEnSwmJA04bMPAF8sdp9wiSnfSewrnr+iVnvlCRJkiRJWnAMaNr37mr7rIhotYz2S6vtlzLzW3PUJ0mSJEmStIAY0LTvzcDtwBrg7yPivgARsSYiXgU8ozrvV7vUP0mSJEmSNM/1drsDC11mDkTED1KmL30HcGNEHAdWUwKwBH41M/+xi92UJEmSJEnzmCNoOiAzvwrcH/gjYBfQDxwCPgw8ITN/v4vdkyRJkiRJ85wjaDokMw8CL64ekiRJkiRJ0+YIGkmSJEmSpC4zoJEkSZIkSeoyAxpJkiRJkqQuM6CRJEmSJEnqMgMaSZIkSZKkLjOgkSRJkiRJ6rLIzG73QdMQEYdWrFix4dprr+12VyRJkiRJUuWb3/wmAwMDhzNzYzvtGNAsEBFxG7AW2N3lrkiSJEmSpDE7geOZeUU7jRjQSJIkSZIkdZk1aCRJkiRJkrrMgEaSJEmSJKnLDGgkSZIkSZK6zIBGkiRJkiSpywxoJEmSJEmSusyARpIkSZIkqcsMaCRJkiRJkrrMgEaSJEmSJKnLDGgkSZIkSZK6zIBGkiRJkiSpywxoJEmSJEmSusyARpIkSZIkqcsMaCRJkiRJkrrMgEZa5CJiR0S8JCI+FBF7ImIwIk5ExFcj4vcjYnO3+yjNRxGxOiL2RkRWj+u73SdpPomIayLi9RHxrYg4FRHHIuKbEfH2iHh0t/sndVtE1CLi2RHx8Yi4OyKGIuJoRHw+In4tItZ0u4/SXIiINRHxtIj4nYj4aETc0/T96j7TuL4WEc+PiH+v/hs6ERFfiYhfjIhlc/Ee5kpkZrf7IGmWRMR24HYgml4+DqwCeqr9I8AzM/NTc9w9aV6LiNcCL2566dmZ+c4udUeaVyLifwGvBhpfjE8CvcDyav9tmfncbvRNmg8iYiXwIeD7ml4+Bqxl7HvZ7cD3ZeauOe6eNKci4oeAv53k8LWZedMU1/YBHwCeXL10FhgBVlT7/0H57+hkh7rbVY6gkRa3RgjzYeBHgA2ZuQ5YSfmf3G3AeuADEbGpO12U5p+I+A7g54DPd7sv0nwTES8AXkcJZP4AuDwz12TmCmAz8NPAv3Wxi9J88BuUcCaBXwEuysyLKCHmTwBHgcuBP+1aD6W5dRfwEeAVwPMv4Lrfpfzccga4nvJzzCrgOuAw8HDgzZ3saDc5gkZaxCJiHbAzM786yfH7AF+hfFl4eWa+Yi77J81HEVGjBDMPofyl/+XqkCNotORFxE7gRsoX5Odn5lu72iFpnoqI24EdwNsz83+0OH498I5qd0NmHpnD7klzKiJ6MnOkaX8n5RfFMMUImuoXyLuBfuDFmflHE47/IGV0TQIPzsyvdbzzc8wRNNIilpnHJgtnquM3AZ+rdh86N72S5r2fBx4G/ElmfqXbnZHmmRdTwpnPG85IU7qs2k7298iXmp6vnOW+SF3VHM5coGdSwpljwFtatPtB4NuUaYP/fcYdnEcMaCQdqrY9U54lLQERsRX4HeBO4Ne73B1pPmp8Ab6hq72Q5r/d1fYhkxxv/GLszszcP/vdkRakx1bbf87MM5Oc84/V9vsmOb6gGNBIS1hE9ALfU+1+vZt9keaJ1wNrgJdm5rFud0aaTyLiKuDSavcrEfFd1QqBhyJiICJuiohXR8SlU7UjLRGNEWbPjohfrqadExHLIuLHgNdQpmW8tFsdlBaA+1bbG6c45xvV9tqIiCnOWxAMaKSl7UXAJqAOvKvLfZG6KiKuA54OfDoz/6Lb/ZHmoaubnj8G+FfgqUAf5QfNayg/bP5nRNxvznsnzS+vBd5ImXrxSuBoRBwFBoD3ADcBT/PvG2lKm6vtgSnOaRxbXT0WNAMaaYmKiAdSvjAAvCEzvzHV+dJiFhGrgDcAQ5TgUtK5Lmp6/luUef/flZlrKV+Kn0xZpWMz8DfVKE1pSapqbrwE+AVguHp5HWM/f60BLulC16SFZFW1HZjinNNNzw1oJC08EbGZUvF8BaVI3S91t0dS1/02ZbWN1xhWSpNq/t6YwNMz8/MAmVnPzI8Cz6mOXwM8Y477J80b1eoznwX+L/CXwIMoPzxeTVl2+0rg7RHxykkbkbTkGNBIS0xEbKAU07oCuBl4yhRFt6RFLyIeTFmZZi8lqJHU2smm5/+Qmd+aeEJmfpgysgbgcXPSK2l++jPgEcDbMvP6zPxaZp7KzFsy8/eBF1TnvcwpgdKkTlXbFVOc07wK2slJz1ogDGikJaQqUPcx4P7AHuDxmXlnd3sldd3rKKuY/RoQEbG6+dF0Xn/1msuhaqlqrgFwTjjT4tj2WeyLNG9FxH2BJ1S7r2l1Tmb+OWUlzRpw3Rx1TVpoGn/vbJninMaxk5l5Ypb7M+sMaKQloqqx8RHgYcBBSjizp7u9kuaFy6vtnwEnWjwa3lTtOwVKS9U3KEXlpytnqyPSPHdt0/PbpjhvV7XdOXtdkRa0xneuqUaZNVZ6+uYs92VOGNBIS0BErAA+BHw35bc1j8/Mm7vbK0nSQpKZp4F/r3avmeLUxrHds9ohaf5qDjJ3THFe4xcEC/63/tIs+VS1/d6IWD7JOY3Rap+Yg/7MOgMaaZGLiGXA+4HHAkeBJ2bmjd3tlTR/ZObOzIzJHk2nPrt6bWe3+irNA39WbZ8UEeeENBHxFODe1e5H5qxX0vzy1abnz2t1QkRcB1xa7X5+1nskLUzvBwYpqwg+d+LB6r+jaygjNm+Y267NDgMaaRGLiB7g3cCTKL+d+YHM/HJ3eyVJWsDeThly3gO8PyIeARARtYh4EvC26rzPYUCjJSozd1EWZAB4SUS8MiIuBahqmV0PvLM6vhv4u7nuozTXIuLixgNY33ToouZjETGaUY+JekYAAA5FSURBVGTmQUqtQIBXRcRPVT/fEBFPBt5RHbshM782F+9jtkWm04OlxSoiHgV8pto9Axyb4vS9mfnw2e+VtLBEROMvymdn5ju72RdpPoiIK4FPM1YE+AQlsGkU0P4GZbTm/rnvnTQ/RMRmypSL5no0J4A1Tft3Un559pW57JvUDU3fp87niszc3XRdH/AB4MnVS4PACGN/5/wH8LjFUCAYHEEjLXbN/40vBy6b4nHJnPdOkrTgVKMDHgD8H0oY00sZXv5l4FeARxjOaKnLzDuAhwIvAf4ZOEz5gfI45b+V3wEeYDgjTS0zhygrnb2QMjpzkPJ3zn8CvwQ8crGEM+AIGkmSJEmSpK5zBI0kSZIkSVKXGdBIkiRJkiR1mQGNJEmSJElSlxnQSJIkSZIkdZkBjSRJkiRJUpcZ0EiSJEmSJHWZAY0kSZIkSVKXGdBIkiRJkiR1mQGNJEmSJElSlxnQSJIkSZIkdZkBjSRJkiRJUpcZ0EiSJEmSJHWZAY0kSbpgEXF9RGREfLrbfZlNEfHwiPhQRNwTEfXqPb+82/3qloh4efUZvLPbfZEkabHp7XYHJElS90REL/CTwI8DDwI2AqeAg8Au4F+AT2bmF7rWyS6JiKuBTwMrgTpwT7U9eQFtbANeBDwRuBewomrnIPC1qv2PZeYdHez6vBURDwP+J/BIYBvll4V3AgeAL1A+j3/KzFMdut9O4HrgaGa+thNtSpI0WwxoJElaoiLiEuAjwMOaXj4DBHANcB/gycAx4KIJlx8DvgXsmf2eds3zKeHMvwBPy8yjF3JxRFwH/CWwpunlo5TPcjPwEOBngNcBL+lEh+eziPht4Ncpf76ghF1HgS3A5cB/A14MPB34QIduuxP4LeB2wIBGkjSvOcVJkqSl6y8o4cwJ4GXA5sxckZkXAeuAJwB/TPkhepzM/NvMvE9m/vRcdniO3a/avncG4cyVwHsp4cyXgKcCKzNzfWaupAQHzwH+iRJULGoR8RPAb1DCmfdS/tz1Z+ZGyqiiB1D+DH69a52UJKnLHEEjSdISFBH3oUy7AXhOZv518/HMPAF8HPh4RPzCXPdvnlhRbac9panJ84HllKlMj8nMcW1k5u3AO4B3RMTytnq5MLy42n44M3+s+UBmjlCCma8Dr14in4ckSedwBI0kSUvTA5qe//1UJ2bmmYmvTVYkOCI+Xb1+vsfLW7S5LCJ+LiL+JSIOR8RgRNweEW+PiGtn+D6JiFpE/I+I+EzV7pmIuC0i3hIR92px/u6ISOAx1UvvaOr37mnetvH5fmZiODNRq8+3qS/3r97/bVW/j0bEZyPihRHRN1W7EXFdRHwwIg5GxNmIuKsqePz957numoi4oTp/ICJuiojfioj+qa47j8bnMeWfNTjv5zHt91T9u/pUtXt5iz+D18/gfUiSNGscQSNJkrYCt3aorcOUoq+TuazVixGxGfgopVAxlGk/p4AdwLOBn4iIZ2Xm+y+kMxGxEvhbxkYLDQGnKVOMngf8VET8eGZ+sOmyuymjXzYAfcBxYKDp2IXYeoHnj4qIn6PUp2n8Qu0ksBr47urxYxHxlMw8PeG6PsronGc1vXwcuIQy1eqpEfGqzPylFvd8FOXfw8qm664AXg58P6WIbztm9HnM8D3dDawF1lP+PE38dzeAJEnziCNoJElamr7U9PyNVcHgtmXmMzJzU6sH5Yd8KCHJJxrXVD98f5ASznyCEj4sz8y1lAKyr6UEJn8eEVddYJf+HyWcGQReCKypauxcQwkblgPvjoh7N72Hh1f9/bfqpRc3vY+HT/O+X6y2j4yIF0VEz4V0OiJ+CHg9JaR6GXBJZq6hBCdPAm6mjPB5TYvLX0UJMm4BfhRYnZnrKGHFz1LVHKrqwjTfcz3wvuoeXwYeXF23mlLM+EHV9TPR+Dx+PiK+dwbXX/B7qv5dPaPa3dviz+RfzfC9SJI0KyIzu90HSZLUBRHxLqBR5PcsZbWizwH/AfxbZk46WqSaHvIOyhSex0zjXt9LCV/6gJ/NzD9pOvZc4K3V/R+XmUMtrn8T8ALgjZn5c9N8fzspI4NqwAsz880Tjq+kLHV9FfDnEwseV9O3Hg08OzPfOZ17Nl17WdX2pdVLdwKfpCwl/QXgS5k5OMm1PVW/LweelJkfa3HOVVX7y4AdjWW6q6XBv0VZyvuhmbm3xbU/DtwA3JiZ9296/TeA3wYOAffJzHsmXPeTwJ9Xu+/KzOvP/0mMXvt44GOM/XLwJuAzlD9rn6/60vJLaZvv6TGUaU63Z+bO6fZXkqRucASNJElL1/MoI0zOUn7Qfxzwa5Qlju+KiC9ExLMiIqZo47wiYgfwN5Rw5s3N4UzlZ6rt61qFM5W/rLZPuIBbP53yXecg8KcTD1ZTg15V7T7jQke5TCUz76SEO41ROJcBP0EZ8fJZ4EhEvDsi7tvi8sdQwpmvtwpnqvZvpYRpvYzVyoESuAXwV62CjMpfU0YU3a+aWtbww9X2rRPDmcpfUparvmCZ+XHgh5quvw8lcPtT4L+AOyLi1RGxscXl7bwnSZIWDAMaSZKWqMw8m5m/AGynTP+5gTJ1pjGS4eGUpbj/KiJm9J2hGqXyAUqtkH8Bfn7C8V7gEdXum6vir+c8gEbtme0XcPvvqLb/Uq0U1Monq+0qyrSnjsnMmzLzeyif4ysoS2ofqg6voAQ2X46IH55w6XdX26sn+zyqz6Rx3vYW1/7MFNfto4Rlo9dGxDLGlhX/zCTvJ4F/vsCPofn6DwH3Ap5Cqa3zOUo9ICgB1kuBr0ZZYazZjN6TJEkLjUWCJUla4jLzLuDN1aMxPec64DcpP+z+CGXUx+tm0Pw7gIdQRk48s8UImQ2U0TsArUZPTLTi/KeMatTV2T/FOftanN9RmflFxmqwEBEPoYwaehHQD7wrIj7bmKYENEaA9DNJUeUJVjY9b1y7pnpM99oNQGME0YEpzp/qszyvzBwGPlI9GsHQoyjLcD+VUkT43RHx0KYpTzN9T5IkLSiOoJEkSeNk5p2Z+aeUESiNFZmec6HtRMSvUgq6ngJ+cJKaNs3fRR6SmXG+x4X2g1IIeN7IzK9k5ksoq1NBCRR+vOmUxmfywel8Hpn58hbX/u9pXvvpWX2z51GN4vp4Zl4HvK16+SHAg5tOW1DvSZKkmTKgkSRJLVV1SBrLT997qnMnioinAr9DmS51fWZ+dZJTDwGN6Uc7ZtLPKTQCoana3dbi/LnybsaWem7+fBuh2Ew+j5lee5ixfw9bpjhvqmPtelvT8059HpIkLRgGNJIkaSqnqu3Z6V4QEddSCsrWgN/NzL+e7NxqylNj+s8PzLSTk/hytf3OqhZOK99XbU9RVgqaM5lZZyygaf58/73aPjAitl5gs41rn3SBfTkL3FjtPqrVOVWx6JbHOuRU0/NWn8cFvadKvdq2VehakqS5YEAjSdISFBFXVEs1T3XOSsrKOwD/Oc12L6KMullLKQ78W9O47J3V9vqIeNB52l8/nX5U3k/5AX0j8PwWba0EfrFx7hSFhC9YRDwyIqacWhURT6LUfoHxn+8ngL2UmjCvPk8bEz+PP6OMWro2Il5wgde+r9o+LyI2TDyfMg1r51RtTnGvx09jNbD/3vS8+fNo5z0dr7brptVRSZK6yIBGkqSl6X7AtyLi/RHxo81LE0fEqoi4jrLq0hXVy9MtEPwe4Grg68BPNRV6ncrbKCv6LAc+GRHPi4i1Tf3ZVC33/RlKMdlpyczbgbdUu78fEc+PiP6qzXsDH6asKnQa+N3ptjtNLwF2R8QfVmHNaHHjiNgcEb8MvLd66QBlmehGv4eAn6OEEj8RER+IiAc3Xd8XEQ+LiFcBtzXfNDO/QVnKG+CPI+KVEbGt6do1EfHEiPgLxgKZhjcCdwEXAx+LiAc23e8ngbcCx2b4ebwH+K+I+MWIeEBjVbCI6ImI+0bEm4CXVed+KDNH31eb7+lmYAhYFxHPnGHfJUmaEzG9702SJGkxiYjvB/5hwssDlKklzaMNRoDfzMzfm3D99ZQVmj6TmY9per3xxeIEY0sot/KHmfmHTdddShnx8j3VS3XgKGUlo1VN1708M18x1Xub0M/GMt9PqF4aokyluajaHwR+LDM/2OLaTwOPBp6dme+c7j2ra29gfOHfpIQbKyjvqWE/cF1mfqVFG88G3sTYKlcD1WMdYysuMbFwckT0AK8H/mfTy8erPqxlbLrPpzPzsROufTTwUcZWyzpGCc76KVONPgP8MvCuzLx+svff4r3cAWxqemmkanvce6GsFva0zDzcwff0LuCnm97P0er5S6eafidJ0lxzmW1JkpagzPxYRFxDWU77kcD9KUscr6b8ALsL+GfgTzPzxkkbmtz5lkRePaE/d1XhwI8BzwIeSpn+cxa4CfgC8PfA311IJzLzdET8AHA9ZWnrB1JWTbod+CfgVZl584W0OU0/BbwdeCLwnZSitxsowdMdlBFGfw+8PTNPTtL3d0TEpyijhp4AXE4JIw4B3wA+RRmZMvG6EeBnI+IvgRcC38tYOLIH+Crwj5Nc+5lqGfBXUOrzrAF2AzcAf0AJZ2biGuDJwGOBh1FGZq2jBGQHKfWC3gv8datRV+28p+r8/cDTKVO0Lq9eX93iXEmSusYRNJIkSZIkSV1mDRpJkiRJkqQuM6CRJEmSJEnqMgMaSZIkSZKkLjOgkSRJkiRJ6jIDGkmSJEmSpC4zoJEkSZIkSeoyAxpJkiRJkqQuM6CRJEmSJEnqMgMaSZIkSZKkLjOgkSRJkiRJ6jIDGkmSJEmSpC4zoJEkSZIkSeoyAxpJkiRJkqQuM6CRJEmSJEnqMgMaSZIkSZKkLjOgkSRJkiRJ6jIDGkmSJEmSpC4zoJEkSZIkSeqy/x/jT3sRrqEYFgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 648x432 with 1 Axes>"
]
},
"metadata": {
"image/png": {
"height": 392,
"width": 564
}
},
"output_type": "display_data"
}
],
"source": [
"lw = 4\n",
"fig = plt.figure(figsize=(9,6))\n",
"ax = fig.add_subplot(111)\n",
"ax.plot(range(1, len(greedy_elapsed) + 1), greedy_elapsed, label=\"Greedy\", color=\"#FBB4AE\", lw=lw)\n",
"ax.plot(range(1, len(celf_elapsed) + 1), celf_elapsed, label=\"CELF\", color=\"#B3CDE3\", lw=lw)\n",
"ax.legend(loc=2)\n",
"plt.ylabel('Computation Time (Seconds)')\n",
"plt.xlabel('Size of Seed Set')\n",
"plt.title('Computation Time')\n",
"plt.tick_params(bottom=False, left=False)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can get some further insight into the superior computational efficiency of CELF by observing how many \"node lookups\" it had to perform during each of the 10 rounds. The list that records this information shows that the first round iterated over all 100 nodes of the network. This is identical to Greedy which is why the graph above shows that the running time is equivalent for $k=1$. However, for subsequent iterations, there are far fewer spread computations because the marginal spread of a node in a previous iteration is a good indicator for its marginal spread in a future iteration. Note the relationship between the values below and the corresponding computation time presented in the graph above. There is a visible jump in the blue line for higher values of the \"node lookups\". This again solidifies the fact that while CELF produces identical solution set as Greedy, it usually has enormous speedups over the standard Greedy procedure."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[100, 1, 4, 9, 2, 7, 4, 1, 5, 13]"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"celf_lookups"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Conclusion"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We implemented both the Greedy and CELF algorithms and showed the following:\n",
"\n",
"- Both correctly identify the influential nodes in simple examples\n",
"- Both result in the same seed set for a larger example.\n",
"- The CELF algorithm runs a lot faster for any seed set $k>1$. The speed arises from the fact that after the first round, CELF performs far fewer spread computations than Greedy.\n",
"- During the Greedy Algorithm section, we mentioned briefly that a natural greedy strategy obtains a solution that is provably within 63% of optimal. We didn't formally proved this statement here, but there are several good notes online that goes more in-depth into the proof behind this. [Notes: N. Buchbinder, M.Feldman - Submodular Functions Maximization Problems (2017)](https://www.openu.ac.il/personal_sites/moran-feldman/publications/Handbook2018.pdf)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Reference"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- [Blog: Influence Maximization in Python - Greedy vs CELF](https://hautahi.com/im_greedycelf)\n",
"- [Blog: The greedy algorithm for monotone submodular maximization](https://homes.cs.washington.edu/~marcotcr/blog/greedy-submodular/)\n",
"- [Paper: D. Kempe, J. Kleinberg, E. Tardos - Maximizing the Spread of Influence through a Social\n",
"Network (2003)](https://www.cs.cornell.edu/home/kleinber/kdd03-inf.pdf)\n",
"- [Notes: N. Buchbinder, M.Feldman - Submodular Functions Maximization Problems (2017)](https://www.openu.ac.il/personal_sites/moran-feldman/publications/Handbook2018.pdf)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
},
"toc": {
"nav_menu": {},
"number_sections": true,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": true,
"toc_position": {
"height": "calc(100% - 180px)",
"left": "10px",
"top": "150px",
"width": "258px"
},
"toc_section_display": true,
"toc_window_display": true
},
"varInspector": {
"cols": {
"lenName": 16,
"lenType": 16,
"lenVar": 40
},
"kernels_config": {
"python": {
"delete_cmd_postfix": "",
"delete_cmd_prefix": "del ",
"library": "var_list.py",
"varRefreshCmd": "print(var_dic_list())"
},
"r": {
"delete_cmd_postfix": ") ",
"delete_cmd_prefix": "rm(",
"library": "var_list.r",
"varRefreshCmd": "cat(var_dic_list()) "
}
},
"types_to_exclude": [
"module",
"function",
"builtin_function_or_method",
"instance",
"_Feature"
],
"window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
jwjohnson314/data-803 | notebooks/Regularization and Model Tuning.ipynb | 1 | 506439 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Regularization\n",
"Regularization is the name for a technique developed at different times and in different ways in statistics and machine learning for improving the predictive quality of a model. The idea is to make a model simpler than it might otherwise be by either making the coefficients small, making the coefficients zero, or perhaps some combination of both at the same time. Regularization is implemented by default in sklearn's linear models."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from IPython.core.pylabtools import figsize\n",
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"plt.style.use('bmh')\n",
"\n",
"from sklearn.datasets import make_classification\n",
"from sklearn.cross_validation import train_test_split, cross_val_score\n",
"from sklearn.grid_search import GridSearchCV\n",
"from sklearn.linear_model import LogisticRegression, LogisticRegressionCV\n",
"from sklearn.metrics import accuracy_score, classification_report, confusion_matrix\n",
"from sklearn.preprocessing import StandardScaler"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's generate some sample data. 100000 observations, 50 features, only 5 of which matter, 7 of which are redundant, split among 2 classes for classification."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"X, y = make_classification(n_samples=100000, \n",
" n_features=50, \n",
" n_informative=5, \n",
" n_redundant=7, \n",
" n_classes=2,\n",
" random_state=2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When building linear models, it's a good idea to standarize all of your predictors (mean at zero, variance 1). "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAs4AAAFwCAYAAACoxP20AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X9w3Hd95/HXe+UtkziuLsAloUlFdeEIDKNmo4o0l+gm\noSJghV6ca+440htocZtjGCiZO67j0OMG7o+j9k091C0tR36Qhk474YjbAhnWSSDBGdNCkioWarCd\n5CqiJNjOQS46Ozl6y+p9f+zKVmRJXmm/331/vvo+HzMZ9Fl//d0PL61Wb69e+q65uwAAAACsrBK9\nAQAAAKAIGJwBAACADjA4AwAAAB1gcAYAAAA6wOAMAAAAdIDBGQAAAOhAJoOzmW02s4Nm9oSZbVvm\nmKvM7DEz+zszezCL+wUAAAB6xbq9jrOZVSQ9IWlM0g8kPSLpPe5+cMEx/ZL+WtI73P05M3utu/+w\nqzsGAAAAeiiLV5wvlfSkuz/t7g1Jd0nasuiYX5W0292fkySGZgAAABRNFoPz+ZKeWbB+tn3bQm+U\n9Goze9DMHjGz92ZwvwAAAEDPbOjh/QxL+iVJGyX9jZn9jbs/1aP7BwAAALqSxeD8nKSBBesL2rct\n9KykH7r7jyX92MweknSxpFMG52uvvdZ//OMf67zzzpMkbdy4UW94wxtUq9UkSfv375ck1jms5z9O\nZT9lW5M/+Zd1PX9bKvsp23r+tlT2U7b1/G2p7Gc9r5966im99NJLkqQjR47owgsv1Gc/+1nTKmTx\ny4F9kg6p9cuBhyU9LOkGdz+w4Jg3SfpDSZslvUrSdyT9G3f/3uLzve997/Ndu3Z1tSeszfbt23Xz\nzTdHb6O0yD8W+cch+1jkH4v849x00036whe+sKrBuetXnN29aWYflnSfWp3p2939gJl9oPXHfou7\nHzSzeyV9V1JT0i1LDc1S618AiDEzMxO9hVIj/1jkH4fsY5F/LPIvlkw6zu6+R9JFi2773KL170n6\nvSzuDwAAAOi1vk9+8pPRe3iF559//pOXXHJJ9DZKqb+/XwMDA6c/ELkg/1jkH4fsY5F/LPKPc/jw\nYV1++eX/ZTV/p+uOc9a+8Y1v+PDwcPQ2AAAAsI5NTExobGxsVR3nTN5yO0sLf8sUvbVv377oLZQa\n+cci/zhkH4v8Y5F/sSQ3OAMAAAApoqoBAACA0lkXVQ0AAAAgRckNznSc49CzikX+scg/DtnHIv9Y\n5F8syQ3OAAAAQIroOAMAAKB06DgDAAAAOUlucKbjHIeeVSzyj0X+ccg+FvnHIv9iSW5wBgAAAFJE\nxxkAAAClQ8cZAAAAyElygzMd5zj0rLLVbEoTE33avbuqiYk+zc2tfDz5xyL/OFlkv9qvN5zEYz8W\n+RfLhugNAOvV5GSfxsc3qdEwVauuev2Yhoeb0dsC1iW+3gD0QnKvONdqtegtlNbo6Gj0FtaV6emK\nGo1WdarRME1Pr/zlRv6xyD9OFtmv9usNJ/HYj0X+xcIzC5CTwcE5VautX76tVl2Dg/zsGMgLX28A\neiG5wZmOcxx6Vtmq1Zqq14/p1luPq14/plpt5R8bk38s8o+TRfar/XrDSTz2Y5F/sdBxBnJSqUjD\nw016lkAP8PUGoBe4jjMAAABKh+s4AwAAADlJbnCm4xyHnlUs8o9F/nHIPhb5xyL/YklucAYAAABS\nRMcZAAAApUPHGQAAAMhJcoMzHec49KxikX8s8o9D9rHIPxb5F0tygzMAAACQIjrOAAAAKB06zgAA\nAEBOkhuc6TjHoWcVi/xjkX8cso9F/rHIv1iSG5wBAACAFNFxBgAAQOmEdZzNbLOZHTSzJ8xs2wrH\nvdXMGmb2K1ncLwAAANArXQ/OZlaR9BlJ75T0Fkk3mNmbljluu6R7VzofHec49KxikX8s8o9D9rHI\nPxb5F0sWrzhfKulJd3/a3RuS7pK0ZYnjfkvS3ZKez+A+AQAAgJ7KYnA+X9IzC9bPtm87wcx+RtJ1\n7v5ZSSt2SWq1WgZbwlqMjo5Gb6HUyD8W+cch+1jkH4v8i6VXV9X4fUkLu8+rKmIDAAAA0TZkcI7n\nJA0sWF/Qvm2hEUl3mZlJeq2kcTNruPtXFp9s165d2rhxowYGWqfs7+/X0NDQiX+RzXeBWGe/Xtiz\nSmE/ZVuTP/mXdT1/Wyr7Kdt6/rZU9lO29fxtqexnPa+npqY0OzsrSZqZmdHIyIjGxsa0Gl1fjs7M\n+iQdkjQm6bCkhyXd4O4Hljn+Dklfdfe/WOrPd+7c6Vu3bu1qT1ibffv2nXiAoffIPxb5xyH7WOQf\ni/zjrOVydJlcx9nMNkvapVb143Z3325mH5Dk7n7LomM/L+me5QZnruMMAACAvK1lcN6QxR27+x5J\nFy267XPLHMvLyQAAACic5N5ym+s4x1nYt0LvkX8s8o9D9rHIPxb5F0tygzMAAACQokw6zlmi4wwA\nAIC8raXjzCvOAAAAQAeSG5zpOMc5Xc+q2ZQmJvq0e3dVExN9mpvr0cZKgp5bLPKPQ/axyD8W+RdL\nJlfVQDlMTvZpfHyTGg1Tteqq149peLgZvS0AAICeSO4V51qtFr2F0jrdBdinpytqNFpVoEbDND2d\n3MOn0LgAfizyj0P2scg/FvkXC5MPOjY4OKdqtfXLpNWqa3CQrgYAACiP5AZnOs5xTtezqtWaqteP\n6dZbj6teP6ZajZpGlui5xSL/OGQfi/xjkX+x0HFGxyoVaXi4Sa8ZAACUEtdxBgAAQOlwHWcAAAAg\nJ8kNznSc49CzikX+scg/DtnHIv9Y5F8syQ3OAAAAQIroOAMAAKB01tJx5qoaAJCgZrP1bp3T0xUN\nDs6pVmuqws8IASBUck/DdJzj0LOKRf6xUst//i3ub7zxLI2Pb9L+/X3RW8pNatmXDfnHIv9iSW5w\nBgDwFvcAkCI6zgCQoImJ1ivOjYapWnXV68d48yEAyBAdZwBYJ+bf4n5hxxkAECu5n/3RcY5DzyoW\n+cdKLf/5t7i//vqGhofX9y8GppZ92ZB/LPIvlnX8VAwAAABkh44zAAAASmctHWdecQYAAAA6kNzg\nTMc5Dj2rWOQfi/zjkH0s8o9F/sWS3OAMAAAApIiOMwAAAEqHjjMAAACQk+QGZzrOcehZxSL/WOQf\nh+xjkX8s8i+W5AZnAAAAIEV0nAEAAFA6dJwBAACAnCQ3ONNxjkPPKhb5xyL/OGQfi/xjkX+xZDI4\nm9lmMztoZk+Y2bYl/vxXzWyy/d8+MxvK4n4BAACAXum642xmFUlPSBqT9ANJj0h6j7sfXHDMZZIO\nuPusmW2W9El3v2yp89FxBgAAQN6iOs6XSnrS3Z9294akuyRtWXiAu3/b3Wfby29LOj+D+wUAAAB6\nJovB+XxJzyxYP6uVB+PflFRf7g/pOMehZxWL/GORfxyyj0X+sci/WDb08s7M7G2S3i9ptJf3CwAA\nAHQri47zZWp1lje31zdLcnffsei4n5e0W9Jmd/+fy53vgx/8oL/44osaGBiQJPX392toaEijo61Z\ne/5fZqxZs2bNmjVr1qxZd7qemprS7GyrOTwzM6ORkRF99KMfXVXHOYvBuU/SIbV+OfCwpIcl3eDu\nBxYcMyDpG5Le6+7fXul8/HIgAAAA8hbyy4Hu3pT0YUn3SXpc0l3ufsDMPmBm/6592H+W9GpJf2xm\nj5nZw8udj45znPl/nSEG+cci/zhkH4v8Y5F/sWzI4iTuvkfSRYtu+9yCj2+UdGMW9wUAAIqp2ZQm\nJ/s0PV3R4OCcarWmKsm9FRuwvK6rGlmjqgEAwPo0MdGn8fFNajRM1aqrXj+m4eFm9LZQUlHXcQYA\nADit6emKGo3WnNJomKanGUNQLMk9Yuk4x6FnFYv8Y5F/HLKP1cv8BwfnVK22ftJdrboGB+d6dt+p\n4vFfLJl0nAEAAE6nVmuqXj/2io4zUCR0nAEAAFA6dJwBAACAnCQ3ONNxjkPPKhb5xyL/OGQfi/xj\nkX+xJDc4AwAAACmi4wwAAIDSoeMMAAAA5CS5wZmOcxx6VrHIPxb5xyH7WOQfi/yLJbnBGQAAAEgR\nHWcAAACUDh1nAAAAICfJDc50nOPQs4pF/rHIPw7ZxyL/WORfLMkNzgAAAECK6DgDAACgdNbScd6Q\n12YAIFKzKU1O9ml6uqLBwTnVak1V+BkbAKALyX0boeMch55VLPLP1uRkn8bHN+nGG8/S+Pgm7d/f\nt+Lx5B+H7GORfyzyL5bkBmcAyML0dEWNRusncI2GaXqapzsAQHfoOANYlyYmWq84NxqmatVVrx/T\n8HAzelsAgETQcQaAtlqtqXr92Cs6zgAAdCO5n13ScY5DzyoW+WerUpGGh5u6/vqGhodP/4uB5B+H\n7GORfyzyLxZecQYAAF3hKjYoCzrOAACgK/xOAYpoLR1n/j0IAAC6wlVsUBbJPbLpOMehZxWL/GOR\nfxyyj5VF/oODc6pWWz/BrlZdg4NzXZ+zLHj8FwsdZwAA0BWuYoOyoOMMAACA0qHjDAAAAOQkucGZ\njnMcelaxyD8W+cch+1jkH4v8iyW5wRkAAABIER1nAAAAlE5Yx9nMNpvZQTN7wsy2LXPMH5jZk2a2\n38xqWdwvAAAA0CtdD85mVpH0GUnvlPQWSTeY2ZsWHTMu6UJ3/6eSPiDpvy93PjrOcehZda7ZbL1T\n1u7dVU1M9Gkug0uWkn+M+c/lpz717cw+l1gdHvuxyD8W+RdLFtdxvlTSk+7+tCSZ2V2Stkg6uOCY\nLZK+IEnu/h0z6zezc939aAb3jwJqNqXJyb5XXPOzUln9MVnfZ6cmJ7N7e9n5fT300AadeWZfV1lk\n+f8x6/xTdfJzeYZ27dqU+1sFR+Rals9lr5Xhc5nyY6fX30cinoeRniwG5/MlPbNg/axaw/RKxzzX\nvu2UwblWo8XRa/Nf5EePvk0TE735Iu9k8Ox0OO30SaqT83V6rqXeXnatw9bJfY1r167ussgys6zz\nT9XJz+VVajS05Ocyy2+YefyjK4vHfqfnyzKLTp97ej38ROTaqSyfxzrJP8vHa9Z6/X0k6+fheaOj\no2sLACF450CEPDF2Mnh2Opx2uv9OztfpuebfXnb+uG7eXjbLLLLMLOv8OxExhHfyuczyG2Y+/+jq\n/rHf6fmyzCKvQWQlWe4r4msky+exXj9eO5XlCxgRz4kRmaF3shicn5M0sGB9Qfu2xcf87GmOkSTt\n2rVLGzdu1MBA65T9/f0aGho68S+y+S4Q6+zWDz20QY3GuKRvqtGQ9uz5vxoevmxN53vooX166qmK\n+vuv1ODgnI4f36tK5dTjBwevbA8re9XX5xoc/IVTzjc4OKe+vgfVbJqq1db5Vt6/1GjsXXb/nZxv\nz55vqdE4Q61XH0179nxLL7/8k1P2f/nlo6rXj2nPnm/pvPPmVKtdvub8Z2crqlavOZHF7OzLkl55\nvk7ykqTZ2b3q6ztTzebbVK26Zmf3at++uVPu/+jRt7Wf2L/ZfpV1RMPDzVzz72R9551/rW3bTu7/\nd3/3a3rjG0/df5bruTmpXr/yxOfy+PE5SavPS+rs8XPy823q63twyc93p/vv9PHa6eOnk/N1+vlu\nDQ9728ddpenpil5+ee8y99c6Zrn9d5r/6p7vlt9/p/eX5ddbp/vv5PGz+sfr8vln+XjtdH3mmVe2\nh9jW4/Xee39hzfl3uv9OHq+dfr47/Xpb2G0eHR1NYh5Y7+upqSnNzs5KkmZmZjQyMqKxsTGtRteX\nozOzPkmHJI1JOizpYUk3uPuBBcdcI+lD7v4uM7tM0u+7+2VLnW/nzp2+devWrvaE1ZmY6DvxJFWt\nXtnVqyEnz7XyKx1zc9L+/Su/otDJMVnfZ6fnytL8vvbs+ZY2b76iqyyyzCzr/Duxe3dVN9541on1\nrbce1/XXN9Z0rtXat2/fsj8y7fT/Y5a5diLLx36n58syi06fe7J8jGX5/zHiayTL57FO8s/y8dqp\nTp8Hev19JOvn4XkrPfcgX2u5HF0m13E2s82Sdql1lY7b3X27mX1Akrv7Le1jPiNps6SXJL3f3SeW\nOhfXce69LJ8YIwafLPcf8U0iQqqZRfzDpRN5fcPs1b6yPF+WWUTkmuW+srzPLKX6eO1U5AsYqWWB\nfIUNzllicC62VAcfFAPfvADwPIBeCXsDlCxxHec4WVxLslZrql4/pltvPa56/ZhqNYbmTnEtT6lS\nkYaHm7r++oaGh3v7zZL845B9rNTyj3weiJBa/lgZV9VApuaf8HiVGQAArDdUNQAAAFA666KqAQAA\nAKQoucGZjnMcelaxyD8W+cch+1jkH4v8iyW5wRkAAABIER1nAAAAlA4dZwAAACAnyQ3OdJzj0LOK\nRf6xyD8O2cci/1jkXyzJDc4AAABAiug4AwAAoHToOAMAAAA5SW5wpuMch55VLPKPRf5xyD4W+cci\n/2JJbnAGAAAAUkTHGQAAAKVDxxkAAADISXKDMx3nOPSsYpF/LPKPQ/axyD8W+RdLcoMzAAAAkCI6\nzgAAACgdOs4AAABATpIbnOk4x6FnFYv8Y5F/HLKPRf6xyL9YkhucAQAAgBTRcQYAAEDp0HEGAAAA\ncpLc4EzHOQ49q1jkH4v845B9LPKPRf7FktzgDAAAAKSIjjMAAABKh44zAAAAkJPkBmc6znHoWcUi\n/1jkH4fsY5F/LPIvluQGZwAAACBFdJwBAABQOnScAQAAgJwkNzjTcY5DzyoW+cci/zhkH4v8Y5F/\nsXQ1OJvZ2WZ2n5kdMrN7zax/iWMuMLMHzOxxM5sys490c58AAABAhK46zma2Q9KP3P2/mdk2SWe7\n+82LjjlP0nnuvt/MzpL0t5K2uPvBpc5JxxkAAAB5i+g4b5F0Z/vjOyVdt/gAdz/i7vvbHx+XdEDS\n+V3eLwAAANBT3Q7O57j7Uak1IEs6Z6WDzeznJNUkfWe5Y+g4x6FnFYv8Y5F/HLKPRf6xyL9YNpzu\nADO7X9K5C2+S5JI+vsThy/Y+2jWNuyXd1H7leUl79+7Vo48+qoGBAUlSf3+/hoaGNDo6KunkA4w1\na9asWa+P9bxU9lO29bxU9lO29bxU9rOe11NTU5qdnZUkzczMaGRkRGNjY1qNbjvOByRd5e5H213m\nB939zUsct0HSPZLq7r5rpXPScQYAAEDeIjrOX5H06+2Pf03Sl5c57vOSvne6oRkAAABIVbeD8w5J\nV5vZIUljkrZLkpm9zszuaX98haR/K+mXzOwxM5sws83LnZCOc5zFPzZCb5F/LPKPQ/axyD8W+RfL\nhm7+sru/IOntS9x+WNIvtz/+lqS+bu4HAAAAiNZVxzkPdJwBAACQt4iOMwAAAFAKyQ3OdJzj0LOK\nRf6xyD8O2cci/1jkXyzJDc4AAABAiug4AwAAoHToOAMAAAA5SW5wpuMch55VLPKPRf5xyD4W+cci\n/2JJbnAGAAAAUkTHGQAAAKVDxxkAAADISXKDMx3nOPSsYpF/LPKPQ/axyD8W+RdLcoMzAAAAkCI6\nzgAAACgdOs4AAABATpIbnOk4x6FnFYv8Y5F/HLKPRf6xyL9YkhucAQAAgBTRcQYAAEDp0HEGAAAA\ncpLc4EzHOQ49q1jkH4v845B9LPKPRf7FktzgDAAAAKSIjjMAAABKh44zAAAAkJPkBmc6znHoWcUi\n/1jkH4fsY5F/LPIvluQGZwAAACBFdJwBAABQOnScAQAAgJwkNzjTcY5DzyoW+cci/zhkH4v8Y5F/\nsSQ3OAMAAAApouMMAACA0qHjDAAAAOQkucGZjnMcelaxyD8W+cch+1jkH4v8iyW5wRkAAABIUVcd\nZzM7W9IXJb1e0vclvdvdZ5c5tiLpUUnPuvu1y52TjjMAAADyFtFxvlnS1939IkkPSPrYCsfeJOl7\nXd4fAAAAEKLbwXmLpDvbH98p6bqlDjKzCyRdI+m2052QjnMcelaxyD8W+cch+1jkH4v8i6Xbwfkc\ndz8qSe5+RNI5yxz3aUm/LSmta98BAAAAHTptx9nM7pd07sKb1BqAPy7pT9z91QuO/ZG7v2bR33+X\npHF3/7CZXSXpo+7+L5a7PzrOAAAAyNtaOs4bTneAu1+93J+Z2VEzO9fdj5rZeZKeX+KwKyRda2bX\nSDpD0iYz+4K7v2+pc95999267bbbNDAwIEnq7+/X0NCQRkdHJZ38kQZr1qxZs2bNmjVr1p2up6am\nNDvbuobFzMyMRkZGNDY2ptXo9qoaOyS94O47zGybpLPd/eYVjr9SrVecl72qxs6dO33r1q1r3hPW\nbt++fSceYOg98o9F/nHIPhb5xyL/OBFX1dgh6WozOyRpTNJ2STKz15nZPV2eGwAAAEhGV68454GO\nMwAAAPIW8YozAAAAUArJDc5cxznOfJEeMcg/FvnHIftY5B+L/IslucEZAAAASBEdZwAAAJQOHWcA\nAAAgJ8kNznSc49CzikX+scg/DtnHIv9Y5F8syQ3OAAAAQIroOAMAAKB06DgDAAAAOUlucKbjHIee\nVSzyj0X+ccg+FvnHIv9iSW5wBgAAAFJExxkAAAClQ8cZAAAAyElygzMd5zj0rGKRfyzyj0P2scg/\nFvkXy4boDQDAajSb0uRkn6anKxocnFOt1lQluZcAAADrER1nAIUyMdGn8fFNajRM1aqrXj+m4eFm\n9LYAAAVDxxnAujc9XVGj0XqeazRM09M8jQEAeiO57zh0nOPQs4pF/p0ZHJxTtdr6SVm16hocnMvk\nvOQfh+xjkX8s8i8WOs4ACqVWa6peP/aKjjMAAL1AxxkAAAClQ8cZAAAAyElygzMd5zj0rGKRfyzy\nj0P2scg/FvkXS3KDMwAAAJAiOs4AAAAoHTrOAAAAQE6SG5zpOMehZxWL/GORfxyyj0X+sci/WJIb\nnAEAAIAU0XEGAABA6dBxBgAAAHKS3OBMxzkOPatY5B+L/OOQfSzyj0X+xZLc4AwAAACkiI4zAAAA\nSoeOMwAAAJCTrgZnMzvbzO4zs0Nmdq+Z9S9zXL+ZfcnMDpjZ42b2i8udk45zHHpWscg/FvnHIftY\n5B+L/Iul21ecb5b0dXe/SNIDkj62zHG7JH3N3d8s6WJJB7q8XwAAAKCnuuo4m9lBSVe6+1EzO0/S\nN939TYuO+WlJj7n7hZ2ck44zAAAA8hbRcT7H3Y9KkrsfkXTOEscMSvqhmd1hZhNmdouZndHl/QIA\nAAA9ddrB2czuN7PvLvhvqv2/1y5x+FIvX2+QNCzpj9x9WNLLalU8lkTHOQ49q1jkH4v845B9LPKP\nRf7FsuF0B7j71cv9mZkdNbNzF1Q1nl/isGclPePuj7bXd0vattw59+7dq0cffVQDAwOSpP7+fg0N\nDWl0dFTSyQcYa9asWbNeH+t5qeynbOt5qeynbOt5qexnPa+npqY0OzsrSZqZmdHIyIjGxsa0Gt12\nnHdIesHdd5jZNklnu/spryab2V5JN7r7E2b2CUlnuvuSwzMdZwAAAOQtouO8Q9LVZnZI0pik7ZJk\nZq8zs3sWHPcRSX9mZvvVuqrGp7q8XwAAAKCnuhqc3f0Fd3+7u1/k7u9w9xfbtx92919ecNyku7/V\n3Wvu/ivuPrvcOek4x1n8YyP0FvnHIv84ZB+L/GORf7HwzoEAAABAB7rqOOeBjjMAAADyFtFxBgAA\nAEohucGZjnMcelaxyD8W+cch+1jkH4v8iyW5wRkAAABIER1nAAAAlA4dZwAAACAnyQ3OdJzj0LOK\nRf6xyD8O2cci/1jkXyzJDc4AAABAiug4AwAAoHToOAMAAAA5SW5wpuMch55VLPKPRf5xyD4W+cci\n/2JJbnAGAAAAUkTHGQAAAKVDxxkAAADISXKDMx3nOPSsYpF/LPKPQ/axyD8W+RdLcoMzAAAAkCI6\nzgAAACgdOs4AAABATpIbnOk4x6FnFYv8Y5F/HLKPRf6xyL9YkhucAQAAgBTRcQYAAEDp0HEGAAAA\ncpLc4EzHOQ49q1jkH4v845B9LPKPRf7FktzgDAAAAKSIjjMAAABKZy0d5w15bQYA5jWb0uRkn6an\nKxocnFOt1lSFn3cBAAomuW9ddJzj0LOKtZ7zn5zs0/j4Jt1441kaH9+k/fv7ord0ivWcf+rIPhb5\nxyL/YklucAaw/kxPV9RotH4a1miYpqd56gEAFA8dZwC5m5hoveLcaJiqVVe9fkzDw83obQEASoyO\nM4Ak1WpN1evHXtFxBgCgaJL7eSkd5zj0rGKt5/wrFWl4uKnrr29oeDjNXwxcz/mnjuxjkX8s8i+W\nBL99AQAAAOnpquNsZmdL+qKk10v6vqR3u/vsEsf9e0m/IWlO0pSk97v7/1vqnHScAQAAkLe1dJy7\nfcX5Zklfd/eLJD0g6WOLDzCzn5H0W5KG3f3n1epVv6fL+wUAAAB6qtvBeYukO9sf3ynpumWO65O0\n0cw2SDpT0g+WOyEd5zj0rGKRfyzyj0P2scg/FvkXS7eD8znuflSS3P2IpHMWH+DuP5C0U9KMpOck\nvejuX+/yfgEAAICeOm3H2czul3TuwpskuaSPS/oTd3/1gmN/5O6vWfT3/5Gk3ZL+taRZSXdL+pK7\n//lS90fHGQAAAHnL5TrO7n71cn9mZkfN7Fx3P2pm50l6fonD3i7p7939hfbf+QtJl0tacnC+++67\nddttt2lgYECS1N/fr6GhIY2Ojko6+SMN1qxZs2bNmjVr1qw7XU9NTWl2tnUNi5mZGY2MjGhsbEyr\n0e1VNXZIesHdd5jZNklnu/vNi465VNLtkt4q6R8k3SHpEXf/o6XOuXPnTt+6deua94S127dv34kH\nGHqP/GORfxyyj0X+scg/TsRVNXZIutrMDkkak7RdkszsdWZ2jyS5+8Nq1TMekzSpVtXjli7vFwAA\nAOiprl5xzgMdZwAAAOQt4hVnAAAAoBSSG5y5jnOc+SI9YpB/LPKPQ/axyD8W+RdLcoMzAAAAkCI6\nzgAAACgdOs4AAABATpIbnOk4x6FnFYv8Y5F/HLKXmk1pYqJPu3dXNTHRp7m53t03+cci/2LZEL0B\nAADKbnKyT+Pjm9RomKpVV71+TMPDzehtAVgkuVeca7Va9BZKi3cuikX+scg/DtlL09MVNRqtqmWj\nYZqe7t20CGbvAAAHJ0lEQVS3Z/KPRf7FktzgDABA2QwOzqlabf2yfrXqGhzsYVcDQMeSG5zpOMeh\nZxWL/GORfxyyl2q1pur1Y7r11uOq14+pVutdTYP8Y5F/sdBxBgAgWKUiDQ836TUDieM6zgAAACgd\nruMMAAAA5CS5wZmOcxx6VrHIPxb5xyH7WOQfi/yLJbnBGQAAAEgRHWcAAACUDh1nAAAAICfJDc50\nnOPQs4pF/rHIPw7ZxyL/WORfLMkNzgAAAECK6DgDAACgdOg4AwAAADlJbnCm4xyHnlUs8o9F/nHI\nPhb5xyL/YklucAYAAABSRMcZAAAApUPHGQAAAMhJcoMzHec49KxikX8s8o9D9rHIPxb5F0tygzMA\nAACQIjrOAAAAKB06zgAAAEBOkhuc6TjHoWcVi/xjkX8cso9F/rHIv1iSG5wBAACAFNFxBgAAQOnQ\ncQYAAABy0tXgbGb/ysz+zsyaZrbsy8RmttnMDprZE2a2baVz0nGOQ88qFvnHIv84ZB+L/GORf7F0\n+4rzlKR/KWnvcgeYWUXSZyS9U9JbJN1gZm9a7vinnnqqyy1hraampqK3UGrkH4v845B9LPKPRf5x\n1vJi7YZu7tDdD0mSma3UD7lU0pPu/nT72LskbZF0cKmDX3rppW62hC7Mzs5Gb6HUyD8W+cch+1jk\nH4v840xOTq767/Si43y+pGcWrJ9t3wYAAAAUxmlfcTaz+yWdu/AmSS7pP7n7V7Pe0JEjR7I+JTo0\nMzMTvYVSI/9Y5B+H7GORfyzyL5bTDs7ufnWX9/GcpIEF6wvaty3pwgsv1E033XRiffHFF6tWq3W5\nBXRiZGREExMT0dsoLfKPRf5xyD4W+cci/97Zv3//K+oZGzduXPU5MrmOs5k9KOk/uvvfLvFnfZIO\nSRqTdFjSw5JucPcDXd8xAAAA0CPdXo7uOjN7RtJlku4xs3r79teZ2T2S5O5NSR+WdJ+kxyXdxdAM\nAACAoknunQMBAACAFCXxzoErvZGKmX3MzJ40swNm9o6oPa53q3mTGnTPzG43s6Nm9t0Ft51tZveZ\n2SEzu9fM+iP3uF6Z2QVm9oCZPW5mU2b2kfbt5N8DZvYqM/uOmT3Wzv8T7dvJv0fMrGJmE2b2lfaa\n7HvEzL5vZpPtx//D7dvIv0fMrN/MvtSeKR83s19cbf5JDM5a5o1UzOzNkt4t6c2SxiX98WmuGY01\nWO2b1CATd6iV90I3S/q6u18k6QFJH+v5rsrhJ5L+g7u/RdI/k/Sh9uOd/HvA3f9B0tvc/RJJNUnj\nZnapyL+XbpL0vQVrsu+dOUlXufsl7n5p+zby751dkr7m7m+WdLFa7ymyqvyTGJzd/ZC7P6nWpe4W\n2qJWJ/on7v59SU+q9YYqyNaJN6lx94ak+TepQU7cfZ+k/73o5i2S7mx/fKek63q6qZJw9yPuvr/9\n8XFJB9S62g/594i7v9z+8FVqXd3JRf49YWYXSLpG0m0Lbib73jGdOnuRfw+Y2U9L+ufufocktWfL\nWa0y/yQG5xUsfvOU58Sbp+SBN6lJwznuflRqDXeSzgnez7pnZj+n1que35Z0Lvn3Rrsq8JikI5Lu\nd/dHRP698mlJv63WP1bmkX3vuKT7zewRM/vN9m3k3xuDkn5oZne0q0q3mNmZWmX+Xb3l9mr0+o1U\ngHWA39zNkZmdJeluSTe5+3EzW5w3+efE3eckXdJ+BegvzewtOjVv8s+Ymb1L0lF3329mV61wKNnn\n5wp3P2xm/1jSfWZ2SDz2e2WDpGFJH3L3R83s02rVNFaVf88G5zW+kcpzkn52wXrFN0/Bmq3qTWqQ\nm6Nmdq67HzWz8yQ9H72h9crMNqg1NP+pu3+5fTP595i7/x8z+6akzSL/XrhC0rVmdo2kMyRtMrM/\nlXSE7HvD3Q+3//d/mdlfqVWV5LHfG89KesbdH22vd6s1OK8q/xSrGgt7zl+R9B4z+ykzG5T0BrXe\nQAXZekTSG8zs9Wb2U5Leo1b2yJfp1Mf7r7c//jVJX178F5CZz0v6nrvvWnAb+feAmb12/rfWzewM\nSVer1TMn/5y5+++4+4C7/xO1nucfcPf3SvqqyD53ZnZm+yddMrONkt6h1sUReOz3QLuO8YyZvbF9\n05ha7y+yqvyTuI6zmV0n6Q8lvVbSi5L2u/t4+88+Juk3JDXU+pHqfWEbXcfMbLNav21akXS7u28P\n3tK6ZmZ/LukqSa+RdFTSJyT9laQvqfVTlqclvdvdX4za43plZldIekitb1je/u931PpH+f8Q+efK\nzIbU+gWcSvu/L7r7fzWzV4v8e8bMrpT0UXe/lux7o/0C4F+q9ZyzQdKfuft28u8dM7tYrV+MrUr6\ne0nvl9SnVeSfxOAMAAAApC7FqgYAAACQHAZnAAAAoAMMzgAAAEAHGJwBAACADjA4AwAAAB1gcAYA\nAAA6wOAMAAAAdIDBGQAAAOjA/wderMc5mM/7BwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1040dfc18>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"figsize(12, 6)\n",
"plt.scatter(range(50), np.mean(X, axis=0));"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"scaler = StandardScaler()\n",
"X = scaler.fit_transform(X)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtsAAAFwCAYAAABpQ7cYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3W2Q3eV53/HvJQlSR0nWJCnCBa/jYBtcqiDoBlNbjUk3\nGIFT5E5T13qRByttmBhapskkiCRTnBedSk5kI5cJtgt2wdMMTshzxpYBP+AqrY2pLEKIJMQUEBBJ\nJMF2EogTGa6+2CO8PuzDkc7Zc/1v7fcz42Hvv/73Obd+WtuXDr89JzITSZIkSaO3ovoAkiRJ0snK\nYVuSJElaIg7bkiRJ0hJx2JYkSZKWiMO2JEmStEQctiVJkqQlMpJhOyI2RMS+iHg4Iq6b5573R8SB\niNgTEesW2xsR50fE/4mIL0XEfRExNYqzSpIkSeMy9LAdESuAm4DLgPOATRFxbt89lwNnZ+ZrgauA\nDwyw9z3ADZl5AXAD8CvDnlWSJEkap1G8sn0RcCAzH8/Mo8AdwMa+ezYCtwNk5heAiYhYs8jeF4CJ\n3tcvB54awVklSZKksVk1gsc4E3hi1vpJZoboxe45c5G9/wn4ZERsBwJ44wjOKkmSJI1N1Q9IxgD3\n/DRwbWZOMjN4f3hpjyRJkiSN1ihe2X4KmJy1PouXVj6eAl45xz2nLrD3xzPzWoDMvDMibp3rya+8\n8sr82te+xhlnnAHA6tWrec1rXsO6dTM/g7lnzx4A10u0vvPOO827cG3+detjX3flPMttbf7mv1zX\nx6515Twn+xrggQce4PDhwwCcffbZ3HzzzYO8aPyiyMzjuf+lDxCxEtgPTAOHgPuATZm5d9Y9VwBX\nZ+ZbI+Ji4MbMvHieve/IzH0R8RDwrsy8NyKmga2Z+f39z/9jP/ZjuWPHjqF+DzpxW7duZcuWLdXH\nWLbMv47Z1zL/WuZfx+xrXXvttdx+++3HNWwP/cp2Zj4fEdcAdzFTS7k1M/dGxFUzv5wfysyPR8QV\nEfEI8CzwzgX27us99L8H3t8byL8G/NRcz3/sbxqqcfDgweojLGvmX8fsa5l/LfOvY/btGUWNhMzc\nCZzTd+2DfetrBt3bu/6/Ad9bW5IkSc1a+e53v7v6DEN5+umn333BBRdUH2PZmpiYYHJycvEbtSTM\nv47Z1zL/WuZfx+xrHTp0iDe+8Y2/fDx7hu5sV/vUpz6VF154YfUxJEmSdJLbvXs309PTx9XZrnrr\nv5GZ/dOiGr9du3ZVH2FZM/86Zl/L/GuZfx2zb0/zw7YkSZLUVdZIJEmSpAEsyxqJJEmS1FXND9t2\ntmvZHatl/nXMvpb51zL/OmbfnuaHbUmSJKmr7GxLkiRJA7CzLUmSJHVI88O2ne1adsdqmX8ds69l\n/rXMv47Zt6f5YVuSJEnqKjvbkiRJ0gDsbEuSJEkd0vywbWe7lt2xWuZfx+xrmX8t869j9u1pftiW\nJEmSusrOtiRJkjQAO9uSJElShzQ/bNvZrmV3rJb51zH7WuZfy/zrmH17mh+2JUmSpK6ysy1JkiQN\nwM62JEmS1CHND9t2tmvZHatl/nXMvpb51zL/OmbfnuaHbUmSJKmr7GxLkiRJA7CzLUmSJHVI88O2\nne1adsdqmX8ds69l/rXMv47Zt6f5YVuSJEnqKjvbkiRJ0gDsbEuSJEkd0vywbWe7lt2xWuZfx+xr\nmX8t869j9u1pftiWJEmSusrOtiRJkjSAss52RGyIiH0R8XBEXDfPPe+PiAMRsSci1g2yNyL+Q0Ts\njYgHI2LrKM4qSZIkjcvQw3ZErABuAi4DzgM2RcS5ffdcDpydma8FrgI+sNjeiLgE+JfA2sxcC/zq\nXM9vZ7uW3bFa5l/H7GuZfy3zr2P27RnFK9sXAQcy8/HMPArcAWzsu2cjcDtAZn4BmIiINYvs/Wlg\na2Z+vbfvL0ZwVkmSJGlsRjFsnwk8MWv9ZO/aIPcstPd1wA9ExOcj4jMRMTXXk69bt26uyxqT9evX\nVx9hWTP/OmZfy/xrmX8ds2/PqqLnHaRYvgo4LTMvjojvB34D+N6lPZYkSZI0OqMYtp8CJmetz+pd\n67/nlXPcc+oCe58EfhsgM78YES9ExHdl5l/OfuAdO3awevVqJidnHmZiYoK1a9e++De/Y90m10uz\nvvnmm827cG3+devZvckunGe5rc3f/Jfr+ti1rpznZF8f+/rgwYMATE1NMT09zfEY+q3/ImIlsB+Y\nBg4B9wGbMnPvrHuuAK7OzLdGxMXAjb1XrOfdGxFXAf8oM2+IiNcBd2fmq/qff/v27bl58+ahfg86\ncbt27XrxG1PjZ/51zL6W+dcy/zpmX+tE3vpvJO+zHREbgB3MdMBvzcytvWE5M/NDvXtuAjYAzwLv\nzMzd8+3tXT8F+DCwDvg74Gcz897+5/Z9tiVJkjQOJzJsrxrFE2fmTuCcvmsf7FtfM+je3vWjwI+O\n4nySJElSheY/rt332a41u9Ok8TP/OmZfy/xrmX8ds29P88O2JEmS1FUj6WxXsrMtSZKkcTiRzrav\nbEuSJElLpPlh2852Lbtjtcy/jtnXMv9a5l/H7NvT/LAtSZIkdZWdbUmSJGkAdrYlSZKkDml+2Laz\nXcvuWC3zr2P2tcy/lvnXMfv2ND9sS5IkSV1lZ1uSJEkagJ1tSZIkqUOaH7btbNeyO1bL/OuYfS3z\nr2X+dcy+Pc0P25IkSVJX2dmWJEmSBmBnW5IkSeqQ5odtO9u17I7VMv86Zl/L/GuZfx2zb0/zw7Yk\nSZLUVXa2JUmSpAHY2ZYkSZI6pPlh2852Lbtjtcy/jtnXMv9a5l/H7NvT/LAtSZIkdZWdbUmSJGkA\ndrYlSZKkDml+2LazXcvuWC3zr2P2tcy/lvnXMfv2ND9sS5IkSV1lZ1uSJEkagJ1tSZIkqUOaH7bt\nbNeyO1bL/OuYfS3zr2X+dcy+Pc0P25IkSVJX2dmWJEmSBmBnW5IkSeqQ5odtO9u17I7VMv86Zl/L\n/GuZfx2zb89Ihu2I2BAR+yLi4Yi4bp573h8RByJiT0SsG3RvRPxsRLwQEd85irNKkiRJ4zJ0Zzsi\nVgAPA9PAnwFfBN6Rmftm3XM5cE1mvjUi3gDsyMyLF9sbEWcBtwDnAP80M5/pf34725IkSRqHqs72\nRcCBzHw8M48CdwAb++7ZCNwOkJlfACYiYs0Ae98H/NwIzihJkiSN3SiG7TOBJ2atn+xdG+SeefdG\nxJXAE5n54EJPbme7lt2xWuZfx+xrmX8t869j9u1ZVfS8C778HhEvA34BuHTQPZIkSVLXjGLYfgqY\nnLU+q3et/55XznHPqfPsPRv4HuCBiIje9f8bERdl5tOzH/iRRx7hXe96F5OTMw8zMTHB2rVrWb9+\nPfCNvwG6Xpr1sWtdOc9yWx+71pXzLKf1+vXrO3We5bY2f/N37Xoc62NfHzx4EICpqSmmp6c5HqP4\nAcmVwH5mfsjxEHAfsCkz98665wrg6t4PSF4M3Nj7AclF9/b2PwpcmJlf7n9+f0BSkiRJ41DyA5KZ\n+TxwDXAX8BBwR2bujYirIuKnevd8HHg0Ih4BPgi8a6G9cz0N89RI7GzXmv03P42f+dcx+1rmX8v8\n65h9e1aN4kEycyczb883+9oH+9bXDLp3jnu+d9gzSpIkSeM2dI2kmjUSSZIkjUPV+2xLkiRJmkPz\nw7ad7Vp2x2qZfx2zr2X+tcy/jtm3p/lhW5IkSeoqO9uSJEnSAOxsS5IkSR3S/LBtZ7uW3bFa5l/H\n7GuZfy3zr2P27Wl+2JYkSZK6ys62JEmSNAA725IkSVKHND9s29muZXeslvnXMfta5l/L/OuYfXua\nH7YlSZKkrrKzLUmSJA3AzrYkSZLUIc0P23a2a9kdq2X+dcy+lvnXMv86Zt+e5odtSZIkqavsbEuS\nJEkDsLMtSZIkdUjzw7ad7Vp2x2qZfx2zr2X+tcy/jtm3p/lhW5IkSeoqO9uSJEnSAOxsS5IkSR3S\n/LBtZ7uW3bFa5l/H7GuZfy3zr2P27Wl+2JYkSZK6ys62JEmSNAA725IkSVKHND9s29muZXeslvnX\nMfta5l/L/OuYfXuaH7YlSZKkrrKzLUmSJA3AzrYkSZLUIc0P23a2a9kdq2X+dcy+lvnXMv86Zt+e\n5odtSZIkqavsbEuSJEkDKOtsR8SGiNgXEQ9HxHXz3PP+iDgQEXsiYt1ieyPiPRGxt3f/b0XEd4zi\nrJIkSdK4DD1sR8QK4CbgMuA8YFNEnNt3z+XA2Zn5WuAq4AMD7L0LOC8z1wEHgOvnen4727XsjtUy\n/zpmX8v8a5l/HbNvzyhe2b4IOJCZj2fmUeAOYGPfPRuB2wEy8wvARESsWWhvZt6TmS/09n8eOGsE\nZ5UkSZLGZhTD9pnAE7PWT/auDXLPIHsBNgOfmOvJ161bN9dljcn69eurj7CsmX8ds69l/rXMv47Z\nt6fq3UgGLpZHxC8CRzPz15fwPJIkSdLIrRrBYzwFTM5an9W71n/PK+e459SF9kbETwBXAP9iviff\nsWMHq1evZnJy5mEmJiZYu3bti3/zO9Ztcr0065tvvtm8C9fmX7ee3ZvswnmW29r8zX+5ro9d68p5\nTvb1sa8PHjwIwNTUFNPT0xyPod/6LyJWAvuBaeAQcB+wKTP3zrrnCuDqzHxrRFwM3JiZFy+0NyI2\nANuBH8jMv5zv+bdv356bN28e6vegE7dr164XvzE1fuZfx+xrmX8t869j9rVO5K3/RvI+273BeAcz\ntZRbM3NrRFwFZGZ+qHfPTcAG4FngnZm5e769vesHmHnl+9ig/fnMfFf/c/s+25IkSRqHExm2V43i\niTNzJ3BO37UP9q2vGXRv7/prR3E2SZIkqUrzH9fu+2zXmt1p0viZfx2zr2X+tcy/jtm3p/lhW5Ik\nSeqqkXS2K9nZliRJ0jicSGfbV7YlSZKkJdL8sG1nu5bdsVrmX8fsa5l/LfOvY/btaX7YliRJkrrK\nzrYkSZI0ADvbkiRJUoc0P2zb2a5ld6yW+dcx+1rmX8v865h9e5oftiVJkqSusrMtSZIkDcDOtiRJ\nktQhzQ/bdrZr2R2rZf51zL6W+dcy/zpm357mh21JkiSpq+xsS5IkSQOwsy1JkiR1SPPDtp3tWnbH\napl/HbOvZf61zL+O2ben+WFbkiRJ6io725IkSdIA7GxLkiRJHdL8sG1nu5bdsVrmX8fsa5l/LfOv\nY/btaX7YliRJkrrKzrYkSZI0ADvbkiRJUoc0P2zb2a5ld6yW+dcx+1rmX8v865h9e5oftiVJkqSu\nsrMtSZIkDcDOtiRJktQhzQ/bdrZr2R2rZf51zL6W+dcy/zpm357mh21JkiSpq+xsS5IkSQOwsy1J\nkiR1SPPDtp3tWnbHapl/HbOvZf61zL+O2bdnJMN2RGyIiH0R8XBEXDfPPe+PiAMRsSci1i22NyJO\ni4i7ImJ/RHwyIiZGcVZJkiRpXIbubEfECuBhYBr4M+CLwDsyc9+sey4HrsnMt0bEG4AdmXnxQnsj\nYhvwl5n5nt4Qflpmbul/fjvbkiRJGocT6WyvGsHzXgQcyMzHASLiDmAjsG/WPRuB2wEy8wsRMRER\na4BXL7B3I/Dm3v7bgM8CLxm2VeP55+GBB1by6KMrePWrX2DduudZMce/JxnkvuXwWK2fv6uP1fr5\nzcIsWnqs1s/fehZq1yiG7TOBJ2atn2RmAF/snjMX2bsmM48AZObhiDh9riffs2cPvrI9fg88sJLL\nL/92jh69l1NOeTOf+MRfc+GFzy9wX3DKKTnnfYPc0/pjLd1zzp9/V7NoI9dBHqtb3/u1WXTre7+N\n87f3WN98n//bU/GcMNPZXr9+/Zy/pm4axbB9Io7r5feeOfsu9957L/fffz+Tk5MATExMsHbt2he/\nEY/9IIHr0a6PHPlBjh4NYA9Hj8Kjj05x4YXPv+T+nTv/iKNHXwZcwtGjwc6df8Rzz339mx7vc59b\nxdGjlwNw9Oi97Nz5t1x44cUvef5HH13B0aP39u67hEcfXcFzz9173M/3zef/7LznH+T56s8/f/6j\nPP8geVX8ebd+/lF+v7Z+/jb++zae83f1z7v187f+37f+H4zsyjxwsq+PfX3w4EEApqammJ6e5niM\norN9MfDuzNzQW28BMjO3zbrnA8BnMvNjvfU+Zioir55vb0TsBS7JzCMRcUZv/+v7n9/Odo3duwf7\nW/gg9y2Hx2r9/F19rNbPbxZm0dJjtX7+1rNQN5xIZ3sUw/ZKYD8zP+R4CLgP2JSZe2fdcwVwde8H\nJC8Gbuz9gOS8e3s/IPlMb/D2ByQ75oUXYM+exftlg9y3HB6r9fN39bFaP79ZmEVLj9X6+VvPQt1Q\nMmzDzNv3ATuYeSvBWzNza0Rcxcyr1B/q3XMTsAF4FnhnZu6eb2/v+ncCvwG8EngceHtmfqX/ubdv\n356bN28e+vegE2N3rJb51zH7WuZfy/zrmH2tqncjITN3Auf0Xftg3/qaQff2rj8D/NAozidJkiRV\nGMkr25WskUiSJGkcTuSVbRtBkiRJ0hJpftjes2dP9RGWtf63ItJ4mX8ds69l/rXMv47Zt6f5YVuS\nJEnqKjvbkiRJ0gDsbEuSJEkd0vywbWe7lt2xWuZfx+xrmX8t869j9u1pftiWJEmSusrOtiRJkjQA\nO9uSJElShzQ/bNvZrmV3rJb51zH7WuZfy/zrmH17mh+2JUmSpK6ysy1JkiQNwM62JEmS1CHND9t2\ntmvZHatl/nXMvpb51zL/OmbfnuaHbUmSJKmr7GxLkiRJA7CzLUmSJHVI88O2ne1adsdqmX8ds69l\n/rXMv47Zt6f5YVuSJEnqKjvbkiRJ0gDsbEuSJEkd0vywbWe7lt2xWuZfx+xrmX8t869j9u1pftiW\nJEmSusrOtiRJkjQAO9uSJElShzQ/bNvZrmV3rJb51zH7WuZfy/zrmH17mh+2JUmSpK6ysy1JkiQN\nwM62JEmS1CHND9t2tmvZHatl/nXMvpb51zL/OmbfnuaHbUmSJKmrhupsR8RpwMeAVwGPAW/PzK/O\ncd8G4EZmhvtbM3PbQvsj4oeArcApwN8DP5+Zn5nrDHa2JUmSNA4Vne0twD2ZeQ7waeD6/hsiYgVw\nE3AZcB6wKSLOXWT/nwM/nJnnAz8BfHTIc0qSJEljN+ywvRG4rff1bcDb5rjnIuBAZj6emUeBO3r7\n5t2fmQ9k5uHe1w8B/yAiTpnrAHa2a9kdq2X+dcy+lvnXMv86Zt+eYYft0zPzCEBvOD59jnvOBJ6Y\ntX6ydw1gzWL7I+JHgN29QV2SJElqxqrFboiIu4E1sy8BCfzSHLcP+6bd37Q/Is4D/itw6Xwb1q1b\nN+RTahjr16+vPsKyZv51zL6W+dcy/zpm355Fh+3MnHfQjYgjEbEmM49ExBnA03Pc9hQwOWt9Vu8a\nwOH59kfEWcBvAz+amY/Nd4Y777yTW265hcnJmaeYmJhg7dq1L34zHvvXLa5du3bt2rVr165dH8/6\n2NcHDx4EYGpqiunpaY7HsO9Gsg14JjO3RcR1wGmZuaXvnpXAfmAaOATcB2zKzL3z7Y+IlwOfBd6d\nmb+70Bm2b9+emzdvPuHfg4aza9euF78xNX7mX8fsa5l/LfOvY/a1Kt6NZBtwaUQcG6a3AkTEKyLi\nDwEy83ngGuAu4CHgjszcu9B+4GrgbOA/R8SXImJ3RHz3kGeVJEmSxmqoV7a7wPfZliRJ0jhUvLIt\nSZIkaR7ND9u+z3at2T9AoPEz/zpmX8v8a5l/HbNvT/PDtiRJktRVdrYlSZKkAdjZliRJkjqk+WHb\nznYtu2O1zL+O2dcy/1rmX8fs29P8sC1JkiR1lZ1tSZIkaQB2tiVJkqQOaX7YtrNdy+5YLfOvY/a1\nzL+W+dcx+/Y0P2xLkiRJXWVnW5IkSRqAnW1JkiSpQ5oftu1s17I7Vsv865h9LfOvZf51zL49zQ/b\nkiRJUlfZ2ZYkSZIGYGdbkiRJ6pDmh20727XsjtUy/zpmX8v8a5l/HbNvT/PDtiRJktRVdrYlSZKk\nAdjZliRJkjqk+WHbznYtu2O1zL+O2dcy/1rmX8fs29P8sC1JkiR1lZ1tSZIkaQB2tiVJkqQOaX7Y\ntrNdy+5YLfOvY/a1zL+W+dcx+/Y0P2xLkiRJXWVnW5IkSRqAnW1JkiSpQ5oftu1s17I7Vsv865h9\nLfOvZf51zL49zQ/bkiRJUlfZ2ZYkSZIGYGdbkiRJ6pChhu2IOC0i7oqI/RHxyYiYmOe+DRGxLyIe\njojrBt0fEZMR8dcR8TPzncHOdi27Y7XMv47Z1zL/WuZfx+zbM+wr21uAezLzHODTwPX9N0TECuAm\n4DLgPGBTRJw74P7twMeHPKMkSZJUYqjOdkTsA96cmUci4gzgs5l5bt89FwM3ZOblvfUWIDNz20L7\nI2Ij8EbgWeBvMvO9c53BzrYkSZLGoaKzfXpmHgHIzMPA6XPccybwxKz1k71rAGv69q8BiIhvA34e\n+GXguH5DkiRJUlcsOmxHxN0R8cez/vNg759XznH7sG9t8kLvnzcA78vM544dY74NdrZr2R2rZf51\nzL6W+dcy/zpm355Vi92QmZfO92sRcSQi1syqgTw9x21PAZOz1mf1rgEcnmf/G4B/HRHvAU4Dno+I\nv83MX+t/8HvvvZf777+fycmZp5iYmGDt2rWsX78e+MY3peulWT/44IOdOs9yW5u/a9euXS+v9TFd\nOc/Jvj729cGDBwGYmppienqa4zFsZ3sb8Eyvf30dcFpmbum7ZyWwH5gGDgH3AZsyc++A+28A/trO\ntiRJkipVdLa3AZdGxLFheitARLwiIv4QIDOfB64B7gIeAu7IzL0L7ZckSZJOBkMN25n5TGb+UGae\nk5lvycyv9K4fyswfnnXfzt49r83MrYvt73uOX57vVW2ws12t/19rabzMv47Z1zL/WuZfx+zb4ydI\nSpIkSUtkqM52F9jZliRJ0jhUdLYlSZIkzaP5YdvOdi27Y7XMv47Z1zL/WuZfx+zb0/ywLUmSJHWV\nnW1JkiRpAHa2JUmSpA5pfti2s13L7lgt869j9rXMv5b51zH79jQ/bEuSJEldZWdbkiRJGoCdbUmS\nJKlDmh+27WzXsjtWy/zrmH0t869l/nXMvj3ND9uSJElSV9nZliRJkgZgZ1uSJEnqkOaHbTvbteyO\n1TL/OmZfy/xrmX8ds29P88O2JEmS1FV2tiVJkqQB2NmWJEmSOqT5YdvOdi27Y7XMv47Z1zL/WuZf\nx+zb0/ywLUmSJHWVnW1JkiRpAHa2JUmSpA5pfti2s13L7lgt869j9rXMv5b51zH79jQ/bEuSJEld\nZWdbkiRJGoCdbUmSJKlDmh+27WzXsjtWy/zrmH0t869l/nXMvj3ND9uSJElSV9nZliRJkgZgZ1uS\nJEnqkOaHbTvbteyO1TL/OmZfy/xrmX8ds29P88O2JEmS1FVDdbYj4jTgY8CrgMeAt2fmV+e4bwNw\nIzPD/a2ZuW2x/RHxfcAHgO8Ange+PzP/vv+x7WxLkiRpHCo621uAezLzHODTwPX9N0TECuAm4DLg\nPGBTRJy70P6IWAl8FPipzPwnwCXA0SHPKkmSJI3VsMP2RuC23te3AW+b456LgAOZ+XhmHgXu6O1b\naP9bgAcy808AMvPLOc9L8Ha2a9kdq2X+dcy+lvnXMv86Zt+eYYft0zPzCEBmHgZOn+OeM4EnZq2f\n7F0DWDPP/tcBRMTOiLg/In5uyHNKkiRJY7dqsRsi4m5gzexLQAK/NMftw75p97H9q4A3AVPA14BP\nRcT9mfmZ/g3r1q0b8ik1jPXr11cfYVkz/zpmX8v8a5l/HbNvz6LDdmZeOt+vRcSRiFiTmUci4gzg\n6TluewqYnLU+q3cN4PA8+58EPpeZX+49z8eBC4GXDNt33nknt9xyC5OTM08xMTHB2rVrX/xmPPav\nW1y7du3atWvXrl27Pp71sa8PHjwIwNTUFNPT0xyPYd+NZBvwTGZui4jrgNMyc0vfPSuB/cA0cAi4\nD9iUmXvn2x8RLwfuAdYDXwc+Abw3Mz/Rf4bt27fn5s2bT/j3oOHs2rXrxW9MjZ/51zH7WuZfy/zr\nmH2tincj2QZcGhHHhumtABHxioj4Q4DMfB64BrgLeAi4IzP3LrQ/M78CvBe4H9gN3D/XoC1JkiR1\n2VCvbHeB77MtSZKkcah4ZVuSJEnSPJoftn2f7Vqzf4BA42f+dcy+lvnXMv86Zt+e5odtSZIkqavs\nbEuSJEkDsLMtSZIkdUjzw7ad7Vp2x2qZfx2zr2X+tcy/jtm3p/lhW5IkSeoqO9uSJEnSAOxsS5Ik\nSR3S/LBtZ7uW3bFa5l/H7GuZfy3zr2P27Wl+2JYkSZK6ys62JEmSNAA725IkSVKHND9s29muZXes\nlvnXMfta5l/L/OuYfXuaH7YlSZKkrrKzLUmSJA3AzrYkSZLUIc0P23a2a9kdq2X+dcy+lvnXMv86\nZt+e5odtSZIkqavsbEuSJEkDsLMtSZIkdUjzw7ad7Vp2x2qZfx2zr2X+tcy/jtm3p/lhW5IkSeoq\nO9uSJEnSAOxsS5IkSR3S/LBtZ7uW3bFa5l/H7GuZfy3zr2P27Wl+2JYkSZK6ys62JEmSNAA725Ik\nSVKHND9s29muZXeslvnXMfta5l/L/OuYfXuaH7YlSZKkrrKzLUmSJA3AzrYkSZLUIUMN2xFxWkTc\nFRH7I+KTETExz30bImJfRDwcEdcttj8iVkXE/4iIP46IhyJiy3xnsLNdy+5YLfOvY/a1zL+W+dcx\n+/YM+8r2FuCezDwH+DRwff8NEbECuAm4DDgP2BQR5y6y/98Ap2bm9wFTwFURMTnXAR555JEhfwsa\nxoMPPlh9hGXN/OuYfS3zr2X+dcy+1om8yDvssL0RuK339W3A2+a45yLgQGY+nplHgTt6+xban8Dq\niFgJfCvwd8BfzXWAZ599dsjfgobx1a9+tfoIy5r51zH7WuZfy/zrmH2tBx544Lj3DDtsn56ZRwAy\n8zBw+hz3nAk8MWv9ZO8awJq+/Wt61+8EngMOAY8Bv5qZXxnyrJIkSdJYrVrshoi4m28MwQDBzCvP\nvzTH7cPjFv64AAAFSElEQVS+tckLvX++Afg6cAbwXcD/ioh7MvOx/g2HDx8e8ik1jIMHD1YfYVkz\n/zpmX8v8a5l/HbNvz6LDdmZeOt+vRcSRiFiTmUci4gzg6TluewqY3bc+q3cN4PA8+zcBOzPzBeDP\nI+KPmOluP9b/4GeffTbXXnvti+vzzz+fdevWLfbb0ohMTU2xe/fu6mMsW+Zfx+xrmX8t869j9uO1\nZ8+eb6qOrF69+rgfY6j32Y6IbcAzmbmt9y4jp2Xmlr57VgL7gWlmaiH3AZsyc2/f/i3AyzNzS0T8\nPHBOZv5kRKzu7fm3mfknJ3xYSZIkacyGHba/E/gN4JXA48DbM/MrEfEK4L9n5g/37tsA7GCmI35r\nZm5dZP9q4CPAP+491Ycz870nfFBJkiSpQPOfIClJkiR1VbOfIBkRPxIRfxIRz0fEhX2/dn1EHIiI\nvRHxlqoznszm+6AiLY2IuLX3MxJ/POvaQB8qpeFFxFkR8eneh2w9GBH/sXfdP4MlFhHfEhFfiIgv\n9bK/oXfd7McoIlZExO6I+P3e2vzHJCIei4gHev8duK93zfzHICImIuI3e/PkQxHxhhPJvtlhG3gQ\n+FfAvbMvRsTrgbcDrwcuB34tIo7rM+y1sEU+qEhL4yPM5D3boh8qpZH5OvAzmXke8M+Aq3vf8/4Z\nLLHM/DvgBzPzAmAdcHlEXITZj9u1wJ/OWpv/+LwAXJKZF2TmRb1r5j8eO4CPZ+brgfOBfZxA9s0O\n25m5PzMPMPNWhLNtBO7IzK/33irwADMfrKPRWeiDirQEMnMX8OW+y4N8qJRGIDMPZ+ae3td/A+xl\n5p2V/DMYg8x8rvfltzDzLlqJ2Y9NRJwFXAHcMuuy+Y9P8NJ5zfyXWER8B/DPM/MjAL258qucQPbN\nDtsL6P8Qnaf4xofoaDQW+qAijc8gHyqlEYuI72HmFdbP89IP5vLPYAn0KgxfAg4Dd2fmFzH7cXof\n8HN882dpmP/4JHB3RHwxIv5d75r5L71XA38RER/pVag+FBHfyglkv+j7bFda4AN1fjEz/6DmVFJn\n+dPOSywivo2ZT7i9NjP/JiL6M/fPYAn0PnPhgt4rTb8TEefx0qzNfglExFuBI5m5JyIuWeBW8186\nb8rMQxHxD4G7ImI/fv+PwyrgQuDqzLw/It7HTIXkuLPv9LC90AfqLOApZt5K8JjZH6Kj0Vjog4o0\nPoN8qJRGJCJWMTNofzQzf6932T+DMcrMv4qIzwIbMPtxeRNwZURcAbwM+PaI+CjzfyidRiwzD/X+\n+ecR8bvMVDn9/l96TwJPZOb9vfVvMTNsH3f2J0uNZHZv+/eBd0TEqRHxauA1zHwojkbni8BrIuJV\nEXEq8A5mctfSCl76vf4Tva9/HPi9/g0aqQ8Df5qZO2Zd889giUXEdx/7af+IeBlwKTOdebMfg8z8\nhcyczMzvZeZ/6z+dmT8K/AHmv+Qi4lt7/0aN3meQvIWZN4jw+3+J9aoiT0TE63qXpoGHOIHsm32f\n7Yh4G/DfgO8GvgLsyczLe792PfCTwFFm/nXvXWUHPUnN90FFWhoR8evAJcB3AUeAG4DfBX6Tvg+F\nqjrjySwi3gR8jpn/k8vef36Bmb/Iv+SDuarOeTKKiLXM/BDSit5/PpaZ/yXm+VC0upOe/CLizcDP\nZuaV5j8evRcNf4eZ/81ZBfzPzNxq/uMREecz84PBpwD/D3gnsJLjzL7ZYVuSJEnqupOlRiJJkiR1\njsO2JEmStEQctiVJkqQl4rAtSZIkLRGHbUmSJGmJOGxLkiRJS8RhW5IkSVoiDtuSJEnSEvn/gifC\nUmW1iiUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1040f3198>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"figsize(12, 6)\n",
"plt.scatter(range(50), np.mean(X, axis=0));"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABB4AAACCCAYAAADhTQsYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+QVeWd5/H3FyzMDwF1VfxBMBpMBjM9kE4Pgxt3TdJE\njTulTpaoSWpiRjNl2WajG8sJZLaKdXaqbLXMZJKM1G4wCaZMGavXHZMZgghJZquzIGrnkp7BUegR\nkF9NCIGGcQKC3/3jnEtfLre774/z6+n+vKoo7/P0Obc/9/HcL5fnnvMcc3dERERERERERNIwKe8A\nIiIiIiIiIjJ+aeJBRERERERERFKjiQcRERERERERSY0mHkREREREREQkNZp4EBEREREREZHUaOJB\nRERERERERFIz5sSDmZ1uZs+b2S/MrN/Mlsb9S81sh5n1xX+urdhniZltNrOXzezqiv52M/ulmb1q\nZl+r6J9iZk/G+6wzs1lJv1ARSY7qgohUU10QkWqj1IWzzGy1mb1iZs+a2fSKfVQXRMahMSce3P0I\n8BF3/wAwD/i4mc2Pf/xVd2+P/6wCMLM5wE3AHODjwKNmZvH2y4Db3f29wHvN7Jq4/3Zgv7tfBnwN\neCih1yciKVBdEJFqqgsiUm2UurAYWOPu7wN+AiwBMLPLUV0QGZfqutTC3d+IH54OnAZ43LYam98A\nPOnux9x9K7AZmG9m5wNT3f2FeLvHgRsr9lkRP+4BOht5ESKSPdUFEammuiAi1UaoC5Xv5RUMv8ev\nR3VBZFyqa+LBzCaZ2S+APcBzFW/6L5hZycyWV5widRHwesXuO+O+i4AdFf074r6T9nH348ABMzu7\nmRckItlQXRCRaqoLIlJthLoww90HAdx9D3BevLnqgsg4Ve8ZD2/Fp0jNJJp1vBx4FLjU3ecRFZJH\nEsxV65sRESkQ1QURqaa6ICLVatSF9zN8NtSJzRL8laoLIgV0WiMbu/uQmf0MuNbdv1rxo28BP4of\n7wTeVfGzmXHfSP2V++wys8nANHffX/3777zzTh8YGOD8888H4J3vfCezZ89m3rx5AJRKJYCG21u2\nbGHRokVN7591O6S8//AP/8Ddd99dmDzKe2obYOPGjezZsweAa665hnvvvbfuv7RVF4rRDinvRHyf\nhZYXVBdqtUN6n4WWdyK+z0LLC8nVBWDQzGa4+2B8GcXeeDPVBdWFE+2J+D4LLS/UXxfMffQJRjM7\nB3jT3Q+a2duBZ4FuoC8+NQoz+6/A77v7p+NvN54A/oDo1KfngMvc3c1sPfBF4AXg74Gvu/sqM+sC\nftfdu8zsFuBGd7+lOsvatWu9vb191LzN6Orq4tFHH038edMSUt6QsoLyAvT19dHZ2TnqBwnVheIJ\nIe/GXYe4b+UW/uUHD3LpzV9u6bkevm42cy+cmlCy0YUwtpVUF1QXykLKG1JWUF5ouS5cRbQg5INm\n9mXgLHdfrLqQvpDyhpQVlBdGrwv1nPFwAbDCzCYRXZrxA3dfaWaPm9k84C1gK3AHgLtvMrOngE3A\nm0CXD89u3AV8F3gbsLK8sjXwGPA9M9sM/Bo4pVikadassO66E1LekLKC8jZAdaFgQsp7+lnn5x2h\nISGNLagupEnHQnpCygrK24CR6sJ64Ckzuw3YRnQnC9WFDISUN6SsoLxjGXPiwd37gVOmB939s6Ps\n8wDwQI3+l4C2Gv1HiAuOiBSf6oKIVFNdEJFqo9SF/cDCEfZRXRgHdg8dYe/hoy09x2/eeJONuw61\nnOW8M6ZwwbTTW34eaU1DazyMV9OnTx97owIJKW9IWUF5ZVhoYxtS3slvf2feERoS0thCeHlDEtrY\nhpQ3pKygvDIstLHNKu/ew0e5b+WWlp5j3unvbPk5ILo8M4uJBx0Lo6vrrhbjXVvbKZOnhRZS3pCy\ngvLKsNDGNqS877hwdt4RGhLS2EJ4eUMS2tiGlDekrKC8Miy0sQ0p76XvuzzvCA0JaWwh+7yaeACu\nvPLKvCM0JKS8IWUF5ZVhoY1tSHmnvWde3hEaEtLYQnh5QxLa2IaUN6SsoLwyLLSxDSlvW8eCvCM0\nJKSxhezzauJBRERERERERFKjiQegt7c37wgNCSlvSFlBeWVYaGMbUt6hgdLYGxVISGML4eUNSWhj\nm0Xe3UNH2LjrUMt/VvztanYPHUk9b1J0LEhZaGMbUt7+F9fnHaEhIY0tZJ93zMUlzex04P8CU+Lt\ne9z9fjM7C/gBcDHR7bFucveD8T5LgNuAY8Dd7r467m/n5Nvg3BP3TwEeBz4I7ANudvftyb1MaUYS\nq9EO7HuDqbsOaTXZcUZ1QUSqqS5MTEksIAcwNLCTefOP6rOCiMg4Vc/tNI+Y2Ufc/Q0zmwz83Mx+\nDPxnYI27P2RmXwaWAIvN7HKiW9rMAWYCa8zssvgevMuA2939BTNbaWbXuPuzwO3Afne/zMxuBh4i\nw3vw6nqc2pL5MHEuT6zcktlqsq3SsVAf1YXiCSmv1nhIl+pCenQspEd1IV2h5Q1JaGMbUt62jgU8\nvea1vGPULaSxhezz1nU7TXd/I354eryPAzcAV8X9K4CfAYuB64En3f0YsNXMNgPzzWwbMNXdX4j3\neRy4EXg2fq6lcX8P8M0WXpOIZEB1QUSqqS5IKyZPgo27DiX2fDrbMn9mNpPoPTwDeAv4X+7+DTNb\nCvwpsDfe9CvuvireR2dCiYxDdU08mNkk4CXgPcDfxN9AzHD3QQB332Nm58WbXwSsq9h9Z9x3DNhR\n0b8j7i/v83r8XMfN7ICZne3u+5t8XQ3p7e0NaoYqpLxDA6WgvsUIaWwh37yqC8USUl7VhXSpLqRH\nx0J6hgZKHPztJdyf4LebaZ5tGdLYQq55jwFfcveSmZ0BvGRmz8U/+6q7f7VyYzObQ2BnQulYSE+0\nxsOMvGPULaSxhezz1rW4pLu/5e4fICoA883s/UTfYpy0WYK5LMHnEpEUqC6ISDXVBRGp5O573L0U\nPz4MvMzwRGKt9+8NxGdCuftWoHwm1PnUPhOqvM+K+HEP0Jn4CxGRltV1xkOZuw+Z2c+Aa4HB8rcY\ncTEonyq1E3hXxW4z476R+iv32RVfFzqt1rcXPT09LF++nFmzZgEwffp02traTszUlFfmVDuZdmnD\nOoYGdp74ZrK8En2jbYhOn1zxt6sBmDf/ihPP30z76o9exQXTTk/t9ZflPf5Z5S0/3r49Oiuxo6OD\nzs76/85WXVC7kXb1HS2aryuzM81flvf4qS6oLhSx3ez7uNbnhWSfL906UZb3+IdSF8zs3cA84Hng\nSuALZvbHwIvAvfGis8GdCRXSN9wQVl6t8ZCurPNadObSKBuYnQO86e4HzeztRNdYdhNdr7nf3R+M\nF4s6y93Li0U9AfwBUSF4DrjM3d3M1gNfBF4A/h74uruvMrMu4HfdvcvMbgFudPdTTpFau3att7e3\nJ/XaZQwbdx1KZKVqgKULkzt98uHrZjP3wqmJPJecqq+vj87OzlG/RVRdkGYkWVNUB7KluiAjKepn\nBVCdSFs9daEsvsziZ8D/cPdnzOxcYF/8fv9L4Hx3/7yZfQNY5+7fj/dbDqwEtgEPuPvVcf+VwJ+5\n+/Vm1g9c4+674p9tAeZXTzyoLmQridqQVE1QLcjOaHWhnkstLgB+amYlohnKZ919JfAg8DEze4Xo\nlKZuAHffBDwFbCIqFF0+PLtxF/AY8CqwubyITNx3Tryw1D1Ei05lpnomuOhCylv9LUbRhTS2kGte\n1YWCCSmv6kK6VBfSo2MhPaoL6cozr5mdRnQJxPfc/RkAd/9Vxfv9W8D8+HErZ0Ix1plQXV1ddHd3\n093dzbJly045m6OZdrmv2f2zbmeVNzpzevh9PTRQarj9zBPfbmn/ynYW47ts2bJMf18R8vb29tLd\n3U1XVxddXV2USiPX8tNG/EnM3fuBU6YH4zf0whH2eQB4oEb/S0Bbjf4jRAvJiEgAVBdEpJrqgoiM\n4NvAJnf/63KHmZ3v7nvi5ieAf4wf/xB4wsz+iuhMqNnAhvjMiINmNp/oTKjPAl+v2OdWognPTwI/\nqRVi0aJFjHbGQ/Vp5/W2qy9NafX50m5nlXfe/CuYtm/4jIfqRaXraV965iClA83v30p+tetvVz7u\n6+tjJGNOPEwEuh4nPSGtXA9hjS2ElzckoY1tSHlVF9IVWt6QhDa2IeVVXUhXXnnN7EPAZ4B+M/sF\n0eKyXwE+bWbziG6xuRW4A6IzocysfCbUm5x6JtR3Gb6dZuWZUN+Lz4T6NRne0QJ0LKRJazykK+u8\nmngQEREREZHEufvPgck1frSqRl95H50JJTIO1XU7zfFO1+mlR9dspiu0vCEJbWxDyqu6kK7Q8oYk\ntLENKa/qQrpCyxuS0MY2pLz9L67PO0JDQhpbyD6vJh5EREREREREJDWaeEDX46RJ12ymK7S8IQlt\nbEPKq7qQrtDyhiS0sQ0pr+pCukLLG5LQxjakvG0dC/KO0JCQxhayzzvmxIOZzTSzn5jZP5lZv5n9\nl7h/qZntMLO++M+1FfssMbPNZvaymV1d0d9uZr80s1fN7GsV/VPM7Ml4n3VmNivpFyoiyVFdEJFq\nqgsiIiIyknrOeDgGfMnd3w9cAXzBzH4n/tlX3b09/rMKwMzmEC3wMgf4OPComVm8/TLgdnd/L/Be\nM7sm7r8d2O/ulwFfAx5K4sXVS9fjpEfXbKYrx7yqCwUTUl7VhXSpLqRHx0J6VBfSFVrekIQ2tiHl\n1RoP6SrcGg/uvsfdS/Hjw8DLRPfVBbAau9wAPOnux9x9K7AZmG9m5wNT3f2FeLvHgRsr9lkRP+4B\nOpt4LSKSEdUFEammuiAiIiIjaWiNBzN7NzAPeD7u+oKZlcxsuZlNj/suAl6v2G1n3HcRsKOifwfD\nH0hO7OPux4EDZnZ2I9laoetx0qNrNtNVhLyqC8UQUl7VhXQVIa/qQjGElFd1IV2h5Q1JaGMbUl6t\n8ZCurPOeVu+GZnYG0bcLd7v7YTN7FPgLd3cz+0vgEeDzCeWq9c0IPT09LF++nFmzoks6p0+fTltb\n24lBK58uonYy7dKGdQwN7DzxYaB8GmTebZhdiPEZL+3y4+3btwPQ0dFBZ2d9XyKqLqjdaFt1IIx2\n+bHqgtr1tBN7Xy+8JNnnU51ItF1+3ExdEBExdx97I7PTgL8Dfuzuf13j5xcDP3L33zOzxYC7+4Px\nz1YBS4FtwE/dfU7cfwtwlbvfWd7G3Z83s8nAbnc/r/r3rF271tvb25t+sSPp7e09UVxDkFXejbsO\ncd/KLS09x9BAiWnvmcfShZdw/5rXEsn18HWzmXvh1ESeq5qOBejr66Ozs7Pmh/lKqgvFEkLeck0p\n14VWpFkHqoUwtpVUF1QXyrLIm8RnBYg+Lzxyxx8l9lkB9HmhUl51wcxmEl0uNQN4C/iWu3/dzM4C\nfgBcDGwFbnL3g/E+S4DbiNaNudvdV8f97cB3gbcBK939nrh/Svw7PgjsA2529+3VWVQXIiH9O+IT\nZw7y9IEZLWfJ6jODjoXR60K9l1p8G9hU+SEivgaz7BPAP8aPfwjcEq88fQnRdPMGd98DHDSz+fHi\nUZ8FnqnY59b48SeBn9SZS0Tyo7ogItVUF0Sk0jFOXnT2rnjR2cXAGnd/H9H7eAmAmV1OYIvOikh9\nThtrAzP7EPAZoN/MfgE48BXg02Y2j2j2citwB4C7bzKzp4BNwJtAlw+fVnEXJ89Uror7HwO+Z2ab\ngV8DtyTy6uoU0swUhJVX12ymK6+8qgvFE1Je1YV0qS6kR8dCelQX0pVX3ngicU/8+LCZvQzMJFoo\n9qp4sxXAz4gmI64nXnQW2Bq/1+eb2TZqLzr7bPxcS+P+HuCbab+uSjoW0tPWsYCnEzwLKm0hjS1k\nn3fMiQd3/zkwucaPVtXoK+/zAPBAjf6XgLYa/UeIZjdFJACqCyJSTXVBREZTsejsemCGuw9CNDlh\nZuVLpi4C1lXsVl509hh1LjprZgfM7Gx335/SSxGRJjR0V4vxqnLRnBCElFf35U5XaHlDEtrYhpRX\ndSFdoeUNSWhjG1Je1YV05Z23etFZojOiKo296FwDv65WZ09PD11dXXR3d9Pd3c2yZctOWTizmXa5\nr9n9s25nlTdapH74fT00UGq4/cwT325p/8p2FuO7bNmyTH9fEfL29vbS3d1NV1cXXV1dlEoj1/Ix\nz3gQERERERFpRrzobA/wPXcvr9cyaGYz3H0wXgdmb9y/E3hXxe4z476R+iv32RUvOjut1tkOixYt\nYrTFJatPO6+3XX0XkFafL+12Vnnnzb+CafuGF5esvpyqnvalZw5SOtD8/q3kV7v+duXjvr4+RqIz\nHtD1OGnSNZvpCi1vSEIb25Dyqi6kK7S8IQltbEPKq7qQrpzznrLoLNFCsZ+LH9/KyQvIBrXorI6F\n9LR1LMg7QkNCGlso4BoPIiIiIiIijRpl0dkHgafM7DaiW+jeBGEuOisi9dEZD+R/3VujQsqrazbT\nFVrekIQ2tiHlVV1IV2h5QxLa2IaUV3UhXXnldfefu/tkd5/n7h9w93Z3X+Xu+919obu/z92vdvcD\nFfs84O6z3X2Ou6+u6H/J3dvc/TJ3v7ui/4i73xT3L3D3rVm+Rh0L6el/cX3eERoS0thC9nnruZ3m\nTKJb1swguhXWt9z962Z2FvAD4GKi22Pd5O4H432WALcRrUB7d7lomFk7J89U3hP3T4l/xweBfcDN\n7r49uZcpIklSXSi23UNH2Hv4aCLPdd4ZU7hg2umJPJeMb6oLIiIiMpJ6LrU4BnzJ3UvxirQvmdlq\n4E+ANe7+kJl9GVgCLDazy4lOl5pDtPDLGjO7LD5Nahlwu7u/YGYrzewad38WuB3Y7+6XmdnNwENk\neJqUrsdJj67ZTFeOeVUXCqYy797DR7lv5ZZRtq7fw9fNTnziQXUhXaoL6dGxkB7VhXSFljckoY1t\nSHnbOhbw9JrX8o5Rt5DGFrLPO+alFu6+x91L8ePDwMtEHxBuAFbEm60AbowfXw886e7H4lOdNgPz\n4xVrp7r7C/F2j1fsU/lcPUBnKy9KRNKluiAi1VQXREREZCQNrfFgZu8G5gHrgRnuPgjRhw3gvHiz\ni4DXK3bbGfddBOyo6N8R9520j7sfBw6Y2dmNZGuFrsdJj67ZTFcR8qouFENIeVUX0lWEvKoLxRBS\nXtWFdIWWNyShjW1IebXGQ7oKt8ZDWXzaZA/RNZiHzcyrNqlut8Jqdfb09LB8+XJmzZoFwPTp02lr\naxvxvrT1tsua3T/rdlZ5SxvWMTSw88Tpj+UPBY2039i1paX9a7WjOyul8/r7+/tz//+bdd7y4+3b\no8ukOzo66Oys70tE1YXitCvzDux7AzgXaP19V9qwjkPnvCOxvEnVhTTrQHVbdUF1YTzUhTR/XxJ/\nv7+xa/jyMH1eKGbe8uNm6oKIiA3foWaUjcxOA/4O+HH5Hrxm9jLwYXcfjE+L/Km7zzGzxYC7+4Px\ndquApUS3yvmpu8+J+28BrnL3O8vbuPvzZjYZ2O3u51XnWLt2rbe3tyfxuqUOG3cdSuw68aULL+H+\nhK7Revi62cy9cGoizyWn6uvro7Ozs+aH+UqqC8WV5Hs3yfdbUXPJ2FQXZCRF/awAqhNpq7cuFIXq\nQraSqA1J1QTVguyMVhfqvdTi28Cm8oeI2A+Bz8WPbwWeqei/xcymmNklRNPNG+LTKw+a2XwzM+Cz\nVfvcGj/+JPCTOnOJSH5UF0SkmuqCiIiInGLMiQcz+xDwGeCjZvYLM+szs2uBB4GPmdkrRIs7dQO4\n+ybgKWATsBLo8uHTKu4CHgNeBTa7+6q4/zHgHDPbDNwDLE7qBdaj+pTEogspr67ZTFdeeVUXiiek\nvKoL6VJdSI+OhfSoLqQrx7rwmJkNmtkvK/qWmtmOuEaU60T5Z0vMbLOZvWxmV1f0t5vZL83sVTP7\nWkX/FDN7Mt5nnZnNyu7VRXQspEdrPKQr67ynjbWBu/8cmDzCjxeOsM8DwAM1+l8C2mr0HyG6pZaI\nBEB1YeKYPCk6XTIJR4+/lcjzQLK5zjtjSuK3DJ2IVBdEpIbvAN8gujtNpa+6+1crO8xsDoHdYlfC\nkMRnBn1WaN2YEw8Tge65mh7dlztdoeUNSWhjm1beg789ntg110sXXgIkUxeSzPXwdbNH/TChY0HK\nQhvbkPLq80K68srr7r1mdnGNH9W6BvwG4lvsAlvjM5vmm9k2at9i99l4n6Vxfw/wzURfQB10LKSn\nrWMBTyfwd30SnxnG+qwAYY0tZJ9XEw8iIiIiIpKlL5jZHwMvAve6+0Gi2+Wuq9imfIvdY9R5i10z\nO2BmZ7v7/rRfwHi1e+gIew8fbfl5kjzLUcYHTTwQXd8S0gxVSHmHBkpBfYsR0thCeHlDEtrYhpRX\ndSFdoeUNSWhjG1LeoYESxGdFhSCksYXC5X0U+At3dzP7S+AR4PMJPfeId9lI8za7V155ZSFum5pE\n3qmXzuW+lVtavq3tJ84cZGhgd0u3xX1m8Kcw4yNN759ku57bi/f393PnnXeO+POitZPIW35cz212\nNfEgIiIiIiKZcPdfVTS/BfwofrwTeFfFz2bGfSP1V+6zK77F7rSRznZYtGgRo91Os3pipt529T/I\nWn2+tNtj5S2vhVD9BUGj7baOBUw78Frd29dqX3rmIKUDze+fZHve/CtOuiVnUf5/FqFd+bivr4+R\n1Hs7zXGtQDPAdQkpb0jfakJYYwvh5Q1JaGMbUl7VhXSFljckoY1tSHlVF9KVc16j4kwEMzu/4mef\nAP4xfhzkLXZ1LKSnrWNB3hEaEtLYQgHXeDCzx4A/BAbd/ffivqXAnwJ7482+Ur7VlZktAW4juh7r\nbndfHfe3A98F3gasdPd74v4pRIvEfBDYB9zs7tuTeoETTVLXZYGuzZKRqS6ISDXVBRGpZmbfBz4M\n/Dsz2060EORHzGwe8BawFbgDolvsmln5Frtvcuotdr/LcF2ovMXu9+KFKH+N7mghUlj1XGox7m+D\nU7Dr3sY0Wt69h49y38otifyepQlca6lrudOVY17VhYIJKa/qQrpUF9KjYyE9WuMhXXnldfdP1+j+\nzijbB3eLXR0L6el/cT0wI+8YdQtpbCH7vGNeauHuvcBvavxo1NvguPtWoHwbnPOpfRuc8j4r4sc9\nQO3VKESkMFQXRKSa6oKIiIiMpJXFJcfNbXBCmpmCsPKG9K0mhDW2UMi8qgs5CSmv6kK6CphXdSEn\ntfImeUkmJHdZpupCukLLG5LQxjakvG0dC3h6zWtjb1gQIY0tFHCNhxGMq9vgjKf2wL43gHOB1m8b\n0//i+pZvg5NGO1prqBjjPR7a5cf13AZnDKoLBWlPiDoQn5KdxPOVNvyKuTdeXff4ToR2+bHqwvhr\n7z18lDu+0QMk875cuvCSQr6vI/q8kGS7/DiBuiAiE5ANr9kyykZmFwM/Ki8WNdLPzGwx4O7+YPyz\nVUSLyGwDfuruc+L+W4Cr3P3O8jbu/nx8G5zd7n5erRxr16710W6D06zxdD3Oxl2HEl3j4f4WZxnL\n13In8VxlD183+6Tb2SRpPB0Lzerr66Ozs3PED/RlqgvFUpm3aHWg+rmSWOMhy5oS8rGQFNWFyHg4\nFpKsD5Dce3FooMQjd/xRYu9r0OeFSnnWhaJQXYiMlTepGpFEbfjEmYM8faD1NR6SyFJPPRlvx0Iz\nRqsL9d5Oc1zfBkdEmqK6ICLVVBdERETkFGNeajERboMT0swUhJVX12ymK6+8qgvFE1Je1YV0qS6k\nR8dCetKoC5MnRd/eJuG8M6ZwwbTTT7RDGlsIL29IQhvbkPJqjYd0ZZ13zImHiXAbHAlLmh8kpD6q\nCyJSTXVBiubgb48nekmWPi+IiDSvlbtajBu6Hic9SVzLXS3NDxIhjS2ElzckoY1tSHnTqAtpCmls\nIby8IQltbEPKOzRQOrG4ZAhCGlvIL6+ZPQb8ITBYXvvFzM4CfgBcTHQm1E3x3W4wsyXAbUR3uLnb\n3VfH/e2cfCbUPXH/FKLb7n4Q2Afc7O7bs3p9oGMhTf0vrgdaX+MhKyGNLWSft941HkRERERERBrx\nHeCaqr7FwBp3fx/RWi1LAMzscqKzmuYAHwcejdd6AVgG3O7u7wXea2bl57wd2O/ulwFfAx5K88WI\nSPM08YCux0lTSN9qQlhjC+HlDUloYxtSXtWFdIWWNyShjW1IeVUX0pVXXnfvBX5T1X0DsCJ+vAK4\nMX58PfCkux9z963AZmB+vEjtVHd/Id7u8Yp9Kp+rB8j8/p46FtLT1rEg7wgNCWlsIfu8mngQERER\nEZGsnOfugwDxnWzKt8W9CHi9Yrudcd9FwI6K/h1x30n7uPtx4ICZnZ1edBFpliYeiK5vCUlIeYcG\nSnlHaEhIYwvh5Q1JaGMbUl7VhXSFljckoY1tSHlVF9JV8Lw+9iZ1s5F+0NPTQ1dXF93d3XR3d7Ns\n2bKTxqW3t7epdrmv2f2zbtebd2igdNL7stF2/4vrW9p/aKDEM098O7E8rbZLG9aNOb7Lli0b9edF\nayeRt7e3l+7ubrq6uujq6qJUGrmW13M7zXG/KIyINEZ1QUSqqS6ISJ0GzWyGuw/Gl1Hsjft3Au+q\n2G5m3DdSf+U+u8xsMjDN3ffX+qWLFi2ivb19xFDVp53X2y7/Y6zZ/bNuj5W3fOe46sufGm23dSxg\n2oHX6t6+VvvSMwcpHWh+/yTb8+ZfwdwLp55oF+X/ZxHalY/7+voYST1nPIz7RWF0PU56dM1munLM\nq7pQMCHlVV1Il+pCenQspEd1IV055zVOPhPhh8Dn4se3As9U9N9iZlPM7BJgNrAhvhzjoJnNj+vE\nZ6v2uTV+/EmiOpMpHQvp0RoP6SrcGg8TYVEYEWmM6oKIVFNdEJFqZvZ94P8RTSJuN7M/AbqBj5nZ\nK0Tv424Ad98EPAVsAlYCXe5evgzjLuAx4FVgs7uvivsfA84xs83APUSTnSJSQM2u8TCuFoUp+HVv\npwgpr67ZTFfB8qou5CikvKoL6SpYXtWFHIWUV3UhXXnldfdPu/uF7n66u89y9++4+2/cfaG7v8/d\nr3b3AxXbDCzPAAAOv0lEQVTbP+Dus919Tvnyq7j/JXdvc/fL3P3uiv4j7n5T3L8gnsjMlI6F9PS/\nuD7vCA0JaWwh+7xjrvFQp8wWhVm+fDmzZs0CYPr06bS1tY14zVK97bJm98+6PVregX1vAOcCw3+J\nl09fbLQdLQqzu+n9hwZKvLFrS0v712qz8JLEnq+04VfMvfHqE+PX39+f+//fRtpJ5C0/3r49ulS6\no6ODzs5EvkhUXciwXZm3aHWgup1EXUizDlSPr+qC6sJ4qAuVP0/q7+Ok60KZPi9MuLogIhOADZ/B\nNMpGZhcDP6pYLOpl4MMVi8L81N3nmNliwN39wXi7VcBSYFt5m7j/FuAqd7+zvI27Px8vCrPb3c87\nNQWsXbvWR1sURqIFYe5buWXsDeuwdOEl3L/mtbE3DPi5Hr5u9kkLxUi0KExnZ+eIH+jLVBeKS3Wg\nMaoDY1NdGD+SrA9Q3Pd10s+nOnGqeutCUagu1CepGpHE+y+p93ASz6MaUJ/R6kK9l1qM60VhRKQp\nqgsiUk11QURERE4x5sTDRFgURtfjpEfXbKYrr7yqC8UTUl7VhXSpLqRHx0J6VBfSFVrekIQ2tiHl\n1RoP6SrcGg/u/ukRfrRwhO0fAB6o0f8S0Faj/wjRLbVEJBCqCyJSTXVBRERERtLsXS3GFd1zNT26\nL3e6QssbktDGNqS8qgvpCi1vSEIb25Dyqi6kK7S8IQltbEPK29axIO8IDQlpbCH7vJp4EBERERER\nEZHUaOIBXY+TJl2zma7Q8oYktLENKa/qQrpCyxuS0MY2pLyqC+kqYl4z22pmG83sF2a2Ie47y8xW\nm9krZvasmU2v2H6JmW02s5fN7OqK/nYz+6WZvWpmX8v6dRRxbEcTUl6t8ZCurPNq4kFERERERLL2\nFtHtdj/g7vPjvsXAGnd/H9Gda5YAmNnlRGu8zAE+Djwa3/kGYBlwu7u/l2hx22uyfBEiUp+WJh7G\ny0ylrsdJj67ZTFcR86ou5COkvKoL6SpiXtWFfISUV3UhXQXNa5z6b5EbgBXx4xXAjfHj64En3f2Y\nu28FNgPzzex8YKq7vxBv93jFPpko6NiOKKS8WuMhXaGt8aCZShGpprogItVUF0SkmgPPmdkLZvb5\nuG+Guw8CuPse4Ly4/yLg9Yp9d8Z9FwE7Kvp3xH0iUjCtTjyMi5lKXY+THl2zma6C5lVdyEFIeVUX\n0lXQvKoLOQgpr+pCugqa90Pu3g5cB9xlZv+BaDKiUnW7cAo6tiMKKa/WeEhX1nlPa3H/8kzlceB/\nuvtyqmYqzaxypnJdxb7lmcpjaKZSZDxRXRCRaqoLInISd98d//dXZva3wHxg0MxmuPtgPNm4N958\nJ/Cuit1nxn0j9Z+ip6eH5cuXM2vWLACmT59OW1vbidPNy/8Ia7Rd1uz+WbfHyjv10rnA8GRg+TKo\nRtv9L65naGB30/sPDZT4lzN+AzNmJJKn1XZpwzoOnfOOUce3v78/9/+/jbSTyFt+vH37dgA6Ojro\n7OykllYnHj7k7rvN7FxgtZm9QoAzlboeJz26ZjNdBc2rupCDkPKqLqSroHlVF3IQUl7VhXQVLa+Z\nvQOY5O6HzeydwNXA/cAPgc8BDwK3As/Eu/wQeMLM/opownE2sMHd3cwOmtl84AXgs8DXa/3ORYsW\n0d7ePmKm6jEKrf2e3/t99h4+ysZdh4DhCYTqdrlvpJ8fPf4WcOp7stF2W8cCph14ren9p71nHjcs\nvITSmtcSydNq+4MLruD4W6eOV2X73186d8zx3z10hAumnZ778XLllVee1NfK81U+7uvrYyQtTTyM\nl5nK8dQe2PcGcC5QjJnKNNosvCSx5ytt+BVzb7y67vEdj+3y43pmKuuhupB/W3VAdUB1QXVhtHZR\n3sdpvq+Tfj7VCU48TqguzAD+j5k50b9HnnD31Wb2IvCUmd0GbCNa7wV332RmTwGbgDeBLncvT1be\nBXwXeBuw0t1XNRsqZHsPH+W+lVtafp6l8ftGTnbwt8e5f81rY284hoevm80F005PIFF4bPg92+CO\np85UriaaqewE9rv7g2b2ZeAsd18cLxb1BPAHRDOVzwGXxTOV64EvEs1U/j3w9VpFY+3atT7aTGWz\nent7CzcTPJrR8m7cdSiRogNR4Wn1DTY0UGLae+Yl8lxJ5ip7+LrZzL1w6on2eDoWmtXX10dnZ6eN\nveWpVBfyU5m3aHWg+rnKdaEouarrQLWQj4WkqC5ExsOxkGR9gOTei0MDJR65448Se1+DPi9UKlpd\nyMN4rwv1vrfH+js4qfdNEs/ziTMHefrAjEJkqec56vl8M9ZnjixlXRdaOeNBM5UJ2T10hL2Hj9a9\n/cC+N5gan7ZTrXx6lEhOVBdEpJrqgoiIyATX9MSDu78GnDKl4+77gYUj7PMA8ECN/peAtmaztCrv\nWcrGT406lydG2L5op0fpms10FS2v6kJ+QspbtLowedLwNZi1TK24ZnM0550xpRCnTxbtWFBdyE9I\neYtWF8YS0thCeHlDEtrYhvRea+tYwNMJngWVtpDGFrI/dltdXFJERCRoum5Tiq7RMyNHozMjRUQk\nD5p4oDjXZtUrieujs1L0rNXfdJY2rGPe/Cuaeq48vu0M7dgNSWhjG1LeoteFaqHlDelYCE1eY9vs\nonG1jt2inRlZNjRQOrEYZBEl+XkBsv/MoLqQntDGNqS/0/pfXE90tV4YQhpbyP7Y1cSDTGjV33QO\nDexk2r7mFt3St50iIiLjU5KfF0CfGURk4pmUd4AiCGmWEsK6fiikrBBe3tCO3ZCENrYh5Q3tfRZa\n3pCOhdCENrYhHbshZYXw8oZ27IYktLEN6dht61iQd4SGhDS2kP2xq4kHEREREREREUlNYSYezOxa\nM/tnM3s1vp93Znp7e7P8dS0bGijlHaFuIWWF8PKGduw2SnWhfiHlDe19FlrekI6FZqgu1C+kYzek\nrBBe3tCO3UapLtQvpGM3WuMhHCGNLWR/7BZi4sHMJgHfBK4B3g98ysx+J6vf39/fn9WvSsQbu5q/\npjBrIWWF8PKGduw2YqLVhd1DR9i461DTf57tfeHE46KvWh/a+yy0vKoL6QltbEM6dkPKCuHlDe3Y\nbYTqQmNCOnb/5ZVNeUdoSEhjC9kfu0VZXHI+sNndtwGY2ZPADcA/Z/HLDx48mMWvSczxf/vXvCPU\nLaSsEF7e0I7dBk2outDsqvVlO/u28fw50f5FXbW+LLT3WWh5VRfSE9rYhnTshpQVwssb2rHboODr\nQhK3zK33S4eQjt1/PTQU0k0t6hrb6jvkNCOpu+JkXReKMvFwEfB6RXsHUREpLN1TWyR1wdUFmdiS\n+DBRlsfteQOhuiAi1YKvC61++QDF/9JBItV3yGlGqHfFKcrEQyaOv+VMslP7t2/fjrs39FyDh4/y\nZy0WiLJGC8WR3+xJ5PdmIaSs0FrePP7RsX379kR+30RS73u9nrrgwOCho4lMQrY6ARnSey2krFB/\n3iQ+TJS18qFCdaFxSdYFiL6c+NW/vtlqrBOarQ8hvddCygqt5836M4PqQjr+7c3jbNu2neNvNfbv\niErN79mckN5rg7t2wOy8U9QvpLGF7OuCNfoP7lRCmC0A/ru7Xxu3FwPu7g9WbvfII4/4xo0bT7Tn\nzp3LvHmt37akVCol8jxZCSlvSFlhYuYtlUpUv6/uvffeGlN02VJdaExIeUPKChMzr+pCbRPxWMhK\nSFlhYuZVXahtIh4LWQkpK0zMvI3UhaJMPEwGXgE6gd3ABuBT7v5yrsFEJDeqCyJSTXVBRKqpLoiE\noRCXWrj7cTP7ArCa6E4bj6lYiExsqgsiUk11QUSqqS6IhKEQZzyIiIiIiIiIyPg0Ke8ARWNm95rZ\nW2Z2dt5ZRmJmD5nZy2ZWMrP/bWbT8s5Ui5lda2b/bGavmtmX884zEjObaWY/MbN/MrN+M/ti3pnq\nYWaTzKzPzH6Yd5bxTnUhOaoL6VJdyI7qQnJCqQsQZm1QXciO6kJyVBfSlUdd0MRDBTObCXwM2JZ3\nljGsBt7v7vOAzcCSnPOcwswmAd8ErgHeD3zKzH4n31QjOgZ8yd3fD1wB3FXgrJXuBjblHWK8U11I\njupCJlQXMqC6kJzA6gKEWRtUFzKgupAc1YVMZF4XNPFwsr8C7ss7xFjcfY27l++ttR6YmWeeEcwH\nNrv7Nnd/E3gSuCHnTDW5+x53L8WPDwMvE90TurDiv9yuA5bnnWUCUF1IjupCilQXMqW6kJxg6gKE\nVxtUFzKlupAc1YUU5VUXNPEQM7PrgdfdvT/vLA26Dfhx3iFquAh4vaK9gwK/AcvM7N3APOD5fJOM\nqfyXmxZpSZHqQuJUF9KlupAB1YXEBVkXIJjaoLqQAdWFxKkupCuXulCIu1pkxcyeA2ZUdhEN+H8D\nvkJ0elTlz3IzStY/d/cfxdv8OfCmu38/h4jjjpmdAfQAd8ezlYVkZv8JGHT3kpl9mJyP1dCpLsho\nVBcmJtUFGUsItUF1IVmqCzIW1YXRTaiJB3f/WK1+M/td4N3ARjMzolOOXjKz+e6+N8OIJ4yUtczM\nPkd0isxHMwnUuJ3ArIr2zLivkMzsNKJC8T13fybvPGP4EHC9mV0HvB2YamaPu/tnc84VJNWFTKku\npEd1IUGqC5kKqi5AULVBdSFBqguZUl1IT251QbfTrMHMXgPa3f03eWepxcyuBR4B/qO7/zrvPLWY\n2WTgFaAT2A1sAD5V1Psqm9njwD53/1LeWRphZlcB97r79XlnGe9UF1qnupAN1YXsqC60LrS6AGHW\nBtWF7KgutE51IRtZ1wWt8VCbU+zT0b4BnAE8F98G5dG8A1Vz9+PAF4hWzv0n4MmiFgsz+xDwGeCj\nZvaLeEyvzTuXFI7qQotUF2QcUl1oUUh1AVQbpC6qCy1SXRifdMaDiIiIiIiIiKRGZzyIiIiIiIiI\nSGo08SAiIiIiIiIiqdHEg4iIiIiIiIikRhMPIiIiIiIiIpIaTTyIiIiIiIiISGo08SAiIiIiIiIi\nqdHEg4iIiIiIiIikRhMPIiIiIiIiIpKa/w+Tvc2bdowe3QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x123f3ec88>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# nice normal looking predictors\n",
"figsize(18, 8)\n",
"ax = plt.subplot(441)\n",
"plt.hist(X[:, 0]);\n",
" \n",
"ax = plt.subplot(442)\n",
"plt.hist(X[:, 1]);\n",
"\n",
"ax = plt.subplot(443)\n",
"plt.hist(X[:, 2]);\n",
"\n",
"ax = plt.subplot(444)\n",
"plt.hist(X[:, 3]);"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1 9 0.726949350643\n",
"1 13 0.606579927635\n",
"1 18 0.255835020937\n",
"1 19 0.810447437735\n",
"1 24 0.380486016381\n",
"1 26 0.42502579766\n",
"1 43 0.655921269696\n",
"9 19 0.456310674759\n",
"9 26 0.288312680355\n",
"9 43 0.616191069381\n",
"13 16 0.376803964405\n",
"13 18 0.425279003734\n",
"13 19 0.674599317708\n",
"13 24 0.389994379041\n",
"16 18 0.778885368515\n",
"16 37 0.729783380122\n",
"19 24 0.451426884508\n",
"19 26 0.277160403695\n",
"19 43 0.687377233213\n",
"24 26 0.544026647404\n",
"24 42 0.311639400533\n",
"24 43 0.486457420514\n",
"26 43 0.794905528454\n",
"32 42 0.311153071282\n",
"37 42 0.392571300964\n"
]
}
],
"source": [
"# multicollinearity\n",
"correlations = np.corrcoef(X, rowvar=0)\n",
"\n",
"corrpairs = {}\n",
"for i in range(50):\n",
" for j in range(i+1, 50, 1):\n",
" if correlations[i, j] > 0.25:\n",
" print(i, j, correlations[i,j])\n",
" corrpairs[(i,j)] = correlations[i,j]"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsEAAAQNCAYAAAC8S5eBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvX14VOW57/991ppJJjNhkLcESCCBIqJNII3Unlqr9vBz\nt/Z3nau7B9uNHPFlW2VrqqiEQmBLm7Q4IEFAjeei4k54keAGtrvn+hXaum2rooUKOQlBBUSTQCDk\njUBmzUsys9bz++PJWjPPzBASCCTC/flHVpxZs2bNncl33ev7fG/GOQdBEARBEARBXE8og30ABEEQ\nBEEQBHG1IRFMEARBEARBXHeQCCYIgiAIgiCuO0gEEwRBEARBENcdJIIJgiAIgiCI6w4SwQRBEARB\nEMR1h20gdsIYqwdwHoABIMQ5v20g9ksQBEEQBEEQV4IBEcEQ4vduznnHAO2PIAiCIAiCIK4YA2WH\nYAO4L4IgCIIgCIK4ogyUcOUA3mGMfcwYe2yA9kkQBEEQBEEQV4SBskN8h3PexBgbAyGGP+Oc741+\nwBNPPMG/+OILjB07FgDgcrkwZcoU5OXlAQCqq6sB4LrYNv89VI6HtofG9vHjx3HfffcNmeOh7aGx\nTd8XtE3fF7Td1+3r+fsCAGpqanDmzBkAwPe//30sXLiQoRcY57y3/99vGGO/BODlnL8U/fN3332X\n5+fnD+hrfVVZuXIllixZMtiHQQwxqC6IRFBdEImguiASQXURoaqqCrNmzepVBF+2HYIx5mSMpfb8\n2wXgHwAcvtz9EgRBEARBEMSVYiDsEOkA3maM8Z79vck5/9MA7Pea5cSJE4N9CMQQhOqCSATVBZEI\nqgsiEVQX/eOyRTDnvA5A3gAcy3VDbm7uYB8CMQShuiASQXVBJILqgkgE1UX/GHBP8IUgTzBBEARB\nEARxNbgqnmCCIAiCIAiC+KpBIngQ2Lt378UfRFx3UF0QiaC6IBJBdUEkguqif5AIJgiCIAiCIK47\nyBNMEARBEARBXFOQJ5ggCIIgCIIgEkAieBAgzw6RCKoLIhFUF0QiqC6IRFBd9A8SwQRBEARBEMR1\nB3mCCYIgCIIgiGsK8gQTBEEQBEEQRAJIBA8C5NkhEkF1QSSC6oJIBNUFkQiqi/5BIpggCIIgCIK4\n7iBPMEEQBEEQBHFNQZ5ggiAIgiAIgkgAieBBgDw7RCKoLohEUF0QiaC6IBJBddE/SAQTBEEQBEEQ\n1x3kCSYIgiAIgiCuKcgTTBAEQRAEQRAJIBE8CJBnh0gE1QWRCKoLIhFUF0QiqC76B4lggiAIgiAI\n4rqDPMEEQRAEQVwyug7U1Kioq1MwaZKBvDwdCrXYiEGmL55g29U6GIIgCIIghg4DJV5ralTce+8w\nhEIMdjvHnj1e5OfrA3/ABDHA0LXaIECeHSIRVBdEIqguiEQMRF2Y4vWxx1Jx773DUF2tXtJ+6uoU\nhEKi4RYKMRw5osAwLv24dB2oqlKxa5cdVVXqZe3reoO+L/oHiWCCIAiCuA6JFa91dZcmCSZNMmC3\nC2ul3c7h9bJLFtTAwIlzgrgYAyaCGWMKY6yKMfZ/Bmqf1yp33HHHYB8CMQShuiASQXVBJGIg6iJW\nvE6adGkt17w8HVu3aigqCqCkJICyMsclC2pg4MT59Qh9X/SPgfQELwDwKQD3AO6TIAiCIIgrQF6e\njj17vJIn+FJQFGDUKI7SUoflC+6LoL6QJ9kU5/3ZF0FcCgNyecUYywTwQwAbB2J/1zrk2SESQXVB\nJILqgkjEpdZFtN+2ulpFXp6O2bNDyM+/vEQHU1C//rqGPXu8fRLUF7I9XMq+CAF9X/SPgeoErwWw\nCMDwAdofQRAEQRADTH+THHpLkEj0//qTCpHI9jBjhk5xa8RV47JFMGPs/wXQzDmvZozdDSBhJtvO\nnTuxceNGTJw4EQAwfPhw5ObmWv4V8+rleti+4447htTx0PbQ2TYZKsdD24O/Td8XtD2Q3xdCeL4H\nAAiF7kZdnQK//70LPr6mRsX3v38Qus5gt9+FPXu81uOdzrt6BPV7UFWOP/7xVuTn630+nkmT7uqx\nPYjnT5p0a6+vN9jn+6uwfT1/X5j/PnHiBABg5syZmDVrFnrjsodlMMZeAPAAgDCAFADDAPwH5/zB\n6MfRsAyCIAiCGFyqqvrXCd61y47HHku1tl9/XcPs2aGL/r++YBhAdbXc9X377cvbJ0GY9GVYxmXf\nZOCcL+WcT+ScTwYwB8CfYwUwIRN7FU8QANUFkRiqCyIRl1oX/fXb9pYgcbnpEooC5OfLnuSBSqy4\nXqHvi/5hG+wDIAiCIAji6qAowIwZQvia0WO9+W57S5Doa7pEfybTDVRiBUH0hcu2Q/QVskMQBEEQ\nxODTX0vEV+31CAK4SnYIgiAIgiC+OlyJYRS9jTqm4RfEUIUqcRAgzw6RCKoLIhFUF0Qsug782799\nlFBw9oVo3212to60NOOS92XS26hj8vlePej7on+QJ5ggCIIgvkIcPqzg6FEFo0eraGtjsNk4pk+P\nCMuLeXCjfbdpaQbuu+/yrQqJur3mfsjnSwxVSAQPAma2HUFEQ3VBJILq4tqkP4vFYmlpUVBR8QNL\nuG7erCEnx7Cef7GBGGYqQ36+jl277BcUr/05xt5GHUe/3qVwOefqeoO+L/oHiWCCIAiCuMr0d3Jb\nNK2tTBKup04pqK5WkZ+vQ9eB9naGwsIgxo41EA4DtbWRccSx4jFWvLrdHFVVYpxy7DHu2OFFa+vF\nu8sD3e29nHNFEL1B11KDAHl2iERQXRCJoLq4Nom1Dxw5ovTZjzttmgFV/QsyM3V4PD4wJoRvKAR8\n9JGKBx5IhceTAr8fWLLEiWefdcX5dE3y8nTs3u3FK69oeOMNDWfOKPjZz1zWEIvoY9y/32Z5fvfu\nlf3DiTJ/BwpaWNd36Puif1AnmCAIgiD6wEDelo/twHZ1MXz4oYqWlr5l6f7qV35kZfnx6KOpUqd2\n/36bJRg7Oy/s0zVRFIAx4LnnXNZ+iosD1nuMPsabbzbg8fhRVpaM/fttSE3FVenI9ma1IIjLgUTw\nIECeHSIRVBdEIqguhg4DeVs+L0/H1q0aqqttcLs5bDb0eYGaogBPPHE7tm9nMSJXhdsNSzC63X0T\nj7GdVq8XuO02w7I4HDmiwOtlWLo0Bc3NCoqL/WAssai+EtDCur5D3xf9g0QwQRAEQfSB3hIQ+oui\nAKNGcZSWOhAKMRQV+fu1b0URtohokTt5so4FC1woLg7A6wVmzAhj924v6usVZGcbsNk4du2yx3Wa\nzU5rerqBgoIgUlMjQ7Ty83XU1Sn4+c9d1s+SkoCdO+0oKgrE7e9KLGK73IV1BHEhSAQPAnv37qWr\nNSIOqgsiEVQXg0MiMTfQt+Vjo8r6s++9e/fi9tvvkDqk06fr2LjRh7o6paeTKxIjbr1VR1WVinvu\ncSfsNJvH0d7O8MADEXvF1q0aRo3iuPFGXTq2CRMMFBUFEnauaRHb4ELfF/2DRDBBEARBxJBIzA30\nbfnoDqdhQBLETU3MSmmI7aTqOnDsmILmZtGF/fGPQ9Zj8vN1zJghxOjbb0e6tIm62ObjzPcTmzpR\nXW1DaakDu3d74973228njlYbyG45QVxpSAQPAnSVRiSC6oJIBNXF4HAhMXelbsubghhAnPiOFas2\nG0dR0Q8v2G1NJOATdbEPH1bw8ccqOjsVtLWxhHFpoRBDfb1ipT6YJNqfrgNpaQaKivxwu4ENG5IT\ndrR1HaiuVnH0qIIxY4QNIzrnmLh06Puif5AIJgiCIIgYBtL6cCGfrK6L6W8tLQpaWxmmTRMdYFN8\np6cbaG9n+POfbXE2hd66um63EJaNjaq1j85Ohp07vejsZBg3jiMvT8e779qwfLnT2u9//IcXxcV+\nJCUBoRBQVuaIyw42hWqirnh1tSpZJHbs8CbsltfUqPjhDyOPKy72Ixwmzy9x9SERPAiQZ4dIBNUF\nkQiqi8FhIKwPpviN9dpG+2c//liVhOiOHV5LfBcUBPHAA6koLAxKore1lUFV/wJd/54l0GO7v8XF\nfrz2mgOrVvml196xQ7wnnw84f162P7S0MNx2m46mJoZhwziWLAnA62VYuNCJ5mZF6jgnWqwW2z1v\nbVWgKPHnLT6NQkFdHR9UEXwlp9JdzYl39H3RP0gEEwRBEEQMA5FIYArTWBEb7Z+NzfL1ekXHtr5e\nRVqagdJSP8JhSF3p9HSOX//ah699zYvWVvHc6A5yKMSQmsqxZo0f1dVq3MALj8cJu52jokKT9puV\nJQvRXbvkVIjaWhWqyqHrLKGg62v3PN52YQxo9u+liM4ruaCPFgsOXUgEDwJ0lUYkguqCSATVxVcX\ns+M5enRicThpkoG2Nhbnw422FJSXa+jsZCgv13DuHMPYsRznzwM33XQXDhwQucA/+1kK1q3zSfsZ\nP56juZlJucHZ2TpycnQUFQXgdnM0NiooLg4gJYUjN1eP63bHitVgkGHfPltc59ocpTx9et+65+aU\nulhP8EBxKaLzSi7ou5qLBfv6fXE1u9NDGRLBBEEQBNHDlZgKN2yYELOnTyvIyDCQnCwEX26ujq4u\njk2bNLS3C09wfb0smD75RLU6t9u3a5gzJxUlJQH8y7+kSBPeWlsVbN+u4cgRkQlcUyM8vKtXJ1u5\nwTNnhjFnjiywH3kk1Vp8Z45KNt+3aQmprVURDDKUlSVj3rzuC3aWTbF5MYFnxrbdeuuVEYKXIjqv\n5FS6oTjxjrrTAhLBgwB5dohEUF0QiaC6uLoM9FS4PXuEZeHBB+WFbV1dHEeOKOjqYrDZgDNnGCZO\nNBJYBcS+zJSGUEgscguF3gNwtzXhLSfHwKlTQgA//HCq1fldt86H1lYF3/ymgWPHZHHY1qZY0W/V\n1Ynfd36+Ds5hLWSL7WqPHs2t/Q2VOLRLEZ1Xcird1Zx419fvC4qyE5AIJgiCIIge6uqUnslpXejs\nZGhvZzAMXLAb3Fvn2PQVb9smZ+q2tMgL5YqL/VY39Z13OrFzpxeff64iK8vAokVOAEB2to7sbBE/\nlpOj93hzhdUhJ0fHl18qmDDBwIEDNuu16utVtLaKeLOaGgU33MAlcZiTE+na9iaKzGP0ehVkZenW\nv91uA6rKrccMhQ4ncGmi80pOpRuKE++GYnd6MCARPAhQV4dIBNUFkQiqi6vLpElidHC07zVRN9gU\nv0eOKPB6GcrKHFKCQrQ4njDBQHa2jvp6FdnZOsaP5ygsDMLt5igrS4bXK1RzKMTw+ecqAKCw0IXM\nTB1PPtmF5GSOsWMNzJkT6fBu3ToThw4Jb+/ixU4880wQp04pkgc4Wty0tChYtswZZY2QPcAXEkW6\nDjQ3Kz2il+PYMRuWLnVaz3v1VQ2vv65d8Q5nfxiKovNq0dfvi6vZnR7KkAgmCIIgiB7y8nQcOXLx\nW8XxkWQBLF3qxJEjCvLy4scH79jhRWOjghEjuCVmzQ5rVpbRs1jNwI03CvvBmjU+cC6GT4wcaWD/\nfrvU4Q2HgdJSh7Wf5GQgI8PAc8+lWEL3m98MY/p0cdytrQz19aolYF99VZO62xcSRTU1qtS1Li+X\nEyWmTTOuS7H5Ved6vlCIhkTwIEAePyIRVBdEIqguri6KAkyb1vutYl1HnFD2esVjvV5mLTCLzcwF\ngMOHbdLPXS5g2TInwmGgoCCIw4dVTJhg4JVXHKivVy2h/I1vhKVj+uKL91FcfLdlS8jIEGLG4/Gj\no4Nh8mSOujoV3d0MY8camDpVfk9paRzvvGOTprUlEkWx7+P8eYbdu72or7++O4hDFfq+6B8kggmC\nIAgiigt1RaMtECNGyP7am2/WUVISQFmZAx6PH2lpsugcNcrAl1+qyMmRxeyIERz19So8Hr9kwTA7\ny6EQA+cMjAGbN2toaRG+3PfeU7B2bSTD9+WXfVi4UDze4/FhwQKX1G2eMSMsTYN77jkxACPRtLZo\nK0fs+7jpJtH5vVLJDoNNb9P9KFLs2oNE8CBAV2lEIqguiERQXVw9YoXOj38cAuewOrtpaYaV4Zud\nraO8XMMnn9gwc2YYCxc6rc6t282xYIFLsiU895zL8gS/+aaIS0tPN5CUJMS0SHyI7iyLY7LbObKz\ndfz0pxFrRUWFhttuuwPZ2Trmz+9CZycwfrxhjUqOHcChKEAgoMBmA7KyDKxa5UBjo/Aee70Kamsh\nDcFISzOwYEHkeKOzgK925/dqT3K7UDrIVyVSjL4v+sdli2DGWDKA9wEk9exvJ+e8+HL3SxAEQRBX\nk0RCB4D1s6Iiv+TLPXpUhdtt4Px5YO1aH06eVJGZqcPvZ7j//m4wBmzZkowxY0S313zeiRNCpC5a\n5ERpqR8ejx9TpujweAx0dgp7Q25uGG+84UVqKtDSIgvktjYFGRk6VqzwW3FoZsd36VIX3G65eztl\nioH775d9vQ88YLemtSUagmF2oqMTJobKZ3IlJ7klSsmYMaNvPnHiq8dlX09xzrsAfI9z/g0AeQDu\nZYzddtlHdg2zd+/ewT4EYghCdUEkguri0hBdPgXvvGPDtm12VFWpMC6SApVIAEX/zExeAMR/8/J0\n/O53SXC7gb//3Qafj6GuTsWDD6bC40nB8uUpePLJILKydOl548cbKCtLxrPPBjFvXirWrXMgEGBY\nvtzZ8zwnjh61ISuL4557whgzhkvP9/uBf/mXj9HUJB9vUhLw0ks+5OTo2LXLi1df1bB1q4bGRvlx\nLS0KKiu9WL3aj6lTdezaZU8wvhnW6w1mfFaiz+RS0HWgqkrFrl2iFkIhoL2dobAwCI/Hj/R0w+oI\nR5/rSZPE4BHT8x3986EIfV/0jwGxQ3DO/T3/TO7ZJx+I/RIEQRDEpVBTo+Ljj9WLRp1FEz+ogsPh\n4Fi/XsOZMypGjdLx1lteNDQImwAAPP10UOqyejz+OGHa1sZQXBwA58JTe/o0wwsvBBAMiscUFHTh\n0CFVeh7nQFOT2E5OjuT05uaG8YtfONHWplqvaf43O1tHKMRw6pSCceMMJCcDo0ZxDBsm+5CzsnRp\nclxxcQCMyR7n//bfwnHRZ7oOHD6soKVFQWurmHB3pb2xA5VnmyitIzar2XyvsX7wt9+2o6zM0WNv\nYcjLC9OCwGuEARHBjDEFwEEAXwNQxjn/eCD2e61Cnh0iEVQXRCKoLi6Nujolrrt5oVvYpje0qYlZ\nUWZeL8PChZHFYx5PCjweHwoKIovPli93orAwKL1G7EIyMenN1vN8vySYN2/W4PH44PezuHzfUAhw\nOsV/XS4DN93E8OWXAGMitxe4Gxs26Ni2TUNVlQ1uN0dDg4olS5woKQngqaciC+N27/Zixw4v6upU\nTJ6so6sL0jEnJ3PcfHM4LvVBUeJj4fp7YRF7jqPFJecX9/sOVJ5tfEdZvuhwOCKPjU3JmDTJQHOz\ngqVLI+Ohh+qiOPq+6B8D1Qk2AHyDMeYG8J+MsVs4559GP2bnzp3YuHEjJk6cCAAYPnw4cnNzrQ/M\nbOHTNm3TNm3TNm1f7vb58wrc7ruRna3jnnvegc8HpKXdDsMAPvpIfvymTR9h8WInxo27EwUFQZw8\n+T5eey0FwN0AgJMn38fcuQrs9jsQCjHcdtuf0NUVxooVd2HyZAOq+hfoOoPdfhecTo7ly3fj9GkF\n3/72d9HRAZw69QGAFHR23tYjvP6KUAg4dOhbKC11YNmyPVi3LhnFxd+G1wsoyl9RXp6EX/3qW/j3\nf7fjzJn3sXFjMpqbZ2H9eg0PPfQH+P0KcnPvAGMcL764D7rOUFQk9l9b+wFCoWSYY5XffvtDjBrF\nMWvWd5CTY6Ci4iOoqhO6/j3Y7RxHjnyAF1+047e//SYAoLr6A2iagTvvlM9vc/P3ei4s3gMAhEJ3\no65Ogd//3kU/j2PHFBQV/RChEIOq/gWrVvmRl/fdnu7se1BVjj/+8Vbk5+vS8xUF8PvfQ3o6kJ9/\nefVgt0de3+v1S9uffdaFxYu/jz17vHHvR9Peg8ejYPjwuzBpkgFNew979w6teqdtWP8+ceIEAGDm\nzJmYNWsWeoNxPrDOBcbY8wB8nPOXon/+7rvv8vz8/AF9ra8qe/dSjh8RD9UFkYhroS4GI17KMMSt\n+/Z2RRpOEdu5DAaBv/3Nhvp6BdnZBjo6gBEjROdw3DiR1/vP/xyEywWcOaNg/HgDqakc//N/RlIi\nVq/249AhFdOm6WhoUDF1qi51fN96y4vPPlNx003yArWSkgCKipx4/XUNKSkcZ84oCIWAsjJH3NQ6\nc6FaZqaOFSsC+OMfP8QPfvAdvPxyMp56qgtHjoj4tWXLnHEL5kpKAli+PAXFxX7cdpuYFFddraK2\nVkUwyFBWloyCgi4sX56S8DzFRsMtWxZJwtizx4sZM/SLfr67dtnx2GOp1vbrr2sAEPezvizAi+7c\nu90cLS0XryvDAPbuVbF/vw1uN/C739mxZEkAdXWRc9DYqPZ6DJfyuleba+H7YqCoqqrCrFmzWG+P\nsV3uizDGRgMIcc7PM8ZSANwDYOXl7pcgCIK4Nria8VKxQsVMYgDEbe+jRxVwDhw9qmD0aA6Xi2Ph\nwsiwiuxsQxLNlZUadB2Sf7Sy0iuNPT55UsG0abolPKNTJEIhhsZGIZAXLhSxaUlJ3BK7drs4htpa\nG7ZsScKTT3Zh3rxupKTIloWkJG5NlTt3juGtt5Lw7W8zHDhgx+nT3SgtdSA93cCqVX5rPLLNJmLP\nysqSkZ5uIDOTo7ZWBedAKMTBOTBxoo6xYw10dsqvF20dqalR8bOfuTB/fhdOnQLWrPHj3DkgK4tb\ngvpin++FvL0XGtXcm6g+fFjBxx+ryMjguO8++QLnQoJcUYDWVgUeT2Tks9cbxOTJOvbts6GgoAsb\nNiT36jk269i8qBjqcWnExblsEQxgHIBNPb5gBcBbnPPdA7Dfaxa6SiMSQXVBJOJaqItEK/yvlGiI\nFSolJQFJaN1wA8cPfxi9KMyPxx/vAmOI8/impxsIhYCWFvn4xXCLFOv5XV0Mhw9HPKax/l6fD9A0\nxRpbnJmpY9UqPwoLg0hPN5CcLKLKon2n27bJ44lDIVivuWWLhldf/SbS03W8+KIPEyYY+N3vOnHq\nlIqOjsh4ZDGAI8XyMD/6qDxAY+lSlyX07XaeUJCan9/8+RfuFPfl8zW9vebFiSlS33mnE59/rsaN\nau5NVLe0KAn92HV1Cnw+YN8+0e1dsSIFGzf6rOcmWvho5j6bi+V68xyb7zM203koxaVdC98XV5PL\nFsGc81oA5HMgCIIgEjJQK/x7w+weHj6soqJCQ0eHECplZcnYuNGHI0dUa/GYHAWmAOBITQVKSgLI\nyIgca0FBEA8+mIo33vDFpCsYPV1ZjuHDOV54wYGCgi7rMRs2JKOyUsPBg7aebrEDzzwTtP5/c7OC\ntjYFgQBw6pSCiRMNfP3rYWzapKGtjcHnY1i1yoGVK/2w2YAxYwy0tirIzNTR2ChyhidPNvBP/xQR\ncFu3itv4VVVq3HGcOCEGZcSmVpjvoa2N4b77wnEL0Mxz2tUVEfXm82trRe5xbq6OMWMMFBX54XYj\nrpsa29UdN47HCVzTfmDGmNXWqglFprmvs2cZKio0GIZ8sRE9zMS0kEQL1NhFdolGW8cuBozGrGO3\nm8e9rmFgyFgiiL4zEJ1gop+QZ4dIBNUFkYhroS76s8I/VjTl5uqorb24n7i6WpU6vJWVXng8PnR2\nKrDZOCorkzB/fhcyM/WYbqCBKVMMMAbcf38q0tMNFBf7kZoK3HCDgYoKTYooy8kJY9GiiCe2vFx4\nW0eMMLBmjR+jRxsYNowD4CgtdVivk5QElJdraG5W0N3NEA4jxvMrOrNFRX7rlv3s2SEsWZIiibpf\n/jIFqgr813/tRSh0LwBTwDHpXJv+3cJCZ0/nWhby0Z3lt94SaQf5+bplJ3j7bbskKmOfHwwy3Hvv\nMOzc6cVPfiJPs7PZImuNYru6a9f6erVdmF38RCIz+v8//XRK1GfFccstBpqa4qfu3XbbhS0WQGI7\nxsXquKGBYds2DYcOqXA6gQULXFLHeTC5Fr4vriYkggmCIIgriimw+iISYkXTzp0itmvECCF0/X7g\n9tsjQtgUN59+KncPT51SsWGDwxr9+9JLPvzTPw1DerphdVjT0gw4nQY0TcGZMwpKSgIoK0vG0qUu\nrFnjg8sFzJkjhPGTTwYxbpyB9nZmTX8LhRjOnlXw4ot+PPSQnDl7yy1irLKmMYwezdHUxGAYQHa2\nbg2viD7eQCDeShHr001OFiLT52PQdVnATZtmSOe6rk7B4cM261jLyhxWR/yWW8IoKnJa+xVDN8TF\nRns7s/zP0d7msjIHtm4V457NhWSmNST6GJuaFPj9DNOni+OJ7baagz8uZLtITzfgdHK8+aaG//t/\nVbjdEZEZa0dobFSxdKkLr7+uIT9fl7rgZtZxbxaL/savRc6tGLjh8aRIx95fETwYC0YJGRLBgwBd\npRGJoLogEjFU6+JK/QGPFU319UL4FhZGuqZbt2oYOVKIqcOHxTSviRNly4XfDzz+eJc1+tcUa42N\nKhYudOG110QHt77eBr8f2LUrCbNnd2Pp0gDS0oyexypYudKPysokMMYQCnFkZ4uhFGYn2OcDmpps\n0jFzzhAMMrS3K8jIMFBa6sCPfhTC6dNATo6OpCTE5QnfcosQUBs2JGPbNg11dcLyEP2Y7m6Ghx9O\nxcaNPuzZ8w/W8Ibp08NoamKoqlKtz2HSJANtbZGsYmHBEH5czs2sYSGkOzsZ9u1Tcd99wySfbbQg\nb25W4HBw5ObqkpiMfR9paQaGD+eWPSDWCpOeblxQeE6aZKCgIIjCQmfPJDdZZF7IjmAK6USi1qzJ\npiaGkpIAOjvFOWhqYsjP7/vFGRCpebebx42mvhSLz5VYMDpUvy+GKiSCCYIgiH5zqX/ALyaeY0VT\nWpqBQ4dkkVldbUNpqfDMdneLjumIEQY2b9Zw6FDEh/vII13wePzo7ASysgxLhBUUBHsENkNZmQPN\nzQrKyzU88kgqSkoCOH+eSVaFigpNihzbvl3DgQMqZszQ0dysICNDtljcdJMckWbu29zetk0DYxGL\nhSmoSkuCWPITAAAgAElEQVR9GD/esOwW2dk63nxTQ329YqU8hEIM584xaRFdSYkfRUUuazAGY0L0\nTZ8extatGlpbGW66yUAoxPGjH7ktG8GoUbwnGULsb9MmDWfOKPB4fCgrc2DDhmSUl2s4elSkWzQ1\nKZgyxcB//mcn9u61w+0Gzp1j0vtwOrlkD4gVpjk5BhQFku0iO1u8/6YmhuxsA4WFQeTkhKWLjehp\nbuZQk9ZWWUj3dsfB7ebSwr633vL228dr1nx6uoHCwgA2b9bQ3h6ZnNdfrsSCUeou9w8SwYMAeXaI\nRFBdEIkYqnVxqX/AE42vjRYz0Z5Wr5ehpUWJ67q53eLfNhvQ1iY6lp99ZkN3NyQfbl6ejoULI4Jy\n2zYRdzZvXrR1QeTvnj4dudUOyFYFkd8b2W5oUHDrrToYEx3qaB/x+PEGampki0Bzc8Rq0diooqpK\nxdixHEuXuqzzUlrqQ1GRSHQwLQz19SrOnFEwYYKBBx+MHDNjwKJFe3DDDXdhwgQDa9Y4esQ+Q1sb\nQ0sLw+rVKWhuVrBnjxf33BMGILJ6o20Emzdr+PRTMQGupCSAgoKISNy0SQPnwLJlTsyf3yVdBGzd\nqlm+5cxMHevX+9DVZeD0aQUNDSrCYVid6bo6BWlpBhwOeSZBbB0UF/vBGJOEanm5hnPn5PHMco2J\nxXLV1RcXfbEJHx9/LBIk+pJxHFvzjY0qnnkmFa+/rmHu3IvnGl+IK7FgdNOmj6yhJBTfdnFIBBME\nQRD95lL/gMeK5/37bfB4REdz82YNY8YI8VpXp+DnP3chM1PH2rU+bNyo4dw5BX5/JF/X7wc8Hiey\ns3W88IIQj9ELlhYudOLxx7vw2mvJmD+/Cy0twpcre3FhHb8psAH5drvZqTS3J040cPYsw/nzkVvs\njDE4HLqVCBFrYxDDKsTCNrc73g7B2IXGLgNr1jhQUSG6tFlZwl6xb58TdrsTFRUa7r+/G0uWOCUB\nW1gYxDPPuKSLE/M9mt3w1laGjAyxHRv7dfYsQ2lpCh5/vAuqKidDtLbKNotgkEkiubjYD7dbToEo\nL9fw7rs2+HzAd76jx9WB1ysWMEb/7Nw5hjlzQr12MmPF9J/+1AldFxdl5uf2+edq3Hl1u0UtAujT\nHQ1dF5/ZhVIwLoWBGgkdTewF21CKbxuKkAgeBIZiV4cYfKguiEQM1bro6x/w2NuzN94Ym84gHhcK\nMRw6JGwOe/Z4LcHW2Khi0SIX1q3zQVEMZGVxeDx+uFwcdXUqNm/WMHy4jk8/tcHrZTh+XMGoURzP\nPCO6rF4vrGloJSUBTJkiv/6MGTo2b9asbqrTyZGRIawVra0Mo0Zx2O0Gyss1fPKJWKhVWOhEaalI\nJYheEFdZqaG93cCGDQ4pCcK0MdhsYnrbhg3JePbZAMrLNZw9K7Jt1651IDtbR2oqx5o1PqSnc9hs\nwlrw7LNBSWRu2qThe9+7DTk5GtaudeDBB7sl4XP6tGItQBs5kmPbNjumTTMwfbr4zNraWEw3XHRh\no8/L+PHiPR8/Hi8gp02L+Hrdbi5lJIdCkWlq5s/S00W6A8Dw6acqhg/ncRdRbrcR5+ueMMFAba2C\nlhYFra1yR9gkVky3tCjSYBMzdSM7W8f27V4cOGCzRGz0Yjvz+RcSjTU1ar8yhftCfxaM9pUf/OA7\nWL/+ysYRXkuQCCYIgiD6TV//gMd26nbv9loCKi3NwIIFQqxG2xw++0zBT34SuuAip6oqeZ/bt2tx\nHt433/TilVccuPXWMLq7GQoLg8jIEIvFzAVlQqwxjBjB8cQTYmCGOVDC4/FZ+ywq8gNg0kKtgwdV\njBtnSALq5EkFU6fqWL9eQzisoLsb0u39yZMNHDxow/z5XVi9OgXPPBOEogA33mhg2bIA0tK4lP27\nbZuGefO6MG6cgfR0A42Nak8nVrG8vE8/HURHR8TH29ysIC2No6NDZOmadpDoLqdpizCPOzUVSE0V\nIrG62ganE3juOXHhMXt2CIaBhJ+FmcjgdMqd73HjRAfb/FlBQRCPPirbKWbNknOJbTaOI0dU6bMx\nDDH4IvqzjZ0Kl5ZmSN7h1tbYmDRRNPX1Ks6eVTBrllhEuH69z3p+b3c0zIu42lpVsrRcLFN4sLgS\n3eVrGRLBg8BQ9fgRgwvVBZGIr3pdxKc9KJg9O4T8fB2GAaxb58Px4yqixwhrmkgruPNOkVt7+LCC\nd9+1Wd3A2H1+8UV8ooSicMydKzqkZkKE6NZ6ce6c8P0CHOPGGejqYmDMACDE8tixBsLhiG1CdKvj\nb6fHxn0Fgwxz5gzrGZSh4p137CgvF7FikycbSE01JM9yKARrQdumTRpOnZLfh4jhckodTXOx4OHD\nHyA19S48/XRkCtzGjT6cPs3Q0SG8yVVVNinOzexyxnZhfT7gllvESOVf/zoyVviLL1SkpgphdaEL\nnrw8HTabELYtLQwjR0bGUBcX++FwIG5QR2srS3gRFQ4z3Huvy7Jr1NWpll3DvACoq1Ogqhwff6yi\ns1MkXpSVaTh9Wk04itntjvxs0iQDM2bo8PlUa6rcG28kJ1xkZxJ7EWfeEbjQgIxLXZg2UAvaPvpI\nfF+QBaJvkAgmCIIgBpToP+ixnbroThvnQGoqkJIioseefFJ0Y3ftSkJRUQDvvGNDc7PIli0qigjZ\nXbsigzDcbgOTJ8sWh+xsXbIPCOEivLqqKg+p8Hj8KCpyYvt2L+bMSbW6wEBETG3YkIzVqyO+5HAY\neOUVB0pLfVi50g9VBUaOFN3X9HQDDQ0K3G5g9uxuKRWiokJDRYWGhgYhdBYtimT1trYKv/OFrCKR\nCW9CwNbVqcjKkkVzezvD5Mmia6woHDk5iYdB5OXp2LpVQ3V1JEnjl78MxJ3HsWMN3HvvsF4XVykK\nejKBDfz+9zY0NSmW8BbDPwIYPTo2Jo3j4EHV8utOmaJbPt6dO0Vqw7PPujB/fhc+/5xh3To/jh1T\nwRjHjTeKRI7oz3DrVg3/+I8h1NSocckRNhvHli1ea1SzzwfJ1lBerqGuTkVurp5QeMZecB09Grkw\nSXReLjU15UrEpREXh0TwIPBV7uoQVw6qCyIRX8W6uFgChCmSowczmIJkyRInCgqCOHZMtYROdraO\n1av9qKtTkJkpOnDRImjNGj8qK0Un1e8HjhyRPaqffKJa09E2bdJihKNidY/Nn3d2KtiyJcm6NX/z\nzTqefdaFxkYVpaU+tLcrKCnx49gxGxiTLQ/FxX587Ws6WloYhg0DCguDPUIzGU1NCoqKnCguDkBR\ngIKCoCXkMzN1LFjgQnFxAIGAEKpHjyrwePzYsCEZU6boGD5cLNLr6uLIzb0Dsd3p6dMjndW9e1Us\nW+bseQ/AN78ZlqLERo2SJ9qlpRkYOdKwxiyPHWtgy5YklJQEUFurgnNYovVCnUq3m6OxMVbIc7zy\nigM7dnjR2CgSP5591onmZpHBvHChGEwSvbBv82YN8+d3xZzXAJYvd2L3bm+c5aG1lfUqIkWHeZhl\nbYmvjXhRa9aomUcd8UPr1nMT+YcvNTVloOLSvorfF4MJiWCCIAiiX1zs1m3sH/TWVmGBMKmpUfDx\nxypUVb5NfvSoirVr/ThxQkFbW2Qf8+d3Ye7ciFguLZWFTHc30NrKkJTE4fMx3HhjvHUh+lhiRVps\nAoTbbcTl8DY2ipi1SZPEiGWnE3C5jLjV+KmposPd3q6goEAei5yWxnt8qoDNxiUhv32713pNj8dn\ndaXNi4g77tChKMKD+/Ofp+IXvxBDPTZtSpxV+8UXYkDI0qWi27x2rU/ysObl6dixw4v9+4UtoL5e\nkTqkxcV+3Hmnjg0bRLLGn/9sw8yZYYwcaeDAARWdneI9ZmUZ6O7mOHrUhqwsA++/b8Pq1X6rMz5x\noo7ly3Wr4//zn6di5swQVq/2o6VFwbZtXoTDkAZZdHTET8vzepllp5k2Tf58R43i+OyzC4vI6HqM\nHgBit3OMHs2teLn2dmZZHExRXVwckHzKDQ0KMjN1FBQE0dUFaUAJcOmpKVciLo24OCSCB4GvuseP\nuDJQXRCJGIp1cbFbtxf7g97SoljZtObjsrOF//fgQRU5OTqcTm5ZHszHAIljxNLSDKSmcoTDwIkT\ndnR0GPB4/GAMyMw0sHixEIIi9UBHcbEfgQDDtGk6NI31jCKG5fe88UYdmzZpqK1VMXo0h6pyrF/v\nQ0aGIYnTTZs0jB+vxwgyA/X1wq8afcxJSUBHh3hMTo6Ohga5W336tGINnbDbYz20CjgXAri2Vu3p\nku5HW9ssvP66hv/1v+KzamOtDZMnRz6fyEWMSLsoK0vGvHlywoRYpIgEHVmRJBG9gC/ar1xeruHk\nSRWPPipbTpqbAZcL8Hh8uPFGHfffLy8AjH4NEZUXmyLCrVrKzRUC/sQJFT4fsGiRuHsgrBbCTxwI\niG74+fNyvZgDQD75RIj6xkaGV15xYP78LlRXq3A4uBThFtvp37nTizVr/NIdjOj6v9SFaQO1oG0o\nfl8MZUgEEwRBEP3iYrdu8/J07N7txdGjIqrLZuPSIiLzdnZZWTKKiwMYMcLAmDHCJ+p2iwENL73k\nw9NPD7M8utGCqKWFWbf58/N1rFrlQE2NDcXFfng8KcjO1rFihR9tbQqcTo7nnguiu1vkvCYnA6+9\n5kBjo/Ctrl3rw9mziiUEt2xJwtixHA6H6BJyDowcCbhcYmJa9PtualKQlRXx1+bkhLFsmRMrVvgR\nDModx+xsA62tDGvW+LF4sRMrV/pjhLzwMmuaiASLTnuYNMmIu/B49NFuZGX50N0NfPCBis5OhnHj\nuNWV/Pa3hVCsq1MxdWoYSUkMu3bZLZ+sua/sbB2rVvnR1CRe0xwfDQghvW+fPK3PTFu40M9aWxW4\nXPJFC4C49I7Y+gmFWE+HtQunT4v9bdkiLkqmTRMXDVu3asjN1bFvn4r9+23IzdXx4otONDaqKCtz\n4M03NQSDkJIoiosD+O1vkyU7xpIlwo7xzjudaGpS44T+1q2aJZxFjYrcY7Pb/vbb9rjjjx268eMf\n955vHMuViEsjLg6J4EGArtKIRFBdEIkYinVxsU6vogCMicVN8bf0gWnTxGK5+fO70NkJ3HQTlya7\nrVjhR11dpFNaVubAxo0+tLUxjBtn4KWXHD32CjHs4oEHunHggN0SY089FZ+rG53nW1zsx2uvOVBQ\nEERqqugkP/JIF265Rce6dSEcPGjDrbca+PnPXdJzbrpJft9jxxooLHTh5Zd9cLsNnDolFoU1NKi4\n4QYDFRUaWlvFxLfVqx1YtCiAOXPE2F23Wx6brCgchw/LcWBvvKEhNVWMEz5/XvbB5ud/F+3tQGOj\nEMApKcDzzzuwbp3P8l/fcYeOO+8U3fUf/nCYJPKirSaxI6HNbnd2to6XXpIvQEaPNtDdzWK6tJEE\nhrQ0EUMXvXAxO1uP8WEz6fOfPDlSD7ET41aujGzv2eNFba0at7BNLHoUr3vypNxh93qF37uxUcGc\nOSFUV6v45S8D1gjncJjh3Xfli5vqahsqK5PivOy9WR76u7DtSo03HorfF0MZEsEEQRBEvzBv3TY1\nMWvVffTCqbQ0QxKxoRDDsWMqwmEGp9NAfr4YtSt7UMX44mefDeLECQUZGZEFSc3NCk6fZj2+XZG6\nENtZXL9eQ1oaR1FRIC5XN3ZkblIS8MILATz6qAslJYG42/0ejxO/+Y3Pek56uoHMTI4TJxRs367h\n+HEFhiFuo7/wghDsAJCcLM4BY8D58wwLFkTivubO7YaqApWVXui6EGdJScDNN+vo6BDHGGuDOH+e\n9Sz2Y5gxQ8cLL/jAmLilP2oUR0GBSzoHq1b58ZOfRM7prl1e3H67WGAXvd+WloiIjfXenjgR6crO\nn9+FxkalJ9FCpDNMnRpGba0N5eUaGhsVTJli4MQJBZs3e+F0chw7ZkNysux3rqz0SpPW0tI4Vqzw\nxyV4NDfLx3n8uIqKCvHzr31Nx9e/Hp9xLJI4ODo7GaZO1RGdTxxtoxg3juPtt+1xXdq8PB0+X/xz\n6uvVOC97bP1HC9hE3eHeRDClQQwNSAQPAuTZIRJBdUEkYijURWzXKjdX/LFOSpLjplav9iEQUPDl\nlwpuvVX2dOo6w/33p6K42A/DCKOxMXZsrnitESMMFBamIj3dQHGxHy4XkJmpo7FRwaJFTthswHPP\nBaXnHj4sOoEPPih3bs1uL2PAmjU+2GzAmTNCTNfXKz0iUO6wBgIMHo8fU6dGun1i2INLEmzr1jmw\nZEkQX36pICPDwCuvOHDffd0oLhYxZrqOnud2xQhCDV1dsbfs/Zg4UQi56HM2fjzHnDnR70kI9p07\nvfjznz9EKHSvddxNTbKITk834PMxVFbaMW4cl2LqMjIM/P73Xhw5olj/z+zKTpyoIztbx1NPBaXE\nBo9HLEb8/HMbpk410NEB3HijjjlzIp//ypXCh93WJp/Tgwcjo7ErK4V4js5hDoUYzpxRwJgsRnNy\ndNx/v9yl9nrlc3TTTYb0mH//d6+1WHDiRAOBgLCgnD6tYNUqYS8xO7xmNFtnp4hVO3VKQWcns/Kq\nL7Q4Lda6cCkjlQcqDSKW3r4vrlT3+asMiWCCIAiiV2K7Vv/5n504dEiFzQZrihYAZGRwVFWJFfil\npQ5UVnrR0CAeFw6LuLApU3R0d4spbdFiJj9fR1FRAB0dQhw0NqpYutSF0lIfgkEGv1/BvHndcLuF\nDSF6EVRSEjBxooHi4gAYEwu9kpOBtWv9WLQoki+8cqXo8mZni0608BpD8t/OmBHG55+raGhQsGmT\nhnPnGLq7ZVF3+rSC554LSuKrokLDkSMqVq5MQWWlBsbE+4sV2U1NDJzHTzU7epShvDwZGzdqOH+e\n4eabDTQ0xD6O9XQ/1QTZuwZUVZ7S9uCDkePbtk1DVZXwXJvT4N55x46HH+6Cx+OXHrt9u9fqopuv\nDcgLxFau9CMQkIWs280xbJhh3RWIdFZhPaa5WXSZu7pYnGhsaWEoL9dw9KjwAR87Fj9opazMIUXX\n1dTIx/n3vwvB7fH48OmnalwmtHlXQtcZ/H6gsNBlWT/WrfOBcwVr1viRnm7g5psNVFXJF3+1tfEi\n8lJGKg9GGgR1n+MhETwIDHZXhxiaUF0QiRjIurhQJ6i/kWeaJg8rKC4OwOUycPy4AoDB6dSxYEEQ\nDQ0qxo4VXs0lS8xxxAaWL3dixoywdQt87FjD6gTHJj8wJqK4ogXYrl1ebN8uOqrRXl9zYlphYQC6\nzjB3bqplswiFGDgXrzF/fheOH1fj/LcihYElEE6yqPva18RADNM2UFDQhTNnFOTl6Sgt9ePsWYbz\n5xUUFweQmSm/n3HjOD7/PJGn1rR9qBgxwoDfH7FXxN7av+EGA4ZxFyorNZw+zeDzMWzbloTHHhOC\nNi2NQ9NkgXrypBjg0dUFlJaKhXAPP9yNhQtduP/+bum9fPGFiq99TR5yMn68PCKac8TZCFwujnnz\nEnfxzUEf2dk6vF5FskJs26bh6FEFSUnAE0+kAgBWrPAjO1uXhPLYsbHRdQE4nfHd48xMHZ2d8Qv4\nAFnIb9wYsbzMn98lWUm2btUsS4t5Dnbu9Epi1xSRiSIBLzZS+UqNN+7t++JKdZ+/ypAIJgiCuE64\nUCeoL5Fn0bfMW1rkDmVSEseUKWEEAioaGoDMTI7Vqx3Yt88upQFkZurWLfvZs0N45JFUq5vrdIph\nC+vXO7B9uxcHDoj8WnMym5kjO3asuM3f2KhAUWSRc+SIitJSR8+CNCbZLLKzdWRlGSgqCiAjQ4/r\ndH7+uejirlkjZxDb7cDUqTo2b9bQ0iIm4Hk8DixeLCK5hN1BXszV3s4wfryBZcuceOqpIDwePzIy\nxOK3jg7RzfR4/HA6RSpEUxPDyJEGSkv9qKxMwqJFAezbZ8Po0cJiYk6ka2hQUVLiR0eHguZmBc3N\nvCchIQXr1vml2LLt2zVJHGZlyfFuxcUBPP10CrZt81o/i30vmzdrOHRIWE2SkuTOfVqagaVLnVZX\ndvr0MM6dY9bnxBhDUpKIi4u2Veza1QnO5SEiDQ0KGGOYMCGMNWt84BzIzpZtDtu2aVi1KroLHMbS\npcIe89ZbXnz8sc1KFhGTB8UVT/QxZ2QYPfXWhc5OUbem0I/1RldX21Ba6rC6x52d8kCVaBF5KV3d\nwUiDoCzieEgEDwJDweNHDD2oLohE9KUu+ur1u1AnKPbnTU1Mug08fbq8kG3HDm9Md9NAMKhKoqW8\nXMO+fXbLr2qmPphRXKYlINYzW16uARApEGPGcKxa5YOiRDp4Ho/PunUfG50msm3F67W3K1ZnsKgo\ngJycsDRwo7xcFokzZuiorPQiGGRxYm/27Ii4rKjQ8NxzQQwbpidczHX0qIqvf12HyyWGesSek/Pn\nhVVh3TrhV16wIOL5feMNDYWFQclnW1wcAMDh9So9kXAG1qxx4Ac/eAfDht2FpCRg8eIgDh6UBdqJ\nE2LaXHu7WDjW0sIkAShymcMIBETnu7g4gORkOdpMRLWlAAD+9//WUFmpoalJRLExxqWubGmpDxkZ\nHE8/HRHR27drOHAg/i5CbFLHpEk6KiqSMXVq2BLM0ZPd0tMNhMPAnDndSE834HQKgbtoUbAnVg7w\neJxWnaekcHzjG2FwDmzdKi6Ipk0T0XAFBcG4ejt7lmH8eJ6wlgC59qJtOOawjOnTL7+rO1B+3d6+\nL65U9/mrDIlggiCIrzh99frFdoKys40en6gsAFwuHre/6IQFr1cMljhzRsGkSToYQ1wahJn1ardz\nTJhg4KWXfFKnsrJSw/PPi25o9PPOnlXw0ksO6xa0mUJgeo+jh1CI6DQNbW0KurthLWhiDJg+PYyK\nCg1JSSKnuL2dxbwOQ2mpHyNGGOjoUFBY6MRvfuPH8OEGyss1nD4tFrylpMg2ANP3u2mThhMnxGCN\n6HM3fbqO1laGefNSUVgoL+D75BMVW7Yko6AgiEWLgkhLk1MsPvtMxbhx8ut5vYDbzVBU5ERmpo7c\nXD/mzu3GsWNiLPPBg0KEGYY8CS893bAm1yUliS5oIgHY1qZYk+W2bZMvbsaMiUSfnTvH8MQTqfB4\nfLj/fpdleUhNBUaPNtDUpKCmRha8J04oyMmRz09ra3xShzk6+cCBSCZx9GS3WH9zcbEfAKwBHRUV\n8gVNbq6O6dPNLmek2xkKAWfOGFIX+swZBYYhHrdypR+ci8eZtZSZaUj1tnWrBgDSsIzoKLVbbtHx\n4YcqvvxSxeTJOr79bR22Piitq+HXpSzieEgEDwLU7SMSQXVBJKIvddFXr19sJ8hm47jnHneMh9PA\noUO2GOEnBK25gGzUKAOapmD8eAPHjglvbawQmTxZrJafOVPH8eMKUlJksXvwoBCEq1b5Jd+nzwc8\n/niX5eM9c0bBunVi0ZpY+BYbnaairCwZTz7ZhWefDWLMGI6ODqC5meGZZ1KtbuqYMbLQ9/kYiopc\n1v+vr1dx9KiKG25QpNv3b70lC8Np03Sr2/zaa+J1zVv0o0cbMAyOcFjBypV+2GzxC8RiO9/R09Zm\nztTR3S0/Z+ZMHatXO6x0i6YmBTYbcNttd0hT2Vau9FsDRG69VUdSkoHZs92SnSA1lVu2lIKCLjQ3\ni7HHZvRaaqp8ATBypIHnn/cjL0+Hx+MAAOkiJDkZMAyRCW2Oko4+9lGjOBYvjlgmbr01jIYGWayL\nPOkguroYRo3iVo2Zk93a2xUoilw7Zh60ud3ezrBypRiO4naLuk5Eba2KefNkMR0KwaqD8nINmiYs\nN2aWcFKSIWUep6cb+Pxz+YJv//5I+sVbb3mli70dO7y4886Li86B8uvS35H+QSKYIAjiK06iDm9N\njZg8Zt4Kjl3ZLkbPCruCmcRQVBRAYaETmzfLgtbrFbFRzz4bxC9+EYTfr6CtjcHnU6yEgLVrHZY9\nYOJEAytXOnDggB2/+Y0P//qvLlRWeiVfcU6OjkWL5KEWb76p4bnnnJg3rwuAKaiEfzQQEB7OG28U\ni88A0YFctkxMDPvtb5OxYoUfR46IZIGODhF1tmuXvWehlEgeaGlRMHq08LMCkdQFU+AePhy5AEhP\nF4MhSkv9GDNGjGZubBR2juxsHYWFQYwZY+DwYdFNB4AHHogIoE2bNGsyXEaGIS1CM1/b5QJeftmH\nMWMMNDYybNmSbF2Q+P0ibmzhwqBk5Vi92heXfcw54PUyuN0GOOf429/k3NqqKtXqysZ6f83otbff\nDuHkSQWdnQp0HfD7xRCOI0cULFwYxKlT3Rg/3sD69RrCYTF5LdrTnZTEsXq1H83NDLfequPUKSXG\nMuHH2rXCZwsA48cLr7HfD3DOYBgi5eO11zRomqjdKVPCCAaVmIsJ0d0VYj6I7m5hn1m7VkwCfP11\nLaoTHCFWaLpcwOrVDmv7k09UzJoV7hGfQoBWVckLKHfv9sb9vkWnX8TeEamrU/skgsmvOzhctghm\njGUC2AwgHeK+w+uc85cvd7/XMuT9JBJBdTH0GYyczb7URaIO79/+Jk8f27HDa61+NyeBBYNMigcz\nfZCKEplmdvPNYbz8sgMvvuiP83JOnKhb2a4HDtjxyCM2lJT4cfq0WPh2zz0h3HyzgVdfFbaE2AEJ\n0avzQyGRYFBQEITLJTpqhgF8+qmKKVN0Keps61YNp04pWLvWgRUr/OjsZEhL43ELv375yxSUl2t4\n5BH5NU+dUtHcHLFr3HyzjpKSgDV4Ifo2fGznEGD45S9TsGWLGK0bfU5KS+VFdadPK9a0NKeTW7fb\no8VOZqaBY8cUNDWJBWhPPRXsyTNWMHWq6ER+9JFd8vNmZHD86U8fwG7/gdRR9XhSkJmp48UX/Rg1\nikvZyDk5ostsDp+QO6vM8utG18ymTRqSk3V0dChWPFlzs9Ij7BPnIFdUaJgwgeOGG3SEwzasWSMu\nIFpaxGI587WjRXj0lDrTKtPaKhYhdnQIW8WmTRqamsTdh2HDDASDLK4mt23TYBgcTidw6JCCnBxD\n+gByuz8AACAASURBVP0Uw1aiLxZ1NDcrlphOTRUXMtEjvmOFc329gh//OGT9vqWlGViwwGXV0qRJ\nsv1j8uS+dXMHyq9Lf0f6x0B0gsMAnuOcVzPGUgEcZIz9iXN+ZAD2TRAEMWS40r69RCK7L8R6/X7/\nexsyMrjkfYzuUM2f3yXdst26VUM4DBw5ovbc+mVYulT8Yfd4/Jg9uxu1tap0K11VAc6B7m4RucWY\n6MwmJYnBGA88IHcadR3QddmXe+4cixElkQQDj8cXF8MWbZFITzcwe3Y3Hn44FSUlAZw4gYTCLlbw\nnTsnJq7FdiM5Z7jpJgOBgBBhJ08qSE01rLQDt1s8xtxvY6MY7hDdNc7IkEVWKAR0dQkRl5IiRCAg\nhHhrK8OECWLBV/T7jBWEFRUavvWtMHJydKvjfOiQirffTpKSEs6eFcdRUBCMu1gxb9Vv26bhJz8Z\nFreg8JZbwnjzTW/cuWprU7BwYfxnwDnAubAuqKp83g8fFiOH16zxo6ZG5BK/9JITpaV+NDcLL3lT\nU7ywjLXKmMdcUaGBMYalS514/PEunDqlgDHhAY/NYK6qUjFsmIiw0zSGQ4dUjBsnvM05OYZ1PjgX\nF4KNjQp27hQXWz/9aeLf60Qd2ujfN8MANm70Wb+zOTk6duzwoq4u4gm+lN9h4upw2SKYc34GwJme\nf2uMsc8AZAAgEXwB6CqNSATVxdDnSudsJhLZfamLWPHsdnPcd58shCZP1i1vo/lH3XwfjY2yD3b7\n9ogPdsOGZCxb5sfEiUBRkR85OTqWLYt0ZSsrNaSkGNLCpdiOaCAAvPZaCtavl8VXerphLc4aM8ZA\nUxNLuABOiFrxXk1rwRdfKHC5xP8zRap8i1psZ2XJIiYzU0dxsR+MMWkKXHFxAHPmpGLLFg12u4GJ\nE4XIf/JJOf7s5EnVEkPR/t2CgiAKC53YuNGHI0fUnosPB+bN60ZpqQNvvKHBZuOSQH3jDc0aDmK+\nz1hBeOqU8OdGd9ArKjScP//fsXRp5HynpxtYu9aHsWPlxXamf9bcl7CIJGHjRh/a2hi6u4GiIiea\nm0W3NfpcjR4du0gv8rm1tIiucUlJQHrO2LEGVqzw48AB1fJ5P/54F5qaRGzcgQO2uMVysR3aaHvB\n4cMiqsz0O7vd4vPesiUJq1b5457X2amguRnS4sriYj/CYZGCsnSpCx6PfEdi61btgr/XF+vQJhKv\nd96p98kCcSWgvyP9Y0A9wYyxbAB5APYP5H4JgiCGAgPl27uQreJSRbYpnk1/ZnKy3J1LTeXQ9UjH\nMbYTOG6cnJ/a3c2wfr0PqalAR4dYsBTdOS4v17BkifDiHjyoYtQoWVTHToObNk3cdj57VixuS0oS\nXdLSUgdmz+6GywWcOBG53W56i03BZXpOd+zw4tw5hoYGBa+84sCyZQF4PCKaa/nyFEsozZypo7lZ\nLJYqLXVg2zax2Gv0aAOrV6fgqaeCOHxYPteBgOhocw40NNgQCsHq+pqPOXtWeG9LSgI4flz4ZiPH\nCtTXqzh9WkFpqUMS46EQ6xG78udy/rzoSP7qV34kJwvBGCvaJ0+ODOYwn9fQoKCyUsPBg0JoKgri\n0hPMxXamf9a8eJg7NxUrVwrLSmenYlkoSkoCaG1VUFGhoaFBBWMiJSTax52fr6O01Ifhwzk+/VSc\nm7KyZCterbtbTAaMFpjmZzJtmmFNwuvqArZv96K+XkVWloH/839s2LQpYoFoaRF3HKItOoEAMH26\n+F04d050+BcvdqK8XMMnn0QE9/z5wbjFlYGAWDzX1SUWd/r98ufa2hofi2daIvrboaXRxF8tBkwE\n91ghdgJYwDnXYv//zp07sXHjRkycOBEAMHz4cOTm5lpXLXv37gWA62Lb/PdQOR7aHhrbtbW1eOKJ\nJ4bM8dB2/Pbtt9+BPXu8+MMfPsTYsQby8m6/pP1t2vQRFi92Qte/B7udw+PZjalTDUyadFfPH+P3\noKockybdGvd9oevi+WfOKPjBD76DvDwdf/jDhwiFUlBQcBuWL3fi4Yf/CFVNtvZ/9uz7+PRThpKS\nu1BWlow1a/Zh8eIupKffCU1jOHhwLx56iKOz826MHWvg/ff3QlXF+01KAv78Z7F/4G6EQgy7d3+I\nH/2IIzPzTtjtgKa9h/T0ZDQ3z4LdzvH3v3+Ahx5imDr1u9B1hv379+JnPwNSU+/Ak0+m4Cc/+RO2\nbUuGx3NbjzAX7/fXv/4Wli51YvfuD/H1r+vYtOlOMAY88MAB6DqD3X4Xyss1/P3vH+CxxzhGjvwu\nnn7aheHD/4x//MdupKaKx8+f/3d0dCj49a+/hX377PjLX/4Lw4ZxTJx4B37602588cX7cDgAu/2H\nCIUYVPUvMIwA/P67esSkOJ7Nm2dKn8eoUTPR1MTQ1vZXjBtnYMaMO+HxOPCNb7zbM8b4XpSVJeOh\nh/6AlBRg/Pg7UVbmgKr+BefOBTB58nel/Y0cObMne1lsV1bOxBtvJGHRoj0IBBjuuOMOVFerMIy/\nSufX53sPf/hDDb73vZ+jrU3B0aPvS5/P6dPvY+5cBf/jf9yO5mYFc+f+ES4Xx5dffren2/w+Ro0y\nMH36nbDbOe699x38679G6mXx4j1obmbYtev/wYoVfjz4YOT8b9zow/79e3uSL+5FY6OK55/fj8cf\nD2LChLug6+L9AUAodDe8XkBR/oonnkjGq69+E8ePK+js/AAvvuiwXm/hwj/gk084XnzxXuvzeP75\nAFJT7wJjQHr6u7DZurBo0ffR3Kxg2bLdePRRBSNG3IUbbjCQnPx+T4zed9HRwfDrX+/DP/xDCMAP\nYLdzGMZfMXduCsaNuxOLFgXQ1fUe5s5VkJt7JzZsSEZb2/t4/nmOUOh7cDqBxx//GIsWBfHP/3x7\nwt+3jz668O93TY2K73//oHW+9uzxwu9/76p9X13P+sL894kTJwAAM2fOxKxZs9AbjPPEUSL9gTFm\nA/D/AdjDOV+f6DHvvvsuz8/Pv+zXuhYg4zqRCKqLax+zS1Rbq+LZZ13Wz19/XcPs2SEYBlBdLXeR\nPvpIrouqqnjLhKpy7Ntng6oCv/iFC5mZOp58sgs2m+j+RdsXzAVjK1eKBUuffWbD9OlhaQBF7EKn\n2E7jypV+ZGXJE70qKzUwxsE5sHJlCmpqbFi50o8lS8QtcwCYOjWMUEikADz0kMjRNYcxAEBRUQCl\npY4eH64YgFBU5JcGIaxbpyEzk+PLL8U5WrVKpFAAwJo1PixcGDmvK1b44XBw2GxiHPO5c6LLfeaM\niOuqr1dx/jxDXp6OlhaGEydU6XheeMEPgMPlAsaMEYkS5nn0ePwoKnJaUWjZ2To++USF1yuitEaN\n4mhrU+BwcEycaKC01IH77+/G6NEGDh+29XiMYaVUAMD69T6cOaNg7FgdGRnc6vRu2JCM1av9OHlS\neKEbGlQEAn/FO+/cg6efDgJA3AKxRYucWLPGL/mLS0pECsSmTRrmzh2GXbs6cfSoCrsdWLQoct7W\nrvVZ9VlUFEj4Ga1e7e+xsIis6NWrU/CjH4WQkaHj0Udl68bixc6ez85v3TkoLHRJ+wS49Dmbn7t5\n5+HUKQWLF4vnvPSSD8OGiTsxN9+sY98+GxoalB5LiAM1NTZrpPS4cRydncCjjw7r8YHzGA+2Fxs3\nJuO//ivJ8jxH/04m+n3rrSu8a5cdjz2WGve7fbWgvyMRqqqqMGvWLNbbYwaqE/xvAD69kAAmZKhA\niURcz3VxvdxCNG0LsT5K01bx/7P37dFRlffaz7v3TDKZIQOBXAi5TRAENAEKqdWjVru6elq7zvq6\n+lmPYou1tSU9RISQIAaqNFFIMAmXUlwrbfyScEmgYlvX+b5i6+lpba21LSAIKDfJ/Z4QyOzZc917\nf3/8Zu+Zd0/wisKR+f2VzGXfZ+/nfd7n9zwTTb2arwuzZOLUKQFz5qicPlO3DKurk9HZKaCuzoO+\nPhHDwww33kjpbykpGioqCNRt3BiJJc7K0jhNaX+/gECAcdPvFosWk1B2+DA1JQHAihV+9PUFkJen\noK1NQktLAu67L4ieHhFZWaqh8aQY5chxmDcvhKoqb3ham2zSokMTSNOrGeDb5VJQWyvjyJEQnE41\nJrhizhyFA+p6yIIOriorvWhqIoA5ZYqGixdj9cMOBzWBHT5sQUeHaOzv6CidB4sF2LrVhhUrfEhI\noJCOoSGGqqokDA4KqKqScfiwBd/4RhDl5Xbs2ycZcgmzLEWWyeFBD6SIlhS89ZaIL3whiEuXBFgs\nGubOvRO33ebBsWNWTJ6soa2N5AXp6Rr6+hh27CCdqz5gSUhQcf68Bbt2UYJaayuJrH/1qwSUlvq4\n7cjNjejHCwpCMVprajhk8HpFPPVUEvbvd6O83IclSyZxIRozZqgoLyfZDO3T5ZP+gFhPZf1Ynzwp\nYt48BdXVMl56yYrcXBWDgwweD/D3v4sc0N+7V0IwSPZyHg/D4CCQk0Ox3+PjDAAvhTh0yIJvfzuA\ngwcTOd25/pv8sBKlq211dj0/Rz5KXQmLtNsBfBvAccbYmwA0AOs0TXv54y47XvGK1/VRn0Za0rVQ\n+gNV11EmJVG61YexQzI3Efn9DKdP88udOlVFWho1IaWmEsAwd/mvXJkU1lNaMGeOGgMWdU1pMEhs\n5YED40hO1qCqDGlpGoLBSLDB4KCAefPoYX/hAgNj1KDk86kYHWV48MEAxyRXV5PFVmIi0NIiYWSE\nnBMuXBAwPk7a3PJyYuQaGhINTW92toLz53mXi2j/3L17Kdq3p4f8i8+dEyZ0dwDIzSE7W8WqVT50\ndAh48cUEfOc7frS00LoYo/1+/HEf8vNDMc1ceuNdVhY5SDzyiIPTL2/fLiMpScXf/mZFQUEIHR20\nLWNjQFubhK4uAbm55Hk8MMBQWKjg8cdpnydqCiwoUODzCZzedt8+CQ0NNhQX+zFlCg1q9PdaWiSs\nW2dHcbEfx46JWLgQcDgoPjkUYjh+XEBhoYING7xYscJhaHdvvTWEUAjGMduxw2awqqmpGjo6RGzf\nLiE7W8XRoxZUVXkxMkIjVv1YM8YgSRpWrbJj+XIfJk1COImNT/q7eFGALNP/FgvQ2irhyBERRUUK\nysrsKCoKorTUh8FBCgh56SUrysp83LU6kc3ejh02bN4sxzC+Ho+A3l4WA7YHBwVUVMj4/OdD2L3b\njcxMzfhNXg7UXm7gHo8m/p9VV8Id4q8AxCuwLddNxacr4jVRXc/XxSftunCtlP5A7ekRsWFD0mXB\nfvQD9tKlV/Hww/9iMOM6SNWn3UURRhqazgCbI4obGyUTqGLIyFDDcbGA1wuO/U1N1bBrl4SxMQK0\n27d7ws1SDImJvMNBczOB2OFhhpERZgCY6M78t97iWWOAGqj06FmXi8Dg+fMUswuoqK2V0ddHIKm0\nlNwLams9mDkzAkrGx/lGszfftBiNcPfdl4y9e90caCR3BzqQJSW+GHeIVasmYft2Dwcmp01T0d8v\nQpYZGhs9GB0la7OzZ8leq6tLRCAwsWduU5OEp5+2w+VSYqQJ9fUyvvUtp3HO29rchnex08kDr4IC\nBZ2dAmy26P19FZ2dn0dxMQVfVFfzjhzDw4LxXvQ+MsbLARobJSM2GQBaW90mizUvTp8W4XJR2IrO\n0D7wAB+BzRhQUsI7aeghLPX1HmRmRvZpcFAIp9fR/5s2UXz2wICA1FQNgqAaA6VowNvcTLKI92pq\ny8tTUVzsQ09PrMvGli1JqK/3oLmZbNoYA3bsoPCOsrJkwykiui4Hai83cL/aVmfX83Pko1Q8MS5e\n8YrXVa+rPYX4adUHZYmiH7CiaMfChaLxUD17VjQ8fAGgrs6DGTMiy01LU/H3v/Oxxxcv8olb5JIg\nX9ZRYNo0Cp7QmU09GKGhIRGPPebjlj04KMDv58MPdEA2Ps6Qna1hbIw/v1lZKgdmiov9HNg5cMCN\nt98WIIoAEFmXxyNAEIIGk2p2UtCn6ru6aH9PnYqA74wMGjA4HCQd0J0nIlZitIwbbggZYEuPDhZF\nASUlEcBcVUXa0bY2N1avjshQzL61fX0Eajs6RHR18aCMGuki2y4IdNwSE8kyrKVFMkDn+vV2bNpE\nDhL6d0SRAN+hQ7T9emhJtJTj0CEL5/qRna3GgMPRUf7aGB6m9yN+0ORQUV4eGdg0N0uGlV1Pj4j+\nfsYxvcEgw+nTohFCYbUSs/yrX7nx+usWOJ1AWZkDy5b5jGuupUVCbq6K8+dFnDplwc6dtstca/x+\nZmSoaG6muOMZMxRoGkNiIiXPuVyKsc0ZGcQa9/czpKSQP/PwsIAVK3wYG4v2ORZRU5P0vqD2ehm4\nf9YrDoKvQsVHafGaqK7n6+KzMIX4QXTN5geqolCj23tZpSnKl9DeLnHm/dG2VZmZKkIhhkWLFCxY\noGDfPmuMjjYUIiuv06dFLFyoYHSUxcTuOhwEqPPyVBw9Kk7IbFZWejlGj/SjsRZeVitQUcGDYj0K\nmAAwQ3r65RldWWYx692wIQkul4J//3en8frOnR5UVnrhcGjGtLrVSpZvTU0SVJX38TWD/uXLIyCs\nsJDAr9/PYtjj5GT6fEICwBhgsVDjln4MdRmKy8VLJrKyaDDncinIzVVRUSEbjW4JCTyjf+GCYHxv\nbIzh7FmKOb50iaG42IfHH7fDYgH27ZPCHrxfQG0tyQOsVg1bt9qMbQwGGWprk1BW5oPT6Ythp6O3\ncfp0FZWVXmgaWdkFAsTMb9woh8M5GMrL7ZzlWLR374YNSUhL09Dby4Ppz30uhJtuUrhj3twscc1v\n0R7Gx4+LSE3VUFbmgMulYPNm2pfoZebkqCgttXM2e7rHcXW1DI9H4BL+dLmP00kWgHqUsrl5raKC\ntOJWKx2DYJChv59N+NvU61oduF/Pz5GPUnEQHK94xeuqlRk4fvObwWumIe7DNOspCvD66yLeeINY\nro0bk9DY6MGCBcp7LuPoURFf/3pkSvW3v3Vj8WKFe8C6XArS01W8+KIVaWkqLlxgqK+XOckBTeES\neJUkYmyjQxu2brWhtNSH+fMVY0q+vt5jAhgK7r8/2UiZm4jZdLsJKOzeTbrbvDxiCIuL/dyyUlL4\nkAVBIPD48ssWPPRQAB6PAJcrZMQImxldSQKn5Z0yhZjR0VHGMZtTp2rYtCkRqamk7V292ofcXBWB\ngAavV0BmpoLmZvKfjU53o30RkJmpoq7Og2AQBshcvZpnHy9cEDA0BNx4owpZJqeIsjKH0bin66I3\nbEhCW5sbbW0SOjsFuFwqRkYYKiq8KCgIGcddl350d4uYOVOF3a7g3DkRU6ZoGBsDUlLAuSs0NkpY\nvjwC2Do6BA5Inj0bRHMzHZu0NA1r1lAjGgCcPx8wAkUi+8NQXS1jdJQ8eD0eBpuNWOUHHiCv6c2b\n5Qm9fgFwjHtiIgV+JCVpxkBBB/VdXQIGB3kZjJl1njcvhOpqGQ0NiXA6YWiLi4v9ePjhSViwIISm\nJglDQwKmT6cI5cFBAevWxbqGjI4yWK2xLPfMmUo4yS0CUs0AtqBAQUWFF06nhs5O0djHaO/tU6cE\nzJ0b1/5+1ioOgq9CxTU78Zqorsfr4lpuiPsw23bsmBj2e42AhvZ2eqBfbhmKApw6xT+0T58WsHix\nwj1gBwZexbe+9XVu2cXFSVyM8NAQw4kTpMn1+xnq6sgKqq4uMoWfnk6JbPr6LBZwoIUxGLZpU6ZE\nrNGiwUJhoQKrFWCMWLj2dgEdHaLBhFosGrKzVQwP80EXogjMmqVi9mw/lixJNsBgba2MBx+MOAo4\nHEBKiopJkzQuqW3XLglLliSjvt6DkpJYZvPkSQu6uwXY7aQhbWuT8NOfknRjYIDAuiCYE+WoeVB/\nbenSAAoKQoaUIlo6ogPkLVs86OoSUVsrY82ayCBk1y5qplu1ygGLBWE9M4H0KVNUeDyMA/yXa0Js\na5NiEuMuXeK3Z8YMfZtfhdV6F1JSIuAuIYHOK0DnbdYsFWfO8N+fNk3Dww9HrouaGkqbO3SIJDQ9\nPSJOnODlNHpjnj5g0Bn3QAB46KFkg+VdtiyaXfXGpPgBNCMxOkpa73Xr7EY4yo9/bEdxMdm96TMD\nhw5Z8Z3vWFFRIUPTBIPtttvBnTurVcP8+XRtRr/mcim4807+N6so5G7yy1+64feTpnhgQMDu3QkY\nHBSwZ49k/PYmmg25VrS/l6vr8TnycSoOguMVr3hdtfo4urr3Y2o/qu1atJfvB90283643cAtt6jv\nuX/HjhFry0sbNPzXf4mYOhW46SYFHg/w5pvmZTNjHUAkCay7W4yJ1q2ulpGfT1Pcb78tYsECxQCn\nKSkqBgYsRrzv44/7sGOHDdu3e3DypIjxcfKr3b/fjfZ2EZmZKhITCfwCiLFk27AhCVVVMhgDyPNV\nRnq6ikceiWiLHQ4CrTabhq4uSlfTgde6dQ5UVMhYuTIZTz7JN3n195MzhMVCACb6vbExhqwsBYrC\nEAoB5eU+BALAunUyTp60YHxcQCAA3HRTKOwTS5KMoSGGNWsiIKyuzobych92704IM58M8+aFMDzM\nUF7uQ1qain/+k5j+NWvseOYZ8kAGqMnPYqFBhNOp4Z//tMBuB+rrKTLY4VANTbF537zeiGY5GKRt\niwZydjudyxMnLCgoCMHtpsHLiRN+FBbSMdYZ3JISH0pLfUhJ0eDxkFMHOTHwswKNjRJOnSKZQG6u\ngpERAUVFESs0c2Oe3uwYCgHLl/uwZo0PKSmq0Uynn6Poa7mgQMGePQkGk6t7+B46ZMWWLR5UVER0\n7UNDAtav9yI9XcWzz/LNjzRgoeO7dGkAjNEgbO1aOyor6XinpVFTHYFkYq0XL1YwebJmJL8pCs28\nnDolYPJkOq7R0ok9eyRMm6Zx94mJZkPa2wVuhic9XcX4ODMcJa6Vmax4fbCKg+CrUPFRWrwmquvx\nuvg4urr3Y2rN70/0kLvccn/wAwc2bpQ5Ded7bZt5P4qKFFgsWszrTqeGI0dIl9veTjHB5qnn1lYJ\nf/iDiEuXqAO/ru6Lhmer06nCbocxhaszc2NjxBiagePoKE3568t3uRS0tpKPKu8AQAxwcbEfHg+v\nx21ro4jk6M/m5amGFlbv4k9PJ7Z1YEDE1q02PPusbDRhmdm0mhoZgQBNp+/d6zZieu3h2e0pU3gG\nUdOA5cv94ZAL/phOnaohIQHwejVORtDaKsWEfugBDT/9qYRQiNhfp5OATnOzBIuFnBkix1rD2BgB\nHbNjwsmTIpYv94MxDd//Pn8sn37abmihR0cFrkFv7lxeNzx3Ll2za9Z40dEhQNOYARz9fiA3NwS3\nW0RKimrokZ97zoaSkjsxPs7Q3T2xM8WePZIBzi0WjYty7usTjbjkTZtkeDwMPT1kTRcMAvn5Cvbs\nkTAwICAlhQYMq1Z5EQoxzJhBYN3hgOFmYbVqYIzCSaKvtfp6Oaxfpua+Zcv8OHbMgtxcNeb8TplC\nUgRFAWpqbNi7V8Kbb0bCQqqrZSQk0IzGwICA+npisAsKSAZ09CjjXC70UA/9vnDsGC89MjumjI8z\nfOUrIeM3rc/GkMyCv0eZ7y2VlV58//uXd3v5NOt6fI58nIqD4HjFK15XrT6Oru79WGTz+0ePWriH\n4nstV9ck6g+5/fvdRqPMRCBa349TpwS43QwrVxLD+Mor49zrZWX0+sGDbuTnqxgcFGKmntvbBSMp\nLRgkdtMMbvbskZCcTBZneXnE5NntPLAIBil4QV8OQC4FR45YAPBsqsMBJCRomDkzhIEBngE3N725\n3QIGBmAwwBUVduzaJZmazrwGgJmITWMMMdZdTz1F6WsAYLfz+tKkJA2KAtx5Zwi9vaLB1OoaTmLF\n+XV0d/PbretNrVYNeXkKgkEBqkqBDikpKsbGBPT0CNyxbmmRUF5uR3k5rxNOSNAwbRqxtpcumXXT\nkWYvqxWYNk1FZmakmbG/X0BzsxQG/oAsM2zd6kFWlsYFZDQ2erB+fRK2b1c5a7X9+91G8prTScdl\nomPc1ydAEDTDc1lnSHVWF9Bt4vjztm6dHfX1HsycqSAUIpY2PV1FWpqGM2dEJCYCnZ0CGhp41rW8\n3I4lSwLGNhQX+zmHkUcf9WHGDNJgu90w2G2nkxL9zH7Pokg64/FxAcXFPgwNMciygMcec3C/BU0D\nBEHDrbeGYgaL0fcF8/1Al+xcbgCuyx1UFTH3qF//2jrh7MwHmcm6XoKB/qdUHARfhYprduI1UV2P\n18XH0dW9H4s8EQv7QR5U+fkqzp/nH5j//KfFSBmbCETr+9HeLuDRRyPTvGfPirj33qDxena2gqoq\nL44fF1FYqOCVV8YxMMA/jHVHAR1AHj78GoLBrxrbMjAgYMGCEAoKVIRCKl5/XcT99ydzSV3p6Sos\nFg1PPinHMI8TpXPJMsMDDySjttaDnBwFFRUyUlM1WCya4UEc+T5tn67hlWWgvz9WDuJ0wtAK5+fz\n25Cbq3I2ZLotl9UK/OQnBNqJ7fRjfFxAXl4I6ekqZFnAyAjDhg0RAF1VJcPpZAD47TQ32+XkRJhz\nj0eIiRlOTCQwZmbTSR7AL5tcCUjHu2+fNOHxoeNKnyNW1MN56xLwJwlJRYWDG6wQSCNHC90CTX+9\nu1tEebkdkyf/N8rKboUgkGPE6CjjwkvoGCfgX/81yDGk27ZJWLbMB7dbgG59FzlvEccIn4/FzADM\nmaNi0iQFCQkCt8yf/1zC5s0yAoHIdaXres0MdVubG+XlDtTXywY7bd73N98UsXt3IpYvJxnK9Omk\ny166NMB97uhRi3G8ExIQM4CpqCC5iKrG3g8Yo9CSwUGGOXNiB+Dv1bQ70b3lg85kfdJ9ENfjc+Tj\nVBwExyte8fofWe/HIpvZWb2Z5/0eVAsXkhbXrEkE3l8bfDlgrr9OgCAC4H73u3FMnapg3z43enpE\npKerUBSgvt6DixcZ9u1z49gxHkCGQkBvr4Djx0XMmKGis5NAkq6rffZZD9rbRWM9LpcS1XAVFMbn\nYQAAIABJREFUSedqaqJmLkUhWUMwyDB1KkxATUZtbRJqamRYLDBszc6csYAxDbNmBSHLIoJB/njp\nzKCuFdatzHT2dmyMYfnyCKPX2kpAMjVVRSBAXsfmBrhf/tJtSEj0ZRUWhpCcrGHFCgdCIRiDAI8H\nqK62Gf+npKiwWhHWCtMx4lliYsOjbdv0xqrqao8hURgboyCRNWsiWtjOTsHQGmdmqnA4aPAxe7Zi\ngMSODtE4TwDpf/XGQEUBioqCYYeCiPwmO1vF0FCEvda3KS2NpCjf/GZwQhu5xkYP+voEnD4t4KGH\nAhwwpUGWhvvuowY2krJEN5eF0NYm4cIFwOuNnQHo69PQ15eAxYtDqK/3YGREMOzH/H7gwgXBsGnT\nrfQmYqjr6jwYHyeHkhkzImx29O9Nv571mOeSEh+ysvjBSEFBKDwTwAexBINkuRY9cC0sVPDLX5L0\nJj2dGPzeXgHl5XYcPOiOYWPfC6zq95bz5wWkptJ5OnDAjfnz3x/Mxv2Fr62Kg+CrUPFRWrwmqvh1\n8eHq/Vhk/f2FCxUcPSpiwwbvB5JcCAJw++0RgJ2ermLlSmJ33w9Em4F5YaFieI3+5jfjkCTBsCDb\nuTMRg4MCOjro6asDmupqDwduDhy4A7t2SXjrrcjU8cMPR6aZzTHKOTl8EEVHh4iBAYYbbwzB7xew\nerUPmZkq1qyxx4DyoSEesEyZoqG01IeLFxkWLw7B52Po7BSRn6+gvV2ELItYs8aO6mo53AhHNl/D\nwwzLlvnhdjPMnx+CIPBpYi0tvB6zq0vAvn2SYfu2fbsUw1J2dYnIyFANiyydhXW7gWXL/IZvrCQx\nA3weOkTOAo89lsyBbXPzWVqahiVLeJeK1FSVOy/6dgO8FjY/X8G//3vE8aKuTkZyMlmpRTs1ROtg\nS0p8HBPd1CRx8pu2NsmwnmtoSORkB3pCWmrqXRNOyZ86JaKuzoaqKi+6uijIJHoA4nbDkA3Y7Sra\n2tw4fJiinSsqIo4X+/a5YxjuqVM1rFhhj7lG6+tl5OWFYLeTvOPSJWD2bBVtbcT2RzPUmZkUyHHx\nIsP4uACPh5aruz7k5CioraUEvPFx0jMzRjKV6POTlaWgv19EcrKKOXM09PSwGCCtHxvdqUU/T/ox\nf+KJpMsC0fcCq/q9Bbi8+8vl6pP2F44/Rz5cxUFwvOIVr890fRTJRfR3VBVobPR8IN2yIAALFtD7\n7e0CPB4Y1mlm4FBZKaO3V8D4eERDCgDj4/zDt7NTQFaWBoBkDF4vNTDl5Sl45x0Rb78torlZgsfD\nMG2aZgRoREsaFIUhEBAMW6/qag8GBwWcPMmwf78b3d3EjqWk0LS9phErOmWKhscecxjAVJYJuFgs\n5PE6kV1Ya6vE/f/88xLGxgRO45uczDN6LpeC8XFqbAKA2tokbNvGs5QZGSoCAWD/fooqTk+nhq2c\nHBWMaeEIaAaHQ4txKcjOVtDTI6K7WwgHYgCtrcSO5+erOHGCZ9MrKmRkZQHHj5utwmhgUFcnY+pU\n8mweGRHQ2uqGz8dgsfAxv21tEs6fJ8lHS0tCOAXOYuhV9eUODvLnvKuLdOmaBmzaJGNkRMDs2eTJ\nrDPe5sGPPiU/f37IiLKeOZOkPeXlDm6biosj1+H+/W7DGUM//iRnYNizh2Km09PJbYJCQrzIyuLT\n9jQN6OwUkZUVsbYzX+86Qz0yQn7GmzcnGddIW5sbTicLNwMyrF/vxf/+3xFwqScQRs92yLKA1av5\nAUpjo4RLlwTMmEHHCqABSHp6rFNLZ6cQltvAkEx82DCMj8Lqxv2Fr62Kg+CrUHHNTrwmqvh18ek3\njXyUlLf3q+hp1Gitow5u9Tja6CljWY6wWGZ7qgsX/owtW75qgLqiIhU9PQRSGhpsKC7248QJilWu\nrrZh9WpfjPOD7kOrNz7t3GnD889LcDiA++9P5gCSWQeqJ4VNm6YZYKq62sOxatGexT091Lk/MMCQ\nlUXgYmAAYIxh9+4E9PSI2LbNg7Y2KdzcReET9fUeI+Z2cFBAby9JEAYGiI2327WwzIPfvqlT+Wa2\n6mqZcymIADCGG24I4dIlERcuMCQlqdi/PwEVFV6kpGjYtcuNsTGy2XI6gcOHRRQV8VKUSZM0fOc7\nfCPZyAiQmAg88ojDaKDTz/H58yQ30Z0RGAPq6myoqeEBvlm/7HIpOH1axK9+lYClS1Wkp6vo7haw\naZOMjg4RLpeKn/zk76iuvg2CQBHBFy6Qw8XQEIOmkf3b7t0SsrNV1Nd7kJqqITFRhaYJ2LhRRlYW\nWZZ1dIjYt4/CT6IZW5uNrN8qKiIzFNFNadHXVWqqirVr7Vi61G9c77LMzyoMDZFuOxBgWLLEgepq\nGeXlDmRkqAAY11hpdm4wM/c5OWrMwOH4cQuqq5Pws59JOHNGMGYidPcP86Bh3jyFu/bNLO4HAasf\nhdX9pP2F48+RD1dxEByveMXrmqlPOzzjk1hfNDsUHV+sg1uzBKGlRUJCgopduyT09wvIy1OMYIVg\nEHj3XcGYFi8u9uPQIQK8w8MMxcX8sqqrZYyM8OBD96ElJpO20WIhS6r29vd3ggA0ZGcrEEUYUg4z\nwIn2LPb5GB54YBJaWym2OBpoVFZ68fOfJyInR41JPnv3XRHPPiujv590lomJGmpqkrBmjReqytDe\nTqlq0UlymsYwOEjhICkpJOfIzlbhdvNMqy4RaG2V8MgjESDX1CTFaKA3bpSxfj1JEc6dIw/hwUEB\naWkaZ3Wm7/f8+Qo0jY5NQUFownOs668BoLbWg8REGDrwtDQVCQkqx5QrCskwWlslnDsn4KGHePCp\naXS8gkEW47Kh64L1AYkOYnX5SDRT3dQkISkJXPpgYyNZxQkCAWBdiuFw8I4iCQnAxo0ezJ1Lsdm1\ntRQjrV/v5obMUIi2VWd19Sop8eHwYf64mp0b9P3Wj4/VGqsjJjmHjJwcFaKo4ZvfjMRrHzjgjlmG\nuZnTzOJq2vv/1uOs7v/8ioPgq1DxUVq8Jqr4dfHxm0Yux+xe7vUr2aSiryPaSaChIREvvODG8LCA\nWbMUHDjgNsCLvs6BAQFbttiwciXpe7u6RLhcCoaGBGzcmITNm29Hb68WA3j37pWQlqZwrB4ATJvG\nSw10H1qrVcOiRQq2b/cgO1uB280gyzyQmD7dHCcbwqRJlMYVzdQ1N0umz9FyZTnSZEfJazwYtdlI\nSvDAA5NilpGVRcBYUYDhYQGDgwKWLAng/PkI+7t3rxuPPcaDS1EEOjoYN+Uf69igTQjyh4ZiQf/Q\nEMlNenoYsrPJX3fFCkqes9vNjVkKJk1SceIEPUpHRhh275aMEBB9uSdPUpOW3gzX00OAuLzcbswY\nRA8IyMWCrkfzDEJiIpCUpGH//sXo6uKBqaZR3PTICDG3OTmqaX8ZN4hwu2kQsWqVD6tWESvLGENv\nLw0mQiFKdcvOVmLkKcEgxWFH27ft2iWhtdWNI0csUFXNGEAEApHrQo9OzspS8dxzJLGJHixareTc\n0NpKeuLp01VcvMiwbl3EdaWiwmuEmuiRz9FAvrVV4nTQ4+N0rqOXsX8/r3k2s7gfZIB8LabGxZ8j\nH67iIDhe8YrXNVMft2nkcg8u/XW9mayzk7r8AwFwU8DR6/uw0ozodehJVnPn6t+jBrlvfSsZLS2S\noXEtKfHBYgFKS32YPVvBvfcmc0CutNSH9evt2LhRRkeHwAGYS5eA5cujbb7cYIxhYIBvhPJ49C58\nAhPBIKBpDCdOkA1VJB1NwdattrB/ayTg4NFHfRgdZRwQGx8n54reXiE8za4hK0sxIpF1QG2OIE5P\nV6FpwPr1XiQnq4ZmNjtbhSRFkr2yshRMnUrevSMjEUBpZmKHhog5N+uojx4VDSlFdMyveUrcHNqQ\nmqoiJ0fF4cOUrtfby/DggwEAwI03hvDuuyIaGz24cIEhN5c0yTabgJdeSsAbb1gNSYnfH+t2kJ1N\nA5Z33xUwaxa5elRVebFzZ+KEIFAHijrjORG7rMtpomUU5gY7XWJCx1/jBhF790q4eJEhP59AHPkG\nO7BgQQirV/uwerUPeXnEVL/9tgUtLRKGhwXDV9k86/DWW3TcPvc5BYLAsGTJJFRVebntnjdPQVWV\njKEhhunTNWRkaCgrs3PNf729DKWl5KldUzOR/lmNSin04uhRkdMzDw3xNnoHD7oRbaHncilITlax\nZw85T+i/0+iKuzhcHxUHwVeh4pqdeE1U8evi400vKgowOsqMKfsXX7RidJThxRetcDp10Ok34n5/\n9KMkDiz09gqQ5UgE7vsxQXoM6+nTNFVut2vYutWDlBSKpl250gcA+PWvrcjPV9HfT4DB56OgAFEE\nF9u6d6/ETesHg9Sw8+1v/w6dnXdh7lw+NIGS3yIP6VCIdJVVVV4OADz/vITRUQFuNwwrKVUFbruN\n0rHILzUBxcU+HDpkxYkTQY6VHB0VDHbbDMSef15CZ6eAKVM0PP98IpqbCXhOn07M9MAAyQlGRwk4\n2WwaB5Srq2WEQrQNJSV8hO26dXZs2uSFLEcAkJmJzcggUG3WUdvtwMmTEa/ZNWt8kGWSluh2Zunp\npJGNbrRLSOC3r6lJwsmTIjweYPJkhlWrJhmsaPS5aGqS8MYbVoMBN9u4rVtHThwPP0znJ1qSUFnp\nRUNDorEuXepSVeXFjh02VFR40dhIxzD6fP/tb69h3rw7sXevhLffFnHzzUoM0334sIi6OhknToiY\nPVuJiQI/flxETU2SweDSoIGhtHRiXbm52U1324gG+z09AvLyIg4lule01aph5kwVp09TSEhtrQ2r\nVvnws5/ZUFfnQW8vaZ0TEjSMjIgoKfFj585EpKSQ/VpNjYzcXBWTJyuwWhl27JAwdapmDBLNswoT\n3UeiHV++8Q0n99s2D3A/aReHT6riz5EPV3EQHK94xesTrQ/DqH6c6cVjx0SuaampSTI1MckGY2j2\nLj12TITdjjBIIL9THTjrHfBmJsgcw1pZKQNgKC1NQkuLBJtN40D0/v1uvPjiOADSzEZrI3VZhCwj\nZlq/piYJiuLAk0/yn+/v5y2h9Kl9HXTYbBr8fprOHhwUsG+fGyUlfIzw7t1k09bcTAyfzhhHL7ew\nMASHg7bfrCF+5x1K4fvlL91YtcpnxDQPD9P+DA4KYCwy7b9xo4djswMBsjPbsoX37R0cpO/6fMBN\nNylobia9tMOhGalygQDD2rV2LF/uh91O2uq+Plrfjh0ErObPJ1lJTo4CxgCvl0GSKPK3t1eAKAqQ\nJGDVKocByqO3QwfvWVlq2GuYBgJmDeuFCwI2b/YgO1uFLJMFmj678MILbtTVyQZANV97iYkkdXni\nCfJVrq/34IYbQpgyRcN995H+ev16OzZv5oFeIAA8+ugk49orLY39jN7gpycQmhnn1FTSWPf3U0Sz\n3Q64XIoRXqJvo80GvPCCG3191PSoacDAACXukcWaxfA3XrHChyNHRKSm0oBFZ2xbWyVomsYN0PLy\nVHR0iAgEGMrL7TGscWWljMmTeclFW5uEKVM07N2biLIyLzZulDE+braBY/jiF0Mx9xH93vLii3zi\n20Qsb1zve31UHARfhYqP0uI1UX1Wr4tPq9nNPH1p1ns6nRrmzQuiupqCE6JlEAsWKMbUrblRSu+A\n15kgnQE+fjwynd3TIxpxuaSrBM6d499vbxcxfbqKs2cJQJn1t+npKo4dsxiMtSxTc87TT38BjMlI\nSDCzoMTEjYwwpKdrhr5XBx179rhx/rwFS5cG4HRqnKwgGCQ5xPLl5Pxw4oQl7C0rG/vtcBArPjws\n4PhxhkWLFGRnT5zC5/MxfO97/IBj82YZNpuGo0cjNmMul8pN1zc1SRPKEjIySCoRDAJvvGExtK1d\nXTQ4mTxZRVkZJbHl5Sk4cUJETo6GG29U8Le/WVBc7Ednp4gnnrAbshO7nQZZmZkqx8S2tkqGhZp5\nAKAnvungq62NmtkAfgDi8ZDE5OGHJ0U1p+kNZhrOniX7MJdLMRq4dNA4Y4ZqNM0RMFSgKIxjYnU2\n/8ABN86do+1cs+ZfjXNpswHbt3sMLe2RI6Kx/Lo6GRUVMgoKFKxfT7ID3VOZIrkjoLO5mSQ4qamx\n5yM61riyUkZ1dVL4uFAQhdvNDNa5oEDBnj0JaGqSMDQkICNDxebNNoyMCOEwDoapUzX09zM0Nkrh\ngZLPWKe+X7pkKdpbu6tLwNiYhm98I4gHH4zYD8bKHy4/AP8gLO+1qPf9IPVZfY58UhUHwfGKV7w+\n0fq0tHXmB9sNN/Dd6XPnxoYf7NkjwWLRcPq0eBmWDti1S8LYGJn2AxMxwAR6KL6VWMDoJjLdEWH6\ndPKjXbxYMTSJOsPpcqm4eBFYvDiE1FQVO3aQ9dnhw6IBXtau9Rq2YgUFCtauJc/YzZtlHDpEzFtt\nrQehEGk8NY13Dpho6pqsoxQsXhxCdbUMxojhW7fOYSxLDxSwWjW8+KLbSARjTPeNlWOYQ6+XQVGI\nbV2wQDGAlKrygGZoiFjoQIDv3BdFkiXon01L07ByJb8vujPBoUMipk/X0NEhQhQJuJw9KxgRyLoU\nYmCAlj08zJ/jri4BmzeTI8TwMAsfYwsKC0N4/PFIMlx3t4CcHBXZ2eRBq2tY9XOhR/pGQivo8VpY\nGEJDgw2lpT7U18fKKNasIaa+sVFCXx8ly5EzSCzjvmuXZNjJRQd2+P0MZ86IRqDE8uU+WK3AihU+\nkL80nY+6OhnnzwuYPTsEWRZiGvh0nXhpqQ91dTLS0ijSOjrtjvYx4m197JgFc+cqSEpCjPMEPzAi\nG72+PgaPh6GkJGK39x//Efk7+hqdNk3jjldlpYy8PBWTJ2tck19CAvDLX7oxMhIBu4oCvP66iDfe\nIJZ640ZyzdADdKKlEf39DEeOiJ+4JWO8rr2Kg+CrUHHNTrwmqmv5uvg4/r0TsS6fhB+w+cE2Ps5w\n4IAb4+MMmZkaFi5U8Otf89Og4+MMAANjEWaTn3JmeOQRSkQbHBTw4osi/H4eoFgslK4limRbpYMv\n/f3ERC3Gt7a1VYIsC9xrlZVe/Md/JKG+XuacIETxj2hpKcLgoACrlY5VTw/ZpiUkaDHLSEgg6zDz\nlH1Pj2DoTnWWsKqKppPNAQ9Wq4Y5cxRcvMg40NreLmDOHBWDgxR4sGYNWYmZGwznzo00aLlcCpqa\nyC7t+9/nAU1Ghmo037lcKgYGAFEk2YJuObZjhw0PPsi7HAwMMM7n1axVbW4mOYrVqiElRXtP54jp\n04mdbmujAZEg0IAnMVHjgGZODjHIlZVeI6HO6QTWriUQq1870aEVADA0RDrkigo7li/3cftx8qQF\nPT0isrMVWK2AKGrIzCSd80SM+9CQAJdLgcUCfPe7L+PGG79oxF7rIFwPlKit9cDlokjfefMUOBya\nMcuhH6+qKm/MwKikxG8Mwo4fpwEXIJg+pxrHZeFCBWVlvEfwRDMxCQkaKipkzJih4dixyHvj40LU\n7AcNQkZGKPilr48fsDgcgNOpYOFCCoWJtt974QU37r03aNwP9EbU6N+GPgCPTnz7wQ8cKC724+23\nKW771ltJO/1peZVf6bqWnyPXYsVBcLzidZ3UxwGe0ZIGl4vssIaG3ns5+vr6+5lhE6Z//ujRKyeR\nMO9Xfr562WVfbhp048YkVFZ6IQgEAjs7eVsnq5XATnGxP6wdjQC+6dOJAb7vvkkTslkul4qjR2P9\neBmjv3XHBZ0ZHhmh9emfV5SIxZYZ7Jk1rG43MG+ehu5uIUb/mZenIBAACgtJ81lTI2NsjMHr5cFK\nXx8xo8EgwyOP8KDV5VLh8TAwRkzw00/LHLDdtYskDJcuRcBLR4eI0VGyPuNBEYzpeadTgarSe1lZ\nagyjaLHw+xIIMHR3ixyQil72hQsM6elAfb1ssNAAAbzOTopoHhoiiczWrTaDEfb7IzMFt94aRGur\nhPZ2ATNnqoYTAmMkIdAZ19WrfcjIoEFXc7OE8XEWbrTkbduamiQIghnc6tvFN6K1tkYY92h3C1kG\nNm6UMTAgoLExCdXVEbbf3BwYCjEDtK9cyfvz6sdL148nJmqYMUNFRYUdS5YEYuz4du+W0NYmob+f\nBo2KQjMAhYUKBgcp6c/sC5yTw29PMAhUV1Pcte6Qom93SYmPu67b2ijNzyxPSU1VYbEwCIIW0yg4\nPCwAiNxDzDNQbjdwyy287KG9XYjZ1xdecOO++yJOMqdOCVEuLx/pFhWva7jiIPgqVHyUFq+J6pO+\nLj6ONjf6gVJc7OcYlolcE44dE3HqlAC3mxlgMfpzV1IiYd6vrVs9McvW1zl7toLf/tZtxOUWFip4\n5x1i6np76aE7ka3TtGlqDJu7axc1Yo2NCRgYiAC8nTttpjQ0uwHG9O9mZqpISKAmpI0bSUeZm0ud\n7nqsceTzd8Hp9AKIBXsul4Lqag/Gx2mq/+abFfT2Cpg2TcVTTxGDrSeKDQwI8HoZpk5VIcvAsWMW\n5OaSNCNao+rxkA42Ou0uGGSYNAno6hKxejUxiI89lmQkpOmfefddAgwWC8+oyzJg1tEGgyycDsfg\ncAgG8K2okA1mcHycQRSBvXsT0NjowalTogFca2tlDkjxx1fjgHRtrQdpaVrY+o2httaGNWt8OHRI\nxL33BjEyQoOZUIgZgPkb3wiivZ0S34aGSHdttWph4CjDZgP8foYtW0jzXVHhRV2dDW1tbni9DH4/\nz2LqbhW63jo3l673+npPzOxBXx8Bb4uFAH9pKckbNA0YHBTCA9EieDzkNEKgX0VLC7mchEKRAZzu\nHRytg9ePV8RmjI7lM89Q09vbb8fOIoyOMsyfT0D3wgWGW25RDL2v1aqhs1NEZaUXXi8wd66CkRGy\n0RseFjB5Ms0a6MvzeJghf7HbNWNAqL9/7JiIp58mX+VduyS89ZYFTqeGtWvt2LDBiwUL1PfV9Zrf\nv/XWUExzW34+xUrz9wvad91J5koM1D/NiuOLD1dxEByveF0n9XGAZ/QDZXwcMcvRlz9rFjXI/O1v\nkW7x5cv9eO65RMOuLD9fxezZPGvkcqk4cuSjsdTm/dK70vVlz5ih4ORJEVOnajh2zILMTFp/QYEa\nw0g/9xy5F2ga0NQkYWSE3A5EUcPhw5EGLx0oWSyALFNXvb7OwUGBS0PLzlYQCvENS+vX27FtmycG\nWEfHGre0SHjnHdGYbgZircBEMVbjfPEiw9iYgGeekcNBEkJMI5j+HYrC5WOTV63S18Wzlikpkaha\nXTttlo/k56vo66OIWh3kzJtHFmHTp6tGeIJuoeZyKcjK4oEITcnzzODevRJCIYoc1l8bGmKGLvfm\nmyllb2SE0uYY0zgZR3q6xjGtlBTH/79liw333hvAqlU+ZGaqxoBEP2bDw4xrKtO0SFOZy6Vg0aIQ\n6upkBALERIuiOYhECwN7AXl5IQiCBq+XAkXS0lRs3y6htjYJg4OC4TKxdClv12ZuPly3zm78vWKF\n05CCRF9TZu/gxkayFvvpTz0IBBhychScPUu2ZYODpKVetIj/faanqwgGRfT1CbBY6HWHg2Yx/H5q\niMvOJgu/qipvzDU9NqbBYgGqq2WMjwMpKRoqK5PCTYbkMBG9PrudfjfFxX4A/HnXwe77uTcsXKjg\n978fx9CQgOFhklKYa+FCBR4Pf55mzqR9N/cHxH2CP5t1RUAwY+x5AP8GYFDTtPlXYpmf5YprduI1\nUX3S18XH8b00622jlzNtWkR+YJ6u122LSkp8nF3Zb3/r5h5gFouGr3wl4tv5+9+PQ1HYhKB4IvlD\n9PYMDvLyi7ExAbLMT01XVsoIhRS0twsc6zh1qoblyyPAZssWD/r7BUydCkyfToBCl0R0dAgGy93a\nKqGmhpp2EhNVnDljMbZJ3/fych+qq5OMY9reLsZIBPT44cFBATYb6S1/85u/YuPG29HZKeCmm0JG\nwMTMmeQmEf39/n6BO/51dXIMe9zdzesxo9/r6hIMHWxDQyL27ZNw6BAB96QkzTj3OvjVWVGHA0hN\npaaznBwN584JYIyWK4o0WFiyJMCBuF27SCese+fqsgW7neQl5v1KSSG5SG8vndfNm204dMgKANi2\nzYOyMkI51dVyjMOHuXEvNtHNgnvvDaKhgbSwJ06I2LhRxtq1ZFvW38+MoAn9PBYVBQ35Q3q6ZjQn\nDg+TZ3Nenort28k3WmdKzU4MPFiU8eyzMhITgbIyB5YsCXDbaNbYnjjxGoCvhq+biDMJAKOpLTlZ\nw7lzPKtLDXsaFi9WwBjJPDIziRWePp0ikPv6BK5R0W7XwrHdPvj9zHBMaW2VDNcIXfttPrYOB0Uc\nm5sCo51XMjJUvPACWfC5XEq4gVKD1wvU19tiwmeAWPcGRUHMQBoAzp+n1D23m/T78+dH7nuCANx+\nOw+m58+n/0dH2Ue+X17NiuOLD1dXigluArADwK4rtLx4xSteV7g+ju9l9ANHVXnT+ZMnL6/NdLuB\nhQtDMR35J06IKCxU8M1vBiEIiPHtHBoSONAcPRVplj+88so49uyRcPQoTZnW1iZhwwYv7r03CEUB\n9u2zTrBdAtrbNcyapWDzZjk8Ta7h9Gle9hHdeNPSImHTJmLfiov9GB8nZ4a1a+04c0aAIFAzWlER\n8MILFOk6ZQo1dE3Emubmqjhzhm84WrRIQU0Nxd329AjweBgOHrRi3z7Sdno8AsdomqOHc3IijKjT\nSaEB5mjkvLwIy2dmlvPyFLS2uvHWWxbY7UBnJ8PnPqdgaIhB0wjQVFbK0DSGpiaahvd4SF6gexEf\nPWoJs9eJHJPa28sPOAAY3rk7dybiZz/zIDVVw7vvEsDXwVFJiQ+MkbdvdDQuNfmF4HSqcLkUY4Ai\nihpnTTdpEtnJRe/nDTfExkP39sbqQ3Xnj9RUcgaprqaBjtWq4d57gwaAj05hiwZ3uh63uVmKmfLX\nwySir8mREaC/n2Qi5uvFbKnncESa06ZPV1BdLSMri29IrK+XJ4zC7u8XEAgASUkUhmJ8OKD8AAAg\nAElEQVQOwFizxo5ly/ywWDTMnk2DuuJiP3butGHp0oCxzdEDqo4OESdPWmK2W7eZM8trHA7gpz/1\nICNDhddLXs26FMg8kF63zoFf/ELiAK+5v2EiudfoKIuZKQF4MDuRFZr5Phf3Cf7s1hUBwZqmvcYY\ny7sSy7oeKj5Ki9dE9UlfF1fK9zJ6OS++aDWcFSYCVbfeGsLtt1MjXPTrPh/DPfckG+A2ms11uRRo\nGvCTn3jhcik4dUoMx/ZSmMWJEyKamyV0dtIUbne3gMxMbcIp02PHREhS7HY5nWrYpYK8XRcsCKGs\nzIehIQGtrW5cuhTLFh4/LiIjQ5sAKBEwimb19Mar7GyK9K2oIJ/f2loPGGOQZYbTpwU891wkWayo\nKISyMgLYPEN4G9atowGFzmhGxxe3tUlG2EdPj4Annog89J97zoOkJKCx0YPhYYbMTGps05Pd5swJ\nYd8+Nw4dsoT1yw4884yMm28mljw3l8IMMjPJJ1ZvBktIIB2nJAlYty6SLnfokMVoftKlHcTkMgPQ\nmhugdG3qpEkROyyXS0FrK0kgzHZz+jKpWZC8ahsaKG3PnMS2YUMS0tK0cJR0hNkcHQUX01tXZ8OK\nFT6cOMGzphYLAeqLFxlWrnQgI0M17MPS01WjIc4MZgFiZUmzTeEeubm8xCArK/aaTE1V4fGIHMuu\nN8e53QwHDowjEBDQ3S0gN/cO/K//dQk9PSKmTNHw0EMRjbYe0azbx9XUyLBaySN5zZrIQIIa1Hhw\n3tEhYONGGR4Pw+goQygEzoM32hli1iwF9fWe8KCLGOPa2iRju9PTNaxbR7MfZnmNLFNTH1kI2sPa\neEvM9rjdsUzsRIA3WhaVkaFidDR2oDE0xKCq+EBSq7hP8PVRcU1wvOJ1leuTsAu7UvV+25afrxrO\nCm43sGBBiGs80z+vs9DHj4vw+SJNO/39DH/5CwVJ7N/vNiKL778/OUZbqHdtR4Ocp55KwgsvuGNY\n7sJCBUeOUKDFzp02lJf70NJCqWipqTQFfOkSjDS40lLe27epSUJamsq5QOTmqkhN1XDkCA+UJk0C\nTp3iXzt6VMS8eQokibdB27tXwrlzBBy3b/egpMQHVaVo3YEBhvp6GV1dZs9damiy22EAJ3N8cV2d\njNpaGzZt8nKDhylTNCxfHpGBkK8qOL0yTe9HgOzJkyLmzqXGupoaGeXlERZPt9+qqPDC7wfXVPfS\nS1YUFCioqPDC6dSgacSeWq0aPB7yLrZazbIEZiSQ6XpjXQva1SXENIzpchEKnYisy2ZDjCWcxULg\nz26nGN558xRcuqRhyhRq0tL1qHV1HnzjG8EJ43cVhYDa3r1uVFV5kZWl4pFHeFlN9CBQZ1orKrwo\nKAhxrP3u3RJaW8l5JCdHhdOpYvduGiylpWkQBNLCvvSSFZWVXlgstP5t2/TGOxmpqRoXWtHUJCE5\nWTMGbNHx1mZdLh07AR0donGMjh+3TOgq8fDDk9DcLKG9XYTFooRdS6hxNDFRM8752bMiN+hqaZGw\ndKkfs2dTAMjwMOPkNbrbhm7rpoPc6IGf2V1lwYIQDh50c0ysWcY0Osq4gbQuQTJbwAUCDH/4gwXT\npmnX1H02Xlev4iD4KlRcsxOv6IqwGq/Car3rmupCfj9HiYULFTQ2etDeLuCWW1QsXKhCEIhdi65o\nX87o5TkcGuc0sX+/G//8J+lcYxtTzIb99P7wsABN49f3zjsC7rmHgPTgoIBVqwjI7d6daDw4U1IA\ngECDmTHSLcmsVg2NjR709TEDPJmBUlqaiuzsyBSwy6VgwQIFhw+LmDaNT8Dq6hLAGIFDSusip4XL\nSRzIE/ZPGB+/GwA1CLW2Stw0dDBItl2lpT488oiDGzy4XBEAk5ZGACYhIcLIlZb64PWabbtgyFdG\nRgglmFk8p1PF7NlqjL+w+X8dpO7cacP69V5kZqqmY0fH7fBhChGxWjUj3GJkREBBQShGLlJX50F+\nvmLofl0uBatX+2K2UVHIyiv6+mpqIuutaP9fl0vF4cMiOjpErF1rNwBofj5pnPftI2uzp56KdcOw\n24GEBBWtrRK6uqiJct06YlrN0/+DgwLKyyMJdg6HgGCQBjZLl04yXl+yJICUFA12u4olSyLbvnix\nYnIyeBV9fZ8HAMOOjGeP+cGDLo/hz6NmNGEODAjw+6MHqEKYabcZrPqBA25cvEg2aYCGixdjtdtO\np4bNm21YsiSAhIRIU6HXyzA4yJCVxc+aOJ0a12y7cyeFgnR3C7jhBhV33hmCxcJrftPTVaxZ4+V0\n/q+8Mm4MhHUvb90CTh9QbN1Kco66Ots1dZ+9khXHFx+uPjUQfODAATQ2NiI3NxcAMHnyZBQWFhon\n67XXXgOA+P/x/6+7/2ka71UARxEM3o32dgGy/OpV2Z7bbrsDx46JePnlv2L6dBUZGV8MP5z+hGAQ\naG8vwoIFClpaXsfAgICvfe12LFyoQJZfhSwDgvDey//CF+7AgQNu/P73f0Vmporu7rtMy/88nE5A\nFP+IkRE/rFZq/BHFP8LtluFyfS2cDEbvu1xfQXq6ih07/oaNG5OgKF+C1aqhouIgJk9ORELCraiu\nlnHp0quYPFnBtm13h4HaqxBFDZs334LmZglnz/4Fohj5/sjInwHYEAzejVOnRFRX/x3Ll3vR0XEP\n1q61Y82ag+joEFBY+EVUVNjxwx8exI9/LMBuvwv5+Sruv/8QFIWhuvrzYdBB67vhhsXw+xmWLz+I\n9nYgGLwnDPbpfAeDd6OzU8R3v/s72O0avvjFO3D//UlQlH9AFDU8/fQX0Nsr4MKFV7ntHRp6NQxI\n+OV1dNyN0VEBq1f/A4pCdms1NTIeeeRlAIDV+kW0tSVg/fqDOHOG9qehIRH33PN7iKINTuctAIBt\n2/6GH//Yh5SUu5GSoqKr68946SURweDXwtv9Kl55xYtg8B7j/1df9eI///NfEQoB99zze7z9NnDH\nHbejpUXCwYN/DUcl3xEGeq9i3rwQWlu/gGAQWLqUjp/LdSf27pXwm9+8DodDRW+vfrxfRjCYBOBu\nFBf7cebMnwEAjY134uJFhlOn/oz6+gT88Ie3cdfX4ODnsXOnDd/97u8gywz/9m//gqEhBkH4E0Qx\nCT09X8KGDUl4+OHfoatLw4wZdyEjI4Tf//6vCAaT4HTewp3PtLQijIwI+O///gsuXWLIy7srzLT+\nCSMjPu76HRnxoqrqbmRlqfje9/5p7N/q1T4Eg6/innt8eOqpyOeXL/ehre2OMJv6Z/zxjwxf+tId\nxvoF4U1kZy+Gw6HhH/94DT/6EcMdd9wBm03DW2/9BaJoN64Pm+1PUFUVY2N3o7lZwhtvvAafD9i5\n818xOCjgj398DRYL0Nj4NWP9777rA3BPePD2Ku67T0Aw+C9h72ja/127irjjMWNGETo6RNx663/h\n8cdtxvp/8IOXkZGhgbG7MDDAUFX1/9DXJ+Kuu+7AhQss/H3a3sFBAW+//Rf8/OeJ2Lv387BY6P5x\n5oyAioqvG9v35JNeZGR8NTyb8yr+7//1Yt26W7FokYL/839ehyjao87ny/jFL5JAdoO0vS+/7MWi\nRbd+qvfX+P+f7P/6311dXQCAoqIifPnLX8Z7FdOnrD5uMcZcAP5T07TCid7/wx/+oC1atOiKrCte\n8fos1ZEjopFaND4OQ0d7NabqjhzhmV+zBOHgQZqP/qh+w+bl79vn5jr5m5slrF9PTTkApZYdOmRB\naqoGi4V0qBkZGpKTVYyOCpg6VcVbb1kgikBiIrGrIyMC5s8n9ih66ljXvkZP/T/5pIy5c8nWLT2d\nmtGysjSuAUv3DN63T0JZmR2lpT5kZSkIBIj5AoCZM0l+MD4esQTr6RFRVBTE44/70N1N0chWq4p7\n73UiI0PFs8/KRiJXNDMWvb5Dh0RueysqZMyfT+lfJ06IhsZ19mwFskzhFmaP4+efl/DQQ8ncPtvt\nFJk8f34IHR0CGhpsWLbMD7cbKCpScO6cgBtvJG02deyr8Hg0vPOOFdXVScjOpobC6O02ux20tUno\n6yPngWgdak0N+QA/8YQd3/ueH08/ze9fZqaKxx6bZLxWV+dBebkj/L4X1dVJaGtzG/IVXSYQPS2v\nhy1kZal46KEIy2q3k6WdLnGpqpIBMDQ0JBr7r8dUFxf7sHOnDZs3k0QlOpLYbidbs337EvDDH/px\n6RLZ0k2bpnIsfG2tbASj5OUpRhS07hJCemENTz1lx09+4oUg0HlxOsl1paTEwZ3PW28NoqzMh64u\nAXl5KhISVJw8aTF01noz3Llz1FzY2UnyoObmBCxZEjBmHFwuBc8+K+PNNy246aYQKiroHNTUyDh5\nUsTixSF0doqc1nflykmoqJC56/EXv5DgdFKynscTOa7R11x2Nq2rvZ1+A6dOke2fzabitdeshpRm\n7Vov3n1XRHq6hrExYNYsBUVFqpHe5vcDjz4auS4qKmQkJ2tGE2L0fUhVgaNHSQ6lquRQMjgY+W2a\nfcvj9dmsI0eO4Mtf/jJ7r89cKYu0VgB3A5jGGOsCsEHTtKYrsex4xeuzUpfT1y5cSAls7xVA8VGW\n+1HK7Lk7PCzEdEibo4fb2wUsWEDNb6dPC0hNpcjZlBQNBQUqty3m5Xd3C4at0syZKp5/PgGrVvmM\nxpZQiBkShmiQ89vfupGZqXGd7eau8ro6fjq6s1OMmTJftCiE8+dFaBpgt5OucMUKB5Yt88PrBebP\nJw/VujoZikKgpaNDwNmzYkxHffT/jY0SLl6kads334yEZmzaJKOtjRq+li6NAJJ9+9zo7xeQkUEW\nW7t2STh6lN9el0tBUREd54IC0sSeOkXT6S0tiXjooQDq68ka61e/cuPsWQHTp2uQJIZdu9wYGxOw\ndasNN9+swGLR0NcnQhA0WK3U2a83uNXVkTtFKMSMWORDh0QUFSlYvDgIlysBHR0i1q+3o7VVQn8/\nAaCtW23GVHxmporycgK+kUAQC1JTqVmsp0dEfb0Mu13lwj5mz1YQCvEa27DTmjF1brVqmDSJfIgT\nE4Hp01WuoS0jQ0UgQEAoKUlDW5sbPT0ivF4YLhZtbTRF7/czyDIFrHR3C7jxRgqC2LxZRlmZHSUl\nZJe2e3ciamtlTJ2qYWyMdMunT4t4+OEATp4UORDa2krXc3o62bh95zsB5OTQoEmPgna5FHR0iBgf\nB3bvJrnB7NkKN2hrbZViZEFvvGFFe3sA06er6O0VMDBgMa5vgBxNeBsyLx54YBKqq3mbuI4OEV1d\nAnbvTsC2bSF873t+zJ2rYGyMwekE+vp4ra/e3Gf+/djt1HSYlKTB4xGwdGkATqcGvz9yDvU0PLPG\nv6VFQkEBpReuWOGDz8dQUcH/pt54gxn3RbNW2OkEkpM1/OIXEmbNUqAoER/yhQuVCeVXBw64sWGD\nN+72EC+jrpQ7xINXYjnXS8U1O9dnXU5fKwgIe4C+CuBuA1h+UBD8cZLgAB5Emz2A8/PVmA7pifyG\njx0T8fWv896sABAKvfd309I07sHY1ETesbwjQKzX7TvvCNiyJQmPPRbRaJo/k5Zmtv9Scfo0ge7T\np0UsWEA2SNEP+8ZGiQOEFRUyXnnFiiee8OHwYRHz5lGIQSgUa6Qf/f+pU9RwZHY2aG8n4KlrNvUm\nsHffFZGVpaK01A6LhTxVb7pJQUWFHd/97u+QlvZFLF6scABn/343Zs5U0Ncn4OGHA9x7jY0S8vJ4\nRruyUsYzz8jh5DgYzObmzXLM+XzggUnYuFGOccKoqZFRWyujp0dAXh6d16QkDTNmaPjud/1IT9cw\nMCCgtzfSgGV2u6ipoUCJo0fJTq6hwWZsY3U1vUf2Z+S7K4oatm/3IDtbxdAQw4EDbni9AtxuAbNn\nh1Bfb8PKlT7DIi0rS+E01mbLsnXr7Dh8mM6/xaKhq0uAqjK0tibijTesBgCzWPRGRAJyigKuKa6p\niZrcoq+7jg4RR45YjOS4r3wlZARKHD9Otmfr19sNFragQMHgIDVKPvkkP2jr749oZvV9Gx+nbXI6\nNfz973/Gl750Owc4zUE2um7eakWMVV5iIln8TeSoYY7jHh2lvxsaErF3L+mHc3IUnDsnIjERSElR\nUVISuU7a2qSwI4UGVWUxYD4YpBQ6RSHG98EHk2P01v39DP39kcGNrhV+6y3RCOJpbPRg0SIlZoZJ\nvwdOZAspCJ9t8BvHFx+u4o1x8YrXp1TvldiWn0+pZIoCA4h81OWeOiV8KDY4GkS7XAoXNDERWzLR\ng8XMDrvdAiZN0riUuIUL+YdSerqKQ4f4sIeTJ0WYgxKcTg033MA3SHk8DM88Q9G1+ut6l7s+9e3x\nEJg6d46Y02hA2NJCbKwOEvR1DQ/zvr233RZCUREPPpubqQkq+nMTNRyZQXlCgoabbw7i6FErNC3i\n+FBezrNfqgo88ADZtm3aJOP11zUUFiro6+O3tbNTRG6uioMHrfjqV0NctzxjDGVlSVi2zG9Yirnd\nFO9ss2mwWlkYiFAzWGOjB+fO0XVz7hxtd1ZWLMOamakaqXerVzuwbJnPAJhNTRIUhfYnuivfDMyi\nk9aigSmBLWKEf/xjO1at8mHqVBUXL1JTn37+zIz/3r0SGNOM9D0zmNIty3RQqLOIQ0MCysoiy2lq\nkvDGG3Qdnz8vxFiu1dbycc6CANx4Ywh+vyXm3AeDLLytSaiuVmN8b/v7BdTV2ZCRQYy23R5pbtM/\nl55O29TVJaC2Vo5xhZgyRUN/vxgOk6Dmr4muQ6uV0v5qa+2GHd/8+fR7MoeteL26tRu/nPnzFbS1\nueF2kyXhyAhDairD9u02lJT4Yho1+/oYysoc2L3bbfwuzf7BuvNGa6uEjAw15v0pUzR4POAGAHa7\nhq9+NYizZ0U0NnqM+9Pl7q3/U23O4vXpVRwEX4WKj9Kuz3qvxLaFCxX87neL0d4ufeipOvNy3W5i\n2T7ojT/6AdLRIWJ4WMC99wYv+/mJHizmbdB9eM0pcYsX0/cWLCBz+5tvVkzfA3THBv21OXNUA7iS\npZMWNu33Iz9fNR7ss2eTJ2t6usYxdm1tktH9D/AslNl9gDEY0b7JyfT6u+/yD1i/H7jxRsXwir14\nkRlSgEmTYGgjS0p8Bihfs4bstTweXkbR3Cxxyz5yhOzJdD9aYjTvQUNDxFNX/66qAmfOCPja12h6\n3azRjdhiwTgnwSCQl6ehs5Nx9m99fQKeftqOLVs8UFX6/tatNqxd64uZ1taXrx/rmhoPZs1S0d1N\ncb8LFoSMrnybTTPCJSLgTo0ZHGRnEyNaWBjC8LCARx/1YepUDY88EtHzPvoogVtZ5gcDAwMCVDVi\nsWYGU9G+tvPmhVBV5UVDQ6LBdhYVBVFa6sPAgIC9e93YscOGWbNUdHTw5z09Pdbn+MCB8ZhrYeNG\n8i6eMUNFRYUXsb63pF+Pvl7q6mywWBBml0XMmaOgu5s0xs89Z8P3vufnljE0JEBV74aqasbMRXW1\njPXr7cZ5LyoiqY9uDagzzvpvaWyMYe5c/vc3d66CkhIfyssjyyksVDA0JGBggGHxYgUlJTyg37nT\nhu3bPaZzTOcgM5OsyH77Wze6usjTurtb4GwSjxwRsXw56a+jnS3GxgQ0NCTGRIsfPOiOuT991DTM\na9me8qNWHF98uIqD4HjF61Oq90ps+ziMxcKFCpeYtnOnDRs2eC+7rPeLHf4gDxDzMubPpwddtCbY\nzA69845gWKcdPUryCZ0J03Wk69fbEQrBeI0xwO/X8I9/WDBnjsoFYixeTOwoYxp2704M+7Pa8cQT\nXm69588LE9pnNTQkoq5ORk2NjBkzVAiChkuXBIyNCbBagWnTVDzwQHKM1+jkyRrXzLdvnxvf+U4A\nM2cqkCQGQMDmzRQ2sGePG4LAjGQ0QdBQXu4Ln6fEmGhWpxO4eJGsy8zBDWfOiAZwCgbJT1mXclBg\ngTm0gQDMtm0eQ8taW2szmtF0EJ6QAGzebIPVSqlkOqCi65JStnp6BIgiD+YAGJZsZmu0w4ctYIyk\nDJpGzOXQkBDWXvMgNRgEamvJK1iSmNG4tnSpPwy+/TH6a35WAMjK0sCYgupqj5FmNzQkGGEW27d7\nkJpKbOP586R7FkXgueckZGRoRjT0+vV21NfL4QAW/neRkEA+vmaWOToKmnxyA3A6yV6tujoJ9fU8\nQPz850Po6xOQl0fNjT/5SbRHM8loeImCHDOQyMhQsXp1MqeTbWgg3XJ3t2CEyOjbSoM0LzSNBpXH\njlFzWnc3MwaRTiddI2aN+LZtHqxZQ8ffbPvmdpP129BQRNt/ww3UsLd1q8fYL8aAH/2IdMGu/8/e\nl0dHcZ/Z3l9V7y0J0C4kpAabxbFYYrCz2U5ycnxmPPNmfGImE+N4y9gPZZDBgAS2IA9G2Fgyklgt\nzyEWASFA8kISn3deMi+eTJ4dkvGJgRgDARmDJNC+IKTurl6r6v3xdS2/amEbG8eJ098/IHWruruq\nuur+7ne/e30yJxPKyAC8XhUbN4aQlaVg9WqvriXfvj2YZI04kVRsomvrRwG4n1RKlqq//EqB4M+g\nUpqdv876MKD7cc8LQQCysiZOTJuorPKHF14I4MABGhSaM+ejsdDaNjTG8swZAbm5amJgS4GqAv/5\nnzzAy8kxnGjee0/Q2/EUviBh+3YPKitDyMsj317GCOg9/jjpU0+c0JLiBMyaZQxe2e0qXn7ZD8aA\nhoYgCgsNkPXlL8dwww0KLlygYaixMWBwUERjIw3bmcFGW5sfmZmGN2t9fRCxGONYzcJCJSlJrqtL\nRCTCuAEprWWtqoxrY1dXS3rKmRa0oAUIFBYq2LXLhXvuicLrVZGRoe2/N2C3fx2MGfGz6ekqhoeN\n96HFJJv3d2mpjLVrabjr0UeN9+VJYK68PDpOXV0CKirCCQsyEatWhZGbq8DhoBCG5ctpIr+mhtcO\nT51KjK5V69nZKeD1121YvDiKeJwhGiWZg90OrF7t4RY+tH9dWLs2jIoKw0O3sjKMadMoCtm6/XPn\nBD2GuahIQUeHAK9XgdvNcP/9RgegtlYCY+SP+8gjVi0vDX7V1kq47z7jsZoaSXfk8PlkHDwYSAws\nkkNCUREPRkdGkgdJc3IUPZkNoHPYnFYnCNTq7+kRMHu2jB/9yA9ZZhBFIDOTNMrm2GenkxwjzGC1\nq4ts2Bob78ChQwFdoqL5WD/5pCcRb6xiaEjA0qVhuFxAcfFE3s685jsW4xeMmZmG17V1MTl3bhyt\nrQEIAqVA0kIJqKhI07+b5jS3xkYn1q0L6Zpvq7ZXUaD7jmvANS2Nf82Jrm0TXVuvphM21wdJ1P5S\nK4Uvrq1SIDhVqfoc1IIFMn75y3EMDlJKE4AJ40FlGRgZYTobmZWl4MQJmz6db7Op3N9cjU3Rbh5W\n14ampgDGxhgmTVITOsogMjOBwUGaIFcUQFWB/Hw+XGLRIhl5eWEUFxtMkMZUJscIh3DhAp98FQ4z\nnV169tmgfpO1DpO1tgbwgx+4E+ANlhsgsU/a76ZNM5wLGFNRWCjjwgVbUvxtcTFZq+XkkIxBS6Hr\n7xcgCMnMofb/tDQ6Rlat51NP0eDU1q0Evk+dCuPeewOorXUlmD96bzabDLvdlZAAKNi922VqhZMG\nurtbTCR1+RGLUfhFVpaCHTuCiMeRxGJeucIwPi5AkgC3G8jMNEDf7t1OPaJ5zhwZV66QpGLyZJVz\neLDbVaxaFU6yS7t8maGtzY+eHgFTp6qorCTWv7w8DFUFfvxjGkYzs4QHD5J2m5esUAvdrNX2+WTU\n1kq6RIMYTRXp6SrOnOGZxN5e47ioajK7vXBhHAcO+DEyIiAeB9xuBS6XivffF5Gfr6C11Y/OThHT\npytJw2Y5OUqig6HqgRz9/YyzFdu/35/w2jWO+fe/T4y6ebhMG1Lz+WSEwwwrVhiP7dsXQHY2SUgo\n1MLYfl+fgGXLwmAMmD1bxtmzNni9tIDjwzZo+MwM0AsLFQwMMBw4QIuMSITp+1I7Bw4eJEnDjBnk\nJuF0UvdC+zcaFbByZRgrV3p1YKl1m7q7RYyNMWzZQnr18XFgxw5D2zsRmP2gDtoH1UcBuB9XRpGq\nz0+lQPBnUKlVWqomqms9L6wAFQCnwZ2I+ThxQuSec/BgAOXlBhN24EAAgMI9X/MwvnCBrLC+9jVZ\nv3lYWbqzZ216qtmPf+zAY4/xrgWaz3BFhaE5tAJV86BUX5+gg9WiIhnl5RE4nSpuuEHGyy+TrZjm\naKFFBzNmJL5t2RJMuhFWV4cQCtHN1dqWN0/aKwo4ZvfAgQCKiujGX10dgsOhclZgGrurDYrFYgBg\nlTsY+tTCQjlpMLC3V0B5eRhut5rwrWX40pfugCwreOCBKEIhYPt20vHW1QX1fThrlozHHw8nBstU\nDA4y3WpOS8OzOiaQrILXmZo/b2urHwDZheXlKUhPV3H+PLkqWBn0FSsMxq2mRkJPTzI7rL3v6uoQ\nJCmOujpiHc3vi5hIPoEsFgPa2gJobxfAGAGxsrKILjEByIFCs5zTPt/s2So2b3Zj+fIwF+18ww2k\nX66pCSIvjwdBhYWKzhKbQSof103ewu3tIubOjXEgcmiIUuEOHgxwMh/za5ATDH/MJ2LUnU5aPKgq\nyTTM7On69R7s3Hkb3G6/6fw1dO0eDwFxux3YuNGtS1as0p7MTFVn+gFg69YgIhGGigonnn02hEcf\nNZh7jZFdvZq6C//8z7y/t3nR09QUSHxfw4hEaOH72mvjaG+3YfbsOF58MYjOTi1l8oN1uB9FKjbR\nYv2jANyPC7D/nCuFL66tUiA4Van6FOpPMXBx6pSAt98WIUkMHo/K+YASIOVdImQZOHuWf053t7Wd\ny/uKd3SQh6fVo/eLX5Tx619fwcDAxJPxfX0Md94Zx9GjPAt35oyAaJRxmsOGBh6omoe5CgsVTJ9O\nrDFpQ4kNszoEaJ6x27fTYNfYGHDwoJ+LCNZuhJ2dJKeoq3NxUgQtUvXQoQD6+xKM0iEAACAASURB\nVInJNb+v/n5Bdz7YuNGNp54KYWTExjHSXi/pTfPyFD2AoLo6BKeTbK5UFdi5M4DCQhqiWrSIH8zT\nJuabmwPYuNH4rOaFi7ZIGBgQ9dCFQ4f8nMdqczPJRsyBElZGevp0/rXNA2t5eQoAxoFdzdrMyiZe\nuMAf45ERpkcgmxcYK1eGUVnphSCo8HoZjh5NjpWeOpUHLpJEEhANlHd2iti0KYTRUWD6dFlnoLW/\nMX++nh4VTzwR5pjltrYAt+A6fNjPgVgNRE4EUs3bttloiCwaZSguVtDbC8gyQ0uLHZs2hdDdTVKH\n8XGGtDQV+/eTrKK4WEEkwp+TmqODVc4SjdL+b2iQ0Nkp4vRpm368ASSCXUjzbAbIu3a5UFYWQVWV\nFw0NQX3QMxazxggDTif/mtOmKfjOd9JhtxObrkktGGPYupU0xwBQWChz2nZr7Pj4OENDg4QHHjAG\nG7UBwU2bPKiqCl3Dle7DayJt70cBuCn3iFSlQPBnUCnNzue/Ps7AxbWeF1bmbt8+fmDI72c4eVKA\nLDPdkkyzYNOec8MNctJN0GxpNn26gnfesQ5okV53aIjM7TU2srRUxpNP0sAVhT4AAOMsjjIzVQwP\n88xVfj4PfL785Tj27/djcJBcC268MY7aWkl/fSDZE9jvF+BwKJAkQR/W2rDBjfnz4/qQ1NSpNKyk\nKEA0CixZEk3S68bjJE+orZWSbKJyc0nu4HAQ2zl9uoL33uOt0oqKZNjtNOClAY+NG91obQ3g6FGb\nroFcvTqMFSu8iaCMAM6fJzeKyZPJ6svhAH760zH4/SLefPMIjDhiBptNTdirkcbabqc0vbY2Skkr\nKFASDgRX13JmZyvwegmcDQ3RueH1Gp+3vJx8kc37WLM2s7KJVsZt0SIZ4bCa8HQ1hjXXrCFGduZM\nRQeiO3YEOCkFhWCQ9nXu3DjWrvXor3/xosgB/Zde8nNBKVbGPRgkPbL5M1idPvr6KMVsaIh8dFeu\n9Cb5JhcWKtw5XFoqIyNDxb33krct7V8VGza4UVsrJYVMLF3qwb59AUQiBGrz8pSEhy6lzvn9QH29\npMtG+vpY4ntCWuTCQlmXwZgdPc6d+w3Wr/8b1NVJiEQYSkvlhDRCwpo1Hv27RdINWZcjaMxwVRW5\ngZi/v8PDtGBatEjG4CBLMOaG1OLiRQHbtklJ3xurNdtNNymcZMqqlb9aMNC1kAfm50YiVmmToIPb\nvzaAm8IX11YpEJyqVF3H0i7MJ0+K3HDLpzFwMTSU7Bvb1BTE2bOiDjxmzJA4FrG5OYCmpiCGhhhK\nShR85SsGW5KTo+CJJww97oED5N9pHQbKy1Nx990EAKxJY9pkfHq6AkBAfX2yxVF9vaSzU1OnKmho\ncOluBFOnKolQAj45S1X5trLG2plBz9Spis7eaq3lo0fteOopAc8+K2FwkI92bWoKcL6vPp+CrVtJ\nYzs8TD7H5mEkQVBRXm6w4hSLG8S+fcTyMQbU1bmxZk0Yvb00vNXZSTdzXjJBLFhVVQgZGSr6+hhk\nmSWFa7S2BvDQQ2l45BF+0WBmi6uqJJSWyli92qtLDe6/n+Jq29r8+t/t3u1EWxsxqTk5KjweBYsX\nm1v8IWRnA/v2kRbU6aRzbCKmmGcTGbq7GSdtaW8XwZiKGTN4Nw9JAmpqPBwrHY+zJAmGxoAfPOjH\nwICgt9VtNmDTphAOH7Zj8eIY5xrQ2OjCnj0ENMk/lyErS0Vamqqns5lZV+313G4Vqgo4HBQLTN8r\nAc3NBnPrditJnsHNzRQGYbNBP4erq0MTOmhoYFuT9XR3i6iooAHHkhIKkxgfBxwOWpz19goIBGix\ntGwZgWzzPiKWX0RDA3kaDwyQ57B2vamrk7BqVRg+n4LeXobZs2Xd8szjUREK0f6y20nOo4VPrF9P\nXY6MDGBggOHSJYpPNu+vkhJyljB/trQ0uhZpntzz5sXR18d0mZJV5mFl1s3XxmshD8zPtS6CUtre\nVH3USoHgz6BSq7TPb1kv4tpwy0e5KN9+++3XxITMmcPf0BkDensZBzysQPnkSdLK2u0qXnnFr0fS\nAmSpZG7tX7ok4MknPdi1K4CmpgCGhw02lYComnTjCQQYZs2S8c47NjidwMqVIZ0R1bYbixkDWTU1\nQZw4YcPixTFd6mBt3Xd0EJu9axfJF86eFVBaKuOll/y4cEFMDEJBj8G1tpbLy8McqNbkBGNjAtas\nCUGSGACyMXvggSiGhwUsXBhHLAbU1Dh1BlBRGLxelQPOoZDmcEELgZoaKWkQ7+JFfr/6/YDPp2DL\nFiPCt77eieXL+ZAHTfP6i1/chR07gpgyxXDNoAE8AYsWxdHZKepxtapK7LDPJ8PpVE2DYnR8S0po\nOMrp5IGM389QVMR0F4WamiB273bq4PbWW+NQFCSxiRs2uNHWFkBHh4pbbiHQe889MSgKWaHt2UPn\nTXExpb3t3x+A12sMHFoH0zo7RT2JLT1dwcGDFMDx0ENGW/3BB6OQaM2kH+OBAQE9PcR4mlnK5uYA\nnn6awii6umggTjtvYjEkZCUC9u8P6CxrTo7C6ZT37g0kSWOGhgRddnD8uIinngohEmFJnRbNL7eo\nSMH06fxjGRnA0aM2vP66PRHwYU1KDCEtjezKzK89PMwS35VvweeTsXBhHDU1ErxeFVu2SDqoratz\nYfnyMC5cEFBWFkFjoxNr1tAQorZYvXKF4eabZfT3CygrC2PnTicWL45Ckuj73dzsQGsrHY/iYgWX\nLwNf+MJEWnoBQ0MqvvjFuM7yasE7Zp293a7ixhvlqwLWa3FrMD+3sdGFAwcCGB9nnxtt78etFL64\ntkqB4FSl6jqW9SLudhv6tI9S18KEWNPXxscZpk1T8POf+3UGEki+8WrvrbtbwH/9F9OZYjOb4vPJ\nKClR8PjjYZw6ZdPZ0717A/B6aZvECBpWV+3tFHZg9tCl51sHVGTs2RNEIABMmaJi69YgsrJU3Vlh\nIk/fDRvcqKuTEAoBkyYB770nIj2dpvFHRwVkZyt48kkP8vMVHDoUwPAwGfMPDhIzaNYvhkJI+MmS\nv+ySJV4OND37rKS3rc2tX59PRkODhJUrCbC0tDgxMODifGutjhPHjomYO5e/6ZeWyhgaYli2jNLc\nTpwQsXRpBMXFyTHPGuicNElNipK+8UaK4zW331tbA4mBNnCDS9owIGMqXnjBhc2b+Zb/TTfRwJ8Z\nVGzeLOnxz4pCGtSmJvIjnj6dgFNLC7k+CAK5EtxzT0yXTNx7r8HSmVnU/fsDV5UxFBSQZtvnU/Df\n/21HRgbJFCZqq9fVSUlWW6tW8QuJ3l6Sh1gXJiMjvGPDu+/SQGdzczLgDYdp0aIN1+3e7URmpsJF\nSmsa9fp6idMYp6craG4m/9zCQhmHD4/jyhXy1WWMJAjZ2SrOnSP2nV+YILFI5UFkLMZ0nXlJiWF5\nVlMTxIoVxrl86FDAIlsIYds2F555RsLp0wyzZilobxcRjarYvt2FZcsiWLEiwgXNVFeH0NsrcOdY\nS4sfr7ziR3e3AL+fgmIGBgTOCg0wgne+/e0Yp82dN+/qWt1rcWswP3dgQEBWloq77op/pOtsqlKl\nVQoEfwaV0ux8fst6EZ8796Nr0o4cOYKBgW9yN8KzZ4WrssIfNNSxcCGZxZ8+LegewNOmkdwBIJDp\n9zP09PAt5aamAM6etaG0NJ50A123zoPTp0W0tBD49XqBeJx8UEdGgNJSJTHNz8cg33FHjLPoikYJ\n1JaVRfDEE2ZLKHJWeO01O1pb/bh4UYQo0mtUVoZRVDSRE0OaDmwGBgSUl0dw//1pun/x1KlKEnic\nNcsADlbWua+P0qw2bQphfJwAkAbOy8oiE7pY9PVRKIYoMvT0CJxus7SU0rba2giQ5+ZSuENdnRv/\n+q8RPTo5Hgdee82ms24+n4J4nBYRv/nNEfT338m9T48HiEbJocD8+/5+hvp6t56upjlqiKKK+fMV\nACpWryb3iZde8uPSJRHxODA6yjg7NEqRMwbvtmwJYu1ar35+VVWFUF/vQlubH8uW0T7ZtSuoLwLM\nLXCrftsc4tDY6NLlJPn5ZEWWnk7aU1pkCLrW3bzNvDwFubnUlVi0KI7RUQoMiUZ5wJibqyYNbXV1\nCUmDe8ZAp5AUTOHxIMlb1+lU0d+v6vKMwkJaaMXj5Mzgcim6fGfVKnJXeecdGxYulLmuRG2thIoK\nGvxra+M1/QsXyli5kh+ujEahg85HHvm/GB6+86r72bog93pVrF8fgttNEg5VBaZMUZCfr8BmI1Y8\neYASmDGDT/gbGhKwZEkMsizjrbdEVFSEMWOGjHnzaPDTCmInuk5d7bp1LW4NWhJde7uAnBzSxU9k\nC/nXVil8cW2VAsGpStV1rE9quTNRBPLjj3snZIU/TDphZZVff30cL74YRHu7kGDcRGRlKTpos9mg\ns6vWEAC/32CStYCLnTsD8PkUjvm1pnkRk0cDSlavX0WBDjYzMiiJrb4+CJ9PwblzIhwOYgF5FwjD\nPs3suXvihKhHssZiDGvWhCFJSEqtS0tTOcbTyjr7fDTxbwXO69Z5k1hejVGORhlsNoaKCgOg79tH\nQKmrS8TwsIBQiHx377vPq+uhZ82SkzyCzWBr3z56XkGBkjQ8mJOjYGBASIqdLihQsXJlGDk59Hyz\no4bdrqKhgZLs3n7bhtJSOTEkyPDUU27k5Sk6s1paKmP9egJgE2lpb7pJxqZNkp7KtmZNGNnZClSV\nobXVD0Ew9qtVv23e1sCAAJeL9jvAuHNJO9ZdXbSIiEaNbVojnA8dCiAYFDB5ssIxsR6PgunTkwcx\ne3qYqYthaGQ1Bw/zNqzMcGenwA3oWe3ByJ6NWFafD1i1imKIJ1p0DQ8b53BXF8NLL/nR3S0iGAR6\neoSk4UpVVROdCIa9e23YuFH+SPvZbidNtiQJWLaM9yJescKLtjY/zp4V9Yhy7fFbbpEhCKrl2BOw\n/cMfRG7A7ec/9+ufX9t3Npv6ka5VWl2LW4MgEFO+apXBXKcS31J1rZUCwZ9BpVZpn98SBGD+fLoI\nd3TQVf6j2qPdfvvtUBQDRGdkqKioMKbjrfo4K8j96U/H4XIZ5vR9fdakLTL4X7XKi337AlyLc//+\nADweVb+pWdvUWjJUZaUBjGIxlsSynT4tJrWoa2pknD1r1aBSK9gMHmiQjCEaBVSVXBCsmlGzfVp2\ntiH38HgolOCGG2Ts3++HzUb+s1Yng8JClXN0oCAJI3GrosKL1av52OWcHFXfpnlb8+bJE7LlsRjD\nqVMi5s2Tdd3o+DjDjTfKyMtTdA3qu+/y+8TqH9vXJ+D55114/PFvIBBQ0NoawIULRrLcd74TxdCQ\nkSRWWhrXgbjPJ+vPN29Tc3jQ3vOrr/rh9zPU1Eg6EwswBIMMzz4r6cyoyyWjuTmAM2coKOPJJymI\nY//+AMrLacFhXjjs2xdAXV0QjDEAKg4fHockkQzA5SIWuqtLRHExOUIMD4vo6eGT0rSFV0mJgooK\nD1auDOvRvNYQEk2//swz5OGblUWDkpWVXmRnK7pDSH4+DT/29wvYulVCR4eAG29UsHIlDZIxRjpd\na7iFlV3m2XchacCyrs6Ff/zHGB5+OA0tLX59sVdaKnODembf6OJiFatXe/H442FUVXlRVCRzA4iV\nlZQG5/MpCc/fr2L9ekO3XVoaR1ubX3ch2bXLpX9uLcHuwQejSYtb7TP4fIo+QOf3ExgdGGCQZXKc\nGBkRMH8+Db0dPy7qqY/attrbSdKxbp3RMXjxxQDmzVM+tXjiz2Pi2yetFL64tkqB4FSl6jrXJ7ng\nm5mQ48dFPXVqIn1cXx/jmNRgkOHb3zZe95VX6OatSQNCIUpua2wkPaxZJxsIMAQCvCZ0/35yCigo\nULBuHaV7LVsWRnq6iqwsNTFopeqvUV4ehtcLOJ3AV78aw+9/b0dZWQR9fQLmzDEYKy0hrrOTBz3H\njxtDe2YgbZWX7N8fwOgoMGOGjM2biTk+e1bErFkqOjoEVFZ6UVNDjJs58rikhKQJHg/0m/rChXG8\n955hA1VUJGPqVJ75mjJFxZIlaZg/P66zsyUlCi5dYhZAAf1Y0YS9wOlGNZbM5yNrNY+Hf52SEsP3\nVmP1li6NwG4HwmGGkRFqY586JWLFijC2bnXhhz8MYWyMJvS9XhVPPy1hYECA10utc3Myn8YgmwFb\nPM641Dgt1rmmJsiFqOzdG8APf0hAVJZpsCo7W8GUKTKGh21JHtWnTom4+WYZ4+PA2JiAYDBZ0wwA\nixen49Ahf1KXYONGN+bOpf29bZsLnZ30XRgYoMWhLPOfq7iYWvZFRQoeeSQNlZUUHNLZKaKzU8QD\nD9hRVSUhHBbQ308DkaoK3WbO41HR1SXox856/FtaArq7iDlBjdhjOvetHQsNYKoq486B1tYAjh2z\noaBAQUGBjH//9wByc+n7VF8vJeQwZMkmScCCBQref5/OpVAI6O8nZnx4mCEehx4vHokI6O4mqcex\nYyLuuSeGH/7Qg+3bgwiFmL7vrDIQDdh3dwuc28uuXQFMny7j5EkjUXJggOGJJwwJEn9u0XXBKocA\nPj2wmkp8S9UnrRQI/gwqpdn5fNfHveBbz4sPi0LWvEk1ANrfLyYxaa++SrZYkgRs2+bWNZbW9m1O\nDg0/mYd/RJHAwfCw4W7wwgsubN8u4dgxAqj19cQ2KQrTB2p8Phn19RLicWIB3W4CGGbG0qqt3bjR\nzQ3tXb7M8NWvxrF8uVdPZ4vFgLVrPYm0NAmBAHnrXrwoYO9e0o8eOECsm6bH1JwM9u8PJA3sPf+8\nC1/9ahQzZ/JtdjMbNneujN5eAjOLF8e4/WbVcC5aJGPXrgAyM9UEKJeTNLtpacDYGC0yKivDaGoK\nYmwMyM6muGozkKqvl1BUJOP3vz+Cb37zdj16+s47YwgGGVatCsPvJ4uxTZtCOHNG5AbOVqzw6mlf\nWnLZ0BDjAJvWnje0w7RAcLt5qcrFiwKeeYYswczJbFqARrJlHVl93XCDgl/8QoTHkxxmoZWVAbfZ\niEnWjnV1dQgnTpDfMKDitdccWLcuhH37AhgZERLezQp27AiAMfLcLSxUcO6ckPSevF4V27dTKto7\n79A5vGaNE0uXRrBxI9nOaXHVWrdi+XIvli6N4Ec/cqK+PgjGgObmgO7jS77XyR0LDWBaHVr6+phu\naXb//enYtCnERSLX1UlJtoLad+TQoQAee4zkUevX/wJr1twJSWKIxwWcOyfA7QYqKz2oq5PQ2yug\ntlbCypVexOMk8cjKUnXZUFERnQ8HDwaQlqZg2jQe/GdmqojHGXbvNroZPp+CoiIZ3d0iBgf5yOW8\nPAWlpcqEcrBPC6x+HhPfPmml8MW1VQoEpypV17mu1wVfECiF6mpRyBp4sE7NazdMr1flNHtau94q\nYXA4kHAr4KNwbTZi8QDobO9zzxEAzs9XEY8D//RPUQgCOL1sWVkkSdsaiwHBIDkqPPggD4icTnqO\nWYMaDDK8956YiA4GCgqAykqjzZqZyQ+87d1L8g5FYfrCQBvekyRMOLC3ZQsB9YEBQ1Lg9aocG7Z1\na1BPMbP6nZ48KaKtLYCjRzUphQcNDUEObFuBck4OhW2Ul4cxMCAgFFIwc6aMJUvSEzZZvJUcDVG5\nsXt3GvbuJb/kK1eEBPNKMc+xGA2iAcnDaJp+u6EhiP5+Aa2tDq4lrrGeVu1wa6uhT9YWNRcuEHCa\nPz+OxYtjGB9nKCggecG6daEEw2nIYLRBwkOHyCaOB6QKiosVVFWFMG0ar2ueMUPBypUktwAo9ONn\nPxtDOCyis1PAmjXhJI9jp1NANAo8/LCxENu5M6j7/drtgKoSqGMsWZ/uctH53dkp4plniE1njOmy\nD7+fJRaTgsU9gUJTNA229vuFC8kB5OWX/ZAkxnVLVJXpw6rasTMf94EBhoEBPk5bY5Vp8FJCY6MT\ng4MMs2ap+me221U0NQXR2Sni+HFyu9i3L4B4HAnmnzyXu7p4t4fm5gAuXBATWmjDF7urS4TTqU7Q\nzaDrSyhE51xamopZs0jHH48zLFiQrOn9tMBqKvEtVZ+0UiD4M6jUKu3zXXPnkj9mR4eoT01/lJro\nvPggVlkD29abqMNBIOb8+WQv2IkGZmIxJNkzdXaKmD07DoeDptGJ7YUOHshHlhiijg4Bc+Yo+F//\ni/xYVZUHuadOGTKHpqYgHA6+ZVpQoGDnThfq6iQuwviuu+K6O8GBA7wuc3Q0GdQuWxbG0JBZnylg\nxow4bDZDhmFO/RoZYZg8mf6+pETG0JCQtG8KChSd7TYPe9ntKmbOlHH0qMjpR637nBhwgy1zOtUE\nUDdAyJ49AcRiyb7LhYXaVP43EIshMaCFpPQtra0NGH9vZWbz8xWsX+/RFwaaLnX3bueEtmAXLxo/\nWxc1e/cGLBKKEEIhhvXrPVi6lPbv5s0SnnzSo29r2zY+EMXhUFFZ6U3olx06UM7PJ3bSLAMqKZER\nDov6YsOaYOj3A0VFKs6cMX7f2Sniv//bjvp6Fw4d8gNgun57IgeEkhIFy5aFwRidS/PmydwiSzs2\ng4PW7xqlA1ZVUSrcqVP0HisrPdi5k4b1FIUWlaoKnDsnoq+PZBWaX671uC9aJHNDgObnFBYquP/+\ntITLye3o7OSP2/CwpucnRlwUYbH0oy5KWxv59w4NCRgZIfmF38+wapUBdjdtIp34qVP8/na7SUuu\nBevU1AS5zs5E8q8UWP3TVQpfXFulQHCqUnWd6+RJEd/5zvUZAjGzyj6fjNxcI9ZY89scGWFJwE0b\nojH/ft68OJqbAwgEGOrrJagqxRiPjjKMjgocW2WzAe3tNsyaFceDD0Zw+bIAwAC34+OG3nXTplCS\nDys//EOfJRZjuHKFwJ4ZGPr9wJo1IY5BbWoiP+Jnn5XAmIpJk4yp/+xsBcXFVosrwG4HsrLo/WsA\n/cQJ8unVPrPV6qq9nZipsTHSk168KGLfPkrkYgwIBID774/C5QLcbsM9ITubLJmyslTOEm3GDB58\nZmerWLeOUuSysshqLTubEsjq6lzo7hYxOsoSvsUMzc0UYzxliprQmxr7MTeXB3qxGA3TvfLKOMJh\nkswcOkQMI2PghqQ0gDowIECWKd3v2DFyiFi7ltrnVo2t9rPVFcMafuJ0qrh8mXEMelWVhO5uMQFi\naRiwstKrs8pdXaIusdGYy5YWB5Yti2DKFAWvvOJHKEQgjTEkOW9YQSOgYvp0FQcP+tHbS8d0fJwk\nHdEo44CcVfNbWiqjq0tEWpoKp1PBrFkq2tuJcRUEYNo0BaOjDD/5yXiSBVssRo4qnZ3kApKeria+\nG2EEgwIeeihNDxXZsyeYtPjZuzeAK1coba29nc6rSIS6Jq2tAXR3U5JjVxdJnbRBx/R0WvRYvaV9\nPln/HtXUBDnpitYJGhhgyMnh2fADBwLIyaHhx8FB8h2nsBU3Vq0Kc68xd66MBQtkNDUFPzCyOFWp\n+kuoFAj+DCql2fl4dS1pap9lfRRN8ESf5Xe/M84L8+OvvurXtZlmeYMGrhUF+PnP/Th7VsCkSSrG\nxhjKyiIJ5o+0jYsWxSFJWrufWr1ZWTJ6egSMjwvIz6cEtnCY6dZTPp+MzZtp2j4YVDFzJh9brDHQ\nVib62DERDQ0Sjh5NttqSJCAnh7TFq1ZRetWkSUiKUj17ltq51dUhbNhAMgNt6rymRsKZM2ISII3F\nKLTB6cSEA2nmmN1YjIIUMjNV3UXCrMuk13UntJ80md/QEERGhoKbbiLA/cADPGjv7RUTzCN5/TIG\njI5Cd0+orOR12MuWkQ61qEjhgIsZKB06FMCvf30E06bdidFRnuH1+chtQpIEzi5MGwqUJD4QgnSq\nRuTyvHm0OPjiF+NIS1N1jW1ODjk2aIuO0lJ+wWG1a8vP13SxvLVWQ0MQ+fkK9uxxoLXVj2iULMG6\nugSUlMic/jwjQzEl0UmQJJFr2VNQiib7AH7yk3FcuGDTo3mjURWZmSyJsd6wwY2GBokDvlZHkPXr\nPSgrC6OwUEZPjwhJova+JPHx3c3NAaxbZ/5O0X7p7CRv6HCYd0bYsiXIfT+sLPKVKwK2bqXFmsbA\n1tQEk9LqzGBVczspKFBRXv427PZvcFZvly9f3Z9Z6wQtWiQnselDQwzj4zb8z/+Zxr3/xYtj2LXL\nhdbWAPr7GWbPJtuzn/6UFuLf/nYM77wjcsc+NZz22VYKX1xbpUBwqv5i6tOy2THX9QDaH0UTPNFn\n+bDHJwLXoqhicJDiZ1evNiJvx8eRxMxpkgQCFCrCYdrWO+8IeOCBODo6jJsZQEDSfAPeuzegawZn\nzJAhinyrVmOR7XYgEqH2KwAsWxbRbZ4aG11YsyaM8vIwB3Ks7B750IZ0i7TCQiNqt7CQgkBGRpge\nHW31jD1+3NoyT56MDwYBrxcJwMizWR4PbefSJQFpaSp27Aji3DmSt6SlqXj7bV6zefasTZduvPtu\nDLW1NMTkdCro6LAlyQ38fgE33hhHWxuxzpoLghW49PUxZGWpcDiA/HwFGRlKou1OgSaaE4L5bwDo\nDL2V8dQkCn19QqLlDjzySFRPd9MY8h/8IA1Ll0YAqHr8Mm2f5DHV1SR9yckhu7YlS6K6c8a0aSRp\nmDpVweCggAULZDDGuGNUVxdERgZpyRsaJAQCKqqqQrjppjh27nRh9eow516SmalwgPTAgQAkCViz\nhobnXn3Vj2CQdzzRFlY5OQq2buXB66VL5AzS2UkMqxYrvXKlV1+I/Nu/hbjhQCvbvWNHENu2uXSJ\nzaJFvP2ZJq3RzjvGeAY6J0fBM89I8PsZ9u2j5D1N460dy/Z2OjcGBwUUF9Og5aZNIVRWevAP/xBD\nUxNpvquqQqipcaOlxZANWSUxt9wSx09+4sfgIOPcWjTmPxTiFzJaUuMrr/hx++10HTx+XMRdd2Vw\n16XUcFqq/pIrBYI/g0qt0j5e/Sk8Ia8H0P4oN4WJPsvixbdf9fG+PobcctenyQAAIABJREFUXIpu\n1ZjPcJgY1PXrPViyxBh2amx0YccOvr2dkQHdAUCrLVvILaKtLaDLGcz+wNY2+OAgDUYFg4Aoki+v\nFk186FAAoRDPnBFTawNjBKSeeILa4VOnKnqIhfaeRkepJXz5MnnU7tzpxOLFUaSlAQ0NQTidKseQ\ntrYGsHQpgX5N47loUQyrVoXR3S1g0aK4BQDG0dVFgRonTojweGg/aTIAKyjIyyNbKk3m0NLiR0GB\ngj/8wYYvfEFOsh4z+71qAH5ggCEzkxjhZPcEBZMng5ORHDoUQG8vD0SmTlVRUXE3x0a6XCrq6106\n+LWC+6lTSUvc2OjU2fK5c2WsW+fRJQrmJD2rRrari7fKqq8PYvt2ClOpr5fw0ENRBIPkDKK5NwDk\nhtDfD847ubaWFl/W18jMBB591M2dKzU1buzYEcSqVXwQRnW1hCtX+O/DO+8YnYJ16zyQJJb0NxoI\nFQQVDQ1B9PYKmDmTwGwoBJw4YcPTTxtMeVVVCEVFMjSnB5+P97FOtgRTkjoO2jmfnW0sWMbGCOR2\ndwuJYyxwAL6pKYhHHknDjh1BFBTw8cyahZuiAGfPihAEYpbLyiJQ1Tv0cy4/nxaJQ0Pk/jI+TuD/\npZf8ePttW8IFw4OlS8NYt86r+0j39zMUFytYscJwkHC5aOCysdGZYIkFCILhfT7RNTil9/3zqRS+\nuLZKgeBU/cXUn8IT8noAbesQiCwTg2IGxdbPkpGh4vhxUWeerY+np1udHijFTGvdm1kmGipS8fLL\n/oTPL4VuWB0ANABhHq7RYmz7+4WktnckwvDoozRcNToq6q/f3EzgzexOEIvRgFFNjVt/zo9+FEBe\nHulvtW1b39OePQGsWJGGmhqJA73kMMEDNe1nrdW9alVYBy3msIgbblA4TWl1tYSqKnrvNEToB2NA\nU1MQV66Q96oGUGpqJFRWehGN8q4ALS0B/fnZ2QqGhgTU1wdhtnHbuzeAhx9Ow6FDfgwPC7rXbE6O\nAlEkHan5M128KGDmzDiXGvbee/xzursFlJbG8eqr5DpQXx+EwwHU1QUhCOQokZ6u6kOA7e0iFi2S\nMTZGALa3l1LVPig1zxobbLer2LaN/Gu7ukj3umKF0Tb3+8mrNhIhv1rz4gYg+YrVE3lwkHF+xYJA\ni7R4HEnBKi4XPWYdbMzLU/QWv9VmLS2NHE9aWwNYudKbWOz5Od25BmrNHQxtUbR5M1mhmZnlM2cE\nPe0vP5/OY+tC0XzOt7YG4HIBjzxinDebNkmw24GqKkM2ceUKS6TB8QsIDTCvX+/B6tVh5OcrSRZ9\nO3cGUFhITi1mF5m9ewMIh4lJ5iUx1Nbq7BTR38/gdAKhEJ3zmpPISy/5uW2Zr7MpX95Ufd4qBYI/\ng0ppdj5e/Snabp/GRf6dd0T83d8ZN9//838oVnbbtiCysoip6u8XsWLFWzh48Fbccouc9Fnb263J\nX5TyNT5OgGPnTmpRp6WRvdgTT3h1P9i8PJp8J91gskbQDHq0qXwAuqbYkDI49VZ+Wpqqvz5j5EFs\nbb+bB+L6+gRMnargj38U9fdUXS0luVJcuUIDesm2UaS7VBQCuJcvM30gbfduJ9raAhyYp5AEATt3\nuvDggxF0doo6MHM4gJ/9bBzhMFmI5eQoSZraNWvCmDKFhgYbGoK4ciUZ7Dz9tAebNweRnU2gubIy\nrEsiAOgewR0dImSZYcUK2kcVFfRaBw/6OWBXUkIMbjBIYLaqikI/RPHXkOVvwm5XIYrA6KiAixeF\nJO2w36/C6UTCz1biLM7q6iT09AiIx4F16zwJ0GdoZM1pdHv2OHTJRUYG2Yrdf78B5KyMqCazWLuW\ntM8TLW5qayUcPBjAH/5ALOmMGXJSwMTevQFIEksC4SUlCjIzZTQ0SBxzXlsroaREQUODpPtCa49N\nnqyip0fA+fOqDrS7u3lwPToK3fXDyiILQjKzXFLCg9AdO4K45RY5aV9UVYWQkUH+wM8950Z1dQiq\nqmL2bAUXLwooLlY42URxsYx//ud0PPUUn1R46RJphgHyeDYv/GIxhv/6ryPIyPgGsrLiSRaA7e0i\n4nEk6bnNHQtzJLt5UZ2XZ3j93nijDFlmScO4KenDn2+l8MW11XUBwYyxvwWwHYAAYI+qqs9dj+2m\nKlXm+jCbneuh550IaH/QdrXH+vqoLT04SM+ZO1fGyZP0ezPrFosxnD0roqIi2df34YdjOvNs/qyy\nDIyN8W3y2bPjOHdOBEDbf+qpEHp7BeTlqaiocKO7W0zyit2/nwcvN99MiVyXLjG0tQX0G3RGhozu\nbkqvOnZMxLx5vCdvdrYCn0/BffelJVg0BY8/HobHo6ClJYATJ0ivah6Ii0aBd9+16fvAeE+89Vks\nBt2Ozfz7adPIGmrTphAHRPbtC8DhoGl6n49PXPN6VaxcGdZbzOaYZk33mZenJCykeE0tDbIZwK+5\nmd93c+bQOejzKfpigVrpxnM8HvoMM2YoOHZMRF6egsJCRWcXDxxwJAG75uYAHn3UiHs+fNiOqqoQ\nMjODKC6mUIi337YjHufPqa4uATNnyhgYEHDffVEuLrmsLJIU76wx/qdOibq7wgsvkL51wQIZLpeK\n1lYHOjvFJClDXx/D/v2Gz+2TTxLznZtrxO6KIm+TZ7MBokiOBprDgjVg4vJlcug4e1bk/GovX2a4\n777JWL+eB4l2u4pz52iwU1W1jgS9D3JB4INhrFHgmZkkR7FqqkMhhkmT+PfvcABdXTyIliQGQVBw\n6BDJCgoKVFRWGh2H5uaALiupqeGdSczDk4EAuVhY7fkiEaC2VoIkAe+/T17HO3YEEI+TFZrLpeLF\nFx2w2eg84s89ir/u6hJ0Scy8eTIyMhS8+GIA6emqHoFOzLmKF18MYPp0CrzQrj/Hj08sD0tJH1L1\nealPDIIZYwKA5wF8C0AvgLcZY6+pqnr2k27781qpVdqnU9dDzzsR0L7ajcD8mpoNkvacV17xY+VK\nLzZvlhAM8gA2O1vhbqaaEX5Ozp3IzY1z70eWgd/9jkCzOcUsFjO8ZnfsCODcOQK9waCCysoQ6uvd\nKC3ldbGjo9C3cdttcYgiuNCBujoJ770nwG4nMOx2KygooHhfs6XZzJmyPhhmDepoawugvt6FvDx6\nHwUFKgYGBEyZosDtJisq/j0JOHCAWszZ2eQfu2ePEw8/HMXBgyTLmDyZ0uzy8pQkhvjUKXKH8Pnk\nxCCP8V5aWohZ1ECQGcxpC4Ty8ghiMR5wT52q4ORJfvDt0iW+FR6JkBeuIABLlkTBGLBzpwt79tCx\nmDNHxvg4Q22thNpacsIoLw8nBS309PCfR0sh0+KefT4ZDz98N/c3c+bISeETsRj51WZlkfSlrCyi\nP25t2fv9xKzb7cBXvhJHNEra8oks5EIhkjiYX6ugQMXKlYbk41//NQKfT9bT6BobXRzTbLfTkJhZ\nivDcc+b3rmlsKbqXseSY4crKMGbO5KO3CwtVHD1KA4/bthHjOjLC4PMB69aRd/HYGB8FbnaF0Lor\nVk31RPt3+nQ65tbPVFFheOVWVrqxdGkEqqpizhxifV991Q+HQ8Hx43buGGhhFk1NQXg8yQEv8Tjt\nd0rdk1FebiQBGuf43di7l1Ly/H7gpZf8uHSJOhtjYwzPPefS/Zq7u0U8/3wAd92lQBAUvP66jfNi\nzstTcdddcf2ao8m3rmZ/9pfi1PPXWCl8cW11PZjg2wCcU1W1CwAYY20A7gGQAsGp+pPWh+l5P+6F\n+4O2qz1mBWfnz4vYvFnC2bMi9u516szWTTfFk8IitJtwaamsW0BpdeKEiLfesqGzU8QLLzhRXh5B\nfz9JC/LyyFZqyhQy59e2t39/AHV1EqqqDOD8pS/FIctAZyfDzTeT9vLCBZ7ZysxUk0AaTZ5LnK6w\noSGos5zWz93Tw3D4sB/nzomYNo0HPnV1QUyfLuOFFwKYMgWJYT8VXq+iSwS01v2lSwJKShQLYy6B\nMR44LVpE+zMQENDXJ3Cx0T09gj4kBvDaV21QbXycoaXFOD7z58fh8ahJg2xFRQqnN96+PQiXiyzm\nsrPJIWHp0jB6egQ8/bQnsSDwY/Fi0oQcOKDg7rvj3L5KT1f1NDozmF22LIwXXnDB6VTR3y9YorAF\ndHUBM2YoaG4O4ORJW0KzSq4b/f0MmzdLCQeHELxeWnSZX4MG9yS4XCpOnzailq2Mb2+vgIoKYss1\nNlELgli2LIJ16zw4fZpe38rOZ2So2LkzCK8XCd9iQ7ve2OhEcbHCxVMvXEjAKhgkeYbZyUHTc2s6\n785OAQUFSlL09tAQw8KFcfT1iVAUkhCkpdECiVLTaGhSO5draiT4fDI8HrK4GxsjZlaSyMVEOyfm\nzo3jiSc82LBBwr59AfT0kGwkPV3BqlXk/3z5soCnn5bgdpN0yPze9u4NYO5ceYJjEEJPj4BQiO+O\n/Nu/SZg5U9aDN955x1iQWd1DBgcJqI6PC7jppjhaWhy4994Y/H6GZ5+V9OHGmpogAJJmLVgg64Db\nHHlsvuZoi34re67Jw/4UTj2pStWfoq4HCC4EcMn0czcIGKfqKpXS7Hw69WF63o974f6g7WqPWdmk\naJQYSM02at06jw4QamvdqK6WMGkSBVucPUu2R6tX/x5tbYt0FiY3V0Ffn+HTOpHOMhplnDcosYkM\nkyerHHC+eJEGrTSWbsMGD6fh9fnkJNmGNkSjgUfzABFAzHFmJr9vcnJIkyyKQE+PFWQD3/0usebL\nlhmfo7nZGHozt+6toMzhADweRbeTCgTIsioa5VPUNHlJSQkNoO3YQaB7eJjhlVf8kGWgp0fASy+R\nd219vUs/PrW1Em68UYbbTel2w8NkB2e2OCsri+DMGTFJzzo4SP6327cHEQoxXL5sBJA8+mgU587x\n7GJmpoqKCq8O+DRt7ZNPhtDQIOnDSaL4azz99JewcaMbGRkKZs0ihw6HgxwatO3F49Bt8GpqaBHU\n2EhuEnV1EvLyFFy5wrBuHclltm4NcqDKOiA3ebKig7OuLjFhaUbOBG63qieTacdH+/fUKRsACgpZ\nsYLfR5cu0QCh16vqCYGlpZTK90//FEVjowvLlkXg9zPMmxfH++8LXKjGxYuUcDYyYrWcA+bNo1AJ\ns/VedbWEhoYgolFKdauvl3T3hddesyfJUfbto/01MCAkvjth9PcLeO450r9fvMh0x5CXXvJP6P9c\nWMhLKXp7BXi9asL9hNLi1q0jZ5aJIqVLS+Wk2HHr4k07L6ZNW2SRuhja3sOH/XjuOQrFMYdmaLZm\n8biMjg5Vl0BoZV70Nza6cOAAuU2YNcB/CqeeVH28SuGLa6vUYFyqPjf1YYNzH/fC/UHb1R57/31q\nDff1CYjHjSEyis012FiHQ8X3vhfFjBkyJk1ScemSkGi/ili+PIx4nHFDdNXVIdTWktWVNVAiPV3F\nyAilpFkBeHr6xO4LBFxVVFaG4XCoeP75YCJyF+jsNG7GPp+M0tI4qqpCcDhI3mG1oWpuDsDhULkW\n8+Ag07W0VhZJCwsYH+edARiDztZpzweSQVlBgYInn6ShLo3BXbkynMSOOZ2qDpTT04nZMzPlZqBw\n6JCfe/8eD1m5rVwZBmMK7HaypyosNPTGdruaBMLIFcCjg73vfz8NP/5xAM3NpOG8cEHgdLg33aTo\nqWmGl3MIAwMU4GEG3bLMYLMRwy+KNKi2c6cLS5dGUF1Nx0fTwQLQtcc1NRLS0sCx8dXVfJKbqvIh\nEs3NAX2I0eMxEuusdmFXs9XTWE5RVJO8kbUuR3+/iI4OoLQ0jqlTgZERAStXhuF0qtyCcdMmYkTN\nOu+ZM+OIROi2xXcEZNTVufDNb/Jsu98voLub7Pwmin82x0PHYlpCnYpXXx1HLCZwz9cWV4ariph0\n7vn9AoaG+O/jtGkk5/ne99KxY0cAVVWGs8bx46QVNw8iWh1BuroILL/7rgiPhzoMPT0CzpwJ67ps\n7blmba/W6Tp8mJdifJitmXnRPzAgICvLkEpM9JyJCIdUpeovpa4HCO4BUGz6uSjxO65effVVNDU1\nobiYnjpp0iTMnTtXX7EcOXIEAP4qfr799tv/rN7P5+3nW26RceTIEfzud/zjY2MC7Pa/01mUsTEJ\nwFc/dHuCAEjSG8jLA265ZeLXe+ed36C83INnnvlSAnS+AVFUcfPNCzE4KMDheAMdHSrWrv17/fW/\n//0wbrjh66bne7Bjh3ZT/X+IxQCX61Zs2hTCH/5wBJMmKaiq+iYyMoDt2/8bvb0RbN58N/LyFDz8\n8H/A6QSKir6Obdtc+O53f4kNGxQ4HN/QtzdpkoyiottQWenBXXe9jq4u4N57v4bKSg+++tX/xC9/\naUN19Vfg9zM4nb/GQw+5dVeCqqpfYGCAIRa7GwAQi72BN98M4Y47bkd/v4Camt8DAKqqvqS/XkOD\njObm2zA0JGB4+A2MjQF2+93IyFBx992/xA9/6NK3/+STv0jYa309cXN9A9u3y2htvQ29vQKGht5A\nZ6eK9eu/jliM4cKFN3H33SpisTuRkaEkHBQY7Pavw+eTcerUEVy4IGDevDsSQOWNxPv+RiJ6+Vf4\n9rdjuHjxDsyeHYfH82bCoux2ZGcreP/9NxGJANnZ30AwyKAo/w8bNnggy99ETU0Qw8P/D6JovP/h\n4TcBuBCLfQNDQwLWrv0F3nqL4Vvf+hpsNgXnzv0W/+N/MAjC7WhpceLuu18HoMJu/1v9fADC2LTp\n6xgaEnDlyhsQRW3/fx3nzv0HJEmB0/lNjI8Df/M3r6O7G6ipuRvz58fxD//wOvr63CgquhPPPSfh\nf//v38LrBaLRO7jzyeu9FVVVEoaH38SyZXY8//ytaGnx4/TpIxgaYgBuTzCpbyAvT8YLL9yGjg4B\nZ8/+BpMmOTE8/C3EYgy/+tURxGJuAN9AY6MLa9f+AuPjDF/+8u3o6hLR0fFGwkv5bv3zDQ6GsHmz\n8fP69SHMm3cH+voYTp78LY4csaG19Us4dsyG4eE30NBgx44dtyUYd/o+bdt2G0pL4zh27AjWr2eI\nRL6B7GwVv/71ESxaRN9PAu6/gSiqyMi4DTk5Ck6d+i26uoBY7G/18/fnPw9j8eKv6eebKKrIzV2E\nkydFXLnyZkIzbDz/1KkIYrG/gd9P7398PISMjK9zf5+RcRsYAx5++D9gswElJXciPV3Bb37zWyxb\nxpCbe7vl+V8CwHD+/BvYssU4v8znc0mJgscf/z0eeyyCadNuh6IA58//BoWFJGMwb+8LX1iYdP2b\nPp3/fkyfrnzg9W7BAhk1NT9Hf7+Av/3br2HBAjnp+YHAG6ipETBpEm0vEHgDR478eVz//9p//mvG\nF9r/L168CABYtGgRvvWtb+GDiqmq+oFP+LBijIkA2kGDcX0Afg9giaqqZ8zP+9WvfqXecsstn+i1\nUpWqT1KxGPDWWyIuXKDkr698RYbtQ5aBH1VHrCikt+vrI4Z2aCj5+YcP27lY0qoqChkw22q1tvo5\nJ4bmZprCz8lRk+JUR0cZli83trd1axCrVxPD+eqrfvzxjyJmz6aUqfFxIREYkTx4VFNDFlNmpq++\nXsITT3i5bRcXKxwz1tYWQEUFxQlrbGNDQ5BrR9fWSqio8Ca0vhQjGwwCoZCAFSu8ln2hoqXFqbfD\nb7pJhtOpcp6lxKyS/OHxx8Noa3PgqadCiEaJxSsqIm3p975naBoBXi6xaRNFQWv7wDxspGmSYzHe\nNmvfvgAuXhTR2OhEfr6CDRtILzoyQq+5ZYsb99wTSySHxfWBKTMzbGZjX3jBhcrKEHJzVQwPC9CS\n2DRHg/XrPVi6NAK/nwY1e3tJe8yzsX60t4soKlKxYQMNZRUVyUmBJebXbm4O4P770/X9vn076bT/\n+Ec6R7KyFFRWGvHUEwVBaMORS5akc+dCNAru3P3Zz8YxOiqgt5c0tIODAlatMo75zp1BTvNdVych\nN1fBmTMivvAFGYKgoqdHxOrVfBTx9OkK1qyhgJiaGnfS+2xr8+vWdw4HeUGvWJGGzZulJDa7rs6F\nf/zHmC5HGR5meOKJNF0yYd6uNvy6fz/pkg8fduCBByLIz1cTDL6CyZNpuO/KFUHXcb/4YgBTpqg4\ncULErbfGEQgwnDwp6oEYy5eHkZNDjgy9vQJmzKAhz+5uunDYbEB/P2l+vV6VY/Zff30c8TjTr0+a\nK421a/XOO6khtlT99dXx48fxrW99i33Qcz4xE6yqqswYexzAL2FYpJ35kD/7q66UZufTr4nA68mT\nIhc48VE0wR9VR6y5SpjeQdJztBaiWVtbUKDgy1+O4Z57Yjh58k3Y7V9FQwNF1AaDFLxQXh7GyZPW\n9rsNCxfy7g8+n4yGhiBmzYpDlimCVVWRpF3V/Gu1bQmC4QlMw0hxxONWRwsVly9DBxi5uQpI96no\nLgGnT4soKZFRXS1BVQlQjowwtLb60dEhIhQSMDTE8NRTniRP4exsBSUlMm66ScbgoIDsbHKziMX4\nz93bK6CtzYH6+iAAhvvui+LcORGNjS48+6yE++5L5yyvGhtd2L49iH37AhgeFjBtmoxolKGnx9iu\nuaWtaZJrang98qlTRkIZYyrnqvHqq36sWBFO8hrWZCFWGYvDATz4YBShEIPLpegSlg0bQpgyRcXF\ni3xi2w9+8AtMmfJ15ORAH4aMxRguXSKLvP5+IyK7qoq3EWtvF3UpzbRppAk2n4OCAESjDLt3u3SX\nA+24fFAQRH29hObmgD58aLMp6OmxcTKXcJhxANzqLzxlCu+SkpWlJHnzWgchZZnh/vvTuIAY83Bm\nXp6CaJShv59BkkTs3u3Ec89JqK8n/bG2eNQGJr/5zTgYo4jvysow6uvJl1cDqObBvf5+hk2byIFC\nC7s4etSOqioJ8+fLSE9XEAoJmDxZxYoVBnjOylLw3e8a58uBAwF88YtkQ7h8OblexGJICvLw+WS8\n956YFC9u7LM38Ic/3Iq5c2V8+9sxPdb4sce8KCuL4MIFAWNjDG63gpERlpgxYADEFBD+HFcKX1xb\nXRdNsKqq/wFg9vXYVqpSdT1qIvA6kSZ4/nz5A5ne6zkAsmCBjJde8iMQYDpbpwFXugG68Mor6bpG\nVZtiJz2kmgSgL19m+gR7fr6CUIgstvLzKWVqIo/X9nYR8+fzk+rFxQricUr9Agg8T54sY+/eAEZG\nKOJ13To3ysvDGBlBkg3ZwADDyAjD/PkEMP1+Yp3NrFtTUxCjo8Rq5eUpiYl8I6HNZgPOneOHzV5+\n2Q9VBRcjW1REE/nxOOOGffbuDehgyDykODAgQJZpSHHTphDa28WkoUDzsJEG/MwJfHY7DT7GYqTN\ndbl4cHj+PLkRmH+nld2uJvm/FhYqGBkh67lIxAjH8HpV3QvZ/HzGgPx8FbIMrF1LbgROJ9nL0WBi\nsuuF9rdz5shYv96DsrIwBgcZ8vNVNDRImDqVZ/Xr6iTIMuB2EwA7dkycIGgB+ufTQGZVFZ2jW7ZQ\np8AcgFFVxQ+IDQ2Rv/DgIIV2uN38MOnoaLK+tqXFgerqEJxOWigYgS1IuHpInD61vDzMsdF79wZw\n/ryIjRvdaGoK4tIlAW43dT/N5091tYSiIkW3Ddu924m6OknXildWerB8eRgbNrgnDAsZGGCQZQGP\nPJKmOy+kpQGTJyvcgisWMyKfm5ooyvnMGRGhEK/tPXFCRFYWeU2bfz8yYuj2RVFFOMzw2GNe7NgR\nxOAgXSeWLw8nDQcCTNcz/8u/uFNuDqlKVaJSg3GfQaVWaZ9+mcFrXh4xIZEI9JSxgQECvR/G9F5t\nAORqMglZptZje7uAnBwCrZr5vCDQEJDZmqysLIKjRzULpG8gFgMuXhSQn6/qA0GlpXHs2uXSAxke\nfZRutM89J6GjA4lUL3CgUxvesQ6XLVgQx+CgAHMYweAgS0rvOnx4HJcuCXA6AYBAttMJDA3xN/SB\nAQEOh4orVxhiMRX/8i8TOzucPSsiI0OBw0FWVeZBtdZW8je1DhlduiQgN5ccJ7KzFezYEQSg4okn\n0rB6NR9woIUB2O1qwmOX0uhsNhU2Gw0Cer0qSkooICQYZGhr8+PoURsmT6b3QDIZOt5kMUaerZJE\njLLdruKGGxTIMr9Pi4sVPSlN+93UqQrq64OYMUNzmggkhq6A0VGGlhYHnntO4gBbQ4PELRBGRxly\nchSMj9+BK1d4F4K9ewO6B25mpqIPTpWWyqitlXDlCsOcOTKCQYb6egl+P3D5soAHHvBOeHwyMxVu\nYfbMMxIkieJ8L14k72Jz+MmiRTK6u1kiHY1kAKpKjhWapZv13MvIULFkSboOzN57z8adh7m51ihx\nYr03bnSjpSXAgdaFC2VkZ1OUcHe30YmwBnCcPi3i5ptl/RysqXGjqioEReFBp8MBdHczmL24R0dJ\nItHXR4xtYaGMQ4cCkCSSUly6ROx6fz8DY0z3fNaszurqgnjoofSkwUFtQXX2rIj6evIuNg+F2u0E\nfjXvbPPv8/MVU4rjl9DYSO4v5g6XtYuhubzQ/9knXsyn6s+7Uvji2ioFglP1uSwrO2TWlR44EEBW\nlooFC2T89KfJk9NmdtjnU/Daa+Nob7dhxgwZN98s48QJAZcvC5y1kgaerRHJ1dUS4nFjCtvnUzA8\nbLR4x8eTXRDy8xX09wsWUEoM8tCQgNpaCTYbkjS8/E1d1Z0dDh0ikFlcTOb+ZWURbNxotGs1P1dz\nKzsaFZJkFIwhKTAgN1dBLAasWOHlZAjWzzR3bhydnSLS02kRsWlTCOPjBH5GRiicIxzm/yYrS52Q\nrSsri2DyZCtgIj9azfuUMWIap0zhNZSaRlljmhctknH0qIhIhGHtWi+KimSOeWxpsePee2NYtSqM\nkhIFdXUuLFkSRXW1hFCI2O/6etL3mn1XnU4Vv/qVDSUlFBWdn6+grc2Bo0ft+Pd/D2DHDgnnz/Me\nwJMnK0kLhL17CbBbFwhmN4qmpiAGB4E5c2ScOyeiooLXWpeXkysVx086AAAgAElEQVQFY7jq8aFF\nDD3W2Sni9GmyOUtLA268kc7dzZsl9PcLKCoirW1/v4iMDBW7d5MUxQzoq6tD2L3badIRq+jqEk3n\nJ5Cbq3C+1IcP+7FvXwAjIwzTplE4RX19EIwBikJa3/PnaaFy+TIwPCwgGoW+mK2poWQ263kxMCDg\n4EE/xscpqnpsjCEvj++sAEBRkYrz51WUltLnKy/nXVpOnLAjP19BYaGMeFxFKATOIaO4eOIFs+YK\nMjwscAsqDQy/+66IhQvjiVhpQytcVhbBrl0uPdL6hhtIcpGZSYsj7by2ylasnQeKSjYAuM8nIzdX\n0aOQU9KIVP01VwoEfwaV0uxcva5XEpHZ1syaejQ+znTLn4mYXis7bLbUeuUVP86cEZNCIjRmRUuh\n0n7v9wvo6FB1EGy3q5wHbX6+Ebt76tSb+Pu//xq2bXPhvvui3HauXGHcwFNTU5B7fMoUvrWs3fCG\nhxl8PoYbb5Rx/jxZcmlpZE6nCp9Pgc2m4o9/FDk2ePPmIAdU/X6G0VEBM2fGOVYzLU1BRwcx29On\nyzh4kOybpk1T8NOfjuO3v7UjIwNYt86DZ56RoCiAKALl5QYIP3QogGBQxcyZsg4WCgrIvsusgXU4\n6NgWFsoIBJjettdAQ02NhBUrjEHB+vogJIk/TjYbsH8/6UL7+w0fZMaMLsHGjdTy1uQCJ07YEoNx\nAt56y4777ouipERrcwPd3QJWrvRi2bIIpkwhpvjSJREPPRTlPFxbW/2orKSWtTVMQWMxnc7kKOGx\nsTdMLgTJ0oShIfJwve++ZCmFmXWcM8eQN2gA9fJlGlqLRq2sLQGn4mIZFy7wC6JDhwLYvNmN5csp\nHKS+XtLt74z9rGLzZkmX5djt2kAiEosnFeGwqjPNJSUK/H76/C4XeToPD4v6+WezMUs4hqTrk1tb\naTGjdQHMwR4amHzkEdIRr1jhTujiBbS2BhCLIQm8P/JIGhoapKTPU1pKg5rxOMOkSQpKSowI7MOH\nHdiwQcLBg8QQFxQo6O6mv6duCTB9ehznztmwZk2YA8MeD/D++yLa2hy4994onE6grk7CuXMiysrC\nAFSsX+9JLLRVCIKCxx7z4uGH/y9ycu7ErbfyswGTJimorZX078+UKQpGRym9bnycYceO4DXPRqTq\nL6dS+OLaKgWCU/VnVdcricgcf3z8uJgEdLXSwHJfH91sOzoIpJjBl7md2NEhchpd6zZzcqxpcApy\ncwkYnToloL+fNKoOh4Ibb1RQU+PG5s0SenoEzJ5NyWNHj9qxeHGU287gIA+uR0f5gSGPR0Frqx/H\njtlw000KhoZ4B4iGBgnFxQq2bAmisJBeZ/nyMI4eFVFYqMDjAVTVAGA+n9WJIIBoVMHFiyJUlVg8\nj0fF5s0erFkTQlUV+Q+bdaYHDwa4pLnRUQZVZUnepn19DNnZ4P720KEAtm51oa6O9k1uLrXcQyGm\ns/pa2/70aRvKyiIQRX7fFxYq+v+1f6dMoVS86moJWVmk7zUPMe3bFwAA7Nnj0L1bS0vjCV0txQNP\nm6bg6FECWVVVHixbFsa6dV5s3OjGpk0hVFV5sGVLMOmYdXeLeOYZShG8Gqu7bx8NRJWVRTA+DmRl\nqejqon/37AlgdJTcKDS2125XMWOGrAemaAscl4vkCR6Pivp6OuYuF3UFurpE5OYSA+92q+jtpXO8\npoZAqpbiV1fnRnm5DFEEx1hfuiSgsjKc5BRi3fddXQIaGiRcvgxkZqro6RHQ2urXAzvKy8N6HLDd\nTs4VS5ak4eWX/VAUxgWqWEGp+TvZ0yNi+nQayLTZSHKUlaVCUUhuZOiIWdL+rq3lt+t00mdhjD+X\nNF35Sy/54XCoeO89GyQJaGlxYGBA0LsAVveO+vogcnNpHzsc1BHYtcuFioowHnwwYgLqYdx7bwzr\n1nnx/PMBeDwK3G4KX4nHoQdcACT16uwU0dTkAuBBS4uf8zGfN0+BwyGjo0NAQYGKBQsoKlmrq/kG\npypVf42VAsGfQaVWaVevTyOJ6IPCLjSwfPz41dlfYsUMwBEOA7t3u3T94Je/HNe3qUXM9veTnnV0\nlLTIv/udiLExns1taQlg+fKw6cZ5N1pb/YjFwhzTuXChjK4uPlUqJ0dBW1tAB2OVlV6sXh3GnDn0\nXv8/e98eHkWZp/tWVXfS6U7CLfcE0iAouCFwkNnRHWd0nnlcZ86efTw7OmdwHvFynIFniCiXBEiy\nwiYKCSThIuI8jGFCQBLwsnNmd4+M67O7o+OMOqKCwBBAJCH3pEMuXV3dne6qOn/8+quuryo4Murg\n0f79A93prntXvd/7vb/39fl4oKnr4Ji0I0f8CAYFTJumIzdXx5IlHo5FtAK13l6aomZd7l6vii1b\nFKxYETamZbdt49npzk7RBoxCIUqOM79fUKChvZ1fX1eXiMceI6ZREKgZb9myEJKS4kC9vV3CwIAY\nc5QQkJJCoMbnI0mC262jvV3gWLFJk6gJLD+ftKQ5ORo34Glrk4zY4x//eBytrUmorlZx773jSErS\nsXWrYovr9XiAXbsCHLs3fXr8mmGfzcrSDGusK7G6Y2OCLcWspuY2ZGZq6OwUMXu2hpMnHTGmkOzu\n1qzxoK5OMYItNm1KQW2tAq/XGi1MA6Gnn3YZILuoSENWlo4zZyhRjX32+ef9NqBbVRXEz3+ejMJC\nzSblaG8na7e2Nmq8LC2NM8DNzbIhw+ntBYqLVZSVhRAO8+BalgUcPiyjvV2ynZfMzImm+BG7flRs\n2ZKCNWtCUNU4s0vWdymm7+i2452baw+aWbIkFa2tsgGqVTXekNfZKSESoYECAJSWhrBqlQdJSWRx\nt2+fjDNnHEYATXm5m5NcCIKO0tIg6utT8NOfhtHWJsWAugtLl44b187Xv67hllvGJ7yfxWevbofT\nSb9fNuAfHwfefDNuA/lXf6Xa7NESQRdf7krgi6urBAhO1BeqPo8btJkVvlIx8F1QoKKkJIzkZODI\nET+ys2n9LIWpuJiS3ubNo2jcgQERug6MjwN//CM9bKZNI6ARjQKrV4egqgLuuSeV08wyoDc0xIPV\nnh7J8E5lTCdpMzVjqtXrJTmArgNTphC4nDcvisxMDYODInRdx/z5qg2AmQFHV5eElpYkrFwZQmen\nyLGIDLCav5+bG5c9AMSwPfBAKv7pn4KGbGLWLM0AYuw7rEs+P1+FppH3bn29wuln+/tFk+l/fHvL\ny6kjX9eBLVsUSBJsDUQzZmgoLSWW9ve/d8Zs4+h8BIMC5sxRoSjx5C+vV0V9vWIBd/EBz4IFFHs8\na5aKjg4JW7YoeOABakQsKwtC02BMge/Zkwy/H7jhBg2BgI78fAGPPhrCdddpqKlxYdMmfj9HRwUU\nFdFym5pIUjJ9Om0/QPulKAIuXuSvCU0jmUBhIe/oUFOjQBB0PPJICJEIsHt3AB0dIvx+ETt2uLB6\nNX+9JSUBAwPEzq5dGwepL73kNyQ6g4MCrrtORXq6ivffTzK+n51N53bNmhDOnRON5lKWopaXR6lo\ntbUpKC0NGVHHNIASsXy5PfJ73Tryj966VcGpU+SGYN4u83lJTaUpfkEACgtVOJ1AQ0MgljQo4Ac/\nGIcoApFIPMJ6xgwVBw7I+OMfSQrS1SUa3tbseA8OioaFHAO72dmkc/d4aMZjYEAwPh+N0j6dOUPn\n0jz7cOKEA243ge2xMbKeYzp7s5yktlbBypUh9PbSdcGO5bx5UVRXB/HYYx40NgaueL/6uEH922/z\nNpBHjvg5ezbGKH9csmaiEvVVqgQIvgaV0Oxcua7VDZqBb2vMMJNjFBfHwXhxsYbf/EbitISHD/u5\nBqwXXvAjHKapewZ+rRIKj0fHzJkqnnlGRmYmpV7l538D9fUKfD7q7h8eFiBJFJbBTz/7bb6i5r+/\n9JIfL7zgx6VLIgIBAWVlbg60ZGRoBgvNGGDWiV9drUCWBcOqLTdXB/M0ZtvPmnGscbqtrTI6Okjj\nGQyS1pZY6DSja50S5uIBIfX1ATQ3J6OlRTbOe3e3aDQGLV8exsmT5HyQlqZxms9z53iAZQ6+cDrJ\nlWFkhPcBfvddnnV2u2kbGCCNRoGdOxWsWeM2zl1JSRiKIuD+++ONXFVVCgoLNaxd60ZdHQ+sa2up\ncY4aISna2uXSwazQUlN1TJpEDH99PYHAWbM0DA8LNqeJ8+d/i8rKO23NjwBsVlgzZmhYvTolBlo1\nPP64grlzaT0sdppdB888Q84C589LGB8XUF9PA6TycgXz5/M2cSUlIYuHL7mPOBwk4aB9TrFZlrGB\nynvv8cecZTQxva51uQy0l5cHUVwcxeCgyDX8bd8ewNq1Hhw65Oe+z8JBXnqJZBcpKQTM2bW6fXsA\nq1aFkJ1N4R0HDybh0Ucp8OLhh93GNcTrhBVs2UI2Y8PDAjZsiC+vvl5BQ4OCzEwtNosj2MA+haHw\n+86s1EpKQigrC6GggAZOx445AQBtbeKEwRfMZWbRIhWK8pqRYMnK7DxDM2nW1x8fmZyo//8rgS+u\nrhIgOFFfqPokrO3nUQx8nzw58UPDWtaHS3u7xLkrhMMCxsfBgV9m3ZWWRkxrd7eEJUvSYuxPCiKR\nFDz7bBqqqhRjSp6BVqvtEZsmZq8vXeIftO+848DChWTvZNblJifTg9nlIo/R0lKyfmLg1evV4Har\nGB2VDK/iQ4f8uPvuNMP/1OMBCgoI6FhlEydOSHC5dJw/T24H5DtMaVuTJsUb9qys7113RbgmMgZ0\nrQxic7MMSSKP2K4uCTU1Ctcdb3VRGB2lhr3ycgU5OTqmTtWg64Jt/boOpKdrscAIxQDKbFvHxgQA\ndlut9evd6OqSbDIehyOeWkeDA9K5DgzQbIMk6fj+99M5oNXdLWJsjPnfMhssAQ0NpOG0Nj8yzTNb\np98vor8fOHyYLLessg3WHFZR4YbfD9uAj11r5LQhGrZ8fj+xovy64tuwfr0b69aFcMcdEQiCgF27\nXIZl2403qvB4NCxaZJeG0PmyLpeuUzaT8PTTLmRkUACGFVg7nbrNg5cFkyiKgI0b3VizJoT6egKp\nLpfOsaJNTTLuvXccDz/sQXa2hro60u/29fFSD79fhM8HTJ+u4cwZfkBlnmGoq1PQ30/uLTt2uNDV\nJcHhAObPj9r2nQ2srA4sGzaI6O8X4fcLeOstYnUZWG5rEzF37sc3C8+axc8AzZxpff3nz6x9Vk3L\niUrUF6kSIPgaVGKU9sUrc+LbJ3loWB8uXq9q89ptbZVRXx9AUhJQVxdANCpg1izybqXGJcaqMnBF\nPsET+Xpa5QlZWRrXQFVYyEsR5s5VDb2w0xm3gtL1OOvNAMGhQ36OxWSuAenpgNerYnBQNAF8EV5v\nFLKMmG8xv11ut47rr1exZEka9u+XjaYzFgrCIppbWvzo7RUxZQolalmbyAYGREOrbX6/t5dsscrK\nQohGgRdeSEJZWcjYx6IiHnAEAgJOnWL2WQGUlsbDDKhjnxg4n49kAiyWl9nYMbcBUYRNl03OEHS8\nmRSEnY/8fF7TqigiZwd24IDM7VdqKpCWpuL663XU16egosJt0rR+B04n6ctZ0xv5NtubMJmm1drw\nxa4jBl6//vUoFEXgpB2M1a2sJKuxzZuJoWbuGeZ1FRdHUV2tGMxyYaGKyZNFDAyQNMHnE/DEE24U\nFKhYvToEr1flpCFTpmjYtUtGfj6/D4sXq0Y4SmWlG/X1NDgYGaFI8WiUgK4gkA6bWZ2x77PrcWCA\nZgi2b4/PJOTm8uEdp09LyMnRjWt76lTY2G4aFGgIh2k2paEhbsFmBvAsadD83Z//PBn5+Rp6egQ0\nN8sYGRGQmqrHAk50m8PM6dMSNm8OoqeH5CZr18ZnIcz3FTY7NdFz5JZbVLzwAiU0zpql4utf/+xm\n1j6rpuVEfb6VwBdXVwkQnKhEmeqTyjH+5m9UHD5MnfaFhaTRtaY7tbdTxO/dd4/D7SYA3NSUjH/9\n12SD1ZyIGTU3/bC/DQwQAAoGaRsdDg2bNyu2qeDTpx0oLo7i8mWBi35lIRtmmUAkQqykIPA61/5+\nEQ4H4HZr2LJFQUeHiNWr+RSqw4f92LSJpt1raxU4nUBGhobUVB2jo9Tw1NvLs2Zm+UZVVRCiqCMQ\nYICfB1m6DvT0EBA2v19YqKG9nRLHdu92ob5eQV2dCzU1lIJWURGPfy4qUrF+vRtLl1KDEWOJWZjB\nrl0B7N+fZOi2rY2DLS1k33X5MrlamK3tZsyg2GgG2OrrycmCB0JxTStzb2DXxsCAaNlfOteDg2Td\nRUEMKg4elHH5MkXeUqoYyRrKytxwOAgYtrdLyMsjPXhdHTVwWRu+2HV0440EXoNBwRZRfN11Knw+\nEfX1AfT0UANYejq5CSxdOm7Y10WjQEODC9///jhWrSL/5A8/lCzXR9zlYsMGag5bsYJkCJmZGjZv\ndmPtWvJENkcTDw0J3MxFT49o+CZbpS5VVUFs25ZsnKecHGJ7q6uDyMzU0Nsr2aQy/DEhTT0bvFo1\n+y4X/UbZce3qkhAIgLN1mwgQRyLkMrF5My+RYf7kxcUajh71Y2hIsG1PW5toOFcwVvdKdowTlcMB\nfOtbKr71rfjfP6uZtc+jaTlRibrWlQDB16C+CpqdazV19mnXeyU5xkRJcLfdpuL4cRjsiPUhG4kA\nq1aF8NBDvG3Y7bdH4XAASUkkTUhJofffeOMN3H77N6BpwOOPKygupvCDffsCqKhIQVcXNRtt3hxA\nUZFu0xqePu1Aa2sSioqiCAYpMGPVqhD6+wVbJO3gIIGwkpKwDQwVFmpYtYoYvvp6BXv2uFBWxgOE\n7m7yHQ0E6IHf3i6hp4eszKZM0fH448lYuTJ0RZDgcukoLCTGuLQ0ZMTj+v0C5s+PwuPRjalg1lw3\nbZrGuQ5UVQUN794f/GAcJ0+SD3JFBYGo8vIg+vtFY1BhjRRWFGDJknE8+KC9abGzU8KOHcQispIk\nAW1tAm66ScX58yI0jUDi2JiAu+6KGA2GbBmpqcBTTwUQCMCWMpeRoaGxMYCuLmp07OsTce6cxDWc\n3XtvGlpb/fD5Xsfo6O02AFhR4cZHH0l46ikXtm5VuJCNlBTdaL6bMUNDf7+A/ftlpKdTeqFVRuDx\nAHV15P1rja/ev1+26XaPHXPi2DEnyssVACKGhvjlHTsmoa5OMWQ6bOBRXh5EWZnbOHfRKEl0kpKo\nmZGxpOYZD8bUSpJdktHeLqGjg37gzL6PfJ7jQSjsOyy0grHbe/cmY/36oCH1sKazORxAR4eEjRtp\nsFdTE8DIiIjublqWwwHDCcY66MjPp4ZP8/aa/ckXLaJG0Rde8OPttx3G9mzerKC8XMHNN0dxyy3q\nhGCZzU79pZ8jCVeJ/z/qq4AvPstKgOBEfS51rabOPs16Pw5AnzjBJ8HV1ioYHVW5RpT4Q9YRY1Vd\n2LAhyIVODAwI2LDBjbq6ALq7JWRkaLH4WyAzkyzIqquDqK1NQX09df+zWGMGkLxeDffck2YLRpg3\nT7Wxkfv3y5AkEfn5PKOanAzDCYIHbjp6e0WsWkWgcObMKEpKQjaLqsxM3XB72LcvYGvQWrYsDIcD\nxhR4URG//uxszYiLTk/X0d8voqKCGLB9+wI4f54HTw0NAZw65eBcB/x+4MYbabmCYE9BKy6O4pe/\nHEM4TPZt06dreO45P44fdxrnhzkoWNl4Yisp7GH16hCmTNEwMiKiuFjF4KCAPXtc2LlTsTUrWgdB\nkQhAumgYoDQUguEgkJqq4dIlMeY9rRmWW34/OQuMj5MEZPJkawhLHGyVlQVjzYaK4d+saeAGX1VV\npDun0A8JSUl2Xfbs2VG4XDpnQxeJUCMjv276TTidFCDR1yfaBhjp6SQfsQInFt7BXDVKSvgZhtpa\nxZQypyElRUdZWRCKIkAU+djz+DkDyss9hgRp3z4Z3d0SWluTsHZtfCDW308+3YsWqbh0iY6X201B\nMQz0miUbWVk0eGhtlTE+bpdKVFS44fOJmDRJR1oaSVwGB6mJ1eHQbYA+LU3Hq686uCj1W29VkZoK\nnDxJrDXTmD/7rAyHQzXA8hfBzSHhKpGoL2MlQPA1qK/CKO0vMXVmBa3z59N0qnlq/5OuV1XJy/dK\nSUq9vQIHZlNSdBsQ7e8XkZqqo77ehexsDatXhzBtmo7Vq1NMQEnGhg1B5OfrKCtLMVjNlhYZHs/t\niETiVmXZ2Ro2bHAbOtMdOxT09Ijo7KTGHVGk73V2EttXX+/CPffwSXNDQ2LM+B+ch25hIYGXadN4\nMDRtmo4HH/SYtjeKjRvdnI7W6dRj51hCdXUQsmxl6MgmLhwGKio8MV2oZjQoSYRjkZHBNwympgKB\nAIwgBasMwppqtnixiqQkBj5ESJKGmhoFQ0PE1ioKEAyK3KCguVlGUVEUHR2UkOf1qtw2pKXRMWhv\nl1BQoGLlSkr3Ki3lHTD6+0WcOMHrlQcGRA5EzZihAhC49be0yPjwQynmCkENj2bHicZGmk3IydGw\ndauCkycl3HrrrfD5+EHEvHkqmptlRKM68vOBd98lDffGjW7U1wdsjZNME6wopPP2+8n9o7eXQFso\nBPzDP0SxZEka9uwJ4NAhP4aHBeTk6OjtFQzw6XAAixerMXsyDenpUQwPOzFnjjZhgl9Xl4DGxgBG\nRgTOR3n+fBWhkG5ruPP5RPh8cfeQp56SkZWlc8eIZEQUk33ggIyGBlesQZIGk0895cKJEw5UVQUx\nPCzguefofGVmavB4dMNm0DoLwa5XVuXlQdTXu9DcLKOra+JBSDBIWuGjR/249dYoNA343e8k2yxG\nIACUlrqNYA0WpW7uRTAP3s0s65Vmp/7Sz5Fr1bScqKurrwK++CwrAYIT9bnUZzV19qfYWfOD48UX\n/UaaGGMkr7Re63KTkoiRLS0NISNDg8NB7AxADEh6us510h86JHOANSWFHuzFxcSWDA4KuP9++zT7\n8eMS5/zA7KDeey/exMasyurrA4amMTtbQ3p6CG43MGeOxvmp7toVQDgM/K//RXG+N98cwVtvOeF0\n6ggEgPLyVGN9DFwwZnTtWpqaTkoiRq2jIw6eGBMZH1S4sGZNCAUFfOwvs8iKs33UJDY+LqC8XEFR\nkWqbTt+0KQV1dQFDD1pYqEFRBCP2eM8eFw4cIL/XvDwC+PffHzZ0qVlZ1NB2993jFku0QIxBFjB9\nuo4LF6ypbSJUlZLUdu50Ydcu2dCUzp6tIhgkhwsGKB95JGRznOjtFXDkiB+hED9N7fEAP/1pHERt\n3hyI+RjHB2UffCChtpYYWRb2YV72yIhgpNaZj1lzs4z9+2X09lLMcXm5G9XVCiRJsAVajI/bbdYY\nazplCmweybJMdnzhMJ3rqVN1w3vZPIDbt0+Gx8O7TrS2ypg6VYcsk9ykqAjw+USsXBmCKFKISyQS\nd09gDY0VFbR8MyPt9aooLo5iYEDEgQPEvmZlkd7YfIx6egjEZmUR0269BpqaZNx3Xxr8fkAQBCxb\nlmpcp+fO0bJCIRoU5OQQGz02Zp+tYKw1k5RYZxmYg4R5kC+KMM4pm8XYti2A8vL4dWGNUmf3mATL\nmqhE/eUrAYKvQX0ZNTtWUMnA4Ke9qX+cvMHKNls9MtPT9Suu17rcw4dlrnHM3NR09KjfBlb6+gQ8\n/rgCtxv41a+cKC8PordXQCBAsbKaJkw4ze6O9fxkZ2soKFBRXh6MpZsBTzzxFhobv27oREUR+OAD\nWp+1Q9wMoCdP1rmp2tZWGd3d45g6lcAS22bzNPb06dRI1d4u4ZlnkrF6dQgpKeBkEyUlIc4vtalJ\nxtCQYGPFentFNDfL8PloW4aHRQwOihgZIVsxc4OcmZUUBPp/erqO9ev5zvv+fhrplJZSw9Jbbznx\n1lvkobptWwD33psGALjjjigH2gWBbLeuv56CF5YvD3PHX1XJx7WxkQYYf/yjwziudo/hADweOn+8\nlENHOCygosLNeRYPD4MDdDfcoNkAp9eroaVFxtatLkOGYF52QYGKY8ccmDbNLFN5DSdP/rUR01xX\nF8CWLQrWraOmP6tUobeX3AXMGuuBAUp06+jg7b8cDiAnh9bFe+MGbQ1Zw8Mizpzh3+vooPO8YIGK\nJ59MwV13RaAowIIFJBth62La3fJyN/bvl404440bg0ZYxaxZ9uM1MCBBEPjBhiCQ/nf9epqhYNId\ntk09PaIxU9DeLsZ+Y7ohqSCLunj4BTvnXq9qDDQikThrrShAX5/IOYq43Ro2boxvq3mwbSUArM4u\n6emabXDOfJPZ/0+dEnH+vPSxfQ1fxudIoj59Ja6Lq6sECE7UZ1JXAqufdurs42QVE5nym1/PnasZ\nDw8rSO/tFThf3/FxcJZWZpsy9h3zsgMBwWB0jxzxG9IIayc6m2ZPSgK8XmrsKiiIp2Slp+v41a+S\n8OijIfzt30aRlERd4fffT1ZeW7cSMLQCEjOgNQN0Ym8pNjk/n7rF2ee+/vUoWlr86OkRY6AjioaG\nAHJzNQNEe70qDh9m07/8VPXp05TqxYAbs11zOgGXS0d+vo5jx0hvO3WqhkcfJRZw1y4ZNTUBQ/fq\ndtP25OVpXDOXy0VR0BcuECByuTTs2xfA8LDAaUFnzYqfC3MzU1lZEN3dBLzPnSNdc309gcHkZIrE\nZczd4KAATdMxfbpuMLWKwh/jtjYJ9fUutLb60dhIkgtmFRaNCohGKaxi1aoQ0tKo2a2hIYCMDB1T\npmg4fdrBLY8a5ajJ8N57x7F6dQgHDiShqYmm63NyNKxd64l5FcebLCVJN5wuGHAbHBRRUhKa0GKs\nu5sGMC+9RM4kPT3UuFVZyTcVbtqUgunTaaBkTZfz+zGhn7OiSNx7Xq+Kc+ccePddacKY5U2bUlBV\nFcS//IsTXi/prJOTgWnTVCxdOo7U1PgArrzcautGv0EmV3C5dGRk6BgehuGRzH6v5m267jqS3jgc\nGsbHGXrUkZ+vwueT0N8vYuZMFS++6MfZs/GBczRKEcmjo1MENXkAACAASURBVAKKi1WsWBGGIMCI\nNK6pSUF5eRBDQyJuvDF6xUE+Y3Xb2sjvd8cOV8xBhQZQTBNsLuv90zoIT0gQEpWoz6cSIPga1Jdx\nlPZ5aYCt4HP2bPKOvXiRGsR+9asxtLVRs0ljYxKqqhSkp+uGqTwr60PmhRf8Nl9f84PHalPmcOix\nBDUH5s1TUVGRYuwrkxAoShw07tnjwr59MoaHyWPX49Hx0UfktqCq4GQbTU1yDAjciRde0LlkMJ9P\nREuLjGDQrodlDhKiGAcr1mQvZueUna3ZbLFaW2Vs2BC3hiooIEurCxdEgyk2rzMjQ4fPJ8Drpall\nUYQtWaumJgVOp46GBsUELgTuOB88KOPAARmiqKOuLoD+fgnp6RqiUd6mrKlJ5rx1ieEWMTgooK4u\nAEGgIIy6ugCmTgWGh2l9Bw8mob9fRGOjbEhLrAl7BQUkeTGDNquso6goiuxsDR0dEpdWVl8fQHm5\n27heGLtpXn5Liwyr7VsgQP7GnZ0CCgtVRCICvvvdKFJSaAB38aJoMKRMDtLbK0LX/xqDg8DSpeOY\nPz+KtDQdsiwYAyUWYJKRwctkWlpkm3ctmz1wOHQDmD3ySAh5ebzP9OLFKnp7BRw+LOPMGRGSREEf\nzHLP7ydt8OXLojHws4NYwVhXWVnIJqFJT9cxMhIfeFgbG9lv0JxkeP/9qca1wAZibreG5mbZ8A9e\nu5bitsfHRe66a2mxX085Ofxvx/z3qirFaLhjA4K404h+xUE+084uXKji+HEJGRnhP+lUY71/JiUR\nY82CWCZaz5fxOZKoT1+J6+LqKgGCE/WZ1Odln2PVyqmqcEXGhB7yHjz7rGx7aFgfMoODItLSdNuD\np7w8iIwMDXPnRrF7twxZFrB2LTW0HDniR329C9XVQWO63ukkqy9inuNSgv5+EZJE7NLFixKnJ7am\nv7GUK/Z6ypR4hDOTA5gtxIqLo/B4NESjEjQNGBkhOcLAAIEA87La20WEw/TaKkvo6KDX7AFvTRBr\nafFzjV6SpOOmmzSUlnoQjcJmm2Zmz83T/D4fz7CeOCEZXqgtLTJEkWywjh93fOxxeffd+PeammS4\nXBrefJPspR5+mE8+q6hwY3RUNOymdB2or1cwZYqG4WERGza4sXZtkFv+2JjAWWhVVrqxYkXINsOQ\nlaUb18vPfiZj0iTdZod16ZJdkkDyhTDS04Hz5wXs3UsWbIGAYJHiEIMaiRCzb9YG798v4/vfT8PW\nrYrBhFZUeLB7Nw0QzO4Z1hRB8+yBqgpQVeDee/kENebKoGk6/H4JY2M6RFFAeTnNYOzcSTMYixdH\ncfmyGHM2uRKI1Y11tbfz23LqlCPGsscHHnv3JuPgQbIcmzpVN+zctm8PGN7I7Pvd3TTIEQSSt7Dm\n0aIiFdEozYBYg1asFnYffSQiOZkaRtlxMf/d5aJ15+RoCASE2MCNpBGUIPjxdTWNZNb7ZyQCrFgR\nxqZNKQkrskQl6nOsBAi+BvVl1OxcbWPHJ/XztT5IXnrJeUXgxTq2CSzzy78SSOcfPILROPb008Qs\nmY37+/uJlfX5qLP+9GkJaWk6PB7qjB8cFAzQk56uY3RUgCTBJmXIy+O35brr2OvX4HTehuFh0Qhl\nYCDVbCHW2irj7/8+Pba9AZunq/VhKorUZGW1VPN6NWzbFkBBgYYXXxzD2bNWECrhmWdchj/xU0/J\nAHTce+84ioqiNu/b9HTSOZeUhOD3C2hqknH2rMQNDohhVQ2d5vnzEgSBPJitIMqupYSxbX19FCbB\n2GkrA8lYwrw80lj+4Ad8UEd7u2S4U7D3R0ZEXLoE7px7PEB6Op92Nnmyhscfp+S79HQN3/9+uu24\nFxZq3Dk7eFBGWVkwNkDQ0dUlGk2P1ubJ5GRqhJNlcktYt+4opk69DYWFKnp6SHZgDmogaQkxzeb3\ncnL4zyxapBqJeFu3unDHHRFjBqCkJIyeHtFogFy6dBz19S40NckYGxNiTYrkvsASAdn1x0IxFAVo\naZExMgJMnUqOKq2tfvT2SjYPXtZ0duKExIWb9PUJCAYFPPyw25AXNTfLcLl0buCZk0MuIx99JNhC\nY6qqFEyZQvIW8zqtg5n8fA27d7uwcmUI/f2iLf0wO1tDd7eIjg4Je/cmY/lysiksKQlBkqiZ9bPy\nP1+4UMVzz8k4fjxur7h2bQhHj/qveC/9Mj5HEvXpK3FdXF0lQHCiPpO6WvucP+XneyWQbPcdjYPZ\nhQujxkPj+HF++a++OjYhSGfvZWVpeOwxj7GszEwdqqpzWtbMTI1jzqqqgnA4dPh8Ek6dklBUpBox\nwU4nJVeRnpOP8h0dJYA4MCAaMo6mJhkvvxzC/PlB7NjhwpYtCvLyeAsx8m+laX8GmqzOBSMjBNA/\n+EDCnDkaKipSjOYp5mThcBDwZlPnFGmsYPp0e5jEihUhg2nPy9ON/d+8OYAbboiDw4wMDbNnq9iy\nRbEl0yUnE/s9Oipg4UKVm7Lfv5+Yv1tuieLiRSkmOSGAGo2S925Xl4T8fNIPs/Pj9WoYHhYwZ46K\nnBwe7BQXR1Fbq6CvT0Rfn2CLy3W5yElkZIRAW18fDUz6+0Vcf71uOQYCRkbIHeD0aUqKe/RRj7H9\n+/bJMUZW5AZAigIcPuzHsWPEVG/Y4MayZfFjyRrqzEw8W+f4OMlWamvJJ/ryZQFFRRoXYuH1qsYg\nY8ECOqbRKAxpBEsCbG0lfXdmJjGp5uOenIwJZwCqqhQUFND1e/mygLw8HSdO0GDm4kWKumZ2gUlJ\nQENDgJOCHDokG9IHNkiz2oWxpjO3G0bzZnl5ELm5NMior1cQjVKSoSDA8Fk+fZquDUmKX4tWGYbH\nQ02KZulGUZGKri6Rs3GrrHRzAJodU2LDdQwOCrjuOg0dHSJ27gxg2jQNs2ZpnJTps9LriiIwbRrZ\nK7Jlz5+fsCNLVKI+70qA4GtQiVHan9YQXwkkmxlnr1fD+LiOHTsCmDVLxS23qEYjmHX5589LuPvu\nCBYsUHHihIRf/tJpgGFmSM+A6eAgReSKIjiWlQEetkyPhxpddu504bHHQhgbEwwNrq7DYJl8PvIq\n7e4macL4uICHHoprD8nbVsTf/d034PPpWLkyhHXr3Ni4kYIDensJuI+NASkp9MBkoMkaUjB5so6e\nHhFPPOFGTY3ChQowbeW+fQEMDAixKWQBRUVRA0Q1Nspoa3MgJ0dDNAoIAnDggIzhYR58U5OfB8uW\nhQEQy1ZTk4If/Yh3K2hroxNSU0OeuMePS9yUfVubBLdbN97r7SXv4rw8DR4PcPq0ZICoFStCSE0l\ngLdmjQfLl4fx0UfAwYNxcK+qAi5elJCcTDZf5uZCM8Nn1gI3NcX1vHEgRIOayko3HnlEx9CQaDRG\nmbd/eJh00wUF1HjGpuVnzEBsv+OssnnW4vJlAYsX8x7FHg+gKPHmPYqu1pGS8k04nRpSUuJSl/Z2\nyXClePfd+DF95hmKb754kWKPX3/dgRUrwjh7lj/uvb0Ujb1/v2xLj0tKIq/m/n6yKjt/XkRTU7KR\nZJeZqXGDPbP+2yo7sEZVb9kSACBg6dIwbrpJ5QY26ekaAgGgsFBHRwevI29tpYbJ9HRi9hVFMBpZ\nrTMI0SggSSR/OXGCzmNHB8Ucj47y54TtO9PDMzZ8795kbN8ewA9/yN+DribC+GrramfTEs+RRE1U\nievi6ioBghN1TepPaYivBJIZ47xggRoLt0ifkJWZaPksEOOtt4id27yZrLLYclVV4FiehoYAtw0D\nA3yjmKKQRGLlypCtQaywUMPy5ZSaVlrqQXV1EAB5DW/YwGtRyU81zvBt3qzEOufJTeCuuyJ4910J\nixer8PmAvDyaLj950gG3G6ipUSCKpB+trHRjyxaFA1cZGQQiOjpEjI8TwNm1K2C4NzAgXlrqgc8n\nGrpnMzvIvs/2v62Njyiurw/grrvGUVBg9VqNn9exMbtudO7cuIew3aJMtoGoXbsC6O8n7SsLLmGy\nA/p+Cqqrg9D1uLVcZaWbc4gYHBS54BNzcxaBSwdqalLQ0BDAzp0BKAr9raYmYDhbsG0sKCBbreFh\nwZbWd+BAvHmLuWjU1CjYuzcZ06ZRCAUD3IIgANAMwF9TEwBAem9iRlNQVsYHiBQVqbFBTpwJt9ra\ntbaSrZ3Xa9eczpihoa9PhKraLciYa0okQtrlFSvCqKhww+8XcOoUr7WdPJlftjlCmA3S2DGgBj4V\nqak6tmxJwSOPhAAAeXnUiFlX50JlZRBOJ69tP3GCGG+rhVpFhQd79yYbjXH5+RqSkljgiYh581Su\nGfSFF/hUv9mz1QnZ8Oef93Oe2ewe9HlGByfCKBKVqL98JUDwNaiEZudPsx5/6mFz4oRkxO4CdlbG\nvPzZs1WoqoAjR5zw+wUcPBhntczfsQLv7Gx+mnrOHBWtrX4oioiBAQGCQKzkhQvWdC4Rvb3g9J5j\nY4LBWM6ZwwPFGTM0LFgQxZ13voqpU28DALz6KjUO7d8v24ImHnmEwhbMU6e7dxNYW748DJ9PiHnC\nSigs1IzoX12HYdp/6RK/zawcDgIXksSDkO5uMTa97kc4TEl0DQ0BuN1kF8f0uykpmtFolJenYWRE\nMGKL8/M1A5BOFM5hlXawdDt2rLxeFRkZWixRjADpjh0uY8p7zhzViMKdMoXO3diYYID1Q4f8ePDB\nVNsxbWmxhn3ohizhwgWJi/V97jkZra2U0kdpe8C5c8TwsgAGtv2DgzT9HonwLhpHjvhx8aIEXQc0\nTcfBg+TZW1CgorExAEEA51JQWXkUd911G5xOFQcOyPjgA4fhrbxli4KNG93GMXC7+fPGBk8sFIVJ\nA9avd+Ohh8KYN0/F9u3xv910E1ms7d5NTXtnzojYvFnB4KAYs20je7Jdu2T09UmGRrqxMYDBQQHT\np1PwDJO5OByIxTnr3D4dOeLHypUh9PaKhnUgk+ZkZdn1zUyKYfY4pkZWBYsXRxEKUfOeGexOmaLj\nrbcctnPy8st+nD0rIjOT4rFfftmPkyf53wP7TZsBfDhMv4+XX/ajvf3ah1okniOJmqgS18XVVQIE\nJ+qalJX1UFUY1mefJGzj4kWRa7jyelVMm6bhpZd4mcOiRWSpxjtKkHuAw0Hep5pGU6zW4ILsbI3b\nBodDR3e3yD3Mm5tlU2NbnP0UBKCqKmjE8pqTqcbHgbq6uFRheFjAmjUhLF2aAlWNa0bvuy/NNlXt\nculG3G1zs4zRUQGTJulITdXh9wscm9XYGEBvL7GmdXUuThaQnW1trNIM5ruiwoOaGl5CoCgEoK1s\nLe/OoWD+fGoKu3RJhNMJSJIeYzGD6OsT8cgjIWRlacjNVTE4SIlpzAPYKu3welX09BCQHBiwh4Ic\nOCCjrk7BBx9IuOkmikKmmGgN06erhraVLXP3bpcRM20F+DU1CnSdgHtHh4gXX/RDVePR0Ax4HT/u\niHkPk11XebmCgweTsWePjGiU9KksNjgri2QXVrlAVxcPrNkx7O8X0dMj2AYDpAnWAQjQNACgZAWH\nAxgeFrFsWRjBIFBcrBpBEfFrEejoEA1pCyBAVeNSi6QkHcuWhYymP0HQEY3Gm/bMoNUsDTDb4dXW\nKtixgxrG+vpEZGQA69e7UVISMvbz8cf5Y/D++w7DZ/vppwNYtiwMv5+kOUuWxK3fWDiFWUfO3DPy\n8zXMnEm/2/ff58HuRx9JmDVLxaxZKucxzQbTq1fHf8MvvODn2GunkxxAKipogDVzpsoNYo4e9ePu\nuyOf050xUYlK1F+yPhUIFgThHgD/BGAegK/puv7eZ7FRX/ZKjNLsdbVhGzNnavjDHySjGamoKGrT\n712J4WXuAaoq4J570nD0KHlHPfaYx2DEbr45iqIismhiOuL333dA03im7cwZCfPmRfH88350dkrI\nzNTgdtMU/e7dLlRUBD/WU5ea0gJob5egqt82lsvAjBVgZ2dr3JT74cOk1x0dFZGaqnOxzz6fgJkz\n4/6vlZVuo/EsKUnnHA+Skmhq+MMPJU5KkZxMzB9zCDCngHV1SRZ3DhHhsGjT2+7cSTrQd98VjTji\nujqFA7TMN/a55wik5ufHgyPY8ers5Nk6WaZmIpau5nDoOH5cxH33RfHhhw7ccIOGYJC2oatLjE3/\nCzaXgIICzWBM+/uJ4VcUe4Lapk0phqsB229yWlAQCIjc/jQ1ybh8mZjhzEx+fZmZGrcfqanEaBYX\nq3A4dESj/Odvu+1WDA0B4bCItra4xrWhQUFdnQtvveVETU0A7e0i9u6NM+OLFqkoK3Ojvl6xeWK3\ntMhwu8n2rrBQwNAQHQefj7Sz775rtRezz3aw//t8oi3RsLmZGiKZ5dyCBfzsx4IFFNQCkOfu5MlR\n9PVJhm0fk7/U1wfQ0yNweubkZB3V1QrKytyxGR0FN9zAL1/XgTNnJDgpZBC7dwcgiuRYkZTEB+O8\n/bYDOTnx30NOjgqPR8NDD4UhCDrn/22dcbqWlXiOJGqiSlwXV1eflgk+CeAfAOz9DLYlUV/hutqw\njYULVQQCwD33TNwhfvGiaCzXyvDeeGMU+/YFUFGRwn02GgWSk3UkJREIOnVKRFGRxgF0c5KX00mO\nFIIAdHaKCASAbdvowVxXF0BdnYJLl0QMDQnQdX6q3DyVu2RJms1ia9YsDQcOyNi/P54olpurQdd1\nTs/a2SkgP5/0pV1dghEUUVWl4JlniJ1bsyaIjAwdKSk6QiFKVEtKAq67TsPx4/S6tNSDbdsUFBbG\nHR8EgZhchwMYGhJgjW0mUGgOFdEMEMP2s6eHrKfMALGqKmjzsGW+sWy5jY0BDvgwxwPzMZoyBTZ2\n8uGHxzkQ/vzzxOjm5fGpeMwFoKgoakzFM3C4ZUsKHn2Uty1zuYjxdDjovBUVqSgoUI3EM6vN2enT\nEubNo+suNZUfcLAo5vh+aHj00TQ8/riCyZMpbY9FCefna/D5gIwMnQubqKoKYsmSVDQ1yfj2tyNw\nu4G6OtLu+v0C5s2LQhBI633hgmjT2BJTT3rj4WERO3a4UF+v4Be/SMZjj4VQXMwfa+tvyHzei4qi\nthmL3l6a8RgbE1BTQ7INs3tGOCzY2HAAuOEGq3ZZsFmX5eVpRmw2QA2HZ8+SG8eFC5LBdJuXf+CA\nbBuExoNx6NjV1io4fVqIHWs+WOfz0gEnKlGJurb1qUCwrutnAUCgro5EfcJKaHbsdbUNJ6IIfOMb\nKl54wY+333agqMj+0GbAddcumQMhQ0PkRdrVJXHrMk/fEiDy4/XXJU4/u2ePC88/70cwSI1yALBm\njYebqq2ocGPqVHCMbVOT1b+XwAGTIOzY4UJl5VG43bchP19DfT05S9x+exQPPcQzv3ygxcSpYH6/\nnZ1raTEDAReam2WuU/7SJXKvYL6nbjeQna3j0iXRNkXPEsdmzlTx7LMypkyhzxUW8sljBOLsoQ3X\nXz+xbyxLGRsc5Ju1MjLI03X/fhoQFBaqNuDl95PPLw/2JOTkUAMYe585K5Dbg8KB7Y4OEY8/rmDa\nNF6TmptLshmzlvjQobi0wmpzdtNNKpKSNBw5QjHVM2ZouHyZ7MGqq1NMbhDA5cuiwY4CAnp6BAQC\ngjGFX1l5FO3tt9tmM7KzySs3J0dDVhYNVp55JhklJSGMjIjweFQEg0BBAZOn8B7Cp045EAgAKSk6\nli0Lo6Mj3uRptjTLz1cxMCBydniFhTSDkZenYWBAMOzWzMdrYEA09O+CAO66tUpEGLN8/Dg1C/b1\nxaOe6+sD3O/X6dQt144GgNhqVRUm9F42R4uz8/Xss7JhjdjVxa4JN8rL+cbVwUHRJs36pD7nn2cl\nniOJmqgS18XVVUITnKgvRF2tPRBAQJgadijNKm6TBSNAoaBAxZQplPLETOg3bAjilluiePZZmVtX\nW1v8QZmdTQ/Wd96hdCxzI5CmwcZssjhaJrUYGBBiDTXUZa/rMKJ+FSXuk8oCDY4dc+L660W0tMTj\nee+5ZxwAD+o++sjOmFvBES2X9ru0NBTb72QbS2t1u5g+nUDVu+9KMWClGRZT4TAPclRVQGVliuF6\nsWKFOY7Wb4AHhwNIStINKQc5BOgAaJDR2SkhO1vDjh0uAwwziUJrq4z2dmJDGxpcWL06hAcfJIC2\nc2cAubl2MGSVOmRmarhwQYQg8KB68WIV27cHbNroSISCHkpLyWIOIDnIyAjZoZmP3/vvx+25eJsz\noKtLQDTqQDgMiKKA9nYgM1M3GhOPHXOioSGA2bM1+HxkrRcOC7YmyIoKN/r6BBQW2tPYrE4QTU0y\nNE3gNOtNTTJSU6mxjMV4M89lNlBpbAygv59Y2AsXeDlCXV0A4+PU3DhnjoZLl4DCQho0mgeMNTWK\n4cDh9RJo7u8XMGsWOVScOycavsYLF6pob7dql2mZhYUadB0YH6dAlM2blVhjY/x3sWWLYuwLSwDc\nsSMZW7YoqKigJj/rrMHMmarluiAZTXExNSOaZ4ysA5qZMzWbNMvaZ3A1fsFfBACdqEQliupPgmBB\nEF4FkG1+C9SZUanr+r9+0hW9+OKLaGxsxIyYgeakSZMwf/58Y8TyxhtvAMBX4vWtt976hdqea/H6\n9dffwIcfipg06TbMnKlBll+DKAJ33/3JPw8AWVm3obxcgc/3OnbtcmLVqltQXu7Gxo0vQ5JSUFLy\n9RgoeA2SpOOJJ/4aM2Zo+Ld/+z1ycjQsXPg3EEVa/siICKfzvyMSEfC97/07lixxQVW/DadTxwMP\n/BqNjSlwOm/Dtm0KIhFafyRyO8bHgZ/85NcIBIDFi7+B1lY/zpz5Lb73PREbN34XkYgASfovbNwY\nxFtvfQd33hnFgw++Ap9PwNjYN9HcLOO3v30DU6fGH76S9F+4fDmIRYu+GXuPtn/mzMXc6/x8/vVN\nN92E5uYofv/7NxAOA0eP/i36+0WUlR1FR4eAmppvYc8eF3p7X8fYmIKqqtvh94vw+X6DtjYNTz5J\n+/+TnxzFL35B++/1qnjwwV9j3ToB2dnfQkGBhjfffAPr1gGKcjvmzNExadJ/wueTEIncjvZ2CevX\n/yFmvXUbnn46gMrKo4hGgY0bv2fs30MPhdDY+D04nTo2bDiK//E/gIKCb+LwYRm/+c0bCIVo+7du\nVfD++2/g//7fcUQid6KkJIxXXvkd/uVfklBTczMAYHT0NYyP60hOvhWNjTLefPMNCAIwOvpN+P0i\nnn3293jggQhuvPGbKCxU8bOfvYlbb1URCt2GpiYZr7zyO8yYoWHPnjuxZk0I7e2/xdmzIezffyci\nEQHZ2f+BFSvCKC+/HenpwM6db8Lni+DgwTtQVRVEZ+drCAR0/PM/34Fjx5z40Y9eAaDj7/7uGzFg\n+xoqKxV4vXdi+fIwTp58HbKsoayMXj/yyNv44Q9p/+i6eg1nzoRQU/NNeL23YtWqN/HAAxHk5n4r\nNmD8HRwOHZHI94zPv/JKCAsWfDMG1H+DSATw+b4Gl0vFW2/9DoEAMHfut9DVJaK9/bfG9Ts4KMDl\n+g1OntRQVHQbdz3NmrUYS5ak4sEHX8HatcnG7+Hhh3+NSCQFADHU7733Bo4cScLBg4tjkcW/RSAg\nIj39VqSm6qioeAdUt6OhIYCLF1/H8uXAnDnfQlaWhrNnX4fPJ2LPnvj1Go3quHTpduTn65Ck/zKu\nJ0HQcf78byFJwOzZ38DYmIA77vh3vPMOsGzZt+D3i/jDH95AZaWGadNuw7x5Gvz+11BTI8Llug1+\nv4CSkj9geFjEK6/chEWLVMjyazh/XsSOHTQTs2nTyxgZEfHd734DCxeqtvvRr3/9O27/f/3r30FR\nop/o/nfihIQ773zX2J+jR/1QlNc+8f1TVYHm5t+jr88Bt5sGFb///Rfr/p54ncAX1+I1+/+lS5cA\nAIsXL8Z3vvMdfFwJuq5/7Ac+SQmC8F8A1n5cY9x//Md/6IsWLfrU60rUl6Pee0/Cj3/sMcIFbr45\nim9848qMyETMCwDuvaYmGRs2uOFwAE89FcClS+SBypLgAPKzdTh0rFqVyjE4bHs2b1Zw6pSEadN0\nlJbGv1deHjQilV96yc/pMw8flrnXzc3Evl28KHHrLi9XkJamQxCEWAwr7fuiRSp8PgHNzclYuZI6\n7FlE7uCggOJiFefPk31USoqGM2ccRnrcSy8l4d57x+FwAFOmULf/0qV2NrG8XEFNjdtg/np6RGRn\nq0hKghG6oCjAE0+4bftbUEBJcAMDIvLyNLS3SygsVG1RtUxjeeCAzGk2Dxzw4+GHSTfLlmldx+bN\nAYhinI1lUoCmJhk+nwhFIW3oww97UFpK3rLmZe3aFYCi8OEmTU0y/vEf3Vi+PITyctq26moFgIAZ\nM/jtZ9dOf7+I5mbyRFYUwTgeNTWKzTfZzKa2tsqGFpl5PQ8NiZg2jeQgfX0iZsxQkZWlcXrTujoF\nU6fqOHNGwvz5UVRU2JfJgkKSkymkpL9fwOgo6brNbOz+/RTUYj4G1dXkegEI2LQpxWh2NH/v8GE/\nHA6yq3O5KKSku1vEdddp6OwUUF+fglWrQtzv4cABmWOc9+2T4fEAjz1GDPr//t+8VzHbD+aXHIlQ\n8Et/P+l3o1GBO59PPSWjoEDDD3+YhuxsDatX0/eysig0hgZuFDiSmalC0yikg3TyZH+Wna1h3jwN\nJ0/GWdfeXgFLl8avzWeflXH33RHb/eWFF/wYHLwyU/tpmOCXXnLiJz9JtW3DJ61Ps+5EJeqrVO+9\n9x6+853vfKxc97OUQyR0wZ+wEpodaliz2jB93M18osY59n/278iIgE2bgsjKomjb5cvDsanauEVS\nJEIet+blLFpEHqTRKMkmMjN1m7Y1PV1DQYGKkpIQBgcFrsmnt5dvevP5qCGssJCfas/IIK1kby9N\n81ZWUkpbRkYIDgfw3e++isrKO9HeLnFxsyUlIbjdpKv0+WhquKBAxYoVYfzoR+MoLNQMEG5tEGTy\niPR0GO+1tUmor3fhwAFqvmK6YLMtmtmurKQkxEUhJcBZqQAAIABJREFUNzXJaGvj3QJSU3Vs3x5A\nbq6G1FR+OpnJCKzTzObmKq9Xu4IUgHSljz3mwcqVIdTXK8jP19DdbdcMt7dLXNNgMAjU1iro6RFx\n4IAfkybpKCkhILd6Na8ZHRoSsW5dEIGAgHXrCAy3tsZ13GNj9sayJ59UjBjfy5eB5mYZg4MkN7CG\nOjA7sfp6/vxMnapxx3b/fhlJSUBysobubikmTfgtKipuj7mIkMRkbEzAzTdH0dws48wZkqyMjpKO\nuLExgLY2yZD/LF06broeRDzzTJIpPATo6pKwYwf5Avf2Sli0SEVyMjAwICAYFFFSEkIkwssxkpPJ\nNq2rS0JGBjvn5LhgThak3yXFU0civIyouVlGZiZp0QH+2igs1Ay9dVeXhLVrPXj6aRl+P50rqy6+\nv1/A3LkMsF5ZtnClJjfr/eXttx3GoHGi+9LVyrfMEoisLP7ecrWNdvFt/Q0ikdu/MG4VifpiVAJf\nXF19Wou0/wlgN4AMAP8mCMJxXde/95lsWaK+1DVzpjahvvXjLNEmeniZ35s7V8OCBSr+8z8dqK4O\nckxVY6OMnh4Je/cmY/NmBZs3K/B6VVy+LOC99yTMmaPaGuNYmtctt0ShqsCWLbTM6mpyMDA/hM3b\nEQgIKC/3wOtVDV/a7GyyGbNqiQUhzspJUgqeeIKSuVgjmrm5jdmpmb1ot2xR0N4ej361NgjOm0eJ\nZpWV8Xja+fOjqK0lZtds37V3bzIOHyY7MYDFOZMzg1VLbLW8ys/XsXZtihF4QNZYDmRkaIbW0qyb\nzcjQkJZGqXyFhaQ9ngi8RyKALAvYvFnhQPKRI340NhLopMGBGJNtxBnHYFCEz0ds+d13j2N4mJof\n9+xxGVpsdlzz87UYGBNins5hdHaKOHxYxtmz9gENi5U+eDAZJSVhlJTEt62mZuKmLwZ6zcsZGZnY\nJYNZxpHUJ4RXX1UxPk5NXwSq3Yb+euFCFZcuEbhyOICeHpELUmGNY+z/LD6bMfbl5UHbgLSqSoHX\nqxlpeUDc23rePArb2LEjgLw8FR0d9Pv58EMnysuDRnAKW9aUKeS2YD0ug4Mi8vJU3HhjFNGogPp6\nBVlZFL7h84k2fffcufSbn+i+sW6dZ0LAagW3EzW5TXR/MQ8aJ7ovXW26m9UC0so0X03FtxV/FohO\nVKISFa9P6w7xfwD8n89oW74ylRilxS3OJgK2E9X8+SpefNFvmOAXF9MUpfWBdvy4hPvus1tWjY4K\nyMjQsH17AJ2dIqZP55nHl1/2Iy1N577D4nOfflpGUZGKs2cFI5KX+cAGAgK2bnUZxv5er4ZVqwhw\ntrdLeO89yQAsVhZQ1/WYrIHeU9Vvw++nZizGxLLoWgBYvjzMTaW3tMgoK3MbjLc5IticDOZwAPX1\nCrq6ROTkUJCHrpP84eBBl+EC4HRS1CwAjI+L2LMnGQCwc6fCAe+cHA3JySy6WTIspkhKQmlmDodu\nxC/v2uUybN5mz1Zx6ZKEU6fInmz3bheiUXBBHgy8kx+xC2VlIc7dIRIR0NEhYfp0DaOj5EDR2SkZ\nTL/VFcOaELd/vwyHA3jxRT/OnZMwa5bGyVmsjhuM+d6/X8bYGM04MLa4tlZBZib5MzNgbA1eMDPe\nKSk6l84mCPaGt0iEmsLiA7I7DbkGA9U0KxFGV5eEYJCXj1y6JOHwYYr9zczUkJKiY2CAtlWSgIaG\nADIzdcOqLT1dtzHdHg9ZBvI2ZkFjBqGhQcHAgID2docRDrNmDX32mWdUbqZkaIjOi3Vfc3I09PSI\niEZ5u7TaWgXj4wI6O3X88z+PQVFEDA5Sc6nTqdvs2/LzNWO7rYB1osHzRODVzOxmZmpYtcpjnLPP\nAmROBMb/3MCN+LYuxsyZ/muaWpeoL14l8MXVVcIdIlHXpJjF2cdNKVqnEB97LG5FZg7TmIj5sU69\nZ2fruOOOKP793x0oLfXYQPKlSwJmzlRx4IAfAwPELjoc9BD0+wWMjwuYM0flQOiBAzIefZS0fceO\nOWOhEBSUATDvXBjrsIYm3HCDhvPnxdj2MecE0tCGQgJqaxXk5cW/YwUqFy9SGhwxrBRFzCKCCwpU\nbNumYM2aELKzNdTWunDihIPTrsZlBx5s305WbWYw0thI+mnz5w8dktHbK6KiwoWaGoWTUpiB5nPP\nyYaF2F13RQybN3viHMke1q93o7lZjmlnefeCqVOJkTQfO5bGxrPq8ahk83GyWqkxtrWlRUY0Chw7\nFmehs7M1RCK8qwazzmIA+ac/jes5nc54xLFZwsIGRbm5GgYHRZSXB5GermNwUITHo6OggFxMwmEW\nrEE+08w1ZMYMPlDj9GnJsPRLT9diQD/Fdhz7+kT8/OfJ2L6dooT/+EcabGzblmIcz9paSrv7+78P\n4/BhcuBYvFjDzTdH8NZbTjideszhgmfnk5NJP5yWpsVkEEBqagSpqcCHH8aT9YJBgZspOXBAhter\nwuEAGhtljI6KiEQose6xx9JslmS6HrdT27VLhqJQip7fLyAlhRII2YxCQYGGujqXIVUKh0kCwXS8\nVtnC/Pkql0zJPmdmdj/4QORS9ByOT983c7UWkB9XV8tCJypRibpyJUDwNaivkmbn4+yA/tTN3DqF\naLYiu5J0gj1s2NQ7ayAjy7O4dZoVJKekAB984LA1VjE2csOGIEIhHlwNDvI2T8EghU7s30/T9F6v\nigsXpBgA0pCWpqGqKgiXi0DvpUsi9uxxxSydNDz00DtG9/2hQ3HWkRhXuxcy21c2vX34cFyWUVIS\nsiWY7dzpQk8Pvw9MdpCXp2FwkP9bW5sEgGfH338/HmrR30/7uHx5GJKkTxgv3Noqc+ljE/kN19Qo\n2Ls3GYODZMWlqnyU7+TJxPQyze2UKeSJu2BBFHffHcHYGEkaMjNVHD7sRzjMA+brruOPW0aGhurq\nIDo6RHi9Ghc1bD1uVVUKmA16JCKgq4s/5+b0N7ZvzF7s8ccV5OYCZWXxa4oa6uKAtLmZ0gQFQcec\nOTpWrw6hsFBDamocNEnSf2H+/MUoLw8iI0OLaaIntsaLRIAnn6RQDwZEb745YgS3MLa6pkbB7Nkq\nx4DTuYoaWuK6Op6dHx8HJAlYtiwNy5eHcf488LWvRY3AGvYb3b3bZUiJiopUpKVphpyFDfamTaPA\njMcfV7j4czbAYftGNn/8wIwd32eflXHbbVFMmhTE0JCA++7jo40XLVJt95hP0lR2/jxvyfbsszKK\niz8dG/znWED+qfoqPUcS9ckrcV1cXSVAcKI+17pSHPInKbsHLr3/cUyK+WFDneQCcnN1FBXR5+fO\npaYUt5t0wiMj8YY4K0AzM4DTpunQNB44RyKwSQ+6uiScOkVNSRcuSByz2twsY9OmFNTWEiBgwQ/P\nPJOMVatCUFXeg5at+9AhGQcPJiEnx2EA4vR0HVu30tT0H/9IXsaBgICaGgVZWTpkmWeNz56VsHp1\nyBaasGhRFK2tfggCkJtrn5pnx9s6XR8MAjfcQBplMztujRe+fFnAokVxkGNuuHM6dSQnA4qiY82a\nEDIydFRUJCMjw4nVq0Po60NMuwv8/OfJhm6VAamlS8djko5k9Pe7DHlINArTAEjA0JDADYgoTSzO\nVD71VMA4j1b9c2oqsH17snEccnI0A+ClpwMjI8IV9+2//bcoOjtFNDYGMDgoGP68y5aFjcFcT4/I\nuZVUVwfR3S0iGhVj51JDV5fCuUZUVwfh9dq132zAtmpVCH6/buiyi4qinLyjpYUCVzZv5uU53d0i\nWluTjPUMDAgcmF2/3o21a0OoqAjC49HR3U3uKwsWRHHsmDMmo9CxcmUI/f0iDh5MxtKl40hLI+mF\nWapSXR1ESUmK4fzQ0BBAdjYNDhUlfs0NDFgHngJ3D2Cx5v/5nw6OvW9rEyd0dfgkyZQTsbaf1ts3\nwd4mKlFfzEqA4GtQX6VR2tXGIZvL+jD62teiOHjQj9xc/YpMyp962CxcqGLXrgDHXtXVkeNARga/\nvsWLVdTXB+D10gPv/HkJra0yTpyQMGeOhoqKFHR1UdpYeTlpeWtqAvB4KGXr4kV+Orm3V8Thw35D\nu9rRIRksMLkd3AbW7GKWUbz/voQVK8IQBB0dHXzTk8MBNDUlo7hYtTG/5n2ZO1dFfz8xz2YQV1bm\njrG6Atxu3ZBVMJsyh4M6+3t7+en6hQtVDA0JNnbc5SJbLvY5lwtYvdptgPc5c1TU1ipQVUBVhZh3\nMC+PEAQ+ma2xUcaTT5LLgxlIWWcI3ntPMgBmRYXHsGDbvFmBKAKjo8DcuaqRHsZ0tcEg2a8lJ2vo\n75e44wYAy5aFDEA9PCxAlgVDBrJrV8AA2E5nvJnwpptURCLAjh0pWL48DEUBZs4Eli0LY8YMugb7\n+gTk5moYHRViEdoq6upcWLs2xIHWffu+hW3bFJw8KRl2ecEgjGjlWbN4+UheHml0PR4dra1JuPfe\nOLDPziYmuLQ0hFmz+OtdUYBt2xTDjq+tTUJWloqcHA3r15MGetYsatCzaqbvuy8uo2B2dMSi0++Y\nBaYwqQr7t6QkzA0Ujx7146//Oj6QtYaZXH+9agu5OXFC4lhgSpcTcPy49IkA7kT3iIl6Db5otmRf\npedIoj55Ja6Lq6sECE7UVdfVsCJ/rhZOjT1fGhoCmDyZbLbWrPGgsTEw4cPnk2zT+Djw9tsSenpE\nzkorN1fDj37ER8USAydg504XSkpCNtDV3S1y2t+iIvLS3bjRjdWrQwgEBFuXPAAsWZKGI0f8qKkJ\nID9fx8MPe7BhQxBNTclGM1FxcRTl5XE3h/R0IDlZhyjCkCLoOnD99Sq6ukRs26bgvfd4wD00JMYA\nmRhrThJQWKhi6dIw+vritmgAMDgo4IYbVEQiAlavTjF8adetCyEvL85eAsDSpeNITyeWcPJkHWlp\nPDuem0vnt7Q0hKwskoCsWBGCy0WNctnZSVixIoTrrtMmbGBMStKhaTwbOzgoIikpnq5n1fyabeAk\nKS6vYA1pzDWCbSOTjVh1tS0tMmSZ2M+BAYqQ3rbNha4ukrQwecfkyfF97usTjMTCFSvCcLl03Hij\nCkBHd7c0getCEA89lMo5PDQ1UXz1U0/JKC0NcfKRSIQkMdOna5g0ia6hn/88mXPL8HpV1NczlxBg\n3Tpqhty8WcHq1SEUFMT1vuaUOeZe8t57DkMCUVoagijqtnjoVatCmDVLxS23qHjuuSRu+wYGSPM8\nb56Kigry+s3O1mK+vCIkCfibv1HR2ipjfJxd0xPrt5n1IfsdFxfbAanZAo19lr+GgJ07Xdi0Kfhn\nWZtNNJD+NIP5RCUqUV/cSoDga1Cfh2bnLxnFeTUShz/XT9Oq8auqCqK9Xbriw+fUKRHvvCNhbIxM\n9B0O3abje/ttCffck4b9+2U8+mgcmDQ0BDgtZ3m5gkcfTTPWa5VJ+P00BR+PyRWwfr0bS5eOG6xf\naWkq1yAViZCeMjtbQyhETJjbTT62hYUa+vtFVFT8AU7nbaitVbBsWdiQWVRWUuADQMECgkABFoyN\nY84NVq3q4CA5YoRCQH6+juPHHcbnzJ8tKNAQDBLgZ+zidddRw9G3vx1Fe7sEQQAH5qqrg3j00RS0\ntvpjzBvpd5OSdIs8gsIpOjtF43PEUtKxKSiwS0zcbmLUx8Zomddfr+LDDyVMmaLh0CFqZuOlAFFU\nVweNAJKNG1Owf7+MtDQd9fUB+Hz8+Tt7VkRVVRCSxOudP/hAgttN4SGLF6tYu9ZtNKPNnx9Fa6uM\n2loXfD5i9Lu7JUybFtdlM3Da1iZh7lwVM2aoePddB7eOYBCorg5CkkiX+9JLTug6zSR4vTQQyc7m\nva2Hh1/D2rX/3djf55/3o6srvk/t7RK6u0n2caVGRQK7UVBQRfx71pkFVQX3mUhEQHu7CFUlRxFB\ngE2KMWMGMcXV1UFjYGiNdD561I/Jk3X8+Mee2CCOmuyiUV6/PXWqPuG9ZcECFSdOSPjlL522+5t1\noB2JCOjvFycccP+5soTPsrHts6qE9jNRE1Xiuri6SoDgL0l9Gu3t1dbVsCJ/rp/mP/1TkGNrmT2S\n9eHDQPPgoMCxtc89JwPQuM9duEAMGwt6YNPhmZnWEAcY+0Y2T/wDsKhIxapVoRibFm8MSk8nDTJg\nb5B64gk3ysuDKCujhixAgKJQQ97lyxS+cepUGN/9boCTWTQ0BFBdHURFRQpycjTU1ysoLSXAwTSQ\nbreOHTvIrQFArMmNvH43bKDPmhugamoUNDYGoGk60tLofHq9NE1+332UpvWzn8m4665I7PMBvPRS\nEqqqFLjdQDAoYM+eZEQiAs6di99CvF4Nly/zUoO0NNJ5dnaS125HBzF1H31Ex2bx4ohhn5abq2Hd\nOmLSzeeytlbB2rUegzX9x390G5KOhQtVuFw6Bgd1LF8eNrZraEiEw6HFmPwwd/4EQUB5uZsLB3E6\ndfzVX6kxJlLEuXMidu+Wce6cA4WFpFN94IFUQ3oxPi5g+3YX6uoCaGyUEQgQeD12jGQmlZVuPPJI\nyNbMOHeuarNrY6+tzhkMyL/zjsDpXTs7JVjDK7KydEyfHjXemyjcIzdXs9m3CQKM4IzMTA0VFe5Y\nOlv8M6pK/sQHDsg4fpx+ay0tlE7n9WrQdQ0tLTJGRoDWVvKZFkXddo/4h3+IoLExYBsQHz3qR1sb\nuT+cPStNeG/5uPvbRH0AR49+ttZhn0djW6ISlahrXwkQfA3q8xil/TnTdX8ue/x5siJsP+xT2H68\n+KLfmC6dP1/FyZNxxthuxM8HGJ44IRn6Qrcb3HS41dLKHCxRVBRFWhqtf3ycpn6HhkS4XDqcTgKE\nrBktFALmzInbnpmBD2MTBQG4/36P0dwFAFOn6vjFL5y4665vAlA5mUVmpobhYUrtSk6G0dlvZtlq\naxU8+aQCTRMsASEBTlPJjk04DDgc5N/a18d7zDJtZ1aWzrHlzc0ykpNpn99804GyshCi0Tg76PGQ\nY8Hs2dQsB5D8JBwW8KMfxbepqiqIDRtII+x06rj7bt4+rb9ftDG3Pl88bKKnh2zhBgZEFBerkCQd\np087MHOmyh2TjAwNx49L2LpVwY4dcS/k3P/H3ruHR1HmacN3VfUp3Uk45UBIgA6CRk2QhayH0ZWZ\nnXVH97re9Z1h5x2dER0dB2aIyCkIAcVJFDuYcHRwlzUOgWASNjBzzfu9L+w7frszvjPjhyswYEDB\nCCQhJOQM6erq7nRX1ffHL1VdT3UnEkFBrfu6vCRJdx2f7rqf33P/7jtLwcqVdH937HDirbeIzJEl\nnsqQ0KoqUSffdXUi7rgjqksvOjvpODZsSMKyZSGMHasyE43S0iB6e3ls2eJCVZWITz6h6rB5+d/o\nf2xecejspPtTXv4QU1mPRICpU2W94S4nh8j+ypVBvdpuJt9er4LDhwWoKo833xSHdNHA5s0u3e/Y\n7Qbmzw9j6lQZpaXkMCHLnGFiQf+NG6cm0ATTyklDgx+PPTaIY8eEuO+I4SbEWmLjM8944iYm2ndL\nRwfHTIo7OmKf7y+i6exGbGyzqn0WEsEaF6ODRYK/IvgsxPSzVo+vVVUkEQnXzsMcy9vRwWPZshiZ\namjw4/vfT9E1pWYjfi1dSsO5czx27HBi1y4Rzc0Cdu4Ucfly7MHKcRwGB1WsWuXGokWxRqieHg4/\n/nEyysqCcfrRYFDF/PlsQ8748Qpyc2MEheMo4rasTMJzz7n1CrK5uYuss8jZoKIigIwMFe3tPMaP\nV+B2A0eOUIVx9WqqMBqvjc0G/PKXLvzTPw0yv790icPSpaG46l9enhJH2NascaOri8cLL0i47TZZ\nj6zVttXTw2HSJGDevOH8fiWsWeOJ+705IMTvJxLo8SioriZfYM1aTYv8jQ+QiIVNaDrr6dNlhEIc\njhyxIS1Nhd9PscVdXdRMVVLiZmzIVJUaG1WVNzS6UcBDZyfJI/r6WK14IBA77iNHBKxeTU17Ph9F\naG/cGICqUuyvqpp1ykBqKpHl9nYBL71ExHv3brZh0ZhcZ15xmDJFiZNTOBzkbvHooymmsRPE4CA3\nJEuhlYHqahEXLlDjXEWFS/cArqsT8ctfurBgQRjz54dRWCjD4SCdt8/n1hsKfT6JGfN5eQp6ezl8\n9BH72fzkE0H/d3c3D56XR/UdIcuISxVMTVX1GGSArqUmdxkYoKY/RcFVSb6+SAmZBQsWbkxYJPg6\n4PPQ7Iz00Bnuy/6zNntcTVVEloFjxwScPs0jK4utnmlLmAcP+tHby2oF09PZauaZM2TOr6VeadU+\n88NTQ26uguPHbYhGY0b+b73lx9KlLLGdPz+M/PwoIhFyb8jIUPXIY+P+jx4VAHBxBKW8nCqDTz8d\nI+x79pAV2/z5g3r4hXl7Z8/y+NGP/g927foOgkEeTzyRNAzZDCIjQzVdGwWLF8fbn2md+loD1Acf\nCLj5ZhktLYk9ZkmvLEAQSCdsTImbNIkCK7Rl+XjSR+zBXM0cN44ldpoDRzDIM5V+zVrt0iUA4IZC\nFbih60XyjIwMcsfQyN2zz8au8c6dop7iVlVFEx3tGNraeGzb5sKGDRLWrqUmP0VRUVIS84L1+4Fb\nblFQVBTbZnW1CABDx02Nbppnrfm+mKOzKQ1Oxf79fjz7bCx9rL+f5Adut4pgEPq49XgAh4MIu0Zc\nAwFaiRCE3+v+0VSRZaUOnZ0cxo8HUwknLTbJMt58M4BDh+z66y9e5IY059wQUedw220KkpLYpjWj\n17aW0vjhh9ToZjzXGTNk/fy0yfdoviOOHxewZIlHt6m7/XYZ997LEtKuLj6uyfBqJV9fpITs84Cl\n/bSQCNa4GB0sEvwVwUgPneG+7K9Hs8fx4wL+4R/oWEpK2CqhRsJnz5ahKGwkss1mJn4qLlwAvN4o\n03CVny8nNLbXyLXfD/31mlWZtv/z52kZmZbwUxiC1dnJEkzSDbPHlJGhYN68CF57zYW9eyniOSOD\nonK1h7fXK2PvXkqEM+suy8uT8NJLYUbPmagpTyNSWuPc5cscJInD/v0O1NWJaGkh/W15uQtALL45\nJYUcJsJhlsRoTV+9vZSKF41y+NGPYoRq1y4R0SiHn/yEXQLXgjIGBug4cnLkuGpmfz+R1lOnBLjd\nVMktK4vZnWnn5XaTrIMSwJLw8MMRDAxQQ9/Jk0TejROm6mqRef/Jk2Qjt2aNG5cvs/dq2jRFd8XQ\niH1XF880nxUWynEBFL29HF55RYLTqWLqVBkXLsRS0QYG+CFJSxgDAxxCIaC21j9kJcdh6VL3kAd0\nQA+qyMpS4PdzuHiRrteJEwIeeIAkMmPGKHA4gJ4e8q3W4qtfe82FJ58MIzc3gLw8st2bM4e8rmOJ\nemrcsTsc5GG8d69fTz7Uxt+kSdSceeutCvr7SVrR28ujpYXH3r1+8LyK+vooAgEeXV20mnHqFK1E\nzJol47e/5ZlY5MuXOfzylyIz+RxNlbWjgxsaR9xQhDMX91qvV8HZs9fWocFyfLBgwYJFgq8DvuhZ\n2nBf9tej2cN4LGZHAyMJV01JpbfdpuDgQT9OnhQgScCaNUno7CSCNVy6kzl2eWCAw5gxFCxw4YKK\nyZPjl5/b2zmYK7zt7Tzy8oi8trcTmTl/nkdmpqpHG3d1cVizhohPba2IcJiaryIRSsUyEiZZ5rBt\nG1md2WyqrruU5W/B5QrglluGD5coLJRhs6k4fZpDfr6C115zYeXKEJqbOSxbFjJFCUs4fNiuk3a3\nGxBFcqXQ5BqTJyu4eJGS7srKgnjmmaQ427L29pgmV/t/VxePysoAmpoEADxaW3lUVkro7ORQX+/H\n4cPkRLF5swsLF4Z1OcALL0g4eNCOkhK2+SoYjPnLGpvFtCqx2Tasp4fXiaDXKyM/n0iszxdAbm4U\n5eUSenp4FBREGQ/dvXv9+MEPYhOcN98UYbMBS5a4sWGDpFfEi4pCGBwkW7meHp6RH2gRzWbrvN27\nRaSlqejoEFBURE16ycmsfraqKoDUVOCf/9mJJ58cRHMzMG0aNd5RGp6Cjg4bCgujOHxYQHOzgKqq\nB+HzSYzrhhaEEUs+ZD9LWVlkTybLZPOmTZoKC2Xm/EtLJQSDHDNuGhqIOBv15Tt3ivr3xtSpKn72\nM9YpJC1N0QmkLAN//rOA996jMbB+fRLeeCOAOXMSf7+kpqpMhbehwR/3GrtdTZiYeDW4ER0fRgOr\n2mchEaxxMTpYJPhrgOG+7K9Hs4d2LJmZZKdVWUkEceJERU91A4avXp86xaOkJFl/XV8fN+yDLFHs\n8lNPJelL7//rf11GQ4Mfzc0CJk+Wcfq0AI7jMGUK+7CVZQ7z5qWgtFTCjBkKHnkkBWVlQTz+OOv/\nqjk6tLTw4PkYaXS7kdBreM0aN7ZuDQBQUF4uoa+Pw6RJKvr6iEh2dfEYHOR0v9+CgiiiUTBkqLZW\nxIoVRPLMlXWPB4ykYeHCEHJyVDzyiId5v0b6NYmGOVJ60iQFPT1sdVVVAUniTY1kAVRUJOFf/kXE\n7Nky2tt53c0CwJCuVEZeHtmPaW4W2dmxZrVIhIuragaD8RMmSQIqKsgfOT+fbaLcuVPElCnKkJ8x\nz0gjWltZMt3VRQ4H8+cPYnAQqK4WIcvmBkO26uxykQTg7Nl43Xo4DNTUOIZ0xhK6u83NbvTvv/u7\naFy1fdIkRSfMd98dwcqVsYmCcXUgM1PRfbQBFd3dFIJSWRm7nkbir401ANi0KRAnY2lpYSc4584J\nSE5m5UenTwuYOzcKgKrBDQ1+neTu2OFEVVWA+dx9//vs5+70aX5YEqyFl2j7ImeT+Cjj0tIkvQI9\na1b0qiftluODBQsWLBJ8HfBFa3Y+z0a20TaSzJol48AB0vwam8oOHvQz2xquep2XF9/kNdy5xZvo\nE/m22aiCK4q8TmhZYunHW2+JQ/6ose54p5OuQSKNsDHSORIBAI4h+xxH/rD799sxb15ED3XgearO\nFhd7EIm8A7t9LkpLg1i0KAm1tSLjrFBbK8aUj1hrAAAgAElEQVQ1rF24ECN5ZqIYjWouGrYh+zAX\nXnpJ0jW12dkKRBEYN04dVgsaiUC3WzP6Ad90EyWvlZUFIUnArbfKEEUOFRUSzp8XsH59Emw2YM2a\nIKM/7e/nMDjIobmZCOS6dUmMv6zdruKmm8z3mLySjZHR27eTTCAlRWUcFkgaYUNlJUVKJyfHS1aM\nP2dnK6ispKaxt97yo7WVj7u3ZnlFdraCM2eEuMlSOEzno5FOimBm74lmN7Zxo9nNhPyttd+1tVGc\n8u7dIv785z+hsPBefTtFRSFGmlJbS3IdSaJtFxeHGOLvcKh46KEwHntsED09rAwkNVXB1KnsNZk2\nTYbHwx53YWGMdPI8cN99MpKT6TNWVRVAQYGMo0fpuyEcRtxn46abTEs7BlxJRTY3V/PSdsPrlXH3\n3ZGEnsGjwY3o+DAaWNpPC4lgjYvRwSLBXwNcqy/7z9pIYibPf/VXMn7zG3tCkqu9NhwG87CePp0e\nsh0dHBoa/OjuZol4ouOIN9EHFi0KQZY5vP66Ez6fhOLiWLVNO5bWVgE33xxFbi6YpezBQSLuFAfL\nVqDnzJFRUiLh1lsVbNvmxKOPDsLnk+D1KsxS886dom4JRoQzgDFjKGGtpyeEgwcV3UGhrY2Pizje\nuDHA7Hfy5BgR09wv2tuJ4Gp6TmMYQmoqGG1tba2I/n5aXu/oIClHXx+HCRNUXLoEjBsHdHURcTXK\nTrZsCWDyZAVFRWw1vKgoCaWlkq7PHTNGRW+vCoADoMLhINnJ7t1+9PWRNVddnQOlpUG4XDRpqK52\nMJHAfj+ln5nP5eab6d6bG7VSU+nf589TzK8mjcjPj+LyZY4h811dHH7+8zAefjiCpiYBVVVOXRZh\nHDelpUG9Kr5qlVuXYdTVkcVaOBybLGmNhhkZih5L7fdzuO22qC6RSU9nx2ZOjoyMDI4hupr/tCC4\n8MADVKXu7SVrM+N4/eADwTBpia/kRyLA008PMveddN7A2LHUbFhXJ+LCBZLHkGxIwYEDfjQ3J57w\nmr9Tjh6l74bMTAUbNkjMCkR+vozMzOGlBlcySTe+ZsIEhYk9/7I1tFmwYOHGgUWCrwO+rLO0z9pI\nkog8D1f9Mb92zx4REyZQBW04Am4k2V4vbbepScCMGTL27BGHktKoerh0aQhbtjhRVBTWu+l9PpZY\nAoDfT1WnN98kGy9jRdjhoEamnTtFnD4tYOxYFTxPOky3W8Xq1UFdQ2qWKJib8VjP1e+gtJQS5EpK\nSCYiirEUMEAL1oiRuJ4eXj+OvDwZzc3UFHf6tIBf/MLNhFF4vUrcPWxtJaL4P/5H7NrW1/uxYoUH\n69dLWLHCjYULw8jJYauemZlKQpcJbYkdIGJq9t6tryddt1ka8q//6kRlpYSzZ3k88sgg1q6NLefv\n3CniRz9KwdatIlOhLimheOBt2wLYtUtEdzc1lW3e7NKrro8+moLSUrL8ysmR8dprAaSmcjhxggJL\nKipcmD9/EJWVZCnW2clj1So34xu9ahVpvRsa/DhzRsCyZSGMG0f+zcXFblRWSsxEZ+bMqB7NrFUv\ntQmHlkDncFB88+HDAiZOVNHcLMBmo8mI1uioXVtZ/hbOniXP59tvH8SlS6wHr9tNemrNfo2t5HPY\nvt2FZctYnXdHB4+JExU8+6xnWL30nj0icnMVFBTIOHZs5BUgbVwVFYUZaUpdnYi0NFbqZMaVTNKN\nE93/+A/WNu7r2tD2ZX2OWPh8YY2L0cEiwRauGJ+1kSQRef7udyMJqz/m1w4McHjggSj2709cOQYS\naX/Js9ZuV7Fvn5+pHmZkUIOaJMWqadu3u7BrF6V+pabS8npjozAURysAYBt3MjJUpKbKkGUeY8eq\nmDpVYchDVVVMd2mWKBh9Ye12Mv03nldyMjkCPPxwBI2NFN9rdALweIDSUmqGGzeO5AWZmQomT1Zw\n4oQNaWkKnE5Vb647fNiOJ5+0oaxMwief8HFSg6wsBefOsdrWw4dtWLAgjFOnBN2WSgsUcblIDtLf\nz2HKFHZbWgWS5BIK6utFtLSw2z5zRohzvHC51DgiqUkKIhHSowJARUUSKisl9PdTg+OyZSFMmaJg\n3jwjgRexbBk1tcUqszQOOzvJQQQwV8eJ1KemKnpld/JkOsdAgMOzz9LqQSjEYfXqGHnfuVNERYWE\nM2d47NoloqeHx9ixCrq6eGze7EJJSZBxURBFoK6OtN48D3R30wRn69YABgeBnh4BkqRgxgwZTU22\nOBnHE08kY88eEQ6HqpNcCvkg7feYMYq+/YwMVfedLioK6dZ82vamTycvaKNs4pNP2HvV0sLj7Flg\ncFDFww+PXHnVvhvMUpL+fg5/+7ejbzgbydZxpIZaCxYsWBgNLBJ8HfBl1ex8Vm1xIvI8XPVnOKI9\nEgE3p0mpKkuijbGsmoNDfb1f315nJw+PR8WDD0Zx5IiAY8c4/UG7f78dK1aEUFkpISNDgctFsohg\nkNcryeZq76VLnE5cd+xwYudOCnFQVSAQ4FBVFUA4DCQnq5Dl2ANdEH6P7OxCLF4cYqppDQ1+SBLp\nRgWBPHMHBng0N1N198gRG2bOlFFW5oDNBlRWBsDzQGWlNBS2oWLJEg+KisKorHQxUoPychdWrw6Z\nyCwwMABMnEi6YpJmUMzx7t0x5wavV8bOnZSGlp8vo6+PG9LhKgiHOV1vbdbTGs+ZtLSIs0wzaqzd\nbqrOk00dIEmc7hFsvvatrdRMaJy0FBTI2LQpgClT6LjWrtUkChj6G3kI9/fzjNZWq8r39vJYty4p\nLpWws5PXSbHZN7iiQsKECSqeeSZ2HPX1IiNJ2L1bhM8XwPjxCoqL2d/v2OHUj9Hl+gNstr9BZial\n8tntKtas8SAnR8arr0p44glW5qAogCCoWLCAGiF/8hOPPonxeACvV8Y998TrfqdNYz9jmn551y5q\nDNSisBsbBagqEImoOH3ahmnTZNx1V2J/75EI6kg9BiPZOq5fn6Rfm7vvvvoGuS8rvqzPEQufL6xx\nMTpYJNjCFeOzaotHQ56He+1I2zBbLNXW+uHzSRgYoL/ZbJrmlyWq+/aRr2tGBjWI/f73NrS0kGds\ndTXpVHNy2DheTdNrtBFL5FygLe1nZ5ON2bPPhtDSwuthDD5fAEVFRE403W9PTxgrVlAinNFSLRLh\nGKJTWyvqKXZGslxVJSI5Gfj4YyEuja6zk8f27U4sWhRCXx8PWQbKy12YN28QTqeC2loRR48Kuo5z\n/XpyGjAHcHR1xSp9zc0CTp4U4PPRcn9ZWRChkIrHH49dH1qaD8LpVDE4SFKFVauCunaZ4+h3r7zC\n6nALCymRzeuVoarAq68GkJ2toLcXmD49yqShGd83ZYqCJUvcuv0cNf9RVDRNFshhQ3NL2LZNxPLl\nITzxROyYNbInCDTmMzJklJUF45LsJk1S9Gthrm4TsY2R7Tlz5Liq/4ULPHbscGH58iDz++5uNszi\nzBkeL79MWvRwmIOqQpftmN0nurt55OQoyMigRL329lgi35o1HlRWBnD+PA+PB5g5M+bykJ8vo7Iy\n3rYvEuF0YqvFjCdacWlo8OP+++P9vUf6rI/UYzCSrWNVVQDnzvG4804r5c2CBQtXB4sEXwd83WZp\nZvIsy9A7yc0VoOGItvb7O+6Qcfy4wHSGmy2WolFu2Id1RYWEYBDo7+cxYYKMKVNkPPxwKqqr2Spd\nXZ2ItjYely6xxOXiRQpJyM+PoqREwsSJqp70ZXQumD8/rJPDXbtoCVvTaAIx0tTWJuDkSRt8viQA\nDwIAMjJYD9pE1U6tys1WoHkkJ8sQBDBkrrWVlusFAbh8GRg7Frh4kcfq1SF9yXzt2iBmzZLR2cmh\nslJCTw83JClw6Uv6BQVR8LzZNUDWr0M0CigKuWC43SSNaGsT8OKLSSgvl6CqHB55ZBAtLQKysxW9\nScxuj4VqdHRQ41dPDzA4SNdHkqA3SNbXi7h8OVax1dLw2tp4TJmioLWVdKm//a0dK1cG0dhow+23\ny0wSnHE8pKWp6Omh66nJOcxkr7ZWxM9+FpOEOJ10bA5HrAHN7Od86RJJDWJkO4DsbFZXHYkACxaE\n9ShoY7XcaGNXVnY/IhHyd66sdAIAqqpEcBw1GxrfO24cpTA2NPjx+OPJuucxxXXTvXvmmWSduPr9\nHO66K4pz5wQcOmTHoUP2hHHJBw/60djIyiU07TeRVAH33y8zn18tHXI4LfFIPQY3kq3jjYqv23PE\nwpXBGhejg0WCLXzhuJq40itpsjNaTUUi1MiWkyOjrU3QtZXG6qlWlTM/kCdNogevMRktN1fBxo0B\nPPYYHcPGjQE9aMLswqBtq72dR28vh8LCxCEY8SlrHOz2GGE2V5q15j+jC4DXKyMtjfS92dmKfszm\nycAtt8iMHZzPJ8FuBzweIsbRKLB0aRKKisJwONjGrvJyCW43vYfjMORh7MJTT4WRkaEymt7qahE+\nn4TsbAUej6o3YGn+t42NAurrRZw+zYPjOL0anJGh4qOPBMyYocDnc+rXfcMGCatWudHSwkNRYtem\nuVnQm7y0Jr6BAWDlyhBWrPAk9E92OICSkiBSUxV0d/MYP56up9ZQ5nQmcl+giu7UqfSedeuSsH+/\nX29SdLtV1NX5ceGCMKQ3Z+/ZhAkkq6ir80OSYkls4bCK3l42ga2rizyGk5OBQIAmAHY7xWNrjXXt\n7QIGBjhMnKgwjZL9/ZxOSiMRbojQu5n7rZ3Xe+/Z9Inavn0xedCOHc6EDiyA2YVD0X83bdqVJ1Vq\nGEniZHn4WrBg4YuARYKvA77ump2riSs16387Ojj8/d9HsW8fxRTn5spx1UqyRgvjxReT4rSn3d28\nXn0zP5AvXOARCJA9Fys7COhyBW072rK/y0VL8pWVLmzdGtBdBNLSVFRUuIakDzadNGkNbzU1Iv73\n//4zHnzwXrS0UEywkZRo70tNJeuy0lLSnNbWivjgA3KGMAdGmJ0o/H4eXV0qc/3cboq9JZ/i2Hvb\n23nYbGAI1owZMgYHgYwMklxQAEcYY8eqcYluJ07EZBL19X6sWUPXxuFgLdrq68mPubJSgt8PLFgQ\n0/qaSfzOnSLcbhXnzrHuCJMnU3BFPOmn5rpEkwjtOCsqnFi5MsREb3u9bMV25kwZR4/Std+82YXl\ny0PYuJGS1l5/3aWHpGzbFgDPqygpSUZOjqyPh3AYusNEXZ3IBHHU1pL7yIsvxo67vJwq1ZoN3fe+\n9zvMnXsfLl7k8OtfD0BVgWPHbMjPj+K111z4x3+MAKBxt2qVWyeldnt8o1pvL/3bPFHTtPNs1Zb9\nTBqJqderYHBQxebNAUybRhrj0X7ORyK6VsX30/F1f45YSAxrXIwOFgm2cMW4FmEZwNXFlSaKWG1s\nFBjf0IqKAKqqAjh1StDlCStWhHDwoB+SxBIijqMI4VAIqK0lQjZpkoK2Ng6TJ8tQVS6O4F26xOGV\nVyT85CfJeuOXtuz/q1+R32pxcQhNTTzT8LRzp4jWVgE1NQ4UFYVx7hyHzEwVa9Yk4ZVXgqitdaKm\nJgV2u4r9+/3YtYvkAVOnsglgZDslQ5Koyux2qzh1ij3GkyeFuJjZ1FQFGRkqnn02dv3q6qgSbnyv\nZremEVkNW7YEsGWLC889F4TDASxbFkI0Sj69EyaophAG6Ns7fNiGlBTosgjjvo4dE+B2A0eOCJg5\nk/xk29oEvTnPLEW5445B3HxzzDM3K0vB4CAwOBj/eq25bscOJ+rqRBw5Qts125pt3uzCyy9LaG+n\ntLWkJLouHR0cxo9X0d1N1frt210oKgoxKwlGaUUkAkydqup6XY5TYbMBaWkqVq4MoaLCFRd20tJC\nzX7l5VSRDwRiFm/Z2Qq+//0U/PSnsYmDuQGvvp78lu+8k0JgXnwxiNxcBbffTnrfYJBtVLv77ije\neENERoaCJUvI99luV5GVpQ4rN9I+48Yoc44D7rpLwT33DH7mz7lFdC1YsHC9YZHg64Av6yztamQM\nRpgrQMa0qU8j14kiVru7WfLT2SkgGFQZecK0aTJ6eqjitXevH729ZG924QJV/7q6ePzsZzFy8etf\nDyAa5XD0qIA5c1gyKUnAxYs2pgJMzUTAmDEqnnqKmqy049H+f/KkgNmzo9iwga3alpaS7ddLL90J\nvz+I/Pwo49+6dWsAL78soauLx9SpMpxOFY2NtrjmN+Mx5ufL2LzZhTffFIcssxSMHavi6FHWY5WC\nHtiJgZbQtn4926wWDJKGNT1dZZLsjESQmvNUrFgRI1hEaIloZ2XFp8GZr8WaNR7s2OHExo3xoRWX\nLtmYAJPyclre377dFRdyMWcOuUJkZSno62P9ls+f5xli/PzzdL6rVrmxZEkI0SjFZxuPTbuWkUhM\nb+10Art3i+jvJ8/htWvJFs3rlePI8qJFoTiLPI6DTkb/+Z9FTJ+uYunSELKyFKSmyti8OQCb7W/0\ne2ZuwOvr4/Hf/3sEx48LaGoS9M/PsWMUXazpmMeMUZGTQ0EYGRkKLl/msGlTAF1dNJGYOTOx3aDx\nMz7az78lafh88WV9jlj4fGGNi9Hhqkgwx3GvAvhvAMIAzgB4UlXVgWtxYBZuPIxGxmCuGlN8L/uz\nIJD+8fe/tzERyg0Nftx3HxFh83aGqy4Zf5eWpiAlJRYzPGWKAo5TsXo1GwzQ3s4jGAS2bXOiqCik\ne8R6vTKcTg7f+16KrretrRXR0kJV4ueec6OoKMxUgHfvJmuqEyeEIZ2vCnPT0sSJKjiOggqqq8lD\nl+OoiqqqQHa2ipYWoKOD9W8VRQrVmD49innzUlFeLsWRoTNnKDSjp4fOSVt+p9hg8q69dEmF02m+\nVlSJNja/NTfT/ik0wugWQA1/5mqmsUHq0iUe48dHUVEhMW4TCxfS9XI4SAbS3i5gwoT4wA2HA9i4\nkXxze3up4nviRKzhcNky1jkjK0tBdzfHhFx4PGSjduEC/U6roLISCqquL1gQhqKQT/Hx4wKKikK4\n5RYZ8+alMA4gkQiHjz6y6fptY/Oc1ytj40YJTz9N2ugNG5x45plQ3DWaMEHBpUsUdhIMcsjLkzEw\nwOGtt/xoaeGRmqoOJcxJSEpSsXBhCpqbBebYzfrx3FwlITnVPquatd3evX5mtaS0NIgXX6T7vnix\nRye0I33GRytjSlTpvVarSRYsWLBwLXC1leDfAVitqqrCcVw5gJKh/yyMgC+rZmc0Mgbzg7mhwY/v\nf5/9+aOPyMpr9WrWIursWUphmzkz/gH/9tsD+kM+I0NBRwdFvRojXgcHVRw/botzBFiwIKwHMLz/\nfqwpaM8eqqIaAy82bowFXlBoBo+SElpGLyoKQZI4VFeLurZ240YXHnlkUI9T3r7dieLiIHbvFvVq\nczSKuECIdeuSUFsrDlU338HWrYVIS1OZ2FlZJh/d9HS6PunpKgYH2XuhKMBjj6XA65Xx8ssSnnwy\njLw8Gb29PHp6iMCuXBmE262gqiqAS5c4RKNAKERhCgMDpPt1OlXMmKEwBL+sTEJJCV2r2bNl8DxL\n7o0NUtnZCr73vVRkZipYtCgEp5M01S0tvG5rtmRJMvbs8cPhUHHzzeZoaw5uN9mPrVzpxrJlIaai\nn5WlMM4Zdju5b1RVBdDdTaTY5VLxyCMsid2+3TXUlMahq4uq35pVms/HBnXU1ZEURbMii1WWo2hv\n51BXJzLkfeHCMKNzrqmJf29qqoJIBGhtFeDzkecwWwEnu7vS0iBEkZwgHn10EKmpKnbu/P+wZ89d\nGBjgMGOGHBdnnCiC3PxZ7e5mJS+xdD8ORkI70mf8amRMw30vWJHHnx1f1ueIhc8X1rgYHa6KBKuq\n+v8afjwEYN7VHY6FGxmjWd6MrxoJcT9r0bB5efGRvJ2dPID4mN+mJgHz5kUAIO5hqv1+/347FCXW\nQJeWpiAnh6qOPp+EHTuccU1BosjuJz2dJXoZGeQJG42CIWB79/rx7LMetLXRcRlDDnJyVPj9wKRJ\nCnp6YtvW/q8RkPPnycu1sZGkBmZP4PZ2HjU1DqxcGUJlZQAej4rx41Wd+OXkEBkpKZFQWBiFIKiY\nORNMJXbRojCiUTbxrK5OhCyDmSzs3esHx6k6eXc4AEUhSUZuroxwGLpVWUsL2cU5HCq2bROH5Ckc\nU4EsKQli+XJa7t+2LYCaGgd8PgmCAPzwh7Rcb/Yo9vkkNDdTY565oi9JrNVcJEK66HCYKrK9vRyy\ns4mIDg7GxlNRUQjt7YLuttDZyevSC7OWuL1dQCgE5OXJesNcfn40TpetjQ/z+zUyrumWMzOJPAoC\nMDCQOFktRkqB229XmKrtE09EMGGCigceiOqVVCMSkVPzZxVgSblm8ZefT4mE2mtG+oxfC3nD1TTF\nWrBgwcK1xrXUBD8FoP4abu8riy/rLG00fr/mB/PUqTJT3bz55iiCQR4lJRIuX+YYi6iWFkGvLg5X\nffo0j1G3W02oNdWaiYya1dxcBYEASxKSk1nrKW0ZWvOU1fbb3Cxg/vwwUlOB3/7WjldfldDWxmPG\nDEpGW7CA9R5mq4Pq0LVRhiqJ38HUqWzj2AcfCHjpJTd8vgBWrSILsMOHBcyeLeta6NWr6fdaBO+4\ncSrjQKBdW7+fJWtHjtgA0PFoGtfmZgHhcIwo7tpFZFdrCjNOADT5RTSKoeqtDIAlnnY7kd+pU6OQ\nJB6PPz4It5sq18XFIT1OOCVFxcAAj4ULQ3A6VV3j29rKx1X0tUq1sTp88SLP3O/aWhHr1iXpgSds\nEhy5RjidwNatAeTksNsLBICSEg9KSiTU1DhRVBTGhQs8Fi8OwWYjKzlZBvbt8+PQIVtcA2JWlopH\nHzVGOfsxOMgNpQaSTZk5xlgbC3ffHY0jyLNm/Q1mzaIJXqJKaiJyav6sRiLQHVSmTJFRUZGEQ4fs\n+qqMRmhHala7Fo1s16KabIHwZX2OWPh8YY2L0eFTSTDHcW8DyDT+CoAKYK2qqv/P0GvWAoioqlo7\n3Hb27duHqqoqTJkyBQAwZswYFBQU6DfsT3/6EwBYP3+Jfv74Yx4lJf+ASIQifzdskPDUU98AAIji\nO/D5eLhcc5GVpeLnP38fnZ0C7Pa5Q1KIP2HVKjdk+Vvw+QJ44YX3IMsc7Pa5KCuTEAq9gz/9ScE3\nvnEfDh7049///c8YO1ZBR8f9OHpUgCj+AYLggSx/C3a7isuX6fX33XcfZs2S8dJLhxCJJAH4JiIR\nDidO/AmAE5HIN9HXx+OZZ/4dFy/yePDBe1FQIKO29s9YvZpHevpcTJki4w9/eBcbN9L7AeDppw/i\niSc4FBTcO/QQfweCoGLixEIsX54CQfg9XnghiOee+w6amwX89KcHEQhwiEQoACMSeQeHDkmorf0b\nfPCBAEX5A86c4VBdfR8++YTHmDH/ie9+N4Jbb72P2f6sWYXYtCmAc+f+Lx54gMO6dd/Rr/fq1UFk\nZMzFsmVBnDr1R/zwhxyys+8dCtN4Z2i/3xxySfjDkIzhIf39PT1hTJt2P+x2FQ899Daef96pX8+V\nKw8O6ZK/ge3bXWhr+yMaG8OIRL6jn8+BA2HMmXMfJk5U0NT0R7S2AnV130FpaRCh0O9x9iyPtLRv\nIjVVwV/+8ie89FLsfj///Pv6/S4vlzA4+A76+zkUFt4LRQHuv/9tnDihwmabO0QI/4BIBPD770JT\nE4aOj0dBwf1Yu9aNBx/8HXO//+f//DP+7u9UOBz3DzWzGa8HnX9fXxCZmXNRUeHCypUH0dfHYe7c\n+7BypRvAH9DTE0JR0d8MEX+6Hy+9dCd8viQIwu/x85+HMHfufejs5LB27UGcO8fj7//+XvT1cfr9\nTEubi8FBDkuX/pc+/nfvFnH27Dt47jke48bNxdSpCt5//4/w+VTce+83cOyYAEH4vX598vIUvPsu\nff46O7/FXI9z5woxe7YMSXoHmZnA7NmJP681Ne/qnzeqLv8fHDrkQiTyTZw7J+CTT/6I6dMV3H//\n5/v9Yfw8T5yoYNasb9ww32fWz9bP1s9f7p+1f7e2tgIACgsL8e1vfxsjgVONvjefARzH/RjATwH8\nraqq4eFe9x//8R/q7Nmzr2pfXxV8VTQ7+/fb8dOfJus/v/GGqEsSAKoSP/QQaTMpES32OgD6e3Ny\nZJSXS+jrI8uwrCwZg4M8U9k6doytgB044AfHUUV4+nQZssyN+HrStXp0DfCECapeMTt+nMehQzYo\nCi2p9/TwSEtTsHYtu/z98ccC0tJkTJig4swZATfdRGl1ra1kxZaaqiAzU8XZszwmT6aQiHnzYsew\naZOESARYvtxjiOZVMW2agqYmHs8//1/IyrofixaFhoISOKiqitdfp6qo2bKsspI8WoNBLq4KanRQ\n0I7d41GQna3ogQ7bt7tgs8Uinp97zqNvu6REgs/nhtcrY/16CSdO2DBnTgQtLQJ6eqg6PnasCkni\nkJmpYOLEKD780IFnn6Vt7N7N+uFWV4v40Y9ShrYdZMZDZWUAskzyA0nimJjq6mqRObeyMgleL8ll\nli6NHa95f2VlQZSUuIdCMVhbvV27qIKdmSnj4kWBuddvveXX9+f1yli+PKSfk/nYKysDqK934Hvf\nG4THA4wbp6K/H5gyRcGpU2x0tVZ9BqjxDyBruc5OHnfeGUFKCvTxO3OmjA8+EHTd+3vv/Ql/+7f3\nJRzXRk1toqYzVaXfNTYKWLYs/v5q12rduqRR6XOtBrfrj6/Kc8TCtYU1LmI4evQovv3tb3MjveZq\n3SEeBLASwP0jEWALX0182tKmJlkwJpsZX6f9rrOTR0qKigcfpFhejTwbH/Rm+UNzM4958yKYPVtO\n+HrzErHNpuKXvxTh93NYsYKcE7SHflcXj3Xr3CgrC8YFTpw8acOtt8ooLiYLrYsXeXCcgm3bXNi6\nVcKzz3p0wrRxY4BJY9u9W0RlpTREjjgoCnR9qNldYNmyEGQ5pqXduDGAHTucWL9ewiuvBLF2rRuv\nvMJagHEckJSkIhTidGnB9u1ONDUJuu+Ya2MAACAASURBVEtCdjbrMbx7t4ikJBWTJqlYtiw0FDXM\nD1UdjcvzdA8XLgzr18TnU+L00C6XCr+fw0MPjR3yuqVtdHWxS/odHbz+N7PDAccB06cr+OQTAZMm\nKbpXcCTCIRDgsHOniL4+mph0d/Po6iIHDOM2PB7S4HZ28rqcQ5MZmH2C16xx4+WXJT31z0hSN292\n4a23yC962jRynjDuJy3NOHaBxYtD6OkhmUMoRA4ffj8Hj0dlzt/hUPWUumnTiOyTnzI1Iz70UKq+\nj9/9jgx2wmHgww8F/Ou/OlFRkTKs9EFDIqkEQNp5zc9a+9vdd0exeXMAoRDZ/I1Wn2s1uFmwYOGr\ngKvVBL8GwAHgbcqxxyFVVRdd9VF9xfFVmaV9WqOMRpK1ONrUVBV5ebHXJdIxAon1vmbCnZys4o9/\nFHDPPcPbOhnN/5uaBKSnqygvT9ITvrTXac1cZi3myZM2VFa6UFYWRHOzgFOnBOzc6cSWLRKWLg2h\nqyvWfJefH8WxY6wH7wcfxFLTdu4Ucfq0gJoaFxoayKXASFzHjVNgt8+FFrfr9SrYuFHCI4+Q53Bz\ns4DnnnMzqXT9/UAgQLHGGsktLZVw880K2tt5JCWp4DhVdxnYv98OVaXz9nhkNDRQsx3pdmMNfYWF\nUV0zbWz6Mtuyvf++DbNny/p5b97s0mOYJ0+Ob3bU3DSyshS89RYFgWRkKEhOJkeJRPrt8eMpjW7i\nRFqx2rzZhWeeCWH7dhdj63b+PI9gkIckUUX5+eeDmDBBRVOTgMWLQ+joYH2CzX7TWrDG8eM2dHTw\nBkcOBRUVAXR2kk59+nRZry5v3+7C0qWhoaY8BTwfc/8wW7JFIoDPl5Swur1nj8gcS1cXj8ceM2qY\n78GaNey4TkQ4E30OtH9rftZJSSoKCmTMmiXD42GbS0ejz7Ua3K4/virPEQvXFta4GB2u1h1ixrU6\nEAs3Bq50mXOk1xn/tm+ff4j4qHHbGu5h7vUqcQRq5kwi3B99xEMUOaxcSdXchgb/iBVpc8XKSLBy\nc6l5LSdH0TvljduZOTOKsjJJryredpuMoqKQTnTeesuvp695vTIqK9lKrdGB4uRJAYWFMsrLk3Dm\njMC4NJSWUrW4rs6PSITcBRSFXBBKS4OYOpWOS7Msq64W46zWNOu35GSgstKlNz2VlkoM+TI6T9TV\niejq4uD1RrFgQUhvArTbySKuuVlgwh3MFdzUVIqxvvXW2PHZ7SSR+MtfbKivFxEI0LL/qVMC3G66\nhgBw6RK5Whw+LCAriyVUycnQ74exiv3rX/vxyitkt9bZSeRfk39kZKh44omY5KG+3o8lSzz6hKe2\n1s8c+9Sp7LkUFsr4xS8k3H67DFkG41tdWhqTQGzbJjKWbZEIB54Hfvzj5DhLtl27RDQ20krCmjVJ\n+vlduGAOfIlty+slCYNxguT3x4/rRJ+/kTy0tbFjrNhejduD1eBmwYKFrwKsxLjrgBtZs3Oly5yj\nTZa64w7SM16JhlAjbxopO3uWh9tNpLmxUUBJSUzbeO6cgPnzB4d9mJsrVikpKjZvJi2tzabiP//T\nplfdtFCM8+dpST0lRYGq8pg/f1AngHZ7rDJqjCpeuDCM4mK3Xk2dPVsearCi8ykokCFJdF6yzLo0\nOJ1Afz+H06f/iFdffYghxwCwdq1bP67JkxVcvGi214pdt0AA+Md/jODQIfvQ32LVwM7OeElJby/9\nbs2a2DXdtCmASZMUeL0yOjt51NSQzGDatCj27vXj/fdtustHRYWEDRtcqKgIIDOTqrWPPx7T5pr1\nybt2iXC7VYwbpzJRwEZClZ6uYNIkunfG0JD/+i8b0tNVpgo8c2YUK1e68eijg8y5tbYK6Ozkh7TX\nIcgyUF9PMoepU6mKbnQkOX2aEgQjEQorMW4rGAR8PgkDAyQvefvtATQ1UdjH8uUefd9G2U9nJw+P\nR9VXEsjyL+albDzfvDyF8b5mQy2oSfTgwfs+VfowHKkd7rNxNW4PVhrc9ceN/ByxcP1gjYvRwSLB\nFhhc6TLnaJOlgHhf3+Eevk1NAkPKSkqC8HiAO+6Q46zWpk2Lt4MyYvp0GT5fQA+DUBRg2bJYxG93\nd+xYm5sFHD1KHwmfLwlbtwaY46isDDAVQLc7RnoGBuj9WvPTCy9IePllCSdPxnSoFRVUhSbJQIwE\neb1kLdbTYya3vOG4YtKK+nq2qjlnDrtEP38+yfOpWhurBk6ebA6mAGpqHNi8mT2ecJjD/PnJTNV8\n714/enpoMjJhgoqMDNIUNzXxWLw4DJtNxeOPJ8elrJFTBasNJpux2Llu3+5CVZWIU6coke3SJQ7p\n6eTt7PXKWLw4BFUlv+XkZBWdnTxef51S/jo7eSxcGGbuhbZ6YLRH05q/jFXwn/889nNZWRDjx1PU\nsVk/e8cdMlN51zypo1Fgy5YAgkEuoexHW73o6ODQ0OBHdzeR3HAY+s9mS7P9+9ngi9RUqp6bx7b2\nGdMaLBsbabIwa1b8a6/W1iwRroVdmgULFixcb1gk+DrgRp6lXeky52iTpUajITS/PzWV4pKPHROw\nfLkHCxeGMTBAXfZ33TVybPOpU0Qka2oc6OyksAztGDTSZd6X5nWbkRH7m9crY9o0GS0tAmprRfj9\nQFISUF4uISODnBKM23G7gZMnWTeH8+d5+HwB7N/vQGmpNOQAQSR39Wo3ysrmDnssRmlFby/PVMod\nDlVfovd6ZRQWyti0KYAZM8ib99VXA8jOVhAMQt9verqCjRvJdaKpidc1y3fcEUVLi4Di4hByclTk\n5MhoaxNw5gw1rbFaVQkcx6Gri+5ZebkUFzJilh0AtG9JEpiqaXIy4HSqura2rU2Ax6PGNRuWl0vY\nuVOEonCMG4TPJw015tH2L13i8PrrTsyfPzg0SWEnGK2tPNMst2OHE8uXhxj9rNOpIjdXRlOTOeiF\nxq7NBtx7r4yTJ3nU1oq4eJFDRgYR8Px8RSeKhlFpHqWfOvbz8hTd9izR64wNllaD2tcLN/JzxML1\ngzUuRgeLBFtgcKXLnJ8lWcr4cM/IoKqsWRIhy4DDoaC+3o+2NmHIfotIRX29HQsXDv/QN+ok45eV\nSTfb28vpx6JVTt98U0R/P4/x4xUkJano66MEt40bXaioIJLb3c3j9GlBD5GorxeZqNz6ej9276Zm\nr4kTFTQ385gzhyU04TCHdeuSUFVFy//t7bzeXGUmX5MmKUhJUdDRQbrqTz4RdHeB8eMV9PbaUFPj\nQFubgNdfF7FzJ6WTpaUpjMzA6OZQW+vH1KkK+vrIqeInPwnHuWGEw5xJrxzEiy8mISdHYarmkQgH\nhwPYt8+OZ5+lxr1IRGuwixH88nLSxra388jIIAux5GSVSdYrKJChqiqcThVdXRwkiYOiUDWYthvb\nZ08PVZKjUVZSoijAtGlKnFaa41T9XrP3graRkgIMDHBYvDiE7GxWe11WFsQPfpCCvXvZynsizbm5\n0vy73w3E2fZdiYXYaD9/jY2JCboFCxYsWPh0WCT4OuBG1uxc6TLnaJOlZs2S0dDgx3vvkZ50yRIP\nqqoCce8/flzA+++zHqsHD/rB80B6uooLFzDsQ9+okywpYZPXtOaiv/7rqG6VphHaMWNUeL0RdHQI\nuHiR4nlfeSUJzc0C5s0bZJrJNDJ95gxLCA8ftjFOEH4/D46T9VQ1WQbq6hxD+lCK9rXbgaKiEDRH\niLa2P+LFF+eiulrEypVuPPdcCCtWuLF7t8gQ0zffFOFwqNiyJYAjR2wYO1ZFdzePixc5XLwYc6gw\nuzlEIqyf8K5drCvByZMCsrJYa6+kJJIOJHLoyMhQsWJFCD/8YbKeEPfII1R5DYdVqCqHBx6IwOEg\nG7RLl6gJ8ZVXkrBgQRh+PzBnjgxAHbo/wLhxQHFxzK6uslJi5CxuNzXemZsns7MVHD/OEkKPR4XD\nQROUri6q/DY385g0SYEoUoMax6lDqXAhrFjhQWlpEDabClmOWYd1dfFx8gUN2gqHudJsdngw+lqP\nRIoTfXYSfV8Yq8xWg9rXEzfyc8TC9YM1LkYHiwRb+ELA80B3N8/IAxJVrc6d4+PIm/a6zEwFBQXD\nV5SNkovUVPZ1t94aRVlZEMuXe1BdLSIa5fDii0EmXMNIWjTSEwqxpFsj01pzkzEe2OeTsH27EydP\nCqipcQxJLaiZqquLGyKIwLZtLl2aYbcDW7ZQo9eJE2E8+KCIVavI+SI7W0ZZWRBtbez1+Ogjsm4j\n5wci3jU1InJygI8/Ht6Pt72djyNqrPyCpATm6/voo6STNTb+5efLWLvWjWeeoSo2LcvHiHpdHTXy\n3XKLjIEBDjNmyAgEOJw/L+CJJ8KQJNI8B4PACy948MorFILR3MySymgUpu364XRStba0VEIwyCEv\nT4Yo0v+Nxy5JwJIlybDb1QSOGjG9c1VVAN3dnK7p9vkkpqrb389j8WJPQqmBNjEwV5o12z3tWp8+\nzWPZsph841rJFqwGNQsWLFj47LBI8HXA13WWdiV649xcBT09XMLX5ecrkCQMhVgIcRVl4/Z37HBi\n714/WloETJmiwOdz4fBhOwBqvNOCNjSYNcvd3RTG8X//r8AcS0EBkenXXnNh504RPA9TpZh0smZS\naCRdMWkGVTdtNsDjUfHgg9/ApUs8KisldHZyGBwk+YS5USs1lf6tqtyQawEHVQW6ujjMmhVBdbWo\np7rt2iWirS1x8MPkybKuBc7Lk9HSwiM5mQh1ezuPcJjTCfjAAMc0/m3ZEsCyZSFEozTZMFdCz5/n\nkZtLBNjpJH20dj3MMo2KCgnRKIf2diLLGzcGdG1xTw97Xy5cEOB0qli/PgmLFoURjXKQZSAU4vDS\nS0n6xCI9neQbmqbZbEtmdM04dYpnJk07djhRX08kXpYBm40sy3p7OUQiQGNjzOUkUfObOQzGbleR\nns5W2EcjWxjp+8JqUPv64uv6HLEwMqxxMTpYJNjCF4YrqVrNmkXWZXv2iOju5phwDZ4HLlwQcPas\nwMTuaoTCuP2MDAVLlniYEInDh+0jkm8z8ZZloKeHY6y0AgEKkHj44Qief96NZctYN4TkZBWbNrni\nLLuMpEurJs+aFUVmpoJbbw3go48EFBezsosPP2SDDjweVY87ttvJVcIobygtlZCeLqC5WcAtt8iQ\nJJagl5dL8PkkcBw5LQBAZqaMpCSVaT6rqxORlaXg8ceTUV0tJqx0BoMUD+xyUXVWc0iIEWwFLS0U\nzyxJHKLRGEk2V/rHj1fwk5+wOmZyd5Di7gtAhHL+/DA4jiQmlZVRrFvnGkqZA0pK4jXN06fLpolE\njKjedVcUvb0c6utFHDsmwO0GVqyghEAAzDVuaPDj+99PYX5mXR5orCoKa01msyVOTbRgwYIFC9cP\nFgm+Dvi6anaupGrF88DMmQqAeJIgy0BGhoLLl4ksaZpejVAYt79/v53xmE1NVfHGGyJycxUUFMg4\nfpzidzWirVX0NNJSUCDj3XcFiGJMN9rZyeNXvxKHmqmgxygbyc1ttynYsIG8gI3OEvn5Ub2xLS9P\nxsGDEV0Xun+/fYgYvgPgm0NEOSbp0Bq1fvvbARw7ZsPy5WQZZvb99ft5HDnCITWVksvMdmU2GzBu\nXIxwUhU2AJ6Pd06YPj2K6moRXV08qqtF9PVxevhDzIptEBMmKCgu9sDrlVFX58eFC0JcVHN1tYjW\n1uFlGpcuxRNkLT76lVckvPmmiI8+ov1GoxweeSQmK6iuFsHzKl57TcTHH9tg9HGORDg4nZq9G6c7\naqSlKcjLi6Kmxo/UVBVdXXTPOzo4vPRSTK5z4oQNgLmCy+qO33svpgU3ShzMY91MikcjW/i6fl9Y\nGBnWuLCQCNa4GB0sEmzhhofm+tDbyzG63d27RaSnqzqhMLtDeL2yTsTIaoped/Ro4uY7I2k5elRg\n3CWqqgJob+cQDHKghHAOssyhrs6hL8FPnEgVv8xMFe++a9ObrHJyFKYie+AAhYc0NvLo6SEJQmqq\nAkFQdfKcny+ju5uauVpbeXi9Mrq6eKxZ40F9vR/z58f72WqWapo0wVy9zcxUMDAQi3pOTVWRlaXi\n7Fm2ijtxooJAgI9zjmhp4Zm0tPz8KHp6eNTV+eF2qxBFDsXFbj3mGSCi2NIiwO1W9ES8/n4O1dUi\nTp0ScOutMjgOwxJkjqPEOW2/JSXSkA47jIEBugfLl7uxZUsAGRmKnloXq7jKaG/nceECu3rwxhsi\nvF4F//APbFXXLDsBWFnDtGnmijL08xxJ4mDJFixYsGDhxoNFgq8DrFna6KC5Ppgrm6LI4TvfiQIg\nAvzuuyxxNQYUdHRwOHKECFJjozBs850Gs0a4s5PDzTdT45axaaq0NBi3BH/ggB+33y7jn/6JrLPM\nNlbNzTw4DjoRz8xUUFwcRE1NIbq7A4hGgc2bXVi2LMQ0c+3cKerEsLRUgqoSmezt5ZCeriI5mc5N\ni3/Wwhs8HiAtTcHZsySTKCqKHX91tcgksBUURLFpkwsPPRQxnT8fl9RWUhKr9tbUiDhxQkhIvsle\njSYPjz/Ons9zz7mxaFFY3+60aQp8Pgk2GxAMkvRj0aKQ/vf8fEqAY/XWQbz3ng133RVlrNfmzCGp\nB0lZ4uUup06Z9cY89uwhLXAkQvu22dhgC+OKgSa5ATAqicOVRpNrsL4vLCSCNS4sJII1LkYHiwRb\nuC4Yjggk+r1GSM3kyuzXeuhQzB4sM1NBOMwhHAY+/DDm76s1riUiRUaYtaiyzKGxUUBycryFmPY6\n7XenT1NT3d69frS387j5ZjWuwtjbS3642tL/0qXJeOEFCbNnRzE4yKG4OBRn+XX6tKBXlwHA7yfp\nwtixKhwO4HvfS9HlF7W11DyYlyejr49e9/rrTjz3XJDZZm8vEdw1a2hJv6yMJB5mp4WpUxXmdbt2\niWhuFvTEsvZ2HoWFMrxemSHfkgSsWZOEoqIQDh+2Mfs+edKGzk6Sm5SUePT9l5R4sHWrCFXlMH/+\nIKZOVfSqtNcrx+mwNemI389hy5bAENlXkJEh49QpG7Zvd6G4OISqqgD6+zlkZ9O46u1lK+BpaSom\nTFCxapULCxaEMX9+GHffHcW998a0vkCsoqsoQFVVYNQShyuNJrdgwYIFC58vLBJ8HWBpdoYnAol+\nrxFScyyt2a/V2OFfVBQypZuRI4Pfz6OmxoHi4hB27SKta14eaYCPHmW7/o2+xjt2OLF4cQgTJ7Lk\nuKAg3qvV7+fw3nvGdDvyqr14kQjrmTMCOE7VK7ba+3p63kFKyr2YPTuK/fvtcTZvbjewbl0S3n57\nALfdJuO99zgAHAYHVaZy3dxMbggzZ0aZhL2tW1mtst2uYtIkcmfo7OQwaxZVTl99VcK2beR+0d7O\n46abFIwfH9VDLzIzyWfX5wsMaXCBTZtokqF58ebkUDxwVhawbBlZyJmv08yZUZSXS5gyhaKw09JU\nCIKKykpKuHM4gNZWFW63in/7N3L68HrluCY8za5t06YA07SmjZ3OTh5Ll8ZI9rhxKngeSElRmOS9\nlBQFs2YpOrG9886Rq7SfVeIwmvREwPq+sJAY1riwkAjWuBgdLBJs4bpgOCKQ6Pff/W4krqnITExy\ncxWsX5+kL4WbK7aaI0NqKulGV6504+BBPx58kOQUR4/Gk+977pGHjlXA1q0BuN0KPvzQpvvK3nyz\nrBPxPXtEHDsWaxorLg5h/XqJ0dXW1bFetfv3+xkSBsS2Zz6fv/7rKAIBDgcP+pGfT1Xr5GS6juEw\nMG4cW22eOFFBby8fl7D3618PMBZzxcVuLFgQhs9HoRyPPUYNdQ8/HMGTT8aOtbpaRH8/h+JiD7Zu\nDSA9XUFRkSdukjEwQKS4rY1HVpaC554jyYTPF2CkCoWFMoJB0inT32MNaVu3BpCWRk1wRm/d0tIg\nli71YNu2AKqqAujt5TBlioKPP6bz/MtfbAnHzoEDfpw+zSM9XUVWlozBQR7799vB8yoAbmivFEfN\n88rnrt290mhyCxYsWLDw+cIiwdcB1ixteCKQ6PefVnGTh35dXBxEejoRq2iUrRbOmhXFwYN+2Gyq\n7gpw7hwxaaPkAogRKABMZbGmRkRxcYyU7dkjQlWpqt3dTRILTXYxZYqM999nSVlrK7uPTz4hBwQN\nb7zxTahqBEePCujrAzZtCqClRcDtt8u45x4ZNlvsfI2SEZtNxccfk4vDhQs8srMVZGfLCId5nD3L\n7rOpyQabDQzp1CYIXV2xhjpJYl0W+vs53H67DJ8vgPHjlTids7aNsWNVLFzojiPH27e7sH59EKdO\n0WRnxYqYnri2VmScNLxeGU1NAlJT6V6S9Rnto7lZwPnzPAYGOAwM8FAU6NeQGhTjx86cOfJQMh07\n2fH5AnjxRTaC+4vAaAMurO8LC4lgjQsLiWCNi9HBIsEWrguGIwIFBSRDOHdOwLRpMmbOZAlCIs3w\nsWMC0+V/4IAff/VX8dvXqsfRKDes5MJIoOKb48yBGlycfGPPHhETJqjo6ODi5Aw33cTKH7xeOW6f\n2vbKyoJMBdeoGzXv88ABPyZOVDFvXoqeYNffTzKPb3wjyuxj8mRyoTDLEt58MwCPR4HPF4AkkTTC\n6K6RlaWgq4vHunXk/mDWZ996K6XbtbaayTGGdMOhoYkC0NnJMe4RTU08U/E2NjdqISMxmzkJWVkK\nKio8eoVZO44dO5zYt8+P8+ep6muzqXqaoAbjPd2+3YU9e0QMDHBfaNraSJO60TbNWbBgwYKFzw6L\nBF8HWJqd4YlAY6MQp+s0viaRZvj0aZacnj7NY84ceViioRGhnBwZK1cSOevro8Qvv59DVlbMds1s\nt2X8OS8vnigPDHB44IEojh4VsH27Xa/OTp8u4667WGcBny8md7j77ihE8R10d39L345xu6dO8UPE\nWsXZs/FuEwA1A27YIOHECQEAh6efTsK2bQFd25udraC/n8PYsao+0cjNleF2Kzh5kjTIRtcFoy9w\nVxcPv5/DHXdEMWdOFB9/zGPnTvIRDoep+a2zk9fDNYx63S1bAmhqEvSEvClT2AnH7beT/dudd5KL\nh9HCLSNDQU0NWbAdPkz67OXLPViwIKxXmI1EFsCI8cS5uWSdp+mkXS4V3/529IYhmonGtyS987X/\nvrAQD+s5YiERrHExOlgk2MINhU9rGkr0dy1iVyMO6enqiPvQqr5FRWFIEmvbZSRN5mq12R6ro4ND\nRkZiWcesWTJKSoJMVVOrEn/3uxH85jd2HDpE/wHkW5uZGTu21FSVIWvjxqm4eJHHU0+54/yBtX0W\nFYVMCXJBnD/PY/x4agS7eJHX455lmdLtkpOBWbNUFBYOorbWzlzb9nYePl+Srgm+dImPs22rq/Nj\ncJBcHGbOjGLjxpiN2pw5URQXu/HSSxJDrn/1KzGuwVFVqSlSa/7TXtvQ4EdyMhhiqE0cAAoMmTBB\nxQMPkLZ7/377sONHk82sWBGEKHKoqXGhsjLphnJnSDS+MzOv80FZsGDBwlcUFgm+DrBmacPj05qG\nEv3dZlOZBrPMzJEbjTRy29gooKtreNKdqFqt/VsjZV6vHBedq73XvO1jx2yorHQNK7+YPfs+KAod\nW0cHh02bAvjBD2Lkb+vWAMrKgpAkoLpahN/PYfr02D7Nvrd+P5Cbq6K9nUdvL4fCQhmvvy6ip4fH\nD38YT/zNk4nsbAX/8i8USNLYKCAlhYi4cR9nzwro76cQjX37/Dh+3KbHU//bv/mxYEEY/f3se/r6\nKPTjjTdEJpzkoYdSsHo1a+F24QIPhwNx53X33VE9AdAoYxhp/JirrJpe+dPcGb5IDDcuLFgww3qO\nWEgEa1yMDhYJtnBD4dOahob7ezQq49w5Ig2ae8Jw0MgtALz/vlny8Omd+mY7snPnBBQUyHH6TTOh\nSU1VR3S8MB+buaqZnq5iyZJYlXT3bpE5p7w8dn/5+TK6ujisXm1sVKPJgnG7LS0cAAEOBzuZcLlU\nOJ0qQ8Tr68U4opyTo6ChwY9wGNi714/WVpJZjB+v4MUXk+IkEmlpSty11q6p2w3Ta8m71/i7wsIo\nOjrIfWLmTBmqCsbe7u23B9DUJMSNH3OVVWvmu5HcGUbbNGfBggULFj47LBJ8HfBl1ux83o07n+YE\nMdzfr8TWynzsM2fKcDgU1NdTJPBNN8U34iWCmdxOmKDi/fcF2GwqZs5UmP3s2+dHby8HpxNoaaFG\nrltuieLYsfhrqI0L7f3m5rOODlYn/MEHscry7NkyU+EOhTisWuXG/PmDJuLHx23X5aLKdmamgkWL\nQpg0SYYocli82IP588PM+8+f51BfT569U6YocLnIgWHRouQ4O7YDB/w4eNCPQAAMuU5Opupzogqu\n5gVN1V/SOefnKzoxnDBBwfLlHr1hT5NLPP00+SGfPcvj7ruj+O53Iwlt9BI5htxIRDPR+P4yf19Y\n+PxgjQsLiWCNi9HBIsEWRoUbKe1qNIQ8UayyZon1yCOJNcEj7evttwdw/LhNT0Tr7KTIXUCJu0YN\nDX4sXaqFVnDo6eEZIjdc819mpsJoZwG2SmqsLM+eLTNVZG3/5mQ8zcZNI5p2O6AowC9+EYTXK+PU\nKaqgbtiQhLY2Ic7hIhjk0dcH/PjHg/rx7t9vR3OzENfM19xMyXkffMDelDFjaLJghLECmpGhYGCA\nGhTz81mLvF27HIyzxLlzlOJnJuCJ7mOiKquqIuGE5GphuTxYsGDBwo0PiwRfB3yZZ2mjTbsaLUZD\nHkZDyM2xytqxa//+tPNJtC9BUFFSkqy/prubthN/jYQ4klZVFUB7O4/t2536PrVxob2/rU1gtLOK\nAjQ0+PHJJwIiEbL4SrScbyR7M2bIOHDAj+bmmKdwWloQGRkKliwhYl5cnIyysqCpqY6syXbscKK+\n3q87M+zY4UR5uYSjRwWdRGZkKCgpkeIS8LTjampi/ZA3bw4gGo3JR8z3vKBARmOjwPg4a2Ng2jR2\nH9OmyUhNVXH5Mvep9zFRlTVRxBgI7wAAIABJREFUSMq1GM/XcrL4Zf6+sPD5wRoXFhLBGhejg0WC\nLYwK1yLtaiSim4g83HGHnPD1oyHk5lhl47Ffyfkk2pdZg6tVa83XaNo0OY6AnzoloLKSKrJX0vwH\nEIm77z4ZY8eq6OzksXp1MC4+WnudmexpYREAMHOmAkUBqqoCeuiFuYqbnKzqUca9vRzmzJHR3Mxj\n4cIQiovd6Ozk9Uq6Vl33emXU1/vR18fqWc3nEwqRT/NwUdn79vnjKvbaudxzD+sjfc89Mj74gCYF\nn2Vcfl6Tus97smjBggULFq4eV0WCOY4rA/AwAAVAJ4Afq6p68Voc2FcZX2bNzrVo3BmpSjZcclui\n14+GkJtjiO++O6of+5WcT6J9DXctElmrAYmlDB4P9Pdp42Kka8zzGJISjEzyPq2ibpROaMdjPL7M\nTBXPPuuGzyehqIiilAHA50vSt2GupDc3C+jrIwmEEdr5fPIJj5QUFadOCSgrC6Kjg4Msx7tadHTw\nuldwWpoCv58kF9p53H8//Wc8DpJ4kDXbrFnRKx6Xn1eE8bXc7pf5+8LC5wdrXFhIBGtcjA5XWwl+\nVVXVdQDAcdxiAC8C+PlVH5WFGxbDNaaNRsYwUpXsSpLbtNePhpDPmiWjqiqAc+colMF4fFfSVJdo\nX9q10CrVv/lNjKiZt3nvvfT+jz7iIYqcLmXwemPHoSisy0Gi5q4rxZUux2vn1dHBMVZvDgelxwkC\nUFYWhMOhYnDws1XStesUCICp8O7f78e778Y3AGZkKFi8OBZ4oUkzhjuP3FwFnZ081qxx66+50uv2\nebkxWC4PFixYsHDj46pIsKqqouFHDz6tPGUBwFdTszMaDeRIVTJzg5QWSGGM8DXKA66EwI72taN9\n/5Wcu/b+mTNlvPuugBUrQvpyvobk5LnXTEd6pcvxxoowIebbawy4qKiQkJREtmy9vRxuv12GLHO6\nA4bWyGYme4ODwHvvCTh7VoAgqKbGOQErVrj1BkCHA5g8WUFvr9nKLFZxTnQeiQjnlU7KrnZcDIdr\nud2v4veFhauHNS4sJII1LkaHq9YEcxz3MoDHAVwC8K2rPiILX0qMRgP5acv9ZocDzWHBHEjxWfB5\ndO2P5txtNsQt53+W7WjncuIEj64uHt3dnK4P5vnhJxpXev7mY1FV/P/s3X18VPWZN/7P95yZPExC\neM4D4SFYUawgKbC1Vqt2uXu3dl+/3V9ru1tta7VqWU2rIsEabLGJq0EhIkV83axxCaCABdbdvX8v\n6ertKhZdvNU0CFQeVMJjSAKGZB4yyeSc7++Pb86ZOTMnTyYwgfm8/4EJkzNnJl8y11zn+l5Xd3Ap\nEAioGuLYrO6WLX7XY733XrQjR2VlMKFfcOwGwLKyEIqLE/sC5+REM869ZZrPx4Y3IiK6ePQZBAsh\nXgcQO7hTAJAAHpFS/m8p5W8A/EYI8WsAvwLwO7fjbN26FdXV1Zg8eTIAYOTIkZg5c6b9qWXnzp0A\nkBK3rb8Pl/MZitutrTug6z4Yxjfh9Uq0tu7Azp2m6/01DQiFdiAvD/Y0rPjj/fGP7yASyQRwIyIR\ngZ0738H113f1eP/+3vb5rGzrDui6xH/+5xzMnm0M6vlPnWpC19+EYQgUFX0DubkmnnhiF/LzTdx+\n+9ftHsB9He/DD/fC630YkYiArr+J1tYQgK/3eP+DBzVEIjd2Z2zV89m2bQ6amzW0tu7AU09JZGff\niKlTTQQCO7BzZ/+ff/zP0zDewocfAmVl30UkInDrrX9EJJJh/3z+8Id38cknBn7+c+f5fvbZX3cH\n02+hqspAdfVXsX+/B6dPv4WDB014vd+1n29WVgjFxer7KytfxalTGr7znWvh8UiUlm5Hfr5p/3tf\nr2f8+vnjH99BKNT1hX6+hgGsW/eufT7FxQbefZe/L3g7ubf37NmDe+65Z9icD28Pj9up/PvC+vvR\no0cBAHPnzsW8efPQGyGl7PUO/SWEmATgVSnlTLd/f+ONN+Ts2bOH5LEudDt3XnyF66Y5tP1Wz1Um\nb9s2L+6+O9rW7PnnAwkbuQYq9rlPmGDgo488aGtTgyGuuaYroSduT95+eyeys2/o92u4bZsXn32m\nOzarlZWFUFnp6/E16+35x2eJPR7pmLz2yivR762sDDlavlVUtGPcODPhtfzTn5y9mV9+2Y+TJzX4\n/QLbtqXh+9/vtPsgWy3XhiJTP5Tr51ytxf5m5S/G3xc0eFwX5IbrIqq2thbz5s0Tvd3HM5gHEEJc\nKqX8pPvm/wvg48EcL1VcjAt0qGsrz9XGonPRDSD2ub/+usdRS2sN0OiPa6+9Drt39/9xp041cfq0\niCsdUP/WUzlFb8/frbY5NqiN/d41a9Lx8st+vP9+tH9wdXUw4RzdWpppmoG6Oh3jxnUkBH+9BZwD\nKWUZyvVzrtqd9beO/mL8fUGDx3VBbrguBmZQQTCApUKIy6De5Y8A+MfBnxLRuduwdK537Tc3O/vt\nWgM0+mOgAxaKiw14PCrQbm4WmDRJDcAAeq6f7e359xXsubV+y8lR31ddHXR9LXuqge7pZ9vbOQzk\n9RnK9XOu2qixlzARUXINKgiWUv5gqE4klfByRfKcq+Da0tMAjf5Qdaw3AehfUBTfM9gagHH4sIai\nIlXOENtfV9N6f/59BXvxlVN9vZaxmduiInXs2PIKtyxub+eQrKAx2Vcl+PuC3HBdkBuui4EZbCaY\niGIMJmDKz+89KOrvAIzZsw3U1ur41rdyBlTH2te5DzRTHX//vvr99nUOViA91BnZvlyoVyWIiKh3\nDIKTgJ/SLl6DCZhuv/3rKC4emiC0p6xpb4F0X+c+0Exs/P376vfb1zlYgbTfrzYdejxDs6k3Wfq7\nVvj7gtxwXZAbrouBYRBMNEwMZRDa06X2gWZz+3PM/t6/r36/fTl0SPUTtjz/fKDfnTeIiIjiDXJM\nAH0RsT3tiCx9rQsrqAT6DiStS+3PPx/A9u1+O6vsFkj3V0/H7O/9r7mmq9/f62Ygz/9iwt8X5Ibr\ngtxwXQwMM8GU8s7FFLlzYSA1pD1llQfT6WCgpR5u9x9M5pY1tERENJSGbFhGXzgsI/kulGDvfEul\nEbtDPdSEiIhoODrnwzLowjKYetCeXAyBdSr1az3XLeKIiIguFBdYuHJxSFbNzmDqQXtiBdZ3352N\nm24agbo6fdDHPN+GS60pa7nIDdcFueG6IDdcFwPDTHAKOReTry6GLCprTYmIiFIPa4JTyLmoB02l\neloiIiK6MLAmmBzORT0os6hERER0IWJNcBJcTDU7VmB9880RzJ594W2KG04upnVBQ4frgtxwXZAb\nrouBYchCRERERCmHNcFEREREdFHpT00wM8FERERElHIYBCcBa3bIDdcFueG6IDdcF+SG62JgGAQT\nERERUcphTTARERERXVRYE0xERERE5IJBcBKwZofccF2QG64LcsN1QW64LgaGQTARERERpRzWBBMR\nERHRRYU1wURERERELhgEJwFrdsgN1wW54bogN1wX5IbrYmCGJAgWQiwUQphCiDFDcbyL3Z49e5J9\nCjQMcV2QG64LcsN1QW64LgZm0EGwEGIigG8BODL400kNra2tyT4FGoa4LsgN1wW54bogN1wXAzMU\nmeAVABYNwXGIiIiIiM6LQQXBQoi/BXBMSsn8+wAcPXo02adAwxDXBbnhuiA3XBfkhutiYDx93UEI\n8TqAvNgvAZAAfgNgMVQpROy/uaqrq8O6devs27NmzUJxcfFAz/eiMHfuXNTW1ib7NGiY4bogN1wX\n5Ibrgtyk8rqoq6vD7t277duzZs3CvHnzev2eL9wnWAgxA8D/ARCCCn4nAjgB4KtSyqYvdFAiIiIi\novNgyIZlCCEOA5gtpWwZkgMSEREREZ0jQ9knWKKXcggiIiIiouHivI1NJiIiIiIaLjgxLsk4aIRi\nCSGeEkJ8LISoE0JsE0LkJPucKDmEEN8RQuwXQhwUQvw62edDySeEmCiE+C8hxD4hxB4hxH3JPica\nPoQQmhCiVgjxH8k+lwsFg+Ak4qARcvEagCullMUADgEoS/L5UBIIITQAzwL4NoArAdwihJie3LOi\nYaALwINSyisBXAOghOuCYtwP4C/JPokLCYPg5OKgEXKQUv4fKaXZfXMXVNcVSj1fBXBISnlEShkB\nsBnA3yX5nCjJpJSnpJR13X8PAPgYQGFyz4qGg+6k2ncBVCf7XC4kDIKThINGqB9+DmB7sk+CkqIQ\nwLGY28fBYIdiCCGKABQDeC+5Z0LDhJVU40avAehzWAZ9cUM1aIQuLr2si0eklP+7+z6PAIhIKTcm\n4RSJaBgTQmQD2Arg/u6MMKUwIcTfAGiUUtYJIW4E44l+YxB8Dkkpv+X29e5BI0UAdgshrEEjHwoh\nOGgkBfS0LixCiNuhLmv99Xk5IRqOTgCYHHPbGkZEKU4I4YEKgDdIKf892edDw8K1AP5WCPFdAJkA\nRggh1kspb0vyeQ17bJE2DHDQCFmEEN8BUAXgeinlmWSfDyWHEEIHcADAPAANAP4vgFuklB8n9cQo\n6YQQ6wGcllI+mOxzoeFHCHEDgIVSyr9N9rlcCFgTPDxw0AhZVgHIBvB6d6ub55J9QnT+SSkNAL+E\n6hayD8BmBsAkhLgWwI8B/LUQ4s/dvyO+k+zzIrpQMRNMRERERCmHmWAiIiIiSjkMgomIiIgo5TAI\nJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkM\ngomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIO\ng2AiIiIiSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo5TAIJiIiIqKU\nwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo\n5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIi\nSjkMgomIiIgo5TAIJiIiIqKUwyCYiIiIiFIOg2AiIiIiSjlDEgQLIUYKIbYIIT4WQuwTQlw9FMcl\nIiIiIjoXPEN0nJUAXpVS/lAI4QHgG6LjEhERERENOSGlHNwBhMgB8Gcp5ZeG5pSIiIiIiM6toSiH\nmArgtBBirRCiVgjxz0KIzCE4LhERERHROTEUmeA5AHYBuEZK+YEQ4hkArVLKR2Pvd88998hPP/0U\n+fn5AICsrCxceumlKC4uBgDU1dUBQErctv4+XM6Ht4fH7U8++QQ/+MEPhs358PbwuM3fF7zN3xe8\n3d/bqfz7AgB2796NU6dOAQC+/e1vY+HChQK9GIogOA/Af0spL+m+fR2AX0sp/5/Y+73xxhty9uzZ\ng3qsi8XSpUvx8MMPJ/s0aJjhuiA3XBfkhuuC3HBdRNXW1mLevHm9BsGDLoeQUjYCOCaEuKz7S/MA\n/GWwx72YHT16NNmnQMMQ1wW54bogN1wX5IbrYmCGqjvEfQBeEkJ4AXwG4I4hOi4RERER0ZAbkiBY\nSrkbwF8NxbFSwa233prsU6BhiOuC3HBdkBuuC3LDdTEwg64J7i/WBBMRERHR+XBeaoJp4Hbu3Jns\nU6BhiOuC3HBdkBuuC3LDdTEwDIKJiIiIKOWwHIKIiIiILioshyAiIiIicsEgOAlYs0NuuC7IDdcF\nueG6IDdcFwPDIJiIiIiIUg5rgomIiIjoosKaYCIiIiIiFwyCk4A1O+SG64LccF2QG64LcsN1MTAM\ngomIiIgo5bAmmIiIiIguKqwJJiIiIiJywSA4CVizQ264LsgN1wW54bogN1wXA8MgmIiIiIhSDmuC\niYiIiOiiwppgIiIiIiIXDIKTgDU75IbrgtxwXZAbrgtyw3UxMAyCiYiIiCjlsCaYiIiIiC4qrAkm\nIiIiInLBIDgJWLNDbrguyA3XBbnhuiA3XBcDwyCYiIiIiFIOa4KJiIiI6KLCmmAiIiIiIhcMgpOA\nNTvkhuuC3HBdkBuuC3LDdTEwDIKJiIiIKOWwJpiIiIiILiqsCSYiIiIicsEgOAlYs0NuuC7IDdcF\nuTnf68IwgNpaHdu2eVFbq8M0z+vDUz/x98XAeJJ9AkRERDS87d6t46abRiASEfB6JbZv92P2bCPZ\np0U0KMwEJ8F1112X7FOgYYjrgtxwXZCb870uDh/WEImo8spIRODwYYYPwxF/XwwMVzERERH1aupU\nE16v2kjv9UpMncp6CLrwMQhOAtbskBuuC3LDdUFuzve6KC42sH27H88/H8D27X4UF7MUYjji74uB\nYU0wERER9UrTgNmzDdYB00WFfYKJiIiI6KLCPsFERERERC4YBCcBa3bIDdcFueG6IDdcF+SG62Jg\nGAQTERERUcphTTARERERXVTOa02wEEITQtQKIf5jqI5JRERERHQuDGU5xP0A/jKEx7tosWaH3HBd\nkBuuC3LDddE7wwBqa3Vs2+ZFba0OM0Vme3BdDMyQ9AkWQkwE8F0AjwN4cCiOSURERPRF7N6t46ab\nRiASEfB6JbZv97PHMSUYqkzwCgCLAJyfAuMLHGd7kxuuC3LDdUFuuC56d/iwhkhElYNGIgKHD6dG\nHwCui4EZdCZYCPE3ABqllHVCiBsBuBYhb926FdXV1Zg8eTIAYOTIkZg5c6b9A7NS+LzN27zN27zN\n27zN24O53dqqwev9LiIRAV1/E62tIQBfHzbnx9tDf9v6+9GjRwEAc+fOxbx589CbQXeHEEI8AeAn\nALoAZAIYAeBfpZS3xd6P3SGidu7caf/wiCxcF+SG64LccF30zjSBujodhw9rmDrVRHGxAS0FksFc\nF1H96Q7hGeyDSCkXA1gMAEKIGwAsjA+AiYiIiM4Fw1A1wPEB7+zZBuuAqVeDDoJp4PgpjdxwXZAb\nrgty47YuegoGL3bcBBfF3xcDM6RBsJRyB4AdQ3lMIiIi6luqBoNum+BS4XnT4KXAZ8ThJ7aIm8jC\ndUFuuC7Ijdu6SKWOCLF9gHNzTXi9an+T1ysxdWqKNAV2wd8XA8NyCCIioovA1KkqGLQywRdzMBib\n9S4qMrBlix/NzdEyEKL+YBCcBKzZITdcF+SG64LcuK2L4mID27f7HTXBF6vYrHd9vY7mZg033xxJ\n8lklH39fDAyDYCIiootAKnVESKWsN507F2/B0DDGmh1yw3VBbrguyE2qrwsr6/388wFs3+6/qLPe\nA5Hq62KgmAkmIiKipBtIi7ehynqnals5UgY9Ma6/ODGOiIho+IoPCGfONLBnz/kLEGtrE1u8zZpl\nDDhIHUhg6/aYqVBOkgrOy8Q4IiIi6tmFkm2M7zO8ZYsfP/zh+QsQe2rxNtAgNf55vPhiAGPHStfX\nvacewxfKz4wGhz/SJGDNDrnhuiA3XBcXPisou/vubNx00wjU1emOf4/teVtbq8PsY4+XYQD/8i/v\nut5/oMeKlRgQ6ue177C12Q2I9vv9Ir2P47+nrs7T4+veU4/hvn5mwxV/XwwMM8FERETnUF8TzXqb\n9BabkczNNdHWJpCTI/HrX/tgGNkJ9+9ralxvGc74jguXXGKc1w4Mbi3egkE4ziE3N/Ec4p/TtGnO\n887JkT2+7vffn4Xy8nb4/cDXvtZlb7DjFLrUwCA4CdjHj9xwXZAbrosLn1s7r9jALSdHYtasLtx8\ncwRtbQJnzgiYptr8FR/UWgGbYXwTQGKANpiAOz4Iveqq89t32G2zW1ub6H7OKvhva0ss8Yx/Tq++\n6sf27X7s36/B7xdYvTrDNYg/fFhDfb2OxYt9AIDnnw9A09RjX6gt2Pj7YmAYBBMR0bBxvmoxz2fN\np1uGs67OGbitXRvAHXdkJ9Sxxge17e3AjBkGyspCyMkB1qxJdwRofQVvfdXANjQI5OaadtnBzJnR\n4Np6LuezNragQOLnP890BO3x4p/TgQMa0tPV62SawCWXhNDcrP7d+nAB9P5apdLgkVTGIDgJdu7c\nyU9rlIDrgtyk2rqIH4e7cmUQTU1DH6ju3q3jrruyMH9+Bz77TEMwCFx7rfvx+wqY3f5dysSvWcFm\nXZ2OPXt0VFS0Y/XqdBw/rqOpKbGOdfnyDGzd6ncEatOnG7j99mxEIjvg9d6ALVucPXL7Ct56Cvys\n172ioh1LlkSDzq1b/fjBDxIzx7FBc06OHPKfUezx+xqJHP+c/H6BX/4yyz7/n/wku1+Z7+LixA1x\n3/te5AutiWTp7ffFcD3nZGIQTEREw0ZsVm/+/A7XAGyoHmf+/A5HwNfT8fuqs3X7dyCxq8GsWQbe\nfVfHrl0eO4t7770dePTRTHzpSwYqK4Noa9OQk2PC51PBcFubsAO13FwTDQ3OYLm5WbMv4QN998/t\nKUi2Xve2NuE4fn194ua42bONHoNmt9fQLWC+9FIDhiF6DMj6es17ek45ORILF/rs8/3sM+f5796t\nIxgErrnGgHBpntXfxx3I+Q0XF+I5n2sMgpMglbI61H9cF+Qm1dZFbFavrQ3nbHPS1KkmPvusf5uf\n+qqz7amDgdvXYoP68vJ2ZGaqYMTjkViyxGf/28qVQVRWBtHaKlBQIO2MZG2ttVHsxgHXqlpZ6AMH\nNIwfL+HxROcEWK97To5M2IjmljnuKWh2ew3dAubKyqDj+cZnmD/5RENFRbu9EbChITFidcva1tXp\naGxUr7Xb5r7OToEf/GAEtm71Iysr8YNKfzfEDdeNc739vhiu55xMDIKJiGjYiM3q9RSADZZhAB6P\nxNy5id0POjuB997T8dlnOi65xMA11xh91tm6/btbV4P4IMTvB776VZW13bbN6/i3vDwTra06TpzQ\n4fcLeDwSV11l9lnu0FtpxpkzwlEaUF4eQleXenzruJ99pmHt2gAOHNDh80n4fNHg0MrebtvmRW6u\niaIiA/n5JqqqgpBStRsbN8501N0C7gFzW5t7QGYFzDU1AfzqV9EM85YtibXAbpnN4mIDr73WhqYm\nDc3NAiNHqo1yn3yissT796sylMZGDUIkflDpz4Y4q7VaT3XZfa29ZJUkXKib/c4lBsFJkGo1ftQ/\nXBfkZriti3PxJu42qQxQwdPWrX60tQlMnGjaAdhgH3fvXg27dnkgpcDatQG0tgpcfrk65jvv6I5s\n7ZYtflx3Xe+Bp1tgun27J6GrQXwQ8rWvdUHXJV5/3YNwGKiqCmLFigw0NqoAMTZT+uKLAQCmXe4Q\nCu3A7NmJ68Jt4MWoURI33TQCpaXhuCBcw+HDErNnq0AZAHTdOUV25EiJK69UwVJTk+YIords8cMw\ngB/9yLnB76WXPCgqUh8gPB73LHNOTvS1KCoykJtrYts2L3JyJPLyTOzfr8oYJk40UFLSgcOHdWRn\nOzfmNTSIhGzx7NmAYahgPy/PRElJGCNGSBQUqDKJ+nodXq/Epk0BjBolE4LC/myI273buUbWrw8A\nQELw7+ZclyT09vuCm/0SMQgmIqJ+Oxdv4vHHdNuMZRii348bf9m/oMBAZ6dmv/n7/UgIMK1jxdeQ\nHj6s4/rrDbvO1jp2fKY1ntXVwArEWlsFJk0y8eqrftTXq+/VdYlduzyOc9m4MYDRoyX274+v/RWO\n53fwoIbGRucHAsNAwve9954HxcVGd+DpDPpyckw7G7h3r4b339ftmuRZs7qQlgZcfrlp1zGPHSsT\n6pE7OpzZ1H37dFRW+lBUZGDVqgBCIZWR3bbNj3AY2LLFb38wePrpIMaNk8jMlHFlIiEIof5eUuKs\n2371VT/mzFE/q5wc6fg3K1tsZZ7V9/pijtuOxYvV7cZGgRtv7EoICvuqqY49vvWcP/pIbWLsz/+F\nZJYk9Oe5pRoGwUkwnLI6NHxwXZCb4bYuzsWbePwx4wPRPXt0TJhgIi/PxPHjep+Pu3u3ju9+t+f2\nY+vXB3oMMONrSKdMMRwZvthg8fRpVabQ1ZUYoM+caWDrVj+OHNExapSJlhYNt9+ejerqIG6+OQIA\n2LjRm1AW0NgoMG9eFwBnOcX06dFSDbVZ7UaUl6ussRV87d6tSiecgS7Q3Kz+vnp1OpYuDcHrVZnR\nrCwThw+rSWjxHwyqqwM4eFCDlNE65srKYELm9MyZxMcD1KbGvXs9rnW/tbXODz2VlSHHa5CdLSGl\nxB/+4MexY4ntz+bMUR9GwmGB0tIw8vNNdHXBzhZbwzLi65X93RUVXq/E5ZebXzgojM/o9zSMoz/f\nO9QlCcPt98VwxyCYiIj67Vy8ifc1qSwcVpe3y8tDWLw4q8/HjQ+qT5503o4P3KZPV8cyDCAzU5Ul\njBsnkZ0t8fzz6cjJ6bCDm6YmLSGLHBts5eWpwHDLFq89qKGxUdXZ/vKXYccgjPHjJfx+53MfP16l\nlYuLDbz6qh8HDmjIy5MIhyXefNOD226LBvNr1wawb5/HPubhwxpWr86wyzCuuMLAkiWZWLkyiDfe\naEVDg47mZoEvf9nA2bMCf/d3OQkfDKzyg9OnNUycKB2jk1evzkB1dQB+v8D06SpzunevhqVLQ5AS\nKCoyUVqqOjO0tQGA83Xfv19l4zs7ndnjvDznaxAMCpSVqZ9zTU0g4fWprXXWN8dvsrOGZcT/nL/2\ntS48/3ygX6UAvZX9WGUFfQ3jcMOShOGFQXASDLcaPxoeuC7IzXBbF+fiTbynSWV79ugIhwVWr063\nL+f3J4iJD6oLC82EoDf28WbONBICK+uy/A03dOHMmWgt8unTorvEoQNtbQJSwjGmt6QkHHcMdQn+\nyBENmiZQV6cjI0Pi2msN5OWZ0DSVdW1uVhu18vJUIKVpgBDAggVZ3V0VsvHYYyG7Bvb06R04ceIb\nqKzMtLOsl15qYNGidoweDTQ1CWRlmVi8uB2ffKIjLU3DmDESbW0aGhqkXXMLOD8YxJcfvPxytE+x\nxwOMGCERCAicPi3wpz8A70vzAAAgAElEQVTpGD1aYs6cLhw6pCMvz8AzzwRx+LCOKVMMHDigO153\nv19g6dIMPPNMyPH1kSMl1q0L4ORJDXl5JsrKoi3OjhzRY4L6LowebeD9973QdaCioh3btnnh9TqD\naqvcpLMTjh7DM2ca2LNHfVgIBtU0uoIC6Vpf3lvZj1X+kp4OTJpkoLIyZB+nL+e6JGG4/b4Y7hgE\nExFRv52LN/HYY8Zm4C65xHDUik6fbvbrcWOzqOPHS0yYYDhqcWNrPwHYl+fdNo6NHWsmbAYrKQkn\nZB63bPHjvfc8CQGZVZ5QVGR2D7lwToTLzzdx6pQqmRg9GtizR0dzs4a8PMOu721rU4H3tGkmfvQj\ndQxdT8fLL5uYOFE9hzNnVI1uYaHELbdEH6emJoCSkixH6cHRoxq+/GUj4YPBq6+qDx6xGeGjR3VH\nHW987a7PF82AdnRouO46A9dfr0pIxoxRNc6nTgmMG6f6Ay9aFMbx4wI1NQGcOKGhsFC1qnvggWz7\nfGNbnKWnq7ZmgITPp7pKxL72NTVqU1pRkWFvesvNNV0D2PgyjPLydvz855mutby9lf1YAXL8xjuA\nAykuNAyCk4Cf0sgN1wW5uZjWRU8BQuzXc3NN3H9/FurrdRQVGX1OC3OjacCcOYa9gar70eNuRx/X\nmt7m80U3jhUVGZgxowunT6vL/R4PcOqUBsMAxo0zHYHi3r2qZvn1171YsCDsCC5nzerC5s0B1NU5\nM6/WRLjXXmtDWprE2bM6mpvhKJ+wAuicHIkFC8L44IPoMQzjm/jwwxDuvbcD6enSDtTLykKOczt1\nSnNMpgNU7e+sWV1Yu1YFnEVFBq66SnVyEAKOjLAV6Pl8QEtLfICvYfLkLkdgbG1c0zTgyitNvPuu\nwMmTOgIB1UrMei1jA/WNGwMoK2tHTo6Epqns85EjOi691IDHY6KuzgtAw6FDGrKznZvz9u5Vr6NV\nGlJc3OXau3jWLMOxaTAvz8TEiSZKS50lKpbeyn562njX05CU87kR7WL6fXE+MAgmIqLzoqdLzPFf\nt0oI6utVVtTaSNaTL5p9i3/cysoQystDyM6WKCyUdtbVynqq0gMVcLmVDtTUBPDIIz4sWxbCmDEm\nzp4V0HUgJ8dAcbGzM4MVSJ86pdl1vkVFBp58MoS9ez3QdeDtt1WbtVGjzO5yEOdmuRkzDHR2AhkZ\nwMMPt2P6dBXIup1beXk7Hn00E7m56vtvuaXTsVlw40Y/NE3g1CmBzZsDjkBvzZoMzJ/fgcJCZ/Y4\nJ8fEmTOJdb9f+YrqmPHOOzp++EOVMV20qB1PPBFCU5PKrsducvzoI90u69i0KYAHH/Rh/vwONDRo\nGDNG2C3Q1qzJwPLlobhzUH/ft08Fwy++GEjogjF1qpmwabCkJIw774xmyF98MYCMDGmXSFglOW5l\nP1aA7BZsW3+P/Rq7MQxfDIKTgDU75IbrgtxcTOuip0vMbkMkANgBTF9Bbk/BdV/fF/+4pqnqPKUE\njh6NP6dogHPggKpT1XVnVrKxUUN9vY72doE773RuYMvMlFi6NAQhgEmTTLS0CFRVBdHVJe2NZRMm\nmGhuFtiwIQ2NjSrY/slPRmDr1jZ0dgo8/bSvuz4W0LS38Mgj30ZVVcgRrFuBfFqaMxjzeiU2bw6g\nq0sFiFI6//3kSR2lpc5WbV6vhGkCjz8ewt69OkaNEti0yY9IRJVeTJpkQNedgXkgIPDmmx6kpUm8\n957HDqRDIYGf/SwadMZucvT5EFN+oWH58hBKS1UgXFLiDORbWoDt21Wpy6hREkeO6KisDOLyyw1U\nVJhYuNAHjwfYulV1lrAm4x06pDs2DVpjqa3nb2Xmly0L4fhx1Wpu+nTTntQXy6phj994N3WqCSmR\n8LXz6WL6fXE+MAgmIqIE56K2sadLzPFfv/rqLjz7bADjx0ukpUX71ObkAI8/nonq6qAd5O7dq2Hf\nvvjevpprhtkafGE9j/jHzc+X0HWJVasyUFoadkwEy8lR5+r1SowaJeHxqKC1rCyEceNUoCWE6lQQ\nCjkzhPv26cjPV7WtPp+JTz7R7H68o0YBP/95NPhctiyIFStC+OgjHR4P8G//1oZjxzRMmWLiV78K\nwzCAnByBqqp0nD6to77eGax3dAhoGlBQ4MzadnWpTXljx0q88EIAXq8zWCssNByDJ/x+YOnSEKZM\nMRNqjGNrm5cuDWHt2gBOndKQmyvR0qJazh07piMnR9XqFhaaOHXK+ZqkpQFlZSHMnduFAwd0PPlk\nCI88Eh1mUV7ejlDIGai2twMjRgCtrapG+pZbRjiC9rKyLHuthcMCy5dnYv78DtTV6Zg7twseD7B4\nsc+164SVUR4zRjoyxG7lDFY9uWkiIVu8d6+G8vIQ/H71840dTU3DD4PgJOCnNHLDdUFukrUuvuhQ\njN7G9sZOgIvdTR/fHcLjkfjhD1UgEt/+qry83RHk7tunYdw4ZzCbm2vaLcNig6j33vMgOzu6IS6+\n1dXixZlobNSwfn3AEfitX68ulVudKTo7JXbv9uDWW53lElZm08qixpYtnD6tweuVGD0ajoxrTU3A\n0W2isFD2eNy1awMwTXRnmed1B+7O53755QZKS31YsCCM6uoAzp7Vukf8+vDgg2E89VQGnnwyBE2T\njmBN0+Aon9i8OYCMDBWwW8Fxfr4JIYDS0jByclTfYY8H8HiAsjKfXdKxfHkIkYiEpgGVlSHcdls2\nKiraHec5YYKJCROA48c1PPecqoOOHWbh9wMzZjgD+eJiA8ePa1ixIgO//KVzE2NjozMr29wsMH9+\nR9xz8uPsWYGRI4FPP42Oh542zbCD46YmZ7C+Z49ur5X4D4Fum0QPHdKxeHE0GH/++QCuuur8ZYP5\nPjIwDIKJiChBfAC5f7/Wr2ywW/AM9L5ZKL47xH/9l8cOtOKzqn6/2nBVW6tj714dY8ZIPPKIr3tj\nlMo+3n9/Fv75n4PdwV9sNhd2r9rY8cxqQ1kWJk5U2dCGBudzP3FCdarIyFBZvRMn9IQhF+3tApWV\nIYRCQHq6xIYNatPZhAkmTp5Utb8zZnTZI5Gt7ztzRnN0mygrC9lBsWkC06aZ+N3vQpg2zUA4DPh8\nwPLlIYwfb6K5WQWEsc/9k080PP54yJGt3bAhgIqKEEaOlFiypB2nTwuMGweMGydx2WVdaGhQGeTY\nOt0jRzS0tAhMn27Yx6qsDOJnP3MG6IWFqoRj+fIQurpU7+PYDxAqIFZt7srL25GRoQaQLFyY5cj6\nLl7sg5SqnKOtTW1sbGoSjtHTBw7oePTRTJSXtyM311n3a7W9a2hQ9z12TENhoRH3nHR0dAD/+I8+\nx3PIyZF49NF25Oaa6Ox0BtPhsBqEYnXz6Ov/QH/7aLuNCt+zh10lzjcGwUnAmh1yw3VBbpK1LuLf\nzP1+dTndLRsc+4YeP0Z3/34N6ek9bxaK/d6iIhORiERdnd69ESodlZXOjVBXXaUC5bvuysLjj4fQ\n0KDqcPft86CyMtM+pwMHNDz4YPSy9tq1AfzmNz7Mnx/G0qUZKCkJ4+OPNZgmunvThjBjhgr44rOW\nhYUmjh3T4PWqzOXUqSZycuJ7DxuOwNPaiLZpUwClpdHz2LzZ7/i+ggIDJ0/q3ZvHwsjLM1FQEEYw\nqC79L1rk656+pmPuXAMLF6qSAV1/E4899lV88IEXR450Ij9fYvRoibNnBQwDjuDv1CnVg3jJkgxU\nVYVw8KCG229X/YedNbchPPdcBhYtUkGmxxPtXXz8eGLgn5amstq/+EUHhJBYssSX0GYuN1e9TseP\nqwC2oiKEDz7wor5et+9jbVi7/HJn6cXmzQHcf3/0/Coq2u0PQuEw7HZqU6aYyMw0EArpOHtW4Phx\nze6yEZtJnzLFxAcfeBznl5Wl2svFbn5z61Ft1Qz3dUWkv320+zMq/ItsqOP7yMAwCCYiGmZiA8PW\nVg1f/zr6lRUayjre4mIDL74YQF2dp/vSdwYefbTd9Y059g09drRuUZGB0aMlPv9cfd0KTKxyBU1L\nDAaqqwPIz5fo6gJ++cswsrIkqqrUxrFQSAWF1qXzI0d0TJ1q2O3MYrO+48Y5N62dOaPh2WcDOHDA\ng6VLQ3ZnBJXdzEJenoknngihtDSMtDSJZctC6OxUr2lTk4bSUh9qagK4/35130ceacf69QE0NQlM\nnGji9GkVIFobvHRdBW3NzSLhPCorQzhzRqC42EBaGpCRIfHMMyqL/NOfOrOo8Zf0raypYQiMH6+6\nOpw+rUpCrI4aXq8aPvHQQ+q1UlljgV/8ogOffqrZwWx8zW1WlsRTT4Vw5IiG225L3MQWH/hHIgL1\n9arrAqCeZ3xnhrNnBdauVYMwLrnExAsvpOEnP+lEUZGB+fM70NYGXH11F15+OYJPP3XWdh84oH7O\n7e3ArFkGDh5Um+BmzFBZ8Vtv7Xk0tvU6ZWdL/K//FUBuromGBpWNLyoy0NUFlJSEEYkATU06Hnss\nHc88E3QM1ohdl1bNcG/lEUD/+2j3NSqcXSXODwbBScBPaeSG64IszsDwuygu7l9WKPb7iooMrFwZ\nRFPTFwuINQ0YO1Zi+fKMPi/tWm/oEyeqoG758hBGj1bBUOyY3+rqAE6e1HH//Vmorg4m9G6NRIQ9\nOe3hh32OAGffPh2VlT77MUeNMjFqlMTJkxqqqoKOy+ubNgWQlWXia1+L4Fe/CttDGdLT1RSxxsZo\n71wrICwp6XB0dCgvD9m7/c+eFXjhhSAyMlRwJdTp2rWuCxdm4vHHQygqMuxOCvn5QFeXtAPtt9/2\n4M47O9DZKRAOC1x9dRekBHbt8mDGDFXHe8stnY7XYvx40x5eYX2tvR3dJQNfxejRhiNzGltTe/Kk\nKovweIBHHvFh+fIQWlsNjBoF1NcDlZVBTJniDGonTpSOINl6zKws4Pe/D2LCBDUdTX0d9rhg1U9Z\nHUOVPYSQlQUUFppoahI4diyama2pCWDVKtWF4dZbs5GXZ2LGDAN79+qYMcNwDL0QQqCszIfKypDj\neS5dGr06YJ1jfJmJlV3+8pfVmo0NaDdtCiAUQkIHj7/8Rbezxq+/3uY6Gtkqjxhs/9++RoV/0a4S\nfB8ZGAbBRETDTG/Tqvr7ffPndwz68qp1adeqs9y/X8OZM6I7cDETuiyUlHQ4glerHtR6Hvv3R0sW\nGhoEgkE9IXNYUGAmDHhobNSQny9RWRm0uyqMHu0MsGMDwA8/1PGd7xhYtCjsaB+2aVMgYZOdEOrx\n43u+ZmUBo0cb+POfvfZjjhkjMGWKCtimTZPIyzPtFmL79+t2a6/6ej1hQ5/qvavbwWP81DkruI59\nLbKyZMLmsFmzooGvNRjDOufY1nK5uWpC2zPPZOD4cR27d6sOCa2tAkIAU6aY6OiAvTnM5wNOnRL4\n0pdMHDwY3znCRGmpD1VVIZSV+ZCXZ2Lp0hB++tMO5OSoIHvp0hDWrQvg4491TJliIjvbxF/+4rFf\nu4qKENLT1cCR0tIwPv00+uEjtoxk7doAGhpU1njhQvWhp63NmbE+fVrDVVd1weuV9jAPrxeOqw1X\nXNGFrVv9KC428MorXkeW/tgxDR6PM4jet0/HlVdGa8QPHdJx880RFBcbqKvTsXBh2FEeMdhMbU+j\nwodyHDn1jUFwErBmh9xwXZAlNkuk629i6tQ5A/6++MDhi7xpW5d2E8fNhtDYaNobhaw39Pis5ejR\nzmxXbJsxawRvXp5p97WdMMF5Sd+qqy0oUJeylyzx2UHPyZPOQDk2AMzJAU6e1PHRR87zOXZMc7QB\nGzXKxJgxJl5+2Y+ODueGqFBIoKlJdwSqmzY5u0Zs2qRG9rplY+OzqR98oDLZ1n3iN/y1twNr16Zj\n2bIg8vJUABsOq3HBGzcGcPy4hsmTVVlDRUU7qqr+Gzk51yR0oVCT18zu6W7A8eO6XbP8l7/oCYG3\ntdFsyZJMrFsXQGOjwJVXGqipUcGo6gah6n6PHFHlCenpEp9/rjky801NGkaONO0ODqrbRM+vndVB\nI/7Dh7XB78wZgWXLgnbQGxvg5uSYGDnSxNq1Aeg6HB+G1q0LIC0N0HWJkSOl4/9F7ACR2LIda80c\nOKDba8jKxMaO1479P9DfDW8DKZsYinHkfB8ZGAbBRETDTGyWqLU1lJAV6umNNvb7rA1JPb1pD6R+\nOD4z3d4u0NkJvPeejrY24MyZaB1l7GO2tGh48cUA2tqE3frMajNmHfP4cXUJuqwshNxcVWNqZezS\n0qKXrq3hDvGjaq1Abs4cA1VVQeTnm1i1KgO33CITJqxNnmw6MsMvvRTAgw9m2T1qrQCvs1Nl/B54\nwLnJ68gR5+tQX584IcwKxuPrZ3NyEHMfgRkzuhIyvD/9aQcmTnR2V1i7NoBbb1VlF7Hn/rOfRbBm\nTTo2bw6gvl6Ve7S3AwUFJkaNMhEMCkgpsXx50D53vz+xZCASEfB4ZPcGvugHkMrKEEpLo62+/H41\nSERt9vMnZK0LC1UZw113qZ+N9bjWY8UPH7EC6okTnWtm7lwDNTVpuPFGiREjhKMbxbp1AaSnAx6P\nCU2TyMhIHGrS0KDh9GmBDRvSUVISxt69qnPE66+34c9/jm6KW706A+vXB/DRR7pdR75yZdBenzNn\nqg9/A83UftHWgpQcDIKTgJ/SyA3XRWqxglCr1CC+dnfWLPXGefjwDaircwapPb3RxmaX3Br5xxrI\nm3V8/aLVCaGioh3/8A/RY7z+ehu2bPHjvffUYIsVKzJQXR3Et77VZT/nri7hGqTPmWPAMGRCxs6q\nJbb+Hp85TE9XNaLHjwssXGj16VVTzT7+WEdNTQBHjmi47DIrO6q+Ny9PTaJ74IFw93mpQQrr1wew\nZEkGSko6IITzEvuUKYajJCMrS2L8eJkQxP32tyGMHasCy8OH1aX9mpo0R/uvUAiO9l/NzWoscnyg\nffq0Kh+Ir4G98spv4JvfDNndIoqKDFRVhdDUBEyYALS0AAUFEpmZJj79VMekSSYOHUJcYC6761HV\nWOHYjg0TJiT+fD7/XGDzZj+6ugRaW2FveCssNCGEKmWxOknEB8lTpiTWvNbXq44bq1cH0damHrOr\nS+Kuuzpw//1ZCb2AT57UUFbmw+bNAXzwgY5RoySmTnUet6DARGennvBhaft2v+NDWmOjBo9Hbcpr\nblY9gw1D2Gt+zx73/x/x/0fiP0w2NCSOUj6fQTDfRwaGQTARURJYQWhFRbsj4LPebHsLUvtTM9zX\nLnW3Y1hfv/RS9T1nz6r+scEgsHmzH0eO6MjPN+0MYnxAumePavV19dVd8PsFVq4MoqFB4E9/0tHU\npAJfqwRi0aJ2vPiianE1erSJEyc0bNiQhvXrVWAVe9y2NrXRb9myECZOdAZn48dLnDihQcrYTLXm\nmPq1cWMABw/quOyyaBBUUhKOqylWHRBaWoAnngg5MpA1NQEcPaqjpcWZKh8/XgXSqtuD1v1hRuCx\nx9RmrpKSTMya1YUFC8K49dZOx+O99FIAjz6a6TjHJ59Mx+OPO1vCqY1wmQmX7ydPVtn0ri6gqioI\njwcIBoGMDKt8IYx/+IdsO1v+wAM+rF4dRHV1AGfOaMjPN9HaKrB5cwCffKJh1iznprTmZmFvSJwx\nw0Bzs8B992WhvDyEjAzVY/iOO6KvcXV1EHfdlWW/jqtWWf2LVXeRjo7oGpoyxbSDdyvbXVKS5Xi9\n58/vQCTiDKRzc62OFBoee8yHoiIDzz0XwKZNARw9qspFsrJM/P73GfjBD5ybDPfv1/D3fx/Bq6+q\nzW4jR6pNldYHNcMQjv9vK1YEe/z/Efth1W0q4RfZ4HYuJjRS3xgEJwFrdsgN10VqsYLQ+EDSCmij\nQepbiERutL9uGHAZAiFRW6v3643TerPt6EBC27LYNmeW2Gza2rUB/Oxn0T668ZvaxoyRaG3VkJ0t\n7X6taWnRscDWJfKSkg6UlmYlfADYuDGA9HSZkIWcMMHEj36kzu1rX4tg8+YAPv1UZViXLs3A7t0e\nrF2r6nNVGYbzNa2tVfW4RUUGNm0KYPdutREs9j7Z2RIvveTH558LnD6d2Nbs3//di4ULw7j3XvfA\nb8OGNJSUhNHZqV6/jg51jAULwrj99uyE/rknTmiOTGp7u9rMaJVlpKWpyXeLF6u629WrM1BTE8D+\n/ercd+7ciUmTrsczz4TiapJDKC9vh6ZJrFwZxKlTGoqKDHzlK12or1edOSzr1wccJRY1NSpAHjdO\nDeJ4+OFMHD+uY/nyIHw+tdExL091zDhxQnNMurM2qWVnA8uXB3HppQY+/VTvfiSJ9HRASoFf/1r1\nEo7vExxbq22aEpMmGWhrE3jpJVUPnZdn2lP3pkwx7f7Ru3d77DW8cWMA99yTjccfD+HoUc2xhjo6\nBD76SGWo4/tH79mjJ2Ta4zP8sf8/Yj+UHj7sfB06OgRef70Nhw7pA9rgNlRlFG+/vRPZ2TcwmO4n\nBsFERElglRjEB5JW5ihaguDcqLN7t+7o+rB2bQALF6p+sNu3+zFrluGaUbKC3zNnBH7yk2jgY03C\nir2M29YWfdeMDQyamlRgbk3/GjHCtLsLXHGFGj07f34H7r03GthWVkY7GFhTvqzAP/4DQG2tjhEj\nJJ57LsPeLBeJqGEPVqAxaZLhCNyWL1fDF1paBNav96OrCxg50vmajhunNkjV1+s4elSDz6d6Djtr\nWk0cPKgGQsTX644da+Khh9rx/vvOQQtWsJyVpdrCxfb4tYZinDihXrP4n/PkyYYd2Fv3b2tT57h4\nsQ9lZe32ZXsA9p9r16ajsVHDww9LPP10RkLdst+vobHRhGEIZGZKVFZmdh8/gIMHnYFh/IjgM2fU\nsBNrCIZ1v6IiA6YpcPYsoOvRgSHxHS6qqwPIygJOnFC1ubGdQtavD9gf7OJfi9xcifvui66Z+E10\nVvY5LU1i2zY/TFP9/KZPVxsFn3kmhN27VeeNri5g714PNmxIs8tNrriiC59/rqGhQaC1NXEjXmWl\nLyHTnpdnOsqJ4sscrAmKbq/D9u1+3HxzZEC/D75oR5h4n3yioayMNcn9xSA4CZjtIzdcF6kltv3Y\nli1+u0m/lTmKbnKbi6lT/fbX498s9+3z4Phx3f43wH1E8e7dOu66K7HOsq1NYOxYibS0aFBodXEA\nnIFiQYFp18QKIZGWJnHsmI6uLrVpatw4MyGwzc2V9mCE06cFamqiGdv4YCgnBwiFopvlqqqCGDtW\ndaGwAo3YoNr6U2WLJRYuVP1wFy7M6g6AYF/Kt+43ebKJDz/UsWFDBlauDGLUKInTp9W/axqQn2+i\nvV1g3TqVpRVCtQB74IFwwkY7K2MdCqnAMBKJtuE6elS3u0d4vYn9c0+dcv4cjx1TE+FifwZr1jhH\nIj/yiA9PPBHCiRMaRo68HosWhTFuXPxVARUAL1mSierqoH38w4dVr961awM4dUpDbq5EVpbpqHGW\nUmLRomw7Y37smCqbMAz1wSl2wlxRkYEFC8JxgaGaqlZeHoIQzg9QJ05omDbNcLwW1oec+M1t8Wvc\n79ewZ4/A736narZjS11qapwBc02N2jy3aVMaFi9W3ThUllmNoNY0LWGUNhDdKBcIqE2cVgtAK4Cs\nrdUdAz5Gj5bYu1cFwvG9rr9IANvfcct9GTnyhiEJplMFg2AionOop1q/2DdYdT8VqL7yite+n1tN\nb/ybZWzbsdiuC0BieYV7naWJ99/XEQoJbNrkh2kKNDerfrjt7SpoPXVKw4QJJgIBgTVrMroDAYHL\nLpN44ol0R23nsWO64/iZmSaqqkKO7O3mzX5s2hRAS4uqE92zx4Np0wwcOaJh1iwTEycamDjRxJQp\nJo4e1TBmjGmXL1jZZOtY48ebqKhox4EDGhYsCKO+XrOzqYC6NC8EsHGjH4GAQCSiOiiUlISRm2vi\nllucWfXGRg333BM7La0d9fV692hlnyO4PntWBcvNzeocvd7ETX3PPhuwyx6+9CUTXq+Jm2/OQUVF\nuyOomjhRDZZYtkxNk5sxQw2maGhIbEVWVpaF5cuDmDatC4GAhtGjVSb7uecCdru43/2uHVlZEr/9\nbQgTJpjIzzdx331hZGQAW7emYdcuL6qqnL2MrUEY9fU6DhxQ67W5WWDCBPU6FBZGN77V1+sJmxvH\njTPtoLWoyJlNj0Rgf7hoblZ14C0tGp59Nh3Ll4dcP1zErvHJk008/rjK1paWhrunGKbbmXZrve/d\nqwLxzZv9OHxYR26uRDAIfOUrXWhp0R09ia2OGIDKtNfXa/irv3L+n7O6oHz2mY6qqhCWLcvArl1e\n+yrKVVeZmD598AFsf8ct92WogulUMeggWAgxEcB6AHkATADPSyl/P9jjXsxY+0luuC4uTv2t9Yu/\n32uvtcEwBP74x3fwne9c69oGLb7tWHGxgWAwMcgF1JvjZ59p2LAhw75MXFzcBdOM1v2uXBlAKCTQ\n1qahrU0gMxN44AFVQ/rUU0GkpyNhjG/s5ie/X2VCN21SHRny81UdZ3ymr6lJQygkICWQnW1i9uwu\n3HdfdOKb1QorNnC2+sq2tAiUl4fg96vsZXa2CoZKSjqQn9+Fri6REHyVlWXZ3RNij7luXSDh0vjY\nsdHa0Lw8ExMnqkxrWprEqlUBvPuu187Kzp8fxj33ZHcHVH6Ul4eg684MaCCgWnYVFRkIhSR8Pg1L\nl6rpcqtWRfD97+c4spiaJjFpkoSuS5imgK6r2u1t29Jw882d8HjU7fr6t1FUdF1CUHfmjMCSJT5U\nVLTbGdLKyiDuuy+29CKAxsaOhF7FZ86ovxcVGbj8cjOh//Gdd0Y3vnm9aphHeXkI7e0C06cbaG1V\njzVtmlqrNTUB7N0bHbv90ENhTJpkOEotNm9Wo6etOuhIRHUVUVPhgNGjTYwcKXHffVmYP78jYTNj\n/EZJa7zx8eM6ysqc9ezx2fejRzWsXBlEOCxgGEBDg4aWFmGP9AZUABxffrRrl9cu09m40YvLLze/\nUB1wrP6OW+5LIBZwGNgAACAASURBVLAD27ffMOhgOlUMRSa4C8CDUso6IUQ2gA+FEK9JKfcPwbGJ\niC44sdnfnBxpZ896uzwZO3q4pKQDp05p3W/4mVi5coQdFFtvbt/7XgRSqsfJyFDZrlde8WLUKIll\ny0LdQwUkGho01NYCV12lAuTlyzPty8QvvhiwL+MDwOjRzlrQmpoAKitDePddHZdcojo4xG8gOnlS\nBbtdXep2ZqZ09JtdvjyUUEYwfrzELbdkOYKZX/yiwzHy1zRVELpkSTvy81Xf2+XLQ5g8WV1SP3TI\ng8mTDWzb5sW993ZgzZp0VFYa9sYyv18950WLVKZv/vwOfPCBc3iGYQAvveS3xyobBpCZCftyuc9n\nOi69b9rkxzXXqKlrVmu1iRMNHD+uo7lZtWGLz7RPmKCmyu3dq2POHCNhI5pbFrO8PITJk03ccYez\nm8SPfxy9feedie3UjhzR7Ix5bFmK2+COK69UQWvsuc6da+Dpp9U45fjXKi1NreOsLGDVqgAKCky0\ntgJCCEybZjqC8aVLQ5gyxUBGhnPsdl6e6iwSm8mtr1fdSM6eFejsFJg82cDPftaBsWMlWlsFRo0y\nceiQB/X1ekKpTUYGkJ2tPsyosc2qnKasLOTIWltrStfhyL5PnqxKHj77THNkxLds8eO664zuf9MT\n1jsAuwymrCz7C9cBnwtDFUynikEHwVLKUwBOdf89IIT4GEAhAAbBPWC2j9xwXVx4eip1iM/qxmbP\nero8aV3GXLQojFAIOHbMClxuRCSiLoPHbmjbvl1NZXBrs1ZeHrI3RFVUtOOmm7Kwfbsf115r4LXX\n2tDcrKGhQUNnpyoNsAKh+I1S0UvL0S4CK1cGHHWk6elqk1L8AIvFi9V0t8JC1YN23boAzp4VGDVK\nJmSG/X4NgOz+ABBGWppqP/bcc0E7QxvfpWLBgiw7+3nihIYVK4I4dsxZCrFtWxtKSsJoa9O6s4TO\noM/nk47NaRs3qsEUsbdjA7bPPtNhGIgpCYE9aGPiRAN793owalR09O/UqSZOnhQYN05i7twuHDni\nDKiam50b1awsptrcBsdEvOh6UN976aXXJ5QNFBSogDu+3tptcEdLi8C0aUZ3Rwhh11TX1+v2h4D4\njPq996oa5GBQoKtLXSlYsiQzofOFlMDp01r3VQG/nf33eiVOnbI2XapBHh4Puq8+qD7Jv/mND7/6\nVRi33pptf1Do6IBdbhF7Tvn5Jm6+Of7n5/xwZf2/Kyw08cgjPjz+eMgRsFdXBxI+JLz3ngfZ2SqY\njO9DfOmlBmpq/BgxQgXPL73kx4oVGcOm9pbvIwMzpDXBQogiAMUA3hvK4xIRDUc9lTo0NDhbPuXm\nmo6SBTdWmUNzs8Btt0XbkFnHbm5ObKVm/T0+Q5aWpsoXdB3weICHH25Ha6vA9u0eZGVJ/PjH2fb4\n4bQ0YPPmAM6eBXy+xGEKkYjqy2odXwjhCEiXLw8lBBFSqvrSwkIjYZf/vfdmu4ysNXHZZSauuirk\nuNytygOQcNm+qUmzM7AffhgdR2x1ZLC+P3Z0b2VlEGvWpNtZ4rlzjYQsX3ygqVqrZdrnPmmSyobH\nl4Rs3hxAQ4OOyZPN7hZmEpdfbjgGiZSXh3DZZc4grrDQsOuQ8/NNrFiRYb8enZ1qc5s1ES8/30wI\nSrOyTGzcqCbGXXKJiWXLMlBa2o7y8hCkVH1+W1oECgrUaOj33/fYG8KeeCKEQ4d0rF6dAY8HuO++\naNsy6z6x9c+//rUPDz0UxqpVGVi4UI2tzs1V2db4DY6RCDB+vMQ773gxc6bh6LlcXR1AKCSxZo0q\nyzl8WCR8gJIS+O1vQ5g+XbVJ8/lUL+aJE01HKczZs851Ef/hKi0NWLEiiJkzDYTDEhUV6gpJ7H3O\nntWQn2/ErUfYQe3YsaajlV12tgkpdUdGf+3aAPLypGPCHFuTXRiGLAjuLoXYCuB+KWUg/t+3bt2K\n6upqTJ48GQAwcuRIzJw50/7UsnPnTgBIidvW34fL+fD28Li9Z88e3HPPPcPmfHi779uNjd/sfkN9\nC5EIcPjwXMyebeDIkbfx6KM+GMY34fVKLFnyKmbNMjF7dt/H37jRi0hkB6qqDJSXX4Pjx3fgkkvU\npWev97uIRAR0/U0cO9aOOXOuQ1GRAU17E7qeaT9eS8sOmKZATs713W2qdkDXJR577Gr4/UAksgM3\n3RTGkiXfto/329+2o7r623jhhQDefXcnDAPYtu1/oLIyiLNnd0DXM1FQcH33+OIdAIBIRGWp/f63\ncPfdwLhxNyInx4RpvoXf/MaHhx76muP18fuvBgBUVe3Cww93YOTIG5CXZ+LTT9/Grl0Cs2d/A6Wl\nYZw+vQOvvOLF3r1fx/LlGXjooe2O59fWtgM/+YnA+PHXY8oUAw88sB2jRkm0tHwDmzcH8MYbO5GX\nZ6Kx8Qb78auqDFRVXY39+zVkZLyF//5v4Ctf+UZ38KNen7y8uY7bOTlXdz/PHTh5sh2jR38DkQiw\nZ8/biEQyoLL0Atu2vYOsLKCmJvp63nNPGJHITfb3793bgdGjr8WyZUE0Nv4JLS2Ax3MtFi3yob7+\nT9B1iRdfnAsAeOedndi8OQ2RyDxkZEjcfvt/orzcg/Lyr8PjkTh06E+orNyHf/qnf8T69Wm46abX\n8cYbAgsXXofjx3U8/fQufO97Efj9N+DLX+7CW2+9g3AY+Pa3r8OpUwI33fQa3n0XGDHiBqxYEcLb\nb+/EmTMSXu9NiEQE1q9/F7ff3gmP5wbMnWuirOw9RCICEyZ8Fbfe2onXXtuJV15JQ2vrX6O8PISq\nql1YuLADQnwTOTkSVVW78D//ZwQbN34HZWUhx3rZv9+Dp57ahTvu6MDp09+A16ten3HjDCxceA0y\nMiTa2t5CY6MGn+96ZGYCCxf+X9xxRwfOnLm+e5PgWwCATZvmOH5e+fnOn19BwVwUFppoa3sbBw9q\nKCv7Lioq2qHrb8IwBLzeGxAKAcHg21i4ECgouAFdXcBTT+3CokVhAF/H/v0e3H33B1BuRFlZCC0t\nOxCJZNo//3ff3Ylp0ww89NDf2D//J58M4ec///p5//2UyvGF9fejR48CAObOnYt58+ahN0JK2esd\n+kMI4QHw/wHYLqVc6XafN954Q86ePXvQj3Ux4AYocsN1ceGprXXPBG/b5sXdd2fb93v++UCv9YKx\nZRV5edFLvEVFBu66648YNeoGGAbg9QIjRki0tKgsnKZJeL3AggVZ+MUvOuD3q0u4ixb50NUFVFSE\nkJ6uBhtMmWIiM1MiFBL46U/V8IbKykz7HFatCqCqKhOVlSGUlfnwi190YOJEA3femW1PPVNjZSXu\nvNO5uUwIODK4L7wQwG23jUBVVTChV+xHH3mQk2Ni1qwu7N7tQXq6qv0F4LhMrdpsCZSV+fDP/6w2\nyjU3CwihesHqOtDRAVx+uYlwGLjjjuyEspC1awP4zW98dunC7NkGTp7UsGlTGhYtCmPZsgz88pdh\nNDZqKCgw8fTTGfj+9yPw+wVmzuzC4sXqdSwpCSMrSw1pCIVUGUMwCHtIgzXE4rHHol0cNm3yO16T\niooQLrlE1U47n2e7Xb5RVhbCnDnO7Pm6dQFHJrWiIoSysizo+pv4p3/6KqZNM1FaGn2Oc+YYOHFC\noLTUvSxg/foA6ut1x+u0fLka9vHAA2E7K+0sGQjC45EJ5/3cc+lYtkx1sJgyxcSBAxqEEFizJh3z\n53egrEy1tIt9rIqKdpSV+VBWFsJVVxmor9ewZk1GQpmC1Rpu9mwDCxb4sGBBGFOnOrPrr7zShrNn\nNXz+uSo5if35XXGFgSVLMrFsWQijR0tcdZWBffs0nD0r0N4usGePxy5zefDBMAoKTIwYoX6+Y8bA\nzuTG/x+vqGjH5MmG41y3bvWjqUkb0P/5c6W/7yOpMKGutrYW8+bNE73dZ6gywf8C4C89BcDkxECH\n3HBdDE+9vVn01NZoIG2KDAN4910dhw6pdk4nTmj4t39rw+efa8jKknj//W9C19Xl6WXLQo6aVavX\nan29jn/9Vy8WLAjj6FENy5eH8MILacjJQUI5QlYW7I1XseeYmytRVRXCyZNqA9qpUwIeD+wA+OhR\n1TEiP19tfJJSTa5LS5M4eNA5RKKlRdV/ejxwXL5ubBR2ecG2bW0AgOZmNaAhPd3ZVSEtDXjmmXR4\nvRKjR0vH866oCME0oyOCKyraUVoaxiWXGPj974Po7BTIzVUjdFesCKK2VpUBLFqkgvtbbulEc7PA\nrbd2QtOAyy4z0NkJ7N7twQcfeO1a48cfD0HTogF+ZWUwYTjEyZO6XWsa+3oGg6odWFOT+mAzYoSJ\njg6Bujrna+X3w66F9npVgK+yxXp39wsTmzf7cfy4akk2YoSJZ58NYPTouVixIg233NKZUJ6xfn0g\n7jGipTPNzRqkdHbAKCw08a1vRXDsmA6fz8TevXrcz1PANEXcMd1GT6sPIZs3B7BsWQYqK0MIhdDd\njUINqli9WpV8zJmj+jevXp2BFStCqK11PqY1xMLaaFdUZOLoUR01NQEcOaLbfYjvuEN9oAsGpePn\nV1GhWtvV1qq6dquG/u//fgSWLg05Nux1dAC33DLC3hQXW9sb+388N9fE/fdnYdw4VSLR1KThS18y\ncM01Bj76CP3+P38u9fd9ZKgm1F3ohqJF2rUAfgxgjxDizwAkgMVSyj8O9thERMnW25tFTzux+9vz\n0wqAY1swlZeHMGaMhoICGbe5rt11iMDMmaofqzWeN3aTkNv929slHnvMh5Urg44ANSNDxp1HOxYs\nyOxuc6Vjw4Z0PPlkyK4Jjd9A5qx1NbFsWQhCSCxenG13vLC6MaxYkYFAwLkjP/4YBQUmHnggjClT\nTLS0CFRVqcC7sNCAEEBdnQdTphj41a/CdgeH+CC1pibgeE0qK0PIzZXweKQju1peHsIVV0RbuxUV\nmfiP//Bg+nTVqszaoGaazlrvEyeim/BaWoQ9Pe/LXzYwYoSJkyd1FBaaOHZM665fRcKGsxkzDDz1\nVMg+H9XKLQghRHd7O4GFC6Pt46wPPkePCvzoR50oKjJx6JDmOK+uLmDVqiBOnlQ/22nTDKxfb6Cl\nBZASuOyyaA1vSUnY8UHpD3/wY9Ik5wckw3BuoPR6Ja64wkjYSOn3q9v19RpKS53H3bAhgNxciV//\n/+y9e3QU550m/FRV39QtCQS6oAtSI5urxeUYfTvObOIzc3K8M9k9uz5ZJzMmE+w4F+sMAmwhiYuI\n4xGJECCJi2OSIYEggaFFCJuT/SP+vuTMTr75sjPOCRDbgM0dCYTuQkhdXd2t7qr6/vj1+3a9VcKx\nZ7Gxnf6dk4Mjtbqqq9/uet7n9/yeZ1M0Fc5iorjYxNCQjN5e2XFdWIhFIkGbMbsG99vf9qOhgXyJ\nc3NNh4Z5zx4fOjpo8O7QoUhKBgTs2KEhJ8cU4pg3bfLzY924oeDxx9OfV2uznCQvKq5cUTBnjom/\n/uupP7ohZp/z90pxfBBs7P1KqPuk1/1wh/jfAJQ/+sBM8cq0vTM1XWXWxcej7Demf8/NgoFjFmFs\nDcCw3uTeekvBG2+4eCTw5KSEsjITqmq1tfoNEom/SN3cneEEkkRDQ5IEwRLq5k0alnK7TT4E53YD\nwaCBYFCHqkqWcyHrp+XLk9iwIcbb211dYciyxBPb9uzxoa4uJrB2RUUkRyCAaSAvz0RLSxa+/OUp\nyDIBU79ftF47fFjF6Kh4XUdGJBw8qOLiRWpTb9rkx+rVUxgbk9He7sPx42HIMmCakgCIrAly9gE6\ne5CCJFGkr6Y5B6iuX1cwNSVKHOzt/4oK3bHRKCvTMTQkpxLE0n7JsixjbExCbW0aoAPOgbOtW6nV\nz9aA223i8mWFn4fdPi4cljF7toG9e9/Aiy9+BqdPK6iuTgpA+fhxFRs2pK/3oUMqbt+WMGcODbH1\n9Sk4ckSF12uip0dkYK9coQhsu/+vLBNDLUkSNA1oaspKrSlxkNLtNjE1JeHMGfF533qLGNkdOzTu\n/PDqqyq6u1UkEsDmzWRtF40SoKyvJ2BKXQrDwRJ3dBDjT10FN1paNAwO0gYmHJZQX29nqWnQzirP\noQHCdCS1222islL8bE+3CZ5O5vBe1mT32kh/GGzs+72PZEI1qDKJcZnKVKYyZSn7jelnPwv/u28W\n97rJMaB97pyCqiqdRwJbjxkIJPGzn4XxT/8Uxec/H8aMGTpeeinAU71KSkiKYE08Y9rPYFBHMGig\np0fmIGP1alFnag+j6O4Oo64uJjCkdsuwgwdV3LlDkghmk1ZVlcTWrX4h6OLJJxMC2LD74Q4NyY6Q\ng8JCE4CJUMiDmpo4Vq+Oo6pKh8tFVmGSBFy+nPaKZeyyx2Pi2LEwensVLFggTvmXlorHYI4LdtaZ\nBWpYNbp2AO3zmbhzRwTZb7+tYNcuDV6viba2LDz5ZAKTk8S03r1LGxkGbhUFeOUVH9asiSMclrBs\nWRJ371JCnK7DsQbYeTD7OIBZnxkoKTHw3/5bwqF/liSy1ksmIVi7vfuu1epOXC8LF4rXqKzMQF+f\nDK8XCATIzo4B8q4uFVNTFOZRXx/Dww/rOHpUxcgIaXLHxiTOmtfViQCZpcm5XGlv5UCA1mBRkYE1\na2LIzkZqU+fD88/T+TPNt50lPn3ahaNHKX553jzDAXhjMTtLLaO3F46fXbok4cQJWj+VlSRtsJZ9\nE3zxovyBmdv3SnF8UGzs/Uqo+6RXBgQ/gMqwfZmarjLr4uNR9hvT5KQ07c3CyhgXFhqYnJRQXGxi\nxQqdh1icO6dwUAAAY2MSTp1yo7DQ4NKDYFBHXZ3os9rbK6OkREq1k7+A11+ntLOvfCWeiteV4fOZ\nDksvn4+8cSUJ3A6rvt6PDRuiwuMGB2Xk54thAhSEAaGtPjoqAomJCQmlpSZ6epy2VoypHBtLe/Gy\nvxsdFf1wg0Edra1ZOH48jGiULM9GRiTk5QEbNsQQiQBHjxLwYoNVoVAYpaU0CNjaGoHHAxurF0VD\ngx9dXeTRW1JiwOcz0NVFPsLJpIT9+72cdT5xIoxbt0hnywI1EgnyuG1tjcDno38ZACwqMjA4KL6O\nRYt0DA6SLrSxMYbTpxV+zTs6NOTmGhzcbtsWxdCQLASVFBUZ+Nu/zUFRkYHGxpgNoKXt4yoqDLS3\nR1BaStHKqiph4cLPOd7TLVvoOHZAKEkSX1fWv5maknDpkoxQiCzACgpoY1VYaNrAMr2/g4MyFMXE\nt74lMuQvv5yFUEhFXp6JurqsFNg1BbmNoiCl7yaZSyIBjI3R+fT1KWhqCuDHPw6jpAT4ylemEAzq\nyMvTMTTk4iyxlT2vqYnzv9u1KyK8rpwcE/n5pg04G6istFuhGViyRMdjj+ncFu3f/g38s7x0qe6I\nhg6HJaxdG7gnczudxOFerOuHwca+3/tIJlSDKgOCM5WpTGXKUuzGxCQEExN0Q/ziFxMOKYNds/v1\nr2cJIRZWlm5oiMIuWAqaFWzaQw9KSkwBsNTUxAXWtrk5inXrAujsFBnNeFzC5cuKA6CWlIiAoKiI\npv+trgH5+Sa8XmDnTi93Gpg/38S+fSra2rIwNCSjtNTE1asyfD47o0bXhM7dwOXLio1d1AVANDws\n4/RpN6LRGHeaoGjfgAN4TUwQuzg1JQnpbe3tmsAIK4qJmpo4hocJ3N26JUPXFR6pbGVNZ8wwuctA\na2tEaIcvWKAL7HdnJ7HmXV0ePPNMHKGQijNniMH//vd9ePLJBCYmJMExo72d2uweT5rB3L+fZBC0\nCTBgmiauX1c4U1xQIK6BJUuSCIVUSBLpkufNM3HzJoF2kn3Y47FNvmmzSz3YgGFFhXiMRx7RcfWq\ngt5eev3DwzJUFdwfmj0H2xgoClBSIiYgMh3w8DDJZjo6NBQUkI67qSnAPy9790bQ3h5JDU0Cr77q\nw969ERw5Qs4KkgQUFoq69OPHCZxbA1B2745g9+4INmwI8IFCr1fcsCxeTHHi1gHO/HwD1dUGfvnL\nMC5dklFQQK+jqsrAm29O/1n+2c/CeOGFAAfgy5dT5DO7LtMxt9N1f+7FumbY2AdfGRD8ACqj/czU\ndJVZFx+sPqyhEnZjGhuThIS2kyfDCIcJtA4PO+OQGRi4c4cCKtraNBQVEegYGZFRXq6jvV2Dx0Ot\n4clJCYsXGxgfB3JydHR3h3H6NLG3DQ3EJBJg+X8xOfkfHCwhMXsK1wNPTRHQWr16SnhsNAqMjyN1\nI6fzZ8llHg/Q3h5BIgFs3OjHc8/FHU4Dzc0aWlq01GvyoaEhhqmp6Ya7ItB1YnX37/fx4y1erOPS\nJUUARO3tEezbF8Hdu2mgbw/cYEzoihUUNbx5s8hm5+XRtbUDXGr5ZwmA5sABL0IhFdevy9B1SUhu\n27/fhyNHKFSioIDYdWtSG0vNO3ZMRTQqpRwaZNy+LePJJxPTJqYBaVcOFgwCAJJEG41kkuzuiovT\nTHFRkcGH3shTWcLQkISxMZKcWLXInZ0qOjp+h+bmz8DrNTE1RYN5Vl2uVRLS2EhJb4ODkrAORkcp\nDrmiQseqVTlobtYgyxJUVXx/7RuDHTs01NezBEQdx46FIUkQPi/24JJoFJg718S3v002fDU1cbz7\nrrhhO3pUlM3cuCE7JC3xODAxQYOS8TgE+c6RIxSu4nKZWLLEQDJJkoOSEhMrVlBE8sqVOlaufG/J\nQzgsoaiINhurVk1BkoCjR71YsUITNkzTMbf3kjhMx7p+GGxs5j7ywSoDgjOVqUx9IuvDsvhhN6ZT\np9zCzex3vyOAageIjEll4MPlgiMpDJCwfn0Ax4+riMXE37e1RaCqCp+QZ+BrdFTC8eMq/tf/iqK6\n2t7GpWNJEskDSksNDrrsEbkrVui4fFnGyy+LXq0MwExNSXj7bRfX19olEOGwjKtXCcyuWjWFK1dk\n/Mu/uDioLC01OCPK7LGsbf9DhyIOBpKe30QgIGqLrY9ZvFjHtm0aEgkavlu+XOdxvgcOeBGLSdzN\nwXq+16/LAkPs8ZhoadEwa1YSkuTC00+LaXxDQzK8XhMzZ8JmP0dtfsaK9veTN3AgYCI7m9h6Nvxl\nB54lJTpn+j0e8gzWNFlgspubNVRV6aCwiLQkYMuWKFpbs/jmpLU1KxU4IcpLxsfpGu/bpwKg5wyF\nVFy+LHOXikWLdLhc9J62tfmxd6+GF18U18F3vpPFWXVmpXb0qBetrRrcborEfvttcciNNkQRVFYa\nME0C/PaNQG8vRWWn/XhpqHLduhj8fhOTkwAgvle3b8sCo1taaqC3V0Fbm4ZZs0iTrevEVD/9dI7j\nmG+/TS4mtbUxnD9vYtEiw9HBAZwbaLssITfXnMb+jTa1f4y5zQycfbIqA4IfQGV2aZmarjLr4oPV\n/RhYea9y3hhJK2h1cqisNPDTn07C7QZu3VJw9CjZLtlBJPvvs2cVACLILCw0bV6+BL7u3JGxdm0W\nfvaz/4ieHgkHD0YwMiJh0aIkJiZk7NypoaKC9McNDemW7fz5eipowIU5c3QkEkA8ToBxchKYMQPo\n7SX3g+FhWZAgtLVFsHKl/XUbKC838Oyz6dCMZ56ZEs65u1vF1avEoP7P/+ni4LSiwsChQx6cO+dK\nBWUoHMTu2ROBYQDr16e10aFQGNevK9B1CU1NWejrU7BvXwTbt2vC8Zi8pLY24IiXZswhY4iZrGVs\nzI3Zs02cOEE65I4ODXl5Bu7ckTE6KjmYaK+X/IiZr200CsiyxLWywaCOtjZi60nqkGZxfT5xs3T8\nuIorV5z67du35WkBWJrBpda73T6srEzHT35SjampMLKzyfFiYkLCwIAsBHZs2RJFQYGBRYvIwWLH\nDh+/dqxzkEhIKbAdgd9vQtNkDA3JaGigAcuWFuo0WI+fl0ca39ZWH1atos7DnDkG39Dk5pL3cDwO\nwY/X7QYiEWBgQEZ1tY7eXnlaffeRIxQ6e/euhEDASG0g/Jb1Fsa2bVF4vemhSEky4fcj9b6nHzvd\n5ti+gf71rycFL+DJSbqe1vcrN9dEVZXBN8n3qgctccjcRz5YZUBwpjKVqU9k2cHDHxtY+aC1YoXO\n9YP5+Sb8fgqy2LtXBGQnToTxN3+TvqHadbq5ueT1yoA0ILKG/f0iOJoxw0AopOLWLRlHjtDE/+io\njPx8ckqIx2WhNR4Kqbxl++ablLA1PCyjujoJj8fAf//vucK5WbXFnZ2q0PpPJiXoOh3/5k0Z5eUG\nsrN1XL9OAQ/Mi9jOwPX0yDAMAlU7dzoB67e/7YLHA1RWkoXahg1RGAbZkrHn6elRcPmygoULDZw+\nraC2No4DB7zQNGBwUAyY6O+XIcv030xr63KZ0HUJySS9rsFBuq52UNTdHXZYn+XlSRgbE4EeQHZs\nW7dGuUyiuFhPBYnIKZ9gGaFQGLdvK8jLMzE+LmHvXh82bBCvz+CghGXLRDafpDLAnTsSmps1+HzE\nePf2Kti2TUN2tsFb7wcOeNHZqWJsTEJJiYmrVxUYhoQFC5LCANt0a6+83MDlyzKXQdy6pWD+fDGV\nrriYNOKhUBh37gDHj6sYHJRQUmLg7l3aqFk13bNmGRgfl/H001Oc5U8mIVznri4V4+Pp4y5blkRO\njoEvfjEX27ZFsW6dmFhnZ3RZUEZXl4q+PlGjnEhIto5MFN/5jh+HDqlIJJybY/ummCUzss3s0JCM\nz38+KXxnnD0r6toXLTLe18Y6M3D2yaoMCH4AldHsZGq6+rSvi/ut4bUyLrm5JvcVterw3u9x3+sx\ndXUBAWSQl2wE4bCEu3cpSau5mSy89u/3YmRExokTYfT0KHjoIWJqr19XEAqp6Ory4C/+IonWVo1b\nnPX2ijfbOXNMAag+++z/jYMHv8ABwenTYmv6zBmFp7ARIBat0KyPtdt+Mb0rY58pSEJCfT1N3585\no6C6Gik3hwgGB+XUMJEoXWDWY83NUX4M1uIeGpLR0aHx51yzJg1eQiERtC1caAiv/fhxFXV1fu6f\na71Gfn+aeOYtqAAAIABJREFUeQwEDMydS4libjcNablcBGrtg2J9fYqg5Y5GgeFhieuYAwETmgbs\n2UMtefs1bW7W+PU+fJiur90DeWxMbOvPmmXi7t20Hjc/34DLBfT1UVwzeS2bkGWSZgSDBn70Ix9n\n91ncs8dj4soVGZOTMkZHf4MFC/6jQ4LAUgFLSigx79w5FxYuNFBfn7axo6AUp0a8r09BY2P6tbS1\nRTB3rol33lEwf76BW7eA8nKK6x4eljE2RqmGJ06EceOGuC5HR+l/fj/wz//sQlVVEpcu0WbG/p7Y\nHRisQRn9/Wm/a/b7kZHpQzrefdflkAOFwxLfHLKaN89wWNLZN84PmtH999an/T5yvysDgjOVqUx9\nJHW/NbxWxuXsWeWeAyvv57jWxwSDOvbti2B4WEYsJrogDAzIePVVH773PY2HIKSZqCw0N9NkvNV5\nwHqjZYCKtej9qc51W5uGoSEJK1fqePNNEUxQ21njAPu9krXs+tjhYdHSyz5kxPSuHg8B/D17fHj6\naYrhPXCAXCJOn1awciVQWanDMChhbOtWvwDQdu70pVrGBoqLTWzZQnpXO+NqBz89PbIAxlgCGQPQ\nt27JqK2N4dQpD5qbNWRnUzu9qSkLdXVpENPaGnHosD0eGgacN09kYDUNWLMmxrXcS5bQWmhsjKKt\nLQtlZQbq62NYvz7G095EwCVGEDNGGiAm1zCQYooNtLdruHFDxuiojLw8g+uyW1sjwhBZc7OGBQsM\nB4NOkhYDuk4btZkzTS5fURQf/uIvJOG1zZuno6dHRlubj28+Nm2i13nyZBiTkxRpXVho4oUXnBrx\noiIxlGLWLDhcSVatykZnp+rwgWbBFexnkYiE737XzzczX/lKWott11BnZ5vcso48hGW89BKFW0Qi\npB/fty8CTZNS1nd2+zOT/7t/v8+hRX755agD4F68+N4evRlG90+jMiD4AVRml5ap6erTvi4+TGN4\nxtoMDBCYunFD5j//Y8fVdfLvbWiIYc4cAwUFBt54g4bgsrPFm20iATz/fNwhYWBMlN9P6VPsd/aY\n3cFBadoW/aFDKoqKKAzC7xdB7pIlj0PTTLz4IoEyxtyGw0B1NSVrMaso+wBaUZGBzk4Vk5MSZs40\n4fMROzw6SkNeTO9aUmIgmZSwevUUNA2YnMS0LhF5eTTMZrWseuklDevWxRGPxzB7tolr18g+zKmN\nhgP8sDZ8WqqgCnpe9nM29X/njoT9+7N4BDOTcjidJej9b2/34ZVXIkISHRvQIlAFNDb6eTLbzp0a\nZBmoq/Ojr4+CUI8cCdsAF22w3G4TsZgkMNL24JDOThpaC4XceOGFGHbs0FBcbEBV/3iQw4ULxPC3\ntkZ40AkNy0mpdfuXGBqK8Hjs0lIDqkqhH6xY5C8x3mkbt2BQ58NzK1boGBiQ0NmpIjtbXD/3ikW2\ndxTGxmQhCW/FCj3lWxxFbq6JoSH6OyZdsUp+5s418KMfefH001OQJOoqNDSIG8za2kAKSAf4+Xd3\nhzE2Rp2J0VGJ67eHhshD26pFtg+nyTKwaNGnc4Dt034fud+VAcGZylSmPpL6MKemGWtz9iwxuoxp\nvXiRbrLBoM6Bif24b72lYNMmatXn5Rm2xLSwA0BRkhk9J/PTrarSEQzqKCoy0N+fZl8rK3VhwvzE\niTC2bNH47wFwbejoqISKCh2/+pULx4+TJnfOHLJpsoKCri7Su1qTtYJBA01NfjQ1RXHsGIVFWAFe\nd3cYpgmuXQ4GdXzvexoPLdi4kR538GAEbW1Z2LlTw/nzIiPt8dB1nj3bFF47SUdIj2vVp7JUNgqC\niKKwkFrooZCKO3eAcFhGJCLh2DEVf/gDDcy1tZEVmZ197e8nfTKb2rf7IJNLhghUKyoMbNsWRUsL\ngWZrEl1FBelkrbZt4bCMsTFimq1dBb+fQPjwsIyKCh2SBHR0RDBnjoE9e2gw7L2CQ7xeE42NMVs6\nnyo4XbDznY7ht26k7H7SxcWG4Ghhl5cUFKQB+/CwqIM1DAmHD3vx3HNxPkz36qsqXz95eXRNp2Nc\n7R2FuXN1tLZquH1bxtKlxFxbJSLsvPr6FB6sYWW9GZDXdQkjI3YPagLQN2+m10RPj4LTp134sz9L\n4nOf02EYwG9/q+C55+JYtEjHzZskSRobu7eU4ZMqd8jU/a0MCH4AldHsZGq6+rSvi4/ipsNYXzvT\nGgrRoM/ChWSif+qUG/PmGVi6VMfYmIS1awkMXrkiAr8bN8ipwMoqPfqojkDAwPbtGp59Ni1t2LAh\nBpfLxIIFFHLQ0yNjeNjOQtPAD/OOpXMVrZi6u8MCmNy48XUkEv+ZP8fAAAF7WTaxYUMMqkoAdd26\nWCq2NksANgBw7ZqCefPSCXE9PQofLtu/38eBkcdjYs2aGEZHZSxdmpYRBIM6iosNjI7KyM420d4e\n4XHNTD4SjYpRvb29Mo4fV5FMAj09Mp55RgTys2bpuHJFwd27kmAN19c35QCExFQDXi8x0VYwFwzq\nUFWJB1TMnm1g5kwTfX3puOEDB7xoa9MEwHj4sHOIbOZMA7t2+blEY+nSJG7fVlL6WB927tTQ0yMj\nGDRw8aKC+voYBgacjDeAFAgl5w+7xdnp02krrw0bYigqMpCTQxHEw8OUdsdCGYLBtKwkGNRx/LiK\ns2cVeL2/QTT6OaHTEI1CGGDLyTHR0hLBwoUGbt4kRxErU01pcuCdBMOgwULAxDe+EeDexYGAidJS\nkpKEQioGBqTUZkZCVhb5FHd0+PDUU1MYHJRhmnYZkYTXXiNXikiE1oO9O7NxY4Cz59MB72DQuUm4\ncUPB44+Tfn9kRIbfD6Gz8F6Sqw8id/iwPMk/jPq030fud2VAcKYylan3rPt1A7ifGrt7nRNjm+3a\n0zNnaADs5MkwvvzlXA4o9uwRtZldXeINuLKSwAhr865cqUPXifU8d44GrBhrCgCNjQFs2BBDSYmO\nkhLDYS1VWEjM3P79Phw6RICHnSP7t6dHBOITE5IDEPr9BsJhGefOkfTAbrEWDIo6WF2X8JWviAlx\nui7B66Xzt2t3Gxqy8ItfTKZszVyOsIaDB9MDdzU1cbzzjj2lTkvpUxXoOgVDWF/T5csKFizQHQzq\nyy9nIR6nQbPDh1XcuUOgySpZWLJEn/acX36Z/G5lGfjXf3VxlrWlJYr+ftnhdXvpEgWNADRENjIi\nIxajTQmz+RoZkdHQ4MehQxHU1sbxta+RrtV67CNHxDVTVaVz2cKNG7QuptNxO10rVITDBOL7+mS0\ntGjQNPrcWDcXfX1kL/bb30qYMQOoqcni67m9nYbi5s1LIjvbRCQCBIOGY30wpjoriwBwW5smbMRa\nWzXuzRuLEft/4wZZ3jU0iCC6qSmbH/vMGWL0/X4RsKqqBFUlycTzz8dRUSGuz9JSQ1jvJNmRUjHR\nMrq7VRQXJ3HiRJjHgR844MW+fRH+nTBvnsE9otlzMenT/+l32IflSZ6pB18ZEPwAKrNLy9R09XFd\nFx+nGwC7mdnT3Ng5WdPe7GwSAyWMRfR4TESjEmdHi4rI+7S9XUNhoYFwmNrw69bFeBta1yVMTMgw\nDBPLlul8SIxJA1paNEQiNKW/ebMfoVCYM3Nz5ujw+01s2RJFfj6xlYODcLSW7SzoX/7lf0RJSZrd\nc7tN3Lkjc32nnWWMRslf9fBhipzV9bQfbHa2id27I4jHJZw65caGDTH09YkJaaz9PDEho6dHRnu7\nz2GJNjkp4dixMMbHqa1uZ0Ozs8lTeWoKXCv72GMJPPlkApOTwNKlSYyNpf+mqMhIOVAQM5lMAhcu\nuFBQYAga13BYRjxuOKQaWVnE9o+M0M9cLgAgHfXICJ3v0qWio8WyZaRbrqzUUxpdiu21DjweOaIi\nFApDlgGPR0p50xoC++rzmYJkZtMmP1avnkIo5EFLi4YtW6Lw+w0+rPXoo0k0Nvq5vy57DadPK8jJ\nAV5+mVw2vvY1GkCzBzaUl+uorw+gp+cLyM5Ov/c1NXHHYB2x7WLoi5WpnjPHQF1dAHV19P6ygUTD\nAAoKDA76a2tFOzIGopn22n7s9naN2+zNnWtg504fnngiybXk1dUJLnsJBg20tfn4OU1MSFizJhtu\nNyXTBYMG7tyRMGOGgj//cwKvN26Qf/RnPiMOu0Ui4maDSZ/uNfjK2OUrVxQOjk3TCZg/zHmG+10f\n1/vIx7UyIDhTmcrUe9bH6QbAbmZ2UMbOibHNhgG8/noYFy/KCIfJ/ioY1PHQQ0ns2aPh7FkFubkS\nmpr82LFDw4ULxHZu2pRmuY4dU/F3fye28AcGZLhcNEh36pSHOylYh7iOHVM5E335cvorNj/fFGQO\njJVlQ0rkawvs2OHjNldz51Lil7Vu35YxOJgGgVaWMRikjUBfn4yhIdIkr1pFGunW1ghMk3THo6MS\n6up0Qf/M2NT8fIPboQWDBo4eVWEY4Ppe1jYHTHg8QDRqOizTioooKMHOdFp1sVY5Qm1tzHYuGrxe\nsuNij3nssQRWrkyit1dOJa2JDPuqVdnYsUMTwj8OHyaf5bExGaoKdHeruHZNRlkZxVUrCqCqEpcI\n2DcUw8My5s3TsX59gK8LeyxzZ6eK/n5FkMysWJFAdXUSp08ryM01sWdPFtaujaG93YdTp8LYsUPj\n19TKDrN1c68BNI8HqK8P4Pnn42hq8mPmzLRmd3LSOVhXXU0SButxli7VUwNrBoaGJKxZE8PDD+sp\niQ6FfbzyCmnf2YbnXiCaDQnaj51IwAHIBwfTtnFvveXCtWtp3fXGjVH8/vcJLF5soKkpiz+PaYru\nFK+/Hsbjj+t4/HHn948sA489puPkSbJrq6zUsWwZPc76HVZTE8eXvuT8HLLnB+DY9GdS4D69lQHB\nD6Aymp1MTVcf13XxcboBsJuZ3WVg3jzD0fJcupQA5MCAjG3bNOTnmwiHZUcbnU3hs///gx94uT2X\nlSG9e5eYzdFRYmS/+tUpRKNO8NHXJ3PfU0lKJ4fZARZj0Xp6FIyNpfW5dXUxmCYxcUNDMq5c+RdU\nV38Oo6PgaVZWVvPAAS/3pi0oEH12jxxRcfiwCkWBwCgyXan1fFwuYlM9HlMAfW1tGvx+muZPJMTn\nOXZMRTgsY+vWLC4ZYTrrZFIET3b7tqEh0gwzz1c72Js/X4ckERtomrQO2WtjG4cLF8j/lWm57VrU\nO3dk7N7tQ0+PgtbWCGpr06D84EEKn9i9289BpV22oGnA+fMK/30iIQ5oJRI0/GZ1RiBnDEWwEGM+\n0t3dYZw/r+CRR8jKjL0PrL1fUxMXdLD2LkEiQXKZrCwTzc2/hN//OI4fp+swf749WpvWFvM/Docl\nLF6cxPCwjNZWAppbtkRRXGwgHpemGTaEcC7sd1VVBKKrqpLweqmzsXKleOxg0BAkHPQZS4dfuN3A\n+Djp19evjyEnh+K9h4ZkbN+uYXxcxp49PhQWipZtf0zecO6cgi9/2dm1mjcvPciqKGLwhtXyjrnK\n2I/5xS8mPjFDdB/X+8jHtTIgOFOZytR71v0eaHsvfZ79d0uW6Pj97xVcv65g3jwdwWASW7Zo8PsJ\nHHm9lOS0YgX561pbnrt3R7h+MBjUMTEh4Z13FNsNEILPbjgMhz0XA1tFRSZeeEEMzhgdlbBggXOI\ni/1+clJKPU52AJqqqiTKyujGr2kAQIyoFTwdPKjC7yfGsr4+7Ym7fXsWDh6M4OJFYho3b/anmDsR\noA0MyIjHkYrzTf/85k0ZixeL51NaauDFF0l729ampQA+6TL7+yWsWhVwMPB9fTLu3pUEy7T29ghM\nE3j4YREYFReLx5uaSuuUFy50gr2LFxUoCqAoJpJJEUT39JAvdG6uif5+iQO2wkIRsBUUGFi1agq5\nuSY0TQTaFy+6BLu5sjJdkC2k3UCmwAbs3G5TYKfZv88/H0N2NiBJSMkh4o51Nn++wTsBJ05MIpmU\ncOuWhEcf1TExQY4TLFTlxg0ZO3ZoyM9PD8tZLe3Kyw38zd9kQdez+RrdtMmPgwcjuHpVxvLlOi5f\nJibf5QKamgiAkowD/LXk5hooKtJx86b9cyEhFPIgFFIxPCxxaUM8Tq9vaEhGe3sEpaUAYELXwSPD\np9MNS1L6uc+dS1/3oSGS69y9C4HBb27W0N6u4c4dSQgdmU7eYAW79+parVhBEogvfSnHEbNttbxj\nz28H9G+++ckYisvUB68MCH4AldmlZWq6+riui/ttGv9eGmP7706cCAshCIcPq5xROnkyjM9+Nn1D\nsrc8rX/X1kZaUzvTV12to7PTg2PHwrh9W8ZDDxm4dUsES4zFsjO5g4N0YK/XxNGjpL+tqDDQ1yeh\noUFsBbe1+eByQWD+tm71Y9cuGszauJEAJFmW2YHaF9DZqWL58iTq6mIYHJS5u4O1BZ+bC8ydKwI0\n0yRJAvPfZT+vqCDASwEUJkpKTFy+TFHF+/d7kZ9v4LnnxNcwHQM/d66BigrYQCF51VrZ2qVLdYTD\nFA/sckHQKYfDMoaGiIVmg1WMFd26NQsnT04imUy3ztlxyssNTE0hlaJGw1QejxjvOzwscZZ/OtcB\nBlCrqnTs2kVuH9u2RW3X1cAjjyRx6tQkpqYk3Lkjobubgh0KCijmWJKAnBwdJSUmdu3SHAORVVU6\n98otK9OhKJKNKSbbPCbPKSszkEgAkYiM1avJgWTNmhgaG2PQNErE0/W/5Oukv59kOnl5OpYsIWeM\nefNIa2sdWDtwwIvduyMIhcLcMk2SSL5gPd9ly5JYuTKB/n4FAwMycnKSKC/XEY9L2LQpivx8Ex6P\nKO9pbdXQ0BDAli1R9PQo/NwCAWDPHi9//+bMIU21NaDlC19I8HVfVGSgrMzE9esEkA8c8GLXLg2F\nhSbfgN8L7LKuFZPtxOMUf7xihc6dWphXsc9ncgeUH/9YFTb41k2/y2XiiSfS0eMf96G4j+t95ONa\nGRCcqUxl6iOt99IYO38nMlT9/bLwu+xsar+fO6cgHgdnjQzDFIaXysr0lCSBnB48HgJrra0+bN4c\nE/SLdsDImGI7gGZRwYcOEVu7aZMfra2aMPBFIJq+Zmtq4rh5UxbswEZGJGiaxAM27GCEAbXJSQlN\nTVHcuKGguNjAvn0qjh718mQ0t5uGyVwuEQQqChtkI2ur3l5iB3/+c1fKYkzGI48kcPWqkkptM9DQ\nEMWdO84wBLfbTAEI0ivn59PA0+hoOia6vNzA5csKT7i7cMGF1tYsdHcTqCB7OE1g2nNzDUxMyNi1\ny4vvfU9Df7+Mmpo4B8mJhIzGRj82bYpyVr28XIeqAi6XhPFxkk8kk0BTUwBr18Ywe7bBnQWqqxN4\n6qkEdxkYGiIHAsaqVlXp2LrVn7LJS4Mkr5cszsbHgWSSHC3stnvt7T6sWxfD7dv0vg4Py1i/Pm0t\nxhj4rVv96OggoFtbS3HU9pb8+DiBwz17SI9r3Xj19Sloagpg374IDhzwoqNDQ0tLhFu1PfSQgVdf\nJQbbeo6HD6t46y0auJucJJY+Hpfw9tsEijdv9mPDhphDMuFymbh9m3UoKN55xgwTa9Zko60tAsDE\n6dMu4TWUlJDkwK4PZx7CIyPEZieTsIWwRAW3iNraGL7xDTEs484dCX/910n+HWKPWWauK9bBWPvg\nLAPIzKt42zbarCxbZmDZMlHiZd30nzolDhZ+nIfiMvXBKwOCH0BlNDuZmq4+7euCSR2sYNXa4gSm\n0x9Pb6XkdlNa1ze/GcDu3WJk7muvqXC5IOhHOzqSGB2V0NKiobdXgd9vYmJCxhNPJKeJGpa4DrWi\nwkBjI7G0THtrdVxYvjwJvx+4eZNCIAIBAoFWNiorC9i7VxPikllIRWWlgevXFRw8GMHIiISHHtLx\n2ms0RKRp1P5WlH9Gbm61Ixa4ri6GyUkJBQWkm3zmmWw0NMS43hMgzafbbWJwUMZzzwU4eHvkEcMS\nOWwIwKmrSwUgMr6zZhmcNS4tJb/gwUH6X1+fghs3FExNSTYrLmqDu90UOMGG2axAOi/PhNdror6e\nEtooJliHpgGrV08hN5fSwGpq4kK7/OBBFc8+mwO3m2QxBQV0TsxezgqyOjtVQQfe2qrBNCkdb9my\nJMJhCTU1Mc7epkFSFM88Q84Ue/ZEHKl0N26Qc4j1uTs7VQG0vvJKBPG4iZYWDefOKejuVhGPm/B4\nJEdYhq4DW7b433PjVV5OVmRPP52Nr33t/8E//MNf8d8dOaI6zrG/n7xzt2yhNXzkSJi7ijCAOXMm\nac+tkgmvl+QrVm/ngwcjCAZ1VFYauHbNOZw4MkK2btZI7epqSo6LRiXk5JiYMcN0bBL9fjP1nUCI\n2+Wyh2UAjzxicG/vFSt0TE5KQtz25CQ9nnWtpgOuX/xiAq+9puLNN+8dpzxdfZxmIt5PfdrvI/e7\nMiA4U5nK1H2te2l+7VKH115T4fOZGBiQeMtyxQodv/rVZApkSVAU4Kc/JZaxslJHVpaBtrYIkkkC\nobW1cbz7riKwvjS8lpY01NTEhbbt4cN0XKbvPXZMjMUtKDARi5H11bVrZMUUj1MLf3hY5t7BfX0K\ndu7UHMlXgITubhWybPKENsbo2b1hX3uN2sHMYm3BAhNDQwrKynRcuqRg/foYbt6MOUI38vKoHe1y\nSTBNKTX8F4XfbwoA3O8nBnjHDh//2/PnFeTlpYeDpgNOubkGB/ylpQTQWNv88mWFb2Cam6P40Y+8\nqKzUceuWwiUJO3ZkITsbUFUCqVevKti924e2NrKf6++XOSPY0kLgx+02sXRpEllZ6evGrunNmyIw\nGh2V0dpKDgsVFQYPsAgGdYebAbluiINsTFKzbVsUBw540d6uYXxc4lHCixYRO8zOa+5cA7GY6MJR\nWWk4Qh9GRmRhLeXnG4hEFEc0tD097s4dsq87cSIMl4vkDFZrtYEBen11dQFurRaJiK9zeDhtocee\n+6GHSBLR2qqlXCLALQEZwBwfl7lsZc4cE8kkYBgUuWx97MSEhFdeieCpp9K6e/Z3VVU610Jb9eFb\ntmj8WjNPYWtQDNNte70mamrSmndRspREa2sW3njDzVnd4mITX/96eqPDXB1YTQdcWdrhveKU7/W9\nlUmW+3RXBgQ/gMrs0jI1XX1a1sX7HVq5fZsGbRig+tWvaGLnzh2Z62ZfeCELzz8fQ1WVDr8fOH/e\njcpKA/X1ftTW0qT3/PliGMDJk2FBuzqdddTixTr/2Z49Phw/Tp6lRUUGduwgC6ejR8MoKyM3hr4+\n2dFmHhqSuYyBPffZs+kp+BMnwhxEMEbPDtDicfIlvn5dxrJlBnSdHCjicQkLFujQdQm6/rij/UtJ\nZDTks2ZNGgx0dak4eFCFxwOHv+zp0wQi5s+nWFn2fHbgJEnkx2t1UgiFVEcLu6nJD5/PREeHJoDW\n5maKY1YUYP36HOzbF0F+voHVq+MoKBBjqUMhFV1dHrS0RHH3Lg2WXb+uCK4cFy4o07gP6LhxQ0FZ\nmfjeh0JhTE1JwmPtvsuPPkruBkuXJrF7tw/JJAGgyUmSneTnE6vZ0UHvS0mJgYEBCpZgjH0wSE4V\n9iGruXN1/piyMtKTapo9DEVcM9eupdPSaEhQT21SDCSTEiYmgDlzDNy4QUw3W9tLl35OOPacOQZf\nAyMjJBnJydFRXx8TkvKslmDV1UnU1weQTJLHtdsNh1Ude2x+Pmmw2bn39CgYHJSxcqUO0zTx3HNx\nLFvmdKhgr5O5MOzf7xP031u3+rF9O/kK375NKX+dnSrOn6ffM0u4N95wC6zuewHTewHX9wK09/re\nut8zER92fVruIx9VZUBwpjKVqftaf2xohd1kyJYpiwOq4WEZ16/LDqumcFjGjRtAQ4PfIm/QOJv2\n0ksaHxq7fVtGMikhK8tARwe1yT0e03FjvntX5pZJk5PgUos333ThqacSGByUMTUl4xvfIEcE9lrY\nv0NDMhYsSCIel+950791S8GaNTE0NQVw4ICXW4xZHx8IpIeLgkEdLS1MUwxkZZmYNcuE3w/09ipC\n+5cBKTuoPndu+iE+j4ekEcuWJXHjhowf/MDH3SUqKw3eik4kwDWp1r+3J3GFw+nBuGvX7L+TMTwM\nLFqUREcHOUXcvCnj6FGv43nPnFHwt387hdFRspUTgTv5FufkmDxBbmxMRn6+kQqLUHgyG3u+nh4F\n8+cn0dlJgKq01MDMmUn89Kdh3LyppGQT5HxQXq6jro5ij69fly3sNsk47J7Gzz2Xlgbs3EnX16of\nrqgw0NnpxZ//uY7JSaC4GNi8OcC1wGkA73TlsF6727fBbd0YqM3KMvHIIwnu9Xz4sIpYjHyPb98m\nVri+nlwburpUaBqwbl0g5eIw/VpYvJgszp5/PoZwmAbr7Kx5dja4bOOVVyg0ZdeuCMrKDCSTJtxu\nCf39pNuePZsYfrZOq6sTqK8nOQl9Nuh1Dg3J6O8nfTirkRECv+QlnIUtW6KCrMfqTcxY3fcCpvf6\n/Xv93cfJDz1TH11lQPADqIxmJ1PT1Ye9Lu5X/PEfK2a8z6JnS0tJozd/vo5f/pJ8Ug2DtH8NDTGU\nlVEbm5K97IAK3I+U/TyZBG7fToM/vx+oqxO1mYcPq1i/nhistrYIurvVVHAB8ItfuNHQEMOGDTFE\nIsDRoz7k5poOppdJEHJzTdg1slNTwLlzLvyP/+FBZyexwuXlJJMAmF2Xgdu3Zezfr2LmTAKukgSc\nOCE6C1hlG2I0cQTvvuvC6OhvUFn5uHB+zOnA7taQm0tWX3a9ZiIhob3dhx/9SMWCBWSbRSEc1P5+\n9VViRJkDQX6+E6hZ///SpUm89pqK/n4Jc+bYz8HA3LkGxsflab1y7edLGmu6ntb33uUysW2bhrIy\n2qxs3uxHXV0M58+70NNDkpGKCgNbtmi8jU+DgKIX9IkTYR7FbH1/7d7JbDNm9Y1l/5K3Lg1SFRcb\nqWHEtH64u1tFT4+Mr31tSgDPzc1RTEyAh0XMm2dgaookHj09JK2xpqXl5hqIRCD4Evf3yxgbk7By\npY6sjFm7AAAgAElEQVQDB9LgeNOm1/H3f/8FrgMvK9OxbVsUg4MySktNNDbG0NbmQ16e6VgLlGaX\nxKVLLkiShKNHPQA82LfPKVVYvz4HAGl27dIfK8Pc1aWiqSmLn98//mMSa9fSBrK42EBuromXXtLg\n95PMwnqc8nId168rmD2bglrY9WW/f+yxpMPB4X7XJ037e6/K4IsPVhkQnKlM/YnURxV/rOui8f6O\nHRrq69OJTEuXkvevFSCdPBlGIADOMKbBFoFjSUr7hdbWxjB7dvrGfuCAF+vXi9ZiVheJoSEFfr+O\nnBxinxsbYw6gYgffY2MyHn44idbWCDRNwvLl+rT+sYODMm7eVODxmJCkNKuWlhgAwaApgIcjR4ip\n27iRLNLuJdsYGSEA/uMfe/CP/0gDc0NDEgoKTGRnG+juDuPSJQXHj6t4++20jrW2Ni4MJ7EwCRYY\nsm5dAC0tmk2nSjKC4WEZFRUURhAKhTkAnJyU0NqqYWJCwooVSYyNSZg9m0Cn32/gBz+IIBqlIT23\n28ShQ158/vNJB3scCnmEDQlzOnjhBTpv63uv6+TmYdWVPvSQjjlzCPhWVelobPTzIAy25uws+B/+\n4MLMmWJAwoULLuTnG47zSzOW4jpkXQvmTuHzmZzxrKpKor5++sS5cBgIBsGt1+zrLpk08eUvT+FL\nX5pCYaEBv9/Eiy8GsHp1PBVhTCAyN5c6IVZwzEJG2EbI7m/d3KxhzZoYfD7Sd1+9qmDp0iRu3ZId\ntmlsUHN4WBY6DorilBWxaOWbN8UwmdFRCe3tGm7elPHQQzpmzDDxb/9GnR2mUZ8xg56LbAmJrZ87\nl9j5qam0NOrUqTCOHKEwE+YDLssfLiub0f7+aVYGBD+AyuzSMjVdfdjr4t/T7rOyx6yNe+WK8p5M\nsv04o6NiItMXv5jAxYuycEO9cUPhAIcxq/E4DRpZGbzOThUTEzRRfvJkGJpGjykrcw4E/ehHFDpQ\nVaXD5zPx/PO5OHYsjNOnRXsqj8fE7Nmm4FihaaSLtbsm2P1jybcVPAzD7zcRDgN+vwlFAQIBAsJM\nG1xUZHAZw86dGpJJCG1+O/va3y8jO/sv0NsbQ0mJgaIik1s/MXDIWsdlZTrWrInD4zGF4aSXXtLw\n3e/Sf//whypqauKOON6+PoVfZwYot22LCqDq0CEV8+bBFv0cRV1dAIcPq4hGSefd0BBAa6sGu/Rj\n6dIkqquTUFUTK1eSRrylRUNWFrkTWF0jmDNGMKijulrHvn0qyspMGAYciX9NTX5hE2N3VFi0SMfY\nGEX2njrlwVNPTWHGDBNFRSJDumwZySh8PhNXrypcJ15RoePOHQqMYCEQra0RvPxyOgmQ+eJO50NN\ncgGndMXlojXCwkyoa0Drr6pKR1ub5mCqrbKAJ574LH7yk7Tbhj0QJRyWUVlJ2vfBQRnLlycRiUgp\nPbn4vG43OUhs2xblr4tprJnlHtNlO8E2i9s2ceWKzK9xTg6xqQSA4zaZk4Zr1ygAx34uTU1+nDun\nQJYJeM+d+9Ewsp807e+9KoMvPlhlQHCmMvUnULpO3ppWW6b3MxltZ4+tgzL3YpLtbUVrIlNhoYGf\n/9zNQx3sN9TubhWXLlHoxNatfnzrW3HB+WFiQsLMmSauX1cwNQV+Yw0GdXR3q7h2jcBoW5sP69fH\nkJtLsbePPZbEiRNhjI9LqK7WhevAwh0YyNZ18p4dHxdBS0+Pwj2GS0sNzsraB700zUR+vuhwsGOH\nhqkpCaWlumBRdfCgiq9+NQft7RFs2uSH1au1sZE0nmzYi4VxLF+exOnTbg64GBNobc2z6x8M6li+\nnAbBcnMNlJUZWL8+4BjoystLs6IMUNpB2927Mt59V/xZNAps20bJX8EghVO43QRWfT5qoZeUGBgZ\nkbBxox8uFw1gnTlDccf9/RL8/rQrw5IlOsbHJZSUkMSFDaBZJSLWzZOikOWZ359ecwcOeNHdreLN\nN9PsOGvRh0IqVq0iVnbXLjHq+O5dCTNmEOtrGEBjox81NXGcPu1CVRUBYQZ29+/34cgRYjKtSXgH\nDnhx/LjK3S/6+sgHejrpSmWlgfPnXZg/X8fUFJCba2LTpihmzDAxOio71h9j9fftiyCZBNrbfTx2\neuZMige3buRyc2lTZt00sG6G/XnLy8mjOCuLuXHImDPHQF+fjKYm0vVWVydw7BhtDKx/7/OZ2L1b\nw8aNtF7tlnTNzZqj0+LxAK++6kVdXcx2LmndtPU5Pu4BFZn65FYGBD+Aymh2MjVdfZjr4q23FHzp\nS2lQdvJkGCtW6Bz8TmcuP52jQzgscwBy7hwBAjsjvGKFjpMnw/jd71zIz6eW6r59kZRpfhb6+mQ0\nNkYRCqmOgavTp8nY/2tfy0YopAKAbfpfRSxmwuUi9pX9bTJJjNr4OHn49vXJGB6WOcC2spvr1mUJ\nz/fii35+/PPn0+4Ox4+LoRmSZGLLlgC2bNGwd68fDQ0xSJKJhoZYSiLhxfXrMubP1x3ewy4XsHlz\nliN2eGKCBvRKStJerTQgl8Tq1VPIzzdw6dL/h3/4h//Mz+PwYRVf/aobBw54eTRzKEQa0+Jiiji2\ntuqt16+ri3xsralZZOOVbv8zKYcdtOXnG5g928my2kFWa6uGYNBwMHx9fRSiYddut7Rk4amnplBQ\nQFZsg4PyPaUN5MygO+QcXV0qQqEwzpxxpRwF/Pje98j2jIYfaRPFANzkpBj1vHdvBA89pGPdugDq\n6mJwu0mjzdYPDWNGhM1TMgns3UvDYgcPRjA+LkHXidEdGqIBr5de0nD4MF3rGTMMwYLNGi3c1aXC\nNMGdKUpLdZSVQTjesmU66ur83JrujTf+N95++z9g2TLdoc1NJmkTd+WKYrt+Ths1xvB+5zvkjWx9\nriNHVA6s33rLhWvXFMeg6Zw51LFgaYOsy8C+J7xeYOHCJIJBnb/ekhIDLS0acnKcbPyJE2H84Q8i\nUM8Mqb3/yuCLD1YZEJypTP0JlB3MjozIkGUdZ88S02sHZ/dydMjNNRzs7euvh7F8uS4wyeGwxKe/\ny8p0bN8exe9/78L69TSN39AQ4OBRfH5wBvLMGQUlJYbjvCordQSDesr3NJ0yZbd2YvGsk5MS3G5w\n8GN9PgZYAPDjs98NDko4eTKMcJgkHXPnGvjhD1UUFJgIhYg9t7arKbTBxNWrMhYudA4HEsB0Asvt\n2zU0NYkBA1b2s77e6QdLrgi0Edizx5dylZCQSCjw+w2hVW/929FRCdu3RyBJxFru2xfhP+/uDqeG\nDpUUKBNZwd27KR3u+PF0FPLwsNOdoqpKx8CAk8UEIOiei4poyv8rX5lCPA7s2pWFv//7GLze9GPs\n8gKPB1zPKr4ukrCw9VNTE0c4LKG83MCFCxIACYCJykpdAPhMq6rrQCxGsc4TEzI8HqCwUOcyFrvX\n9PHjKkZHySXkxRepi7BtW5RrmFn3Y9EinW9umHwFgCNaeGBAFjobVo0z2ywMDVEwCUDaeUUh5xD7\nZ7u/X8aWLfS3dg9simwGjhwhBrmggJw3mGuH/fPx9tsutLf70NWlwus1MTxMnRYWOlFVlURTUxrM\nNzdrqKycvstz8mQYfX0ywmGJs8a/+tUkXn89jIsX6eeNjdQt2L1bHND7sIbUPqph4Ux9fCsDgh9A\nZXZpmZquPsx1YQezwaCBs2cVnDunTAvO7DGk7CbhcpnTsjQABNnEyZNhbkHmdpu4fVvC0aNewbIp\nN9fkKWwXLqSHdGpq4qn4Vd3hJpBMSqivD6CjI4L8fGJy+/vT58L+zc42MTJCwOfoUS9qa2McdFqf\nr7xc50AvGBQn9fPzqa3/9a+LjOb69Vno6lIFJpqxvU1NWRgaktHdHbZF7NL1sOo3580jv+NVq6YE\nVvLAAVWQgMyY8bjtnA2k3SpkvPhijFuQMYusHTvI87WkRHy9kQgBwu98JytlsyV2AKxyF/v0P9Nr\nnj1LAJgxz9bnX7zY4A4K1p9XVZEkw+paYd+4MAb5ypW07RyzlqP3R4dhAJcuKQ73i7lzdRiG09Zs\nYkJyuGocPKgiEiEJhmmK728opOKb3/Q7rod9aLG3V4YsQ4hhPnXKg9bWCAIBoKDAwN69EUQiaVZ+\n6dL0OdvZ2IICA+++6+IMKtu0seNR9LbJ1+ajjybxwx/+XwiHTcd7LElpnbmmQRh0GxyU+aawooJk\nKj09CvLzzVRIBWySCpNvknbv9vPo75UrdYRCHqxaBQHMZ2eTTKO5OQpFEYcRR0ZkeL3A2rUB/r3U\n1yejuJg9Lu0/HIlIH8mQ2kc1LPxRVgZffLDKgOBMZepPoKYDs088kcu1oQyc+XzE0A0MyDh7lv7O\nPiySTOqCx25hoeFgo3p6FEecMQNReXl00z51yo2WFg3DwzKqq8kFoqNDw6VLZEf1zDMUM5welpL4\n34jDWZojECESkbjOt7k5mjLoD8PvT7ObxcUGsrJM/Nf/mvbp3b07glu3aFI/J8fA5ct2/aSUYjxd\nWLw46QAytbVxnDrlxtSUJMgkzpxxYft2jbep29p82Lw5irq6GAoKDLS3RyBJwMmTHuTnm1i7Voz9\ntbLEqgpkZQGAhCtXZM4279kTwdmzbgBkP8ccKw4eVHHjBgHHwUEJRUWkK75wQbEAEDHQIJGQHNrP\ntHsC+bqOjkrIyZHQ1UX2X0VFBvbsobZ5KBTGjh0aRkdlVFUlsXWrH8kk0Nioo7OTHs+uHXt+gEAJ\nkw+QNlpPuSLEEI1KuHgxrfO1ul94vQYmJhThml+6pHA3AtaaHxwkVvvuXRlr1tBQoR3cWv+/xwMe\n9mF9r+068sJCExs3xrBxIwHFgYG05vnll7NQVGRg794EB6fFxTpOnCBmlNw+TMyZkx48sw8V5uYa\nWLDA4Cx+YyM5i9TWBrB8eZJb+pWXG/D5DMTjEvLzDYyNyZAkE7/+tRtPPTWFWbPIfcK6UaDNJRxD\noL29NKhHa9tEe7tokcY2EfbPwBtvuPHGG260tor+yIzNFV+XaZs5oCG74mLzIxlSy3gDZyoDgh9A\nZTQ7mZquPsx1YZ98PnWK0peYNjQQoGQr08QfHUhZsYKGc6wa45/9TGy7RqOSgzGORoGOjgjGx2Uc\nOUKpZlbmjiyTJCxcqKO/n25OfX0KmpqI+WWaxfPnFdiBW18fuMa4rMzAxo3EqhYV0TDYN78ZhyRJ\nePdd0Zqts1PlIKmlRbOBdg3z59vlICZnlMfHZT45n59PoRyTk8DmzTGbHpbCF86dc3GWbGiIGLDL\nlyXHYN2bb4qv71//9bd47LHPIivLxM2bMsrLqS09c6bobXzwoIrW1ix+zNmzaVguP9/A/Pm6A8Dk\n5BCzbgdbAAEVZ9JaknvlEsPuw86dGs6dSyd/Pf98HKdPu3HmjAuf+UwSBQWkdd6+XYPXawqbF+Z1\nzP4/SV8ULh9gEoOeHgWmSXpbxs4nkxDcL5YvdybkLVhgIB4HB5asy3D+PAHUYFB3dEDsQRYEhE1s\n3ernHYvFiw00NWXx9+f8eXpfOzo0riMuKjKQmxuDxwN0dqpwuYBVq0SwV1amo74+wDdgHR0RtLdT\nrHRHhy8FIoG8PFpr9fV0fbdsodf9T//0WyQSX8BTTyXw3HPiGrpyRbZ1Imgg0C57unRJ4R7H1p+/\n+66CZct0rF8fQ2UlpSg+8UTCwU7PmWPwzwAbxLOy+CdOhDE2JrK51s24HYRmZdF3jpX5/TAlC58W\nb2BrZfDFB6sMCM5Upv4Ei335M0eBX/xiMpVW5WRG7HrfFSt0HiTBHjc5SfrZa9cUzJlDjCANGFmH\nXsQBHrLRsvq5pofSmMMB02y6XNR6Hh6WANhT2gwsWqTjnXcUTE6SZtGV+marrY3hG99wJn2xY9IA\nUwSzZ5PzhChDMDE0RG3zkREZc+fqiMcl7niwb58Pa9fG0N9PsbYM5Nh1uF4v4HIZcLvp+WfONLBt\nG4HHeFzUYF6/LsPvF9mymTNNvPQSsaFMqtDWpnGfWPa3lLqV3hhcuiTh8GEvGhpi8HpN4bWx9nh9\nfZpRXblSR1+fnHKSMBGJgAOcpUuT3JM3GNSxfbvmkGEw9pbJHzRNEpwwjhxRhfOdmKBrOTYmY/Hi\nJDwekscw8Mds0gic6g7HAXYtli+nGGjrcwcCQHY2MfmhUBi9vYow6MbkHhMTtHnq65NTEdngvst+\nP8lz2to0NDdriEaB6uok4nHJpiOn96qgwMDAAG1g7JZgBw+Kr900Tdy9mz5nu+a4uVlDQwMNYb7w\nQg7/3Fot0vLzCXAyHS9ju3t7KSzDasvHPtd20L94sY5k0nTIV1as0Ln3MQPtdmlSfr6BvDwTg4MK\n985ety7G9cvz5un47Gd1uFziJtrO8Fqfc+lSJ/v7YUoWMt7AmcqA4AdQmV1apqar/5N1YWdLli7V\nce7cvdkT65d/YaGBNWuyuf+pXepw4YLs0Ps6B+ZMvPBCgDNtdXUxqCpS2lkJJSWmA7QVFoo35Ece\n0XHsWBgXL5JbBbFlhgBiOztV7Nzp5TG/LMksGpUspvwGNmwgmcHdu+IxmTUbez4WghAKqYjHgRde\nEEHS2bMuhMMGvF7gyhWXAKIOH1axebMftbUxXLyYZm/tw1wVFYbD4aKlJSs1OS+ez9y5ZDN27JiK\nP/yB6aT/Cs8/HxekCrNmEWi3a0EBMaK2r09BY6Mf3d0q1q8XXTGuXlUELXJ7e4QPVLndJjo6NDz8\nsIHeXmBsLG0PVlMTtw0hsqQ1YPHiJLZti2LrVj82bBBZx+Fhmbsd/OIXbsyYYULTSB9LEhlwych3\nvpOFtWspvS4vj9hk63NlZ6fTxy5flrFggdNj+exZFwfKnZ2qo4Nw9iwxuKFQGAUF4nvErMBaW2mz\nMTEhpwBxBKOjMnbsoI3Q8DBp3VtbIxgdJfs9KzBlx7K/V4sWGbh8Ob2Zs2uOAwFg164IHnpoOm21\nhupqHZOTnxOiuKcLy2hqCqC2NsaHSEUvZnLbaGgg2dHBgyouXqQwmEuXFEHry4JOGBu+bBm9TpHd\nJjnVrVsymKb5jzG27weEfpiSBVkGli/X+XHYOX2Sh+My+OKDVQYEZypT76M+7lPEdrbk5Mkwvvzl\ntNZ1374IhofFc2df/ufOEUu2f78Xp0550NGhCTKF114TWazf/c6F//SfEgKIHhiQp00hu3yZbqSr\nVjm9acfHwT1VNY1uymNjEpJJCYGAie3bvVi7VgRSFy8qWLuWmOFZs0x4PNRiZ21eOwNntzm7e1fi\nXr8lJQSSDx2KADBx5YrLBpIULi8IhVSHI8HgoIzVq6fg95tYuDA99MSGudjg2NCQCIjeekvBmjUx\n7N/vQ0NDNDWpLyORAO7elbhzRmtrFn9/vV5yNti3L4LBQQpa6OpKa2erqpKYmJDQ3h5BaSnpmWMx\nCR0dEZSXGw63hrfeUhyMc2Wlzs+lsNDA+Di5FjQ2BnDq1OQ9ARtjf1eu1PHii37uYMC03+z5NQ2c\n6WftebY+29s1XLsmp9hLAtwNDQEuU7EzlSUlJqamaIBz5kwTg4PE2Pf3UydAUUxu50cbsjRAtW7c\nEgkJt29T2pn1Nd28SR/unp50gEVzcxTRqIT6enF9bdiQHvALBknzLMtOVwvrAObwsIT9+0ka43KZ\n3FHByrL+3d/lIBjUBVu1yUlKL3zhBbrO7e0RzJhh4NSpMFRV1KEHAsArr0RgmkBbm4+vlWDQQDhM\n8dKJBL3uvj4F/f0KD4OhIbn0+SxZkkRLC4Vt5OaSh/Lq1VOOjcns2eYH8vd9PwEV00kW7uf38adx\nOC5T778yIPgBVEaz88mrj+KLcrp18X6/7J1sSRqw1dTEHR7BDOhYf04tT9ORqDYyYteNUgiA309B\nAO+8o+DUKQ9WrUrfFIuKDExNScjJMTFrFnnpejzUxtd1oKzMgGEAvb0EfNra/Ni+PSqEX7zySgTh\nsCR4pc6fbyAWo1ZwT48Cv1/C8uVJ5OZSy7y01BCAwMCAhFCIBpDmzqVBsdFRmo5ngz8EcDTMny+C\npKoqHWVl7D2mQR37zViSgLIyE6YJQRvpchEb+cwz2Rz8M2mH200pWHv3RjAyIsPjMSHLJsrL0z62\n1ra1ovwzpqb+DKtXZ+P4cRVHj/oQCnnR0qLh/HkXcnMN5OSY2LPHh9OnaXBw4ULRX9kaoOF2k7UW\n04O73aQN3rCB4pStIG/HDo1fg9ZWDYWFphBMwVrq27Zp8HhMQSYwYwYNWPX3yygpSeu0EwlxAK2m\nJu5gytnzDw3J6O9XUFioc5BbWWlwj91gUEdrq4Z4XEJeHklH2OdmzhySBzANOAOU4+PEpPf2UucD\nIGbW+pqsg29WptsuAzp71sX/GyBng4EBGa++6oN1cE+SRNY0FFK59rm1NYLLl8W44okJictSbt6U\n8d3vMo00eevW1saxd++/IZF4DN/6Vo7DUq25WUNZGQWNsDATq856yxY/2tsjKCwUgz5OnCDpyMKF\nSS4LWbKEvnMGB0nisH17Fvr6FMHhIhjUUVFh4No18bvjfrC207HFb755/76PP23DcRl88cEqA4Iz\nlan3UQ/qi/L9gm8nW5IGbHbm7ne/c6XidjUeaTo5KWHePPLeBRRH65YxoQyMvvJKAhcuKDAMugE+\n+2wc+fkm9u1TMTiooKoqyQFgXZ3YopUk4Pp1hQ8Q1dZS29vlSusYe3oUqKoksErHjqnYsMGPnTvF\nATYmS9i5U3PoRiMRCYYhobLSwIULCh5+WLeBBQZwZMTjBmdwg0ED167J2LWL2uGrVuVwp4rsbJI4\nXL2qYHSU/F3z802erAVQyEFxMXkcM7BJ18k5MLd+fYBfBzaYxdrWXi9w8SKx9Aw8shCN73/fhyef\nTGByUoKqSvj2tzW8+64Lfj/padm1TCQkXLpEtm23b5NetK3Nl3rfgZUrSTO6atVUipFOr5XcXBN7\n94puHK2tGrq6KC2NWZpJEp2blZlevz6AZJKS38bGKCa6t1eBJJnChsO+Pt96i4a1Tp9OrzerM4E1\nprimJu7wah4bk1OvS8fgYNpnuqdHwYULLixZQm4VLESjooKYWWJ6gSVLdD6YNjkpoazM4JZ9VlcL\nxian7eroZ4WFhkNmYhhOi7Xjx8NIJoltLy83hPCMbds03oXo7laxa1cElZU6+vsV9PfLAEysX0+D\nd1u2RAVvZSanuHRJFtYf25ht2uTn59vU5Mdrr6mpzz/JqHJzgRs3FBQWGtixI8sRn8020fPn6/jl\nL8Po6UlvqO3dnvsxaDYdW3w/v48/jcNxmXr/lQHBD6Ayu7RPXn0UX5TTrYv3+2VvZ0u83vTUtt1T\n1erZWlsbE0DhyZNhfPe76TjZlSt1TE2ZKCnREYkAFy+6UFMT5+c0d67hSAAbHCQmbvnypIOZ9fmA\nQMBATg7Q0BDj9lk1NZRA9+qrEdy8qWBgQHL48N68SWEB9uG94WEZL70UdehGfT5g926yIpszhyyg\n7MN4adsvA4EAeKSunZlkr+HUKQ/q62OIRCTBZcLKXjK2nA0useFD5o/Mjh2N0jmmgQPQ0eHjms2y\nMkrY6uz8K4GhbGhI61xpMM2XildWHWzgD37g4+zz1JSE+fN1XL+uYN26GH/fWAIbszljGxmm1T1z\nRpSJAGSRVlZGjhjz5+t4+20X5s83sWEDbWxefNFIacw14To1NxPb390dRkeHhqkpOFwo5s83kEjQ\n2rp1S0ZHh8aZ47IyXVjPdgDtdgOjo6TLbmjwo71dEzTuVVU6D9OwD8mdPSth5coE4nEJTz89hUQC\n+PWv3cjNJY25ogDz5yfR1aXi8mUFjzyiY3SUBuL27YtA0ySUlBiORLV58+jzav1ZRYWB/n7FIa0Y\nGKAAi8bGNGv+5psKvvtdv4Pt7ep6HM8+60/Zr4l2ZAUFBjRNEdbfkSPEPm/YQDrrnBzaoLhcJv7L\nf0ninXcU/OY3Lu4bHQxS8qO1q0TSCRlPP53gHamVK3WH20xWFg25fViDZvfz+/jTNhyXwRcfrDIg\nOFOZeh/1oL4o38+X/XSSiZ//3M2ZybIynbM9s2cb2LAhwFvJ9uGl27dl/OQndLO8fVtGb6+M73/f\nj927I5gxw+SawVCIwiDslksXLpCOluk8iT2mqf81a2IwTSA7G5wR3bJFw7p1MQ6UrDd6uy7R66WW\nvP2aFBWRLIGBTnYDLy83sHp1HMXFJmfFrMN4waCO6uoEOjp0FBSkh5kMA4KTwrVrMmflOjtVPPNM\ntgNMDwxIjtCPPXsi6OwkxnTePCMlwxAjhwHY2OsompoC2Lcvgjt3JCgKUgDt3tZcjM2eziFh+3ZN\ncGg4fFjF5CRZylnlCFZA3NamIZGga6rrzkE/KxBvbtZQXm5gxgyTs6llZQbGxyl0QVGc+uFEQsLp\n0y48+ii5haQZdkCS0oEjhw+raG3144c/VFFUlE4hs3oE23W+kUhad9zcHEVPj4yOjojAZHd3qwiH\nRY/it9+mdXvkiC4MYh4+rAr2YwcPqti6lboO0wWJHD8exv/P3reHV1Gf674zs25ZKwRCriQhrERA\nqAlQwVZ3W23r9tSe8+zjaTl9lFbU2haeEq4SwIBKg0ICSQiieDZtaBIuSajSHvc5j7h3zz5uL9ta\nBZSbBlByIfcLCVmzZl1n5vzxrZk1v5mIYt3H2/qex0eSrDVr1sysNe/v/d7vfUtLPfr+FRXJWLXK\ng7w8BU1Nov4Zrax0xYA2m/RWW+tCdbXEyErchIcxNsae36EhXu/kmOUUgkDXoHE/+vt5rFvnxtGj\nPly5AuaYHD7sw7lzAgSBrv09e5xobxcwOMgzIR92OzmLvPOOoC/GZZkGaI2ypbo6/39op+zT/D7+\nOLrkRH15KwGCP4NKaHa+ePX/44tyvOvC/GVfXExRx8Yv//EkE0ag2N/PIy1NxR13RHHkiF1vJbe3\nC5bhpUmTVASDNBCkhTCsXh1EW5uA7Gwy+KebI4UuzJnDBkbMny/j0UclzJolm7xyA0hOBpKSVOJ+\nyK8AACAASURBVGZKPyWFvIm1n7UbfV6eDLcberAC2Z6RrlILB+jv53U7tl/+MoRJk1Rdt2q3qxZN\nLLkJKLpTQFGRPK5vrdmOq6lJBBAfhotEOItdVGYm2Y0tW0Yt9m3bJASDrJyjsVFEXZ0fo6McMjNp\nKC8cNscL02MBFZMnAxcvchgefhVZWbfC6VRRUhLUz4vbzT5HA4ra6403lHf5ModJkxR4vfHFgJFN\nXbo0xIC7xkaRAVNz5sgMS+nz8RgZIVnA8DCP3/7WiS1bAjEduHUYUtM6p6RA1z9rXtBlZRImTCBH\niwULInC5yFc6J0dBOAxUVpLExOgRvH+/D4cOkcXZtGkyolFODx4JhWgfzTpVTWbBss+y7gRhBqba\n9VhSEsLwMHke22zU6Vi4MMJIJpxOFU88Iel+whs20ABbV5eA/v4QcnNpSHHt2qCFMU5NJZ37+fO8\nnkiYlqZg0yZ37LPCnt/Tp1/BsmW3xq4HMMz2wYM+PPGEpKfrbdjgxtq1Qbzwgg82m4qBAYFZ6A0N\n8RaZ0ObNSfp3jBaTrFmhbd4c0L8LT54UmNmCw4d9mDPnPxZQJoDrh1cCX1xbfSogmOO4OwHsAsAD\n2Keq6vZPY7uJStRXvcxf9idOWAHveJKJggJKEMvIIHBUVKSMy9i43Sqj9920iSQDZo/T1FQFoRCP\nu+8mgFRT40dJSTDG/mmyi6iuazR75fp8iFl4cQwAef55O9atC8SGdGjoyut1YOnSEEpL2da+z8fH\nQIwd995rR1mZhLVrJ8TavwGLbtUMfDSGsKZGimmi2bQwjX00Dz91d5N+s7eXR2EhhSzU1rr0+ONI\nhIMgqMzw0f79osVx4PRpwcBSkn2Vme2eNy+KhgYRihIPEhGEJBw+TCERxvOiJXLRYFoAtbUuHDxI\nMb6pqSpcLnJRqKjw68C5oEDBj388gUniy8//cHlBXx+PJ56QMDrKoaiIhh1Zj1wFkyfTYOC2bU5s\n2ybh/vvjoQxae9zlIgnAuXM8tmwJYO9eGuwzy3Q6OsjRwRg4Mt7Ql2Z95nbHJSzt7WwQyuHDPvT3\nU6iIWapi3K9QiEC1FndtfKzm2jCe/diaNUHLYsluRyzxkD5HNhti2mIgO1tldL+HD/uYYcqREdqO\nFqzy0ks2bNok6R0VtxuxbgOB0fp6O77/fQUDAxQeUlUlob+fw5w5Mnp7yWZw7lwZ588LKCkJYsaM\nKOx24I47UtDcbLXMM553m40CcLRB3LS0eBfI3JEyf/+89ZYNKSlgmOLPs7NOor7a9TeDYI7jeABP\nA7gdQA+AtziOe15V1da/ddtf1kqs0hI1Xn2c6+LDAK9R95iWpuCXv6ShpJKSIAYHyXYMAMPYNDSI\naG8XkJSk4sABJ0pKQuMOR125wmN0lEdqqqKzX6EQ2Zj19Qm6lVdZWUBnmc1Mm8ZG7dghYedONqDB\nHBJQVSVZWvsEFFgws2CBjP/xP0SkpBCDVllJoKOvjwa2vF5ZBxwpKdC3pUXgmreXm0tMIs9TK19z\njsjLUyxpa8QIA7t2aXpcFtB4PLRt4/bz8xXDsJWKvDwZR4440NREnrTagNbKlR5GZiLL30N7u1Va\nwHEUIHLuHA+OA4aGeESj0FPINHBjBJAHDoh6u3vjRg+qq/2QZaCqyo/Jk4GREY5571OmxB0uzp7l\n8PzzDl3icd11CoaHOXR0CAgEgCVLQvq1ox1bTY+6ZUsAq1YRU+5wEICvqXExEpJNm9yoqpKwY4eE\nvr54cInmOau97+Rk8tB1OqFfJ2Nj5AFtZDf7+3msXOnB7t1+NDeLsbQ9GkAz6mQXLYqHUZw7Z2P2\nqbrapXsGG/fB4RjfKYJ8h6mjcOSI3RI1rMkm6LMrID9fwdmzHGbOlHHunKAvELZtk5CdTQvP48dp\n8QQQoI7bmN2C++6Ln9v9+0UUFakIhVScOiWguNiaEuj3a1Ialh3v7GQH/goLafATAL7xDRk2G1kl\nDg5ymDWLlR9YPcPBzC4kLMj+/1YCX1xbfRpM8DcAXFBVtQMAOI5rAXAXgAQITlSirqE+DmNivuFM\nny5Dljk89BCxmtnZwFtv2bBtm4TBQZ5hU2tq/MyNT9OUNjWJWLMmrsutqWHZSb8/bhdl1EhWVPiZ\nFq3x33v3OnU7qvR0FTwPrF4dhNutYuPGAEZHORQXKzh50hqBfOIEZwHRKSlKzFc1zr6uXevWmUcj\niDZ6+548Sf6qWkvZbidv4eZmEefP8zHmlI8BY+hDQZoUwOmkNr+ZHS0okNHVJaCqSoLLpUIQVMyc\nqeD4cQ4AAdmnnvIzwDg3V8HKlWzwh8MBi/zACCK130cisHjler0K46DwxBMSE9oRibBWZCQ94PHY\nY0l6uzszkxwkAgEOv/hFErNvggBcvEjPVxQaYFu9OojFi1k3Bo9HwYwZaozFpcWH5m6RnEya9EuX\nePz85yFMm0ZJcg4HcPKkDWfP2hg/5K4uHoJADLbmKmJmy3NzZTgcKs6csennNCVFRUaGyoSdHDpE\nx1KSOHR3A8nJKlSVnBdGRkhK43IpqKkhL93MTIr9PX/epoNOAHj77ai+cNK2PWWKguFhnlkwUCck\niHAY+OMfybfX7C1tTHzLyKD46/nzZfzTP9nxox9FIEkcHnooiKEh+uBfvMgzn4W9e526RtzsCDE4\nyOHv/z6Kw4ft43Y6+vp4uFx0XTmd7OeLLP5IUzxnTpRhrFtafMxC9ehRnyV459lnffjrX22MJlir\nL5sFWaK+XPVpgOBcAJcMP3eBgHGiPqQSmp1EjVeNja+jrOw/X5UxMWuEZZljWBYCge6YjIEFvda2\nMP2bEt3iLg7NzcT2tbaSR6hRA2p0YNizx4Vdu/yorxcxPMxjyhQZzz03hrExHv399F9hoYzWVsES\nYJGeTu3U2bPNAQYKgHgb3emkUAubjSyhCgoUbN9OfrgAdG2yZvOmMaxdXQKOHxdw441RyDKHNWuC\nmDJFgcul4v33iYEDOESj5CCxdGkIgsAOS50+LcQYZNUCPo2goKrKj0CAx4QJCoqKZFy4IGDrVgnn\nzwuMbZp5EdLeLsDlUk1Ahhg5I4js7X0FbvetqK11oaGBQPu0aQoTa9vYSLrl9HRa7NTWumCzAV4v\ne3xzchRkZdHxbG4WY+9NwalTLFjr7aXUr+uvJ/mH10sLiW3bJMbtw24HMjNVBshr/rIcx0EUVSgK\nBYAY2dCtWylQJBxmwdjUqWS5duYMe501Nor6+Vi71oMVK4Jwu+MhEKoK9PVxJtBHg5der4KqKhfe\neMOuA3xtcVhT4ze5V0iYPt0aqjF5cnywrbBQQXV1fHuNjbSYMQLHxkbqFpgXczfeKMe06RQWk55O\n2nUaRuSY0I2qKgk9PTyiUVWXOixYIOtyi9/85gXY7T80LA5UvP66YNBds9ctxwE33CDjuedI2nP4\nsA/Dw3zM0o3H0BCvL2SNaXHt7Vf3/uV54NvflpGcTIC3rs5/VaY4YUH2H1sJfHFtlRiMS1SiPiel\nDV0B8ZvN3LkyzpzhMTDAM61I7SakWRNpzzFG646Osm4EIyN0g6LhH+DIEQcqKsj1wei1Wl4uQZY5\nuN00IGfUgHq9Ch59VMLs2TJGR4n1NE7Pt7SIePDB+M/794tQFM40hMMhK0vF3XdPwN//fRjNzdRm\nzcxU0dvLITVVwbp1QdTWulBR4YfDwVkkE319PNatCyAvT7XYvGksZ0oKYgwn+940PWl5eQBnzgi6\nXZZ1iAsYG6NYXI0l+9rXorh8mQVbaWkqHnwwyeKJbLZNM1uBeb2ypQ2dlyfr5yg3V8HAAI8dO1yQ\nZdrnzk4K+Fi3LsgAlZ4enok81oBZVVUSEzJRXe3CsmVB5OYq6OrisWuXC//4jyJuusnKPGsOEE1N\nNHhmjUuWkJ5O2zGzz2lpZPO1ZUtgHGkLAatLl0j/29AgoreXAjXOn+fxzDMubN8e1wv39/OIRjmG\nnR0a4jF3bpTRYZv1vMQiu/UOxhtv0GdlZCR+PRqHMrXPz+nTXGyQk7oge/a4sGOH1Q1C297QEC0a\njOdjYIAG9daujTtFfP3rMgYHSa+dn6/oITRZWQomT1Zw4gQbcGN8vYYGEVOnAkNDHGbMoOvo8mWO\ncYQYGwNEUcDAAIeGBooBp1AO6sZkZSmIRjlGEnX0KFHTxkXKH/4QP47aAmjrVj+8XgWtreQfrChg\n2OCrDap92SzIEvXlqk8DBHcDyDf8nBf7HVPPPfcc6urqkJ9PD504cSKKi4v1Fctrr70GAF+Jn7/9\n7W9/rvYn8fPn4+fs7DggEoSXcOWKhJMnv4O33hLwyCNvQpY52O234ehRHyTpZQBAQcFtsee8DEFQ\nkZLyDeTlyfjhD/8Fra1AS8u3EI0Cr77672htBWbNuhXPPefAnXf+GXfeCTz22A9j+lPaXiTyXTgc\nwNtvv4qhIQ4vvXRHDCy+iuuuk7F27Q/Q3i5AEF7Cz38ewv/5P3egvl7Ea6+9hilTVHR03Ba7kf8b\nIhFgYOAmeL0y7rvvmL7/zc0i/u///XdEIkm49975WLQoGQ888M/4/e+dkOXvwW5Xcf/9L+KnP1Xh\ncHw7lmAX37+8PAW/+tU/48wZDrW1/ykWrRz/u82m4oEH/hm7dtmxcePNzP74fN+MPe5lnDkTQnHx\nd2LDYC+jpkZGefktcLlUXL78MnbtcmL16ltiQOtNCIKKJ574JgoKZAjCS/r7GRnhEIm8jNOnQ4hE\nfqBv/6WXAqiv/zYGBngMD7+MHTtsKC//Fjwe4MyZV/Dii+zxJU3wdyBJHKqq3sDPfx7CwYM/wOOP\nfwPDw0cxYYIKSfoutm+X8Je/vAZBcOnHa3j4FUQiSQC+i0iEw//+3/+OtDQVd911W2yRQtfH449/\nEx4PcOHCK/D7OaxZcxvOnrXB5/s33H8/j4yM72L27CgeeuhNAAIike/i1CkBfX2vxPSkd+rvr7Mz\ngOLiv0NODpjjEYkAIyMv44EHeOzdewe2bpWYv5OF10sYG5NQU/OfsHJlECdOvIrhYRXZ2beiv5/H\nqlVvYt26EFT1u0hJAd5881Xm/Q4N/RvOnVNQXv5d+Hw8bLaX8PrrQF3drRgc5HDlysuoqHACuB2R\nCIdXX30NQBLs9tswZYqKVav+ClnmUFFxk+XzA3B45JG/YsWKIDIzb8PixWG8/vprzPE9c+YVAC59\ne6dPvwJBiF+/5869AklSsGQJ7d/Q0L/h/HkFjzzyX1BRIeHuu42fBx/OnHkNNht0Zvf06VcQibj0\n13v1Vfr73r13IitLwZIlLyItTYXPh1igyV/w61+HsHXrD/Xvj0cfDWDq1O/g+usViOLLGBsD+vu/\nx3we2toW6OdT+/yQU8QL6Ovjcfvt38Ldd0/AAw/8Mx57LP7+KipewMyZysf6fuN5QJJeRlYWcOON\nn5/v2y/rz19lfKH9u7OzEwCwYMEC3H777bhacaqqXvUBH1UcxwkAzoEG43oBvAlgkaqq7xkf96//\n+q/qjTfe+De9VqIS9UWsjzsdrSjAO+9QUERKCukFU1LIUuzxx+Ms2O9+J2LhwgjznLY28gyVZSAU\n4hjdppH9PHhQBM+TDrW0NIiKiiRUVEjYu9epD9bNny8jKUlBIMAzgzWNjSJ++tP4EFF1tR+7drnw\n61+HMH26jP5+Djk5rDVZZSUlxD30UFwW8JvfSEhNVXRt6Nq1HpSVBRhtaFlZAACQnq7AZqMENEni\nMGuWDJuN3jPA6ftvnNzX9L7XX0+MlZFR27JF0vXN2hBSTY2kOzFoz3c4FJw/b4PHQylbV64QI8lx\nFJhw5oxN1/rOnEnDfeZkLe3n5mYfzp8X9MdPnKhidJT0s0ZPWooeBh5+2B1jIsmNwetV0NHBM237\nigoJ4TCnazgHBljJwZYtlFBH/rduw3GVdDut5mYRNpsCv59HXx+PcJhkKGYnhIYGERs2uFFby7Kh\nzc0iqqtd6OrisXWrhNZWmy6TWL8+CFEEZswg+co994TB80B+Pg3Taczl5Mns+amspAhknw/4u7+L\nQJJ4vPOODdnZFKDBcUBOjoLkZAWiyOPUKXrNSZNYvXVjo8iw1uR+AIyOcggGOaxZE/fQ3rZNwuXL\n9PlJTqbo6kmTSD6gdUiam31Mt4QcVei109IUbNuWhCVLQvqwZ1cXD1mma1urmhp/7FqXmHNSXe2P\nxRhL8PuhO60YnScqKyXU1rqwdWsA/f3UJTA7U5w9K+A3v2HP9YQJwObNSTh61Ie5c2W8/rowLhP8\nYYNrR47Y8atfJVs+n8bvoEQl6vNaJ06cwO23385d7TF/MxOsqqrMcdxyAP+CuEXaex/xtK90JTQ7\nX636qOloDSS/+OK/4wc/+BbS0hTcdVcKA0I+TFOntSHnzpV1oK35owJWiURPDw+bTRtkU3X9qTly\n+NAhkYnBTUlR4XRaW+bLlgUxbZrCpExpGuHsbNKtlpSEmOc5nYDDQcA2P398p4Zp0yjAor2dwKJR\n//rkk37Mnx9FKESaT7c7Drbz86mlPmMG6UA3bgzEfIFtmDJFwZQpMnbu9GPqVAJjS5cG0d3N6XrP\n3FySDPz61zTg5PWquHCBtd5qbBQZre+2bRLKyyVMnEht98FBciGIRkkecvEi6WMPHHCgq0vQQdDN\nN0fQ0kK+y/n5FDAhSXzsnAGzZino7+dx8uSrSEm5jTmnw8PxVn9Liw85OaouK+A44NlnHdi4MYr5\n81l9a3GxHBuYDEKSAI+Hs4R10PCVD4EAh5ERHoIALFsWAs/TgkpVOV3KsWJFEBs2uNHTIzAWWn4/\nDdJFo9CT/4zAevdussRrb2elEsSGqpg+XYGq0kCecbuaM0VuLhhQWl8vMpKbgQFej7jOyaHAE0Uh\nTezZs/FYcC0UJj9fgcdDEcvBIAeHQ9WDSHw+Sjlsbo5rgo0a4wMHxBgAptemBY81yMPrVfSkRuPv\nMzPp3319vA40NVlMfz8HWQYEAejvp8G2669X8MYbthh7S0zxiRM2i4+wJufRpFUAsGpVXJ5x881R\nXZrwYXIFTc9r/nwmdL2f30rgi2urT0UTrKrqiwCu/zS2lahEfdnqo6aj4yA5CU8+OQF1daxnZzAI\niz2RLEPXCg8NcZgyRcHdd0+I6SD9ppsh3bDohqvok+Ha8JXHg3EcEDgUFLDWYP/zf46hpcWHS5dI\nF3jlCoEWo1VUe7uAs2dtAFTk5kKP1n3ySQI9nZ08bDa6yfv9Nng8FF4xMkJAtK+P9IvJySp+/OMJ\nDDjTrKVycohFNsc19/fzFjuq06cpLGD27CgGBnh0dgqYNSsae78EmpOTVYYd07yCr7+eXAgUhT02\nPT2sjpfjyD2jrCyA6moX9u3z4557ktHUJDIMs6ZVXrCAgPi0aYrF2zgzU0VZmYQFC2Ts2JGEFSuC\nWL48CU88weq7tejrlBQa9HM66Zjm5CgYGiJwunBh3A/Y4UDM0YJ1DDFHOTudNIQVjbJa6ooKCQMD\ntEjguPGB86FDIt5+Ox6osHhxGNXVLh24Gl9n4kQV99yTbNFhp6cTw6mx6Mb91/TGHAecO0f6WS3E\nYmCAB0BWf1qENED+ucZroqFBxJ49lMoGAKmpKkZGOGzY4Ma6dUHm2DQ2iohGOQwMcPD7ebS18di4\n0QOvl9jjn/wkjHCYwOnmzcYOgISiIgUOh4yWFhHt7WTZZ7fLSEvj4XSSR/DFi4LBG1tmgGZ/P4+e\nHtLcl5VRYuPRoz79s68ogCCokGXEFjdROByk533zzbhLw9KlIR20trWRblkLGvnd70TwPH0PfZSe\nt7eXw7PP+jA4mND1JurLVYnBuM+gEqu0L2Z9UtP3j5qOjoPk7yISge4QEGdFVcsN6sQJASdPCnjq\nKXI28Pvjw1p79rh0L9vcXHrtbdskcJyKwUEahtJM9zmOQ3a2jGiUnWJPSyNjf2Ps6ugobwI/EmbM\noKEeK+gme6hHHpFw5Qq120MhFU1NDpw8aWMkGk1NPmRkAJEIoCgcXC7rsFVKioJDh3xobRUQjXJ4\n7734EFFWlgJFIcZM88Dt6hJgs6m47jryOzUyufv3iwzA27ePXXRQ9LNbb0NHoxzjw5yTo+Dpp/1I\nSVHR20uM97ZtfsyYoaC62h/TCHMWb1mnk17L7ZaRkwMLCwqAkUfU1fnR18dDlr+HPXtkndEuKopi\n06Y4M64l4OXlcfD7KRGuu5tn/IB37vQjHCYPZONrZmYqpmtNweXLxIYaH8dxwMSJdP2YXRg04Dwy\nwjGsreY+cuaMgOxsNrRDu16NLiDZ2YruM6wxmF1dAp55xoVt2wJ47z0OCxYoqKtz4Je/DKOsTEJR\nkcwcC22x1NPDYe1aDyorWZA/PMzFNMcePPmkiO5uslDbvl2C38/px0yrS5dIjvLuuwLmzZPx+99T\nAEdvLy0+KyrcyMuT9eCN9PQ4qDbLR+rrRZSW0rmYPl1mBhm14dCWFh+6uwVkZFCi4NatLtjtKubM\nIZAaDgOvvy7A5+PQ0rIA7e2UqOfxKFi1KhkNDSJuvz2Kixd57Nzpx9gYh8OHieXNzGS9szMzFRw5\nYr/qd5nWaTJ8C370F16iPtNK4ItrqwQITlSiPmZ9UtP3j5qONoNkjoMOPr/97QgATr9ZFRfLePdd\ncoqw2ShKdmwMSE0lEDt3bhRr1gRjLWhg3TpKwqqqkhAIcAiHVSxdGkIoBBQVRdHaKoDjKGDjwAFy\nAcjJUSAIYOJpy8okpKWpDPDMyyNmd9o0Gc3NPvT0CEhPV2Kt5CQsWhRGKMQC54YGET/72QT4fLzO\n4nV3C8jKUhgNZ0uLj0m2y85WLYyedsxKSoIMeNQY19xc8tEtKLCGKBiBkXnRUVQk6zZrqooPlYv8\n7GcsG/rTnxL7u327E3a7qks9tMeEw8B9903QE9DMLGhursLs15UrHLKzaRtdXQL6+nhUV7uQlaVg\n2bIgkpNV5OUpeOghjw5s9u8XTU4fAfz2t05kZZEN2vz5MgOEHA5Vd4/IzVWQlKRgeNiGvDzzvpN9\n1759InJzwSwKpk0jCcrMmQr++McxXLhgQyhEizHteJr9kLXzZwzTeOCBZN1Rw8iKms/v/v0sw15R\nIel6aC1CetIk6F0D4/vIySFLO4+HWODjx3k9qGPJkhA2byYPZY5Tcf/9yfp+Ga/LBx/0IC9PRm0t\nOVgAAMepEARiZ/1+HiUlQctCTusgqCos/s0nT1IinFHXfPiwD5s3B/TvDFkmAHz33Vb9eV2diF27\n/CgqUnQw+8Mf0uN+9av44zQ2NzNTwapV8esmEWCRqK9qJUDwZ1AJzc4Xsz6p6ft49kFGOYPfDxw+\n7MO//uu/4/bbv4XBQQ5DQ6TxM/sAP/ecD+++y/ru1teLWLeOWNsZM2SLldPGjW5MnqziF79gW70d\nHTzq66l9XFkpxTSL9BivV8b27RLOnKH9uOEGWQcY4wGTlhYRa9eyzBagoqOD9RgdGyO5htMJ7Nol\n4fx5HoEAAQTj444dszH2VuZQjbheGfB4WHbT46E2f18fjz//2Y6HHw6irY2m6LVBOFarKevR0dnZ\nKvr6eKxeHUQkAkydSmDYnLBlZnF9PmIuT5wQsH59EL29HOx2Bc3NPkQiZJkVjZJkYWyMt7CgGRlk\nh2bcL78fUBQe99//Im688TtITaX3lZFBi5S+PtLMtrcLyMuTsW5d0JL253Sq2LqVBfDNzSRPkCSg\noiIJ994bQl6egp4e0pyqKi2KGhtJ35yRQdKXrCwFfX3Uzq+p8Zts6wJYtCgZ5eUSiotl+P0c1q8P\nIi9PxtAQb4mQbm0VUF4egM2mQpbpWGhgkHx/aT81SYDxueakNq3sdoqdrq6m81tWJkFRgKYmX0wz\nS16+a9YEkZqqWKQz2jm02VQ9iEKS2Guru5vXFwCDgxzq60WoKhhbwPLyAB57zG2xyCssVHDwIEVi\nqyrbeZk1Sx4nxY2kPJqe12ZT8dZbNgNTHtcEDw7yCIdVXd6gfVdpjLq2zcFBHgsXRnDkiJ2xdEsE\nWHx5KoEvrq0SIDhRifqY9Wmavp88KeCtt1gwe//9HO6+ewIqKqTY9DyPtjb2JnzxoqCDKO13PT1x\nrd+OHWwggwZcR0fpZqixr11dPBwO4JlnRIyOChgZ4QBQ+39oyDqd3tQk4i9/EXD4sA+dncQes/vF\n7tPx45TUNnUqe8xycxWMjgoYHKQBPrcbWLcuCY2NLGAwxhyfO0csmfHv11+voLOT2EdNF6n9TZLi\nCXcNDaIF7PT1sf6qAwM8QiFqbZvDEw4f9qGqyo/CQtnyPtj9VfX9fvttARMmAG+/zaO4OIr2dl6X\nAZSWBhEIgGFBGxpEdHYKOiiOA0PS1dbVJWH/frOXM7Hd2nErKQlBIpkrs19TpiiWBUZvL53rnBzg\nnnvCyMtTLcfovfdsCIfBXJ91dSJsNmJN16wJWq4zAt2Az0eDZTt3urBkCaUEmpllt5t0w7TQErBm\nTVAf2KQFAqspNj7XLOHIyVFi+mgFgkDn33is6upExo0BwLhJbto5lGViiTVwamaSq6v9uHBBwKVL\nAlJSSFM+3rEYHSWf3o4OCjeRJBVuN3DxogBJIi9fv5+DywW4XASSjQl0+fkyswA+eFDUwzfIZi6u\nCeY4MN9HVxtok2VKxzN2WlJSVJw4IXxsiVeiEvVlqQQI/gwqsUr7Ytanafre1sYzYHbu3Ch+8INv\nYeZMYmS1RCrzkFthoYxgEBZAprFTRrDh9cqYPz+KmhoKNdAeY2yj1teLOqOrtekjEXJdMN7YT5wQ\n8L3vyXjoIQ+WLg1ZUrXMC4SUFNI2p6QoTLtdkjgTsCLQ7nCoesRwcXFUl2HY7Sq+9jXST2psbVGR\nzLhFPPusT3/u7Nnx50YinCWAxOcDZs5UUVXl1J+/b188/tkcntDWJiAnRwHHEdvd3U3MfW0tRThP\nmEDA6Nw50uA+/7wdK1YEY9HKBEqM77ehQcTYGGk/BwZ4ZGaq6Omh9w8gJg2QUFbmNoCYJjeSLwAA\nIABJREFU2zA6Ko0LtHp7iREXBApDOXDAgfLyABwOcu9Yv96NkpKgBcgZ5QRaWpm27UCA3DvMi63W\nVpvumKDJNLRtaLHCmmyivFzCE09I6OwUMHky6csrKgilk4ZVtUhM2CATCRzHxVh/gYn0DYXAxFFf\nuULOGyUlIXR00ILJuN+joyzDnpmpQJIE5nfz58u4fJmLLfKI7dZiv8vLAwgEgK99TQbHqejuFuBw\nAAcOONDfz6OpybyAU2NAnx3Ka2nxIRw2X/8i7rtvgmVh43KpFsZ7cJBikzWm/A9/mI++PlEPwigq\nioPgqw20vfOOYBkEXbuWZFMJWcQXvxL44toqAYITlaiPWVdLRbrWKihQMDQUlxesWRO0DNG88YYd\ne/a4cPAgASevV4HLpaC4WNUZJq9XhtutoLpawqJFyfo0vcdD7JvWstZiWM3pXUaW0JjsVlTEakdT\nUoCuLh7bt0vo6+PA86TNHBwkf1VBoAG3U6dsmDVLRkcHaYs1VnBkhIMsCzFwxt7Y7XYV3d3E6p48\nySE5WcWSJUEd5NjtpGM+eZIG1srKAroEoKQkhA8+EDBjhoKLF+NWUgABaDNYKyqSUVpKnqwjIxzc\nbhWtrQImTVJx5IgPfj9nAoxKTLIi4Le/deKpp0SEwxzuuCMCjuNQU+NCdTUNxZ04IWDFiqBFA218\nv8PDPJqaHFi3LgiPhwWjDQ0iOA5ITVXw5JN+5ObKMYZaQm6uNcpX06Nu3OiOdQ8UPUHN6EW7Z48L\ndXUihoZ4FBTIumWZtk9ZWewxmjVLjkX+WtlubSHhdisMEJ02TdaHyiIRTrc383hU2GwqolF6LeMC\nzOxMYbTy83iAF18UYotA+l1zswPFxVGkpRG7rVUoBMbb2LxwjEahDw+mpEDffy2Zr6BAxqpVHixe\nHEZbG68Pu5WWBpGXp2DNGtIst7fzlmTCjRvdGByMA+W5cykVbv9+EcPDrBTh2DEbo6vX5Anx90+P\nHxnhsHo165zh9VJXpbQ0gIyMOOjV5A8f9l0Vr/i/zbKus2dt6OoS9L8lQHCivkqVAMGfQSU0O4ma\nN0+GzUYtzqEhLjasFdf4aTf5/n6KoL3jjihOnBDw/e9PtAzFtLTENbNdXQI2bvRg/34Rx47Z9Jud\nFsM63jCW9nNhocy0kVtafPjgAwG5uQqeesqFu+4KAwDS01X4/ayFVl2diORkFTfdFMXChRP0AT2/\nn2KF//xnO/r6eOzYITFtWE2Pe/KkgMxMGenpKi5eFBgf3l27KEygokJiAOC6deR1OzTEIxwGbrgh\nClkmANLTQ+EPtbUug98qTe13dQno7CRvWCNTt3+/iIEBjgF3SUkKcnOBS5d4HTiPjrIBFMeP29Hc\n7EBVlWTRCvf1We3U1q0L4J57JuDhhwMmplVAZWUSWlp8UFV6LAHql+H1fgdNTSJ6e+Nxyo2NInbv\ndqGiQoIkEeg5dMiHvj6BGQjr7ydbutpailueOpUF1MnJZFM3PExhJ9rQpSAQUz86StpYbdCtuFjG\n+fM2yzkyXpNer2xhec3MckaGwgzYzZ8vY8GCCE6etEGSgF/8Isycn/p6usba2tjX3r3bzyyuCPTH\nz/lTT7mwZUtAP2dmyUt1tYT+fgqmAeJSlXXr3PjjH8di7gqCZfGgSY0CAU6PbtY+mzRcx3Zsiopk\nffvG60H7nXZdZ2erMUkIsb5JSdQBMrK3L7zgQ0PD65g48bZrcqoBrLIuo4Viwv/3i18JfHFtlQDB\nifpK1ye1Pftbi+eBOXMUAHTTefVVgdH4FRaSZs9oaN/bS0ytpp0ENIZJsBjwDw1xun4wEuFi0cDs\nMFZeHjHL+/aJGB0lxwnjdtvbBaxfT+1pbZhKlgmYUdSytVWuyRvWrCFGdO7cKNauDWLx4jBycxUL\nqOnoYO3LNDBttNOaOpXe/969TtTXE6PZ0iIiFALjKEEhFm5Eo9C1pgsXRjA0RPZpRpCWn69YdKH9\n/eS+sGxZCGlplFD2wQc2Zv+am30ArAxpNAoEAoDTCUbXCQCHDok4fZo00leukI1ZVpZi0ZvOnSuj\nulrCBx+Qo8Xly3Q+0tMJKLa10fF3OFR0dgrIzlawcmXQ5KpBQHn/fpcuQykooNS2vDwl5npBx29g\ngENmporf/taF//W/nPp5ppRCHhUV8VS1rVslfdExnsRi6lQFlZWSDr47O9lj6/HQdozPGRzkUFXF\n2ogdOiTigw8E7NnjsuiOL1/mIUkqUlPZ4+/3k3zDCPp7eqhzAgBPPulHMBhn+M1DeooCbNkiYc8e\nF2w26PaBKSmUSnfffbR4NDPjX/taFI2NpOttaiLJQVWVSwfIzc0OXYowebKCtWs9iEYRC/EgS8CZ\nM6PYudOPrCwFHR0CtmwJYHSU1YxrEqxIJK7pP31awLlzPI4eTbLIGIzfadOny5Bljvl+M8u6bDYV\nv/udmPD/TdRXshIg+DOoxCrt81Of1Pbsby0z+P7mN2UcOTIfH3zgR3a2gspKF/r6eMybJ+NPf7LD\n61UwYYKKxx5LsrC5KSnUEm5qEnHpEjGcDoeKtjYe+/aJGBnhda1w3JJKgiAAAwMCysuTsGZNEDk5\n7BBNXp6CigopNmEOAOSLG4lwloEbrVVulDdoYFhjl806454e3uJbe+UKj7ExVkd74ICIsrIA5syJ\nYmyMw9SpFFNsBuKDgzyWLAkZGFR6/h//OAZVhX4s0tMVjIywiwS7nVrMJSVBHDniwNq1QQwMkDNC\nVpaCri6ycSMQxaOhgUC40wm0tgoWfWtDA8VTa5KFSZNUCzNq1LpS0hiBZk0X29wswuuVsXXrN/DA\nA2yMcUVFEux2sgdjFy5k+bVwYRg//znL1Hs8wD33TNDfp90OtLdzuP/+EIqKFKSkqBgdJZBtTJrr\n7+fh8QBDQzRwCBDb2thIlnqFhWyiX2OjqEsstNfiOOigt7+fw5w5Mtatc2PlyqBl/zU9tFnKkpam\n4MwZAbfcQjr3cJj0xYODPJKSVNTUSFBVICODhtW2bEnCyZM2HDpE4Sc1NZL+NzOAt9sVVFVRIMjE\niQqKiqLo7SVHj6wsBXv2OFFaGkRDAy3ColHg8uV48AidJwmLF4eRkqLg+utl3H57JLaolrF/v0N3\nY9i40YPqaj9KSz2orfUjFGLDR44e9VlmDwRBNUhDgJ07Xejvv1OXZBhlDMbvNKPO3+uV8eSTfgwM\n0HZ/9KOIvuCnBXmivgyVwBfXVgkQnKivdF2L7dknYY0/7Dnjge9bb5WRnAz88pcePenp4kVeZxVr\naohlPXLEzsT8PvWUCytWsNZoBw+Kuneq3U7DT3V1Ilpb44leq1cH4XBAB3DNzT5GCgCw7GllpaS7\nPWhpcxqjVVvr0tu75eUSCgsVBgwDJKMwg49IhAWiGRmKxebr5ElimZubRYgiB59PGBeIOxzEEpqH\n4S5etKG2lrS73d3QAyeef96uJ4dpjgPPP+/Ahg1Bk80cDWyVlAQZuUhTk6g/zgzwh4bYZDbt3Gl/\ndziAzEyZkZRUV0tITVX1JLjRUWDrVslinWXUkZpdKrxeAqTLl1sXCIOD9G/Sz7qZ96eB6oYGEapK\nVmDGQcXSUrd+TWrAuKODjyXlSYzd1unTNjQ3O1BfT3ZgrGzGHxu8I79m8/5fd52CRx+VMGuWDFHk\nGMb69GnS9K5c6UFNjcToqevq/BgeZjXH5eUBHDtGMhyjfV99vWhyB+GQmsrr59YIHLXHnzsn6FZx\nWoz3okVh/RgvXRoy2dCxi+mCApYFnzJFiXV85HGjjM2aXlnmxtUja5IMo4zB+J1mlKAsXRpiJBWJ\nIbhEJSoBgj+TSmh2Pj91LbZnH4c1NoNem03Vn+P1UlwuuSaoKC0NxgCpE6dPC3jnnVdx331/h6ef\nFnH6tA3DwwRGN24M4MoVXmdqFy6M4Kc/TdZZtgcfDMHpBB5+OAC3m8IdNCCotU/DYcBmA5qbHTpj\nF4kApaUeHcBVViZh9eoghocpKMMMJm02YHSU00EBxwFOpwpR5FFaGsTUqQoGBjhkZ6sAlJiGldfl\nATabyoDs/n4O1dVJenTz5MkKampIt2o8J/PmRbF/vwi3W4HdzmHSJDb2mQClipERYOVKq+45M1NB\ne7sAWY57ynZ28igrCyAc5iwhDmZLMYeDdKQ2G8taGxPhxmOVjel1ZpZdA38tLT4cO0YettEomxjX\n1ETDj0NDr8Bu/4Fh8UCRydnZMiZMULB/P0lVOA6oqnLF3B7Y/YlEgOnT6TXN3rHGgbTWVmK8OY78\nl73eKIaGSBpjlNLk5ChYt8497ntPSVHR3i7oWmRWcsLpCySNTTfaiNntCtLTOT06efly6nysXMmC\nW7P2emQkLvmJvy96/KRJbAjJwAAPjlMBkFUcx4EJUDFrl40JguXlAaxaRbrt+LG1vjZp+uPfDbfc\nIuPZZ0lbPG0aJTQePerDnDky6ur8aGvj8Y1vfPjC2rxY9/k4CMJLmD17AZ57zsfIGIzfaUYJh3kf\nE0NwX85K4ItrqwQITtRXuq7F9uzjsMZmoHzwYNwdYOnSkJ72tHy58aYuIRjk8MgjbsybJ0AUOYut\n1qpVSWho8KGpSdQdHjRGb8uWAEpK2O1pw0/GqXmtxX7xYlwnCkCPtJUkisedPFmB2012V0ZwM3ky\nyQLa2ihGecMGNxYvDqO52YGaGgnHjhFTt32706L11IIXjANNZWUBfZBv926KIV68OAS3mwXLvb00\nLe/1yqipoXZ6U5OIU6cEcByHp592Yts2CYA1hGLaNAU+H4E00gWzgSHmVC8tHMQMIGfOpFQ04++N\niXB79zoZdv7KFU4fkNq8OSk2cBdnH0dHSY7h9wMLFkRx7JgN6eksSDl1SoDbreKf/smuM4ULFkRR\nVZWk2+f96EcpDNt/110RtLXxEASgudmH48ftOvP/yCMBNDWJFoBsHIyaNUtGSoqCH/84hbn+zFKa\nnh5e1zzv3etEQwOd30AgPkCnhXoYX0uWaTG2cCG7fVZ3TXIKDaxbQTtigDm+3exsBVOnsq81ezY5\nVoyM8JbHGnXUzc0+yHL8Wre6YsDw2rQvw8MklTl0SMTbb1s1+bm5KhQFOqC12YBbb5Vx660UffzX\nvwo4fVqA308A+aPAqHmxPnu2jAcfDGHjRjc2bw4wLhHG77QZM2S88IIP7e28xV85MQSXqEQlQPBn\nUolV2uenrsX2zHwjysxUmBsdQEBZc0bo7iYwcvPNEbzxhl1nYsw3dYcD2LXLCVn+Hs6e9YPj2MG3\n4WFiWl0uDvfcE2c6PwwkJCcDkgS0tIgWxuz48TirVV8v4uGHeTgcKqLROEhxu+lns1NCaiq5EgA8\nOjt5PP44hXrMmRO1xNia2dT+ft4SnGEEX5MnkzQiI0PF66/bGPeFsrKAPpxlfJ1Dh2hBsGIFRQgn\nJckmsEYpZlVVfpSXB3SZhcaO9/XxuO4665CbZkvX30/64QkTVHzwAclSNCB7ww1ROBwK6uoI/E2b\nRsyoxrIfOhTXxTY0iBAEYNWq+GJk3z4/OjtJyxoIkC2X5n6hPYZYfRd27vwGhofJL7mri8cbb9gB\nWBlLcyogDbkpUBQO27eTg0Q4DFy4IKCpScSFCzycTjrfTz7pR2oqDVS6XOz11NEh6I4bRgaY9pcs\n3YaGeFx3XRSnT9t0XazbraKyMknXYqemKkhNVfH++6y8o6+Pj3U1QhgbIyeK0tIAAgFePyfG4zJ/\nvozKyvi5mD2b5BraUNvlyxxyc1Vdp3zzzRF98UihFexio71dwOTJ5Gfd30/AUUscLCqKYtOmuGe1\nti+ZmQp+8hPSpVdUJCEvT9aDTpxOoL2dR0+PHbNnW9ndv/6V9el99lmSQl2tjMA2Hnl857hg1vid\npnWmAGL2//znMVy4ICSG4L7ElcAX11YJEJyoRH3MmjePWpp//Su1r1et8qCuzm/S/im6M4IRjPT1\nhfTJefNNnYbOyFVAlq1ge9IkBX4/h74+LU2LmE5NZzje9jhufNcII6t19qyAHTskcBzpLI1MssdD\nrfXKSglnz3JwuwGfj4+5TqjYu9eF6mpp3AE1gEC4ecFQWupmGM1Ll3g96WvSJAWqCqgqh6wslXFY\nSEkhgGTUxmZlUfIVzwP5+Qr+8Ac7/tt/i+h+uOFwPIqX5xFzw7Cy416vjKYmAniaDVh/Pw3shcP0\nvGeeceLBB8O6B692To1sZnU1q4t9+20By5aRz+zgIIUvGNnSjRtpqr+uzg+Hg9VZezxg9sXpJOeJ\n3l4e2dmqbjFH8pD4MR4ZYcFrby+ndwo0eYHZWo8YQhVr1ybpAH7/fpGxseM4NTaw5kFNjV+XDkQi\n0GO2NWmHsbq6BJw8aYPbDfj9BA7tdgVTp7IdBq+XZD1mlr69nUBtdzeP5uY4iAVUnDxpw7Fjdtjt\nZEum+dyePWtDaqqCVauSsGxZCD4fhxtvjDJdCXOccSRCA46dnQL27nVi61aJGXh74gkJ584J+PrX\noxgZ4XDwoAhBII18Rkbcr5njVPA8kJ6uWAbdjN8RFy+yi4C2NgG33ipfdeZAVePH1eMh3+OPA2bH\nk3AtXBj5OF93iUrUV6ISIPgzqIRm54tZPE8paEaW0iyJKC6Wcfasw8Q08YhEgJERDn/84xjCYYpM\n7e8n1wZBULF+fRDvvfcKZs26Fe+9J+jMVThMYQj9/QQEjODkH/9RRHOziPPneTQ1+RAMko1UZqaC\nJ5904a67Iujo4HXXiKwsGqKrqfFDVQGvVwbHAR0d5ghZHgUF0djwE0kcUlOtsb2aLMMMwnNziS2s\nq/OjtZWsvABg0aIwOA44cMCJwkJKj9Pq/fcFTJ2qWCQUDgcAqLH9iIMn85Bafb2I6uokrFgRhCDQ\ncwB6j7m5Crq7CU386U9jOH8+7p/c3i7gxAkb8vNl5OSQ93B6OsvqlpdLWLPGreuPCwoUvPMOe8y0\nxDTjYsPppLCIU6c4pKRw4Dg63prDAkCOCYWF8eAJp5NsswYHeaxeTa4KL774Gv7hH76FaJRjmPDD\nh31oafGhq0uAJMHS7p4yRdOCjt8xOHaM1bpu3EjAr7ub139/6BClly1bRvtcW0sxxq2t1mQ2iu6O\nv7edO/2orCRAuXWrhPffF1BYCCQnK3j2WR8kiezKABUeD7utoSEemzcnMdeCzUaLg0mT4nIZK1Or\nIDdXYRYsZgeNkycFy5Do+vWkQ1+6NITaWheamkT093NIT1fhdKq4/XYCjnffzbouaOE0BQXKh7qg\nmL8jzBHchYVWVwczeB7vb1lZL+HGG69+H7mWwd9EfTkqgS+urRIgOFFf2fokbg/jDdIZt5OZSUyV\n+TFr19J0/cgIAWKN5WtqErF2LblBXLnCISdHwYULAt5/nwCRETBpUoabb46gpkbC6dM25OaSnZMo\n8njwQRYUGi2ymppErFnjxq5dku7Vq93IrZZrZLFWXy/C5aLo19/8JqCnyaWkqFBVFdOmyRYGMy9P\ngdOpxLxayXdXYyKNTLPTqWLjxmT9vZWVBfSYXCDuaFBV5cLixSEd+GtMshmA9fTwWLWKBcb795M7\ngZaap7GAVsCqYHSUx8qVSaipkXDmjI1hdT0e4Ne/DmHaNAWtrQLCYWDqVIXxMk5LU/RYZ21fq6sl\nLFwYf20KwVCYhUxhoaxLYmbPluF0qjh/3sY4S2zaRL67PT3s8enq4rF2rUdvyW/bJsUidQn8X7pE\nQ4luN9vKH68rYLMRWCTmN/77zk6SJGj6X40lnzUrHvygDWjabDAMQQLZ2YpuTVZVRYuy++4j7+iH\nH2b9jffvZ9nZ/HwZu3f74fdzFqlJVZUf06cr6O0Fhoa4mJ8wkJurIClJhSAQaB4aog7GpEns+3a7\ngZ4eAdXVLv13mv2aBv4dDhVr1rBs7niuC5qmfefOuPuHeVDQLFcwDskVFsq45RY6llcDrOP9LSvr\no77hrm3wN1GJ+ipWAgR/BpVYpX0+6qPcHozg1uulm0lvL6cb4GvA+Z132O1UVEi6XrG4OIr33+ex\ndGnIYt+k+XvG/3YnXn9d1m2xFiywRhcDwIoVQYYRbG6mMAajrpLnofvbaiDx8cclBkhpN3JjMhW1\n77W/ky5YawubJR5VVTT45XAQyIhGiV385jdp2KivL85CG2/gyckAx4EBkTNnypZBvIwMAtPz55MW\ntrraj3CY3ktGhvXmbrRjIzkAD0VhwfLx4wL+/Ge7zsTn55NGdHCQdNc5OQpUVWWSzPLyFHR1cRYf\n4JKSuISEWGsV3/xmFO+/T6EH2rHTXtvv5xn3h0OHCKTfey+7eKmtdaGlRdQHDffu/QGWLw9awFVu\nroqtW8mO7uabI+A4srSrrGQ9ixsbRbS0iDh3jtedPb7+dVaO4nQCpaVJaG4WUVoaZ1YjEQ67drl0\nf1xARU8PyWLmz4/qARnGxUddnR82m8qA3PLygM5EL1wYsQSVtLUJuqZWljmsXk02aK2tdB6Ni5Jo\nlMP77/Pw+aAHegC0kCoujuL+++NeyAANH1ZUSLHnA0eOOLBoURg7d/oxZQrJSAQB+Na3IvjTn8bQ\n3c0jGOSYz4+2UNaOiXl4zsju7t3rREuLiL4+Dtdfb5UrGIfkjHU1wDre3z6KBQaubfA3UV+OSuCL\na6sECE7UV7Y+qlVoBsmaX6wZMJu3MzzM6YzSli0BuN0qIhF22E2zb8rNVRitq9VvlEDLrFkyTp8W\ncOiQD2NjHGO/1dnJIz1dtegqjfsrSUBaGmkLn3xSRGoqyTNqavyorXVh82ayfdJY6UuXeCxYIGNg\ngMBQaysLWtrbaUDrjTfsuq8tC/Ljr93SwrJ8HEfDWBqrvHevC8uXB+HxsK4Qyck0sBUOE2jmOE4H\nVl6vjIYGGoKaMkXF5cscpk4lMHjXXRGMjdEiYGiIBdYUJBFhjjENCLJ6VLO7RUODyLx/o6VWJELe\nuJqX8dNPu7B0aQi5uWzb2wyKe3vj1mTa/y9f5rF+fQCRCMlGNK1rZqaCxx4jTXUgQODGGFDR1CRi\ndBS67tjMkrtcBJrPnrVhzpwoeB6Mj3R1tRR7LIdt2yQMDfFQVVrYLF4cQnIy2d5RWArtG9nbBSxW\neq2tPAD2vdrtNNB2880R5OZSFLX5mtCCYMrKCIR3dNDis7OTZxYlU6YoSE6mNDcjqz57tqy/d7MX\nsgb+586VUVoaxOLFLEBftoys+gAKs/B65VjqILmFzJgho6hIGdd1oaBAwZw5VrB5rcmTVwOsnxTM\nXsvgb6IS9VWsBAj+DCqh2fl81Ee1CqnlGGdX8/LUWOyswABm83ZuuimK6mq/3sZdsYLatcbHzJ4d\nxZYtATz1lAtr12q+uC9jbOwbDHjo7uYxa5bMML+a7Zb2/6wsYm/NusrkZDXmJ6sgGqVW9pQpBGSM\nLgL79pF7QWenYGGsW1p8qK6WLKEGZlbsat6zw8Osy0R+fhTvvmuDzQbk58tYvz6ASZNUDAzwuOEG\nGZJE78fv55CWpupMqVFr2d4uYHiYh98PLFrEeusawWtFhYT9+0U9/W3jRjbkYDxASx6vVo2q8f2b\nLbq0xLyOjjizr+lFk5OJjeQ467Bgezu7Xb8fsNs5XLnCYfXqYIyJ/Qvc7ptQXe1HZ6cAr1fBBx+w\n7CgthGQ4nRwmT7a6mAgCYkONxK5zHJhrOzOTFhCqyqGjg4PTCUybFh+YMwdIVFRIKC31wOGwJrsV\nF8elEtrvolEOixYlo7lZxKJFyfqx8XhIxnD5MhcbyIuz0NOmKTh2TMCBA05LIl9Tk2j5eft2FxYu\nDMNut3ohG71+zRphzfZMu2YB62L0hRd84wLK+fPj/x4PbF6L5OpqgHW8vyXuI4karxLXxbVVAgQn\n6gtfn0TbC3w0uzJ9umy5+WrA0wiYjdvxekkTGw7TdH51tYTOTtZeq7g4CoeDdIg/+UkY27e7Yu1i\nCQsWRBl2KzdXht/PMcEa2k07NZV0qGfOCLj+elmXJRjb5b29KtLTFWzaFGcNzSBgYIDH00+7xk0n\na20VwPMcurooveviRbLJamhwoKUlrmtU1Q/3nk1KYvW/TU0+S/rVqlUE6t99V2D+VldHWsu8PBlF\nRTJzbNLTFfT22pj9NUsvhoc5FBRQEIUocqiokCz7qqV3GVlJM7DLzFQMzhYyJAm6FETTeHu9sg5Q\nNaZ+40YPnn5aRH6+io6OuBxh9mwZbW08nnnGpQ8QGpP8jMdgw4YQIhEOTU0O3H9/GJ2d1qS1KVMU\nRKM8SkuTUF3tt1jbffABDR5q+uimJp+lc9DcLOoDhBTLy6OqSkIgQHIBY/fBbgfKyiRMmaIgECAG\nWluUrF/vjgWz0PUiy3Gnjo4OVktbViZh1aoJOtu+fHkQmZkqPB4FFy8KSE8nPfKZM1c/zydOCLj3\n3jBkGfqibTwpEV1L1gWMds3m5ysoK4tr5LXntLfzDOD9uHU1ydUn/d5KVKIS9elVAgR/BpVYpX26\n9XGS3Marj2oVyjJnkQF4PAqee44AL0AAWFUBQaCbaUcHh0mTBJw9S9PzpaUU5GCcVt+yJYC9eylQ\nIhgENmwIYnCQw6xZ38bdd8f1jA89RO4AxtjZ8nIJHEf/Tk9X9SE3u13Fnj1+HWgXFUWZdrlx+t/s\nIpCVpWDp0hA2bbJ61c6cSY4NW7YEcM89cYa4vl6TOABvvWVHerqCpiYfOjooSS4pScXu3X6kpysM\nONccKcygPiuLQEtvL8+ArcFBer2SkpCF+XO5FIs20wxob7opirY2AUNDPLKzoygrcyMaRWw4j+zV\nnE6FAY3XXUf7YQy3aGsTsHEjsZS7d4vw+zmdhV+2LIh168gObTzGPjVV1YeutNqxww+vlx0gNA6Y\nGY+BLH8P991H3sUAAfTdu12orydrt8JCBcPDgM9HDg2rV3uwbBnJMaZMUdDWJiAri9wyNJ3rlSsc\n7HaW7b54kcf69R7mepk8WTFdf/SeJAmM33RSkor33+dw220yVq4MIjdXwb59Djw6jqCTAAAgAElE\nQVT4YJhh5o0BI16vtrAJxD47vC6haW4WEY1ycLvJi5nn2YWLcTsayM3MNIdgaLZqMtauJe2w3U5u\nD88950NnJ1nOjYxw+P3vRaSmKli+PFlnvq/WJfq4dTXJ1Sf93tIqcR9J1HiVuC6urRIgOFFf+LpW\nG6CPy8C0tZEUwXgznDpVYYzujx4lb9S33hJ0p4Vf/zoOFuvq/HC5KDmuu5tHKESsWElJiAEHpPXk\nLHpGs92Sx0P+sPv2jTdwpurJcWVlrG+tL2bharermDSJJBCjo8SK2WzAu+8SW0r7LGJ0lEc0Cpw6\nRYuA8drLCxawCWyHD/uQm0uOAFlZCqqqknDXXRE9uOPyZQ5ut9lqjUB9SUnQMki1eXMSOA66NZmZ\n+Zs/X0VRUVQPrOA4YOJEAk3Dwzyys8l72Kj31cDdxo0ePPqohIwM4NIlmynJjthmo0XXli2Sfvwy\nMlTs2JGk63NnziT5hvl8OJ2kh6ZUOPY6ys4mAF9eLkFVKYpaEGCxodu8OUmXWvT18SgtdevAe3iY\njw2RubF+fVBnh7WwkIYGkXHGKC+XYr7PNoTD0H2m450DRQ8SEQTyag4G2fNus5Fmev16t/67y5d5\niKKK226L4p13yBd40yY3liwJguPoMzAyAkydqoLn4wuO+fOjzCKuvl7Ut9nXx+H55+1YtCiMnh6e\ncQYpKpLhditoaKAuiNYZWL6c9avu6eFw331hAIix7Tx8Pg4rVnjQ38/j4EERP/nJBP2819b69c/M\nnj0uNDbSNTtr1icfKLua5CphX5aoRH32lQDBn0ElNDufbl2rDZCZgfmXfxmDLHMWUFxQoODNNwWG\nERwYsN64UlJUvV2sqlrLlcBEfz+Hnh4BX/uajMJCGT/5yYQYqGRBncOhwud7GXb7DxnAaXYEMLKN\nZrbK4SADf1W1xsrGGTcFFy/ykCRK8Dp3zganU8WCBTJSUoJYtGgCA8I0ey2zrVhRkWyJHL54UWDC\nE8w2bfv2iZa2tscDOBwkHzEDyKYmESMjHMJh+r2Z+evuFiAIKpYvJ6lFXp6MykqJSXAz63+Ni4G5\nc2UsWpQ8jkUcdMcMm43CHDhOxY4dfuTm0lCWxuxXVPgZyznjdrzeuDWeqsblBhkZClwuFRcuEPjW\nrhWnk23Bu1wEvmtq3oDd/n1kZCiMlGDHDj/KytwxYK6grMzNAENzF8Pn43HuHF3HfX08Cgpk3Y/a\n61VQVeWyxGxrkcnG64/joFumad2AtDSVAdyNjQT+u7p49PcLmD+fOhOrVwdjsdKwWL6dOyfo25w1\nS8HDDwfw3nsUYLFkSUgHwBs2uLFxYwCZmZTmNzbGY8sWOu9mthiId3za2ngsX856NBsfb3R46O+n\nEJE774xe47cRW1eTXP2t9mWJ+0iixqvEdXFtlQDBifrC17VOTpsZmIEBnrGp0tqS8+bJ8PvBML9/\n+IPPohU1/l2TCYwHJjZtcqOxkVhLLT0uzjDLaG9XcOiQCFmGPg2vsajvv0/BGkaHgT17XKirE3Hl\nCk3sV1Ym6Wl12uCRwwE9vEJzGigrCwBQcf31KlaujCenkd8qCxgPHHCiqsqPwkKFYVy15DP2WLAg\nTotO1kDe4CCFGxi1mhkZCq5cseo0vV4Z99wzQWc9Nf2z0Yd36dIgpk+PSy1KSoIM6C4vD1iG0W66\nKa65Pn+etYiz2YgN3bTJrbOplZUSeB7M4uDAAVGP2DVKCjT2sK+Pzu/YGMa1xistTca+fX5dlrJu\nXRCSBKSnqxZQ9u67Av77fw9j2jTJovkuLFTw29+KmDCB4o4rKiS4XCpuuSWKv/zFNk5aIGleze4j\nDz/sRnW1hP/6X8MQBHZx1toq6Hrf9HQF69e7sW5dUGdzZ8+OYmSEt2jJe3oIWJOtGjk9RKNAIMCh\nv9+G4uKoZdhw3jwZTz0lIidHwfvv85g0ScWRI44YAKZ45NpaF0pKgohGwYRzaB7HRrZ49Wo20dEM\nOmfNUpgo4lAIFvvDv7WuJrlK2JclKlGffSVA8GdQiVXap1vXagNkvhkODrKMlNaW5HngW9+SmRtl\nTw/P6EeHhtjnXr4cT4Mz/n54mMcDD4QQjQIHDjhw770hHDpEXqJ+P7F7jzzyX3RAWlMjMfrS+nqa\nhm9u9jH+uh6Pis2bKcL4xz8Oxyys4mxhdbUfDofKMHcpKYpuPaXtY3u7gNRUFmTdeKMMmy2EvDyV\nCX3QmPEDBxyoq/Ojv59Dbq7Vjuy665RxFwSHDhH7yHGkY01PV3HpEqdrXHNzlZjmVEJmpgq3W0FH\nh4AtW7ThPRuWLg1hzx4XHn44oHvAmjWuGogvL5fgdgMZGUpsOI5a+Zr+WQO8W7YEsGmTGzU1Erq7\nacjLZqPOgVkK8vjjbpSVBRiGvL+fR28vBVjY7SSFOH+e3SePhwYTBwc5PPusE83NIsJh4P77WceE\nvDxyRpg9W0FKyncwZYqMQABoafGhvV1Afr6Cy5eBtDRFXyyUlARht5PMIStLwcgIh8ZGEb29PDIy\nVEycqODsWfa9aNdAXx+PiookiyZ83jwZly9zyM2V4XAgNiwXj9MWBKCvj7N0LLKzFUQiwNgYkJJC\nwSrmQbymJh8aG0WcPm2LOYwAOTkqjh2jWPKGBjvWrAnqNmVut4rVq+MLHSPzvnevE7t2+dHWJoDj\nOGzY4La4uIwHOjUZ1HjaXFkGTpz4jxtc+1vtyxL3kUSNV4nr4toqAYIT9ZUr880Q+PCEJ+ON6sgR\nOzo7BVRUJOl/P3yYmOGsLAVr1pA5v8tFzhLGbfr9wG9+Ex8k4jjSJofDHMrKPCgrCzCA9IMPrLZd\nkQilqJmtqtrbBRw/TsNPWVkKqqv9yMyk18zNpSn7xkbSAE+aRKB/3To3SkqCOuOsKComTVJiWmFi\nltescesOAWZwmZKixoa6uFjgBIfCQplha6uq4sNbxudfukQMaiBA7Ofp0wKKi1kbuC1bJJSVefTW\nunZcADBJX6mpKjo7ed1j1izZKC0NIhDgUF1NQ2bNzT4GODU1iTh1inyYOzoEbNsmoaLChaEhHk88\nQQONmiRE26728+zZUUycSGln3d08Jk6k419TQ0NvqqqguJh9riRBf18VFRJkGbq3rXHhcs89yWho\nEC2hFxUVLjz8cBAdHRT00dkpxFjwkMVxg+OANWvii489e0TMnDn+IKHmkKCl/zkc5MdrHK7cv19E\ndbWEjAyShHz968DoKIcFC8iz2MjCOp0qw54fPChaUv5OnLBh/vwo0tJIYnH5Mo8lS+Lvwfz+NamP\nkXnfv1+EKNKw59gYXYPGzsyHfZaN9WHa3L91cC1RiUrU578SIPgzqIRm57Mt881QUcCA4uJieVwG\nqKDAynY6HOSlGwpxzGBXZaWkg4Ibb5SxfbsLFRUSxsaIPRsYoASx/HxZByGC8BJk+Xuw21WLBdZ1\n15F7gt/PMs/Dw7yuY508WbEMnY2MCPrEfXl5AJcuQWdCjxxxYPduP0ZHOYyM8LhwQYDNRszejTfK\nWLYsBI4jYGfcl/nzZQwOkq8rz9PjVZXDP/zDRDz6qMS4INxxR8QCIsNhIBSi8AsN+Hq9MurrRZw9\na8MNN0QxPMzrrgHERNI+1Na6dCnCtGnkiiAIqi5rICaTnAJEkdNDGLTXTk6mczM0xMds3FRUVhoH\n4AI4dswOAHqwRFmZW7c2mzVLhihCt4tzuxVEIip27aI2/ZUr5I6hqip6egQUFCioqZEQDgM5OQoz\nUAZQWlxlJcu+clzcI5oe92+IRL6LwUEeCxeGmWEyTbNrHlyk69KB8nIJkyapyMpS0d3NobubGPDh\nYQ5z5shITaUBM0ni0Nwsor2dXnPXLicWLw4zw5WnTgmMI8TEiSp+9jNisNevpwWg10shJ+ZgkI4O\nGuIza6+PH7ejuprOaVcXz0Rza10NbRuqCl1GpDHfAwMUpLFqlQft7QK8XpmRNHzYZ9lY06fLTHdl\nxowPjyqeO1f+3NiaJe4jiRqvEtfFtVUCBCfqK1fjuUMYQfGJE+MzQPPmybDZiNUaGOAgivFJc7P3\n7ugoB7cboOQsYPHiEJPQVVkpIT9fxsSJqu4QsGFDAOnpfkydqqCmxhUDhcSqrl3rRnW1X3++9n8t\ndGPvXuc4mt743TkSoWGzoqKofsOfMycKv5+zWLBpQOfQIWqlv/iiDS0tBJCmTSPrq6NHnSgrC6Ci\nIkkfSNMYUKPmd9YsGmSqqxPR2mrTvXAXLw7r+wUQy6vpR10uoLTU2DYX4XLF0+QuXaLErvZ2Abt2\nuVBVJens98gIHfP77ktGebmEZ54hnW5PDw06XbzIQxCgs/k7d/r1SOC8PBnDw5w+QOh2q+B5Fbt3\nixBFGmjjeWKvjUNgLS0+1NRIjK7cmJjX2Chi40Y3tm6VsHhxSNc05+QoyPp/7L17eFT1vS7+rrVm\nMpckwyV3EkgAEagJUEBrq9Xu093dy96/46na1ragVrulm8g9URKKNFEYJAFExXOQ2ISLCRY4nj6/\np/prPT17az0ePYUUGpCbkgsh90CSWbNmMjNrrd8fn1lr5rvWcAmggK73eXwktzVr1nyTedf7fT/v\nm0VKpddL9cO9vRyqqlz6tfN6/WhqGkZRkR+TJkVw6lRssFC7Odm5k5Ty+HVBSn4w2rQHU3Sb1+vG\n9u0+ADzOniULSlKSgvx86Kklxvi5+Kzdo0cFFBbKuoLt93PMzUZDAztQN2mSgpISN7Omydc9rB9v\n7tyI6bqyvnkFyclkGcnLU5kKai31o6VFiN4shCHLwAcfCKY0F3OhBceo6G+9RdOTiQbXLHXYgoUv\nFiwSfB1g3aVdW4w0dP5S6RCdnRf2CM+YoQBQ8Ic/2CCKPObPD8HjMefTTpsmM1u5GlEKhYDx4xXY\nbCra26nOtqBAQVOTAI/nW3jxRQeqq/148MEQenp4RlXt6BCgqkSgBYE8rklJKoaHqSBAlhMXVgDQ\nt75tNpqaP3uWFHBj2oVGnLOyFARJ3MN//s8RU0XvsWM2TJwYweuv+8BxYFRwTdH1eFRIEtXu2mys\njYHOjTORnNJSN1auDDBELxiE7vXctSsJ7e0CNm3yR20AQZP6rcWppaQApaVEBONTK2pqYqRxwgQZ\np04JGBriIUmUb7xrVxKKi4MAONhsZFmJf35axbB2zVpaBGabPv46hsNUj5yoDttuV0xlLA0NIkpL\ng5g8OQK/n8fQEIeiom9i2zYH1q6VmNSP4uIgfv7zVF1Jj/lr6UajtDQIVQVCIeO5xWwd8deuoYHS\nOCoqAnA4qB2RVGMeM2dGsHJlrM3N44G+CxEOm9NO2tr4uIrnCM6cIXvJ2bM8vv71MCIRDuvWUR7z\nxo1+2GzAmTOsX/mTTwR9N+XOOyNRf74NAIeuLrP/Wzs3zQJx+LCADz9k00gSxZAZFV+tGCORh/jN\nN+2XPN7nBet9xEIiWOtiZLBIsIWbHonUmYttWxrf9Lq7ecyfHyMDe/f6TAoQwJLttDSFUb7q6314\n8UW/7rm12WLFBPRmGYsPM1bQvvqqiDlzZLS28ti4UUJdnQPf+lZEz3HVtn4VhVSr/HyZ8VvW1lIV\n7cyZET19IjNTgctFW+urV0uYMUNGaSmlALDkXExInIuLg6aSBK1so7FRQHW1P6owpqKkhFWgjx4V\ndCIpSRzuvDOC4WEOGzeSn3RggMPwMIfhYXr87m4OWVkqPvmEx549IlSVTXx47DFzdu6tt0bQ3GxD\nOJyYfNrtqv6aGYcUBwZ4lJVJmDuXlExjQ53RX7txI0t6jWUj+fnkiU50HbWvHzzIEryDB21ITzcP\nVh48mLgmuKbGH71p4XRfrijGfjaRXzo9nZIgjHaL6dNlVFYGTBFqBw8KSEtT8eqrDmza5Ed7u4DM\nTBq+HDVKQXW1xKRzeL0xy48xB1lVoZeL/O53QygooNKOadNkuFwcDhxgmwF376ac5PhjKAqnH2P7\ndhE8LyMnR8Vjj5n933feGcH27SKTskDxhRf2+2u4UFRZIg/x1caaWbBg4caCRYKvAyzPzoVxJVWi\nibx7ADvxvXu3iLQ0mnaPfyMrKJChKGyDWW8vnzC6KJ5sG0ssWlsFTJwom8oJtC3x/HxFJ8WSxBKf\n1FREfZ7vwm6/F3V1tP0fDkMfCjMqrfHeSa1xbdkytnBi927yWY4aRf7KSARMIkQ4zKGnh9OJzMyZ\nMgRBRVkZ+WovpLR5PMDp0zGvqDZUpT1uUZGMrVv9+PhjAV1dvE7G4s+/rY1qgnlexahR7HY9kStK\nSTCSXJuNhuZCIQ7Ll7sTZPwqyM1VUF9PZPrTTwUUFLDEJTtbgSQJWLHCbbKQ9Paai0GMGclut6rb\nQwoKFLz3noBvfjNW2jF+PO0maLaKc+eITLHnqUZ9yarh80Bx8bAhcuxdHD/+NVRXO5k19frr7A1M\nb2/stZwzR0ZyMqnDDgftHths5KktLXUnbEXzeABBoF2Fn/yEXcfnz9uQnAw9l3fBgiDsdjWan63A\n7Vbwu99RC1tenmJoaAPuvJOsPz09PD79lMfQELsO29t52Gz02g8Ocpg1K4ITJwQ9+kwjm5o629nJ\nmeLMeD5WR9zYSOtr7VoHoyYniiEbSVTZjRRrZr2PWEgEa12MDBYJtnBD4Uo8d4nUGSMxPnTIhupq\nJ95+24dZs2T87nc++Hz0xss2lUmYOFFhFCDtTbWpKUZMjApTTk5sUl97zJSUWPtYaakbCxcGUV6e\nbGqha21lz5W8saruITYS7nPneIMKLaK4OIgjR4SoajyMoSH6fptNhSjS8NDy5UFMmECe3UiE1N5w\nmMP48TJGj1bR1GTDbbeFUVREzzv+HOfOjTC+29xcBcPDWuoAJQpkZBBBPHZMwIwZ8gVb744epYQN\nzc9qzJjt76e4rhde8JsIrCxzKCtz63aIrVsd2LLFjzFjiASOG6fi00+JiAoCh/37k1BeHsDrr1PD\n3rhx5CvNzeXw5JNB0wBibq5iUnpTUxXU1lK6RnY2pVGIIoetW53o7ib12lgUkZ2torsbADhUVrqx\nalUAO3eK0SQI6Hm327Y5GeJaUkIFHx6Pqid3NDUFUVgYQVaWwtgsurtJXVdVYMwYBeXlsSzoF1/0\nY9w4FUlJQGurgFCIQ0ODHfPmhbBuHRVLuN0qGhp8OHjQpqu7VVWSSbXWHvOVV5KwcOEwxoxRMHmy\nAq/XpQ8RbtjghywDX/96BIWFCl5+WcS5czx6enh88gnZaA4ftmHbNifWrZOgKIDX69evYSjEYeVK\nt17QEn89GxpE2GwqFCWmzsZg/tug/Q3RMqY9HhV33HHhG+qRRJVdbayZBQsWbixYJPg6wLpLuzCu\npEr0QuqMUXmLPx7PA48/nmzayh81StV/XlOl+/s5zJvHNott2+ZAbS0VI+TkKHjpJSdKSoLMY44Z\no2Dx4lgta0aGgoYGH7q6eNTXizh1ipIEYn7ib8Fupxit/HxS7zZvdpoId0aGgtde8+P8eQ5VVU50\ndmpDeDBlsdbUiEhPJ3IV7+kNh1l1ec8eH1591YHKSgWPP57MZNZmZio4d47Hyy87sWDBMIaGgMxM\nSh/Ys0dEczNl/o4dq+oNafGvo/H8Z82SsW8fqYYdHeYt68JCKrTIy6NhqvjoraefduvKut1OGb+D\ngxyWLGGHpB55hAbj7r8/hBMnbPpNw5YtIhSFx7Fj9LhaMgENZsk4cULAjBlhPY+3oEDB4CCPX/yC\nXv/4yLGKigBeecWBUIjdSWhqouiv6mqnbmWha6Fi8uQIIhEOy5YFMXVqBNXVElpbeTgcQH8/KblJ\nSSrKymiQjhT072HvXq1iGvrazsoiwi9JQG4uZRpTMQl5gQGOed0rKgIoLXVjzx4RkgSUlCTrRNHh\nANauldDXR5Fn8cONmrVDy1NuaBBRVeXE/feHcOCAHXY7NSauWuXGzp20rseOVRk7TUMD2R0WLBhm\n1l1dHSWMlJbSmg0EqL47/nfy8GEBbjePI0dUvcL4YrtD2trTIue2bxe/kKTVeh+xkAjWuhgZLBJs\n4YbClXjuEqkzGjE+fpyHz0eqnd2u4pZbKDLp9GkBlZUBuN3sdnRenqK/wWqKkkaU33tPQEMDRWPl\n5ZEnk+dp+v5HPwrh5MnYMNDMmTJkmT322LEwFWCsXOlGXp6CnTtF/P3vbHpCQ0MSnn9eQns7qY3t\n7UR4Skspv7e2VsSqVQFkZqpoayNrhzFW6vhxW3QbPd7TawPAtrsdOGBDVZWkZ/pqBOLFF0XY7cDp\n07yp/ay2VsTHH1MFs8ej4sABQf8e4w1DXZ0YPTegq4vX0x+8Xj/T9KVlzra0CCgrk6KtYMTwX3zR\nj5KSADIyVHR3c3psmdm6QXYGp5MG3TIyFGza5Ed6Onmk4/3fFRUBdHcTIT5xgkhefb2Mn/0sRbeY\n2O3Aa6/5Tf5dn888mFdTI8Jmo5KIiooA8vIUQ4oBFXuUlyfj9dd9ePRRItfx17W6WoLXK5nylR0O\nsiuUlUmYPVuG06madgSMNzfxr7vDQaTT76eMXa30JC9PQW8vbxrQ6+iIVTy3tgpRtZfD0qWkOD/4\nYEi3fGhNc2fP8igpSTap/5qX2DhAd+QIrcX2diLcM2fSLkn8741xyPRSu0OWb9eCBQuXC4sEXwdY\nnp0Lo6iIcj6bmwVMmiRjxozLV3AS+YlnzZJx6JCANWsCuOUWGUNDHBOZpPlPtUQBzUYgy6TMlZQE\n9arfhx8OobraicWLg+jspLiw7GwZ27c78dOfhtDVxSMri873pz+NNYClpAC5ubLJLnH0qIDnn5fQ\n1cUjKUnFhg0f6jnBHo+KBQuGsWoVKasHDlChxFNPxba8tagprfpYU3QTKeDxnt4ZMyJISjIq5cCZ\nMzxjDygokJGbq6K5mY+qpCwpO3eOx/TpCk6dQtSfHCM58VXE48cr4HmySixcmIKysoBu25AkGvQ6\neVJAdjb5oDU7gPEGxe8Hxo9XGUJUURFAOGxW/UkpJYtK/PUxJjsEAsDUqQo+/ZTH5MkK3nxzEKdP\nU6JAcfEwVq5kyxviH2f6dNmUh6vddNTViVizxmXaaYiPrdNygLVr5XCoCIU4bN7sxIIFlE5Bj0de\n8UmTZEQiHGSZbib6+9nXI9HNTfzrHgpxePTRFOzb50NxcVDPxXW7VcgyS04PHrTpHuSpU8lHbCTr\ndBNDUXNlZQHceWcYBQUKNmygmm1WTQa2bqWBP6OH+5ZbFD0TenAQuO8+9ga2tZW1+fT3c7o1IhFu\nJN/uZwnrfcRCIljrYmSwSLCFGwpNTQJ+9KPEnuBLDc1dyE+s/dfYaI5M0pTcF14gb+Lbb/v0Y8Xn\nvjY0UCvYokXs8Fl9vQ+PPhrCgQNESFetcuPJJ4OMmlpWFsCKFe4ESQxEhGSZyPfq1QGkpPgRDiOq\nBg9j0aKgTsQKCmQ8/7wUVyNLqqrRTxsj9dAV8LlzZfzmNxKmTCGlrarKhfp6sjLk5pKdY9GiIAQh\nlsdbWBhhlGvj+fv9dKPgclHhQGkpbeFrNgWqIiY195lnXNi3z4eNG/3IyVFQXKwYGs6kaJwaWzhS\nXy+isTGmkC9ezJJKm03FlCkyGhp8aGsjskQVywG0tgq6Kqx9v7EaetYstqmuoUGE30//1gbkyGIw\njPPnOdTXk3Vi0iQZ5eXuaFWx+abj+HEBtbW01W8kfRq0G454m8HBgzZUVkq6+l1REUBrawD/9E/k\ni/3xj1mvrPGxAfbxiopkbNzoRyhEZDsc5iBJbCJGQ4OI8eONmcDazROP/n4q1NCef0cHh9xcFSUl\nsci0GTMimDs3bPLyHjxoQ2FhBKtW0c3bqlVu7N5N/mzyl3M4dYrXPeK7d4v6zo52A9vfz5lsPhdT\ngy3frgULFi4XFgm+DrDu0i6Mi3mCLzU0dyk/caLIpBkzZKgqsHIlbbNrAzidnRyTwNDeTtvGxiG2\ncJgzbT9nZsaIVkGBjDlzIjo5fOMNH/7619gg0qJFQfz3/25HeXkEbvfdEAQZw8McnnoqgHHjVL3B\nC4Apa7aujra/4weMUlNVPPFECvLyqPFt+fIgcnIUcJyKqVNlPPxwCkpKgrjvvrBeilBQQETp2DEB\n06YpGDNGxdSpYZNy3drKm7JoN26UcO4ctYmtXUsDT7SVziE9XUVvL4+qqhj50si2prxrx05JUU1e\nUFUF+vo4JvZr8mTzIFtnJxEqYwrF+vUS8vPZIUQtB9fppHxlYyZ0ayuvWwUKCuhnKTIt3gtMOc2L\nF5OXliLIoNsMNHJ94oSA9HQFu3ZRw11mpgKHg9bXli1+ZGTIqK8nQpifr6CvjwYZk5NjsW5r1riw\nf/834PcDLS3sDVxHBxdNZBAgSfTYNhvicpoV9PRwyMlRmDUaa6KLWRVmzqRzaWvjEQrFnofHo6C/\nn0dfH/RUil27RHCcinXrJBw7JsDtJh9vV5d5vQB0o7Z1q6g36AHAvHmswr56taS38TU2CvoN7uzZ\nlN7S23vj5PPeKLDeRywkgrUuRgaLBFu4oXAxP9+lSO6lvICZmQrWrnXp/tPbb4/oatOyZTHf5ttv\n+5CcrJoasEpKYkqn9nma9me3n4lokQ1i3DiFqbl94w0fEzMlCMCiRUEcPcrmpr72msjUBZNVw+in\njNXY7thB3l2Xi1UX9+0bQijEo7mZhrxefVWEwwEm6WLBgmFDtFsAixcnm7b/h4cBu53NorXZSH2M\nRKggIT2dSkCGhoBx42Rs3uzU/Z7d3byubBujzbKyVJw+zWbtZmbSVr2mTHs8lKurkdgJE2hwbsGC\nYSxZ4mKG+XJyFLhcChYtStGHzcJhoKqKbhZee82Phx9Oweuvs/aR/HwF3d08ysvdePVVH3bsIC9z\nZWUAW7c60N4uwOUiYudwUCrD6NEKQiGqwV66NKjXJq9ZE1s/O3bQTsK4ceQlj0SAY8fsyM1VIAjk\np961y4Hi4mF0dsb8zjNnyjh1ypbwmvn9HPx+Go5cuHAY8+eHUFQUYSwzmywVrTkAACAASURBVDb5\n4fMBNTUiBgfJ49vRwTPH8XjIWjNlCmU4T58uY/XqAFwu6MOXK1cG8PLLInw+Grbr7qYdB5eLbua2\nbPHD7WZ//3Jy6LpoXuof/jAMnqeSlj/9aQg9PTx6ezmkpqqYPTvCqNzxN7g8D0ybZvl8LViwcO1h\nkeDrgC+SZ+dKcn0vhov5+S5Fci/2s7JMquITTwxHs02JRPA8kWuj53BgwFxi8MQTw9i8mfye3d08\nJkxQTC1tc+dG0N/PY+xYFenpMo4dMypYZJEAaJJ/3boAurq03NR3AXwL4TCH3l66iIEA4uwJxqxZ\n6Mft6uIxZUoEwSCn1wDn5irw+3lTxvBTT7kZb6aRXGsWgtZWAVVVEjIzFfT08JBlwOejil+7HZAk\nmLbWd+wQsXBhjPzV1Ym6fWP8eBnNzUS+4z3DsgwkJysYPZpDTY0fvb2c7iNubY1dL4C8p9XVTuzc\nSWpzS4ug2xY0+8natRI+/ZSHw8Hrg3V5eTKqqiQsXx7E8DCH8+fp/DZvpnSInh5aA6+9lqTbSdLS\nzHXDa9a4MHmyjKNHqeZZkogIx5eXVFRIcDjA2FJ6e3m9LGXjRj9WrnTryREOB8WjZWcHmGrtqioa\nijx48H2Ew981XDMa9nzqqSBsNiqm0K53d3esMIRIPQeO4zB6NP2+vPSS01RfvHGjn7kRqq0V8Ytf\nxJ77tGkUO/jkk7HXwucjdXvLFj8efDAVM2dG9GuZn6+gv5+tUtaILc9T6Uu83Wj3bvGiN7hfFp/v\nSPBFeh+xcO1grYuRwSLBFq4K8ZmcxcVBHD/OX1aM0YVwMT/fpd4I439WloFDh2Lk3GajoP54dU7z\n/95yi2xq6HrjDeOAGQ19HThgx6OP2vDaayIEQUV1tUuPSps4Uca5c0Sit251RTNkzUqj9jG1spHi\nGgoBgqDqpHriRDlKQl1YuzaA9nYVDgcpxOfPE8GN92SOG6cgFOL1KfwPPhDwyCMhdHbyqKsTsXmz\nEwcO2NHRwaO9XcDTT7tRV0fnHX9Omh/UbqckhUCATRtoaBDR3Mzh9tsjCAQ4kyfZqIx3dvL68NRv\nf+sz+WArKwMoK3OjutrPVBvX14v42c9SdfVTW18uF1BXJ2LLFieWLAky56v9bEGBrKcuaJ/v7ubR\n0kI3LqtWubFoURBer4TcXAUpKSreeMOGr3+dfKhTpihYtsyNpUtZ/7HTSSTT5zMTf6O1o6VFQFIS\nKdIpKSpOnowp71rFsrGZjuwtseNkZSloaeGRnGy8ZhLKyty6L/u55yQmqq+2VkRrKxV5HDokRJNK\naPBx6tQInngiiLY2AbfdRut1wYJhnDjBWhkGBzm89ZYPLS2JYwcLCmQUFkZw/jyHYJDO9cABO+bN\ns2P7dhGjRpG6fSFia9zV6e1ldwGMN7gX+7twrW/ELViw8OWBRYKvA75Id2nam5nxDf1ySi5GipEM\nvBj9w7t3i7rXU4sw6+ykCmCbTTUVNrS1CdHBnphaVl0tYdMmvz58NXlyBCUlAZw6JSA3V8VDD8Vu\nBkpKgsjIUJCSouD116ldLDeXlMa6OlLLeJ4ea/NmJ55+OoCdO+eiv19EXp4SVZplfPWrEdhsRIBP\nnRJ036fXK+HJJ4MYN05BUpIKSeIgy8CYMeSTLSyM4P77jcqeDZMmURzb+fOkjBcUKGhvJ/tGIEBb\n4ZJEvt7z5wFJYslKSwuPadNkLF6cjEgEqKpi7SF5eeZKYS1GiywNcsLBvcxMNtXgzBk2OWHiRJmJ\nItOizbRrWV8voq+PFPwzZ8i+IEnQB7p8PvL6lpcHsG6dxBD79eslfP3rsp5F3NFBpJnjWJU/PV3B\nkSM2pKUpzLn29fFMEgKthWSG3MZfF62Mw9hM19/P2hTIS+tESck9qKnxY3CQhulUFXqawtatTixf\nTjFuTz/txsKFw+jo4MHzHHNTV1Xlj+5o2FFUFEFPDw+nE9i504EDB+xRdT/22LfequiZxBpmzZLx\n1ls+nDjBIydHNajksSY7jYj6/ReuLDbu6kybplyx0nslBTtfBHyR3kcsXDtY62JkuCoSzHHcBgD/\nD4BhAJ8C+IWqqkPX4sQs3BzQ3syMb+jXe3DFqDT19HBYujSIzEwVbje7fb17t4j0dFZNlGXg7Fny\nK0oSh7VrJQQCQH6+ggMHKM6rvV2ALfob1N6e+GagoYHIWW6uguPHBXzve2E4nXT8zEyKkTpwwI6f\n/cyGujqqdo6vrKU2Mpb8cRwYQtjQIMLtBuM9NqqT3d08du4UsX69E4cP21BRIeHWW2VIEoeqKheW\nLg0iJUWF3Q7827+xx46/LuEwkSvtPMrKYmUWVA2sYP16CX19lC6hVfTa7SpefNEPVaVrKIoc0tJU\n/OIXw3C7gfPnWcKUlcWqnxs3stFmPh9w662s37q2VkRqqgqnE6bPP/kkKacZGappbfT1xdTqjRv9\nuPVWGbt2EXnWvLlTpig4f558yUZyHA4DGzZI+NvfbNFBMs50fK117tw5HqNHE2nMy1NNx4lvj4tE\naEBu6dJk/TV96CFSx+N92cPDAMDpXmav12+yuIwdCzz+ODvcNzDA4/BhWsDbtjmYGmKbTcV3vuMx\nEcs5c+i//ftZm4/Ho2L7dpFRYu+668I7N4l2dcxtcFf2u369//ZYsGDh5sHVKsF/ArBSVVWF47j1\nAMqi/1m4CL5Inh3tzay//+LbmZ83jNW3osihrIzIRE2NaCApHPLzZWYASxCAXbsc+PWvA4hEyBNc\nWBiL0/J6/QzZra0VE94MnD5NCrCmynm9flPFLgCIIoePP/4Lxo69F5WVAezfb8cDD4SZdAjNr2vM\ngj18WMCYMaqJeMU//+xsBc3Ngl5z6/PxOHiQw+zZMmw2+hmOM1c4d3VxUfJGpFWLH1NVujmIL7PQ\n/Lp1dVQx3N9PnlztWKNHq/jZz2LPvarKjxkzZD1FwOuV0N9PVgtVBV55xY+xY1WcPUtJE/Fq69y5\nNNAYf65Hj1K2rVaprH2+p4dHWZmEuXNl1NQk4Z57jN5qWquacq0p6F6vH4sXJ+v/3rbNiaVLg8jO\nlvWBOYAqkJcuDepEuqGBtcBEIsCoUSpUlcOKFW69pW14GNi5k26ScnLIMsFxtO4yMoK49dYI1q+X\ncOrUe8jPv0e3nmjquNNJqv+KFbE4NZeLrpMsI0qGYwOF7DrisWtXkv4zRUVylIgSeTSS3OZmHjNn\nyrrtwPj7NW2aYiKeF9u5uZYxZl/Wcowv0vuIhWsHa12MDFdFglVV/Z9xH34I4IGrOx0LNxviY4xu\npMGVoSFOb8SaPl1GeTkRFPIfxghiQYGMnBwFn3wigOM47NqVhPZ2AWVlAfz0pyEcOxZLbYhvwaJB\nthhJOHFCQEWFhIkTSd3V6oVzc9lYNePPNTURcauvF/Fv/+aCLCczg0nGRIAZMyKw22EgIOaa6Oxs\nhckB3rzZie98J6x/HxE/Dh0dPDMU5fX6meP4fDyWLXNFG+3YQSpV5Qxkkv6tDcIZt8PPn6fYOUWB\n3m4XiahITlbxb/+Wor92mj+4sjLADNlp0V8zZkQQDNLzjj9+YWEEWVkK0tJYhXV4mIPX60ZZmYRv\nflPWG+z6+nikp5OdZPVqCTNnyjh5Mvb6bN3qRE2NH598wmPKFBlVVX50dgpQVfIHxxdpxNcZ+3yc\nXrs8YYICh4NuQDQSG8uPlnDbbTLS0lRGua6okDA8zOGHP/Rg714f+vupmCMQ4Bh1fPdu2jnQ4tRe\nfZVSGs6c4ZGWpjI3aUZv+owZETz1lIJQCNEUBxVvv21DTg7FuyUilvG2g4ICmVGOr+fvuzU0Z8GC\nhSvFtfQEPwZgzzU83hcWX8S7tBstoD4nR8Xq1Q4sWDCMnh4aQtOydDkOeOMNH/r7SdGKb5DTEgCm\nT5cxMEBDP1pecGGhrKuR2dkyo7Tdeiu1eY0aRSkEWgZvvEpM28aJSwmam3nI8j8AiNkX4lU/m03F\n5MlyNHmCfL1nz9JzaW/nsXdvEmprqep24kQF584BKSlU3qE91sqVQbz4oh+jR9PW/ubNDixYEMTZ\nswJD/LSEgeHhWMFCTw+PlBRgwgQZixcHEQpx+va9Fj+m+XtnzIjg7FkeL7wQq+adMYPU3SVLaBgu\n3q8af30KCmQUFCgoKQkiN1dBVpaC9nZBv9GornbitddEuN2cfvPQ2BgrKlm4MIjBQU4/L1Ji6Qam\nsFCGKHJYtiyI5GQVKSkRSBKPs2cFfPWrEbS18eC4GLHv7ubR0cHh2WfdujVkxYpYcUlDg4jDhwV9\nrTQ0+PQIsHi1f+dOEV1dgmmAz+MBOjooai3+xsjtBjhOjT53HtOnfxMcp6Kvj8OOHSIEAejqomG0\nwsKYlzZ+La9d62dyrgMBYP9+H/7P/6GM6p4eTq+u1og3wOGxx1x4+21fQmL55psxdbilRUBvL48H\nHghfl9/veNxof3s+L3wR30csXD2sdTEyXJIEcxz3DoCs+E8BUAGsUlX1/41+zyoAYVVV6y90nH37\n9qGmpgYTJkwAAIwaNQpFRUX6C/b+++8DgPWx9fFlf6woQErKvWhu5jE4+C5uuUXBPffQ10XxXfzy\nlzyeeeYHCIc5CMK/o7Q0gNtv/ybS0hQMDLyHrCygu/sfom/s/4FwGLDZbkddnYjnnvsIP/lJCFOm\nfDNK2N6FIKjYvXsuOA44deo9/OY3br3m+Je//P8QiXCoq/tutCr3XQBAOPwtnDghYNWqt9HVxcHt\nvgc7d4r44IP3EQwCW7f+EwoKZEjSuxAEl368c+fo4/b2f8CaNS48+ugf0dKiYvv27yEc5jB9+v/E\nT34SQmrqvbjlFgV/+9v7mDePg91Odoq2tnfhdAJe7z1QFODUqb+guNiObdtuhyRx+Oij9/Gd76jY\nuvU7eP55CYLw75BlDt3d96KtTUAo9O+orIw9v+PH30MkwuE3v/mufj1Xrw5g7drvIytLwfe+9yf8\ny78A+fn3ICVFQUvL+/j+9wGf71vweBR88sl70eSI70ctI+z1eeSRPyIpScW3v3131HJC1/vZZ+9A\neXkyBOHfIQgBVFbeizFjFLzzzgcoKuLQ2HgPvF43gP9AerqMgoI70N/PIRT6DwwMAF/72jejQ2p0\nvD175uLvf+fR0/M+eB5Yv/77+vNZs0bCb3/7PVRUBHDkyHuYOlXGV75yNzZs8GNw8F38r//FIRz+\nPvLyZPzLv/wJhw6pyMy8N5qA8SHOn+fx7LNfg88H5vn5fBx4/t/x8cc86uvvwqlTPJqb/4IXXrBj\n+/bbEQpx+vW32+9FIMDh17/+CL/4RRA+3z3w+Xj8+tcf6V+vqJAgy/+BgQEFPH83Zs+m9fPeezaE\nw98HAEjSu1i/PraeSkvfRlIS4PX+AADws5/9EeGwA1ok35Ej70fP97tobuYhSXT+DzxAv0/vvfc+\nurt52O2x36fBQQnAN26YvwfWx9bH1sdf7o+1f7e1tQEA5s6di29/+9u4GDhVVS/6DZcCx3GPAvhX\nAP9JVdXhC33fn//8Z3X27NlX9VhfFFienStHfBxSZqaCJUuSdZ+oNryjfU9Tk4BgkNNLDqqrKdnh\nn/85oh+vsVHAL3+ZrNsX5s6VMTQEeDzAihVuLF4cxPLl5pza6moJS5awnwcAr9cFr1fCM8+49KQI\nrVHLZgNKStzYs8eHFSuS8cQTw0hKolKBVavc+Md/fAcZGfdgzhwZSUkKhod5XeUkC4KEQ4eooWvr\nVgcWLqSfD4U4TJggM7mvCxZQy1lFhQSO41BWRr7R1aslTJ8uG2LPfAA4Jgnjv/03H0RRQGsrFTyU\nlroxf35I970CwEsvUVyYzYZobi1d59WrJcyaFWHUUK9XQk6OokeXxefHah/v3u2DqnJob49V6rrd\nKtraeLjdQGoqtdmtWuVGdbWkn692LKNPWxsyI5JMqK72o7+f1HuHA8xru2WLH7m5CnMdnngiqKce\naEOKlZUBAKrpscrL3XpqQ/zz27OHFOT4NdbXxyEjQ8HZswI2bnRG86spneLpp6nsYssWP6qqnLjn\nnv+J+vrvMmtt0iTZpMI2NsbsCqtXS3j22djz/s1vJEydKuuWFrdbYTKJKytJCX7mGVfCdAXt90Q7\nzzvvjOCuu6wosusJ633EQiJY6yKGxsZGfPvb3+Yu9j1Xmw7xPQClAO65GAG2YGGkSJT9qaqUf/vh\nh7Slu3atC088MYzycjczFW6MTNIsDuEwkJys4p13bOjt5TB1qgKnU0F1tYTqaqrz/fRTHpMnKxga\noi3f4WGz7zUrS8G4cUZbA3ls7XY1amGQUFDA1tXu2CGirk5Ea6vAlDiUlATR0iKgpsYJwI1Nm/wY\nHuYhSWTBGBykdIqqKifuuy+MoSHg+eclvayB41T8+tduPPEEkay1ayU8/TRdk5QUYNMmBwDyq37l\nKzJ8vphf2uOhocFRo1RkZ1NL28svi9i924GvfjU2YNTdzZu288eOJc9wdraCxx+PEcJp0yjjOH6L\nH4Ae7RYKcaivF6MtZTQYV1cnQlE4QwyahHHjVPzrv8bsCIcPC1iwYBj9/UQmV6xw67F3ycmsrSAp\nSUV6ujnJwet1wW6nLOL4r2Vmku81njSrKgevV8LQEA0Oal7fvj7zwKK2PrZtc+ilEcPDlFet3ZRo\nj6Vl8HZ08Mxw4YYNfhQXD2PbNgfGj6ehxYkTzYN8aWkK9u+3M8kKRUXk021uFkx10VOmsBFz+/b5\n9LizjAwVY8bIGBwUsHmzHwBZOuIJbnMze57bt4v6EJ0FCxYs3Ky4Wk/wSwCSALzD0WTIh6qqLrzq\ns/qCw7pLuzQSZX8CMPl3ffRpZircGJnkcFAW7ObNTqxYEcRTT7GpDidOCFi0KMj4VBsaRJSVSRg9\nWsGuXURo/H7yvRYXB1FaykaDORwqenu5aJkEj0iEw7FjLBHs6+MhihQRpnmLu7upypYIy7eiCQWy\nSUU9c0bAffeFGSK1a5eIpCQV/f081q2T0NRkw5w5YbS2Cpg/P6T7j9etk9DbyyM7W4bdjqgvWsWu\nXY5ooYfIVNbW1or4wQ8iKC9360UKe/aIGBgA9uwR0d5OaQ02G/Dqqw69eCIvj6K1Dh+2YdYsloTl\n5CiYNy9FH27r6OBQVBRBS4uAvDw6ljGr2efjcfasivp6H/r6eLS28qitpXOurxdRVeXEc89J6Ojg\nMWuWgpMneRPhdbnUaN6zTa8U1o7f28vpNcuRCKJkkb250Yo36GMnKiok5OfTQFn8902fHsGePSJO\nnOCxYMEwfv1rauX7yU9SoySaJegnTvBwuVTMmRPB6tUS3G5SnmWZ1NjaWhEbNriwaZMfy5d/F16v\nBAB6LvTy5eYdkKYmAT/6UWxwbf9+ItoZGVSqYUzMeOCBMObMISLb2CgwPnbj0NuXNYHhRob1PmIh\nEax1MTJcbTrElGt1Iha+vEik+hqJbGcnh6QkoKQkGC0JcOjbsvH5pIA5MikUIkWvu5vH+PEKKisD\n+tZ9RwdFP50+zT5eWxudS3MzFTwEAnSM+fNDsNuRMBqsoiKAX/3KxWybx5+H3w8AlLMbrxRu3uzU\nCyQKChRTe1d/Pym2RiI1NMQhEOAwZgzV8qanK+jt5ZnUAq9Xgt/P6WkL8SS6psaPjg4ig/FDVFpl\n9KJFQdOxfvUrt/78srIUU9NeRQVtwxcUyDrh9XhUXRk+elSA1+tCQYGMdeskqCrlMd96q2JKe6Cq\nZQUnTwr6AGJ5eQALF6agtZXHffeF447P62kOx48LepHE0qVBJCUpqK52Yv16iakUTkujFI3+fg6p\nqbQWu7s57N3rQyBA14XnwQzn+Xw8BgdV3HqrjJ07RfT2UrxZcjJlH3/lKzJ6e3nU1Phhs6n6zkB8\nTbWWIOHz8fjVr9iKaU3BP3rUhg8/tKO1NYSWFgElJcn6WgNUJnpO2wGJ/52JRIBAgIPLBWRkqMjJ\nUS9KYo2/bx99ZIPX69ZJtpXAYMGChS8irMa46wDLs8MikeprJLIej2pQgSleinyJsTdkWQaSkhTs\n2CGiqcmmk6HFi4OorAzg5EmKl9IsErJMU/IbN7LRYFlZ1Mzl9RKhi3lQiUwY48gqKwMQBPK3Dg6S\nvzQtzXwe8+eHkJWlQFGoPrewMIKpU2WcOSOgt/ddBAJ3R1vWJN2XOneujIEB4NZbWfVx7FgVp07x\n2LzZqftN58xhExUAwG5HNNuXJdF9fXRjkZGhYtGiGBmrrxfB8+ZSCe3/2g1De7uAI0dsJvUWoJsE\njfDa7aTEa4kIeXky1q6V0NQU896uWhWA3w/s3k1VzhkZCnp7OagqTNXCGomLLxGprxejaQ48UyQR\nDpPyXVERwPAwp1dc0xCkCkEA+vp4DA5Sg93+/UlYtixoIvaaL9jjUZCbq1zCD0vrMT420O2mcz9y\nRMD06QrKy12YPz/EXLsjRwS0twv6erfbVUyaJEeH5mjAbdasCFJSFCaZZMoU881fcXEQ8+bFnsNb\nb/kuSmLNv2/Qz0sj2V/GBIYbGdb7iIVEsNbFyGCRYAufG4yKb1ERbeE2NbHK5/HjPH784zDzpm0k\nZB6PyhAR7djHj/MYM4bipOLJkLbNXFkZQDjMYcwYBXV1Io4fJ7+my8XWG2/e7MSPfxwCACxYMGxq\nY9O2p8NhUt3iFdbaWhEOh4p588ztXh6PiuLiIB5/3Fy6IQgu7NnDmeLVVqxwY906Cd3d5OVVVWDS\nJBltbTyGhniT3zSetBUUkD93aIhsG2y9LxGfjg5zQUYkwulfj3lmiZjF+6HNkW+x4om5c2W88oqI\nQIDKSOrqRKxa5UZx8bCBZAZw+jQR5uee82PqVAXd3Rxyc1Umvk2zlKxfL+HcOTMxr6gIIDWV8pHP\nnOGRnh4briNPeGwQr6zMjZdfFpGZqZpIttGW4XDQQF1mpoL0dAV33EE3SI2N7O6FkRTHR3c1Ngr4\nv/+X/MZer5TQY63tamRmKhga4vD22z7MmCHj+ecljBoV2+04dEhgzvmtt8gTFK/WDg+z16elhb+o\nhSH+Z7WBU+11tKwPFixY+KLCIsHXATfzXVoi68LlTogbFd99+3x48MFUxjZQUCBj7FgVb7xhR2Ym\nDfQUFsaIVWz4SmEI8AcfCIxSvGOHiOpqCbIMTJigYGAAui9YI3TxSuKmTQpEkWfI5LJlQQCAJLGE\n4tgxAc8+644qmgFTG9cnnwhwu+lctZxfjTxKEse0ymnlGXl5MoqLv4a2NpWxaxw9aosOYnHw+zms\nWUNE/uGHyW7h8SimlrqUFFVXkltbBcbSsGePD21tAiZMkJGUBHzwgQ1FRawNQWvX27JFZFr0HA5S\nvF96yRn12QoYPZqudVcXj/x8Kk3RHnvFCjeeeCIIgMPhwzakpRFB7+83DpVBJ4TTp7MK7+9+x5Y8\nZGUpeOihVOzcyQ61KQpdm9/+VkQoBN1WYLdTLXZtrYjeXj4aS+fU19CxY+y5nD3Lw+Nh11ooFEvX\noIEwhUliiPflXgizZsl6eYg2OJmZqZi8t4mGzR577BsAYkkQxhvClhYec+bIJtId/xzS0hT88pdm\nH7GG+J9VFKCmxn9J68PV/C2wcPW4md9HLHx2sNbFyGCRYAsjQiLrwuVukca/eWdlESEsKQnC7Sa/\nqaJQw1p8okJFhYRIRL6oJ/HwYUqMMBLVadNkHDkiYPJkFf/8zzI++kjA8uVBjB9PW+3x35+RoWLj\nRoc+7EYxVuTBnDlTNhBwemxt+33CBPbrt90m64NWWrtXZWUAP/95Kn77Wx8KCmIKoMdDQ3Jr10o4\nckSAx8Nh2zaKP1uzxqWTw9GjVWzYQDYOQYgR7JKSIKZMMQ6hqVi8OOZXjn+eBw7YomokKdBZWQqe\nfjqIjRslpKcrcDhUXQWsqnJFUyiApCQVnZ00eLZwYRDnznG6qrl4sUu/gVm2LMikK5A9QsXs2aRc\nd3TwSEpiSebcuTIGB4HXXvNDVVXGznH+PIedO6miODubCH9ZmQS3W2Fucs6d47B+vYSyMjdsNmD/\n/iFIEo/2dvrvpZco/WP6dBlr1gT0NZSo7jt+6HHOHBklJfR84lVRIxFtbub1zycihDwP3HWXeQ3T\n94zMYnA5Q2qzZlFSxEcfUZLK8uXJCZNUEuFyyyeu5m+BBQsWLNwIsEjwdcDN7NlJ9OZ/uW98Rs+i\nMQ6L45DQY9rcrOqPPX16GD09AnbsSMLEiTK+8Q0ZnZ0UJRbvo502TWa23Pft8+mT85rNIL7eOClJ\nRXW1Hy0tAoqKFHi9TsybF0JRUSSaIkCRYtnZCmw2YPNmP8aPV6AoKgYHeSZy7NQpHq+84tSTB9LT\nFTz9NA0ZpaYCJ07Evn/KFBoQI+L/LqgMIQCnk/JlP/mEx2uv+XH+PI/ubh7l5W692ri9XUBpqRtb\ntviZx+/t5RiSbSTIr7/uQ1cXj8rKQDRpIKaa1teLmD9/WL+ObW0CnnnGhddeEzEwIOD3v7ejpCSI\n8+fJyiFJsZuJlhYhLukiZo+49VYFb75pw49/HIbfz0EUKUWjrY2HqgJVVURQtZuAkpIAli5Ngd2u\nwuWi427b5sDatRKKi2PZtg0NImNTqa0V9fMIBHjMn89aLhwOFXffzaqtWVmKrnYXFkZMmb3V1U68\n8IIfvb08Cgoo/WL/fjsyM41WEeWShPBKm82Mfy8uZ0iN52lYkr0hof9fK4vD1fwtsHD1uJnfRyx8\ndrDWxchgkWALI8LVRCVdzLPocJDPNRQyk6j4rdx9+3wM8dmzxwe3W8WBAzaduD33nITWVvYN+tNP\nWZ9nVxeP6mqJOVZdnah/z+HDNjzwQBiPPEK2A81T6vX6mYGjujoRfX2cyXPa3i6gvDwZZWUS8vNV\nrFsXwPnzlHLBcZxuuygrUwFwBuIP3Qf99NPJ8Hol/P73dtTXU/za+PEKXnnFj0CAY9Rb7fHXr5f0\ntInkZLpGn34qYNIkBUlJCh54wKN/r9crMY/d2CjoqQC1taJupRgYmoaNDwAAIABJREFU4DE0BCxa\nFGSuWUMDa0tISSH7QXs7j5wcJTpECHzta1TmoVVXNzT4MDxM1pBFi4JYtcqtb9XX1Yl45RURo0aR\n+pybS8q68QbJ+BofPSroCrpR6ff5gDvuUEzb9dOnKxgYkNHcDIwZo+DZZwNoaeFx222kOj/3XEC3\nKTQ2CvjOdzy66q1ZGTIzFXR28oyN5UKE8FpYCC6XTBt/VxMlqVwNrNg0CxYs3OywSPB1wM18l3Y1\nUUkX8yyGQkBqKjBrVgRvveXDsWM8Ro9Wcf48z2zlGonPmTOkhsYrfr29vCluKyvLPOTV0sIe68gR\nG6qrnXj5ZT/q6rQUAbIdVFVJOtmprpYQiVCqAMdRooCmxM6eHUFpaWz73OMBfD4Ojz+erJPobdtY\n20Us35ZyggsLZSQnqzqJ3LrVgc2bJWZgzuuVMG6cgqYmG7KzFezeLaKjgwjy+fOA201+4Jwchckc\n3rFDZJ6zufQD+teOHo2lFYwfLyMtjdMVZI3sacN6gQAwbZoc9dTS66ndQLBDewF9S944TLhyJTWl\n9fXxiETAEHut+S7+XLOzzefudqt4550hRCKciQAmWqvx2bqagmtsYtMQr3y2tAi6lzdRMcuFCOGV\nWAiu9O9Fot/Va1lwYcWmXV/czO8jFj47WOtiZLBIsIUR4Uq3dI0K2IwZMtNYlZWloLCQlLo5c2S0\ntPB4+OFU/ee1rdyCAjO5NSp+t90mY2goZmGYPl2OZvEG4HarCASA8nIXiouDzEDenDkRvd5XkjjY\n7cDGjX5s3uxEIADdq2yu542lMVRXS3juOQlHjwrIzlYRidC2tEYct251Yt06CT09PIqKFNhsCm67\nTUFtrYj+fh5jx5Ky29VF8mBtLamqxgQHAIbqY1EvAdm40Y+FC91RpZlVevv62EIJ2jKXYLORHzue\nwM+eLWPDBj8mTlQwMMDhiSdSTGQvK0vF0qXkeX70UcoOXrYsCIcjlmXMvj708z09F1ZxtRuM+K97\nPCpGjVLwxhukakcinP6a2myU/kF10UFEIpxO0Do76Wd7engcOgRdeY2v1r7cLf1EyqfREuByxXJ1\nE+HztBBc6e/qjXJ8CxYsWPisYZHg64Avo2cnkQI2Z46sN1Zp0MhJfHxUQYGM22+PYPNmP3geqKry\no7tb0P2u8cSksJAIcE6Oiscei1kYDh+24cABO6qr/Sgro8EvKlcQMTBAsWjaNr+R5MarwkAs0QHQ\n0hiAV18VkZ6uoLubh9NJFcRjxqi6AhxPHAUBePllJ5YtCyISAc6f5zF+vIyTJ/8D4fC3wHGkaK5d\nS0Q9OZmKHeKfZ24uS/7PnImdk1Z2AcCUdJCZqaCigrzA4TD5cbu7iaSXltKgW28vj7Q0IsSaRaG6\nmsg0pVgMw+FQsXOnCKdTwf/4H0M4etQW9XoPY+VKt574YYwBmz5dK5lgybjHAzgc5El2uxVIEvv1\nadMUzJ4tIxymfGVN3T582KY3wi1YMIytW53R+DpBj/uKTw3RlFdtPRoLTS43Rixe+Yz/+aKii5PC\nK7EQfBn/Xli4NKx1YSERrHUxMlgk2MJnDlkG+vs5pu3tQgqYRk60gSWPR8X48YqpLtnrdQEA/ut/\nFfHGGz787W82uN3ASy85UVYWQHMzj337fBga4pCWpmD9egl9fTzy8mIkhNIdiOS1tV2Y5Pb2klp9\noWGz0aMVCAI9z4EBDosXpyZUYR0OItRDQxwWLBiGJAElJTF19ZFHeFRWJut2h2XLYo1t8Q1sRUVU\nmBB/DhMmxAo28vNjavm2bQ7U14tRGwkVRKxZ48LMmREsWxbE8uVB5OcrEEXA65WwZQs1qx09KjCt\nZJmZsRQLY5HExIkKZJk+1pRfLRouNVXBnj0iDh0S4HZTnnJVlYQNG5zR50OFGb//vR1lZQH09PAY\nM4aDxyMz8Ww2Gw1HNjUJWLEiWbeT3H57BGPHqqYsZu2Gy/gaGNvVtPN0uYjAXmxLP175lGXg0CEB\nnZ2cKebsYrAsBBYsWLBw48AiwdcBX5a7NE3V7e/nmGEyjTglgkZOtMGy7dtF09Z5/JT7wACH6dNV\n3HtvBM3NPMrKAiblr6hIQThM2+ApKYqecasN0i1aFMSECRcugMjIoPKMmhoRx48T2fZ6Kc0iFALK\ny93o7uZRXy/ittsiqK4m/7DTaVZvm5t55OcraGsDAPZ5ZWR8S//34CCH9HSyexQXD2NoiIOicGho\nSMKcORGoKuUeqyowbpyCnh4O2dkqurooTzg+LeL8eQ6pqSrS0xX4/ZTMEA7DkM5BKvXevT4UFioY\nHGQ9tXa7iqoqCY2NguG14NHTA93nrNlVYtFwVNvsclGD2tq1EtrbeVRVSUhJUXDHHSr6+syv2+7d\nIsrLk/V1sX27iBkz6PrFV1Zv3y7innsuXKxiVMK1dacpstp5jjTe60rjwa7EQvBl+XthYWSw1oWF\nRLDWxchgkWALnxk0olBSEjT5Oy+kgN1yi2yqhDUOOc2ZI6OsLIDsbAWRCHDokA0TJ8pwOlXGFqAp\nfwAYgrV3rw+pqWq0bS2IlBQFTic1yPX3cygoULBrF3lxOQ5YtcqNJ54YRkeHwCiOr70mMr7lv/9d\nwLRpQFcXD0miIb/aWiLxOTkKUlIUPPMM+Waff15CW5vREhArBZk5U8apUzyKi4PYto1qkY8dI/KY\nmipjcJBHQYHMDL1VVEh6BnB8WsWOHSJ8Pg6hEMWTuVzmljifj9P//7e/CWhuFlBXJ6K1VQDHASdP\n2mCzqSZS6fEoyM+XsWWLH4ODVMVcVydicJBDIMBBEICxYxU8/niK7hvWfvatt3xRO4yM/fvtBvWd\nfc0zM6lqOpGdIBGxjFfCEym1V6vIWvFgFixYsHDzwyLB1wFfFs+ORhSMvtCpUxUcOmSuT9Y8nL//\nfRLuuy+MoSEOAwMcvvENlrDYbLT9vX69xLShUdyXWfkzEpZPPxUYlXH//iE0Ndl04n36NI/+fh7P\nPhufsUoqbEODD2fPCsjOVuBysc/LmE28Y4cIj0fF66/bcP/9IfT22nSV++mn3aiullBT48fAANUK\nNzX9BRs3fgvjxlHCw9atTixdGjTVIu/b58M//qOMnTuTTKosQD+3Y4eIpiYbPB4VTz1Ftctay9yS\nJS6TF3b6dLr5GDVKxQ9+wFpPqG5aQm6uglWr2CIJp1PBk0/SceP9z7t2iUhJkeH38xBFoKFBNL0O\nJ0/yaGnhccstsil3d+pUGoL7618p+m7JkmTU1Pgvi7xeTirC1Q51fZ7xYF+WvxcWRgZrXVhIBGtd\njAwWCf4S4fOuOdWIglYT6/HQgJPNpup5qxqpi1dq6+tFJg7s7bd9KCyk2tlPPuGRkaFg0ya/bhfQ\n2sUAIoC7d5Pv1ji8RNaCIGw2wOv165m14TDHDMLt2iUiL49NoSgqiqCwMMLUEBcUyNizx6dnFBvj\n2zo6eIRCwC9/GUJrK89YLrq7eTQ3UxFFQ4OIkycFyDKHl15yoqVFwOuv+/RzGxpiM5VPn6bBQWNT\nnaYkd3fzcLtZn+zgIBc9FuvZdTjUqKXDhe5uHps3+5nHstloAG7UKAWiyOnFEXfcQdf2zTft0eE+\nNgWir49DejqHH/4whXldWS+1ip//PDUaG+fUyfWdd0Zgt6v461/tTNmDprZeirx+HqkFlrfXggUL\nFm5+WCT4OuB63aV93jWniRU5mLa+T582x1TFf3z8OI9QSMWDD9I0/6JFbH6sFk+Wmamiu5tHWpqK\n73wnAoCIPwBUV1Oubjy5rqsTwXHQyab2eN3dPARBZfJvz53j4PGwyQva4JhmrSgsZElpUhL5YP1+\nYNMmJ2w2UkQPH6ZK59ZWHg0NIkpKtBSG7+tDbFrEW2qqgltuYRXnYJDDhx/aGOI4d24ESUkqNm70\nY+JEGXfcIeNPfxpCTw+P3l4O48crTFqD5oXduVPET38as3TEDwDa7SpkmT43e7aiX8/Dh6HbTKZM\nkVFcHNRrouPTHIyvY18f61VubaXrNzRk9vn29FzYz3sxfF43ep9nPJil6lhIBGtdWEgEa12MDBYJ\n/hLh8/YxXogoGLeSJ02SDR+zX/f5qLEsXsnUnkNSElBWFoDHoyA1VcFbb/mQlKTgnXdsOvnTVGZj\nUkBXF6mzxqrfjAwlWoShIj0djMWhrk5kVGXyzHLYtSsJQJI+POfxUKWyLPN4/PEUeL0SSkqS0d9P\nFc9nzvDIy1PR08MxKQyNjVTY0dAgYvFisi1UV8fKNQoLZTz9tBvz54cY4kjRbzE1++23aXpw3jzy\nIJeWBqIKORHx7m4OU6eSKh//3JOTFdTXi+js5JCVpSInR0YoxGP/frtuRYm/kXrrLfJXr1/v0gnu\nrFmRhPFh48YpWLw4dgNTWSkBgGkQsaBAgSQBbW181JfM47bbLp7coOHzvtGzYMGCBQs3LywSfB1w\nvTw7N0rNqVEhnjFDZvyf1dWsp3XrVieeeipx7iw9JyAzU8GYMRSj9b//t10fJjtxgtOLKozK4rhx\nCj75hMekSQoTx9Xby2HJkmSd9MYnNAgCsGuXCEVhyyqqqiQEAlSMoZ3z0qVB7N9vR2VlABxHxRtp\naQrOnhUwbpyCM2d43HKLopPq73//T0hLuweVlQEMD9MA38cfC3juOQknTgiYOzeCFSuS0d4umIjj\nuHGK6QZH+3dx8TBKSmLk849/HILdzqGpScDkyTJ+//sh/OUvdhQWynjyyRQ9G/jtt30IhXiGVO7e\nzTbOtbTwmDaN8pHLy936z/F84tc5vsCivZ3HG2/4MG4cFae0tND3CYKKBx9k7TJ33XV5iu7FbvQ+\nbzvQtYLl8bOQCNa6sJAI1roYGSwS/CXCjeJjTKQQ9/fzjP+zuDjIeFqzs8lT2tPDob5exNmz5A3u\n6eFQUuJmSNrQEI9ly4KQJCqi8HgUlJQE8cILlE3b3c0jFOLA88Azz7iRlaVg4cIgJk6UkZam4tAh\nAV6vhK1bHejspIQGtiEuoKcpALEc3XhSXFFBQ3oPPBA21AbH7Bs7dohob+dQU+NHUpKKefOckOVk\nPcHi7rtl2Gwqzp3jMWqUio4OAVVVfjQ22jBzJtVLHz/OQxQpy7igQMaCBcMYGqKbglGj6IbBqJ73\n9PCYP59tm/N63SgrCzCqdDyR1v5vTG3Q1lGidZXoddYqsy9WnFJfz9plzpzhL7vu92I3epZKbMGC\nBQsW4mGR4OuA63WX9nn5GK9EcTOSl7Q0Bbt3E+kNhTgsX05ZvBUVASxd6sL69RKSk831u729lPM7\nZozCFFHU1YlYtCgISeKQn6/g4EFBb4HTMon37PHhoYdYIstxgN3OEsFAACgqiujlFNu2OdDba2yR\nU6EolCOcKMFBI6OlpUSuV6+WIMv/EPc8iPj5/WSn0M6ppsYPr9eNSZNE/Jf/Esa5cxw6OgQkJSmo\nrvajpCQZCxYM48MPbfja1yJ4550hdHezUWxGD3RrKw+v1w+3O7EH1+j1TeTzNpZIXOy1v5Qtx+hL\nzshQL3vtXexG72aNNbNUHQuJYK0LC4lgrYuRwSLBFq45jIrbvn0+BINEUKdNS0yMzORFAc8r+MMf\nbGhv5zF/fggej4rMTBl1dSKOHxcwPMzhq1+NmEiazabi73+3MYSns5MIUH8/UFycrGf1xhPZvj6z\n33jzZieKi4PMY8yYITMDdrW1ItxuM3GTZUBR2M/HZwFnZcUsDNOmsb7ozEz6vt5e9pw0JXbiRAWH\nDwtMCUlNjWiKU3v7bR++/e0Ic20liSW2oRCHZ55xob5eTJipeyHSezmvfSK11RiHpj1XDVpboGZP\nycq6fNvOxW70bhQ7kAULFixYuDFgkeDrgC+6Z8eouJ06JZiGtmbOlE1qcSLy4vGoDKkzxqf94Q8+\n7N3rQ3OzgEmTZMyYIcNmA8JhllROmSLjk08E9PXxuk921Sq3bh/YtMkPm82shK5cGUBhIXlWjx3j\n4ffT84l/fkeP2jBhgswkHzQ3C3jlFQdKSoKoqxPR2Ul2hd5eHps2+TF+vIKBgVhUW2srj0ce+SMy\nMu5FejqVgLz+uh3jxrEkOj9fibbgydi7l7UNDA2Z49QSxYpFIsDevT58+qmAUIji0sJhymR+4IEI\nAPY1GMnuweWorVryhXathoY45uuFhQoiERnNzfQaFBaayeqV7DbcKHagkeKL/vfCwpXBWhcWEsFa\nFyODRYItXHMYFbfMTDXh0Nbl+DONdgdjI9zJkzyqq126BQAA7rpLxle/GiM8t9wiQ5Y5JCWpKCyM\noKBAxtAQZ1JNq6r8qKgIIClJRTgMLFlCFgzNs9rVxUEUeeTlKSZ11+NRsXhx7Fha8gHHqeB5slTI\nMoeMDAVnz/IMkd+5k5Tk1asdkGUXvF6/3gRXUCCjtlbEwACrojc2CvD5WH/u9OkKk0V8IbXTZgPu\nuUdGSgr7GlwLZfRy1NacHBWPPcaq1fG4HNvOlfh7P89YMwsWLFiwcOPDIsHXAV/0u7R4xS0zU0FL\ni3loq7OTu6RiCJhJ1eTJrMKbk6Oa2sq0oTKN8Bw8KDAtaA0NPoTDHP7+d1bR7e4W4PW6UFYWgNfr\n0s9BOzeNvM2cGcHu3TRgl5FBdcivvhrL7J09WwbHqdiwQUJrK4+HH2ZzjXNz2ZuCri6ye/zxj3PQ\n1OSHLMfU3JYWAUeP2jBpEkvempt5bN3qTBhLdrlq52ehjF5po9tIcbP6e68EX/S/FxauDNa6sJAI\n1roYGSwSbOGyoW1BaxFXfX0cRo8Gurooc1ZTKXkemDmTCIlGdF56yY/7709liOrl+DMvFLMVT7CH\nh2MxaO3tAj76yIYxYxQMDPA4fVqAIJhJ50MPhU0+Xs2va4wf085NOxefD5AkDp2dHPx+Adu2ubF2\nrQRZ5nD+PKVOPPRQKkpKgvpjav/3+Xj09ppzkuN9tn/9q2A6L+P1mTjRHEumqqxFoKhIvuiQ2meh\njF7OMa/F41r+XgsWLFiwcLWwSPB1wM3q2dG2oCsrA3jmGSpy+NWvXAm3pI3b1cZ82Z4e3uTljYfR\n8/nDH4bB87EGOADgOCKjQ0M8srNlbNnih9/P4fx5Hv39PJYvT0ZLiwCv128aWlNVYNQoOq/eXg45\nOQrOnBFQXU3f6/VKerGFzaYy5zN2rMoUaFRUBHDkCJVcVFRI6OoildvjUQGYiXZuroKaGhGDg6SQ\n33knPan3338f3/jG3bDZVD0ZIzubyjuMvthEauqhQ+aBxPg66i9SJNjN6u+9Etysfy8sfLaw1oWF\nRLDWxchgkWALlw1tC1rLnTXmz8ZvSRu3q435sh6PimPHBGzd6tR9t/EEzUiiNYtD/Od37vTp+b1e\nrx8nTwqmPN/ycje2bnUyTW5JSSo++EDAkiXJejHE3r0+lJa68ZvfBPTnplX7ShKHSITTH9fYPOfz\n0QBfOMwhNVXF1KmkUm7d6kBJSQA7d4ro6+OQmamiq4ti0drbBWzfLuLuu1nyxvPAjBkKgBjpvVDs\nmFFNNV7zRHXUN2I83pXA8vdasGDBgoWrhUWCrwNu1rs0bQtaa21L1N5m/F5jvuzx4zx8Pg7V1U48\n/vgwqqokdHfzGBqi1AJbdEV2dpLFQSOjH38sICWFJXrxQ3NDQ+ZiB1903qq7m0dSEjBjBsWprV3r\nwuHDNp0kE0knIj44yDFZwbW1IrKzVeZxjc1zWpWxNpyWSKXUhtnmzXMnvF7AhdfF5Q6BXaqO+vOw\nDFiFFNceN+vfCwufLax1YSERrHUxMlgk2MJlo6hIxr59PnR2Ut3twACHhgYR3d0xT7CGCxHB5mYe\nTz6ZDK9XwsAAh8WL2YG2e+6hYxij0WprRf1YGrGjIgv6d3q6glCIJae33x7Bli1+SBJQWqqVbUi4\n//4wDhyw6yRZI4izZ8vYt4+NHRsc5PC970X07wuHOWzb5mDydG02FWvWBEwqrRYD9+abdpOfeSRb\n+JcaAotXX/ft82FoiENOjnrFj3c1+DINrFmwYMGChZsbFgm+DrhZPTtNTcJle0wvtF2tkVjKhjXa\nKQSdBBuj0U6cEHDvvRGGXE+ZQvm9LS08cnNlnDwpoKbGj95eDrm5CsaOVdHfr2LJkhT98bXGNrtd\nxZ13RrB9u8gQxKwsVk3Ny1PA8xci9bHnRhYGFhdSRS90zRKtC1k2l0sYFd2Lqa+ft2XAGli79rhZ\n/15Y+GxhrQsLiWCti5HBIsEWLhvXQuXTyGR/P4fTp3nT9r0GI5maOzdyQS/snDky9u+3Y+nSGNld\nvVqCKHKm43g8CiZNImtGPJGVZbIrdHbyqK0VceKEALebih1G4nON/97h4cTFFZcLWYbuXdbi1+68\nM2JSdG8k9fXLNLBmwYIFCxZublgk+DrgZr1LuxYqnxafdvQoD6eTiiJ6enhMnBhLSQBi1ovTpyk9\n4utfv/iAlVEtnTZNRlaWilmzSC0+cYJHRgZVFRcWKqZjGdXUigpKwHjrLR8++ODyFfD44xhTKS51\nvYzr4vBhAR9+aENLi4DycjcAYPt2kVGggRtLfbUG1q49bta/FxY+W1jrwkIiWOtiZLBIsIXLxrVS\n+S5neGok1gvAXMUbDEJXbOfMkTFnzsXP1aimulz0mDabig8/tF+20hp/HEql8OP4cT6hgnspNDfz\npiG8RATXUl8tWLBgwYKFkeMzCC+ycCm8//771/sULgjNFrB/vx2NjQKUOM6lqXwPPBDG7NlXHn2V\naPve+PhNTWy8V1OTYDqfeOTkqFizxgWv14VnnnEhP18d0flpaipApLOoiNTMU6cEnYhqX7uY0hp/\nnO5uHh0dPLxeN3p6+Euej3FdTJyoYNs2ByoqAigrk7Bvny8hwb1Wr4uFGxM38t8LC9cP1rqwkAjW\nuhgZLCXYAoPPI+LKuH2fmalAUYjMHTnC469/FZCby8avBYOU07t7t4i0NNXky71SNTS+BS8+8UH7\n+YkTFaxd67qoJzceRUUy9u71RfOFSQ2+FHHWzuG992xwuwX9uc2aJaOmxo/mZh533PHZZe5asGDB\nggULX0Zwqqp+Lg/05z//WZ09e/bn8lhfRlyrkoL9++3413+NDZht3y7igQfC1/BMAUUB3n+f6o09\nHmDbNgdqavyYPVvGO+/YMG9eCrKyFCxcGERyMrXCaZXI1dV+9PdzuPPOCO666+pJYWPjxUm/oiQu\nqrjU8bTz93goI/liP3epc7BgwYIFCxYsjAyNjf8/e3cfHlV57ov/+6w1k5dJGOQlCZCAAa1iJZID\n1OpPjrbb02vXnmvbq5f2VN2+tW6lNVJEghqoeJJTDJQgsmvaiy3dvCnEAqe73dfR7nbvfbb+rD/d\nBQoGK1QkL4SXvAFm3pLMrPX8/ngya2bNTGAFAhky388/dcJkzTN3FvSeO/dzP/tw5513inM9h3Wl\nUSJawX388XzcddcY7N+vX9B1EtsCLnST1fnaKlTvrurlXbCgDydPqvu0s1ONTWtr07FsWR40Tc0L\nbmvTByrDQG2tB/fee+HvMd65WjOiax1Kq0H0etH1Z2fjvN93vjUQERHR8GM7xAi4FHP8zjUmayhV\n4su1+S3xMIydO9XJFTNnDn7SnNcrrSkJwzUKbLgnK1zI9WLf8w7c7js4W5dsOPeTUuF9Qanwvhga\nJsGjxLmSr6H0+Q7XiKvzza5NPAyjs1MDYAx60lx5uYE//EFHe3vssIvhSBaHe7LChVwv+j2//W0I\nX/966s1vRERENLyYBI+AS/Ep7VzJ10gcpnC+iuhgfz5YEq5pwG23Df8osOGea3sh14t9zy0AmACT\nHas6lArvC0qF98XQMAkeJc6VfI3EYQrnq4heSMWUBzEQERHRcBmWHThCiCVCCFMIMX44rjfaXe45\nftGE87XX/NZxwZfa+TaUcbZtMs53pFR4X1AqvC8oFd4XQ3PRlWAhRAmArwFoufjl0KWQbhXU4Rrn\nRkRERHShLnpOsBBiJ4AaAL8BMFdKeTrV8zgnmKI4F5eIiIgupUs+J1gIcTeAY1LKxou5DmUWzsUl\nIiKikXbedgghxO8BFMV/CYAE8CMAy6BaIeL/LKVdu3Zh48aNmDZtGgBg7NixKCsrs3YyRvtYMuFx\nfM9OOqxnOB6/++57OHJEw9ixas6t3/8ONC3186dPN6Hr/xeGIay5uCO9/nR43NjYiB/84Adpsx4+\nTo/Ho/HfCz7mvxd8zH8vhvtx9L9bW1sBAPPmzcOdd96Jc7ngdgghxCwA/wogCJX8lgA4DuBmKWVH\n4vPZDhHz3nujb5j1UFochnoUcaYYjfcFXTzeF5QK7wtKhfdFjJN2CNeFXlxKeRDApOhjIUQTgDlS\nyjMXes1MMRpv0KHMIk63jXrpYjTeF3TxeF9QKrwvKBXeF0NzwUlwChLnaIeg0W0kZhGnwskTRERE\n5MSwpQdSyhmDTYYgu/j+ldFiJGYRpxI9Ivrxx/Nx111jsH+/PiLruBCj8b6gi8f7glLhfUGp8L4Y\nmuGsBFMGS5cWh5E4IpqIiIiuPEyCR0C69OyMxtaBdGnLuBDpcl9QeuF9QanwvqBUeF8MDZPgDBZt\nHRhNh1ZE2zLiE3siIiKiRFd43e/KlC49O6Px0IpoW8Y994QxZ86VVdlOl/uC0gvvC0qF9wWlwvti\naK6gFIGGW7R1AMAV1zpAREREdDEu+LCMoeJhGemHh1YQERHRaHRJD8ugK1+6THQgIiIiutxY9xsB\n7NmhVHhfUCq8LygV3heUCu+LoWESTEREREQZhz3BRERERDSqOOkJZiWYiIiIiDIOk+ARwJ4dSoX3\nBaXC+4JS4X1BqfC+GBomwURERESUcdgTTERERESjCnuCiYiIiIhSYBI8AtizQ6nwvqBUeF9QKrwv\nKBXeF0PDJJiIiIiIMg57gomIiIhoVGFPMBERERFRCkyCRwB7digV3heUCu8LSoX3BaXC+2JomAQT\nERERUcZhTzARERERjSrsCSYiIiIiSoFJ8Ahgzw6lwvuCUuEcIUxFAAAgAElEQVR9QanwvqBUeF8M\nDZNgIiIiIso47AkmIiIiolGFPcFERERERCkwCR4B7NmhVHhfUCq8LygV3heUCu+LoWESTEREREQZ\nhz3BRERERDSqsCeYiIiIiCgFJsEjgD07lArvC0qF9wWlwvuCUuF9MTRMgomIiIgo47AnmIiIiIhG\nFfYEExERERGlwCR4BLBnh1LhfUGp8L6gVHhfUCq8L4aGSTARERERZRz2BBMRERHRqMKeYCIiIiKi\nFJgEjwD27FAqvC8oFd4XlArvC0qF98XQXHQSLIRYKIT4RAjRKIRYNRyLGu0aGxtHegmUhnhfUCq8\nLygV3heUCu+LoXFdzDcLIb4C4G8AlEkpI0KIicOyqlHu888/H+klUBrifUGp8L6gVHhfUCq8L4bm\nYivBPwCwSkoZAQApZdfFL4mIiIiI6NK62CT4OgC3CyE+EEL8XyHEvOFY1GjX2to60kugNMT7glLh\nfUGp8L6gVHhfDM152yGEEL8HUBT/JQASwI8Gvn+clPIWIcSXAPwSwIxU19m/fz+2bNliPZ49ezbK\ny8svYulXrnnz5mHfvn0jvQxKM7wvKBXeF5QK7wtKJZPvi/379+PAgQPW49mzZ+POO+885/dc1Jxg\nIcRbAFZLKd8ZeHwEwJellN0XfFEiIiIiokvsYtsh/gnAXwGAEOI6AG4mwERERESU7i5qOgSATQD+\nUQjRCKAPwMMXvyQiIiIiokvrsh2bTERERESULnhi3AgTQiwRQphCiPEjvRYaeUKInwwcPrNfCLFb\nCOEd6TXRyBBCfF0IcUgI8RchxHMjvR4aeUKIEiHEvwshPh44oOqHI70mSh9CCE0IsU8I8ZuRXsuV\ngknwCBJClAD4GoCWkV4LpY3fAbhRSlkO4FMAVSO8HhoBQggNwKsA/hrAjQDuF0LMHNlVURqIAHhG\nSnkjgFsBVPC+oDiLAPx5pBdxJWESPLLWAVg60oug9CGl/FcppTnw8AMAJSO5HhoxNwP4VErZIqUM\nA2gA8M0RXhONMCnlKSnl/oH/9gP4BEDxyK6K0sFAUe0bADaO9FquJEyCR4gQ4m4Ax6SUPOibBvM9\nAG+P9CJoRBQDOBb3uA1MdiiOEKIUQDmAD0d2JZQmokU1bvQagoudDkHncJ6DRpZBtULE/xllgHPc\nF8ullP888JzlAMJSyu0jsEQiSmNCiHwAuwAsGqgIUwYTQvx3AO1Syv1CiK+A+YRjTIIvISnl11J9\nXQgxC0ApgANCCAH1K++9QoibpZQdl3GJNAIGuy+ihBCPQv1a668uy4IoHR0HMC3uccnA1yjDCSFc\nUAnwNinlr0d6PZQWbgNwtxDiGwByAYwRQmyVUnJs7XlwRFoaEEI0AZgjpTwz0muhkSWE+DqAtQBu\n58EzmUsIoQM4DOBOACcB/CeA+6WUn4zowmjECSG2AuiSUj4z0muh9COEuAPAEinl3SO9lisBe4LT\ngwR/fUHKTwHkA/j9wKibn430gujyk1IaAJ6CmhbyMYAGJsAkhLgNwN8C+CshxJ8G/o34+kivi+hK\nxUowEREREWUcVoKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKi\njMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiI\nKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIi\nIso4TIKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKijMMkmIiI\niIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYi\nIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJiIiIKOMwCSYiIiKijMMkmIiIiIgyDpNgIiIiIso4TIKJ\niIiIKOMMSxIshBgrhNgphPhECPGxEOLLw3FdIiIiIqJLwTVM11kP4C0p5beFEC4AnmG6LhERERHR\nsBNSyou7gBBeAH+SUl4zPEsiIiIiIrq0hqMdYjqALiHEJiHEPiHEPwghcofhukREREREl8RwVILn\nAvgAwK1Syj1CiFcAfC6lfDH+eXfffbfs7e3FpEmTAAB5eXm49tprUV5eDgDYv38/AGT84+jX0mU9\n6fz4yJEjuPfee9NmPen6OPHeGun1pPPjxJiN9HrS9fGuXbv477eDx9Gvpct60vkx/z3nv+fD8fft\nwIEDOHXqFADgmmuuwc9//nOBcxiOJLgIwP8npZwx8Hg+gOeklH8T/7yHH35Yrl+//qJeKxOsWrUK\nzz///Egv44rAWDnDODnHWDnDODnDODnHWDnDODm3aNEibN269ZxJ8EW3Q0gp2wEcE0JcN/ClOwH8\n+WKvS0RERER0qQzXdIgfAnhDCOEGcBTAdxOfEC1P07m1traO9BKuGIyVM4yTc4yVM4yTM4yTc4yV\nM4zT8BqWJFhKeQDAl871nGuu4fAIJ8rKykZ6CVcMxsoZxsk5xsoZxskZxsk5xsoZxsm52bNnn/c5\nF90T7NS//du/yTlz5lyW1yIiIiKizLVv3z7ceeedl7YnmIiIiIjoSnPZkuD4ERY0uPfee2+kl3DF\nYKycYZycY6ycYZycYZycY6ycYZyGFyvBRERERJRx2BNMRERERKMKe4KJiIiIiFJgT3CaYb+Pc4yV\nM4yTc4yVM4yTM4yTc4yVM4zT8GIlmIiIiIgyDnuCiYiIiGhUYU8wEREREVEK7AlOM+z3cY6xcoZx\nco6xcoZxcoZxco6xcoZxGl6sBBMRERFRxmFPMBERERElMQzgwAEdTU0apk83UV5uQLtCyqdOeoJd\nl2sxRERERHTlOHBAx113jUE4LOB2S7z9tg9z5hgjvaxhw57gNMN+H+cYK2cYJ+cYK2cYJ2cYJ+cY\nK2cud5yamjSEw6qYGg4LNDVdIWVgh0bXuyEiIiKiYTF9ugm3W7XNut0S06ebI7yi4cWeYCIiIiJK\nYprA/v3sCSYiIiKiDKJpwJw5xqjqA47HnuA0w74o5xgrZxgn5xgrZxgnZxgn5xgrZxin4XWFFLWJ\niIiIiIYPe4KJiIiIaFRx0hPMSjARERERZRz2BKcZ9vs4x1g5wzg5x1g5wzg5wzg5x1g5M5xxMgxg\n3z4du3e7sW+fDnN0TT9zhNMhiIiIiDLMaD8Nzgn2BBMRERFlmN273Xj88Xzr8Wuv+XHPPeERXNHw\nYk8wERERESUZ7afBOcGe4DTDvijnGCtnGCfnGCtnGCdnGCfnGCtnhjNO5eUG3n7bh9de8+Ptt30o\nL8+sVgiAPcFEREREGWe0nwbnBHuCiYiIiGhUYU8wEREREVEK7AlOM+yLco6xcoZxco6xcoZxcoZx\nci6dYzWc83Qv9lojGafROFeYPcFEREREgxjOebpX8mzeK3ntg7lsleDy8vLL9VJXtPnz54/0Eq4Y\njJUzjJNzjJUzjJMzjJNz6RyrpiYN4bBqLQ2HBZqaLjx1uthrjWSchjMO6eLKfwdEREREl8hwztO9\nkmfzXslrHwx7gtNMOvdFpRvGyhnGyTnGyhnGyRnGybl0jtVwztO92GuNZJxG41xh9gQTERERDWI4\n5+le7tm8hqF6eZuaNEyfbqK83ICUyV/THJRER+NcYc4JJiIiIhqF9u1L3swGYNRtcEvFyZxgVoKJ\niIiIUkhVSXVSNU2XtQy2mS3xa6MxCXaCPcFpJp37otINY+UM4+QcY+UM4+QM4+RcusYqOhbs8cfz\ncdddY7B/v37JX3OwebwHDuj467/ea62lsVE779zeVJvZRuMGtwvFSjARERFRCqkqqeeqmg5H5fjA\nAR1/93d5WLCgD0ePaggEgNtuM9DUpMEwYmvp6NDw4IP552xriG5mi18PgJRfy0TD1hMshNAA7AHQ\nJqW8O/HP2RNMRESU/tKpBWC4XOh7StVTe64keKjPT7XGxkYdvb0CK1bknrOXd926AJ56Kt/6/tde\n8+Oee8KOXisTXO6e4EUA/gzAO4zXJCIiosvoSj0Z7FyJ7oW+p8EqqYMZauU4XnSNNTUh9PQk9+1+\n61th21oA1c4QfU+Z3NZwoYbls50QogTANwBsHOw57Al2Jl37otIRY+UM4+QcY+UM4+TMlRqnkTgZ\n7GJiFe2hffNNN/74Rx3V1blJ/bsX+p6iY8HuuSeMOXPOXz2+kH7b6PobG3XU1ISwe7cbs2YZSdfR\nNCAYfMday2ic23u5DVcleB2ApQDGDtP1iIiIaAREE7nLUWGMVm/ffdcFj0e/4B7a+Crvxo0BnDih\n4eTJ2G/CB3tPw936MdTKcar1V1eHsHy5Bzt3+tDZOfh1RuPc3svtonuChRD/HcBdUsqnhBBfAbBE\nSvk3ic9jTzAREVH6M01g//7L0xN8MT20Ubt3u/H447He2KqqEOrqcrBzpw+3366uNdh72rcvtgmt\npwe45ZYIbrvt8vZAJ65/3boAysqMQeM+Gnu2L4XL1RN8G4C7hRDfAJALYIwQYquU8uH4J+3atQsb\nN27EtGnTAABjx45FWVkZ5s+fDyD2qxA+5mM+5mM+5mM+HrnH77+vHt9zz6V7PdME8vPvQGOjjkcf\n/Rf86ldudHXdiaYmDcHgO0O63uefvwNd98Awvgq3W6Kr6x2Ewzno7JwHwLA9f84c9fj999XjpiYN\nX/va7/GjH2Vb319b+xauu84ctvf77rvv4cgRDWPH3oHSUhMHD76L48d1fP3rt6G83Ehav2H8B4JB\nE5qW+npbtryP557zDGm90Xg3NWn4/PN3cO21Jm6/PT3ut+F6HP3v1tZWAMC8efNw55134lyG9cQ4\nIcQdUJXgpOkQa9euld/73veG7bVGq/fee8/6wdK5MVbOME7OMVbOME7OME6DO3BAwwcfuNDTo2HS\nJANdXe8iEvnKBVVio1XeQ4c0+HwC9fU5aG/XHFWVDxzQsHevC5WVedbXLmTKwrmqs4nV7urqIJYt\ny7Mq3+XlhuPK+3vvvYf29q/aKsdO1jscFfcrDU+MIyIiorRiGEBnp4YVKzwIhwVqawN46aVcGIbn\nghK0aG9sNJl88cUQpk83UVZmYN++5OSyvx/48EMdR4/quPpqA+GwsykL0UT35EkBr1eioyN23XNN\nn0jclOfzxU5tU33LQ2ttuJCe7YuZWjGaDWsSLKV8B8A7qf6svLx8OF9q1GLVwDnGyhnGyTnGyhnG\nyZkrKU6Xs89UJZIaiopMVFT0QdcBw/gqAOcJ2mDrnT07lnj29ADf+U5yYvrhhzruvVd9vaoqiG3b\nslFdHYLPJ3DDDRG4XMm/ITcM4P33dXzwgQuzZhnW90eve64kMzFpLS8P4403Ijh0SEdensSPfpSL\nb34zbDsYY7DYz58/H6Y59M13l3Oz45WElWAiIqIMdzlnAzc1aRg/3kRFRS9WrPCgpiY05ARtsPXG\nf72qKpgyMT16VLe+7vUC7e0ali1TVeiamhD6+gRuusm0JdqFhaaV+L7wQvJ1z5VklpcbeP11P44d\n0xAOA21tOp5/3mM9d9MmP7773XOf/BbvQqZCXMjUikxw2fYTck6wM/EN3nRujJUzjJNzjJUzjJMz\nV1KcLtdsYMMACgtNZGVJuN3qterrs/HII/+Cn/wkgNdf9ztK0OLXW1RkortbYPduN3w+YNWqIKqq\nQiln7QLAjBmxr2/YkI2GBh+qqoKoqQlhw4ZseL0S+/bpVkL9+OP5+OADl/V6M2far1tYaFpJ5rZt\nPuzc6cPhwxp+/3sXPvpIxXHCBInuboGqqjx0ddljfeKE89g7uaeic4d373Zj3z4dpjn0eceZgpVg\nIiKiDHe5fl1+4IBqRSgqMrF6dRBut0Rbm45Nm7Lx4x8DOTnSUYIWv96Kil48+KCqpK5f70d/v3pO\nV5fAjh0+7N3rwi23RKzk+tZbDezc6UNTk44ZMwx8+csGxo4FDh3SsGBBL5Ys8aC9XcO6dQFbxTj6\nei0tGtasCWL8eImODoG+PgHTVElm4ga0jRv9CASArCxgyhQTtbUBZGXZe5CvucYYttjHt214vcDK\nlbnYuDHA/t9BDOt0iHPhnGAiIqL0dLlmA8fPxC0pMfCTnwTR2amhoEBVh00T+G//bfCELbFFoadH\n4PPPBZ56Sl1z61Y/Hnssz0oot2zxo7BQOno/ifN633zTZyXXpaUGXnklgLY2DePGSbS2xjb2ud3S\nmkmcamax12vanrtjhw+9vQKHD+vweIBp0yJoadHh82nwek3MnGlgzBhc0M8geRJFCAUF5pCnXYwG\nnA5BRERE5+Wkz3Q4Ns9Nn26itNSwDqfIzpZYty4Hzc26lUye6/Xff19P2pTm9UqrktrRIWytBd3d\nAoGAepy43sT384Uv2CuyRUUm3n7bZ5sGUVAgsWZNDh58sD+hhUHH7bcbSRV1r1eip8fe7nDqlIbF\ni2OJ+rZtfixbFhvRFj3s4/XX/ZgwwVkCH5U8iQK4+WZughvMZUuC9+/fD1aCz49zJZ1jrJxhnJxj\nrJxhnJwZbXEayua5wRLm8nID69cHbIlsdXUIy5b9J8Lhr6CzUwNgpLxOYaGJPXtcSf2zOTnSmu5Q\nXGxPQvv7BRYuVDN533rLh7lzY9dOfD9vveXD737Xg44ODZ2dApGIGGihSJ7zW1Bgf50ZM9R1y8sN\nvPWWD4cOafD71cziiope23NnzjStTWqFhSba29WYuJ4eVQn2eNR727/fhbq6HFucz3dPJSbh8W0g\n5/q5ZCpWgomIiOi8zjUGLDG5crlkyoRZ04COjuRqJYCU/bCJiermzf6kSmtOjsRvfuPGN78ZRlOT\nhjff9KG7W8OYMRKVlR7rdQ4f1mxJcOL7aW5Wa4+2QAw2/ixaeW5o8KG1VfUV33qrum400RdC9Riv\nXRvElCkqMY5ev7zcQLQTtbFRHxgVF2uXqK1VvdKzZkVQVGQOaaZvNAk/fFhVrceOtbe8Xs4pIFeC\ny5YEc06wM6OpanCpMVbOME7OMVbOME7OjGScBqv4XUwlMLHKOGaMmqKQ6rCI11/3O56be8stEbz2\n2jxce20PAOD3v3ehs1Ng5kwzKQFtadEGqr7ArFmGtYntl7/04X/8D3tV9/RpgfZ29ebcbomCAntC\nWFhoX0dhYfLrpRp/VlAgMX48UFZmoLFRJdMffRRrt0iVaM6da9gS8Pje3cRRbqYJ1NSEsHy5B08+\n2Wv7YHDrrfNTHgASpWmAELC1W5zr4I5MPzSDlWAiIqJRxskc3fivO0mOy8vVVIXPPtPR3w9UVqoE\nNFrljE+uOjuFLXG86qpYwpxqZq2UBt5/X8eRI/YZujt3+qwe4mAQuP56Az09Atdfr6qoFRV9qK/P\nRmurbnv9w4c1zJploLo6aG04Kyqyz/6dNMnEpk1+nDqlQQigp0ekTIyj640eyxxNvLdu9aO5WbOO\naf7d73pgGAKNjfo5E03DALq7BSore+H1yoFxcbHXNAyBqipVwfZ6VU9wdN3d3SKpUp348+vrg+MP\nIJl+aAZ7gtPMaOshu5QYK2cYJ+cYK2cYJ2dGMk6DVfwG+7qTX5NrmjruWEqgqiq2kevwYQ0zZ9qT\nqylTTKxZE0B7uw6v18Tp0wJHjmg4dEg9t7zcvgnvH//xfXR3fxUTJkjb/N/+foFVq4J46KFY4rdp\nkx/33Rd7XF0dxNSphq2vtrTUQH+/QH6+RGlpZGDqgpn0PqurQ/iHf8jGypVBnD0rkJ0NrFkTRHu7\nNrCpTVibBk+eVEceP/RQP7xeiaYmHS++mDvQ0+xBR4eGBx/MR01NyLb5r7DQtGb1AipZjU9k16wJ\nYOdOHzo7VY/wokUqttH+YU2LVY6//e3fIRz+63P+/GprA+c8uIOHZsSwEkxERDTKpKpoAoNXAp3+\nmnz6dBMnToik9oBolfjDD9V82meeycOPfxxEXV0W2tp0bN3qt40JS1XBLClR644mkG63xGefaQgG\n7RMfEg+XGDNGwuWC7foNDT5861v2zWyRiIHOzthxzT09AiUlJhYu7MWjj9qT6traXGudUV6vxIoV\nubZkPBwWCIWA2toAjh/XrMM/Vq8O2q45WEtCUZGJSZMkfD5Vhe7o0LB+fQA9PQKTJ0srSY1+T16e\nPO/Pr74+B1u2+HH6tLA+cERdyGlzoxl7gtMMqyvOMVbOME7OMVbOME7OjGScenqENTEhWtEEBq8E\nOv01eVmZgd5ezdZmMG6cgX/7NxeOH9fg9QL19dloa9Px8cc6nnyyDy++mJs0uuyTTzRr9NiiRXlY\nsOAObNiQjbq6AFautCeQiZvhEidAFBZKdHYK1NSE0NOjrtncbG9J8Pk0NDWp9UePa47O/128uNf2\n3OxsNaasvNw+WSFxQ9/hw2qsW3m5gfvuy7eOf25r03Hw4OAtEYkHfTz0kPre+AQ7sRIf/Z633/4a\nqquD8HqlLcGNv2Z7u4aWFh0rVuTi7bd9jnu+M3FyBCvBREREo8zkyRLf+549qQIGrwQmJsdlZQb2\n7tWtKQNFRSZmzTLR2Kjjqafy8MQTfQAkrr/eQGOj29bHW10dwosv5mLiRNUW8fLLAUyZYq9g+v0C\n48er/62qCuF//a9cPPlkH7q6NPT323ta29o0bNrkR0eHhmnTTOvx4cM6brhBbY5bvTqIFStyUVRk\nYunSEIqL7a83a1YEEyYYOHNGx1VXqcT60CEdM2caOHVKsz130iQTzz/vSUogEz8ozJplWHOEoxXg\n6uoQsrPVNeJbIsaPlzh4UKC/X0NTk4Zdu3zWQR/hsEBPjxg0aU7180lMUKN/fuSImopx6JCOmpoQ\nTp4851kRNpk4OYI9wWmGvXbOMVbOME7OMVbOME7OjGSchtr7mZgc79un4xvfSG4naGrS0NysY9ky\ntXFr3boAurpUhbSkxEBFRR+ysiR27PAjK8vEPfd4rYrrG2/48ac/ueD1StTX5+Chh/pRV5eDnTt9\nuOuu38Pnux033qj6gO3HCpuorPRYm+OWLo0/fc0PADh0SLeOYm5t1VBZmWtNkZgzx8DatTmorOzF\nAw+oqusPfxj7gLBmTdCqmt9wg4EzZwRqaoJwuezTJFJv6AMCAR1VVUF4vcCGDdlYuzaAJUvykira\nmzb58d3v2lskJk+WKC01MGtW5JyV+OjPJxh8B3PmJN9T0T8PBGCbwXyuw0cSZeLkCFaCiYiIRpmL\nPQEuMSGSUp2+1ten+l+jExFmzDDQ26s2cVVU9Nl+pb9xY2xMWnOzjtZWDXV1ObYZv6qnVuAf/zEb\nhuGB2y3x61/3YNMmP06c0FBcbOLsWWDBgj6r0ltdHURWllpXZaUHTz7ZByEkKip6cfCgDkDYEvWq\nqiDuvjuMo0e1lFVXdViFeu2amiA8HgAQ+NOfXIhEDCsuqWK6b5+elHROmGCitjaIkyftMUzsZW5q\n0vCtb4Wxfn0AixblWUl74gEXTn9uhgEcO5Y4pcN++Mi5ZOLkCPYEpxlWV5xjrJxhnJxjrJxhnJy5\n1HEaag/n+Q60eP11PwoLTRiGQEGBaZu2kHiIxI4dfkycqJKk3FyJLVv8aGtLTsDikyohgOrqIPLy\ngOJiE//0Ty6sX68quc8+ewu83iDq67Px2Wc6nnkmz/Zan30WbY3QsWxZHqqqQqitzQUAZGWpampb\nmz7wTs2E9gaJceNMnD2robY2gAkTpO293XRTBK++qo4o7uhQJ8XFJ/PR0WdOPiy0tWn49rdVTNeu\ntU9pmDo1OcmMHh4Sn7S/9pofmpacuBoG4PHcgX//99Rj0g4c0OHziQtOZDNxcgQrwURERFegVD2c\ns2cbgybGic/fssV+oMWRIzoiEeDgQR3z5kWwYUPOQE+rSNrYtnevjjvvlGhq0vD00/nYutUPw0DS\nmLS1a1U/8OnTAhMmmOjuFqipUXN2Gxr8aGtTJ7UpEpWVIUyYoHp2W1p0CAHrYAx7YmugtjaInh6g\ntNTE8eMaPB4JXQekVInz6dMCvb0CQgCPPWZP4CsqYkn2L3/pw6xZBh59NB9PPNEHl0va3mt7u4bn\nn/dg4cJe7N+vo6tLYNIk1SNdWpqccNfVBbFmTQ48HmnbQDhmjIl16wK2HmvAeQU2+vOrrLRv5Isf\nf1dfn2O1diRu7DufTJwcwZ7gNMNeO+cYK2cYJ+cYK2cYJ2cuJk5OqryJVchDh9QTBtvcFH1+tHf3\n5EkN69f7IYRAf7+qznZ0CGzblo1x46TVgpBq9mxZmYHOToHiYgPr1/sRiUh88YsmNm/2o7tbtTEs\nWeJBJAJUVPTC7Qa6u3Vce22sYtvRITBlisQDD+QhHH4Hbvcd2LzZj2efVUlydbWamLB1qx/jxxvY\nscOPlhYNpaUGdB349rdjiWx1dRAFBaYtud20yY9gUM35jY9Ta6uWlPxPm2YiElGnrU2aZN9U19am\nYcGCvoTNf6pHOvo6H3+sY9IkiZYWNUd59eogTp3SsGxZbJ5yVVXQaruIbrozDMDlUlX46Cl5gyWu\n6uf3Drzem1MmzdOnm2hv17Bsmf01aHCsBBMREaUZJzv1p0+3TyCYNEni00+TE+NoIh2tOMb37tbW\nBmzzdVetCmL16iC6ujSMG2egqMhEW5tuzZ49dUqdSBZLVIMAgGBQw4IFubbrNDfrqK0N2q6/ebNq\nf4iONtuzxz5K7ORJzUqSfT5hVWKzsyXuvz9/YMZvL7Kz1dHC0XFsPp+GtjZ7svvxxzpqaz3YutVn\nSxqnTbNXXmfMMPH55ypxPXhQR1aWwKuv+jFmDHDihEq6Q6HYCW/19dkDI9fUxrnWVg21tZ6B9xqL\nwdat9tFuXi+stUWrtwcPavjgA5fVmuFySVviGv9hqLDQhK6r11+1KoisLBVDl0vCNAdvZ8jE0WdO\nsSc4zbC64hxj5Qzj5Bxj5Qzj5MzFxCmxatvYqBLD+ASd3FIAACAASURBVASmvNzA2rVB2+lpmzbZ\nEy+fT+Cpp/JQWmrgZz/zY+tWv23DVk+PPWkWQiV1PT0agkHghReCOH1aR08PICWQny/xzDP51jp9\nPrWY/Hxpm9NbUqISzegmtOj7OHVKjQfLyjLR2qrD6422UHzF6hsGgNJSA3PnRvCTnwQwdaoJv1/N\nAS4uNvGzn2Vj4cJeHD+u4ZVXgqiry4HXa2LGDDNl0nnmjH2u8enTsE2OOHsWGDdO4jvfGWOL4yOP\n5Kf8oFBdHYQQsCqwHo+0vddoLDUt1g4xa1YEy5ernt/o4SW7d7sxfry0Xfv11/0AYu0Q8R+GSksN\n7N49F21tIUyeLG0/9507fZg/30jZzpCJo8+cYiWYiIgozUSrtkuX9iIYVJun/vhH9avzm25SSZKm\nwZpRC8QOcKiuDiE3V/XkLlmiEq/Fi3tx4ICqOMaP4/J67Ynj1KkmHnjA3j/71FOx6uYbbyRWN00U\nF5vweID7749935YtflRXB3H99QZqa0243UA4DKxbp6ZKbNrkR1GRRF1dtpWQzp1rDIwsC2DGDLX2\nBQv6sGePjnnzDGzYkI377+9POuEtOo6tt1dg1y4fPvtMx9VXG2hr01BVFUJWlkrKm5uBadNMrF6d\ngz173ABUi8LcuQZaW+0V6RMnYifL6bq96pyXB0ybZsDlUi0g//zPLlRXh6zEP7quU6d0XHONiZ4e\ntTFPHccsMHWqOhq5uVmNVrNvJrTP9Y1veWlu1tHWpmHx4rykvuAPP3QhPx8pk9tMHH3mFHuC0wx7\n7ZxjrJxhnJxjrJxhnJy5kDhFf3V98qTAzp0+hEICDz8cS/i2bvWjp0fgs890zJhh4Prr7YnXDTcY\nOHFCw+TJaiNWSYlK5OTAyNtt27LgcmVhyxY/Ghtd8HiAurogNE1iyhSJ7m575balRbMlgG1tGmpr\ng3C7MXDMr8CyZR5897t9tkTr1CkNV19tQkokVFFDWLbMgxMnNIwdK/HEE3246ioTgcC7OHDgK/B4\nJL7wBQMtLbqtJzn6vULAOp44+lpHj2qYMQPo7BSYOFFtjmtu1vHTn6qNfYGAwF/+oltj3TZu9OPE\niTA2bMjGvHkGGht1lJUZKC010NysWy0S8SfLxR8CEgwC3/qW16rA5ucD3/++Gt8W7Q/2elXCv3Gj\nmkZx111e6zrr1gXQ3Kwq+7FKuPqzmTPtm+ISN811dLyLcPgb8HplwocRnPOo60wbfeYUK8FERDTq\npUtf5PnWkfir65dfDtgSvo4ODevWqeTugw9cuO22MHbt8mHPHhdmzzZQWRm/GU3DsmVBfPqpC5GI\n2vj2yisBPP10HrKzVRX31CnVIjBrlomFC/MGEtzkmb/RBFBKoKrKg7q6AADg1CndOiAjPtHq6xP4\n278dg1desa8/OsJrxgwTLS0aXnwxF7/4RQCrVuVac4K3bPGjqMhMOnrY5wO2bctGfX3ANuJsxgwD\nwaAan9bTY2L6dAMHDrhTJtHLlnlw6JALdXU52LHDjyVLPFbi+8YbaszbpEkm+vok8vLsUyJyclS7\nQrS6Hu07zskBamuDKCkxUVxsoKhIorlZw8aNAZSXG/jVr9y26xQXx8bPeTwmdu3yoaMj9ViyxD7f\nxkaV0NbXZ9sS7g0bsrFxYyDlPZeJo8+cYk9wmmF1xTnGyhnGyTnGypkrMU4j0ReZKk7nW0f8r66L\nilSrQXxyOXGiiYULe61JBaWlqi84EhEIBgUiEVgtFN3dGvx+LWmqwZNP9iIvz8S0aQLHj6vkWEo1\nDaKqyoPq6hB03Z4A5uVJ/OpXPfj8c4EdO/xobdXQ3CwGKstAXV0AW7eqCQfhsMC6dTlwu9UoMPtU\niQgaGvzo6BBwu4EdO3xoa9NhGF+1XquzU8O2bVl47rle2/fOm2egoKA3qbr8xhs+HD8e+yThcgHz\n5kWSNt25XGo+sMejHre0qPm80ap3c7MGwwDGjjXx5S+b2L8fCYk9kJMj0d6uXsvtligtNW2tGW+/\n7cPcuQbmzjVgGMD+/brtgBGXC0nrf+stH+65J5zyHkocW1ZefhvKylRCW1JiorBQ4i9/0bB6ddDa\nIJf44U7TgNmzYxNC1HW4OQ5gJZiIiDJAuvRFphprFp+QxP/quqKiF888EztJbNYsA11dAlLGpiAs\nWNBn2yBVXR3EpEkmjh5VF+zstL+ez6ehoMCE36/bkrft2/3o6YF1aEO0Ihz9c0AiFNLQ3a0hEIDV\nWhBtUbj/fvumsoce6ofXq6qpW7ao098KCyWysiSWLMmzJloUFwPZ2fYqckmJga99LYyuLoEdO3zY\nu9eFiRMl2toETBNobdWtft2eHgHDENiwIceq6G7cGMCLL+bi5ZftY90MQx2CEX1vV1+dPC0jWone\nv1/gxhvVWLajR9XIt3XrclBS0mtVVQsLTezZ4xr0vtq/33709PbtfmRlSXzwgf17mps1zJ3r7F5M\ndbz14sV5tiQ81X3NzXGpsSc4zbDXzjnGyhnGyTnGypkrMU4j0ReZKk6J6+jrE/jwQ1Wx7ewUuO46\nE//0Tz04dkxHf38sKS0pMbBmTRAul6rclpYaAy0O6uslJab1624hYhMHEuf7zpoVQXd38qzc1lbN\ndiDFhg3Z2LzZj4MHXfB6JSIRMTDPVwxsXgsiFBLQdYlJk0xrlFo4LNDdrcHlUonz55+rim9VlVpP\nVVUwqU1hxw4fliz5LSZOvB3TpxtYsiTPSmi3bfPB61XV02BQYPfuLFRW9qbs1122zGNtLmtu1iGl\nOqHO5QIMQ6C+PhvhsEqkGxp8OHJEx+bNfrS322PR2KjaJXbt8qGyUm3OO3hQx+LFvSguNnHjjere\naWrS8F/+S8QW38JC06rGHj5sv257u0B2tkjqAx7sXkzVOvP++/Z7yumHuwv5EJguLUSXEivBREQ0\n6qVLX2R5uYFf/tIHn08bOCzCxJEjOior7Qc/CCEAxCqkFRW9tg1ymzb5YZoCK1Z4UFcXxN69qje0\nstKDZ54JWQlPfX0Otm5ViV5JiYnKStUDu2OHfXZuaamJw4d17NjhxyefaLjpJgPhsEBdXY6VvMYn\nUePHSzz2mH2+cH+/QE8PUFJiDhw4AfT1qUkL0c11Xi/Q02Of53v8uI5IRCIcVkl/JIKB0+BUAp1Y\npZUSyM62X8PnU/EtLTUwZYqJqqogjh9XRyyvXRvA8uWxa+g6sGePyzq44s037bHweuXAhrvkzXnb\nt/vxhz8I62jkW24Jo6FBTaRQvb65+PGPQ5gzx0BBgb3CXVAgMWGCxMqVuVZ1/5ZbBj/VLVX1NpHT\nD3cX8iEwE6rH7AlOM1dadWUkMVbOME7OMVbOXIlxGsqRsMNVAYuPU/w1J0ww8dhjsaR348aAbSKD\nrgOTJpn4+7/Pto7AjfaxAqpXWNOA9naBlSuDttFk1dUhTJwYS75UlROoq8vB00/3WlMJfD6BTZtU\nm0JxsYmuLlgnjW3e7Mef/6xjw4YcK1mbN89+bPGZM/bRbG438PzzsWSxocGPpqbEfuQQfv1rN5Yu\n7U1IDk2UlPxXRCIGdF3Yqrx1dWbKKu3mzfZRbbNmGVi7NoDSUgP33TfGVgV3uWCbE6zrEl5v7JqR\nCPDmmz40N+uYOtXEmTOq13r6dAMffmhvXdi3zwUg1i/9zW+GsWZNrjW3uLKyF6dPw/o5xb9u9Kjk\njRsDaGrScPPN9nsr8b5LVb295x773z2nH+4u5ENgurQQXUqsBBMREcW50ArYuZLn+P7QF16wV1W7\nu8UgExmC+NnPclBR0QtNk9bmqoqKXusgh8QKrc+nDq6IT3D7+2FtnIpOJcjNlXj+eY91OtsLLwSt\na/T0CBQXS9x/fz+EUBMZxozptRLiL30pAintv9KfODGWrBYVmQgMDCqIH6+WnS2xcGEvlixRm++y\nslT1N3r6XEODH/v367jhhthJdYWFMul1ampCOHNGJfGHD+uYOdPA8uUerFypTqmLr4Jv2aIOB4k/\nvvjv/96PDRuyAcBKkuMPyqiuDqKuLoi8PBNlZfbk3+tVs+ZKSw0sXNgLAKis7LV9EGlo8GHfPjXm\n7otfNNDZqSqvs2aZ5/wwlnjf7drlO2/11umHu6F8CIzKhNFq7AlOM1dir91IYaycYZycY6ycGe1x\nOl8FbLBkNzGJqap6G3PnzkdfH3DqVOyaN9xgT6xKSw28/rr9JLdwWMDjkVi/3n4i3I4dfpw9C+t0\ntvg+XjVBIQJA4rvfja1jyxZ1+tmqVcGkk8+WLcuDmk9roKTEwNKlIRQUyITqsjr0Qo3xkpASWLJE\nbdgLhVSVUQh768Zjj9mr0y++mIuCAhMHD7qsPueqqhBqa3MHovof2LPnZqtFIbq2M2dUFTcrSx22\n4XIlVpxVb+/KlUEsX676d+Or4EIAU6aYCfFWo+Kam3Vcc00ER4/aq72hkMDevS7U1eVjzZqgLWGP\nTnhYsyaIBx7Ix+zZETz0UL/t+9vadOzZI6zRZa+8Ekj6bUKqeyjxvuvpEUnV28v5dy9dWoguJVaC\niYiIEEtM4g8iKC01MGGCiS1bsjBjhoFbbzXw0Uc6/u7v1ISDo0c1+P3AVVdJNDbaR3IdOaKjtnYM\nNm3y46qrYtc8e1ZYbQ5erzqgYvp0CZfLnqwVF8ukMV979+qYO9fAD36QG9eT6kdLizqcYs2aXHz1\nqxHb9AQhgNmzIzh71t7CkJMDrFwZRGmpAZ9PYP36IFpaNASD0rbRLStLJb1PPNGLH/wgHy+8ELRN\nkbjvvnzbQRHqdDj7fN1t2/zIy5O2E+ri/1u1KMD6nvx8NXatuNi0PohMm2YmfVBobdXxox95UFmp\nWj3q61ULiddrYvJkEy0tOqZNM7Blix+ffKLD45Ho71fTLGpqQjh4UKVB8XGfOTN2glx7u0BtrQeP\nPBLC3XeHsXhxL0pLDXz+uYrl4sW9aG3VbN8fDCIumQ+huVmDaQItLbrtHkr8bUNhYeKxz3LI1dvh\ndCHV4ysNe4LTzGiurgw3xsoZxsk5xsqZ0RqnaCU32svp9UpMnmzaflW+c6cPnZ1a0oYptVHNnkzN\nnTsfZWUhtLertoQ1awIIBNSosGPHAK9XYsOGbNTWBnHXXWOwbl3Alhx3dCRXer1eoLk5dqSv263m\nxEZHltXWBjF5somXXorYqrHRDWXx1yoqUodlPPpoPmpqQli40N6KEa0Sh8Nq2kJWFjBvXhizZxt4\n4YUgZs40rN7gtjYdzz/vwbp1QYRCyfN177tvDEpLDaxfH8DmzX6cOqXhuusiA4mzC3PnzkVLi0RV\nlUpgpZTo79dw//1j8L//dw+uuw5oa9MwY0byMc/bt/sRiajXbGvT8eKLudi61W/1Bkc37l1/vTqJ\nDhBYvjyEq69WJ8T97Gex3usbbjAQCKgxdLW1AcyeHcGMGX6MH2/artfQoFoVTpxQsY9+f1lZBM8+\nGztMw+cDrrtOpryHEn/bMHasic2b/Th+XN0vfX3J9+jF/t3LhIkPQ8FKMBEREWJtEG1taqrAq6/6\nU8yBVUfsHj2q2aqtpql6caurQ8jLU9XAMWMkuruBri4N/f3AF79ooKfH3mqwaZMf+fkSlZW9mDRJ\nYvHi+NFhflRWepJOBqutDQ46IgwAHn00H5WVvbZ1d3UJaBpsSXZPj4DLFfvVe/zzs7OB9esDKCgw\n0dmpobTUGGjx6MWePWoty5d78OMfB62EuqKiF8eOqX7jLVv8VtK6alUOADX54cgR1YPscgHvv++G\n16s27a1aZdo20dXWBuHziYGYu7BkiQc1NSGrnzg6N7mtTUMoBBQUmNZmvMmTzaSqt5SwYhgf/+3b\n1eSM6KbAmhrVG71smQelpQZefjkAwwCOH7dX5I8dU5M0hIDt+xsa/NZhGqWl6tCMlpbEhFdP6jWe\nPl31Uf/t3+bbkuXhlgkTH4aCPcFpZrT32g0nxsoZxsk5xsqZ0RqnxI1ABQUSPp+9qjl5skpW5s6N\nwOuVtkR02zY/cnMNTJ0awdmzOv793/+AL31pPjweYN26HKxcqWbrrloVhJRAYaFEbq4amfXBB26r\ntaG5WSWd2dlqc1p3t4YJEyQ0DXj55QCysiTy8uyJVVaWRFVVEKWlagpBfEuH2y0xZYrEp5+qKmn0\na5s3+2Ga0vrVe2LfbPyRwlu2+JGVhYSDOUI4fFhHdXUIpaWGtVkvsZKskvgIvF4TLpca47ZxYwDB\noJpHXF0dwl/+8i7C4bus99PdLaw1RTfd9fQIqw0DiLVLPPywqmRHW0SiyW38+yksNBEO60nJ/kcf\nqXFxJ07omDjRRH6+RE2N6lNesKAP3/mOapuIH1fndktcfbWBQ4d0FBaatk2IoZC0JkKUlUVw//35\n2LrVvpZrrjFS9tsmHq/c2akBsCeoF/t3LxMmPgwFK8FERERI3gjkckk895x9kkFlpZpkoObsIiFp\nUTNxr7pK4tAhHd3dGo4fV5XRp5/uhaap6nBFhX0m8L339uOb3wyjuNi0JZk7d/pQVhZBZ6fqh83N\nVdXb73xnDH7xC/shGOFwrA910yY/XnklB9XVQeTlqSqpaUpMn67GiBUUqJPbDAMD1eEgNA1oaPBb\nVd4lSzx44ok+6wCKEydUX2v8+/X5AK9XzfFdsyZxSoVm/ffHH+uorc2F2y2xfn0ANTUhdHerxP3p\np3vR3i4webI9yZw710Bnp5oAMWaM+rNJk0xruoXXaw60TajpDNHvjb7msWOabTzZVVdJrFiRbds4\n53ZLeDyqQh09zMPtlnj1VT8WL+7FqVMaNm/249NPdWzcGGt5uOmmCEwT2LBBfbA5eDBWGV+9OmhN\noqirC8T1gMfW4nLJlP22l2IaQ2L7QyZMfBgK9gSnmdFYXblUGCtnGCfnGCtn0jlO0f/TP3ky2lfr\nvPcxMTExTWDjxgBOnhQ4c0agsjLfem5Lix6XgEarxBKrV2ejrMwYqBD/NdxuiV/8wo/cXIkHHkhu\nU/D5NEycaAKQaGuzV+mCQWGrrr75ps863ay3F9i0yY+uLg3jx5tWdTSadEY3bK1Zo6YZrF0btP2q\nfePGAE6cECgqMgGoDYDNzRpqaz3We4weQBFNsgGRlKiePi1QU6OS6PjNhLNmRaz+Xs/AJaMb3hYt\nsh9+UVICmOZt2LHDbx36UVeXg4ULe3HypIYzZ4AdO3zo6xO2o543b/Zb8Uk8GU9Ktd6CAhPFxSb8\nftXeEQwKrF0bQGGhhBDA6dMCxcUmKit74fVK1NdnY8KE87dM9PSovvD49TQ0+BAICGuUXXSjW2ur\nHjcFA1i3LoBbbulPuv+cTGMY6t+9xPaH3/++Z9RPfBgKVoKJiGjUOHBATW5YuTKIRYtiExwCAeC2\n286dCBsGcPCgho4ODe3tAkVFEmPGmAOtCBqqqoJWX+7VVxs4flzDxo0BdHaqROrMGZVoJfaPnjmj\n4ZNPxMBEBHvF0+s1MWmSieXL1clv8X924oQ9KT56VMd11xmorQ3A51MtA1Kqo3grKnqtCumkSSaE\nAExTYPXqINrbtaRfgx86pKOuLgc7dvixYEEuXn/dj6uvNpOS3J//3I+JEyU++kjHVVep45L7+1Ws\nsrIkcnOBqqp8rF8fwKZNKlmcPNm0Je87dviwdm0AXV2xDXnRyRPRiQ15eSqG06aZGDtWYunSiG0j\n2ubNySPkjh+PPa6vz7GOQO7rU+0nqmLvR2urWtORI1pS33FVlQfV1UGrUl1dHUzq4e3qEmho8KGx\n0YXrrzewdKlnoBfcXhnfs8eFMWOAF1/MRUODD5qmTr5LjOuMGcagG9SGexpD4s/900913HNPOKNb\nIOKxJzjNjNZeu0uBsXKGcXKOsXImnePU1KQqdAcPJh95u3OnD/PnD54IHzig48AB3ZYorVoVxJQp\npq3ip3pAdVRWJh4bDOTmmhgzRv3avrHxPZSVzcfUqQaCQRfcbjkwwiuI/HzgqqtMnDmjYfly1Xpw\n4ICO7dv9+MtfdJSWGknTJgoLJYJBdVRydCNaXp7qXV69Otfq392xw4/771d9stF1J1ZKb7opgrq6\nIMJh4De/+RzBoIbWVn2g6ikwbpza1FdYKBP6gNWRzlVVHrzwQhCzZxuoqwtg/HgTr7ySg4ce6scn\nn9g/BIRCIuHkuFi/8OzZxkDV9R2Ulv5XvPRSEI2NOm66ybAlywcPumwj1VRvbexxe7uG1lY1qeHJ\nJ3vx9NO9mDIldkx0XV3AWk/0f91u1UpRUiJRUmKgrU0l+oWF0vaBx+uV8Ps1bNyYjVdeUR8q6uuz\nsXp1MOEDDaDrEjU1IUQiAg8+mG9Vxnfs8OPkSYGrrzZxyy3GBW9QG+rfvcT2B69XYt8+PeOnQkSx\nEkxERGnnQkY5GQYwZYqa4er1iqRK3YcfupCfj0GTjaYmDVLav0dKoKPDXk37+GM1ZivxefX1Ofjh\nD3txzTUGnnjCg3A4G263B1u2+K0NYKEQcP31Js6eVRMHenoEFizog5TRgy4Err/ewN69OiZOlFiz\nJoBIRM369XhMa36tOl0ueTpEOCysSmb8JrD6+hxs3BjAoUMa5s0zbJveNm/225L86uoQnnrKg7q6\nAPr67L22WVnAK69kw+2WuOEGA59+qlkHSLz0UhCGAUycaE/eE49YzstT/bKTJ5s4fTr2ZwsW9Nkq\nyBs3qg8b0UQ09h7ULOdgULV59PcDkyerzYAPPdQHIQRefTUbNTUh65jowkKJxM1t48aZWLQoz3rP\nL76Yi7FjZVIrxOrVObjvvn5UVPSisjI2nSI/X+KXv/ThP//TZSXM0Q9ea9fGeqSbm3UcPao+7Lz5\npg+//rUbfX32++xSbVCLtlgcOqTB5xNYskT1tGf6VIgo9gSnmXStrqQjxsoZxsk5xsqZyxGnwSpl\n50qODxzQceiQjnBYJSQrVyZX6hobVVJUVqYOLDh8WENBgfoV/fTpJk6csPe9FhebyMqyJ0/z5hkI\nBOyJnhAYON4YaGqKVkK/gnAY+OQTHa++6kcopOHYMQ29vcDYsRLf/759HFogoKGlRUtKbvPy1PVb\nWnTr9DPTjJ0a5/VK5OaaqK0NIhgESktNvPRSwPZr+PZ2DVlZqhJ4/LiwksPEtgLVpxyLQarT1p59\ntheBQOy44+rqEIQAHnlEHZqxbFnINoptypTko48ffTQfDQ2q6XjlygBKS+fixAl7wn3okAt1dTnY\nvt2Pjz7SUVHRi7NngdraXJSWGqirC6K9XZ0k99xzHisRDwQE1qwJ4uRJ1f+7bl0OzpwBioulbYOa\nx6MqwAAGNg0GIQRsFeiWFg0ul6qotrRotukUP/2pH9/+dhhjxqj7asGCPtTXZyMcFkkHX0QP/fjj\nH12orfUkVeanTzdt7TidnQIzZyZ/+Bvq371oi0VTk4annoodHZ3pUyGiWAkmIqK0YhjAoUOpRznF\nJ8fRwxeim99OnhTo6tKwbVsWnnyyDy0tOhoa/Ni/X4fHE6vU3XXXGOza5cO9946x2gpOntQwdaqB\niRNNW6KUn29i4cJ8q/o3Z46Bs2cBv1/Dtm3qgIyuLtXPumRJHpqb9aQE58YbDfT1CTzwQKzCuHWr\n3/b+jh3TEIkAPT2JCSkgBFBVpSqWa9aoAzW+8AXDdr2GBj/uuy/XljwvX+7B9u1+fPaZhqlTTfT0\nCFx3nTqEITFBi39cVhbBqlVB/PSnOfiHf/Bh+3bVV3v11SbGjlVV6m3bsq0ZySUlJtraYodmfP65\nZhvF9rOf2Q8BiW4qPH5ct+b/Rg/sSPzV/ezZEQBqqsaMGSohXLs2kDTCLVoJF0L9PJ58MjaBY8cO\nP7KzTUQi6v3v3Svg8agPFU8/3YvJk01UVcVfK/6gEODZZ0PWqLT49fn9AgcP6pgzx4CmSXz4oQsP\nPdQPr9fElCkGdu70oblZR0mJic8+07B+vX+g1SIEjwfYvt2Ps2eF9WFu/34df/yjbvsQNFwVW06F\nSO2ik2AhRAmArQCKAJgAXpNS/n3i89gT7Ew699qlG8bKGcbJOcbKmUsdpwMHdFs1UvXDmti9242J\nE02sWhXE2bMC8+ZF8Oc/6+jp0dDVJTB7tppFG7+T/9e/7kFurgZdBxYv7kUkovpAo4nY0qW9CAbV\ngQehEFBeHrGtRdclXnopiBMnNMyda6KrS6CgQOL731fJW7TnuLTUQG1tEMePq4SzocGH//iPP+DW\nW+cjL0/i/fdjh26oiQyw9Z1Onaq+Fj35LH5z2tNPxyY/9Paq1ojmZg01NSHU12ejrU39uj0+ec7J\nUTOGe3sBjwdWkvnUU7nWiXj5+cDEiSYmTDDwy1/6cOyYqop7PGp+8dq1Afh8ui3Z3r7dD69XxTK+\nz/fNN30oLTWs1o6dO30IhQQ6OjRMmGDaktJoMllQEJv/Gw6/g927b8PmzX709KgYHzyo4/nne62+\n3trawKAtINH75fhxDcGgvf1i714dN94IPPjgGFRVBQcqsUFbv3j8tTweDEy2UC0YS5aoiR7RI5mz\ns9W4tnXrcjBxYh/mzDHg9wvb2nbv9uH22w3k58P60FZbG8DDD8fisHOnD/fcE7vfmpq0pA9BiRXb\nC/2752TyRCYajkpwBMAzUsr9Qoh8AHuFEL+TUh4ahmsTEVGGaWqyH0U7b14EixblJSVCW7f6bInH\n1q1qFFl0YsN11xno7tawbFneQKtA7HCLaLV23DiJyspYYrJ5s9+a8woA27f7Eg6BCKGlJfmUtQUL\n+vDww/YNZPn5quoZbcWIJrcVFb22527f7kdnp8D48SauvdbA5s1q9FlhoRqdFj2BzO2WuPZaE/ff\nn29VsJctC2HsWGkbURadwPDMM6qaqTbAxdYbPRFv/foAGht1zJ2rku8lS+zzi8eNU/OB40/Gi0SA\nX//ajfvv70c4LFBSYqCiog/NzTpefllNgMjJEWhp0REMwuoX3r7dj5YWVU32+YDNm/3o6FA/B49H\nfdi4556wlaz/8IfJCWqqKnk0LrNnR7B5sx/9l//d6gAAIABJREFU/UBpqT0WXi9w4oSKYfTnkHho\nRvy1CgpMLF0au69mzFCnu0WPZK6pUVX2lSuDOHNGYN8+Hc3NekLyqmP+fMM2nSF+/UVFJvr6BHbv\ndltJ6fTppjVBY7grtpdi8sRocNFJsJTyFIBTA//tF0J8AqAYgC0JZk+wM6xCOcdYOcM4OcdYOTNY\nnC5kM1sq115rYPHiXkgJ3HCDAUAiMlAwi08kEjesdXRoqKvLQVubjpIS1ePZ0yPwxhs+tLVpyMmJ\nbUbavTsL27f7ceyY/Rrd3ZqVhJSWGujqsieBU6caOH1aPSf+8Ibo90Svow6L+CpWrFA9rUuXxjZU\neTz2TVEtLRqqqjzYudOHTz7RrVFnHR0aAgGB6uoQpFTH8EY3vUU3xtXUhLBoUay6m5enEtozZwRq\na4Oor89GQYFptRckVtf7+tRIscRY+nwaOjqASZPMpCOad+xQGWNtbQDFxRKPPRZLnrds8eORR/KS\nEtiWFg2vvKLGliVuxNu0yY8tW+bh5EmZ9OEiPkFNnA5x002q5aCzU21MXL7cg5deCto2r82aZQyM\nnwtYPdPbt/shhITbnWNda9Yswzrc4qc/zbGOqp43z8D48SbeesuHgwd19PaqinBFhX1GcOKpcNFq\nf2lpbM3x66+o6LWmR0TbHsrLDbhcEq+/7rf1BDv5u0cXZlh7goUQpQDKAXw4nNclIqL0l7iZ7fXX\n/ZgwQQ45GTaM5JFaTz7Zi2XL8jBtmmElnlOmmAOHPOhWUhd9XmKSsX27H5omrQRl8eJePPBAch+q\nx6MOPdizx4VZswy0tmpYujSEYFAAEGhrUyfCbd/ugxDCmiSQ2AccPaWspiaEtjYNa9cGcfiwhkmT\nYCWl8ZvqwmE1Siw+2dy82Y9x4wQeeywPq1YFbX2z0Y1x0ZFc9fXZWLYsD1VVQYwZI9Hfr2HFilyr\nIl1dHcRVV6mE8/BhNZu3o0Pg2WfzrJ7ixPWXlBjweEx0d9uT0pMn1RHBK1Z48D//Z8i2Qe/UqeTj\nnEtLDYTDatOaxyOT5iifOqWhoSELixf3xh20EWsVmTPHwE9+EsD110fQ0OBDS4uOoiITa9fm4MAB\nF6qr1QeBNWuCyMlR7SvRPnE1QUKNR4tvf2ho8MUdX22ioMBATo5Ec7OOyspe/OIXWXj77WxUVYVQ\nV5ePt97yoazMsO7vxMkjOTn245OLi1XyGr1/fT4NHo/Erl0+dHRog06HuOkmE6qzlC6HYUuCB1oh\ndgFYJKX0J/75+vXrkZeXh2nTpgEAxo4di7KyMutTzXvvvQcAGf84+rV0WU86P25sbMQPfvCDtFlP\nuj5OvLdGej3p/DgxZiO9nsTHt946HwcO6Pjtb/+ASZNMPPro/wNNu/zr+fnPf57y3+/29q8O/B/7\nfyAcBvbv/zLq6nJQW/sWrrvOdHz93/72DwiHc6GmKwgcPPgexo838dJLd6CoyMRTT+2FYQi43Xeg\nocGHf/3XP6CoSGLr1jtx7739WLHiLRw7JhAO3wUACIffwa9+1Yubb56PzZv9OHTo/8X/+T8awuGv\no74+G4888i/IypKYOvUOBAICy5f/EX/zN2GcPPlfUV+fg0cf/RfU1ubCML4Kt1viuefexp//LJCf\nf4f1fteuNbBly804cUJDd/e7OH4cCAYlVq26C+HwO9B1iW3b5iErC3jhhQ/xyCMRFBTcjnnzDFRV\nfQhd19HRcbMtfqdOfQluN/DEE79FUxMQDt9lrTf8/7P37vFRnGeW8KmqvqlbakDohu7iZjASJoZJ\niOPYyefxJM5v15m14wQcYzt2FnbBYGTERWJtR9jQgCQEBryjRHy6gSQCJOvZ3XgSb34ZO7bjtYFB\nXGxuBknofkGgrq7uVndV7R9PV3W/1RKWbezgTD//gKTuquq3qqvOe97znBNQsHnzAwgEOAjCn/Cz\nn/lRV/c9OJ1AZ+dbaG62IBC4D1YrsH79+1iyxIfExHtD0op/haoqCAa/i+JiLwYG3sTRowoaGr6N\njg4eg4NvQlFUDAzci6tXBfj9b0IQwp+/r+8t9PYCqanfQ16ejCVLjkacDxGC8Cf950AAePTR36Oi\nwooNGxYiK0vB6dNvQRBs+vbOnXsLc+eewMDASpSVSVi0KLy9piYR//Iv74DjAKv12yFvZhrPl176\nBo4eNePjj9/Ck08CwLfh9XJ47rn30dsr6Mfzl7+8g64uDoHA9/Xr4X/8Dx9mz/424uOBP//5baSm\nqti//3tYtsyP3/zmHSxcqMBkug/5+UE88sgf8NZbMlau/CZ+9zs3/uf/fAc2mwqzmcY/NfWPOHnS\nh5df/oF+Pp5/3gu//25cvsyjpOQDUH0Hv/qViNTUP+H8eR5mc/j1169LAO76xO9H7H5+4/v322+/\njfb2dgDAggULcN999+FGxamULfi5iuM4E4D/BeB1VVV3jfaaiooK9amnnvrc+/pbr1hjzvgrNlbj\nq9g4jb9u9bE6fvyzGezf7BprnIzHt2mTF8XFdvzqVyIefjgw7u1Hb0cCAMyYQRZmq1aF44t37fKg\np4fkA4mJCpKTVXzwAbG4xojdzk4emZkKrlzhoSgc09RWXk5NbcnJCtats6OjQ8CBA248+WQ8XC4J\nRUVhnXBk8EIku1hfL2Lx4gT9dYWFryMl5V6dJVVVShPTJAIANcfNmkWfa+ZMmUlJ0xrvysokZGYq\neqRwVZUVhYVePPtseBw0P+GqKiu2bfPg0iUThofJCm7dOju2b5cMKW4iiorsWLaMks/+7u+CMJlU\neDxk0ZWQQGPZ0UFykNZWAWlpCvr7OZSVxYWs0STYbMBzz4XHprraDYcDOHnSpMcQL1kygvJySnTr\n6eFRWWnD8uX+kN47gJERDu+88zYyMu6BJHF46aVwdLPWyGY2k2/wE08kRPzNi/JyGxoaRCxZwuq2\ntfEtK/PAagU8HvZcaddmRYUHIyMcTCYVwSD7moMH3XjuOUodlCTga18LYmiIZDdHjliwerUPZ84I\nyM+Xcfq0wERO79jhwSuv2LBrlwc/+lH0d1ZRgBMnWOmQqoblRCkp5OYxZQq7knKr36NupTp+/Dju\nu+8+7kavuVlM8P8P4MOxADAQ0wSPt2IX9/grNlbjq9g4jb9u9bEyRqD+tbw+xxonozH/3r22cTX3\nyDIBgrNneSQlqUhKkvG//zfpY9PTCQBcukS+tlOmsLrW5GQFksShqsqG8nIJP/lJ2D6tqUnEuXM8\nbrtNQUsL2aSVlNjx8ssS/tt/C+tGFyyQmVS0mhoRGzaQjrW2lhY2jfKFKVMUlJSw2lOzOSy3WLHC\nhxkz7sbixXHMdo1NWE4ncPUqJYm5XHGoqxPR0cFDlqlpatMmLwDgwgUeb7xhxsMPj6Cw0IfMzGj/\n3pMnBaxc6YPFAoPzgYT+fvbaaWvjoxL1GhvFqOY+juOwahWr8e3ooHPhcERLOyZOpGMtLw/rbQsK\ngti3j/x6N2zwMhHPHAc8/ng8UlP/AStW+JCUpMLl8mDvXtIPO53Qj/naNZ7ZF22XGuzGanLLy1Og\nqkBFhU2XK0ydqmDrVro2R0YI+DY1iTh2jJVpXLkSnTqohWqUlnpx4IAFP//5CFpbecyfLzPSnNRU\nBUuXko58NFeG0RrVjJO/0lIvnnoqjpns3ur3qK9a3QyLtG8B+CmAUxzH/RsAFUCJqqr/8nm3HatY\nxSpWsQrXF+31OZ7Gthu9RltYtFqBrCwZO3YQC3f5Mr2goEDGqVPR721pEfCDHyQw4Ov222XcfruM\nvj4OTz4ZdkNISiIWs7OTQ2Ym6VqnT5fxT/8k4qOPTLo+trVVwPnzPGbNYtnVsjIJggA895wXycn0\n/hMnWPBz5oyA7dslWK3AmjV2rF7tQ2OjiOPHBaSlUZNefz+n63ydTg4bN9pRWOjFgQMifD7g6afj\nsWGDl9nuuXMEkO68U0ZxsaRvy2QiS7L1673o7haQlUW+tZEATGOrjx0jAFpWFodDh9wYHiZmsqeH\nx4IFQbS1Cfj4Y/bzxMdTYEWkzjYtTcHp0+zr2tujm+O0/4d/R+fYbFaRnq7AZqPzZbFQaMX58wJe\nfdWqO3vMnh1EQoKC4WEeq1b5Qux5WPesOVcYE/Dq6kS92U3bX0YG2ePl5CiwWBSsWhWP1lYB9fVu\n5nsxf76MV17xIDVVgderYu/eOKxc6YtaGWhvF/Rwi+vXaTJkbBz88EPB8Pk5/d/HHhthJk9NTW5I\nEoehIe1Lo2LKFHXcrgzGSa62r1iwxRdXN8Md4h0Awie9LuYTPL6KLXWMv2JjNb6KjdP461Yfqy/a\n63OslDbja773vWO6njPyNcb3a4EU2s+HDrnxyCPhn//wh2HIModTp4xAg0dfn4K0tHCjlREkNTaK\nUextYWE4AveXv7SGUr4Ext0hM1PRfWe119rtYaaXGrNk9PSQ3+/GjV7Y7SoSEmQkJJBcwigr6Ori\n4XJJcLs5KArQ308evu3tb8Js/r7+2jvukPGb37hx8KAZt9+uYvJkBT/7WXhbW7dKWLOGPsOBA8QI\na+OybJmfifOlCGYOTz/NMrdkB8c26aWnq4ytWmGhD4IALFgQZF6XlsZOspxOBQBr2bVgAU1usrMp\nSOQXv7Bj5Uofenp4ABwcDpXxaW5uJiZ940Z7qEmQZW01JvnUqT8jEPie/vuBAQ6iSBONtjYe2dns\neWtqEpGUpGDZMj9EkWMa/jo7+ZBDhIQZMxSsXOkLJQlyEdvnUVVlBQC90XLiRApfiY8HfD4VFouK\n5GQjM62GgHZQd+rQttnZKYQ0y2E5xaf5jhonudq+Iie7t/o96qtWscS4WMUqVrH6Euvz2Ih9Fq/P\nT7O/seQWkdvw+8m9IfI1gqCir49HZ6cxwCHaO1X7OTVVwdWrPI4eFXQpQeQyd0KCgocecqK2llwL\njLZZRtZS84ENBMiKqrxcwuLF5KZgtPhiQxaAN94wo7FRxOXLtFRuBJsvvhin+wdXVHiijmP9+rD3\n8IoVYenA0qXQrbacTqCoyI6yMgl33qkgO1uJsmcTBOi2Zq2tdCzauBjdCNzu0W3NAPLmra8X8eGH\nJAE5f56dSGhg2G4HmppEDA0B8fFAfb1FlwxMmyYjLo58jg8edOua4I4ODjt2ECBsbBTxox+NYGCA\njkFRiK3dtk1CWpqC+HgVq1Y5sHjxCJYt8+Pppx1RbhzXr3NobBTR0sJeAxMnqli1Kl6f4Fy6xDNR\nz5cu8Vi92sdMIjR2t6yM2F27ndL2Ojt5zJsn62Eew8Mk4ygv90CSjBMJcppoahKZFYR9+0QIAjA8\nzKGujlYipkxhQWtKimK4NgScOIFxf8cjJ7maJlizTovVF1NfGgiOaYLHV7EZ3vgrNlbjq9g4jb++\njLEaD9v619rfWHKLyG0Qy0hd/9qD//hxE3bvtukAY/t2CSUlduTksMAmO1vRl+QtFlVncnNzZV1u\n4HQipLWlZfLKSvLZ1fYXqYGN/HnaNBmNjaQjTktTdeC3d68VRUW+MZf08/NlzJ6t6KloxcXSqEvS\nAwO8/hmMnykQoAYvo/9vTs49GBwE0zB1/LigN3oZvWVTUkhnvHy5D7LM4fx5Hrt2eTBxIumQWUY2\niM5OgfldUpICl0vC8DBgt6u4/XYZJ09Sk2BurqxPJIysemkpveeee4IMqNQmAI2Nog70IycR2mfZ\ntYtCKrKyVGYCUVsroqJCgtWq4J13zPr5KC31wmYjO7opUxScOycgOfleJq5akxSkppKmN3JCoEkj\nenujPZ6rqrQ4ZyArKxytnJtLvtGRqweNjRRKMtr5NrK8H31kQnm5DZs2Sfiv/5XA+Z49HtTUiOjt\n5ZGXJ0MQ2HPk9XJ44IGEcX/HxzPJ1e5RN8uT+997xZjgWMUqVrH6EuvLam7THpJGqcGN9jea3EKW\ngcFBDkVFPjidKo4csWD/foq2zctT0N1NQQWjNVm99poZzc0UVJGRoYb0s6RJfe65sF62tVVAezv9\nTWOR/X5OX6YeGgImTyb96KRJBJBqay1obhbR2sojLU1BZ6eANWvCQK2mhgBmR4cQ1byVny+juNiL\nuXODqK+34L77gvqxRCa7RS5JZ2VRkpvXS2ELra3kUzxhAvkWT5+u4OJFtnFLloG8vLCvsdOpwB7C\nw4EAeehGAr/+fg5Ll/phtQKVlQTmJkwgYLxypQ8ul4T0dAUWi4qrVzmoqhpimk3Izw/CalWxeHF4\nssIGXIh6JLORVbfZAJMJul+x9nuvV2sQiwaKWlMfAEyaRCy3cbJx+jQBx6YmEXffPYIDB2R0dpKP\nbkKCggcfnKDHE1dWWrF0qR+AihkzSPoAACtW+PDUU/G4446gztZnZCjYvduGtWtZVnnyZAVbtrAu\nGJqzR2urgNZW9nOcPClg3rzgqOc7J4e9ZubNC6KhQdSPKxDg0NoqoLzchsOH3bjrLhlnzvDYv59c\nSPx+Ttcbf97v+GiA98ueTP+t1pcGgmOa4PFVTO8z/oqN1fgqNk7jr7HG6mayLl90c5tW2kPSuPx8\no/1pjW02mwqPB3j9dRMcDpUJnSgtlXDmzJ9xzz13Y948GYLAQxAQBba7unjceaeC8+eFUSUGkyax\nLg9al77LJWHPHhsSE1VcvkwaTLebx5YtxDT39Ai4804ZTzzhx5o1Dl0j6nKFGVyNPXS5JKSkKEhJ\nIaa5s5OH1wusX29Hby+PTZskPPbYCIAw8K2qsqK5WcSJEwJmz5Zx7RqnxzFfvixgYIBHUpKCmTNl\nXLggwGZT8dprFjzyyAj27rXB5aJAiJQUFW+99TZyc+9GVZVNP86KCklna1WVroeTJ0lPW1Zmw5Il\nfmRmkob5tdfM+PGPVSxb5o8KDykpIe1wQ4MIp1PB4CCP7m4Ct5mZMsxmFtD293OYNInGyQjwUlMV\nPPlkvC490X4/a5Y8KvtdUBDUU/AAYGCAC8lQ1ChAqUkXpk4F05jW1OTWX1NVZcXf//0bUNVvY8EC\nBe3tPLZskXDtGodgkLbd08OjvZ2H1Upgfd06cuWIXEHQjiPycwMIRTv7kJ7Ofo7Zs8mWrK5OxPnz\nAgoKZHR3c6itFbFvnwXV1R6cPUtA+b77gjhxQmAirOfODeLwYTe++U05arUkckL4eb/jkdsWhD/h\n97+ff8s4xXzVK8YExypWsYrVJ9SnZV1uBJo/b3ObcdtjOS5oD8kjR8z6ku306TLmzJFx/Pjo709J\nUfCjHyXo/rTl5RJUVdFZ4L17rbBYgB07rKivd6CiQkJXF2kjCwpY6YMkAcXFDn1ZXANnK1b4IQgq\nJk5UcPCgG34/uRskJZGO12ZTsXmzxIDmbdukUayqJCxd6te1vSkpYQCmsYfaa+vqRNhsKrKzZXi9\nHFav9oHjgMpKG5YsGcHp0zyam0UMDwNOJ+lg582TYbEoeOIJ55jMqsOhwu/n8OijfqSnqzCZgKIi\nakx79lkHAoE4/Pf/Hq9brmnWYpGfo6lJNNiJyejv5zE8DKxZ44PJpOL9900GJjasf+7t5VFVZcPO\nnR4kJdE2VqzwR8lHJkxQdS/d3FxZ1/7KMoe2NiEkARB0VweafJD+1eFQdMY6KYmY6JYWEzZvlnD9\nenjsSeogIT4e8HigW+RlZChR8oK2NgFNTW4IArBli4x33yWwGClXqKsT9cQ540SgsVHE2bMmZGXJ\nmDxZxeAgWeH5/WwjX0aGonska9HS2vGtW0eTobo6EXffHQQAZv/33COjvNyG1193Q1UxaqSx9r2O\nBKV799qY1ZLPq+mN3LYsc/p398uYTP+tV0wTfItVjLEbf8XGanwVG6fx11hj9WlZlxuB5vE2t40G\npFUVePddAe+9Z4LTCWzeHIedOz2M44K2L+0huWTJCK5c4TE8zGNkBLDZFBw/LmB4mMfAAAe/X8U/\n/mMCo4fVlssTExUGTJaWSpgyRUFh4Tdx220Sjh7VGr7iUFbmQXW1B9eucUhKUrB+fXjZuLeX18EZ\nBT34MDTE49o1XgdLvb08qqtFxMcjCjDl5MiQJI4B4yMjHKZOlUPL6QomTZLR3OzGlStC1LL+qVO0\nLL91q6QzzpFs5aJFZHVVVxduhtI0pBs2kHuE388yjFpwxapVLKA9dkyA1art/zsIBIAzZwQsX+7H\niy/GITmZbZ7q6+NCTg/AHXeQJZwkAQ0NVpSX8/jtb4ejXBzItYFA7qRJ5Efb1ibA46EmsytXeOzY\nYdMB7dy5QfT3h4+/tVUINevRWG7bJqG4WEJOjoyNG8MODHV1Ih59NAG5uTK2b5fQ3g5kZytYvDiB\naa7z+8l6rreXR06OguZmC37ykxGsWuXD1KkKysttKCryMZ9hyhQFFy4IEROL72PGDGnU89bYKEY1\nQra2koTk+nUOWVkK/H5AVTnwPCsxMZvJYUSLduY4DjyvYO/eON0xhOMI4ObnK6M2phUUyMz3rqrK\niupqD7MaFAlKe3t5TJ6s4v77g7oH9udZRWIB773Iy3N/4U4x/14qxgTHKlaxitUnlPYQ0h78fj81\nOI31QLsZS5UtLQJ+/nNKq7p0icDihAkqYzlWWuplHBci96U9JPv7OSYAoalJZBjNhgZRf39amhpq\nfCPbqKEhFvjFx5PV1Wh2XcePm/XGIQDMsnFOjoI9e0QkJADPPONDUpLCeP+WlHgxYYKK7m4eXV3A\nnDksqwwgCozPnMlKLFwuCcXFFF7BcSrjBJCfLyM1VYHTqWLCBAUVFRKSkxX09VH62bPPkpa1u5u1\nJDM2UbFAFKM6ViQkqMjKYlm6tDRqequooLGJDFVISVHR10cA2DimJSV2XLhgwvTpMg4cICDIcYAg\nUJJafr4Mj4cY9oEBHjk5Mnp7iZmPtCmrqxPh8bAM6fz5MhwO0tBGyhQaG0V8/DHZw5EDhBvXr5OP\n7p49Njz3nC/Etkc317lccbqf8bVr1MzW2spj5UofJkwI6uxzRoYCt5vD8DD7PZk0yajdDqKoyAcv\n5YUwf5s6lb5PJ06YoCjkbrFoEV1Ty5f7MHmyou8nLU1FYSGrVzc6hjQ2ijhxghsVrB4/LuDZZx36\n9bR5s4TubjaIbCxQejO0u6Nt+7M4xcQqumKa4FusYvrN8VdsrMZXsXEaf401VtpDaHCQY/Sxoz3Q\nZBlISRl9qXIsdnc06cTly+FELw3A2e1gLMjc7mjAmJen6Pvp7uaigKyRUevvDzegJSdTE5b2sJ85\nM9oCKilJQWfnmwgEHtC3YbGo+NrXgmhqCsDvJyeFw4cpOKCvj4csq0hKAo4eJSZNY3o1ILVpE9lS\naQxsebmE8nICqh4P6Ysjj9liAcNsBgLkDEBSAQ4NDVbs2iXpoGjFCh9WryZg1NtLjHggQCCtrMwD\ni4XD9u0e5OaGx9JoSTYwwOnMan5+UJ8MRI6Ppjnt7+dRUyPid797BwUF9yAYBDMRqakR0dYm4Lbb\nZD3JrqUlOpRB0+M+9BAxr6tX+7BmTTiieNcuT5RvcWmpF+XlVkbu0NpKARZGu7YdOzxRNmuavjYS\nGJeWSrjtNmpMHKu5zmKBzsp3dPBITGQnKfX1Iq5cEeD3U5jK8DAwf34QCxcG8N57ZqSm/hETJy5A\nUxOBfaMvcFmZhNJSL6xWcgaJj1fwH/7DBGZMAwEOHR0CXn3Vhi1bJAwNcUhNVaMa4s6cEZCYqDK/\n6+7mdIcQ43c78ruo/f3QITfzvR8LlN6MCXHktt9++23wfOx+frMqxgTHKlaxitUnlPYQOnLE/IkP\ntJYWYo20ON2FC4M3ZIUAjMoU5eUpuHQpDBarqqItyBYuDOLrX5dx+LAbly8LyM6mxh6PJ8xcAWyz\nUk6OwjCRGRlkUQUAgqBiyxYJp04JSEpSMTgI1NeL6O7moapAfLyCwkIf/vVfWVYuEACCQbKV0ti1\nSA2tUU+rOTdoQGp4mNMDLcxmFRcu8LpE4vBhty7V0JaiAwFENWHl5weRmyvD6aSwBg3sj8ZYlpQ4\nkJsrw+WiOOGJExVYrZTC1txMY2m0YEtJUXXpgwbUh4bIZ7elRcDcuTK2bbOhsNCHyZNVrF1rx9//\nPYG9KVNYQN3TQ6yt3w8kJKi6W4KxaauuTtSb3To6hIjxpn+DQRr3SJmI280hGKRr1mYDPB4VDgcx\n82fOmOByxenX6pUrfJTX7fz58ijJZTwuXwaKi+347W+HUVMjQlGio6STkqghMSVF0ZvUtG309/NR\n8cOrVmmpdz588MEI3G5eXyFYvdrH+AL39vKhlQYvFi2KZxohtUlQpCb86afj9cmVsTm0oEBGVxfr\n5JGUxILiyO925Hcx8vMAnyxpSklRmGs3pt29tSqmCb7FKsbYjb9iYzW+io3T+OuTxmo8zSiXL5Op\nf0kJaWJ/9SsRPB9mlIwPWu3/kb/T5AyiGGbdjEzUb387DEXhcOiQhdHVulwSnnqKZAHDw8SKRjKA\na9bY9Yam5GRK17JYgIYGC5xOJQowLl3q0JfU/X4CcK+//g8RsbgySkriUFjoY5a3x/p/IEDxwQcO\nhC27nE51zEALj4djmM4DB0QIggpFoTSyjz/mkZmpQBSBjRu9SElRUF9PKWWjMZZaU9myZX6GnS0t\nlfDggwFIEofiYrveRGW3U7DC8DA5EXR08MjOlmGxqABoW8nJCoJBYMmSETz5ZDzKyiRs3iyhs/Pb\nyMggZt+oh7XZ6FwsW+bH6dMCFiwAfvMbN06eJDeN7m4eU6YQE6xNWqqqrDronj2bGuieftrBfAaO\n40ISkzCjP306eSj7fCyIzsxUsWaNXZ+w5efLKCqyo7xcitIgp6cr2LTJi+5uHpcumdDQYNGvgYIC\n0hwXFYWPxeg0MXGiYjgPdF7CYRUPID4+HKFsbOwrKAjqqyCpqUqUw8WUKYpumZeTo+COO4L6uY9s\nDs3Lk8HzKqZOVVBXF5Zn9PWxY5OSokBRaDIxb54MjwdRfz9yxHxDnW9LixCVmPh5tbux+/nNrRgT\nHKtYxSpW46x582T87ndunDvHIzlZhcl/z+nAAAAgAElEQVSk6g9KrW4ElI3s4vTpFGAwGlPE88DE\niRSlO2WKglOn2Phfn48fVUPK8ySZEATywzWZLOjp4ZnAhoEBHsEg8OijYdDickm6pADQfGK5kJ0X\n/Y4svWRGb7ppkxe9vTxuuy2InBwee/aISEtTceUKr8fNag1K2r7mzZPhctnQ08OjtNSLiRMVjIwY\nwSq91hhm8G//JmD+/CA4jtcb80pK7Fi61AeOI9mClopWWipFjbnWVBadwMYjK0sOOTxozCq5R6xd\na0dNjYhHH41HaakX589TQ1d5uYSBAQL5Ho+C/Pwg9u3zwG5nQyOOHHHrgIvjgN27bXqKWuTEprnZ\njalTFR2cL1wYQFGRD6tW+ZCdrcDhkNHaasKkSSosFgocifwM8fGAKBLzG+2m4cWrr1p12y+nU0Vf\nH8dM2IqLvWhtFXDtGvDrX1OTYXIyuUGYzSoEgUdiImAyBdHba9Ovgf37RVgs0JvPnE6ShNTWijh9\n2gSnU8XQEG84D2rU+dU8mrXJWyTItljISq2jQ4DL5cHatWHwvmABTUoeeijc1FhWRnHLLpcHFguY\nEJDf/c6N+fNlHD/O4YknyN84EtTPni3j2WcdqK724M47CeB+61tsmtuzz4bt+cbS+Ronvf39vD4h\njtWtUTFN8C1WMf3m+Cs2VuOr2DiNvz5prHiePEoLCx261vT0aZWxSxqrQWZkhGyZysrIu/b6ddLr\n/uQnYzNFFy4IGBkh3e78+UHk58s4fZoAzGga0txcGdnZSsi5gMPu3TZUVEg4f54FIJMmEQCKfL/Z\nDMydy7oQzJolM9rQrVslzJwpY82a15GSci/S0hR4PEBjI0kWtJjiyCakpiZyK2huFnHuHA+O43Q2\n+vRpEziO5AAXLrDpZ3PnBkPhFCxDt2ABsaIjI+Sg0NvLh8CLNhMJywdKShzYskVCaakEi4W0qLm5\nQVRUeEYFxykpdBxUKiorPejqEnT2OjVVQWamgp4eDps2efUGP20bDQ0i7PZIDeq/IhD4Dv7yF5Oe\nElda6sUPfxiAJEUD8c5OdmVg5UofA6abmkRs2xaHZcv8OHaM/JIXLgxg8eIRTJ5MMdQ5OQri4lR8\n8IHRVo0kBV1dHFyuOF2ny0oCaEwmTADOnhVGlZFoYD3SgSE+XoHJxDNOGTU1ZEun2b/l5spoahJx\n+rSAOXOoga+pSYQsawzrm6iq+jaamih9LhJka5Z9jY0kzQFUBrzv2OFhNOLLlvkZfW9ZGSudOHeO\n179nlZUeTJmioqnJwuyvtVVgJBGRutwjR8yMVGMsne8XYWMWu5/f3IoxwbGKVaz+JuvzBFzc6L0a\nu7N2rQ+SBHR2CnC7OZhMKubOVZiHZaQ90uTJCgN4a2pEXLzIAlkjUzR9uoy4OBV9fRSmEAm4jMvN\ns2fLUf66LpekW0fV1tJycFoaMXupqSy4nDxZ0QFOMEiAieeB8nIJZWU2dHSQ9dhDDyVgwgQr1qwB\nurqIFeM4oL+f1xnoyOa9Y8cEBgAWFxNwIYsrYv1GRjjMmRNERYWEkRHSUcbHqxga4pCRIeu2X7m5\nMq5c4TEwQOCrstKD48fNyMyUMTTEQZIIIEV+rpkzg+A4aghMT1ewebMdP/xhACdOCGhudmNggEdc\nHDA0RMx3JPCrrg7HNdvtCGlNw+x5eTkLrjo6eBQX2yM0qJrcA/pr3G4OgIqGBhu2bZMM50BFe3t4\nwmJsCGxri27Qam4W4fGwTGdZmQf5+WzDZEFBEAcPumGzKbrjg9Wq6g2IFosKi4VkL52dfJSExWSi\n8JG9e60hABpu0Kuvp7jqyNf39fGYPZscIXp6iAHv6eHwi1+EVyR27vRg/35iYE+f9uOBByQAKkpK\nSFNvMqmQ5XDyWns7j5ERasIz6nkj/YGNk4vUVBaMJierUfr8Q4co2dDt5nR/47FA63jBbczG7Nav\nmCb4FqvYDG/8FRur8dW/13H6LNZE2ljd6L3aA3DSJBWVlXEh3aXmTqAwwRUmk6pvZ/t2D/NgJksr\n9mE6bZqMP/9ZwKVLAnJyZAhCGNxoHr7a+/v7Ob2TPidHwbVrwNAQC1wAGJwDJDz6aALMZhW/+Q3L\n5sXFqVi0KByUEfkezeM2J0fGrl0epKR8He3tJI84dMiCJ58cQWKiihUr2OX3F1+MMwBA+r/ZrOK2\n21j3gNpaMfQ64JVXbHj44RE4HGQHpnnX1te7Gd1pdbWos5p1dSJEUUFaGmk9Bwc5TJ5M4Mg4eRjr\n5/Jyj2GMKQ2vqUlEZyeFQqSmKnqTmjGOOSWF/k+hEV6YTH+HjAwRGzfa9c89dy4t7ZeXx2H9ejtK\nSyU4HIAkUYDEq69a4XJJzLWmMam5uQo+/phnJhkff0yTlcjj7u0VUF5u0YFkRoaCdevsMJmINe3q\nomsmclJWWiohI0PFiy/GoaxMQmIi+9lkmfyVS0ujE+f6+viouGm/n8Nbb5kjJkAS0tLYCUpysoKW\nFhOOHjXDbP4HPPQQBZBUVHhw+bKAnByFYXQ1j+eyMgnV1SKuX6dzfP06OZSQVzGHBQtkw/FxjO45\nNZUYf+O5XrSIJkcvvui9IWgdL7j9ImzM/r3ez7+oijHBsYpVrP4m6/NYE93ovdoD8MwZIYqVO3zY\nzTTCNDWJOmjKyDCyUdRsdfBgWHt5/TqHH/84/P66urCHr9MJxvs2K4uamjRdouaPG7mPjIxwM1Jq\nqoK8PLIES09X4HYDM2fKuHQJoUQvAgWSNLpWtraWbL1SU1nrquZmEYsWxWPbNhakW63EKmuWXmYz\nOQ+88ooHqqpGBWKcPh1mjI1AVdM7iyLH6E79fvLI7egQ0NVFTU+rVpErRmIiORV0dbGgsbOTNwBG\nXp8MZGZGN1tZrWA+rxa4MTxMzg4HD7rR2krjYjLR5+zoEPDii+RKsH69HVu3SnpjYnGxHatXe3VQ\ndtttCsrKbHjvPTN27SL/2sFBmph4vapudTZ1KpumVlrqxS9/aUVGBjXRafrr3l4+ZFMWPobTp03o\n6BBQUeHRga9xUuV28xgcVHQpgaap1gC6xsY6HMC+fRb9b9r+9+yxMhrdYFBFTw/ts7LSFtIrc3rw\nRU6OgoQEOaQbDtu2lZd70NYmMM2JNhuFlWjH0NvLITOT3Eq0cBPtusnMBGprLTh0iFw+Jk9WUVIS\np6f17d4t4v77FQSD7EpIXp4ybtAa8+j926mYJvgWq5jeZ/wVG6vx1VdtnD6PjCGyjEuWTqc6asBF\n5P6uX38TTz55V9R7jZ3g2sPvj39kdZeXLrHs0rFjApYv96GkxIHdu22orxfx4YcC7riDuvCXLfNj\n+fIwiDbaPg0M8LozwGuvmVFRIUUBIS02WPPHra8XQ/IJCpnQmu7sdoVxQ2hsFHH+PK/rPDV96KxZ\nsmHcFKSksI1eTzzxe1RXfx+BAKfrX1WVZQIBYoqXLvXpbDNAEoGRkWjZQiRjHO0LrOL55yWkpqrY\nvt2qA9LaWlFnqQMBYuM3b6bwh02bvHjmmWhmetq0aKDb1cXj1VctaGiwoKGBZCOSBKxfb0dmJsU5\nX7pELgKyjJCbQbiZzWSCbu2l6Y9zc2X88Y/vYMmS70BRSL+sAbHBQR52OwDQpGPRIj8WLx5BaqqK\nJUvCTHddnagz+UbQarWq+meNBIE2mwqzGXj+eXK2eO01M1au9KG42AuTKTzBMTK3Tiex6KdOCSFp\nB0keyss9zEQvM1PBd78bREaGgt27bXjhBQk5OSpznlVVxaVLgg7KS0sl5OUFMTLC4fJlASkpKq5e\nBQSBR28vj/x8GX/60ztYtuweDAzwerOcdgz19W5mzDUXi1WrfIaJFCXMHTrkxt13y4iPBz74QGCC\nW0SRw8mTwldWqvBVu5/f6hVjgmMVq1jdUnUzEpaAMGN79izp/NassaO3l9e3p4Hfs2d5+P2keTx+\nXMCMGQK++U22E/w3vzHjwQcDOHNGQH8/h7Q0BXPnyvD7VT1owulUMG2aEUCSvvXgQTf6+kjLOHGi\nimPHBLS2ClH2XSkpLDD0eIDycg86O4lJPnGCBdkjIwi5NwDz58uYOTOof35J4vH442Hwsn+/aOje\n55CZqaK42IvsbNIeu1wSrFZVdzJIT1fQ308sbeR+AwHah9ms6g1mlZU2/X0pKSqGhoC+Pp7RjmqA\nfHgYaGhgY301rbDZTPZVkeMQCAAvvWSH1uTk9XJ63O3MmUGUlUmQZSArK4gzZ8whXSgXBRo3bfKi\nttais+8pKQocDnL42LlTQnm5DYpC2lXNTWPbNimqOY1dJQg3SGmgrbjYC44DfvlLG2Q5TpcDaBOO\nWbNk7N5tw8qVPnR2Esvr9apRQSZXrvBoahLR1sZHNfLl5FADZOTrz54VkJCgIhjkEBdHiXZFRV69\n2S9SvkF2a8Ri0/nicPUqh/nz2WuY44DSUi9sNrJrM64+/PnPZqSlqYbz7EV5uU2fpDkc5GccydrW\n1IjMqscTTwAvvBAX0jizn3VoiJwmzp4VMGsW6b8LC31RchSnU9WlDTxPNoMmk8o4c1RW2kJyk883\n0b5Zk/VPu8/z53n09t7Ymi1W46+YJvgWq9gMb/wVG6vx1VdtnD6LjCEyIY2sn8IPpsuXeTzzDD2g\nMzNlDA6Sb6jR5qiszIOCgnvw3nv0wJ48WcF/+k8BvP66CQ8+GGQe4KWlEoJBGaqqMsdhNitobnbj\nxAmTzsKtXRvE0aMmpKWpaG0l4JafL+vBDuzDnvSn584JyM2VcfasAK+XQ1mZDUuW+EdpdpIZZrim\nRsTjj8dj/34Rfj+YEIXe3nBYQW6ujIoKTyjBTcXICPDIIyxA2bPHhpdflmA2AwUF7H7/43/8Fh58\ncBgAcO6cgOZmEcPDgNWqorjYzgBG46Rg714rtm2TGJu12loRS5f64XbT+ZMkFU1NbrS3k0xEA8iB\nAIfERIVhBSPBZVOTiJkzgzogitx3erqCS5cEPPmkH34/h6IiO2prRTz8MCtfcTgUFBSEWVKjfKKt\njXXamDFDhiRx2LHDg7w8GYoCtLUJyMpS8LWv3Y2jR+l9EyeqqK93Y2iIdMZFRV4sXszuW5bZJfpp\n0zSnD6CszIbGRgJzkgRs3WpDcbGPeb3dTu/xeIAXXqCVBtLR0jnZtUtkdOBWK5jzRf7KBBqJjSXQ\n2NvLY/9+NySJx+LFI/o1ZTKpyM9XonyQk5IUfXUiN1dGZqYStUpiZPuTk+9FIMDhxAkBX/96AE1N\nov7ZKytt2LHDg3vvDeLsWR6TJqlob+dQUkI2aWQVh6iGNp4H5s4l6UNJCYXNLFnih8Oh4uc//2SL\nsxvVzZqsf9p9Fhf/4BP3+dcA6F/VijHBsYpVrG6pMkoRcnMVHD8+9g1dloF33yVTemNT1+uvuzF9\nuqyztfn5QaxfzzJZmpwgMRF4+mm2ISwYJKB68SLr0ZuZSQ9hs5l1E9C0rFrq2Jo1Ph08j5aa1t7O\n4+BBem1ysgq7XUFnJw+eV6M0sRxHccMae+p0qnqaGBANLCKB4oED1KG/dauEykoCA5GgvrqabQjz\neoGKCglHjwrIz5dRVmZjGovOnye9aU2NCLebx/nz5GRx9KjJcDwcGhvd6OnhkZ5OGuaODgEbN9r1\nY/J4CDxrkgZNqrF1qw1r1vigKGCWs43Nf5o1miY/yc8HDhwQMTDAob5eRH8/hYL09XGw2aj57xe/\n8GLTJi96eli98OXLPDIzAUkCmpspGMOo5Z4yRdHje9PSFFy8KGDDBtKvbtsm6frWtWvtePllCY89\nZg5pwFWmyau2lmWU29t5HDlihsslwWQirW2kFrm01IvBQQ4ZGQpaW3ls2OCD16syrDZJIVS0tppQ\nWEjuJd3d4fEqK4sLHSO5jQwMcHr4ht0O9PVxKCpiJ1Xa5EtRuKhgDlmmpsPDh9kmS0FAaJIWREFB\nEIsWxUelthnHVZu02O3ApUsm5OQEsWABWaHt2OHBXXfJsFhoQvZ//68Aq5Ws0PbutQKg6zWyoc0I\nBF95xcNMeCK/+58lyvhmxCF/2hrvPv8aAP2rWjFN8C1WMb3P+Cs2VuOrv8Y4fR4mwqjVM5lU3H+/\nM+qGHiln8PnC8bvGh8T06eGbf3s7j9WrfVi92hECUPR7s1nzzX0TwHcQCJA8YnCQw4QJMnJzOaxe\n7UMgEPambWoSI/xgwxre1FQKfhgc5ACMnZpGjVwKtmyJw0MPBfDRRzzS0jg0NFiwZMlIFChNTydt\nbiTza7RJ02QEHR3RARORNmVGC6mBAZaBTEzEqNrjzEwZW7ZIaG9/E5s23Yv2dl53Z6itFaN0ph4P\nj5ER0mGuWRMXYnsJSG/fToERdjsx72VlEjweYg7b2wnkXb1Kf9MS7/LzZfT0GEMXFP0cOp2kt1UU\nAqG1tSLWrGEDQTQm3DjJePHFOEydyi73l5VJ2LrVptvLpaYq2LHDhpYWE+rrRVy6RIxvUZEP+fnB\nqG2+++7bKC+/B4EAcPIky4RGxvyazeQ6UVjo0+3ETp4UGC9aVSU2+/p1DmYzQpHLwJkzAmbMINnK\n9esCpk6VsWEDy+5q++nt5UPBKXTOKiok9PQAEyaQ7MFsZq8LLWZ51y5PVAyyxQLs3EmNaufPs5Zp\n27d7sG+fB+vW2fVrWXPMsNloIuFwKHC5KLlw7lwZv//929i06V5UVVmxZQsl3917r4zvfjf8/ZVl\n4L332BQ27dxNnqzi/vvDcqDjx1kgWFHBTvQiv/s38u8d6172RXgAf1Ll5SkQhD9Blr97w33+NQD6\nV7ViTHCsYhWrm16fh4kwdl4fOWLWb+ipqcqocgaXyzPqEnhenoK+Pj7K+xWgh983vhHE7t0iRkY4\npKcrEARVN+/XNLgLFowOCHt7uRBwCO/PYlGxc6cnpMEkj9tdu2hp+Y47ZL3JzWwmy6lAAGhpMaGn\nh8eKFT4A0IFQ5HbnzZOxZo0d27ZJOHBAxL/9G7GNu3fb0NzsDskagLo60rtGeqZq4BDQ/F5VzJ9v\nZNtlhsnr6jKmt9H7ySc3HoFAHMzmONTWirp37OAg6Uw1e6+MDAVuNwdBIJszjbXr6BBQXOzFww8H\ndLCWm0sex7LMhxhRi26Rlp6uoLzchgcfDKCtjcecOTL27aPmv4wMBXa7yiTuLVvmw/TpClJTyb94\nwwYvZs2S0dYm6NZeZ8+ygJScLER4PCqeecang7YpUxQsWeKHxQL4fJTQ9uyzPly9ysNiUTF1qozH\nH6eGuNWrWSeOzEwZ3d1ASoqKV16xorCQlS4EAtDB/Z13yti2zYb77w+ivNyGrVslzJolM24gs2aR\ntMdoEZeTo2DtWjuWLqUGwUiwl5pK0b8ul4SMDPIC1hjyvj66PtesCcsCamqM8hU1JMsIIjOTZ8Y5\nEAA6OgR9tcY4GZMkLuRUoYYmZrR6sHWrhCtXeEybFpZi5ObKePRRet2yZT6sW0f6/UOH3PjmN2Wc\nOiWEGumA1lb23MXF0f1Fa2zTQKvW4JeZKWPFCj8UhWMcNBYuDOJXvxI/sSlurHvZWI11X6QUYd48\nGdu2SZgw4cbH/dcA6F/VimmCb7GKMZvjr9hYja/+GuN0M5mIyBv6ihU+PPZYNCDdu9eG6moPOjs5\nHDzoxuBg+AHU1GRmjmV4mJboBwY4PfJ4ZIRDRYUNL730DVitHqSlKbo3bXGxZJBCKMjNlZGSoiI+\nPojDh92QJE5vmJMkDq+9ZsHKlT5cuUJNTw0NZmzdGsc0nIkiEBcHVFR4kJ6uoqjIjmCQgOaECQRI\nzp0TMHOmjLg4BVu2EHjQnAcmT1bx7LMyOjupu35ggMd3vhPET36SoLsUxMerSE9Xcf48D5dLQlWV\nFdOmKRgcBJqa3Dh2jMDzuXMsk9fU5NbZyRUrfHA4oMsaaCy/g0AAejd+aamE9HQVL78swWJR8fHH\nAk6eNCE/P4glS9jz9c//bMaCBUG0tlKzU2WlDQ8/HGBY1EhXBLNZxeHDw5AkanD0eDhcuCDAbif2\nvqHBhsJCH06fNoWANv28ZYtk8Ej2Yu1aOxoaRCgKO3kZGeGwaFE8tm6VQtcINcSZTCokidfjpY2S\nFg1wrljhhxaMoV2nNFl4QAeXGzfaGUnJ+vXEkrpccXj+eQktLSY8/HAgxPpSeIfR/cEoWzl71qQ3\noFksKoqKfEhPV/XJ1ooVvij3iKtXhag4ZU0W0NFB50Rr1uvuJku6c+dMDLtcWytCEFTs2uVBYqKC\nbdvCTY4FBUEIgooXXqDPq6qq7metqjRxKy+XUF1NNmtWK33/9u79nj4eWl28KKC9nQ+tECj46U+j\nZRVTp9LkACCQqIFW7XUrVrA2htXVHthsKr71LXlcEcZj3cvGskn7IqUIPA889dRdAAI3fN1X1fni\nr1ExJjhWsYrVTa/PykSMxqLMmyfjj3+8jv5+Aa2trIZTYyg1b9SJE6E3xRUUyDhxQkBSUnSDVKQe\n1uWS8MILcaGlcoRYWiAYWll1OgmYGvW8FouKDz80Y2QEBmAkYeVKFnzU1Ih47LEE9PfzOvvlcnmw\nYoWdASNWq8qAja1bJfA89O7+lBQ1xOCpOH+ejbXdulWKAK5+DA/zyM0NMrrSw4fdUBTgyhUTHA4Z\n8+cH0dZGTXhms4o77giisNCHa9e4kAsCdKZzxQpfVEiC1o1vsRBYSE+nJiTtuIy2XjabirVrfTqz\nnpsro6xMigIamo5VY/HI6YIAUGQgR329iOee84WSz2z673NyFFy6xG5DEFQsW+ZHfLyCZ56J18Gw\n5hqg+fweOmTGD38YwOnTxNCqapgVN0paJk6ka2t4mOzpNCBotxvDK3gm5re42MuwpHfcIWPTJklv\n7KLPgSjNd3+/keFXdanElCkKBgd5XLjAo6yMvHa192n/DgzwUVKYSFlAVpYyqj9zcbGXec/p0yRN\nqay0YfNmSQ+8yM2VkZ8fxJUrZFXX1kYpg1evcvD7adK3ebOEujoLHntsBKdPmzBnTgAXLwpYsmQE\n8+cHUFGh6ImAZrOKVavidWlKIECrQDU1JE/JzVXgcsXhvffMOuDUriVNfkFNc5ETBx733RccNzv7\nae9lt4IUIeZjPP6KaYJvsYrpXMdfsbEaX33Z4ySH7ruVlR4kJxMoy8//ZBAsy8D77/M4eVLA8DCP\ngYFwFPHQEM9IEjTAGh9PcacOhwK3m2dY4kOH3HjkkQTGu1UDJJEPKe1fiwVYv/59XW+nuQ5UVdFS\ntlErOXmyosf+ssBIYZqRAgFOlzckJys6MDPqL91uwGZjf2c2qzCZSKPb0cGjqCgMLgGjRpNYXyNg\nj2T6rl/nDA1zbuTkKGhtJYcHu13Bgw+G9ddaLDCxaeHwgq6ut5CRcY8O2jQA1t7Ow2od24tWEKC7\nVqSlKUhOpqZHo+uFBrY1Fq+oyKez+JGf+eRJYkJ//Ws3mpvJTSI7W0FfH6cHXxiZwLo6YklVNTpN\nT5LAgHSzmZr0tGPTgFkgwGHhwgDsdmKMc3IU/OlPJrz6qlWXtbhcHlRUvIfr1/8/5OQojJRg7twg\namtF9PcT83rlCo8ZMxS88IIXKSkKVq924LnnfAy7rEl09u0Tce1a2LnBbFYxaxYbpFFd7QkFbrAT\nQApMYW39ZsyQUV7uwdSpcpSWXAPIkZ/bbFZ1Jrujg2z+tOa6WbPkKOa5vV2ALJOLSm8vD68XePxx\nPx59VGsYVULX65twuf6OuXY1aQ3JS2gM8/Oj9dzvvWfWAacGWjX5hVE3v3BhcExmdKxJ+KdhVb9o\nKULsuXdzK8YExypWsRqzPou+bbTlQO09xu0VFMh6zHBKCjX9RD4E9+8XAUTbK2nsTleXAFFUEBdH\nUbGRr/n4Y0FnjTXvVpcrjmkUMptV3Zs3NVXGU0/5kZTkhdOpIjFRRXm5BxkZFKagvSc3V8bcuUH0\n9/NISFCRmKgYtL6jPwhdLglxcSp27SJXgClT2NcUFMiwWsFsKyODmtzIOisMLtPSVCQlscBxyhRy\nX9A0rdo4eL3Arl0eTJpEDFskk97TI2DNmvB4NzayjgUpKXSMWoqc5oO7ahW5Qaxb50N6OutiUFcX\nHt+qKqu+vC4I5JmsBXa4XB4dhObmynoy2rRp1DRVWipBEBACnyqjUQ2DsSBSUxV8+KEJeXkyVJVA\ntqrStfbP/3wdFy6wjhXUGOaJmqjExwP19RYsXsw2JZ48KWDPHg8SE+lcHDlC0gyTCVH+wZLEOiis\nW+fH7beLzPhoutvFixOwdSsrd2hqckNVgZ07RbS3m7B3L+ulPDTEQZI4ZGVRw+jq1b5Q2Ec0Y+x0\nKqH30wRwyhQ6T4WF7CSpqckNUeSgKBRBHDm+d94po7LSg6wsGQ0N5JaRnq6gpMSu64GTkyn9b+vW\n8GRFOw5NJ75li4RVq8LjEumMEcmuG5l2ai6llRhtrKOT7ujeon3PjP7glZU0Bk4nTRbGCsvp7qYJ\n7NAQTRZbWgR9Ev5pWNWYFOGrVTFN8C1WsRne+Cs2VqOXEWjedddnH6fPom+70XJgS4uAn/+cYm0v\nXaKl2eeec+ja28mT2aXLvj7S7U6dygK+9HQVixeHH6r79onwetkHOPmjxund45qLgM+n6sAsI0NB\nQoKCpiYRPA/U1n5Pf39NjYhnnnHA5ZKQm0sgwO3GKM4JEl5+WcKZMybcfnsQEyeq+PBDQQcv+flB\nQ8CAhFdfJd1qRYUHqakqBEFFS4sJdjv5FR8/bobTqeLcOXpal5Q44HJ59EappCSF0ZgWFMjo7eX0\npqHIcZg3T0ZrK2/w1qUx0fxctfHu6uLx/PNSqJGMh8OhgVqWkbznnrvh9wM7dpDDQzCohXZQI1xT\nkxtdXQIyM8npIS2NPJADgbB3caTMoLWVYo8zMhScOyfgL3+x4Omn/fB6aX+0tE3XR3OziBMnyNJr\n40Y7li/3ITdXidL/PvsssYAeDzsefj9dF8bJ0MSJCh56aCRqcjJrFk1ONBCm6YI3b2bBWHs7j/5+\nY/jJvTh7lmNcHgjoy9izxwOnU4DnDbAAACAASURBVGW8nFtbBYyMADNnKpg4UWG8lJuaxKhJYmmp\nFz/9aQIOHHAbJl0yAgEOS5aMgOM47NxpxZIlI+joEPQ0Nu14jh0z6c4hZWWSDpqnTqVJhSBQ8MrE\niQr27LEhGCSP45QUFV1dpPO124m1NcplkpNJN21sZhsYCE8qwyzzd+B0eqIY5+JiiZGXGFcXvvGN\nIPbsEZGcTKsmAPTGNZJD+W84gY/UEHd08KNOwj8NGRApRZBl4NQpHn19dG2MBsI/bcWeeze3Ykxw\nrGL1N1Y3szHjk/Rtoz0cbrQcePkyj2XLohtVurp4TJ6sID6eBbKiSOb53/ymjEOH3GhrEyBJCNmZ\nhY/r2jXyWNXArSyTJjAQoM7/2loRCQkqfvELAlJGTXBxsV1vitK2ee6coLNReXkcBEFFYiKHo0fZ\nB7qqEosGkMdpezsPReF039viYokBQW43jxUr/Iz2t7RU0hPRqqtF3cJKS3gDKAhg1y4PFi1KwEsv\nSSHXAGJJr1zhMX26wgDG+HiSKVy9So1WkcdstRLra7Wy4y1JbDLbmTMENlNTFezZ40FcHI29308A\ndOlSPzguWjO9f7+IjAwZly8LephESgqY2GajE4HmOVtbKyInR4bHw2HjRjsaG0UcP06+sF4veSXb\n7dDZbIsFUfZdbjf93NvLM2zq7NkySkrovPC8yjhiDA3xcDgAUeRQVuZBYiJ9Vp6nBDkjW2n0uc3O\nVpCaiqjxnDePncBlZCg4etSE+fNlhkkuLaUGTFWlpLjsbBkNDW50dJCu1uFQYDYb5Qr0XquVvkf9\n/ZwuTXE4VADkWLJ2rTcE4KlxMfJ4Ip1DenvJPq28nBrw2CZUCZs3S+jr45GZqUYde0mJA7m5Mhob\nRT1QpKuLZE3z57POKBwHVFcTqM/MVPDrX7vx/vsUMLN1Kx1jVhY5wcybR2mGkasLhw650d9P9xyL\nRcFHHwno7BRCE90g5s5Vxq2L1e5xkgQEg+z49vfT/z/rPbWlRcAHH7Da/Zhn761VMU3wLVYxvc/4\nKzZWo5cRuP7Lv7yDO+9cOObrb8RyfJK+zfhw+MMfhmEyEQiKZD60mj5dhtXKsl8dHRQO4fXSQ72s\nTMLgIIc77qBQBrebPFP7+0kysXatfVS7qV/8QoLfz4PnoWsQiREGfvrTBB14tbaywRcpKaSVTE0N\ne3Dm5sq44w4ZlZUisrMVXWs6PAxGv5qbK+O221gwU1MjoqzMqrO0xhja2bOD6OsbO/BheJhDfb0b\nfX3UsJWWRmPe28ujs5MA+PTpCrPP5mYCHrW1YqgZiYMoUte93Q5YrdEMXVcXj7lzR9DURJrUrCwF\n588LuuVZYqLKLO3X1Ij42c9on4LwJ7z00jegqiri46mJMPLzXLnCNgC+8II9aql8aIhDQwNNWtLS\nFFRWUmPb1askd5k8GVi+nPS1b7xhZizVtMmLFt+cnm4EdprEhWVTN22S0NFBjYCKwsHhADIzgxga\n4lFZSa4FWkpZZHDKaLrgykqb3qCVlkbXhtNJzPmpU5TEV1PzF7hcX0d1tYihIfIZLi4Ou45EjofF\nAsTFGcGlVw8lefddM+x2FmTPnRtEc7PI2JzRqobKTDgiU/WOHHGjrk7ERx8JuvWe9l3Rxm3KFCUq\nKc/t5tHXB2RnK/j449Gv39ZWASdPCggGaXIWOdnVJjNOJ9DYaEFRkQ+DgxQ7bberEMU3kZJyNyZM\nUPC1ryk4e5b20dND4TSHD7t1r+bhYU6/V/3xjyYGZDY3i/g//4fCb8bDuublKfr3XZLY8Z01Sxn1\nnqq5UXwSM3z5Mh8l8fi8jXKx597NrRgTHKtY/Y2VEbimpd14Oe9GLMcn6duuXgUjLRge5nQj+9xc\nGbt2efDb35Knr8ZavvACKw3IyYnuSLfbgaIiin39+GMBWiRqby+P0lJJ1/lZLGTwHwwCbjfPPPib\nmkR0dXFITVVDtmkcbDbynY1uHpNgs6n42c98SE72Ij8/iMWLyY1g0SIH84Bds8aO8vKwF+6xYywz\nLEkctmyRMDDAY9YsGb/6lVW3RgsEgJISO1as8BlAWzjwIT2dDcRoanJj82YPZs1S0NFBeta2NvbB\nevQoG4bxwgtx2LvXA6sV6O8nto1lPSkV7dQpCxITFaSlsaC6rMyDoSGWXY0E7rJMQNViATwehM4D\n24ClvVZRyGbLyJwmJqpR9mktLRQvbTKp+PGPw9dkQ4OIlhZW22sysT6zTU0iurs5pKWpuHCB9OCV\nlTbU1Yno7iYt69AQMfMLFrAx2LW1IsrLJQiCgvnzoTtLaPs6c0ZAYyN562ZnyyGfXR69vbweK9zU\nJGLxYlpW15wq/vN/DhiS+UR9VcC4rJ+bSwzuaIx2Wxs1nZ09K4QmOjxycsgDu6eHY+QosqyC4zhm\nohk5ybp8WUBPDzXNXb8OLF3qg9dLLLnHQ0l5587xoziBKMjKUkZNf4u8fufOlcFxapQEoqODx9e+\nRj0AK1f6opjk3bvj8E//FI/f/c6NM2eiGdTqahFJSQoTlHHokDtqFeDoUQFz5sh44IH4cbGu8+bR\nfepHPwo30Wr+1Nr9znhPTUlRxsUM5+UpUUE0Mc/eW6timuBbrGIzvPFXbKxGLw24dncT6Ozruxfv\nvss+PCJv2jeSPIy2pBgJqBMTFaxbFwa19fXhhpdly/yjJjtFuhU4HGT/ZXzwm0xqlGxCe5/DAZSU\neDFhgoqNG+366zZsYG2cjh2LBIZSaF8kX3A4WO2xw0G+rNOm3QtJInBXWhp+0Guva2sjqytJ4nTX\nAmOzlsOh4oknwrZiDzwQhMUCjIxA9+Ldu9cWYgzJwk0QqAmPEsGgyyCcThVXr/JISADOn+f1iUBz\nszHUAPoxWiw0ATCZqGFp0iQa49tukzE4qMJmo8+6d68Na9cSGDc2FaamqmhtZR/ekaAoN/fbyMiQ\n9MmPw6FZWNGEJHL5WktnS01VUF0t4uxZYknb2th9arpSQVBx5Qr7t74+HrffHtS3uXBhAFlZCjZv\nljB1qoyuLkGXEAwO8uA4VR8rgJoNBwao+W3yZDXKgq2ri0cwCMyZo6KwkPS+kW4O+fnEEqalqXjo\nobB7RmOjiNWrfeA4Oj+BQNiay2pVIQj3MJ/j+vWwFraqyhoKPjHB6VSgqnSuR2O0jQl3hw+7cfEi\nOVzMny9j3jwPHnvM6LYQBpgcHUJo8kFe1sPDQE4OYLcDbjdgtVLa3po1FKt99iwB/4GBsBXc1avR\nnxEg3XBFhQfZ2QpsNgUeD034WLmIjKtXecydSzpx1uqQh+Y9ffYsj2CQbQQNBMgTGQh/HzVGWJbB\nhGA4ndDjwyPvZWMRAaoK+HyRkwYblizxY84cVScKjGSA0bpuLHZ33jz5hitjn6Viz72bWzEmOFax\n+hsrDbhGxoYal17PnuX1h8D06TJcLg8kicOsWTJ8PuDYMQK1Fy4IUczxiRMCfvADVlOrpVj19YUf\n4tF+pFzoX9qOppmcM4eVC8yZE0RcXDQ493rpPZMmkTVZe7uA557z6jZss2bJYwLDkREOM2fK+lJ3\nMBhtPcVxKpYvj0NqqoK1a73IzZXR38+josKjs30aENSsupxOFVVVrPShvZ2OW7MVi2SmNZZ0xQof\nurvpwXnhAg+O41FVZcXWrQS8li0Lg/+aGhFLl8br/9+wwQ6fT0VzsxutrZSCVlQUXtKeNk1GYSE1\n9EkSp9uqmc0qDhwQ8dOfhsHUpEkqLl0Sopjcri5WS1tQEMTgILGNg4PcqHpWq5WYr9Wr7XjhBS9+\n/WuSdPB8uBnu2jVeZ0m1lD9tG14vUFxMDYDaZ9H+lpREevG6Okrfy8gIW4IZAyy0ydb+/SKCQeCj\nj2i5ffp0GY8+Su9pbKRGMqN9Wm2tiGXL/AbHBhETJsgAhCg9eHc3uUQkJyu668TevTbdmotcPSJl\nKCwj393N6+EQzz9PevWaGhFXr3JIT1dx9SqHHTukKFs/j4djpCGRIRrG5XeHA1BVFcXFXjidCiZN\nUvDUU6yVYGoqh85O0o4XFvp0fezFixQ73t4uQBBUpKay6W/79ol4/PEEfeyOHxcwdy7JlyJ9kwsK\nglizhhpily+PizpXkUzyyAh9X+neQuNpMiHkac3jwAF3KGBlhGn2rK4W0dUloKrKis2bpSjWdawV\nr5YWIUr7PGeOzIBVIxlw/LgwLnaX54G5cxUAMfb3Vq2YJvgWq5jeZ/z1VR+rLzJeE4gEkf8Kp/Pr\nUQzTO+8I+Na3ZMhydMf5f/kvcYyOUHtgyDJ0rR5AD1mO05ZigawsGW+8MYwLFwQkJ0cHK5jNKhYs\nkLFzpwfJyQrOnqVu+F//2o3LlwXExamYMEHFu++aorS0WqCAJieoqiLGqrubvFo7OnjGkWHjxjAw\njHwIDw/Tg6m5mRrtpkyh5hpavn0TK1Z8HZLE4Ykn2HhakwkoK7PpIRJmMy01L1/uQ3w8wHHA6tV2\nrF3rhcvlgSCAYbva23lUV4uwWBAl27h8mUd5uQSvV0V3Nwu0Ll4U9KVuRaHOfKsVOH+emtYAFUuX\n+nRgNTJCLHxnZ7QesaeHY0CY3a5AVU0wmdQIL2W6flgtLUksampE7Nxpx/DwHxAIPKBv1+3m4XBQ\nvPG2bRK6u3kkJnIQRQ7PPBMex61bJTQ2uuH18rh2jZbeL16kyUVvL4/iYi/MZmDnznAKWiAAPUa3\nsdGN5GQFra1j22ppk62eHp6ZAETacl27xqG01AtBYJn+wcHoMIljxwTk5wOnTwuMhIFS+8h2rr09\nzNLX1oqw2ehauXjxLZSWLkR8PMlGKipsIQcKahS7cMGkg1O7XUVDA3lSB4McRkZokrh6NU1oIr8L\nRnu3yBANo6dvSoqia1gBQBTZ9w4Ph72jXS6yBCwqCq9kdHYKyM1V4PGQC0Tk9TNpkort2+k9u3eT\nUwjPa24l4eunro5kIEafZ5uNWO3Ll3k8+ujv8f3v3xUF8PfvFyEIrB3dgQOiPtnUtnX9Oq2CVFR4\nIAhslDJ7P2TZW+PvnU66B/32t+Yx78tftg1a5LPi+vU38eSTd93UZ8W/54oxwbGK1V+pvsh4TSBS\nx0ZLuk1NYgg8kC61t5dnEpYAI2MbqSOkB8bp02R3FfmQzcykdC6Ax7lzAhYuDOIf/zGA998n0Dc4\nyCM7W8H587QEumaNPSoO9vBhN/LyZPh8HB56iMZk506R0RtLEskIyKA/2mXi0CE3PvpIAMBhYIBD\nebkHLS0m3HYbBVO89JLEMGAHD7rxyisEpM1m0owKghpyYzD6rmq+sCMYGSE3guZmt96F39bG61KH\nyMS0SLbL7weeeCIBO3aw0bctLYLuyFBa6gXHseM7Z06YwdRAcyDAprK5XHZkZsooLPShp0dATo6M\n+HgVFy6wjGpyshqyIQMADkVFjpC9m6BvY/lyP+x2so1ra+NDkbbWkHMBhUkMDRkb0RSkpCh45JER\n5rxS81qkkwbQ3i4wIKepyR3SsIYb6TQAtXmzBzxPVl9OJ7kKPP54PBOAYAR92mQrJSWsS9bS4MrL\nPUhJUTFhgoLt2+OwbJlft50bHgYyMmQkJ3OG7QGdnbwujaiu9uDsWQH5+cFR09XCUdJe7NgBcBzp\ndLOzyYItJ4cAY1GRjxmHujoR69f7os61NtmK9PvVwle013EcdDZ+xgyy8+vrI3lIfz/HRGK/8oqH\nkXpEar337rVh3TrfqCsZjY3UBJidraCri/Tw8fEy8vI4HD8u4Ic/DCAYBB57LD4qoEYD6UbpkKoC\nJpOK/HwFHR0KJkxQo5pGNSeYyN91dfFROl2Ph0NxMTtpH/1+SK+fPl0ONeqxx5SVpeD++8OSl9G2\n9WUnskU+KwTBjnnzhJjDxE2qmCb4FquvMrP5ZddXfay+6HjNMFuxAHl5HphMqq6TjTwG48MhHEwQ\nXqLUlvv6+nisXx/2p83PJ/uiyIdlfb2I4WEOzz4bZl6zs1VYrQhpXyXdyaCy0oajR824coVHYaGD\ncRBITlajlqV37ZLQ3k4Pd83CTBs/v5/T2eGeHh7JycSsbd4s4eGHE6LcCa5cERggnZsro65uAVQ1\niI4OFmQEAkBOjoKLF3nGjzbSCUB7vbFRx2SiMVm7lsY9LS3ah1Z7rdvN4Y03zGhqEkP+ugrc7mhm\nMhKkO52ked28WdLZypISO5Yu9WHOHBl1dZRMJknERD788IjO+CYlKRAEAlYulwdHjljAcbQkffUq\n6YDPneOxbRstyXd08KHl6e/h4EE3Ll0SkJJCHsB2uwqTiT3W9HT2s+bkKFHXvWZpFwnE9u0jN4XM\nTDYJra6OJgCaM0NfH48ZM2RUVEj/j713D4+ivPvGPzOzu9nshnDKOYEEEIQSlEdoa6tiWy/faq+3\nr215bdGKqLXyloiCCYdEW35JCwGSgGjBhzY8CQJJEGhf3+uq2vZqqxZ97CMiCDwCiZCQ84kcdnb2\nODO/P757z849E9QqKtbc/2jY3Znde07f+/P9HGKcS+LuNjQQB3PbNhnRqIDUVM3W8t68WYktlhSL\nKFDh2vi9veQgUlzMLOEootl6PjG7MhZl7PMBhYVf4xZqNTUy1qzxoKAgZBNUnjjhwPjxvG/z+fOi\n4UCRmqqjpISoE0VFQdTWMtoECepSUwGPR8PChWO4/U2YYC08dSQnE12pqkpBT0+86O/uFg0BoxW1\nbW2l89F8/h886MOFCyImTqRFRzjMh6qwgJqcHBW7dskIhQTU1MhoaiLrPL+feNJZWRrWrr0eANnp\n8eeMaiz2WOGek6OhsNDD0ZBWrPAY39VM97LfD+mep6oCbr89LoZjYRqdnQLnHtPfTx2YzxJ5NV8z\nqvpNnD8vjxbBl2mMIsGjY3R8RuOTjte0ohWaBgwNRW37ZA+Hc+dEpKSQ4nz/fh96ewWjVRsK6Th0\nyIlgkGyQSkrogfPUUzL6++0uAl1dAldgMt5mba1ssxO7/36HEZKRnKwbyJy15XvhAhXgVpTM3CK2\nosN1dTJOnaJiIyND4+Jic3JUHDvm4B54mibgqacScM89YdTX+xAOE+8TIPTX2nrv6yPqRWuraCDt\n1uOana3B5aICsbxcwcWLVAicOUN0hpYW2j4roBYuDNvmyLw9lhbHioLnn3eiokLhEEQqDkQ0NZF7\nBvFVE1Ferth4ytbUM/b3vn0+wyFjJMSzu5tQ4nffJaeB06epWDB/195e0RAl5uSQ+EtV+ffk5Oho\na4v/m8OBmFARaG/nz63OTlqcHDnixP33O1BfL2P5ci8eeiiEaJRipxMS4j7Ql7Jn8/lEvP028ZNZ\nNDR7rbtbMASVtFBLxFNP+bFhg4KODhGqCuzeLUMQ+N8xZ07UWNg5nRT0YLUZ6+qiY012avzn8/Oj\ntm3m5WmIRoEDByjJrqAgiOFhih4eHhZQVZWIykoFsizA69VsjgynTkmYNy+KfftkNDaKmDFDQzAI\nFBXFr5E9e2Rj0ZWbqyIaBUf5Ye/LzKTkRrNoMxDgqQt2waYWEx8G0dMjIi9PRUuLhKQknaOQlJYq\niEbpXjVmDM+bjkQEzmGjrk7G2bMSdx+qrPQb19fwMDB+vI6TJ8UYH3fk++Ef/uAwfosgCBg7VjO0\nFFb3mM/a2/eTflZ8kccoJ/gKG593nuunOT7vc/Vp8crYPIkicMMN9n3qJPBGOAycOSMZD6aaGhl7\n9rgA0MNlaEhAbq6G66+P4M47w9B1ICVFx5gxVLhGoxSaIAg65szRMDhoDxiwFgWM5+l2I5YMRS30\ne++12zClpNidGurqZJw7J0LTiI985Ahf1EYiJKjJy1ORmqrhxAlqfz7/vAurV5OobtMmBY8/7on5\nB/8FW7Z8BY2NEiZNEjjUq6FBhtcbtRRwGn70I7LFYsVjXp6KhgYfjhxxIDmZQiU2blRsFBBmZVZf\nL2P7dhkZGUSrsKKpZ87E0+euuSaKjg6R205dnYx33rHHSk+cSEUUtYoxIrpntQJraYmr9tmxsn7G\n5yOf4NTU+XjkEV5UtmaNBzU1JF6bMEHHwICAHTvcWLw4jKIiDw4c8CErS0VDg4wjRwi1ZlHP7DfO\nmxc10N+qKl485/HoBjIaDhNSai6Gqqr8XDAIO++sLe/kZA3Z2cR1TknRLMWoGlv8kYPF0qUhDl1l\nCwWGIDK+L+Mt19YSfzwxUcfw8CtwOm/nOgoVFWSvV1zMJ/6VlHiwZYsfdXXk25yermHTJjeOH3eg\nrk6GqoKzlKutlWOi1Lg7i5kmwqgcFy6Qx3Zyso67706yLQja2uKezuz3Ebc9yBWjPp9gc6moqlJs\n5w/rEGRmkpixvDxOQxpJxFhS4oHPJ+Kll17FddddD0URDMrF1KmqzUXk/HmiIJkXtF6vbru+6utl\naJp2SQTX6mN84AApdufOVW26h8vdpftnh/lZMTT0CubO/fpn9l3+1cYoEjw6RsdlHB81XvNy78f8\nene3iKEhBzIzKULXuk+zi4T5wXTqlIRly6j9+8ADcaHMo48GbUb8GzYoiEbBqbVH4m1avWLz8lQI\nAomOAAGKoht0AmbD5HaThZjLpXMt0XBYwN13J2HfPhLOVFQkYvnyoA3F2bhRsSGltbUyfvQj+2/+\nX/8rYjxIrY4aR44wxTsVPhkZmsFfNBeKzc0Szp3jaSenT0sIhfhikiXZMT/kFSviqLm18GNcx/37\nfRAEvkju7CRKgJW+wT5TW0v+qnV18oiuGOa/zVHT7DVrATlrlooHHgihrU1ERYWCCRN09PTQ93E4\nSCC4apXVoot++9mzUiwxjeayoCCEu+4KIzubFk0zZuiQ5fjvczjAFWIpKRruvnuMIdSzFn0ZGRou\nXLBH8m7fTs4bzMmBeLKJxiKModUkCvMYCzqXC0hLoyCVtjaJWziwln9VlR/FxXHOLSX0CSgs9GDs\n2ASOG7t9O8VlT5+u4le/UmKBKAJWr/agrU3Cm286DXT6xz8eY2yzpUXE0BB//jDuMeNdDw8LBhqq\naeTlzBxHdD2eqmc9ntnZPAXjwgURBQVB+P2CsbgAgC1b/PD7+e8wfjx//oRCQCBAXHMAmD8/gnvv\nDRufYZ7RDEnWddYB0eB0Ero5YQJw++3xbkR6ur2z0tXFxxuXlys2odxbb0kYN06/5P3Vyj3u7RUB\n0H105swrC3k1PysOH750YT86/vkxygm+wsbnGdn8tMeVOFcfRez2UVwi3m8/qgq89pqEO+9kr38H\nNTUyHnzQi+pqv+37jCSMY8irx0MPgkgkLpQZqbXc10etb/O/s7Z/f78Il4u4wKoK1NURbSAri3w+\nExIwopUYs2HaskVBdrbGFa3MKowVgaoKLF8eRG8vRd+av4euw0ataG8XDcRY00hM9POfK5gx4wa8\n+CIVPNZ2dXIyuMInEsElC0Vz+zIvT8W//VvUsH1i78nKogdrNAquiGYewt3dIqZMoXNhyxY/cnM1\nPPaYNybkMwuCgM2bCYE9dUrCrFmawR1l8/Pkk4Tu//rXfgNJzcvTUFvrQmlpAA6HzkVNOxwkNKqt\nJX53QwN5Gk+frsZcAG5CVpaGQIBf+DQ0+HDsGB9q4XIBTz6ZAKdTx4wZFJ2bnGyPWi4tDeCRRxI5\nmktXl8AtJmjeBRw65ERNjYxwGIaAj6XOdXWJMfGaiPx8Ffv2yWhrExEKCdi6NQGLF4cNWzIARixx\nRQVZcf3qV1REmn+X2SnFunCwcrwnTIgv5Pr6bkFJCQzxIltoLFw4ZsSgGEqA85kWM/FFjd0CMN4Z\n4f20absnTzqwdGkQbjddx/n5fKy2y0U896QklUNVJYmux7o6Gd/9bghLloSNcA6Ph/8OFy8S8n3y\npMPw2F29Oh4Es3Bh2OhCsGvB2sXYtYsWaV/5CqGbc+eqeOEFH86cEWOLFBdqaihsZto0DWlpqq2A\nFUV7MmNyMt4Xwb2UUI7dh5nLzafh/vDPjCvxufd5HqNI8OgYHZdxfBSx2/HjEh58kIqbc+dE+P1E\nW3i/Qvj99nP8uIR//IMvRM6ckbB+vYITJyit6v2ikWfNIisySdJjfrwC10ofqbWcmakjNZV/CMmy\ngPHjyeO1v18w0tXMRc1vfiPD7eZjlM+elQxkTlEEbNrkxs9/HuAQpAsXRLS1UQtYUeKoZ0WFYmtv\nZ2by6KDTqWPatHhqXFlZwMKnpYJn584E1NUxriTvxRsOC7jvviTU1fmMqGIm1AqFYLNr++//lrBz\npxtmQeGqVR6DDykIvDips1M04pr9fgp46O4mnrWuAzU1JHZLT9cMFHHtWk8s9QxGSITTScdq0yYF\nJ086MGGCjlWr4u3zhgYf2toInTVzg7OzNaxZ40FGhoa1a4M4f17E7NkqhobIHeLsWRF3351kCyjp\n6BAxd26UK6pmzoxizZoAMjJo3gIBQvIfftguLKPfT8U3+TKr2LZNRleXhORkDbNmRVFVRfxPTWMt\neAFOJ3DhgoiuLiqcXC4dX/qSis5OASkpdA6yotbqJpGeTugyGz09IhwOnnpDhbwfgQCwdaubK/xY\nKl1vr4iEBD3mYsHvY948FVVVfsNpIxIRkJREyXgs0S4jQ0MkAnR2StiyxW24ULDictmyEGpqZHR1\nkcPL9u1uYzHFvmt6uoYpUzScOUPuFS0tZEsmisCaNR5s2+bHuHG6EUG+aRPZmllRVXYs77svbEkv\nlDnruooKQraZ97PTSdwqc5pjRUXcb9qqH2hpoYLT46HF+7Fj8SJ00aIIXntNwvHjDtxzD3kRHzzo\nw+zZOkIh/l4TCpGDB1sImp08LjUuJZQzAwsLF0be9949Oj7/Y5QTfIWNzzvP9dMcV+JcfRQBw/nz\ndkHXByHIVqQxLU3DoUNOXHWViv5+AbNmxV+XpL9h5sz5BgLD4ox7eujmf8019DA4cUJCMEht4rY2\nCU895cfwMIzQhJycOJLEHsbkDCCgsVHEjh1uLhFs+3Y3HnssiFCIitnMTBX5+fzDy+vVbdSKyZM1\nCAIVch6PjpUrg5g4UcfDZa7d9wAAIABJREFUD8fnp6FBxjPPyBg7Vsfq1VScpqdryM7W0NhID8PO\nTkqeammRsGMHUSsCAeCaa1R0dAgGYsxzXl+By/VlgxM6MEDCn/R0DcuWBeH1snY6FaCtrRImT1Yx\nZgwtEiZN0tDVRYr9wkIvmpslFBcrAASOu1pcHEBbGy1IkpKAMWMo9vf4cRLLORzgCvPdu2UkJFDR\n5HaTwGrqVEpHYwVvdzch4mvXergCyuWiAhGg/zLruJkzVXR2ilAUAbt3u1BfLxthIozH3N8vorFR\nxKuvOnDPPWH4/SKGhoATJw4jEvm2DZ3MzCS7LnNRtX+/D7IsYNWqRDz8cNAo6KzOEWxxlZ6u24I4\nyssT4XSSiMssxKqpkVFQEPchrq2VIYrEt21ullBe7kdBgcfg7zL+OrMQEwSgt1fkbNJYEpkViXU6\nEbPPikAUwRV+nZ0i1q71oKFBxg9+MAaVlQpKSxW8++7fcdttN2BgQDAWUmzx5vcLiEYFDhmtqZGR\nnk6eyR0dIrePvDyyvQuHNbjdwC9+EcCECTra2+MhHQUFcaqS2TFk/nwVDgcwNCTi0Uf5sIq+Pn5B\n3d8vGotLsx8zK1p/85sErFlDiY2rVgWRm6viuefIJSInR0dTE1E8nnwyAU8+6TfEfGSjZ6diPPoo\nLQZ/8YsXsGvXbRwY8NWvqjhwgDzEp05V8bWv2ePck5N1FBbSdVVUFMScOSouXhRQXe3H3Lkq12lj\n8e2ZmTrmzOHvrx82Be6zHlfic+/zPC5LESwIwm0AngQgAtil6/qmy7Hd0TE6Pi/DfKM9eNBn3Gg/\nTBttyhTNJlC61A3Yup9QiAqmN94gEZaiAEVFXs6ns7k5CAB4/PEA8vPJN1SWiS94/LgDe/eSjdKU\nKaqJQqFj3DhCaHJyNCQk6IY3LoAYPxIGr7KsLAAAMS/W+IN70iSNK+Z27ZINdDUvz/673W6KYH3n\nHSrGXC4da9d6bIjjiRMSrrpKRUtLvAgsKIh7rF5/fQSrVgVx5IiE/HwqAEpKPCgv9xvvYaIrM7JN\n4QnAnj0uFBQEEQgIhlCMLJ8UPProGKM4C4UENDZKBqJsLjBqawkdnDSJPJKt6DkAg86QmkrHbuNG\nSqxbsSJo+b3E/6ytlXHfffGir76e+KyBANmDdXeTUGxwkBDP4WERubk6HnnEayp8FM6XeN06CsGw\novRdXXEaRV2djKoqN5YvD6KrS8SMGVT8trTERXts0XDuHC9kam2N+zo7nbpRFLlcxNf2+QTMnk2x\nxoSwWmO0437VVmEli8dlf588SY+0aBSxCGbesuvZZ3222ONNm9yGGJP9+7PPyti2jZDbCRM0jBtH\nc3jXXWHD8ovFBofDZNkWiQhG0VhRQYW+le6wezdZtg0M0HseeYQ/zmfOSJg8WcO+fRQiUlNDVI7p\n0zUcO0YLpJ07E1BZqSA1VcMPfxi/XvfsIVs4tj1r8l1Dgz1gIhCADRmfNUvFrl1+lJQk4sknFQMt\nLygIwukkW7W2Nl40WlsrIztbR1sbiVS3b08w+OE81cnHcbzJdk8yzreRwIAFC1QsWHBpn96jRyUj\nUW/VKg9efNGH226LGu8dSfPwwAOJOHjQx8W6Hzjg+6cBjNHx+R8fuwgWBEEE8GsAtwDoAPCmIAjP\n67p+2vy+UU7whxujK7wPP66kufpnucBWHvDXvma3LrvUfszUifnzo3jsMa/R3t6zR7bZ/txww40W\ntJW4l4xXGwoJ+OtfJVxzjYr6el/MZikeqNHQIHMtUTM/srpaRlISKfwLCkJ4/HFe8T4wwKMrTieP\ncNbV8cKm9HSN+66sNevx8Pzc6dNV9PURGrp/vw9tbSJ0Pb6v5cuD3Heuq6NiQlXtoitdFwwqQ1bW\nfHR16diwIYCf/MTLzRnFu8L4LYzrev/9oREQZSrQJk3S0NMjYOzYeFGcm6tC02CgzQwxlyT6Pjk5\nOtrbeSSS8T+tReCFCxIEgRDFCxcIlXY6dUSjVHxQBDQvfDIXlXEKgmjjQEciwLJlIezYkYBIBHjk\nkaBR+Hz3u7egoYHmVFGAPXsS0N0tYvdu2badtDQKOhkeFuBymYNEKH2vo4MS1+rrXfjBD8KxcJOR\nFwyTJ9tFUvb3ChzVxfy6lUt6/ryIRYvCtn9/5x0Js2ercLmIIwvo2LBBMSzMGF/dem3k5anc61VV\nN4+4mCktDXCevOzzHo+OhAQdb7/tMHjL5eWKjZIQjQLt7fxioatLNLo1dD7y3PgjRyTMmcPP7dy5\nKlyueBw1W9gWFATR3S1i1y4X6urILs1c9Jpjmtm+rcEfXq+OoSGBozqdOydxwR3UJaE5veWWG/Dm\nm7Adnw9CYz/IZedSYUDWxVp7u8gV6A6H/r77/azGlfTc+1cYlwMJ/gqARl3XWwBAEIQGAHcAOP2+\nnxodo+NfaPyzXOCTJ0W8+SYhZH19Am68MfKh7NJGok4wZ4NIhERg5tf276dW4kgPgY4OMVYsUHLW\nO+9Q2zQcBvegsrZEzUXU0JAAQENpaQD9/YLFQ9hvKLsZkjSSQM2MDLe28oVkWppdzONyAUlJOrq6\nSAE/NEQpbenpGvLyVCxfHkQ4DCNtLidHg9erIiODWt9VVf6YgIoXXRUXK0hJEbBiRRKKi3nk2e2m\n4sPMC2bxwtdeq9oQZSpEBSxenIT6eh9CIcEIsti0KRGrVgUB0EPW4QAmT6ZW+UMPhdDVFaegMO4l\n439ai6bMTIoQZkXo//2/w6irk9HXJxgFYEoKzUtzs4S8PBX5+VEUFweQkaHGQiBISNXbK2DPHhnH\nj8fpLIsXh7FyJRW/ZkHkokU8V5TREHp6ROzcmcBxn8eM0TB7toZwWLQFRLS0UItaFIEf/pBcIsj/\nloqjtDQNiYk6nn5aRkqKDq9Xw+7dsrHAAEgsN368jsREKj4VRUdSEnNjSOB4olYf3uxsij1WFLsI\nsqVFxNVXa2hvFzBxIqHeXq+G+nriUaemaia+KyGTQ0MCh4xbnQ3YYsbtJrTZ5wP27KHFRHY2uY0E\ng0LsGJETiq7H+cnp6cQbfucde0E7YYKOs2fNXHS7UIzFRbPv198voKCAR6rLyxUMDAior6cwDlW1\nC0tDIZr3vj4qGFmgBXu9rY2uO6u48KqrVDz7rM+gosyYoWL9ej+mTNHQ0iLZxG2XAgNGEhN/WAEc\nu06nTuX3lZKio6Agyfjcb38rcz7Do+Nfc1yOIjgbQKvp7zZQYcyNUU7whxujfJ8PP66kufpnucA9\nPbzFz969Mm69NfqBqMdI1AkfMRTgdOq29nBrq4TBwVdg9iplD4Fp0zRDbGUNmLAWWpdu5QvIziZx\nkvV9kyerCAQEbNniR1aWjkWL7N6/6ekkWnM4gCNH6CH4zDMy1q8nmsXYsRr27KGiJz2d1P8rVwbx\nv//3GKOw9ngAXSef4/JyxYi4tSLBZoR5zx4ZTidf+Mybp+I///PvcDpvtxW0oRDF+m7eTFZMkyZp\nEEUdmzeTT2t5OXkc19fL6OwkKkxPj4CNG6mYM7ela2tl23cbGADWr1cwPCwgNVU3WsnRKDBjBtEj\nSAAFA7Xz+2GI61hbX5ZF3HMPxQqbPXypEHTguuuiBhJfXu7HvffyNImUFEpDu/baqJESl5lJFmHm\nOXn11cOIRG43zrP2dhHTpqnIziZR5eCggKlTiR/83nsSsrI0VFW5UVgY5OY1L4/OJet8NDVRMc14\nuvPnU3u7vV3CuHEaMjM1qCqPTj73nA8TJ2oQBHIeYYX/E0+QYPDCBREzZkSxf78PTU0kBnz6aaIt\nVFQkGsXh7NlR+HwCxo2zcpMDKCry4tlnCYk9edKBN95w4o03nACoKJw8WUNZWQKiUWDlyiAOHz6M\n+vobcfEiicLYYobRmLxe4Nw5cqcYGKCUxaoqP8dzNrtlmDm/27bJHHI5MEDdH3MCIjsfU1NJWBkO\nCxAE3Vg00cIujtT29YkoLOSjku++237der069x0bGngqgaraqSpJSUBrq2jQtQoKgjh3TkJenoaS\nEg+am/+OvLybUFMjY3BQwMyZlwYD/pnOmxkpZpzgF1/0GVoIVkg7HHaHlytxXEnPvX+F8akJ4155\n5RUcOXIEkydPBgCMHTsWc+bMMQ7m4cOHAeAL/zcbV8r3uZL/PnHixBXzfWT5FZSXixg79makpWn4\n618P49gxHfPn34jGRglDQ6/gqqs0LFhA73/ttcOIRBIBfAORiIDXXjuMxMSobftf+9qNOH5cwksv\nvYbsbBX5+QuQmanhpz99Eb//vQtDQ99Cfr6KpUtfhKYJAG6K3chfgSTpUJSv4JlnErBkyUvweICb\nb74RZ86IuO++P2LZMie2b/8KZJneDwCRyDfQ1SVgyZKXIAjAt799I/r7BTzxxAvo6RHxrW/dCF3X\ncffdf4TXq+PQoVvwyCNBHDlyGDNmRFFXdxMiEQGvv34YR47o2Lv322hulnD33S8hEnFj+/abUFoa\nQEfHK1BVoKdnAfr6BIjiyzh0yIXk5K/B5QIefPCPEAQdirIA996bhLFj/4rvfz+Me+5ZAFEExo79\nK773vTA8npswcaKON944jMFBHfn5N8LpBP78Z35+//pX/u/Dhw/jwAEXSku/Bp8PEMWXUVCQgJ/+\nFGho8OHw4dfw+OM6xoy5GeGwgKqq/0Rfn4Tm5i9DVYGTJ/+ODRsSUVLyVTQ3SygqehMpKSqqq7+M\nCROA3/3uNXi9wJ//fCs2bFC4+SVKQ/zvo0cllJf/F9LTVWzf/hX09Ai4774/4oknEvGrX301ViDS\n8dy9ez4SEnS8++6reOYZ+j05OSqOHv07rr9egKbdiPR0DS+99BoiEbfxe1944XXs3+/Cpk1fiRUm\nL+PEiRAikW/HvscrOHkyBLf7RlRU+DE09Cr+8AcRc+YsQHGxB7fd9idUVblQU/MVtLSIaGw8Dkly\nQ1W/CadTRyDwCl5+WUBW1gJs3+5GJPIyHnwwBE37JpKTNbz77qu49VYRHR03o75exuHDhyEIQHPz\nAgDAfff9Eb//vRN9fbego0PEe++9gltvFfCLX3wbkQiJO++/P4jq6tvhdOp44okX0dQkIhK5zfj+\nf/tbAM88c5vx/jVrAtD1b+Kaa6J4+eXDuHhRRCh0I770pSjOnv073ntPx513LoDHo6Gz81WUlAhw\nOun7LVnyJn70ozA3Py0tAZSV3YzBQQGK8jL6+kQ4nfH9nT4dwtq1344JDA9j9Wo3VDUR//7vSXjw\nwZeQnq5j8eJvIjlZR1XVG/jhD8N44YX/geZmCZL0N/z85wHU1d0U47fGz4/jxyUsWfIS3G7A5Vpg\nHL9f/lLFtm1fQX+/jhMn/o7f/96FpKRvoL5eNs6/oqJb8dhjQZw58yrKyhKN41VS8iIEQUdR0W3G\n/u+/P4iUlBsRiQhISfkLvv/9CC5cuAllZQHU1LyOwsIIBOEbSE7WbefXK6+8hlWrdKSk3IxQiK6X\nO+8Mc/PT3R2Apn0TkYiA22//M554IsH4PkuW/BHV1afR3PwNnDrlQCTyMiZPjkIUR77f0v7j1/P/\n+3+vQZajxv3V/H5dB44d+zu6ukRMmXIDbrghitdfP4w33qDXyXv3MDQNePHFm41AClnWAFwZz5fR\nvz98/XT48GFcuHABADB//nzccssteL8h6PrH470IgnA9gP9P1/XbYn+vBaBbxXF/+ctf9FEkeHRc\nKeOjePN+mGEXYcT5swcO+HDjjbQf6/usSAb7fqdPi/D5BEP5bUaPd+2ikIjhYQFpaaSQXr48CF0H\nsrKIy1hY6DGEJ8XFASQlaRBFwWRWryMhAZboUx+OHHFi3rwoKivduOOOCIaHqbXd0ODCffeFjXnr\n7xcAUPu5rY18PAsL4xZcjKpBcb1xhIohtqzVz5K2rIhpVxclgzGBnHleGXeW95ol5HXGDM0WB8xC\nKYaHyVN0xQp+bsrLE1FV5cdVV0URjYqGqI6lyeXlqaioUNDaSvZlZ89KmD2b7M+Gh0Xk50ehqlZ/\nWQr7sMY9m79bWVkAxcX8HDFfWfa92NiyxY81azxGWARDdM1zUF0tw+WCTeilxYAtNsfWz9XWykhM\npAADc0wto2X094uYOJH4xc8/78TDDwcN71brMSdBVOIlf3N1tQyvFzakdd26RJSVKZg+3W6nZ56L\nDRv8uPpqjUOQKYXOYaCaK1YE0d8v4pprorj33iSuc5CdTWLPkyfJuu6hh0Lw+Qhx7ugQsXx5Enc8\nnE4S8YXDgNerw+kE8vKiGBiQ0NVFHsTbtyegrU3Cli1+9PZaqTYBTJyocclszFpvx44ErFoVRGqq\nFptPFStXxnn+7Px45hkZqam65dxRcOiQCytWxGOJu7tF/Oxn8bb+tm3+Eak/c+aonDVcZaUfTidQ\nVMSfX/Fjqhs8c7Lci1uRVVYq6Owkd5QVK7zc9XL0KB0Tj4ccJ5jXODuWOTkqNmxQ8O67DiQna/B4\ndMyerb1vV8x6/ywrU/DlL49Mifige+3o+NcdR48exS233CK833suBxL8JoCrBEHIBdAJYBGAuy7D\ndkfH6PjExkcJtfgwwy7CiPNn//EPB5KSiEPqcBAFord35Laf9fvt3Suju5vnyzY2Sti4MREbNyp4\n9NFEbNqk2OyWzH6x+flRuFywJaclJOhcW7W1VTQsqWpqZNx/P19M8iK5AHJzVa4tzQrf9HQNOTkU\nQety0SKgp4fidK3Fz44dCRAEcK3ZkyclI2CACeTYb09KovYxi8W1znd/v2aEKOTmahg7NorKSsVm\nvcUWKKzVn5WlQZZF2zz294uxtDLefqq5mYroPXtcWLyYooqtVJW8PM2wZ5s7N4qeHgpzGBwkznNx\nMRUnZiETE5fFbcOogHM4gLKyAA4dcqKiQkFamobOznjUcVubhKYmCddeG0V1NX3vyZM1aJqOe+8d\nY7iGeL0USbtxo2LwOnt7RaxaRdQB62+YP1/D0JCAKVMo7c1KA2DzQO8XbD67LS38cTp92gGAf4/D\nocd+hxsrVgRx3XWXFsh5vQBAAq3eXgGCAJw5Ez9vS0sV5OXFk7VYMIq56N+zR4bHA47H/vOfK5g7\nl/Zr5qFnZhJ32Cr+ikYp4td8XmVkaEhPt3KMyfavtDSA8eM1pKZSAT51qopf/CIAr1ePRXoDK1d6\nDfpGKBTng7OFLuMgs4UcQPZ4DgcQCgmcOM7p1JGaqkFRJBs/uLeXdyxhdofl5YotldDh0DFtGolQ\ng0F7nHhTkwhNE7BiRSJ+9SsFTU2S4USTnx/F1q1u9PWJ2LnTh4YGCjkxUzzMC8eDB30f6KozZw5R\nPc6dIy711q1upKSERryHfxTv9tHxxRkfuwjWdV0VBOFhAH9C3CLtXev7RjnBH26M8n0+/Pg4c/VJ\n3RjtIoz4g5slGAHAE09QxK+iMBU3cOpUHJm28n67ukRbCMTcuSoqK/3IytKQkaHZxCsXLwqor/fh\n+PHDSEm5GV1doiGKY+8hSyndhlqx1628Pmsx4/PZHQsYR9n6cCsvp6LNKo7y+ehByBfSFCDB3mP1\nlM3K0qBpGEHQRPOdksLzTHfvJlSZFUPDw1TQbdrkR06OhpYWQqKXL/8v/PSnX+O+36lTEjIzdTQ3\nS4bzRn5+lCuUGfppFV7NmaOitVWE10v81/Z2Cr9Yv57Q7/JyBQ89FILHQ3ZyTAz1/PNONDT40NlJ\nNlm6DjzwAL+/QAC2xce6dYmYOVPFXXeNMdDeu+6Ki9qYVdjmzX60tRHKTkOAotDvnTCBn+v586MY\nP17FzJkUZjBvnor09L+gu/sWjMQZnzVLjaGl8X/LzbWLk9h1YS4e29slLnqZ0F2a/9xc1ZifaNSK\nVvPnC1EB4uh0RYUf0Sh/7vf0iLbY35kzVRQW0kIAIGFeUpKO9esT8c1vRrnPM6eHX//az4nNmpvJ\nM3vjRgXnz7+Kr3/9Rsgy4POJ8PmAq6/WbW4P1kVhSwsVtboOLF4cRnKyhra2uPA0J0fFnDkKFi8O\nIT+fT2HbuFExQlDS0jR4vTp27kzAvn0y3n47jt6uX68YC6JoFAgGgfHjNQwMUGHJONVOJwkIz5xx\nwOHQMTDAX+9HjsQXq6WlAZw65UB+ftTWiRk3TgcgYtEiQuWZYNHpZAX3y4hEvoGeHhGi+P734hMn\nJNuC9lIc3o/i3X4lj9Ea4fKOy8IJ1nX9JQBXX45tjY4v5vik6AmXGiMpho8elT72fq12PaGQzhU2\nxcUBnDghoagoyN3EGxp83EN9/35eaJKeruHiRUJpRJFM+/v6iAbR2CgZPro8AkSK9g0bEqGqXqMY\ntBYskmRPgAOoQJk2zfoAsUe3Wh0L5s+Por7eZxTlOTkqCgpCMfGP3Ypr1iwVPT18gZKUBGzZkmB8\nD5eLEKdz50j0VFnpRmFhANOnqwZSy5wkWHqYueAVRYpGLikhk//TpyUjuhkgkZLLBSxZEuaCRpxO\nEsyxGGFWbBQXK9z2c3I07NiRgKKiAOrqZBw9SsVGSYkHVVUKzp4VR0TL+/upTb1vn89WGFGRpuO+\n+5JsUdUOhw5R5NE6t5vawi0t8UUGQ8qtQj9VJR9hq3jO6SSXBWtnABC4sJWf/SyE9HRqz7e1kY3e\nmTOiIcx6/PEAVxh2dgqGCwiLN+7rE7FvnxwL7Ihb8tXVUYdk6dIQenoE7NmTgIKCEN5+24H58ykF\nTlX588XrBbZujZ8v48frHDqdnq6juZm/PljcNEN709J0tLSQz7KiCBwdoKaG3C+s534kIiAxEVi3\nzhzk4sOKFUGkpuoYHNRRUuLB+vUKCgo8xrlj/u5W716fj+g8VjqI+Z5gXjRat9fXR84LU6eq8PkE\nHD3qQFWVAlHUkJIiQteBsjIKDvF6dfT1ifB4gP5+4Be/8HK/ububjtfTTxM673AAjY12Jw3zd09O\n1mwL49ZWEd/6VhiHDjmNxdipU2QDV16uxLaHD12kWkGM5ORLe7J/kIXa6Phij09NGDfqE/zhxhd1\nhfdR6AkfZ67YjZFxbgsL6QH8cWgR5kI+L4/Uxp2dIr761Sh6e0UUFwcMc/bNm3mfTfLmjReMLS0S\n6upkNDZSYeHx6AaKDPCUhoYGGX4/qdnNxYsgEL9TVb9p7GdoiDxxAwHa5unTEsaN03Ho0DCamwlx\nGxgQ8PvfD0PTgI4OKnB6egQMDoqxlm48nMHvJ+Swro7slJKSqPAOhWB4+zI7sPHjicLgclG8cXc3\n2TitWUMew3xrVovxNAWkpFArmYUFPP44WYkR15C4p2VlAY4DW18v2zjUDC00B1pYfV5ram7E2rWJ\nKC1V4HZTG/3sWRH5+bQ4YnQNj0e3bb++nri4584JmD8/itZWKdZa1qEofNHmdutGWEddnc8w+2ev\nswIoL0/Fvn0yVNVu7aWqfFGXmakZvF/27ywIgbX2ExJgRPcyf2O2z74+OtbNzRKSkoAZMyI4d05C\ndrbOWdeRm8jtKCsLcEV0fb0PiiLg4YeD8Hp1LFt26XmurpbhcACPPebB4sUhrtgjoaDH+Jz9OBI/\n1bpIrKpSjHNkYICfr95e0bCd8/kEXHNNFKtWeQxkvLiYuhS5ubRdq+fzxYsipk+PGgWz2baOgi/o\n8x0ddI0cPOjCHXdEAHwDVVUK10GxLgIzMqyLSEo8Y9Z77N8lKX59x9FT+/aSkzVMmqRBUQSue1Be\nriAzkw/vqKuTMWGCiv/+bwkAfw4yW7n77ktCaWkAPT0C6uoSUFgYX+gxzjw7566/PoqxY3UjdY7t\nZ+pUuqeawQfruelyfRnTp38wFcK6HULwtUuCF+ZgjX+F8UWtET6p8akVwaNjdLzf+DR5W+ZiFQCK\ni+OeuB9nv9ZC3sw5ZUgE+41W9DQ3V0N5uR8uF0bgHQJNTRJcLiAxUUdrK08nOHJEwnXXRTE4KMQK\nYPJ4XbeOWoQMid65MwFZWRqamiRkZmocMllfLyMcFtDUNLIIr6FBxqZNCXj4YR0lJV6jWJckHT6f\nA1ddFUVysmgLuigtDSA1legGRUW8qC8nB0aM7M6dCairIzsnQEBSkoZ16+ICLqtQi3nQbt3qNsRn\n5jnp7aWADR5hi/Oz2X+tHsg9PSIeeSSIqVNVCAJiQivE0HaPgYRu2KCgq4vn4l64IOKqq6LIztZt\nrfprruELmvR0DY8/TkK9zk5g/nz+dUoN86G9nYqqujoX56dcWOhBNEoLkqQkcHZp+/f7sH+/L6b6\nB/buldHaKhqRtewYeTx8IZmaql0yFKWhId5BYNxleziIhC1b3IYoyoyIWyNpBwdFVFS40dYm2Yq4\n/HzVCBI5d04c4TgK+POfnaivp/nIzaWuyLhxhGIPD9NnmP9uZibZYnV3i9ixIwEFBUH09pJHNhNl\nzpunor1dxJ49LpSWBmwdD7+fuhglJV7Mnx9BYWHQELMNDQlQFJ4ny7j0jMudlxe/3nfuTDD4rNOm\nqRgepqS8/n4SirIYYXO62qxZURw/7sAvf0kFZxw9jW+vuTkeY97bK3D0j/R0DWlphNCaz9mjR4k/\nPn9+FGfPSrbjwASdPh8wZYqON95w4s47ncjJUbF1q4LhYaCykha0V18d7+BFo9oHxh1Pn67ihRd8\nOHNGRGoqXRP5+ZcuZs3j00B3P+3u5Oj4bManVgSPcoI/3Pii8n0+Cm/ro86VuVgtL/d/JL7YSDfI\n9xPFsfexfT39tJtrD+/a5cKCBVGbIEWWyV90eJjQ3cmT6aFrbUdGIoLNmD4pCYa9Flk/+dDRQeIe\na3v9zBkRbjfgdAKbN1PcbHo6zUVBQQjNzWIMuaSCZeXKIFesHzw4DIAXtvX3UwqYOb6W7W9wUMCO\nHcRLbG8XMXWqhosXaXFw5IgDWVmCgVwmJuoGF5c5WuTnawYi/JvfJBioKvs+g4MiPB5aWLC5I3U6\nj1BZuar9/a9g/frv2JwTNm2Kt5yXLg2NyMXNy1MxOCiit9d+HjQ2kr/viROklG9pkTh/ZlY0treL\nmDSJHuhnz5LrhKqa+kb8AAAgAElEQVQC994bwtmzEtxuCi9hrf6SEi+2bvVzCzkWaZ2RQXO0YYOC\n/n4qiJ5/3hmLJnZg2jRy6QBI+GVN9zOfv11dAicSk6S/ITn5q7ZC8aGHKGFu6dIQWluJ+rJ9ewI2\nbVK49+bkaIZoky2A3nsvHg+cnEw81ooKhRNRMRrC4sUhNDaKGB4m8Vhioo5f/tKDZcuCSE8nFNTh\noA5Ce7uIhAQqHLOy+MXfnj2ycS17PDrWrAng6FEHvF5y1HjnnXhwyOrV5HG8cGHEksBIvFp+QUDn\nwPe+9ycAC3D+vGTQdrKzNYOvbD3PampkFBSEsH17Atrb4+lq5eUKUlLi57PHEw8NiUQAQdA554nn\nnvNx3QMrP5+dsxkZOsJhEV1dhI4zAS5xgCUUFISwc2cC8vNVjB0bv1a6u+k7NDU50NQUT1hjRaLD\ngQ+MO2Zj3jz6/8OHDxuWaB80zNtRVeoSXe5i9ZMST3/c8UWtET6pMYoEj44rYnyavC1zsbp9uxt7\n98qGUMq8X3Ohy0zWMzNJ7PTGGxLeeINQwvXrE1FdTalHeXmqYcOVn69i/vwIFi4MIxSibf7pT8M4\ne1bCxIk6LlwgTuqqVR5DuW41pZ84UceGDYmxbZIZ/r/9W9R4AAoC8PTTFLtrfgh7vbCJ2pqbJaSm\nslYkjwLm5WkWoZeCZcuCnPm+00miG/YwN2/b77dyXhVMmqShqio6YkhGaqqOO+6IcPvcvVtGUxMh\ng+fOSdixw42dO30IBiW0toIrjDZtcmPp0hBcLh2VlQp6eigpy+EgvuuhQ0489lgQS5Z4jSKTFPe6\nid4hYONGN0pLFXg8QE6Ohs2bHaiq8kOSgF27/LFWtxuTJl06jtbr1VFVpUBVBQwMUGpfebnfhDJG\nceECFWKVlW5j8WVGUpubJRw9SkKr+nofIhHBZl/GjpF1Lq1RwuPGkcCsocGFqqp45C5ztOjsJDu3\noSEqyNxuHT/84Rjbdhk3PC9PRUaGjkCAAlG2bnVj7doAxo0jGsw77xAFgRLmQrFzmbfXYou+3l7i\n57a2ioarQE4OXQPWqOvycgXvvSdi1iwV1dUyBgdF5OSoBqptDvqorZWxeHEYggB4PDoCAREtLRLC\n4bgFX3U1iwaOH7vubr5DUV0tG1SM+nrZOF4MvWcCS+tiYcqUqPGegoIg3G5g3z4fGhs1i32dH2+9\n5TAWMVZ3k/5+Ki5LSgLIyNCwZYsfGRlUYCYm6vjBD5JN3RsfGhpcOHLEiQ0bFDz7LHF4J03S8Jvf\nJOC226LYuJGcHhwOu9tDWVkA0Si4ePADB3xITeVFh/X1MlJSNHzpSxp3j+7vtwf+AJ++6OzTcvoZ\ndZX41xyjnOArbHxRV3gfhbf1UefKjMh2d4uYOFHHrbdGOUQhL09DIAAsXMi34R94IBEHD/oMbi9r\n7VNLlHxcf/Sj+GuHDvlw6pSE9nYJPh/xaFNSdFvbmT0MrTGvx45JI8QkK/jd71xYsyaAaFTAY48F\nuYQsp1NHNApDKBaJfANOJ1kg9fQIHA8vKQnIzlZx7JjD9mCn9C2aJ0Z/UFVA0wRkZ6scympFP5OS\ngEAAxr/T/oi2kJ6uGZ6h5s+cOCHhq1+N4r33yCFg82YFwaBos2Tr7RWwdm0Qb70lITmZktw2bFDw\nyCOJhr9pWRkJEM3orVmIuGcPFVW33hqFINCx03Xg+9+/weZHvGxZEIODgoGaWtFjRSFKjZVCsHu3\njIQEGB66eXkqGhqoRTxligpdtyL6egyVd2DMGJ7ewVrl5rlkBX9rq4B9+6ir4HQS/3V4GLj33nAs\nUCI+B4yCcfKkhOuuU9HYSOd6erqGQ4echhhq2jS6DrdupRQ03gdYwZQpN8Hp1BAKCYhSmBscDkL1\nWlr4lrvbrcfoAyQQ4znYMrZudeNXv1JsCyunkzoD7FrLy1NRVeWHKAo2IWVfH3VUFAXw+fiFW3W1\nHx0dItrbJRuXePx4fp5Zod3WJuHiRYHj2DscOu65Z4yR4MYKXtYdaWjwwe/nOzK1tQu47ff2xrmw\ntBi1n0u6LsS463yaX3a2xm3r+HEHVq4M4uTJCHJzVQwO0nUaCgn47ncjGD9eN4ritjb+XLvqKqJ/\nqKrACTyHh4VYJ8HsTCPgW9+i4tZ8j66rc9p+28cZV7rTz5XiKvFFrRE+qTGKBI+Oz8X4IH7WP8Pf\nmjtXxZ/+NIyeHtG4cWsaff7BB71YujSEc+dEzJmjIj1dMx4KLhc9+M6d4x8S775LCB7jqppfk2Ue\n0Yu3MPmCccaMCKqqNOg6LQj27KECorxcsSGPLhewaFEY4bBg87Pt6xMxebIKTYMhYovHqhLa2dBA\ngrvcXBLyhMOELltRwEhEQG4ucSOt6N7+/T4LZ5h3s/D7gcxMPRYQEOckL10axI9/PCZW0PAt8vx8\nFYoicEXoSJ61eXm6JXjBD6+XhQ+QpVhnp4jk5PiD3zqHmsaHOdTVyUhOVuH12ikBEydqSEnRsGxZ\nvBh79lkZvb1kW7d6tcfEkabWNUXQEi8zGkXsOFJsrdOp48IFCZMmxZ0tFCUutJoyRUVnJ0/bAGDQ\nAtrapFioRLzg7+rS0d8vICXFHnxingP7giqAJUuSDNEg84S2tumZmwUh30BVlRt33RW27auwMB7y\nQPQPCRkZGv7jP1xYv16xoaj9/SQYXbRoDHbt4ikt48dr3LWydGnIQCit9JdJk6hwdTpho96cPi2h\nstKNmhoZa9d6sGsXHbtwmJB7axG6bBlRbMaN0xEMCsjLiyIpScdzzzljcy3guefIL9dMi6istP++\nri7+OObkkGXZnj2yEW7BIq0Z7WLx4rDxefN52NsLXH99BMuXB2Mx1Rpqa134+tdVnDwp4ctfjhqx\nxGVlAU4AWl6ucIvrxx6jeOZwWLDx/5lLCCvyARIrzpmj4sSJ+D326qv5InH2bBVHj376HNpPqlgd\ndZX4YoxRTvAVNkb5PiOPkcIjWltfxeLFX8eJExL6+wXcc0/8gXSplhgrlkd6//nz4oioK0P2IhFg\n5UoSTY2E4DE7KPNrVoS0u1u0fT4SATo6JBsCWVLixc6dCbZiMRIh5HH9ej/HlW1vF5GZqceKdODQ\nIRfuuiuMzs6XMWfOjejtFVBZ6cbChWHk5mrcA7yiwo/du6k4YF6hW7cmYOXKoEkRH0eEz5/nFwJn\nzkiorvbj9GnJeJhv2KBwqFh9vWyY+y9dGuKM/6+7TsWqVR7cdVeY225qKv+AmzNHRV8fX6iePi2h\nvp6slnw+Ea2ttGDZuTPB2L5VeGY9Li0tIqZM0dHU9HewqFe2GMjK0uDzweBwM8/iLVvcWL9eQXe3\nOELCloKsLB2A3UXCfE7V1Mhwuch+jfnBdnWJhuDP5xMwa5aKkhJK12Jdh8xMQvU3blTw9NNubN3q\nR3a2YEPFWlqIi9rVRQKxkyftHs2RiBBDnuOFlz2EhK4fVijOnfsX9PXdzL2nuVnibMk6OkSDWlBT\nQ2mAtbW8RZ+iAMEgoZGsWCNxFwnRzP7Q5oXM1q3u2PlGorbERAqSYAX8yAi7hO5uQoQBWgSx8BCX\nCwZtIBoleosV/b7jjgiamqiro6qw8ffT0jSbb3VT06uor78Rzc1iLAzGEzvOurH/TZsUjnYxa1YU\nkjRy2MaqVTxlpK5O5pxidu2SY3PFXyOaRh0ctrgGyCWkuNiDhx+26gMkw3fXfI84cMCHO++M34P/\n/OdhrkhUVeFj0RI+6rPvkypWr1RXidEa4fKOUSR4dHwuhvXhfuyYA5s3e3DVVRLuvHOMTeh1qZYY\nK6ZHev9IIRVeLwylOoljyGd2JKskxlllwqPkZN0WnjBpEvmumhHa7GzNZpHlcgGbN/uhqgKGhoCN\nGxUjDpkhj1dfzSdVWR+IpaUBFBZ6cffdVJAUFXljUbB2YVx3twRRJM/gxESgp4cKVabgr6/3cYiw\nlT+am0vFm/lh3tPD/6b2dtEQQw0P80ldVVV+RKNAfn6UQ45DIXDJULIswO+30wiWLg3ZivrNmxW0\ntYmYMUPD0BBQU0MovKoSOssvLAQsWjQGjz+uGXOdlqZh/Hiilpw7Jxn/lpSk4913JYNeUFoagCTp\ntuOnKMCYMTrcbr5YCgR4G6qJE3VDAAXAsEwrKaECsqxMiaGcOtrbJbhcOlasSMSyZSHoOsXiRiIC\njh+X8KUv8cV+SoqOU6ckAAKefNJtE6ixRVtmps5RBaxt+muuIfSbcaQXLBBs4S1WbnJamm78Tobo\nbt3q5gSC27e7sWZNAAUFQe741dTIeOKJRGzb5jdoOxMn8jQmQSBRKKPDsDnevt2NZ5+VuVhup5N8\nZDdtIpuwujoX6utlvPWWhNzcuFPH2rU8Ss7Qb59PRCQS5/eWl/sB2AvVOXM0o0uQnq7h9GkNLpeG\n4uIkbs6Hh+MpdrSII5760JCAkhIPHA6gvt6H9nbJoDXRfZBfxFg9hgcHRRQXK8jPVzl6lKoK+MlP\nPNwCrK8vbs1o/h3Tp2vGtcrfI/l9NzZKWLgwYtxnmQfwB92DL/e4UovV0fH5GKOc4CtsfF5WeFdC\nuIWqfhPnz/tjD23d8gAeuSXGimnr+9lvsDovZGWRkpu1BnWduKvMJmzZshAefTSIadNUyLKAykoF\nHR1URGzf7obDAa7dGQrpSE0FurqoTSwIQFeXaIs6jUQovEFVdVy8SCheS4sIr5eQo64uER0dPNrD\n7I/iLgqIoacLkJ1NxRFDiKy/PzlZw8SJOn784zFwOonuYOY2s8KEBWBYeamPP+7BihVx1DgzU7O1\ngqNRKvACAdHYJnstI4Pmd6TY54ce4oVL27cnGolp8+ZFEQgItuhgQEBnJ4nU7rorCZWVCsaP15CR\noeMnP/Hg2mujXKy0w0HOFjNmLMDq1W4DLdu82Y+MDJ1D6TduVDBtGsUHs0LebFlFRSUd2x/+cIwN\n/Zw5kx7WNO9m7ja9TjHWAcMjecaMKJ55hoIp2tuFWNEWwMWLImbOjMbCHYCamgSsWhWwUWDy81Xo\nOtDd7caaNR5UV1ORRucUpeCdPSuBkgMVeDw60tPJxzglRUdvr2DYr5WWBtDdLeI73/k6xo5VjX3N\nmxeBqhJvOiODxHYXLhCdZ+fOBOP67eoS4XKBWyylpenQNP5c7u4WsX69gr4+ASUlXjzzDFF9qqv9\n6O+nqOKzZyUIAqWddXTEz7XubgqEePJJN0pKAqioUNDbK6K5mRB2FsjR0UFBJew6ttrsBSg40bg+\nzKK64eG4nRrzHW5qYiEbZmrBApSVEaqfkEDn+fCwgOnTdSQnB22iuWXL4ouht95yYuJEHo01W9U5\nnTpnveZ0Eg2Joe91dWQRFwzS9cqu+9/+VsaUKXHU2hwPnZenYcUKOtYHD/IUJ2sHy0o7+Li0hM/L\ns++zHqPzdHnHKBI8Oj7S+LTtY6zhFgzdmTEjiqoqQmV276bWcnu7hOHhuEjD6vJgvvEnJ5PR+pw5\nKo4dkzA4iJhnJyGOAwMkjpk2jVDiri5S1judPDezo4O+186dbsMdYutWCkooKorzJM2hAWbeZV6e\nitpaKjIZAqkoPGWjvl6GoohGoWht+06axPu87tsno6wsgJ07idZQWysbAQvs93u9QGqqBpeLkFsm\nCgLAod0bNyZi4cIwpk+PC+IEQUdCAvmaAsRZFQQBTz5J+3M4qH3/7ru0ANi61Y0NG4g2sHx5EOXl\nJPbp6RGxd68Lt93Gx9J2ddl9fYeGBCNWd+xYPsWNoXfr1iUawRE9PSJ27fLD49FQVOQ1vHXz8sgq\nq6wsAEAfkYrC0E2GaJvFgU6nhvnz40ggi6W9cEHElCkqCgu9+OlPQygrC6CzU4zxlaloUxSBQ7uf\nesqP/ft9OHeO/Jt7ekQugYxEfAIeeYQXSiUl6YaNWnKyhqKiICoqErFhg4LBQSAlhfin//7vCbj3\n3rBBNaCgBXAJcIzWwWzxrOI1Nv/MVaC/X8SpU4IRclFVpV1yDuvrZVy8COM6CoVgoj0IhqjUfC4z\nvntdnWwUyosWeY3z3hqZm52tGXSe7GzyeF69OoC0NJ4/Xl6uoKjIa/gL//zn5Ayyc2cCKiv5hczc\nuSp27JCRlKRj3DhyxzAj5Wa0vrZWRleXZDtfOzpELFwYwc6dCSgvJzvArCwNSUkaXC4eae3ttXY4\nNJsYjnU0WJJbdbXLsBLMzKQuEXvv0aMS5s+Pck4PM2dqxn36D39wGPHQqakaxowhZ5F16wKYMkXD\nNdfwNAPr31bawSiHdnR8HscoJ/gKG58Xvs/HUeR+FBSZtbwcDh2vv+7A4sVh9PW9DFW1q/kBYPZs\n3fisuWDPy1Nx4IAPvb38vt96S8J3vhN/WFRVKdB1AX19hKSFw2SIn58fNWJimb1Tby8hU7IsYOXK\nIKJRYM8eNyorRZSXK3joIUKZGJprRpPY/zc3S+jsFKFpQHu7hHHjojh2TOKU25EIOOHN9u1u1NbS\ngz8QAOcEQIiYAEnScc89f0RGxg1wOEQcOyZySXRbtyYYRXtyso5ly0JYty7RlKQVQHl5Iqqq/Fi7\n1oONGxUOvdq4keabWq5AcbHHQKiam4lfnJysYXiYwgmCQcTazvwxW7BAtRVCkYiAyZN59CkzU+ds\nv6yRsQ4H8SLb2kTbPpiHrSAIxjwyKzXmb1xV9Z/weq/HU0/5EYkAHo+GrCwYLebHH6eQioKCIMaO\nJbRtYADweoETJ8hrtr9fNNwgzAU6uRRQwh4Tff3ylzR/ZNVFKODtt4fQ0EAiv/R0cikxJ4QxSkVe\nnsrZ0lVX+2P+rcBPfsLbq/FUEQXTp8dtx1JTee/c8nJ+Tk+dkozzgh3ju+9+CXPmLDCOjZWnbfYY\nfvddEWPHkqfxs8/KnCVXaamC8eNhpLmxzgJDLtvbaQFhbvtb+cpeL9DdLWDSJB1FRR6On209P9i5\nmptrpxIFAvTf8+eJelNR4cbPfhbCwADZ4L37roRDh3zw+ahwr62VDdQ5IYFEoJmZPBra2Ph31NZ+\nGw0NMioq3HjjDafxu6dP5987dWpcKMnOEdbNYe8ZGKB7TloaLXD+5/+MYHhYiC0wFaOz4XRS3PcN\nN1y6MM3M1PHAA/Hz5MUXfZg9W8fs2RHjPVaawfvRDj4uLeHz8uz7rMfoPF3eMYoEj46PND5O6+vj\noMiNjZKJP5mImTOtQh9Cgsw3e3PB3twsobdXxPe+F8Hx4xJ+/3snpkzR0NMDjkrgdBKfMilJx/nz\n8XYzawkvWpRkUAbKygI4dYpHgTdtUrBmjccIjKisVPDWWw7Mmxd3YbDyLs0UiPfekzBvnmprmTJk\njAo+wO0ma6/JkzU4HPwDc8IEHWvWJOL22wXMns1bjTU0UDhBebmCwUEBXi+J0IJBGMp3RjvJy1OR\nmUlII0t2Yo4ZDgdxUr1eShyrqvIjL09DKESfCwTIS5TRSYJBsmQzbyMxEZg0ScV775Gzw5kzEqZP\nV1FSQuEHrOWcnKyjsVHkOLbWtDFVhdEJsBdldk7zwoURrgBcsiSMaJT4mv39Inw+Qt7Z91+5Mmgr\nGuvrZa6gYhZap0/z5yZzKdi/n1RmhYVeY7seT9xb+J57wpy3b1WVgv5+3nv42mtVGx1mcFBAQ4OM\n4WFw1BCrY0F3t4C0NAFLlozBtm1+m1sJS5aLI5JU5D31lB/jxunYvNmPQEDD8887sW0b/ZuV+848\nhp1OHbNmURBKebkfvb0C9928XorSZqgqdUfiKHhOjoa33pI4YaP1uklJIVrHkSP2JDvr+ZGVRYhx\nWxv/mzs6qIj+0Y/4rkJ3N/mHMzTV6ppRWyvD7Y776ublqQaXd/x4Hf/1X3S9HDkiYdGiMO64g4rW\nnBw9FkASF27+9rcJuOkmFW63jowMHbIs4OxZ4gtTmAd5gm/b5sett9L9TdOog7VuXQApKRpHhUlJ\n0eByXbowHUVuR8foGOUEX3Hj87LC+zg30I+DIpuL77y8m5CbaxX6aLYceWvBnpWl4vXX+bCLqiqF\ne/jW1MgQBNiQto4OQn4iEcGILybqhWBzlqipkeH16pg3LxrztNWxe7cLBw+Sn6gsC9i7l5T7EyZo\nSEwk9LqoiGzamNDJXDA2N4tcXKw1XIBRHBSFnAGo6LsNKSm8EO7IEYlT7q9dm4jubkK4dR1wu4l/\n294uoaJCsQju4q1uQaCi9uJFwUCtQiEgKQkIBnV0dtL3ZmEgI21j0iQrKudDNCpg9eogsrN5j1qi\nvPA0hPp6EkGlpZH/8KOP0vxZzwviTwKlpQG4XISIqiqPsM6cuQAOBwyrsPXr/di4UcGYMeQp29pK\nCW7XXhvFwoVU0JAAK76Nzk4B9fU+AHYBXyQi4M03Hbj2WhVlZQFkZ2scMsrQRbY9sgUzn4MyOjok\nFBXZecjRKNEYGCWE/dfqa5yfr8LlokK3q0u08cMHBgTOTou18l0ucxz07Who8EHTBNx9d5LhsuD1\nwkApGeWjqMiDqio/Cgp4y7V16xIRjQL19S7jmMsy0NDgw4ULEudPbC4us7NVPPecDy0tJBobGuIL\nXvPv2bkzwcTJp5b/D35gDwZJTdXx9ttWr2wgJQWX7N4QAi4iI0PFxo0K+vrEmFYBpgCO2wz7uQkT\nNJtbCukHdDQ1ibjpJhXr1iVi716696xcSefxW2+Rp3Nvr2CE5rDB0Ndrr1Vx6hQl7nV1xUWJmoZL\ndtmuNEHZ5+XZ91mP0Xm6vGMUCR4dH2l8nBvoP4sim+kTLG/+5El6ABYVeTg0ZeJEyp83j7lziQLx\nj39Q0Xv6tMPSKg9wDzoqZERbC9rsN0o8Rc146AK6DX08dYq8NUdqNZeUkBr9/Hmax5UrSYxSWalg\n+fLgJfmVWVnEqXzqKTfKygK2mOLy8kRs3OgHoMPlAtLSCImyC+FgfM+uLhErVlCR3NMjYNMmD55+\nWkZSkoB16xJtThJJScCTT/oRCAjQdSqMysoCWLaMtwibMUMz5sg6N243qd8HBwntYq8RJ1XAO+9Q\nAVZY6EFlpT9ma6Wjs5Ospurribc9ZowOr1dFRgZi8csqKiqIFsBiorOyyE6so0PEgQMuLF8exMmT\nEvLzVXg8/LxEIuBCG6ZOJWFSWVkABQX8AsfsqWulbDQ2Sti5020U3Myyjt5LQrydOxNslnD9/SLX\nUrf6G58+7UB5OdmlnT8vGSj57NlR9PeLKCoikSajqdTXy/B6VcMmbepUFV1dIjIydCOZrriYrqFw\nGJgzJ4ozZyQAIlJSiD+8dCkFXSxeHLKgp+S1G4kIBn1m82Y/7r2XhIiMLwzAcCFgn01IIK5zV5eA\nwsIgmpokm1ctEx6yz7e3S9i6lbot2dlkqWd+/xNPeLB7N/Gn6+tldHZSOl1iIl2rkyZpOHjQaXDv\n48mBRF/xeHjUeN48FU4nRQNfCoVmziFWdNj8W10u4Ne/TsBjjwW4f29uJnHdqlUBpKaSbd+zz8rI\nyYni7bedtkU1ObtQWI91sO6a1arvT38ahqoKttTLT8vDd3SMjit9jHKCr7DxReD7mFHkvDxKYjp0\nyHlJfvBI9Ik5c1T8x3+8jubm27BjRwIKCkK4cEHE2LG6bX+6DoRC1LqfPFnFwIC1VQ7MmMEnoDGL\nq5GQvK4uEWVlivHw7esjTjCFW8Rb1vn5quGmwPblchH/2PqAI1SIwhdGCtN46il6sKoq+acuXRqy\ncSsFgf7/S1+K4tQpR6yY0/Dggy/B4/mGEdSRm0sxtQCMwo8lnjU0+PDYYwHIsgi3m1rHJATjFehX\nX63i/HnJ8Eq1FrkuF9DbK2DSJHIQyMnhi81QiIIGampkDA7Gt19QELTZvLW0SAbKZvXiXbo0yWhR\nmxO8IhEBlZWJqKhQOJSZ+dWyv3/3u2E0NMhobqbggjNnXsWcOTcb34cdC+vvM9u/MW52eztxSfv6\nBAwPi4ZzRE4OWXM98kiQQwJLSwM2GsHEiRrOnydv34sXBUycaHfxYMdNEHTjuNXWygb6aA+6UDB5\nsoZf/9qNyko/UlMpSSw1lRDIykoFAwMCxo3T0dZGFx8hxBpyc1U0NtJjwkwtkKS/wen8MrKyeM42\nE3KNH88XixkZ/N/hMF2TK1YkYds2vw1h7egQbVSG7GwS8J08KSE7W+A6JD09dE2sXu1BW5uE4mIF\nY8YAssyHotTW8se/tlbG4KAOr5e8h/ftk/H225KBYK9fryA3l1DolhYJubkqdu+mYx2NEhd38WJ+\nIWN2RZGkvyEraz4qKhRIkt2RpqgoiJQUHSUlca55T48L2dkahod5twpNi1O2rIN110Y6T83iWpZ6\n+UkLmT/K+CI8+y7HGJ2nyztGkeDR8akPUQSuvZZuwGa3h+5uES+84MO8efzNeST6xPe/HzE8Ua1p\nZtYb/PHjEvcgYEgu+3vuXBUdHTyaQ6lfbkNxbk70ysoiNwVVJWP5a69VOTux6moZDgcM71Erf3Hi\nRNj4oozzJ8uiDSlPSSHHgIwMaue2t8OGEHq9QEaGiu3b/YhERO63rF5N0cINDTKKi6lY3LhRwalT\nEmbN0lBSkmg4H5w7JyEaFbBlSwIeeiiIyZM1KIpg83ZdvDiE8nKPgYJakeZIhFDo7m4RkydrGBwU\njLCJcDgufOroEDmLJkJNrQlxGsJhOyrKxFesgLJTLgJobbWHlZj/PnPGgeLi+Gd+8hMJWVnA3r1y\nrFDURvx95qKuu1vEhQsSioup4N22TcHAAP+6202uJdbftmcPH19tTlyrrFSwZk2igfbm50eRkKCj\nuJj4n5JEMd25uSpaWuLbtgddiGhpAdavJ7/hQADweIC77oovop59loR4rJvABrkn6FixImjQUfr6\nRPT0BJCdTYs8s1vB1q1u5OWpcDoRs6UjesXevS7O73nrVjcWLQobHRXrgjM7WzM8mH0+imOORq1O\nILyLh3mxk5wMDA8LSE9XuQXK0BBfJJ48SWmPe/fKqKryo7VV4hBsWsQCHg8Te0oIhymMhd1zrOhw\nXp6K/ft9eE+NK4AAACAASURBVPttB7q6QkbXJz2dEPmeHlqI8mEctCAyn7+MW87+VlWKg37xRTsS\nfNVVtIgfO1bHvn0+nD5NIk27YFEw7qFXWhE8OkbHZzFGOcFX2PiirPCs6C4zpj9zRsTcuSrnHjF9\nut2fUhSB//N/vo7rr/fhxAm+uDDf4FWVCm2+8JFMSnRAknR0dsYfFunplBJ2//0URrBnjws/+EEY\nq1YFoSjA6tUerFoVgKJQLK6VSjE8TP/e3CwZfrpuN3FlV6/2xLi3vAdnfr6Kri76nM9HnMymJhKI\nDQ6SG8Djj3uM4twaepCSouGee6htf/48XyxOnrwAZWUBNDfHvXSffNKN1avJyWKkxLOaGhnDw1Sk\nTp2qQRB0zts1JYUWCrouYN8+KqCshXJRURCBgGBsl4m8zBzXadM0LF4cNqzVKirsUcqSRHQPe9AD\noaKsCLGL4Qixfj9EMi1N5477rbfeAL8faG0l2sW4cbRgSEwky7nuboo+3rLFjepqGUNDouElzRDf\n2loXHnwwZCygolFK5/L7+UKPztEQBIEWHRs2KFzEclYWiR3/f/a+PrqKs173mZm9s7+SzUdCEtgJ\n2aGlhTYhLEBPe+yXx+Oyeu/RpainrcVWOcI9pLQEQmmCtiaWBkhCaJF6UZBAaBKkvV2uc67o0Xtt\nKyoqRShg+WghCfn+IJC99+zPmbl//PY7e96Z0MaCXrT7t1ZXE7L37Jl3Zs887/M+v+dhNlw//GFQ\nP15ixlXMmqXgiSc83NiYQVlJSWJcfbtxrIaG6HjN750zh3e4qKuTMTIioK7uM9iwIYTCQgrjyM9X\n0dcn4stfjsHnU1FVRcCvv1/AggUKPvOZhIWRdzopCCQjgyQLO3eGdKcVh0PFhg0yRkZEZGUBq1a5\n8bWv8XIM8hsOwedTEYloeviF1wv8+Md2rFlD17fZZ9doT2dc3Ukk6N5kvtckEkB3t6hbtNntpCdn\nNnWaBn1cFi6kicyqVRGUlipIJO7B8uXRZPJjCBkZJFPq7BS5dD1K5OOv344OUbdxLCwkKcPBg4Fx\n+y8IILstcckHDgRM3xlNP64brT4sz75rrfQ4Xd9KM8Hp+v9SZnY3EEg1qBw/LuHf/o2aQs6fF3HH\nHQn8+MdjOHPGhlmzFMybRw8BpksGrA8ugADwb34j6dtmf3e7oTsEVFW5sWVLCHfckXJtKC+PcICB\nLMUkTJum6MutU6akml8aG3lN6IwZKjSNfmZewq2tQXzpS1n68ZPLRKqTu6+PbM7MThBr1xKYUFVi\nBru7RWzaROb/zc2U4JWfT53mDICbWcvsbA2PPcYnYQmChq98JdXQ5HDwwPnUKQm3365gxYpM2O0a\nXn11LCldIE1hZye5Lbz4IjH4O3eGLCEIPp+Kigo36utl5OYScBsZAWdDNTICS8ock23k5hKT5fdr\nePLJCCZNUtHWRu8VRSTBVjjprCBzEbt2O6Wcud0alxTH4oiZFdfoKC/FOHuWXxHYsyeI6dOJyY5E\nBEyfrmLVKg8GBkT09kpQVQ2XLgmor5eTnwE8+GAMX/wiP8G7eFHUbcBYuEJPj8CxjkNDoiVi2djU\nNTJClmlmtrC8PIqmJmcyqZBWFBobSRM8fbo6bhz15cs0KWFL8IAGn0+Dy5Xy283NVS2JZCMjgq4n\n9/tVCzN7663kp22W+zQ2Wm3XysoU3HILjW1BAX3vZ8+m70JlJQ+YlyyJYv58s10escUNDbTteBzI\nyyNmee1a8sc169mtDaH089SpZEf29NN8lPeaNW7d8cW4HeaJHY+TywcrlnyYSACapiErS8PYmIiK\nCmJ6z5yxgbnAGI9l0SIFsZj1PjZp0sT0u1eTQwQCgi49Y5rgqwHpdKXrw1hpTfANVtdb7/PXTnab\naJmTjkpKEqitlZGXp+LcOatm1rj0yeQOhw4dwp133gVNo4fPtGkasrJUXLpERvEAcPiwLbnkTOCj\nrCyBQEBAQ0MIiQT5iBYVqZg6VcW+fUEcO2ZLBkSkHiRHj0rIyiImraZGxosvOnVdcUGBgqKiVHJW\nTg6xd+fP8wEJZiP8zExw6VBVVWH985g0oauLUrMefZQYXj4gIIxHHyVNbWeniFgM8PsVlJQk0NmZ\nshqbPz+B1177NeLxT+vbdzhYYEKqoYnFIhuXk7u7RbzwQgiahiRYJzP9z3/ey4HEEydsyMjQMGmS\nogNOn4/Sytjyu3FS0dwchChS4EV+voof/YiCImIxiuQFgA0bwhgcJJBRXu5JNrqR7pW5VdTWhjkA\n3dYW4CYWBFQpJWzTJlkHbMeP27BnD7GqU6dSE5mi0KTq6NFDiMc/BYCY4USCfG5LShSsW+dOAn5y\naNixw4ENG2R0dYkoL/fobHdFRcQERICSEj5cobZWxs0389+BggLFEk3b30/NU93dEurrQxaN+fHj\nEjZudKG+PgSHAwCEpHTHgRUroujsFPU4auNnyTIB5e5ukvps3kzuIMaGPzYRM4O1+nonvvGNn6K3\n927O7szhoEZGpts1elybJyheL92XSksVuFwAoGHjRldS8wruvZJEDYojIySpYRO0gQFKaMzKUiCK\nIidJamwcP0nS3BC6ZEkMXq+KyZOJ0V22LKJfP7T6QWPEPH2Z7lwUycrQnKKWn69ixYoIPB6aAHd1\nvYH77rsLXq+Kz30u9b0hJjk1GVuzhhIX9+5NNTDeeacC21We0Ob7OpNQmY93+nTthnKAeK9Ka10n\nVulxur6VZoL/zuuvnew20WLAlj1w3G4NH/mIgrlzSbdnbl6z2ZCUAjg4ucPx43zIBYVlkKtBQwMt\nexrBx8svB7B1qxNr1kTw0EOp5U1a6qZ9MRveM31hPE7a2+efDyEaFfQAhbNnU97FdXWyhQV8+mkX\nXnghpNtfFRURA+r3KzrLVFrKbKucnMaZmf2Px/DE4yRXcDiAzEzVIjVobSW7s0iEZ5iKilScO8dH\nGg8OpjxLWSjEc8/JHHhlSWvG/ejtJQ2p3U7BGZmZxGBdvEha4K1biRkzvufkyRQbRy4S5EN84gRZ\nuu3Y4YDdrsFuF1BZ6cGiRXFs2iSjs5N8jR0OFTt3BhEKCbpdXDQKHD9uw3e+k2JWybNYwdNPE3PO\nGuDy81Vs2eLE8LCI+nqytpo3j0DimTOpc19eHjE1H5JkZ2hIREYGAaR33hFRWKga0tg0dHTwY7to\nkYKLF6266lWrImhtJU/m0VFqtDI3ysXj0IMqbr5Zgaryf588mX7Oy9Ms4Q+BADWzrVoVwfCwwKX3\nGXXdxmMza6bPnRO56+LKFWDt2jC+/GUHFMWjv/eZZ1zIzydvWqeTjtnoce33K2hvJ8cHJkWorQ0j\nkSC5zMaNBAo1jRhYsz/2nj002bt8WcC3v506x6SPTo032+9p0+hcGJMRCwpIh8vuP0VFtGIkCDTh\ni8Xo/dnZKuJx6Ix/TY0Mp1NFa2vQIq/42c/GxtU6T56sJRP+XNi1KxP79vGOEeQE49RXowAK/Cgp\n0fCpT8Xe9/5pvq///OdjOHgwgL4+wRIGlK50pevqldYE32B1vWd41+LJa6zrzSjzoRfAD34QxL33\nxnH0qIQvftHq4+nzUQLZ1q0yBgaInf3Hf7wLr77KH5/NRuxiXh5FD7Pl70AAuOOOBMbGBBw+bMfR\no3xE7x//mAJm27eHLD6py5dH4fcr8PlURKMCBw6NjXbmZVOHg5asEwlgyZJM7qHOGE3GLk2erOlJ\nYYxhG8/7lDFOdXXE/k2ZomJ0VMSRIzxQHh0lZ4n8/Ht1Vrq4mDx9jUvzpaUJXeYBEHhcuTKCkRFr\n4MTQkLWBif1d04CpUzXO3aG5mRhXv1/Rm4CMbFwgICIW48MnDhwIIBYjv1kGZLu7RQwPE+M9dSo1\nEJJfM0VnqyoQi/HgMxYT8MADWWhpCWLqVFVf2j55UkJFRQTDw6Jh/FW43cA///Nd+NSnAujtlRCL\n8ecyI0PTVw6cTg0bNriwdm2Yi6Vlmm3j2A4MkAtCXZ3MMdfxuGCxBquvD2HnzhBOn5Z0sPrUU2E0\nNwdx8SLpj42TR0mi8zE0xH8POjsJlBmBcXNzkPt8/jyMr5mePZvcSqZPJx3+5csigkFAUT5u+M5R\nlPL69W48+6yMBx7IQllZgnNN6OiQMDICLFqUQEeHhA0bZDQ1OXH8uA27dwdx5YqgR0X7/QpWr+bZ\n9KEhavbcuNGqhZ82TdN9j1OTOtEQ+03JiE1NIdTXy+joIJ27sTFt//4AgkEB/f02ZGerqKpK3Zu8\nXg133KHixAngzTd5L+F335VQXEyyDPbZixfHDQ2Z9yEet64EzZuXQHt7kAPlJSWUiDmRMt/Xz52T\nsHhx3PCKvz3wm2Y3J1bpcbq+lWaC/87rWpLdjHUtjLKiACdPihgcFDE0JGDOHPWq+8Vu7qyhzOGg\nB/P69W5UVERw7pyIsTERY2MColHNsh1FEbB0qRs1NWT7tGpVBHl5ZFsViwnIzrYuG5KMQEFVVRhe\nr4ZJkzSsW+fGsmXE0jY0yAA0vPBCAosXW3WGrNGOdbEb92faNJJ3yDIPqPr7RT2FraQkoUseHn+c\n1+4ys//hYWIyz5+nSUg8zjNSu3YFIcsS99lTp2omCQWBgqwsjWPH9+8P6Ez72BhNItatc1ua1Lxe\n8v1NyTw0uN300GYazY4O/uHMuu/37w8gGk01YD3/fAj9/UKSXUxJS8rLo+jokDBtGq833b07iPr6\nDAwMUOzzY4+lQMfOnUFkZpK22MharltHrxkcFNHXlwozSaW0pUC6WdsKCCgq4s9lPA5OT1pVFbb4\n3zJHDDa2u3YFUVBAYD4aFXTrs1CIXDHM9lqCIFiaEKdM0fT9q6ri/Xe3bg3hf/2vAOJxK4NsZnU7\nOyUu0GJwkMZ8YICY8L17g2htzdAlLbNmqWhocOJzn4sl09RSqWnm7xxjM5l13JEjdlRURLjXZWdr\n3IShpiaMI0fsOHVKwqJFCbS0UDKa1wvL8eTm0gpEVpbGuT1kZpJjQ3ExnTebjZrEWloysHhxHKJI\nMpOGhhA6OyUkEsT8iiJJJjo7KZQjI0PD0qXjHx8L31EUwbJfjBAw+pDv2OFAQwP/3Zk5U+Um1lVV\nbjQ3B7Fpk4xjx4idX7fOjWeeCWPevPe/R1+v+3q60vVhr7Qm+Aar6633uV7RmB+UUWbNaefOSYjH\noVuhseU7836xmztrKHv55QAOH7aho0PC1Kkq1zBTWXkQn/rUx/CTn5BDRDSast7KyADq652oqIhw\nYHHfviCam4l5amsL6sv2RhnBK68E8OyztEwuCNSZPjAg6ib4ZlZ2/nwFZ85QzLERiC1aRP8uCBpu\nu41/aOXlqfp+XU3y4PWSxOHYMQlz5igcc2VuNLp8WcSOHeSuMHWqisuXRUOS2WuIx++Dy0XnY2hI\nwP79AWgadJ/VhoYQHnyQl5V4PGS31Ncn6aBp7Vq3Hh1dVeXBli0hvdueNSnxwJl+vnhRMqRoEePp\n9ZI0YuFCBX6/woWEsDFhx3fqlKS7TZibtU6ftunjznx5n3tO1vWeM2YoCIVsOktvtlJjASa0vdcR\nCPwDvF6Ns+hiDCabKLHEPrPWdXQUejBFPE7ODuZmtz17glizhiY7+fm8P/WsWQpWrvTonztvHu81\nbfbODYcpNMPlUvHyy2OIxUR0ddEEy8yO3nSTAkmiCa0sk6Z50yYZogiIogpJErB0aRRvvy1hbEzE\nuXPAmjVhVFR4sHZtauK3fbsTa9YchCB8HCUlCaxfn2IzZ85MjUdnp6gz4jRm/IQhI4PsxLxe6Ncq\nA/gFBWRtdvo0XfujowROPR6Nm7Ds2RNEbq6G8+dpZYkFSpjdTlpaaDIyOChg0iQNR4/aMGeOghde\ncCbPq8wdH/kHC7j11tS96cIFvrlx/vyEviJ21130mt/9zobly6NoaHDiwIEADh36Ne6//2Po6xPw\npz+lgk4AWg0rLla5Cc9EwezfY+RxWus6sUqP0/WtNBP8d17XKxrzz2UeYjHgd7+T8O671CDT3p6B\n48dtOlBhy3fm/TLf3G+/XYGiAFVVMkZHrY4Sf/yjDaWl5BhhZKqLi8l6y6wV7OsTuaSpmpqwxWLt\n/HkJa9e6UVkZ4R5alCJHOkMjq7NmjRsrV0Zw6ZKAp54KIxwmxrOjQ8SLLzowMCCipSWgx75OnUq6\nZ9b84/NdvanFCM7Z2MXj1jCC7GwVy5ZFMXWqpgcypBgtAijmeGJjs+F4KVePP+7BqlVh+P0KZFlA\nfz9pdrdvd+jL54WFKrZscaO8PIoHH4xBkmhbw8O8t/KUKfx5mDoVWLqUDzEYHr462PN6kTw2t0Uq\nw4B2IGmfSlpefuLjdqsoKqLxNU82mJY3HhcgScR4k8VbGLm5WjIqW+BS/JqbKdr2/HkRr7wyhlCI\nVjpyczU0NjrxyU/GdUBn9u3t6qIJVX+/CJ9P4/x6W1pIJjMwIKC4WIPDoelx1PE4xQCTC4RR2xvD\nggUq4nGRk6K88kqqUbCkJIHubtGSlNjXR4B5aEjCtGmaxaFk505K32PJf/E48z0GolGK1964UUZP\nD00ms7MTuh+0389PLs22gLm5KurrZTQ2OvG5z8UBaNxniCL5GRtBr3ny19sr6qwq+24aZRDsdQMD\nIiorrRZi7DtlvN6Y73NOjsrdn4qL+ebGgwcDuiSMAeHMTALLzz4bTgLkBBYsUHD0qITubus99IOC\n2Rst8jhd6fpbrbQm+AarG3WG9+ferH/3O4lrENu9O4iHH87SwdPVQLT55n70qKQvwz7/fJBjzWbP\n/hjOnRPw6U9n4ec/H8N//deYLrmw2zW0tWVYlvTz8vjGLhZCYHwNS70yg1JBIHuv/n6SMxiXpe12\nDeXlHgsDxR6yg4MSfD6FS/ViDCGzKZs6lRr0+vrIZeLYMWu4AvusSZNoebWvj5atQyFAEDScO8cn\nme3cGcQ773wUc+YEMTRk1fiyn4eHRRNA0bB8eRTTpml4+20J5gQyv1/VLdp4ptOJtrYgfD5qGHz8\n8QgUxeqRS84PPEiZOTPFirrdqqWRikU7m72XGdBesICWvc1x18eOEVPc1hbA3r1BfR9S7K2gywQS\niY9CkoCvfS2KwkJNn+AYddrd3RIGBkRdbmFOaGtuDsLpTB2v2Xu3sFDl5A3Gfe3upia/W2+l5sLC\nQhWzZyewc2cQp08T8O3vF02ezSpGR1PNkmxbRt19QYHCsbnselq0yBrQYXzNlSvQATsvg7kXTU0Z\nWLQoju5uMTlZEOB0SjoQ9/sVfbJYWqrA61V1+zvGkjNHiq1bnXjwwRgaGshOLzOT0uvMGnsWXmL8\nPtfWhjE0RNZ6g4MiCgtT+nMj4B5vtYV9p3bscKCtjeQYc+Yo6Owk4K+q0IHu+90DxwOm7H4+fz7p\nffftC+qSMMYiXw3M3qjOPn+pulGffTdapcfp+laaCU7XhGoizIPxpm1+IPf2EsgqK0v8WT6VRhlG\nIiFgxw5n0lGBOulfecUOWm4nCy9jMlx7ewChkMC5MoyO8gDI69Usy7aXLwscq+TxALIsYNs2J7Zt\nCyIWs+nsLXvYz5ihobIyAp9P1eNc8/JUFBSoqKqS4fMp3AN4+3YKqyDgI+HFF53YvJnstmbMIJ2j\n280Dx5ISio299dYEYjGRs7JiHfrGlKmBARE2GzBtmqZrjvljT0Xw5uaqnJ6W4mCjEEVAknggkplJ\nmk1JAkZHBbjd/N97ekS4XBpuvZWSwL7+9Uw0NMicjVxxsWIBM8bELL+fAO2cOQquXBF1ttHoqHHL\nLSo0TdNDTCoq3LpmeDymeHCQYrWffppS2MJhkhucOyfB4UhZlBUWKigsBN59l6z6zOzpM8+4MGOG\nqkfYmkH36dMSSkoSOuDz+xXU1cm4ckXAnDkK18RmZrzjcUAUBY6x37kzhN5eEW1tGVi+PIrLlwW0\nt1NwR16emgyU0ODx8JO2oiKevTVes+x6OnPGxoU2mBvjCgpUznps794gVBXo7KTmNl7jKydT2lL2\nZqoqoKWFJjCKQh7dFLaRmkCeOiVhyZIYZBn6CsKsWQo2bHBZAlIyMugceDxk81ZVlQLSfX3UONnZ\nKeHmmxW0tATR3U2SpsHB1LVg3N5HPpLAli0h5OWp2LUrAw8/HOOYZ2Pvw7Wwr6KIpNZ34trdG9XZ\nJ13p+nuqtCb4BqsbXe/zXuyE8ab90kv80udNN6k6+P1z2AyjDGN4WOD8gyXpl/jOd/4Bx48TQ3b4\nMN+5TUu9ms4mMi9OBoDKyhQMDRHwNT74mpuDOigWBAF2uwq7HaitDUOWaUm5rCzBRaDysgXyEjZ6\n0xIzzadVFRamgCAL6GBNWx6PBiCV0LVoES1nOxwaolHBErvMJh2Dg4IemsB0uv/9v/8X4vFPc82G\nxcUkM9m8OYTiYhWbNjlx5IgdANlOLVkSQ06Ohq9+1QqeJ09W0dNDmtJly6LJ/Uwx9Pn5Cs6ft+G5\n5xx4/vkQ9u4lgPLii2T/NjwsoqBARWsruTAkEhQUMW0aNQp6vdRwZ9Qot7UFkZVFzUxG4LVnTxCR\nCLhuforppYlPKJRiiqdN07B2LTU8Mha0ro6Ou66OAbrXUVf3ET19y8xE2myU3OZ2p2JzzY1U8+cn\nEIkIevOWx6Nx0czt7SmQzhofqTmMNOTm6OihIUH3JOavpwDOniX9bn6+guJiRZciTJ9OExCjk0RG\nhspNRLKyCPgb993l0vT9yckhUM7OyfbtDvT3i3jySTfi8dexYcNH9ImA16tB0wSMjFgDP2pqiN11\nuwXdR9j4mQsWKBbrsT17gigvj6CzU8Lu3UGMjIiQZUHvFXjqqTBnhzc4SBM+s2SlsjLFhO/cGcLg\nIE0gurpo5SGRoImQzabhC1+IW6wZL1wQUVamWBp7J3ofu5b7+fVy9vlbqRv92XejVHqcrm+lmeB0\nTagY+B0ZETi21chOGG/aTU1OvfGsuFhBdraK06fpcvtzgPD8+YoeYlFSouDkyRT4UxQBHg95ZJ47\nJ3Gsmt+vID9f45bTly2LYmCAmKmKigh6egh4BYOp2NOSEgXDw6Ju18TARmenhOFhsmCLxwUsXhzX\nmVjzknZmJrB5s2zRGr/5ZsqGrbU1mAQpBMg9HgaGo5aldUEQ0dPDN5YxDaSR7fT7FeTmUtOW1wt9\n6X7KFGK/GIBoaQli9WoPnn2WHDRuvVVNjgdF3iqKBptN0PffLD+ornbDZgM2bJD1MayuTjXtseak\n1tYAZJkY2Jkz6TOMIKW1NQiPR4XLhXFifXmN8pkzIkRRQDAocCEkly8LFoZzZITAGDvnS5ZEUVKi\n4OJFiqqtribwtGFDCBUVEZw8mYDPpyQZ/JSGd7yoZorZBueCsX27E3v2BDE8TOl9ACyTH5Z0V1xM\nTiXGFLunniJ7Oub8YAbVgkAhDtRsZ5RO8DKVlpYgFAVJJxQJmqZxNoTf+pasB1Pk56uorSUwuXNn\nCJcvC0gkgNpaFx54IJbcDxkPP8wzvfn5KvbuDeLXvw7j1ltVSxTypUvEthvB8aRJGqZMUXH2LLHO\n69bRtu12YOpUVV8lMh7b8LBoaSZkk8SaGtnSoxCNWrXXQ0Op7bLglKefduHgwQBKSxULy7p4MVk0\nmnW7x49L+MMf+LH+a7CyaQeIdKXrL19pTfAHqL+kVutGneExlvfb3w5zD7i+PkF/jfGmffy4DZMn\na/inf4rh6FEJS5Zk6THIoRDwsY+lxsw4nizac/r0VFxodjZZRuXlqSZQci9kWdatz6JR6IlSpaWK\npaksHKblzHnzZI51euklYhPnzVPQ2OjE9OmkRx0cFJCbSw9pgMBPLEbMn6alGCPzknZ2toq335Ys\n/270ZT16VMLChQkIgoZEQsSMGeM3bbFgCTPQTkk4iNEMhcgui3X2e73Eqq5d68ZHPnKXJZgkkQBU\nVQAgIJEQOdDW3h5ARwelpPn9CnJyVBQVKUndror8fBWLF8e59zCHhbExajTLy1MRDgtcg5pZb/rW\nW5RoN1687eXLvEbZGtEbTgLtIPr6BD2wID9fQ3W1C0uWxDjAy/yG33ubMl588W6UlMg6Y79tm1OX\nNcyYQayuKFIsrhFgCQLF59bWhi1MbleXiJtvJo/pN9+UUFKiYNs2J1aujHCfz64P5k5w7pyE2bNJ\nRuPzaejpMeu2eX27psF0HvmJUlmZgvPnRSxcqGLjRvLozcig5DOAAiaWLInpx2a+Fj0emqzV1rqw\nePE9OH6c//vICP08ebLGNZ+1tQWxcmWmzgCTIwk4dtw8qaPACn7bZFWIZNqdU9dJ5+SocLk0+P28\ntl9RwFkXShJNmEtKVLz6qn1clnU83e+rr9otAHuirOy13M//Hh0g3qtu1GffjVbpcbq+lWaCP0B9\nGLVajOX1+xXuQXvgQEB/zdVu2hcuiJYY5IMHAygrU8Zll1tbg3j9dRuuXCFwO29ears+XyremHXH\nr1sXxurVHm6f3n3X2lRGTUBuLFkS5f5mDMrYsycIhwN44AHm22tMDEu5Kbz0Er+kbWzi2rbNibVr\nydO4rY1SyoqLKSWO+bJ6vUBXV4pdevFFkmAUFPDsz7x5Cl5+OQBF4QH17NkqOjtFzJtHpv/LlkVQ\nUKBZWOTaWhn9/SLHCL7wQpBLQzMD7CNHbBxjLQiwMH6nTvHjC8ASc808Y9lrjA4DdruGOXMU3WfX\nrNXMy1PR1kZxyrNmERvHn08CYH19AmbMIPZbUQT09AA2mzUmeOZMFUNDIl55JYDLl4mdVlXo+m0G\n8jZvli1BKE8+SbrTffso9KS+3oWqqjDq60OYOpUs5xwOAuY+n9WaLD9fxalTkuXcBIOC3mg5Y4am\nBycMDIgYHhbgcAAnT9KEzuPRsG0bb7/HdK5sm+bGx2PHJLS2UvhKcTHfANfWFoAgkGTD69UwPExx\nyy4XjVVbG61UGLdfUKAmAXAcLhdwyy38pEKWiWllkcVsPzo6iIFvanJi926SqZh11H19pOV+6y3S\nwpsbKHJgGQAAIABJREFUNYuKVN2jmzm29PbGuQbBhgYZu3YFMTSUmrRmZGjJ1Dw6h8zRwXwt5uYS\nyzqe7pex939tVjbtAJGudP3lK60J/gD1l9Rq3ah6H8bymrWo9MAZv3FEUcjdwevVcP48/9B76y0J\noRDwxS9aWcALF0S43aThramhhqKPfSy13WPHAK9XxYkTh1Befpfu5sDCFjo7JUuDD71XQ0NDSP+3\n8Rja/n6yZmKspnG/wmEhGShBS8evvBLAO++Q2f6xYxJaWhwoL49ixYqoDqLNlmQbNsjo7ZXw4x/b\nsXZtWI/bdbtVPPGER1/uzczUEAqlfHmffz6kA4hYTEBFBVtCDyORAAoKCAQZHQyGh8VkRPIbsNs/\no++HIBDguxqTnZ+v6ccZDgMjI/z1PjBAOknje9g5YK8hpwV+u0zmcPmyiEQC6OwUceutdJ62b3eg\nvj6EvDxK+yLQDzgcNOmcP18xnTPa3rRpdNw335zAlSsiwmEBjY1y8tohwLhggYK1a0musW1bCKtX\n83pVNrHx+RQcPXoIlZUf1zWwIyMivva1KNxuDU4nORZ87nNx3ZrPvNqwdKkHL7wQ0uUON92kYmRE\ngCzz1xLTC/f2knVXWVkCzz4rJzXmCuJxAUuWpCYVu3YF0dgo48wZETk5gM2mYsoUQXdu8PsVqCp/\nXbvdwNmzEkSR2NeVKyOw2YD+fhGAYJjopT5n584Qjh61oaXFgcpKSqrr6yOm+9IlAYsXx7BjhxNf\n+crPIMv3YvfuIM6ckTBvnoLeXhF5eSpycsxWf3SOjxyx42tfsyUBNr+v8biAhx7KRE2NjKoqD/x+\nRQfFJSUKPvIRmgyGQqnXM0eHN9+kyWdTE+nwb75Z0Z1pzOEi7F49NibA2Aw7NpZa0TLX1ZwdJlI3\n6v38Rqz0WE2s0uN0fSvNBH+A+jBqtRjLOzLCP7z8fhVHj753o5xVxkDNXayRzcwCKkqqEainR0Rv\nLzBpkqYnKQWDQpJVc8Bud2P/fmrCIz1tKnqVsWB2OzGFw8OC7nxQUyMjK4u8eCsrU2b/RUUqzp4V\nOaBlZC7NEoCqKjd++MMgysqUpIUXdJsyqx0TxQ6PjQmWuN3GRllf0r/pJrLHMjZ7ybKAJ56wWrB5\nvRrH6jIw9swzLiQSwEMPZSEvz4nW1lTsrsejIRjkwcRLLwXxxz/aUFKSQH+/qEdFv/02NWyZWTlA\n4yQWmZn8WPl8Knp6RDQ2ykgkiHGtrEwxkTU1Mm65hYBbQ4OMadNoG4sX8xpUAPjOd9z6+eztpaau\nzk4JtbUEGisr3WhtDeJb33LrwQdGKcTmzSHdASEa5SdjHg/0idHwsIhNm1xQFJf++VOmqMjJAdat\no6bK4mIFq1aNz6AzdjqRIBZSFEk7vG2b09IMpigCHn00E62tQeTlqThyxI6HH7ajsTGkNygat/32\n22TzRiy8DYANPp+CkydtyM9Xkvpo6DZfbjfGbaarqZFRV+e6akALNYpSiMqqVZloaAihspJA6ZYt\nIQQC5AqxerUDAwMe/Xrr7BTx3e86sWJFBENDoj6Ry8nRkJ2t4KWX6NwVFKiorHQjkaCmPbcbCIf5\nkJuqKhklJUqyiTGC7GwNp06R5SKbJJIPMJCXp+ATn9Bw4YKInTtDOjhlK0dmxpfdq6dP1/D1r/Mr\nU1erD+LskK50petvo9Ka4A9Qf0mt1o06w9OSkfaxGHDgQACDg8T6BIPAl788vjSEMebd3dQMs2cP\nWRYpCj30WKwqsyLLySGbp9On6UG7fn2q2WrfviDYQ+j8ecZG34d4nBKzGEvKHugdHRLeekvCpEmp\nZVojSKyu9qC9PYDKSqNbQAIjIyJeeSVD98BlzX25uSpCIR4waBqwZ08QTqfG2UgxfaMZRJeUJJLb\nYCCOWFsAyMlR0dVFnr/vvCPi5pvNy7X0s7FJrahIxZkzIhwOHjDZ7dQkNTAgJhPO7sTAgIrCQgWi\nKOALX+DBhMNBy+BMd712bYSTrzAAyuQo3d1kRWWUWHzve0Gd/fT5yJlA0wi8FxeT7MVoxeXxkJWV\nsVGOefiy1wQCIqZMUVFXJ2P7dgc6O0W0t2fgC1+IITOTnAvq62mfo1GgoiKCKVOIVff7U16xPp+q\nW6uZE96mTqUABEnSEIsJUJSP65+fkZHyst25MwiPB1zqmVXzTed7xgwKOWFOH489FoHTSVIbsvFK\ngb6jRyWsWBHR2eiiIhWxGI2pedtspaKlheKj29qCmD5dRXY2f/21ttL3rLqazu+GDTJ8PhVNTU7d\nG5rtu/kanTVLwerVHv3zfT6y+Fu4UOE+o6bmTlRXp6RGXi+wbFkUHg8QClH0s91O18Dx43b4fKoe\nQMOug+pqYs2N3814XEhq4CmS2uvVdF0uu5dUV3vQ1ESAd+5cDaJolQywFSlVxbj36r+W3vZGvZ/f\niJUeq4lVepyub6WZ4A9QH0atlpHVZRZef/qTxDWImaUhRsZ8YECEx0PNKuyhZ7Ol2ERBALKzVZPv\naCohbWgotVw5cybPTM6cqeJLX8qydNXfdpsCux14802rntRu1zAwIFoYQ0UBFi+OWZqwHn00E3v3\npnTAfj81Op04QUvBRm1pZ6eUBPWkrTx5khqc2PL/c8+5dIBWX08s6IkTtKTLQPmaNcRwd3RIKCxU\nIYq8wwPbF7dbg8/HA5lEglwsmpqcnKduJAJkZADr14cxe7aC7m7SimoaTSR+9KMA+vtpcvOHP6Ts\n5tiEwu1OaVSzsjRuLHJzU04c69e70dgYQiRClmTbt4csbHJBQUoPzM6L0SWAAJoKRRGSvr4y4nHg\nC1+Io7rag6oqYvK7uyXU1YVMnsky6utlXLxIcpBQCGhslHVgamQSJ03S4HIpuqbVvETf3U2AjUUz\nG32Ymb3ZmTNS0s+YJk0DA/SdMDt91NSEk17IRiafZB8MaG7c6MTDD0dRWEguDEzn29TkTH4usGJF\nFNXVbvT2kia6r4+3BuzsJHmEIAicXGP3bprQFRQocLsp7CQUEtDeTu4nM2fSNbJsWURn+J1ODaWl\ndO3y3yH6LtLkjlZXHn88gsFB+i5v3+7EqlURXVPPmGcz6M7OJn9qaiZM2dmx191+u4JjxyREo0Bd\nXUiPXS8tpfsvk1yZV6LMzcuf/3yca17+MN7D05WudFkrrQm+wep66n2up4sFY3XND/bdu/mubqM0\nZP58hUtxc7uBu+6K69o6gGcT6+tDV33QzpyZSm8KhUjPd/Lkr1BaejdGRgTs3UsOD8x6KSdHRVUV\nLbuapRiLFsWxZ08CgsCzbUVF9Bl9ffwDn7FrgpAC7SUlCa6ByqgtZcAyM1PFb39rh9cLC6hm4D43\nVzVthwDBgw/GcPGihNWrPSgoUNDQIOv64dFR6tJ/+20Jqipg7VoH6upIOsB8aflmxNdht5N+0xir\nW1NDkozdu4PYvJnARU1NGJs2UXOTcWzKyhRO39zeHsC+faRHLShQLJOXY8dsuP12BbW1pLt87jkK\nqBBFauo7dsyGOXN4YAxA9/fNyaFGtvr61DL51q1OPQrb66VI3YaGEAQBputGRHc3sZAMBDIQxpjE\nzZtDAAQ8/rgHK1dGktHBAh555KeYPv1elJUpnEyGLMXCuHiRktO6u8kpY+1atw6Uq6rCuHgRekKc\nVQ4joK0tg9Ox7thB587vBzZuJM/iI0fsqKqScfvtClpbHVi5MoIlS2JcTLLdTlHUoRAA8Ox2PA6E\nQiT/MX7+wIAIl8va/Ge8dtvaApg1S0VfHxCJkKxj8mQFDgf/XXE6X0NDw72Ix0kqYo6qZt7AZtac\njzUmO7fqapK7bN0awjPPhHWHmIMHA1AUgWtC3rcviOxsTWdur9akfKM0L6f1mxOv9FhNrNLjdH0r\nzQT/Hde1PgjM1mXjPdjPnCHW0+vVLA0jxMhYfYU/+ckEAFg8Oc1L1YsWJbB5cwiFhdRc9Itf2DA8\nLGDWLAWDg4TmMzIoNvbNN21YsEBJdtVrOHkylYTFpBipBiLgxAkJ+fkaNm6UkZFB2uBLl8iKKSOD\nf+AnEgKOHqWvCutMr6oKc+Pg8TAbLhWyrMHlEtDfL1m8jc3g3uygwJaW6+pcOrNdXh7FkiU8eD1x\ngvx9OzsJ7NrtsPgInzzJg0OKq7VqWE+dknR2MRwm5ndwUNQ1m1Onqjh7lj+GI0dsmDOHZA+dnfzf\nwmFgzhwFPT0iANJ/M8b9pZcCOjBlsbrML3fbNicaGkKYPFlFIiFwx8NA3Ny5CdTWhnXN8tNP8yl5\njEEuLFTx7rtXT2ZTFAFVVQRyh4eJvdyyxYn77xeQSAhQFOCxxyLJY6ImPyODu2dPEAA5ObBzSQl8\nQjKuOpSUBBhXJhJ47rkEolENCxcq6OoS0dgYQnOzA488EsMnPxnH4sVx7NjhgNcL9PZSE15XFx+T\nPG9eAu3tQYiiih07SKu8Z08QJ06kHFNIv8x/n/LzyRKusdGsZU7FZ7/5Jvlxz5ypICMDEEUNo6MS\ntm1zcs1+DQ02/Ou/AtOmqXjyybBlRcjjoYmo3U5OH4x5vnRJQGGhikCAbBBtNg0/+EHQMEnn708s\nEZJtd2xM0O8fwNWblD9sQRPpSle6PlilNcE3WF3PGd61PgiMINrvV3DgQADRKN8YV1Ki6MzMeCzz\ne+3D/Pm0zfPnKWJ4aEhMGu4LKChQsXmzC4cP21FXFwKQitStqwslf/4UDhxgzT5unZkeGRF0No7J\nN0ZGBBQV0WdcukSBGYz5zMvjTf/r62U9WS0/X9WZLiAFpNj2U8v7KuJxcMvPbW1BVFZaE7JKS5Vk\nMxYs1mcLFypYtYrAGQNTbHmdjSFFG6uWaF3ja4aGaJxp2/fp+s7xNKxeL5Lxv0xCQg1NGza40NAg\nQ1VhAXReL1mDjY1Rmt17scZGkNrTw+u2T51KTRTq64nN7umhdLDm5iCuXCHf4cFBARs3yrh0ifS7\ny5dHdV3t0JCAtrYAentFTJ6sYXSUmuUYm81AGAu08PlSdmR0DScwPExJZ9u3fxIDAyJqa1MuBfX1\nsuU67usT0dTk5Bj4wUEB9fVO3Td4dFREXZ0MUQRmzFBhs1EKXkpSRGPwyCMxiwXdN79J183JkxJa\nWpg1moC5cxO6Y8j+/QFs3kyyD6dT44BycTHpaFmCnN+v4soVoLmZ0u7MkwY2Fl4vcPKkDbm51Kj4\n+c/H0d4uobtbxMWLUtJFQcHatXfgD38QEA5LSScT/jr2+xVkZAhoagohP5+aT5kE6ODBAO65JwVk\nWcPrePV+TchX+/uN0rycZuwmXumxmlilx+n6VpoJ/juua30QGB/8HR0ShoZEfP7zcb2h5OabFSgK\nAVtg/CS499oHUQTuuou0qV/5Spb+71VVYaxZ40FNTRiHD5NRPZBiNc3G9UYm69QpYnhLShTs3BmE\n3Q6L3OCZZ1y6JCEQGN8CrKGBAgtGRkT8+79H4PeruHyZNJ99fQKmT1eTKXOiHhqSkQEuSCQe17Bh\ng6x7oA4NCbhyRcDlywK2bnVi61YZZ8+Kuq60rExBRgYBJBZ4cfmyAEniAUZJiWKxqrt8mZ+cTJtG\nS/VGm7CeHvqs4WFqXjt3TtRZ1draMGprCazv3RtEOKxh0yYZS5ZkJp0dwti7N4jLlylUoaODgFV7\nuxNtbQ7dtSAnR4UgaFzUbldXyi3ArF9etEjBwAA1zwkChZGY/XRXraKEuoYGsgi79VYKnSgvj2LH\nDgcuXyZXh9WrI/jqVzP166inR9S9l59+2qXro32+BF54IYgLF2yYMUPV7dMYw9vXJ0KS6DosLU1g\naMiaSjdjBp2nrVudyeuF5BVr10ZQUKAgFiO3CbebdNsPPJCFDRtChghq6BIUc4jIyIiIJ56IwOXS\ncOedCTQ0uFBdTZO82towurslFBSQ5CYSIdkHA8VM2/vOOxJuv5002RQJnfoOtLQEk+eDWO6ZMxUu\nznvlygjy8kgPrKrAnDmqKQqZgiqY9VhVVRgtLRk6UC8rS2DSJA2f/KSX+94xCdCfMxl/vwa2q/39\nwxY0ka50peuDVVoTfIPVeHqfD6rtvdYHwXgA1thQcvTo+8st3m8fRJEesmaGkjGeBQUKSkoS6OpK\nNS2lWFjSupqZLEUhf1RNS4FHgJcAsOa40lLFwsaWlibQ3BxEe3sGHnkkht5eAapKzN7ly8SSimIq\n8crvV9DYGEJPjwRA01nm9vYg1qxxY/nyKI4eJaux555zYdWqSJIt1JCRQb6tJSUKRFHTJRzMAWD/\nftJO1NTICIcFzJmjIBgULHra3FwC5VeuCJg/nxqZUk1/r6Gq6qM6W97SEkRmpoJbbiE2t6GBGEeH\nAxgdFTA2RlZqb71FQJvZZW3ZEkJRkWppttq61QmHA5gyRUVRkcqFMtTUyJgxg2yxVqyIYnhY0e3a\n8vJU1NU5MTws6o1rZs/o4WERzz0XxugoMb6iKFhY06eecqO8PGphI6dN07BmjQuVlRFLWEtzcxD1\n9U7OrSAeF/Cb3xyCz3ePPgkZGhLwxBOZuOOOONraiFXNy1PR2EiJa83NQSiKgOpql27RZ7axY3pu\nv1/lkgoZMDTbeMkyUFVFGt329gDq6oiN9/lUrF9PwLO8PIKzZ/kAjp07yW7NfH7MkhtyjiBd9JNP\nkuZ8xYooMjI0LF8ewcyZCioqPBgYEHHgQAB33aXg9Gl+G7/97SHY7ffr38eBAVEH6gcPBnDu3NUl\nQH/OZPz9Gtiu9vcbpfEtrd+ceKXHamKVHqfrW2km+G+gPqi291ofBO8HYCcit5jIPrDPOX1aRCAg\n6B3iixYpuO02skpbtSqCnTtpedxuJ2uy//zPCP7bfwsiI0PjmKyGBlkHSi+9FBhXAjBvXgJ79wb1\ndC+j521GhoY337RZlqlrasLYscOJhgYZ3d3UIDU0JKKwkG8Mq6uTk5641qQ8Bgr37AnqIF2WBUSj\nvHaaAaSBAdJju92A308OBG63hv5+YhCnTFExOiqiqopcJb7zHTe+//0giopSIFmSaCzZGD31lBtb\ntoTw4IPWsIT29gAyM1X09REwN46dppHvrfGc9/aKqKiIWBruGOuXkUH2aytWkEY1I0PDmjUezJ2b\nwNKlUSxZEkNurqpv1+wekEgAS5d6ko1WGrq6eJ3zqVMSursljI3BIhu4fFlATQ2BzxMneFA2MiJi\nyZKoJaEvJ4dP3WNyh899Lm65Fo4csWNkREB2NjmNML28WTcfj5Oe+KmnSEfOQl0kSUNdXQgej6pf\nf6WlCTz5pFt/b0+PhKoqNxoaZAwPC/rKgiCQltksgVFVfnwuXRKRnc0fI2sIZew2QHIXSQIAAefO\n2fRmvwsXJNxzj2KZqAoC0N4ewJEjNrjd0LX1c+em7hPG199xR4LT/qYrXelK141Q1wSCBUHYDOBf\nAEQBvAvga5qmjY332rQmeGI13gzv/0eTRywG/O53UjK2VsG8eVbrodxc3o91PIZHUYCTJ0XdIYI1\nzxmZbOZB7HAAM2YoWLkygoIC8sBluslVq8hF4tvfpkQokhjcj9JSGTt2OLBsGS11b9ggc01cZFcW\n1pu1RkcFfVk/FBJ0gOl2A4EAuVCsWuVBd7eEzZvNbhUCli+PcmCouTmICxd4gMUsr/x+FUeO8H9z\nOABBIIeLLVucWLMmgq9+1WNhQBlTnZtLS+lMR2q3U+TrM8849XGvq5OxfHkKVE2frmDlykxDxO4i\nDA5SCAJLk2P2ZGbA1tsr6hHUrHHt1CmygRscFPVmJ3b8N91E/sbGbYTDwPPPh3SAHokImDFDhcul\noatLQl2dDI9HQ3+/AJ9PQU9PKuGPuQdkZtIYNTWRD3BxMbGNxKaHIAhkUbZwoYIXXghixgwNDQ0p\nNrK5OYgNG1zo7pbw4otBlJbygD4eB+rq3PiXf4li//4ALl6UMG2aiitX7uGOBaDViLExswNFim2u\nqnInZRcKN9EySifi8RR7bwx1YWxtdTUxsk1NCSxZEtUndNnZKl5+eQyJhMBNtJqbg4jFYAGmZtlG\nKATMmAFdxuPzkcSmvZ2YcLbfRmeH3bup6c9uJ99ggCaqLHyGHEruwfCwhqwsWsnwemk1wqj3N0+g\nzU1vH4ZKM3YTr/RYTazS43R961qZ4P8C8JSmaaogCBsBVCX/S9d1rPFkCdfT/my8+t3vJD161G7X\ncOBAAPfcY7UeOnAggKEhK1PM9u/0aRFTpmhc8IWRyVYU4Pe/F/HWWxLGxsjWae7cBN5+24ZwWMAt\ntygc0J49m1LbmLZy+3YHVqyIIDOTxqmx0YmKiojOemZkaFwgQ3t7ENEodP9Sxs76fJqeZtXdTZ9V\nWGiVaZjBUE+PiPx8HvRMmaLiiSeykjIJvikuFhPw1a9mYv/+ANavD+sA2gyc5s5VUFsr6/6s43nO\nMrbVbge++12HPka7dgU5/2MWHWvURM+cqSaZT3N4REo+0tEhYWBATAJUSlsLhQS0tgaTcdgUbd3Q\nwB/j/PkKzp4VUVnJA6svfYlPg5s9myYczz0XtrgP2O0qFi8mTWldXcgiI2CuEG63ipkzBXR1UXjE\npUsCpk6lJrHycpoYTZumYXhY4Nh+l0tL2ulpCIdTThRmr+l4nFhOs51eaWkCbW1BdHennC8KChTd\nPo0FVkQixNDa7Ro6O2kCYLZ06+8XdXBsZNR37w4iK4tmiOaJVmenpDf7DQ2RRMNmI/cWcgbhnSLi\ncfIjBoDaWrIOrKigGOVLl/hJzOgoNbTNmqXgzjtTkehTpmh46KHUNfjyywE89ljqe2RMXbtR5Ajp\nSle60vVedU0gWNO0Xxh+PQxg8dVem9YET6zG0/uMx6ocO/aX9cFMpbIx9pmWRc2sNAPAfX0CQiGy\n1iouViFJGrd/5saYsjIC1CMjAqJRcACvrS1o8SLu7BR12609e4JwuTSsW3cQkyffi3hcwJYtFBFr\nDLpgUa8NDbLe7b5hgwsPPhgzsXoiTp/W8POf2/HcczKGhsRkjK+qA6DCQmLQbr2VB42zZqno6eEB\n1ugozUYSCUDTCJSOjopIJCjAIh4XcP48LXMbwTzzT/X5yELK59P0Tn6r5yydJ6YhXbYsqo/v4CAf\n+jA8/AaA+5GXp+puB6KooaUlAEHg993h0PD880EkEgKGh6kBUBDAsd91dbLeFAUAo6O0NN7dTWzq\n4KBgaV7s7xe5pkFNY6wzBa8sXRpNglOgs1NEUZGmNx6Sp6xV133+vAhFEblrpbU1iMFBAWvW8BKN\n+nqZ86R+/vkQxsYAr1fgmgwbGw9jz56PWuzGvvtdp86ExuPAk0+SVKW1NeV8MTAgoqtLwtNPu7Bn\nD0lSVq8mH2KmCT53LmWpxvbN51P1hjxe6mGDzUYTPwKxxomwgo4OEU8+6cLAgIhdu0J44IEsbN4c\nwqxZKucU4ferFh31qVM2xGICZs1K4PRp3qpw7lx13HuJ8T505crruPPOfxxXLnWtE/S/9AT/r1lp\n/ebEKz1WE6v0OF3fup6a4K8DaL+O20tXssZjVa6XROJqD5xZsxQT2LOmwNFyvYpPfzrL0gxkjcCl\nz2NMNmOUKysjyM5Wudea06l6e8mJgA9kkNHfT/KKhx8mZ4nOTimZPEXvXb48aop6lfHZz8YtrJ7X\nq+K22xSUlpLPcEGBgv5+EYJA3f2XL5NPcHFxAnY72UwND4sQRcDjUaFpEnw+DUNDKoqLFaxZQ2Cr\nvDyCBx/kP5+xzMYYZOYOUVREvr+MsVu61IOysgTa2gKIxXj3hwULlGQkMgtQiOrjO316KqmutFTB\nihV2fX+MThkstMEIaGmbKgcsN27k3QvMOlq3Gzh71qaf/7q6kMVCzgjEGBDv6xOQn6/hzBk6v7GY\nYNLdyqirc11V1z1rlmq5Vo4elZKxu/w+T53KM+2yDJ0dZzHXxILS+BtB5IwZKpYvj8DpVDEywo8X\nY337+0kbfPGimGSIRcyaRcfJwLjfr2D16gg2b05pl0tLE7hwgRwvrBZ25Ds8OChi+3b+PQMD5LdL\nIRoqRkdT8pSxMejWaPn5vF8ygWsJdXUunc29886EHmBj9vo2lvE+dOiQCpttfLb3Wv3Jb5Sgi3Sl\nK11///W+IFgQhJ8DyDP+EwANwHpN0/4j+Zr1AOKaprVebTvvvPMOVqxYgZkzZwIAJk2ahNLSUn1G\nc+jQIQBI/z7B369ceR2S5IaifBx2u4YrV17HoUPqn709t/ve5APndUiShp/9bCEWLFCgqq/j6adF\nZGbeh1mz6PdDh4B//Me78JOfBPAf//FrTJ6sYXj4bsTjAk6c+BXicQeA+xCPC/jVrw6hqkpDfv69\naGpywuF4Df/jfwiYPfse2Gwa/vM/f4NJkzJQUvJRAIAk/RKKIsBuvxfTp6vc74oi4H//718jHnfq\n2z958hAAaqR7+eUAfvGLQ9A0BX7/vaiqkjE8/Ab+9CcgHr8fABCPv46urjBKSu6Gogh47LGfIpGg\n45k0ScWbbx7Ct7+dGs9HHvkZdu92oKVlUVI68TrWr5dRXv5pxOMCJOmXeOqpMBTl3qRe+TUAwO7d\nC/HcczLeeOMQOjuBePzT3OdXVd2LBQsUvP76IUiSE8A9GBkR4HD8Eq+9JiIn5z6cOwdEo6/hkUck\nzJ17NwDg9Ok38OSTAqZMuReCALz++iF873tOfX9Fkca3qOgerFvnRl/fG/jWt8IYHb0bTzxxJ06e\n/Bk6O1Vuf3784wjuv/9jSeBF59/r/Ycki/t68nX3oaCAPx82m4ZHHvkpZFlEaeldyMrScPHi64jH\nXQDuw/btTnzjGz/FunUCcnPvhc+n4De/OYR43A3gPixfHsUDDxzRt1dTE0ZFxe/x7/8eRWXlx+H1\namhs/C16emLYsuUejI0JWLv2IC5eFHH//R9DZ6eIb37zIMrLHVi16k7L/gPA8PAbkCSHPj6///2v\n8MgjAqZNuwfz5ilYufL3ACTE4/ehs1NEdfVBXLpE1+foKH98kgScP/8GFEVBScm93OdFIv+Ahx43\n+KwfAAAgAElEQVTKxNKlP8X//J8uNDZ+BA8+mIlHH/0Z1qxx4Mkn70gC0NfQ0QFMm7Yw6aTwe0iS\nhmef/Siqqz2QpF+itlbG/v134/x5CVeuvI5oVENGxsfh86no63sD1dUC/P67UVqawLvv/gqBgIqi\nonuRm6vi1Kk38MwzAkZG7kVOjoqf/OTX8PsViOK9KCzkz5/XCwCvIR4HBgcX4e674zh06A3MnAks\nWDCx+wf7t/H+ThP01PVz4YIIWX59wve3a31/+ve/3d9Z3Sj7cyP+ftddd91Q+3Mj/c5+7urqAkD9\nMJ/4xCfwXiVorCvpA5YgCI8C+AaAf9I0LXq11/2f//N/tLQc4vpVPA789rcSLlyQdO2e7QPw+q+8\nYsc3vpHyVv3BD4JYvDj+nu8xWqOx4AozE8x+r6mRMXOmmvQ+9eifcfPNCnp7RTz6aCbKyhJYtSqC\nwUERRUUKmpsduPNOYqITCWJLzc1EtbXUtV9UlIodToVopPS/Rruo2loZN91EzNiiRTGMjUm6r2pP\nD1lhsfr2t2U4HEB+voKsLOhMOYu2BSghLhbjpRyvvDKGQEDEyZOkmTWPSVWVG88/H9LP4U03KZBl\nAYLA+xk3NweT2meKgY7HBb0BkDlaxOOUcLdwIWlwMzOBvXszUFERQU+PiFmzVITDxFZu3+5EeXkE\nO3Y4db/ckhIFTU1OfOELcbjdGsJh6K/jjymAkyclg2QCWL06JS3YsiUETQOnvd63jyQrPT3UNGU8\nPqZRZsUYbbOLRlERSTEkiVL/li2LIhAASksVXLok4LHHMnV7LyYrqK4m7bnfr2DzZhl//CN5F0sS\nrXr4fCT5+PKXU0xja2sQDoeGxx/36O999llZT7JjzYTf+paM7GzyYO7vFxGLpf7GjqmhIYTKSg+2\nbg1h2jQKZ2HjyvyEc3I0DA+LmDJFxQsvOLF4cRxjY6SFd7s1fPGLXrS1BXQdNLPg6+iga9XsxPHM\nMy68/HKA0/DX1IQhCOR0kZenYsUKCucgfb2I/n4JXq+KO+9M6GEV10uGMBHrxL/k+9OVrnSlCwCO\nHj2KT3ziE8J7veZa3SHuB7AWwD3vBYCBtCZ4ojVRvc+JExLXaPRBHxQfJFDDKMXYvt2JffuoU/3A\ngQA6OiSEw4Ke5hUIiBgd1dDU5ASQkkMoioCLF0VdE3vxoqgDhba2II4fJ3nA+vXkASvL1OE+OgpM\nnUoTt//7f38Nv/8u5OUxn2BeOzo4KGDXriDefpvXd7rdGsbGJE5e0d7OR++WlCiorHRzdmtMT/nw\nw3bY7RqKilSsWuXmUsNCIRHr11Pa1/r1bj15LhaDbv2Wm5vyiz1wIIBHH7X6446M0Nhs3+5Efb2s\nW6CFwwReZVnA4CCwcCGBer+fAGNFRUTXRLP9/eY3f4+XXloEu12zHA8DUQ0NIWga2YaVlCSwcaOM\n4WECvcSUpkBvWxsvT5g+nazPKLqXwP+6dW6sXh2Bz0e+tXl5ZAPmdAJ5ee/fcJiZSXHNZ85ImDVL\nxbJlER2EDw5SYIfdrqG7W8Izz5A3b3U1TTCuXCFZgyRpaGvL4IIw7HYNFRUe3Tlj4UIFqqoB0PDs\nszIOHz6Ee+65C6JIjZLGicm8eSSXcToJCC9dmpn0DA4lwXQAmZmUllZQwOtw9+wJorNTQn29C2vW\nRGC3a+jpkbB4cYybcOzZE0RdXQjd3XxQzbFjNnznO25LXHdKH81r+DMyNFy5Qn/r7pZQXe3B88+H\n4PEAlZWpZraf/CTVzPbnyBDe6z51rf7kf09BF2n95sQrPVYTq/Q4Xd+6Vk3wNgAZAH4uCAIAHNY0\nbcU171W63reuVRNsZH1efjmAsTEB06drE3rgGIHzwABRRey9Hg/wmc9kGQCOirlzVezcGeIeaq++\nasfNN6sWQFZd7cabb0rIygL27cvQQxRSUbMaBEHD6tUedHS48P3vZ6KmRoYgkB+rEVzl5amIRARO\n3xmP0+uOHLFZADPTXHq9GgIBslt7803J9Dox2XxEaXlLlkT1yNy33rIhP19FR4ekR+oODop6utfX\nvhaF2w00NlIa3enTkh4aUVLCRw8LApIMeAR9fSI2bJARiwEZGcAf/kDerDk5qfGrqpLx85/b8dBD\nfNNff7+Ir389ClUFHnggywK2HQ4NjY0y8vJU9PeTGwdAThCszFpVh4P8hMmxAHqMb2trACUl1Ly4\nYYOMaBQ4dkzigNhLLwWwbRs1mXV00PXQ3S3gllustmKf/awXtbVh/Pa3IsccNzaGEAymtNm5uSqG\nhyn0Q5YFzu6LgLkNCxfG0dkpQRCgRy4zdresTMEf/mDD5MnkhawowFe+kqUDd48HkGWgosKNTZtk\n3bKupkZGcbE5AEPGs8/KFq1yTw95OdvtFNACAP/2by5UVPDnY2hI1FdWjOMxZ46CggLForUuKUmg\nqkrmfKHp/7AEqhQXWxtbOzpELFyoXJd7CqtrdYZIO0ukK13p+mvVtbpDzJ7oa9M+wROric7wrjUS\n+VqaT8zhFmvWEAg6eDCgN1JpGvnZ5uSomD9fhaaRH/Dp0yJGRsgf9vRpHogy71WvFxgbAx5+OIbT\np4kR9flULF1qtDULo7r6PsTjBAxVVcMLLzh1Jwm/n8CopgH19TIGBgQsWEASDE0DZs9OYO/eAAYH\nKXigoEDlbNPa24M4coRYTeM4UyKaGytXRrjlf9bExVjBxYvjFnDkcml6ElhXl4Tdux14/vkQyssj\nOmvMlvsDAQFbtxII93qB9evd2Lo1hLfflpBICABUTJ2qorWVXAV8PgUNDS6sWxexNKRVVX0KOTkE\ntsxWbLGYgG3bHMnoXiAaFXD2rMQxv6+8MsY5SKgq0NsrYWRERF2dS39dIiFwLHRbWxC33cYDMYdD\nw9q1EU6m0toaxM6dGXozl9+vQlGoWZK5SRi3kZ9PKwTLl1OcdU+PqDfemUF+X5+YBI4wnS9iwOfO\nVQBo2LiRSTHuxy23yBxw37o1hKoqGo+eHlH/24svOsfxdxbR3w/4/dbvJ2s6DATIbuwHPwhZ4q7z\n8ui4yS2ErSIIWL/ejc2bKRFwzx6ykisupmuRSTj27g3irbdSqx7V1WFs3CjDZiMZxB13KHjrLbPL\nROq+8efcU9JM1MQqPU4Tr/RYTazS43R9K50Y9zda17pkeC2sD2NqLlwQ8dhjKbB04QKxwswdASD9\nryiqOHpU4hji3buDmD6df+iS92oAfX0SMjMpmvjWWxVUVnrw2GNmsEHbZ+8HgIEBEadOkQbUCMYa\nGsgz+MIFEYoClJXFIcsSxxi+8EII7e1BvPuuCJ9PxcWLgh5YwMBpSYmCNWvcqK8nvagZ/BQU0Pg1\nNsrIyVGRl6eiu1vS/56draKhIYR4PKW9ra934etfjyZ1ugT4Ll4UUVhoZcllWeCWzvfuDSIzU8PQ\nkIAZM4gZtdlobPv6SBM8NCRw4Ndoxcas7caTfBjPCwN85LsrQpY1aJpmYSXN8bwXLojIyODT+DQN\nlnCNt96S8ItfZOCeexL6JIFZj3m9GnbscOihHWxCwGzeVBW4ciXlKDIeyGeWZcbPdDrpMwANDQ0u\nzqM4kUhdV36/gsJCOm+5uRomTyabueXLo8mgD96Ozuslh5CsLFWPh545k9eSV1WF0dBAMqKsLJUb\nH7udl3ns2xfE+fMSHnwwBlEENm1y6aB3zZqwHvnc0SEhkeBdLa5cIfb5Bz8I4u67rx5iwervSYaQ\nrnSlK10Tqb8aCE5rgidW76X3Ga9x5YMuGX5QJtmYJFdUpOCOO+Lo7hZRXh5BNEp+usZwC7+fALA5\ntvbUKQktLcZ0MPJeNTdl7doVxPLlUYvUYdEiBStWHMTHPnYX9u3LwD//cwIvvhjE1KnA4KDAedK6\nXJoehsAYSrPMIRwW8MADHu41lZXUiGazafB6BaxbR0EaR49KlgQyr1dFeXnUwg5XV3v0vzOGb8WK\nKNavDyMWE3D4sB0rV0ZQXu7iPtscTxwIjB+TW1VFjW7Hj9tQVqZg0yYXPvvZOAoKFDzwQCaam4OQ\npF9i+/Z79LGePFnFlCkaVq6kRjCzndjAgKiz5yUlCpxODZs2ydzEoq6OpAA7d4YwOiqgsFCx2LjN\nmKHi5EkbxxY3NIQsLOlttynYtSuoh3vE4wRqm5uDCIUEPPusjIEBXhJx8aKIoiKSQZSVpXx0Gch3\nu8Fp01lghZHRP3ZMwm23Kfj616O4eFHE2JiIn/70DSxadLeuX545U+VY640bZTQ2hnRpSUtLBmdd\n5nIRMP/lLzP0SdSzz8o4fpxutQzYx+MCjh2zAdC449q/P2Bh3Y0NgyycJjdXxZ/+xPv7ulyabnVm\njB83frffS2rw58gQ0rrEiVV6nCZe6bGaWKXH6frWh5IJ/ls1Y7+e/pkflPU5fJhvyNu/PwBNEzig\n8OqrYwiFKCY5HKZ0tuXLoybQCH25uakptdxsDlkYHRUxNga0tPA+qbQM7MJPfuJGY6OMI0ck5OdT\ngtmGDTIefzwFHFpbeRawq0u0yBymT+e9it99l3St/f3ktWoEgCUlCsdw5uSomDlTQVeXNSK5oSGE\nGTOocayy0qMzfG1tQZw7R9szhjXE4wJOnpQwezYPshctoq5+syxg+fKUawbz371wQcToKI1jU5MT\n69aFkZ0dQX6+iqYmYiS/972gzj6XlPCfFYsR+MvNJZbVZgNOnuT3cWREQDxOwRDt7QGMjIj4/veJ\nsWUpc01NTixeHLPIMzIzFZ159fkolOTkSbuuL2fnQ1FIDrFsWaYuM0ltR8G//iv5Uz/+uEvX6GZm\navD5qNHN2PiYl0fMbG8vMfb19S4cPmzXr4/ycpoASZITn/qUhpEREdOnK+jv50NKhodFPfHN69WS\ndmek9a2tlTm3Esbgj44K+NGPAujuFhEMpsCp16vpx8te398vAqA479JSBWfOWCc+ixfH8cords47\neO5cBWfPSvjoRxV84hMJHDsm4Zlnwu/73f5bvRemK13pStf1qL8aCL6RNME3shk7m+GN93C6Xo0r\nALE+ZWWphhgAE3oAmrvQOzokfcmd/VsoJOLhh3kgsH27A3V1MjIyCKScOSOirk7Gjh0OrqnHvMQu\nCNTB39CQAhs//GEwuQx8H5YvlzkAXlMTtoDK/n6eoZw5kxK1mpuDupWYw8F/7s03k9YUAKfXXbiQ\nXCMSCWDFCgr6yMqi95nlHdOmaejpoWa6hgYntmyR8cc/0pJ+V1cqAMEcPjF7tsJ95qJFCkZGBLjd\nqRS1uXMTcDh4V4Xly1Oxuyz+98gRO44f/7RuF1dWlsBLLwUwPCwC0NDS4oDNlqE3kPHhGwLq6ly6\nhZkZlA8PC9i7l+zFwmHg+HEbHn6Y4qJJYhGD369g//4A3n5bgt9PISnz55NF2OgoWZDNmqVxspNF\nixTY7QSM2bXR1OTUZRx0Tum7wJL02ISqoSGERIIS9mpqwsnwFKCyknTrNTUyzpyR8NnPxnH4sB3x\nOLmUsDFUlI/j/PkQiooUVFW5LeDb61X1yGnGOns8pPEdHQWGh63JfoJAbhdz56o4fVpEQwOx7PX1\nLths5KrS3U36+vp6p66vZ9/t8VZsiotVCwC//XZF/w5PlNH9oPfCNBM1sUqP08QrPVYTq/Q4Xd/6\nUDLB1xNM/qVqvIfTtTbDTeQz3m8cGAAwLitrGs9QmkFxIICkl6rb4mfa2hrE0JCIAwcC6OmhaGGW\noDZnDnkfV1a6OV1uZmYKkMmyOVIXFpY3L4+Wkd99V0IsJmDXrgxLc1Z7ewCtrUEcPfr/2rv34Kiu\nO0/g33O7W08kMBiJl7EEfuCYhwLYwTGTOEMxNrO1yWSdqkk2dmbjOCZePzAGjMFOWEhskRiMicNm\nKJiAgQFiUHmyD8jEeZQ3lIPLRhEGj8FQvF+SeIlutSTU95794/S9fW+/dCS11C30/VS5jKRW9+lf\n31b/7rm/8zsqSZ03rwjPPdeCigrL2Up53DgT588bOHHCh1GjTKiOKBJDhkhPGzDVTUBg8eJCDBtm\nYeHCVjz7bCsMA3j33QAuXLDLDVQSU1FhYvNmNYN6000WmprUyYVdHmD3oLWT/BUrCrBsWQvq62U0\nYZTRhDAWizVrCrB+fTMOHfI5LciWLm3B7bebCX1mFy8ugml660nHjzejmyvE6nLdr0FDg/AsJKyu\nDntm6gEJvx/46KMAysstGIZ30Zy9kNCu2bZjfNddJq5fl2hrM+D3q2R582a1A9uIEarv7htv5OPV\nV1ucsblf65EjLZSUWDhzxo8lSwoxf36rpxwjGLTP8mKzsPGdFUxTjXXp0hY0NBjOQrSyMpXoXr6s\ntpouLVWv/YIFqkwGADZtSmy1t3BhEV58sQVz58bitWNHMG6m1kw6ezthgokdO4JOP/CJE2O1vbt2\nBXH4sIGhQ2W0w4jV6VncvvC3kIiop/TLmuBMJ5OZZNf7xH84HTjgw+c/H8GuXUGntVRXF67Ys8zx\ndbodfQCaJjBggHfBz6VLwMiREWzbZndlMFFW5o3vtGkRrFsXQmWllfC87G1uAwHVs9TvV5eiIxHg\n1CkfpJSIRADVgU/ANAUuXwbWr2/GX/7yZ1RVTU+YoWxoEE4iXVQkcf68qqFUG1uo0oGpU03POM6c\n8eHCBeHUZ44aZaK8XOLcOZV8jRxp4vRplfzaC6Ps+/rZz5o9s5G//GUI4TDw5JNtGDdOJTdFRSqZ\n/8lPwjh9Wp0QuGc+z541nLplexbXXTpij9PvV5turF2bj9mz2zBvXpEzi+sua6ivN3DunJrJ9fn+\nhLffnoonnijEK69463/tjhyFhfYss8CECepE4+BBAxs2qNlyu+TEXpj26qve+7l0STivo3ujlOrq\nQlRXNyf0AS4uVsl9aSmwalUBZs9uRWEhcOiQD4GA6iySn69i9tZbISxa5O3scOUKsHRpGAMHSs9r\n3dAgcPy4aiFXXR1OsRUxcNttarHbqFEWhg9XieZnn/lw5MifsWbNTLS3q167Q4damD+/GE880YZP\nP1UdRubOVUnvunUhFBVJp4yjokLFf+VKtYiuvl7VkdfXq0Q1WVmDW7LZ21T9wA1DXZWw25t1VVf/\nFrIuUQ/jpI+x0sM4ZVa/nAnuC6ug4z+cWlsFZs4sxe7dwQ53dOuIPQMc34s03QegaQLvv+/D3r1+\nZ8HPE0+0YcmSwoSd2X7966CzQGfcOLvOMBbjVAneZ58Znk0G1E5ZapbQ7uRgf++jj3wwTYGrV+Hp\n73v0qIH8fGDgQImBA1U5xapVBZg7txU1NXlOCcTYsd74Dh5sIRz2OfWjP/1pOKHFmb3I7Te/aUI4\n7MMrr4Sdmcf4Mohnny3GsmUtCaUajY0G8vOlZ6b39debYVneWdy33lI9cIcMUe3A7LiNHWvhxAlV\nr7xqVQFOnPAhLw/Yti0PzzxjOYlfKCRQVmZi06Yg3n+/FefOqT6+huGN/8SJESxb1oL589UGEu3t\nAi+8oGYuR4+2oh0T1A5tJSXAtWsCs2e3IT/fOwM7frwZ3UHPu1GK/XxWrQp7bh+JqCRu3z5/tG9v\nAV59tQXf+14xysstLFjQgrIyCytXhiEEPJ027Nric+fUbnQXLxq44w4Tly8beO21Qjz66HUEg6rU\n4403mrFhQwiXL6va7fx8iTNnDMydq5LTDRtCaG72Yfp0E0IAixblwzTtBWfA2bM+LF0axqFDfpSW\nqoV4Z874nPfL3XebePvtIE6d8mHkSG9HD3u21+5jXF3d7GwIo5ts9vRMbV/4W0hE1FP6ZU1wTzVj\nz8QiE/sMz/5wOnDAh9bWWGKRiQ9B+4PV7kVaWKga+Kf7ANy/35ewLWswKFBebiVsDHD0qA8//7lq\nAXbokLfe2P2hO3iwxLx5sQRv2DCJvXtjvYNnz27DN7/p7f1qf0+N40E89FAQP/iBd2viBQsKnf6o\ngwdbeP75VgwdauFb37ruXJKvqDCdvrSVlWqh2w9/WBSt0TUTFoLZCZ0qwfB5kp3Nm0OumXDLWUxl\n16vG7gO4804Ln30W36nA21mhvt5AXh5QUCDR2GhEk2eBW26J9YW1X4P9+/24fFngtdfCcWUOYeTn\n+6K9lWchEJBYv161VHN3H7hyRWDRIvUaHDpkOLO5w4ZJ5zlWV6ttnpcsicX5nXeuedqWvflmAV54\noQUffujHU0+1Ye3afGfWtb5elTbYMbr1VgslJSZaW1VdMgD4/aqrR3u7iO4QKPCd7xR7no99EhKJ\nqJZg8a3wli5tQX29el533GFh0qQwvvWtEs99FBR4t3w+fNiHxkZ1snTvvSa2bJmKjz9u8dRGl5Wp\njUkAYPRo07mqUVWlZvntLZjju2w0Nqq/A+6Soy1bQhgyRG9TGqDnr1p19W8hZ6L0ME76GCs9jFNm\n9cuZ4J6SyQV39ocTAM99ZuJD0P5gtTsV6IwzfkZK1d5KPPVUa8I2uCNHqnZh7lZn7su4kyebmDTJ\nxF/+4sMzz7Ri+HALPp/ElSvCU89rX0J3133G1wAfOOD31BCfPKm2XX7uuSJnDLNnt+H8eR8mTjSd\nGcUTJ3yeUoytW4PO1rxXriR2j7ATukBAJvS5PXfOwMKFsedqb8EcX686ZUoEkYhAOCywcaPaRvfO\nOyM4d84Hn897WV8IieJiOF0LAgHVF9juC1tebjkL0FpbBU6f9ibceXnAlSve7zU1Gbh4EZ6NMBYt\nCjvPa+pU0+lj/NlnsZOAa9eMhFZgQqhWaxMnApcuCSxa1OI5Sdq4UdV6//CHYVRVmTh2zOdpH7dh\nQwjf/a53w4zr19U4rl0TALxjHzBAYvXqZgwdamHAAIlXXy3EV74S8dymoEBGa6sF5swpwne/2+b5\neWmpxODB0ilnuXZN7ap28aKBWbNKsHOnKjWKr42urxe4fl04PXfdV2Lc74v4YyZZ+c+1awIzZ0Zg\nmkBtrTphLiuzPDs2uk+cOVNLRNRz+mVNcE/JxKXL+HqfnvgQdN/nbbepBVA1NYG0s9fxM1L33BPB\n5csCV68aWLWqwGl5NWaM6rwQn6DEx2L/fh8efrjE2Q45EFDb8+blRfCv/6pqju1+svYq/JIS1XvW\nHofP9yfcffdUtLQI7N4dQFEREAwKRCIW/P7YpXt3n1Vv7164xhfbJW3lymZnIVhLCzB5cgRtbard\nmRBIWEg1erS3vZq9BbOUwNatIXz8saoJPnnSl9BH2LIEnn++yJM8njploKhIbRayaVMIly6pspJg\nMJZkPfVUq6cV18aN3gVZFRUWzp+3Z5zfQyDwZZSXq7jEv46/+EUIN98skZcn0dQk8OMfF2H16uZo\nLa+B8eMj8PvzXJ0IWvCjHw3A7t1BfPGLEVy/DuzYEfDE4Px5A5cuqVnZoiILfn/iiYP765MnDVy/\nLrBtWwimCRw75p0tHzXKwj/+o3dBZUuLt+vHxImqg8qcOQMAJG4bfMst6th59dWwJ3bV1WoG99gx\nH1au3IulS+9z2o4tXFiE555rxZo1+UlPQt3vi7Vr850+vu73arKZ3PgT5qVLW/DYY4knpLm6hTDr\nEvUwTvoYKz2MU2ZxJjiDdC5ddrZkItMfgvGPLwSSzl7H327iRG8y7vdLPP98MV55Jey0xgoEJHbu\nDGL5ctX5IF0s7BOG+BnjjRvVrm1r1hTA74ezLXBFhYnSUon33/c7M5IXL7bhyBE1mx0/s7hjRxBt\nbQJ1dd6yhgEDJFatUi2w7Mvi9uy1Pd433yxw+u2OG2dh0CATly/7IITaDldKlYQdP25EE/fY76qF\ngRKnTqmZwZUr1da6x44Z8Pu9s9h5ecD5894Zz0uXDFRVRXD0qB9tbWqB2JgxJiZMsLBvn+GUIAQC\niEsifZ6escuXF2Dx4jC2bg3hj39swcyZQUQiwLBhJrZvD+LECR8qK00MG6biYM+M2t0mIhF4Xpdt\n29TzjURipTkHDqhZ6XAYCIW8Cakqo1BdGewFcO6fjx1rOkn2sGEqZh9/7MeRIwamT29HebnlqSuP\nj1NDg8CIEZbnJCE+6Tx50vDUi1+7JvDggya2b/ceE4Ba1DZmjIkrVwxPsl9fb+D2282UPXftE8rz\n59VjNDR439epTmITr6yILp84ExFR1/TLmuCeojNr21HJRE+f4cU//pYt3o0k7A/hVOO0x1pTE8CJ\nEz4sXFjkqQ2dM6cY69c3Y8aMSNJY2Mn1oEHqsvTIkRbmz2+N1mDm4+BBP1asKHBad129KvDII9ed\nxxRCuGZ2H8SyZS3RpChxU4Gvf70dBQXekoRbb7Vw//1qLGvWhNDUpPqzFhSoGeBBg4CBAy3MmVPs\n1N6uX9+Mc+e8WxZv3x7ESy+pr6dNa3eS4rFjrYTWa4DqqBC/ELG9XST0CG5uVm28Vq5UO8F9+qkP\n48cDH30EPPXUALzwQgvGj1eLuNy/J4R0thxetkzVCre2GtEZz1lYv169hi0tPs8mEtu2haJbUqsN\nSbZtg1O76525FRg92vL0f25tFZg1qwQrVoQ9GzdMnBhx6oztGXe7/ry4WHVcaGgwnHhWVzd76n+3\nbAlh5swIgNiJU22td3e0UaPUa2Qn77fcom7rfg+WlVmeEo3du4Pw+4HPfc6Kex2AN95oxn33mfj3\nf5+C48dDTonC7t1Bz8JOdxmDe9fG2trk75dUJ7HxJ8x26UwudapJhzNRehgnfYyVHsYpszgTnEE6\ns7bZ7ssZ//iNjd4ZPPtDuKNxuuuKP/nE59n61b5tsljYyfWKFWG88ko4oXesEMKZGQsEJMrKYknB\nbbeZCIdVe7SrV1V9sL37VnxdcmWl6pl6//2q/dUHH/g9SfrkySZCIZUkLlvWgqefjpVMbNwYq721\nYxS/k93hw/bMq+pycOaMmtmNTx6PH1czritXhjFihNo44q9/VS281q7Nx5tvNmPLlhDq6mIbVbz0\nUktCbN56S42pqclAU5PE2rUFzuNPnKgW9q1ZE8KgQRInT/qwbFnY2VDC/Rra/7b/v2+fz6TqV54A\nABhNSURBVNODePHiIpw6pVp6ueNZXi4xfLiZsCNce7taHOneuKGmJoj165udRHTOnNhOef/8zyFE\nIrGZTyBxl8DGRpFw3MaX8Fy8aHiS9xUrCj0napMnm7As4He/u4aGBsO5T8tS9xUf8yVLWuD3e49Z\n+4TtnXdipULJTiKHDJHa72v3FZadO4PO1t7uhJuIiHoHa4J7WUclEz1d7xP/+OPGWUlnbFONM9WH\nuO4KdjtZuHDBSEjS8vKAN95QtZcTJkSwfHk4ukgK0ccWmD+/2Ck7eOyx32LBggdQVmahtVX1hW1q\nEqiqMnH+vOpBXFVlorHR8CTp9s/OnvXuOmaP4+JFbylHcbHE8OER57L+2rX5ECLWVWHlymb4/Sph\nV48Va4VVUWF5Zl6XLw/jzjtNfPKJ35nFHDBAehZjDR0qsW9f4jbF9qKxzZvzsXx52Jl9X7SoCOvX\nN+PyZeDb3y5xnue2bUFPTbD9unhnIOE8hn3iMXas2qLZ3UWivNzCpUsGTp82EA4LDB8OPPFEG559\nthVDhpjYuTOIY8fUhg7TpqlNTuxE1E6IKystNDcD3/jGAM+s+M03e4+1O+9MPH7cJ5j79vmSbvgR\nn3gahjpm3LPXdqI8ZIg35nZs3O+/ZFdD4pPdujp15WLnzqDzHOxe2cnq7HN5t8rOYF2iHsZJH2Ol\nh3HKLM4E97KuLnTLRPu1VI/v7kTR0TiTfYh35jnZyXVpqVqI5U5+7rjDxIsvqkvqmzfn4ZFHrqO+\n3sCf/+zDffd5t40+ccKHa9cMPP30dc+l6OrqZk85gnunPfciPHef5PgkPhKJbcQwapSF69eFJ+na\nvj2I114rxOrVzbjpJgtXrxoYMUJ62qZt3BhCQQEQDsuEBFv1jC10aqjnzCl2ZnXvuSeC06cTu1PY\nJyuXLgls25aH+noDQ4ao8W3cGML48YkJ7vDh6nd++9sWPPRQbJbRXS4wZ06sLrqqSpWwTJxoYuBA\ntQlEY6N67PHjLfz+935PScjSpS1YskRtinHvvSb+6Z+uJ7ze9vbcPp+qlz171sCyZS2oqQlg6dIW\n5OerFnGvvdaMwYNVm7SWFjVjm+r4Pnw4sZ421clXqhlanWM22e8mK2OwT6TSlWHY769sXwkiIqIY\n1gT3so5KJlKd4WVqBkl3oV2q2yX7EJ80SX8c7oVEN91keWYbS0rULOCnnxp4/PHrnmR2x45gwk50\nf/M39wPwJjRtbUgY39e/3u4kkI88Eus7vGZNPjZsUN0Y7PZkkyaZaGoCbr011q6qpsbb+eDCBQPz\n57fiyBED8+erMcb3iLVrm99+OxiXNFkYPdrCokVhTJsWQUOD4dk4Y926EO6+28Ljjxc6ifEXvhCB\n3y/xySdqQ4bXX2/2dErYvTuYdBGWvY3u5MnTAMReI3e5gHuW1n1iNXGiBXdNLgBcvBjf99guXTFw\n/LhMeUzt3+/Dhx/6kibQy5a1YN++AEpLJb73vUKt4zu+VOOuuyLYudNbSmCfNLa1IekmFamOb/f7\nL9nVEDvGhw6pWnK7HGf4cOncX/zx4k50c3m3ys7gTJQexkkfY6WHccoszgT3ET05g9SZWWb3h7h9\n2ffXvw44CUF9vZE2gXHPOtfUBDw9a3/xixDmzlXlDvZWxLHnqzZHiF/t775Pe4FSstpgd3Jiz/ye\nOePDyy8X4Y03mnHmjIHx403cfLOFBx6wPM8/fia5pUXVI0sZSwoT+wqrf589a2DXriAOH1Yztw0N\nqqewve1uqkTLTk7vucdCe7vE734XQGkpMHduYbQWNvFYSJbYpXttO3v7ceOSL+YqLbU6LIGJr/st\nLIzNgttlIbrHd3m5hfXrQ9Fd3CR+/vMCLFjQqlW725ma23RXTeyNMpJ1jUiX6LLvLxFR7mBNcI5J\nVe/TkzNInZllTrf6PlVtZrzr14EPPvBhwADvjN7QobHSAXfLskBA9eL1+yWKiy0Egz4AEmfPvoea\nmgdStqQqK7M8tcF2DO2+w6WlMum2zqmesz2TbI9pw4ZYb961a9Ws8sWLBlpaYgv2hg6VmDLFxJQp\nKkH/zneKEhLeVImWndR/7WulnhiXlenXYO/f78ODD+6DaX5F6wpCumOhqkotMty3z4+77jJx9arA\n5s0hDBtmOeUYyVRWqm2D3SdPY8aYaGgwsHp1M9rakNC/ON1zGj/eQlOTcGp6q6ubE+p+U21S0RH3\n+8+9sUv8Arl0V1TSJbq52ve3s1iXqIdx0sdY6WGcMoszwX1EV2aQdGd4OzPL7P4Qj7/sm6420+2D\nD9QWzOXlqhwiLw9obwdKSry9erduVZtmlJdbqK4uwP79fixdGnbqaR9/3IcXXxyQ0JJq0iQzugCr\n49rljuqq3TGML7VoaDCwaVMIFy8KhEICL75YhAULWiClwKOPXsewYSYKC6WzQCq+17I7mUqVaCXb\nqe/KFSTdlCGZ48cNmKb+FYR0x4JhAI2NBn7849giw3XrQvi7v0v/eldVmfD7pdP395ZbEmtmO3N8\n210/0pXAZPKksbOlSDdKoktEdKNjTXCOSXWG15UPVt0P764mDPG/Zy+s6ihBP3ZMdT44c0bt0rZo\nUQuqqwuxeXMQu3YFceqUwKBBwIULAnl50tPxIBiMtfkaNOgB59/uZG3/fh/27vUnTea6E8Pq6mbP\n8x071sT996uNRfbu9WHevFZUVqra5qNHfSgrs/Dww6l7Lad6HPdt42M8daqJIUPset+On4f6/S+j\nvR1ar226Y8E0gREjTGzaFERDgwEhgJEjVW2xlOnLLtw1xqlqZjvz2nRUAqOTVCc7SUz2/uNitkSc\nidLDOOljrPQwTpnFmeAbmO6Hd1frFLsyswoAY8Z4t7O1a0vtxUVCpE48S0tjXRDsf8e3pFK7d+lf\nXk/HHcM1awqwZUsI164Jz/Otq/MlzGw+/HB72gVS6R6noy4GnekK0tnXNt2W2n6/2tUtfoe/7dt9\nSWd3Uz3XTJf2dFRSkkq6k0R3ghy/ILOvLmYjIiIv1gTnmO7U+8TPbN1+u6n14d3Vy7dd/b377lO1\npSdO+DB6tInmZu9GAekST79fOgvKDhz4f1i37gEMGeJNwHbsCGLt2nynu8K0aRFUVSVuBa2TULoT\nNrstWXxtaaoEtjPJXqrbdvfSumEA4fB7ePhhvWMqfoY1fnFZ/AK3gwfVZhvx3THSJfyZWByW7LXs\nbIySvW7h8HuYPn26J0GuqDC1y0/6C9Yl6mGc9DFWehinzOJM8A0kfmZr165gTq5E9/uBL33JxJe+\n1PFMYbLEU11aVz14i4os/OEP3tKHxkbD6a5w772xZDfV1rbp6CRsqRJY9+9WVKgEPtkGCrqPk6le\n0br3mWx3wdLS+A4R6radmXnPRM1sJloGJnvdwmH1s/ie1I2NBh5+uL3L4yUiotzDmuAc050zvPik\n5cQJ9cGdLjnIRGKVyeTMNOFZRGV3b0hm+vTpqKlJ3FiistLS7nHc1X7JbqkS2PhZ1ZkzS1Mmbd29\nfJ9OumPq4EEDH36oNh65eFHA75fOSUay3QXt16ahQWDECIl589QiubVr8z2zpRMmqOfsLqvo6oLE\nZL+TiTrd5GUU05M+d5ZAeHEmSg/jpI+x0sM4ZRZngntJT8zixevKB3cmZtQyuRVs/H3t2BFM6Jjg\nVllp4ZVXChNKH5LpqcRGJ4HNRNKWqQVa7mOxpER6any3bAnBXsCWrN3c8OHAjBkRGAZSbLahxhO/\ni5/7MXSOj46OqUy8ll1tc0ZERDeGDKdhqdXV1fXWQ+Uk+0P9+98fgFmzSlBX50t6uz179nT5MewP\n7nXrQlpdGoDkiVVnZeI+Ut3XBx/4U8Zsz549zsYSQ4damDEjgvvvT31y0ZX4ZIqdtAF6XRq6ex+m\nqRLRmpoAfvWr92G5buo+Fs+cSSx5sNlJYmWlqrl+9NESz+tg/9y+2pBqpja+jljn+Eh2TLmfk9+v\nyn0y/Vra7790zy0Z99hqa32eeN+IuvN3qj9hnPQxVnoYp8ziTHAv6Y02S12ptczEjFomZ1jj78uu\nOU0Vs848Z7uHMAAnEeuJGflkOppZ1LlS0JnZSfdMqs9XhKoqnxMj97EoBBJKHuJ15dh1v47xdcQ6\nx0eyYyrZ7LC7Trc3rrakksmrIURE1DtYE9xLdBPF3q73ycRl30xeOo6/BD9njtpWOVnMuhKrbCUr\nHSXrOuPqTMLvTlxN8ys4fjzk/J77WHzzzQJs2BDC1aup66+7cpLjfh1vv93Erl1BnDihf3wkO6be\neSd9y7lMvLZdff/1t17CrEvUwzjpY6z0ME6ZxZngXpKrNYaZWKmfyR2y3PeVrOa0u3I1Wcn0uNIl\nrlVVJrZsCaGuzo/SUokXXyzCkiUtGW1pluyYmDJF//kk+/2OkvFsvrZcSEdE1PewT3Av0U0U2QMw\npqOYdSVWuZqsVFT03AYSTU3voarqi87PDAMYMkRixYqCXmtplgkdJeOZeG27+v7L1ZPcnsK/U3oY\nJ32MlR7GKbM4E0z9Sq4mK4GAxNKlYQSDBkpLVSuy7nAnrnv2WN2qL84VHSXj2XxOuXKiQERE+oSU\n3fuw1fWHP/xB9ueZYKJ0amoC+P73Bzhfr1sX4uYMREREXVRbW4sZM2aIdLfptRZpRJRaJlqoERER\nkT72Cc4x7AGo70aKVU/2ML6R4tTTGCs9jJMexkkfY6WHccos1gQT5QDWlBIREfUu1gQTZUE2N3Yg\nIiK60enUBHMmmCgLuMMYERFRdrEmOMew3kdfX45Vso0dekpfjlNvY6z0ME56GCd9jJUeximzeAGW\nKAvYDYKIiCi7WBNMlAWWBdTVsSaYiIioJ/RaTbAQYh6A1wDcLKW8nIn7JLqRsRsEERFRdnV77kkI\nMQrATAAn092ONcF6WO+jj7HSwzjpY6z0ME56GCd9jJUeximzMnEBdhWABRm4H0rCNIHaWh9qagKo\nrfXBYukoERERUbd1qyZYCPFVAA9IKZ8XQhwHMCVVOQRrgrumtpattIiIiIg6IyM1wUKIdwGUu78F\nQAJ4GcBiqFII988og5K10mISTERERNQ9HSbBUsqZyb4vhBgPoALAfiGEADAKwD4hxL1Syob4269e\nvRrFxcUYPXo0AGDgwIGYMGECpk+fDiBW59Lfv7a/Z39dWfllBAIS7e3vweeTqKycklPjzebXBw4c\nwJNPPpkz48nVr+OPrWyPJ5e/jo9ZtseTq1//8pe/5N9vja/t7+XKeHL5a/4959/zTLzf9uzZg1On\nTgEApk6dihkzZiCdjLVIi5ZDTJZSXkn285UrV8rHHnssI491I9uzZ4/zwgJspZVOfKwoOcZJH2Ol\nh3HSwzjpY6z0ME76dMohMpkEHwMwlTXBRERERJRNvdYnGACklGMydV9ERERERD2p1y6ss0+wHndt\nC6XHWOlhnPQxVnoYJz2Mkz7GSg/jlFmsLiUiIiKifidjNcEdYU0wEREREfUGnZpgzgQTERERUb/D\nmuAcw3offYyVHsZJH2Olh3HSwzjpY6z0ME6ZxZlgIiIiIup3WBNMRERERDcU1gQTERERESXBmuAc\nw3offYyVHsZJH2Olh3HSwzjpY6z0ME6ZlbEd44huRKYJ7N/vw/HjBiorLVRVmTAM/Z8TERFRbmJN\nMFEatbU+zJpVgvZ2gUBAYvfuICZPNrV/TkRERL2PNcFE3XT8uIH2dvUeam8XOH7c6NTPiYiIKDex\nJjjHsN5HX2/EqrLSQiCgrpYEAhKVlVanfp4LeEzpY6z0ME56GCd9jJUeximzWBNMlEZVlYndu4Oe\nmt/O/JyIiIhyE2uCiYiIiOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgT\nTERERET9DmuCiYiIiOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgTTERE\nRET9DmuCiYiIiOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgTTERERET9\nDmuCiYiIiOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgTTERERET9DmuC\niYiIiOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgTTERERET9DmuCiYiI\niOiGwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYpszgTTERERET9DmuCiYiIiOiG\nwppgIiIiIqIkWBOcY1jvo4+x0sM46WOs9DBOehgnfYyVHsYps7qdBAshnhFCfCqEOCCEWJ7qdkeP\nHu3uQ/ULBw4cyPYQ+gzGSg/jpI+x0sM46WGc9DFWehgnfTqTr/7uPIAQ4gEA/xnABCllRAhxc6rb\nNjc3d+eh+o2mpqZsD6HPYKz0ME76GCs9jJMexkkfY6WHcdK3f//+Dm/T3ZngJwEsl1JGAEBKebGb\n90dERERE1OO6mwTfAeBLQoi9Qog/CSGmprrhhQsXuvlQ/cOpU6eyPYQ+g7HSwzjpY6z0ME56GCd9\njJUeximzOiyHEEK8C6Dc/S0AEsDL0d+/SUo5TQhxD4C3AYxJdj9jx47FnDlznK8nTZqEqqqqbgz9\nxjR16lTU1tZmexh9AmOlh3HSx1jpYZz0ME76GCs9jFNqdXV1nhKI4uLiDn+nW32ChRC7APxUSvle\n9OujAL4gpbzU5TslIiIiIuph3S2H+DcAfwsAQog7AASYABMRERFRrutWdwgAGwD8SghxAEAbgO90\nf0hERERERD2r17ZNJiIiIiLKFb26bbIQYokQ4owQojb630O9+fh9jRBinhDCEkIMzvZYcpEQYpkQ\nYr8Q4q9CiN8KIYZle0y5Sgjxs+imNnVCiBohRGm2x5SLhBDfEEIcFEKYQojJ2R5PrhFCPCSEOCSE\n+EwIsTDb48lVQoh/EULUCyE+zvZYcpkQYpQQ4o9CiE+iG249m+0x5SohRL4Q4oPo590BIcSSbI8p\nlwkhjGie+b/S3a5Xk+Co16WUk6P//TYLj98nCCFGAZgJ4GS2x5LDfialnCSl/DyA/wuAfxRS+x2A\nu6WUVQCOAFiU5fHkqgMAvg7gvWwPJNcIIQwAvwDwIIC7AXxLCDEuu6PKWRug4kTpRQA8L6W8G8B9\nAJ7iMZWclLINwFein3dVAGYJIe7N8rBy2RwA/9HRjbKRBIssPGZftArAgmwPIpdJKUOuL4sBWNka\nS66TUv5eSmnHZy+AUdkcT66SUh6WUh4B/04lcy+AI1LKk1LKdgDbAXwty2PKSVLKPQCuZHscuU5K\neUFKWRf9dwjApwBGZndUuUtKGY7+Mx9qTRfrWZOITiL+PYD1Hd02G0nw09FLsuuFEAOz8Pg5Twjx\nVQCnpZTcJLwDQoifCCFOAfivAH6U7fH0EY8B2J3tQVCfMxLAadfXZ8CEhTJECFEBNcP5QXZHkrui\nl/j/CuACgHellB9me0w5yp5E7PAkobvdIRKk2VzjJQD/E8AyKaUUQvwEwOsAvpfpMfQFHWxCshiq\nFML9s34p3fEkpfzfUsqXAbwcrU98BsD/6P1R5oaOYhW9zUsA2qWUW7MwxJygEyci6j1CiAEAdgKY\nE3eFj1yiV/M+H13T8W9CiM9JKTu85N+fCCH+E4B6KWWdEOIBdJA/ZTwJllLO7PhWAIB1APrtB06q\nOAkhxgOoALBfCCGgLlvvE0LcK6Vs6MUh5oROHE9bAexCP06CO4qVEOK/QV0i+tteGVCO6sQxRV5n\nAYx2fT0q+j2iLhNC+KES4M1Syt9kezx9gZTymhDiTwAegkbdaz9zP4CvCiH+HkAhgBIhxCYpZdIW\nvr3dHcK9ev+/ADjYm4/fF0gpD0oph0kpx0gpK6EuOX6+PybAHRFC3Ob68h+g6skoiWgnlgUAvhpd\nYEEd67dXYFL4EMBtQohbhRB5AL4JIO3K635OgMeQjl8B+A8p5epsDySXCSFutktIhRCFUFeLD2V3\nVLlHSrlYSjlaSjkG6m/UH1MlwEAPzAR34GdCiCqoBUwnAMzu5cfviyT4hzSV5dGdCi2oLho/yPJ4\nctmbAPIAvKsuMGCvlPK/Z3dIuUcI8Q9QsboZwP8RQtRJKWdleVg5QUppCiGehuo0YgD4FyklTzyT\nEEJsBfAAgCHRNQtLpJQbsjuq3COEuB/AtwEciNa6SgCL2TkqqeEA3op2aTEA/FpKuSvLY+rzuFkG\nEREREfU72egOQURERESUVUyCiYiIiKjfYRJMRERERP0Ok2AiIiIi6neYBBMRERFRv8MkmIiIiIj6\nHSbBRERERNTv/H8D5LsadHS+zgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x123f31fd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# plot is slow - 1 min or more\n",
"figsize(12, 18)\n",
"\n",
"plt.subplot(311)\n",
"plt.scatter(X[:, 16], X[:, 37])\n",
"\n",
"plt.subplot(312)\n",
"plt.scatter(X[:, 16], X[:, 18])\n",
"\n",
"plt.subplot(313)\n",
"plt.scatter(X[:, 26], X[:, 43]);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's perform a train-test split for cross-validation."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Xtr, Xte, ytr, yte = train_test_split(X, y, test_size=0.2, random_state=0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next let's build a model using the default parameters and look at several different measures of performance."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy: 0.8397\n",
"\n",
" precision recall f1-score support\n",
"\n",
" 0 0.85 0.83 0.84 9912\n",
" 1 0.83 0.85 0.84 10088\n",
"\n",
"avg / total 0.84 0.84 0.84 20000\n",
"\n",
"Confusion Matrix:\n",
"\n",
" [[8179 1733]\n",
" [1473 8615]]\n",
"\n"
]
}
],
"source": [
"default_model = LogisticRegression(random_state=0).fit(Xtr,ytr) # instantiate and fit\n",
"pred = default_model.predict(Xte) # make predictions\n",
"print('Accuracy: %s\\n' % default_model.score(Xte, yte)) \n",
"print(classification_report(yte, pred)) \n",
"print('Confusion Matrix:\\n\\n %s\\n' % confusion_matrix(yte, pred)); "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the sklearn implementation, this default model <i>is</i> a regularized model, using $\\mathcal{l}2$ regularization with $C = 1$. That is, the cost function to be minimized is $$-\\frac{1}{n}\\sum_{i=1}^n[y_i\\log(p_i) - (1-y_i)\\log(y_i - p_i)]+\\frac{1}{C}\\cdot\\sum_{j=1}^m w_j^2.$$ Here, $y_i$ is the $i^{th}$ response (target), $p_i$ is the predicted probability of that target, and $w_j$ are the coefficients of the linear model. In a traditional statistical implementation, the second sum wouldn't be there as it biases the model. This is the regularization.\n",
"\n",
"There is no reason to believe that $C = 1$ is the ideal choice; it may be better to increase or decrease $C$. One way to search for better values by doing a grid search over a set of possible values for $C$, assessing the best choice using cross-validation."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[10, 100, 1, 0.1, 0.01, 0.001, 0.0001]\n"
]
}
],
"source": [
"cs = [10**(i+1) for i in range(2)] + [10**(-i) for i in range(5)] # create a list of C's\n",
"print(cs)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Fitting 5 folds for each of 7 candidates, totalling 35 fits\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 35 out of 35 | elapsed: 10.6s finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Best score: 0.8416375\n",
"Best choice of C: 0.001\n"
]
}
],
"source": [
"lm = LogisticRegression(random_state=0) \n",
"\n",
"grid = GridSearchCV(estimator=lm, \n",
" param_grid=dict(C=cs), \n",
" scoring='accuracy',\n",
" verbose=1,\n",
" cv=5, \n",
" n_jobs=-1, # parallelize over all cores\n",
" refit=True) # instatiate the grid search (note model input)\n",
"\n",
"grid.fit(Xtr, ytr) # fit \n",
"print(\"Best score: %s\" % grid.best_score_)\n",
"print(\"Best choice of C: %s\" % grid.best_estimator_.C)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Fitting 5 folds for each of 7 candidates, totalling 35 fits\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 35 out of 35 | elapsed: 10.2s finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Best score: 0.831911995219\n",
"Best choice of C: 0.1\n"
]
}
],
"source": [
"# change the metric\n",
"grid_prec = GridSearchCV(estimator=lm, \n",
" param_grid=dict(C=cs), \n",
" scoring='precision',\n",
" verbose=1,\n",
" cv=5, \n",
" n_jobs=-1, # parallelize over all cores\n",
" refit=True) # instatiate the grid search (note model input)\n",
"\n",
"grid_prec.fit(Xtr, ytr) # fit \n",
"print(\"Best score: %s\" % grid_prec.best_score_)\n",
"print(\"Best choice of C: %s\" % grid_prec.best_estimator_.C)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Fitting 5 folds for each of 7 candidates, totalling 35 fits\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 35 out of 35 | elapsed: 10.1s finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Best score: 0.915052639594\n",
"Best choice of C: 0.01\n"
]
}
],
"source": [
"# change the metric\n",
"grid_auc = GridSearchCV(estimator=lm, \n",
" param_grid=dict(C=cs), \n",
" scoring='roc_auc',\n",
" verbose=1,\n",
" cv=5, \n",
" n_jobs=-1, # parallelize over all cores\n",
" refit=True) # instatiate the grid search (note model input)\n",
"\n",
"grid_auc.fit(Xtr, ytr) # fit \n",
"print(\"Best score: %s\" % grid_auc.best_score_)\n",
"print(\"Best choice of C: %s\" % grid_auc.best_estimator_.C)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy: 0.8396\n",
"\n",
" precision recall f1-score support\n",
"\n",
" 0 0.85 0.82 0.84 9912\n",
" 1 0.83 0.86 0.84 10088\n",
"\n",
"avg / total 0.84 0.84 0.84 20000\n",
"\n",
"Confusion Matrix:\n",
"\n",
" [[8150 1762]\n",
" [1446 8642]]\n",
"\n"
]
}
],
"source": [
"grid_preds = grid.predict(Xte) \n",
"print('Accuracy: %s\\n' % accuracy_score(grid.predict(Xte), yte))\n",
"print(classification_report(yte, grid_preds))\n",
"print('Confusion Matrix:\\n\\n %s\\n' % confusion_matrix(yte, grid_preds));"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([[ -1.94881362e-03, 6.11894799e-01, 5.56016366e-03,\n",
" 9.66391259e-03, -3.37593417e-03, -2.84746983e-03,\n",
" 5.43636937e-03, 1.05682075e-02, 1.27804594e-02,\n",
" 3.79970966e-01, 1.32455604e-03, 7.75931819e-03,\n",
" 6.03182136e-03, 7.69719240e-01, -4.38522147e-03,\n",
" -9.10312768e-03, 3.89346423e-01, -6.07929488e-03,\n",
" 1.31749101e-01, 7.11110748e-01, -3.30808982e-04,\n",
" -9.19102612e-03, -2.18644108e-03, -1.24054210e-02,\n",
" 2.09419123e-01, 4.55561566e-03, -3.91681865e-01,\n",
" 9.15080966e-03, -7.85568577e-05, 3.33015315e-03,\n",
" 1.74126013e-02, 1.42947252e-02, -2.87393846e-01,\n",
" -4.92830888e-03, 5.10965364e-03, 6.32300394e-03,\n",
" -1.04355603e-02, 1.28024019e-01, 1.72433861e-03,\n",
" 7.28022705e-03, 3.71547934e-03, 3.40682893e-03,\n",
" -9.82192133e-02, 7.91444907e-02, 1.13302578e-02,\n",
" -2.20890918e-03, 1.70834618e-02, 1.40809490e-02,\n",
" -3.82096528e-03, 1.79161201e-02]])"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"grid.best_estimator_.coef_"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAuAAAAGCCAYAAAChCnbFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X98ZHV97/HXJ9loFdYVagEVFyNWsHavIa4UcSvoVmXR\nQltbK9aftGhvtdJrf4jaVuttFdqLilqpAnrV1lJlb+uPayjWH8tdrSKNu26VX1sjy29F7LpIbcfk\nc/+YE5gNSZgkM/M9M3k9H488ds6ZkzOffeck+eTMZ85EZiJJkiSpN4ZKFyBJkiStJjbgkiRJUg/Z\ngEuSJEk9ZAMuSZIk9ZANuCRJktRDNuCSJElSD9WqAY+IiyLitoj42iLbvCMirouIHREx1sv6JEmS\npJWqVQMOvB945kJ3RsQW4MjM/Eng5cBf9aowSZIkqRNq1YBn5nbge4tscirwwWrbLwPrIuLQXtQm\nSZIkdUKtGvA2PBy4oWX5pmqdJEmS1Bf6rQGXJEmS+tqa0gUs0U3AI1qWD6/W3cspp5ySP/zhDzns\nsMMAOOCAA3j0ox/N2FjzdZs7duwAcLkLy7O361LPals2f/Nfrcuz6+pSz2pbnl1Xl3pW2/LsurrU\nM8jLu3fv5gc/+AEAt956K0ceeSTnn39+sASRmUvZvusi4pHAJzJzwzz3nQy8IjOfFRHHAW/PzOPm\n28+LXvSiPO+887paq+Z39tlnc9ZZZ5UuY9Uy/7LMvxyzL8v8yzL/cs4880w++MEPLqkBr9UZ8Ij4\nMHAi8OMRsQd4A3A/IDPzvZn5qYg4OSJ2Az8AXrrQvm699dZelKx57Nmzp3QJq5r5l2X+5Zh9WeZf\nlvn3l1o14Jn5/Da2eWUvapEkSZK6YfiNb3xj6Rq64tvf/vYbjznmmNJlrErr1q1j/fr1pctYtcy/\nLPMvx+zLMv+yzL+cW265heOPP/5PlvI5tZsB75TPfOYzOT4+XroMSZIkDbDJyUk2b968pBnwgb0M\nYeurgtVb27dvL13Cqmb+ZZl/OWZflvmXZf79ZWAbcEmSJKmOHEGRJEmSlskRFEmSJKnmBrYBdwa8\nHOfQyjL/ssy/HLMvy/zLMv/+MrANuCRJklRHzoBLkiRJy+QMuCRJklRzA9uAOwNejnNoZZl/WeZf\njtmXZf5lmX9/GdgGXJIkSaojZ8AlSZKkZXIGXJIkSaq5gW3AnQEvxzm0ssy/LPMvx+zLMv+yzL+/\nDGwDLkmSJNWRM+CSJEnSMjkDLkmSJNXcwDbgzoCX4xxaWeZflvmXY/ZlmX9Z5t9fBrYBlyRJkurI\nGXBJkiRpmZwBlyRJkmpuYBtwZ8DLcQ6tLPMvy/zLMfuyzL8s8+8vA9uAS5IkSXXkDLgkSZK0TM6A\nS5IkSTU3sA24M+DlOIdWlvmXZf7lmH1Z5l+W+feXgW3AJUmSpDpyBlySJElaJmfAJUmSpJob2Abc\nGfBynEMry/zLMv9yzL4s8y/L/PvLwDbgkiRJUh05Ay5JkiQtU9/PgEfESRFxdURcGxGvmef+B0XE\nxyNiR0TsioiXFChTkiRJWrbaNOARMQS8C3gm8DjgtIg4es5mrwC+npljwFOBcyNizXz7cwa8HOfQ\nyjL/ssy/HLMvy/zLMv/+UpsGHDgWuC4zr8/MBnAxcOqcbRJYW91eC3w3M3/UwxolSZKkFanNDHhE\nPAd4Zma+rFp+AXBsZr6qZZsDgY8DRwMHAr+amRPz7c8ZcEmSJHVb38+At+GZwFcz82HAMcBfVk25\nJEmS1BfmnZ8u5CZgfcvy4dW6Vi8F3gKQmf8WEVM0z4ZfOXdn5513HgcccADr1zd3uW7dOjZs2MCm\nTZuAe2alXO78cuscWh3qWW3L5m/+q3V5dl1d6llty7Pr6lLPalueXVeXegZ5edeuXezduxeAPXv2\nsHHjRjZv3sxS1GkEZRi4BtgM3AJcAZyWmVe1bPOXwLcz808i4lCajffjM/OOufs799xz8/TTT+9N\n8drP9u3b7z5Q1XvmX5b5l2P2ZZl/WeZfznJGUGrTgEPzMoTAeTRHYy7KzLMj4uVAZuZ7I+KhwP8G\nHlp9ylsy82/n25cz4JIkSeq25TTga7pVzHJk5qXAUXPWvafl9i0058AlSZKkvtRvL8Jsm9cBL6d1\nHk2918v8p6dhcnKYrVtHmJwcZmamZw9dWx7/5Zh9WeZflvn3l1qdAZfUX3buHGbLlrU0GsHISDIx\nsY/x8enSZUmSVGsDewZ8bGysdAmrli8CKauX+U9NDdFoNMfeGo1gampgf6S0zeO/HLMvy/zLMv/+\n4m9LScs2OjrDyEjzhdwjI8noqDMokiTdl4FtwJ0BL8c5tLJ6mf/Y2DQTE/u44II7mZjYx9iY4yce\n/+WYfVnmX5b59xdnwCUt29AQjI9PO/ctSdIS1Oo64J3kdcAlSZLUbcu5DvjAjqBIkiRJdTSwDbgz\n4OU4h1aW+Zdl/uWYfVnmX5b595eBbcAlSZKkOnIGXJIkSVomZ8AlSZKkmhvYBtwZ8HKcQyvL/Dtr\nehomJ4fZunWEyclhZu7jvYbMvxyzL8v8yzL//uJ1wCVpETt3DrNly1oajWBkJJmY2Od1zyVJKzKw\nZ8DHxsZKl7Bqbdq0qXQJq5r5d9bU1BCNRnO0r9EIpqYW/7Fp/uWYfVnmX5b595eBbcAlqRNGR2cY\nGWm+WH1kJBkdvY8ZFEmS7sPANuDOgJfjHFpZ5t9ZY2PTTEzs44IL7mRiYh9jY4uPn5h/OWZflvmX\nZf79xRlwSVrE0BCMj0879y1J6hivAy5JkiQtk9cBlyRJkmpuYBtwZ8DLcQ6tLPMvy/zLMfuyzL8s\n8+8vA9uAS5IkSXXkDLgkSZK0TM6AS5IkSTU3sA24M+DlOIdWlvmXZf7lmH1Z5l+W+feXgW3AJUmS\npDpyBlySJElaJmfAJUmSpJob2AbcGfBynEMry/zLMv9yzL4s8y/L/PvLwDbgkiRJUh05Ay5JkiQt\nkzPgkiRJUs0NbAPuDHg5zqGVZf5lmX85Zl+W+Zdl/v2lVg14RJwUEVdHxLUR8ZoFtjkxIr4aEf8a\nEZ/rdY1auelpmJwcZuvWESYnh5mZKV2RJElS79RmBjwihoBrgc3AzcBXgOdl5tUt26wDvgg8IzNv\nioiHZObt8+3PGfD6mpwcZsuWtTQawchIMjGxj/Hx6dJlSZIkLVm/z4AfC1yXmddnZgO4GDh1zjbP\nB7Zm5k0ACzXfqrepqSEajeZx2mgEU1N1OgwlSZK6q06dz8OBG1qWb6zWtXoMcHBEfC4ivhIRL1xo\nZ86Al3Nfc2ijozOMjDSfeRkZSUZHnUHpJOcAyzL/csy+LPMvy/z7y5rSBSzRGmAceBpwAPDPEfHP\nmbm7bFlairGxaSYm9jE1NcTo6AxjY46fSJKk1aNODfhNwPqW5cOrda1uBG7PzB8CP4yIy4HHA/dq\nwHfv3s1v/dZvsX59c5fr1q1jw4YNbNq0CbjnL0WXO7+8adOmRe8fGoK77trGoYfC+Hj5egdt+b7y\nd9n8XXbZZZddXv7yrl272Lt3LwB79uxh48aNbN68maWo04swh4FraL4I8xbgCuC0zLyqZZujgXcC\nJwH3B74M/GpmfmPu/nwRpiRJkrqtr1+EmZnTwCuBy4CvAxdn5lUR8fKIeFm1zdXAPwJfA74EvHe+\n5hucAS9p9q9FlWH+ZZl/OWZflvmXZf79ZU3pAlpl5qXAUXPWvWfO8v8C/lcv65IkSZI6pTYjKJ3m\nCIokSZK6ra9HUCRJkqTVYGAbcGfAy3EOrSzzL8v8yzH7ssy/LPPvLwPbgEuSJEl15Ay4JEmStEzO\ngEuSJEk1N7ANuDPg5TiHVpb5l2X+5Zh9WeZflvn3l4FtwCVJkqQ6cgZckiRJWiZnwCVJkqSaG9gG\n3BnwcpxDK8v8yzL/csy+LPMvy/z7y8A24JIkSVIdOQMuSZIkLZMz4JIkSVLNDWwD7gx4Oc6hlWX+\nZZl/OWZflvmXZf79ZWAbcEmSJKmOnAGXJEmSlskZcEmSJKnmBrYBdwa8HOfQyjL/ssy/HLMvy/zL\nMv/+MrANuCRJklRHzoBLkiRJy+QMuCRJklRzA9uAOwNejnNoZZl/WeZfjtmXZf5lmX9/aasBj4h3\nLLD+7Z0tR5IkSRpsbc2AR8T3M/NB86z/bmb+eFcqWyFnwCVJktRty5kBX7PYnRFx+ux2LbdnPQq4\nfSkPJkmSJK129zWC8sLq434tt18IvAA4EnhxV6tbAWfAy3EOrSzzL8v8yzH7ssy/LPPvL4ueAc/M\npwJExJ9m5h/2piRJkiRpcC3pOuARcQhwYOu6zPxmp4vqBGfAJUmS1G0dnwGfFRHPBN4HPHTOXQkM\nL+UBJUmSpNWs3euAvxv4n8ABmTnU8lHb5tsZ8HKcQyvL/Msy/3LMvizzL8v8+0tbZ8CBg4D35KC+\nb70kSZLUI+1eB/wvgKsy833dL6kznAGXJElSty1nBrzdEZTjgPMj4tqIuLz1Y+llLiwiToqIq6vH\nec0i2z0xIhoR8UudfHxJkiSp29ptwC8EXgb8GXDRnI+OiIgh4F3AM4HHAadFxNELbHc28I+L7c8Z\n8HKcQyvL/Msy/3LMvizzL8v8+0tbM+CZ+YFuFwIcC1yXmdcDRMTFwKnA1XO2+23gEuCJPahJkiRJ\n6qi2zoBH0xkR8dmI+Fq17ikR8dwO1vJw4IaW5Rurda11PAz4hcw8H1h01mZsbKyDpWkpNm3aVLqE\nVc38yzL/csy+LPMvy/z7S7sjKG8Cfh14L7C+WncjsOCcdpe8fc5jLmngXZIkSSqt3csQvgQ4JjNv\nj4jzq3VTwKM6WMtN3NPcAxxerWu1Ebg4IgJ4CLAlIhqZ+fG5OzvvvPM44IADWL++uct169axYcOG\nu/9CnJ2Vcrnzy61zaHWoZ7UtD3L+T3rSJnbuHObSS7/AYYfN8JKXHM/QUH3qG/T86748u64u9ay2\n5dl1dalntS3PrqtLPYO8vGvXLvbu3QvAnj172LhxI5s3b2Yp2r0M4c3AozLzhxFxR2YeHBFrgW9k\n5iOW9IgLP8YwcA2wGbgFuAI4LTOvWmD79wOfyMz/M9/95557bp5++umdKE1LtH379rsPVPXeIOc/\nOTnMli1raTSCkZFkYmIf4+PTpcvazyDnX3dmX5b5l2X+5XTzMoSfAt4aEfeH5kw4zXfG/MTSSlxY\nZk4DrwQuA74OXJyZV0XEyyPiZfN9ymL7cwa8HH8AdNb0dLPx3Lp1hMnJYWZmFt9+kPOfmhqi0Wj+\njGs0gqmpdn+E9c4g5193Zl+W+Zdl/v1lTZvbvRr4ALAXGAHupNkov6iTxWTmpcBRc9a9Z4FtPb2t\nVWHnzvqf9e2V0dEZRkby7ixGR+/jrxFJkmqordNHmfn9zPxF4Aiab8pzZGb+Ymbu62p1K+B1wMtp\nnUfTyi31rO8g5z82Ns3ExD4uuOBOJib2MTZWvz9EBjn/ujP7ssy/LPPvLwueAY+IyGpAvHrzG4Dv\nVB93r8tMT0FJXeRZ33sMDcH4+PSqfQZAkjQYFnwRZkR8PzMfVN2e4d4z1wFkZg53t8Tl+cxnPpPj\n4+Oly5BWbGYGduwYZmpqiNHRGcbGphmq3+izJEmr0nJehLnYDPjjWm6PLq8kSSvlWV9JkgbLgufR\nMrP1XSlvBW7OzOtnP4Cbq/W15Ax4Oc6hlWX+ZZl/OWZflvmXZf79pd0nsj8NPGHOuicA/9jZciRJ\nkqTB1u4b8XwPODhbNq5ehPndzDyoi/UtmzPgkiRJ6rZuvhHPXuDQOesOBX6wlAeTJEmSVrt2G/Ct\nwIcj4qcj4oERsQH4IPCR7pW2Ms6Al+McWlnmX5b5l2P2ZZl/WebfX9ptwF8PXAVcAewDvgRcA7yu\nS3VJkiRJA6mtGfC7N44I4CHA7bmUTyzAGXBJkiR1W0evAx4Rj8zMb1W3HzXn7rXNXhwy85tLrFOS\nJElatRYbQdnVcns3cF31b+vHdd0rbWWcAS/HObSyzL8s8y/H7Msy/7LMv78s9k6YR8zeyEzf+FqS\nJEnqgAVnwCPi+5n5oOr2P2Xmz/W0shVyBlySJEnd1unrgN9VXXZwGDg2mobmfqysZEmSJGl1WayB\n/hOalx38L+AA4EdAo+VjdrmWnAEvxzm0ssy/LPMvx+zLMv+yzL+/LDgDnpnnR8QFwGHA1cDjelaV\nJEmSNKAWmwH/UmYeV93+m8z8tZ5WtkLOgEuSJKnbOj0D/piI+LHq9s8vvyxJkiRJsxZrwD8GXBsR\nlwMPiIjL5/voUZ1L5gx4Oc6hlWX+ZZl/OWZflvmXZf79ZbEZ8JdGxCbgkcATgYt6VZQkSZI0qBac\nAd9vo4jTM/N9PainY5wBlyRJUrd1egb8bpn5voh4ekRcFBGfAIiIjRHxtOUUKkmSJK1WbTXgEfHb\nwPnAdcBTqtX/Afxpl+paMWfAy3EOrSzzL8v8yzH7ssy/LPPvL+2+k+XvAD+XmWcDM9W6q4GjulKV\nJEmSNKDanQH/NvDQzJyOiDsy8+DqEoVTmfnQrle5DM6AS5Ikqdu6NgMOXA6cNWfdq4DPLeXBJEmS\npNWu3Qb8t4FfjIhvAWsj4hrgucCru1XYSjkDXo5zaGWZf1nmX47Zl2X+ZZl/f1nwOuCtMvOWiHgi\nzeuBHwHcAFyRmTOLf6YkSZKkVm3NgANExBrgeODhwE3AFzPzR12sbUWcAZckSVK3LWcGvK0z4BFx\nNPAJ4MeAG4FHAD+MiJ/PzKuWXKkkSZK0SrU7A/5u4L3A+sx8UmYeDvxVtb6WnAEvxzm0ssy/LPMv\nx+zLMv+yzL+/tNuAjwFvzf3nVd5ere+YiDgpIq6OiGsj4jXz3P/8iNhZfWyPiA2dfHxJGjTT0zA5\nOczWrSNMTg4z4yt3JKm4dq8D/q/AqzLzsy3rngq8KzMf15FCIoaAa4HNwM3AV4DnZebVLdscB1yV\nmXsj4iTgjZl53Hz7cwZckprN95Yta2k0gpGRZGJiH+Pj06XLkqSB0bUZcOB1wMcj4pPA9TSvhPIs\n4AVLK3FRxwLXZeb1ABFxMXAqzXfcBCAzv9Sy/ZdoviBUkrSAqakhGo3m74VGI5iaGrIBl6TC2hpB\nycyPA+PAvwJrq3+fkJkf62AtD6d5ecNZN7J4g/0bwMRCdzoDXo5zaGWZf1l1y390dIaRkeYznSMj\nyejo4M6g1C371cb8yzL//tLuVVDuT/Nt5/+0Zd1IRNw/M/+za9UtXM9TgZcCmxbaZtu2bVx55ZWs\nX78egHXr1rFhwwY2bWp+yuyB6rLLLrs8yMtjY9O85S2f4tZbhzjppCczNjZdq/o6uTyrLvWstuVZ\ndalntS3Pqks9g7y8a9cu9u7dC8CePXvYuHEjmzdvZinanQG/HPiD1hGQah777Mw8cUmPuPBjHEdz\npvukavksIDPznDnb/TdgK3BSZv7bQvtzBlySJEndtpwZ8HavgrIB+PKcdVcAj1/Kg92HrwCPjogj\nIuJ+wPOAj7duEBHraTbfL1ys+ZYkSZLqqt0GfC9w6Jx1hwI/6FQhmTkNvBK4DPg6cHFmXhURL4+I\nl1Wb/RFwMPDuiPhqRFyx0P6cAS9n7tNh6i3zL8v8yzH7ssy/LPPvL2va3G4r8OGIeBXwTeBI4K3A\nRzpZTGZeChw1Z917Wm6fAZzRyceUJEmSeqndGfAfA86l+cLH+wM/BN4H/F6JF2G2wxlwSZIkdVvX\nrgOemT8EXhERrwQeAtye7XTukiRJkvbT7gw40LwkSWZ+px+ab2fAy3EOrSzzL8v8yzH7ssy/LPPv\nL0tqwCVJkiStTFsz4P3IGXBJkiR1W0evAx4Rf9Fy+2krKUySJElS02IjKC9ruf0P3S6k05wBL8c5\ntLLMvyzzL8fsyzL/ssy/vyx2FZSdEXEJ8A3g/hHxpvk2ysw/7kplkiRJ0gBacAY8Ig6heRb8CODF\nwN/Ms1lm5undK2/5nAGXtJjpadi5c5ipqSFGR2cYG5tmyJelq895XEu919HrgGfmt4E/BYiINZn5\n0hXWJ0m1sXPnMFu2rKXRCEZGkomJfYyPT5cuS1oRj2upP7T1d3FmvjQiDoqIF0XEa6t/D+52cSvh\nDHg5zqGVZf7tmZoaotFonrBoNIKpqc6cJjT/csy+e8d1O8y/LPPvL219Z0bEk4B/A34T+G/Ay4Hd\n1XpJ6jujozOMjDRH8EZGktHRmcIVSSvncS31h7auAx4RXwbelpkXt6z7VeD3MvOJXaxv2ZwBl7SY\nmRnYscNZWQ0Wj2up9zo6Az7HY4CPzFl3CfBXS3kwSaqLoSEYH592PlYDxeNa6g/t/l18HfC8Oet+\nheZYSi05A16Oc2hlmX9Z5l+O2Zdl/mWZf39p9wz47wCfjIhXAdcDjwR+Enh2l+qSJEmSBlJbM+AA\nEXEQ8CzgYcDNwKcy844u1rYizoBLkiSp27o5A05mfg/46yVXJUmSJOluA/vaaGfAy3EOrSzzL8v8\nyzH7ssy/LPPvL22fAZckSaqD6enmu356uUX1q7ZnwPuNM+CSJA2myclhtmxZS6MRjIwkExP7vPSi\nilnODHjbfy9GxEhE/Gz1BjxExAERccBSi5QkSVqJqakhGo1mv9NoBFNTnv5Wf2n3reg3ANcCFwAX\nVatPAN7XpbpWzBnwcpxDK8v8yzL/csy+rF7mPzo6w8hI8xn8kZFkdHSmZ49dVx7//aXdGfDzgT/O\nzA9FxPeqddtoNuSSJEk9MzY2zcTEvv1mwKV+0tYMeNV0H5yZGRF3ZObB1fq7b9eNM+CSJEnqtm7O\ngH8LeELriog4Fti9lAeTJEmSVrt2G/A/Av5vRPwJcL+IeC3wUeAPu1bZCjkDXo5zaGWZf1nmX47Z\nl2X+ZZl/f2mrAc/MTwInAT9Bc/b7COCXMvOyLtYmSZIkDRyvAy5JkiQt03JmwNu6CkpEvGmh+zLz\nj5fygJIkSdJq1u4M+CPmfDwR+D3gyC7VtWLOgJfjHFpZ5l+W+Zdj9mWZf1nm31/aOgOemS+duy4i\nTgJO63hFkiRJ0gBb9gx4RAwB38vMdR0rptnUv53mmfmLMvOcebZ5B7AF+AHwksyc91S3M+CStDpM\nT8POncP7vSnL0DzP77a7nTRXiWPM47V/dHMG/FFzVj0QeD5ww1Ie7D4eYwh4F7AZuBn4SkR8LDOv\nbtlmC3BkZv5kRPwM8FfAcZ2qQf2nrj+gbAi0mvX6uN65c5gtW9bSaAQjI8nExD7Gx+/9zojtbqfB\n0MnjsMQx5vE62No9FHcD11X/7ga+BPws8OIO1nIscF1mXp+ZDeBi4NQ525wKfBAgM78MrIuIQ+fb\nmTPg5XRiDm16GiYnh9m6dYTJyWFmZubfbvYH1BlnHMiWLWvZsWN4xY/didrarasb9S+Wf7u5trud\n7q0f5zA7/fXu9ffl1NQQjUYAn6fRCKam5v/Vds92LLpdp/T799tS63/zm79Uq/o7eRy2e+x08hhb\n6r768WfPatbuDHgvzsk9nP3PqN9IsylfbJubqnW3dbc09Vq7f/nP9wOq22cI2qmt3bo6Wf/s2Z7L\nL1/DAx84PO/ZHs8Udk87+ddVp7/e7RzXnXyWaHR0hpGRpNGAkZFkdHT+DvCe7WLR7Tqlzt9v7eS6\n9PofwHnnrZ13uxLP9nXy52u7x04nj7FeH6/qrbYa8H40NjZWuoRVZ/YH7G23PZXJyZX9gG33B2c7\nP6A6PQ7STm0lfljf80twC+edV78/DAZ9zKad/NvV68w6/YdsO8d1J5vTsbFpJib2MTW1kdHRfYyN\nzV/7Pdvdk+tytfM1KvH91q7unEg4kUaDebcr8UdGuz9f2/latnvstLNdu9/fSz1eN23atOj9qpcF\nG/CIuAG4z1doZub6DtVyE9C6r8OrdXO3ecR9bAPAJZdcwoUXXsj69c1drlu3jg0bNtx9gM4+VeNy\n55avvXaI1772ZBqNYHj4c5xzzl2cfvrxy9rf3r3bGB5+INPTT2VkJNm7dxvbt8/ca/vjj9/ExMQ+\nLr30Cxx22AxjY/d+vJ07h3nmM/+F6elgZOQEJib2cddd25Zd/+joDMPDn7t7f6OjM/eq/847t/GW\ntwyxbl3z/jvv3Mb27ff+/7ZTf7vLl1++hkZjCwCNxjYuvfQ/GB8/br/tR0dPqH4hbWN4OBkdfcKK\n8m9nud38Z2bgwANPYGpqiL17t/HoR8/wlKcs73i8/PLt7N69f/5DQ909/tvJ/0lPauYx+/V+yUuO\nZ2jo3vv7wAe+yGtec0/+b3nLp3jMY5aXfzvLnfx6Q3vHfzt5bdq0qWrutlXbncjU1NC9jp8vfrG5\n/XOec9/1jY9Pc9dd27jrLhga6u7Pu05/v7V7/NTx50W7X+9OLrf783Up32/j49Ns376dL35x/scf\nGoK77trGoYfC+Pj89S318TpxvLrc2eVdu3axd+9eAPbs2cPGjRvZvHkzS7HgVVAi4oR2dpCZ25b0\niAsVEjEMXEPzRZi3AFcAp2XmVS3bnAy8IjOfFRHHAW/PzHlfhHnuuefm6aef3onS1KatW0c444wD\ngc8DJ3LBBXfynOc0lrWvmRnYsaMzZwDvqatpobra3a6TtXXS5OTsGaZtdze6c88wtVt7ifzvqX/l\nZ8g6ua+lP+bC+bdbVzuZdfIseYljut0slvK13L59e8/OArbzNer091uvv0eWWv+ll36Bk0568rzb\nlfiebFe7P6Pq/ni9PP61v45eBaVTjXW7MnM6Il4JXMY9lyG8KiJe3rw735uZn4qIkyNiN83LEN7r\n+uQqp905zHYMDcH4+HRHfkB3ehykk7V10uzTlZde+h+cdNL8T8O3W3uJ/Dv5NHyJp/Tbyb+To1Wd\nfEq/xDHdyaf0S2jna9Tp77dOHtft5LrU+u+660cLblvXryP0ftba2W7BEq4DHhFjNK988hDg7i6/\nrm9F73XAe6+uZ4ZLnPXVPep6dq+EdutqJ7Nen7XT/ur8rIGWptdfS3/XDJ7lnAFvqwGPiJcBb6N5\ndnoLMAE8A/hYZj5/GbV2nQ241F86+Uuprr/gOlmXzdjqU9fjWlrtltOAt/ut+wfASZn5i8B/VP/+\nMlDb0y38mSkNAAAXdUlEQVReB7wcr0VaVr/mP/s09nOe02B8fGWNRSf3tVSL5d/Jumaf0r/ggjuZ\nmFj4yh+rSb8e++0qeVy3Y9Dzrzvz7y/tXobwkMz8f9XtmYgYysyJiPibbhUmSVpYXV+LIEm6b+2O\noHwDODkzvxUR/wz8OXA78NHMPKzLNS6LIyiSJEnqto5eBWWOPwceC3wLeBNwCXA/4FVLeTBJkiRp\ntWtrgiwz/3dmTlS3J4CDgIMy8/xuFrcSzoCX4xxaWeZflvmXY/ZlmX9Z5t9f2mrAI+LtEfHE2eXM\n/K/MvLN7ZUmSJEmDqd0Z8POAX6H55jcfBj6cmdd0ubYVcQZckiRJ3da1yxBm5pnA4cBvAY8AvhQR\n/xIRr156mZIkSdLq1fZVRDNzJjM/nZmnAz8NfBf4i65VtkLOgJfjHFpZ5l+W+Zdj9mWZf1nm31/a\nbsAj4oCIeEFE/F/gWuBHwIu7VpkkSZI0gNqdAf8ozbegnwT+lub1v2/vcm0r4gy4JEmSuq2b1wH/\nCvC7mbln6WVJkiRJmtXuizD/vN+ab2fAy3EOrSzzL8v8yzH7ssy/LPPvL23PgEuSJElaubZmwPuR\nM+CSJPWX6WnYuXOYqakhRkdnGBubZshThaq5bs6AS5IkddXOncNs2bKWRiMYGUkmJvYxPj5duiyp\n4wb270pnwMtxDq0s8y/L/Msx+7I6kf/U1BCNRvNEYqMRTE0NbJvScR7//cUjW5Ik1cLo6AwjI83R\n2JGRZHR0pnBFUnc4Ay5JkmphZgZ27HAGXP3FGXBJktS3hoZgfHzauW8NvIH9u9IZ8HKcQyvL/Msy\n/3LMvizzL8v8+8vANuCSJElSHTkDLkmSJC3TcmbAPQMuSZIk9dDANuDOgJfjHFpZ5l+W+Zdj9mWZ\nf1nm318GtgGXJEmS6sgZcEmSJGmZnAGXJEmSam5gG3BnwMtxDq0s8y/L/Msx+7LMvyzz7y8D24BL\nkiRJdeQMuCRJkrRMzoBLkiRJNVeLBjwiDoqIyyLimoj4x4hYN882h0fEZyPi6xGxKyJetdg+nQEv\nxzm0ssy/LPMvx+zLMv+yzL+/1KIBB84C/ikzjwI+C7x2nm1+BLw6Mx8HPAl4RUQc3cMaJUmSpBWr\nxQx4RFwNnJCZt0XEYcDnM3PR5joi/gF4Z2Z+Zr77nQGXJElSt/XzDPghmXkbQGbeChyy2MYR8Uhg\nDPhy1yuTJEmSOqhnDXhEfDoivtbysav695R5Nl/wtHxEHAhcApyZmXcutJ0z4OU4h1aW+Zdl/uWY\nfVnmX5b595c1vXqgzHz6QvdFxG0RcWjLCMq3F9huDc3m+0OZ+bHFHm/btm1ceeWVrF+/HoB169ax\nYcMGNm3aBNxzoLrssssuuzwYy7PqUs9qW55Vl3pW2/KsutQzyMu7du1i7969AOzZs4eNGzeyefNm\nlqIuM+DnAHdk5jkR8RrgoMw8a57tPgjcnpmvvq99OgMuSZKkbuvnGfBzgKdHxDXAZuBsgIh4aER8\nsrr9ZODXgKdFxFcjYjIiTipWsSRJkrQMtWjAM/OOzPy5zDwqM5+Rmf9erb8lM59d3f5CZg5n5lhm\nHpOZ45l56UL7dAa8nLlPh6m3zL8s8y/H7Msy/7LMv7/UogGXJEmSVotazIB3gzPgkiRJ6rZ+ngGX\nJEmSVoWBbcCdAS/HObSyzL8s8y/H7Msy/7LMv78MbAMuSZIk1ZEz4JIkSdIyOQMuSZIk1dzANuDO\ngJfjHFpZ5l+W+Zdj9mWZf1nm318GtgGXJEmS6sgZcEmSJGmZnAGXJEmSam5gG3BnwMtxDq0s8y/L\n/Msx+7LMvyzz7y9rShcgSVJdTE/Dzp3DTE0NMTo6w9jYNEMDe6pKUinOgEuSVJmcHGbLlrU0GsHI\nSDIxsY/x8enSZUmqMWfAJUlagampIRqN5u/RRiOYmvLXpKTOG9ifLM6Al+McWlnmX5b5l9OJ7EdH\nZxgZaT4zPDKSjI7OrHifq4XHflnm31+cAZckqTI2Ns3ExL79ZsAlqdOcAZckSZKWyRlwSZIkqeYG\ntgF3Brwc59DKMv+yzL8csy/L/Msy//4ysA24JEmSVEfOgEuSJEnL5Ay4JEmSVHMD24A7A16Oc2hl\nmX9Z5l+O2Zdl/mWZf38Z2AZckiRJqiNnwCVJkqRlcgZckiRJqrmBbcCdAS/HObSyzL8s8y/H7Msy\n/7LMv78MbAMuSZIk1ZEz4JIkSdIyOQMuSZIk1dzANuDOgJfjHFpZ5l+W+Zdj9mWZf1nm318GtgGX\nJEmS6qgWM+ARcRDwd8ARwLeA52bm3gW2HQKuBG7MzFMW2qcz4JIkSeq2fp4BPwv4p8w8Cvgs8NpF\ntj0T+EZPqpIk3W16GiYnh9m6dYTJyWFmZkpXJEn9qS4N+KnAB6rbHwB+Yb6NIuJw4GTgwvvaoTPg\n5TiHVpb5lzXI+e/cOcyWLWs544wD2bJlLTt2DJcuaT+DnH0/MP+yzL+/1KUBPyQzbwPIzFuBQxbY\n7m3A7wPl52YkaZWZmhqi0Wg+y9poBFNTdfkVIkn9ZU2vHigiPg0c2rqKZiP9h/Nsfq8GOyKeBdyW\nmTsi4sTq8xc0Nja2/GK1Ips2bSpdwqpm/mUNcv6jozOMjCSNRjAykoyO1msGZZCz7wfmX5b595ee\nNeCZ+fSF7ouI2yLi0My8LSIOA749z2ZPBk6JiJOBBwBrI+KDmfmi+fZ5ySWXcOGFF7J+/XoA1q1b\nx4YNG+4+QGefqnHZZZdddrm95eOP38TExD4uvfQLHHbYDGNjx9eqPpdddtnlXizv2rWLvXub1wrZ\ns2cPGzduZPPmzSxFXa6Ccg5wR2aeExGvAQ7KzLMW2f4E4HcXuwrKueeem6effnoXqtV92b59+90H\nqnrP/Msy/3LMvizzL8v8y+nnq6CcAzw9Iq4BNgNnA0TEQyPik0UrkyRJkjqoFmfAu8HrgEuSJKnb\n+vkMuCRJkrQqDGwD7nXAy5l9wYLKMP+yzL8csy/L/Msy//4ysA24JEmSVEfOgEuSJEnL5Ay4JEmS\nVHMD24A7A16Oc2hlmX9Z5l+O2Zdl/mWZf38Z2AZckiRJqiNnwCVJkqRlcgZckiRJqrmBbcCdAS/H\nObSyzL8s8y/H7Msy/7LMv78MbAMuSZIk1ZEz4JIkSdIyOQMuSZIk1dzANuDOgJfjHFpZ5l+W+Zdj\n9mWZf1nm318GtgGXJEmS6sgZcEmSJGmZnAGXJEmSam5gG3BnwMtxDq0s8y/L/Msx+7LMvyzz7y8D\n24BLkiRJdeQMuCRJkrRMzoBLkiRJNTewDbgz4OU4h1aW+Zdl/uWYfVnmX5b595eBbcAlSZKkOnIG\nXJIkSVomZ8AlSZKkmhvYBtwZ8HKcQyvL/Msy/3LMvizzL8v8+8vANuCSJElSHTkDLkmSJC2TM+CS\nJElSzQ1sA+4MeDnOoZVl/mWZfzlmX5b5l2X+/WVgG3BJkiSpjpwBlyRJkpbJGXBJkiSp5mrRgEfE\nQRFxWURcExH/GBHrFthuXUR8NCKuioivR8TPLLRPZ8DLcQ6tLPMvy/zLMfuyzL8s8+8vtWjAgbOA\nf8rMo4DPAq9dYLvzgE9l5mOBxwNXLbTD3bt3d7xItWfXrl2lS1jVzL8s8y/H7Msy/7LMv5zlnPSt\nSwN+KvCB6vYHgF+Yu0FEPAj42cx8P0Bm/igzv7/QDn/wgx90o061Ye/evaVLWNXMvyzzL8fsyzL/\nssy/nJ07dy75c+rSgB+SmbcBZOatwCHzbDMK3B4R74+IyYh4b0Q8oKdVSpIkSSvUswY8Ij4dEV9r\n+dhV/XvKPJvPd2mWNcA48JeZOQ7cRXN0ZV633nprZwrXku3Zs6d0Caua+Zdl/uWYfVnmX5b595c1\nvXqgzHz6QvdFxG0RcWhm3hYRhwHfnmezG4EbMvPKavkS4DUL7fPII4/kzDPPvHv58Y9/PGNjY8sr\nXkuyceNGJicnS5exapl/WeZfjtmXZf5lmX/v7NixY7+xkwMOOGDJ+6jFdcAj4hzgjsw8JyJeAxyU\nmfc6ux0R24AzMvPaiHgD8MDMXLAJlyRJkuqmLg34wcBHgEcA1wPPzcx/j4iHAhdk5rOr7R4PXAiM\nAN8EXpqZvupAkiRJfaMWDbgkSZK0WtTlKigdERG/HBH/GhHTETE+577XRsR11Zv4PKNUjYMuIk6K\niKsj4tpqnEhdFBEXVa+h+FrLurbe2EorExGHR8RnqzcF2xURr6rWm38PRMT9I+LLEfHVKv83VOvN\nv0ciYqi6KtnHq2Wz75GI+FZE7KyO/yuqdebfI/O9MeRS8x+oBhzYBfwisK11ZUQ8Fngu8FhgC/Du\niIjelzfYImIIeBfwTOBxwGkRcXTZqgbe+2nm3ardN7bSyvwIeHVmPg54EvCK6ng3/x7IzP8EnpqZ\nxwBjwJaIOBbz76UzgW+0LJt978wAJ2bmMZl5bLXO/Htn7htDXs0S8x+oBjwzr8nM64C5zfWpwMXV\nm/d8C7gOOHbu52vFjgWuy8zrM7MBXEwze3VJZm4Hvjdn9X2+sZVWLjNvzcwd1e07ab4z7+GYf89k\n5l3VzfvTvKpXYv49ERGHAyfTfF3WLLPvneDePZz598ACbwy5lyXmP1AN+CIeDtzQsnxTtU6dNTfn\nGzHnEtp5Yyt1UEQ8kuZZ2C8Bh5p/b1QjEF8FbgU+nZlfwfx75W3A77P/+3aYfe8k8OmI+EpE/Ea1\nzvx7Y743hnwgS8y/Z9cB75SI+DRwaOsqmgfi6zPzE2WqkmrNV1p3UUQcSPN9Cc7MzDsjYm7e5t8l\nmTkDHFOdkfr7iHgc987b/DssIp4F3JaZOyLixEU2NfvueXJm3hIRPwFcFhHX4LHfK7NvDPmKzLwy\nIt5Gc/xkSfn3XQO+2Bv6LOImmpc4nHV4tU6ddROwvmXZnMto542t1AERsYZm8/2hzPxYtdr8eywz\nvx8RnwdOwvx74cnAKRFxMvAAYG1EfAi41ex7IzNvqf79TkT8A80RUI/93pj7xpBbaTbgS8p/kEdQ\nWufAPw48LyLuFxGjwKOBK8qUNdC+Ajw6Io6IiPsBz6OZvboruPfx/pLq9ouBj839BHXM+4BvZOZ5\nLevMvwci4iGzVxmIiAcAT6c5h2/+XZaZr8vM9Zn5KJo/5z+bmS8EPoHZd11EPLB65o2IOAB4Bs2L\nUHjs90A1ZnJDRDymWrUZ+DpLzH+grgMeEb8AvBN4CPDvwI7M3FLd91rg14EGzaeKLytW6ACLiJNo\nvjp4CLgoM88uXNJAi4gPAycCPw7cBrwB+Afgo8x5Y6tSNQ6qiHgycDnNX3xZfbyO5h/393pjsVJ1\nDqqI2EDzhU5D1cffZeafxQJv7Fau0sEWEScAv5uZp5h9b1QnEv+e5s+cNcDfZObZ5t87Mc8bQwLD\nLCH/gWrAJUmSpLob5BEUSZIkqXZswCVJkqQesgGXJEmSesgGXJIkSeohG3BJkiSph2zAJUmSpB6y\nAZekFYiI90fEm6rbmyLiqtI1dUJE/GtEPKXNbWci4lEL3PfiiPh/K6jj5RHx1ur2IyLi+xER9/V5\nC+xrKiKettxaqn3cLyKuiogfX8l+JK1uNuCS1CGZuT0zH3tf2620Ke2FzPzpzLy83c1XeP+8ImIE\neD3w51VNN2Tmg7LgG1hk5n8BFwGvLVWDpP5nAy5JlYgY7tVDscymFLpb5zL3vawz0m04FbgqM2/t\n0v6X62+BF1d/IEjSktmASxpo1djBWRHx9Yj4bkRcFBH3q+47ISJuiIg/iIhbgPdV658dEV+NiO9F\nxPbqbc9n93dMRPxLROyNiIuBH2u574SIuKFl+fCI2BoR346I70TEOyLiaOB84EkRsS8i7qi2fVBE\nfLDadioiXt+ynxdXdbw1Im4H3jDn//jQiLgrIh48p87vRMRwRDwqIj4TEbdX+//riHjQnIz+ICJ2\nAndWn3P3uEZEPDEivljlcVNEvDMi1syJ+lkR8W/V/v98ka/H0RFxWfW1uCoifmWRL98WYFvL5x5R\njbsMVcufi4g3Vdl8PyIurd6Oe3b7F0bEt6ocXjenjqiOi93V/RfP5hcRz42Ib0bEgdXyloi4ZXbs\nJDNvAu4AjlukdklakA24pNXg+cDTgSOBo4A/bLnvMODBwHrgZRFxDM0RgzOAg4H3AB+PiJHqjOff\nAx+o7vso8Jw5j5UAVZP4SWCq2vfDgYsz82rgN4F/zsy1mTnbML4LWAs8EjgReFFEvLRlvz8D7AYO\nAf5svwfMvAX44pxaTgM+mpnTNM9Qv7n6vz4WOBx445y6n0ez4X1w9TmtpoHfqf7PTwKeBvzWnG1+\nARivPk6NiNPn3E9EPBC4DPhr4CHVY/5l9UfJfDYA18xZN/eZg9OAFwM/Adwf+L3qsX4KeDfwa8DD\ngB+n+TWY9SrgFOBnq/u/V21PZn4E+ALwjqqhvxA4PTO/2/L5VwOPX6BuSVqUDbik1eCdmXlzZv47\nzeb1tJb7poE3ZGYjM/+TZuP9V5l5ZTZ9CPhPmmc7jwPWZOY7MnM6M7cCX1ngMX8GeCjwB5n5w8z8\nr8z84nwbVs36rwJnZeZdmXk9cC7wwpbNbsrMd2fmTFXnXH9L8w+NWc8DPgyQmf+WmZ/JzB9VTeTb\ngBPmfP55VUb32ndmTmbmFVUee4D3zvP5Z2fm3sy8EXg7+2c869nAVGZ+sNrXTuD/AAudBX8wsG+B\n+2a9v/r//SfwEWCsWv8c4BOZ+YXMbAB/xP7N+8uB12fmLdX9bwJ+efbsOvBKYDPweeBjmTkx53H3\nVfVJ0pLNfQpRkgbRjS23r6d5xnPWd6oGbNYRNM8+/3a1HMBIy+fcNGff1y/wmIcD12fmTBv1PYTm\nz+M9c/bbesb2Bha3leYZ20OBo4HpzNwOEBGHAOfRPNt7IDBMc4Si1Y0sICJ+EngrsBF4QFXrvyzy\n+XMznnUEcNzs2A3NbIeBDy3w0N+j+azAYlrnw++i+f+jevy7M8vMuyKi9Qz2EcDfR8Ts1yeABnAo\ncEtm7o2IjwL/A/ileR53LfDv91GbJM3LM+CSVoNHtNw+Ari5ZXnuSMMNwJ9l5sHVx0GZeWBm/h1w\nC/s3xdAcL5nPDcD6ljOqreY+5u00m78j5tTZ2uwv+qLN6uz+ZTTPfJ8GXNxy95uBGeBxmflg4AXc\n+4WTi+3/fOAq4Mjq818/z+e3Zrye/TOedQPw+TnZPigzX7HA434NeMwidS3mltaaqvGX1ksH7gG2\nzKnlgGqch4gYA06n+czCO+fZ/2OBncusTdIqZwMuaTV4RUQ8vJrnfR37N6dzXQD8ZkQcCxARB0TE\nyRFxAPDPwI8i4rcjYk1E/BJw7AL7uYJmE3h2RDwwIu4fEcdX990GHF7NlFOdJf8I8GcRcWBEHEHz\nzOtCZ4YX8rfAi2iOX3y4Zf1a4E5gX0Q8HPj9Je53LfD96izy0cB/n2eb34+IB0fEI4AzmT/jTwKP\niYgXVPmNRMTGRWbAP0VzHr5Vu1dcuQR4dkQcX+X8pjmf+x7gzRGxHiAifiIiTqlu/xjN7M+i2YQ/\nLCLu/j9HxMOAg4AvtVmLJO3HBlzSavBhmmeHdwPXMedFjK0y819ozoG/qxqVuJbmi/yoRlV+CXgp\n8F2as8tbF9jPDPDzwE/SPNt6A/Dc6u7PAl8Hbo2Ib1frXkVzhOKbwOXAX2fm+5f4//x49Xi3ZOau\nlvV/AjyB5sjEJ+apeb6z363rfg/4tYj4Ps3GdW5zncDHaI6lTFaP8b577TDzTuAZNM/S31x9nA3c\nb4H/zyeAoyLisAXqWvCsfWZ+A3gFzT9Kbqb59WodkzmvqvmyiNhL80Wss39MvZnm+NB7q+t+vxD4\nnxFxZHX/rwEfmDO6JElti4LvZyBJXRcRU8CvZ+ZnS9eipYuI3wB+KjNfXboWaL4TJrADeEpm3l66\nHkn9yRdhSpJqKzMvLF1Dq+qM+E+VrkNSf3MERdKg82k+SVKtOIIiSZIk9ZBnwCVJkqQesgGXJEmS\nesgGXJIkSeohG3BJkiSph2zAJUmSpB6yAZckSZJ66P8Dv6yIxJzKniAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1244705f8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"figsize(12, 6)\n",
"plt.scatter(range(grid.best_estimator_.coef_.shape[1]),\n",
" grid.best_estimator_.coef_)\n",
"plt.ylabel('value of coefficient')\n",
"plt.xlabel('predictor variable (index)');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Another way to do this is with the 'LogisticRegressionCV' function. This is a logistic regression function built with tuning $C$ via cross-validation in mind. This time, we'll set the penalty to $\\mathcal{l}1$, we'll let python pick 10 possible $C$'s, we'll use all cores on my machine ('n_jobs=-1'), and we'll use the liblinear solver (which is the only one of the three possible choice which can optimize with the l1 penalty). The $\\mathcal{l}1$ penalty is $$-\\frac{1}{n}\\sum_{i=1}^n[y_i\\log(p_i) - (1-y_i)\\log(y_i - p_i)]+\\frac{1}{C}\\cdot\\sum_{j=1}^m |w_j|.$$ This will take a minute or two to run."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cvmodel = LogisticRegressionCV(penalty='l1', \n",
" Cs=10, \n",
" n_jobs=-1,\n",
" verbose=1,\n",
" scoring='accuracy',\n",
" solver='liblinear') # liblinear only for l1 penalty"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 59.0s finished\n"
]
}
],
"source": [
"# takes about a minute\n",
"cv_fit = cvmodel.fit(Xtr,ytr)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 0.00599484])"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cvmodel.C_"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0. , 0.64766949, 0. , 0. , 0. ,\n",
" 0. , 0. , 0. , 0. , 0.12835093,\n",
" 0. , 0. , 0. , 0.53989798, 0. ,\n",
" 0. , 0.65691285, 0. , 0. , 1.4445903 ,\n",
" 0. , 0. , 0. , 0. , 0. ,\n",
" 0. , -0.39762551, 0. , 0. , 0. ,\n",
" 0.00386294, 0. , 0. , 0. , 0. ,\n",
" 0. , 0. , 0. , 0. , 0. ,\n",
" 0. , 0. , 0. , 0. , 0. ,\n",
" 0. , 0.00242243, 0. , 0. , 0.00376126]])"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cvmodel.coef_ # now all very small, most effectively 0"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAuAAAAGNCAYAAABQXMQQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYZGV9/v/3Z4YBEXAEjYDAwIgb4sRmHBEVBSUq4wLR\nGOOuYDSJG4kxBpe4YEyI+aFgjEYUSDASvigxiGYMRBTEKIjjjBNljS3DjriMLC5Nz+f3xzmNNUV3\nT3V1VT2nqt+v66pr6pw6dc7TdxfN06fvOhWZiSRJkqTBWFR6AJIkSdJC4gRckiRJGiAn4JIkSdIA\nOQGXJEmSBsgJuCRJkjRATsAlSZKkAXICLqmRIuLREXFJRPwiIn5Qr9szIr4cEXdExGS9bjwi3j6H\n/c5p+yaLiL0jYnNEPHEr2707Iq7uYv+nRcR53Y+wOSLiKxFxco/2tTkiXtKLfTXhOJIGb5vSA5Ck\nGXwA2AQ8HLirXvd24IHAbwN31OtWtTzeiblu35F6gvupzDyu1/uexUZgN+DH9Rj2AK4DDs3Mi9q2\nnfeHPkTEo4D3AGPAvsApmfna+e53CO0G/KxXO4uI84HrMvPofh5HUnM4AZfUVA8D/jkzr2tbd2lm\n/mBqRWb+eC47nev2TZbVJ6nd2rIq6MFEexb3Ba4FzgHe3O1OImJJZk70bFQDMjXuzLx161vP36CO\nI2nwrKBImrOIeH1EfC8ifhkRt0TEZ1oe2zEiPh4Rt9aPfysint72/AdFxD/X2/w8Ir4WEU+uH9s7\nIjYDDwHeFxGTdYViM/A04NX1ulPr7beolETE4nr7a+rjXxcRJ7U83r79NhHxnoj4QV132RARW5zV\nrasAfxIRp9fjvS4ijm15/CtUZ4TfXW87GRHL6n1/sN7+lxFxY0ScMUuux0XExS3Lh9b7O65l3fsj\n4uutWbVUUDbW/361Xv8DWkTEERFxeV3h+UpEPHSmsUwnMy/LzL/IzE8DP+/0eXXm74uIf4yI24CL\n6vU7RMRJEXF9RNwZEd+OiOe1PfeAiPhG/b25PCKeN8338F5VjYg4f+o1MsOYfqfO4McR8bOI+GpE\nPK5tm80R8caI+HRE/Aw4vf14U6/N+nu+ueU29frcJyLOjogb6q/xuxHxspZjnAYcBryyZT9Pme7r\niojdIuLMiPhpRNxVj/+xLY8fUj/ndyLiwvp434uIwzv9XkkaDCfgkuYkIt4L/C3wEeDRwNOBb7ds\nclq97iXAY4CvA1+IiIfXz78P8BWqs6nPpKoz/CdwXkQ8gt/UKm4Ajgd2B/6+XvdN4NP1/WNmGOKp\nwJ8A7wL2A34X+L9ZvqRP1tu8BngkcBxwfEQc1bbdu4AL66/pb4G/iYin1o89H/ghcEI9tt2B64E3\nAS+os3go8Nz6a5jJV4BVEXHfevlpVGe4n9ayzVOBC1qWW894r6Q6C/68ehytE8oHA38MvBh4ArAT\ncMosY+m1NwK3AAcBU9l+AVgB/D6wP/Ax4N+mco2I7YEv1s9bBbwSeAvwWz0Yz47APwKPp8rjKuBL\nEbFz23bvonoNHwC8c5r9TL02d6//PQKY4Dffox2BL1O91h8NfBw4NSIOqR8/BvgacBawa72f/5lh\nzOdQVbKeRfW9vQU4PyJ2mWZMf01V1boEODMils6wT0klZKY3b968dXSjmjTfBfzZDI/vC2wGntm2\n/tvAJ+v7r6KaZC9q2+bLwAdblseBt7dt8xXg5LZ192xHNcndDDxvlq+hdfvlwCTw8LZt/gr4Tsvy\nZuBDbdt8H3h/y/LVwLvatjkR+O855Lsd8Avg8Hr5Yqqqxy/r7HcEfg08tX5873psT6yX96iXn9K2\n33fXz9ulZd0LgbuBbWcZz2nAeTM8dq/vxVYyP79t3aH1a2mntvWnAP9e338N1Zn2HVsef0T9Nb69\nZd1m4CVt+zkfOLXT8VKdkPoJ8OK2/d7rOdMdr16/F3Aj8LdbyeM/gI/PNNbpjkN1lnwSeETL49vW\nx3tnvXxI/ZwjW7Z5UL3u6Z2+Dr1589b/mx1wSXOxP9Uk8fwZHn8U1RnZr7Wtv4jqzCdUZzJ3BzZF\nROs22zL/N0ceUB9/pvG1eyzVGePLYsvBbEN1FrPV+rblG6nOWM7mNKozlNfUYzofODdn6D9n5q8i\n4hvA0yLia1RZvYDqjPFTqCaJd1OdkZ2rGzPzJ23jD6oJ2vVd7G+uLm1bXkX1Wrqx7XWwhOpsNFR/\nwbg8M6fecEtmXlnXQeYlIvYB3kf1unwQVbbbU/1S0+pbHe5vB+Bc4OuZ+baW9dtT/QL0HKrX/bb1\n7StzHPKjgB9n5pVTKzLz1xFxCdV/l/espuW1mpm3RnXFoK29ViUNkBNwSYO2iOrs8e9STQBb9fzq\nJB2MJakqCL9oe6z9zYy/nubxWWt8mbm+nug9nao6ciJVr/3xrZPKNhdQVUguAH6QmTfXHfPDqPL6\nRma2j6UT042frX0NPXRn2/Iiqit8rOLer4PWsXbyptKcZh9LtvKcL1LVe15HdeWYX1P9YrNt23bt\n476X+pe3M6n+UvHytof/P6rq0Z9R/WJxJ/BB4H5b2+88TPf6sHIqNYj/QUqai+8DvwKeMcPj36v/\nfUrb+qcAG+r7l1G9wfL2zPxB2+3meY5vLdVEbKbxtZvqru89zVjG53jsXwOL21dm5l2ZeU5m/ilV\nb3c/qqrATL5C1Yv/fapaDlST8afVtwtmeN7UGJhuHA10GXB/YPtpsp86I/99YL+I2GnqSfX7BO7f\ntq9bqTruU9tsR3XGeFp1Z3o/4PjMPD8zr6DK7kFdfi0nUHXZn5uZv2x77MnApzPz7MzcQFXHeXjb\nNtO+dtp8D3hARDyy5evYjqrDvmHGZ0lqJCfgkjqWmXdSTTbeExGvi4iHRcRjor4iSFaXB/ws8NGI\neEZEPCKqK5DsT3UmEKo3UY4DX4yIp9dX8jgwIo6NiCPmOb7/q/f/0Yh4aUQ8JCIeFxFvmmX704BP\nRMTLImLfiPjtiDgqIt46x8OPA0+KiL0i4gFReUtEvCQiHlWfCX81VYXkqln2cwnVXwJexm8m21+l\nmuD9NrNPwG+juj76MyJi14hon6i2az9rPPvGEUvq7/cYVR99l3p5v7nsByAzLwD+G/j3iDgyIpZH\nxMqIeENEvLre7NNUZ4w/FRErIuLxVG+avYstz4z/N/DHEXFQRDya6nvafia71U+BHwGvqV/DTwDO\noIu/wETEq6je9PuHwKI6910jYuoM95XAkfXr8FHAybT8slAbBx5bv14fEBHT/SJ3AVUd5oyIeGL9\ndZ5OVeP5p9YhzfVrkDR4TsAlzUlm/hXwDqqrWmwAvkTVvZ7yauC/gE8B66jqHc/OzKvq5/+K6gzw\nZVRXLLkSOJvq7PC1rYea7vAdrHsV1ZUm3kd1BvVsYJ9Ztn8N8CGqD/n5HtVk7hVseeWUTmoQ76Y6\nM3sl1RnZvajeQPhmqqtafBc4Enh+Zs74qZSZOdXxXkTdE87Mn9XPv4N7d6mz5blJVal4IVWve+1W\nxjzXa4Y/GPgO1V8OVlJVZdZS1Tm6Oc4RwL9TVTIup7oqyrOos8/MXwCrqc5MX0o14TyRalLeeqb5\nLcD/Ur0Wv0h1tZqt5fQCqjcNr6d6HX4IuKnDcWfLY4dQTfb/i6pXP3U7sX78z6he1xdQvQfgeuAz\nbOkEql+e1lO9dp40w/GPBK6gyukSqlx+p63b3+l/N5IKiurnUHkRsSfVD9ddqd6x/YnM/PA0232Y\n6gfyncCrMnPdQAcqSSomIvamOmP83Mzc2sRfkhqpSW/CvBt4c2aui4gdgW9HxHl1Nw+AiFgN7JuZ\nD6v/FPlP/ObKCpKkERMRL6W6Jvw41V8y/q6+f17BYUnSvDSmgpKZN0+dza6vDnA51TVtWx1J/Ulk\nmXkJsDQivLSSJI2uB1D1vi+n6oT/EDhkpks5StIwaNIZ8HvUb1Yao+q4tdqD6nJRU26o190ykIFJ\nkgaqriLeq44oScOsMWfAp9T1k88Cx8xynVxJkiRpKDXqDHhEbEM1+f5UZp4zzSY3UF1ZYMqe9bp7\nOeKII/KXv/wlu+22GwA77LADD33oQxkbGwNg3brqvZsu93556n5TxrPQls3f/Bfq8tS6poxnoS1P\nrWvKeBba8tS6poxnlJevueYa7ryz+oyum2++mX333ZePfexjc7usa1OuggIQEacDt2Xmm2d4/FnA\n6zPz2RFxEHBiZk77JsxXvOIVedJJJ/VxtJrJ8ccfz7HHHlt6GAuW+Zdl/uWYfVnmX5b5l3PMMcdw\n+umnz2kC3pgz4BHxJOClwIaI+A7VdUvfDuxNddnWkzPzPyPiWRFxDdVlCI+aaX833zzfD9RTtzZu\n3Fh6CAua+Zdl/uWYfVnmX5b5D5fGTMAz8+t08PHJmfmGAQxHkiRJ6ovF73nPe0qPoS9uvfXW9xxw\nwAFb31A9t3TpUpYtW1Z6GAuW+Zdl/uWYfVnmX5b5l3PTTTfxxCc+8b1zeU6jOuC99OUvfzlXrlxZ\nehiSJEkaYWvXruWwww6bUwe8cZch7JXWdwVrsC6++OLSQ1jQzL8s8y/H7Msy/7LMf7iM7ARckiRJ\naiIrKJIkSVKXrKBIkiRJDTeyE3A74OXYQyvL/Msy/3LMvizzL8v8h8vITsAlSZKkJrIDLkmSJHXJ\nDrgkSZLUcCM7AbcDXo49tLLMvyzzL8fsyzL/ssx/uIzsBFySJElqIjvgkiRJUpfsgEuSJEkNN7IT\ncDvg5dhDK8v8yzL/csy+LPMvy/yHy8hOwCVJkqQmsgMuSZIkdckOuCRJktRwIzsBtwNejj20ssy/\nLPMvx+zLMv+yzH+4jOwEXJIkSWoiO+CSJElSl+yAS5IkSQ03shNwO+Dl2EMry/zLMv9yzL4s8y/L\n/IfLyE7AJUmSpCayAy5JkiR1yQ64JEmS1HAjOwG3A16OPbSyzL8s8y/H7Msy/7LMf7iM7ARckiRJ\naiI74JIkSVKX7IBLkiRJDTeyE3A74OXYQyvL/Msy/3LMvizzL8v8h8vITsAlSZKkJrIDLkmSJHXJ\nDrgkSZLUcCM7AbcDXo49tLLMvyzzL8fsyzL/ssx/uIzsBFySJElqIjvgkiRJUpfsgEuSJEkNN7IT\ncDvg5dhDK8v8yzL/csy+LPMvy/yHy8hOwCVJkqQmsgMuSZIkdckOuCRJktRwIzsBtwNejj20ssy/\nLPMvx+zLMv+yzH+4jOwEXJIkSWoiO+CSJElSl+yAS5IkSQ03shNwO+Dl2EMry/zLMv9yzL4s8y/L\n/IfLyE7AJUmSpCayAy5JkiR1yQ64JEmS1HAjOwG3A16OPbSyzL8s8y/H7Msy/7LMf7iM7ARckiRJ\naiI74JIkSVKX7IBLkiRJDTeyE3A74OXYQyvL/Msy/3LMvizzL8v8h8vITsAlSZKkJrIDLkmSJHXJ\nDrgkSZLUcI2agEfEKRFxS0R8d4bHD4mIn0XE2vr2zpn2ZQe8HHtoZZl/WeZfjtmXZf5lmf9w2ab0\nANqcBvwDcPos21yUmUcMaDySJElSTzWuAx4RewPnZuZvT/PYIcBbMvO5W9uPHXBJkiT120LpgD8h\nItZFxBcj4lGlByNJkiTNxbBNwL8NLMvMMeAjwH/MtKEd8HLsoZVl/mWZfzlmX5b5l2X+w6VpHfBZ\nZeYdLffXRMRHI2KXzPxJ+7YXXnghl112GcuWLQNg6dKlrFixgoMPPhj4zQvVZZdddtnl0Vie0pTx\nLLTlKU0Zz0JbntKU8Yzy8oYNG9i0aRMAGzduZNWqVRx22GHMRRM74PtQdcBXTPPYrpl5S33/QOCs\nzNxnuv3YAZckSVK/ddMB36Zfg+lGRJwBHAo8ICI2Au8GtgUyM08GXhARfwJMAL8A/qDUWCVJkqRu\nNKoDnpkvycwHZ+Z2mbksM0/LzI/Xk28y8x8z89GZeUBmPjEzL5lpX3bAy2n/c5gGy/zLMv9yzL4s\n8y/L/IdLoybgkiRJ0qhrXAe8V+yAS+qFyUlYv34x4+OLWL58M2Njkyzy1IUkqTb0HXBJapr16xez\nevVOTEwES5Yka9bczsqVk6WHJUkaYiN7HscOeDn20Moy/94aH1/ExER1YmNiIhgfn/3HpvmXY/Zl\nmX9Z5j9cRnYCLkm9sHz5ZpYsqap6S5Yky5dvLjwiSdKwswMuSbPYvBnWrbMDLkmanh1wSeqxRYtg\n5cpJe9+SpJ4Z2fM4dsDLsYdWlvmXZf7lmH1Z5l+W+Q+XkZ2AS5IkSU1kB1ySJEnqUjcdcM+AS5Ik\nSQM0shNwO+Dl2EMry/zLMv9yzL4s8y/L/IfLyE7AJUmSpCayAy5JkiR1yQ64JEmS1HAjOwG3A16O\nPbSyzL8s8y/H7Msy/7LMf7iM7ARckiRJaiI74JIkSVKX7IBLkiRJDTeyE3A74OXYQyvL/Msy/3LM\nvizzL8v8h8vITsAlSZKkJrIDLkmSJHXJDrgkSZLUcCM7AbcDXo49tLLMvyzzL8fsyzL/ssx/uIzs\nBFySJElqIjvgkiRJUpfsgEuSJEkNN7ITcDvg5dhDK8v8yzL/csy+LPMvy/yHy8hOwCVJkqQmsgMu\nSZIkdckOuCRJktRwIzsBtwNejj20ssy/LPMvx+zLMv+yzH+4jOwEXJIkSWoiO+CSJElSl+yAS5Ik\nSQ03shNwO+Dl2EMry/zLMv9yzL4s8y/L/IfLyE7AJUmSpCayAy5JkiR1yQ64JEmS1HAjOwG3A16O\nPbSyzL8s8y/H7Msy/7LMf7h0NAGPiA/PsP7E3g5HkiRJGm0ddcAj4ueZeb9p1v84Mx/Ql5HNkx1w\nSZIk9Vs3HfBtZnswIo6e2q7l/pSHALfN5WCSJEnSQre1CsrL69u2LfdfDrwM2Bd4ZV9HNw92wMux\nh1aW+Zdl/uWYfVnmX5b5D5dZz4Bn5lMBIuKvM/OdgxmSJEmSNLrmdB3wiHgQsGPrusz8Qa8H1Qt2\nwCVJktRvPe+AT4mIZwKnAru3PZTA4rkcUJIkSVrIOr0O+EeB9wE7ZOailltjJ992wMuxh1aW+Zdl\n/uWYfVnmX5b5D5eOzoADOwMfz1H93HpJkiRpQDq9DvjfA5dn5qn9H1Jv2AGXJElSv/WtAw4cBLwp\nIo4Fbm59IDOfMpcDSpIkSQtZpx3wTwKvBd4PnNJ2ayQ74OXYQyvL/Msy/3LMvizzL8v8h0tHZ8Az\n81/6PRBJkiRpIei0Ax7AHwIvBh6Ymb8dEU8BdsvMs/o8xq7YAZckSVK/ddMB77SCchzwauBkYFm9\n7nrgL+dyMEmSJGmh63QC/irgOZl5JtWH7wCMAw/px6B6wQ54OfbQyjL/ssy/HLMvy/zLMv/h0ukE\nfDFwR31/agK+Y8s6SZIkSR3otAP+SeDXwJ8BNwEPAD4EbJuZr+vrCLtkB1ySJEn91s8O+JuB3YFN\nwFKqM9970+MOeEScEhG3RMR3Z9nmwxFxdUSsi4ixXh5fkiRJ6reOJuCZ+fPMfB7VpPsgYN/MfF5m\n3t7j8ZwGPHOmByNidX3shwF/BPzTTNvaAS/HHlpZ5l+W+Zdj9mWZf1nmP1xmvA54RETW/ZSImJqo\n/6i+3bMuMzf3ajCZeXFE7D3LJkcCp9fbXhIRSyNi18y8pVdjkCRJkvpptjPgm1ru3w1MtN2m1g3S\nHsB1Lcs31OvuZWzMdkopBx98cOkhLGjmX5b5l2P2ZZl/WeY/XGb7JMz9W+4v7/dAJEmSpIVgxgl4\nZraeab4Z2JyZ95zxjogldP4mzl65AdirZXnPet29nHTSSeywww4sW1Z9btDSpUtZsWLFPb8hTnWl\nXO79cmsPrQnjWWjL5m/+C3V5al1TxrPQlqfWNWU8C215al1TxjPKyxs2bGDTpqoosnHjRlatWsVh\nhx3GXHR6GcKLgLdm5jdb1h0EHJ+Zh87piFs/1j7AuZm5YprHngW8PjOfXR//xMw8aLr9nHDCCXn0\n0Uf3cmjq0MUXX3zPC1WDZ/5lmX85Zl+W+Zdl/uV0cxnCTifgPwV2yZaN6zdh/jgzd57zSGc+zhnA\noVTXGb8FeDewLZCZeXK9zUeAw4E7gaMyc+10+/I64JIkSeq3bibg23S43SZgV6oqypRdqSbBPZOZ\nL+lgmzf08piSJEnSIHXa4T4bOCMiHh0R942IFVSXAzyrf0ObH68DXk5rH02DZ/5lmX85Zl+W+Zdl\n/sOl0wn4O4DLgUuB24FvAlcCb+/TuCRJkqSR1FEH/J6NIwJ4IHBbzuWJBdgBlyRJUr/1tAMeEftk\n5g/r+w9pe3inai4OmfmDOY5TkiRJWrBmq6BsaLl/DXB1/W/r7er+DW1+7ICXYw+tLPMvy/zLMfuy\nzL8s8x8us10FZe+pO5k56A/ckSRJkkbSjB3wiPh5Zt6vvv/fmfk7Ax3ZPNkBlyRJUr910wGf7cz2\nXfVlBxcDB0ZlUfttfkOWJEmSFpbZJtDvpbrs4K+BHYC7gYmW29RyI9kBL8ceWlnmX5b5l2P2ZZl/\nWeY/XGbsgGfmxyLiE8BuwBXA/gMblSRJkjSiZuuAfzMzD6rvfzozXzrQkc2THXBJkiT1W6874A+P\niPvU95/b/bAkSZIkTZltAn4OcFVEXARsHxEXTXcb0DjnzA54OfbQyjL/ssy/HLMvy/zLMv/hMlsH\n/KiIOBjYB3gccMqgBiVJkiSNqhk74FtsFHF0Zp46gPH0jB1wSZIk9VuvO+D3yMxTI+LpEXFKRJwL\nEBGrIuJp3QxUkiRJWqg6moBHxBuBjwFXA0+pV/8C+Os+jWve7ICXYw+tLPMvy/zLMfuyzL8s8x8u\nnX6S5Z8Cv5OZxwOb63VXAI/oy6gkSZKkEdVpB/xWYPfMnIyIn2TmLvUlCsczc/e+j7ILdsAlSZLU\nb33rgAMXAce2rXsT8JW5HEySJEla6DqdgL8ReF5E/BDYKSKuBF4IvLlfA5svO+Dl2EMry/zLMv9y\nzL4s8y/L/IfLjNcBb5WZN0XE46iuB743cB1waWZunv2ZkiRJklp11AEHiIhtgCcCewA3AP+TmXf3\ncWzzYgdckiRJ/dZNB7yjM+AR8UjgXOA+wPXAXsAvI+K5mXn5nEcqSZIkLVCddsA/CpwMLMvMJ2Tm\nnsA/1esbyQ54OfbQyjL/ssy/HLMvy/zLMv/h0ukEfAz4YG7ZVzmxXi9JkiSpQ51eB/x/gTdl5gUt\n654KfCQz9+/j+LpmB1ySJEn91rcOOPB24PMR8QXgWqoroTwbeNnchihJkiQtbB1VUDLz88BK4H+B\nnep/H5uZ5/RxbPNiB7wce2hlmX9Z5l+O2Zdl/mWZ/3Dp9Coo21F97Pxft6xbEhHbZeav+jY6SZIk\nacR02gG/CHhrZn6zZd1BwPGZeWj/htc9O+CSJEnqt2464J1eBWUFcEnbukuBx8zlYJIkSdJC1+kE\nfBOwa9u6XYE7ezuc3rEDXo49tLLMvyzzL8fsyzL/ssx/uHQ6AT8bOCMiHh0R942IFcDpwFn9G5ok\nSZI0ejrtgN8HOAE4CtgO+CVwKvCWpr4J0w64JEmS+q1v1wHPzF8Cr4+INwAPBG7LTmbukiRJkrbQ\naQUFgKz8aBgm33bAy7GHVpb5l2X+5Zh9WeZflvkPlzlNwCVJkiTNT0cd8GFkB1ySJEn91tPrgEfE\n37fcf9p8BiZJkiSpMlsF5bUt9/+j3wPpNTvg5dhDK2uU85+chLVrF3P22UtYu3YxmzeXHtG9jXL+\nTWf2ZZl/WeY/XGa7Csr6iPgs8H1gu4g4brqNMvNdfRmZRtbkJKxfv5jx8UUsX76ZsbFJFvluBHVg\n/frFrF69ExMTwZIlyZo1t7Ny5WTpYUmSNCezTcBfQHUWfG8ggL2m2aaxBfKxsbHSQ1iwDj744Fkf\ndxLVX1vLf5iNjy9iYqKq2U1MBOPjixr32hnl/JvO7Msy/7LMf7jMOAHPzFuBvwaIiG0y86iBjUoj\nbRgmUWqm5cs3s2RJ3vPL2/LlDeygSJK0FR394T8zj4qInSPiFRHxtvrfXfo9uPmwA17O1npoU5Mo\nwElUH4xyD3BsbJI1a27nE5+4gzVrbmdsrHm/uI1y/k1n9mWZf1nmP1w6+iTMiHgC8EXgCuBa4DnA\niRHx7Mz8Rh/HpxE0NYlq7YBLnVi0CFaunPQvJpKkodbRdcAj4hLgQ5l5Zsu6PwDekpmP6+P4uuZ1\nwCVJktRvPb0OeJuHA2e1rfss8NC5HEySJEla6DqdgF8NvKht3e8D/9fb4fSOHfBy7KGVZf5lmX85\nZl+W+Zdl/sOlow448KfAFyLiTVQd8H2Ah1F1wSVJkiR1qKMOOEBE7Aw8G3gwcCPwn5n5kz6ObV7s\ngEuSJKnfuumAd3oGnMz8KfCvcx6VJEmSpHuM7AeA2wEvxx5aWeZflvmXY/ZlmX9Z5j9cRnYCLkmS\nJDVRxx3wYWMHXJIkSf3Wz+uAExFLIuLJ9QfwEBE7RMQOcx2kJEmStJB1NAGPiBXAVcAngFPq1YcA\np/ZpXPNmB7wce2hlDTL/yUlYu3YxZ5+9hLVrF7N588AO3Vi+/ssx+7LMvyzzHy6dXgXlY8C7MvNT\nEfHTet2FVBNySQvU+vWLWb16JyYmgiVLkjVrbmflysnSw5IkqdE6raDsz28uQZgAmXknsH0vBxMR\nh0fEFRFxVUT85TSPHxIRP4uItfXtnTPta2xsrJdD0xwcfPDBpYewoA0y//HxRUxMVLW3iYlgfNz3\ndfv6L8fsyzL/ssx/uHR6BvyHwGOBy6ZWRMSBwDW9GkhELAI+AhxG9UE/34qIczLzirZNL8rMI3p1\nXEndW758M0uW5D1nwJcvt4MiSdLWdHq66q+AL0bEe4FtI+JtwGeAGc9Ad+FA4OrMvDYzJ4AzgSOn\n2a6jd5naAS/HHlpZg8x/bGySNWtu5xOfuIM1a25nbMz6ia//csy+LPMvy/yHS0dnwDPzCxFxOPAa\nqu733sDzM/PbPRzLHsB1LcvXU03K2z0hItYBNwB/kZnf7+EYJM3BokWwcuWkvW9JkuagMdcBj4jf\nA56Zma+tl18GHJiZb2rZZkdgc2beFRGrgZMy8+HT7c/rgEuSJKnfurkOeEdnwCPiuJkey8x3zeWA\ns7gBWNZN1hvSAAAZL0lEQVSyvGe9rvVYd7TcXxMRH42IXTLzJ+07++xnP8snP/lJli2rdrl06VJW\nrFhxz5sUpv5U47LLLrvssssuu+yyy50ub9iwgU2bNgGwceNGVq1axWGHHcZcdHQGPCJOa1u1G9V1\nwD+XmS+d0xFnPsZi4EqqN2HeBFwKvDgzL2/ZZtfMvKW+fyBwVmbuM93+TjjhhDz66KN7MTTN0cUX\nX3zPC1WDZ/5lmX85Zl+W+Zdl/uX07Qx4Zh7Vvq7uhL94LgfbyjEmI+INwHlUbw49JTMvj4g/qh7O\nk4EXRMSfABPAL4A/6NXxJUmSpEHougNeXzbwp5m5tLdD6g074JIkSeq3fnbAH9K26r7AS9jyqiWS\nJEmStqLT64BfA1xd/3sN8E3gycAr+zSuefM64OVMvWFBZZh/WeZfjtmXZf5lmf9w6bQD7udLS5Ik\nST3QmOuA95odcEmSJPVbTzvgEXEdsNXZeWYu29o2kiRJkiqzVUteBry8g1sj2QEvxx5aWeZflvmX\nY/ZlmX9Z5j9cZjwDnpkXDnIgkiRJ0kLQcQc8IsaornzyQOCenksPP4q+p+yAS5Ikqd+66YB3dHWT\niHgt8HXgacBfAiuAPwceOtdBSpIkSQtZp5cXfCtweGY+D/hF/e8LqD4SvpHsgJdjD60s8y/L/Msx\n+7LMvyzzHy6dTsAflJlfq+9vjohFmbkGeG6fxiVJkiSNpI464BHxfeBZmfnDiPgG8AHgNuAzmblb\nn8fYFTvgkiRJ6reeXge8zQeA/YAfAscBnwW2Bd40l4NJkiRJC11HFZTM/Oe6ckL9787Azpn5sX4O\nbj7sgJdjD60s8y/L/Msx+7LMvyzzHy6dXgXlxIh43NRyZv46M+/o37AkSZKk0dRpB/wk4PeBO4Ez\ngDMy88o+j21e7IBLkiSp3/p2HfDMPAbYE3gdsBfwzYj4dkS8ee7DlCRJkhauTi9DSGZuzszzM/No\n4NHAj4G/79vI5skOeDn20Moy/7LMvxyzL8v8yzL/4dLxBDwidoiIl0XEF4GrgLuBV/ZtZJIkSdII\n6rQD/hlgNbAW+Deq63/f1uexzYsdcEmSJPVbP68D/i3gzzNz49yHJUmSJGlKp2/C/MCwTb7tgJdj\nD60s8y/L/Msx+7LMvyzzHy4dd8AlSZIkzV9HHfBhZAdckiRJ/da364BLkiRJ6o2RnYDbAS/HHlpZ\n5l+W+Zdj9mWZf1nmP1xGdgIuSZIkNZEdcEmSJKlLdsAlSZKkhhvZCbgd8HLsoZVl/mWZfzlmX5b5\nl2X+w2VkJ+CSJElSE9kBlyRJkrpkB1ySJElquJGdgNsBL8ceWlnmX5b5l2P2ZZl/WeY/XEZ2Ai5J\nkiQ1kR1wSZIkqUt2wCVJkqSGG9kJuB3wcuyhlWX+ZZl/OWZflvmXZf7DZWQn4JIkSVIT2QGXJEmS\numQHXJIkSWq4kZ2A2wEvxx5aWeZflvmXY/ZlmX9Z5j9cRnYCLkmSJDWRHXBJkiSpS910wLfp12Ak\n9cbkJKxfv5jx8UUsX76ZsbFJFvm3K0mShtbI/m/cDng59tB6a/36xaxevROvec2OrF69E+vWLZ51\ne/Mvy/zLMfuyzL8s8x8uIzsBl0bF+PgiJiaqv2xNTATj4/5nK0nSMLMDLjXc2rXVGfCJiWDJkmTN\nmttZuXKy9LAkSRJ2wKWRNDY2yZo1t2/RAZckScNrZP+WbQe8HHtovbVoEaxcOcnv/d4EK1du/Q2Y\n5l+W+Zdj9mWZf1nmP1xGdgIuSZIkNZEdcEmSJKlL3XTAPQMuSZIkDdDITsDtgJdjD60s8y/L/Msx\n+7LMvyzzHy4jOwGXJEmSmsgOuCRJktQlO+CSJElSw43sBNwOeDn20Moy/7LMvxyzL8v8yzL/4dKo\nCXhEHB4RV0TEVRHxlzNs8+GIuDoi1kXE2KDHKEmSJM1HYzrgEbEIuAo4DLgR+Bbwosy8omWb1cAb\nMvPZEfF44KTMPGi6/dkBlyRJUr910wHfpl+D6cKBwNWZeS1ARJwJHAlc0bLNkcDpAJl5SUQsjYhd\nM/OWgY9WktQIk5Owfv1ixscXsXz5ZsbGJlnUqL/vSnPn63q0NWkCvgdwXcvy9VST8tm2uaFed68J\n+Lp16/AM+GBN/bD40pe+zuGHP2lePyw6/cHTyXa93FepY3aik/xLjqtpx+z1/9wGnX+Jfc01i0GN\nf/36xaxevRMTExeyZMkhrFlzOytXThYf17D/7Jnrvgb5s6fpWfRiX795XQdLluSMr+spF198MQcf\nfPCMj6tZmjQB15D7zQ+L7TnppJ22+sOis33N/oOnk+16ua9Sx+xEJ/mXHVezjtnL4225v8HkX2Jf\nc89iMOMfH1/ExET119+JiWB8fNFQ5drUY859X4P72dP8LOa/r05f1xpOTZqA3wAsa1nes17Xvs1e\nW9kGgGuuuYbXve51LFtW7XLp0qWsWLHint8Op94t7HLvli+6aBsmJlYDhzIx8VW+9KVfsHLlQV3t\n70tf+joTE9vX+wq+9KWvc9ddd99r+1tueWr9A+qrTEzA+PgqVq6c3GJ/1Q+xCwGYmDiU8fFF3HXX\nhbOMHyYmLpxx/J3sr5fj72X+nR6v0/F3stzr/DtZ7mT8vTxeifxLvF5L5N/J+DdtupDFi+/L5ORT\nWbIk2bTpQi6+eHPxnxe9/u9tOMZP37/fJfIv8d/b8uWHsGRJMjFxIYsXJ8uXP/Zex3O5zPKGDRvY\ntGkTABs3bmTVqlUcdthhzEWT3oS5GLiS6k2YNwGXAi/OzMtbtnkW8Pr6TZgHASf6JszmWLu2d2fR\nOt1XJ9v1cl+ljtmJYR5XiWP28ni9PmZT99XULDZvhnXrtv4n/abm2tRjNnVfwz7+TvfV6eta5XXz\nJszGTMChugwhcBLV5RFPyczjI+KPgMzMk+ttPgIcDtwJHJWZa6fb1wknnJBHH330gEYu+M0Pi150\nwDv9wdPJdr3cV6ljdqKT/EuOq2nH7PX/3Aadf4l9zTWLQf83srUObFNzbeox57qvQf7saXoWg/zv\nbYod8HKGfgLeS07Ay/GHQFnmX5b5l2P2ZZl/WeZfjhPwFlZQJEmS1G/dTMBtE0mSJEkDNLIT8HXr\n1pUewoI19Y5hlWH+ZZl/OWZflvmXZf7DZWQn4JIkSVIT2QGXJEmSumQHXJIkSWq4kZ2A2wEvxx5a\nWeZflvmXY/ZlmX9Z5j9cRnYCLkmSJDWRHXBJkiSpS3bAJUmSpIYb2Qm4HfBy7KGVZf5lmX85Zl+W\n+Zdl/sNlZCfgkiRJUhPZAZckSZK6ZAdckiRJariRnYDbAS/HHlpZ5l+W+Zdj9mWZf1nmP1xGdgIu\nSZIkNZEdcEmSJKlLdsAlSZKkhhvZCbgd8HLsoZVl/mWZfzlmX5b5l2X+w2VkJ+CSJElSE9kBlyRJ\nkrpkB1ySJElquJGdgNsBL8ceWlnmX5b5l2P2ZZl/WeY/XEZ2Ai5JkiQ1kR1wSZIkqUt2wCVJkqSG\nG9kJuB3wcuyhlWX+ZZl/OWZflvmXZf7DZWQn4JIkSVIT2QGXJEmSumQHXJIkSWq4kZ2A2wEvxx5a\nWeZflvmXY/ZlmX9Z5j9cRnYCLkmSJDWRHXBJkiSpS3bAJUmSpIYb2Qm4HfBy7KGVZf5lmX85Zl+W\n+Zdl/sNlZCfgkiRJUhPZAZckSZK6ZAdckiRJariRnYDbAS/HHlpZ5l+W+Zdj9mWZf1nmP1xGdgIu\nSZIkNZEdcEmSJKlLdsAlSZKkhhvZCbgd8HLsoZVl/mWZfzlmX5b5l2X+w2VkJ+CSJElSE9kBlyRJ\nkrpkB1ySJElquJGdgNsBL8ceWlnmX5b5l2P2ZZl/WeY/XLYpPQBJ0nCYnIT16xczPr6I5cs3MzY2\nyaKRPY0jSf1jB1yS1JG1axezevVOTEwES5Yka9bczsqVk6WHJUlF2QGXJPXN+PgiJiaq/8dMTATj\n4/4vRJK6MbI/Pe2Al2MPrSzzL2uU81++fDNLllR/NV2yJFm+fHPhEW1plLMfBuZflvkPFzvgkqSO\njI1NsmbN7Vt0wCVJc2cHXJIkSeqSHXBJkiSp4UZ2Am4HvBx7aGWZf1nmX47Zl2X+ZZn/cBnZCbgk\nSZLURHbAJUmSpC7ZAZckSZIarhET8IjYOSLOi4grI+K/ImLpDNv9MCLWR8R3IuLS2fZpB7wce2hl\nmX9Z5l+O2Zdl/mWZ/3BpxAQcOBb478x8BHAB8LYZttsMHJqZB2TmgbPt8JprrunxENWpDRs2lB7C\ngmb+ZZl/OWZflvmXZf7ldHPStykT8COBf6nv/wvwuzNsF3Q45jvvvLMHw1I3Nm3aVHoIC5r5l2X+\n5Zh9WeZflvmXs379+jk/pykT8Adl5i0AmXkz8KAZtkvg/Ij4VkS8ZmCjkyRJknpkYB9FHxHnA7u2\nrqKaUL9zms1nujTLkzLzpoj4LaqJ+OWZOW3p6eabb57XeNW9jRs3lh7Cgmb+ZZl/OWZflvmXZf7D\nZWAT8Mx8+kyPRcQtEbFrZt4SEbsBt86wj5vqf38UEZ8DDgSmnYDvu+++HHPMMfcsP+Yxj2FsbGw+\nX4I6tGrVKtauXVt6GAuW+Zdl/uWYfVnmX5b5D866deu2qJ3ssMMOc95HI64DHhF/B/wkM/8uIv4S\n2Dkzj23b5r7Aosy8IyJ2AM4D3puZ5xUYsiRJktSVpkzAdwHOAvYCrgVemJk/i4jdgU9k5nMiYjnw\nOap6yjbApzPz+GKDliRJkrrQiAm4JEmStFA05SooPRERL4iI/42IyYhY2fbY2yLi6oi4PCKeUWqM\noy4iDo+IKyLiqrpOpD6KiFPq91B8t2VdRx9spfmJiD0j4oKI+F5EbIiIN9XrzX8AImK7iLik/mC2\nDRHx7nq9+Q9IRCyKiLUR8fl62ewHZLoPJjT/wYmIpRHxmXpO+b2IePxc8x+pCTiwAXgecGHryojY\nD3ghsB+wGvhoRMTghzfaImIR8BHgmcD+wIsj4pFlRzXyTqPKu1WnH2yl+bkbeHNm7g88AXh9/Xo3\n/wHIzF8BT83MA4AxYHVEHIj5D9IxwPdbls1+cKb7YELzH5yTgP/MzP2AxwBXMMf8R2oCnplXZubV\nVJc4bHUkcGZm3p2ZPwSuprqCinrrQODqzLw2MyeAM6myV5/Ul+H8advqTj/YSvOQmTdn5rr6/h3A\n5cCemP/AZOZd9d3tqN4blJj/QETEnsCzgE+2rDb7wZnugwnNfwAi4n7AkzPzNIB6brmJOeY/UhPw\nWewBXNeyfEO9Tr3VnvP1mHMJnX6wlXokIvahOgv7TWBX8x+MugLxHeBm4PzM/BbmPygfAv6CLT+3\nw+wHp/WDCf+wXmf+g7EcuC0iTqsrWCfXV+qbU/4Duw54r8zygT7vyMxzy4xKajTfad1HEbEj8Fng\nmPoyqe15m3+fZOZm4ID6jNTnImJ/7p23+fdYRDwbuCUz10XEobNsavb90/rBhOdFxJX42h+UbYCV\nwOsz87KI+BBV/WRO+Q/dBHy2D/SZxQ1Ulzicsme9Tr11A7CsZdmcy+jog600fxGxDdXk+1OZeU69\n2vwHLDN/HhFfBQ7H/AfhScAREfEsYHtgp4j4FHCz2Q9G2wcT/gdVBdTX/mBcD1yXmZfVy2dTTcDn\nlP8oV1Bae+CfB14UEdvW1xN/KHBpmWGNtG8BD42IvSNiW+BFVNmrv4J7v95fVd9/JXBO+xPUM6cC\n38/Mk1rWmf8ARMQDp64yEBHbA0+n6uGbf59l5tszc1lmPoTq5/wFmfly4FzMvu8i4r71X96oP5jw\nGVQXofC1PwB1zeS6iHh4veow4HvMMf+Rug54RPwu8A/AA4GfAesyc3X92NuAVwMTVH8q9hM0+yAi\nDqd6d/Ai4BQ/LKm/IuIM4FDgAcAtwLuB/wA+Q9sHW5Ua46iKiCcBF1H9jy/r29upfrm/1weLlRrn\nqIqIFVRvdFpU3/5fZr4/Zvhgt3IjHW0RcQjw55l5hNkPRszwwYTmPzgR8RiqNyAvAX4AHAUsZg75\nj9QEXJIkSWq6Ua6gSJIkSY3jBFySJEkaICfgkiRJ0gA5AZckSZIGyAm4JEmSNEBOwCVJkqQBcgIu\nSfMQEadFxHH1/YMj4vLSY+qFiPjfiHhKh9tujoiHzPDYKyPia/MYxx9FxAfr+3tFxM8jIrb2vBn2\nNR4RT+t2LPU+to2IyyPiAfPZj6SFzQm4JPVIZl6cmfttbbv5TkoHITMfnZkXdbr5PB+fVkQsAd4B\nfKAe03WZeb8s+AEWmflr4BTgbaXGIGn4OQGXpFpELB7UoehyUgr9HWeX++7qjHQHjgQuz8yb+7T/\nbv0b8Mr6FwRJmjMn4JJGWl07ODYivhcRP46IUyJi2/qxQyLiuoh4a0TcBJxar39ORHwnIn4aERfX\nH3s+tb8DIuLbEbEpIs4E7tPy2CERcV3L8p4RcXZE3BoRP4qID0fEI4GPAU+IiNsj4if1tveLiNPr\nbccj4h0t+3llPY4PRsRtwLvbvsbdI+KuiLh/2zh/FBGLI+IhEfHliLit3v+/RsT92jJ6a0SsB+6o\nn3NPXSMiHhcR/1PncUNE/ENEbNMW9bMj4v/q/X9glu/HIyPivPp7cXlE/P4s377VwIUtz927rrss\nqpe/EhHH1dn8PCK+VH8c99T2L4+IH9Y5vL1tHFG/Lq6pHz9zKr+IeGFE/CAidqyXV0fETVO1k8y8\nAfgJcNAsY5ekGTkBl7QQvAR4OrAv8AjgnS2P7QbcH1gGvDYiDqCqGLwG2AX4OPD5iFhSn/H8HPAv\n9WOfAX6v7VgJUE8SvwCM1/veAzgzM68A/hj4RmbulJlTE8aPADsB+wCHAq+IiKNa9vt44BrgQcD7\ntzhg5k3A/7SN5cXAZzJzkuoM9d/UX+t+wJ7Ae9rG/SKqCe/96+e0mgT+tP6anwA8DXhd2za/C6ys\nb0dGxNFtjxMR9wXOA/4VeGB9zH+sfymZzgrgyrZ17X85eDHwSuC3gO2At9THehTwUeClwIOBB1B9\nD6a8CTgCeHL9+E/r7cnMs4CvAx+uJ/SfBI7OzB+3PP8K4DEzjFuSZuUEXNJC8A+ZeWNm/oxq8vri\nlscmgXdn5kRm/opq4v1PmXlZVj4F/IrqbOdBwDaZ+eHMnMzMs4FvzXDMxwO7A2/NzF9m5q8z83+m\n27CerP8BcGxm3pWZ1wInAC9v2eyGzPxoZm6ux9nu36h+0ZjyIuAMgMz8v8z8cmbeXU8iPwQc0vb8\nk+qM7rXvzFybmZfWeWwETp7m+cdn5qbMvB44kS0znvIcYDwzT6/3tR74d2Cms+D3B26f4bEpp9Vf\n36+As4Cxev3vAedm5tczcwL4K7acvP8R8I7MvKl+/DjgBVNn14E3AIcBXwXOycw1bce9vR6fJM1Z\n+58QJWkUXd9y/1qqM55TflRPwKbsTXX2+Y31cgBLWp5zQ9u+r53hmHsC12bm5g7G90Cqn8cb2/bb\nesb2OmZ3NtUZ212BRwKTmXkxQEQ8CDiJ6mzvjsBiqgpFq+uZQUQ8DPggsArYvh7rt2d5fnvGU/YG\nDpqq3VBluxj41AyH/inVXwVm09oPv4vq66M+/j2ZZeZdEdF6Bntv4HMRMfX9CWAC2BW4KTM3RcRn\ngD8Dnj/NcXcCfraVsUnStDwDLmkh2Kvl/t7AjS3L7ZWG64D3Z+Yu9W3nzNwxM/8fcBNbToqhqpdM\n5zpgWcsZ1Vbtx7yNavK3d9s4Wyf7s75psz67fx7Vme8XA2e2PPw3wGZg/8y8P/Ay7v3Gydn2/zHg\ncmDf+vnvmOb5rRkvY8uMp1wHfLUt2/tl5utnOO53gYfPMq7Z3NQ6prr+0nrpwI3A6rax7FDXeYiI\nMeBoqr8s/MM0+98PWN/l2CQtcE7AJS0Er4+IPeo+79vZcnLa7hPAH0fEgQARsUNEPCsidgC+Adwd\nEW+MiG0i4vnAgTPs51KqSeDxEXHfiNguIp5YP3YLsGfdKac+S34W8P6I2DEi9qY68zrTmeGZ/Bvw\nCqr6xRkt63cC7gBuj4g9gL+Y4353An5en0V+JPAn02zzFxFx/4jYCziG6TP+AvDwiHhZnd+SiFg1\nSwf8P6n68K06veLKZ4HnRMQT65yPa3vux4G/iYhlABHxWxFxRH3/PlTZH0s1CX9wRNzzNUfEg4Gd\ngW92OBZJ2oITcEkLwRlUZ4evAa6m7U2MrTLz21Q98I/UVYmrqN7kR11VeT5wFPBjqu7y2TPsZzPw\nXOBhVGdbrwNeWD98AfA94OaIuLVe9yaqCsUPgIuAf83M0+b4dX6+Pt5NmbmhZf17gcdSVSbOnWbM\n0539bl33FuClEfFzqolr++Q6gXOoailr62Oceq8dZt4BPIPqLP2N9e14YNsZvp5zgUdExG4zjGvG\ns/aZ+X3g9VS/lNxI9f1qrcmcVI/5vIjYRPUm1qlfpv6Gqj50cn3d75cD74uIfevHXwr8S1t1SZI6\nFgU/z0CS+i4ixoFXZ+YFpceiuYuIPwQelZlvLj0WqD4JE1gHPCUzbys9HknDyTdhSpIaKzM/WXoM\nreoz4o8qPQ5Jw80KiqRR55/5JEmNYgVFkiRJGiDPgEuSJEkD5ARckiRJGiAn4JIkSdIAOQGXJEmS\nBsgJuCRJkjRATsAlSZKkAfr/AX5FLpff2qxuAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x124f10400>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.scatter(range(cvmodel.coef_.shape[1]), cvmodel.coef_[0])\n",
"plt.ylabel('value of coefficient')\n",
"plt.xlabel('predictor variable (index)')\n",
"plt.title('coefficients with l1 regularization');"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.841\n"
]
}
],
"source": [
"cv_preds = cvmodel.predict(Xte)\n",
"print(accuracy_score(cv_preds, yte))"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[CV] no parameters to be set .........................................\n",
"[CV] no parameters to be set .........................................\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/jwj2/anaconda/envs/snowflakes/lib/python3.5/site-packages/sklearn/linear_model/logistic.py:1583: UserWarning: Multiprocessing-backed parallel loops cannot be nested, setting n_jobs=1\n",
" for label in iter_labels\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[CV] no parameters to be set .........................................\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/jwj2/anaconda/envs/snowflakes/lib/python3.5/site-packages/sklearn/linear_model/logistic.py:1583: UserWarning: Multiprocessing-backed parallel loops cannot be nested, setting n_jobs=1\n",
" for label in iter_labels\n",
"/Users/jwj2/anaconda/envs/snowflakes/lib/python3.5/site-packages/sklearn/linear_model/logistic.py:1583: UserWarning: Multiprocessing-backed parallel loops cannot be nested, setting n_jobs=1\n",
" for label in iter_labels\n",
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 1.2min finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][CV] ................................ no parameters to be set - 1.2min\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 1.2min finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][CV] ................................ no parameters to be set - 1.2min\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 1.3min finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][LibLinear][CV] ................................ no parameters to be set - 1.3min\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 1.3min finished\n"
]
}
],
"source": [
"tuned_cv_scores = cross_val_score(cv_fit, X, y, scoring='accuracy',n_jobs=-1, verbose=2)"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0.84049319 0.84231842 0.84345843]\n",
"0.842090015968\n"
]
}
],
"source": [
"print(tuned_cv_scores)\n",
"print(np.mean(tuned_cv_scores))"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[CV] no parameters to be set .........................................\n",
"[CV] no parameters to be set .........................................\n",
"[CV] no parameters to be set .........................................\n",
"[CV] ................................ no parameters to be set - 0.9s\n",
"[CV] ................................ no parameters to be set - 1.0s\n",
"[CV] ................................ no parameters to be set - 1.1s\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 1.5s finished\n"
]
}
],
"source": [
"default_cv_scores = cross_val_score(default_model.fit(Xtr, ytr), X, y, scoring='accuracy',n_jobs=-1, verbose=2)"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0.83890322 0.84084841 0.84261843]\n",
"0.840790018868\n"
]
}
],
"source": [
"print(default_cv_scores)\n",
"print(np.mean(default_cv_scores))"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA78AAAGNCAYAAADZzcYVAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XuYZGdZ7/3v3ZPmlISRgyQIDgzhKAaGJsQAIwlGJAPK\nwaCCchA0sAUEFV45qSBbFHRzFEWJwIYNiEC2nAeCAgMBOYRhxgGSkGwaEkISQGDIEJCm+37/WFWT\nSqe6u6p6VXfV83w/11XX9Fq1etXzq6rpez1VddeKzESSJEmSpJLNbPYAJEmSJEkaNye/kiRJkqTi\nOfmVJEmSJBXPya8kSZIkqXhOfiVJkiRJxXPyK0mSJEkqnpNfVSMibhkR/x4RhyJisbPu6Ij414j4\nbkQsRsS2iPhwRLx6iP0Otf2ki4iliPjNNbb57YhYGGHfz42IC0cf3eSJiJM799lPbfZYJGnaWJsH\nY20ejrVZK3Hyq00VETeOiL+OiPMj4gcRcXlEfCQiHhURbT8/nw3cFLgLcPPOut8Dfg64V2fdJcBD\ngT8aYr/Dbj+QiPhgRLy27f0O4Fjg7T3jWIiIRy/bJjuXURz+vYh4UES8NyIui4jvR8TnI+Ipa+0g\nIl7XKWpLnfF9JSJeFRE3HnFM69Wb6d6dcW3bpLFI0rpYm1dWSW0+NiLe2KnJCxFx9iA7sDZrGhyx\n2QNQvSLilsDHgR8BfwrsAxZoit3TgP3Af7Z4k7cDPp2ZX1627guZ+cWedd8dZqeZOdT2ky4zv7GB\nN3cK8Ang+cAVwH2AV0XEdTPzb9b43Y8CvwbMAncH/gm4JfArYxvtYILRDz4kaVNZmyfTBtfm6wL/\nBbwY+HVgyxC/a23WZMtML1425QK8G/g6cFSf67YA1+/8fATwQuBrwH8DXwAesWz7I4GXd7b5PvBZ\n4KE91y8Biz3/vhaY7yx3Lx/qbPsR4NXL9v+kzu3+kGaS9rae6z7cZ/vfB84DfgBcQPPK9pae6+eB\nPwdeRlNgLgdeAsx0rn9dnzHfp3Pds4H/1xnLN4DdwHVXuI8fB1zSs3zrzv7e0LPuDODSZffVb/aM\nc7F3HJ31j6E5MLpX577+PnAucMIaj/lzgS+tsc3Lgc+ssc3rgLOXrXs2zQHadTvLNwP+d+c++h7w\nMeDne7Y/uZPpF4E9nQxfAE5btt+/AL7Yuf5i4FXADZftZxH4KeBWfR63D3W2+TFwi2X7fjTNAd31\nN/v/oxcvXrxkWpuxNi+/7lr1dpX9WJu9TPzFjz1rU0TEjYBdwN9m5qHl12fmYmb+oLP4V8DvAE8B\n7gy8EXhjRNy351feAxxP82rjnWn+CP5zzzbHAp8E3tT5+anACcBbaV6lPAb41e7NLxvrn3fG8Erg\nZ4H70RSVlbI9j+ajVs8A7ti5rccDf7Zs0yfTHGCc2Pn5yTSFi87vfKwzvmNoPvb1iYj41c5+fx+4\nLU1x2L3SWGiK/09FxO06y78AfBPove/uS1ME+rkHTaF4Ks39dvOe67YAf9kZy91oCtm/tPCRuJ+g\nKWbD+iFNK8cREXE9muw3AO4P7ADeB5wdEXdY9nt/Q1NE7wJ8CnhLRGztuf4q4HeBO9E8PifTHMz1\ncwnw4M7PJ9DcX7+amXuAL9Ec8PT6XeCNPc91Sdo01mbA2tw2a7Mmy2bPvr3UeeHqP9wPWWO769P8\n4XzCsvX/F/i3zs+n0PwRPHrZNq8B/m/Pcr9Xgfu9Snl4O5o/0FcBf7jKGHu3vz7NxO2Xlm3zKOA7\nPcvzwDuWbfM+4E09yx8EXrtsmz8AzqfnleoB7ut54H90fn4jzSu83wVu31l3GfDYnu0Pv7rcWV4A\nHr1sn4+heeX0rj3rTuysu90qY1n1nd/OY/nfwAPWyHSNxw34GeAi4OOd5d+meSV4Ztnv/Tvwks7P\n3VeXH9xz/c066+63ym0/BPhBz/LhV5c7y/fuLG9b9nt/CMz3LN+xc1t3Gcf/MS9evHgZ9oK12dp8\n7etGfufX2uxlEi++86vNEgNud1uavpGPLVu/h+ZVZGhexbsu8PWIuLJ7AX6Lpm9oPe7c2fcHh9j+\n+sBZy8byj8DREXGTnm33Lfvdr9O8kryatwLXAS7ufLHEIyPiqDV+58M0rypD80ryB2juz1+IiJ+h\nKSorvbq8muSafV9fp3lc18rQV0ScBPwr8NzMfN8Av3Lfzv17VWccFwGP7FzXfWX34LLHYSfXfE4k\nTf9as9D0VC32ZoiIX42IPRFxaWcfbwKuExHHDhnx9cAxEXH/zvLvAudmZpu9c5K0HtZma/N6WZs1\n0fzCK22WC2leWfsZ4B1rbLtWMZ6hebX0hD7b/mik0Y2u+4LSw2gyLvftnp+Xjy1Z4xvYM/PrnY8G\n3ZemaP4J8KKIODEzL13h1z4EvDQi7gQcBXyapuieSvM34CuZ+dXVbncFS5nZ+zG07s9Dv6gWEacA\n7wJekJkvGvDXPknTl7MIfD0zf9xz3QxNL9BDuPZz4qply/2eIzOdcf0czUHNC4CnA98B7knTr3Sd\nAccJQGZ+OyLeDpwRER+iecfh2cPsQ5LGzNpsbV4va7MmmpNfbYrM/E5E7AaeHBGvzMzv9V4fEUfQ\nvKp8Ec3HYO9D8wez6xTg852fz6XpE71+XvObIdvwxc7t/1LP7a2m+8Ubx2XmB9Z52z+izzcsZuYC\ncDZNj8yf0XzJx0OAv1thPx8GbkLT6/TRzFzq/IF/Fs3fgLVeWe47jrZExANpithzMvNlQ/zqDzJz\nfoXrzqUpYFdm5rfWMbx7A9/MzOd2V0TEr6/xO92C3e8++0eax+MJwPWAt6xjbJLUKmvzQKqozetg\nbdZE82PP2kxPpOlZOTciHhERd4qI4yLikTR/IG+XzZcNvAL4nxHxsIi4XUQ8m+Yr818AkJkfAv4N\n+L8R8eCI2B4RcxHx5Ij4nfUMMDO/T/NV/8+LiCd2bv+uEfHMVbb/S+AvO9vfPiJ+JiJ+IyJeOOTN\nzwN3j4jbRMRNIuKIiHhcRPxuRNwlmnPVPZLmFeMVDyw6rzpfSNML9KHOun00r7o+gLUL7DzNx5hu\nvuyjYesWEb9G0yP2NzRfgnJM53LTde76TTTjfm9E3C8ibhURJ0bEMyPiQb1DWGM/FwA/2bnft0dz\nTsXf6xel5+ev0rxz8oCI+MmIuGH3isz8eGef/wv4587zRZImibV5dcXXZoDO/bkDuDFwVGf5ruvc\nrbVZm853frVpMvOSiJij+YbE5wLbaL72/gLg77n61dzn0Hx85qXAT9K84vxbmfmRnt09qLOPlwC3\noPkI0z7gr3tvctChLRvnn0bEN2i+OfElNB+v+egq2/9FRHyd5hsi/xfNKRW+RPNxnGHG8mKab7Dc\nT/PlHvft3PbTgRfR9Dt9GTgjMz+8xr4+TNOj1VtMP0LzqvTyArt8bE+jyf0Vmr8Zq73SPOh93PXE\nzj7/tHPp+ipwmyH3dfUgMv87Ik6m+abI19I8b75J87Gy3m/g7Dfew+sy870R8QKag7mjaPrZng68\neZXf+UZEPAt4Js3pMj7G1X1dAGfSPJdfPVI4SRoja/OaaqjNAJ9b9nvd5ZHfbbY2axLENdsCNk80\nJ1V/A00z+xJwZma+os92r6D5Gv7vA7/deZVMkqZCRPw1cGpm3n2zxyJJkqzNNZmkd35/DPxRZu6L\n5hvyPhsRZ2fm+d0NImIXTb/G7aJpdv8H4KRNGq8kDazzEas7AGfQvPMgSZI2kbW5PhPT85uZl3ff\nxc3mxOrn0XxEpteDad4dJjM/BWyNiI366nZJWo930nyc7azMfNMmj0WSJFmbqzNJ7/weFhG3BnYA\nn1p21S2AS3qWL+2su2JDBiZJI8rM+272GCRJ0tWszfWZmHd+uzofeX478NTOO8CSJEmSJK3LRL3z\n2zl/3NuB/5OZ7+yzyaXAT/cs37Kz7loe9KAH5Q9/+EOOPfZYAI488khue9vbsmPHDgD27Wu+J2va\nl7vrJmU841p++9vfXuTj17t80UUX8bCHPWxixjOu5eXP3c0ez7iWfTyne/miiy7i+99vznZx+eWX\nc9xxx/GqV71qrdNvaA3W5rKWrc3lLJf6t3z5so/ndC+3UZsn5tueASLiDcC3MvOPVrj+AcCTMvOB\nEXES8LLM7PuFV49+9KPz5S9/+RhHOxle+MIX8sxn9j2tXVFqyFlDRjBnaWrJ+dSnPpU3vOENTn7X\nydpclhpy1pARzFmaWnKOUpsn5p3fiLg38FvAgYjonkvs2cCtgMzMV2fm+yLiARFxEc2pjh670v4u\nv/zyjRj2prv44os3ewgbooacNWQEc5amlpxqh7W5LDXkrCEjmLM0teQcxcRMfjPz4wxw4uzM9GvI\nJUmSJElD2fK85z1vs8cwFt/4xjeed7e73W2zhzF2W7duZdu2bZs9jLGrIWcNGcGcpakl52WXXca9\n7nWvP9/scUw7a3NZashZQ0YwZ2lqyTlKbZ6ont82/fu//3vOzc1t9jAkSQXYu3cvp556qj2/62Rt\nliS1ZZTaPHGnOmpL77ecleycc87Z7CFsiBpy1pARzFmaWnKqHdbmstSQs4aMYM7S1JJzFMVOfiVJ\nkiRJ6vJjz5IkrcGPPbfD2ixJaosfe5YkSZIkqY9iJ7/2FZWlhpw1ZARzlqaWnGqHtbksNeSsISOY\nszS15BxFsZNfSZIkSZK67PmVJGkN9vy2w9osSWqLPb+SJEmSJPVR7OTXvqKy1JCzhoxgztLUklPt\nsDaXpYacNWQEc5amlpyjKHbyK0mSJElSlz2/kiStwZ7fdlibJUltsedXkiRJkqQ+ip382ldUlhpy\n1pARzFmaWnKqHdbmstSQs4aMYM7S1JJzFMVOfiVJkiRJ6rLnV5KkNdjz2w5rsySpLfb8SpIkSZLU\nR7GTX/uKylJDzhoygjlLU0tOtcPaXJYactaQEcxZmlpyjqLYya8kSZIkSV32/EqStAZ7ftthbZYk\ntcWeX0mSJEmS+ih28mtfUVlqyFlDRjBnaWrJqXZYm8tSQ84aMoI5S1NLzlEUO/mVJEmSJKnLnl9J\nktZgz287rM2SpLbY8ytJkiRJUh/FTn7tKypLDTlryAjmLE0tOdUOa3NZashZQ0YwZ2lqyTmKYie/\nkiRJkiR12fMrSdIa7Plth7VZktQWe34lSZIkSeqj2MmvfUVlqSFnDRnBnKWpJafaYW0uSw05a8gI\n5ixNLTlHUezkV5IkSZKkLnt+JUlagz2/7bA2S5LaYs+vJEmSJEl9FDv5ta+oLDXkrCEjmLM0teRU\nO6zNZakhZw0ZwZylqSXnKIqd/EqSJEmS1GXPryRJa7Dntx3WZklSW+z5lSRJkiSpj2Inv/YVlaWG\nnDVkBHOWppacaoe1uSw15KwhI5izNLXkHEWxk19JkiRJkrrs+ZUkaQ32/LbD2ixJaos9v5IkSZIk\n9VHs5Ne+orLUkLOGjGDO0tSSU+2wNpelhpw1ZARzlqaWnKModvIrSZIkSVKXPb+SJK3Bnt92WJsl\nSW2x51eSJEmSpD6KnfzaV1SWGnLWkBHMWZpacqod1uay1JCzhoxgztLUknMUEzX5jYjXRMQVEfGf\nK1x/ckR8NyL2di5/stFjlCRJkiRNn4nq+Y2IncAh4A2ZeZc+158MPC0zH7TWvuwrkiS1xZ7fdlib\nJUltmfqe38w8B/jOGpt58CFJkiRJGspETX4HdM+I2BcR742In1lpI/uKylJDzhoygjlLU0tOtcPa\nXJYactaQEcxZmlpyjuKIzR7AkD4LbMvMqyJiF/AO4PabPCZJkiRJ0oSbqslvZh7q+Xl3RPx9RNw4\nM7+9fNuLLrqIJz7xiWzbtg2ArVu3cvzxx7Nz507g6ldEXJ6O5e66SRnPuJZ7s07CeMaxvHPnzoka\nzziXuyZlPD6egy8fOHCAgwcPAnDxxRdzwgkncOqpp6L1sTaXtdxdNynj8W+5f8sHWe6alPH4eG5s\nbZ6oL7wCiIhbA+/OzOP7XHdMZl7R+flE4K2Zeet++/FLNSRJbfELr9phbZYktWXqv/AqIt4MfAK4\nfURcHBGPjYgnRMTjO5s8LCI+HxGfA14G/MZK+7KvqCw15KwhI5izNLXkVDuszWWpIWcNGcGcpakl\n5yiO2OwB9MrM31zj+r8D/m6DhiNJkiRJKsTEfey5LX60SpLUFj/23A5rsybR4iLs37+F+fkZtm9f\nYseORWYm6rORkvoZpTZP1Du/kiRJ0kbav38Lu3YdzcJCMDub7N59JXNzi5s9LEljUOzrWvYVlaWG\nnDVkBHOWppacaoe1uSyl5Jyfn2FhoXnzaGEhmJ+/+vC4lIxrMWdZask5imInv5IkSdJatm9fYna2\naQOcnU22b1/a5BFJGhd7fiVJWoM9v+2wNmsSLS3Bvn32/ErTxp5fSZIkaQgzMzA3t2ifr1SBYl/X\nsq+oLDXkrCEjmLM0teRUO6zNZakhZw0ZwZylqSXnKIqd/EqSJEmS1GXPryRJa7Dntx3WZklSW0ap\nzb7zK0mSJEkqXrGTX/uKylJDzhoygjlLU0tOtcPaXJYactaQEcxZmlpyjqLYya8kSZIkSV32/EqS\ntAZ7ftthbZYktcWeX0mSJEmS+ih28mtfUVlqyFlDRjBnaWrJqXZYm8tSQ84aMoI5S1NLzlEUO/mV\nJEmSJKnLnl9JktZgz287rM2SpLbY8ytJkiRJUh/FTn7tKypLDTlryAjmLE0tOdUOa3NZashZQ0Yw\nZ2lqyTmKYie/kiRJkiR12fMrSdIa7Plth7VZktQWe34lSZIkSeqj2MmvfUVlqSFnDRnBnKWpJafa\nYW0uSw05a8gI5ixNLTlHUezkV5IkSZKkLnt+JUlagz2/7bA2S5LaYs+vJEmSJEl9FDv5ta+oLDXk\nrCEjmLM0teRUO6zNZakhZw0ZwZylqSXnKIqd/EqSJEmS1GXPryRJa7Dntx3WZklSW+z5lSRJkiSp\nj2Inv/YVlaWGnDVkBHOWppacaoe1uSw15KwhI5izNLXkHEWxk19JkiRJkrrs+ZUkaQ32/LbD2ixJ\naos9v5IkSZIk9VHs5Ne+orLUkLOGjGDO0tSSU+2wNpelhpw1ZARzlqaWnKModvIrSZIkSVKXPb+S\nJK3Bnt92WJslSW2x51eSJEmSpD6KnfzaV1SWGnLWkBHMWZpacqod1uay1JCzhoxgztLUknMUxU5+\nJUmSJEnqsudXkqQ12PPbDmuzJKkt9vxKkiRJktRHsZNf+4rKUkPOGjKCOUtTS061w9pclhpy1pAR\nzFmaWnKOotjJryRJkiRJXfb8SpK0Bnt+22FtliS1xZ5fSZIkSZL6KHbya19RWWrIWUNGMGdpasmp\ndliby1JDzhoygjlLU0vOUUzU5DciXhMRV0TEf66yzSsi4sKI2BcROzZyfJIkSZKk6TRRPb8RsRM4\nBLwhM+/S5/pdwJMz84ER8XPAyzPzpH77sq9IktQWe37bYW2WJLVl6nt+M/Mc4DurbPJg4A2dbT8F\nbI2IYzZibJIkSZKk6TVRk98B3AK4pGf50s66a7GvqCw15KwhI5izNLXkVDuszWWpIWcNGcGcpakl\n5ygGmvxGxCtWWP+ydocjSZImlccDkqRpNlDPb0R8LzNv2Gf9f2XmTVodUMStgHev0PP7D8CHM/Nf\nOsvnAydn5hXLt/293/u9/O53v8u2bdsA2Lp1K8cffzw7d+4Ern5FxGWXXXbZZZeXLx84cICDBw8C\ncPHFF3PCCSfwtKc9rfqe3/UeD1ibXXbZZZddHnW5jdq86uQ3Ih7X+fGVwJOXXX0b4Ncy8w7D3OCa\nA4q4Nc3k9/g+1z0AeFLnC69OAl7mF15Jksat9i+8aut4wNosSWrLOL7w6lGdy3V6fn4U8EjgOOAx\nI4xzRRHxZuATwO0j4uKIeGxEPCEiHg+Qme8D5iPiIuAfgSeutC/7ispSQ84aMoI5S1NLTrVzPGBt\nLksNOWvICOYsTS05R3HEaldm5n0BIuIvMvNPxj2YzPzNAbZZ/oqzJEkao40+HpAkaRyGOs9vRNwM\nOKp3XWZ+ue1BtcGPVkmS2lL7x56XG/V4wNosSWrLKLV51Xd+uyLi/sBrgZsvuyqBLcPcoCRJmk4e\nD0iSptmg5/n9e+B/Akdm5kzPZWILnX1FZakhZw0ZwZylqSWnDlvX8YC1uSw15KwhI5izNLXkHMVA\n7/wCNwL+MYf5jLQkSSqNxwOSpKk16Hl+/wY4LzNfO/4htcO+IklSW+z5baz3eMDaLElqy9h6foGT\ngKdExDOBy3uvyMz7DHODkiRpank8IEmaWoP2/P4T8HjgBcBrll0mkn1FZakhZw0ZwZylqSWnDlvX\n8YC1uSw15KwhI5izNLXkHMVA7/xm5uvHPRBJkjTZPB6QJE2zQXt+A/hd4BHATTPzLhFxH+DYzHzr\nmMc4EvuKJEltsee3sd7jAWuzJKkto9TmQT/2/Hzgd4BXA9s6674GPGOYG5MkSVPN4wFJ0tQadPL7\n28AvZ+ZbaE5kDzAP3GYcg2qDfUVlqSFnDRnBnKWpJacO+23WcTxgbS5LDTlryAjmLE0tOUcx6OR3\nC3Co83O32B3Vs06SJJXP4wFJ0tQatOf3n4AfAX8IXAbcBHgpcJ3MfOJYRzgi+4okSW2x57ex3uMB\na7MkqS3j7Pn9I+DmwEFgK80rvLfCHh9Jkmri8YAkaWoNNPnNzO9l5kNpCtxJwHGZ+dDMvHKso1sH\n+4rKUkPOGjKCOUtTS0411ns8YG0uSw05a8gI5ixNLTlHseJ5fiMisvOZ6IjoTpK/2bkcXpeZS+Me\npCRJ2hweD0iSSrFiz29EfC8zb9j5eYmrv9ji8CZAZuaW8Q5xNPYVSZLaUnPPb5vHA9ZmSVJbRqnN\nK77zC9y55+ftow1JkiRNOY8HJElFWLHnNzMv6Vm8HPh6Zn61ewG+3lk/kewrKksNOWvICOYsTS05\na9bm8YC1uSw15KwhI5izNLXkHMWg3/b8QeDuy9bdHfhAu8OR2re4CHv3buGss2bZu3cLS3alSdKo\nPB6QJE2tQc/z+x3gxtmzcecLLv4rM280xvGNzL4ide3du4Vdu45mYSGYnU12776SubnFzR6WpClS\nc89vr/UeD1ibJUltGed5fg8Cxyxbdwzw/WFuTNoM8/MzLCw0/y8WFoL5+UGf9pKkZTwekCRNrUFn\nAWcBb46In42IG0TE8cAbgLeOb2jrY19RWdaTc/v2JWZnmzcpZmeT7dsn83PPPpZlMacKta7jAWtz\nWWrIWUNGMGdpask5itW+7bnXc4AXA58Grgv8EHgd8OwxjUtqzY4di+zefSXz8zNs377Ejh1+5FmS\nRuTxgCRpag3U83t444gAbgp8K4f5xU1gX5EkqS32/F7TqMcD1mZJUltaPc9vRNw6M7/S+fk2y64+\nuql7kJlfHnKckiRpSng8IEkqxWo9vwd6fr4IuLDzb+/lwvENbX3sKypLKTlXO+1SKRnXYs6y1JKz\ncq0dD1iby1JDzhoygjlLU0vOUazW83ur7g+Z6dfjSi3Yv9/TLkmaOh4PSJKKsGLPb0R8LzNv2Pn5\n3zLzFzd0ZOtkX5Em0VlnzXLGGUcdXj7zzEOcfvrCJo5I0iBq7vlt83jA2ixJakvb5/m9qnMqgy3A\nidGYWX5Z35ClukzLaZckqYfHA5KkIqxWrP6c5lQGPwKOBH4MLPRcussTyb6ispSSs3vapTPPPMTu\n3Vde47RLpWRciznLUkvOyrV2PGBtLksNOWvICOYsTS05R7Fiz29mvioizgSOBc4H7rxho5IKNTMD\nc3OL9vlKmhoeD0iSSrFaz+8nM/Okzs9vyszf2tCRrZN9RZKktlTe89va8YC1WW1aXGy+SHJ+fobt\n25fYsWORGT+AL1Wj1fP8ArePiOtl5g+BX1nf0CRJ0pTyeGAdnKCNj2dQkDSs1f78vhP4UkR8FLh+\nRHy032WDxjk0+4rKUkPOGjKCOUtTS87KtXY8UGNt7k7QzjjjKHbtOpp9+7Zs4sjatdn//+fnZ1hY\naN70WVgI5ufbf1VhszNuFHOWpZaco1it5/exEbETuDVwD+A1GzUoSZI0GTweWJ9+EzTfnWxH9wwK\n3Xd+PYOCpLWs2PN7jY0iHpeZr92A8bTGviJJUltq7vnttd7jgRpr8969fjR3XJaWYN8+P1Iu1art\nnt/DMvO1EXE/4OHAzTLzVyLiBOCGmfmhEcaqMbCvSJI0Th4PDK97irve2qx2eAYFScMaaGoUEb8P\nvAq4ELhPZ/UPgL8Y07jWzb4i+4qmTQ0ZwZylqSWnGus9HqixNncnaKefvsDcXFkvStfw/7+GjGDO\n0tSScxSD/gn+A+AXM/OFQLeh4nzgDmMZlUayEV/8IEmqmscDkqSpNWjP7zeAm2fmYkR8OzNvHBHX\nA+Yz8+ZjH+UI7Cuyr0iS2mLPb2O9xwM11mZJ0niMUpsHfWvwo8Azl617CvDhYW5M49XtKzrzzEPs\n3n2lfUWSpLZ5PCBJmlqDTn5/H3hoRHwFODoiLgB+HfijcQ1svewrsq9o2tSQEcxZmlpy6rB1HQ/U\nWJtLVkPOGjKCOUtTS85RDPptz5dFxD1ozu93K+AS4NOZ6QnVJEmqhMcDkqRpNlDPL0BEHAHcC7gF\ncCnwicz88RjHti72FUmS2mLP79XWczxgbZYktWVs5/mNiDsC7wauB3wN+GnghxHxK5l53tAjlSRJ\nU8fjAbVlcbE5RWPv+Y9LateSNJkG/TPz98CrgW2Zec/MvCXwD531E8m+orLUkLOGjGDO0tSSU4et\n63jA2lyW9eTcv785Q8UZZxzFrl1Hs2/flhZH1h4fy7KYU4NOfncAL8lrfkb6ZZ31rYmI0yLi/Ij4\nUkQ8o8/1J0fEdyNib+fyJ23eviRJWtWGHA+ofPPzMywsNJ9WXFgI5ud921fS+A16nt/PA0/JzA/1\nrLsv8MrMvHMrA4mYAb4EnAp8HfgM8PDMPL9nm5OBp2Xmg9ban31FkqS22PPbWO/xgLVZXXv3Nu/8\nLiwEs7PJ7t1XMjfnKRolDW5sPb/As4F3RcR7gK/SfMPjA4FHDjfEVZ0IXJiZXwWIiLcADwbOX7Zd\n9QcfkiTZ27n4AAAgAElEQVRtko04HlAFduxYZPfuK6/R8ytJ4zbQZ0wy813AHPB54OjOv3fPzHe2\nOJZb0JwyoetrnXXL3TMi9kXEeyPiZ1bamX1FZakhZw0ZwZylqSWnGus9HrA2l2U9OWdmYG5ukdNP\nX2BubnK/7MrHsizm1KDf9nxdYD4z/6Jn3WxEXDcz/3tso7u2z9J8ycZVEbELeAdw+34b7tmzh3PP\nPZdt27YBsHXrVo4//nh27twJXP2kmPblrkkZz7iWDxw4MFHjGcfygQMHJmo8Lvt41rx84MABDh48\nCMDFF1/MCSecwKmnnkrt1ns8YG0ua9na7PK0Lft4TvdyG7V50J7fjwJ/nJmf7Fl3EvDCzDxlqFtc\n+TZOAp6Xmad1lp8JZGa+aJXfmad5xfnby6+zr0iS1BZ7fhvrPR6wNkuS2jJKbR70QybHA59atu7T\nwF2HubE1fAa4bUTcKiKuAzwceFfvBhFxTM/PJ9JM3q818ZUkSWOxEccDkiSNxaCT34PAMcvWHQN8\nv62BZOYi8GTgbOALwFsy87yIeEJEPL6z2cMi4vMR8TmaUyv8xkr7s6+oLDXkrCEjmLM0teTUYes6\nHrA2l6WGnDVkBHOWppacozhiwO3OAt4cEU8BvgwcB7wEeGubg8nM9wN3WLbuH3t+/jvg79q8TUmS\nNLANOR6QJGkcBu35vR7wYuCxwHWBHwKvBZ6+wV94NTD7iiRJbbHnt7He4wFrsySpLWM7z29m/hB4\nUkQ8Gbgp8K0cZNYsSZKK4fGAJGmaDXVWtWx8cxoKnX1FZakhZw0ZwZylqSWnrmnU4wFrc1lqyFlD\nRjBnaWrJOYoJPaW4JEmSJEntGajndxrZVyRJaos9v+2wNkuS2tLqeX4j4m96fv6F9QxMkiRNJ48H\nJEmlWO1jz4/v+fkd4x5I2+wrKstm51xchL17t3DWWbPs3buFpaX2b2OzM24Uc5allpyVa+14wNpc\nlhpy1pARzFmaWnKOYrVve94fEW8HvghcNyKe32+jzPyzsYxMVVlchP37tzA/P8P27Uvs2LHIzAR1\npO/fv4Vdu45mYSGYnU12776SubnFzR6WJG0EjwckSUVYsec3Im5G82rvrYDHAG/qs1lm5uPGN7zR\n2Vc0XfbunezJ5VlnzXLGGUcdXj7zzEOcfvrCJo5I0kaquee3zeMBa7MkqS2tnuc3M78B/AVARByR\nmY9d5/ikFc3Pz7Cw0Dx3FxaC+fmZiZr8bt++xOxsHp6cb98+hs89S9IE8nhAklSKgT5YmpmPjYgb\nRcSjI+JZnX9vPO7BrYd9RdOlO7kE+k4uNzvnjh2L7N59JWeeeYjdu69kx472J+abnXGjmLMsteRU\nY73HA9bmstSQs4aMYM7S1JJzFKv1/B4WEfcE3gucD3wV+GXgZRHxwMz8jzGOT5XoTi57e34nycwM\nzM0tTtS70ZK00TwekCRNs4HO8xsRnwJemplv6Vn3G8DTM/MeYxzfyOwrkiS1peae317rPR6wNkuS\n2tLqeX6XuT3w1mXr3g7cdpgbkyRJU83jAUnS1Bp08nsh8PBl634N+H/tDqc99hWVpYacNWQEc5am\nlpw6bF3HA9bmstSQs4aMYM7S1JJzFAP1/AJ/ALwnIp5C0+Nza+B2NL0+kiSpDh4PSJKm1kA9vwAR\ncSPggcBPAV8H3peZ3x7j2NbFviJJUlvs+b3aeo4HrM2SpLa0ep7f5TLzO8Abhx6VJEkqhscDkqRp\nNWjP79Sxr6gsNeSsISOYszS15FQ7rM1lqSFnDRnBnKWpJecoip38SpIkSZLUNXDP77Sxr0iS1BZ7\nftthbZYktWWc5/klImYj4uc7J7MnIo6MiCOHHaQkSZpeHg9IkqbVQJPfiDge+BJwJvCazuqTgdeO\naVzrZl9RWWrIWUNGMGdpasmpxnqPB6zNZakhZw0ZwZylqSXnKAZ95/dVwJ9l5h2Bhc66PcDOsYxK\nkiRNIo8HJElTa6Ce34j4DnDjzMyI+HZm3riz/vDPk8a+IklSW+z5baz3eMDaLElqyzh7fr8C3L13\nRUScCFw0zI1JkqSp9hU8HpAkTalBJ79/Crw3Iv4cuE5EPAt4G/AnYxvZOtlXVJYaco4r4+Ii7N27\nhbPOmmXv3i0sLY3lZgZWw2MJ5lSx1nU8YG0uSw05a8gI5ixNLTlHccQgG2XmeyLiNOAMmt6eWwG/\nmpmfHefgJK3f/v1b2LXraBYWgtnZZPfuK5mbW9zsYUmaQh4PSJKmmef5lQp31lmznHHGUYeXzzzz\nEKefvrDKb0hazp7fdlibJUltGaU2D/TOb0Q8f6XrMvPPhrlBSRtr+/YlZmfz8Du/27dv8ueeJU0t\njwckSdNs0J7fn152uQfwdOC4MY1r3ewrKksNOceVcceORXbvvpIzzzzE7t1XsmPH5n7kuYbHEsyp\nYq3reMDaXJYactaQEcxZmlpyjmLQnt/HLl/X6fl5ROsjktSqmRmYm1u0z1fSunk8IEmaZiP3/EbE\nDPCdzNza7pDaYV+RJKkt9vyubJjjAWuzJKkt4+z5vc2yVTcAfhO4ZJgbkyRJ08vjAUnSNBu05/ci\n4MLOvxcBnwR+HnjMmMa1bvYVlWXaco5ybt1pyzgqc5allpw6bF3HA9bmstSQs4aMYM7S1JJzFIP2\n/A46SZaE59adVouLzWM3Pz/D9u1L7NixyIx//aTDPB6oi38TJZXG8/xKY+C5dafT3r2+aKH+7Plt\nh7V5uvg3UdIka7XnNyIuAdacGWfmtmFuUKqB59adTvPzMywsNH9DFxaC+fkZD/RUPY8H6uXfREml\nWe3DK48EHjXAZSLZV1SWacs5yrl1py3jqCY5Z/dFC2DdL1pMcs421ZKzcq0dD1ibp8tafxNLybma\nGjKCOUtTS85RrPjOb2bu2ciBSCXx3LrTqfuiRW9/m1Q7jwfq5d9ESaUZuOc3InbQfKPjTYHDn63O\nzD8bz9DWx74iSdPML5qZLPb8Xm09xwPWZklSW8Z5nt/HAy8FzgZ2AbuBXwLeOewgJUlr8xvDNYk8\nHpAkTbNB30f4Y+C0zHwo8IPOvw8DJvbra+0rKksNOWvICOYcVL8vmplEtTyeOmxdxwPW5rLUkLOG\njGDO0tSScxSDHk3dLDM/1vl5KSJmMnM38CtjGpckVa3NL9+SWuTxgCRpag3U8xsRXwQekJlfiYj/\nAP4a+Bbwtsw8dsxjHIl9RZKm2dIS7Ntnz++ksOe3sd7jAWuzJKktY+v5pSludwK+AjwfeDtwHeAp\nw9yYJGkwfmO4JpTHA5KkqTXQ+wiZ+b87H2ui8++NgBtl5qvaHExEnBYR50fElyLiGSts84qIuDAi\n9nW+cbIv+4rKUkPOGjKCOUtTS0411ns8YG0uSw05a8gI5ixNLTlHMdDkNyJeFhH36C5n5o8y81Cb\nA4mIGeCVwP2BOwOPiIg7LttmF3BcZt4OeALwD22OQdL4LC7C3r1b+OhHj2Dv3i0s2cI6dt37/Kyz\nZtd1n7e1H02/jTgekCRpXAbt+X058GvA94E3A2/OzAtaHUjEScBzM3NXZ/mZQGbmi3q2+Qfgw5n5\nL53l84BTMvOK5fuzr2ht4zyP6Er7buM2Pf/pxmvjPt+7t/+pezbjediWzXguDnObbd3nK+2nJvb8\nNtZ7PGBtliS1ZWw9v5n51Ij4Q+BU4BHAJyPiy8CbMvMlww+1r1sAl/Qsfw04cY1tLu2su9bkt3TD\nHLyutG0b5xEddt/D3ma//a+0j2mdFA877s14AWHY+7zf+n6n7hnlOTFMpnHue6Xn+V3vuji2F35g\nuNts6z5faT+qzwYdD0ytNmpzG+sz29n3MDmHvc029j3s4zApj8+wj1tbOcf5XPE2J+M2p+G4d7MN\n+oVXZOYS8EHggxHxp8DrgL8BJrLY7du3j5JfXb764HUPs7Mnr3rwutKB7koHtMP8Jxt238MeRPfL\n2dYB/TiL4zBWeizH+aJFW5OfYV7k6J66p5uze+qeYZ8Tw9wvwz7Hh72/VjoXb7/Hs62J+Oq3ec19\nX32fxzVOlzTs/bLSfqDpK9q5c+fQOTS91nM8YG3ut+1gLxIPsx76/01o64XpfjmHvc219712nmH2\nMexYVnosN+Nxayvn6re5+Tk35jbLztl9vlibVzbw5DcijgQeSvNK7ynAHuAxLY7lUmBbz/ItO+uW\nb/PTa2wDwJ49ezj33HPZtq3Z5datWzn++OMPPxG6jeDTuvz+93+chYXrA83B6/vf/3GuuurHfbdv\nDnT3dLY9hfn5Ga66ag8HD84wO/sAFhaCLVs+zMGDVwH3Yv/+Ldz//p9lcTEO/4G46qo9fOlLMzzr\nWVdv/6IXXcXWrSd3DqI/wsICzM+fwNzcIgcP7mHLlhuwuHhfZmeTgwf3cM45S2zffvLhCdCWLcn2\n7XdfNe8VV9y3s/99h/e/ffsSW7Z8+PD4tm9f4pxzzuGjHz2ChYVdnZx7eP/7f8Dc3Ekr7r9fnsc9\nbuX8/cZ3gxucfPiP6ZYtyQc+cHfm5haHejyvfnz2XePxWWl8Kz2eS0tw1FEnMz8/w8GDe7jtbZe4\nz33Wev6csubzB1jx8bz68bnm499v/zt3/pjdu0/m/e//Acce+z4OHVoCdq74eK50f630+PR7/E87\n7d59n2+vf/0neMYzrs7zV3/1Pm5/+6UB/r9d8/7q93xe6fEc9vm50nK/+2ul8d3rXjvZvftK3v/+\nj3PssUvs2HGvVR/PlZ7Phw7t4a/+aoatW5vbO3RoD+ecMzl/D8exfODAAQ4ePAjAxRdfzAknnMCp\np56K1nc8YG1euzav9LdimO3vcIefH/hv81VX/XjFv+XD1Obu7Q+aZ6X7c5g8a49vsPzD1OY2Hp+V\ntr/ggo8NVZuHfTz7bd/c/njyjPv5Ocz2Vz8/N//xbCPPsM/nUpbbqM2D9vy+DdgF7AX+meZ8ft8a\n6pbWvo0twAU0H6W6DPg08IjMPK9nmwcAT8rMB3Z6hF+WmSf121/pfUXD9OCttO1K5xE966xZzjjj\nqMO/f+aZhzj99IW+67dvXxpq38Oeu7Tf2HfsWOy7j2H7EofJefrpC0PtYxgrjXulfa+0fRvPiZWs\n9Li1MZZhnxPD3C8rPVeGfdyG+T+0b9/675PVDHObw+xjlPulJvb8NtZ7PGBtXnvbNtZD/3ec2vib\nvdLYh73NNvY97OMwKY/PsI9bWznH+VzxNifjNmtrSRqlNg86+f1j4C2ZefGogxtoMBGnAS+n+Rbq\n12TmCyPiCTRffPXqzjavBE6j+bKNx2bm3n77Kr3ADjNhaGPCudJ/spUmF6XlbGsSOcy423rRoo37\natixt7X/foa9X4bZx7A5h9l2nPdJW/u2kK7MyW9jvccD1ua1t21jPbSz72FyDnubbex72MdhUh6f\nYR+3tnKO87nibU7GbdbW8zu2ye80evGLX5yPe9zjNnsYYzeOz/RP4n+ySc3Z5n2yPGNbk/lJs97H\nso37fCOey9PYbzPK/TKNOUfh5Lcd1uay1JCzhoxgztLUknNs3/asuszMwNzc4rUmTiutn1Zt5Bzn\nfTLsvnfsWDz8JU+9rzqWpo37vLTnclu8XyRJUsmKfee39I9WSZI2ju/8tsPaLElqyyi1ubJPhkuS\nJEmSalTs5Hffvn2bPYQN0f0a8NLVkLOGjGDO0tSSU+2wNpelhpw1ZARzlqaWnKModvIrSZIkSVKX\nPb+StIkWF2H//rpPVTAN7Plth7VZktQWv+1ZkqbM/v3TcYoqSZKkaVfs+wv2FZWlhpw1ZARzLjc/\nP8PCQvOi5cJCMD8/XX+Wa3k81Q5rc1lqyFlDRjBnaWrJOYrpOsqSpMJs377E7GzTfjI7m2zfvrTJ\nI5IkSSqTPb+StImWlmDfPnt+J509v+2wNkuS2mLPryRNmZkZmJtbtM9XkiRpzIp9f8G+orLUkLOG\njGDO0tSSU+2wNpelhpw1ZARzlqaWnKModvIrSZIkSVKXPb+SJK3Bnt92WJslSW0ZpTb7zq8kSZIk\nqXjFTn7tKypLDTlryAjmLE0tOdUOa3NZashZQ0YwZ2lqyTmKYie/kiRJkiR12fMrSdIa7Plth7VZ\nktQWe34lSZIkSeqj2MmvfUVlqSFnDRnBnKWpJafaYW0uSw05a8gI5ixNLTlHUezkV5IkSZKkLnt+\nJUlagz2/7bA2S5LaYs+vJEmSJEl9FDv5ta+oLDXkrCEjmLM0teRUO6zNZakhZw0ZwZylqSXnKIqd\n/EqSJEmS1GXPryRJa7Dntx3WZklSW0apzUeMazCStB6Li7B//xbm52fYvn2JHTsWmfGzKpIkSRpR\nsYeS9hWVpYacNWSEwXPu37+FXbuO5owzjmLXrqPZt2/LmEfWLh9P6dqszWWpIWcNGcGcpakl5yiK\nnfxKmm7z8zMsLDSfZFlYCObn/XMlSZKk0dnzK2ki7d3bvPO7sBDMzia7d1/J3NziZg9LlbLntx3W\nZklSW+z5lVSMHTsW2b37ymv0/EqSJEmjKvZzhPYVlaWGnDVkhMFzzszA3Nwip5++wNzc9H3ZlY+n\ndG3W5rLUkLOGjGDO0tSScxRTdjgpSZIkSdLw7PmVJGkN9vy2w9osSWrLKLXZd34lSZIkScUrdvJr\nX1FZashZQ0YwZ2lqyal2WJvLUkPOGjKCOUtTS85RFDv5lSRJkiSpy55fSZLWYM9vO6zNkqS2eJ5f\nSeuyuAj792+5xrl1p+0UQ5IkSVI/xR7W2ldUlhpyTkLG/fu3sGvX0ZxxxlHs2nU0+/Ztaf02JiHn\nRjCndG3W5rLUkHMSMi4uwt69WzjrrFn27t3C0lL7tzEJOTeCOeU7v5IOm5+fYWGh+fTIwkIwPz/D\n3NziJo9KkqR6dV+YXlgIZmeT3buvtDZLI7LnV9Jhe/daYKV+7Plth7VZGt5ZZ81yxhlHHV4+88xD\nnH76wiaOSJoM9vxKWpcdOxbZvfvKa/T8SpKkzbN9+xKzs3n4hent28fwuWepEvb8TrlaPtNfQ85J\nyDgzA3Nzi5x++gJzc+P5sqtJyLkRzCldm7W5LDXknISM3RemzzzzELt3XzmWF6YnIedGMKd851eS\nJEmaUN0Xpm1DktbPnl9JktZgz287rM2SpLaMUpuL/dizJEmSJEldEzH5jYgbRcTZEXFBRHwgIrau\nsN1XImJ/RHwuIj692j7tKypLDTlryAjmLE0tOdUOa3NZashZQ0YwZ2lqyTmKiZj8As8E/i0z7wB8\nCHjWCtstAadk5t0y88QNG50kSZIkaapNRM9vRJwPnJyZV0TEscBHMvOOfbabB07IzP9aa5/2FUmS\n2mLPbzuszZKktkxzz+/NMvMKgMy8HLjZCtsl8MGI+ExEnLFho5MkSZIkTbUNm/xGxAcj4j97Lgc6\n/z6oz+YrvR1978ycAx4APCkidq50e/YVlaWGnDVkBHOWppacaoe1uSw15KwhI5izNLXkHMWGnec3\nM++30nURcUVEHNPzsedvrLCPyzr/fjMi/hU4Eej76O7Zs4dzzz2Xbdu2AbB161aOP/54du5s5svd\nJ8W0L3dNynjGtXzgwIGJGs84lg8cODBR43HZx7Pm5QMHDnDw4EEALr74Yk444QROPfVUtD7W5rKW\nrc0uT9uyj+d0L7dRmyel5/dFwLcz80UR8QzgRpn5zGXb3ACYycxDEXEkcDbw55l5dr992lckSWqL\nPb/tsDZLktoyzT2/LwLuFxEXAKcCLwSIiJtHxHs62xwDnBMRnwM+Cbx7pYmvJEmSJEm9JmLym5nf\nzsxfzMw7ZOYvZeZ3O+svy8xf7vw8n5k7Oqc5Oj4zX7jaPu0rKksNOWvICOYsTS051Q5rc1lqyFlD\nRjBnaWrJOYqJmPxKkiRJkjROE9HzOw72FUmS2mLPbzuszZKktkxzz68kSZIkSWNT7OTXvqKy1JCz\nhoxgztLUklPtsDaXpYacNWQEc5amlpyjKHbyK0mSJElSlz2/kiStwZ7fdlibJUltsedXkiRJkqQ+\nip382ldUlhpy1pARzFmaWnKqHdbmstSQs4aMYM7S1JJzFMVOfiVJkiRJ6rLnV5KkNdjz2w5rsySp\nLfb8SpIkSZLUR7GTX/uKylJDzhoygjlLU0tOtcPaXJYactaQEcxZmlpyjqLYya8kSZIkSV32/EqS\ntAZ7ftthbZYktcWeX0mSJEmS+ih28mtfUVlqyFlDRjBnaWrJqXZYm8tSQ84aMoI5S1NLzlEUO/mV\nJEmSJKnLnl9JktZgz287rM2SpLbY8ytJkiRJUh/FTn7tKypLDTlryAjmLE0tOdUOa3NZashZQ0Yw\nZ2lqyTmKYie/kiRJkiR12fMrSdIa7Plth7VZktQWe34lSZIkSeqj2MmvfUVlqSFnDRnBnKWpJafa\nYW0uSw05a8gI5ixNLTlHUezkV5IkSZKkLnt+JUlagz2/7bA2S5LaYs+vJEmSJEl9FDv5ta+oLDXk\nrCEjmLM0teRUO6zNZakhZw0ZwZylqSXnKIqd/EqSJEmS1GXPryRJa7Dntx3WZklSW+z5lSRJkiSp\nj2Inv/YVlaWGnDVkBHOWppacaoe1uSw15KwhI5izNLXkHEWxk19JkiRJkrrs+ZUkaQ32/LbD2ixJ\naos9v5IkSZIk9VHs5Ne+orLUkLOGjGDO0tSSU+2wNpelhpw1ZARzlqaWnKModvIrSZIkSVKXPb+S\nJK3Bnt92WJslSW2x51eSJEmSpD6KnfzaV1SWGnLWkBHMWZpacqod1uay1JCzhoxgztLUknMUxU5+\nJUmSJEnqsudXkqQ12PPbDmuzJKkt9vxKkiRJktRHsZNf+4rKUkPOGjKCOUtTS061w9pclhpy1pAR\nzFmaWnKOotjJryRJkiRJXfb8SpK0Bnt+22FtliS1xZ5fSZIkSZL6mIjJb0Q8LCI+HxGLEbHiS8IR\ncVpEnB8RX4qIZ6y2T/uKylJDzhoygjlLU0tOtcPaXJYactaQEcxZmlpyjmIiJr/AAeChwJ6VNoiI\nGeCVwP2BOwOPiIg7rrT9RRdd1PYYJ9KBAwc2ewgbooacNWQEc5amlpy1TNrGzdpclhpy1pARzFma\nWnKOUpuPGMM4hpaZFwBExGqf2T4RuDAzv9rZ9i3Ag4Hz+238/e9/v+1hTqSDBw9u9hA2RA05a8gI\n5ixNLTn379+/2UMogrW5LDXkrCEjmLM0teQcpTZPyju/g7gFcEnP8tc66yRJkiRJWtWGvfMbER8E\njuldBSTwnMx8d9u3d/nll7e9y4l08cUXb/YQNkQNOWvICOYsTS051Q5rc1lqyFlDRjBnaWrJOYoN\nm/xm5v3WuYtLgW09y7fsrOvruOOO46lPferh5bve9a7s2LFjnUOYPCeccAJ79+7d7GGMXQ05a8gI\n5ixNqTn37dt3jY9THXnkkZs4mnJYm8tSQ84aMoI5S1NqzjZq80Sd5zciPgw8PTM/2+e6LcAFwKnA\nZcCngUdk5nkbO0pJkiRJ0rSZiJ7fiHhIRFwCnAS8JyJ2d9bfPCLeA5CZi8CTgbOBLwBvceIrSZIk\nSRrERL3zK0mSJEnSOEzEO79tiYiHRcTnI2IxIuaWXfesiLgwIs6LiF/arDG2JSJOi4jzI+JLEfGM\nzR5PWyLiNRFxRUT8Z8+6G0XE2RFxQUR8ICK2buYY2xARt4yID0XEFyLiQEQ8pbO+qKwRcd2I+FRE\nfK6T87md9UXl7IqImYjYGxHv6iwXlzMivhIR+zuP6ac760rMuTUi3tapGV+IiJ8rMedGsDZPP2tz\nWVlrqs011GWwNg+Ts6jJL3AAeCiwp3dlRNwJ+HXgTsAu4O8jVj2n8ESLiBnglcD9gTsDj4iIO27u\nqFrzOppcvZ4J/Ftm3gH4EPCsDR9V+34M/FFm3hm4J/CkzmNYVNbM/G/gvpl5N2AHsCsiTqSwnD2e\nCnyxZ7nEnEvAKZl5t8w8sbOuxJwvB96XmXcC7kpzTvkSc24Ea/P0szYXlLWy2lxDXQZr88A5i5r8\nZuYFmXkhzWmUej2Ypkf4x5n5FeBC4MTlvz9FTgQuzMyvZuYC8BaajFMvM88BvrNs9YOB13d+fj3w\nkA0d1Bhk5uWZua/z8yHgPJpvMC8x61WdH69L8w3zSYE5I+KWwAOAf+pZXVxOmr+vy2tHUTkj4obA\nz2fm6wA6teMgheXcKNbm6WdtLjJr8bW5oroM1uaBcxY1+V3FLYBLepYv7aybVsvzfI3pzrOWm2Xm\nFdAUJuBmmzyeVkXErWleef0kcExpWTsfOfoccDnwwcz8DAXmBF4K/H80BxBdJeZM4IMR8ZmI+N3O\nutJybge+FRGv63xc7tURcQPKy7nZrM3Tzdo8xSqpzbXUZbA2D5xzw87z25aI+CBwTO8qmgf8OZn5\n7s0ZlTZYMd/SFhFHAW8HnpqZhyJiebapz5qZS8DdOq/Y/WtE3Jlr55rqnBHxQOCKzNwXEaessulU\n5+y4d2ZeFhE/CZwdERdQ2ONJUxvngCdl5rkR8VKaj1WVlrM11mZR0P8Ha/PVm238yNpRWV0Ga3Ov\nVXNO3eQ3M+83wq9dCvx0z/ItO+um1aXAtp7lac+zlisi4pjMvCIijgW+sdkDakNEHEFTXP9PZr6z\ns7rIrACZ+b2I+AhwGuXlvDfwoIh4AHB94OiI+D/A5YXlJDMv6/z7zYh4B81HPUt7PL8GXJKZ53aW\nz6IpsKXlbI21GbA2F/H/wdpcTM5q6jJYm4fJWfLHnnt7i94FPDwirhMR24HbAp/enGG14jPAbSPi\nVhFxHeDhNBlLEVz78fvtzs+PAd65/Bem1GuBL2bmy3vWFZU1Im7a/da9iLg+cD+aHqqicmbmszNz\nW2behub/44cy81HAuykoZ0TcoPOOCBFxJPBLNF9mVNrjeQVwSUTcvrPqVJrzyxeVc5NYm6eXtbkx\n9VlrqM211GWwNjNkzqLO8xsRDwH+Frgp8F1gX2bu6lz3LOB3gAWaj7GcvWkDbUFEnEbzjWczwGsy\n84EkY4EAAAjMSURBVIWbPKRWRMSbgVOAmwBXAM8F3gG8jeYdgq8Cv56Z392sMbYhIu4NfJTmj1N2\nLs+mOfB7K4VkjYjjab58YKZz+ZfMfEFE3JiCcvaKiJOBp2Xmg0rL2Zmg/CvN8/UI4E2Z+cLScgJE\nxF1pviRlFvgy8FhgC4Xl3AjW5ulnbbY2T7OS6zJYmxmyNhc1+ZUkSZIkqZ+SP/YsSZIkSRLg5FeS\nJEmSVAEnv5IkSZKk4jn5lSRJkiQVz8mvJEmSJKl4Tn4lSZIkScVz8isNKSJeFxHP7/y8MyLO2+wx\ntSEiPh8R9xlw26WIuM0K1z0mIj62jnE8ISJe0vn5pyPiexERI+5rPiJ+YdSxdPZxnYg4LyJusp79\nSJLGx9psbZYG4eRXWofMPCcz77TWdustOhshM382Mz866ObrvL6viJgFngP8dWdMl2TmDXMTT0ie\nmT8CXgM8a7PGIEkanLV55Ov7sjarJE5+VbWI2LJRN8WIRQfGO84R9z3Sq70DeDBwXmZePqb9j+qf\ngcd0DgAkSWNkbbY2D8jarKE5+VVxOh+neWZEfCEi/isiXhMR1+lcd3JEXBIRfxwRlwGv7az/5Yj4\nXER8JyLOiYjje/Z3t4j4bEQcjIi3ANfrue7kiLikZ/mWEXFWRHwjIr4ZEa+IiDsCrwLuGRFXRsS3\nO9veMCLe0Nl2PiKe07Ofx3TG8ZKI+Bbw3GUZbx4RV0XETywb5zcjYktE3CYi/j0ivtXZ/xsj4obL\n7qM/joj9wKHO7xz+GFJE3CMiPtG5Py6NiL+NiCOW3dUPjIj/19n/X6/yeNwxIs7uPBbnRcSvrfLw\n7QL29PzurTof45rpLH84Ip7fuW++FxHvj4gb92z/qIj4Sud+ePaycUTneXFR5/q3dO+/iPj1iPhy\nRBzVWd4VEZd1P06VmZcC3wZOWmXskqQVWJutzdZmTQInvyrVbwL3A44D7gD8Sc91xwI/AWwDHh8R\nd6P56MwZwI2BfwTeFRGz0bya+K/A6zvXvQ04fdltJUCnCLwHmO/s+xbAWzLzfOB/AP+RmUdnZrcg\nvBI4Grg1cArw6Ih4bM9+fw64CLgZ8IJr3GDmZcAnlo3lEcDbMnOR5tXfv+xkvRNwS+B5y8b9cJqC\n9hOd3+m1CPxBJ/M9gV8Anrhsm4cAc53LgyPiccuuJyJuAJwN/P/t3WuIVHUYx/HvQ9pNDS3N8rYv\nRDMjEpKSoHoRBIX5wqIStciCCtMoNCSJyFB808UuViZJF6wsCzMKhEQiK6wki+4X0dXdLopXJDP3\n14v/f+TscWZ0gxgdfh9YmD1nzvk/5z/sPHOefc6ZV4C+ecyn84eOas4HfigtK1flJwA3A/2Ak4AZ\neayRwEJgIjAAOIP0GlRMB8YBl+b1O/LzkbQMWAs8kRP2YmCKpO2F7b8HLqgRt5mZHZlzs3Ozc7M1\nlE9+rVk9KalN0k5ScppQWHcQeFDSAUn7SYn1WUmfK3kZ2E+qJI4Bukl6QtJBScuBz2qMeTFwNnCf\npL8k/S3p42pPzMn4BmCWpH2SNgGPAJMLT9sqaaGkjhxn2aukDxIVNwJLAST9IukDSf/kJPEYcHlp\n+wV5jg7bt6T1ktbl+dgMLKqy/XxJuyRtAR6n8xxXjAU2Snop72sD8BZQq8LcG9hTY13Fknx8+4Fl\nwKi8/FpgpaS1kg4AD9A5Od8OzJbUntfPAa6rVK6Bu4ArgDXACknvl8bdk+MzM7P/xrnZudm52Rqq\n3Cph1iy2FB5vIlUTK/7Mb7AVLaTK7rT8ewDdC9tsLe17U40xBwGbJHUcRXx9SX9/m0v7LVZDW6lv\nOaka2h8YARyU9BFARJwJLCBVUnsCJ5Bag4q2UENEDAMeBUYDp+RYv6izfXmOK1qAMZV2MtLcngC8\nXGPoHaSKez3Fa472kY6PPP6hOZO0LyKK1eEW4O2IqLw+ARwA+gPtknZFxBvAPcD4KuP2AnYeITYz\nM6vNudm52bnZGsr/+bVmNbjwuAVoK/xebtVpBeZKOj3/9JHUU9LrQDudkx6ktqlqWoEhhWplUXnM\nbaQ395ZSnMVkXvcmHLlyvopUVZ4AvFZYPQ/oAM6T1BuYxOE3wqi3/2eA74ChefvZVbYvzvEQOs9x\nRSuwpjS3p0maWmPcr4DhdeKqp70YU27rKn4FwmbgqlIsPZTa1IiIUcAUUtX+ySr7PxfY8B9jMzMz\n52bnZudmazCf/FqzmhoRA/M1IvfTOfmUPQ/cEREXAUREj4i4OiJ6AJ8A/0TEtIjoFhHjgYtq7Gcd\n6U1+fkScGhEnRcQled3vwKB8nRK5Ar0MmBsRPSOihVTVrFV1reVV4CZSW9HSwvJewF5gT0QMBGZ2\ncb+9gN25QjsCuLPKc2ZGRO+IGAzcTfU5fhcYHhGT8vx1j4jRda4reo90jVXR0d698k1gbERckud5\nTmnb54B5ETEEICL6RcS4/Phk0tzPIiXZARFx6JgjYgDQB/j0KGMxM7PDOTc7Nzs3W0P55Nea1VJS\n5fVn4CdKN6UokvQF6dqip3IL0I+kmzaQW7DGA7cA20nXwyyvsZ8O4BpgGKmS2Qpcn1evBr4BfouI\nP/Ky6aTWoF+BD4FXJC3p4nG+k8drl/R1YflDwIWkVqCVVWKuVlkuLpsBTIyI3aTEVE6eAlaQ2q3W\n5zFeOGyH0l7gSlIFvC3/zAdOrHE8K4FzIuKsGnHVrIhL+haYSvrQ0UZ6vYrtXwtyzKsiYhfppiSV\nD0vzSG1xi5S+O3Ay8HBEDM3rJwIvllryzMysa5ybnZudm62hQo37fmqz/0VEbARulbS60bFY10XE\nbcBISfc2OhaASF/F8SVwmaRtjY7HzOx45Nx8fHNutmbhG16Z2TFF0uJGx1CUq80jGx2HmZlZozg3\nW7Nw27M1I7czmJmZHVucm82s4dz2bGZmZmZmZk3P//k1MzMzMzOzpueTXzMzMzMzM2t6Pvk1MzMz\nMzOzpueTXzMzMzMzM2t6Pvk1MzMzMzOzpueTXzMzMzMzM2t6/wJV7TdMMGdOzwAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x124405c50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(1,2, sharey=True, figsize=(16, 6))\n",
"\n",
"ax[0].scatter(range(grid.best_estimator_.coef_.shape[1]),\n",
" grid.best_estimator_.coef_)\n",
"ax[0].set_ylabel('value of coefficient')\n",
"ax[0].set_xlabel('predictor variable (index)')\n",
"ax[0].set_title('Coefficients with l2 Penalty')\n",
"\n",
"ax[1].scatter(range(cvmodel.coef_.shape[1]), cvmodel.coef_[0])\n",
"ax[1].set_ylabel('value of coefficient')\n",
"ax[1].set_xlabel('predictor variable (index)')\n",
"ax[1].set_title('Coefficients with l1 Penalty');"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"trivial = np.isclose(cvmodel.coef_, np.zeros(shape=cvmodel.coef_.shape)).flatten()\n",
"nontrivial = []\n",
"for i in range(len(trivial)):\n",
" if not trivial[i]:\n",
" nontrivial.append(i)"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[1, 9, 13, 16, 19, 26, 30, 46, 49]"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"nontrivial"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"final = LogisticRegression(C=cvmodel.C_[0], penalty='l1', solver='liblinear').fit(X[:, nontrivial], y)"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# thanks StackOverflow! \n",
"# see http://stackoverflow.com/questions/36373266/change-in-running-behavior-of-sklearn-code-between-laptop-and-desktop/37259431 \n",
"import warnings\n",
"warnings.filterwarnings(\"ignore\")\n",
"\n",
"final_cv_scores = cross_val_score(final, X[:, nontrivial], y, scoring='accuracy', n_jobs=-1)"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0.84049319 0.84240842 0.84348843]\n",
"0.842130016368\n"
]
}
],
"source": [
"print(final_cv_scores)\n",
"print(np.mean(final_cv_scores))"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 4.0s finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[LibLinear]"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 6.2s finished\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[LibLinear][LibLinear][ 0.84049319 0.84237842 0.84345843]\n",
"0.842110016168\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"[Parallel(n_jobs=-1)]: Done 3 out of 3 | elapsed: 3.9s finished\n"
]
}
],
"source": [
"alt = cross_val_score(LogisticRegressionCV(penalty='l1', solver='liblinear', verbose=2, n_jobs=-1), X[:, nontrivial], y, scoring='accuracy')\n",
"print(alt)\n",
"print(np.mean(alt))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python [snowflakes]",
"language": "python",
"name": "Python [snowflakes]"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
othersite/document | machinelearning/deep-learning-book/code/model_zoo/multilayer-perceptron-dropout.ipynb | 1 | 17923 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*Accompanying code examples of the book \"Introduction to Artificial Neural Networks and Deep Learning: A Practical Guide with Applications in Python\" by [Sebastian Raschka](https://sebastianraschka.com). All code examples are released under the [MIT license](https://github.com/rasbt/deep-learning-book/blob/master/LICENSE). If you find this content useful, please consider supporting the work by buying a [copy of the book](https://leanpub.com/ann-and-deeplearning).*\n",
" \n",
"Other code examples and content are available on [GitHub](https://github.com/rasbt/deep-learning-book). The PDF and ebook versions of the book are available through [Leanpub](https://leanpub.com/ann-and-deeplearning)."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sebastian Raschka \n",
"\n",
"CPython 3.6.1\n",
"IPython 6.0.0\n",
"\n",
"tensorflow 1.2.0\n"
]
}
],
"source": [
"%load_ext watermark\n",
"%watermark -a 'Sebastian Raschka' -v -p tensorflow"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Model Zoo -- Multilayer Perceptron with Dropout"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Typically, dropout is applied after the non-linear activation function (a). However, when using rectified linear units (ReLUs), it might make sense to apply dropout before the non-linear activation (b) for reasons of computational efficiency depending on the particular code implementation.\n",
"\n",
"> (a): Fully connected, linear activation -> ReLU -> Dropout -> ... \n",
"> (b): Fully connected, linear activation -> Dropout -> ReLU -> ...\n",
"\n",
"Why do (a) and (b) produce the same results in case of ReLU?. Let's answer this question with a simple example starting with the following *logits* (outputs of the linear activation of the fully connected layer):\n",
"\n",
"> `[-1, -2, -3, 4, 5, 6]`\n",
"\n",
"Let's walk through scenario (a), applying the ReLU activation first. The output of the non-linear ReLU functions are as follows:\n",
"\n",
"> `[0, 0, 0, 4, 5, 6]`\n",
"\n",
"Remember, the ReLU activation function is defined as $f(x) = max(0, x)$; thus, all non-zero values will be changed to zeros. Now, applying dropout with a probability 0f 50%, let's assume that the units being deactivated are units 2, 4, and 6:\n",
"\n",
"\n",
"> `[0*2, 0, 0*2, 0, 0*2, 0] = [0, 0, 0, 0, 10, 0]`\n",
"\n",
"\n",
"Note that in dropout, units are deactivated randomly by default. In the preceding example, we assumed that the 2nd, 4th, and 6th unit were deactivated during the training iteration. Also, because we applied dropout with 50% dropout probability, we scaled the remaining units by a factor of 2.\n",
"\n",
"Now, let's take a look at scenario (b). Again, we assume a 50% dropout rate and that units 2, 4, and 6 are deactivated:\n",
"\n",
"> `[-1, -2, -3, 4, 5, 6] -> [-1*2, 0, -3*2, 0, 5*2, 0]`\n",
"\n",
"\n",
"Now, if we pass this array to the ReLU function, the resulting array will look exactly like the one in scenario (a):\n",
"\n",
"\n",
"> `[-2, 0, -6, 0, 10, 0] -> [0, 0, 0, 0, 10, 0]`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Low-level Implementation"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting ./train-images-idx3-ubyte.gz\n",
"Extracting ./train-labels-idx1-ubyte.gz\n",
"Extracting ./t10k-images-idx3-ubyte.gz\n",
"Extracting ./t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"import tensorflow as tf\n",
"from tensorflow.examples.tutorials.mnist import input_data\n",
"\n",
"\n",
"##########################\n",
"### DATASET\n",
"##########################\n",
"\n",
"mnist = input_data.read_data_sets(\"./\", one_hot=True)\n",
"\n",
"\n",
"##########################\n",
"### SETTINGS\n",
"##########################\n",
"\n",
"# Hyperparameters\n",
"learning_rate = 0.1\n",
"training_epochs = 20\n",
"batch_size = 64\n",
"dropout_keep_proba = 0.5\n",
"\n",
"# Architecture\n",
"n_hidden_1 = 128\n",
"n_hidden_2 = 256\n",
"n_input = 784\n",
"n_classes = 10\n",
"\n",
"# Other\n",
"random_seed = 123\n",
"\n",
"\n",
"##########################\n",
"### GRAPH DEFINITION\n",
"##########################\n",
"\n",
"g = tf.Graph()\n",
"with g.as_default():\n",
" \n",
" tf.set_random_seed(random_seed)\n",
"\n",
" # Dropout settings\n",
" keep_proba = tf.placeholder(tf.float32, None, name='keep_proba')\n",
" \n",
" # Input data\n",
" tf_x = tf.placeholder(tf.float32, [None, n_input], name='features')\n",
" tf_y = tf.placeholder(tf.float32, [None, n_classes], name='targets')\n",
"\n",
" # Model parameters\n",
" weights = {\n",
" 'h1': tf.Variable(tf.truncated_normal([n_input, n_hidden_1], stddev=0.1)),\n",
" 'h2': tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2], stddev=0.1)),\n",
" 'out': tf.Variable(tf.truncated_normal([n_hidden_2, n_classes], stddev=0.1))\n",
" }\n",
" biases = {\n",
" 'b1': tf.Variable(tf.zeros([n_hidden_1])),\n",
" 'b2': tf.Variable(tf.zeros([n_hidden_2])),\n",
" 'out': tf.Variable(tf.zeros([n_classes]))\n",
" }\n",
"\n",
" # Multilayer perceptron\n",
" layer_1 = tf.add(tf.matmul(tf_x, weights['h1']), biases['b1'])\n",
" layer_1 = tf.nn.relu(layer_1)\n",
" layer_1 = tf.nn.dropout(layer_1, keep_prob=keep_proba)\n",
" \n",
" layer_2 = tf.add(tf.matmul(layer_1, weights['h2']), biases['b2'])\n",
" layer_2 = tf.nn.relu(layer_2)\n",
" layer_2 = tf.nn.dropout(layer_2, keep_prob=keep_proba)\n",
" \n",
" out_layer = tf.add(tf.matmul(layer_2, weights['out']), biases['out'], name='logits')\n",
"\n",
" # Loss and optimizer\n",
" loss = tf.nn.softmax_cross_entropy_with_logits(logits=out_layer, labels=tf_y)\n",
" cost = tf.reduce_mean(loss, name='cost')\n",
" optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)\n",
" train = optimizer.minimize(cost, name='train')\n",
"\n",
" # Prediction\n",
" correct_prediction = tf.equal(tf.argmax(tf_y, 1), tf.argmax(out_layer, 1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name='accuracy')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch: 001 | AvgCost: 0.669 | Train/Valid ACC: 0.927/0.935\n",
"Epoch: 002 | AvgCost: 0.372 | Train/Valid ACC: 0.944/0.953\n",
"Epoch: 003 | AvgCost: 0.308 | Train/Valid ACC: 0.952/0.956\n",
"Epoch: 004 | AvgCost: 0.271 | Train/Valid ACC: 0.962/0.961\n",
"Epoch: 005 | AvgCost: 0.251 | Train/Valid ACC: 0.964/0.966\n",
"Epoch: 006 | AvgCost: 0.231 | Train/Valid ACC: 0.968/0.966\n",
"Epoch: 007 | AvgCost: 0.219 | Train/Valid ACC: 0.970/0.970\n",
"Epoch: 008 | AvgCost: 0.204 | Train/Valid ACC: 0.972/0.971\n",
"Epoch: 009 | AvgCost: 0.194 | Train/Valid ACC: 0.974/0.970\n",
"Epoch: 010 | AvgCost: 0.187 | Train/Valid ACC: 0.976/0.970\n",
"Epoch: 011 | AvgCost: 0.178 | Train/Valid ACC: 0.977/0.972\n",
"Epoch: 012 | AvgCost: 0.175 | Train/Valid ACC: 0.978/0.972\n",
"Epoch: 013 | AvgCost: 0.170 | Train/Valid ACC: 0.979/0.973\n",
"Epoch: 014 | AvgCost: 0.162 | Train/Valid ACC: 0.980/0.975\n",
"Epoch: 015 | AvgCost: 0.157 | Train/Valid ACC: 0.980/0.974\n",
"Epoch: 016 | AvgCost: 0.153 | Train/Valid ACC: 0.982/0.976\n",
"Epoch: 017 | AvgCost: 0.151 | Train/Valid ACC: 0.982/0.976\n",
"Epoch: 018 | AvgCost: 0.147 | Train/Valid ACC: 0.983/0.973\n",
"Epoch: 019 | AvgCost: 0.144 | Train/Valid ACC: 0.984/0.974\n",
"Epoch: 020 | AvgCost: 0.143 | Train/Valid ACC: 0.985/0.975\n",
"Test ACC: 0.974\n"
]
}
],
"source": [
"from numpy.random import seed\n",
"\n",
"##########################\n",
"### TRAINING & EVALUATION\n",
"##########################\n",
"\n",
"with tf.Session(graph=g) as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
"\n",
" seed(random_seed) # random seed for mnist iterator\n",
" for epoch in range(training_epochs):\n",
" avg_cost = 0.\n",
" total_batch = mnist.train.num_examples // batch_size\n",
"\n",
" for i in range(total_batch):\n",
" batch_x, batch_y = mnist.train.next_batch(batch_size)\n",
" _, c = sess.run(['train', 'cost:0'], feed_dict={'features:0': batch_x,\n",
" 'targets:0': batch_y,\n",
" 'keep_proba:0': dropout_keep_proba})\n",
" avg_cost += c\n",
" \n",
" train_acc = sess.run('accuracy:0', feed_dict={'features:0': mnist.train.images,\n",
" 'targets:0': mnist.train.labels,\n",
" 'keep_proba:0': 1.0})\n",
" valid_acc = sess.run('accuracy:0', feed_dict={'features:0': mnist.validation.images,\n",
" 'targets:0': mnist.validation.labels,\n",
" 'keep_proba:0': 1.0})\n",
" \n",
" print(\"Epoch: %03d | AvgCost: %.3f\" % (epoch + 1, avg_cost / (i + 1)), end=\"\")\n",
" print(\" | Train/Valid ACC: %.3f/%.3f\" % (train_acc, valid_acc))\n",
" \n",
" test_acc = sess.run(accuracy, feed_dict={'features:0': mnist.test.images,\n",
" 'targets:0': mnist.test.labels,\n",
" 'keep_proba:0': 1.0}) \n",
" print('Test ACC: %.3f' % test_acc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### tensorflow.layers Abstraction"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bote that we define the *dropout rate*, not the *keep probability* when we are using dropout from `tf.layers`."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting ./train-images-idx3-ubyte.gz\n",
"Extracting ./train-labels-idx1-ubyte.gz\n",
"Extracting ./t10k-images-idx3-ubyte.gz\n",
"Extracting ./t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"import tensorflow as tf\n",
"from tensorflow.examples.tutorials.mnist import input_data\n",
"\n",
"\n",
"##########################\n",
"### DATASET\n",
"##########################\n",
"\n",
"mnist = input_data.read_data_sets(\"./\", one_hot=True)\n",
"\n",
"\n",
"##########################\n",
"### SETTINGS\n",
"##########################\n",
"\n",
"# Hyperparameters\n",
"learning_rate = 0.1\n",
"training_epochs = 20\n",
"batch_size = 64\n",
"dropout_rate = 0.5 \n",
"# note that we define the dropout rate, not\n",
"# the \"keep probability\" when using\n",
"# dropout from tf.layers\n",
"\n",
"# Architecture\n",
"n_hidden_1 = 128\n",
"n_hidden_2 = 256\n",
"n_input = 784\n",
"training_epochs = 15\n",
"\n",
"# Other\n",
"random_seed = 123\n",
"\n",
"\n",
"##########################\n",
"### GRAPH DEFINITION\n",
"##########################\n",
"\n",
"g = tf.Graph()\n",
"with g.as_default():\n",
" \n",
" tf.set_random_seed(random_seed)\n",
"\n",
" # Dropout settings\n",
" is_training = tf.placeholder(tf.bool, name='is_training')\n",
" \n",
" # Input data\n",
" tf_x = tf.placeholder(tf.float32, [None, n_input], name='features')\n",
" tf_y = tf.placeholder(tf.float32, [None, n_classes], name='targets')\n",
"\n",
" # Multilayer perceptron\n",
" layer_1 = tf.layers.dense(tf_x, n_hidden_1, activation=tf.nn.relu, \n",
" kernel_initializer=tf.truncated_normal_initializer(stddev=0.1))\n",
" layer_1 = tf.layers.dropout(layer_1, rate=dropout_rate, training=is_training)\n",
" \n",
" layer_2 = tf.layers.dense(layer_1, n_hidden_2, activation=tf.nn.relu,\n",
" kernel_initializer=tf.truncated_normal_initializer(stddev=0.1))\n",
" layer_2 = tf.layers.dropout(layer_1, rate=dropout_rate, training=is_training)\n",
" \n",
" out_layer = tf.layers.dense(layer_2, n_classes, activation=None, name='logits')\n",
"\n",
" # Loss and optimizer\n",
" loss = tf.nn.softmax_cross_entropy_with_logits(logits=out_layer, labels=tf_y)\n",
" cost = tf.reduce_mean(loss, name='cost')\n",
" optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)\n",
" train = optimizer.minimize(cost, name='train')\n",
"\n",
" # Prediction\n",
" correct_prediction = tf.equal(tf.argmax(tf_y, 1), tf.argmax(out_layer, 1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name='accuracy')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch: 001 | AvgCost: 0.814 | Train/Valid ACC: 0.917/0.925\n",
"Epoch: 002 | AvgCost: 0.520 | Train/Valid ACC: 0.931/0.938\n",
"Epoch: 003 | AvgCost: 0.457 | Train/Valid ACC: 0.940/0.945\n",
"Epoch: 004 | AvgCost: 0.408 | Train/Valid ACC: 0.948/0.952\n",
"Epoch: 005 | AvgCost: 0.393 | Train/Valid ACC: 0.952/0.956\n",
"Epoch: 006 | AvgCost: 0.376 | Train/Valid ACC: 0.954/0.957\n",
"Epoch: 007 | AvgCost: 0.355 | Train/Valid ACC: 0.956/0.958\n",
"Epoch: 008 | AvgCost: 0.348 | Train/Valid ACC: 0.958/0.960\n",
"Epoch: 009 | AvgCost: 0.338 | Train/Valid ACC: 0.961/0.964\n",
"Epoch: 010 | AvgCost: 0.334 | Train/Valid ACC: 0.962/0.964\n",
"Epoch: 011 | AvgCost: 0.324 | Train/Valid ACC: 0.963/0.965\n",
"Epoch: 012 | AvgCost: 0.315 | Train/Valid ACC: 0.964/0.963\n",
"Epoch: 013 | AvgCost: 0.310 | Train/Valid ACC: 0.965/0.965\n",
"Epoch: 014 | AvgCost: 0.305 | Train/Valid ACC: 0.966/0.965\n",
"Epoch: 015 | AvgCost: 0.305 | Train/Valid ACC: 0.967/0.965\n",
"Test ACC: 0.961\n"
]
}
],
"source": [
"from numpy.random import seed\n",
"\n",
"##########################\n",
"### TRAINING & EVALUATION\n",
"##########################\n",
" \n",
"with tf.Session(graph=g) as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
"\n",
" seed(random_seed) # random seed for mnist iterator\n",
" for epoch in range(training_epochs):\n",
" avg_cost = 0.\n",
" total_batch = mnist.train.num_examples // batch_size\n",
"\n",
" for i in range(total_batch):\n",
" batch_x, batch_y = mnist.train.next_batch(batch_size)\n",
" _, c = sess.run(['train', 'cost:0'], feed_dict={'features:0': batch_x,\n",
" 'targets:0': batch_y,\n",
" 'is_training:0': True})\n",
" avg_cost += c\n",
" \n",
" train_acc = sess.run('accuracy:0', feed_dict={'features:0': mnist.train.images,\n",
" 'targets:0': mnist.train.labels,\n",
" 'is_training:0': False})\n",
" \n",
" valid_acc = sess.run('accuracy:0', feed_dict={'features:0': mnist.validation.images,\n",
" 'targets:0': mnist.validation.labels,\n",
" 'is_training:0': False})\n",
" \n",
" print(\"Epoch: %03d | AvgCost: %.3f\" % (epoch + 1, avg_cost / (i + 1)), end=\"\")\n",
" print(\" | Train/Valid ACC: %.3f/%.3f\" % (train_acc, valid_acc))\n",
" \n",
" test_acc = sess.run('accuracy:0', feed_dict={'features:0': mnist.test.images,\n",
" 'targets:0': mnist.test.labels,\n",
" 'is_training:0': False})\n",
" print('Test ACC: %.3f' % test_acc)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
InsightLab/data-science-cookbook | 2019/02-python-bibliotecas-manipulacao-dados/pandas_basico.ipynb | 3 | 31111 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Pandas"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Importando o Pandas e o NumPy"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Series\n",
"Uma Series é um objeto semelhante a uma vetor que possui um vetor de dados e um vetor de labels associadas chamado index.\n",
"Sua documentação completa se encontra em: http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series\n",
"### Instanciando uma Series"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0 4\n",
"1 7\n",
"2 -5\n",
"3 3\n",
"dtype: int64"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Apenas a partir dos valores \"\"\"\n",
"\n",
"obj = pd.Series([4, 7, -5, 3])\n",
"obj"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 4, 7, -5, 3], dtype=int64)"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj.values"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"RangeIndex(start=0, stop=4, step=1)"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj.index"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"d 4\n",
"b 7\n",
"a -5\n",
"c 3\n",
"dtype: int64"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir dos valores e dos índices \"\"\"\n",
"\n",
"obj2 = pd.Series([4, 7, -5, 3], index=['d','b','a','c'])\n",
"obj2"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Index([u'd', u'b', u'a', u'c'], dtype='object')"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj2.index"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Ohio 35000\n",
"Oregon 16000\n",
"Texas 71000\n",
"Utah 5000\n",
"dtype: int64"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary \"\"\"\n",
"\n",
"sdata = {'Ohio': 35000, 'Texas': 71000, 'Oregon': 16000, 'Utah': 5000}\n",
"obj3 = pd.Series(sdata)\n",
"obj3"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"California NaN\n",
"Ohio 35000.0\n",
"Oregon 16000.0\n",
"Texas 71000.0\n",
"dtype: float64"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary e dos índices \"\"\"\n",
"\n",
"states = ['California', 'Ohio', 'Oregon', 'Texas']\n",
"obj4 = pd.Series(sdata, index=states)\n",
"obj4"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Acessando elementos de uma Series"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"-5"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj2['a']"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"6"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj2['d'] = 6\n",
"obj2['d']"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"c 3\n",
"a -5\n",
"d 6\n",
"dtype: int64"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj2[['c','a','d']]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"d 6\n",
"b 7\n",
"c 3\n",
"dtype: int64"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj2[obj2 > 0]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Algumas operações permitidas em uma Series"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"d 12\n",
"b 14\n",
"a -10\n",
"c 6\n",
"dtype: int64"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Multiplicação por um escalar \"\"\"\n",
"\n",
"obj2 * 2"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"d 403.428793\n",
"b 1096.633158\n",
"a 0.006738\n",
"c 20.085537\n",
"dtype: float64"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Operações de vetor do numpy \"\"\"\n",
"\n",
"import numpy as np\n",
"\n",
"np.exp(obj2)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Funções que funcionam com dictionaries \"\"\"\n",
"\n",
"'b' in obj2"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"False"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"'e' in obj2"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"California True\n",
"Ohio False\n",
"Oregon False\n",
"Texas False\n",
"dtype: bool"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Funções para identificar dados faltando \"\"\"\n",
"\n",
"obj4.isnull()"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"California False\n",
"Ohio True\n",
"Oregon True\n",
"Texas True\n",
"dtype: bool"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"obj4.notnull()"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"California NaN\n",
"Ohio 70000.0\n",
"Oregon 32000.0\n",
"Texas 142000.0\n",
"Utah NaN\n",
"dtype: float64"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Operações aritméticas com alinhamento automático dos índices \"\"\"\n",
"\n",
"obj3 + obj4"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## DataFrame\n",
"Um DataFrame representa uma estrutura de dados tabular, semelhante a uma planilha de excel, contendo um conjunto ordenado de colunas, podendo ser cada uma de tipos de valores diferente. Um DataFrame possui um índice de linhas e um de colunas e pode ser encarado como um dict de Series.\n",
"Sua documentação completa se encontra em: http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Instanciando um DataFrame"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>pop</th>\n",
" <th>state</th>\n",
" <th>year</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1.5</td>\n",
" <td>Ohio</td>\n",
" <td>2000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1.7</td>\n",
" <td>Ohio</td>\n",
" <td>2001</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3.6</td>\n",
" <td>Ohio</td>\n",
" <td>2002</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2.4</td>\n",
" <td>Nevada</td>\n",
" <td>2001</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>2.9</td>\n",
" <td>Nevada</td>\n",
" <td>2002</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" pop state year\n",
"0 1.5 Ohio 2000\n",
"1 1.7 Ohio 2001\n",
"2 3.6 Ohio 2002\n",
"3 2.4 Nevada 2001\n",
"4 2.9 Nevada 2002"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary de vetores \"\"\"\n",
"\n",
"data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada'], \\\n",
" 'year': [2000, 2001, 2002, 2001, 2002], \\\n",
" 'pop': [1.5, 1.7, 3.6, 2.4, 2.9]}\n",
"\n",
"frame = pd.DataFrame(data)\n",
"frame"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop\n",
"0 2000 Ohio 1.5\n",
"1 2001 Ohio 1.7\n",
"2 2002 Ohio 3.6\n",
"3 2001 Nevada 2.4\n",
"4 2002 Nevada 2.9"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary em uma ordem específica das colunas \"\"\"\n",
"\n",
"pd.DataFrame(data, columns=['year', 'state', 'pop'])"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" <th>debt</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>one</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>two</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>three</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>four</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>five</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop debt\n",
"one 2000 Ohio 1.5 NaN\n",
"two 2001 Ohio 1.7 NaN\n",
"three 2002 Ohio 3.6 NaN\n",
"four 2001 Nevada 2.4 NaN\n",
"five 2002 Nevada 2.9 NaN"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary e dos índices das colunas e/ou dos índices das linhas \"\"\"\n",
"\n",
"frame2 = pd.DataFrame(data, columns=['year', 'state', 'pop', 'debt'], index=['one', 'two', 'three', 'four', 'five'])\n",
"frame2"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Nevada</th>\n",
" <th>Ohio</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2000</th>\n",
" <td>NaN</td>\n",
" <td>1.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2001</th>\n",
" <td>2.4</td>\n",
" <td>1.7</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2002</th>\n",
" <td>2.9</td>\n",
" <td>3.6</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Nevada Ohio\n",
"2000 NaN 1.5\n",
"2001 2.4 1.7\n",
"2002 2.9 3.6"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" A partir de um dictionary de dictionaries aninhados \"\"\"\n",
"\n",
"pop = {'Nevada': {2001: 2.4, 2002: 2.9}, 'Ohio': {2000: 1.5, 2001: 1.7, 2002: 3.6}}\n",
"\n",
"frame3 = pd.DataFrame(pop)\n",
"frame3"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note que estas não são todas as formas possíveis de se fazê-lo. Para uma visão mais completa veja a seguinte tabela com as possíveis entradas para o construtor do DataFrame:\n",
"\n",
"Type |Notes\n",
"-----|-----\n",
"2D ndarray | A matrix of data, passing optional row and column labels\n",
"dict of arrays, lists, or tuples | Each sequence becomes a column in the DataFrame. All sequences must be the same length.\n",
"NumPy structured/record array | Treated as the “dict of arrays” case\n",
"dict of Series | Each value becomes a column. Indexes from each Series are unioned together to form the result’s row index if no explicit index is passed.\n",
"dict of dicts | Each inner dict becomes a column. Keys are unioned to form the row index as in the “dict of Series” case.\n",
"list of dicts or Series | Each item becomes a row in the DataFrame. Union of dict keys or Series indexes become the DataFrame’s column labels\n",
"List of lists or tuples | Treated as the “2D ndarray” case\n",
"Another DataFrame | The DataFrame’s indexes are used unless different ones are passed\n",
"NumPy MaskedArray | Like the “2D ndarray” case except masked values become NA/missing in the DataFrame result\n",
"\n",
"### Manipulando linhas e colunas de um DataFrame"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"one Ohio\n",
"two Ohio\n",
"three Ohio\n",
"four Nevada\n",
"five Nevada\n",
"Name: state, dtype: object"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Acessando colunas como em uma Series ou dictionary \"\"\"\n",
"\n",
"frame2['state']"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"one 2000\n",
"two 2001\n",
"three 2002\n",
"four 2001\n",
"five 2002\n",
"Name: year, dtype: int64"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Como colunas como um atributo \"\"\"\n",
"\n",
"frame2.year"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"year 2002\n",
"state Ohio\n",
"pop 3.6\n",
"debt NaN\n",
"Name: three, dtype: object"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Acessando linhas com o nome da linha \"\"\"\n",
"\n",
"frame2.ix['three']"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"year 2001\n",
"state Nevada\n",
"pop 2.4\n",
"debt NaN\n",
"Name: four, dtype: object"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Acessando linhas com o índice da linha \"\"\"\n",
"\n",
"frame2.ix[3]"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" <th>debt</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>one</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" <td>16.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>two</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" <td>16.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>three</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" <td>16.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>four</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" <td>16.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>five</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" <td>16.5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop debt\n",
"one 2000 Ohio 1.5 16.5\n",
"two 2001 Ohio 1.7 16.5\n",
"three 2002 Ohio 3.6 16.5\n",
"four 2001 Nevada 2.4 16.5\n",
"five 2002 Nevada 2.9 16.5"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Modificando uma coluna com um valor \"\"\"\n",
"\n",
"frame2['debt'] = 16.5\n",
"frame2"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" <th>debt</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>one</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>two</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" <td>1.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>three</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>four</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" <td>3.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>five</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" <td>4.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop debt\n",
"one 2000 Ohio 1.5 0.0\n",
"two 2001 Ohio 1.7 1.0\n",
"three 2002 Ohio 3.6 2.0\n",
"four 2001 Nevada 2.4 3.0\n",
"five 2002 Nevada 2.9 4.0"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Modificando uma coluna com um vetor \"\"\"\n",
"\n",
"frame2['debt'] = np.arange(5.)\n",
"frame2"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" <th>debt</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>one</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>two</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" <td>-1.2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>three</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>four</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" <td>-1.5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>five</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" <td>-1.7</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop debt\n",
"one 2000 Ohio 1.5 NaN\n",
"two 2001 Ohio 1.7 -1.2\n",
"three 2002 Ohio 3.6 NaN\n",
"four 2001 Nevada 2.4 -1.5\n",
"five 2002 Nevada 2.9 -1.7"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Modificando uma coluna com uma Series \"\"\"\n",
"\n",
"val = pd.Series([-1.2, -1.5, -1.7], index=['two', 'four', 'five'])\n",
"\n",
"frame2['debt'] = val\n",
"frame2"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>state</th>\n",
" <th>pop</th>\n",
" <th>debt</th>\n",
" <th>eastern</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>one</th>\n",
" <td>2000</td>\n",
" <td>Ohio</td>\n",
" <td>1.5</td>\n",
" <td>NaN</td>\n",
" <td>True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>two</th>\n",
" <td>2001</td>\n",
" <td>Ohio</td>\n",
" <td>1.7</td>\n",
" <td>-1.2</td>\n",
" <td>True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>three</th>\n",
" <td>2002</td>\n",
" <td>Ohio</td>\n",
" <td>3.6</td>\n",
" <td>NaN</td>\n",
" <td>True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>four</th>\n",
" <td>2001</td>\n",
" <td>Nevada</td>\n",
" <td>2.4</td>\n",
" <td>-1.5</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>five</th>\n",
" <td>2002</td>\n",
" <td>Nevada</td>\n",
" <td>2.9</td>\n",
" <td>-1.7</td>\n",
" <td>False</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year state pop debt eastern\n",
"one 2000 Ohio 1.5 NaN True\n",
"two 2001 Ohio 1.7 -1.2 True\n",
"three 2002 Ohio 3.6 NaN True\n",
"four 2001 Nevada 2.4 -1.5 False\n",
"five 2002 Nevada 2.9 -1.7 False"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Adicionando uma coluna que não existe \"\"\"\n",
"\n",
"frame2['eastern'] = frame2.state == 'Ohio'\n",
"frame2"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Index([u'year', u'state', u'pop', u'debt'], dtype='object')"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"\"\" Deletando uma coluna \"\"\"\n",
"\n",
"del frame2['eastern']\n",
"frame2.columns"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
gaufung/Data_Analytics_Learning_Note | Data_Analytics_in_Action/pandasIO.ipynb | 1 | 68175 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Pandas 数据读写"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# API\n",
"读取 | 写入 \n",
"--- | ---\n",
"read_csv | to_csv\n",
"read_excel | to_excel\n",
"read_hdf | to_hdf\n",
"read_sql | to_sql\n",
"read_json | to_json\n",
"read_html | to_html\n",
"read_stata | to_stata\n",
"read_clipboard | to_clipboard\n",
"read_pickle | to_pickle"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# CVS 文件读写"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"csv 文件内容\n",
"```\n",
"white,read,blue,green,animal\n",
"1,5,2,3,cat\n",
"2,7,8,5,dog\n",
"3,3,6,7,horse\n",
"2,2,8,3,duck\n",
"4,4,2,1,mouse\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>read</th>\n",
" <th>blue</th>\n",
" <th>green</th>\n",
" <th>animal</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>horse</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>2</td>\n",
" <td>1</td>\n",
" <td>mouse</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white read blue green animal\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 3 3 6 7 horse\n",
"3 2 2 8 3 duck\n",
"4 4 4 2 1 mouse"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"csvframe=pd.read_csv('myCSV_01.csv')\n",
"csvframe"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>read</th>\n",
" <th>blue</th>\n",
" <th>green</th>\n",
" <th>animal</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>horse</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>2</td>\n",
" <td>1</td>\n",
" <td>mouse</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white read blue green animal\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 3 3 6 7 horse\n",
"3 2 2 8 3 duck\n",
"4 4 4 2 1 mouse"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# 也可以通过read_table来读写数据\n",
"pd.read_table('myCSV_01.csv',sep=',')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 读取没有head的数据\n",
"```\n",
"1,5,2,3,cat\n",
"2,7,8,5,dog\n",
"3,3,6,7,horse\n",
"2,2,8,3,duck\n",
"4,4,2,1,mouse\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" <th>1</th>\n",
" <th>2</th>\n",
" <th>3</th>\n",
" <th>4</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>horse</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>2</td>\n",
" <td>1</td>\n",
" <td>mouse</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0 1 2 3 4\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 3 3 6 7 horse\n",
"3 2 2 8 3 duck\n",
"4 4 4 2 1 mouse"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_02.csv',header=None)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"可以指定header"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>blue</th>\n",
" <th>green</th>\n",
" <th>animal</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>horse</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>2</td>\n",
" <td>1</td>\n",
" <td>mouse</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white red blue green animal\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 3 3 6 7 horse\n",
"3 2 2 8 3 duck\n",
"4 4 4 2 1 mouse"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_02.csv',names=['white','red','blue','green','animal'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"创建一个具有等级结构的DataFrame对象,可以添加index_col选项,数据文件格式\n",
"```\n",
"colors,status,item1,item2,item3\n",
"black,up,3,4,6\n",
"black,down,2,6,7\n",
"white,up,5,5,5\n",
"white,down,3,3,2\n",
"red,up,2,2,2\n",
"red,down,1,1,4\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th></th>\n",
" <th>item1</th>\n",
" <th>item2</th>\n",
" <th>item3</th>\n",
" </tr>\n",
" <tr>\n",
" <th>colors</th>\n",
" <th>status</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">black</th>\n",
" <th>up</th>\n",
" <td>3</td>\n",
" <td>4</td>\n",
" <td>6</td>\n",
" </tr>\n",
" <tr>\n",
" <th>down</th>\n",
" <td>2</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">white</th>\n",
" <th>up</th>\n",
" <td>5</td>\n",
" <td>5</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>down</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">red</th>\n",
" <th>up</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>down</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" item1 item2 item3\n",
"colors status \n",
"black up 3 4 6\n",
" down 2 6 7\n",
"white up 5 5 5\n",
" down 3 3 2\n",
"red up 2 2 2\n",
" down 1 1 4"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_03.csv',index_col=['colors','status'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Regexp 解析TXT文件\n",
"使用正则表达式指定sep,来达到解析数据文件的目的。\n",
"\n",
"正则元素 | 功能\n",
"--- | ---\n",
". | 换行符以外所有元素\n",
"\\d | 数字\n",
"\\D | 非数字\n",
"\\s | 空白字符\n",
"\\S | 非空白字符\n",
"\\n | 换行符\n",
"\\t | 制表符\n",
"\\uxxxx | 使用十六进制表示ideaUnicode字符 \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"数据文件随机以制表符和空格分隔\n",
"```\n",
"white red blue green\n",
"1 4 3 2\n",
"2 4 6 7\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>blue</th>\n",
" <th>green</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" <td>3</td>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white red blue green\n",
"0 1 4 3 2\n",
"1 2 4 6 7"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_04.csv',sep='\\s+')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"读取有字母分隔的数据\n",
"```\n",
"000end123aaa122\n",
"001end125aaa144\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" <th>1</th>\n",
" <th>2</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>123</td>\n",
" <td>122</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>125</td>\n",
" <td>144</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0 1 2\n",
"0 0 123 122\n",
"1 1 125 144"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_05.csv',sep='\\D*',header=None,engine='python')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"读取文本文件跳过一些不必要的行\n",
"```\n",
"##### log file #####\n",
"this file has been generate by automatic system\n",
"white,red,blue,green,animal\n",
"12-feb-2015:counting of animals inside the house\n",
"1,3,5,2,cat\n",
"2,4,8,5,dog\n",
"13-feb-2015:counting of animals inside the house\n",
"3,3,6,7,horse\n",
"2,2,8,3,duck\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>blue</th>\n",
" <th>green</th>\n",
" <th>animal</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>horse</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white red blue green animal\n",
"0 1 3 5 2 cat\n",
"1 2 4 8 5 dog\n",
"2 3 3 6 7 horse\n",
"3 2 2 8 3 duck"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_table('myCSV_06.csv',sep=',',skiprows=[0,1,3,6])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 从TXT文件中读取部分数据\n",
"只想读文件的一部分,可明确指定解析的行号,这时候用到`nrows`和`skiprows`选项,从指定的行开始和从起始行往后读多少行(norow=i)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" <th>1</th>\n",
" <th>2</th>\n",
" <th>3</th>\n",
" <th>4</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>cat</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>dog</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>duck</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0 1 2 3 4\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 2 2 8 3 duck"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_csv('myCSV_02.csv',skiprows=[2],nrows=3,header=None)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**实例** :\n",
"对于一列数据,每隔两行取一个累加起来,最后把和插入到列的Series对象中"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" white read blue green animal\n",
"0 1 5 2 3 cat\n",
"1 2 7 8 5 dog\n",
"2 3 3 6 7 horse\n",
" white read blue green animal\n",
"0 2 2 8 3 duck\n",
"1 4 4 2 1 mouse\n"
]
},
{
"data": {
"text/plain": [
"0 6\n",
"1 6\n",
"dtype: int64"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"out = pd.Series()\n",
"i=0\n",
"pieces = pd.read_csv('myCSV_01.csv',chunksize=3)\n",
"for piece in pieces:\n",
" print piece\n",
" out.set_value(i,piece['white'].sum())\n",
" i += 1\n",
"out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 写入文件\n",
"+ to_csv(filenmae)\n",
"+ to_csv(filename,index=False,header=False)\n",
"+ to_csv(filename,na_rep='NaN')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# HTML文件读写"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 写入HTML文件"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" <th>1</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n"
]
}
],
"source": [
"frame = pd.DataFrame(np.arange(4).reshape((2,2)))\n",
"print frame.to_html()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"创建复杂的DataFrame"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>up</th>\n",
" <th>down</th>\n",
" <th>left</th>\n",
" <th>right</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>white</th>\n",
" <td>0.812351</td>\n",
" <td>0.909022</td>\n",
" <td>0.957337</td>\n",
" <td>0.277063</td>\n",
" </tr>\n",
" <tr>\n",
" <th>black</th>\n",
" <td>0.390331</td>\n",
" <td>0.181537</td>\n",
" <td>0.697226</td>\n",
" <td>0.867162</td>\n",
" </tr>\n",
" <tr>\n",
" <th>red</th>\n",
" <td>0.647759</td>\n",
" <td>0.505687</td>\n",
" <td>0.189957</td>\n",
" <td>0.217562</td>\n",
" </tr>\n",
" <tr>\n",
" <th>blue</th>\n",
" <td>0.540899</td>\n",
" <td>0.416303</td>\n",
" <td>0.681703</td>\n",
" <td>0.973349</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" up down left right\n",
"white 0.812351 0.909022 0.957337 0.277063\n",
"black 0.390331 0.181537 0.697226 0.867162\n",
"red 0.647759 0.505687 0.189957 0.217562\n",
"blue 0.540899 0.416303 0.681703 0.973349"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"frame = pd.DataFrame(np.random.random((4,4)),\n",
" index=['white','black','red','blue'],\n",
" columns=['up','down','left','right'])\n",
"frame"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"s = ['<HTML>']\n",
"s.append('<HEAD><TITLE>MY DATAFRAME</TITLE></HEAD>')\n",
"s.append('<BODY>')\n",
"s.append(frame.to_html())\n",
"s.append('</BODY></HTML>')\n",
"html=''.join(s)\n",
"with open('myFrame.html','w') as html_file:\n",
" html_file.write(html)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## HTML读表格"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Unnamed: 0</th>\n",
" <th>up</th>\n",
" <th>down</th>\n",
" <th>left</th>\n",
" <th>right</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>white</td>\n",
" <td>0.812351</td>\n",
" <td>0.909022</td>\n",
" <td>0.957337</td>\n",
" <td>0.277063</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>black</td>\n",
" <td>0.390331</td>\n",
" <td>0.181537</td>\n",
" <td>0.697226</td>\n",
" <td>0.867162</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>red</td>\n",
" <td>0.647759</td>\n",
" <td>0.505687</td>\n",
" <td>0.189957</td>\n",
" <td>0.217562</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>blue</td>\n",
" <td>0.540899</td>\n",
" <td>0.416303</td>\n",
" <td>0.681703</td>\n",
" <td>0.973349</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Unnamed: 0 up down left right\n",
"0 white 0.812351 0.909022 0.957337 0.277063\n",
"1 black 0.390331 0.181537 0.697226 0.867162\n",
"2 red 0.647759 0.505687 0.189957 0.217562\n",
"3 blue 0.540899 0.416303 0.681703 0.973349"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"web_frames = pd.read_html('myFrame.html')\n",
"web_frames[0]"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Position</th>\n",
" <th>Name</th>\n",
" <th>Points</th>\n",
" <th>Rank</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>Fabio Nelli</td>\n",
" <td>16682</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>admin</td>\n",
" <td>9029</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>BrunoOrsini</td>\n",
" <td>2078</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>4</td>\n",
" <td>Berserker</td>\n",
" <td>700</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>5</td>\n",
" <td>albertosallusti</td>\n",
" <td>277</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>6</td>\n",
" <td>Dnocioni</td>\n",
" <td>194</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>7</td>\n",
" <td>Jon</td>\n",
" <td>181</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>8</td>\n",
" <td>Mr.Y</td>\n",
" <td>180</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>9</td>\n",
" <td>michele sisinni</td>\n",
" <td>150</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>10</td>\n",
" <td>Selina</td>\n",
" <td>133</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>11</td>\n",
" <td>stefano gustin</td>\n",
" <td>120</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>12</td>\n",
" <td>Pietro Baima</td>\n",
" <td>107</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>13</td>\n",
" <td>Cecilia Lalatta Costerbosa</td>\n",
" <td>106</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>14</td>\n",
" <td>Davide Aloisi</td>\n",
" <td>106</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>15</td>\n",
" <td>Leonardo Zampi</td>\n",
" <td>106</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>16</td>\n",
" <td>gildalombardi</td>\n",
" <td>105</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>17</td>\n",
" <td>Marco Contigiani</td>\n",
" <td>101</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>18</td>\n",
" <td>Maurizio Andreoli</td>\n",
" <td>100</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>19</td>\n",
" <td>Telerobotlabs</td>\n",
" <td>100</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>20</td>\n",
" <td>ron</td>\n",
" <td>55</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>21</td>\n",
" <td>EnricoSx</td>\n",
" <td>30</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>22</td>\n",
" <td>guz</td>\n",
" <td>30</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>23</td>\n",
" <td>Frankie842</td>\n",
" <td>24</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>24</td>\n",
" <td>dan_bar</td>\n",
" <td>23</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>25</td>\n",
" <td>carlo71</td>\n",
" <td>23</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>26</td>\n",
" <td>Gilles</td>\n",
" <td>23</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>27</td>\n",
" <td>Forno92</td>\n",
" <td>23</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>28</td>\n",
" <td>robertozz</td>\n",
" <td>21</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>29</td>\n",
" <td>ciro66</td>\n",
" <td>20</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>30</td>\n",
" <td>rocruss</td>\n",
" <td>20</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>93</th>\n",
" <td>94</td>\n",
" <td>Andrea Ficicchia</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>94</th>\n",
" <td>95</td>\n",
" <td>Nicola Secciani</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>95</th>\n",
" <td>96</td>\n",
" <td>vietcusc</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>96</th>\n",
" <td>97</td>\n",
" <td>abramelek</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>97</th>\n",
" <td>98</td>\n",
" <td>stefanodebiasio</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>98</th>\n",
" <td>99</td>\n",
" <td>Fabrizio</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>99</th>\n",
" <td>100</td>\n",
" <td>drogo75</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>100</th>\n",
" <td>101</td>\n",
" <td>federico</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>101</th>\n",
" <td>102</td>\n",
" <td>Archimede_2000</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>102</th>\n",
" <td>103</td>\n",
" <td>phuocdai</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>103</th>\n",
" <td>104</td>\n",
" <td>darkakushi</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>104</th>\n",
" <td>105</td>\n",
" <td>vinicio.nigro</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>105</th>\n",
" <td>106</td>\n",
" <td>Enry</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>106</th>\n",
" <td>107</td>\n",
" <td>sbnmc</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>107</th>\n",
" <td>108</td>\n",
" <td>ANDREAFFI</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>108</th>\n",
" <td>109</td>\n",
" <td>brunoli</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>109</th>\n",
" <td>110</td>\n",
" <td>alexit71</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>110</th>\n",
" <td>111</td>\n",
" <td>Giuseppe</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>111</th>\n",
" <td>112</td>\n",
" <td>jo bach</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>112</th>\n",
" <td>113</td>\n",
" <td>franco</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>113</th>\n",
" <td>114</td>\n",
" <td>toledo</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>114</th>\n",
" <td>115</td>\n",
" <td>Michele Domanico</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>115</th>\n",
" <td>116</td>\n",
" <td>Goffredo Geymet</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>116</th>\n",
" <td>117</td>\n",
" <td>michele007</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>117</th>\n",
" <td>118</td>\n",
" <td>francis_bell</td>\n",
" <td>10</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>118</th>\n",
" <td>119</td>\n",
" <td>edsel2016</td>\n",
" <td>7</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>119</th>\n",
" <td>120</td>\n",
" <td>pierpaolo</td>\n",
" <td>6</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>120</th>\n",
" <td>121</td>\n",
" <td>fdaniele</td>\n",
" <td>4</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>121</th>\n",
" <td>122</td>\n",
" <td>squarewheel7</td>\n",
" <td>4</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>122</th>\n",
" <td>123</td>\n",
" <td>Marco Corbetta</td>\n",
" <td>1</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>123 rows × 4 columns</p>\n",
"</div>"
],
"text/plain": [
" Position Name Points Rank\n",
"0 1 Fabio Nelli 16682 NaN\n",
"1 2 admin 9029 NaN\n",
"2 3 BrunoOrsini 2078 NaN\n",
"3 4 Berserker 700 NaN\n",
"4 5 albertosallusti 277 NaN\n",
"5 6 Dnocioni 194 NaN\n",
"6 7 Jon 181 NaN\n",
"7 8 Mr.Y 180 NaN\n",
"8 9 michele sisinni 150 NaN\n",
"9 10 Selina 133 NaN\n",
"10 11 stefano gustin 120 NaN\n",
"11 12 Pietro Baima 107 NaN\n",
"12 13 Cecilia Lalatta Costerbosa 106 NaN\n",
"13 14 Davide Aloisi 106 NaN\n",
"14 15 Leonardo Zampi 106 NaN\n",
"15 16 gildalombardi 105 NaN\n",
"16 17 Marco Contigiani 101 NaN\n",
"17 18 Maurizio Andreoli 100 NaN\n",
"18 19 Telerobotlabs 100 NaN\n",
"19 20 ron 55 NaN\n",
"20 21 EnricoSx 30 NaN\n",
"21 22 guz 30 NaN\n",
"22 23 Frankie842 24 NaN\n",
"23 24 dan_bar 23 NaN\n",
"24 25 carlo71 23 NaN\n",
"25 26 Gilles 23 NaN\n",
"26 27 Forno92 23 NaN\n",
"27 28 robertozz 21 NaN\n",
"28 29 ciro66 20 NaN\n",
"29 30 rocruss 20 NaN\n",
".. ... ... ... ...\n",
"93 94 Andrea Ficicchia 10 NaN\n",
"94 95 Nicola Secciani 10 NaN\n",
"95 96 vietcusc 10 NaN\n",
"96 97 abramelek 10 NaN\n",
"97 98 stefanodebiasio 10 NaN\n",
"98 99 Fabrizio 10 NaN\n",
"99 100 drogo75 10 NaN\n",
"100 101 federico 10 NaN\n",
"101 102 Archimede_2000 10 NaN\n",
"102 103 phuocdai 10 NaN\n",
"103 104 darkakushi 10 NaN\n",
"104 105 vinicio.nigro 10 NaN\n",
"105 106 Enry 10 NaN\n",
"106 107 sbnmc 10 NaN\n",
"107 108 ANDREAFFI 10 NaN\n",
"108 109 brunoli 10 NaN\n",
"109 110 alexit71 10 NaN\n",
"110 111 Giuseppe 10 NaN\n",
"111 112 jo bach 10 NaN\n",
"112 113 franco 10 NaN\n",
"113 114 toledo 10 NaN\n",
"114 115 Michele Domanico 10 NaN\n",
"115 116 Goffredo Geymet 10 NaN\n",
"116 117 michele007 10 NaN\n",
"117 118 francis_bell 10 NaN\n",
"118 119 edsel2016 7 NaN\n",
"119 120 pierpaolo 6 NaN\n",
"120 121 fdaniele 4 NaN\n",
"121 122 squarewheel7 4 NaN\n",
"122 123 Marco Corbetta 1 NaN\n",
"\n",
"[123 rows x 4 columns]"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# 以网址作为参数\n",
"ranking = pd.read_html('http://www.meccanismocomplesso.org/en/meccanismo-complesso-sito-2/classifica-punteggio/')\n",
"ranking[0]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 读写xml文件\n",
"使用的第三方的库 lxml"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<lxml.etree._ElementTree at 0x9bcd8c8>"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from lxml import objectify\n",
"xml = objectify.parse('books.xml')\n",
"xml"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"root =xml.getroot()"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'EnRoss Mark'"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"root.Book.Author"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'2014-22-01'"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"root.Book.PublishDate"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<Element Book at 0x9bcaa08>, <Element Book at 0x9bcaac8>]"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"root.getchildren()"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"['Author', 'Title', 'Genre', 'Price', 'PublishDate']"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"[child.tag for child in root.Book.getchildren()]"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"['EnRoss Mark', 'xml cookbook', 'Computer', '23.56', '2014-22-01']"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"[child.text for child in root.Book.getchildren()]"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Author</th>\n",
" <th>Title</th>\n",
" <th>Genre</th>\n",
" <th>Price</th>\n",
" <th>PublishDate</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>EnRoss Mark</td>\n",
" <td>xml cookbook</td>\n",
" <td>Computer</td>\n",
" <td>23.56</td>\n",
" <td>2014-22-01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>Barbara</td>\n",
" <td>xml for dummies</td>\n",
" <td>Computer</td>\n",
" <td>35.95</td>\n",
" <td>2014-12-06</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Author Title Genre Price PublishDate\n",
"0 EnRoss Mark xml cookbook Computer 23.56 2014-22-01\n",
"1 Barbara xml for dummies Computer 35.95 2014-12-06"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def etree2df(root):\n",
" column_names=[]\n",
" for i in range(0,len(root.getchildren()[0].getchildren())):\n",
" column_names.append(root.getchildren()[0].getchildren()[i].tag)\n",
" xml_frame = pd.DataFrame(columns=column_names)\n",
" for j in range(0,len(root.getchildren())):\n",
" obj = root.getchildren()[j].getchildren()\n",
" texts = []\n",
" for k in range(0,len(column_names)):\n",
" texts.append(obj[k].text)\n",
" row = dict(zip(column_names,texts))\n",
" row_s=pd.Series(row)\n",
" row_s.name=j\n",
" xml_frame = xml_frame.append(row_s)\n",
" return xml_frame\n",
"etree2df(root)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 读写Excel文件"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>green</th>\n",
" <th>black</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td>12</td>\n",
" <td>23</td>\n",
" <td>17</td>\n",
" <td>18</td>\n",
" </tr>\n",
" <tr>\n",
" <th>b</th>\n",
" <td>22</td>\n",
" <td>16</td>\n",
" <td>19</td>\n",
" <td>18</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td>14</td>\n",
" <td>23</td>\n",
" <td>22</td>\n",
" <td>21</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white red green black\n",
"a 12 23 17 18\n",
"b 22 16 19 18\n",
"c 14 23 22 21"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_excel('data.xlsx')"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>yellow</th>\n",
" <th>purple</th>\n",
" <th>blue</th>\n",
" <th>orange</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>A</th>\n",
" <td>11</td>\n",
" <td>16</td>\n",
" <td>44</td>\n",
" <td>22</td>\n",
" </tr>\n",
" <tr>\n",
" <th>B</th>\n",
" <td>20</td>\n",
" <td>22</td>\n",
" <td>23</td>\n",
" <td>44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C</th>\n",
" <td>30</td>\n",
" <td>31</td>\n",
" <td>37</td>\n",
" <td>32</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" yellow purple blue orange\n",
"A 11 16 44 22\n",
"B 20 22 23 44\n",
"C 30 31 37 32"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_excel('data.xlsx','Sheet2')"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Jan2015</th>\n",
" <th>Feb2015</th>\n",
" <th>Mar2015</th>\n",
" <th>Apr2015</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>exp1</th>\n",
" <td>0.696097</td>\n",
" <td>0.333292</td>\n",
" <td>0.799803</td>\n",
" <td>0.945701</td>\n",
" </tr>\n",
" <tr>\n",
" <th>exp2</th>\n",
" <td>0.409402</td>\n",
" <td>0.778060</td>\n",
" <td>0.695790</td>\n",
" <td>0.725668</td>\n",
" </tr>\n",
" <tr>\n",
" <th>exp3</th>\n",
" <td>0.458230</td>\n",
" <td>0.398461</td>\n",
" <td>0.064312</td>\n",
" <td>0.797225</td>\n",
" </tr>\n",
" <tr>\n",
" <th>exp4</th>\n",
" <td>0.031586</td>\n",
" <td>0.230344</td>\n",
" <td>0.446283</td>\n",
" <td>0.128528</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Jan2015 Feb2015 Mar2015 Apr2015\n",
"exp1 0.696097 0.333292 0.799803 0.945701\n",
"exp2 0.409402 0.778060 0.695790 0.725668\n",
"exp3 0.458230 0.398461 0.064312 0.797225\n",
"exp4 0.031586 0.230344 0.446283 0.128528"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"frame = pd.DataFrame(np.random.random((4,4)),\n",
" index=['exp1','exp2','exp3','exp4'],\n",
" columns=['Jan2015','Feb2015','Mar2015','Apr2015'])\n",
"frame"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"frame.to_excel('data2.xlsx')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# JSON数据"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"frame = pd.DataFrame(np.arange(16).reshape((4,4)),\n",
" index=['white','black','red','blue'],\n",
" columns=['up','down','right','left'])\n",
"frame.to_json('frame.json')"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>down</th>\n",
" <th>left</th>\n",
" <th>right</th>\n",
" <th>up</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>black</th>\n",
" <td>5</td>\n",
" <td>7</td>\n",
" <td>6</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>blue</th>\n",
" <td>13</td>\n",
" <td>15</td>\n",
" <td>14</td>\n",
" <td>12</td>\n",
" </tr>\n",
" <tr>\n",
" <th>red</th>\n",
" <td>9</td>\n",
" <td>11</td>\n",
" <td>10</td>\n",
" <td>8</td>\n",
" </tr>\n",
" <tr>\n",
" <th>white</th>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" down left right up\n",
"black 5 7 6 4\n",
"blue 13 15 14 12\n",
"red 9 11 10 8\n",
"white 1 3 2 0"
]
},
"execution_count": 59,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# 读取json\n",
"pd.read_json('frame.json')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# HDF5数据"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"HDF文件(hierarchical data from)等级数据格式,用二进制文件存储数据。"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from pandas.io.pytables import HDFStore\n",
"store = HDFStore('mydata.h5')\n",
"store['obj1']=frame"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>up</th>\n",
" <th>down</th>\n",
" <th>right</th>\n",
" <th>left</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>white</th>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>black</th>\n",
" <td>4</td>\n",
" <td>5</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" </tr>\n",
" <tr>\n",
" <th>red</th>\n",
" <td>8</td>\n",
" <td>9</td>\n",
" <td>10</td>\n",
" <td>11</td>\n",
" </tr>\n",
" <tr>\n",
" <th>blue</th>\n",
" <td>12</td>\n",
" <td>13</td>\n",
" <td>14</td>\n",
" <td>15</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" up down right left\n",
"white 0 1 2 3\n",
"black 4 5 6 7\n",
"red 8 9 10 11\n",
"blue 12 13 14 15"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"store['obj1']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# pickle数据"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"frame.to_pickle('frame.pkl')"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>up</th>\n",
" <th>down</th>\n",
" <th>right</th>\n",
" <th>left</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>white</th>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>black</th>\n",
" <td>4</td>\n",
" <td>5</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" </tr>\n",
" <tr>\n",
" <th>red</th>\n",
" <td>8</td>\n",
" <td>9</td>\n",
" <td>10</td>\n",
" <td>11</td>\n",
" </tr>\n",
" <tr>\n",
" <th>blue</th>\n",
" <td>12</td>\n",
" <td>13</td>\n",
" <td>14</td>\n",
" <td>15</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" up down right left\n",
"white 0 1 2 3\n",
"black 4 5 6 7\n",
"red 8 9 10 11\n",
"blue 12 13 14 15"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_pickle('frame.pkl')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 数据库连接\n",
"以sqlite3为例介绍"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>blue</th>\n",
" <th>black</th>\n",
" <th>green</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>5</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>9</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>10</td>\n",
" <td>11</td>\n",
" <td>12</td>\n",
" <td>13</td>\n",
" <td>14</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>15</td>\n",
" <td>16</td>\n",
" <td>17</td>\n",
" <td>18</td>\n",
" <td>19</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" white red blue black green\n",
"0 0 1 2 3 4\n",
"1 5 6 7 8 9\n",
"2 10 11 12 13 14\n",
"3 15 16 17 18 19"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"frame=pd.DataFrame(np.arange(20).reshape((4,5)),\n",
" columns=['white','red','blue','black','green'])\n",
"frame"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sqlalchemy import create_engine\n",
"enegine=create_engine('sqlite:///foo.db')"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"frame.to_sql('colors',enegine)"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>index</th>\n",
" <th>white</th>\n",
" <th>red</th>\n",
" <th>blue</th>\n",
" <th>black</th>\n",
" <th>green</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" <td>6</td>\n",
" <td>7</td>\n",
" <td>8</td>\n",
" <td>9</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>10</td>\n",
" <td>11</td>\n",
" <td>12</td>\n",
" <td>13</td>\n",
" <td>14</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>3</td>\n",
" <td>15</td>\n",
" <td>16</td>\n",
" <td>17</td>\n",
" <td>18</td>\n",
" <td>19</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" index white red blue black green\n",
"0 0 0 1 2 3 4\n",
"1 1 5 6 7 8 9\n",
"2 2 10 11 12 13 14\n",
"3 3 15 16 17 18 19"
]
},
"execution_count": 73,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.read_sql('colors',enegine)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
yskmurakami/MPMaximizer | MPMiximizer.ipynb | 1 | 20625 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"A = np.array(\n",
"[[4.0, 0.0],\n",
" [3.0, 2.0]]\n",
")\n",
"\n",
"B = np.array(\n",
"[[ 7.0, 0.0, 0.0],\n",
" [ 4.0, 1.0, 2.0],\n",
" [ 0.0, 0.0, 8.0]]\n",
")\n",
"\n",
"C = np.array(\n",
"[[ 13.0, 3.0, 0.0],\n",
" [ 5.0, 0.0, 13.0],\n",
" [ 0.0, 2.0, 16.0]]\n",
")\n",
"\n",
"D = np.array(\n",
"[[13.0, 0.0, 0.0, 0.0],\n",
" [11.0, 1.0, 4.0, 0.0],\n",
" [ 7.0, 0.0, 3.0, 9.0],\n",
" [ 0.0, 2.0, 3.0, 16.0]]\n",
")\n",
"\n",
"a = MPMaximizer(B)\n",
"a.find(False) #strict\u306aMP-maximizer\u3092\u8abf\u3079\u308b\u306b\u306fTrue\u3092\u5165\u308c\u308b."
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"a-star = (0, 0)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (0, 1)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (0, 2)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (1, 0)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (1, 1)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (1, 2)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (2, 0)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (2, 1)\n",
"This a-star does not seem to be MP-maximizer."
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"a-star = (2, 2)\n",
"[[ 0.96146275 0.52472772 0.30786694]\n",
" [ 0.52472772 0.12679931 0.38007753]\n",
" [ 0.30786694 0.38007753 1. ]]"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"\"\"\"\n",
"\u4ed5\u69d8\n",
"\u30fbrandom_matrix\u306f\u4eca\u306e\u3068\u3053\u308d\u5bfe\u79f0\u884c\u5217\u306e\u307f\u3092\u751f\u3058\u3066\u304a\u308a\u3001\u305d\u3046\u3067\u306a\u3044\u5834\u5408\u306f\u307e\u3060\u4e0d\u5341\u5206.\n",
"\u30fbrandom_matrix\u306b\u9006\u884c\u5217\u3092\u6301\u305f\u306a\u3044\u3082\u306e\u306f\u8abf\u3079\u3089\u308c\u306a\u3044.\n",
"\u30fb\u5bfe\u89d2\u6210\u5206\u3067\u306a\u3044\u3068\u3053\u308d\u304cMPMaximizer\u3060\u3063\u305f\u5834\u5408\u306f\u307e\u3060\u4e0d\u6b63\u78ba.\n",
"\u30fbpayoff_matrix\u306f\u6b21\u5143\u304c\u5897\u3048\u3066\u3082\u5bfe\u5fdc.\u305f\u3060\u3057\u3001\u5229\u5f97\u304c\u5bfe\u79f0\u306a\u30b2\u30fc\u30e0\u306b\u9650\u308b.\n",
"\u30fb\u305d\u308c\u305e\u308c\u306e\u6226\u7565\u306e\u7d44\u306b\u5bfe\u3057\u3066\u3001random_matrix\u306f\u6700\u5927\u3067100\u56de\u767a\u751f\u3055\u305b\u308b.\n",
"\u30fb\u8a08\u7b97\u306b\u304b\u304b\u308b\u6642\u9593\u306f\u624b\u5143\u306e\u30ce\u30fc\u30c8PC\u4e0a\u3067\u306f\uff12\u6b21\u5143\u3067\uff11\u79d2\u4ee5\u5185\u3001\uff13\u6b21\u5143\u3067\u7d04\uff12\u79d2\u3001\uff14\u6b21\u5143\u3067\u7d0418\u79d2.\n",
"\"\"\"\n",
"\n",
"import numpy as np\n",
"from random import uniform\n",
"from __future__ import division\n",
"from math import floor\n",
"from itertools import combinations\n",
"\n",
"class MPMaximizer:\n",
" def __init__(self, mat):\n",
" self.payoff_matrix = mat\n",
" self.dim = mat.shape[0]\n",
" self.strategies = self.gen_strategies()\n",
" self.trial = 100\n",
" \n",
" def find(self, strict):\n",
" \"\"\"\n",
" \u5bfe\u89d2\u6210\u5206\u3067\u306a\u3044\u3068\u3053\u308d\u304cMPMaximizer\u3060\u3063\u305f\u5834\u5408\u306f\u300c\u7a7a\u632f\u308b\u300d\u6050\u308c\u304c\u3042\u308b.\n",
" \u767a\u751f\u3059\u308b\u884c\u5217\u306f\u5bfe\u79f0\u306a\u884c\u5217\u306a\u306e\u3067\u3001\u5bfe\u89d2\u6210\u5206\u306b\u95a2\u3057\u3066\u306f\u300c\u7a7a\u632f\u308a\u300d\u306f\u306a\u3044.\n",
" \u3044\u305a\u308c\u306b\u3057\u3066\u3082\u3001trial\u3092\u7121\u9650\u306b\u5927\u304d\u304f\u3057\u306a\u3044\u9650\u308a\u3001\u300c\u898b\u9003\u3057\u300d\u306e\u53ef\u80fd\u6027\u306f\u6d88\u3048\u306a\u3044.\n",
" \"\"\"\n",
" for i in range(len(self.strategies)):\n",
" print \"a-star = \" + str(self.strategies[i])\n",
"\n",
" self.strategy = self.strategies[i][0]\n",
" self.setstrategy = self.strategies[i]\n",
" \n",
" self.degU_payoff_matrix = self.degen_matrix(self.payoff_matrix, True)\n",
" self.degL_payoff_matrix = self.degen_matrix(self.payoff_matrix, False) \n",
" \n",
" for j in range(self.trial): \n",
" self.random_matrix = self.gen_random_matrix()\n",
" \n",
" self.degU_random_matrix = self.degen_matrix(self.random_matrix, True)\n",
" self.degL_random_matrix = self.degen_matrix(self.random_matrix, False)\n",
" \n",
" self.equilibria = self.gen_equilibria()\n",
" \n",
" self.br1st_random = self.cal_br(self.degU_random_matrix, True)\n",
" self.br2nd_random = self.cal_br(self.degL_random_matrix, False)\n",
" \n",
" if strict:\n",
" self.br1st_payoff = self.cal_br(self.degU_payoff_matrix, False)\n",
" self.br2nd_payoff = self.cal_br(self.degL_payoff_matrix, True)\n",
" else:\n",
" self.br1st_payoff = self.cal_br(self.degU_payoff_matrix, True)\n",
" self.br2nd_payoff = self.cal_br(self.degL_payoff_matrix, False)\n",
" \n",
" self.cond1st = self.compare(self.br1st_random, self.br1st_payoff)\n",
" self.cond2nd = self.compare(self.br2nd_payoff, self.br2nd_random)\n",
" \n",
" if self.cond1st and self.cond2nd:\n",
" print self.random_matrix\n",
" break\n",
" \n",
" if j == self.trial - 1:\n",
" print \"This a-star does not seem to be MP-maximizer.\"\n",
" \n",
" def set_trial(self, trial):\n",
" self.trial = trial\n",
" \n",
" def gen_equilibria(self):\n",
" \"\"\"\n",
" \uff12\u3064\u4ee5\u4e0a\u306e\u6226\u7565\u304c\u7121\u5dee\u5225\u306b\u306a\u308b\u7a7a\u9593\u3068\u3001dim\u6b21\u5143\u306e(0,1)\u7a7a\u9593\u306e\u5883\u754c\u90e8\u5206\u3068\u306e\u5171\u901a\u70b9\u3092\u5168\u3066\u6319\u3052\u308b.\n",
" (\u4f8b)dim = 3\u306a\u3089\u3070\u3001\u307e\u305a\uff13\u3064\u306e\u6226\u7565\u304c\u7121\u5dee\u5225\u306b\u306a\u308b\u70b9\u3092\u63a2\u3059.\n",
" \u6b21\u306b\u3001\uff12\u3064\u306e\u6226\u7565\u304c\u7121\u5dee\u5225\u306b\u306a\u308b\u76f4\u7dda\u304c\uff13\u672c\uff08(0,1),(0,2),(1,2)\u305d\u308c\u305e\u308c\uff09\u3042\u308a\u3001\n",
" \u3053\u308c\u3068\u306e\uff13\u6b21\u5143\u7a7a\u9593\u306e(0,1)\u3068\u306e\u5883\u754c\u90e8\u5206\u306f\u591a\u304f\u3066\u76f4\u7dda\uff11\u672c\u306b\u3064\u304d\uff12\u30f6\u6240\u3060\u304b\u3089\uff16\u70b9\u304c\u52a0\u308f\u308a\u3001\n",
" \u9ad8\u3005\uff17\u70b9\u304cequilibria\u306b\u52a0\u3048\u3089\u308c\u308b.\n",
" \"\"\"\n",
" equilibria = []\n",
" \n",
" for i in range(self.dim - 1):\n",
" rawcolumns = self.gen_deletelist(i)\n",
" for j1 in range(len(rawcolumns)):\n",
" for j2 in range(len(rawcolumns)):\n",
" self.cut_matrix(rawcolumns[j1], rawcolumns[j2])\n",
" equilibrium = self.cal_equilibrium()\n",
" \n",
" if self.test_area(equilibrium):\n",
" for k in rawcolumns[j2]:\n",
" equilibrium = np.insert(equilibrium, k, 0)\n",
" equilibria.append(equilibrium)\n",
" \n",
" for i in range(self.dim):\n",
" zeros = np.zeros(self.dim - 1)\n",
" zeros = np.insert(zeros, i, 1)\n",
" equilibria.append(zeros)\n",
" \n",
" return equilibria\n",
" \n",
" def test_area(self, vec, epsilon=1E-7):\n",
" \"\"\"\n",
" \u4e0e\u3048\u3089\u308c\u305f\u6df7\u5408\u6226\u7565\u304c\u78ba\u7387\u5206\u5e03\u306a\u3089\u3070True\u3001\u305d\u3046\u3067\u306a\u3051\u308c\u3070False\u3092\u8fd4\u3059.\n",
" \u3059\u306a\u308f\u3061\u3001\u5168\u3066\u306e\u6226\u7565\u306e\u5272\u5408\u304c\u975e\u8ca0\u306a\u3089\u3070True.\n",
" \"\"\"\n",
" boolvec = vec > -epsilon\n",
" return self.cut_dim - np.count_nonzero(boolvec) == 0 \n",
" \n",
" def get_dim(self):\n",
" return self.dim\n",
" \n",
" def gen_deletelist(self, dim):\n",
" \"\"\"\n",
" equilibria\u3092\u6c42\u3081\u308b\u306e\u306b\u5fc5\u8981.\n",
" (\u4f8b)combinations(range(6), 4)\u306f\u3001range(6)=(0, 1, 2, 3, 4, 5)\u304b\u30894\u3064\u3092\u9078\u3073\u9806\u756a\u306b\u4e26\u3079\u308b\u7d44\u3092\u5168\u3066\u8fd4\u3059.\n",
" \u3059\u306a\u308f\u3061\u3053\u306e\u5834\u5408\u3001deletelist\u306b\u52a0\u3048\u3089\u308c\u308b\u306e\u306f\n",
" (0, 1, 2, 3), (0, 1, 2, 4), (0, 1, 2, 5), (0, 1, 3, 4), (0, 1, 3, 5), (0, 1, 4, 5),\n",
" (0, 2, 3, 4), (0, 2, 3, 5), (0, 2, 4, 5), (0, 3, 4, 5),\n",
" (1, 2, 3, 4), (1, 2, 3, 5), (1, 2, 4, 5), (1, 3, 4, 5), (2, 3, 4, 5)\u306e15\u500b.\n",
" \"\"\"\n",
" deletelist = []\n",
" for i in combinations(range(self.dim), dim):\n",
" deletelist.append(i)\n",
" return deletelist\n",
" \n",
" def cut_matrix(self, raws, columns):\n",
" \"\"\"\n",
" equilibria\u3092\u6c42\u3081\u308b\u306e\u306b\u5fc5\u8981.\n",
" \u5f15\u6570\u306e\u300c\u884c\u300d\u300c\u5217\u300d\u3092\u53d6\u308a\u9664\u304f.\n",
" \"\"\"\n",
" self.cutmatrix = self.random_matrix\n",
" self.cutmatrix = np.delete(self.cutmatrix, raws, 0)\n",
" self.cutmatrix = np.delete(self.cutmatrix, columns, 1)\n",
" self.cut_dim = self.cutmatrix.shape[0]\n",
" \n",
" def gen_random_matrix(self):\n",
" \"\"\"\n",
" \u767a\u751f\u3055\u305b\u3066\u3044\u308b\u306e\u306f\u5bfe\u79f0\u884c\u5217\u306erandom_matrix.\n",
" \"\"\"\n",
" random_matrix = np.random.uniform(0, 1, (self.dim, self.dim))\n",
" random_matrix = (random_matrix + random_matrix.T) * 0.5\n",
" random_matrix[self.setstrategy] = 1\n",
" return random_matrix\n",
" \n",
" def cal_equilibrium(self):\n",
" \"\"\"\n",
" \u4e0e\u3048\u3089\u308c\u305f\u5229\u5f97\u884c\u5217\u306b\u5bfe\u3057\u3001BR\u304c\u5168\u3066\u306e\u6226\u7565\u306b\u306a\u308b\u3088\u3046\u306a\u76f8\u624b\u306e\u6df7\u5408\u6226\u7565\uff08\u8ca0\u306e\u5024\u3092\u8a8d\u3081\u308b\uff09\u3092\u6c42\u3081\u308b.\n",
" \u6761\u4ef6\u306f\u3001\u5229\u5f97\u884c\u5217\u304c\u9006\u884c\u5217\u3092\u6301\u3064\u3053\u3068.\n",
" \u5f0f\u3067\u66f8\u304f\u3068\u3001\n",
" M = \u4e0e\u3048\u3089\u308c\u305f\u884c\u5217\uff08dim*dim\u6b21\u5143\u306e\u884c\u5217\uff09\n",
" x = \u6c42\u3081\u308b\u6df7\u5408\u6226\u7565\uff08dim\u6b21\u5143\u30d9\u30af\u30c8\u30eb\uff09\n",
" 1 = \u5168\u3066\u306e\u6210\u5206\u304c1\u306edim\u6b21\u5143\u30d9\u30af\u30c8\u30eb\n",
" c = \u5b9f\u6570\u5b9a\u6570\n",
" \u3068\u3057\u305f\u3068\u304d\u306b\u3001\n",
" Mx = c1 and x'1 = 1\n",
" \u3092\u6e80\u305f\u3059c\u3068x\u3092\u6c42\u3081\u3001x\u3092\u8fd4\u3059.\n",
" \"\"\"\n",
" ones = np.ones(self.cut_dim)\n",
" inversemat = np.linalg.inv(self.cutmatrix)\n",
" x = np.dot(inversemat, ones)\n",
" c = np.dot(x.T, ones)\n",
" return x / c\n",
" \n",
" def gen_strategies(self):\n",
" \"\"\"\n",
" \u6b21\u5143\u3092\u4e0e\u3048\u308b\u3068\u3001\u53d6\u308a\u3046\u308b\u5168\u3066\u306e\u7d14\u7c8b\u6226\u7565\u306e\u7d44\u3092\u8fd4\u3059.\n",
" player\u304c\uff12\u4eba\u306e\u5834\u5408\u306b\u306e\u307f\u5bfe\u5fdc.\n",
" (\u4f8b)dim = 2\u306a\u3089\u3070\u3001(0, 0), (0, 1), (1, 0), (1, 1)\u306e4\u3064\u3092\u30ea\u30b9\u30c8\u4e2d\u306e\u30bf\u30d7\u30eb\u3068\u3057\u3066\u8fd4\u3059.\n",
" \"\"\"\n",
" strategies = []\n",
" for i in range(self.dim):\n",
" for j in range(self.dim):\n",
" strategies.append((i,j))\n",
" return strategies\n",
"\n",
" def degen_matrix(self, mat, upper, HUGE=1E+7):\n",
" \"\"\"\n",
" \u884c\u5217\u3092\u9000\u5316\u3055\u305b\u308b\u95a2\u6570.BestResponse\u3092\u6c42\u3081\u308b\u304c\u3001MPMaximizer\u306e\u6226\u7565a-star\u306b\u3088\u3063\u3066\u3001\n",
" \u6761\u4ef6\u5f0f\u3067\u53d6\u308c\u308b\u6226\u7565\u3092\u9650\u308b\u5fc5\u8981\u304c\u3042\u308b\u306e\u3067\u3001\u3053\u306e\u95a2\u6570\u304c\u5fc5\u8981.\n",
" \u547d\u540d\u306fupper\u304cTrue\u306a\u3089\u4e0b\u306e\u4f8b\u3067\u306e\uff11\u3064\u76ee\u3001False\u306a\u3089\uff12\u3064\u76ee\u306b\u306a\u308b\u3088\u3046\u8fd4\u3059.\n",
" (\u4f8b)A_i = {0, 1, 2, 3}\u3067a-star_i = 2\u3068\u3059\u308b\u3068\u3001\uff12\u3064\u3042\u308b\u6761\u4ef6\u306e\u3046\u3061\u306e\uff11\u3064\u76ee\n",
" br{pi_i|[0,2]}\u306f\u30010\u304b\u30892\u307e\u3067\u306e\u6226\u7565\u306e\u4e2d\u304b\u3089br\u3092\u9078\u3076\u3068\u3044\u3046\u3053\u3068\u306a\u306e\u3067\u3001\n",
" \u5229\u5f97\u884c\u5217\u3092\u3001\n",
" [ ## ## ## ##\n",
" ## ## ## ##\n",
" ## ## ## ##\n",
" -- -- -- -- ]\n",
" \uff08\u305f\u3060\u3057##\u306f\u5143\u306e\u5024\u3001--\u306f##\u306b\u6bd4\u3079\u3066\u660e\u3089\u304b\u306b\u5c0f\u3055\u3044\u5024\uff08-- << ##\uff09\uff09\n",
" \u3068\u3059\u308b\u3053\u3068\u30673\u3068\u3044\u3046\u6226\u7565\u304c\u4ed6\u306b\u652f\u914d\u3055\u308c\u308b\u3088\u3046\u306b\u3067\u304d\u308b.\u540c\u69d8\u306b\u3001\uff12\u3064\u76ee\u306e\u6761\u4ef6\n",
" br{pi_i|[2,3]}\u306f\u3001\u5229\u5f97\u884c\u5217\u3092\n",
" [ -- -- -- --\n",
" -- -- -- --\n",
" ## ## ## ##\n",
" ## ## ## ## ]\n",
" \u3068\u3059\u308b.\n",
" \"\"\"\n",
" degen = HUGE * np.ones((self.dim, self.dim))\n",
" if upper:\n",
" for i in range(self.strategy+1):\n",
" degen[i, :] = 0\n",
" else:\n",
" for i in range(self.strategy, self.dim):\n",
" degen[i, :] = 0\n",
" return mat - degen\n",
"\n",
" def cal_br(self, deg_mat, maximum, epsilon=10E-7):\n",
" \"\"\"\n",
" \u305d\u308c\u305e\u308c\u306e\u6df7\u5408\u6226\u7565\u306b\u5bfe\u5fdc\u3057\u305f\u9806\u756a\u306bBestResponse\u3092\u8fd4\u3059\u95a2\u6570.\n",
" BestResponse\u304c\u8907\u6570\u3042\u308b\u5834\u5408\u306fmaximum\u304cTrue\u306a\u3089\u6700\u5927\u5024\u3092\u3001\u305d\u3046\u3067\u306a\u3051\u308c\u3070\u6700\u5c0f\u5024\u3092\u8fd4\u3059.\n",
" \"\"\"\n",
" best_responses = []\n",
" for i in range(len(self.equilibria)):\n",
" A = np.dot(deg_mat, self.equilibria[i])\n",
" br = 0\n",
" value = A[0]\n",
" for now_number in range(self.dim):\n",
" if maximum:\n",
" if A[now_number] - value > -epsilon:\n",
" br = now_number\n",
" value = A[now_number]\n",
" else:\n",
" if A[now_number] - value > epsilon:\n",
" br = now_number\n",
" value = A[now_number]\n",
" best_responses.append(br)\n",
" return best_responses \n",
" \n",
" A = np.dot(deg_mat, self.equilibria)\n",
" number_of_colomns = len(test[0])\n",
" best_responses = []\n",
" for i in range(number_of_colomns):\n",
" br = 0\n",
" value = A[0][i]\n",
" for now_number in range(dim):\n",
" if maximum:\n",
" if A[now_number][i] - value > -epsilon:\n",
" br = now_number\n",
" value = A[now_number][i]\n",
" else:\n",
" if A[now_number][i] - value > epsilon:\n",
" br = now_number\n",
" value = A[now_number][i]\n",
" best_responses.append(br)\n",
" return best_responses\n",
"\n",
" def compare(self, smaller, bigger):\n",
" \"\"\"\n",
" \u30ea\u30b9\u30c8\u5185\u306e\u5bfe\u5fdc\u3059\u308b\u8981\u7d20\u306e\u5927\u5c0f\u3092\u6bd4\u3079\u308b.\u5168\u3066\u306e\u8981\u7d20\u3067smaller\u5074\u304cbigger\u5074\u3088\u308a\u3082\u300c<=\u300d\u306a\u3089\u3070True\u3001\n",
" \uff11\u30f6\u6240\u3067\u3082\u305d\u3046\u306a\u3063\u3066\u3044\u306a\u3051\u308c\u3070False\u3092\u8fd4\u3059.\n",
" \"\"\"\n",
" X = []\n",
" for i in range(len(smaller)):\n",
" X.append(smaller[i] <= bigger[i])\n",
" return all(X)\n",
" \n",
" def get_1st(self):\n",
" print self.br1st_payoff\n",
" print self.br1st_random\n",
" \n",
" def get_2nd(self):\n",
" print self.br2nd_payoff\n",
" print self.br2nd_random\n",
" \n",
" def get_equilibria(self):\n",
" print self.equilibria"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
SergioSantGre/project_portfolio | document_similarity2.ipynb | 1 | 6273504 | null | lgpl-3.0 |
jljones/portfolio | ds/Webscraping_Craigslist_multi.ipynb | 1 | 285850 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Webscraping Craigslist for Housing Listings in the East Bay\n",
"\n",
"### Jennifer Jones"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
}
],
"source": [
"%pylab inline\n",
"import numpy as np\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import requests\n",
"from bs4 import BeautifulSoup as bs4"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Craigslist houses for sale\n",
"\n",
"Look on the Craigslist website, select relevant search criteria, and then take a look at the web address:\n",
"\n",
"Houses for sale in the East Bay: \n",
"[http://sfbay.craigslist.org/search/eby/rea?housing_type=6](http://sfbay.craigslist.org/search/eby/rea?housing_type=6)\n",
"\n",
"Houses for sale in selected neighborhoods in the East Bay: \n",
"[http://sfbay.craigslist.org/search/eby/rea?nh=46&nh=47&nh=48&nh=49&nh=112&nh=54&nh=55&nh=60&nh=62&nh=63&nh=66&housing_type=6](http://sfbay.craigslist.org/search/eby/rea?nh=46&nh=47&nh=48&nh=49&nh=112&nh=54&nh=55&nh=60&nh=62&nh=63&nh=66&housing_type=6) \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## General Procedure\n",
"\n",
"```python\n",
"\n",
"# Get the data using the requests module \n",
"url = 'http://sfbay.craigslist.org/search/eby/rea?housing_type=6'\n",
"resp = requests.get(url) \n",
"\n",
"# BeautifulSoup can quickly parse the text, specify text is html\n",
"txt = bs4(resp.text, 'html.parser')\n",
"\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## House entries\n",
"\n",
"Looked through output via `print(txt.prettify())` to display the html in a more readable way, to note the structure of housing listings\n",
"\n",
"Saw housing entries contained in `<p class=\"row\">`\n",
"\n",
"`houses = txt.find_all('p', attrs={'class': 'row'})`\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Get data from multiple pages on Craigslist\n",
"\n",
"\n",
"First page: \n",
"url = 'http://sfbay.craigslist.org/search/eby/rea?housing_type=6'\n",
"\n",
"For multiple pages, the pattern is: \n",
"http://sfbay.craigslist.org/search/eby/rea?s=100&housing_type=6 \n",
"http://sfbay.craigslist.org/search/eby/rea?s=200&housing_type=6 \n",
"etc."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Get the data using the requests module \n",
"npgs = np.arange(0,10,1)\n",
"npg = 100\n",
"\n",
"base_url = 'http://sfbay.craigslist.org/search/eby/rea?'\n",
"urls = [base_url + 'housing_type=6']\n",
"\n",
"for pg in range(len(npgs)):\n",
" url = base_url + 's=' + str(npg) + '&housing_type=6'\n",
" urls.append(url)\n",
" npg += 100\n",
"\n",
"more_reqs = []\n",
"for p in range(len(npgs)+1):\n",
" more_req = requests.get(urls[p]) \n",
" more_reqs.append(more_req)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['http://sfbay.craigslist.org/search/eby/rea?housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=100&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=200&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=300&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=400&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=500&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=600&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=700&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=800&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=900&housing_type=6', 'http://sfbay.craigslist.org/search/eby/rea?s=1000&housing_type=6']\n"
]
}
],
"source": [
"print(urls)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"11\n",
"100\n"
]
}
],
"source": [
"# USe BeautifulSoup to parse the text\n",
"more_txts = []\n",
"for p in range(len(npgs)+1):\n",
" more_txt = bs4(more_reqs[p].text, 'html.parser')\n",
" more_txts.append(more_txt)\n",
"\n",
"# Save the housing entries to a list\n",
"more_houses = [more_txts[h].findAll(attrs={'class': \"row\"}) for h in range(len(more_txts))] \n",
"print(len(more_houses))\n",
"print(len(more_houses[0]))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1100\n"
]
}
],
"source": [
"# Make a list of housing entries from all of the pages of data\n",
"npg = len(more_houses)\n",
"\n",
"houses_all = [] \n",
"for n in range(npg):\n",
" houses_all.extend(more_houses[n])\n",
"print(len(houses_all))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"# Extract and clean data to put in a database"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Define 4 functions for the price, neighborhood, sq footage & # bedrooms, and time\n",
"# that can deal with missing values (to prevent errors from showing up when running the code)\n",
"\n",
"# Prices\n",
"def find_prices(results):\n",
" prices = []\n",
" for rw in results:\n",
" price = rw.find('span', {'class': 'price'})\n",
" if price is not None:\n",
" price = float(price.text.strip('$'))\n",
" else:\n",
" price = np.nan\n",
" prices.append(price)\n",
" return prices\n",
"\n",
"# Define a function for neighborhood in case a field is missing in 'class': 'pnr'\n",
"def find_neighborhood(results):\n",
" neighborhoods = []\n",
" for rw in results:\n",
" split = rw.find('span', {'class': 'pnr'}).text.strip(' (').split(')')\n",
" #split = rw.find(attrs={'class': 'pnr'}).text.strip(' (').split(')')\n",
" if len(split) == 2:\n",
" neighborhood = split[0]\n",
" elif 'pic map' or 'pic' or 'map' in split[0]:\n",
" neighborhood = np.nan\n",
" neighborhoods.append(neighborhood)\n",
" return neighborhoods\n",
"\n",
"# Make a function to deal with size in case #br or ft2 is missing\n",
"def find_size_and_brs(results):\n",
" sqft = []\n",
" bedrooms = []\n",
" for rw in results:\n",
" split = rw.find('span', attrs={'class': 'housing'})\n",
" # If the field doesn't exist altogether in a housing entry\n",
" if split is not None:\n",
" #if rw.find('span', {'class': 'housing'}) is not None:\n",
" # Removes leading and trailing spaces and dashes, splits br & ft\n",
" #split = rw.find('span', attrs={'class': 'housing'}).text.strip('/- ').split(' - ')\n",
" split = split.text.strip('/- ').split(' - ')\n",
" if len(split) == 2:\n",
" n_brs = split[0].replace('br', '')\n",
" size = split[1].replace('ft2', '')\n",
" elif 'br' in split[0]: # in case 'size' field is missing\n",
" n_brs = split[0].replace('br', '')\n",
" size = np.nan\n",
" elif 'ft2' in split[0]: # in case 'br' field is missing\n",
" size = split[0].replace('ft2', '')\n",
" n_brs = np.nan\n",
" else:\n",
" size = np.nan\n",
" n_brs = np.nan\n",
" sqft.append(float(size))\n",
" bedrooms.append(float(n_brs))\n",
" return sqft, bedrooms\n",
"\n",
"# Time posted\n",
"def find_times(results):\n",
" times = []\n",
" for rw in results:\n",
" time = rw.findAll(attrs={'class': 'pl'})[0].time['datetime']\n",
" if time is not None:\n",
" time# = time\n",
" else:\n",
" time = np.nan\n",
" times.append(time)\n",
" return pd.to_datetime(times)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1100\n"
]
}
],
"source": [
"# Apply functions to data to extract useful information\n",
"prices_all = find_prices(houses_all)\n",
"neighborhoods_all = find_neighborhood(houses_all) \n",
"sqft_all, bedrooms_all = find_size_and_brs(houses_all)\n",
"times_all = find_times(houses_all)\n",
"\n",
"# Check\n",
"print(len(prices_all))\n",
"#print(len(neighborhoods_all))\n",
"#print(len(sqft_all))\n",
"#print(len(bedrooms_all))\n",
"#print(len(times_all))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Add data to pandas database"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(1100, 3)\n"
]
}
],
"source": [
"# Make a dataframe to export cleaned data\n",
"data = np.array([sqft_all, bedrooms_all, prices_all]).T\n",
"print(data.shape)"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>SqFeet</th>\n",
" <th>nBedrooms</th>\n",
" <th>Price</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1890</td>\n",
" <td>4</td>\n",
" <td>539999</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>NaN</td>\n",
" <td>4</td>\n",
" <td>499950</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3288</td>\n",
" <td>5</td>\n",
" <td>609000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1200</td>\n",
" <td>3</td>\n",
" <td>635000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" SqFeet nBedrooms Price\n",
"0 1890 4 539999\n",
"1 NaN 4 499950\n",
"2 3288 5 609000\n",
"3 1200 3 635000"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"alldata = pd.DataFrame(data = data, columns = ['SqFeet', 'nBedrooms', 'Price'])\n",
"alldata.head(4)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"alldata['DatePosted'] = times_all\n",
"alldata['Neighborhood'] = neighborhoods_all"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>SqFeet</th>\n",
" <th>nBedrooms</th>\n",
" <th>Price</th>\n",
" <th>DatePosted</th>\n",
" <th>Neighborhood</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1890</td>\n",
" <td>4</td>\n",
" <td>539999</td>\n",
" <td>2016-04-08 10:02:00</td>\n",
" <td>hayward / castro valley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>NaN</td>\n",
" <td>4</td>\n",
" <td>499950</td>\n",
" <td>2016-04-08 10:02:00</td>\n",
" <td>hercules, pinole, san pablo, el sob</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3288</td>\n",
" <td>5</td>\n",
" <td>609000</td>\n",
" <td>2016-04-08 10:00:00</td>\n",
" <td>brentwood / oakley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1200</td>\n",
" <td>3</td>\n",
" <td>635000</td>\n",
" <td>2016-04-08 10:00:00</td>\n",
" <td>walnut creek</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" SqFeet nBedrooms Price DatePosted \\\n",
"0 1890 4 539999 2016-04-08 10:02:00 \n",
"1 NaN 4 499950 2016-04-08 10:02:00 \n",
"2 3288 5 609000 2016-04-08 10:00:00 \n",
"3 1200 3 635000 2016-04-08 10:00:00 \n",
"\n",
" Neighborhood \n",
"0 hayward / castro valley \n",
"1 hercules, pinole, san pablo, el sob \n",
"2 brentwood / oakley \n",
"3 walnut creek "
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"alldata.head(4)"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"SqFeet float64\n",
"nBedrooms float64\n",
"Price float64\n",
"DatePosted datetime64[ns]\n",
"Neighborhood object\n",
"dtype: object\n",
"<class 'pandas.tslib.Timestamp'>\n",
"<class 'numpy.float64'>\n",
"<class 'numpy.float64'>\n",
"<class 'str'>\n",
"<class 'numpy.float64'>\n"
]
}
],
"source": [
"# Check data types\n",
"print(alldata.dtypes)\n",
"print(type(alldata.DatePosted[0]))\n",
"print(type(alldata.SqFeet[0]))\n",
"print(type(alldata.nBedrooms[0]))\n",
"print(type(alldata.Neighborhood[0]))\n",
"print(type(alldata.Price[0]))"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# To change index to/from time field\n",
"# alldata.set_index('DatePosted', inplace = True)\n",
"# alldata.reset_index(inplace=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Download data to csv file"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"alldata.to_csv('./webscraping_craigslist.csv', sep=',', na_rep=np.nan, header=True, index=False)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data for Berkeley"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"11\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Price</th>\n",
" <th>SqFeet</th>\n",
" <th>nBedrooms</th>\n",
" <th>DatePosted</th>\n",
" <th>Neighborhood</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>113</th>\n",
" <td>849000</td>\n",
" <td>1438</td>\n",
" <td>3</td>\n",
" <td>2016-04-07 09:44:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>292</th>\n",
" <td>1175000</td>\n",
" <td>2192</td>\n",
" <td>4</td>\n",
" <td>2016-04-06 13:53:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>392</th>\n",
" <td>1358888</td>\n",
" <td>3921</td>\n",
" <td>5</td>\n",
" <td>2016-04-06 07:18:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>415</th>\n",
" <td>1565000</td>\n",
" <td>3507</td>\n",
" <td>5</td>\n",
" <td>2016-04-06 06:49:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>597</th>\n",
" <td>600000</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>2016-04-04 19:56:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>655</th>\n",
" <td>725000</td>\n",
" <td>NaN</td>\n",
" <td>2</td>\n",
" <td>2016-04-04 12:51:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>704</th>\n",
" <td>780000</td>\n",
" <td>4200</td>\n",
" <td>4</td>\n",
" <td>2016-04-04 08:12:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>824</th>\n",
" <td>929000</td>\n",
" <td>NaN</td>\n",
" <td>3</td>\n",
" <td>2016-04-02 09:36:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>883</th>\n",
" <td>545000</td>\n",
" <td>NaN</td>\n",
" <td>2</td>\n",
" <td>2016-04-01 16:59:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>887</th>\n",
" <td>1325000</td>\n",
" <td>NaN</td>\n",
" <td>3</td>\n",
" <td>2016-04-01 16:47:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1012</th>\n",
" <td>449000</td>\n",
" <td>1360</td>\n",
" <td>3</td>\n",
" <td>2016-04-01 07:58:00</td>\n",
" <td>berkeley</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Price SqFeet nBedrooms DatePosted Neighborhood\n",
"113 849000 1438 3 2016-04-07 09:44:00 berkeley\n",
"292 1175000 2192 4 2016-04-06 13:53:00 berkeley\n",
"392 1358888 3921 5 2016-04-06 07:18:00 berkeley\n",
"415 1565000 3507 5 2016-04-06 06:49:00 berkeley\n",
"597 600000 NaN NaN 2016-04-04 19:56:00 berkeley\n",
"655 725000 NaN 2 2016-04-04 12:51:00 berkeley\n",
"704 780000 4200 4 2016-04-04 08:12:00 berkeley\n",
"824 929000 NaN 3 2016-04-02 09:36:00 berkeley\n",
"883 545000 NaN 2 2016-04-01 16:59:00 berkeley\n",
"887 1325000 NaN 3 2016-04-01 16:47:00 berkeley\n",
"1012 449000 1360 3 2016-04-01 07:58:00 berkeley"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Get houses listed in Berkeley\n",
"print(len(alldata[alldata['Neighborhood'] == 'berkeley']))\n",
"alldata[alldata['Neighborhood'] == 'berkeley']"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The average home price in berkeley is: $ 936,444 \n",
"\n",
"The most expensive home price in berkeley is: $ 1,565,000 \n",
"\n",
"The least expensive home price in berkeley is: $ 449,000 \n",
"\n"
]
}
],
"source": [
"# Home prices in Berkeley (or the baseline)\n",
"\n",
"# Choose a baseline, based on proximity to current location\n",
"# 'berkeley', 'berkeley north / hills', 'albany / el cerrito'\n",
"neighborhood_name = 'berkeley'\n",
"\n",
"print('The average home price in %s is: $' %neighborhood_name, '{0:8,.0f}'.format(alldata.groupby('Neighborhood').mean().Price.ix[neighborhood_name]), '\\n')\n",
"print('The most expensive home price in %s is: $' %neighborhood_name, '{0:8,.0f}'.format(alldata.groupby('Neighborhood').max().Price.ix[neighborhood_name]), '\\n')\n",
"print('The least expensive home price in %s is: $' %neighborhood_name, '{0:9,.0f}'.format(alldata.groupby('Neighborhood').min().Price.ix[neighborhood_name]), '\\n')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Scatter plots"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Plot house prices in the East Bay\n",
"\n",
"def scatterplot(X, Y, labels, xmax): # =X.max()): # labels=[]\n",
" \n",
" # Set up the figure\n",
" fig = plt.figure(figsize=(15,8)) # width, height\n",
"\n",
" fntsz=20\n",
" titlefntsz=25\n",
" lablsz=20\n",
" mrkrsz=8\n",
" matplotlib.rc('xtick', labelsize = lablsz); matplotlib.rc('ytick', labelsize = lablsz)\n",
"\n",
" # Plot a scatter plot\n",
" ax = fig.add_subplot(111) # row column position \n",
" ax.plot(X,Y,'bo')\n",
"\n",
" # Grid\n",
" ax.grid(b = True, which='major', axis='y') # which='major','both'; options/kwargs: color='r', linestyle='-', linewidth=2)\n",
"\n",
" # Format x axis\n",
" #ax.set_xticks(range(0,len(X))); \n",
" ax.set_xlabel(labels[0], fontsize = titlefntsz)\n",
" #ax.set_xticklabels(X.index, rotation='vertical') # 90, 45, 'vertical'\n",
" ax.set_xlim(0,xmax)\n",
"\n",
" # Format y axis\n",
" #minor_yticks = np.arange(0, 1600000, 100000)\n",
" #ax.set_yticks(minor_yticks, minor = True) \n",
" ax.set_ylabel(labels[1], fontsize = titlefntsz)\n",
" \n",
" # Set Title\n",
" ax.set_title('$\\mathrm{Average \\; Home \\; Prices \\; in \\; the \\; East \\; Bay \\; (Source: Craigslist)}$', fontsize = titlefntsz)\n",
" #fig.suptitle('Home Prices in the East Bay (Source: Craigslist)')\n",
" \n",
" # Save figure\n",
" #plt.savefig(\"home_prices.pdf\",bbox_inches='tight')\n",
"\n",
" # Return plot object\n",
" return fig, ax\n"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA80AAAIdCAYAAAAH/59uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xm8HFWZ8PHfk4QQkCXiwg5BNEREh8gAgg6rvi6IjKgQ\nUJRFcFdknBFHBsEFRRllxlcBR5AXRwmbjiuDsomDiIqJKAoRZXEBVJgISiCEPO8fp5p0Ol339nb3\n3/fz6U/fqjqnzqm+1dX99Dl1TmQmkiRJkiRpTdPGugKSJEmSJI1XBs2SJEmSJNUwaJYkSZIkqYZB\nsyRJkiRJNQyaJUmSJEmqYdAsSZIkSVINg2ZJkiRJkmoYNEuSJE0gEfHKiNhwrOshSVPFjLGugDQV\nRMQTgUMz89/Hui6SxqeIWA8gM/8y1nXR+BUR7wI2yMyL22zbFtgXeDxwJ3B5Zv6x2rZ/Zn5tVCs7\niVU/WuwNbAXMBJYA387MZdX2dYE9MvO/x66WI28sr1sR8QrgaZn5kdEuW1OPLc3S6DgSOD0injHW\nFZlMImJuRFwXEXdHxMqmx30R8f2I+Nsq3TERsSgiHmpJ98uIuHSsj2OQal6ThyPifyLiyupxbUTc\nGBGXRsQRETG9zzIvqsrbbVDHMdLGS50j4hkRcVdEPAzcDxw3imXXvX9+1HSuXBUR10fEnU3bx31Q\nX3Nsy1veB1dExPeqdP8YEY8b63oPJyIOBZ6XmSe2rJ8ZEWcCFwAPAT8GZgMXRcR7IuIY4J2jXuFJ\nKCK2iYiFwK3AS4E/AouBjYELI+KtVdIzgYNGqU6jej0b7ro1WvXJzEuAtSPi/SNZjgRAZvrw4WOE\nH8Ai4FHgg2Ndl8n6AC6tXuOfAjNq0mwOrKzSvXus6zyKr8kZNdv3p3zhuRHYoscyNmp6TT8x1sc8\nHusM7AT8zRDbZwKnVvU5cYzPlR8MkeYpwLeqdBuNYt2GfP26OLazarb/PfBX4DfADmPx+nd4HFsD\nvwOe2Gbb54DvA2u12fZJYAVw5Vgfw0R/AAcDDwKXAZvUpDke+F51jTlnFOo0JtfguuvWIOvTyXsf\nCOBKYL+xPj98TO6HLc3SCIuI7YC/qRYXjGVdJrm7KR+ef8zMFe0SZObvmhbvGpVaja27q+dl7TZm\n6ar5IWAH4JsR0fVnQmbeB5wC/A+lZWXcG4M678eqa0C7+iynBHYxCnWp03j/1LYiZ+avgVdUabcc\npXrBMK9fBxrvg7+225iZ/0U5HzYHvh4Rs/ooayR9AjgzM//UvDIidgJeB5ycmY+0yfcO4OejUL9J\nrWrl/yIlIH5pZt7dLl2WrsK3ATka9Rqra3DddWvA9Rn2vZ+ZSTnHz/Y+f40kg2Zp5B0KXEz5YNkm\nInYd4/pIzS6vnp9BaXnuWmaekJl7ZuYtg6vWyBrlOj+vgzSj8gW7X5n5AKUL8FajWGwnr1+/vlg9\nbwm8bBTK60pEPBN4Me2DkJdRzp9ft8ubmSsprc3qUUTMBT5DaWU+vObHiWbvBJaPeMUqY3gNbnvd\nGmB9OnrvZ+ZPKT9mjNrtLZp6DJqlkbcA+EfKL89QgmhpvPhz09/bjlktJqmIeDplYKbJ5PuMUtA8\niq/f75v+3noUyuvW0ZTu1X9ss22T6vlvh8j/7cFXaUr5ELAOcHFm/na4xJn5B8qPS+pRD+/9zwBv\nH8c9RTTBGTRLI6gaiOq+zLwDuJDS2vyqiBjLbphSsyc3/b2klx1ExLSIeEJEzB5QnUbcSNc5IqZH\nxHOAS0Zi/6MpIj4UEXs0rfo58MQRLnO0X78dm/4ej12ZX0l94Hs75bPl5IjYvF2CzLwdW5t7EhGb\nAAdWi92MPj5qo2aPt2twP/Xp471/JTCd0iNDGjiDZmlkHUIJlml63hjYp13iapTnm5tGe10aEac1\nbT80IpZV2/4aEae25D+wGhH22xHxw4i4OiL2a0mzW0R8JyJ+EWWU6b+r8n0nIu6IiOOa0u4UEadF\nxCXVfhdHxH9ExDZ1B1yN4vqOagTe71aj1X4gIp4bEQujjGL9g4iY0ZRn2HqPpojYpRr98/tVXa6L\niOObR9eNiG2rEXh/FhH3RMQ/RMSGEXF6RHw9Im6qtu9Spd80Ij4TEd+MiCURcU1E1HY9G8XX5BXV\n84+Ab1Rld3SORMTsiLgXeIQyguzba47lbyLii1FGYb4iIr4VEf8eEWvcF9vhOTwzIv6lOreuqtJ/\nOCI+FuW+w1pD1XmI/+knIuJr1fqrorNbLN4CfBhotHocH6tGoz57mDpuFBGfiohvVGU+dh7VpB/p\nc2XT5oXM/FlmntxSh46vFR3+/3p+/Xr0fkpX029n5jf6OLbDI+Lnseoafn9EfKJp+4JY/Rr+r8NV\nLMq4GJtQ3qPtLKScz08BbqzO1xdHxPrNiTLzyzX7H/Z6V6WbG2Xk/b9W9T+nadvOVf7l1bYTm7Z1\n/JlTpe/4elGl7+n8j/I59aeIeNswSV/Eqvt2bxxuv02uofrc7+E16Oiciw6uwdHlZ3KH78+2hqvP\nSL73q3usf0AZ2E8avLEeicyHj8n6oHzI/gbYvGndEsqIkmcPk/eTVbrXt9l2KKUlZOOW9f9GmZfz\nqU3rDqGMmnp407onAC8EvluV8e6qvI2q5eWUX2s3pQwg9WOq0agpH2IXUbr07tymbtMpXxT+CGxZ\nrVubMiDIvVXZ2wPnNe2zo3p38Hp/jjJi55AjxLJqVM/X1mx/G/C/wIub1s0GvkAZmXuLat16wPOB\nL1f7Own4PLB102vxA+A+YB6lq94m1bYZwA8pI1dv2qYOg3xNHgU+3mbbBpT7vx6htGBt1LSto3Ok\n6XX4CDUjPwOHUabAeXfTupnA1ZRbFqb1cA5fTBkUaXrTuudSBrFq+39tqVPbOnfxP70XeFKH/4P3\nVfs6bJh0e1bn5kcp99c23j8zKMFS2zIHfK6s8f6hDMJzL2W+2bq8XV0ruvn/dfr69fE+mEMZCflh\nyhf1mf0cW1O+j1dlvrPNtiOAW6gZfblN+ldX+1pj1OymNG+u/uePVv/HlZT39g+BdwGzavJ1dL1r\nyXMYNSNDA//S5n3VzfWk4+tFv+c/ZZqoR4FFw6T7CKs+Nx7X4znYzWvQ7fup9hpMb5/J3bw/G9et\n1utoXX1G9L1PuX7e3Mv/yIeP4R5jXgEfPibrA9gL+J+WdR+oPmDuo83UIE3pnlqlu6zNtn8ADmhZ\n99oq/YI26b8C/AlYu2X9UVWenwFrUYL8zwOfqrZvQxlt9nfAOk35ZlO+1FzXpqyDqn3+R8v6xpes\nD/Rb7yFes8aX/vso3bSuqp6bH1cxRNBMaVF4FDimzbYAbgKuY/VAb99qn78Hnt2S5/hq26+BrVq2\nvYc2P4yM0Gvy25bX4brqcRawzxD5hzxHmtLtQ8sXp2r9/Opc+VrL+h1Z9aV+djfHDaxfpXtmm3Qf\na/d/rTm2tnXu8H/6KPDqDstpfPEbsl6s+vJ5H7B9zbny6pb1I/n++Q7wq6b3y1BBc8fXim7/f52+\nfh0e250t74Nrq//x7yg/IG3Qz7G15NuKEri1u06+C3hlF/VvBKLThkl3IOUa9WjToxFALwIe35K+\n6+tdy7naLmh+3RDvq+E+czq+Xgzi/Kd0eb8eOHCY1/WspvdB9HoedvIa9HrOUX8N7vYzudv35xpB\nc119eth31+994E3VedL2RyIfPvp52D1bGjmHsqpLdkNjYJANKVMptJWZt1J+Wd83Iua0bH4Ja95X\ndQLlw+grbXZ3JfB4YLeW9Y1pmb6XmY9kcVhmvqWqw22UKVielpmPTVmUmUspU7g8u01Zja5jf2hZ\nf0/1PH8A9R7O4szcJzP3rp6bH3sPk/fD1fMa91JlZlb13IVV97fBqtfxt5n545ZsjdfhR5l5Z8u2\neyhfmDZuWT8Sr8mVLa/DbtXjDZl55RD5hjxHmjxak/9EyhfDc5tXZuZi4PXAQdX5BJ0fd+PL88kR\n0Xpf7X8BNw9xPJ3UGYb/nwYjN1jUTzKz9Z7axrnSWuZIvn/2zMxtgZ0pPSJqdXmtGNT/r1tJGcSp\n+X3w3MzcjPLF/2Dgzoh4/WqZersOUr3fLwN2iYhntWx+GaU3Q6eeBPwlyyjY9QeY+aXMfEZVp+Mo\n58VSyrE/C/h0S5Zernf9GO560s31Avo8/zPz4szcNTO/NEy972v6e51h0g5n2Gtqj+dc3fWs28/k\nkby+jsZ7/y7KraebDWBf0mpmDJ9EUrciYi3g5ZRfSh+TmT+LiF9QuuseQvmgqPNZSmv16ylfDoiI\n5wLfb/7yVAXVT6V8GH8jIoLVp4FYD7iD+g/7n9VVIDOXRsTaEXEApfXtGZTrxsa0v358t3puHVm3\n8WX/hgHWe6AiYgtKV9SHMvPemmR3UoKXV1C6mTVrN4jWox1sm95UhzmMo9ekSe05Uqeqe2NAlsWt\n2zOz+X7IOXR43Jn514g4hfIF+6UR8eNq/5cBXxkusOjSUP+3kfr8bDdFyxpljta5kpk3RMQaQUlE\nrAesyMyHqnQdXStG+f/Xkcy8NSJeQvl/nxUR0zPzrKbt3V4HG86kvAfeSOk+TUTsA3w3M4f60abV\nuqw+yv1wx/MT4CfAv0XETOBUyjy2r4qI92XmkgFc7/qxxvWkm+tFlX4Oo3etbA7mNqFmaq9WETEd\nmJuZv2izechrah/nXKuOP5Orckfs/TlK7/0Hq2fna9bAGTRLI+OFlF87vxCrD5QdlC6mAewXEY/L\nzL/W7OMSyj1PR0TEidUHylGULt7NGi2VKzKz7QBjw6j9MhYRhwGnUbowfhR4X2b+b0TcRpspZzLz\nexHxWeCgiHhmZv40IjalfGH7CdA86E2/9R60LarnoebWbMzN2W5AmqHydTpf53h7TRo6/sLe5EmU\nexGTcs/kULo67sw8OSKuo3TP3JfSGnoMsCgiXpKZ9wy5g86N2jyrPZQ5mudKuyl2TgT+k2pgpG6u\nFaP4/+tYZt4bEV8A3gqcGhH/2bg2d3sdbPINymv36oj4x2p/R1O623djOUMM3BoRLwauafdZkmVw\npHdGmed5b8rrvYT+r3f9aHc96eZ6AaN7/v83qwLyHegwaKbcK3wUcGybbUNeU/s451bT5WdyI8+I\nvT9H4b3fOGdH+4dlTQF2z5ZGxqHAsdm+e/AelG5K61Bao9vKzIcp9zptAuwfERsAT6i6bjX7XfW8\ndkRs1GU9k9V/nX9MRLwd+H+Ue9p2zszzM7OTLzMbUu4Ve19EXAmcX+1nt8xs7ubZT71HQqP72rpD\npHlS9dxurtRBGG+vCQxxjgzjXla1kA437UjHxx0RMyJibmZ+KzNfk5mbUlpNTqB8Sf1MD3UdVRHx\ntojYuc/djNq5kpknZOY1Lat3BH4B3V0rBvH/G9Dr185N1fP6wHZVWb1eB6l+6PwspdXz0Ih4MmUg\nqdu7rNefgccNsf0gSqvrUM6l/Fi7XrU8Ute76cNsr7uedHO9gNE9/++hDMIVlK71ndqB9tOXDXlN\n7eecq9HpZ/KIXl9H6b3fOJ/rGiOknhk0SwMWEetSftFvO8dgZv6eMlpxULpoD+U/qnTHUALxL7TZ\n328pvxgDPKemTu3uqxvOP1E+2N+VmStats1s2vcLIuIF1d/rAnMy8/LMfGX1Q8FemfmxRjfOUah3\nTzLz18CtwPRY8z7yhm0pr8mlI1SHcfWa9KPqfnpFtdh2iqaI2CwintLlcW/Omvc8/jYzG93+9h1A\n9Qep0eWwucvJEyg9Tno2ludKlKmMnpiZjVadjq8VlJGjz21OMMz/b0RevxrNcxw3Wte7vg62+Czl\nGN5AOfbP9VCv24ENImLWEGmGmwbtT9Xzr6Hv691QP6LV7WtIXVwvtq3Sj/b5fwIlEDsoaubCbuMg\n4Ks9lNXvOUdTmo4/kysjeX3tdt+9vPcb3bJb7+GW+jbhguaIeF2smv+w7vFIm3y7R5kf9d6IeDAi\nfhJl3rqhujy9Lso8gQ9EmS/3qhhi7r+ImBURJ0eZZ3dZlHk+L4iIeYM6fk0IBwCXZuaDQ6Q5t3p+\nfkQ8oS5RZt5EGd3zhZRRSesGj3lv9XxkzfZ/pkx/1Y3GHJ+rffhExNMord8NmzUtzwLmR8SOHZYx\nEvXux4nV86taN1TXiv0p97edN4J1GPRr0ksr8aCcTPni8+Yhtjeuwd0c964RsUObNLexKjgYL+6g\nfOl7UtO6zSndLvs1Vu+f41j9fu9urhWbUgbH6vT/N5Kv32Oqnjyvo7xfLsrMxrH0ch18TPUj6dcp\ngze9lt6CqEYL+BrzQjc5Nsr9y3V2BR5g9QC41+td43+0bkueoMyRm/R2+18n14vmAKqv8z8iXhVl\nTuph5/XNMjjnUZRjPifKuCW1IuKlwM8z8+7h9t1GX+dci24/k2Fkr6/d7LuX9/6WlPv07+qrllIb\nEy5opgwacFLN40rKxfqbzRmiDKTwHeB5wJco94muRZkr7vx2hUTEaZRfhDehdBn5PKWrzdciYo0L\nevVhdTllaog/A6dTWhNfDvxohLqSaZyJiK0p5+JwXdQuY9UXizcNk/Y/KO/V/2lq2VlNZn6TMhXV\nyyLijU31mRkRHwe+3KZ714a0H725odGq/b7qyxARsRllcJuvV8tzKK0Rt1b1uI8S5P8gIm6JiF9E\nxM+qLyZfiIjXV79891PvNVRf8DatFjeKMgBLu3TNx7rG6JqZuZDSovDeiNi3Kd90ypQYD1Cm+2r+\nhb7xy/b6rKmxbYNOt43AaxLApkP9QDiE4c6RhkZ3ytVeg8y8jnJ+7xIR/7fRUhbFscAfqi+j3R53\nAP9ZfYlspNuYMpXPGvfodVPnSq//03a+Tvky+PfVcc+mzN3eel9k12WO0PunthUnIjaKiBMo75Hm\ngYy6uVZcTrmedfr/6/T1G+7YGuNJtEuzDeV7wxaU7wpH93hst9ZU48zq+ZLsbgCwhh9S7tVsHem4\n2XbAxdXrs5rqc+ntwD81/5jb4/WOLKO7LwZ2izIgXMMJlM+2oLTI/n1VdsOQ15NurhdV+n7P/3+h\n/Jhw4hBpmut3IWWU9ecCX41yb/AaIuKFwIJq/606uab2cs7VXYO7+kxuHAKdvz/rrod119du9t3L\ne397yrz20uDlOJj3alAP4HuUe2L2a1q3PuXXumXA/Kb1MylzND5KmcageT+NaU1uoWneRsrgC3+i\njM7Xbs7VlcDClvX7V+t/Otavj48RPfe2pcyDuZxV82PeTsvcppRffa+tzsnmuTRvAb5as+91KdMo\nbNdBPXah3Hv1A0qLwpeAfVvS7EH5ErasqfxfAJ9ps783UT5wf0H5EegiyofSZtX6G4G3t+R5R8ux\ntc4ZejOwSbf1rjneuZT7vu5uKeeP1fXgb6t0x1BGCf1LS7olwDfb7HdXynRh11THfRXlC9D6LWV/\nn/LFsrG/GymtHjtXx9J4jR8Bfkxp0Wl9/R/bNsKvyT3VazKvg310dI5Qzvvrm17XRyhfWP62Jd1O\nlOnWfkbpgvk1aubeHO64KQHQ16vz8MvVsV5ePV7e4Xu1bZ17/Z92UOazquNeVB3TvKZt7cpcDLyG\n0u10LM6V61lzXu9bq/IfpYxY/Pe9XCt6+f8N9fp1eWwPAv/TcmyLKC1XlwKH1Oyr6+tgS/6gtJpt\nNVy9h9jH14CzarZ9jvLj/h6Uz5dPULoGP796zX81TP2Gvd61yfNE4OPV8X+7+p8eUNXhPspn2ncp\nwWPHnzndXi/6PP+PozRyvLPL/8VWlMD2D9XrfijwAkpPhc9T5nKPljzdvgadvp+GvQbTxWcyHb4/\nWfO61bg2HVdXn0733c97n3IP+Um9vs98+BjqEZlj2XNvcKruHjdS7kPaOqsDi4gjKfcUnZuZR7bk\n2ZvyZvxONs3fGhHnAa8GjsjM81rynEz5NfX9mXly0/o7KL9SPyUz72jJ02jl3iczvzOgQ5bGnYg4\nl9IN8eCsptmofilfnzJQzQsov+qfn5mvr9uPJE0WVSvhGZl5QB/7OJgSpG6RLV/cIuL5wLVZzelb\ndcXdiRLY3k35YXCkBi+csqJ06d+HEkSvRflh6ds59K1Zo2oqfSZHxFaUxoodcs257qW+TaYpp95A\n6e762ZYPlL2r9Ze1yXMN5Zfn3SNirVzV9bURQLfLcynlF9h9KPfXEGVgii2BW1oD5qY8f1flMWjW\npBQRT6fcs7drNs1LWb0f76f8Cv3j6oNt97GppSSNnKo7+F7A95uCp6OBs/vc9cXAKZTRm1ebNzsz\nL29ZXkybuY41WFlGnv6vsa5HnSn4mXwI5ccjA2aNiIl4T/MaqvteXk3pCtL6wbRd9bykZT1Z7i26\njfLjwVOqfa1LGWjgL9l+vrhfVs9zOyljiDzSZHM/pavXcPe/bkLpqihJk83RlO6mH4XHRhrfMzN7\nGQDsMdX3lX+m9HSTOjFlPpMjYgbwRuCDY10XTV6TImimDMwwmzJi8e9atjUGKaibSL6xvjFoQbfp\ne80jTSrVe++fgP+IiKMiYp3m7RExJyLOogyo946xqKMkjbB7gYeAayNibcrtYacMYseZeQHwu4g4\nZhD70+Q2xT6T3wIszsx2PUSlgZgs3bOPoXTBPmusKyJNZZn58Yj4JmVqjssjYgWlB8hawFJKV7a3\nZebyMaymJI2IzLw4Ip5DuWXsLcAnWrtP9+kw4LKIuC4zfzrA/WoSmgqfyRHxVOD1lFsgpREz4YPm\niNieMtr1b1h9/sGGRivvhm22Na9f2mP6XvOsJiImx4hs0tBeCny2mkVDkia7547Q9e5Gr6MagMn0\nmfyHSXIcAjJz3P0zJ3zQTP0AYA23UEaRnEsZsv4x1VyE21Cmz/g1QGY+GBG/AzaLiI3b3NfcmFuu\n+f7lW6rnunuW2+VZw2QZyVwaCyeddBInnXTSWFdDmrB8D0n98300eq6++mq23nprttlmm7GuigZo\nvP74MaHvaa7uF3oNpavJOTXJrqTMkfiiNtv2pMyBe23TyNmNPNTkeUn1fEVjRWb+CrgTmBsRW9fk\nyab9SpIkSerRXnvtZcCsUTOhg2bgIODxlDkIWwcAa7gY+BOwICJ2aqysAu4PUoLZM1rynEkJtN8b\nEbOb8syh3KP0EHBuTZ6PRtNPJBFxAGWO5puco1mSJEmSJpaJ3j27MQDYZ+oSZOYDEXE0cBFwdUQs\nBO6jzHU4F7goMy9qyXNdRHwceCflvqGLgZmsGqX7rZl5Z0tRH6fcG/JK4PqIuALYulr+C3Bkvwcr\nqd5ee+011lWQJjTfQ1L/fB9Jk1NM1PtoI2Ie8HNKt+htau5nbk6/G/BeyqBhs4BbKXM6f7Iub0S8\nltKyvD1lrrsbgI9lZrsBxxrzRR9PmWB9K8oceVcBJ2XmzcPUb7hDkCRJkqRJKyLG5UBgEzZonmwM\nmiVJkiRNZeM1aJ7o9zRLkiRJkjRiDJolSZIkSaph0CxJkiRJUg2DZkmSJEmSahg0S5IkSZJUw6BZ\nkiRJkqQaBs2SJEmSJNUwaJYkSZIkqYZBsyRJkiRJNQyaJUmSJEmqYdAsSZIkSVINg2ZJkiRJkmoY\nNEuSJEmSVMOgWZIkSZKkGgbNkiRJkiTVMGiWJEmSJKmGQbMkSZIkSTUMmiVJkiRJqmHQLEmSJElS\nDYNmSZIkSZJqGDRLkiRJklTDoFmSJEmSpBoGzZIkSZIk1TBoliRJkiSphkGzJEmSJEk1DJolSZIk\nSaph0CxJkiRJUg2DZkmSJEmSahg0S5IkSZJUw6BZkiRJkqQaBs2SJEmSJNUwaJYkSZIkqYZBsyRJ\nkiRJNQyaJUmSJEmqYdAsSZIkSVINg2ZJkiRJkmoYNEuSJEmSVMOgWZIkSZKkGgbNkiRJkiTVMGiW\nJEmSJKnGjLGugCRJ0mSwfPlyTj31VADe/e53M3PmzDGukSRpEGxpliRJ6tMpp3yKWbNewYknbseJ\nJ27HrFmv4JRTPjXW1ZIkDUBk5ljXQUBEpP8LSZImnuXLlzNr1ivI/Aqr2iNWEnEADz10iS3OktSh\niCAzY6zr0cqWZkmSpD6ceuqpZB7G6l+rppH5mse6a0uSJi6DZkmSJEmSatg9e5ywe7YkSROT3bMl\naTDsni1JkjQJzZw5kw9+8EVEHABcAFxAxMv44AdfZMAsSZOALc3jhC3NkiRNbE45JUn9Ga8tzQbN\n44RBsyRJkqSpbLwGzRO6e3ZE7BsRX46IuyLioYj4XUT8d0S8qE3a3SPimxFxb0Q8GBE/iYh3RETt\naxARr4uI6yPigYhYGhFXRcR+Q6SfFREnR8TNEbEsIu6JiAsiYt6gjlmSJEmSNHombEtzRHwUeBfw\nG+BS4E/Ak4CdgMsz8/imtAcAFwPLKDcb3QfsD8wDLsrMg9vs/zTguGr/FwMzgQXAE4C3ZuanW9LP\nBK4Edgd+WP29JXAQsBzYOzN/OMTx2NIsSZIkacoary3NEzJojoijgbOAzwFvyMwVLdunZ+aj1d/r\nA78C1gd2z8xF1fqZwFXAc4BDMvPCpvy7AdcCvwR2zsz7q/VbAT8G1gXmZeadTXneA3wIuDAzFzSt\n3x/4CnBTZj5ziGMyaJYkSZI0ZY3XoHnCdc+ugt0PAnfQJmAGaATMlVcBTwTObwTMVZrlwAlAAG9q\n2cWbgAQ+1AiYqzx3Ap8C1gaOaMnzxirPu1vq8jXgu8D2EbFn50cqSZIkSRprEy5oBl5A6YZ9CZAR\nsV9E/FNEvD0intMm/d6UYPayNtuuAR4Edo+ItVryUJPnUkqgvU9jRURsS+mKvSQz7+gkjyRJkiRp\n/Jsx1hXowc6UIHg5sAjYoVoGiIi4BnhlZv6pWrdd9bykdUeZ+WhE3AZsDzwFuCUi1gU2Bx7IzHva\nlP/L6nlu07raMobII0mSJEka5yZiS/OTKa22/wisBJ5LuV/5WZSW4T2AC5vSb1g9/7lmf431s3tM\n32seSZIkSdI4NxGD5kadHwH2z8zrMvPBzLwJOBD4LbBnROw6ZjWUJEmSJE0KE7F79tLqeVFm/qZ5\nQ2Yui4jLgCOBXYDrWdXKuyHtNdY39ttt+l7zrOHwww9nzpw5AMyePZsdd9yRvfbaC4Crr74awGWX\nXXbZZZfM/ngMAAAgAElEQVRddtlll112eVIsL168mKVLS4h0++23M15NuCmnIuII4Gzg0szcr832\njwL/ALwnMz8aEZ8HDgUOzcwLWtJOpwS8awHrZeYj1frfAJsBm7Xe11wNNvY94LuZuWe1blvKfcu3\nZObT29TpeOAU4AOZ+b6a43LKKUmSJElTllNODc4VlIG/tq/ZvkP1fFv1fCXlHugXtUm7J2XO5Wsb\nAXNTHmryvKSpHgBk5q+AO4G5EbF1TZ5s2q8kSZIkaQKYcEFzNVfy14CtIuLY5m0R8X+AFwL/C/x3\ntfpi4E/AgojYqSnt2pT5nhM4o6WYMymB9nsjYnZTnjnAW4CHgHNr8nw0IqIpzwHA84CbMvM7XR+w\nJEmSJGnMTLju2QARsTlwLWVu5CspU089BTiAMqL2wZn5X03pDwAuAh4GFgL3AS+jTAF1UWYuaFPG\nacA7gd9RAu+ZwMHARsBbM/OMlvQzq7rsBtxAaYneGnglJcjeJzN/NMQx2T1bkiRJ0pQ1XrtnT8ig\nGSAingCcSAl+NwXuB64BPtIuOI2I3YD3UoLaWcCtlHujP1kXrUbEaykty9tTgvEbgI9l5qU16WcB\nxwOHAFtVdboKOCkzbx7meAyaJUmSJE1ZBs0akkGzJEmSpKlsvAbNE+6eZkmSJEmSRotBsyRJkiRJ\nNQyaJUmSJEmqYdAsSZIkSVINg2ZJkiRJkmoYNEuSJEmSVMOgWZIkSZKkGgbNkiRJkiTVMGiWJEmS\nJKmGQbMkSZIkSTUMmiVJkiRJqmHQLEmSJElSDYNmSZIkSZJqGDRLkiRJklTDoFmSJEmSpBozBrWj\niJgFbAZsCKwD/BX4Q2beNagyJEmSJEkaTT0HzVWQ/GLg74FdgW1p03IdEQ8BPwKuAi7MzJ/3WqYk\nSZIkSaMpMrO7DBEbAscBbwemAz8AfgzcBtwFPAg8AqxLaXXeEtge2BmYB1wLfDAzLxvMIUwOEZHd\n/i8kSZIkabKICDIzxroerbpqaY6I/YCzge8BhwBXZubyLvJvVeU7MyIWA8dk5h+7qYMkSZIkSaOl\n45bmiHg/8DzgHZn5074KjZgBvAV4PXCwXbZtaZYkSZI0tY3XluaOguaIOB5YG3j/ICO7iHgqcAal\nxfm2Qe13IjJoliRJkjSVTfSg+RWZecmIVCBiNrBjZl49EvufKAyaJUmSJE1lEzpo1sgzaJYkSZI0\nlY3XoHmNKaIkSZIkSVLRd9AcEYdGxGurxy7Vuo0j4isR8ZeIuD0i3tZ/VSVJkiRJGl2DaGmeD3wa\neCawVkRMA74J/B/gZOBdwKsj4uUDKEuSJEmSpFHT1TzNNVYAL8zMawGq4Hg+cEJmfqxa913gC8CX\nB1CeJEmSJEmjYhAtzbs0AubKC4EEzmusyMx7BlCOJEmSJEmjahBBc+s+dgT+kJm/bVn/uAGUJUmS\nJEnSqBlE0LxWREwHiIgnAs8GrmhOEBFPA+4eQFmSJEmSJI2aQQTNlwGnRcQzgc8A02nqmh0ROwAX\nAe8dQFmSJEmSJI2aQQTNpwJbAj8B9gPen5nfioi5EfG9av2zgI8OoCxJkiRJkkZNZGb/Oynds9cF\nVmbmX6t1M4DNm5Itz8y7+i5skoqIHMT/QpIkSZImooggM2Os69Gq75bmiDgOWAZ8pBEwA2Tmisy8\no+lhwCxJkiRJmlAG0T37HZT7mDcYwL4kSZIkSRo3BhE03w48CXjtUIki4jMDKEuSJEmSpFEziKD5\n34CTgRnDpPu7AZQlSZIkSdKoGS7Q7cQfgd8Ci6rRsn8G/BloHtVqY2DuAMqSJEmSJGnU9D16dkTc\nB2wItI5y1rzjADIzp/dV2CTm6NmSJEmSprLxOnr2IFqa7wFuAs4FVtSk2ZAyn7MkSZIkSRPGIILm\nPwCnZOZlQyWKiMMGUJYkSZIkSaNmEN2zdwOWZOa9w6TbIzOv6auwSczu2ZIkSZKmsvHaPbvvoHnI\nnUe8ANgEuDUzrxuxgiYBg2ZJkiRJU9l4DZoHMeVUJ2W8OCLePgplSZIkSZI0MCPa0vxYIRFzgK9m\n5rNGvLAJypZmSZIkSVPZpG5pjoidI+K6iHg4Ih5tfQC/ApYNoixJkiRJkkZL36NnR8Q2wOXA2sBd\nwMbA3dXmmZR7mr8OvKnfsiRJkiRJGk2DaGn+Z+BbwCaZOQf4QWZuUz02B+YB6wGzB1CWJEmSJEmj\nZhBB887AYZm5tFpeERGPb2zMzF8ChwEnD6AsSZIkSZJGzSCC5nsz86Gm5ZuAFzUnyMzfM8CW5oi4\nPSJW1jx+X5Nn94j4ZkTcGxEPRsRPIuIdEVH7GkTE6yLi+oh4ICKWRsRVEbHfEOlnRcTJEXFzRCyL\niHsi4oKImDeI45YkSZIkja6+72kGlkbEDGCtzFwGXAGcFBEXZeYKgIgIYIsBlNWQwFLgE0Dr6Gp/\naU0cEQcAF1MGI7sAuA/Yv8q/O3BwmzynAccBvwE+Q7k/ewHwtYh4a2Z+uiX9TMq93bsDPwROB7YE\nDgL2i4i9M/OHPR6vJEmSJGkM9D3lVBVc7kMZAOxpwKPAncB1wLuAPwDvA56Xmbv2VdiqMm8DMjOf\n0kHa9Smjd68P7J6Zi6r1M4GrgOcAh2TmhU15dgOuBX4J7JyZ91frtwJ+DKwLzMvMO5vyvAf4EHBh\nZi5oWr8/8BXgpsx85hD1dMopSZIkSVPWZJ5y6nzg6ZTu1zMz82FKsPwy4Bbgf4FjgXMHUFYvXgU8\nETi/ETADZOZy4ARKS3XryN5vorRmf6gRMFd57gQ+RRkp/IiWPG+s8ry7eWVmfg34LrB9ROw5iAOS\nJEmSJI2OvoPmzLwBeAqwQ2MwsMz8PCVQvovSXfqszDyj37JarB0Rr46I90TE2yNir5r7k/emBLOX\ntdl2DfAgsHtErNWSh5o8l1IC7X0aKyJiW0pX7CWZeUcneSRJkiRJ498g7mkmM+9qs+7fgX8fxP5r\nbAKc17QcwG0RcURmXtO0frvqeUnrDjLz0aqr9/aUwP+WiFgX2Bx4IDPvaVPuL6vnuZ2UMUQeSZIk\nSdI4N4ju2R2JiAMHuLtzgH0pgfPjgGcCZwJzgG9GRPO9wxtWz3+u2VdjfWN0727T95pHkiRJkjTO\njVrQTLl/eCAy8wOZeXVm/jEzH8rMn2fmm4GPUwbpOmlQZUmSJEmSpq6OumdHxHqU6Zd6tQGlNXik\nnQn8A7BH07pGK++GayZfbf3SHtP3mmcNhx9+OHPmzAFg9uzZ7Ljjjuy1114AXH311QAuu+yyyy67\n7LLLLrvsssuTYnnx4sUsXVpCpNtvv53xqqMpp6qg+X7KgFq9DgGemTm9x7wdiYgNKIHpQ5m5brXu\n88ChwKGZeUFL+umUgHctYL3MfKRa/xtgM2Cz1vuaI+I5wPeA72bmntW6bSn3Ld+SmU9vU6/jgVOA\nD2Tm+2rq7pRTkiRJkqas8TrlVEctzZn5l4h4BDidMhJ0t9HdhsAXuszTi92q5183rbsSeDXwIuCC\nlvR7UrpzX90ImJvyvKbK8/9a8ryker6isSIzfxURdwJzI2LrNiNov4Tyml3Z3eFIkiRJksZSRy3N\nABFxF7B1Nb9x9wVFfD8zn9NL3pb9zAPuzMwHW9bPAb5NGQX7nzPz1Gr9+sCvgPWB51VTZBERawNX\nAbsCCzLzoqZ97QZcC9wK7NKYSqsq4wZgHWBeNW9zI0+jNfmian9ZrT8A+DLws8x81hDHZUuzJEmS\npClrvLY0dxM0PyMzb+q5oIi5mVk3JVM3+3kf5b7la4A7gAeAbYH9gLWBbwAHZuaKpjwHUILZh4GF\nwH3AyyhTQF2UmQvalHMa8E7gd8DFwEzgYGAj4K2t805HxExKS/JulMD6CmBr4JXAQ8A+mfmjIY7L\noFmSJEnSlDXhg+a+C4o4MDO/NID97AG8AZjPqimnlgKLgfMys2038Kr1+L2UoHYWpRX5bOCTddFq\nRLwWeAtlHueVlGD4Y5l5aU36WcDxwCHAVpT7wK8CTsrMm4c5LoNmSZIkSVOWQXPEjzPz2aNS2ARk\n0CxJkiRpKhuvQfNkm3JKkiRJkqSBmVRTTk1ktjRLkiRJmsomdEvzBJpySpIkSZKkgekoaK7cB/xL\nH1NO9TzytiRJkiRJY2FaF2mf32vAXHltH3klSZIkSRp1Axs9OyKmAQcCrwC2BP5I6cp9XmY+NJBC\nJjHvaZYkSZI0lY3Xe5oHEjRHxBbARcAurD5QWAI3Awdk5q19FzSJGTRLkiRJmsombdAcEY8Dvk/p\n6v0V4E7gEeBJwLbA/sADwLMz84G+CpvEDJolSZIkTWWTOWg+njIH82vaRX1Vt+2PAUsz8wN9FTaJ\nGTRLkiRJmsomc9B8HfDizFw6RJrpwOWZuXdfhU1iBs2SJEmSprLxGjR3M3p2nYeHCpgBMvNRYMUA\nypIkSZIkadQMImie1WG6tQdQliRJkiRJo2YQQfNvIuLFQyWIiH2BuwdQliRJkiRJo2YQQfPHgC9G\nxDER8YTmDRExJyL+EbgE+NcBlCVJkiRJ0qgZ1DzNbwNOrxYfBpYD6wLTq3UnZOaH+y5oEnMgMEmS\nJElT2WQeCIzM/CSwH3Aj5R7nDYAZwK+AVxswS5IkSZImooG0NK+2w4gtgC2AP2Tmrwe680nMlmZJ\nkiRJU9l4bWkeeNCs3hg0S5IkSZrKxmvQPKOfzBGxEbAv8DfAE4AHgF8C387M2/uunSRJkiRJY6in\noDkitgY+CLwKWKsmzTeB4zPzpt6rJ0mSJEnS2Om6e3ZEvAr4LLB+B8kfAt6SmZ/roW5Tit2zJUmS\nJE1l47V7dlejZ0fEy4EvAgl8AnghMIcSQM+gTDO1GfB3wAeAPwP/ERELBldlSZIkSZJGR8ctzRHx\nZODnwA3AazLzjx3kWR84F9gbeHpm3tN7VSc3W5olSZIkTWWToaX5DcCvgZd0EjADZOYDwEHAzcCb\nuq+eJEmSJEljp5ug+eXAOzPz0W4KqNL/I3BAN/kkSZIkSRpr3QTN62bmtb0UUuVbp5e8kiRJkiSN\nlW6C5vv6LOvePvNLkiRJkjSqugmaH+qzrIf7zC9JkiRJ0qjqasopSZIkSZKmkm6C5pl9ltVvfkmS\nJEmSRtWMLtLuEhFnAg/2UM7awLN7yCdJkiRJ0piJzOwsYcRKoLPEbbIDmZnTe8w/6UVEdvq/kCRJ\nkqTJJiLIzBjrerTqpqUZ4FvA3T2Usynwgh7ySZIkSZI0Zrppab47MzfpqZCIacDve80/FdjSLEmS\nJGkqG68tzd0MBHZbr4Vk5sp+8kuSJEmSNBa6aWmem5lLei6oz/yTnS3NkiRJkqay8drS3HHQrJFl\n0CxJkiRpKhuvQXM33bMlSZIkSZpSDJolSZIkSaph0CxJkiRJUg2DZkmSJEmSanQUNEfEzIj4RkTc\nHRE7jHSlJEmSJEkaDzptaT4I2Bl4MrBJ84aI2HXQlZIkSZIkaTzoNGjeDHgT8MzMvLxl24c72UFE\nXNpNxSRJkiRJGmudBs0/AF4L/LyPsrbrI68kSZIkSaNuRieJMvPqiHgvsDgivgjc1bR5TkT8CzDU\nJNQbA1v3Xk1JkiRJkkZfZGZnCSM2As4HXtBjWZmZ03vMO+lFRHb6v5AkSZKkySYiyMyhGmPHRMdB\n82MZIuZSBgOL6vEJ4Nhhsj0e+M/MXK+XSk4FBs2SJEmSprLxGjR31D27WWYuAZY0liNiaWZ+Z7h8\nEXFTt2VJkiRJkjSWOh0IbChHdJju0AGUVSsiXhMRK6vHkTVpdo+Ib0bEvRHxYET8JCLeERG1r0NE\nvC4iro+IByJiaURcFRH7DZF+VkScHBE3R8SyiLgnIi6IiHmDOE5JkiRJ0ujpunt27Y5K4Hkg8Apg\nS+CPwKXAeZn50EAKqS97S+BGyo8A6wFHZ+Y5LWkOAC4GlgEXAPcB+wPzgIsy8+A2+z0NOA74TZV3\nJrAAeALw1sz8dEv6mcCVwO7AD6u/t6TMc70c2Dszf1hzDHbPliRJkjRljdfu2QMJmiNiC+AiYBdW\nH0U7gZuBAzLz1r4Lqi//csro3F8C3kVL0BwR6wO/AtYHds/MRdX6mcBVwHOAQzLzwqY8uwHXAr8E\nds7M+6v1WwE/BtYF5mXmnU153gN8CLgwMxc0rd8f+ApwU2Y+s+YYDJolSZIkTVnjNWjuu3t2RDyO\n0qK8AXAq8GbgaOCfgXMorbKXVoHrwEXEO4C9KN3EH6xJ9irgicD5jYAZIDOXAydQAv03teR5EyXo\n/1AjYK7y3Al8ClibNbumv7HK8+7mlZn5NeC7wPYRsWcXhydJkiRJGkODuKf5bZSu0Ttk5j9n5pmZ\neXZmfiQzjwY2A77K8CNsdy0ing58GDg9M/9niKR7U4LZy9psu4YSbO8eEWu15KEmz6WUQHufprps\nS+mKvSQz7+gkjyRJkiRpfBtE0HwA8Ja6vsWZuRL4JwYcLEbEdODzwO3Ae4dJvl31vKR1Q2Y+CtxG\nGUn8KdW+1wU2B/6Smfe02d8vq+e5nZQxRB5JkiRJ0jjW9ZRTbTycmUuHSpCZj0bEigGU1ex9wN8A\nz83Mh4dJu2H1/Oea7Y31s3tM32seSZIkSdI4NoiW5lkdplt7AGUBEBG7Au8BTsvMHwxqv5IkSZIk\nNRtES/NvIuLFmXlpXYKI2Be4ewBlNbplnwfcApzYurkmW6OVd8Oa7Y31jRbzbtP3mmc1hx9+OHPm\nzAFg9uzZ7Ljjjuy1114AXH311QAuu+yyyy677LLLLrvsssuTYnnx4sUsXVrCo9tvv53xqu8ppyJi\nF8pgWe8GLsnMe5u2zaGMXP1e4IWZeX1fhZV9bgj8L2Vgr3ZBcvP60zPzuIj4PHAocGhmXtCyv+mU\ngHctYL3MfKRa/xvKIGabtd7XHBHPAb4HfDcz96zWbUu5b/mWzHx6m3ofD5wCfCAz39dmu1NOSZIk\nSZqyxuuUU323NGfmDyLiROAM4IyIeBhYTpnHeHqV7IRBBMyVh4HP1mx7NjCfMr3TLcB11forgVcD\nLwIuaMmzZ1XXqxsBc1Oe11R5/l9LnpdUz1c0VmTmryLiTmBuRGzdZgTtl1AC+iuHPDpJkiRJ0rjR\nd0vzYzuKeBFl+qe/aVp9K3BiZi4cSCHD1+F9lC7bR2fmOU3r1wd+BawPPC8zb6jWrw1cBewKLMjM\ni5ry7AZcWx3DLo3BzqrW8xuAdYB51bzNjTyN1uSLqv1ltf4A4MvAzzLzWTV1t6VZkiRJ0pQ1aVua\nGzLzv4H/jogtgC2AP2Tmrwe1/y6s8SJn5gMRcTQlmL06IhYC9wEvo0wBdVFzwFzluS4iPg68E7gx\nIi4GZgIHU0bAfmtzwFz5OPBS4JXA9RFxBbB1tfwX4MjBHaY0WCtXrmTRokUAzJ8/n2nTpo1xjSRJ\nkqSxN/BvxZn528z8/hgFzFC6QK+5MvMrlK7Y3wEOBN5K6Ub+TuCQmjzvAo4A7gKOBg4Dfgq8NDPP\naJN+OfB84AOUgb+OBfYFvkRprf5RPwcmjZRFi25ip52OZY897mCPPe5gp52OZdGim8a6WpIkSdKY\nG1j3bPXH7tkaKytXrmSnnY5l8eLTWfU72kp23PFYbrjhdFucNaZWrFjBwoXlDp8FCxYwY8bAOkhJ\nkqRxZrx2z/bbsDTFLVq0iCVL9mL1y8E0lizZ87Hu2tJYOP/8r7LBBgdx2GEzOeywmWywwUGcf/5X\nx7pakiRpijFoliSNOytWrOCoo85l2bKLgYOAg1i27GKOOupcVqxYMdbVkyRJU4hBszTFzZ8/n7lz\nrwZWNq1dydy532H+/PljUylNeQsXLmTZsgW09oBYtuzgx7prS5IkjQZvDpOmuGnTpnHOOW/gyCOP\nZcmSPQF42tOu5pxz3uj9zJIkSZryHAhsnHAgMI01p5zSeLJixQo22OCgqnv2qgHq1lnnldx//4UO\nCCZJ0iQ0XgcC6/tbR0Qc2rSfmzPzBxGxMfAZynRLfwL+NTM/2W9ZkkbOtGnT2Gmnnca6GhIAM2bM\n4OyzD+eoo17JsmUHAzBr1kLOPvsIA2ZJkjSq+m5pjoiPAW8CzgD+C7gO+CGwPXAicBvwLuDUzPxy\nX4VNYrY0S9KanHJKkqSpY7y2NA8iaP4w8PXMvLZafjlwCXBCZp5SrdsY+EJmPr/P+k5aBs2SJEmS\nprLxGjQP4qbFXRoBc+WFQALnNVZk5j0DKEeS1IGVK1dyww03cMMNN7By5crhM0iSJKnWIILm1n3s\nCPwhM3/bsv5xAyhLkjSERYtuYqedjmWPPe5gjz3uYKedjmXRopvGulqSJEkT1rBBc0QcHhFvjoj1\na5KsFRHTq7RPBJ4NXNGyj6cBd/dbWUlSvZUrV3LkkWexePHpPPjggTz44IEsXnw6Rx55li3OkiRJ\nPeqkpflfgU8Cv4uI/xsR81q2XwacFhHPpIyYPZ2mrtkRsQNwEfDewVRZktTOokWLWLJkL1a/tE9j\nyZI9H5tOTJIkSd3pJGh+EfAp4LfAm4GbIuKKiPj7iJgGnApsCfwE2A94f2Z+KyLmRsT3qvXPAj46\nIkcgSZIkSdII6Wr07IjYnDLQ1/MpczA/BHw6M0+tum+vzMy/VmlnAJs3ZV+emXcNrOaTjKNnS+rX\nypUr2WmnY1m8+HRW/Sa6kh13PJYbbjidadMGMYyFJEnSyBivo2f3NeVURMwHdsjMzw+uSlOTQbOk\nQVi06CaOPPIslizZE4CnPe1qPve5NzJ//jPGuGaSJElDm5RBswbHoFnSoKxcufKxe5jnz59vC7Mk\nSZoQDJo1JINmSZIkSVPZeA2aZ/SaMSLWA+YDmwKPB2YDK4G/UAYNuyUzlwyikpIkSZIkjYWug+aI\neDFwHLAXw4y+HRG/BxYCH8rMpb1UUJIkSZKksdLt6NlnAsdUi/cBd1bPDwGPAutWj8cBG1cPgLuA\nV2Xm9wZT7cnH7tmSJEmSprLx2j2746A5Io4BPgJ8AvjPzLytgzxPAg6kzO+8MbBtY0oqrc6gWZIk\nSdJUNhmC5uuBwzPzF10XEjEN+CpwXmZe2G3+qcCgWdKKFStYuHAhAAsWLGDGjJ6HnZAkSZpwxmvQ\n3M08JH/tJWAGyMyVwJnANr3kl6TJ7vzzv8oGGxzEYYfN5LDDZrLBBgdx/vlfHetqSZIkTXndtDQv\nysz5PRcU8WZgZWae2es+JjNbmqWpa8WKFWywwUEsW3Yxq37LXMk667yS+++/0BZnSZI0JUyGluZb\nI+KMiFi320IiYk/gA4ADgUlSi4ULF7Js2QJWvyRPY9mygx/rri1JkqSx0U3zxb8A1wGHRMSXgR8B\nd7Bq9OwVTWlnAk8GdgBeCjwXuCQzbxxEpSVJkiRJGg3dTjm1HfBZShDcScagBNNnAO/OzId6qeRU\nYPdsaeqye7YkSdL47Z7d1TexzLwF+LuIeA5lKqkdgacCG1HmZl4JPECZv/km4Brgy5n5p0FWWpLG\n0qBHub799tt56KGvUC6lpwHrM2vWQs4++wgDZkmSpDHWVUuzRo4tzdLEcP75X+Woo86t7kGGddZZ\nyNlnH84hh7ysp/1FzKHcyfLaas15wI088sivDZglSdKUMl5bmg2axwmDZmn8G3Q36ltvvZWnPe1Y\nyjT2q/YHL+OXvzydpz71qQOruyRJ0ng3XoPmnpsxImI9YD6wKfB4YDbl295fgN8Ct2TmkkFUUpLG\ng+FGuX7Na17T1f7mzZsHfHGN/cFhzJs3jxUrVrTPKEmSpFHTddAcES8GjgP2YpgpqyLi98BC4EOZ\nubSXCkqSJEmSNFa6HT37TOCYavE+yoBfjSmnHgXWrR6PAzauHgB3Aa/KTOdprmH3bGn8s3u2JEnS\nyBmv3bM7Dpoj4hjgI8AngP/MzNs6yPMkyijbb6YE0Ntm5l97r+7kZdAsTQyrBgI7GIBZsxZyzjlH\nDGAgsMOqNecBN5F5e991lSRJmkgmQ9B8PXB4Zv6i60IiplGaUs7LzAu7zT8VGDRLE8egp5y69dZb\nq/ub4eabb7aFWZIkTUmTIWi+MjP36bmgiJcCz8jMU3vdx2Rm0CxJkiRpKhuvQfOQA3m1eHyfZW0F\n/LnPfUiSJEmSNGq6CZpvjYgzImLdbguJiD2BDwAOBCZJkiRJmjC66Z49D7gOCODLwI+AO1g1enbz\nhKIzgSdTRrd5KfBc4JLMPGhgNZ9k7J4tSZIkaSobr92zu51yajvgs5QguJOMQQmm/z979x4fVXXu\nf/yzhhCSVAG11jsgSIBSJemUIhYD2vsNVDCCgmK8YNVTU2tLW22tVnvqqW3xtKeKSlBACDf9SVvt\nTQ2obSkOE2wpEES5tdqLRcUmIST7+f2xd5KZZCbXIZkk3/frlVfYe/baa+0h8Mozz1rPuh+Yb2bV\nHRlkX6CgWURERERE+rJeETQ3NHLubPytpPKAM4Bj8fdm9oCD+Ps3bwU2AE+Y2b9SNeDeSkGziIiI\niIj0Zb0qaJbUU9AsIiIiIiJ9WboGzR3eXNQ5dxSQD5yEX1l7MH6m+V1gP7DDzCpSMUgRERERERGR\n7tDuoNk592ngZmAKrVTfds79DSgF7jaztzoyQBEREREREZHu0t5CYA8A1waH/8Zfu1xfPbsOyAm+\n3gOcEHwBvA5cbGbacioJTc8WEREREZG+LF2nZ7dny6lrge8BPwKWmdlrbWhzPH7BsOvxA+gRZvaf\njg+391LQLCIiIiIifVlvCJo3AnPNbFu7O3EuBKwDlpjZqva27wsUNIuIiIiISF+WrkFzi2uSm/hP\nRwJmADPzgAeA0zvSXkRERERERKQ7tCdoPqaTfQ0B3u7kPQBwzt3jnPutc26vc67SOfemc26zc+5b\nzrljk7Q5xzn3VHBtpXNui3PupiALnqyfK5xzG51zB51zbznnnnPOfbaF67Occ3c457Y756qcc393\nzq10zo1OxXOLiIiIiIhI12rP9OzVwL+AL5tZZbs6cW4y8Dhwnpm93O5RNr/fISAC/AX4B37hsbOB\n8dtyo8EAACAASURBVMBfgbPN7K8x108D1gBVwEr84mWfB0YDq83skgR93ItfJXxf0DYTmAkcB9xo\nZj9tcn0m8CxwDrAp+PNpQCFQEzz7phaeSdOzRURERESkz0rX6dntCZpHA78HHPAE8BKwh8bq2bUx\nl2cC7wM+AHwO+Aiw1swKUzJo5zLNrCbB+buAbwA/NbMbg3NHA7uAo4FzzCxafw/gOfxge1bsWmvn\n3ETgRWAnMN7M3gnODwE241cIH21me2PafB24G1hlZjNjzn8eeBLYamZntvBMCppFRERERKTP6vFB\nM4BzbhTwMH4Q3JaGDj+Yvh+Yb2bVHRlkWznnzgLKgd+Y2SeDc0X4Y37EzIqaXH8e8Ayw3szOizm/\nBLgMuNLMljRpcwdwG3Cnmd0Rc34PcCow3Mz2NGmzHpgEnG9m65OMXUGziIiIiIj0WekaNLdnTTNm\ntsPMzsWfgvwD/IBzD3AQ8PAD5APAFmA5MA842cxuOtIBc2Bq8H1LzLnz8AP8XyW4fgNQCZzjnOvf\npA1J2jyN/2HA+fUnnHMj8KdiVzQNmJO1ERERERERkfSX0ZFGZvYH4A8pHku7OeduwV/PPAj4EH42\ntxy4J+ayUcH3iqbtzazOOfca8H5gOLDDOZcDnAIcNLO/J+h2Z/A9ty19tNBGRERERERE0lyHguY0\n8mX8tdP1nsbfS/rNmHODgu/JKnfXnx/cwes72kZERERERETSXLumZ6cbMzvJzPoBJwIXASOAcudc\nXveOTERERERERHqDLss0O+fmm9k9rV/Zfmb2T+BJ51wUf4r0EuCs4OX6LO+gRG1jzr/Vwes72qaZ\nuXPnMmzYMAAGDx5MXl4eU6ZMAaCsrAxAxzrWsY51rGMd61jHOtaxjnvFcXl5OW+95YdIu3fvJl21\nq3p2pzpybqOZTeiCfjYD44DjzezfzrmlwKXApWa2ssm1/fAD3v7AUWZ2ODi/DzgZv4jZ35u0ORv4\nHfC8mU0Ozo3AX7e8w8zGJBjT14DvAt8xs9uTjFvVs0VEREREpM/qFdWzO+n0Lurn5OB7XfD9WfzK\n1Z9KcO1k/D2XX6wPmGPakKTNZ4Lvz9SfMLNdwF4g1zk3NEkbi7mviIiIiIiI9ABtzjQ7576On5Ht\niCH4ex7362D72HGMBP5uZu80Oe+Au4CvAy+YWUFw/mhgF3A0MMnMIsH5AcBzwARgppmtjrnXROBF\n4BXgw2b2VnB+GBABsoHRZrY3pk19Nnl1cD8Lzk8DngD+bGb1U8YTPZcyzSK9jOd5RKNRAPLz8wmF\nuvJzShEREZGeJV0zze0Jmn8CXI+fMW3Pg9RfbykKmm8C/ht4AXgNeBM4AT9rPBz4G/AxM9se02Ya\nfjB7CCgF/o2/p3MusNrMZibo517gS8BfgTVAJnAJcCxwo5nd3+T6TPxM8kT8wPoZYCgwA6gGzjez\nl1p4LgXNPZQCI0kkGt1KUdFCKiqmAJCbW0ZJyTzy88d267hERERE0lWPD5oBnHPPAe8CSYO/JE4j\ndZnmscA8/D2ZT8Xfxuk/+AXAfg78uD4z3KTdROBW/KA2Cz+LvCi4PuGb4Jy7HLgBfx9nDz8Y/r6Z\nPZ3k+izga8As/Oz6O/jZ7G/HBvFJ2ipo7oEUGEkinucRDhdTXr6AxlUwHnl5xUQiC/TBioiIiEgC\nvSVo/ij+1ONr2tWJP3X672b2vlYv7qMUNPc8CowkmUgkQkHBHiorL4o7n5Ozlg0bhhEOh7tpZCIi\nIiLpK12D5vb+Vl8GjGpvJ0E0+Fp724mks2g0GmSYY/8ZhaiomNwwXVtERERERHq2dgXNZlYHbOlg\nX090sJ2ISI+Sn59Pbm4Z/qqOeh65uevJz8/vnkGJiIiISId02T7N0jJNz+55ND27Z6itraW0tBSA\nmTNnkpGR0SX9Nq53nwzAyJFlLF58nda7i4iIiCSRrtOzFTSnCQXNPZMCo/S2YsU6rrrqEaqq/AL5\n2dmlLFo0l1mzpnZJ/6qsLiIiItJ2CpqlRQqaey4FRumptraWgQMLqapaQ+xMgOzsGbzzzqouyziL\niIiISNuka9Cs3+5FOikUChEOhwmHwwqY00hpaWmQYY4v1FZVdUnDdG0RERERkdboN3wRERERERGR\nJDQ9O01oerZIaml6toiIiEjPounZIiJdKCMjg0WL5pKdPQNYCawkK2s6ixbNVcAsIiIiIm3WZZlm\n59zFZra6SzrrgZRplt6uuwqmddeWUyIiIiLSPumaae7KoHmzmX2wSzrrgRQ0S2/WuDXXFAByc8so\nKZmnrblEREREpEGvDpqdc8cDnwCGAonSOAOBm8ysf6c766UUNEtv5Xke4XAx5eULiF1bnJdXTCSy\nQBXHRURERARI36C50/MUnXMTgKeAwUBLD6iIUKQPikajQYY5fuuniorJRKNRwuFwN41MRERERKR1\nqVjc9z1gF/A48A+gLsE1g4B7UtCXiIiIiIiISJdJRdB8PDDOzBIFyw2cc7NT0JeI9DD5+fnk5j5K\nefkFxE7Pzs1dT37+hd05NBERERGRVqUiaH6ttYA5cEMK+hKRJLqrOnVrQqEQJSXzKCoqpqJiMgAj\nR5ZRUnJd2oxRRERERCSZThcCc879CFhgZntaua7IzEo61VkvpkJg0hk9oTp1ugb1IiIiIpIe0rUQ\nWCqC5kHAT4AfmdnmFq572czO6lRnvZiCZukoVacWERERkd4gXYPmVEzPvhq/ENjPnXP7gQqgpsk1\nRwPpk/IS6UVUnVpERERE5MhJRdD8VeC9+NtNnQh8KMl1SqOKiIiIiIhIj5KKoPmfwO/wp2jXJrlm\nEPBYCvoSkSZUnVpERERE5MhJRdD8D+D/zOyZli5yzm1NQV8i0oSqU4uIiIiIHDmpKAQ2Avi7mb3b\nynW5ZlbRqc56MRUCk85SdWoRERER6cnStRBYp4PmNnfk3IfM7KUu6awHUtAsIiIiIiJ9WboGzV2Z\ninqgC/sSERERERER6bQ2r2l2zk0ECoEHzGxHcG4w8MU2ND8aGNehEYqIiIiIiIh0kzZPz3bOvQEc\nD7xgZpODc8fhV882/C2nWmJm1q8TY+3VND1bRERERET6snSdnt2e6tnPA9OD7/UO4AfM3wd+DdQl\naTsYbTklIiIiIiIiPUy7CoE55441s383OfcmMLQN1bM3mtmEjg2z91OmWaT9uqtieG1tLaWlpQDM\nnDmTjIxU7N4nIiIi0rela6a5Xb9hNg2YAyNaC5gDl7anLxGRlkSjWwmHiyko2ENBwR7C4WKi0SO/\nHfyKFesYOLCQOXMymTMnk4EDC1mxYt0R71dEREREukeXbTklLVOmWaTtPM8jHC6mvHwBjZ/9eeTl\nFROJLDhiGefa2loGDiykqmpNXL/Z2TN4551VyjiLiIiIdEKPzTQ75wYdyQEc6fuLSPrzPI9IJEIk\nEsHzvFavj0ajVFRMIf6/sBAVFZMbpmsfCaWlpVRVzWzWb1XVJQ3TtUVERESkd2lLOubjzrk7j0Tn\nzrkzgUVH4t4i0jN01zRrEREREZG2aNP0bOfcLcAk4Goz+1dKOnbuWmAu8Lkka6X7FE3Plr6oo9Os\nNT1bREREpPfpsdOzAczsXmAVsMU5903n3PEd6cz5pjnnNgGfAT6pgFmk7+roNOtQKERJyTzy8orJ\nyVlLTs5axo27iZKSeUe0gnZGRgaLFs0lO3sGsBJYSVbWdBYtmquAWURERKSXau+WU0OBHwGfBp4F\nfgO8BGwH/m1mXpPrs4DTgXxgMvA5oBr4hpmtTMUD9BbKNEtfFIlEKCjYQ2XlRXHnc3LWsmHDMMLh\ncIvtteWUiIiISO+RrpnmDlXPDtYiXwPMAE4E6m/yLvA2ftroPcDA4Pxh/AB7GbDGzOo6N+zeR0Gz\n9EXdNc1aRERERNJPrwqa427g3CjgQ8Bw4HggB6jBD553A1uBTWZ2qFMd9XIKmqWvika3UlS0kIqK\nyQCMHFnG4sXXkZ8/tptHJiIiIiJdqdcGzZIaCpqlL+uuadYiIiIikj4UNEuLFDSLiIiIiEhflq5B\ns9I5IiIiIiIiIkmo5KtID6YqziIiIiIiR5YyzSI91IoV6xg4sJA5czKZMyeTgQMLWbFiXXcPS0RE\nRESkV9Ga5jShNc3SHrW1tQwcWEhV1Rpit2rKzp7BO++sUsZZRERERHocrWkWkZQpLS2lqmom8f+E\nQ1RVXdIwXTsdeJ5HJBIhEongeV53D0dEREREpN0UNIvIERGNbiUcLqagYA8FBXsIh4uJRrd297BE\nRERERNolZdOznXMDgIlAtpk9HZw7C9hnZgdS0kkvpunZ0h7pPD27Prs8e/YPqKhYRmO9QY+8vGIi\nkQXah1lEREREmunV07Odc3OBvwLPAP8X81IWsNg5d0Uq+hERX0ZGBosWzSU7ewawElhJVtZ0Fi2a\n260Bc2N2eTcVFRcBNwP12eUQFRWTiUaj3TY+EREREZH26nSm2Tn3WeBJ4BfAs8BlZvbhJtf8EPiF\nmT3Tqc56MWWapSPSacspz/MIh4spL19AbPYbigH/XE7OWjZsGEY4HO62cYqIiIhIeurNmeavAHPM\nbJqZ3Qe8m+CarwE3pKAvnHPHOueuds497pzb6ZyrdM695Zx73jlX5JxL+CY7585xzj3lnHszaLPF\nOXeTcy7pe+Ccu8I5t9E5dzDo47ngQ4Jk12c55+5wzm13zlU55/7unFvpnBudimcXaSojI4PZs2cz\ne/bsbq+YHY1GqaiYQtPiZDAZiAIeubnryc/P747hiYiIiIh0SCqC5veY2YqWLjCzGiA7BX0BXAw8\nCHwY+APwI2ANMBZ4GH+uahzn3DRgPTAJeBz4MdA/aJtw7M65e4HFwIlBf0uBDwA/c85dn+D6TOC3\nwDeBt/FTa78BLgRecs6N7+gDi/RstWRlPcO4cTdRUjJP65lFREREpEdJxfTs35jZx2OOnzWz8xNc\n98em07Y72N8U/ED9F03Ovw/YBJwKzDCzJ4LzRwO7gKOBc8wsGpzPBJ4DzgZmmdmqmHtNBF4EdgLj\nzeyd4PwQYDOQA4w2s70xbb4O3A2sMrOZMec/jz99fauZndnCc2l6tvRoyaZn5+Zey7Jl8wiHwwqY\nRURERCSp3jw9O+ScOyPmuNlDOueuA/akoC/MrKxpwByc/wfwQND/lJiXLgbeC6yoD5iD62uA24Lr\nv9Dkdl8ADLi7PmAO2uzFL3Q2ALiySZvrgjbzm4zrZ8DzwPudc5Pb/KAiPUwoFKKkZB55ecXk5Kwl\nJ2ct48bdRGnplxg/frwCZhERERHpkVKxCPL/gGedc1/Fz6ga+GuP8bO4RcBU/KnRR9rh4HttzLnz\ngjH9KsH1G4BK4BznXH8zOxzThiRtnsafgn0+cAeAc24EcBqww8wSfTjwNHBu0GZ9m59GpAfxPA/P\nq+bBB+cAfhCdn39fp4Nlz/MaKm6PGzeOLVu2AJCfn98jAvHY8feUMYuIiIhIo04HzWb2eJBBXY5f\nKtdzzlXiZ2PrfdnM/tjZvlrinOsHXIEfIP8y5qVRwfeKpm3MrM459xrwfmA4sMM5lwOcAhw0s78n\n6Gpn8D23LX200Eak14hGt1JUtDAoBAa5uWUpWb8ce1/P83DubjxvCv36nUpu7qOUlMwjP39s5x/g\nCGn+vqT/mEVEREQkXqfXNDfcyLnL8ac7x07V3gLcamZPpaSTlvu/F39T2J+b2dSY8zuCMY00s1cT\ntHsBmIi/3nmjc+4k/D2n95vZkATXZwA1wCEzyw7OzQIeA5aZ2eUJ2nwM+DXwKzP7dJLxa02z9EjJ\n1jLn5RUTiSzocODc+hZWdLqPI+lIvS8iIiIivVVvXtMMgJktMbNc/IztRGCImeV3UcD8RfyA+S9A\ns6BVRI6cZFtNVVRMbpiWnMr7Nm5h1fk+jqQj9b6IiIiISNdKycauwV7HA83sLTPbDewOzg8HQmb2\nSir6SdL3jfhppz8DHzOzt5pc8nbwfVCSW9Sfr2/X3us72qaZuXPnMmzYMAAGDx5MXl4eU6ZMAaCs\nrAxAxzpOy+O6uj8Dx9JYg68sODesw/ffsWMHcHzD/Xz1938JOEi97n7+9o7/pZde4uDBg2k1Xh3r\nWMc61rGOdazjrj4uLy/nrbf8EGn37t2kq1RsOXUafkGtU4HC+q2egtdOxi+W9Q8zu7VTHSXuuxj4\nIfAyfsD8rwTXLAUuBS41s5VNXuuHH/D2B46qLwTmnNsHnAyc3HRds3PubOB3wPNmNjk4NwJ/3fIO\nMxuTYAxfA74LfMfMbk/yLJqeLV0qVQWqND07MU3PFhEREWmf3jw9+yv420n1A46JfcHM/mZm1wD/\nDNY8p4xzbj5+wLwZOC9RwBx4Fn9bqU8leG0y/p7LL8ZUzq5vQ5I2nwm+P1N/wsx2AXuBXOfc0CRt\nLOa+It0qGt1KOFxMQcEeCgr2EA4XE41u7dC9km011dlCYE3vm5W1mqys6QwYMIKcnCdS0seRdKTe\nFxERERHpWqnINP8a+BzwfjMrT3KNA9aZ2ec71Vnj/b6Jn8HeBHwywZTs2GuPBnYBRwOTzCwSnB8A\nPAdMAGaa2eqYNhOBF4FXgA/X3985NwyIANnA6GDf5vo29dnk1cH96rfemgY8AfzZzM5qYZzKNEuX\nOJKZ4SOxtZK2nBIRERHpG9I105yKoPkZM/toqq5rw32uABbj78X8ExrXE8fabWaPxrSZhh/MHgJK\ngX/j7x2dC6w2s5kJ+rkX+BJ+Je01QCZwCf7CzRvN7P4m12fiZ5In4gfWzwBDgRlANXC+mb3UwnMp\naJYuEYlEmDTpNaqrZ8Sdz8pazQsvDCc/P19BnoiIiIh0uXQNmlNRCOyo1i5wzmUBJ6SgL/ArCxn+\ndPCbklyzHmgIms3syWAv6VuBi4As/Czyl4AfJ7qBmd3inHsZuAG4Bn8xZQT4vpk9neD6mmBrqa8B\ns/AXXr4DPA5828y2t/tJRY4Az/M4dOhws/OHDh3mL395hauvflT7CouIiIiIBFKRaV4ObDGze1q4\n5ifA8WZ2Sac668WUaU5ve/fuJTc3F4CKigqGDGm2hXe7dOeU3U2bNjFhwo8xe4T4AltXMHLkAHbu\nfBAVrhIRERGRrtabM833ABudc5OAR4By4AAwGH+98PXAh4FzUtCXSJcbMGAENTVjgCUADB16PZmZ\n2zh0aFeH7heNbqWoaGG3ZXNDoRCZmR/i0KFi/Fp4AGX0738C+/ZNINm+wuFwuEvGJyIiIiKSTjqd\nOjKzLfjTlz8OrAIqgH/ib8G0DDgbuKG+AJdIT7J3794gYF4HFAZf66ipGcPevXtbbpyA53kUFS2k\nvHwBlZUXUVl5EeXlCygqWojneS22raiooF+/fvTr14+KioqOPA7gZ7bHjHkFv/j8sODrR5x++n5l\nk0VEREREmkjJb8hmthS/ANY64DD+Fk8e8BugwMweTkU/Il3Nn5J9OU2zrzCnYbp2e0Sj0SDDnDib\nW8/zPCKRCJFIBM/zcG4oo0bdjOetwPNWMGrUzSTe3ax1jVsh3UxOzm5ycnYzbtyXWL78VnJz1+P/\n020YCbm568nPz+9QXyIiIiIiPV0qpmcDYGZR4MJge6njgTfNrC5V9xfpK5pO3z711PuBM/E/k6oP\ntmcAU6moqOhQ8J6fP5ZIZEHMuur7GoLpoqJiKir8adsjR5ZRUnKdMtAiIiIi0md1uhBYmzty7kMt\nbbnU16kQWHrau3cvQ4deT3zA6gFT2bPnp+0uCNbaHslAgtfnAR/FnxoeayWh0KXU1aXms6n64mT1\n08RDoZC2nBIRERGRLtObC4G11QPAh7qwP5FOGzJkCJmZ26ipmQrMCc4uITNze4cqaLeUzQVYvnw5\n27efS/Pp4EdWNLqVuXPvZ/v2fgCMHl3HI498QQGziIiIiPR5bc40O+cm4qe6HjCzHcG5wcAX29D8\naKDYzPp3dKC9nTLN6e1Ibzm1Zcs2iooWsn37aVRXDyU+q1yNPx27ebZ7x44fdmh6dtOxDBs2nX37\nDgN/D86ewGmn9Wf37rUKnEVERESkS6Rrprk9QfMb+GuVXzCzycG54/ArZRt+8a+WmJn168RYezUF\nzX1X/JRtgGIgfvo2TAEG0pjtfhTYitmeTve/ceNGzj57LjACv+gZ+Ntr7eIPf3iECRMmdLoPERER\nEZHWpGvQ3J7p2c8D04Pv9Q7gB8zfB34NJFtcORh4rCMDFOltmmaZm1fUnocfOE8Mzr0A3I8f1H4J\n2M6aNTcyffr0lIxn9erVwb2bFxpbvXq1gmYRERER6dPaVQjMOXesmf27ybk3gaFm9m4rbTeamX77\nTkKZ5r6haWXs3NwybrllEtdem0Fl5UUxV3pkZhYDp1BT8xVi1zXn5Kxlw4ZhhMPhlIwpJ+doqqoW\nkajQ2FFHXc3BgwdT0o+IiIiISEt6Q6aZpgFzYARQ1Ybml7anL5HexvM8iooWxlXGLi+/gO9//yZG\njoQtWy4gNjgeM8aA/WzZEneXYN/kC1M2ppqa05K+PmDAgJT0IyIiIiLSU6WievaVwD3OuYfM7IZk\nF5nZrhT0JdJjNZ+GDRBi584pPPigx733xlfUXrzYr6h9JPdNjkajhEKXUVf3GP6U7Nh11MtZvnx5\nSvoREREREempUhE0FwP98KsUiUirPCAa/DkfgNGjhxOJTI9Z63xfQ2AciSxIeD5V+vXL5PDhM/GD\n5kuCs6VALscdd1xK+xIRERER6WnataY54Q2cWw9cCBxoaVGuc+5BM7u2U531YlrT3Pt5nseYMXOp\nqBgEnBecfY7c3LfZtu2RbtnayfM8PvjBm4Ip4D8AVgWvFDJu3JfZvDn1QbqIiIiISCLpuqY5Fb8N\n3wfcQetZ63NT0JdID5eF/0/mouDrvuBc9wiFQixefB25uW/j3NVAf5wLkZt7A4sXp24auIiIiIhI\nT5WKTPO5wDn4G8j+Dvgz8Db+VlT1TgC+p32ak1OmufeLRCIUFOxpUiU79dWwO8LzPCKRCDt27GDU\nqFGEw2EFzCIiIiLSpdI105yKNc1PAoMAB7w/5nxsBOiaHItIjPqgFfy9m7s6YA2FQowfP57x48d3\nab8iIiIiIukuFZnmbcC/gEeA2iSXDQLuMbPsTnXWiynT3Pt5nkc4XBy35ZS/hdR1ZGcPYOdOf51z\nbm4ZJSXzyM8f267779+/n9zcXAAqKio49dRTUzd4EREREZEjLF0zzakqBPZdM/tVK9dtMjOlsZJQ\n0Nw3RKNbKSpaGLOF1HNUVb1DRcUjxAbSeXnFRCIL2pxxzsnJpaoqF7g8OLOE7OwKKisrOjVeBeIi\nIiIi0lV6c9A8Eagwszdbua7AzDZ0qrNeTEFz+qmtraW0tBSAmTNnkpGRitUMfsa5fgspz/OYMmVf\nh9Y5199n//79XHDBQ8A64vdZnsq+fQ90ONA9UoG4iIiIiEgi6Ro0d3rhpJn9vrWAObhOAbP0GCtW\nrGPgwELmzMlkzpxMBg4sZMWKdSm5dygUIhwOd6rYVjS6lXC4mIKCPVxwwSX4gW3svULAnIYscXvt\n378/CJjXAYXB1zqqqnLZv39/h+4pIiIiItITtfs3dudcyDk3zTl3s3Puc865tPskQKSjPM9j48aN\nzJ1bQlXVGuoDxqqqNVx11SPU1iZbtt8x+fn55OaW4WeGG0ZBbu568vPzm40tEomwadMmrrzyAcrL\nFwQZ6v4pHRMQBNuzaR6IX9bhQFxEREREpCdqV9DsnDsVKAceB76PXzn7D865Y4/A2ES6VGP2djk1\nNZfSNGCsqrqkYbp2qoRCIUpK5pGXV0xOzlpyctYybtxNlJTMi8tCx2aWCwp28/LLbwPbgld3AEto\nGnjDUioq4qdS7927l6ysLLKysti7d2/ScflLBbwEr3hoGYGIiIiI9CVtXqTpnOsHPAV8oMlL44GV\nwMdTOC6RLuV5HkVFC4PK1su7tO/8/LFEIgsa1jnn598XFzDHj63+/HSgGFgAnAzsAqbib5cO/vrj\nnXHrmQcMGEFNzRj8ABuGDr2ezMxtHDq0q9mY5s2bx333PQXMJH6d9NPMmzcvJc8tIiIiItITtKey\n0eXAMODrwG+Bt4H34f/2/kXn3Plm9mzKRyjSBaLRKBUVU/ADxJn407JnEBswZmevZObMVUek//p1\nzq2PraEFUABEgTCwleHDi3j99SuB5pWu9+7dS03NaOKLhc2gpmYqe/fuZciQIXF9HnfcccAp+IH5\n5OBsGTCO446r7viDioiIiIj0MO0JmguBy8zsZzHnXgF+55z7K3AJoKBZeoEMYC5+0HwJAFlZpSxa\ndGXKKmingnM1DBjwDKHQbkaOLGPx4q+Qn/9IwmuHDn0/sJBkxcKqq+MD4fnz53P77dMxewLYEpz9\nEc5dyPz5a1P+LCIiIiIi6ao9a5pPaRIwx3oYOCsF4xHpFs0Lck0FShkyZBGPPnqIgwdXM2vW1G4e\nWy0QCb5qOeus37Nhw3ls2DCMzZvvIz9/bML2r776KpAHZLW5z8zMTO6661M4dyH+Z2Ov4NwF3HXX\np8jMzOzcA4mIiIiI9CDtSZsdTPaCmb2jItrSk9UX5CoqKqaiwp+O7Gdvf5Q0GO3KsX3kI4MoL58G\nnBuc/RaTJn2Q8ePHt9p+1KhRwFJgPXAh8WuUF7FqVeIp59/4xg3ccss13HPPPQDMn/+4AmYRERER\n6XNcWyvhOueeNbPzO/H6aDPb3oEx9gnOOVNV4u7neV5MQa78Du+j3N4+6s/t3buXwsJCAHbs2MHw\n4cOpqalhwIBPAWOB84K7PAds5dChX8YFsonu3b9/f2prHwvaL6RxjfITwC956aVfJV1P3Vm1tbUN\nFcdnzpzZML29K95nEREREelZnHOYWdplY7syaP6dmZ3TgTH2CQqa+4ZodCtFRQuDwl6Qm1vGV7/6\nMf7nf35LefmfgPfg19wDWEIotJXbbrucO+98DXiE+CzxFXzrW8O54447kt67pGQegwZlM2LEbUQo\nGwAAIABJREFUF/GLgIFfPMwDvs3IkSeyfftDRyRoXbFiHVdd9QhVVTMByM4uZdGiuYwePSLhOLs7\noy8iIiIi3as3BM0vmNmkFl5PGjQ750LA62Z2QseG2fspaE6ut2QlPc8jHC5usnWUR3b2DKqqSoDZ\nxFe39oCpTJjwLzZuvBm/Fl+slZx//oM888wzSe+dl1dMJLKA/v1H4Hljid2SCrazefO6uGC1srKS\nyy/3g/YlS5aQk5PToWetra1l4MBCqqrWxI0nK2s6o0adypYt9yUcZ0/9uxURERGRzkvXoLk9a5rH\nO+fuB6qSvJ7rnFuS5LWTgPe2a2QiJMqePtrjspL1Qf/WrVvZvv1U/ExvPvVBY1XVeOAc4Nskqm69\nceNM4HCCO9fykY98BM/zWL58Odu3n9bk9RAVFZOJRqPU1b3Gq6++yqhRozAzVq9ezbRp0+KC1Esu\nuZ5Vq/ZSn+leu7aQwsIhrFz503Y/c2lpaZBhjn+e6uoPs23biGbn68d5pKaJi4iIiIh0VHuC5v7A\ntS287vBTZU1Z8JrSqNIunudRVLQwLntaXn4BRUU9JytZH/Rv23YGNTW/w+wiYDdwP/ABYBd+ca+T\nk96jX79+1NUtA2YRn4VexhlnXE04XMz27edSXT0Uf1/lefjrl+MNHz6cw4cTBd9+htkPmOP3cV61\naiqLF1d2OOMsIiIiItLTtWd6tgf8CnijA/2cBHzczPp1oG2foOnZzUUiEQoK9lBZeVHc+ZyctWzY\nMCzts5KNU6Z/CNwMxE+d9itZr8X/7Koaf1/o5tOzd+36X1aseIrbbvsljdOrnweuITv7jmZToP3A\neQFAm6c9z5gxg7VrC0k0BXz69NWsWbOmXc+u6dkiIiIi0l69YXr2P8zs0x3pJFjT/LeOtBVJpSO1\nPjpRlehoNBpMK98CTKH51OtLg9fC+Hso5+PvD9247jgU+gvDhw/nU5+ayN13n0BV1fDgtYuBaMIp\n0HA2GRmXMmbMcZSUXN8tgWhGRgaLFs3lqqtmUFV1CQBZWaWUlFwZFAKL39qrpOQ6BcwiIiIikpba\n81vqax3txMy8zrSXvik/P5/c3DL87Gk9j9zc9eTn5+N5HpFIhEgkgud5iW8SIxrdSjhcTEHBHgoK\n9hAOFxONbm33fZpasWIdAwcWMmdOJnPmZDJwYCErVqxrvWEz36Ffv4vp1+8yMjJms2vXj6mra/xn\n41w//AA7TMv/dPtRW5vHzp2vs337rjb1vGTJEvziYPHvNSwNXmu/WbOm8s47q1i69DBLlx7m4MHV\nzJo1lfz8sUQiC9iwYRgbNgxj8+b7etQadRERERHpW9ozPTvXzCo63FEn2/d2mp6dWGMhsMas5OLF\n1wE027bo4YevAWqA5lnkZNWlc3Pnkp09iJ07z2u4T3sKjSWbhpydPYO33iplwoRbWpiePQNYReOE\nj+TTlBOPv5bs7OZ9x07Pzs6ewTvvrGrYH7kljYXAGjPdhYVDO1QITERERESkvdJ1enabg2Y5shQ0\nJ9d0SjWQIID8E1lZtxMKXQa4ZsFv4vXRHs7NxewRYoPOceNu4qGHLicUCrU6hXvZsmXMmZNJorXA\nS5ceZuzY/KAQ2AhqaiKYfRIYAKwHPg78Bucmkp2dyciR61m8+LqkAXuiDxDmz/8499zzG7ZunUht\nbT/gBeA6GguB+eOYPTtRjb7mUrXllIiIiIhIe6Vr0NyeNc0i3SIUCsUV/YpEIkGGOTa7+hDV1Y0Z\n17ZV2Y5i9jmargl++eWJFBSUEQqN6PQWV/VTkaPRKJ53Djt2vMp3vrOGffum49xhzjjD+OpXMxg9\n+nTy8y9qMUCPvZd/fB8rV/6cHTv2U1v7InAaEFtgq/1ycnLaXfRLRERERKQ3U6Y5TSjT3HZ+1ng3\nlZXT688Ae4DkVbYTT2/ehHOvYDarSQ9rgNPx1w63XNm5penZyaZFp6oYWXzf0Dgtu23jEBERERFJ\nJ+maaVa5Wulx8vPzOfXUp4kvWtXyBw6hUIiSknnk5RWTk7OWnJy1nHXWo4wc+RzNi1+tB7YCy4BX\nKC//P/r3788rr7zS7L71VaKzs2cAK4GVZGVN56GHLmfLli0Ji4vVZ87D4XCnKkaXlpY2qZ49Cb8i\n9wpgBVlZ01m0aG7CgLmyspIZM2YwY8YMKisrOzwGEREREZHeTpnmNKFMc/s89thq5sz5GWbT8APd\nFfgZ4pb3/m2a5d2yZVvDOmHPq6O6ehVwELgK+DowBrg8aL0E+DNmu5uNJ3bLqVGjzuTaaxfFFSnr\nzBTvZBrXU48FFuJva2XASs4//z/86ldPJgyYGwt+NT5XYeEQFfwSERERkW6VrplmBc1poi1B85Ha\nY7g7JdrfuC08z+ODH7yJLVsuxw+UM4EHgTDO/YL3vOcvPP30YiZN+nCzdk3fw/pzhw8fZuLEu4B1\nwBvAtcGfY9dOT2XnzgWcccYZSceVqEp3S1O8O6q2tpajjrqYQ4dOJX4ts0dW1gwOHmw+LbuyspL3\nvKcw4XP95z+rVPhLRERERLpNugbNPT/q6kVa2iM42R7DPVln9jcOhUIsXnwdeXlLycnZTU5OBdnZ\nLwJrMLuYd9+9nXPPvZNPfOKyhjbJ3sP66dL+9Ov6IDwXmE3TImEwh9GjRzeceeONNzjmmGM45phj\neOONN4hGo02KlPntKiomNwTrqZKRkUFR0XDg7Gb9VVdf0vBhRCy/Mvblza6HOQ1Vs0VEREREpJGq\nA6WRcLg44TRez/MoKloYl71sW3Xo9FVbW8tVVz0SV0CrqmoGV101g4sv/kyrGWfP8/C8ah580N9T\nuLKykilTTiY+gzqD3/xmKu+++y45OTnteA+/CYymtc+UjjnmTN56ayj+1Gg46aSrOeqoXcDdbX8j\nOumcc/K5//7+XdafiIiIiEhf0/OirV6svHwBRUULm2WcuzJ72VWaF7ECCFFVlThDGis2Yzxlyj6u\nvXYpt9zyNZJlUKdNm9am99CfHr4Uvxr3H/D3PG5aJGwp27dv54033ggC5nX4ezT7U57ffXcEJ5/8\n82btcnPXN+wxnUozZ84kO7u0WX/Z2SuZOXNms+uXLFmCvza7+XP5r4mIiIiISCxlmtNKYxAXuy+x\nNEqWdT/qqLM6fe+MjAze+95y3njjHvx/GvPwt3GaDNQCi4HtnHHGGRxzzDH4GebmQfobb1xNXt5R\nVFRMBmDkyDJKSq47IjMC6qt3X3XVDKqqLgEgK6uURYuuTJitz8nJobBwCKtWTQXmBGeXUFg4VOuZ\nRUREREQSUCGwNOGcM7C4vYXrdWVxqa7S1v2NX331VUaNGgXAjh07OHDgAJMmvUJ19eGgzUwggwED\nlnPo0HISFbg6eLCUnJyc4D38HvDl4PUfkJf3tbj38JhjjuGttxbiZ47r7xEFfgmsIC/vfEpK5nH+\n+ZOaXFdvJYMHX8ebb77ZpUXb2ltQrbKysmEN85IlSzocMPfG4nQiIiIi0j3StRCYguY04QfNdUkD\n4Wh0a8PWSOBnLxcvvi7l2xh1pRUr1gXrmhszpCUlVzJr1lQA+vU7Hc8bS/yWTy8D+UB9ga9SYC45\nOYf5wAdK+OMfHbEZ1I9/fDC//OVSotEo06Zdw1//ehJ+gS+AZQwf/g67dj3fMKYrr7ySRx45HPQV\nG3xfDnwUuIK8vGJ+8Yuvccopiatrv/76w5x44ompepvSVuPP5BTgyG2tJSIiIiJ9g4LmFHLOTcef\nM5sHjAOOBpaZWdLyv865c4DbgAlANrATKAF+bGYJy1Y7564ArgfeD9ThpxzvNbNfJLk+C39z30uA\nocA7QBlwu5ltb+WZbNy4G1sMhHtjVi9ZhvTVV19lxIgvkigohVVATsy5GZx55kmUl/+YyspKpk2b\nBsCTTz7Jzp17KCpayPbtH6G6+lHg503u9xkOHChl8ODBAFRXV5Od/SngTPx9jwGeA/4C/BrIaJgN\n8LGPzQ3WNTcG6YMH7+XAgT+l9D1KR71x9oOIiIiIdC8FzSnknIsCZwHvAvvxSx0/lixods5NA9YA\nVcBK4N/A54N2q83skgRt7gVuBvYFbTPx5wIfB9xoZj9tcn0m8CxwDrAp+PNp+PN3a4DzzGxTC89k\ndXV1CjYC/fv3p7b2MRJNf/Y/h7g/7tx1173A/ff/OO7K+MBuKf465cuI9xhnnPFtdu7c2dBm5sx5\nrF69Dzg3uGYTUIQfsBM3hf6NN95gzJgxAGzbti2tM8wd3RM7kUgkQkHBHiorL4o7n2h5gYiIiIhI\nW6Rr0NxTI7RiINfMBuFngpO+sc65o4GH8Cs5TTaza8xsPn6W+vfADOdcYZM2E/ED5p3AmWb2ZTP7\nLyCMH3Df65wb0qSrL+MHzKvMbIKZfd3MZgPT8dOiJa09lALmjjv55Pc1OxdfMfsPQKKtmTLYvXs3\nAJHInxgz5lp+9rNPkJ19FccdV8agQU/gZ7anBtfHV8I+8cQTOXDgAAcOHOjygNnzPCKRCJFIpMU9\nvqFze2KLiIiIiPRlPTJKM7P1ZrarjZdfDLwXWGFmDfszmVkN/nRtB3yhSZsvAAbcbWbvxLTZC/wf\nMAC4skmb64I285uM9WfA88D7nXOT2zjmPm/Hjh0k2xoJfhB3zrllzJ8f97YnMAF/anbT+/2ck046\niUjkT5x77u1UVDxIdfXFVFVdzJtv/ooTTvgg48Z9mZycteTkrGXcuJsoKZnX7R9wxG67VVCwh3C4\nmGh0a8Jr4/fE9rfHqqpaw1VXPUJtbW2H+s/Pzyc3t4yu2lpLRERERKS79IUtp87DD2Z/leC1DUAl\ncI5zrr+ZHY5pQ5I2TwPfBM4H7gBwzo3An4q9w8z2JGlzbtBmfQefo1fyPI9Nmzbx61//mqFDh3Lp\npZcSCoU4cOAA8Gf8DG/9muFHgT/j3CX4SXxwbil33fVpMjMz4+4ZjUbxPI+RI59jy5YL8It/LQdu\nIn6t8n42b97MRz5yI1VVl9F0C6n9+z9BWdnQhiA5P/++dgXMR2IderJtt4qKitm06Yds2bIlrr/W\n9sSePXt2sz5aEwqFKCmZR1FRMTt2TKKu7lVOOOH3PPjgnd3+gYKIiIiISCr1hd9uRwXfK5q+YGZ1\nwGv4Hx4MB3DO5QCnAO+a2d8T3G9n8D23LX200KbPi0a3Mnz4lZx99i6+9a1RXHHFb8nO/jTDhl1K\nQcEeBgy4GT/+WggsJDf3FDZvfprq6rXceWcFd95ZQXX143zjGzfE3bM+Aztlyj6qqt4mN/c6cnKe\nxJ+R/yr+X1MFsIvhw2vZs2cPe/eGSTTL3/M8QqEQ4XCYcDjcroCwPdng9oifdl4vxPbt5zJ27OyU\n95dMfv5YbrnlfOrqllFTM4x9+y5j8uQ7NO1bRERERHqVHlkILFYw5fk5klTPds7tAM4ARprZqwle\nfwGYCJxjZhudcycBfwX2m1nTdcs45zLwC3sdMrPs4Nws4LEWxvAx/NLLvzKzTyd5Duvpfxft4Xke\nH/zgTWzZch/x1axvwp8YsAB/WXl9NrUWeIxBg37Az3/+U84555yGADY2s3zNNUua3LOWkSMv47bb\nPsuYMWM4/fTTGT9+POAXszr22GOJRCKce+5rVFVtiOnPH09u7rVs2/YgoVCoXYW0jmR16WRFuJxb\njtlIYHxcfxs33svgwTNb3RO7vdq617aIiIiISFuoEJj0Ou0pRNVUNBpl27Zz8X8EPSCCv6NXATAE\nf//lKcHr64AZQDZvv30b5577fd73vk8TjW5tks3dzcsvvw1sC3rZCtzMzp3TueqqEB/+8HSOP/54\ndu/ezTPPPMOxxx4L+NOYR43aAFyDX2NuLbCGrKzpLF9+E6FQqN2FtJJng8+hsLCQL3zhC1RXV7fr\nPauXbD0x/BK/Vl1jfxUVk/nTn/7EokVzyc6egV99fCVZWdNZtGhupwLb1qZ9i4iIiIj0Bn0hFfR2\n8H1Qktfrz7/Vwes72qaZuXPnMmzYMAAGDx5MXl4eU6ZMAaCsrAwgbY4femgx99zzM15/3V8Pe9JJ\ndzN//ue55por29T+pZdewvP+hh/YLsSv1QbwCnAC/ls6AH9NcwnwRfzgbAowgzffLOCii25l0KDT\ngszyhqD9I/iB7zT8mm1rgPuprX0Ifxb9vUAtI0bMxLm9eN4bhEIhrr8+n3vuuZ2//W0WZrs47rin\n+eY35xAOn0ltbS1z536fmpo78JelQ1XVe5k793YuvvgzZGRkJHy+urq/A/XZ4DLgRaqr/8jatZcB\nW3nggfO44YaP8ZOffKdd73/jeGfw+uv+FlrHHLOIf/xjBIcPh2L6a3TSSQP52c9u4PXXXw+Ob6Rf\nv34Nr3fk52Hbtm3426TH9ue/vm3bNsrKytLm51XHOtaxjnWsYx3rWMfpd1xeXs5bb/khUv2ONumo\nL0zPXgpcClxqZiubvNYPPzrrDxxVXwjMObcPOBk4uem6Zufc2cDvgOfNbHJwbgT+uuUdZjYmwRi+\nBnwX+I6Z3Z7kOXrM9OxUTD32PI/8/C/y8ssOaDpFewZ+pvkW/MxpNon2a3aujAEDhlNd/ZWgXX1x\n9F34M+hzgM8BF+IvWW/az+fZtevHDB8+vGFMTYt2eZ7H3Xffzbe+NSrhGJYuPdxQSCt2+nZhYSET\nJtwS8x7VBu3jpzLDVKqq1pCVldXqe9ZU7HjHjRvH+PE3H5Hp4MloeraIiIiIpJKmZ3efZ/ErPH0q\nwWuT8SOrF2MqZ9e3IUmbzwTfn6k/EWx/tRfIdc4NTdLGYu7boyWbelxRMbkhiGtNKBTiq18twF9O\nHn8fmE5W1gIyM08Hvp70Ho2fZ2zFzy7vCb5+RkbGr/ED1XuAj+AXRG/az2zOOGN03JhiC37VT/2+\n665/tfo8TadvDx48k4svHkVeXjE5OWvp168Y/8OA5cCyYGwhYA5f+tKXmt2vLVPfY8ebkZFBScm8\nhv7auz1WR6bah0Ihbr21gMzMi0jltG8RERGR3qAzSxklvfSFoHkN8C9gpnOuYcGnc24AcBd+MHt/\nkzYP4AfatzrnBse0GQbcAFTjzwNO1OZ/nHMups00YBKw1cy03VSM0aNHkJMzoNn5nJwB3HorDBu2\nFX+d8WM0X7+7nH799pGbuwf/rV+APxX6IuBRTj7Z6N9/aZN2zZmdzsaNG5v9Rxa7rVNNzQ/wM9/x\nY8jOXsnMmTOT7oN8113PsHHjvWzYMIwTTijDDywzg69C/LXazXW06va4cWN48ME5LFxYRVnZEDZv\nvo/8/LGttutIf/VtvvvdIUAhxx13F9OnP86BAyuYNWtqq32KiIiI9GZHahcV6SZm1uO+8BesLg6+\nnsaPZl6JOff9BNfXAAeBh/DTj9uAOqA0SR/3Bq/vBX4I/AT4Z3DuCwmuzwReCF7/I/Df+GnFGuAd\n4EOtPJP1FHV1dZaX918GdQYWfPnn6urqWm370ksv2UsvvWSHDx9OeJ9x4260ceNuDM7XGVxgcKFB\nafB1gcFEGzr0Elu6tNScWx7XHl4yuMvg+wbTDD5vcGOzfvx7LrXMzO9ZXt5/2ebNf24Y49KlSy0r\na1XM9U/GjSEr6wJbvvxJMzNbunSpwcqYa+u/Sm3p0qX2n//8x+CzSfr/lFVVVXX6vd28+c+Wl/df\nlpOz1nJy1sY9T6r/LuPb1L8vKw1WWlbWhQ3vi4iIiEhf1Jnflfu6ICbq9niz6VdPzTTnAZcHX5/A\nzxafHnMubi8eM3sSfyr2+uC1G/GD2S8BsxJ1YGa3AFcCr+OnO+cAfwI+Z2ZNM9OYWQ3wMeA7+IW/\nioGPAo8DHzazlzrzwOkkFAp1aCpw00rXY8dex4wZpzNu3E1x9/nKV85l58766dQh/AkBJwPPA2XA\nu8AA/vnPi4HDZGdnBj38CX/5+rP4Pw4v4L/9V+N/RnI5frb3MfzPUeYC2dTUfIzy8gUUFS0kEvkT\n4XAx11zzOtXVsWvMpwKryMx8kTvvrODgwdVtzqhefnn9j2XT6eGXMHz4nrj1zB2Z+h6bFa+svIjK\nyosanqe1qUAd6a+xjYc/4aIxw15dvYarrnqE2traFvsVERER6a1SsZRR0kuPDJrN7A4z69fC14gE\nbX5vZp8zs+PM7D1mNs7M/jf4RCNZP0vMbIKZHW1mg8zsfDN7uoXrq83s22Y2ysyyzewEM5tpZttT\n9ezpIj9/LJHIAjZsGMaGDcNanQrcPLCbTkXFg9x222befHMv8+dX8Oyzp/LQQ5djVoNZbLA3Fvhf\n/K2oJuIXBrsOgFGjRpGbux7YAtwOXAyMwJ/6PBv/R3wq8BTwBn5AXQs8gV8kbD2QD4TYseNcLr30\nPsrLF1Bd/WX8oDt2HCHe/3649dZb49bszpw5k+zs5NO3W34f39/i621xpP5jbn0dTimgLadERERE\npHfrkUGzdL9ElaZbEo1G2b69gPgfuW2AY//+2dx+ewbnnvtdCgr2MG9eNmbL8TPHsfbjB8KXA48z\ncmQZ4XCYhx++hszMb+JnPKfjTyb4MhBb2y0Tv3p2JX6x9LXATcC8hjGZvcrevZ+kMcM9D3/CwEqy\nslYlzaZnZGS0uA/ykiVLgCU0X5e9NHitUbI9mHNz15Ofn5/0/e2oZP2deuqTXHPNkoTrcBK3ERER\nERHo+t/n5MhT0Czt1pHCBp7ncehQbBDr4e/P/Ah+oLuPw4efoLp6BpWV06muXgPcBqzAXxo+j8YA\n1wFn8ZWvnBsEsDWEQnOI/3EO07jcvd4YzjprELffXsGJJz4C/Ag/i+2Pp7r653he7MSDscACsrL2\n8NBDNUmz6Z7nkZt7Cs89N59HHz3E0qWH46Zv5+TkUFg4BD/jvTL4+jyFhUPIycmJu1dHpr639B/z\nuHHjWswWJ+rvrLO+CGSxZct9Cad717c566w/kqhIW1sy7CIiIiK9VUeXMkr66vH7NPcWPWWf5vbu\n0Vy/d/GuXbu4445XMHs0aBcBduMHzBH8raLilqLjZ46rgVH4mdr7gvPFZGdP4vnnRxAOh4lEIhQU\n7Kaycjrx+zWvp3//ZzG7jFAoxNChv8G5Gvbvv4Da2r3U1PwWf12zw18rfTVwK/407xD+tG1a3Os4\nGt1KUdHCYHo05OaWUVIyL2FwXVlZGaxvhiVLljQLmJu+z+3L5NePYzIAI0eWMX/+x/mf//ltMDbj\n1FOf5lvf+iSzZk1vdr/Y/jzPY8qUfVRWxv995OSsZcOGYYTD4Ybr/vu//5c77yyjpsYvDZCVVcrD\nD1/B6NGntXnsIiIiIr1Re3+fk/Tdp1lBc5roKUGzH6DuaTWgAn/vYn8rppk0ZpZPw9/+eh/+GuVZ\nJA+a1wLD8LPGK4Nr9gHXMnbsT9m/fwXOObZu3cpnP/s9ysuvwS+OPgW/NtzD9OtXS13dR4P7vYAf\nGF8Q9PkqMDx4LR9/uvh38DPCGTj3c844A1aunJ80w9yeDxCOtNj/mMeNG8f48Tc3G5tzcznrrEEs\nXnxd0jXo7fk7hsYPRgBGjTqTa69d1KYPEUREREREYqVr0JzR+iUiydTiF4MCz+sf/0rc3sX1QdsI\noAL/x24zsBW4BD9gfRQ/mG0M8PwiXRc29JWZuZ9+/Qo4dOhmtm6tAx4E4JRTruU973mF/v33cPjw\nEzH3uJC6upuArwbnPGAGfgEw8APrbcGfz8Tf73k5jWucZ5CTcxPjxo1J+PR+Aa7JJCvA1TS4bEkq\nPokMhUINfUYikYTFwcymsWXLkKBSeOLA3p/u/Sjl5fF/H/46nAubXZ+RkcGll15KJBJh9uz/pqJi\nGfX/tZSXX0BRUfd8iCAiIiIikgr6LVbapXH97P/D32YoE8jk0KFlbN++r+G6ZcuWUVX1Ifyp0vVr\nXuvXGc/AX6v8eeBa/MB7eHB+ObAU+C8a1zB7ZGauZsOGy3jiiYF4XibwW+q3OYJ1/Oc/x3P4cCHN\nt3WaTON0bX+bJ7+/fUE/mcHXxUBOMNZlwZfHzp1T2LRpE8uWLWPZsmVxWylt376LqqqaJu+QR23t\nTp566qlm2y4lqkbteR6PPbaaMWOupaBgN5MmvcqYMdcSiTQtgta61qtdN74vLVXWbu86nMY17rup\nqLgIuBn/A5HW+xIRERERSXeanp0mesr0bIBNm7YwYcJt+NtfN2Yis7Nn8M47q1i9+imuuOJBDh++\nHD/jWIYfAI8F7gV+R+NWRb/E3wo7EzgEFAT324C/tdQEYC/9+4/gxRcncf755/Puu7fiZ4/Bn2a9\nI7jnRPzttGMtD8ZQGByvBKrwt6SKzYJ7+Hs398Pf6xmgFOdGkpn5Rw4d+gIA2dmlLPr/7d15fJTl\n1f/xzxlCCKlVu2lbkUUkaFFCTHGXxVZt64aCsqiIuKB1AVu39rGlLq2PtrViH1utGgUFQcGlVevS\nCsRq2x/GEBWB4AbiUx+XarUlASZz/f449zBLZkICIQnJ9/163a8k93rNZO5MzlzXdc6dkxg79hj2\n228qNTXgc61jeKB4a9SOgk37jh9/XM65z5dd9k2uv/5pXnrpX4Rwd6Pn8tlnr6K8fN/N/j6g8dzq\nAQMWUle3ntraW7Me4zTgJoqLH6Sysl+TveHN6f3ON0Q9eR2I5R3WLSIiIiKSrqMOz1bQ3EFsT0Hz\ntdf+Nz/60R6kAtGkedx9dz3nnfdI1rDsZBB1I0VFJzNgwFd4+eVJpJJtrcOD6N+TGXweiAfTlRQU\nfJY99ngvGg7dA+9pfh/4LD7cegOeyfmxrOtOjb5PJhE7Dg/GR0fXzGy/B+4T044/Dg+uizat69lz\nDAsXXs7hh7/DunUD8bnahwF/wLOBZwa/H388lwMOuKRRYNmz5xjq6i4H3iFXErSSkvksXz5ns8Oa\n4/E4gwadSm3t9/HefO+dLymZRM+eO/HSSwcRQiE+3P1cYO8WB+X55Jv/nJqPXtZuc7xFREREZPvS\nUYNm/RcrLZJIJLj99mfybn/++eejxF/Zw6QPolu3ofzXfx3CmDG9gJ/gibjm44FzMlBmrqS/AAAg\nAElEQVRdgpeCmgGcgg+bnkFDw8vU1t6MZ9xeifdiGh6knkyqfvMxwA3AA3jAfC5wKHA9cCTweVKB\nZS7Juc9V+LDu8cDPo58TQIy6urE89dRT0f6Dorasx4ebZz7uurqxXH/99TnnF9fVjQVW5WmHsWbN\nfpsd1lxdvYxBg86NhkW/jX84sQyIsXbt8dx++0RmzepGjx634IH9CmAqdXVXcdZZt29mGPfmJRIJ\nEomGHFviFBX9WeUVRERERGS7p/9kpUWqq6t5772z8HnBmfV5YTaPP/56jqOWAY9jdjk//vFX+clP\nlgPfBJ4E1uIJxd7BA75FeHALHqhWARDCeOAovPzUwOj7k0i9hJcBf8ZLSPWLzn0OHtQ24HOUv4IH\n2ZfhmbSz2z8HTwg2Dc/U/RxwPzAg+jkZkEKfPn3SaiPHgL3ZsttpYPSYs9uyGLN+TR6ZSCSiIdm/\nwz84OBEP4G/bdL5YLMbee+9JLHY+noitL/6BxL5bPde4unoZZ589i/Xr/9Co/SUlT1NZOTJvbWsR\nERERke2FsmdLi8ViBXhwOgZPrAU+NPpw1q79LmajCWEMHkTGgauBS4jHkz28Y/EA9FY82KvB5xH/\nHu/dfS7aPiI690y8VNWNwNBoXT/gFbxEVAL4AM+mnQxcR5McEg730r//3rzxxncIIbl9SrT9EDzR\n2Fw2bHgfuIP0etCQno17FDCVoqK1TJjwAPvuW87kydOorR1OCA3U188ihBPIHII9j8svn8uDD17S\nKBt1z57zqKu7H09ANg2fz70Bn589hYEDb6esbHTe34Nn7x5B41794UDVpmzX1dXVmMXwHvbWkQzY\na2pm4BnIvf1mGxg8+HnuuutiBcsiIiIi0imop1lapKysjAEDFuLDoO8HNuJDk3sDFwGFdOs2mMLC\nE/GA9RS8bNQiPDB+mVRgV4MH0L+P9osBpdG+N+E9p8ne07/gw7iT/o4PwX4PeBXYn8bB4yHABGKx\nOiZOLKd7925p231YdUHBG1x99Wv85z8LOPfcQ/B51DE8eB+R45wHcuWVh1FQUEBZ2SCqqm6isrIv\nzz7bn3vuOYuePcfgc6PnUVQ0mjvvnERhYWHObNR33jmJIUO+R3HxCnr0OITCwlvo3v1FevYcTmnp\n77ZiWHOcAQN+sen4VMbz7N7gxZSVleU+xWZkBuzJIer96NFjLbfffroCZhERERHpNNTTLC1SU7Oc\nurp/YTaJEI7G5xU/i/c0eoDXrduX2HHH7rz//rN4L/PteAC6BzAduAoP4Jbjw553w3tbIdXrnB2s\njou2leO9sXOBXfB5ugk8Adh+eACXZMClhFDLz362lo0bH8V7x1Pn3mOP1/nBD26loKCAQw4p5dZb\nM+tNZysu7sG3vjU81bK02sjl5eWMHXsMc+d67epx4x6goMBvsWSAncpGPYNYLMbYscdsWlda+jQ1\nno6bsrLRmw2Y89dTfpply2ZvunYsFuOOO85mwoQJrFmzH2b9KCmppKLi3Faca+w92bHYW5q/LCIi\nIiKdirJndxDtnT275eWFIFWDeSZwM8nh2GajCGE6HhBXkiw9FJ0F7z2O4b3L6/FkYIX4nOLq6Ljs\nbMyzgRJ8ePZ0YCmZQ6eTmbKT5Z/Syx49iA/nLgJuxeyg6Jg/Ulg4lL33fo2KiinE4+s44IBfR+Wf\nIL1sUvIauTJBpz93paWlaYFv7udxa6VfDwo566zbWbnyMEJ4k913r+K++67MyIqdKkc1nEQiQe/e\nTzJnztQWZ87OfpxDh36vUUZwZcoWERERkS3VUbNnK2juINozaM5VQ7iiYkqjIbb5ywvNBtbgPcm/\nBs4D9sITc+1JZgCcwLNczyIz4D0O2An4FvAUHoinbz8F+BSvw3wj8H0al7yaDbwGfA0P1r28Umbw\nmwCuw+dIn7pp3ZAh01iy5Ea+9rXJrFr1b7y3+x28TNN4zDZGc3XPy3he0p+7RCKB2RwSiRF069Yr\n7/PYUvF4fFPv9cCB+3LOOXdm/K4uueRwrr76UdasOYpYLEZJyeJN181XR7mlwW1V1ctMmPBT1qwp\nx6wfAwdWctll3+SGG/4UlQGDAQMWcddd52potoiIiIhsEQXN0qT2CppbElQ1DpoTeM/w08CX8czT\ncTxwHY8Hy6fgwTT4nORq4HVy1Xj24dpH46Wo7sOD2gRe//gKPIv19cCL0flznWMZ3botAs6me/ce\nrF//B0K4gsxh2/PwYD6VGKu4eAGVlX1ZseJ1Tj11PT60G3w493wKC/9OZeWpHHDAAZt97lJBOlvc\n85rs1X3iicVce+2z1NePB8DsHkL4Gf5cA8Tp2fPkRnWxk9etrq6Ofmej8OceoIzi4oeorOy7aWh5\nU6qqXuaww6ZTV3dK9LwsAs5myJDbWbLkxm3esy5tpzkjTkRERES2lY4aNOs/oi4uXwbmXOWISktL\n6dXrcTwwXIYHh2/hScB+j/fMDgWeiPb5HN5j/Bapkk2v4SWgctkzOn5PPNjuFy074z3GhcCP8KB3\nJrlKXsGPaWg4n4aGR4nHr6dXL6JjU/uZPUZmUrF0htnT+Bzrf+I9zkVs2HAYo0b9iurqZZv2bDp7\ndTX5nsfNqa5eRnn5NIYNe4srr/wy9fW98KD/ZEJ4BJ8jnnzsNTnrYqdft6FhLakyWv578HXRM5JI\nUFVVRVVVVaO6zYlEggkTZkRB+WhSidl8SHhNTQ3l5eWUl5dvNsBq6jrS/lKvu9UMG7aa8vJpGa93\nERERka5KicCkWZLDkFevHgycDgQyh1iPw0sy7Yr3Oh8LfAEPptNLNo0GvohnzU7vnZ0D/BCvy5wA\nupHqCU6WZDok+vlZ4B8UFp7Ihg3jo3VzgbPwl3QDUE48Poa33/4NAwacwzvvfBuAAQMWUlcHtbXp\nj84zSZeWHs+ZZ96dNac51YP77rtjOOOMqbz44oxt1gOXLOWU2Xs9jswh5smgfPO9xKWlpcRiPyX9\nccAoYrExlJaen2No/syMIeXV1dWsWXMUuT4YCOF1UqMImra560j7yvW6W7p0FJMna466iIiIiP4T\n6uKaU44o/R/q9esvwHuC9846UzKx1zP4MOurSSX8yt7nSHxe82y813g88AmpntBZwMNRmxJAfXTc\nfDxx2OnApdxyyzF8+cu/jdY9gM+LTgB/BS4BTgL+zJtvvsdtt8WprOzLiy/ezNy5lzcq/1RRMYWa\nmhpWrRpJUyWnXn31YJYsWbKpt9TLb2X3eC/Ge7JbXtZp873X4B9YJJXSs+fcRm3o1euPm4bahtA4\nG3kI46murt70e1237kTWrTuRpUtvYvLk2zJ6gnMHTIHevV9s1mNLf/00dR1pPy0ZcSIiIiLS1ain\nuYuLxWJUVExh8uRpGQmd0ssRpf6hXo5npx6Bv3SmAVNIzReO4Qm2ziD/5zEG9AH+hc9/bgC+hM9h\nTu+RPg7vrf5c9P0avCZ0ET7c+3F+9KPVfPTRGMz+RAjdouMfx4Pqnnhw+RDx+Klcc82DLF8+h0Qi\nwbJl1Vx88dcZOLBXVG/Ze46rqqo2+3xt3Bhj+PArgFGYfZWdd15D796n88EHx5NIBBKJe0kkdiQW\nm8bAgQ1UVHy3lXvpEpjNpKjoNMzeYsCARVx++SRuuGEatbXDiMcbgPtYvXokI0a8Ta9e9+PzsjPF\nYjFWrlzZZKBUXl6eVtbqBNJHBhQVzWHOnKua9dg2F5A1Z161iIiIiEh7UU+zbKohXFnZN+qNndFo\n2GwICeDWaJmAJ+G6CbiNVI/wfXiyLsN7WhfRuBf2ETyZ1w7AZ/Hg9hM8IE+KAZOA7niv8xigFi8d\ndTLegzyTd98tYf36C6Lh1P2BG/Ch2z/Dh3/fC3wM3MYbb+zGBRdczmc+M4bTTivk9NOLGDnyempr\n39kU+KV63eNRW++Pvk9v/3OsX/8069e/Tn39aN599yHWrPkXX/hCBZMnv0gs1o14/Fg2bDiUVav+\nwYoVr/uRzZzPm6/n33veaykqGs0995zJs8/23/S7Gj/+OO6442x22+0BNmyYxYYN81m/firr1p1I\nbe29mM1pdL6SksUMHDgwbzs2/SaiD1W8Z34+RUX3M2DA2fzlL1e1uGSVdFzNGXEiIiIi0lUpe3YH\n0d51mpsSj8fp3/87rFnzDeBSMuciXw/8b/R9CXAwcA8eUC/Hg+ph+BDqh/F5uK/QuORUdk3k+4E3\ngcuBJaQycqebgwfpQ6Ofx+FlqfYgs15zFXAhPt86s7Zzz55j+OST+yko8EEXP/vZLVx55ROEcFp0\n7L3A4Xjv+CLgHGADXk5rZHTt+cA8zOqjRF2Z51+48EdMnHhLzpJQuaTXVQbYc8+FnHRSb/r2/Srj\nxo3b1NakVBbv04C3ya5x3aPHDPr0eZm1a5Pzur00VGnp3s3OnL41WZVbq+yVbFvZrzuVEBMREZG2\n1lGzZyto7iA6atCc/Ef61VcPZcMGgL/gQ7LBA+JD8SHWD+DznE/Es1xPx3uE43i2553xOsyD8QA0\nu1zUfDxTdjkerJ4DHBWd4158OPiAaN8yPPiahwfjE6NjCvBe5pKoHS/jwfNRwCqgL95Lnm4eM2eu\nZ9CgQcTjcYYNu44NGx4kM6Afh39YUBQ9lhHR43oKuBhYET3+UTnb2L37z9m48f/RkoCxJUFqqhRY\nH3xOeGbQXFy8gEWLemf0qKeG3rdNoKSAbPugklMiIiLSnhQ0S5M6UtAcj8eZO3cuiUSCG29cQk1N\nstcWUgFtwAPI9PXH4Qm7nsczWV8B7Ij3PH8fD2CryRXYeVKwNXj5qr/igfnteO/zTXiCsTNIrxPs\nw7E/A9xMKnv2j/A51gPwwD2ZNboKnws9Ouu689h99zv48MPziMdXsWHD7jQOrGfjyc9mk9kbHo8e\nL/gHBYYHzkRtnIL3qj8XtTGluHg+lZX9WmU+bypoHkXjHvvWDdC3hgIyEREREWlKRw2alQhMMtx3\n3+8588y7o9q/bwAH0TiT8+H40Ons9afhva4T8eC4Dz7X+M/Aq8D5wC+Bu/HgMj3g/hvdu7/Mj398\nLPPnG6tW1dLQ0J8QTmTDhkDj0lXH4WWphuAB+HjgLmABPv95Ax7QJo8pw2s7n5B13Xt4++3H8KA3\nGVhni/GFL1zMhx9OSzt2Gd7TPppUjej0odmjgKnA6zQeVk6rZo1OJesahQfq04BhmG1g8ODnqag4\nr8kANRaLtUkyrra6joiIiIhIa1LQLJvE4/EoYM7unc0W8IA1WwIfvr1jdOx38HnMi0kN6T4ZTwA2\nCTg+WrcIOJfu3Zfz7W/344c/LIt6JPvyyis7M2lST3IH6K/jvdbpAfV4PKA+AO/5TT9mCh7Qfxt/\n6f8h2mcV3judL7CezfXXn8kFFxj19cl1t5Hq0a2KHk92Gw/Ek5w9TWYAn6B376coK/tdjuew5bIz\noIdwGL16PcD06aMZP/5m9eiKiIiIiGwFBc1dVHIINrApudTcuXOjHubN9c7+Le371HqzOYTwGF4j\neRbe2zuHzKB2DB7UjsXnGEMqadcKILNHcvnyZFbtBKk6xclsvg34/GLwwDW5bSIeUC8is0d7b7zU\n1Z74S39WtD59SPMUPAA+Bv9gYBEwnH322Ye99prN0qWjyV3DOdcokh7ARfhc6Kl4EN2DoqLZzJlz\ndasGs8kM6Knhz/cpWBYRERERaQUKmrugzCHYcM45J3P77RN58803SSWyglQQeTrdun2LhoZkHeQr\nou3TgOH43N676NbtKOLxl0kFlBfjAWyuXuJL8F7iVNA9YMAiyspmbNozHo8Tj8fp1m0mDQ3P4tmq\nwYd31wJXA3+P2jEi2jYTTyj2d+CatDYG4A7gCLwXOt0wPBAuxwPrnaJzxIAZFBY+QEFBwabe3BUr\nelFf3zft+OSHC9lDzp/AS3QV4B8MXM+OO97BM888vE3KNWn4s4iIiIhI61PQ3MU0HoINdXVjOO20\n4+nR41TgUXwIdap3tkePf3PaaYu4447u+JDqZMbjm/Bg8wmgL/H4Li1oSQ/gdOBbQAFmj1JXZ9TU\nLKesbBD33PMgkyffRDx+JB7EpicjG4X3BpfhJa/mZ207Ac/q/UM8qddy4KXoermsB57AbCUhPIAH\n48mgNsHee/+FsrKTiMViVFXdRFVVFaeeehu1tWOi68aAs+nZcwwhjKe+fkP0nAwFvod/8DAI2INx\n476p+sYiIiIiItsRjd/sYhoPwQaIEcLp1NfviWfG3gn4EvBbYCK77NKDQw89HO8ZXoz3ohKdowxP\nCvYu8CRQig9pTgC/wodApye98uRb8F/48O0SYA9CuIja2gs544xbmTVrARMnVhCPT8WD69GN2gtH\n4jWhT86x7VQ8WdlDwP9E57gUH5b9TKP2FBbez6xZ/bnnngIGDNgBs5/jdZfnUFIyhbvuOnfTUOdY\nLMbQoUOZO/dihgyZRnHxAoqLF1Ba+jsWL55O794Losc0Ex+afRM+/zkO3MOMGTMQEREREZHth3qa\nJWLAecAuwJ3RulnAx7z9diU//ekUunX7lIaGWrzH9hg8EHwQ+DfwR7xH93vAHqQSbn0Gn8N8Wto5\nd8LLMJ2AZ9Z+Bi8XVUBNzUdMmnQbPrR6FbArntk6W/do/ds5tiWD6ALgu/ic6v7RuvXABAoKjicW\ni9Gnz1Pcd9+1m3p/x48fQ1VVFStXrmTgwIGUl4/LOTe48RziGVRXV7N27cl4D3N6Ww4BRnD++SMp\nKirK0V4REREREemoVKe5g2irOs3xeJwddzw5Y3i297xOAf5BZtKuZO3lWXhQXAA8iwfYy/Es2aXA\n14CT0o6pBh7DS07tg88TvhgfsnwlPlT6s3jZpmSd47n4kOs6vIf4eDwR1x/w5F0PZ7VrGnAj3gu9\ngNTnP8ltycRe8/BAeWLa9lHcffdo9tlnn1atF5yql5xZg7qgYA6LF/fl4IMPbtZ5VM9YRERERLqi\njlqnWf+NdzEFBQXceeckevYcgweU8zA7Dg+K8yXtKseD0j2Bm/HEWX2i9UV4oL0s7ZhyYCAeMJcD\nxfgQ5Rui4w8CXsGD45OjZT5eZ/kp4F58iHP/aN3OwLFRexfgmainRG0aF22bHS0XRdtieID8KB60\nQyqg35+99tqL8vLyVs5gXUZJySKyh3/vs8/fOPDAA5t1jurqZZSXT2PYsNUMG7aa8vJpVFcv2/yB\nIiIiIiKyTainuYNoq57mpGTJqUQiweuvr+bqq68hVce4nFTwPA/Pln0YnrUavEd4J1LZrBfivcF3\nkwpWJ6X9nDQPH879EnAVHiynuw4fdr2GVDbsRXjwvBzPaP1NfB518rzzo312wTNm98tq19romsvx\nwH0EEKek5Cnmzr2YsrJkUrPWUV29jMmTb6O2djgAAwYs4q67zm3WdRKJBOXl01i6NNlLDpBgyJBp\nVFXdpB5nEREREenUOmpPs4LmDqKtg2bwAG/cuOuprf0UHy59DF77eCHem7s3Pjx7V+BTfAh1FfBr\nMgPiBD7PuYSiooF88YsPs3btu8CfyB7qbVZOCL8HfkDjoPlqfB7zzKzjJuHzpJfgw7XTt00F3sOH\naQ/CSzztHm1bjNn7hPA8XuKqbYLRLR1enW94d3HxAior+6qclIiIiIh0ah01aFYisC4qkUhwxhm3\nUlu7I41LOo3Fg+APgTeA6UAhZscTQl88uM4exn0McB3x+DjWrj0aqCAzAdhMiopeZf361Xgm67nA\nGDID4Ffw5GDZ5/4WPqc5ORx7NJ6E7I/4fOUf40O/x0SPYwGeyftUevToQSIxhg0bRjY6b23tcKqr\nq1s9GFW9ZBERERGRzkNBcxdVXV3NypW9o5/60zhQPQLYDfiAoqKFDBz4NpdeeiZXXHELa9fmmp8b\nB24lHk9uGw9cCKyguPg+1q3bk/r6G6Jts4HBeJA7ltTc4/QgOl2Itm3Eg/iZeM/3/ngQPYjdd9/I\n+++Pob7+JOBxkr3V9fUAJ2I2iRASec7fMfic6JksXTqK9A8TSkoWU1Z2Qns2TURERESky+q4EYS0\nsQQ+9Loq+r4I2JGSkqeprBzJiy/O4JRTRjF//rX4EOns2st/wLNdJ8XwWslHsm7dnniysGTSr4fw\nxGFz8ED4Obw3eQxQmePcf4y2FeBzlh/F60W/RlHRG5SWTuWRR37Ep5/ez9VXv0Zh4bHk7q2uyjiv\nB6NlW/JkbROxWIyKiilZ9Z+nUlExRfOZRURERETaieY0dxBtPac5kUiw335TqakJwCc0Tuy1lsGD\nd+Puu8/LSGI1e/b9nHrqGmA1nhwMPNDdAxiOJxFLmgf8Fg9YjyAzgdc8vHzVYXivMHgwnEzYNQzY\ngAfWPwX2JbOUFBQWzuPOOzcyYcKETUFlvnnBRUUP0Lv3Atau9dJYLUnQ1dZUckpEREREuqKOOqdZ\nQXMH0V6JwMaO/W9WrfqI7PrMvXtP4vXXKygoSI3gTwXaAL8CaqItpZidQAgPkRrx/zBeXmpnfAh1\nAZ7legqesGseUAt8Byile/ej2bjxs6TmNM8C3icVbP8Bz+KdCnKLixewaFHvTUFlstc4XwbqJUtu\npMYbr2BURERERKSDUdAsTWqPoBlgyZIlDBv2VjQXOCU7Y3MikWDOnDmcfXYP6uu/hvcGD8fnG88C\nJgPPROs2Avfgvc/pCcYSeG/xjfgw7ftJBtnFxfP57W/XEULgrbfeol+/fgwYMIiRIy9h/fqj8OHc\nmVm1S0rOpWfPHqxa5T3kJSWLqKiYArDFZZ9ERERERKR9dNSgWYnAurhYLEYs1q3JfZK1h1es2J36\n+j54b+9NQDUezB6Il3m6Ee99fhwfdl1C47nFh+DDwC8l8+VnDBo0qFHW6eeeu5kJE37Km2/uTjw+\nCfgWPXp0Z+DAxdTV1VNTc+umayxdOorJk72MVFXVTWlDnGeoV1lERERERLaIguYubnMZmxOJBJMn\n3xYNdwbvKU5muS7C5zMfic9xnokPv+4HrM1zxTg77/xvPv74K3jPc4ymMkSXl+/L8uVzqK6uJpHw\nBGGxWIxEoi8jRrxNU2WkVPZJRERERES2loLmLio92dQdd5zNWWdNyxjOXFFxLrFYjKqqKmprR5AK\nTr+JB82ZpZ3cKDyoTtZMfidalz48+z7q6n6A2WvAryksLGevvV7bdL1cctU9rqqqyrmvZFJSMRER\nERGRraOguQtKDrf2YNjnAt9xx9l4tuqmhjMngD/hc5HnAsfRuGrZV9h992OZMuV4pk9/hIaG04Fj\n8DrOs4HrWb9+32jfsfTpcw4vvHBro4Rjmwv0VNN48xr/nmdSUTFFc7tFRERERFpAicA6iLZKBJZI\nJPJml66quqlRgJq5fzU+DPtEvOZx8nvwuc23AYdSVGTstdez/O53Z/LKKy/y2GOP8fnPf5577z2C\nurqmE47lCujzBXqpfZXwK1tLf88iIiIiIu2toyYCU9DcQbRV0JyvjnF28JoulQisF/X1ffHM18lM\n2OlznfMHaM257pYEehp+nNuW/J5FRERERNpTRw2aFWHIZpWVDaKq6iYqK0dSUvIUqQReU4CpwHXA\noeRLyuXnKKOkZFF0bFJyOLXXV66urs6aP934PNmS853Ly8sVMIuIiIiISKtTlNHFNCd4zSUWizF0\n6FDmzr2YIUOmUVy8gOLiFQweHLjmmm4UFTX9gVAsFqOiYkrasQsoLZ1KRcUUBbvbwJb+nkVERERE\nJJOGZ7cyM9sNuAY4CvgC8A/gYeCqEMLHTRzXJsOzYevnAmcPiQaaPay6qeHUmofbujTnW0RERES2\nJx11eLaC5lZkZnsAfwW+iAfKK4H9gcOBFcAhIYSP8hzbZkEztP5c4NYK0BTotS7N+RYRERGR7YWC\n5i7AzJ7ECxlfGEL4Tdr6XwIXA7eGEL6b59g2DZq3hdYK0BToiYiIiIh0PQqaO7mol/k14M0QQv+s\nbTvgw7QBdgkh1OU4frsPmmX7pg8rRERERKQ9ddSguaC9G9CJjIy+PpW9IYTwbzN7DjgCOBBY2JYN\n25zmBEu55jFXV1eTSCQa7Que+Ct5ruSxyX3TtzW3DfmuD1BaWkpNTU2zj01ub8k1N3eN7V3j+tgz\n89bH7qgWLVrEiBEj2rsZItst3UMiW0/3kUjnpKC59QwEAlCbZ/sqPGguoQMFzc0JlrL36dVrBlDE\nmjVHsn79RuCPhDAYeA6zIuA4evTozl57zeSyy77JDTf8iRUrhm3at7Dw6+y9d+o6m2tD4+vfBtSz\ndu0oGhrWEov9lBAmEIvFNntscjvQ7Gtu7hrbu0QiweTJt2UkYFu6dBSTJ29fCdj0j4rI1tE9JLL1\ndB+JdFIhBC2tsAC3AQ3A5Dzbr422X55ne2hrDQ0NYciQCwM0BAjR4usaGhry7NMQ4IJGx/i68xut\n79nzhAAbs/a9MMDGMGTIhWHjxo1NtiFfG/16G6NztezY0tILQmlp48eQ+7iGJq/RGbzwwguhuHhB\n2uPzpbh4fnjhhRfau3nNNn369PZugsh2TfeQyNbTfSSydaKYqN1ju+xFPc1dWHV1ddTTmt6TGKO2\ndjjV1dWUl5fn2KcaH4meeQwcBqxutL6ubixQA5Sn7TscqKG2djhz585tsg1Azu0wApgbfW3ZsStX\n5m5r7uOqmrxGeXk5IiIiIiLSeSkRWCsxsxuA7wOXhBB+lWP7r4HvAt8NIdyWY7t+ESIiIiIi0qUF\nJQLr1FYChs9ZzmVA9DXnnOeO+OIQERERERHp6tTT3Eq2tuSUiIiIiIiIdDzbR1rc7UAI4Q283FRf\nM7sga/PVwGeAWQqYRUREREREth/qaW5FUW/zc8AuwO+B5Xhd5hHACuCQEMJH7dZAERERERERaRH1\nNLeiqLf568DdwP7A94B+wK+Ag7IDZjPbzcwqzOwdM6s3szfN7FdmtnNbt12kLZjZW2aWyLP8b55j\nDjazx83sQzNbZ2Y1ZjbVzPL+/TKz083s72b2qZl9bGYLzezoJvYvMrOrzGyFmZsCnHAAAA74SURB\nVNWZ2f+Z2Twz26s1HrdIS5nZaDO72cwqzexf0T0yazPHdMh7Re910h5acg+ZWZ8m3psSZjanievo\nHpJOx8w+b2ZnmdmDZrYqek/52MyeNbPJZpYzF1Nnfh9ST3M7Me+V/ivwReBhPJHY/sDhqFdaOikz\nexPYCf8gKfsP7r9DCDdm7X88MB+oA+YB/wSOBfYCHgghjM1xjV/gH1i9HR1bCIwDvgBcEEL4Tdb+\nhcAzwMHAkuj73YGTgQ3AyBDCki1/1CItZ2bVwGDg38Ba/DU/O4QwMc/+HfJe0XudtJeW3ENm1gd4\nE1iKv06zvRJCeDDHcbqHpFMysynAb4H/BRYCa4BdgROBnYH5IYSTs47p3O9D7V0ouqsuwJNAA16C\nKn39L4EE8Jv2bqMWLa294P+UvNHMfT8LvBf98S1LW1+IT4NoAE7OOuag6P5ZCeyYtr438AGwDuid\ndcwPomPmZq0/Nlr/cns/b1q63oIXtO+f9n0Cz4uRa98Oe6/ovU5Ley0tvIf6RNsrWnB+3UNaOu2C\nTy09Osf6XYDV0WvyhLT1nf59qN1/KV1xAfaIfkmv59i2A/BptPRs77Zq0dKaCy0Lmifn+ycGGBlt\nW5i1flb0h3FijmOuirZNz1qf/OPfJ8cxi6Ntw9v7udPSdZdm/MPfIe8Vvddp6ShLM+6hLQmadQ9p\n6ZJLWuA6I21dp38f0pzm9jEy+vpU9oYQwr/xT2SK8SRiIp1NDzM7xcx+YGYXmdmIPHNdRgIB/4Qw\nWyX+CeTBZtY96xjyHPNHfEj44ckVZtYfH9ZTG0JY3ZxjRDqgjnqv6L1OtjdfNbNzovenc8xs3yb2\n1T0kXdXG6Gs8bV2nfx9S0Nw+BuIvrNo821dFX0vapjkiberL+KeL1+Jzm58BVpnZsKz9BkZfG90n\nIYQGvNe6AP8UETMrBnbD50b/X47r5rqv8l6jiWNEOpqOeq/ovU62N0fg8zivjb7WmNkzZrZ7+k66\nh6SrMrNuwOn46/KJtE2d/n1IQXP72Cn6+q8825PrlRVROpsK4Bt44PwZYF/gVqAv8HjWp/otvU+2\n5L7SvSidQUe9V3R/yfZiHXA1UA58LlqG4x/qjgD+ZGY90/bXPSRd1fXAIOCxEMLTaes7/fuQgmYR\naTMhhGtCCItCCO+HEOpDCK+GEL4L3IgPj/lJ+7ZQRES6mug96SchhKUhhE+i5S/AUcDfgT2Bs9q3\nlSLty8wuwjNdvwrkrOTQmSlobh/JTzV2yrM9uf7jNmiLSEdwa/Q1fYh2S++TLbmvdC9KZ9BR7xXd\nX7Jdi4aV3oHPk9ya96e2PEak1ZnZBcBNwCvA4SGE7Ndcp38fUtDcPlbif4DzjZ8fEH3NN/5epLN5\nP/r6mbR1K6Ovje6TaE5NPzwJxRsAIYR1wDvADma2a45r5Lqv8l6jiWNEOpqOeq/ovU46g0bvT7qH\npCsxs2nAzcBLeMD8Xo7dOv37kILm9rEw+npk9gYz2wE4BJ9f87e2bJRIOzoo+vpG2rpn8D9038qx\n/3B8OPdzIYSNWceQ55jvRF//nFwRQngdWAOUmFmfPMeEtPOKdEQd9V7Re510Brnen0D3kHQBZnY5\nPoXuRWBkCOGDPLt2/veh9q711VUXPONcA3BB1vob8Xpit7R3G7Voac0F2AsozrG+L569sAG4PG39\nZ4H3gDqgPG19D+D5aP+Tss51UHT/1AI7Z13jw+gPY++sY66IjpkHWNr646P1L7X3c6elay9svsZs\nh71X9F6npSMszbiHytJf02nrvxHdVw3AgVnbdA9p6dQL8KPoNfb39Nd4nn07/fuQRQdJGzOzPfDa\nYLsAvweW4zXCRgArgENCCB+1WwNFWpmZTQe+j9frW40Xk+8PHI3/UX0MODGEEE875njgAWA9MBf4\nJ3AcPszmgRDCuBzX+QVwMT7sZz5QCIwFPo//wfxt1v6F+KeSBwFV+KeafYAxQD0+FOmFVnkSRJop\neu2Pin78Mp6Q6A3g2WjdByGES7P273D3it7rpL205B4ys4X4MM3ngbXR9sF4vdcAXBlCuC7HNXQP\nSadkZqcDd+FDqv+H3Nmn3wohzEw7pnO/D7X3pxhdecHrk90ZvVDq8RpmvwR2au+2adHS2gueRGU2\nnnXxn9Ef1f/Di9qf0sRxBwGP4p86/geoAS4iR69A2jET8U9GP8X/0D8DfLuJ/YvwzN0r8U9J/w//\ng79Xez9vWrrmAkzHPxnPt7ye45gOea/ovU5LeywtuYeAM/B/pt8APole228Bc/B/qJu6ju4hLZ1u\nacb90wA8k+O4Tvs+pJ5mERERERERkTyUCExEREREREQkDwXNIiIiIiIiInkoaBYRERERERHJQ0Gz\niIiIiIiISB4KmkVERERERETyUNAsIiIiIiIikoeCZhEREREREZE8FDSLiIiIiIiI5KGgWURERERE\nRCQPBc0iIiIiIiIieRS0dwNEREQ6KjPrD3wD+BywBvhTCOH9aNuxIYQ/tGf7REREZNuzEEJ7t0FE\nRKRDMbNC4Gbg69HXfwB7AmOBJ4EPgXEhhMPbrZEdkJmVADOBfsAuaZteBD6Jvo8BnwF6A1+K1t0b\nQpjYVu0UERFpCQXNIiIiWczsLmBv4LAQwsasbb8GzgMqFTTnZ2Z/BI4EXgghHJBnn6F4kP1BCGFY\nG7WrHIiHEGra4noiIrL905xmERGRNFFQdTpwVXbAHJkKvNq2rdouvQsY8J98O4QQluC9933aqlHA\n0UBpG15PRES2cwqaRUREMh0HBOCNXBtDCAng123aok4shPAy8J6ZtVWelUPb6DoiItJJKGgWERHJ\n9OXo69eb2OfptmhIF7IEn+O8TZnZ3nhiNxERkWZT0CwiIpLpLXxY8VVmtluuHUIIb6He5i1mZrPN\nLD1IfmQbX6+bmR0ILNiW1xERkc5JQbOIiEimucBGYA/gJTP7lZl928w+m75TCOGh7APN7GtmdpeZ\nvWRmz5jZo2Y2Mtp2tZlNTNu3xMyeM7P/mFnCzCrStg01s7+Z2YZo24+zrlNuZr8wswVm9mczW2pm\nt5tZvxxtOsjMFpvZcjP7p5kdZmYnRutWm9n3chxzYnTep81siZktMrOjt+C5zOfL6T+EEJ4MIWQM\nh29JG5qx7/nAdUBR9PMV0e9noZnd2YqPS0REOiEFzSIiImlCCG8CFwMJYGc88ddjwD+jgOwSMyvK\nPs7MTgGq8MDsoCiz9hjgdDM7CTgn6zq1IYRDgHNztGFJCOFA4Bp8fnX6db4C/AU4HBgbQvgGcGDU\n1qVRRup0tcDPgA+AnYCDgZHACUAv4L/NrFva+WcANwFTQghHhBCGArcBj5jZpCafvGYwsxHAIZvZ\np9ltaM6+IYSbQwgj8UzdANeFEA4PIYwMIZy5tY9JREQ6NwXNIiIiWUIIvwFOBlbgQWvA3zPLgRuA\nv5rZ55L7m9nXgQrgbeC0EMJ/ovPU48HydFI1ibOtaaIpa/Ch4umK8IB+V6B72nXOBnrgdaXTH8uH\nIYQngbujc50GfA/4CJgD3B5CaIgex0TgQuCyEMJraee4D//g4Bdm1qOJ9uYyJOrVrTSz1cAzyXbn\n0pI2bEV7s59TERGRvBQ0i4iI5BBCeDCEMAjYDw8yHwE+xgPowcBv0nafDhQAvwkhxLPOswG4rxXb\n9SawGzAghFCXtv5jvMzTfnkOTbbr+RDCxuBOCyGcn7bPlXhAnmuO8TPA54CDWtjkpVGv7rAQQh+8\nl3tDE/u3pA3bor0iIiIZ2qq8g4iIyHYphFAD1AAzzKwQuB4fsn2SmU0HXgOOinZflOc0H7dymz42\nsx5mdjyeDXoQ/p6+K5t/b38l10oz6wvsiQfXj5mZkTk0fAdgNdBzK9u+2Mye29o2tFV7RUREFDSL\niIikMbNvA5XJIdbpol7ji81sX7zH9BvAJ/j7aQDWtlEbTwN+AfwvPlx8egjhIzN7k82XbvpXnvW7\nRl/j0XzsbendrW2DmR3Q3H1FRES2hoZni4iIZDoZ78Fsyt34vNgdgH/i2bYh/7zlLdUte4WZXYQn\ntPorMDSEcF8I4aNmni85PzuXd6KvPczs8y1uaQuEEE4NIeSay92SNrRKe83swhzJ00RERDZR0Cwi\nItLYAZvZ/kH09fWo93lh9PNhefZvFPymyRfEAvTNse6y6JhLsudPA4XJb8zsCDM7oolzZzYihLX4\nMHTwbNyNmNn+Zja4uedsqZa0YQvbm0huSlv3BTyBmoiISE4KmkVERBqbFs1fzucA4FPgiejnq/FA\n9rtmlvHeamYFwBlNnCsZgBdnHWfAqOi86dOpkvWi38vafwCZ9Y+/mvVzc/xX9HVynu0/xDOEb0st\naUNL27saD5jTRwTshg9zFxERyUlBs4iISGMDgflmtnP2BjPrA1yElzlaBxBCeD5aNwj4nyhQJipL\ndQ8+hDunEMKrwFLgIDPbIW3TlcCTeJB3spmNiq49O9o+PQqsMbOvArcCj0Y/9wX640nKknaKzrUr\neYQQHge+DxxnZpvqR5tZoZndCDzUnKHg0QcHX4l+/FKuutat0YYtaO+j+IcUo8ztDOwWQnijue0T\nEZGux0JoalSYiIhI12Jmd+FzlO8FrgP+Hz5/+J/A1/DM2TNCCDfnOHZ/4Ad40P0u8CHwU+B44MfA\nGSGEWTmO+yLeK3oInlhsPXA7Xkv5YeB9vGf5lhDCXDM7D5gE7IgnH/sYL3v1MfAQnjH6jhDCzWY2\nDPglsA+p4du1wLMhhHPyPAf7A5cCfaLHUBdd+8+bee5K8PnW/cjszV0HrALeCCGMaeocW9KGFu47\nGPgV8Hn8d3RxCGFFc9okIiJdk4JmERGRNGb2TeC5ZA1kMxsClANfxIOsx0MI77fwnNNpImgWERGR\njkslp0RERNKEEP6U9fNSfPi0iIiIdEGa0ywiIiIiIiKSh4JmERGRbe9LeBKuRonFREREpGNT0Cwi\nIrKNmNlYM3sZOA8vHfVzM1tiZge3c9NERESkmZQITERERERERCQP9TSLiIiIiIiI5KGgWURERERE\nRCQPBc0iIiIiIiIieShoFhEREREREclDQbOIiIiIiIhIHgqaRURERERERPJQ0CwiIiIiIiKSh4Jm\nERERERERkTz+P+ir091VJnjdAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f576be58e80>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"X = alldata.SqFeet\n",
"Y = alldata.Price/1000 # in 1000's of Dollars\n",
"labels = ['$\\mathrm{Square \\; Feet}$', '$\\mathrm{Price \\; (in \\; 1000\\'s \\; of \\; Dollars)}$']\n",
"ax = scatterplot(X,Y,labels,20000)"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7QAAAIaCAYAAAAQpgGEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcXFWZ+P/Pk4QQIkvEhR2CSIyImsgAgg4E0K8LIooI\nAUURFcUVGR1RGRAXFHWUGX8KqCCDC7uOK6IsEQVEjYkLChHZXFgUJoISCKGf3x/nFqlUqrqrqquX\n6v68X696dd97z7nn3Kpbt+qpc+45kZlIkiRJktRvpox1BSRJkiRJ6oYBrSRJkiSpLxnQSpIkSZL6\nkgGtJEmSJKkvGdBKkiRJkvqSAa0kSZIkqS8Z0EqSJEmS+pIBrSRJUh+JiAMjYqOxrockjQfTxroC\n0mQQEY8FDs3M/x7rukganyJifYDM/MdY10XjV0S8E9gwMy9ssm07YB/g0cBtwKWZ+ddq236Z+a1R\nrewEVv2gsBewNTAdWAb8IDNXVNtnAntk5vfGrpYjbyyvWxHxMmD7zPzoaJet8cUWWml0HAGcEhFP\nGeuKTCQRMSciromIOyJioO5xT0T8JCL+pUp3ZEQsiYgHGtL9PiIuHuvj6KUWz8mDEfHjiLi8elwV\nEb+KiIsj4jURMXWYZV5Qlbdbr45jpI2XOkfEUyLi9oh4ELgXOGYUy271/vl53blyRURcGxG31W0f\n9wF3i2Nb2fA+uCwirq7SvSsiHjXW9R5KRBwKPDszj29YPz0iTgPOAx4AfgHMAi6IiPdExJHAO0a9\nwhNQRGwbEecCNwIvAv4KLAU2Ac6PiLdUSU8DDhqlOo3q9Wyo69Zo1SczLwLWjYgPjGQ56gOZ6cOH\njxF+AEuAh4EPjXVdJuoDuLh6jn8NTGuRZgtgoEr37rGu8yg+J6e22L4f5cvIr4Atuyxj47rn9FNj\nfczjsc7ATsDTB9k+HTi5qs/xY3yu/HSQNE8Avl+l23gU6zbo89fBsZ3eYvtLgH8CfwR2HIvnv83j\n2Ab4M/DYJtu+CPwEWKfJtk8Dq4DLx/oY+v0BHAzcD1wCbNoizbHA1dU15sxRqNOYXINbXbd6WZ92\n3vtAAJcD+471+eFj7B620EojLCKeBDy9Wlw4lnWZ4O6gfLD9NTNXNUuQmX+uW7x9VGo1tu6o/q5o\ntjFL98MPAzsC342Ijj8TMvMe4CTgx5QWiXFvDOq8L6uvAc3qs5ISdMUo1KWV2vunZetrZt4EvKxK\nu9Uo1QuGeP7aUHsf/LPZxsz8X8r5sAXw7YiYMYyyRtKngNMy82/1KyNiJ+DVwImZ+VCTfG8HfjsK\n9ZvQqtbxr1KC1Rdl5h3N0mXp/nozkKNRr7G6Bre6bvW4PkO+9zMzKef4Gd5XPnkZ0Eoj71DgQspF\nf9uI2HWM6yPVu7T6+xRKi23HMvO4zNwzM2/oXbVG1ijX+dltpBmVL7/DlZn3Ubq1bj2Kxbbz/A3X\nV6u/WwEvHoXyOhIRTwVeQPMA4cWU8+emZnkzc4DSSqsuRcQc4HOU1tnDW/xwUO8dwMoRr1hlDK/B\nTa9bPaxPW+/9zPw15YeGUbtlQ+OLAa008hYC76L8YgslwJXGi7/X/b/dmNVigoqIJ1MG6ZlIfsIo\nBbSj+Pz9pe7/bUahvE69ntJl+K9Ntm1a/f2XQfL/oPdVmlQ+DKwHXJiZfxoqcWbeRfnhR13q4r3/\nOeBt47iHhUaQAa00gqpBie7JzFuB8ymttC+PiLHsWijVe3zd/8u62UFETImIx0TErB7VacSNdJ0j\nYmpEPBO4aCT2P5oi4sMRsUfdqt8Cjx3hMkf7+ZtX9/947J57IK2D0lsony0nRsQWzRJk5i3YStuV\niNgUOKBa7GSU6FEb3Xi8XYOHU59hvPcvB6ZSejJokjGglUbWIZRAlrq/mwB7N0tcjcZ7fd2onMsj\n4hN12w+NiBXVtn9GxMkN+Q+oRu78QUT8LCIWRcS+DWl2i4gfRsTvoowG/K9Vvh9GxK0RcUxd2p0i\n4hMRcVG136UR8fmI2LbVAVejbb69Gin1R9Wooh+MiGdFxLlRRhv+aURMq8szZL1HU0TsUo3S+JOq\nLtdExLH1o6BGxHbVSKm/iYg7I+LfImKjiDglIr4dEddV23ep0m8WEZ+LiO9GxLKIuDIiWnanGsXn\n5GXV358D36nKbusciYhZEXE38BBlpM+3tTiWp0fEV6OMlntZRHw/Iv47Ita6D7PNc3h6RPxHdW5d\nUaX/SER8PMp9bi0NVudBXtNPRcS3qvVXRHu3DbwZ+AhQay04NlaPGnzGEHXcOCI+ExHfqcp85Dxq\nkX6kz5XN6hcy8zeZeWJDHdq+VrT5+nX9/HXpA5Tukz/IzO8M49gOj4jfxupr+L0R8am67QtjzWv4\nfw5VsSjjMGxKeY82cy7lfH4C8KvqfH1BRGxQnygzv95i/0Ne76p0c6KMkP7Pqv5n1m3bucq/stp2\nfN22tj9zqvRtXy+q9F2d/1E+p/4WEW8dIunzWX2f6K+G2m+dK6k+97t4Dto656KNa3B0+Jnc5vuz\nqaHqM5Lv/eqe3p9SBnnTZDPWo1L58DFRH5QPwD8CW9StW0YZ+e+MIfJ+ukr3uibbDqW0IGzSsP6/\nKPMOPrFu3SGU0S0Pr1v3GOB5wI+qMt5dlbdxtbyS8ivnZpTBhH5BNWow5QPmAko31Z2b1G0q5UP8\nr8BW1bp1KYND3F2VvQNwdt0+26p3G8/3FykjKw46kierR198VYvtbwX+D3hB3bpZwFcoIyhvWa1b\nH3gO8PVqf+8HvgRsU/dc/BS4B5hL6X62abVtGvAzygjDmzWpQy+fk4eBTzbZtiHlfqOHKC0/G9dt\na+scqXsePkqLEXqBwyjTiLy7bt10YBGlG/6ULs7hCykD5EytW/csyoBGTV/Xhjo1rXMHr+ndwOPa\nfA1OqPZ12BDp9qzOzY9R7uesvX+mUQKZpmX2+FxZ6/1DGZDlbsp8mq3ydnSt6OT1a/f5G8b7YDZl\nxNoHKV+ipw/n2OryfbIq8x1Ntr0GuIEWo+Q2Sf+Kal9rjW5cl+ZN1Wv+cPU6DlDe2z8D3gnMaJGv\nretdQ57DaDGCL/AfTd5XnVxP2r5eDPf8p0y18zCwZIh0H2X158ajujwHO3kOOn0/tbwG091ncifv\nz9p1q/E62qo+I/rep1w/r+/mNfLR348xr4APHxP1ASwAftyw7oPVxf8emkyvUJfuiVW6S5ps+zdg\n/4Z1r6rSL2yS/hvA34B1G9a/tsrzG2AdSgD+JeAz1fZtKaOC/hlYry7fLMoXjmualHVQtc/PN6yv\nfQH64HDrPchzVvtCfg+l69EV1d/6xxUMEtBSfol/GDiyybYArgOuYc0gbJ9qn38BntGQ59hq203A\n1g3b3kOTHy1G6Dn5U8PzcE31OB3Ye5D8g54jden2puFLTbV+fnWufKth/TxWf+Ge1clxAxtU6Z7a\nJN3Hm72uLY6taZ3bfE0fBl7RZjm1L2WD1ovVXwzvAXZoca68omH9SL5/fgj8oe79MlhA2/a1otPX\nr93nr81ju63hfXBV9Rr/mfLjzobDObaGfFtTgqpm18l3Agd2UP9akDhliHQHUK5RD9c9asHtEuDR\nDek7vt41nKvNAtpXD/K+Guozp+3rRS/Of0o37muBA4Z4Xk+vex9Et+dhO89Bt+ccra/BnX4md/r+\nXCugbVWfLvbd8XsfOKo6T5r+gONj4j7sciyNnENZ3c24pjZIxEaU4eibyswbKb9I7xMRsxs2v5C1\n7+M5jvJB8Y0mu7sceDTQOMF5bWqbqzPzoSwOy8w3V3W4mTKNxfaZ+ci0L5m5nDINxjOalFXrDnVX\nw/o7q7/ze1DvoSzNzL0zc6/qb/1jryHyfqT6u9a9O5mZVT13YfX9VLD6efxTZv6iIVvtefh5Zt7W\nsO1OypeZTRrWj8RzcnnD87Bb9XhDZl4+SL5Bz5E6D7fIfzzlS9tZ9SszcynwOuCg6nyC9o+79sX2\nxIhovI/zf4HrBzmeduoMQ7+mwcgNHPTLzGy8h7N2rjSWOZLvnz0zcztgZ0pPgpY6vFb06vXrVFIG\n9Kl/HzwrMzenfCk/GLgtIl63RqburoNU7/dLgF0i4mkNm19M6QXQrscB/8gyWnHrA8z8WmY+parT\nMZTzYjnl2J8GfLYhSzfXu+EY6nrSyfUChnn+Z+aFmblrZn5tiHrfU/f/ekOkHcqQ19Quz7lW17NO\nP5NH8vo6Gu/92ym3U27eg32pj0wbOomkTkXEOsBLKb8wPiIzfxMRv6N0QT2EchFv5QuUVt7XUT64\niYhnAT+p/2JTBbxPpHxQficigjWH0l8fuJXWH8S/aVWBzFweEetGxP6UVqunUK4bm9D8+vGj6m/j\nCKi1L+KLe1jvnoqILSndKx/IzLtbJLuNEli8jNJ1ql6zAZUebmPb1Lo6zGYcPSd1Wp4jrVR1rw3O\nsbRxe2bW3383mzaPOzP/GREnUb78vigiflHt/xLgG0N96e/QYK/bSH1+NpvmYq0yR+tcyczFEbFW\nwBAR6wOrMvOBKl1b14pRfv3akpk3RsQLKa/36RExNTNPr9ve6XWw5jTKe+CNlC7BRMTewI8yc7Af\nVBrNZM3RyIc6nl8CvwT+KyKmAydT5ul8eUSckJnLenC9G461riedXC+q9LMZvWtlfaC1KS2mR2oU\nEVOBOZn5uyabB72mDuOca9T2Z3JV7oi9P0fpvX9/9df5aCcZA1ppZDyP8ivhV2LNAY2D0m0ygH0j\n4lGZ+c8W+7iIco/NayLi+Opi/1pKt+V6tRa+VZnZdLCpIbT8ohQRhwGfoHTL+xhwQmb+X0TcTJNp\nOzLz6oj4AnBQRDw1M38dEZtRvkz9EqgfAGW49e61Lau/g80dWJt7sNngJIPla3c+wvH2nNS0/WW6\nzuMo974l5R69wXR03Jl5YkRcQ+lyuA+lFfFIYElEvDAz7xx0B+0btXkkuyhzNM+VZtOUHA98mWqQ\nnE6uFaP4+rUtM++OiK8AbwFOjogv167NnV4H63yH8ty9IiLeVe3v9ZQu5J1YySCDeEbEC4Arm32W\nZBko5x1R5rHdi/J8L2P417vhaHY96eR6AaN7/n+P1cHyjrQZ0FLuTX0tcHSTbYNeU4dxzq2hw8/k\nWp4Re3+Ownu/ds6O9o++GmN2OZZGxqHA0dm8y+selK4361FacZvKzAcp99ZsCuwXERsCj6m6I9X7\nc/V33YjYuMN6Ji0mRo+ItwH/Q7mHaufMPCcz2/misRHl3qQTIuJy4JxqP7tlZn3XxeHUeyTUumTN\nHCTN46q/zeaC7IXx9pzAIOfIEO5mdcviUFM3tH3cETEtIuZk5vcz85WZuRmlteE4yhfIz3VR11EV\nEW+NiJ2HuZtRO1cy87jMvLJh9Tzgd9DZtaIXr1+Pnr9mrqv+bgA8qSqr2+sg1Y+QX6C0Fh4aEY+n\nDCp0S4f1+jvwqEG2H0RprRzMWZQfUtevlkfqejd1iO2triedXC9gdM//OykDMgWlu3i7dqT5FFCD\nXlOHc8610O5n8oheX0fpvV87n1s1FGiCMqCVeiwiZlJ+CW86h1pm/oUyqmxQuh0P5vNVuiMpQfJX\nmuzvT5RfWgGe2aJOze7jGsq/Uz5035mZqxq2Ta/b93Mj4rnV/zOB2Zl5aWYeWAXxCzLz47WuiaNQ\n765k5k3AjcDUWPu+5ZrtKM/JxSNUh3H1nAxH1aXysmqx6TQ3EbF5RDyhw+PegrXvsftTZta6su3T\ng+r3Uq0bXX1XjcdQemp0bSzPlSjTwTw2M2utIW1fKygj/J5Vn2CI129Enr8W6udwrbVKd3wdbPAF\nyjG8gXLsX+yiXrcAG0bEjEHSDDWV1N+qvzfBsK93g/3A1Wpfg+rgerFdlX60z//jKEHSQdFirt8m\nDgK+2UVZwz3nqEvT9mdyZSSvr53uu5v3fq2rceM9w5rg+i6gjYhXx+r53Vo9HmqSb/co8z/eHRH3\nR8Qvo8zLNVg3nldHmQftvijzgV4Rg8xtFhEzIuLEKPOIrogyj+F5ETG3V8evvrA/cHFm3j9ImrOq\nv8+JiMe0SpSZ11FGYXweZfTIVgOJvK/6e0SL7e+lTCHUidochmt8METE9pRW45rN65ZnAPMjYl6b\nZYxEvYfj+Orvyxs3VNeK/Sj3U509gnXo9XPSTetqr5xI+VLypkG2167BnRz3rhGxY5M0N7P6i/t4\ncSvlC9nj6tZtQelKOFxj9f45hjXvL+7kWrEZZaCkdl+/kXz+HlH1gHk15f1yQWbWjqWb6+Ajqh8w\nv00ZyOdVdBfg1FqOW87/DRwd5X7ZVnYF7mPN4LTb613tNZrZkCcoc4Am3d3S1s71oj64Gdb5HxEv\njzLn7pDzlmYZqPG1lGM+M8o4GS1FxIuA32bmHUPtu4lhnXMNOv1MhpG9vnay727e+1tR7gu/fVi1\nVN/pu4CWcgP5+1s8LqdcSL9bnyHKTfU/BJ4NfI1yX+I6lLmwzmlWSER8gvJL6qaUbhBfonQf+VZE\nrHWxrT5ILqUMr/934BRKK9xLgZ+PUPcojTMRsQ3lXByq29UlrP7QP2qItJ+nvFd/XNcisobM/C5l\nOp8XR8Qb6+ozPSI+CXy9SZeljWg+ym5NrTX4hOqLChGxOWWgk29Xy7Mpv+LfWNXjHkoA/tOIuCHK\nJPK/qb40fCUiXlf9Yjyceq+l+vK1WbW4cZTBOJqlqz/WtUZBzMxzKb/Evy8i9qnLN5UyrcB9lCmT\n6n/Zrv0ivAFrq23bsN1tI/CcBLDZYD/eDWKoc6Sm1kVwjecgM6+hnN+7RMT/V2thiuJo4K7qi2Kn\nxx3Al6sveLV0m1CmQ1nrnrBO6lzp9jVt5tuUL2ovqY57FmVu6sb78Douc4TePy1bPyJi44g4jvIe\nqR/UppNrxaWU61m7r1+7z99Qx1Ybv6BZmm0p3xu2pHxXeH2Xx3Zji2qcVv29KDsbDKrmZ5R7AxtH\npK33JODC6vlZQ/W59Dbg3+t/aO3yekeWUbiXArtFGRys5jjKZ1tQWjJfUpVdM+j1pJPrRZV+uOf/\nf1AC/eMHSVNfv/Mpo2E/C/hmlHtR1xIRzwMWVvtv1M41tZtzrtU1uKPP5Noh0P77s9X1sNX1tZN9\nd/Pe34Eyb7cmmxwHcwf16gFcTbkHY9+6dRtQfuVaAcyvWz+dMgfdw5Sh4Ov3U5sa4gbq5qWj3Ij/\nN8ooas3mlBwAzm1Yv1+1/tdj/fz4GNFzbzvKPH8rWT3/3y00zN1I+bX0quqcrJ8r8Abgmy32PZMy\nFP2T2qjHLpR7fX5K+SX+a8A+DWn2oHxBWlFX/u+AzzXZ31GUD8PfUX6guYDygbF5tf5XwNsa8ry9\n4dga50S8Hti003q3ON45lPuM7mgo56/V9eBfqnRHUkZz/EdDumXAd5vsd1fKlEtXVsd9BeXLyQYN\nZf+E8qWvtr9fUVoLdq6OpfYcPwT8gtIS0vj8P7JthJ+TO6vnZG4b+2jrHKGc99fWPa8PUb5M/EtD\nup0oU1b9htKt8Fu0mFtwqOOmBCffrs7Dr1fHemn1eGmb79Wmde72NW2jzKdVx72kOqa5ddualbkU\neCWlK+VYnCvXsva8xTdW5T9MGVn2Jd1cK7p5/QZ7/jo8tvuBHzcc2xJKi8/FwCEt9tXxdbAhf1Ba\nm7Yeqt6D7ONbwOkttn2R8sP7HpTPl09Rurs+p3rO/zBE/Ya83jXJ81jgk9Xx/6B6Tfev6nAP5TPt\nR5TAru3PnE6vF8M8/4+hNEC8o8PXYmtK0HlX9bwfCjyX0sL/Jcpc1dGQp9PnoN3305DXYDr4TKbN\n9ydrX7dq16ZjWtWn3X0P571PuWf5/d2+z3z07yOqE6DvVV0YfkW572WbrA4sIo6g3MNyVmYe0ZBn\nL8ob5YdZNz9lRJwNvAJ4TWae3ZDnRMqvkB/IzBPr1t9K+XX3CZl5a0OeWuvw3pn5wx4dsjTuRMRZ\nlK51B2c1VUH1C/MGlEFLnkv5NfyczHxdq/1I0kRRta6dmpn7D2MfB1MCyC2z4YtbRDwHuCqrOUur\n7qU7UYLOOyg/2o3UQHaTVpRu6ntTAtx1KD/6/CAHv91oVE2mz+SI2JrSkLBjrj2Xtya4iTRtzxso\nXTi/0HCx36taf0mTPFdSfrHdPSLWydXdOWvBbbM8F1N+udybcj8HUQYp2Aq4oTGYrcvzr1UeA1pN\nSBHxZMo9Yrtm3bx71fvxXsqvt7+oPnR2H5taStLIqbo4L6DMF14LbF4PnDHMXV8InEQZZXeNeYEz\n89KG5aU0mctVvZVlhODB5pIfU5PwM/kQyg87BrOTUD/eQ7uW6j6LV1C6NzR+aDyp+rusYT1Z7mW5\nmRLYP6Ha10zKTef/yObzYf2++junnTIGySNNNPdSui8Ndb/lppTud5I00bye0oXyY/DIiNB7ZmY3\ng0E9ovq+8l5KDzGpHZPmMzkipgFvBD401nXR2JgQAS3lJv1ZlJFl/9ywrXbDeqtJrGvrazewd5q+\n2zzShFK99/4d+HxEvDYi1pjYPCJmR8TplMHV3j4WdZSkEXY38ABwVUSsS7nl6aRe7DgzzwP+HBFH\n9mJ/mtgm2Wfym4GlmdmsZ6UmgYnS5fhISrfi08e6ItJklpmfjIjvUqY3uDQiVlF6TqwDLKd0z3pr\nZq4cw2pK0ojIzAsj4pmU26DeDHyqsUvwMB0GXBIR12Tmr3u4X01Ak+EzOSKeCLyOclufJqm+D2gj\nYgfKqMR/ZO3Jv2F16+hGTbbVr1/eZfpu86whIibG6FzS4F4EfKGaiUCSJrpnjdD17ldeR9UDE+kz\n+a4JchwCMrOjF3MidDluNRhUzQ3V37XuX63mWtuWMgXBTQDVIA5/BtaPNeesrKnNnVV/v2zLMgbJ\ns5axHvLaR+vHCSecMOZ18OFr1O8PX6Px/fD1Gf8PX6Px//A1Gr3HFVdcwU033eTrM8Ee3ejrgLa6\nP+WVlO4TZ7ZIdjllDrjnN9m2J2WOz6ty9QjHtTy0yPPC6u9ltRWZ+QfgNmBOwyTi9Xmybr+SJEmS\nurRgwQK23Xbbsa6GxoG+DmgpE4c/mjLHWuNgUDUXAn8DFkbETrWVVTD8IUqgeWpDntMoQfD7ImJW\nXZ7ZlHtiHgDOapHnY1HX5yEi9qfMQXtdOgetJEmSJPVMv99DWxsM6nOtEmTmfRHxeuACYFFEnAvc\nQ5nLbQ5wQWZe0JDnmoj4JPAOyn0qFwLTWT2a8lsy87aGoj5JuRfhQODaiLgM2KZa/gdwxHAPVmNn\nwYIFY10FDcHXaPzzNRrffH3GP1+j8c/XaHzz9ZmYotu+ymMtIuYCv6V09d02hziQiNgNeB9lAKkZ\nwI2UOWs/3SpvRLyK0iK7A2Uur8XAxzOz2eBTtflwj6VM7rw1ZQ6wK4D3Z+b1Q9RvqEOQJEmSpAkr\nIsgOB4Xq24B2ojGglSRJkjSZdRPQ9vs9tJIkSZKkScqAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSX\nDGglSZIkSX3JgFaSJEmS1JcMaCVJkiRJfcmAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSXDGglSZIk\nSX3JgFaSJEmS1JcMaCVJkiRJfcmAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSXDGglSZIkSX3JgFaS\nJEmS1JcMaCVJkiRJfcmAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSXDGglSZIkSX3JgFaSJEmS1JcM\naCVJkiRJfcmAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSXDGglSZIkSX3JgFaSJEmS1JcMaCVJkiRJ\nfcmAVpIkSZLUlwxoJUmSJEl9yYBWkiRJktSXDGglSZIkSX3JgFaSJEmS1JcMaCVJkiRJfcmAVpIk\nSZLUlwxoJUmSJEl9yYBWkiRJktSXpo11BSRJkiRppKxcuZKTTz4ZgHe/+91Mnz59jGukXrKFVpIk\nSdKEdNJJn2HGjJdx/PFP4vjjn8SMGS/jpJM+M9bVUg9FZo51HQRERPpaSJIkSb2xcuVKZsx4GZnf\nYHU73gAR+/PAAxfZUjsORQSZGZ3ksYVWkiRJ0oRz8sknk3kYa4Y8U8h85SNdkNX/DGglSZIkSX3J\nLsfjhF2OJUmSpN6xy3H/scuxJEmSJAHTp0/nQx96PhH7A+cB5xHxYj70oecbzE4gttCOE7bQSpIk\nSb3ntD39o5sWWgPaccKAVpIkSdJkNum6HEfEPhHx9Yi4PSIeiIg/R8T3IuL5TdLuHhHfjYi7I+L+\niPhlRLw9Ilo+BxHx6oi4NiLui4jlEXFFROw7SPoZEXFiRFwfESsi4s6IOC8i5vbqmCVJkiRJRd+2\n0EbEx4B3An8ELgb+BjwO2Am4NDOPrUu7P3AhsILSgf4eYD9gLnBBZh7cZP+fAI6p9n8hMB1YCDwG\neEtmfrYh/XTgcmB34GfV/1sBBwErgb0y82eDHI8ttJIkSZImrUnT5TgiXg+cDnwReENmrmrYPjUz\nH67+3wD4A7ABsHtmLqnWTweuAJ4JHJKZ59fl3w24Cvg9sHNm3lut3xr4BTATmJuZt9XleQ/wYeD8\nzFxYt34/4BvAdZn51EGOyYBWkiRJ0qQ1KbocV4Hoh4BbaRLMAtSC2crLgccC59SC2SrNSuA4IICj\nGnZxFJDAh2vBbJXnNuAzwLrAaxryvLHK8+6GunwL+BGwQ0Ts2f6RSpIkSZIG03cBLfBcStfii4CM\niH0j4t8j4m0R8cwm6feiBJqXNNl2JXA/sHtErNOQhxZ5LqYEwXvXVkTEdpTuxcsy89Z28kiSJEmS\nhmfaWFegCztTAtSVwBJgx2oZICLiSuDAzPxbte5J1d9ljTvKzIcj4mZgB+AJwA0RMRPYArgvM+9s\nUv7vq79z6ta1LGOQPJIkSZKkYejHFtrHU1o73wUMAM+i3B/7NEqL6h7A+XXpN6r+/r3F/mrrZ3WZ\nvts8kiRJkqRh6MeAtlbnh4D9MvOazLw/M68DDgD+BOwZEbuOWQ0lSZIkSSOuH7scL6/+LsnMP9Zv\nyMwVEXEJcASwC3Atq1tHN6K52vrafjtN322etRx++OHMnj0bgFmzZjFv3jwWLFgAwKJFiwBcdtll\nl1122WXxLBV3AAAgAElEQVSXXXbZZZcnxPLSpUtZvryESLfccgvd6LtpeyLiNcAZwMWZuW+T7R8D\n/g14T2Z+LCK+BBwKHJqZ5zWknUoJRtcB1s/Mh6r1fwQ2BzZvvI+2GnjqauBHmblntW47yn2yN2Tm\nk5vU6VjgJOCDmXlCi+Ny2h5JkiRJk9akmLYHuIwyCNQOLbbvWP29ufp7OeWe2+c3SbsnZU7Zq2rB\nbF0eWuR5YV09AMjMPwC3AXMiYpsWebJuv5IkSZKkYeq7gLaaC/ZbwNYRcXT9toj4f8DzgP8Dvlet\nvhD4G7AwInaqS7suZT7bBE5tKOY0ShD8voiYVZdnNvBm4AHgrBZ5PhYRUZdnf+DZwHWZ+cOOD1iS\nJEmS1FTfdTkGiIgtgKsoc79eTpm+5wnA/pSRjw/OzP+tS78/cAHwIHAucA/wYso0Ohdk5sImZXwC\neAfwZ0pQPB04GNgYeEtmntqQfnpVl92AxZQW3G2AAykB8N6Z+fNBjskux5IkSZImrW66HPdlQAsQ\nEY8BjqcEppsB9wJXAh9tFjhGxG7A+ygB5wzgRsq9uJ9uFUlGxKsoLbI7UALlxcDHM/PiFulnAMcC\nhwBbV3W6Anh/Zl4/xPEY0EqSJEmatCZVQDvRGNBKkiRJmswmy6BQkiRJkiQZ0EqSJEmS+pMBrSRJ\nkiSpLxnQSpIkSZL6kgGtJEmSJKkvGdBKkiRJkvqSAa0kSZIkqS8Z0EqSJEmS+pIBrSRJkiSpLxnQ\nSpIkSZL6kgGtJEmSJKkvGdBKkiRJkvqSAa0kSZIkqS8Z0EqSJEmS+pIBrSRJkiSpL03r1Y4iYgaw\nObARsB7wT+CuzLy9V2VIkiRJklTTdUBbBbAvAF4C7ApsR5MW34h4APg5cAVwfmb+ttsyJUmSJEmq\niczsLEPERsAxwNuAqcBPgV8ANwO3A/cDDwEzKa21WwE7ADsDc4GrgA9l5iW9OYSJISKy09dCkiRJ\nkiaKiCAzo5M8HbXQRsS+wBnA1cAhwOWZubKD/FtX+U6LiKXAkZn5107qIEmSJEkSdNBCGxEfAJ4N\nvD0zfz2sQiOmAW8GXgccbDdkW2glSZIkTW7dtNC2FdBGxLHAusAHehl1RcQTgVMpLbU392q//ciA\nVpIkSdJkNpIB7csy86Kuazb4vmcB8zJz0Ujsv18Y0EqSJEmazEYsoNXIM6CVJEmSNJl1E9CuNc2O\nJEmSJEn9YNgBbUQcGhGvqh67VOs2iYhvRMQ/IuKWiHjr8KsqSZIkSdJqvWihnQ98FngqsE5ETAG+\nC/w/4ETgncArIuKlPShLkiRJkiSgw3loW1gFPC8zrwKoAtf5wHGZ+fFq3Y+ArwBf70F5kiRJkiT1\npIV2l1owW3kekMDZtRWZeWcPypEkSZIk6RG9CGgb9zEPuCsz/9Sw/lE9KEuSJEmSJKA3Ae06ETEV\nICIeCzwDuKw+QURsD9zRg7IkSZIkSQJ6E9BeAnwiIp4KfA6YSl1344jYEbgAeF8PypIkSZIkCehN\nQHsysBXwS2Bf4AOZ+f2ImBMRV1frnwZ8rAdlSZIkSZIEQGTm8HdSuhzPBAYy85/VumnAFnXJVmbm\n7cMubIKKiOzFayFJkiRJ/SgiyMzoJM+wW2gj4hhgBfDRWjALkJmrMvPWuofBrCRJkiSpZ3rR5fjt\nlPtmN+zBviRJkiRJaksvAtpbgMcBrxosUUR8rgdlSZIkSZIE9Cag/S/gRGDaEOn+tQdlSZIkSZIE\nDB2EtuOvwJ+AJdWoxr8B/g7Uj3C0CTCnB2VJkiRJkgT0YJTjiLgH2AhoHI2qfscBZGZOHVZhE5ij\nHEuSJEmazLoZ5bgXLbR3AtcBZwGrWqTZiDJfrSRJkiRJPdGLgPYu4KTMvGSwRBFxWA/KkiRJkiQJ\n6E2X492AZZl59xDp9sjMK4dV2ARml2NJkiRJk1k3XY6HHdAOuvOI5wKbAjdm5jUjVtAEYEArSZIk\naTLrJqDtxbQ97ZTxgoh42yiUJUmSJEmaJEa0hfaRQiJmA9/MzKeNeGF9yhZaSZIkSZPZmLXQRsTO\nEXFNRDwYEQ83PoA/ACt6UZYkSZIkSdCDUY4jYlvgUmBd4HZgE+COavN0yj203waOGm5ZkiRJkiTV\n9KKF9r3A94FNM3M28NPM3LZ6bAHMBdYHZvWgLEmSJEmSgN4EtDsDh2Xm8mp5VUQ8urYxM38PHAac\n2IOyJEmSJEkCehPQ3p2ZD9QtXwc8vz5BZv6FHrbQRsQtETHQ4vGXFnl2j4jvRsTdEXF/RPwyIt4e\nES2fg4h4dURcGxH3RcTyiLgiIvYdJP2MiDgxIq6PiBURcWdEnBcRc3tx3JIkSZKk1YZ9Dy2wPCKm\nAetk5grgMuD9EXFBZq4CiIgAtuxBWTUJLAc+BTSOgvWPxsQRsT9wIWVgqvOAe4D9qvy7Awc3yfMJ\n4Bjgj8DnKPcDLwS+FRFvyczPNqSfTrmXeHfgZ8ApwFbAQcC+EbFXZv6sy+OVJEmSJDUY9rQ9VeC3\nN2UwqO2Bh4HbgGuAdwJ3AScAz87MXYdV2OoybwYyM5/QRtoNKKMsbwDsnplLqvXTgSuAZwKHZOb5\ndXl2A64Cfg/snJn3Vuu3Bn4BzATmZuZtdXneA3wYOD8zF9at3w/4BnBdZj51kHo6bY8kSZKkSWus\npu05B3gypUvx9Mx8kBLIvhi4Afg/4GjgrB6U1Y2XA48FzqkFswCZuRI4jtLC2zgC81GUVuAP14LZ\nKs9twGcoIzq/piHPG6s8765fmZnfAn4E7BARe/bigCRJkiRJPQhoM3Mx8ARgx9rAUJn5JUoQezul\nC/DpmXnqcMtqsG5EvCIi3hMRb4uIBS3uh92LEmhe0mTblcD9wO4RsU5DHlrkuZgSBO9dWxER21G6\nFy/LzFvbySNJkiRJGp5e3ENLZt7eZN1/A//di/23sClwdt1yADdHxGsy88q69U+q/i5r3EFmPlx1\nX96BEpTfEBEzgS2A+zLzzibl/r76O6edMgbJI0mSJEkahl50OW5LRBzQw92dCexDCWofBTwVOA2Y\nDXw3IurvVd2o+vv3Fvuqra+Nwtxp+m7zSJIkSZKGYdQCWsr9qj2RmR/MzEWZ+dfMfCAzf5uZbwI+\nSRmw6f29KkuSJEmSND611eU4ItanTGHTrQ0pragj7TTg34A96tbVWkc3Wjv5GuuXd5m+2zxrOfzw\nw5k9ezYAs2bNYt68eSxYsACARYsWAbjssssuu+yyyy677LLLLk+I5aVLl7J8eQmRbrnlFrrR1rQ9\nVUB7L2VwpY6GUa6TmTm1y7xtiYgNKUHjA5k5s1r3JeBQ4NDMPK8h/VRKMLoOsH5mPlSt/yOwObB5\n4320EfFM4GrgR5m5Z7VuO8p9sjdk5pOb1OtY4CTgg5l5Qou6O22PJEmSpEmrm2l72mqhzcx/RMRD\nwCmUEXs7jbw2Ar7SYZ5u7Fb9valu3eXAK4DnA+c1pN+T0kV5US2YrcvzyirP/zTkeWH197Laisz8\nQ0TcBsyJiG2ajHT8QspzdnlnhyNJkiRJaqWtFlqAiLgd2Kaav7XzgiJ+kpnP7CZvw37mArdl5v0N\n62cDP6CMVvzezDy5Wr8B8AdgA+DZ1TRDRMS6wBXArsDCzLygbl+7AVcBNwK71KYjqspYDKwHzK3m\npa3lqbXCXlDtL6v1+wNfB36TmU8b5LhsoZUkSZI0aXXTQttJQPuUzLyuq5qV/HMys9W0Np3s5wTK\nfbJXArcC9wHbAfsC6wLfAQ7IzFV1efanBJoPAucC9wAvpkyjc0FmLmxSzieAdwB/Bi4EpgMHAxsD\nb2mcVzciplNaYHejBL2XAdsABwIPAHtn5s8HOS4DWkmSJEmT1ogGtMMVEQdk5td6sJ89gDcA81k9\nbc9yYClwdmY27dpctbq+jxJwzqC0vp4BfLpVJBkRrwLeTJmndoASqH48My9ukX4GcCxwCLA15b7j\nK4D3Z+b1QxyXAa0kSZKkSWu8B7S/yMxnjEphfciAVpIkSdJkNmKDQvXRtD2SJEmSpEliQk3b089s\noZUkSZI0mTltjyRJkiRp0mgroK3cA/zHMKbt6XqEZEmSJEmSGk3pIO1zug1mK68aRl5JkiRJktbQ\ns1GOI2IKcADwMmAr4K+U7slnZ+YDPSlkAvMeWkmSJEmT2ZhN2xMRWwIXALuw5qBRCVwP7J+ZNw67\noAnMgFaSJEnSZDYmAW1EPAr4CaX78jeA24CHgMcB2wH7AfcBz8jM+4ZV2ARmQCtJkiRpMhurgPZY\nyhyzr2wWkVVdkT8OLM/MDw6rsAnMgFaSJEnSZDZWAe01wAsyc/kgaaYCl2bmXsMqbAIzoJUkSZI0\nmXUT0HYyynErDw4WzAJk5sPAqh6UJUmSJEkS0JuAdkab6dbtQVmSJEmSJAG9CWj/GBEvGCxBROwD\n3NGDsiRJkiRJAnoT0H4c+GpEHBkRj6nfEBGzI+JdwEXAf/agLEmSJEmSgN7NQ/tW4JRq8UFgJTAT\nmFqtOy4zPzLsgiYwB4WSJEmSNJmN1aBQZOangX2BX1Huqd0QmAb8AXiFwawkSZIkqdd60kK7xg4j\ntgS2BO7KzJt6uvMJzBZaSZIkSZPZmMxDq94woJUkSZI0mXUT0E4bZoEbA/sATwceA9wH/B74QWbe\nMpx9S5IkSZI0mK4C2ojYBvgQ8HJgnRZpvgscm5nXdV89SZIkSZKa67jLcUS8HPgCsEEbyR8A3pyZ\nX+yibpOKXY4lSZIkTWYjPspxRLwU+CqQwKeA5wGzKcHtNMpUPZsD/wp8EPg78PmIWNhJOZIkSZIk\nDaXtFtqIeDzwW2Ax8MrM/GsbeTYAzgL2Ap6cmXd2X9WJzRZaSZIkSZPZSLfQvgG4CXhhO8EsQGbe\nBxwEXA8c1UnFJEmSJEkaTCcB7UuBd2Tmw50UUKV/F7B/J/kkSZIkSRpMJwHtzMy8qptCqnzrdZNX\nkiRJkqRmOglo7xlmWXcPM78kSZIkSY/oJKB9YJhlPTjM/JIkSZIkPaKjaXskSZIkSRovOglopw+z\nrOHmlyRJkiTpEdM6SLtLRJwG3N9FOesCz+ginyRJkiRJTUVmtpcwYgBoL3GT7EBm5tQu8094EZHt\nvhaSJEmSNNFEBJkZneTppIUW4PvAHR3mAdgMeG4X+SRJkiRJaqqTFto7MnPTrgqJmAL8pdv8k4Et\ntJIkSZIms25aaDsZFOrmDuvziMwcGE5+SZIkSZIaddJCOyczl3Vd0DDzT3S20EqSJEmazLppoW07\noNXIMqCVJEmSNJmNdJdjSZIkSZLGDQNaSZIkSVJfMqCVJEmSJPUlA1pJkiRJUl9qK6CNiOkR8Z2I\nuCMidhzpSkmSJEmSNJR2W2gPAnYGHg9sWr8hInbtdaUkSZIkSRpKuwHt5sBRwFMz89KGbR9pZwcR\ncXEnFZMkSZIkaTDtBrQ/BV4F/HYYZT1pGHklSZIkSVrDtHYSZeaiiHgfsDQivgrcXrd5dkT8BzDY\nBLibANt0X01JkiRJktYUmdlewoiNgXOA53ZZVmbm1C7zTngRke2+FpIkSZI00UQEmTlYQ+naeToN\noiJiDmVgqKgenwKOHiLbo4EvZ+b6HRU2iRjQSpIkSZrMuglo2+pyXC8zlwHL6gpdnpk/bKNy13Va\nliRJkiRJrbQ7KNRgXtNmukN7UFZLEfHKiBioHke0SLN7RHw3Iu6OiPsj4pcR8faIaPk8RMSrI+La\niLgvIpZHxBURse8g6WdExIkRcX1ErIiIOyPivIiY24vjlCRJkiQVHXc5brmjEhQeALwM2Ar4K3Ax\ncHZmPtCTQlqXvRXwK0qAvj7w+sw8syHN/sCFwArgPOAeYD9gLnBBZh7cZL+fAI4B/ljlnQ4sBB4D\nvCUzP9uQfjpwObA78LPq/60o8/iuBPbKzJ+1OAa7HEuSJEmatEblHtoWBW8JXADswpqjHSdwPbB/\nZt447IJal38pZRTlrwHvpCGgjYgNgD8AGwC7Z+aSav104ArgmcAhmXl+XZ7dgKuA3wM7Z+a91fqt\ngV8AM4G5mXlbXZ73AB8Gzs/MhXXr9wO+AVyXmU9tcQwGtJIkSZImrW4C2mF3OY6IR1FaYjcETgbe\nBLweeC9wJqU18+IqqOy5iHg7sIDS9fn+FsleDjwWOKcWzAJk5krgOEoQflRDnqMoAfmHa8Fslec2\n4DPAuqzd3fqNVZ5316/MzG8BPwJ2iIg9Ozg8SZIkSVILvbiH9q2U7r47ZuZ7M/O0zDwjMz+ama8H\nNge+ydAjIXcsIp4MfAQ4JTN/PEjSvSiB5iVNtl1JCYR3j4h1GvLQIs/FlCB477q6bEfpXrwsM29t\nJ48kSZIkqXu9CGj3B97cqr9sZg4A/06PA7mImAp8CbgFeN8QyZ9U/V3WuCEzHwZupoz4/IRq3zOB\nLYB/ZOadTfb3++rvnHbKGCSPJEmSJKlLHU/b08SDmbl8sASZ+XBErOpBWfVOAJ4OPCszHxwi7UbV\n37+32F5bP6vL9N3mkSRJkiR1qRcttDPaTLduD8oCICJ2Bd4DfCIzf9qr/UqSJEmS+kcvWmj/GBEv\nyMyLWyWIiH2AO3pQVq2r8dnADcDxjZtbZKu1jm7UYnttfa2ludP03eZZw+GHH87s2bMBmDVrFvPm\nzWPBggUALFq0CMBll1122WWXXXbZZZdddnlCLC9dupTly0t4dMstt9CNYU/bExG7UAZOejdwUWbe\nXbdtNmWE4fcBz8vMa4dVWNnnRsD/UQZ5ahbA1q8/JTOPiYgvAYcCh2bmeQ37m0oJRtcB1s/Mh6r1\nf6QMaLV54320EfFM4GrgR5m5Z7VuO8p9sjdk5pOb1PtY4CTgg5l5QpPtTtsjSZIkadLqZtqeYbfQ\nZuZPI+J44FTg1Ih4EFhJmad1apXsuF4Es5UHgS+02PYMYD5lipwbgGuq9ZcDrwCeD5zXkGfPqq6L\nasFsXZ5XVnn+pyHPC6u/l9VWZOYfIuI2YE5EbNNkpOMXUoLtywc9OkmSJElSW4bdQvvIjiKeT5lC\n5+l1q28Ejs/Mc3tSyNB1OIHSDfn1mXlm3foNgD8AGwDPzszF1fp1gSuAXYGFmXlBXZ7dgKuqY9il\nNvBV1eq8GFgPmFvNS1vLU2uFvaDaX1br9we+DvwmM5/Wou620EqSpLUMDAywZMkSAObPn8+UKVPG\nuEaSNDLGpIW2JjO/B3wvIrYEtgTuysyberX/Dqz1BGTmfRHxekqguSgizgXuAV5MmUbngvpgtspz\nTUR8EngH8KuIuBCYDhxMGan4LfXBbOWTwIuAA4FrI+IyYJtq+R/AEb07TEmShs9gaXxbsuQ6jjji\ndJYtWwDAnDn/w5lnvoH5858ythWTpHGiZy2040GrFtq67btR7ufdjTI6843AGcCnWzWPRsSrgDcD\nOwADlNbZj7caBCsiZgDHAocAWwP3UlqB35+Z1w9Sd1toJUmjau1gaZHB0jgyMDDATjsdzdKlp7B6\nYooB5s07msWLT/HHB0kTTjcttBMqoO1nBrSSpNFksDT+LV68mD32uJX77z9gjfUzZ17ElVfOZqed\ndhqjmqnRqlWrOPfccofdwoULmTatZ50gpUmlm4DWTytJkiahJUuWVC2z9V8FprBs2Z6PdEGWNLRz\nzvkmG254EIcdNp3DDpvOhhsexDnnfHOsqyVNGga0kiRJ49D8+fOZM2cR5Y6nmgHmzPkh8+fPH5tK\naQ2rVq3ita89ixUrLgQOAg5ixYoLee1rz2LVqlVjXT1pUjCglSRpEjJYGv+mTJnCmWe+gXnzjmbm\nzIuYOfMinv70t3PmmW+wS/g4ce6557JixUIaezqsWHHwI12QJY0sO/hLkjQJ1YKlI444mmXL9gRg\n++0XceaZbzRYGkfmz38KixefUjcS9X/5+khSHQeFGiccFEqSNBactkfq3qpVq9hww4OqLserB1db\nb70Duffe8x0cSurQmMxDGxGH1u3n+sz8aURsAnwO2Af4G/Cfmfnp4ZYlSZJ6a8qUKY6WK3Vp2rRp\nnHHG4bz2tQeyYsXBAMyYcS5nnPEag1lplAy7hTYiPg4cBZwK/C9wDfAzyrytxwM3A+8ETs7Mrw+r\nsAnMFlpJkqT+5LQ9Um+MyTy0EfER4NuZeVW1/FLgIuC4zDypWrcJ8JXMfM6wCpvADGglSZIkTWZj\nNQ/tLrVgtvI8IIGzaysy884elCNJkjTpDAwMsHjxYhYvXszAwMDQGSRpEulFQNu4j3nAXZn5p4b1\nj+pBWZIkSZPGkiXXsdNOR7PHHreyxx63stNOR7NkyXVjXS1JGjeGDGgj4vCIeFNEbNAiyToRMbVK\n+1jgGcBlDfvYHrhjuJWVJEmaLAYGBjjiiNNZuvQU7r//AO6//wCWLj2FI4443ZZaSaq000L7n8Cn\ngT9HxP8XEXMbtl8CfCIinkoZ2Xgqdd2NI2JH4ALgfb2psiRJ0sS3ZMkSli1bwJpf16awbNmej0y1\nJEmTXTsB7fOBzwB/At4EXBcRl0XESyJiCnAysBXwS2Bf4AOZ+f2ImBMRV1frnwZ8bESOQJIkSZI0\nKXU0ynFEbEEZ9Ok5lDlmHwA+m5knV12SBzLzn1XaacAWddlXZubtPav5BOMox5Ikqd7AwAA77XQ0\nS5eewuo2iAHmzTuaxYtPYcqUXgyFIknjx6hP2xMR84EdM/NLXe9EgAGtJEla25Il13HEEaezbNme\nAGy//SK++MU3Mn/+U8a4ZpLUe2MyD616w4BWkiQ1MzAw8Mg9s/Pnz7dlVtKEZUDbxwxoJUmSJE1m\n3QS004ZR2PrAfGAz4NHALGAA+AdlAKkbMnNZt/uXJEmSJGkwHQe0EfEC4BhgAUOMkhwRfwHOBT6c\nmcu7qaAkSZIkSc10OsrxacCR1eI9wG3V3weAh4GZ1eNRwCbVA+B24OWZeXVvqj3x2OVYkiRJ0mQ2\novfQRsSRwEeBTwFfzsyb28jzOOAAyvy1mwDb1ab10ZoMaCVJkiRNZiMd0F4LHJ6Zv+uiYlOAbwJn\nZ+b5neafDAxoJUlSM6tWreLcc88FYOHChUyb1vUQKJI0rnUT0HYy7vs/uwlmATJzADgN2Lab/JIk\nSZPROed8kw03PIjDDpvOYYdNZ8MND+Kcc7451tWSpHGjkxbaJZk5v+uCIt4EDGTmad3uYyKzhVaS\nJNVbtWoVG254ECtWXMjqNogB1lvvQO6993xbaiVNOCPdQntjRJwaETM7rBcRsSfwQcBBoSRJktpw\n7rnnsmLFQtb8ujaFFSsOfqQLsiRNdp38tPcfwDXAIRHxdeDnwK2sHuV4VV3a6cDjgR2BFwHPAi7K\nzF/1otKSJEmSJHU6bc+TgC9QAtR2MgYl0D0VeHdmPtBNJScDuxxLkqR6djmWNNl00+W4oythZt4A\n/GtEPJMyHc884InAxpS5ZweA+yjz014HXAl8PTP/1kk5kiRpdAwMDLBkyRIA5s+fz5QpndyNpJE0\nbdo0zjjjcA499EVAbbbE2ZxxxlEGs5JU6aiFViPHFlpJ0mhbsuQ6jjjidJYtWwDAnDmLOPPMNzB/\n/lPGtF5aLWI25Q6uV1VrzgZ+Q+YtY1QjSRo5IzoPrUaWAa0kaTQNDAyw005Hs3TpKdR3Z50372gW\nLz7Fltpx4MYbb2T77Y8Gvkn9awQv5ve/P4UnPvGJY1c5SRoBI97luKGw9YH5wGbAo4FZlKvsP4A/\nATdk5rJu9y9JkkbOkiVLqpbZNUfQXbZsT5YsWcJOO+00RjVTzdy5c4Gv0vgawWHMnTuXVatWNc8o\nSZNIxwFtRLwAOAZYwBDT/kTEX4BzgQ9n5vJuKihJkiRJUjMd9SeKiNOA7wD7AH8HfglcAVwMfBu4\nHPgJ8GvgLmAL4N+A6yJi995VW5IkDcf8+fOZM2cRpXNVzQBz5vyQ+fPnj02ltIbrr7+ecs/smq8R\nfKnaJklq+x7aiDgS+CjwKeDLmXnzEFmIiMdRRkN+E7AJsF1m/rP76k5c3kMrSRptqweF2hOA7bdf\nxBe/+EYHhRpHVg8KdVi15mzgOgeFkjQhjeigUBFxLXB4Zv6ui4pNoYxocHZmnt9p/snAgFaSNBac\ntmf8u/HGG6v7aUurrYNBSZqoRjqgvTwz9+6qZiX/i4CnZObJ3e5jIjOglSRJkjSZdRPQdvIz7KM7\nrE+jrSn33UqSJEmSNGydBLQ3RsSpETGz00IiYk/gg8DVneaVJEmSJKmZTroczwWuAQL4OvBz4Fbg\nHuABoH4ytOnA4ymjGLwIeBbw/7N37+FRVff+x99rCDGJNWh7vKOiaJBSCdOUWq0NeOkpbRUREIOC\n2ngUW/sTam3p1d449liroqcXsTVeQLl5qWirtloB62mtjJOoiESpgLd6aZXYJhCG+f7+2GvIMEmA\nJJPsneTzep79hL3XXrNX2M9k5rvXWt91t5lNyVvL+xgNORYRERERkf6sW+fQ+gsMA35NEKDuTkVH\nEOj+EphtZps70rj+RAGtiIiIiIj0Z90e0GZd6BMEy/GMAo4EPgjsSbA42vvARmA1sBK418ze6fBF\n+hkFtCIiIiIi0p/1WEAr+aeAVkRERERE+rPOBLQFXbjYB4A4cCBBBuS9CXpo/wW8Cqw1s/rOvr6I\niIiIiIjIznQ4oHXOfRa4DBjLLrIkO+deBxYB/21m73WmgSIiIiIiIiJt6WhSqBuBi/zuPwnmymay\nHG8DSvy2J7C/3wDeAM40My3b0w4NORYRERERkf6sW+fQOucuAv4HuA5YYGYv70adfQmSR32JILgd\namb/7kgD+wsFtCIiIiIi0p91d0D7JHC+ma3pRMNiwDLgdjNb0tH6/YECWhERERER6c86E9DudA5s\njn93JpgFMLM0cCNweGfqi4iIiIiIiOTqSEC7TxevdSiwqYuvAYBz7irn3CPOuY3OuUbn3D+cc087\n565wzn2wnTrHO+d+589tdM7VOedm+t7j9q5znnPuSefc+86595xzjznnPr+T84uccz9wzr3gnGty\nzqfLfHQAACAASURBVL3pnFvsnDs6H7+3iIiIiIiItOjIkOOlwDvAV82ssUMXcW4McA9wopk90+FW\ntn69LUACeB54iyAJ1SeA0cBrwCfM7LWs808H7gKagMUEiaxOA44GlprZWW1c46cE2Zxf8XULgSrg\nQ8CXzewXOecXAn8Ejgee8v8+BJgCNPvf/amd/E4aciwiIiIiIv1Wd8+hPRr4M+CAe4FVwAZashyn\nsk4vBPYDPgKcCnwSuNvMpnSkcTtpS6GZNbdxfA7wLeAXZvZlf2wvYB2wF3C8mSUzrwE8RhAIT82e\n2+ucOw54AngRGG1mDf74ocDTBJmcjzazjVl1vgn8N7DEzKqyjp8G3AesNrNjdvI7KaAVEREREZF+\nq1sDWn+BYcCvCQLU3anoCALdXwKzzWxzRxrXUc65kUAt8Acz+4w/Vk3Q5lvNrDrn/BOBR4EVZnZi\n1vHbgXOAL5jZ7Tl1fgB8B/ihmf0g6/gGYDBwhJltyKmzAjgBOMnMVrTTdgW0IiIiIiLSb3V3UijM\nbK2ZfYpgWO01BMHgBuB9IE0QvL4L1AF3AjOAg8xsZncHs954/7Mu69iJBMH3w22cvxJoBI53zg3M\nqUM7dR4kCNRPyhxwzg0lGF5cnxvMtldHREREREREuqagM5XM7C/AX/Lclg5zzl1OMH92EPAxgl7Q\nWuCqrNOG+Z/1ufXNbJtz7mXgw8ARwFrnXAlwMPC+mb3ZxmVf9D/LducaO6kjIiIiIiIiXdCpgDZC\nvkowVzfjQYK1cv+RdWyQ/9lehuXM8b07eX5n64iIiIiIiEgXdGjIcdSY2YFmNgA4AJgIDAVqnXOj\nwm2ZiIiIiIiIdLce66F1zs02s6t2fWbHmdnbwH3OuSTBsN/bgZG+ONM7OqitulnH3+vk+Z2t08r5\n55/PkCFDANh7770ZNWoUY8eOBWD58uUA2te+9rWvfe1rX/va1772td8n9mtra3nvvSBEWr9+PZ3R\noSzHXeGce9LMju2B6zwNlAP7mtk/nXPzgbOBs81scc65AwiC0YHAB8xsqz/+CnAQQUKrN3PqfAL4\nP+BxMxvjjw0lmCe71syGt9GmbwBXAj8ys++1025lORYRERERkX6r27Mcd9HhPXSdg/zPbf7nHwky\nDI9r49wxBGvKPpEJZrPq0E6dz/mfj2YOmNk6YCNQ5pw7rJ06lvW6IiIiIiIi0kW73UPrnPsmQU9m\nZxxKsKbrgE7Wz27HUcCbZtaQc9wBc4BvAn8ys0p/fC9gHbAXcIKZJfzxPYDHgGOBKjNbmvVaxwFP\nAC8BHzez9/zxIUACKAaONrONWXUyvbBL/euZP346cC/wnJllhkG39Xuph1ZERERaSafTJJNJAOLx\nOLFYT/ZHyO7QPRLJj8700HYkoP0Z8CWCnsaOXCRzvuUpoJ0J/Bj4E/Ay8A9gf4Le1iOA14FTzOyF\nrDqnEwSaW4BFwD8J1qwtA5aaWVUb1/kp8BXgNeAuoBA4C/gg8GUz+2XO+YUEPbDHEQS9jwKHAZOB\nzcBJZrZqJ7+XAloRERHZQTK5mi984UbWrq0EYNiwldxyy8XE4yNCbplkJJOrqa6eR339WADKypZT\nUzND90ikE7o1oPUXeAz4F9BuYNaOQ8hfD+0IYAbBmrODCZbC+TdBMqgHgP/N9Kjm1DsO+DZBwFlE\n0Pt6sz+/zf8E59y5wCUE69SmCQLVq83swXbOLwK+AUwl6JVuIOgF/n52gN1OXQW0IiIisl06nWb4\n8Iupr7+RllliacrKLmbNmhvVCxgB6XSaiopZ1NbOJfsejRo1i0Riru6RSAf1REB7MsFw2gs72DBH\nMEx4v12e3E8poBUREZFsTz31FMce+xJmU3c47tydPPnkUYwePTqklklGIpGgsnIDjY0TdzheUnI3\nK1cOoaKiIqSWifROPZEUajkwrIN18JHayx2tJyIiItJfrV27lrYGt5kNYO3atSG0SEQkejoU0JrZ\nNqCuk9e6t5P1RERERPqdYcOG4dwDBLOeMtI491uGDetw/4J0g3g8TlnZcnLvUVnZCuLxeDiNEuln\nemwdWtk5DTkWERGRbMEc2vOprx8EjPVHH6OsrIE1a27V/MyIaEkKNQaAo45arsRdEaMs1L1Ht8+h\nle6jgFZERERyLVy4jOrqW9i8+eMA7LHHk9xySzVTp44PuWWSTQFTdCkLde+igLYXU0ArIiIi2Voy\n6F5Ly4yvckaNukwZdEV2g7JQ9z49kRRKRERERHpAMpn0vUoFQIXfCqivH7O9N1BE2tfyHsoOeWJ6\nD/UxCmhFRERERESkV1JAKyIiIhJByqAr0jV6D/UPmkMbEZpDKyIiIrmUQVeka/Qe6l0inRTKOXem\nmS3tkYv1QgpoRUREpC3KoBt9ukfRpvvTe0Q9oH3azD7aIxfrhRTQioiIiPQ+WhZGJH9CC2idc/sC\n/wkcRpCKL1cpMNPMBnb5Yn2UAloRERGR3kXLwojkV2cC2raCz45e9Fjgd8DewM4urmhNRERERPqM\nXS0LU1FREVLLRPqPLge0wP8A64B7gLeAbW2cMwi4Kg/XEhEREREREQHyE9DuC5SbWVuB7HbOuWl5\nuJaIiIiISCQEy8LcRm3tBLKHHAfLwpwRZtNE+o18BLQv7yqY9S7Jw7VEREQkj5T9U6TzYrEYNTUz\nqK6etcOyMDU1F+u9JNJDupwUyjl3HTDXzDbs4rxqM6vp0sX6MCWFEhGRnqbsrCL5oQdDIvkRSpZj\n59wg4GfAdWb29E7Oe8bMRnbpYn2YAloREelJys4qIiJRE0qWY+C/CJJCPeCcexWoB5pzztkL0ONe\nERGRiFB2VhER6QvyEdB+HfgPgiV7DgA+1s556n4UERERERGRvMlHQPs28H8Ew45T7ZwzCLgjD9cS\nERGRPFB2VhER6QvyEdC+BfzczB7d2UnOudV5uJaIiIjkgbKziohIX5CPpFBDgTfN7F+7OK/MzOq7\ndLE+TEmhREQkDMrOKiIiURFKluPdvpBzHzOzVT1ysV5IAa2IiIiIiPRnnQloe/Ix7I09eC0RERER\nERHp43Z7Dq1z7jhgCnCjma31x/YGLt2N6nsB5Z1qoYiIiIiIiEgbdnvIsXPu78C+wJ/MbIw/9iGC\nLMdGsGzPzpiZDehCW/s0DTkWEREREZH+rDNDjjuS5fhxYJL/mfEuQTB7NfB7YFs7dfdGy/aIiIiI\niIhIHnUoKZRz7oNm9s+cY/8ADtuNLMdPmtmxnWtm36ceWhEREWlLc3MzV111FQCzZ8+msLAw5BaJ\niHSPbk8KlRvMekN3Fcx6Z3fkWiIiIiL93ZVX/pyioklcccUwrrhiGEVFk7jyyp+H3SwRkcjosWV7\nZOfUQysiIiLZmpubKSqahNl9tPRBpHHudDZvvls9tSLS53RLD61zblDnm7Rr3f36IiIi0r50Ok0i\nkSCRSJBOp8NujmS56qqrMJvOjl/XYphN2z4EWUSkv9udIcefds79sDsu7pw7Bri5O15bREREdi6Z\nXE1FxSwqKzdQWbmBiopZJJOrw26WiIjIbtutIcfOucuBE4D/MrN38nJh5y4CzgdObWdubr+iIcci\nItKT0uk0FRWzqK2dS/Zw1lGjZpFIzCUW61CaDekGGnIsIv1NtyWFMrOfAkuAOufcd51z+3aygc45\nd7pz7ingc8BnFMyKiIj0vGQySX39WHKHs9bXjyGZTIbUKslWWFjInDnjcO50YDGwGOfGM2fOOAWz\nIiLebq9Da2Z3OueeAK4DNjrn/gj8AVgFvAD808x2mHzjnCsCDgfiwBjgVGAz8C0zW5yfX0FERESk\nb/rWty7h8ssvzFq25x4FsyIiWTqV5djPfb0QmAwcAGRe5F/AJoLHvXsCpf74VoLgdwFwl5lt61qz\n+x4NORYRkZ6kIcciIhI1nRly3OVle5xzw4CPAUcA+wIlQDNBYLseWA08ZWZbunShPk4BrYiI9LRk\ncjXV1fOorx8DwFFHLeeWWy4mHh8RcstERKQ/CiWglfxQQCsiImFIp9Pb58zG43H1zIqISGgU0PZi\nCmhFRERERKQ/67YsxyIiIiIiIiJRs9tZjkVERKTvSaVSLFq0CICqqioKCvTVQEREeg/10IqIiPRT\nCxcuo7R0CtOnFzJ9eiGlpVNYuHBZ2M0SERHZbZpDGxGaQysiIj0plUpRWjqFpqa7yF62p7h4Mg0N\nS9RTKyIiPU5zaEVERGS3LFq0iKamKnb8KhCjqems7UOQJRrS6TSJRIJEIkE6nQ67OSIikaKAVkRE\nRCSiksnVVFTMorJyA5WVG6iomEUyuTrsZomIREbehhw75/YAjgOKzexBf2wk8IqZvZuXi/RhGnIs\nIiI9SUOOoy+dTlNRMYva2rlk36NRo2aRSMzVmsEi0ueENuTYOXc+8BrwKPDzrKIi4Bbn3Hn5uI6I\niIjkR0FBAd/5zsk4dzqwGFiMc+P5zndOVjAbEclkkvr6seQOC6+vH0MymQypVSIi0dLlgNY593ng\n18ATwGXAO5kyM/urmU0Ayp1zJ3f1WiIiIpIf6XSapUvXYnYvcCRwJGa/YenStZqnKSIivUY+emi/\nBkw3s9PN7HrgX22c8w3gkjxcC+fcB51z/+Wcu8c596JzrtE5955z7nHnXLVzrs0uaufc8c653znn\n/uHr1DnnZjrn2v0/cM6d55x70jn3vr/GYz6Ab+/8IufcD5xzLzjnmpxzbzrnFjvnjs7H7y4iIpIv\nLb1/BUCF3wrU+xch8XicsrLlQPYDhjRlZSuIx+PhNEpEJGLyEdDuaWYLd3aCmTUDxXm4FsCZwE3A\nx4G/ANcBdwEjCHqKF+dWcMF4qhXACcA9wP8CA33dNtvunPspcAtwgL/efOAjwP3OuS+1cX4h8Ajw\nXWATMBf4A3AGsMo5N7qzv7CIiIj0P7FYjJqaGZSXz6SoaAlFRUsoL7+UmpoZmj8rIuLl46/he7t5\n3ofycC2AtcBpZjbYzKab2bfN7L+Ao4FXgEnOuTMyJzvn9gJ+BaSAMWZ2oZnNBkYBfwYmO+emZF/A\nOXccwfDpF4FjzOyrZvb/CB5f/xP4qXPu0Jx2fRU4HlhiZsea2TfNbBowCSgBavL0+4uIiHSZev96\nmw1+61CuFBGRPi8fAW3MOXdk1n6rv7TOuYsJ/gp3mZktN7PftnH8LeBGf/2xWUVnAv8BLDSzZNb5\nzcB3/PlfzHm5LwIG/LeZNWTV2UiQ9GoP4As5dS72dWbntOt+4HHgw865Mbv9i4qIiHSjTO/fqFGz\nKCm5m5KSuykvn6nevwhJp9NUV8+jru56Nm/+Gps3f426uuuprp6nec4iIl4+PrF+DvzROVflnCsm\nCOoyc10/55y7C7gBuDoP19qVrf5nKuvYib5ND7dx/kqgETjeOTcwpw7t1HmQIAg+KXPAOTcUOASo\nN7O2AvdWdURERMIWj4/gqaeuZd68JubNa2LVquuIx0eE3SzxWuY5AyT8huY5i4hk6XJAa2b3APcC\ndwLvAyc45xqBt4H7CeaQft3M/trVa+2Mc24AcB5B8PpQVtEw/7M+t46ZbQNeJsiIcYR/nRLgYOBf\nZvZmG5d60f8s251r7KSOiIhIqJLJ1YwefRkzZpQwY0YJo0dfRjK5OuxmSZbm5g3ALFqGHM/yx0RE\nBIJArsvMbKZzLkEwhPfIrNetA75tZr/Lx3V24SqCxFAPmNkfso4P8j83tVMvc3zvTp7f2ToiIiKh\nyQxnra2dS+b5dm3tBKqrZ5FIzNWw4wgYMWIEqdT3gGW09EFMIJUaz4gRrfJTioj0S3n7tDKz282s\njKCn8zjgUDOL90Qw65y7lCCJ0/PAud19PRERkd6uZThr9leBmIazRsjVV18NTCP3HsE5vkxERPLS\nQ+vXci01s/fMbD2w3h8/AoiZ2Uv5uE471/4ywRI5zwGnmFlu1uVM7+gg2pY5nqnX0fM7W6eV888/\nnyFDhgCw9957M2rUKMaOHQvA8uXLAbSvfe1rX/vaz8v+XnvtRWC5/xmUb9v2HKtWvUNFRUWk2ttf\n92ENwT3K7C/3xwZGon3a1772td+V/draWt57LwiR1q9fT2c4M+tUxe0v4NwhBMmVBgNTzOzerLKD\ngB8Ab5nZt7t0obavPQu4FniGIJh9p41z5gNnA2eb2eKcsgEEwehA4ANmttUffwU4CDgodx6tc+4T\nwP8Bj5vZGH9sKME82bVmNryNNnwDuBL4kZl9r53fxbp6L0RERHZXOp2momLWDkOOIc2oURpyHBXN\nzc0UFU3C7D6y75Fzp7N5890UFhaG2TwRkbxzzmFmHVqfLB+fVl8jyFIwANgnu8DMXjezC4G3nXN5\nHQrsnJtNEMw+DZzYVjDr/ZEgw/C4NsrGEKwR+0QmmM2qQzt1Pud/Ppo5YGbrgI1AmXPusHbqWNbr\nioiIhCoWi/H1r59CcfFkYDGwmKKiSXz966comI2IwsJC5swZh3Onk7lHzo1nzpxxCmZFRLx89ND+\nHjgV+LCZ1bZzjgOWmdlpXbpYy+t9l6Dn9yngM20MM84+dy9gHbAXcIKZJfzxPYDHgGOBKjNbmlXn\nOOAJ4CXg45nXd84NIciZXwwc7delzdTJ9MIu9a+XWb7odIIs0M+Z2cidtFM9tCIi0mNaemivJcjh\nCFDOqFGXqYc2YhobGzn33KBf4Pbbb6ekpCTkFomIdI/O9NDmI6B91MxOztd5u/E65wG3EKw1+zPa\nziy83sxuy6pzOkGguQVYBPwTGE+wjM5SM6tq4zo/Bb4CvAbcBRQCZwEfBL5sZr/MOb+QoAf2OIKg\n91HgMGAysBk4ycxW7eT3UkArIiI9JpFIUFm5gcbGCUAmCVSckpJ7WblyyPY5tBKuhQuXccEFt9LU\nFHxVKS5exM03n8/UqeNDbpmISP6FFdA+aWbH7uKcImCVmX2kSxcLXut7wBW7OG2FmZ2UU+844NsE\nAWcRQe/rzcD/thdJ+mHSlwAfBtIEgerVZvZgO+cXAd8ApgKHAg0EvcDfN7MXdvF7KaAVEZEek0gk\n+OQnn2DLlpfITji0xx5DeeKJExTQRkAqlaK0dApNTXeRPYe2uHgyDQ1LKCjIS25PEZHICCugvROo\nM7OrdnLOz4B9zeysLl2sD1NAKyJ91caNGykrKwOgvr6eQw89NOQWCShY6g0WLFjA9OmFwJScksXM\nn7+VadOmhdEsEZFu05mANh+fVlcBTzrnTgBuBWqBd4G9Ceanfgn4OHB8Hq4lIiK9yB57DKW5eThw\nOwCHHfYlCgvXsGXLunAbJtTV1bFtWxW5a5xu23YWdXV16qEVEZFeocsBrZnVOecuBH5FSwbgbGng\ni5lkTCIi0j9s3LjRB7PLaAmaJtPcPJ6NGzeqpzZk6XSarVu3tTq+des20ul0CC2SXFVVVVx00RSa\nmkYRzH4CeJ7i4sVUVS0Js2kiIpGRlxSGZjafYG7qMmArwTI5aeAPQKWZ/Tof1xERkd4jGGZ8Lrk9\ngDB9+xBkCduDBDkWE35LAQ+F2iJpUVBQQFPTKuAy4E6/XUZT0yoNCRcR8fL219DMksAZfomefYF/\nmFnrR78iIiISulgsxoABh5JKTQEyyf7/mwEDhmvJnoior68HRpI7ygHGU19frwdDIiLkISnUbl/I\nuY/tbNma/k5JoUSkr9m4cSOHHfYldvwyngbGs2HDLzTkOGRKChV9AwYMIJ1eSFtJoWKxs9m2Tf0G\nItK3dCYpVE8+gr2xB68lIiIhO/TQQyksXEOw7Pdiv51GYeEaBbMRsKukUCIiIr3Bbj9+9eu4TgFu\nNLO1/tjewKW7UX0voLxTLRQRkV5ry5Z1rF+/fodle4YMGRJuowQIkkI1N28lmDe7yB+tork5paRQ\nEbFmzRqGDbuMYJhx9iiH+axZsya8homIREhHxhPdSzA39qPAGH9sAPB9wAgSQe2MxtOKiPQzyeRq\nqqvnMXBgEDCdcca11NTMIB4fEXLLpLm5Gfg5cDctc2inAH+nufnq0NolLY488kjgWYJRDtP90duB\n53yZiIjs9hxa59xSYBJwpZl9xx+LEWQ1vhr4PdDeZI69gTvM7ANdbnEfpTm0ItLXpNNpKipmUVs7\nl+zepVGjZpFIzFXioZBNmzaNO+5oAH7Djr1/EzjnnFIWLFgQXuMEgEQiQWXlBhobPwEM80fXUlLy\nZ1auHKK1giMknU6TTCYBiMfj+vsm0kmdmUO72z20Znamc+6DZvbPrGNp59x7wBwz+9cuGre6Iw0T\nEZHeLZlMUl8/ltw5mvX1Y0gmk/oyHrJ77rkHuJXWyyqdwz33fCGUNklrW7duBJYDt/kj/8PWrUcA\nQ8JqkuTIjEQJ/t5BWdltGoki0oM6lMIwO5jNMhRo2o3qZ3fkWiIiItJ9SkpKaGrn07ukpKRnGyNt\nOuaYY0ilvg/cR8uDhwmkUqdzzDFfCq9hsl06naa6et4OI1FqaydQXa2RKCI9JR/vsi8ATc65n+/s\nJDNbl4driYhILxGPxykrW04wjDUjTVnZCuLxeDiNku2ef/55gl6/He8P3O7LJGxLlizBbBq5vehm\n57BkyZKwmiVZdjUSRUS6Xz4WmZtFkByqNA+vJSIifUQsFqOmZgbV1bOorw9yCR511HJqai5Wr0UE\n7Lfffuy77xu8/XZ2wqHb2Hffv7PffvuF2TTZQVtTyTo0vUxEpE/b7aRQ7b6AcyuAM4B3d5bVyDl3\nk5ld1KWL9WFKCiUifZWSpUTbW2+9xYgRwVy/1atXK5iNkFQqxZ57TqK5+V6yE3cVFp7Bv/99NwUF\n+eiXkK5Q8juR/OpMUqh8BLQTgROBy8xs607OW2Nmw7t0sT5MAa2IiIhkS6fTDBlyNq+8si8w1h99\njEMOeYf16+9UsBQRLUmhWkai3HLLxUoKJdIJYQW0nwKOJxiv9H/Ac8Amdlx3dn/gf8xsQJcu1ocp\noBUREZFsLcv2TAAy8zHjlJTcq2V7IkYjUUTyo1uX7dmJ+4BBBBM6Ppx1PDs6czn7IiIiIrJbYoCC\n1yiLxWJ6wCASknz00K4B3iFYzC7VzmmDgKvMrLhLF+vD1EMrIiIi2dLpNMOHX0x9/Q3A1f7o1ygr\nu5Q1a25UL6CI9DlhDTleAVxpZg/v4rynzGx0ly7WhymgFRERkWzpdJoBAw4HjgGm+aMLgGfZtu1l\nBbQi0ud0JqDNx1/CbwCrduO8r+bhWiIiIpJHqVSKBQsWsGDBAlKp9gZaSRjuv/9+gtlcy4Aqvy0D\nPuzLRESkyz20kh/qoRURkZ62cOEyLrjgVpqaqgAoLl7EzTefz9Sp40NumQAMHDiQVOo24Oyckjso\nKDifrVvbXVxCRKRX6pEhx865GHAaMBSoB36rSKzrFNCKSF+l7J/RlEqlKC2dQlPTXWSvn1lcPJmG\nhiVa4zQCnHPAYmBKTslioAp9bxCRvqbbhxw75wYDtcA9BNkJ7gP+4pz7YEdeR0RE+odkcjUVFbOo\nrNxAZeUGKipmkUyuDrtZAixatMj3zKaAH/ktRVPTWSxatCjcxkmWZUA6az8NaLixiEjGbge0zrkB\nwO+AjxAsw5PZRhM8KhQREdkunU5TXT2P2tq5NDZOpLFxIrW1c6munkc6nd71C0i3Cu7BH4BJwDC/\nTQIe0f2JiHPOOQd4H5gJ3O23S4H3fZmIiHRkPNG5wBDgm8AjwCZgP4JPv0udcyeZ2R/z3kIREemV\nkskk9fVj2fHZaYz6+jEkk0mt2Riy4uJi4A2CHsDMPZoMjPdlErajjjoKKAE2AuuySk7gqKMaw2mU\niEjE7PYcWufcg8AvzKzVOBfn3GXAMDObkef29RuaQysifU0ikaCycgONjRN3OF5ScjcrVw5RQBuy\nwsJCtm69DZiaU7KQgQPPo7m5OYxmSZbm5mb22GMi8Bugzh8tByawZcs9FBYWhtc4EZFu0N1zaA9u\nK5j1fg2M7MiFRUSkb4vH45SVLSd3/l9Z2Qri8Xg4jZLttm3bxo73JiPtyyRsBQUF7L8/BEmh1vpt\nMvvvj5J2iYh4HQlo32+vwMwa8tAWERHpQ2KxGDU1Mxg1ahYlJXdTUnI35eUzqamZoUzHERDMk32Y\n1gmHHtIc2ohIJpO8885IgvvyZ7/BO++M3J45XESkv+vI470tuyhv2lmhc+5oM3uhA9cTEZFeLh4f\nwVNPXbs9a25V1XXqWYqIAQMGsG1bHJgFjPFHlwNxBgxYGFq7pEVzczPbtv0VGA6c6I8+xrZtf6W5\n+bQQWyYiEh09+Yi8pgevJSIiEZBMrmb06MuYMaOEGTNKGD36Mi3bExEvvPAC8HvgWoKcj0OA64A/\n+DIJ24MPPggcCFwPTPTb9cCBvkxERDoS0HY684BzLgYM7Wx9ERHpfbRsT7Rt3rwZ2Ax8BVjvt1nA\nZl8mYXv88ceB08jNFA6n+jIREenIuK/Rzrlf0v7Q4jLn3O3tlB0I/EeHWiYiIr2alu2JtmOOOYZg\nGfnJQGY+5g3AUo455hiUeT98gwYNAlJtlKR8mYiIdCSgHQhctJNyB0xr47j5Mn0yioiIREqa4IFD\nRc4xiYJx48Zx333LgCpaHgylgfsZN25ceA0TEYmQjmbm+D3w905c50Dg052oJyIivVQ8Hmfw4HnU\n108g+8v44MEPE4/fGGbTBLjpppu46KIFBEvCZAdLd3DTTTeF1zDZ7qGHHgIagJnAp/zRlcBbPPTQ\nQ1x88cWhtU1EJCo6EtC+ZWaf7cxF/Bza1ztTV0REerPNBF/Gx/r9x/wxCduqVasIshvnZjkew6pV\nq7jwwgvDapp4r732GkHv7Hq/ZXyO115bHEaTREQipyNJoV7u7EXMLN2V+iIi0vskk0lefXUCQVbW\nIX67gVdfPV1raEbGYcBcWu7P9cChIbZHsgU9sAcT3JeT/XYDcLB6Z0VEvI4EtOd18VpdrS8iIr1M\nkM04M0ezAogpw3FETJ8+HcjkcszcH4D5vkzCNnXqVGCB38u+R3f4MhER2e2A1szqu3KhrtYXTBrt\nHQAAIABJREFUEZHepby8HOfuZMckQ2mcW0h5eXlYzRLvpZdeAhoJhoTf7bdLgUZfJmG75pprgBMJ\nhoVn7lEwhD8oExGRjvTQioiI7La6ujpSqUpyv4ynUpXU1dWF2zhhw4YNwAXkDgmHC3yZRMMhtB4W\nfkiI7RERiRYFtCIi0i3S6TSp1P7kfhlPpfbTsOMIGDx4MMGKfDsOCYcCXyZhmz17Ns7N93stQ46d\nW8Ds2bNDa5eISJQooBURkW70oP+ZPf/voZDaItmeeuop4AGCrNM/8ttm4AFfJmErLCxkzpxxwKnA\nF/32eebMGUdhYWG4jRMRiQgFtCIi0i1isRgFBR8ld8hxQcFHicX08RO2Aw88EPgLMBkY5rfJwJO+\nTKJg2bLfE3xdO9FvA/wxEREBcGYWdhsEcM6Z7oWI9CWpVIrS0ik0NS0ClvijUygurqKhYQkFBR1Z\nCl3y7ZlnnqG8/FvAMlqeb6eB8dTVXcnIkSPDa5wA0NDQwKBBZ9PWPdq06U5KS0vDa5yISDdwzmFm\nriN19IhcRHq1dDpNIpEgkUhoXmbE1NXVsWXL/sBE4FW/ncGWLfspKVQEjBo1CpjGjl8FYsA5vkzC\ndvLJJwPn0voeTfdlIiKigFZEeq1kcjUVFbOorNxAZeUGKipmkUyuDrtZ4qVSKdLpl4DDgTK/HUE6\nvY5UKhVu44RgVNC2NkrSaMSQiIj0FgpoRaRXSqfTVFfPo7Z2Lo2NE2lsnEht7Vyqq+eppzYi1qxZ\nAxxIsMzIRL9dDxzgyyRM+++/P7CQ3HWCYaEvk7A9+uijwO20vkfzfZmIiCigFZFeKZlMUl8/ltyh\nePX1Y0gmkyG1SrK98sorBNlZc4dLnurLJExvvvkmcDK5SbvgJF8mYSstLeXYYwcA44HFfjuNY48d\noPmzIiKeAloREekW//mf/wm0NbQ45cskfAeTu05wcEyi4i9/uY9E4odAFVBFIvEj/vKX+8JulohI\nZCigFZFeKR6PU1a2nNyheGVlK4jH4+E0SnYwevRoBg1aSu49GjToLkaPHh1Ws8QbO3YscJvfy14n\n+HZfJlHg3BAqKq4g00NbUXEFzg0JtU0iIlHSKwNa59wk59wNzrmVzrlNzrm0c+72XdQ53jn3O+fc\nP5xzjc65OufcTOdcu/8HzrnznHNPOufed86955x7zDn3+Z2cX+Sc+4Fz7gXnXJNz7k3n3GLn3NFd\n+X1FpLVYLEZNzQxGjZpFScndlJTcTXn5TGpqZmiN04hIpVJs2tRAMIw1M6T1UjZtalBSqAi4/PLL\ngX8SrD2bGc46CfinL5OwvfTSS8BHCJbtmeK3ZcBHfJmIiPTKdWidc0lgJPAvgnUgjgbuMLNz2zn/\ndOAuoIngE/ufwGm+3lIzO6uNOj8FLgNe8XULCcb7fAj4spn9Iuf8QuCPwPHAU/7fhxB8+jQDJ5rZ\nUzv5nbQOrUgnpNPp7XNm4/G4gtkI+dGPfsQVVwwjCJgy85rjwFJ++MN6vvvd74bXOGHw4MG89tpV\nwFnAIn+0CljMwQfP5tVXXw2vcQJAQUEB27bdSfBVIttiBgw4Rw+GRKTP6cw6tL11VftZwKtmts45\nNwZ4rL0TnXN7Ab8imMg1xsyS/vh3fb3JzrkpZrYkq85xBMHsi8BoM2vwx68GngZ+6px7wMw2Zl3q\nqwTB7BIzq8p6rcXAfUANcEzXf3URyRaLxaioqNj1iRKiGC3DWSUq/v73vwMDCb4KTMsqKfBlIiIi\n0dcruzLMbIWZrdvN088E/gNYmAlm/Ws0A98BHPDFnDpfBAz470ww6+tsBH4O7AF8IafOxb7O7Jy2\n3g88DnzYB98iIv3C7NmzcW4+uXNonVvA7Nmz26smPWSfffYB7qf1kjD3+zIJ2wsvvEB7y/YEZSIi\n0isD2g46kSDQfLiNspVAI3C8c25gTh3aqfMgQRB8UuaAc24owfDiejPbsDt1RET6usLCQubMGUcw\n6yOYo+nceObMGUdhYWHYzev3qqurgffJneMM7/syCdsRRxwBPMOOy/acCjzjy0REpD8EtMP8z/rc\nAjPbBrxMMN7qCADnXAnBmgX/MrO2FuJ70f8s251r7KSOiEifV1e3muBP7Z+AP2GWpq5uddjNEqCh\noQH4lN9b5zeAT/kyCVsymaSg4FxgALDCbwMpKJiu9bZFRLz+ENAO8j83tVOeOb53J8/vbB0RkT6t\nsbGRJUs2EmRlPd9vy1iyZCONjY1hNk2AyZMnE6SS+DHwV7/9D7Dcl0nYUqkUqdSzwL3AL/x2L6nU\nc0oIJSLi9YeAVkREQnDuuecSzOC4FPiJ3y4FxvoyCdPPfvYz4C2CLMcf89tZwJu+TMK2du1a4Bx2\n/LoWA872ZSIi0luzHHdEpnd0UDvlmePvdfL8ztZp5fzzz2fIkCEA7L333owaNWr74vbLly8H0L72\nta/9XrOfTqcJ5mUa8J/ACGA+sII33/wgGVFpb3/bf/vtt4EPEKxK10yw3ulrwOs7rHEalfb2x/1g\nGbLVwHIgKA/+vZpYrCz09mlf+9rXflf3a2tree+9IERav349ndEr16HNlrVsz4K21qF1QYrNs4Gz\nzWxxTtkAgmB0IPABM9vqj78CHAQclDuP1jn3CeD/gMfNbIw/NpRgnuxaMxveRhu+AVwJ/MjMvtfO\n76F1aEU6QevQRtePf/xjvvWtJwiGHGfuSxoYz5VXfpJvfvOb4TVO/Dq0JwG3suP9OY+DD35M69BG\nQCqVorR0Ck1Nd5F9j4qLJ9PQsISCgv7QL9E76LNIJD86sw5tf3i3/ZEgw/C4NsrGACXAE5lgNqsO\n7dT5nP/5aOaAX0JoI1DmnDusnTqW9boikgfJ5Go++tGZnHDC3zjhhL/x0Y/OJJlUwqGouOKKK4Bz\naT1ccrovkzC99tprBBlzc+/Pqb5MwlZQUEB19Qh2zHJ8GtXVIxTMRkgyuZqKillUVm6gsnIDFRWz\n9Fkk0oP6Q0B7F/AOUOWcq8gcdM7tAcwhCDR/mVPnRoIg+NvOub2z6gwBLgE2EzzSbqvOT5xzLqvO\n6cAJwGozW5GX30hESKfTVFVdT13d9WzefCabN59JXd31VFVd74e6Sth21kOh3ouo2NrGMSUbiopU\nKsWvfvUccA/BvdoK3MuvfqWkUFGRTqeprp5Hbe1cGhsn0tg4kdrauVRXz9NnkUgP6ZXfKJxzpzvn\nbnHO3QJ8wx8+PnPMOXd15lwzex+4kCDn/XLn3K+cc1cBtcCxwFIzW5r9+mb2Z+BaYCjwjHPuWufc\nz4CnCDIVf9XMNuY061qCociTgSedcz92zt0JLAX+BVTn9T9BpJ9LJBK8+OKJ5PYuvfjiWBKJRFjN\nkiwLFiwAbicYxpqRBub7MgnTl7/8Zdq+P7f7MgnbnXfeSXPzCcDlBAPKSoDLaW7+JHfeeWe4jRMg\nWFqpvn4suZ9F9fVjtLSSSA/preNVRhGMY8sw4HC/AawHvra90Ow+P9f228BEoAh4CfgK8L9tXcDM\nLnfOPUPQI3shwad8ArjazB5s4/xm59wpBAH2VGAW0EDwWPX7ZvZCZ39ZEWlt7dq1mBW2Om42gLVr\n1zJ69OgQWiXZbrzxRoLMuZMJsucCLAJGcOONN3LmmWeG1jaBRx55BPgkwXDWqf7oncAhvkzCtm7d\nOuBvwG20BEwTgHNZt25oaO0SEYmSXtlDa2Y/MLMBO9la/ZU3sz+b2alm9iEz29PMys3shp1lYjKz\n283sWDPby8wGmdlJbQWzWedvNrPvm9kwMys2s/3NrErBrEj+DRs2DOceILd3ybnfMmzYsLCaJVk+\n8IEPACOBJbQMl1wKjPRlEqbg46+Z4P78yW9LgS0oSWE0vP7668BnaT3P+bO+TMIWj8cpK1tO7mdR\nWdkK4vF4OI0S6Wd6ZUArIlJRUcHgwc3ATIKlYe4GLmXw4GYqKip2Xll6xIgRI4D7CT5qpvktBtzv\nyyRMkyZNAg4guC8n+m0acKAvk7ANHjyYtr+qxXyZhC0Wi1FTM4Py8pkUFS2hqGgJ5eWXUlMzQ7kC\nRHqI3mki0msVFxcSPBVf7re0PyZR8PzzzwNbyH3oAJt9mYRp6NChwBqC3IlT/HYXsMaXSdhmz54N\nLKD1POc7fJlEywa/dWjFERHpIgW0ItIrJZNJ/va3Q4HXgQP99gZ/+9shSsQREcGw1TOB64EhfrsB\nOFNDWiMgSMhfRevhrGeRlaxfQvTss88S/G0bDyz023jgAF8mYctkOQ4y7n+NzZu/Rl3d9cpyHDGp\nVIoFCxawYMECZQjvgxTQikivlEqlSKWeBAYDR/ttMKnUX/VhFRENDQ0EOftiQIXfYoD5MgnT+vXr\nabsnyfkyCdvatWuB4QQPgzK9f0OA4b5MwqYsx9G3cOEySkunMH16IdOnF1JaOoWFC5eF3SzJIwW0\nItIrrVmzhqDn4hqg0W/XAAf4MgnbJz7xCYKsubnDJRf6MgnTG2+8ATxEsO5swm8p4CFfJmELhn7/\nkWBkwzf8dgPwmIaFi+yGVCrFBRfcSlNTy9SKpqa7uOCCW/Xwuw9RQCuyE+l0mkQiQSKR0NChiHnl\nlVeAgwmGTBb6rQo42JdJ2IKlX04iWMUsM4d2JnCiloWJgGDY9wEEX/LW+W0KcKCGhEfEiy++SEsy\ntYwYcI4vk7DF43EGD36I3Ad3gwc/rCzHEbBo0SKamlpPrWhqOotFixaF1SzJMwW0Iu1IJldTUTGL\nysoNVFZuoKJiFsnk6rCbJd5JJ50EPE9bCW2CMgnbqlWrCAKmubTMob0eONCXSZhGjhwJrKb1e2i1\nL5OwBVly23q4YMqgGymbaSv5nYj0DP01FGlDJslDbe1cGhsn0tg4kdrauUryECHr1q0DzqF1z8XZ\nvkyiYYn/mZlDm31MwnTTTTcBZ9PWeygok7BNnDgRuIPWw8Lv9GUStmQyyauvTiA3+d2rr56uObQR\nUFVVRXHxInJ70IuLF1NVVRVWsyTPFNCKtEFJHqJvZ70T6rmIhuLiYqCSoOfiJ367FPiUL5MwPffc\nc8DANkoKfJmE7ZprrgGOofWw8I/4MomO3OR3EgUFBQXcfPP5FBdPBhYDiykqmsTNN59PQUFB2M2T\nPNE7TkR6pSlTpgC30zrh0HxfJmELHixk7s8Qvzk0XDIagnvwAK3fQw/o/kREMCLoNVoPC39No4Ui\nIh6PU1a2nNz3UVnZCs2hjYipU8fT0LCE+fO3Mn/+Vt5/fylTp44Pu1mSR/rEEmmDPqCir66uDmgG\nWp66wiSg2ZdJ2M4++2xgBcFQvMyX8euBFb5MwjRs2DBgE0GveWaN0/8HNPgyCdtnPvMZ4DO0HhY+\nzpdJ2GKxGDU1Mxg1ahYlJXdTUnI35eUzqamZoQdDEVJQUMC0adOYNm2aemb7IL3TRNqgD6joC9Zg\n/C+C+Zhb/bYUuEDrM0bE/PnzaXuO5lRfJmFqbGwEXicYxvobv/0NeN2XSdgGDhzIwIGtv3wPHDiA\ngQPbGi4uYYjHR5BIzGXlyiGsXDmEp5++nnh8RNjNEuk39IhCpB2ZD6jMnNl4/HoFsxEybNgwnHsJ\nswKCZS0Czm1T71JEBGv8tfUxU6D1/yJgn332YcOGQqCYYHQDwCKgkH322Se8hsl28Xicww+fR339\nmbQ8GEpz+OF/JB7X1IooicViVFRU7PpEEck7BbQiO6EPqOiKx+MUFPyArVvPBDJDjMspKLiTePw3\nYTZNvLFjx/LII/cQDAtv+TIO9zJ27NjQ2iWB8vJyamvfJZiTmbk/k4EzKC9XQBsdmwmGhR/s919F\nS8JETzqdznoAHtcDcJEepHebiPRKyWSSrVsbgDNoyf45ga1bG5SJOiI2bNgAvE3r9Rnf9mUSpk2b\nNtHe0ldBmYQtmUzy0kt7Ai8TrEdrwHpeeqlEf+ciROvWR186nSaRSJBIJJRQrQ9SQCsivdLq1auB\nfYB7gaF++w2wjy+TsL333ntANXAd0OS3uUC1L5Mw7bXXXp0qk57T3NxMOr0WOJxgiaWBwOGk0/U0\nNzeH2zgBstetv5bGxsNobDyM2tprtW59hOiBQ9+ngFZEeqWgh68SuAzY4LfLgE+p9y8i3n//feAt\n4CvAHn77CvCmL5MwPfnkk8BttF6253ZfJmF76KGHgFKC5a4yD+4csJcvk7Alk0nWrDmS4G/b3/z2\nFdasGape9AhoeeAwl8bGiTQ2TqS2dq4eOPQxmkMrshOaExNdBx98MMGSMLfR8mxuAnAuBx88Nqxm\nSZY99tiDzZsfBZbRco8mAePZY489wmuYAOCcA0YQzJs9yx9dBIzAuXWhtUta1NbWAoMIlrvK/jt3\nni+TsKXTaZqb/wzcQfbfuebmc0injw+xZQLBA4f6+rHkTq2orx9DMplUnpQ+Qt/ORdqhISrRFvQg\nfZbW8/8+q96liAjmYU6lrWV7NEczfEceeSQwitZLX5X7Mgnba6+9BpxK6/fQqb5MwpZOpzE7jdx7\nZHaqegBFeogCWpE2aIhK9L377rsEQ+9yOV8m0TCAYBhrwm9p9NETDQUFBcCDQDPwhN+agYd8mYTt\nkEMOAdpa4irlyyRsL774Iu0tTxaUSZji8ThlZcvJnVpRVraCeDweTqMk7/StQqQNuxqiIuG75JJL\nCIZ45c7/u9OXSdj2228/4GaCLMeZec4zgRpfJmEaPnw4QXbwKcAYv00B1vkyCdsdd9wBLKD137k7\nfJmELVgT/QFy75Fzv9Wa6BEQi8X4+tdPobh4MrAYWExR0SS+/vVTNI2sD9GdFJFeaeXKlcDJBAHS\nT/x2KXCSL5Owbdu2DfgQQZbjw/x2HfAhXyZh+tOf/kQwP/M3wFF++w0wyJdJ2IqKiigt/TcwHrjT\nb+MpLf03RUVF4TZOgKAHcODAN8ldnmzgwDfVAxgB6XSan/zkEZqalgBHAkeyefNSfvKTRzTirg9R\nQCvSBg1R6W0O91tbQ5AlLMHSPMfSOhP1x7VsTwQEQetJtL4/JymgjYhkMsmWLZMIHgZlhoUfxpYt\nEzVaKCLq6upw7vN+L7MmOjj3Oerq6kJrlwRaRtwVABV+K9CIuz5Gk2RE2hCLxaipmUF19Szq68cA\ncNRRy6mpuVhDVCLilFNO4fvf/zFtZdA95ZRvhtcw2W7gwIFs25YAbic3E/XAgQPDa5hkeRa4ldwM\nuhIN6XSaLVv+AAwBTvRHH2PLlkeUQTdCBgwYDHwZyARIcQYMuDfEFon0L/pmLtKOeHwEicRcVq4c\nwsqVQ3j66euJx0eE3SzxXnjhBdrOoFvlyyRsW7ZsIchEnSaYB5iZC/hZXyZhKi4uBj5D6/fQOF8m\nYUulUsDewDVAo9+uAQb5Mglby4guaOkBRCO6IkIj7voHBbQiOxGLxaioqKCiokI9sxGzbNky2sty\nHJRJNDxDkGio0G9T/DEJ2wEHHNCpMuk5jzzyCDAYqKLlPVQFDPZlErbMiK5Ro2ZRUnI3JSV3U14+\nk5qaGfreEAG6P/2DhhyLSK8UzE0aRPDlLvOhlAYe0ryliDj66KNZs2Y1Ow4LnwyM5+ijjw6vYQLA\n1q1bCdagPQvIvGfKgSW+TKLheeBednwPnQF8LLQWyY4yI7oyczLj8esVLEWI7k/f58ws7DYI4Jwz\n3QuR3Td27FhWrPg88ArBciMAy4FDGTPmtyxfvjysponnnCNYJmFKTslioAr9zQvXgQceyN//fj6w\nluDBEMAioIwDDriNN954I7S2SUDvIRHpb5xzmFmHsnzq8YSI9Erf+973gMeAawkSpgwhWBLmMV8m\nIjtTXl5O8EDoLoKAaYr/96u+TEREJPoU0IpIr/TYY48Bm4GvAOv9NgvY7MskbJ/+9KcJMhzvmIwD\n5vsyCdOGDRuAz9E6KdRnfZmELZHIZAlv/R4KykRERAGtiPRKjz/+OFANXE9LD+0NwBd8mYQtCIoM\nGE8wRHIxcBpgCpgioKioiLYTq8V8mYTtt7/9LUEAm/seSvsyERFRUigR6ZVavozHyCyTENCX8aho\naGggyNC6gWBoOMA+wKE0NDwdWrsksG3bNuAOgqRQ2YnV7vBlEg3nA6cC5/r9pcD9QH1YDRIRiRQl\nhYoIJYUS6ZhBgwbR0HA6cCs7fhk/j9LSZWzatCm0tkngIx/5CKtXDwF+w45ZdCcwYsR6nnvuudDa\nJnDQQQfxxhuXARvZMbHaYRx44LW8/vrrobVNAs3NzRQVTcLsPrL/zjl3Ops3301hYWGYzRMRyTsl\nhRKRfiNYVuRggiUsFvptEnCwlhyJiPfffx84GbiMoJd2g//3Sb5MwrTnnnsCBwJzaRm2fz1woC+T\nsBUWFjJnzjicO53MkGPnxjNnzjgFsyIinoYci0ivVFlZycMP/wUYAbzqjx4MPEllZWV4DZPtgmGr\nSXbsRZ8AnKchrREwfPhwXnrpQWAqLcP208CDDB8+PLyGyQ6+9a1LuPzyC7nqqqsAmD37HgWzIiJZ\nFNCKSK80YcIEHn74TwSJoLKHHJ/LhAknhNcw2e6tt94CPkPrLLrjeOutxeE0SrYbOXIk998/iCA7\nePaQ43JGjtSQ/SgpLCzku9/9btjNEBHpNqlUikWLFnWqroYci0iv9PDDDxNk/swNlk7zZRK29pNz\nmRJ3RcCAAQOAZ2m9lvMzvkxERKT7LVy4jNLSKUyf3rnRJwpoRaRXeu+994AUQa9swm9pIOXLJGzH\nHXccQTbW3DU0H/BlEqYjjjgCiBPMa17vt68AcV8mIiLSvVKpFBdccCtNTXcBUzr1GgpoRaRXOuGE\nE4BfATNpSTg0E/i1L5Ow/eMf/yCYmzkTWOK3S4EKXyZhOvroo4HHgJ8CTX67Bljuy0RERLrXokWL\naGqqoithqQJaEemVTjnlFKCQICvrRL9dDxT6MglbPB4HniQYxjrUb3OBJ32ZhKmgoADYk+C9U+i3\niUCJLxMREYk+rUMbEVqHVqRjZsyYwU03nQhU5ZQs5KKLljNv3rwQWiXZGhoaGDRoAkEm6kyv+ePA\n82za9BtKS0vDa5zQ2NjInntOAZaxY2K18fz730soKSkJr3EiItIvpFIpSkun+CHHMUDr0IpIPxGL\nxWj7T1jMl0nYrrvuOuBYgmWV/ua3V4GP+zIJ01e/+lXgXFonVpvuy0RERLpXQUEBN998PsXFkwnW\n2+44fesTkV4pCIhup3XCofkKliLi9ddfJ0g6tJgggVeKYB5t3JeJiIhIfzd16ngaGpYwf/7WTtXX\nkOOI0JBjkY5Jp9Pss8+naWgYBJzpjy6htLSBd9/9g3ppI6CmpoYLLlhAMOT4RH/0MWA1N988jerq\n6vAaJ2zevNk/EW895Lip6S4trSTSAel0mmQyCQT5A/QZJNI5zmnIsYj0E4lEgoaGzwIHARv9djAN\nDeNIJBLhNk4AGDFiBFBK68Rdpb5MwlRUVMQll8QJ1nNe6LfTuOSSuIJZkQ5IJldTUTGLysoNVFZu\noKJiFsnk6rCbJdJvKI2hiPRKa9asAZ4BbmXH3qXzWLNmf0aPHh1W08QLeiim0HqO5pnqvYiICy6o\nYuXKd1mz5mUAhg8/nAsuyE20JiLtSafTVFfPo7Z2Lpm/dbW1E6iunkUiMVd/60R6gN5lItKLjaN1\nsDQupLZIW5xrPWqorWPS8zJfxJ999gZSqW+RSn2LZ5+9gerqeaTT6V2/gIiQTCaprx9L7mdRff2Y\n7UOQRaR7KaAVkV5p+PDhtBUXOReUSVQ8SOvEXQ+F1BbJpi/iIiLSFyigFZFeqaKigqOOWk5usHTU\nUSuoqKgIqVWSLRaLUVj4/9u78zA5qnKP499fEhMIEGSRRUCCQJTNEJGwKsgmiwZFBS4SkEUQjCAg\nV5RF3ECuQhDEC4gJhC0XUBJW2SQsAQUlLoSdBCIBRULCEjKQIe/945wmnU73ZHrSM9Uz8/s8Tz01\nU6e66p1T3dP11qk65xPAt4Df5ulY+vffwrfhmVmPMGzYMIYMmUTld9GQIfcwbNiwYoIy62V8RtFg\nktaSNEbSTEktkqZLGi3p/UXHZtaT9OnTh/Hjj2Xo0GNZZplrWGaZaxg69BjGjz/WyVKTGDZsGBtt\n9AxwDjA4T6PZaKNnfaLXBHwibrb0+vTpw5gxR7L55t9i4MDfMnDgbxk69FjGjDnS30VmXcTD9jSQ\npA8DDwKrAhOAJ4HhwE7AE8B2ETG7xms9bI9ZB3iohOY2ZcpUDj30Ip56agcANtxwEmPHfp1hw9zL\ncTPw8TFrDH8XmTVGR4btcULbQJJuA3YBvhkRvypbfjZwHHBhRBxd47VOaM2sR/KJXnPz8TEzs2bh\nhLZAuXX2GWB6RKxfUbY88FL+dbWImFfl9U5ozcysy7W2tjJ+/HgA9t9/f/r184h+ZmZWjI4ktL4M\n2zifzvPbKwsi4k1gMjAQ2Lorg7LGmDRpUtEhWA0tLS0cddRRjBgxgpaWlqLDsSrmzJnDxhtvzLrr\nrsucOXOKDsfKXH31DQwc+EVGjpzIyJG/ZuDAL3L11TcUHZZVaG1t5YorruDkk0+mtbW16HCsDT5f\naG4+Pj2TE9rG+QgQwFM1yp/O8yFdE441kv8BNqdRo05l2WW/xIUXfpobbxzAsst+iVGjTi06LCuz\n2Wa7stJKB/L446czY8ZwVlrpQDbbbNeiwzJSknTAAT9i/vwFwJeB1Zg/fwEHHPAjJ01N5Oqrb2DQ\noH0ZObI/Z5zxFIMG7euLDk3M5wvNzcenZ3JC2zgr5vlrNcpLy93bsVkDtLS0cMEFU4AbgH2BTYAb\nuOCCKW6pbRJz5szh0UcHUHmMHn10gFtqm8DYsWOB1YGJLDw+E4HVc5kVrbW1lcMOu5R5866jdIzm\nzbuOww671BcdzMwyJ7Rm1i0dd9xxwEEs+m+sDzAyl1nRtt12W2odo1RmRbr44oupdXxSmRVt/Pjx\nzJu3P5XHaN68/d577tnMrLdzp1ANIul/gBOAb0fE6Crl5wNHA0dHxEVVyn0gzMzMzMzHP4oGAAAS\nvUlEQVSsV6u3Uyh3Zdg4TwKi9jOyG+Z51Wds6z1wZmZmZmZmvZ1baBtkaYftMTMzMzMzs/r4GdoG\niYhppCF7BksaVVH8Q2A5YJyTWTMzMzMzs8ZwC20D5VbaycBqpG49HyeNO7sj8ASwXUTMLixAMzMz\nMzOzHsQttA2UW2k/AVwKDAeOB9YDRgPbVCazktaSNEbSTEktkqZLGi3JQ/sUTNIXJZ0n6V5Jr0la\nIGlc0XFZImllSYdL+p2kpyW9JWmOpPskHSrJz6Q3AUlnSbpT0ox8jGZJekTSaZJWLjo+W5ykA/P/\nuwWSDi06nt5O0nNlx6NyerHo+GwhSTtLul7SS/mcbqak30vavejYeitJB7fx+SlN84uO00DSXpJu\nl/TPfL7wrKRrJG3drte7hbYYuTX3QWBVYAKpU6nhwE64NbdwkqYAHwPeBF4APgpcGREHFRqYASDp\nSOB/gReBu4EZpAE19yGN9XxdROxbXIQGIOlt4C/AY8DLpEcvtga2BGYCW0fEzOIitHKS1gH+TrrY\nvTzwtYgYU2xUvZuk6aRx7keTOp4s92ZEnNP1UVmlPNLFt4F/ArcCrwAfALYA7oyIkwoMr9eSNBTY\nu0bxp4BPAzdFRK11rAtIOgs4kfS5mZDnGwAjgPcBIyPiqja34YS2GJJuA3YBvhkRvypbfjZwHHBh\nRBxdVHy9naQdgBci4tn8893AFU5om4OkHYHlIuLmiuWrAQ8DawNfiojrCwjPMkn9I+KdKst/DHwP\n+FVEVPY5YAWRdCewLvA70sm5E9qC5YQ2IuLDRcdi1Un6GnARMBY4MiJaK8r7RsS7hQRnNUl6ANgK\nGFF5LmFdR9LqpAvcLwObRcSssrLS+fe0iNigre34luMC5NbZXYHnypPZ7PvAXGCkpGW7PDgDICLu\niYhni47DqouISdW+gCLiZeBCUkvGjl0dly2qWjKbXZPnG9Yoty4m6VjSZ+YQ4K1iozHrHiT1B34M\nPE+VZBbAyWzzkbQp6W6hmcAtBYfT261Lykf/VJ7MQjoXB94g3e3QJo9DW4xP5/ntlQUR8aakyaSE\nd2vSlQkza7/S8zCLnVhY0xiR538rNAoDQNJGwJnAuRFxv6Sdi47JFjFA0leAD5EueP8duDciFhQb\nlpHO1T4AnAOEpL2ATYAW4KGI+GORwVlNRwIBXBK+VbVoTwPvAMMlrVLRQvspYAXSXUNtckJbjI+Q\nPkhP1Sh/mvRPcghOaM3aTVJf4GDS5+v3BYdjmaRvk56fXZHUcd72wF+Bs4qMy977zFwOPAecXGw0\nVsMaQHmnhAKmSzokIu4tKCZLtiR937wDTAE2zb8DSNK9pMdfXikoPqsgaRngK8C7wG8KDqfXi4jZ\nkv6bdFHoMUkTgFmkZ2g/B9wGfH1J23FCW4wV8/y1GuWl5e7t2Kw+Z5Gujt8UEXcUHYy95wTScGYl\ntwJfrby9yArxfWAoqSPCt4sOxhYzBrgPmEq69e7DwChSC9MtkraJiH8UGF9vtxrpAsOJpGO0HenO\nk/WAnwOfIT1isVNRAdpi9iOdX9/oTgmbQ0ScJ+l50v+7w8uKngEua88FIT9Da2Y9gqRjSENlPQa4\n864mEhFrRkRfUkvTPsD6wF8lbV5sZL2bpK2A7wI/j4iHio7HFhcRP8p9BvwnIloi4rHcYeQ5wEDg\n9GIj7PVK59Hzgc9FxIMR8VZETCX9r3sB2CF/1qw5HEFqRb+o6EAsyS2015ES2vVJd3RtAUwHrpL0\n0yVtwwltMUotsCvWKC8tn9MFsZh1e5JGAecCjwI7RYQ/O00on5RPBHYDVmHR2yitC+VbjceRhow7\nrbK46yOyOl2Y558qNAorfddMiYh/lhdExDzS7ZKQhmW0gknaGNiGdKHh1oLDMd7ryfinwISIODEi\nnssX7/4KfIHUcdcJkga3tR0ntMV4knTCMKRGeannz1rP2JpZJulbwHmkjlJ2yj0dWxOLiBmklvRN\nJK1cdDy91PKk75qNgLclLShNLExwL8nLPNZp8/lPni9XaBT2ZJ7Xuog6O889akVzcGdQzeezpGMy\nqbIgXxR6iJSvDmtrI36Gthiljp52qyyQtDzpGYy3APeOZ9YGSd8h9c76CLBrRMxewkuseXwwzz2k\nRTHeBi6pUfZx0snDfaQT9ge7Kihrt23yfFqhUdhdpJPxjWuUb5rn07smHKtF0gDgQNJ3jsfXbh4D\n8rzW0Dyl5bWGAQTcQluIiJhGGrJncL5VstwPSVdcx+UrE2ZWhaRTScnsw8AuTmabi6QNJQ2qslyS\nfkLqTGVyRNTqHM86Ub6l64hqE3BjXu2yvOzaImPtrSR9VNLAKssHA78kJVKXd3FYVibfbXIj8KF8\nt9B7JO1G6hRqNu51vxnsC6wE3OLOoJrKfaS7Vo+Q9MHyAkl7kBr5WoAH2tqIW2iLczQwGfhFHvPv\ncdK4szsCTwCnFBeaSdob+Hz+dY0831bS2PzzKxFxYtdHZgCSDgZ+QBprdjJwrLTYY3/PRcRlXR2b\nvWdP4ExJ95NaJ2YBqwM7kHpqfZHUOYc1Jz9HW7z9SM+O3Qs8T+rleH1gL1Krxs3A2cWFZ9k3gM2B\ns/M4tFNI/+P2Jn1HHR4RbxQYnyWlzqAuLjoQW8R1wB3ALsDjkq4H/kW662GvvM53ltRo4YS2IBEx\nTdInSC2yuwN7AC8Bo4EfutWicJuzaE+5QeqGf738+3OkbvqtGINJx6QvcGyNde4BnNAW507Syff2\npM/T+4G5pL4BLgPOd+ddTc3PlxXvblJfG8OAbUl3b80htWiMi4grC4zNsoiYKWkL0rPnI4BPAq8D\nE4GfRsSfi4zP0t0OpJa+GbgzqKYSESFpT9KFof1JjUkDgVeBm4DzIuKuJW1HfibazMzMzMzMuiM/\nQ2tmZmZmZmbdkhNaMzMzMzMz65ac0JqZmZmZmVm35ITWzMzMzMzMuiUntGZmZmZmZtYtOaE1MzMz\nMzOzbskJrZmZmZmZmXVLTmjNzMzMzMysW3JCa2ZmZmZmZt1Sv6IDMDMza3aSBgHzI2Je0bE0mqQd\ngeHAi8A1EfFOsRG1X08+LmZm1j5uoTUzs6UmaYik+yX9RdLrkhZIeknSKjXWv0/S7LzeAkmzJN3R\n1XG3RdLukl6WNB+YA3y56JgaSdLKuc6PA54FzgGur7LeEEkPSvpX2fF6Jx/vP+TpLkkP5PVOlLRc\nJ8a9d08+LmZmVh9FRNExmJlZDyJpLLAj8CHgdxFRNeGQ1A+4FmgF9ouIBV0WZDtJGgj8GtgfOCQi\nxhUcUsNIug1YA9gc2Bj4B/ByRKzRxmtuBXYDLomII6uUfx64EngV2CMiHu2k2JcDLqYHHhczM6uP\nW2jNzKwzHAW8Dewj6YBqK0REK3ADcFMzJrMAEfEW0FQtx40gaQiwK3BVJFNJieouS3jpv/J8brXC\niJgAnAGsBdwkaZkGhVy5n7n0wONiZmb1c0JrZmad4THgFEDA+ZLWrLHeAqDZbxVq9vg6otQK+1Jp\nQUTc2aAW1avyfB1gRAO2V0tPPC5mZlYnJ7RmZtZZRgP3ASsBvyk4FluUOnHbL5b9vG4n7sfMzMwJ\nrZmZdY5InTR8FXgT+IykI4qNyMp0ZkK7ednPj3XifszMzJzQmplZ54mI6cCJpATq55IGt7V+7lF3\nsqS5uTfdMWVlW0r6Y+5hd4Gk08rK1s+97T4q6d+STpC0oqRzJd0kaWouH57XX1PSxZJukfSUpHsl\nbb+kvyf3sDtR0p2SnpZ0vaQt21h/n9wD8B2SHpY0SdJeZeXbSLpH0uOSXpX0yfyaeyQ9L+n4JcWU\ntzNc0rW5fibl3oZPquxtWNJgSXeTWs8BTi/rqXir9uyrHX5Iuh34joi4uUa8bdZLxbofycfqz7le\n7skXR0RFYt6R+mxv3dW7fme9JyX1l3SqUi/Td+d6PFPSz1TjeXUzsx4tIjx58uTJk6eGTcBY4EMV\ny24lPS87qWL5wcBBVbYxMq8/pkrZqcC7wGlly5YndWh0fS47HbgcWDeX9wUeIvW++1Hg/4A1clk/\n4GHgdWDNKvs7OMfyMPA9oH/ZNs8g9dJ8SJXX/QKYAWxQtuy/8vpfzb+vAnyGdGv2u8B3gPOBlfPv\n7wB9l1Df3wRmk3oVLi17P6m34X8Aa1d5zQ75bzq1A8f2XeCcKmWDgdtInYGdWaqnjtRLxfK5wA9K\n9UC6GH8S8HSO5aCy9euqz3rrrp71O+s9CVxHuiBR/ndsR7oTYrHPkidPnjz19KnwADx58uTJU8+a\nqJ7QfjCfuL8LHF+2vFZCW0q4qiW0pQTztCplO+eyF4GPV5SdlMumVYnvuzm2w9vY3y9r/L035iTu\nY2XLDsqv2b/K+hOBV4ABZcsOy+s/CryP1PJ4OXDBEup69xz3EVXKBEwFHgT61KjfxeqwHcd2ASkh\n/UPZNDnX+UzgeGBQjde3u16ALYEW4OYa27qEioS2nvqst+6Woq4b9p4EVsjrb1Ylhp9VqwtPnjx5\n6umTbzk2M7NOFxEvklq3BPxY0kadtKvWPH8hIh6pKHs5z/8cETMqyv6dY1u9jW1Pq7H8ClLS9N2y\nZaeQEo+JVdb/A6mjrG2qxP1ARMyPZGREfKONeCC1hAL8trIgIiLvfziwzxK2U48ArouIncqm7SLi\ng6REeT9ghqTDq7y2nnr5Pqlea3Uo9s82YmxPfdZbdx2t60a+JxcA84EfSFq1Yv0JwBOVsZmZ9XT9\nig7AzMx6h4i4UtI+wBeAcZK27sTdPVVl2bvtKOvbgX09k+d7QHpOFdiAlMjcLEksOsTM8sDzwLJV\nttXuYXMkrQ0MBVoiYlaN1WaQkqIvkm5V7VQR8YykPUl1fJGkvhFxUY53MO2sF0l9SOPiAkxZipCq\n1me9dSfpj/WsT/W6Xur3ZETMlXQGcBrwWUmPAH8l3eo9MZp0PGczs87khNbMzLrSkcD2wMdJrXXP\nddJ+3ulgWUfMyfMVJPVnYYtaa0TsVOe2Xqtj3bXzvK2/Z36er1NnHB0WEbMkXQmMAs6SdEVEzKWO\nepG0OukcJUjPrHZUrfqst+4aUdcNeU9GxA8kPUi6fXtn0q3ZRwBTJO0ZEf9u77bMzHoC33JsZmZd\nJiJeISW1InWwtEUHNtORVtTOtGKevxoR75CeIwUYIGnlOrYTLNpiuSSl21UHtrHOB/L8P3VstxGm\n5vkKwEfyz/XUyyssvFV3QAdjaKs+6627pqhrSf0kDYmI2yPiwIhYkzTW7ynAxsDFnbVvM7Nm5YTW\nzMy6VERMIHXQ8z7g6FqrtbGJwY2OaSmVxl29ASAiXgD+lpdVva06D/3ysaXZaURMI93u3Fe1h0Na\nn1SXty7NvjpgrbKfX4D66iUi3gXuyIs3aXRw9dZdE9X1WsCl5Qsi4oWIKN2GvHMn7tvMrCk5oTUz\ns0brQ8X4oFUcQ0p0aq33Sp4v0iKWn7v8PClx6OrHZjausfww4A0WdhoEcHKeH1rjNd+j7U6N2qs0\nFu+XKwvyc6ifI3UUNK4B+2oXSYNIPUMHcG1EvFxWXE+9/JjUCdLIGuuWWvc72mJfb901S11vJWnT\nKsuns/BzY2bWazihNTOzhsnPPn6SKif95SLiNVIiWKv8MVJnN9tIWr6s6BRSBzgC9pX0eUnrlpWX\nbv9docpmS2WD6iwDmAfMlXR8Tl6QNEDSL0gtiPtFRKlzKCLiFuAEYISkr5eWS+ov6Rzg+ogofzZ0\nRZbcy/JiImI8qU5OlvRe65ykvqRhXN4A9o6IloqXrpTn7d5f/rvXzHFWvQ1Y0nrALaRnTu8BvlYR\nb7vrJSIeBL4BHCBpVL6YgaTlJI0mPasq4CBJO0gqP+ZLrM96624p6rrR70kBV0jasCyG1YFvA2dX\n/2vNzHoupZ7mzczMOk7SEGA8sBHQPy+eSWqhO6GN151PGlrl6iplq5Ja7LYDXieN9fprUidBE1j4\nbOMFwCOklrFNWNiqOxU4F/hHXmezHNuCvOxM0tAoZwObVpZFxLU5joOBLSLiGElfAQ7M+1ge+BPw\ns4iYXuPvGw6cSHrOcRYpMb4gIu7K5Z+q2D+kHm/vi4gjatVblf1sRUoU18j11I80DM65EfFG2Xrr\nA1fleir1svw88GRE7FFj20OAy4D1WPic6NukOi/vzGglUgL5N2BctWNats0266Vi3S1JQyKtQ3of\nzAFGk4YIOob0HvgPqROqVamzPttbd/Wun+utoe9J4H7SZ+C/gZ/kGObmbV8QEddX+xvNzHoyJ7Rm\nZmZmZmbWLfmWYzMzMzMzM+uWnNCamZmZmZlZt+SE1szMzMzMzLolJ7RmZmZmZmbWLTmhNTMzMzMz\ns27JCa2ZmZmZmZl1S05ozczMzMzMrFtyQmtmZmZmZmbdkhNaMzMzMzMz65ac0JqZmZmZmVm35ITW\nzMzMzMzMuqX/B0RXhCxwpLybAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f57660e0b00>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"X = alldata.nBedrooms\n",
"Y = alldata.Price/1000 # in 1000's of Dollars\n",
"labels = ['$\\mathrm{Number \\; of \\; Bedrooms}$', '$\\mathrm{Price \\; (in \\; 1000\\'s \\; of \\; Dollars)}$']\n",
"ax = scatterplot(X,Y,labels,X.max())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Price"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"SqFeet 367\n",
"nBedrooms 421\n",
"Price 439\n",
"DatePosted 439\n",
"Neighborhood 432\n",
"dtype: int64\n"
]
},
{
"data": {
"text/plain": [
"{'El Dorado Hills',\n",
" nan,\n",
" 'richmond / point / annex',\n",
" 'Glorieta, NM',\n",
" 'hercules, pinole, san pablo, el sob',\n",
" 'Sonora',\n",
" 'Discovery Bay',\n",
" 'Lower Laurel District',\n",
" '2664 Tronero Way Rancho Cordova CA',\n",
" 'albany / el cerrito',\n",
" 'oakland downtown',\n",
" 'LAS VEGAS',\n",
" 'san leandro',\n",
" 'Hesperian Gardens',\n",
" 'DAVIS',\n",
" 'pittsburg / antioch',\n",
" 'Clio/Graeagle',\n",
" 'Manteca, CA',\n",
" 'fremont / union city / newark',\n",
" 'walnut creek',\n",
" '5448 Bloom Dr. Marysville CA',\n",
" 'brentwood / oakley',\n",
" 'oakland west',\n",
" 'vallejo / benicia',\n",
" 'berkeley north / hills',\n",
" 'oakland north / temescal',\n",
" 'oakland hills / mills',\n",
" 'Elk Grove',\n",
" 'Fernley',\n",
" 'ELK GROVE',\n",
" 'berkeley',\n",
" 'oakland lake merritt / grand',\n",
" 'sacramento',\n",
" '8954 N. Camden Dr. Elk Grove CA',\n",
" 'San Pedro, Belize',\n",
" 'South Lake Tahoe',\n",
" 'OAKLAND',\n",
" 'Oakland',\n",
" 'concord / pleasant hill / martinez',\n",
" 'Soda Springs, CA',\n",
" 'alameda',\n",
" 'Somerset, CA',\n",
" 'dublin / pleasanton / livermore',\n",
" 'Rio Vista',\n",
" 'Mariposa',\n",
" 'Vallejo Hercules Oakland',\n",
" 'hayward / castro valley',\n",
" 'Mi Wuk Vlg Ca',\n",
" 'Tracy, CA',\n",
" '3873 Linden Ln.',\n",
" 'Oakland Berkeley San Francisco',\n",
" 'danville / san ramon',\n",
" 'Lake Wildwood',\n",
" 'oakland rockridge / claremont',\n",
" 'Eastmont',\n",
" 'Stockton',\n",
" 'Folsom',\n",
" 'Tracy',\n",
" 'Brentwood',\n",
" 'pioneer',\n",
" 'Patterson',\n",
" 'Twain Harte, CA',\n",
" 'Manteca',\n",
" 'oakland east',\n",
" 'fairfield / vacaville',\n",
" 'Pinole, Hercules, Richmond, San Francisc'}"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# How many houses for sale are under $700k?\n",
"price_baseline = 700000\n",
"print(alldata[(alldata.Price < price_baseline)].count())\n",
"\n",
"# Return entries for houses under $700k\n",
"# alldata[(alldata.Price < price_baseline)]\n",
"# In which neighborhoods are these houses located?\n",
"set(alldata[(alldata.Price < price_baseline)].Neighborhood)\n"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Would automate this later, just do \"quick and dirty\" solution for now, to take a fast look\n",
"# Neighborhoods to plot\n",
"neighborhoodsplt = ['El Dorado Hills',\n",
" 'richmond / point / annex',\n",
" 'hercules, pinole, san pablo, el sob',\n",
" 'albany / el cerrito',\n",
" 'oakland downtown',\n",
" 'san leandro',\n",
" 'pittsburg / antioch',\n",
" 'fremont / union city / newark',\n",
" 'walnut creek',\n",
" 'brentwood / oakley',\n",
" 'oakland west',\n",
" 'vallejo / benicia',\n",
" 'berkeley north / hills',\n",
" 'oakland north / temescal',\n",
" 'oakland hills / mills',\n",
" 'berkeley',\n",
" 'oakland lake merritt / grand',\n",
" 'sacramento',\n",
" 'Oakland',\n",
" 'concord / pleasant hill / martinez',\n",
" 'alameda',\n",
" 'dublin / pleasanton / livermore',\n",
" 'hayward / castro valley',\n",
" 'Tracy, CA',\n",
" 'Oakland Berkeley San Francisco',\n",
" 'danville / san ramon',\n",
" 'oakland rockridge / claremont',\n",
" 'Eastmont',\n",
" 'Stockton',\n",
" 'Folsom',\n",
" 'Tracy',\n",
" 'Brentwood',\n",
" 'Twain Harte, CA',\n",
" 'oakland east',\n",
" 'fairfield / vacaville',\n",
" 'Pinole, Hercules, Richmond, San Francisc']"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#neighborhoodsplt = set(alldata[(alldata.Price < price_baseline)].Neighborhood.sort_values(ascending=True, inplace=True))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Group results by neighborhood and plot"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"by_neighborhood = alldata.groupby('Neighborhood').Price.mean()\n",
"#by_neighborhood"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#alldata.groupby('Neighborhood').Price.mean().ix[neighborhoodsplt]"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f5765fb8c50>"
]
},
"execution_count": 79,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2MAAAOICAYAAABbsilIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmYK1WZ+PHvy4ULIpsgcgGBCygyqLiCAo4s6igq4oqI\nA7gy7iiOI47I5qijorj8VFRcxp1lVNwQF1CRTVRQYQRkuSDovSKIgOzw/v44FW46N+lOp9Jd6fT3\n8zx50qk6W1VXKnlzqs6JzESSJEmSNLtWaroBkiRJkjQfGYxJkiRJUgMMxiRJkiSpAQZjkiRJktQA\ngzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkjSDIuL5EbF20+2QNHpWbroB0iiKiPsD+2TmR5pu\ni6TRFBFrAGTmzU23RaMrIv4dWCszT+yybkvgScD9gKuAH2XmtdW6PTLz27Pa2DFWBcO7ApsCC4FL\ngB9m5q3V+tWBJ2bm95tr5cxr8rwVEc8DHpyZ/z3bdY8ye8ak7l4GfCgiHtp0Q8ZJRGwVEWdFxNKI\nuKftcX1EnB0Rj63SHRAR50XEbR3p/hARJze9HcPUY5/cHhE/j4hTq8cZEfHbiDg5Il4aEQtq1nlC\nVd8Ow9qOmTYqbY6Ih0bEnyPiduBG4KBZrLvX++eXbcfKaRFxTkRc1bZ+5IPFHtt2R8f74McRcWaV\n7i0Rcd+m2z2ViNgHeEJmHtqxfGFEHAMcB9wG/BpYBzghIt4WEQcAb5r1Bo+hiNg8Ir4GXAo8E7gW\nOB/YADg+Il5XJT0G2GuW2jSr57Opzluz1Z7M/F9g1Yg4cibrmXMy04cPHx0P4DzgbuC/mm7LuD6A\nk6t9/Dtg5R5pNgbuqdK9tek2z+I++USP9XtQPkh/CzxwwDrWbdunRze9zaPYZuAxwCMmWb8QeG/V\nnkMbPlZ+MUmaLYAfVOnWncW2Tbr/prFtn+yx/tnAP4A/Ag9rYv/3uR2bAdcA9++y7nPA2cAqXdZ9\nFLgLOLXpbZjrD+CFwC3AKcCiHmkOBs6szjGfnYU2NXIO7nXeGmZ7+nnvAwGcCjyj6eNjVB72jEkd\nIuIhwCOql3s32ZYxt5RyUr42M+/qliAzr2l7+edZaVWzllbPt3ZbmeWSpXcBDwO+FxHTPodn5vXA\nu4GfU34JHnkNtPkZLD8HdGvPHZSAIWahLb203j89e70y83LgeVXaTWapXTDF/utD633wj24rM/Ob\nlONhY+A7EbFajbpm0tHAMZn51/aFEfEYYH/giMy8s0u+A4H/m4X2jbWqV/IrlEDrmZm5tFu6LJfM\nXQHkbLSrqXNwr/PWkNsz5Xs/S0R2IPAZ76MsDMakFe0DnEg5YW0eEY9ruD1Sux9Vzw+l9JRNW2Ye\nkpk7Z+bFw2vWzJrlNj+hjzSz8sWtrsy8iXIp3KazWG0/+6+ur1TPmwDPmoX6piUiHg7sTvcvt8+i\nHD+Xd8ubmfdQesc0oIjYCvgUpVfsJT2C3nZvAu6Y8YZVGjwHdz1vDbE9fb33M/N3lCB51i7zHmUG\nY9KK9gbeQvmlDEpwJo2Kv7f9vWVjrRhTEfFPlAEVxsnZzFIwNov7709tf282C/VN1ysplxle22Xd\nour5sZPk/+HwmzSvvAu4D3BiZl49VeLM/AvlRwsNaID3/qeAN4xwz/asMRiT2lQDSFyfmVcCx1N6\nx14QEU1ejiS1e0Db35cMUkBErBQR60XEOkNq04yb6TZHxIKIeDzwvzNR/myKiHdFxBPbFv0fcP8Z\nrnO2998j2/4exUv6nk/vgGoJ5bPliIjYuFuCzFyCvWMDiYhFwHOrl9MZjXLWRlEctXNwnfbUeO+f\nCiyg9CDPawZj0kQvogRhtD1vAOzWLXE16t9FbaN/3RARR7Wt3ycibq3W/SMi3tuR/7nVCGE/jIhz\nI+InEfGMjjQ7RMRPI+L3UUYd/Ocq308j4sqIOKgt7WMi4qiI+N+q3PMj4tMRsXmvDa5G9TqwGpHt\n9Gr0sndGxE4R8bUooxr+IiJWbsszZbtnU0RsX40GdXbVlrMi4uD20dYiYstqRLYLImJZRLw5ItaO\niA9FxHci4sJq/fZV+g0j4lMR8b2IuCQifhYRPS/BmMV98rzq+ZfAd6u6+zpGImKdiLgOuJMyotgb\nemzLIyLiK1FG5ftxRPwgIj4SESvcd9TnMbwwIt5RHVunVenfExHvj3JfR0+TtXmS/+nREfHtavlp\n0d+lxq8F3gO0fqU9OJaPTviZKdq4bkR8LCK+W9V573HUI/1MHysbtr/IzAsy84iONvR9rujz/zfw\n/hvQkZRLrn6Ymd+tsW0viYj/i+Xn8Bsj4ui29XvHxHP4B6ZqWJT7jhdR3qPdfI1yPG8B/LY6XneP\niDXbE2XmN3qUP+X5rkq3VZSRWP9Rtf+zbeu2q/LfUa07tG1d3585Vfq+zxdV+oGO/yifU3+NiNdP\nkfRpLL8v6rdTldvmZ1Sf+wPsg76OuejjHBzT/Ezu8/3Z1VTtmcn3fnUP2y8oA/LMb02PIOLDx6g8\nKCfvPwIbty27hDLC0GemyPvRKt0ruqzbh/LL7QYdyz9MmVfmQW3LXkQZReslbcvWA54KnF7V8daq\nvnWr13dQfl3akDLww6+pRieknBxPoFzatl2Xti2gfABdC2xSLVuVciPvdVXd2wBfaCuzr3b3sb8/\nRxnBadIRw1g+ytN+Pda/HvgbsHvbsnWAL1NGanxgtWwN4MnAN6ryDge+CGzWti9+AVwPbE25ZGVR\ntW5l4FzKSIYbdmnDMPfJ3cAHu6xbi3J9/Z2UX9zXbVvX1zHSth/+mx4jAQL7UobafmvbsoXATyiX\n7q40wDF8ImUwgwVty3aiDD7R9f/a0aaubZ7G//Q6YP0+/weHVWXtO0W6natj832U+5da75+VKV/C\nu9Y55GNlhfcP5eb56yjzJfXKO61zxXT+f/3uvxrvg8WUkfFup3wBXFhn29ryfbCq801d1r0UuJge\no/F1Sf/iqqwVRlFsS/Oa6n9+d/V/vIfy3j4X+HdgtR75+jrfdeTZlx4jBQLv6PK+ms75pO/zRd3j\nnzIc/d3AeVOk+2+Wf27cd8BjcDr7YLrvp57nYAb7TJ7O+7N13uo8j/Zqz4y+9ynnz4sG+R+N06Px\nBvjwMSoPYBfg5x3L3lmduK6nyxDEbekeVKU7pcu6NwN7dizbr0q/d5f0JwF/BVbtWP7yKs8FwCqU\n4PGLwMeq9ZtTRh+7BrhPW751KB+WZ3Wpa6+qzE93LG99eL+zbrsn2WetL5PXUy5XOK16bn+cxiTB\nGOUX0LuBA7qsC+BC4CwmBhBPqsr8E/DojjwHV+suBzbtWPc2ugTcM7RPru7YD2dVj08Cu02Sf9Jj\npC3dbnR8IFfLH1UdK9/uWP5Iln9ZXGc62w2sWaV7eJd07+/2f+2xbV3b3Of/9G7gxX3W0/pCMWm7\nWP6l5npgmx7Hyos7ls/k++enwGVt75fJgrG+zxXT/f/1u//63LarOt4HZ1T/42soP0ysVWfbOvJt\nSgkIup0n/x14/jTa3wpwVpoi3XMp56i72x6twOw84H4d6ad9vus4VrsFY/tP8r6a6jOn7/PFMI5/\nyqWf5wDPnWK/frLtfRCDHof97INBjzl6n4On+5k83ffnCsFYr/YMUPa03/vAq6vjpOuPD/Pl4WWK\n0nL7sPzSxJbWDb1rU4Zs7SozL6X8EvikiFjcsfrprHjd+iGUk9xJXYo7Fbgf0Dn5Ymv49zMz884s\n9s3M11ZtuIIy1PODM/PeodEz8wbKUNGP7lJX6xKKv3QsX1Y9P2oI7Z7K+Zm5W2buWj23P3adIu97\nqucVrlXPcqY/Cdie5fcPwPL9eHVm/rojW2s//DIzr+pYt4zyQbxBx/KZ2CenduyHHarHv2XmqZPk\nm/QYaXN3j/yHUr5wfL59YWaeD7wC2Ks6nqD/7W59KTsiIjrvW/omcNEk29NPm2Hq/2kwc4M8/CYz\nO+9Zah0rnXXO5Ptn58zcEtiO0oPb0zTPFcP6/01XUgZfaH8f7JSZG1G+UL4QuCoiXjEh02DnQar3\n+ynA9hGxbcfqZ1F6X/u1PnBzllERe29g5tcz86FVmw6iHBc3ULZ9W+DjHVkGOd/VMdX5ZDrnC6h5\n/GfmiZn5uMz8+hTtvr7t7/tMkXYqU55TBzzmep3PpvuZPJPn19l47/+ZcsvURkMoa85aeeok0viL\niFWA51B+2blXZl4QEb+nXLb2IsoJqJdjKb1rr6B86BAROwFnt38oV8Hagygn+e9GRDBxuNk1gCvp\n/SFyQa8GZOYNEbFqROxJ6S14KOV9vgHd3++nV8+dI621vkT+aojtHqqIeCDlkqzbMvO6Hsmuonwp\nfh7lcot23Qa/uLuPdQva2rCYEdonbXoeI71UbW/dSH1+5/rMbL/fZDF9bndm/iMi3k354vbMiPh1\nVf4pwElTfWGdpsn+bzP1eddtKOgV6pytYyUzfxURK3zZjYg1gLsy87YqXV/niln+//UlMy+NiKdT\n/t+fjIgFmfnJtvXTPQ+2HEN5D7yKchkhEbEbcHpmTvZjQKfVmTjq6VTb8xvgN8CHI6I1Me+BlMGj\nDsvMS4ZwvqtjhfPJdM4XVfrFzN65sj1IWESPKQQ6RcQCYKvM/H2X1ZOeU2scc536/kyu6p2x9+cs\nvfdvqZ7n9XxjBmNS8VTKrzNfjokDJwblUqsAnhER983MrhORUn6t/Cjw0og4tDpRvZxyqWO7Vs/K\nXZnZdWCQKfT8kI+IfYGjKJfyvA84LDP/FhFX0GVo68w8MyKOBfaKiIdn5u8iYkPKF4HfAO03q9dt\n97A9sHqebG6Y1twy3W4knyxfv/PNjNo+aen7i2Cb9Sn3eiTlnpTJTGu7M/OIiDiLcpnSkyi9NwcA\n50XE0zNz2aQF9G/W5gkaoM7ZPFa6DeV9KPAlqgENpnOumMX/X98y87qI+DLwOuC9EfGl1rl5uufB\nNt+l7LsXR8RbqvJeSbnsdDruYJIB0iJid+Bn3T5Lsgxq8KYo85TtStnfl1D/fFdHt/PJdM4XMLvH\n//dZHug9jD6DMcq9WC8H3thl3aTn1BrH3ATT/Exu5Zmx9+csvPdbx+xs/2A5UrxMUSr2Ad6Y3S+T\neyKlu/4+lN6zrjLzdsq15IuAPSJiLWC96hKGdtdUz6tGxLrTbGfSY9LGiHgD8D+Uewa2y8yvZmY/\nH5JrU67FPywiTgW+WpWzQ2a2X+5Up90zoXUZx+qTpFm/eu42188wjNo+gUmOkSlcx/IenamGN+57\nuyNi5YjYKjN/kJn/mpkbUn7lPYTy5edTA7R1VkXE6yNiu5rFzNqxkmUC1591LH4k8HuY3rliGP+/\nIe2/bi6sntcEHlLVNeh5kOoHtGMpvTT7RMQDKANALJlmu/4O3HeS9XtReokm83nKj4BrVK9n6ny3\nYIr1vc4n0zlfwOwe/8sog2cE05sQ/GF0nyZh0nNqnWOuh34/k2f0/DpL7/3W8dzrR+55wWBM815E\nrE75BbLrHBmZ+SfK6HVBuVRxMp+u0h1ACfC+3KW8qym/cAE8vkebut23MJX/oHxg/Htm3tWxbmFb\n2U+JiKdUf68OLM7MH2Xm86sAdJfMfH/rcqZZaPdAMvNy4FJgQax4n17LlpR9cvIMtWGk9kkd1WVY\nP65edh0KPiI2iogtprndG7PiPSVXZ2br8pdRm2C5delNexf5epQe8oE1eaxEGTL9/pnZ+hW673MF\nZSTBz7cnmOL/NyP7r4f2ObpavYHTPg92OJayDf9G2fbPDdCuJcBaMflktlNNt/DX6vlyqH2+m+zH\nmV5lTWoa54stq/SzffwfQvmCv1f0mMuti72Abw1QV91jjrY0fX8mV2by/Drdsgd577cuT+y8R25e\nmVPBWJS5XF4REV+PiD9ExC1R5nU6PSJeFtF9Yt6I2DHKXEHXVXl+E2UOh8kuI9g/ypwZN1V1nBaT\nzIMREatFxBFR5py6NcqcN8dFxNaT5Nk4Ij4bEddExG0RcUWU+UZ6/so0G9syD+0JnJyZt0yS5vPV\n85MjYr1eiTLzQspoT0+ljFLV66bvt1fPL+ux/j8pw+xPR2uOmgkntYh4MKW3rmWjtterAY+KiPYJ\nVCczE+2u49Dq+QWdK6r3xB6U+we+MINtGPY+GaRXa1iOoHygvmaS9a1zzXS2+3ER8bAuaa5g+ZfO\nUXEl5cvE+m3LNqZcflRXU++fg5h4P910zhUbUga16Pf/N5P7717VlQf7U94vJ2Rma1sGOQ/eq/rx\n7TuUQRf2Y7Av560eu57zOwJvjHJ/WC+PA25iYmA16Pmu9T9avSNPUOZ4Sga7baWf80X797Jax39E\nvCDKnGpTzkuVZVCtl1O2+bNR7gvvKSKeCfxfZi6dquwuah1zHab7mQwze36dTtmDvPc3odwH+eda\nrZzj5lQwRjkBfYoyWtDZlLkPTqTcKHksy0e+u1eUmyl/CjwB+Drlnp5Vqrxf7VZJlEl7P0d503yK\ncunZw4BvR8QKJ53qhPojynC2fwc+ROlJeQ7wy25dtBGxBWVOiv2rbfkgZVjiA4EzI+J+TWzLfBMR\nm1HmJprqUo1TWP6B9eop0n6a8t76edsv0RNk5vcoQ94/KyJe1daehRHxQeAbXS5zWJvuo/m1tHrh\nDmv9MBERG1FuSv9O9Xox5dfTS6t2XE8JHn8RERdHmeDyguoD78vVjx/3foAP2O4VVF8cWhPTrhvl\nxulu6dq3dYXRljLza5RfQN8eEU9qy7eAMvTuTZRpBdp/UWz9EjdhgtWOdWv1u24G9kkAG072A8sk\npjpGWlo/+HROMnsW5fjePiL+X+uX/SjeCPyl+pIz3e0O4EvVl5NWug0oQ4ZPOYnuZG2uDPo/7eY7\nlC8Zz662ex3K3IOd951Mu84Zev/0/NU5yg+Yh1DeI+0DEEznXPEjyvms3/9fv/tvqm1r3a/bLc3m\nwPco91H9lHJf1yDbdmmPZhxTPf9vTm/gjpZzKffCdI581+4hwIndfnytPpfeAPxH+4+EA57vyDLa\n5/nADlEGcmk5hPLZFpQepGdXdbdMej6ZzvmiSl/3+H8HJUg9dJI07e07njLq5k7At6Lce7WCiHgq\nsHdVfqd+zqmDHHO9zsHT+kxubQL9vz97nQ97nV+nU/Yg7/1t6D05+vyRIzC+fr8Pykh1z+iy/AGU\niPxu4Dlty9ek/FJxK/CotuULKfOV3E0ZerW9rNZQzBfTNocJ5QbMv1JGfuk2/9A9wNc6lu9RLf9d\nlzafUtX/mo7lH6jyfLxj+axsy3x5UE6K51Fuhm7N77KEjrl5KL9SnVHt+/a5YC4GvtWj7NUpw7U+\npI92bE+5tv0XlF9Avw48qSPNEykf7re21f974FNdyns15UT+e8oPAidQTnYbVct/C7yhI8+BHdvW\nOefNRXRMdtpPu3ts71aU6+qXdtRzLXAm8Ngq3QGUUaNu7kh3CfC9LuU+jjItwc+q7T6N8sG6Zkfd\nZ1O+sLTK+y3lV9rtqm1p7eM7KT+WvKDL/r933Qzvk2XVPtm6jzL6OkYox/05bfv1TsoH4WM70j2G\n8uPWBZRLkb5N70m3J91uyhfr71TH4Teqbf1R9XhOH9vWs82D/k/7qHPbarvPq7Zp67Z13eo8H/hX\nyuVXTRwr57DivHSXVvXfTRnB7tmDnCsG+f9Ntv+muW23UCa7bd+28yi/tJ8MvKhHWdM+D3bkD8p3\nioE/HynvmU/2WPc5yo+jT6R8vhxNuUTuydU+v2yK9k15vuuS5/6UH33PqfJ8h3JVyBMpQ8FfTBnJ\nb2+m8Zkz3fNFzeP/IMoP3itMzD1Fvk0pAdNfqv2+D/AUyo/hX6TMRRgdeaa7D/p9P015DmYan8n0\n+f5kxfNW69x0UK/29Ft2nfc+5R69wwd9n43Lo/EGDG1DlgdEH25b9jJ6T3S4a7XutI7lX6D3BLNH\nVOsO61jeCgQ365Lnp9W6nduWbVHVfVmX9GtUb5abmDh54Kxsi4/59aBcfvlb4J/algXlV7NHA2+l\nXHd/bNNt9eHDh4/ZeFRfoE+qWcYLKYNWrDDpMCXoav98fyTlkrq3UgKE9ZveB+P4qD7Xnk0Jit5M\nCUZXb7pdHW2cN5/JlCD5HmCbptvS9GOuXaY4mdblYO03T+5KubTslC7pf0b51W3HjmuJW5PMdstz\nMuVNce+wrFFuTt0EuCQzr+wnT1sdP+hMnJk3U34pW52JN7nO+LZofomIf6LcE/HybJtXJYsbM/PX\nmfleyofDYxpqpiTNmIhYKSJ267j065XAZ2oWfSJwG11G88syOEP75MDnZ+ZnMvO9mfk/mTlTo7/O\na9Xn2jcz8yOZ+YHMPCknv1d8Vs3Dz+QXAWdkuYx2XhuLYKy6Xrp1I+/321Y9pHpeYSLQLNeBX0G5\nB2iLqpzVKTcb3pzd5074Q/W8VT91TJEnB8jTtZ4hbovmlxspv0pNdX/RIkrvrySNm1dSLrt6H9w7\n8uTOmTnIwB33qj6X/5NyX5bUj3nzmRwRK1MmV/+vptsyCsYiGKPMVv9Q4LuZ+cO25a0bFXtN1tda\n3rpxcbrpRznPIHVoHsnMayhD8n46Il4eERMmXYyIxRHxScqALwc20UZJmmHXUXqwzoiIVSmDgb17\nGAVn5nHANRFxwDDK03ibZ5/JrwXOz8xuV27NO4MMZTpSoky2dxDlJsD9Gm6ONKdk5gcj4nuU+xV+\nFBF3Ue4lXAW4Afgm8PrMvKPBZkrSjMjMEyPi8ZR5xV4LHJ2ZPxpiFfsCp0TEWZn5uyGWqzE0Hz6T\nI+JBwCvwNpl7zelgLCJeRxlG/gLgyZl5Q0eSVu/P2nTXWt7KN930o5xnkDomiIgm5zvSaHgmcGx0\nn8JPksbNTjN0vvut51ENwTh9Jv9lTLajb5nZdYPn7GWK1RwWH6GMOrNbLp/wsd3F1fMK90VV95lt\nThnwozXD/S2U0Y/W6JjfqKU1z0L7fVs965giTwyQp2s9Q9yWFQxrpJjDDjtsqCPPDLO8UW7bfNrW\nUW7bfNrWUW7bfNrWUW7bfNrWUW7bfNrWUW6b29r/47TTTuPyyy8fybbN9H6bzJwMxiLirZT5Mn4N\n7JqZvWYYP5US9Dyty7qdKSMWnpETJ+Y9tXrulufp1fOPWwsy8zLgKmCrjskS2/NkW7lQ5gQB+JfO\nxNWEjDtRRkc8eza3RZIkSZoJu+yyC5tvvnnTzRg5cy4Yi4h3AO+hTMb35Jx8tvYTKZMb7x0R9w4D\nWt2k+1+UIOkTHXmOoQQ9b69mD2/lWUy5nvw2yrCi3fK8L9r6XCNiT+AJwIWZ+dPW8iyzkf8AWFxd\natnuSOC+wBeybejbWdwWSZIkSbNgTt0zFhH7UyYrvosyF9eBXa43XZKZ/wOQmTdFxCspM6H/JCK+\nRplp/lmUy/1OyMwT2jNn5lkR8UHgTZRrvE8EFlImcFwHeF1mXtVR5wcp1/E+HzgnIn4MbFa9vpky\nYXOn11Tb8OGIeBJl1vbHA7tQZlefMBzuLG7LjNhll11GtrxRbtuwy7Nto1GebRuN8mzbaJRn20aj\nPNs2GuWNctuGXd58attkYqrrGEdJRBwGHDpFsp9m5oQRWiJiB+DtwA7AasCllAkdP5o9dkBE7Efp\nPdqGMu/Dr4D3Z+bJPdKvBhxMmcRuU8p8EacBh2fmRT3ybEzpCXsasB7wZ+DrwJGZ2XVI+tnYlrZ8\nvYqUJEmS1IeIIHsM4DGngjHNLoMxSZIkqZ7JgrE5d8+YJEmSJI0DgzFJkiRJaoDBmCRJkiQ1wGBM\nkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJ\nkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJ\naoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQA\ngzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZj\nkiRJktQAgzFJkiRJaoDBmCRJkqR5Y9GixUTEwI9FixYPrS2RmUMrTOMlItLjQ5IkSeMkIoA633GD\n6XxHjggyM7qts2dMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQA\ngzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZj\nkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJ\nkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJ\nUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAYkyRJkqQG\nGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJkiRJDTAY\nkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJkhpgMCZJ\nkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAQZjkiRJktQAgzFJkiRJaoDBmCRJkiQ1wGBMkiRJ\nkhpgMCZJkiRJDTAYkyRJkqQGGIxJkiRJUgMMxiRJkiSpAXMqGIuI50XERyLiZxHx94i4JyK+0CPt\nZtX6Xo+vTFLP/hFxTkTcFBE3RMRpEfGMSdKvFhFHRMRFEXFrRCyLiOMiYutJ8mwcEZ+NiGsi4raI\nuCIijo6IdSbJs2NEfC8irouIWyLiNxFxYET0/D9Od1skSZIkzY7IzKbb0LeIOA/YFrgZuBrYGvhy\nZu7XJe1mwBXA+cA3uxR3QWZ+vUu+o4CDgD8CJwILgb2B9YDXZebHO9IvBE4FdgTOrf7eBNgLuAPY\nNTPP7ciuiN3oAAAgAElEQVSzBXAWcP+qbRcD2wO7ARcBO2Xm3zry7Fm151bgOOB6YI9qH5yQmS+s\nuy1d8udcOj4kSZKkqUQEUOc7bjCd78gRQWZG13Vz6ct2ROwMXJ2Zl1V/nwZ8aYpg7POZ+bI+y98B\nOAP4A7BdZt5YLd8U+DWwOrB1Zl7VludtwLuA4zNz77blewAnARdm5sM76jkFeDLw+vaAKCI+ALwJ\nOCYzX9O2fE3gMmBNYMfMPK9avrDaB48HXpSZx9fZli77w2BMkiRJY2WUgrE5dZliZv40My+bwSpe\nTfnPvKsVvFT1XgV8DFgVeGlHnldVed7a0dZvA6cD21SBI3Bvr9hTgCVdeqYOA/4B7BsR92lb/gJK\nL9pXW4FYVccdwCFAVG2vuy2SJEmSZsmcCsYGtFFEHBARb6ueHz5J2l2r51O6rDuZEvTs1loQEVtS\nLkm8JDOv7CdPWx0/6EycmTdTerNWp/R2tefJHu36GXALsGNErDLotkiSJEmaXSs33YBZ8JTq0RIR\n8RNg/8z8Y9vC1YGNgZsyc1mXcv5QPW/Vtuwh1fMlPerulSenyPOUKs9pU9WTmXdHxBXANsAWwMUD\nboskSZKkWTTOPWO3AEcCjwHuVz12pgywsQvwo45LAdeunv/eo7zW8vbRDkc1zyB1SJIkSZpFYxuM\nZea1mXl4Zp6fmTdWj58DTwXOAR4EvKLZVkqSJEmar+bDZYoTVJf1HQs8Dngi8NFqVau3aO2uGZcv\nv6Ft2ajmGaSOrl7ykpewePFiANZZZx0e+chHsssuuwDwk5/8BMDXvva1r33ta1/72te+nlOvl2u9\n3mWar+lZ/vnnn88NN5Sv2UuWLGEyc2po+3ZTDW0/Rd5nUeb3+n5mPr1t+R+BjYCNOu+1iojHA2cC\np2fmztWyLSn3X12cmf/UpZ6DgXcD78zMw6plLwc+DXwyMztHQCQivk+5Z+zJmXlateyLwD7APpl5\nXEf6BZTgaxVgjcy8c5Bt6bGfHNpekiRJY8Wh7Zu3Q/V8ecfyU6vnp3XJ0wraftxaUA2zfxWwVTWv\nWbc82VYuLB+U4186E0fEGsBOlPvdzu5oV/Ro186U0RfPaAVig2yLJEmSpNk1tsFYRDwqStjbufxJ\nwBspQdKXOlYfQwl63h4R67TlWQy8FrgN+HyPPO9rry8i9gSeQJn0+aet5Zl5OWVY+8UR8bqOso4E\n7gt8ITNvbVt+IvBXYO+IeExbHasC/1VtyyeGsC2SJEmSZsmcukyxCnCeXb1cRBmM43LK5MoAf83M\nt1RpTwMeTLkc7+pq/baUubUSOCQz39OljqOANwHXUIKghcALgXWB12XmJzrSL6T0Qu0A/IrS27QZ\n8HxKwLNbZv6yI88WlPnEHgB8C/g9ZV6xXYCLgJ0y829dtv0E4Hbga8D1wLMow9OfkJl7192WLvm9\nTFGSJEljZZQuU5xrwdhhwKGTJFmSmVtWaV8KPAd4GHB/yj1VyyjB2ccy84xJ6tmP0nu0DXAPJch6\nf2ae3CP9asDBwIuATYEbKZcjHp6ZF/XIszGlJ+xpwHrAn4GvA0dmZtch6SNiB+DtlMBvNeBS4DPA\nR3tFTdPdlo68BmOSJEkaKwZjmhMMxiRJkjRuRikYG9t7xiRJkiRplBmMSZIkSVIDDMYkSZIkqQEG\nY5IkSZLUAIMxSZIkSWqAwZgkSZIkNcBgTJIkSZIaYDAmSZIkSQ0wGJMkSZKkBhiMSZIkSVIDDMYk\nSZIkqQEGY5IkSZLUAIMxSZIkSWqAwZgkSZIkNcBgTJIkSZIaYDAmSZIkSQ0wGJMkSZKkBhiMSZIk\nSVIDDMYkSZIkqQEGY5IkSZLUAIMxSZIkSWqAwZgkSZIkNcBgTJIkSZIaYDAmSZIkSQ0wGJMkSZKk\nBhiMSZIkSVIDDMYkSZIkqQEGY5IkSZLUgJWHUUhErAZsBKwN3Af4B/CXzPzzMMqXJEmSpHEzUDBW\nBV+7A88GHgdsSZdetoi4DfglcBpwfGb+3+BNlSRJkqTxEZnZf+KItYGDgDcAC4BfAL8GrgD+DNwC\n3AmsTukl2wTYBtgO2Bo4A/ivzDxleJugmRIROZ3jQ5IkSRp1EQHU+Y4bTDOGIjOj27q+e8Yi4hnA\nZ4AzgRcBp2bmHdPIv2mV75iIOB84IDOv7Te/JEmSJI2TvnrGIuJI4AnAgZn5u1oVRqwMvBZ4BfBC\nL10cXfaMSZIkadyMUs/YlMFYRBwMrAocOcxv5hHxIOATlB6yK4ZVrobHYEySJEnjZpSCsX6Gtv9D\nZh4x7G/lmXkp8AJgs2GWK0mSJElzwbQG8ND8Ys+YJEmSxs1c6xmbrOB9ImK/6rF9tWyDiDgpIm6O\niCUR8fo6dUiSJEnSOKoVjAGPAj4OPBxYJSJWAr4H/AtwBPDvwIsj4jk165EkSZKksTLQpM9t7gKe\nmplnAFRB16OAQzLz/dWy04EvA9+oWZckSZKkeWjRosUsW3blwPk32GAzli5dMrwGDUndnrHtW4FY\n5amUCzC/0FqQmctq1iFJkiRpHiuBWA78qBPIzaS6wVhn/kcCf8nMqzuW37dmPZIkSZI0VuoGY6tE\nxAKAiLg/8Gjgx+0JIuLBwNKa9UiSJEnSWKkbjJ0CHBURDwc+BSyg7RLFiHgYcALw9pr1SJIkSdJY\nqRuMvRfYBPgN8AzgyMz8QURsFRFnVsu3Bd5Xsx5JkiRJGitDmfQ5ItYE7snMf1SvVwY2bktyR2b+\nuXZFmlVO+ixJkqRRMMyJmkdp0ufawVhELMjMu2sVopFkMCZJkqRRMK7BWK3LFCPiIODWiPhYnXIk\nSZIkab6pe8/YgZRBO9YaQlskSZIkad6oG4wtAdYH9pssUUR8qmY9kiRJkjRW6gZjHwaOAFaeIt0/\n16xHkiRJksbKVEHUVK4FrgbOq4ayvwD4OxPviNsA2KpmPZIkSZI0VmqNphgR1wNrA52jg7QXGkBm\n5oKBK1IjHE1RkiRJo2BcR1Os2zO2DLgQ+DxwV480a1Mmh5YkSZIkVeoGY38B3p2Zp0yWKCL2rVmP\nJEmSJI2VusHYwcAlfaR7c816JEmSJGms1LpnbNKCI54CLAIuzcyzZqQSzSjvGZMkSdIoGNd7xuoO\nbT+VlYDdI+INM1yPJEmSJM0pM9Yzdm8FEYuBb2XmtjNakYbOnjFJkiSNAnvGehe+XUScFRG3R8Td\nnQ/gMuDWuvVIkiRJ0jipNYBHRGwO/AhYFfgzZYLnpdXqhZR7xr4DvLpOPZIkSZI0bur2jP0n8ANg\nUWYuBn6RmZtXj42BrYE1gHVq1iNJkiRJY6VuMLYdsG9m3lC9visi7tdamZl/APYFjqhZjyRJkiSN\nlbrB2HWZeVvb6wuBp7UnyMw/Yc+YJEmSJE1QNxi7ISJWjoj7VK9/DPxHRNx7L1qU4UoeWLMeSZIk\nSRordYOxK4BfAJdGxOrA94GNgBMj4kERsRZwFHBjzXokSZIkaazUmmcsIh4D/By4B9g4M2+IiH2B\n/2Hi4P2vy8xP1GqpZp3zjEmSJGkUjOs8Y7UnfY6IDYHVMvOKtmVvAP4DWBP4cma+plYlaoTBmCRJ\nkkaBwZjmHYMxSZIkjYJxDcbq3jPWbwOeOxv1SJIkSdJcMSvBGHDILNUjSZIkSXPCylMliIg1gINq\n1LEW8PAa+SVJkiRp7Ex5z1gVjN1IubCy67WOfcjMXDBgXjXEe8YkSZI0Csb1nrEpe8Yy8+aIuBP4\nEHAy02/52sCXp5lHkiRJksbalMFY5XrgHZl5xyCVRMSFg+STJEmSpHHV7wAeTx40EKvsVyOvJEmS\nJI2dvoKxzKzbs/WwmvklSZIkzRGLFi0mIgZ+LFq0uOlNmBWzMulzRPw6Mx894xVpqBzAQ5IkSYMY\n9iAZ83YAD4e2lyRJksbfokWLWbbsyoHybrDBZixdumS4DZoHHNpePdkzJkmSNH/U6zGauZ6sYZc3\np3rGHNpekiRJkobPoe0lSZIkqQEObS9JkiRJDRjKaIoRsRLwXOB5wCbAtZRLGr+QmbfVrkCN8J4x\nSZKk+cN7xgZr25SpJ7lnrHYwFhEPBE4AtmfiAB8JXATsmZmX1qpEjTAYkyRJmj8MxgZr25SpZyoY\ni4j7AmdTLnc8CbgKuBNYH9gS2AO4CXh0Zt40cEVqhMGYJEnS/GEwNljbpkw9g8HYwZQ5xP6127f2\n6vLF9wM3ZOY7B65IjTAYkyRJmj8MxgZr25SpZzAYOwvYPTNvmCTNAuBHmbnrwBWpEQZjkiRJ84fB\n2GBtmzL1JMFYv6Mp9nL7ZIEYQGbeDdxVsx5JkiRJGit1g7HV+ky3as16JEmSJGms1A3G/hgRu0+W\nICKeBCytWY8kSZIkjZW6wdj7ga9ExAERsV77iohYHBFvAf4X+EDNeiRJkiRprAxjnrHXAx+qXt4O\n3AGsDiyolh2Sme+pVYka4QAekiRJo2vRosUsW3blwPk32GAzli5dcu9rB/AYrG1Tpp7JSZ+rCp4G\nvAd4RNviS4FDM/NrtStQIwzGJEmSRtdoBTwGYz1Tz3Qw1lbRA4EHAn/JzMuHVrAaYTAmSZI0ukYr\n4DEY65l6Boe2nyAzr87Msw3EJEmSpIkWLVpMRAz8WLRocdOboCEbuGcsItYFnkS5NHE94CbgD8AP\nM3PJsBqo5tgzJkmSNDyj3FtUv7xRbtvE8uZ0z1hEbBYRXwT+BHwNeBtwAPBm4Bjgsoj4dkQ8dLpl\n91H38yLiIxHxs4j4e0TcExFfmCLPjhHxvYi4LiJuiYjfRMSBEdFz2yNi/4g4JyJuiogbIuK0iHjG\nJOlXi4gjIuKiiLg1IpZFxHERsfUkeTaOiM9GxDURcVtEXBERR0fEOk1uiyRJkqTZMa2esYh4AXAs\nsGYfyW8DXpuZnxuwbd3qPw/YFrgZuBrYGvhyZu7XI/2ewInArcBxwPXAHlW+EzLzhV3yHAUcBPyx\nyrsQ2JvS+/e6zPx4R/qFwKnAjsC51d+bAHtRRpbcNTPP7cizBXAWcH/gm8DFwPbAbsBFwE6Z+bfZ\n3pYu+e0ZkyRJGpJR7i2qX94ot21ieaPUM9Z3MBYRzwGOB/4BfAb4PiWIuI4SICwE1gG2BP6F0lu2\nPvCvwxpRMSJ2Bq7OzMuqv08DvtQtGIuINYHLKIHjjpl5XrV8YZXv8cCLMvP4tjw7AGdQLrfcLjNv\nrJZvCvyaMmT/1pl5VVuetwHvAo7PzL3blu8BnARcmJkP72jbKcCTgde3B0QR8QHgTcAxmfma2d6W\nLvvQYEySJGlIRjlAqV/eKLdtYnmjFIz1dZliRDwA+DSl1+fBmfnmzPxhZl6Vmf/IzHsy87bMXJqZ\nZ2TmYcBWlGDk4xGxQd+tnURm/jQzL+sz+QsoPU9fbQUvVRl3AIcAAby6I8+rKf+Zd7WClyrPVcDH\ngFWBl3bkeVWV560dbf02cDqwTRU4Avf2ij0FWNKlZ+owSrC7b0Tcp4FtkSRJkjRL+r1n7N+Ay4Gn\nZ+a1/WTIzJsol+pdxIqBwmzYlRKMnNJl3c+AW4AdI2KVjjz0yHMyJejZrbUgIrakXJJ4SWZ2m3Fv\nhTxtdfygM3Fm3kzpzVqd0ts1a9siSZIkaXb1G4w9B3hTZt49ncKr9G8B9pxuw4bgIdXzJZ0rqnZd\nAawMbAEQEasDGwM3Z+ayLuX9oXreqp86psiTA+TpWs8Qt0WSJEnSLOo3GFs9M88YpIIq332mTDh8\na1fPf++xvrW8NXrhdNOPcp5B6pAkSZI0i/oNxq6vWc91NfNLkiRJ0lhZuc90t9Ws5/aa+QfR6v1Z\nu8f61vIbBkw/ynkGqaOrl7zkJSxevBiAddZZh0c+8pHssssuAPzkJz8B8LWvfe1rX/va1772dZ+v\n4SfV82CvR7c8JpTXtmRelNf+/z7//PO54YbyNXvJkiVMpq+h7SPi1MzcbcqEM5S/R5lTDW3/RWAf\nYJ/MPK5j3QJKwLIKsEZm3lkt/yOwEbBR571WEfF44Ezg9MzcuVq2JeX+q4sz85+6tOFg4N3AO6sR\nJomIl1NGpvxkZq4wsElEfJ8y2uKTM/O02dqWbhzaXpIkaXhGebj3+uWNctsmljfnhranzCFWR938\ngziVMmLg07qs25kyYuEZreClLQ898jy9ev5xa0E1zP5VwFYRsVmPPNlWLpQAEspcbBNExBrATpTR\nEc+ezW2RJEmSNLv67Rm7A/gsJUiYrlWBl2bm6gPknaxN05n0+QmZ+atq+apVvscBe2fmCW15WhMl\nXwpsn5k3VMsXA7+iDETSOelzq/frhKq8rJbvCXwDuCAzt+1oW6v368DM/H9tyz8IvBH4RGa+dra3\npcs+tGdMkiRpSEa5t6h+eaPctonljVLPWL/B2D3U+c9AZuaCAfO3t2NP4NnVy0XAUynzn51eLftr\nZr6lI/0JlHvWvkYZiORZlCHdT8jMvbvUcRTwJuAa4ERKr94LgXWB12XmJzrSL6T0Qu1ACXJ+DGwG\nPJ9yr91umfnLjjxbUAKlBwDfAn5PmVdsF8q8bDtl5t+6bPuMbkuX/AZjkiRJQzLKAUr98ka5bRPL\nm6vB2CnA0r5rXW5D4ClDCsYOAw6dJMmSzNyyI88OwNspwdJqlJ6izwAf7RVpRMR+wGuBbYB7KEHW\n+zPz5B7pVwMOBl4EbArcSOmxOjwzL+qRZ2PgSMplhOsBfwa+DhyZmV2HpJ+NbenIazAmSZI0JKMc\noNQvb5TbNrG8uRiMLc3MRf03cELelYA/DZpfzTEYkyRJGp5RDlDqlzfKbZtY3igFY/0O4HFF37V1\nyMx76uSXJEmSpHHUbzC2f8166uaXJEmSpLHS12WKmp+8TFGSJGl4RvnSvfrljXLbJpY3Zy5TjIi1\np9myaZnp8lVfxIqPww/vnvbww01vetOb3vSmN73pxzN9xOFERJfH4ZOmX7RocfeKBpJTtn+62re3\nXoBy2HAadK+csD+HVX7Zb3U7G3Jax89kJu0Zi4jnA9tm5mQjGA4kIh4OHJaZzx922RoOe8YkSdJ8\nN8o9MqNV3ii3bWJ5c6ZnLDNPBG6MiG9GxP2n18hJG3QA8EnggGGVKUmSJElzyZQDeGTmUcDxwG8i\n4h0Rsf4gFUWxZ0ScCzwdeGpmXj9IWZIkSZI01/U9gEdEbAYcDewOnAr8EPglcBFwfTWEfXv61YDN\ngUcBOwPPBG4D/jMzjxvWBmjmeJmiJEma70b58rjRKm+U2zaxvFG6THHaoylW93q9Eng+sIjlW3Iz\n8HdKb9t9gbWq5XdSArcvASdm5t3TqlCNMRiTJEnz3SgHAaNV3ii3bWJ5czoY6yj4IcBjgS2A9YHV\ngTsoQdkS4ELg3My8feBK1BiDMUmSNN+NchAwWuWNctsmljc2wZjGm8GYJEma70Y5CBit8ka5bRPL\nG6VgbMoBPCRJkiRJw2cwJkmSJEkNMBiTJEmSpAYYjEmSJElSAwzGJEmSJKkBBmOSJEmS1ACDMUmS\nJElqwFCCsYhYNSJ2iYjd25ZtGxH3G0b5kiRJkjRuagdjEfES4Brgx8DH2latBnwuIvavW4ckSZIk\njZtawVhEPAM4FjgDOAj4a2tdZv4iM58NPCIinlSrlZIkSZI0Zur2jL0F2Dcz98zMDwM3d0lzMPDa\nmvVIkiRJ0lipG4zdNzO/OlmCzLwDuE/NeiRJkiRprNQNxm7oM916NeuRJEmSpLFSNxhbKSIe1PY6\nOhNExKuAK2vWI0mSJEljZeWa+T8GnBoR/wGcBCRARKwLPB54GfAs4Ak165EkSZKksVIrGMvMr0fE\nzsBXgHuAeyLiFmDVtmRvzsxf1KlHkiRJksZN7XnGMvNA4CXA5ZTgbjXK5Yq/BfbIzA/VrUOSJEmS\nxk1k5vAKi1gMbABck5lXD61gNSIicpjHhyRJ0lwTEVR34gxaAq3vU8Msa/TKG+W2TSxv2G2bMnUE\nmbnC2BpQ/54xImIlYK3MvCEzlwBLquVbACtl5qV165AkSZKkcVPrMsWI2AS4DLg2Ip7Tsfo24K0R\n8a46dUiSJEnSOKp7z9hbKMPWLwDu174iM/+Uma+kBGr71axHkiRJksZK3WBsa+BfgEdn5md7pPkw\n8IKa9UiSJEnSWKkbjC3IzDsy8/xeCaoRIFavWY8kSZIkjZW6wdgaUyWIiNUoIyxKkiRJkip1g7HL\nIuKtU6Q5CriwZj2SJEmSNFbqDm3/XuCciHgC8HngfOBvwDrA44DXANsDO9asR5IkSZLGSu1JnyNi\nX+DTwCpdVt8DvDozj61ViRrhpM+SJGm+G+XJhkervFFu28TyRmnS57qXKZKZXwR2AL4F3AkEJQj7\nIfBEAzFJkiRJWlHtnrEJhZUwc33gusy8e2gFqxH2jEmSpLlm0aLFLFt25cD5N9hgM5YuXXLv61Hu\nkRmt8ka5bRPLG6WesaEGY5M04LGZ+csZr0hDZTAmSZLmmvkUBIxWeaPctonljVIwVvsyxT4dM0v1\nSJIkSdKc0NdoihGxA7AXcExmXlwtWwd4Qx/Z1wQeMXALJUmSJGkM9XWZYkQspdwL9vPM3Llath5w\nLaWPr2u3W5vMzAU126pZ5mWKkiRprplPl8eNVnmj3LaJ5Y3SZYr9zjN2OvC86rnlb5SteD/wA6DX\ngB3rAF/usx5JkiRJmhf6HsAjItbNzOs7ll0HbJaZN0+R95zMfNzgzVQT7BmTJElzzXzqkRmt8ka5\nbRPLG6Wesb4H8OgMxCpbArf2kX2ffuuRJEmSpPmg7miKLwVujYiPTZYoMy+rWY8kSZIkjZW6wdgb\ngQXAWkNoiyRJkiTNG3WDsSWUURb3myxRRHyqZj2SJEmSNFbqBmMfBo5g6lEZ/7lmPZIkSZI0Vvod\n2r6Xa4GrgfMi4kzgAuDvTByeZANgq5r1SJIkSdJY6Xto+66ZI64H1mbFSZ/bCw2c9HlOcmh7SZI0\n18ynIdVHq7xRbtvE8kZpaPu6PWPLgAuBzwN39UizNvDemvVIkiRJ0lipG4z9BXh3Zp4yWaKI2Ldm\nPZIkSZI0VuoGYwcDl/SR7s0165EkSZKksVLrnjGNN+8ZkyRJc818uldptMob5bZNLG/O3jMWESsB\newBbUnrEvuu3dUmSJEmavr6DsYh4IPA94KFti38ZEbtn5vVDb5kkSZIkjbG+Jn2OiAWUQOxhlKHq\nW4/tgONmrHWSJEmSNKb6CsaA/YDFwNsoAdhWwBOAo4FdImK3GWmdJEmSJI2pfi9T3At4cWZ+u23Z\npcCZEXEN8ELg1GE3TpIkSZLGVb89Yxt3BGLtjgW2HVJ7JEmSJGle6DcYu6nXisy8cUhtkSRJkqR5\no99g7PYp1t862cqI2LrPeiRJkiRpXug3GKvrs7NUjyRJkiTNCf0GYwsHraCaKHrLQfNLkiRpvC1a\ntJiIGOixaNHippsvDSwyc+pEEbdTerd6XY64F71HU9wQ2C0zFwzUQjUmIrKf40OSJKmOiAAG/c4R\ntH9fqVfWzJY3ym2rX94ot21iecNu25SpI8jM6Lquz2DsHiZvcdfCqzwBpMHY3GMwJkmSZoNBQPNt\nq1/eKLdtYnmjFIz1O88YwA+ApdNI37Ih8JQB8kmSJEnS2Oo3GPtLZu4+SAXVPWN/GiSvJEmSRs+i\nRYtZtuzKgfNvsMFmLF26ZHgNkuaofoOxKwatIDPviYiB80uSJGm0lEBs8Mu8li3rdYeLNL/0O5ri\n/jXrqZtfkiRJksZKX8FYZl5Sp5K6+SVJkiRp3MzWpM+SJElqSJ15vJzLS5o5fQ1tr/nJoe0lSRoP\nozzMeP3yRrltE8sb5bbVL2+U2zaxvFEa2t6eMUmSpBFkb5Y0/uwZU0/2jEmS1JxR7gkYrfJGuW0T\nyxvlttUvb5TbNrE8e8YkSZLGjD1ZkqbLnjH1ZM+YJEn9m089AaNV3ii3bWJ5o9y2+uWNctsmlmfP\nmCRJkiTNcwZjkiRp3qpzaaGXFUqqa+WmGyBJktSUZcuuZNDLlZYt63rVkST1zZ4xSZI0Y4Y9qIWD\nZEgaJw7goZ4cwEOSVNco38Rfv7xRbtvE8ka5bfXLG+W2TSxvlNtWv7xRbtvE8hzAQ5IkSZLmOYMx\nSZIkSWqAwZgkSZIkNcBgTJIkTeBw75I0OwzGJEma44Y9wuDy4d6n/yh5JUn9cJ4xSZLmuDpzZZX8\nzpclSU2wZ0ySJEmSGmAwJkmSJEkNMBiTJEmSpAYYjEmSJElSAwzGJEmSJKkBBmOSJDXAubwkSfMi\nGIuIJRFxT4/Hn3rk2TEivhcR10XELRHxm4g4MCJ67rOI2D8izomImyLihog4LSKeMUn61SLiiIi4\nKCJujYhlEXFcRGw9SZ6NI+KzEXFNRNwWEVdExNERsc4keaa9LZKkmeVcXpKkyBx8XpK5IiKuANYG\njgY6J1O5OTM/2JF+T+BE4FbgOOB6YA9ga+CEzHxhlzqOAg4C/ljlXQjsDawHvC4zP96RfiFwKrAj\ncG719ybAXsAdwK6ZeW5Hni2As4D7A98ELga2B3YDLgJ2ysy/1d2Wtrw5H44PSWpCRDD43GBB+/m5\nXlnDLm+U2zbs8ka5bRPLG+W21S9vlNs2sbxRblv98ka5bRPLG3bbpkwdQWZ2ndBxPgVjmZlb9JF2\nTeAyYE1gx8w8r1q+EDgNeDzwosw8vi3PDsAZwB+A7TLzxmr5psCvgdWBrTPzqrY8bwPeBRyfmXu3\nLd8DOAm4MDMf3tG2U4AnA69vD+4i4gPAm4BjMvM1dbaloz6DMUmaIeP7pWeU2zbs8ka5bRPLG+W2\n1S9vlNs2sbxRblv98ka5bRPLG6VgzMvUVvQCSs/TV1vBC0Bm3gEcQulZe3VHnldT/qPvagViVZ6r\ngI8BqwIv7cjzqirPW9sXZua3gdOBbSJi59byqlfsKcCSzl424DDgH/x/9s48zI6q6MNvyb4vIrsQ\nQFYBQRAQIiSILOL2gSKLIOCGgqKgoiIQUERwQURERBFBRBFlFUQFwi4Igux7wp4gW1iSQMjU90ed\nmx5RXBYAACAASURBVOnp6Xu77709c4fk9z5PPzPdt7u6ejvn1Kk6dWBPM1ugy2sRQgghhBBCDANz\nkjE2n5ntYWbfNLMvmdmYJmOmxhJG0mUFv10NTAU2N7N5csfQ5JhLCaNn68YGM1uNCEm8392LAv8H\nHZM5x9/zO7v7y4RnbkHC29XNtQghxGxBNwkyipJk1C1PCCGEmJOMsWWBM4DvEmPHrgAeMLMtc/ut\nmf7enxfg7jOBCcDcwKoAZrYgsAIx9mxywXkfSH/XqHKOkmO8g2MKz1N0LUII0WvqzDDYTYKMoiQZ\ndcsTQggh5hRj7DTgvYRBthCwHvALYBRwiZllx2Ytlv5OaSKrsb2RvbDd/Uf6MUII0TOUYVAIIcSc\nxBxhjLn7d9x9vLv/z92nu/vdKdHFj4nQvnG91VAIId6YKHRPCCGE6Jy5e61Aj/kFcDCQDVVseIsW\nG7z7gO0vdLj/SD9mAHvvvTejRo0CYPHFF2eDDTZgzJgxAIwfPx5A61rX+htsfdllR3XsRVpmmZWZ\nNGniLHn9nqzxaY8x6W+19cmTxw7Qr5/O5M06eraXFzIaz7d/n3b1GRp5+fev8/s10uUxQF5mi+QN\nq7yR/T0Mltfu8QPX9T2MTHnZ+va2227jhReieT1x4kRaMUektm+GmS1KGCLT3X3BtO1MYHdgd3f/\nY27/uQgDZx5gYXefkbY/BiwPLJ8fN2ZmmwHXA9e4+1Zp22rEGK/73H3tAr2+AXwP+I67H5G2fQo4\nFTjF3QdlQDSzvxHZFrdx9ys7vZbcPkptL0QHdGPsQL/BM1TyZt/UxSNZt7rlSbeRIW8k6zZQ3kjW\nrXt5I1m3gfJGsm7dyxvJug2Up9T2I4d3p78PZ7ZdQWQy3L5g/62IsMbrcsbLFelv0THvT38vb2xw\n94eAR4E1zGzlJsd4Ri7EvGAA2+Z3NrOFgS2I7Ij/6vJahBBdosQRQgghhKjCbG+MmdlaKeNhfvso\n4GdEa+XMzE/nAs8Au5rZRpn95yMyMTpwck7cLwij51AzWzxzzChgf2A6cHqTY46zMM8bx3wYGE1M\n+nxVY7u7P0yktR9lZgfkZB1FJCY5w92ndXktQgghhBBCiGFgtg9TNLMjiHFhVwOPAC8BqwE7EpMx\n/xXYyd1fzxzzYeBPwKvAH4DngA8RaeP/5O67Fpznh8BXgCcII2he4OPAksAB7n5ybv95Cc/Vu4Fb\nCM/ZysBHCeNta3e/OXfMqsR8YksDFwL3EPOKjQHuBbZw9+dzx7R9LZljFaYoRAeM5NCM7uVJt5Eh\nT7qNDHkjWbeB8kaybt3LG8m6DZQ3knXrXt5I1m2gvJEUpjgnGGNbAp8DNqQ/tf0LwG2EJ+msJse9\nGziUMJbmBx4Efg2c2MxCMbO9CE/YOkAfYWT9wN0vbbL//MA3gN2AlYAXiXDEce5+b5NjViA8YdsD\nbwaeAv4CHOXuhSnsO7mWdJyMMSE6YCRXQN3Lk24jQ550GxnyRrJuA+WNZN26lzeSdRsobyTr1r28\nkazbQHkyxsQbAhljQnTGSK6Aupcn3UaGPOk2MuSNZN0GyhvJunUvbyTrNlDeSNate3kjWbeB8kaS\nMTbbjxkTQogqdDNflubKEkIIIUQnzOnzjAkhBJDNWNjJsYWdXUIIIYQQLZFnTAghhBBCCCF6gIwx\nIYQQQgghhOgBMsaEEMNGneOyupGlcV5CCCGEGAkom6JoirIpirqZfbM0jWTd6pYn3UaGPOk2MuSN\nZN0GyhvJunUvbyTrNlDeSNate3kjWbeB8pRNUQghhBBCCCHmcGSMCSGaolBAIYQQQoihQ6nthRBN\n6SbdexyvlO9CCCGEEM2QZ0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBC\niB4gY0wIIYQQQggheoCMMSFmI5SKXgghhBDijYNS2wsxG6FU9EIIIYQQbxzkGROix3TjzZInSwgh\nhBDijYs8Y0L0mG68WfJkCSGEEEK8cZFnTAghhBBCCCF6gIwxIYQQQgghhOgBMsaEaBNlLBRCCCGE\nEHWgMWNCtIkyFgohhBBCiDqQZ0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQggh\nhBBCiB4gY0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wIIYQQ\nQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wIIYQQQggheoCMMSGEEEII\nIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGE\nEKIHyBgTQgghhBBCiB4gY0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBC\niB4gY0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wIIYQQQggh\neoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0zMESy77CjMrKNl2WVH9Vp9IYQQ\nQggxGzJ3rxUQYjiYPPkRwDs81upVRgghhBBCCOQZEyOUbjxZ8mYJIYQQQog3AvKMiRFJN56sOF7e\nLCGEEEIIMbKRZ0wIIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wI\nIYQQQggheoCMMSGEEEIIIYToATLGhBBCCCGEEKIHyBgTQgghhBBCiB4gY0wIIYQQQggheoCMMSGE\nEEIIIYToATLGhBBCCCGEEKIHyBgTtbDssqMws46XZZcd1etLEEIIIYQQYliZu9cKiNmDyZMfAbyL\n460+ZYQQQgghhHgDIM+YEEIIIYQQQvQAGWNCCCGEEEII0QNkjAkhhBBCCCFED5AxJoQQQgghhBA9\nQMaYEEIIIYQQQvQAGWNCCCGEEEII0QNkjAkhhBBCCCFED5AxJoQQQgghhBA9QMaYEEIIIYQQQvQA\nGWNCCCGEEEII0QNkjAkhhBBCCCFED5AxJoQQQgghhBA9QMaYEEIIIYQQQvQAGWNCCCGEEEII0QNk\njAkhhBBCCCFED5AxJoQQQgghhBA9QMaYEEIIIYQQQvQAGWNCCCGEEEII0QNkjAkhhBBCCCFED5Ax\nJoQQQgghhBA9QMaYEEIIIYQQQvQAGWNCCCGEEEII0QNkjAkhhBBCCCFED5AxJoQQQgghhBA9QMaY\nEEIIIYQQQvQAGWNCCCGEEEII0QNkjM0BmNkKZnaamT1hZtPNbIKZHW9mi/daNyGEEEIIIeZU5u61\nAmJoMbNVgRuApYDzgfuATYADge3MbAt3f76HKgohhBBCCDFHIs/Y7M/JhCH2RXff2d2/5e7bAMcD\nawFH91Q7IYQQQggh5lBkjM3GJK/Y+4CJ7v7z3M9HAK8Ae5rZAsOunBBCCCGEEHM4MsZmb8amv3/P\n/+DuLwPXAQsCmw29KuNHsLw6ZY10eXXKqltenbJGurw6ZdUtr05ZI11enbLqllenrJEur05Zdcur\nU9ZIl1enrLrl1SlrpMurU9ZIl1enrLrl1SmrNTLGZm/WBBy4v8nvD6S/awy9KuNHsLw6ZY10eXXK\nqltenbJGurw6ZdUtr05ZI11enbLqllenrJEur05ZdcurU9ZIl1enrLrl1SlrpMurU9ZIl1enrLrl\n1SmrNTLGZm8WS3+nNPm9sV1ZFYUQQgghhBhmZIwJIYQQQgghRA8wd++1DmKIMLPjgIOBr7r78QW/\nnwh8AfiCu59S8LteDiGEEEIIIbrE3a1ou+YZm725DzCajwlbPf0tHFPW7KURQgghhBBCdI88Y7Mx\nKbX9g8AEd18t99vCwFNpdWl3nzbc+gkhhBBCCDEnozFjszHu/jCR1n6UmR2Q+/koYCHgDBliQggh\nhBBCDD/yjM3mJO/YdcDSwIXAPcS8YmOAe4Et3P35nikohJijMLNF3P2lXushhBBCjATkGZvNSd6x\njYHTgU2Ag4BVgOOBd7+RDTEzW97MDjOzCb3WZXbGzA43sy1L9nmPmR0+XDplzlurbmY2DHPujUzM\nbBEze6uZLTpE8jc1s18DTwyF/JJzL1Vxv42HWhcxMjGzg8xsyV7r0Q5mNo+ZbWhma/ZaF9E+ZrZS\nWXmbyuWVqsiqeM4dquo3UjGzStMxmdlGQ61LXcgzJt5QmJkBOwKfAXYgktC4u8/VI33mIibXXgIo\n1MHdrx5WpZil13zuPjW3fWvgw8BU4JfuXmrImlkfMM7dj2qxz6HAUcP9HOrWLcm7EjgF+Iu7v16j\nrmsBawMLu/uZXcgZDewDbEjMJTgF+A9wurtf26asuYGvAp8mOmkaTAB+Bfywm3tgZosBexLf67pE\nQqFp7r5QpzI71ONxYPdW36KZHQR8z93nHz7NhhYzWxFYAZiv6PeyssnMHgZeAfZ193832edA4EB3\nX7VN3ZYDNiDmuZwC3OruT7U+asDxnyHe3bHu/mTB7ysAVwDfd/ffVJDXB0wHzgVOcffrquoy1JjZ\nLsBHgf3c/bm0bTXgUqAxHvwCYJc6y6yKul0InAz8zWtsUJrZrkS51CjnXgRuAX7t7n9ocVwlo6QI\nd3+002M7wcxmEvXXd1rsU6n+MrO7gM3dvdm8spjZNsCF7r5gBd2WAJYDHnL3VzPb9wE+QpQLP3H3\nm8pk5eTOA7yX/rrwO2n7/MCiwDPu3lci4xrgve7+Wot91geucPdKHXE9x921aBnxC/BWYBzwKDAT\n6AMmAccBa/RIp8OA55I+TZc2ZW4JrFThXmxZss/xRMNiscy2XTP3rg/4H/DWCjr1AYeX7DMOmNGD\nZ1CrboQh1pfu02TgGGDVLnXcALi56J0AtiIM4w9WlHVi7hlml5nAT9vQa16isToTeB2YCNyQ/r6e\nto8H5u3gmrcgvPEvZ/T9DzGVxmLtyqvhPZkKzAAOJ3VCZn5bggjh7iMaHvljH+5wGSSrhX7zEI3t\n44BTgdMKll+3IW9b4K6i8qjoPSz5vvqIhtf/NdnniCqyMvuvCFzcRKeLKSn/MnKuAq4r2ecaokFW\nRd7BRAbixrd0B3BAL97XAt3+Btye23Z+0vWfwK1J58/0QLfG/ZoIHAos26U8A87MlBsziGRjMzLn\nOquCPu0ur7eh40HAkjXdu7L669CK3+r09E0UltfAe4jy+MmKup0MvAQskNn2xcxz6SPK1XXauN7t\niciIhoxsXbhZ2r5bBTkzgXNa/L4O8DQwpQ3dai2D234XhkqwFi3dLkQY7YeBv6aCuNFo7AP+Aszd\npfx5gPVSIbU+ME8bx3496fE80ej8DtEoGbS0qdPMOgpnogfx0ty2e4BngU8QPcozgOMr6FSlwrgQ\neKrF71t2ugy1bgX7rw78MBXmfemduwzYCZirzee5BvBCqtR+TGqEZn434HHgtxVkfTHp8yDwSWBl\nwuOxMrB32j4T2L+ibt9I8i4EVs/9thrR2JsJfKOivCWAA4E76a9sn0t/z2jnvtW9EF65u5NeV5Aa\njMBoooOnDzgHWLTg2ImEpzC7PEF/gyTfWOxLv0+oqNvy9BtORUb2LGO7orzNgNeSDiekY68EfpHO\n05ee7REVZPURnqLH0ndwUME+lY0xYBngkST3EeB3wA/S3wlp+6PAMhVkTQZ+XrLPz2jj20/HjAHO\nBqalZ/IK0RDbtIfv76NkGoKEB+E14A9pfZ70bK/vgW7vBH5JeK76gFfTO/O+DuXtl+T8G9iaVOYS\nkSdbAzel57Jfk+NPB37TydKGjg1D5Axi3H2n965K/XUi8GIFWbvTxEhJZcKLRJ1WyXgCbgfOz217\nJL2LownDZSrwq4ryNiYMxseBL6VvfmZunweL9C+Q9bV0735S8NvqwJPpu23ZfsgcU2sZ3NG7MFSC\ntczZC130MhCNy+8ysAflbuAQIuSmjwix61S3RYmGySsM7Bl7JW1fvIKMB4gGyltqvm9VCudvU9KL\nlwrdEzPrqybZ4zLbLgTuaXL8FZmlj+jpv6JguSr9NhP4Xcl1ddJbOajwq1u3FjrPC+zGQG/Zk4Th\nvXJFGWeR6T2koOEK/Am4u4Ksu4iKrPD9BJZM38xdFXW7PS1vavL7m9Lvd5TI2ZKoWKfS32FyKfBx\nYP4avtcFCUP014RRXPSsL68gZwGi0dVHNOR/RjRopwKfa0OfRYkG4fWEZzPbWBxDeBdvBBapKO/s\npNNZ6fjViDJw0FJR3gVEw2v5zLd3ePrfiEy6LwNvryCrj/AmrgD8Nz3fk8h4F4ve6RbyTkwyv0mu\nM40IOW90EJxYQdZ04OiSfY4Gpnf43r2Zwd6y2whjYeE2ZS1HdIIdku5nfjms5PhpwHcz69slnT6S\n2fYTYHKJnIc7XEq9vMDCwOeIjsDG/XqQ6LisXE+mb+thMh6Z3O8LAA8B/+7kudaxFLwXlb2owF6Z\npdGxvFfBsk/6tp6nxAOckd3oJD4+s22jJONZ4B1tXOOzOTnrJNlfy2z7I3B/RXkXEJ1zjY6worrw\nbOC+ivJ+mu79wZltqxDtsmm00RlAzWVwR+9Ur15mLbPvQhe9DEQ4RsP79RzhKt80t0/HjTuiIXVH\nkjGFCMM6O/19IW2/k4Ie8pyc6VRoMHSgXxVj7FTg+Qr6HZ1Z3zM9j80y244BXmqhx6zn1OIZvk40\nbH9PiwqXCBU8IrdckmQ8QDSSj0l/H0jb/0pB733dulV8LqsTPfjPpHPOILxc25ccN4mMIUhxBfRj\n4IUKOkwDTijZ56fEmKwq1zQVOLZkn2OBqS1+vyfzDBodJssXPK9Ov9f10z2srceSaEg13p3JVDBK\ncsefCNxP83Cg+dM7XClklGj0jO/m/czJezr3zg3ohEnb/g2cW0FW1pBbmDCy+4CLgIWavdMt5E0A\n/l6yz2VU8CoSHssLS/a5EHi8hnv6PqKR1+gkeokw5lescOyRhLco28nUl/+/wjPNdq59Lx27VGbb\n91t9q5l7NoEh8vJmzrMR/d6ymUR99AdgTIVjXwZ+VLLPj4CXu32uNbwXY2jTi5p79q2Wxv1/Gdi2\nDZ0aoewHE5E/zxJtm3e1eW1TgWMy659JcjfMvYevVJT3DHBaZr2oLjyOCl7AtK8Bfybq+Y8T4c8T\n0rf2gTavtdYyuJNlboSonx8RgzPPJgyHRohLFbYlCqBjgCO9xQDNDvkm8HbCyDvU3V9o/JCSDXwX\n2D/t980WciZDPd9PQaa/MZGnZBBzASsRY7/KEjU8xcCEDNsQFcYtmW0L0+S5uPusTKtVkmSU4e7j\nsutmthlxfw8ETvLMgF0zexPhCfk+0Ys/pLpV5C3E9BALkpJQAO8HdjCz64Fd3b0oS+AShDerFUZ4\n4cp4lvDktOI1otKrwmvEO9CKhYiGWTPWJL7X7xON9pkVz12VnxD3/ggiJOiJbs5hZtsSIS4QDeql\ngK+b2Rfc/ZWKYv4POLtZ2eTu083sAuI7/VIFefMTnrS6WIwIJWrwGvEcs1xHhDVVxt1fNrMdgZ8D\nnwWuNrMPtKnbckTnSCtuJjyOZVwJfMLM3u3uN+R/NLPNiW+07HxNMbNViEboPkSI5WtEJ9I7iPGP\ne5nZR9z9iibH70GMLb6C8Cj+mQij+zvRkP8U4Rk/pUSVB4iyZj7AgV2IMWTZb31lwmhriruPyum3\nKDHm7BGiPL7W3WemBFDvIerhNxH1R2Xc/Rbgs2Z2OuE9WSHp/DEzu5vwBJ7f7HCiTGxF2e/DgruP\nB8ab2ZuJUPHPpr+fNLM7iEib37n7y5nD9kl/jTDczie8RnlmEmX+Ddl2SgW+RNzvY4khDfMSnYaF\nCXha8ASwVmZ9O8K4/m9m2xJEXViFhSmvmxakYpZ3d3cz2x24nPimJhEG2a7ufnFFnRrUXQa3Ty8t\nQS2z50IXvQyE4dboOfo3YRgtkdunm572+yiJqycaKi1d74SX5EEiY2G396uqp6exPAZsVCLzbKJH\n7QNERfoKuV5kwrNzZwX9Pkkb4Q0Vr/kfwMUl+/wVuGy4dcvIXpQIPbkj81yuJ8KN5iXGIZ2Rtl/Q\nRMajZDwQFPcG/p0KoRlET/x9NBnbmHS6n4oeW+BqolOh0GtIGCqTgKtbyLgh894+mb6Lt+f26eZ7\nnUqFMQQV5MxFGIyvEw2K3dL1NTw99wIbVJQ1jYKxCrl9TqC6h/JG0tifmt7bx4CTc+/gX3L7nEQT\nr3jBsxvkqSfCoWYm2X/Kv9Mt5D0NnFmyzxnA0xVkrZXej2lEj/rWROfA1uk9nEabCQaS3DcRBnc2\nSmMi8C1g6bSPEcbF88AtLWRdm+7R3EX3k2jgvk5JAh+inOtLsh5K9/5LuX3uB/7a5rXW6uXNHPNJ\noqxslJu3EkbC6fR7kb7Y5Pib0v1uFab4MHBTm9f6LiLE/2SGMDkDbXhRiQ6Fveo4b07ufOnde4XI\nNtqJjF8SXqYDiKyWrxGdUNl9/k5kQa0i76Hs+0lxXXgtuUQ1FeQuQURlzCAy5nZyrbWWwR3p0MuT\na5k9l1QAtAx/anHsm4APEmEwjaQd04jB9TsQjapuGnfTifTVrfb5HiUNKaIH55qk5ypd3q+t0jIm\nXdtpmW3ZZTThcSwc45OTuR79Y3gaYXWbZn6fnwjT7KoCSgXhQh0cN4XMGIgm+xxNG9mQatRt0/QM\nXk7P4yWi57rQ6CMaj4V6Eo2PV4E10/qACohoIMykQmOH/rFKVwGb0z81iRHZC6+mvbFKu6Trm0D0\n0K9KNHRWIXpvG42+XUrkrEs06hrJOmYmPT9PpC3v5nt9GvhBN+9oknN90uMW4G25375ONDSmkWvg\nNpF1J+HtLBwfkt67dsbuNQbCt2U0tJB3OZlQQKLsfImUdRZYljCy/1NBVtOw6YzelTIzpmPOS/e5\nMIyLGOQ/jZzx2ELeh9K15UO/+giju1KW0iRrJWI86BMZOZcQ9ZE1OeZYWoxJI8q5X+Tu55G5ff5K\niw6PzH7fIzwLzxDGfnbc3uZJ9lfbfFceL/u+iGRGpaGexJiiE+jPMDyNyIq4eW6/txLhzROayMkm\n8Hgv/YbsXMBY4F+0SOBRIM+A32bei3yHZ6VQ0QrnWSU9o6eSvOnEeLCHMu/j1t2cI3e+h0uWp4g6\nLL+9UpbXdD3P5r6nNTO/L0p8/ydVlPczouNhdFrP14U7pPMMap9RPE44u9yVdM1vLx1LnOTXWgZ3\n9Dx7dWIts+9CTb0MxNizw+nPvjWT/ory9A5lPktJ9h8itPLZ3Laiwi7b+/Vck30qp7dO5/kN8KGa\nnsN6REX6Q3Lx4sC7iYbRNhXkbE30PC+R2bY0YRTMJIyNH7ep24vketkK9vkjJcZY3boRA/Qblc9d\nRK9gS+OGlHSgyW9rEp0Tkwnj5JQk/+1pfRIRzz8onXeT9+nxzDv3avoesuNRHm/nnSMaD83GMPQR\nczRVlTU/MfD82ozMRi/4uTRp0JbI/AMVGqoV5PQR4+maeQA2I4zSKimkD0jy7kvXO4owYkcRHoH7\n0zV/oaJuW6Z3/QVifNGH6CCzaEbe19I7sWRa34JoBL1CNHBfSPqV9shTUh4R5cjdwMMVdds46fZa\nkr0X4UnYk0jQ8mpaKo9vIb73Q4iG7xXpb1tJI5Kcxjv/P6JMKe1ko8W3n36fysCxu425mbL7HEsX\nnU5JxrxEeGpbGYapwcubnt01mfv3ULr/S7U4ZhxNklARxtNZmTJkBlF+zsico3L7gv4stKcTmR/7\niHG6m6Xn9wIRyrpyB/e9Ni9qB+eeyODxf5WWNs6xLFHeHUCujkr38viq3yoROvlM+iaOJcq8mcS8\nsccShuMTRe8N5dFCzZaqnUS1lsEdPc+hEqxlzl2ov6fXiF6T84hKvFFI30D06Ff2fqRCcwq5VN6Z\n31dLv/8tt33IC76RuhAx7Q/mtjXC8+4nwtNKPSgFz+E1mgy0TYXhDOCS4dQt6fRHYKs2rmVVYMcW\nv29PVMT5wft9hBFf2Fs6XO8c0Sg5lRir80D6eyrw7i7embWIivqZzPU+TngeKnuS0739H9FoatuY\ny8gpnCMrt8/iVEhqkfY9IXNdRUZsy0QrOVn53vqmg/oryluU8O4uktn2f4RHbxrhlfhsp/ey24WY\nMPb5gmttfA+lz2qI9LqBMCy6Dj3PyHyIgUkL7iE37xnhPXq2rnO2qV/XXl76kyVdRIzRK/1OSVlq\nK+zzj1SGzEh//0GFeahycm4mkzWYwaGiGxIdAPu0IbM2LyoR9XIxEQUwg+Jvv/IcaCN5IQy4B8kZ\nTPQn8lqvR3rVWgZ3sjTCXISoDTPbkhjrtR3RaLmF6HEYhLtf3absZQkDbF/Cje5EVqXFKh7/XiLO\n+SUitOpKwp2/LBEm+EWih3E7d/9nO7rVjZktSFSGcxX97u6PFm0fAj0mAFe5+95pfQHCw3iNu29n\nZosQ46oedvetK8rciAirm5/wYjXGLy1DVE5bEg3H97j7rcOlm5kt4+6Tq1xDO5jZ4oTXZDMiZfYU\nItzmN+7+XN3nGymY2bzAx4gkCFumzTPdfZ42ZKxJhBm+QHgupxTs5u7+qS7VbQszezdRDm1IlBlT\niImtT3f369uQM44ox0px9yPb17Q+zGwJIq37Y13KWYQwEN9J/727lQhPfKkGPRchGrBVkwsMCWZ2\nLuFR2CStn0QkediX8OCNIbzG17l7W0kyatLvAMJj/AARFp4vhw8lOii/6O4/byLje8Ap7v7IsCjd\nJmb2MjGP4/5pvY8IkT88s8+fief0rooyZxKdxM8SHt6T3X1CyTHfIELwsgmodiQ6FOcixgM2TXbm\n7mNL5K8EvObuk6pcQ69IyWF2JLzq2brwAnevmuitbp3G0eMyWMaYqJ1U2Dn9GY+avmTuXmhoVDzP\ntkTF9kF3n6+N4z5HGIn5BqERPVNfdveTO9WrW8xsTyLsZu0Wu7m7z8rmaGZ7dXo+dz+jRJ9XDhM4\nlAAAIABJREFUiJ7+b6X1MUQ40B7ufnba9jOiR3uFqudN2c5OIyZGhoHvzH3Ap8oatUOl25yAmT1M\nTAy+/zCdb3ViHqK93H3pisesSPSGr1myq1ctS8xsIeKdW9jdr6lyzJyMmS1MhO7sQWS2nFX2mNmm\nxNiPb7v7f4ZZr7FEiOMP3P35tG0pwrM9hijLf+ruX+9Adi3viJntTWSffLu7TzCztxJG5xKZ3WYQ\nKd//lTmuUYe2y4B6oaKOJxCdkEXnMyIh0IEd6NIRqS67zd1vb7HPekSK9ZZ1V9r3ZeI9aNQRLxHG\n2QGZfb4P7O/ui1TU8QbiuZ7j7q9WOaaJnH8TIesfcfe/dyonyZpJXNe+HR5/ePlehbi7f6eC/DeE\nsdgrlNpeDAVH0VlF0hap8Pq7mb2lzeNOMbNLiZCUbK/2rUQa2p718KXK+zTCJX4N1acFOJ3277ml\nY8oqtFeJMTEN3pOOy3o1XyQmHa5MMrTWSkZZtof8P214FmrVzcz2Ab4M7ODuTxb8vgIRjvIDd/9d\nRR2HhNT7vzgx3uTFDkS8hWIv05Dg7g8AXzWzVlNG5PkJYYidRgzCf5Lq02QMIBl2JxChRHMR70nD\nqBhNZA/7gke6asGs6T6uJRqMtxGhYtlOojuIb243wis4nHyJSKrzrcy2HxJJHiYQ6fwPNrOb3P3c\nKgLrfkfc/XSibG6sP2Zm7yLmgFqNCEX+ubvfkTv0aoahDk06HWhmf6BLL6+ZzUMk3FibMGK/k7bP\nT4TOPuOZKUxacDoxpqypMUaEsR9Fed0FEUqY7Yh7mJgHLcvqxHi+Srj7u6vuW8K6xPi3rgyxxAtU\nn9akiHEdHudEyGYZE4gyvCNjMU+aAmd/opNobWK4SuNb3ZCIxviJu99fx/mGGhljonY8N6dUu5jZ\nJ4lG5s/dvXCOoxT+9Hki1r7tRnEK8Tu6Cx2/TfQIr9yi0T6BmE/l2DZEf5UYTzHa3e9p47h9ynfp\nmAlEoowGOwMP+MB5td5KhxVBquwrh3UNsW57EYPVBz1TAHd/IvW07g0Meu9SiG5HVAnZNbO5iXfk\n02TmkUvhmr8CfthGqMddRIOwK1KP6kKEd6TV9/pdYkLP77YhfmtieoNPd6njckRioWWIiYCXJsJk\nGtyYtn2cmAC+isy5CEOxVShxlWd6OjHX05VePFdd2fEPEw2ibZL35eGKh7q7lz3/QwlDbG93P8PM\njiCSKjUETDWzq4hGeBVdv0XMu7Vai3LzAWKy9x+UiNuATKdLavR/jMgmuS3QCFH+PBEKWKZb7e9I\nESmc7YCSfcZ0Kr8TPOZpGzRXW1XMbHsiAcuy9HfyNRroGxDTxXyCmHKlDhqGchVuYqDxdSnwNTM7\njP5Q0Q8T47bapksv6svEOMk6+BdhTHdKyzDIGujWWJxFqk8uJZ7dc8Swk+ycmRMIo+9/RDutHdmj\nifu4OP2dw2XzunaPj4BBfVq0NBb6U323THue9j0m7dtyzq3cMadRkq2QmJvrtJJ9bgT+UbLPZcSE\nje1c/3QyqZBHwkL0QPela25kzTo8t89/gX++0XUjshueXLLPScCTTX5rOfi31VJBt3mJEMyZhHdo\nItGAmpjWZxKNxMKMgQXydicS7azfxf1/bzrvVyrs+9W075g25L8AHFfDe/ILIhxsbFo/In/PiQRB\nlea4IQyKRgrvbhNuZN+Ze4nwp51J2RArHD+RaHysklvvOtELMdj+0sx60X07CZhcUdcby75FYkxv\ny7kg034vk0mDTYxx6iMz11DS7YlevCNzykJkyJxOJAL5EtFJlb9vD1JxvkBaTKeQ2ed3wP8qyvsI\nkTil8X0sSXjHskkbngHWavO6VyQm8X6NXJINYhqau8vKOiJbbOm7XlGfd6Xn8OlevxNN9PsrJW2m\nNmQd2nhPiIyW4wreub8D/2pD5kbpmeUTbc1M2zceyvsjz5gYUjroZdibqGSreJOOIdzU+xJJQqqw\nN9FYubDFPu8gki20cqe/jQLPSI67id7AdniOCL0bSZxMJJ74ONHreRGZ52Nm6xJp9NuKOU9hLR8G\nNqG5d8G9dWKGunVbnPKeyhdoHvY4lCG6BxE9gRcDB3uE/QFgZqsBPyLCqw4iJjgu43HCI3OdmZ1C\npD2fRIH+3tzD8wnifp1U4XwnElkRP0l1z8K/iFCebnk/Men5lS32eZQIuWuJmX2dGEM1hciEVzWU\nuBnrEEbtNoRBsR8xts7N7HbSfDlEiv9BoVTuPqrVepc0GpyteJkIbavCakQa8VbcTXQUlPEakQCo\nQVGI8hSqh093/Y6kcTEd4cOUkKkIM9uM8LZn6+pbiARDZVELhxGdOhu7+6TkPc3zbyIUvdn5T8tt\n+oiZjSrYdS4ik+F7iMZ9Ke5+PpEko7H+XCaMrREqeoa7P1VFXtK3Li/qIcBNKdLmaE9WQYfskM51\nipl9nvAIFpXn7hXGeA0B44BrzOzT7v6rLmXtQSS9OQrAzIru2wSiPizFzN5GlLGLEmHZVxCJ3ZYj\nojNGA/8ws02y9W6dyBgTQ0LKlncm/QPvG6ELmNl9xCD+mwsO3ZJI/VuaUcvdXzSzK4gGTJ3MR/SG\ntGIBogJqxXQiVKYdLgbGmJl1WTDXhkfo2e5mtl+sDno2k4hKfGJVmWa2PJGYYS36k3YUnp7Injlc\nuk0mGsetWIfIolWkz7iK5+mE3YlU1B/x3NgLd3/IzHYixvXsQTVjbDz9SVMOorUR2Sw5xubE9/pa\n2cnc/VUzu5yY96oqhxIV+K7u/oc2jsuzDBH+1ooZRLhlGZ8hxqG8093/14VOALj7vYRH7CQzM6KH\n9r1p2ZzoHPpK0m/+ZnKGiJeIRmUrVqF6+NFClI/NmUa1cnMiA0OrdiamuXg8s23FNnSr4x2ZSIeJ\nN8i0x4Y6mUIWM/su8E0Gl8MbAPua2bE+cFxeni2A8711YobHiAx6zdg787+nc2/QZF8njJ2vtJDX\nEnefQowv7JQjiO/ife5+ZTJAZxlj7j7DzK6hvKw7gggXP5K417dRnHm6rFMSBo752pDmIYtVx3jV\nTZ3G4iqUG+PPUb0j5jCizPm4u/8p99s4M/so4cX8NtGZWDsyxkTtdNnLMIqIBa7K/USPcjs0rSzN\nbD7CICzL+PM44ZFpxWZEo60dvknE1//CzA5295erHNTGOJE87uXjRho7FiaJcPdnaD8W/EfEoNuz\niTmtuvIu1KjbVcCuZraRuw/ytqbB9x8AzulI0e54G5HZrHAQvLv3pcQ0X6worw4v3orEuIuqVO6t\nTOxIlB9nJYP7Fpqntm9VgT9HjB1sxRqUf/ckOafWYYjlSR0wNwM3p2e5I3Ag0fCrPB1Ajfwb+ICZ\nLVLUQZY8BO+n+nibxwhPeCs2IeqLMs4Afmxm1xFesvUZ3Mhcj6gjqlDHO3IGg7+pVYg6ZQrRWTKJ\nGFu1AeFRvJr4LrKMq6TxYNpqaJvZx4gJih9Jx+Xr6sOAQ8zsNndvVuYtTHkZuyARTtaMxvhXI0II\nf0IkUskzE3i+yEM8zNTlad878/+otBTRslMy0dWYr2HI4Dku83+3xuJ0woPbipVoMqVSAdsA5xUY\nYqGQ+7lmdgHttzUrI2NMDAXd9DLMQ7lXKstMmvfaA4WGyldS1rw8cxEZ5uYjxg+04m/A/mb2cXf/\nY8E5dyU8doVzs7TgT4TH7dOEx+cBmveUZQfNv4nOCtJWXqmhZFsi7GqPOoSljJo7059V6dOZ7asA\nd3i1OYeOA3YBrjazHxHPuZGNawfCgzSTamG0dfMaAwcpF7EQ0XtfSk1ePKPk+yvYv533dFzm/y3p\nn6ssT1kFfh3wITNbtqgH3yLt/vaUhx5DeE9rrzvNbBX6PWJjibLICG/Lr4kOripy6kwudALROXaJ\nmX02J2dtoiNlfmKuqipcBnzBzHZ290Hhj6luGEt5+QtRtm5OfPeW9JzlETaztxNexaoD+Lt+RzzN\nd5g5Zk1iXOfxwJHZTiMzW5TwiOxFTNGSZaiTKTT4IvE+vyt1XDWYCJxmZhcS3vj9ad4B9QSR5KUV\nGxBGViGeyWBsZkcSyWxqyWqcOnG+RsxZ2ex7uJoYf/jrimLr8rSvUvJ7Zdz9qi5FDHUGzzrf6duA\nbc1s3qKojJQFdjuqJwZbiohOaMW9REfskCBjTAwF3fQyPEN7BVSVEJmsodIIyyoyQmYQ2bcuJzK/\nteJYIhzs92b2cQY32j9E9LRWCRfLMibz/0K0DtXoX6l3nMggUsaoLxAF3AqEwTpIp6peNqIBd2NN\nun2KaAzOT39jv5F9bxmiMfRZokHbEne/08w+QaTgPTQts05FhFB9wpvMgZPCZjshb1wXcTvwUTMb\nV+SVsZhj6aNEwpLh4mn654mrwprpmKrUVYH/gBifeJWZfZnoqW+811sSjeU+wmNbxjnA/5nZfN7F\nHEMNzOxUwgBbmXjHJhNl0BXA5e4+sU2RHwTGFzU8YVZG0CuJxAYtjTF3vyw1jo8gGuUzks7PEOM8\nDTikwriiBo1y8xyLiXbz5eZORDbZY8oEpUbYLhYTUbu75zutniaSGjxUUbc635EG3yc6gg4u0P9F\nomNwo7TfTpnfum1YV+UdxHipwjrU3Z8xsz8RBmMzLgX2M7PRRePBzWwHwmiuVBd6/ZPq7g48VfI9\nPE6Mf61qjNXiaa/L4KwDH+IMnjW/078EziIiJgZ4DM1scWIi7iWo1qkDkXWxbHjCWtSUDbIQHwFZ\nVrTMXguRgKJlNkQirfyrBdvPJ8bjLFzhPAsTheJ5behWmqmpDVkbEz3M+Qx6faS5THr9LGq6zsWJ\nhlgf4aXrIxpMr6T/+4iwzQltyLyRmF+lW93el+75rYQBfBKDsyrdDlzUptwViAboJUTv2iVEEpDl\nK7xfnSxVsinukvadQISsrEqMXVyFmNrgoXQvdhnGd+MPxLiiN1fYdyki2cPZPXqP901lU1Hmw1eJ\nicKryFmQyNx5ESlDW5d6NcqPvwGb1iDvWWIi9Fb7HE/FbHRp/7FEJsGnCA/t/9L1b92BfpsSIVxF\n5eYjwCa9eD/qfEdyz+Lokn2+R0zR0ovrfQU4tmSfY4FXWvy+AtFInZr2/WO6Xzum9ZcJg3upJsev\nlJa5cuulS8VrnAycVLLPiYTBVvW+nZvKvWXT+oDMm8S8Za9RkpVZS1fv7mmpzHiVMHpnEiHe09L2\nE9uQdQYxTGLXJr/vnH7/7VBdjzxjYijoppfhHKJRfTwxUL4VPyZi7geFCbZgLG0kmmiFu99sZmsQ\nPdGbEUbLC0QGuIu8yZxLb0C+TTzPTxETcs4kns93iIbVz4hKfbs2ZP4AOMPM1nH3u7vQ7RCigbiV\nR0KXojj02xmY6aoUj/me2u6hdfdW4yK6wt3PMbMNiIyEvyzYxYg08IXhREPktTuTMBJPN7Odmr3z\nFvOjnUYYj1Umaq0ddz8tDar/AvG9vpkYx/Mv4Gfufl9FUXcS4dTLA+83syk0DyWu4im+hviOtgXG\nmtlNhGfsciI1c7vlSO3JhTzGxrQaH1MZd78xjSv+CIPLzfO9QjKYoaLGd6TBfMT4sFYsR3GkwXDw\nEDEm8JteMBbVYmLd99PCu+jhWdqWqLu/lvnpQqJMegjYyZt43+hPerI2Mb6vsV7GgKQnLViM8rFD\nLxKelKrU6kXtMptlVs5yRH3diGCZt2A392pjvIYEi4yje5HLsg2c6W14Ct19XzO7mhhTuz7xrr2T\nSIjyY3f/TRtqHUU8z7PMbH+irHuK+HbHEHkOXqI8YqpjLFl9QtSGmZ1BhAZ8wgsyoJnZzoQBdZa7\nfzL325sIr8k7ifEFRwE3enpRU7axTYlxadsTPSGb+Rz+IptZI4zkPHd/KbNeiru3bByb2f3EvFpj\n0nofMM7708ouTYR3/tLdD6uo75bEOITtiHEpt9CkwvQWE+ea2QuEh22/tH4E4fmcK7PP94EvunuV\nTHkjnlRxf4qozBYjKrNbiV7YphO3pudWRCN0t9l2z97PArmXEs/xdiIU6Qp3fzr99hYiBO8QosK8\nzN3f3/ICi89RSwVeB2Y2kYpjK9y9Usi1mS1ADPbfhugw2pAIr55KJEG6nLivpVN4pO/1CXdvGuKZ\nwhRXqmgsjgjSdTmwnbtPTOtVcHdfs3y3+kmG3TuB0e5+a8HvGxHG+M3uvmVme8Njvo67399GcoW2\nGtpm9g3CM/dX4CAfPF1Gw+g41N1bhhlaTIK+I9HxlTViL/AWE9FbTHruwDfcfXJmvRR3Lxr7nZc/\nAbjT3ZsmDjKzi4AN3L0s9DB7zL7E1CpF9/t1YF93P6uCnGbZLCHuQ1k2y4acFYgMhcsQBsl6hKf5\nVSKKYm5irNWUorLBIoOnE17E56x6Rk/3ihk8zewzxJCCeRl8va8BB7r7KRXPm5W7AGFMT/EOk7tY\nJOc6g/4M4Nl68T7gk+5+UyeyK51/Dm/DiiEg9XreQoQRXk/zXoZ3ecGcDWa2IpH2fE3ig3iF/tjr\nZYmxVEZ8INskL0a7Om5M+fxW7WSlWoTUSPQmmf3a1G9X+nvKFiN67m4Bft3EwG1U1mu3UXmXNrST\n7GnAzz2NezCz14kK4tDMPqcDW7j76hWvr6Ffo7BrqmuJITCVmKS5oVuRMfYLYiLYRavoljlucZqP\nj8Pd/9OOvJGGmc1L9GavS3g5x9Of6W0sMV7uTiLssal3Jt2nC+if5wn6M2M2GipGDBD/sEda6Xb0\nHJIKfCST7ulYIqPdx4hkHpUa2mb2U6KjY3dvnlzo98Q3fUAbOi1I8/IS72KerNSQXweY6u6FXpg0\nrseBLd19Qma9lHYa2XViZtsQ4acziTEuVxNhc8sQCZ52J4zu7d398sxx44lr29PdH8+sl9LKCC/Q\nb15ictwtCePvSfrr6hWSbtcS9WzPPJbdYDGH2Z7EZN5FY9reQ7RRfue5BCwVZK9OF15Ui2yWf6R1\nNsuVgN2aRTxkZJ1CtBm2c/d/ZjtNU5vqVCJb4+bu/nzB8UVtiCqUtiGS/PcS79pLRHmev9YvEW3G\n7bLfwnBjZpsTHSizOjrd/bohP6+MMTEUdNvLkIybbxEegKVyPz8D/Ao4xivMR5aTuyiRinssgxt2\nWaoYKXMDXyUKwGwP+ISk3w9b9Qg2kWnEfds96TeTuN6liEaQE56gPXLH7Z1++0vyjFWeC8Pdf1ui\n07OE1+VrmfXzPTPviZkdS3ifFqxyTjMbR/XGRdNwQTO7G3g647UrMsZuBV5393dV1G00EV6ycYle\ng96P5PEDuMndp2fWS2nlARwKzOw7xFizdX1w8gPMbEnC4/lrd2/ZS5oa058mEqW8g/401n1Eb+wv\nk5x2MqXWXoEnPdektVExrM8hj0VCirGEl+y9xPgTqN7oWYHwUjaM5KLkQs8TnoDHm8nJyNuT8Gyu\n3WK3qobizsT4iwPc/bm0bRViTGYjEcyficZnW+9Ku9gwTdBskSHyFOKdy5Z5RjyHz3pBZsnhwszm\nIeqxfYlJkBs8RIQW/7BVZ8wQ6LMXMNndL6tJ3pqEF30uIgNn/nv4PFHPbuzu99RxzjZ0u5r4vtfz\ngjBOi6RMdwL3uftWJbImAne5+45pPR/BsnCSdaG7f6ng+Ib8G1Pd1fJ8WbxCcg4z+xthtG5U1OGS\nPLG3EKHZ21c5r9WXRbnnyBgTQ0odvQxmthbR+IIYZFuWgrSVrFOIsWjXEBl3ms5v1aqAST2KfyN6\nN51IYNFoJK5IVLTXANu206NokYb350ShdAhwlbvPTI3IrYgwsI2A/d29aqagrrCYiPJed981rV9D\n9Jyu6WmcgcVcP8u5+6rDoVNGt2OArxMDb/+UN8YspjD4FRXCbNL+7yS8uS8RYx72IbIxTiAygo0i\nGo73NIzT3PGdeCiB1h7AJHtDIgTorIZ3yWKMws+JUKKphMeyaH6eInkPE2MbD2yxzwnAB9t5rsmD\nskxanezuZeOXWsmqrQI3s8OIiWIXa7VfFYOnTqw/RLGR1n4DmJXx9UXCm3I5kVnxzooyNyamyViZ\nwQbAROBjXi3kcW+iQT6TSP3eqrysEjJ2KbCiu6+X2XYe8f5eTUzS+nbCQKma2a4j2vk2c1QyPHPn\nWoi4xmxd+B8ihK/Xc2bNIjXYFyMiPArnuLQ2QuDzeElIfJL/OpF8oeNJnQtk7kh4gxdh8PfwIuFF\nvqSu87Wh1xQim2XTuSHN7ERgL3dvWW6Z2XTgp+7+9bQ+gzCkv5nZ51SiTbJyLRfQBmb2HHCuu+en\nccjucyqws7uXTtZsBVmUM/X+ukRW4SEvR+pCCTzEkOIx+LTyANQmMu6lfA6IqnyYqATHepPJcyty\nEBFyeTFwsA+Otf8RkdjjINpLb78v0VjaMtujk3qJr0i9VXcSHsNhMcaIiZB3MTPz6L35I1EIXmIR\naz+GaDCfPEz6ZDkO2BU4O/VALwZgZgcQDdydiPlgTqwo71tEw3OTFAq1DzHO6ajkCf0+ce+bNRQa\nEyk/k1uvg0OIuXKyc9cdQ4TgvEyEyfzYzO5x979XkLc8EebXihn0d4RUIhlfE9o5pgWbAOc0C11z\n94csUm/v3EqImX2dSMgyhUg60tUk40nmfETq9FahrFWSlbxA1MVGJNYYT39q+393Uk55fcmFvkp4\nb0bX5DV4O/DPxkqKgNgR+LO7fyx5af5LlIND3YgqmqB5SEgG1+/TMmJJBlihEZbhdNq/b40pR6p8\nD5NoPUF027j7X81sVWKS5U0Z+D381t2fbXX8EHpR56Y82c5UqrXVX2Rgwo7nibIpyxQi5LkXLEB5\navj/pf1aYmbvI6ItbicyWW4H7Nf43WOKmruIJEGVyxEz+yDRGbYikaQpj2cjgupEnjFRO6nH/Sfu\n3nQiUIuMNQf3wJMyjYjnHuTVaFNOY56pDYoaSxaJSG4jvrH18r+3kPsycIoXzEuT2edHwOfcvWwC\n4FpI3qLPEJNiPpaMknOIgq7BdYQHpeqM93XqtxJRyReFBF5D9HpWGldoZpOICUd3S+t9xGStR6Z1\nI5JlzPIUDhdm9iDhAfpEWp+HqNzuIQziJZNu/3b30skpk7w+IkyxaOLM+QjD39z9bXVdRzuk7/V4\nbzGA3cy+B3zF3ZtW4haTp88PvNML5mjrQK99iY6AZhnYKo3HTLJuIAyUK4DrvYa5y+oi9baf7ilB\nTg3yphGZzg5N69sSEQY7u/t5adtPCE93yyyEZvYtYkzNat58Mt8HgCPc/Qd16N8tKQR1YXd/rMK+\nHXmgKnYA5M+1INFxlU+Qc17ec2dthMAX6NYyJD7J/xXRCVNYt/aCofKipnbEXESYYrN2xH+TnPVL\ndPw38Ki775zW/0GE763h7lMzbZL53b2duSEb70dX40XN7F7gBXffrMU+NwBLeknCHTP7J5GRex2P\nLMpFwxN+B7zbKyQpMrOViak63g7dDV/pFHnGxFAwiijQW7E4EUIz3DxAfwhVN7yNCKUorCzcvS+F\n5DQNP2hCs8x2Wcp+j53MNiG8KY2enqLvvTTkxiNRxecz668DO1lkAnsb4clruwc/GTYfpXwi6ZaT\nIaeKYIyZrU8uk1eVUKwcSzDQqzODSBgzSxkzu4rwxg03SxPhsA02JsJuTnH36cCTFpOpV4q3Jya2\nPpLwuH4LuM77Q2JHE3MBrkr0PPaKR4ixYa0YS8xb1Yq3AqfWZIhtT4S+3kXcox8R8yPeRBjF2xIh\ngpXCnty9rWkXhpnniGxsdfESkE2ksyVR5l2T2TY9t08zPky8s60m870W+D8iK2AtmNmSnsa7Vdx/\nYeI724OUiIVUFpvZpsT39W0fnBDodDozANoyxszs/URZsCQD6xYHjjezfdz94lkbKxhUXXIo4bH6\ntZl9zZunxO+aZBy/ViFUdKi8qL8nslleYGbNslmuQ9yTMi4HPmtm8yTP928Jva9Phtlowtj4XlXl\nrOJ4UarZEucBXzeznwPfynbcWozl/w5hhB9XQdbGxNj5VsnSHqd8WokGPyUSWZ1G3LMn6DJyol1k\njIlesQjlIVJDwUnA981sharekia8RiQOaMVCRGO+He4hDJ1DvWDgaRpf8hGg5dxcKWTvD0S4x0Si\noVhr4ZIMnXaNHWCW1+USovHaCGHJNwQa26vqczsRttANzzBwTNHTMCA5C8Q9rZQm32LOqN8QFceg\nDFZtkq/0Rqdt2bGN/6N6GEpj/OGHiGxifSmuf0niGo0YN9dOmG3d1FWBT6a++u5gYjLfzT2S5fwI\nuM1jTOL301iGX1A9NHYA1mZmVhvCaS2IMOwxmRDlbnkQ2M5izK0Tc9TdkWtwr0R8d2WsRnnY391E\nMqRSzOxEbzF2J+2zOJFQpmVyn8z+ixHZCN9OeCWeYWDD9g4inHo3whOVpcgA2ICYIqKWufpS1MNf\nCI/HWQxOkLMbcK6ZbdFBx1annE10pu0F7GqRmGISg+9FaUcdgEUSoO2IhF/Pp21LEx0mo4HXzewk\ndz+omQxvM8tiG/yY6DzbEdjBzJpls/xxBVm/JkITlyLG1v8udZh+kXhnINoER1dRzAaOF72G7kO7\njyHqmv2APczsv/Rf6zuIDph7035lzEtk2W7F4oTuVdiaGI7w6Yr714+PgJm0tbzxF6ICbSx9ROGx\nUsGyCpGI4gEi808v9PwjYaDsQxRSRXquVCKnkaL4LU1+X4qoQK5uU7/90v37NzGYf+60fS7CA/Av\nooDZr0TOnUSFNrrm+7cQEcryni7lHJ6u80ii8d+Xti1LeJ0mEg2tuUrk7A28tcbrGw9cmln/CzG2\nYOW0/mai1+y/FeW9np7XNKLy37HsmlrIugO4NrN+LfBIbp/fEHPCtSN3d2IqiWeIzoNniAbnbnW+\nOx1e86KEB6ovvc9Xp+/3qvRc+ogG96Ilcn5AGALz1aBTI7toY72Rtazpe1RB5tzEZN4PpvelsTyY\nts/d4ti+tO8aufVWSx8ws4JebyYaSKcQ4XXd3rt90rknEhP8zgS+nNvnPuCSCrKmEQ3hTLTPAAAg\nAElEQVTsVvscA0yrqFsf8LUWvy9MKn/buN7jkty90voR+eMJg/c/FeUNOr7L5/HndB83a/L7pun3\nP9d1zorPocpS6T4QXusHc9vOSDLuJ9L5zySm8BiWa8zpMg8xz9gDuet7IG2fp0v5b0nPcZk2j7sz\nlXVr13iti6Wy5OXctb6cti9RUc7dwPjMetF31QjZryLvOeC4Xjz/WTr08uRaZp8l1wCo2hj4cg/1\nLNPx9RI5uyQZE4iEDqsSA09XIRocD3VSwBPeiLMy+s0gjL4ZGb3/UEHOdOAXNd63FVPF/Vr+/hC9\ni3cDY9qQdwcx0Wn2uRyeWV+VGJB8cMXn+QDhjdgFWKqL6/wG0fhYLK2PTfKfJ7xHT6f1z1SUtxyR\n7fGujK6TiNC2d7Sp22FJxrnA75KsH+X2+RdwzVB+Q8O9UEMFDixI9O5eBKzSpT7TgaMz61OJcVDZ\nfX4IPFdR3ryER2ImYbxPJDJ4TqTfmB8PzNvk+L2BTwKLpPVPVl0q6HYF4bGZSYQY/idtyy+Xt3H/\njiMM6ReISIU3ZX7bjBKjKLPv/WXnJUK3Hq6o17npfu/a4v3po6RMyh33IAM7d4oajScRWUeryKvb\nGHuayObXap8zielDGusPd7g8VJfebV7jBGLcY2N9gfTNXpbWF0nf2hUdyl+LCIXdswZdFyY8Yl13\nfNSgS61tiJzseYiwwC3S37YMTqKTZSaRFXbQd0G0wWYSE4lXkXcRFTqAhnJRmKKoi0ZIhRHhBbcT\nYRl5ZhK9LZd7tYxvdVNL7Le7n2NmGxCN918W7GJET0vLiRoL5Drhwr+YyCi2IeE5mkL09Jzm7mdX\nEDWJ9kMkCzGz5YAbibF2FxJjl7LjXG5M2z5ONBqrsBoxCWUDJ5O9yN0fNrO/Eg3NH7WQsz/hQRxD\nzHH1GcBTJqVGRrqrvPp8dL8kvJKW9LgyDVj/LuHRfYJoKJ7aXETmotyfIhqfx6WQkb0Jz99XgC+n\nAdynA7/38vFMxxMhLTul9duIbI0AWMzX9C6qhXm8YfBI4/+5lCFzTfpTg9/n1bMC3km8X8sD77dI\nKV2UbMa9fMD3JAaGgj5F/3yKDRajyWD3ArrKzOrup+fW6xzTMybz/0JEmFwRlctUj9TbX2/y823E\nvS0NzwQuA75gZjt7wTxdKVR7LNWzzu5BJFI53cwmufv4JGd+orG2BdFh1Ko8ytPoxGrFy5RMtzCE\nLEaEn7XiUQaO4XsTndWhlcY6DwFLE96vBpsSyXxOB/AI7b2YMKgqk+r/XxF1dIMz029bAZcCH3f3\ni6rK9GrZLJvpM454f//lbc5v2oS6x4vOIpXblabpaELdWZQPB64xs13d/Q9d6NUxyqYoasdykw3O\nzpjZZoRnbEMyc6kRRtMNPdTrB0QDbn1vY56zJrJ+QVzjtsk4OYLBmYvOI7Katcz4lNl/CtHrdkha\nf4Hw+O2X2ef7xETSpeOzUjKQDeifq2k00Xh0ogPgZnffvNIFNz/HXF7DRLQpC+IHCO/EDkSI2gx3\nn7/i8eumf+/2TNIUMxtFxN7f7G2Oh6wjW9ZIJo07qVTZuXt+jGBe1l+Jnuut0vrpRMPgfe5+TXo+\n1xFh2KXvnA1RZtbZHTNbkej0W4wwePKT+e5EGNwbeIXshUnm4sRULMsRjbr7CENsWyKb7Lfb1PF/\nwMWe5mBrUnaeQ4w/XLGCvEHHd4OZTSBC+N7XYp/LiBDYlt9FXZjZTKIu2KMmec8R6eu/ktYPA8YR\nQxGeSNtKM7LmZK5BjMOei+hUXAPYwfvnuTLCyL3c3T9Zx3VU0KmR8XEa4cW9kuiQ/I930NA3s18S\nhusGnRw/1FiNWZSTvE2BvxJRO/8h2nJ53N2/04G65fTSLadl9lxIRn6F/Zbs8jzvJIyNnl/zSFuI\nsJp/EfHyK3cp61EyYwYoDrU5AXimDZl3Ab/LrN9EbhwW0fP9WIc6zwscSHgx2hlf8FPg88P0jBYh\nPKuvVtVvCHTYk+ih7Dhkt41z7UQM4F6gjWPmAhYs2L51eueOocuwww6u4wAinG35tL4OMZh8JpFA\npRFO/P6K8hqTdbfa51hgai/ekZG8EI3FRxkcdt5HZOLcpAOZKxOelMeIJEN95MJQ25B1SXonGiGk\n+XCq5QhPSGnoedHxNdy/k9L9+ga5sayEB+zg9PtJw/hMX6BkLGCb8m7J1i1Ex8a9uX3ObKeuIYYS\nTCVSqzerE/9EdJiVydqE6Ex4qFEXdFIGE1ETP6Q/rLjxTTxHjH0+gDbGf1HzeNEkc0XC03850dHR\ndTgrMe7/c8QcofsDG3Wg12JJp1rGKXayKExRDAU/pSSle7tZqZpwMxGSdjcRvnO2t5Fe3czWIjJb\nLezuZ3ahx5CQeteWpXjyQbyFt8JjXpHPEr1jDyfPU7OenrKwrGUIl38rBqSAr8B1wDaZ9fOB71rM\nMXMeER61DW1Mkmpmb6PfMzaW/lTNDxEFbRU+R4QDDgnpmW5LeMU+TITLONX1q1OXvak3W1YZ5xLX\n+qyZnUDM91f0Tmb5IfB5M1umsa+Z7Uo0hhphT582s3d6Re9HDZxCNLSeB3D3u1PGtm8T4bc3E/Ms\nXlZRXu2ZWVOY1NeIht4SFE+i614yrUW3mNkM+ueyeyCtV+lld3cvnEg7t9ON6bv/CIMntz7fO4gK\ncPdHzGwHIlnMdsDJ3iLTXgknEOFql6TyeBZmtjbhVZmfqDN7wXeIe3c0EQp8Df0Z7kYT09RMIsK0\nh4tbiQ6Ouvgt8BMzu5H41tYjEkdlWZ8wDqryXuAv7t4qq/FjQFOPI9Sb9djd/0Z4hzGzJYkOq0Z9\n+BGiviGF4OYng8bMrigQOxX4NLC7xVyNzUK7q2S1HEN0TsxPXONkiq+1NJzVzLYEXnT327yeLMrH\nE22GfxKG+ZNNdBsyFKYoaie5yw/xJhNtWsy78k/gXd5FuIWZ3Ux8uGsSnqAJFQyLwlhv7w8vKIz1\nTi5xgCc85mJaiYq0Mpqa6PcxoqdyXZqn427ZkDKz0UTBvCCtCz68PCzrKWJw8x5pvSjU5kJi4spK\noSypYD6E8EJNTGFyVxJjnhpjDx8ExnqLUAMz24P+CmfFdNxTpKQCSe/K9z9VOOPd/TNVj6kodx3C\nANuD6A03wsD9LXDmMBoSWZ3uTLqMdvd7huF85xLXvR4xP91L7t5yrIyZ3UIkD9ghs+0eYhzIgUSj\n8RjCsPvKUOk+lJjZ1UQZtq4XjBs0s6UI7+X97l4UkpPff0eic2MuwmvU1Mh297G5Yxvyb3L36Zn1\nUtz96gJdriW+593c/fHMehV576l67k4ws8NLdnkPEfr8Mwbq7N5GqFIqL49IMmYQnWvPE0ay0aSu\nbHLv9yHGZI+hSaO16DmU6DeK6GAoMhz+QWTunVBBznxE+d1szki8woTUFvP4XUR4lv9Rtn8FefMQ\n5ezHiXt2EZFY69X0+7pEY/5wd69kdJrZq8Rk9N9I60V14vHA59x9wRZy7iTmQNzR3a/t5Poq6LoE\n8c58kyg3vajdldptnVAor0D+TUQY/aeIMdKdnq8RynqKu3+hUxk5eU8T5evoOuR1gjxjYij4C3CM\nmT3mucGQqdF9KdFj+7VuTuLuGyeZcyd5VRoqaxBJJuYiei3XIMYXNLiacOt/lCi0G0wkKtO1iSxe\njfVSNWnjOzOz/Yle0tcJ71Gnkw8eS1T6e9FlwZf0+JCZLevuk/I/mtnqRIjE76oK9BgcPz6zPtXM\ntiB67xoTSV/k7lNLRJ1J3OMrCO/ole5+b1U9CvgjsJeZLeLVk340xcy+SDyDdxINgSlER8Bv3f36\nbuV3yduILGNDbogBuPtHG/9bJIXZqsJhbyXG8DSOW5UwXI5y99+lbVsS71+pMWZmG9PvLSpqQJQ2\ntFMP8nXuflgF/avwM6J3/CYz+y7RKdHwTowhPG5vAb5UUd44otG/o7efJGk8A8u5xnoVBt3PfOOm\nl42dAsZV3O+I3LoTHqVKuPuRyeD+EuG9e3OScQnRoC/ySEDze280T5TUVn2T9JtIzP22Armxz606\nwgYoZLYvkVRhiWa7JN2qzI+2NNGReKmZnU8kVCqaZ6ySceeRLGJ3M9svVgeV65OI655YQbcGk4ny\nsxVvpzw5SqMMrs0Qs0g4M5r+TsoNCc/bq0QHZWEUhrsXec/rZD0ieqlyO6EFzxBj4+piATL1TC+Q\nMSaGgqHIStUUj8xB11PtYzqCGE+0cQovOoKMMebubmY3ED18WRpZGKfk1uvmK0S64c2r9Ea24B3U\nV/D9gDCSrjKzLxPeNsxsIcIAPp4IRerqeabnWJZ5LM9rxPPcigj1Wt7MLgeu7yREiQjH2Qz4h5l9\ng5inpGxyyVacQNybfxC9s+e5+/Qu5NXJkGXLKsMjy2SVrFWLMjCz3hbEd/e3zLa7iBCTplhMEP2X\ntF+rMJgqDe3NiDC4WvD6M7OuS4xB6iRb7VHEPXgmtz5iSfeuzMAuyjDa8p2pE3e/kjCy2+FqhvHe\nJ8OrrcQ/MMuT9SviOzyaqAfOJ0LuxhBh2X8ijM8qnE5/dMRO9GePzd6Ldoy7OLjJBOoeE44/U/Rb\nC64AdjOzNd19UHijmb2LMIROKpFTZ9bjQ9M53014Jl8nDNnvEwZYp3ViXTxP1Dl1MB7oKiFXjluJ\n6XR6hsIUxZBgNWelqlGvScA/3f0Tab0ovODHwL7uvngP9JsGnOruVXvBm8mZRHjEOh3rkJe3L3Ay\nxR04rxP366w6ztUOycDfgv5ewHcSvYDTifev0RN4s1co7MzsxXT8gvRX/lMZ3CjyshC7JO8QIgzx\nybJ9hxurOVuWma3h7vd3r9kAmROAG9x997T+W2BnYm6xGWnbicAn3L1Zrzxmdgox7cE1xMTYrUL3\nrirR6b/A7e6+Z/tX1FJuLZlZLTL4neHuB9epXx2kULY3A//zgmkJzGxeYCng2UYYWQtZixDjEBtj\nT5sZ2ZXCqOZErIZ06Gb2DyKcc1WPNPEDsimb2aeI6QXGVvEAWUwlUglvYxoHM3sLUXasDSzk7p/O\nbF8FuMPdK3lbzGxNIlHGy4SHdQNibNX6RAflEcTYqPVbhclbvVmPG9kU/0FE11ztkSp/RJDqm43c\nfaMaZK1OTKlzEhEl0ZVBa2bvI6YWee9QhYuW6iBjTAwVZrYyMXnpTCJd6PbEwPa2DASLAdq70l+I\nfiRtX5Eo/K5t1utVIKuWWO+hwszuJ0LtPtelnNOISYW7LvgyMlcHvkB/qM0UwkPws6Lewdyxe3V6\n3iqhKJnzLEr0eG+dlsZA8CnuvmSF42+m+piWvPf0DYWZvZkIQb2KmN+qq4o7NQauJMaf/KXTxl1O\n5tlEY2VXwsC+gEgX/aHMPhcDo9x93WIpszonHiey63UTstsIPT2SMGJHXMp/M/sDkba7655ji7Gx\nL7QqX5NRtESVe2FmRxPzpa3o7s8W/P5m4jkd5+758MD8vicTCXduoNzAHvYEOXnMOk/INFRYDenQ\nzexZ4AJ33zcj8yh3H5fZZzwwzTNjP4eTZBD+lDCQjIyBnsaM/Rf4rLv/ug2Z2wNn0z8HW8NbZ0Si\ni4+2CEFtyFiQ8LJNAg5090faua6crEeIsG6SvEZHZFvjpocKi7Gv/yKyJH+9m4iT1L55G9ERO5l4\nfkWhrO7un6ogby8i+ueDRNKwWyhOeNZWe6QtfIjSNGrR4u4Q4XJT6DA9LjE56GsUpBYFVk9yK6ci\nJwa0n5tZL0pJ+3diQtlWcmYCh5XscyhtpgVPxzxKSoXcxX1fmkgQcRJhwPb6Pcinnq6ydJRKljAU\ndyFCviZ3Kmd2X4hGQCMN8kvp/ysKlssryrsy85wnE4k1Vu1Sx/UIz2TjnZgBbPr/7J13uFxV1cZ/\ni96E0PlAISAiSJGOICV0EKUJitJCB0ERkV4SCE1AmoCAAqFIh4Sa0EIglNBBmtSE3kOvIVnfH+8+\nmXPnnjpzZu4NzPs857l3zuzZZ5++11rvelfs++nC8+XcnH6+AE6o6Lj1RcXPX0Vy0SshOfT565eC\n/R0OrJ7TZjXkNCrS3wLh+B8KxcqMZPRV9DlXtHTEo6juVlab64CHC/T1Zrhmpyyy7Z5agC3R5C5N\ntryy8hENjK1pOXTkJDk69vlz6koBhG2M66F9XDfs06OotMYZ9dcrEvC4voG++yAhoUvRvOFKVA6g\ncNke5FB+P4zxfZqQe0dqrrui3OdJ7z40FzgrXItz9MR5CONbOOzjJ+GeaOh9Q74EfSkp+thx6vJb\nKpiPFF06OWMdNA3LV6V6AIXx36lr656RLG9mmyG+812ohsRmyKsa/fh5M3sUeTT+WXC4VXG9jezc\nk3i7MjgOUe1uM7P9kYeyESGJy9ADb3ckSPEc6dL2ubK0FWCHVnUcy12LqIpLUjs/HxGiKRm/3w6I\nJHJbNb4/IJnsNKUx9zol0DZEE/vF/p8R3aOJ3RXc5poherobEi05ANgv5PCdjbznpYpmu/sTpmKc\nEXXpcnd/MNZkGXRPX5rT1fOoREMVeImaB/zUjHZFxRQGhiVLBS+iPh1ZoL8BKH/nCGBHM3uMdEnq\nPK9x0edcUSyIzlcWnkMe7zz0QbUKmy7EHiEIyxxK7V6dJqGZe8GSABUKMrUE3qQcesBbSGAmwptI\nZCeOWUgpKJ+GCmmFB4QxreHuH5vZMglt/otyrUrB3T9Ez4Cs50AqrLvq8eck32+F7kF3fxGVcjkn\n9L8UOpdrIXbBLsioSIzOthJmtjhy2EV08qTzAMXeN1UXIG/Z/KQoOsZYB1VgYMF2ZVWp9kEKRxu4\nZJaTpHefooCKYgzHIu/QXYEvPy9MelBEE55PkCevWcyKvIaF4ZLNPwN52EaEsaU0zZwQ9Iv9PyPN\nPfiahpfg9peBqS7OiuhZZigCcjs1aftHPJ+WNhhdw5UbYyF38m5El/wYUVo+QpO86UOzN0hO4h5M\n+fNTOLHdW6Ce5e7PA381s4PRRGpX5JleB3jbzM4F/u0l6Dju/gTw15Tv7kNOmjycARxnZvN5QYW4\nDLRKvCcLU6NJVBH0j/3fNyxJcJSj1izmQUWvi2Bq5GXOwkRq90YWXkAMgEpgUhN8ABntTyGnycso\norUQesY8Rgp9KQVVCTK1HO4+DuXgXWXd5dDnyfjpU3Q1vkYBW5nZau4+KtAAfxPaFUISrRDlZIHO\nz33o2VKEVrg8ErTJSmV4jex9rB/f2l6A+mpmR3g23bZK1eMkTBX6nyb8NZJrDrYDJyHWyuFIzOqN\nRh0pZd4fBftryfykDDrGWAdVoFWqVEsj8YMsg+YNSni83f1ZM/s18qSfHlYbmohHXO/NPYFjbd3r\nvvRNWAfyAM6PVCXLFJLEzDZBL8QpgTE0WHywFRPtKmFmfYJXMa/dcu7+cEaTlVAib2R83edNJvNW\njEORIbYTMq4mIPXJQWjsp6OJ7PoJv+1xb12jcCWjXwpcGqJlu6L9ORg40MxuRrmGwzO6qRLDkHf4\nHjM7AlFkEq+/pHu/7vv+lY8uH8tSXPGtKa9xQkR26ZQobfSc2wblBBfBGPJLGqyBqNp5+CcwyMz+\nz6XO2SwORxPy9d39tpD7dL67Hxnyk/+FDNsyTIL5kCBTrzbErEE59IBhqKjyvC6houORw3OkmY0D\nZkPv1qI1vNZFkZ3/Iufo+ojhAYC7P2lmT6HIXRFjbBrynQV9yHcSxHF1MDZTr/vgkDqU7k7oOKpU\nPcZUuic6h/2o1bJzZAznnctWYmWUS9zOAuKTDTrGWAdNw3PUx5rAlChfLAtzFGjTBe4+3MwWRNSn\nejGK84OHMAkjqXnEPfw+TfnJkIe3rKLZQERVaFkRyF6C64N3MfXcBYrFzegcp2FWb056vtXYGKla\nnQ+1KKeLqD7azH6BJrKHAF3qVvUGb11FmBN512egFr38BbChmd0LbBVFq1pIzRxLjVr476xuaMN7\n0VSrLI7+pkLo9ZgSJeUvQD4VE6jEazyYrs+5TcJSjyhk/zmiRBbBdcABZvYXdz+pW4dmf0WRjCLM\nhGuR4XZ3YDlkGdhF1EzXB4a7+20Jv3/NzLZExbePoHjNt1dJKYDcG2DVyKGfjZgcHwC4SsasjQyR\nHwIPIeGumwsOq2pa4VggT8hqJco5Tj8DbjKzld39tfovzWwfZHzek9PPp1Qk925mryKmT3RfvoRK\nxYxAIh7dCson9HFq+M2o8I6qEl9TrpZbKsK9uAdS0e12b4co94VIp+CaKrbZanSMsQ56M15ExlIi\ngjrVKkDporUNcr2jmjuGvKgjkRJdPaJE3Du8fAHiHyNZ6m+zIQY6bxcj+ko3mNlPkORyJre9lxti\noIl0vHj4RGKTM3d/x8yGIT5/VUWESyN4/tPy2XD3rHympP5mRtSb3VBk0JCz40zgClRsfX8UVTmT\n2mR/MK2hZvYEtTAL/WL/O+l0wonoWXI5BYpaV4QoImvAeahm1LUJ7aLn3H1FotwBJ6JzfoKZ/QaJ\nHryOrr31kSH2Goqu5OFVas/jwRntihrY86BrM8IEYnRJd//UJOO+CcWNsQuA3ayiIvItwCCalEMP\nTIS369aNBn7Z4JiqphVeC+xvZlu6+5X1X5rZDkhE45ASY/wFevcPM7NV3X0SddXM9kC11h4kVsM0\nBTeRHykuiimREmAkgtGIguKeSLTlfTO7DhgC3FrAIC+CkSiloArsDPRJc7K4++tmNktoV8gYazS3\nuyp0jLEOKkfwim0NHJritZgXeY0u9FAQOgVXAQPMbHd3Pyvh+z8Di1I++tQQvKtU7/bAUHc/reLN\nvEfJSN9kigOBv5nZKe7+5/gXgdZ2G8p1a5cUch+TjHdhFHzZfU7XXJ+P6D6JeBs9/AuhwsR2zGw9\nRJtcNKdpoeT7ILaxGzKyZ0Ae5H8DZ7r747GmTyJhGegadWkJNbNKamGQVc7DRJQj+AxSaXurbjyT\naMRWV5epwnH+Cj2Ho+tk4bB+MSTh/J+k/Ll4RDb2nKtEztndx4UI4KVoYrYiNYMKlLP1e0+QvU/A\nJVRrYH9MV8GOD+h+X35EV7GKPFQlyNQqvIocRushg+T2ILhTWA69KOW8BKqmFR6PnF2XmtkWSEwE\nM9sLqZRujgR+/lF0gO7+eEh3uAm41szWc/evzWxnRD1/HNFd8wzbAxF1+gyalHt393kb/W0M8yL6\n52bIabID8JmZ3YQMs5uauH73B+43swOBvzUZeVsS1QXLwoPoOZeLJnO7K0GnzlgHlcPMhgKLunvq\nBM/MngGedvdfZ7SZEb2cF0VelamRytYg9BDthxKqVy7ruTHVvFgM+D7pdV9aU08iA6YaZxugIpC9\nKfepcpjZacgTt7+7/z2sWxCpys0BbOzut7ZhHFGtnTJwL6CoFpTs/ufuW4XPo5Ax9uMoWdvM7gH+\nz90XKtBfZfVyTEWG7wLeRY6PPyJv77Po/loM0coedfdcGlrY10jJ8hmU03NB1ss7vJiP6e05jnHU\nXS9J6jpet348ckydkNLf9ugYVyIgExgDg9FkCkQLnT52ncyDIguHuPvfcvo6HxW4PrmKsdX1vSJi\nPvRB9MLR7v5A1dspMZ4HgVeid1KIgi0GLOLun5vZFOh9M527L1Ki37UQja9PRrOiz5P5UcR5mdDf\nR4ieeXGj9FQz+yFd84zmRNfwS9RyjO5w98ScRTP7Aj0nLkA0z2br+D0NvOPu/cLnpFqgj6JyAIVq\nPYbjdiHJYl+jkAOgtLCPmW2D9vsq4EYUSX4WlarIdSgEunIflDv2OVIS7UnV4/jYvoeMmc1QtGgm\najmEQ4DrilAfY/2dh5yFqyO6YpoYjnuOyquZfQmc6O6HZrQ5Cviru09XYGwnIqXueG73QBJyuz1b\nw6BxeA/VG+gs394FJV+fl9PmX8DLBfqaAz3o6mtATETc5sL1PEJ/0yFltS+ouL5VRcduRuBeRA3q\n29PnssX7auEcfgP8FhnGY9AD/5dtHMdE5AUfU2Yp2PepKP8hcnztFbY3HBmiV4Zr7vQCfVVaLwfR\ndz4G5o0dh8Nj5+ZIlNOweMH+vkZ0ujVKHPuFUH5kj1+PJca8IKK+vIMESVZH9OLVEdXpnXBdr4Ck\npF8J522TNo1vz3Au/42iAAMTrpM7ESUtr68vgWN7+pi36bgdh/J3pg6ftwnH8THgBKTgNwEYVKLP\nTZAxPhHR7qPCyt2WAn3tQu29Vf8u/BLYraLjsBSixF6PjOQJwPiM9s9Qq8v0ZjhWSzax/WNDX1uG\nzwPi1y+K1kwADmxw33YL9+2ewHIVHK8DY/v/HDBPid9WXS9rCuRUG40MnW9i3y2DKOGLNLCP0yLD\n7HzkvJsYruu7UJ21Bdq5r8iZdHlOm8uBtwru33PAyLqxHh77PBdisBS+98suHZpiB63AXCikm4W3\nKSBL7PLGbRESMruIbXhjnsATUOLnM+hmbbjuS6DT7Y2oNrOSTOVyL8cxfgJF6lYCfmVmH5LuPWoJ\ndzlBXKAo3Et479zdzez3yNM2GNWr+T4SdMijIFSNk71imljABYjq8H1ECToLqfptiqhBoCTvVA9f\nDFUntq+MvJvxe3UKmCQwcriZbYgEC7Yo0N8P3P3t/GY1uHtU1DQTZjYDohPFIwKPAEO8BLXHVEcw\nLycgT+59UxQ5XNq7etOfRSUzLkQG8yh3P8WkHPk0MsSTcq+isc2F8mXSniV4sWj9TihCuku4x5Ki\nvs+TrOBZj7FUKB/fy3EucsrMAbzp7heb2XJocrtUaHMZcHSJPgdSgSBToP6fhcqunIDygt4E/g89\nT/4EnGFmL3gByfUclJJDd/fFwn3VHznV9gX+EiLlFyDJ9qJKoNACWmFsrP+lgRImORT2S9AcYDVk\nKE4Tb+8ZdE+vkBFgZtMgZct+yKnwCYpmRRgD7IiMqSyFx25w96+QcX59iBCvgSJmmyCa+0lm9pi7\nZwmlVFkb7B5gYzNb1BPy8gMVexO65mtnocdzuzvGWAetwEfo4s7CDyhem4Yw6dNAfl0AACAASURB\nVLm6mUEF/AY9jFfwJmiAZrYyymuaHhlzb5Ns1JUtmDpF6Cf+AG+4CGSD6Jeyvp5+Vb++NOfZ3b8K\nuS33AD8Ctnf3Ks5zr4C7P4KM/+jzN8DmYZK3MJrsPujFqD1VJ7bPQtfr7GsUmY3jHuD3RTora4gV\nhUlx8gJqEtmTNgmcbGY75BnvddS96Fqt7ytan2eM7Qpc6Sm0Jnd/1cyuDO1OcfdXzOwGFNlMGtvU\naKK9HemT3sL141CU7uxgUKfhHYrlPl0C7G5ms7r7BwXa58LMpkLiDnlOrN0K9rcM+QZ2bl+uGnl/\nq1u3j5kdgyK4Yxu4xqsSZNoPTa6XcxX2jfAskpC/ANEV96OkdLlVIIfuKsT+oJn9GUXtt0d0+1OQ\nWMswYLC7D80bj7t/YGZroGt9y9hXUX52RCtsp3jTWPLfb0b3wu1tUWcN2A+VGRqIcvIPJ2Y4uPuH\nZnYXuldKGWNxhHdVFNH9k5ktjwzkTXN+V2VtsBPDNu82syMR0yQSAtoQ7feUFK8XW3lud1l0jLEO\nWoEHgE3NbB6vS1yHSQIem5Ij+2pmHwNHe0Zeg5nth/IxZik4thmROlCz+VjHohf/7oiS2VB0rR7u\n3rfR31pFsrT13rrgcbsCWAJxqEeiKNY86OF/CBJkSFRGDH3kRdscUeZ2DknQseG0lyvfDrhqp2XV\nT0tC1Ynt76CJV/xzfbR1aooV4I1Uyf4MbOjpcsM3ASd4wbo6ZrYsogROCfyH7hGB36EitT/37Hp0\newHbogneaQS5bXRd90NUo5tQkds89CW/8O+HdPUEj6WrlzqOQcij/iLax1dpMFof8A2iY2dhPkRB\nzcOxyAlwh5kdihwHDRvdIV/tVmoKm2lwRCfL6isqU9CffAO7kGGXOBDlxRTOjalDVYJMKwJX1Bli\nk+DuLwYHQGoOdhKsAjn0unGMD7+/2iQotDW67zZGBnihOWeIJvUzlTdZma6MmLLPTWCSoM3SpOeJ\nZ0XFe5saaxK2Bu6JGB4pEfExFBS1KAp3fwg9Tw/OamdmLwHD3H3PCrb5oJn9AVH1Tw5LHBOAPdz9\n/oJdRkI2EZ4GVjezKWKO0lXRvKc1aBX/sbN8dxdEv5qIqAQbA9OG9dOi0PEL6GbZIKefLrzdlDaH\nUCK/CxUIvriCffwMRSl6/HjHxvRNOK7voEnKRsA0FfQ7CEVc+qR8PxvySh2Zcy4bWVqeu1fkOmui\n7+lRYdzE8xDuifmRKEBeX0/Tldc+oP74IHrcgwXHdjtwS+zzFcj7vkj4PA96+TxSsL870GQpq809\nwG0ljt/VKE/mZynfrxS+vzqnn4eAZ9LOOaI/fgXsUGBMrwIP5bR5GHgt9vksJEqQ1PYV4H9IZKOK\na+6+cK1EeYr1OTfThX24tUBfXfJoM5ZvCo7tP6Gvy4F1UOToh0lLgb6i3LiLkbEyERnYqyLa78co\nspfbV0Lf30eT1siQ+H6D5+JkRImfuslz+gUSuslqcwzwRcl+3wAuQs6A+au4/mJ9G4oGXxzurZ7K\nw14AsWGScu3a+q5JGV8leV7hGjkh9jnp/XAs8GUP7ecneddwA30uhuiqD6C8rweQs22xkv1Ultvd\n6NKJjHVQOdz9FjMbhELFQwA3sw+o0R8MJUIOr2Bzs6AHfVGcCAw2s0Xc/bkmtvs1XSlelSBEkAZ7\nRm5IUHDa0d3XqvuqVbK0W6PJblpB1XFmdlXY5uEpbSrhxrcrn61CHI6iRfORXNxzRjQRP5GUYxdD\n1fVyhgNHmdlsrkLnpyLqx6NB0exHwPeQJHERLIausyw8hq7PolgNUQJHJ33p7veHay8v/2lRRHWM\nY9L7z90fDVTCP6Ak9Sxcjeg5FwMHeywnJOSKHIs88PGcluWQcyoJcyHp/0LlCArgIqT+dbKZ/SX+\nhZlNCZyEnhUHFuhrFNVGBNYH7nb331bQV3/gOXffBogKqo9zUQLvNrPhSAzpZhR1zIWZLYCKGHej\nlAZ1xd3dfWyJMR6KHAZXmtmfS/42jpdRJDgLa1LyneTVyKF3gZktimiK21CLur1A9/sv7ffTIwrt\nW56gkmxm0wJzI+dGEWW70xCr4zwU4Wo4Tzw2hu2At714Ieu0fqrM8/qSbMVOkOOvyjIEZfAU3ZkX\nTcHdn0GGbLOoMre7MfSEhdxZvhtLuIivR5Gar8Pf64B1M36zbGyZGG6KZROWFRAl41Xg8ZLj+hPi\n/w5A3s/Vk5acPm6kgGe5gWNWSTQQTaJ/jzw6H4d+v0C1OXYC5iwxpi+JedxS2pxISa9sE8cn0auZ\ns76nvJ6PkaNuGO6J3OgTcmaMQROJy5ExNQF58S5H6lb/QzWlioxtZjRR/F5s3WaIcvoF8ujvWvI6\nOTqnzdGU8MwiR0vTfSJK3jGxz59Q5+VEanqfFDxuD1NTFBuLIu5jqSnnPQLMHNr/HzIKdk/p7zng\n3xVec1OGa2Mimnj+L1wnV6EI90QkfNIT98NnqMZQFX19ApwR+zyRuug8org+ULC/edD7ZCKi6w1G\nhvVgZMxNDMevjFreS6HPKIL4flhXv7yY00+kMHgmdQyFcD2eGr4vpXyJDJSNc9r8knx15FmRI+N+\nas/cD4FzgFVKjunY8PxJVEpGTIzP6891znUyrOLr+Bsk+tRsP4eEY3U4ipANpHs06xZyGAeh3R3I\naJ8mfK6PiM+CaLPXVXksSuzr78N5W6ontt/gmJdDojQrAVO0dFs9vbOdpbPEF/LpMEky9DuW3MYA\nNDnL7Dunj5+iicW2Ldj/PGPsKOCrEn02JUuLvJrPkU21ex54oQeul2lQGYAXkDd2gTCeBZDn/HkU\nrWmKJtTE+D4E/p7T5kTk0S/S3/woZy/J8LwTmK8n9jOM7WVyJvnhXLxeos8x5Dg9UORjTE6bZ1HN\ns+jz48B9dW2uprgU8rQo8v9C3Tl4AU2scmmnsb4ORkbTLBWei6nQxO69uvGNQ+qYU/XQNfIAcGlF\nfVVmYIe2Z4RjtB8wZd13UwJ/Dd8XpiohA31MkSWnn5lRZGEiorLdhRwwd4ZnzERETZ255DFs2vlH\njUo8ARkpN6NczsL3QF1/lTmwQttxwPEVX8evAadW0M/TKMc7+pxELTwbeKNAX78L5/PKcL1M6gtF\nzIaEc/SLKo9FiX1dPZy3T9A777dIlbGUI7yFY1u6J45LtHRoih30NpxELfH6Lyj/4d6EdpGXcYSX\nSOg1s4PQQ+p99DJ7g8YoC5ugJOfBQXDiYZLD/+7ug0r2nUgLCgnr8wO/QN7WYp01L0t7AZrAjTCz\ng1GS8IRAeVoVRSYWokGFJjP7PulKaLh7vUJVHIchgYElvCuN8mV0bq5D5QIOI58G2ApMTVeVpiQ4\n+YILatiCxPYKcSewlZktlzSWIH/9S5SbVhQ3ITW/A1F0dpI4SbiW90G5R2fl9PMA8nJGGAbsZ2aH\noehJP3Q/FCqpEO6pQcCgUBx1ZuBjb4wGfBxy7txmZvsDD3u2YmaR8X0DDDSzI4BFqF0n/4sfwx7A\n34Hz0iSpS+INuqqbjUGsiTgWRt74ItgI5VB2K84djtmJZrYOuob3KtKhNyHIVNfPx2a2CpJ93xo9\ndyN8jup2HtjsdZOCackWBdqM4OwALvIGiifXoS/5ipDP0fUYZOEeRFOsEsOBNesEHhrBgohlk4Vx\nKBqYCXe/1MzWRU7IjVGZBszsIWBxdB7PcPebmhhvMxhJ17ldFv05sbRHC3EHMnr/0ObtTkKUrNZB\nB5Uj5E9sR/faQBd5AZlTM3sXUVqKypMWGdMY9GJZzt3zFNGy+in6AHZ3z3ywhL6iG7GIRLwhj3DT\n/OW4LK27/ySlzdTI27ZxGFvkYZ8NUSsMeby28BKqkma2HjIGF81ql3X8gkLT9e6+d0abU4FfuftC\nRcdWFczsCUTfXDGjzYPATO6+WPtG1mX7cyLK72KI4rhzbP2CwBNeIJ/JzJZAQhkT0KS7Xm74L+gl\nu6Kr3k+Rsc2DHB3zoHyYUSjReh40GeuLREaWd/c3M/rZFNGffuHuY8xstjDWvtQmCOOAVSswEkrB\nzKKJbt697+7eIw5UM/s/JH2eJR+f63QKBsXeiMJ+EulOLNw9yQkX7+ti4KfuvmT4/DcUvTqUmoF9\nOqKobVxgbF+iKHZqzqWZHQ3s6+6FnCetQHge/xjRzj4CnvUG1YHDu2dA2rkL+Vk3Awu5+/wpbVby\n4qp1Rcb0Gcqh3C+jzQnAnu4+Q4H+lkHPjZ3d/bKKxjg3EtwYCezn5eqoxfv5ALjK3XcJnwegSOWU\nsTb/AdZ290IlS8ysP7rHlqKmkvkUcJK7n9/IOKuAmQ2kYP6pux/R2tF0hZm9jYTd9m3ndruMoWOM\nddAKmNkuKHF2GrpLGH8N7O3uZ+f0sS/wiieIFTQxri+Af7r7X3IbZ/ezRtG27n5nTl8jqT2kVkeT\nzrEJTaNo4O0ox6QZj1xpmAo074CM62gi8AhwvrtfWrKvnyGqzbsol+WPKLLyLBJtWAwZeI9mPZjD\nBOofOS/uE9GLu5BEe5UIk7cDgYPc/fiE7w9EkcXj3b2IrHrV49sJ3afTEYyBaCIQjKvHUd7YuQX7\n2wJ5yOsnq4aoTNu7+1Ulx9iXFFEFJJO+u7uPKdNn6HcWYBeUVD4W1YNKNehahbr7PxPuvmbJvlej\n6/36qLuPKtnHEegajhuCccOxy3WT01fkeMp1OhVwYm2O6oKtFwzs2ZFxF0lUGzL0VnX3pwuM7W1E\nid0mo81FYXtz5/XXWxEcWBH6omOUZBBPiYQ0pgXO8gokyYugFQ4sM1sJRaCeQO+sJEdsYRZLEJKa\nDVgSzWfGIqdQ/TXtniEcZWZ3IFbJj9z963pjLDyjXgTuLeJQqOt7epTL95G3tybbZAczuxypia7c\nY2PoGGMdVA0zWxslnX6CJnoj6Fob6E9IMWh9d0+lI5jZeMTL/muFY3sKuN/dd6yqzyoRJisDPdQK\n+bbCzK5F6l+Luvsb8f0OdMwjUCRlJXd/KqOfKGdnCU9X3noSPesWbsW+ZMHMZkVy8z8If2+hFi1a\nH6nuvQIs6xUV1S0xtnVR9Oq/iGK6PjJs4l7Z/wIvu3vh2jSmemI7o6TnPmiiNxo5ELrVHyvZb71h\n0Swl6lsJM/s5EmeIrvm48fM8yrPNjDyFfrZG6owjUE7V1UjQ4hYUedoJRc3PznM6hf6OorjheVh+\nq279z4pqikUG9uCi14iZXY2oimslHZswob8TuNHdy9bzmhaJTmXRsYsU9G4aZjaW2jmYHwk8JRlj\nceffUe5elO7Z7PgqdWAFg+Ya9L7JQiGHQuizEmaMmf0OlXu4Gt1L+xCMMTPrg/K8N0bMjrbTC83s\nRyjKllegvVKVxHYj7Of96Bl3ZKOR5qbG0DHGOqgaJknhnyEqYDdJYTP7IfJgjnb3DTL6eRm4oUqP\nnJnthSaeS3pCQeqehkla+cNmKJSTA8zsHZSfEclSR0poA2NtHkSGwBYZ/RyGDLd7kRBCUj7byoiK\nc1Sr9icLIbJzCbonoGtx2nuBbbxxyetmxnUbooj+xJWTkkSRuRhYeXJ/2X6XYGbLIVrWdMh4GEnX\nIu2royjlau7+SE5fd6MJ+0Lu/k29s8jM1kcRh83c/frW7FF7YCowfi+acF6G8kgiSmw/agIJeQXG\n6/vdEeV6zZrWhLpJu7WphEdvdP5V7cAys/NQHtVtyLGQmidexKFQNWLjG4/yvOZE+x3P86pCvr3s\nuFZGx2x6dLzeJv24LZi0PqXfqRHleTEU3RwU1k+Hcm/fy2P9mFJgPvSMHElTLu+sHis9ktE2clz9\nHO3n46RHOtMKgzcH70H1kM7y7VxQ7sU5OW3+RY6CHKrT8z8qKFwc63MBRIt7CT0Al0STjW5LTx/H\nunHPjhKl16dO6avN45gBvRSbOmZIsjyuhNZNPh8VcE0slBtrMzVSU4xUOMejh+l4amqbQ+kh9bi6\nsS6LEoQPDn+X7eHxfIjoR9HnJCWv44DP2jyu7ZiM5I8r2N/+wA8q7G84ok79KuX7TcL9kSv3jSKQ\n8WtkInBEXZsbgbt64Lh9hfKPq+zzlygaVK/qOxEpU2bKwCf0t0H47RMo6jERRWkOpFZ+4HJE343/\nri0lPJCY0wLtPncFxtUXGcZJ+3030LdEX++g2nY9vl8ZY+yPDLD4fj5BgSL0CefzhrDP0Tuw0QLt\nI5HxtWtV789wP7yedL0iZ+UE4HcF+pkAHJbTJrcEUKxt2v3W7T5r1TXQUVPsoBWYHr24svBuaJeF\nw5FH8nIz28eriR6MoRaZyMqDcci+P0JS+6HIQJoP5cd168dLJN2b2R7owbyhqxBv5OkeTk1R6SEz\nW8vbyAM3s22BA5A3Kw25xyyGd+jqKX6H7gUhpybnGnHRCTaty2ebjSby2VoFVxQiMxLRZkyDyjNk\noQ/ZSmqJCBSbLEpW1nEYjGTZJ4l8mNn2aMKaV/h2csR5gIdcntsRJXCENygKAKwCXOMpkSp3v9bM\nhpBfKBt0D74f+/wFoonG8SSweyMDbRJfIInxyuDuNwSv+ybIeTKJEgsMbeCZuy86fqu4+ydm9nfg\nMXc/Djgu5GyeRdcC4bj7FPHPpuLAVyBVwEF0j3Yegs7Db8oMznsgElQE4V2/SohW/owY3Tnn2ZGE\n6UlWZO41cPfBSP234TwvM9sIOR6nRJHDZ2muuPUKSFzknCb6mASTWNhQNDfcB1Effxd97+6jTQJr\nmwF572yjuxZBMygc2WsVOsZYB63Ayyg3LAtrogdGFu5ED9KNgY3NbBzpoeOfFhzbhQm/L42Qv/IA\nMDdSKpoW7fdXKCF3KlQvpSzd8Ldof8bF1p2AHtDnh+1thCY/f29iFwojqDOdhyblo5CsfjMPeZA0\ncdz4Gg1saGaLuPtzJhW9X6P8lly4+yWICthBcYylq9x7ElZCL/VCMLNV0XW5fE7TstLFfZHXt0dg\nZsu4+6Mt6n5PRNvph7zQuyDj7ClqxtmdXlw2P6p3loXnkaJhHqJc3wivIJW2OOalxPMg5IRuSs2J\nlabOmGcsPka2c6ghhElwVc+TZYFr687dJEPL3c8Njq5DkOJoGlpawiNMlPPygsqWaGkaFTmwHkXv\n5EphKq2xJyo1ECnRThW+Wwbdx6e4+3MZfZyH1GpPBnCp1uYq16ZgIIqGbeTutzTYRxxfkz9HK4PD\nUBmG5d39rUCLr8eDdC9P0SjmId/ZCIAXUPduNTrGWAetwBBgfzM7Ezg4/vIws5mRZ29FxKPPwrzI\ncIobJoXkXdPg7v2b+X0Mh6OxrO/utwXu/fkuAYrvIxpmXzTJKoMfEas7YmZzoEnov919t7DuflTN\nvi3GGJKL/gCpkj1TUZ/DgaPMbLZgeJ6KJPYfNbOn0XH4HrB/RdvrUVhF0uAV41p0n27pCYqlZrYD\nmninSn3XtV8W5Rh8gqJbO6A6gWNQtKYvqhtW1TXUTjwchA+GIO/u3R74Lc3C3f8J/DMYKUuj62Rt\nlPO4JEqgn2BmD7n7KgW6fAjVLcvCT5EzKQ+P0rVG0whg12BARPLxW6BaTrkIEZ4b0P5FoiJxD3ch\npcWA44FrA0ug0RyrVmNGZNBG+BLlxcTxEJAnKLU1cHWdITYJ7j7OzK4CtqGEMRbex5G4RVakwdF7\ne3LEIOAGM1vV3e+uosNwHQ9D1/849MybKdZkDDqn75Jdf/P3qLxLFVgCuKwiQwwUTVymor5A+VhD\nPTtX/1XkbO4GM9uubtXSCetAzoT50b3wRCMD7Ql0jLEOWoFjUTRrd2BrM3ucWiL0T9HL6H+hXSrc\nfY4Wj7MZrA8Md/fb6r9w99fMbEtEGzkCqUcWxeyIshfh5+HvkNi6UYjKmIogYDGt1ylgmdlaiILz\nOcrrKyIJvjBSJatyEn02krYfD+Du94RjNgi9VMYC+3sJhTEzm4F0zy5eIJG3FbCC0uC0f7JzPLAV\ncKlJkn4WmCRysxoyjp+njkKVgYNR9HRFl9T4DsDNwUExFco/ixTDJjccgKI5fw7LuyZF0CHA7V6B\n+lYw7h4Ny4lhwrcHcBAwF4pSFsGhwEgz2yMYel1gZvFIXB5uAM40swXDs+I4FL0fHBbQPVy05uH+\nqEj3scgB8xZwJPDvMJ5jUE5Q/wJ99UET4puDEuKDJDMnosh5T+AtJMgQ4U1UIyyOWciPFM+LIhVZ\nGE/XKGYRnIBYLKMQ86Ip1kOIjHepK1qVAdQE/g9dxyPM7BIkHpbIWCnxvtkPGbADgaOQATxJ/dPd\nPzSzu9A8IcsYG4vu7SrwKV0d183iYOBeM9vW3S+qoL+ZyE9fmYFY5LgOg6nd247mMZsktIucCp+j\n+ddkgY4x1kHlcCmzrYIme1sjD2+Ez1HU6EDPUMKZDDAP4vBHmEAsv8ndPzWzW9HDoowxNg6IG6Fr\nINpRnPPudK/jVI8TgT3MbG4PyoxmthWS0Y0eVjub2bLu/mqBMX1VcPyFEM79/XXrhtDV6CyEFuSz\nVQaTNPhhFJAGr2BbE9BE6jLgWM8pXuzuH5jq5V0IbBn76rTwdxTw+xK5C6sC19UZ+Ba29Y2Z7Ycm\n4oOQEdhSmIp9Xw2MajaK5e4nACcE+uymyFDtjyT8PzGzm1CEYVgzuZxmtjC1yNiaKP/RUK2hxDIg\nZpYUCRkBnG5mf0bn8W1EcV4VRZ2HI5piZrHeKJcl9vlVM1sB5UJF8vFnuntRD/RvUUmCQ8LYASa6\n+2vAxWZ2H6If7kl+xOBiapG034Sl/jxHjo6eMsaeoqvxNQrYysxWc/dRplp+vwntsvAasImZHeLp\nJTw2QeIIZbAJogGu6U3UrQx5zRdR29dJziYzexbYzt0farT/JjGY2nWyXVjSrpOixtjWSLk3UhVN\ner6MAfJKglwC7G5ms3rzpU1uR8rBDSHjOTLYzHYmvUB7UVbH60ghMgtLI3G1JOwQDRWlTQxF7I56\nRCUZ7kuLJPdGdIyxDlqCYADsFrzsP6aWCP1sFV7kZhEmFHk5C1kSph/TVbDjg9BXHB/R1StaBM8A\nvzKzQ9BDZSvgwTrDtS/yuGZhdeAO7yqRPwA9TPdGxuSxqJZXXqTiBqCfmVlV1CyAYAj8HHl9QZLD\nd7v7XSX66E/1+WxVYg80kdogGCQAY939MuCyIKRwI/kJy0VgSHBhWxSRvtZz6iGFaGE/M1sKvchn\nR9ftaC8h3x0wK5qARBiPaFrRttzM7qSYIVbFdbYnsBfwfsipGYKK+uZFGNIHJYrNWcBZpvpFv0IJ\n5xuj/frSVDJgCDJM30/tLCAY7JEB9n10Ht9EBtPtSMwjK6o7MOO7H4WlHhsiZbPS0dhgbO9V9ncB\nC9FVOMnRNRv1/aKZ3YgoXnnG2C4NjqGdGAacYmbzumrsHY8cHyNDDnRkbOeV3bgAeflHmFlaCY+F\nyI7CJGEWpEjZjCG2MLpOZ0ZRzfq6oqsCt5rZiu5eKAe4YuyQ36Q0FiSWTpCC6Pxm4ViUC3iHmR2K\n3vVvNzimA4AHQj9HN/CuHpjx3WphSUJRVscwZHgm0kXNbENEZz8ucSPuF8Tabo8oj22pzdcOdIyx\nDiqHxWpABMPryYQ2ZWpATIFyV7LU2a4pODZDnrJtyM9ZyDLGXkZ1UCI8DqxlZjO4++dhzOtRXu3r\nVOTxeQ0ZFTPQPW/qZ+Tne/yAWDTNzBZCRvGR7n5xWLc6mpDlGWMHoZyQs8xsX3f/tNiuJCMYYf+k\nqxcVap7U/wF7FDTKWpHPViWWBC5197iBOImS5O43m9nNiPbSVJ0md58iXN9Loqjb6iV++19i6oUN\n4j26Ku29Q3eVqimIGWgZGGhmA+tXhuhfEty7q5bOi6JYm6H7fQfgsxDFGgLc5MVFMZI2+BGKzlxs\nqpGzQdjWRkgifYKpTtc17p5F9bwIXfsj0ETkjryoZh3yitn2JnyD2BERPqW7w2os+REF3D1LDbe3\n4GwU+f4AwN2fNrO1Ea3zhyhf7BR3vzmnn+OQ2M7GqP7ZxJgxNwV6hl5HykQ2A8+jiGkzOAzl9/42\nIfd0YKBAX4b2efsmt1Ua8Ul8hfgSUTGzMD/JkaT6fkDn71qYFC2uR9LzrR4DUIT1CGBHM3ssZftp\njuZWP0eORQ6rW8zsH8ipHKlAro6cZ28CJ+V15O6T0zOvEDrGWAetwBjkZcnylvwJ5QpkcuXN7LdI\nqCKNCx8ZTkXV2fZCkYMLER3rIVTP6go0gT0QiQwclNPP7SiRfepgcF4Q+rw30BNXRSH5YwqOCwB3\nv87MdkeqagD/iYwnADPrh7jXeS/vmVH0LsLP0XEaHlv3FMUewFeiCdTOwO/N7HnSH/KZgiVm9msU\nBZoKPXjvQNEskAHZD9ENbzOzrQoY2a3IZ6sSbZUGD97QyLA6Lad51XierqplDwLrmtkC7v6ymc2O\n6H3dCsEnoKxscbf27v4OcA5wTnD+RFGsXyBq2Fdmdju1KNa7JbcZ39aXyIkyNEQr1gzb2gQ9X7KM\nsa9RlH0NdG/PG8Z1b5EonrdBnjw4l+ZDkbupk9oUdJ68HvqI8By1YugRfkowXiZ3hHfD23XrRiNj\nvWw/rSjhcQaS2J/P3ctSHCOsAwxJMMQAcPerQn7lOg323xvxGLCemU2TQhudBTFv8iT1R1ENCwC6\n5ln2DUsSEh3NrX6OuPvrZrYemmvtF/vqOmpU7M298ZIekzU6xlgHrUAlNSCC2MQliEM8EHl8hqEE\n94jidjWquVIU2yOqZP+wDVAUbzQwOkQpRgO3ooTmNJyLJgxzAG+6+8WBN/9HatLPlyH6SCm46nok\n1vZw95F0rc+VhjfpGpVYBxkCcerZTBSj9PWL/T8j4nUnDi+rEzObFxmt36Dj9G93n1DXZgr0ojgF\nuNDMRgd6Txoqz2erGJVLgzeKlJyAIiiaEzAcGGBms4So0T+QMfJY8NIujmiQA3M2lpbA3TBCBOwS\n4JKQX7MeMgx/iYyzs0K+0tWI/tKw1HG4pm8Ly55mtmLOT/qgZ1lEVTwQvw1tZgAAIABJREFUJc9/\naWb3IsfP7cBDVdKEiyLk+v2VrrmsSSjiELuHrg6ga4EjzexsauqM65FC2zVJgQ919+sKbCsXwUi4\nGrjBu5YT6ZXw6kt4DENUwntMQkNpeUFZAkhzIEGuLPyPkgZo1TCzOVG5lEiGfufY+gWRxHxRWflz\nUP71f0y14uLb6YPmDrMiSnMq3L1fmX3IQaW1skxKhY8F1kRamyWAZYvSBd39ETP7MWIPdKHFoxIQ\nhd6DppqMBTfp9fVLeye8F1Qf7yzfrgUJThye0+YfwMc5bYahyfasSf2i3KevgBVKjO1T4Iy6sR5Z\n1+ZqxN1uZN/nRKpnc/fwObg07OsvkSH2GfL+x9vcADzZxjEdH473ZgXabhra/i2n3TmIImo9ebwz\nxncV8EDs8xkol2pbZNhuhIzk20r2uyoyaA9DUeZVC/xmYoPLhIJjmg0ZE31i67ZBtLOJKAL6l54+\nJ3VjngIZB6ch6vFElH/4cA+OaWZkxJ6KpJknhGVcD4xlYDgm76LczEGIDtVtKdjfWsjR1Td8nhGx\nE6LjPhF5yL+fcQ0fXrduAPBNg/v3Qejza2Tw7gnM19PXZRvPb/y4T8hYUo8votRfk7Odq4HXU76b\nv9GlxH7uhN6Bk/Y19t0SYf1OJY/deaGvr1AO94RwLX8R1v+jp89vBddG3jzukKLvh4rHNhYxsOqX\n6H6eGK7LMT19HIsunchYB5XAWlMDYgVkQMQpK/GCmaea2W+QrGxujkEMcVGLz+ieZFu0IGo3uKhO\nDdOd4gh0pzlIz5PLyrc7Bk3oIrWhicSidCHHZTVkLLQLGwD3u1QTM+HuQ0311DZEiclpqDSfrQWo\nVBq8SdWylvLsXZGF2+vWRTlVU3pdFLQ3wCVccEdY/mQqfrs5cgb01Jg+Drlm0yKF1rmQk6ee3toO\n7ISYCct5VzGghuCqBzYi9vkzM1sZHfOF0STr2gbu40aZGHMiAzESYfkHcJqZPYQidUPdvUzR84k0\nRjtzz88JagUupHma3AhEX9/KJUzUBYGavgmKJCVhbINjKKSQa2brIqfdf5Hhvj4xWri7P2kqsL4p\nXcVlsjfuvqNJvn5vxHYwVLD4KeAkd89i1nxbMCUFz52Z/QG4xCtQOHT3vhnbWRg512ZE57oQzOxH\n6FzmFT9vSaStY4x1UBUGU30NiJnoKtX7FUoUjmM0xWrSRHidrqqHL6HE6Dh+RMHK7a2AmS2JJu1r\nkmKIkfMicvcnzGwlagnTl7v7g7Emy6CXaBUqfkWxAKonVBT3kq+YVlk+WyvgFUqDN6ta5i3OCTCz\n04BnPKG2VW80xJIQDNmHEE2wbTCzGVESe0RVXJIa3fsj5FRJlLZvMWYHzqrCEINJVOXxHsvPc+VD\nXV5F/2XhokXdEpY9TCVZNkMT82OBY4KgUGSY5SmM3kV1OUBdYCocfyg1FeBpEpqVMuo80PWbxJEE\nY8tUw+4OanVF+6Hn0iekK0ZWYRBm4YAwnjWCoyOpkPF/aUAWPnq+m9n0aAL/kTdQ2iKc27XJVnfu\njUW3F6F4fufpwN/N7HqUrjDMm1DxTIO7v2Bmm6Nc7AHk5/8THEK3IefXNyjPM4ky2XT6TRo6xlgH\nVaEVNSDepmuewpt0l2meiZSE8hQ8QFfjaxiwn5kdRi1nYRMU0Wg7zGwxakm/t6KI3+PoWCyLjscd\nKPcoE2GC/9eU7+5Dk46y4/s+2aqWWUn8U5NfuDSO8eTnofSL/d9wPls74Y1Lg/dq1TJgN/LlyDuo\ng5mNQt7YqdDz8wuCpH34+0grJi0F8QLFclSL4lU0+W6F3HjTcPd70fN3v5AP82tkmB0CHGxmrxEM\nM+AuD5yp2O/7tWJcZjYfenfNjSIv0yJa7VdINGcqJCpRidFcBmHyuw46rz+nJhYVTVyfBbZPchCF\n3/dv8RCXBy7z7LqmryHjsRTMbCb0Hl2GUL7HzB5Bhnuh6G7I1TuQrvPxSYyH2P8tN8ZCTmYcm5pZ\n34SmEcNpNfIl/iMchN5LW6D76h0z+w9woWfkpTUCd/8yCKn9jgLGGHK8TIsipud5wdy1StHTPMnO\n8u1bkLGwXQX9DEcyz9Hni1EUZNnweWGUU3Z/iT43RbW8FgyfZ0PRsTh3/j1g0R46dv9BcrdLhs+T\neNvI2DgXGaU/aPO41kOTgKy8gkzuOMoFuaHENq8HXuyJ81DhcftJhX29DlyV0yY1N6MN+/o88K+e\nPuaT24IcFKMQU2B1YOqeHlNsbLsj2vU8FfX3Pjl5oDm/T8sZa2neClKm+0s4T9+E593bbTwPZ4dt\nrlN/HJA65bDwXpu1iW0sigyLbZvoYxXkaDok/P15u45Rxpg+B/6edb0goY3MHPaEfrcM13M0b5iU\nYxvWb1Ggj63Db24Lx34icmZvFcY0Hgm2rNGmY1W/H5m5xMhxsVDJbSyPomTvxfp5BOU+z1HhvvwD\n+LJg28+Qwd5j12knMtZB5fCEGhBmtjGiUhlwpxerCzYMONHM5nYVQjwReVUeMLNXkQrd1JSoreLu\nQ5FXM/o8LtAWdqFGG7vQ3d8s2mfF6IcMljhtzWBSfsVuiFIxiBg9MyU/rxA8RwnJzH6GIoXvoofo\nH4E7kcdzNaROdR1SuczCXYhKuKjn1FEKEcL1Sc8zmFzwpJk9iGgZl3lzim29XbXscmA7M/ueN1G/\n6zuIWb0BalMcZrYZov18mdu4BNz9LDNbBKntHYkmTYnRFy9QMxK4H0URmkFfU43ESZ8BzGw1UmhE\nXqKQfMrvx6L6RyeZ2VzIqVc4r7ACGtr6wHB3vy3hh6+Z2ZaIlnUEmtQWhpktjejj8fNyUfhuDfQe\n/q27J9ZBDOfiY3d/zGuRxUpgZoui98tM7n5Rg92MpXsqQj1WQu+zouNaF1H8J6KI4Egk4jEPSi/4\nPXCpmX2YdM5i2ANF5TZw92+CuvNYV+7dZWY2BEWe2pVOECkyGnJSn4KEhOoxAfigkeeWByq4me2D\nmD/bo3zyU4ATzGyYuzeVs2tmcyDj9tW8tgFfU4Bt1FL0pCXYWb49C7qp7iLBg4NyZuJelgnA1QX6\nnA4ZSNPF1q2JHnyvIi/l5j297xUfx6+AY2Ofv6bOk4wU+d6oW5enhpW0FFLKQ3TTj4F5Y9uKvLKG\ncgY+BRbP6We58NsXyIgYoZfvC2GMy/f0OWnyfA5D3s0JKOJ5JTKWpmygr6ZUy9qwr9MhD+9o5FSY\nsaePf4v2cwQ5kX8kUDSijWOaGO7Bq8O2+1TY9/aIgdCQ2l5dXyuFZ1z/JvYz9VnWzNhaeG6OCPuc\nNt7c53B4dhwf+zw+/p4I6/4FvFxybIugHNtPkLF5Q3ws4fn+GnBBRh8TUN5rlcdsaZS72Y11gcra\nfA78qmBfx4Y+tgyfB9T1t0P4/sAS4xuFoinLpny/fBjjXTn9fIRyMuPX9xF1bW7M66dF1+0AYPU2\nbWsORK//Ku9eCO0PT1mORGUFoufV/gW3fyNwa7uPcXzpRMY6qAobo5ym++MrzeyXwHbowXUyeujv\nirjIv/OMQpUuL++Ldesi5bOGYGYTUIRi6wZ+O4W3PndjHMqDi/Ae4mbH8TXdldVamYOxMlK1jNf7\nmgImFRk+3Mw2RJOOLdI6cfeHzewEVPDxETO7BuXExIs+r4M8WtMgakmaMmA3NJnP1hK4+4ZmNg+S\nst8eceU3B94LfPkL3P3xgt01q1rWaryDrosZCGITZvY53fP13N17QhmwKvQjv7bhAmjSWBghAr0z\nilD0QRO1h1FB37xow2+pFbTeDBhvZnei/KZrvcFIv5ntjChy36B9foPmauKtja7jc03F7R9EEYWk\na+TYhN+3TCCjFTCzrVGu5wjkRLsaOSdvQdfRTshBc3ZOVx/TVbDjA7oKUYGulzlLDnFA6Hd5d3/a\nzAYgBVtAJyHU31sho4/3UJ5jJQiR2JEoL+lUZDBuGGtyF3pPboGo7Hk4HtH+Lg15tbOE7eyFmB2b\nI4p1VmH2eiyDRLEeSfrS3R8ysyvIeB8GTI0ojRG+oPu7/Uli6o9xhOjS1V4sKl0W/ZGSa8vem6ZQ\n4Lro3bgJOh5FxJ4G5nz/MXCUux9fcCgHA/ea2bbeeAS2KXSMsQ6qworAKO9Ok9kRvTx3cPerAMzs\nImRkbU171fxAxmCjD653zOw6YAhwi7u3otjwiwTaTcDDwLpmNpe7vxNU1zZBNTUmwd0vaMFYIsxC\n12P2Ncpfi+MeRM3IhLsfYGafIS/YVmgSGYehh/Eg8h+4+oHZesjQXzSnaZGitJXD3d8CTkAUjGXR\nS24r4M/A3mb2BDDY3U/J6apZ1bJW4zl66UTZzOZHxd1Tk/jN7HuIMljFxCZS5So6vqNQonk9zW5p\nYEcz+5u7pyo8ugRdrjSzqZHBszlykK0DnB6oslFB6xdK7MdfkZG9ikt4plnEr80Vw5IERxGNritb\nJJDRQlRFQ3sZOasiPA6sZWYzuPvnZjYFyut9reT41kbR9qcz2ryKJsxpGIlyxapCFQbiJLj7B4Fu\neSHK84pwWvg7Cvi9l6PcfYWevVl4I7TLQqSGG+EVJJMfx7ykP0v+jlI5Hqem+PlkzjaLYg5aJAgT\n0hC2R1H8/0PPvefROSpSQDqtTMtE5Kj4n5cT4dgEOUwGBwdUWvFz91apWvZkWK6zfHsWpPZ3YsL6\n95Dnx+rWX0EP0KnQBPbaBn97I/JcTUCT3iuRWs/MFY7vcEQ3mjF83gg9YF4P23spbP/PbTxmrwL/\njH1+hTq6HPL6flKizwVQJO02JAzyFIqmHEEQVynYz8+Qcfg68qJGdaPOCn1ORDmCA9p9reWMeyr0\nArg6jL8ozWsFlKiflGT9DLBiT+9bb1zCcTosp02hAqbhWCf2hSYVC6DcqhcKjm3L0OcY5Lzqi6K7\nfcPnMWH8vym5z4YM9L8jJ090vTwR7rOlC/TxBRUWr6Um3Z+79PQ1U9H+VkJDQ3nR4wjiLmgSOxEp\nKJ4A3BfO7aCS4/sKOC72OUnc4mTg84w+fhTGNogKxGdQpPTinDGdhJwrZfteCqm+HowKfC/X4BiH\nAiNz2twJDMlpcxXwQOzzGYiCui1yeG4U7sHbUn6/PKop+nTs/n4uXC8/a/I8jEbRv6ruhdnCMX+A\n2nvrQ1QDbpWqttPg2LKESrqIlrRqDJ3IWAdVYVbqZMuDN3o24HoPV3wMY5DnlrrfNCJx6u7+04Jt\n/wZcb2bruvutJTeyUZCy3QhRgTZEtLOvzWwkNUrQ22X6rcO/UCLx9MBn7n5joCIMCNv6POzDaeld\nVI7nUO5ehNHAhma2iLs/F2h4v0aerUJw95fRPjWLg1A+xQru/oaZ/REpcB4ZKBBHIBW0QyrYVpWY\nAVFA5kKGWaGIkqtW3GKhHtKyBDll4FF3v6dFY01FEI55zCuWJm4Boppdjf24ezHfgWY2MGd7xxTs\n/o/ImbWCu78XWz8WOC9E459EE5krio45PHPvDsu+ZvZTagWtDwMONbOX0YRx35RuXqdc6ZC8MfVE\nrbSeRFM0tBjORR7/OYA33f1iUwH4P1KLpFwGHF1yfG8jVeIsLE62EMJBaB8OBnYKUZo06ulOBcY0\nK/kRPiO5zlomwnOqimfVAcB9ZnYcMoAnRdUCe2UAsAT5EcMbgDPNbEFX5Pk4xBYZTK0+5XjEJOkG\nj9VFNLMfUyvFsD8qz/AWYvIMQcZjmXqPpwH/NrOlKnq+v0ntXXcb2r8hXrHoUINIi7S1DR1jrIOq\n8AmS2I0jUjBKU9lLugmXaGDbZahRcyHJ/GFmNpT0nAU8QWXQVTvkcuByM5sG0Tc2QwIm66EH62hq\nlIGXSu2Icjsur1t3qpmdjl7E7yQYtphZqe107T63ovxw4Cgzm82lBngqmtQ9amZPI8/o99ALoN2o\nJJ+tHQjG4fqInrExErxwFBEcXKYvr0i1zMxmQ9GXFdEkKInK6Z5eMHswopP2dmOsCOYhvdh7PFdp\ndRQdHpvQLpK1vp3iBc5/ihRc30v60t3fM7MrUe5tw3DlJj4ODDCzH6J7eDNgb1SEPAkXAjt3FDIb\nRrM0NABcNbr+VrduHzM7BtUZG9ugE3AE8Dsz+7G7d1MTNBWoXxtFbNLQP/b/PKTX63KUI5eHKgzE\nSQjvxlPcPdWBGWjf+7r7Qinf19ffAj3z9gN2NdUWexvVgYucZHehd2LqPnsoGh37/Go45vtSU3c+\n07uqK6f19SxyAB0T8qc3Q/f4bogu+6GZ3YDmJjcXMIJeQ0bTPWZ2NtlzpSJ5ZWPQvl7k7q8XaJ8L\nM5sS+DHp765CY3P3O6sYTzPoGGMdVIUngI3MbCavFTvcDN24dye0X5BkzvWSCev+gDyH9S+xRjCY\nWkHKzcMCXR8wUZHFTO6yu3+NKCY3hon26mifN0Ey/CeEfKDIMGt4who8Wlkv2ykoZ5RGKBItOBu9\nWMaHsdwTpJQHIeN5LFItKsL1rhqV5bO1Cma2ODLAtkYTlYgffwGahJfN86hqXIuifI85yb4OemUe\nWB6se7mHpRPWQa2A6TboOdYNHstVClGy8939yIqGOhWKeGfhcyp8X7v7i9TyGLOK3R6Dnru3mdkB\nwMNljTIzG4FyIi+MrZsZKT72rJx06/EoXR2MI9DkfVv0XuiHnESZUe1w3b7t7jfH17v7u6jkSKM4\nFtFk7wqR3nnD9hZH77MByNF6YkYfC2Z81wiqMBDj6IsEcbLQB9GL09A/57drJaxfAx3DIgboJIQI\n2V5lfpPQx2tIkOQfZjY7cv5ths71NsAXZnazu/86o5uR1OZKfyH7PZCbj+3ueTndpWBmhwH70D3S\nXI8eyRUvC0twsnfQQWmY2S5o0v4ommQugrwxbwHzx8PjwXB5Hbgv52EQtR+ApNSbvqnMbPuibb0J\nUQxT7bKIMvATdZc8flOdlrFFJyaBbvTTHjJ+ehVM9eZucPc9wudXgIfcffNYmzOQFPn3emB8DyMR\nBkN0wivQxPS+Ar89vMHNuhdIMg5e0l8gasw5wKslaSyRYTKwQsOkMiRQC1Obhr+fo1IZt+T0uwCq\nsZMqBlIGgZo9JSr03k2tNYgzPI7OaxUOqTJji66HyEGVBnf3RGMx6Rqp8pnem2Fm/YEzUdmPMWb2\nA/SOnDXWbDzQz91HZ/TzDcrd26cFY9wACYjMHK2iNgn/EBUvHlH1djPG82OUc/kpirovjVRGl6Jm\nIE4HLFXknVnkGRXohnu7+/Qp32cZapkIlPxegUChjBRXf+HuqUZqMM6L0uePqGSABWFm+6P31keo\n9M6rpESX2z22RtGJjHVQFc5FUab1qU0+x6MHXP0Eb20UIcgqhtgSNGNgldzOo+ile6hJqjeriOEd\niEYXn6wcgKJNsye03xQJfXznjTFakM9WMZYGbkUR2aEl+fEDG9ymo6hlHlYDbvQMlb7JHFG5BwPO\nQ0n31ya0i6iF97l7koJWPe5ABUobpj3V4RIUgbrWzP4SKGlRPz9EEayf0DN5j6OYTCOjeWgxtTtq\nOJhqaGhvEejXVcPdh5vZgih6/zNgdjTJHY0iwJmF6oPTaGQWHcxUkHvNIk4bd3/WVKbjUuD0qAtE\nC4wMxM2zDLGQrx5Hn4R1UIuK/xqJY6WNqRKDKmUMhVBFFDnktsWVV7PaDmxmW+G6cOAMdx9XwrlY\nxJm4C3LoLxuiw03DVJj9UDSHnY/knMRUp1Oz6BhjHVQCd59oZhshdcFV0OTmGnd/LKH5HCjv6Lo2\nDrHH4O7PoVonaUiiiE1HPrWig96dzwbwg7p8tjJodVKxIRWuZpE20UlFO+hpccdLiIgPrSia3Jfm\naU9xnARsgISBNjSzN6iVLJgPTcLvDu3aCp/8pOTLIInaPQ21HK8JSA14DmpUpzepE6oqiwZpaMOB\nNa1FtS6DE+LUsJTFwLBk5eZEEa1CEfRmDURk5MbP7d5hSUNExWs1xtKYc8OpeL7u7uOr7C8BA9G4\nL0dqmwML/q6IM/EHwL8qNMTmQyqPcyMV5mlROYmvUE7mVEi5tCVS/9AxxjqoEOEl8R9yis56qLHS\nlkHVIShQbQScnZTwHCIpuyJRiCRDslcilgszxN0/ScmNSUT9BLUdHuMK0Zvz2WjCEGtHUvHDKPm5\nWeRNdOpR+cQid4Pu7VbL+h4FJ+3u/rWZrYtqeu2IIiaRGNKLKKp3YhsmT98puHvf+OeQx3YbmoQd\nBNzt7hOCSMBqKL9qClS7rd04BBki55rZfp4i9lIWgYZ6mbtvXUV/GZgaSYMXRpMG4oXUqJbboaha\n0vt8kuBOHj25IkTjmqxgZqvStRj9I+6epAUQR/TMfaXucxV4m2rfIYcj59f67n5bPC84iKH8Cznh\n0oSsmkbHGOvgu4Z9Ue2dNM/L2yjhdmGaVC9rMwajh/xolHAdfc5CmlBJK8VAKkXI27m/bl0k5dtB\nNo4Ebjazfu4+sol+Pia5QOa3BlXTnuoRDK1jgWNN5TNmAT7ymhhSBxkwsxnIVlQrEok9Gk02l3CJ\nM0W/nQCMNLM1kcDL0cCfmh50OVyKJsHbAVuZ2VjS5ePLTBg/oasAUquwLIoytgXu3j/6Pzgmh/SG\nvNb4uCYHBOf1RdScdpNyR83sWZSL/VDSb+udiRU7F68ANjOzad09r7B2EawPDHf3bqkz7v5acPA+\nidJJWnLvd4yxDr5rWBnVoUo0Ntzdg/rX6u0dVtPYET0kI4XKHTLaZqLeY9xB74KZ9UVFQZchVmcM\nFUodU6KrH6AcqlvM7FIUKUs0qnIiiyf3holOHsxsDSRFHcn4J+XgpOUEjKVNtKdggH3bjLB6Jcul\nAYKqYKITp0g0O/z+AGCxjGZFI7GbAZfGDbG68XxpZtcCW9F+Y6xf7P9p0eQ4Kapd1on2KMpHLIXw\njoyjv5n1S2g6JXrOLIAMyrbD3VuSa/dth5ktjEp0zIxo0iOolWpYCzm1bzWzFeN5rm3CAERfvcrM\n/lTyvZeEeehaw3ECqvUK6JlsZrcipeyOMdbBtx+mAqf1WCTjO9AEapOCm5iH/IKSb9C1NkyvR0gU\nj39ui1BJB+2Fme2LPPNT03USuykSiznI3YvmFg2mRuXZNiz1k7lCZR56O0I+61A0OXwFFVbPrO1U\nh95Ke8pESNJflBq96JkeojtuEpY4jOz6epnXXFAqPA8d81FkKKoVxOzkF7ieOrRrK1poUPwNuN7M\n1nX3W0v8rl/sf0cUrr4J7Sai++FyJEPeQQxmNidyJDzqCSUjAnV2aeDpqqipJXAYolv/1t2vrPtu\noJltgdJNDkW5fe3Ek+henBf4hZl9RLIjsWjqxMd0Fez4AOXrxvERKgPTEnSMsQ56G37ZwHdlvIGf\nk39DzYkSN9uJXssjN7Ot3T0zDzC0O8/dd2zxWCanfLZKYWa/Q8p6HyAlv5GIqjQP4uP/CdWNet3d\nL0/rJ4aGo6eTIQaivMKNGjGSqqQ9teMaDpO445GBPV3sqy/N7CLgQC+mHFkFWuUY+iu6F1Z192cq\n6O9FYAszG+Du3RL1zWxWVBOs0fPXGzEXEgcZZmZDyS7se2Hs/0nGYW8ubzEZ4FBUwyzN+TsBuB4V\nkE8rzN4qrIOec/WGGADuflWIFCfmUJYoLZLQda5i4RTI8RKn2CZF2IumTryMIrgRHgfWMrMZ3P3z\nUF5kPfId+Q2jU2esg16F4MEuDXe/sWD/tyNhhx8m5WOESczzyBPVlqT/Rh9a3qYaPWb2JbChu9+R\n0eYsYJdWjynkSjT00HL3qouTthVm9hAqsLqsJ0gtB/Wxh4EX3X2FNo1pspiImdkXSKigxw3QlGu4\nkIpfkWs4PMPuARZHOUGPUqMXLY1oR08Dq3hFtdJ6AuG5NNjdd6+ov72Qk+N5FH2+C+UQz40K+B6C\nxFX+6O5nVrHNnkbs3VM/aY1fn0Z2ncztgcfc/fHWjPLbi6D4+7S7b5HR5kpgMXdfIq1NaHcd8E+U\n+9T0xN7MvgJOcPdDM9ocDfzV3adN+G4kjb+r2yq4FOrM7QrM7e7jzWwbFJn/LypNsyqitx/j7oe1\nYgydyFgHvQpFjaomcA7irt9qZru5+3+jL0zFlM9Gk6BzsjopKOU9Efi44ISnrPhF7kOuyRyZOF4E\nhpjZqu7+ZMJ2TkYPsmtyR90kJod8NjM7FbgaGFXFSzGGnwAXJBliIMns8OLetsJtflvwKZJX7nG0\nQcXvIGSI/RM4JB4BM7NZgKOAPUO7g5ramZ7FOCpkMLj76Wb2I+CPwPkJTQwVXu4xQ8zMtkIFkKN8\n0Y+RA+Zcl0pxWTTtnMiixIdo4teu+lYddMcPUOQrCy+hqEwefomUol81s3+ha+KtJsb2Lvn5hIuS\nIszik1dZjHNRlH0O4E13vziIl/wRFRsHUTKPbtUAOpGxDr5zMLPBKO/DkefzdcQPnhu9cC/MUz0q\nGc16CxkqR7SL952QI5NVoT7TCxUMz/uQcfkzd3899t1xqIbXjcBm7t5Mzsa3Amb2DbqO3ke19IYA\nt6YJA5To923gPHdPnUCH89Hf3edpZlvfNpjZZcD87r5KA789D93rB7v72+FzEbi771Sg/38gNa8l\nkq4RM5sOqfgNc/fc5PGgcvZ+1r6a2T3AnO6+SMJ3jyNnwtC4s6q3wczOAVYClq7S6WFmKyNBpLhA\nziMoCndvVdspOSZDnvrfo2dLffTUaY9EfdLY1kJ18o519w/CurlQceFV0XvnDHdPFbRpoQOrV8PM\nPkZGU2o+XXB27uLuM+X0tSywOxKYmQnRsq9HZXzK5ANG/UXX2zZJhr6pMPflwH/cvd05Y21ByOlb\nCBjrCaWQKt3Wd+i676CDSTCzXZHXY/HY6ieB09z93wV+PxgpRK2BEkcfo0ZpWRolzI8EPgOWRHLX\nLwMrekWFCnPG9yDat02rEBIIUcM7kVH3c3f/2MyOQEm+twG/bNbYaHBcvSafLbatuZCgxmYol2tq\ndB3chAyzm5KStQv0exGwuLsvm/K9IS/5k+5eqCyDmc0I/AEZA/OP8vKKAAAgAElEQVQhpbZ6fBvy\n7RZART3/ARxdZsIXc7ws5u7Phc9FkErtquv/NaTit19GmxOBrdz9+2ltYm2/BE5y94Mz2hwD7OPu\n0yd89xQSFXCkInkNyh3pEUMkDWY2O6Jj3gnsm0Q7/7bAzHYHzkT39wHAnbHo6RrAccBywJ7uflab\nxzYUORIWjq27ENgGeAEZBnMDv3P3K1L6qNSBZS0qjl01wnt6RndPjECFZ/pTKLq4dME+ZwK2RmyV\nZdB9PAaxfc4vOv8wqSk+jM7fvcAd1IrR90OG9ifACt5iNUUrUTe1Ht5DNUbLomOMdfCdhqk+TR/g\nQ3f/vMTvfoyiRWehyd1nse9mREbKLkhK/4XweQBwSpaHsCq0IkfGzNZBEbD7kMztQKRitoG7f1HV\ndkqOqdfks6Vs+3vAr5Bhtj56sX2FJIOHoOLiRV+O/4deiqORAMPLse/mR8poK6FcoFx6ipn1QZLF\nP0F0p5lRFGAaarK+bwDjvwX5duchtbc1kFPkMdLVt7pEs4IhB/C6u38T+5yLNEppXf9fIO/1nzPa\nnArsmmQ8JbR9HxlPO2e0+RewubsnKgMGut7myKmwYlj9Doq2DwFG9HQU3CSv3gf4KRJmep70c9qy\nYq3tgJk9gKJgiyc9a81seuRMHOdN5oua2XyoLtgUwL15zyczG4OMw/6xsbyPolzrh2fgE8BL7r5W\nSh+VOrDM7D1qRt0tXk0tqsphZgcgGvKZwH7xcxuO44ko2nWoux/bQP/LAbuhaNmMKFo2FDjLC9SW\nNLMVUEQ2KqMQzy98Ftje3R8oO66yKMlEmvQzCjrEMra7KLAher5c5gnCPlWhY4x10EEDMLMhQJ8s\nip+Z3QF84O6bh8+PAN9z9x+1YXzvIrplpQpMIbE1yhG4H1i3J/MBghd/PqSolpbPtjdwjWckSbcD\nZjYt4v5vjvj9syO60X3UaGFxA6u+lg8o92+p8LtXqEVj50d0pf+iCVnu5DNEW/6CipwPDn0ORAXR\nVwJORxOi9d39y7L725tQdTSrSpjZk8ioWDzpZR/ybp5EDqPF679PaD8cOYGWT/JYm9kPEe3uPnff\noEB/86JJ8mao/uKUyHi/AU12h5dxZFWFVp1TM/sZtbysqCTAwyiq0FM0xU+RwZ76PDezvwO75dHZ\nQtulgD8j5eAHgb+7+2dmNgjRzqM84vHAQe5+ckZfnwGnRpFYU72xEcDW7n5pWHc6orHXy4Un9de0\nA8vMbkS1sKZBE+nhKMJ7o/ci0ZpgcN2H2DNvItGYKG1idSTd/jhysDXs8DSzVRClMDr+jkR8DnP3\noQV/vyyxupbufk+j4ykLk0hMQ/ACZX7M7HBgD/QMHhfWrYNonpHk/VjEbHq/0bHkDbSzdJbOUnJB\nnr+jc9ocjXI3os9nAl+0aXyXIa9mI79dPWe5BiX3blz/XQ+ch/nRy+tVYL66745DeW7XA1P19DVT\nN7YpkAf4NBSpmYiMoYdjbSY2uEwoOIbngJF12zs89nkuZOwN6unjVcHxXqDoUqCvl1AOTFVj2ysc\n+2dRLmtfFJnsi+r3PBeujT8U7G/t0P5DZFivhWiHawJHIOGLCcA6DYy1TxjTUGSoTwx/h4Sxz9bT\n57rJc3FUODaJ9xVSU+uJcX2CqKdZbU4CPi3Q16LImJ4Q26+hKHoyMWzrISTcFH2/VkZ/41Dh9+jz\nYeE388XWHUMD7z5Em/4VElR5N4xnPDJa9s66X5ER91v0Lvwo/PZLZJhFynm94ZrrA//P3nmGS1JV\nbfteIBkk+oEgOYiIkhWJQ5acg4CCoITXHBCUHFQQeAEzQRgyLxkkxwEEyQOSFAlDFJCMkpnn+/Hs\nnlOnp0N1d3U4M3Vf17lmqrt61+7uquq90rM4C9fWZc+3D4EzsNO3nXGnTdfqbZnveixugTIaeCc9\n/p1+fwb9/sMG8Y1Vj92FDfn9sGNyPHBI1+bQ7w+h/Cv/ev2Hw/V74VqnR/Diqvrv8SZj/AcX3jba\n5+TsjyPu+/NWj97j/HghvR8pAt7Cays/wI3+au7Tp+9zKbzwfAD4eHrs4DTHa4Cp+33O5XgPy6cF\ny8M9POY72CNe2f6QKgdD+tH+Z78/n0H6w4vVQhflwHENrrvxOPLQyni7p4VnrbHeA/YsYM7T4Sjv\nGXhBPh54r9/fTwfvZ+v0Hp7EAh4LYGNggbT9ZPoMt+nD3O7EnvnpGnwXTwB35hhrdHqfv8YR+uPS\n+3oAR59mzuy7WXruwgbj3QPcn9m+D/h71T6nA890+Bk0dWA1eO3UWGnwJPy7WDF2/oKzAxYagPPv\nE8AGWDRjA2CONsdZIn2nFafLO+nzX6lqv3nx+ufJfr/3fv/hqOTvM9vzpHPkqMxj1wF/69YcyjTF\nksmKoupkkhrZUlhdsFZ63OexR+o+Saukx87FqUMLFfeOJhyvlsLbArRXI3MQ7fcHObid13XKINaz\nDTqptuhkJeGItH1x9nyIiCOw53T6Pk1z4IiI24GnJG1b8LiFqvilOsKvVo03FjhDOWrZWjzWx3AE\nbjNJ/1Pk2L0iIm4GFgU+pxqqtxExB04X/Yek1Xs8t6yAxz64RuvDJOCxGq47WoEcAh6pxutZSatm\nHrsFWAn4oqS7q/a/DFhGdVIMI+K7wLE4kvB+GudgZXoPhhU6/y0pb3uGpkTE8qS6RtURwKjzusCf\n2ebApthxKWyMXsiAq4jWIyK+iiN+K+F6qSdxq56Ta53P6TUH4Xq0mu1tImIq/BlV2uPUSvedaA0x\n0ki150cp9VSLiG1wC6S1lGrr0m/h7pJm6cocSmOsZHKiqDqZiFgPFxe/jz3DtzJUv7MKVjOaCthQ\n0tUpN/xfwJ8lFd4HqoX6iWqkPghbdINBq2cbdCKi4sHeLm3fgpWyPq2kRJacDp/shgOhm8RQH8Dn\nZNW5PH0BAZD0dJOxt8ce9hVH4qJtEEhGxKepv8BD0s0tjPcp6quB5horIt7AdbbfabDPb4CvSZo5\n79yKIBkQZwBfwYbDeBz5mA1HjAI4t3ItNxnrXZxm+6PMY0fjGrIZq51XEfEr4PuSpqYGacF+Kk4J\nDJwWvo2SaEZELIlrWQ+QdFgr77sXRMQywJY4CrgEI/Q3Ma0BxgNX4h6DV6rJAj8ivoKFgSaqfU+1\notfitNZGfVDrfl7RxTYZUaAScEQ8A1ynJHgWEX/APfhmrVwPqf58V0kfL+gtDKNs+lwy0KQfofVo\n7pn5Xs4hNwFulnRKGn/CAMDtEbEB9pDti3Pfa5IMrB3wTW9X7NGeMG3shd5V0tXpsanxj9U/cs6z\nVUa02l1eImK1Bk8/DVyCG+UeDixX+X6htcXdoFPE4hNLgm8TEZHO///DKUBXRMSfsXzxivgcH2mM\nI8nR45qrynYzRPPfxWdxysqtEXE8jgi8UGv8SemcK4qI2B/4AY7WNSJPW4B1gWPwgrGjsfD33kyI\n5G36sG5K1+cOKUpViZ7OxlC082QlsYwcTJ1el+XNdJxaWQT/pcHnJ+kDYPsUvZMmVj18Ic13XM75\n9RRJY/FnuF9ELIaNspHI4VjkJXfUO50z9c6bo/H982zgRBr0Km3Ax7Cz+8CIGEdBbTJayXDKOeR9\nwCbJcfAuXqv9pep6WAA71LtCGRkrGVjCDfeuwn272vLM1BjzHZwb/KO0/SFwhKR9M/uMxr20mqoe\nhnt6bMpQKtCb+MZ+SY0fpZIOySlxG7X2GYnezmryLj7zvNdwk9Bv4vqnZ1Kq2bkMX4zcCmwsqVaK\n68CSrmHhFgAvZraboibtIDLnYOWeVHfcXpxzGQfFnZLebeKwqOY9nLL2XNM9CyAifoIXjW9gx0mj\nZvQNU56T6uHNWNjhfNw38ibs8FoVLyQvxcpvTdOnI+Jv2Oj4nGr0qIqIKbCynSR9vtl4g0o6fw+q\nSiM8EEeuJjpfGz1XMjik6P/raqAWmZQqZ20W/U/7vgI8IGlUh/MqvE1GURlOmfFWxX3UsuvMjSRd\nmZ6fEhti16pLjdXLyFjJIHM0NnIuxWlB7Xhmqnkbh/IrvIFTs7K8yJAEbE3Sje99uZ/TmelvkiVF\nKLeieUpAt/v5HEKb9WwjnbT4vAwvPn9Lg8VnnvEk3YvlfCvbHwJbhHvTLII92XfVWpgOOko9j+pt\nd8ignYNjGB4FrGznJiLuALaU1DXPb+KbWP10WeXsr9eAn2Iv9gqSno+I72BFtEPS/epgvGDbt9Eg\nGc7CIjqXRMQPlWkLEG4HcCT2xOcdb5AZpPO3pBieZMggqcd38f0rj2E9LU7374h0HR0BHBHD22Ts\nimvc3kwR31baZBSS4ZSZ4y0RsRG+Pwk4s2KIJVbC962LcsytLcrIWMnAEu6V9aiklQscs5A6mYj4\nCDhV0i719plUCPfHugKnrVWiTlkPUmV7RObajxQi4hKsJrZ4WnxO8HBXLT6/KOmhfs61pHfEkODO\nbyS9Gq0J8EyLa7c2AS5QwaIk1aR6pRMb1WW1MNZLuKHvjmm7Ij19UGafu7DYStMegxExNVZfXQ07\n7J7H3vC5sANqCpwatbak9zudfytExJw4uvAFrLon7JS5A6d9vdTCWO000G0Y5S2yfqekPWpFPGvs\nsy++RvJkTtyBlRab1iG2Q0o13BQbZuvg9MJ38DV4EXCZUs+vGq8tNMNpECgjYyWDzAw4TapIiqqT\neR2oqVA0CbI3NgIOxZK5L2MP3An48zocK0cWLkxSMowv4Yanz2cemwImeAQPiIj1sVHWdoPriJgd\nL0jfxkXNH7U/5cEj1dtlG/reK+nZFl5/AF6knN6lKbZE1viotZ2HiDgVNyTvNi9S3LpjZlwnWuF9\n/JuR5VYsFd4USe9HxDrAj3Fd1sLAp9LTj+NWJUelGqmekVI7D8CL1ep0/Z2AoyPiAEn/28qwLU6j\nrvHWhfqdSZqImKKP2QZz4fS9PBwJnBYRS0h6uOiJpNT3U4FTwwJn62OHwwbYSPuAOjXRFJThNEiU\nxljJIPMwxV9Mp+IfiU/htMc/kiSZGVqM3Ir7czXidrygmxzYGi9YD4RhKQEvAOdExJ24APb7OLW0\npDsUuviMiD2BnYH1Kx7IlKJ4FRYHALg7ItbUJKBKGRHzY6nndWo8dy2wh6RxOYbaD0t5T0pch/sO\ndZtzgc0jYholtb0OeAmLOmW3qyMvUzFkEDQlGVq/BH6Z6oFnBt6Q9J8O59oWEbF3mg/Y4BmD06UC\nmBs7yVYGjkwOxqb3X0lTFDzN/bAhlq3fOYYa9TsFH3ek8lJEXIqjP9d0ch1ExNeqHlq6xmPgtMT5\ngB1x+l6ueWJlzNsi4jjcVqFm7XCnQkVJKONC4MLItMlo8JJnGH6/ehhYrcrQXQWLx4wIyjTFkoEl\nqRUeDywl6fEuH6ulOpmIWAH3sfq2pJO6Obd+ExFv49Si76Xtj7Dow/6Zfc4GlpT0uT7Mb1Dq2YiI\nG9p8adP5heV3L5O0Z9p+Grhb0haZfX6HpbdnyjHXMcC0klasmv9qeFE1J26UuleeRd4gExFzYdXD\nefA1fjNOQfskrrdbEHvvl09OhkZjPQlcLWmPbs65U8KS42vhWrIZJR2aHp8WRy9e7rWHPiKmB67G\ni7rvSnqyg7Gux43m103b52Lv+nKSHk3f+X3A85KW7Xz2vSXV1zwO/AfYWqnfUY391gTOw0bnwj2o\n+6s+/qP4Mx6Vtoely0XE/8MGwAnZ34wG492PnaRnaBIUwYqIy7GxMTWO8FyFDZHLG4lv1Bkrb8pp\nJRL6NrCFpGtaGHsghIqyJONwG2BuSYqIb+MMp2uwATkKR9n+IOnbvZxbu5SRsZJB5hHcyPf2cK+T\nRp6Zezs81jjsOZqFfCkc62Mv5fEpwnAnteWtVVkEjWA+wIXyFd7CdQtZnsJ1Jz2llXq2Hk1pVJ3H\nq+dV/Xie+T3KcM//7cD6EbFYZvG5JfDPmq+emEXx9QVAuKnt6sBJknZPj92BI20j2hjDRdzz4JTb\n/82mXialrB8Av8Je/mY/3hdhGeTpNKANxSPiy8CfcOpO5fyq3IeWxhHUHamStW63ngjf5/KsJx7E\n0aq5gQ3Cvb3qNaNvVl90FXBYRMyWIrvH4QXY2Ih4GJ/fMwE/yfsmYILBuAVVqay4NquXEeId8YJ9\nt3qGGICkGyLim1hRcgfgqN5MbwLz4gVwhfFkHGKSXoqIK4HtyCGmgKNsvwV+FRHnYLn2u5u8ZsQg\nacMUdd0Q10utj+/b7ycH2YVYjfnFHMNVlF8Dp9FejFVKq/kIeAX4q/Ir4w6aUFGWojKcBoYyMlYy\nsFR5ZhqeqHk9M3lTs4CGqVmRv8nyiBe1iIiHsDx0pVD+TmAaSUtl9rkaWEJSL1KdsnM7gCEFqYb1\nbP2ofUqiAOcCS6Y5jsFG+1w4xWhfvEDdplktSkTsBRyGxWVejYiVcQ3kezhNo7L4/Lqk03LM7V1c\nA7Nf2t4ULwQ2lHRVeuwoYGdJc7T41geKcI+bv0v6coN9rsLiKAs0GWsm4AbcdPdHkh5scS5di56m\n8ZfHKW0vYwPzC8BXsvehiHgMpx5vU/XaMbS5AFONxrE15jYu7/iSGvZOjIiP46jfw5UISkRsjq+z\nhbGD7RhJJ+Q5Xnr9BnihNxsTO3VexdfWZXnH64QUQVk8r+hFRDwOPCJpo+7ObKLjvoL7nO2V2b5Y\n0q6ZfY4AviNp+hzjzYlTHr+BezsJK8QeD5zVrkEcBTcaL4r0G7EONsw2xo7O8djZdiH+LJ/IMc6N\nwCl57v2TKq1mOA0SpTFWMrCkhWDeH+69co45hgJSsyJi9TzHS3O7Ke++g0hEnIAVxBZK2z/DRsHJ\nOEowCqv4nSWppyIeEfEA8J6k5dN2dYrMQjhV6eB+pNpFxKHYe7lkLY9kRMyGU3j+JOmAJmMVuviM\niOexIMgeaft/sVz+7JV0mYg4EthT0ox5xhxUkuF5tDJqWzX2+Tk2rqZtMtYT2Cv7yfTQu7i+olZU\nfKKFdANHTtPoaR7HTlh1c1XsHHkhavSJSmnFy0r6dLPxJhfCffduwwv1s7HBXUllXRP4Co4wrCzp\nnh7MZxyW765VA1Rr/9OAVZsZsUUTBSkU1xl7PSx/vjH+Xv6D28icIOm+FsbJ1Wi8347TlHK/GjbM\nNgXmx9f/AwwZZn/r3wxLukWZplgysEj6cReGLSQ1a9AMrC57288C5o2IBWSBg2PxD8Uu2NAI4DFg\nnzbn0AkLAydmtoXToLwhPZE8zDvTn1S7HbBkeL302lcj4nycktTQGEsG0h1Vj11E+71PHgE2Dssd\nf4TTiO6qqltYgBFUBN2AN/DCphHzpf2aMQVO3a1unFptSNVMd1aVgEIr0dMccwMLOlzcpPbtGex0\nKhliX3z/WFXS7VXPjU71mGOAn+G0sm4zKzYG8/I8Q9kdvaQoheKJkHQ1cHUmWrYrsDuwe7htwR+B\nc9SgsW9YjfJgfG2fTjH9SrtC+vxuSn/fj4hl8Lm2Gc74OJB8PcImaSJiZ+B6Sc90MMZxwAXALRqA\nqFRpjJVMbsyOvdgVKj3MsgvaW/DifSQxqs7jHdcqpXqFMZntt1OK3KYMpQT8WfmaNRbNwNazJebG\nqoeN+IChKEsvOQ7XGDyLFyfTM3F9zYq4HnKk8xdgq4j4vaTbqp+MiC9i1dDLJ3plFc3SGNtgf2B5\nJo6ePoWNgEuxZ3x/mhjsiRlp3nZjelJbhEmJiNgER7ECR5UuaOHlqwLn1TDEAJB0R3Kc9EoVcEby\ny5CDezRVq6v2gq7X70h6MSJ+CTyE68nmwem3K2AlyZ9LqqdwWmSj8Z4iaSxO0dwvIhYjozCYIvTC\nWStPpu2cw474fm8nA0rv+Xocxb5BUivthr6F64NfiSF1y2vV4x6CFUpjrGRy41UgW/+yOs7Pzi7Q\nhJuhjhh64G2vPt6H2KvUb55lePuDR3E/rizL4O+9HzwLbBoR+9a6yScBkk3xYiEXqfh7c/y+ZsYe\n37FYYCC3BLekSyNiD5wGBHCmpDMyxxmFF4RX5x1zgPk5jgTdlEQBbmSooe8onII2HvhFH+ZWWPQ0\n8Rzw2Sb7LA1MtHhLNZjtILUgVJTO+xWor35KrdqXiNgY2AvYvzo7ISJOAb7GkPPp2xFxsaS8UayZ\nsTHRiKexEmUvaLUXWLuv6QhZPGvPzPaHwBZF1e9ExDy4fmxXfL6MBy7FC/JlgT1wr7XZVVutcV6s\nBjyiDLFqJD2Ka0ArTMFwZ2r1dj16fo50gW9hpdhR+Pfrm9g4e4gh4+wmNVbjnBsbt5vje+vXgf9G\nxBXYMLuiyesLpawZKxkYkndCuEbl+bSdB0naNOcxrgcWBz6PU7MeBsZJWimzz3nAMpIWaTBOXtUx\nKZ/KWKEUWatU47UzkVTG1KIUb9EMcj1bms/+OEXmNpzedKukj1Ix+SrYSPgScKCkw3KMtzX2PFer\nfgqr0u0u6fxi38WkQURshL34szL82g1srO8iKe89JzvurFg6vq2UmVTP9ptGda+pfvZbkpr2zIqI\n3+IF6ihJf6muGQs3Br8cOFzSz6pe227Be656tnSMXfCictZ6u9QbLyJOxIbzHNnUtPTdXoojScfg\nCPluwELAjpLOrh6rxthPAo9JmqgPXWafq4HFelGXlb6LMWSyEpqwBrBav+ueiiDVTq2PUxLXx4GD\nF4GTcL3YM5l9Z8IL8E9JmrvGWE/hhfWe1c+V9IewYmkjIZXqFPB64wR2LK2V/lbB0WHh9d3d2bVd\ng3FmwnWJm+PI94xYGOt6vI64tNvGfGmMlQwMGQPnM7JUd+GKhSmN5WJ8oVVSs3aqigg8A9zZyKMa\n9VXHZgEWwz1f7gdeVw6VsaJJ4fs/K/UGq7PPccDGeYqqw40Yf4w9lNmFyJP4B/Ko5BHtKSl6szc2\n4Melm/yN2OteScV8DFhDUu7oU4Hzmwr3ANokzWc8XvjPhj2ZgReRWzX7/CJiHeDKNMaZTBzt3D6N\nt76k67rwdkY8ETEDjkQuy/Co4sVqQaUtRScPxlGtT5BxuqSUxwOB/ZSj5UZY2XA8dpzUi54+iH+v\n6zqIMvvPg+890wO/wXV/W+FzcDXsVX4D9298ueq1uYWJqslTRxuW3L8Cp5udjOs4L8apsKNwWtt5\nePF8ao3X3497Wq1f9fiF+HvdtuKMCLd6eBy4UTkUBlNN2B44a+BIDW9/MAVD7Q/+KOlbzcbrlBYN\n45ZEXookIqbD18ALDc7fOYGXGtV2ZfbfH0fB5iWlmwK/By6sd49MrzmojgF/JF5kf1adNxov6YCI\n+Cr+vf5Mg93admCnjKA9gZ8C/482rod0vq6L21tshEtbPgL+irOBLpb0VDvza3jc0hgrGRTSQonK\noqiynYcWF1K7MTw165jMc6OwJ2RvtSCJXDX+TNg7uxJW3nqtnXE6oUhve7rBXYVTOoVT7yoqY5/C\nP5i3AOv2K986SzIcB6GeLTun7XGkMptaeC+WIm7qtU9j3IKNiFVrLfLDkuY3Y2/gakXNvWQ4ETEz\nrkH7LFbqnBo7kCqRp+mxF/+Pja6/zHiFRk/TmMviNOWso6WyYH8cN359IM9YRRIR12JP9kKS3oqJ\n1U93xZHfNST9pcbrXwROV5W4U0S8jN/bHMosasKNoFeWNA9NSMbbPdi58TS+p1VSWVdhSMxmefWg\nsXKKaLaMpIOLnksjUi3X94F5lNrFVD0/G/7NOCpPFkY6J97EYht/kPRwjtdsgBtjf73Gc4U1Gi9p\nn7DoxsnYsLmVBkIqtb7HBuMuwlBkbA2G2lI8jkU+9uhgzlPgdU9F3XJefB+9T9Jy7Y5bE0nlX/lX\n/hX8h6MefwN+36fjP4brp6au8/w0uDnwYznG2oehPP1Fq55bGHu2PwL26ffnPin/YVnnk5vsMxr4\nT7/nOuh/uO5nXuDjbbz2V+l6+FraPhD4qGqfy3AfrzzjTZWuofHpOvoAG3MfpO3x6fmPtTjPKXE0\n7Je4796RWJmtpXEK/twrPakq2xVjLLvPGODKOq9/H/hF1WPzpXEuqbH/EcC7LcxvAbxwH1/j72pg\nwX6fu4P2hx0Sf26yz6UtXA+7ATN0MJ8navw9k66lj3BmQq19Hu/3Z9nh97BfumfMXef5edL1s3fO\n8X4IzFbg/B5M1/9nChhrB2zYPZW5Rz6HDfidgfm69Bkvj+uKHy567ElOTamkZBCQi5VvJKN+1GNO\nxZGhGyJiteRlJyKmTKlI12Ov+egcY22Pb6SbSfpn9glJj+Nw/kP4BtlXImKmiJg33JNrUuM9mktd\nP5/2K6kiIqaOiH3DzXFfw1HT1yLi8fT41DmH2gK4Wo2bqz7FcGGZukj6QNJmuIj8Bhw1nS39ez2w\ng6TN1GIasKSPJF0q6aeSdpO0l6QLWh2nYGZg+Dn8LhMLYtwNfLHO69/C0fgsFQ/12DqvaZoaV0HS\nOEnrYUN9E+Cr6d95Ja2nMqpSiwWw468Rj6b9miLpBLXZ2DlRSf/O/n2Io51P4+uq+vlg5KuLbgyM\nkfR8rSflNP1W1iRHAc9GxGlh9eROWQSrlT5SwFinAzvh8+rbuKfiPJK+Kmm0ctactYqkuyX9TNIS\nRY9dqimWjAgiYhYaK281rc3oA9NSv0i92xyOFymb4Bvw+IioVat0eI6xFsEpjzVrGCSNj4grccPg\nnlOvni0V5Petnq0L3MJQK4Z6rIxTFUsyZIr8l8NpJk8zVG83P3AIsElErKXmipSformS6H9o0mC2\nGkln4Z5+fSOliI3Hi5tK3W6RQkUvMLz1xL+A6sbTM1O/l9IDwIYRMWPme9o8zXGitEZ8P2g5pTAt\nXHteYzpCmQqfM43omUKxim89MVJYBDijyT4PY6dPHvbCUcodgR0i4mHgeJwmnKcfYzWvUpyj8H2c\nHr46FtuYO4mz3aYBKJVoh9IYKxloImIVXOS9fJNdB0pBKiIWx32LHuvH8SV9AGxWVatU8ba3VKuE\nb3wzNtlnBpwi0VNq1LM9w1A92wK43ubLEdGTerYWFq/V5DK5WqsAACAASURBVFnM7g38NSIOBw7N\neo9TfeWBuJVBU/WoyZCD8T3kQmCvbIQjIhbEXuDN034/ajLWW7g4vBEL0rzXVyFExNfafW2N6N7N\n+Px9u2q7KB5iuPF1C7BdRKwq6ZaIWBK323iozuvPxAvCmyLiVCyWtAM28m7M7piU1lbBhfdNiYiD\ngOuA2ycR502veALffxsxCkeLc5GyN/bCvcRmpXbUKq8DYOAJt2zYAQtbzKAk1BMRn8ERrzPVXIBq\nOoau23q8C8yUZ06SjsYtA0ZhVcvNcG/KIyLi/4DjJd2RZ6zEZcCoiAnNwTthFux4rNSK7YPrbd+N\niNuw4+16XD89IoQxSgGPkoElFaHfhhc/l2Kj4q9YwW8lvNi+AnhEOQrlC57byXWe+hhOcVkZG4jf\nkHRKzybWBSLiZryAWlI15F0jYg6cxvioeiwcERH74Bzuy4AfZdMoI2JhbMhvDOwrKU8UsNP5jKHN\nxauaqG6mc24h3Jy2YlS/iJXKKuqAN+Pro2po7drOnCYVkkLqvyUtW+f5wJ/nHJLmbTLWFVitsyJC\nUS0d/0lcj3mZpO1anGfLks9tOgD6pbz3beBYXNPxfEQsAdyFoyaVyH0AG0m6osbrp8Cy/OsxJEjy\nAU7lPL9q37WBa7BI0R9yzK3yOb6DjcQb8YLu3pGyoOsHEfFzvBj+qaRf1Xh+H+wU+5Wkn+YYb0Nc\nIzkljmA3EnpoqlQcETcAoxulFUfEjri1xZrNxiuSdN8ZzVC06h1gusy9ZC4sfrKvpCOajPUo8Fyj\nzyQibsTXXstNnyNidlyPtRuwKL5WHsCCO2c0yyhIr78VuAn/VufuiZljbh/H4h1rpr9KGuEbkmYr\n6jjdpDTGSgaWcKPT9bER8GRWeSulph2OJXC/UF3L1IO5NUvL+DuWRx7RhhhARGwDnIM9m4cxccPc\n/bBh/BVJ5/Z4bn9L/126VhplWrzdh+91n+vl3IomxzlXj54vugeNiHgHOLbRYjBFHL8rafomY62H\nWwzcihcm25CMseTJPhFYEfd8uq3+SMPGbFvyOSJ2ynOMOgNOJB/fTcKtHmYDXqtEqiNiRXwPWRjX\n8R0rqW6j8XRNfwU75F7Bkuf31dhvO1x7dlSOqEJFdn9tvJhbimSwYsfHGFzPd31BNS+TDOE+e2Ox\nE3IsNoCfw2UF62H1zKeBZZVDWTgi7sJKpZtJuqaA+Q1T7Kyzz77AIX1wTnwLt584GUfkf4Abmk+Z\n2ecm/PvV0NEZEb/GbSu2l/R/NZ7fDqdB/17Stzuc9zppzpW+bm/jOvXDJT1b5zU34IjWUmn/f2KF\ny2okaa025jQ7jpKtjZUPKy1HRsRvX2mMlQwsEfEC7hHzlbQ9HjhYSbo3eZXGAn9v1QNdwNzmr/PU\neLzQKMzr0ynteNtrjPEL7P2sdcMI7PXcp5N5tkNEvI3r2fZusM8RwHeaLbIHnQbnXFPUhb4oI4mI\neAQXt9dt/BoRfwBWz1OcnaJhB+Lr4QNcN/Mavs4CK5YdmXNuO9MFyeeS9gnLsa/JUBrUIgzd+15Q\nDqn8yYmIWAAv9FdMD1WiluDslh0ljcs51jvAOUWd6zmNscNw+nLNmvRuERH34s9pWUmqjrKnfU4C\n1ssRsZ8HKzjPAlyC0/crRvH6uH78Ney4rGkw5ZjvgsA3cZbSnLiE4QpsYC2Ia2U3k3RDjdcW2jc2\npeavxtA1+jmGxFgqDpTrJf0253H7yiSRb1syyTIrw1OuPsC1SYCv2OQ16qkhlo498IvbvN52ctwH\nJP0sIi7Fkchsr6yxWKo6V11GFxjYerZq0o/HYsCMkm5p9fUj4ZwbYE4E9o2In9daiETEfMC2wKF5\nBpN0cErf/S5egM6Or6UrgGNqLUYa8GO8SFplEKMuKZq1KUP1O7UWSpNUKqzcL+t84PwU+fkaQ41k\n5+rn3AaRZGitlEoLVsQGweu4/q5Vca3/4JTVIqkZdUgO3fmADbATpNd8GtdeNYqKvMRw0ZuaSHou\nRe3Pw/Vdm2aeDhx13rpVQyxFojfFdWNr4/q9p3E0+yRJL6XPcWtcz3kkQwqn2fkVplYZ7rn5Bbx2\nCZzeeT0peo1Ti9vNJOkLpTFWMsi8zHBFspfIqOUlpiBjoJWYKm/7LTTwtudF0u3A7R1Prlj+BmwV\nEQc1qGfbCri/5zMbmsOncOHzxnghO8EADgvUnAD8j6Qx/ZrjZMCF2It6b0Qci2vrKvV2qwPfw7UM\nFyXDbAL1IseSbqRKNKJNFsE1LYNoiM0NXAsszlCkoxbCjppWx58K2BNHoQJ/B7+T1Lf2DBExLRb+\nqHjcl8G/M+8xJAxQUoNkeHWqbHw9bnLeNjXqKA9KAi11X4Jrj3vNhzRXmZwHG6hNkXR3RCyGf2uG\nGcW4F1xup2S6D34T2IUhB8TVwB9wPeyEzzf9/9yIWA7fS7vNF4E7GDK+/trKe6tHuh+thR3YM0o6\nND0+LW7B8XK3jLzSGCsZZP6JBQsq3AWsExHzS3oq5QhvgTut94WI2AHfrJbBF+ubDKkVntmveTHg\n3vYC+S2uZ7szpZrUqmf7BI5g9Jwk5nAHXvRfij3r2YXGHemxbXFaRUl3eIKh1Kla0a/AaTybVD2e\nK3LcIR1JPkfEE22+VDkK+Y/GC5OzcXSxZadOWO3xMODrkq7PPD4FFt5ZmyFDbyNgy4hYXT1WNEx1\nQ2vh63Ma/D7vwrXJPZXNjoi2hZAkjfTWFnvj+/l+wM+bRI3qkVUBXR1HcsbV2O8jXHd4PW6D0mse\npoHCYDIC1qR+D72JSEbJhemvE57E1+Ur+D7wBzXvs/calpzvNrOqs150E5FqRv+E1w6VetHKb8XS\nOIV8R3wvLJyyZqxkYEkqTAcCc0l6IyLWwNLDb2JRhs/i9KA9JJ3Y47lNhdNYNsIX7kc4kjcHQ9GP\ny4CtivDYtDG/d7G3fY9eH7vXDGo9G0BE/BFHDNaVdGOdmoCLgIUlfb4fc5wciIjRtK9yWbd2JaXn\nzIVrxmq9Nk895gnY07t0OwvPiBhH+++tOtOgeuxXgAckjWpn/DTG6fg+OYekjzKP74Cbt76AnSZv\nYQGDL+JI8fHtHrPNeVaiKdcCvwZu7lftb43ITm5GimBBPcKqsQtgI+op/FtfT+ihaTQ2T81Yv4iI\n/8EOxV8DPwT2Z0gMaEos7rE78LVeO3cj4q/A74Fzi4xUJyGRbzBU7vAmcA/wJ0nnFHWcFue0PO5T\n+DLwK5wC+ZWq3+nHcPrjNl2ZQ2mMlQwqqYh6GeAeSa+nx3bEXtb5cHHqMZL+tw9zOwA4CIf/fwr8\nRdJH6Qa6KvBLfEEfKOmwPszvedztvhcpA30nKbINWj0bEfE0cJekLdN2LWPsOCzNPUefplnSIhGx\nNXYALEn9yJmUow9SdFHyuVMi4r/AbxsJ5OQY4yHgMUmbVj1+JbAuFie4Lj02I45ijFUbimqdEBFP\nYUVAsIFYSUm8IY9RXfBcDqJ9Y+zgYmfTW7og9LATcL9qKG72m7ReuBxfB//CDolFgYtwmuHcwCWS\nNu/bJAsiOa5OA7anvgP7HEk79GFul+B12xKSXqjzO302FlqpblJfCGWaYsnAkoqor6967AzgjIiY\nMutl7QNfww2dR2VTV9KcxoQbJT6I+3L03Bij2AaLA8+A1rOB0xObtV0YJkxTMtiE5ah/jdPYbsVO\noU5S6s7DUs/fALaPiEIlnzvkQaBtFc/EnPh+VM1KwIsVQwxA0n8iorI47SmS5g/3JqzUiq2LG/Eq\npYJWjLMbJXW1obekg7o5/oDTMFrbBn8i1eUWPG7HJAfuRjgy/G3gk+mpLfA94FByigp1k07FpxK7\n4+vpHpyKelPGgb06TgfeLiJukfTHIubdAisDF0t6ocE+zwAbdmsCpTFWMiLpsyEG8CksqV6zhkDS\ne8nb8q3eTmsCP8ULxT9GxEB52yczXmXI216PxbAnvmRk8AMsJrRSjhqKPIzK/H8GXJ9Qi344VY4E\nTouIJSQ93OYYH6dq7hGxCDAT7klVzbNYeKDnSHoc1yCfABARn8eG2ZpYtfebuH1JzbTUks5R8aqx\nr2C1vYEk1UYeFBEH49+C2XFmx9/7vc4pWHxqF1y3t5qkCd9Heo83RMTq2PmzK24k3UtmxFG6RkyP\nhXy6QmmMlQwsEXEZrhG7UVLf1PDq8DzNf5CnSvv1g0H2tk9O3ApsEhFz1fK6RcSiwJeBM3o+s5J2\nmQc4sSBDrFDJ5ywRMQ2wAp5vzf5Jkk6rek21cMRLwJ+B21I67T3Uvo80Eo54jYmjHSukf2sJE3yM\nnOpxPeBj+D4+dfo36OKCLEv6LsblTZGMiKWApaq/0xLG4CjsQJMyWP7R73lU6IL41BJYxr+mYSzp\nnYi4GEfQes1zWIOgEUtjIaiuUBpjJYPMBrhZYaWQ/EYsZXqDpGapX93mLGDniDhA0pvVT0bELFhS\n/U89n5kZlfn/oHnbJyeOxD1aboqI72PvWrZh5THY035032ZY0irPUMe4GRQiYhdciD5rvV3wtV+9\ncB9DfSGc/es8V6Fe/c5YYMOI+KSkf6XHtktj3VRj/0Vx/UxHJCGID4Gz5TYEeV6zGENpiqMYauIt\n4CF6K21/I3AwMEF4IiL2Bn4iafYa+28GHMDE32nhRMT9wAU4tetvXTzOlLimqJ4zIY+huh9wR0Qc\nChzSD0GtEcqB2NhaJyM+NcEYk/RBuN/XyjnHyzYCr0ez57vFlcAeEbGKpL9UPxkR62OD/vBuTaA0\nxkoGmTlxesja6d+t058i4jmGekzcIOm5Hs/tEFy8f2dEHMLEfYv2B+6kT/ne3fK2l7SGpDsiYndS\nb5bMUxUD/kNgF0kP5RkvRdK+R/MGvM0ky0va51Rg94iYSdJb/Z5MNUmi+SRsPPwcG/oX4/vRKFwL\ndR5uUF3NIRTvoPlTOuZfI+JCbGxtiEU9bq2a+8dwIf1VBRx35/TvrhFxJ/ALSX+ut3NEPIMFEyoL\nwiewwVFxAE7Ux7DL1FqYTkufUjir+BgWsDowqXleCFwk6bYiBo+Iz+GF7xrUd3zkbTvxU5z+9jN8\nLtyP08Krz/Nc6oxFEhF5msOPx78Xj+DP+O7uzmoCGwCXNnFkPI2v1zw8AmwREfvWio5FxHTYodBu\nOnQn/BI7iK6JiN9gNU8iYkPsNP0WdhB1TSyuVFMsGTFExPwMGWZrYMMHcqqWdXjselLD0eTxrs+t\nZPBJRtT/YIWsSk3A7VipLldqSkR8CaftToeNuBepIxzRTLK8pH2St/5cXDf6Eyx3XIhRlmo0GqUV\nNu0hFRHX4kj4QpLeqpb2johKTcYatbzA3SDJ938j89AbwGaSbqrab3NsAO0iaXSHx9wJpxR+Dhuh\nn5NUN7U8KdBeT3Ly9VpBscZ8JpJkr6Xylue5Ls1vUSw0sRl2DoHTWi/GaoA3qI1ecRHxGew4AH8X\nGwP34/vdsjhSdiPwtBq0nciMV6g6Y5Fk5lYvalT9uIA/SmpYix4R01PfWZe35cZ7WK16n7RdS2Hw\nKOBbkqbLMd4eWCr/HqxEe5OkD9P9dDVsEK2Qxut1zRgRsSy+r2d721Y+/8eBLSQ90K3jl4vEkhGD\n3Oj5dNyM8Gng6ziM3guyTSRLSloipdX+oMNhfokX6Xtgyf6eNsUdaUTEFJLyLsRykxTAfoejSzek\nY9XZNZ8jJiLWxSmrizfZNc9icVksh501ECdEyiX9KSK+CuxLSgPvNpJ2i4hTcarPK8BVkmrV076N\nr5NLCzjmqdntiPh4k/3n7vSYkxPpnnYEcEREzA1snv52BXYD3kx13xfh7/vtnEPvh+vzVpD0QDJY\nLpJ0SErv/jWO2uycc7xBdkxNC5yDG6sfintdVTJsVsWfxcPAd3BN0+E4ne5uSadUD5au673TePXI\nG1EsWnzqePyevoKFe8ZHxKvAbPj+FLinWc8NMQBJ90bEp3HU/ksMd5pe0u3f29IYKxloUm+K5RnK\n418J38AE3AucQg9y+NVB09N+U4S3vWQgWAE4X9IJ/Z7ICOGliLgULwavUUGNSyNiU9zwfUrsGHqe\nDqTtwz3yLgP+jRvAfgfXUv0DL14+g42TWmIXtZiB4TVX72JFwyx3Y3WznpFSEm9tss/VwNVdOv5E\ntb1ZUo3ZxZLqGoJJhnwLST397AadZFj/DvhdqpfeFBtmW2A583ci4hp8LV4mt62px6i0TzYKEek4\n/01p33/DxsvOOeZWtDpjkeyP1zdLVp2fTwNnJmP2QWAPSQdExL34vvANvPaZQETsDJyM+3fdgmtb\nOzEgChWfSgIlO6T3tAvuCTobw3uCnt3BfDsmKTteSgHOoFYpjbGSgSUiLsL1VzPjm/HDuBbiBmCM\npDf6OL2Bp2Bve0kOImK+9N/nUgRlvoYvyJAjdeR9/CNdko87sBd2J+DtiLgK17Zc3mxh3oSDcARn\nw4LS/H6KDaYVJD0fEd/BCrKHJGfUwcAPcSQrDy8An8hs/wuoblQ6M+V1X83OWHq70UJsKXw+lcZY\nHSS9jusqT011QOtjo2wDbKR9QGMBnDkY3pvxQ5LwURr/w4i4ERt7I50dgAvr3Y8kvRERFwA74hTB\nV8LN0jeusfuPsXLpKpIeKWBuXRGfSgZXX42uQaQ0xkoGmU1xBOxaYF9J9/R5Pk2JiNnxjept4Dr1\nqU9IF7ztJfkYh8/ZzwCPZrabkSd15DbsTSzJgaQNI2JGnHayOV4Ubgm8HxFjsGF2iaQXWxz608Bp\nBdZbfQkXymfT9qaACd7kA5Ka18FYobUZDzHc+LoFN1NdVdItEbEksE3ab8QQEV9r97UqTu59Ghx5\n6BUjOjU+CTVcCFyYxFnWxDVmjXgV932q8DJQ7dR6HzsUcpN+E7+B76Gz4IjMPcApRQmPtMHc2Dht\nxAcMNYMG9+GbtsZ+iwCjCzLEuiE+9TXgvkbqm0m4ZZkCr9dGc2mLbs2tFPAoGViSR2gULkQV9pZd\nh9MSx0h6rY9z2xN7UtevpFxExHJYBWy2tNvdwJqS/tuH+V2CRU4WT972CcXgVd72L+a9mZY0JyJG\n43N1H0kvZrab0qwYPdxH6DacsnJ6h1Od7IiIqYF1sGG2MY4ejcc1ARfiFLWmfWQi4um073cLmtd7\nwNGSfpa238UN5ffK7HMssL2kpjWyEfFt4FhgvnTtLwHchRdwlRqNADaSVEtRcSCpIaJUTzyJ6n3y\nCDOk8Q+UVFMBN9y37WosjJI74t0uDUSjGtJrEYqiiYi/AK9J2jht/xk7LJaQ9FKKzDwAvC1pyZxj\nHoYj0PVEMo6oXH+9JCIex8bWkrVqkiJiKpym+DElhdyIOAlfu3NV7fs8cJ6k7xU8x47Fp9I4EwnS\n1NhnX9x+oKvncJvXVu57STuUkbGSgUXSlslwWAarKK6BDaD/wcWf9zEkbd+VOoMGbOspDst9PxIb\njqfgAtwNsdhCP3pIFe1tL8mBpJ0bbXfIpjhFd3REfIP6DXhVb0E5OSPpfeBy4PJ0X1kNG2abAkcB\nR0bEAwwZZvU8uBcAX46IqVRMz6KXGN4P7CWgujXBVFhFMw/HY3GR1wAkPRwRa2ExgIWxk+jYPtwz\nO6WWs2ILbFjfhHukvQDMhX8rVsPR/4vqDRgR1cb3DyKi1nGmxMb7NFiJsle02ndpUvCuXwP8JCJm\nSI7MP+Lf0rERcRuwHDA/8KM8g0XE1ljW/ilcZ3YDTt39JI7U7Q/sHRH3STq36DfThNNxb7hrI2I/\n4K+SxkfEFLg+/jAc8crez1eidlT7MmBURIQKjLKoGPGpvExJb87hpiqcvaaMjJWMKJKnaEVsnO2O\nfyClHsvHh/ucXS5pt7Q9B1ZBOknS7umxO7BHa7lezi0du1Bve0k+UoH1HySdmLabpma0MPbASjSP\ndCJiGZzCuBmwBA0+w+SZvxYbTd+XNK7DY18PfCRp3bR9Lk6pXE7SoxExF3Af8LykZTs51qRERGyA\nDa2tVKN/WBJaORfYVFLNvmXhHlmVRdB8OAWrloPjI6wCeT1wmPIrA5a0SER8EhvS10t6OT32PdyE\neBZcAvBrYD/lUEuNiJtxb7vPVcaren4OHH36h6TVC3sjOUjR+gtxPZ1wpL5aYfAq3Abi/fTZ/C9w\ngaTzq8aaHYtu3AT8SNJ/evZGcpAzMnYGsJ6kT9TbZ1KljIyVjBgiYmGsqFiJks1eeaoP05kdL8Yq\nVLrQZ72wt5Bffrdoiva2l+RjaYbn94/Ggg8dG2P4nC/pApLG4vrJ/SJiMRrXtTyAr50vAhtHxOs4\ndafGsLmab18FHBYRs6VI+3E44jM2Ih7GC8mZcE+zpkTELElEoWPCTWlHN6qTiIgdce3ImkUcswX2\nxZLnNRs5S7okIi7GkY+axpikBSr/T4vFYxotFku6j6R/Af9X9dhxEfFbLO7xUouRn6VwjedEhlga\n++WIOA9ou46oXVK0fqOwJP1O+PdjNuwUGIvnfVpm/39hUaJanIcN1W8A20fEP6mfObFW9YOtiE3V\nGLCmsFRYoTTLZhGxQI1dp8TOkFVx9sJkR2mMlQwsETEnQ5L2a+GeFxXD62ngzww16ew1r+Ifhgqr\nY69WthBY1C607QWPMtz4uh1YPyIWy3jbt2S4alVJ57zC8POiMFTVILekO0h6FPhVg12mwMXr2QVI\nLYdQXifR8biP4Qfp+Lem1KpDgSWxCMxPWigc/1dY0v9U3N+pk15ro3D6XyPmx/e/phSY2gleZN/Y\nZJ/HcNQhD2vgz7pkAJHFsFoV2wGvc5tFMt+mj+vhVAPcaR3wqMz/Z8CGXc3D1Xl8XIPnGtFIfGrn\nqv2WbjKvO+hdSuRAURpjJYPMvxjqgP5v7Pmp1Ig93s+JAY9gr/i+OIVlO+AuDZeoXYD8DRGLplBv\ne0lu7gO+mtJYK72els6j3tRtBamSYshGUwoa7028CMk+dhENap2aMA7YGteCvpRSf07T8L5NRTId\n+fsZPRcRpwAnSnqsw+O+jw2yRixFc7U6oHR2DCIRsSquGZ+Z1I9K0i0tDvM4jj79tJZjItVnbZD2\nG7FImqL5Xg05jeLrtSoNtwN4AgsLHVdjv4+waEtPxM5q1IrmJW+2Q8uUNWMlA0tSUboOG1/dWki0\nRURsAlwMvMdQH5SdJJ2R2ecZ4E5JW/Zhfh/H8uoPS3orPbY59rYvjBdsx6hsIFwoSVHzClItIwUr\nvpWU5CEiVsBe6W1x2pOwo+BU4Kx6KVs1xqmrMJhEUObDRuPHJS2SY7yXM/O5AYszXKw2WoCk1LIt\ngO8Bv8umrqW5VVQlL5C0TQvjLg98Aad517omS4GcLhMRK+MGxpVzKnsf/SdOi80lRx8R+wC/wOlv\nP0yCFJXnFmaon9a+kg4v5h2UVBMRB+L+iTcPwFzG0abhKWnB5nu1TmmMlQwURQoedJuI2A3YLW2e\nKemYzHOj8CJl79LgmbyIiJnwYm4eXDN2MXBJs9dJOjXH2J/EqnjrpfGnrj1UbwVtSgaTJHi0Ca5H\n+TLOhvkAuBLXgl1c4zVZ2ee8zoRfSNovx3ymxhG73bBIg3A968k4Wjau+buaMNbCOKI4K/Ak8Bec\nxjYnsAr2yr+K23fkaVnwcSymsAaNU0xLx0kXSQ6tW3CKfz2VzHeAVSXdm2O8qbFC42q4lOB5nLUw\nF76HToHPnbVTDVfXaLddAeU9fZKnNMZKBoo8ijslJSOFIs/niJgHuBMvNh8CPoflmt8DFsIL7fuA\nNySVYh8DSr9SZCLiE8AOwFdx6tf4Wgu8cEPsysJgNVwbN67GkFmFwZNarU1LQim7Y+GE2fFC+Rpc\nQ/fnnEp5iwC/x6JO1VwLfCtvOmREHA98ExsCpwDPUCf9cnJOaey2QRERV2HJ+S0bqGSeD1wnaf08\nB05OiR8DuzC8lvpx7Ag4qsBaxkbzGMPEn92swOfx+f8MQ4bnvNhQ/BtO4ct1T4+I7Rhqbj0zFgO5\nB/iTpHPanPfiONNmRnXY4zIipsRN6etFnhmE6FmvKY2xkoFipBhjEXEAbjxd96YREavgps8D/V5K\nukdE7ATcL+m+AsY6Hv/IrifpuhjeyPtTwIm4TnEl9bEheklj+pUik1L31sZRsq1x242GEZ5e3I8z\n0bJvYiEQ4cjFScAJGt4rsd4Y8zBxbdFzLc7jBeBZ4Asdip5M0nTboIiIN4ErJG3XYJ9z8X1w5jbm\nPyPpPFGf5d9TpsNt2FjaS9KTmecWxP0Pl8H39Ib15+n6Pg3YHkd2PwJexoJSlf5d50jaoYX5LY2v\nw2Uqj1XuGRGxOo6wb1tP0bTGePtjgY6G39vkGHkuw54lJe1xUPpr5MFZHfdG6boxNogFqSUA/Ak4\nATcq75T1sDreddVPSHo2KfA9iBt5f7eA45V0gaIFQJqRvNo7ATsCc+OF2mO4fqwZC1JbHrsw5P5J\nl+NF46J4jnPjZrg/jYg/4HTv9xqM8RzQkvFVg5mB00tDrDGSRmW3MwbFhTQ2KL6c8xDj8fnZiH8C\n6+YcbxjJABuUHlxHYCN1q+onJD0ZEVsB96b9dmoy1u448n0PsDdwk6SPUiRqdeBwYLuIuEVS08bl\nKXI9BhtyxwGL4f6HFW7GacBbYWXrZuP9BP82vYGVI+tGnrtNRlDrIklv5RHYqtAtoa3SGCsp6R5T\n4R+WXjAF7Xnb+9GjbXLiFVzfUARz4Sa2FT4i0ydO0n8i4lpcjD5ZG2Pd6JkzkoiIWXE/op2A5fF1\n/iZ2DozOK34g6amuTRKIiBXxInIbXCP0Jm7oezKwLPBD4DvANMCe3ZwLXuDP2eVjTIoUaVAA3E0+\nlcw7W53oALIePtdrIkkRcTXw9Rxj7YLTiVeTNOE3J4nj3JAiWQ8Cu2LhnGYciGuSl5f0cBLgmGCM\npbn9FVghx1jgyPdzwLKS/p3zNd1iNF4v3Q68ldluRKV+tjTGSiYbZml1MTWgC6hlcZpA1+m1t70k\nN2OAlQoa602GC3a8hgvQs7yBlRwnd8ZRfM+crhARxp9digAAIABJREFUO0g6M8d+J0vaJcd+F2Cp\n7qnx+7kOLzYukvRuG/ObChv4zRQGd8053ky4bm133EctcIPb32Olx8pC8m8RcTpu07EVNYyxiJgN\nL0KbzW2iJrc1+B1weETM02qK42ROkQYFWKBoTETsKekP1U9GxLdw39FReSeYDJG9GDpPasnA90Mk\nYyaapOyl52fKMdYSwPFZQyyLpHfCTdB3zzm3tYALJT3cYJ9ngHVyjjcvFunptyEGvmdU0qEh/7nZ\nNUpjrGQQ+V76y0tPFlARUd1ceuekmljNlPjGMz9wdrfnVTLQ7AfcERGHAod0WCT+FD6vKtwPrBkR\n00t6O/XLWRfXvUzu1OqZsyAWpHgDC51U6lqWxguem7EqX6/5U0Q8L6luA+OI+COOKjQ1xoDNgX/g\nNMTTOzEsImJuLISxOE0UBrHHvdl4f8JRsOmx8MzpwO8l1YxypDSrMVjQoXqsxbGz4xM55paHK9Nx\nbo2Ig3G6V80UzQF1/vWLjgyKVH9dzQ3AbyPi+1hQJauSuSg20Nelqj9fnfE3xIq2U2Ixmn/Qp/S4\nGjwCbBsRv5T0TPWTETE/bk/RyCCqUGml0ohWMmFmpflvSVBb0bcWLzIgNoek0VXbeVK2u0op4FEy\nUKSC8TdosU6hW70fsqS5TTgk9W9s4xlSGftePzxBRXvbS9ojIiq9clbGP0b3YyOg+sbbNLIQEYdj\nSfA5JX0QETtio+NveMG8Cvb8/kLS/oW+kRFORHwa+CtWyTtYmebsSdL8YKzq9yVJj+Yc8/O4WP4z\nwAyS1k6PL4C/h2vzCKlExEM4wrmKpAdrPH8Mdk5dWCsVrMb+X5TUdJGah4g4Gy8Gz8YCMY0UBpum\nNKZ76OM4TeoUuSF9s9esjGXHD656/DIcATwc12U+ozb6lVXNLU9vwH5EUAaWiLgHCwct3cCgGAs8\nIWn5Gs+3m8qvPEIPEXEX8FlgM0nXtHmsrpCUD8/CtVe/xg6hiuG5Ok7RnRXYXtL/NRnrTuD/AZ+p\nFR2LiOmwCu/Lkr6QY25P4z6pW6XtA4EDsp95RFwDzC/p0znGOxI7ij7bqP6zH0TEFP2uFS2NsZKB\nYgSpKQ70PCPiXWD9HN72b06OykW9ooWFRtOFRUQsipvcnibpX+mxY/APdiXt5hzcELXldLRJmYi4\nCJhN0uoN9rkZL1S2yDHeIcDPGPrcJ3x/EbEQrj/6vqTf5BhrPmwojgdWzEaykgH+E9ywdnNJPfXo\nR8QrwAPVog0djLduUQviiHgDuFnSxgWNN5qcUTRJfU9rGhQ6NShSCmFbKEeLgYh4B6sIDuR3FhE/\nwA6FagM/cE/AfZTpYdpgnD1wqu89wD5YwOPDJOCxGvBLXN/1rZwCHqNx3ennJf2j2hgLN5a/HTdc\nb1qjHBHTA1djR/t3s0Iv/SYingPOwL+tD/VlDqUxVjJIDLqRUyEsWT5WA9qcumhve0l7JK9wLtoV\nSwj3j1oIGCfpxXbGmNRJRsUfJe3bYJ9fALtLmr3JWJXF59VYtWxbvGDKeozvAN6UlKueIiKWwg1u\nnwFWlvRmSpXbH9d8baQuN6StM6//Ar+VtHevj92MsAT6HwZxbpMbRRkU3SAi/o0X2T/qx/HzkH4n\ndmR4e4Z7gTPz/i5ERGCD4ivYqTAeG8izYadRAOeqQcuAqvE+nebwH6wcvTRurfJ5bNwdiEV3Pp8n\nbTes+DwVVkqF+hlQUo8VniPiNfy5C7/n0cDZeSL3RVGG2ktK2mN1LKBQ1xiLiI2ALfqUBrg+9rZf\nGRG1vO3fw972XDfmkvZo18Bq8Rj/BgahKHqQmQbXhzXik2m/ZnwXS29vKsuyb15jn0doQWBA0v1J\nde5y4NJUn7o/rpfZtB+GWOJBXPtaKAWleN6Dm8eW9BlJx0TEhXRoUHSJ64Ev9fH4TUmfz887HEPA\nDil9dxf8PcxG6rsHnCwpdw17ioZtiVOUf5seDrzmCWxIbdFC/eQUOMU5u3+tUo9+KDzPCWyG63LX\nxRHeo8MtN04FLu8kBToPZWSsZKAYQZGxpvOMiH2xaENf0gAH1dteUixJyGB94G2cjvNGn6c0cETE\nLVjddBVJY2s8vxw2fO6WtFqTsd7C8vDfSdu1ail+AfxA0nR1hqk39o4M9f+6A1hH0n9bGaNIkoF4\nGkneuqAxC0nxjIg1cHRyXUljiphbZuzFsaE4o6TTixy7pLekqNOdwG+An6tc9LZERMyCjZQVgdmx\ncXc7OWs+RxoRMSd2KuyE1V6FVbHPwhHWiX4/iqCMjJWUdI9pcC+ovjDA3vZJlhhqyfCcrASXu0VD\nMw9jUh3bExdAv5oeWxs33KwoWv0kIr4g6ZXWZz9JczBWYLs9Is5k4rqW7bFxcHDdEYYImvcPnBOo\nWbcXEY2MvaeBS4BVcdrXcs4+MpIaNZnvBi/h8+u2iDiOxgqDTeeWUjz3oyrFMzPGExFxN7AJXjw3\nYl78WV2ThEYazS1Xb6CIWBo4CUcVKpyenlsdKy5uK6lpk9vJhYj4CDuBdmjz9RXhlFbJK6RyIBau\nOBjYJSLuo356XK72DO2SufbvlPRuk3vBMPpw7VeO+zpu+nxcP47fa1Kq/9E4MrYMNsq2w9lE36FL\ndlMZGSspaYP0A3KgpEPrPD8NXnAsJKntBrRFMGje9kmZzMLiM5IebWGh0XRhEW6w+a6kNTKPVZTC\nfoHT8P4HOExSLbnoyZrkmDgeiwlkv5PAKce7SbogxzhjgQ8lrZC2qwvbp8Bpiv+WtEqN1+c5J2oq\n+vU6yh7DFQapNacKeeYWEbcBcwBLphTPWlHF0cAoNemdWGNuteYX5FfdWwxHUKbEypGLYRGkyvca\nOMvgekl5mhdPFkTE67h276dtvn4M7RljZO+FDcYvTESpUzr4fejHtb+WpOtz7HewpAN7Mad+kISz\nvgF8H/hYt76HMjJWUpKTVICa5QcRUUuhaUrc+2Ya8nW675gR5m2flKn0t3qjarsIFgAuqmxExDzA\ncsD/SjosPbY4zn0vjbEqJJ0fEVfiBsbLMryu5ZIWHBTnAodFxI8kHV3j+Z/hdgb1PMmHUNw50W2K\nnuvncIpno6j88ziy2Iyi1fEOxBHm5SU9nAzF9StPSlJyiKxQ8HFHOmNxw+G2UEFKnQ3oetubFqhc\nTy9XbbdMMuTGA0sU7fhLXBARq0p6oMEcfoYj3bmNseSoXgELjNWs0c0bye4WETEzjobtBHwxPfwW\ncF63jlkaYyUl+ZmCoZtdxSNbq9j0A+ABXDh8WG+mxhjyedsvqvF4KW1fEJJ2brTdIbNidawKK+Pv\n/LLMY/cAuxd4zEmKZHCdlf7a5Vhga+BXEbEN6bqLiKOww2N5XFNxQp05HNTBsXtKF+baUYpnFhXf\nqHUtrC7bqDbuGSCXQuZkxBHAnyNiHUnX9nsy1fRZPGQY1ddTh9fXzfje83bVdlH8F7giIr4kaaLm\nz0lB8zDg1rwDRsQuwK/wb1nNXfB76LkxljIavowNsI2xoSi8jhsNXKQa/duKojTGSkpykk2bSV6o\nYwZIaGQkedtL2uPf2JtYYQ1s+Gcb/E7NkDBCSReQ9E4SjzgO2IEhZ8YPsaFxBvBt9bgn2Ajhn8BK\n9Z5MC6JVcI1Pr5kVmGjRWUUwVJ9ZYv4frse8MiIuBu6idmP7vkc8Bo1UB/xkOyIx1RHFLkQYN8AC\nYFdGxCpZYaiI2BPXVd1FJnrciIj4Mq7HfAgrRx4NXIxTg0dhFcPzgCuKewv5iIijcd3w/8PX+KO4\ntOP0WoZoNyiNsZKS9lgDGNfvSVQYSd72kra5D9gkIpbEkYNtgb9UeesWAP7Vh7mNCCJieSydPiu1\nI8KqVwdatdMbwM4R8UOcclNRGbtTbjVQUptOUzwnItxMdgssujELQ6mnF7VYG/tiOnYjPoujYyVD\njGYoU2SL9AcT12W2FPGIiE/iaGW9dLZc1+qAsx+OtA8cSQBsS2wcXRJu2P5+RHwDS93fD6wn6T85\nh/wR8AqwkqS3kgF0n6TDgcMjYldc1tFMuKcb/ADfN04ETpX0115PoBTwKCkpKekyEbECsB6NFxYN\nlbwiYlXgRoanxm4k6cr0/JTYELu2XWWzSZWI+DhwIXaiNOpjU1gRf0TMllf6OYlDbEXzc2StIubW\nCkXOLSKmw2lNSwF34wX6CsAxDE/xXD1PZDEiNsAe7NmYWMjjVeDrki6r9doaY43GDXM/L/dYqhZm\nWSHN7XeSvptnzMmBiMgtZpI3tTS1YNmH4QGDrKhNbmGWQSYingSulrRHv+dSj4wA2PlYmflk4B/A\naq2o9kbEK7g2d5e0PR63/jkos88Y4B1JuaJtRRER2wIXS3qvl8fNUkbGSkpyEBFfS/+9KHl1vtbw\nBRnK1IzJl7SQHY37llQWE9WLxsrjDY0xSbeEG4l/M+1/ZsUQS6wEPEftusDJnSOBNXFbh1NwdKOt\nNMKI+I1Sj7EG+8wCXIONi2bjTYO9z6Nofo70lKLnVmSKZ0Qsiw3sKYEzgRuwM+KT+Lv+CnB+RKws\n6Z4c0/slrgW8OSIOAuZOx/kssBoWKXgLOCrPe51cKLp2LyJ2wC1YbgB+B1yA76HX4PNwV5zOdnyR\nx+0TF+Fsh+mKqEeKiKmwQFGz6H9uCX9JZ0TEp7Bi71bA48BarRhiiRkYnrXxLvDxqn3uxg2re4qk\n/+v1MaspI2MlJTloU5K2r967Qfa2Ty5ExHfwwvM04Nf4x+ZYnK41Cnt/rwB+OkiF5pMaEfECrgf6\ngqS8Utf1xhoP7C3pyDrPz4ibqq+QU1L9AOAg4FB8rryctk/A58jhwG3AVyX1tG9hN+cWEbPRQYpn\nRFyA61rWkHR7jee/iIWNrpC0Zc4xvwyczdAiMWuAvg5sJemGvHMsaZ2I+AswH24L82G63g6q1GdH\nxHo4QrO5Rni/t4iYCRudrwI/kvRgB2PNDVwLLE4b0f9o3hPzWBy93oyqVF016ZGZxh8HXCNpt7T9\nOPB3SRtm9jkR2EbSzM3G6xYp7bmeIZvrvbZDGRkrKcnHLvhHueLZKVpWuVAG2ds+mbET8I+KqmJq\nKfB6WjzeHhFX49Sna3HEpqQ7zIyLsTsyxBIXAr+MiGcknZN9Iv2QX4k903vlHG9r4F6lXj2VthOS\nXgDOiYg7cb3g93HRey/p2txSCufVHcxtVeC8WoZYGv+OiDgfO6PyzumqiFgQX7crMmQo3g6ckjft\ntKQjPgecXRUdnbAwlnR1um/uhRuSj2Tux4IwywL3R8S7uNF69e+yJC3cZKyjgc9gZ8KJtB79H1fj\nuNUEVm0cNjfy2RIPAZ/ObN8CbJfk829JtdDb0B/xHiLiq7gR/Wca7Jb3vbZMaYyVlORA0uiq7aJl\nlYtmb1wf09Sj3Z/pTTYszlDD7QoT7ruSxkbEZbhZc2mMdY9/kq93VR52wJGv0RHxgqQxABExLV4c\nroxrjfIaJwvjxVMFAVNN2JCeiIjLgZ3pvTE2yHObmeZiGk8zcSpUQyS9ju+ZuUVEJnciYgZ8D2uW\nhdHMoACfX9kUuHfwd53lQWBg66xaYAqsiFsdbamObDWKdFVYF7i5g3rhInti1uJK4NiImFvS81ji\nfmtgTES8ylDdZ6/aAU0gInbGtXAfYSOx7TT2dimNsZKSSZNB9rZPbryR+f9/8Y9Oln/iH9KS7vE7\nrNg1j6TnOhlI0nsRsTF2ZlyUhFX+gWWa1wB+odSEOycfMLyv1lu4aXyWp4BN2p9123Q0t4g4uc3j\n5qlreR5HIBuxPDnVRSPiI+CcUvymNVJ95F9w4+c3sfH7Bo74TJd2ex6fS3mo1P1VeBr4fNU+c9Pj\nxXI3UKZdTgFMy/A2Jy2hYnti1uJ4XOv3WjrewxGxFlaUXJiUwi+pk2h5u/w4zWsVSY/04filMVZS\n0gmpPmRzLKs8M/4RGouFPvJKvnaDQfZoT048x/DeYE8Ay1Xtsyg20kq6x5VY1OHWpNR2D64Bmog8\nNQGSXo+I9YG/prEfwAb1sZL2a3FuzzL8HHkU+FLVPsswvOF3r+h0bju3edymgjY4DXuPiNgHODJb\ns5b6lf0AWBvLZefhLSaOUJQ0Zz9siO2KhTY+wuqYhwJfxDLo/yV/uuhYYMnM9g3AbimN7EKc2bEV\ndZoNR0S7NX0jvX76QWD+ogZLImUvFmUcSfoAt4/IPnY7sFER43fIIsDofhliUBpjJSVtExFb4x/6\nWZi4HuvYiNhd0vl9mdxge9snJ+5kuPF1JbBXROzP0MJiUyCX/HZJ24xjqE7ypAb75a4JkPRUMshu\nxgvNP0j6YRtzuxUbDRUuxr24TsJqa6PS82e1MXandDq3Bbs4t0OxmMDPgd0j4hYcVZkLN45eADcf\nzhulHIuNipLW2ASnx50Cw7IwhOtiN8DOin2xSmIzLgN+HxELSnoSp9Rviw290WmfD7ARWItRdR6v\nrpuufrwfaqU7SDozx34nVyThG3AkcFpELCHp4QKmdzLu+dWPSFWveRXom6w9lGqKJSVtERHr4IX1\neCyrPAb/8M+FU5W2xzf49SVd14f5PQSMlbRj2r4TmEbSUpl9rgaWkDRvr+c3uRARm2HJ7A0kPZkU\n5O7GC8XKIuBVnB7x975NdBIn9ZDKK78+TJwnKQo2YlVgaRwByB5DytGUNiJG4RrPPSWNSyIgN2Kl\nwco58hhWDewoxbJVBnluaX4L4PSndWo8fS2wR1rQ5xnry7jmbwNJ1xY1x0mdiHgH+L2kH6XtD4Ej\nJO2b2Wc0sLKkRds8xoK4afDC2LHye0kP5Hzt1Fi9dklswI9h+G/1vjiqtE2K3vSMJNixvqQbG+zz\nR+CbzZRZI2I14FvYMXQcjaP/1SIctcZ7FrhA0vea7ZuHdK0uAdyk1Iw9Ij6GDfTNcPT0SEk9b80S\nESfgKO7S6pNRVBpjJSVtkLywywKrSrq3xvPLY4/53ZJW68P8TgDWlrRQ2v4Z9hCfzJBH+4fAWZJK\nEY8eEhEz415hlYXFaZJy1bWU9J4krd0Obbe1SIuUTXH6zDjgz5LebnMehTKIc4uIeahKFW/VOExp\nWVsD6+MI4F140T7RIkll78gJ/H/2zjtMsrJo3/ezCCgZREAQXIIEBSQLkhbhR1SRoJ+CAcEAKKDy\nkdMuoAKCgIABleSnIAoSBSQuWUSSgBIks0RRQIkuz++POr3T29vhzExPh5m6r2uu3XPO2++pCX36\nrbeqnlI08z3F9l5Vx+dV1/xJOhLYzfZsXbDvMEL9ePlCnKX2+nxE5O7ntlttvLTbtnuINOB16sna\nSzoW2AM41/a2LeaqtNupRP8aLu7LPJeK6PcahIMybBVaSacSUdQFK0qZin5+1T/zqcSaqq5C6kgh\n6Z1EFsBkosVAx0tM0hlLkiEg6d/A2c1SB4rdwG1tz9ExwwbuPYEe3tEerUjaHbjZ9i3dtiVpD5LW\nH+prbU9upy2jhUIAZXtCRnp220sV55cDPkY0NO90FLB2MVuhepHU1d6RvYikO4h+UZ8ujq8jok7L\nVBbxkm4A3l3ZHOywfQ8RGwYNIzySjgc+1mn7it5eNxEZNmtW/81LOgLYm4Geak0FSwrHpmz0f1IJ\n2xYkWjpcA+xl+/kyczeZ72/AXbY/VRyPIzY7nifqbRciVGovs/0/w7nXEGy7iig3+SDwCiGqVS+q\nOGJ1hVkzliRD43Vaq3RNoUt5yIXc9jVVx69IWpse29EehRxHtBC4BaYptE0sk642XIoPlP8SfWZ+\n0erDe6wi6T1EFGUeIopym+0nGo3vtEOlaAQ7D/Ci7Zc6ee+ySJqZSPt6xfZ9g3idiLqfzxanXmVA\ncQ9C0ew7hNNzZFuMLU9P947sYSYDn5KkIsXr10SD+99LupDIwlgT+FGX7FsYeKPFmDeZXsGxI9h+\nrKipmwxcKmlt2y8VIkN7E87JNmWe5bYnttm8M4nn4+eJfmCPUD9SXNZBWZCoU6+wEjA/MKl4/j4h\n6Xwi7bvTTKj6/+yFbfUYsehVOmNJMjSuI/oJNWNtZmyQ2DWKB/o53bZjlPMa0/fYEeV6xLSDCcW/\nGwITJR1t+4QO3bvnkfReGtQXSarUFz3SabuK+7+NkFf+ElWiF5IeJgRHju6Gcy3pU4Ry3c4uGh5L\nWpKol12yOD6fqLcpY9+uRG/DU4gaoG9SJepg++kiirIFJZyxIuK/E7F4eg9VirFVlFosuvd7R/Yq\npxMy9u8h+jP9mFAu/QQDLTtuoLHgxkjzBLClpANsz+CUSZqV2KTsSoaI7TslbUtEwC4oNtUOItYY\nW9azuUNMqPr/rETD5mXqjCvroMxcM3bt4rha/fIJuuMUj+v0PWtJZyxJhsY+wE1FKsFhlYJUmNYA\n8xBi5/jDXbJvOvpht32U8DCwiaQf2K7I+HYqF3wDoonoCsQH6YGEGtaYR9JCRC+kRYio8LUM9DNa\nl1g0Xi9pNUcvvk7aNgtwKbA+8bfyeJVt4wm1wE0lbdyFhdmOwMIVR6zgGCK6fhXwTmIh+0Wmb6XR\niJ2AOwlBAkuq9954gBIy6JJWBP5AqMQ22/DIWowRpKiZ3qXq+L/A1pJWZSAL40/tqDsaIqcDk4Cr\nitrpG2xPlTQTobr5bWAJ4jO7K9i+QtJOha3rEumBm9t+tYs2tdtBeYLp+8VtDjzv6eXkFyB61Y05\nsmYsSYaAopnpEsSD80XgNqKHxoKEsMfcxIKvVsnLbt3MtF021t1tL2zq2m77aKaoGTuOgQVgWclk\n287NsRFC0knEgnEf4PuevifVTESE5ihCpe3rJeZ7N+HsbkI4eLPUGVbqd6rok/UdQtJ7T9sPVF1b\nknB+PgYcYPuIVvO1E0mPAZdXnlmS5iJqPM61/ekiXfEOYpOn5caTpP8AP3HRAkDSIcDB1TVYkr4D\nfMv221vMdRXhwB4CnAE8Wf17HSrq3d6RyRAo/kZ/Q4hHmKjPegGYj9i8EnABUd89op+HheJhM75B\nrCl2oqZmqZUCosr3VxuxuqdmSDqaeM4eS2SQ7AucavvLVWMmA++w3aqZ+6gjnbEkGQLdUFgbDHV2\n259gYLf9PcQH0HVAN3bbRzWSPk2kWS1MRKseJXaHm2J7g5G1bOxS1Dv8zfamTcZcCixre3yLuRYh\nagIXBO4hIpGPEvWhSxAZJxUHpeXvVNJdxX/rqpYVhe53EJ/XK7Sar50UsuXHuGhkLWkTIkVxa9vn\nFeeOAz5je8ES871IiHPsWhzXc8ZOB7awPX+LuV4BLqoIArQDNe8d+S+gm70jexJJOwBX2n6827Y0\nQ9J2RAS32sm+jXAIzuyQDRWRmKbD6o1ptW4osSaZ1k+tGwI0khYAbiSekRBpoR+yPaXq+hPAD2z/\nb6ftq1DUFC/C9OUG02jlFA+V3IlNkqExks1M28G3iFS1Vrvt3yKaaiZtwvZZwFkw7QPyVNuHtvMe\nRSrs0sActq9r59yjlIWIfoDN+DONG8ZWc3Ax3yZFetG033HxQf5TIr2w7O7zUsAJjdK4bL8l6RJg\nt5LztZOXiYVrhcrmzvVV514D5iw5373AhCqxh+mQ9Hai3uj2EnP9m+kFAYaFonfkmUTk5Azq9448\nU9K/3IXekT3MKYAL1cIrifTVq4arvtdubP+K7jROr+ZQRihttlFaoaKVyupEDeb9DIjntKTYCPoa\n0yufvq24tjLRouU42/eXsO9ZSSsw8FycbPvlqiHzA3vRpSbTkjYmonbLthg6Io5sOmNJMgRst20R\nMEJsRzSy/ETtIs/23yVtTey2b086YyPJJKpULYdLsdg/nnCkZyI+2CsfjusAJwO7FmqayQAvAu9t\nMWaxYlwrNgEurbcgt/1EEV25m/jd715ivjeAVu0vZicU3zrNA8BmhciBgU8R8tTVC+33As+WnO8X\nRHPsYyV9q/pCkS76fSKivG+Jua4iGrW2i4OJ6Ga93pGnSzqRSD0/mFC5S4KvEQvsCcBXiAW6FT20\nKs5Z7cJ7TDICiodl7vkicEWx2XA3IZxzVKvXFdk1lxC/1xeIjZnq59TDRE3pc5Sstytq4C5qcO1e\nYrOm40hak7DrOeL5tBuhcHkfkTa6HJHKWmaTaEh0XUEkSZIRYSngkma77VQpoiUjg+1J7UprKOqU\n/kgIJlxE9KepTqX6I1EA3dEeLX3C9cC2kurWNUn6ENHw9/p612tYiEhPrDCVKnn2oq7ocuL3VIa7\nCtve1cC2+QlFwztLztdOTibSih4A/kpkBJxaM2ZVpv95NOMnhOjG7oRQyWcAJP2WiHLtDFxgu1UU\nE2B/YDlJ+xaS+cNlZeDXdRwxAGzfCpxN1AQnBbZ/5GhI/C7ib2Ef4u9/CaIG6nzgH5Ju7J6VgaTZ\nJC0iabF6X922byQpRHh+T9SQl2EvIiI8iUjJ/lnNfP8iNidaiu30AfsREf7VPdCP7mrbOxNCbIcD\nGwEjlqKckbEkGZ308m57MjQOIZyt/2f76qLeZq3KRdtvKhqutmq5MBb5NlHHN1nSWUQD9KcIx2oC\n4RS8RQhptOIlphfs+CdRY1DNi8TitAwnEmmtt0g6vI5tBxZzlYmytRXbp0tahoh4VGydptBZOLdL\nEU5bmfmmSvoo8T19nQEZ662JmqzDiq8ycz1URINvBL6saD5cL7JZVjSpp3tH9jpF2untxdfRRWRl\nF2KhuwDtjWIOCkmfI5zE5ZoMm5Zl0CmKkoG1gYtt/6PO9fkJ1cHrbT/Uhlu+RGQAlGF7Qnny0MKW\neumVDxNZGqWRtDoDwkf16rI6JnJWxVrEJtCUqnPjKsYAB0vajHBMtx0JA9IZS5LRSWW3faLt52ov\ndnm3PRkamxMfGFc3GfMY3Wma2dPYvq3o5XM6scjYruqyiDScHW3/ucR0jwKLVh3fCXxE0myO5urj\nCKn8ho2ka2w7W9JKRGpePadGwFG2zy4zX7uxvT8RharHrcC8wH8aXK8333+JPniTiLrHdxJO1N8G\no4ZYpOyeV9x/XhrX8ZpQp2tF3/WO7DUkLUWEOn6sAAAgAElEQVSkLG5IRFXmI/5+/06kLHbDph2I\nurapxO/4caBXVIT3JfqxNRIQeRE4mugPukuDMaWQ9A5iQ6psSvHiRO+zZlRUKcvcv7rhe0WkpFYk\np3K+087Y3MRnZ4U3iM3qam5g+s+NtpLOWJKMTnp2tz0ZMgsS6WLNeJMZP0QSwPZFRSrSlgy0n6jI\nlp/nql6BLbgS+IqkmW2/STh4ZwA3KppHrwN8gHJRtopt+0u6gFiE1Eqqn2L7prJzdZJCibW0Gquk\nWW2/XrzWRE1GvXHj3boB93FEE9pTiN/BFIa3yO6r3pG9gqTtGXDAKkq9TxFqvlcSYh6PNZ5hxPlf\nInq9jqfvadULTACuKJ4jM1BkO1xOiNo0RdLnG1x6G7F5tB0RxT66pG2vEaqizViMGgn+JnydaPh+\nBvADYiPnOCL1dwLhmP6eiKR2mmeJDZ3q49oSjpmpSkdvN+mMJckopNd325Mh8QLTR2TqsTShAJfU\noVhgD1dV7efE4m5+4Cnb/6docLsbA01NzyJSIwdj281Es9fRzC9pkeYjaVFC9GGJZuOIBepltsvW\nwNTe55Q6p+8iamW+IqlR78i96fzOfS/zCyKacRUhBnW17b9116TpWAo4rQcdMYhUvVZ1SI8RPdJa\ncRr1lRor0ae3gP8jNmLLcAewsaRZ6rW/KVQaNyHShMvwBeA+2zsUrwf4V+W5J+ky4vl3OTPWpY40\n9zO983UzIVy0tO37JS0EbEPrzdAhk85YkoxS+nW3PWnIDcDHJS1kewaHS9L7gE2JD9xkhCjaRBxZ\nc+6bimbFSwCP2H6mK8aNAGpjg2tga0nHVxXJ195rIWJRX1uDV49xwF9KjGvEDk2uzUP9aMT6wHqk\nM1bNG8TfxPpEnfLCkq4Ebqy3iO8CL9C7dX5vAHO1GDMn5eTwv9jg/FvE5tGt9T43mnAysXnyS0nT\n/b1LmodwmOYl+vKVYVkigl3NtGeG7dslXQTsSuedsUuBwyXNVwidHE/Usd4u6V7gfcTvYe+RMiCd\nsSQZxYyR3faxwveIFLvJkr4BzAbTUqjWI3qkvEX0kEvqIGlF4INEOtXMdYbYdikBiTovfI6QRh41\naMYG17PSoMF1ySlPAL4u6XHb06VLFU1fryZqVbYvMdfNRNrgUOn1XpH9wjxELV0lVXFfosbwtUJB\n8cri69Z6veU6wEU06W3XZe4GtpD0jXqpioUIykcpIfluu9bRGRa2zyzk8HcgInP/LGy6lUjDnhU4\nyfbvBzFt9XPiP8xYb/YAUW/baX5CRL3fBLB9Q9Gi5DDiGfMIsLftM0bKAPXe32aSJElSD0k7Aj+i\n/kbafwkRijKy4GMKSfMR6VSbVk41GGrbI9LUsx+R9BNCCru6wfVEz9jg+sO2/1liPhFpWVsCn3U0\nSK/8fq4hFnlfLLPoKVJDryP+5s8ayveXtB9JcxHiHR8pvt5fXHrRdimxhzbb804iq2AysGfReqIn\nkLQz8ENC/n+X6shVESX+MaFWuJvtH3bJxh2APYgU7Mpz8x7g+7ZLR7Ak3QfcbPsLxfGdwCu216oa\ncw6wtu2F2mR+35DOWJIkSR9RpCPuCqzJgBLdzcCJtusKIox1JJ1BqHhdQaRxPkkDsQfbk2teW6+2\nqAzdkGhuK5IeAe6xvUVxPM0ZK47nIHb3L7BdSgxI0UD6SmA1wjm+nUhNXBnY2XYpmXxJBwNrAJsR\nTtmfaSxtP6RoZzI0CgdoQ6I305aEWFRXNjokXUVE7z4IvEJEX+qJTtj2hh22bRyRIrdRYdtdxLNp\nEcL5mY14Zm3qBj1DO0Whxjgv4VSXVk+tev0vgJVtL18cH0HUZ04EziVEPI4HLrL9iTaZ3TekM5Yk\nSZKMaiS9ANxre50hvHaoi6C+j7JJeg34ge29i+M3gaNt71c15qfAxrbfO4h55yOiFQsBDxGO2Ddt\nHz+IOcr+Xvr+99DrVKVKV1IVVyCiKCIc5GuAK22f2AXbevrvRNLMRP+qXYi67gr/IqJmkxqpLfYT\nkj4BfBfY3PbDxTPgViKyXpG1f4FQvewlAZiOkDVjSZIkyWhnJsqrftUylmuL2t3gGgDbL0jaBLgJ\nWAnYbzCOWMEGgxyfjABFo/k1iPWkgFcpJO2Lf2/rZlTH9rhu3bsMhaO1v6QDCZGLeQhH7G/djobB\ntOj3VswoAva7waR82j6P6AtYOX5B0srAlwklw0eAM2y3arw+bCQNtYG2bddK3reFjIwlSZL0IEVP\nrCHR5b4+PYekq4F/2G4qq55Mj6Q/AY/Z3qY4vhxYDljaAw2u7wDebnvpOq9vleK5LKFUdmHN+b5P\n8RwrSHoD+CMDztdNoyGSk0AhYvFjwkGsbdD8L+CrtltJ8/ccRfp1rfMzC/Du4v9TgeeJ9iWVaOlT\nwBu2R2RzLp2xJEmSHqRIrxnKA7qszPiYQdJHiIaiG9m+vtv29AtFXcdXgAWLBrSfJZq23kX0A1qH\niIp8x/ZBdV4/ZlM8xwqSZh9KDVEyPZLWIaJP8xDRp9u6+awqlBQvIRR6f0mkmj5NpBZvQDSRFrCZ\n7Su6ZGZbKERnriDqiPcDrrc9VdJMwLpEeuU44vPj5RGxIZ2xJEmS3kPSaQzNGcN2o54zY5aiZuGn\nhNT1bTSQYx9J+eJ+oxCL2Zqq9CFJxxINrivpX2cRioav1Xl96TqyWmw/Ogg7ZyPEBeo6cBkpHjkk\nrWL7tm7bUYZCAXQRQpZ9Bmxf21mLpqmC/gJYpnKKgef+fcDnbd/a4LVbAZfUe++1wa7riGbn69b7\n/UpajZCDv9X2eiXnHAd8jWhdsRwwe2XjsCpl8Tjb97fnuyiHpBOIPorL1+uNJ+ntRE/DS8oKFQ3a\nhnTGkiRJktFM0a/nJ8DnGHAiaj/8REZkSiHpXfRAg2tJnwP2IRZ2jchI8QhSRD//RLy/zrL9SpdN\nmgFJGxN9GJdtNq7T731JSxEiFnMB1xOpnk8R6XIfISLPLwJrOJrN177+LUKF8TLgd4QSYT2lyKHY\n9m/gbNs7NhlzGrCt7TlKzDcLEWmbwEAj7ndXfuZFI+mngSNtHzLsb2AQSHoCONP2Xk3GHA182vZ7\nRsKGfEAlSZIko53vAl8gmqf+GphCA2n7pDUeYoPronD+EttfG64NRf+jU4j6juuAx8nfaTe4mGhR\n8FPg+4WE+cm2/9JdswJJaxLR8OeAE4mo7mQi6rQu4chfQIhSdJqDgDmB/7H9m5prEyVtS0SeDySe\nX7X8DyGusXnx75uSJhNS8ecPUwzjdcIxbMaUYlwZ9iLSGycChwMHE98/ALb/JelaIkLVUWeMaBEz\nc4sxMxfjRoSMjCVJkvQZRbpNbX3BE921qneR9CRRkL16vTSUpDWSliUWrnPY/sUQ53gZOMH2/m2w\n524igrCO7b8Od75k6BTPoy8BOwLvIaLONxPRsl/bLrtgHwnbziecgGVtT6lpXC5CVv5bwIds39Nh\n254kBE8aCgsVjZDXtF2rYlo9ZmaipcDWwMeBBYharz8B5wDn2X5wkLadB8xje0KTMZOBF2xvVWK+\newkRpXWL40OAg6ujkUWT+Y/ZXngwtg6X4lkyD/AB2zOkr0ual+in+C/bHxgJG3pa8jNJkiQZQNJ7\nJV0KPErIBJ9GpKc8KulSSeO7Z11PMw/wh3TEBo+klSTdCtwD/Jb4m6tcW1/SK5I+VnK6ewgZ63aw\nFPCbdMS6j+0nbE8kekZtSYjlrAGcCkyRdKykZqmkI8laRFPyKVXnxkHkr9o+GPgr4ZR1mvmBVj21\n/laMa4jtN21favsrxAbFekQD5QWAo4D7JP1F0iRJK5W0bR9gRUlHFH3kpiFpdklHAcsD+5acb3HC\nQW/GC8B8JedrJz8GFgZukfR5SeMlvaP49wuEWuhCwEkjZUCmKSZJkvQBkhYi6goWIXqyXMtAfcG6\nwMbA9ZJWs/10t+zsUf7KgGxxUhJJSxMqajMRi7ulgc2qhlxLLKC2ZUZ5+nr8APiZpBVt3zVM8yp1\nJ0mPUPTFuhC4sIiW7QTsDOwO7F6IQpzYYTn0uYFqAZc3gNlrxtxAqAN2mueA97cYsywR1S+FI93t\n+uJrT0kfJCJmnyDSAg+U9CjRJ2zPyusatKG4i0gv/Iqk24BngAUJYY+5iff/3sTvuRWvEZtizViM\nkMzvKLZPLMSKdiM2EGoREdH/4UjZkM5YkiRJf3AQ4YjtA3zf9tTKhUKC95vELuiBwNe7YmHvcgzw\nU0lLd1qpq885hOi/s5rte4vUomnOmG1LuglYveR8TxAS0jcUKUl/Ior2Z6iXKKFsdxEwQZKc9Ra9\nyPuBFYk6GxEOxbrAupLuALax/UgH7HiWUNqsPq6Nzs4MvKMDttRyFbCdpE/bPqv2oqRtiEjjL4d6\nA9t3AncCh0haknDMtgL2APasGrpDk2nmIQRFalmfiMKVccbuADaWNEsDxcK5iXqxG0vM1XZs7yHp\nLCLVtrrB9W3AabZH1K6sGUuSJOkDikaVf7O9aZMxlxK1EeM7ZVc/IGk9Ynd+QyLC82caS9tP5wRI\numqIt7XtDYf42p5A0tPAFbY/WxzXq/P4PiFt32rXu7p3XqWBbMMFSCtlO0nvJCIak4E9bf+71f2T\nkUXSAsRi9stEyiJEI+gfEiIZ7yUiLV8FLrO9eQdsuhKYanvj4vhsYkNhVdv3FxkHdwBTbK8y0vbU\n2LYU8Syag3BCriayHRYiVAfXAV4mal1nUFMc5r0Xqs6gGOk2FJI+QziV5xDO2zcpniWFkuKpRL3b\nx2z/fqi29CsZGUuSJOkPFqL1DumfiQ/xZHquYcAJOJjm/dtqnYAJDcZVOxX1zo+Gnc55iWhWM0RE\nz8pwKEP8uTRwil8hhCO2k/QA9VOc+t4p7nUkbUg4WFsSUaZ/AscBP6oRjngY2FXSrMCnOmTepcDh\nkuaz/QKxGbM1cHshKvE+QtFw7w7ZMw3bD0raiGikvnbxVf1cuQ/4QrsdseLeT9ccl+7rN8T7nalo\nJL0D4XT9E6CoR/0A0fvtpLHoiEE6Y0mSJP3Ci8TOcjMWo0HEZ4wzZCfA9nRCV0W/nLOJ4vXDCEfv\nacJZ3gA4gFDe6tRicyR5hhDKaMYHCFn5lhQiD0NlQpNrswONhAlGg1PcsxRO8BKEA3ErEQU7q0Uj\n4geYsW5rpPgJUdv0JoDtGyR9knjvLk/U3+7drWbvtv8ELCfpwwzUYr0I3G77hm7YNFLY3rGQr9+D\nSGEV8T3fQ6Te16vXGhNkmmKSJEkfUEgcbwF8pF7+uqQPESlbF9veptP2jRUkHQZ8EVi+XoNVSfMB\nfwF+Xii19S1FU9fPACvavq82TVHS6oRC2km2d++epUm3kPQKcCbwQ9t/LvmaRYElbE8eUeN6nCJ9\n+iXbd3Tblk4j6R1E5P1F2//ptj3dJp2xJEmSPkDSKkRdwUxEI9Da+oLPEL1l1i67KEoGT9G4+ELb\nezQZczxR+7BE5yxrP5KWIQrY/000a12JSAtckSjcPwR4O+GsPdZgmnrzVvoiVfqWHVacfzswF/B8\nocyX9DiS5qm3KZG0RtJU4Ce2d+22LUl3yTTFJEmSPsD2bZK2BU4Htmd6KWYRUt87piM24ixMyGM3\n401GgZR+EQ3bhoh8nFicFiF5LaJGa+tBOmKbAj8nNhEqtXWHFZdXIkQ5PlvcM+lx0hEbFs8Dr3bb\niKT7ZGQsSZKkjygacG5JTX0BcF6mezSm6COzB9GMdl5mFOqAEHto2pRY0oNEBHL5BhLNsxI1Y7Ld\nqt6qLyjUzr4ArElIlb9IpCeeWogilJ1nNaL/0fNEG4Y1gM/UqDM+CNxmu2nNnaSdCWW+dWsa+lau\nL0LUCn3H9s/L2pgMnaK32CKEGMMMlGhX0A4bHhriS1u+99uNpF8Di9leq5P37QT99HvoBdIZS5Ik\nSUY1ktYi+lu9A/gvIUzx33pjbS/eYq6DgElEyuj+wA22pxa93tYBvg2sBRxi+/C2fROjAEnnE72m\n3m/76QZS+WcCq9hepsVc1wLjbK/TZMxk4C3bG7TnO0jqIWlj4FiiQXFDWrUraJMtjzB0sZ6m7/12\nU2wQ/RE4CTjU9pvDmOsh4DjbP2gy5mtEG4gRT5/up99DL5BpikmSJMlo57vEbv3OwCm26zpiJTkC\nWJWQZ74aeEvSC8B8wDgi9e6CYlwyPWsTEdynm4x5nBCqacUywG9bjLkL2LakbckQkLQm0YD7OSKV\ndTdCSOg+wvFejng/3N4Je/qsx+J+RBR9f2AnSXdSvwm6bbdqrDyeaM7cjHlorcjbFvrs99B10hlL\nkiTpI4pUr1apdofVOT+WWR34re2ThztRsXv9CUnbEaqKKxOO2IuE2MWptvuy3qlQdxsSJVPQ5iBS\nFJsxG+HUtmJu6vcVq+Yl4n2SjBz7Aa8RjYmnSNoNuNr2oZJERJG/RbR8SKZnh6r/L1R81cNEo+Th\nMiet612TLpDOWJIkSR8gaS7gXKKXVb1mwxWqBRGS4A2gtMhEGWz/CvhVO+fsAa5h6H25yqSgPUn0\nJWvGSkCZepOnCFXHZqxIRGySkWMt4IKaur1xELtCwMGSNiOcso5HKSVtb/uXJcadYnvHTthUxbDS\n8SQtVnNqnjrnIN6biwHbUO69NeIUn2dzE9L2L3Xbnm6TzliSJEl/8D3gI8B1wKlEOtdw0u3GEjcS\nEaykOUNujl2SS4CdJa1j+/rai8Wi/cOUS/G8Gvhck7nWBTYD/m+YNifNmZvpNzreYMaGzjcwvfpr\nJ/m5pCm2r240QNKPCYGajjpjth8d5hSPMP37dY/iqxEiopRdQdIshOjOjkRaZeX8I8ApwPfqiSKN\nBVLAI0mSpA+Q9DTwBLBG9mAaHJI+SDhkO9v+RRvnnY3G6aIMRvJ9LFAoHN5JpCKeQCzItiXq79YD\nvkake37QdtN0xqoeaDMBPwQuJSJvixBO2C7AVGA1238dgW8nASQ9Dlxke5fi+DHgVttbV405Cfi8\n7Tm7YN89xN/EOrbvrnP9WMKBOdd2X9UXFk3ZTThZnyfeW/UaSE8F/gFcafsPHTOwCklzAlcS9bYm\nNhOfJlIzFyW+h1uBDW3/uxs2dpN0xpIkSfoASa8CJ9req9u29DqSDq5zenVgc0Ja/c/UrzcqVW8n\n6XPAPoQ4QSNsO7NPaiial58NVCu6VRaUfyf6lv2l5FxbEKmiczJ9hEBEvdh2tn/fDruT+ki6Ephq\ne+Pi+GzCGV7V9v2SFiIchCm2V+mCfYsBNxHtKNa0/WTVtSOAvYGLga2GKezTVSS9BUy0fWi3bamH\npO8D3yBS7fey/XDVtcWBo4GtgGNt79kdK7tHOmNJkiR9gKS7gDtsf77btvQ6xcJkKLiV/LakHYiU\nmqlE+lXDdFHbXxyiHT1Hkfa3MlW97WxfN8S5ZiIUE9di+r5l5w92QSzpnYQQwocItbh/FXOdbvsf\nQ7EvKY+kvYDDgXfbfkHS2oSa4uvAvcD7CGf5i7bP6JKNHyxsehxY2/ZLkiYBBxEtLz46VtPjOkUR\nQX2ukUNeiL3cBsxve9GOGtcDpDOWJEnSB0j6KlFLs3z17m4yI5LWH+prbU9uMffdwLuJtKdRn/5W\nLK5PASoNrMVAFOoBYEfbN3bDtqT7FEIMywH32n65OLcVISK0JFHXdGw7lEyHg6SNiAjYTcBVwESi\n/nZT26920bQxQZHZcZzt/ZqMOQLY3fZsnbOsN0hnLEmSpA8o0m2+R0QAJtE41S5rlUYQSa8Bp9ne\nudu2jDSSViUWrG8nIgvXMFDnsQFR5/UqsK7t27pkZpKUQtJngdOLwz8C/8/2f7poUluRNB8hjtGq\n9cmGHTUMkPRX4JpKbWGDMT8C1rf9/s5Z1hukM5YkSdIHFKl3ldqaZg/urFUaQSRNAX5ju5lq2ahA\n0qWEguc2ti+sc31LovHyFbY3azHXYsC7gPsqBfqFoMeBxOJxHKGQ+J164h1VPdBusf3aYHqileyB\nlowCSvxdfINoRr0TNZtZ/fx3ImlZYrPkXbRofdIqFXskkFTpNfdB20/Uub4YUVt4mO1jO21ft0ln\nLEmSpA+oUs5qyWiqVWoHkjYEtgcOrOmHVLm+MFH3cobta1rMdTIRnVzJo/wDVNJLwO9tf7rJmLOB\nTWzP3eD6TMBpDEibv0TUeN0K3EKkfFYwIeKxWm3voarNiOUKYYjKcUu6sfhMukPJv4u6G1r9/Hci\n6SJCoOgI4GTgcdtTu2vVAJLGA8cRrSuOA64FngEWBNYnFC1vAL5JiK1MYyxkeuTuaZIkSR9ge4du\n29DH7AYsW88RA7A9RdJahDjFNS3m2o9YNPxY0p6jXIb5LeDBFmMeADZucv2rhCP8H+A+YBngZ4Si\n4nzAt4mUsXkJafvVgT2BQ2rmqfRAe77mOOkyRY3mXgykx42rM6xTEfux+nexLnCx7f27bUgDHmIg\ns6OeYq2IFhcfrzlvxoCvkpGxJEmSZFRT9D66wnbDpq6SfgpsbPu9Lea6ilDt+yDwCuGMNJLJ73ht\nRjuRdAXwqu2PNRlzETBLRdq8zvUbgGUp0pMkLQrcTijsfcP2j6rGzkr8PP9hO5t09wFFe4HziPqk\nx2iuLrpBB03rOYpnx1Bo+Swpotg/sr3PEO8xogwms6OWsZDpMeq9zSRJkmTMswBQNypWxTPFuFZM\nqPr/7MBKDcaNhp3OA4FrJO1S7TRVkPQ1YEOm/5nU8gHgd5U6EduPS7qQaFJ7XvVA269LuoSBlMak\n95kIvAls0a2Gwn3EhAbnKxGjRufLPEv+TESde5LM7GhOOmNJkiQ9iKRTiA/h/W0/UxyXwbZ3GkHT\n+pEXgVa9axYlUumaYrteCtZoZWNCBvxESd8glBUrdR7rED2kLgU2kbRJ1euqm2fPSURLqqk4Zk/V\nuedTQFukrSVtTAgCfKgd8yV1WR44Kx2x1tQ+OyTNQqTrLk+k7l3D9GqlBwB3A58qMf2hwGWSJrSq\ne016j3TGkiRJepMdCGfsSGIBvEPJ15lQCksGuAX4hKSFbD9de7EQ8PgEUQuWDDCx6v/vK75q2az4\nqsYM1IWIGdPWmjV2LhVRLGS836z0tqq5thZRizbkfnNJaf4NvNBtI5pRNBTeFtgEWASYtc6wbqQV\nHwSsRvSOrE51fhQ4TdIFwF+KcQe3mGtR4HzgD5LOpHnrk640304ak85YkiRJb7J48e+TNcfJ4DkB\n2AK4TtKewGVFStyswKbAMcAcwA+6aGMv0nM1PpK2AY4CxhfHfwG+avuPkhYAfghsRTiBd9B6EZsM\njyuBtbptRCOK9/jviRTBSspfdUrgYFIB2832wDk1jtg0bL8g6bfAZ2n9d3waA9/L54qv2u+p8n2m\nM9ZjpDOWJEnSg9h+tNlxUh7bf5B0GLHD/DvAkv5JKL+p+DrM9qWDmVfSe2i8097XfYsAbE9u01QT\nIjgxcAwg6SBmrJWZ0GgSSesSaV3Vr1kRuETSBOBCIkJwD3CI7XOHaXfSmn2AWyQdCHy7B9s97ENs\nKhwGHE+ocU4k5N8nEFLwNxLOS6dZGHijxZg3mb79QyNGvcjFaCbVFJMkSZIxQVFDtBvRJ2weIo3n\nZuAE25cPcp5jCZXAhvRz36J2UfR9Ksu0KEW9n52kc4io137Az4vTOxP1Mi8Q0c1vAT+2PZj7JiVp\nULs6nkgJfZSIRjZSF+14+nQROX3d9mrF8VvARNuHFsdLEDZPsn1Mh217kGgfsbztGZyyIqp3N7FW\nX6qTtiWdJZ2xJEmSPkLSOsQu6MpEX6wXgduA02xf303bxgKS1iQalj4H/JZw7iYTPbTWBZYDLgBu\ntz2pW3b2CpJq+4WVot7PTtKTwL22/1/N+SuJKMdXbP+89nVJ+xikc11NXQd7pJH0CvBT23sUx1OB\n79g+qGrMmYRDtEKHbTsImERE5vYHbrA9tWiUvg5R97gWEeU9vJO2JZ0l0xSTJEn6BEknALsyY2rX\nSsAXJZ1ke/fOWzam2A94DVi9aBa9G3C17UMLoYBJRHTmgG4a2Su02SF9FyFMUMuthDN2ThvvldSn\n32pX3yTerxVeJv6OqnmUGZsNd4IjgFWLe18NvCXpBaIZ+jjiOX9BMa4UkmYDtiY26+ZhYLPud7Zb\nqsW2E0njMkJdjnTGkiRJ+oBi0f814CHqyyAfCHxN0n22T+qWnWOAtYALbFf3LRsHsfUPHCxpM8Ip\n27YL9o1m3kY02q7lFYBGQghJ++jD2tUniLrOCvczo+DIynRBEdL2m4TK63YMZDvMx4ADdartM8vO\nJ2lz4PRijlqRkmMlfdH2Re2yvwTPFoqQvwP+YPv1Dt67r0hnLEmSpD/YmWhcvFoLGeRdgTHtjBWp\nVG8B77d9f3FcJifftlt9Ls4NPFZ1/AbR/LmaG8jGxUnSC9wAbFR1fB5wuKSfEU7ChOL6rzpvWmD7\nV8O9v6RVgHOBmYBfEv0BnyLEPz4CfAb4raS1bdeLLo8Efyzu+wXgFUmXFjZebPulDtnQF6QzliRJ\n0h8sAZzcQgb5HODLnTWrJ7mWcL5eqTluB88SKozVx0vWjJkZeEeb7pdMzw6FcmI14wEkXVVnfDf6\nRyW9w6+ARSWNt/0IcBywJbAjEY0S8CCwb9csbA8HEM+4dW3fXHPtNEknEdkU+wPbdMIg21tImoNo\nK7IV0Y9wG+ANSdcQjtn5tp/phD29TAp4JEmS9AGSngDOtL1XkzFHA/9je9HOWTa2KMQiptreuDg+\nm1hkrFpE4RYi1Nmm2F6li6YOCUlbAZfYfq3l4A4zRPGIrghHJL2LpLcRDtlSwCPAhbbrpb920qbZ\niE2eun+rth+rd77q9c8Cl9r+fJMxvwA2sb3AcGwdKpJmAf4f4Zh9jKjde4tQtD0XOM/2Q92wrduk\nM5YkSdIHSDqR+CBbvqg1qL0+CyGDfJnt3TptXy8jaT3gJdt3tGGuvYDDgXcX0ci1CTXF14F7gfcB\ncwJftN13zVULh+cV4DIijeuiXqnFkjmQXcQAACAASURBVLT+UF7Xxn5pSdJWJH2O6IW2XJNhLdOn\nJb0OHG27oXCQpG8De9p++5CMbSOF2NF6hGO2JfBeIrL3FwYcs7u6Z2FnSWcsSZKkD5A0F3AF8Cqh\n6HeTbRcfah8Gvks0H97I9svds7T3KOSsf2J71zbMNRexcLq38nMuokmHEemKjwDH2j55uPfqBpI+\nSSyQNgfmItToJjOQUvRUF81LkmEhaU4KlcFu1y1J2gE4BZhK1LY9Dvy33ljbTZs6S3oYeLC27UPN\nmMuApW33nCKmpJWJFMZPAO9njEW00xlLkiTpAyQ9BMxCFGRDfGg/D8zPQP3vU4SgRDW2XVvTNKaQ\n9Azwf7b37LYt/YKkmYENCZnsjwMLEClFfyIk5M+z/WD3LEySchRpif8LfInppfkfBn5GRJTqOkEj\nbNfdxPN8Hdt/HeZcJxEiTwcA37M9teraOOCbwFFEQ/SvDedeI42kpYFP2D6q27Z0inTGkiRJ+gBJ\njzBEEYpe3AntJJJ+DSxmu1bSOilBEX1dm4iYfYJY0JpIyzyX6GE07BTQJGk3Rfr2pcD6xN/sEwyo\nDL6HEPC4DtjYdu1G1kjb9hpwmu2d2zDXQkQPvoUItdfriO9zIaKB9HiiFcpqGd3uPdIZS5IkSUY1\nkt5HyCyfBBxar+YuKY+kDxIRs08AKxCL3EcJp2zPqnHrDfUetq8drp1JImlf4DvARUS91ANV15YE\njiHEJA6wXbq5cptsmwL8xvYebZpvPPATora4lsuBnW0/3I57Je0lnbEkSZJkVCPpFEI5bW3gGeBO\nYpe49gPQtneqee1Q1b3GRHposaDdmoiarVEtNDCI/m4zMJbqRZKRQ1JFBGIl2zOocRYpfHcQ6+EV\nOmzbycCHCtvathiXtAjRQHpuooH07bafbNf8SftJZyxJkiQZ1QxCEn2GovFMDy2PpIVsP111PJEZ\nf3YfAjYF/g5cTzjFlVSqJYFLgFtsT+qEzcnoRtIrwAm292ky5khgN9uzdc4ykPROQrhjMhG1+3cn\n75/0Dtn0OUmSJBntDNkpsj2+jXaMaqodseJ4YvWxpDUJJdA9gJOqIxVFhGI34Ajg0BE3NhkrvAHM\n0WLM7IRqaKf5DdFG4kvAdpIeAOq1kcjG5aOcjIwlSZIkSTLiSLoceN32R5uMuRh4m+1NOmdZMlqR\ndC2wDNGf8bk61+cn+jPeb3vINY5DtG3IEfsG880G7ASsRIiTzNxgrnTseoyMjCVJkiRJSSRtb/uX\nJcadYnvHTtjUR6wBnNBizB3A1ztgSzI2OBE4C7hF0uHA1QyoDE4ADgTeBezeacNsj2vXXJJWBP5A\nfC9qdtt23TNpH+mMJUmSJEl5fi5piu2rGw2Q9GPgC0A6Y9Mjoi6sGUu15UbS54lefBfbfrEdcyb9\nh+2zJa0E7AvUa8Qu4CjbZ3fWsrZzHOGIHQKcATxZ3WusV5A0ExGpnBeoG+0bi0qqmaaYJEmSJCWR\ndA+wCNGo9e46148laqLOtb1tp+3rZSRdCnwE2Nr2RXWuf5xoKH257c2Hea+KkuPLwI+AY20/O5w5\nk/6lqFfciRqVQeAU2zd107Z2UAiVXGT7U922pRGSDiKaT8/dbNxYVFJNZyxJkiRJSiJpMeAm4C1g\nzWrJaElHAHsDFwNb2f5vd6zsTSStClwLvJ1QkLuWaDWwINGUdz3gVWBd27cP816nEVGPFYAVgTc6\nrZaXJGWR9B5ik2fWetdbRYskPQucbnuvETBv2EjamxDneRE4H3iciFzPwFhUUk1nLEmSJEkGQdH0\neDKxoFjb9kuSJgEHAVcAH7X9Rjdt7FUkfRg4BVi6OGUGalzuA3ayfWOb7zk34eDNEI1Lkm4iaWPg\nWGDZZuNaRYsknQUs3GkRkrIUSpFvB1apJ6Qy1klnLEmSZBRQNCd+kyhWP972C102aVQjaSMiAnYT\ncBUwEbgO2NT2q100bchIOniIL7XtwwZ5rw8DqzCQMnZbu52wJOllitTJa4HngN8SrR0mE5sS6wLL\nARcQTZubRoskLQH8ETgGOLKdTaTbgaTXgJ/a3q3btvQi6YwlSZKMAmpkkv8DnGx7z27ZMxaQ9Fng\n9OLwj8D/s/2fLpo0LBpIbVcvElTnvCgpvZ0kyQCSzgc2AJa1PaV4/020fagkAZOAbwEfsn1PifmW\nAW4kepXdQWxy1GLbO7XtmyiJpEeB39vepdP37gdSTTFJkmR0sDgwjqiRmUDU4CTDRFKztJ/HiPqH\ndYl6iFVjDRX0oSrYBnXOfRPYHPglcA3wNCELvgGwHREdPK5D9k1D0srAWsAvK2qJkmYHfghsSTTT\nPdL28Z22LUlKshZwge0pVefGQXhMwMGSNiOcsqZiQEXN2XmESuG8NG50b0LIpNOcDWwlaVbbr3fh\n/j1NRsaSJEmSpAFVqnxNh9Ub0+/RokIe/kdEvdVtda6vRqRZfdX2L0rOOTPhLK1BY3nrlrv3RY3M\nurYXqTr3A6JH2b8JIYS3AZvZ/kMZ25Kkk0h6HTjG9v7F8WvACdUiHJKOA7azvUCLuX4LbE3UY54O\nTKGxQMaj7fkOylM0pL6MiNrtbvvhTtvQy2RkLEmSJEkacyhjt1HqN4Ff13PEAGzfKunsYlxLZ0zS\nwsDlhFhBq8a0rXbvVyMa+Fbmnpno7XYLERmej5Au351ohpskvcazxIZE9XFtH76ZgXeUmOsjwGW2\nv9Qm29rN3cT3sjCwuaQXCcesFttu1Ytw1JHOWJIkSR8jaVlgMyIt66xscNtebE/stg1dZBng9y3G\nTAE+WXK+YwhRgjOBn9JE3roECwBPVB2vBswJ/MT2a8CUoiZn0yHOnyQjzf1M73zdDGwmaWnb90ta\nCNgGeKDEXOOAv4yAje1iHPFef6zqXL0NmWabNKOWdMaSJEn6gELpbhfgAxWlxELR70JglmLY3pLW\nsP2PLpmZjC5eAtZuMWYdIi2wDBsD19reflhWBWb6Ncw6xbnJVeeeA97VhnslyUhwKXC4pPmKZ/rx\nRKrh7ZLuBd5HbDDsXWKum4HlR8zSYWJ7fLdt6GXGdduAJEmSpBSbAX+rkaz/LrEAPYSo7Vkc2KML\ntiWjk4uBdSUdLWnO6guS5pR0DOGsXVhyvrcTqpPt4DFgzarjLYEnbD9UdW5h4J9tul+StJufEI3O\n3wSwfQMRZX6YcKyeAnaxfUaJuQ4AJkj69AjZmowgKeCRJEnSB0h6Cvid7V2L40WINK/v2/7f4twV\nwAK2V+yepaOfQnZ6W2ATYBFCLKIW296wo4a1GUkLEH3UxgMvE3LZzwALAisBcwEPAR+2/WyJ+f4I\nPGx72AtGSQcRKnPnAq8BnwGOq27nIOlm4E3b6w73fknSyxSZE2sQm3bXAX+msbT9oHoCJiNPOmNJ\nkiR9QKG0dbTtA4vjTxG1NxvavqY4dyShbDdP1wwd5UialaijmsCAimJt/61R03tL0juJCOx2wGxV\nl14h5O73L5sWK2lb4AxgNdv3DtOuOQh1trWKU3cAG1TJ3C8OPAh8t/KeSZLRSoMegfXoyHOpUGKF\n2EB8ueq4JSUjgaOKrBlLkiTpD54jojAVNiDSW6rTvmYh089Hmn2In/1hRI3H88BE4GTCQTuCaLz6\nue6Y114KR+srknYlVBDnJnbc/2Z7sOIbzxIpjTdKOp7Yva+nqNayR5vtfwNrS6rUydxru3pBaqL+\n5tZB2pgk/Ui9HoHd5DTiPXgzEVWvHDejsrk15pyxjIwlSZL0AZIuBD5MNHN+jZDwvs32RlVjfge8\n3/Yy3bFy9CPpL8Drtlcrjt8CJto+tDhegojSTLJ9TPcsHT5F6tPDZXuIlZiv0rOtEklsuAAZDVHF\nJKlG0kOtR9Wl7+TeJe1AvL/PLSJjXyj7Wtunj5hhPUpGxpIkSfqDo4i+SndWnZu22Jc0EyGmcHmH\n7RprLEnIslcw0T8nDuyHJF0M7EDV76dPORA4ro3ztb1nW9FfbENCMn+OSj2MpLcTNW3P10TMkqRb\njGNof/99J/du+7Sa4zHnYA2GdMaSJEn6ANvXSfoo8GXiA/2Xti+pGvJh4Engd92wbwzxJhGZrPAy\nM8qnPwp8vGMWjRxPEg5NW2h3zzZJmwI/BxZiIMWpIk6wEnAD8FmitjJJukon5N0lrUjUdy4HzF7J\nnJA0nhD4uNx2Koz2GJmmmCRJkiQlkXQPcLvtzxbHtwCz2v5g1ZjLiHTRRbtkZluQ9H3CqVzB9qvd\ntqcaSasB1xM1e0cRC83PVKc3SnqQSOX9VHesTJLOIelQYH8G6oaniXUU6dMPAN+wfUKXTEwakIXe\nSZIkSVKeG4goZIXzgBUk/UzSFpK+B2wEXNMN49rMIUSfrvOqhDJ6hYMIRcfVbP+AWGjW8ifgg3XO\nJ0nXkVSq+bmkU0qM+TSRVnw5ERX+bvX1ov/erXQoYi/poSF+/b0T9vUamaaYJEnSJ0gaB3wN2J6B\nNJS3FddWJlIYj7N9f/esHPX8ClhU0njbjxA1VVsCOwJfJNLlHgT27ZqF7eNOQqFzFeDOor3Cs8xY\n91JaYKCNPdrWBs6z/XSTMY8DW5SxK0m6wM8lTbF9daMBkn4MfIF4vjRjd+K5s6XtNyRtVWfMXwnF\n104wZurj2kE6Y0mSJH2ApFmAS4gP0xeIWqU5qoY8THxgP0dENJIRoOjpdk3V8SuS1iYcsqWAR4AL\nbb/SDfvazDiiRu6xmvO1C6ZSC6jB9GgrMd0cRIpiM2YjM4CS3uXvwO8krWP77tqLko4FvkI0Nm/F\nCsBptt9oMmYK0bB9xOlEfdxoIh9SSZIk/cFeRC+ZScQH6s+qL9r+F3AtEXFIOojt/9o+x/aRtn89\nShwxbI+3vXiZr5JTVnq0HQ7MTzheE4GFCdGBx4GziGhcK54EPtBizErAUOXEk2Sk2Qz4D3CJpOoe\nkkg6AtgDuBj4dIm5BLRSDV2Q6cWHkh4hnbEkSZL+YHvgBtuHFlLd9aIHDwOLddassY2kOSUtKqlt\nqoOjmE8SghqH2H6hctL207bPAj4CfBT4Rom5LgE2kbROvYuSNiNq+y4avtlJ0n5sPwZsDswJXFp5\nhkiaBOwNXAFsU7K5+gNMX8s6HUWK+zrAPcO1ux1ImiufmwOkM5YkSdIfLA7c3GLMC8B8HbBlTCPp\nbZL2LdT6/kWkJv5T0oPF+VFZAtAGx3NJQgClwgw92ohIwA4l5vou8bP/g6QjgfcXNm5RHP8GeAr4\n/hBtTZIRx/adRA3l0sAFRaP1g4DrKOq/Sk51NrCKpD0bXN+fSKP+1TBNHjKSZpF0QCHS8U8Gnpt/\nL86XiYiPSkblB0aSJMko5DVgnhZjFiMWqMkIUSwYLgXWJ5yJx4lF/7uB8cC3gU0lbTyIhVTPUjiW\n/wt8idgQqJx/mEiVPbrkzj20sUeb7SclbUwsQvequnQBkbL1d2Br263qypKkq9i+QtJOwOnAusSm\n2+aDbCdxHBF5PkrSpygyJyQdXcy5WjHvye20vSyS5gSuBFYtbHsMeJroEfheoiH8xyVtaPvf3bCx\nm6QzliRJ0h/cAWwsaZZ6i3xJcxP1Yjd23LKxxbcIAYqLgD1tT5NUl7QkcAzwsWLcEd0wsF2MgOP5\nBKGgWOF+YK2aMSsTEd6W2L5N0jKEYuJawDuBF4lF5/mDcBKTZMSRtF6Ty48B5xOO0xHAqiE8Gti+\nttnctl+VtAFwPJHSXum39y2iluz/gK938T0xiXAIzwX2sv1w5YKkxYGjga2KcY2ie6OWbPqcJEnS\nB0j6DPBL4BxgJ+CbwMG2Z5I0D3AqEVH4mO3fd8/S0Y2ku4r/rlTU7tVeH0c4zrK9QkeNazOS9gW+\nQ2vH8wDbLR1PSScDG9leojjenxDzOAX4HeHkfgv4le3Ptfe7SZLuIqlRre90w+qNqW5mXuI+8wGr\nM7A5cYvt5wZhatuR9DjwnO1VGlwXcBswv+1FO2pcD5DOWJIkSZ9QNP/cgUj3+ieR4nU7oSo3K3CS\n7d26ZuAYQNIrwAm292ky5khgN9uzdc6y9tNux1PSBEJRcRfbj0iaDbiaWDhWZO0fBDaw/WR7vosk\n6Q0kTWRovbewPanF3J8HnrF92VDmH2kkvUr0wNyvyZgjgN37/bk5FDJNMUmSpE+wvaOkawnJ4xWJ\nxesqhELW922f2k37xghvMH1/t3rMTjjM/c5ShONZVzLb9luSLgFKbQAMp0dbsdgcErbPGOprk6Rd\n2J44gtOfApwA9KQzRry3W9U8z12MG3OkM5YkSdJH2D4NOE3SO4B5gRdt/6e7Vo0p7gK2lTSxXuqP\npPkJdbQ7O25Z+xlxx7OoYTmnxNDTGHxUoZLylc5YMtp5mt5WSP8pcICkb9t+ovaipMWA/wEO67hl\nPUA6Y0mSJH1IobQ1GLWtpD2cSDQmvkXS4USa3VOEKtgE4EAifXT3bhnYRnrJ8fxiB+6RJP3KpcAG\nksY1imR3ksK5quZcYD3gNknHAdcCzxCNqNcnsj0mE7WjY46sGUuSJEmSQSDpO8C+1I/UCDjK9r6d\ntar9FBLZZxFy840cz/HAZ2yfXef1mVqYJE0ohCu2JZRwFyFqf2ux7Q1bzLMgoSJ6DaFW2NWWDk3E\nSuoKlBTnAd6yPeYCRemMJUmS9CCSHhriS217ybYak8yApDUJVcuViVqHFwkxlVNs39RN29rJcBzP\nkupx9eb0YNTjkqQfkTQr8HtiY6PipKhqSOW45ftB0lXAfMAKRHrxI0TqYu37r6Vj1w4knVbn3qWw\nPeai4OmMJUmS9CCSHmHoH2aLtx6VJOUYquMp6QtDvaft04f62iTpByQdDEwk6qSOB54vjk8mHLQj\niL6Rn7M9tcVcZVMTc6OjB0lnLEmSJEmSvmIQkeOMFCc9iaS/AK/bXq04fguYaPvQ4ngJonXEJNvH\ndM/SZKTpZeWVJEmSJElGCUVz8jLjVi0xbByRwlX7NS9RxzYemIVc5yS9y5LADVXHBmaedmA/BFxM\n9JacDkm7S1pjpA1MOsOYK5JLkiRJkqQ1kj4J7AJ81vaUOtcXIWTjT7J9bokpL5S0oe03mtxzRaJX\n0vzNJrI9vskcSwE/IGT3NylhV5J0gzeB16qOXyaUWKt5FPh4ndceR6Q03gIgaSoRVetJaXhJp5Qc\nats7jagxPUg6Y0mSJH3AYJTpUokuaRNfAuap54gB2H5S0tzFuDLO2IeB/wM+Ve+ipPcDV1AVHRgK\nth+UtDVwN3AIsN9w5kuSEeIJQkGxwv3AWjVjVgZeqPPa15heebESGe5VdmhxfZpYCVGfOqZIZyxJ\nkqQ/OI3Wgh7Z5DZpJysAF7UY8yfgYyXn2xc4UtJxtr9RfUHS+whHbHZgs8EaWovt1yRdDnyGdMaS\n3uQGYKOq4/OAwyX9jOi3NaG4/qs6r30Y2ETSD2w/U5zrZRGIRqJS8wCrAwcRYiV93xJkKKQzliRJ\n0h80kvutfJh9GjiHqDFIknYwH/BsizH/oEVKYQXb35O0KLCbpMcrogSSFgeuIuq9Pm772mHYXM1/\niZ5oSdKL/ApYVNJ4248QqYdbAjsSz3sBD1LfQflJMX5KtCoDYKKkiS3u6W708bL9aINLjwJ3SrqM\naDJ/BfDzjhnWI6SaYpIkyShA0oaEI7aR7eu7bU/S/0h6ArjB9v80GfNrYH3bpZyeosntb4lF5/ZE\ndOA6YGFgG9utInGlkDQ/oUT3qu33tWPOJBlpJL2NeG8sRfQKu9D2Kw3GfhrYgnjvbEA4No+0uoft\nDdpkbluRdAawku0Vu21Lp0lnLEmSZJQg6TxgLtsf6bYtSf9TOFofB1a2/bc615cj+o1daPuTg5h3\nVuBKYFWiMe17gE/bPmcQcxzc4NLbgEWJBe3cwH62jyo7b5L0I7Wy+P2IpO8BX7f9jm7b0mnSGUuS\nJBklSDoK2Nn2XN22Jel/JK1O1HG8CBwKXAo8SYgObEbUecwNrGP7j4Oce14iKvY+4Au269XFNHt9\nqya3LwHH2z5kMPMmSbeQNCeRdv6i7ZcG+dpDgKvbmOLbUSTNRChDLlI2yj6aSGcsSZJklCDpImBd\n23N325ZkdCDpy8BJwEx1Lk8FdrX9swavvarF9AsSNV131py37Q1b2LV+g0tvAf8E/mb7vy3unyRd\npUhL/F9CkbRa5OJh4GfA0aPh71jSeg0uVSLZXwTWBX5m+6sdM6xHSGcsSZKkj5E0jvgw+zKhGneJ\n7Y9216pkNFGkI+4KfIjYuf8XcDPwI9t/bfK6VtGrRth2PecvSUYNkmYhos3rE0qITwBPAe8mUndF\n1FNu3Kw3Xz9QPAuaORwCriUEfAYVFRwNpDOWJEnSB5T8MPsHsF6zBXKSJEnSfSTtC3yHaB+xp+0H\nqq4tCRxDtI04wPYR3bGyPRQqj/U+vyqR7Fts39JRo3qIdMaSJEn6AEnX0OLDDDjV9nOdtCtJuoGk\nTwK7AJ+t15Ra0iJEv72TbJdpSJ0kHUXSXcV/V7I9QxS5yHq4g1irr9BR45KOkn3GkiRJ+gDbE7pt\nQzI2KYrrlyH6gNVNH+yCcMCXgHnqOWKFPU9KmrsYl85Y0ossBZxQzxEDsP2WpEuA3TprVtJp0hlL\nkiRJkqQukg4CvkmoJjZjUDVekt5DqDLOWu96CeduBSK9qxl/ItK8kqQXeQOYo8WY2YE3O2BL0kXS\nGUuSJOkDJL0LWA643fbLda7PBawE3Gv7+U7bl4w+JO0NTCKk7X8BPA4MS9lN0sbAscCyLYa2cu7m\nA55tMeYfwPwlTUuSTnMXsK2kifXSy4vG5dsyo9pozyPpoSG+1LaXbKsxfUA6Y0mSJP3BgcAOhNJW\nPaYCFxJyyHt2yKZkdPNloq/YKu2oRZS0JhHNeg44kUi/+v/t3XmQpVV5x/Hvb1gEIWERA4gsYwJK\ncEECKo4RUAEJEQqXiCZxAVOlaESTGIyloqClJagxgAtSuFQBhlKCSALBBRBHBxA0llEQFQQEXIJM\nFGMCM0/+OC9FO9zpvt3T9Hvfnu+n6tblvufc009X0Xfu855znnM5cD2trPXuwAW0g6Rn8nPaGWXT\n2ZVW+VGaRKcCnwKuSvIO4FJaNcXtgP1pn/kPB17bV4DrYAkP3OO8Mff/+7WK9je8DfffeLmdNlu4\n3lnSdwCSpLEcCHy+qn49qrGq7gYuAQ5e0Ki0mO0InD+PRWH+AfgNsE9VHdtdu7SqXgk8FngH8Czg\n02OMtRw4LMnIGbauHP/htNLg0sSpqnOBdwM7A6cDNwC/Ar5Pu6m2FDip6zcoVbVLVS297wE8gXZj\nZwVwALBJVW0PbAI8A7iSVtr/8X3F3CeTMUkahh2BH8zQ54ddP2k+/IT5XUGzL3DBGkU3lkBbm1RV\nbwW+S1saOZOTu9i+kuS1SXZLsln3fCwtCdug6ydNpKp6E/BU4EzajPAPu+czgWVV9cYew5tP76Sd\nUbh/VV1eVasAqmpVVV1GS9C27vqtd1ymKEnDULRlHtPZmFkWUpCmcS5wRJKHVNX/zsN4WwA3T3n9\nf7QCBVMtB14800BVdXWSY4DTaHvQ3r9Gl1XAq6rqyrmHKz34qmoFbcZoMTsCOGdth1dX1W+SfBY4\nkmEuy1wnzoxJ0jBczzRLEJOka//+gkWkxe542j6OTydZOg/j/ZRWHn/q6zU3628EbDrOYFX1Udry\npw8C19Bmjq+hJWhPqKoz1jVgSfPiYbS/7els1PVb73josyQNQJLjgHfRvni+oar+Z0rbprTlWK8E\n3lxV7+onSi0mXUW0jYBHdJdWMrogxlgV0JJ8EVhVVQd1r88FDgH+qKq+l2Q72iG3t1XVXvPxO0jq\nX5Jv05Yp7lFVK0e0bwV8G7irqvZY6Pj65syYJA3DP9FKIb8KuCHJ2UlOSnI2beP3q7r2f+wxRi0u\nS2il7G/uHiuBjHiM+13iYmC/JFt3rz9AmwX7RpKrgeto1eNm/H84yQ+TnDb+ryKpRx+m3dS5KslL\nkuySZNPu+aW0Ah7b0Wa11zvOjEnSQCTZkjYz9mf89hfg1bQSya+pKkt5ayJ1Z+HtTjsL75fdtSOA\nE2nLFW8C3l9Vp48x1i+BU7oCCJImXJIP0I6zGJV4hPb3fOyItkXPZEySBqY7AHof2rKPu4CrPOhZ\n65MkK4AfVdUL+45F0niS7AscBTyRVtBnJXAt8PGq+mqfsfXJZEySBiDJS4CfVNW/9x2L1k9Jfod2\nA2BlVf13z7G8mHYW01Oq6lt9xiJJ68LS9pI0DGcCpwAmY1owSTYE/g54Be0Q2vuu30hLhk6uqntn\nMd5+wDLuLwpyG7C8qi6fZWi3Al8Alif5CHA1cAcjlkBV1ZdnObYkLRhnxiRpAJLcCnxmfV1Tr4WX\nZGO6ohu0JOdWWqn77YFH0vZ5XAEctLbzg6aMtR/wIeDR913qnu/7EnId7VywsRKnJKu79645zgNU\nlWfvSZpYzoxJ0jBcDByQZElVre47GK0X/gbYH7gQ+NuquuG+hiS/D7wXeE7X791rGyTJ84BzaN85\nbgcuBW7pmnfsfsbuwBeSHFlV540R2wlMk4BJ0lA4MyZJA5BkW2AFcBntnDELduhBleS+vVh7jroB\nkGQJ7VywVNXj1jLGI4Dv0ap/vh44o6pWjRjnaFpJ+wJ2q6rb5u0XkaQJ5syYJA3DObTKUy8Bjkxy\nE6P3yFRVPXOBY9Pi9Ae0ctMjZ2KranWSi2jlqtfmdcBDgedV1b+sbRzgo0l+BpwHHAsct06RS9JA\nODMmSQPQ7ZEZR7lHRvMhyV3AWVX16mn6nAr8ZVVtsZb2bwF3V9W+Y/7MrwGbVdXjx+y/EfBM2jLH\nzavqxO76JsDvAj93Wa+kSbZk5i6SpL5V1ZIxHyZimi/fAp7fnWv3AEm2AZ4P/Mc0Y+wMzOb8oK8C\nu4zTMcmzaQdF/ytt/9rbpjTvSduf5jlkkiaayZgkSRrlVODhwFVJjk7yqCSbJlma5OXAlV37qdOM\nsREwbaXFNdwDzHhDIcnewPm0a0uvxgAACjBJREFUZbqvB86e2l5VK4AbgSNm8bMlacG5Z0ySJD1A\nVZ2bZE/gjcDpI7oEeE9VnTvNMLcDI4t7rMUetL2QM3kL8Gtg76q6I8nxI/pcDew1i58tSQvOmTFJ\nGogkS5L8dZIVSVYmuXdK2xOTfDDJbn3GqMWlqt4EPJV26Pg3gB92z2cCy6rqjTMM8WXgwCSPmeln\nJdkdOLh7z0yWAedX1XSJ2y20M9EkaWI5MyZJA9AdwHsR7UymO4FfAptP6XIjcBTwM2DULIE0J92S\nvxVzfPupwEuBC5McVlXfGdWpS8Q+R1uieNoY424OzHS8w0PxprOkCeeHlCQNwxuAA4C3A9sCZ0xt\nrKq7aDMKBy98aNJoVXUNcBLwKODaJGd3+88O6h5HJzmHNtv2KOB9VfX1MYb+MW1J43T2pM3kSdLE\nMhmTpGH4c2B5VZ3QleoedS7JjcBOCxuWFqskL0jype7g5lHtOyT5YpLnTjdOVR1Hq3S4BDiStv/s\nou5xOq3i4QbAicDfjxneRcDBSZ62ltgOoS2vvHDM8SSpFy5TlKRhWEor4T2dO4GtFyAWrR9eAWxZ\nVbeNaqyqHyfZout33nQDVdUJST5BW0q7jPv3ct0BfAX4eFXdOIvY3kVL7C5JcgpdOfwkhwJPB15N\nKx7yvlmMKUkLzmRMkobhN8CWM/TZCbhrAWLR+uFxzDyzdDXwnHEGq6ofMU/7GbtE8CDgXNoS3vtc\nQKvy+APguVU1074ySeqVyZgkDcM3gYOSbFxVDzi3qZuhOJjZHbArTWdr4Kcz9PkvYJsFiOUBqura\nJI8GDgX2BR4GrKQVG/lsVd073fslaRKYjEnSMJwOnAWcleToqQ1JtgQ+BmwFfLiH2LQ4/RzYdYY+\nu9LjbGxVraLNhl3QVwyStC5MxiRpAKrqnCQHAi8DDgN+AZDk67Sqcg8BTquqf+stSC02y4HDkjym\nqq5bs7ErR384rSS9JGkOUjWqIJckaRIleRlwLPB42t4YgP+klQT/WF9xafFJsg9t2etK4ATgYlpJ\n+R2AQ4C3AFsAT6uqKxcgnqfP5X1VNc4h0pLUC5MxSRqgJJvSliWurKq7+45Hi1OSv6IdwrzBiOZV\nwDFVdcaItgcjlrUd6TCdqipXAUmaWCZjkiRprbrliMcAT6ZV9LyLViTjQ1X13QWM4zIemIztAuwM\nXL6291XVAQ9eVJK0bkzGJEnSICU5HnhrVY2auZOkibek7wAkSeNJsl+SC5P8NMk9SVaNeFjOW5Kk\ngXAdtSQNQJJDgfNpe3duBq4HTLwkSRowkzFJGoa3AfcAh1bVJT3HIkmS5oHLFCVpGB4L/LOJmCRJ\ni4fJmCQNw6+AO/sOQpIkzR+XKUrSMHwR2LfvIKS+JNlpxOUtu7Yduf8Q9N9SVTc/mHFJ0rqwtL0k\nDUCSnYGrgFOAd5Yf3lrPeOizpMXIZEySJlCSM0dc3gXYD/gR8E3a4btrqqo6+kEMTepFkpuYfTJG\nVS2d/2gkaX6YjEnSBOpmAeaiPABXkqRhcOpekiaTd/MlSVrknBmTJEmSpB5Y2l6SJEmSemAyJkmS\nJEk9MBmTJEmSpB6YjEmSJElSD0zGJEmSJKkHJmOSJEmS1AOTMUmSJEnqgcmYJElaVJJ8KcklSV6e\nZMO+45GktfHQZ0mStKgkWd39ZwG3AidX1Sk9hiRJI5mMSZKkRSXJfrTVP48D9geWVdW2vQYlSSOY\njEmSJElSD9wzJkmSJEk9cFOrJEkarCSbAbsBm1fVFX3HI0mz4cyYJEkanCSPTPIZ4BfA14FLp7Q9\nLcl3kuzfV3ySNA6TMUmSNChJtgeuBA4HLgS+BmRKlyuB3wNeuPDRSdL4TMYkSdLQHE9Ltg6squcC\nn5/aWFX3AFcAy3qITZLGZjImSZKG5k+AC6rq0mn63Aw8YoHikaQ5MRmTJElDsy1wwwx97gE2W4BY\nJGnOTMYkSdLQ3AnsOEOf3YA7FiAWSZozkzFJkjQ0y4HDkmw3qjHJrsCzmVJhUZImkcmYJEkampOA\nTYDLkxwCPBTamWPd688Bq4H39heiJM0sVdV3DJIkSbOS5CjgQ8CGI5rvBY6qqrMWNipJmh2TMUmS\nNEjdcsRjgKcADwNWAiuAU6vq+j5jk6RxmIxJkiRJUg/cMyZJkiRJPRi1zlqSJGliJNlpru+tqpvn\nMxZJmk8uU5QkSRMtyWpgLl9Yqqq88SxpYvkBJUmSJt0nmVsyJkkTzZkxSZIkSeqBBTwkSZIkqQcu\nU5QkSYOV5JHAE4EtaeeMXVtVt/YblSSNx2WKkiRpcJLsDHwEOHBE8+eBV1bVTQsalCTNksmYJEka\nlCTbAVcDOwA3AV8Gbge2B/4YWArcBuxdVXf0FKYkzchlipIkaWjeQkvEjgPeV1Wr7mtIsgHweuA9\nwJuB1/QSoSSNwZkxSZI0KEluAq6rqmdP0+di4DFVtctCxSVJs2U1RUmSNDTbAdfM0Oearp8kTSyT\nMUmSNDQrgZ1n6LNT10+SJpbJmCRJGpqvAM9P8tRRjUmeDLyg6ydJE8s9Y5IkaVCS7AV8FdgA+BRw\nKa2a4nbA/sCLgNXAsqqaaTmjJPXGZEySJA1Okj8FPgFsBUz9MhPgTuCoqrqgj9gkaVwmY5IkaZCS\nbAYcDuwFbEHbI/YN4PyqurvP2CRpHCZjkiRJktQDC3hIkiRJUg827DsASZKkuUiyN/Ak2r6xDUZ0\nqao6cWGjkqTxuUxRkiQNSpLfBc4DDqAV7FibqqpRSZokTQRnxiRJ0tCcBDwDuAL4GHALcG+vEUnS\nHDgzJkmSBiXJHcCtwJOqanXf8UjSXFnAQ5IkDc0WwKUmYpKGzmRMkiQNzQ3Atn0HIUnrymRMkiQN\nzWnAc5Ls0HcgkrQuLOAhSZKG5iJaAY/lSd4OXAPcNapjVd28kIFJ0mxYwEOSJA1KktVA0craT/dF\npqrKG8+SJpYfUJIkaWg+yfRJmCQNgjNjkiRJktQDC3hIkiRJUg9MxiRJkiSpB+4ZkyRJEy3JmbQ9\nYm+qqp90r8dRVXX0gxiaJK0T94xJkqSJNqV64u5V9b3u9TiqqjZ4EEOTpHXizJgkSZp0S7vnH6/x\nWpIGzZkxSZIkSeqBM2OSJGkwkuwE7ENbtnh1Vd3Sc0iSNGfOjEmSpEFIcjLwOiDdpQLeX1Vv6C8q\nSZo7kzFJkjTxkrwIOIuWgF1HS8ge3TX/RVWd01dskjRXnjMmSZKG4BXAvcCzqmqPqvpD4GBgNWD5\nekmD5MyYJEmaeEl+BlxWVS9Y4/qngf2rapt+IpOkuXNmTJIkDcFWtOWJa7oO2HKBY5GkeWEyJkmS\nhmAJcM+I6/dwf0EPSRoUkzFJkjQU7q2QtKi4Z0ySJE28JKuZfTJWVeWZqpImlh9QkiRpKGa7HNHl\ni5ImmjNjkiRJktQD94xJkiRJUg9MxiRJkiSpByZjkiRJktQDkzFJkiRJ6oHJmCRJkiT1wGRMkiRJ\nknpgMiZJkiRJPfh/FFhsmoxxPuAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f5765fb0978>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Home prices in the East Bay\n",
"\n",
"# Group the results by neighborhood, and then take the average home price in each neighborhood\n",
"by_neighborhood = alldata.groupby('Neighborhood').Price.mean().ix[neighborhoodsplt]\n",
"by_neighborhood_sort_price = by_neighborhood.sort_values(ascending = True) # uncomment\n",
"by_neighborhood_sort_price.index # a list of the neighborhoods sorted by price\n",
"\n",
"# Plot average home price for each neighborhood in the East Bay\n",
"fig = plt.figure()\n",
"fig.set_figheight(8.0)\n",
"fig.set_figwidth(13.0)\n",
"\n",
"fntsz=20\n",
"titlefntsz=25\n",
"lablsz=20\n",
"mrkrsz=8\n",
"\n",
"matplotlib.rc('xtick', labelsize = lablsz); matplotlib.rc('ytick', labelsize = lablsz)\n",
"\n",
"ax = fig.add_subplot(111) # row column position \n",
"\n",
"# Plot a bar chart\n",
"ax.bar(range(len(by_neighborhood_sort_price.index)), by_neighborhood_sort_price, align='center')\n",
"\n",
"# Add a horizontal line for Berkeley's average home price, corresponds with Berkeley bar\n",
"ax.axhline(y=by_neighborhood.ix['berkeley'], linestyle='--')\n",
"\n",
"# Add a grid\n",
"ax.grid(b = True, which='major', axis='y') # which='major','both'; options/kwargs: color='r', linestyle='-', linewidth=2)\n",
"\n",
"# Format x axis\n",
"ax.set_xticks(range(0,len(by_neighborhood))); \n",
"ax.set_xticklabels(by_neighborhood_sort_price.index, rotation='vertical') # 90, 45, 'vertical'\n",
"ax.set_xlim(-1, len(by_neighborhood_sort_price.index))\n",
"\n",
"# Format y axis\n",
"ax.set_ylabel('$\\mathrm{Price \\; (Dollars)}$', fontsize = titlefntsz) # in Hundreds of Thousands of Dollars\n",
"\n",
"# Set figure title\n",
"ax.set_title('$\\mathrm{Average \\; Home \\; Prices \\; in \\; the \\; East \\; Bay \\; (Source: Craigslist)}$', fontsize = titlefntsz)\n",
"\n",
"# Save figure\n",
"#plt.savefig(\"home_prices.pdf\",bbox_inches='tight')\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
basnijholt/holoviews | examples/reference/elements/bokeh/TriMesh.ipynb | 1 | 5623 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div class=\"contentcontainer med left\" style=\"margin-left: -50px;\">\n",
"<dl class=\"dl-horizontal\">\n",
" <dt>Title</dt> <dd> TriMesh Element</dd>\n",
" <dt>Dependencies</dt> <dd>Bokeh</dd>\n",
" <dt>Backends</dt> <dd><a href='./TriMesh.ipynb'>Bokeh</a></dd> <dd><a href='../matplotlib/TriMesh.ipynb'>Matplotlib</a></dd>\n",
"</dl>\n",
"</div>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import holoviews as hv\n",
"from holoviews import opts\n",
"from scipy.spatial import Delaunay\n",
"\n",
"hv.extension('bokeh')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A ``TriMesh`` represents a mesh of triangles represented as the simplexes and vertexes. The simplexes represent the indices into the vertex data, made up of three indices per triangle. The mesh therefore follows a datastructure very similar to a graph, with the abstract connectivity between nodes stored on the ``TriMesh`` element itself, the node or vertex positions stored on a ``Nodes`` element and the concrete ``EdgePaths`` making up each triangle generated when required by accessing the edgepaths attribute.\n",
"\n",
"Unlike a Graph each simplex is represented as the node indices of the three corners of each triangle rather than the usual source and target node.\n",
"\n",
"We will begin with a simple random mesh, generated by sampling some random integers and then applying Delaunay triangulation, which is available in SciPy. We can then construct the ``TriMesh`` by passing it the **simplexes** and the **vertices** (or **nodes**)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"n_verts = 100\n",
"pts = np.random.randint(1, n_verts, (n_verts, 2))\n",
"tris = Delaunay(pts)\n",
"\n",
"trimesh = hv.TriMesh((tris.simplices, pts))\n",
"trimesh"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To make this easier TriMesh also provides a convenient ``from_vertices`` method, which will apply the Delaunay triangulation and construct the ``TriMesh`` for us:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"hv.TriMesh.from_vertices(np.random.randn(100, 2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Just like the ``Graph`` element we can access the ``Nodes`` and ``EdgePaths`` via the ``.nodes`` and ``.edgepaths`` attributes respectively."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"trimesh.nodes + trimesh.edgepaths"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let's make a slightly more interesting example by generating a more complex geometry. Here we will compute a geometry, then apply Delaunay triangulation again and finally apply a mask to drop nodes in the center."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# First create the x and y coordinates of the points.\n",
"n_angles = 36\n",
"n_radii = 8\n",
"min_radius = 0.25\n",
"radii = np.linspace(min_radius, 0.95, n_radii)\n",
"\n",
"angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)\n",
"angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)\n",
"angles[:, 1::2] += np.pi/n_angles\n",
"\n",
"x = (radii*np.cos(angles)).flatten()\n",
"y = (radii*np.sin(angles)).flatten()\n",
"z = (np.cos(radii)*np.cos(angles*3.0)).flatten()\n",
"nodes = np.column_stack([x, y, z])\n",
"\n",
"# Apply Delaunay triangulation\n",
"delauney = Delaunay(np.column_stack([x, y]))\n",
"\n",
"# Mask off unwanted triangles.\n",
"xmid = x[delauney.simplices].mean(axis=1)\n",
"ymid = y[delauney.simplices].mean(axis=1)\n",
"mask = np.where(xmid*xmid + ymid*ymid < min_radius*min_radius, 1, 0)\n",
"simplices = delauney.simplices[np.logical_not(mask)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once again we can simply supply the simplices and nodes to the ``TriMesh``."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"nodes = hv.Points(nodes, vdims='z')\n",
"hv.TriMesh((simplices, nodes))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also do something more interesting, e.g. by adding a value dimension to the vertices and coloring the edges by the vertex averaged value using the ``edge_color_index`` plot option:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"trimesh = hv.TriMesh((simplices, nodes))\n",
"\n",
"trimesh.opts(\n",
" opts.TriMesh(cmap='viridis', edge_color='z', filled=True, height=400, \n",
" inspection_policy='edges', tools=['hover'], width=400))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For full documentation and the available style and plot options, use ``hv.help(hv.TriMesh).``"
]
}
],
"metadata": {
"language_info": {
"name": "python",
"pygments_lexer": "ipython3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
awni/tensorflow | tensorflow/tools/docker/notebooks/2_getting_started.ipynb | 1 | 147269 | {
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"version": "0.3.2",
"views": {},
"default_view": {},
"name": "Untitled",
"provenance": []
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "6TuWv0Y0sY8n",
"colab_type": "text"
},
"source": [
"# Getting Started in TensorFlow\n",
"## A look at a very simple neural network in TensorFlow"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "u9J5e2mQsYsQ",
"colab_type": "text"
},
"source": [
"This is an introduction to working with TensorFlow. It works through an example of a very simple neural network, walking through the steps of setting up the input, adding operators, setting up gradient descent, and running the computation graph. \n",
"\n",
"This tutorial presumes some familiarity with the TensorFlow computational model, which is introduced in the [Hello, TensorFlow](../notebooks/1_hello_tensorflow.ipynb) notebook, also available in this bundle."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Dr2Sv0vD8rT-",
"colab_type": "text"
},
"source": [
"## A simple neural network\n",
"\n",
"Let's start with code. We're going to construct a very simple neural network computing a linear regression between two variables, y and x. The function it tries to compute is the best $w_1$ and $w_2$ it can find for the function $y = w_2 x + w_1$ for the data. The data we're going to give it is toy data, linear perturbed with random noise.\n",
"\n",
"This is what the network looks like:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "q09my4JYtKXw",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{}
]
},
"cellView": "both",
"outputId": "22b94683-437b-45ed-f6b8-4abf3b76ce38"
},
"source": [
"from IPython.display import Image\n",
"import base64\n",
"Image(data=base64.decodestring(\"iVBORw0KGgoAAAANSUhEUgAAAJYAAABkCAYAAABkW8nwAAAO90lEQVR4Xu2dT5Dc1J3Hv+YQT8VJZUhVdprLWs4FTSrGGv4ql9CuHBCH4GaTFCLZwnIcjOAy8l6Q/1SlU4XHcg6xJgtY2OOik2KxSGoTGWrXzYFC2T2MDAtWitRavmQ0e9k2SYGowom4hNRPtqA9TE+rW3/cPfPepcfup6f3fu/Tv9/T+/PVpo8//vhjsMQsULAFNjGwCrYoKy6xAAOLgVCKBRhYpZiVFcrAYgyUYgEGVilmZYUysBgDpViAgVWKWVmhDCzGQCkWGEuwrly5gtf++zW887/vYOn/lnD5T5cT40x9ZQrb/nEbxDtFiHeI2LJlSylGY4X2t8BYgUVAvfzqy3i5/TI+vPLhmq37wpYv4AHpATxw3wMMsP4cFJ5jbMAiqA4eOYg/Lv8xMcL26e34+vTXk8+vbv1q8n/03TsX38EfLv4h+aRE380dmmNwFY7O2gWOBVgE1Y/2/yjxUls+vwXaY1oS7tZK3v94MJ8zceUvV0Dea+H4AoOrQrhGHqxuT0Xjp0P7D2HqH6Yymejyu5dx5PiRZBxGnmt+bj7TdSxTfgv0ASuAzglwmyE8pfbZu3VaEDkDdT+AweevzGolvPjvL+LMb84knmr+yHxmqNKyCK7ZQ7OJ5yIo+3m6clqx8UrNB1bso2W64FQN9cnijdcdAvNAQWGRPBcLicX3Ua8S84FVcj3PnjuLhRcWkgH63OG5XHc7+NTBZEBP47NvffNbucpiF/e3QCaw2g0NfNvES5c+wtQ9u2G0LCj8BLAiFEaeBU0zYJ9fxkfYjKl7FZgtCzIHIA7QUmXov/g9LmMztt6rwLBMyFROj3TkZ0fgveXh4X96GN//zvf7t2aNHGlI7VlW0pYmRC+AKUwAsQu5thOuvIjQEjGBGJ7CQYptdOw6etc6VzXXzcUZwJrGseWt2P28DV2I4OgyDgQKFgMTYtQ1xqq10eDuR6j8Fi1NxGTkwpAfRos7h05bQscQIFgibEeHMBHCVhs4EBtY8lQQd6ulvbN78e6f302mC7Z/bXsuo9NkKk1X9PZ+IUyeR0sN4GscYl8DPzOP5VuPYynQwMU+dL4O3wzRbpQQ93O1bvQuzgRWS0p/tQA6Nuqcilq7A5u3Px28T7qw7BB1VUHqhEKTB2+pCAIVHZVD3dPgujpE6peOBzesQRS5nr/+b//g24nF7JN27qkCGq/J++RknHXm5JlVeiKGr/MQPQMdV0ZkCRBbNUwEMYzQhRyZEHgHOv29ynPM6HXtja1Rf7B4AZ7RgZv+SuMAOj+NtrYEX3avfyqMfDi2DdcLEAQBvPOX8MGtR3Ex0MEFJiRxP373wWZsvaeBhixDVRrg1/jxlwEWPV3ap+xVrR57Cjgpht2xEDV4mLIFvqkiaoUwwzp4U4Hv9/awN7YrR+vuGcAS4ZsdtKV0VNEFVqMLrIkWJGEPPP4hKA0RgiCAc1XsdJQErGQ2Ig7hOQ5sx4Hz0u+wvHX2akjtMWCpNhQCiCicq+AcCx1Fh9B2IegcNN6B4Teg1z0EeknzKqPFRe7a9AeLm4ajXvzUoJEDqUahMESrKxSqbQHbDBGLoXUNlBiuUsNOT8fFQEVsNdHmdOjStTgSGOCnLTQuBDBosLxKqnTwntw/glPnoHMS4E6iFVjgbBGcwUGMPAjtawP73GZf/wVkAutYtAvPezYUPoKjipBdGZ5vQOgavGteHbfsiXD09TZUIUbg6JD3vITlrU/iYthErPOYaQk44ZhocDF8U0HDqsEOHfQaC7/2X68lyzJVTjd0WiJu2XMem++7+tAxSd52+hguTe3GYtjq6V3XPyqDtbA/WLyAtqRg0rHhLceo3avCsk0kjqd7uoEL0FJkaC/9Hh/gS9ixS0dTCaDKHVidNhoTNN2gQP/FedAmly/t2IWm2YK2xswqDbj3antzz5oToD/915/i5smbcdo8vfaDQGiC37YfEyeW4KtcMu2g1HbCrp9Dx5Fw3ZCw04ZSb0Jse6CsLH1qgZFfK0znn+hpznzKHGpJRzus4YJ/AX/78G94ofUC7r777pwMxAhdE6pyAK8u78CJJZ+BtcKiIw8Wea0DTx34ZCH5oHYwM1y0TjhnziXbaWgB+4cP/RCPPfYYtm/fjpMnT+Kmm24aDrDYhdpoQdAbaMtNSB4Da6UhRx4sqnB3SCTPNbtvtu9iMoU/Wg5Kt9p0h8DTp09j3759ePrpp/H4448PB1fylOtC5jTUGVifseFYgJXClXou+jcN6Gk2nj7JG1Gi7TG0Hkiz7OlGP/ru6OGjq46rnnjiCSwuLibe66677hocMAZWT5uNDVgpXGfbZ5OtybQNZq1EE6G0NXmXtGvNwbrv+4n3uu222wYPjwys9QFW2goKjbQ4Tdth6CAFeSpK5J3oQMUwhynS8PjMM89AVdVs3ouBtb7Aytbrw+WiMZfnednCIwOLgTUIZml43LFjB5577rnhnx4Huek6yztWY6yqbb+wsJBMTwwUHquu5Ijej4GVoWMoPJ4/fz7xXkM9PWa4x3rLwsDK2KMXLlxIvBeFR5qe2LRpU8YrN2Y2BtaA/U7hkaYnnn322exPjwPeYz1kZ2AN2YtpeCTvdeeddw5Zyvq9jIGVo28pPJL3ok2NLDxeb0gGVg6w0kvT8HjixIlkHJY1lauaE8GRangwsvD/noKqt+kzsLJSkCEfzdi/8cYbifdaKzxWoppDmxJ5FT54NH06YZShAQVmYWAVaEwqKg2PMzMzyfTEyqfHqlRzAoOH6OqwJnXoNQeBSWcjq0sMrJJsferUqSQsdofHylRzYg8aLyG0QtiTOvhGhFZglyKD0Mt8DKySwEqLpfD45ptvYn5+Hr/+z19/sukwj2pOP72vyJXBy4BNME340Pg6AiNAu8IDkQysksGi4t9++2189wffxee++DkIO4TcqjlrSw504Eg81FobYetq+KOwKDgagjVOnRdtBgZW0RZdpbw0BL73/nv4yZM/6bv7tVeVxkk1h4FVAVgbUTWHgVUBWGUcvCVV6EP/cuiztQ9NCNsMiIshrPSIeaK3oUNIlXQqaDMDqwIjlyEV0Fv6MoQlbENT/FTIhWSXOF2AF5jocei8cCswsAo36WcLLEPchO7yyr+9smrt6TQ3geQmcgcd2CQbIHoIDKGyuSwG1joEi06oU+jj3RAWR2HQgFiiTuxqJmRgVQBWGaGQDo78/OjPe9T+qpfSeBeeqIM3JPip4k8F7aVbMLAqMHSlg/dr7YkcCZxWg1Jz0G5UL7/EwKoArBuhmoNEbupBvPrRDhxf8qFVLFrCwKoArFQi4P3o/VwTpCmgdBi3r2oOIrQbNdwfGljytZ46r2U1n4FVlmW7yn3rrbfwvX/+XrKkMyPM5FLNIS2KbCrSNI8loKX48G6AxhIDq2SwaIcDgWWaJn71H78qRDWnlxbF1aaQxJILj6TRjRhm0L4hYrwMrJLAos1+BBXtyaLty5SKVs1Zverx1RB4dhIPPe/CVioeXF2rFAOrYLDIOxFQd9xxRwLVytSt90XfFaGaU3ATCimOgVWIGa8WkoY9AorA6pUIrqJVcwpsRiFFMbAKMONqYS9LsWWo5mS5bxV5GFg5rExhj8ZPdHBitbCXo+ixv5SBNWQXpmGPvNXtt98+ZCnr9zIG1oB9O2zYG/A2Y5+dgZWxC1nYy2goNt2Q3VA0jqIDESzsZbcZ81hr2CoNe/T56KOPZrcqy8m2zazGAAt7+X8ZzGOtsCELe/mhohLGEqwyVFpY2CsGqLSUsQKrDJUWFvaKBWrswCpDpYWFvXKgKiYUxh5U/huwhd8idBqYRARX4bHTldd8Le8gTSpapYWWX0is47qnveTdi02I6aFOejlAbSdcOT2fF8NTOEixDTqnV6Uk0CC2GpW8hYTCyFXA72yj8XoAAzoE+nsxgNnrZc8DtL7bU9HJlDwqLY9855FkbY8ktS3LWlGLECbPo6UG8DUOsa+Bn5nH8q3HsRRo4GISL6vDN0O0e70SdoB2rfeshYBF71Juyzzu90TcF59FIC8WJvSVvgiT9nnPH5nP/K7CtOPonYWzh2aTF2Fu+usmvPjLF3us7cXwdR6iZ6DjyogsAWKrhokghhG6kCMTAu9Ap7+r1l0cQwoLAote4+ugwT+IsxO78XrQKkTkqzsEkqeily8Nk0il5cfHfowv3/xlLBxf6Pk2sNhTwEkx7I6FqMHDlC3wTRVRK4QZ1sGbCnxfrfxgwjBtvtHXFAZW7OsQZo7hEm7Fkxf8nm+mH6TBlau0RG00OBWcY6Gj6BDaLgSdDn46MPwG9Hr15/MGsdco5S0GrDiAIU7D5M/AgIo9gY6Lng4+5wi3jIOea59wieCQzgEnAe4kWoEFzhbBGRzEyIPQDmBWpaoxSpQMUZdCwCLh1OlmDWcCBzJsSNzDiIyL8LR8Ur1lHE2nPeZzh+d6mooENW7Zcx6b7zuHTlvCJB1Nnz6GS1O7sUhKxDl/LEP00Vhekh8sUjThNUyYAdxr59dCSwSvAWbg5Xq7exkqLfRO6TMnz/TurNAEv20/Jk4swaf2xC6U2k7Y9XPoOBIm6crYh6UoaLodABOoSU3YlpLbQ48lQT0qnR+sEq1RBlj0dGmfsnPVOtB51IMmfEdGLQ7RkkSYkps8VbJ01QIjDdaNCIVZwOi4DnxOgsRRXIzhazwakY3gmphsljLWe56RBqv6wfvg3R0HFqS6CcHxC5kQHrwGo3nFSIN1Q1RaBuinyDchSyYmDRcthWPLPF22G2mwuo+k55kgHUylJRtZoa1A0kI0bAdGPRnSszQuYFE90yUdepoznzKHWtLRDmsglZY8cHZTE7UVCGqEpmtDScZZLK20wEh7LKpst9YBKQUf1A5mhovWCefMuU9eM9JbWnEQMAIY/DQOXLr+mqmHXkfIdj18YpSRByuFa6+2F1f+cgXkuWb3zfZdN6Twt/DCQuKpsgmVDQIXy9vPAmMB1krPRf9eryot/TpsXL4fG7BSuNa7Ssu4gNOvnmMFVtqY9azS0q/DxuX7sQRrXIy7kevJwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3Ixf9d0NIelzdt4X5AAAAAElFTkSuQmCC\"), embed=True)"
],
"outputs": [
{
"output_type": "execute_result",
"execution_count": 1,
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJYAAABkCAYAAABkW8nwAAAO90lEQVR4Xu2dT5Dc1J3Hv+YQT8VJ\nZUhVdprLWs4FTSrGGv4ql9CuHBCH4GaTFCLZwnIcjOAy8l6Q/1SlU4XHcg6xJgtY2OOik2KxSGoT\nGWrXzYFC2T2MDAtWitRavmQ0e9k2SYGowom4hNRPtqA9TE+rW3/cPfPepcfup6f3fu/Tv9/T+/PV\npo8//vhjsMQsULAFNjGwCrYoKy6xAAOLgVCKBRhYpZiVFcrAYgyUYgEGVilmZYUysBgDpViAgVWK\nWVmhDCzGQCkWGEuwrly5gtf++zW887/vYOn/lnD5T5cT40x9ZQrb/nEbxDtFiHeI2LJlSylGY4X2\nt8BYgUVAvfzqy3i5/TI+vPLhmq37wpYv4AHpATxw3wMMsP4cFJ5jbMAiqA4eOYg/Lv8xMcL26e34\n+vTXk8+vbv1q8n/03TsX38EfLv4h+aRE380dmmNwFY7O2gWOBVgE1Y/2/yjxUls+vwXaY1oS7tZK\n3v94MJ8zceUvV0Dea+H4AoOrQrhGHqxuT0Xjp0P7D2HqH6Yymejyu5dx5PiRZBxGnmt+bj7TdSxT\nfgv0ASuAzglwmyE8pfbZu3VaEDkDdT+AweevzGolvPjvL+LMb84knmr+yHxmqNKyCK7ZQ7OJ5yIo\n+3m6clqx8UrNB1bso2W64FQN9cnijdcdAvNAQWGRPBcLicX3Ua8S84FVcj3PnjuLhRcWkgH63OG5\nXHc7+NTBZEBP47NvffNbucpiF/e3QCaw2g0NfNvES5c+wtQ9u2G0LCj8BLAiFEaeBU0zYJ9fxkfY\njKl7FZgtCzIHIA7QUmXov/g9LmMztt6rwLBMyFROj3TkZ0fgveXh4X96GN//zvf7t2aNHGlI7VlW\n0pYmRC+AKUwAsQu5thOuvIjQEjGBGJ7CQYptdOw6etc6VzXXzcUZwJrGseWt2P28DV2I4OgyDgQK\nFgMTYtQ1xqq10eDuR6j8Fi1NxGTkwpAfRos7h05bQscQIFgibEeHMBHCVhs4EBtY8lQQd6ulvbN7\n8e6f302mC7Z/bXsuo9NkKk1X9PZ+IUyeR0sN4GscYl8DPzOP5VuPYynQwMU+dL4O3wzRbpQQ93O1\nbvQuzgRWS0p/tQA6Nuqcilq7A5u3Px28T7qw7BB1VUHqhEKTB2+pCAIVHZVD3dPgujpE6peOBzes\nQRS5nr/+b//g24nF7JN27qkCGq/J++RknHXm5JlVeiKGr/MQPQMdV0ZkCRBbNUwEMYzQhRyZEHgH\nOv29ynPM6HXtja1Rf7B4AZ7RgZv+SuMAOj+NtrYEX3avfyqMfDi2DdcLEAQBvPOX8MGtR3Ex0MEF\nJiRxP373wWZsvaeBhixDVRrg1/jxlwEWPV3ap+xVrR57Cjgpht2xEDV4mLIFvqkiaoUwwzp4U4Hv\n9/awN7YrR+vuGcAS4ZsdtKV0VNEFVqMLrIkWJGEPPP4hKA0RgiCAc1XsdJQErGQ2Ig7hOQ5sx4Hz\n0u+wvHX2akjtMWCpNhQCiCicq+AcCx1Fh9B2IegcNN6B4Teg1z0EeknzKqPFRe7a9AeLm4ajXvzU\noJEDqUahMESrKxSqbQHbDBGLoXUNlBiuUsNOT8fFQEVsNdHmdOjStTgSGOCnLTQuBDBosLxKqnTw\nntw/glPnoHMS4E6iFVjgbBGcwUGMPAjtawP73GZf/wVkAutYtAvPezYUPoKjipBdGZ5vQOgavGte\nHbfsiXD09TZUIUbg6JD3vITlrU/iYthErPOYaQk44ZhocDF8U0HDqsEOHfQaC7/2X68lyzJVTjd0\nWiJu2XMem++7+tAxSd52+hguTe3GYtjq6V3XPyqDtbA/WLyAtqRg0rHhLceo3avCsk0kjqd7uoEL\n0FJkaC/9Hh/gS9ixS0dTCaDKHVidNhoTNN2gQP/FedAmly/t2IWm2YK2xswqDbj3antzz5oToD/9\n15/i5smbcdo8vfaDQGiC37YfEyeW4KtcMu2g1HbCrp9Dx5Fw3ZCw04ZSb0Jse6CsLH1qgZFfK0zn\nn+hpznzKHGpJRzus4YJ/AX/78G94ofUC7r777pwMxAhdE6pyAK8u78CJJZ+BtcKiIw8Wea0DTx34\nZCH5oHYwM1y0TjhnziXbaWgB+4cP/RCPPfYYtm/fjpMnT+Kmm24aDrDYhdpoQdAbaMtNSB4Da6Uh\nRx4sqnB3SCTPNbtvtu9iMoU/Wg5Kt9p0h8DTp09j3759ePrpp/H4448PB1fylOtC5jTUGVifseFY\ngJXClXou+jcN6Gk2nj7JG1Gi7TG0Hkiz7OlGP/ru6OGjq46rnnjiCSwuLibe66677hocMAZWT5uN\nDVgpXGfbZ5OtybQNZq1EE6G0NXmXtGvNwbrv+4n3uu222wYPjwys9QFW2goKjbQ4Tdth6CAFeSpK\n5J3oQMUwhynS8PjMM89AVdVs3ouBtb7Aytbrw+WiMZfnednCIwOLgTUIZml43LFjB5577rnhnx4H\nuek6yztWY6yqbb+wsJBMTwwUHquu5Ijej4GVoWMoPJ4/fz7xXkM9PWa4x3rLwsDK2KMXLlxIvBeF\nR5qe2LRpU8YrN2Y2BtaA/U7hkaYnnn322exPjwPeYz1kZ2AN2YtpeCTvdeeddw5Zyvq9jIGVo28p\nPJL3ok2NLDxeb0gGVg6w0kvT8HjixIlkHJY1lauaE8GRangwsvD/noKqt+kzsLJSkCEfzdi/8cYb\nifdaKzxWoppDmxJ5FT54NH06YZShAQVmYWAVaEwqKg2PMzMzyfTEyqfHqlRzAoOH6OqwJnXoNQeB\nSWcjq0sMrJJsferUqSQsdofHylRzYg8aLyG0QtiTOvhGhFZglyKD0Mt8DKySwEqLpfD45ptvYn5+\nHr/+z19/sukwj2pOP72vyJXBy4BNME340Pg6AiNAu8IDkQysksGi4t9++2189wffxee++DkIO4Tc\nqjlrSw504Eg81FobYetq+KOwKDgagjVOnRdtBgZW0RZdpbw0BL73/nv4yZM/6bv7tVeVxkk1h4FV\nAVgbUTWHgVUBWGUcvCVV6EP/cuiztQ9NCNsMiIshrPSIeaK3oUNIlXQqaDMDqwIjlyEV0Fv6MoQl\nbENT/FTIhWSXOF2AF5jocei8cCswsAo36WcLLEPchO7yyr+9smrt6TQ3geQmcgcd2CQbIHoIDKGy\nuSwG1joEi06oU+jj3RAWR2HQgFiiTuxqJmRgVQBWGaGQDo78/OjPe9T+qpfSeBeeqIM3JPip4k8F\n7aVbMLAqMHSlg/dr7YkcCZxWg1Jz0G5UL7/EwKoArBuhmoNEbupBvPrRDhxf8qFVLFrCwKoArFQi\n4P3o/VwTpCmgdBi3r2oOIrQbNdwfGljytZ46r2U1n4FVlmW7yn3rrbfwvX/+XrKkMyPM5FLNIS2K\nbCrSNI8loKX48G6AxhIDq2SwaIcDgWWaJn71H78qRDWnlxbF1aaQxJILj6TRjRhm0L4hYrwMrJLA\nos1+BBXtyaLty5SKVs1Zverx1RB4dhIPPe/CVioeXF2rFAOrYLDIOxFQd9xxRwLVytSt90XfFaGa\nU3ATCimOgVWIGa8WkoY9AorA6pUIrqJVcwpsRiFFMbAKMONqYS9LsWWo5mS5bxV5GFg5rExhj8ZP\ndHBitbCXo+ixv5SBNWQXpmGPvNXtt98+ZCnr9zIG1oB9O2zYG/A2Y5+dgZWxC1nYy2goNt2Q3VA0\njqIDESzsZbcZ81hr2CoNe/T56KOPZrcqy8m2zazGAAt7+X8ZzGOtsCELe/mhohLGEqwyVFpY2CsG\nqLSUsQKrDJUWFvaKBWrswCpDpYWFvXKgKiYUxh5U/huwhd8idBqYRARX4bHTldd8Le8gTSpapYWW\nX0is47qnveTdi02I6aFOejlAbSdcOT2fF8NTOEixDTqnV6Uk0CC2GpW8hYTCyFXA72yj8XoAAzoE\n+nsxgNnrZc8DtL7bU9HJlDwqLY9855FkbY8ktS3LWlGLECbPo6UG8DUOsa+Bn5nH8q3HsRRo4GIS\nL6vDN0O0e70SdoB2rfeshYBF71Juyzzu90TcF59FIC8WJvSVvgiT9nnPH5nP/K7CtOPonYWzh2aT\nF2Fu+usmvPjLF3us7cXwdR6iZ6DjyogsAWKrhokghhG6kCMTAu9Ap7+r1l0cQwoLAote4+ugwT+I\nsxO78XrQKkTkqzsEkqeily8Nk0il5cfHfowv3/xlLBxf6Pk2sNhTwEkx7I6FqMHDlC3wTRVRK4QZ\n1sGbCnxfrfxgwjBtvtHXFAZW7OsQZo7hEm7Fkxf8nm+mH6TBlau0RG00OBWcY6Gj6BDaLgSdDn46\nMPwG9Hr15/MGsdco5S0GrDiAIU7D5M/AgIo9gY6Lng4+5wi3jIOea59wieCQzgEnAe4kWoEFzhbB\nGRzEyIPQDmBWpaoxSpQMUZdCwCLh1OlmDWcCBzJsSNzDiIyL8LR8Ur1lHE2nPeZzh+d6mooENW7Z\ncx6b7zuHTlvCJB1Nnz6GS1O7sUhKxDl/LEP00Vhekh8sUjThNUyYAdxr59dCSwSvAWbg5Xq7exkq\nLfRO6TMnz/TurNAEv20/Jk4swaf2xC6U2k7Y9XPoOBIm6crYh6UoaLodABOoSU3YlpLbQ48lQT0q\nnR+sEq1RBlj0dGmfsnPVOtB51IMmfEdGLQ7RkkSYkps8VbJ01QIjDdaNCIVZwOi4DnxOgsRRXIzh\nazwakY3gmphsljLWe56RBqv6wfvg3R0HFqS6CcHxC5kQHrwGo3nFSIN1Q1RaBuinyDchSyYmDRct\nhWPLPF22G2mwuo+k55kgHUylJRtZoa1A0kI0bAdGPRnSszQuYFE90yUdepoznzKHWtLRDmsglZY8\ncHZTE7UVCGqEpmtDScZZLK20wEh7LKpst9YBKQUf1A5mhovWCefMuU9eM9JbWnEQMAIY/DQOXLr+\nmqmHXkfIdj18YpSRByuFa6+2F1f+cgXkuWb3zfZdN6Twt/DCQuKpsgmVDQIXy9vPAmMB1krPRf9e\nryot/TpsXL4fG7BSuNa7Ssu4gNOvnmMFVtqY9azS0q/DxuX7sQRrXIy7kevJwNrIvV9i2xlYJRp3\nIxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3Ixf9d0NIelzdt4X5\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
}
}
],
"execution_count": 1
},
{
"cell_type": "markdown",
"metadata": {
"id": "fBQq_R8B8rRf",
"colab_type": "text"
},
"source": [
"Here is the TensorFlow code for this simple neural network and the results of running this code:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "Dy8pFefa_Ho_",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 665,
"status": "ok",
"timestamp": 1446658971218,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "5a95f8c8-0c32-411d-956d-bb81aeed8e50"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"import tensorflow as tf\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"%matplotlib inline\n",
"\n",
"# Set up the data with a noisy linear relationship between X and Y.\n",
"num_examples = 50\n",
"X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)])\n",
"X += np.random.randn(2, num_examples)\n",
"x, y = X\n",
"x_with_bias = np.array([(1., a) for a in x]).astype(np.float32)\n",
"\n",
"losses = []\n",
"training_steps = 50\n",
"learning_rate = 0.002\n",
"\n",
"with tf.Session() as sess:\n",
" # Set up all the tensors, variables, and operations.\n",
" input = tf.constant(x_with_bias)\n",
" target = tf.constant(np.transpose([y]).astype(np.float32))\n",
" weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))\n",
" \n",
" tf.initialize_all_variables().run()\n",
" \n",
" yhat = tf.matmul(input, weights)\n",
" yerror = tf.sub(yhat, target)\n",
" loss = tf.reduce_mean(tf.nn.l2_loss(yerror))\n",
" \n",
" update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)\n",
" \n",
" for _ in range(training_steps):\n",
" # Repeatedly run the operations, updating the TensorFlow variable.\n",
" update_weights.run()\n",
" losses.append(loss.eval())\n",
"\n",
" # Training is done, get the final values for the graphs\n",
" betas = weights.eval()\n",
" yhat = yhat.eval()\n",
"\n",
"# Show the fit and the loss over time.\n",
"fig, (ax1, ax2) = plt.subplots(1, 2)\n",
"plt.subplots_adjust(wspace=.3)\n",
"fig.set_size_inches(10, 4)\n",
"ax1.scatter(x, y, alpha=.7)\n",
"ax1.scatter(x, np.transpose(yhat)[0], c=\"g\", alpha=.6)\n",
"line_x_range = (-4, 6)\n",
"ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], \"g\", alpha=0.6)\n",
"ax2.plot(range(0, training_steps), losses)\n",
"ax2.set_ylabel(\"Loss\")\n",
"ax2.set_xlabel(\"Training steps\")\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlsAAAEPCAYAAAB1MgENAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYVNW1///36oFuZpFmUFBQQGVwQkVQgx0cUENEo5HM\nIRqvSuKAibZmuOD3l1wFjWg0XjVxilfjnGCIUVDpoAmIiiIWCCjz1NDMMz2s3x+nWsumm56q6lRV\nf17Pc56qOnXqnFVAb1bvvc/a5u6IiIiISGJkhR2AiIiISCZTsiUiIiKSQEq2RERERBJIyZaIiIhI\nAinZEhEREUkgJVsiIiIiCRSXZMvMHjGzEjP7KGZfBzObamYLzew1M2sfj2uJiCSSmXU3szfNLGJm\n88zs2uj+iWa2wMw+NLMXzaxdzGduNbPF0ffPDS96EUlF8erZegwYXm3fLcDr7n408CZwa5yuJSKS\nSOXAje7eHxgC/NTMjgGmAv3d/QRgMdE2zcz6AZcBfYHzgQfMzEKJXERSUlySLXd/G9hcbfdI4Ino\n8yeAi+JxLRGRRHL3de7+YfT5DmAB0M3dX3f3yuhhs4Du0ecXAs+4e7m7LyNIxAYlOWwRSWGJnLPV\n2d1LIGi8gM4JvJaISNyZWU/gBOCdam9dDrwSfd4NWBnz3uroPhERILkT5LUukIikDTNrA7wAXB/t\n4ara/0ugzN3/ElpwIpJWchJ47hIz6+LuJWbWFVhf00FmpiRMJEO4e0bMVTKzHIJE60l3nxyzfzRw\nATAs5vDVwGExr7tH99V0XrV3IhmgoW1dPHu2LLpVeRkYHX3+Q2By9Q9UcfeU2MaNGxd6DKkWS6rE\noVhSOw73jMshHgXmu/u9VTvM7DzgJuBCd98bc+zLwLfMrIWZHQH0BmbXduKw/54y5d9bc/0O6R5/\nJnyHxohLz5aZPQ0UAh3NbAUwDrgDeN7MLgeWE9ytIyKS0szsdOC7wDwz+4BgCsQvgd8DLYBp0ZsN\nZ7n7GHefb2bPAfOBMmCMN7ZFFpGMFJdky92/U8tbZ8fj/CIiyeLu/waya3irzwE+cztwe8KCEpG0\npgryMQoLC8MO4XOpEkuqxAGKpSapEoc0D5nw7y3dv0O6xw+Z8R0aysLu7TYz9biLZAAzwzNkgnyi\nqL0TSX+NaevUsyUiIiKSQEq2RERERBJIyZaIiIhIAinZEhEREUkgJVsiIiIiCaRkS0RERCSBlGyJ\niIiIJJCSLREREZEEUrIlIiIikkBKtkREREQSSMmWiIiISAIp2RIRERFJICVbIiJJpHWoRZofJVsi\nIkm0c2fYEYhIsinZEhFJopKSsCMQkWRTsiUikkTr14cdgYgkm5ItEZEkUrIl0vwo2RIRSSINI4o0\nPzlhByAijROJRJgybQoAI84ZQf/+/UOOSOpDPVsizY96tkTSUCQS4eY7b2Zm2Uxmls3k5jtvJhKJ\nhB2W1IOSLZHmR8mWSJqJRCL8fNzPWdpyKbmdc+lyTBdy++d+3sslqU3DiCLNj5ItkTRS1aO1onIF\n67PW88aCN9i8eXPYYWUUM+tuZm+aWcTM5pnZddH9HcxsqpktNLPXzKx9zGduNbPFZrbAzM490PnV\nsyXS/CjZEkkjU6ZNIbd/Lt3O7Ma+8n3kbMvh45kfUxYpY8Q5I8IOL1OUAze6e39gCPATMzsGuAV4\n3d2PBt4EbgUws37AZUBf4HzgATOz2k6uni2R5kfJlkia2V65nZIWJZze/3Q6retEjw09mHjTRE2Q\njxN3X+fuH0af7wAWAN2BkcAT0cOeAC6KPr8QeMbdy919GbAYGFTb+dWzJdL8KNkSSSPHDj6WpSVL\n6bStE3l78+jZrid33XaXEq0EMbOewAnALKCLu5dAkJABnaOHdQNWxnxsdXRfjbZuhfLyREQrIqlK\npR9E0sSSzUt4c9ub3PPNe1jwzgIARtykkg+JYmZtgBeA6919h5lVX0K6UUtKt2gxnqIiaNsWCgsL\nKSwsbGqoIpJAxcXFFBcXN+kc5iEvQW9mHnYMIqlu+Zbl3Df7PkafMJoBnQeEHU6NzAx3r3WuUjox\nsxxgCvBPd783um8BUOjuJWbWFZju7n3N7BbA3X1C9LhXgXHu/k4N5/Vjj3WefBKOPz5530dE4qcx\nbZ2GEUVS3Kptq7h/9v18/7jvp2yilYEeBeZXJVpRLwOjo89/CEyO2f8tM2thZkcAvYHZtZ24c2fN\n2xJpbjSMKJLC1m5fy72z7uVbA77F8V3VFZIMZnY68F1gnpl9QDBc+AtgAvCcmV0OLCe4AxF3n29m\nzwHzgTJgzIG66zt31h2JIs2Nki2RFFWyo4R7Zt3DN/t/k5MOPSnscJoNd/83kF3L22fX8pnbgdvr\nc/4uXdSzJdLcaBhRJAWV7ipl0qxJjDxmJIO61VpFQNKQhhFFmh/1bImkmI27NnL3zLu5oM8FnHbY\nafu9P2fOHJ599jXWrVuNWTZdunRl1KjhDBw4MIRopaE6d4ZFi8KOQkSSScmWSArZsmcLk2ZN4uwj\nz2Zoj6H7vT9nzhyuvnoSe/aczpIls4DzOeKIQ5k+fRIPPjhWCVca0DCiSPOjYUSRFLFt7zbunnk3\nQ3sMZdgRw2o85tlnXyM7ezS7dm0mN/c6cnMvYffuvmRnj+bZZ19LarzSOBpGFGl+1LMlEqJIJMKU\naVPY63tZ120dI04cwbm9DriOsaS5Ll10N6JIc6OeLZGQRCIRbr7zZt7a9xZ/2f0XZhfPpse+Hgf8\nzKhRw6moeJxWrTpQVvZ7yspepGXLBVRUPM6oUcOTFLk0RadOQc+WajmLNB+qIC/NQtWkciBlJpNP\nuGcCb+97m5IOJbTPa0+rda04rcVpFN1QdMDPpeoE+UyqIJ8oVe1d27awahW0bx92RCLSUI1p6zSM\nKBmvalJ5dvZogJSZTF7mZSwpX0LXFl054qAjWF9Sv4k8AwcODD12aZqqSfJKtkSaBw0jSsarmlRe\nUHAWBQVnpcRk8r3le9nSYwu5q3NpU9KG9QvXUxYpY8Q5I0KNS5JDk+RFmhf1bIkkWVlFGQ+8+wDH\nHnkso48azT9e/wcAI24aQf/+/UOOTpJBS/aINC9KtiTjjRo1nOnTJ1FaGrwOJpOPDSWW8spy/ve9\n/6VdXju+f/z3ybIsBgzQ4tLNjWptiTQvSrYk4w0cOJAHHxwbM0E+nPlaFZUVPPz+w+Rl5/GjE39E\nlmkUv7nSMKJI86JkS5qFsCeVV3olf5rzJ9ydK066QolWM9elCyxYEHYUIpIsavFFEqzSK3nsg8fY\nW7GXq06+ipws/Y7T3KlnS6R5UbIlkkDuzpNzn2Tb3m1cc/I1SrQEULIl0twkvOU3s2XAVqASKHP3\nQYm+pkgqcHeenvc0G3Zt4NpB15KbnRt2SJIitGSPSPOSjF+zK4FCd9+chGuJ1CqZVeTdneciz7Fq\n2yquH3w9eTl5CbuWpB/1bIk0LwlfrsfMlgInu/vGWt7Xcj2ScNWryFdUPB7XKvJVC0oDfO3sr7Ew\nayELNy7khsE30Cq3VVyukeq0XE/dqtq7ykrIz4cdO6BFi7CjEpGGSNXlehyYZmYVwMPu/sckXFPk\nS2KryAOUlgb74pFsVS0onds/GCZ8/oHnGfLVIdwx8o5mk2hJw2RlQUEBbNgA3bqFHY2IJFoykq3T\n3X2tmXUiSLoWuPvbsQeMHz/+8+eFhYUUFhYmISyR+JgybQq5/XPpckwXVmxdwY59O+i0qhOtW7QO\nO7SEKi4upri4OOww0lbVUKKSLZHMl/Bky93XRh83mNlfgUFArcmWSCIko4r8qm2rWL9zPb1ye5Fn\nmT9Hq/ovRrfddlt4waQhLdkj0nwkNNkys1ZAlrvvMLPWwLmAWmSJq/pMfE9EFfmqeVola0tYsm4J\ne/ftpXdub5gfrHMociBaskek+Uh0z1YX4K9m5tFrPeXuUxN8TWlGqk98nz59Uq0T3+NZRT4SiXDV\nr66ipP0mdufvojxnDxfvuJieXXpqQWmpF92RKNJ8JDTZcvelwAmJvIY0b4mc+H4gDz3+EJGyZVir\nw9nbch85nxm5B+dSdENRg86TzHIUUn9m9ggwAihx9+Oi+04B/gDkAmXAGHd/L/rercDlQDlwfX1+\nqVStLZHmQxXkRRph7txFVLQ5mPK2u+iwbwjZFUcyd+6iBp2jqlduxoxBzJgxiKuvnsScOXMSFLE0\n0GPA8Gr7JgK/cvcTgXHAnQBm1g+4DOgLnA88YGZ13hauni2R5kPJlqS1UaOGU1HxOKWlb1Ba+kZ0\n4nv1/yPj76AjD2afl5K3vAvla7fjn1TQ+7BjGnSO2F65goKzyM4e/Xkvl4Qresd09ULMa4H20ecH\nAaujzy8EnnH3cndfBiwmuBHogJRsiTQfWqhN0lpTJr43dghv7rq5tDs9m5739WPXlsMB6JRfwU9+\n8oNGfANJI7cA/zaz3wEGnBbd3w2YGXPc6ui+A9IwokjzoWRL0l5jJr43ZGJ9bHX4YwYdw1s73uI3\nX/8NG/tvjEnWrmlwDMkoRyFx9Qhwrbv/zcwuBR4FzmnoSapK3WzdCitXFgKF8YtQROIuHjUFE75c\nT50BaLmeZqshPUvxnkheVHQ7M2YMiplY/wZDh85mwoRbv3RcbHX47ZXbWVqylAdGPcB5p54Xl/gy\naYJ8pi3XY2Y9gL/HTJDf5u7tYt7f4u4HmdktgLv7hOj+V4Fx7v5ODef8vL3bswfatw8e657hJSKp\nIlWX6xHZT0N6lhpybLxVVYfP75nP0tKlHMmRzJ0590vJVlPii2c5Cok7i25VFpvZme7+LzM7i2Bu\nFsDLwFNmNolg+LA3MLuuk+fnQ+vWwZI9nTvHO3QRSSVKtiQUDSnZkIjyDg0ZwttZuZOlpUs5puAY\n9u7Ym5T4JFxm9jTB+F5HM1tBcPfhfxHcadgC2BN9jbvPN7PngPl8URKiXt31AwfCe+/BBRck4EuI\nSMpQsiXNUn0n1g88bSAPPfMQPenJ3h17KYuUqTp8M+Du36nlrVNrOf524PaGXmfwYJg1S8mWSKZT\nsiWhqG/P0pw5cygpWceyZb9m587FtG7dJ24Tyesawlu5dSVTt0zlrkvuYvG7wYhRTdXhNdFdGmvw\nYPj978OOQkQSTRPkJTR1TQ6PnQu1Y8dOSkvv5dxz+3L99ZcnfIhuzfY1TJo5iW8f+20GHlL3tTJp\nontjZdoE+USo3t5t2AB9+sCmTZClqociaUET5CWt1NWz9OWin9CmTWu6dp2d8ESmZEcJ9866l2/2\n/2a9Ei3QRHdpnE6doKAAFiwALacpkrmUbEmzF1tH67Shp/GPTf9g5DEjGdStziLgIk02ZEgwb0vJ\nlkjmUse1pKy6luKZM2cORUW3U1R0e6PXFKyqozWzbCb/2vcvfvTkj+iX04/TDjut7g+LxEHVJHkR\nyVzq2ZKUdaA7BuNVe2vKtCns7LaT0q3b2JC1jq6tO7H2w7Uq6i1JM3gwPPhg2FGISCIp2ZKUVttc\nqHjUtopEIrz8ysu8v2keNqgDeXYYK5avZnXf1XV/WCROjjsOli6FbdugXbu6jxeR9KNkS1JWIu/w\nqxo+XNFpDfsOLyP70620phcVS7uzs4tG1yV5cnPhxBPh3XfhrLPCjkZEEkH/q0hKqhomnDFjEDNm\nDOLqqyd9aV5WXfO56jJl2hSsn1Heq4zWLXqRn3MoWYvzOLzVlRQUdEnEVxKpleZtiWQ2JVuSkr5c\n9uEssrNHf97LBV/M5xo6dDZDh85u8Hytfb6PJeVL6NGlO/l79pCb3YH83O7k5RU3KGkTiQclWyKZ\nTcOIknYaM7wYiUR45P8eYcHiBfTp1YetvbaS/2k+XXK6kH9IPivnr6PwK635yU+uqbG4anMvWCqJ\nNWQIXH01uIOpLKxIxlEFeYmreCUm1e82rKh4nAcfDJbAqWn/ga4TiUQYM24Mn+R+grUzduzcQfec\n7txx0R0sXLYQgBHn7L8Mz4HiUMK1P1WQr9uB2rvDD4fp06FXryQHJSINogryEqp4lWOA2ss+FBXd\n3uC7EKdMm8KGThvI75bPnvw95Jfmk7Uoi4XLFlJ0Q9EB44jHXY8i9TF4MMycqWRLJBMp2ZK4iXdi\nEs8lcBxnu28nz/LIL8vHUAeMpJaqeVvf+17YkYhIvCnZkrQyatRwpk+fRGlp8Dq4C3HsfsfFLsHT\np2cfyueXU766nBbegj0L9tCjQw9GnDMibtcTaarBg+Hpp8OOQkQSQXO2JG6SNb+prnlhVTW0cvvn\n4u4sWbmE0044jZaftmTh4oX07dWXK35wRY1ztBpzPQlozlbdDtTe7d4dLEq9YQO0apXkwESk3hrT\n1inZkrhKhcRkwj0TmFk2k85Hd2bhxoVsXruZb7X8Fr8Y+4ukx9KcKNmqW13t3aBBcPfdcMYZSQxK\nRBpEE+QldPGcZ9UU7s7iTYspqyyjZ05Psi077JBE6jRkSDBvS8mWSGZRsiUZo2qe1rq161i4cSE5\n5TkcmXMkFfMrGHFT3fOzRMI2eDC8+GLYUYhIvGkYUTJC1TytnH45rK5YzcalG/l6x6/TrUu3Wmto\nSXxpGLFudbV3S5fCaafBmjUqbiqSqjSMKM1SJBLh5+N+zvLK5bTPaU9WhywGZA+gW4tuddbREkkl\nRxwBBx0E770Hp5wSdjQiEi9aG1HSWlWP1vJOy1l72Frmz59Pt73dNEdL0tbFF8NLL4UdhYjEk5It\nSVtVPVpLWy4lv08+la0qyc/JZ9GbiyiLlNWrjpZIqvnGN4J5W5pdIZI5lGxJWqrq0VpRuYJ1uev4\nrPQzTj7kZDpaRw7POpyJN03UPC1pNDN7xMxKzOyjavuvNbMFZjbPzO6I2X+rmS2OvnduU6590kmw\nZw/Mn9+Us4hIKlGyJWkntker5cCWVOyuIH9TPmsXrOWI3Udw1213KdGSpnoMGB67w8wKga8Dx7r7\nscBd0f19gcuAvsD5wANmjZ/ebhb0bmkoUSRzKNmStBLbo1WSU8KiXYs4qedJFKwvoMeGHurRkrhw\n97eBzdV2XwPc4e7l0WOiizgxEnjG3cvdfRmwGBjUlOt/4xvw17825Qwikkp0N6KEpjHV5qdMm0Ju\n/1w653Zm5fyVtCxvybrN6zii3RFKtCTRjgKGmtn/ALuBn7v7+0A3YGbMcauj+xrt9NNh1aqgFMQR\nRzTlTCKSCpRsSSiqr6M4ffqkA66jWFWwtPjtYtYfuZ6KIys489gzWTJ9STBH6zYlWpJwOUAHdx9s\nZqcAzwNHNvQk48eP//x5YWEhhYWF+x2TnQ0jRwa9Wzfe2Oh4RSQOiouLKS4ubtI5VNRUQlFUdDsz\nZgyioOAsAEpL32Do0NlMmHDrfsfefffd/OZPt2NHGwd1a8vaLWs5seuJdOrSibJImXq0UkSmFTU1\nsx7A3939uOjrV4AJ7v6v6OvFwGDgSgB3vyO6/1VgnLu/U8M5693e/fOf8Nvfwttvx+PbiEi8NKat\n05wtSWl33303N99+K1ta7WBr+30sy1nBYe0Oo92ydgzJHaJESxLJoluVvwHDAMzsKKCFu28EXgZG\nmVkLMzsC6A3MburFhw2DSATWrm3qmUQkbEq2JBSjRg2nouJxSkvfoLT0DSoqHmfUqC/d/MV9991H\n0T23UHFcOX5MOZW+E9vYhtK1myk8o5CiG4qUaElCmNnTwH+Ao8xshZn9CHgUONLM5gFPAz8AcPf5\nwHPAfOAVYEw8uuvz8uCCC2Dy5KaeSUTCpmFECc2BJshPnjyZ79zwHXafvBvv4pANbMjFFmVz0K42\nvPV8sRKtFJNpw4iJ0ND27oUX4OGHYerUBAYlIg3SmLZOyZaknEgkwsU/vJhlOcvgBCjrVBbchL8g\ni+yPcph46+3cqFnDKUfJVt0a2t7t2AGHHgrLlsHBBycuLhGpP83ZkrRXVUdri2+h8tBKyveUk7sh\nFysxchZnK9GSZqVNm2Du1pQpYUciIk2h0g+SMiKRCFeNvYpFGxeR0z4Hb+Fk7ciCT6BlSUvuuOkO\nrr322lo/35i6XSKprmqtxB/8IOxIRKSxNIwoKSESiTBm3BjeL3uffQfto5JKWi5sSe6OXAryC7jz\n13cycuTIWj9fvW7Xtm2/45RT+tClS1clXkmSisOIZtYLWOXue6PL7RwH/Nndt4QUT4Pbu61boUcP\nWLQIOndOUGAiUm8aRpS0NWXaFFa2WYn3goruFWTlZ0EL6Ny+M3994q8HTLQAnn32NbKzR1NQcBa5\nuR1YvjyXqVMHMmPGIK6+ehJz5sxJzheRVPMiUGFmvYGHgcMI7iRMG+3bw0UXwZNPhh2JiDSWki1J\nCatXr2b1hg3syXWy93WgcgvkVuRywdALGnzX4Zo1rwE/oFWr0ygoOIvs7NGfDy9Ks1MZXcvwYuA+\nd78JOCTkmBrsiivgT38CDQKIpCclWxKKOXPmcPbZX6dDjwJ6DOjBv995D1q1JGtJHrYsF/u4Nbkb\n89m6vpKiotvr7JmKrdu1a9cyYAOHHqoxF6HMzL4N/BCommaeG2I8jXLGGVBZCTNn1n2siKSehM/Z\nMrPzgHsIErtH3H1Ctfc1Z6uZmTNnDl/72g9YlzsfBkVraJVBx2XDaLf7eHbsWUDl3n2wbwd9+vwP\nABUVjx9w7cSq8z777GusW7ea999fQ9u2P6n3Z6XpUnTOVj/gamCmu/8lWuH9surtUBLjaXR7N3Ei\nfPIJPPponIMSkQZJuTpbZpYFLALOAtYA7wLfcvdPYo5RstXMXHHFDTz61wfgrDI4OgvMYYWT+4/W\nnNQnKJe9bNmvKSi4hZ49LwQOvHZiTXRnYvKlYrIVy8w6AIe5+0chxtDo9m7dOjjmGFixAtq1i3Ng\nIlJvjWnrEl36YRCw2N2XA5jZM8BI4JMDfkrSQmMTmk9XfgK50R6tbKDSYCfk5+UwdGiwpNzRR5/C\nwoWtGx3bwIEDlWAJZlYMXEjQ1r0PrDezf7t72hVr69oVvvpVePZZuPLKsKMRkYZI9JytbsDKmNer\novskzVWVWpgxY1CD7/g7/vijsINzYA+w0uETh9kwqO9XmDDhViZMuJXrrvthnWsnitRDe3ffBnyD\noOTDqcDZIcfUaFdcAY88EnYUItJQKVHUdPz48Z8/LywspLCwMLRYpH5iSy0AlJYG++rTm/T9732f\n5zY+x/ollfhMoMzomtebiRNv+/yYgQMH8uCDY2N6zjTnKtUUFxdTXFwcdhh1yTGzQ4DLgF+GHUxT\nnXceXHUVfPwxDBgQdjQiUl+JTrZWA4fHvO4e3fclscmWZLZdZbuYunUqt3zrFj6b9hkftVhM78OO\n4Sc/+cF+yZSGAlNb9V+MbrvtttoPDs//A14D/u3u75rZkcDikGNqtJwcGD066N2aNCnsaESkvhI9\nQT4bWEgwQX4tMBv4trsviDlGE+TTUPWK7fW5429P+R4mzZxEr4N78c1+38QsZedSSyOk+gT5VBCP\n9u6zz2DwYFi1CvLy4hSYiNRbyt2NCJ+XfriXL0o/3FHtfSVbaaohE+T3lu/l3nfupXu77nx7wLeV\naGWgVEy2zKw7cB9wenTXW8D17r4qpHji0t4NGwZXXw2XXRaHoESkQVIy2aozACVbGW9fxT7un30/\nBa0K+P5x31eilaFSNNmaRrA8T9ViN98Dvuvu54QUT1zau2eegQcfhNSfMieSeZRsZbh0rB1VVlHG\nA+8+QNu8tow+YTRZpkULMlWKJlsfuvsJde1LYjxxae/KyqBXL3jpJTj55DgEJiL1poWoM1hTSi2E\npbyynIfff5iWuS2VaElYNprZ98wsO7p9D9gYdlBNlZsLN9wAd90VdiQiUh8pUfpB6taUUgvJFIlE\nmDJtCpVeye5euznkkEO44sQrlGhJWC4nmLM1CXDgP8DoMAOKlx//GH77W1i2DHr2DDsaETkQ/Q8o\ncROJRLj5zpv5z77/8Nye53jx9Rc5Lf80srOyww5Nmil3X+7uF7p7J3fv7O4XAZeEHVc8tGsXJFwq\nASGS+pRspYlRo4andEX1yZMnc/EPL2b2ztl8lvUZLTu3pFf3Xrz6xqthhyZSXdot1VOb666DJ5+E\nTZvCjkREDkTDiGkizIrqdU3Mnzx5MleOv5JdbXexp+MetqzYQmFeoYYOJVWl1CT+pujWDS68EB56\nCG6t3xrtIhIC3Y0oB1Sf4qXnX3o+H3T8gMrOlWxZvgUq4aC9B3FK61OYeNNE+vfvH07wklSpeDdi\nTcxshbsfXveRCbl23Nu7efNg+HBYulRFTkWSQXcjStzFTswvKDiL7OzRn/dyRSIRJtwzgU+XfcrO\n8p3QDg49/FDyVuRx0NKDlGhJaMxsu5ltq2HbDhxaj88/YmYlZvZRDe/9zMwqzezgmH23mtliM1tg\nZufG+esc0LHHwnHHwVNPJfOqItIQSrakUWInw9tZxq6Nu6h4t4K9G/bScntL7vz1nUq0JDTu3tbd\n29WwtXX3+kyfeAzYb1JktCL9OcDymH19CRa67gucDzxgSa7ce9NNQRmIyspkXlVE6kvJlhxQ9Yn5\nO3bcw+7Ktfx83M/Zc/ge9h66l3a92nFirxPpuKQjJ2w8gT+O/yMjR45s1PXmzJlDUdHtFBXdnvJ1\nxCRzufvbwOYa3poE3FRt30jgGXcvd/dlBAtdD0pshF82bFgwhPjKK8m8qojUlybIywHFTswvLS1h\n4abNrOiczYrPVrB6zWq6dezGoB6D2Lx1M0O+N4SiG4oafa3q88OmT59U5+LWIsliZhcCK919XrWO\nq27AzJjXq6P7khgb/OIXMH48fO1rwWsRSR1KtqROAwcOZODAgUy4ZwIbywrockwXNuVsYtncZZQv\nLGfzvs2URcoYcdOIJl0nXQq3SvNjZi2BXxAMITbJ+PHjP39eWFhIYWFhU08JwCWXwB13wIsvwqWX\nxuWUIgIUFxdT3MSFSJVsSYOt2b6G7S23M7DjQNosb8OQo4Yw4qYRmqMlmawX0BOYG52P1R2YY2aD\nCHqyYu9u7B7dV6PYZCuesrLgf/4Hrr8eLroIctS6i8RF9V+KbrvttgafQz+OUqeqJXhKSkqY/8l8\nNvTcRIceGWcDAAAgAElEQVStB9N6c2vu+s1d9O/f//O5VtD4RbJHjRrO9OmTKC0NXgeFW8fG86uI\nNIRFN9z9Y6Dr52+YLQUGuvtmM3sZeMrM7iYYPuwNzA4hXs49Fw45BJ54Aq64IowIRKQmqrPVzNVV\nsLTqrsPc/rms2LqCjz/5hIPmDSPfD6F93jqeeCLI8OuqxRWveCR1pUudrfows6eBQqAjUAKMc/fH\nYt5fApzs7puir28FrgDKgOvdfWot5014ezdrFnzzm7B4MeTnJ/RSIs1SY9o6JVvNWF0FSyORCD8f\n93OWd1rOoQMP5aOVEfZ93J1Dll5K7+5FlJa+wdChwS/wM2YMiplrFeyfMEElrZuTTEq2EiVZ7d3I\nkXDmmXBjxixMJJI6VNRUGuRABUsnT57MJWMu4f0N77O2ci2zl86m7e72ZJW1CDVmEanbb38LEybA\ntm1hRyIioGRLajB58mR+fNOPWd15NeX9y9m+Zzs5G3LwDfuo/GQZLSoLvrQYdqovki3S3AwYECzh\n87vfhR2JiICGEZu1moYRb7rpQn59/69Z7aspO6qMioMraLe9Hdnzszmp00lcPupy3nvvU+DLc6o0\n10o0jFi3ZLZ3S5fCySfDggXQuXNSLinSLGjOljRYbJJ08sm9efTZR3l/w/uUH1HO9uztZJNN7rZc\nuq3vxosPvKjyDlIrJVt1S3Z7d8MNsGMH/OlPSbukSMZTsiWNVnXX4dKWS1lXsY5te7fR1tpSvqSc\n/HX5/OnOPzV6CR5pHpRs1S3Z7d3WrdCvHzz3HJx+etIuK5LRNEFeGqXqrsOlLZdScEwB5QXltM1v\nS+7SXLpZNyVaImmqfftg3tY110BZWdjRiDRf6tlq5iZPnkzRxCI27dlE2dFlVPSsYEDnAWxZuIUe\nG3pw12131WvoUHO2RD1bdQujvXMPip2edx787GdJvbRIRtIwYjMRr8QmEolwyZhL2HrMVipzKykt\nLSWnPJc2Fe3oy1E89JuH6p1oxauoqaQvJVt1C6u9W7wYhgyBDz6Aww5L+uVFMoqGEZuBqsRmxoxB\nzJgxiKuvnsScOXMada4p06aQ1S+L7MOy2XPoHiw3h8r3W1IxuydbP+3A3r1763WeA9XrEpHw9ekD\nP/1pMGFeRJJPyVaaiXdi07FTR7bt2kb5lkpsd2taVHThhD6P0abNDUqYRDLILbfARx/BK6+EHYlI\n86Nkqxk7fejprNm+hj45fchf3JKc99rQr8sE2rZtWHkHFTUVSX35+fCHPwQ9XLt2hR2NSPOiOVtp\npinzoyKRCFOmTQHgK2d+hX9s+ge9s3qzfu56Vq9ezfRXl9KmzQ0NPm9VXJog37xpzlbdUqG9+973\ngrsU//CHUMMQSVuaIN9MNCaxqaqjlds/lzIvY9GaRRRdWMSPh/24SecVqaJkq26p0N5t2QInnAD3\n3w8jRoQaikhaUrIlNaqqo7W803KOPvVoVuxdQYvNLbgo/yKKbiiq9XNKvqQhlGzVLVXau7ffhm9+\nM7g7sWvXsKMRSS+6G1H2U9WjtaJyBRt9I28ufJOW3pIu2V0O+Ll43vUoIqnljDPgyith9GiorAw7\nGpHMp2Qrw02ZNoXc/rkcNewo9pTvIWtXFhvnbqQsUsaIc2ofQ1A5B5HM9utfB0OK998fdiQimS8n\n7AAkcSKRCMVvF7PMl5EzOId+/fqx9e2t9MjqwcTbJmpRaZFmLDcXnnoKBg+Gr34Vjj027IhEMpeS\nrQwViUS46ldXsaLVGtbkrySr2OiS050eWYfWawmeUaOGM336JEpLg9dBOYexSYhcRJKlVy+46y74\n9rfhnXegdeuwIxLJTBpGzFAPPf4QH5cvpbRjCyq9G2U7WrD5nZb1rgw/cOBAHnxwLEOHzmbo0Nla\nfkckQ/3gB3DyyZq/JZJIuhsxQ31l+Lm8330x3qITFRuOxjcuod2ithx1+E0MHTqbCRNuDTtEyTC6\nG7Fuqdre7dkDw4bB8OEwblzY0Yiktsa0dRpGzEDlleWUH1MGiwyraIuXlcLCClrnHBN2aCKSgvLz\n4aWX4NRToV+/oCyEiMSPkq00VlMdrIrKCv74/h/56plD2P5ma0q3dWTT5m3klLfkoN7HaO6ViNSo\na1f429/g3HOhd2848cSwIxLJHBpGTFM1LdvzwP9ezwd8wN6KvVx98tV89OFHPPvsa5SUrMO9gq5d\nu6k4qSSMhhHrlg7t3QsvwI03wuzZKngqUhNVkG9GiopuZ8aMQRQUnAXAhtJpHPzVhxh+4VcYc8oY\ncrNzG31uVY6XxsikZMvMHgFGACXuflx030Tg68Be4DPgR+6+LfrercDlQDlwvbtPreW8adHe3XYb\n/POf8Prr0KZN2NGIpBZVkG9mdu1axqerJrB41R2sKXiG3baLa065psmJlirHi/AYMLzavqlAf3c/\nAVgM3ApgZv2Ay4C+wPnAA2aW1knnf/839O8PI0fC7t1hRyOS/pRspaFIJMKqDR+zsHQsq9v/hVXH\nPcqGrOe58rjv0SK7RZPOrcrxIuDubwObq+173d2riiPMArpHn18IPOPu5e6+jCARG5SsWBPBDB5+\nGLp0gUsugXpUixGRA1CylWaq1jr8IO8DWg/PpazDIloWbOOUASewcu3KsMMTaS4uB16JPu8GxP7w\nrY7uS2vZ2fDEE8Gdit/5DpSXhx2RSPrS3YgprPrcqby8PH4+7uesqFxB1kFZZB+aTV6XFvTY3J2D\nux4cl2uqcrzIgZnZL4Eyd/9LYz4/fvz4z58XFhZSWFgYn8ASIDcX/vIXuPhi+OEP4c9/DpIwkeak\nuLiY4uLiJp1DE+RTVPW7DXfsuIf2vTezqesmNlduZs/mPZQfUk6rva0oWF9Az3Y9mXjTgdc7rO/E\nd02Ql8bIpAnyAGbWA/h71QT56L7RwJXAMHffG913C+DuPiH6+lVgnLu/U8M507K9270bvvY16NED\n/vhHyNGv6dKM6W7EDFL9bsO5C68k77R/c+KwAUyPTGd3xW46LexE3rY8Lhh8AVf84Io6E63qpSK0\nBI/EUwYmWz0Jkq1jo6/PA34HDHX3jTHH9QOeAk4lGD6cBvSpqWFL5/Zux45g/lZeHjzzDLRqFXZE\nIuFQBfkMtX17hG0755K9tZSS3SV0OrQTFQsrODLvSO56oO5FpeHLE98BSkuDfUq2RPZnZk8DhUBH\nM1sBjAN+AbQApkVvNpzl7mPcfb6ZPQfMB8qAMWmbUR1Amzbw97/DFVfA2WcHzzt2DDsqkfSQsAny\nZjbOzFaZ2Zzodl6irpWJRo0aTkXF46xY8QhzV19BZe/llO3bw3sfv0fBxgJ67+rNXbfVL9ESkYZx\n9++4+6Hunufuh7v7Y+7ex917uPvA6DYm5vjb3b23u/etrcZWJmjRIpg0/5WvwBlnwPLlYUckkh4S\nfTfi3TEN06sJvlZGGThwIDfddCHbKiaQ1XkJR519GIeeeSjd13Wn9fzWdc7Pqq4qeSstfYPS0jei\nE9+rlxESETmwrCyYMAGuuipIuObODTsikdSXsDlbZjYO2OHuv6vjuEzscW+yyZMnUzSxiE05m9jb\nYy/e0jlzwJlk78lmSO4Qim4oavA5NfFdEinT5mwlQqa1d88+Cz/9KdxzD3z3u2FHI5IcKTVBPpps\njQa2Au8BP3P3rTUcl1GNTzxEIhEuGXMJW4/ZSnmrcjZv3Ey7snYcsveQet11KBIGJVt1y8T2bu5c\nuPRSGD4cfve7YAK9SCZL+gR5M5sGdIndBTjwS+AB4P+5u5vZb4C7gStqOk861Z1JhinTppDVLwvr\nZlS2qKTAC6j8oJLDOx3eLBIt9cClh3jUnpH0d/zx8O67MHo0nHkmPP88HHZY2FGJpJaklH6oqV5N\nzHsZ95teU024ZwIvbXqJBeULaNeqHRUrK2j/cXtefPjFZpFoqURFelLPVt0yub1zhzvvhLvvhkcf\nhQsuCDsikcRIqYWozaxrzMtvAB8n6lqZpu+pfdmwYwMDcgbQbnU78j7Mo1+XU/jzn1/O+EWhtTaj\nSHoyg5tvDuZx/eQn8KMfwZYtYUclkhoSeTfiRDP7yMw+BM4EtOZLPSwsXciM7TP4w6g/MPLgkZzd\n5mza7jqWtWtHM2PGIK6+elLGJ1wikr7OPBPmzQuKnh57LLzySt2fEcl0qiCfQj7d9CkPvvcg/3XS\nf3FUx6OA/SvJl5a+wdChs5kw4dYwQ00YDSOmLw0j1q25tXdvvhkUQS0sDCbPHxyfJVxFQpVSw4jS\nMEs3L+XB9x7kihOv+DzRCtOcOXMoKrqdoqLbk9qTNnDgQB58cCxDh85m6NDZSrRE0tiwYUEvV9u2\n0Lcv3H8/lJeHHZVI8qlnKwWs2LqC37/ze0afMJoBnQd86b0wenrUuySNoZ6tujXn9m7ePBg7Ftau\nhUmT4Nxzw45IpHFSqs5WvQNoxo0PwKptq7h31r1897jvckLXE2o8JtmlEJrb0KXEh5KtujX39s4d\nXn4ZfvazoKfrt7+F4/a7R10ktWkh6jSzdvta7p11L6MGjKo10YJgaE29SiKS7sxg5Eg47zz4wx+C\nQqhDhsB//zecUHsTKJL2NGcrJOt3rueeWfdwab9LOfnQk8MO50u0jqKIJFJeHtx4I3z2WbCo9QUX\nBEnY+++HHZlIYmgYMUkikQhTpk0B4PShpzNl0xS+ftTXOf3w00OOrGaq4i4NpWHEujWX9q6hdu+G\nP/4RJk6EXr3g2mvhoosgR2MvkoI0ZytFRSIRbr7zZnL757LP97Fo7SJ+eeEv+dFXfxR2aCJxo2Sr\nbs2hvWuKsjL461/hvvtg2TK45hq48kro1CnsyES+oNIPKWrKtCnk9s/loN4Hsa79Orp06cL6uevD\nDktEJKXk5sJll8FbbwUT6T/7DPr0gW98AyZPhn37wo5QpHGUbCVJmZcxb/08urbpSqds/ZomInIg\nJ54IjzwCy5fD174WrLnYrRv89KcwcyZUVoYdoUj9KdlKgmFfHcbiNYvJ3ZxLizUtKIuUMeKcEWGH\nJSKS8tq3D6rQ/+tfMHs2dOkCP/4xHHYYjBkDr78eDD+KpDLN2UqA2Mnww746jNe2vka7Pe3YFdmF\nmTHinBH0798/5ChF4ktztuqWie1dWBYtCuZ3vfQSfPppUEbi3HPhnHOCHjCRRNEE+RQQOxm+witY\ntHoRV11wFWPPHYuZ/h+SzKVkq26Z1t6litWr4Z//hGnTgp6uQw4Jkq5hw+C006Bjx7AjlEyiZCsF\nTLhnAjPLZtLxqI58vP5jKkoruDT/Us4989wGlVJQ6QVJN0q26pZp7V0qqqiAOXNg6tRg6HHWrGDI\n8Ywzgu3UU6F3b8jSJBppJCVbKWDCPRP4975/s+HgDbTMaUnb9W3psaEHs/61ud5rDWptQklHSrbq\nlmntXTooL4ePPoK33w7ucnz3XdiyBQYOhJNOCrbjjw/uelRdL6kPLdeTAoafNZwn/vgEeRV5dM7u\nTPn8cnZmZ5GdPTpmrUF49tnXak2enn32tQYdLyIiNcvJCRKrgQPhuuuCfaWlQbX6996DZ5+FX/0K\n1qyBo4+GAQPg2GOD50cdFRRZbdEi3O8g6U/JVhyVV5bz1q63GHXuKFosbkGWZTHiphH8+c8vhx3a\nAWnIUuTLzOwRYARQ4u7HRfd1AJ4FegDLgMvcfWv0vVuBy4Fy4Hp3nxpG3FI/BQXBhPrhMauQ7dwJ\n8+fDxx8H24wZwST8FSuge/cg8TriiC9vPXtChw7Bmo8iB6JhxDipqKzgofcfIsuyuHLglWRnZX/+\nXkOHBZM5jKghS4mXTBpGNLMzgB3An2OSrQnARnefaGZFQAd3v8XM+gFPAacA3YHXgT41NWyZ0t41\nJ/v2wdKlsHhx8LhkSfC4dGlQA6ysLEjGDjss2Lp1g65dg0n6VY+dO0Pr1krKMoXmbIWk0iv505w/\nUVZRxlUnX0VO1v4dhg3tPUpWb1NR0e3MmDEoZsjyDYYOnc2ECbcm5HqSuTIp2QIwsx7A32OSrU+A\nM929xMy6AsXufoyZ3QK4u0+IHvdPYLy7v1PDOdO+vZMv274dVq2ClSuDbc0aWLsW1q0LHteuhfXr\nwT1YdqhTpyD56tgRDj74i8eDD4aDDvpia98+eFSSlno0ZysElV7J4x8+zu6y3Yw5ZQw5WTk1JkpV\nW3019HgRSbjO7l4C4O7rzKxzdH83YGbMcauj+6QZaNsW+vYNtgPZuTNIujZsCLZNm4Jt40ZYuDB4\nvmVLsG3d+sXzPXugTRto1y64Vrt2QQLWps0XW+vW0KrVF1vLll/e8vO/eKza8vKCxxYtgue5ubpD\nM5GUbDWBu/N/H/0fW/Zs4dpB15KbnbvfsNz06ZNSelhu1KjhTJ8+idLS4HVFxeOMGjU23KBE0kOj\nuqjGjx//+fPCwkIKCwvjFI6kstatv5jr1RDl5bBjB2zbFvSibdsWJG47dnz5cdeu4Pn69cHrPXtg\n9+5gq3q+Zw/s3Rs8Vm379n2x5eYGyVeLFl88z82tecvJ+eIxdsvO3v+xti0ra//nWVkH3sy+/Fh9\nX/X3q79X0wa1v5edDXl5xRQXFzfp71/DiI3k7vzl47+wettqrjv1OvJy8oD0HJbTBHmJh2YwjLgA\nKIwZRpzu7n1rGEZ8FRinYURJJ+7B/LO9e4PHffu+eNy3L0j6ysqCrep5efmXt7KyoM5ZRcUX+6pe\nV98qK/d/HbtVVAQx1bSv+v7YfbGPscdVva6+VX332racHPj737/8Z6VhxCRxd56f/zwrtq7ghsE3\nfJ5opSsNWYrUyKJblZeB0cAE4IfA5Jj9T5nZJILhw97A7OSFKdJ0Zl/0akn8KdlqIHfnr5/8lcUb\nFzN2yFjyc/K/9L6G5UTSn5k9DRQCHc1sBTAOuAN43swuB5YDlwG4+3wzew6YD5QBY9R9JSKxNIzY\nQH9f+Hc+WPcBPxvyM1q3aF3jMRqWk+Yo04YREyHd2jsR2Z9KPyTYPxf/k3dWv8PPhvyMtnltww5H\nJKUo2apbOrV3IlKzxrR1utGznqZ9No3/rPwPYwePVaIlIiIi9aZkqx6mL51O8bJibhxyI+3z24cd\njoiIiKQRJVt1eGv5W0z9bCo3DrmRDi07hB2OiIiIpBklWwcwc+VM/rH4H4wdMpaOrTqGHY6IiIik\nISVbtXh39bv87ZO/ccPgG+jcunPdHxARERGpgZKtGsxZO4fnIs9x/eDr6dqma9jhiIiISBpTslXN\nRyUf8fS8p7nu1Os4tO2hYYcjIiIiaU7JVozI+gh/nvtnfjropxzW/rCwwxEREZEMoGQr6pPST3js\nw8e45uRr6HlQz7DDERERkQyhCvJRCzYsIDsrm6M6HhV2KCJpSRXk65Yq7Z2INJ6W6xGR0CjZqpva\nO5H0p+V6RERERFKMki0RERGRBFKyJSIiIpJASrZEREREEkjJloiIiEgCKdkSERERSSAlWyIiIiIJ\npGRLREREJIGUbImIiIgkkJItERERkQRqUrJlZpea2cdmVmFmA6u9d6uZLTazBWZ2btPCFBFJDdG2\nLWJmH5nZU2bWwsw6mNlUM1toZq+ZWfuw4xSR1NHUnq15wMXAv2J3mllf4DKgL3A+8ICZpfyaacXF\nxWGH8LlUiSVV4gDFUpNUiaO5MLMewJXAie5+HJADfBu4BXjd3Y8G3gRuDS/KxMmEf2/p/h3SPX7I\njO/QUE1Kttx9obsvBqonUiOBZ9y93N2XAYuBQU25VjKk0j+AVIklVeIAxVKTVImjGdkG7ANam1kO\n0BJYTdDmPRE95gngonDCS6xM+PeW7t8h3eOHzPgODZWoOVvdgJUxr1dH94mIpC133wz8DlhB0K5t\ndffXgS7uXhI9Zh3QObwoRSTV5NR1gJlNA7rE7gIc+KW7/z1RgYmIpBozOxIYC/QAtgLPm9l3CdrE\nWNVfi0gzZu5NbxPMbDrwM3efE319C+DuPiH6+lVgnLu/U8Nn1SiJZAh3T/m5mU1hZpcB57j7ldHX\n3wcGA8OAQncvMbOuwHR371vD59XeiWSAhrZ1dfZsNUDshV8GnjKzSQTDh72B2TV9KNMbZxHJKAuB\nX5tZPrAXOAt4F9gBjAYmAD8EJtf0YbV3Is1Tk5ItM7sIuA8oAKaY2Yfufr67zzez54D5QBkwxuPR\nhSYiEiJ3n2tmfwbeByqAD4CHgbbAc2Z2ObCc4G5sEREgTsOIIiIiIlKzlKkgb2bXRgugzjOzO1Ig\nnp+ZWaWZHRzS9SdG/zw+NLMXzaxdCDGcZ2afmNkiMytK9vVj4uhuZm9GC0nOM7PrwoolGk+Wmc0x\ns5dDjqO9mT0f/XcSMbNTQ4pjvyKfYcSRylLlZ6khzOwRMysxs49i9qVN8dba2o00+w55ZvaOmX0Q\n/R7/E92fNt8B9m8z0zD+ZWY2N/r3MDu6r0HfISWSLTMrBL4OHOvuxwJ3hRxPd+AcguGAsEwF+rv7\nCQR1ypJaJNHMsoD7geFAf+DbZnZMMmOIUQ7c6O79gSHAT0KMBeB6giHysN0LvBKdiH08sCDZAdRS\n5PNbyY4jlaXYz1JDPEYQc6x0Kt5aW7uRNt/B3fcCX3X3E4HjgGFmdjpp9B2iqreZ6RZ/JcENMCe6\ne1XN0AZ9h5RItoBrgDvcvRzA3UtDjmcScFOYAbj76+5eGX05C+ie5BAGAYvdfbm7lwHPEBRuTDp3\nX+fuH0af7yBIKkKp2xZNxC8A/hTG9WPiaAd8xd0fA4gWEN4WQijVi3y2AtaEEEcqS5mfpYZw97eB\nzdV2p03x1lraje6k0XcAcPdd0ad5BP9nbyaNvkMtbWbaxB9l7J8vNeg7pEqydRQw1Mxmmdl0Mzs5\nrEDM7EJgpbvPCyuGGlwO/DPJ16xemHYVKVCY1sx6AicA+5URSZKqRDzsyY5HAKVm9li0e/5hM2uZ\n7CBqKPK5JVrkU76Qkj9LjdQ5HYu3xrQbs0izArTRIbgPgHVAsbvPJ72+Q01tZjrFD0Hs08zsXTP7\ncXRfg75DPEs/HJDVXhz1V9E4Orj7YDM7BXgOODKkWH5BMIQY+16y4/i8YKyZ/RIoc/enExVHujCz\nNsALwPXR31STff2vASXu/mF06DvM2/hzgIHAT9z9PTO7h6Bbe1wyg7D9i3y+YGbf0b/XZiPsXzrq\nVL3dsP1rnaX0d4iOcJwY7c1+Ldr2pMV3qKHNrE1Kxh/jdHdfa2adgKlmtpAG/h0kLdly93Nqe8/M\nrgZeih73bnRiekd335jMWMxsANATmGtmRtDl/L6ZDXL39cmKIyae0QTdr8Pife16WA0cHvO6e3Rf\nKKJDVC8AT7p7jTWMkuB04EIzu4BgTby2ZvZnd/9BCLGsIuiBfS/6+gUgjInXJwP/dvdNAGb2EnAa\noGTrCyn1s9REJWbWJaZ4a9zbxXiqpd1Iq+9Qxd23mdkrBD9z6fIdamoznwTWpUn8ALj72ujjBjP7\nG8HUgAb9HaTKMOLfiCYUZnYUkJuoROtA3P1jd+/q7ke6+xEE/6GdmIhEqy5mdh5B1+uF0UmSyfYu\n0NvMekTvLvsWQbHasDwKzHf3e8MKwN1/4e6Hu/uRBH8eb4aUaBHtvl4Z/XmBoLhmGJP2FwKDzSw/\n+gvKWYQwUT/FpdrPUkMY+xesHh19Xmvx1hRSU7uRNt/BzAqq7nKLThM4h6C2W1p8h1razO8DfycN\n4gcws1bR3lHMrDVwLjCPBv4dJK1nqw6PAY+a2TyCqsyh/AdWAye8oaL7gBYE48QAs9x9TLIu7u4V\nZvZTgrsis4BH3D2U/0Sjd998F5gXnbvgwC/c/dUw4kkh1xGs1JALLAF+lOwADlDkU6JS6WepIczs\naaAQ6GhmKwiGqO8gWA8y5Yu31tZuEFT5T5cCtIcAT0R/kcki6KF7I/p90uU71OQO0if+LsBfo8PP\nOcBT7j7VzN6jAd9BRU1FREREEihVhhFFREREMpKSLREREZEEUrIlIiIikkBKtkREREQSSMmWiIiI\nSAIp2RIRERFJICVbIiKStszsYDP7ILpG6FozWxXzul61JM3sETPrU8cxY8zs2/GJusbzXxxTpFgy\njOpsiYhIRjCz/wZ2uPvdNbxnnsL/4UWXsXkhxOXIJIHUsyUiIpni8xU/zKyXmUXM7P/M7GOgq5k9\nZGazzWyemf0q5ti3zOw4M8s2s81mdruZfWhm/zazgugx/5+ZXRdz/O1m9o6ZLTCzwdH9rczsBTP7\n2MyeN7N3zey4/YI0uzMa24fR85xBsA7u3dEeucPNrLeZvRo9R7GZ9Y5+9kkze8DM3jOzT6JLu2Fm\nA6LfbU70vD0T9qcsDZYqy/WIiIjE29HA99z9AwAzK3L3LWaWDUw3sxfc/ZNqn2kPTHf3W83sd8Dl\nwMSaTu7up5rZ1wmWMjofuBZY6+6XRpOs96t/xsw6A+e7e//o63Yxi0w/7+4vR/e/CVzh7kvN7DTg\nD8Dw6Gm6u/vJ0WHH182sFzAGuNPdn48u4RXWUnNSAyVbIiKSqT6rSrSivhtdyy6HYN3BfkD1ZGuX\nu0+NPn8fOKOWc78Uc0yP6PMzCNb9w90/MrNIDZ/bBFSY2cPAK8CU6gdEF58eDLwYXRcRvjwS9Vz0\nGoui61b2Af4D/Drao/WSu39WS9wSAg0jiohIptpZ9SQ6DHcdUOjuxwOvAfk1fGZfzPMKau+U2FuP\nY/brXXL3cuBk4G/ARcA/avncBncf6O4nRrfjY09T7Vh39/+Lnm8v8Gp0aFJShJItERHJVLHJTjtg\nG7DDzA7hiyG5A32mof4NjAIws2OBvvud3KwN0N7dXwFuBE6IvrU9GiPuvgVYa2YXRT9j1eZ+fTO6\n/yigO7DYzI5w9yXu/nuC3rL95opJeDSMKCIimerzHiB3n2NmC4AFwHLg7ZqOq/a8zvNWcx/wRHRC\n/vzotrXaMe2Bl8wsjyCxGxvd/xfgITO7kaCH6lvAg2Y2HsgF/g/4KHrsajN7D2gNXOnu5Wb2nWhp\nig7DR7AAAAB7SURBVDJgNcE8MkkRKv0gIiISB9GJ9znuvjc6bPka0MfdK+N4jSeJmUgv6UE9WyIi\nIvHRBngjppjqf8Uz0YpSD0kaUs+WiIiISAJpgryIiIhIAinZEhEREUkgJVsiIiIiCaRkS0RERCSB\nlGyJiIiIJJCSLREREZEE+v8BDWQFu2iG7q0AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f804039d090>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "vNtkU8h18rOv",
"colab_type": "text"
},
"source": [
"In the remainder of this notebook, we'll go through this example in more detail."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "r6rsv-q5gnn-",
"colab_type": "text"
},
"source": [
"## From the beginning\n",
"\n",
"Let's walk through exactly what this is doing from the beginning. We'll start with what the data looks like, then we'll look at this neural network, what is executed when, what gradient descent is doing, and how it all works together."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "UgtkJKqAjuDj",
"colab_type": "text"
},
"source": [
"## The data\n",
"\n",
"This is a toy data set here. We have 50 (x,y) data points. At first, the data is perfectly linear."
]
},
{
"cell_type": "code",
"metadata": {
"id": "-uoBWol3klhA",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "form",
"executionInfo": {
"elapsed": 398,
"status": "ok",
"timestamp": 1446659128547,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "efef4adf-42de-4e6f-e0c3-07ddd3083d85"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"num_examples = 50\n",
"X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)])\n",
"plt.figure(figsize=(4,4))\n",
"plt.scatter(X[0], X[1])\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQMAAAEACAYAAAC3RRNlAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEGpJREFUeJzt3XuMHeV5x/Hv4xinBgIN2Yq0WCFFJK1EUzC3otAWC4JB\nRHESkUq0qRKIBG2jAE1cZBKoQL0kBGSRtEr/IBdE2iDUEkhMLrJNqS1BBeF+dYA2KbcALYUWIVyu\nT/8447Ase9a7O+/MOTPn+5Esn4Nn552F9Y9553nP80ZmIklLRn0BksaDYSAJMAwkVQwDSYBhIKli\nGEgCCoVBRHw2Iu6NiLsi4lsRsazEeSW1p3YYRMS+wKnAysz8TWApcFLd80pq19IC53gWeBHYLSJe\nBXYFflbgvJJaVPvOIDOfAdYDDwOPAf+TmdfWPa+kdpWYJuwHfBrYF/gVYPeI+IO655XUrhLThEOB\nGzLzaYCIuAp4L3D59IMiwg9BSCOSmbGzY0pUE+4HjoiIX4iIAI4Btg25oNZ+nXfeeY7X0fH6/L2N\nYrz5KvHM4E7gm8CtwJ1AAJfUPa+kdpWYJpCZFwEXlTiXpNHo7QrEVatWOV5Hx+vz9zaK8eYrFjKn\nqDVQRLY1lqTXRATZ0gNEST1gGEgCDANJFcNAEmAYSKoYBpIAw0BSxTCQBBgGkiqGgSTAMJBUMQwk\nAYaBpIphIAkwDCRVDANJgGEgqVJqr8U9I+KfImJbtefib5U4r6T2FGmICnwZ+EFm/l5ELGWwxZqk\nDimxo9IewO9k5qUAmflyZj5b+8qkntm4cSOrV5/I6tUnsnHjxlFfzhvUbogaEQcy2CfhPuBA4Bbg\nzMzcPuM4G6JqYm3cuJEPf/jjbN/+RQCWL1/H1VdfxnHHHdf42G02RF0KHAx8JTMPBp4Hzi5wXqk3\n1q+/pAqCjwODUFi/frz2GirxzOBR4JHMvKV6fyWwbrYDzz///J+/XrVq1dj2j5dK2bhxI+vXX8Kt\nt94JrGllzC1btrBly5YFf12RfRMiYitwamY+EBHnAbtm5roZxzhN0ER5/dTgbuCrwN8A4zlNKFVN\nOAP4VkTsAvwEOKXQeaXOev3UYGCvvf6SQw45kLVr2wmChSi11+KdwGElziV12Y5pAcBTT/33jD99\nD4cc8lM2bfp2+xc2D6XuDKSJN7NisGzZn7Js2Vm8+OLgz5cvX8fatZeN8ArnZhhIhcycFrz4Iqxc\n+VWmpjYAjOXUYDrDQGrQ1NTeYzstmMkwkGra8Zzgqaee7NS0YCa3ZJdqmO05wQEHHMjU1NtYu/a0\nsZgWtF1alCbSbM8JpqY2dGZqMJ39DKRF2PGho8HKwn7wzkBaoNdPDX6VwZq7ga49J5jOMJAWqGsr\nC+fLMJBqG++VhfNlGEjzMH2Z8VFHHcz1169je9Wxo8tTg+ksLUo7MVtjknPOOZ2tW28DGJsS4jCW\nFqVCZj4j2L4dtm7tZvlwLpYWpSH6WD6ci3cG0iz6Wj6ci2EgzaKv5cO5GAZSpcuNSUowDCS635ik\nBMNAovuNSUooFgYRsYTBBiqPZmY7PaGlBnWpMUkJJe8MzmSwq9IeBc8pNaovjUlKKBIGEbECOAH4\na+AzJc4pNW225wQrV15aNSbp/7RgplJ3BhcDZwF7Fjqf1Lg+NSYpoXYYRMT7gScz846IWAUMXQPt\n9moaB6PY8qxNI9teLSI+D/wh8DKwHHgLcFVmfmzGcX5QSSM3LluetWm+H1Qq+qnFiDgKWDtbNcEw\n0DhYvfpENm9ew2srC/+Mvfb6TrWycLw/fbhYfmpRmpf+ryycr6JhkJlbga0lzynVNQmNSUqwuYl6\nreuNSUpwmiAxOY1JSrC5iXpp0hqTlOCdgXpnEhuTlGAYqHcmsTFJCYaBemHSG5OUYBio82xMUoZh\noM6zMUkZhoF6adIak5RgGKizbExSlisQ1UmzPSc44IADq8Yk/V9VuBCuQFSv2ZikPMNAnTF3+VB1\nGQbqBMuHzTMM1AmWD5tnGKizLB+WZRhorFk+bI+lRY0ty4dlWFpU51k+bFft5iYRsSIirouIeyPi\n7og4Y+dfJQ1nY5LRKHFn8DLwmWoTld2BWyNiU2b+uMC5NWFsTDI6tcMgM58AnqhePxcR24B9AMNA\nC2ZjktEp+swgIt4JHATcVPK8mmQ2JmlLsTCopghXAmdm5nOzHeNei5qN+xqUNbK9FgEiYinwPeCH\nmfnlIcdYWtQbuK9B89ouLX4DuG9YEEjDuK/B+ChRWjwS+ChwdETcHhG3RcTx9S9NfWb5cPyUqCbc\nALypwLVoQlg+HE+uQFTrLB+OJ8NArXBfg/FnGKhxNibpBsNAjbMxSTcYBhoJG5OMH8NAjbExSbfY\n3ESNsDHJ+LC5iUbKxiTdU3sFojSdKwu7yzsDFePKwm4zDFSMKwu7zTBQg1xZ2CWGgWqxMUl/WFrU\notmYpBssLapxNibpF0uLWjDLh/3knYEWxPJhfxkGWhDLh/1lGGinbEwyGYqEQdUA9UsMnkF8PTO/\nWOK8Gj0bk0yO2qXFiFgCPAAcA/wMuBk4aeZei5YWu2n16hPZvHkNr00LLqsak+wNWD7sgjZLi4cD\nD2bmQ9XAVwAfxL0We8vGJP1UIgz2AR6Z9v5RBgGhDrMxyeRp9QGiey12w2zPCVauvLRqTGLFYNyN\nbK/FiDgCOD8zj6/enw3kzIeIPjPojtmeExx7rCsLu6rNZwY3A/tHxL7A48BJwO8XOK9aNHf5UJOg\nxPZqr0TEp4BNvFZa3Fb7ytQay4cCP7UoLB/2nZ9aVC2WDyePYTDBLB9qOqcJE8p9DSaH0wTNyX0N\nNJPNTSaMjUk0jHcGE8TGJJqLYTBBbEyiuRgGE83GJHqNYdBz7mug+bK02GPuayCwtCjc10ALY2mx\nhywfajG8M+gZy4daLMOgZywfarEMgx5wXwOVYBh0nI1JVIph0HGzfeBo0JhkA4BTA82bYdBDNibR\nYhgGHWVjEpVWawViRFwIfAB4Afh34JTMfHbIsa5ALMTGJFqI+a5ArBsG7wOuy8xXI+ICBvslfHbI\nsYZBIe5roIWYbxjUWoGYmddm5qvV2xuBFXXOp7m5slBNKvnM4BPAFQXPp2lcWaim7TQMImIzsPf0\nfwQkcE5mXlMdcw7wUmZePte53Gtx8VxZqPka5V6LJwOnAkdn5gtzHOczgxp8TqDFauUjzBFxPHAW\n8LtzBYEWx8YkalPdasKDwDJgx4L4GzPzk0OO9c5gAWxMolJauTPIzHfV+XoNZ2MStc3mJmPG8qFG\nxeXIY8TyoUbJMBgjlg81SobBiNmYROPCMBghG5NonBgGI2RjEo0Tw2DM2JhEo2IYjICNSTSO3F6t\nZTYmUdvcXm1MzfacYGrKlYUaPcOgBXOXD6XxYBg0zPKhusIwaJjlQ3WFYTAClg81jgyDhlg+VNdY\nWmyA5UONE0uLI2T5UF1kc5OCbEyiLvPOoBAbk6jrioRBRKwFLgKmMvPpEufsGhuTqOtqh0FErACO\nBR6qfzl9YmMSdUuJO4OLGeydsKHAuTrFfQ3UJ3U3UVkDPJKZd0fstHLRKzPLh9dfv2NfA1cWqpvq\n7LV4LvA5BlOE6X82VJ/2WnRfA42r1vdajIjfAK4FnmcQAiuAx4DDM/M/Zzm+F4uOdkwNbr31Tp5+\n+s9x70ONu8YXHWXmPcDbpw34U+DgzHxmseccd5YP1Wcl1xkkO5kmdJ3lQ/VZsTDIzP1KnWucuK+B\nJoUrEOdgYxJNEsNgDjYm0SQxDBbIxiTqK8NgFjYm0SSyuckMNiZR39jcZJFsTKJJZXOTio1JNOm8\nM8CVhRIYBoArCyUwDIZwZaEmz8SGgY1JpNebyNLizPLh8uU7GpPcBmAJUb1iaXEONiaR3miiSouW\nD6XhJubOwPKhNLeJCQPLh9Lceh0GNiaR5q+3YWBjEmlhSuyodDrwSeBl4PuZeXbtqyrAxiTSwtTd\nRGUV8AHgPZn5ckRMFbmqhtiYRBqu7p3BnwAXZObLAJn5VP1LqsfGJNLi1FqBGBG3A98Fjge2A2dl\n5i1Djm18BaKNSaQ3KrYCcSfbqy0F3pqZR0TEYcA/AiNrmW5jEmnxdhoGmXnssD+LiD8GrqqOuzki\nXo2It2XmzDoe0K+9FqVx1fpeiwARcRqwT2aeFxHvBjZn5r5Djm19mrB8+TquvtqqgSbbfKcJdcNg\nF+AbwEHAC8DazNw65NhWPrU4faGRzwmklsJgIcbpI8zSJJlvGEzUpxYlDWcYSAIMA0kVw0ASYBhI\nqhgGkgDDQFLFMJAEGAaSKoaBJMAwkFQxDCQBhoGkimEgCTAMJFUMA0mAYSCpYhhIAgwDSZVaYRAR\nh0XEjyLi9ur3Q0tdmKR21b0zuBA4NzNXAucBF9W/pDIW0zfe8cZjvD5/b6MYb77qhsHjwJ7V618E\nHqt5vmL6/h+4z+P1+XsbxXjzVXfj1bOBGyJiPYNt195b/5IkjULdvRZPB07PzO9ExEcYbKgydDs2\nSeOr7o5Kz2bmHtPe/29m7jnkWHdQkUakyC7MO/FgRByVmVsj4hjggToXI2l06obBHwFfiYhlwP8B\np9W/JEmj0Npei5LGW6srECPiLyLizoi4IyKujYgVDY93YURsq8b7dkTssfOvWvRYH4mIeyLilYg4\nuMFxjo+IH0fEAxGxrqlxqrG+HhFPRsRdTY4zbbwVEXFdRNwbEXdHxBkNj/fmiLipWjR3b0R8vsnx\nqjGXRMRtEbGh6bGq8f6j+jt3e0T8aM6DM7O1X8Du016fDnyt4fHeByypXl8AfKHBsX4NeBdwHXBw\nQ2MsAf4N2BfYBbgD+PUGv6ffBg4C7mrp5+PtwEE7flaA+5v8/qpxdq1+fxNwI3Bkw+N9GvgHYENL\n/05/Arx1Pse2emeQmc9Ne7sb8FTD412bma9Wb28EGrsTycz7M/NBBqXXphwOPJiZD2XmS8AVwAeb\nGiwzrweeaer8s4z3RGbeUb1+DtgG7NPwmM9XL9/MIGwb+36rO+ETgK81NcZswzLPGUDrH1SKiL+K\niIeBk4EvtDj0J4AftjheE/YBHpn2/lEa/ssyKhHxTgZ3JTc1PM6SiLgdeALYkpn3NTjcxcBZDNbp\ntCWBzRFxc0ScOteBdasJbzDHIqVzMvOazDwXOLea734JOKXJ8apjzgFeyszLmx5L9UXE7sCVwJkz\n7iaLq+4cV1bPkzbtKJWXHici3g88mZl3RMQqmr2DnO7IzHw8In6JQShsq+743qB4GGTmfFcgXg78\noOnxIuJkBrdmRzc9VgseA94x7f0KxujzICVExFIGQfD3mfndtsbNzGcj4vvAoUDxMACOBNZExAnA\ncuAtEfHNzPxYA2P9XGY+Xv3+XxFxNYOp5qxh0HY1Yf9pbz/E4AFYk+Mdz+C2bE1mvtDkWDOHbui8\nNwP7R8S+1dqOk4Cmn0oH7f1fDAZL2u/LzC83PVBETEXEntXr5QyW0jfyM5mZn8vMd2Tmfgz+u13X\ndBBExK7VXRYRsRuwGrhn2PFtPzO4ICLuquZoq4C1DY/3twyeSm+uyjl/19RAEfGhiHgEOAL4XkQU\nfz6Rma8AnwI2AfcCV2TmttLj7BARlwP/Crw7Ih6OiFpTunmMdyTwUeDoqhR2WxXoTfll4F+qn8cb\nGTzh/+cGx2vb3sD1076/azJz07CDXXQkCbDtmaSKYSAJMAwkVQwDSYBhIKliGEgCDANJFcNAEgD/\nDzcvNav5fpAxAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8030785b10>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "AId3xHBNlcnk",
"colab_type": "text"
},
"source": [
"Then we perturb it with noise:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "fXcGNNtjlX63",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "form",
"executionInfo": {
"elapsed": 327,
"status": "ok",
"timestamp": 1446659134929,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "231c945e-e4a4-409e-b75b-8a8fe1fdfc30"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"X += np.random.randn(2, num_examples)\n",
"plt.figure(figsize=(4,4))\n",
"plt.scatter(X[0], X[1])\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQkAAAEACAYAAACgZ4OsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEptJREFUeJzt3X+MpVV9x/H3B5dJx6rYFbNGNqjUX2S1wFbRipWNZHYo\nhtUV02B/iJq4bbBI64QssCZLSmyKdKOGYixRYW3cUH/Rbi3MMgZ3G0ypRUC3gLCt1gKKBrES063L\nj2//uHfWu8OdZ+7Mvec553nu55Xc7Nx7n5nnTLL3O+d8z/eco4jAzGwxR+VugJmVzUHCzCo5SJhZ\nJQcJM6vkIGFmlRwkzKxS8iAh6RJJd0v6tqTPSZpIfU8zG52kQULSi4D3AadExG8Aq4BzU97TzEZr\nVeKf/xhwCPhVSU8BzwR+kPieZjZCSXsSEfFTYAfw38BDwP9ExFdT3tPMRiv1cOME4M+AFwEvBJ4l\n6fdS3tPMRiv1cOM1wNcj4lEASV8G3gDsmr9AkhePmGUUEap6P/Xsxn3A6yX9iiQBZwD3LrwoIhr1\n2L59e/Y2tL3NTWtvU9s8iNQ5iW8BnwW+CXwLEHBNynua2WilHm4QEVcCV6a+j5ml4YrLFdiwYUPu\nJixb09rctPZCM9s8CA06LknWAClyt8FsXEkiMicuzazhHCTMrJKDhJlVcpAws0oOEmZWyUHCzCo5\nSJhZJQcJM6vkIGFmlRwkzKySg4SZVXKQMLNKDhJmVslBwswq1XE4zzGSviDp3u4hPa9LfU8zG506\nehIfB26MiBOBk+izx6VZ2+3Zs4eNG89h48Zz2LNnT+7mLEvSTWckPQe4MyJ+veIabzpjrbZnzx42\nbz6PgwevAGBycis33LCT6enpzC0rY9OZlwCPSLpW0h2SrpE0mfieZkXZseOaboA4D+gEix07mrMf\ndOqNcFcB64H3R8Ttkj4GXAxs773osssuO/z1hg0bWrtXoFlue/fuZe/evcv6ntTDjTXAv0TECd3n\nbwS2RsTZPdd4uGGt1vThRvKNcCXtA94XEfdL2g48MyK29rzvIGGtt2fPnsNDjJmZLUUECCgnSJwE\nfAo4Gvgu8J6I+FnP+w4SVqxSP9yjUkSQWIqDhJUq5TChlODjIGE2hI0bz2FubhOdWQmAnUxN7ebm\nm7801M8tKUcxSJBIfsyfmR3pyClROHiw81qpQxkHCbMevcOA009fz623buXgwc57k5NbmZnZmbF1\neThImHUtHAbceutWtm27gH37dgMwMzOaIcHMzBZuvfW8xgQf5yRs7CyWNEyVg1hOG+rmnIS10jAf\nsKf3Fs7LkjScnp4uNgfxNBGR9dFpgtlgZmdnY3JyTcB1AdfF5OSamJ2dHfj7p6be3v3e6D6ui6mp\nt4/kZzdR9/NX+Rl1T8IaJeXMwPT0NDfcsLOnl1JG6XRuDhI2VpZKGjZqGFATJy6tUUZRiFRK0rAE\nrri0Vqr6kLcxAKT8nQYJEk5cWmu0MfGY+ndigMSlexLWGnXWOdQl9e9UwvZ1ZtZwnt2w1mhaufMg\nSvidPNywxnHist7EZR07Ux0F3A48GBGb+rzvIGEDK2kvhjYoJSdxIXBPDfexMdD07embKGmQkLQW\nOIvOHpdm1kCpexIfBS4CPJ6wkZiZ2cLk5FZgJ7Czm8jbsuT3NfmYvdySzW5Iegvwo4i4S9IGYNFx\njw/nsUGtZBFWKcvDS1DU4TyS/gL4A+AJYBJ4NvDliHjXguucuLSk2lhkNSpZE5cRcWlEHB+d07vO\nBW5ZGCDMrHwuprLWK6EgqclcTGUr1qTCpSa1tU5FFFMtxUGimVzU1A4OEpaMk4HtUErFpZk1mBOX\ntiJOBo4P9yRsxV75ypeyevXlnHLKtc5HtJh7ErZsC5OWBw9uzdwiS8k9CVu23CsxvQ6jXg4S1ijz\nvZi5uU3MzW1i8+bzDgcKB49EltopN/UD75bdODl3pV7smL7UbZqdnY2pqbcfvldb4GP+LIUSj8NL\nefzfuK8idZCwFcl1HN5iU68pcyIpA1ATOEhYo1T1Yly3kYbLsq01Ui3iavM6Fa/dMBuRtq4idZAw\ns0pe4GVmQ0u+pb6kWyTdLWm/pA+kvJ+ZjV7S4YakFwAviM6O2c8Cvgm8NSK+03ONhxtmmWQfbkTE\nwxFxV/frnwP3AselvKdZPy7ZXrnaEpeSXgzsBV7VDRjzr7snYUm1eQpzWIP0JGoppuoONb4IXNgb\nIOb5cB5LadwrJnsVdTjP4RtIq4CvADdFxMf7vO+ehCXl/TgXV0pP4jPAPf0ChFkdvNXecFLPbpwG\n/DOwn86hwQFcGhGzPde4JzHm6qhmbGvF5LBccWnFc1Ixr+xToDbeBpl2zL0V3ii1dZrVS8UtiXHb\nqKXVv+9SW1elfuDt61ppsW3mFsq5Fd4oDfr7loYBtq/zcMOymt9EZmpqN1NTu5f917etXfyiLBVF\nUj9wT6KV6ughlNQLKakty8EAPQkHCRvYcneMTr3DdGld/CbuqD1IkHDi0gaynMTcuNYk5NocOLml\nokjqB+5JNEKqROQwf32b2sUvCe5JWN2Ws5hq2GnDEs//aCMHCRtIivUPo1id2doufkEcJGwgS/3V\nns9DPPLIj5iYuIhDhzqvezFV83nthg1t4bBhYuJPWbfuJI499nmViUuv28jPC7ysFsPs1zCuMyGl\nKGU/CbNFOadQPpdl29BmZrYwObkV2Ans7OYhtuRu1ki47Lue7evOBD5GJyB9OiKuWPC+hxst0MZh\nwzjkTLLnJCQdBdwPnAH8APg34NzwuRvWAOOwN2YJm86cChyIiO9HxOPA9cBbE9/TzEYodeLyOOCB\nnucP0gkcZsXzBrodnt0wW4TLvjtSB4mHgON7nq/tvnYEH87TPm1JZLZtira4w3kkPQO4j07i8ofA\nN4B3RsS9Pdc4cdkyy50VaEtAaaJBEpd1LAU/k06gOABc3Of9Uax4tYIsZzMYL/fOixL2uIyI2Yh4\nRUS8LCL+MvX9rFnq2lLfRVEr58SljVxpswKt3u6+Dkt1NVI/8HCjlQbdcaqO4UZpe2GWBO9MZbkM\nOivgacbyeam4td44rMFYqexrNwbhIGF18DRrfw4SZlaphAVelpin9iw19yQazGNtG5Z7Eg2ykh7B\nKAuR3COxxThIFGC+RzA3t4m5uU1s3nze4Q9qHR/eqvubuZiqAIsV+yxVaDSqQiQXG40vXEzVbEud\ncOVCJKuDg0QBFlvrMEh+YRT7HczMbGHfvnM5dOiTAExMfIeZmeuH+pnWHg4SBajqEdS3UOpo4I+7\nX1+U6B7WRJ4CLVwdlYLjsCu09ecTvFqgbdunWfMkCxKSPgKcDfwC+E/gPRHxWKr72cqVtv+DlSVl\nncTNwLqIOJnO1nWXJLxXI5RasDSfE5ma2s3U1G5XbdoRaslJSHobcE5E/GGf98YiJ+ESaitRSWXZ\n7wVuquleRaprL0ezURsqSEiak/Ttnsf+7r9n91yzDXg8InYN3dqMSh0qmKU2VOIyIqaq3pf0buAs\n4M1V15V+OM8oNlJ1ctBKUNThPJLOBHYAb4qIn1RcV3xOYlR1BN4dyUqTu07iKmACmJMEcFtEnJ/w\nfsVbTs2DA4qVIlmQiIiXpfrZdat7qOBzIqwkLsseUJ1/2V0mbXXJPdxoFZdH27jyzlQjMOrp0ZmZ\nLUxObgV2Aju7w5stQ/9cs5XwcGNIqSopnbi0OvjcjRr0yx+sXn05u3Zd7Q+2Fa+ksuyx8uijz/dm\nstYa7kkMaeFwA+ZzCQ97RsKK555EDeaXWa9efTnwSToBwsMMaw8HiRGYnp5m166rmZz8HvAwnpGw\nNvFwY4Q8I2FN49kNM6vknISZDc1BoiG86Y3l4uFGA3h/TEvFOYmW8KpQS8U5CTMbWvIgIWlG0lOS\nVqe+10o0YazvVaGWU9LhhqS1wKeAVwC/GRGP9rkm23CjSWN912BYCtlzEpK+APw5sJsCg0Tusb4/\n+JZb1p2pJG0CHoiI/d2NcK2H97G0phgqSEiaA9b0vgQE8CHgUmBqwXt95Tp3I+dZGEee6AUHD3Ze\nc5CwlIo5d0PSq4CvAv9LJzisBR4CTo2IHy+4NusUaK4u//r1b+TOO58EXghsoY6l5R7e2EKDDDeI\niOQP4HvAry3yXoyb2dnZmJh4fsB13cexMTHx3JidnU16z8nJNYfvOTm5Jun9rBm6n7/Kz29du2UH\nFcONcbNjxzUcOnQlv0yYwrp11yb9y+7hja1ULUEiIk6o4z5Nduyxz8vdBLO+fO5GBjkSpj6w2FbK\nazcyyZFEdOLSFspeTDWIcQ0STeLg0l4OEja0JpWu2/J5FegimrCoqxRHzop0gsV8r8LGw9glLl0O\nbbY8Y9eTKOkvYxN6NF6mbmPXkyhFU3o084cP/TJxWV4bLa2xS1yWkojLvUzdDDIvFS+V/zKaLc/Y\n9SRK0a9Hs23bBezbdwfgegSrh+skCtdbpHT66ev58Ievyj4MsvHiINEgzlFYDi6mMrOhjV3islRe\npWml8nCjIF5IZXXLnpOQdAFwPvAE8E8RcXGfaxwkzDLJmpOQtAE4G3h1RLwa+KtU9ypVE8quzZaS\nrCch6e+Av4mIW5a4rpU9iVIqO82q5J7deDnwJkm3SfqapNckvFdxSlpIZjaMlIfzrKKzjf7rJb0W\n+DzQd0PcXIfzmI2bYg7nAZB0I3BFROzrPv8P4HUR8ZMF13m4YZZJ1tkNSVuA4yJiu6SXA3MR8aI+\n17UySICnNK18uYPE0cBngJOBXwAz872KBddlDxL+MNu4yl4nMYjcQcLDAhtnDhID8MIqG2e5p0DN\nrAXGfoGXF1aZVRv74QY4cWnjyzkJM6vknISZDc1BwswqOUiYWSUHCTOr5CBRGG9UY6Xx7EZBXCJu\ndfMUaMO4RNzq5ilQMxva2Jdll8Ql4lYiDzcK4xJxq5NzEmZWKfe5G6+V9A1Jd3b/Havdss3aImXi\n8iPAhyLiFGA7cGXCe5lZIimDxA+BY7pfPxd4KOG9zCyRlBvhHg98nc45HALeEBEP9LnOOQmzTAbJ\nSaQ8nOcC4IKI+HtJ76Czc/ZUv5/jw3nM6lHa4TyPRcRzep7/LCKO6XOdexJmmeSuuDwg6fRuQ84A\n7k94LzNLJGXF5R8BV0uaAP4P2JLwXmaWiIupzMZY7uGGmbWAg4SZVXKQMLNKDhJmVslBwswqOUiY\nWSUHCTOr5CBhZpUcJMyskoOEmVVykDCzSg4SZlbJQcLMKjlImFklBwkzqzRUkJD0Dkn/LulJSesX\nvHeJpAOS7pW0cbhmmlkuw/Yk9gObgX29L0o6Efhd4ETgd4BPSKrc2KJJlruRaAma1uamtRea2eZB\nDBUkIuK+iDhAZ5fsXm8Fro+IJyLiv4ADwKnD3KskTfzP0LQ2N6290Mw2DyJVTuI4oPeMjYe6r5lZ\nwyy5EW7F2RrbIuIfUzXMzMowko1wJX0NmImIO7rPLwYiIq7oPp8FtkfEv/b5Xu+Ca5ZR0hO8Fui9\n0W7gc5I+SmeY8VLgG/2+aakGmllew06Bvk3SA8Drga9IugkgIu4BPg/cA9wInO99882aKfu5G2ZW\ntqIqLiXNSHpK0urcbVmKpI90C8XukvQlSc9Z+rvqJ+lMSd+RdL+krbnbsxRJayXdIuluSfslfSB3\nmwYh6ShJd0janbstg5B0jKQvdP8P3y3pdYtdW0yQkLSWzqnj38/dlgHdDKyLiJPp1IFckrk9TyPp\nKOCvgWlgHfBOSa/M26olPQF8MCLWAb8FvL8BbQa4kM7wuik+DtwYEScCJwH3LnZhMUEC+ChwUe5G\nDCoivhoRT3Wf3gaszdmeRZwKHIiI70fE48D1dArdihURD0fEXd2vf07nP2/RNTbdP3BnAZ/K3ZZB\ndHu9vx0R1wJ0ix4fW+z6IoKEpE3AAxGxP3dbVui9wE25G9HHwqK2Byn8A9dL0ouBk4GnTZ0XZv4P\nXFMSfC8BHpF0bXeIdI2kycUuTnmq+BEqirI+BFxKZ6jR+152gxSSSdoGPB4RuzI0sbUkPQv4InBh\nt0dRJElvAX4UEXdJ2kAh/3eXsApYD7w/Im6X9DHgYmD7YhfXIiKm+r0u6VXAi4FvdReBrQW+KenU\niPhxXe3rZ7E2z5P0bjrdzDfX0qDlewg4vuf52u5rRZO0ik6A+NuI+Ifc7VnCacAmSWcBk8CzJX02\nIt6VuV1VHqTTc7+9+/yLwKJJ7eKmQCV9D1gfET/N3ZYqks4EdgBvioif5G5PP5KeAdwHnAH8kE5B\n2zsjYtEkVQkkfRZ4JCI+mLstyyHpdDqVx5tyt2UpkvYB74uI+yVtB54ZEX0DRW09iWUImtFluwqY\nAOa6q+Bvi4jz8zbpSBHxpKQ/oTMTcxTw6QYEiNOA3wf2S7qTzv+HSyNiNm/LWucDdKqijwa+C7xn\nsQuL60mYWVmKmN0ws3I5SJhZJQcJM6vkIGFmlRwkzKySg4SZVXKQMLNKDhJmVun/AUYHTBJb9HcU\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8040158790>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "3dc1cl5imNLM",
"colab_type": "text"
},
"source": [
"## What we want to do\n",
"\n",
"What we're trying to do is calculate the green line below:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "P0m-3Mf8sQaA",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "form",
"executionInfo": {
"elapsed": 414,
"status": "ok",
"timestamp": 1446659137254,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "74e74f19-6ff8-4a8c-81c7-9021a08b78b5"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"weights = np.polyfit(X[0], X[1], 1)\n",
"plt.figure(figsize=(4,4))\n",
"plt.scatter(X[0], X[1])\n",
"line_x_range = (-3, 5)\n",
"plt.plot(line_x_range, [weights[1] + a * weights[0] for a in line_x_range], \"g\", alpha=0.8)\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQMAAAEACAYAAAC3RRNlAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHvdJREFUeJzt3Xl4VPX1+PH3CRCNRVCgUpWK4iOlRWWxipVa0BDCIsHt\nZ22lLLbybRECGBYXFBBbQeQBRCoWGkWptrUUxQoJQYQWLVKURREBFUGggKDsS0jm/P6YgULMJDOZ\nO3eZnNfzzNNMcrn3tM2cfO7nc+75iKpijDFpXgdgjPEHSwbGGMCSgTEmwpKBMQawZGCMibBkYIwB\n4kgGIvJHEdkpImtO+d65IrJARNaLSKGI1E1OmMaYZItnZPAckF3me/cDC1X1e8Ai4AGnAjPGuEvi\nKToSkcbA66p6ZeT9x0A7Vd0pIt8BFqtqs+SEaoxJpkTnDM5T1Z0AqroDOC/xkIwxXnB6AtFqm40J\nqJoJ/vudItLwlNuEXdEOFBFLFMZ4RFWlsmPiHRlI5HXCXKB35OtewGuVBBSo18iRIz2PIZXjtZjd\necUqnqXFl4B3gKYiskVE+gBjgSwRWQ9kRt4bYwIo5tsEVf15lB91cCgWY4yHrAKxAu3bt/c6hLgE\nLV6wmP0krjqDhC4kom5dyxjzPyKCJmEC0RiToiwZGGMASwbGmAhLBsYYwJKBMSbCkoExBrBkYIyJ\nsGRgjAEsGRhjIiwZGGMASwbGmAhLBsYYwJKBMSbCkoExBnAoGYjIAyKyVkTWiMifRCTdifMaY9yT\ncDKI7KVwD9BKw/sp1ATuTPS8xhh3JdodGWA/UAx8S0RCwFnAdgfOa4xxUcIjA1X9GpgAbAG2AXtV\ndWGi5zXGuCvhkYGINAEGA42BfcDfROTnqvpS2WNHjRp18uv27dunbC85Y7y0ePFiFi9eHPe/S7gH\noojcAWSp6j2R978A2qhq/zLHWQ9EYzzgZg/E9cC1InKmiAjh/RPWOXBeY4yLnJgzWA28ALwHrCa8\n49IfEj2vMcZd1ird+FZhYSETJoT/ruTl9SU7O9vjiIIp1tsESwbGlwoLC7nlll4cOTIOgIyM4cyZ\nM9MSQhVYMjCB1rHjbRQV5RDezxdgJllZc1mwYLaXYQWSbaJijA8UFhbSseNtdOx4G4WFhV6HUyEn\nKhCNcVxeXl+WLu3FkSPh9xkZw8nLm+ltUHEqe6uzdGkvX9/q2G2C8a2gTyD65VYn1tsEGxkY38rO\nzg5cAggySwbGJEnQbnXsNsGYJPLDrY4tLRpjAFtaNMbEyZKBMQawZGCMibBkYIwPFH1axPYD3nYL\ntGRgjIdUlRdXv8ikdydxtOSop7FYMjCBFKSa/2hCGmLisom8vuF18nPyaXJuE0/jsaVFEzip8Hhz\ncWkxoxaP4stDXzIhewJ1zqiTtGu5urQoInVF5BURWRfZTKWNE+c1pjwTJvwhkgh6AeGkcKKwJwgO\nFh8kd34uJaESpnadmtREEA+nypEnA/NU9f+JSE3CeycYY8r48tCX5Bbk0rJhS4a2HUqa+OdO3YlW\n6XWA61W1N4CqlhDeWMWYpAhazf8Jn+/9nNz5udzc7Gb6tOxDuH+wfzjRKr0F4QaoHwEtgBXAQFU9\nUuY4mzMwjvFDzX881uxcw5AFQxhwzQC6fa+bq9d27dkEEbkKWAb8SFVXiMgkYJ+qjixznI4c+b9v\n2SYqprr45+Z/8uiSR3n0hke57rvXJf16ZTdRGT16tGvJoCHwb1VtEnn/Y2C4qnYrc5yNDEy1M2fd\nHKa9N42J2RP5wbd/4EkMrjU3UdWdIvKFiDRV1Q2EN1H5KNHzGhNkqsr096fzxsY3mN5tOhfVvcjr\nkCrl1GpCLvAnEakFfAb0cei8xgROaaiUsUvHsm73Op7r/hz1Mup5HVJMrOjIGAcdLTnKg28+yLGS\nY4zvOJ6zanm/ym79DIxx2b6j+/jNG7+hdnptJnWa5ItEEA/rgWiMA7Yf2M6A+QNo17gd/a/p76ti\nolhZMjAmQRv2bGBQwSB6tujJnZff6XU4VWbJwJgE/Gfbf3hw0YMMu24YWZdmeR1OQiwZGFNFCz5d\nwPh3xjM2cyxXXXCV1+EkzJKBMVXw0gcvMWvNLH7f5fdcVv8yr8NxRPBmOYyJUTIaoIQ0xKRlk5jz\n8Rzyu+enTCIAqzMwKSoZDVCOlx5n9JLRbD+wnUmdJvmmD0FlrM7A+Fqy25Y53QDlUPEhBhYM5GjJ\nUZ7p+kxgEkE8bM7AuC5oW5XvObyHAfMHcPl5l3P/j+8PZA1BTFTVlVf4UsaoZmXdqvC8gkZez2tW\n1q2OXqOgoEAzMhpGrvO8ZmQ01IKCgrjPs3nvZu32Ujed/t50DYVCjsbolshnr9LPqI0MTErKzs5m\nzpyZpzRAiX/k8eGuD7mv8D76Xd2Pm5vdnIwwfcUmEI3rgtDdeOmWpYxaPIqR7UZyfePrvQ4nIbYL\ns/E1P7ctm7t+Lk8vf5oJHSdwRcMrvA4nYZYMjImTqpK/Mp/X1r/GlM5TaHxOY69DcoQtLRoTh5CG\nGLt0LG9uepP87vm+SgRu7R7lWDIQkTQReV9E5jp1TpM6/Lwd2rGSYwwrGsYX+79gerfpNDirgdch\nnXRifqWoKIeiohxuuaVX8v73i2XJIZYXMBiYBcyN8vNkrJqYAHBqmS8Z9h3dp3e/erc+9OZDWlxS\n7HU43+DEMiwxLi06tb1aI6ALMMOJ85nU4pft0MqOTnYc3MEv5/6SKxpewaM3PEqtGrVcj8lPnKoz\nmAgMBeo6dD5jKhXPikTZ5cx/fngXVw5vwqAbB/HzK37uSrxV4ebuUU5sr9YV2Kmqq0SkPRB11nLU\nqFEnv7ZNVKqPsr/QaWmDadcuL6FzxlvSfNro5Pz3ONbhO3w17yg/H+jfRABVK54qu4lKzGK5l6jo\nBfwO2EK4Rfp/gYPAC+UcV9XbJpMCHnvsMU1Lq69wrUJewvMG8d5Lnzy+SZHyiw7KBY9oWlp938xd\nJBNuzRmo6oOqepGGd1S6E1ikqj0TPa9JLUuWvE8oNAH4N/Ckg/MGhcBtwDR2794Z9ai8vL7I5ffC\nj/JgXgfY/iyhUO9AbeWebFZnYHyrouXIvLy+pKcPAnoAOcCvWbt2Q7nLbqrKhnM2UOe6M2FuTdiz\nHJgJBL+60FGxDB+ceGG3CdVavMuLsRzfqlW7Sm8Vjpce14cXPay9X+2tf/vH33y7xJlM2FOLxk/i\nnQg7fTkSjhwJf+/Uf9OgQf0Kr3n4+GGGFQ2jVlotnun6DGfWPJPac2on9CRjSoslYzjxwkYGJg6x\nTBBWNHrYc3iP9vh7Dx2zZIyWlJZ84/wFBQWalXWrZmXdmvKjA2IcGVgyML4U621FQUGBtmrVTuvV\nu1RbtWqrBQUFumXvFu3+cnd9dsWz5TYk8XNFZDJYMjCBF8tf77If7DMa1dfWE1vr7I9mRz2vG52W\n/CTWZGBzBsa3srOzK72nP21u4bvvcOyGhqQtrc2tg251J8gUYsnApIamr0ObKVD4M869cmWFh7pZ\n4hsk1tzEBFpBQQE5I3/K8Usvgfk9yDj2ZEwt1Pzcaclp1unIpLyQhhj/9njmr5oP82qTXnJGyn+w\nq8KSgUlpxaXFjFg0gv3H9vNkxyepnV7b65B8y9qemZS1/9h++s/rTw2pwVOdn7JE4BBLBiZQdh3a\nxa/m/opmDZrx28zfkl4j3euQUoatJpjA+OzrzxgwfwB3Nr+THlf2QKTSka+JgyUDEwgr/7uS4QuH\nM/jawXS+rLPX4aQku00wvlLeY8uLNi1i2MJhjLlhjCWCJLLVBOMb5W27NnjGL3lf32di9kSaNWiW\ntOumcs1BrKsJTjxz0AhYBKwFPgByoxyXhKprk0pOf2YgpFz9Cz1vwAW6dd/WpF2zOjy0hIvPJpQA\n92m4IWpt4D0RWaCqHztwblMdpZXA9b+Fcz/jBxtbc2GdC5N2qVj6JlQXCScDVd0B7Ih8fVBE1gEX\nApYMTFzy8vryr2U9OfrjWaDCmW9u5P5XXvA6rGrD0dUEEbkYaAm86+R5TfVw9U+upu3jV7Dp/W00\n+aIZQ155Iel/oe2hpf9xbAIxcouwGBijqq+V83N16lom9Wzbv43+8/vTsUlHfv3DX7taQ2ATiJHj\nnPiAikhN4B/AfFWdHOUYHTly5Mn3tomKOWHdl+sYXDiYX7X+Fbf/4Havwwm8spuojB492tVk8AKw\nW1Xvq+AYGxmYb1i2dRkjFo3goesf4oZLbvA6nJTk2oNKItIWuAu4UURWRrZl75ToeU3s/LzdeUXm\nbZzHI289wpMdn7RE4AexrD868cLqDBJWXk/AIK6Th0Ihnblqpnb9U1f99KtPvQ4n5WENUVNLtA99\n0Jp7loZKdfzb4/WOV+7QnQd3eh1OtRBrMrAHlQIiWnFMkBSXFvPIW4/w1ZGvmNFtBmefcXbSrpXq\nKwTJYA8qBVxeXl8yMoYT3jtwZmSdvK/XYX3DgWMH6D+vP6rK012eTloiKCwspHXr9nTpchdFRZdQ\nVJTDLbf0CtRcimdiGT448cJuExJS0dyA33cH2nlwp/70lZ/qE0uf0NJQadKuU/Z/I2ioUOD7W6dk\nI8bbBHtqMUCCOPTd9PUmcgtyuf37t9OzRc+kFhN17HgbRUU5nLiVCo+W5gI5ZGXNZcGC2Um7tp/F\nurRocwYBEsumIn6yesdqhhYNZdC1g+hyWRePotherUuM42FzBqZcidYuLP58MUOKhjC6/WjXEkHZ\n+ZO0tMG0alUjpn0UDDZnYL4p0dqF2R/N1uwXs3XtrrVJjLJ8fp8/8QI2Z2Cqqrx771juuVWVZ997\nloJPCni6y9M0qtMo6bGaytmcgXFVaaiU3/3rd2z8aiP53fOpl1HP65BMnCwZmG+I9xn/I8eP8MCb\nD1AaKmXaTdM4q9ZZLkVqnGS3CaZcsS5j7j26l0EFg2hctzEPt3uYmmn298VvbK9Fk3TbD2yn/7z+\nZF6SSb+r+9mmJj5lcwYmqdbvXs+gwkH0admHO5rf4XU4xgGWDEzclm9bzkOLHuL+tveT2STT63CM\nQ6zoKAUls9lJwScFjFg0gnEdxlkiSDFOtT3rBEwinFz+qKrjyjnG5gxcUN6uRE5V4M1aM4uXP3yZ\npzo9xaX1Lk34fMYdrk0gikgasAHIBLYD/wHu1DKbqFgycEdVC4YqEtIQk5ZNYtnWZUzpPIWGtRs6\nEqtxh5sTiNcAG1V1c+TCfwa6Y5uopITi0mJGLR7Fl4e+ZEbODOqcUcfrkEySODFncCHwxSnvt0a+\nZxwSzxyAk81ODhUfYuD8gZSESpjadaolghRnqwk+V3YOYOnSXhXOAWRnZzNnzsxTCoaqNl+w+/Bu\ncufn0qJhC4a2HUqa2FxzqnMiGWwDLjrlfaPI975h1KhRJ7+2TVRiU5WNQU/te3BiVAGxN0TZvHcz\nA+YP4OZmN9OnZR8rJgqYspuoxCyWRxsregE1gE+AxkA6sAr4fjnHOflUZrWRSPfjqjyKvHrHas16\nIUtf+/g1J8I3PoCbrdKBTsB6YCNwf5Rjkv/fOgUl0lsg3kSy5PMlmjkzU5duXupU+MYHYk0GjswZ\nqGoB8D0nzmVO59QcQGVe/fhVnlnxDJM7Tab5ec0dP7/xP3tQKYWUfdIQqLQASVWZ/v503tj4BlM6\nT+GiuhdVeE5rHxY8sdYZWNuzFBHtdqKiNmAlpSX62JLH9K7Zd+mew3tiPqcJFmx7tdQU7cMd7/zA\nkeNHdHDBYO33j356qPhQuccEbes2U75Yk4HVGQRI2ZqDJUt+QfPmTWnQoCG7d++J+Tz7ju5jcOFg\nGtVpxLgO46hVo1ayQjZBEkvGcOKFjQwSVt5farhW4XlNTz9H09O/XemQfvv+7XrrX27VycsmV7q7\nkd0mpAZsZFBdXAD0orgYWrWaToMGc4HyVx027NnAoIJB9GzRkzsvv7PSM7u1kmH8wVYTAqTsbQIM\nAWYB2VT2dOKK7St44M0HGHbdMLIuzXIpYuMH1gMxRZ1Y6tu9ew9r166muHgSUHHfggWfLmD8O+MZ\nmzmWqy64yu2QjccsGVQDsdQAvPTBS8xaM4vJnSZzWf3Lkn494z+WDKq5kIaY8u4U/rXlX0zpPIXz\nzz4/ofM51UHJEor7rOioGisuKdYRb47QPq/20b1H9jpyTidqDmx1whvEuJpgD6kHXNnGJ4ePH2Zg\nwUAOHz/MM12foe6Zdb0O8aTTH8cOjzJOjBKM92xpMcDKDt3/teIX/OjRy+nQogPD2w6nRloNx64V\n75ZrJoBiGT448cJuExx32tC97mblZy31+z1aaSgUSsr1Et3u3G4TvIEVHVUj530IHfNgxfU0+u62\npHUmOrWDUlX/vRUx+ZetJgRYYWEhOf1/RvF158Pi7mR8me/YHgkmdcS6mpDQBKKIPCEi60RklYjM\nFhFrn+uiYxcf4/J7L+HafeeT9b31lghMQhIaGYhIB2CRqoZEZCzhe5MHohxrIwOHqCr5K/N5bf1r\nTOk8hcbnNPY6JONjrmyioqoLT3m7DLgtkfOZyoU0xBNvP8GanWvI755Pg7MaeB2SSRFOTiDeDfzZ\nwfOZMo6VHGPEohEcOn6I6d2m8630b3kdkkkhlSYDESkCTt1cTwAFHlLV1yPHPAQcV9WXKjqX7ZtQ\ndfuP7WdwwWC+U/s7/C7zd9aQxERV1X0TnNh4tTdwD3Cjqh6r4LjAzxl4VVe/4+AOBswfQNvvtiW3\nTa7tbmTi4sqzCYT3S1gL1I/hWEcLKdzmVcHMxj0btfOszjpr9aykX8ttiRYxmdjgRkNUwpumbAbe\nj7x+X8GxLvzXdtapv6ytWrVzvTnoe9vf0w4vdNCCjan3QbFqRPfEmgwSXU1I7AF5Hytb95+Wlufq\n9Rd+tpBxb4/jtzf+lmsuvMbVa7uhKntImuSycuQoyv6yhkIfkJY2mFAo/PNkPqjzlw//wszVM5na\nZSpN6zdNyjWMKcuSQcyuoEWLH1TYcDRRqsrU/0zlrc/fYkbODC44+4Jyj0uFBiH2FKQPxXIv4cSL\ngM0ZuH1Pe7z0uD6y6BHt/Wpv/frI176JK5lsAtEdxDhnYA8qVcCtv8CHjx9meNFwaqbV5PEOj3Nm\nzTOjHtu69Y9ZubKUcIv0vsCOCrsiR5MKowsTG2t7FhB7Du/RHn/voWOWjNGS0pIKjy0oKNC0tHNP\njgqgoUKetR8zFcL2WvS/LXu3aPeXu+uzK56NqSFJeX0I09Lqx/1Btj0Uq5dYk4GVsnnkoy8/4p7X\n76Fni570vaovIvKNfoaxaNHichviG2fEkjGceGEjg5Pe3vK2Zs7M1CWfLzn5vViG7k4N7+02oXrB\nJhD96R8b/sFT7z7Fkx2f5MqGV578fseOt1FUlMOJuoZTt0s7dbKvXbvWLFnyPpDYxJ9NIFYfrvQz\nMLFTVZ5f9Tx///jvPHvTs1xy7iUx/buylZBLl1Zt85KyEu1naFKPJQMXhDTEk+88ycodK8nPyefb\n3/r2N46JVoRjZbvGLTaBmGTFpcXcv/B+Pv3qU6Z3m15uIoD/dQ7OyppLVtZc62doXGdzBkl04NgB\n8hbkUT+jPqNvGE16jfS4z+HUHoem+rKNVz2269AuBswfQJsL2zDo2kEVNiSpbDLPJvtMIiwZeOiz\nrz8jd34uP23+U3pc2aPCTU3sL79JNksGHlm1YxXDioYx+NrBdL6sc6XHV7SkaIwTXNlE5ZSL5YlI\nSETqOXG+oFq0aRFDi4Yy5oYxMSUCY/wk4WQgIo2ALMLtz1JGvKXBr6x9hfHvjGdK5ym0adQm5uvk\n5fUlI2M4MBOYGVlS7Fv1wI2pqljKFCt6Aa8AVwCbgHoVHOdoiWUyxVOuGwqFdOryqXrLn2/Rrfu2\nVvl69ly/SRbcKEcWkRygvareJyKbgKtU9asox2oi13JTrKXBg+77JSsyVvDJV58wudNkzs0417OY\njYnGsXLkCjZRGQE8SPgW4dSfRRX0TVROm/mvWcyiM27npps68vLdL5NRK8Pr8IwBPNhERUQuBxYC\nhwkngUbANuAaVd1VzvGBGRlEW+6bMOEP4RHDmTnQeSB8dZDMdGXhgjkeR2xMdElfTVDVD1X1O6ra\nRFUvAbYCrcpLBEFTYWnw2V9D97th67WwJIc0q+g2KcKxOgMR+Qz4YSrMGUQz49UZ/N+cewmtuAc+\nupr09EE0b96CBg3qW2Wg8S1X6wwAIiOEchNBKnh367v85cBfeLzrGLIu/C+tWk0HarFyZR+KinK4\n5ZZeMXcnckJVuiIZU6FYlhyceBGgpcWy3tjwhma9kKUr/7vy5Pe87CNonYpMPHBje7VUp6q8uOZF\n/rr2r0y7aRpNzm3idUiAbU1mksOSQRQhDTHx3xNZvn05+d3zOe9b5532c9sRyKQae1CpHMWlxYx8\nayR7juxhQscJnH3G2eUe59Wjxfako4mHPbVYRQeLD5JXmMc5Z57DmBvHVKkhiRusx4GJlSWDKth1\naBe583O56vyryLsur8KGJMYEhXVHjtOmrzeRW5DL7d+/nZ4telbYkMSYVGTJAFizcw1DFgxhYJuB\ndG3a1etwjPFEtR8HL/l8CXkL8hjVfhRdm3a1Yh5TfcVSjODECx8WHc3+aLZmv5ita3etVVX/FvNY\nvwOTCGwX5uhCoZBO+8807f5yd92yd8vJ7/txd2K/JigTHLEmg2o3Z1AaKuXxpY+zYc8G8rvnUy/D\n320brdrQuKVaJYOjJUd5YOEDlIRKmHbTNM6qddZpP7eqQlOdVZs6g71H9zK4cDAX1bmIh9s9TM20\n8vOg34p5rNrQJMqKjk6x/cB2+s/rT+YlmfS7ul/gagj8lqBMsFgyiNiwZwODCgbRu2Vv7mh+h+vX\nN8ZrrjU3EZEBIrJORD4QkbGJns9Jy7ct595595L3ozxLBMZUIqEJRBFpD3QDrlDVEhFp4EhUDij8\npJAJ/57AuA7jaH1+a6/DMcb3El1N+A0wVlVLAFR1d+IhJW7Wmlm8/OHLPNP1GS6td6nX4RgTCIne\nJjQFfiIiy0TkLRH5oRNBVdWJhiRz188lPyffEoExcUh0E5WawLmqeq2IXA38FYjaGyyZm6gUlxYz\nevFodh7ayYycGdQ5o45j5zYmSFzfRAVAROYB41R1SeT9J0AbVd1TzrFJW004VHyIIQuGUDu9No/d\n+Bhn1DwjKdcxJojcWk14FbgxcsGmQK3yEkEy7T68m3tev4eLz7mYcVnjLBEYU0WJTiA+B+SLyAfA\nMaBn4iHFbuv+rfR7ox83N7uZPi37BK6YyBg/CXTR0YFjB1i+bTmZTTIdPa+TrHrQeM0qEH2g7HMF\n6elDad68KQ0aNLTEYFzj+vZqbglSJ6LTHz/uRXHxeFauLPVkOzZjKhOoZHDiL21RUU6AP1AXAOHR\nwonbB2P8IFD9DILW6KNsfwQYAszyMCJjogvUyCBosrOzmTNnJllZc2nV6jnS00uAHcDMSOOUvl6H\naMxJgZpADHqjD1tZMF5I2dUE+0AZE5+UTQbGmPik7NKiMSY5LBkYYwBLBsaYCEsGxhjAkoExJsKS\ngTEGsGRgjIlIKBmIyNUislxEVkb+09OGqMaYqkt0ZPAEMEJVWwEjgfGJh+QfVWkq6aWgxQsWs58k\nmgz+C9SNfH0OsC3B8/lK0P5PD1q8YDH7SaKPMN8PvC0iEwi3UL8u8ZCMMV5IdN+EAcAAVX1VRG4H\n8oGsZARqjEmuRPdN2K+qdU55v09V60Y51p5SMsYjsTyolOhtwkYRaaeqS0QkE9iQSDDGGO8kmgz+\nD5gqIunAUcBa9xgTUK71MzDG+JsnFYgikiciIRGp58X1YyUiT4jIOhFZJSKzRcS3u7mKSCcR+VhE\nNojIcK/jqYiINBKRRSKyVkQ+EJFcr2OKlYikicj7IjLX61hiISJ1ReSVyO/xWhFpE+1Y15OBiDQi\nvOKw2e1rV8ECoLmqtgQ2Ag94HE+5RCQNeBrIBpoDPxORZt5GVaES4D5VbQ78CLjX5/GeaiDwkddB\nxGEyME9Vvw+0ANZFO9CLkcFEYKgH142bqi5U1VDk7TKgkZfxVOAaYKOqblbV48Cfge4exxSVqu5Q\n1VWRrw8S/gW90NuoKhf5Q9YFmOF1LLGIjGSvV9XnAFS1RFX3Rzve1WQgIjnAF6r6gZvXdcjdwHyv\ng4jiQuCLU95vJQAfLgARuRhoCbzrbSQxOfGHLCgTbZcAu0XkucitzR9EJCPawY5volJJkdKDnF6U\n5PlyYwXxPqSqr0eOeQg4rqoveRBiyhKR2sDfgIGREYJviUhXYKeqrhKR9vjgdzcGNYHWwL2qukJE\nJhGuGh4Z7WBHqWq5FYgicjlwMbBawnunNwLeE5FrVHWX03HEKlq8J4hIb8JDwxtdCahqtgEXnfK+\nET5/TkREahJOBC+q6mtexxODtkCOiHQBMoCzReQFVe3pcVwV2Up4JL4i8v5vQNTJZc+WFkVkE9Ba\nVb/2JIAYiEgnYALwE1Xd43U80YhIDWA9kEn44bHlwM9UNepkkddE5AVgt6re53Us8RKRdkCequZ4\nHUtlRGQJcI+qbhCRkcBZqlpuQvByr0XF/0OtKUA6UBQezLBMVft5G9I3qWqpiPQnvPqRBvzR54mg\nLXAX8IGIrCT8u/CgqhZ4G1lKygX+JCK1gM+APtEOtKIjYwxgbc+MMRGWDIwxgCUDY0yEJQNjDGDJ\nwBgTYcnAGANYMjDGRFgyMMYA8P8BB4YEUxpBpuwAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f80640172d0>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "VYUr2uPA9ah8",
"colab_type": "text"
},
"source": [
"Remember that our simple network looks like this:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "gt8UuSQA9frA",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "form",
"executionInfo": {
"elapsed": 170,
"status": "ok",
"timestamp": 1446659140755,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "080025d5-d110-4975-e105-7635afaa3ce9"
},
"source": [
"from IPython.display import Image\n",
"import base64\n",
"Image(data=base64.decodestring(\"iVBORw0KGgoAAAANSUhEUgAAAJYAAABkCAYAAABkW8nwAAAO90lEQVR4Xu2dT5Dc1J3Hv+YQT8VJZUhVdprLWs4FTSrGGv4ql9CuHBCH4GaTFCLZwnIcjOAy8l6Q/1SlU4XHcg6xJgtY2OOik2KxSGoTGWrXzYFC2T2MDAtWitRavmQ0e9k2SYGowom4hNRPtqA9TE+rW3/cPfPepcfup6f3fu/Tv9/T+/PVpo8//vhjsMQsULAFNjGwCrYoKy6xAAOLgVCKBRhYpZiVFcrAYgyUYgEGVilmZYUysBgDpViAgVWKWVmhDCzGQCkWGEuwrly5gtf++zW887/vYOn/lnD5T5cT40x9ZQrb/nEbxDtFiHeI2LJlSylGY4X2t8BYgUVAvfzqy3i5/TI+vPLhmq37wpYv4AHpATxw3wMMsP4cFJ5jbMAiqA4eOYg/Lv8xMcL26e34+vTXk8+vbv1q8n/03TsX38EfLv4h+aRE380dmmNwFY7O2gWOBVgE1Y/2/yjxUls+vwXaY1oS7tZK3v94MJ8zceUvV0Dea+H4AoOrQrhGHqxuT0Xjp0P7D2HqH6Yymejyu5dx5PiRZBxGnmt+bj7TdSxTfgv0ASuAzglwmyE8pfbZu3VaEDkDdT+AweevzGolvPjvL+LMb84knmr+yHxmqNKyCK7ZQ7OJ5yIo+3m6clqx8UrNB1bso2W64FQN9cnijdcdAvNAQWGRPBcLicX3Ua8S84FVcj3PnjuLhRcWkgH63OG5XHc7+NTBZEBP47NvffNbucpiF/e3QCaw2g0NfNvES5c+wtQ9u2G0LCj8BLAiFEaeBU0zYJ9fxkfYjKl7FZgtCzIHIA7QUmXov/g9LmMztt6rwLBMyFROj3TkZ0fgveXh4X96GN//zvf7t2aNHGlI7VlW0pYmRC+AKUwAsQu5thOuvIjQEjGBGJ7CQYptdOw6etc6VzXXzcUZwJrGseWt2P28DV2I4OgyDgQKFgMTYtQ1xqq10eDuR6j8Fi1NxGTkwpAfRos7h05bQscQIFgibEeHMBHCVhs4EBtY8lQQd6ulvbN78e6f302mC7Z/bXsuo9NkKk1X9PZ+IUyeR0sN4GscYl8DPzOP5VuPYynQwMU+dL4O3wzRbpQQ93O1bvQuzgRWS0p/tQA6Nuqcilq7A5u3Px28T7qw7BB1VUHqhEKTB2+pCAIVHZVD3dPgujpE6peOBzesQRS5nr/+b//g24nF7JN27qkCGq/J++RknHXm5JlVeiKGr/MQPQMdV0ZkCRBbNUwEMYzQhRyZEHgHOv29ynPM6HXtja1Rf7B4AZ7RgZv+SuMAOj+NtrYEX3avfyqMfDi2DdcLEAQBvPOX8MGtR3Ex0MEFJiRxP373wWZsvaeBhixDVRrg1/jxlwEWPV3ap+xVrR57Cjgpht2xEDV4mLIFvqkiaoUwwzp4U4Hv9/awN7YrR+vuGcAS4ZsdtKV0VNEFVqMLrIkWJGEPPP4hKA0RgiCAc1XsdJQErGQ2Ig7hOQ5sx4Hz0u+wvHX2akjtMWCpNhQCiCicq+AcCx1Fh9B2IegcNN6B4Teg1z0EeknzKqPFRe7a9AeLm4ajXvzUoJEDqUahMESrKxSqbQHbDBGLoXUNlBiuUsNOT8fFQEVsNdHmdOjStTgSGOCnLTQuBDBosLxKqnTwntw/glPnoHMS4E6iFVjgbBGcwUGMPAjtawP73GZf/wVkAutYtAvPezYUPoKjipBdGZ5vQOgavGteHbfsiXD09TZUIUbg6JD3vITlrU/iYthErPOYaQk44ZhocDF8U0HDqsEOHfQaC7/2X68lyzJVTjd0WiJu2XMem++7+tAxSd52+hguTe3GYtjq6V3XPyqDtbA/WLyAtqRg0rHhLceo3avCsk0kjqd7uoEL0FJkaC/9Hh/gS9ixS0dTCaDKHVidNhoTNN2gQP/FedAmly/t2IWm2YK2xswqDbj3antzz5oToD/915/i5smbcdo8vfaDQGiC37YfEyeW4KtcMu2g1HbCrp9Dx5Fw3ZCw04ZSb0Jse6CsLH1qgZFfK0znn+hpznzKHGpJRzus4YJ/AX/78G94ofUC7r777pwMxAhdE6pyAK8u78CJJZ+BtcKiIw8Wea0DTx34ZCH5oHYwM1y0TjhnziXbaWgB+4cP/RCPPfYYtm/fjpMnT+Kmm24aDrDYhdpoQdAbaMtNSB4Da6UhRx4sqnB3SCTPNbtvtu9iMoU/Wg5Kt9p0h8DTp09j3759ePrpp/H4448PB1fylOtC5jTUGVifseFYgJXClXou+jcN6Gk2nj7JG1Gi7TG0Hkiz7OlGP/ru6OGjq46rnnjiCSwuLibe66677hocMAZWT5uNDVgpXGfbZ5OtybQNZq1EE6G0NXmXtGvNwbrv+4n3uu222wYPjwys9QFW2goKjbQ4Tdth6CAFeSpK5J3oQMUwhynS8PjMM89AVdVs3ouBtb7Aytbrw+WiMZfnednCIwOLgTUIZml43LFjB5577rnhnx4Huek6yztWY6yqbb+wsJBMTwwUHquu5Ijej4GVoWMoPJ4/fz7xXkM9PWa4x3rLwsDK2KMXLlxIvBeFR5qe2LRpU8YrN2Y2BtaA/U7hkaYnnn322exPjwPeYz1kZ2AN2YtpeCTvdeeddw5Zyvq9jIGVo28pPJL3ok2NLDxeb0gGVg6w0kvT8HjixIlkHJY1lauaE8GRangwsvD/noKqt+kzsLJSkCEfzdi/8cYbifdaKzxWoppDmxJ5FT54NH06YZShAQVmYWAVaEwqKg2PMzMzyfTEyqfHqlRzAoOH6OqwJnXoNQeBSWcjq0sMrJJsferUqSQsdofHylRzYg8aLyG0QtiTOvhGhFZglyKD0Mt8DKySwEqLpfD45ptvYn5+Hr/+z19/sukwj2pOP72vyJXBy4BNME340Pg6AiNAu8IDkQysksGi4t9++2189wffxee++DkIO4TcqjlrSw504Eg81FobYetq+KOwKDgagjVOnRdtBgZW0RZdpbw0BL73/nv4yZM/6bv7tVeVxkk1h4FVAVgbUTWHgVUBWGUcvCVV6EP/cuiztQ9NCNsMiIshrPSIeaK3oUNIlXQqaDMDqwIjlyEV0Fv6MoQlbENT/FTIhWSXOF2AF5jocei8cCswsAo36WcLLEPchO7yyr+9smrt6TQ3geQmcgcd2CQbIHoIDKGyuSwG1joEi06oU+jj3RAWR2HQgFiiTuxqJmRgVQBWGaGQDo78/OjPe9T+qpfSeBeeqIM3JPip4k8F7aVbMLAqMHSlg/dr7YkcCZxWg1Jz0G5UL7/EwKoArBuhmoNEbupBvPrRDhxf8qFVLFrCwKoArFQi4P3o/VwTpCmgdBi3r2oOIrQbNdwfGljytZ46r2U1n4FVlmW7yn3rrbfwvX/+XrKkMyPM5FLNIS2KbCrSNI8loKX48G6AxhIDq2SwaIcDgWWaJn71H78qRDWnlxbF1aaQxJILj6TRjRhm0L4hYrwMrJLAos1+BBXtyaLty5SKVs1Zverx1RB4dhIPPe/CVioeXF2rFAOrYLDIOxFQd9xxRwLVytSt90XfFaGaU3ATCimOgVWIGa8WkoY9AorA6pUIrqJVcwpsRiFFMbAKMONqYS9LsWWo5mS5bxV5GFg5rExhj8ZPdHBitbCXo+ixv5SBNWQXpmGPvNXtt98+ZCnr9zIG1oB9O2zYG/A2Y5+dgZWxC1nYy2goNt2Q3VA0jqIDESzsZbcZ81hr2CoNe/T56KOPZrcqy8m2zazGAAt7+X8ZzGOtsCELe/mhohLGEqwyVFpY2CsGqLSUsQKrDJUWFvaKBWrswCpDpYWFvXKgKiYUxh5U/huwhd8idBqYRARX4bHTldd8Le8gTSpapYWWX0is47qnveTdi02I6aFOejlAbSdcOT2fF8NTOEixDTqnV6Uk0CC2GpW8hYTCyFXA72yj8XoAAzoE+nsxgNnrZc8DtL7bU9HJlDwqLY9855FkbY8ktS3LWlGLECbPo6UG8DUOsa+Bn5nH8q3HsRRo4GISL6vDN0O0e70SdoB2rfeshYBF71Juyzzu90TcF59FIC8WJvSVvgiT9nnPH5nP/K7CtOPonYWzh2aTF2Fu+usmvPjLF3us7cXwdR6iZ6DjyogsAWKrhokghhG6kCMTAu9Ap7+r1l0cQwoLAote4+ugwT+IsxO78XrQKkTkqzsEkqeily8Nk0il5cfHfowv3/xlLBxf6Pk2sNhTwEkx7I6FqMHDlC3wTRVRK4QZ1sGbCnxfrfxgwjBtvtHXFAZW7OsQZo7hEm7Fkxf8nm+mH6TBlau0RG00OBWcY6Gj6BDaLgSdDn46MPwG9Hr15/MGsdco5S0GrDiAIU7D5M/AgIo9gY6Lng4+5wi3jIOea59wieCQzgEnAe4kWoEFzhbBGRzEyIPQDmBWpaoxSpQMUZdCwCLh1OlmDWcCBzJsSNzDiIyL8LR8Ur1lHE2nPeZzh+d6mooENW7Zcx6b7zuHTlvCJB1Nnz6GS1O7sUhKxDl/LEP00Vhekh8sUjThNUyYAdxr59dCSwSvAWbg5Xq7exkqLfRO6TMnz/TurNAEv20/Jk4swaf2xC6U2k7Y9XPoOBIm6crYh6UoaLodABOoSU3YlpLbQ48lQT0qnR+sEq1RBlj0dGmfsnPVOtB51IMmfEdGLQ7RkkSYkps8VbJ01QIjDdaNCIVZwOi4DnxOgsRRXIzhazwakY3gmphsljLWe56RBqv6wfvg3R0HFqS6CcHxC5kQHrwGo3nFSIN1Q1RaBuinyDchSyYmDRcthWPLPF22G2mwuo+k55kgHUylJRtZoa1A0kI0bAdGPRnSszQuYFE90yUdepoznzKHWtLRDmsglZY8cHZTE7UVCGqEpmtDScZZLK20wEh7LKpst9YBKQUf1A5mhovWCefMuU9eM9JbWnEQMAIY/DQOXLr+mqmHXkfIdj18YpSRByuFa6+2F1f+cgXkuWb3zfZdN6Twt/DCQuKpsgmVDQIXy9vPAmMB1krPRf9eryot/TpsXL4fG7BSuNa7Ssu4gNOvnmMFVtqY9azS0q/DxuX7sQRrXIy7kevJwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3Ixf9d0NIelzdt4X5AAAAAElFTkSuQmCC\"), embed=True)"
],
"outputs": [
{
"output_type": "execute_result",
"execution_count": 6,
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJYAAABkCAYAAABkW8nwAAAO90lEQVR4Xu2dT5Dc1J3Hv+YQT8VJ\nZUhVdprLWs4FTSrGGv4ql9CuHBCH4GaTFCLZwnIcjOAy8l6Q/1SlU4XHcg6xJgtY2OOik2KxSGoT\nGWrXzYFC2T2MDAtWitRavmQ0e9k2SYGowom4hNRPtqA9TE+rW3/cPfPepcfup6f3fu/Tv9/T+/PV\npo8//vhjsMQsULAFNjGwCrYoKy6xAAOLgVCKBRhYpZiVFcrAYgyUYgEGVilmZYUysBgDpViAgVWK\nWVmhDCzGQCkWGEuwrly5gtf++zW887/vYOn/lnD5T5cT40x9ZQrb/nEbxDtFiHeI2LJlSylGY4X2\nt8BYgUVAvfzqy3i5/TI+vPLhmq37wpYv4AHpATxw3wMMsP4cFJ5jbMAiqA4eOYg/Lv8xMcL26e34\n+vTXk8+vbv1q8n/03TsX38EfLv4h+aRE380dmmNwFY7O2gWOBVgE1Y/2/yjxUls+vwXaY1oS7tZK\n3v94MJ8zceUvV0Dea+H4AoOrQrhGHqxuT0Xjp0P7D2HqH6Yymejyu5dx5PiRZBxGnmt+bj7TdSxT\nfgv0ASuAzglwmyE8pfbZu3VaEDkDdT+AweevzGolvPjvL+LMb84knmr+yHxmqNKyCK7ZQ7OJ5yIo\n+3m6clqx8UrNB1bso2W64FQN9cnijdcdAvNAQWGRPBcLicX3Ua8S84FVcj3PnjuLhRcWkgH63OG5\nXHc7+NTBZEBP47NvffNbucpiF/e3QCaw2g0NfNvES5c+wtQ9u2G0LCj8BLAiFEaeBU0zYJ9fxkfY\njKl7FZgtCzIHIA7QUmXov/g9LmMztt6rwLBMyFROj3TkZ0fgveXh4X96GN//zvf7t2aNHGlI7VlW\n0pYmRC+AKUwAsQu5thOuvIjQEjGBGJ7CQYptdOw6etc6VzXXzcUZwJrGseWt2P28DV2I4OgyDgQK\nFgMTYtQ1xqq10eDuR6j8Fi1NxGTkwpAfRos7h05bQscQIFgibEeHMBHCVhs4EBtY8lQQd6ulvbN7\n8e6f302mC7Z/bXsuo9NkKk1X9PZ+IUyeR0sN4GscYl8DPzOP5VuPYynQwMU+dL4O3wzRbpQQ93O1\nbvQuzgRWS0p/tQA6Nuqcilq7A5u3Px28T7qw7BB1VUHqhEKTB2+pCAIVHZVD3dPgujpE6peOBzes\nQRS5nr/+b//g24nF7JN27qkCGq/J++RknHXm5JlVeiKGr/MQPQMdV0ZkCRBbNUwEMYzQhRyZEHgH\nOv29ynPM6HXtja1Rf7B4AZ7RgZv+SuMAOj+NtrYEX3avfyqMfDi2DdcLEAQBvPOX8MGtR3Ex0MEF\nJiRxP373wWZsvaeBhixDVRrg1/jxlwEWPV3ap+xVrR57Cjgpht2xEDV4mLIFvqkiaoUwwzp4U4Hv\n9/awN7YrR+vuGcAS4ZsdtKV0VNEFVqMLrIkWJGEPPP4hKA0RgiCAc1XsdJQErGQ2Ig7hOQ5sx4Hz\n0u+wvHX2akjtMWCpNhQCiCicq+AcCx1Fh9B2IegcNN6B4Teg1z0EeknzKqPFRe7a9AeLm4ajXvzU\noJEDqUahMESrKxSqbQHbDBGLoXUNlBiuUsNOT8fFQEVsNdHmdOjStTgSGOCnLTQuBDBosLxKqnTw\nntw/glPnoHMS4E6iFVjgbBGcwUGMPAjtawP73GZf/wVkAutYtAvPezYUPoKjipBdGZ5vQOgavGte\nHbfsiXD09TZUIUbg6JD3vITlrU/iYthErPOYaQk44ZhocDF8U0HDqsEOHfQaC7/2X68lyzJVTjd0\nWiJu2XMem++7+tAxSd52+hguTe3GYtjq6V3XPyqDtbA/WLyAtqRg0rHhLceo3avCsk0kjqd7uoEL\n0FJkaC/9Hh/gS9ixS0dTCaDKHVidNhoTNN2gQP/FedAmly/t2IWm2YK2xswqDbj3antzz5oToD/9\n15/i5smbcdo8vfaDQGiC37YfEyeW4KtcMu2g1HbCrp9Dx5Fw3ZCw04ZSb0Jse6CsLH1qgZFfK0zn\nn+hpznzKHGpJRzus4YJ/AX/78G94ofUC7r777pwMxAhdE6pyAK8u78CJJZ+BtcKiIw8Wea0DTx34\nZCH5oHYwM1y0TjhnziXbaWgB+4cP/RCPPfYYtm/fjpMnT+Kmm24aDrDYhdpoQdAbaMtNSB4Da6Uh\nRx4sqnB3SCTPNbtvtu9iMoU/Wg5Kt9p0h8DTp09j3759ePrpp/H4448PB1fylOtC5jTUGVifseFY\ngJXClXou+jcN6Gk2nj7JG1Gi7TG0Hkiz7OlGP/ru6OGjq46rnnjiCSwuLibe66677hocMAZWT5uN\nDVgpXGfbZ5OtybQNZq1EE6G0NXmXtGvNwbrv+4n3uu222wYPjwys9QFW2goKjbQ4Tdth6CAFeSpK\n5J3oQMUwhynS8PjMM89AVdVs3ouBtb7Aytbrw+WiMZfnednCIwOLgTUIZml43LFjB5577rnhnx4H\nuek6yztWY6yqbb+wsJBMTwwUHquu5Ijej4GVoWMoPJ4/fz7xXkM9PWa4x3rLwsDK2KMXLlxIvBeF\nR5qe2LRpU8YrN2Y2BtaA/U7hkaYnnn322exPjwPeYz1kZ2AN2YtpeCTvdeeddw5Zyvq9jIGVo28p\nPJL3ok2NLDxeb0gGVg6w0kvT8HjixIlkHJY1lauaE8GRangwsvD/noKqt+kzsLJSkCEfzdi/8cYb\nifdaKzxWoppDmxJ5FT54NH06YZShAQVmYWAVaEwqKg2PMzMzyfTEyqfHqlRzAoOH6OqwJnXoNQeB\nSWcjq0sMrJJsferUqSQsdofHylRzYg8aLyG0QtiTOvhGhFZglyKD0Mt8DKySwEqLpfD45ptvYn5+\nHr/+z19/sukwj2pOP72vyJXBy4BNME340Pg6AiNAu8IDkQysksGi4t9++2189wffxee++DkIO4Tc\nqjlrSw504Eg81FobYetq+KOwKDgagjVOnRdtBgZW0RZdpbw0BL73/nv4yZM/6bv7tVeVxkk1h4FV\nAVgbUTWHgVUBWGUcvCVV6EP/cuiztQ9NCNsMiIshrPSIeaK3oUNIlXQqaDMDqwIjlyEV0Fv6MoQl\nbENT/FTIhWSXOF2AF5jocei8cCswsAo36WcLLEPchO7yyr+9smrt6TQ3geQmcgcd2CQbIHoIDKGy\nuSwG1joEi06oU+jj3RAWR2HQgFiiTuxqJmRgVQBWGaGQDo78/OjPe9T+qpfSeBeeqIM3JPip4k8F\n7aVbMLAqMHSlg/dr7YkcCZxWg1Jz0G5UL7/EwKoArBuhmoNEbupBvPrRDhxf8qFVLFrCwKoArFQi\n4P3o/VwTpCmgdBi3r2oOIrQbNdwfGljytZ46r2U1n4FVlmW7yn3rrbfwvX/+XrKkMyPM5FLNIS2K\nbCrSNI8loKX48G6AxhIDq2SwaIcDgWWaJn71H78qRDWnlxbF1aaQxJILj6TRjRhm0L4hYrwMrJLA\nos1+BBXtyaLty5SKVs1Zverx1RB4dhIPPe/CVioeXF2rFAOrYLDIOxFQd9xxRwLVytSt90XfFaGa\nU3ATCimOgVWIGa8WkoY9AorA6pUIrqJVcwpsRiFFMbAKMONqYS9LsWWo5mS5bxV5GFg5rExhj8ZP\ndHBitbCXo+ixv5SBNWQXpmGPvNXtt98+ZCnr9zIG1oB9O2zYG/A2Y5+dgZWxC1nYy2goNt2Q3VA0\njqIDESzsZbcZ81hr2CoNe/T56KOPZrcqy8m2zazGAAt7+X8ZzGOtsCELe/mhohLGEqwyVFpY2CsG\nqLSUsQKrDJUWFvaKBWrswCpDpYWFvXKgKiYUxh5U/huwhd8idBqYRARX4bHTldd8Le8gTSpapYWW\nX0is47qnveTdi02I6aFOejlAbSdcOT2fF8NTOEixDTqnV6Uk0CC2GpW8hYTCyFXA72yj8XoAAzoE\n+nsxgNnrZc8DtL7bU9HJlDwqLY9855FkbY8ktS3LWlGLECbPo6UG8DUOsa+Bn5nH8q3HsRRo4GIS\nL6vDN0O0e70SdoB2rfeshYBF71Juyzzu90TcF59FIC8WJvSVvgiT9nnPH5nP/K7CtOPonYWzh2aT\nF2Fu+usmvPjLF3us7cXwdR6iZ6DjyogsAWKrhokghhG6kCMTAu9Ap7+r1l0cQwoLAote4+ugwT+I\nsxO78XrQKkTkqzsEkqeily8Nk0il5cfHfowv3/xlLBxf6Pk2sNhTwEkx7I6FqMHDlC3wTRVRK4QZ\n1sGbCnxfrfxgwjBtvtHXFAZW7OsQZo7hEm7Fkxf8nm+mH6TBlau0RG00OBWcY6Gj6BDaLgSdDn46\nMPwG9Hr15/MGsdco5S0GrDiAIU7D5M/AgIo9gY6Lng4+5wi3jIOea59wieCQzgEnAe4kWoEFzhbB\nGRzEyIPQDmBWpaoxSpQMUZdCwCLh1OlmDWcCBzJsSNzDiIyL8LR8Ur1lHE2nPeZzh+d6mooENW7Z\ncx6b7zuHTlvCJB1Nnz6GS1O7sUhKxDl/LEP00Vhekh8sUjThNUyYAdxr59dCSwSvAWbg5Xq7exkq\nLfRO6TMnz/TurNAEv20/Jk4swaf2xC6U2k7Y9XPoOBIm6crYh6UoaLodABOoSU3YlpLbQ48lQT0q\nnR+sEq1RBlj0dGmfsnPVOtB51IMmfEdGLQ7RkkSYkps8VbJ01QIjDdaNCIVZwOi4DnxOgsRRXIzh\nazwakY3gmphsljLWe56RBqv6wfvg3R0HFqS6CcHxC5kQHrwGo3nFSIN1Q1RaBuinyDchSyYmDRct\nhWPLPF22G2mwuo+k55kgHUylJRtZoa1A0kI0bAdGPRnSszQuYFE90yUdepoznzKHWtLRDmsglZY8\ncHZTE7UVCGqEpmtDScZZLK20wEh7LKpst9YBKQUf1A5mhovWCefMuU9eM9JbWnEQMAIY/DQOXLr+\nmqmHXkfIdj18YpSRByuFa6+2F1f+cgXkuWb3zfZdN6Twt/DCQuKpsgmVDQIXy9vPAmMB1krPRf9e\nryot/TpsXL4fG7BSuNa7Ssu4gNOvnmMFVtqY9azS0q/DxuX7sQRrXIy7kevJwNrIvV9i2xlYJRp3\nIxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3IxfNwNrIvV9i2xlYJRp3Ixf9d0NIelzdt4X5\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
}
}
],
"execution_count": 6
},
{
"cell_type": "markdown",
"metadata": {
"id": "Ft95NDUZy4Rr",
"colab_type": "text"
},
"source": [
"That's equivalent to the function $\\hat{y} = w_2 x + w_1$. What we're trying to do is find the \"best\" weights $w_1$ and $w_2$. That will give us that green regression line above.\n",
"\n",
"What are the best weights? They're the weights that minimize the difference between our estimate $\\hat{y}$ and the actual y. Specifically, we want to minimize the sum of the squared errors, so minimize $\\sum{(\\hat{y} - y)^2}$, which is known as the *L2 loss*. So, the best weights are the weights that minimize the L2 loss."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "RHDGz_14vGNg",
"colab_type": "text"
},
"source": [
"## Gradient descent\n",
"\n",
"What gradient descent does is start with random weights for $\\hat{y} = w_2 x + w_1$ and gradually moves those weights toward better values.\n",
"\n",
"It does that by following the downward slope of the error curves. Imagine that the possible errors we could get with different weights as a landscape. From whatever weights we have, moving in some directions will increase the error, like going uphill, and some directions will decrease the error, like going downhill. We want to roll downhill, always moving the weights toward lower error.\n",
"\n",
"How does gradient descent know which way is downhill? It follows the partial derivatives of the L2 loss. The partial derivative is like a velocity, saying which way the error will change if we change the weight. We want to move in the direction of lower error. The partial derivative points the way.\n",
"\n",
"So, what gradient descent does is start with random weights and gradually walk those weights toward lower error, using the partial derivatives to know which direction to go."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "W7SgnPAWBX2M",
"colab_type": "text"
},
"source": [
"## The code again\n",
"\n",
"Let's go back to the code now, walking through it with many more comments in the code this time:"
]
},
{
"cell_type": "code",
"metadata": {
"id": "4qtXAPGmBWUW",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 718,
"status": "ok",
"timestamp": 1446659172854,
"user": {
"color": "#1FA15D",
"displayName": "Michael Piatek",
"isAnonymous": false,
"isMe": true,
"permissionId": "00327059602783983041",
"photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg",
"sessionId": "4896c353dcc58d9f",
"userId": "106975671469698476657"
},
"user_tz": 480
},
"outputId": "0664707f-ea8a-453b-fc3f-48d5ca0f76dc"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"import tensorflow as tf\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"# Set up the data with a noisy linear relationship between X and Y.\n",
"num_examples = 50\n",
"X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)])\n",
"# Add random noise (gaussian, mean 0, stdev 1)\n",
"X += np.random.randn(2, num_examples)\n",
"# Split into x and y\n",
"x, y = X\n",
"# Add the bias node which always has a value of 1\n",
"x_with_bias = np.array([(1., a) for a in x]).astype(np.float32)\n",
"\n",
"# Keep track of the loss at each iteration so we can chart it later\n",
"losses = []\n",
"# How many iterations to run our training\n",
"training_steps = 50\n",
"# The learning rate. Also known has the step size. This changes how far\n",
"# we move down the gradient toward lower error at each step. Too large\n",
"# jumps risk inaccuracy, too small slow the learning.\n",
"mu = 0.002\n",
"\n",
"# In TensorFlow, we need to run everything in the context of a session.\n",
"with tf.Session() as sess:\n",
" # Set up all the tensors.\n",
" # Our input layer is the x value and the bias node.\n",
" input = tf.constant(x_with_bias)\n",
" # Our target is the y values. They need to be massaged to the right shape.\n",
" target = tf.constant(np.transpose([y]).astype(np.float32))\n",
" # Weights are a variable. They change every time through the loop.\n",
" # Weights are initialized to random values (gaussian, mean 0, stdev 0.1)\n",
" weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))\n",
"\n",
" # Initialize all the variables defined above.\n",
" tf.initialize_all_variables().run()\n",
" \n",
" # Set up all operations that will run in the loop.\n",
" # For all x values, generate our estimate on all y given our current\n",
" # weights. So, this is computing y = w2 * x + w1 * bias\n",
" yhat = tf.matmul(input, weights)\n",
" # Compute the error, which is just the difference between our \n",
" # estimate of y and what y actually is.\n",
" yerror = tf.sub(yhat, target)\n",
" # We are going to minimize the L2 loss. The L2 loss is the sum of the\n",
" # squared error for all our estimates of y. This penalizes large errors\n",
" # a lot, but small errors only a little.\n",
" loss = tf.reduce_mean(tf.nn.l2_loss(yerror))\n",
"\n",
" # Perform gradient descent. \n",
" # This essentially just updates weights, like weights += grads * mu\n",
" # using the partial derivative of the loss with respect to the\n",
" # weights. It's the direction we want to go to move toward lower error.\n",
" update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)\n",
" \n",
" # At this point, we've defined all our tensors and run our initialization\n",
" # operations. We've also set up the operations that will repeatedly be run\n",
" # inside the training loop. All the training loop is going to do is \n",
" # repeatedly call run, inducing the gradient descent operation, which has the effect of\n",
" # repeatedly changing weights by a small amount in the direction (the\n",
" # partial derivative or gradient) that will reduce the error (the L2 loss).\n",
" for _ in range(training_steps):\n",
" # Repeatedly run the operations, updating the TensorFlow variable.\n",
" sess.run(update_weights)\n",
" \n",
" # Here, we're keeping a history of the losses to plot later\n",
" # so we can see the change in loss as training progresses.\n",
" losses.append(loss.eval())\n",
"\n",
" # Training is done, get the final values for the charts\n",
" betas = weights.eval()\n",
" yhat = yhat.eval()\n",
"\n",
"# Show the results.\n",
"fig, (ax1, ax2) = plt.subplots(1, 2)\n",
"plt.subplots_adjust(wspace=.3)\n",
"fig.set_size_inches(10, 4)\n",
"ax1.scatter(x, y, alpha=.7)\n",
"ax1.scatter(x, np.transpose(yhat)[0], c=\"g\", alpha=.6)\n",
"line_x_range = (-4, 6)\n",
"ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], \"g\", alpha=0.6)\n",
"ax2.plot(range(0, training_steps), losses)\n",
"ax2.set_ylabel(\"Loss\")\n",
"ax2.set_xlabel(\"Training steps\")\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlUAAAEPCAYAAABr+zG+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8VPW9//HXJwtLIKwBQVAEEdlETBUXLM2VKlZR22uv\n2NpatNdb6lqtGm17L1j7uwgu1KU+qPe617Vqi3LdEIm4VFHjggNaXNjXsIU1ZPn8/pgJjiEJSWY5\nk5n38/GYR2bOnDnnM0K+fviez/l8zd0RERERkdhkBR2AiIiISDpQUiUiIiISB0qqREREROJASZWI\niIhIHCipEhEREYkDJVUiIiIicRCXpMrMrjezkJl9bGaPmFmbeBxXRCRRzKyvmb0aGbsWmtnlke1d\nzexlM/vMzF4ys85Rn7nezJaY2WIzOyW46EUkFcWcVJlZP+Ai4Ch3HwHkAOfGelwRkQSrAq5y92HA\n8cAlZjYYuA54xd0PB14Frgcws6HAOcAQ4HvA3WZmgUQuIikpHjNV5cAeoIOZ5QB5wOo4HFdEJGHc\nfa27fxh5vh1YDPQFzgIejOz2IPD9yPMzgcfdvcrdlwJLgFFJDVpEUlrMSZW7bwZuBZYDq4At7v5K\nrMcVEUkWMzsEGAm8DRzg7usgnHgBPSO79QFWRH1sVWSbiAgQn8t/A4ArgX7AgUBHM/txrMcVEUkG\nM+sIPAVcEZmxqrt2l9byEpEmyYnDMY4G3nT3TQBm9gxwAvBo9E5mpoFJJE24e1rUEkVKFp4CHnb3\nWZHN68zsAHdfZ2a9gPWR7auAg6I+3jeyre4xNdaJpInmjnXxqKn6DDjOzNpFijbHEq5NqC+4lHhM\nnjw58BhSKQ7FktpxpFosaeY+YJG73x617VlgYuT5z4BZUdvPNbM2ZtYfGAgsqO+gQf8ZpdPft0yM\nPx2+Q2uP371lY13MM1Xu/pGZPQS8D1QDHwD3xHpcEZFEMrPRwHnAQjP7gPBlvt8A04AnzexCYBnh\nO/5w90Vm9iSwCKgELvaWjrwikpbicfkPd78ZuDkexxIRSQZ3fxPIbuDt7zbwmanA1IQFJSKtWkZ2\nVC8qKgo6BCB14gDFUp9UiQNSKxZJf63971trjx9a/3do7fG3lCVr9trMNFMukgbMDE+TQvVE0Fgn\nkh5aMtZl5EyViIiISLwpqRIRERGJAyVVIimuoqqixbf3iohI8iipEklhVTVV3LXgLhasqrcdkoiI\npBAlVSIpyt154MMH6NCmA8f0OSbocEREZD+UVImkqGcWP8OmXZv4+VE/J8v0qyoikuo0UoukoHlf\nzeOjdR9xyTGXkJudG3Q4IiLSBEqqRFLMB2s+4MXPX+TyYy+nQ5sOQYcjIiJNpKRKJIV8sekL/vLx\nX7j4mIspyCsIOhwREWkGJVUiKWLd9nXMfG8mFxx1Af269As6HBERaSYlVSIpoLyinDveuYPvD/4+\nw3sODzocERFpASVVIgGrqKrgrgV3cVzf4xh98OigwxERkRZSUiUSoBqv4Z7376Fvp76MHzQ+6HBE\nRCQGSqpEAuLuPPLxIzjOeUech1mzFkMXEZEUo6RKJCDPL3me5VuX84tv/YLsrOygwxERkRgpqRIJ\nwFsr3uLNFW9y2bGX0TanbdDhiIhIHCipEkmy0PoQzyx+hsuPvZxObTsFHY6IiMRJXJIqM+tsZn81\ns8VmFjKzY+NxXJF0s3zrcu774D4mHT2JXh17BR1ORjOze81snZl9HLVthJm9ZWYfmdksM+sY9d71\nZrYkMs6d0tix3RMZuYikKvM4/Pab2QPAa+5+v5nlAHnuXl5nH4/HuURKS0t54omXAJgwYRyFhYUB\nR9Q0G3duZPqb05kwfAKFvVtHzPUxM9y91VfVm9mJwHbgIXcfEdm2ALjK3d8ws4nAAHf/LzMbCjwC\nHAP0BV4BDqtvUDMz377d6aAVhkRatZaMdTHPVJlZJ+Db7n4/gLtX1U2oROKltLSUSZNmMH/+KObP\nH8WkSTMoLS0NOqz92rFnB3e8cwfjBo5r1QlVOnH3N4DNdTYfFtkO4cTp7MjzM4HHI+PbUmAJMKqh\nY2/bFudgRaRViMflv/5AmZndb2alZnaPmbWPw3FF9vHEEy+RnT2RgoKxFBSMJTt74t5Zq1RVWV3J\n3e/ezREHHMFJ/U8KOhxpXMjMzow8P4fwrBRAH2BF1H6rItvqpaRKJDPlxOkYhcAl7v6emf0RuA6Y\nHIdji7Rq7s59H9xHl3ZdOHvI2fv/gATtQuBOM/tP4FlgT0sOcsstU+jdO/y8qKiIoqKieMUnIglS\nUlJCSUlJTMeIR1K1Eljh7u9FXj8FFNe345QpU/Y+10AjLTFhwjjmzZtBWVn4dXX1A0yYcGWwQdUR\nCoWYPWc2ALlDcqnJr+GKY69otc094zHQtBbu/k9gHICZHQacHnlrFXBQ1K59I9vq9eMfT+E730lU\nlCKSCHXzkhtuuKHZx4hXofprwEXu/k8zm0y4UL24zj4qVJe4eOSRR7jjjicAuPzyCZx33nlxPX4s\nhfChUIhrb76W3GG5rK9ez4a1G3jsgsc4+sij4xpjkNKlUB3AzA4BnnP3IyKve7j7BjPLAu4H5rn7\nA1GF6scSvuw3h0YK1Z97zhmvVYdEWrWWjHXxmKkCuBx4xMxygS+BC+J0XJFvKC0t5fbbXyQ7+woA\nbr/9AYYMGbI38Yn1zsDaQvjs7IkAzJs3g5kzr2zycWbPmU3usFyyDspi55adHJZ1GHPnzU2rpCpd\nmNmjQBHQ3cyWEy5ZyDezSwAHnnH3BwDcfZGZPQksAiqBixv7V6JqqkQyU1ySKnf/iPCtxiIJFV2o\nDlBWFt5WWFgYc0K0v+M31faa7WzYvIHhPYezY9uOJn9Oksvdf9zAW3c0sP9UYGpTjq2kSiQzqaO6\npI1UuDPw2BOP5ct1X1JQXsCOL3dQGapk/Mm6DpRplFSJZKZ4Xf4TSYpEF6rHcvwtu7fw8taX+cP3\n/8CK0vDd9+OvGc+wYcPiFp+0DkqqRDJTXArVm3QiFapLnDRUN1X38l919QPNvvzX2PEbs7tqN7e8\ndQuFvQs57bDTmnW+1iadCtUTwcz8qqucW28NOhIRiUVLxjolVZJWgljCprqmmrsW3EX3vO6cd8R5\nrbZ1QlMpqWqcmflFFzn33BN0JCISiyDv/hNJCYWFhQlLpOpL2Nydhz9+mOysbH58xI8xs1a7NqHE\njy7/iWQmJVUiTdDQnYUrO6xkzbY1XHX8VWRZVlzuQJTWr1yrn4pkJCVVIk1QX6uFW/46kwEn96R4\ndDFtc9o2uF9zWzJI66eZKpHMpJYKIi2ws+OXfJ79KZcfezn5bfODDkdSjJIqkcykmSqRJpgwYRzP\nPz+ZVRsfp6rDNvYMfZf7xs2gZ4ee++yX6msTSuIpqRLJTEqqROoRXWx+9NED+cd7/2Bb3kJqRi5k\nV8E2Dll7MId2O3SfzxUWFjJz5pVRheqqp8pESqpEMpNaKojUEV1svnPnUpbt/C+6DWzLjn472N1t\nN0f1O4ou5V04Pvd4in9VvN/jpRu1VGicmXn79s7OnUFHIiKxaMlYp5oqkTqii833ZJWRNfgQdloF\ne7ruoW37tuzatCvoECXFVVRAVVXQUYhIsimpEtkPx/HDHVtlZK3MYtvybVrTTxrVsSNs3x50FCKS\nbEqqROqYMGEcZWU38nrpKFasepid2z8mv2MeI3qMoMsnXTi1y6lMv2a61vSTBuXnq65KJBOpUF2a\nJRO6hb/55pus3PMO1X2q4VDDKmDUulEcOfRIxl+oBZJl/5RUiWQmJVXSZJnQLTwUCvH7//k9NSfW\nkNM9h6rtVXSo6cjmTZszsihdWkZJlUhmUlIlTZYJ3cJnz5mNHW5YX6Mmv4bcmlwqP6+Envv/rEgt\nJVUimUk1VSJ19OnXh6rKKtgGVZurqFpWRfuaAoqLp1JaWhp0eNIKKKkSyUxKqqTJJkwYR3X1A5SV\nzaWsbG6kW/i4oMOKq29/59uUV5dzePbhdPqyE3kf5NHDh7NmzUTmzx/FpEkzlFjJfimpEslMcbv8\nZ2ZZwHvASnc/M17HldSRrt3CQ6EQs+fMptIrWdt3LcXji9m8cDP0gX92WsOiRWek9SXPTGVm9wLj\ngXXuPiKy7RjgT0AuUAlc7O7vRd67HrgQqAKucPeXGzq2kiqRzBTPmqorgEVApzgeU1JMYWFhWiUU\noVCIa2++luyh2XxV9RU5JTlM+uUkho8dDkBx8dSAI5QEuh+4E3goatt04Hfu/rKZfQ+4GfgXMxsK\nnAMMAfoCr5jZYQ0tE5GfD+XliQ1eRFJPXJIqM+sLnAb8P+CqeBxTJFGi20LsqllDztActvTYQmfv\nTPec7vzfK//H8OHhpEoLJKcvd3/DzPrV2bwG6Bx53gVYFXl+JvC4u1cBS81sCTAKeKe+Y2umSiQz\nxWumagZwDV8PRiIpqW5biBUbrqbLuZV06NqBI3oeQdnGsm/sn66XPKVB1wFvmtmtgAEnRLb3Af4R\ntd+qyLZ65efDunUJi1FEUlTMSZWZnU64JuFDMysiPBDVa8qUKXufFxUVUVRUFOvpRZrliSdeoqKi\niD1Z7wFgvY9i1bJnGd3pOMq2lIWXn7nmm8vPpNslz+YqKSmhpKQk6DCS5V7gMnf/u5n9ELgPOLm5\nB3n11SksWwZTpmisE2kt4jHWWQMlAU0/gNl/Az8hXLzZHsgHnnH38+vs11D5gUjS/Pznv+KZ+W/T\n9sheVLbbyo49nzHWRzNm9NEAjD9ZHdP3pyUrt6eqyOW/56IK1cvdvVPU+1vcvYuZXQe4u0+LbH8R\nmOzu+1z+MzN/8knn8cfh6aeT9EVEJO5aMtbFPFPl7r8BfhMJ4DvAr+smVCK1YlnmJh5L5HToVgOH\nr6Sqex678pfR5ssaDj20t7qlZy7jm7PrS8zsO+7+mpmNBZZEtj8LPGJmMwhf9hsILGjooJ06qaZK\nJBOpo7okTSzL3MRjiZxQKMSSr5bQqWc22woWcpAdQO8hB8Oer+/yS9f1DGVfZvYoUAR0N7PlwGTg\nP4C7zawNsDvyGndfZGZPEr7DubbVQoNT7ypUF8lMcU2q3P014LV4HlPSRyzL3MS6RE5t64Qd/XZQ\ntrGMNmva0LfvAVQsrGDe51/RseNZQHquZyj1c/cfN/DWsQ3sPxVoUo8NJVUimUkzVZIRZs+ZTdbQ\nLHZ33c3IbSPZ8sYW2pS34ZBuR7Coo5p7SnwpqRLJTEqqJGla2vOptLSUtWtXsXTpf7N9+w46duzQ\n7H5RNV7DsqpldMvtxqCBg1hfvZ7jc49n05qaln4dkQYpqRLJTEqqJGla0vMpupaqR4/hbNhwE9/6\n1jFcfnnTL9G5O1mDs6h6oYpOOZ1Yv2H93tYJFRUVau4pcVebVLmDpcV9kiLSFDG3VGjyidRSQVqg\nuHgq8+ePiro8N5cxYxYwbdr1TT7GC0te4P0173Nal9OY8+oc4JutE+JxV2EmSaeWColQO9a1bQtb\nt0K7dkFHJCItEUhLBZFU9vbKt3l9+etcO/paurTrQuGIfROmTG/uKYlRO1ulpEokc2QFHYBIYyZM\nGEd19QOUlc2lrGxu5PLcuCZ9dvGGxTy16CkuG3UZXdp1SXCkIt+kuiqRzKOZKklpza3DCoVCzJ4z\nm601W1ndazW/Hfdbeuf3Tla4InspqRLJPEqqJOU19fJcbS8qH+osqVxCz5Ke7DlyD3RPQpAideTn\nQ3l50FGISDLp8p+kjdlzZmNDjXWd1zHokEH0OKwHs+fMDjosyVCaqRLJPEqqJG1UezVLq5bStX1X\n+uT3CTocyXBKqkQyj5IqSQvuTuXASmyN0WFtB9Z/FulFdfL4oEOTDKWkSiTzqKZK0sIzi58hr1se\nD//Hw7w0N1zUPv6ar3tRiSRbp05KqkQyjZKqNJVJDS1f/epVPl73MdeOvpYObTow8oiRQYckopkq\nkQykpCoNRS/tAjBv3gxmzmz6si6pbtasWcx8eCYAp5x9CmsL1u5NqERSRX4+bNgQdBQikkxKqtLQ\nE0+8RHb2xKilXcLbmpJUpfoM16xZs7hoykVkj8qmKruK155/jTvOvIPueeqbIKklPx++/DLoKEQk\nmVSoLnvVznDNnz+K+fNHMWnSDEpLS4MOa69QKMQ1N17DrvxdtOnRhppDasjrlMfTTzwddGgi+9Dl\nP5HMo5mqNDRhwjjmzZtBWVn4dXhplyv3+7lYZrgSrbax55b+W6hoV8GaVWsosAK8Sot0S2pSUiWS\neZRUpaHmLu2Saupegmzbti1XT76aZT2Wcejhh/Le2vdgF2x7bRvtt7Vn0pRJAUcssi8lVSKZR0lV\nmmrq0i7RWjrDFU91i+yff34ynQduZrNtZlPNJtaUr+GQnoew5cMtdN3ZlZun3MxZZ52V1BhFmkJJ\nlUjmibmmysz6mtmrZhYys4Vmdnk8ApPkq53hGjNmAWPGLAjkjsHoS5AFBWPZWtGLdZ03MeSkIVTu\nrKS6opqclTmM6jCKvz34NyVU0mJmdq+ZrTOzj6O2PW5mpZHHV2ZWGvXe9Wa2xMwWm9kp+zu+kiqR\nzBOPmaoq4Cp3/9DMOgLvm9nL7v5pHI4tSdaSGa5k2N5lO71H9Kb67WoOsUOYfsN0NfaUWN0P3Ak8\nVLvB3c+tfW5mtwBbIs+HAOcAQ4C+wCtmdpi7N1jUp6RKJPPEnFS5+1pgbeT5djNbDPQBlFRJs9Ve\ngvznP99k3fbZVFV+RcGmDny57EsOyz0M8mH6NUqoJHbu/oaZ9Wtkl3OAosjzs4DH3b0KWGpmS4BR\nwDsNfVhJlUjmiWtNlZkdAoykkYFGWqdk9a8qLCykqKg3M578A1ZotC1ow9pd2zhjxRkcPfhoLT0j\nSWFm3wbWunttp6k+wD+idlkV2dagjh1h506oqYEsNa8RyQhxS6oil/6eAq5w9+317TNlypS9z4uK\niigqKorX6SWBktmhPRQKcf9z95M12sg5JIfdlbvJ35jP9rLtFP+qOO7nk/0rKSmhpKQk6DCS7UfA\nYy39cO1Yl50NL7xQxOmnF8UnKhFJmHiMddZISUDTD2KWA8wGXnD32xvYp7HyA0lhxcVTmT9/VFT/\nqrmMGbOAadOub9HxGpv1mvbHadz6t1vZNngbfpCTtTuL7M+yOdFP5IWnXoj9y0jMzAx3t6DjiIfI\n5b/n3H1E1LZswjNRhe6+OrLtOsDdfVrk9YvAZHffZ1Y+eqzr3Rveew/6NDqnJSKpqCVjXbwmpe8D\nFjWUUInUakrX9oOHHkzljkp8rVP9VTX+kTPpp+pFJQlhkUe0k4HFtQlVxLPAuWbWxsz6AwOBBfs7\neKdOqqsSySTxaKkwGjgPOMnMPojcinxq7KFJqpgwYRzV1Q9QVjaXsrK5kf5V41p0rLotE7KzJ+6d\ntQIYN3Yc29tsp39Bfzov7Eyn0k5MvWyqWidI3JnZo8BbwCAzW25mF0TemkCdS3/uvgh4ElgEPA9c\n3JSpdxWri2SWeNz99yaQHYdYJEUlq0O7u/NOxTv86Ls/ou3nbbFDjPEnB1OYnuoLS0vs3P3HDWy/\noIHtU4GpzTmHkiqRzKKO6tIk8epf1VDXdnfnr4v+yvY92/nt6b8lJyu4v5rJLMyX9KakSiSzKKmS\npGpo1uuVL19h8YbFXDP6mkATKkjthaWldVFSJZJZlFRJ0tWd9Xpv9Xu88uUrXDv6WvJy8wKMTCS+\nlFSJZBYlVZJ0oVCI2XNmA3DEcUfwavmr/Oq4X9GtfbeAIwtLhYWlJT0oqRLJLEqqJKlmzZpF8W3F\nZA3NoluPbvz5yT/zx3/7I3079Q06tL2SVZgv6U9JlUhmUVIlSRMKhSieXszW4VvJ7ZPLyp0rGdRx\nEIvfWcyZx58ZdHjfkKoLS0vrkp8Py5YFHYWIJItWpJKkmT1nNtkHZNOmYxt2td1F+/bt2blhZ9Bh\niSSMZqpEMouSKkmqHv17UL6pHC9zbKVRs6iG8SePDzoskYRQUiWSWZRUSdKc/t3T2VSxiR4H9KDn\nkp50+aQL066aFkhzT5FkUFIlkllUUyVx1Vgn8i9yvuCkfzmJHst7kNMrJ7Bu6SLJoqRKJLMoqZK4\naawT+evLXufd1e9y4/gbyW+bH2icIsmSnw/l5UFHISLJoqRK4qahTuQ5fXJ49rNnuWb0NUqoJKN0\n6qSZKpFMoqRK4m7bthDrts5mx47P+WpzNQ9++CCXjrqUnh16Bh2aSFLp8p9IZlFSJd/QWE3U/kyY\nMI5nnrmKlTu/hJ5G9sE7eSunLbd3vJ3+XfsnKmSRlKWkSiSzKKlKA7EkQnWP01BNVFO0bduWym5L\nyTp6M1l52ThV9OjYl8/f/RxGtygkkVatbVuoqYE9e6BNm6CjEZFEU0uFVq42EZo/fxTz549i0qQZ\nlJaWtuhY0TVRBQVjyc6euDdZa4rZc2aTV5hHwbButB/chryCPPZ8vqdFsYg0lZkdamZtI8+LzOxy\nM+sSdFwAZpqtEskkSqpauVgToXjr1aMX5dvLqdldQ9aWLKrXVau5pyTa00C1mQ0E7gEOAh4NNqSv\nKakSyRxKqgQIz3itW7eWpUv/k2XLZlJWNpfq6geYMGFck49x+ndPZ/PGzRS0LaDH6h50+bQL065V\nc09JuBp3rwJ+ANzp7tcAvQOOaS8lVSKZQzVVrdyECeOYN28GZWXh1+FE6Momfba2Fmvt2lW8//5q\n8vMvoaBgLBs23M5RRw3hiiuaXk8FsKrdKkYXjabXyl7kds1l/KVq7ilJUWlmPwJ+BpwR2ZYbYDzf\noKRKJHPEJakys1OBPxKe+brX3afF47iyf4WFhcyceWVUoXrTEqHoovRly56kvPwUCguP5pBDOtOx\nYwd69VrQrIRqwaoFzFs6jxvH30jX9l1b+nVEWuICYBLw/9z9KzPrDzy8vw+Z2b3AeGCdu4+I2n4Z\ncDFQBfyfu18X2X49cGFk+xXu/nJTglNSJZI5Yk6qzCwLuAsYC6wG3jWzWe7+aazHlqYpLCxs9h1/\n0bVYGzYsoLy8B6tXr6dz585N+nwoFGLabdN4+6O36di3IwefcjB3//RuJVSSdO6+CLgcwMy6AvlN\n/Ifd/cCdwEO1G8ysiPBs1xHuXmVmBZHtQ4BzgCFAX+AVMzvM3X1/J1FSJZI54lFTNQpY4u7L3L0S\neBw4Kw7HlSQ58MBxwEPs3PlWk2qpQqEQ5196Pk+88QRLhy3lo4M/Yt5f5vHuq+8mL2iRCDMrMbNO\nZtYNKAX+x8xu29/n3P0NYHOdzb8EborUaOHukQvrnAU87u5V7r4UWEJ47NsvJVUimSMeSVUfYEXU\n65WRbZLCJkwYR3X1A5SVzaWycjP9+lVyyimljBmzoNHeVKFQiKsnX82nyz6FYZB1WBZtu7elZkAN\nMx+eCYQvLRYXT6W4eGqL2zuINENndy8H/hV4yN2PBb7bwmMNAsaY2dtmNs/MvhXZXnecW0UTxzkl\nVSKZI6mF6lOmTNn7vKioiKKiomSeXqLsW4v1h/1eQgyFQlx787Us67GMyqGVVLapJHtDDlkdHas2\nIPYGopJ6SkpKKCkpCTqMxuSYWW/Cl+d+G+uxgK7ufpyZHQP8FRjQ3INEj3WbNhWxbVtRjGGJSKLF\nY6yzJpQENH4As+OAKe5+auT1dYDXrWkws6aUH0iKqp2hWtZjGX2G9uGNL95g9/rd4YsgfXPILjWm\nX3ET69ZVMH/+qKhFlecyZswCpk27PtgvIHFjZri7BR1HLTP7N+A/gTfd/ZdmNgC42d3PbsJn+wHP\n1Raqm9nzwDR3fy3yeglwHHARgLvfFNn+IjDZ3d+p55jfGOumToWtW+Gmm2L8oiKSVC0Z6+IxU/Uu\nMDAyOK0BzgV+FIfjSoqonaFaXrOcTTWbWLtqLXm5+VSt64AthY5rB9Mj7xTWrasIOlTJQO7+V8Iz\nSrWvvwT2m1BFWORR6+/AScBrZjYIaOPuG83sWeCRSK1WH2AgsKApJ+jUCVas2P9+ItL6xVxT5e7V\nwKXAy0CIcDHn4liPK6lj9pzZ5A7LZejYoVRtq6KyshL/3Om4fCAnDHuN0SPfoFu38OJ+0bVaLWkg\nKtJcZtbXzP5mZusjj6fNrG8TPvco8BYwyMyWm9kFwH3AADNbSLgr+/mw9w7DJ4FFwPPAxU2deldN\nlUjmiEtNlbu/CBwej2NJ6trddTc9R/bEFzjddnSjvF03KirWUlGxdm/T0Zb2zRKJwf2EE6B/i7z+\nSWTbyY19yN1/3MBbP21g/6nA1OYG16lT+PKfiKS/mGuqmnwi1VS1WqFQiEm3T2Jtv7UMzB1I1qIs\npl8znYqKiqjkaVxck6fabu+JOLbEJgVrqj5095H725bEeL4x1n30EZx3HnzySRDRiEhLtWSsU1Il\n9QqFQsyeMxuAI48/kse/eJxea3vRNasr409O7PIzde8grK5+QHcQppAUTKrmEp6Zeiyy6UfABe4+\nNqB4vjHW7dwJ3buHLwHmaGEwkVYjqEJ1STO1hem5w3LZ7bv58+N/5rZ/u43v//j7STl/dLd3gLKy\n8DYlVdKACwl3Rp8BOOE6qYlBBhQtLw969YKlS2HgwKCjEZFEUlIl31DbOmF5zXIOa3cY63LX0aem\nD58t+AxOCDq62OiSYnpy92XAmdHbzOxXhNcjTQmDB8OnnyqpEkl38eioLmkiFApx8eSLed/eZ1nO\nMua+O5e8nXl0z+6e1DgScQdh7SXF+fNHMX/+KCZNmqFu7+ntqqADiFabVIlIetNMVZqJZTbm3r/c\ny6e5n5IzKIeK3RX4emfNC2vo0qcL468Zn6iQ95GIOwh1STHjpEzNF4STqne1NKZI2lNSlUZiWSKm\ntjB9R/8d5LXNo3P7zuxetZuczTlM/+P0hBam16ewsFAJj8Qipe6KGTwYHn446ChEJNGUVKWRls7G\n1BamVx9aTUV5BRXLKyjIKiB7eTbjxzZ8p19rqlGaMGEc8+bNoKws/Lq2r5a0Xma2jfqTJwPaJzmc\nRunyn0hmUFKV4aLX9Cs4soB1y9bBR1BdXs3gvoP5+fk/r/dzrW3hZDUlTT/unh90DE3VsydUV4f/\noVNQEHTQ56HpAAAgAElEQVQ0IpIoSqrSSHNnY2bNmkXx9GI27d5EZZdKVm5YydEDjmZ9xXr6bejH\nLTfc0uAsVWusUdIlRQmK2dezVSeeGHQ0IpIoSqrSSHNmY2bNmsW//+e/s/vw3eS2zWXbjm10WteJ\n9ZvX039Xf6bfkPw6KpF0pqRKJP0pqUpBsdQqNWU2JhQKUTy9mN0jdlN1YBUVVJC/Pp+cD3Po178f\n028IL0FTXDy1wRhUoyTSPKqrEkl/SqpSTDJqlWbPmU32Adl07NaRje02YnuMqh1VHNDuAG654RYq\nKir2G4NqlESaZ/BgeP31oKMQkURSUpViklWr1KN/D1ZtXkXHNh2pXFtJu8/aMe3GaQwbNozi4qlN\nikE1SiJNp5kqkfSnpCqD1PaiWrtmLavLV9OrZy+y/plFzboapt04jbPOOivoEEXS1oABsHIl7N4N\n7doFHY2IJIKSqhSTqFql6EWSV3dZTdWmKs6wM/BDnR1ds3jrrUUcdNBBFBYWql5KJAFyc6F/f/j8\ncxg+POhoRCQRzD05jYfNzJN1rtauvkL1WBttTvvjNP5R+Q+qDqxizfY19N7amwEbBvD2a5v31k5V\nVz+wt3aqNTX2lOQyM9w9pZaBSSWNjXU/+AGcdx788IdJDkpEmq0lY52SqhTRWBJTt3g9OvnZn9pL\nfiVvlFDWv4zKQys58oAj2fr5VjbP2c2ebddE1U7NZcyYBUybdn3cv5+kDyVVjWtsrLv+eujQAX73\nuyQHJSLN1pKxTpf/UsD+7vhrafH6rFmzKL6tmKyhWeQeksuStUsY6SPZum0rlaFKBh40mEWLEvjF\nROQbBg+GOXOCjkJEEiUrlg+b2XQzW2xmH5rZ02bWKV6BZZLopKmgYCzZ2RP3zlq1VG0vqq2Dt7Kt\nzza+avMVA3sNpPPSzhyfezzTr5nOJZecT3X1A5SVzaWsbG6kdmpcXL6TSKozs3vNbJ2ZfRy1bbKZ\nrTSz0sjj1Kj3rjezJZEx75SWnFN3AIqkt1hnql4GrnP3GjO7Cbg+8pA4aknh+L0P3cum3ZvYs2wP\nHAB5eXlUraqi6MQiin9VvHc/9ZqSDHY/cCfwUJ3tt7n7bdEbzGwIcA4wBOgLvGJmhzW3puHww+Gz\nz8A9vHSNiKSXmJIqd38l6uXbwNmxhZOZ9pc0NbfRZigU4vm3n6fmiBp2tNuBlRo57XOoWV/D+EvH\nf2Nf9ZqSTOXub5hZv3reqi/dOQt43N2rgKVmtgQYBbzTnHN26QIdO8KqVdC3b/NjFpHUFs+aqguB\nx+N4vIzRlKSpqclPKBTi6slXs2fAHvYU7KFju45UbqzEPjKm3TxN6/mJ7N+lZvZT4D3g1+6+FegD\n/CNqn1WRbc1WewlQSZVI+tlvUmVmc4ADojcBDvzW3Z+L7PNboNLdH23sWFOmTNn7vKioiKKiouZH\nnKbiMWNUW5i+kY3s7r0bM6Ov96W6oJpTzz61VTX3VEuH1FFSUkJJSUnQYSTL3cDv3d3N7A/ArcC/\nN/cgjY11tUnVd78bc6wiEkfxGOtibqlgZhOBi4CT3L2ikf3UUiGBQqEQZ//H2WwdvpWKjhVsW72N\nzu0707NtT/rv6s/0a6a3mlmqWFpISOKlU0uFyOW/59x9RGPvmdl1gLv7tMh7LwKT3X2fy3/7G+tu\nvx2WLIG77orb1xCRBGjJWBfr3X+nAtcAZzaWUEli1V7y27R7E5VeSdYBWXTv2Z2sL7Lot6Ffq0qo\nIDF3Q4o0wIiqoTKzXlHv/SvwSeT5s8C5ZtbGzPoDA4EFLTmh7gAUSV+x1lTdCbQB5lj4Vpa33f3i\nmKOSJqu95Lep5yZ2j9jNzm076f5pdyzX6EY3brnhlnoTKl1ek0xnZo8CRUB3M1sOTAb+xcxGAjXA\nUuAXAO6+yMyeBBYBlcDFLZ16V1Ilkr7UUb0Vi77kV1NQw8ZdG8nblEe7he3o1q4b066tf5HkVL+8\nlurxZbp0uvyXCPsb62pqID8f1q4N/xSR1JT0y38SnFmzZvGDn/2AFWtWsKd6D1Wdq+iW1412O9rx\nrf7f4ul7nm6wMD3VL6/V3g05ZswCxoxZoIRK0kpWFgwaFO5XJSLpRcvUtEKzZs3ioikXsWvYLiq2\nVrBz4046fdWJNjVt6Ly+M7fcXf8lv9ZE/bMkndVeAjz66KAjEZF40kxVKzTz4Zlkj8qmx1E9yBqZ\nRVaHLKpeqqLzJ52ZdtX+e1FNmDBOy9OIBGjIEFi4MOgoRCTeVFPVCn3vh9/jg+4fwGFQXVXNrk92\nceCnB/K3B//W5BkqFapLS6mmqnFNGeveew/OPTfcWkHL1YikppaMdUqqWqG///3vnP+/58MgyNuR\nR82CGv5nyv+0quae0nopqWpcU8Y69/AlwIcegmOPTVJgItIsSqrSWCgUYvac2QB0G9GNV5e8ysZX\nNpLt2Uz66SQlVJI0Sqoa19Sx7sYbYf16uPPOJAQlIs2mpCpN1faiyhqaRYceHdi0bRMPn/8wJxx1\nQtChSQZSUtW4po51X34Jxx0XXlw5NzcJgYlIs6ilQhoKhUIUTy9m6+CtbO2zlc+qPqNXfi9ef+31\noEMTkRgMGAADB8KcOUFHIiLxoqQqxc2eM5vsA7LJzs9md5vd5Ofls3nD5qDDEpE4+MlP4C9/CToK\nEYkXJVWtQLf+3SgvL6dNWRtqVtRQs6iG8SePDzosEYnROefA88/Dtm1BRyIi8aCkKsWdfNLJrKte\nR/+u/en2ebcm96ISkdRXUADf/jb8/e9BRyIi8aBC9RRUe6dftVdT3r+cbm27UfNpDWbG+JPHM2zY\nMPWZksCoUL1xzR3rnngC7rsPXkqdlaJEBN39lxZCoRDX3nwtOUNzWF69nMrVlTz2i8c4YvgRe/cp\nLS3l/PP/wKZN4TYK3brN4qGHfqfESpJCSVXjmjvW7dwJffrA4sXQq1cCAxORZtHdf61cKBTi6slX\n81X7ryjLL6NNQRsGHDSA5195/hv73XHHgyxdegq7dp3Grl2nsXTpKdxxx4NJjbW0tJTi4qkUF0+l\ntLQ0qecWSSd5eXDWWfD440FHIiKxUlKVImbNmsXZ/3E273/1PqtrVvPJik84MPdAsmzfP6LFi78C\netCmTfgBPSLbkqO0tJRJk2Ywf/4o5s8fxaRJM5RYicRAdwGKpAclVSkgFApRfFsxW4dvxQud7eXb\nyVmTw2fvfEZlqHKfO/0GDz4YeIg9e+ayZ89c4KHItuR44omXyM6eSEHBWAoKxpKdPXFvfZeINN+/\n/AusXg2ffhp0JCISCyVVKWD2nNlkDc0i+6BsqgdW0y2vG9kfZ9NvQz+mXzN9nzv9rrjiQvr1q6R9\n+ydp3/5J+vWr5IorLgwoehGJVXY2XHghTJsWdCQiEoucoAOQsO49urNy50o65nXEc5zO7Tpzyw23\n1Ns6obCwkIcf/kPU3X+/SGqR+oQJ45g3bwZlZeHX1dUPMGHClUk7v0g6uvZaGDIE3n47vHyNiLQ+\nuvsvBSz4cAHnPXAe+Z3y2b1hNzWLaph21bSUXiRZLR0yl+7+a1wsY91f/gJ//CO880549kpEghNY\nSwUz+zVwM1Dg7psa2EdJVT32VO/htn/cRt7OPHYt2gWwtxeVSCpKl6TKzO4FxgPr3H1Enff2GdPM\n7HrgQqAKuMLdX27guC0e69zDzUB/9jO46KIWHUJE4iSQpMrM+gL/CxwOfEtJVdPVeA0z35tJ+5z2\nTBw5EbNW//8pyQBplFSdCGwHHopOquob08xsCPAocAzQF3gFOKy+QS3Wse6DD+B73wv3reratcWH\nEZEYBdWnagZwTRyOk1Hcncc/eZyKqgp+euRPlVCJJJm7vwHUtzp5fWPaWcDj7l7l7kuBJcCoRMR1\n1FHwr/8K//VfiTi6iCRSTIXqZnYmsMLdFyopaJ6XvniJLzZ9wdUnXE1OVviPQXVKIsFqZEzrA/wj\n6vWqyLaEuPFGGDoU/v3f4cgjE3UWEYm3/SZVZjYHOCB6E+DA74DfACfXea9BU6ZM2fu8qKiIoqKi\npkeaRt5Z+Q6vLX2N4hOLaZ/bHvi6oWZ29kQA5s2bwcyZV8acWClRk1iVlJRQUlISdBgJZ2bt2XdM\na5FYx7ru3eGGG+Cyy+C110D/ZhVJvHiMdS2uqTKz4YTrCnYSTqb6Ev7X2yh3X1/P/hlbU1W7QDLA\n0GOH8tq217jq+Ks4MP/AvfsUF09l/vxRFBSMBaCsbC5jxixg2rTrW3zeuoladfUDcUnUJLOlS00V\ngJn1A55z9xGNjWmEC9Rx95sin3sRmOzu79RzzLiMddXVcOyxcMEFcMklMR9ORJqpJWNdiy//ufsn\nwN7lP83sK6DQ3eurUchYtQsk5w7LZVfNLv781z9z5zl3fiOhSpTozucAZWXhbUqqRPayyKPRMc3M\nngUeMbPbCF/2GwgsSGRg2dnh9QBPOCFcZ3XCCYk8m4jEQzw7qjv7ufyXie596F6Wli9lxRcrWGbL\nOKjnQXzy9if77Ddhwjiqqx+grGwuZWVzIw01xwFavFgkEczsUeAtYJCZLTezC+rssndMc/dFwJPA\nIuB54OJkTL0PHAj33w/nnANr1iT6bCISKzX/TKBQKMTZF5/NliFb2N11N22+asPwPsMZd9A4in9V\nvM/+9dU/xXIJT5f/JBHS6fJfIiRirPv97+Hll+HVV6FNm7geWkQaEFjzzyadKAOTqml/nMaLm17k\ng8oPyM3LJXtlNl0+6cLT9zzd5OaesdZaqVBd4k1JVeMSMdbV1MD3vw8HHwx33RXXQ4tIA5JaUyX7\n5+5sab+FQ3seSnZ5NtuztnPqmFOT2i29sLBQiZRIK5eVBQ8/DMccAw8+GO64LiKpR0lVArUb1o5d\n/7eLQdmDyMrNonJXJT+/9OfNOoYWLxYRgM6d4e9/h6Ii6N8fxowJOiIRqUuX/xJk3lfzmLd0Hmd0\nO4NX570KtHxNP13Ck1Siy3+NS/RY9+qrcO65MGsWHH98wk4jkvFUU5UiPljzAY998hjXjr6WgryC\noMMRiSslVY1Lxlj34otw/vnwf/8XviQoIvGnpCoFfLn5S/604E9cfuzl9OvSD0jeTJNmtCQZlFQ1\nLllj3XPPhZexeeklGDky4acTyThKqgK2bvs6bnnrFn428mcM7zkcSF5bA7VPkGRRUtW4ZI51Tz8N\nl14Kc+bA8OFJOaVIxmjJWBfP5p8ZrbyinDveuYOzBp+1N6ECuP32+1i5Mo8NGxaQm9uV7OyJe2eT\n4im6e3pBwdiEnUdEUsfZZ8Ntt8Epp8C77wYdjYjo7r84qKiq4K4Fd3Fc3+M48eAT924vLS3l5ZcX\ns23bxeza1YWyshkcfPDoACMVkXTzox9BXh6cdhr87//CWWcFHZFI5lJSFaMar+Ge9++hT34fxg8a\n/433nnjiJQoKrmDXroOAvlRVfZ8NG25lwoT4d+9T6wWRzHXWWdCnT/jn0qVwxRVBRySSmZRUxcDd\neXThozjOT0b8BLN9L7127NiBESMGsHr1enbu3M4ppxyTkDqnwsJCZs68MqpQXfVUIpnk6KPhrbfg\n9NPhiy9gxozwoswikjwqVI/B80uep3RNKVefcDXtctrt837QxeN17wYEdHegxEyF6o0LeqzbuhV+\n+MPwGoEPPQTduwcWikirprv/kuitFW8x+5+zKR5dTOd2nRvcL6g2B3UTuvLyWzFrR37+JYDuDpSW\nU1LVuFQY6yor4Te/gSeegL/8Rd3XRVpCa/8lyaINi3hm8TP8+vhfN5pQQXBr70XfDQiwbNmTwAn0\n71+7MHN4HyVVIuknNxduvhlOOgkmTIBJk+B3v9PlQJFEU0uFZlqxdQX3lt7LpKMn0Tu/d9DhiIg0\n6Hvfg9JSmD8fxo6FlSuDjkgkvSmpaoaNOzdy14K7OG/EeQzsNjDocBo1YcI4qqsfoKxsLmVlc+na\ndQXdus3a+zp8d+C4oMMUkQTr3Rtefjncy+qoo+BPf4Lq6qCjEklPqqlqoh17dnDzWzfz7YO/zdgB\nY4MOp0lUqC6JoJqqxqXyWLdoEfziF7BnD/z5z1reRqQxKlRPkMrqSm5/53b6de7Hvw37t6DDEQmU\nkqrGpfpYV1MD998fLmT/yU/ghhugY8egoxJJPYEsU2Nml5nZYjNbaGY3xXq8VOPu3P/h/XRu25kf\nDv1h0OGISJyY2b1mts7MPo7a9nsz+8jMPjSzV8ysb9R715vZksh4d0owUccuKwt+/nP45JPwDSuH\nHRa+JLhnT9CRibR+MSVVZlYEnAEc4e5HALfEI6hU8tSipyivKGfiyIn1NvcUkVbrfqBuYeF0dz/S\n3UcCs4DJAGY2FDgHGAJ8D7jbWvmA0KMHPPggPP88zJ4NgweH2y+o3kqk5WKdqfolcJO7VwG4e1ns\nIaWOuV/OJbQhxC+P/iW52blBhyMiceTubwCb62zbHvWyA7Ax8vxM4HF3r3L3pcASYFQy4ky0o46C\nF14IXxK8++5wndVf/wpVVUFHJtL6xJpUDQLGmNnbZjbPzI6OR1Cp4P3V7/PyFy9z2ajL6NCmQ9Dh\niEiSmNkfzGw5MBGYGtncB1gRtduqyLa08Z3vwJtvwn//N9x+e/iy4B13wPbt+/+siITtN6kyszlm\n9nHUY2Hk55mEm4d2dffjgGuBJxMdcDIs2biExz55jEtHXUr3PK3xIJJJ3P137n4w4cuDfww6nmQy\ngzPOgDfegMceg9dfh0MOgeuuCy/ULCKN229HdXc/uaH3zGwS8Exkv3fNrMbMurv7xvr2nzJlyt7n\nRUVFFBUVNTfehFuzbQ1/fv/PXHjUhRzU+aCgwxEJXElJCSUlJUGHEYRHgecjz1cB0QNC38i2erWG\nsW5/jjsufBnwyy/hzjvhmGPgyCPhwgvhBz+A9u2DjlAkvuIx1sXUUsHM/gPo4+6TzWwQMMfd+zWw\nb0rfZgywdfdWpr05jTMGncHxBx0fdDgiKSmdWiqY2SHAc5EbbTCzge7+eeT5ZcAod/9ppFD9EeBY\nwpf95gCH1TeotYaxriV274Znn4X77oN334VzzoFzz4UTT9TyN5Kekt6nysxygfuAkUAF8Gt3f62B\nfVN6oNldtZtb3rqFwt6FnHbYaUGHI5Ky0iWpMrNHgSKgO7CO8J1+pwOHA1XAl8Av3X19ZP/rgZ8D\nlcAV7v5yA8dN6bEuHpYvh4cfhqeegtWrwzNXP/xhuC4rV/f0SJpQ888Wqq6p5k/v/olu7btx3hHn\nqXWCSCPSJalKlFQe6xLhiy/g6afDj88/h+9+F8aNCz/6pFUpv2QaJVUt4O489NFDbNuzjYuPuZgs\n03KIIo1RUtW4VB3rkmHVqvA6gy++CK+8El538JRT4NvfhtGjoWfPoCMUaTolVS3w3GfPsXD9Qn59\n/K9pm9M26HBEUp6Sqsal6liXbNXV8N57MHdu+G7Ct96CXr3CNVgnnABHHw1Dh0LOfm+XEgmGkqpm\nemP5G7yw5AWKTyymU9tOQYfTInUXTdYiyZJoSqoal4pjXSqorg4vjfP66/D22/D+++HarBEj4Fvf\nCjcdHT4chg2D/PygoxVRUtUsn6z/hAc/fJCrT7iaAzoeEHQ4LVJaWsqkSTPIzp4IQHX1A8yceaUS\nK0koJVWNS7WxLpWVl8MHH4QTrI8+glAIFi8OL6EzfDgcfjgMGhRuRDpoEBx4YHjtQpFkaMlYl5ET\nr8u2LOP+D+7nklGXtNqECuCJJ14iO3siBQVjgfDiqE888ZKSKhFpFTp1Ct8x+J3vfL2tuhq++io8\nq/XZZ+H2DY8+Cv/8ZzgJ69cv3JA0+mffvuGi+AMPhLaq4pAAZVxSVbazjD+9+yd+euRPGdB1QNDh\niIhIlOxsGDgw/Khr+/ZwZ/fax7Jl4bqtlSvDRfJr10LnzuEE64AD9n107w4FBV//7NQp3EVeJF4y\nKqmq8Rr+tOBPnHbYaYzsNTLocGI2YcI45s2bQVlkGevq6geYMOHKYIMSEUmQjh3DlwWHD6///Zoa\n2LAhnGCtW/f1Y/Vq+PBD2LgxPKNf+3PXrnAS1qULdO0a/tmlSzjZ6tQp/F6nTuEar44dv3506BB+\n5OV9/bN9ezVBlQysqdqwYwM9OvQIOoy4UaG6JJtqqhqXKmOd7F9lJWzZAps3f/1z69bwZcby8q+f\nb9/+zce2bbBz59ePHTvCCVpuLrRrF06w2rcPP699tG379c82bb7+WfvIzQ0/op/n5obvjox+XvvI\nzm74Z+0jK2vf59E/G3qY7fvc7JvP63uvsUdrpEJ1EUk4JVWN01iXmdyhoiK8nM+uXeHH7t1fb4v+\nuWdP+FH7vKIinODVPvbsCf+sqvrm9urq8LboR3X119ujf9bUfP1e7evabbU/3b/eXneb+9evo7fV\n/mxoW91HXfUlW409r7ut7vaGttX3Xt04on/+7Gdw661191FSJSIJpqSqcRrrRPbVUMLV2PO62+pu\nb2hbfe/VjaXue23b7tvKQ3f/iYiISMppzZcBm0MdP0RERETiQEmViIiISBwoqRIRERGJAyVVIiIi\nInGgpEpEREQkDpRUiYiIiMSBkioRERGROFBSJSIiIhIHMSVVZnaMmS0wsw8iP4+OV2AiIolkZvea\n2Toz+zhq23QzW2xmH5rZ02bWKeq9681sSeT9U4KJWkRSWawzVdOB37n7UcBk4ObYQ0q8kpKSoEMA\nUicOUCz1SZU4ILViSSP3A+PqbHsZGObuI4ElwPUAZjYUOAcYAnwPuNssfftDt/a/b609fmj936G1\nx99SsSZVa4DOkeddgFUxHi8pUuUPO1XiAMVSn1SJA1IrlnTh7m8Am+tse8XdayIv3wb6Rp6fCTzu\n7lXuvpRwwjUqWbEmW2v/+9ba44fW/x1ae/wtFevaf9cBb5rZrYABJ8QekohISrgQeCzyvA/wj6j3\nVkW2iYjstd+kyszmAAdEbwIc+B1wGXCZu//dzH4I3AecnIhARUSSxcx+C1S6+2P73VlEJMLcveUf\nNit39+hCzq3u3rmBfVt+IhFJKe6eFvVEZtYPeM7dR0RtmwhcBJzk7hWRbdcB7u7TIq9fBCa7+zv1\nHFNjnUiaaO5YF+vlvyVm9h13f83MxgL/jFdgIiJJYJFH+IXZqcA1wJjahCriWeARM5tB+LLfQGBB\nfQfUWCeSuWJNqn4B/MnM2gC7gf+IPSQRkcQzs0eBIqC7mS0nfAfzb4A2wJzIzX1vu/vF7r7IzJ4E\nFgGVwMUeyzS/iKSlmC7/iYiIiEhY0juqm9llkeZ5C83spmSfv04svzazGjPrFmAMDTYbTNL5TzWz\nT83sn2ZWnMxz14mjr5m9amahyN+Ny4OKJRJPlpmVmtmzAcfR2cz+Gvk7EjKzYwOM5fpIDB+b2SOR\nGWqJkiq/T83RQBPUrmb2spl9ZmYvmVm9tbKpoKGxo7V8BzNra2bvRJpoh8zsvyPbW0X8teqOma0w\n/qVm9lFtM/PItmZ/h6QmVWZWBJwBHOHuRwC3JPP8dWLpS/hOxWVBxRBRb7PBZDCzLOAuwg0QhwE/\nMrPByTp/HVXAVe4+DDgeuCTAWACuIHypJ2i3A8+7+xDgSGBxEEFECrovAo6KFHXnAOcGEUuqSrHf\np+aorwnqdcAr7n448CpJHJdaoKGxo1V8h0jt3r9EmmiPAE4ys9G0kvij1B0zW1v8NUCRux/l7rU9\n6Jr9HZI9U/VL4CZ3rwJw97Iknz/aDMIFqYFqpNlgMowClrj7MnevBB4Hzkri+fdy97Xu/mHk+XbC\nyUMgfYAiCfdpwP8Gcf6oODoB33b3+wEijSfLAwqnHNgDdDCzHCAPWB1QLKkqZX6fmqO+JqiE434w\n8vxB4PtJDaoZGhg7+tK6vsPOyNO2hP+/vJlWFH8DY2ariT/C2DcnavZ3SHZSNQgYY2Zvm9k8C2it\nQDM7E1jh7guDOH8jLgReSOL5+gArol6vJAUaGprZIcBIYJ/b1ZOkNuEOuuCwP1BmZvdHptXvMbP2\nQQTi7puBW4HlhBtfbnH3V4KIJYWl5O9TC/V093UQTlqAngHH0yRRY8fbwAGt5TtELp19AKwFStx9\nEa0ofuofM1tT/BCOfY6ZvWtm/x7Z1uzvEOvdf/uwxpuF5gBd3f04MzsGeBIYEO8YmhDHb/hmk9KE\n3gLdSCy/dffnIvvUNht8NJGxpDoz6wg8BVwR+Vdnss9/OrDO3T+MXK4O8vb4HKAQuMTd3zOzPxKe\njp6c7EDMbABwJdAP2Ao8ZWY/zvS/rxkk6H9g7FfdscP27ReWst8hcrXiqMjs9EuRsadVxF/PmNmQ\nlIw/ymh3X2NmPYCXzewzWvBnEPekyt0b7KhuZpOAZyL7vRspEu/u7huTFYeZDQcOAT4yMyM8Tfy+\nmY1y9/XxjqOxWKJimkh46vSkRJy/EauAg6Ne9yXA9Rsjl5WeAh5291kBhTEaONPMTgPaA/lm9pC7\nnx9ALCsJz6i+F3n9FBBU8fPRwJvuvgnAzJ4hvCyVkqqvpdTvU4zWmdkB7r7OzHoBCRkb46WBsaNV\nfQcAdy83s+cJ/761lvjrGzMfBta2kvgBcPc1kZ8bzOzvhC/nN/vPINmX//5OJHEws0FAbiISqsa4\n+yfu3svdB7h7f8L/4zoqUQnV/tjXzQbPrNNsMBneBQaaWb/InVznEm5yGJT7gEXufntQAbj7b9z9\nYHcfQPi/x6sBJVREpp1XRH5XAMYSXPH8Z8BxZtYu8o+RsQRUNJ/CUu33qTm+0QSVcNwTI89/BgT1\nj5ymqm/saBXfwcwKau8qi1zePxn4gFYSfwNj5k+B52gF8QOYWV5kphMz6wCcAiykBX8GcZ+p2o/7\ngfvMbCFQAQTyP6s6nGAv8dxJPc0Gk3Fid682s0sJ34GYBdzr7kHdXTYaOA9YGKktcOA37v5iEPGk\nkMsJd/LOBb4ELggiCHf/yMweAt4HqgkP+vcEEUuqSqXfp+aw+pug3gT81cwuJHyH9DnBRdi4hsYO\nYMjnsCMAAAPrSURBVBrwZCv4Dr2BByP/WMkiPNs2N/JdWkP8DbmJ1hP/AcDfIpeMc4BH3P1lM3uP\nZn4HNf8UERERiYOkN/8UERERSUdKqkRERETiQEmViIiISBwoqRIRERGJAyVVIiIiInGgpEpEREQk\nDpRUiYhIyjOzbmb2QWQdzDVmtjLqdZN6LprZvWZ22H72udjMfhSfqOs9/g+iGvpKmlGfKhERaVXM\n7L+A7e5+Wz3vmafw/9giS7g8FeBSXJJAmqkSEZHWZu8qGGZ2qJmFzOwvZvYJ0MvM/mxmC8xsoZn9\nLmrf181shJllm9lmM5tqZh+a2ZtmVhDZ50Yzuzxq/6lm9o6ZLTaz4yLb88zsKTP7xMz+ambvmtmI\nfYI0uzkS24eR45xIeJ3X2yIzbAeb2UAzezFyjBIzGxj57MNmdreZvWdmn0aWNMPMhke+W2nkuIck\n7L+yNFuyl6kRERGJt8OBn7j7BwBmVuzuW8wsG5hnZk+5+6d1PtP5/7d3PyE2hWEcx79PjSjTzE6p\nKUmjkAZNkSzsNAs1CyJ2xEJRZmehrMmGFHYypUwmicnInw1WxmKKKRqymGah5H8NM34W9xmuM/di\n6tTMrd+nTr333Pd9z1k+Pc/beYAHko5FxGlgH3Cy1uaSNkbEdiotfLqAw8C4pB0ZTA0V10TEEqBL\n0pr83VLVMLlP0o28fx/YL+l1RGwGzgHbcps2SZ1ZLrwbESuAQ8ApSX3Zvmou26xZgYMqMzNrdKPT\nAVXam/3amqj01lsNFIOqr5Lu5HgI2FJn7/6qOctyvIVKbzskDUfEsxrr3gFTEXERGABuFidkI+VN\nwLXs/Qd/VpCu5jNeZF/GduAxcDwzVP2SRuu8t80Bl//MzKzRfZkeZPnsCLBVUgcwCCyqseZb1XiK\n+kmGif+YMyNbJGkS6ASuA93ArTrr3kraIGl9Xh3V2xTmSlJv7jcB3M6Sos0TDqrMzKzRVQc1LcBH\n4HNELOV3Ke1va2brEbALICLWAqtmbB7RDLRKGgB6gHX516d8RyS9B8YjojvXROFs1s68vxJoA15G\nxHJJrySdoZL9mnGWy+aOy39mZtbofmV0JD2NiBFgBHgDPKw1rzD+574FZ4FLeTD+eV4fCnNagf6I\nWEglgDua968AFyKih0rGaTdwPiJOAAuAXmA4545FxBNgMXBA0mRE7MlPPnwHxqic87J5wp9UMDMz\nm4U8AN8kaSLLjYNAu6QfJT7jMlUH2q0xOFNlZmY2O83AvaqPjh4sM6BKzng0IGeqzMzMzErgg+pm\nZmZmJXBQZWZmZlYCB1VmZmZmJXBQZWZmZlYCB1VmZmZmJXBQZWZmZlaCn3k/n05X32zbAAAAAElF\nTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8047207c10>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "lSWT9YsLP1de",
"colab_type": "text"
},
"source": [
"This version of the code has a lot more comments at each step. Read through the code and the comments.\n",
"\n",
"The core piece is the loop, which contains a single `run` call. `run` executes the operations necessary for the `GradientDescentOptimizer` operation. That includes several other operations, all of which are also executed each time through the loop. The `GradientDescentOptimizer` execution has a side effect of assigning to weights, so the variable weights changes each time in the loop.\n",
"\n",
"The result is that, in each iteration of the loop, the code processes the entire input data set, generates all the estimates $\\hat{y}$ for each $x$ given the current weights $w_i$, finds all the errors and L2 losses $(\\hat{y} - y)^2$, and then changes the weights $w_i$ by a small amount in the direction of that will reduce the L2 loss.\n",
"\n",
"After many iterations of the loop, the amount we are changing the weights gets smaller and smaller, and the loss gets smaller and smaller, as we narrow in on near optimal values for the weights. By the end of the loop, we should be near the lowest possible values for the L2 loss, and near the best possible weights we could have."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "dFOk7ERATLk2",
"colab_type": "text"
},
"source": [
"## The details\n",
"\n",
"This code works, but there are still a few black boxes that are worth diving into here. `l2_loss`? `GradientDescentOptimizer`? What exactly are those doing?\n",
"\n",
"One way to understand exactly what those are doing is to do the same thing without using those functions. Here is equivalent code that calculates the gradients (derivatives), L2 loss (sum squared error), and `GradientDescentOptimizer` from scratch without using those functions."
]
},
{
"cell_type": "code",
"metadata": {
"id": "_geHN4sPTeRk",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 657,
"status": "ok",
"timestamp": 1446499870301,
"user": {
"color": "",
"displayName": "",
"isAnonymous": false,
"isMe": true,
"permissionId": "",
"photoUrl": "",
"sessionId": "0",
"userId": ""
},
"user_tz": 480
},
"outputId": "85c49bf6-8d07-401a-ae08-79c6933adff5"
},
"source": [
"#@test {\"output\": \"ignore\"}\n",
"\n",
"# Use the same input data and parameters as the examples above.\n",
"# We're going to build up a list of the errors over time as we train to display later.\n",
"losses = []\n",
"\n",
"with tf.Session() as sess:\n",
" # Set up all the tensors.\n",
" # The input is the x values with the bias appended on to each x.\n",
" input = tf.constant(x_with_bias)\n",
" # We're trying to find the best fit for the target y values.\n",
" target = tf.constant(np.transpose([y]).astype(np.float32))\n",
" # Let's set up the weights randomly\n",
" weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))\n",
"\n",
" tf.initialize_all_variables().run()\n",
" \n",
" # mu is the learning rate (step size), so how much we jump from the current spot\n",
" mu = 0.002\n",
" \n",
" # The operations in the operation graph.\n",
" # Compute the predicted y values given our current weights\n",
" yhat = tf.matmul(input, weights)\n",
" # How much does this differ from the actual y?\n",
" yerror = tf.sub(yhat, target)\n",
" # Change the weights by subtracting derivative with respect to that weight\n",
" loss = 0.5 * tf.reduce_sum(tf.mul(yerror, yerror))\n",
" gradient = tf.reduce_sum(tf.transpose(tf.mul(input, yerror)), 1, keep_dims=True)\n",
" update_weights = tf.assign_sub(weights, mu * gradient)\n",
" \n",
" # Repeatedly run the operation graph over the training data and weights.\n",
" for _ in range(training_steps):\n",
" sess.run(update_weights)\n",
"\n",
" # Here, we're keeping a history of the losses to plot later\n",
" # so we can see the change in loss as training progresses.\n",
" losses.append(loss.eval())\n",
"\n",
" # Training is done, compute final values for the graph.\n",
" betas = weights.eval()\n",
" yhat = yhat.eval()\n",
"\n",
"# Show the results.\n",
"fig, (ax1, ax2) = plt.subplots(1, 2)\n",
"plt.subplots_adjust(wspace=.3)\n",
"fig.set_size_inches(10, 4)\n",
"ax1.scatter(x, y, alpha=.7)\n",
"ax1.scatter(x, np.transpose(yhat)[0], c=\"g\", alpha=.6)\n",
"line_x_range = (-4, 6)\n",
"ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], \"g\", alpha=0.6)\n",
"ax2.plot(range(0, training_steps), losses)\n",
"ax2.set_ylabel(\"Loss\")\n",
"ax2.set_xlabel(\"Training steps\")\n",
"plt.show()"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlUAAAEPCAYAAABr+zG+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8VPXZ///XlYUlLEEIIIsCCqKAqCmgFkvTUkUrLnft\nXay2va12obZK9RZTWr8/oO19K2pLXWqxLWqxWnGrWEpVVCK3K2pcBxSs7MgSdgiELNfvj5ngGJKQ\nZCZzZnk/H4/zyJkzZ865RuDjlc/5fK6PuTsiIiIiEpusoAMQERERSQdKqkRERETiQEmViIiISBwo\nqRIRERGJAyVVIiIiInGgpEpEREQkDuKSVJnZFDMLmdm7ZvaAmbWJx3VFRFqLmc02s01m9m7UseFm\n9rKZvWNm88ysY9R7U8xshZktM7OzgolaRJJZzEmVmfUDvg+c4u7DgRzg4livKyLSyu4FxtU59mfg\nenc/Cfg7cD2AmQ0BvgGcAJwD3GVmlsBYRSQFxKOnahdwAOhgZjlAHrAhDtcVEWk17v4isL3O4UGR\n4wDPAhdF9s8HHnL3KndfBawARiUkUBFJGTEnVe6+HfgNsAZYD+xw92djva6ISABCZnZ+ZP8bQN/I\nfh9gbdR56yPHREQOisfjv2OAa4B+QG+go5ldEut1RUQCcDnwYzN7HehAuBdeRKRJcuJwjRHAS+6+\nDcDMHgc+DzwYfZKZaZFBkTTh7mk5nsjdlxMZZ2Vmg4BzI2+tB46KOrVv5Ngh1NaJpI/mtnXxGFP1\nIXCambWLDNwcCyxrILik2KZOnRp4DMkUh2JJ7jiSLZY0Y5Et/MKse+RnFnADMCvy1pPAxWbWxswG\nAAOBJQ1dNOg/o3T6+5aJ8afDd0j1+N1b1tbF3FPl7u+Y2RzgTaAaeAv4Y6zXFRFpTWb2IFAEdDOz\nNcBUoJOZ/Rhw4HF3vw/A3Zea2cPAUqASuNJb2uqKSNqKx+M/3P0W4JZ4XEtEJBHcvaGxn7c3cP6N\nwI2tF5GIpLqMrKheVFQUdAhA8sQBiqU+yRIHJFcskv5S/e9bqscPqf8dUj3+lrJE9WCbmXrLRdKA\nmeFpOlA9HtTWiaSHlrR1GdlTJSIiIhJvSqpERERE4kBJlUiSq6yubPH0XhERSRwlVSJJrKqmijuX\n3MmS9Q2WRBIRkSShpEokSbk7c96ZQ7ucdozsMzLocERE5DCUVIkkqSc+eIIte7fwvcLvkWX6pyoi\nkuzUUoskoZJVJZR+UsqPR/2Y3OzcoMMREZEmUFIlkmTe2fgOC1YsYNJpk+jYpmPQ4YiISBMpqRJJ\nIh9v/5j7372fH4/8MQV5BUGHIyIizaCkSiRJbN67mT+8/gcuO/ky+nXpF3Q4IiLSTEqqRJLA7ord\n3PbqbZw/+HyG9RgWdDgiItICSqpEAlZRVcGdS+7k1L6n8oV+Xwg6HBERaSElVSIBqvEa/lz6Z3p3\n6s15x50XdDgSJzU1QUcgIkFQUiUSEHfnwfcepKqmim8N/xZmzVoMXZLY7t1BRyAiQVBSJRKQf330\nL1btWMUPR/yQ7KzsoMORONqxI+gIRCQISqpEAvDK2ld4cc2LXDXqKtrltAs6HIkzJVUimUlJlUiC\nLduyjMeWPcZVo64iv11+0OFIK1BSJZKZ4pJUmVm+mT1iZsvMLGRmp8bjuiLpZu3Otcx+azYTR0yk\nV6deQYcjrURJlUhmyonTdW4DFrj7f5pZDpAXp+uKHKK0tJS5c58GYMKEcRQWFgYcUdNsLd/KnUvu\n5JITL2Fg14FBhyOtaOfOoCMQkSDEnFSZWWfgC+5+GYC7VwG7Yr2uSH1KS0uZOHEm2dmXAbBo0Uxm\nzbom6ROr8spy7lhyB2cdexaFvZI7VomdeqpEMlM8Hv8NAMrM7F4zKzWzP5pZ+zhcV+QQc+c+TXb2\nZRQUjKWgYCzZ2Zcd7LVKVpXVldz1+l0M7T6UsceMDTocSQAlVSKZKR5JVQ5QCPze3QuBcuBncbiu\nSMpzd+57+z7y2+bz9SFfDzociWJms81sk5m9G3VspJktMbO3Ij9HRL03xcxWRMaOntXYtZVUiWSm\neIypWgesdfc3Iq8fBYrrO3HatGkH94uKiigqKorD7SWTTJgwjkWLZlJWFn5dXX0fEyZcE2xQdYRC\nIeYvnA9A7gm51HSqYdKpk1K2uGdJSQklJSVBh9Ea7gXuAOZEHbsZuMHdnzGzc4BbgC+Z2RDgG8AJ\nQF/gWTMb5O5e34WVVIlkppiTKnffZGZrzew4d18OjAWW1ndudFIl0hKFhYVMmnQ2t99+GwCTJk2I\n+3iqWAbCh0Ihrr/lenKH5rKlegub/7WZB7/7ILnZuXGNMZHq/gI0ffr04IKJI3d/0cz61Tn8CVBb\n56ILsD6yfz7wUGTM6CozWwGMAl6r79pKqkQyU7xm/10NPGBmucDHwHfjdF2RzygtLeW2254iO3sS\nALfddh8nnHDCwcQn1pmBsQ6En79wPrlDc8k+Opu92/cyKGsQzy96npEnjWxWHBKYnwEvmdlvAAM+\nHzneB3gl6rz1kWP10uw/kcwUl6TK3d8B9H8NaXXRA9UBysrCxwoLC+MyM7Cx6zfVnpo9bNm2hWE9\nhrF3994mf06SwmzgKnd/wsy+DtwDnNnciyxdOo3ajnkNdRBJDfEY6hCvniqRwMUjIYrVqWecyt0P\n3k1/+rN3z14qQ5WMnzw+YfeXmJ3q7mcCuPujZvbnyPH1wFFR5/Xl00eDh8jL+zSpEpHUEI+hDkqq\nJKW09kD1WK6/c/9Ontn5DL+68FesK10HwPjJ4xk6dGjc4pO4s8hWa4WZfdHdXzCzscCKyPEnCQ9x\nmEn4sd9AYElDF9WYKpHMZA1MXon/jcwamigj0iwNjZuq+/ivuvq+FhUGbcm4rP1V+7n15Vsp7FXI\nVwd9tVn3SzVmhrun5lTGKGb2IFAEdAM2AVOBd4G7gDbAfuBKd38rcv4U4AqgEpjk7s80cF3PznYq\nKyFFJ3yKCC1r65RUSVoJYgmb6ppqfv/67+naviuXnnhpypZOaKp0Sapai5l5hw7Oxo3QsWPQ0YhI\nSympEmlF9SVs7s6cd+aw+8Burhx5JVmWlbJrEzaVkqrGmZn36eO8+ir07Rt0NCLSUi1p6zSmSqQJ\nGppZuL7Dejbs3sC1p197MKFKxbUJJb66dAmPq1JSJZJZlFSJNEF9Mwt/88jdDDizO8Wji2mb07bB\n8xI9A1GCl5+vweoimSgea/+JZJzyjitZkb2Mq0+9mk5tOwUdjiSZ2p4qEcks6qkSaYIJE8axYMFU\n1m99iKoOuzkw5HXuGTeTHh16HHJesq9NKK1PSZVIZlJSJVKP6MHmI0YM5JU3XmF33nvUnPwe+wp2\n03/j0Rzb9dhDPldYWMisWddEDVTXeKpM1KWLlqoRyURKqkTqiB5sXl6+irsf/yldB7Zl3yn72N91\nP4X9Csnvnc/8hfPrLexZWFioRCrDqadKJDNpTJVIHdGDzQ9klZF1fH/KrYIDRxygbfu2lG8rDzpE\nSXJKqkQyk5IqkcNwHB/s2Hoja10Wu9fsDq/pd6bW9JP6afafSGbS4z+ROiZMGMfjj1/LsjVTqKos\np7LLKrp1PJK+Wcex8dWNnD3mbK74yRVa008apJ4qkcykpEqaJd2rhQO89NJLrDvwGtV9quFYwypg\n1KZRnDTkJMZfrgWS5fA0UF0kMympkibLhGrhoVCIX/7pl9ScUUNOtxyq9lTRoaYj27dtp/inxUGH\nJylCPVUimUlJlTRZJlQLn79wPjbYsL5GTacacmtyqfyoEnoc/rMitZRUiWQmDVQXqaNPvz5UVVbB\nbqjaXkXV6ira1xRQXHwjpaWlQYcnKUAD1UUyk5IqabIJE8ZRXX0fZWXPUVb2XKRa+Ligw4qrL3zx\nC+yq3sXg7MF0/rgzeW/l0d2H8cknl7F48SgmTpypxEoOqzapcg86EhFJJPM4/as3syzgDWCdu59f\nz/ser3tJcNJxoHooFGL+wvlUeiUb+25keNfhbH9vOwDL3/uEpUvPi3rk+RxjxixhxowpQYYcKDPD\n3S3oOJJVbVvXvj1s3Qp5eUFHJCIt0ZK2Lp5jqiYBS4HOcbymJJl0qxYeCoW4/pbryR6SzcdVH5Nb\nksvEH01k2NhhABQX3xhwhJKqamcAKqkSyRxxSarMrC/wVeB/gGvjcU2R1hLd27av5hNyhuSwo/sO\njvAj6JrTlX8++0+GDQsnVVogWVqqdrB6r15BRyIiiRKvnqqZwGQgP07XE2kVdctCrN1yHV0urqTD\nER0Y3nM4W7Zu+cz5WiBZWkozAEUyT8xJlZmdC2xy97fNrAho8PnjtGnTDu4XFRVRVFQU6+1FmmXu\n3KepqCjiQNYbAFivk1m/+h+M7nwaW3ZsCS8/M/mzy8+k2yPP5iopKaGkpCToMFKOZgCKZJ6YB6qb\n2f8C3wKqgPZAJ+Bxd/9OnfM0UF0Cd8UVP+Xxxa/S9qQjqWy3k70HPmSsj2bM6BEAjD9TFdMPRwPV\nG1fb1l18MVxwAXzzm0FHJCItEchAdXf/OfDzSABfBP67bkIlUiuW2YPxmHnYoWsNDF5HVbc89nVa\nTduPazj22F6qli5xp6VqRDKPKqpLwsSyzE08lsgJhUKsWLmCzj2y2V3wHkdZT3qdcDQc+HSWX7qU\niZDgaUyVSOaJa/FPd3+hvhpVIvDZZW4KCsaSnX3ZwZ6n1vwsfFo6YW+/vZTVlOGfVNE3qydVS6tY\n9NRKFi8epeKeGcbMZpvZJjN7N+rYQ2ZWGtlWmllp1HtTzGyFmS0zs7MOd30lVSKZRz1VkhHmL5xP\n1pAs9h+xn5N3n8yOF3fQZlcb+nc9kaUdz0vr9QylQfcCdwBzag+4+8W1+2Z2K7Ajsn8C8A3gBKAv\n8KyZDWpsoGh+Pqxa1TqBi0hyUlIlCdPSmk+lpaVs3LieVav+lz179tKxY4dm14uq8RpWV62mW243\nBg0cxObqzZyeezrbPqlp6deRFOfuL5pZv0ZO+QZQFNm/AHjI3auAVWa2AhgFvNbQh9VTJZJ5lFRJ\nwrSk5lP0WKru3YexZctNfO5zI7n66qaPp3J3bLBR/VQ1nXM6s3nL5oOlEyoqKlTcUw5hZl8ANrr7\nx5FDfYBXok5ZHznWICVVIplHSZUkVHNrPtUdS9WhwyB69lzSrGv866N/UdWxivu/dz8Ln18IwPjJ\nn5ZOUHFPqcc3gb+19MPTpk1j7Vp4/30oKVFNPpFUEI+afEqqJK29vPZlXlzzIsWji8lvl0/h8EMT\npkwv7imfZWbZwNeA6L8U64Gjol73jRyr17Rp01i2DF5+GZRPiaSGukXJp0+f3uxrxHX2n0i8TZgw\njurq+ygre46ysucij+fGNemzS7cs5fFlj3PVqKvIb6cVlKRexqGrQJwJLHP3DVHHngQuNrM2ZjYA\nGAgsaezCevwnknlirqje5Buporq0UHOKfoZCIeYvnM+Omh18cuQn3HD2DQzsOjBRoWaEdKmobmYP\nEh6I3g3YBEx193vN7F7gFXf/Y53zpwBXAJXAJHd/poHrurtTXg7dusG+fa36NUSklbSkrVNSJWmj\nthaVD3FWVK6g5+qe3D3pbi07E2fpklS1ltq2zh3atoXdu8M/RSS1tKSt0+M/SRvzF87Hhhib8jcx\nuP9gCgYVMH/h/KDDkgxlpqVqRDKNkipJG9VezaqqVXRt35U+nRud7S6SEBpXJZJZlFRJWnB3Dgw8\ngH1i5G3MY9MHm8K1qM4cH3RoksGUVIlkFpVUkLTw6NJH6ditI/f/4H6efi48qD26FpVIEPLzlVSJ\nZBIlVWmqOTPmUt2zHz9LaEuI60dfT15uHiefeHLQIYkA6qkSyTRKqtJQ9NIuAIsWzWTWrPSpFD5v\n3jxm3T8LgK9c9BU2F2ym+Ixi8nLzAo5M5LOUVIlkFiVVaSh6aReAsrLwsaYkVcnewzVv3jy+P+37\nZI/Kpiq7ihf++QK3X3A7Xdt3DTo0kUNo9p9IZtFAdTmotodr8eJRLF48iokTZ1JaWhp0WAeFQiEm\n/2oy+zrtI7d7LjX9a+iQ34HH5j4WdGgi9VJPlUhmUU9VGpowYRyLFs2krCz8Ory0yzWH/VwsPVyt\nrbaw544BO6hoV8HGDRspsAK8SgVlJXl16QIbNhz+PBFJD0qq0lBhYSGzZl0T9RgvtcZT1X0E2bZt\nW66beh2ru6/m2MHH8samN6Acdr+wm/a72zNx2sSAIxapn2b/iWQWJVVpqrCwsNmJVEt7uOKp7iD7\nBQumkj9wO9ttO9tqtvHJrk8Y0H0A29/ezhHlR3DLtFu44IILEhqjSFPp8Z9IZol5TJWZ9TWz580s\nZGbvmdnV8QhMEq+2h2vMmCWMGbMkkBmD0Y8gCwrGsrPiSDblb+OEL59A5b5KqvdXk70um1EdRvH3\nv/xdCZUkNQ1UF8ks8eipqgKudfe3zawj8KaZPePuH8Th2pJgLenhSoTd+bvpfWJvql6tor/15+bp\nN6uwpyQ99VSJZJaYkyp33whsjOzvMbNlQB9ASZU0W+0jyOXLX2LTnvlUVa6kYFsHVq1ZxcDcgdAJ\nbp6shEpSg5IqkcwS1zFVZtYfOBl4LZ7XleAlqn5VYWEhRUW9mPnwr7FCo21BGzbu2815a89jxPEj\ntPSMpBQNVBfJLHFLqiKP/h4FJrn7nvrOmTZt2sH9oqIiioqK4nV7aUWJrNAeCoW49x/3kjXayOmf\nw/7K/XTa2ok9ZXso/mlx3O8nh1dSUkJJSUnQYaSkjh1h/36orITc3KCjEZHWFpekysxyCCdU97v7\nvIbOi06qJHXEu35VY71e8xfOx3oYWR2zqG5fTa7lUrmrMubvIC1X9xeg6dOnBxdMijEL91bt3AkF\nBUFHIyKtLV4V1e8Blrr7bXG6nqSpplRtP3rI0VTurcQ/capXVuPvOBO/rVpUkpo0A1Akc8SjpMJo\n4FLgy2b2lpmVmtnZsYcmyWLChHFUV99HWdlzlJU9F6lfNa5F16pbMiE7+7KDvVYA48aOY0+bPRzT\n7Rjy38+nc2lnbrzqRpVOkJSlweoimSMes/9eArLjEIskqURVaK/xGl7e/zKXnnkpuStysQHG+DOD\nGZie7AtLS+pQUiWSOVRRXZokXvWrGqra7u7MfX8uFVUVTPnqFHKygvurmciB+ZL+NANQJHMoqZKE\naqjX6+mPnuajbR9x3eevCzShguReWFpSj3qqRDKHkipJuLq9XkvWL6FkVQnFZxTTPrd9gJGJxJ8G\nqotkDiVVknChUIj5C+cDMOTUIbyw+wWuPf1aurTrEnBkYcmwsLS0PjObDYwHNrn78KjjVwFXEl6C\n65/u/rPI8SnA5ZHjk9z9mabcRz1VIplDSZUk1Lx58yj+bTFZQ7Lo2r0rdz9yN3d84w56d+oddGgH\nJWpgvgTuXuAOYE7tATMrAs4DTnT3KjMriBw/AfgGcALQF3jWzAa5ux/uJl26wEcftUL0IpJ0lFRJ\nwoRCIYpvLmbnsJ3k9MlhXfk6BncczPuvvs+5p50bdHifkawLS0v8uPuLZtavzuEfATe5e1XknEh/\nJRcAD0WOrzKzFcAomrAklwaqi2SOeBX/FDms+Qvnk90zm9yOuexvu5/27duzd8veoMMSiXYcMMbM\nXjWzRWb2ucjxPsDaqPPWR44dVrdusGVLnKMUkaSknipJqO4DurN++3pyc3KxHUbNBzWM/8n4oMMS\nqZUDHOHup5nZSOAR4JjmXiR6Sa5jjy3iww+L4hWfiLSSeKxzak0YEhAXZtaU4QeSxt5//30umXUJ\nFR0ryF6eTc2mGmZcP0PV0lOMmeHuFnQc8RB5/PeP2oHqZrYAmOHuL0RerwBOA74P4O43RY4/BUx1\n90Me/9Vt66qqoFOncGmODh1a+xuJSLy0pK1TT5XEVWOVyJdnL+fML59Jt9XdyD4yO7Bq6SJRLLLV\negL4MvCCmR0HtHH3rWb2JPCAmf2W8GO/gcCSptwgJwcGDYIPPwQN0xNJb0qqJG4aq0ResqqEtze+\nzS/H/5IObfTrugTPzB4EioBuZrYGmEp4cfh7zew9oAL4DoC7LzWzh4GlQCVwZXO63ocMgaVLlVSJ\npDslVRI3DVUit17GghULuH709UqoJGm4+yUNvPXtBs6/EbixJfeqTapEJL0pqZK42707xKad89m7\n9yM+3l7FX98t4+pTr6YgryDo0EQCMWQI/PWvQUchIq1NSZV8RmNjog5nwoRxPP74tawr/xh6GNlH\nl/Nybhsu7fR7+nWpWw5IJHOop0okMyipSgOxJEJ1r9PQmKimaNu2LZVdV5E1YjtZedk4VfTscBQf\nLvkQPt+ikETSwsCBsGYN7N8P7doFHY2ItBYV/0xxtYnQ4sWjWLx4FBMnzqS0tLRF14oeE1VQMJbs\n7MsOJmtNMX/hfPIK8ygY2pV2x+eSV5BHxUcVLYpFpKnM7FgzaxvZLzKzq80sORaSjGjTBo45BpYv\nDzoSEWlNSqpSXKyJULwd2f1Idu3Zhe93snZkUb2pmvFnqrintKrHgGozGwj8ETgKeDDYkA41dCiE\nQkFHISKtSUmVAOEer02bNrJq1f9j9epZlJU9R3X1fUyYMK7J1zj3K+eybes2urftTvcN3enyQRdm\nXD9DtaiktdVE1uT7D+AOd58M9Ao4pkNoXJVI+tOYqhQ3YcI4Fi2aSVlk2ddwInRNkz5bOxZr48b1\nvPnmBjp1+jEFBWPZsuU2TjnlBCZNavp4KoDVbVYz5ktj6Lm2JzlH5DD+JyruKQlRaWbfBP4LOC9y\nLDfAeOo1ZAg8/HDQUYhIa4pLUmVmZwO/I9zzNdvdZ8TjunJ4hYWFzJp1TdRA9aYlQtGD0levfphd\nu86isHAE/fvn07FjB448cslhrzNv3jxm3T8LgKKvFbGz505+fd6v6dy2c8zfS6QZvgtMBP7H3Vea\n2QDg/oBjOoR6qkTSX8xJlZllAXcCY4ENwOtmNs/dP4j12tI0hYWFzZ7xFz0Wa8uWJeza1Z0NGzaT\nn5/fpM/fcccdTLlzCjbSyOmQwwsLXuCuC+9SQiUJ5+5LgasBzOwIoFMy/mJ33HGwciUcOBAeuC4i\n6SceY6pGASvcfbW7VwIPAVohN4X07j0OmEN5+ctNGksVCoX45R2/pHJEJTWDatjTcw/t8tox96G5\niQtaJMLMSsyss5l1BUqBP0XW6EsqbdtCv36wYkXQkYhIa4nH478+wNqo1+sIJ1qSxOqOxerXr5KR\nI0vp2XNDo48QQ6EQ1029jvKqctgH1dnV5JJLZXnlwXPiVTdLpIny3X2XmX0PmOPuU83s3aCDqk/t\nI0ANNRRJTwkdqD5t2rSD+0VFRRQVFSXy9hLl0LFYvz5s8hMKhbj+lutZ3X01uaflUr6vHHs/iyw3\ncktzmXjrxJgLiEryKSkpoaSkJOgwGpNjZr2AbwC/CDqYxmhclUh6i0dStR44Oup138ixQ0QnVRK8\n5ozFqu2hWt19NX2G9GHt2rVkfZKNP5uLVbWle/tBHHXUUQ0uqqykKnXV/QVo+vTpwQVTv18CTwMv\nufvrZnYMkJQP2YYMgSefDDoKEWkt8UiqXgcGmlk/4BPgYuCbcbiuJInaHqo1NWvYVrONjes30tbb\nU7m5K53bDWFIv1upqNgYaNFRyVzu/gjwSNTrj4GLgouoYUOGwE03BR2FiLSWmAequ3s18BPgGSAE\nPOTuy2K9riSP+Qvnkzs0lyFjh1C1p4qqA1XUfOS0/7gXQ/rdSqdOnw4QmTBhHNXV91FW9lyLCoiK\nNJeZ9TWzv5vZ5sj2mJn1DTqu+gweDB99BFVVQUciIq0hLmOq3P0pYHA8riXJq7xLOT1O6oG/5nTd\n25Vd7bpSUbGRioqNB4uOtrRulkgM7iW8LM1/Rl5/K3LszMAiakBeHvTuHU6sjj8+6GhEJN7M3RNz\nIzNP1L0kvkKhED+47Qds7reZQbmDsKXGzZNvpqKiotVm+WkGYfIyM9zdgo6jlpm97e4nH+5YAuNp\ntK077zz47nfha19LYFAi0mwtaeu0TI3UKxQKMX/hfABOPO1EBhUNYszGMXTJ6sL4yZ8uP9MayY5m\nEEozbTWzbwF/i7z+JrA1wHgaVTsDUEmVSPpRUiWHqB2Ynjs0l/2+n7sfvpvf/efvOP+S8xNyf80g\nlGa6HLgDmAk48DJwWZABNWbIEHhaczpE0lI8KqpLGqktnbBq1yq8nbOp8yb69ujLstdSf+5BaWkp\nxcU3Ulx8I6WlpUGHI3ESWc3hfHfv7u493P1CknT2H4QLf6pWlUh6UlIlB4VCIa6ceiVv2puszlnN\n8288T4d9Heia3TWhcbTGDMLaR4qLF49i8eJRTJw4U4lVers26AAacvzxsHw5VFcHHYmIxJse/6WZ\nWAZ4z/7rbD7I/YCc43Ko2F+Bb3I2LNhAfp98xk8e31ohH6I1ZhDqkWLGSZqB9HV17Ag9eoQXVx44\nMOhoRCSelFSlkVgGeNcOTN87YC/t27Qnv30++9fvJ2d7Djf/7uaDA9MTpTnV3kXqkdRTjWsHqyup\nEkkvevyXRqJ7YwoKxpKdfVmTqpzXDkyvPraaivIKdqzdQe6aXDqs6cD4seMbTKhSaYySipKmHzPb\nbWa76tl2A72b8PnZZrYpevFlM5tqZuvMrDSynR313hQzW2Fmy8zsrFhiHzIEQqFYriAiyUhJVYar\nHZi+sv1Kup3WjbaD2tL2w7ZUv1bN4CMGc8V3rqj3c6k2Rqn2keKYMUsYM2aJSjSkAXfv5O6d69k6\nuXtTeuHvBerLrH/r7oWR7SkAMzuB8ILNJwDnAHeZWYsfMZ5+Oixa1NJPi0iy0uO/NDJhwjgWLZpJ\nWVn4dW2V84bMmzeP4puL2bZ/G5VHVFK9pZoRx4xgc8Vm+m3px63Tb22wlyoVxyjpkaJEc/cXI2uW\n1lVfsnQB4SW4qoBVZrYCGAW81pJ7jxsXLgC6Ywd06dKSK4hIMlJPVRppTm/MvHnz+N7/+x7re6+n\nakgVu/fuJmdTDpuXbWbAvgGNJlQiae4nZva2mf3ZzPIjx/oAa6POWR851iIdO0JRESxYEEOUIpJ0\n1FOVhGLoBo+PAAAgAElEQVSZwdeU3phQKETxzcXsH76fqt5VVFBBp02dyHk7h34D+nHz9PASNMXF\nNzYYQ3N7xURSxF3AL93dzezXwG+A7zX3ItOmTTu4X1RURFFR0SHnXHghPPEEXHJJi2MVkTgqKSmh\npKQkpmto7b8kU3cGX3X1fXEf/zPjdzOYs3gO2/puY2uXrdgBo82/29BnQx8e++NjVFRUNCkGrc+X\nmZJt7b9YRB7//cPdhzf2npn9DHB3nxF57ylgqrsf8vivqW3dli0waBBs3Ajt2sX8VUQkzrT2XxpI\n1Fil7gO6s37HejrmdqRyUyXtPmzHjF/NYOjQoRQX39ikGDRGSdKAETWGysyOdPeNkZdfA96P7D8J\nPGBmMwk/9hsILInlxt27w/Dh8NxzcO65sVxJRJKFkqoMUluLauMnG1m/ez29uvfClhs1m2qY8asZ\nXHDBBUGHKJIwZvYgUAR0M7M1wFTgS2Z2MlADrAJ+CODuS83sYWApUAlcGY+u99pHgEqqRNKDHv8l\nmdZ6/FdbiypnSA7rq9ez/ePtnFdwHjVVNezdlkVBQc+Dj/AS8QhSUlc6Pf5rDc1p6z7+OFxeYcMG\nyM5u5cBEpFla0tYpqUpC9Y1VinX80ozfzeCVylc40PsAW/Zu4cgdRzJgywBefWF7vcmTxktJQ5RU\nNa65bd1JJ8Fdd8Ho0a0YlIg0m5KqFNZYEhNLz1HtI7+SF0vYfMxmao6p4aSeJ7Hjox1sX7ifA7sn\nR42deo4xY5YwY8aUuH8/SR9KqhrX3LZu6lQoL4dbbmnFoESk2VrS1qlOVRI4XHXyli4/M2/ePC66\n8iL+8uFfWD9gPcs2LCPvozx2fLSDylAlA486vvW+lIg0yYUXwt//DvqdUyT1xTRQ3cxuBs4DKoB/\nA991913xCCyTtMaMv9paVDuH7SS7Tza7yncxsNdAOq/szOl9T2f85PEHSyeo1pRIcE4+GaqqwmsB\nDhsWdDQiEotYZ/89A/zM3WvM7CZgSmSTOGpJoc3Zc2azbf82KlZXYD2NDnkdqFpfRdEZRRT/tPjg\nebNmXRP12FGD0UUSzezTWYBKqkRSW9zGVJnZhcBF7v7tBt7XmKoGNGXMVHMGjodCIS668iLKBpSx\ns/1ObLXRuUNnCjYX8Nhdj2n5GYmJxlQ1riVtXUkJXHcdvPFG68QkIs0X6EB1M3uS8IKjDzbwvpKq\nRsRjtl0oFGL2nNnMf24+5YPL2dV7FzntcjjwwQHav9OeP9/yZ9WikpgpqWpcS9q6qio48kh46y04\n6qhWCkxEmqVVKqqb2UKgZ/QhwIFfuPs/Iuf8AqhsKKGq1ZT1sDJVrNXJQ6EQP/r5j/hw+4fszdvL\n/o77aVfTjj7eh+qCas6+6OyUSqhU0iF5xGM9LGlcTg6cfz787W9w/fVBRyMiLRVzT5WZXQZ8H/iy\nu1c0cp56qlpJKBTiuqnX8ebKN8kZlkP10dVs+3gbba0tR3c6mgH7BnDz5JtT5rGfio8mN/VUNa6l\nbd2bb4bHVn38MeTmtkJgItIsCS+pYGZnA5OB8xtLqKT11FZKX919NfuO2UfZ5jIO2AG6detG3to8\n+m3pl1IJFbS8hIRIKvvc58ILLM+dG3QkItJSsc7+uwNoAyw0M4BX3f3KmKOSJpv919msbL+SnG45\n5OTkUF5VTuVLlbTp0YYTup/ArdNvrTeh0uM1keRz3XXw85/DpZeGZwWKSGqJqafK3Qe5ez93L4xs\nSqgSKBQKsWDxArbXbGdru60cyDtAj/Ie9N7Zm0v7X8pd0+9qMKFqrNho0CZMGEd19X2UlT1HWdlz\nkRIS44IOS6TVnX02VFbCc88FHYmItESsPVUSkHnz5jH5V5MpKy/DPjCqulXRfk978lfl89hfGi+b\n0BrFRuOpsLBQ9bMkI2VlwX//N9x6K3zlK0FHIyLNpaQqBc2bN4/vT/s++4buo8IqqC6vpteKXuRX\n5zPutHEpNX6qIbHOhhRJVZdeCjfcAO++C8OHBx2NiDSH1v5LQbPun0X2qGy6n9Id+kNWtywOfHyA\n/p37c8V3rjjs5/V4TSR5tW0LV10Fv/1t0JGISHPFrfjnYW+kkgpxc87Xz+Gtbm/hgxyvdsrfK6f3\nB735+1/+3uReKg1Ul5ZSSYXGxaOt27YNBg6E996DPn3iFJiINEugFdUPeyMlVXHzxBNP8J17vgMD\nIW9vHjVLavjTtD+lVHFPSV1KqhoXr7Zu0iRo1w5mzIhDUCLSbEqq0lgoFGL+wvkAdBrWiZf//TJb\nnt1Clmcx8dsTlVBJwiipaly82rqVK2HEiPDPzp3jEJiINIuSqjQ1b948in9bTNaQLPK657Fj9w4e\n+K8HOPXkU4MOTTKQkqrGxbOt+/a3YcAA+OUv43I5EWmGhFdUl9YXCoUovrmYncfvZEefHSyvWk6v\nTr20FptIBvjf/4Xf/x5Wrw46EhFpCiVVSW7+wvlk98wmu1M2+3P30ymvE1u3bA06LBFJgKOOCs8E\nLC4OOhIRaQolVSmg6zFd2bV7F23L2lKztoaapTWMP3N80GGJSAJcfz28/DK8+GLQkYjI4SipSnJf\n/tKX2Vi1kWPzj6Xrv7uS/34+M66dkRYFPkXk8PLy4Kab4Kc/hZqaoKMRkcZooHoSqp3pV+3VbO23\nlaM6HEXFsgoAxp85nqFDh6rOlAQmXQaqm9lsYDywyd2H13nvv4FbgAJ33xY5NgW4HKgCJrn7Mw1c\nN+5tnTuMHg3f/z5897txvbSINECz/9JAKBTi+luuJ2dIDqurVlP9STV/++HfGDZs2MFzSktL+c53\nfs22beEyCl27zmPOnBuUWElCpFFSdQawB5gTnVSZWV/gz8Bg4HPuvs3MTgAeBEYCfYFngUH1NWqt\n1da9/jpccAF8+CF06hT3y4tIHZr9l+JCoRDXTb2Ole1XsrnjZtr3aM+Aowbwz2f/+Znzbr/9L6xa\ndRb79n2Vffu+yqpVZ3H77X9JaKylpaUUF99IcfGNlJaWJvTeIvHg7i8C2+t5ayYwuc6xC4CH3L3K\n3VcBK4BRrRvhZ40cCWeeGZ4RKCLJSUlVkpg3bx4X/eAi3lz5Jut9PUvXLqVXTi+y7NA/omXLVgLd\nadMmvEH3yLHEKC0tZeLEmSxePIrFi0cxceJMJVaSFszsfGCtu79X560+wNqo1+sjxxLqxhvhT3+C\nDz5I9J1FpClygg5AIrWoflvMzmE7qampYe+OveRX5PPBjg8YsG8A4yd/dqbf8ccfTSg0hwMHukSO\nzOH4449OWLxz5z5NdvZlFBSMBaCsLHxMjx8llZlZe+DnwJmxXmvatGkH94uKiigqKor1kgD07g2/\n+lW4KOjLL0NublwuKyJASUlJzDUglVQlgfkL55M1JIusPll4G6fbB93wd5x+A/px8/SbD5npN2nS\n5bzxxg1s3/4wAL17VzJp0uVBhC6STo4F+gPvmJkRHjtVamajCPdMRf/m0jdyrF7RSVW8TZwI8+aF\nHwNOndpqtxHJOHV/AZo+fXqzr6GkKkl07d6VdeXr6EQnanJryG+Xz63Tb623dEJhYSH33//rqNl/\nP0xoL9GECeNYtGgmZWXh19XV9zFhwjUJu79IHFlkw93fB448+IbZSqDQ3beb2ZPAA2b2W8KP/QYC\nSwKIFzO45x445RT46lfDY61EJDlo9l8SeOWtV/j2nG/TpVMXyreUU7O0hhnXzkjqRZJV0iFzpdHs\nvweBIqAbsAmY6u73Rr3/MTCiTkmFK4BKElxSoT5z54Z7qkpLw7WsRCS+AiupUF9Nl3rOUVJVj/1V\n+7nlpVvoXtmdne/vBD6tRSWSjNIlqWotiWzrLrkECgrg9tsTcjuRjBJIUlVfTZcGzlNSVUdVTRV3\nLrmT7nndueTESwgP4xBJbkqqGpfItm7bNjjpJLj3XvjKVxJyS5GMEVSdqvpqushhuDv3v3M/uVm5\nfPPEbyqhEpFm69oVZs8OV1nftCnoaEQkpoHq0TVdlBQ0z5MfPsnGPRu59vRrD9ai0jglEWmus86C\nyy6Diy6C55+HNm2Cjkgkcx02qTKzhUDP6EOAAzdwaE2XRjOr1qrdkmoWr17MGxve4PrR19M2py3w\naUHN7OzLAFi0aCazZl0Tc2KlRE1iFY/aLdK6pk+H996Dn/wE7r47PENQRBKvxWOqzGwY4fWvygkn\nU7V1W0a5++Z6zs/YMVW1CyQDDBo5iFf2vsLk0ZPp0aHHwXOKi29k8eJRUQU1n2PMmCXMmDGlxfet\nm6hVV98Xl0RNMpvGVDUuqLZu9244/XS48srwJiKxaUlb1+LHf43VdGnpNdNR7QLJuUNzKa8p5+7H\n7uYPF//hMwlVa1Hlc5HM0alTuCjo6NEwZAhk6IMAkUDFc+0/5zCP/zLR7DmzWbVrFWs+XsNqW02/\nnv14++W3DzlvwoRxVFffR1nZc5SVPRcpqDkO0OLFItI0xx4LDzwAF18MKxO3HKiIRMStorq7HxOv\na6WLUCjEglcXsP2E7VQcUUGbN9rQ56g+cNSh5xYWFjJr1jVR45/Cj+liGWulyucimWfsWPjFL2D8\neFi8GLp1CzoikcyhZWpa0fyF8+n1xV5srNxIm/ZtyD4imw2vbmD85ePrPb+wsPCQZCmWR3gNJWoi\nkt5+8hPYsCE8M/C556BLl8N/RkRip6SqFdV4DdvabWNQz0HYTmNP1h7OHnN2Qqul15eoiUh6Mwsv\nuFxeDuecA888Ex5zJSKtK55jqiSKu5N9fDaVGyvptbcXvXN7M2DfAK741hXNuk5jY61ERBpiBr/7\nHZx4Ipx/fjjBEpHWpQWVW8lTHz3F6+tf59wjzmXh8wuBlq/pp1pTkkxUUqFxydbWVVeHi4Nu2RKe\nHdi2bdARiaSGwBZUbtKNkqyhaU2vrXuNJz54guIziunSToMZJL0oqWpcMrZ1VVXwzW/C3r3wyCPQ\noUPQEYkkPyVVSeCDsg/4c+mfufb0a+ndqTeQuJ4m9WhJIiipalyytnWVlfDDH4Yrr//zn9Cj9Uvl\niaQ0JVUBW7drHb979Xf84HM/4LhuxwGJq2qu6umSKEqqGpfMbZ17eEmbv/4V/vUvGDQo6IhEkldL\n2joNVI+T7fu2c+eSO7l42MUHEyqA2267h3Xr8tiyZQm5uUeQnX3Zwd6keIouvVBQMLbV7iMiqcsM\npk2DKVNgzBh49dWgIxJJL0qq4qC8spzbX7udsQPGMqL3iIPHS0tLeeaZZezadRZbt47i3Xdnsnfv\nigAjFRGBK66Ae+4Jzwp85JGgoxFJH0qqYlRVU8UfXv8Dxxccz1eO+cpn3ps792kKCiaRk3MMMJyq\nqgvZsmVOq5REUOkFEWmOc86Bp56C4mKYNAkqKoKOSCT1KamKgbtz39v30aFNB/5z6H9iduij144d\nOzB8+DF067aDzp33MG7cyFYZ51RbPX3MmCWMGbNE46lE5LAKC+HNN2HNGjjjDK0XKBIrDVSPwWNL\nH+Pf2//NNaddQ2527iHvBz14vO5sQECzAyVmGqjeuFRs69zhttvCVdjvvhv+4z+CjkgkeJr9l0CL\nVi5i0apFFI8upkObhou+BFXmoG5Ct2vXbzBrR6dOPwY0O1BaTklV41K5rXvtNbj4YjjzTLj5Zq0Z\nKJmtJW2d1v5rgbc+eYunPnqKyaMnN5pQQXBr79VdiHn16oeBzzNgQPMXZhaRzHDqqfD22/Czn8HQ\noXDHHfC1rwUdlUjq0JiqZvr3tn/z13f/ypUjr6QgryDocERE4io/H/7wB3joIfj5z8NJ1YYNQUcl\nkhqUVDXDpj2bmPXGLC4/5XL6dekXdDiNqjsb8Igj1tK16zzNDhSJMLPZZrbJzN6NOvZLM3vHzN42\ns2fNrG/Ue1PMbIWZLTOzs4KJOnG+8IVwr9WwYXDSSfCb38D+/UFHJZLcNKaqiXZV7GLGizP46qCv\nMvro0UGH0yQaqC6tIV3GVJnZGcAeYI67D48c6+jueyL7VwHD3f37ZjYEeAAYCfQFngUG1deopXpb\nV59ly8KPBN95B379a7jkEsjSr+SS5jRQvZVUVFXwm1d+w/Cewxl/3PigwxEJVLokVQBm1g/4R21S\nVee9nwFd3P1nkX139xmR9/4FTHP31+r5XMq2dYfzf/8HkyeHa1rNmBEe0F5PJRmRtBDIMjVmdlWk\nO/w9M7sp1uslm+qaau5+8276du7LuYPODTocEWllZvZrM1sDXAbcGDncB1gbddr6yLGM8oUvwCuv\nwA03wFVXwWmnweOPQ3V10JGJJIeYZv+ZWRFwHnCiu1eZWVqN3HZ3HnjvAQzj0hMvrbe4p4ikF3e/\nAbjBzIqB3wHfbe41pk2bdnC/qKiIoqKieIUXODO46CK48EKYNy/cYzVlClx3HXz729CuXdARirRM\nSUkJJSUlMV0jpsd/ZjYXuNvdn2/CuSnXJT5/+Xze2fgO133+OtrmtA06HJGkkEGP/44CFrj7ifU8\n/nsKmJppj//q4w4vvBCua1VaCt/9Lnzve3DssUFHJhKbIB7/HQeMMbNXzWyRmY047CdSxEtrXuKV\nta9w1alXKaESSV8W2cIvzAZGvXch8HZk/0ngYjNrY2YDgIHAkoRFmcTMoKgIFiyARYvgwAE4/XQY\nOzZclkFrCkomOWxPlZktBHpGHwIcuAH4H+B5d59kZiOBue5+TAPXSZnf3kKbQ9z39n1c9/nr6Nmx\n5+E/IJJB0qWnysweBIqAbsAmYCpwLjAYqAI+Bn7k7psj508BrgAqgUnu/kwD102Ztq61VFSEHw3+\n6U/h3qsLLoBvfCOcaOUeuqKXSFJK+Ow/M1sAzHD3FyKvPwJOdfet9ZzrU6dOPfg6WccZrNm5htte\nvY0rR17JsV3Vfy1Sd5zB9OnT0yKpai1Kqj5r3Tp49FF4+GFYvjw8FutrX4MvfQnatw86OpGGBZFU\n/QDo4+5Tzew4YKG711sVMxUamq3lW7n5pZu5eNjFnNLrlKDDEUlK6dJT1VpSoa0Lypo14QRr3jx4\n6y0YPRrOOSe8DRoUdHQinxVEUpUL3AOcDFQA/13ba1XPuUnd0Ow9sJcZL83gS/2/xJcGfCnocESS\nlpKqxiV7W5csduyAZ5+Ff/0rvLVpA2PGwBe/GP45cKBqYEmwVPyzhSqrK5n56kyOPeJYLhpyUdDh\niCQ1JVWNS+a2Llm5w4cfwuLF4ZmEL7wQrn11+ukwcmR4GzECunQJOlLJJEqqWqDGa/jjm38kJyuH\nK065QrWoRA5DSVXjkrWtSyXusGoVvPYavP56eHvrLejdO7wO4YknfroNGKAlc6R1KKlqJnfn4dDD\nrNu1jkmnTSInK6ZaqCIZQUlV45KxrUsH1dXhNQjffRfee+/TbevW8HiswYPhuOPC26BB4WSre3c9\nQpSWU1LVTAv/vZCX177M5NGTycvNCzqcFqm7aLIWSZbWpqSqccnY1qWzXbvCswqXLw8/QqzdX7ky\nXDOrf/9wgtW/P/TtC336hH/27Rvu+cpLzaZfEkBJVTO8vv51Hlv2GMWjizmi/RFBh9MipaWlTJw4\nk+zsywCorr6PWbOuUWIlrUpJVeOSra3LZDt3hh8jrlwJq1fD+vXhEg+124YN4QHyPXvCkUeGtx49\noKDgs1vXrnDEEeEtP1+PGzNFS9q6jHzetXzrcuaG5vLT036asgkVwNy5T5OdfRkFBWMBKCsLH1NS\nJSISToBOOim81cc93NO1ceOn25Yt4bb0ww/hpZfCr7dtg+3bw9uePdC5c/jatVvt644doVOnT392\n6PDplpf36c/27Q/dcnP1qDIdZFxStWH3Bv745h/5XuH36Nu5b9DhiIhIQMw+TYwGD27aZ6qqwj1g\nO3eGE7Lo/T17YPfu8M8NG8L75eWwd+9nf+7bd+hWXQ1t24a3du0+3W/T5tOfbdqEk6/an/VtOTmf\n/ozesrPDW/R+3S0rq+GfdffNDt2veyz6eFO32vNr/3yit9pj0e/Vtx/9s6nHOnSIz+zSjEqqamf6\nfX3I1zm+4Pigw4nZhAnjWLRoJmVl4dfV1fcxYcI1wQYlIpLGcnKgW7fwFk81NeHlffbvD28VFeEx\nYQcOhPcrKqCyMrzVHq99XbtVVX36M3qr/Ux1dXirqvp0v3arqWn4Z91j7uH92p8N7bsfun+4raYm\n/N+j7vHaY9Hv1bcf/bM5xy69NLwoeKwybkzVropddG7bOegw4kYD1SXRNKaqccnS1olIbDRQXURa\nnZKqxqmtE0kPLWnrNIdBREREJA6UVImIiIjEgZIqERERkThQUiUiIiISB0qqREREROJASZWIiIhI\nHCipEhEREYkDJVUiIiIicaCkSkRERCQOlFSJiIiIxEFMSZWZjTSzJWb2VuTniHgFJiLSmsxstplt\nMrN3o47dbGbLzOxtM3vMzDpHvTfFzFZE3j8rmKhFJJnF2lN1M3CDu58CTAVuiT2k1ldSUhJ0CEDy\nxAGKpT7JEgckVyxp5F5gXJ1jzwBD3f1kYAUwBcDMhgDfAE4AzgHuMrO0Xf8w1f++pXr8kPrfIdXj\nb6lYk6pPgPzIfhdgfYzXS4hk+cNOljhAsdQnWeKA5IolXbj7i8D2OseedfeayMtXgb6R/fOBh9y9\nyt1XEU64RiUq1kRL9b9vqR4/pP53SPX4Wyonxs//DHjJzH4DGPD52EMSEUkKlwN/i+z3AV6Jem99\n5JiIyEGHTarMbCHQM/oQ4MANwFXAVe7+hJl9HbgHOLM1AhURSRQz+wVQ6e5/O+zJIiIR5u4t/7DZ\nLnePHsi5093zGzi35TcSkaTi7mkxnsjM+gH/cPfhUccuA74PfNndKyLHfga4u8+IvH4KmOrur9Vz\nTbV1ImmiuW1drI//VpjZF939BTMbCyyPV2AiIglgkS38wuxsYDIwpjahingSeMDMZhJ+7DcQWFLf\nBdXWiWSuWJOqHwK/N7M2wH7gB7GHJCLS+szsQaAI6GZmawjPYP450AZYGJnc96q7X+nuS83sYWAp\nUAlc6bF084tIWorp8Z+IiIiIhCW8orqZXRUpnveemd2U6PvXieW/zazGzLoGGEODxQYTdP+zzewD\nM1tuZsWJvHedOPqa2fNmFor83bg6qFgi8WSZWamZPRlwHPlm9kjk70jIzE4NMJYpkRjeNbMHIj3U\nEiVZ/j01RwNFUI8ws2fM7EMze9rM6h0rmwwaajtS5TuYWVszey1SRDtkZv8bOZ4S8deq22amYPyr\nzOyd2mLmkWPN/g4JTarMrAg4DzjR3U8Ebk3k/evE0pfwTMXVQcUQUW+xwUQwsyzgTsIFEIcC3zSz\n4xN1/zqqgGvdfShwOvDjAGMBmET4UU/QbgMWuPsJwEnAsiCCiAzo/j5wSmRQdw5wcRCxJKsk+/fU\nHPUVQf0Z8Ky7DwaeJ4HtUgs01HakxHeIjN37UqSI9nDgy2Y2mhSJP0rdNjPV4q8Bitz9FHevrUHX\n7O+Q6J6qHwE3uXsVgLuXJfj+0WYSHpAaqEaKDSbCKGCFu69290rgIeCCBN7/IHff6O5vR/b3EE4e\nAqkDFEm4vwr8OYj7R8XRGfiCu98LECk8uSugcHYBB4AOZpYD5AEbAoolWSXNv6fmqK8IKuG4/xLZ\n/wtwYUKDaoYG2o6+pNZ3KI/stiX8/+XtpFD8DbSZKRN/hHFoTtTs75DopOo4YIyZvWpmiyygtQLN\n7Hxgrbu/F8T9G3E58K8E3q8PsDbq9TqSoKChmfUHTgYOma6eILUJd9ADDgcAZWZ2b6Rb/Y9m1j6I\nQNx9O/AbYA3hwpc73P3ZIGJJYkn576mFerj7JggnLUCPgONpkqi241WgZ6p8h8ijs7eAjUCJuy8l\nheKn/jYzleKHcOwLzex1M/te5Fizv0Oss/8OYY0XC80BjnD308xsJPAwcEy8Y2hCHD/ns0VKW3UK\ndCOx/MLd/xE5p7bY4IOtGUuyM7OOwKPApMhvnYm+/7nAJnd/O/K4Osjp8TlAIfBjd3/DzH5HuDt6\naqIDMbNjgGuAfsBO4FEzuyTT/75mkKB/wTisum2HHVovLGm/Q+RpxSmR3umnI21PSsRfT5vZkKSM\nP8pod//EzLoDz5jZh7TgzyDuSZW7N1hR3cwmAo9Hzns9Mki8m7tvTVQcZjYM6A+8Y2ZGuJv4TTMb\n5e6b4x1HY7FExXQZ4a7TL7fG/RuxHjg66nVfAly/MfJY6VHgfnefF1AYo4HzzeyrQHugk5nNcffv\nBBDLOsI9qm9EXj8KBDX4eQTwkrtvAzCzxwkvS6Wk6lNJ9e8pRpvMrKe7bzKzI4FWaRvjpYG2I6W+\nA4C77zKzBYT/vaVK/PW1mfcDG1MkfgDc/ZPIzy1m9gThx/nN/jNI9OO/J4gkDmZ2HJDbGglVY9z9\nfXc/0t2PcfcBhP/HdUprJVSHY58WGzy/TrHBRHgdGGhm/SIzuS4mXOQwKPcAS939tqACcPefu/vR\n7n4M4f8ezweUUBHpdl4b+bcCMJbgBs9/CJxmZu0iv4yMJaBB80ks2f49NcdniqASjvuyyP5/AUH9\nktNU9bUdKfEdzKygdlZZ5PH+mcBbpEj8DbSZ3wb+QQrED2BmeZGeTsysA3AW8B4t+DOIe0/VYdwL\n3GNm7wEVQCD/s6rDCfYRzx3UU2wwETd292oz+wnhGYhZwGx3D2p22WjgUuC9yNgCB37u7k8FEU8S\nuZpwJe9c4GPgu0EE4e7vmNkc4E2gmnCj/8cgYklWyfTvqTms/iKoNwGPmNnlhGdIfyO4CBvXUNsB\nzAAeToHv0Av4S+SXlSzCvW3PRb5LKsTfkJtInfh7An+PPDLOAR5w92fM7A2a+R1U/FNEREQkDhJe\n/FNEREQkHSmpEhEREYkDJVUiIiIicaCkSkRERCQOlFSJiIiIxIGSKhEREZE4UFIlIiJJz8y6mtlb\nkXUwPzGzdVGvm1Rz0cxmm9mgw5xzpZl9Mz5R13v9/4gq6CtpRnWqREQkpZjZ/wfscfff1vOeeRL/\nj/Hvu0AAAAM/SURBVC2yhMujAS7FJa1IPVUiIpJqDq6CYWbHmlnIzP5qZu8DR5rZ3Wa2xMzeM7Mb\nos79PzMbbmbZZrbdzG40s7fN7CUzK4ic8yszuzrq/BvN7DUzW2Zmp0WO55nZo2b2vpk9Ymavm9nw\nQ4I0uyUS29uR65xBeJ3X30Z62I42s4Fm9lTkGiVmNjDy2fvN7C4ze8PMPogsaYaZDYt8t9LIdfu3\n2n9labZEL1MjIiISb4OBb7n7WwBmVuzuO8wsG1hkZo+6+wd1PpMPLHL3KWb2G+By4Ob6Lu7up5rZ\neYSX8DkHuAr4xN2/Hkmm3qz7GTPrAZzj7kMjrztHLZj8iLs/GTn+PHCFu680s88DvwfGRS7T191H\nRB4XPmtmxwJXAre4+yOR5auCXGZN6lBSJSIiqe7ftQlVxKWR9dpyCK+tNwSom1SVu/szkf03gTMa\nuPbjUef0i+yfQXhtO9z9XTML1fO5bUC1mf0RWADMr3tCZCHl04DHImv/wWefID0cucfyyLqMg4CX\ngf8X6aF63N3/3UDcEgA9/hMRkVS3t3Yn8vjsaqDI3U8Cngba1fOZA1H71TTcyVDRhHMO6S1y9yr+\n/3bun7WKIArD+HNAsUgwtWCTIgEL8Q9+kDSSYJ/0ySfIZ0gaLcWAndgoWthpFywsTCEIFiFFGjU2\nQfG1uINeNtFwYcBceH6wsOzOzG75cuYwcAd4CiwBz/4y7zDJ7SS32nVjfJnB2CTZaesdAy/alqLO\nCUOVJGnajYeay8BX4FtVXeHPVtq/5kzqDbAMUFXXgWsnFq+aBeaSPAc2gJvt1VH7R5J8Bg6qaqnN\nqUFv1t32fBG4CnyoqvkkH5NsMap+nejl0v/j9p8kadr9rugkeVtVe8Ae8Al4fdq4wf2Z6w5sAw9b\nY/z7dn0ZjJkDnlTVJUYBbr09fww8qKoNRhWnFeB+VW0CF4Ed4F0bu19Vu8AMsJrkR1Xda0c+fAf2\nGfV56ZzwSAVJkibQGuAvJDlu240vgYUkPzt+4xFjDe2aDlaqJEmazCzwauzQ0bWegaqx4jGFrFRJ\nkiR1YKO6JElSB4YqSZKkDgxVkiRJHRiqJEmSOjBUSZIkdWCokiRJ6uAX5JpS92QHQFAAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8040158550>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "TzIETgHwTexL",
"colab_type": "text"
},
"source": [
"This code looks very similar to the code above, but without using `l2_loss` or `GradientDescentOptimizer`. Let's look at exactly what it is doing instead.\n",
"\n",
"This code is the key difference:\n",
"\n",
">`loss = 0.5 * tf.reduce_sum(tf.mul(yerror, yerror))`\n",
"\n",
">`gradient = tf.reduce_sum(tf.transpose(tf.mul(input, yerror)), 1, keep_dims=True)`\n",
"\n",
">`update_weights = tf.assign_sub(weights, mu * gradient)`\n",
"\n",
"The first line calculates the L2 loss manually. It's the same as `l2_loss(yerror)`, which is half of the sum of the squared error, so $\\frac{1}{2} \\sum (\\hat{y} - y)^2$. With this code, you can see exactly what the `l2_loss` operation does. It's the total of all the squared differences between the target and our estimates. And minimizing the L2 loss will minimize how much our estimates of $y$ differ from the true values of $y$.\n",
"\n",
"The second line calculates $\\begin{bmatrix}\\sum{(\\hat{y} - y)*1} \\\\ \\sum{(\\hat{y} - y)*x_i}\\end{bmatrix}$. What is that? It's the partial derivatives of the L2 loss with respect to $w_1$ and $w_2$, the same thing as what `gradients(loss, weights)` does in the earlier code. Not sure about that? Let's look at it in more detail. The gradient calculation is going to get the partial derivatives of loss with respect to each of the weights so we can change those weights in the direction that will reduce the loss. L2 loss is $\\frac{1}{2} \\sum (\\hat{y} - y)^2$, where $\\hat{y} = w_2 x + w_1$. So, using the chain rule and substituting in for $\\hat{y}$ in the derivative, $\\frac{\\partial}{\\partial w_2} = \\sum{(\\hat{y} - y)\\, *x_i}$ and $\\frac{\\partial}{\\partial w_1} = \\sum{(\\hat{y} - y)\\, *1}$. `GradientDescentOptimizer` does these calculations automatically for you based on the graph structure.\n",
"\n",
"The third line is equivalent to `weights -= mu * gradient`, so it subtracts a constant the gradient after scaling by the learning rate (to avoid jumping too far each time, which risks moving in the wrong direction). It's also the same thing that `GradientDescentOptimizer(learning_rate).minimize(loss)` does in the earlier code. Gradient descent updates its first parameter based on the values in the second after scaling by the third, so it's equivalent to the `assign_sub(weights, mu * gradient)`.\n",
"\n",
"Hopefully, this other code gives you a better understanding of what the operations we used previously are actually doing. In practice, you'll want to use those high level operators most of the time rather than calculating things yourself. For this toy example and simple network, it's not too bad to compute and apply the gradients yourself from scratch, but things get more complicated with larger networks."
]
}
]
} | apache-2.0 |
kaushik94/tardis | docs/research/code_comparison/plasma_compare/plasma_compare.ipynb | 2 | 74046 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Plasma comparison ###"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/tqdm/autonotebook/__init__.py:14: TqdmExperimentalWarning: Using `tqdm.autonotebook.tqdm` in notebook mode. Use `tqdm.tqdm` instead to force console mode (e.g. in jupyter console)\n",
" \" (e.g. in jupyter console)\", TqdmExperimentalWarning)\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/importlib/_bootstrap.py:219: QAWarning: pyne.data is not yet QA compliant.\n",
" return f(*args, **kwds)\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/importlib/_bootstrap.py:219: QAWarning: pyne.material is not yet QA compliant.\n",
" return f(*args, **kwds)\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n"
]
}
],
"source": [
"from tardis.simulation import Simulation\n",
"from tardis.io.config_reader import Configuration\n",
"from IPython.display import FileLinks"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**The example tardis_example can be downloaded here**\n",
"\n",
"[tardis_example.yml](tardis_example.yml)\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/astropy/units/quantity.py:1067: AstropyDeprecationWarning: The truth value of a Quantity is ambiguous. In the future this will raise a ValueError.\n",
" AstropyDeprecationWarning)\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mtardis.plasma.standard_plasmas\u001b[0m][\u001b[1;37mINFO\u001b[0m ] Reading Atomic Data from kurucz_cd23_chianti_H_He.h5 (\u001b[1mstandard_plasmas.py\u001b[0m:74)\n",
"[\u001b[1mtardis.io.atom_data.util\u001b[0m][\u001b[1;37mINFO\u001b[0m ] Atom Data kurucz_cd23_chianti_H_He.h5 not found in local path. Exists in TARDIS Data repo /Users/wkerzend/projects/tardis/tardis-data/kurucz_cd23_chianti_H_He.h5 (\u001b[1mutil.py\u001b[0m:29)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/IPython/core/interactiveshell.py:3185: PerformanceWarning: indexing past lexsort depth may impact performance.\n",
" if (yield from self.run_code(code, result)):\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mtardis.io.atom_data.base\u001b[0m][\u001b[1;37mINFO\u001b[0m ] Read Atom Data with UUID=6f7b09e887a311e7a06b246e96350010 and MD5=864f1753714343c41f99cb065710cace. (\u001b[1mbase.py\u001b[0m:184)\n",
"[\u001b[1mtardis.io.atom_data.base\u001b[0m][\u001b[1;37mINFO\u001b[0m ] Non provided atomic data: synpp_refs, photoionization_data (\u001b[1mbase.py\u001b[0m:187)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/astropy/units/quantity.py:1067: AstropyDeprecationWarning: The truth value of a Quantity is ambiguous. In the future this will raise a ValueError.\n",
" AstropyDeprecationWarning)\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/python/tardis/tardis/plasma/properties/ion_population.py:63: FutureWarning: \n",
"Passing list-likes to .loc or [] with any missing label will raise\n",
"KeyError in the future, you can use .reindex() as an alternative.\n",
"\n",
"See the documentation here:\n",
"https://pandas.pydata.org/pandas-docs/stable/indexing.html#deprecate-loc-reindex-listlike\n",
" partition_function.index].dropna())\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/astropy/units/equivalencies.py:90: RuntimeWarning: divide by zero encountered in double_scalars\n",
" (si.m, si.Hz, lambda x: _si.c.value / x),\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n",
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/miniconda/envs/tardis3/lib/python3.6/site-packages/astropy/units/quantity.py:1067: AstropyDeprecationWarning: The truth value of a Quantity is ambiguous. In the future this will raise a ValueError.\n",
" AstropyDeprecationWarning)\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n"
]
}
],
"source": [
"config = Configuration.from_yaml('tardis_example.yml')\n",
"sim = Simulation.from_config(config)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Accessing the plasma states ####\n",
"In this example, we are accessing Si and also the unionized number density (0)"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" </tr>\n",
" <tr>\n",
" <th>ion_number</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>3.406539e-13</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>9.307653e-04</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2.293418e+04</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2.468681e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>8.681218e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0\n",
"ion_number \n",
"0 3.406539e-13\n",
"1 9.307653e-04\n",
"2 2.293418e+04\n",
"3 2.468681e+08\n",
"4 8.681218e+08\n",
"5 0.000000e+00\n",
"6 0.000000e+00\n",
"7 0.000000e+00\n",
"8 0.000000e+00\n",
"9 0.000000e+00\n",
"10 0.000000e+00\n",
"11 0.000000e+00\n",
"12 0.000000e+00\n",
"13 0.000000e+00\n",
"14 0.000000e+00"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# All Si ionization states\n",
"sim.plasma.ion_number_density.loc[14]"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" </tr>\n",
" <tr>\n",
" <th>ion_number</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>3.055157e-22</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>8.347575e-13</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2.056853e-05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2.214038e-01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>7.785756e-01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0\n",
"ion_number \n",
"0 3.055157e-22\n",
"1 8.347575e-13\n",
"2 2.056853e-05\n",
"3 2.214038e-01\n",
"4 7.785756e-01\n",
"5 0.000000e+00\n",
"6 0.000000e+00\n",
"7 0.000000e+00\n",
"8 0.000000e+00\n",
"9 0.000000e+00\n",
"10 0.000000e+00\n",
"11 0.000000e+00\n",
"12 0.000000e+00\n",
"13 0.000000e+00\n",
"14 0.000000e+00"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Normalizing by si number density\n",
"sim.plasma.ion_number_density.loc[14] / sim.plasma.number_density.loc[14]"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0 0.000931\n",
"Name: (14, 1), dtype: float64"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Accessing the first ionization state\n",
"\n",
"sim.plasma.ion_number_density.loc[14, 1]"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"sim.plasma.update(density=[1e-13])"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th></th>\n",
" <th>0</th>\n",
" </tr>\n",
" <tr>\n",
" <th>atomic_number</th>\n",
" <th>ion_number</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th rowspan=\"9\" valign=\"top\">8</th>\n",
" <th>0</th>\n",
" <td>1.288175e+04</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>7.151416e+08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1.598774e+03</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>6.741210e-14</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"13\" valign=\"top\">12</th>\n",
" <th>0</th>\n",
" <td>3.800017e-05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6.545794e+03</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>7.432405e+07</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"8\" valign=\"top\">14</th>\n",
" <th>0</th>\n",
" <td>3.172104e-02</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1.332867e+06</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1.113664e+09</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1.601707e+04</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>5.800053e-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"9\" valign=\"top\">18</th>\n",
" <th>10</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"21\" valign=\"top\">20</th>\n",
" <th>0</th>\n",
" <td>2.144981e-07</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1.601330e+02</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>4.507800e+07</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1.833649e-06</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>94 rows × 1 columns</p>\n",
"</div>"
],
"text/plain": [
" 0\n",
"atomic_number ion_number \n",
"8 0 1.288175e+04\n",
" 1 7.151416e+08\n",
" 2 1.598774e+03\n",
" 3 6.741210e-14\n",
" 4 0.000000e+00\n",
" 5 0.000000e+00\n",
" 6 0.000000e+00\n",
" 7 0.000000e+00\n",
" 8 0.000000e+00\n",
"12 0 3.800017e-05\n",
" 1 6.545794e+03\n",
" 2 7.432405e+07\n",
" 3 0.000000e+00\n",
" 4 0.000000e+00\n",
" 5 0.000000e+00\n",
" 6 0.000000e+00\n",
" 7 0.000000e+00\n",
" 8 0.000000e+00\n",
" 9 0.000000e+00\n",
" 10 0.000000e+00\n",
" 11 0.000000e+00\n",
" 12 0.000000e+00\n",
"14 0 3.172104e-02\n",
" 1 1.332867e+06\n",
" 2 1.113664e+09\n",
" 3 1.601707e+04\n",
" 4 5.800053e-08\n",
" 5 0.000000e+00\n",
" 6 0.000000e+00\n",
" 7 0.000000e+00\n",
"... ...\n",
"18 10 0.000000e+00\n",
" 11 0.000000e+00\n",
" 12 0.000000e+00\n",
" 13 0.000000e+00\n",
" 14 0.000000e+00\n",
" 15 0.000000e+00\n",
" 16 0.000000e+00\n",
" 17 0.000000e+00\n",
" 18 0.000000e+00\n",
"20 0 2.144981e-07\n",
" 1 1.601330e+02\n",
" 2 4.507800e+07\n",
" 3 1.833649e-06\n",
" 4 0.000000e+00\n",
" 5 0.000000e+00\n",
" 6 0.000000e+00\n",
" 7 0.000000e+00\n",
" 8 0.000000e+00\n",
" 9 0.000000e+00\n",
" 10 0.000000e+00\n",
" 11 0.000000e+00\n",
" 12 0.000000e+00\n",
" 13 0.000000e+00\n",
" 14 0.000000e+00\n",
" 15 0.000000e+00\n",
" 16 0.000000e+00\n",
" 17 0.000000e+00\n",
" 18 0.000000e+00\n",
" 19 0.000000e+00\n",
" 20 0.000000e+00\n",
"\n",
"[94 rows x 1 columns]"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sim.plasma.ion_number_density"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Updating the plasma state ####\n",
"\n",
"It is possible to update the plasma state with different temperatures or dilution factors (as well as different densities.). We are updating the radiative temperatures and plotting the evolution of the ionization state"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[\u001b[1mpy.warnings \u001b[0m][\u001b[1;33mWARNING\u001b[0m] /Users/wkerzend/python/tardis/tardis/plasma/properties/ion_population.py:63: FutureWarning: \n",
"Passing list-likes to .loc or [] with any missing label will raise\n",
"KeyError in the future, you can use .reindex() as an alternative.\n",
"\n",
"See the documentation here:\n",
"https://pandas.pydata.org/pandas-docs/stable/indexing.html#deprecate-loc-reindex-listlike\n",
" partition_function.index].dropna())\n",
" (\u001b[1mwarnings.py\u001b[0m:99)\n"
]
}
],
"source": [
"si_ionization_state = None\n",
"for cur_t_rad in range(1000, 20000, 100):\n",
" sim.plasma.update(t_rad=[cur_t_rad])\n",
" if si_ionization_state is None:\n",
" si_ionization_state = sim.plasma.ion_number_density.loc[14].copy()\n",
" si_ionization_state.columns = [cur_t_rad]\n",
" else:\n",
" si_ionization_state[cur_t_rad] = sim.plasma.ion_number_density.loc[14].copy()"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
},
{
"data": {
"text/plain": [
"Text(0, 0.5, 'Number density [1/cm$^3$]')"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmoAAAJXCAYAAAAjNngMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xuc3GV99//XNaed0543yc7u5kQgJIFgOCQKqIBowUOlglKR3lbFaj30Z28rVn+9q9S7Vq3aaiu2t63+6qHi4a4orVSBCgUEDCEICknklMMmG5LseXd2d2Z3rt8f35nJJmw2M7vfme98J+/n47GP2Zmdnfm4mM07n+t7fS5jrUVEREREak/A6wJEREREZG4KaiIiIiI1SkFNREREpEYpqImIiIjUKAU1ERERkRqloCYiIiJSo+oqqBljvmaMOWSM+XUJz11pjPkvY8zjxph7jDE91ahRREREpFR1FdSAfwGuLPG5nwO+Ya09B/gE8KlKFSUiIiKyEHUV1Ky19wIDsx8zxqwxxvzEGPOIMeY+Y8y6/Jc2AP+V//xu4KoqlioiIiJyUnUV1E7gK8AfWWvPBz4EfDn/+GPANfnP3wA0GmPaPahPREREZE4hrwuoJGNMErgI+L4xpvBwQ/72Q8CXjDFvA+4F9gPT1a5RRERE5ETqOqjhdAyHrLWbjv+CtfYAcDUUA9011trhKtcnIiIickJ1vfRprR0BnjPGvAnAOF6U/7zDGFP43/9R4GselSkiIiIyp7oKasaYW4AHgTONMb3GmBuA64EbjDGPAU9wdNPApcAuY8xvgGXAJz0oWUREROSEjLXW6xpEREREZA511VETERERqSd1s5mgo6PDrlq1yusyRERERE7qkUceOWKtXXKy59VNUFu1ahXbtm3zugwRERGRkzLG7CnleVr6FBEREalRCmoiIiIiNUpBTURERKRG1c01aiIiIlI7stksvb29TE5Oel2Kp6LRKD09PYTD4QV9v4KaiIiIuK63t5fGxkZWrVrFrPO2TynWWvr7++nt7WX16tULeg0tfYqIiIjrJicnaW9vP2VDGoAxhvb29kV1FRXUREREpCJO5ZBWsNifgYKaiIiISI1SUBMRERGpUQpqIiIiUhUXXXSR1yWU5KabbuJzn/uc12UACmoiIiJSJQ888IDXJVSctZZcLufa6ymoiYiISFUkk0nACTM33ngjZ599Nhs3buS73/0uAPfccw+XXnopb3zjG1m3bh3XX3891toTvt6qVav4+Mc/znnnncfGjRvZuXMn8MKO2Nlnn83u3bvZvXs369at453vfCdnn302119/PXfddRcXX3wxZ5xxBlu3bi1+z2OPPcYrXvEKzjjjDP7pn/6p+PhnP/tZNm/ezDnnnMPHP/5xAHbv3s369et573vfy3nnnce+fftc+5kpqImIiEhV/eAHP+CXv/wljz32GHfddRc33ngjfX19ADz66KN84Qtf4Mknn+TZZ5/l5z//+byv1dHRwfbt23nPe95T0nLl008/zQc+8AEef/xxdu7cybe//W3uv/9+Pve5z/FXf/VXxec9/vjj/PjHP+bBBx/kE5/4BAcOHOCOO+7gqaeeYuvWrfzyl7/kkUce4d577wVg165dvPWtb+XRRx9l5cqVi/jpHEtBTURERKrq/vvv57rrriMYDLJs2TIuueQSHn74YQC2bNlCT08PgUCATZs2sXv37nlf6+qrrwbg/PPPP+lzAVavXs3GjRsJBAKcddZZXH755Rhj2Lhx4zHff9VVVxGLxejo6OCyyy5j69at3HHHHdxxxx2ce+65nHfeeezcuZOnnnoKgJUrV/KSl7xkQT+P+ehkAhEREamq+ZYzGxoaip8Hg0Gmp6fnfa3C82c/NxQKHXOd2OyBs7NfPxAIFO8HAoFj3uv4+WfGGKy1fPSjH+Xd7373MV/bvXs3iURi3joXSh01ERERqaqXv/zlfPe732VmZobDhw9z7733smXLFtdef9WqVWzfvh2A7du389xzz5X9Gj/60Y+YnJykv7+fe+65h82bN3PFFVfwta99jbGxMQD279/PoUOHXKt7LuqoiYiISFW94Q1v4MEHH+RFL3oRxhj++q//ms7OzuJmgMW65ppr+MY3vsGmTZvYvHkza9euLfs1tmzZwmtf+1r27t3Ln//5n9PV1UVXVxc7duzgwgsvBJzNEd/61rcIBoOu1D0XM1/70U8uuOACu23bNq/LEBEREWDHjh2sX7/e6zJqwlw/C2PMI9baC072vVr6FBEREalRWvoUERGRmvaGN7zhBdeZfeYzn+GKK67wqKLqUVATERGRmnbrrbd6XYJntPQpIiIiUqPqpqP2m+dHufzz9xzz2PEzUACOf2SOp2A4fnZKaTW8YObKcV8PBgyxSJB4JEhbPMKapUnOWJpk04oWljZGS3sTP5sYhJE+mBxyPp/I304OQWYcZjL5j2z+I3P0NpeF4ze+GEPxp1z82c+6H4o6H+E4hKMQjjmfx1oh3u58tKyElhUQilTrpyAustYyMT1Bejrt3Gad29mPZWeyZHNZpnPTzod1bguPzeRmsNji6xVfm7k/NxjCgTCRYIRIMHL080D+fjBMPBSnKdJEU0MTzZFmmhqaCAfC1fvBiEjdqJugFg0HWZdqOvrAHJtZ7XEPzrXh9fjHjv+eE35fCc+ZzuWYyMwwMJ5h18FRfvDofgAiwQDXbVnO+y47naVNdRDYrIXDu6B3K+zbCs//GgaecwLZXEwAwgkIhiEYyX8UPg85t4EwBIKzfrD22M8L7zv7azOHITsB2UnIpmE6fzvX+zcvh+7zYfmLYeWF0HlO6QldXJfOpukd66V31Pk4MnGEgckBBqcGGZzMf0wNMp4dX9T7hEyIYCBIwMy9uDD7H22Ff4jlbK4Y8soRD8Vpi7axLLGMzkQnXYkuVjevZnXzak5rPo14OL7w/yEiUrfqJqitaItz81vO87qMsoxOZnnq0Bjf39bLv/5iL9/dto//+cq1vPuSNV6XtjAjB+CxW+DRb8HAs85jsVZIbYKzr4G21dDU7TwWa4VYC0RboKEJAlVahc/lnMCYHoDxQzC4x6n1yG+cUPnED5znta6CjW+Cc34XOs6oTm2noHQ2zRP9T7BzYCc7B3aye3g3vWO9DEwOHPO8SCBCa7SVtmgbLQ0tLG9cTmu0lWQ4STwcJxaKEQ/F5/w8HAgTCoSKt8UPE5qz616qnM2RmcmQyWXIzGTIzmSLn09MTzCSGWF4arh4Ozw1TP9kP8+PP88vD/2Sn4z/hBk7A0DABDit+TQ2tG/gvKXncXH3xXQmOhf1sxWRhfnJT37CBz7wAWZmZnjnO9/JRz7yEU/r0Ry1GrGnf5y//PEO7nzyef7+unP57Rd1eV1S6TLjcNdN8PA/g83ByovhnGud2/bT/dWZGu6FZ/8bfvV9eO6/nf89G6+FV34cmnu8rs73ZnIzbD+0nfv338+2g9t4ov+JYljpiHWwpnkNPY09xY/lyeV0J7tpbmheVKiqRdmZLPtG9/HcyHPsGtjFE/1P8Osjvy6G1NXNq3nF8lfw+jWv57SW0zyuVqR8fpyjNjMzw9q1a7nzzjvp6elh8+bN3HLLLWzYsGFRr7uYOWoKajUkM53jun96iJ19I/zo/Rdz+tJGr0s6uT0PwA/fA4O7YfM74SXvhXafdgSPN3oQtn4FHviSszx68Qfg5Tc6y7FSMmstjx56lH9/9t/52d6fMTA5QMiEOLvjbDZ3bmbT0k2sb1vPkvgSr0v1nLWWZ4ae4YEDD3D//vvZenArM3aGDe0bePOZb+Z1a16na93EN/wY1B588EFuuukmfvrTnwLwqU99CoCPfvSji3rdxQQ1/Y1TQyKhADe/5Txe+3f38Yff2s6P3ncxiYYa/k+0/Ztw2x85F+O/7cew6qVeV+Suxk64/GNw/tvgzo/Df38aDu+Ea/7ZuYZO5jU1M8Xtz97OLTtvYcfADmKhGJf0XMKrVr6Kl3a/VNdkzcEYw+mtp3N66+m89ay3cmTiCP/53H9y69O38rEHPsY/PPYPvOPsd3D1GVcTCWoDjNSvv/j3J3jywIirr7mhq4mP//ZZ8z5n//79LF++vHi/p6eHX/ziF67WUS6N56gxnc1R/u66c3n28Bif+PcnvS7nxPY8CP/xP+G0S+A9D9RfSJutZQW86f+D3/pLePKH8L3fh+kpr6uqWdZafvLcT3j9ra/nYw98jGwuy8cu/Bj3XHsPn73ks/zWqt9SSCtRR6yD/7Hhf/Bvv/1v3Hz5zSyNL+WTv/gk19x2DdsO+nsFQaQWzbXK6PVlFzXcrjl1XXx6B9e/eCXf3baP//c162mO11j3ZmgffPf38gHmX6Ah6XVF1XHRHznjPm7/EHznerjuO1oGPc6ugV385UN/yS8P/5K1rWv5xwv/kYu6LvL8F53fGWN4ec/LeVn3y7h///188hef5O0/fTvXnHENf3LBn9AY8cFlEiJlOFnnq1J6enrYt29f8X5vby9dXd5eM66OWo269oLlZKZz/PhXfV6XcqxMGr7zFme22XXfcXZvnkq2/AG89vPw9J3w4N97XU3NsNbyvV3f4y0/fgt7R/dy04U38b3XfY+Luy9WSHORMYaX9byMH7z+B7z9rLfzw6d/yFt+/BZ2D+/2ujSRurB582aeeuopnnvuOTKZDN/5znd4/etf72lNCmo16uzuJs5YmuQH23u9LuVYD94MBx93rtNastbrarxxwQ2w/rfh7k/Bkae8rsZz49lxPnzvh/nfD/1vNndu5tarbuWatdcQDAS9Lq1uxcNxPnjBB/nqFV9leGqYt9z+Fh448IDXZYn4XigU4ktf+hJXXHEF69ev59prr+Wss7zp7hUoqNUoYwxvOK+bbXsG2dO/uKGersmMw0NfhjOugLX1fxDuCRkDr/m8c9LBbX/kzGY7RY1kRviDO/6AO/fcyQfO+wBffuWXaYu2eV3WKeP8Zedzy+tuoTPRyXvvei+3PXOb1yWJ+N5rXvMafvOb3/DMM8/wZ3/2Z16Xo6BWy35nUzfGwA+27/e6FMf2b8DEALzsg15X4r3GZXDlp2Hvg878uFPQSGaEd9/xbnYM7OBvL/1b3rnxnSec8C+V053s5luv/habOzfz5z//c+7ac5fXJYmIi/RbtYZ1tcS4aE07tz66f86dKFU1nYEH/h5WXAQrXuJtLbXiRW+G01/pDPtND5z06fVkJDPCu+54FzsHd/K3l/4tl624zOuSTmnxcJwvXvZFNnZs5MZ7b+SB/VoGFakXCmo17upze9g7kOaRPYPeFvKr78HIfnjZn3hbRy0xxhnZkR13uo2niJzN8ZF7P8KuwV184dIvcOnyS70uSXDC2pdf+WXWNK/hj+/5Y3595NdelyQiLlBQq3FXnt1JLBwsHuDuidwM3P8F56Dy0y/3ro5atHQ9rHoZPPxV5+d0Cvjar7/Gffvv4083/ymXLL/E63JklqZIE//4qn+ktaGVD/33hxjNjHpdkogskoJajUs0hLhoTTsPP+fh0tozd0P/U/DSP/bXuZ3V8uJ3w/Be2PWfXldScdsObuNLj36JK1ddye+e+btelyNz6Ih18JmXf4aD4we56YGbvL9sQkQWRUHNB87qauLZI+NMZj3q2Dx7NwQb4MzXevP+tW7tq6GpB7b+H68rqaj+iX4+fO+H6Wns4eMXflzz0WrYpqWbeP+57+eOPXfwb0/9m9fliMgiKKj5wIauJmZylt8879Eyxu77oGczhKPevH+tC4Zg8w3w3L1waKfX1VTM3zzyNwxNDfH5Sz5PMnKKnEbhY+84+x28JPUSPr310zw79KzX5Yj4wjve8Q6WLl3K2Wef7XUpRQpqPrAh1Qzg+gG1JZkYgr7HYfXLqv/efnLe7ztdx61f8bqSinii/wlue+Y2fm/D73Fm25lelyMlCJgAn3rZp4gEI3x666e1BCpSgre97W385Cc/8bqMYyio+UBPa4xkQ4gn+zwIansfBGx9H7ruhkQ7bHwjPPYdyE54XY2rrLX89da/pi3axrs2vsvrcqQMHbEO3rfpfTzY9yB377vb63JEat7LX/5y2tpqa2i3TpT2gUDAsD7VyA4vgtru+51OUfcF1X9vvznravjlv8Kenzvz1erEnXvuZPuh7Xzswo9pydOHrj3zWr6/6/t89uHPcnH3xTQEG7wuSeTk/vMjcPBX7r5m50Z49afdfc0qUEfNJzakmtjRN0ouV+Xli933wfItuj6tFKsuhlAUnqqfyfBTM1P8zSN/w9rWtVx9+tVelyMLEA6E+fCWD9M71ss3n/ym1+WISJnUUfOJDV1NfP3BPewbTLOyPVGdNy1cn3bpR6rzfn4XjjlLxE/XT1C79alb2T+2n6+86is6ZN3HLuq6iMuWX8ZXHv8KV625iiXxJV6XJDI/H3a+KkUdNZ9Yn2oCqryhQNenle/0Vzoz5wZ3e13JouVsjm/v/DYbOzZyYdeFXpcji/ShCz5EZibD15/4uteliEgZFNR8Yu2yRoIBU90NBbo+rXynv8q5fepOb+twwUMHHuK54ee4bt11XpciLljRtILfWvVbfP8332d4atjrckRq0nXXXceFF17Irl276Onp4atf/arXJSmo+UU0HGTNkkR1NxQ8d6+uTytX+xpoWQlP/5fXlSzat3d+m/ZoO1esusLrUsQl7zj7HaSn03z/N9/3uhSRmnTLLbfQ19dHNpult7eXG264weuSFNT8ZH2qqXpLnxODzo6bVZqfVhZj4IxXOSF3esrrahZs38g+7u29lzed+SYiwYjX5YhL1rWt46Kui/jWk99iasa///8UOZUoqPnIhlQTB4YnGRzPVP7N9m8HLKzUtUllO/1VkB3PX+PnT7fsuoWgCfKmtW/yuhRx2TvOfgf9k/386OkfeV2KiJRAQc1HNnQ5Gwqqsvw5kD9ypkNT6Mu2+mUQjPj2OrV0Ns0Pn/ohr1r1KpbGl3pdjrhsS+cWzmo/i68/8XVmch6dHywiJVNQ85Hizs9qBbVwApL6i7pskQSsvMi3Yzru3HMno9lRbSKoU8YY3n7229k7upf79t/ndTkichIKaj7SkWxgaWND9YJa22nONVdSvtWXwOGdkB7wupKy3bX3LlKJFJuWbPK6FKmQV6x4BW3RNi1/iviAgprPrGpP0DtQhbMkB56FttWVf5961ZMfabL/EW/rKNN4dpwH9j/A5Ssuxyik161wIMxrT3st9/Tew+DkoNfliMg8FNR8JtUSpW+kwkEtN+MMbG07rbLvU8+6zgUTgN5tXldSlvt67yOTy/DKlfVzVqnM7ao1VzGdm+b25273uhSRmrFv3z4uu+wy1q9fz1lnncUXv/hFr0tSUPObVHOMg8OTlT3zc2Q/zGQU1BajoRGWrIf9/gpqd+29i/Zou5Y9TwFntp3J+rb1Wv4UmSUUCvH5z3+eHTt28NBDD3HzzTfz5JNPelqTgprPdLVEyc5YjoxXcAZSYcengtri9JzvLH3aCoZqF01OT3Jv771cvuJynet5irjq9KvYMbCDXQO7vC5FpCakUinOO+88ABobG1m/fj379+/3tCYdyu4zqeYYAH1DkyxtrNCJAQpq7ui+ALZ/w/l5tq/xupqTevDAg0xMT3D5ysu9LkWq5DWrX8Pntn2O2565jRvbbvS6HJGiz2z9DDsHdrr6muva1vGnW/605Ofv3r2bRx99lBe/+MWu1lEuddR8JtXshLO+4QpepzbwLISi0Jiq3HucCgobCnxyndpde++iKdLE5s7NXpciVdIabeWSnkv4j2f/g2wu63U5IjVjbGyMa665hi984Qs0NTV5Wos6aj5zNKhNVu5NBp6D1tUQUI5flCXrIJKE3ofhRb/rdTXzys5kuXvf3Vy2/DLCgbDX5UgVvX7N6/mvvf/F1r6tXNx9sdfliACU1flyWzab5ZprruH666/n6quv9qyOAv1N7DNtiQgNoUCFg9qzWvZ0QyDo7P70wYaC7Ye2M5oZ5ZUrtNvzVHNR10XEQjHu3ne316WIeM5ayw033MD69ev54Ac/6HU5gIKa7xhjSDVHOTBUoaXPXM7pqGmGmju6z4eDv4ZsBYO1Cx4++DBBE2RLaovXpUiVRUNRLkxdyD377sH6ZOOLSKX8/Oc/55vf/CY/+9nP2LRpE5s2beL2270dYaOlTx9KNccq11EbOwjTE+qouaXnAshl4eDjsLx2Q9C257exvm09iXDC61LEA5etuIyf7fsZTw48yVntZ3ldjohnXvrSl9bcP1jUUfOhVEuUvkp11Io7PtVRc0V37W8omJqZ4leHf8UFnRd4XYp45OU9LydgAty9V8ufIrVGQc2HuppjPD86xUwlht5qNIe7mlLQ1F3T16k9fvhxMrkM5y873+tSxCNt0TY2LdnEPfvu8boUETmOgpoPdTZHmclZDo9WYOht/zMQCENTj/uvfarqPr+mz/x85PlHMBjOW3ae16WIhy5bfhm7Bnexf8zb4Z5SX2ptGdELi/0ZKKj5UFeLM6LjQCVmqQ08C60rIajLF12z7GwY3APZCp/RukDbnt/GmW1n0hTxdlaQeOuyFZcBqKsmrolGo/T395/SYc1aS39/P9HowgfU629jH5p9OgErXH7xgee07Om29jWAdX62yzZ4Xc0xsjNZHjv0GG9c+0avSxGPrWxayWnNp3H3vru5fv31XpcjdaCnp4fe3l4OHz7sdSmeikaj9PQsfJVKQc2HugpBze2OmrVOR22Vhl66qv1057b/6ZoLak/0P8HkzKSuTxMALl1+Kd944huMZEbUYZVFC4fDrF6tjWmLpaVPH2qKhYhHghwYcnlEx9ghyI6ro+a2wjmf/U97W8cctj3vbHJQUBNwdn9O22kePviw16WISJ6Cmg8Vht4eHHG5oza017ltWenu657qGhoh2els1Kgx257fxuktp9MabfW6FKkBGzs2Eg1GFdREakjVg5ox5mvGmEPGmF+f4OvGGPN3xpinjTGPG2O0FW0OqeaY+x218fx1BMkl7r6uOMufNdZRm85N8+jzj6qbJkWRYIRzl57LL/p+4XUpIpLnRUftX4Ar5/n6q4Ez8h/vAv6hCjX5Tqo56v41aul+5zbe4e7rirP8WWNBbdfgLtLTaS5YpkG3ctSW1BaeHnqa/ol+r0sRETwIatbae4GBeZ5yFfAN63gIaDHGpKpTnX+kWmIcGp0iO5Nz70XTR5zbhIKa69pPd36+E4NeV1K0s38nAGd16MggOWpLp3PU2cPPa/lTpBbU4jVq3cC+Wfd784+9gDHmXcaYbcaYbafa9t+u5ijWwvMjLi5/pvshFIVw3L3XFEfHGc5tDV2ntmNgB8lwku7knH+85BS1oX0DiXCCrX1bvS5FRKjNoGbmeGzOaXnW2q9Yay+w1l6wZMmpdV1VqqUwosPFoDbe7yx7mrn+E8iizB7RUSN2DexibetaAqYWfw2IV0KBEOcvO18bCkRqRC3+hu4Fls+63wMc8KiWmtXV7Ew5djWopY9Aot2915OjWlaCCdZMUMvZHLsGd7G+fb3XpUgN2tK5hd0ju3l+/HmvSxE55dViULsNeGt+9+dLgGFrbZ/XRdWazkJQG3JxQ0G6H+IKahURijhHc9VIUNs7speJ6QnObD3T61KkBhWuU9t6UMufIl7zYjzHLcCDwJnGmF5jzA3GmD80xvxh/im3A88CTwP/BLy32jX6QWM0TGNDyOWlzyPa8VlJNTSiY+egs5FgXds6jyuRWlQ4+1VBTcR7VT9Cylp73Um+boH3VakcX1vS1MDhsSn3XjDdrx2fldR+Ouy+3zmqy+PrAHcN7CJkQqxpWeNpHVKbAibA5s7Nuk5NpAbU4tKnlKg1HmFwPOPOi2UnITMG8TZ3Xk9eqH0NZNMw6v1K/o6BHaxpWUMkGPG6FKlRmzs3s39sPwfGdImwiJcU1HysNR5mMJ1158U07Lbyamjn566BXZzZpuvT5MQ2Ld0EwOOHH/e4EpFTm4Kaj7XGIwylXeqoadht5dVIUDsycYQjE0d0fZrMa23rWhqCDTx+REFNxEsKaj7Wmogw6FpQK3TUtOuzYhq7nGHCHg+93TWwC9BGAplfOBBmQ/sGfnX4V16XInJKU1DzsZZ4mMlsjonMzOJfbFxLnxUXCECb92d+7hjYAaClTzmpjR0bebL/SbIzLl1iISJlU1Dzsda4cyG4K101LX1WR/tpnge1XQO76E520xRp8rQOqX0bl2wkk8vwm8HfeF2KyClLQc3HWuNhwK2g1g8mANGWxb+WnFjLShjaB7mcZyXsHNipQbdSkhd1vAiAxw4/5nElIqcuBTUfa8l31Ibc2Pk5fgRibc7ynFROywqYmYLxQ568fTqbZs/IHta16/o0ObnORCcdsQ5+dUTXqYl4RX8r+1hbwuWlTy17Vl7LCud2aJ8nb//s8LNYLGtb1nry/uIvxhjO6ThHIzpEPKSg5mMtxaVPFzpq6QHt+KyG5uXO7fBeT95+98huAFY1r/Lk/cV/Ni7ZyN7RvQxNDnldisgpSUHNx1pi+aVPN04nGD+ioFYNLfmgNuRNUNszsgeDYXnjck/eX/znnI5zALT8KeIRBTUfi4QCJBtCDLi1mUBLn5XX0AixVs+WPveM7KEr2aWjo6RkZ3WcRcAENPhWxCMKaj7XEg8vfjNBLgcTWvqsmublMOxdUFvVtMqT9xZ/SoQTrGlZo8G3Ih5RUPO51rgLpxNMDILNadhttbSs8GTp01rLnpE9rGhaUfX3Fn87p+McHj/yODnr3VgZkVOVgprPOcdILbKjVjg+Skuf1dGywln6tLaqb9s/2c94dpyVTSur+r7if2d3nM1oZpT9o/u9LkXklKOg5nOt8fDiD2YvnEoQb1t8QXJyzcshO+50Mqtoz8geAC19StkK58LuHNzpcSUipx4FNZ9rjUcYXOyuz/FCUFNHrSqKOz/3VPVtC0FNHTUp1+ktpxMwAXYN7PK6FJFTjoKaz7XEw4xMTjM9s4hrRwpLn9pMUB0eDb3dPbKbcCBMKpGq6vuK/0VDUVY3rVZQE/GAgprPFQ5mH5pYxHVqOpC9uopDb6sb1PaO7GV543KCgWBV31fqw9qN6ah/AAAgAElEQVS2tVr6FPGAgprPFU4nWNR1auP9EGmEUINLVcm8Yq0QSVZ95+eekT1a9pQFW9e2joPjBxmeGva6FJFTioKazx0973MxHbV+bSSoJmOcrloVlz5zNsfekb3aSCALtq7V2VCg5U+R6lJQ87nC0ueiNhToQPbqa1lR1fM+D44fJJPLqKMmC7a2bS0AOwe0/ClSTQpqPnf0YPbFLH0e0Y7PamtZXtWlz8Jh7Bp2KwvVEetgSWwJuwbVUROpJgU1nyt21Ba19Knjo6queTlMDsPkSFXeTjPUxA1r29Zq6VOkyhTUfC4eCRIJBhbeUbM2v/SpoFZVhREdVdr5uWdkD/FQnI6YOqeycOta1/HM8DNkZxZ5GoqIlExBzeeMMc7B7OML/MWZTcP0pJY+q604S606y5+FHZ/GmKq8n9SndW3rmM5N88zwM16XInLKUFCrA22JRRzMXjyVQB21qirMUqvSzk+N5hA3nNl2JqANBSLVpKBWB1riYYYWeo3a5JBzG2t1ryA5ueRSCEWrsvMzO5Nl/9h+BTVZtBWNK4gGo7pOTaSKFNTqQGs8wsBCO2qFi9mjTe4VJCdnDDT3VGXp88D4AXI2px2fsmjBQJC1rWu181OkihTU6kBLPLLwkwmmRp3bhkb3CpLSVGnobd94H4DO+BRXnNl2JjsHdmKt9boUkVOCglodaM0vfS7oF2cxqKmjVnVNXTD2fMXfpm9MQU3cs6ZlDaOZUfon+70uReSUoKBWB1rjEaZzltGp6fK/eSq/9KmgVn3JpTB2CHK5ir5N33gfBsOyxLKKvo+cGgrXOhZm84lIZSmo1YHW/HmfCxrRUQxqWvqsuuQyyGWPbuiokL7xPpbElxAOhCv6PnJqUFATqS4FtTrQuphjpKZGIRiBcNTlquSkkkud2wovf/aN92nZU1yTSqQIBUIKaiJVoqBWB1ryx0gtaOfn5Ii6aV5J5pciKx3UxhTUxD2hQIjljcvZO1K9s2pFTmUKanWg0FFb0M7PqVEFNa8Ug9qhir1FzuY4OH5QQU1ctbJxJbtHdntdhsgpQUGtDhQPZl/QNWqj2kjglSosfQ5MDpDJZUglFdTEPSuaVrBvdB85W9mNMCKioFYXmmJhAmahHbURBTWvNDQ5pxNUMKgdHD8IaDSHuGtl00qmZqY4lK5cN1hEHApqdSAYMDTFwgxNLHDXp5Y+vWHM0REdFXJg7ACgoCbuKuz81PKnSOUpqNWJZEOIsckFzFGbHNHxUV5KLqtoR61wKkFnorNi7yGnnkJQ04YCkcpTUKsTyYYQYwsaeKvNBJ5KLqtoR+3g+EHioThNEYVxcc/S+FKiwahGdIhUgYJanVhQULNWQc1ryaUV76h1JbswxlTsPeTUEzABljctV1ATqQIFtTqRaAgxXm5Qm550JuNrM4F3kssg3Q8zC7i+sAQHxg5o2VMqYmXjSgU1kSpQUKsTyWio/LM+iweyq6PmmcKIjvHDFXl5zVCTSlnZtJLesV6mcwu45EJESqagVieSkQV01IpBTR01z1TwdIKJ6QkGpwYV1KQiVjatZDo3Td9Yn9eliNQ1BbU6kYwuYNfn5LBzq12f3qng6QSFGWpa+pRKWNG0AoA9o1r+FKkkBbU6kWgIMZ6ZIZezpX+Tlj69V8HTCQqdjq5kl+uvLVIY0aHr1EQqS0GtTjQ2hABIZ2dK/yYFNe8lKhjU8jPUtPQpldAebScRTiioiVSYglqdSOSDWlnLn1Mjzq2uUfNOOArR5oosffaN9xEwAZbEl7j+2iLGGFY0rtDQW5EKU1CrE4mGIEB5s9S0maA2VOh0gr7xPpbElhAOhF1/bRGAVU2r1FETqTAFtTrRGM131MoKaoWOmpY+PVWh0wn6xvu07CkVtaJpBQfGD5Ct0BxAEVFQqxuJiBPUyhrRMTkCoSiEIhWqSkpSodMJ+sb6SCUV1KRyVjatJGdz7Bvb53UpInVLQa1OJPMdtdGyrlHT8VE1oQIdtZzNcTCtYbdSWTqcXaTyFNTqRLJhAR01BbXakFwKmTGYGnPtJQcmB5jOTbMsvsy11xQ5nkZ0iFSeglqdKAa1TJnXqGkjgfcKQ2/H3euqHU47R1ItjS917TVFjtfc0ExLQ4uCmkgFKajVicJ4Di19+lBx6K2LQW3CCWodsQ7XXlNkLiuaViioiVSQglqdaAgFCAfNApY+1VHzXAXO+zwycQRAM9Sk4lY2rlRQE6kgBbU6YYwh0RAqbzzH5IjO+awFFTjvs7D0qY6aVNrKppU8n36eiekJr0sRqUsKanUkESkzqE2NaOmzFsTbwQRc7agdnjhMU6SJhmCDa68pMhft/BSpLAW1OtIYDZV+hJS1ukatVgSCEO9wfelzSUzLnlJ5K5pWALB3VEFNpBIU1OpIoiFU+q7PbBrsjK5RqxUuz1I7PHFYy55SFRrRIVJZCmp1JNkQYmxqprQnF8/5VEetJiSXuBrU+if66YgrqEnlJcIJOmIdCmoiFaKgVkeSDSHGJks8c2+ycM6nOmo1Id4B6X5XXspay+H0YS19StWsaFyha9REKkRBrY4kG0KMl9tR067P2hBvdy2ojWRGyOQyWvqUqlnVvEodNZEKUVCrI2WN55gqdNS09FkTEu3OMVLZyUW/VHGGmjpqUiUrGlfQP9nPWMa9Y9BExKGgVkeSUWczQS5nT/5kBbXaEm93bicGFv1ShVMJNOxWqmVV0yoA9oyqqybiNgW1OpJsCGItpLMlLH8WNxNo6bMmFC78Hz+y6JfSsFuptuKIDl2nJuI6BbU6Ujjvs6RjpLTrs7YUOmouXKempU+ptuWNywHYPbLb20JE6pCCWh1J5oNaSdepTWrps6Yk8t0vF4La4YnDxEIxEuHEol9LpBTRUJRUIqWOmkgFKKjVkWJQK+V0gqkRCMchGK5wVVISNztq6SN0xDowxiz6tURKtaJJIzpEKkFBrY4ky136VDetdsRaAeNaR03LnlJtKxtXajOBSAUoqNWRwjVqoyUFNR3IXlMCQSesubCZ4MjEEW0kkKpb3ric4alhRjIjXpciUlcU1OpIY7Tcjpp2fNYUl4be6pxP8UJPYw8A+0f3e1yJSH1RUKsjiXI2E2jps/YkFn+MVDqbZjw7rhlqUnWFoNY71utxJSL1RUGtjpS961NBrba40FHrn3C+Xx01qbbuZDcAvaMKaiJuUlCrIw2hAKGAKXHX5yhEmytflJQu3rbooFY8lUCbCaTKGiONtDS0KKiJuExBrY4YY0g0hLTr06/i+aVPW8IRYCdQCGrqqIkXepI9WvoUcZmCWp1JNoQYmzrJEVK5nHZ91qJ4O+SmYXJ4wS9RPJVA16iJB3oae9RRE3GZglqdcYJadv4nZccBq12ftcaF0wkOpw8TMiFaGlpcKkqkdD2NPRwYP8BMroTzhkWkJApqdSYZDTF+so5a8ZzPZOULktK5cDrB4YnDtMfaCRj90Zbq60n2MJ2b5lD6kNeliNQNT36bG2OuNMbsMsY8bYz5yBxfX2GMudsY86gx5nFjzGu8qNOPEg2hkw+8zYw7txEtfdYUF4LakYkj2kggntGIDhH3VT2oGWOCwM3Aq4ENwHXGmA3HPe1/Ad+z1p4LvBn4cnWr9K/GUjYTFINavPIFSekKQW0RpxMcnjhMR1wbCcQbxaCm69REXONFR20L8LS19llrbQb4DnDVcc+xQOECqmbgQBXr87VEQ/Dk4zmyaec2rKBWU9zoqKXVURPvLIsvI2RC7Bvd53UpInXDi6DWDcz+U9ybf2y2m4DfM8b0ArcDfzTXCxlj3mWM2WaM2Xb48OFK1Oo7JY3nyOSDWiRR+YKkdJEEhKKQXlhHLZvLMjg1qNEc4plQIEQqmdLSp4iLvAhqZo7Hjh8cdR3wL9baHuA1wDeNeeHV0dbar1hrL7DWXrBkiboI4Cx9jmWmsfPN4srmlz7VUastxuRPJxhY0LcPTQ4B0B5td7MqkbL0JHt03qeIi7wIar3A8ln3e3jh0uYNwPcArLUPAlFAbYISJBpCWAvpzDw7P4sdNQW1mrOIY6QGJp2A1xptdbMikbL0NGrorYibvAhqDwNnGGNWG2MiOJsFbjvuOXuBywGMMetxgprWNkuQjDrnfc67/JkZc27DWvqsOfH2BW8mUFCTWtDT2MPA5ADjhc69iCxK1YOatXYaeD/wU2AHzu7OJ4wxnzDGvD7/tD8B/sAY8xhwC/A2O+9anhQUDmafd0RHVh21mrWIjtrg5CCgpU/xVk9SOz9F3BTy4k2ttbfjbBKY/djHZn3+JHBxteuqB4WgNn9HTbs+a1aiQ0uf4muzZ6md2Xamx9WI+J/Gl9eZRD6ozTuiIzvu7C4MBKtUlZQs3u6cwzqdKftbByYHCJgAzQ3NFShMpDSapSbiLgW1OlPoqI2drKOmblptWsQstcGpQVoaWnR8lHiqKdJEU6RJQU3EJfqNXmeKS5+Zk1yjphlqtWkRQW1gYoC2aJvLBYmUTzs/RdyjoFZnSlr6zIyro1arEvkpNAvsqCmoSS3oTnaroybiEgW1OtMYLSx9zjNHLZvWjs9aVeyolT+iY3ByUBsJpCb0JHvoG++bf/C2iJREQa3ONIQCBAOGsansiZ+USWuGWq0qBrXyTyfon+yntUFBTbzXlexiamaK/smFn1srIg4FtTpjjCEeCc5/MkF2XB21WhXLL12WOfQ2m8symhmlLaalT/FeV7ILgP1jOkpKZLEU1OpQPBJk4mRHSOkatdoUDEG0pexr1ArnfLY1KKiJ97oSTlA7MHb86YAiUi4FtToUj4RO0lHTrs+atoChtxp2K7Wk0FFTUBNZPAW1OhQLn2TpU7s+a1u8vezNBIWgpl2fUgvi4TitDa0KaiIuUFCrQ/FIkInsyeaoKajVrFgrTAyW9S2Fcz4V1KRWdCW72D+ua9REFktBrQ7FIkHGTzSeY2YaZjLa9VnLYm0wMVTWt2jpU2pNV7JLHTURFyio1aF5NxNkx51bddRqV6y17PEcOudTak1Xoou+Mc1SE1ksBbU6FI+ESJ9o6TOTdm51jVrtirU6gXp6quRvGZgc0DmfUlO6kl1MzkwWu70isjD6rV6HYvN21PJBTbs+a1c8v3xZxvLn4KSOj5La0p3sBrTzU2SxFNTqUHy+XZ+Z/NKnOmq1K1YIaqV3InTOp9SaVDIFoA0FIoukoFaHnF2fM3NfG1LsqCmo1azC6QJl7PwcmBzQRgKpKRp6K+IOBbU6FIuEsBYms7kXfrHYUdPSZ80qdNTK2FAwMDmgjprUlGQkSXNDs4KayCIpqNWheCQIQDozx4YCddRqX3Hps7SOWnbGOedTHTWpNV0JjegQWSwFtToUKwa1Oa5TK+76VEetZsXLW/ocnMoPu9U5n1JjupPdCmoii6SgVocKHbWJ7BxBTXPUal8kCYFQyZsJiqcSxBTUpLakkikOjB/QLDWRRVBQq0PxkjpqCmo1y5j86QSlddSKpxI0aOlTakt3spuJ6Yli11dEyqegVodi4RBwsmvUtPRZ08o4nUAHskut0s5PkcVTUKtDxaXPOTtq4xCMQDBc5aqkLPHSO2o6kF1qVVdSQU1ksRTU6tC8S5/ZtJY9/SDWWvLJBAOTAwRNkKaGpgoXJVIeBTWRxVNQq0OxeTtqaS17+kGsteTNBDrnU2pVY6SRxkgj+8d0OoHIQuk3ex2KR+a7Rm1cHTU/iLWWtfSpGWpSq7qT3RwYV0dNZKEU1OpQcelzrvEcmbRGc/hBrNVZps5OnvSpOudTalkqkdLSp8giKKjVoYZQAGNOsPSZTWvYrR+UMfRWx0dJLetKdnFw/KDXZYj4loJaHTLGEA8HTzBHbVwdNT8o4xgpHcgutSyVSDGWHWM0M+p1KSK+pKBWp2KRkHZ9+lkxqM2/oSCby5/zqWG3UqM6E52Adn6KLJSCWp2KR4JMzLWZQLs+/SFW2tLn8NQwAC3RlkpXJLIgqUQKQMufIgukoFan4pETLH1q16c/FDpqJzmdoBjUGhTUpDYVglrfeJ/HlYj4k4JanYpFgnMfyq5dn/5Q4maCoSlnKG5zQ3OlKxJZkPZYO6FASEFNZIEU1OrUnB21XA6mJ7Tr0w/CceeorxKDmjpqUqsCJkBnvFNBTWSBFNTqVCw8x2aC4oHs6qjVPGNKOp1gaFJBTWpfKpnSNWoiC6SgVqfm3ExQCGq6Rs0fYic/mF0dNfGDVCKljprIAimo1ak5lz4zY86tdn36Q6wV0iff9RkJRIiFYlUqSqR8qUSKQ+lDTOfm2IkuIvNSUKtTsUjwhScTZNRR85V4aR21loYWjDFVKkqkfKlEipzNcTh92OtSRHxHQa1OxSNB0tkZrLVHHyxeo6aOmi/EWkoKas1R7fiU2qYRHSILp6BWp+KREDM5S2Ymd/TBzLhzq46aP5SymSDfUROpZZ1J53QCBTWR8imo1alYOAgcdzC7dn36S6wNpichO3HCpyioiR90xhXURBZKQa1OJRqcoHbMhoLiNWpa+vSFEk4nGJ4aVlCTmhcPx2lpaNGIDpEFCJXyJGNMWwlPy1lrhxZZj7gkFnH+0x4T1LL5pU911Pxh9ukEzd0v+LK1VkFNfCOVSOlgdpEFKCmoAQfyH/NtLQsCKxZdkbgiHi501GZth9euT38pdNROcJ3aaHaUGTuj46PEFzoTnewb3ed1GSK+U2pQ22GtPXe+JxhjHnWhHnFJPDLH0mexo6alT1+IzX/ep04lED9JJVI8fPBhr8sQ8Z1Sr1G70KXnSJXEInNsJsikwQSdMySl9hU7aicIavlTCVqjrdWqSGTBUokUY9kxRjOjXpci4isnDWrGmD8E/t4Y82ZjzH8YY94z1/OstZOuVycLFp/zGrW0003TcFR/OMlmgkJQ09Kn+IFGdIgsTCkdtVcA7wLeb619HfCiypYkbji69Dn7GrVxXZ/mJ5E4hKIn7KgNTw0DWvoUfygMvdXOT5HylBLU+q0z3v4z+ftTFaxHXFJc+swe31FTUPOVeYbeDk46AU5BTfygeDrBmDpqIuUoJah9EcBa++/5+z+oXDniljk3E2TSmqHmN7E2mJh76s3Q1BABE6Ax0ljlokTK1xHrIBQIaelTpEwnDWrW2p3H3f/vypUjbomGTrDrUx01f4m1nDCoDU8N0xxpJmA0t1pqX8AE6Ix3KqiJlKnU8RwAGGMuAP4MWJn/XgNYa+05FahNFiEQMMTCQSaOn6PWoO6Lr8RaYeC5Ob80NDWkjQTiK6lkSteoiZSprKAG/CtwI/ArIHeS54rH4pHgC3d9NnZ6V5CUL9oy72YCXZ8mfqJZaiLlKzeoHbbW3laRSsR1sUjwuDlq2vXpO7EWmJx76XNwapCuRFeVCxJZuM5EJ4fSh5jOTRMKlPvXj8ipqdw/KR83xvwz8F/M2v1prdUGgxo0Z0dN16j5S6zF+e82PQWhhmO+NDQ1xIb2DR4VJlK+VCLFjJ3hyMQROhPq7ouUotyg9nZgHRDm6NKnRTtBa1IsEiKdPW7XZyTpXUFSvuLpBEPQuOyYL2npU/ymOKJjvE9BTaRE5Qa1F1lrN1akEnFdfPZmAmudzoyWPv1l9jFSs4LaxPQEUzNT2kwgvlIIagfGDnDu0nmPjxaRvHL39T9kjNFai08cs/SZnQCslj79JprvmB23oUAHsosfFbpoGtEhUrpyO2ovBX7fGPMczjVqGs9Rw47ZTJBNO7caeOsvhY7acRsKCud8KqiJn8TDcZobmjWiQ6QM5Qa1KytShVTEMR21zLhzq46av8RO0FFTUBOfSiVS6qiJlKGsoGat3VOpQsR98Ujo6KHsxY6agpqvzN5MMIsOZBe/6kx0sn9sv9dliPhGWdeoGWO+boxpmXW/1RjzNffLEjfEIsGjh7Jn8kEtoqVPX2loBsyJO2pRBTXxl1QixcExLX2KlKrczQTnWGuL/7S31g4C2rpTo+LhINkZS3Ym55zzCeqo+U0gANHmFwS1wSnnfnNEuz7FX1KJFKPZUUYzo16XIuIL5Qa1gDGmtXDHGNNG+de5SZXEIrMOZi921BTUfCfW+oLNBMNTwyTCCcLBsEdFiSxMYUSHNhSIlKbckPV54EFjzPdxBt1eC3zS9arEFfGI8593IjNDc7GjpqVP34m98LzPoakhXZ8mvjR7RMcZrWd4XI1I7SspqBljLgQestZ+wxizDXgFzmiOq621T1ayQFm4eLGjNq2Omp/FWl+wmUBBTfyqK+mcT6uOmkhpSu2o/T5wszHmN8BPgP9rrdWfshp3zNKn5qj5V7QFBo/dcD00qaAm/tQR6yAUCGlEh0iJSgpq1to/BDDGrANeDfyLMaYZuBsnuP3cWjszz0uIBwodtYnsjOao+Vmsdc6lz5VNKz0qSGThAibAsvgyBTWREpW1mcBau9Na+7fW2itxlj/vB94E/KISxcnixF/QUTMQinpblJSvsJkglys+NDw1TGu0dZ5vEqldqUSKvjEFNZFSlLvrs8haO2GtvR3Ybq29wMWaxCWxcGEzQf4atUgCjPG4KilbrAVsDvLjDLK5LGPZMR3ILr6l0wlESrfgoDbLX7jwGlIBx3bUxjVDza+OO51ApxKI33UmOjmUPsR0btrrUkRqXqm7Ph8/0ZeAZe6VI26KHz9HTden+VN01nmfrSsZmtQ5n+JvqWSKGTvDkYkjxXEdIjK3Und9LgOuAAaPe9wAD7hakbimsOtzonCNmnZ8+lOxo+b88SscH6WlT/GrwtDbvvE+BTWRkyh16fM/gKS1ds9xH7uBeypWnSxKYeCt01EbV0fNr2L5ztnksUufrQ3aTCD+VAxq2lAgclKljue4YZ6vvcW9csRNwYAhEgqQzk7nO2oKar50go6alj7Fr2afTiAi83NjM4HUsHgk6Cx9FnZ9iv8ct5mgeCC7lj7FpxLhBE2RJgU1kRKUFNSMMdvdeI5UXzwc1K5PvwvHINhQ7KgNTw0TCUSIhWIeFyaycBrRIVKaUjcTrJ9n5yc4mwr0z/saFIsE82d96ho1X5t1OkHhnE+jmXjiY93JbvaO7vW6DJGaV2pQW1fCc0o+QsoYcyXwRSAI/LO19tNzPOda4CbAAo/pWriFiUdCR8dzaNenf8VaipsJhqaGaInq+jTxt57GHh448ADWWv2jQ2QepW4m2HPyZ5XGGBMEbgZeBfQCDxtjbrPWPjnrOWcAHwUuttYOGmOWuvX+p5pYJEh6atpZ+lRHzb9irccMvNVGAvG77mQ3kzOT9E/20xHr8LockZrlxWaCLcDT1tpnrbUZ4DvAVcc95w+Am621gwDW2kNVrrFuxCNBpjOTzhFEukbNv6ItxaXPwclBbSQQ3+tp7AGgd7TX40pEapsXQa0b2Dfrfm/+sdnWAmuNMT83xjyUXyp9AWPMu4wx24wx2w4fPlyhcv0tHgliM2POHe369C911KTOFIPamIKayHzKCmrGmPcbYxY7ZXOuixHscfdDwBnApcB1wD8bY17wN5O19ivW2gustRcsWbJkkWXVp3gk5FyfBuqo+Vl+M0HO5hjOKKiJ/3UnnX+fq6MmMr9yO2qdONeUfc8Yc6VZ2BWgvcDyWfd7gANzPOdH1tqstfY5YBdOcJMyxSNBZ9gtqKPmZ7EWyI4zmh4gZ3MKauJ7DcEGlsaWKqiJnERZQc1a+79wAtNXgbcBTxlj/soYs6aMl3kYOMMYs9oYEwHeDNx23HN+CFwGYIzpwFkKfbacWsURiwQxWXXUfC8/9HZoxBlnoF2fUg96Gnu09ClyEmVfo2attcDB/Mc00Ar8X2PMX5f4/dPA+4GfAjuA71lrnzDGfMIY8/r8034K9BtjngTuBm601vaXW6tAPBwiPDPp3NGuT//KB7Oh0f2Ajo+S+tDT2MP+sf1elyFS00qdowaAMeb/AX4fOAL8M06AyhpjAsBTwIdLeR1r7e3A7cc99rFZn1vgg/kPWYR4JEjM5IOa5qj5V76jNjx2ENDxUVIfupPdPD/+PJmZDJFgxOtyRGpSWUEN6ACuPn6umrU2Z4x5nXtliVtikSBxppw76qj5V2HpM/08oI6a1Ieexh4slgNjB1jVvMrrckRqUrlLnw3HhzRjzGcArLU7XKtKXBOPBImbfFDTNWr+FcsvfU44VwAoqEk96Ek6Izq0/ClyYuUGtVfN8dir3ShEKiMeCRIrdtSS3hYjC1foqE0OEDABGiONHhcksngaeityciUtfRpj3gO8FzjtuMPZG4GfV6IwcUcsEtLSZz2IOtekDWVGaI40EzBezKoWcVdHrINIIKKdnyLzKPUatW8D/wl8CvjIrMdHrbUDrlclrjlm6TMU87YYWbhAEBqaGcqM0RzVRgKpDwEToLuxWx01kXmUeij7MDCMc0qA+Egs7Cx9TgdjhALqwvharIXhmTSt0ZTXlYi4piepER0i8ynpb25jzP3521FjzEj+Y7Rwv7IlymLEI0HiTDITVDfN9+JtDM1MajSH1JWexh72je7DmcokIscrKahZa1+av2201jblPxoL9ytboixGPBIiZqbIKqj5X6yNIZvVjk+pK93JbsayY4xk9G9+kbmUeyj7m4wxjfnP/5cx5gfGmHMrU5q4oTBHLROIel2KLJKNtTKEVVCTuqKdnyLzK/eipT+31o4aY14KXAF8HfhH98sSt8QV1OrGRKyZjNGpBFJfCrPUtPNTZG7lBrWZ/O1rgX+w1v4I0LkfNSwcDBA3U0wZBTW/G25w5uC1hnW1gdQPddRE5lduUNtvjPk/wLXA7caYhgW8hlRZMpBhEgU1vxsMNwDQQtDjSkTckwgnaG1oVUdN5ATKDVnXAj8FrrTWDgFtwI2uVyWuijPFhGnwugxZpKGQM01HC59Sb7qT3ewf1YgOkbmUdSi7tTYN/GDW/T6gz+2ixF1xM8V+q6Dmd8NBp5PWMpPzuBIRd6WSKZ4afMrrMkRqUllBLb/UeQ2warGpY1YAACAASURBVPb3Wms/4W5Z4qYYk6QV1HxvyDhzplqmsx5XIuKuVCLFfb33Ya3FGON1OSI1pdylzx8BVwHTwPisD6lhUTvFuIKa7w3hdNKas5MeVyLirq5kF5MzkwxODXpdikjNKaujBvRYa6+sSCVSGTNZQkwzmtPmXL8byk2RzOUITwx5XYqIq1IJ51i0vrE+2qJtHlcjUlvK7ag9YIzZWJFKpDIyTsNzTEHN94ay4zTncjAx4HUpIq4qBLUD4wc8rkSk9pTbUXsp8HZjzLPAFGAAa609x/XKxB3ZNAAjMwpqfjc8NUyLDUBay0NSX7qSXQAcGFNQEzleuUHt1RWpQionkw9q02GPC5HFGpoaoiUQVkdN6k5TpIl4KM7B8YNelyJSc8pd+twLvAz4fWvtHsACy1yvStyTdZY+h6bVUfO7oakhmgMNkFZQk/pijKEr2aWOmsgcyg1qXwYuBK7L3x8Fbna1InFXvqM2NBMml7MeFyOLMTI1QksoAel+r0sRcV1nopO+cY3lFDleuUHtxdba9wGTANbaQXTWZ23Ld9TStoHJ6ZmTPFlq1UxuhtHsKE3hpJY+pS51JboU1ETmUG5QyxpjgjhLnhhjlgAak17L8h21CRpIZxTU/Go0MwpAc0MzTAxCTn/spL6kkimGpoZI5zdAiYij3KD2d8CtwDJjzCeB+4G/cr0qcU/+l16aBtJTCmp+NZwZBqA51gY2B1PDHlck4q7iLDV11USOUe5Zn/9qjHkEuDz/0O9Ya3e4X5a4JnN06TOdnfa4GFmokakRAJpi7c4D6QGItXpYkYi7Zo/oWNOyxuNqRGpHSUHNGPPBE3zp1caYV1tr/8bFmsRNWS191oNiRy2R32SdHoB2/WUm9UMdNZG5ldpRa8zfnglsBm7L3/9t4F63ixIXZQpLn1EmFNR8azi/1NmU6HQe0IYCqTNLYksImZCCmshxSgpq1tq/ADDG3AGcZ60dzd+/Cfh+xaqTxcuOkws2kCOgjpqPjWTyS59NPc4DmqUmdSYYCLIssUyz1ESOU+5mghVAZtb9DLDKtWrEfZk0NhQDIJ3RNWp+VeioNTctdx5QR03qUCqR0ukEIscp9wipbwJbjTG34ozoeAPwdderEvdk09hIAkBLnz42khkhFooRjneACWjordSlrmQXWw9u9boMkZpS7q7PTxpj/hPnGCmAt1trH3W/LHFNZgwTjgNo6dPHhqeGnRlqgYCz21NLn1KHOhOdHEofIpvLEg7ofGIRKL+jhrV2O7C9ArVIJWTSmEJHLaug5lcjUyM0RZqcO7E2LX1KXepKdJGzOQ6lD9Gd7Pa6HJGaUO41auI32TSmIU7A6Bo1PxvJjDgdNYB4uzpqUpdSyfyIjjHt/BQpKDmoGcfyShYjFZAZx4QTxCMhLX362PDUMM2RQlBrc46REqkzXQln6K1GdIgcVXJQs9Za4IcVrEUqIZuGSJxYJKjNBD42khmhqWHW0qc2E0gd6szPCdSIDpGjyl36fMgYs7kilUhlZNIQSZKIBNVR87FjO2r5zQTWeluUiMuioSht0TZ11ERmKXczwWXAu40xe4BxwOA0285xvTJxR3YcwnFiWvr0rcnpSTK5zLEdtZmpfLc04W1xIi7rSnQpqInMUm5Qe3VFqpDKyThLn/FIkAkdyu5LxeOjCrs+47MOZldQkzqTSqZ4avApr8sQqRnlzlHbU6lCpAJyM07nJZwgHgkyNqWg5kfFA9kbZm0mAGdER4v290h9SSVS3Nd7H9ZajDFelyPiubKuUcvv/Pw9Y8zH8vdXGGO2VKY0WbTMuHMbiRMLazOBX41M5c/5nD1HDbShQOpSV7KLyZlJBqe0s1kEyt9M8GXgQuC6/P1R4GZXKxL3ZNPObdhZ+tQ1av50wo6aZqlJHSrs/NQsNRFHuUHtxdba9wGTANbaQSDielXijmJHLaHNBD5W6KgdM/AWNEtN6lJhltqBcY3oEIHyg1rWGBPEOZAdY8wSIOd6VeKO4zpqEzqZwJdGMscvfbY6t+qoSR3qSuaH3qqjJgKUH9T+DrgVWGaM+SRwP/BXrlcl7sjkg1p+12c6O4PV7C3fGZ4aJmiCJMNJ54FgGBqadN6n1KWmSBPxUFwjOkTyyt31+a/GmEeAy/MP/Y61dof7ZYkrsvmlz3CCWCSItTA1nSMaDnpbl5RlJDNCY6Tx2B1wsVZtJpC6ZIwhlUjpdAKRvLKCmjEmCrwGeBnOkmfEGPOctXayEsXJIs3uqOXDWTozo6DmM8NTw0evTyuIt2npU+pWKplSR00kr9ylz28AZ+EsgX4JWA980+2ixCXFa9ScQ9kB0rpOzXdGMiNHj48qiLdr6VPqlk4nEDmq3JMJzrTWvmjW/buNMY+5WZC4aPYctfzeXM1S85/hqWFaoi3HPhhrgyOa3i71KZVMMTQ1RDqbJh6Oe12OiKfK7ag9aox5SeGOMebFwM/dLUlcc9yuT0AjOnxo7o6alj6lfqUSKQB11UQosaNmjPkVzkiOMPBWY8ze/P2VwJOVK08WpXiNWoJYxFnyVFDzn+Gp4aOjOQpibZAZhekMhDTKUOpLcUTHeB9rWtZ4XI2It0pd+nxdRauQysiOQyAMwXDxGjUdzO4vOZtjNDM692YCcIbeNi6rfmEiFVToqGnnp0iJQU2HsftUJg0R5/oOLX3602hmFIudJ6gNKKhJ3VkSW0LIhLT0KUL54zkuAP4MZ8kzBBjAWmvPqUBtsljZcQgnAIiFFdT86AUHshfEdN6n1K9gIMiyxDIFNRHK3/X5r8CNwK/Q0VG1b46OmnZ9+kvh+KgTdtQ09FbqVCqR0jFSIpQf1A5ba2+rSCXivmwawoWgVpijpqDmJ8NTw8A8HTXNUpM6lfr/27vvKMfu+v7/z7c00sxo2s7ObG+zxV6X9bp3m26DMTYE+MYmAfxNA0w4gYT8EjjkmxASggklCSGJISS0hNgOBmIHG8c2JRhwL7tui3e9s73NTm+aos/vj3s1q92dopmRdK+uXo9zdK50dXX11l3NzHs/7V23jMcOPRZ0GCKBm22i9mdm9hXgQSCd3emc+05Bo5LCGBmApNf1WZOIYYYKs5eZqVvUWrytuj4lopbVL+PwzsOMZkZJxBJBhyMSmNkmar8BnIa3TEe269MBStTCaHQQ/IVSzYzaRFwtamUm26J2UqKWTEFVjVrUJLKW1y0n4zIcGTwysVyHSCWabaJ2tnPurKJEIoU3MgiNx37BpZJxBpSolZWekSm6PsHr/hzsKnFEIqWxrP7YEh1K1KSSzbYywcNmdkZRIpHCy5n1CVCbjKvrs8z0pnupraolGZ9kUdvUQk0mkMhSdQIRz2xb1K4A/q+ZvYw3Rk3Lc4RZzqxPgFSiSl2fZaZnpIeGZMPkT6YWqutTIkuJmohntonaG4oShRRHzqxP8FvURpWolZPedO/J49OyahfCoedKG5BIidRU1bCwZqGqE0jFm22idtMU+z8x30CkwDIZL1FLHuv6TCU1maDc9Iz0nFyQPUstahJxK+tXsrd/b9BhiARqtmPUBnJu48A1QFuBY5JCGBvytjktakrUyk/vSO/kEwnAa1Eb6vKScpEIWlG/gn19+4IOQyRQs2pRc859LvexmX0W0AK4YTQy6G2TuZMJqjSZoMz0DPewqWXT5E+mFoLLwHD3sUoFIhGyomEF9++6n/HMOPFYPOhwRAIx2xa1E6WAdYUIRApsdMDb5raoaR21stMz0sOC6gWTP5ld9HZIS3RINK2oX8GYG+PQ4KGgQxEJzGyLsm/FW+AWIA4sAv6i0EFJAUy0qJ0wmUCJWtkYGhsiPZ6msXqark/wqhO0rC9dYCIlsqJ+BQD7+vdpLTWpWLOdTPCmnPtjwCHnnPrSwmjUT9QSJ0wmGB3HOYeZBRSY5CtblWDqFjXV+5RoW1m/EoC9fXu5cOmFAUcjEoy8EjUz+9NpnnPOObWqhc2I3/WZPH4ywXjGMTKeobpK4z3CbsryUVm1zd5Wi95KRC2tW4ph7OvXhAKpXPmOURuY5OaA3wL+uDihybxMtKjldn16ebm6P8vDRKI25fIcKswu0ZaIJ1hSt0SJmlS0vFrUcmd7mlkD8EHgN4HbgM9N9ToJ0ESLWv3ErlTSa0UbHBlnQWqyF0mYZOt8TtmiVtMEFlfXp0TaivoVStSkouU969PMFprZXwJb8BK885xzf+ycO1y06GTuRk+eTJCbqEn4dae7gWkSNTOv+1MtahJhWktNKl2+Y9Q+A7wV+DJwlnOuv6hRyfyNnLw8R23CS9TU9VkeZpxMAKpOIJG3sn4lh4cOkx5PUx2vDjockZLLt0Xtw8By4E+A/WbW69/6zKy3eOHJnE10febO+vTy8kEtelsWetI9VMerqamqmfqg2oVqUZNIW9HgLdGhmp9SqfIdozbfhXGl1EYHvfFL8eTErtps16cKs5eFnnTP1N2eWakW6GovSTwiQchdS21t09qAoxEpPSVgUTXiF2TPWS8tO0ZNXZ/lIb9ErVldnxJpE4maxqlJhVKiFlWjA8eNTwNNJig33enuqZfmyMp2fTo3/XEiZWpxajGJWEIzP6ViKVGLqpHB42Z8wrExairMXh56R3qnn0gA3mSC8fSxWb4iEROzGMvrlytRk4qlRC2qRgePKx8FalErN93p7pm7Pifqfao6gUSX1lKTSqZELapGBk5qUcsuz6FELfycc/lPJgDN/JRIU6ImlSyQRM3M3mBm28xsu5l9ZJrj3m5mzswuKGV8kTA6eNIYtVjMqEnEGNKsz9AbGhtiNDOaR6KmwuwSfSvqV9Cd7mZgdCDoUERKruSJmpnFgX8ArgHOAN5hZmdMclwD8HvAI6WNMCKysz5PkEpWaR21MjBjnc+sia5PJWoSXdm11Pb27Q04EpHSC6JF7SJgu3PuZefcCF690DdPctxfAH8NDJcyuMiYZNYneN2f6voMv2ydz7wmEwAMdRU5IpHgrKxfCaDuT6lIQSRqK4A9OY/3+vsmmNm5wCrn3H9PdyIze4+ZPW5mjx85cqTwkZazSWZ9gjehQOuohV+2zmdjdeP0B9Y2e1tNJpAIy130VqTSBJGo2ST7JhaBMrMY8Dd4Zaum5Zz7snPuAufcBYsWLSpgiBEwyaxP8BI1taiFX151PgHiCahpUqImkbagegF1iTp1fUpFCiJR2wusynm8Esgt4tYAbAJ+bGbtwCXAXZpQMAvOTTrrE7wyUmpRC7+JMWozTSYASLXCQEeRIxIJjpmxqmEVe/r2zHywSMQEkag9BpxiZmvNLAncCNyVfdI51+Oca3XOtTnn2oCHgeudc48HEGt5GhsG3KRj1FLJKgZHNZkg7GaVqNUtggF1/Uu0KVGTSlXyRM05NwZ8ALgPeAG4wzn3nJl9wsyuL3U8kTTir1I/yazPWnV9loWedA+1VbVUx6tnPriuVV2fEnkrG1ayt38v4xn9/pLKUhXEmzrn7gHuOWHfn05x7KtKEVOkZNcamqxFLaGuz3LQne6mMTnDRIKsVAvsebS4AYkEbHXDasYyYxwaPMTy+uVBhyNSMqpMEEUTLWqTz/pUi1r49Yz0zDyRIKtukdeilskUNyiRAK1q8IY27+7bHXAkIqWlRC2KJlrUJuv6rFKLWhnoTffmNz4NvK5PNw7D3cUNSiRA2URN49Sk0ihRi6IZWtRGxjOMjqv1JczyKsielWr1tppQIBG2JLWERCyhRE0qjhK1KBr1E7Up1lEDFWYPu7wKsmfVZRM1LdEh0RWPxVlRv0JrqUnFUaIWRSN+1+cU66gB6v4MMeecl6jNVOczK5uoDSpRk2hb1bCK3b0aoyaVRYlaFE20qE3e9QmoMHuIDY4NMubG8p9MoK5PqRCrG1ezp28PzrmZDxaJCCVqUTTdOmoJb0UWdX2GV7bOZ/5j1Fq87YDWUpNoW9WwisGxQTqHO4MORaRklKhF0XTrqGW7PkeVqIVVtirBjAXZs6qSfr1PdX1KtGnmp1QiJWpRNDIIGCRqT3pKkwnCL++C7LlSrer6lMhToiaVSIlaFI0Oeq1pZic9dWwygcaohdVEnc98JxOAX+9TLWoSbSvqV2CYEjWpKErUomhkYNIZn+AVZQe1qIXZRItazSxa1FTvUypAMp5kad1SVSeQiqJELYqyLWqTUNdn+GUnE+Rd6xO8CQXq+pQKsLphtVrUpKIoUYuikYFJZ3yC1lErBz0jPdRW1ZKMJ/N/kep9SoVY2bBSi95KRVGiFkXTtagl1KIWdj3pWRRkz6prBZeBoa7iBCUSEqsaVtE53En/SH/QoYiUhBK1KBoZnLJFrSoeIxmPMTiqyQRhNavyUVl1i7ytluiQiFvduBrQzE+pHErUomh06q5P8Lo/1fUZXrMqH5U1seitEjWJNi3RIZVGiVoUjUzd9QnehAJ1fYZXd7qb5prm2b2oTmWkpDJkEzXN/JRKoUQtikYHp1yeA9SiFnadw51zGKOmrk+pDHWJOlprW9nVuyvoUERKQolaFI0MQmLqrk+vRU1j1MJoLDNG70jv7FvUVO9TKsiaxjVK1KRiKFGLGudgpH/aFrVUokpdnyGVXUNt1olaPOHV+1TXp1SAtsY22nvagw5DpCSUqEXN2DC4cahumPKQ2mRcRdlDqnvYT9SqZ5mogb+Wmro+JfraGtvoSndNVPEQiTIlalGT7vO2yfopD9FkgvDqSnvroM26RQ38wuxK1CT62praAGjvbQ80DpFSUKIWNdlErXrq8kOaTBBeXcNeojbryQTgzfxUoiYVYE3jGgCNU5OKoEQtarKrdVfP1KKmyQRhNOcxauAXZleiJtG3smElcYtrnJpUBCVqUZNX16cmE4RV53AnMMcxaqlW1fuUipCIJVjZsFJdn1IRlKhFTTrbojbNZIJEnPRYhvGMK1FQkq/udDf1iXoS8cTsX6x6n1JB2hrblKhJRVCiFjUTY9SmTtRSSa8wu2Z+hk/ncOfcuj1Bi95KRVnTuIbdvbvJOLUgS7QpUYuakfwTNY1TC5/u4e65dXtCzqK3WktNoq+tqY30eJpDA4eCDkWkqJSoRU2eY9QAzfwMoTnV+cyaqPepFjWJvrbGNgB29u4MNhCRIlOiFjXpfsAgOX0JKUATCkJoTnU+s9T1KRUkm6hpiQ6JOiVqUZPu87o9zaY8pFaJWig55+bXopbt+uxX16dEX2ttK6mqlJbokMhTohY1I33TdnuCuj7DamhsiPR4eu6JWjzhJWv9GrMj0WdmtDW1qUVNIk+JWtSk+6edSACaTBBWE+Wj5jqZAKB+qRI1qRhrGtdoiQ6JPCVqUZPum7YqARzr+tTyHOEyUZB9ri1qAA1LoO9ggSISCbe1jWvZ37+f9Hg66FBEikaJWtSMzNyiVud3ffan1aIWJtmqBHOeTABqUZOKsqZxDQ7H7t7dQYciUjRK1KImPfMYtfoaL1EbUKIWKvOq85nVsMRL1FRGSipAW1MboJmfEm1K1KIm3Q/VjdMekkrEMYO+YSVqYTJR53M+iVr9UsiMwVBngaISCa/sEh0v97wcbCAiRaRELWrSvTOOUYvFjPrqKiVqIdOd7qbKqmhITN91Pa2GJd5W49SkAqQSKZbVLVOiJpGmRC1KnPPGqM3Q9QnQUF2lMWoh0zXcxYKaBdg0a+DNqH6pt+1XoiaVYd2Cdezo3hF0GCJFo0QtSsaGvW6vGSYTgDdOrW94tARBSb66hrvmN5EAclrUNKFAKsOGpg3s7NnJeEaz2CWalKhFSbrf2+aRqDXUJNSiFjLzqkqQVe8nampRkwqxfsF60uNp9vfvDzoUkaJQohYlI35B9nxa1Kqr6NcYtVDpHO6c32K34NV4TTZA/+HCBCUScusXrAdge/f2gCMRKQ4lalGS9hO1PMaoeV2fStTCpCAtaqBFb6WirGtaB8COHo1Tk2hSohYls+j6bKypok9dn6ExnhmnJ91TmERNi95KBalP1rMktUQTCiSylKhFSbZFbYblOUBdn2HTM9KDw81/MgGoRU0qzoYFG5SoSWQpUYuSkWyL2vQL3gLUVycYGh1ndFwr2IfBRJ3P+Y5Rg2Mtas7N/1wiZWDdgnXs7NlJxun3mUSPErUoSfd623zWUVMZqVApSFWCrIYlMDp4rIVVJOLWN61neHyYff37gg5FpOCUqEXJxBi1/CYTgMpIhUVB6nxmTSx6q3FqUhmyMz9f7laFAokeJWpRMtIPGCTqZjy0oVqJWphMtKgVoutTZaSkwqxb4M381BIdEkVK1KIk3ed1e8Zm/mdtqEkAaNHbkMi2qC2oKcBkArWoSYVpTDayOLVYNT8lkpSoRUm6L6+lOeBY12d/WmWkwqBruItUVYrqePX8T6YWNalA65vWa+anRJIStShJ9+U1Pg285TlAXZ9h0ZXuKsz4NICaBRCvVhkpqSjrF6zn5Z6XNfNTIkeJWpSM9OfdotaoyQSh0jXcVZjxaQBm/lpq6vqUyrF+wXqGxoY4MHAg6FBECkqJWpRkx6jl4VjXpxK1MDg6dJSW2pbCnbB+icaoSUXJzvxU96dEjRK1KEnn36JWm4gTjxl9wxqjFgYdQx201rYW7oRK1KTCZBO1X3b9MuBIRApLiVqUzGIygZmpjFRIjGfG6Up3FbZFrWGpJhNIRWlMNrK8bjm/7FSiJtGiRC1KRvLv+gRvQoEKswevK91FxmUK3KK2FIa7YXS4cOcUCblTF57Ktq5tQYchUlBK1KLCuVl1fYJXRkqTCYJ3dOgoQGETtewSHer+lApy2sLTaO9tZ3hM/0GR6FCiFhVjaciM5r08B3iJmro+g9cx1AEUOFHTordSgTY2byTjMqpQIJGiRC0qRrJ1Phvzfkl9dZVmfYbARKJWU4QWNY1TkwqysXkjANs61f0p0aFELSrSvd52FmPUGmoSmvUZAtlErbDLc/gtakrUpIKsaFhBqirFi50vBh2KSMEoUYuKdLZFbRaTCWrUohYGHUMdpKpSpBKpwp20bhHEEtC7r3DnFAm5mMXYuHCjluiQSFGiFhXpPm87m8kE1ZpMEAZHh44WdnwaQCwGTSugZ29hzysScqc2ezM/VUpKokKJWlRkx6glZzfrMz2WYWRMv9CC1DFc4MVus5pWKVGTirNx4UYGRgfY16/WZIkGJWpRMYcWtWxhdnV/BqtjqKOw49OymlZBz57Cn1ckxE5rPg1AC99KZChRi4qJRG02Y9QSAFqiI2AFLx+V1bQS+g7AuCaMSOXY0LyBmMW08K1EhhK1qJhYnmN2XZ8AvZr5GZj0eJq+kb7iJWou4yVrIhWitqqW1Q2rNfNTIkOJWlRkW9QSdXm/pEFdn4ErSlWCrKaV3lbj1KTCnLbwNM38lMhQohYV6X5vDbVY/v+k9X6Lmro+g1OUqgRZC1Z7226NU5PKsnHhRvb176N3pDfoUETmTYlaVKR7Z9XtCd6CtwB9aXV9BqUoi91mNa7wtppQIBXm1OZTAU0okGhQohYVI/2zqkoAObM+1aIWmKKUj8pKpiDVoq5PqTinLzwdgBc6Xwg4EpH5U6IWFem+ObSoeYlan8aoBSY7Rm1h7cLivEHTSiVqUnEWpRaxJLWErR1bgw5FZN6UqEVFun9WS3MAVFfFSMRN1QkC1DHUQXN1M4lYojhvoEVvpUJtat3Ecx3PBR2GyLwpUYuKkX6obpzVS8yM+uoqdX0GqGiL3WZlF711rnjvIRJCm1o3sbtvNz3pnqBDEZkXJWpRke6d9Rg1UGH2oBWtfFRW00oviR/uLt57iITQptZNAGpVk7KnRC0q5jBGDaChOkGfFrwNTFEKsufSWmpSoc5oOQOAZ48+G3AkIvOjRC0KMuMw3AO1zbN+aX1NlcaoBcQ5V7zyUVkLVnlbJWpSYRqTjbQ1tmlCgZQ9JWpRMNzjlQpKzX7mYKO6PgPTP9pPejxd5BY1JWpSuTShQKJAiVoUDHZ62zks8VBfrRa1oBR1sdusVCvEq6F7d/HeQySkNrVu4sjQEQ4NHAo6FJE5CyRRM7M3mNk2M9tuZh+Z5Pk/MLPnzWyLmT1oZmuCiLNsDPmJ2hxa1DSZIDhFLR+VFYtB0wq1qElFyk4oeLZD49SkfJU8UTOzOPAPwDXAGcA7zOyMEw57CrjAObcZ+Dbw16WNsswMzj1Ra6hJaHmOgEwUZC9GVYJcWktNKtRpC0+jyqo0oUDKWhAtahcB251zLzvnRoDbgDfnHuCc+5FzbtB/+DCwssQxlpeh+XV9joxnGB4dL3BQMpOStKiBEjWpWNXxak5pPkUTCqSsBZGorQByq0Tv9fdN5beAeyd7wszeY2aPm9njR44cKWCIZWbQa5mZW4uaX+9T3Z8l1zHUQVWsisZZLlQ8a00roe8AjGsZFqk8m1o38XzH82RcJuhQROYkiETNJtk36bLpZvZO4ALgM5M975z7snPuAufcBYsWLSpgiGVmsBNiVbOuTAA5iZq6P0uuY6iDlpoWYlbkH8OmlYCD3n3FfR+RENrUuom+0T529e4KOhSROQkiUdsLrMp5vBLYf+JBZvY64GPA9c65dIliK09Dnd4aajZZDjy9+mqvxqRmfpbe4cHDLKotwX8wtJaaVLCzWs8CYMuRLQFHIjI3QSRqjwGnmNlaM0sCNwJ35R5gZucCX8JL0g4HEGN5Geyc0/g08MaoAfSl1S1WagcGDrCsflnx3yi7llr3numPE4mg9QvW05hs5MnDTwYdisiclDxRc86NAR8A7gNeAO5wzj1nZp8ws+v9wz4D1AP/aWZPm9ldU5xOAIa6IDW3tbiyXZ9qUSst5xwHBg6won664ZkF0rQKLAadLxf/vURCJmYxzl18Lk8eUqIm5akqiDd1zt0D3HPCvj/Nuf+6kgdVzgY7YeHaOb20qdbr+uwZVItaKR0dPkp6PM2yuhK0qFUlYcEaOLq9+O8lEkLnLTmPn+z9SfFLtokUgSoTRMHg0TnVwcGQ9AAAIABJREFU+QRoqU8C0Dk4UsiIZAb7+71hmcvrl5fmDVs2QOeO0ryXSMict/g8AJ4+/HTAkYjMnhK1cuecN5lgDktzANQm4lRXxegcUKJWSvsHSp2orYejO7zvi0iFObPlTKrj1Txx6ImgQxGZNSVq5W5kAMZH5jyZwMxoqUtytF+JWilNtKjVlbBFbaQf+lXzUCpPIp7grNazNKFAypIStXI3jzqfWc11SbrU9VlS+/v305BsoD5ZX5o3bFnvbTVOTSrUeUvO48XOFxkYHQg6FJFZUaJW7ibqfM5t1ifAwrokR9X1WVIlm/GZ1bLB2x7VODWpTOcvPp+My/DM4WeCDkVkVpSolbt51PnMaqlL0jmgNYVLaX///tLM+MxqXAnxarWoScXavGgzMYvxxGGNU5PyokSt3A0WqOtzQMtzlIpzjv39+0s3kQAgFoOF69SiJhWrPlnPxuaNPHX4qaBDEZkVJWrlbrAwLWr96THSY+MFCkqm0zvSy+DYYOkmEmS1rFeLmlS085ecz5YjWxgd139MpXwoUSt3E12fc1tHDWBhXTWAlugokZKvoZbVsh66dkJGCblUpvOWnEd6PM2zR58NOhSRvClRK3eDnVDTBPG5F5lYWOdVJ1CiVhrZRK0kdT5ztWzwlnLpUc1PqUwXLrkQw3h4/8NBhyKSNyVq5W5o7gXZs9SiVlrZxW5X1JVw1ifkzPxU96dUpgU1Czij5Qx+ceAXQYcikjclauVucO5VCbIW1vllpJSolcT+/v3UVtXSVN1U2jfWEh0iXLb8MrYc2ULfSF/QoYjkRYlauRs8WoAWNSVqpbS/fz/L65ZjZqV947pFkGxQi5pUtEuXX8q4G+fRg48GHYpIXpSolbt51PnMWlCbIGZK1ErlwMCB0k8kADA7VvNTpEKds+gcaqtq+cV+dX9KeVCiVu4Gu+bdohaLGc2ppBK1Etk/UOI11HK1bFCLmlS0RDzBhUsvVKImZUOJWjkbG4GRvnmVj8pqrlOiVgoDowP0pHtKW5UgV8t66N4NY6pEIZXrsuWXsbtvN3v6NANawk+JWjkb6vK2qbmvoZalep+lkV2ao6R1PnO1bAAcdO4M5v1FQuDS5ZcCqFVNyoIStXJWgDqfWQtTSbqUqBXdgYEDQABrqGW1rPe2R18K5v1FQmBt41qW1i1VoiZlQYlaORs86m3nOZkAYGG9uj5LYaIqQanLR2W1bgQMDj0fzPuLhICZcdnyy3jk4COMZcaCDkdkWkrUylkB6nxmtdQl6RocIZNx8z6XTG1//36SsSQttfMfVzgn1fVe9+fBLcG8v0hIXLr8UvpG+tjasTXoUESmpUStnGW7PgvQotacSpJx0DOkYsXFtLd/L8vqlxGzAH/0lp6lRE0q3uXLL6cqVsUPd/8w6FBEpqVErZwVskWt3lv0VhMKimt3727WNK4JNoilZ3kzP4e6g41DJEANyQYuXnoxD+5+EOfUkyDhpUStnA11QlUtJFPzPpWqExRfxmXY3bebtsa2YANZttnbHlSXj1S216x+DXv69rC9W2sLSngpUStng10F6fYEr+sTlKgV0+HBwwyNDYWgRU2JmgjAq1e9GkDdnxJqStTKWQHqfGZluz6VqBVPe287QPAtavWLoX6JEjWpeItSi9i8aDMP7n4w6FBEpqRErZwNdRZksVvIbVHTivXFsqtnF0DwLWrgTyhQoiby2tWv5YXOFzjQfyDoUEQmpUStnA12FqR8FEBNIk5dMk7ngGZ9Fkt7bzu1VbUsTi0OOhSv+/PICyolJRXvNateA8AP96j7U8JJiVo56z8EdYX7o+8teqs/3MWyq3cXaxrXYGZBh+K1qGXG4MiLQUciEqi2pjbWN63XODUJLSVq5Wq4F9K90FS4mpEL66q1PEcRZRO1UNCEApEJr1n9Gp449ARdw11BhyJyEiVq5arXK0VEYwETtVSCrkElasUwOj7Kvv594UnUFq6DRJ0SNRHg6rarGXfj3Nd+X9ChiJxEiVq56t3rbQuZqNVV09mvRK0Y9vbvZdyNBz/jMysWg6Wb4IAqFIhsbN7IKc2ncPeOu4MOReQkStTKVc8+b1vArs+W+iRHB0a0SncR7OoN0YzPrOzMz0wm6EhEAmVmXLfuOrZ0bKG9pz3ocESOo0StXPXuAwwalhXslM2pJOmxDEOj4wU7p3iyv/zDlahthpE+6N4VdCQigbt23bXELMbdL6tVTcJFiVq56tkHDUshnijYKVv8MlJH1f1ZcO297TRXN9NU3RR0KMdkS0ntfzLYOERCYHFqMRcvvZjvv/x9Mk6tzBIeStTKVe/ego5PA2hWvc+i2dW7i7amtqDDON6SsyDZALt+HnQkIqFw3frr2Ne/jycP6T8vEh5K1MpV7/6Cjk+DY2WkOvq1llqhhWppjqx4Fay+GNp/FnQkIqHw2tWvpbaqlv9++b+DDkVkghK1cuSc1/VZ4Ba1lc21AOzpHCzoeSvdwOgAR4aOhC9RA1hzmVehYOBo0JGIBC6VSHHVmqu4r/0+hsaGgg5HBFCiVp6Gu2F0oOCJ2qL6alLJOO1HlagVUnbGZ2iW5si15gpvu0utaiIAb9nwFvpH+7l3571BhyICKFErT0VYmgO8KeprWurYdXSgoOetdKFcmiNr+blQVatxaiK+C5ZcwIYFG/jWC9/SUkUSCkrUylGvn6g1riz4qdtaUuxSi1pBtfe2YxirGlYFHcrJqpKw6iLY9VDQkYiEgpnxa6f/Gtu6tvHkYU0qkOApUStHPX5VggK3qAGsaaljT9cgY+Oanl4oL3W9xIr6FdRU1QQdyuTaroCDz8KQ6hyKAFy79loakg1864VvBR2KiBK1stS7HywO9UsKfuq1rSlGxx0HeoYLfu5KteXIFs5qPSvoMKa25jLAwe6Hg45EJBRSiRRv3fBWHtz9IAcHDgYdjlQ4JWrlqHefV5EgFi/4qde01AHQrnFqBXF48DCHBg9x1qIQJ2orLoB4tSYUiOS44bQbyLgMd2y7I+hQpMIpUStHPXuL0u0J0OYnahqnVhhbj2wFCHeLWqIGVl6g9dREcqxqWMUrV76SO1+6k+Ex9TBIcJSolaPewq+hlrW4oZqaREwzPwtkS8cWqmJVnN5yetChTG/N5XDgGUj3BR2JSGi8+8x30zncyZ0v3Rl0KFLBlKiVG+eKUpUgKxYz1iys01pqBbK1YysbmzdSHa8OOpTptV0Bbhx2/jToSERC48KlF3Lh0gv5l63/olY1CYwStXIzeBTGhouyNEfWmpaUWtQKYDwzznMdz4W72zNr9aVQ0wQv3B10JCKhcvPZN3Nk6Iha1SQwStTKzcQaasuL9hZtrXXsOjpIJqPFHudjR88OBscG2bxoc9ChzKwqCRvfCNvugfHRoKMRCY3cVrX0uOogS+kpUSs3RapKkGtNS4r0WIZDfWrqn4+ymEiQ6/TrvfJk7er+FMmVbVX79i+/HXQoUoGUqJWbIlYlyMrO/Gzv0Di1+djasZXGZGM4S0dNZv2rIVGn7k+RE+S2qg2O6veilJYStXLTsxdiCahbVLS3WNOSAtA4tXna0uEtdGtmQYeSn0QtnHo1vPDfkBkPOhqRUPm9c3+PI0NH+MrWrwQdilQYJWrlpnefNz4tVrx/umVNtSTjMc38nIfB0UF2dO8I90K3kzn9Ohg4DHseCToSkVA5Z/E5vGndm/jac19jT++eoMORCqJErdz0FG8Ntax4zFi1sFYtavPw3NHnyLhM+YxPyzrlaq9Kgbo/RU7y++f/PlWxKj7z+GeCDkUqiBK1ctP5MjQXf8xTW4vWUpuPZ448A5TRRIKs6gbY8FovUXOa9SuSa3FqMe/d/F5+tOdH/GyfKnlIaShRKyf9R6D/ICwt/h//NS117Do6gNMf6zl55MAjrG9aT3NNc9ChzN7p10HPHnV/ikziXWe8i9UNq7nl0Vu0CK6UhBK1cnLIW+6BJZuK/lZtrSkGR8Y50q91g2ZrcHSQJw49wRUrrgg6lLk5/XqoboJH/znoSERCJxlP8rGLP0Z7bztfeOoLQYcjFUCJWjk56CdqJWhRyy7Rsf1wf9HfK2oeO/gYo5lRLl9xedChzE11PZz7Tnj+e9B7IOhoRELnshWXccPGG/jm89/k0QOPBh2ORJwStXJycKu3flpqYdHf6uyVCzCDx3Z2Ff29ouan+35KbVUt5y85P+hQ5u6i3/aW6Hjiq0FHIhJKf3D+H7CmcQ1/8rM/oW+kL+hwJMKUqJWTg8+WpDUNoCmV4IxljTz88tGSvF9UOOd4aN9DXLz0YpLxZNDhzN3CdXDq6+Hxr8KYur9FTpRKpPjkFZ/k0OAhPvXIpzSeV4pGiVq5GB2Cjl/C0uKPT8u6dF0LT+zuYnhUi5/ma1fvLvb17yvfbs9cF73HW1Ptue8FHYlIKJ296Gzeu/m93P3y3dy+7fagw5GIUqJWLg6/AG68ZC1qAJesa2FkLMPTe7pL9p7l7qF9DwFEI1Fb/xpoPRUe/VLQkYiE1ns3v5dXrHwFn3700zx28LGgw5EIUqJWLg49621LmKhduHYhZqj7cxYe2v8QbY1trGpYFXQo82fmtartewJ2/CjoaERCKR6Lc8uVt7CqcRUf/vGH2de/L+iQJGKUqJWLg1sh2QAL2kr2lk21Cc5crnFq+RoeG+bxg4+X77Ickzn3XbBgNdz3MdX/FJlCQ7KBL7z6C4xlxvjAgx+ge1i9EFI4StTKxcGt3vi0Itb4nMwla1t4cne3xqnl4fFDj5MeT0crUUvUwFV/AYefgye/EXQ0IqHV1tTG51/9eXb37uZ9D7xPM0GlYJSolYNMxpvxWYKFbk+kcWr5+8HOH5T/shyTOePNsPoy+OFfwnBP0NGIhNYlyy7h86/6PNs6t/H+B97P4KjK8Mn8KVErB927YKSvpOPTsjROLT9dw13cu/Nerl9/PTVVNUGHU1hm8Ia/gsGj8NPPBR2NSKi9ctUr+fQrPs2Wji3c/MDN9I70Bh2SlDklauWghBUJTpQdp/aLHUrUpnPnS3cykhnhHae9I+hQimP5uXD2O+Dhfzr2fRSRSV3ddjW3XHkLWzq2cNO9N3GgXxU+ZO6UqJWDg1vB4rD49EDe/tJ1LTy1R+PUpjKWGeP2bbdz8dKLWb9gfdDhFM9Vn4BUC9xxEwyrlUBkOtesvYZbX3crBwcO8s573smLnS8GHZKUKSVq5eDgFmg9BRK1gbz95RtaGRnLcP/zhwJ5/7D7yZ6fcHDgIO84PaKtaVn1i+Bt/wJd7XD3B0ErsYtM6+JlF/P1a76OmfGue97Fd176jioYyKwpUQu7dD/s/F9YfWlgIVx5yiLWLarjn368Q79kJvGtF7/F8rrlvGrlq4IOpfjaLofX/Ak89x147CtBRyMSeqc2n8ptb7qNsxefzZ/9/M/46EMfZWB0IOiwpIwoUQu7F+6G0UE4+8bAQojHjPe9cj3PH+jlJ788ElgcYbS9azuPHnyUG067gXgsHnQ4pXH5h+CUq+EHH4VtPwg6GpHQa61t5Uuv+xK/e87vcu/Oe3nbXW+bqGIiMhMlamH3zH9AcxusujjQMN5yzgqWNdXwjz/aEWgcYeKc47NPfJbaqlreuuGtQYdTOrEYvPWfvXX9bn8nbLs36IhEQi8ei/O+s9/HV1//VRKxBDc/cDN/9L9/RMdQR9ChScgpUQuznr1et+fmG70lEgKUrIrxO1eu49H2Th5v7ww0lrC4++W7+dm+n/HB8z7IgpoFQYdTWrUL4F3f82Yi3/4uePGeoCMSKQvnLTmPO6+/k/ef/X4e2PUAb/zOG/niU1+kf6Q/6NAkpJSohdmWOwAHZ98QdCQA3HjRKppTCf7xx2pV6xjq4NOPfppzF58b3SU5ZlK7AN79PVi22WtZ++nnvMWZRWRayXiSm8+5me+++bu8YuUr+NKWL3HNd67hK1u/Qk9ai0rL8ZSohZVzsOV2WHUJLFwXdDQApJJV/Obla/nhi4f54YuVPQP0kw9/kuGxYf78sj8nZhX8Y1TTBO/+L696wYOfgH9/O/RrHKNIPtY0ruGzr/wst117G2e2nMnfPfl3XPXtq/jUI5+ivac96PAkJCr4L0zIHXgajrwY6CSCyfz2les4c3kjH/yPp9l+uDJr2d2x7Q4e2P0AN59zM2ub1gYdTvCqG+Dt/wpv+htofwj+6VJ44msq4i6SpzNbz+TWq27l29d9m6vWXMUd2+7guu9dx0333sR3X/quukUrnEVluYULLrjAPf7440GHUTjf/zA8+U34w21Q2xx0NMfZ1z3Em7/4EA01Cb73/stpSiWCDqlk/uPF/+CvHvkrrlhxBX//mr+nKlYVdEjhcnCr993d84hXm/Z1fw4bXhv4GEuRcnJk8Ah37biL723/Hu297SRiCS5dfimvW/06rlx5Ja21rUGHKAVgZk845y6Y8TglaiH08o/hm78C5/w6vPmLQUczqcfaO/m1f36Yi9e2cOu7zqe+OvoJy9ef+zqfffyzvHrVq/nsKz9LMp4MOqRwcg6e+y7c/2fQsxsWnQ4Xvwc23wDJuqCjEykbzjmeOfIM9++6nwd2PcD+gf0AbGzeyGXLL+Pcxedy1qKzlLiVKSVq5ap3P9x6pVeq53d+CNX1QUc0pTse28Mff2cLKxbU8pm3n82l61uCDqko9vfv52+f+Fvubb+Xq9dczS2vuIVErHJaEedsdBievRMeudWrrpGog1Ov9sazbbgq1N9tkbBxzvFi54v8bP/P+Pn+n/PU4acYy4wBsLxuOWctOouzWs9i86LNbFiwgYZkQ8ARy0yUqJWjsRH42rVw+Hn4nR/BolODjmhGj+7s5P/79jPsOjrIuy5Zw29dsZa21mi0mnQMdfCtF77FN57/BgC/sek3eO/m96q7c7ac87pCn7nNW8B5sANiVbD8PFh7pTdhZtlmaFgadKQiZWNobIjnjz7P1iNb2dKxha0dWzk4cHDi+UW1i1jbtHbi1tbYxrK6ZSytW0oqkQowcskKdaJmZm8A/g6IA19xzt1ywvPVwDeA84GjwA3Oufbpzln2idrRHfA//w+2fR/e/lXYVD4LqA6OjPHpe1/kmw/vIuPgoraFvOXcFVy0diHrWuuIxcpnfNLBgYM8cuAR7tl5Dw8feJiMy3Dtumv50HkfYmmdEol5y4zDrp/Djge9iQf7ngTnTzqoWwyLT/MWeD7uttYbp6lxbiLTOjJ4hGc7nmVn70529ni3l3tepm/k+IlfjclGltYtZWndUpakltBc00xzdTNN1U0T9xfULKC5upnaqlpMP3tFEdpEzcziwC+Bq4C9wGPAO5xzz+cc835gs3PufWZ2I/ArzrlpFxMry0RtuAeObIOn/s27xZPw6o/C5R8MOrI5OdQ7zJ1P7uU/H9/Lzg6vll1TbYKzVjSxpiXFmpYUy5pqWZBKsKA2SVNtgqbaBA01VSVL5pxz9I320TXcRedwJ3v79rK7bzftPe08c+QZDgwcAGBF/QquXXct1667lnVN4VgeJZLS/XDgGa9r9MAWOPqSV/R94IQlPuLV3nCAuhZItUJdq/e4utEb95asg2Q9JFM59+sgkYKqaoglIO7fYgnvZy2mSe8Sfc45Ooc72dW7iwMDBzg4cPDYbfAghwcP053uJuMmXwMxEUvQVN1EXaKOVFXK2yZS1FV521TC21dbVUt1vJpkPEkyljx2P37sfnW8mmTM25eIJYjH4sQtTjwWp8qqjj22eEUkh2FO1C4FPu6ce73/+KMAzrlP5Rxzn3/ML8ysCjgILHLTBLt0XYP79U+cc9y+k4+e/OVuikeTHe0mecJNcfTJb+/AjXmtCuMjMDrk7Y7FoGkVLFzv/VGZeP0k55zkEkx23JT7J92V3/tMeewkF2RwdIy+oTH60mMMpMcYHh1nLOMmDwCvnmjMwDDMvMaTmIGZ9ziGgf9ze9yPrx37UCf+WDsbI8OIf0sz7m9PjsGopoUGW0cDG2iyU6ljTWh+UYQkjFmxk/41Zqc6M8TC0YO0ju6ndXQ/TeNHqR/roT7TQ/14N/Xj3rY2Mzjn98gQY8yqGLcqxvG3VoXDcBbDYWSIHffYEcNZzn7/sTvuOCYeZywG2AnfuGPXxp10nXKey3lq2uOmudZuquNO+FLlH59EUQbHoGXoj2Xot3H6Yhn6bJz+mHd/wMYZNsewZXK2/v1YhrQVPo+IOYhjxIC4836jxIGYM2+LTezPfkuz//UyDHNMPHfsefOfz7k5m+T1/jlg4jyQ+5Mx2b2T/wbl7pvsua+999G8ErUgBtusAPbkPN4LnFjIcuIY59yYmfUALcBxRdHM7D3AewAa19SwfeSEFZ3Nu8gnOv4P/fS/iKa78DPt8/af8IzFsHgMEvVQ3wJVNd7/+uMJGOmBkRMOnyS+yf4ITvWHMd/XT75rinNO9v4nvE9VHBbWx1lYHwe85HMsk2F03DGecYyNO8YyjrFMhvGMYzzjJYcOL5/NOOfltTmPyT7OfSMHzmV/5I5Pss2lMLeAmEsQJ0kyk8RIYpkUMVdPzNVTNd5CPLMQw5scMOzfYGDSz15q5TiEtHAht/q3zd7D7G/q+LEjzGWoZoQaN0Qtw9S6YWrcsH9/iBqXJsEoVYwRd+MkGKMqe3PjxBmjyo3ipWpjVLkxL8VyXhrmpWAZzPnbbArmjqVqx9K23H3jxx032dWxE9KgqVKnqdO8E5/L77gTz0eex033OqlsGSBtMJpzGzEYxd/m7Ms+HjPvdeMG40DG33qPzX/scvYdOya7HfO/5M6PAf+56fa53Ofs+H25z7lJnjvR8f+ZOn573HFT3M9XEInaZH/9T27imPkYnHNfBr4MXtfnf/1mmXV9ioiISEWy9+TXYh3EII29wKqcxyuB/VMd43d9NgGqBC4iIiIVJYhE7THgFDNba2ZJ4EbgrhOOuQu4yb//duCH041PExEREYmiknd9+mPOPgDchzfa5F+dc8+Z2SeAx51zdwH/AnzTzLbjtaSFq+CliIiISAkEsnKnc+4e4J4T9v1pzv1h4P+UOi4RERGRMNFCQiIiIiIhpURNREREJKSUqImIiIiElBI1ERERkZBSoiYiIiISUkrUREREREJKiZqIiIhISClRExEREQkpJWoiIiIiIaVETURERCSklKiJiIiIhJQSNREREZGQUqImIiIiElJK1ERERERCSomaiIiISEgpURMREREJKSVqIiIiIiGlRE1EREQkpJSoiYiIiISUOeeCjqEgzOwIsCvoOGahFegIOogyoOuUH12n/Og6zUzXKD+6TvnRdZraGufcopkOikyiVm7M7HHn3AVBxxF2uk750XXKj67TzHSN8qPrlB9dp/lT16eIiIhISClRExEREQkpJWrB+XLQAZQJXaf86DrlR9dpZrpG+dF1yo+u0zxpjJqIiIhISKlFTURERCSklKiJiIiIhJQStQIxs1Vm9iMze8HMnjOzD/r7P25m+8zsaf/2xpzXfNTMtpvZNjN7fc7+N/j7tpvZR4L4PMVkZu1mttW/Ho/7+xaa2f1m9pK/bfb3m5l9wb8WW8zsvJzz3OQf/5KZ3RTU5ykGM9uY85152sx6zexD+j6Bmf2rmR02s2dz9hXs+2Nm5/vfz+3+a620n7AwprhOnzGzF/1r8V0zW+DvbzOzoZzv1a05r5n0ekx1zcvNFNepYD9nZrbWzB7xr9PtZpYs3acrjCmu0e0516fdzJ7291fsd6lonHO6FeAGLAPO8+83AL8EzgA+DvzhJMefATwDVANrgR1A3L/tANYBSf+YM4L+fAW+Vu1A6wn7/hr4iH//I8Cn/ftvBO4FDLgEeMTfvxB42d82+/ebg/5sRbpeceAgsEbfJwfwCuA84NlifH+AR4FL/dfcC1wT9Gcu4HW6Gqjy73865zq15R53wnkmvR5TXfNyu01xnQr2cwbcAdzo378VuDnoz1yIa3TC858D/rTSv0vFuqlFrUCccwecc0/69/uAF4AV07zkzcBtzrm0c24nsB24yL9td8697JwbAW7zj426NwNf9+9/HXhLzv5vOM/DwAIzWwa8HrjfOdfpnOsC7gfeUOqgS+S1wA7n3HSVNyrm++Sc+1+g84TdBfn++M81Oud+4by/Gt/IOVdZmew6Oef+xzk35j98GFg53TlmuB5TXfOyMsX3aSqz+jnzW4xeA3zbf31ZXqfprpH/GX8V+I/pzlEJ36ViUaJWBGbWBpwLPOLv+oDf1fCvOU26K4A9OS/b6++ban+UOOB/zOwJM3uPv2+Jc+4AeEkvsNjfX8nXKetGjv8lqO/TyQr1/Vnh3z9xfxT9Jl6rRtZaM3vKzH5iZlf6+6a7HlNd86goxM9ZC9CdkxxH8ft0JXDIOfdSzj59lwpIiVqBmVk9cCfwIedcL/BPwHrgHOAAXhMxeE2/J3LT7I+Sy51z5wHXAL9rZq+Y5thKvk7441muB/7T36Xv0+zM9rpUxPUys48BY8C/+7sOAKudc+cCfwB8y8waqZDrMYlC/ZxVwvV7B8f/R1LfpQJTolZAZpbAS9L+3Tn3HQDn3CHn3LhzLgP8M14TOXj/m1iV8/KVwP5p9keGc26/vz0MfBfvmhzym8azTeSH/cMr9jr5rgGedM4dAn2fplGo789eju8OjNz18idOvAn4db8LCr8r76h//wm88VanMv31mOqal70C/px14HW3V52wPxL8z/VW4PbsPn2XCk+JWoH4/fT/ArzgnPt8zv5lOYf9CpCdNXMXcKOZVZvZWuAUvIGWjwGn+DOFknjdXneV4jOUgpnVmVlD9j7e4OZn8T5jdubdTcB/+ffvAt5tnkuAHr9p/D7gajNr9rslrvb3Rc1x/1vV92lKBfn++M/1mdkl/s/0u3POVfbM7A3AHwPXO+cGc/YvMrO4f38d3vfn5Rmux1TXvOwV6ufMT4R/BLzdf32krhPwOuBF59xEl6Yc3h9lAAAGK0lEQVS+S0UQ9GyGqNyAK/CacbcAT/u3NwLfBLb6++8CluW85mN4/9vYRs7MMv91v/Sf+1jQn63A12kd3oyoZ4Dnsp8PbyzHg8BL/nahv9+Af/CvxVbggpxz/SbeYN7twG8E/dmKcK1SwFGgKWdfxX+f8BLXA8Ao3v/Sf6uQ3x/gArw/zDuAL+JXcCm32xTXaTveWKrs76hb/WPf5v88PgM8CVw30/WY6pqX222K61SwnzP/d96j/rX/T6A66M9ciGvk7/8a8L4Tjq3Y71KxbiohJSIiIhJS6voUERERCSklaiIiIiIhpURNREREJKSUqImIiIiElBI1ERERkZBSoiYiBWdmrzKz//bvX29mH8nj+MtyHr/PzN49zxg+ZmZP+7fxnPu/N5/zFpOZrTOzG4t4/n8zs51m9tv+4780sw/592vN7If+dWvwr9WImS0oVjwiMrOqmQ8REZlY1Nmct1p73pxzdzHzIruvAvqBn/uvuXUuMZ7wvp8EPglgZv3OuXPme85CMLMqd6z244nW4S2Wetsszxl3zo3nefjvO+e+d8Lrq/GqhPzcv24A55jZ3pNeLSIlpRY1EZmSmbWZ2Qtm9o94i1euMrN/MrPHzew5M/vznGPfYGYvmtlDeGVlsvv/r5l90b9/nZk94hdsfsDMlphZG/A+4Pf9VpwrzezjZvaHZna6mT16Qjxb/Pvnm1f0+Qkzu++E1eRn+lxLzOw7/ud41K9akG1h+pqZ/Y+ZtZvZW8zsc2b2rJl93/xSQGa218xu8V/7iL8C+0zn/ZKZ3Q981czWm9lP/evwhJld7Id2C/DqbMufmf22mf1tTtw/MLMrzKzKzLr98z4KXGRmF+Zcj3vNbEmelyMB3AE855z7k3yvoYiUhhI1EZnJRuAbzrlznXO78FZdvwDYDLzSzDabWQ1eTcTrgCuBpVOc6yHgEucVbL4N+CPnXDtwK/A3zrlznHM/zR7snHsBSGYTIeAG4A7z6ur+PfB259z5wL/it57l6QvAX/uf41eBr+Q8txZvlfm3Ad8CfuCc2wRkgDfkHNflnLsI+BKQLRs33XnPxVul/V14q7xf5V+HX/dfB/AR4Ef+dfgC02vCqwN7EV4S/XfA2/zr8W/AX+R3KfgoMOCc+3Cex4tICanrU0Rmsss593DO4181s/fg/f5YBpyB95++nc65l8AbCwW8Z5JzrQRu91u/ksDOPN7/Dryk5xa8RO0GvORxE3C/1yNLHC/5ydfrgI3+awGazazWv3+Pc27MzLYCOOfu9/dvBdpyzpGtwfrvfmwznfe/nHPD/v1q4ItmdjYwBqyfRexZI3jdlQCnA2cCD+Rcj3y7Lf8XuMLMNjjnts8hDhEpIiVqIjKTgewd8wpR/yFwoXOuy8y+BtT4T+dTj+7vgc875+4ys1cBH8/jNbcD/2lm3wGcc+4lMzsLr6vu0vw/xnEMuMg5N3LcTi/JSfsPM3jJEDmPc39nTvZ5pzvvQM6uD+PV3HwnXtdj/xRxjnF8z0dNzv0hd6wGoAFbnHNXTnGe6fwYL+m818yudM4dnMM5RKRI1PUpIrPRiJdw9PhjoK7x978IrDWzbMvQO6Z4fROwz79/U87+PqBhshc453YA48D/w0vawCuIvcjMLgUws4SZnTmLz/EA8LvZB2Y2l4kGN/jbdwA/m+V5m4ADfqJ1E16iBSdfh3bgXPO0AedPcb7ngRVmdpH/vsnZXA/n3O14Xaf3mlljvq8TkeJToiYieXPOPQM8BTyHNy7sZ/7+Ybyuzu/7kwl2TXGKj+O1jv0U6MjZfzfwK9nJBJO87na81qc7/PcbAd4OfNrMngGeBi6b5HVT+V3gcjPbYmbPA78zi9dmpfyB/DfjtZDN5rxfBH7bzB4G1nCsFe8pIG5mz5i3jMhP8BLbrXjdq09PdjLnXBrvenzevx5PARdPduxUnHNfBL4P/Jd5s0BFJATsWMu5iIjkw7xlKzY557qDjmU2/LGD3z5xeY5pji/LzykSJWpRExGpHN3Ap8xf8HYq5i94i9clO6t180SksNSiJiIiIhJSalETERERCSklaiIiIiIhpURNREREJKSUqImIiIiElBI1ERERkZD6/wHwZLy0MFdVwgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 720x720 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"%pylab inline\n",
"\n",
"fig = figure(0, figsize=(10, 10))\n",
"ax = fig.add_subplot(111)\n",
"si_ionization_state.T.iloc[:, :3].plot(ax=ax)\n",
"xlabel('radiative Temperature [K]')\n",
"ylabel('Number density [1/cm$^3$]')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.8"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
kriukov/interval-methods | ipynb/asin-extension.ipynb | 1 | 388777 | {
"metadata": {
"language": "Julia",
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Resolution of the asin() problemResolution of the asin() problem"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's take the example function"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f(x) = asin(x)/x - pi/3"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 1,
"text": [
"f (generic function with 1 method)"
]
}
],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It has two symmetrical roots, -1/2 and 1/2."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The zero-finding algorithms will encounter the roots as long as we start with the intervals fitting in the domain of arcsin:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"using KrawczykMethod"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Syntax: krawczyk(function, Interval(lo, hi), precision [default is 64])\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"krawczyk(f, Interval(-0.9, 0.9))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Unique zero in Interval(-4.99999999999999468768e-01 with 64 bits of precision,-4.99999999999999462507e-01 with 64 bits of precision)\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Maybe a zero in Interval(-3.12198595744902126454e-15 with 64 bits of precision,-2.32258541169002204847e-15 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(-2.32258541169002204885e-15 with 64 bits of precision,-1.52318486593102283268e-15 with 64 bits of precision)\n",
"Maybe a zero in Interval(-1.52318486593102283287e-15 with 64 bits of precision,-7.23784320172023617034e-16 with 64 bits of precision)\n",
"Maybe a zero in Interval(-7.23784320172023617226e-16 with 64 bits of precision,7.56162255869755988157e-17 with 64 bits of precision)\n",
"Maybe a zero in Interval(7.56162255869755988037e-17 with 64 bits of precision,8.75016771345974814737e-16 with 64 bits of precision)\n",
"Maybe a zero in Interval(8.75016771345974814689e-16 with 64 bits of precision,1.67441731710497403067e-15 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.67441731710497403048e-15 with 64 bits of precision,2.47381786286397324665e-15 with 64 bits of precision)\n",
"Maybe a zero in Interval(2.47381786286397324646e-15 with 64 bits of precision,3.27321840862297246234e-15 with 64 bits of precision)\n",
"Unique zero in Interval(4.99999999999999461721e-01 with 64 bits of precision,4.99999999999999468741e-01 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 3,
"text": [
"10-element Array{Any,1}:\n",
" {Interval(-4.99999999999999468768e-01 with 64 bits of precision,-4.99999999999999462507e-01 with 64 bits of precision),:unique} \n",
" {Interval(-3.12198595744902126454e-15 with 64 bits of precision,-2.32258541169002204847e-15 with 64 bits of precision),:possible}\n",
" {Interval(-2.32258541169002204885e-15 with 64 bits of precision,-1.52318486593102283268e-15 with 64 bits of precision),:possible}\n",
" {Interval(-1.52318486593102283287e-15 with 64 bits of precision,-7.23784320172023617034e-16 with 64 bits of precision),:possible}\n",
" {Interval(-7.23784320172023617226e-16 with 64 bits of precision,7.56162255869755988157e-17 with 64 bits of precision),:possible} \n",
" {Interval(7.56162255869755988037e-17 with 64 bits of precision,8.75016771345974814737e-16 with 64 bits of precision),:possible} \n",
" {Interval(8.75016771345974814689e-16 with 64 bits of precision,1.67441731710497403067e-15 with 64 bits of precision),:possible} \n",
" {Interval(1.67441731710497403048e-15 with 64 bits of precision,2.47381786286397324665e-15 with 64 bits of precision),:possible} \n",
" {Interval(2.47381786286397324646e-15 with 64 bits of precision,3.27321840862297246234e-15 with 64 bits of precision),:possible} \n",
" {Interval(4.99999999999999461721e-01 with 64 bits of precision,4.99999999999999468741e-01 with 64 bits of precision),:unique} "
]
}
],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"using NewtonMethod"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Syntax: newton(function, Interval(lo, hi), precision [default is 64])\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"newton(f, Interval(-0.9, 0.9))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Function calls: 13"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 5,
"text": [
"2-element Array{Interval,1}:\n",
" Interval(-4.99999999999999321696e-01 with 64 bits of precision,-4.99999999999999319094e-01 with 64 bits of precision)\n",
" Interval(4.99999999999999319094e-01 with 64 bits of precision,4.99999999999999321181e-01 with 64 bits of precision) "
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But if we set the interval which goes outside of the domain, we get errors."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"krawczyk(f, Interval(-2, 2))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "LoadError",
"evalue": "DomainError\nwhile loading In[6], in expression starting on line 1",
"output_type": "pyerr",
"traceback": [
"DomainError\nwhile loading In[6], in expression starting on line 1",
"",
" in asin at mpfr.jl:573",
" in asin at /home/kriukov/main/work/mexico/unam/interval-methods/modules/IntervalArithmetic.jl:507",
" in f at In[1]:1",
" in differentiate at /home/kriukov/main/work/mexico/unam/interval-methods/modules/AutoDiff.jl:101",
" in krawczyk_internal at /home/kriukov/main/work/mexico/unam/interval-methods/modules/KrawczykMethod.jl:37",
" in krawczyk at /home/kriukov/main/work/mexico/unam/interval-methods/modules/KrawczykMethod.jl:64",
" in krawczyk at /home/kriukov/main/work/mexico/unam/interval-methods/modules/KrawczykMethod.jl:25"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"newton(f, Interval(-2, 2))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "LoadError",
"evalue": "DomainError\nwhile loading In[7], in expression starting on line 1",
"output_type": "pyerr",
"traceback": [
"DomainError\nwhile loading In[7], in expression starting on line 1",
"",
" in asin at mpfr.jl:573",
" in asin at /home/kriukov/main/work/mexico/unam/interval-methods/modules/IntervalArithmetic.jl:507",
" in f at In[1]:1",
" in differentiate at /home/kriukov/main/work/mexico/unam/interval-methods/modules/AutoDiff.jl:101",
" in N at /home/kriukov/main/work/mexico/unam/interval-methods/modules/NewtonMethod.jl:16",
" in newton at /home/kriukov/main/work/mexico/unam/interval-methods/modules/NewtonMethod.jl:33",
" in newton at /home/kriukov/main/work/mexico/unam/interval-methods/modules/NewtonMethod.jl:13"
]
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can try to create an extension of asin(). One option is to set it to $-\\infty$ for $x < -1$ and to $+\\infty$ for $x > 1$. But since its derivative involved square root, we need to extend one too: "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"\tfunction arcsin(x::Real)\n",
"\t\tif abs(x) <= 1\n",
"\t\t\treturn asin(x)\n",
"\t\telseif x < -1\n",
"\t\t\treturn -Inf\n",
"\t\telseif x > 1\n",
"\t\t\treturn Inf\n",
"\t\tend\n",
"\tend\n",
"\n",
"\tfunction arcsin(x::Interval)\n",
"\t\tif x.lo >= -1 && x.lo <= 1 && x.hi <= 1 && x.hi >= -1 \n",
"\t\t\treturn Interval(asin(x.lo), asin(x.hi))\n",
"\t\telseif x.lo < -1 && x.hi <= 1 && x.hi >= -1 \n",
"\t\t\treturn Interval(-Inf, asin(x.hi))\n",
"\t\telseif x.lo >= -1 && x.lo <= 1 && x.hi > 1\n",
"\t\t\treturn Interval(asin(x.lo), Inf)\n",
"\t\telseif x.lo < -1 && x.hi > 1\n",
"\t\t\treturn Interval(-Inf, Inf)\n",
"\t\telseif x.lo < -1 && x.hi < -1 \n",
"\t\t\treturn Interval(-Inf, -Inf)\n",
"\t\telseif x.lo > 1 && x.hi > 1\n",
"\t\t\treturn Interval(Inf, Inf)\t\t\n",
"\t\tend\n",
"\tend\n",
"\t\n",
"\tfunction sqrt1(x::Real)\n",
"\t\tif x >= 0\n",
"\t\t\treturn sqrt(x)\n",
"\t\telse\n",
"\t\t\treturn -Inf\n",
"\t\tend\n",
"\tend\n",
"\t\n",
"\tfunction sqrt1(x::Interval)\n",
"\t\tif x.lo < 0 && x.hi < 0\n",
"\t\t\treturn Interval(-Inf, -Inf)\n",
"\t\telseif x.lo < 0 && x.hi >= 0\n",
"\t\t\treturn Interval(-Inf, sqrt(x.hi))\n",
"\t\telseif x.lo >= 0 && x.hi >= 0\n",
"\t\t\treturn sqrt(x)\n",
"\t\tend\n",
"\tend"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 3,
"text": [
"sqrt1 (generic function with 2 methods)"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Also add the differentiation"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"arcsin(x::Ad) = Ad(arcsin(x.u), x.up/sqrt1(1 - x.u^2))\n",
"sqrt1(x::Ad) = Ad(sqrt1(x.u), x.up/(2sqrt1(x.u)))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
"sqrt1 (generic function with 3 methods)"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"using AutoDiff"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"g(x) = arcsin(x)/x - pi/3"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 8,
"text": [
"g (generic function with 1 method)"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"krawczyk(g, Interval(0,2))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Maybe a zero in Interval(0e+00 with 64 bits of precision,8.88178419700125234072e-16 with 64 bits of precision)\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Maybe a zero in Interval(8.88178419700125233976e-16 with 64 bits of precision,1.77635683940025046795e-15 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.77635683940025046757e-15 with 64 bits of precision,2.66453525910037570183e-15 with 64 bits of precision)\n",
"Maybe a zero in Interval(2.66453525910037570145e-15 with 64 bits of precision,3.55271367880050093513e-15 with 64 bits of precision)\n",
"Unique zero in Interval(4.99999999999999465136e-01 with 64 bits of precision,4.99999999999999465407e-01 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(9.99999999999999111822e-01 with 64 bits of precision,1e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1e+00 with 64 bits of precision,1.0000000000000008885e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000088829e+00 with 64 bits of precision,1.00000000000000177657e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000177647e+00 with 64 bits of precision,1.00000000000000266464e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000266454e+00 with 64 bits of precision,1.00000000000000355282e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000355261e+00 with 64 bits of precision,1.000000000000004441e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000444078e+00 with 64 bits of precision,1.0000000000000053295e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000532918e+00 with 64 bits of precision,1.00000000000000621757e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000621747e+00 with 64 bits of precision,1.00000000000000710564e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000710554e+00 with 64 bits of precision,1.00000000000000799393e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000799371e+00 with 64 bits of precision,1.00000000000000888243e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000000888211e+00 with 64 bits of precision,1.0000000000000097705e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000000097704e+00 with 64 bits of precision,1.00000000000001065857e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001065836e+00 with 64 bits of precision,1.00000000000001154664e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001154654e+00 with 64 bits of precision,1.00000000000001243471e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001243461e+00 with 64 bits of precision,1.00000000000001332289e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001332268e+00 with 64 bits of precision,1.00000000000001421107e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001421075e+00 with 64 bits of precision,1.00000000000001509914e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001509892e+00 with 64 bits of precision,1.00000000000001598775e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001598732e+00 with 64 bits of precision,1.00000000000001687582e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001687561e+00 with 64 bits of precision,1.00000000000001776389e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001776379e+00 with 64 bits of precision,1.00000000000001865218e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001865196e+00 with 64 bits of precision,1.00000000000001954068e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000001954036e+00 with 64 bits of precision,1.00000000000002042875e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002042865e+00 with 64 bits of precision,1.00000000000002131682e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000213165e+00 with 64 bits of precision,1.00000000000002220489e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002220479e+00 with 64 bits of precision,1.00000000000002309296e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002309286e+00 with 64 bits of precision,1.00000000000002398114e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002398093e+00 with 64 bits of precision,1.00000000000002486932e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000024869e+00 with 64 bits of precision,1.00000000000002575739e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002575717e+00 with 64 bits of precision,1.00000000000002664589e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002664557e+00 with 64 bits of precision,1.00000000000002753396e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002753386e+00 with 64 bits of precision,1.00000000000002842203e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000002842193e+00 with 64 bits of precision,1.00000000000002931032e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000293101e+00 with 64 bits of precision,1.00000000000003019893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000301985e+00 with 64 bits of precision,1.000000000000031087e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003108679e+00 with 64 bits of precision,1.00000000000003197507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003197475e+00 with 64 bits of precision,1.00000000000003286314e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003286304e+00 with 64 bits of precision,1.00000000000003375121e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003375111e+00 with 64 bits of precision,1.00000000000003463939e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003463918e+00 with 64 bits of precision,1.00000000000003552757e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003552725e+00 with 64 bits of precision,1.00000000000003641564e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003641542e+00 with 64 bits of precision,1.00000000000003730414e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003730382e+00 with 64 bits of precision,1.00000000000003819221e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003819211e+00 with 64 bits of precision,1.00000000000003908028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003908018e+00 with 64 bits of precision,1.00000000000003996857e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000003996835e+00 with 64 bits of precision,1.00000000000004085707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004085675e+00 with 64 bits of precision,1.00000000000004174514e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004174504e+00 with 64 bits of precision,1.00000000000004263321e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004263289e+00 with 64 bits of precision,1.00000000000004352128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004352118e+00 with 64 bits of precision,1.00000000000004440935e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004440925e+00 with 64 bits of precision,1.00000000000004529753e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004529732e+00 with 64 bits of precision,1.00000000000004618571e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004618539e+00 with 64 bits of precision,1.00000000000004707411e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004707389e+00 with 64 bits of precision,1.00000000000004796239e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004796207e+00 with 64 bits of precision,1.00000000000004885046e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004885036e+00 with 64 bits of precision,1.00000000000004973853e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000004973832e+00 with 64 bits of precision,1.0000000000000506266e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000506265e+00 with 64 bits of precision,1.00000000000005151467e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005151457e+00 with 64 bits of precision,1.00000000000005240285e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000005240264e+00 with 64 bits of precision,1.00000000000005329103e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005329071e+00 with 64 bits of precision,1.0000000000000541791e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005417888e+00 with 64 bits of precision,1.0000000000000550676e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005506728e+00 with 64 bits of precision,1.00000000000005595567e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005595557e+00 with 64 bits of precision,1.00000000000005684374e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005684353e+00 with 64 bits of precision,1.00000000000005773181e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005773171e+00 with 64 bits of precision,1.0000000000000586201e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005861978e+00 with 64 bits of precision,1.0000000000000595085e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000005950828e+00 with 64 bits of precision,1.00000000000006039667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006039635e+00 with 64 bits of precision,1.00000000000006128474e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006128464e+00 with 64 bits of precision,1.00000000000006217281e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006217271e+00 with 64 bits of precision,1.00000000000006306088e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006306078e+00 with 64 bits of precision,1.00000000000006394906e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006394885e+00 with 64 bits of precision,1.00000000000006483724e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006483702e+00 with 64 bits of precision,1.00000000000006572585e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006572542e+00 with 64 bits of precision,1.00000000000006661392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006661371e+00 with 64 bits of precision,1.00000000000006750199e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006750167e+00 with 64 bits of precision,1.00000000000006839006e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006838996e+00 with 64 bits of precision,1.00000000000006927813e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000006927803e+00 with 64 bits of precision,1.00000000000007016631e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000701661e+00 with 64 bits of precision,1.00000000000007105449e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007105417e+00 with 64 bits of precision,1.00000000000007194256e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007194234e+00 with 64 bits of precision,1.00000000000007283106e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007283074e+00 with 64 bits of precision,1.00000000000007371913e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007371903e+00 with 64 bits of precision,1.0000000000000746072e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000746071e+00 with 64 bits of precision,1.00000000000007549549e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007549527e+00 with 64 bits of precision,1.00000000000007638399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007638367e+00 with 64 bits of precision,1.00000000000007727206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007727196e+00 with 64 bits of precision,1.00000000000007816013e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007815992e+00 with 64 bits of precision,1.0000000000000790482e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000790481e+00 with 64 bits of precision,1.00000000000007993649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000007993617e+00 with 64 bits of precision,1.000000000000080825e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008082478e+00 with 64 bits of precision,1.00000000000008171317e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008171274e+00 with 64 bits of precision,1.00000000000008260124e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008260103e+00 with 64 bits of precision,1.00000000000008348931e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000834891e+00 with 64 bits of precision,1.00000000000008437738e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008437728e+00 with 64 bits of precision,1.00000000000008526545e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008526535e+00 with 64 bits of precision,1.00000000000008615374e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008615352e+00 with 64 bits of precision,1.00000000000008704224e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008704192e+00 with 64 bits of precision,1.00000000000008793031e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008793021e+00 with 64 bits of precision,1.00000000000008881838e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008881817e+00 with 64 bits of precision,1.00000000000008970645e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000008970635e+00 with 64 bits of precision,1.00000000000009059452e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009059442e+00 with 64 bits of precision,1.0000000000000914827e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009148249e+00 with 64 bits of precision,1.00000000000009237088e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009237056e+00 with 64 bits of precision,1.00000000000009325895e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000009325873e+00 with 64 bits of precision,1.00000000000009414745e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009414713e+00 with 64 bits of precision,1.00000000000009503552e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009503542e+00 with 64 bits of precision,1.0000000000000959237e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009592349e+00 with 64 bits of precision,1.00000000000009681188e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009681166e+00 with 64 bits of precision,1.00000000000009770049e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009770006e+00 with 64 bits of precision,1.00000000000009858856e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000009858835e+00 with 64 bits of precision,1.00000000000009947663e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000000994762e+00 with 64 bits of precision,1.0000000000001003647e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010036449e+00 with 64 bits of precision,1.00000000000010125277e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010125267e+00 with 64 bits of precision,1.00000000000010214084e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010214074e+00 with 64 bits of precision,1.00000000000010302902e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010302881e+00 with 64 bits of precision,1.0000000000001039172e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010391698e+00 with 64 bits of precision,1.0000000000001048057e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010480538e+00 with 64 bits of precision,1.00000000000010569377e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010569367e+00 with 64 bits of precision,1.00000000000010658184e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010658163e+00 with 64 bits of precision,1.00000000000010746991e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010746981e+00 with 64 bits of precision,1.00000000000010835798e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010835788e+00 with 64 bits of precision,1.00000000000010924616e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000010924595e+00 with 64 bits of precision,1.00000000000011013434e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011013402e+00 with 64 bits of precision,1.00000000000011102241e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011102219e+00 with 64 bits of precision,1.00000000000011191091e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011191059e+00 with 64 bits of precision,1.00000000000011279898e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011279888e+00 with 64 bits of precision,1.00000000000011368705e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011368695e+00 with 64 bits of precision,1.00000000000011457534e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011457512e+00 with 64 bits of precision,1.00000000000011546395e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011546352e+00 with 64 bits of precision,1.00000000000011635202e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011635181e+00 with 64 bits of precision,1.00000000000011724009e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011723977e+00 with 64 bits of precision,1.00000000000011812816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011812806e+00 with 64 bits of precision,1.00000000000011901623e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000011901613e+00 with 64 bits of precision,1.00000000000011990441e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001199042e+00 with 64 bits of precision,1.00000000000012079259e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012079227e+00 with 64 bits of precision,1.00000000000012168066e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012168044e+00 with 64 bits of precision,1.00000000000012256916e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012256884e+00 with 64 bits of precision,1.00000000000012345723e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012345713e+00 with 64 bits of precision,1.0000000000001243453e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001243452e+00 with 64 bits of precision,1.00000000000012523359e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012523337e+00 with 64 bits of precision,1.00000000000012612209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012612177e+00 with 64 bits of precision,1.00000000000012701016e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012701006e+00 with 64 bits of precision,1.00000000000012789823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012789791e+00 with 64 bits of precision,1.0000000000001287863e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001287862e+00 with 64 bits of precision,1.00000000000012967437e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000012967427e+00 with 64 bits of precision,1.00000000000013056255e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013056234e+00 with 64 bits of precision,1.00000000000013145073e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013145041e+00 with 64 bits of precision,1.00000000000013233913e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013233891e+00 with 64 bits of precision,1.00000000000013322741e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000013322709e+00 with 64 bits of precision,1.00000000000013411548e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013411538e+00 with 64 bits of precision,1.00000000000013500355e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013500334e+00 with 64 bits of precision,1.00000000000013589162e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013589152e+00 with 64 bits of precision,1.00000000000013677969e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013677959e+00 with 64 bits of precision,1.00000000000013766787e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013766766e+00 with 64 bits of precision,1.00000000000013855605e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000013855573e+00 with 64 bits of precision,1.00000000000013944412e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001394439e+00 with 64 bits of precision,1.00000000000014033262e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001403323e+00 with 64 bits of precision,1.00000000000014122069e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014122059e+00 with 64 bits of precision,1.00000000000014210876e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014210866e+00 with 64 bits of precision,1.00000000000014299705e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014299683e+00 with 64 bits of precision,1.00000000000014388555e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014388523e+00 with 64 bits of precision,1.00000000000014477362e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014477352e+00 with 64 bits of precision,1.00000000000014566169e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014566159e+00 with 64 bits of precision,1.00000000000014654998e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014654976e+00 with 64 bits of precision,1.00000000000014743859e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014743816e+00 with 64 bits of precision,1.00000000000014832666e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000014832645e+00 with 64 bits of precision,1.00000000000014921473e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001492143e+00 with 64 bits of precision,1.0000000000001501028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015010259e+00 with 64 bits of precision,1.00000000000015099087e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015099077e+00 with 64 bits of precision,1.00000000000015187894e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015187884e+00 with 64 bits of precision,1.00000000000015276712e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015276691e+00 with 64 bits of precision,1.0000000000001536553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015365508e+00 with 64 bits of precision,1.0000000000001545438e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015454348e+00 with 64 bits of precision,1.00000000000015543187e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015543177e+00 with 64 bits of precision,1.00000000000015631994e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015631962e+00 with 64 bits of precision,1.00000000000015720801e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015720791e+00 with 64 bits of precision,1.00000000000015809608e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015809598e+00 with 64 bits of precision,1.00000000000015898426e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015898405e+00 with 64 bits of precision,1.00000000000015987244e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000015987212e+00 with 64 bits of precision,1.00000000000016076051e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016076029e+00 with 64 bits of precision,1.00000000000016164901e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016164869e+00 with 64 bits of precision,1.00000000000016253708e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016253698e+00 with 64 bits of precision,1.00000000000016342515e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016342505e+00 with 64 bits of precision,1.00000000000016431333e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016431312e+00 with 64 bits of precision,1.00000000000016520151e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016520119e+00 with 64 bits of precision,1.00000000000016609002e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001660898e+00 with 64 bits of precision,1.00000000000016697819e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016697776e+00 with 64 bits of precision,1.00000000000016786626e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016786605e+00 with 64 bits of precision,1.00000000000016875433e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000016875412e+00 with 64 bits of precision,1.0000000000001696424e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001696423e+00 with 64 bits of precision,1.00000000000017053047e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017053037e+00 with 64 bits of precision,1.00000000000017141876e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000017141854e+00 with 64 bits of precision,1.00000000000017230726e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017230694e+00 with 64 bits of precision,1.00000000000017319533e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017319523e+00 with 64 bits of precision,1.0000000000001740834e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001740833e+00 with 64 bits of precision,1.00000000000017497169e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017497147e+00 with 64 bits of precision,1.00000000000017586019e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017585987e+00 with 64 bits of precision,1.00000000000017674826e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017674816e+00 with 64 bits of precision,1.00000000000017763633e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017763601e+00 with 64 bits of precision,1.0000000000001785244e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001785243e+00 with 64 bits of precision,1.00000000000017941247e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000017941237e+00 with 64 bits of precision,1.00000000000018030065e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018030044e+00 with 64 bits of precision,1.00000000000018118883e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018118851e+00 with 64 bits of precision,1.0000000000001820769e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018207668e+00 with 64 bits of precision,1.0000000000001829654e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018296508e+00 with 64 bits of precision,1.00000000000018385347e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018385337e+00 with 64 bits of precision,1.00000000000018474154e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018474133e+00 with 64 bits of precision,1.00000000000018562961e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018562951e+00 with 64 bits of precision,1.00000000000018651779e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018651758e+00 with 64 bits of precision,1.00000000000018740586e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018740565e+00 with 64 bits of precision,1.00000000000018829415e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000018829372e+00 with 64 bits of precision,1.00000000000018918222e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000189182e+00 with 64 bits of precision,1.00000000000019007072e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001900704e+00 with 64 bits of precision,1.00000000000019095879e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019095869e+00 with 64 bits of precision,1.00000000000019184686e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019184676e+00 with 64 bits of precision,1.00000000000019273504e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019273483e+00 with 64 bits of precision,1.00000000000019362322e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001936229e+00 with 64 bits of precision,1.00000000000019451162e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001945114e+00 with 64 bits of precision,1.00000000000019539979e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019539947e+00 with 64 bits of precision,1.00000000000019628786e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019628776e+00 with 64 bits of precision,1.00000000000019717593e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019717583e+00 with 64 bits of precision,1.000000000000198064e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000001980639e+00 with 64 bits of precision,1.00000000000019895218e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019895197e+00 with 64 bits of precision,1.00000000000019984036e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000019984014e+00 with 64 bits of precision,1.00000000000020072886e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020072854e+00 with 64 bits of precision,1.00000000000020161693e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020161683e+00 with 64 bits of precision,1.000000000000202505e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020250479e+00 with 64 bits of precision,1.00000000000020339307e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020339297e+00 with 64 bits of precision,1.00000000000020428125e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020428104e+00 with 64 bits of precision,1.00000000000020516932e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020516911e+00 with 64 bits of precision,1.00000000000020605761e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020605718e+00 with 64 bits of precision,1.00000000000020694546e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020694525e+00 with 64 bits of precision,1.00000000000020783375e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000020783332e+00 with 64 bits of precision,1.00000000000020872215e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020872193e+00 with 64 bits of precision,1.00000000000020961032e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000020961022e+00 with 64 bits of precision,1.00000000000021049861e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021049839e+00 with 64 bits of precision,1.00000000000021138711e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021138679e+00 with 64 bits of precision,1.00000000000021227518e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021227508e+00 with 64 bits of precision,1.00000000000021316325e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021316293e+00 with 64 bits of precision,1.00000000000021405132e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021405122e+00 with 64 bits of precision,1.00000000000021493939e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021493929e+00 with 64 bits of precision,1.00000000000021582757e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021582736e+00 with 64 bits of precision,1.00000000000021671575e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021671543e+00 with 64 bits of precision,1.00000000000021760382e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002176036e+00 with 64 bits of precision,1.00000000000021849232e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000218492e+00 with 64 bits of precision,1.00000000000021938039e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000021938029e+00 with 64 bits of precision,1.00000000000022026846e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022026836e+00 with 64 bits of precision,1.00000000000022115664e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022115643e+00 with 64 bits of precision,1.00000000000022204493e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002220445e+00 with 64 bits of precision,1.00000000000022293333e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022293311e+00 with 64 bits of precision,1.0000000000002238215e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022382118e+00 with 64 bits of precision,1.00000000000022470957e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022470947e+00 with 64 bits of precision,1.00000000000022559764e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022559754e+00 with 64 bits of precision,1.00000000000022648571e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022648561e+00 with 64 bits of precision,1.00000000000022737389e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022737368e+00 with 64 bits of precision,1.00000000000022826207e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022826185e+00 with 64 bits of precision,1.00000000000022915057e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000022915025e+00 with 64 bits of precision,1.00000000000023003864e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023003854e+00 with 64 bits of precision,1.00000000000023092671e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023092661e+00 with 64 bits of precision,1.000000000000231815e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023181478e+00 with 64 bits of precision,1.0000000000002327035e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023270318e+00 with 64 bits of precision,1.00000000000023359157e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023359147e+00 with 64 bits of precision,1.00000000000023447964e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023447932e+00 with 64 bits of precision,1.00000000000023536771e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023536761e+00 with 64 bits of precision,1.00000000000023625578e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023625568e+00 with 64 bits of precision,1.00000000000023714396e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023714375e+00 with 64 bits of precision,1.00000000000023803214e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000023803182e+00 with 64 bits of precision,1.00000000000023892032e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002389201e+00 with 64 bits of precision,1.00000000000023980882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002398085e+00 with 64 bits of precision,1.00000000000024069689e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024069679e+00 with 64 bits of precision,1.00000000000024158496e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024158464e+00 with 64 bits of precision,1.00000000000024247303e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000024247293e+00 with 64 bits of precision,1.0000000000002433611e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000243361e+00 with 64 bits of precision,1.00000000000024424928e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024424907e+00 with 64 bits of precision,1.00000000000024513746e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024513714e+00 with 64 bits of precision,1.00000000000024602553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024602531e+00 with 64 bits of precision,1.00000000000024691403e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024691371e+00 with 64 bits of precision,1.0000000000002478021e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000247802e+00 with 64 bits of precision,1.00000000000024869017e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000024869007e+00 with 64 bits of precision,1.00000000000024957835e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000024957814e+00 with 64 bits of precision,1.00000000000025046653e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025046621e+00 with 64 bits of precision,1.00000000000025135493e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025135471e+00 with 64 bits of precision,1.0000000000002522431e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025224278e+00 with 64 bits of precision,1.00000000000025313117e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025313107e+00 with 64 bits of precision,1.00000000000025401924e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025401914e+00 with 64 bits of precision,1.00000000000025490731e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025490721e+00 with 64 bits of precision,1.00000000000025579549e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025579528e+00 with 64 bits of precision,1.00000000000025668356e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025668335e+00 with 64 bits of precision,1.00000000000025757185e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025757142e+00 with 64 bits of precision,1.00000000000025846025e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000025846003e+00 with 64 bits of precision,1.00000000000025934842e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002593481e+00 with 64 bits of precision,1.00000000000026023649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026023639e+00 with 64 bits of precision,1.00000000000026112456e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026112446e+00 with 64 bits of precision,1.00000000000026201274e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026201253e+00 with 64 bits of precision,1.00000000000026290092e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002629006e+00 with 64 bits of precision,1.00000000000026378899e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026378877e+00 with 64 bits of precision,1.00000000000026467749e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026467717e+00 with 64 bits of precision,1.00000000000026556556e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026556546e+00 with 64 bits of precision,1.00000000000026645363e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026645353e+00 with 64 bits of precision,1.00000000000026734192e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002673417e+00 with 64 bits of precision,1.00000000000026823042e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002682301e+00 with 64 bits of precision,1.00000000000026911849e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000026911839e+00 with 64 bits of precision,1.00000000000027000656e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027000624e+00 with 64 bits of precision,1.00000000000027089463e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027089453e+00 with 64 bits of precision,1.0000000000002717827e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002717826e+00 with 64 bits of precision,1.00000000000027267088e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027267067e+00 with 64 bits of precision,1.00000000000027355906e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027355874e+00 with 64 bits of precision,1.00000000000027444724e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027444702e+00 with 64 bits of precision,1.00000000000027533574e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027533542e+00 with 64 bits of precision,1.00000000000027622381e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027622371e+00 with 64 bits of precision,1.00000000000027711188e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027711178e+00 with 64 bits of precision,1.00000000000027800006e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027799985e+00 with 64 bits of precision,1.00000000000027888824e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027888792e+00 with 64 bits of precision,1.00000000000027977664e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000027977642e+00 with 64 bits of precision,1.00000000000028066481e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028066449e+00 with 64 bits of precision,1.00000000000028155288e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028155278e+00 with 64 bits of precision,1.00000000000028244095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028244085e+00 with 64 bits of precision,1.00000000000028332902e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000028332892e+00 with 64 bits of precision,1.0000000000002842172e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028421699e+00 with 64 bits of precision,1.00000000000028510538e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028510516e+00 with 64 bits of precision,1.00000000000028599388e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028599356e+00 with 64 bits of precision,1.00000000000028688195e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028688185e+00 with 64 bits of precision,1.00000000000028777002e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028776981e+00 with 64 bits of precision,1.00000000000028865809e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028865799e+00 with 64 bits of precision,1.00000000000028954627e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000028954606e+00 with 64 bits of precision,1.00000000000029043434e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029043413e+00 with 64 bits of precision,1.00000000000029132263e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002913222e+00 with 64 bits of precision,1.00000000000029221048e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029221027e+00 with 64 bits of precision,1.00000000000029309877e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029309834e+00 with 64 bits of precision,1.00000000000029398717e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029398695e+00 with 64 bits of precision,1.00000000000029487534e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029487524e+00 with 64 bits of precision,1.00000000000029576363e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029576341e+00 with 64 bits of precision,1.00000000000029665213e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029665181e+00 with 64 bits of precision,1.0000000000002975402e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000002975401e+00 with 64 bits of precision,1.00000000000029842827e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029842795e+00 with 64 bits of precision,1.00000000000029931634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000029931624e+00 with 64 bits of precision,1.00000000000030020441e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030020431e+00 with 64 bits of precision,1.00000000000030109259e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030109238e+00 with 64 bits of precision,1.00000000000030198077e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030198045e+00 with 64 bits of precision,1.00000000000030286884e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030286862e+00 with 64 bits of precision,1.00000000000030375734e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030375702e+00 with 64 bits of precision,1.00000000000030464541e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030464531e+00 with 64 bits of precision,1.00000000000030553348e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030553338e+00 with 64 bits of precision,1.00000000000030642166e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030642145e+00 with 64 bits of precision,1.00000000000030730995e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030730952e+00 with 64 bits of precision,1.00000000000030819835e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030819813e+00 with 64 bits of precision,1.00000000000030908652e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003090862e+00 with 64 bits of precision,1.00000000000030997459e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000030997449e+00 with 64 bits of precision,1.00000000000031086266e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031086256e+00 with 64 bits of precision,1.00000000000031175073e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031175063e+00 with 64 bits of precision,1.00000000000031263891e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003126387e+00 with 64 bits of precision,1.00000000000031352709e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031352687e+00 with 64 bits of precision,1.00000000000031441559e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031441527e+00 with 64 bits of precision,1.00000000000031530366e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031530356e+00 with 64 bits of precision,1.00000000000031619173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031619163e+00 with 64 bits of precision,1.00000000000031708002e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003170798e+00 with 64 bits of precision,1.00000000000031796852e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003179682e+00 with 64 bits of precision,1.00000000000031885659e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031885649e+00 with 64 bits of precision,1.00000000000031974466e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000031974434e+00 with 64 bits of precision,1.00000000000032063273e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032063263e+00 with 64 bits of precision,1.0000000000003215208e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003215207e+00 with 64 bits of precision,1.00000000000032240898e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032240877e+00 with 64 bits of precision,1.00000000000032329716e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032329684e+00 with 64 bits of precision,1.00000000000032418534e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000032418512e+00 with 64 bits of precision,1.00000000000032507384e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032507352e+00 with 64 bits of precision,1.00000000000032596191e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032596181e+00 with 64 bits of precision,1.00000000000032684998e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032684977e+00 with 64 bits of precision,1.00000000000032773805e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032773795e+00 with 64 bits of precision,1.00000000000032862634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032862602e+00 with 64 bits of precision,1.00000000000032951474e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000032951452e+00 with 64 bits of precision,1.00000000000033040291e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033040259e+00 with 64 bits of precision,1.00000000000033129098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033129088e+00 with 64 bits of precision,1.00000000000033217905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033217895e+00 with 64 bits of precision,1.00000000000033306712e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033306702e+00 with 64 bits of precision,1.0000000000003339553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033395509e+00 with 64 bits of precision,1.00000000000033484348e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033484326e+00 with 64 bits of precision,1.00000000000033573198e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033573166e+00 with 64 bits of precision,1.00000000000033662005e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033661995e+00 with 64 bits of precision,1.00000000000033750812e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033750791e+00 with 64 bits of precision,1.00000000000033839619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033839609e+00 with 64 bits of precision,1.00000000000033928437e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000033928416e+00 with 64 bits of precision,1.00000000000034017244e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034017223e+00 with 64 bits of precision,1.00000000000034106073e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003410603e+00 with 64 bits of precision,1.00000000000034194858e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034194837e+00 with 64 bits of precision,1.00000000000034283687e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034283644e+00 with 64 bits of precision,1.00000000000034372527e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034372505e+00 with 64 bits of precision,1.00000000000034461344e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034461312e+00 with 64 bits of precision,1.00000000000034550151e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034550141e+00 with 64 bits of precision,1.00000000000034638958e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034638948e+00 with 64 bits of precision,1.00000000000034727776e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034727755e+00 with 64 bits of precision,1.00000000000034816594e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034816562e+00 with 64 bits of precision,1.00000000000034905401e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034905379e+00 with 64 bits of precision,1.00000000000034994251e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000034994219e+00 with 64 bits of precision,1.00000000000035083058e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035083048e+00 with 64 bits of precision,1.00000000000035171865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035171855e+00 with 64 bits of precision,1.00000000000035260694e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035260672e+00 with 64 bits of precision,1.00000000000035349544e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035349512e+00 with 64 bits of precision,1.00000000000035438351e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035438341e+00 with 64 bits of precision,1.00000000000035527158e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035527137e+00 with 64 bits of precision,1.00000000000035615965e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035615955e+00 with 64 bits of precision,1.00000000000035704794e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035704762e+00 with 64 bits of precision,1.00000000000035793645e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035793623e+00 with 64 bits of precision,1.00000000000035882462e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035882419e+00 with 64 bits of precision,1.00000000000035971269e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000035971248e+00 with 64 bits of precision,1.00000000000036060076e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036060055e+00 with 64 bits of precision,1.00000000000036148883e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036148873e+00 with 64 bits of precision,1.0000000000003623769e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003623768e+00 with 64 bits of precision,1.00000000000036326519e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000036326497e+00 with 64 bits of precision,1.00000000000036415369e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036415337e+00 with 64 bits of precision,1.00000000000036504176e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036504166e+00 with 64 bits of precision,1.00000000000036592983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036592962e+00 with 64 bits of precision,1.0000000000003668179e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003668178e+00 with 64 bits of precision,1.00000000000036770597e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036770587e+00 with 64 bits of precision,1.00000000000036859415e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036859394e+00 with 64 bits of precision,1.00000000000036948233e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000036948201e+00 with 64 bits of precision,1.0000000000003703704e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037037018e+00 with 64 bits of precision,1.0000000000003712589e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037125858e+00 with 64 bits of precision,1.00000000000037214697e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037214687e+00 with 64 bits of precision,1.00000000000037303504e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037303494e+00 with 64 bits of precision,1.00000000000037392333e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037392311e+00 with 64 bits of precision,1.00000000000037481194e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037481151e+00 with 64 bits of precision,1.00000000000037570001e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003756998e+00 with 64 bits of precision,1.00000000000037658808e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037658765e+00 with 64 bits of precision,1.00000000000037747615e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037747594e+00 with 64 bits of precision,1.00000000000037836422e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037836412e+00 with 64 bits of precision,1.00000000000037925229e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000037925219e+00 with 64 bits of precision,1.00000000000038014047e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038014026e+00 with 64 bits of precision,1.00000000000038102865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038102843e+00 with 64 bits of precision,1.00000000000038191715e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038191683e+00 with 64 bits of precision,1.00000000000038280522e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038280512e+00 with 64 bits of precision,1.00000000000038369329e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038369319e+00 with 64 bits of precision,1.00000000000038458158e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038458136e+00 with 64 bits of precision,1.00000000000038547008e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038546976e+00 with 64 bits of precision,1.00000000000038635815e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038635805e+00 with 64 bits of precision,1.00000000000038724622e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038724612e+00 with 64 bits of precision,1.00000000000038813451e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038813429e+00 with 64 bits of precision,1.00000000000038902312e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038902269e+00 with 64 bits of precision,1.00000000000038991119e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000038991098e+00 with 64 bits of precision,1.00000000000039079926e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039079883e+00 with 64 bits of precision,1.00000000000039168733e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039168712e+00 with 64 bits of precision,1.0000000000003925754e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003925753e+00 with 64 bits of precision,1.00000000000039346347e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039346337e+00 with 64 bits of precision,1.00000000000039435165e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039435144e+00 with 64 bits of precision,1.00000000000039523983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039523961e+00 with 64 bits of precision,1.00000000000039612833e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039612801e+00 with 64 bits of precision,1.0000000000003970164e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000003970163e+00 with 64 bits of precision,1.00000000000039790447e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039790415e+00 with 64 bits of precision,1.00000000000039879254e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039879244e+00 with 64 bits of precision,1.00000000000039968061e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000039968051e+00 with 64 bits of precision,1.00000000000040056879e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040056858e+00 with 64 bits of precision,1.00000000000040145697e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040145665e+00 with 64 bits of precision,1.00000000000040234504e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040234482e+00 with 64 bits of precision,1.00000000000040323354e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040323322e+00 with 64 bits of precision,1.00000000000040412161e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040412151e+00 with 64 bits of precision,1.00000000000040500968e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040500958e+00 with 64 bits of precision,1.00000000000040589797e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000040589775e+00 with 64 bits of precision,1.00000000000040678658e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040678615e+00 with 64 bits of precision,1.00000000000040767465e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040767444e+00 with 64 bits of precision,1.00000000000040856272e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004085624e+00 with 64 bits of precision,1.00000000000040945079e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000040945069e+00 with 64 bits of precision,1.00000000000041033886e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041033876e+00 with 64 bits of precision,1.00000000000041122704e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041122683e+00 with 64 bits of precision,1.00000000000041211522e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004121149e+00 with 64 bits of precision,1.00000000000041300329e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041300307e+00 with 64 bits of precision,1.00000000000041389179e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041389147e+00 with 64 bits of precision,1.00000000000041477986e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041477976e+00 with 64 bits of precision,1.00000000000041566793e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041566783e+00 with 64 bits of precision,1.00000000000041655622e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000416556e+00 with 64 bits of precision,1.00000000000041744472e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004174444e+00 with 64 bits of precision,1.00000000000041833279e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041833269e+00 with 64 bits of precision,1.00000000000041922086e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000041922065e+00 with 64 bits of precision,1.00000000000042010893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042010883e+00 with 64 bits of precision,1.00000000000042099722e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004209969e+00 with 64 bits of precision,1.00000000000042188573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042188551e+00 with 64 bits of precision,1.0000000000004227739e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042277347e+00 with 64 bits of precision,1.00000000000042366197e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042366176e+00 with 64 bits of precision,1.00000000000042455004e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042454983e+00 with 64 bits of precision,1.00000000000042543811e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042543801e+00 with 64 bits of precision,1.00000000000042632618e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042632597e+00 with 64 bits of precision,1.00000000000042721425e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042721415e+00 with 64 bits of precision,1.00000000000042810254e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042810222e+00 with 64 bits of precision,1.00000000000042899094e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042899072e+00 with 64 bits of precision,1.00000000000042987911e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000042987879e+00 with 64 bits of precision,1.00000000000043076718e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043076708e+00 with 64 bits of precision,1.00000000000043165525e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043165515e+00 with 64 bits of precision,1.00000000000043254343e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043254322e+00 with 64 bits of precision,1.00000000000043343161e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043343129e+00 with 64 bits of precision,1.00000000000043431968e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043431946e+00 with 64 bits of precision,1.00000000000043520818e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043520786e+00 with 64 bits of precision,1.00000000000043609625e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043609615e+00 with 64 bits of precision,1.00000000000043698443e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043698422e+00 with 64 bits of precision,1.00000000000043787261e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043787239e+00 with 64 bits of precision,1.00000000000043876122e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043876079e+00 with 64 bits of precision,1.00000000000043964929e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000043964908e+00 with 64 bits of precision,1.00000000000044053736e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000044053693e+00 with 64 bits of precision,1.00000000000044142543e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044142522e+00 with 64 bits of precision,1.0000000000004423135e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004423134e+00 with 64 bits of precision,1.00000000000044320157e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044320147e+00 with 64 bits of precision,1.00000000000044408975e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044408954e+00 with 64 bits of precision,1.00000000000044497793e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044497771e+00 with 64 bits of precision,1.00000000000044586643e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044586611e+00 with 64 bits of precision,1.0000000000004467545e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004467544e+00 with 64 bits of precision,1.00000000000044764257e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044764236e+00 with 64 bits of precision,1.00000000000044853064e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044853054e+00 with 64 bits of precision,1.00000000000044941871e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000044941861e+00 with 64 bits of precision,1.00000000000045030689e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045030668e+00 with 64 bits of precision,1.00000000000045119507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045119475e+00 with 64 bits of precision,1.00000000000045208314e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045208292e+00 with 64 bits of precision,1.00000000000045297164e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045297132e+00 with 64 bits of precision,1.00000000000045385971e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045385961e+00 with 64 bits of precision,1.00000000000045474778e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045474746e+00 with 64 bits of precision,1.00000000000045563585e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045563575e+00 with 64 bits of precision,1.00000000000045652392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045652382e+00 with 64 bits of precision,1.0000000000004574121e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045741189e+00 with 64 bits of precision,1.00000000000045830028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045829996e+00 with 64 bits of precision,1.00000000000045918868e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000045918846e+00 with 64 bits of precision,1.00000000000046007696e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046007664e+00 with 64 bits of precision,1.00000000000046096503e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046096493e+00 with 64 bits of precision,1.0000000000004618531e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000461853e+00 with 64 bits of precision,1.00000000000046274139e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046274117e+00 with 64 bits of precision,1.00000000000046362989e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046362957e+00 with 64 bits of precision,1.00000000000046451796e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046451786e+00 with 64 bits of precision,1.00000000000046540603e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046540582e+00 with 64 bits of precision,1.0000000000004662941e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000466294e+00 with 64 bits of precision,1.00000000000046718217e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046718207e+00 with 64 bits of precision,1.00000000000046807035e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046807014e+00 with 64 bits of precision,1.00000000000046895853e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046895821e+00 with 64 bits of precision,1.0000000000004698466e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000046984638e+00 with 64 bits of precision,1.0000000000004707351e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047073478e+00 with 64 bits of precision,1.00000000000047162317e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047162307e+00 with 64 bits of precision,1.00000000000047251124e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047251114e+00 with 64 bits of precision,1.00000000000047339953e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047339931e+00 with 64 bits of precision,1.00000000000047428814e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047428771e+00 with 64 bits of precision,1.00000000000047517621e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000475176e+00 with 64 bits of precision,1.00000000000047606428e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047606396e+00 with 64 bits of precision,1.00000000000047695235e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047695225e+00 with 64 bits of precision,1.00000000000047784042e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047784032e+00 with 64 bits of precision,1.0000000000004787286e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000047872839e+00 with 64 bits of precision,1.00000000000047961678e+00 with 64 bits of precision)\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Maybe a zero in Interval(1.00000000000047961646e+00 with 64 bits of precision,1.00000000000048050485e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048050463e+00 with 64 bits of precision,1.00000000000048139335e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048139303e+00 with 64 bits of precision,1.00000000000048228142e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048228132e+00 with 64 bits of precision,1.00000000000048316949e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048316939e+00 with 64 bits of precision,1.00000000000048405778e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048405756e+00 with 64 bits of precision,1.00000000000048494628e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048494596e+00 with 64 bits of precision,1.00000000000048583435e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048583425e+00 with 64 bits of precision,1.00000000000048672242e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048672232e+00 with 64 bits of precision,1.00000000000048761071e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048761049e+00 with 64 bits of precision,1.00000000000048849932e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048849889e+00 with 64 bits of precision,1.00000000000048938739e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000048938718e+00 with 64 bits of precision,1.00000000000049027546e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049027503e+00 with 64 bits of precision,1.00000000000049116353e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049116332e+00 with 64 bits of precision,1.0000000000004920516e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004920515e+00 with 64 bits of precision,1.00000000000049293967e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049293957e+00 with 64 bits of precision,1.00000000000049382785e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049382764e+00 with 64 bits of precision,1.00000000000049471603e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049471581e+00 with 64 bits of precision,1.00000000000049560453e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049560421e+00 with 64 bits of precision,1.0000000000004964926e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000004964925e+00 with 64 bits of precision,1.00000000000049738067e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049738035e+00 with 64 bits of precision,1.00000000000049826874e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049826864e+00 with 64 bits of precision,1.00000000000049915681e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000049915671e+00 with 64 bits of precision,1.00000000000050004499e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050004478e+00 with 64 bits of precision,1.00000000000050093317e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050093285e+00 with 64 bits of precision,1.00000000000050182124e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050182102e+00 with 64 bits of precision,1.00000000000050270974e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050270942e+00 with 64 bits of precision,1.00000000000050359781e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050359771e+00 with 64 bits of precision,1.00000000000050448588e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050448578e+00 with 64 bits of precision,1.00000000000050537406e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050537385e+00 with 64 bits of precision,1.00000000000050626224e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050626192e+00 with 64 bits of precision,1.00000000000050715075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050715053e+00 with 64 bits of precision,1.00000000000050803892e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050803849e+00 with 64 bits of precision,1.00000000000050892699e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050892678e+00 with 64 bits of precision,1.00000000000050981506e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000050981485e+00 with 64 bits of precision,1.00000000000051070313e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051070303e+00 with 64 bits of precision,1.0000000000005115912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051159099e+00 with 64 bits of precision,1.00000000000051247927e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051247917e+00 with 64 bits of precision,1.00000000000051336756e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051336724e+00 with 64 bits of precision,1.00000000000051425596e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051425574e+00 with 64 bits of precision,1.00000000000051514413e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051514381e+00 with 64 bits of precision,1.0000000000005160322e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000005160321e+00 with 64 bits of precision,1.00000000000051692027e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051692017e+00 with 64 bits of precision,1.00000000000051780845e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051780824e+00 with 64 bits of precision,1.00000000000051869663e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051869631e+00 with 64 bits of precision,1.0000000000005195847e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000051958448e+00 with 64 bits of precision,1.0000000000005204732e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052047288e+00 with 64 bits of precision,1.00000000000052136127e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052136117e+00 with 64 bits of precision,1.00000000000052224934e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052224924e+00 with 64 bits of precision,1.00000000000052313763e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052313741e+00 with 64 bits of precision,1.00000000000052402613e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052402581e+00 with 64 bits of precision,1.0000000000005249142e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005249141e+00 with 64 bits of precision,1.00000000000052580227e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052580195e+00 with 64 bits of precision,1.00000000000052669034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052669024e+00 with 64 bits of precision,1.00000000000052757841e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052757831e+00 with 64 bits of precision,1.00000000000052846659e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052846638e+00 with 64 bits of precision,1.00000000000052935477e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000052935445e+00 with 64 bits of precision,1.00000000000053024295e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053024273e+00 with 64 bits of precision,1.00000000000053113145e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053113113e+00 with 64 bits of precision,1.00000000000053201952e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053201942e+00 with 64 bits of precision,1.00000000000053290759e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053290738e+00 with 64 bits of precision,1.00000000000053379566e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053379556e+00 with 64 bits of precision,1.00000000000053468373e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053468363e+00 with 64 bits of precision,1.00000000000053557191e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005355717e+00 with 64 bits of precision,1.00000000000053646009e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053645977e+00 with 64 bits of precision,1.00000000000053734816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053734794e+00 with 64 bits of precision,1.00000000000053823666e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053823634e+00 with 64 bits of precision,1.00000000000053912473e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000053912463e+00 with 64 bits of precision,1.0000000000005400128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005400127e+00 with 64 bits of precision,1.00000000000054090109e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054090087e+00 with 64 bits of precision,1.00000000000054178959e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054178927e+00 with 64 bits of precision,1.00000000000054267766e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054267756e+00 with 64 bits of precision,1.00000000000054356573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054356552e+00 with 64 bits of precision,1.0000000000005444538e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005444537e+00 with 64 bits of precision,1.00000000000054534198e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054534177e+00 with 64 bits of precision,1.00000000000054623005e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054622984e+00 with 64 bits of precision,1.00000000000054711834e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054711791e+00 with 64 bits of precision,1.00000000000054800619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054800598e+00 with 64 bits of precision,1.00000000000054889448e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054889405e+00 with 64 bits of precision,1.00000000000054978288e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000054978266e+00 with 64 bits of precision,1.00000000000055067105e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055067095e+00 with 64 bits of precision,1.00000000000055155934e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055155912e+00 with 64 bits of precision,1.00000000000055244784e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055244752e+00 with 64 bits of precision,1.00000000000055333591e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055333581e+00 with 64 bits of precision,1.00000000000055422398e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055422366e+00 with 64 bits of precision,1.00000000000055511205e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000055511195e+00 with 64 bits of precision,1.00000000000055600012e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055600002e+00 with 64 bits of precision,1.0000000000005568883e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055688809e+00 with 64 bits of precision,1.00000000000055777648e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055777616e+00 with 64 bits of precision,1.00000000000055866455e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055866433e+00 with 64 bits of precision,1.00000000000055955305e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000055955273e+00 with 64 bits of precision,1.00000000000056044112e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056044102e+00 with 64 bits of precision,1.00000000000056132919e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056132909e+00 with 64 bits of precision,1.00000000000056221726e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000056221716e+00 with 64 bits of precision,1.00000000000056310544e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056310523e+00 with 64 bits of precision,1.00000000000056399351e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005639933e+00 with 64 bits of precision,1.0000000000005648818e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056488137e+00 with 64 bits of precision,1.00000000000056576987e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056576965e+00 with 64 bits of precision,1.00000000000056665837e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056665805e+00 with 64 bits of precision,1.00000000000056754644e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056754634e+00 with 64 bits of precision,1.00000000000056843451e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005684343e+00 with 64 bits of precision,1.00000000000056932258e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000056932248e+00 with 64 bits of precision,1.00000000000057021087e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057021055e+00 with 64 bits of precision,1.00000000000057109927e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057109905e+00 with 64 bits of precision,1.00000000000057198744e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057198712e+00 with 64 bits of precision,1.00000000000057287551e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057287541e+00 with 64 bits of precision,1.00000000000057376358e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057376348e+00 with 64 bits of precision,1.00000000000057465165e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057465155e+00 with 64 bits of precision,1.00000000000057553983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057553962e+00 with 64 bits of precision,1.00000000000057642801e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057642779e+00 with 64 bits of precision,1.00000000000057731651e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057731619e+00 with 64 bits of precision,1.00000000000057820458e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057820448e+00 with 64 bits of precision,1.00000000000057909265e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057909244e+00 with 64 bits of precision,1.00000000000057998072e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000057998062e+00 with 64 bits of precision,1.0000000000005808689e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058086869e+00 with 64 bits of precision,1.00000000000058175697e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058175676e+00 with 64 bits of precision,1.00000000000058264526e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058264483e+00 with 64 bits of precision,1.00000000000058353311e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000005835329e+00 with 64 bits of precision,1.0000000000005844214e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058442097e+00 with 64 bits of precision,1.0000000000005853098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058530958e+00 with 64 bits of precision,1.00000000000058619797e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058619787e+00 with 64 bits of precision,1.00000000000058708626e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058708604e+00 with 64 bits of precision,1.00000000000058797476e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058797444e+00 with 64 bits of precision,1.00000000000058886283e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058886273e+00 with 64 bits of precision,1.0000000000005897509e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000058975058e+00 with 64 bits of precision,1.00000000000059063897e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059063887e+00 with 64 bits of precision,1.00000000000059152704e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059152694e+00 with 64 bits of precision,1.00000000000059241522e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059241501e+00 with 64 bits of precision,1.0000000000005933034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059330308e+00 with 64 bits of precision,1.00000000000059419147e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059419125e+00 with 64 bits of precision,1.00000000000059507997e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059507965e+00 with 64 bits of precision,1.00000000000059596804e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059596794e+00 with 64 bits of precision,1.00000000000059685611e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059685601e+00 with 64 bits of precision,1.00000000000059774429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059774408e+00 with 64 bits of precision,1.00000000000059863258e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059863215e+00 with 64 bits of precision,1.00000000000059952098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000059952076e+00 with 64 bits of precision,1.00000000000060040915e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060040883e+00 with 64 bits of precision,1.00000000000060129722e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060129712e+00 with 64 bits of precision,1.00000000000060218529e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060218519e+00 with 64 bits of precision,1.00000000000060307347e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060307326e+00 with 64 bits of precision,1.00000000000060396165e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000060396133e+00 with 64 bits of precision,1.00000000000060484972e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006048495e+00 with 64 bits of precision,1.00000000000060573822e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006057379e+00 with 64 bits of precision,1.00000000000060662629e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060662619e+00 with 64 bits of precision,1.00000000000060751436e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060751426e+00 with 64 bits of precision,1.00000000000060840265e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060840243e+00 with 64 bits of precision,1.00000000000060929115e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000060929083e+00 with 64 bits of precision,1.00000000000061017922e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061017912e+00 with 64 bits of precision,1.00000000000061106729e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061106697e+00 with 64 bits of precision,1.00000000000061195536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061195526e+00 with 64 bits of precision,1.00000000000061284343e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061284333e+00 with 64 bits of precision,1.00000000000061373161e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006137314e+00 with 64 bits of precision,1.00000000000061461979e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061461947e+00 with 64 bits of precision,1.00000000000061550797e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061550775e+00 with 64 bits of precision,1.00000000000061639647e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061639615e+00 with 64 bits of precision,1.00000000000061728454e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061728444e+00 with 64 bits of precision,1.00000000000061817261e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006181724e+00 with 64 bits of precision,1.00000000000061906068e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061906058e+00 with 64 bits of precision,1.00000000000061994875e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000061994865e+00 with 64 bits of precision,1.00000000000062083693e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062083672e+00 with 64 bits of precision,1.00000000000062172511e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062172479e+00 with 64 bits of precision,1.00000000000062261318e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062261296e+00 with 64 bits of precision,1.00000000000062350168e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062350136e+00 with 64 bits of precision,1.00000000000062438975e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062438965e+00 with 64 bits of precision,1.00000000000062527782e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062527772e+00 with 64 bits of precision,1.00000000000062616611e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062616589e+00 with 64 bits of precision,1.00000000000062705461e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062705429e+00 with 64 bits of precision,1.00000000000062794268e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062794258e+00 with 64 bits of precision,1.00000000000062883075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062883054e+00 with 64 bits of precision,1.00000000000062971882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000062971872e+00 with 64 bits of precision,1.000000000000630607e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063060679e+00 with 64 bits of precision,1.00000000000063149507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063149486e+00 with 64 bits of precision,1.00000000000063238336e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063238293e+00 with 64 bits of precision,1.00000000000063327121e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000633271e+00 with 64 bits of precision,1.0000000000006341595e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063415907e+00 with 64 bits of precision,1.0000000000006350479e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063504768e+00 with 64 bits of precision,1.00000000000063593607e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063593597e+00 with 64 bits of precision,1.00000000000063682436e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063682414e+00 with 64 bits of precision,1.00000000000063771286e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063771254e+00 with 64 bits of precision,1.00000000000063860093e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063860083e+00 with 64 bits of precision,1.000000000000639489e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000063948868e+00 with 64 bits of precision,1.00000000000064037707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064037697e+00 with 64 bits of precision,1.00000000000064126514e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000064126504e+00 with 64 bits of precision,1.00000000000064215332e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064215311e+00 with 64 bits of precision,1.0000000000006430415e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064304118e+00 with 64 bits of precision,1.00000000000064392957e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064392935e+00 with 64 bits of precision,1.00000000000064481807e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064481775e+00 with 64 bits of precision,1.00000000000064570614e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064570604e+00 with 64 bits of precision,1.00000000000064659421e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064659411e+00 with 64 bits of precision,1.00000000000064748228e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064748218e+00 with 64 bits of precision,1.00000000000064837046e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064837025e+00 with 64 bits of precision,1.00000000000064925853e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000064925832e+00 with 64 bits of precision,1.00000000000065014682e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065014639e+00 with 64 bits of precision,1.00000000000065103489e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065103467e+00 with 64 bits of precision,1.00000000000065192339e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065192307e+00 with 64 bits of precision,1.00000000000065281146e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065281136e+00 with 64 bits of precision,1.00000000000065369953e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065369943e+00 with 64 bits of precision,1.00000000000065458771e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006545875e+00 with 64 bits of precision,1.00000000000065547589e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065547557e+00 with 64 bits of precision,1.00000000000065636429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065636407e+00 with 64 bits of precision,1.00000000000065725246e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065725214e+00 with 64 bits of precision,1.00000000000065814053e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065814043e+00 with 64 bits of precision,1.0000000000006590286e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006590285e+00 with 64 bits of precision,1.00000000000065991667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000065991657e+00 with 64 bits of precision,1.00000000000066080485e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066080464e+00 with 64 bits of precision,1.00000000000066169303e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066169281e+00 with 64 bits of precision,1.00000000000066258153e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066258121e+00 with 64 bits of precision,1.0000000000006634696e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006634695e+00 with 64 bits of precision,1.00000000000066435767e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066435746e+00 with 64 bits of precision,1.00000000000066524574e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066524564e+00 with 64 bits of precision,1.00000000000066613392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066613371e+00 with 64 bits of precision,1.00000000000066702199e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066702178e+00 with 64 bits of precision,1.00000000000066791028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066790985e+00 with 64 bits of precision,1.00000000000066879813e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066879792e+00 with 64 bits of precision,1.00000000000066968642e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000066968599e+00 with 64 bits of precision,1.00000000000067057482e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006705746e+00 with 64 bits of precision,1.00000000000067146299e+00 with 64 bits of precision)\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Maybe a zero in Interval(1.00000000000067146289e+00 with 64 bits of precision,1.00000000000067235128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067235106e+00 with 64 bits of precision,1.00000000000067323978e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067323946e+00 with 64 bits of precision,1.00000000000067412785e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067412775e+00 with 64 bits of precision,1.00000000000067501592e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006750156e+00 with 64 bits of precision,1.00000000000067590399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067590389e+00 with 64 bits of precision,1.00000000000067679206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067679196e+00 with 64 bits of precision,1.00000000000067768024e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067768003e+00 with 64 bits of precision,1.00000000000067856842e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006785681e+00 with 64 bits of precision,1.00000000000067945649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000067945627e+00 with 64 bits of precision,1.00000000000068034499e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068034467e+00 with 64 bits of precision,1.00000000000068123306e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068123296e+00 with 64 bits of precision,1.00000000000068212113e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068212103e+00 with 64 bits of precision,1.00000000000068300931e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000006830091e+00 with 64 bits of precision,1.0000000000006838976e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068389717e+00 with 64 bits of precision,1.000000000000684786e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068478578e+00 with 64 bits of precision,1.00000000000068567417e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068567385e+00 with 64 bits of precision,1.00000000000068656224e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068656214e+00 with 64 bits of precision,1.00000000000068745031e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068745021e+00 with 64 bits of precision,1.00000000000068833849e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068833828e+00 with 64 bits of precision,1.00000000000068922667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000068922635e+00 with 64 bits of precision,1.00000000000069011474e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069011452e+00 with 64 bits of precision,1.00000000000069100324e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069100292e+00 with 64 bits of precision,1.00000000000069189131e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069189121e+00 with 64 bits of precision,1.00000000000069277938e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069277928e+00 with 64 bits of precision,1.00000000000069366767e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069366745e+00 with 64 bits of precision,1.00000000000069455617e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069455585e+00 with 64 bits of precision,1.00000000000069544424e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069544414e+00 with 64 bits of precision,1.00000000000069633231e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069633199e+00 with 64 bits of precision,1.00000000000069722038e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069722028e+00 with 64 bits of precision,1.00000000000069810845e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069810835e+00 with 64 bits of precision,1.00000000000069899663e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069899642e+00 with 64 bits of precision,1.00000000000069988481e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000069988449e+00 with 64 bits of precision,1.00000000000070077321e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070077299e+00 with 64 bits of precision,1.00000000000070166149e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070166117e+00 with 64 bits of precision,1.00000000000070254956e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070254946e+00 with 64 bits of precision,1.00000000000070343763e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070343742e+00 with 64 bits of precision,1.0000000000007043257e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007043256e+00 with 64 bits of precision,1.00000000000070521377e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070521367e+00 with 64 bits of precision,1.00000000000070610195e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070610174e+00 with 64 bits of precision,1.00000000000070699013e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070698981e+00 with 64 bits of precision,1.0000000000007078782e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070787798e+00 with 64 bits of precision,1.0000000000007087667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070876638e+00 with 64 bits of precision,1.00000000000070965477e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000070965467e+00 with 64 bits of precision,1.00000000000071054284e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071054274e+00 with 64 bits of precision,1.00000000000071143113e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000071143091e+00 with 64 bits of precision,1.00000000000071231963e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071231931e+00 with 64 bits of precision,1.0000000000007132077e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007132076e+00 with 64 bits of precision,1.00000000000071409577e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071409567e+00 with 64 bits of precision,1.00000000000071498406e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071498384e+00 with 64 bits of precision,1.00000000000071587267e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071587224e+00 with 64 bits of precision,1.00000000000071676074e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071676053e+00 with 64 bits of precision,1.00000000000071764881e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071764838e+00 with 64 bits of precision,1.00000000000071853688e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071853667e+00 with 64 bits of precision,1.00000000000071942495e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000071942485e+00 with 64 bits of precision,1.00000000000072031302e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072031292e+00 with 64 bits of precision,1.0000000000007212012e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072120099e+00 with 64 bits of precision,1.00000000000072208938e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072208916e+00 with 64 bits of precision,1.00000000000072297788e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072297756e+00 with 64 bits of precision,1.00000000000072386595e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072386585e+00 with 64 bits of precision,1.00000000000072475402e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007247537e+00 with 64 bits of precision,1.00000000000072564209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072564199e+00 with 64 bits of precision,1.00000000000072653016e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072653006e+00 with 64 bits of precision,1.00000000000072741834e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072741813e+00 with 64 bits of precision,1.00000000000072830652e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007283062e+00 with 64 bits of precision,1.00000000000072919459e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000072919437e+00 with 64 bits of precision,1.00000000000073008309e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073008277e+00 with 64 bits of precision,1.00000000000073097116e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073097106e+00 with 64 bits of precision,1.00000000000073185923e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073185913e+00 with 64 bits of precision,1.00000000000073274741e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007327472e+00 with 64 bits of precision,1.00000000000073363559e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073363527e+00 with 64 bits of precision,1.0000000000007345241e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073452388e+00 with 64 bits of precision,1.00000000000073541227e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073541184e+00 with 64 bits of precision,1.00000000000073630034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073630013e+00 with 64 bits of precision,1.00000000000073718841e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007371882e+00 with 64 bits of precision,1.00000000000073807648e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073807638e+00 with 64 bits of precision,1.00000000000073896455e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073896445e+00 with 64 bits of precision,1.00000000000073985284e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000073985262e+00 with 64 bits of precision,1.00000000000074074134e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074074102e+00 with 64 bits of precision,1.00000000000074162941e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074162931e+00 with 64 bits of precision,1.00000000000074251748e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074251738e+00 with 64 bits of precision,1.00000000000074340577e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074340555e+00 with 64 bits of precision,1.00000000000074429427e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074429395e+00 with 64 bits of precision,1.00000000000074518234e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074518224e+00 with 64 bits of precision,1.00000000000074607041e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074607009e+00 with 64 bits of precision,1.00000000000074695848e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074695838e+00 with 64 bits of precision,1.00000000000074784655e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074784645e+00 with 64 bits of precision,1.00000000000074873473e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074873452e+00 with 64 bits of precision,1.00000000000074962291e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000074962259e+00 with 64 bits of precision,1.00000000000075051131e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075051109e+00 with 64 bits of precision,1.00000000000075139959e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075139927e+00 with 64 bits of precision,1.00000000000075228766e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000075228756e+00 with 64 bits of precision,1.00000000000075317573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075317541e+00 with 64 bits of precision,1.0000000000007540638e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007540637e+00 with 64 bits of precision,1.00000000000075495187e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075495177e+00 with 64 bits of precision,1.00000000000075584005e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075583984e+00 with 64 bits of precision,1.00000000000075672823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075672791e+00 with 64 bits of precision,1.0000000000007576163e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075761608e+00 with 64 bits of precision,1.0000000000007585048e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075850448e+00 with 64 bits of precision,1.00000000000075939287e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000075939277e+00 with 64 bits of precision,1.00000000000076028094e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076028084e+00 with 64 bits of precision,1.00000000000076116912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076116891e+00 with 64 bits of precision,1.0000000000007620573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076205698e+00 with 64 bits of precision,1.0000000000007629457e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076294548e+00 with 64 bits of precision,1.00000000000076383387e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076383355e+00 with 64 bits of precision,1.00000000000076472194e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076472184e+00 with 64 bits of precision,1.00000000000076561001e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076560991e+00 with 64 bits of precision,1.00000000000076649808e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076649798e+00 with 64 bits of precision,1.00000000000076738626e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076738605e+00 with 64 bits of precision,1.00000000000076827444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076827422e+00 with 64 bits of precision,1.00000000000076916305e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000076916262e+00 with 64 bits of precision,1.00000000000077005112e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077005091e+00 with 64 bits of precision,1.00000000000077093919e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077093887e+00 with 64 bits of precision,1.00000000000077182726e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077182716e+00 with 64 bits of precision,1.00000000000077271533e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077271523e+00 with 64 bits of precision,1.00000000000077360351e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007736033e+00 with 64 bits of precision,1.00000000000077449169e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077449137e+00 with 64 bits of precision,1.00000000000077537976e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077537954e+00 with 64 bits of precision,1.00000000000077626826e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077626794e+00 with 64 bits of precision,1.00000000000077715633e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077715623e+00 with 64 bits of precision,1.0000000000007780444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007780443e+00 with 64 bits of precision,1.00000000000077893269e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077893247e+00 with 64 bits of precision,1.00000000000077982119e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000077982087e+00 with 64 bits of precision,1.00000000000078070926e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078070916e+00 with 64 bits of precision,1.00000000000078159733e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078159701e+00 with 64 bits of precision,1.0000000000007824854e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000007824853e+00 with 64 bits of precision,1.00000000000078337347e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078337337e+00 with 64 bits of precision,1.00000000000078426165e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078426144e+00 with 64 bits of precision,1.00000000000078514983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078514951e+00 with 64 bits of precision,1.00000000000078603823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078603801e+00 with 64 bits of precision,1.00000000000078692651e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078692619e+00 with 64 bits of precision,1.00000000000078781458e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078781448e+00 with 64 bits of precision,1.00000000000078870265e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078870255e+00 with 64 bits of precision,1.00000000000078959083e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000078959062e+00 with 64 bits of precision,1.00000000000079047901e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079047869e+00 with 64 bits of precision,1.00000000000079136741e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079136719e+00 with 64 bits of precision,1.00000000000079225558e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079225526e+00 with 64 bits of precision,1.00000000000079314365e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079314355e+00 with 64 bits of precision,1.00000000000079403172e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000079403162e+00 with 64 bits of precision,1.00000000000079491979e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079491969e+00 with 64 bits of precision,1.00000000000079580797e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079580776e+00 with 64 bits of precision,1.00000000000079669615e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079669593e+00 with 64 bits of precision,1.00000000000079758465e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079758433e+00 with 64 bits of precision,1.00000000000079847272e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079847262e+00 with 64 bits of precision,1.00000000000079936079e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000079936069e+00 with 64 bits of precision,1.00000000000080024908e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080024886e+00 with 64 bits of precision,1.00000000000080113769e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080113726e+00 with 64 bits of precision,1.00000000000080202576e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080202555e+00 with 64 bits of precision,1.00000000000080291383e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008029134e+00 with 64 bits of precision,1.0000000000008038019e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080380169e+00 with 64 bits of precision,1.00000000000080468997e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080468987e+00 with 64 bits of precision,1.00000000000080557804e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080557794e+00 with 64 bits of precision,1.00000000000080646622e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080646601e+00 with 64 bits of precision,1.0000000000008073544e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080735418e+00 with 64 bits of precision,1.0000000000008082429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080824258e+00 with 64 bits of precision,1.00000000000080913097e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000080913087e+00 with 64 bits of precision,1.00000000000081001904e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081001872e+00 with 64 bits of precision,1.00000000000081090711e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081090701e+00 with 64 bits of precision,1.00000000000081179518e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081179508e+00 with 64 bits of precision,1.00000000000081268336e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081268315e+00 with 64 bits of precision,1.00000000000081357154e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081357122e+00 with 64 bits of precision,1.00000000000081445961e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081445939e+00 with 64 bits of precision,1.00000000000081534811e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081534779e+00 with 64 bits of precision,1.00000000000081623618e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081623608e+00 with 64 bits of precision,1.00000000000081712425e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081712415e+00 with 64 bits of precision,1.00000000000081801243e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081801222e+00 with 64 bits of precision,1.00000000000081890061e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000081890029e+00 with 64 bits of precision,1.00000000000081978912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008197889e+00 with 64 bits of precision,1.00000000000082067729e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082067686e+00 with 64 bits of precision,1.00000000000082156536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082156515e+00 with 64 bits of precision,1.00000000000082245343e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082245322e+00 with 64 bits of precision,1.0000000000008233415e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008233414e+00 with 64 bits of precision,1.00000000000082422957e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082422947e+00 with 64 bits of precision,1.00000000000082511786e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082511764e+00 with 64 bits of precision,1.00000000000082600636e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082600604e+00 with 64 bits of precision,1.00000000000082689443e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082689433e+00 with 64 bits of precision,1.0000000000008277825e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008277824e+00 with 64 bits of precision,1.00000000000082867079e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082867057e+00 with 64 bits of precision,1.00000000000082955929e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000082955897e+00 with 64 bits of precision,1.00000000000083044736e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083044726e+00 with 64 bits of precision,1.00000000000083133543e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083133511e+00 with 64 bits of precision,1.0000000000008322235e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000008322234e+00 with 64 bits of precision,1.00000000000083311157e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083311147e+00 with 64 bits of precision,1.00000000000083399975e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083399954e+00 with 64 bits of precision,1.00000000000083488793e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083488761e+00 with 64 bits of precision,1.00000000000083577633e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083577611e+00 with 64 bits of precision,1.00000000000083666461e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083666429e+00 with 64 bits of precision,1.00000000000083755268e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083755258e+00 with 64 bits of precision,1.00000000000083844075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083844043e+00 with 64 bits of precision,1.00000000000083932882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000083932872e+00 with 64 bits of precision,1.00000000000084021689e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084021679e+00 with 64 bits of precision,1.00000000000084110507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084110486e+00 with 64 bits of precision,1.00000000000084199325e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084199293e+00 with 64 bits of precision,1.00000000000084288132e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008428811e+00 with 64 bits of precision,1.00000000000084376982e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008437695e+00 with 64 bits of precision,1.00000000000084465789e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084465779e+00 with 64 bits of precision,1.00000000000084554596e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084554586e+00 with 64 bits of precision,1.00000000000084643414e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084643393e+00 with 64 bits of precision,1.00000000000084732232e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000847322e+00 with 64 bits of precision,1.00000000000084821072e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008482105e+00 with 64 bits of precision,1.00000000000084909889e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084909857e+00 with 64 bits of precision,1.00000000000084998696e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000084998686e+00 with 64 bits of precision,1.00000000000085087503e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085087493e+00 with 64 bits of precision,1.0000000000008517631e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000000851763e+00 with 64 bits of precision,1.00000000000085265128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085265107e+00 with 64 bits of precision,1.00000000000085353946e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085353924e+00 with 64 bits of precision,1.00000000000085442807e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085442764e+00 with 64 bits of precision,1.00000000000085531614e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085531593e+00 with 64 bits of precision,1.00000000000085620421e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085620389e+00 with 64 bits of precision,1.00000000000085709228e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085709218e+00 with 64 bits of precision,1.00000000000085798035e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085798025e+00 with 64 bits of precision,1.00000000000085886853e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085886832e+00 with 64 bits of precision,1.00000000000085975671e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000085975639e+00 with 64 bits of precision,1.00000000000086064478e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086064456e+00 with 64 bits of precision,1.00000000000086153328e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086153296e+00 with 64 bits of precision,1.00000000000086242135e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086242125e+00 with 64 bits of precision,1.00000000000086330942e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086330932e+00 with 64 bits of precision,1.00000000000086419771e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086419749e+00 with 64 bits of precision,1.00000000000086508621e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086508589e+00 with 64 bits of precision,1.00000000000086597428e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086597418e+00 with 64 bits of precision,1.00000000000086686235e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086686203e+00 with 64 bits of precision,1.00000000000086775042e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086775032e+00 with 64 bits of precision,1.00000000000086863849e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000086863839e+00 with 64 bits of precision,1.00000000000086952667e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000086952646e+00 with 64 bits of precision,1.00000000000087041485e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087041453e+00 with 64 bits of precision,1.00000000000087130292e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008713027e+00 with 64 bits of precision,1.00000000000087219142e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008721911e+00 with 64 bits of precision,1.00000000000087307949e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087307939e+00 with 64 bits of precision,1.00000000000087396756e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087396746e+00 with 64 bits of precision,1.00000000000087485574e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087485553e+00 with 64 bits of precision,1.00000000000087574403e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008757436e+00 with 64 bits of precision,1.00000000000087663243e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000087663221e+00 with 64 bits of precision,1.0000000000008775206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087752028e+00 with 64 bits of precision,1.00000000000087840867e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087840857e+00 with 64 bits of precision,1.00000000000087929674e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000087929664e+00 with 64 bits of precision,1.00000000000088018481e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088018471e+00 with 64 bits of precision,1.00000000000088107299e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088107278e+00 with 64 bits of precision,1.00000000000088196117e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088196095e+00 with 64 bits of precision,1.00000000000088284967e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088284935e+00 with 64 bits of precision,1.00000000000088373774e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088373764e+00 with 64 bits of precision,1.00000000000088462581e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088462571e+00 with 64 bits of precision,1.0000000000008855141e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088551388e+00 with 64 bits of precision,1.0000000000008864026e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088640228e+00 with 64 bits of precision,1.00000000000088729067e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088729057e+00 with 64 bits of precision,1.00000000000088817874e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088817842e+00 with 64 bits of precision,1.00000000000088906681e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088906671e+00 with 64 bits of precision,1.00000000000088995488e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000088995478e+00 with 64 bits of precision,1.00000000000089084306e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089084285e+00 with 64 bits of precision,1.00000000000089173124e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089173092e+00 with 64 bits of precision,1.00000000000089261942e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008926192e+00 with 64 bits of precision,1.00000000000089350792e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008935076e+00 with 64 bits of precision,1.00000000000089439599e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089439589e+00 with 64 bits of precision,1.00000000000089528406e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089528385e+00 with 64 bits of precision,1.00000000000089617213e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089617203e+00 with 64 bits of precision,1.00000000000089706042e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008970601e+00 with 64 bits of precision,1.00000000000089794882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000008979486e+00 with 64 bits of precision,1.00000000000089883699e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089883667e+00 with 64 bits of precision,1.00000000000089972506e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000089972496e+00 with 64 bits of precision,1.00000000000090061313e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090061303e+00 with 64 bits of precision,1.0000000000009015012e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009015011e+00 with 64 bits of precision,1.00000000000090238938e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090238917e+00 with 64 bits of precision,1.00000000000090327756e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090327734e+00 with 64 bits of precision,1.00000000000090416606e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090416574e+00 with 64 bits of precision,1.00000000000090505413e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090505403e+00 with 64 bits of precision,1.0000000000009059422e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090594199e+00 with 64 bits of precision,1.00000000000090683027e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090683017e+00 with 64 bits of precision,1.00000000000090771845e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090771824e+00 with 64 bits of precision,1.00000000000090860652e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090860631e+00 with 64 bits of precision,1.00000000000090949481e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000090949438e+00 with 64 bits of precision,1.00000000000091038266e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091038245e+00 with 64 bits of precision,1.00000000000091127095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091127052e+00 with 64 bits of precision,1.00000000000091215935e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091215913e+00 with 64 bits of precision,1.00000000000091304752e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009130472e+00 with 64 bits of precision,1.00000000000091393559e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091393549e+00 with 64 bits of precision,1.00000000000091482366e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091482356e+00 with 64 bits of precision,1.00000000000091571184e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091571163e+00 with 64 bits of precision,1.00000000000091660002e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009165997e+00 with 64 bits of precision,1.00000000000091748809e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000091748787e+00 with 64 bits of precision,1.00000000000091837659e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091837627e+00 with 64 bits of precision,1.00000000000091926466e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000091926456e+00 with 64 bits of precision,1.00000000000092015273e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092015263e+00 with 64 bits of precision,1.00000000000092104102e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009210408e+00 with 64 bits of precision,1.00000000000092192952e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009219292e+00 with 64 bits of precision,1.00000000000092281759e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092281749e+00 with 64 bits of precision,1.00000000000092370566e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092370534e+00 with 64 bits of precision,1.00000000000092459373e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092459363e+00 with 64 bits of precision,1.0000000000009254818e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009254817e+00 with 64 bits of precision,1.00000000000092636998e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092636977e+00 with 64 bits of precision,1.00000000000092725816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092725784e+00 with 64 bits of precision,1.00000000000092814634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092814612e+00 with 64 bits of precision,1.00000000000092903484e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092903452e+00 with 64 bits of precision,1.00000000000092992291e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000092992281e+00 with 64 bits of precision,1.00000000000093081098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093081077e+00 with 64 bits of precision,1.00000000000093169905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093169895e+00 with 64 bits of precision,1.00000000000093258712e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093258702e+00 with 64 bits of precision,1.0000000000009334753e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093347509e+00 with 64 bits of precision,1.00000000000093436348e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093436316e+00 with 64 bits of precision,1.00000000000093525155e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093525133e+00 with 64 bits of precision,1.00000000000093614005e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093613973e+00 with 64 bits of precision,1.00000000000093702812e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093702802e+00 with 64 bits of precision,1.00000000000093791619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093791609e+00 with 64 bits of precision,1.00000000000093880448e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093880426e+00 with 64 bits of precision,1.00000000000093969298e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000093969266e+00 with 64 bits of precision,1.00000000000094058105e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094058095e+00 with 64 bits of precision,1.00000000000094146912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094146891e+00 with 64 bits of precision,1.00000000000094235719e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094235709e+00 with 64 bits of precision,1.00000000000094324537e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094324516e+00 with 64 bits of precision,1.00000000000094413344e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094413323e+00 with 64 bits of precision,1.00000000000094502173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009450213e+00 with 64 bits of precision,1.00000000000094590958e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094590937e+00 with 64 bits of precision,1.00000000000094679787e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094679744e+00 with 64 bits of precision,1.00000000000094768627e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094768605e+00 with 64 bits of precision,1.00000000000094857444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094857434e+00 with 64 bits of precision,1.00000000000094946273e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000094946251e+00 with 64 bits of precision,1.00000000000095035123e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095035091e+00 with 64 bits of precision,1.0000000000009512393e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009512392e+00 with 64 bits of precision,1.00000000000095212737e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095212705e+00 with 64 bits of precision,1.00000000000095301544e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095301534e+00 with 64 bits of precision,1.00000000000095390351e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095390341e+00 with 64 bits of precision,1.00000000000095479169e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095479148e+00 with 64 bits of precision,1.00000000000095567987e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095567955e+00 with 64 bits of precision,1.00000000000095656794e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095656772e+00 with 64 bits of precision,1.00000000000095745644e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095745612e+00 with 64 bits of precision,1.00000000000095834451e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095834441e+00 with 64 bits of precision,1.00000000000095923258e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000095923248e+00 with 64 bits of precision,1.00000000000096012065e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000096012055e+00 with 64 bits of precision,1.00000000000096100883e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096100862e+00 with 64 bits of precision,1.0000000000009618969e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096189669e+00 with 64 bits of precision,1.00000000000096278519e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096278476e+00 with 64 bits of precision,1.00000000000096367326e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096367304e+00 with 64 bits of precision,1.00000000000096456176e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096456144e+00 with 64 bits of precision,1.00000000000096544983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096544973e+00 with 64 bits of precision,1.0000000000009663379e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009663378e+00 with 64 bits of precision,1.00000000000096722619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096722597e+00 with 64 bits of precision,1.00000000000096811469e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096811437e+00 with 64 bits of precision,1.00000000000096900276e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096900266e+00 with 64 bits of precision,1.00000000000096989083e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000096989073e+00 with 64 bits of precision,1.00000000000097077912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009707789e+00 with 64 bits of precision,1.00000000000097166762e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009716673e+00 with 64 bits of precision,1.00000000000097255569e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097255559e+00 with 64 bits of precision,1.00000000000097344376e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097344344e+00 with 64 bits of precision,1.00000000000097433183e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097433173e+00 with 64 bits of precision,1.0000000000009752199e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009752198e+00 with 64 bits of precision,1.00000000000097610808e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097610787e+00 with 64 bits of precision,1.00000000000097699626e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097699594e+00 with 64 bits of precision,1.00000000000097788444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097788422e+00 with 64 bits of precision,1.00000000000097877294e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097877262e+00 with 64 bits of precision,1.00000000000097966101e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000097966091e+00 with 64 bits of precision,1.00000000000098054908e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098054876e+00 with 64 bits of precision,1.00000000000098143715e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098143705e+00 with 64 bits of precision,1.00000000000098232522e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098232512e+00 with 64 bits of precision,1.0000000000009832134e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098321319e+00 with 64 bits of precision,1.00000000000098410158e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098410126e+00 with 64 bits of precision,1.00000000000098498965e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098498943e+00 with 64 bits of precision,1.00000000000098587815e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098587783e+00 with 64 bits of precision,1.00000000000098676622e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098676612e+00 with 64 bits of precision,1.00000000000098765429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098765419e+00 with 64 bits of precision,1.00000000000098854247e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098854226e+00 with 64 bits of precision,1.00000000000098943065e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000098943033e+00 with 64 bits of precision,1.00000000000099031905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099031883e+00 with 64 bits of precision,1.00000000000099120722e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009912069e+00 with 64 bits of precision,1.00000000000099209529e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099209519e+00 with 64 bits of precision,1.00000000000099298336e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099298326e+00 with 64 bits of precision,1.00000000000099387143e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099387133e+00 with 64 bits of precision,1.00000000000099475961e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000009947594e+00 with 64 bits of precision,1.00000000000099564768e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099564747e+00 with 64 bits of precision,1.00000000000099653597e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099653554e+00 with 64 bits of precision,1.00000000000099742437e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099742415e+00 with 64 bits of precision,1.00000000000099831254e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099831222e+00 with 64 bits of precision,1.00000000000099920061e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000099920051e+00 with 64 bits of precision,1.00000000000100008868e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100008858e+00 with 64 bits of precision,1.00000000000100097686e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000100097665e+00 with 64 bits of precision,1.00000000000100186504e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100186472e+00 with 64 bits of precision,1.00000000000100275311e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100275289e+00 with 64 bits of precision,1.00000000000100364161e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100364129e+00 with 64 bits of precision,1.00000000000100452968e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100452958e+00 with 64 bits of precision,1.00000000000100541775e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100541765e+00 with 64 bits of precision,1.00000000000100630604e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100630582e+00 with 64 bits of precision,1.00000000000100719454e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100719422e+00 with 64 bits of precision,1.00000000000100808261e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100808251e+00 with 64 bits of precision,1.00000000000100897068e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100897047e+00 with 64 bits of precision,1.00000000000100985875e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000100985865e+00 with 64 bits of precision,1.00000000000101074693e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101074672e+00 with 64 bits of precision,1.000000000001011635e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101163479e+00 with 64 bits of precision,1.00000000000101252329e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101252286e+00 with 64 bits of precision,1.00000000000101341136e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101341114e+00 with 64 bits of precision,1.00000000000101429986e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101429954e+00 with 64 bits of precision,1.00000000000101518793e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101518783e+00 with 64 bits of precision,1.000000000001016076e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010160759e+00 with 64 bits of precision,1.00000000000101696429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101696407e+00 with 64 bits of precision,1.00000000000101785279e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101785247e+00 with 64 bits of precision,1.00000000000101874086e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101874076e+00 with 64 bits of precision,1.00000000000101962893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000101962872e+00 with 64 bits of precision,1.000000000001020517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010205169e+00 with 64 bits of precision,1.00000000000102140507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102140497e+00 with 64 bits of precision,1.00000000000102229325e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102229304e+00 with 64 bits of precision,1.00000000000102318143e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102318111e+00 with 64 bits of precision,1.0000000000010240695e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102406928e+00 with 64 bits of precision,1.000000000001024958e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102495768e+00 with 64 bits of precision,1.00000000000102584607e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102584597e+00 with 64 bits of precision,1.00000000000102673414e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102673393e+00 with 64 bits of precision,1.00000000000102762221e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102762211e+00 with 64 bits of precision,1.00000000000102851039e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102851018e+00 with 64 bits of precision,1.00000000000102939846e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000102939825e+00 with 64 bits of precision,1.00000000000103028675e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103028632e+00 with 64 bits of precision,1.0000000000010311746e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103117439e+00 with 64 bits of precision,1.00000000000103206289e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103206246e+00 with 64 bits of precision,1.00000000000103295129e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103295107e+00 with 64 bits of precision,1.00000000000103383946e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103383936e+00 with 64 bits of precision,1.00000000000103472775e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103472753e+00 with 64 bits of precision,1.00000000000103561625e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103561593e+00 with 64 bits of precision,1.00000000000103650432e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103650422e+00 with 64 bits of precision,1.00000000000103739239e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103739218e+00 with 64 bits of precision,1.00000000000103828046e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103828036e+00 with 64 bits of precision,1.00000000000103916875e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000103916843e+00 with 64 bits of precision,1.00000000000104005715e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104005693e+00 with 64 bits of precision,1.00000000000104094532e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001040945e+00 with 64 bits of precision,1.00000000000104183339e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000104183329e+00 with 64 bits of precision,1.00000000000104272146e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104272136e+00 with 64 bits of precision,1.00000000000104360953e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104360943e+00 with 64 bits of precision,1.00000000000104449771e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010444975e+00 with 64 bits of precision,1.00000000000104538589e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104538567e+00 with 64 bits of precision,1.0000000000010462745e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104627407e+00 with 64 bits of precision,1.00000000000104716257e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104716236e+00 with 64 bits of precision,1.00000000000104805064e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104805032e+00 with 64 bits of precision,1.00000000000104893871e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104893861e+00 with 64 bits of precision,1.00000000000104982678e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000104982668e+00 with 64 bits of precision,1.00000000000105071496e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105071475e+00 with 64 bits of precision,1.00000000000105160314e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105160282e+00 with 64 bits of precision,1.00000000000105249121e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105249099e+00 with 64 bits of precision,1.00000000000105337971e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105337939e+00 with 64 bits of precision,1.00000000000105426778e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105426768e+00 with 64 bits of precision,1.00000000000105515585e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105515575e+00 with 64 bits of precision,1.00000000000105604414e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105604392e+00 with 64 bits of precision,1.00000000000105693264e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105693232e+00 with 64 bits of precision,1.00000000000105782071e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105782061e+00 with 64 bits of precision,1.00000000000105870878e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105870846e+00 with 64 bits of precision,1.00000000000105959685e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000105959675e+00 with 64 bits of precision,1.00000000000106048492e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106048482e+00 with 64 bits of precision,1.0000000000010613731e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106137289e+00 with 64 bits of precision,1.00000000000106226128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106226096e+00 with 64 bits of precision,1.00000000000106314968e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106314946e+00 with 64 bits of precision,1.00000000000106403796e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106403764e+00 with 64 bits of precision,1.00000000000106492603e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106492593e+00 with 64 bits of precision,1.0000000000010658141e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001065814e+00 with 64 bits of precision,1.00000000000106670239e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106670217e+00 with 64 bits of precision,1.00000000000106759089e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106759057e+00 with 64 bits of precision,1.00000000000106847896e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106847886e+00 with 64 bits of precision,1.00000000000106936703e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000106936693e+00 with 64 bits of precision,1.00000000000107025532e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010702551e+00 with 64 bits of precision,1.00000000000107114382e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010711435e+00 with 64 bits of precision,1.00000000000107203189e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107203179e+00 with 64 bits of precision,1.00000000000107291996e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107291964e+00 with 64 bits of precision,1.00000000000107380803e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107380793e+00 with 64 bits of precision,1.0000000000010746961e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001074696e+00 with 64 bits of precision,1.00000000000107558428e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107558407e+00 with 64 bits of precision,1.00000000000107647246e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107647214e+00 with 64 bits of precision,1.00000000000107736086e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107736064e+00 with 64 bits of precision,1.00000000000107824914e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107824882e+00 with 64 bits of precision,1.00000000000107913721e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000107913711e+00 with 64 bits of precision,1.00000000000108002528e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108002496e+00 with 64 bits of precision,1.00000000000108091335e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108091325e+00 with 64 bits of precision,1.00000000000108180142e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000108180132e+00 with 64 bits of precision,1.0000000000010826896e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108268939e+00 with 64 bits of precision,1.00000000000108357778e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108357746e+00 with 64 bits of precision,1.00000000000108446585e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108446563e+00 with 64 bits of precision,1.00000000000108535435e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108535403e+00 with 64 bits of precision,1.00000000000108624242e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108624232e+00 with 64 bits of precision,1.00000000000108713049e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108713039e+00 with 64 bits of precision,1.00000000000108801878e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108801856e+00 with 64 bits of precision,1.00000000000108890728e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108890696e+00 with 64 bits of precision,1.00000000000108979535e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000108979525e+00 with 64 bits of precision,1.00000000000109068342e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109068321e+00 with 64 bits of precision,1.00000000000109157149e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109157139e+00 with 64 bits of precision,1.00000000000109245956e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109245946e+00 with 64 bits of precision,1.00000000000109334774e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109334753e+00 with 64 bits of precision,1.00000000000109423592e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000010942356e+00 with 64 bits of precision,1.00000000000109512399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109512377e+00 with 64 bits of precision,1.0000000000010960126e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109601217e+00 with 64 bits of precision,1.00000000000109690067e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109690046e+00 with 64 bits of precision,1.00000000000109778874e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109778864e+00 with 64 bits of precision,1.00000000000109867703e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109867681e+00 with 64 bits of precision,1.00000000000109956553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000109956521e+00 with 64 bits of precision,1.0000000000011004536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011004535e+00 with 64 bits of precision,1.00000000000110134167e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110134135e+00 with 64 bits of precision,1.00000000000110222974e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110222964e+00 with 64 bits of precision,1.00000000000110311781e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110311771e+00 with 64 bits of precision,1.00000000000110400599e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110400578e+00 with 64 bits of precision,1.00000000000110489417e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110489385e+00 with 64 bits of precision,1.00000000000110578224e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110578202e+00 with 64 bits of precision,1.00000000000110667074e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110667042e+00 with 64 bits of precision,1.00000000000110755881e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110755871e+00 with 64 bits of precision,1.00000000000110844688e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110844678e+00 with 64 bits of precision,1.00000000000110933517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000110933495e+00 with 64 bits of precision,1.00000000000111022378e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111022335e+00 with 64 bits of precision,1.00000000000111111185e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111111164e+00 with 64 bits of precision,1.00000000000111199992e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011119996e+00 with 64 bits of precision,1.00000000000111288799e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111288789e+00 with 64 bits of precision,1.00000000000111377606e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111377596e+00 with 64 bits of precision,1.00000000000111466424e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111466403e+00 with 64 bits of precision,1.00000000000111555242e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011155521e+00 with 64 bits of precision,1.00000000000111644049e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111644027e+00 with 64 bits of precision,1.00000000000111732899e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111732867e+00 with 64 bits of precision,1.00000000000111821706e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111821696e+00 with 64 bits of precision,1.00000000000111910513e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000111910503e+00 with 64 bits of precision,1.00000000000111999342e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011199932e+00 with 64 bits of precision,1.00000000000112088192e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011208816e+00 with 64 bits of precision,1.00000000000112176999e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000112176989e+00 with 64 bits of precision,1.00000000000112265806e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112265774e+00 with 64 bits of precision,1.00000000000112354613e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112354603e+00 with 64 bits of precision,1.0000000000011244342e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011244341e+00 with 64 bits of precision,1.00000000000112532238e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112532217e+00 with 64 bits of precision,1.00000000000112621056e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112621024e+00 with 64 bits of precision,1.00000000000112709896e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112709874e+00 with 64 bits of precision,1.00000000000112798724e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112798692e+00 with 64 bits of precision,1.00000000000112887531e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112887521e+00 with 64 bits of precision,1.00000000000112976338e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000112976317e+00 with 64 bits of precision,1.00000000000113065145e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113065135e+00 with 64 bits of precision,1.00000000000113153952e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113153942e+00 with 64 bits of precision,1.0000000000011324277e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113242749e+00 with 64 bits of precision,1.00000000000113331588e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113331556e+00 with 64 bits of precision,1.00000000000113420395e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113420373e+00 with 64 bits of precision,1.00000000000113509245e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113509213e+00 with 64 bits of precision,1.00000000000113598052e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113598042e+00 with 64 bits of precision,1.00000000000113686859e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113686827e+00 with 64 bits of precision,1.00000000000113775666e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113775656e+00 with 64 bits of precision,1.00000000000113864473e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000113864463e+00 with 64 bits of precision,1.00000000000113953291e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011395327e+00 with 64 bits of precision,1.00000000000114042109e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114042077e+00 with 64 bits of precision,1.00000000000114130916e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114130894e+00 with 64 bits of precision,1.00000000000114219766e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114219734e+00 with 64 bits of precision,1.00000000000114308573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114308563e+00 with 64 bits of precision,1.0000000000011439738e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011439737e+00 with 64 bits of precision,1.00000000000114486209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114486187e+00 with 64 bits of precision,1.0000000000011457507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114575027e+00 with 64 bits of precision,1.00000000000114663877e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114663856e+00 with 64 bits of precision,1.00000000000114752684e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114752652e+00 with 64 bits of precision,1.00000000000114841491e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114841481e+00 with 64 bits of precision,1.00000000000114930298e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000114930288e+00 with 64 bits of precision,1.00000000000115019116e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115019095e+00 with 64 bits of precision,1.00000000000115107934e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115107902e+00 with 64 bits of precision,1.00000000000115196741e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115196719e+00 with 64 bits of precision,1.00000000000115285591e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115285559e+00 with 64 bits of precision,1.00000000000115374398e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115374388e+00 with 64 bits of precision,1.00000000000115463205e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115463195e+00 with 64 bits of precision,1.00000000000115552034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115552012e+00 with 64 bits of precision,1.00000000000115640884e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115640852e+00 with 64 bits of precision,1.00000000000115729691e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000115729681e+00 with 64 bits of precision,1.00000000000115818498e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115818477e+00 with 64 bits of precision,1.00000000000115907305e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115907295e+00 with 64 bits of precision,1.00000000000115996134e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000115996102e+00 with 64 bits of precision,1.00000000000116084985e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116084963e+00 with 64 bits of precision,1.00000000000116173802e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116173759e+00 with 64 bits of precision,1.00000000000116262609e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116262588e+00 with 64 bits of precision,1.00000000000116351416e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116351395e+00 with 64 bits of precision,1.00000000000116440223e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116440213e+00 with 64 bits of precision,1.0000000000011652903e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116529009e+00 with 64 bits of precision,1.00000000000116617837e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116617827e+00 with 64 bits of precision,1.00000000000116706666e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116706634e+00 with 64 bits of precision,1.00000000000116795506e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116795484e+00 with 64 bits of precision,1.00000000000116884323e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000116884291e+00 with 64 bits of precision,1.0000000000011697313e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011697312e+00 with 64 bits of precision,1.00000000000117061937e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117061927e+00 with 64 bits of precision,1.00000000000117150755e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117150734e+00 with 64 bits of precision,1.00000000000117239573e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117239541e+00 with 64 bits of precision,1.0000000000011732838e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117328358e+00 with 64 bits of precision,1.0000000000011741723e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117417198e+00 with 64 bits of precision,1.00000000000117506037e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117506027e+00 with 64 bits of precision,1.00000000000117594855e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117594834e+00 with 64 bits of precision,1.00000000000117683673e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117683651e+00 with 64 bits of precision,1.00000000000117772534e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117772491e+00 with 64 bits of precision,1.00000000000117861341e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011786132e+00 with 64 bits of precision,1.00000000000117950148e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000117950105e+00 with 64 bits of precision,1.00000000000118038955e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118038934e+00 with 64 bits of precision,1.00000000000118127762e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118127752e+00 with 64 bits of precision,1.00000000000118216569e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118216559e+00 with 64 bits of precision,1.00000000000118305387e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118305366e+00 with 64 bits of precision,1.00000000000118394205e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118394183e+00 with 64 bits of precision,1.00000000000118483055e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118483023e+00 with 64 bits of precision,1.00000000000118571862e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118571852e+00 with 64 bits of precision,1.00000000000118660669e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118660648e+00 with 64 bits of precision,1.00000000000118749476e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118749466e+00 with 64 bits of precision,1.00000000000118838283e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000118838273e+00 with 64 bits of precision,1.00000000000118927101e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000011892708e+00 with 64 bits of precision,1.00000000000119015919e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119015887e+00 with 64 bits of precision,1.00000000000119104726e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119104704e+00 with 64 bits of precision,1.00000000000119193576e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119193544e+00 with 64 bits of precision,1.00000000000119282383e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119282373e+00 with 64 bits of precision,1.0000000000011937119e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000011937118e+00 with 64 bits of precision,1.00000000000119460019e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119459997e+00 with 64 bits of precision,1.0000000000011954888e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119548837e+00 with 64 bits of precision,1.00000000000119637687e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119637666e+00 with 64 bits of precision,1.00000000000119726494e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119726462e+00 with 64 bits of precision,1.00000000000119815301e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119815291e+00 with 64 bits of precision,1.00000000000119904108e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119904098e+00 with 64 bits of precision,1.00000000000119992926e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000119992905e+00 with 64 bits of precision,1.00000000000120081744e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120081712e+00 with 64 bits of precision,1.00000000000120170551e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120170529e+00 with 64 bits of precision,1.00000000000120259401e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120259369e+00 with 64 bits of precision,1.00000000000120348208e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120348198e+00 with 64 bits of precision,1.00000000000120437015e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120437005e+00 with 64 bits of precision,1.00000000000120525844e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120525822e+00 with 64 bits of precision,1.00000000000120614694e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120614662e+00 with 64 bits of precision,1.00000000000120703501e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120703491e+00 with 64 bits of precision,1.00000000000120792308e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120792276e+00 with 64 bits of precision,1.00000000000120881115e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120881105e+00 with 64 bits of precision,1.00000000000120969922e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000120969912e+00 with 64 bits of precision,1.0000000000012105874e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121058719e+00 with 64 bits of precision,1.00000000000121147558e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121147526e+00 with 64 bits of precision,1.00000000000121236365e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121236343e+00 with 64 bits of precision,1.00000000000121325215e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121325183e+00 with 64 bits of precision,1.00000000000121414022e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121414012e+00 with 64 bits of precision,1.00000000000121502829e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121502819e+00 with 64 bits of precision,1.00000000000121591636e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121591626e+00 with 64 bits of precision,1.00000000000121680454e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121680433e+00 with 64 bits of precision,1.00000000000121769261e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000012176924e+00 with 64 bits of precision,1.0000000000012185809e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121858047e+00 with 64 bits of precision,1.00000000000121946897e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000121946875e+00 with 64 bits of precision,1.00000000000122035747e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122035715e+00 with 64 bits of precision,1.00000000000122124554e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122124544e+00 with 64 bits of precision,1.00000000000122213361e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122213351e+00 with 64 bits of precision,1.00000000000122302179e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122302158e+00 with 64 bits of precision,1.00000000000122390997e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122390965e+00 with 64 bits of precision,1.00000000000122479837e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122479815e+00 with 64 bits of precision,1.00000000000122568654e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122568622e+00 with 64 bits of precision,1.00000000000122657461e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122657451e+00 with 64 bits of precision,1.00000000000122746268e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122746258e+00 with 64 bits of precision,1.00000000000122835075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122835065e+00 with 64 bits of precision,1.00000000000122923893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000122923872e+00 with 64 bits of precision,1.00000000000123012711e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000123012689e+00 with 64 bits of precision,1.00000000000123101561e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123101529e+00 with 64 bits of precision,1.00000000000123190368e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123190358e+00 with 64 bits of precision,1.00000000000123279175e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123279154e+00 with 64 bits of precision,1.00000000000123367982e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123367972e+00 with 64 bits of precision,1.000000000001234568e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123456779e+00 with 64 bits of precision,1.00000000000123545607e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123545586e+00 with 64 bits of precision,1.00000000000123634436e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123634393e+00 with 64 bits of precision,1.00000000000123723221e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001237232e+00 with 64 bits of precision,1.0000000000012381205e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123812007e+00 with 64 bits of precision,1.0000000000012390089e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123900868e+00 with 64 bits of precision,1.00000000000123989707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000123989697e+00 with 64 bits of precision,1.00000000000124078536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124078514e+00 with 64 bits of precision,1.00000000000124167386e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124167354e+00 with 64 bits of precision,1.00000000000124256193e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124256183e+00 with 64 bits of precision,1.00000000000124345e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124344968e+00 with 64 bits of precision,1.00000000000124433807e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124433797e+00 with 64 bits of precision,1.00000000000124522614e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124522604e+00 with 64 bits of precision,1.00000000000124611432e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124611411e+00 with 64 bits of precision,1.0000000000012470025e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124700218e+00 with 64 bits of precision,1.00000000000124789057e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124789035e+00 with 64 bits of precision,1.00000000000124877907e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124877875e+00 with 64 bits of precision,1.00000000000124966714e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000124966704e+00 with 64 bits of precision,1.00000000000125055521e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125055511e+00 with 64 bits of precision,1.00000000000125144339e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125144318e+00 with 64 bits of precision,1.00000000000125233168e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125233125e+00 with 64 bits of precision,1.00000000000125322008e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125321986e+00 with 64 bits of precision,1.00000000000125410825e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125410793e+00 with 64 bits of precision,1.00000000000125499632e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125499622e+00 with 64 bits of precision,1.00000000000125588439e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125588429e+00 with 64 bits of precision,1.00000000000125677257e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125677236e+00 with 64 bits of precision,1.00000000000125766075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000125766043e+00 with 64 bits of precision,1.00000000000125854882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000012585486e+00 with 64 bits of precision,1.00000000000125943732e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001259437e+00 with 64 bits of precision,1.00000000000126032539e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126032529e+00 with 64 bits of precision,1.00000000000126121346e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126121336e+00 with 64 bits of precision,1.00000000000126210175e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126210153e+00 with 64 bits of precision,1.00000000000126299025e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126298993e+00 with 64 bits of precision,1.00000000000126387832e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126387822e+00 with 64 bits of precision,1.00000000000126476639e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126476607e+00 with 64 bits of precision,1.00000000000126565446e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126565436e+00 with 64 bits of precision,1.00000000000126654253e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126654243e+00 with 64 bits of precision,1.00000000000126743071e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000012674305e+00 with 64 bits of precision,1.00000000000126831889e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126831857e+00 with 64 bits of precision,1.00000000000126920707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000126920685e+00 with 64 bits of precision,1.00000000000127009557e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127009525e+00 with 64 bits of precision,1.00000000000127098364e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127098354e+00 with 64 bits of precision,1.00000000000127187171e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000012718715e+00 with 64 bits of precision,1.00000000000127275978e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127275968e+00 with 64 bits of precision,1.00000000000127364785e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127364775e+00 with 64 bits of precision,1.00000000000127453603e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127453582e+00 with 64 bits of precision,1.00000000000127542421e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127542389e+00 with 64 bits of precision,1.00000000000127631228e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127631206e+00 with 64 bits of precision,1.00000000000127720078e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127720046e+00 with 64 bits of precision,1.00000000000127808885e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127808875e+00 with 64 bits of precision,1.00000000000127897692e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127897682e+00 with 64 bits of precision,1.00000000000127986521e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000127986499e+00 with 64 bits of precision,1.00000000000128075371e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128075339e+00 with 64 bits of precision,1.00000000000128164178e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128164168e+00 with 64 bits of precision,1.00000000000128252985e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128252964e+00 with 64 bits of precision,1.00000000000128341792e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128341782e+00 with 64 bits of precision,1.0000000000012843061e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128430589e+00 with 64 bits of precision,1.00000000000128519417e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128519396e+00 with 64 bits of precision,1.00000000000128608246e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128608203e+00 with 64 bits of precision,1.00000000000128697031e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000012869701e+00 with 64 bits of precision,1.0000000000012878586e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128785817e+00 with 64 bits of precision,1.000000000001288747e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128874678e+00 with 64 bits of precision,1.00000000000128963517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000128963507e+00 with 64 bits of precision,1.00000000000129052346e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129052324e+00 with 64 bits of precision,1.00000000000129141196e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129141164e+00 with 64 bits of precision,1.00000000000129230003e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129229993e+00 with 64 bits of precision,1.0000000000012931881e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129318778e+00 with 64 bits of precision,1.00000000000129407617e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129407607e+00 with 64 bits of precision,1.00000000000129496424e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129496414e+00 with 64 bits of precision,1.00000000000129585242e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129585221e+00 with 64 bits of precision,1.0000000000012967406e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129674028e+00 with 64 bits of precision,1.00000000000129762867e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129762845e+00 with 64 bits of precision,1.00000000000129851717e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129851685e+00 with 64 bits of precision,1.00000000000129940524e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000129940514e+00 with 64 bits of precision,1.00000000000130029331e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130029321e+00 with 64 bits of precision,1.00000000000130118138e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130118128e+00 with 64 bits of precision,1.00000000000130206956e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130206935e+00 with 64 bits of precision,1.00000000000130295763e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130295742e+00 with 64 bits of precision,1.00000000000130384592e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130384549e+00 with 64 bits of precision,1.00000000000130473399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130473377e+00 with 64 bits of precision,1.00000000000130562249e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130562217e+00 with 64 bits of precision,1.00000000000130651056e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130651046e+00 with 64 bits of precision,1.00000000000130739863e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000130739853e+00 with 64 bits of precision,1.00000000000130828692e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013082867e+00 with 64 bits of precision,1.00000000000130917542e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013091751e+00 with 64 bits of precision,1.00000000000131006349e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131006339e+00 with 64 bits of precision,1.00000000000131095156e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131095146e+00 with 64 bits of precision,1.00000000000131183985e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000131183963e+00 with 64 bits of precision,1.00000000000131272835e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131272803e+00 with 64 bits of precision,1.00000000000131361642e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131361632e+00 with 64 bits of precision,1.00000000000131450449e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131450417e+00 with 64 bits of precision,1.00000000000131539256e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131539246e+00 with 64 bits of precision,1.00000000000131628063e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131628053e+00 with 64 bits of precision,1.00000000000131716881e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013171686e+00 with 64 bits of precision,1.00000000000131805699e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131805667e+00 with 64 bits of precision,1.00000000000131894517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131894495e+00 with 64 bits of precision,1.00000000000131983367e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000131983335e+00 with 64 bits of precision,1.00000000000132072174e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132072164e+00 with 64 bits of precision,1.00000000000132160981e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132160949e+00 with 64 bits of precision,1.00000000000132249788e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132249778e+00 with 64 bits of precision,1.00000000000132338595e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132338585e+00 with 64 bits of precision,1.00000000000132427413e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132427392e+00 with 64 bits of precision,1.00000000000132516231e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132516199e+00 with 64 bits of precision,1.00000000000132605038e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132605016e+00 with 64 bits of precision,1.00000000000132693888e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132693856e+00 with 64 bits of precision,1.00000000000132782695e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132782685e+00 with 64 bits of precision,1.00000000000132871502e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132871492e+00 with 64 bits of precision,1.0000000000013296032e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000132960299e+00 with 64 bits of precision,1.00000000000133049138e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133049106e+00 with 64 bits of precision,1.00000000000133137978e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133137956e+00 with 64 bits of precision,1.00000000000133226795e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133226763e+00 with 64 bits of precision,1.00000000000133315602e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133315592e+00 with 64 bits of precision,1.00000000000133404409e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133404399e+00 with 64 bits of precision,1.00000000000133493216e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133493206e+00 with 64 bits of precision,1.00000000000133582034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133582013e+00 with 64 bits of precision,1.00000000000133670841e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013367082e+00 with 64 bits of precision,1.0000000000013375967e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133759627e+00 with 64 bits of precision,1.0000000000013384851e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133848488e+00 with 64 bits of precision,1.00000000000133937327e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000133937295e+00 with 64 bits of precision,1.00000000000134026134e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134026124e+00 with 64 bits of precision,1.00000000000134114941e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134114931e+00 with 64 bits of precision,1.00000000000134203759e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134203738e+00 with 64 bits of precision,1.00000000000134292577e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134292545e+00 with 64 bits of precision,1.00000000000134381384e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134381362e+00 with 64 bits of precision,1.00000000000134470234e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134470202e+00 with 64 bits of precision,1.00000000000134559041e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134559031e+00 with 64 bits of precision,1.00000000000134647848e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134647838e+00 with 64 bits of precision,1.00000000000134736677e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134736655e+00 with 64 bits of precision,1.00000000000134825527e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134825495e+00 with 64 bits of precision,1.00000000000134914334e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000134914324e+00 with 64 bits of precision,1.00000000000135003141e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135003109e+00 with 64 bits of precision,1.00000000000135091948e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135091938e+00 with 64 bits of precision,1.00000000000135180755e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135180745e+00 with 64 bits of precision,1.00000000000135269573e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000135269552e+00 with 64 bits of precision,1.00000000000135358391e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135358359e+00 with 64 bits of precision,1.00000000000135447209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135447187e+00 with 64 bits of precision,1.00000000000135536059e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135536027e+00 with 64 bits of precision,1.00000000000135624866e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135624856e+00 with 64 bits of precision,1.00000000000135713673e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135713663e+00 with 64 bits of precision,1.00000000000135802491e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013580247e+00 with 64 bits of precision,1.00000000000135891309e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135891277e+00 with 64 bits of precision,1.00000000000135980149e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000135980127e+00 with 64 bits of precision,1.00000000000136068966e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136068934e+00 with 64 bits of precision,1.00000000000136157773e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136157763e+00 with 64 bits of precision,1.0000000000013624658e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013624657e+00 with 64 bits of precision,1.00000000000136335387e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136335377e+00 with 64 bits of precision,1.00000000000136424205e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136424184e+00 with 64 bits of precision,1.00000000000136513023e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136513001e+00 with 64 bits of precision,1.00000000000136601873e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136601841e+00 with 64 bits of precision,1.0000000000013669068e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013669067e+00 with 64 bits of precision,1.00000000000136779487e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136779466e+00 with 64 bits of precision,1.00000000000136868294e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136868284e+00 with 64 bits of precision,1.00000000000136957112e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000136957091e+00 with 64 bits of precision,1.00000000000137045919e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137045898e+00 with 64 bits of precision,1.00000000000137134748e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137134705e+00 with 64 bits of precision,1.00000000000137223533e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137223512e+00 with 64 bits of precision,1.00000000000137312362e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137312319e+00 with 64 bits of precision,1.00000000000137401202e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013740118e+00 with 64 bits of precision,1.00000000000137490019e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137490009e+00 with 64 bits of precision,1.00000000000137578848e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137578826e+00 with 64 bits of precision,1.00000000000137667698e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137667666e+00 with 64 bits of precision,1.00000000000137756505e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137756495e+00 with 64 bits of precision,1.00000000000137845312e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013784528e+00 with 64 bits of precision,1.00000000000137934119e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000137934109e+00 with 64 bits of precision,1.00000000000138022926e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138022916e+00 with 64 bits of precision,1.00000000000138111744e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138111723e+00 with 64 bits of precision,1.00000000000138200562e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013820053e+00 with 64 bits of precision,1.00000000000138289369e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138289347e+00 with 64 bits of precision,1.00000000000138378219e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138378187e+00 with 64 bits of precision,1.00000000000138467026e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138467016e+00 with 64 bits of precision,1.00000000000138555833e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138555823e+00 with 64 bits of precision,1.00000000000138644651e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013864463e+00 with 64 bits of precision,1.00000000000138733469e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138733437e+00 with 64 bits of precision,1.0000000000013882232e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138822298e+00 with 64 bits of precision,1.00000000000138911137e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138911094e+00 with 64 bits of precision,1.00000000000138999944e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000138999923e+00 with 64 bits of precision,1.00000000000139088751e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000013908873e+00 with 64 bits of precision,1.00000000000139177558e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000139177548e+00 with 64 bits of precision,1.00000000000139266365e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139266355e+00 with 64 bits of precision,1.00000000000139355194e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139355172e+00 with 64 bits of precision,1.00000000000139444044e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139444012e+00 with 64 bits of precision,1.00000000000139532851e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139532841e+00 with 64 bits of precision,1.00000000000139621658e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139621648e+00 with 64 bits of precision,1.00000000000139710487e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139710465e+00 with 64 bits of precision,1.00000000000139799337e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139799305e+00 with 64 bits of precision,1.00000000000139888144e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139888134e+00 with 64 bits of precision,1.00000000000139976951e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000139976919e+00 with 64 bits of precision,1.00000000000140065758e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140065748e+00 with 64 bits of precision,1.00000000000140154565e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140154555e+00 with 64 bits of precision,1.00000000000140243383e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140243362e+00 with 64 bits of precision,1.00000000000140332201e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140332169e+00 with 64 bits of precision,1.00000000000140421041e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140421019e+00 with 64 bits of precision,1.00000000000140509869e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140509837e+00 with 64 bits of precision,1.00000000000140598676e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140598666e+00 with 64 bits of precision,1.00000000000140687483e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140687451e+00 with 64 bits of precision,1.0000000000014077629e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014077628e+00 with 64 bits of precision,1.00000000000140865097e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140865087e+00 with 64 bits of precision,1.00000000000140953915e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000140953894e+00 with 64 bits of precision,1.00000000000141042733e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141042701e+00 with 64 bits of precision,1.0000000000014113154e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141131518e+00 with 64 bits of precision,1.0000000000014122039e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141220358e+00 with 64 bits of precision,1.00000000000141309197e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141309187e+00 with 64 bits of precision,1.00000000000141398004e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141397994e+00 with 64 bits of precision,1.00000000000141486822e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141486801e+00 with 64 bits of precision,1.0000000000014157564e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141575608e+00 with 64 bits of precision,1.0000000000014166448e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141664458e+00 with 64 bits of precision,1.00000000000141753297e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141753265e+00 with 64 bits of precision,1.00000000000141842104e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141842094e+00 with 64 bits of precision,1.00000000000141930911e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000141930901e+00 with 64 bits of precision,1.00000000000142019718e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142019708e+00 with 64 bits of precision,1.00000000000142108536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142108515e+00 with 64 bits of precision,1.00000000000142197354e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142197332e+00 with 64 bits of precision,1.00000000000142286215e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142286172e+00 with 64 bits of precision,1.00000000000142375022e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142375001e+00 with 64 bits of precision,1.00000000000142463829e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142463797e+00 with 64 bits of precision,1.00000000000142552636e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142552626e+00 with 64 bits of precision,1.00000000000142641443e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000142641433e+00 with 64 bits of precision,1.00000000000142730261e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014273024e+00 with 64 bits of precision,1.00000000000142819079e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142819047e+00 with 64 bits of precision,1.00000000000142907886e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142907864e+00 with 64 bits of precision,1.00000000000142996736e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000142996704e+00 with 64 bits of precision,1.00000000000143085543e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143085533e+00 with 64 bits of precision,1.0000000000014317435e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014317434e+00 with 64 bits of precision,1.00000000000143263179e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143263157e+00 with 64 bits of precision,1.00000000000143352029e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143351997e+00 with 64 bits of precision,1.00000000000143440836e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143440826e+00 with 64 bits of precision,1.00000000000143529643e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143529611e+00 with 64 bits of precision,1.0000000000014361845e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014361844e+00 with 64 bits of precision,1.00000000000143707257e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143707247e+00 with 64 bits of precision,1.00000000000143796075e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143796054e+00 with 64 bits of precision,1.00000000000143884893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143884861e+00 with 64 bits of precision,1.00000000000143973733e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000143973711e+00 with 64 bits of precision,1.00000000000144062561e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144062529e+00 with 64 bits of precision,1.00000000000144151368e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144151358e+00 with 64 bits of precision,1.00000000000144240175e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144240165e+00 with 64 bits of precision,1.00000000000144328993e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144328972e+00 with 64 bits of precision,1.00000000000144417811e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144417779e+00 with 64 bits of precision,1.00000000000144506651e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144506629e+00 with 64 bits of precision,1.00000000000144595468e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144595436e+00 with 64 bits of precision,1.00000000000144684275e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144684265e+00 with 64 bits of precision,1.00000000000144773082e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144773072e+00 with 64 bits of precision,1.00000000000144861889e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144861879e+00 with 64 bits of precision,1.00000000000144950707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000144950686e+00 with 64 bits of precision,1.00000000000145039525e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145039503e+00 with 64 bits of precision,1.00000000000145128375e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000145128343e+00 with 64 bits of precision,1.00000000000145217182e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145217172e+00 with 64 bits of precision,1.00000000000145305989e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145305979e+00 with 64 bits of precision,1.00000000000145394818e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145394796e+00 with 64 bits of precision,1.00000000000145483679e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145483636e+00 with 64 bits of precision,1.00000000000145572486e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145572465e+00 with 64 bits of precision,1.00000000000145661293e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014566125e+00 with 64 bits of precision,1.000000000001457501e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145750079e+00 with 64 bits of precision,1.00000000000145838907e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145838897e+00 with 64 bits of precision,1.00000000000145927714e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000145927704e+00 with 64 bits of precision,1.00000000000146016532e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146016511e+00 with 64 bits of precision,1.0000000000014610535e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146105328e+00 with 64 bits of precision,1.000000000001461942e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146194168e+00 with 64 bits of precision,1.00000000000146283007e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146282997e+00 with 64 bits of precision,1.00000000000146371814e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146371793e+00 with 64 bits of precision,1.00000000000146460621e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146460611e+00 with 64 bits of precision,1.0000000000014654945e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146549418e+00 with 64 bits of precision,1.0000000000014663829e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146638268e+00 with 64 bits of precision,1.00000000000146727107e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146727075e+00 with 64 bits of precision,1.00000000000146815914e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146815904e+00 with 64 bits of precision,1.00000000000146904721e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146904711e+00 with 64 bits of precision,1.00000000000146993528e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000146993518e+00 with 64 bits of precision,1.00000000000147082346e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147082325e+00 with 64 bits of precision,1.00000000000147171164e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147171142e+00 with 64 bits of precision,1.00000000000147260025e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147259982e+00 with 64 bits of precision,1.00000000000147348832e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147348811e+00 with 64 bits of precision,1.00000000000147437639e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147437607e+00 with 64 bits of precision,1.00000000000147526446e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147526436e+00 with 64 bits of precision,1.00000000000147615253e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147615243e+00 with 64 bits of precision,1.00000000000147704071e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014770405e+00 with 64 bits of precision,1.00000000000147792889e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147792857e+00 with 64 bits of precision,1.00000000000147881696e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147881674e+00 with 64 bits of precision,1.00000000000147970546e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000147970514e+00 with 64 bits of precision,1.00000000000148059353e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148059343e+00 with 64 bits of precision,1.0000000000014814816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014814815e+00 with 64 bits of precision,1.00000000000148236989e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148236967e+00 with 64 bits of precision,1.00000000000148325839e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148325807e+00 with 64 bits of precision,1.00000000000148414646e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148414636e+00 with 64 bits of precision,1.00000000000148503453e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148503421e+00 with 64 bits of precision,1.0000000000014859226e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000014859225e+00 with 64 bits of precision,1.00000000000148681067e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148681057e+00 with 64 bits of precision,1.00000000000148769885e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148769864e+00 with 64 bits of precision,1.00000000000148858703e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148858671e+00 with 64 bits of precision,1.00000000000148947543e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000148947521e+00 with 64 bits of precision,1.00000000000149036371e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000149036339e+00 with 64 bits of precision,1.00000000000149125178e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149125168e+00 with 64 bits of precision,1.00000000000149213985e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149213975e+00 with 64 bits of precision,1.00000000000149302814e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149302792e+00 with 64 bits of precision,1.00000000000149391664e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149391632e+00 with 64 bits of precision,1.00000000000149480471e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149480461e+00 with 64 bits of precision,1.00000000000149569278e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149569268e+00 with 64 bits of precision,1.00000000000149658107e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149658085e+00 with 64 bits of precision,1.00000000000149746957e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149746925e+00 with 64 bits of precision,1.00000000000149835764e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149835754e+00 with 64 bits of precision,1.00000000000149924571e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000149924539e+00 with 64 bits of precision,1.00000000000150013378e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150013368e+00 with 64 bits of precision,1.00000000000150102185e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150102175e+00 with 64 bits of precision,1.00000000000150191003e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150190982e+00 with 64 bits of precision,1.00000000000150279821e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150279789e+00 with 64 bits of precision,1.00000000000150368661e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000150368639e+00 with 64 bits of precision,1.00000000000150457489e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150457457e+00 with 64 bits of precision,1.00000000000150546296e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150546286e+00 with 64 bits of precision,1.00000000000150635103e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015063506e+00 with 64 bits of precision,1.0000000000015072391e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150723889e+00 with 64 bits of precision,1.00000000000150812717e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150812707e+00 with 64 bits of precision,1.00000000000150901524e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150901514e+00 with 64 bits of precision,1.00000000000150990342e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000150990321e+00 with 64 bits of precision,1.0000000000015107916e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151079138e+00 with 64 bits of precision,1.0000000000015116801e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151167978e+00 with 64 bits of precision,1.00000000000151256817e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151256807e+00 with 64 bits of precision,1.00000000000151345624e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151345614e+00 with 64 bits of precision,1.00000000000151434453e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151434431e+00 with 64 bits of precision,1.00000000000151523303e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151523271e+00 with 64 bits of precision,1.0000000000015161211e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001516121e+00 with 64 bits of precision,1.00000000000151700917e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151700896e+00 with 64 bits of precision,1.00000000000151789724e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151789714e+00 with 64 bits of precision,1.00000000000151878531e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151878521e+00 with 64 bits of precision,1.00000000000151967349e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000151967328e+00 with 64 bits of precision,1.00000000000152056167e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152056135e+00 with 64 bits of precision,1.00000000000152144974e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152144952e+00 with 64 bits of precision,1.00000000000152233835e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152233792e+00 with 64 bits of precision,1.00000000000152322642e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152322621e+00 with 64 bits of precision,1.00000000000152411449e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152411439e+00 with 64 bits of precision,1.00000000000152500278e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152500256e+00 with 64 bits of precision,1.00000000000152589128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152589096e+00 with 64 bits of precision,1.00000000000152677935e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152677925e+00 with 64 bits of precision,1.00000000000152766742e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015276671e+00 with 64 bits of precision,1.00000000000152855549e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152855539e+00 with 64 bits of precision,1.00000000000152944356e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000152944346e+00 with 64 bits of precision,1.00000000000153033174e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153033153e+00 with 64 bits of precision,1.00000000000153121992e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015312196e+00 with 64 bits of precision,1.00000000000153210799e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153210777e+00 with 64 bits of precision,1.00000000000153299649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153299617e+00 with 64 bits of precision,1.00000000000153388456e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153388446e+00 with 64 bits of precision,1.00000000000153477263e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153477231e+00 with 64 bits of precision,1.0000000000015356607e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015356606e+00 with 64 bits of precision,1.00000000000153654877e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153654867e+00 with 64 bits of precision,1.00000000000153743695e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153743674e+00 with 64 bits of precision,1.00000000000153832513e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153832481e+00 with 64 bits of precision,1.00000000000153921353e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000153921331e+00 with 64 bits of precision,1.00000000000154010181e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154010149e+00 with 64 bits of precision,1.00000000000154098988e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154098978e+00 with 64 bits of precision,1.00000000000154187795e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154187785e+00 with 64 bits of precision,1.00000000000154276624e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154276602e+00 with 64 bits of precision,1.00000000000154365474e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000154365442e+00 with 64 bits of precision,1.00000000000154454281e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154454271e+00 with 64 bits of precision,1.00000000000154543088e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154543067e+00 with 64 bits of precision,1.00000000000154631895e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154631885e+00 with 64 bits of precision,1.00000000000154720702e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154720692e+00 with 64 bits of precision,1.0000000000015480952e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154809499e+00 with 64 bits of precision,1.00000000000154898338e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154898306e+00 with 64 bits of precision,1.00000000000154987145e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000154987123e+00 with 64 bits of precision,1.00000000000155075995e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155075963e+00 with 64 bits of precision,1.00000000000155164802e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155164792e+00 with 64 bits of precision,1.00000000000155253609e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155253599e+00 with 64 bits of precision,1.00000000000155342438e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155342416e+00 with 64 bits of precision,1.00000000000155431288e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155431256e+00 with 64 bits of precision,1.00000000000155520095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155520085e+00 with 64 bits of precision,1.00000000000155608902e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155608881e+00 with 64 bits of precision,1.00000000000155697709e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155697699e+00 with 64 bits of precision,1.00000000000155786527e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155786506e+00 with 64 bits of precision,1.00000000000155875334e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000155875313e+00 with 64 bits of precision,1.00000000000155964163e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015596412e+00 with 64 bits of precision,1.0000000000015605297e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156052948e+00 with 64 bits of precision,1.0000000000015614182e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156141788e+00 with 64 bits of precision,1.00000000000156230627e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156230617e+00 with 64 bits of precision,1.00000000000156319434e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156319413e+00 with 64 bits of precision,1.00000000000156408241e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156408231e+00 with 64 bits of precision,1.0000000000015649707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156497038e+00 with 64 bits of precision,1.0000000000015658591e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156585888e+00 with 64 bits of precision,1.00000000000156674727e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156674695e+00 with 64 bits of precision,1.00000000000156763534e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156763524e+00 with 64 bits of precision,1.00000000000156852341e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156852331e+00 with 64 bits of precision,1.00000000000156941148e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000156941138e+00 with 64 bits of precision,1.00000000000157029966e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157029945e+00 with 64 bits of precision,1.00000000000157118784e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157118762e+00 with 64 bits of precision,1.00000000000157207634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157207602e+00 with 64 bits of precision,1.00000000000157296441e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157296431e+00 with 64 bits of precision,1.00000000000157385248e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157385227e+00 with 64 bits of precision,1.00000000000157474055e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157474045e+00 with 64 bits of precision,1.00000000000157562873e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157562852e+00 with 64 bits of precision,1.0000000000015765168e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157651659e+00 with 64 bits of precision,1.00000000000157740509e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157740466e+00 with 64 bits of precision,1.00000000000157829294e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000157829273e+00 with 64 bits of precision,1.00000000000157918123e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015791808e+00 with 64 bits of precision,1.00000000000158006963e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158006941e+00 with 64 bits of precision,1.0000000000015809578e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015809577e+00 with 64 bits of precision,1.00000000000158184609e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158184587e+00 with 64 bits of precision,1.00000000000158273459e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158273427e+00 with 64 bits of precision,1.00000000000158362266e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158362256e+00 with 64 bits of precision,1.00000000000158451073e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158451041e+00 with 64 bits of precision,1.0000000000015853988e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.0000000000015853987e+00 with 64 bits of precision,1.00000000000158628687e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158628677e+00 with 64 bits of precision,1.00000000000158717505e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158717484e+00 with 64 bits of precision,1.00000000000158806323e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158806291e+00 with 64 bits of precision,1.0000000000015889513e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158895108e+00 with 64 bits of precision,1.0000000000015898398e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000158983948e+00 with 64 bits of precision,1.00000000000159072787e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159072777e+00 with 64 bits of precision,1.00000000000159161594e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159161573e+00 with 64 bits of precision,1.00000000000159250401e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159250391e+00 with 64 bits of precision,1.00000000000159339219e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159339198e+00 with 64 bits of precision,1.00000000000159428026e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159428005e+00 with 64 bits of precision,1.00000000000159516855e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159516812e+00 with 64 bits of precision,1.00000000000159605662e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015960564e+00 with 64 bits of precision,1.00000000000159694512e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000015969448e+00 with 64 bits of precision,1.00000000000159783319e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159783309e+00 with 64 bits of precision,1.00000000000159872126e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159872116e+00 with 64 bits of precision,1.00000000000159960955e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000159960933e+00 with 64 bits of precision,1.00000000000160049805e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160049773e+00 with 64 bits of precision,1.00000000000160138612e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160138602e+00 with 64 bits of precision,1.00000000000160227419e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160227398e+00 with 64 bits of precision,1.00000000000160316226e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160316216e+00 with 64 bits of precision,1.00000000000160405033e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160405023e+00 with 64 bits of precision,1.00000000000160493851e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016049383e+00 with 64 bits of precision,1.00000000000160582669e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160582637e+00 with 64 bits of precision,1.00000000000160671476e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160671454e+00 with 64 bits of precision,1.00000000000160760326e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160760294e+00 with 64 bits of precision,1.00000000000160849133e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000160849123e+00 with 64 bits of precision,1.0000000000016093794e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016093793e+00 with 64 bits of precision,1.00000000000161026758e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161026737e+00 with 64 bits of precision,1.00000000000161115587e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161115544e+00 with 64 bits of precision,1.00000000000161204427e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161204405e+00 with 64 bits of precision,1.00000000000161293244e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161293212e+00 with 64 bits of precision,1.00000000000161382051e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161382041e+00 with 64 bits of precision,1.00000000000161470858e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161470848e+00 with 64 bits of precision,1.00000000000161559676e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161559655e+00 with 64 bits of precision,1.00000000000161648494e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161648462e+00 with 64 bits of precision,1.00000000000161737301e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161737279e+00 with 64 bits of precision,1.00000000000161826151e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161826119e+00 with 64 bits of precision,1.00000000000161914958e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000161914948e+00 with 64 bits of precision,1.00000000000162003765e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162003755e+00 with 64 bits of precision,1.00000000000162092594e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162092572e+00 with 64 bits of precision,1.00000000000162181444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162181412e+00 with 64 bits of precision,1.00000000000162270251e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162270241e+00 with 64 bits of precision,1.00000000000162359058e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162359037e+00 with 64 bits of precision,1.00000000000162447865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162447855e+00 with 64 bits of precision,1.00000000000162536683e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162536662e+00 with 64 bits of precision,1.0000000000016262549e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000162625469e+00 with 64 bits of precision,1.00000000000162714319e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162714276e+00 with 64 bits of precision,1.00000000000162803104e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162803083e+00 with 64 bits of precision,1.00000000000162891933e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016289189e+00 with 64 bits of precision,1.00000000000162980773e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000162980751e+00 with 64 bits of precision,1.0000000000016306959e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016306958e+00 with 64 bits of precision,1.00000000000163158419e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163158397e+00 with 64 bits of precision,1.00000000000163247269e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163247237e+00 with 64 bits of precision,1.00000000000163336076e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163336066e+00 with 64 bits of precision,1.00000000000163424883e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163424851e+00 with 64 bits of precision,1.0000000000016351369e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016351368e+00 with 64 bits of precision,1.00000000000163602497e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163602487e+00 with 64 bits of precision,1.00000000000163691315e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163691294e+00 with 64 bits of precision,1.00000000000163780133e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163780101e+00 with 64 bits of precision,1.0000000000016386894e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163868918e+00 with 64 bits of precision,1.0000000000016395779e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000163957758e+00 with 64 bits of precision,1.00000000000164046597e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164046587e+00 with 64 bits of precision,1.00000000000164135404e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164135394e+00 with 64 bits of precision,1.00000000000164224211e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164224201e+00 with 64 bits of precision,1.00000000000164313029e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164313008e+00 with 64 bits of precision,1.00000000000164401836e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164401815e+00 with 64 bits of precision,1.00000000000164490665e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164490622e+00 with 64 bits of precision,1.00000000000164579472e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016457945e+00 with 64 bits of precision,1.00000000000164668322e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016466829e+00 with 64 bits of precision,1.00000000000164757129e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164757119e+00 with 64 bits of precision,1.00000000000164845936e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164845926e+00 with 64 bits of precision,1.00000000000164934754e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000164934733e+00 with 64 bits of precision,1.00000000000165023572e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016502354e+00 with 64 bits of precision,1.00000000000165112412e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016511239e+00 with 64 bits of precision,1.00000000000165201229e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165201197e+00 with 64 bits of precision,1.00000000000165290036e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165290026e+00 with 64 bits of precision,1.00000000000165378843e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165378833e+00 with 64 bits of precision,1.0000000000016546765e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016546764e+00 with 64 bits of precision,1.00000000000165556468e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165556447e+00 with 64 bits of precision,1.00000000000165645286e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165645264e+00 with 64 bits of precision,1.00000000000165734136e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165734104e+00 with 64 bits of precision,1.00000000000165822943e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165822933e+00 with 64 bits of precision,1.0000000000016591175e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000165911729e+00 with 64 bits of precision,1.00000000000166000557e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166000547e+00 with 64 bits of precision,1.00000000000166089375e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166089354e+00 with 64 bits of precision,1.00000000000166178182e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166178161e+00 with 64 bits of precision,1.00000000000166267011e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166266968e+00 with 64 bits of precision,1.00000000000166355796e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166355775e+00 with 64 bits of precision,1.00000000000166444625e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166444582e+00 with 64 bits of precision,1.00000000000166533465e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166533443e+00 with 64 bits of precision,1.00000000000166622282e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166622272e+00 with 64 bits of precision,1.00000000000166711111e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000166711089e+00 with 64 bits of precision,1.00000000000166799961e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166799929e+00 with 64 bits of precision,1.00000000000166888768e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166888758e+00 with 64 bits of precision,1.00000000000166977575e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000166977543e+00 with 64 bits of precision,1.00000000000167066382e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167066372e+00 with 64 bits of precision,1.00000000000167155189e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167155179e+00 with 64 bits of precision,1.00000000000167244007e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167243986e+00 with 64 bits of precision,1.00000000000167332825e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167332793e+00 with 64 bits of precision,1.00000000000167421632e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016742161e+00 with 64 bits of precision,1.00000000000167510482e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016751045e+00 with 64 bits of precision,1.00000000000167599289e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167599279e+00 with 64 bits of precision,1.00000000000167688096e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167688086e+00 with 64 bits of precision,1.00000000000167776914e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167776893e+00 with 64 bits of precision,1.00000000000167865743e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001678657e+00 with 64 bits of precision,1.00000000000167954583e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000167954561e+00 with 64 bits of precision,1.000000000001680434e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168043368e+00 with 64 bits of precision,1.00000000000168132207e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168132197e+00 with 64 bits of precision,1.00000000000168221014e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168221004e+00 with 64 bits of precision,1.00000000000168309832e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168309811e+00 with 64 bits of precision,1.0000000000016839865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168398618e+00 with 64 bits of precision,1.00000000000168487457e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168487435e+00 with 64 bits of precision,1.00000000000168576307e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168576275e+00 with 64 bits of precision,1.00000000000168665114e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168665104e+00 with 64 bits of precision,1.00000000000168753921e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168753911e+00 with 64 bits of precision,1.0000000000016884275e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168842728e+00 with 64 bits of precision,1.000000000001689316e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000168931568e+00 with 64 bits of precision,1.00000000000169020407e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169020397e+00 with 64 bits of precision,1.00000000000169109214e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169109182e+00 with 64 bits of precision,1.00000000000169198021e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169198011e+00 with 64 bits of precision,1.00000000000169286828e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169286818e+00 with 64 bits of precision,1.00000000000169375646e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169375625e+00 with 64 bits of precision,1.00000000000169464464e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169464432e+00 with 64 bits of precision,1.00000000000169553282e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016955326e+00 with 64 bits of precision,1.00000000000169642132e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001696421e+00 with 64 bits of precision,1.00000000000169730939e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169730929e+00 with 64 bits of precision,1.00000000000169819746e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169819725e+00 with 64 bits of precision,1.00000000000169908553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000169908543e+00 with 64 bits of precision,1.0000000000016999736e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000016999735e+00 with 64 bits of precision,1.00000000000170086178e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170086157e+00 with 64 bits of precision,1.00000000000170174996e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170174964e+00 with 64 bits of precision,1.00000000000170263803e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170263781e+00 with 64 bits of precision,1.00000000000170352653e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170352621e+00 with 64 bits of precision,1.0000000000017044146e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017044145e+00 with 64 bits of precision,1.00000000000170530267e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170530257e+00 with 64 bits of precision,1.00000000000170619096e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000170619074e+00 with 64 bits of precision,1.00000000000170707946e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170707914e+00 with 64 bits of precision,1.00000000000170796753e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170796743e+00 with 64 bits of precision,1.0000000000017088556e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170885539e+00 with 64 bits of precision,1.00000000000170974367e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000170974357e+00 with 64 bits of precision,1.00000000000171063185e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171063164e+00 with 64 bits of precision,1.00000000000171151992e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171151971e+00 with 64 bits of precision,1.00000000000171240821e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171240778e+00 with 64 bits of precision,1.00000000000171329606e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171329585e+00 with 64 bits of precision,1.00000000000171418435e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171418392e+00 with 64 bits of precision,1.00000000000171507275e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171507253e+00 with 64 bits of precision,1.00000000000171596092e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171596082e+00 with 64 bits of precision,1.00000000000171684921e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171684899e+00 with 64 bits of precision,1.00000000000171773771e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171773739e+00 with 64 bits of precision,1.00000000000171862578e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171862568e+00 with 64 bits of precision,1.00000000000171951385e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000171951353e+00 with 64 bits of precision,1.00000000000172040192e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172040182e+00 with 64 bits of precision,1.00000000000172128999e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172128989e+00 with 64 bits of precision,1.00000000000172217817e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172217796e+00 with 64 bits of precision,1.00000000000172306635e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172306603e+00 with 64 bits of precision,1.00000000000172395442e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017239542e+00 with 64 bits of precision,1.00000000000172484292e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017248426e+00 with 64 bits of precision,1.00000000000172573099e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172573089e+00 with 64 bits of precision,1.00000000000172661906e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172661896e+00 with 64 bits of precision,1.00000000000172750724e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172750703e+00 with 64 bits of precision,1.00000000000172839542e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017283951e+00 with 64 bits of precision,1.00000000000172928393e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000172928371e+00 with 64 bits of precision,1.0000000000017301721e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173017167e+00 with 64 bits of precision,1.00000000000173106017e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173105996e+00 with 64 bits of precision,1.00000000000173194824e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173194803e+00 with 64 bits of precision,1.00000000000173283631e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173283621e+00 with 64 bits of precision,1.00000000000173372438e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173372428e+00 with 64 bits of precision,1.00000000000173461267e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173461245e+00 with 64 bits of precision,1.00000000000173550117e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173550085e+00 with 64 bits of precision,1.00000000000173638924e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173638914e+00 with 64 bits of precision,1.00000000000173727731e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173727721e+00 with 64 bits of precision,1.0000000000017381656e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173816538e+00 with 64 bits of precision,1.0000000000017390541e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173905378e+00 with 64 bits of precision,1.00000000000173994217e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000173994207e+00 with 64 bits of precision,1.00000000000174083024e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174082992e+00 with 64 bits of precision,1.00000000000174171831e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174171821e+00 with 64 bits of precision,1.00000000000174260638e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174260628e+00 with 64 bits of precision,1.00000000000174349456e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174349435e+00 with 64 bits of precision,1.00000000000174438274e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174438242e+00 with 64 bits of precision,1.00000000000174527114e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174527092e+00 with 64 bits of precision,1.00000000000174615942e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017461591e+00 with 64 bits of precision,1.00000000000174704749e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174704739e+00 with 64 bits of precision,1.00000000000174793556e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000174793524e+00 with 64 bits of precision,1.00000000000174882363e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000174882353e+00 with 64 bits of precision,1.0000000000017497117e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017497116e+00 with 64 bits of precision,1.00000000000175059988e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175059967e+00 with 64 bits of precision,1.00000000000175148806e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175148774e+00 with 64 bits of precision,1.00000000000175237613e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175237591e+00 with 64 bits of precision,1.00000000000175326463e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175326431e+00 with 64 bits of precision,1.0000000000017541527e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017541526e+00 with 64 bits of precision,1.00000000000175504077e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175504067e+00 with 64 bits of precision,1.00000000000175592895e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175592874e+00 with 64 bits of precision,1.00000000000175681713e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175681681e+00 with 64 bits of precision,1.00000000000175770553e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175770531e+00 with 64 bits of precision,1.0000000000017585937e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175859338e+00 with 64 bits of precision,1.00000000000175948177e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000175948167e+00 with 64 bits of precision,1.00000000000176036984e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176036974e+00 with 64 bits of precision,1.00000000000176125791e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176125781e+00 with 64 bits of precision,1.00000000000176214609e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176214588e+00 with 64 bits of precision,1.00000000000176303427e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176303405e+00 with 64 bits of precision,1.00000000000176392288e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176392245e+00 with 64 bits of precision,1.00000000000176481095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176481074e+00 with 64 bits of precision,1.00000000000176569902e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017656987e+00 with 64 bits of precision,1.00000000000176658709e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176658699e+00 with 64 bits of precision,1.00000000000176747516e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176747506e+00 with 64 bits of precision,1.00000000000176836334e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000176836313e+00 with 64 bits of precision,1.00000000000176925152e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017692512e+00 with 64 bits of precision,1.00000000000177013959e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177013937e+00 with 64 bits of precision,1.00000000000177102809e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177102777e+00 with 64 bits of precision,1.00000000000177191616e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177191606e+00 with 64 bits of precision,1.00000000000177280423e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177280413e+00 with 64 bits of precision,1.00000000000177369252e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017736923e+00 with 64 bits of precision,1.00000000000177458102e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017745807e+00 with 64 bits of precision,1.00000000000177546909e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177546899e+00 with 64 bits of precision,1.00000000000177635716e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177635684e+00 with 64 bits of precision,1.00000000000177724523e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000177724513e+00 with 64 bits of precision,1.0000000000017781333e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017781332e+00 with 64 bits of precision,1.00000000000177902148e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177902127e+00 with 64 bits of precision,1.00000000000177990966e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000177990934e+00 with 64 bits of precision,1.00000000000178079806e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178079784e+00 with 64 bits of precision,1.00000000000178168634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178168602e+00 with 64 bits of precision,1.00000000000178257441e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178257431e+00 with 64 bits of precision,1.00000000000178346248e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178346227e+00 with 64 bits of precision,1.00000000000178435055e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178435045e+00 with 64 bits of precision,1.00000000000178523862e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178523852e+00 with 64 bits of precision,1.0000000000017861268e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178612659e+00 with 64 bits of precision,1.00000000000178701498e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178701466e+00 with 64 bits of precision,1.00000000000178790305e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178790283e+00 with 64 bits of precision,1.00000000000178879155e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178879123e+00 with 64 bits of precision,1.00000000000178967962e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000178967952e+00 with 64 bits of precision,1.00000000000179056769e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179056759e+00 with 64 bits of precision,1.00000000000179145598e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179145576e+00 with 64 bits of precision,1.00000000000179234448e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179234416e+00 with 64 bits of precision,1.00000000000179323255e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179323245e+00 with 64 bits of precision,1.00000000000179412062e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179412052e+00 with 64 bits of precision,1.00000000000179500891e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179500869e+00 with 64 bits of precision,1.00000000000179589752e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179589709e+00 with 64 bits of precision,1.00000000000179678559e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179678538e+00 with 64 bits of precision,1.00000000000179767366e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179767323e+00 with 64 bits of precision,1.00000000000179856173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000179856152e+00 with 64 bits of precision,1.0000000000017994498e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000017994497e+00 with 64 bits of precision,1.00000000000180033787e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180033777e+00 with 64 bits of precision,1.00000000000180122605e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180122584e+00 with 64 bits of precision,1.00000000000180211423e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180211401e+00 with 64 bits of precision,1.00000000000180300273e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180300241e+00 with 64 bits of precision,1.0000000000018038908e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018038907e+00 with 64 bits of precision,1.00000000000180477887e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180477855e+00 with 64 bits of precision,1.00000000000180566694e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000180566684e+00 with 64 bits of precision,1.00000000000180655501e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180655491e+00 with 64 bits of precision,1.00000000000180744319e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180744298e+00 with 64 bits of precision,1.00000000000180833137e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180833105e+00 with 64 bits of precision,1.00000000000180921944e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000180921922e+00 with 64 bits of precision,1.00000000000181010794e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181010762e+00 with 64 bits of precision,1.00000000000181099601e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181099591e+00 with 64 bits of precision,1.00000000000181188408e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181188398e+00 with 64 bits of precision,1.00000000000181277237e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181277215e+00 with 64 bits of precision,1.00000000000181366098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181366055e+00 with 64 bits of precision,1.00000000000181454905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181454884e+00 with 64 bits of precision,1.00000000000181543712e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018154368e+00 with 64 bits of precision,1.00000000000181632519e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181632509e+00 with 64 bits of precision,1.00000000000181721326e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181721316e+00 with 64 bits of precision,1.00000000000181810133e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000181810123e+00 with 64 bits of precision,1.00000000000181898951e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018189893e+00 with 64 bits of precision,1.00000000000181987769e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000181987747e+00 with 64 bits of precision,1.00000000000182076619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182076587e+00 with 64 bits of precision,1.00000000000182165426e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182165416e+00 with 64 bits of precision,1.00000000000182254233e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182254223e+00 with 64 bits of precision,1.00000000000182343062e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018234304e+00 with 64 bits of precision,1.00000000000182431912e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018243188e+00 with 64 bits of precision,1.00000000000182520719e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182520709e+00 with 64 bits of precision,1.00000000000182609526e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182609494e+00 with 64 bits of precision,1.00000000000182698333e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182698323e+00 with 64 bits of precision,1.0000000000018278714e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018278713e+00 with 64 bits of precision,1.00000000000182875958e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182875937e+00 with 64 bits of precision,1.00000000000182964776e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000182964744e+00 with 64 bits of precision,1.00000000000183053616e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183053594e+00 with 64 bits of precision,1.00000000000183142444e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183142412e+00 with 64 bits of precision,1.00000000000183231251e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183231241e+00 with 64 bits of precision,1.00000000000183320058e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183320026e+00 with 64 bits of precision,1.00000000000183408865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183408855e+00 with 64 bits of precision,1.00000000000183497672e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183497662e+00 with 64 bits of precision,1.0000000000018358649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183586469e+00 with 64 bits of precision,1.00000000000183675308e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183675276e+00 with 64 bits of precision,1.00000000000183764115e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183764093e+00 with 64 bits of precision,1.00000000000183852965e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183852933e+00 with 64 bits of precision,1.00000000000183941772e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000183941762e+00 with 64 bits of precision,1.00000000000184030579e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184030569e+00 with 64 bits of precision,1.00000000000184119397e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184119376e+00 with 64 bits of precision,1.00000000000184208215e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184208183e+00 with 64 bits of precision,1.00000000000184297055e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184297033e+00 with 64 bits of precision,1.00000000000184385872e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018438584e+00 with 64 bits of precision,1.00000000000184474679e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184474669e+00 with 64 bits of precision,1.00000000000184563486e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184563476e+00 with 64 bits of precision,1.00000000000184652293e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184652283e+00 with 64 bits of precision,1.00000000000184741111e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018474109e+00 with 64 bits of precision,1.00000000000184829929e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184829907e+00 with 64 bits of precision,1.0000000000018491879e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000184918747e+00 with 64 bits of precision,1.00000000000185007597e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185007576e+00 with 64 bits of precision,1.00000000000185096404e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185096372e+00 with 64 bits of precision,1.00000000000185185211e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185185201e+00 with 64 bits of precision,1.00000000000185274018e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185274008e+00 with 64 bits of precision,1.00000000000185362836e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185362815e+00 with 64 bits of precision,1.00000000000185451654e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185451622e+00 with 64 bits of precision,1.00000000000185540461e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185540439e+00 with 64 bits of precision,1.00000000000185629311e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185629279e+00 with 64 bits of precision,1.00000000000185718118e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000185718108e+00 with 64 bits of precision,1.00000000000185806925e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185806915e+00 with 64 bits of precision,1.00000000000185895754e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185895732e+00 with 64 bits of precision,1.00000000000185984604e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000185984572e+00 with 64 bits of precision,1.00000000000186073411e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186073401e+00 with 64 bits of precision,1.00000000000186162218e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186162197e+00 with 64 bits of precision,1.00000000000186251025e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186251015e+00 with 64 bits of precision,1.00000000000186339854e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186339822e+00 with 64 bits of precision,1.00000000000186428705e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186428683e+00 with 64 bits of precision,1.00000000000186517522e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186517479e+00 with 64 bits of precision,1.00000000000186606329e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186606308e+00 with 64 bits of precision,1.00000000000186695136e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186695115e+00 with 64 bits of precision,1.00000000000186783943e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186783933e+00 with 64 bits of precision,1.0000000000018687275e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018687274e+00 with 64 bits of precision,1.00000000000186961579e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000186961557e+00 with 64 bits of precision,1.00000000000187050429e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187050397e+00 with 64 bits of precision,1.00000000000187139236e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187139226e+00 with 64 bits of precision,1.00000000000187228043e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187228022e+00 with 64 bits of precision,1.0000000000018731685e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018731684e+00 with 64 bits of precision,1.00000000000187405657e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187405647e+00 with 64 bits of precision,1.00000000000187494475e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187494454e+00 with 64 bits of precision,1.00000000000187583293e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187583261e+00 with 64 bits of precision,1.000000000001876721e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187672078e+00 with 64 bits of precision,1.0000000000018776095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187760918e+00 with 64 bits of precision,1.00000000000187849757e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187849747e+00 with 64 bits of precision,1.00000000000187938564e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000187938554e+00 with 64 bits of precision,1.00000000000188027393e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188027371e+00 with 64 bits of precision,1.00000000000188116254e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188116211e+00 with 64 bits of precision,1.00000000000188205061e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000018820504e+00 with 64 bits of precision,1.00000000000188293868e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188293825e+00 with 64 bits of precision,1.00000000000188382675e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188382654e+00 with 64 bits of precision,1.00000000000188471482e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188471472e+00 with 64 bits of precision,1.00000000000188560289e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188560279e+00 with 64 bits of precision,1.00000000000188649107e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188649086e+00 with 64 bits of precision,1.00000000000188737925e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188737903e+00 with 64 bits of precision,1.00000000000188826775e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188826743e+00 with 64 bits of precision,1.00000000000188915582e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000188915572e+00 with 64 bits of precision,1.00000000000189004389e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189004379e+00 with 64 bits of precision,1.00000000000189093218e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189093196e+00 with 64 bits of precision,1.00000000000189182068e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189182036e+00 with 64 bits of precision,1.00000000000189270875e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189270865e+00 with 64 bits of precision,1.00000000000189359682e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189359672e+00 with 64 bits of precision,1.00000000000189448511e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189448489e+00 with 64 bits of precision,1.00000000000189537372e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189537329e+00 with 64 bits of precision,1.00000000000189626179e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189626158e+00 with 64 bits of precision,1.00000000000189714986e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189714943e+00 with 64 bits of precision,1.00000000000189803793e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189803772e+00 with 64 bits of precision,1.00000000000189892589e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000189892579e+00 with 64 bits of precision,1.00000000000189981407e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000189981386e+00 with 64 bits of precision,1.00000000000190070225e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190070193e+00 with 64 bits of precision,1.00000000000190159043e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190159021e+00 with 64 bits of precision,1.00000000000190247893e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190247861e+00 with 64 bits of precision,1.000000000001903367e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019033669e+00 with 64 bits of precision,1.00000000000190425507e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190425475e+00 with 64 bits of precision,1.00000000000190514314e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190514304e+00 with 64 bits of precision,1.00000000000190603121e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190603111e+00 with 64 bits of precision,1.00000000000190691939e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190691918e+00 with 64 bits of precision,1.00000000000190780757e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190780725e+00 with 64 bits of precision,1.00000000000190869564e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190869542e+00 with 64 bits of precision,1.00000000000190958414e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000190958382e+00 with 64 bits of precision,1.00000000000191047221e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191047211e+00 with 64 bits of precision,1.00000000000191136028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191136018e+00 with 64 bits of precision,1.00000000000191224857e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191224835e+00 with 64 bits of precision,1.00000000000191313707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191313675e+00 with 64 bits of precision,1.00000000000191402514e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191402504e+00 with 64 bits of precision,1.00000000000191491321e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001914913e+00 with 64 bits of precision,1.00000000000191580128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191580118e+00 with 64 bits of precision,1.00000000000191668935e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191668925e+00 with 64 bits of precision,1.00000000000191757753e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191757732e+00 with 64 bits of precision,1.00000000000191846571e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191846539e+00 with 64 bits of precision,1.00000000000191935367e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000191935346e+00 with 64 bits of precision,1.00000000000192024196e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192024153e+00 with 64 bits of precision,1.00000000000192113036e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192113014e+00 with 64 bits of precision,1.00000000000192201853e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192201843e+00 with 64 bits of precision,1.00000000000192290682e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019229066e+00 with 64 bits of precision,1.00000000000192379532e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000001923795e+00 with 64 bits of precision,1.00000000000192468339e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192468329e+00 with 64 bits of precision,1.00000000000192557146e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192557114e+00 with 64 bits of precision,1.00000000000192645953e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192645943e+00 with 64 bits of precision,1.0000000000019273476e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019273475e+00 with 64 bits of precision,1.00000000000192823578e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192823557e+00 with 64 bits of precision,1.00000000000192912396e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000192912364e+00 with 64 bits of precision,1.00000000000193001203e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193001181e+00 with 64 bits of precision,1.00000000000193090053e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193090021e+00 with 64 bits of precision,1.0000000000019317886e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019317885e+00 with 64 bits of precision,1.00000000000193267667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193267635e+00 with 64 bits of precision,1.00000000000193356474e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193356464e+00 with 64 bits of precision,1.00000000000193445281e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193445271e+00 with 64 bits of precision,1.00000000000193534099e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193534078e+00 with 64 bits of precision,1.00000000000193622917e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193622885e+00 with 64 bits of precision,1.00000000000193711735e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000193711713e+00 with 64 bits of precision,1.00000000000193800585e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193800553e+00 with 64 bits of precision,1.00000000000193889392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193889382e+00 with 64 bits of precision,1.00000000000193978199e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000193978189e+00 with 64 bits of precision,1.00000000000194067028e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194067006e+00 with 64 bits of precision,1.00000000000194155878e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194155846e+00 with 64 bits of precision,1.00000000000194244685e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194244675e+00 with 64 bits of precision,1.00000000000194333492e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194333471e+00 with 64 bits of precision,1.00000000000194422299e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194422289e+00 with 64 bits of precision,1.00000000000194511106e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194511096e+00 with 64 bits of precision,1.00000000000194599924e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194599903e+00 with 64 bits of precision,1.00000000000194688742e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019468871e+00 with 64 bits of precision,1.00000000000194777549e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194777527e+00 with 64 bits of precision,1.00000000000194866399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194866367e+00 with 64 bits of precision,1.00000000000194955206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000194955196e+00 with 64 bits of precision,1.00000000000195044013e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195044003e+00 with 64 bits of precision,1.00000000000195132831e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019513281e+00 with 64 bits of precision,1.0000000000019522166e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195221617e+00 with 64 bits of precision,1.000000000001953105e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195310478e+00 with 64 bits of precision,1.00000000000195399317e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195399285e+00 with 64 bits of precision,1.00000000000195488124e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195488114e+00 with 64 bits of precision,1.00000000000195576931e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195576921e+00 with 64 bits of precision,1.00000000000195665749e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195665728e+00 with 64 bits of precision,1.00000000000195754567e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195754535e+00 with 64 bits of precision,1.00000000000195843374e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195843352e+00 with 64 bits of precision,1.00000000000195932224e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000195932192e+00 with 64 bits of precision,1.00000000000196021031e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196021021e+00 with 64 bits of precision,1.00000000000196109838e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196109828e+00 with 64 bits of precision,1.00000000000196198667e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196198645e+00 with 64 bits of precision,1.00000000000196287517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196287485e+00 with 64 bits of precision,1.00000000000196376324e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196376314e+00 with 64 bits of precision,1.00000000000196465131e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019646511e+00 with 64 bits of precision,1.00000000000196553938e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196553928e+00 with 64 bits of precision,1.00000000000196642756e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196642735e+00 with 64 bits of precision,1.00000000000196731563e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196731542e+00 with 64 bits of precision,1.00000000000196820392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196820349e+00 with 64 bits of precision,1.00000000000196909177e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196909156e+00 with 64 bits of precision,1.00000000000196998006e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000196997963e+00 with 64 bits of precision,1.00000000000197086846e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197086824e+00 with 64 bits of precision,1.00000000000197175663e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197175653e+00 with 64 bits of precision,1.00000000000197264492e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019726447e+00 with 64 bits of precision,1.00000000000197353342e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019735331e+00 with 64 bits of precision,1.00000000000197442149e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197442139e+00 with 64 bits of precision,1.00000000000197530956e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197530924e+00 with 64 bits of precision,1.00000000000197619763e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197619753e+00 with 64 bits of precision,1.0000000000019770857e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019770856e+00 with 64 bits of precision,1.00000000000197797388e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000197797367e+00 with 64 bits of precision,1.00000000000197886206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197886174e+00 with 64 bits of precision,1.00000000000197975013e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000197974991e+00 with 64 bits of precision,1.00000000000198063863e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198063831e+00 with 64 bits of precision,1.0000000000019815267e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019815266e+00 with 64 bits of precision,1.00000000000198241477e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198241467e+00 with 64 bits of precision,1.00000000000198330284e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198330274e+00 with 64 bits of precision,1.00000000000198419102e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198419081e+00 with 64 bits of precision,1.00000000000198507909e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198507888e+00 with 64 bits of precision,1.00000000000198596738e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198596695e+00 with 64 bits of precision,1.00000000000198685545e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198685523e+00 with 64 bits of precision,1.00000000000198774395e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198774363e+00 with 64 bits of precision,1.00000000000198863202e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198863192e+00 with 64 bits of precision,1.00000000000198952009e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000198951988e+00 with 64 bits of precision,1.00000000000199040816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199040806e+00 with 64 bits of precision,1.00000000000199129645e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199129613e+00 with 64 bits of precision,1.00000000000199218485e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199218463e+00 with 64 bits of precision,1.00000000000199307302e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019930727e+00 with 64 bits of precision,1.00000000000199396109e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199396099e+00 with 64 bits of precision,1.00000000000199484916e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199484906e+00 with 64 bits of precision,1.00000000000199573723e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199573713e+00 with 64 bits of precision,1.00000000000199662541e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000019966252e+00 with 64 bits of precision,1.00000000000199751359e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199751337e+00 with 64 bits of precision,1.00000000000199840209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199840177e+00 with 64 bits of precision,1.00000000000199929016e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000199929006e+00 with 64 bits of precision,1.00000000000200017823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200017802e+00 with 64 bits of precision,1.0000000000020010663e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020010662e+00 with 64 bits of precision,1.00000000000200195448e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200195427e+00 with 64 bits of precision,1.00000000000200284255e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200284234e+00 with 64 bits of precision,1.00000000000200373084e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200373041e+00 with 64 bits of precision,1.00000000000200461869e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200461848e+00 with 64 bits of precision,1.00000000000200550698e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200550655e+00 with 64 bits of precision,1.00000000000200639538e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200639516e+00 with 64 bits of precision,1.00000000000200728355e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200728345e+00 with 64 bits of precision,1.00000000000200817184e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200817162e+00 with 64 bits of precision,1.00000000000200906034e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200906002e+00 with 64 bits of precision,1.00000000000200994841e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000200994831e+00 with 64 bits of precision,1.00000000000201083648e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201083616e+00 with 64 bits of precision,1.00000000000201172455e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201172445e+00 with 64 bits of precision,1.00000000000201261262e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201261252e+00 with 64 bits of precision,1.0000000000020135008e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201350059e+00 with 64 bits of precision,1.00000000000201438898e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201438866e+00 with 64 bits of precision,1.00000000000201527705e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201527683e+00 with 64 bits of precision,1.00000000000201616555e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201616523e+00 with 64 bits of precision,1.00000000000201705362e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201705352e+00 with 64 bits of precision,1.00000000000201794169e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201794159e+00 with 64 bits of precision,1.00000000000201882987e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000201882966e+00 with 64 bits of precision,1.00000000000201971816e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000201971773e+00 with 64 bits of precision,1.00000000000202060656e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202060634e+00 with 64 bits of precision,1.00000000000202149473e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202149441e+00 with 64 bits of precision,1.0000000000020223828e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020223827e+00 with 64 bits of precision,1.00000000000202327087e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202327077e+00 with 64 bits of precision,1.00000000000202415905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202415884e+00 with 64 bits of precision,1.00000000000202504723e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202504691e+00 with 64 bits of precision,1.0000000000020259353e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202593508e+00 with 64 bits of precision,1.0000000000020268238e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202682348e+00 with 64 bits of precision,1.00000000000202771187e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202771177e+00 with 64 bits of precision,1.00000000000202859994e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202859984e+00 with 64 bits of precision,1.00000000000202948823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000202948801e+00 with 64 bits of precision,1.00000000000203037673e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203037641e+00 with 64 bits of precision,1.0000000000020312648e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020312647e+00 with 64 bits of precision,1.00000000000203215287e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203215255e+00 with 64 bits of precision,1.00000000000203304094e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203304084e+00 with 64 bits of precision,1.00000000000203392901e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203392891e+00 with 64 bits of precision,1.00000000000203481719e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203481698e+00 with 64 bits of precision,1.00000000000203570537e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203570505e+00 with 64 bits of precision,1.00000000000203659355e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203659333e+00 with 64 bits of precision,1.00000000000203748205e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203748173e+00 with 64 bits of precision,1.00000000000203837012e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203837002e+00 with 64 bits of precision,1.00000000000203925819e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000203925798e+00 with 64 bits of precision,1.00000000000204014626e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204014616e+00 with 64 bits of precision,1.00000000000204103433e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204103423e+00 with 64 bits of precision,1.00000000000204192251e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020419223e+00 with 64 bits of precision,1.00000000000204281069e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204281037e+00 with 64 bits of precision,1.00000000000204369876e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204369854e+00 with 64 bits of precision,1.00000000000204458726e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204458694e+00 with 64 bits of precision,1.00000000000204547533e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204547523e+00 with 64 bits of precision,1.0000000000020463634e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204636308e+00 with 64 bits of precision,1.00000000000204725147e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204725137e+00 with 64 bits of precision,1.00000000000204813954e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204813944e+00 with 64 bits of precision,1.00000000000204902772e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204902751e+00 with 64 bits of precision,1.0000000000020499159e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000204991558e+00 with 64 bits of precision,1.00000000000205080397e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205080375e+00 with 64 bits of precision,1.00000000000205169247e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205169215e+00 with 64 bits of precision,1.00000000000205258054e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205258044e+00 with 64 bits of precision,1.00000000000205346861e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205346851e+00 with 64 bits of precision,1.00000000000205435679e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205435658e+00 with 64 bits of precision,1.00000000000205524508e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205524465e+00 with 64 bits of precision,1.00000000000205613348e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205613326e+00 with 64 bits of precision,1.00000000000205702165e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205702133e+00 with 64 bits of precision,1.00000000000205790972e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205790962e+00 with 64 bits of precision,1.00000000000205879779e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000205879769e+00 with 64 bits of precision,1.00000000000205968597e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000205968576e+00 with 64 bits of precision,1.00000000000206057415e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206057383e+00 with 64 bits of precision,1.00000000000206146222e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000002061462e+00 with 64 bits of precision,1.00000000000206235072e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020623504e+00 with 64 bits of precision,1.00000000000206323879e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206323869e+00 with 64 bits of precision,1.00000000000206412686e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206412676e+00 with 64 bits of precision,1.00000000000206501515e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206501493e+00 with 64 bits of precision,1.00000000000206590365e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206590333e+00 with 64 bits of precision,1.00000000000206679172e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206679162e+00 with 64 bits of precision,1.00000000000206767979e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206767958e+00 with 64 bits of precision,1.00000000000206856786e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206856776e+00 with 64 bits of precision,1.00000000000206945604e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000206945583e+00 with 64 bits of precision,1.00000000000207034411e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020703439e+00 with 64 bits of precision,1.0000000000020712324e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207123197e+00 with 64 bits of precision,1.00000000000207212047e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207212025e+00 with 64 bits of precision,1.00000000000207300897e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207300865e+00 with 64 bits of precision,1.00000000000207389704e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207389694e+00 with 64 bits of precision,1.00000000000207478511e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020747849e+00 with 64 bits of precision,1.00000000000207567318e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207567308e+00 with 64 bits of precision,1.00000000000207656147e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207656115e+00 with 64 bits of precision,1.00000000000207744987e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207744965e+00 with 64 bits of precision,1.00000000000207833804e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207833772e+00 with 64 bits of precision,1.00000000000207922611e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000207922601e+00 with 64 bits of precision,1.00000000000208011418e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208011408e+00 with 64 bits of precision,1.00000000000208100236e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208100215e+00 with 64 bits of precision,1.00000000000208189054e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208189022e+00 with 64 bits of precision,1.00000000000208277861e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208277839e+00 with 64 bits of precision,1.00000000000208366711e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208366679e+00 with 64 bits of precision,1.00000000000208455518e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208455508e+00 with 64 bits of precision,1.00000000000208544336e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208544315e+00 with 64 bits of precision,1.00000000000208633154e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208633132e+00 with 64 bits of precision,1.00000000000208722015e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208721972e+00 with 64 bits of precision,1.00000000000208810822e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208810801e+00 with 64 bits of precision,1.00000000000208899629e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208899586e+00 with 64 bits of precision,1.00000000000208988436e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000208988415e+00 with 64 bits of precision,1.00000000000209077243e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209077233e+00 with 64 bits of precision,1.0000000000020916605e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000020916604e+00 with 64 bits of precision,1.00000000000209254868e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209254847e+00 with 64 bits of precision,1.00000000000209343686e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209343664e+00 with 64 bits of precision,1.00000000000209432536e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209432504e+00 with 64 bits of precision,1.00000000000209521343e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209521333e+00 with 64 bits of precision,1.0000000000020961015e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209610129e+00 with 64 bits of precision,1.00000000000209698957e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209698947e+00 with 64 bits of precision,1.00000000000209787764e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209787754e+00 with 64 bits of precision,1.00000000000209876582e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000209876561e+00 with 64 bits of precision,1.000000000002099654e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000209965368e+00 with 64 bits of precision,1.00000000000210054207e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210054185e+00 with 64 bits of precision,1.00000000000210143057e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210143025e+00 with 64 bits of precision,1.00000000000210231864e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210231854e+00 with 64 bits of precision,1.00000000000210320671e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210320661e+00 with 64 bits of precision,1.000000000002104095e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210409478e+00 with 64 bits of precision,1.00000000000210498361e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210498318e+00 with 64 bits of precision,1.00000000000210587168e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210587147e+00 with 64 bits of precision,1.00000000000210675975e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210675943e+00 with 64 bits of precision,1.00000000000210764782e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210764772e+00 with 64 bits of precision,1.00000000000210853589e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210853579e+00 with 64 bits of precision,1.00000000000210942407e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000210942386e+00 with 64 bits of precision,1.00000000000211031225e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211031193e+00 with 64 bits of precision,1.00000000000211120032e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021112001e+00 with 64 bits of precision,1.00000000000211208882e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021120885e+00 with 64 bits of precision,1.00000000000211297689e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211297679e+00 with 64 bits of precision,1.00000000000211386496e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211386486e+00 with 64 bits of precision,1.00000000000211475325e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211475303e+00 with 64 bits of precision,1.00000000000211564175e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211564143e+00 with 64 bits of precision,1.00000000000211652982e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211652972e+00 with 64 bits of precision,1.00000000000211741789e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211741757e+00 with 64 bits of precision,1.00000000000211830596e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211830586e+00 with 64 bits of precision,1.00000000000211919403e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000211919393e+00 with 64 bits of precision,1.00000000000212008221e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000002120082e+00 with 64 bits of precision,1.00000000000212097039e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212097007e+00 with 64 bits of precision,1.00000000000212185879e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212185857e+00 with 64 bits of precision,1.00000000000212274707e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212274675e+00 with 64 bits of precision,1.00000000000212363514e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212363504e+00 with 64 bits of precision,1.00000000000212452321e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.000000000002124523e+00 with 64 bits of precision,1.00000000000212541128e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212541118e+00 with 64 bits of precision,1.00000000000212629935e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212629925e+00 with 64 bits of precision,1.00000000000212718753e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212718732e+00 with 64 bits of precision,1.00000000000212807571e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212807539e+00 with 64 bits of precision,1.00000000000212896378e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000212896356e+00 with 64 bits of precision,1.00000000000212985228e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000212985196e+00 with 64 bits of precision,1.00000000000213074035e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213074025e+00 with 64 bits of precision,1.00000000000213162842e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213162832e+00 with 64 bits of precision,1.00000000000213251671e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213251649e+00 with 64 bits of precision,1.00000000000213340521e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213340489e+00 with 64 bits of precision,1.00000000000213429328e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213429318e+00 with 64 bits of precision,1.00000000000213518135e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213518125e+00 with 64 bits of precision,1.00000000000213606964e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213606942e+00 with 64 bits of precision,1.00000000000213695825e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213695782e+00 with 64 bits of precision,1.00000000000213784632e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213784611e+00 with 64 bits of precision,1.00000000000213873439e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213873396e+00 with 64 bits of precision,1.00000000000213962246e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000213962225e+00 with 64 bits of precision,1.00000000000214051053e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214051043e+00 with 64 bits of precision,1.0000000000021413986e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021413985e+00 with 64 bits of precision,1.00000000000214228678e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214228657e+00 with 64 bits of precision,1.00000000000214317496e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214317474e+00 with 64 bits of precision,1.00000000000214406346e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214406314e+00 with 64 bits of precision,1.00000000000214495153e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214495143e+00 with 64 bits of precision,1.0000000000021458396e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214583928e+00 with 64 bits of precision,1.00000000000214672767e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214672757e+00 with 64 bits of precision,1.00000000000214761574e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214761564e+00 with 64 bits of precision,1.00000000000214850392e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214850371e+00 with 64 bits of precision,1.0000000000021493921e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000214939178e+00 with 64 bits of precision,1.00000000000215028017e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215027995e+00 with 64 bits of precision,1.00000000000215116867e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215116835e+00 with 64 bits of precision,1.00000000000215205674e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215205664e+00 with 64 bits of precision,1.00000000000215294481e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215294471e+00 with 64 bits of precision,1.00000000000215383299e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215383278e+00 with 64 bits of precision,1.00000000000215472117e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215472085e+00 with 64 bits of precision,1.00000000000215560968e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215560946e+00 with 64 bits of precision,1.00000000000215649785e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215649742e+00 with 64 bits of precision,1.00000000000215738592e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215738571e+00 with 64 bits of precision,1.00000000000215827399e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215827378e+00 with 64 bits of precision,1.00000000000215916206e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000215916196e+00 with 64 bits of precision,1.00000000000216005013e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216004992e+00 with 64 bits of precision,1.0000000000021609382e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021609381e+00 with 64 bits of precision,1.00000000000216182649e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216182617e+00 with 64 bits of precision,1.00000000000216271489e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216271467e+00 with 64 bits of precision,1.00000000000216360306e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216360274e+00 with 64 bits of precision,1.00000000000216449113e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216449103e+00 with 64 bits of precision,1.0000000000021653792e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021653791e+00 with 64 bits of precision,1.00000000000216626738e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216626717e+00 with 64 bits of precision,1.00000000000216715556e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216715524e+00 with 64 bits of precision,1.00000000000216804363e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216804341e+00 with 64 bits of precision,1.00000000000216893213e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000216893181e+00 with 64 bits of precision,1.0000000000021698202e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021698201e+00 with 64 bits of precision,1.00000000000217070838e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217070817e+00 with 64 bits of precision,1.00000000000217159656e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000217159634e+00 with 64 bits of precision,1.00000000000217248517e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217248474e+00 with 64 bits of precision,1.00000000000217337324e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217337303e+00 with 64 bits of precision,1.00000000000217426131e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217426088e+00 with 64 bits of precision,1.00000000000217514938e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217514917e+00 with 64 bits of precision,1.00000000000217603745e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217603735e+00 with 64 bits of precision,1.00000000000217692552e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217692542e+00 with 64 bits of precision,1.0000000000021778137e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217781349e+00 with 64 bits of precision,1.00000000000217870188e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217870166e+00 with 64 bits of precision,1.00000000000217959038e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000217959006e+00 with 64 bits of precision,1.00000000000218047845e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218047835e+00 with 64 bits of precision,1.00000000000218136652e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218136631e+00 with 64 bits of precision,1.00000000000218225459e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218225449e+00 with 64 bits of precision,1.00000000000218314266e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218314256e+00 with 64 bits of precision,1.00000000000218403084e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218403063e+00 with 64 bits of precision,1.00000000000218491902e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021849187e+00 with 64 bits of precision,1.00000000000218580709e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218580687e+00 with 64 bits of precision,1.00000000000218669559e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218669527e+00 with 64 bits of precision,1.00000000000218758366e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218758356e+00 with 64 bits of precision,1.00000000000218847173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000218847163e+00 with 64 bits of precision,1.00000000000218936002e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021893598e+00 with 64 bits of precision,1.00000000000219024863e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000021902482e+00 with 64 bits of precision,1.0000000000021911367e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219113649e+00 with 64 bits of precision,1.00000000000219202477e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219202445e+00 with 64 bits of precision,1.00000000000219291284e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219291274e+00 with 64 bits of precision,1.00000000000219380091e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219380081e+00 with 64 bits of precision,1.00000000000219468909e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219468888e+00 with 64 bits of precision,1.00000000000219557727e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219557695e+00 with 64 bits of precision,1.00000000000219646534e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219646512e+00 with 64 bits of precision,1.00000000000219735384e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219735352e+00 with 64 bits of precision,1.00000000000219824191e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219824181e+00 with 64 bits of precision,1.00000000000219912998e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000219912988e+00 with 64 bits of precision,1.00000000000220001827e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220001805e+00 with 64 bits of precision,1.00000000000220090677e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220090645e+00 with 64 bits of precision,1.00000000000220179484e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220179474e+00 with 64 bits of precision,1.00000000000220268291e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220268259e+00 with 64 bits of precision,1.00000000000220357098e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220357088e+00 with 64 bits of precision,1.00000000000220445905e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220445895e+00 with 64 bits of precision,1.00000000000220534723e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220534702e+00 with 64 bits of precision,1.00000000000220623541e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220623509e+00 with 64 bits of precision,1.00000000000220712381e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220712359e+00 with 64 bits of precision,1.00000000000220801209e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220801177e+00 with 64 bits of precision,1.00000000000220890016e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220890006e+00 with 64 bits of precision,1.00000000000220978823e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000220978802e+00 with 64 bits of precision,1.0000000000022106763e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022106762e+00 with 64 bits of precision,1.00000000000221156437e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221156427e+00 with 64 bits of precision,1.00000000000221245255e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221245234e+00 with 64 bits of precision,1.00000000000221334073e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221334041e+00 with 64 bits of precision,1.0000000000022142288e+00 with 64 bits of precision)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Maybe a zero in Interval(1.00000000000221422858e+00 with 64 bits of precision,1.0000000000022151173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221511698e+00 with 64 bits of precision,1.00000000000221600537e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221600527e+00 with 64 bits of precision,1.00000000000221689344e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221689334e+00 with 64 bits of precision,1.00000000000221778173e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221778151e+00 with 64 bits of precision,1.00000000000221867023e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000221866991e+00 with 64 bits of precision,1.0000000000022195583e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022195582e+00 with 64 bits of precision,1.00000000000222044637e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222044627e+00 with 64 bits of precision,1.00000000000222133466e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222133444e+00 with 64 bits of precision,1.00000000000222222327e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222222284e+00 with 64 bits of precision,1.00000000000222311134e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222311113e+00 with 64 bits of precision,1.00000000000222399941e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222399898e+00 with 64 bits of precision,1.00000000000222488748e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222488727e+00 with 64 bits of precision,1.00000000000222577555e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222577545e+00 with 64 bits of precision,1.00000000000222666362e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222666352e+00 with 64 bits of precision,1.0000000000022275518e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222755159e+00 with 64 bits of precision,1.00000000000222843998e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222843976e+00 with 64 bits of precision,1.00000000000222932848e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000222932816e+00 with 64 bits of precision,1.00000000000223021655e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223021645e+00 with 64 bits of precision,1.00000000000223110462e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022311043e+00 with 64 bits of precision,1.00000000000223199269e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223199259e+00 with 64 bits of precision,1.00000000000223288076e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223288066e+00 with 64 bits of precision,1.00000000000223376894e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223376873e+00 with 64 bits of precision,1.00000000000223465712e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022346568e+00 with 64 bits of precision,1.00000000000223554519e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223554497e+00 with 64 bits of precision,1.00000000000223643369e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223643337e+00 with 64 bits of precision,1.00000000000223732176e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223732166e+00 with 64 bits of precision,1.00000000000223820983e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223820973e+00 with 64 bits of precision,1.00000000000223909801e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022390978e+00 with 64 bits of precision,1.00000000000223998619e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000223998587e+00 with 64 bits of precision,1.0000000000022408747e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224087448e+00 with 64 bits of precision,1.00000000000224176287e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224176244e+00 with 64 bits of precision,1.00000000000224265094e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224265073e+00 with 64 bits of precision,1.00000000000224353901e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.0000000000022435388e+00 with 64 bits of precision,1.00000000000224442708e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224442698e+00 with 64 bits of precision,1.00000000000224531515e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224531505e+00 with 64 bits of precision,1.00000000000224620344e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224620322e+00 with 64 bits of precision,1.00000000000224709194e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224709162e+00 with 64 bits of precision,1.00000000000224798001e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224797991e+00 with 64 bits of precision,1.00000000000224886808e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224886787e+00 with 64 bits of precision,1.00000000000224975615e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000224975605e+00 with 64 bits of precision,1.00000000000225064422e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000225064412e+00 with 64 bits of precision,1.0000000000022515324e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000225153219e+00 with 64 bits of precision,1.00000000000225242058e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000225242026e+00 with 64 bits of precision,1.00000000000225330865e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000225330843e+00 with 64 bits of precision,1.00000000000225419715e+00 with 64 bits of precision)\n",
"Maybe a zero in Interval(1.00000000000225419683e+00 with 64 bits of precision,1.00000000000225508522e+00 with 64 bits of precision)"
]
}
],
"prompt_number": "*"
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | gpl-3.0 |
neurodata/ndmg | tutorials/Overview.ipynb | 1 | 22964 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Ndmg Tutorial: Running Inside Python"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This tutorial provides a basic overview of how to run ndmg manually within Python. <br>\n",
"We begin by checking for dependencies,\n",
"then we set our input parameters,\n",
"then we smiply run the pipeline.\n",
"\n",
"Running the pipeline is quite simple: call `ndmg_dwi_pipeline.ndmg_dwi_worker` with the correct arguments. <br>\n",
"\n",
"\n",
"Note that, although you can run the pipeline in Python, the absolute easiest way (outside Gigantum) is to run the pipeline from the command line once all dependencies are installed using the following command: <br>\n",
"`ndmg_bids </absolute/input/dir> </absolute/output/dir>`. <br>\n",
"This will run a single session from the input directory, and output the results into your output directory.\n",
"\n",
"But for now, let's look at running in Python -- <br>\n",
"Let's begin!"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"import os\n",
"import os.path as op\n",
"import glob\n",
"import shutil\n",
"import warnings\n",
"import subprocess\n",
"from pathlib import Path\n",
"\n",
"from ndmg.scripts import ndmg_dwi_pipeline\n",
"from ndmg.scripts.ndmg_bids import get_atlas\n",
"from ndmg.utils import cloud_utils"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Check for dependencies, Set Directories"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The below code is a simple check that makes sure AFNI and FSL are installed. <br>\n",
"We also set the input, data, and atlas paths."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Make sure that AFNI and FSL are installed"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your fsl directory is located here: /usr/local/fsl\n",
"Your AFNI directory is located here: /Users/alex/abin/afni\n",
"\n"
]
}
],
"source": [
"# FSL\n",
"try:\n",
" print(f\"Your fsl directory is located here: {os.environ['FSLDIR']}\")\n",
"except KeyError:\n",
" raise AssertionError(\"You do not have FSL installed! See installation instructions here: https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation\")\n",
" \n",
"# AFNI\n",
"try:\n",
" print(f\"Your AFNI directory is located here: {subprocess.check_output('which afni', shell=True, universal_newlines=True)}\")\n",
"except subprocess.CalledProcessError:\n",
" raise AssertionError(\"You do not have AFNI installed! See installation instructions here: https://afni.nimh.nih.gov/pub/dist/doc/htmldoc/background_install/main_toc.html\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Set Input, Output, and Atlas Locations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here, you set:\n",
"1. the input_dir - this is where your input data lives.\n",
"2. the out_dir - this is where your output data will go."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your input and output directory will be : /Users/alex/.ndmg/input and /Users/alex/.ndmg/output\n"
]
}
],
"source": [
"# get atlases\n",
"ndmg_dir = Path.home() / \".ndmg\"\n",
"atlas_dir = ndmg_dir / \"ndmg_atlases\"\n",
"get_atlas(str(atlas_dir), \"2mm\")\n",
"\n",
"# These\n",
"input_dir = ndmg_dir / \"input\"\n",
"out_dir = ndmg_dir / \"output\"\n",
"\n",
"print(f\"Your input and output directory will be : {input_dir} and {out_dir}\")\n",
"\n",
"assert op.exists(input_dir), f\"You must have an input directory with data. Your input directory is located here: {input_dir}\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Choose input parameters"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Naming Conventions\n",
"Here, we define input variables to the pipeline.\n",
"To run the `ndmg` pipeline, you need four files:\n",
"1. a `t1w` - this is a high-resolution anatomical image.\n",
"2. a `dwi` - the diffusion image.\n",
"3. bvecs - this is a text file that defines the gradient vectors created by a DWI scan.\n",
"4. bvals - this is a text file that defines magnitudes for the gradient vectors created by a DWI scan.\n",
"\n",
"The naming convention is in the [BIDs](https://bids.neuroimaging.io/) spec."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your anatomical image location: /Users/alex/.ndmg/input/sub-0025864/ses-1/anat/sub-0025864_ses-1_T1w.nii.gz\n",
"Your dwi image location: /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.nii.gz\n",
"Your bvector location: /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.bvec\n",
"Your bvalue location: /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.bval\n"
]
}
],
"source": [
"# Specify base directory and paths to input files (dwi, bvecs, bvals, and t1w required)\n",
"subject_id = 'sub-0025864'\n",
"\n",
"# Define the location of our input files.\n",
"t1w = str(input_dir / f\"{subject_id}/ses-1/anat/{subject_id}_ses-1_T1w.nii.gz\")\n",
"dwi = str(input_dir / f\"{subject_id}/ses-1/dwi/{subject_id}_ses-1_dwi.nii.gz\")\n",
"bvecs = str(input_dir / f\"{subject_id}/ses-1/dwi/{subject_id}_ses-1_dwi.bvec\")\n",
"bvals = str(input_dir / f\"{subject_id}/ses-1/dwi/{subject_id}_ses-1_dwi.bval\")\n",
"\n",
"print(f\"Your anatomical image location: {t1w}\")\n",
"print(f\"Your dwi image location: {dwi}\")\n",
"print(f\"Your bvector location: {bvecs}\")\n",
"print(f\"Your bvalue location: {bvals}\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Parameter Choices and Output Directory\n",
"Here, we choose the parameters to run the pipeline with.\n",
"If you are inexperienced with diffusion MRI theory, feel free to just use the default parameters.\n",
"\n",
"- *atlases = ['desikan', 'CPAC200', 'DKT', 'HarvardOxfordcort', 'HarvardOxfordsub', 'JHU', 'Schaefer2018-200', 'Talairach', 'aal', 'brodmann', 'glasser', 'yeo-7-liberal', 'yeo-17-liberal']* : The atlas that defines the node location of the graph you create.\n",
"- *mod_types = ['det', 'prob']* : Deterministic or probablistic tractography.\n",
"- *track_types = ['local', 'particle']* : Local or particle tracking.\n",
"- *mods = ['csa', 'csd']* : [Constant Solid Angle](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4360965/) or [Constrained Spherical Deconvolution](https://onlinelibrary.wiley.com/doi/10.1002/ima.22005).\n",
"- regs = *['native', 'native_dsn', 'mni']* : Registration style. If native, do all registration in each scan's space; if mni, register scans to the MNI atlas; if native_dsn, do registration in native space, and then fit the streamlines to MNI space.\n",
"- vox_size = *['1mm', '2mm']* : Whether our voxels are 1mm or 2mm.\n",
"- seeds = int : Seeding density for tractography. More seeds generally results in a better graph, but at a much higher computational cost."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [],
"source": [
"# Use the default parameters.\n",
"atlas = 'desikan'\n",
"mod_type = 'prob'\n",
"track_type = 'local'\n",
"mod_func = 'csd'\n",
"reg_style = 'native'\n",
"vox_size = '2mm'\n",
"seeds = 1\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Get masks and labels\n",
"The pipeline needs these two variables as input. <br>\n",
"Running the pipeline via `ndmg_bids` does this for you."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"mask location : /Users/alex/.ndmg/ndmg_atlases/atlases/mask/MNI152NLin6_res-2x2x2_T1w_descr-brainmask.nii.gz\n",
"atlas location : ['/Users/alex/.ndmg/ndmg_atlases/atlases/label/Human/desikan_space-MNI152NLin6_res-2x2x2.nii.gz']\n"
]
}
],
"source": [
"# Auto-set paths to neuroparc files\n",
"mask = str(atlas_dir / \"atlases/mask/MNI152NLin6_res-2x2x2_T1w_descr-brainmask.nii.gz\")\n",
"labels = [str(i) for i in (atlas_dir / \"atlases/label/Human/\").glob(f\"*{atlas}*2x2x2.nii.gz\")]\n",
"\n",
"print(f\"mask location : {mask}\")\n",
"print(f\"atlas location : {labels}\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Run the pipeline!"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"dwi = /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.nii.gz\n",
"bvals = /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.bval\n",
"bvecs = /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.bvec\n",
"t1w = /Users/alex/.ndmg/input/sub-0025864/ses-1/anat/sub-0025864_ses-1_T1w.nii.gz\n",
"atlas = desikan\n",
"mask = /Users/alex/.ndmg/ndmg_atlases/atlases/mask/MNI152NLin6_res-2x2x2_T1w_descr-brainmask.nii.gz\n",
"labels = ['/Users/alex/.ndmg/ndmg_atlases/atlases/label/Human/desikan_space-MNI152NLin6_res-2x2x2.nii.gz']\n",
"outdir = /Users/alex/.ndmg/output\n",
"vox_size = 2mm\n",
"mod_type = prob\n",
"track_type = local\n",
"mod_func = csd\n",
"seeds = 1\n",
"reg_style = native\n",
"clean = False\n",
"skip eddy = True\n",
"skip registration = True\n",
"Output directory: /Users/alex/.ndmg/output\n",
"Adding directory tree...\n",
"Connectomes downsampled to given labels: /Users/alex/.ndmg/output/dwi/roi-connectomes/desikan_space-MNI152NLin6_res-2x2x2/sub-0025864_ses-1_dwi_desikan_space-MNI152NLin6_res-2x2x2_measure-spatial-ds_adj.csv\n",
"Performing eddy correction...\n",
"eddy_correct /Users/alex/.ndmg/input/sub-0025864/ses-1/dwi/sub-0025864_ses-1_dwi.nii.gz /Users/alex/.ndmg/output/dwi/preproc/eddy_corrected_data.nii.gz 0\n"
]
},
{
"ename": "KeyboardInterrupt",
"evalue": "",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mKeyboardInterrupt\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-28-f45eb063a997>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mndmg_dwi_pipeline\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mndmg_dwi_worker\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdwi\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mdwi\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mbvals\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mbvals\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mbvecs\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mbvecs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mt1w\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mt1w\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0matlas\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0matlas\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mmask\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mmask\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mlabels\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mlabels\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0moutdir\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mstr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mout_dir\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mvox_size\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mvox_size\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mmod_type\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mmod_type\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtrack_type\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mtrack_type\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mmod_func\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mmod_func\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mseeds\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mseeds\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mreg_style\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mreg_style\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mclean\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mFalse\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mskipeddy\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mTrue\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mskipreg\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m~/Dropbox/NeuroData/ndmg-top/ndmg/ndmg/scripts/ndmg_dwi_pipeline.py\u001b[0m in \u001b[0;36mndmg_dwi_worker\u001b[0;34m(dwi, bvals, bvecs, t1w, atlas, mask, labels, outdir, vox_size, mod_type, track_type, mod_func, seeds, reg_style, clean, skipeddy, skipreg, buck, remo, push, creds, debug, modif)\u001b[0m\n\u001b[1;32m 242\u001b[0m \u001b[0mcmd\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m\"eddy_correct \"\u001b[0m \u001b[0;34m+\u001b[0m \u001b[0mdwi\u001b[0m \u001b[0;34m+\u001b[0m \u001b[0;34m\" \"\u001b[0m \u001b[0;34m+\u001b[0m \u001b[0mdwi_prep\u001b[0m \u001b[0;34m+\u001b[0m \u001b[0;34m\" 0\"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 243\u001b[0m \u001b[0mprint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mcmd\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 244\u001b[0;31m \u001b[0msts\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mPopen\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mcmd\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mshell\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mwait\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 245\u001b[0m \u001b[0mprint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0msts\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 246\u001b[0m \u001b[0mts\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtime\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtime\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/Caskroom/miniconda/base/envs/ndmg/lib/python3.6/subprocess.py\u001b[0m in \u001b[0;36mwait\u001b[0;34m(self, timeout, endtime)\u001b[0m\n\u001b[1;32m 1475\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mreturncode\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0;32mNone\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1476\u001b[0m \u001b[0;32mbreak\u001b[0m \u001b[0;31m# Another thread waited.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1477\u001b[0;31m \u001b[0;34m(\u001b[0m\u001b[0mpid\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0msts\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_try_wait\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1478\u001b[0m \u001b[0;31m# Check the pid and loop as waitpid has been known to\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1479\u001b[0m \u001b[0;31m# return 0 even without WNOHANG in odd situations.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/Caskroom/miniconda/base/envs/ndmg/lib/python3.6/subprocess.py\u001b[0m in \u001b[0;36m_try_wait\u001b[0;34m(self, wait_flags)\u001b[0m\n\u001b[1;32m 1422\u001b[0m \u001b[0;34m\"\"\"All callers to this function MUST hold self._waitpid_lock.\"\"\"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1423\u001b[0m \u001b[0;32mtry\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1424\u001b[0;31m \u001b[0;34m(\u001b[0m\u001b[0mpid\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0msts\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mos\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mwaitpid\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpid\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mwait_flags\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1425\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0mChildProcessError\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1426\u001b[0m \u001b[0;31m# This happens if SIGCLD is set to be ignored or waiting\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mKeyboardInterrupt\u001b[0m: "
]
}
],
"source": [
"ndmg_dwi_pipeline.ndmg_dwi_worker(dwi=dwi, bvals=bvals, bvecs=bvecs, t1w=t1w, atlas=atlas, mask=mask, labels=labels, outdir=str(out_dir), vox_size=vox_size, mod_type=mod_type, track_type=track_type, mod_func=mod_func, seeds=seeds, reg_style=reg_style, clean=False, skipeddy=True, skipreg=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Try It Yourself : Command Line"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`ndmg` runs best as a standalone program on the command line.\n",
"\n",
"The simplest form of the command, given that you have input data, pass an output folder, and have all dependencies installed, is the following:\n",
" \n",
" ndmg_bids </absolute/input/dir> </absolute/output/dir>\n",
" \n",
"Here, we'll show you how to set this up yourself."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Setup: Running Locally"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. install [FSL](https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation)\n",
"2. install [AFNI](https://afni.nimh.nih.gov/pub/dist/doc/htmldoc/background_install/install_instructs/index.html)\n",
"3. `git clone https://github.com/neurodata/ndmg.git`\n",
"4. `cd ndmg`\n",
"5. `pip install -r requirements.txt`\n",
"6. `pip install .`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Running Locally"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Most Basic"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This will run the first session from your input dataset, and put the results into the output dataset.\n",
"We still recommend the `--atlas` flag so that graphs don't get generated on all possible atlases.\n",
"\n",
" ndmg_bids --atlas desikan </absolute/input/dir> </absolute/output/dir>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Specifying Participant and Session\n",
"\n",
"You can also specify a particular participant and session.\n",
"(This is extremely useful for setting up batch scripts to run large datasets).\n",
"\n",
" ndmg_bids --atlas desikan --participant_label <label> --session_label <number> </absolute/input/dir> </absolute/output/dir>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Different Registration Styles, Diffusion Models, Tractography Styles"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can use:\n",
"- the `--sp` flag to set the registration space;\n",
"- the `--mf` flag to set the diffusion model; and\n",
"- the `--mod` flag to set deterministic / probablistic tracking;\n",
"\n",
"\n",
" ndmg_bids --atlas desikan --sp <space> --mf <model> --mod <tracking style> </absolute/input/dir> </absolute/output/dir>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Setup: Running in Docker"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you're having problems installing the program locally, it's often easier to use Docker.\n",
"\n",
"1. install [docker](https://docs.docker.com/install/)\n",
"2. `docker pull neurodata/ndmg_dev:latest`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Running in Docker"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Option A (Docker executable approach):\n",
"Once you've downloaded the docker image, you can:\n",
"Attach your local input and output folders with `-v`, <br>\n",
"Run the image, <br>\n",
"and input your participant and session labels into the container.\n",
"\n",
" docker run -ti --rm --privileged -e DISPLAY=$DISPLAY -v <absolute/path/to/input/data>:/input -v <absolute/path/to/output/data>:/outputs neurodata/ndmg_dev:latest --participant_label <label> --session_label <number> --atlas desikan /input /output"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Option B (Inside Docker container):\n",
"\n",
"You can also enter the container yourself and then run `ndmg` from inside the container.\n",
"\n",
" docker run -ti --rm --privileged --entrypoint /bin/bash -e DISPLAY=$DISPLAY -v <absolute/path/to/input/data>/input -v <absolute/path/to/output/data>/output ndmg_dev:latest\n",
"\n",
" ndmg_bids --participant_label <label> --session_label <number> --atlas desikan /input /output"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "ndmg",
"language": "python",
"name": "ndmg"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.8"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| apache-2.0 |
mirjalil/DataScience | algorithms-in-C++/data-structures_00_overview.ipynb | 1 | 769 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Data Structures in C++\n",
"=======\n",
"\n",
"## C++ STL\n",
"\n",
"**Containers:** "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
ahwkuepper/stdme | code/app_model_chlamydia.ipynb | 1 | 92068 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# A first simple model"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import pickle\n",
"import numpy as np\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Plain Seaborn figures with matplotlib color codes mapped to the default seaborn palette \n",
"sns.set(style=\"white\", color_codes=True)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>FIPS</th>\n",
" <th>Population</th>\n",
" <th>hd01s001</th>\n",
" <th>hd02s002</th>\n",
" <th>hd02s005</th>\n",
" <th>hd02s006</th>\n",
" <th>hd02s007</th>\n",
" <th>hd02s008</th>\n",
" <th>hd02s009</th>\n",
" <th>hd02s010</th>\n",
" <th>...</th>\n",
" <th>hd01s168</th>\n",
" <th>hd02s181</th>\n",
" <th>hd02s184</th>\n",
" <th>hd01vd01</th>\n",
" <th>d002</th>\n",
" <th>d014</th>\n",
" <th>d019</th>\n",
" <th>d024</th>\n",
" <th>d029</th>\n",
" <th>lnd110210d</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1001</td>\n",
" <td>55246</td>\n",
" <td>4.736962</td>\n",
" <td>21.8</td>\n",
" <td>7.9</td>\n",
" <td>5.6</td>\n",
" <td>5.8</td>\n",
" <td>6.1</td>\n",
" <td>7.6</td>\n",
" <td>7.5</td>\n",
" <td>...</td>\n",
" <td>3.13</td>\n",
" <td>75.4</td>\n",
" <td>24.6</td>\n",
" <td>52475</td>\n",
" <td>0.562138</td>\n",
" <td>0.003017</td>\n",
" <td>0.020029</td>\n",
" <td>0.002868</td>\n",
" <td>0.017704</td>\n",
" <td>92.781808</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1003</td>\n",
" <td>195540</td>\n",
" <td>5.260703</td>\n",
" <td>19.0</td>\n",
" <td>6.4</td>\n",
" <td>5.2</td>\n",
" <td>5.6</td>\n",
" <td>5.9</td>\n",
" <td>6.3</td>\n",
" <td>6.6</td>\n",
" <td>...</td>\n",
" <td>2.93</td>\n",
" <td>72.5</td>\n",
" <td>27.5</td>\n",
" <td>50183</td>\n",
" <td>0.545409</td>\n",
" <td>0.002747</td>\n",
" <td>0.023886</td>\n",
" <td>0.003444</td>\n",
" <td>0.020292</td>\n",
" <td>122.920831</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1005</td>\n",
" <td>27076</td>\n",
" <td>4.438653</td>\n",
" <td>18.0</td>\n",
" <td>6.3</td>\n",
" <td>6.5</td>\n",
" <td>7.3</td>\n",
" <td>6.6</td>\n",
" <td>6.6</td>\n",
" <td>6.6</td>\n",
" <td>...</td>\n",
" <td>3.01</td>\n",
" <td>66.8</td>\n",
" <td>33.2</td>\n",
" <td>35634</td>\n",
" <td>0.437169</td>\n",
" <td>0.002342</td>\n",
" <td>0.019348</td>\n",
" <td>0.003666</td>\n",
" <td>0.022200</td>\n",
" <td>30.563959</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1007</td>\n",
" <td>22512</td>\n",
" <td>4.360120</td>\n",
" <td>18.4</td>\n",
" <td>6.7</td>\n",
" <td>6.5</td>\n",
" <td>7.0</td>\n",
" <td>7.2</td>\n",
" <td>7.6</td>\n",
" <td>7.1</td>\n",
" <td>...</td>\n",
" <td>3.09</td>\n",
" <td>75.6</td>\n",
" <td>24.4</td>\n",
" <td>37984</td>\n",
" <td>0.524582</td>\n",
" <td>0.001886</td>\n",
" <td>0.020244</td>\n",
" <td>0.002012</td>\n",
" <td>0.020370</td>\n",
" <td>36.101222</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1009</td>\n",
" <td>57872</td>\n",
" <td>4.758321</td>\n",
" <td>20.2</td>\n",
" <td>7.0</td>\n",
" <td>5.4</td>\n",
" <td>6.0</td>\n",
" <td>6.0</td>\n",
" <td>6.8</td>\n",
" <td>7.0</td>\n",
" <td>...</td>\n",
" <td>3.07</td>\n",
" <td>80.6</td>\n",
" <td>19.4</td>\n",
" <td>44409</td>\n",
" <td>0.606034</td>\n",
" <td>0.001946</td>\n",
" <td>0.017981</td>\n",
" <td>0.003707</td>\n",
" <td>0.013440</td>\n",
" <td>89.615659</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>5 rows × 46 columns</p>\n",
"</div>"
],
"text/plain": [
" FIPS Population hd01s001 hd02s002 hd02s005 hd02s006 hd02s007 \\\n",
"0 1001 55246 4.736962 21.8 7.9 5.6 5.8 \n",
"1 1003 195540 5.260703 19.0 6.4 5.2 5.6 \n",
"2 1005 27076 4.438653 18.0 6.3 6.5 7.3 \n",
"3 1007 22512 4.360120 18.4 6.7 6.5 7.0 \n",
"4 1009 57872 4.758321 20.2 7.0 5.4 6.0 \n",
"\n",
" hd02s008 hd02s009 hd02s010 ... hd01s168 hd02s181 hd02s184 \\\n",
"0 6.1 7.6 7.5 ... 3.13 75.4 24.6 \n",
"1 5.9 6.3 6.6 ... 2.93 72.5 27.5 \n",
"2 6.6 6.6 6.6 ... 3.01 66.8 33.2 \n",
"3 7.2 7.6 7.1 ... 3.09 75.6 24.4 \n",
"4 6.0 6.8 7.0 ... 3.07 80.6 19.4 \n",
"\n",
" hd01vd01 d002 d014 d019 d024 d029 lnd110210d \n",
"0 52475 0.562138 0.003017 0.020029 0.002868 0.017704 92.781808 \n",
"1 50183 0.545409 0.002747 0.023886 0.003444 0.020292 122.920831 \n",
"2 35634 0.437169 0.002342 0.019348 0.003666 0.022200 30.563959 \n",
"3 37984 0.524582 0.001886 0.020244 0.002012 0.020370 36.101222 \n",
"4 44409 0.606034 0.001946 0.017981 0.003707 0.013440 89.615659 \n",
"\n",
"[5 rows x 46 columns]"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_merged = pd.read_csv(\"../data/chlamydia_cdc_census.csv\")\n",
"df_merged.drop(\"Cases\", axis=1, inplace=True)\n",
"df_merged.head()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df_zipfips= pd.read_csv(\"../data/ZIP_COUNTY_122014.csv\", usecols={0,1})"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"zip2fips = dict(zip(df_zipfips[\"ZIP\"], df_zipfips[\"COUNTY\"]))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"fips = zip2fips[10027]"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(1, 46)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"target = df_merged[df_merged['FIPS']==fips]\n",
"target.shape"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"target_params = target.values[0]"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model = pickle.load(open('../data/randomforest_params.pickle', \"rb\" ))"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model2 = pickle.load(open('../data/gradientboosting_params.pickle', \"rb\" ))"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Ymean = pickle.load(open('../data/Ymean.pickle', \"rb\"))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Ystd = pickle.load(open('../data/Ystd.pickle', \"rb\"))"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
}
],
"source": [
"chlamydia_rate = model.predict(target_params[1:])"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(0.04390608807429472,\n",
" 3.960329144301384,\n",
" 5.454453321469633,\n",
" 2.5821170396492725,\n",
" 1.1687800645377253,\n",
" 0.5883415801955493,\n",
" 0.2886825290884878,\n",
" 0.12425422925025406,\n",
" 0.036442053101664616,\n",
" 0.007024974091887155)"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"gender_rate = {}\n",
"gender_factor = {}\n",
"gender_number = {}\n",
"gender_rate[\"Male\"] = 278.4e-5\n",
"gender_rate[\"Female\"] = 627.2e-5\n",
"gender_number[\"Male\"] = 155651602\n",
"gender_number[\"Female\"] = 160477237\n",
"rate_average = (gender_rate[\"Male\"]*gender_number[\"Male\"]+gender_rate[\"Female\"]*gender_number[\"Male\"])/(gender_number[\"Male\"]+gender_number[\"Female\"])\n",
"gender_factor[\"Male\"] = gender_rate[\"Male\"]/rate_average\n",
"gender_factor[\"Female\"] = gender_rate[\"Female\"]/rate_average\n",
"gender_factor[\"Female\"], gender_factor[\"Male\"]\n",
"race_rate = {}\n",
"race_factor = {}\n",
"race_number = {}\n",
"race_number[\"Native\"] = 1942876.0\n",
"race_number[\"Asian\"] = 12721721.0\n",
"race_number[\"Black\"] = 29489649.0\n",
"race_number[\"Hispanic\"] = 46407173.0\n",
"race_number[\"Multiple\"] = 5145135.0\n",
"race_number[\"Pacific\"] = 473703.0\n",
"race_number[\"White\"] = 161443167.0\n",
"race_rate[\"Native\"] = 689.1e-5\n",
"race_rate[\"Asian\"] = 115.8e-5\n",
"race_rate[\"Black\"] = 1152.6e-5\n",
"race_rate[\"Hispanic\"] = 376.2e-5\n",
"race_rate[\"Multiple\"] = 116.1e-5\n",
"race_rate[\"Pacific\"] = 641.5e-5\n",
"race_rate[\"White\"] = 187.0e-5\n",
"US_number = race_number[\"Native\"] + race_number[\"Asian\"] + race_number[\"Black\"] + race_number[\"Hispanic\"] + race_number[\"Multiple\"] + race_number[\"Pacific\"] + race_number[\"White\"]\n",
"rate_average = (race_rate[\"Native\"]*race_number[\"Native\"]+race_rate[\"Asian\"]*race_number[\"Asian\"]+race_rate[\"Black\"]*race_number[\"Black\"]+race_rate[\"Hispanic\"]*race_number[\"Hispanic\"]+race_rate[\"Multiple\"]*race_number[\"Multiple\"]+race_rate[\"Pacific\"]*race_number[\"Multiple\"]+race_rate[\"White\"]*race_number[\"White\"])/US_number \n",
"race_factor[\"Native\"] = race_rate[\"Native\"]/rate_average\n",
"race_factor[\"Asian\"] = race_rate[\"Asian\"]/rate_average\n",
"race_factor[\"Black\"] = race_rate[\"Black\"]/rate_average\n",
"race_factor[\"Hispanic\"] = race_rate[\"Hispanic\"]/rate_average\n",
"race_factor[\"Multiple\"] = race_rate[\"Multiple\"]/rate_average\n",
"race_factor[\"Pacific\"] = race_rate[\"Pacific\"]/rate_average\n",
"race_factor[\"White\"] = race_rate[\"White\"]/rate_average\n",
"\n",
"age_rate = {}\n",
"age_factor = {}\n",
"age_number = {}\n",
"age_number[\"0-14\"] = 61089123.0\n",
"age_number[\"15-19\"] = 21158964.0\n",
"age_number[\"20-24\"] = 22795438.0\n",
"age_number[\"25-29\"] = 21580198.0\n",
"age_number[\"30-34\"] = 21264389.0\n",
"age_number[\"35-39\"] = 19603770.0\n",
"age_number[\"40-44\"] = 20848920.0\n",
"age_number[\"45-54\"] = 43767532.0\n",
"age_number[\"55-64\"] = 39316431.0\n",
"age_number[\"65+\"] = 44704074.0\n",
"\n",
"age_rate[\"0-14\"] = 20.0e-5\n",
"age_rate[\"15-19\"] = 1804.0e-5\n",
"age_rate[\"20-24\"] = 2484.6e-5\n",
"age_rate[\"25-29\"] = 1176.2e-5\n",
"age_rate[\"30-34\"] = 532.4e-5\n",
"age_rate[\"35-39\"] = 268.0e-5\n",
"age_rate[\"40-44\"] = 131.5e-5\n",
"age_rate[\"45-54\"] = 56.6e-5\n",
"age_rate[\"55-64\"] = 16.6e-5\n",
"age_rate[\"65+\"] = 3.2e-5\n",
"\n",
"US_age_number = age_number[\"0-14\"] + age_number[\"15-19\"] + age_number[\"20-24\"] + age_number[\"25-29\"] + age_number[\"30-34\"] + age_number[\"35-39\"] + age_number[\"40-44\"] + age_number[\"45-54\"] + age_number[\"55-64\"] + age_number[\"65+\"]\n",
"rate_average = (age_rate[\"0-14\"]*age_number[\"0-14\"]+age_rate[\"15-19\"]*age_number[\"15-19\"]+age_rate[\"20-24\"]*age_number[\"20-24\"]+age_rate[\"25-29\"]*age_number[\"25-29\"]+age_rate[\"30-34\"]*age_number[\"30-34\"]+age_rate[\"35-39\"]*age_number[\"35-39\"]+age_rate[\"40-44\"]*age_number[\"40-44\"]+age_rate[\"45-54\"]*age_number[\"45-54\"]+age_rate[\"55-64\"]*age_number[\"55-64\"]+age_rate[\"65+\"]*age_number[\"65+\"])/US_age_number \n",
"age_factor[\"0-14\"] = age_rate[\"0-14\"]/rate_average\n",
"age_factor[\"15-19\"] = age_rate[\"15-19\"]/rate_average\n",
"age_factor[\"20-24\"] = age_rate[\"20-24\"]/rate_average\n",
"age_factor[\"25-29\"] = age_rate[\"25-29\"]/rate_average\n",
"age_factor[\"30-34\"] = age_rate[\"30-34\"]/rate_average\n",
"age_factor[\"35-39\"] = age_rate[\"35-39\"]/rate_average\n",
"age_factor[\"40-44\"] = age_rate[\"40-44\"]/rate_average\n",
"age_factor[\"45-54\"] = age_rate[\"45-54\"]/rate_average\n",
"age_factor[\"55-64\"] = age_rate[\"55-64\"]/rate_average\n",
"age_factor[\"65+\"] = age_rate[\"65+\"]/rate_average\n",
"\n",
"race_factor[\"Native\"], race_factor[\"Asian\"], race_factor[\"Black\"], race_factor[\"Hispanic\"], race_factor[\"Multiple\"], race_factor[\"Pacific\"], race_factor[\"White\"]\n",
"age_factor[\"0-14\"], age_factor[\"15-19\"], age_factor[\"20-24\"], age_factor[\"25-29\"], age_factor[\"30-34\"], age_factor[\"35-39\"], age_factor[\"40-44\"], age_factor[\"45-54\"], age_factor[\"55-64\"], age_factor[\"65+\"]"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your individual chance of having Chlamydia is 4.74 percent\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
}
],
"source": [
"def calculate_rate(Zipcode, Race, Gender, Age):\n",
" fips = zip2fips[int(Zipcode)]\n",
" target = df_merged[df_merged['FIPS']==fips]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])\n",
" return chlamydia_rate*gender_factor[Gender]*race_factor[Race]*age_factor[Age]\n",
"\n",
"Race = \"White\"\n",
"Gender = \"Male\"\n",
"Age = \"35-39\"\n",
"Zipcode = \"02139\"\n",
"print(\"Your individual chance of having Chlamydia is %.2f percent\"%(calculate_rate(Zipcode, Race, Gender, Age)*100))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## ZIP code census data base CSV file"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df_zipcode = pd.read_csv(\"../data/census_zipcode.csv\")\n",
"df_zipcode_unnormalized = pd.read_csv(\"../data/census_zipcode_unnormalized.csv\")"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>geoid2</th>\n",
" <th>Population</th>\n",
" <th>hd01s001</th>\n",
" <th>hd02s002</th>\n",
" <th>hd02s005</th>\n",
" <th>hd02s006</th>\n",
" <th>hd02s007</th>\n",
" <th>hd02s008</th>\n",
" <th>hd02s009</th>\n",
" <th>hd02s010</th>\n",
" <th>...</th>\n",
" <th>hd01s168</th>\n",
" <th>hd02s181</th>\n",
" <th>hd02s184</th>\n",
" <th>hd01vd01</th>\n",
" <th>d002</th>\n",
" <th>d014</th>\n",
" <th>d019</th>\n",
" <th>d024</th>\n",
" <th>d029</th>\n",
" <th>landsqmi</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>602</td>\n",
" <td>-0.187985</td>\n",
" <td>0.202049</td>\n",
" <td>-0.140291</td>\n",
" <td>0.868417</td>\n",
" <td>0.458393</td>\n",
" <td>0.369554</td>\n",
" <td>1.049363</td>\n",
" <td>0.316382</td>\n",
" <td>0.966525</td>\n",
" <td>...</td>\n",
" <td>1.155430</td>\n",
" <td>0.683548</td>\n",
" <td>-0.683573</td>\n",
" <td>-2.522258</td>\n",
" <td>0.550821</td>\n",
" <td>-0.475777</td>\n",
" <td>-1.064918</td>\n",
" <td>-0.417037</td>\n",
" <td>-1.132623</td>\n",
" <td>0.653718</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>603</td>\n",
" <td>-0.147833</td>\n",
" <td>0.401021</td>\n",
" <td>0.001670</td>\n",
" <td>0.241583</td>\n",
" <td>0.222605</td>\n",
" <td>0.452316</td>\n",
" <td>0.835698</td>\n",
" <td>0.668510</td>\n",
" <td>-0.023418</td>\n",
" <td>...</td>\n",
" <td>0.376440</td>\n",
" <td>-1.061493</td>\n",
" <td>1.061497</td>\n",
" <td>-2.524746</td>\n",
" <td>-1.301043</td>\n",
" <td>-0.781474</td>\n",
" <td>-1.519258</td>\n",
" <td>-0.905455</td>\n",
" <td>0.099090</td>\n",
" <td>0.876386</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>606</td>\n",
" <td>-0.294408</td>\n",
" <td>-1.124613</td>\n",
" <td>0.356574</td>\n",
" <td>0.689322</td>\n",
" <td>0.694182</td>\n",
" <td>0.866131</td>\n",
" <td>0.408369</td>\n",
" <td>0.081630</td>\n",
" <td>0.100325</td>\n",
" <td>...</td>\n",
" <td>1.377999</td>\n",
" <td>-0.036628</td>\n",
" <td>0.036615</td>\n",
" <td>-2.705957</td>\n",
" <td>-0.339241</td>\n",
" <td>-0.015301</td>\n",
" <td>0.107207</td>\n",
" <td>-1.278090</td>\n",
" <td>-0.523061</td>\n",
" <td>-0.057227</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>610</td>\n",
" <td>-0.226109</td>\n",
" <td>-0.056754</td>\n",
" <td>0.072651</td>\n",
" <td>0.510226</td>\n",
" <td>0.144009</td>\n",
" <td>0.286791</td>\n",
" <td>1.049363</td>\n",
" <td>0.903262</td>\n",
" <td>0.966525</td>\n",
" <td>...</td>\n",
" <td>0.821577</td>\n",
" <td>0.683548</td>\n",
" <td>-0.683573</td>\n",
" <td>-2.446622</td>\n",
" <td>-0.395512</td>\n",
" <td>-0.547272</td>\n",
" <td>-0.622365</td>\n",
" <td>-0.760020</td>\n",
" <td>0.785830</td>\n",
" <td>0.330580</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>612</td>\n",
" <td>-0.110268</td>\n",
" <td>0.547769</td>\n",
" <td>-0.317743</td>\n",
" <td>0.420679</td>\n",
" <td>0.183307</td>\n",
" <td>0.121265</td>\n",
" <td>0.622034</td>\n",
" <td>0.433758</td>\n",
" <td>0.224068</td>\n",
" <td>...</td>\n",
" <td>0.320798</td>\n",
" <td>0.032620</td>\n",
" <td>-0.032634</td>\n",
" <td>-2.406234</td>\n",
" <td>-1.282855</td>\n",
" <td>-0.831928</td>\n",
" <td>-1.189636</td>\n",
" <td>-1.009735</td>\n",
" <td>0.851580</td>\n",
" <td>0.447418</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>5 rows × 46 columns</p>\n",
"</div>"
],
"text/plain": [
" geoid2 Population hd01s001 hd02s002 hd02s005 hd02s006 hd02s007 \\\n",
"0 602 -0.187985 0.202049 -0.140291 0.868417 0.458393 0.369554 \n",
"1 603 -0.147833 0.401021 0.001670 0.241583 0.222605 0.452316 \n",
"2 606 -0.294408 -1.124613 0.356574 0.689322 0.694182 0.866131 \n",
"3 610 -0.226109 -0.056754 0.072651 0.510226 0.144009 0.286791 \n",
"4 612 -0.110268 0.547769 -0.317743 0.420679 0.183307 0.121265 \n",
"\n",
" hd02s008 hd02s009 hd02s010 ... hd01s168 hd02s181 hd02s184 \\\n",
"0 1.049363 0.316382 0.966525 ... 1.155430 0.683548 -0.683573 \n",
"1 0.835698 0.668510 -0.023418 ... 0.376440 -1.061493 1.061497 \n",
"2 0.408369 0.081630 0.100325 ... 1.377999 -0.036628 0.036615 \n",
"3 1.049363 0.903262 0.966525 ... 0.821577 0.683548 -0.683573 \n",
"4 0.622034 0.433758 0.224068 ... 0.320798 0.032620 -0.032634 \n",
"\n",
" hd01vd01 d002 d014 d019 d024 d029 landsqmi \n",
"0 -2.522258 0.550821 -0.475777 -1.064918 -0.417037 -1.132623 0.653718 \n",
"1 -2.524746 -1.301043 -0.781474 -1.519258 -0.905455 0.099090 0.876386 \n",
"2 -2.705957 -0.339241 -0.015301 0.107207 -1.278090 -0.523061 -0.057227 \n",
"3 -2.446622 -0.395512 -0.547272 -0.622365 -0.760020 0.785830 0.330580 \n",
"4 -2.406234 -1.282855 -0.831928 -1.189636 -1.009735 0.851580 0.447418 \n",
"\n",
"[5 rows x 46 columns]"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_zipcode.head()"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>geoid2</th>\n",
" <th>Population</th>\n",
" <th>hd01s001</th>\n",
" <th>hd02s002</th>\n",
" <th>hd02s005</th>\n",
" <th>hd02s006</th>\n",
" <th>hd02s007</th>\n",
" <th>hd02s008</th>\n",
" <th>hd02s009</th>\n",
" <th>hd02s010</th>\n",
" <th>...</th>\n",
" <th>hd01s168</th>\n",
" <th>hd02s181</th>\n",
" <th>hd02s184</th>\n",
" <th>hd01vd01</th>\n",
" <th>d002</th>\n",
" <th>d014</th>\n",
" <th>d019</th>\n",
" <th>d024</th>\n",
" <th>d029</th>\n",
" <th>landsqmi</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>487</th>\n",
" <td>2139</td>\n",
" <td>36349</td>\n",
" <td>4.560492</td>\n",
" <td>9.6</td>\n",
" <td>6.7</td>\n",
" <td>16.8</td>\n",
" <td>19.1</td>\n",
" <td>12.1</td>\n",
" <td>7</td>\n",
" <td>4.9</td>\n",
" <td>...</td>\n",
" <td>2.81</td>\n",
" <td>32.2</td>\n",
" <td>67.8</td>\n",
" <td>73819</td>\n",
" <td>0.258902</td>\n",
" <td>0.007714</td>\n",
" <td>0.039328</td>\n",
" <td>0.009229</td>\n",
" <td>0.038983</td>\n",
" <td>14198.828125</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1 rows × 46 columns</p>\n",
"</div>"
],
"text/plain": [
" geoid2 Population hd01s001 hd02s002 hd02s005 hd02s006 hd02s007 \\\n",
"487 2139 36349 4.560492 9.6 6.7 16.8 19.1 \n",
"\n",
" hd02s008 hd02s009 hd02s010 ... hd01s168 hd02s181 hd02s184 \\\n",
"487 12.1 7 4.9 ... 2.81 32.2 67.8 \n",
"\n",
" hd01vd01 d002 d014 d019 d024 d029 landsqmi \n",
"487 73819 0.258902 0.007714 0.039328 0.009229 0.038983 14198.828125 \n",
"\n",
"[1 rows x 46 columns]"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_zipcode_unnormalized[df_zipcode_unnormalized[\"geoid2\"]==int(Zipcode)]"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your individual chance of having Chlamydia is 0.28 percent\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
},
{
"data": {
"text/plain": [
"(487 36349\n",
" Name: Population, dtype: int64, 487 18283.547\n",
" dtype: float64, 487 22645.427\n",
" dtype: float64, 487 2544.43\n",
" dtype: float64)"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def calculate_rate(Zipcode):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(Zipcode)]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" return chlamydia_rate\n",
"\n",
"Race = \"White\"\n",
"Gender = \"Male\"\n",
"Age = \"35-39\"\n",
"Zipcode = \"02139\"\n",
"zipcoderate = calculate_rate(Zipcode)\n",
"\n",
"target_unnormalized = df_zipcode_unnormalized[df_zipcode_unnormalized[\"geoid2\"]==int(Zipcode)]\n",
"\n",
"TOTALNR = target_unnormalized[\"Population\"]\n",
"\n",
"if Gender == \"Male\":\n",
" gender_table = \"hd02s026\"\n",
"else:\n",
" gender_table = \"hd02s051\"\n",
"\n",
"GENDERNR = TOTALNR*target_unnormalized[gender_table]/100.0\n",
"\n",
"if Race == \"White\":\n",
" race_table = \"hd02s078\"\n",
"elif Race == \"Black\":\n",
" race_table = \"hd02s079\"\n",
"elif Race == \"Native\":\n",
" race_table = \"hd02s080\"\n",
"elif Race == \"Asian\":\n",
" race_table = \"hd02s081\"\n",
"elif Race == \"Pacific\":\n",
" race_table = \"hd02s089\"\n",
"elif Race == \"Multiple\":\n",
" race_table = \"hd02s095\"\n",
"elif Race == \"Hispanic\":\n",
" race_table = \"hd02s107\"\n",
"\n",
"RACENR = TOTALNR*target_unnormalized[race_table]/100.0\n",
"\n",
"if Age == \"0-14\":\n",
" age_table = \"hd02s002\"\n",
"elif Age == \"15-19\":\n",
" age_table = \"hd02s005\"\n",
"elif Age == \"20-24\":\n",
" age_table = \"hd02s006\"\n",
"elif Age == \"25-29\":\n",
" age_table = \"hd02s007\"\n",
"elif Age == \"30-34\":\n",
" age_table = \"hd02s008\"\n",
"elif Age == \"35-39\":\n",
" age_table = \"hd02s009\"\n",
"elif Age == \"40-44\":\n",
" age_table = \"hd02s010\"\n",
"elif Age == \"45-54\":\n",
" age_table = \"hd02s011\"\n",
"elif Age == \"55-64\":\n",
" age_table = \"hd02s013\"\n",
"elif Age == \"65+\":\n",
" age_table = \"hd02s015\"\n",
"\n",
"AGENR = TOTALNR*target_unnormalized[age_table]/100.0\n",
"\n",
"the_result = 100*(zipcoderate/TOTALNR + gender_rate[Gender]/GENDERNR + race_rate[Race]/RACENR + age_rate[Age]/AGENR)/(1.0/TOTALNR+1.0/GENDERNR+1.0/RACENR+1.0/AGENR)\n",
"\n",
"print(\"Your individual chance of having Chlamydia is %.2f percent\"%(the_result))\n",
"TOTALNR, GENDERNR, RACENR, AGENR"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Model validation with Boston Public Health Commission data"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"df_boston = np.genfromtxt(\"../data/zipcodes_boston.txt\", dtype=[('Neighborhood','O'),('zip1','i8'),('zip2','i8'),('zip3','i8'),('zip4','i8'),('zip5','i8'),('zip6','i8')], delimiter=\",\")"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(array([(b'HydePark', 2136, 0, 0, 0, 0, 0),\n",
" (b'WestRoxbury', 2132, 0, 0, 0, 0, 0),\n",
" (b'Roslindale', 2131, 0, 0, 0, 0, 0),\n",
" (b'Mattapan', 2126, 0, 0, 0, 0, 0),\n",
" (b'JamaicaPlain', 2130, 0, 0, 0, 0, 0),\n",
" (b'SouthDorchester', 2124, 2122, 0, 0, 0, 0),\n",
" (b'NorthDorchester', 2121, 2125, 0, 0, 0, 0),\n",
" (b'Roxbury', 2119, 2120, 0, 0, 0, 0),\n",
" (b'Fenway', 2215, 2115, 0, 0, 0, 0),\n",
" (b'SouthEnd', 2118, 2111, 0, 0, 0, 0),\n",
" (b'SouthBoston', 2127, 2210, 0, 0, 0, 0),\n",
" (b'BackBay', 2199, 2116, 2110, 2113, 2114, 2109),\n",
" (b'Charlestown', 2129, 0, 0, 0, 0, 0),\n",
" (b'Allston', 2134, 2135, 2163, 0, 0, 0),\n",
" (b'EastBoston', 2128, 0, 0, 0, 0, 0)], \n",
" dtype=[('Neighborhood', 'O'), ('zip1', '<i8'), ('zip2', '<i8'), ('zip3', '<i8'), ('zip4', '<i8'), ('zip5', '<i8'), ('zip6', '<i8')]),\n",
" 15)"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_boston, len(df_boston)"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"b'HydePark' 2136 715.0\n",
"b'WestRoxbury' 2132 343.0\n",
"b'Roslindale' 2131 639.0\n",
"b'Mattapan' 2126 749.0\n",
"b'JamaicaPlain' 2130 551.0\n",
"b'SouthDorchester' 2124 729.0\n",
"b'SouthDorchester' 2122 705.0\n",
"b'NorthDorchester' 2121 698.0\n",
"b'NorthDorchester' 2125 665.0\n",
"b'Roxbury' 2119 696.0\n",
"b'Roxbury' 2120 586.0\n",
"b'Fenway' 2215 470.0\n",
"b'Fenway' 2115 487.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"b'SouthEnd' 2118 429.0\n",
"b'SouthEnd' 2111 515.0\n",
"b'SouthBoston' 2127 452.0\n",
"b'SouthBoston' 2210 411.0\n",
"b'BackBay' 2199 401.0\n",
"b'BackBay' 2116 480.0\n",
"b'BackBay' 2110 324.0\n",
"b'BackBay' 2113 405.0\n",
"b'BackBay' 2114 458.0\n",
"b'BackBay' 2109 420.0\n",
"b'Charlestown' 2129 458.0\n",
"b'Allston' 2134 497.0\n",
"b'Allston' 2135 501.0\n",
"b'Allston' 2163 497.0\n",
"b'EastBoston' 2128 605.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n",
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
}
],
"source": [
"predictions = np.zeros(len(df_boston))\n",
"i = 0\n",
"for hood in df_boston:\n",
" average = 0.0\n",
" count = 0\n",
" if (hood[\"zip1\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip1\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip1\"],round(chlamydia_rate[0]*1e5))\n",
" if (hood[\"zip2\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip2\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip2\"],round(chlamydia_rate[0]*1e5))\n",
" if (hood[\"zip3\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip3\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip3\"],round(chlamydia_rate[0]*1e5))\n",
" if (hood[\"zip4\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip4\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip4\"],round(chlamydia_rate[0]*1e5))\n",
" if (hood[\"zip5\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip5\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip5\"],round(chlamydia_rate[0]*1e5))\n",
" if (hood[\"zip6\"]):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(hood[\"zip6\"])]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" average += chlamydia_rate[0]*1e5\n",
" count += 1\n",
" print(hood[\"Neighborhood\"], hood[\"zip6\"],round(chlamydia_rate[0]*1e5))\n",
" average /= count\n",
" predictions[i] = average\n",
" i+=1"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(15,)"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(predictions), "
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"df_boston_rates = np.genfromtxt(\"../data/rate_boston.txt\", dtype=[('Neighborhood','S20'),('mean','i8'),('error','i8')], delimiter=\",\")"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"labels = df_boston[\"Neighborhood\"]"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.50231504327178955"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"R2 = 1.0-np.sum((predictions-df_boston_rates[\"mean\"])**2)/np.sum((df_boston_rates[\"mean\"]-np.mean(df_boston_rates[\"mean\"]))**2)\n",
"R2"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/matplotlib/collections.py:590: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison\n",
" if self._edgecolors == str('face'):\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmcAAAG2CAYAAAA6OCEGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVPXixvFn2ERZSk0poNDIretyI8ElU69bZGqkmaJp\nXSuvmktSXUlzaXEpMzVt9ZYmmkqFuy2KKWmmeTHTTL2ZWoApihqDIcvM7w9+TJLioMGcA3zer5cv\nZ84MnofhyDzzPed8j8Vut9sFAAAAU3AzOgAAAAD+QDkDAAAwEcoZAACAiVDOAAAATIRyBgAAYCKU\nMwAAABMp03K2e/duDRgwoMiy1atXq2/fvo778fHx6tWrl/r06aNNmzZJkrKzszVixAj1799fgwcP\nVkZGRlnGBAAAMI0yK2fz5s3Ts88+q9zcXMeyffv26eOPP3bcT09PV1xcnJYuXap3331XM2bMUE5O\njpYsWaIGDRpo8eLFioqK0ptvvllWMQEAAEylzMpZSEiI5s6dq8I5bk+fPq2ZM2dq7NixjmXfffed\nwsLC5OnpKV9fX4WEhOjAgQNKTk5W27ZtJUl33nmntm3bVlYxAQAATMWjrP7hLl26KCUlRZJks9k0\nbtw4xcbGqkqVKo7nWK1W+fn5Oe77+PjIarXKarXKx8fHsSwzM/Oy68rOztbevXtVq1Ytubu7l8F3\nAwAAUDry8/OVnp6uxo0by9vb+6LHy6ycXWjv3r36+eefNWnSJOXk5OjHH3/U1KlT1aJFC2VlZTme\nl5WVJT8/P/n6+jqWZ2Vlyd/f3+m/379//zL9HgAAAErT4sWL1bx584uWu6ScNW3aVGvWrJEkpaam\nKiYmRs8884zS09M1c+ZM5eTk6Pz58zp06JDq16+vsLAwJSUlqWnTpkpKSrpk8AvVqlVLUsE3ef31\n15f59wMAAHC1fv31V/Xv39/RX/6szMuZxWIpct9utzuW1apVSwMHDlS/fv1ks9kUExMjLy8vRUdH\na8yYMerXr5+8vLw0Y8aMy66jcFfm9ddfr+Dg4LL5RgAAAEpRcYdiWeyFR+eXYykpKerYsaMSExMp\nZwAAwNSc9RYmoQUAADARyhkAAICJUM4AAABMhHIGAABgIpQzAAAAE6GcAQAAmAjlDAAAwEQoZwAA\nACZCOQMAADARyhkAAICJUM4AAABMhHIGAABgIpQzAAAAE6GcAQAAmAjlDAAAwEQoZwAAACZCOQMA\nADARyhkAAICJUM4AAABMhHIGAABgIpQzAAAAE6GcAQAAmAjlDAAAFPHzzz9ryJAhioiIULt27fTS\nSy8pJyfH6FiVhofRAQAAgHnk5ORoyJAhqlevnpYuXapTp05p7NixkqQxY8YYnK5yYOQMAAA4fPfd\nd/rll180bdo03XzzzQoPD9eoUaO0evVqo6NVGpQzAADgcPPNN+udd95R1apViyz/7bffDEpU+VDO\nAACAQ40aNdSqVSvHfZvNpkWLFql169YGpqpcOOYMAAAUa+rUqTpw4IA++ugjo6NUGpQzAAAqqISE\nBMfB/H/m5eWla6+9Vk2bNtVjjz2mZs2aFXncbrdr8uTJWrp0qV577TWFhoa6IrIkKS8vT4sWLVJ8\nfLxSU1NVq1Yt9ezZU4MHD5aHR8mqy6xZs/TWW29d8rGuXbvq1VdfLdX1lSbKGQAAFVxERIQiIiKK\nLMvMzNTu3bu1YcMGbdq0Se+//75uv/12SQW7MseNG6fVq1dr1qxZ6tChg0vzPv/884qPj1fz5s3V\nqVMn/fe//9Vrr72m/fv367XXXivRv7F//355eXlp8ODBFz1Wv379Ul9faaKcAQBQwUVERGj48OGX\nfOy1117TG2+8oenTp2vp0qWSpGnTpmnt2rV6/fXX1a5dO1dGVXJysuLj4xUZGalZs2Y5lsfGxmrF\nihXatGmT2rdv7/TfOXjwoG655ZZiv+/SXl9p4oQAAAAqsaFDh8rDw0O7d+9WTk6Ovv32Wy1cuFAj\nRozQrbfeqvT0dMcfV1i8eLEkXVSqYmJiZLFY9OGHHzr9N6xWq9LS0tSgQQOXrK+0MXKGyqVOnYK/\njxwxMgUuh58R4FKenp7y9fXV2bNnlZ2drc8++0ySNGPGDM2YMcPxPIvFou+//15ubiUf1+nQoYPS\n0tIu+5z77rtPU6dOddzfuXOnatSooVtuuaXI82rXrq2QkBDt3LnT6Xr3798vSSUqZ6WxvtJGOQMA\noBLbu3evzpw5o8DAQPn7+2vMmDGldiWAhx56SJmZmZd9TqNGjRy3c3JydPz4cf3973+/5HODgoJ0\n5MgRnT59WtWrVy/23zxw4IAkKSMjQ//85z+1d+9eWSwWtWzZUqNHj1bdunVLdX2ljXIGAEAlY7fb\nlZmZqV27dunFF1+UxWJxemzW1XjooYeu6PlnzpyRJPn5+V3y8cLlVqu1ROXsvffeU4cOHdSnTx/t\n379fn3/+ubZt26a4uDg1bNiw1NZX2ihnAABUcHPnztXcuXMv+VjhaFnPnj1dnOpieXl5kgqm+biU\nwuXnz5+/7L/j4eGhoKAgTZs2TeHh4Y7lq1ev1tNPP62xY8cqISGh1NZX2ihnAABUcBdOpZGVlaVP\nPvlEv/76q+6991698MILxZaTv2rBggUl2q3ZqVMnSZK3t7ckKTc395LPzcnJkaSLLi31ZxMmTLjk\n8u7duys+Pl7ffPONjhw5In9//1JZX2mjnAEAUMH9eSqNkSNHavDgwVq5cqV8fX01fvz4MlnvwoUL\nL3tCgMViUVRUlKOc+fr6ymKxFFvoMjMzZbFYit0NWRKNGjXSN998o5SUFEVERJT5+q4G5QwAgEqm\natWqmjVrlu69914tXrxY9evXV58+fUp9PRs3bryi53t5eSkwMFApKSmXfDwlJUU1atRwjHhdSn5+\nvr7//ntJUtOmTS96PDs7W5JUpUqVUllfWWCeMwAAKqGaNWtq0qRJkgomnU1NTTU20P9r3ry50tPT\ndeRP0+kcP35cR48evegyU3+Wn5+vfv366bHHHpPNZivymN1u165du+Th4eE4S/Svrq8slGk52717\ntwYMGCBJ+uGHH9S/f38NGDBAjzzyiE6dOiVJio+PV69evdSnTx9t2rRJUkGrHTFihPr376/Bgwcr\nIyOjLGMCAFApderUSV26dNHvv//uKGpGi4qKkiS9+uqrstvtkgpKVeG1MJ2N8Hl5ealDhw46e/as\n3nnnnSKPvffee/rf//6n7t27y9fXt1TWVxbKbLfmvHnztGrVKvn4+EiSpkyZovHjx6thw4ZatmyZ\n5s2bp0cffVRxcXFKSEjQ+fPnFR0drdatW2vJkiVq0KCBhg8frnXr1unNN9/UuHHjyioqAACV1rhx\n4/TVV1/pyy+/1Nq1a3XPPfcYmqdVq1bq2rWr1q1bpz59+igiIkK7du3Sf//7X0VGRha5nFRmZqYW\nLFggf3//ItN2jBkzRsnJyZo1a5Z27NihBg0aaO/evfrmm29Ur149xcbGXtX6XKXMRs5CQkI0d+5c\nRwt99dVX1bBhQ0kFp8pWqVJF3333ncLCwhyzE4eEhOjAgQNKTk5W27ZtJUl33nmntm3bVlYxAQCo\nsCwWiywWy2WfExAQoNGjR0uSpk6d6vTsSld4+eWXNXLkSJ0+fVoLFy7UqVOnNGrUKE2fPr3I886e\nPavXX39dCxcuLLI8KChIH3/8sXr16qWDBw8qLi5OaWlpGjRokJYsWaJrrrnmqtbnKmU2ctalS5ci\nB9jVqlVLUsEFRhcvXqzFixfryy+/LHIGhI+Pj6xWq6xWq2PEzcfHxxQbCgAA5c19992n++67z+nz\n+vfvr/79+7sgUcl4eHho2LBhGjZs2GWfFxwc7LhU058FBARo8uTJpbo+V3Hp2Zrr1q3TW2+9pXfe\neUfVq1eXr6+vsrKyHI9nZWXJz8+vyPKsrCyXnyUBAABgFJedrbly5UotXrxYcXFxCg4OllRwiuvO\nnTuVk5OjzMxMHTp0SPXr11dYWJiSkpIkSUlJSWrevLmrYgIAABiqzEfOLBaLbDabpkyZosDAQMck\neC1atNDw4cM1cOBA9evXTzabTTExMfLy8lJ0dLTGjBmjfv36ycvLSzNmzCjrmAAAAKZQpuUsODhY\nS5culSRt3779ks/p3bu3evfuXWSZt7e3Zs+eXZbRAAAATIlJaAEAAEyEcgYAAGAilDMAAAAToZwB\nAACYCOUMAADARChnAAAAJkI5AwAAMBHKGQAAgIlQzgAAAEyEcgYAAGAilDMAAAAToZyh8ujcWTp6\ntOBP585Gp8Gl8DMCAMoZKonOnaUNG/64v2GDFBwsJScblwlF8TMCAEmUM1QWiYkXL0tNlXr0cH0W\nXBo/IwCQRDkDAAAwFcoZKoeOHS9eFhQkrVrl+iy4NH5GACBJ8jA6AOAS69cXHL+UmlpwPyhISkkx\nNhOK4mcEAJIYOUNlsmqV5O5e8IfRGHPiZwQAjJyhEgkLKxiZKbwN8+FnBACMnAEAAJgJ5QwAAMBE\nKGcAAAAmQjkDAAAwEcoZAACAiVDOAAAATIRyBgAAYCKUMwAAABOhnAEAAJgI5QwAAMBEKGcAAAAm\nQjkDAAAwEcoZAACAiVDOAAAATIRyBgAAYCKUMwAAABOhnAEAAJgI5QwAAMBEKGcAAAAmQjkDAAAw\nEcoZAACAiZRpOdu9e7cGDBggSTp69Kiio6PVv39/TZo0SXa7XZIUHx+vXr16qU+fPtq0aZMkKTs7\nWyNGjFD//v01ePBgZWRklGVMAAAA0/Ao7oG0tLQS/QOBgYGXXD5v3jytWrVKPj4+kqSpU6cqJiZG\n4eHhmjhxohITE9WsWTPFxcUpISFB58+fV3R0tFq3bq0lS5aoQYMGGj58uNatW6c333xT48aNu4pv\nDwAAoHwptpx16dJFtWvXvuwXp6ena8+ePZd8LCQkRHPnztW///1vSdK+ffsUHh4uSWrbtq22bt0q\nNzc3hYWFydPTU56engoJCdGBAweUnJysxx57TJJ055136o033riqbw4AAKC8KbachYaGauXKlZf9\n4nvvvbfYx7p06aKUlBTH/cLdmJLk4+OjzMxMWa1W+fn5FVlutVpltVodI26FzwUAAKgMii1n8fHx\nkqRff/1Vv/76q9zc3FS7dm1df/31Fz2nJNzc/ji8zWq1yt/fX76+vsrKynIsz8rKkp+fX5HlWVlZ\n8vf3L/l3BFzOkSNGJzCnOnUK/jbD62OGDIXM9LoAqDSKLWepqamKjY3V6dOnVatWLUkFuzG9vb31\n8ssvq1GjRqpSpUqJV9SoUSPt2LFDERERSkpKUqtWrdS0aVPNnDlTOTk5On/+vA4dOqT69esrLCxM\nSUlJatq0qZKSktS8efO//p0CAACUA8WWs6eeekpjx469qBjt3LlT48aNU0JCQolWYLFYJEmxsbEa\nP368cnNzFRoaqsjISFksFg0cOFD9+vWTzWZTTEyMvLy8FB0drTFjxqhfv37y8vLSjBkz/sK3CAAA\nUH4UW86ys7MvOWLVvHlz5eTklOgfDw4O1tKlSyVJderUUVxc3EXP6d27t3r37l1kmbe3t2bPnl2i\ndQAAAFQkxZazv/3tb5o0aZK6d+/uOGvzxIkTWrlypRo3buyygAAAAJVJseVs8uTJiouL0+zZs3Xi\nxAnZ7XYFBASoXbt2jollAQAAULqKLWdeXl565JFH9NBDDykjI0Nubm669tpr5eFR7JcAAADgLyq2\naZ08eVKTJ09WUlKSfH19JRVMgREeHq4JEyYUe2UAAAAAXL1ir635xBNPqH379tq+fbs2b96szZs3\na/v27erataueeuopV2YEAACoNIotZxkZGbr33nuL7Mb08PBQjx499Ntvv7kkHAAAQGVTbDkLDg7W\nvHnzdPz4cdlsNtlsNh0/flxvv/22brzxRldmBAAAqDSKPebslVde0axZs9SvX7+LztacNm2aKzMC\nAABUGsWWM39/f02YMMGVWQAAACq9YsvZuXPn9MYbb+jTTz8tcuHzdu3a6YknnpCfn58rcwIAAFQK\nxR5z9tRTT6latWpatGiRvv32WyUnJysuLk7XXXedYmJiXJkRAACg0ii2nB0+fFjDhg3T9ddfLw8P\nD3l4eOiGG27Q0KFDlZaW5sqMAAAAlUax5axGjRpat26dbDabY5ndbteaNWtUo0YNl4QDAACobIo9\n5mz69Ol67rnnNH78+CJXCGjevLleeukllwUEAACoTIotZ4GBgXr77beVm5ur06dPy263q0aNGvL0\n9HRlPgAAgErF6VXMPT09Vbt27SLLNm7cKHd3d7Vq1UpeXl5lFg4AAKCyKfaYs8vZuHGjcnNzlZiY\nWNp5AAAAKjWnI2eX8uKLL5Z2DgAAAMhJOUtKStKnn36q48ePy2KxOCahveuuu1yVDwAAoFIptpzN\nmjVLe/bsUY8ePVSrVi1J0okTJ/TRRx9p165dio2NdVlIAACAyqLYcvbJJ59o3bp1cnd3L7K8e/fu\nuueeeyhnAAAAZaDYEwKqVKmiX3/99aLlqampqlKlSpmGAgAAqKyKHTmLjY3Vgw8+qJCQEMduzZMn\nT+rw4cOaOnWqywICKGOdO0tHj/5xe/16Y/OYBa8LAIMUW85at26tTz75RHv27NGJEydkt9sVEBCg\npk2bMnIGVBSdO0sbNvxxf8MGKThYWrVKCgszLpfReF0AGOiyZ2umpqZqx44djrM1AwIC5O3trSZN\nmrgqH4CydKm5ClNTpR49pJQU1+cxC14XAAYq9pizxYsXKyYmRhaLRU2aNFHjxo1lt9s1fvx4vfvu\nu67MCAAAUGkUO3L2/vvva+XKlapatWqR5YMGDVJUVJQeeeSRMg8HoIx17Fh0950kBQUV7L6rzHhd\nABio2HLm6emp3Nzci8rZ77//zvU0gYpi/fqCY6lSUwvuBwWx207idQFgqGLL2ZAhQ3TfffepVatW\nuu666yQVnK25bds2jR492mUBAZSxVaukiIg/bqMArwsAgxRbzrp3766IiAh99dVXSk9Pl91uV/Pm\nzTVixAgFBAS4MiOAshQWVjBKVHgbBXhdABjksmdrBgQE6L777nNVFgAAgEqv2LM1AQAA4HrFjpy1\nadNGp06dkt1uv+gxi8WiH374oUyDAQAAVEbFlrOPP/5YAwcO1Ny5c1WvXj1XZgIAAKi0it2tGRAQ\noLFjx2rOnDmuzAMAAFCpXfaEgHbt2qldu3auygIAAFDpcUIAAACAiVDOAAAATIRyBgAAYCJOy9mg\nQYNckQMAAAByckKAJGVnZystLU2BgYF/eWW5ubmKjY1Vamqq3N3d9cILL8jd3V2xsbFyc3NTvXr1\nNHHiRFksFsXHx2vZsmXy8PDQ0KFD1b59+7+8fgAAALNzWs4yMjLUoUMH1axZU1WqVJFUMAltYmLi\nFa9s8+bNys/P19KlS/XVV19p5syZysvLU0xMjMLDwzVx4kQlJiaqWbNmiouLU0JCgs6fP6/o6Gi1\nbt1aXl5eV/4dAgAAlCNOy9l//vMfSQWF7FJXC7gSdevWVX5+vux2uzIzM+Xp6andu3crPDxcktS2\nbVtt3bpVbm5uCgsLk6enpzw9PRUSEqIDBw6oSZMmf2n9AAAAZuf0mLPg4GAlJycrPj5eNWrU0M6d\nOxUcHHxVK6tWrZpSU1MVGRmpCRMmaMCAAUUKn4+PjzIzM2W1WuXn51dkudVqvap1AgAAlCdOy9n0\n6dO1efNmff7558rPz9fHH3+sqVOnXtXKFixYoDvvvFOfffaZVq5cqTFjxigvL8/xuNVqlb+/v3x9\nfZWVleVYnpWVJX9//6taJwAAQHnitJxt2bJF06dPV5UqVeTn56f58+crKSnpqlZ2zTXXyMfHR5Lk\n7++vvLw83XrrrdqxY4ckKSkpSc2bN1fTpk21c+dO5eTkKDMzU4cOHeL6ngAAoFJwesyZu7t7kfs5\nOTkXLSuphx9+WGPHjlX//v2Vm5urJ598Un/72980fvx45ebmKjQ0VJGRkbJYLBo4cKD69esnm82m\nmJgYTgYAAACVgtNyFhkZqdGjR+vs2bNasGCBVq5cqXvuueeqVlatWjXNmjXrouVxcXEXLevdu7d6\n9+59VesBAAAor5yWs8GDByspKUmBgYE6duyYRo4cqX/84x+uyAYAAFDplOjyTefPn1dOTo7sdju7\nFwEAAMqQ03I2bdo0vfvuu6pTp44CAwM1e/ZsvfXWW67IBgAAUOk43a35xRdfaM2aNfL09JQkRUdH\n695779WQIUPKPBwAAEBl43TkrGbNmsrMzHTcz83NVfXq1cs0FFAWsrOztfSj1Vr60WplZ2cbHQcA\ngEtyOnLm7++vHj16qGPHjnJ3d1dSUpJq1qypZ555RpKuekJawJWys7M18tk5SssPlSRt/HqOXntx\nhLy9vQ1OBgBAUU7LWZcuXdSlSxfH/caNGztuWyyWskkFlLIVa9YrLT9UFreCOfpS827WijXr1ff+\n7gYnAwCgqGLL2auvvqqYmBj17Nmz2C+eMWNGmYQq1+rUKfj7yBEjUwBXhu310nhdLo3fcyiPytF2\nW2w5S0hIcDptxvLly/Xkk0+WeiigtEV166yNX89Rat7NkqQgj58U1W2EwakAALhYseWsT58+Tr+4\nb9++pRoGKCve3t567cURWrFmvSQpqhvHmwEAzKnYcjZiBKMKqFi8vb05xgwAYHolukIAAAAAXMPp\n2ZoAKrbs7OwLdvd2ZncvABisRCNnOTk5kqQjR45o06ZNstlsZRqqvMrOzlbWud+Vde53JjlFuVA4\n/9uirblatDVXI5+dw7YLAAZzWs7mzp2rcePGKTU1VQ8++KAWLFigCRMmuCJbuVL4JmfNtsuabedN\nDuXChfO/WdzcHfO/AQCM47Scbdy4UZMnT9batWvVvXt3LViwQPv27XNFtnKl8E1OFkkW8SYHAACu\nitNylp+fLy8vL33xxRdq166d8vPz9fvvv7siG4AyFtWtswLdD8mWnydbft7/z//W2ehYAFCpOS1n\nrVu3Vrdu3ZSTk6OIiAgNGDBA//jHP1yRrVwpfJOTXZJdvMmhXCic/21AGy8NaOPF9UYBwAQsdrvd\n7uxJaWlpCggIkLu7u3744Qc1atTIFdlKLCUlRR07dlRiYqKCg4MNy5Gdna38m0IkSe4/H+VNDkDF\nVI4ugwM4mGi7ddZbnI6cnTlzRm+88YYefvhhZWRkaOHChTp79myZhC3vvL295VOtqnyqVaWYAQCA\nq+K0nI0fP16NGzfWmTNn5Ovrq9q1a+vpp592RTYAAIBKx2k5S0lJUd++feXu7i4vLy+NHj1ax44d\nc0U2AJVMdna2ln60Wks/Ws1UNAAqLadXCPDw8FBmZqbj/pEjR+Tu7l6moQBUPoVzBablh0qSNn49\nhxMUAFRKTkfORowYoQEDBujYsWMaOnSooqOjNWrUKFdkA1CJMCEuABRwOnLWtm1bNW7cWLt375bN\nZtMLL7yg6667zhXZAAAAKh2nI2dHjx7Vli1b1K5dO23atEn/+te/tHPnTldkA1CJMCEuABRwWs6e\neeYZeXh4aOPGjTpy5IhiY2P10ksvuSIbgEqECXEBoIDT3Zrnz59X165dNW7cOHXr1k3h4eHKz893\nRTYAlYy3t7f63t/d6BgAYCinI2ceHh769NNPtWnTJrVv314bNmyQm5vTLwMAAMBVcNqynnvuOW3e\nvFkTJkxQQECA1q5dqxdffNEV2QAAACodp7s1GzZsqH//+9/Kzs5WWlqaYmJilJKS4opsAGCY7Oxs\nx1QeUd06c/wbAJdxWs5mzJihDz74QLm5uapevbqOHz+uJk2a6MMPP3RFPlQAvMmhvGFCXABGcrpb\nc+3atdq0aZO6du2quLg4LViwQNWrV3dFNlQAhW9yi7bmatHWXI18dg6X5YHpMSEuACM5LWe1atWS\nn5+f6tevrx9++EEtW7bUyZMnXZENFQBvcgAAXBmn5czX11crVqzQrbfeqtWrV2vXrl1FrrWJC3Tu\nLB09WvCnM5NnAuUVE+JeBr/nUB6Vs+3WaTmbMmWKMjIy1LJlSwUHB2vixIl64oknXJGtfOncWdqw\n4Y/7GzZIwcFScrJxmUyANzmUR0yIWwx+z6E8KofbrcVut9sv94S8vDxt2rRJnTp1UkZGhhITE9Wr\nVy9TzXWWkpKijh07KjExUcHBwcaEcHOTLvVSBgVJlfzsVk4IACoIfs+hPDLhduustzg9W3P8+PHK\nz89Xp06dJEnbt2/Xnj179Pzzz5d+WlRIzPoOAEDJOR3+2rNnj15++WVJUo0aNfTKK69o165dZR6s\n3OnY8eJlQUHSqlWuzwIAZYHfcyiPyuF263TkzG636/jx4woICJAknTx50lS7NE1j/fqCfdipqQX3\nGeYHUNHwew7l0fr1sgcFyZKWJkmyBwbKYvLt1mk5GzJkiHr27Knbb79ddrtdu3fv1rhx4656hW+/\n/ba++OIL5eTkqF+/fgoPD1dsbKzc3NxUr149TZw4URaLRfHx8Vq2bJk8PDw0dOhQtW/f/qrX6TKr\nVkkREX/cBoCKht9zKGeys7P1Sof79cziuZKkqR3u11PZ2aY+/tlpOevevbsiIiK0a9cueXp66tln\nn3WMol2p7du3a9euXVq6dKnOnTun9957T9OmTVNMTIzCw8M1ceJEJSYmqlmzZoqLi1NCQoLOnz+v\n6OhotW7dWl5eXle1XpcJCyv4VFl4GwAqGn7PoZxZsWa9vr6unU76LZEkbavZVivWrDf1sdBOy5kk\nBQQEKDIy8i+vbOvWrWrQoIGGDRsmq9Wqf//734qPj1d4eLgkqW3bttq6davc3NwUFhYmT09PeXp6\nKiQkRAcOHFCTJk3+cgYAAAAzK1E5Ky0ZGRk6duyY3n77bf3yyy8aMmSILpzJw8fHR5mZmbJarfLz\n8yuy3Gq1ujIqAACoAKK6ddbGr+dI/183CubbHGFsKCdcemR/9erV1aZNG3l4eKhu3bqqUqVKkdJl\ntVrl7+8vX19fZWVlOZZnZWXJ39/flVEBAEAFUDiptK+3Rb7elnIxqbTTkbOTJ09q9erVOnfunOx2\nu/Lz85VfDG6HAAAgAElEQVSamuqYXuNK3H777Vq4cKH++c9/6vjx48rOzlbLli21Y8cORUREKCkp\nSa1atVLTpk01c+ZM5eTk6Pz58zp06JDq1at3Vd8gAACo3Ly9vaVqVQvvGBumBJyWs+HDhyskJETf\nfvutOnXqpC1btqhRo0ZXtbL27dvrm2++0f333y+bzaaJEycqKChI48ePV25urkJDQxUZGSmLxaKB\nAweqX79+stlsiomJMf/JAAAAAKXAaTk7ffq0li5dqmnTpqlz584aMmSIHnrooate4dNPP33Rsri4\nuIuW9e7dW717977q9QAAAJRHTo85u/baayVJdevW1YEDB+Tn56e8vLwyDwYAAFAZOR05a9mypUaO\nHKkxY8Zo0KBB+v77701/IB0AAEB55bScjR49Wj///LOCgoI0Y8YM7dy5U48//rgrsgEAAFQ6xe7W\n3LhxoyRp+fLlSk5O1vLly/W///1P11xzjbZt2+aygAAAAJVJsSNne/fuVYcOHbR9+3ZZLJaLHo+K\niirTYEBFlp2drRVr1ksqmCCRQwUAAIWKLWcjR46UJE2bNs1lYYDKIDs7WyOfnaO0/FBJ0sav55SL\nSREBAK5RbDnr0KGD47bFYilymSWLxaLExMSyTQZUUCvWrFdafqgsbu6SpNS8m01/EV4AgOsUW84W\nLlwoSXr99dd14403qmfPnnJzc9OaNWv0yy+/uCwgAABAZVLsCQHBwcEKDg7WgQMHNGzYMF1//fWq\nXbu2Bg0apG+//daVGYEKJapbZwW6H5ItP0+2/Lz/vwhvZ6NjAQBMwukktHa7vcjZmZs3b5aHh9MZ\nOAAUo/AivAPaeGlAGy+ONwMAFOG0ZU2ePFljxozRiRMnJEmBgYGaPn16mQcDKjJvb2+OMQMAXJLT\ncpaXl6fVq1crIyNDFotF1atXd0UuAACASsnpbs3p06erW7duSkhI4JqaAAAAZczpyFlcXJxSU1O1\nYsUKDRo0SIGBgbrvvvvUsWNHeXp6uiIjAABApeF05EySgoKCFBUVpW7duungwYNauHChunXrps8/\n/7ys8wEAAFQqTkfO4uPjtWrVKp04cUJRUVFasmSJrr/+eh0/flxRUVHq0qWLK3ICAABUCk7L2Tff\nfKMRI0aoRYsWRZYHBARo4sSJZRYMAACgMnJazqZPn679+/frm2++KbI8PDxckZGRZRYMAACUX9nZ\n2VqxZr2kgsm3mc+x5JyWs9GjR2vfvn2qXbt2keVxcXFlFgoAAJRf2dnZGvnsHKXlh0qSNn49hwm3\nr4DTcrZ//36tW7dO7u7urshT/h05YnQCc6pTp+BvXp8/8JrgSphpezFDhkJmeV3MkkMyRZYVa9Yr\nLT9U7743RJI06J9vasWa9cZOvm2Gn00JOT1bs1mzZjpSjr4hAACA8szpyFnLli3VvXt31apVyzF6\nZrFYlJiYWObhAAAFu4jyz/0uSXLPzmbXEEwvqltnbfx6jmQvuB/k8ZOiuo0wNlQ54rSczZo1S++/\n/75uuOEGV+QBAFyg8NidF7IL3uXGP8uxOzA/b29vvfbiCOUvfEWS2GavkNNyVqNGDd1+++1ycyvR\nfLUAgFJUeOyOLAX3U/NuNvTYHc7AQ0l5e3tL1aoW3jE2TDnjtJw1aNBAffr0UevWrYtcrmn48OFl\nGgwAYC6cgQe4htPhsMDAQLVt21YeHh6y2+2y2+2uyAUAUMHoVKD7oYJjd+yFx+50NiRL4Siexc1d\nFjd3xygegNLldORsxIiiB/DZbDalpKSUWSAAwB84dgdXgpNHKganI2dxcXEKCwtTo0aN1LBhQ916\n660aNGiQK7IBAFRQ0HyqVZVPtaqGvtkWjuLZ8vNky88zdBQPFyvc7WzNtsuabdfIZ+coOzvb6Fi4\nCk7L2fz587Vy5Urdfffd2rBhg6ZMmaJmzZq5IhsAwEQKR/EGtPHSgDZejOKZTJGTRyxit3M5VqKz\nNW+88UY1bNhQBw8eVM+ePbVo0SJXZAMAmIy3t7exs7wDlYDTkbNq1arp66+/Vv369fXFF1/oxIkT\n+u2331yRDQAAlJCZTh7BX+O0nD377LPauHGj2rZtqzNnzujuu+/Wgw8+6IpsAACghAp3O/t6W+Tr\nbWG3cznmdLdm/fr1NXbsWEnSnDlzyjwQAAC4Okz8WjEUW846dOhQ7BdxbU0AgNGYNgIVVbHlbOHC\nhcV+kcViKZMwAACUBNccRUVWbDkLDg6WJOXk5Gjbtm06ffq0JMlut8tisSgoKMg1CQEA+BOzXXMU\nKE1OjzkbNWqUTp48qdDQ0CIjZlFRUWUaDAAAoDJyWs4OHz6sTz75hF2ZAADTiOrWWRu/nlMwbYQK\np40YcfkvKiMc+4bS5nQqjZtuuklpaWmuyAIAQImYZdoILpmEslDsyNmAAQMkSadPn1b37t3VsGFD\nubu7Syo4IeByJww4c+rUKfXs2VMLFiyQm5ubYmNj5ebmpnr16mnixImyWCyKj4/XsmXL5OHhoaFD\nh6p9+/ZXvT4AQMVjhmkjOPYNZaHYcjZ8+PCLllksFscJAVcrNzdXEyZMUNWqVWW32zV16lTFxMQo\nPDxcEydOVGJiopo1a6a4uDglJCTo/Pnzio6OVuvWreXl5XXV6wUAACgPit2t2aJFCzVs2FD16tVT\nixYt1KJFC9ntdtWrV08RERFXvcKXX35Z0dHRqlWrliRp3759Cg8PlyS1bdtWX331lfbs2aOwsDB5\nenrK19dXISEhOnDgwFWvEwCAssAlk1AWii1n+/btU9euXbV3717Hsq1bt6pHjx7av3//Va0sISFB\nNWrUUJs2bSQVTMtht9sdj/v4+CgzM1NWq1V+fn5Fllut1qtaJwAAZcUsx76hYil2t+a0adP06quv\nqkWLFo5lhbsfp02bpgULFlzxyhISEmSxWPTVV19p//79io2NdcyfJklWq1X+/v7y9fVVVlaWY3lW\nVpb8/f2veH0AAJQ1Mxz7hoql2JGz3377rUgxK3TnnXcqIyPjqla2aNEixcXFKS4uTg0bNtRLL72k\nNm3aaMeOHZKkpKQkNW/eXE2bNtXOnTuVk5OjzMxMHTp0SPXq1buqdQIAAJQnxY6c5efny2azyc2t\naH+z2WzKy8srlZVbLBbFxsZq/Pjxys3NVWhoqCIjI2WxWDRw4ED169dPNptNMTExnAwAAAAqhWLL\nWfPmzTV37lyNHDmyyPI33nhDjRs3/ssrjouLu+TtQr1791bv3r3/8npgAp07S0eP/nF7/Xpj85gB\nrwmuBNvLpZnldTFLDrJUGMXu1nzyySe1bds2derUSTExMXriiSfUpUsXbdmyRc8884wrM6I869xZ\n2rDhj/sbNkjBwVJysnGZjMZrgivB9nJpZnldzJKDLBWKxX7h6ZJ/YrPZtH37du3bt0/u7u5q3Lix\nmjdv7sp8JZKSkqKOHTsqMTHRccF2mISbm3SpTSwoSEpJcX0eM+A1wZVge7k0s7wuZslBlnLFWW+5\n7LU13dzc1KpVK7Vq1arMAgIAAOAPTq+tCfwlHTtevCwoSFq1yvVZzILXBFeC7eXSzPK6mCUHWSqU\ny46cAX/Z+vUFxxmkphbcZ0ib1wRXhu3l0szyupglB1kqFEbOUPZWrZLc3Qv+8KmpAK8JrgTby6WZ\n5XUxSw6yVBiMnKHshYUVfIIqvA1eE1wZtpdLM8vrYpYcZKkwKGcVVHZ2tlasKZhTJqpbZ671BgBA\nOUE5q4Cys7M18tk5SssPlSRt/HoOF+MFAKCc4JizCmjFmvVKyw+Vxc1dFjd3pebd7BhFAwAA5kY5\nAwAAMBHKWQUU1a2zAt0PyZafJ1t+noI8flJUt85GxwIAACXAMWcVkLe3t157ccQFJwRwvBkAAOUF\n5ayC8vb2Vt/7uxsdAwAAXCF2awIAAJgI5QwAAMBEKGcAAAAmQjkDAAAwEcoZAACAiVDOAAAATIRy\nBgAAYCKUMwAAABOhnAEAAJgI5QwAAMBEKGcAAAAmQjkDAAAwEcoZAACAiVDOAAAATIRyBgAAYCKU\nMwAAABOhnAEAAJgI5QwAAMBEPIwOgDJUp07B30eOGJmigBkymA2vCa4E28ulmeV1MUsOiSwVACNn\nAAAAJkI5AwAAMBHKGQAAgIlQzgAAAEyEcgYAAGAilDMAAAAToZwBAACYiEvnOcvNzdXYsWOVlpam\nnJwcDR06VKGhoYqNjZWbm5vq1auniRMnymKxKD4+XsuWLZOHh4eGDh2q9u3buzIqAACAIVxazlav\nXq0aNWpo+vTpOnv2rO699141atRIMTExCg8P18SJE5WYmKhmzZopLi5OCQkJOn/+vKKjo9W6dWt5\neXm5Mi4AAIDLubScRUZG6q677pIk2Ww2eXh4aN++fQoPD5cktW3bVlu3bpWbm5vCwsLk6ekpT09P\nhYSE6MCBA2rSpIkr4wIAALicS485q1atmnx8fGS1WjVq1Cg98cQTstlsjsd9fHyUmZkpq9UqPz+/\nIsutVqsrowIAABjC5ScEHDt2TA899JCioqLUrVs3ubn9EcFqtcrf31++vr7KyspyLM/KypK/v7+r\nowIAALicS8vZyZMnNWjQID399NPq2bOnJKlRo0basWOHJCkpKUnNmzdX06ZNtXPnTuXk5CgzM1OH\nDh1SvXr1XBkVAADAEC495uytt95SZmamXn/9db3++uuSpHHjxmny5MnKzc1VaGioIiMjZbFYNHDg\nQPXr1082m00xMTGcDAAAACoFi91utxsd4q9KSUlRx44dlZiYqODgYKPjmEedOgV/HzliZAoAAHAB\nZ72FSWgBAABMhHIGAABgIpQzAAAAE6GcAQAAmAjlDAAAwEQoZwAAACZCOQMAADARyhkAAICJUM4A\nAABMhHIGAABgIpQzAAAAE6GcVVSdO0tHjxb86dzZ6DQAAKCEKGcVUefO0oYNf9zfsEEKDpaSk43L\nBAAASoRyVhElJl68LDVV6tHD9VkAAMAVoZwBAACYCOWsIurY8eJlQUHSqlWuzwIAAK6Ih9EBUAbW\nry84xiw1teB+UJCUkmJsJgAAUCKMnFVUq1ZJ7u4FfxgxAwCg3GDkrKIKCysYPSu8DQAAygVGzgAA\nAEyEcgYAAGAilDMAAAAToZwBAACYCOUMAADARChnAAAAJkI5AwAAMBHKGQAAgIlQzgAAAEyEcgYA\nAGAilDMAAAAToZwBAACYCOUMAADARChnAAAAJkI5AwAAMBHKGQAAgIlQzgAAAEyEcgYAAGAilDMA\nAAAToZwBAACYCOUMAADARDyMDlAcm82mSZMm6eDBg/L09NTkyZN10003GR0LAACgTJl25GzDhg3K\nzc3V0qVL9dRTT2natGlGRwIAAChzpi1nycnJuvPOOyVJzZo10969ew1OBAAAUPZMu1vTarXK19fX\ncd/d3V02m01ubhf3yfz8fEnSr7/+6rJ85UpKitEJAADA/yvsK4X95c9MW858fX2VlZXluF9cMZOk\n9PR0SVL//v1dkq3cqFKl4O+OHY3NAQAALpKenq6QkJCLlpu2nIWFhemLL77Q3XffrW+//VYNGjQo\n9rmNGzfW4sWLVatWLbm7u7swJQAAwJXJz89Xenq6GjdufMnHLXa73e7iTCVit9s1adIkHThwQJI0\ndepU1a1b1+BUAAAAZcu05QwAAKAyMu3ZmgAAAJUR5QwAAMBEKGcAAAAmQjkDAAAwEdNOpVGe/HnC\n3OTkZIWFhRmS5bnnntMDDzygRo0aGbL+C+Xl5Wn58uVKS0tTixYtVL9+fdWoUcOQLFarVUlJSTp/\n/rwkyWKxKCoqypAsW7Zs0YIFC4pkWbhwoSFZLjd/oKtt27ZNrVq1MjqGcnJy5OXlZXQM00hLSyv2\nscDAQBcm+YOZ/g+ZbXs5deqU43WRjPsZ7du3T8uWLVNOTo5j2dSpUw3JYqbtpaQoZ6Vg2LBheued\nd+Tu7q7XXntNX375pVasWGFIlvbt2+vNN9/UiRMn1KNHD/Xo0aNIcXSlCRMmKCAgQFu3blWTJk00\nZswYzZs3z5AsQ4cOVUBAgG644QZD1n+hqVOnaty4cQoICDA6ih555BHNnz/f6BiSpDlz5piinPXq\n1UstW7ZU7969Vb9+fUOz9OzZUz169FBUVJSuvfZaQzI88cQTslgsOn36tLKyslS/fn39+OOPuu66\n67R8+XJDMpnp/5CZtpdJkyYpKSlJtWrVcixbtmyZIVliY2M1YMAAx8/IYrEYkkMy1/ZSUpSzUvDw\nww/r8ccf12+//aY77rhDH374oWFZ2rVrp3bt2ikjI0OTJ0/Wyy+/rMjISA0bNkw33XSTS7P88ssv\nmjJlinbu3KkOHTronXfecen6/+yVV14xdP2FAgMD1bp1a6NjSJKuueYabdiwQXXr1nWMoBk1n6DF\nYtGwYcMcWSwWi2JiYlyeY8WKFfryyy81d+5cnT59Wt27d9c999wjHx8fl2eZP3++1qxZoyFDhuiG\nG27Q/fffrzvuuMOlGeLj4yVJjz/+uF566SX5+vrq3LlzhvxsCpnp/5CZtpfvvvtOGzZsMMVoeK1a\ntdS7d2+jY0gy1/ZSUpSzv+Cnn36SxWJRnTp1FBERoW3btunee+9VSkqKYW9wP/74o5YvX66NGzeq\nRYsW+uCDD5SXl6dRo0a5/FNufn6+MjIyJBXsVjTyF0aDBg307bff6tZbb3UsM2pXRM2aNTVhwgQ1\natRIFotFFotFffr0MSTLqVOn9P777xdZFhcXZ0iWXr16GfrpupC7u7vatm0ri8WiDz/8UIsWLVJC\nQoLuueceDRgwwKVZrrnmGvXv318tW7bU66+/rqeeekpBQUEaPHiwunTp4tIsx44dc4zCV61aVSdO\nnHDp+i9kpv9DZtpebrrpJmVnZ6tatWouXe+lBAUF6Z133nEcYmOxWNSmTRtDsphpeykpytlfMHHi\nxIuWTZgwQZJxb3Djx49X79699fjjjxf5D9qrVy+XZ3niiScUHR2t9PR0PfDAAxo3bpzLMxTavn27\nNm7cWGTZn++7SlBQkCwWi06dOmXI+i8UFxenzMxMpaam6sYbbzTk036hHj16aPny5UpNTVXLli0N\n20X08ssvKzExUeHh4Ro8eLCaNm0qm82mnj17uvzNdvHixVq5cqV8fHzUu3dvvfTSS8rLy9MDDzzg\n8nJ25513qn///mrcuLG+++47de7c2aXrv5CZ/g+ZaXs5duyY/vGPfygkJMRRQpYuXerSDIVycnJ0\n+PBhHT582LHMqHJmpu2lpLhCQCn4z3/+o0cffdToGJKkmJgYvfrqq0bHKCIjI0PVq1c3xaiIkY4d\nO6YbbrhBP/3000WP3XzzzQYkkj799FO99dZbys/P11133SU3NzcNGzbMkCxjx451HKM4ZMgQLVmy\nxJBjFBcuXKhevXpdVFR/+eUX3XjjjS7NMnPmTN1///0Xrdeok4727Nmjo0eP6pZbblHDhg1dvv4L\nbdq0Sf/73/9Ut25dderUybAc8fHxl9yNacT2cvjwYccegcK39uDgYJdmuNDBgwf1448/qk6dOkX2\nWhjBLNtLSVHOSsGAAQM0f/58eXgYPxA5YsQIPf7446pbt66jDLl6911xw8VGforbsGGDYxev3W7X\nmTNntHr1apdmmDJlisaOHXvJT9NGjbT27dtX77//vh599FG9//776tWrl2EHeQ8YMEBxcXGOv/v2\n7WvI9mLUei/l9OnT2rJli/Lz82Wz2ZSenq5//etfhmRJS0vTmjVripx9N3z4cEOyvPLKKzp69Khu\nv/127dy5U8HBwYqNjTUky5EjR/Tpp586frekp6fr+eefNyRLz549VbduXXXp0kXt2rWTt7e3ITmk\ngg85a9asUbNmzbRr1y5FRkYaNohhpu2lpIxvExXAmTNndOeddyo4ONhxILNRv9wPHz580ciHq3ff\nzZgxw3HbLKNls2fP1vPPP6+lS5cqIiJCX331lcszjB07VtLFRezCNztXc3NzU5UqVRy3jTxWxSzH\nKFarVk1TpkxRnTp1HP+fjTo+Zfjw4QoNDdXBgwdVpUoVVa1a1ZAckjRq1Ci1bt3aFGc879y50/E7\n9qGHHjL0wPMnn3xSXbp0UXJysmrXrq2srCzDsiQkJOjHH3/Uxo0b9fDDD6tmzZp6/fXXDcmyZs0a\nffDBB/Lw8FBubq769OljWDkz0/ZSUpSzUvDmm2+apoSsWbPG6AiOYXQzfaKsVauWbrvtNi1ZssTQ\n0SFJWrJkiRYsWOB4XTw8PPT5558bkuX2229XTEyMTpw4oQkTJqhJkyaG5JDMc4zibbfdJovF4iiK\nRrLb7Xr++ef1zDPP6MUXX1T//v0Ny+Lr66vRo0cbtv4L5eXlKT8/X+7u7obP1VetWjX961//0pEj\nRzR16lRFR0cbluWHH37Q1q1btX37dklSaGioYVkkOfYmeXp6GjoXnJm2l5KinJWCvLw805SQP+8y\nM3KyPTN9ovTy8tKOHTuUn5+vpKQknTlzxrAsH3zwgRYuXKi33npLd911l6GTIT755JPavHmzGjVq\npNDQUHXo0MGwLN7e3vrss8+UkZGha6+9Vt98840hOXr27GnIei/Fw8ND2dnZOnfunNzc3JSfn29Y\nlnr16mnt2rWOM94k46Zd6dq1q6Kjo9WsWTN999136tq1qyE5pIIR5xMnTigrK0vnzp3T77//bliW\n/v3768Ybb9To0aPVrl07QwcNwsLCNGLECN1+++1KTk7WbbfdZlgWM20vJUU5KwVmKiGTJk1y3P7+\n++/1ww8/GJbFTJ8oJ02apMOHD2vo0KGaPXu2hg4daliW2rVrKyAgQFar1TFFgqvl5eXJZrM5TiBp\n1aqVbDabBg4c6PKyuHPnTv34449asGCB/vnPf0oq2MW5ePFirV271qVZJDnm77Lb7UpJSVFISIiW\nLFni8hyS1K9fP73//vtq06aN2rVrZ9iVR6SCUZk//z4x6ljJAQMG6I477tDhw4fVu3dvQycXffzx\nx7Vhwwb16NFDnTp1Uo8ePQzLsn37dv33v//Vli1bNH/+fNWoUUMzZ840JEtsbKy++OIL/fTTT+rZ\ns6fat29vSA7JXNtLSVHOSoGZSsiFw9ihoaGGTohrpk+UAQEB2rNnj/bs2aP77rvP0BEiX19frV+/\nXm5ublqyZIkho3gff/yx3n77bZ08eVKRkZGSCn5ezZs3d3kWf39/paenKycnR+np6ZIKRnz//e9/\nuzyLVHRG9d9++03jx483JIdUsN0W/nwiIyPl5+dnWJY/F7ELLxHkKidOnJDValVsbKxeeukl1a9f\nX3a7XY888og++ugjl+eRpIiICEVERCgnJ0dffPGF4xhOI2RmZur48eNKS0vTuXPnDDlM4c8f/O64\n4w7DPviZcXspKcpZKTBTCbnwRIT09HRDs5jpE+W4ceN07tw53XbbbVq5cqW+/vprxwH6rjZ58mT9\n/PPPiomJ0fz58/Xss8+6PEOfPn3Up08fffjhh4YfHFu/fn3Vr19fDzzwgOMTbVpammHXBLyQr6+v\nfvnlF8PW//HHH+uFF17Q3//+d3Xp0kUREREuP15m1KhRmj17tiTpvffe06BBgyRJjz32mMvfbHfv\n3q2FCxfq8OHDjjkl3dzcDJk/64cfftDs2bNVs2ZNde3a1THi+swzzxh23d5HH31UHTt21NChQ1Wv\nXj1DMpjpg5+ZtpcrxVQapWDHjh368ccfVbt2bU2YMEE9evQw7DTdOXPmFJlCo2vXrobOc2MWvXv3\nLjKK+MADDzguS+MqX375paSCUaEL/9sZOXP2/v37HcczvfrqqxoyZIhhlzmZN2+e/P399dtvv2n5\n8uVq06aNIQX6wjMzT506pdatWxt2DGmhnTt3avr06fr555+1bds2l667cGqTy912tc2bN6tdu3aG\nrLtQnz59NHLkSJ09e1Zjx47V8uXLVbNmTT3yyCOG7bHIzc1VfHy8Yz6v6Ohoww7EN8MHv0Jm2F6u\nFCNnf5HValWTJk0UEREhSYZPbjdixAht3LhRhw8fVv369Q0pZn/eZejp6anc3FxVqVJFn3zyicvz\nSAWXNSmcFPLkyZO6/vrrXZ5h7dq1xR6ga1Q5mzhxoiZMmKDXXntNo0eP1vTp0w0rZ59//rkWL16s\nRx55RGvXrtXAgQMNyTFjxgzHz6lKlSq67rrrDMkhSQsWLNDXX3+tU6dO6fbbbzdsXjGz8fDw0ObN\nm2W32/XCCy9o1KhRLh+Z9/LyclzndOHChY6TI4y8ysaECRPk7++vNm3aaPv27Xr22Wf18ssvG5Kl\nSZMmSk5ONsUHPzNsL1eKcvYXLFq0SO+9957c3d01fvx4tW3b1uhImjRpks6cOaPbbrtNH374ob76\n6iuNGTPGpRkKC9hzzz2nvn37qmnTptq3b58++OADl+a40Lfffqu7775bgYGBOn78uLy8vByFaMuW\nLS7JMG3aNB04cEBVq1Z1+UXoi+Pl5aVbbrlFeXl5uu222+Tu7m5YFnd3d508eVK1atWSxWIx5Jgm\nSbLZbJo+fbrjA87TTz9t2NxeX375pTIzM3XXXXepTZs2hs/KbxYzZ87Uq6++queee05LlizRE088\nYeibraenp+O2kWfUHj161PF7tlOnToZeP9JMH/zMtr2UBOXsL1i9erU+/fRTWa1WPf3006YoZwcO\nHHCcWfbQQw+pb9++Ls9QeEDszz//rKZNm0qSbr311ktetshVEhMTDVt3oZkzZ2r79u3KycnRwIED\nDTsu5UKFB963bdtW69atK/Im42otWrTQgw8+qFdeeUVTpkwxbDfEuHHj9Oijj+q2227Tzp07NXbs\nWM2fP9+QLO+++67Onz+vr7/+WpMnT9bhw4dd9mGi0I8//qgnn3xSdrtdhw4dchxbdejQIZfmuFDV\nqlVVo0YNeXh4qHbt2obMW2XG1yUnJ0fnzp1TtWrV9Pvvv8tmsxmWxUwf/MywvVwpytlfUKVKFXl5\neY1lJqkAAB/MSURBVKlGjRrKy8szOo4k6YYbbnBcwzE9Pd3QU4b9/Pw0a9YsNWnSRN9++61q165t\nWJZdu3YpISGhyFx07777rkszbN++XUuWLFF2draGDRtminI2a9Ys7dmzR23bttX27dsNvS7r6NGj\nNXr0aJ0+fVpPPfWUYcfKuLu7O4phhw4d9P777xuSQ5I+++wzJSUlad++fWrcuLEee+wxl2eYNWuW\n4zjJC0dijPjgV8jHx0ePPvqo+vbtq8WLF6tGjRouz2DG16XwQ98tt9yiQ4cOacSIEYZlMdMHPzNs\nL1eKcvYXXHhQt5GfUCTpjjvucOwK2rBhg2644QYdP35c1157rWGZXnnlFS1dulSbN29WaGioob8o\nJk2apMcee0yfffaZ6tWrp9zcXJdn8PLyksViUdWqVQ3d9XEhLy8vJScn69NPP1X79u119uxZw7aZ\nHTt26Pnnn3dchD0oKMilBxQXnrBRtWpVzZs3T82bN9d3332nmjVruizDnyUnJ+u+++7Tiy++aNiE\noi1atDBkvZcze/Zs/fLLL7rlllt08OBBQw48N+PrEh4ermXLliklJUVBQUE6ffq0YVnM9MHPDNvL\nlaKc/QXFDWtbLJYi15d0ha1bt0qS4xIVhaxWq0tzXKhq1apq3ry5Y66d3bt3Kzw83JAs1atXV7du\n3bRlyxaNHDnSkMvgXFjmzXKS9NixY9W2bVvt2LFDtWrV0tixY7V48WJDssya9X/t3XtYTen7P/D3\n7uhQoqjPkFHEhGZ8kEMZFzNIomI6CNPhU2kkp4kmHZCm1B5icskUM4aOKmqkHLpoyGGQnIuyOxcd\npt0R2dXevz/67fUtme80Xz7rWep5/TPZ/bHu65rV2vd6nvu57x8RFRWFDRs2YM2aNVixYgWrD1Hp\ngY3BgwejsLAQhYWFkEgkRPtW2dvbIzU1FTdu3GA+o4cCAKFQiP3790MgEEBbWxteXl59+lR6Xl4e\nqqursWfPHnh4eEAikUAoFCIkJAQpKSmsxvLmXGlp38CSkhJiNXAf4v1Ck7N38FfL2iRHZtjZ2WHv\n3r3Q0NDA/fv34e3tTaTLOtBxclQoFHYppiaVnMnKyiI/Px8tLS0oKChAY2Mj6zHk5OQw94lAIGB+\n5vF43R5obKmrq4OlpSVOnTqFKVOmEE0aZWRkMGTIEAAdo5yUlJRYvX5wcDAAIDc3FxMmTGA+z8jI\nYDWOzjoPG5dIJJyZ4Uuar68vVq5cCX19fWRlZcHHx4fo9nNnra2trG/hNTU1IS0tDbW1tczznsfj\nEXkJramp4dx9yuX75a/Q5OwdcHFZe926dXBxccH06dPx8OFD7N+/n1gstbW1xJKON3l6ekIgEODr\nr7+Gh4cHLCwsWI+B7TfYnuDxeEwBc2VlJdGi3Y8//hh79uxBfX09IiIiiDWh9fX1hY2NDZYuXQo+\nn4+CggJiEyW4NGz8wYMHSE5ORktLC/NZUFAQkVhEIhHmzZsHoONUIqkDGwBw6NAhuLi4AOhYwfL0\n9MRvv/3Gagz6+vrQ19dHTk4OJk6cCKD7LgpbFi9ezPo1/w6X7peeoslZL6OjowM1NTVcv34ds2bN\nItqyQVtbG1VVVZyYY3b//n1miywpKYnIWxMXl9F9fHzg5eXFFA93ns3Ktp07dyIxMRH6+voYMGAA\nvv/+eyJxxMTEwNPTEz/++CPs7OyIjm/i0rBxPz8/2NraMjV4JFdH2tvb8eTJE+jq6iIvL49oLE+f\nPkVcXBxevHiBU6dOEf0bEggEKCoqgkgkwu7du+Hk5ARnZ2dWY9ixY0e3z+rq6lBSUoKHDx+yGosU\nl+6XnqITAnqZhQsXwsPDA/PmzcORI0eQlpaGpKQkIrEYGRmhvLwcQ4YMYf4Y2G4DkJqaioyMDNy4\ncQMzZ84E0HF4Iz8/H2fOnGE1Fup/19jYiGvXrjErMzwej8iJ1vj4eERHR8PU1BRpaWnYtm0bkdEz\nQEcX/jeR6spvb2/Pma2g3Nxc+Pr6oqamBurq6ggICMD48eOJxCIWi7FlyxYIhUJEREQQrVG0sLDA\nzz//jG+//RYRERFwdHQkVkMKdKy2RkVF4dq1a1i4cOFbEzc2cOl+6Sm6cvYeVFZWYs+ePRAKhVi4\ncCF0dXUxadIkIrEcPXqUqfFycnJiJheQkJ6eTuzaUrNnz8awYcNQX18PGxsbSCQSyMjIcKYJLGkH\nDhxAdHQ05OT+51HAdgIt5ebmBk1NTaId+QHg+vXriI2NhbKyMhYtWgQPDw9i2/NRUVFoampCRUUF\nRo4cSaT7vPQUq7KyMsLDw5ltM5JjxyZMmICkpCSmUTGJhKhznXFrayvy8/NhZ2dHtIa0X79+ADq2\nwxUVFYmcCheJREhLS0NMTAwUFBTQ3NyMjIwMJjYSuHC//FM0OXsPtm3bBkdHRxw8eBDTpk2Dp6cn\nsdlqDQ0NWLduHSorKzFs2DAEBgayHkNYWBjc3NyY06tSJE6xqqioYMaMGbh9+3aXRDUkJASbN29m\nNRYpLvRck8rIyMClS5eIPjg7I1XD1FloaCjy8/Nx5coVaGtrIzo6mlgs586dQ3h4ONNeREZGBmvX\nrmU1BukpVmVlZZSUlKCkpIT5HdvJWedh44sXL2bq8UgMG5c+yzrPym1tbSXWnw/oqNu0traGt7c3\nDhw4gE8++YT1GL788kssWbIEu3fvhra2NpydnYk9X7h0v/xTNDl7D1paWmBgYICDBw9i9OjRRL/o\nAgMDERgYCF1dXTx+/Bg7d+5k/S1OWnhJshmjVGJiIk6cOAGBQIDMzEwAHdsQra2txJIzLvRck1JT\nUyN6CADoeNMGOmry7ty5Az09PeZ3JL7oIiMjkZqaikmTJuHIkSMwNjZmvW5H6ujRo4iPj4ezszPW\nrl0LCwsL1pMz6SnWhIQEWFtbM5+T2OL08/Njho2vXbu2y7Bxtr9spTWk8fHxKC4uhqenJxwdHWFm\nZoYRI0awGotUUFAQXrx4gYEDB0JPTw/Dhg1jPQZ7e3ukpKSgoqIClpaWRE+Ac+l++adocvYe9OvX\nD5mZmRCLxbh79y7RNyeJRMLM3xs/fnyX7Sq23Lt3D/fu3ev2OY/HY32b1dzcHAYGBggPD4erqyuz\nrUly64wLPdekq5q1tbVYtmwZxo4dCx6PR2R109jYmPn55s2bXX5Hoo1FamoqYmNjIScnh9bWVixf\nvpxYciYjI8NswcjIyGDAgAGsx9C5blPab01at2lvb89qLFwcNh4XF8fslERERGDVqlXEvvjz8/Ph\n5+eHxsZGmJqaYty4cfjiiy9YjWH16tVYvXo1bt68icTERDx69Ai7d++Gubk5xo0bx2osXLxfeoom\nZ++Bv78/+Hw+6urqcOTIEaKndWRkZJCRkYFp06YhKyuLSKLIpT43CgoK0NTUxI4dO/Dw4UO0t7dD\nIpHgzp07WLJkCZGYuNBzbfny5V3+H5HsoSVNwCQSCSorK/HRRx/hwYMHzFxWEqQvNfLy8kRftqZO\nnQp3d3dUV1dj+/btTENnNknrNuvq6pi6TVlZWYwcOZL1WDrjyrBxWVlZ5n6Rk5MjOrcxICAAu3bt\nwrZt22BpaYnVq1eznpxJzZgxAzNmzEBDQwNSUlLg4eGBU6dOEYkF4M790lP0tGYvU15ejh9++AGF\nhYUYPXo0PD09iS2xSyQSNDc3g8fj4cKFC5g7dy6x0UDffPMN2traUFVVBbFYDHV1dRw9epRILPn5\n+RAIBFBXV8euXbtgZmYGBwcHIrFcvHgRjx49wsaNG+Hk5AQHBwfMnj2bSCzbt2/HqFGj4OTkhICA\nAAAdPcfYFhwcjIqKCkydOhV37tzBiBEj4OnpyWoM0rpNADh9+jQqKysxZswYYv3WAKCioqJbAs92\nLzoDAwMYGhpCIpF0OYF948YNXL9+ndVYpA4ePIgrV67gs88+Q25uLmbPns30PWObnZ0dIiMjYWtr\ni6ioKOa/fRUX75eeosnZO5DOsxSJRHj16hUzz1JVVRW///476fAAAJcvX2aGOLNt06ZNmDt3Lu7e\nvQuJRILa2lqEhYURicXa2hoJCQnw8fGBr68vHB0dERcXRyQWoVCIx48fY9asWYiOjoaZmRkGDRpE\nJJalS5ciMjISgwYNQlNTE5ydnZlxK2yzsLDAyZMnmX+vXLkSsbGxrF2/tbUVGRkZGDRoEF6/fo2C\nggIMHToUGRkZCA0NZS0OAF2+VLnyBSs9nSiRSFBeXo5Ro0ax/jd08+bNLgX4UiRKJjrLzc1FcXEx\nRo8ezZSVkLBhwwYYGBjg5MmTcHBwwNmzZ4k9c7mAq/dLT9BtzXcgnWe5ZcsWbN68mUnOSJw4S0pK\nwt69e9GvXz+EhoZi5MiR2LZtGwoKCoglZ9XV1Vi6dClOnjyJqKgoYqtDQMecT4lEgpcvX6J///7E\n4gA66r3s7OwAAIMGDYKHhwciIiKIxCIvL88khsrKykQPB/B4PAiFQqiqqqKhoQFisZjV62/ZsgVy\ncnKoqamBkZERRo8eDV9f37f2GuuLOiftjY2NRJrzcnEqS3FxMTIzM9HW1oaCggLExsbC39+fSCyB\ngYEIDw+HqqoqHj16ROS0Ppdw8X7pKZqcvQdlZWVMbzENDQ08e/aM9Rh+/fVXpKWloaamBsHBwaiq\nqsL8+fOxZ88e1mORamtrQ3p6OnR0dCAUCvHixQtisRgZGSEsLAzjx4+HtbU1kcJqqZaWFmZ7yszM\njFjbFQD49NNP4e7ujn//+994+PBhl5mSbHNzc4OlpSVUVFTQ2NjIesPKsrIyJCUlQSQSwcLCAvLy\n8oiMjMSYMWNYjeNDoKSkhLKyMtJhcMLmzZthZGSEO3fuQF1dnchzrrCwkNly7jyarq6ujlgpCfVu\naHL2HowZMwZbtmzBZ599hnv37nVpBcCWwYMHQ0VFBSoqKigoKICfnx+xFTMpZ2dnpKWlwcvLC1FR\nUay3AAA6+tlIicViyMjIQF1dncgpVik5OTlcvXqVSYhIrlZt2rQJN2/eRFFREYyNjZk2KCQ0NjYi\nPT0ddXV1UFNTY72wWjpoXUFBAWKxGEeOHCH2xZaTk8NsIwoEAuZnkg1OOzddra2thaGhIZE4uGbA\ngAH45ptvUFxcjKCgIKxYsYL1GP63FxkubImT9uYw+sbGRmKlJD1Fk7P3ICAgAOnp6SgpKYGJiQnm\nz59PNJ7hw4cTT8yAjtUqLS0t3LlzBwsWLCCyKvPo0SO0tLTA1NQUkydPZv36bxMQEAA+n4/AwECM\nGTOG2BYI0HFQglTt3ZsSEhJgbm5OpDcTgC51KaqqqkRXHFJSUohd+6+EhIQwqzOKiopE29FwaQi7\njIwMqqur8eLFC7x8+RKvXr1iPQZpAvbzzz8Ta/vCRdXV1WhubsbWrVvB5/MBdLykf/fdd13qW7mI\nJmfvgaWlJczMzGBtbY0hQ4YQiaGhoQFXr16FRCJBU1MT8zPJEStcaOZ5+vRp5OXlISUlBYcPH4a+\nvj7Mzc0xatQoVuMA/uftbfjw4awXmP8VFRUVHDt2DNra2kyfM1L3i0gkgrm5ObS1tSEjI8N6zzWB\nQIDNmzdDIpGgoKCA6QVHovebtMEpl8jKyiIoKAgCgQDa2trw8vIiFieXhrC7ubnhwoULMDMzw/z5\n82FmZkYslsuXL8PBwYHozgCX3L9/H5GRkSgqKsL27dsBdCTTpE6k/xP0tOZ70NDQgNTUVJw+fRof\nffQRLC0tmcZ3bNm6dSvzgHqzZxWpN0pra+tuzTxJDWGXysrKQlRUFCorK5GQkMDqtd3d3bF37963\ntkMg0WwV6HrfSJG6X6Qnqzpj80TVh3yyiw1OTk5YuXIl9PX1mb8jUoPQuTSEXUokEkEikRCd22hq\naoo///wTmpqazAsOqW1wLiHZteD/iiZn71FBQQHCwsLwxx9/YMSIEXBxcYGRkRHpsIiRtq+QsrGx\nIfagaG5uRnp6OtLS0vDq1SuYmJjg66+/JhIL10j7rmlpaRE9ENDU1ISDBw8yKzNr166lxcwc8mZL\nj1WrViEmJobVGKRD2OPj46Gnp0d0CHvnuY0mJibMSivJuY3l5eXdXnBI9bnkkmvXrjGzjL///nts\n3LiR6ApnT9C1z/cgJiYGp06dwsCBA2FlZQU+n4+2tjZYW1v36eRsypQpWL9+PdPMk0TN15kzZ5CW\nlobnz5/DyMgIfn5+xDubX7hwAbGxsczDor6+HqdPnyYSCxe2nqW8vb0xbdo0mJqa4tatW9i6dSvC\nw8OJxEJ1197ejidPnkBXVxd5eXlEthK5NIS989xGNzc3TsxtbGtrw7lz55hnS01NDdGaVq7Yt28f\n9u7di507dyIuLg6bNm2iyVlfUF1djZCQkC5f+vLy8ti5cyfBqMiRNvOcM2cO08xz3rx5RLbu3N3d\nmcaQ+fn5yM/PB0CmjkgqNDQU/v7+OH78OKZPn060UzWX5kjW19cz/d8mTJiA8+fPE4mDejtfX194\ne3ujpqYG6urqzBQHNnFpCDsX5zZyoa0HF/Xv3x+qqqqQk5ODuro60RFbPUWTs3eQnJwMANDS0kJ2\ndjays7OZeq+lS5diypQprMd08ODBLi0rQkJCsHnzZlZj4FIzT+lDu3M9Xud/kzBs2DBMnjwZcXFx\nsLCwYO4jUrgyR/L169eorq6Guro6ampqutV+UWRNmDABSUlJaGhogKysLNN6hE1cGsLeGVfmNnKh\nrQcXDRw4EM7OzrCxsUFMTAxUVVVJh/S3aHL2DgoKCpgv+dTUVGKDtAEgMTERJ06cgEAgwOXLlwF0\nPLRaW1tZT8641MyTix2iFRQUcOvWLbS3tyMzMxP19fXEYuHC1rPUxo0bsWLFCigpKaG5uZnIygzV\nXU5ODry9vZGYmIhLly5hx44dGDRoEL777jvW++JxaQj7X53uLSgoYD0WKS609eCi0NBQlJWVQUdH\nB/n5+bCysiId0t+iBwLeE9Lz70QiEaqrqxEeHg5XV1fmoaWmpsb6aoh0+C4ALF68GDExMbSwu5PK\nykoUFRVh6NCh2L9/P4yNjbF48WJi8Vy6dAkFBQUYM2YM5s6dSywOKekIJ4ob7Ozs4O3tDV1dXSxa\ntAi7d++GlpYWnJ2diR3w4cIQdi6e7r116xYEAgHU1dWxfft2mJmZYevWrURi4ZLi4uIPrhaPrpz1\nEgoKCtDU1ISXlxcaGxshJyeH+Ph4LFu2jPXTOlxq5slFQ4cORX19PV6+fAlnZ2diW6xPnjzBuXPn\nUFdXh3/961/Q0tIiEodIJMK+fftw/vx5iEQiDBw4ECYmJnBzc6P9mjhAIpFAV1cXVVVVaGlpYSag\nkCwNkK5SkRzCzsVV+enTpzOJIelm6FzyIdbi0SdfL7NhwwasWLEC58+fh46ODrZv345ffvmF1Ri4\n1MyTi1xcXNDa2tplfEhYWBirMZw9exaHDx+GjY0NPv30U1RUVGD9+vXYuHEj6w/14OBgqKur4+zZ\ns1BUVERzczMOHz4MPp8PHx8fVmOhupMmyFeuXIGBgQGAjkM/L1++JBYTF4awc9GBAwcQHR3d5aXm\n6tWrBCPihg+xFo8mZ+9AmnQA4EwS0tLSgnnz5iEyMhK7d+/GH3/8wXoMP/74I7Pc33keH8k3bS4R\niUSIjo4mGsOxY8cQHR3dZQD8V199BVdXV9aTs5ycHKZ7N9Ax4/Lbb7+lfeg4wsDAADY2Nnj+/Dl+\n+uknlJaWwt/fH4sWLSIdGgA6hL2zjIwMXLp0Cf369SMdCqd8iLV4NDl7B8uXL+dcEtLa2opjx45h\n4sSJePr0KZGbkIvL/Vyir6+PzMxM6OjoMJ+xXS8jLy/fJTEDOr7kSAxh/6uayA/huHtf4OLigi+/\n/BLKysrQ0NBAaWkpli9fjgULFhCLiQ5hfzs1NTUif8Ncx6URWz1Fk7N3wMUkxNPTExcvXoSrqytS\nUlLothAH1dbWIigoqMu2ZudtGpJItAGQSCQQiUTdPheLxazHQr1d5xeJjz/+GB9//DHBaLg1hJ0L\npLs2tbW1WLZsGcaOHcvMyqWlJN1r8V6/fk04or9Hk7NeZurUqXj9+jXOnj0LfX19YkXe1F8rLCzE\n2bNnicYgEAi6bMtLkWgD8OzZMxgbG7N+XerDxaUh7FxgbW2N4uJiWFhYQE5ODllZWVBVVSXSvohL\nNm7ciNDQUADAkSNH4OjoCABYvXo101GAq2hy1suEhISgqqoKAoEACgoKOHToEPbu3Us6LKqTTz75\nBHfv3mXmAgJ/vbX339K5LrAzGxsbVuMAyA19pz5cvr6+XYaw+/j4cG4QOpuysrKQn58PPp+PAQMG\nYPjw4eDz+RAKhZzc4WGLUChkfv7999+Z5OxD6CBGk7NeJjs7G7GxsbC1tcWyZctYP15O/b2srCxc\nunSpy2dsJyh9+YFNffhEIhHTAHf+/Pn49ddfCUdE1uXLl5GQkMDUaY4cORL79u3D8uXLsW7dOsLR\nUf8XNDnrZcRiMbOf3t7eTouqOYjUkHOK6i24MISdSwYMGNDtWS8vL090zif1bmhy1svY29vjq6++\nglAohJWVFRwcHEiHRL3hwoULiI2NZbpV19fX04SNov4BLgxh55L+/fujtLS0y0GNsrKyPv9yzsUR\nWz1Fxzf1EtK3SACor69HaWkpNDU16RgcDjI1NYW/vz+OHz+O6dOn4/r168ROVD148ADJycloaWlh\nPgsKCiISC22gSf1TJIewc8nTp0/h7u4OAwMDaGpq4vnz57h69SqCg4O71Lb2NVwcsdVTdOWslwgM\nDMSzZ88wffp0zJ49G59//nmXVg0UdwwbNgyTJ09GXFwcLCwskJycTCwWPz8/2NraQk1NDQDZHn20\ngSb1d7g0hJ1Lxo4di5iYGFy8eBE1NTWYOHEi3Nzc+nzS+iHX1tLkrJeIiorC69evcffuXWRlZSEh\nIQESiQTTpk2jBaEco6CggFu3bqG9vR2ZmZmor68nFouysjKWLVtG7Pqd0Qaa1N/h8/ng8/lQUFDA\nvn37cPjwYWYIe19OzgBg0KBBnPlbpt4dTc56EUVFRejp6aGxsRHNzc3Izc3F48ePSYdFvcHPzw9F\nRUVYs2YN9u/fD1dXV9ZjuHLlCoCO5Cw8PJzZ+uDxePj8889ZjYU20KR6iotD2Cnqv4EmZ73EL7/8\ngsuXL6OpqQkGBgb44osvsGXLFsjLy5MOjfr/CgsLmS8RDQ0NyMjIICAgACoqKqzHkpaWBh6PB2Vl\nZZSUlKCkpIT5HdvJmXQUz9tqQyiqMy4OYaeo/wZ6IKCXmDp1KmbPng0rKytMmzaN9aam1N+ztbXt\n9plQKISxsTHWr19PICIgISEB1tbWzL+PHTsGe3t7VmNoa2uDWCyGu7s70zBZLBZj9erViIqKYjUW\nitsOHTqEjIwMZgi7kpIS/P39oa+vjzVr1pAOj6LeG5qc9RIikQjZ2dnIzMxEVlYWhg4dijlz5mDO\nnDmsD9Wmek4sFsPKygonT55k9bqpqanIyMjAjRs3MHPmTCaW/Px8nDlzhtVY4uPjERERgT///JOZ\nkSgjIwN9fX0EBwezGgvFfQKBoMsQ9ry8PKJD2Cnqv4EmZ71UZmYmwsPDcffuXVp3xlFtbW3Izs7G\nDz/8wHpy1tDQgCdPniA8PByurq6QSCSQlZXFyJEjoaGhwWosUjExMVi1ahWRa1MURXEJTc56iQcP\nHiA7Oxu3b99GYWEhdHV1YWhoCENDQ4wYMYJ0eNRbvHjxAl5eXvjPf/6DyZMnE4mhoqKiWzE1qZVW\nGxsbHD9+nMi1KYqiuIQmZ72Eg4MDDA0NMWvWLIwfP77Pd4amekZajC+RSFBeXo5Ro0YRm8fq6OgI\nHR0daGlpQUZGBjwej4mPoiiqL6GnNXuJo0ePkg6B+gDFx8czPzc2NmLbtm3EYpk8eTJ4PB6EQiGx\nGCiKoriALq9QFAUAUFJSQllZGbHrr1+/Hnp6elBUVISuri5tnkxRVJ9FV84oqg/rvG1YW1sLQ0ND\nYrHs2bMHJSUlmDp1Kn777Tfcvn0bW7duJRYPRVEUKbTmjKL6sPLycuZAgKKiItPKgoTOBwIkEgms\nrKxw4sQJYvFQFEWRQlfOKKoPk5WVRVBQEAQCAbS1teHl5QVNTU0isbS1taG9vR2ysrIQi8X0UAtF\nUX0WTc4oqg/z9fXFypUroa+vj6ysLPj4+ODYsWNEYjExMcGKFSswadIkPHjwACYmJkTioCiKIo1u\na1JUH2Zra9tlRNKqVasQExNDLJ68vDwUFRVh9OjRGDduHLE4KIqiSKIrZxTVh7W3t+PJkyfQ1dVF\nXl5et4a0bEhOTu72WW5uLnJzc7F06VLW46EoiiKNJmcU1Yf5+vrC29sbNTU1UFdXR0BAAOsxFBQU\ndEkKxWIxkpOT0a9fP5qcURTVJ9FtTYqi0NDQAFlZWSgpKRGNo7S0FJ6entDW1oa3tzfxeCiKokig\nx6Eoqg/KycmBubk5RCIR0tPTYWxsDAsLC1y8eJFYTDExMXBycoKLiwt27dpFEzOKovosuq1JUX0Q\nn88Hn8+HgoIC9u3bh8OHD0NLSwvOzs6YN28eq7FUVlbCy8sLgwcPRmJiIgYPHszq9SmKoriGJmcU\n1QdJJBLo6uqiqqoKLS0t0NPTAwAiBwKWLFkCBQUFzJw5E/7+/sznPB4PISEhrMdDURRFGk3OKKoP\nkpPr+NO/cuUKDAwMAACtra14+fIl67GEhYUB6EjGOpfAkkgUKYqiuIAmZxTVBxkYGMDGxgbPnz/H\nTz/9hNLSUvj7+2PRokWsxzJjxgzWr0lRFMVl9LQmRfVRAoEAysrK0NDQQGlpKfLy8rBgwQLSYVEU\nRfV5NDmjKIqiKIriENpKg6IoiqIoikNockZRFEVRFMUhNDmjKIqiKIriEJqcURRFURRFccj/AwXW\nArqMEIWFAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1031e0a58>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig = plt.figure(figsize=(10, 6))\n",
"data = np.arange(len(df_boston_rates['Neighborhood']))\n",
"ax1 = plt.scatter(data,predictions)\n",
"#plt.xlabel(\"Neighborhood\")\n",
"plt.ylabel(\"Chlamydia cases [per 100,000]\")\n",
"ax2 = plt.errorbar(data, df_boston_rates[\"mean\"], yerr=df_boston_rates[\"error\"],fmt='o', color='red')\n",
"plt.xlim([-1,15])\n",
"plt.ylim([0,1400])\n",
"\n",
"x = np.arange(15)\n",
"labels = ['Hyde Park', 'West Roxbury', 'Roslindale', 'Mattapan','Jamaica Plain', 'South Dorchester', 'North Dorchester', 'Roxbury','Fenway', 'South End', 'South Boston', 'Back Bay','Charlestown', 'Allston', 'East Boston']\n",
"plt.xticks(x, labels, rotation='vertical')\n",
"\n",
"plt.text(12, 1200, r'$R^2 = $%.2f'%(R2), fontsize=20)\n",
"\n",
"plt.savefig('../graphics/boston_comparison.png', bbox_inches='tight', dpi=150)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Plots for website"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/akuepper/anaconda/lib/python3.5/site-packages/sklearn/utils/validation.py:386: DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and willraise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.\n",
" DeprecationWarning)\n"
]
},
{
"data": {
"text/plain": [
"array(['You', 'Your gender', 'Your age group', 'Your race / ethnicity',\n",
" 'Your location'], \n",
" dtype='<U21')"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def calculate_rate(Zipcode):\n",
" target = df_zipcode[df_zipcode[\"geoid2\"]==int(Zipcode)]\n",
" target_params = target.values[0]\n",
" chlamydia_rate = model.predict(target_params[1:])*Ystd+Ymean\n",
" return chlamydia_rate\n",
"\n",
"Race = \"Black\"\n",
"Gender = \"Male\"\n",
"Age = \"30-34\"\n",
"Zipcode = \"02474\"\n",
"\n",
"\n",
"target_unnormalized = df_zipcode_unnormalized[df_zipcode_unnormalized[\"geoid2\"]==int(Zipcode)]\n",
"\n",
"TOTALNR = target_unnormalized[\"Population\"]\n",
"\n",
"if Gender == \"Male\":\n",
" gender_table = \"hd02s026\"\n",
"else:\n",
" gender_table = \"hd02s051\"\n",
"\n",
"GENDERNR = TOTALNR*target_unnormalized[gender_table]/100.0\n",
"\n",
"if Race == \"White\":\n",
" race_table = \"hd02s078\"\n",
"elif Race == \"Black\":\n",
" race_table = \"hd02s079\"\n",
"elif Race == \"Native\":\n",
" race_table = \"hd02s080\"\n",
"elif Race == \"Asian\":\n",
" race_table = \"hd02s081\"\n",
"elif Race == \"Pacific\":\n",
" race_table = \"hd02s089\"\n",
"elif Race == \"Multiple\":\n",
" race_table = \"hd02s095\"\n",
"elif Race == \"Hispanic\":\n",
" race_table = \"hd02s107\"\n",
"\n",
"RACENR = TOTALNR*target_unnormalized[race_table]/100.0\n",
"\n",
"if Age == \"0-14\":\n",
" age_table = \"hd02s002\"\n",
"elif Age == \"15-19\":\n",
" age_table = \"hd02s005\"\n",
"elif Age == \"20-24\":\n",
" age_table = \"hd02s006\"\n",
"elif Age == \"25-29\":\n",
" age_table = \"hd02s007\"\n",
"elif Age == \"30-34\":\n",
" age_table = \"hd02s008\"\n",
"elif Age == \"35-39\":\n",
" age_table = \"hd02s009\"\n",
"elif Age == \"40-44\":\n",
" age_table = \"hd02s010\"\n",
"elif Age == \"45-54\":\n",
" age_table = \"hd02s011\"\n",
"elif Age == \"55-64\":\n",
" age_table = \"hd02s013\"\n",
"elif Age == \"65+\":\n",
" age_table = \"hd02s015\"\n",
"\n",
"AGENR = TOTALNR*target_unnormalized[age_table]/100.0\n",
"\n",
"\n",
"\n",
"zipcoderate = calculate_rate(Zipcode)*100\n",
"genderrate = gender_rate[Gender]*100\n",
"agerate = age_rate[Age]*100\n",
"racerate = race_rate[Race]*100\n",
"\n",
"the_result = (zipcoderate/TOTALNR.values + genderrate/GENDERNR.values + racerate/RACENR.values + agerate/AGENR.values)/(1.0/TOTALNR.values+1.0/GENDERNR.values+1.0/RACENR.values+1.0/AGENR.values)\n",
"\n",
"d = np.array([the_result[0], genderrate, agerate, racerate, zipcoderate[0]])\n",
"d_label = np.array([\"You\", \"Your gender\", \"Your age group\", \"Your race / ethnicity\", \"Your location\"])\n",
"d_label"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'sns' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-1-2a9e1e284dae>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0msns\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mset\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mstyle\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m\"white\"\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcontext\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m\"talk\"\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3\u001b[0m \u001b[0mfig\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0max\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msubplots\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mfigsize\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m10\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m6\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0msharex\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0msns\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mbarplot\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0md_label\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0md\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpalette\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m\"RdBu_r\"\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0max\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0max\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0max\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mset_ylabel\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"Risk\"\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mfontsize\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m20\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mNameError\u001b[0m: name 'sns' is not defined"
]
}
],
"source": [
"sns.set(style=\"white\", context=\"talk\")\n",
"\n",
"fig, ax = plt.subplots(1, 1, figsize=(10, 6), sharex=True)\n",
"sns.barplot(d_label, d, palette=\"RdBu_r\", ax=ax)\n",
"ax.set_ylabel(\"Risk\", fontsize=20)\n",
"plt.title(r'Chlamydia', fontsize=20)\n",
"ax.plot([-1, len(d)], [0,0], \"k-\", linewidth=1.0)\n",
"sns.despine(bottom=True)\n",
"plt.setp(fig.axes, yticks=[])\n",
"plt.tight_layout(h_pad=3)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
dseuss/notebooks | Ellipsoid Method.ipynb | 1 | 287207 | {
"cells": [
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import cdd\n",
"import itertools as it\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib\n",
"from matplotlib.patches import Polygon, Ellipse\n",
"from matplotlib.collections import PatchCollection"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Helper Methods"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def h2v(A, b):\n",
" \"\"\"Converts the halfspace representation Ax <= b of a polyhedron P\n",
" to a vertex-representation \n",
" \n",
" :param A: ndarray of shape (m, d)\n",
" :param b: ndarray of shape (d)\n",
" :returns: ndarray of shape (n, d)\n",
" \"\"\"\n",
" assert len(A) == len(b)\n",
" mat = cdd.Matrix([[b_i] + list(-A_i) for (b_i, A_i) in zip(b, A)],\n",
" number_type='float')\n",
" mat.rep_type = cdd.RepType.INEQUALITY\n",
" vertices = cdd.Polyhedron(mat).get_generators()\n",
" result = []\n",
" for v in vertices:\n",
" assert v[0] == 1.0\n",
" result.append(v[1:])\n",
" return np.array(result)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def proj(ket):\n",
" return ket[:, None] * ket.conj()[None, :]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def plot_poly(A, b, ax=None):\n",
" ax = ax if ax is not None else pl.gca()\n",
" \n",
" vertices = h2v(A, b)\n",
" poly = Polygon(vertices, closed=True)\n",
" p = PatchCollection([poly])\n",
" \n",
" ax.add_collection(p)\n",
" \n",
"def plot_hyperplane(c, x, ax=None):\n",
" ax = ax if ax is not None else pl.gca()\n",
"\n",
" t = np.linspace(-1, 1, 20)\n",
" xs = x[0] + t * c[1]\n",
" ys = x[1] - t * c[0] \n",
" ax.plot(xs, ys)\n",
" ax.arrow(x[0], x[1], c[0], c[1], fc='k', ec='k')\n",
" \n",
"def plot_ellipse(x, A, ax=None):\n",
" ax = ax if ax is not None else pl.gca()\n",
"\n",
" vals, vecs = np.linalg.eigh(A)\n",
" phi = np.arccos(vecs[0][0])\n",
" ell = Ellipse(x, width=vals[0], height=vals[1], angle=phi / np.pi * 180,\n",
" fill=False, linestyle='solid', linewidth=1, edgecolor='k')\n",
" ax.add_artist(ell)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def normalize_hrep(A, b):\n",
" norm = np.linalg.norm(A, axis=-1)\n",
" return A / norm[:, None], b / norm"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"SQUARE2D = (np.array([[1,0], [-1,0], [0,1], [0,-1]], dtype=np.float64),\n",
" np.ones(4, dtype=np.float64))\n",
"SQUARE2D = normalize_hrep(*SQUARE2D)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Separation Oracle"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def contained(x, poly, delta=1e-6):\n",
" A, b = poly\n",
" violated = A.dot(x) > b + delta\n",
" \n",
" if not np.any(violated):\n",
" return True\n",
" else:\n",
" return A[violated][0]"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3X2M1eWB9//PjNwzPEnHBwYYBTXNggz+CGsybqWBihtr\nG+qdTTpM2T+aNoY7xkJi2P1jYypZCWk0adb9x7Rh162RNJGnEO+NKF3btGrqA8YWRsEOPuHTsDOy\nSFGRAUd+f5jh7ggoD+fMORe+Xklj5/qeueY6p5en857v+Z7TcPTo0aMBAAAAitJY6wUAAAAAp0/Q\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIFG1XoBSfLBBx/k2WefzR//+Me8+eab2bdvX0aNGpVp\n06bluuuuy4IFC9LQ0HBKcy1dujR79+494bGWlpasXr26kksHAACAmqiLM/RPP/10/u3f/i2vvPJK\n/uqv/ioLFy7M1772tbz11ltZvXp1/vVf//W05hs7dmwWLVp03H9uuummiq57/fr1FZ0PEvuK6rG3\nqAb7imqxt6gG+4pqqdXeajh69OjRmvzkv7Bjx44MDAzk6quvHjb+5z//Obfffnv+53/+J//4j/+Y\na6655gvnWrp0aRoaGnLvvfdWa7nHdHV1eVKg4uwrqsXeohrsK6rF3qIa7CuqpVZ7qy7O0M+aNeu4\nmE+Sr3zlK7nhhhuSfBr9AAAAwKfq4hr6z3PeeecN++epOHLkSJ588sns3bs3zc3NueyyyzJz5sw0\nNtbF3y8AAADgrNV10H/yySd5/PHHkyRz5sw55e/bv3//cS+5b21tza233pr29vaKrhEAAABqoa6D\n/pe//GXefvvtXH311Zk9e/Ypfc+CBQsyc+bMTJ06NaNHj05/f3+2bNmSxx57LHfddVd+8pOfZNq0\naVVeOQAAAFRX3b4G/ZFHHsnmzZtz6aWXZtmyZaf8fZ2dnZk1a1YmTJiQpqamXHrppVmyZEm+853v\n5PDhw94EAwAAgHNCXbzL/Wdt2bIl999/f6ZOnZoVK1bkK1/5ylnP+d///d+57bbbMn78+PzHf/xH\nBVYJAAAAtVN3L7nfvHlz1qxZk2nTpmXFihWZMGFCReYdmmdgYOCUv2f9+vXZuHHjSY8BAABA8ulH\n151MZ2fn5x4/U3V1hv6hhx7Kgw8+mCuuuCJ33HFHxo8fX7G5t23blrvuuiuXXnpp/uVf/qVi8/b2\n9lZsLkiStrY2+4qqsLeoBvuKarG3qAb7impoa2ur2c+um2voN27cmAcffDBf/epXs2LFis+N+cHB\nwfT29qavr2/Y+DvvvHPCM/D9/f35xS9+kSSZN29eZRcOAAAANVAXL7n/3e9+lw0bNqSxsTEzZszI\nI488ctxtJk6cmOuuuy5Jsm/fvixfvjwTJ04c9vF0Tz31VB5++OHMnDkzF198ccaMGZO+vr784Q9/\nyJEjR3L11VfnpptuGqm7BQAAAFVTF0H/7rvvJvn0c+dPFPNJ0t7efizohzQ0NAz7etasWdmzZ09e\nf/319PT0ZGBgIOPGjcvMmTMzf/58Z+cBAAA4Z9TVNfQlcg0OlebaLqrF3qIa7Cuqxd6iGuwrqsE1\n9AAAAMBpEfQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAA\nBRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAA\nAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFGlXrBQAAAFC/\nBv/P/x729Xn//p81Wgmf5Qw9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUaFStF5AkH3zwQZ599tn88Y9/zJtvvpl9\n+/Zl1KhRmTZtWq677rosWLAgDQ0Npzzfvn37snbt2mzfvj0ffPBBWlpa0tHRkUWLFmXcuHFVvCcA\nAAAwMuoi6J9++uncd999ueCCCzJr1qxcfPHF+fOf/5xnn302q1evzrZt2/IP//APpzRXX19f7rjj\njhw4cCAdHR1pa2vLq6++mkcffTTbt2/PqlWrMn78+CrfIwAAAKiuugj6tra2/NM//VOuvvrqYeN/\n//d/n9tvvz3PPvtstm7dmmuuueYL57rvvvty4MCB3HzzzbnxxhuPja9ZsyabN2/O2rVrs2TJkorf\nBwAAABhJdXEN/axZs46L+ST5yle+khtuuCFJsmPHji+cp6+vL93d3WltbR0W80nS1dWV5ubmPPHE\nEzl8+HBlFg4AAAA1UhdB/3nOO++8Yf/8PEPRP3v27OOOjR49OjNmzMjAwEB27dpV2UUCAADACKvr\noP/kk0/y+OOPJ0nmzJnzhbfv7e1NkkyZMuWEx4fG9+zZU6EVAgAAQG3UddD/8pe/zNtvv52rr776\nhGfdP+vgwYNJkrFjx57w+ND4hx9+WLlFAgAAQA3UbdA/8sgj2bx5cy699NIsW7as1ssBAACAulIX\n73L/WVu2bMkDDzyQqVOnZsWKFaf82fFDZ+CHztR/1tD4qc63fv36bNy48aTHkk/foR8qzb6iWuwt\nqsG+olrsLarBvjp9b33ma4/hiXV1dZ30WGdn5+ceP1N1F/SbN2/OmjVrMm3atKxYsSITJkw45e8d\n2lgnu0Z+aPxk19h/VldX1xc+6EPX7UOltLW12VdUhb1FNdhXVIu9RTXYV5XhMRxuqEOHTvqOpLoK\n+oceeigPPvhgrrjiitxxxx0ZP378aX3/rFmzkiTd3d3HHTt06FB6enrS3Nyc6dOnV2S9AAAAUCt1\ncw39xo0b8+CDD+arX/1qVqxY8bkxPzg4mN7e3vT19Q0bnzRpUmbPnp3+/v5s2bJl2LF169ZlYGAg\n8+fPT1NTU1XuAwAAAIyUujhD/7vf/S4bNmxIY2NjZsyYkUceeeS420ycODHXXXddkmTfvn1Zvnx5\nJk6cmHvvvXfY7ZYsWZIVK1bk/vvvzwsvvJBLLrkkL7/8cnbu3Jm2trYsXrx4JO4SAAAAVFVdBP27\n776b5NPPnT9RzCdJe3v7saAf0tDQcNztJk2alLvvvjvr1q3Ltm3bsm3btrS0tGThwoXp7Ow86Ufa\nAQAAQEnqIugXLVqURYsWnfLtJ06cmHXr1p30+IUXXphbb721EksDAACAulQ319ADAAAAp07QAwAA\nQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0A\nAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQ\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAA\nFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFGhUrReQJM8880x27tyZN954I7t3786hQ4cyb968LFu27LTmWbp0afbu3XvCYy0tLVm9enUl\nlgsAAAA1VxdBv2nTprzxxhsZPXp0LrroorzzzjtnPNfYsWOzcOHC48ZHjx59NksEAACAulIXQf/D\nH/4wF154YSZPnpydO3dm5cqVZzzXuHHj0tnZWcHVAQAAQP2pi6Bvb2+v9RIAAACgKHUR9JV05MiR\nPPnkk9m7d2+am5tz2WWXZebMmWls9P5/AAAAnDvOuaDfv39/7r333mFjra2tufXWW70SAAAAgHPG\nORX0CxYsyMyZMzN16tSMHj06/f392bJlSx577LHcdddd+clPfpJp06bVepkAAABw1s6p16F3dnZm\n1qxZmTBhQpqamnLppZdmyZIl+c53vpPDhw9n/fr1tV4iAAAAVMQ5dYb+ZG644YY8/PDDeemll07r\n+9avX5+NGzee9FiStLW1nfX64LPsK6rF3qIa7Cuqxd6iGuyr0/fWZ772GJ5YV1fXSY91dnZ+7vEz\n9aUI+gkTJiRJBgYGTuv7urq6vvBB7+3tPeN1wYm0tbXZV1SFvUU12FdUi71FNdhXleExHG7oDxy1\neEX4OfWS+5PZtWtXkmTSpEk1XgkAAABURnFBPzg4mN7e3vT19Q0bf+edd054Br6/vz+/+MUvkiTz\n5s0bkTUCAABAtdXFS+6fe+65PPfcc0k+/di5JOnp6cnPfvazJMn555+f73//+0mSffv2Zfny5Zk4\nceKwj6d76qmn8vDDD2fmzJm5+OKLM2bMmPT19eUPf/hDjhw5kquvvjo33XTTCN8zAAAAqI66CPrd\nu3fn8ccfHzbW39+f/v7+JJ9+jvxQ0A9paGgY9vWsWbOyZ8+evP766+np6cnAwEDGjRuXmTNnZv78\n+c7OAwAAcE6pi6BftGhRFi1adEq3nThxYtatW3fceHt7e9rb2yu9NAAAAKhLxV1DDwAAAAh6AAAA\nKJKgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcA\nAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAOCEjh4dddxYQ8OYE44z8gQ9AAAAxzl6dFT6+pqOG/+bv5mQ\nvr4mUV8HBD0AAADHaWz8X/m7vzv/uPG33jovf/d356eh4X/VYFX8JX9SAQAAYJjzzjsvTz99Xt56\n67zk//vs0TF5663k8suPptEp4hw6dKhmP1vQAwAAMExDQ0Neeum8kxz9NGCPHBm59XBigh4AAIBh\njh49mpkzB092NEny0EMH8rWvfZTBwZPdjmrzAgkAAACGGRwczN/8zWCmTj1xrE+dOpiOjkExX2OC\nHgAAgON88smRPPTQ+8eNT506mP/7f9/P0aNec19rXnIPAADAcRoaPs6kScknnxl/9tkD+eSTI2lo\n+Lgm6+L/EfQAAACc0Imi/ejRj9LQUIPFcBwvuQcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAKNqvUCkuSZZ57Jzp0788Ybb2T37t05dOhQ5s2bl2XLlp32XPv27cvatWuzffv2fPDBB2lp\naUlHR0cWLVqUcePGVWH1AAAAMPLqIug3bdqUN954I6NHj85FF12Ud95554zm6evryx133JEDBw6k\no6MjbW1tefXVV/Poo49m+/btWbVqVcaPH1/h1QMAAMDIq4ug/+EPf5gLL7wwkydPzs6dO7Ny5coz\nmue+++7LgQMHcvPNN+fGG288Nr5mzZps3rw5a9euzZIlSyq1bAAAAKiZuriGvr29PZMnTz6rOfr6\n+tLd3Z3W1tZhMZ8kXV1daW5uzhNPPJHDhw+f1c8BAACAelAXQV8JO3bsSJLMnj37uGOjR4/OjBkz\nMjAwkF27do300gAAAKDizpmg7+3tTZJMmTLlhMeHxvfs2TNiawIAAIBqOWeC/uDBg0mSsWPHnvD4\n0PiHH344YmsCAACAajlngh4AAAC+TOriXe4rYegM/NCZ+s8aGj+dz6Jfv359Nm7ceNJjSdLW1nY6\ny4QvtHffexkzZkytl8E56L337C0qz76iWuwtqmHvvvf8/n4G3vrM1x7DE+vq6jrpsc7Ozs89fqbO\nmaAf2lQnu0Z+aPxk19ifSFdX1xc+6EPX7kOljBkzJt+874+1XgYAwDnnv5b8td/fK8BjONxQiw6d\n9B1J58xL7mfNmpUk6e7uPu7YoUOH0tPTk+bm5kyfPn2klwYAAAAVV1zQDw4Opre3N319fcPGJ02a\nlNmzZ6e/vz9btmwZdmzdunUZGBjI/Pnz09TUNJLLBQAAgKqoi5fcP/fcc3nuueeSJPv370+S9PT0\n5Gc/+1mS5Pzzz8/3v//9JMm+ffuyfPnyTJw4Mffee++weZYsWZIVK1bk/vvvzwsvvJBLLrkkL7/8\ncnbu3Jm2trYsXrx4BO8VAAAAVE9dBP3u3bvz+OOPDxvr7+9Pf39/kqS1tfVY0A9paGg4bp5Jkybl\n7rvvzrp167Jt27Zs27YtLS0tWbhwYTo7O0/6kXYAAABQmoajR48erfUiSuYNIag0b4oHAFAd/7Xk\nr/PRRx/VehnFGfw//3vY1+f9+3/WaCX1qZbv+l/cNfQAAACAoAcAAIAiCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAKNqvUC/tK+ffuydu3abN++PR98\n8EFaWlrS0dGRRYsWZdy4cac0x9KlS7N3794THmtpacnq1asruWQAAACoiboJ+r6+vtxxxx05cOBA\nOjo60tbWlldffTWPPvpotm/fnlWrVmX8+PGnNNfYsWOzcOHC48ZHjx5d6WUDAABATdRN0N933305\ncOBAbr755tx4443HxtesWZPNmzdn7dq1WbJkySnNNW7cuHR2dlZrqQAAAFBzdXENfV9fX7q7u9Pa\n2jos5pOkq6srzc3NeeKJJ3L48OEarRAAAADqS12cod+xY0eSZPbs2ccdGz16dGbMmJHu7u7s2rUr\nV1111RfOd+TIkTz55JPZu3dvmpubc9lll2XmzJlpbKyLv18AAADAWauLoO/t7U2STJky5YTHp0yZ\nku7u7uzZs+eUgn7//v259957h421trbm1ltvTXt7+9kvGAAAAGqsLoL+4MGDST59M7sTGRr/8MMP\nv3CuBQsWZObMmZk6dWpGjx6d/v7+bNmyJY899ljuuuuu/OQnP8m0adMqt3gAAACogXPuNeidnZ2Z\nNWtWJkyYkKamplx66aVZsmRJvvOd7+Tw4cNZv359rZcIAAAAZ60ugn7oDPzQmfrPGho/1c+iP5Eb\nbrghSfLSSy+d8RwAAABQL+riJfdtbW1Jkj179pzw+ND4ya6xPxUTJkxIkgwMDJzy96xfvz4bN248\n6bHk/60dKuW9996r9RIAAM5Zfn8/fW995muP4Yl1dXWd9FhnZ+fnHj9TdRH0s2bNSpJ0d3cfd+zQ\noUPp6elJc3Nzpk+ffsY/Y9euXUmSSZMmnfL3dHV1feGDPvSGflApY8aMqfUSAADOWX5/P3sew+GG\n/sBRi8u76+Il95MmTcrs2bOPvYHdX1q3bl0GBgYyf/78NDU1JUkGBwfT29ubvr6+Ybd95513TngG\nvr+/P7/4xS+SJPPmzavSvQAAAICRUxdn6JNkyZIlWbFiRe6///688MILueSSS/Lyyy9n586daWtr\ny+LFi4/ddt++fVm+fHkmTpw47OPpnnrqqTz88MOZOXNmLr744owZMyZ9fX35wx/+kCNHjuTqq6/O\nTTfdVIu7BwAAABVVN0E/adKk3H333Vm3bl22bduWbdu2paWlJQsXLkxnZ+cJP9KuoaFh2NezZs3K\nnj178vrrr6enpycDAwMZN25cZs6cmfnz5zs7DwAAwDmjboI+SS688MLceuutX3i7iRMnZt26dceN\nt7e3p729vRpLAwAAgLpSF9fQAwAAAKdH0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEE\nPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAU\nSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFGhUrRcAAABA/Trv3/+z1kvgJJyhBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAKNqvUC/tK+ffuydu3a\nbN++PR988EFaWlrS0dGRRYsWZdy4cSM+DwAAANSrugn6vr6+3HHHHTlw4EA6OjrS1taWV199NY8+\n+mi2b9+eVatWZfz48SM2DwAAANSzugn6++67LwcOHMjNN9+cG2+88dj4mjVrsnnz5qxduzZLliwZ\nsXkAAACgntXFNfR9fX3p7u5Oa2vrsAhPkq6urjQ3N+eJJ57I4cOHR2QeAAAAqHd1EfQ7duxIksye\nPfu4Y6NHj86MGTMyMDCQXbt2jcg8AAAAUO/qIuh7e3uTJFOmTDnh8aHxPXv2jMg8AAAAUO/qIugP\nHjyYJBk7duwJjw+Nf/jhhyMyDwAAANS7ugh6AAAA4PTUxbvcD505HzrD/llD41/0GfKVmmfI+vXr\ns3HjxpMeS5K2trZTmgtO1XvvvVfrJQAAnLP8/k61dHV1nfRYZ2fn5x4/U3UR9EP/Up3s2vah8ZNd\nG1/peYZ0dXV94YM+dN0+VMqYMWNqvQQAgHOW39+ptKEOHTrpO5Lq4iX3s2bNSpJ0d3cfd+zQoUPp\n6elJc3Nzpk+fPiLzAAAAQL2ri6CfNGlSZs+enf7+/mzZsmXYsXXr1mVgYCDz589PU1NTkmRwcDC9\nvb3p6+s7q3kAAACgVHXxkvskWbJkSVasWJH7778/L7zwQi655JK8/PLL2blzZ9ra2rJ48eJjt923\nb1+WL1+eiRMn5t577z3jeQAAAKBUdRP0kyZNyt13351169Zl27Zt2bZtW1paWrJw4cJ0dnae8KPo\nGhoaKjIPAAAAlKbh6NGjR2u9iJJ5Uw0qbcyYMfnmfX+s9TIAAM45/7Xkr/PRRx/VehmcY2r5yQl1\ncQ09AAAAcHoEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNAD\nAABAgQQ9AAAAFEjQAwAAQIFG1XoBQ3p6erJp06a8/PLLOXz4cKZMmZIFCxbkW9/6VhobT+3vDu++\n+26WLVt20uNz587NbbfdVqklAwAAQM3URdA/99xzueeee9LU1JRrr70248ePz/PPP58HHnggPT09\nWb58+WnNd/nll6ejo+O48alTp1ZqyQAAAFBTNQ/6jz76KKtXr05jY2PuvPPOXHHFFUmSxYsXZ+XK\nlXnmmWfy1FNPZe7cuac852WXXZbOzs5qLRkAAABqrubX0D/99NN5//338/Wvf/1YzCfJqFGj8r3v\nfS9J8thjj9VqeQAAAFCXan6GfseOHUmSOXPmHHesvb09TU1N6enpyccff5xRo05tue+9915+/etf\n5/3338/555+f6dOnZ9q0aRVdNwAAANRSzYO+t7c3STJlypTjjjU2Nqa1tTVvv/12+vv709bWdkpz\ndnd3p7u7e9hYe3t7li5dmosvvvjsFw0AAAA1VvOgP3jwYJJk7NixJzw+NP7hhx9+4VzNzc357ne/\nm2uuuSatra1JkjfffDMbNmzIiy++mFWrVuWnP/1pmpqaKrR6AAAAqI2KBP3SpUuzd+/eU779vHnz\nPvfj5c7UhAkT0tXVNWzsyiuvzI9//OOsWLEir7zySn7zm9/k29/+dsV/NgAAAIykigT95MmTT+us\n9wUXXHAbMHPmAAAUlklEQVTsvw+dgR86U/9ZQ+Pjxo074/U1Njbmb//2b/PKK6/kpZdeOuWgX79+\nfTZu3HjSY0lO+TIAOFXvvfderZcAAHDO8vs71fLZk8t/qbOz83OPn6mKBP2KFSvO+Hvb2try2muv\nZc+ePcPe5T5JPvnkk/T39+e888479hL6MzVhwoQkycDAwCl/T1dX1xc+6EPvAQCVMmbMmFovAQDg\nnOX3dypt6I9EQyd9R1LNP7buqquuSpJs27btuGM7d+7M4cOHM2PGjFN+h/uT2bVrV5Kc9R8GAAAA\noB7UPOi/9rWv5fzzz8/vf//7vPbaa8fGjxw5krVr1yZJvvnNbw77noMHD6a3tzf79+8fNv7666/n\n6NGjx/2MF154IZs3b07y6fX7AAAAULqav8v9mDFjcsstt+See+7JnXfemblz52b8+PF5/vnn09vb\nm2uvvTbXXnvtsO/ZunVrfv7zn+cb3/hGfvSjHx0bX7NmTfbs2ZPp06fnoosuSvLpu9y/+OKLSZLF\nixdn+vTpI3fnAAAAoEpqHvRJ0tHRkZUrV2bTpk3ZunVrjhw5ksmTJ+cHP/jB576BXUNDw7Cv58+f\nn61bt+a1117L9u3b8/HHH6elpSVz587NjTfemCuvvLLadwUAAABGRMPRE71GnVPmTTWotDFjxuSb\n9/2x1ssAADjn/NeSv85HH31U62VwjqnlJyfU/Bp6AAAA4PQJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAKNqvUCBgcH86tf/Sq7\nd+/O7t278/bbb2dwcDC33HJLrr/++jOas6enJ5s2bcrLL7+cw4cPZ8qUKVmwYEG+9a1vpbHR3zAA\nAAAoX82DfmBgIA888ECSpKWlJRdccEH27t17xvM999xzueeee9LU1JRrr70248ePz/PPP58HHngg\nPT09Wb58eaWWDgAAADVT86BvamrK7bffnssvvzwtLS3ZsGFDNm7ceEZzffTRR1m9enUaGxtz5513\n5oorrkiSLF68OCtXrswzzzyTp556KnPnzq3kXQAAAIARV/PXn48aNSpz5sxJS0vLWc/19NNP5/33\n38/Xv/71YzE/9DO+973vJUkee+yxs/45AAAAUGs1D/pK2rFjR5Jkzpw5xx1rb29PU1NTenp68vHH\nH4/00gAAAKCizqmg7+3tTZJMmTLluGONjY1pbW3N4OBg+vv7R3ppAAAAUFHnVNAfPHgwSTJ27NgT\nHh8a//DDD0dsTQAAAFANFXlTvKVLl57WO9PPmzcvy5Ytq8SPBgAAgC+ligT95MmT09TUdMq3v/DC\nCyvxY48zdAZ+6Ez9Zw2Njxs37pTmW79+/UnfcX/9+vVJkra2ttNdJnyuvfvey38t+etaLwMA4Jwz\neNTv71RPV1fXSY91dnZ+7vEzVZGgX7FiRSWmOWttbW157bXXsmfPnmHvcp8kn3zySfr7+3Peeeel\ntbX1lObr6ur6wgd96Lp9qJS2tjb7iqqwt6gG+4pqsbeoBvuKahj6I9HQSd+RdE5dQ3/VVVclSbZt\n23bcsZ07d+bw4cOZMWNGRo2qyN8xAAAAoGaKDPqDBw+mt7c3+/fvHzb+ta99Leeff35+//vf57XX\nXjs2fuTIkaxduzZJ8s1vfnNE1woAAADVUBenqh966KFjL33ZvXt3kuS3v/1t/vSnPyVJrrzyylx/\n/fXHbr9169b8/Oc/zze+8Y386Ec/OjY+ZsyY3HLLLbnnnnty5513Zu7cuRk/fnyef/759Pb25tpr\nr8211147cncMAAAAqqQugn779u3ZuXPnsLFdu3Zl165dx77+y6Af0tDQcNxYR0dHVq5cmU2bNmXr\n1q05cuRIJk+enB/84Af59re/XfnFAwAAQA00HD169GitF1Eyb6pBpXmzFqrF3qIa7Cuqxd6iGuwr\nqqGWn5xQ5DX0AAAA8GUn6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIe\nAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok\n6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACg\nQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECjar2AwcHB/OpXv8ru3buze/fuvP322xkcHMwtt9yS66+//rTmevfd\nd7Ns2bKTHp87d25uu+22s10yAAAA1FzNg35gYCAPPPBAkqSlpSUXXHBB9u7de1ZzXn755eno6Dhu\nfOrUqWc1LwAAANSLmgd9U1NTbr/99lx++eVpaWnJhg0bsnHjxrOa87LLLktnZ2eFVggAAAD1p+ZB\nP2rUqMyZM6fWywAAAICi1Dzoq+G9997Lr3/967z//vs5//zzM3369EybNq3WywIAAICKOSeDvru7\nO93d3cPG2tvbs3Tp0lx88cU1WhUAAABUzjkV9M3Nzfnud7+ba665Jq2trUmSN998Mxs2bMiLL76Y\nVatW5ac//WmamppqvFIAAAA4OxUJ+qVLl57WO9PPmzfvcz9e7kxNmDAhXV1dw8auvPLK/PjHP86K\nFSvyyiuv5De/+U2+/e1vV/xnAwAAwEiqSNBPnjz5tM56X3jhhZX4saessbExf/u3f5tXXnklL730\nUkWDvq2trWJzwRD7imqxt6gG+4pqsbeoBvuKc0lFgn7FihWVmKaqJkyYkOTTz70/VevXrz/pR+it\nX7++IusCAACgfJ99tfhf6uzs/NzjZ+qcuob+8+zatStJjl1bfyq6uro+90Hv6uoS9lScfUW12FtU\ng31FtdhbVIN9RbXUam81jvhPrICDBw+mt7c3+/fvHzb++uuv5+jRo8fd/oUXXsjmzZuTfHr9PgAA\nAJSuLs7QP/TQQ+nt7U2S7N69O0ny29/+Nn/605+SfPrGdtdff/2x22/dujU///nP841vfCM/+tGP\njo2vWbMme/bsyfTp03PRRRcl+fRd7l988cUkyeLFizN9+vSRuEsAAABQVXUR9Nu3b8/OnTuHje3a\ntevYy+STDAv6IQ0NDcO+nj9/frZu3ZrXXnst27dvz8cff5yWlpbMnTs3N954Y6688srq3AEAAAAY\nYXUR9P/8z/98Wre/7rrrct111x03vmDBgixYsKBCqwIAAID6VeQ19AAAAPBlJ+gBAACgQOfdeeed\nd9Z6EaU6evRoZs2aVetlcI6xr6gWe4tqsK+oFnuLarCvqJZa7a2Goyf6nDcAAACgrnnJPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRoVK0XUO8GBwfzq1/9Krt3787u\n3bvz9ttvZ3BwMLfcckuuv/7605rr3XffzbJly056fO7cubntttvOdskUoJL7akhPT082bdqUl19+\nOYcPH86UKVOyYMGCfOtb30pjo7/dfdlUYj94zvpy2rdvX9auXZvt27fngw8+SEtLSzo6OrJo0aKM\nGzduxOfh3FCJ/bB06dLs3bv3hMdaWlqyevXqSi6ZAjzzzDPZuXNn3njjjezevTuHDh3KvHnzPvf/\nu07GcxZDKrWvRuo5S9B/gYGBgTzwwANJPn3gL7jggpP+D3OqLr/88nR0dBw3PnXq1LOal3JUel89\n99xzueeee9LU1JRrr70248ePz/PPP58HHnggPT09Wb58eaWWTgEqvR88Z3159PX15Y477siBAwfS\n0dGRtra2vPrqq3n00Uezffv2rFq1KuPHjx+xeTg3VHI/jB07NgsXLjxufPTo0ZVeNgXYtGlT3njj\njYwePToXXXRR3nnnnTOax3MWf6lS+yoZmecsQf8Fmpqacvvtt+fyyy9PS0tLNmzYkI0bN57VnJdd\ndlk6OzsrtEJKVMl99dFHH2X16tVpbGzMnXfemSuuuCJJsnjx4qxcuTLPPPNMnnrqqcydO7eSd4E6\nVY394Dnry+O+++7LgQMHcvPNN+fGG288Nr5mzZps3rw5a9euzZIlS0ZsHs4NldwP48aN83zEMT/8\n4Q9z4YUXZvLkydm5c2dWrlx5RvN4zuIvVWpfJSPznOV1uF9g1KhRmTNnTlpaWmq9FM4hldxXTz/9\ndN5///18/etfPxZvQz/je9/7XpLkscceO+ufQxnsB85UX19furu709raOuwX2iTp6upKc3Nznnji\niRw+fHhE5uHcYD9QTe3t7Zk8efJZzWGP8lmV2FcjyRn6Gnjvvffy61//Ou+//37OP//8TJ8+PdOm\nTav1sijUjh07kiRz5sw57lh7e3uamprS09OTjz/+OKNG+Vf+XFeN/eA568thaO/Mnj37uGOjR4/O\njBkz0t3dnV27duWqq66q+jycGyq9H44cOZInn3wye/fuTXNzcy677LLMnDnTe8VwxjxnUU0j8Zzl\nt/sa6O7uTnd397Cx9vb2LF26NBdffHGNVkWpent7kyRTpkw57lhjY2NaW1vz9ttvp7+/P21tbSO9\nPEZYNfaD56wvh8/bO0Pj3d3d2bNnz+f+UlupeTg3VHo/7N+/P/fee++wsdbW1tx6661pb28/+wXz\npeM5i2oaiecsQT+Cmpub893vfjfXXHNNWltbkyRvvvlmNmzYkBdffDGrVq3KT3/60zQ1NdV4pZTk\n4MGDST59040TGRr/8MMPR2xN1E4l94PnrC+XSu0dz0n8/+3dPUgbYRzH8Z8VUfEFta2KL2uaIDiU\nFqpDxBYVcRJEXMTFqXRwcJMMIqKTazdnrSAOKRSKoIOLoSVBifhC1MGEnIsuUptWO0iCqWmt9rzk\nku9n0ifhyR38+ZF/7u55rjOzHtrb2+VyudTY2KiioiIZhqFPnz7p8+fPmpqa0uTkJHcP4c7ILDwU\nqzIrJxr6v20ZkMp9t7u4TXl5ufr7+5PGnE6nxsbG5PF4tLe3p+XlZXV3d5v+2TBfptQVsk+m1BaZ\nBSCT/L6wVENDg4aHh1VYWCiv16sPHz5odHQ0TUcHAMmsyqycaOhra2vvdAWpqqrqAY/mpkePHunN\nmzfa29vT1tYWX45tIlPqKv7LcfwX5t/Fx9lD1T7uWluVlZWJv62oBzIrO5lVO2QSrrOiHjo6OuT1\nerW1tXXvOZC7yCxYzezMyomG3uPxpPsQblVeXi7pan9y2EOm1FVdXZ1CoZAikUjSquaSdHFxIcMw\nlJ+fn7hlGpnvf2rLqnogs7JPfE2FSCSS8vX4+J+eMzV7HmQHK+qBPML/ILNgNbMziyVBM8TOzo4k\n0XThzuILtPj9/huvBYNBff/+Xc+ePWOF+xxhVT2QWdmnqalJkm4sgChJ37590/b2tgoLC+VwOCyZ\nB9nBinqI51FNTc2950DuIrNgNbMzi4b+AZydnSkcDuvk5CRpfH9/X5eXlzfev7GxoY8fP0q6ehYW\nSOVPdfXq1SuVlZVpbW1NoVAoMR6LxTQ3NydJ6uzstPRYkT73qQcyC9LVF4vm5ubEoj3Xzc/P6/z8\nXG63O/E4yM+fPxUOhxWNRv9rHmQ3s+rq6Ogo5dUswzA0OzsriTzC35FZeAiZkFl5l6m+rSHJ0tJS\nYkuLg4MDHR4eyuFwJG69cTqdev36deL9Kysrev/+vdra2vT27dvE+Pj4uCKRiBwOhx4/fizpasXo\nzc1NSdLAwIB6e3utOi2kmVl1JUk+n08zMzMqKChQa2urSktL9eXLF4XDYbW0tGhkZMS6E0Pa3bUe\nyCzERaNReTwenZ6e6sWLF6qvr9fu7q6CwaDq6uo0MTGh0tJSSdLx8bHevXunp0+f3tiS5y7zIPuZ\nUVcLCwvyer1yuVx68uSJiouLFY1G9fXrV8ViMT1//lyjo6PKz89P12kiDXw+n3w+n6Sr7cECgYCq\nq6vlcrkkSWVlZRocHJREZuHfmVFXVmYW9+D+g0AgoGAwmDS2s7OTuF1CUlLjFZeXl5f0v9vt1vr6\nukKhkAKBgH78+KGKigq1traqq6tLTqfzYU4AGcmsupKkly9fanx8XIuLi1pfX1csFlNtba2GhoZY\nsCwH3bceyCzU1NRoenpa8/Pz8vv98vv9qqioUE9Pj/r6+lJu65Qqk+4zD7KXGXXV1NSkSCSi/f19\nbW9v6/z8XCUlJXK5XHK73Vydz1EHBwdaXV1NGjMMQ4ZhSLp6LCzeeMWRWbiNGXVlZWZxhR4AAAAA\nABviGXoAAAAAAGyIhh4AAAAAABuioQcAAAAAwIZo6AEAAAAAsCEaegAAAAAAbIiGHgAAAAAAG6Kh\nBwAAAADAhmjoAQAAAACwIRp6AAAAAABsiIYeAAAAAAAboqEHAAAAAMCGaOgBAAAAALAhGnoAAAAA\nAGyIhh4AAAAAABuioQcAAAAAwIZo6AEAAAAAsCEaegAAAAAAbOgXssgaGdlBV9IAAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1076ee470>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
}
],
"source": [
"POINT = np.array([ 1.26403501, 1.26403501])\n",
"plot_poly(*SQUARE2D)\n",
"pl.scatter([POINT[0]], [POINT[1]])\n",
"\n",
"res = contained(POINT, SQUARE2D)\n",
"if not (res is True):\n",
" plot_hyperplane(res, POINT)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Ellipsoid Method"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def ellipsoid_iter(c, oracle, ball):\n",
" n = len(c)\n",
" x, R = ball\n",
" A = R**2 * np.eye(n)\n",
" \n",
" while True:\n",
" sep = oracle(x)\n",
" yield x, A, sep\n",
" a = c if sep is True else -sep\n",
" x += 1. / (n+1) * A.dot(a) / np.sqrt(a.dot(A.dot(a)))\n",
" A = n**2 / (n**2 - 1) * (A - 2. / (n+1) * A.dot(proj(a).dot(A)) / a.dot(A.dot(a)))"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3XmYl3W9//HXIA4MIA0uLOOe/TTAOLZwDLwEFfelUnHU\nslzCy1PgKcrOLzVNJdPUPJl2jCNaeloAiaxUSkSTcv9ZQImBG5YOMZLiwjqO8/ujazgRoggzfOeD\nj8d1cV1y3zP39z3jfV18n997q2ppaWkJAAAAUJROlR4AAAAAePsEPQAAABRI0AMAAECBBD0AAAAU\nSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQAAABSoc6UHSJIHHnggc+fOzTPPPJMFCxZkxYoV2XfffTNmzJi3tZ3Ro0dn8eLFb7iutrY2\n48ePb4txAQAAoOI6xBH6qVOn5le/+lUWLFiQbbbZZqO21a1btxx33HFr/TnqqKPaaNr/NXny5Dbf\nJtivaC/2LdqD/Yr2Yt+iPdivaC+V2rc6RNCfcsopueqqq3LjjTdm1KhRG7Wt7t27Z+TIkWv9OfLI\nI9to2v81ZcqUNt8m2K9oL/Yt2oP9ivZi36I92K9oL5XatzrEKfcDBgyo9AgAAABQlA4R9G2pqakp\nv/nNb7J48eJ06dIlO++8c/r3759OnTrEyQgAAADQJja7oF+yZEmuueaaNZb17t07n/nMZ5wJAAAA\nwGZjswr6/fffP/3798+OO+6Yrl27prGxMb/85S8zffr0XHLJJbn44ouz0047VXpMAAAA2Gib1Xno\nI0eOzMCBA9OzZ89UV1dnhx12yKhRo3LkkUdm1apV7moJAADAZqOqpaWlpdJD/KO5c+fmwgsv3KDn\n0K/LX//613zuc59Ljx49cv3117fJNgEAAKCSNqtT7telZ8+eSZKVK1e+re+bPHnyOh8/4Gg/AAAA\nrerr69e5buTIkW+6fkO9I4J+/vz5SZI+ffq8re+rr69/y196Q0PDBs9VKS0tLbnzzjszbty4PPnk\nk0mSvffeO+eff3722muvCk9HXV1dkfsVHZ99i/Zgv6K92LdoD/arynvttdcyceLEXH755Vm8eHGS\n5CMf+UjOPvvsYu93VldXl6QyB32Lu4a+ubk5DQ0NWbRo0RrLn3vuuTc8At/Y2JgbbrghSbLvvvtu\nkhk7sj/+8Y85/vjjc8opp+TJJ5/MLrvskuuuuy4/+clPxDwAANCuOnfunJNOOim//e1vc+aZZ6Zr\n1675+c9/nuHDh+drX/taXnrppUqPWJQOcQ39ww8/nIcffjjJ3x87N3v27PTu3Tv9+/dPkmy11Vb5\n5Cc/mSR5/vnnM2bMmGy33XZrPJ7u5ptvzq233pr+/ftn2223TU1NTRYtWpTf/e53aWpqygc+8IGc\nddZZ2WKLLdp09lI+4Vu4cGEuu+yy3HzzzWlpaUltbW0+//nP5+STT051dXWlx+Mf+OSY9mLfoj3Y\nr2gv9i3ag/2q43nuuedy6aWXZurUqUmSXr165ayzzsonPvGJbLnllhWebv20HqGvhA5xyv2CBQty\nzz33rLGssbExjY2NSf7+HPnWoG9VVVW1xt8HDhyYhQsX5umnn868efOycuXKdO/ePf3798+wYcPe\nsUfnly1blmuvvTbXXnttli9fni233DInn3xyPv/5z6dXr16VHg8AAHgH23777XP11Vfn05/+dC66\n6KI8+OCDOffcc3PDDTfkK1/5Sg466KC12o//1SGO0Jeso37C19zcnJtvvjmXXXbZ6ssTDj/88Jxz\nzjnZddddKzwdb8Ynx7QX+xbtwX5Fe7Fv0R7sVx1bS0tLpk2blosvvjgLFixIkgwdOjRf/epXs+ee\ne1Z2uDdRySP0xV1Dz1ubOXNmDj300Hzxi1/MokWL8i//8i+ZOnVqrrvuOjEPAAB0SFVVVTn88MNz\n991354ILLkhtbW3uu+++HHrooRk7dmwWLlxY6RE7HEG/GXn88cfzqU99KieeeGLmzp2burq6XH31\n1bn11luz9957V3o8AACAt1RdXZ3TTz89v/3tb3P66aenc+fOmTx5cvbdd99cccUVWbp0aaVH7DAE\n/Wbg5Zdfzvnnn58RI0ZkxowZ6d69e7785S9n5syZOeaYY9Kpk//NAABAWXr16pULLrggd999dw4/\n/PAsX748//mf/5l99903t9xyS1w9LuiL1tLSkltuuSXDhw/P9ddfn5aWlpx00km59957c+aZZ6am\npqbSIwIAAGyUXXfdNdddd12mTp2avfbaK4sWLcro0aNz/PHH54knnqj0eBUl6Av1+OOPp76+PqNH\nj05jY2M++MEPZtq0afnGN76R7bbbrtLjAQAAtKm99947v/jFL3L55ZentrY29957bw488MBccskl\nWb58eaXHqwhBX5hly5blkksuyUEHHZT77rsvvXr1yhVXXJFbbrmlQ9/5EQAAYGN16tQpH//4x/Ob\n3/wmH//4x9PU1JRrrrkm++23X+64445Kj7fJCfpCtLS05Fe/+lX222+/XHPNNWlqasonPvGJzJw5\nMyeeeKLr5AEAgHeMrbfeOpdffnl+9rOfZeDAgXn22Wdz6qmn5uSTT86f//znSo+3yajAAvz5z3/O\nKaecktNOOy3PPfdc9txzz/z85z/PZZddlq233rrS4wEAAFTEhz70odx+++256KKLstVWW+XOO+/M\n/vvvn6uuuiorV66s9HjtTtB3YCtXrsy3vvWt7L///rnzzjuz1VZbZdy4cbntttvywQ9+sNLjAQAA\nVFznzp3z6U9/Ovfcc0+OOeaYrFixIpdddlkOPPDAzJw5s9LjtStB30E9+OCDOfjgg3P55ZdnxYoV\nOeaYYzJz5sycdtpp6dy5c6XHAwAA6FD69OmTq6++OpMnT8573vOePPXUUznxxBNz5pln5m9/+1ul\nx2sXgr6DefHFF/OlL30pxxxzTJ544onstttumTx5cq6++ur07t270uMBAAB0aPvss0+mT5+eL3/5\ny+natWumTp2aYcOGZdKkSZvds+sFfQfR0tKSn/70p9lvv/3yox/9KNXV1fnCF76Q6dOnZ5999qn0\neAAAAMWorq7OmWeemRkzZmTYsGFZsmRJvvCFL+S4447brJ5dL+g7gGeeeSYnnXRSxowZk8WLF+fD\nH/5wpk+fni9+8Yvp0qVLpccDAAAo0i677JIf/ehHufrqq7PNNtvk/vvvz0EHHZQrr7xys7hpnqCv\noKampnznO9/JAQcckF//+tepra3NFVdckZtvvjnvec97Kj0eAABA8aqqqnLMMcfknnvuyQknnJBV\nq1blm9/8Zg4++OA88MADlR5vowj6CnnkkUdy2GGH5etf//rqm97dc889nikPAADQDnr16pVvfvOb\nmTJlSnbbbbc88cQTOfbYY3PWWWflxRdfrPR4G0Q5bmLLly/P+eefn49+9KN57LHHsvPOO68+BWTb\nbbet9HgAAACbtSFDhqy+xLm6ujo//vGPM3z48Nx6662VHu1tE/Sb0COPPJKDDjoo119/fbbYYouM\nGTMmM2bMyPDhwys9GgAAwDtGly5dVt+EfMiQIfnb3/6WM844I2PGjMmSJUsqPd56E/SbwMqVK3PJ\nJZfkYx/7WJ5++unsscceufXWW3P22Wenpqam0uMBAAC8I73nPe/J5MmTc/HFF6empiY//elPM2LE\niNx9992VHm29CPp29uijj+aII47INddck5aWlnz2s5/NtGnT8r73va/SowEAALzjderUKaecckru\nuOOOfOhDH8pf//rXnHTSSfm///f/ZunSpZUe700J+nby2muv5dvf/naOOOKIPPbYY9lll13y05/+\nNOeee65H0QEAAHQw7373uzN16tScc845qa6uzg9+8IMceOCBefDBBys92joJ+nbw5JNP5uijj843\nvvGNNDU15eSTT84dd9yRwYMHV3o0AAAA1mGLLbbI6NGjc/vtt2fgwIH585//nGOPPTYXXXRRVqxY\nUenx1iLo29Drr7+eG264IQcffHB+97vfpW/fvvnRj36Ur3/96+nevXulxwMAAGA99O/fP7feems+\n97nPpVOnThk/fnwOPfTQzJ49u9KjrUHQt5Fnn302J5xwQs4777ysWLEixx57bO666y53sAcAAChQ\ndXV1/uM//iM/+9nPsttuu+Xxxx/PUUcdlW9+85tpamqq9HhJBP1Ga2lpyaRJkzJixIjce++92Wab\nbTJhwoR8+9vfzrve9a5KjwcAAMBGeP/7359f/epXGTVqVJqbm3PllVfmIx/5SObPn1/p0QT9xjr1\n1FPzhS98Ia+++moOO+yw3HXXXTnssMMqPRYAAABtpKamJhdeeGFuvvnm7LDDDpkzZ04OPfTQfPe7\n363oXIJ+I02fPj09e/bMVVddleuuuy7bbrttpUcCAACgHQwdOjR33nlnTjzxxKxcuTLjxo2r6DyC\nfiMNGzYsM2bMyMiRI1NVVVXpcQAAAGhHW221Va644orceOON6d27d0Vn6VzRV98M/OhHPxLyAAAA\n7zAHHnhgZsyYUdEZHKHfSGIeAADgnWnrrbeu6OsLegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAAChQ50oPkCQPPPBA5s6dm2eeeSYLFizIihUrsu+++2bMmDFve1svvPBCJk6cmNmzZ+fVV19N\nbW1tBg8enOOOOy7du3dvh+kBAABg0+sQQT916tQ888wz6dq1a7bZZps899xzG7SdRYsW5Stf+Upe\nfvnlDB48OHV1dXnyySczbdq0zJ49O+PGjUuPHj3aeHoAAADY9DpE0J9yyinZeuut07dv38ydOzcX\nXnjhBm1nwoQJefnll3PaaaflkEMOWb38pptuym233ZaJEydm1KhRbTU2AAAAVEyHuIZ+wIAB6du3\n70ZtY9GiRZkzZ0569+69RswnSX19fbp06ZKZM2dm1apVG/U6AAAA0BF0iKBvC48++miSZNCgQWut\n69q1a/bYY4+sXLky8+fP39SjAQAAQJvbbIK+oaEhSdKvX783XN+6fOHChZtsJgAAAGgvm03QL1u2\nLEnSrVu3N1zfunzp0qWbbCYAAABoL5tN0AMAAMA7yWYT9K1H4FuP1P+z1uWeRQ8AAMDmoEM8tq4t\n1NXVJVn3NfKty9d1jf0bmTx5cqZMmbLOdf/4utBWFr/wYmpqaio9BpuhF1+0b9H27Fe0F/sW7WHx\nCy96/067qa+vX+e6kSNHvun6DbXZBP3AgQOTJHPmzFlr3YoVKzJv3rx06dIlu++++3pvs76+/i1/\n6a0344O2UlNTk4Mn/L7SYwAAbHbuGPV+799pc60fErUe9N2Uijvlvrm5OQ0NDVm0aNEay/v06ZNB\ngwalsbExv/zlL9dYN2nSpKxcuTLDhg1LdXX1phwXAAAA2kWHOEL/8MMP5+GHH06SLFmyJEkyb968\n/Nd//VeSZKuttsonP/nJJMkLL7yQsWPHZrvttss111yzxnZGjRqV8847L9/73vfyhz/8Idtvv30e\nf/zxzJ07N3V1dTnhhBM24U8FAAAA7adDBP2CBQtyzz33rLGssbExjY2NSZLevXuvDvpWVVVVa22n\nT58+ufTSSzNp0qTMmjUrs2bNSm1tbY444oiMHDlynY+0AwAAgNJUtbS0tFR6iJK5Boe25hp6AID2\ncceo92f58uWVHoPNTCVvtFjcNfQAAACAoAcAAIAiCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIAC\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAA\nKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcA\nAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAJ1rvQA/+iFF17IxIkTM3v27Lz66qupra3N4MGDc9xxx6V79+7rtY3Ro0dn8eLF\nb7iutrY248ePb8uRAQAAoCI6TNAvWrQoX/nKV/Lyyy9n8ODBqaury5NPPplp06Zl9uzZGTduXHr0\n6LFe2+rWrVuOOOKItZZ37dq1rccGAACAiugwQT9hwoS8/PLLOe2003LIIYesXn7TTTfltttuy8SJ\nEzNq1Kj12lb37t0zcuTI9hoVAAAAKq5DXEO/aNGizJkzJ717914j5pOkvr4+Xbp0ycyZM7Nq1aoK\nTQgAAAAdS4c4Qv/oo48mSQYNGrTWuq5du2aPPfbInDlzMn/+/Oy5555vub2mpqb85je/yeLFi9Ol\nS5fsvPPO6d+/fzp16hCfXwAAAMBG6xBB39DQkCTp16/fG67v169f5syZk4ULF65X0C9ZsiTXXHPN\nGst69+6dz3zmMxkwYMDGDwwAAAAV1iGCftmyZUn+fjO7N9K6fOnSpW+5rf333z/9+/fPjjvumK5d\nu6axsTG//OUvM3369FxyySW5+OKLs9NOO7Xd8AAAAFABm9056CNHjszAgQPTs2fPVFdXZ4cddsio\nUaNy5JFHZtWqVZk8eXKlRwQAAICN1iGCvvUIfOuR+n/Wunx9n0X/Rg466KAkyWOPPbbB2wAAAICO\nokOccl9XV5ckWbhw4Ruub12+rmvs10fPnj2TJCtXrlzv75k8eXKmTJmyznXJ/84ObeXFF1+s9AgA\nAJst799pL/X19etcN3LkyDddv6E6RNAPHDgwSTJnzpy11q1YsSLz5s1Lly5dsvvuu2/wa8yfPz9J\n0qdPn/X+nvr6+rf8pbfe0A/aSk1NTaVHAADYbHn/Tltr/ZCoEpd3d4hT7vv06ZNBgwatvoHdP5o0\naVJWrlyZYcOGpbq6OknS3NychoaGLFq0aI2vfe65597wCHxjY2NuuOGGJMm+++7bTj8FAAAAbDod\n4gh9kowaNSrnnXdevve97+UPf/hDtt9++zz++OOZO3du6urqcsIJJ6z+2hdeeCFjx47Ndtttt8bj\n6e67777ceuut6d+/f7bddtvU1NRk0aJF+d3vfpempqZ84AMfyFFHHVWJHw8AAADaVIcJ+j59+uTS\nSy/NpEmTMmvWrMyaNSu1tbU54ogjMnLkyDd8pF1VVdUafx84cGAWLlyYp59+OvPmzcvKlSvTvXv3\n9O/fP8OGDXN0HgAAgM1GVUtLS0ulhyiZa3BoazU1NTl4wu8rPQYAwGbnjlHvz/Llyys9BpuZSt5o\nsUNcQw8AAAC8PYIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiTo\nAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBA\ngh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAA\nCiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIe\nAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok\n6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACg\nQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAK1LnS\nA/yjF154IRMnTszs2bPz6quvpra2NoMHD85xxx2X7t27b/LtAAAAQEfVYYJ+0aJF+cpXvpKXX345\ngwcPTl1dXZ588slMmzYts2fPzrhx49KjR49Nth0AAADoyDpM0E+YMCEvv/xyTjvttBxyyCGrl990\n00257bbbMnHixIwaNWqTbQcAAAA6sg5xDf2iRYsyZ86c9O7de40IT5L6+vp06dIlM2fOzKpVqzbJ\ndgAAAKCj6xBB/+ijjyZJBg0atNa6rl27Zo899sjKlSszf/78TbIdAODN1WzZKQe+Z+scN6h3DnzP\n1qnZskO8pQCAd5QO8a9vQ0NDkqRfv35vuL51+cKFCzfJdgCAdTt+wNaZfOz/ydjmp/Jv/+8XGdv8\nVCYf+39y/ICtKz0aALyjdIhr6JctW5Yk6dat2xuub12+dOnSTbIdAOCNHT9g63yyd3O23WdItvjL\nX5IkPZM077hjPvmTnybZOpPmvlDRGQHgnaJDHKEHADq+mi075aRB22XbY49eHfOttvjLX7LtsUfn\nE+/bLl07e3sBAJtCh/gXt/XIeesR9n/WuvytniHfVtsBANa2z8616fTgg2vFfKst/vKXdHroweyz\ny7s28WQA8M7UIU65r6urS7Lua9tbl6/r2vi23k6ryZMnZ8qUKetc94+vCW3lxRdfrPQIAG+oV7fO\n6fr/5r3p19TMn5etP7j7JpoI4O3z/p32Ul9fv851I0eOfNP1G6pDBP3AgQOTJHPmzFlr3YoVKzJv\n3rx06dIlu+/+5m8Q2mo7rerr69/yl956Iz5oKzU1NZUeAeANvbjstazYY4/0fJOvWb77HnlhWdMm\nmwng7fL+nbbW+iFR60HfTalDnHLfp0+fDBo0KI2NjfnlL3+5xrpJkyZl5cqVGTZsWKqrq5Mkzc3N\naWhoyKJFizZqOwDA+rv3mSV5fe+907zjjm+4vnnHHfP6v+6dexe8tIknA4B3pqqWlpaWSg+RJIsW\nLcp5552Xl156KR/60Iey/fbb5/HHH8/cuXNTV1eXcePGpUePHkmS559/PmPGjMl2222Xa665ZoO3\n0xZ8wkdbq6mpycETfl/pMQDe0Oq73P/TjfGad9wxi3/y0/xP4xbucg90WHeMen+WL19e6THYzFTy\nMo4Occp98vej65deemkmTZqUWbNmZdasWamtrc0RRxyRkSNHvuGj6KqqqtpkOwDA+vl7rG+dk+69\nP1UPPpia+fOyfPc90rL33vnBnOfFPABsQh3mCH2pHKGnrTlCD5SgZstOGbrzu7J1ty3zwrKm3Lvg\npax47fVKjwXwphyhpz04Qg8AFGV50+uZ8YSncgBAJXWIm+IBAAAAb4+gBwAAgAIJegAAACiQoAcA\nAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAoUOdKD9Bq3rx5mTp1ah5//PGsWrUq/fr1y/77759DDz00nTqt\n3+cOzz//fMaMGbPO9UOHDs3nPve5thoZAAAAKqZDBP3DDz+cK6+8MtXV1RkyZEh69OiRRx55JDfe\neGPmzZuXsWPHvq3t7bLLLhk8ePBay3fccce2GhkAAAAqquJBv3z58owfPz6dOnXKBRdckF133TVJ\ncsIJJ+TCCy/MAw88kPvuuy9Dhw5d723uvPPOGTlyZHuNDAAAABVX8Wvo77///rzyyivZZ599Vsd8\nknTu3DkMWv4aAAAfd0lEQVTHH398kmT69OmVGg8AAAA6pIofoX/00UeTJHvttdda6wYMGJDq6urM\nmzcvr732Wjp3Xr9xX3zxxdx555155ZVXstVWW2X33XfPTjvt1KZzAwAAQCVVPOgbGhqSJP369Vtr\nXadOndK7d+88++yzaWxsTF1d3Xptc86cOZkzZ84aywYMGJDRo0dn22233fihAQAAoMIqHvTLli1L\nknTr1u0N17cuX7p06Vtuq0uXLjn22GPzr//6r+ndu3eS5M9//nNuvvnm/PGPf8y4ceNy+eWXp7q6\nuo2mBwAAgMpok6AfPXp0Fi9evN5fv++++77p4+U2VM+ePVNfX7/Gsve+970599xzc9555+WJJ57I\njBkzcthhh7X5awMAAMCm1CZB37dv37d11LtXr16r/7v1CHzrkfp/1rq8e/fuGzxfp06dMmLEiDzx\nxBN57LHHBD0AAADFa5OgP++88zb4e+vq6vLUU09l4cKFa9zlPklef/31NDY2Zosttlh9Cv2G6tmz\nZ5Jk5cqV6/09kydPzpQpU9a5Lsl6X9cP6+vFF1+s9AgAAJst799pL/98tvg/Gjly5Juu31AVv4Z+\nzz33zG9/+9vMmjVrrWfNz507N6tWrcqAAQPW+w736zJ//vwkeVsfDNTX17/lL731pn7QVmpqaio9\nAgDAZsv7d9pa64dErQd9N6WKP4f+wx/+cLbaaqvce++9eeqpp1Yvb2pqysSJE5MkBx988Brfs2zZ\nsjQ0NGTJkiVrLH/66afT0tKy1mv84Q9/yG233Zbk79fvAwAAQOkqfoS+pqYmZ5xxRq688spccMEF\nGTp0aHr06JFHHnkkDQ0NGTJkSIYMGbLG9zz00EO59tprM3z48Hz2s59dvfymm27KwoULs/vuu2eb\nbbZJ8ve73P/xj39MkpxwwgnZfffdN90PBwAAAO2k4kGfJIMHD86FF16YqVOn5qGHHkpTU1P69u2b\nk08++U1vYFdVVbXG34cNG5aHHnooTz31VGbPnp3XXnsttbW1GTp0aA455JC8973vbe8fBQAAADaJ\nqpY3Oked9eYaHNpaTU1NDp7w+0qPAQCw2blj1PuzfPnySo/BZqaSN1qs+DX0AAAAwNsn6AEAAKBA\ngh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAA\nCiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIe\nAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok\n6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACg\nQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECdKz1Ac3NzfvWrX2XBggVZsGBB\nnn322TQ3N+eMM87IAQccsEHbnDdvXqZOnZrHH388q1atSr9+/bL//vvn0EMPTadOPsMAAACgfBUP\n+pUrV+bGG29MktTW1qZXr15ZvHjxBm/v4YcfzpVXXpnq6uoMGTIkPXr0yCOPPJIbb7wx8+bNy9ix\nY9tqdAAAAKiYigd9dXV1zj777Oyyyy6pra3NzTffnClTpmzQtpYvX57x48enU6dOueCCC7Lrrrsm\nSU444YRceOGFeeCBB3Lfffdl6NChbfkjAAAAwCZX8fPPO3funL322iu1tbUbva37778/r7zySvbZ\nZ5/VMd/6Gscff3ySZPr06Rv9OgAAAFBpFQ/6tvToo48mSfbaa6+11g0YMCDV1dWZN29eXnvttU09\nGgAAALSpzSroGxoakiT9+vVba12nTp3Su3fvNDc3p7GxcVOPBgAAAG1qswr6ZcuWJUm6dev2hutb\nly9dunSTzQQAAADtoU1uijd69Oi3dWf6fffdN2PGjGmLlwYAAIB3pDYJ+r59+6a6unq9v37rrbdu\ni5ddS+sR+NYj9f+sdXn37t3b5fUBAABgU2mToD/vvPPaYjMbra6uLk899VQWLly4xl3uk+T1119P\nY2Njtthii/Tu3Xu9tjd58uR1PkJv8uTJq18T2tLiF17MHaPeX+kxAAA2O80t3r/Tfurr69e5buTI\nkW+6fkNV/Dn0bWnPPffMb3/728yaNWutZ83PnTs3q1atyoABA9K58/r92PX19W/5S2+9ER+0lbq6\nOvsV7cK+RXuwX9Fe7Fu0B/sV7aH1Q6LWg76bUpE3xVu2bFkaGhqyZMmSNZZ/+MMfzlZbbZV77703\nTz311OrlTU1NmThxYpLk4IMP3qSzAgAAQHvoEEfob7nlltWflC1YsCBJcvfdd+dPf/pTkuS9731v\nDjjggNVf/9BDD+Xaa6/N8OHD89nPfnb18pqampxxxhm58sorc8EFF2To0KHp0aNHHnnkkTQ0NGTI\nkCEZMmTIpvvBAAAAoJ10iKCfPXt25s6du8ay+fPnZ/78+av//o9B36qqqmqtZYMHD86FF16YqVOn\n5qGHHkpTU1P69u2bk08+OYcddljbDw8AAAAVUNXS0tJS6SFK5hoc2ppru2gv9i3ag/2K9mLfoj3Y\nr2gPlbzRYpHX0AMAAMA7naAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAANgAzc3NFX19Qb+RLrnkkqxcubLSYwAAALAJPf300zn22GMrOoOg30jXXHNNjjji\niPzxj3+s9CgAAAC0s5aWltx444056KCD8vDDD1d0FkG/kXbZZZc89thjOfLII3PVVVfltddeq/RI\nAAAAtIOGhoZ8/OMfzznnnJPly5fnYx/7WEXnEfQbafr06Tn11FPT1NSUyy67LB/72MfyxBNPVHos\nAAAA2khLS0umTJmSESNGZObMmenVq1e++93v5jvf+U5F5xL0G6lbt2752te+lh//+Mepq6vL73//\n+xxyyCGZMGFCXn/99UqPBwAAwEZYvHhxTj/99Hzuc5/Lyy+/nIMOOih33XVXjjrqqEqPJujbyrBh\nwzJjxowcd9xxWbFiRb761a+mvr4+f/nLXyo9GgAAABtg2rRpOeCAAzJt2rT06NEjV155Zb73ve+l\nd+/elR4tiaBvUz179sy3vvWt3HDDDdl2221z//3358ADD8yPf/zjtLS0VHo8AAAA1sNLL72Uf//3\nf8+oUaPyt7/9LUOHDs2MGTNy/PHHp6qqqtLjrSbo28EhhxySu+66K4cffnheffXVnHXWWTn55JOz\naNGiSo8GAADAm5g5c2ZGjBiRn/zkJ+natWvGjRuXSZMmZYcddqj0aGsR9O1km222yX//93/n6quv\nzrve9a7MmDEjBxxwQH72s59VejQAAAD+ybJly3L22WfnxBNPzMKFC/P+978/d9xxR0477bR06tQx\n07ljTrWZqKqqyjHHHJMZM2Zkv/32y5IlS/LZz342n/nMZ/LCCy9UejwAAACSPPzwwznooINy0003\nZcstt8yXv/zl3HLLLdltt90qPdqbEvSbQL9+/fKDH/wgl156abp165af//znGTFiRH7xi1+4th4A\nAKBCli5dmq9+9as5+uijs2DBgvTv3z+33XZbzjzzzHTu3LnS470lQb+JVFVV5ZOf/GTuvPPO7L33\n3mlsbMy//du/5eSTT86zzz5b6fEAAADeUe64447st99+mTBhQqqqqjJmzJjcdtttGThwYKVHW2+C\nfhPbeeedM2XKlFxyySXp2bPn6tPxx48fn9dee63S4wEAAGzW/vrXv+b000/PqaeemoaGhgwaNCi3\n3357zj777HTp0qXS470tgr4COnXqlE996lP59a9/naOOOirLly/PRRddlCOPPDJz5syp9HgAAACb\nnebm5nz/+9/Pfvvtl9tvvz3dunXLBRdckF/84hd53/veV+nxNoigr6A+ffrku9/9bm666abssMMO\n+cMf/pAjjjgi559/fl599dVKjwcAALBZmDt3bj760Y/m3HPPzSuvvJKDDz44v/71r3P66acXca38\nugj6DmDEiBG5++67c8YZZyRJrr/++uy///654447KjwZAABAuZYvX56vf/3rOeyww/L73/8+ffv2\nzXXXXZcbbrgh22+/faXH22iCvoPo1q1bzj///EybNi2DBg1KQ0NDTj311Jx++ulZuHBhpccDAAAo\nyj333JMRI0bkO9/5Tpqbm3PKKafk7rvvzuGHH56qqqpKj9cmBH0Hs+eee+bWW2/NhRdemG7duuX2\n22/P8OHDM378+DQ1NVV6PAAAgA5t4cKFOeOMM/Lxj388zzzzTPr375+f/exnufjii9OzZ89Kj9em\nBH0HtMUWW2TUqFH59a9/nUMPPTRLly7NRRddlMMOOywPPfRQpccDAADocJqamjJ+/PgMHz48t956\na2pqanLOOedk2rRp+eAHP1jp8dqFoO/Att9++1x//fW58cYbs9NOO+Wxxx7L0UcfnbFjx+Zvf/tb\npccDAADoEB566KEceuihueiii7J06dIcdthhueeeezJ69OhsueWWlR6v3Qj6Ahx44IG566678vnP\nfz7V1dWZPHlyhg0blv/5n/9Jc3NzpccDAACoiMWLF2fs2LE5+uij86c//Sk77bRTbrzxxkyYMGGz\nuOndWxH0haipqcmXvvSlzJgxI8OHD8+SJUvy5S9/OR/5yEc8ux4AAHhHaW5uzk033ZRhw4Zl8uTJ\nqa6uztixY3PXXXflwAMPrPR4m4ygL8y73/3u/PCHP8z48ePTt2/fzJo1K4cffnjOPffcvPTSS5Ue\nDwAAoF3NmTMnH/nIR3L22WfnpZdeyn777ZcZM2bkrLPOSk1NTaXH26QEfYGqqqpy5JFH5p577skZ\nZ5yRTp065fvf/36GDRuWH/7wh07DBwAANjvPP/98/uM//iOHH354/n979x5Tdf3HcfwlKKAiO4Ai\nUiY1h1yccy0sUVFwSk5baxJYrumazRSWealmelTGvM3NrdYyf7OLllNE0TWNnJpaVgazcZBQkBCd\nwkCWpnnhJr8/GEzEG/A958v38Hz8pZ9z9jnvoy/fnjfne8nLy1NwcLA2b96s7777Ts8995zZ5ZmC\ngd7CfH19tWLFCh08eFAvvviiqqur9eGHH2ry5Mk6duyY2eUBAAAAQKfdvn1bn376qcaMGaPt27fL\nw8ND7777ro4fP65p06a5zT3lO6Kn2QU0NDTo4MGDKisrU1lZmS5duqSGhgbNnTtX8fHx7drrypUr\nSk1NfejjMTExWrBgQWdL7nIiIiK0Z88eff/991q7dq3Onj2rmTNnKi4uTna7XcOGDTO7RAAAAABo\nl7t372rv3r1at26dysvLJUmTJk3S8uXLNXToUJOr6xpMH+hramq0detWSZLNZpO/v7+qq6s7tWdo\naKiio6PbrA8ePLhT+3ZlPXr00KuvvqqEhAR9/fXX+uSTT3T06FEdP35cb7zxhj744AMNGDDA7DIB\nAAAA4LH++OMPpaWlyeFwSJKioqK0YsUKjR071uTKuhbTB3ovLy8tXbpUoaGhstlsyszM1O7duzu1\n55AhQ5SYmGhQhdbi4+OjefPmKSkpSRs3btS3336r7du3a9++fUpNTdU777zT7S4UAQAAAMAaSktL\ntWbNGmVnZ0uSBg4cqI8++kiJiYny9PQ0ubqux/Rz6Hv27KmRI0fKZrOZXYpbCQwM1OrVq/XTTz9p\n0qRJunnzptavX6/Y2Fjt2bNHd+/eNbtEAAAAAJAkXb16VStXrlR8fLyys7PVu3dvLV68WCdOnFBy\ncjLD/EOYPtA7w9WrV3X48GHt3btXhw8f1sWLF80uyTRDhw7VN998o4yMDEVFRam8vFzvvfeepk2b\nppMnT5pdHgAAAIBurLa2Vv/73/80duxYbdmyRfX19UpOTtaJEye0aNEi9enTx+wSuzTTD7l3hvz8\nfOXn57dai4yMVEpKivr3729SVeYaO3assrOztXv3bq1fv14Oh0PTp0/XlClT9PHHH3fb2zwAAAAA\ncL3Gxkb98MMPWrNmjcrKyiQ1zSx2u13Dhw83tzgLcauB3tvbW9OnT9eoUaMUFBQkSbp48aIyMzNV\nUFCg9PR0bdiwQV5eXiZXag5PT08lJyfrlVde0RdffKHPP/9c2dnZOnTokGbNmqWFCxfK39/f7DIB\nAAAAuLG8vDylpaUpJydHUtNRxXa7XRMnTuzWt6DrCEMG+pSUlHZdmX7cuHGPvL1cR/n5+SkpKanV\nWnh4uJYtWya73a6SkhIdOXJEU6ZMMfy1raRPnz5atGiR3nzzTW3YsEEZGRn68ssvtWfPHi1YsECz\nZ8/utj/0AAAAAOAcly9f1tq1a7V3715JUkBAgBYvXqyZM2eqV69eJldnTYYM9MHBwe0aAAMCAox4\n2Sfm4eGhiRMnqqSkRGfOnDF0oA8JCTFsL1cLCQnRjh07tGPHDrNLwX2snCt0bWQLzkCu4CxkC85A\nrswTEhKirKwss8twK4YM9Ha73YhtnMrPz09S033vn9SuXbseegu9Xbt2GVIXAAAAAMD67j9a/F6J\niYmPfLyj3Ooc+kcpLi6WpJZz659EUlLSI//Qk5KSGOxhOHIFZyFbcAZyBWchW3AGcgVnMStblrxt\n3a1bt1ReXq5r1661Wj9//rwaGxvbPP/06dM6cOCApKbz9wEAAAAAsLou8Q39vn37VF5eLkkttyw4\nevSozp49K6npwnbx8fEtz8/JydGmTZs0fvx4zZ8/v2V927ZtqqioUFhYmAIDAyU1XeW+oKBAkjRj\nxgyFhYW54i0BAAAAAOBUXWKgdzgcKiwsbLVWXFzccpi8pFYDfbP7b2kQGxurnJwclZaWyuFwqL6+\nXjabTTExMUpISFB4eLhz3gAAAAAAAC7WJQb6lStXtuv5EyZM0IQJE9qsx8XFKS4uzqCqAAAAAADo\nuix5Dj0AAAAAAN0dAz0AAAAAABbkuWrVqlVmF2FVjY2NioqKMrsMuBlyBWchW3AGcgVnIVtwBnIF\nZzErWz0aH3SfNwAAAAAA0KVxyD0AAAAAABbEQA8AAAAAgAUx0AMAAAAAYEEM9AAAAAAAWBADPQAA\nAAAAFsRADwAAAACABTHQAwAAAABgQT3NLqCra2ho0MGDB1VWVqaysjJdunRJDQ0Nmjt3ruLj49u1\n15UrV5SamvrQx2NiYrRgwYLOlgwLMDJXzYqKipSVlaVz586ptrZWgwYNUlxcnF5++WV5ePCzu+7G\niDzQs7qnf/75Rzt37pTD4dB///0nm82m6Ohovf766+rbt6/L94F7MCIPKSkpqq6ufuBjNptNmzdv\nNrJkWMDJkydVWFioCxcuqKysTHfu3NG4ceMe+X/Xw9Cz0MyoXLmqZzHQP0ZNTY22bt0qqekP3t/f\n/6F/MU8qNDRU0dHRbdYHDx7cqX1hHUbnKjc3Vxs3bpSXl5dGjx4tX19fnTp1Slu3blVRUZEWLlxo\nVOmwAKPzQM/qPiorK7V8+XJdv35d0dHRCgkJ0d9//63s7Gw5HA6lp6fL19fXZfvAPRiZhz59+mjq\n1Klt1n18fIwuGxaQlZWlCxcuyMfHR4GBgbp8+XKH9qFn4V5G5UpyTc9ioH8MLy8vLV26VKGhobLZ\nbMrMzNTu3bs7teeQIUOUmJhoUIWwIiNzdfv2bW3evFkeHh5atWqVnn32WUnSjBkzlJaWppMnT+q3\n335TTEyMkW8BXZQz8kDP6j62bNmi69ev6+2331ZCQkLL+rZt23TgwAHt3LlTc+bMcdk+cA9G5qFv\n3770I7SYPXu2AgICFBwcrMLCQqWlpXVoH3oW7mVUriTX9CyOw32Mnj17auTIkbLZbGaXAjdiZK5+\n//133bhxQ2PGjGkZ3ppfIzk5WZJ06NChTr8OrIE8oKMqKyuVn5+voKCgVh9oJSkpKUne3t76+eef\nVVtb65J94B7IA5wpMjJSwcHBndqDjOJ+RuTKlfiG3gRXr17V4cOHdePGDfXr109hYWF65plnzC4L\nFvXXX39JkkaOHNnmscjISHl5eamoqEj19fXq2ZN/8u7OGXmgZ3UPzdkZMWJEm8d8fHw0bNgw5efn\nq7i4WMOHD3f6PnAPRuehrq5Ov/zyi6qrq+Xt7a0hQ4YoIiKCa8Wgw+hZcCZX9Cw+3ZsgPz9f+fn5\nrdYiIyOVkpKi/v37m1QVrKq8vFySNGjQoDaPeXh4KCgoSJcuXVJVVZVCQkJcXR5czBl5oGd1D4/K\nTvN6fn6+KioqHvmh1qh94B6MzsO1a9f02WeftVoLCgrSvHnzFBkZ2fmC0e3Qs+BMruhZDPQu5O3t\nrenTp2vUqFEKCgqSJF28eFGZmZkqKChQenq6NmzYIC8vL5MrhZXcunVLUtNFNx6kef3mzZsuqwnm\nMTIP9Kzuxajs0JNwLyPzEBcXp4iICA0ePFg+Pj6qqqrSjz/+qEOHDmnt2rVavXo1Rw+h3ehZcBZX\n9axuMdA/6pYBD9LR2108jp+fn5KSklqthYeHa9myZbLb7SopKdGRI0c0ZcoUw18bxusquYL76SrZ\nomcB6Eruv7DU008/rTlz5sjb21v79+/Xrl27tGTJEpOqA4DWXNWzusVAHxwc3K5vkAICApxYTVse\nHh6aOHGiSkpKdObMGT4cW0RXyVXzT46bf8J8v+Z17qFqHe3Nlr+/f8uvXZEHepZ7Mio79CTcyxV5\nmDRpkvbv368zZ850eA90X/QsuJrRPatbDPR2u93sEh7Lz89PUtP9yWENXSVXISEhKi0tVUVFRaur\nmkvS3bt3VVVVJU9Pz5ZDptH1dSZbrsoDPcv9NF9ToaKi4oGPN68/7DxTo/eBe3BFHuhH6Ax6FlzN\n6J7FJUG7iOLiYkli6EK7NV+gJS8vr81jhYWFqq2t1bBhw7jCfTfhqjzQs9xPVFSUJLW5AKIk3blz\nR0VFRfL29lZYWJhL9oF7cEUemvvRwIEDO7wHui96FlzN6J7FQO8Et27dUnl5ua5du9Zq/fz582ps\nbGzz/NOnT+vAgQOSms6FBR7kYbl66aWX1K9fP/36668qLS1tWa+rq9POnTslSZMnT3ZprTBPR/JA\nz4LU9MFixIgRLRftuVdGRoZqamoUGxvbcjpIQ0ODysvLVVlZ2al94N6MytXly5cf+G1WVVWVvvrq\nK0n0IzwaPQvO0BV6Vo/GB31aQyv79u1ruaVFWVmZLly4oLCwsJZDb8LDwxUfH9/y/GPHjmnTpk0a\nP3685s+f37KelpamiooKhYWFKTAwUFLTFaMLCgokSTNmzNBrr73mqrcFkxmVK0nKzc3Vxo0b1atX\nL8XExMjX11enTp1SeXm5Ro8erffff991bwyma28e6FloVllZKbvdrn///VcvvPCCnnrqKZ07d06F\nhYUKCQlRenq6fH19JUlXrlxRamqqBgwY0OaWPO3ZB+7PiFxlZmZq//79ioiIUP/+/dW7d29VVlbq\nzz//VF1dnZ5//nktWbJEnp6eZr1NmCA3N1e5ubmSmm4P5nA4FBQUpIiICElSv3799NZbb0miZ+HJ\nGZErV/YsjsF9Ag6HQ4WFha3WiouLWw6XkNRq8GrWo0ePVr+PjY1VTk6OSktL5XA4VF9fL5vNppiY\nGCUkJCg8PNw5bwBdklG5kqTo6GilpaUpKytLOTk5qqurU3BwsGbNmsUFy7qhjuaBnoWBAwdq3bp1\nysjIUF5envLy8mSz2TR16lQlJiY+8LZOD+pJHdkH7suIXEVFRamiokLnz59XUVGRampq1LdvX0VE\nRCg2NpZv57upsrIyHT9+vNVaVVWVqqqqJDWdFtY8eDWjZ+FxjMiVK3sW39ADAAAAAGBBnEMPAAAA\nAIAFMdADAAAAAGBBDPQAAAAAAFgQAz0AAAAAABbEQA8AAAAAgAUx0AMAAAAAYEEM9AAAAAAAWBAD\nPQAAAAAAFsRADwAAAACABTHQAwAAAABgQQz0AAAAAABYEAM9AAAAAAAWxEAPAAAAAIAFMdADAAAA\nAGBBDPQAAAAAAFgQAz0AAAAAABbEQA8AAAAAgAX9HzFg8OS/6q1mAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1076cd278>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0. 0.] 16.0\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3Wd4VHXChvFn0guE0AIEQksWjaCuKOLqgmVRWcVXUeBV\nERIgGEpQmiJSA9IEUSD0HkEBe0fXVRAVXVgFVFhKIJQACSEJIX0yc94PvrDrCkpJ8j+T3L/r8suM\nDDdcEzJPZs45DsuyLAEAAAAAAI/iZToAAAAAAABcPAY9AAAAAAAeiEEPAAAAAIAHYtADAAAAAOCB\nGPQAAAAAAHggBj0AAAAAAB6IQQ8AAAAAgAdi0AMAAAAA4IEY9AAAAAAAeCAGPQAAAAAAHohBDwAA\nAACAB2LQAwAAAADggRj0AAAAAAB4IAY9AAAAAAAeyMd0gCR988032rlzpw4ePKjU1FQVFRWpXbt2\nSkhIuKjHGThwoDIzM895X2hoqBYuXFgWuQAAAAAAGGeLd+jffPNNffzxx0pNTVXt2rUv67GCgoLU\ntWvXX/133333lVHtv61bt67MHxPgeYXywnML5YHnFcoLzy2UB55XKC+mnlu2GPSxsbGaNWuWVq5c\nqbi4uMt6rODgYHXp0uVX/3Xq1KmMav/t9ddfL/PHBHheobzw3EJ54HmF8sJzC+WB5xXKi6nnli0+\ncn/VVVeZTgAAAAAAwKPYYtCXJafTqU2bNikzM1P+/v5q0qSJoqOj5eVliw8jAAAAAABQJirdoM/J\nyVFSUtIvbgsLC1P//v35JAAAAAAAoNKoVIP+9ttvV3R0tCIiIhQQEKCMjAytX79ef/vb3zRlyhRN\nmjRJjRs3Np0JAAAAAMBlq1SfQ+/SpYtatmypkJAQ+fn5qVGjRoqLi1OnTp1UUlLCWS0BAAAAAJWG\nw7Isy3TEf9q5c6cSExMv6Tr053P8+HE9+eSTqlatmpYuXVomjwkAAAAAgEmV6iP35xMSEiJJKi4u\nvqhft27duvNefoB3+wEAAAAAZ3Tr1u2893Xp0uU3779UVWLQ79mzR5JUr169i/p13bp1+92/9KNH\nj15yF3Au4eHhZf68SklJ0f3336/s7Gx1795d06ZNk8PhKNPfA/ZXHs8t2E9hYaHuuece7dmzR927\nd9fzzz9frr8fzyuUF55bKA88r1AewsPDJZl509fjjqF3uVw6evSo0tPTf3F7WlraOd+Bz8jI0LJl\nyyRJ7dq1q5BGwE4yMzPVo0cPZWdn6y9/+YsmT57MmAcqsQkTJmjPnj2KiorS+PHjTecAAIByZIt3\n6Lds2aItW7ZI+vmyc5K0e/duzZs3T5JUvXp19ejRQ5KUlZWlIUOGqG7dur+4PN3XX3+t999/X9HR\n0apTp44CAwOVnp6u7777Tk6nU61bt9Z9991XwX8ywKyCggLFxsbq4MGDuuaaazR//nz5+Njiyx5A\nOfj444+VnJwsPz8/zZ07V0FBQaaTAABAObLFK/vU1FRt3LjxF7dlZGQoIyND0s/XkT8z6M/473cY\nW7ZsqWPHjunAgQPavXu3iouLFRwcrOjoaLVv355351HluFwuDRw4UN9//70iIiK0cuVKBQcHm84C\nUE6OHTumoUOHSpJGjhypVq1aGS4CAADlzXZnufc0HIODslYWx3ZZlqVRo0Zp5cqVCg0N1TvvvKOo\nqKgyKoSn4rjBysvtduuRRx7Rl19+qVtvvVWrVq2Sl1fFHFXH8wrlhecWygPPK5SHM8fQm+Bxx9AD\n+H3z58/XypUr5e/vr+XLlzPmgUpu4cKF+vLLL1W7dm299NJLFTbmAQCAWXzHByqZt99+W5MmTZLD\n4dCsWbN04403mk4CUI62b9+uqVOnSpJmzpypsLAww0UAAKCiMOiBSmTz5s0aMmSIJGnMmDGcCBKo\n5PLz8zVw4ECVlpaqd+/e6tChg+kkAABQgRj0QCWxd+9e9enTRyUlJerdu7cef/xx00kAytnYsWN1\n4MABXXnllRo1apTpHAAAUMEY9EAlkJmZqZ49e+rUqVPq2LGjxo8fz7XmgUruvffe05o1axQQEKC5\nc+cqICDAdBIAAKhgDHrAwxUVFal37946dOiQrr32WiUlJcnb29t0FoBylJaWphEjRkj6+fCaK6+8\n0nARAAAwgUEPeDC3262hQ4fqn//8p8LDw7V8+XIFBgaazgJQjlwulwYNGqRTp06pQ4cOiomJMZ0E\nAAAMYdADHmzGjBl65513VK1aNSUnJ6tevXqmkwCUszlz5ujbb79VWFiYZs6cyeE1AABUYQx6wEOt\nW7dOs2bNkpeXlxYsWKDo6GjTSQDK2datWzVz5kxJ0qxZs1S7dm3DRQAAwCQGPeCBNm/erKefflqS\nNHHiRN1+++2GiwCUt9zcXCUkJMjlcqlfv35q37696SQAAGAYgx7wMCkpKYqLi5PT6VRcXJxiY2NN\nJwGoAKNGjdLhw4fVqlWrsyfEAwAAVRuDHvAgWVlZ6tmzp3JycnTXXXdp7NixppMAVIDXXntNb775\npgIDAzV37lz5+fmZTgIAADbAoAc8RHFxsfr06aPU1FS1atWKy9MBVcS+ffs0cuRIST8fYhMVFWW4\nCAAA2AWDHvAAlmVp+PDh+sc//qH69etrxYoVCg4ONp0FoJwVFhaqX79+Kiws1IMPPqiHH37YdBIA\nALARBj3gAV566SW9+eabCgoK0sqVK9WgQQPTSQAqwPjx47Vr1y41a9ZMU6ZM4RJ1AADgFxj0gM29\n9dZbmjFjhry8vDRv3jy1atXKdBKACvDOO+9o1apV8vf314IFC1StWjXTSQAAwGYY9ICN/eMf/9DQ\noUMlSePGjdOdd95puAhARUhNTT17acqxY8fygzwAAHBODHrAplJTU9W7d2+VlJQoNjZWffr0MZ0E\noAIUFxerf//+ysvL0z333KOYmBjTSQAAwKYY9IAN5eTkqGfPnsrOztYdd9yhxMREjp0FqohJkyZp\nx44dioiI0IwZM/jaBwAA58WgB2ympKREcXFxSklJUXR0tObPny8fHx/TWQAqwCeffKKlS5fKx8dH\n8+bNU40aNUwnAQAAG2PQAzZiWZbi4+O1efNmhYWFaeXKlZwIC6gi0tLSNGTIEEnSyJEj1bp1a8NF\nAADA7hj0gI0kJSVpxYoVCggI0IoVK9SwYUPTSQAqgNPp1IABA5STk6O//OUvevzxx00nAQAAD8Cg\nB2zi3Xff1dSpU+VwODR37lxde+21ppMAVJAZM2Zo69atql+/vl566SV5efHtGQAA/D5eMQA28M9/\n/lODBw+WJE2fPl0dO3Y0XASgomzYsEFJSUny8vLSvHnzVKtWLdNJAADAQzDoAcMOHTqkXr16qbi4\nWN27dz973XkAld/x48f1xBNPSJKGDx+utm3bGi4CAACehEEPGHTq1CnFxMTo5MmTat++vSZNmsQl\nqoAqwuVyKSEhQSdPnlS7du2UkJBgOgkAAHgYBj1giNPpVHx8vPbs2aMWLVpo4cKF8vX1NZ0FoILM\nmjVLmzdvVt26dTV79mx5e3ubTgIAAB6GQQ8YYFmWRo0apU2bNqlOnTpKTk5WSEiI6SwAFeSrr77S\nzJkz5XA4NHv2bIWFhZlOAgAAHohBDxiwcOFCrV69WgEBAVq+fLkiIiJMJwGoIJmZmRo0aJAsy9IT\nTzyh9u3bm04CAAAeikEPVLCPPvpIzz33nKSfP3LbunVrw0UAKorb7dbgwYOVnp6utm3bchJMAABw\nWRj0QAXatm2bEhISZFmWRo4cqU6dOplOAlCBFixYoM8//1w1a9ZUUlKSfHx8TCcBAAAPxqAHKkha\nWpp69eqloqIiPfzwwxo4cKDpJAAVaMuWLZo6daok6aWXXlJ4eLjhIgAA4OkY9EAFOH36tGJiYpSR\nkaGbb75ZU6ZM4fJ0QBWSnZ2tgQMHyuVyKT4+Xh06dDCdBAAAKgEGPVDOSktL1b9/f+3atUtRUVFa\nvHix/Pz8TGcBqCCWZWnYsGFKS0vTddddp2eeecZ0EgAAqCQY9EA5sixLY8eO1eeff65atWpp5cqV\nCg0NNZ0FoAItW7ZMH3/8sUJCQjRv3jx+oAcAAMoMgx4oR0uWLNHKlSvl5+enZcuWqWnTpqaTAFSg\n7du3a+LEiZKkGTNmqHHjxoaLAABAZcKgB8rJJ598osTEREnSiy++qDZt2hguAlCRcnNz1b9/fzmd\nTsXGxuree+81nQQAACoZBj1QDn788UcNHDhQlmVp+PDheuCBB0wnAahAlmVpxIgROnjwoFq2bKkx\nY8aYTgIAAJUQgx4oY0ePHlVMTIwKCgr00EMPafDgwaaTAFSwV155Re+++66Cg4M1f/58BQQEmE4C\nAACVEIMeKEP5+fmKjY3V8ePHddNNN2n69Olcng6oYnbt2qWxY8dKkqZNm6bIyEjDRQAAoLJi0ANl\nxOVyacCAAfrpp5/UrFkzLV68WP7+/qazAFSggoIC9evXT0VFRXr44YfVuXNn00kAAKASY9ADZSQx\nMVGffvqpQkNDlZycrFq1aplOAlDBRo0apX379qlFixZnz24PAABQXhj0QBlYsWKFli5dKl9fXy1d\nulTNmzc3nQSggr322mtat26dAgICtGDBAgUFBZlOAgAAlRyDHrhMf//738+ewXr69Om66aabDBcB\nqGj79u3Ts88+K0l67rnndMUVVxguAgAAVQGDHrgMO3fuVP/+/eV2uzV48GB17drVdBKAClZYWKh+\n/fqpoKBAnTt31sMPP2w6CQAAVBEMeuASpaenKyYmRvn5+XrggQc0fPhw00kADEhMTNSuXbvUtGlT\nTZ06lStbAACACsOgBy5BQUGBYmNjdfToUd1www164YUXeBEPVEHvvvuuXn75Zfn5+WnhwoWqVq2a\n6SQAAFCFMOiBi+RyuTRo0CDt2LFDTZo00bJlyxQQEGA6C0AFO3jwoJ5++mlJ0rhx49SqVSvDRQAA\noKph0AMXafLkyVq/fr1CQkKUnJys2rVrm04CUMFKSkrUv39/nT59Wvfcc49iYmJMJwEAgCqIQQ9c\nhFWrVmnBggXy8fHR4sWLFRUVZToJgAGTJ0/W9u3bFRERoRkzZnDIDQAAMIJBD1ygjRs3nr0s1bRp\n0/TnP//ZcBEAEz755BMtXrxYPj4+mjdvnmrUqGE6CQAAVFEMeuAC7N69W/Hx8XK5XEpISOCyVEAV\nlZaWpiFDhkiSRo4cqdatWxsuAgAAVRmDHvgdJ06cUM+ePXX69Gnde++9GjFihOkkAAY4nU4NGDBA\nOTk5uuOOO/T444+bTgIAAFUcgx74DYWFherVq5eOHDmi6667TrNmzZKXF182QFU0Y8YMbd26VfXr\n1+ffAgAAYAu8GgHOw+1268knn9T333+vRo0aafny5QoMDDSdBcCADRs2KCkpSV5eXpo7d65q1apl\nOgkAAIBBD5zPtGnT9MEHH6h69epKTk5W3bp1TScBMCA9PV1PPPGEJGnYsGG66aabDBcBAAD8jEEP\nnMPatWuVlJQkb29vLVy4UFdccYXpJAAGnDkR5smTJ/XnP/9ZgwYNMp0EAABwFoMe+C9ffvmlnn76\naUnSpEmTdOuttxouAmDK7Nmz9fXXX6tOnTqaM2eOvL29TScBAACcxaAH/sO+ffv0+OOPq7S0VPHx\n8erRo4fpJACGbN68WTNnzpTD4dCcOXMUFhZmOgkAAOAXGPTA/8vKylLPnj116tQpdezYUaNGjTKd\nBMCQkydPKiEhQW63W4MGDVL79u1NJwEAAPwKgx6QVFJSor59++rgwYO65ppr+GgtUIW53W4NHjxY\nx48f14033qhhw4aZTgIAADgnBj2qPMuy9Oyzz+qbb75R/fr1tXz5cgUFBZnOAmDIwoUL9dlnnyk0\nNFRz586Vj4+P6SQAAIBzYtCjylu8eLFeffVVBQQEaOnSpapfv77pJACGbN26VVOnTpUkvfjiiwoP\nDzdcBAAAcH4MelRpn332mSZOnChJmjlzpv74xz8aLgJgSk5OjgYMGKDS0lI9/vjjuuuuu0wnAQAA\n/CYGPaqsPXv2aMCAAXK73RoyZIjuv/9+00kADLEsS8OGDVNaWpr++Mc/auTIkaaTAAAAfheDHlVS\nVlaWevXqpdOnT+vee+/V0KFDTScBMGj58uVav369QkJCNH/+fPn5+ZlOAgAA+F0MelQ5JSUlevzx\nx5Wamqqrr75as2bNkpcXXwpAVfXDDz+cPfRm+vTpaty4seEiAACAC8OKQZViWZZGjx6tzZs3q169\nelq2bJkCAwNNZwEwJDc3V/369VNJSYliYmLUqVMn00kAAAAXjEGPKmXZsmVavXq1/P39tXTpUs5g\nDVRhlmVp6NChSk1NVcuWLTV27FjTSQAAABeFQY8qY8OGDRo/frwk6YUXXtB1111nNgiAUYsWLdJH\nH32kkJAQLVq0SAEBAaaTAAAALgqDHlXCvn371L9/f7ndbj3xxBPq3Lmz6SQABm3ZskWTJ0+W9PP1\n5ps2bWo2CAAA4BIw6FHpZWdnKyYmRrm5ufrrX/+qp556ynQSAIMyMzPVr18/lZaWKj4+Xh07djSd\nBAAAcEkY9KjUnE6n4uPjzx4jO3v2bM5oD1RhLpdLCQkJOn78uNq0acP15gEAgEdj2aBSGzt2rL76\n6ivVrVtXy5cvV1BQkOkkAAa9+OKL2rRpk2rXrq358+fL19fXdBIAAMAlY9Cj0lqxYoWSk5PPntG+\nYcOGppMAGLRhwwa99NJLcjgcmjt3rho0aGA6CQAA4LIw6FEpffHFF2cvQTV9+nRdf/31hosAmJSW\nlqaEhARZlqVhw4apXbt2ppMAAAAuG4MelU5KSor69et39ljZhx56yHQSAINKSkrUr18/ZWdn67bb\nbtOTTz5pOgkAAKBMMOhRqeTk5Cg2NlanTp3S3XffrREjRphOAmDYpEmT9N133yk8PFxz5szhxJgA\nAKDS8DEdIEnffPONdu7cqYMHDyo1NVVFRUVq166dEhISLvqxsrKytGbNGm3fvl15eXkKDQ1VmzZt\n1LVrVwUHB5dDPeyitLRU/fr10/79+xUdHc0LdwB6//33tWTJEvn6+mrBggWqVauW6SQAAIAyY4tB\n/+abb+rgwYMKCAhQ7dq1lZaWdkmPk56ertGjRys3N1dt2rRReHi4UlJS9NFHH2n79u2aOHGiqlWr\nVsb1sIvx48dr06ZNqlOnjlasWMEPcIAqLiUlRcOGDZMkjRkzhnNpAACASscWgz42Nla1atVS/fr1\ntXPnTiUmJl7S4yxZskS5ubnq3bu37r777rO3Jycn64MPPtCaNWsUFxdXVtmwkeTkZC1fvlx+fn5a\nsmSJGjVqZDoJgEGFhYWKj49XXl6eOnXqpN69e5tOAgAAKHO2+DzyVVddpfr161/WY6Snp2vHjh0K\nCwv7xZiXpG7dusnf319ffPGFSkpKLuv3gf18+eWXGj16tCRp2rRpatOmjeEiAKaNGjVKu3btUvPm\nzTVjxgw5HA7TSQAAAGXOFoO+LPz000+SpGuuueZX9wUEBOiKK65QcXGx9uzZU9FpKEf79+9XfHy8\nXC6X+vfvr27duplOAmDYmjVrtHbtWgUEBGjRokWqXr266SQAAIByUWkG/dGjRyVJDRo0OOf9Z24/\nduxYhTWhfJ06dUqxsbHKyclRhw4dNHLkSNNJAAz78ccfNWrUKEnSlClTFB0dbbgIAACg/FSaQV9Q\nUCBJCgoKOuf9Z27Pz8+vsCaUn9LSUg0YMEApKSm68sorNXfuXHl7e5vOAmBQbm6u4uPjVVRUpEcf\nfZRP7AAAgEqv0gx6VC0TJkzQhg0bVKtWLa1YsYKrFwBVnGVZGjZsmFJTU9WyZUtNmDDBdBIAAEC5\nqzSD/sw78Gfeqf9vZ27nUmaeb/Xq1Vq6dKl8fX21dOlSRUREmE4CYNjixYv14Ycfqnr16lq0aJEC\nAwNNJwEAAJQ7W1y2riyEh4dLOv8x8mduP98x9ueybt06vf766+e97z9/X1SMDRs26Nlnn5UkLVy4\nUA888IDhorKXmZXNGEG5yM6unM+tb7/9VpMmTZIkzZ07l+PmK1hlfV7BPJ5bKA+ZWdm8fke5+a3D\n/bp06VIuhwNWmkHfsmVLSdKOHTt+dV9RUZF2794tf39/tWjR4oIfs1u3br/7l37mZHwof6mpqerc\nubNKS0sVHx+vu+++u1L+/QcGBuquJd+bzgA8gjMvRztnxau0tFT12nfV7OMNNZuvHwDAeXwSd12l\nfP0Is878kOjMm74VyeM+cu9yuXT06FGlp6f/4vZ69erpmmuuUUZGhtavX/+L+9auXavi4mK1b99e\nfn5+FZmLMpKbm3v2jPZ33HHH2bNYA6i6LLdLB16dLOepTFVr2koN/xpnOgkAAKBC2eId+i1btmjL\nli2SpJycHEnS7t27NW/ePElS9erV1aNHD0lSVlaWhgwZorp16yopKekXjxMXF6cxY8Zo+fLl+uGH\nH9SwYUPt3btXO3fuVHh4uB5++OEK/FOhrLhcLg0cOFB79+5VixYtNG/ePM5oD0BHP12l3L3/lE9w\nqJp3Hy0vb1t8SwMAAKgwtnj1k5qaqo0bN/7itoyMDGVkZEiSwsLCzg76MxwOx68ep169epo6darW\nrl2rbdu2adu2bQoNDdW9996rLl26nPeSdrC35557Tp999plq1qypFStWqHr16qaTABh2as9WHfv7\ny5LDoeaPPiu/GnVNJwEAAFQ4h2VZlukIT8YxOOXr1Vdf1fDhw+Xj46M1a9boT3/6k+mkcscx9MBv\nK8nJ0M6X4lVakKvwu2IV3qHH7/8iAAD08zH0hYWFpjNQyZg80aLHHUOPquObb77RyJEjJUlTpkyp\nEmMewG9zlzqVsnqiSgtyFdKijRrc0d10EgAAgDEMetjSoUOH1LdvXzmdTsXFxenRRx81nQTABo58\nuFj5B3fKt0ZdNXtkpBxefBsDAABVF6+EYDunT59WbGyssrKydNttt2nMmDGmkwDYQNaOjcr48g05\nvLwV+dhY+QbXMJ0EAABgFIMetuJyuZSQkKDdu3crKipK8+fPl4+PLc7dCMCgohNHlPraDElSo079\nVK3JVYaLAAAAzGPQw1amTJmiTz/9VKGhoVqxYoVCQkJMJwEwzFVSpJRViXIXF6jmNbcq7JbOppMA\nAABsgUEP21i7du3Zd+QXLVqkZs2amU4CYAOH3p6jwmP75V+noZp2GXbOy5YCAABURQx62MKWLVv0\nzDPPSPr5uvO33HKL4SIAdpC55SOd3LpeXr7+iuwxXt4BwaaTAAAAbINBD+MOHz6sPn36qKSkRL17\n91aPHlxTGoBUcDRFB9+aLUlq3PlJBTVobrgIAADAXhj0MCovL0+9evXSyZMn1b59e40bN850EgAb\nKC3MU8rLibJKS1SnzV9V54a7TScBAADYDoMexrjdbg0aNEi7du1S8+bNOaM9AEmSZVlKfW2Gik+m\nKbBBpBo/MMh0EgAAgC0x6GHMtGnT9Mknn6hGjRpasWKFQkNDTScBsIGML99Uzo+b5B0QrMge4+Tl\n6286CQAAwJYY9DDi9ddfV1JSkry9vbVgwQJFRkaaTgJgA3mpP+nIBwslSU27PqWAOg0NFwEAANgX\ngx4VbuvWrXrqqackSRMmTFD79u0NFwGwA2dejlJWT5Dldqleuy6qeXU700kAAAC2xqBHhUpLSzt7\nRvuYmBjFxsaaTgJgA5bbpQOvTpbzVKaCm7RUw3v6mk4CAACwPQY9Kkx+fr5iY2OVmZmpP//5z0pM\nTDSdBMAmjv19tXL3/lM+waGKfGyMvLw5QSYAAMDvYdCjQrjdbj3xxBPauXOnmjZtqgULFsjX19d0\nFgAbOLVnq45+miw5HGr+6LPyq1HXdBIAAIBHYNCjQkyfPl3r169XSEiIVq5cqZo1a5pOAmADJTkZ\nOvDKJMmyFN6hp0L+cL3pJAAAAI/BoEe5e+uttzR79uyzZ7SPiooynQTABtyuUqWsnqjSglyFtGij\nBn95zHQSAACAR2HQo1x99913GjZsmCRp/PjxuvXWWw0XAbCLtA8XKf/gTvnWqKtmj4yUw4tvSQAA\nABeDV08oN2fOaF9cXKzHHntMvXr1Mp0EwCayf/hC6ZvekMPLW5GPjZFvcA3TSQAAAB6HQY9yUVBQ\noN69eysjI0M333yznnvuOTkcDtNZAGyg6MQRHVg3XZLUqFO8qjVpabgIAADAMzHoUebcbreefPJJ\n/fjjj2ratKkWLlzIGe0BSJLczmKlrEqUu7hANa9ur7BbHjSdBAAA4LEY9ChzM2fO1Icffqjq1atr\nxYoVqlWrlukkADZx6O3ZKjy2X/51Gqpp1+F8cgcAAOAyMOhRpt555x29+OKL8vLy0vz58/WHP/zB\ndBIAm8jc8pEyt6yXw8dPkT3GyTsg2HQSAACAR2PQo8xs375dQ4cOlSSNHTtWt99+u+EiAHZRcDRF\nB9+aLUlq8uCTCmoQabgIAADA8zHoUSYyMjLUp08fFRUV6ZFHHlFcXJzpJAA2UVqYp5SXE2WVlqhO\nm7+qzg0dTScBAABUCgx6XLbi4mL17dtXx44dU5s2bTR58mSOiwUgSbIsSwdfn6Hik2kKbBCpxg8M\nMp0EAABQaTDocVksy9Lo0aO1detWNWjQQIsXL5afn5/pLAA2kfHlm8r+YZO8A4IV+dhYefn6m04C\nAACoNBj0uCwrV67UK6+8ooCAAC1dulR169Y1nQTAJvJSf9KRDxZKkpp2fUoBdRsZLgIAAKhcGPS4\nZF9//bXGjRsnSZo+fbquvfZaw0UA7MKZl6OU1RNluV2q166Lal7dznQSAABApcOgxyU5fPiw4uPj\nVVpaqv79++vBBx80nQTAJiy3SwfWTJHz1AkFN2mphvf0NZ0EAABQKTHocdEKCgrUq1cvZWVl6fbb\nb9fIkSNNJwGwkWN/X63cPVvlE1xDkd3HyMvbx3QSAABApcSgx0WxLEuDBw/Wrl271KxZM82dO1fe\n3t6mswDYRM6ub3X002TJ4VCzR56VXyjn1QAAACgvDHpclNmzZ+uDDz5Q9erVtWLFCtWoUcN0EgCb\nKDp5VAcfMBbcAAAgAElEQVTWTJYsS+F39VKNFjeYTgIAAKjUGPS4YJ988omef/55ORwOzZkzR1FR\nUaaTANiEq6RIKcnj5CrMU+hVN6vB7Y+YTgIAAKj0GPS4IHv27NGgQYMkSSNGjNCdd95puAiAXViW\npYNvzFThsf3yr9NQTf93hBxefHsBAAAob7ziwu/KyclRr169lJeXp//5n/9RQkKC6SQANpLx9dvK\n+v7v8vILUFTPCfIJrGY6CQAAoEpg0OM3lZaWasCAAUpNTVXLli31wgsvyOFwmM4CYBOnD/ygI+/N\nlyQ17fqUAus3NRsEAABQhTDo8ZumTJmijRs3qlatWlq2bJmCgoJMJwGwiZLck9q/aoIst0v12ndV\nrWtvM50EAABQpTDocV5vvPGGFixYIB8fHy1atEiNGjUynQTAJtylTu1fNUHO01mq3vxaNfprX9NJ\nAAAAVQ6DHue0fft2PfXUU5KkCRMm6E9/+pPhIgB2cuT9BcpL/VG+Neqo+WNj5PD2Np0EAABQ5TDo\n8SsZGRnq3bu3iouL1b17d/Xs2dN0EgAbOfnd35Tx9dtyePsqssd4+VaraToJAACgSmLQ4xeKi4vV\nt29fHT9+XDfeeKOee+45ToIH4KyCo/t08I0XJUmN709QtcbRhosAAACqLgY9zrIsS6NGjdLWrVsV\nHh6uRYsWyc/Pz3QWAJsoLcjVvuTxcjuLVadNR9Vpe6/pJAAAgCqNQY+zVqxYoVdffVUBAQFatmyZ\n6tatazoJgE1Ybpf2vzpZJVnHFNToCjV+4Ek+vQMAAGAYgx6SpK+++krjxo2TJL3wwgu6+uqrDRcB\nsJOjf0tW7u4t8gkKUWSPcfLy5dM7AAAApjHooUOHDik+Pl4ul0sDBw7UAw88YDoJgI3k7Pxax/6+\nSnJ4qXn30fKvWc90EgAAAMSgr/Ly8/PVu3dvZWdn64477tCIESNMJwGwkaITR3RgzVRJUsOOvRXy\nh+sNFwEAAOAMBn0VZlmWBg8erF27dql58+ZKSkqSN9eSBvD/XCWFSnl5vFxF+Qpt1U71b3vYdBIA\nAAD+A4O+Cps1a5Y+/PBDVa9eXcuXL1eNGjVMJwGwCcuydPC1F1R4/IACwhqrWbenOAkeAACAzTDo\nq6iPP/5Y06dPl8PhUFJSkqKiokwnAbCR9E1vKGv75/LyC1Rkz0R5BwSbTgIAAMB/YdBXQbt379ag\nQYMkSc8884w6dOhguAiAnZxO2a4jHy6UJDX73xEKDGtsuAgAAADnwqCvYrKzs9W7d2/l5+fr/vvv\n18CBA00nAbCRkpwTSlk9QXK7Vf+2h1Xz6namkwAAAHAeDPoqpLS0VAMHDlRqaqpatWqlF154gWNi\nAZzlLi1RyqpEleblqHpUazW8u7fpJAAAAPwGBn0VMmXKFG3cuFG1a9fWsmXLFBgYaDoJgI0cfnee\n8g/tkl9omJo/OkoOrnoBAABgawz6KuKtt97SggUL5OPjo0WLFqlhw4amkwDYSObW9TrxzXty+Pgq\nssd4+VYLNZ0EAACA38GgrwJ++OEHDR8+XJKUmJiom266yXARADvJP7JHB998SZLUpPOTCo64wnAR\nAAAALgSDvpI7efKk+vTpo6KiIj3yyCOKiYkxnQTARkrzTynl5fGySp2q0/Ze1WnzV9NJAAAAuEAM\n+krM6XQqPj5eaWlpat26tSZNmsRJ8ACcZbld2v/KJJVkpys44ko1vj/BdBIAAAAuAoO+EpswYYI2\nb96ssLAwLV68WP7+/qaTANhI2sfLlbv3n/IJDlVkj/Hy8vEznQQAAICLwKCvpNauXatly5bJ19dX\nixcvVv369U0nAbCR7B+/1PHPX5UcXmrefbT8QuuaTgIAAMBFYtBXQt99952eeeYZSdLkyZN1ww03\nGC4CYCeFGYd0YO00SVKje/oqJOo6w0UAAAC4FAz6SiYjI0N9+/ZVSUmJevbsqUcffdR0EgAbcRUV\nKCV5nNzFBap5zW2q176r6SQAAABcIgZ9JVJSUqK+ffvq+PHjuvHGG5WYmGg6CYCNWJal1Nemqyjj\nkALqNVHTrsM5USYAAIAHY9BXImPGjNHWrVvVoEEDLVq0SH5+nOAKwL+lb1yn7B++kHdAsKJ6Jsrb\nP9B0EgAAAC4Dg76SePnll7Vq1Sr5+/tr6dKlqluXE1wB+Lfcfd/ryEdLJElN/3eEAupGGC4CAADA\n5WLQVwJbtmzRmDFjJEnTpk3Ttddea7gIgJ0UZ6dr/+qJkuVWgzu6q2bLW0wnAQAAoAww6D3c0aNH\n1bdvXzmdTsXFxalrV05wBeDf3M4SpaxKVGn+KYW0aKPwu2JMJwEAAKCMMOg9WFFRkfr27asTJ07o\nlltuOfsuPQCcceidJBUc3i2/mvXV/JGRcnh5m04CAABAGWHQeyjLsvTMM89o27ZtatSokRYsWCAf\nHx/TWQBs5MS3HyjzHx/I4eOnqJ7j5RNcw3QSAAAAyhCD3kMtX75cr732mgICArR06VLVqlXLdBIA\nG8k79C8denuOJKnJg4MV1PAPhosAAABQ1hj0Hujrr7/W+PHjJUkzZ85Uq1atzAYBsBVnXo72r0qU\n5XKq7p/+R3VuuNt0EgAAAMoBg97DHDlyRPHx8XK5XBo4cKDuv/9+00kAbMRyubT/ledUkpOh4CZX\nKeK+AaaTAAAAUE4Y9B6ksLBQffr0UVZWlm677TaNGDHCdBIAmzmyfolO7/tePtVqKvKxcfLy8TWd\nBAAAgHLCoPcQlmVp+PDh+vHHH9W0aVPNnTtX3t6crRrAv2Xt2Kj0jeskLy9FPjZWfjXqmE4CAABA\nOWLQe4iFCxfq7bffVlBQkJYtW6bQ0FDTSQBspDA9VanrpkuSIjr1U/Xm1xguAgAAQHlj0HuAjRs3\natKkSZKkWbNm6YorrjBcBMBOXEX52rdynNwlhar1x78o7JYHTScBAACgAjDobS41NVUDBgyQ2+3W\n4MGDdc8995hOAmAjltutA2unqTjziALrN1OTLkPkcDhMZwEAAKAC+JgO+E9ZWVlas2aNtm/frry8\nPIWGhqpNmzbq2rWrgoODL+gxBg4cqMzMzHPeFxoaqoULF5ZlcrnKz89Xnz59lJOTow4dOmjYsGGm\nkwDYzPENa5Tz01fyDghWZM9EefsFmk4CAABABbHNoE9PT9fo0aOVm5urNm3aKDw8XCkpKfroo4+0\nfft2TZw4UdWqVbugxwoKCtK99977q9sDAgLKOrvcWJalwYMH61//+pciIyM1Z84ceXnxgQoA/3Zq\nz1alfbxcktTskWcVUKeh4SIAAABUJNsM+iVLlig3N1e9e/fW3Xffffb25ORkffDBB1qzZo3i4uIu\n6LGCg4PVpUuX8kqtEHPmzNGHH36o6tWra9myZQoJCTGdBMBGirOOa/8rz0mWWw069FRo9E2mkwAA\nAFDBbPGWb3p6unbs2KGwsLBfjHlJ6tatm/z9/fXFF1+opKTEUGHF+vTTT/X888/L4XAoKSlJUVFR\nppMA2IjbWayUl8fLVXBaNa5sq/AOPUwnAQAAwABbvEP/008/SZKuuebXl1kKCAjQFVdcoR07dmjP\nnj1q1arV7z6e0+nUpk2blJmZKX9/fzVp0kTR0dEe8ZH1ffv2KSEhQZZl6emnn1aHDh1MJ8GADlG1\nVDPIR9kFpfrqYI4KnW7TSbAJy7J08K1ZKkjbK/9aDdTs4ZFyeMC/bQAAACh7thj0R48elSQ1aNDg\nnPc3aNBAO3bs0LFjxy5o0Ofk5CgpKekXt4WFhal///666qqrLj+4nOTl5SkuLk6nT5/WPffcoyee\neMJ0EiqYj2VJRUUa4tqvgK27VXTFFXryobZateOE1u7MMp0HGzjxzfs6ufVjefn6KzImUT5B1U0n\nAQAAwBBbDPqCggJJP5/M7lzO3J6fn/+7j3X77bcrOjpaERERCggIUEZGhtavX6+//e1vmjJliiZN\nmqTGjRuXXXwZsSxLQ4YM0d69e9WiRQu99NJLXHqqivGxLPmlp6v6Aw/I+/BhSVKIJFdEhHq88Zak\nWoz6Ki7v4E4dfvfnH1Y2eWioghpEGi4CAACASZXuc5pdunRRy5YtFRISIj8/PzVq1EhxcXHq1KmT\nSkpKtG7dOtOJ5zR//vyzJ8FbsmTJBV+mD5WHr5fXL8b8Gd6HD6vOQ53V/eq6CvCpdF+yuEDO01lK\neXm8LFepwm7prNqtORwHAACgqrPFOjjzDvyZd+r/25nbL2fk3nnnnZKkXbt2XfJjlJdNmzZpypQp\nkqRZs2YpMpJ33aoab29veX/77a/G/Nn7Dx+W1z++1S1Na1RwGezA7SpVyurn5Mw9qWpNW6lRp36m\nkwAAAGADtvjIfXh4uCTp2LFj57z/zO3nO8b+Qpy57FtxcfEF/5p169bp9ddfP+990r/bL9WhQ4eU\nkJAgt9utUaNGqVevXpf1ePBMRUVFcv/OD5sC9+xWretbVFAR7CTtw0XK279dvtVrq/ljY+XlbYt/\nugEA8EiX+/odOJ9u3bqd974uXbr85v2XyhavClu2bClJ2rFjx6/uKyoq0u7du+Xv768WLS59zOzZ\ns0eSVK9evQv+Nd26dfvdv/QzJ/S7FEVFRXrwwQeVmZmp2267TfHx8Zf1ePBc3t7eCoyO/s3/p7DF\nFcoqcFZQEewia9tnSt/0hhxe3orsMU5+IbVNJwEA4NF4vY2yduaHRCYO77bFR+7r1auna6655uwJ\n7P7T2rVrVVxcrPbt28vPz0+S5HK5dPToUaWnp//i/01LSzvnO/AZGRlatmyZJKldu3bl9Ke4eGPG\njNH27dsVERGhpKQkeXt7m06CIS6XS662beWKiDj3/RERct/YVl+lnqrgMphUePyAUl97QZIU8T8D\nVK1pS8NFAAAAsBNbvEMvSXFxcRozZoyWL1+uH374QQ0bNtTevXu1c+dOhYeH6+GHHz77/2ZlZWnI\nkCGqW7fuLy5P9/XXX+v9999XdHS06tSpo8DAQKWnp+u7776T0+lU69atdd9995n44/3K6tWr9cor\nryggIEBLlixRzZo1TSfBMKfbrdNvv/2rE+O5IiKU+cZbWv3DCRWVcj36qqK04LT2rRwnt7NItVvf\nqbp/ut90EgAAAGzGNoO+Xr16mjp1qtauXatt27Zp27ZtCg0N1b333qsuXbqc85J2/31Zt5YtW+rY\nsWM6cOCAdu/ereLiYgUHBys6Olrt27e3zbvz33//vUaPHi1JmjJlilq1amW4CHZQ6nBI9eop99tv\nVfLVZgXu2a3CFlfIast16Ksay+3S/lcmqfhkmoLCo9T4wcFcxhIAAAC/4rAsyzId4cku9hiczMxM\ndezYUceOHVNMTIwmT55cTmXwVIGBgZq2IVW1gnyVVeDUV6mneGe+ijny4WId37BGPsE1FP3EfPnX\nvPBzfwAAgPP7JO46FRYWms5AJWPyRIu2eYe+KigtLVX//v117NgxXX/99Ro/frzpJNjU3/dlm06A\nIVnbPtfxDWskLy81f2wsYx4AAADnZYuT4lUVU6dO1ddff626detq0aJFZ0/yBwCSVHA0RamvTZck\nRdw3QCGRfzRcBAAAADtj0FeQ9957T/Pnz5ePj48WLlyo+vXrm04CYCPO/FPat3KM3M5i1b7hboXd\n/IDpJAAAANgcg74C7NmzR0OHDpX086Xq2rZta7gIgJ1YLpf2r5qgkux0BUdcqSadOQkeAAAAfh+D\nvpzl5uaqT58+KigoUOfOndWnTx/TSQBs5vAHC3U6ZZt8qtVUZM/x8vLlcBwAAAD8PgZ9OXK73Ro8\neLD279+v6OhoPf/887zrBuAXMv/5iTK+fEMObx9F9hwvvxp1TScBAADAQzDoy1FSUpI+/vhjhYSE\naPHixQoKCjKdBMBG8g/v1sE3ZkqSGt8/SNWbtjJcBAAAAE/CoC8nGzdu1PPPPy9JmjNnjpo1a2a4\nCICdOE9naV/yOFmlTtVt20l1b+pkOgkAAAAehkFfDg4fPqwBAwbIsiwNHTpUHTp0MJ0EwEbcpU6l\nvJwo56kTqta0lSLuTzCdBAAAAA/EoC9jhYWFiouLU05Oju644w4NGTLEdBIAmzn83jzlpf4o3xp1\nFNljnLx8fE0nAQAAwAMx6MuQZVkaOXKkfvzxRzVp0kRz5syRlxd/xQD+7cS3H+jE5nfl8PFVVM9E\n+VavZToJAAAAHoq1WYaSk5P12muvKSAgQEuWLFFoaKjpJAA2kpf6kw69PVuS1OTBwQqOuNJwEQAA\nADwZg76MbN26VePGjZMkTZ8+XVdddZXhIgB2UnIqUykvj5flKlXYLZ1V54aOppMAAADg4Rj0ZeDE\niROKj4+X0+lUnz599OCDD5pOAmAj7tISpbw8Xs7TWare/Fo16tTPdBIAAAAqAQb9ZXI6nerXr5+O\nHz+utm3basyYMaaTANiIZVk69NYs5R/aJb/QMDV/bKy8vH1MZwEAAKASYNBfpkmTJumbb75RvXr1\ntGDBAvn6crZqAP92YvO7ytyyXl6+/oqKmSDfapxbAwAAAGWDQX+ZFi9eLF9fXy1cuFBhYWGmcwDY\nyOn9O3T43bmSpCZdhimo4R8MFwEAAKAyYdCXgfHjx6tNmzamMwDYSHF2ulJeTpTldqle+26qfd1f\nTCcBAACgkmHQX6aHHnpIMTExpjMA2IjbWayU5HEqzc9RSIsb1OieONNJAAAAqIQY9Jdp2rRpcjgc\npjMA2IRlWUp9Y6YK0vbKv1YDNX90lBxe3qazAAAAUAkx6C9TYGCg6QQANpK+6Q1lffepvPwCFBkz\nQT5BIaaTAAAAUEkx6AGgjOTu/aeOfLBQktTsf0coqEFzw0UAAACozBj0AFAGik8eVcrqiZLlVoM7\nuqvm1e1NJwEAAKCSY9ADwGVylRRq38qxchWcVo0r2yr8Lk6UCQAAgPLHoAeAy2BZllLXTVfh8QPy\nr9NIzR55lpPgAQAAoEIw6AHgMhzfsEbZOzbKyz9IUbET5RNYzXQSAAAAqggGPQBcolP/+lZp65dK\nkpo/MlKBYY0NFwEAAKAqYdADwCUoyjis/a9MkixL4XfGKPSqm00nAQAAoIph0APARSotzNO+lWPk\nKspXzavbqcFfHjOdBAAAgCqIQQ8AF8Fyu3Tg1ckqOnFYgfWbqWm3EXJ48U8pAAAAKh6vQgHgIqR9\nvFyn/vWtvIOqKyp2orz9A00nAQAAoIpi0APABcra9pmOf/6q5OWlyMfGyb9WA9NJAAAAqMIY9ABw\nAfKP7FHqazMkSRH3DVBI1HWGiwAAAFDVMegB4Hc487KVkjxObmex6rTpqLCbHzCdBAAAADDoAeC3\nuEudSnk5USU5GQpuHK3GnZ+Uw+EwnQUAAAAw6AHgtxx+d67yDvwg35DaiuyZKC8fP9NJAAAAgCQG\nPQCcV8bm93Tim/fk8PFVZM8J8gupbToJAAAAOItBDwDncPrADh1+Z44kqclDQ1Wt8ZWGiwAAAIBf\nYtADwH8pzk5XSnKiLLdL9dp1UZ3r7zKdBAAAAPwKgx4A/oOrpEgpK8eqND9HIX+4Xo3uedx0EgAA\nAHBODHoA+H+WZengazNUcHSf/Gs3VPPuY+Tw9jadBQAAAJwTgx4A/t/xDWuUtf1zefkFKip2gnyC\nqptOAgAAAM6LQQ8AknJ2fau09UslSc0feVaB9ZqaDQIAAAB+B4MeQJVXlHFYB16dJFmWwu/updCW\nN5tOAgAAAH4Xgx5AlVZamKe9K0bLVZSvmle3V4M7uptOAgAAAC4Igx5AlWW5XTrw6mQVZx5RYIPm\natrtaTkcDtNZAAAAwAVh0AOostI+Xq5T//pWPkEhioqZIG//QNNJAAAAwAVj0AOokk5+/5mOf/6q\n5OWl5o+NlX+tBqaTAAAAgIvCoAdQ5eQf2aODr8+QJDW+b6BCoq4zXAQAAABcPAY9gCrFeTpL+1aO\nldtZrDpt/qq6N99vOgkAAAC4JAx6AFWGu9SplJcT5Tx1QsFNrlLjzk9wEjwAAAB4LAY9gCrj8DtJ\nykv9Ub416iiyx3h5+fiZTgIAAAAuGYMeQJWQsfk9nfj2fTl8fBXVM1F+IbVNJwEAAACXhUEPoNI7\nvX+HDr8zR5LUtMswBUdcabgIAAAAuHwMegCVWnF2ulJeTpTldqle+26q3fpO00kAAABAmWDQA6i0\nXCVF2rdyrErzcxTS4gY1uifOdBIAAABQZhj0AColy+1W6tppKjy6T/61G6r5o6Pl8PI2nQUAAACU\nGQY9gErp6KfJyv7hC3kHBCsqdqJ8gqqbTgIAAADKFIMeQKWTte1zHfv0ZcnhpebdRyuwXhPTSQAA\nAECZY9ADqFTyD/9LB9Y9L0mKuK+falxxo+EiAAAAoHww6AFUGiWnTmjfirGySktU58Z7FHbLg6aT\nAAAAgHLDoAdQKfx8Rvtxcp4+qWrNr1XjB56Qw+EwnQUAAACUGwY9AI9nWZZSX5uugiO75V+rgSJ7\njJOXj6/pLAAAAKBcMegBeLxjn76s7O0b5OUfpKjY5+QbXMN0EgAAAFDuGPQAPFrWjo06+reVP5/R\n/tHRCqzf1HQSAAAAUCEY9AA8Vv6RPUpdO02S1OjexxUa3dZwEQAAAFBxGPQAPFJJ7kntWzlGbmex\nat/QUfXadTGdBAAAAFQoBj0Aj+N2FmvfyjFynspUtaat1OTBJzmjPQAAAKocBj0Aj/LzGe1nqODw\nbvnVrK/Inony8vEznQUAAABUOAY9AI9y7LNXlLXtM3n5BeoPvZ6Tb7VQ00kAAACAEQx6AB4j+4dN\nOvrxMsnhUPNHRymwfjPTSQAAAIAxDHoAHqEgba8OrJkqSWr0174KvepPhosAAAAAsxj0AGzPeTpL\ne1eMkdtZpNrX36V6t3YznQQAAAAYx6AHYGtuZ4n2rRwr56kTCm7SUk0eGsIZ7QEAAAAx6AHYmGVZ\nSn3jBeUf2iW/0DBFxXBGewAAAOAMBj0A2zq+YY2yvvtUXn4Biur1nHyr1TSdBAAAANgGgx6ALWX/\n9JXS1i+VHA41e+RZBTWINJ0EAAAA2AqDHoDtFBxN0YFXJ0uWpYYd+6hmy1tMJwEAAAC242M64D9l\nZWVpzZo12r59u/Ly8hQaGqo2bdqoa9euCg4OrvDHAVDxnKeztG/FaLlLilSrdQfVv+1h00kAAACA\nLdlm0Kenp2v06NHKzc1VmzZtFB4erpSUFH300Ufavn27Jk6cqGrVqlXY4wCoeO7SEu1LHq+SnAwF\nN45W04eGcUZ7AAAA4DxsM+iXLFmi3Nxc9e7dW3fffffZ25OTk/XBBx9ozZo1iouLq7DHAVCxLMvS\nwTdmKv/gT/9/RvsJ8vLljPYAAADA+djiGPr09HTt2LFDYWFhvxjhktStWzf5+/vriy++UMn/tXfv\ncVGWifvHrwHkIGjgAQFTcS0PaGVt9kv6qmmltfXa2k2RPIGnrDTNNbdM2VAqK8tO5mFTE5XCw9dO\nup2sdrcyw2wVT4GEaAorkpIoZ5jfH37hlXmGmbnnGT7vv+p58J5r6PZurnlm7qe83CXjAHC9w/9a\nrZ+3fiqvRv66Ij5JjZo0Mx0JAAAAcGtuUeh37dolSbr66qvPOOfv769OnTqprKxMmZmZLhkHgGsV\n7t6kgx++IUlqH/u4GkdcYTgRAAAA4P7cotDn5uZKksLDw896vuZ4Xl6eS8YB4DrFednKfuvUjvYR\nA0Yp5KpepiMBAAAAluAWhb64uFiS1Lhx47Oerzl+8uRJl4wDwDUqThQqa1mCqstL1Kz7LQrvN8R0\nJAAAAMAy3KLQA2h4qivL9ePyJ1V+7L8KbNNZkYPY0R4AAAC4FG5R6GuunNdcYf+tmuMXuoe8o8YB\n4Fx2u137172iEzk71eiyFuoQN0tejfxMxwIAAAAsxS1uWxcRESHp3N9trzl+ru/GO3qcGqtXr9ba\ntWvPee7Xjwk4yrFjx0xHcLrDX67Vz999JK9GfroiLkm+TZubjgQAABoIXr/DWWJiYs55buDAgec9\nX1duUei7du0qSUpPTz/jXGlpqTIyMuTn56eOHTu6ZJwaMTExF/yl12zEBzhKQECA6QhOVbjnWx3c\n8HdJUuTgxxR4+cX9fQQAAHAEXr/D0WreJKq56OtKbvGR+1atWunqq69Wfn6+Pvroo9POrVq1SmVl\nZerdu7d8fX0lSVVVVcrNzdXhw4frNQ4A1yr5b46y33pKslcr4rY4Nbu6j+lIAAAAgGW5xRV6SRoz\nZowSEhL05ptvaseOHWrdurX27t2r3bt3KyIiQrGxsbU/e/ToUU2ePFktW7bUvHnz6jwOANepOPmL\n9i6boeqyYoVcc7PCbx1uOhIAAABgaW5T6Fu1aqVnn31Wq1at0rZt27Rt2zYFBwfrzjvv1MCBA896\nK7qz7Yhdl3EAOFd1ZYV+XJ6o8qN5anx5J7WP+Ss72gMAAAD1ZLPb7XbTIayM7+DA0QICAtR/8X9M\nx3AYu92u/f87VwVp/1CjJs3VZeLr8r2spelYAACgAfpkzLUqKSkxHQMexuRGi27xHXoAniv/63Uq\nSPuHbD6+uiJ+FmUeAAAAcBAKPQCn+SUjTT99sFCS1D7mrwps09lwIgAAAMBzUOgBOEXJ4f3KTjm1\no334rcPVrHtf05EAAAAAj0KhB+BwlSd/UdayGaoqPamQq3or4tYRpiMBAAAAHodCD8Chqqsq9eOK\nmSr7OVeNW1+pyMGPyebFUgMAAAA4Gq+yATiM3W7XT+++pqLs7WrUpJmuiEuSt6+/6VgAAACAR6LQ\nA3CY/E3v6si362XzaaQOcbPkG8yO9gAAAICzUOgBOMQvmd/pp/fnS5IiB01VUNsuhhMBAAAAno1C\nD6DeSvN/UvbKWad2tO83VM2vvcV0JAAAAMDjUegB1Etl8XHtXTZdVaUnFdztfxTRP950JAAAAKBB\noNADqLPqqkr9uDJJZQWHFBBxhdrHPs6O9gAAAICL8MobQJ399P7rKsr6Xj5BIboibpa8fQNMRwIA\nACBMxlAAACAASURBVAAaDAo9gDrJ3/SejnzzvmzejXRF3Ez5hbQyHQkAAABoUCj0AC7Z8b3f68D7\n8yRJkYOmKKhdV8OJAAAAgIaHQg/gkpQeOagfV86SqqsV1vc+Nb/uNtORAAAAgAaJQg/golWWnFDW\nshmqKilScNdotR4wynQkAAAAoMGi0AO4KPaqKmWnJKn0yE8KCP+d2sc+wY72AAAAgEG8GgdwUX5a\nv0DHM7+TT2Cwroh/St5+7GgPAAAAmEShB3BBRzZ/oPyv35HNu5E6sKM9AAAA4BYo9ADO63jWf3Tg\n3dckSe3unawmkd0MJwIAAAAgUegBnMepHe1nyl5dpVZ9YtTi+gGmIwEAAAD4PxR6AGdVWXxce998\nQlXFRbqsy426/I4xpiMBAAAA+BUKPYAzVFdWKGt5osoKDikgvIN+d9902by8TccCAAAA8CsUegCn\nsdvt2v+/L+pE9nY1atpcV458Wt7+jU3HAgAAAPAbFHoAp8n7PEU/b/1UXo38dUX8U/INbmk6EgAA\nAICzoNADqHV02+fK/fhNyWbT74ZMV+DlHU1HAgAAAHAOFHoAkqQTObu0b/XzkqTL73xAwV2jDScC\nAAAAcD4UegAq+zlXWckJsldWqGXPP6pVr3tNRwIAAABwARR6oIGrLC7S3jenq/LkL2raqYfa/nGC\nbDab6VgAAAAALoBCDzRg1VWV+nHlTJXmH1BAWHt1GJogmze3pwMAAACsgEIPNFB2u10H1r2soqz/\nyCcoRFeMfFre/oGmYwEAAAC4SBR6oIH67z9TVbDlQ3k18tOVI5+SX0gr05EAAAAAXAIKPdAAHU3/\nlw59uFiS1D52mgLbdDacCAAAAMClotADDcyJAz9oX+qzkqTWfxirkKt6GU4EAAAAoC4o9EADUnbs\nsLKWzZC9slwtbviDwvoMNh0JAAAAQB1R6IEGorLkhPYufUKVJ46pyZXXqe2fJnF7OgAAAMDCKPRA\nA1BdVanslCSVHs6Rf2hbdRj2pLy8fUzHAgAAAFAPFHrAw9ntdv307ms6nvmdfAKDdeWoZ+QTEGQ6\nFgAAAIB6otADHu7wl2t15Nv1svk00hXxs+TXLNx0JAAAAAAOQKEHPNixnV/p4IZFkqT2gx9XULuu\nhhMBAAAAcBQKPeChTh7M1L63Z0t2u1rfPkrNrrnZdCQAAAAADkShBzxQeWG+st6coeqKUjX/fX+F\n9R1iOhIAAAAAB6PQAx6mqrRYe9+croqin9Xkd9eo3b1/4fZ0AAAAgAei0AMexF5Vpey3nlJJXrb8\nWlyuDiMS5eXTyHQsAAAAAE5AoQc8yE8fzNcvP3wrn8ZNT92ernFT05EAAAAAOAmFHvAQh79+R/mb\n3pXNu5E6xM2Sf4vWpiMBAAAAcCIKPeABCvds1k/vz5ckRQ56VE3aX2U4EQAAAABno9ADFlecm6Xs\nlCTJXq2I2+LU/LpbTUcCAAAA4AIUesDCyn85or1vTld1eamaXXuLwm8dbjoSAAAAABeh0AMWVVVW\noqw3Z6jilwIFRXZT5KBHuT0dAAAA0IBQ6AELsldXad/bz6g4N0t+zSPUIW6WvHx8TccCAAAA4EIU\nesCCDm5YpMLdm+Qd0ERXjnxGjQIvMx0JAAAAgItR6AGLyf/mfR3+8n9l8/ZRhxGJ8g9tYzoSAAAA\nAAMo9ICF/JKRpgPvvSZJanfvX9S0Q3fDiQAAAACYQqEHLKI4L1s/rkySqqsV3m+oWlw/wHQkAAAA\nAAZR6AELqCg6qqw3p6u6rFgh19ysiP7xpiMBAAAAMIxCD7i5qvJS7V02Q+WF+Qps20XtY/4qmxd/\ndQEAAICGjlYAuDF7dbX2pT6r4p8y5NssXFfEJ8mrkZ/pWAAAAADcAIUecGOHPlqswp1fyts/UFeO\nfEqNgkJMRwIAAADgJij0gJs68u0G/fefq2Tz8laH4U8qoFWk6UgAAAAA3AiFHnBDx/du1YF3XpEk\ntf3TJDW98veGEwEAAABwNxR6wM388MMP+nHFTNmrqxR282C1/H93mo4EAAAAwA1R6AE3UlBQoNjY\nWFWVnlRwt15qffsY05EAAAAAuCkKPeAmSkpKNHLkSB04cECN23RS+9jHuT0dAAAAgHPyMR0AgFRd\nXa2//OUv+v7773X55ZerefxT8vb1Nx0LAAAAgBvj8h/gBubMmaP3339fQUFBSk1NVaMmzUxHAgAA\nAODmKPSAYatWrdKrr74qb29vLVy4UFFRUaYjAQAAALAACj1g0KZNm/TYY49JkpKSktS3b1/DiQAA\nAABYBYUeMCQrK0tjx45VRUWFxo4dq7i4ONORAAAAAFgIhR4w4OjRo4qLi1NhYaH69++vhIQE05EA\nAAAAWAyFHnCxsrIyjR49Wjk5OerWrZvmzZsnb29v07EAAAAAWAyFHnAhu92uKVOmKC0tTWFhYVq2\nbJkCAwNNxwIAAABgQRR6wIVeeuklvfPOO2rcuLGSk5MVHh5uOhIAAAAAi6LQAy6ybt06vfjii/Ly\n8tL8+fPVrVs305EAAAAAWBiFHnCBb7/9VlOmTJEkJSYm6rbbbjOcCAAAAIDVUegBJ9u3b59Gjx6t\n8vJyjRw5UqNHjzYdCQAAAIAHoNADTnTs2DGNGDFCx44dU79+/ZSYmGg6EgAAAAAPQaEHnKS0tFSj\nRo1Sdna2unTpogULFsjHx8d0LAAAAAAewm3aRUZGhtatW6e9e/eqvLxc4eHh6tu3r26//XZ5eV3c\n+w5HjhzRhAkTznk+OjpakyZNclRk4Jyqq6v1yCOP1N6ebvny5QoKCjIdCwAAAIAHcYtCv2XLFs2d\nO1e+vr7q2bOngoKCtHXrViUnJysjI0OTJ0++pPEiIyPVo0ePM463adPGUZGB83rqqaf0wQcfqEmT\nJlqxYoUiIiJMRwIAAADgYYwX+pKSEi1atEheXl5KTExU+/btJUmxsbGaOXOmNm/erE2bNik6Ovqi\nx2zXrp0GDhzorMjAeS1dulSLFi2Sj4+P3njjDUVFRZmOBAAAAMADGf8O/TfffKOioiLddNNNtWVe\nknx8fDR48GBJ0qeffmoqHnBJPvzwQ/3tb3+TJL3wwgvq1auX4UQAAAAAPJXxK/S7du2SJHXv3v2M\nc1FRUfL19VVGRoYqKysvekOxY8eOaePGjSoqKlKTJk3UsWNHtW3b1qG5gd/67rvvNGHCBNntdk2d\nOlWDBg0yHQkAAACABzNe6HNzcyVJ4eHhZ5zz8vJSaGioDh48qPz8/Iv+HnJ6errS09NPOxYVFaXx\n48erRYsW9Q8N/EZ2drbi4+NVWlqqIUOGsPkiAAAAAKczXuiLi4slSY0bNz7r+ZrjJ0+evOBYfn5+\nuvfee3XDDTcoNDRUknTgwAGtWbNGO3fuVFJSkubMmSNfX18HpQekgoICDR8+vPZe87Nnz5bNZjMd\nCwAAAICHc0ihHz9+vAoKCi7653v16nXe28vVVdOmTRUTE3Pasc6dO2v69OlKSEhQVlaWPvvsM91x\nxx0Of2w0TCUlJYqPj1dOTo6uuuoqLVy4kHvNAwAAAHAJhzSPsLCwS7rqHRISUvvPNVfga67U/1bN\n8cDAwDrn8/Ly0i233KKsrCzt2bOHQg+HqKqq0vjx4/Wf//xHl19+uZYvX16veQoAAAAAl8IhhT4h\nIaHOfzYiIkLZ2dnKy8s7bZd7SaqurlZ+fr68vb1rP0JfV02bNpUklZWVXfSfWb16tdauXXvOc5K4\nv3gDZbfbNXHiRH388ccKDg7WJ598oi5dujhk7GPHjjlkHAAAAJyJ1+9wlt9+WvzXBg4ceN7zdWX8\ns8HdunXTV199pW3btp1xr/ndu3ervLxcUVFR9f4Yc2ZmpiRd0hsDMTExF/yl12zqh4Zl4cKFmjdv\nnnx9fbVkyRJddtllDpsLAQEBDhkHAAAAZ+L1Oxyt5k2imou+rmT8PvQ33nijmjRpoq+//lrZ2dm1\nxysqKpSamipJ6t+//2l/pri4WLm5uSosLDzt+L59+2S32894jB07dmjDhg2SxH3BUW/vvfeekpKS\nJEkvv/yybrzxRsOJAAAAADRExq/QBwQEaNy4cZo7d64SExMVHR2toKAgbd26Vbm5uerZs6d69ux5\n2p9JS0vTggUL1KdPHz300EO1x5cvX668vDx17NhRzZs3l3Rql/udO3dKkmJjY9WxY0fXPTl4nM2b\nN+uRRx6RJM2YMUN333234UQAAAAAGirjhV6SevTooZkzZ2rdunVKS0tTRUWFwsLCFBcXd94N7H57\na7DevXsrLS1N2dnZ2r59uyorKxUcHKzo6GgNGDBAnTt3dvZTgQfbu3evRo0apfLycsXHx+uBBx4w\nHQkAAABAA2azn+0z6rhofAenYTh8+LD++Mc/6uDBgxowYIDeeOMNeXt7O+WxAgIC1H/xf5wyNgAA\nQEP2yZhrVVJSYjoGPIzJjRaNf4cecHcnT55UXFycDh48qGuvvVavv/6608o8AAAAAFwsCj1wHpWV\nlXrggQe0Y8cORUZGKjk5mV3oAQAAALgFCj1wDna7XU888YQ+//xzNWvWTCtWrKjdbBEAAAAATKPQ\nA+fw6quvKiUlRf7+/lq2bJl+97vfmY4EAAAAALUo9MBZrF27Vs8//7xsNpvmzZun3//+96YjAQAA\nAMBpKPTAb3z55ZeaMmWKJGnmzJnnvXUiAAAAAJhCoQd+Zc+ePRo7dqwqKyt1//33a/To0aYjAQAA\nAMBZUeiB/5Obm6thw4apqKhId911lxISEkxHAgAAAIBzotADko4fP64RI0bov//9r2644Qa98sor\n8vLirwcAAAAA90VjQYNXXl6u+++/X3v27FGHDh20dOlS+fv7m44FAAAAAOdFoUeDZrfbNXXqVH35\n5Zdq2bKlVq5cqZCQENOxAAAAAOCCKPRo0F544QWtXbtWAQEBSk5OVtu2bU1HAgAAAICLQqFHg/XW\nW2/p5ZdflpeXlxYuXKhrrrnGdCQAAAAAuGgUejRIn3/+uR5//HFJ0uzZs3XrrbcaTgQAAAAAl4ZC\njwZnx44dGjdunKqqqvTwww9r2LBhpiMBAAAAwCWj0KNB+emnnzRixAgVFxfrz3/+sx577DHTkQAA\nAACgTij0aDAKCws1fPhw5efnKzo6Wi+++KJsNpvpWAAAAABQJxR6NAhlZWUaPXq09u7dq06dOmnx\n4sXy9fU1HQsAAAAA6oxCD49XXV2tyZMna/PmzQoLC9OKFSt02WWXmY4FAAAAAPVCoYfHmz17tt57\n7z0FBQVp+fLlat26telIAAAAAFBvFHp4tGXLlmn+/Pny8fHRG2+8oa5du5qOBAAAAAAOQaGHx/rk\nk0+UkJAgSXr++efVu3dvw4kAAAAAwHEo9PBI33//vR588EFVV1fr0Ucf1eDBg01HAgAAAACHotDD\n4+Tk5Cg+Pl6lpaW677779Mgjj5iOBAAAAAAOR6GHRzl69KiGDRumn3/+WTfffLNmz57NveYBAAAA\neCQKPTxGSUmJ4uPjtW/fPnXt2lWLFi1So0aNTMcCAAAAAKeg0MMjVFVVaeLEidq6datat26t5cuX\nKygoyHQsAAAAAHAaCj08wsyZM/WPf/xDTZs21YoVKxQWFmY6EgAAAAA4FYUelvf3v/9dS5Yska+v\nr5YsWaJOnTqZjgQAAAAATkehh6WtX79es2bNkiS99NJLio6ONpwIAAAAAFyDQg/LSktL08SJE2W3\n2/XEE0/onnvuMR0JAAAAAFyGQg9LysrK0siRI1VWVqYRI0booYceMh0JAAAAAFyKQg/LOXLkiIYP\nH67CwkLddtttSkpK4l7zAAAAABocCj0spbi4WHFxcTpw4IC6d++u+fPny8fHx3QsAAAAAHA5Cj0s\no7KyUg8++KC2b9+udu3aKTk5WY0bNzYdCwAAAACMoNDDEux2u2bMmKGNGzcqODhYK1asUIsWLUzH\nAgAAAABjKPSwhNdff10rVqyQn5+fli1bpg4dOpiOBAAAAABGUejh9t555x3Nnj1bNptNr732mnr0\n6GE6EgAAAAAYR6GHW/v3v/+tyZMnS5KefPJJ3XnnnYYTAQAAAIB7oNDDbaWnp2vMmDGqqKjQ/fff\nr7Fjx5qOBAAAAABug0IPt7Rv3z4NHz5cJ0+e1J///GclJCSYjgQAAAAAboVCD7eTn5+voUOHqqCg\nQH369NGLL74oLy+mKgAAAAD8Gi0JbqWoqEjDhw/X/v37dc011+iNN96Qr6+v6VgAAAAA4HYo9HAb\nZWVlGj16tHbu3Kn27dtr+fLlCgwMNB0LAAAAANwShR5uobq6WpMmTdLXX3+t0NBQvfXWW2rRooXp\nWAAAAADgtij0MM5ut+vJJ5/UBx98oKCgIK1YsUJt27Y1HQsAAAAA3BqFHsbNmzdPS5cula+vr5Yu\nXapu3bqZjgQAAAAAbo9CD6NSU1P17LPPymaz6bXXXtNNN91kOhIAAAAAWAKFHsZ88skn+utf/ypJ\neuqpp3TXXXcZTgQAAAAA1kGhhxFbtmzRgw8+qKqqKk2aNEnx8fGmIwEAAACApVDo4XKZmZmKj49X\naWmphgwZoqlTp5qOBAAAAACWQ6GHSx06dEhDhgxRYWGh+vfvr9mzZ8tms5mOBQAAAACWQ6GHyxw7\ndkzDhg1TXl6ebrjhBs2fP18+Pj6mYwEAAACAJVHo4RIlJSWKj49XZmamOnXqpDfffFMBAQGmYwEA\nAACAZVHo4XSVlZV68MEH9d133ykiIkIrV65UcHCw6VgAAAAAYGkUejiV3W7XY489pk8//VTBwcF6\n6623FBERYToWAAAAAFgehR5O9fzzzys1NVX+/v5KTk7WlVdeaToSAAAAAHgECj2cZunSpXr11Vfl\n7e2tRYsW6frrrzcdCQAAAAA8BoUeTvH+++/rb3/7myRpzpw5uvXWWw0nAgAAAADPQqGHw3311Vea\nNGmS7Ha7pk2bpsGDB5uOBAAAAAAeh0IPh9q5c6dGjx6t8vJyjR49WuPHjzcdCQAAAAA8EoUeDrN/\n/34NGzZMJ06c0N13363ExETZbDbTsQAAAADAI1Ho4RBHjhzRkCFDdOTIEfXq1UsvvfSSvLyYXgAA\nAADgLDQu1NuJEyc0fPhw5eTk6KqrrtLixYvl5+dnOhYAAAAAeDQKPeqlvLxcY8aM0Y4dOxQZGakV\nK1YoKCjIdCwAAAAA8HgUetRZdXW1Jk+erC+//FItWrRQSkqKWrZsaToWAAAAADQIFHrUid1uV2Ji\not59910FBgZq5cqVioyMNB0LAAAAABoMCj3qZP78+VqyZIkaNWqkJUuW6KqrrjIdCQAAAAAaFAo9\nLtmqVav0zDPPyGaz6ZVXXlGvXr1MRwIAAACABodCj0uyceNGTZ06VZI0a9Ys3X333YYTAQAAAEDD\nRKHHRdu6davGjRunqqoqTZgwQaNGjTIdCQAAAAAaLAo9LsrevXs1YsQIlZaWKjY2Vo8//rjpSAAA\nAADQoFHocUG5ubkaMmSICgsLdeutt+q5556TzWYzHQsAAAAAGjQKPc6rsLBQw4YNU25urn7/+99r\n4cKF8vHxMR0LAAAAABo8Cj3OqaSkRCNHjlRGRoauvPJKJScnKyAgwHQsAAAAAIAo9DiHyspKjR8/\nXmlpaQoPD1dKSopCQkJMxwIAAAAA/B8KPc5gt9v1xBNP6OOPP9Zll12mlJQUtW7d2nQsAAAAAMCv\nUOhxhhdeeEEpKSny9/dXcnKyOnXqZDoSAAAAAOA3jO9uVlVVpY8//lg5OTnKycnRwYMHVVVVpXHj\nxqlfv351GjMjI0Pr1q3T3r17VV5ervDwcPXt21e33367vLx4D+N8li1bppdfflleXl5asGCBevTo\nYToSAAAAAOAsjBf6srIyJScnS5KCg4MVEhKigoKCOo+3ZcsWzZ07V76+vurZs6eCgoK0detWJScn\nKyMjQ5MnT3ZUdI+zfv16zZgxQ5L0/PPPq3///oYTAQAAAADOxXih9/X11bRp0xQZGang4GCtWbNG\na9eurdNYJSUlWrRokby8vJSYmKj27dtLkmJjYzVz5kxt3rxZmzZtUnR0tCOfgkfYtGmTHn74Ydnt\ndv31r3/VfffdZzoSAAAAAOA8jH/+3MfHR927d1dwcHC9x/rmm29UVFSkm266qbbM1zzG4MGDJUmf\nfvppvR/H0+zatUujRo1SeXm54uPjNXHiRNORAAAAAAAXYLzQO9KuXbskSd27dz/jXFRUlHx9fZWR\nkaHKykpXR3NbBw4c0LBhw1RUVKS77rpLs2bNks1mMx0LAAAAAHABHlXoc3NzJUnh4eFnnPPy8lJo\naKiqqqqUn5/v6mhu6eeff9aQIUOUn5+v6Ohovfrqq/L29jYdCwAAAABwETyq0BcXF0uSGjdufNbz\nNcdPnjzpskzu6uTJkxo+fLj27dunrl27asmSJfLz8zMdCwAAAABwkRyyKd748eMvaWf6Xr16acKE\nCY54aNRBeXm5xo4dq+3bt6tt27ZauXKlmjZtajoWAAAAAOASOKTQh4WFydfX96J/vlmzZo542DPU\nXIGvuVL/WzXHAwMDnfL4VlBdXa0pU6boX//6l5o3b66UlBSFhoaajgUAAAAAuEQOKfQJCQmOGKbe\nIiIilJ2drby8vNN2uZdOFdn8/Hx5e3tfdIFdvXr1OW+ht3r16trHtJIpU6Zo3bp1CgwM1EcffaTr\nr7/edCT8RsHRY/pkzLWmYwAAAHicKrv1Xr/DOmJiYs55buDAgec9X1fG70PvSN26ddNXX32lbdu2\nnXGv+d27d6u8vFxRUVHy8bm4px0TE3PBX3rNRnxWsHDhQs2dO1eNGjXS4sWLFRERYan8DQX/XeAs\nzC04A/MKzsLcgjMwr+AMNW8S1Vz0dSVLbopXXFys3NxcFRYWnnb8xhtvVJMmTfT1118rOzu79nhF\nRYVSU1MlSf3793dpVnexdu1aJSUlSZJefvll9e7d23AiAAAAAEB9uMUV+nfffbf2nbKcnBxJ0hdf\nfKEffvhBktS5c2f169ev9ufT0tK0YMEC9enTRw899FDt8YCAAI0bN05z585VYmKioqOjFRQUpK1b\ntyo3N1c9e/ZUz549XffE3MTGjRs1ZcoUSVJiYqLuuecew4kAAAAAAPXlFoV++/bt2r1792nHMjMz\nlZmZWfvvvy70NWw22xnHevTooZkzZ2rdunVKS0tTRUWFwsLCFBcXpzvuuMPx4d3cN998o3Hjxqmy\nslLjx4/X2LFjTUcCAAAAADiAzW63202HsDJ3/g5Oenq6Bg0apBMnTmjo0KF67rnnzvomCNwL3+2C\nszC34AzMKzgLcwvOwLyCM5jcaNGS36HHhWVlZWno0KE6ceKE/vjHP2r27NmUeQAAAADwIBR6D3Tw\n4EHFxsbq6NGj6tevn1555RV5e3ubjgUAAAAAcCAKvYc5cuSIYmNjlZeXpx49eujvf/+7fH19TccC\nAAAAADgYhd6D/PLLLxoyZIj27dunrl27Kjk5WQEBAaZjAQAAAACcgELvIUpKShQXF6fdu3erffv2\nSklJ0WWXXWY6FgAAAADASSj0HqC8vFxjx47Vli1bFB4erlWrVqlly5amYwEAAAAAnIhCb3FVVVWa\nOHGivvjiCzVr1kypqalq3bq16VgAAAAAACej0FuY3W7XtGnT9MEHHygoKEgpKSm64oorTMcCAAAA\nALgAhd7CnnnmGaWkpMjf31/Jycm6+uqrTUcCAAAAALgIhd6iXn/9dc2fP18+Pj5atGiRbrzxRtOR\nAAAAAAAuRKG3oBUrVuiZZ56RzWbTK6+8oltvvdV0JAAAAACAi1HoLea9997TtGnTJElPP/207rnn\nHsOJAAAAAAAmUOgt5LPPPtPEiRNlt9v12GOPKS4uznQkAAAAAIAhFHqL+Pbbb3X//fersrJSDzzw\ngB5++GHTkQAAAAAABlHoLWDnzp2Ki4tTaWmp7rvvPs2YMUM2m810LAAAAACAQRR6N5eVlaUhQ4ao\nqKhId955p5577jnKPAAAAACAQu/ODh06pPvuu08///yz+vTpo9dee03e3t6mYwEAAAAA3ACF3k0V\nFBQoNjZWubm5uv7667V48WL5+fmZjgUAAAAAcBMUejd0/PhxDR06VNnZ2erSpYuSk5PVuHFj07EA\nAAAAAG6EQu9mSkpKFB8fr507dyoyMlJvv/22goODTccCAAAAALgZCr0bKS8v1/33369vv/1WYWFh\nSk1NVcuWLU3HAgAAAAC4IQq9m6iqqtIjjzyizz//XCEhIUpNTVWbNm1MxwIAAAAAuCkKvRuw2+2a\nPn263nvvPQUFBSklJUVXXnml6VgAAAAAADdGoXcDzz77rFasWCE/Pz+9+eabuuaaa0xHAgAAAAC4\nOQq9YQsWLNC8efPk7e2thQsXKjo62nQkAAAAAIAFUOgNSklJ0VNPPSVJeumll9S/f3/DiQAAAAAA\nVkGhN+SDDz7QY489Jkl6+umnde+99xpOBAAAAACwEgq9AV988YUefvhh2e12TZ06VfHx8aYjAQAA\nAAAshkLvYlu2bNGYMWNUUVGhsWPHatKkSaYjAQAAAAAsiELvQrt27dKIESNUWlqqwYMH68knn5TN\nZjMdCwAAAABgQRR6F8nOztaQIUN0/Phx/eEPf9Dzzz9PmQcAAAAA1BmF3gVyc3MVGxurgoIC9erV\nS/PmzZOPj4/pWAAAAAAAC6PQO9nRo0d133336dChQ7ruuuu0ZMkS+fn5mY4FAAAAALA4Cr0TFRUV\naejQocrKylLnzp21fPlyBQYGmo4FAAAAAPAAFHonKSkp0ciRI5Wenq7IyEi99dZbCgkJMR0LAAAA\nAOAhKPROUFFRoQceeEDffPONWrVqpbffflutWrUyHQsAAAAA4EEo9A5WXV2tv/zlL9q4caOCg4P1\n9ttvq23btqZjAQAAAAA8DIXegex2uxISErRu3ToFBgZq5cqV6tSpk+lYAAAAAAAPRKF3oDlzWbNS\nswAADg1JREFU5mjZsmXy8/PT0qVLde2115qOBAAAAADwUBR6B1m0aJFeeeUVeXt7a8GCBfqf//kf\n05EAAAAAAB6MQu8AqampmjVrliTpxRdf1IABAwwnAgAAAAB4Ogp9PW3YsEFTp06VJM2aNUuDBg0y\nnAgAAAAA0BBQ6OtpwoQJqq6u1pQpUzR69GjTcQAAAAAADQSFvp7Ky8s1evRoTZ482XQUAAAAAEAD\nQqGvp0GDBikxMVE2m810FAAAAABAA0Khr6cXXnhBXl78GgEAAAAArkUTrScfHx/TEQAAAAAADRCF\nHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegBAAAAALAgCj0AAAAAABZEoQcAAAAA\nwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegBAAAAALAgCj0A\nAAAAABZEoQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAF\nUegBAAAAALAgCj0AAAAAABZEoQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAA\nAAAsiEIPAAAAAIAFUegBAAAAALAgCj0AAAAAABZEoQcAAAAAwIJ8TAeoqqrSxx9/rJycHOXk5Ojg\nwYOqqqrSuHHj1K9fv0sa68iRI5owYcI5z0dHR2vSpEn1jQwAAAAAgHHGC31ZWZmSk5MlScHBwQoJ\nCVFBQUG9xoyMjFSPHj3OON6mTZt6jQsAAAAAgLswXuh9fX01bdo0RUZGKjg4WGvWrNHatWvrNWa7\ndu00cOBAByUEAAAAAMD9GC/0Pj4+6t69u+kYAAAAAABYivFC7wzHjh3Txo0bVVRUpCZNmqhjx45q\n27at6VgAAAAAADiMRxb69PR0paenn3YsKipK48ePV4sWLQylAgAAAADAcTyq0Pv5+enee+/VDTfc\noNDQUEnSgQMHtGbNGu3cuVNJSUmaM2eOfH19DScFAAAAAKB+HFLox48ff0k70/fq1eu8t5erq6ZN\nmyomJua0Y507d9b06dOVkJCgrKwsffbZZ7rjjjsc/tgAAAAAALiSQwp9WFjYJV31btasmSMe9qJ5\neXnplltuUVZWlvbs2ePQQh8REeGwsYAazCs4C3MLzsC8grMwt+AMzCt4EocU+oSEBEcM41RNmzaV\ndOq+9xdr9erV57yF3urVqx2SCwAAAABgfb/9tPivDRw48Lzn68qjvkN/PpmZmZJU+936ixETE3Pe\nX3pMTAzFHg7HvIKzMLfgDMwrOAtzC87AvIKzmJpbXi5/RAcoLi5Wbm6uCgsLTzu+b98+2e32M35+\nx44d2rBhg6RT398HAAAAAMDq3OIK/bvvvqvc3FxJUk5OjiTpiy++0A8//CDp1MZ2/fr1q/35tLQ0\nLViwQH369NFDDz1Ue3z58uXKy8tTx44d1bx5c0mndrnfuXOnJCk2NlYdO3Z0xVMCAAAAAMCp3KLQ\nb9++Xbt37z7tWGZmZu3H5CWdVuhr2Gy20/69d+/eSktLU3Z2trZv367KykoFBwcrOjpaAwYMUOfO\nnZ3zBAAAAAAAcDG3KPRPPvnkJf38zTffrJtvvvmM43379lXfvn0dlAoAAAAAAPdlye/QAwAAAADQ\n0FHoAQAAAACwIO/ExMRE0yGsym63q2vXrqZjwMMwr+AszC04A/MKzsLcgjMwr+AspuaWzX62+7wB\nAAAAAAC3xkfuAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAA\nYEEUegAAAAAALMjHdAB3V1VVpY8//lg5OTnKycnRwYMHVVVVpXHjxqlfv36XNNaRI0c0YcKEc56P\njo7WpEmT6hsZFuDIeVUjIyND69at0969e1VeXq7w8HD17dtXt99+u7y8eO+uoXHEfGDNapiOHj2q\n1NRUbd++XSdOnFBwcLB69OihQYMGKTAw0OXjwDM4Yj6MHz9eBQUFZz0XHBysRYsWOTIyLGDz5s3a\nvXu39u/fr5ycHJWWlqpXr17n/X/XubBmoYaj5pWr1iwK/QWUlZUpOTlZ0qlffEhIyDn/w1ysyMhI\n9ejR44zjbdq0qde4sA5Hz6stW7Zo7ty58vX1Vc+ePRUUFKStW7cqOTlZGRkZmjx5sqOiwwIcPR9Y\nsxqOw4cPa8aMGTp+/Lh69OihiIgI/fjjj/rwww+1fft2JSUlKSgoyGXjwDM4cj40btxYd9555xnH\n/f39HR0bFrBu3Trt379f/v7+at68uQ4dOlSncViz8GuOmleSa9YsCv0F+Pr6atq0aYqMjFRwcLDW\nrFmjtWvX1mvMdu3aaeDAgQ5KCCty5LwqKSnRokWL5OXlpcTERLVv316SFBsbq5kzZ2rz5s3atGmT\noqOjHfkU4KacMR9YsxqOxYsX6/jx4xo1apQGDBhQe3z58uXasGGDUlNTNWbMGJeNA8/gyPkQGBjI\neoRa8fHxatasmcLCwrR7927NnDmzTuOwZuHXHDWvJNesWXwO9wJ8fHzUvXt3BQcHm44CD+LIefXN\nN9+oqKhIN910U215q3mMwYMHS5I+/fTTej8OrIH5gLo6fPiw0tPTFRoaetoLWkmKiYmRn5+f/v3v\nf6u8vNwl48AzMB/gTFFRUQoLC6vXGMxR/JYj5pUrcYXegGPHjmnjxo0qKipSkyZN1LFjR7Vt29Z0\nLFjUrl27JEndu3c/41xUVJR8fX2VkZGhyspK+fjwV97TOWM+sGY1DDVz5+qrrz7jnL+/vzp16qT0\n9HRlZmaqW7duTh8HnsHR86GiokJffvmlCgoK5Ofnp3bt2qlLly7sFYM6Y82CM7lizeLVvQHp6elK\nT08/7VhUVJTGjx+vFi1aGEoFq8rNzZUkhYeHn3HOy8tLoaGhOnjwoPLz8xUREeHqeHAxZ8wH1qyG\n4Xxzp+Z4enq68vLyzvui1lHjwDM4ej4UFhZq3rx5px0LDQ3Vgw8+qKioqPoHRoPDmgVncsWaRaF3\nIT8/P91777264YYbFBoaKkk6cOCA1qxZo507dyopKUlz5syRr6+v4aSwkuLiYkmnNt04m5rjJ0+e\ndFkmmOPI+cCa1bA4au6wJuHXHDkf+vbtqy5duqhNmzby9/dXfn6+PvroI3366aeaPXu2nn76aT49\nhEvGmgVncdWa1SAK/fluGXA2db3dxYU0bdpUMTExpx3r3Lmzpk+froSEBGVlZemzzz7THXfc4fDH\nhuO5y7yC53GXucWaBcCd/HZjqcsvv1xjxoyRn5+f1q9fr9WrV+vRRx81lA4ATueqNatBFPqwsLBL\nuoLUrFkzJ6Y5k5eXl2655RZlZWVpz549vDi2CHeZVzXvHNe8w/xbNce5h6p1XOrcCgkJqf1nV8wH\n1izP5Ki5w5qEX3PFfLjtttu0fv167dmzp85joOFizYKrOXrNahCFPiEhwXSEC2ratKmkU/cnhzW4\ny7yKiIhQdna28vLyTtvVXJKqq6uVn58vb2/v2o9Mw/3VZ265aj6wZnmemj0V8vLyznq+5vi5vmfq\n6HHgGVwxH1iPUB+sWXA1R69ZbAnqJjIzMyWJ0oVLVrNBy7Zt2844t3v3bpWXl6tTp07scN9AuGo+\nsGZ5nq5du0rSGRsgSlJpaakyMjLk5+enjh07umQceAZXzIea9ahVq1Z1HgMNF2sWXM3RaxaF3gmK\ni4uVm5urwsLC047v27dPdrv9jJ/fsWOHNmzYIOnUd2GBsznXvLrxxhvVpEkTff3118rOzq49XlFR\nodTUVElS//79XZoV5tRlPrBmQTr1wuLqq6+u3bTn11atWqWysjL17t279usgVVVVys3N1eHDh+s1\nDjybo+bVoUOHzno1Kz8/X0uXLpXEeoTzY82CM7jDmmWzn+3VGk7z7rvv1t7SIicnR/v371fHjh1r\nP3rTuXNn9evXr/bn//nPf2rBggXq06ePHnroodrjM2fOVF5enjp27KjmzZtLOrVj9M6dOyVJsbGx\n+tOf/uSqpwXDHDWvJGnLli2aO3euGjVqpOjoaAUFBWnr1q3Kzc1Vz5499cgjj7juicG4S50PrFmo\ncfjwYSUkJOiXX37R9ddfr9atW2vv3r3avXu3IiIilJSUpKCgIEnSkSNHNGHCBLVs2fKMW/Jcyjjw\nfI6YV2vWrNH69evVpUsXtWjRQgEBATp8+LC+//57VVRU6LrrrtOjjz4qb29vU08TBmzZskVbtmyR\ndOr2YNu3b1doaKi6dOkiSWrSpImGDx8uiTULF88R88qVaxafwb0I27dv1+7du087lpmZWftxCUmn\nFa8aNpvttH/v3bu30tLSlJ2dre3bt6uyslLBwcGKjo7WgAED1LlzZ+c8AbglR80rSerRo4dmzpyp\ndevWKS0tTRUVFQoLC1NcXBwbljVAdZ0PrFlo1aqVnn32Wa1atUrbtm3Ttm3bFBwcrDvvvFMDBw48\n622dzrYm1WUceC5HzKuuXbsqLy9P+/btU0ZGhsrKyhQYGKguXbqod+/eXJ1voHJycvSvf/3rtGP5\n+fnKz8+XdOprYTXFqwZrFi7EEfPKlWsWV+gBAAAAALAgvkMPAAAAAIAFUegBAAAAALAgCj0AAAAA\nABZEoQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegB\nAAAAALAgCj0AAAAAABZEoQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAs\niEIPAAAAAIAF/X+p84Hc6c4EeAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1077b8e10>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.99380799 0.49690399] 5.61865569273\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3X9gzvX+//HHtc1+YrOxzWZ+dE7kR4pDTucT+nGSE5WY\nHTmVRCdC5ciPMWM2GyvHz4p+0Emnw7BUFPrUiQrlVMyPzlAMGxvNzNjP67q+f/jwTVFo9rqu632/\n/XM67/eut8e2t7kee7/fr6fN6XQ6BQAAAAAA3IqX6QAAAAAAAODyUegBAAAAAHBDFHoAAAAAANwQ\nhR4AAAAAADdEoQcAAAAAwA1R6AEAAAAAcEMUegAAAAAA3BCFHgAAAAAAN0ShBwAAAADADVHoAQAA\nAABwQxR6AAAAAADcEIUeAAAAAAA3RKEHAAAAAMANUegBAAAAAHBDPqYDSFJJSYk+//xzff311zpw\n4IAKCwvl4+Ojxo0b69Zbb9Vtt90mm812yccrLCzUkiVLtG3bNpWUlCgkJEQdO3ZU3759FRQUdBU/\nEwAAAAAAaoZLXKHftGmTXnrpJe3du1fXXnutevTood///vc6ePCgFixYoJkzZ17ysfLz8zV27Fit\nX7/+3LEiIyP1/vvvKyEhQSUlJdWWOyMjo9qOBffEOQDOAXAOgHMAnAPgHICpc8AlCn1UVJTGjh2r\n+fPna8SIEXrggQc0ZMgQzZo1S2FhYfr888/1xRdfXNKxXnnlFRUXF+vRRx/VM888o/79+2vixInq\n0aOH8vLytGTJkmrLvXz58mo7FtwT5wA4B8A5AM4BcA6AcwCmzgGXKPStW7dW+/btf7I9ODhYd955\npyRp586dv3ic/Px8ZWVlKTw8XHfdddd5++Li4uTn56cNGzaooqKieoIDAAAAAGCISxT6n+Pt7X3e\n//6cs6W/bdu2P9nn7++vFi1aqLy8XLt3767ekAAAAAAA1DCXLvQOh0Pr16+XJN14442/+PF5eXmS\npIYNG15w/9nthw8frqaEAAAAAACY4dKF/o033tChQ4fUvn37C151/7HTp09LkgIDAy+4/+z2U6dO\nVV9IAAAAAAAMcNlC/95772n16tVq1KiRhg8fbjoOAAAAAAAuxeZ0Op2mQ/zYmjVrtGjRIsXExGji\nxIkKDg6+pNe98cYbevfdd/XQQw+pZ8+eP9m/cOFCrV27VoMHDz632B4AAAAAAO7Ix3SAH1u9erVe\nf/11NW7cWBMnTlTdunUv+bVRUVGSLv6M/NntF3vG/scyMjIuOn6AWZMAAAAAgLPi4uIuui82NvZn\n918plyr0K1eu1L/+9S81a9ZMCQkJql279mW9vnXr1pKkrKysn+wrKytTdna2/Pz81Lx580s6Xlxc\n3C9+0c8uxAdrioqK4hywOCudA9HR0ef+e/78+brnnnsMpnEdJs6BnTt3qnv37vLy8tKHH36o3/72\ntzX65+N8Vvo5gAvjHADngLWdvbBs4qKvyzxDv3z5cv3rX//Sb37zG02cOPFny7zdbldeXp7y8/PP\n2x4REaG2bduqoKBAa9asOW/f0qVLVV5eri5dusjX1/eqfA4AYAW33377BR9rQs1wOp2aNGmSHA6H\nBgwYQJkHAMDCXOIK/ccff6xly5bJy8tLLVq00HvvvfeTj2nQoIFuvfVWSVJhYaFGjhypBg0aaN68\need93ODBgzVx4kQtWrRI27dvV3R0tPbs2aNdu3YpKipK/fr1q4lPCQA8yscff3zuv1NTU2Wz2cyF\nsbg1a9Zo06ZNCgkJ0ciRI03HAQAABrlEoT969KikM3PnL1TmJalVq1bnCv1ZF3pDGRERoWnTpmnp\n0qXaunWrtm7dqpCQEPXo0UOxsbEXHWkHALiw0tJSjR8/XpLk5+enmJgYw4msq7y8XMnJyZKk0aNH\nq169eoYTAQAAk1yi0Pft21d9+/a95I9v0KCBli5detH9oaGhGjp0aHVEAwDLmz17tnJyciSdKfQw\n59VXX1VOTo6aN2+uBx980HQcAABgmMs8Qw8AcD3Z2dl68cUXTceAztzNNnv2bEnS5MmT5ePjEr+T\nBwAABlHoAQAX5HA4NG7cOFVVVXE12AWkp6erpKREf/zjH9W1a1fTcQAAgAug0AMALmjJkiX64osv\n1KBBA8XHx5uOY2k7duzQv/71L/n4+GjixImm4wAAABdBoQcA/MSxY8c0depUSWdu7w4JCTGcyLrO\njqlzOp0aOHAgY+oAAMA5FHoAwE8kJSWpqKhIXbt21X333Wc6jqW999572rx5s+rVq8eYOgAAcB4K\nPQDgPJ988okyMzPl7+/PzHnDysrKzhtTFxwcbDgRAABwJRR6AMA5ZWVl556Xf+qpp9S0aVOzgSzu\nlVde0cGDB3XdddfpL3/5i+k4AADAxVDoAQDnzJs3T/v27VPz5s01ZMgQ03EsLT8/X3PmzJEkTZo0\niTF1AADgJyj0AABJ0t69ezVv3jxJ0rRp0+Tr62s4kbVNnz5dp06dUrdu3dSlSxfTcQAAgAui0AMA\n5HQ6NW7cOFVWVuqBBx5Qp06dTEeytKysLGVkZKhWrVqMqQMAABdFoQcAKCMjQ5s2bVJYWJgmTJhg\nOo6l/XBM3aOPPqprrrnGdCQAAOCiKPQAYHGFhYXnVlJPTExUvXr1DCeytlWrVumLL75QWFiYnn76\nadNxAACAC6PQA4DFTZs2TcePH9fNN9+sPn36mI5jaaWlpUpJSZEkjRkzRnXr1jWcCAAAuDIKPQBY\n2Jdffqk333xTPj4+SktLY+a8YS+99JIOHTqkli1b6oEHHjAdBwAAuDgKPQBYVFVVleLj4+V0OjVk\nyBBde+21piNZ2pEjR85NGUhKSpK3t7fhRAAAwNVR6AHAov7xj39o586datSoEc9qu4Bp06bp9OnT\n6t69u/7nf/7HdBwAAOAGKPQAYEH5+flKT0+XJCUnJysgIMBwImvbtm2bli1bJl9fX8bUAQCAS0ah\nBwALmjJlikpKSnTnnXeqW7dupuNY2tkxdZI0ePBgNW3a1GwgAADgNij0AGAxGzZs0MqVK+Xv739u\nXB3Meeedd7RlyxbVr19fTz75pOk4AADAjVDoAcBCysvLNWHCBEnS008/rZiYGMOJrO2HY+rGjh2r\nOnXqGE4EAADcCYUeACxk/vz5+u677/Tb3/5Wjz/+uOk4ljd//nzl5eWpVatW+vOf/2w6DgAAcDMU\negCwiAMHDmjOnDmSpKlTp8rX19dwIms7fPiwnn/+eUln1jRgTB0AALhcFHoAsACn06mEhASVlZXp\n/vvv1y233GI6kuWlpaWptLRUd999t26++WbTcQAAgBui0AOABaxdu1Yffvih6tSpo8TERNNxLO+r\nr77SihUr5Ovrq4SEBNNxAACAm6LQA4CHO3369LnZ5mPHjlV4eLjhRNb2wzF1f/3rX9WkSRPDiQAA\ngLui0AOAh5s1a5by8vLUpk0bPfzww6bjWN7KlSv11VdfqUGDBhoxYoTpOAAAwI1R6AHAg2VnZ2vB\nggWy2WyaNm0aC68ZVlpaqqlTp0qSxo0bp9q1axtOBAAA3BmFHgA8lNPp1Pjx41VVVaUHH3xQ7dq1\nMx3J8l588UUdPnxYbdq0UVxcnOk4AADAzVHoAcBDrVixQps3b1ZYWJjGjRtnOo7l5ebmnjemzsuL\nf4IBAMCvw7sJAPBARUVFSk5OliQlJCQoJCTEcCJMmzZNZWVl6tmzpzp16mQ6DgAA8AAUegDwQNOn\nT9exY8fUqVMn9e3b13Qcy/vyyy+VmZkpPz8/xtQBAIBqQ6EHAA+zdetWLV68WD4+PkpNTZXNZjMd\nydIcDocSExMlnRlTFxMTYzgRAADwFBR6APAgdrtd8fHxcjqdeuyxx3TdddeZjmR5y5Yt09atWxUZ\nGcmYOgAAUK0o9ADgQRYvXqysrCxFRUVp5MiRpuNYXnFxsVJTUyWdWcsgKCjIcCIAAOBJKPQA4CEK\nCgo0ffp0SWdWUac8mjdz5kwdO3ZMHTt2VK9evUzHAQAAHoZCDwAeIjk5WcXFxbr99tvVvXt303Es\nb+/evVq4cKFsNptSUlJYywAAAFQ7Cj0AeICNGzcqMzNT/v7+lEcX4HQ6lZiYqKqqKvXv319t2rQx\nHQkAAHggCj0AuLmKigqNHz9ekjR8+HA1adLEcCJ88MEHWr9+vYKDgzV27FjTcQAAgIei0AOAm3vp\npZe0Z88eNWvWTE888YTpOJZXVlamyZMnS5KeeeYZhYWFmQ0EAAA8FoUeANzYoUOHNHPmTElSamqq\n/Pz8DCfCSy+9pJycHLVo0UIPP/yw6TgAAMCDUegBwI0lJiaqrKxM9957r7p06WI6juXl5eVpzpw5\nkqSkpCT5+PgYTgQAADwZhR4A3NS6deu0du1a1a5dW5MmTTIdBzpzl0Rpaanuvvtude7c2XQcAADg\n4Sj0AOCGSktLlZiYKEkaPXq0IiMjDSfCF198obfeekv+/v7nvjcAAABXE4UeANzQ7NmzdfDgQbVq\n1UqPPPKI6TiWZ7fblZCQIEl64oknFBMTYzgRAACwAgo9ALiZvXv3av78+ZKktLQ0ntN2AW+++aZ2\n7typqKgoJg0AAIAaQ6EHADfidDo1fvx4VVZWqn///urQoYPpSJZ3/PhxTZ8+XdKZRQoDAgIMJwIA\nAFZBoQcAN7Jy5Up99tlnqlevnuLj403HgaRJkybp+PHjuvnmm9WzZ0/TcQAAgIVQ6AHATRQXFysp\nKUmSlJCQoNDQUMOJ8M033+iFF16Ql5eXkpOTZbPZTEcCAAAWQqEHADfx7LPP6ujRo+rQoYPi4uJM\nx7E8p9OpxMRE2e12DRgwQC1btjQdCQAAWAyFHgDcwPbt2/Xaa6/J29tbaWlp8vLix7dpq1ev1saN\nGxUWFqZRo0aZjgMAACyId4QA4OIcDofi4+PlcDg0aNAgtWrVynQkyystLdWUKVMkSSkpKapXr57h\nRAAAwIoo9ADg4pYuXaqvv/5aERER+tvf/mY6DiS9+OKLys3NVatWrfTYY4+ZjgMAACyKQg8ALuz4\n8eOaOnWqpDMj0erUqWM4EQ4dOqTnn39e0pmr897e3oYTAQAAq6LQA4ALS09PPzcS7b777jMdB5Km\nTJmisrIy9erVS506dTIdBwAAWBiFHgBcVFZWlhYvXiwfHx9NnTqVkWgu4NNPP9Xq1asVEBCgCRMm\nmI4DAAAsjkIPAC7I4XBo/PjxcjqdGjRokFq0aGE6kuVVVVUpMTFRkjRixAhFRUUZTgQAAKyOQg8A\nLoiF8FzP66+/ruzsbDVu3FiPP/646TgAAAAUegBwNcePH1dqaqqkMwvh1a5d23AiFBYW6rnnnpMk\nTZ48Wf7+/oYTAQAAUOgBwOWkp6ersLCQhfBcyPTp03XixAl17dpV3bp1Mx0HAABAEoUeAFzK2YXw\nvL29WQjPRezYsUP//Oc/5ePjo6SkJL4nAADAZVDoAcBFsBCe63E6nUpISJDT6dTAgQN17bXXmo4E\nAABwDoUeAFxERkYGC+G5mJUrV2rLli2qX78+3xMAAOByKPQA4AKOHz+uqVOnSpImTpyoOnXqGE6E\nU6dOKSUlRZIUHx+vunXrGk4EAABwPgo9ALiAZ5999txCeL169TIdB5Lmzp2rI0eO6IYbblBcXJzp\nOAAAAD9BoQcAw7Zv367XX39d3t7eSklJYdE1F7B//34tWLBAkjRlyhR5efHPJQAAcD0+pgNI0ubN\nm7Vr1y7l5ORo//79KisrU+fOnTV8+PDLOs6wYcN07NixC+4LCQk59+YMAFzFjxfCu+6660xHgqSk\npCRVVFQoNjZWHTp0MB0HAADgglyi0GdmZionJ0f+/v4KCwtTbm7uFR8rMDBQPXr0+Ml2f3//XxMR\nAK6KjIwMffXVVwoPD2fRNRfx8ccfa926dQoKCtL48eNNxwEAALgolyj0jzzyiEJDQxUZGaldu3Yp\nKSnpio8VFBSk2NjYakwHAFfHDxfCS0xMZCE8F1BRUaHExERJ0siRIxUREWE4EQAAwMW5RKFv1aqV\n6QgAUONYCM/1LFq0SN9++62aNWumQYMGmY4DAADws1yi0FenyspKffLJJzp27Jj8/PzUpEkTtWzZ\nkgWNALgUFsJzPQUFBfr73/8u6cwz9L6+voYTAQAA/DyPK/RFRUWaN2/eedvCw8M1dOhQ7gQA4BIc\nDocmTJggp9OpRx99lIXwXERaWppKSkp0xx136I477jAdBwAA4Bd5VKG/7bbb1LJlS8XExMjf318F\nBQVas2aNPvjgA6WlpWnq1Klq3Lix6ZgALG7ZsmX68ssvFR4erlGjRpmOA0n/+c9/lJGRIV9fX02e\nPNl0HAAAgEviUfehx8bGqnXr1qpbt658fX3VqFEjDR48WD179lRFRYUyMjJMRwRgcSdOnFBqaqok\nKSEhgYXwXIDdbldCQoIk6fHHH9c111xjOBEAAMCl8agr9Bdz5513atWqVfrmm28u63UZGRlavnz5\nRfdJUlRU1K/OB/fGOYDLOQemT5+uY8eO6ZZbbtHw4cPd7tl5Ly8vjzvn58+fr+3btysmJkZpaWkK\nCgq67GN42tcEl49zAJwD4BxAXFzcRffFxsb+7P4rZYlCX7duXUlSeXn5Zb0uLi7uF7/oeXl5V5wL\n7i8qKopzwOIu5xzYtWuX5s2bJy8vLyUmJurw4cNXOV31czgcHnXOFxYWKj4+XtKZOyZOnDihEydO\nXNYx+DkAzgFwDoBzwNrO/jLHxB3hHnXL/cXs3r1bkpgnDMAYp9OphIQEORwODRgwQK1btzYdCZKm\nTZumoqIi3XLLLerRo4fpOAAAAJfF7Qq93W5XXl6e8vPzz9uem5t7wSvwBQUFWrhwoSSpc+fONZIR\nAH5s5cqV+vzzzxUWFqbRo0ebjvOreHt7m45QLbZt26Y333xTPj4+jA4EAABuySVuud+yZYu2bNki\n6czYOUnKzs7WCy+8IEmqU6eOHnroIUlnbo8cOXKkGjRocN54uo0bN2rVqlVq2bKl6tevr4CAAOXn\n5+urr75SZWWl2rdvr3vuuaeGPzMAkE6ePKnk5GRJ0oQJExQcHGw40eXxcTpVy+vM739tFRUK2LRJ\n9k6dVOlwqMpNS/APRwcOHjxY1157relIAAAAl80lCv3+/fu1fv3687YVFBSooKBA0pk58mcL/Vk/\nvpLSunVrHT58WPv27VN2drbKy8sVFBSkli1bqkuXLlydB2DMrFmzlJ+fr3bt2qlv376m41wWH6dT\nvvn5qtOrlyTJVlamuvffL3tMjE6uXClFRLhlqc/IyNDXX3+tiIgIjRw50nQcAACAK2JzOp1O0yHc\nmRUWv7A/dq/pCAAAwMV4v/yO6QgugwXRwDlgbSYnHLjdM/QAAAAAAIBCDwAAAACAW6LQAwAAAADg\nhlxiUTy4Np6Ruziel8LFzoFp06Zp7ty5atu2rVatWuW2o94CbDbV7dRJ3gcP/mSfPSZGxZs3q9RA\nriuxfPlyPfXUU6pfv742bNhQbdMG+DkAzgEAgClcoQeAavbdd99pwYIFkqSUlBS3LfOSVOlw6OTK\nlbLHxJy33R4To5Nvv61KN1lX9eTJk0pJSZHknqMDAQAALoQr9ABQjZxOpxITE1VRUaF+/frpd7/7\nnelIv0qVzSZFRKj488/l/cUX8t61S/ZWrWS/6Sa3mkM/Y8YMHT16VB06dFBsbKzpOAAAANWCQg8A\n1WjdunX697//reDgYMXHx5uOUy2qbDZVOZ3y/v3vZbv5ZjmdTtntdslNynx2drYWLlwoLy8vTZ06\nVV5e3JwGAAA8A4UeAKpJaWmpJk2aJEkaPXq06tevbzhR9bLb7aYjXDan06mEhATZ7XYNGDBAbdq0\nMR0JAACg2nCZAgCqyQsvvKCDBw+qZcuWeuihh0zHgaR33nlHGzduVL169TR69GjTcQAAAKoVhR4A\nqsGBAwf0/PPPS5JSU1Pl48MNUKadOnVKU6ZMkSSNHz9e9erVM5wIAACgelHoAaAaJCUlqby8XL17\n99ZNN91kOg4kzZ49W0eOHNGNN96ofv36mY4DAABQ7Sj0APArbdiwQWvWrFFQUJAmTJhgOg4k7d27\nVwsWLJDNZmMhPAAA4LF4hwMAv0JlZaUSExMlSU8//bQiIyMNJ8LZhfCqqqrUv39/3XjjjaYjAQAA\nXBUUegD4FZ5//nnt2bNHzZo106BBg0zHgaRVq1bpk08+UUhIiMaNG2c6DgAAwFVDoQeAK3Ts2LFz\nY+qSkpLk5+dnOBFOnTqlpKQkSVJ8fLxCQ0MNJwIAALh6KPQAcIWmTZum4uJi3X777brjjjtMx4HO\nLIR3+PBh3XDDDXrggQdMxwEAALiqKPQAcAW2bdumJUuWqFatWpo8ebLpOND5C+GlpqbK29vbdCQA\nAICrikIPAJfJ4XBo4sSJcjqdGjlypH7zm9+YjmR5LIQHAACsiEIPAJcpMzNTX375pcLDw5WQkGA6\nDsRCeAAAwJoo9ABwGUpKSjR16lRJ0oQJE1SnTh3DifDDhfDGjRvHQngAAMAyKPQAcBlmz56tgoIC\ntW/fXr179zYdBzp/Ibz+/fubjgMAAFBjKPQAcIm+/fZbvfzyy7LZbEpOTpaXFz9CTdu7d69eeukl\n2Ww2TZ06lYXwAACApfBuFAAu0eTJk1VZWal+/fqx6JoLOLsQXmVlpfr376927dqZjgQAAFCjKPQA\ncAn+93//Vx999JHq1KnDomsugoXwAACA1VHoAeAXlJeXn5s1P2rUKNWvX99sILAQHgAAgCj0APCL\nXn31Ve3bt0/XXnutHnnkEdNxoP+/EF7btm1ZCA8AAFgWhR4AfsaRI0c0a9YsSdKUKVNUq1Ytw4nw\nw4XwUlNTWQgPAABYFoUeAH5GamqqTp06pe7du6tLly6m41geC+EBAAD8fxR6ALiI//znP1qxYoX8\n/PyUmJhoOg4krV69moXwAAAA/g+FHgAuwOFwaOLEiZKkIUOGqEmTJoYT4dSpU+cWJ2QhPAAAAAo9\nAFzQ0qVLlZWVpYYNG2r48OGm40AshAcAAPBjFHoA+JETJ04oLS1NkjRx4kQFBgYaToTs7GwtWLCA\nhfAAAAB+gEIPAD/y97//Xd9//706deqke++913Qcy3M6nRo/fryqqqr04IMPshAeAADA/6HQA8AP\n7N69W4sWLZKXl5emTJkim81mOpLlrVixQps3b1ZYWBgL4QEAAPwAhR4A/o/T6VRiYqLsdrsefPBB\ntWnTxnQkyysqKlJycrIkKSEhQSEhIYYTAQAAuA4KPQD8n7Vr154biTZ69GjTcSBp+vTpOnbsmDp1\n6qS+ffuajgMAAOBSKPQAIKm0tPTcSLTRo0czEs0FbN26VYsXL5aPj49SU1N5/AEAAOBHKPQAIGnB\nggU6ePCgWrZsqQcffNB0HMuz2+2Kj4+X0+nUY489puuuu850JAAAAJdDoQdgebm5uZo7d64kacqU\nKfLx8TGcCIsXL1ZWVpaioqI0cuRI03EAAABcEoUegOWlpKSorKxM99xzj/7whz+YjmN5BQUFmj59\nuqQzv2AJCgoynAgAAMA1UegBWNqmTZv0zjvvyN/fXxMnTjQdB5KSk5NVXFys22+/Xd27dzcdBwAA\nwGVR6AFYVlVV1bkSP3z4cEVHRxtOhI0bNyozM1P+/v5KSUlhITwAAICfQaEHYFn//Oc/9c033ygm\nJkZDhgwxHcfyKioqNH78eElnfsHSpEkTw4kAAABcG4UegCUVFhYqPT1dkpSYmKiAgADDifDSSy9p\nz549atasmZ544gnTcQAAAFwehR6AJT333HMqKirSLbfcoj/96U+m41jeoUOHNHPmTElSamqq/Pz8\nDCcCAABwfRR6AJazc+dOLV68WN7e3poyZQrPabuAxMRElZWV6d5771WXLl1MxwEAAHALFHoAluJ0\nOpWYmCiHw6FHHnlELVq0MB3J8tatW6e1a9eqdu3amjRpkuk4AAAAboNCD8BS3n33XW3evFmhoaEa\nNWqU6TiWV1paqsTEREnSM888o8jISMOJAAAA3AeFHoBlnD59WsnJyZKkcePGKTg42HAizJ49WwcP\nHlSrVq00cOBA03EAAADcCoUegGW88MILysvL0/XXX69+/fqZjmN5e/fu1fz58yVJaWlp8vHxMZwI\nAADAvVDoAVhCbm6uXnzxRUlScnKyvL29DSeyNqfTqfHjx6uyslL9+/dXhw4dTEcCAABwOxR6AJYw\nderUc6uod+zY0XQcy1u5cqU+++wz1atXT/Hx8abjAAAAuCUKPQCPt2XLFr399tvy9/dXQkKC6TiW\nV1xcrKSkJElSQkKCQkNDDScCAABwTxR6AB7N4XCcG4U2ZMgQRUdHG06EZ599VkePHlWHDh0UFxdn\nOg4AAIDbotAD8GgrVqzQtm3bFBkZqSeeeMJ0HMvbvn27XnvtNXl7eystLU1eXvwzBAAAcKV4JwXA\nY506dUppaWmSpPj4eAUFBRlOZG12u13x8fFyOBx69NFH1apVK9ORAAAA3BqFHoDHmjdvnvLz89Wu\nXTv17t3bdBzLe/PNN/X1118rMjJSzzzzjOk4AAAAbo9CD8AjHTp0SAsWLJAkTZ48mVu7DTt27Jim\nTZsm6cz3o3bt2oYTAQAAuD/e4QLwSCkpKSovL1evXr2Yce4Cpk6dqqKiInXt2lU9e/Y0HQcAAMAj\nUOgBeJwvvvhC7777rvz9/TV+/HjTcSzv888/V0ZGhvz8/JSSkiKbzWY6EgAAgEeg0APwKD8cU/fE\nE08wps6wyspKxcfHS5KGDRuma665xnAiAAAAz0GhB+BRli1bpqysLEVGRmro0KGm41jeq6++quzs\nbDVt2pSxgQAAANWMQg/AY5SUlJxbeG3ChAkKDAw0nMjacnNzNWPGDElScnKyAgICDCcCAADwLBR6\nAB5j7ty5KigoULt27dSrVy/TcSxv8uTJOn36tO6++27dfvvtpuMAAAB4HAo9AI9w4MABvfzyy5Kk\npKQkxtQZ9uGHH+q9995TYGCgJk+ebDoOAACAR/IxHUCSNm/erF27diknJ0f79+9XWVmZOnfurOHD\nh1/2sQowH1ViAAAgAElEQVQLC7VkyRJt27ZNJSUlCgkJUceOHdW3b18FBQVdhfQAXMHZMXW9e/fW\n7373O9NxLK20tFQTJ06UJI0aNYqFCQEAAK4Slyj0mZmZysnJkb+/v8LCwpSbm3tFx8nPz1dCQoKK\ni4vVsWNHRUVF6dtvv9X777+vbdu2KTk5WbVr167m9ABM27x5s1avXq2AgIBzK6rDnOeff145OTm6\n7rrrNGjQINNxAAAAPJZLFPpHHnlEoaGhioyM1K5du5SUlHRFx3nllVdUXFysRx99VHfddde57a+/\n/rpWr16tJUuWaPDgwdUVG4ALsNvt58bUDRs2TFFRUYYTWdu3336r559/XpKUlpamWrVqGU4EAADg\nuVziIdNWrVopMjLyVx0jPz9fWVlZCg8PP6/MS1JcXJz8/Py0YcMGVVRU/Ko/B4BrycjI0I4dOxQV\nFaUhQ4aYjmNpTqdTEyZMUEVFheLi4nTTTTeZjgQAAODRXKLQV4edO3dKktq2bfuTff7+/mrRooXK\ny8u1e/fumo4G4Co5efKkpk+fLunMmDrGopn1zjvv6JNPPlFISIgSEhJMxwEAAPB4HlPo8/LyJEkN\nGza84P6z2w8fPlxjmQBcXXPnztXRo0f1u9/9Tvfdd5/pOJZ24sSJc6vZx8fHKywszGwgAAAAC/CY\nQn/69GlJUmBg4AX3n91+6tSpGssE4OrJyck5b0ydzWYznMjapk2bpoKCAnXo0EH9+/c3HQcAAMAS\nPKbQA7CWlJQUVVRUqE+fPmrXrp3pOJb25ZdfavHixfLx8dH06dPl5cU/LQAAADXBJVa5rw5nr8Cf\nvVL/Y2e3X84s+oyMDC1fvvyi+ySxojY4Bwz4+OOP9d577ykwMFCzZ882+j04Vnjc0s/uV1ZWKj4+\nXk6nU8OHD7fkL1eOH7f2OQDOAXAO4Mz7Ad4TIi4u7qL7YmNjf3b/lfKYQn/2L9DFnpE/u/1iz9hf\nSFxc3C9+0c8+uw9rioqK4hyoYXa7XcOGDZN0ZkydzWYz+j0ICAhQt1e+Nvbnm3ZkfYYO7dwp39CG\nWl//Tkt/LQAA1rVucDveE1rY2S569qJvTfKY+yJbt24tScrKyvrJvrKyMmVnZ8vPz0/Nmzev6WgA\nqtGSJUu0a9cuRUdH6/HHHzcdx9LKj+crb90/JElNeo2Qt6+/4UQAAADW4naF3m63Ky8vT/n5+edt\nj4iIUNu2bVVQUKA1a9act2/p0qUqLy9Xly5d5OvrW5NxAVSj4uJixtS5CKfTqQNvzZajskz12t6q\n4Os6mY4EAABgOS5xy/2WLVu0ZcsWSVJRUZEkKTs7Wy+88IIkqU6dOnrooYckSYWFhRo5cqQaNGig\nefPmnXecwYMHa+LEiVq0aJG2b9+u6Oho7dmzR7t27VJUVJT69etXg58VgOo2Z84cff/99+rYsaPu\nvfde03EsrWjHJzrx38/l7R+kmHufMB0HAADAklyi0O/fv1/r168/b1tBQYEKCgokSeHh4ecK/VkX\nGlEVERGhadOmaenSpdq6dau2bt2qkJAQ9ejRQ7GxsRcdaQfA9e3bt0+vvPKKJMbUmWYvO6UDb5/5\nhWp090HyrcvMeQAAABNcotD37dtXffv2vaSPbdCggZYuXXrR/aGhoRo6dGh1RQPgIlJSUlRZWam+\nffvqhhtuMB3H0nLXLlJl8fcKatxSDX7f03QcAAAAy3K7Z+gBWM+nn36qNWvWKDAwUOPGjTMdx9JO\nHfyvCjaulLy81KT3SNm8vE1HAgAAsCwKPQCXZrfbNXnyZEnSiBEjFBkZaTaQhTntduWsmCk5nYq4\nJVaBUb8xHQkAAMDSKPQAXNqbb76pb775Ro0aNdJjjz1mOo6lFWxcqdN5e+UbEq6obg+bjgMAAGB5\nFHoALqu4uFjp6emSpISEBMbUGVRRVKDctQslSY17PSlvX74XAAAAplHoAbisWbNmqbCwUJ06dVLP\nniy+ZtKBt+fJUVGmkDadFdLqZtNxAAAAIAo9ABf13XffaeHChbLZbJo8eTJj6gw6vvMzFe38TF5+\ngWp83zDTcQAAAPB/KPQAXFJycrIqKysVFxentm3bmo5jWfay0zqwcq4kKfqugfINbmA4EQAAAM6i\n0ANwORs2bNC6desUFBTEmDrD8j54TZUnjiowurnC/3Cf6TgAAAD4AQo9AJdit9s1ZcoUSWfG1IWH\nhxtOZF2nc/co/9O3JJuXmvRh5jwAAICrodADcClLly5lTJ0LcDrs2r9ipuR0KPx/7ldQo+amIwEA\nAOBHKPQAXEZJSYmeffZZSdL48ePl7+9vOJF1Hd30rk4fylat4AaK7vaI6TgAAAC4AAo9AJfxwgsv\nqKCgQO3atdO9995rOo5lVZw4qkNrXpUkNb5vuLz9Aw0nAgAAwIVQ6AG4hLy8PC1YsECSNGnSJMbU\nGXTwnRfkKD+tkNZ/UL02t5iOAwAAgIug0ANwCdOnT1dZWZl69Oihjh07mo5jWUXfbNbx7Rvk5euv\nxveNMB0HAAAAP4NCD8C4rKwsLV++XL6+vho/frzpOJZlryjVgZVzJElR3QbKN4QJAwAAAK6MQg/A\nKKfTeW5M3cCBA9W0aVOzgSws74PXVXE8XwFRv1XE/9xvOg4AAAB+AYUegFHr1q3Tpk2bFBISoief\nfNJ0HMs6ffhb5X+yXLLZ1LTPSNm8mTkPAADg6ij0AIyprKxUSkqKJGnUqFEKCQkxnMianA6HclbM\nlBwOhd98n4JirjMdCQAAAJeAQg/AmMWLF+u7777TNddco4ceesh0HMs6+vlqnTrwjWrVDVPUXQNN\nxwEAAMAlotADMKKoqEgzZsyQJCUkJKhWrVqGE1lT5clC5b7/siQp5t5h8gmobTgRAAAALhWFHoAR\nc+bMUVFRkW6++WZ169bNdBzLOvjOC7KXnVLwdZ1U7/oupuMAAADgMlDoAdS4nJwcLVq0SDabTZMm\nTZLNZjMdyZJOZG9R4bZ/y6uWnxr3epLvAwAAgJuh0AOocampqaqoqFCfPn10/fXXm45jSfaKMuW8\nNVuSFHXnAPmFRhpOBAAAgMtFoQdQo7Zs2aJVq1bJ399fY8eONR3Hsg5/+IYqCg8rILKZwjv3MR0H\nAAAAV4BCD6DGOJ1OJSUlSZKGDBmiqKgow4msqfTIfuWvz5BsNjXpM1Je3j6mIwEAAOAKUOgB1Jh3\n3nlHX3/9tcLDw/XEE0+YjmNJTodDOZkz5XTY1aBTT9Vu0tp0JAAAAFwhCj2AGlFWVqbU1FRJ0ujR\noxUUFGQ4kTUd2/K+SvbvkE/teor+02DTcQAAAPArUOgB1IhXX31Vhw4dUsuWLfXnP//ZdBxLqiw5\nrkPvnZk53/jeJ5g5DwAA4OYo9ACuuu+//15z586VJCUmJsrb29twIms6+M4LspeeVN3mHVXvhttM\nxwEAAMCvRKEHcNXNmDFDJ0+e1O23364uXbqYjmNJJ/77uQq3fiSvWv5q0vspZs4DAAB4AAo9gKtq\nz549euONN+Tl5aWEhATTcSzJXl6qnMxZkqSobgPkF9rQcCIAAABUBwo9gKsqOTlZdrtdf/nLX9Si\nRQvTcSwpd+0iVRQVKDC6uSJuYeY8AACAp6DQA7hqPvnkE3344YeqXbu2nnnmGdNxLOnUwf+q4LO3\nJC8vNY39m2ysXwAAAOAxKPQArgq73a4pU6ZIkoYPH6769esbTmQ9DnuV9i+fITkdirglVoHR15qO\nBAAAgGpEoQdwVSxbtky7du1SdHS0Bg9m3rkJ+RuWqfTwd/INbaiobgNMxwEAAEA1o9ADqHanTp1S\nenq6JCk+Pl4BAQGGE1lP2bFc5X3wuiSpSe+n5e3rbzgRAAAAqhuFHkC1mz9/vvLz83XjjTfqvvvu\nMx3HcpxOp3IyZ8pZVaGw9ncquHkH05EAAABwFVDoAVSrw4cP68UXX5QkTZo0SV5e/Jipad//Z61O\n7v1aPkHBanTPUNNxAAAAcJXwThtAtUpPT1dpaanuvvtu3XTTTabjWE7lyUIdXDVfkhRzz1DVCgo2\nnAgAAABXC4UeQLXZsWOHli1bplq1amnChAmm41jSwXdflL30pOo276jQdn80HQcAAABXEYUeQLVw\nOp2aMmWKnE6nHnnkETVt2tR0JMs58d/PVbj1I3nV8leT3k/JZrOZjgQAAICriEIPoFp88MEH+uyz\nzxQSEqKnnnrKdBzLsZeXKidzliQpqtsA+YU2NJwIAAAAVxuFHsCvVllZqZSUFEnSyJEjVa9ePcOJ\nrCd37SJVFBUoMLq5Im7pYzoOAAAAagCFHsCv9s9//lPffvutmjZtqocffth0HMs5dfC/KvjsLcnL\nS01j/yabt7fpSAAAAKgBFHoAv8qJEyc0Y8YMSVJCQoJ8fX0NJ7IWh71K+5fPkJwORXSOVWD0taYj\nAQAAoIZQ6AH8KnPnzlVhYaF+//vfq3v37qbjWE7+hmUqPfydfEMbKurOAabjAAAAoAZR6AFcsUOH\nDmnhwoWSpMTERFZVr2Flx3KV98HrkqQmvZ+Wt6+/4UQAAACoSRR6AFcsPT1d5eXluv/++3XDDTeY\njmMpTqdTOZkz5ayqUFj7OxXcvIPpSAAAAKhhFHoAV2THjh3KzMyUr6+vxowZYzqO5Xz/n7U6ufdr\n+QQFq9E9Q03HAQAAgAEUegBXJDU1VU6nUwMGDFDjxo1Nx7GUypOFOrhqviQp5p6hqhUUbDgRAAAA\nTKDQA7hs69ev1/r161W3bl09+eSTpuNYzsF3X5S99KTqNu+o0HZ/NB0HAAAAhlDoAVwWh8OhlJQU\nSdKIESMUGhpqOJG1nPjv5yrc+pG8avmrSe+nWIgQAADAwij0AC5LZmamdu3apaioKA0cONB0HEux\nl5cqJ3OWJCmq2wD5hTY0nAgAAAAmUegBXLKysjKlp6dLkkaPHq2AgADDiawld+0iVRQVKDC6uSJu\n6WM6DgAAAAyj0AO4ZK+99ppyc3PVsmVL9elDoaxJpw7+VwWfvSV5ealp7N9k8/Y2HQkAAACGUegB\nXJLjx49rzpw5kqSEhAR5UyhrjMNepf3LZ0hOhyI6xyow+lrTkQAAAOACKPQALsncuXN14sQJde7c\nWV27djUdx1LyNyxT6eHv5BfaUFF3DjAdBwAAAC6CQg/gFx08eFCLFi2SJE2YMIGV1WtQ2bFc5X3w\nuiSpce+n5e3rbzgRAAAAXAWFHsAvSk9PV0VFhXr37q3rr7/edBzLcDqdysmcKWdVhcLa36ng5h1M\nRwIAAIALodAD+Fk7duxQZmamfH19NWbMGNNxLOX7/6zVyb1fyycoWI3uGWo6DgAAAFwMhR7ARTmd\nTiUnJ0uSBg4cqJiYGMOJrKPyZKEOrpovSYq5Z6hqBQUbTgQAAABXQ6EHcFHr16/Xp59+quDgYI0Y\nMcJ0HEs5+O6LspeeVN3mHRXa7o+m4wAAAMAFUegBXJDdbldKSookacSIEapXr57hRNZx4r+fq3Dr\nR/Kq5a8mvZ9iEUIAAABcEIUewAWtWLFC33zzjaKjozVw4EDTcSzDXl6qnMxZkqSobgPkF9rQcCIA\nAAC4Kgo9gJ8oLS3Vs88+K0kaM2aM/P0ZlVZTctcuUkVRgQKjmyvilj6m4wAAAMCF+ZgO8EOFhYVa\nsmSJtm3bppKSEoWEhKhjx47q27evgoKCLukYw4YN07Fjxy64LyQkRAsWLKjOyIBHWrRokfLy8tSq\nVSv17t3bdBzLKMnZpYLPMiUvLzWN/Zts3t6mIwEAAMCFuUyhz8/PV0JCgoqLi9WxY0dFRUXp22+/\n1fvvv69t27YpOTlZtWvXvqRjBQYGqkePHj/ZzlVG4JcVFhZq7ty5kqSEhAR5eXEjT01wVFVo//Ln\nJKdTkV3/rMDoa01HAgAAgItzmUL/yiuvqLi4WI8++qjuuuuuc9tff/11rV69WkuWLNHgwYMv6VhB\nQUGKjY29WlEBjzZnzhwVFxerS5cu6tq1q+k4lnH4ozdVlp8jv/qNFHXnw6bjAAAAwA24xKW3/Px8\nZWVlKTw8/LwyL0lxcXHy8/PThg0bVFFRYSghYA0HDhzQa6+9JpvNpgkTJpiOYxmnD3+rIx+9KUlq\n2neUvGr5GU4EAAAAd+ASV+h37twpSWrbtu1P9vn7+6tFixbKysrS7t271aZNm188XmVlpT755BMd\nO3ZMfn5+atKkiVq2bMmtw8AvSE9PV2Vlpfr06XNJf9fw6zntdu3PeE5Oh10N/nCf6jT76c9BAAAA\n4EJcotDn5eVJkho2vPB4poYNGyorK0uHDx++pJJRVFSkefPmnbctPDxcQ4cOVatWrX59YMADZWVl\n6a233pKfn5/GjBljOo5l5H+yXKdzd8s3JFyNul/aY0UAAACA5CKF/vTp05LOLGZ3IWe3nzp16heP\nddttt6lly5aKiYmRv7+/CgoKtGbNGn3wwQdKS0vT1KlT1bhx4+oLD3gAp9Op5ORkSdLAgQPVqFEj\nw4msoezoQeWue02S1KTPSHn7X/hnIAAAAHAhHncPemxsrFq3bq26devK19dXjRo10uDBg9WzZ09V\nVFQoIyPDdETA5fz73//Wxo0bFRISohEjRpiOYwlOh0P7l/9dzqoKhf3uTgW3uMl0JAAAALgZl7hC\nf/YK/Nkr9T92dvulzqK/kDvvvFOrVq3SN998c8mvycjI0PLlyy+6T5KioqKuOBM8g7ufA3a7XdOn\nT5d0Zkwdj6VcnuPHj1/R645+vkol+7LkUztEMfc8Uc2pAABATXP394T49eLi4i66LzY29mf3XymX\nKPRnT/7Dhw9fcP/Z7Rd7xv5S1K1bV5JUXl5+ya+Ji4v7xS/62ef/YU1RUVFufw4sXbpUO3bsUKNG\njXT//fe7/edT0wICAi77NeXH83Vo9UuSpMa9npRPYN3qjgUAAGoY76Gs62yfNXE3uEvcct+6dWtJ\nZxbl+rGysjJlZ2fLz89PzZs3v+I/Y/fu3ZKkiIiIKz4G4GlKS0uVnp4uSRozZoz8/f0NJ/J8TqdT\nOZmz5KgoVUibzgpt29V0JAAAALgplyj0ERERatu27bkF7H5o6dKlKi8vV5cuXeTr6yvpzC3CeXl5\nys/PP+9jc3NzL3gFvqCgQAsXLpQkde7c+Sp9FoD7efXVV3XkyBG1bt1a999/v+k4llD49f+qOPsL\neQfUVuNerFcAAACAK+cSt9xL0uDBgzVx4kQtWrRI27dvV3R0tPbs2aNdu3YpKipK/fr1O/exhYWF\nGjlypBo0aHDeeLqNGzdq1apVatmyperXr6+AgADl5+frq6++UmVlpdq3b6977rnHxKcHuJzCwsJz\nf38SEhLk5eUSv9/zaJUnC3XgneclSTH3DJVv3TDDiQAAAODOXKbQR0REaNq0aVq6dKm2bt2qrVu3\nKiQkRD169FBsbOwFR9rZbLbz/n/r1q11+PBh7du3T9nZ2SovL1dQUJBatmypLl26cHUe+IFZs2bp\n5MmTuvXWW9WlSxfTcSzhwNvPy376pOo276Cw391lOg4AAADcnM3pdDpNh3BnLH5hbe66KF5OTo66\ndu2qqqoqrV279tw6Frh8AQEB6vbK17/4ccd3fKpvX58kL19/tf7bq/ILjayBdAAAoCasG9xOpaWl\npmPAEJMTDrjHFrCg6dOnq7KyUn369KHM14Cq0yd14K3ZkqRGf3qMMg8AAIBqQaEHLGbr1q16++23\n5efnpzFjxpiOYwmHVs9X5clC1W7aRg1uvtd0HAAAAHgICj1gIU6nU1OnTpUkDRo0SNHR0YYTeb4T\nu/+jY1vWyOZTS01jn5GNxQcBAABQTXhnCVjIhg0btHHjRgUHB2vYsGGm43g8e3mpclbMlCRF/fFh\n+YfHGE4EAAAAT0KhByzC4XAoLS1NkjR8+HCFhIQYTuT5cte8qorjRxQY9VtFdI0zHQcAAAAehkIP\nWMSqVau0fft2RUZGauDAgabjeLyS/TtVsHGl5OWlpn2fkZe3y0wJBQAAgIeg0AMWUFlZqfT0dEnS\nyJEjFRAQYDiRZ3NUVmj/8uckp1ORt/ZTYPS1piMBAADAA1HoAQtYunSp9u3bp2bNmunPf/6z6Tge\n7/CHb6is4ID8wxsr6o6HTMcBAACAh6LQAx6utLRUM2eeWZhtzJgxqlWrluFEnu103l4d/vhfks2m\nJrGj5FXL13QkAAAAeCgKPeDhFi1apCNHjuj6669Xz549TcfxaE67XfsznpUcDoX/oZfqNG1jOhIA\nAAA8GIUe8GBFRUWaN2+eJCk+Pl5ezEC/qo5syNDpvL3yrReh6O6DTMcBAACAh+PdPeDBXnzxRZ04\ncUJ/+MMf1KVLF9NxPFpZwUHlffAPSVKTPn+Ttx8LDwIAAODqotADHio/P1+vvPKKpDNX5202m+FE\nnsvpcGj/8ufkrKpUWIfuCm7ewXQkAAAAWACFHvBQs2bNUllZmf70pz+pffv2puN4tKOb3lHJ/h2q\nVSdUMT2HmI4DAAAAi6DQAx5o3759evPNN+Xl5aUxY8aYjuPRDh48qEPvvyxJanz/U/IJrGM4EQAA\nAKyCQg94oOeee05VVVXq27evmjdvbjqOx3I6nXr66aflqChTveu7qF6bW0xHAgAAgIVQ6AEPs2PH\nDq1cuVK+vr4aNWqU6TgebdmyZfr3v/8t78A6atxrhOk4AAAAsBgKPeBhpk+fLkkaMGCAoqOjDafx\nXAUFBUpKSpIkNb5nmGrVCTWcCAAAAFbjYzoAgOqzadMmffTRR6pdu7ZGjOCK8dU0YcIEFRUV6Y47\n7lBR+z+ajgMAAAAL4go94CGcTqfS0tIkSY8//rjCwsIMJ/Jcq1ev1nvvvaegoCDNnDmTkYAAAAAw\ngkIPeIgPPvhAX375pUJDQ/XXv/7VdByPdfz4cU2YMEGSNH78eDVq1MhwIgAAAFgVhR7wAHa7XdOm\nTZMkPfXUU6pdu7bhRJ4rMTFRR48eVadOnfTwww+bjgMAAAALo9ADHiAzM1PZ2dmKjo7WQw89ZDqO\nx1q7dq0yMzPl7++vGTNmyMuLH6EAAAAwh3ejgJsrLy/Xc889J0l65pln5OfnZziRZzp+/LjGjRsn\nSYqPj1ezZs0MJwIAAIDVUegBN/fGG2/o0KFDat68ufr06WM6jsdKTExUQUGBbrrpJj366KOm4wAA\nAAAUesCdlZSUaPbs2ZKkcePGydvb23Aiz7Ru3TputQcAAIDL4V0p4MZefvllff/992rfvr26detm\nOo5HOn78uMaOHSvpzC9NrrnmGsOJAAAAgDMo9ICb+v777zV//nxJZ8anMQv96vjhrfaDBg0yHQcA\nAAA4h0IPuKm5c+eqpKREt912m26++WbTcTwSt9oDAADAlfHuFHBDubm5+sc//iFJ51ZeR/XiVnsA\nAAC4Ogo94IZmzJihiooK3XfffWrTpo3pOB5p0qRJKigoUMeOHVnVHgAAAC6JQg+4md27d2vZsmXy\n8fHR6NGjTcfxSOvWrdOKFSvk7++vv//970wPAAAAgEui0ANuJj09XQ6HQw888ICaNWtmOo7H+eGt\n9mPHjuVWewAAALgsCj3gRr766iu9//778vf319NPP206jkf64a32rGoPAAAAV0ahB9yE0+lUamqq\nJGnw4MGKjIw0nMjz/PBW+xkzZnCrPQAAAFwahR5wExs2bNCmTZsUHBysoUOHmo7jcYqKis5NDBg7\ndqx+85vfGE4EAAAA/DwKPeAGHA6H0tLSJEnDhg1TSEiI4USeZ9KkScrPz+dWewAAALgNCj3gBlav\nXq3t27crIiKCEWpXwbp167R8+XJutQcAAIBbodADLs5ut+u5556TJD311FMKCAgwnMiz/PBW+zFj\nxnCrPQDg/7V353FZlYn//98ssigiLiHi2syEC+ZopZOYmpal2TKORNrouG+AW2pm5ajZlB8tScc1\nMwfbFB11ZrLFJbNyTxPXwA3LQFEBRQXZ7t8ffuGXuSHe3Nd9bl7Pv+rceN1vOBfncb8551wHACyD\nQg84uZUrV+rw4cOqXbu2unfvbjqOyym81P6BBx5Q//79TccBAAAAio1CDzix3NxcxcTESJJGjhwp\nLy8vw4lcy68vtZ8+fTqX2gMAAMBSKPSAE1u2bJmSkpL0u9/9Tl27djUdx6VwqT0AAACsjkIPOKnL\nly8XnZ0fNWqUPD09DSdyLVxqDwAAAKuj0ANO6uOPP1ZycrIaNGigp59+2nQcl7J27VpWtQcAAIDl\nUegBJ5SVlaWZM2dKkkaPHi13d35V7SUjI0Njx46VJI0ZM0Z/+MMfDCcCAAAASoaWADih2NhYpaam\n6t5771XHjh1Nx3EpEydO1KlTp3T//fdrwIABpuMAAAAAJUahB5zMhQsXNHv2bElXFmtzc3MznMh1\nrFu3TsuWLWNVewAAALgECj3gZBYuXKi0tDQ98MADateunek4LoNL7QEAAOBqKPSAE8nIyNC8efMk\nXSmdnJ23n4kTJ+rkyZNcag8AAACXQaEHnMi7776r8+fPKywsTA899JDpOC6j8FJ7b29vLrUHAACA\ny6DQA04iLS1N7733nqQr987DPn59qf2LL77IpfYAAABwGRR6wEnMmTNHFy9eVPv27dW8eXPTcVzG\npEmTdPLkSd13331cag8AAACXQqEHnMCpU6e0aNEiSVfunYd9rFu3TnFxcfL29lZMTAyX2gMAAMCl\nUOgBJzBr1ixlZ2erU6dOatKkiek4LuHcuXNcag8AAACXRqEHDPvll1/04Ycfys3NTaNGjTIdx2UU\nrmrPpfYAAABwVRR6wLAZM2YoJydHTz/9tBo2bGg6jktYs2YNl9oDAADA5VHoAYOSkpK0dOlSubu7\n64UXXjAdxyWkpaUVPSVg7NixXGoPAAAAl0WhBwyKiYlRXl6ewsPDKZ52YLPZ9NJLL+n06dN68MEH\nudQeAAAALo1CDxhy6NAhrVixQp6enho5cqTpOC5h1apVWr16tSpUqKCYmBi5u3OIAwAAgOvi0y5g\nyJERqbgAACAASURBVNtvv62CggJ1795dderUMR3H8lJSUvTKK69IkiZMmMDPFAAAAC6PQg8YsH//\nfv3vf/+Tt7e3hg0bZjqO5dlsNo0ZM0bnzp1T+/bt9fzzz5uOBAAAAJQ6Cj1gwFtvvSVJ6tGjh4KD\ngw2nsb4PP/xQGzZsUEBAgKZNmyY3NzfTkQAAAIBSR6EHHGz37t1as2aNfH19FR0dbTqO5SUlJem1\n116TJL3xxhsKCgoynAgAAABwDAo94GDTpk2TJPXt21eBgYGG01hbfn6+Ro4cqUuXLumpp57SM888\nYzoSAAAA4DCepgP8WlpampYsWaL4+HhduHBBAQEBat68uZ599llVqFDB4eMA9rZt2zZ9/fXX8vPz\n0+DBg03HsbwFCxZo+/btCgwM1BtvvGE6DgAAAOBQTlPoT506pVdffVXnz59X8+bNFRwcrCNHjujz\nzz9XfHy8Jk+eLD8/P4eNA9ibzWbT1KlTJUkDBw5UlSpVDCeytoSEBP3f//2fpCtXPfDzBAAAQFnj\nNIX+vffe0/nz59W3b189/vjjRdsXL16s1atXa8mSJerfv7/DxgHs7dtvv9XWrVsVEBCgAQMGmI5j\nabm5uRo+fLhycnLUvXt3Pfroo6YjAQAAAA7nFPfQnzp1Snv27FFgYOBVJVySIiIi5O3trW+++UY5\nOTkOGQewN5vNVnTv/ODBg+Xv7284kbXNnDlTe/fuVa1atTRhwgTTcQAAAAAjnKLQ79+/X5LUpEmT\na17z8fFR/fr1dfnyZSUmJjpkHMDe1q9fr127dqlq1arq27ev6TiWFh8frxkzZkiSpk+frooVKxpO\nBAAAAJjhFIU+OTlZklSjRo3rvl64PSUlxSHjAPZUUFBQdHY+OjqahRnvQFZWloYPH678/Hz169dP\nrVq1Mh0JAAAAMMYpCv2lS5ckSeXLl7/u64XbL1686JBxAHv6/PPPtW/fPgUFBalnz56m41ja1KlT\ndejQIf3+97/XuHHjTMcBAAAAjHKKQg+4qoKCAsXExEiShg4dKl9fX8OJrGvLli1asGCBPDw8NGPG\nDH6WAAAAKPOcYpX7wjPnhWfYf6tw+60uVbbXOIXi4uK0fPnyG74mScHBwcUaC67rZnNgxYoVOnjw\noGrWrKlRo0bJ29vbgclcR2ZmpkaPHi2bzaZx48apc+fOpiMVSU9PNx0BAAA4AXoBIiIibvhaeHj4\nTV8vKaco9IWT/0b3thduv9G98fYep1BERMQtf+iF9+2jbAoODr7hHCgoKND48eMlSUOGDNHZs2cd\nGc2lvPjii0pKSlLjxo3Vr18/p/q940oBAAAg0QvKssIeWnjS15Gc4pL70NBQSdKePXuueS07O1sJ\nCQny9vZWSEiIQ8YB7GHNmjU6cOCAgoKC1L17d9NxLGv9+vX66KOP5OXlpRkzZsjLy8t0JAAAAMAp\nOEWhr169upo0aaLU1FR98cUXV722dOlSXb58WW3atCn6IJ+fn6/k5GSdOnXqjsYBSovNZiu6dz4y\nMlI+Pj6GE1lTenq6xowZI0kaM2aMGjRoYDgRAAAA4Dyc4pJ7Serfv7/Gjx+vRYsWae/evapZs6YO\nHTqkAwcOKDg4WN26dSv62rS0NI0cOVJ33XWXZs2aVeJxgNKydu1a7du3T9WrV9fzzz9vOo5lvfLK\nKzp16pSaN2+uQYMGmY4DAAAAOBWnKfTVq1fXlClTtHTpUu3evVu7d+9WQECAOnfurPDw8Os+is7N\nzc0u4wD2ZLPZNH36dElXzs5zj3XJ/Pe//9V//vMf+fr6KiYmRh4eHqYjAQAAAE7FzWaz2UyHsDIW\nvyjbrrco3tq1a9W7d28FBgZq8+bNFPoSSE1NVfv27ZWenq433nhDvXr1Mh3phnx9ffXYez+YjgEA\nAAxa07+ZsrKyTMeAISafcOAU99ADruLX984PGTKEMl8CNptNY8aMUXp6utq2bau//e1vpiMBAAAA\nTolCD9jRV199pfj4eN11113q2bOn6TiWtHTpUq1bt07+/v566623rntrDQAAAAAKPWA3vz47P3jw\nYM7Ol8DPP/+sCRMmSJJef/11o5cvAQAAAM6OQg/YyYYNG/TDDz+oatWqXCZeAgUFBRo5cqQuXLig\nJ554Qn/5y19MRwIAAACcGoUesINfr2w/ZMgQnqZQAu+//762bNmiqlWrasqUKVxqDwAAANwChR6w\ng40bN+qHH35QlSpVnHpFdmd1+PBhvfnmm5KkqVOnqmrVqoYTAQAAAM6PQg/coV+fnR88eDBn529T\nXl6eRowYoezsbIWHh6tjx46mIwEAAACWQKEH7tC3336rnTt3qnLlyurdu7fpOJYza9Ys/fDDD6pR\no4Zee+0103EAAAAAy6DQA3fgt2fnK1SoYDiRtcTHxxc9GWD69OmqVKmS4UQAAACAdVDogTvw1Vdf\naceOHQoICODs/G26dOmSoqOjlZeXp379+qlNmzamIwEAAACWQqEHSshms2nSpEmSpEGDBsnPz89w\nImuZPHmyjh49qvr162vcuHGm4wAAAACWQ6EHSmjz5s369ttvFRAQoD59+piOYynr1q3T4sWL5eXl\npX/+85/y9fU1HQkAAACwHAo9UEKF934PGDBAFStWNJzGOs6cOaNRo0ZJksaOHavQ0FDDiQAAAABr\notADJbB582Zt2bJFAQEB6tu3r+k4lmGz2TR69GidOXNGYWFhGjhwoOlIAAAAgGVR6IESKFzZfuTI\nkfL39zecxjo++ugjrV27Vv7+/nrnnXfk7s4hCAAAACgpPk0Dt2nr1q3asmWL/P39NWzYMNNxLOPI\nkSOaOHGiJGnKlCmqWbOm2UAAAACAxVHogdtUeHa+f//+CggIMJzGGnJzczV06FBlZWXpL3/5i555\n5hnTkQAAAADLo9ADt2H79u3atGmT/P391b9/f9NxLCMmJkbx8fGqWbOmXn/9ddNxAAAAAJdAoQdu\nQ+HZ+X79+qlSpUqG01jDjh079M9//lNubm6aMWMGPzcAAADATij0QDHt2LFD3377rSpWrMjZ+WLK\nzMzUsGHDVFBQoMjISLVs2dJ0JAAAAMBlUOiBYip87nzfvn25d76Y/v73v+unn35SaGioRo8ebToO\nAAAA4FIo9EAx7Ny5Uxs3bpSfn58GDBhgOo4lfPrpp4qLi5OPj49mzZolLy8v05EAAAAAl0KhB4qh\n8Ox8nz59VLlyZcNpnF9KSorGjh0rSXr11VcVEhJiOBEAAADgeij0wC3Ex8drw4YNKl++vAYOHGg6\njtMrKCjQCy+8oIyMDLVr1069e/c2HQkAAABwSRR64BZmzZolSerVq5eqVKliOI3ze//99/XNN9+o\nSpUqmj59utzc3ExHAgAAAFwShR64icTERH322Wfy9vbm3vli+PHHH/XGG29IkqZNm6bAwEDDiQAA\nAADXRaEHbqLw7Pxzzz2n6tWrG07j3C5fvqzo6GhdvnxZzz//vDp27Gg6EgAAAODSKPTADRw/flyr\nVq2Sh4eHIiMjTcdxelOnTtXBgwdVr149TZw40XQcAAAAwOVR6IEbmDNnjvLz89WlSxfVrl3bdByn\n9t1332n+/Pny8PDQzJkzVaFCBdORAAAAAJdHoQeu4+TJk4qLi5Obm5uio6NNx3FqGRkZGj58uGw2\nm0aMGKH777/fdCQAAACgTKDQA9cxf/585eTkqFOnTrrnnntMx3FaNptNL730kk6ePKlmzZpp2LBh\npiMBAAAAZQaFHviNtLQ0ffDBB5JEQb2FFStW6H//+5/Kly+vf/7zn/L09DQdCQAAACgzKPTAbyxc\nuFBZWVlq166d7r33XtNxnNbPP/+sV155RZL02muv6e677zacCAAAAChbKPTAr2RmZmrRokWSODt/\nM/n5+Ro+fLgyMzPVsWNHdevWzXQkAAAAoMyh0AO/snjxYp07d05/+tOf1KJFC9NxnNbcuXO1bds2\nBQYGatq0aXJzczMdCQAAAChzKPTA/5OVlaV3331XEmfnb2bv3r2aNm2aJGn69OmqUqWK4UQAAABA\n2UShB/6fJUuW6MyZM2rSpInatm1rOo5TysrKUnR0tPLy8tSnTx+1a9fOdCQAAACgzKLQA5Jyc3M1\nd+5cSdLQoUO5hPwGJk+erMOHD+uee+4pWhAPAAAAgBkUekDSypUr9csvv+gPf/iDOnbsaDqOU1qz\nZo1iY2NVrlw5zZo1S76+vqYjAQAAAGUahR5lXkFBgebMmSNJioyMlLs7vxa/lZKSohdeeEGS9NJL\nL6lx48aGEwEAAACguaDMW7NmjQ4dOqTg4GB16dLFdBynU/iIuvT0dLVt21YDBw40HQkAAACAKPQo\n42w2m2bNmiVJGjRokLy8vAwncj5z587Vpk2bVK1aNb3zzjtcwQAAAAA4CT6Zo0zbvHmzfvjhB1Wu\nXFnPP/+86ThO54cffih6RF1MTIwCAwMNJwIAAABQiEKPMm327NmSpH79+ql8+fKG0ziXzMxMRUVF\nKS8vT/3791f79u1NRwIAAADwKxR6lFl79uzRxo0bVb58efXu3dt0HKfz8ssv6/jx4woNDdXLL79s\nOg4AAACA36DQo8wqPDvfo0cPVa5c2XAa5/Lvf/9bK1askK+vr+bMmSNvb2/TkQAAAAD8BoUeZdLR\no0e1evVqlStXjlXbfyMpKUnjxo2TJL322mv6wx/+YDgRAAAAgOuh0KNMmjt3rmw2m8LDw1WjRg3T\ncZxGbm6uoqOjdfHiRXXu3Fndu3c3HQkAAADADVDoUeakpKRo2bJlcnNz05AhQ0zHcSpvvfWWfvjh\nB9WsWVNTp06Vm5ub6UgAAAAAboBCjzJnwYIFys3NVefOnfX73//edByn8d1332n27Nlyd3fXrFmz\nFBAQYDoSAAAAgJug0KNMSU9P14cffihJio6ONpzGeaSlpWnYsGGy2WwaMWKEWrRoYToSAAAAgFug\n0KNMiY2N1cWLF9W2bVvde++9puM4BZvNplGjRunUqVNq0aKFhg8fbjoSAAAAgGKg0KPMyM7O1qJF\niyRJkZGRhtM4j0WLFmnNmjWqVKmSZs2aJU9PT9ORAAAAABQDhR5lxsqVK3XmzBk1btxYrVq1Mh3H\nKezbt0+TJ0+WJE2bNk01a9Y0nAgAAABAcVHoUSbYbDa9++67kqSBAweyerukixcvKjIyUjk5OerZ\ns6c6d+5sOhIAAACA20ChR5mwYcMGJSYmKigoSE8//bTpOE7h1Vdf1ZEjR9SgQQNNmDDBdBwAAAAA\nt4lCjzJh/vz5kqR+/fqpXLlyhtOYt3LlSsXFxcnHx0dz5syRr6+v6UgAAAAAbhOFHi5v//79+u67\n71S+fHn99a9/NR3HuGPHjumll16SJL322muqX7++4UQAAAAASoJCD5dXeO989+7dValSJcNpzMrJ\nyVFUVJQuXLigJ598Us8//7zpSAAAAABKiEIPl3by5En95z//kbu7u/r37286jnFTpkxRfHy8atWq\npalTp7I4IAAAAGBhFHq4tEWLFik3N1edOnVSnTp1TMcx6quvvtL8+fPl4eGhOXPmlPmrFQAAAACr\no9DDZV28eFEffPCBJGnQoEGG05h16tQpjRgxQpL04osv6v777zecCAAAAMCdotDDZcXFxencuXO6\n//77y3SBLSgo0LBhw3T27Fm1bt1akZGRpiMBAAAAsAMKPVxSfn6+FixYIImz87Nnz9Z3332natWq\naebMmXJ359ceAAAAcAV8sodL+vLLL3X8+HHVrVtXHTt2NB3HmB07dmjatGmSpBkzZigwMNBwIgAA\nAAD24mk6QKGEhAStWLFChw4dUk5OjmrUqKF27dqpY8eOxT6jePr0aUVHR9/w9bCwMA0fPtxekeHE\nCh9V179/f3l4eBhOY0Z6erqioqKUn5+vwYMH6+GHHzYdCQAAAIAdOUWh37Fjh6ZPny4vLy+1bNlS\nfn5+2rlzp2JjY5WQkKCRI0fe1nj16tVT8+bNr9leu3Zte0WGE9u1a5d27NihSpUq6bnnnjMdx4iC\nggKNGDFCv/zyi5o1a6axY8eajgQAAADAzowX+qysLM2fP1/u7u6aOHGi7r77bklSt27dNGnSJG3d\nulWbN29WWFhYscesW7euwsPDSysynNz8+fMlST169FCFChUMpzFj/vz5WrdunQICAjRv3jx5eXmZ\njgQAAADAzozfQ79lyxZlZmaqVatWRWVekjw9PYvOrq5du9ZUPFjMTz/9pM8++0yenp7q06eP6ThG\nbN++XW+++aYk6Z133lGtWrUMJwIAAABQGoyfod+/f78kqWnTpte81qhRI3l5eSkhIUF5eXny9Cxe\n3PT0dK1bt06ZmZmqWLGiQkJCVKdOHbvmhnNauHChCgoK1KVLF9WoUcN0HIc7e/ashgwZovz8fEVG\nRqpDhw6mIwEAAAAoJcYLfXJysiRdt3y5u7srMDBQJ06cUGpqqoKDg4s15p49e7Rnz56rtjVq1EhR\nUVGqVq3anYeGUzp37pw++eQTSdLAgQMNp3G8goICDR06VCdPnlSLFi304osvmo4EAAAAoBQZL/SX\nLl2SJJUvX/66rxduv3jx4i3H8vb2VteuXdWiRYuix3P99NNPWrZsmfbt26fJkydr2rRp3E/soj7+\n+GNdvHhRrVq1UuPGjU3HcbiZM2dq48aNqlKliubMmaNy5cqZjgQAAACgFNml0EdFRenMmTPF/vrW\nrVvf9PFyJeXv76+IiIirtjVo0ECvvPKKxo8fr8OHD2v9+vXq1KmT3d8bZuXm5mrhwoWSpEGDBhlO\n43jfffed3n77bbm5uWnWrFll8nYDAAAAoKyxS6EPCgq6rbPelStXLvrvwjPwhWfqf6tw+52sVu7u\n7q5HHnlEhw8f1sGDB4td6OPi4rR8+fIbviap2LcBoHR9/PHHSklJUcOGDfXXv/5V7u6OW+/R9BxI\nSUnRsGHDVFBQoPHjx6t79+5G85Q16enppiMAAAAnYPozIcz77cnlXwsPD7/p6yVll0I/fvz4Ev/b\n4OBgHT16VCkpKVetci9duSc4NTVVHh4eRZfQl5S/v78k6fLly8X+NxEREbf8oReuAQBzbDabpkyZ\nIknq06ePTp486bD3Dg4ONjoH8vLy1K1bN506dUphYWEaMGAAc9LBfH19TUcAAABOgM9gZVfhH3MK\nT/o6kvHH1hXe67x79+5rXjtw4IBycnJUv379Yq9wfyOJiYmSdMd/GIDz2bJli/bu3auqVauqa9eu\npuM41PTp07Vlyxbdddddmj17tjw8PExHAgAAAOAgxgv9gw8+qIoVK2rTpk06evRo0fbc3FwtWbJE\nkvTYY49d9W8uXbqk5ORkZWRkXLX92LFjstls17zH3r17tXr1aklX7t+Ha5k/f74kqXfv3vLx8TGc\nxnE2bNigGTNmyN3dXbNnz+aPVQAAAEAZY3yVe19fXw0aNEjTp0/XxIkTFRYWJj8/P+3cuVPJyclq\n2bKlWrZsedW/2b59u+bOnau2bdsqMjKyaPvixYuVkpKikJAQVa1aVdKVVe737dsnSerWrZtCQkIc\n982h1B05ckTr1q2Tt7e3evXqZTqOwyQnJ2vo0KGSpNGjR6tVq1aGEwEAAABwNOOFXpKaN2+uSZMm\nacWKFdq+fbtyc3MVFBSkXr163XQBOzc3t6v+v02bNtq+fbuOHj2q+Ph45eXlKSAgQGFhYXr88cfV\noEGD0v5W4GCLFy+WJP3lL38p+iOOq8vNzVVkZKTS09P18MMPFxV7AAAAAGWLm+1616ij2Fj8wpxL\nly7p/vvv1/nz5/XFF1/o3nvvdXgGE4vivf7665o7d66CgoK0Zs2aMvOHDGfl6+urx977wXQMAABg\n0Jr+zZSVlWU6Bgwx+YQD4/fQAyW1atUqnT9/Xvfdd5+RMm/CmjVrNHfuXHl4eGjevHmUeQAAAKAM\no9DDkmw2m/71r39JurIYXlnw888/a8SIEZKkl19+Wc2bNzecCAAAAIBJFHpY0s6dO7V//35VqVJF\nnTt3Nh2n1OXk5Gjw4ME6d+6cOnTooEGDBpmOBAAAAMAwCj0sKTY2VpLUvXv3MvGoutdff127d+9W\nrVq1FBMTc82CkAAAAADKHgo9LOfs2bP69NNP5ebmpp49e5qOU+o+/fRTLVy4UOXKldO8efNUuXJl\n05EAAAAAOAEKPSznk08+UU5Ojh555BHVrl3bdJxSdezYMY0ePVqSNH78eDVr1sxwIgAAAADOgkIP\nS8nPz9cHH3wgSerVq5fhNKUrOztbgwYNUmZmpp544gn17dvXdCQAAAAAToRCD0v56quvdOLECdWt\nW1cPP/yw6TilasKECdq/f7/q1aunt99+m/vmAQAAAFyFQg9LKVwM729/+5vc3V13+q5cuVIffvih\nvL29NX/+fPn7+5uOBAAAAMDJuG4jgstJSkrShg0b5OPjo4iICNNxSk1iYqJefPFFSdKkSZPUuHFj\nw4kAAAAAOCMKPSyj8N75p59+WlWqVDGcpnScP39effv21aVLl9SlSxf16NHDdCQAAAAATopCD0vI\nysrSkiVLJLnuYngFBQUaNmyYjh07poYNG2ratGncNw8AAADghij0sIT//ve/ysjI0B//+Ec1bdrU\ndJxS8c4772jt2rUKCAjQwoUL5evrazoSAAAAACdGoYclLF68WJLrnp1fu3Zt0Ur2s2fPVt26dU1H\nAgAAAODkKPRwert379bu3bsVEBCgp59+2nQcuzty5IiGDh0qSRo7dqzLP44PAAAAgH1Q6OH0Ch9V\n161bN5e7DP3ChQvq37+/MjMz9cQTTyg6Otp0JAAAAAAWQaGHU0tLS9N///tfSVLPnj0Np7Evm82m\nkSNHKjExUSEhIYqJiWERPAAAAADFRqGHU4uLi1N2drbatWunevXqmY5jV7Nnz9Znn32mihUr6r33\n3pOfn5/pSAAAAAAshEIPp1VQUOCyi+F9/fXXmjJliiRp5syZ+v3vf284EQAAAACrodDDaW3cuFHH\njx9XrVq11L59e9Nx7Ob48eOKioqSzWbTCy+8oMcee8x0JAAAAAAWRKGH0/rwww8lST169JCHh4fh\nNPaRlZWl/v37KyMjQ48++qhGjhxpOhIAAAAAi6LQwymlpaVp/fr18vDwUEREhOk4dmGz2TRmzBgd\nOHBAd999t2bOnCl3d34FAQAAAJQMbQJOadWqVcrNzVXbtm1VvXp103HsYsGCBVq5cqXKly+vhQsX\nqlKlSqYjAQAAALAwCj2cUlxcnCTp2WefNZzEPjZt2qTXX39dkhQTE6P69esbTgQAAADA6ij0cDo/\n/vij9u7dq0qVKrnEgnG//PKLhgwZovz8fEVHR+vJJ580HQkAAACAC6DQw+ksW7ZMkvTUU0/Jx8fH\ncJo7k52drQEDBujs2bNq27atXnzxRdORAAAAALgICj2cSl5enlasWCFJll8Mz2azady4cYqPj1ed\nOnU0e/Zsl1mtHwAAAIB5FHo4lY0bNyo1NVW/+93vdN9995mOc0diY2MVFxcnHx8fvffee6pcubLp\nSAAAAABcCIUeTqXwcvtnn31Wbm5uhtOU3I4dOzRhwgRJ0ltvvaXQ0FDDiQAAAAC4Ggo9nEZGRobW\nrFkjNzc3de3a1XScEjt58qQGDhyovLw8DRgwQF26dDEdCQAAAIALotDDafzvf//T5cuX9dBDD6lm\nzZqm45RI4SJ4qampatmypV599VXTkQAAAAC4KAo9nIbVnz1vs9k0atQo7dq1S8HBwZo3b548PT1N\nxwIAAADgoij0cAqHDx/Wrl27VKFCBXXq1Ml0nBKJiYnRqlWrVKFCBcXGxqpatWqmIwEAAABwYRR6\nOIXly5dLkp588kmVL1/ecJrbt2rVKr399ttyd3fXnDlz1KhRI9ORAAAAALg4Cj2My8/PLyr0Vrzc\n/vvvv9cLL7wgSZowYYIeffRRw4kAAAAAlAUUehi3adMmpaSkqE6dOvrTn/5kOs5tSUpKUt++fXX5\n8mX17NlT/fr1Mx0JAAAAQBlBoYdxhc+eDw8Pl7u7dabk+fPn9eSTT+rs2bNq06aNJk+eLDc3N9Ox\nAAAAAJQR1mlPcEmZmZn67LPPJF0p9FaRl5enyMhI7d+/X/fcc4/mzZuncuXKmY4FAAAAoAyh0MOo\n1atXKzs7W3/6059Ut25d03GKbeLEidqwYYOqVaum2NhYVapUyXQkAAAAAGUMhR5GFS6GFxERYThJ\n8S1atEiLFi2Sl5eXVq5caak/RAAAAABwHRR6GJOWlqZt27apXLlyeuKJJ0zHKZYNGzbo73//uyTp\nrbfe0kMPPWQ4EQAAAICyikIPY9auXauCggKFhYXJ39/fdJxb+vHHHzV48GAVFBRo+PDh6tq1q+lI\nAAAAAMowCj2MWbNmjSTp8ccfN5zk1s6cOaNevXrpwoULeuqppzR69GjTkQAAAACUcRR6GJGVlaWv\nv/5akvTYY4+ZDXML2dnZ6tu3r06cOKFmzZopJibGUo/XAwAAAOCaaCUw4ttvv1V2draaNm2qGjVq\nmI5zQzabTaNGjdLOnTsVHBys999/X76+vqZjAQAAAACFHmZ88cUXkpz/7HxMTIxWrVqlChUqKDY2\nVoGBgaYjAQAAAIAkCj0MyM/P19q1ayVJHTt2NJzmxlatWqW3335b7u7umjNnjho1amQ6EgAAAAAU\nodDD4b7//nulpaWpXr16CgkJMR3nur7//nu98MILkqQJEybo0UcfNZwIAAAAAK5GoYfDffnll5Ku\nrG7v5uZmOM21Dh06pF69euny5cvq2bOn+vXrZzoSAAAAAFyDQg+HstlsVxV6Z3PixAl169ZNGRkZ\neuSRRzR58mSn/KMDAAAAAFDo4VCJiYlKSkpSlSpV9MADD5iOc5WzZ8+qe/fuOnnypFq0aKH58+er\nXLlypmMBAAAAwHVR6OFQhavbd+jQQR4eHobT/P8yMzPVo0cPHT16VI0aNdK//vUvHk8HAAAAxTEO\nVQAAGBVJREFUwKlR6OFQa9askeRcq9tnZ2erb9++2rNnj+rVq6ePPvpIlSpVMh0LAAAAAG6KQg+H\nSUlJ0e7du+Xj46PWrVubjiNJysvLU1RUlDZv3qzq1avrk08+4VnzAAAAACyBQg+HKTw7//DDDzvF\n5ew2m01jx47VF198oUqVKumjjz5SnTp1TMcCAAAAgGKh0MNh1q1bJ0l67LHHDCe54o033tCSJUvk\n4+Oj2NhYNWzY0HQkAAAAACg2Cj0coqCgQN9//70kOcXl9nPmzNGcOXPk6empBQsWqHnz5qYjAQAA\nAMBtodDDIQ4dOqTz588rODhYwcHBRrN8/PHH+sc//iE3NzfNmDFD7du3N5oHAAAAAEqCQg+HKDw7\nf//99xvN8dlnn2ns2LGSpNdff11//vOfjeYBAAAAgJKi0MMhdu7cKUl64IEHjGX47rvvFBUVpYKC\nAo0ePVq9e/c2lgUAAAAA7hSFHg5h+gx9fHy8+vbtq5ycHPXt21cjRowwkgMAAAAA7IVCj1KXlpam\nI0eOyMfHR6GhoQ5//8OHD6tHjx66ePGiunTpokmTJsnNzc3hOQAAAADAnij0KHW7du2SJDVp0kRe\nXl4Ofe8ff/xR4eHhSktLU/v27RUTEyN3d6Y9AAAAAOuj2aDUFd4/7+jL7ePj49W1a1edPn1aDz30\nkN59912VK1fOoRkAAAAAoLRQ6FHqCu+fd+SCeNu3b1dERIQyMjLUoUMHxcbGytfX12HvDwAAAACl\nzdN0gPz8fH355ZdKSkpSUlKSTpw4ofz8fA0aNKjEzwdPSEjQihUrdOjQIeXk5KhGjRpq166dOnbs\nyOXWBhw4cECS9Mc//tEh7/fNN9+oT58+ys7O1tNPP62ZM2dyZh4AAACAyzFe6C9fvqzY2FhJUkBA\ngCpXrqwzZ86UeLwdO3Zo+vTp8vLyUsuWLeXn56edO3cqNjZWCQkJGjlypL2ioxjS09OVkZEhX19f\nBQUFlfr7ffnllxo8eLBycnLUrVs3TZ06VR4eHqX+vgAAAADgaMYLvZeXl8aNG6d69eopICBAy5Yt\n0/Lly0s0VlZWlubPny93d3dNnDhRd999tySpW7dumjRpkrZu3arNmzcrLCzMnt8CbiIpKUmSVK9e\nvVJfWX7VqlUaNmyY8vPz1a9fP02cOJErMgAAAAC4LONtx9PTU02bNlVAQMAdj7VlyxZlZmaqVatW\nRWW+8D2ee+45SdLatWvv+H1QfIWF/tf7ozR8/PHHio6OVn5+voYOHapJkyZR5gEAAAC4NJdqPPv3\n75ckNW3a9JrXGjVqJC8vLyUkJCgvL8/R0cosRxT6BQsWaMyYMbLZbHrppZf00ksv8Zx5AAAAAC7P\npQp9cnKyJKlGjRrXvObu7q7AwEDl5+crNTXV0dHKrBMnTkiSateubfexbTabZsyYoYkTJ0qSJk+e\nrKFDh9r9fQAAAADAGRm/h96eLl26JEkqX778dV8v3H7x4kWHZSrrCvdJxYoV7TquzWbTm2++qdmz\nZ8vd3V3Tpk1Tt27d7PoeAAAAAODM7FLoo6Kibmtl+tatWys6Otoebw0nl5WVJUl2fQZ8dna2Xn75\nZS1dulSenp6aOXOmnnnmGbuNDwAAAABWYJdCHxQUJC8vr2J/fZUqVezxttcoPANfeFb4twq3V6hQ\noVjjxcXF3XDF/bi4OElScHDw7cYsU2w2mySpZs2advlZHTt2TM8++6x27dolHx8fxcXF6amnnrrj\nce8Ec6BsO5OWrjX9m5mOAQAADMq38ZkQUkRExA1fCw8Pv+nrJWWXQj9+/Hh7DHPHgoODdfToUaWk\npFyzCFtBQYFSU1Pl4eGhwMDAYo0XERFxyx964X37uL5z585Jki5cuHDHP6v169dr2LBhysjIUN26\ndbVgwQKFhoYa3QfBwcHMgTKOOQDmAJgDYA6AOVC2Ff4xp/CkryO51KJ4jRs3liTt3r37mtcOHDig\nnJwc1a9fX56eLrV0gFOrVKmSJCk9Pb3EY+Tn5+utt95Sr169lJGRoQ4dOujzzz9XaGiovWICAAAA\ngOVYstBfunRJycnJysjIuGr7gw8+qIoVK2rTpk06evRo0fbc3FwtWbJEkvTYY485NGtZV7i6/c8/\n/1yif5+Wlqa//e1viomJkZubm8aOHav333+/6A8FAAAAAFBWOcWp6lWrVhVdolL43PINGzboxx9/\nlCQ1aNBA7du3L/r67du3a+7cuWrbtq0iIyOLtvv6+mrQoEGaPn26Jk6cqLCwMPn5+Wnnzp1KTk5W\ny5Yt1bJlS8d9Y1CtWrUklazQb968WSNHjtSJEydUpUoVzZ49W23atLF3RAAAAACwJKco9PHx8Tpw\n4MBV2xITE5WYmFj0/78u9IXc3Nyu2da8eXNNmjRJK1as0Pbt25Wbm6ugoCD16tVLnTp1sn943FRI\nSIikK3+gKSgokLv7rS8KOXv2rF577bWiBQmbNWum+fPnq2bNmqWaFQAAAACsxM1WuAw5SoTFL24u\nLy9PDz74oFJSUvTJJ5/c9Ax7Xl6e4uLi9I9//EMZGRny9vbW0KFDFRkZKW9vbwemLj4WQAFzAMwB\nMAfAHABzoGwz+YQDS95DD+vw9PRUjx49JEnjxo277qX36enpmjNnjsLCwjRmzBhlZGSoTZs2Wr9+\nvUaOHOm0ZR4AAAAATHKKS+7h2nr16qXPPvtM+/fv11NPPaWuXbuqTp06On78uBISErRt2zZlZWVJ\nku6++26NHj1azzzzzHVvqQAAAAAAXEGhR6mrXLmyli9frj59+mjr1q2aN2/eNV/Ttm1b9evXT+3a\ntSvWffYAAAAAUNZR6OEQ/v7+Wrp0qbZs2aItW7bo5MmTqlOnjho0aKDGjRsXrYYPAAAAACgeCj0c\nxtPTU61bt1br1q1NRwEAAAAAy+PaZgAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEH\nAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACw\nIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAA\nAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEU\negAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAA\nAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQA\nAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAW\nRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAA\nAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhC\nDwAAAACABVHoAQAAAACwIE/TAfLz8/Xll18qKSlJSUlJOnHihPLz8zVo0CC1b9/+tsY6ffq0oqOj\nb/h6WFiYhg8ffqeRAQAAAAAwznihv3z5smJjYyVJAQEBqly5ss6cOXNHY9arV0/Nmze/Znvt2rXv\naFwAAAAAAJyF8ULv5eWlcePGqV69egoICNCyZcu0fPnyOxqzbt26Cg8Pt1NCAAAAAACcj/FC7+np\nqaZNm5qOAQAAAACApRgv9KUhPT1d69atU2ZmpipWrKiQkBDVqVPHdCwAAAAAAOzGJQv9nj17tGfP\nnqu2NWrUSFFRUapWrZqhVAAAAAAA2I9LFXpvb2917dpVLVq0UGBgoCTpp59+0rJly7Rv3z5NnjxZ\n06ZNk5eXl+GkAAAAAADcGbsU+qioqNtamb5169Y3fbxcSfn7+ysiIuKqbQ0aNNArr7yi8ePH6/Dh\nw1q/fr06depk9/cGAAAAAMCR7FLog4KCbuusd5UqVezxtsXm7u6uRx55RIcPH9bBgwftWuiDg4Pt\nNhasiTkA5gCYA2AOgDkA5gBMsEuhHz9+vD2GKVX+/v6Srjz3vrji4uJu+Ai9uLg4u+QCAAAAAFjf\nb68W/7Xw8PCbvl5SLnUP/c0kJiZKUtG99cURERFx0x96REQExb6MYw6AOQDmAJgDYA6AOQBTc8Dd\n4e9oB5cuXVJycrIyMjKu2n7s2DHZbLZrvn7v3r1avXq1pCv37wMAAAAAYHVOcYZ+1apVSk5OliQl\nJSVJkjZs2KAff/xR0pWF7dq3b1/09du3b9fcuXPVtm1bRUZGFm1fvHixUlJSFBISoqpVq0q6ssr9\nvn37JEndunVTSEiII74lAAAAAABKlVMU+vj4eB04cOCqbYmJiUWXyUu6qtAXcnNzu+r/27Rpo+3b\nt+vo0aOKj49XXl6eAgICFBYWpscff1wNGjQonW8AAAAAAAAHc4pCP2HChNv6+ocfflgPP/zwNdvb\ntWundu3a2SkVAAAAAADOy5L30AMAAAAAUNZR6AEAAAAAsCCPiRMnTjQdwqpsNptCQ0NNx4BBzAEw\nB8AcAHMAzAEwB2BqDrjZrvecNwAAAAAA4NS45B4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAA\nAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCPE0HcHYnT57U1q1btWfPHqWkpOjcuXOqUKGC\n7rnnHnXu3FmhoaG3PWZCQoJWrFihQ4cOKScnRzVq1FC7du3UsWNHubvzNxZnk5+fry+//FJJSUlK\nSkrSiRMnlJ+fr0GDBql9+/a3Ndbp06cVHR19w9fDwsI0fPjwO40MO7PnHCjEccCa7LHfOA44t7S0\nNC1ZskTx8fG6cOGCAgIC1Lx5cz377LOqUKGCw8eB49lj30VFRenMmTPXfS0gIEDz58+3Z2TY0dat\nW3XgwAEdP35cSUlJys7OVuvWrW963L4RjgPWZK854KjjAIX+FpYsWaItW7aoVq1auu++++Tn56fk\n5GR9//332rlzp/r06aOOHTsWe7wdO3Zo+vTp8vLyUsuWLeXn56edO3cqNjZWCQkJGjlyZCl+NyiJ\ny5cvKzY2VtKVX77KlSvf8JezuOrVq6fmzZtfs7127dp3NC5Kh73nAMcBa7L3fuM44HxOnTqlV199\nVefPn1fz5s0VHBysI0eO6PPPP1d8fLwmT54sPz8/h40Dx7Pnvitfvrw6d+58zXYfHx97x4YdrVix\nQsePH5ePj4+qVq2qX375pUTjcBywLnvNAckxxwEK/S00a9ZMf/7zn1WvXr2rth88eFCTJ0/WBx98\noAcffFABAQG3HCsrK0vz58+Xu7u7Jk6cqLvvvluS1K1bN02aNElbt27V5s2bFRYWVhrfCkrIy8tL\n48aNU7169RQQEKBly5Zp+fLldzRm3bp1FR4ebqeEKG32nAMcB6ypNPYbxwHn89577+n8+fPq27ev\nHn/88aLtixcv1urVq7VkyRL179/fYePA8ey57ypUqMDvuAX17t1bVapUUVBQkA4cOKBJkyaVaByO\nA9ZlrzkgOeY4wHWdt9C2bdtryrwkNWzYUKGhocrLy1NiYmKxxtqyZYsyMzPVqlWrog+DkuTp6ann\nnntOkrR27Vq75Ib9eHp6qmnTpsX6ow1ckz3nAMcBa2K/ub5Tp05pz549CgwMvOrDtyRFRETI29tb\n33zzjXJychwyDhyPfQdJatSokYKCgu5oDOaStdljDjgSZ+jvgIeHhyQV+77J/fv3S5KaNm16zWuN\nGjWSl5eXEhISlJeXJ09Pdo0rS09P17p165SZmamKFSsqJCREderUMR0LDsBxwJpKY79xHHAuhfu4\nSZMm17zm4+Oj+vXra8+ePUpMTFTjxo1LfRw4nr33XW5urr799ludOXNG3t7eqlu3rho2bMg6KWUA\nxwEUcsRxgE+LJXT69Gnt3btX3t7eatSoUbH+TXJysiSpRo0a17zm7u6uwMBAnThxQqmpqQoODrZr\nXjiXPXv2aM+ePVdta9SokaKiolStWjVDqeAIHAesqTT2G8cB53KzfVy4vXCB3Jt9ALfXOHA8e++7\njIwMzZo166ptgYGBGjJkSLE/O8KaOA6gkCOOAxT6EsjLy9PMmTOVl5en7t27q3z58sX6d5cuXZKk\nG3594faLFy/aJyicjre3t7p27aoWLVooMDBQkvTTTz9p2bJl2rdvnyZPnqxp06bJy8vLcFKUFo4D\n1mTP/cZxwDnZax/zO25d9tx37dq1U8OGDVW7dm35+PgoNTVVX3zxhdauXas333xT//jHP7gix4Vx\nHIDkuONAmSj0N3tkwPXc7LEEBQUFmjlzphITE9WqVSs9+eST9oqJUmTPOXAn/P39FRERcdW2Bg0a\n6JVXXtH48eN1+PBhrV+/Xp06dbL7e5d1zjIHYI6zzAGOA4Dr++0iWLVq1VL//v3l7e2tTz/9VHFx\ncRo9erShdAAcwVHHgTJR6IOCgm7rTEeVKlWuu72wzG/btk1hYWG3/UGv8K9xhX+1+63C7TyX0v7s\nNQdKi7u7ux555BEdPnxYBw8e5IN8KXCWOcBxwJzbnQOVK1cu+m9H7DeOA2bZax/zO25djth3HTp0\n0KeffqqDBw+WeAw4P44DuBl7HwfKRKEfP378HY+Rn5+vGTNmaNu2bWrdurWioqLk5uZ2W2MEBwfr\n6NGjSklJuWqVZOnKHwtSU1Pl4eFRdAkm7Mcec6C0+fv7S7ryzHPYn7PMAY4D5tzJHHDUfuM4YE7h\n2gcpKSnXfb1w+43uibX3OHA8R+w7fsfLBo4DuBl7HwdYZrMY8vLy9Pbbb2vbtm1q27atoqOjb7vM\nSypa9GL37t3XvHbgwAHl5OSofv36rGxdRhU+/pAi59o4DliTo/YbxwFzQkNDJemahQolKTs7WwkJ\nCfL29lZISIhDxoHjOWLfFf6OV69evcRjwPlxHMDN2Ps4QKG/hby8PE2bNk07d+7UI488osjIyFv+\nm0uXLik5OVkZGRlXbX/wwQdVsWJFbdq0SUePHi3anpubqyVLlkiSHnvsMft+AzDiRnPg2LFjstls\n13z93r17tXr1aklX7tuF9XEccC0l2W8cB6ylevXqatKkSdGiRb+2dOlSXb58WW3atCm6bSM/P1/J\nyck6derUHY0D52GvOfDLL79c98xbamqq3n//fUn8jrsKjgNwhuOAm+16nypQZM6cOdq4caP8/f3V\noUOH656ZDw0NveqxA19//bXmzp2rtm3bXvMHgB07dmj69OkqV66cwsLC5Ofnp507dyo5OVktW7bU\niBEjSv17wu1btWpV0SNIkpKSdPz4cYWEhBRdKtWgQQO1b9++6OtvNAcmTZqklJQUhYSEqGrVqpKu\nrG69b98+SVK3bt3UpUsXR31buA32mgMSxwGrut39xnHAek6dOqXx48fr3LlzeuCBB1SzZk0dOnRI\nBw4cUHBwsCZPniw/Pz9JVx5fGx0drbvuuuuaRxLdzjhwLvaYA8uWLdOnn36qhg0bqlq1avL19dWp\nU6e0a9cu5ebm6r777tPo0aPl4eFh6tvETezYsUM7duyQdOWRY/Hx8QoMDFTDhg0lSRUrVlTPnj0l\ncRxwVfaYA448DnBN5y2cPn1aknT+/Hn9+9//vu7XuLm5Xfc5gtcr/82bN9ekSZO0YsUKbd++Xbm5\nuQoKClKvXr1YAMmJxcfH68CBA1dtS0xMLLpkRtJVZa7Qb+dAmzZttH37dh09elTx8fHKy8tTQECA\nwsLC9Pjjj6tBgwal8w3gjtlrDkgcB6yqpPuN44B1VK9eXVOmTNHSpUu1e/du7d69WwEBAercubPC\nw8Ov+wiq6/2Ol2QcOAd7zIHQ0FClpKTo2LFjSkhI0OXLl1WhQgU1bNhQbdq04ey8k0tKStLGjRuv\n2paamqrU1FRJV26JKixzhTgOuBZ7zAFHHgc4Qw8AAAAAgAVxDz0AAAAAABZEoQcAAAAAwIIo9AAA\nAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegBAAAAALAgCj0AAAAAABZE\noQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegBAAAA\nALAgCj0AAAAAABb0/wGl6BP/gye8ZQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x108aa0c18>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.76697557 1.45444689] 1.97308073709\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3XlwnPWh5vunW1K3WpslWYsl7wuyZRkDBmEwtsH4gGGw\nzyVBVnzuTOZQjGsyhMxNcebeOzN1YCoUNxOqMpNbOcXNGc6QMOEssR0gyQkEs5iwGBtsbCTZlpFX\neZOsxdq3Xt/7h9yyHcvYlrv71+/b308VVfC+1qvHqkbVT/82l2VZlgAAAAAAgK24TQcAAAAAAADX\nj0IPAAAAAIANUegBAAAAALAhCj0AAAAAADZEoQcAAAAAwIYo9AAAAAAA2BCFHgAAAAAAG6LQAwAA\nAABgQxR6AAAAAABsiEIPAAAAAIANUegBAAAAALAhCj0AAAAAADZEoQcAAAAAwIYo9AAAAAAA2FC6\n6QCS9Nlnn6mxsVEnTpxQc3OzRkZGtGLFCn3ve9+7ruc89dRT6uzsHPdefn6+XnrppVjEBQAAAADA\nuKQYoX/jjTf0zjvvqLm5WZMnT76hZ2VlZWn9+vWX/bNu3boYpb1gy5YtMX8mwOsK8cJrC/HA6wrx\nwmsL8cDrCvFi6rWVFIX+8ccf109/+lP98pe/1MaNG2/oWdnZ2aqpqbnsn7Vr18Yo7QWvvfZazJ8J\n8LpCvPDaQjzwukK88NpCPPC6QryYem0lxZT7hQsXmo4AAAAAAICtJEWhj6VgMKhPPvlEnZ2d8nq9\nmjlzpiorK+V2J8VkBAAAAAAAYsJxhb6np0cvvvjiJddKSkr05JNPMhMAAAAAAOAYjir0q1atUmVl\npaZPn67MzEy1t7dr69ateu+99/SjH/1IP/zhDzVjxgzTMQEAAAAAuGGOmodeU1Ojqqoq5eXlyePx\naNq0adq4caPWrl2rQCDArpYAAAAAAMdwWZZlmQ5xscbGRj333HMTOof+Ss6ePavvf//7ysnJ0c9/\n/vOYPBMAAAAAAJMcNeX+SvLy8iRJfr//ur5uy5YtVzx+gNF+AAAAAEBUbW3tFe/V1NR87f2JSolC\nf+jQIUlSaWnpdX1dbW3tVX/oLS0tE84FjKe8vJzXlSTLsrR8+XI1NzfrV7/6lVauXGk6km2FQiHN\nmzdPwWBQR44ckc/nMx0JDsLvLMQLry3EA68rxEN5ebkkM4O+tltDHw6H1dLSora2tkuunzlzZtwR\n+Pb2dv3iF7+QJK1YsSIhGQHcuC+//FLNzc0qKSnRPffcYzqOrZ08eVLBYFAzZsygzAMAADhIUozQ\n7969W7t375Y0euycJDU1NelnP/uZJCk3N1ff/va3JUldXV16+umnVVxcfMnxdDt27NCbb76pyspK\nFRUVyefzqa2tTXv37lUwGNSSJUu0bt26BP/NAEzUG2+8IUl69NFHlZaWZjiNvR09elSSNH/+fMNJ\nAAAAEEtJUeibm5v10UcfXXKtvb1d7e3tkkbPkY8W+iiXy3XJf1dVVam1tVXHjx9XU1OT/H6/srOz\nVVlZqZUrVzI6D9hIMBjU7373O0nSY489ZjiN/VHoAQAAnCkpCv369eu1fv36a/qzxcXF2rx582XX\nFy5cqIULF8Y6GgADPvroI3V1damiokJVVVWm49jesWPHJFHoAQAAnMZ2a+gBOF90uv03v/nNy2bj\n4PoxQg8AAOBMFHoASWVgYEDvvPOOJOkb3/iG4TTOcPjwYUkUegAAAKeh0ANIKm+//bZGRka0dOlS\nTZs2zXQc2+vo6NC5c+eUm5ur6dOnm44DAACAGKLQA0gqF0+3x407ePCgJGnBggUsXwAAAHAYCj2A\npHH27Flt375dHo9Ha9euNR3HEaKFvrKy0nASAAAAxBqFHkDS+N3vfqdIJKLVq1crPz/fdBxHuHiE\nHgAAAM5CoQeQNJhuH3tfffWVJHGsJwAAgANR6AEkhUOHDmn//v2aNGmS7r//ftNxHCEUCrHDPQAA\ngINR6AEkhejo/Nq1a5WZmWk4jTM0NzdrZGRE06ZNU15enuk4AAAAiDEKPQDjIpGIfvOb30hiun0s\nsX4eAADA2Sj0AIzbvXu3Tp8+rfLyct15552m4zgGO9wDAAA4G4UegHGvv/66pNHRebebX0uxEt0Q\nj0IPAADgTLxzBmBUKBTSH/7wB0nSo48+ajiNszDlHgAAwNko9ACM2rFjh7q7uzVv3jyKZwwNDAzo\n5MmT8ng8mjNnjuk4AAAAiAMKPQCj3nzzTUnSunXr5HK5DKdxjuh0+3nz5ikjI8NwGgAAAMQDhR6A\nMcFgcGy6/dq1aw2ncRbWzwMAADgfhR6AMdHp9jfddJPmz59vOo6jsMM9AACA81HoARgTnW6/du1a\nptvHGCP0AAAAzkehB2DExdPt161bZziNs1iWxQ73AAAAKYBCD8CIHTt2qKenRxUVFUy3j7HW1lb1\n9vaqoKBApaWlpuMAAAAgTij0AIz4/e9/L4nN8OKhsbFR0ujoPEsZAAAAnItCDyDhgsGg3n77bUkU\n+njYt2+fJOnmm282nAQAAADxRKEHkHCffvop0+3jqKGhQZJ0yy23GE4CAACAeKLQA0i46HR7NsOL\nj2ihZ4QeAADA2Sj0ABIqGAxq69atkphuHw9tbW06e/ascnNzNXv2bNNxAAAAEEcUegAJtX37dvX0\n9Gj+/PmqqKgwHcdxoqPzixYtktvNr3gAAAAn490egIR68803JTE6Hy+snwcAAEgdFHoACcN0+/iL\nFvrFixcbTgIAAIB4o9ADSJjodPsFCxYw3T5OKPQAAACpg0IPIGGiu9szOh8fZ8+eVXt7u/Ly8jRr\n1izTcQAAABBnFHoACREIBJhuH2cXH1fncrkMpwEAAEC8UegBJMSOHTvU29urBQsW6KabbjIdx5GY\nbg8AAJBaKPQAEiI6Ov/www8bTuJc9fX1kij0AAAAqYJCDyDuIpGI3n33XUnSmjVrDKdxJsuytG/f\nPkkcWQcAAJAqKPQA4q6+vl5tbW0qLy/XokWLTMdxpNbWVnV0dCg/P18zZswwHQcAAAAJQKEHEHfR\n6fYPPfQQm7XFSXR0ng3xAAAAUgeFHkDcvfPOO5KkBx980HAS52L9PAAAQOqh0AOIq6NHj+rw4cOa\nNGmS7rrrLtNxHCs6Qk+hBwAASB0UegBxFd0Mb/Xq1crIyDCcxpksy2KEHgAAIAVR6AHEVXT9PLvb\nx09LS4vOnTun/Px8TZ8+3XQcAAAAJAiFHkDcdHR0aM+ePfJ6vbrvvvtMx3Gsuro6SaOj82yIBwAA\nkDoo9ADi5r333pNlWVq+fLlycnJMx3GsPXv2SJJuv/12w0kAAACQSBR6AHFz8XF1iJ8vvvhCEoUe\nAAAg1VDoAcTF4OCgtm/fLpfLpQceeMB0HMfy+/1jO9zfdttthtMAAAAgkSj0AOLiww8/lN/v1+23\n367i4mLTcRxr//79CgQCqqioUH5+vuk4AAAASCAKPYC4YLp9YjDdHgAAIHVR6AHEXDAY1AcffCBJ\nevDBBw2ncTY2xAMAAEhdFHoAMff555+rp6dHN910k+bOnWs6jmNZljVW6O+44w7DaQAAAJBoFHoA\nMffOO+9IktasWWM4ibO1tLTo7NmzmjRpEh+cAAAApCAKPYCYsiyLQp8g0fXzS5YskdvNr3MAAIBU\nwztAADF14MABnTlzRqWlpbr11ltNx3E01s8DAACkNgo9gJiKjs4/8MADjBrH2d69eyVR6AEAAFIV\n77YBxFR0d/sHHnjAcBJnGx4e1r59++RyuXTbbbeZjgMAAAADKPQAYqajo0N1dXXyer265557TMdx\ntH379ikUCmnBggXKzc01HQcAAAAGUOgBxMyHH34oSVq2bJl8Pp/ZMA7H+nkAAABQ6AHETHS6/f33\n3284ifNFd7in0AMAAKQuCj2AmAiFQvroo48kSatWrTKcxtksy2KEHgAAABR6ALGxd+9e9fb2as6c\nOZo9e7bpOI526tQpdXR0qKCgQHPmzDEdBwAAAIZQ6AHExLZt2yQx3T4RLp5u73K5DKcBAACAKRR6\nADERXT+/evVqw0mcj+n2AAAAkCj0AGKgtbVVjY2N8vl8Wrp0qek4jseGeAAAAJAo9ABi4I9//KMk\nacWKFfJ6vYbTOFtfX58aGxuVkZGhJUuWmI4DAAAAgyj0AG4Yx9Ulzq5duxSJRHTLLbfI5/OZjgMA\nAACDKPQAbkggENDHH38siUKfCJ999pkk6a677jKcBAAAAKZR6AHckF27dmlwcFALFizQ1KlTTcdx\nPAo9AAAAoij0AG4I0+0TZ2BgQA0NDUpLS1N1dbXpOAAAADCMQg/ghlDoE+eLL75QOBzWzTffrJyc\nHNNxAAAAYBiFHsCEnTx5UocPH1Zubq7uuOMO03Ecb+fOnZKYbg8AAIBRFHoAExYdnV+5cqUyMjIM\np3E+1s8DAADgYhR6ABO2bds2SdLq1asNJ3G+4eFh1dfXy+Vy6c477zQdBwAAAEmAQg9gQoaHh7Vj\nxw5J0n333Wc2TArYs2ePgsGgqqqqNGnSJNNxAAAAkAQo9AAmZOfOnRoZGdHNN9+s0tJS03Ecj+n2\nAAAA+FMUegAT8uGHH0qSVq1aZTZIiogW+rvvvttwEgAAACQLCj2ACfn4448lSffee6/hJM43MjKi\nvXv3ShLr5wEAADCGQg/gurW0tOjw4cPKzs7WkiVLTMdxvLq6Ovn9flVWVqqwsNB0HAAAACQJCj2A\n6/bJJ59IGp3+7fF4DKdxPs6fBwAAwHgo9ACuW3S6/cqVKw0nSQ1siAcAAIDxUOgBXJdIJDI2Qs/6\n+fgLBAL64osvJFHoAQAAcKl00wGk0dGnxsZGnThxQs3NzRoZGdGKFSv0ve9977qf1dXVpU2bNqm+\nvl4DAwPKz89XdXW11q9fr+zs7DikB1JLY2Ojzp07p7KyMs2dO9d0HMdraGjQyMiI5s2bp6KiItNx\nAAAAkESSotC/8cYbOnHihDIzMzV58mSdOXNmQs9pa2vTM888o76+PlVXV6u8vFxHjx7V22+/rfr6\nej3//PPKycmJcXogtVy8u73L5TKcxvmYbg8AAIArSYpC//jjj6uwsFBTpkxRY2OjnnvuuQk95+WX\nX1ZfX5+eeOIJrVmzZuz6q6++qrfeekubNm3Sxo0bYxUbSEmsn08szp8HAADAlSTFGvqFCxdqypQp\nN/SMtrY2NTQ0qKSk5JIyL0m1tbXyer36+OOPFQgEbuj7AKlseHhYu3btksvl0ooVK0zHcbxgMKhd\nu3ZJYoQeAAAAl0uKQh8LBw4ckCQtXrz4snuZmZmaP3++/H6/Dh06lOhogGPs3r1bfr9fixYtstV5\n6GlpaUpPT1daWprpKNelrq5Og4ODmjdv3g1/6AkAAADncUyhb2lpkSSVlZWNez96vbW1NWGZAKeJ\n7m5vl+n26ZYln8sl386dyv75z+XbuVM+l0vplmU62jXZvn27JGn58uWGkwAAACAZJcUa+lgYGhqS\nJGVlZY17P3p9cHAwYZkAp4kWejsUzHTLkqetTbmPPqq0U6fGroenT1f/b38rlZYqlOSb+kV/3ixv\nAAAAwHgcM0IPIL66urq0f/9+eb1eVVdXm45zVRlu92VlXpLSTp1S7qOPKiPJy/zg4KD27t0rt9vN\nhngAAAAYl2MKfXQEPjpS/6ei1zmLHpiYHTt2yLIs3X777fL5fKbjfK20tDSlff75ZWV+7P6pU0rb\nvTup19R//vnnCgaDuuWWWzRp0iTTcQAAAJCEHDPlvry8XNKV18hHr19pjf14tmzZotdee+2K9y7+\nvkCsdHZ1J2Vhjh6ftmrVqqTM96fSDx686n1PEu8FEP1533fffTH7eXd3J+drC/bG6wrxwmsL8dDZ\n1c37d8RNbW3tFe/V1NR87f2Jckyhr6qqkiQ1NDRcdm9kZERNTU3yer2qqKi45mfW1tZe9Yce3YwP\niBWfz6cHX/7SdIzL7PvndyVJr/eW6Z0kzHexP5tXqKdvmq/xd9QY1T+vQv/vh83adqQ7Ybmux4E3\ntkqS3hqcqk+S/OcNAIBdvLvxNt6/I+aiHxJFB30TyXZT7sPhsFpaWtTW1nbJ9dLSUi1evFjt7e3a\nunXrJfc2b94sv9+vlStXyuPxJDIu4Aj+7jb5z51RWma2sqde+4dipnx6okeRpUsVnj593Pvh6dMV\nuXOpPm3uTXCyaxMc6NFw61G50j3KmVllOg4AAACSVFKM0O/evVu7d++WJPX09EiSmpqa9LOf/UyS\nlJubq29/+9uSRjfmevrpp1VcXKwXX3zxkuds3LhRzz77rF555RXt27dPU6dO1eHDh9XY2Kjy8nJt\n2LAhgX8rwDn6j+yVJOXOvUWuJF53HjUcjOgfGjr07dd/o6LHvnHZLvedr/9G/7ivQyOhiMGUV9Z/\nZHREPmfWIrkz+BASAAAA40uKQt/c3KyPPvrokmvt7e1qb2+XJJWUlIwV+ijXODtUl5aW6oUXXtDm\nzZtVV1enuro65efn65FHHlFNTc0Vj7QD8PX6Do8WzNx5SwwnuXabG7skFepffbpTrs8/l+9Qk4Yr\n5staulT/0NBx/n5y6jtf6PNuss/PGwAAAInnsizLMh3CzliDg1hLtjX0lmWp/vn1Cg10q+o//EK+\n0pmmI10XX4Zby2ZOUmFWhrqGgvq0uTdpR+al0Z/3vhf+pQLdbar89z9T9vT5piMBAOAY7268TcPD\nw6ZjwGFMbrSYFCP0AJLXSPsJhQa6lZE7WZklM0zHuW7DwUjSbnw3Hn/nGQW625SWlausqfNMxwEA\nAEASs92meAASq//Y6MkRuXMWj7vUBbHVd3iPJClv3u1yuZN/vwIAAACYQ6EH8LX6j9VLknLm3GI4\nSWoYK/SsnwcAAMBVUOgBXJFlWRq4aIQe8WWFw+o/WidJyqu4w3AaAAAAJDsKPYAr8neeVrC/S+nZ\n+bZcP283g6e+UnhkUN6iafIWlJqOAwAAgCRHoQdwRRfWz9/M+vkEGJtuX3G74SQAAACwAwo9gCvq\nPz5a6Fk/nxi9h76QJE26ien2AAAAuDoKPYBxsX4+sULDAxo8dVByu5U7lw9QAAAAcHUUegDjCnSf\nVaCnXWlZufKVzjYdx/H6j9ZJkYhyZixUWma26TgAAACwAQo9gHFFj6vLnX2zXG5+VcRb3/np9nk3\nsX4eAAAA14Z36QDGFd0QL2c207/jzbIs9X71uSRp0oKlhtMAAADALij0AMbVz/r5hBlpO6FAT7vS\nc/KVNfUm03EAAABgExR6AJcJ9LQr0NWqtMxsZZXPNR3H8cZG5+ffyfIGAAAAXDPeOQK4THT9fM6s\nRXK50wyncT6m2wMAAGAiKPQALjO2fp7p9nEXGh7QQPN+ye1mQzwAAABcFwo9gMuM7XA/hw3x4q3/\nyF5ZkbByZlYpPSvXdBwAAADYCIUewCUCfefk7zwjtyeTDdoSgOn2AAAAmCgKPYBLDFy0ft6dlm44\njbONHle3S5I0acGdhtMAAADAbij0AC7BcXWJM9xyRMH+LmVMKpJvyhzTcQAAAGAzFHoAl+g/Ht0Q\nj/Xz8dYTHZ2fv1Qul8twGgAAANgNhR7AmOBAj0baTsid4VX2tPmm4zjehfXzTLcHAADA9aPQAxgz\ncOKAJClr+gK50zMMp3G20GCvBk8elCstXXnzlpiOAwAAABui0AMYM3iiUZKUM3Oh4STO13toj2RF\nlDN7sdIys0zHAQAAgA1R6AGMGaDQJ0xvE9PtAQAAcGMo9AAkSZFwSEOnmyRJ2TOrDKdxNisSVl/T\nbkmcPw8AAICJo9ADkCQNtxxVJOiXt2iqMrInmY7jaIOnDyk02CtPYZkyi6ebjgMAAACbotADkCQN\nnGS6faJcvLs9x9UBAABgoij0ACRd2BAvewbT7eOt96Lz5wEAAICJotADkHThyLqcWYzQx1Owv0tD\np5vkSvcod+4tpuMAAADAxij0ABToO6dAd5vc3iz5SmeZjuNovU2jo/O5c29VmifTcBoAAADYGYUe\nwIXp9tMXyOVOM5zG2Xoad0qS8iuZbg8AAIAbQ6EHwPnzCRIJ+tXX9IUkKX/hMsNpAAAAYHcUegAX\n1s9T6OOq7/AeRYIjyppaIU9+iek4AAAAsDkKPZDiIqGghs4ckiRlz6DQx1PPgU8lSfmL7jGcBAAA\nAE5AoQdS3FDLEVmhoDJLZig9K9d0HMeyImH1NH4mSSqootADAADgxlHogRQ30Mx0+0QYONGo0GCP\nvIVlyuQkAQAAAMQAhR5IcYMnz+9wz3T7uBqbbl91j1wul+E0AAAAcAIKPZDixna4n1VlOIlzWZbF\n+nkAAADEHIUeSGGBnnYFezuU5stRZvEM03Eca6TthPznWpSePUk5M/ngBAAAALFBoQdSWHR0Pnt6\npVxufh3ES/f50flJlXfL5U4znAYAAABOwTt4IIWNTbdnQ7y4ik63Z3d7AAAAxBKFHkhhg6e+kiRl\nz6g0nMS5Aj0dGjrdJHdGpvIqbjcdBwAAAA5CoQdSlBUOa7jliCQpe1qF4TTO1dO4Q5KUV3G73Ble\nw2kAAADgJBR6IEUNt59QJOiXp7BM6dmTTMdxrIuPqwMAAABiiUIPpKihM4ckSdlTbzKcxLlCwwPq\nP1onudzKr7zLdBwAAAA4DIUeSFGDp0cLfRbT7eOm96tdsiJh5c6+mVkQAAAAiDkKPZCihs4XetbP\nxw/T7QEAABBPFHogBVnhsIZajkqSsqZS6OMhEgqot2mXJCm/apnhNAAAAHAiCj2Qgobbm2WFAvIW\nlik9K9d0HEfqP1qniH9IvrK58haWmY4DAAAAB6LQAyloaGz9/HzDSZyrZ390uj2j8wAAAIgPCj2Q\ngi5siMcO9/FgRcLqPrBdklSwaLnhNAAAAHAqCj2Qgi5siMcIfTz0H2tQaKBH3slT5SubazoOAAAA\nHIpCD6SYSDikodbohniM0MdDd8NHkqSCW+6Vy+UynAYAAABORaEHUsxIW7OsUFDeyVOV7ssxHcdx\nrHBY3fs/kSQVLr7XcBoAAAA4GYUeSDGDnD8fV/3Hz0+3L2K6PQAAAOKLQg+kmAs73FPo42Fsuv1i\nptsDAAAgvij0QIoZPEOhjxcrHFb3vuh0+/vMhgEAAIDjUeiBFBIJBTXcckySlFU+z3Aa5+k/3qDQ\nYHS6/RzTcQAAAOBwFHoghYy0NcsKB+UtmsaGeHHQXf+hpNHReabbAwAAIN4o9EAKYUO8+Ll4d/sC\ndrcHAABAAlDogRTChnjx03+sXqHBXnmLpjHdHgAAAAlBoQdSyFDrUUmsn4+HroYPJY2ePc90ewAA\nACQChR5IEVYkouGzxyVJWYwgx5QVDqtn/3ZJUsEtTLcHAABAYlDogRTh7z6rSGBEGXmTlZ49yXQc\nR+k/Vndhuv0UPiwBAABAYlDogRQx3Dp6XB2FM/a6Gj6SJBXewu72AAAASBwKPZAixgp92WzDSZzl\nkun2i1caTgMAAIBUQqEHUsTY+nlG6GMqOt0+s3g6sx8AAACQUBR6IEUMMUIfF131o9PtC9jdHgAA\nAAlGoQdSQDgwIv+5FsntVmbJDNNxHCMSDqln/yeSRgs9AAAAkEgUeiAFjLSdkKyIMouny53uMR3H\nMfqPfKnQUN/56fbMfAAAAEBiUeiBFMD6+fjo+nKbJKnw1vuZbg8AAICEo9ADKYD187EXDgyr+/x0\n+8LbVhtOAwAAgFREoQdSQHSEnl3YY6fnwA5FAiPKnlGpzKKppuMAAAAgBVHogRRw4Qx6Cn2sRKfb\nT17yZ4aTAAAAIFVR6AGHC/Z3KTTYo7TMbHnyS0zHcYTgQLd6D+2Wy52mgsX3mY4DAACAFEWhBxxu\nbP38lNls3BYjXfUfSpGI8uZXKyMn33QcAAAApCgKPeBwY+vnmW4fM11735ckTb6N6fYAAAAwh0IP\nONzwRSP0uHEjHac0eOoruT0+TVp4t+k4AAAASGHppgNcrKurS5s2bVJ9fb0GBgaUn5+v6upqrV+/\nXtnZ2df0jKeeekqdnZ3j3svPz9dLL70Uy8hA0mOEPrbOnd8Mr+DmFUrzZBpOAwAAgFSWNIW+ra1N\nzzzzjPr6+lRdXa3y8nIdPXpUb7/9turr6/X8888rJyfnmp6VlZWlRx555LLrmZm8+UZqscJhDbc1\nS5J8pbOMZnECy7LY3R4AAABJI2kK/csvv6y+vj498cQTWrNmzdj1V199VW+99ZY2bdqkjRs3XtOz\nsrOzVVNTE6+ogG34u1plhYLy5Jco3XdtH4jhygZPHpT/XIsycicrd+6tpuMAAAAgxSXFGvq2tjY1\nNDSopKTkkjIvSbW1tfJ6vfr4448VCAQMJQTsaaTjlCTJWzzNcBJnOPfl6GZ4hbfdL5c7zXAaAAAA\npLqkGKE/cOCAJGnx4sWX3cvMzNT8+fPV0NCgQ4cOadGiRVd9XjAY1CeffKLOzk55vV7NnDlTlZWV\ncruT4vMLIGGihT6zeLrhJPYXCYfUXfdHSUy3BwAAQHJIikLf0tIiSSorKxv3fllZmRoaGtTa2npN\nhb6np0cvvvjiJddKSkr05JNPauHChTceGLCJkY7Tkij0sdDXtFuhoT5lls6Sr2yu6TgAAABAchT6\noaEhSaOb2Y0nen1wcPCqz1q1apUqKys1ffp0ZWZmqr29XVu3btV7772nH/3oR/rhD3+oGTNmxC48\nkMQYoY+d6HT7yUv+TC6Xy3AaAAAAIEnW0MdSTU2NqqqqlJeXJ4/Ho2nTpmnjxo1au3atAoGAtmzZ\nYjoikDAU+tgIjwyq58AOSVLhrfcbTgMAAACMSopCHx2Bj47U/6no9Ws9i348DzzwgCTp4MGDE34G\nYCeh4QGFBrrlzvDKM6nYdBxb696/XVYooJzZi+UtKDUdBwAAAJCUJFPuy8vLJUmtra3j3o9ev9Ia\n+2uRl5cnSfL7/df8NVu2bNFrr712xXvShexArHR3d8fkOf7O0fXz3qKpcrEh5A25eLo9AACwN96/\nI15qa2uveK+mpuZr709UUhT6qqoqSVJDQ8Nl90ZGRtTU1CSv16uKiooJf49Dhw5JkkpLr310rba2\n9qo/9OjFHtM2AAAgAElEQVSGfkCs+Hy+mDyH6faxEehpV/+RL+VKy1DBzStNxwEAADeI9++IteiH\nRCaWdyfFsF1paakWL148toHdxTZv3iy/36+VK1fK4/FIksLhsFpaWtTW1nbJnz1z5sy4I/Dt7e36\nxS9+IUlasWJFnP4WQHJhh/vY6NzzrmRZyq+6R+lZuabjAAAAAGOSYoRekjZu3Khnn31Wr7zyivbt\n26epU6fq8OHDamxsVHl5uTZs2DD2Z7u6uvT000+ruLj4kuPpduzYoTfffFOVlZUqKiqSz+dTW1ub\n9u7dq2AwqCVLlmjdunUm/npAwo2N0BdNM5zEvqxIRJ27Rz9kLLrzYcNpAAAAgEslTaEvLS3VCy+8\noM2bN6uurk51dXXKz8/XI488opqamnGPtPvTo6OqqqrU2tqq48ePq6mpSX6/X9nZ2aqsrNTKlSsZ\nnUdKiRZ6LyP0E9Z/rF6BrlZ58kuUN+8203EAAACASyRNoZekwsJCPfnkk1f9c8XFxdq8efNl1xcu\nXKiFCxfGIxpgK1YkIn/nGUlSZjEj9BPVufttSdLkO9bI5U4znAYAAAC4VFKsoQcQW4HeDkWCfqXn\nFCjdl2M6ji2FhgfUve8TyeVS0R0PmY4DAAAAXIZCDzgQO9zfuK4vt8kKBZQ77zZ5C6eYjgMAAABc\nhkIPOJCfHe5v2NhmeHewGR4AAACSE4UecKALI/Ssn5+IoZajGjpzSGm+HBUsWm46DgAAADAuCj3g\nQEy5vzHRzfAKb1std4bHcBoAAABgfBR6wIFGOqNT7hmhv16RYEDn9r4vSSquZro9AAAAkheFHnAY\nKxxWoLdDcrnkKSg1Hcd2eg58qvBwv7LK5ylr6k2m4wAAAABXRKEHHCbQ2yFFIsrImyx3OtPFr1fn\nF+c3w2N0HgAAAEmOQg84TKC7TZLkyWd0/nr5u9vUd3iPXOkZKrxttek4AAAAwNei0AMO4+8+K0ny\nFnB2+vU698U7kmWpYNEKpWflmo4DAAAAfC0KPeAwYyP0hYzQXw8rErlouv1DhtMAAAAAV0ehBxzG\nf77Qe5lyf136j36pQHebPAVTlDv3NtNxAAAAgKui0AMOEzg/5d5TyJT769G5a/Ts+aI71sjl5lcj\nAAAAkh/vWgGHGRuh58i6axYc6FH3/u2Sy6XJd6wxHQcAAAC4JhR6wEGsSFjBnnZJ7HJ/PTp3vy0r\nHNSkBUv5IAQAAAC2QaEHHCTYd05WJKyM3EK5MziD/lpYkbA6PntTklRy958bTgMAAABcOwo94CDR\nI+s8jDJfs96vdinQfVbewjLlVVSbjgMAAABcMwo94CBjR9ZR6K9Z+85/liQV3/3nbIYHAAAAW+Hd\nK+AgFzbEY4f7azFyrkV9h3bLlZ6hIjbDAwAAgM1Q6AEHCXRFp9xT6K9Fx87fS5alwltWKT17kuk4\nAAAAwHWh0AMOMjZCX8iU+6uJBP3q/GL07PmSZf+b4TQAAADA9aPQAw4ytoaeI+uuqqv+Q4WH+pU1\nbb6ypy8wHQcAAAC4bhR6wCGsSESB6Bn0bIp3Ve07fyeJo+oAAABgXxR6wCFCQ72ywkGlZeUqzZNp\nOk5SGzz1lYZONSnNl6uCW+4zHQcAAACYEAo94BDB/m5JUkZOgeEkya995+8lSUXVD/HhBwAAAGyL\nQg84RGjgfKHPLTScJLmFhvrUVfeBJKn4rnWG0wAAAAATR6EHHCLY3yWJEfqr6dy9VVYooLyKamUW\nTTUdBwAAAJgwCj3gENEp9+m5FPorsSIRdXw2Ot2+ZBmb4QEAAMDeKPSAQwSZcn9VfYf3yH+uRZ78\nEk1asNR0HAAAAOCGUOgBhwixKd5Vte8YPaqu+K51crnTDKcBAAAAbgyFHnCI6Ah9OoV+XCOdZ9T7\n1WdypWWo6M6HTccBAAAAbhiFHnCIsU3xWEM/rrbtr0uWpcLbVjOLAQAAAI5AoQccYuwcegr9ZUKD\nvTq3e6skacrKGsNpAAAAgNig0AMOYEXCCg32SmLK/XjaP3tTkaBfeRXV8k2ZbToOAAAAEBMUesAB\nQoO9khVRelae3GnppuMklUgooI4dv5UkTbl3veE0AAAAQOxQ6AEHGNsQj+n2l+n68gMF+7vkK5uj\n3HlLTMcBAAAAYoZCDzhAkCPrxmVZlto+eU2SVLpyvVwul+FEAAAAQOxQ6AEHGDuDPrfQcJLk0nfo\nCw2fPa6MvMkqvGWV6TgAAABATFHoAQfgDPrxtX38a0lSyT3fkDs9w3AaAAAAILYo9IADhAZ7JEkZ\nOfmGkySPoZaj6ju8R25PpoqXrjUdBwAAAIg5Cj3gAKHhAUlSmi/HcJLk0fbJ6Oh8UfXDSs/KNZwG\nAAAAiD0KPeAA4eFBSVJaJoVekgK9neqq+6Pkcqt0+TdNxwEAAADigkIPOEB4JFrosw0nSQ7tO34r\nKxxSwaLl8k4uNx0HAAAAiAsKPeAA4ZHolHsKfdg/rI7Pfi9p9Kg6AAAAwKko9IADREfo05lyr84v\ntio8PKDsmVXKmbnQdBwAAAAgbij0gANcWEOf2iP0Vjis9k9elyRNYXQeAAAADkehBxzgwpT71B6h\n72r4UP6uVnknlyu/apnpOAAAAEBcUegBm7PCYUWCfsnlktuTaTqOMVYkotYP/lGSNGXVX8jlTjOc\nCAAAAIgvCj1gc+HAsCTJ7fHJ5XIZTmNOz4FPNdJ2Qp78Ek1e8oDpOAAAAEDcUegBm4ucL/RpHp/h\nJOZYlnVhdP7eb8mdnmE4EQAAABB/FHrA5iL+EUlK6en2fU27NHTmsNJzClR058Om4wAAAAAJQaEH\nbG5syr03NUfoLctSy7bzo/Mr18ud4TWcCAAAAEgMCj1gc5HA6Ah9WoqO0Pcfq9fgiQNKy8pV8V3r\nTMcBAAAAEoZCD9hc2J/aI/St7/+9JKn0nm8qLTPLcBoAAAAgcSj0gM1FgufX0Gek3gh9/7EG9R+t\nU1pmtkqWf9N0HAAAACChKPSA3UUikiSXO/X+d255/1VJUsnyx5TuyzGcBgAAAEis1GsAgMNYljX6\nLyl2Bn3/8Qb1H/lSaZnZKl3xmOk4AAAAQMJR6AHbGy30Lldq/e/c8t7o2nlG5wEAAJCqUqsBAE5k\njU65T6UR+v7j+9R/ZO/o6Dxr5wEAAJCiKPSAzUWn3KfSCP2FtfPfVHpWruE0AAAAgBmp0wAAp0qx\nEfr+o/XqPxwdnWftPAAAAFIXhR6wu7FN8Zz/v7NlWTr9h7+TJJWuXM/oPAAAAFKa8xsA4HBW9Ni6\nFBih7973sQZPfaX0nAKVrqwxHQcAAAAwikIP2F2KjNBHwiGdefvnkqTyB/5SaR6f4UQAAACAWc5u\nAEAKuLApnrNH6Ds/f0v+c2fkLZqmojsfNh0HAAAAMI5CD9hddFM8t3P/dw77h8d2tp/28Ea509IN\nJwIAAADMc24DAFLF2JR7547Qt338a4UGepQ9o1L5i5abjgMAAAAkBQo9YHPW+RF6l5xZ6IP9XTr7\n0WZJ0rRH/q3jlxYAAAAA14pCD9icKy1DkhQJBw0niY+Wbf+gSGBEkyrvVu7sxabjAAAAAEmDQg/Y\nXJp3dLf3iH/YcJLYG+k4rc7P3pRcbk17eKPpOAAAAEBSodADNpfmzZIkhf1DhpPE3pl3XpEVCavo\njgflmzLLdBwAAAAgqVDoAZtznx+hDztshH7w1FfqbvhQrnSPyh943HQcAAAAIOlQ6AGbuzDl3jkj\n9JZl6fRbfydJKl3+TXnyiw0nAgAAAJIPhR6wObcDp9z37P9E/cfqlZaVqymr/sJ0HAAAACApUegB\nm7swQj9iOElshP3DOvnP/58kaeqaf6N0X47hRAAAAEByotADNue0TfFa3n9Vwd5OZU2br+Kl/8J0\nHAAAACBpUegBm3N7zo/QB4ZlRSKG09yY4bPNav/kdcnl0sxvfF8ud5rpSAAAAEDSotADNudyu+X2\nZEqSIgH7Tru3LEsnfvs3siJhFS9dq+zp801HAgAAAJJauukAF+vq6tKmTZtUX1+vgYEB5efnq7q6\nWuvXr1d2dnbCnwPYRZo3S5HAiML+IaVlZpmOMyFdX27TwLF6pWdP0tSHnjAdBwAAAEh6SVPo29ra\n9Mwzz6ivr0/V1dUqLy/X0aNH9fbbb6u+vl7PP/+8cnKuvjlWrJ4D2Inb65P67buOPjQ8oFNv/g9J\n0rR/8W+VnpVnOBEAAACQ/JKm0L/88svq6+vTE088oTVr1oxdf/XVV/XWW29p06ZN2rhxY8KeA9hJ\nRu5k+TvPKNjbKV/JDNNxrlvLu/9LoYFuZc+s0uTbHzQdBwAAALCFpFhD39bWpoaGBpWUlFxSwiWp\ntrZWXq9XH3/8sQKBQEKeA9iNt3CKJMnf1Wo4yfUbOnNY7Tt+J7nc5zfCS4pfSwAAAEDSS4p3zgcO\nHJAkLV68+LJ7mZmZmj9/vvx+vw4dOpSQ5wB24ykYLfSB7jbDSa6PFYnoxG9+KlkRldzzqLLK55qO\nBAAAANhGUhT6lpYWSVJZWdm496PXW1u/fvQxVs8B7MZbWCpJ8nefNZzk+nR+sVWDJw8qI3eypj74\nuOk4AAAAgK0kRaEfGhrdyCsra/zduaPXBwcHE/IcwG6iI/T+LvsU+kBPu06/9ZIkadraf6e0TE6g\nAAAAAK5HUhR6ADfGWzg6+yRgkxF6KxLR8S0/Vnh4QJMq71LhratMRwIAAABsJykKfXTkPDrC/qei\n1692hnysngPYjSevSHK7Few7p0go+Td9bN/xG/Uf2av07EmaVfMf5HK5TEcCAAAAbCcpjq0rLy+X\ndOW17dHrV1obH+vnRG3ZskWvvfbaFe9d/D2BWOnu7r7ur3GlpckzqUSB7rMKdLcps3h6HJLFxnBb\ns07/4X9KkmY+9lfKyC00nAgAAKQS3r8jXmpra694r6am5mvvT1RSFPqqqipJUkNDw2X3RkZG1NTU\nJK/Xq4qKioQ8J6q2tvaqP/ToRnxArPh8vgl9nbegVIHus/IncaGPhII6/qsfyQoFNfmOh1SwaLnp\nSAAAIMXw/h2xFv2QKDrom0hJMeW+tLRUixcvVnt7u7Zu3XrJvc2bN8vv92vlypXyeDySpHA4rJaW\nFrW1td3QcwAn8UTPoj+XvKc4tL7/9xpqOSJPwRTN+PPvmo4DAAAA2FpSjNBL0saNG/Xss8/qlVde\n0b59+zR16lQdPnxYjY2NKi8v14YNG8b+bFdXl55++mkVFxfrxRdfnPBzACfxTZkjSRo6/ZWkdWbD\njGOg+YBa//gryeXS7A3/kV3tAQAAgBuUNIW+tLRUL7zwgjZv3qy6ujrV1dUpPz9fjzzyiGpqasY9\nim68jbQm8hzACXJnL5Ik9R/fbzjJ5cL+YR3f9CPJimjKfd9S7uzFpiMBAAAAtpc0hV6SCgsL9eST\nT171zxUXF2vz5s03/BzASXzl8+TOyJS/87SCA93KyCkwHWnMqd//rfxdrfKVzVH5g4+bjgMAAAA4\nQlKsoQdw49xp6cqeWSlpdHp7suiq+0Cdu96SKy1Dszf8Z7nT2cMCAAAAiAUKPeAgObNGp90PHN9n\nOMmowVNNOr7lx5KkaWu/o6yyOYYTAQAAAM5BoQccZKzQN5tfRx/oO6cjr/4XWaGAiqofVsmyR01H\nAgAAAByFQg84SM6MhZLLraEzhxUODBvLEQkGdPSX/0XB3k7lzFqkGd/4/ribWAIAAACYOAo94CBp\nmVnKKp8rKxLW4MmvjGSwLEvNr/93DZ76Sp78Es391z+QOz3DSBYAAADAySj0gMPkzrtNktRV90cj\n3//sR5vVtfd9uT2Zmvf4/5NUu+0DAAAATkKhBxymqPphSVJX3TaFRwYT+r17GnfqzNsvS5Jmb/jP\nyiqfm9DvDwAAAKQSCj3gML6SGcqZc4sigRGd+3Jbwr7v0JnDOvar/ypZlsoffFwFi5Yn7HsDAAAA\nqYhCDzhQyV1rJUkdn70py7Li/v0GTh5U09/9n4r4h1Sw+D6Vrf5Xcf+eAAAAQKqj0AMOlL9oudKz\nJ2m49agGTx6M6/fqP9agQ3/3fyk8PKD8Rcs1e8N/ZEd7AAAAIAEo9IADudM9mnzHGklSx+dvxu37\n9B76Qod//p8UCQyr8Nb7NedfPit3uidu3w8AAADABRR6wKGKl45Ou+/6cpuGWo/F/Pk9jTt05JVn\nFAn6VVT9sGZv+E9yp6XH/PsAAAAAGB+FHnCozKKpKl66VlY4pOObXlAkFIzZs7saPtLRV38gKxxU\nyT3f0MzH/koud1rMng8AAADg6ij0gINNW/vv5C0s03DrUbW+//c3/LxIKKBTb72kY//4vKxIWFPu\n26Dpf/6UXG5+lQAAAACJxrtwwMHSvD7N+tb/Lblcav3jr9TbtHvCzxpqPaqDf/NdtX20RXK5NPXh\njZr68EY2wAMAAAAModADDpc7e7Gm3LdBsiI68stn1fvV59f19ZFQUK0fbtLBv3lKw2ePyzt5qhY8\n+VOVrfoLyjwAAABgEDtYASlg6kP/RuGRQXXs/Gcd/l/PaMp9G1S++ttyZ1x5R/pIKKhze95V67Z/\nUKCnXZJUfNc6TVv7HaV5fImKDgAAAOAKKPRACnC5XJrx6P+htMxsnf1wk85+8E/q2vu+Cpf8mQqq\n7pF3crlcaRkK9LRppOO0ehp3qqfxU4WH+iVJmaUzNf2R72jSgqWG/yYAAAAAoij0QIpwuVya9vBG\n5VferebX/ptG2k/q7Af/pLMf/NMVv8Y3ZbbK7v/fVbD4XnaxBwAAAJIMhR5IMTmzqlT1Vz9X//EG\ndX25TYMnDyrQ065IKChPfrE8BaXKnb1YBTevkK90lum4AAAAAK6AQg+kIJfbrby5typv7q2mowAA\nAACYIHa5BwAAAADAhij0AAAAAADYEIUeAAAAAAAbotADAAAAAGBDFHoAAAAAAGyIQg8AAAAAgA1R\n6AEAAAAAsCEKPQAAAAAANkShBwAAAADAhij0AAAAAADYEIUeAAAAAAAbotADAAAAAGBDFHoAAAAA\nAGyIQg8AAAAAgA1R6AEAAAAAsCEKPQAAAAAANkShBwAAAADAhij0AAAAAADYEIUeAAAAAAAbotAD\nAAAAAGBDFHoAAAAAAGyIQg8AAAAAgA1R6AEAAAAAsCEKPQAAAAAANkShBwAAAADAhij0AAAAAADY\nEIUeAAAAAAAbotADAAAAAGBDFHoAAAAAAGyIQg8AAAAAgA1R6AEAAAAAsCEKPQAAAAAANkShBwAA\nAADAhij0AAAAAADYEIUeAAAAAAAbotADAAAAAGBDFHoAAAAAAGyIQg8AAAAAgA1R6AEAAAAAsCEK\nPQAAAAAANkShBwAAAADAhij0AAAAAADYEIUeAAAAAAAbotADAAAAAGBDFHoAAAAAAGyIQg8AAAAA\ngA1R6AEAAAAAsCEKPQAAAAAANkShBwAAAADAhij0AAAAAADYEIUeAAAAAAAbotADAAAAAGBDFHoA\nAAAAAGyIQg8AAAAAgA1R6AEAAAAAsCEKPQAAAAAANkShBwAAAADAhtJNB4hqamrSG2+8ocOHDysQ\nCKisrEyrVq3SQw89JLf72j536Ojo0Pe+970r3l+2bJm+//3vxyoyAAAAAADGJEWh3717t37yk5/I\n4/Ho7rvvVk5Ojvbs2aNf/vKXampq0tNPP31dz5s1a5aqq6svuz59+vRYRQYAAAAAwCjjhX54eFgv\nvfSS3G63fvCDH2j27NmSpA0bNui5557TZ599ph07dmjZsmXX/MyZM2eqpqYmXpEBAAAAADDO+Br6\nnTt3qr+/X/fcc89YmZek9PR0fetb35Ikvffee6biAQAAAACQlIyP0B84cECSdOutt152b+HChfJ4\nPGpqalIoFFJ6+rXF7e7u1vvvv6/+/n7l5uaqoqJCM2bMiGluAAAAAABMMl7oW1paJEllZWWX3XO7\n3SopKdHp06fV3t6u8vLya3pmQ0ODGhoaLrm2cOFCPfXUUyoqKrrx0AAAAAAAGGa80A8NDUmSsrKy\nxr0fvT44OHjVZ3m9Xj322GO68847VVJSIkk6efKkfv3rX2v//v16/vnn9eMf/1gejydG6QEAAAAA\nMCMmhf6pp55SZ2fnNf/5FStWfO3xchOVl5en2traS64tWLBAf/3Xf61nn31WR44c0bZt2/Twww/H\n/HsDAAAAAJBIMSn0U6ZMua5R74KCgrF/j47AR0fq/1T0enZ29oTzud1urV69WkeOHNHBgwcp9AAA\nAAAA24tJoX/22Wcn/LXl5eU6duyYWltbL9nlXpIikYja29uVlpY2NoV+ovLy8iRJfr//mr9my5Yt\neu211654T9I1r+sHrlV3d7fpCAAAAI7F+3fEy5/OFr9YTU3N196fKONr6BctWqTt27errq7usrPm\nGxsbFQgEtHDhwmve4f5KDh06JEnX9cFAbW3tVX/o0U39gFjx+XymIwAAADgW798Ra9EPiaKDvolk\n/Bz6u+66S7m5ufr000917NixsevBYFCbNm2SJD344IOXfM3Q0JBaWlrU09NzyfXjx4/LsqzLvse+\nffv01ltvSRpdvw8AAAAAgN0ZH6H3+Xz6zne+o5/85Cf6wQ9+oGXLliknJ0d79uxRS0uL7r77bt19\n992XfM2uXbv0t3/7t7r33nv13e9+d+z6q6++qtbWVlVUVGjy5MmSRne5379/vyRpw4YNqqioSNxf\nDgAAAACAODFe6CWpurpazz33nN544w3t2rVLwWBQU6ZM0V/+5V9+7QZ2Lpfrkv9euXKldu3apWPH\njqm+vl6hUEj5+flatmyZ1qxZowULFsT7rwIAAAAAQEK4rPHmqOOasQYHsebz+fTgy1+ajgEAAOA4\n7268TcPDw6ZjwGFMbrRofA09AAAAAAC4fhR6AAAAAABsiEIPAAAAAIANUegBAAAAALAhCj0AAAAA\nADZEoQcAAAAAwIYo9AAAAAAA2BCFHgAAAAAAG6LQAwAAAABgQxR6AAAAAABsiEIPAAAAAIANUegB\nAAAAALAhCj0AAAAAADZEoQcAAAAAwIYo9AAAAAAA2BCFHgAAAAAAG6LQAwAAAABgQxR6AAAAAABs\niEIPAAAAAIANUegBAAAAALAhCj0AAAAAADZEoQcAAAAAwIYo9AAAAAAA2BCFHgAAAADw/7d3d7Fd\nlvf/wN8UVlAeUtDV0k3FkwrFGH7LMFIjCmY+xKNFVjlZXBYTMiFxJp4YRwYhy5aYcLTEmCxL8AjB\nEA80m3817smHQFhoxWorw2KwDZUok4nyUPkfkDZWEAW+D73a1+vIXvc3131968eP33fv733dFEig\nBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACA\nAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQA\nAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAg\ngR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAA\nAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQ\nAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABA\ngQR6AAAAKJBADwAAAAWaVu8FDA8P58UXX0x/f3/6+/tz8ODBDA8PZ82aNVm5cuVFzdnb25sdO3bk\nvffey4kTJzJ//vysWLEid999dxoa/A0DAACA8tU90B8/fjxbtmxJkjQ1NWXu3Lk5fPjwRc+3a9eu\nbN68OY2NjVm2bFlmzZqV3bt3Z8uWLent7c0jjzxSqaUDAABA3dQ90Dc2Nuaxxx7LggUL0tTUlO3b\nt+fZZ5+9qLk+//zzPPXUU2loaMiGDRty3XXXJUlWr16djRs35s0338zrr7+ejo6OSr4FAAAAqLm6\nf/982rRpWbJkSZqami55rjfeeCNHjx7NLbfcMhrmR85x//33J0leeumlSz4PAAAA1FvdA30lvf32\n20mSJUuWnHWsvb09jY2N6e3tzalTp2q9NAAAAKioCRXoBwYGkiTz588/61hDQ0Oam5szPDycoaGh\nWi8NAAAAKmpCBfpjx44lSS6//PJzHh8Z/+yzz2q2JgAAAKiGimyKt3bt2gvamf7WW2/NunXrKnFq\nAAAAmJQqEuhbWlrS2Nj4nV8/b968Spz2LCNX4Eeu1H/dyPjMmTOrcn4AAAColYoE+vXr11dimkvW\n2tqa/fv3Z3BwcMwu90ny5ZdfZmhoKFOnTk1zc/N3mm/btm3f+Ai9bdu2jZ4TKunwx5/k/z34f/Ve\nBgDAhDN82ud3qqezs/Mbj61ateq8xy9W3Z9DX0k33HBD/vWvf2XPnj1nPWu+p6cnJ06cSHt7e6ZN\n+25vu7Oz81t/6SMb8UGltLa2qiuqQm1RDeqKalFbVIO6ohpG/kg0ctG3lorcFO/YsWMZGBjIkSNH\nxozffPPNmT17dl577bXs379/dPzkyZPZunVrkuTOO++s6VoBAACgGsbFFfrnnntu9C9l/f39SZJX\nX3017777bpJk4cKFWbly5ejrd+7cmSeffDK33XZbHnroodHxyy67LGvWrMnmzZuzYcOGdHR0ZNas\nWdm9e3cGBgaybNmyLFu2rHZvDAAAAKpkXAT6rq6u9PT0jBnr6+tLX1/f6M9fDfQjpkyZctbY0qVL\ns3HjxuzYsSM7d+7MyZMn09LSkgceeCD33HNP5RcPAAAAdTDl9OnTp+u9iJK5B4dKc28X1aK2qAZ1\nRbWoLapBXVEN9dxosch76AEAAGCyE+gBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNAD\nANndVn4AAA30SURBVABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCB\nHgAAAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAA\nCiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNAD\nAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMAAECB\nBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEEegAA\nACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBA\nDwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAokEAPAAAA\nBRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAFEugB\nAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKNK3eCxgeHs6LL76Y/v7+9Pf35+DBgxkeHs6a\nNWuycuXKC5rro48+yrp1677xeEdHRx5++OFLXTIAAADUXd0D/fHjx7Nly5YkSVNTU+bOnZvDhw9f\n0pwLFizI0qVLzxq/+uqrL2leAAAAGC/qHugbGxvz2GOPZcGCBWlqasr27dvz7LPPXtKc1157bVat\nWlWhFQIAAMD4U/dAP23atCxZsqTeywAAAICi1D3QV8Mnn3ySl19+OUePHs3s2bPT1taWa665pt7L\nAgAAgIqZkIG+u7s73d3dY8ba29uzdu3aXHnllXVaFQAAAFTOhAr006dPz3333Zebbropzc3NSZIP\nPvgg27dvz969e7Np06Y88cQTaWxsrPNKAQAA4NJUJNCvXbv2gnamv/XWW8/7eLmLNWfOnHR2do4Z\nW7hwYR5//PGsX78++/btyyuvvJJ77rmn4ucGAACAWqpIoG9pabmgq97z5s2rxGm/s4aGhtxxxx3Z\nt29f3nnnnYoG+tbW1orNBSPUFdWitqgGdUW1qC2qQV0xkVQk0K9fv74S01TVnDlzkpx57v13tW3b\ntm98hN62bdsqsi4AAADK9/Vvi3/VqlWrznv8Yk2oe+jPp6+vL0lG763/Ljo7O8/7S+/s7BTsqTh1\nRbWoLapBXVEtaotqUFdUS71qq6HmZ6yAY8eOZWBgIEeOHBkz/v777+f06dNnvf6tt97KCy+8kOTM\n/fsAAABQunFxhf65557LwMBAkqS/vz9J8uqrr+bdd99NcmZju5UrV46+fufOnXnyySdz22235aGH\nHhodf/rppzM4OJi2trZcccUVSc7scr93794kyerVq9PW1laLtwQAAABVNS4CfVdXV3p6esaM9fX1\njX5NPsmYQD9iypQpY35evnx5du7cmf3796erqyunTp1KU1NTOjo6ctddd2XhwoXVeQMAAABQY+Mi\n0P/2t7+9oNfffvvtuf32288aX7FiRVasWFGhVQEAAMD4VeQ99AAAADDZCfQAAABQoKkbNmzYUO9F\nlOr06dNZvHhxvZfBBKOuqBa1RTWoK6pFbVEN6opqqVdtTTl9rue8AQAAAOOar9wDAABAgQR6AAAA\nKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUKBp9V7AeDc8PJwXX3wx/f396e/vz8GD\nBzM8PJw1a9Zk5cqVFzTXRx99lHXr1n3j8Y6Ojjz88MOXumQKUMm6GtHb25sdO3bkvffey4kTJzJ/\n/vysWLEid999dxoa/O1usqlEPehZk9PHH3+crVu3pqurK//73//S1NSUpUuX5mc/+1lmzpxZ83mY\nGCpRD2vXrs3hw4fPeaypqSlPPfVUJZdMAd5888309PTkwIED6e/vzxdffJFbb731vP/v+iZ6FiMq\nVVe16lkC/bc4fvx4tmzZkuTML37u3Lnf+C/mu1qwYEGWLl161vjVV199SfNSjkrX1a5du7J58+Y0\nNjZm2bJlmTVrVnbv3p0tW7akt7c3jzzySKWWTgEqXQ961uRx6NCh/OY3v8mnn36apUuXprW1Nf/5\nz3/yl7/8JV1dXdm0aVNmzZpVs3mYGCpZD5dffnnuvffes8ZnzJhR6WVTgB07duTAgQOZMWNGrrji\ninz44YcXNY+exVdVqq6S2vQsgf5bNDY25rHHHsuCBQvS1NSU7du359lnn72kOa+99tqsWrWqQiuk\nRJWsq88//zxPPfVUGhoasmHDhlx33XVJktWrV2fjxo1588038/rrr6ejo6OSb4Fxqhr1oGdNHn/6\n05/y6aef5pe//GXuuuuu0fGnn346L7zwQrZu3ZoHH3ywZvMwMVSyHmbOnKkfMeoXv/hF5s2bl5aW\nlvT09GTjxo0XNY+exVdVqq6S2vQs38P9FtOmTcuSJUvS1NRU76UwgVSyrt54440cPXo0t9xyy2h4\nGznH/fffnyR56aWXLvk8lEE9cLEOHTqU7u7uNDc3j/lAmySdnZ2ZPn16/vGPf+TEiRM1mYeJQT1Q\nTe3t7WlpabmkOdQoX1eJuqolV+jr4JNPPsnLL7+co0ePZvbs2Wlra8s111xT72VRqLfffjtJsmTJ\nkrOOtbe3p7GxMb29vTl16lSmTfOf/ERXjXrQsyaHkdq58cYbzzo2Y8aMXH/99enu7k5fX19uuOGG\nqs/DxFDpejh58mT++c9/5vDhw5k+fXquvfbaLFq0yF4xXDQ9i2qqRc/y6b4Ouru7093dPWasvb09\na9euzZVXXlmnVVGqgYGBJMn8+fPPOtbQ0JDm5uYcPHgwQ0NDaW1trfXyqLFq1IOeNTmcr3ZGxru7\nuzM4OHjeD7WVmoeJodL1cOTIkfzxj38cM9bc3Jxf/epXaW9vv/QFM+noWVRTLXqWQF9D06dPz333\n3Zebbropzc3NSZIPPvgg27dvz969e7Np06Y88cQTaWxsrPNKKcmxY8eSnNl041xGxj/77LOarYn6\nqWQ96FmTS6VqR0/iqypZDytWrMiiRYty9dVXZ8aMGRkaGspf//rXvPTSS/n973+f3/3ud749xAXT\ns6iWWvWsSRHoz/fIgHO52MddfJs5c+aks7NzzNjChQvz+OOPZ/369dm3b19eeeWV3HPPPRU/N5U3\nXuqKiWe81JaeBYwnX99Y6oc//GEefPDBTJ8+Pc8//3y2bduWRx99tE6rAxirVj1rUgT6lpaWC7qC\nNG/evCqu5mwNDQ254447sm/fvrzzzjs+HBdivNTVyF+OR/7C/HUj456hWo4Lra25c+eO/nMt6kHP\nmpgqVTt6El9Vi3r4yU9+kueffz7vvPPORc/B5KVnUWuV7lmTItCvX7++3kv4VnPmzEly5vnklGG8\n1FVra2v279+fwcHBMbuaJ8mXX36ZoaGhTJ06dfQr04x/l1JbtaoHPWviGdlTYXBw8JzHR8a/6T7T\nSs/DxFCLetCPuBR6FrVW6Z5lS9Bxoq+vL0mELi7YyAYte/bsOetYT09PTpw4keuvv94O95NErepB\nz5p4Fi9enCRnbYCYJF988UV6e3szffr0tLW11WQeJoZa1MNIP7rqqqsueg4mLz2LWqt0zxLoq+DY\nsWMZGBjIkSNHxoy///77OX369Fmvf+utt/LCCy8kOXMvLJzLN9XVzTffnNmzZ+e1117L/v37R8dP\nnjyZrVu3JknuvPPOmq6V+rmYetCzSM58sLjxxhtHN+35qmeeeSbHjx/P8uXLR28HGR4ezsDAQA4d\nOnRJ8zCxVaquPvzww3NezRoaGsqf//znJPoR56dnUQ3joWdNOX2uT2uM8dxzz40+0qK/vz8HDhxI\nW1vb6FdvFi5cmJUrV46+/m9/+1uefPLJ3HbbbXnooYdGxzdu3JjBwcG0tbXliiuuSHJmx+i9e/cm\nSVavXp2f/vSntXpb1Fml6ipJdu3alc2bN+d73/teOjo6MmvWrOzevTsDAwNZtmxZfv3rX9fujVF3\nF1oPehYjDh06lPXr1+e///1vfvzjH+cHP/hB3nvvvfT09KS1tTWbNm3KrFmzkiQfffRR1q1bl+9/\n//tnPZLnQuZh4qtEXW3fvj3PP/98Fi1alCuvvDKXXXZZDh06lH//+985efJkfvSjH+XRRx/N1KlT\n6/U2qYNdu3Zl165dSc48HqyrqyvNzc1ZtGhRkmT27Nn5+c9/nkTP4rurRF3Vsmf5Du530NXVlZ6e\nnjFjfX19o1+XSDImeI2YMmXKmJ+XL1+enTt3Zv/+/enq6sqpU6fS1NSUjo6O3HXXXVm4cGF13gDj\nUqXqKkmWLl2ajRs3ZseOHdm5c2dOnjyZlpaWPPDAAzYsm4Quth70LK666qr84Q9/yDPPPJM9e/Zk\nz549aWpqyr333ptVq1ad87FO5+pJFzMPE1cl6mrx4sUZHBzM+++/n97e3hw/fjwzZ87MokWLsnz5\nclfnJ6n+/v78/e9/HzM2NDSUoaGhJGduCxsJXiP0LL5NJeqqlj3LFXoAAAAokHvoAQAAoEACPQAA\nABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEig\nBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBA/x9OrfVtAx1KhAAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1077b26d8>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.71708006 0.99618873] 0.692878832229\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3Xl4VNXh//HPJCHJZIEQtiQQNi0IAdwIighWrEBZjNUQ\nkKUoRGVRKe4o9Csqi1apWgqiIIuKECmIZRPQn0JZhKIkAWzYEpYkJEAIkWxkmd8fNFRkh5mcuZP3\n63n6PPXe5M5n0muf+cy55xybw+FwCAAAAAAAWIqX6QAAAAAAAODKUegBAAAAALAgCj0AAAAAABZE\noQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC6LQAwAAAABgQRR6AAAAAAAsiEIPAAAAAIAFUegBAAAA\nALAgCj0AAAAAABZEoQcAAAAAwIIo9AAAAAAAWBCFHgAAAAAAC/IxHUCSNm3apJ07d2r//v1KS0tT\nUVGROnbsqCeeeOKKrjNixAgdPXr0vOdCQkI0ffp0Z8QFAAAAAMA4txihX7Rokb766iulpaWpVq1a\n13StgIAA9e7d+5z/9OrVy0lp/ychIcHp1wS4r+Aq3FtwBe4ruAr3FlyB+wquYurecotC//DDD+vd\nd9/VnDlzFB8ff03XCgwMVGxs7Dn/6dmzp5PS/s/ChQudfk2A+wquwr0FV+C+gqtwb8EVuK/gKqbu\nLbd45L5ly5amIwAAAAAAYCluUeidqaSkROvWrdPRo0fl5+enRo0aqUWLFvLycouHEQAAAAAAcAqP\nK/S5ubmaMmXKWcfq1q2rYcOG8SQAAAAAAMBjeFShv/vuu9WiRQtFRkbK399f2dnZWrlypVavXq2J\nEydq/PjxatiwoemYAAAAAABcM496Dj02NlZRUVGqXr26fH191aBBA8XHx6tnz546deoUq1oCAAAA\nADyGzeFwOEyH+KWdO3dq3LhxV7UP/YUcPnxYI0eOVFBQkGbOnOmUawIAAAAAYJJHPXJ/IdWrV5ck\nFRcXX9HvJSQkXHD7AUb7AQAAAAAV4uLiLnguNjb2ouevVpUo9Lt27ZIk1atX74p+Ly4u7pJ/9IyM\njKvOBZxPREQE9xVcgnsLrsB9BVfh3oIrcF/BFSIiIiSZGfS13Bz6srIyZWRkKCsr66zj6enp5x2B\nz87O1kcffSRJ6tixY6VkBAAAAADA1dxihH7Lli3asmWLpNPbzklSSkqKpk6dKkkKDg7WwIEDJUk5\nOTkaNWqU6tSpc9b2dBs2bNDSpUvVokUL1a5dW3a7XVlZWfrhhx9UUlKiW265Rb169arkdwYAAAAA\ngGu4RaFPS0vTd999d9ax7OxsZWdnSzq9j3xFoa9gs9nO+ueoqChlZmYqNTVVKSkpKi4uVmBgoFq0\naKFOnToxOg8AAAAA8Chut8q91TAHB87G3C64CvcWXIH7Cq7CvQVX4L6CK1TMoTfBcnPoAQAAAAAA\nhR4AAAAAAEui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAA\nAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9\nAAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACA\nBVHoAQAAAACwIB/TAQDgfLKyspScnKzk5GTt2LFDO3bsUH5+viTJZrPJ29tbzZo1U3R0tLp27aqo\nqCjZbDbDqQEAAIDKQ6EH4DYyMzP15Zdf6osvvlBSUtIlfz4rK0vr1q3T5MmT1bZtW02ePFnXXXdd\nJSQFAAAAzKPQAzCqsLBQixYt0uLFi7Vp0yY5HA5JUkBAgG688Ua1bt1arVu3VqtWrRQaGnrmfHFx\nsZKTk/Xdd99p6dKl+ve//60uXbro+eefV3x8vLy9vU2+LQAAAMDlKPQAjMjNzdXs2bM1c+ZM5eTk\nSJL8/Px0zz33KCYmRvfcc4/sdvtFr9GgQQP9/ve/14svvqhXXnlFn3/+uV599VXl5eXpueeeq4y3\nAQAAABhDoQdQqbKysvTBBx/o448/PjMn/uabb9agQYPUrVs3BQcHX/E1Q0JC9M477+jee+/V0KFD\n9e677yo6Olq//e1vnZweAAAAcB+scg+gUuTl5enVV1/V7bffrvfff1/5+fnq1KmTEhIS9M9//lO9\ne/e+qjL/Sz169NDTTz8th8OhJ598UllZWU5KDwAAALgfCj0AlyorK9O8efN05513avr06SopKVH3\n7t21fPlyffbZZ+rQoYNTV6cfOXKkOnTooJycHH366adOuy4AAADgbij0AFzm+++/V/fu3fXcc8/p\n2LFjateunVasWKEPP/xQN954o0te08vLS0888YQkKSEhQeXl5S55HQAAAMA0Cj0Apzty5IiGDx+u\nBx54QNu3b1d4eLimTp2qRYsWqXXr1i5//Q4dOigiIkIHDx7Uxo0bXf56AAAAgAkUegBO43A4tGTJ\nEt19991asmSJ/P399fTTT2vdunWKiYlx6qP1F+Pt7a3Y2FhJ0ooVKyrlNQEAAIDKxir3AJzi2LFj\nGj16tJYtWyZJ6tixo/7yl78oMjLSSJ5bbrlFkrRnzx4jrw8AAAC4GoUewDVbtmyZRo8erWPHjikw\nMFB//vOf1b9//0obkT+fJk2aSJJSU1ONZQAAAABciUIP4Krl5ubqpZde0pIlSySdnrv+9ttvGxuV\n/6WGDRvK29tb6enpKioqkr+/v+lIAAAAgFMxhx7AVUlMTFS3bt20ZMkSBQQEaPz48Zo/f75blHlJ\n8vX1Vf369eVwOHTo0CHTcQAAAACnY4QewBVxOByaNWuWXn31VZWUlKhNmzaaNm2aGjdubDraOapV\nqybpdGYAAADA01DoAVy2vLw8Pfvss2cWvnvkkUc0duxY+fn5GU52fmVlZZIkHx/+rw4AAACeh0+5\nAC5LcnKyhg4dqrS0NAUFBemtt95Sr169TMe6qNLSUkkUegAAAHgm5tADuKR58+YpJiZGaWlpioqK\n0ooVK9y+zEv/K/Te3t6GkwAAAADOx7AVgAsqKSnRuHHjNGvWLEnSgAEDNG7cOMusGF9YWChJbjsl\nAAAAALgWFHoA55WTk6OhQ4dq/fr18vX11aRJk9SnTx/TsS7biRMndOLECQUEBCg0NNR0HAAAAMDp\nKPQAzrFnzx4NGjRIaWlpqlOnjj788ENFR0ebjnVF9u/fL0lq1KiRbDab4TQAAACA8zGHHsBZNmzY\ncGa+fKtWrbRs2TLLlXlJSktLk3S60AMAAACeiEIP4IyEhAT169dPubm56tKlixYvXqz69eubjnVV\nfjlCDwAAAHgiCj0AORwOvfnmmxo1apRKSkr06KOPasaMGQoICDAd7aoxQg8AAABPxxx6oIorKirS\n008/rSVLlsjLy0uvv/66Bg0aZDrWNUtMTJQk3XDDDYaTAAAAAK5BoQeqsJycHD3yyCP697//rcDA\nQL3//vvq3Lmz6VjX7MSJE/rPf/4jX19f3XjjjabjAAAAAC5BoQeqqMOHD6tPnz7as2ePIiIiNGfO\nHLVs2dJ0LKf44Ycf5HA41Lp1a/n7+5uOAwAAALgEhR6ogtLT0xUXF6e0tDS1aNFCn3zyicLCwkzH\ncprNmzdLkiVX5wcAAAAuF4UeqGIOHjyouLg4HThwQK1bt9a8efMUGhpqOpZTbdmyRZLUrl07w0kA\nAAAA12GVe6AKSU1N1QMPPKADBw7o5ptv1oIFCzyuzJeUlOjHH3+UJLVt29ZwGgAAAMB1KPRAFbFn\nzx7FxsYqIyNDbdu21WeffaYaNWqYjuV0mzdvVlFRkZo1a6ZatWqZjgMAAAC4DIUeqAJSUlIUGxur\nw4cPq3379po3b56Cg4NNx3KJNWvWSJJ+97vfGU4CAAAAuBaFHvBwO3bsUGxsrI4cOaKOHTvq448/\nVmBgoOlYLrN69WpJFHoAAAB4Pgo94MGSkpIUFxennJwcde7cWbNnz5bdbjcdy2X27Nmj1NRUhYSE\n6NZbbzUdBwAAAHApCj3gobZu3ao+ffooNzdXXbp00YwZMzx+T/Zly5ZJku699175+LCJBwAAADwb\nhR7wQJs3b1a/fv2Ul5en7t27a/r06fLz8zMdy+VWrFghSerevbvhJAAAAIDrUegBD7Nhwwb1799f\nJ0+e1P33369p06bJ19fXdCyX279/v5KTkxUYGKhOnTqZjgMAAAC4HIUe8CBr167VwIEDVVBQoN69\ne+u9996rMo+eL1y4UJLUtWtXj59aAAAAAEgUesBjfP3113r44YdVVFSkfv36afLkyfL29jYdq1KU\nl5crISFBkhQXF2c4DQAAAFA5KPSAB/j66681ZMgQFRcXa9CgQXrjjTfk5VV1/vXeuHGjDh06pPr1\n66tDhw6m4wAAAACVoup84gc81A8//KDHHntMJSUlio+P1/jx46tUmZekBQsWSJJ69+5d5d47AAAA\nqi4++QIWtmfPHv3xj39UUVGR+vTpo1deeUU2m810rEr1888/n9murnfv3obTAAAAAJWHQg9Y1OHD\nh9W/f38dP35c99xzj958880qV+YlaenSpSoqKtLtt9+uxo0bm44DAAAAVBoKPWBBJ06c0IABA3To\n0CHdcsstmj59epVZzf7XKh63ZzE8AAAAVDUUesBiioqKNHjwYP3000+6/vrrNWfOHNntdtOxjEhO\nTtaWLVsUFBSknj17mo4DAAAAVCoKPWAhZWVlevLJJ7Vp0yaFhYVp3rx5Cg0NNR3LmA8++ECS9NBD\nDykwMNBwGgAAAKByUegBi3A4HBozZoyWL1+u6tWr65NPPlH9+vVNxzImMzNTX375pby8vDRkyBDT\ncQAAAIBKR6EHLOKdd97R3Llz5efnp1mzZqlFixamIxk1e/ZslZaWqnv37oqMjDQdBwAAAKh0FHrA\nAj799FO99dZb8vLy0pQpU3T77bebjmRUfn6+Pv74Y0nSY489ZjgNAAAAYAaFHnBzX331lV588UVJ\n0vjx49W9e3fDicz7/PPPdeLECd1666269dZbTccBAAAAjKDQA25sy5YtGj58uMrLyzVq1Cj98Y9/\nNB3JuPLycn344YeSGJ0HAABA1UahB9xUSkqKBg0apKKiIvXv31/PPPOM6UhuYc2aNUpLS1NkZKS6\ndetmOg4AAABgDIUecEPp6enq37+/Tpw4oa5du2rChAmy2WymY7mFiq3qhgwZIh8fH8NpAAAAAHMo\n9ICbycnJ0YABA5SZmal27drp73//O8X1v5KSkrRx40YFBwerb9++puMAAAAARlHoATdSVFSk++67\nT7t27VLz5s01a9Ys2e1207HcRsXc+X79+ik4ONhwGgAAAMAsCj3gJhwOh1566SWtX79e4eHh+uST\nTxQSEmI6ltvYv3+/vvzyS3l7e2vw4MGm4wAAAADGucVzvJs2bdLOnTu1f/9+paWlqaioSB07dtQT\nTzxxxdfKycnR/PnzlZiYqJMnTyokJETR0dHq3bu3AgMDXZAecI45c+ZowYIFstvtmj17tiIiIkxH\ncit/+ctfVFpaqt69e6tBgwam4wAAAADGuUWhX7Rokfbv3y9/f3/VqlVL6enpV3WdrKwsjRkzRnl5\neYqOjlZERIT27t2rFStWKDExUa+99pqCgoKcnB64dps2bdL//d//SZJmzpypVq1aGU7kXrZv367F\nixfL19dXzz77rOk4AAAAgFtwi0L/8MMPKzQ0VGFhYdq5c6fGjRt3VdeZMWOG8vLyNHjwYHXt2vXM\n8blz52rZsmWaP3++4uPjnRUbcIr09HQ9/vjjKi0t1eOPP66HHnpIGRkZpmO5lYkTJ0qSBg0axOg8\nAAAA8F9uMYe+ZcuWCgsLu6ZrZGVlKSkpSXXr1j2rzEtSXFyc/Pz8tHbtWp06deqaXgdwpqKiIj32\n2GM6evSo7rzzTr300kumI7md9evX69tvv1VwcLCeeuop03EAAAAAt+EWhd4ZduzYIUlq06bNOef8\n/f3VvHlzFRcXa9euXZUdDTgvh8Oh0aNHa9u2bYqMjNS0adPYnu5XHA7HmdH5YcOGKTQ01HAiAAAA\nwH14TKGveEQ5PDz8vOcrjmdmZlZaJuBiZs+erYSEBPn7+2vmzJmU1fNYvny5fvzxR9WtW1ePPvqo\n6TgAAACAW/GYQl9QUCBJCggIOO/5iuP5+fmVlgm4kI0bN55ZBG/y5MmKiooynMj9lJaWatKkSZKk\nP/3pTxf8dxsAAACoqjym0ANWUbEIXllZmYYNG6aYmBjTkdzS/PnztW/fPjVu3Fj9+vUzHQcAAABw\nOx5T6CtG7ypG6n+t4jh70cOkwsJCxcfH69ixY+rUqZNGjx5tOpJbKiws1OTJkyVJzz//vKpVq2Y4\nEQAAAOB+PGYFroiICEkXniNfcfxCc+zPJyEhQQsXLrzguV++LnApDodDDz/8sJKSktSkSRMtXrz4\nvPPmj+Ycl91uN5DQfUyfPl1ZWVm66aabFBcXJy8vj/nu0ajjx7m34HzcV3AV7i24wtGc43x+h8vE\nxcVd8FxsbOxFz18tjyn0FXOQk5KSzjlXVFSklJQU+fn5qVmzZpd9zbi4uEv+0dkvHJdr5syZmjt3\nrux2uz744AMVFRWd9/6x2+3qMuNHAwndQ2lBnpLffFuSVBDdT90+SjScCAAAeIpV8Tfz+R1OV/El\nUcWgb2Wy3LBXWVmZMjIylJWVddbxevXqqU2bNsrOztbKlSvPOrdgwQIVFxerU6dO8vX1rcy4gCRp\nw4YNGjdunKTTi+C1bNnScCL3lfn/PlNZUb6Cf3OLqv/mVtNxAAAAALflFiP0W7Zs0ZYtWyRJubm5\nkqSUlBRNnTpVkhQcHKyBAwdKknJycjRq1CjVqVNHU6ZMOes68fHxGjt2rGbNmqXk5GTVr19fu3fv\n1s6dOxUREaG+fftW4rsCTvvlInjDhw/XfffdZzqS2zqVm63s9YslSQ1+zzZ1AAAAwMW4RaFPS0vT\nd999d9ax7OxsZWdnS5Lq1q17ptBXsNls51ynXr16mjRpkhYsWKBt27Zp27ZtCgkJUY8ePRQbG8u2\nV6h0hYWFGjJkiHJycnTXXXfpxRdfNB3JrWWsniNHaYlqtvmtAhtc/vQYAAAAoCqyORwOh+kQVsYc\nHFyIw+HQU089pUWLFqlRo0ZatmyZatasecnfq6pz6Auz0rRj8qOy2WyKeuYj+ddpYDoSAADwMKvi\nb1ZhYaHpGPAwJhdatNwcesAq5syZo0WLFikgIEAzZ868rDJflaWvnCk5ylX7th6UeQAAAOAyUOgB\nF/jpp5/06quvSpLeeusttWjRwnAi95a7c6Nyd2yQl6+/wu8ZYDoOAAAAYAkUesDJCgsLNXz4cBUX\nF6tfv36KiYkxHcmtlZ0q1IEv3pMkRXR5RL7VaxlOBAAAAFgDhR5wsldeeUW7du3S9ddff2arOlxY\nxqq5OpWbrYCI61Wvwx9MxwEAAAAsg0IPONHy5cv1ySefyNfXV1OnTmVnhUsoyNijrH8tlGxeavTg\n07J5e5uOBAAAAFgGhR5wkvT0dD377LOSpDFjxigqKspwIvfmKC/T/n/8VSovV907YhQY2dx0JAAA\nAMBSKPSAE5SWlurJJ5/UiRMndM8992jw4MGmI7m9I5v+qfyD/1G1GrVVv+sjpuMAAAAAlkOhB5zg\nvffe0/fff6969erpr3/9q2w2m+lIbu3UiaM6tGKmJKlhzJPy9g80nAgAAACwHgo9cI2+//77MyX+\n3XffVa1arNJ+KQe//LvKiwsU0vIOhUR1MB0HAAAAsCQKPXAN8vLy9OSTT6q8vFwjRoxQx44dTUdy\ne7k7N+p48lp5+forMuYJnmYAAAAArhKFHrgGY8eOVXp6um688cYzC+Lhwn6957xfzXqGEwEAAADW\nRaEHrtLSpUu1cOFC+fv767333lO1atVMR3J77DkPAAAAOA+FHrgKhw8f1gsvvCDp9Cj99ddfbziR\n+2PPeQAAAMC5fEwHAKzG4XDomWeeUW5urn77299q0KBBRvPYq3mpQ6MQ1Qzw0fGCUq3fn6vCknKj\nmX7trD3nO/yBPecBAAAAJ6DQA1dozpw5+vbbbxUSEqK3337b6KJufVqGakCbOvL6/nv5/ztFRc2b\na+SDt+mTpCNasDPHWK5fY895AAAAwPko9MAV2LNnj1577TVJ0ptvvqmwsDBjWfq0DNXAumWq3aG9\nvA8elCRVl1QWGamB/1gsKdQtSj17zgMAAACuwRx64DKVlJToqaeeUlFRkWJjY9WjRw9jWezVvDSg\nTR3VfvAPZ8p8Be+DB1X7wT+of+s68vcx/684e84DAAAArmH+0z5gEe+++64SExPVoEGDM6P0pnRo\nFCKv778/p8xX8D54UF6bv1eHxjUqOdnZcn/axJ7zAAAAgItQ6IHLkJKSor/97W+y2Wx65513VL16\ndaN5agb4yD8l5aI/Y9+VotAAc1vplRbkaf8/Jktiz3kAAADAFSj0wCWUl5frhRdeUGlpqQYOHKj2\n7dubjqTjBaUqan7xleILmzVXTkFJJSU6m8Ph0P5F76gk75gCG0Wp3p3sOQ8AAAA4G4UeuITPPvtM\nW7ZsUd26dfXiiy+ajiNJWr8/V+W33aayyMjzni+LjFR5u9u0Pu1EJSc7LefHr3U86Tt5+drVtO+L\nsnmx5zwAAADgbBR64CKOHDmi8ePHS5LGjRunGjXMzkmvUFhSrk+SjujoPxafU+rLIiN19B+L9Wny\nERWVVv5+9MXHs3Tgi/ckSQ1jRsivVkSlZwAAAACqAratAy5i3LhxOnHihDp37qxevXqZjnOW01vS\nhWrA+o2yff+97LtSVNisuRy3mduH3lFerrQFb6isKF8hUXeoVttulZ4BAAAAqCoo9MAFfPfdd1q8\neLH8/f01fvx4t1yhfcHOHH25O1d3NGqi0FubKaegROsX7jYyMi9JWesW6ud9ifIJClGjB592y78Z\nAAAA4Cko9MB5FBYWavTo0ZKkZ555Rg0bNjSc6MIKS8r19Z7jpmOoIHOf0ld+JElqHPuMqgXVNJwI\nAAAA8GzMoQfO491339X+/fvVokULPfroo6bjuL3y0lNKnT9RjrIS1W7XQyEt7zAdCQAAAPB4FHrg\nV1JSUjRt2jTZbDZNmjRJ1aqZ28vdKtK/mqXCzH3yqxWhyF7DTMcBAAAAqgQKPfALv95zvm3btqYj\nub0Tu/6trO8SJJuXmvR9Ud5+dtORAAAAgCqBQg/8gjvuOe/OSk4eV+r8SZKkiHv/qKBGUYYTAQAA\nAFUHhR74L3fdc95dOcrLlbrgTZWePK6gJm0U3rmf6UgAAABAlUKhB/7Lnfecd0fZ6xcrL2WzvAOC\n1fShl2Tz8jYdCQAAAKhSKPSArLHnvDvJP7RLh5Z/IElqHPusfEPqGE4EAAAAVD0UelR5Vtpz3h2U\nFRdq37zxcpSVqk77+1Sz1Z2mIwEAAABVEoUeVR57zl+ZA0umqPjoIdnDmiiy51DTcQAAAIAqi0KP\nKo0956/MsR+/0bF/r5TNx1dN+42RVzU/05EAAACAKotCjyrtlVdeUWlpqQYMGMCe85dQlH1QBxa/\nI0lqeN9w2cMamw0EAAAAVHEUelRZ69at09q1axUcHKznn3/edBy3VlaUrz1z/6yyonzVbN1JtW/r\naToSAAAAUOVR6FElORwOTZw4UZI0YsQIhYaGGk7kvk7vNz9JRdkH5F+vsRrHPc8uAAAAAIAboNCj\nSlq6dKkSExNVr149xcfHm47j1jK//kS5OzbI2x6k6we9Km8/u+lIAAAAAEShRxVUUlKiN954Q5I0\natQo2e0U1AvJ3bFBGavnSDabmvZ7Wf6165uOBAAAAOC/KPSocj777DOlpqaqSZMm6tu3r+k4bqsw\n+4D2zT89LaF+tyGq0byd4UQAAAAAfolCjyqloKBAf/3rXyVJL7zwAtvUXUBp4UntnfNnlRcXqGab\nuxT2W774AAAAANwNhR5VyowZM5Sdna0bb7xRPXuyUvv5OMrLlTp/koqOHJQ9rIka936ORfAAAAAA\nN0ShR5WRk5OjqVOnSpJeeuklSuoFZKz5WCd+2ihve7CuYxE8AAAAwG1R6FFlTJkyRT///LPuuusu\n3XnnnabjuKXjO9Yrc81cyealpv3HyL9WhOlIAAAAAC6AQo8qIT09XbNnz5Z0enQe5yrM2q/U+ZMk\nSfV/P0Q1mrU1nAgAAADAxVDoUSW89dZbKi4uVkxMjFq1amU6jtspLTypPRWL4N34W4Xd1cd0JAAA\nAACXQKGHx0tJSdHChQvl4+Oj5557znQct3N6EbyJKj56SPbwpmrc+1nWFwAAAAAsgEIPjzdp0iSV\nl5drwIABatKkiek4bidj9Ryd+GmTvAOCdf0fx8nbl0XwAAAAACug0MOjbdmyRatWrVJAQID+9Kc/\nmY7jdo5v/5cyv/5Esnnpuv5j5ccieAAAAIBlUOjhsRwOhyZMmCBJeuyxx1SnTh3DidxLYVbamUXw\nGnR/VNV/c6vhRAAAAACuBIUeHuubb77R5s2bFRoaqqFDh5qO41ZKC34+vQjeqUKF3tRZ9Tr1Nh0J\nAAAAwBWi0MNjTZs2TZI0YsQIBQcHG07jPspLirVnzlgVH02XPfw6NYp9hkXwAAAAAAui0MMjJScn\na+PGjQoKClL//v1Nx3EbjvIy7ftsgk6mJqtajdq6/uHX5O3rbzoWAAAAgKtAoYdH+uCDDyRJ/fr1\nY3T+vxwOhw4sfk+52/8lb3uQmg15Q34165mOBQAAAOAqUejhcTIzM/Xll1/Ky8tLQ4YMMR3HbWSu\n+VhHvl8qm4+vrn/4ddnDGpuOBAAAAOAaUOjhcWbPnq3S0lL16NFDDRo0MB3HLRzZ9E9lrJ4j2bzU\ntP8YBTdpbToSAAAAgGtEoYdHyc/P18cffyzp9FZ1OL3X/P7F70mSGj3wJ9WM6mA4EQAAAABnoNDD\no3z++ec6ceKE2rZtq1tuucV0HON+Tk3WvnnjJUe5Iu4dpDq39TAdCQAAAICTUOjhMcrKyvThhx9K\nkh599FEG8nPiAAAgAElEQVTDacwrPJyqPbPHyFF6SnVu76Xw3w00HQkAAACAE1Ho4THWrFmjtLQ0\nRUZGqlu3bqbjGFV8PEu7Zr6ossKTCml1pxre/yR7zQMAAAAehkIPj1GxVd2QIUPk4+NjOI05pQV5\n2j3zRZWcOKqgJq3V9KGXZfPyNh0LAAAAgJNR6OEREhMTtWnTJgUHB6tv376m4xhTdqpIu2e9rKLs\nA7KHNdH1D78ur2q+pmMBAAAAcAEKPTzC7NmzJUkPPfSQgoODzYYxxFFWpn2fvqb8/TvlG1JXvxky\nUT72INOxAAAAALgIhR6Wl5+fr6VLl0qSBg6smgu/ORwO7V80WSd+2iTvgGD9Jv4N+daoYzoWAAAA\nABei0MPyli5dqoKCAkVHR6tp06am4xiR8dUsHd2yUl7V/PSbR8bLXreh6UgAAAAAXIxCD8tLSEiQ\nJPXp08dwEjOyN3yhzG8+lby81LT/WAU1ijIdCQAAAEAloNDD0tLS0rRp0ybZ7Xb16tXLdJxKd2TT\nP3Xgi79Jkho/+IxCWrY3nAgAAABAZam6e3vBI3z++eeSpO7duysoqGotAJe1frEOLpkiSWrQc6hq\nR3cznAgAAABAZaLQw7LKy8vPFPqq9rj94e8SdGjZdElSw5gnVbfD/YYTAQAAAKhsFHpY1saNG5We\nnq7IyEi1b191HjXP+PpTZXz1kSSp0QOjVOf2noYTAQAAADCBQg/LWrZsmSQpJiZGXl6evxyEw+FQ\nxuo5ylzzsWSzqXHsszxmDwAAAFRhFHpYUnl5uVauXClJ6tGjh+E0rudwOJS+cqYO/7/PJJuXmvR5\nQbVu+Z3pWAAAAAAMotDDkrZu3aqsrCw1aNBArVu3Nh3HpRwOhw4tnaasdf+QzctbTfq9rNA2d5mO\nBQAAAMAwCj0sadWqVZKkbt26yWazGU7jOo7ych34coqObFgim7ePmg74s2pGdTAdCwAAAIAboNDD\nklavXi1J6tKli+EkruMoL9f+RX/V0c3LZfOppusGjlNIi9tMxwIAAADgJij0sJy0tDTt3r1b1atX\nV7t27UzHcQlHeZnSPn9Lx7auks3HV9c//JpqNGtrOhYAAAAAN0Khh+V8++23kqS77rpL1apVMxvG\nBUpLS5U6f5Jytn0jr2r+uv6R11X9+ptNxwIAAADgZtyq0Ofk5Gj+/PlKTEzUyZMnFRISoujoaPXu\n3VuBgYGXdY0RI0bo6NGj5z0XEhKi6dOnOzMyDNi8ebMkqUMHz5tLXlJSomHDhp0u834B+s3gCQpu\n4tmL/gEAAAC4Om5T6LOysjRmzBjl5eUpOjpaERER2rt3r1asWKHExES99tprCgoKuqxrBQQEnHcr\nM39/f2fHhgFbtmyRJEVHRxtO4lzFxcUaOnSoVq1aJW//QP0m/g0FNWxhOhYAAAAAN+U2hX7GjBnK\ny8vT4MGD1bVr1zPH586dq2XLlmn+/PmKj4+/rGsFBgYqNjbWVVFhUHp6ujIyMlSjRg01a9bMdByn\nycvL02OPPaZ169apZs2aChs4QYENPOf9AQAAAHA+L9MBpNOj80lJSapbt+5ZZV6S4uLi5Ofnp7Vr\n1+rUqVOGEsJdVIzO33rrrfLycovb95odPHhQMTExWrdunWrXrq0lS5ZQ5gEAAABckls0oh07dkiS\n2rRpc845f39/NW/eXMXFxdq1a9dlXa+kpETr1q3T4sWLtXz5cu3YsUPl5eVOzQwzPO1x+x9//FE9\ne/bUrl271KxZMy1dulStWrUyHQsAAACABbjFI/cZGRmSpPDw8POeDw8PV1JSkjIzMy+r7OTm5mrK\nlClnHatbt66GDRumli1bXntgGLN161ZJnlHoly1bpqeeekpFRUXq2LGjpk+frho1apiOBQAAAMAi\n3KLQFxQUSDq9mN35VBzPz8+/5LXuvvtutWjRQpGRkfL391d2drZWrlyp1atXa+LEiRo/frwaNmzo\nvPCoNA6HQ3v37pUk3XDDDYbTXD2Hw6H3339fr7/+uiSpX79+mjBhgkduwQcAAADAddzikXtnio2N\nVVRUlKpXry5fX181aNBA8fHx6tmzp06dOqWEhATTEXGVjh49qoKCAtWoUUM1a9Y0HeeqlJSU6IUX\nXjhT5l9++WW9+eablHkAAAAAV8wtCn3FCHzFSP2vVRy/3L3oz+fee++VJP30009XfQ2YlZaWJklq\n1KiR2SBXKScnR/369dOnn34qf39/TZ8+XcOHD5fNZjMdDQAAAIAFucUj9xEREZKkzMzM856vOH6h\nOfaXo3r16pJO7/V9uRISErRw4cILnpP+lx2ul5eXJ+n04/ZW+7tv375d9913n1JTUxUWFqYvvvhC\nt91223l/9vjx45WcDgAAoOqw2udIWEdcXNwFz8XGxl70/NVyi0IfFRUlSUpKSjrnXFFRkVJSUuTn\n53dN+45XrJBfr169y/6duLi4S/7RKxb0g+tt27ZN0un/Da30d1+5cqWeeuop5efnq02bNpo5c6Yi\nIiIu+B7sdnslJwQAAKg6rPQ5EtZQ8SWRiendbvHIfb169dSmTZszC9j90oIFC1RcXKxOnTrJ19dX\nklRWVqaMjAxlZWWd9bPp6ennHYHPzs7WRx99JEnq2LGji94FXC07O1uSFBYWZjjJ5SkpKdG4ceM0\nZMgQ5efn6/7779eiRYv4VhgAAACAU7jFCL0kxcfHa+zYsZo1a5aSk5NVv3597d69Wzt37lRERIT6\n9u175mdzcnI0atQo1alT56zt6TZs2KClS5eqRYsWql27tux2u7KysvTDDz+opKREt9xyi3r16mXi\n7cEJysrKJOnMFzvuLD09XUOHDtUPP/wgHx8fjR49Wo8//jjz5QEAAAA4jdsU+nr16mnSpElasGCB\ntm3bpm3btikkJEQ9evRQbGzsebe0+3U5ioqKUmZmplJTU5WSkqLi4mIFBgaqRYsW6tSpE6PzFldS\nUiJJ8vb2Npzk4tasWaORI0cqNzdX4eHhev/999W2bVvTsQAAAAB4GLcp9JIUGhqqYcOGXfLn6tSp\nowULFpxzvGXLlmrZsqUrosENVIzQ+/i41W17Rmlpqd588039/e9/lyR17txZ7777rkJDQw0nAwAA\nAOCJ3LMZAedRWloqyT0L/YEDBzRy5Eht3rxZ3t7eev755zV8+HB5ebnFMhUAAAAAPJD7NSPgAgID\nAyVJubm5hpP8T3l5uT7++GO9/vrrKigoUFhYmKZOnXrBLekAAAAAwFko9LCMJk2aSJL27dtnOMlp\nhw4d0jPPPKN//etfkqT77rtP48eP5xF7AAAAAJWCQg/LqCj0qampRnM4HA59+umnevXVV5Wfn6/Q\n0FBNmDCBHRQAAAAAVCoKPSyjadOmksyO0O/du1djxozR2rVrJUndu3fXxIkTVbt2bWOZAAAAAFRN\nFHpYRpMmTRQQEKDU1FTt3btX1113XaW9dl5ent555x199NFHKikpUUhIiCZMmKD77ruPveUBAAAA\nGMES3LAMf39/9ezZU5KUkJBQKa9ZVlamefPm6c4779T06dNVWlqqhx56SN9++61iYmIo8wAAAACM\nodDDUvr06SNJWrhw4Zl96V3B4XBo/fr16t69u5577jkdO3ZM0dHRWr58ud566y3VqVPHZa8NAAAA\nAJeDQg9Lue2229S4cWMdPnxYf/vb35x+/fLycq1atUoxMTGKi4vT9u3bFR4erqlTp2rx4sVq06aN\n018TAAAAAK4GhR6WYrPZNGHCBNlsNr399ttntoy7VqWlpVq0aJHuvfdePfLII9q6datCQkL07LPP\nat26dTxeDwAAAMDtsCgeLOeuu+7SyJEj9c4772jo0KGaPHmyunTpcsXXcTgc2rlzp5YsWaLFixcr\nIyNDkhQWFqbHH39c/fv3V2BgoLPjAwAAAIBTUOhhSU8//bSSkpL0zTff6JFHHtGDDz6o0aNHKzw8\n/KK/V1JSol27dmnVqlVasmSJdu/efeZckyZNNGLECD3wwAPy8/Nz9VsAAAAAgGticzgcDtMhrKxi\nVBeVr6ysTDNnztQbb7yhoqIi2Ww23XTTTWrXrp0iIiJks9lks9lUWlqqPXv2aPv27frPf/6j4uLi\nM9eoWbOmevbsqfvvv1/t2rWTl5f5WSh2u11dZvxoOgYAAIDHWRV/swoLC03HgIeJiIgw9toU+mtE\noTdv3759mjhxor7++uuzyvqFNG7cWG3btlVMTIw6duyoatWqVULKy0ehBwAAcA0KPVzBZKHnkXtY\nXtOmTfXhhx/q5MmT2rx5s3744QedOHFCDodDFd9XNWrUSK1atVJUVJRq1KhhODEAAAAAXDsKPTxG\nUFCQOnfurM6dO5uOAgAAAAAuZ37CMAAAAAAAuGIUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9\nAAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACA\nBVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAA\nAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui\n0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAA\nAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEH\nAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAAAACABVHoAQAAAACw\nIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEUegAAAAAALIhCDwAA\nAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCKPQAAAAAAFgQhR4AAAAAAAui0AMAAAAAYEEU\negAAAAAALIhCDwAAAACABVHoAQAAAACwIAo9AAAAAAAWRKEHAAAAAMCCfEwH+KWcnBzNnz9fiYmJ\nOnnypEJCQhQdHa3evXsrMDCw0q8DAAAAAIC7cptCn5WVpTFjxigvL0/R0dGKiIjQ3r17tWLFCiUm\nJuq1115TUFBQpV0HAAAAAAB35jaFfsaMGcrLy9PgwYPVtWvXM8fnzp2rZcuWaf78+YqPj6+06wAA\nAAAA4M7cYg59VlaWkpKSVLdu3bNKuCTFxcXJz89Pa9eu1alTpyrlOgAAAAAAuDu3KPQ7duyQJLVp\n0+acc/7+/mrevLmKi4u1a9euSrkOAAAAAADuzi0KfUZGhiQpPDz8vOcrjmdmZlbKdQAAAAAAcHdu\nUegLCgokSQEBAec9X3E8Pz+/Uq4DAAAAAIC7c4tCDwAAAAAAroxbFPqKkfOKEfZfqzh+qT3knXUd\nAAAAAADcnVtsWxcRESHpwnPbK45faG68s69TISEhQQsXLrzguV++JuAsx48fNx0BAADAY/H5Ha4S\nFxd3wXOxsbEXPX+13KLQR0VFSZKSkpLOOVdUVKSUlBT5+fmpWbNmlXKdCnFxcZf8o1csxAc4i91u\nNx0BAADAY/H5Hc5W8SVRxaBvZXKLR+7r1aunNm3aKDs7WytXrjzr3IIFC1RcXKxOnTrJ19dXklRW\nVqaMjAxlZWVd03UAAAAAALAqtxihl6T4+HiNHTtWs2bNUnJysurXr6/du3dr586dioiIUN++fc/8\nbE5OjkaNGqU6depoypQpV30dAAAAAACsym0Kfb169TRp0iQtWLBA27Zt07Zt2xQSEqIePXooNjb2\nvFvR2Ww2p1wHAAAAAACrsTkcDofpEFbGHBw4m91uV5cZP5qOAQAA4HFWxd+swsJC0zHgYUwutOgW\nc+gBAAAAAMCVodADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkShBwAA\nAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAK\nPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAA\ngAVR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoA\nAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAAAAAL\notADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADAgij0AAAA\nAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkSh\nBwAAAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAA\nsCAKPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8A\nAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAAAAALotADAAAAAGBB\nFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADAgij0AAAAAABYEIUeAAAA\nAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAAAAAAFuRjOkCFlJQULVq0\nSLt379apU6cUHh6uu+++W926dZOX1+V973DkyBE98cQTFzx/xx13aOTIkc6KDAAAAACAMW5R6Lds\n2aLJkyfL19dX7du3V1BQkLZu3ao5c+YoJSVFo0aNuqLrNW7cWNHR0eccj4yMdFZkAAAAAACMMl7o\nCwsLNX36dHl5eemVV15RkyZNJEl9+/bVuHHjtGnTJm3YsEF33HHHZV+zUaNGio2NdVVkAAAAAACM\nMz6HfuPGjfr555/VoUOHM2Veknx8fNSnTx9J0urVq03FAwAAAADALRkfod+xY4ck6aabbjrnXMuW\nLeXr66uUlBSVlpbKx+fy4h4/flxr1qzRzz//rODgYDVr1kwNGzZ0am4AAAAAAEwyXugzMjIkSeHh\n4eec8/LyUt26dXXo0CFlZ2crIiLisq6ZlJSkpKSks461bNlSI0aMUO3ata89NAAAAAAAhhkv9AUF\nBZKkgICA856vOJ6fn3/Ja/n5+enBBx9Uu3btVLduXUnSgQMH9Pnnn2v79u167bXX9Je//EW+vr5O\nSg8AAAAAgBlOKfQjRozQ0aNHL/vnO3bseNHt5a5W9erVFRcXd9axG264QS+//LLGjh2rPXv26Ouv\nv9bvf/97p782AAAAAACVySmFPiws7IpGvWvWrHnmv1eMwFeM1P9axfHAwMCrzufl5aV77rlHe/bs\n0U8//UShBwAAAABYnlMK/dixY6/6dyMiIrRv3z5lZmaetcq9JJWXlys7O1ve3t5nHqG/WtWrV5ck\nFRcXX/bvJCQkaOHChRc8J+my5/UDl+v48eOmIwAAAHgsPr/DVX79tPgvxcbGXvT81TI+h75Vq1b6\n17/+pW3btp2z1/zOnTt16tQptWzZ8rJXuL+QXbt2SdIVfTEQFxd3yT96xaJ+gLPY7XbTEQAAADwW\nn9/hbBVfElUM+lYm4/vQ33777QoODtb69eu1b9++M8dLSko0f/58SVKXLl3O+p2CggJlZGQoNzf3\nrOOpqalyOBznvEZycrKWLVsm6fT8fQAAAAAArM74CL3dbtfjjz+uyZMn65VXXtEdd9yhoKAgbd26\nVRkZGWrfvr3at29/1u9s3rxZ06ZN01133aXhw4efOT537lxlZmaqWbNmqlWrlqTTq9xv375dktS3\nb181a9as8t4cAAAAAAAuYrzQS1J0dLTGjRunRYsWafPmzSopKVFYWJgGDRp00QXsbDbbWf/cqVMn\nbd68Wfv27VNiYqJKS0sVEhKiO+64Q127dtUNN9zg6rcCAAAAAEClsDnO94w6LhtzcOBsdrtdXWb8\naDoGAACAx1kVf7MKCwtNx4CHMbnQovE59AAAAAAA4MpR6AEAAAAAsCAKPQAAAAAAFkShBwAAAADA\ngij0AAAAAABYEIUeAAAAAAALotADAAAAAGBBFHoAAAAAACyIQg8AAAAAgAVR6AEAAAAAsCAKPQAA\nAAAAFkShBwAAAADAgij0AAAAAABYEIUe+P/t3V1sl+X9P/A3hRWUhxR0tXRT8aRCMYbfMozUiIKZ\nD/FokVVOFpfFhExInIknxpFByLIlJhwtMSbLEjxCMMQDzeZfjXvyIRAWWrHayrAYbEMlymSiPFT+\nB6SNFUSB70Ov9vU6stf9zXVf3/rx4/fd+3tfNwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAA\nFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAH\nAACAAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIAC\nCfQAAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAA\nAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCB\nHgAAAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAA\nCiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNAD\nAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMAAECB\nptV7AcPDw3nxxRfT39+f/v7+HDx4MMPDw1mzZk1Wrlx5UXP29vZmx44dee+993LixInMnz8/K1as\nyN13352GBn/DAAAAoHx1D/THjx/Pli1bkiRNTU2ZO3duDh8+fNHz7dq1K5s3b05jY2OWLVuWWbNm\nZffu3dmyZUt6e3vzyCOPVGrpAAAAUDd1D/SNjY157LHHsmDBgjQ1NWX79u159tlnL2quzz//PE89\n9VQaGhqyYcOGXHfddUmS1atXZ+PGjXnzzTfz+uuvp6Ojo5JvAQAAAGqu7t8/nzZtWpYsWZKmpqZL\nnuuNN97I0aNHc8stt4yG+ZFz3H///UmSl1566ZLPAwAAAPVW90BfSW+//XaSZMmSJWcda29vT2Nj\nY3p7e3Pq1KlaLw0AAAAqakIF+oGBgSTJ/PnzzzrW0NCQ5ubmDA8PZ2hoqNZLAwAAgIqaUIH+2LFj\nSZLLL7/8nMdHxj/77LOarQkAAACqoSKb4q1du/aCdqa/9dZbs27dukqcGgAAACaligT6lpaWNDY2\nfufXz5s3rxKnPcvIFfiRK/VfNzI+c+bMqpwfAAAAaqUigX79+vWVmOaStba2Zv/+/RkcHByzy32S\nfPnllxkaGsrUqVPT3Nz8nebbtm3bNz5Cb9u2baPnhEo6/PEn+X8P/l+9lwEAMOEMn/b5nerp7Oz8\nxmOrVq067/GLVffn0FfSDTfckH/961/Zs2fPWc+a7+npyYkTJ9Le3p5p077b2+7s7PzWX/rIRnxQ\nKa2treqKqlBbVIO6olrUFtWgrqiGkT8SjVz0raUiN8U7duxYBgYGcuTIkTHjN998c2bPnp3XXnst\n+/fvHx0/efJktm7dmiS58847a7pWAAAAqIZxcYX+ueeeG/1LWX9/f5Lk1VdfzbvvvpskWbhwYVau\nXDn6+p07d+bJJ5/Mbbfdloceemh0/LLLLsuaNWuyefPmbNiwIR0dHZk1a1Z2796dgYGBLFu2LMuW\nLavdGwMAAIAqGReBvqurKz09PWPG+vr60tfXN/rzVwP9iClTppw1tnTp0mzcuDE7duzIzp07c/Lk\nybS0tOSBBx7IPffcU/nFAwAAQB1MOX369Ol6L6Jk7sGh0tzbRbWoLapBXVEtaotqUFdUQz03Wizy\nHnoAAACY7AR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMA\nAECBBHoAAAAokEAPAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEE\negAAACiQQA8AAAAFEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAA\nKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAokEAP\nAAAABRLoAQAAoEACPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAF\nEugBAACgQAI9AAAAFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEA\nAKBAAj0AAAAUSKAHAACAAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAokEAPAAAABRLoAQAAoEAC\nPQAAABRIoAcAAIACCfQAAABQIIEeAAAACiTQAwAAQIEEegAAACiQQA8AAAAFEugBAACgQAI9AAAA\nFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAH\nAACAAk2r9wKGh4fz4osvpr+/P/39/Tl48GCGh4ezZs2arFy58oLm+uijj7Ju3bpvPN7R0ZGHH374\nUiaGbjEAAAvlSURBVJcMAAAAdVf3QH/8+PFs2bIlSdLU1JS5c+fm8OHDlzTnggULsnTp0rPGr776\n6kuaFwAAAMaLugf6xsbGPPbYY1mwYEGampqyffv2PPvss5c057XXXptVq1ZVaIUAAAAw/tQ90E+b\nNi1Lliyp9zIAAACgKHUP9NXwySef5OWXX87Ro0cze/bstLW15Zprrqn3sgAAAKBiJmSg7+7uTnd3\n95ix9vb2rF27NldeeWWdVgUAAACVM6EC/fTp03PfffflpptuSnNzc5Lkgw8+yPbt27N3795s2rQp\nTzzxRBobG+u8UgAAALg0FQn0a9euvaCd6W+99dbzPl7uYs2ZMyednZ1jxhYuXJjHH38869evz759\n+/LKK6/knnvuqfi5AQAAoJYqEuhbWlou6Kr3vHnzKnHa76yhoSF33HFH9u3bl3feeaeigb61tbVi\nc8EIdUW1qC2qQV1RLWqLalBXTCQVCfTr16+vxDRVNWfOnCRnnnv/XW3btu0bH6G3bdu2iqwLAACA\n8n392+JftWrVqvMev1gT6h768+nr60uS0Xvrv4vOzs7z/tI7OzsFeypOXVEtaotqUFdUi9qiGtQV\n1VKv2mqo+Rkr4NixYxkYGMiRI0fGjL///vs5ffr0Wa9/66238sILLyQ5c/8+AAAAlG5cXKF/7rnn\nMjAwkCTp7+9Pkrz66qt59913k5zZ2G7lypWjr9+5c2eefPLJ3HbbbXnooYdGx59++ukMDg6mra0t\nV1xxRZIzu9zv3bs3SbJ69eq0tbXV4i0BAABAVY2LQN/V1ZWenp4xY319faNfk08yJtCPmDJlypif\nly9fnp07d2b//v3p6urKqVOn0tTUlI6Ojtx1111ZuHBhdd4AAAAA1Ni4CPS//e1vL+j1t99+e26/\n/fazxlesWJEVK1ZUaFUAAAAwfhV5Dz0AAABMdgI9AAAAFGjqhg0bNtR7EaU6ffp0Fi9eXO9lMMGo\nK6pFbVEN6opqUVtUg7qiWupVW1NOn+s5bwAAAMC45iv3AAAAUCCBHgAAAAok0AMAAECBBHoAAAAo\nkEAPAAAABRLoAQAAoEACPQAAABRoWr0XMN4NDw/nxRdfTH9/f/r7+3Pw4MEMDw9nzZo1Wbly5QXN\n9dFHH2XdunXfeLyjoyMPP/zwpS6ZAlSyrkb09vZmx44dee+993LixInMnz8/K1asyN13352GBn+7\nm2wqUQ961uT08ccfZ+vWrenq6sr//ve/NDU1ZenSpfnZz36WmTNn1nweJoZK1MPatWtz+PDhcx5r\namrKU089VcklU4A333wzPT09OXDgQPr7+/PFF1/k1ltvPe//u76JnsWIStVVrXqWQP8tjh8/ni1b\ntiQ584ufO3fuN/6L+a4WLFiQpUuXnjV+9dVXX9K8lKPSdbVr165s3rw5jY2NWbZsWWbNmpXdu3dn\ny5Yt6e3tzSOPPFKppVOASteDnjV5HDp0KL/5zW/y6aefZunSpWltbc1//vOf/OUvf0lXV1c2bdqU\nWbNm1WweJoZK1sPll1+ee++996zxGTNmVHrZFGDHjh05cOBAZsyYkSuuuCIffvjhRc2jZ/FVlaqr\npDY9S6D/Fo2NjXnssceyYMGCNDU1Zfv27Xn22Wcvac5rr702q1atqtAKKVEl6+rzzz/PU089lYaG\nhmzYsCHXXXddkmT16tXZuHFj3nzzzbz++uvp6Oio5FtgnKpGPehZk8ef/vSnfPrpp/nlL3+Zu+66\na3T86aefzgsvvJCtW7fmwQcfrNk8TAyVrIeZM2fqR4z6xS9+kXnz5qWlpSU9PT3ZuHHjRc2jZ/FV\nlaqrpDY9y/dwv8W0adOyZMmSNDU11XspTCCVrKs33ngjR48ezS233DIa3kbOcf/99ydJXnrppUs+\nD2VQD1ysQ4cOpbu7O83NzWM+0CZJZ2dnpk+fnn/84x85ceJETeZhYlAPVFN7e3taWlouaQ41ytdV\noq5qyRX6Ovjkk0/y8ssv5+jRo5k9e3ba2tpyzTXX1HtZFOrtt99OkixZsuSsY+3t7WlsbExvb29O\nnTqVadP8Jz/RVaMe9KzJYaR2brzxxrOOzZgxI9dff326u7vT19eXG264oerzMDFUuh5OnjyZf/7z\nnzl8+HCmT5+ea6+9NosWLbJXDBdNz6KaatGzfLqvg+7u7nR3d48Za29vz9q1a3PllVfWaVWUamBg\nIEkyf/78s441NDSkubk5Bw8ezNDQUFpbW2u9PGqsGvWgZ00O56udkfHu7u4MDg6e90NtpeZhYqh0\nPRw5ciR//OMfx4w1NzfnV7/6Vdrb2y99wUw6ehbVVIueJdDX0PTp03PfffflpptuSnNzc5Lkgw8+\nyPbt27N3795s2rQpTzzxRBobG+u8Ukpy7NixJGc23TiXkfHPPvusZmuifipZD3rW5FKp2tGT+KpK\n1sOKFSuyaNGiXH311ZkxY0aGhoby17/+NS+99FJ+//vf53e/+51vD3HB9CyqpVY9a1IE+vM9MuBc\nLvZxF99mzpw56ezsHDO2cOHCPP7441m/fn327duXV155Jffcc0/Fz03ljZe6YuIZL7WlZwHjydc3\nlvrhD3+YBx98MNOnT8/zzz+fbdu25dFHH63T6gDGqlXPmhSBvqWl5YKuIM2bN6+KqzlbQ0ND7rjj\njuzbty/vvPOOD8eFGC91NfKX45G/MH/dyLhnqJbjQmtr7ty5o/9ci3rQsyamStWOnsRX1aIefvKT\nn+T555/PO++8c9FzMHnpWdRapXvWpAj069evr/cSvtWcOXOSnHk+OWUYL3XV2tqa/fv3Z3BwcMyu\n5kny5ZdfZmhoKFOnTh39yjTj36XUVq3qQc+aeEb2VBgcHDzn8ZHxb7rPtNLzMDHUoh70Iy6FnkWt\nVbpn2RJ0nOjr60sSoYsLNrJBy549e8461tPTkxMnTuT666+3w/0kUat60LMmnsWLFyfJWRsgJskX\nX3yR3t7eTJ8+PW1tbTWZh4mhFvUw0o+uuuqqi56DyUvPotYq3bME+io4duxYBgYGcuTIkTHj77//\nfk6fPn3W699666288MILSc7cCwvn8k11dfPNN2f27Nl57bXXsn///tHxkydPZuvWrUmSO++8s6Zr\npX4uph70LJIzHyxuvPHG0U17vuqZZ57J8ePHs3z58tHbQYaHhzMwMJBDhw5d0jxMbJWqqw8//PCc\nV7OGhoby5z//OYl+xPnpWVTDeOhZU06f69MaYzz33HOjj7To7+/PgQMH0tbWNvrVm4ULF2blypWj\nr//b3/6WJ598Mrfddlseeuih0fGNGzdmcHAwbW1tueKKK5Kc2TF67969SZLVq1fnpz/9aa3eFnVW\nqbpKkl27dmXz5s353ve+l46OjsyaNSu7d+/OwMBAli1bll//+te1e2PU3YXWg57FiEOHDmX9+vX5\n73//mx//+Mf5wQ9+kPfeey89PT1pbW3Npk2bMmvWrCTJRx99lHXr1uX73//+WY/kuZB5mPgqUVfb\nt2/P888/n0WLFuXKK6/MZZddlkOHDuXf//53Tp48mR/96Ed59NFHM3Xq1Hq9Tepg165d2bVrV5Iz\njwfr6upKc3NzFi1alCSZPXt2fv7znyfRs/juKlFXtexZvoP7HXR1daWnp2fMWF9f3+jXJZKMCV4j\npkyZMubn5cuXZ+fOndm/f3+6urpy6tSpNDU1paOjI3fddVcWLlxYnTfAuFSpukqSpUuXZuPGjdmx\nY0d27tyZkydPpqWlJQ888IANyyahi60HPYurrroqf/jDH/LMM89kz5492bNnT5qamnLvvfdm1apV\n53ys07l60sXMw8RVibpavHhxBgcH8/7776e3tzfHjx/PzJkzs2jRoixfvtzV+Umqv78/f//738eM\nDQ0NZWhoKMmZ28JGgtcIPYtvU4m6qmXPcoUeAAAACuQeegAAACiQQA8AAAAFEugBAACgQAI9AAAA\nFEigBwAAgAIJ9AAAAFAggR4AAAAKJNADAABAgQR6AAAAKJBADwAAAAUS6AEAAKBAAj0AAAAUSKAH\nAACAAgn0AAAAUCCBHgAAAAok0AMAAECBBHoAAAAo0P8HxfUHyP0AobUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10775ee80>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.9555404 0.86702672] 0.243315474692\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3Xtw1vWd//1XAMOZxgOnWMTWFgUsVbeoYEGhrcfatWug\n9jRtHX7TaXXb2792O1tndZxOO7Pz628602nv3ne3rv5mu4DUs7dYra4niiIKqHSDVqmH0FAKFggk\ngZj7D39hpUgFciXX9Ukfjxln5Pu9rnc+4TuOeeZ7uOq6u7u7AwAAABRlULUXAAAAABw+QQ8AAAAF\nEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAA\nUCBBDwAAAAUS9AAAAFAgQQ8AAAAFGlLtBSTJypUrs379+vzud7/Lxo0b097enjlz5uTqq68+rDlX\nXXVVtmzZ8o77Ghoa8pOf/KQSywUAAICqq4kz9Lfeemvuu+++bNy4Mccee2yvZo0YMSILFiw44J9L\nL720Qqv9b0uXLq34TPqXY1g+x7Bsjl/5HMPyOYblcwzL5xiWr1rHsCaC/stf/nJ+8IMf5Kabbsqi\nRYt6NWvkyJFpamo64J9PfvKTFVrtf1u2bFnFZ9K/HMPyOYZlc/zK5xiWzzEsn2NYPsewfNU6hjVx\nyf20adOqvQQAAAAoSk0EfSXt2bMnjz76aLZs2ZKhQ4dm8uTJmTp1agYNqomLEQAAAKAiBlzQv/HG\nG/nhD3+437Zx48bla1/7misBAAAAGDAGVNDPmzcvU6dOzaRJkzJs2LBs3rw5y5cvz/3335/vfve7\n+c53vpMTTjih2ssEAACAXhtQ16E3NTVl+vTpGTNmTOrr6/Pe9743ixYtyic/+cl0dnZ6eiQAAAAD\nRl13d3d3tRfxduvXr8/1119/RJ9DfzC///3v881vfjOjRo3Kv/7rv1ZkJgAAAFTTgLrk/mDGjBmT\nJOno6Dis9y1duvSgHz/gbD8AAAA9Fi5ceNB9TU1Nf3H/kfqrCPoNGzYkScaPH39Y71u4cOG7/qW3\ntLQc8bqovsbGRsewcI5h2fry+G3dujUf+tCH8vDDD+cDH/jAvu0vv/xy5syZk/r6+jz11FM55phj\njmj+c889lwsuuCCTJk3KypUrK7Xs4vhvsHyOYfkcw/I5hmVrbGxMUp2TvsXdQ9/V1ZWWlpa0trbu\nt/31119/xzPwmzdvzs9+9rMkyZw5c/pljQDUrn/7t39Ld3d3LrvssiOO+SR57LHHkiTnnHNOpZYG\nAHBYauIM/apVq7Jq1aokb33sXJI0NzfnRz/6UZJk9OjR+eIXv5jkrTMu11xzTcaOHbvfx9OtWLEi\nd999d6ZOnZrjjjsuw4cPT2tra55++uns2bMnZ5xxRi699NJ+/s4AqCVtbW1ZsmRJkuTKK6/s1azH\nH388iaAHAKqnJoJ+48aNefjhh/fbtnnz5mzevDnJW58j3xP0Perq6vb78/Tp07Np06a8/PLLaW5u\nTkdHR0aOHJmpU6dm7ty5zs4DkFtuuSU7duzImWeemVNPPfWI5+zZsydPPPFEkmT27NmVWh4AwGGp\niaBfsGBBFixYcEivHTt27L6zK283bdq0TJs2rdJLA2CA6O7uzs0335wk+cpXvtKrWWvXrk1bW1tO\nOumkTJgwoRLLAwA4bMXdQw8AR2L16tVpbm7OcccdlwsvvLBXs1xuDwDUAkEPwF+Fn//850ne+gST\n+vr6Xs1asWJFEkEPAFSXoAdgwNuxY0fuvPPOJMlnP/vZXs1qb2/PU089lcT98wBAdQl6AAa82267\nLbt3786sWbPy/ve/v1eznnrqqbS3t2fq1Km9+tg7AIDeEvQADHg9l9t/7nOf6/Wshx56KEly3nnn\n9XoWAEBvCHoABrQNGzbk2WefTUNDQy6++OJez3vwwQeTJPPnz+/1LACA3hD0AAxod999d5Lk8ssv\nz7Bhw3o169VXX82GDRsyatSozJw5sxLLAwA4YoIegAHtgQceSFKZy+17zs7PnTs3Rx11VK/nAQD0\nhqAHYEBra2vLGWeckVNOOaXXs3run3e5PQBQCwQ9AAPe5z//+V7PaG9vz2OPPZYkmTdvXq/nAQD0\nlqAHYEB68cUXkyTDhw/PpZde2ut5TzzxRHbv3p3p06dnwoQJvZ4HANBbgh6AAekXv/hFkuTjH/94\nRo4c2et5PffPOzsPANQKQQ/AgNPR0ZE777wzSSpydj7576D/2Mc+VpF5AAC9JegBGHCWL1+e7du3\nJ0lOPvnkXs97+eWX89JLL+U973lPzjjjjF7PAwCoBEEPwICzePHiis7rebr9ueeemyFDhlR0NgDA\nkRL0AAwomzZtyqOPPlrRz4nvCXr3zwMAtUTQAzCg3Hbbbenu7s65555bkXm7d+/OihUrkgh6AKC2\nCHoABozu7u4sW7YsSfKpT32qIjNXrFiR9vb2fPjDH87YsWMrMhMAoBIEPQADxvPPP5/m5uYcffTR\n+ehHP1qRmT1Pt58/f35F5gEAVIqgB2DAuOWWW5Ikl112WUXuoe/u7s59992XxMfVAQC1R9ADMCDs\n3bs3t99+e5KkqampIjPXrl2bTZs2ZcKECfnwhz9ckZkAAJUi6AEYEB5++OFs2bIlJ510UsXie/ny\n5UmSCy+8MIMG+V8mAFBb/HQCwIDQ8zC8pqam1NXVVWTm24MeAKDWCHoAivenP/1p373ul19+eUVm\nvvjii3nhhRfS0NCQs88+uyIzAQAqSdADULx77rknHR0dmT17do4//viKzHz7w/Aq8YA9AIBKE/QA\nFO8Xv/hFkso9DC9J7r333iQutwcAapegB6Bor7zySlauXJlhw4bl4osvrsjMTZs25ZlnnsmwYcNy\n3nnnVWQmAEClCXoAitZzdv6iiy7K6NGjKzLzl7/8ZZLk3HPPzYgRIyoyEwCg0gQ9AMXq7u7e7+n2\nldLzdPsLLrigYjMBACpN0ANQrKeffjobN27MuHHj8tGPfrQiM994442sWLEigwcPzic+8YmKzAQA\n6AuCHoBi3XrrrUmSyy67LEOGDKnIzAcffDB79+7NWWedlWOOOaYiMwEA+oKgB6BIe/fuzd13350k\n+bu/+7uKzfV0ewCgFIIegCKtWLEiW7Zsyfvf//6ceuqpFZm5e/fuPPTQQ0kEPQBQ+wQ9AEW64447\nkiR/+7d/m7q6uorMfPTRR7N79+7MmDEjxx9/fEVmAgD0FUEPQHE6Ojr2XRr/qU99qmJzPd0eACiJ\noAegOA8//HD+9Kc/ZerUqZkyZUpFZu7Zsyf33XdfkuTiiy+uyEwAgL4k6AEozp133pnkrcvt382Q\nIUMyePDgd33do48+mjfeeCMnn3xyxX5JAADQlwQ9AEXZvXv3vjPpB7vcfkh3d4b/n/vqhy9bluG/\n/nWG19VlSHf3QefeddddSZJLL720wisGAOgbgh6Aotx///3ZtWtXTj/99EyePPmA/UO6u1Pf2prR\n55+fJBnxv/5Xxnz60xlz1lmpb219x6jv7Ozcd//8Jz/5yb79BgAAKqSuu/svnK7gXbW0tFR7CfRC\nY2NjnxzDrv9RuYd0AcBAMPj/vbPaSxiw+urnGfqPY1i2xsbGqn1tZ+gBAACgQIIeAAAACiToAQAA\noEBDqr0AGIjcJ9h/3HNWtsM5fjt37syMGTPS2dmZVatWZeLEie/4uuF1dRlz1lkZ/OqrB+zrmjQp\n21euzO63bfv7v//73HrrrfmHf/iHfOMb3ziSb+Ovmv8Gy+cYApTLGXoAinD//feno6MjZ5555kFj\nPkn2vPlmdtx+e7omTdpve9ekSdlxxx3Z87ZnwR7KR+ABANQqZ+gBKMKdd7515cu7fU783rq6ZPz4\nbH/iiQx+8skMXr8+XdOmpevMM7PnzTff2v9/PPDAA2lra8vpp5+eE088sS+XDwBQcYIegJq3ffv2\n/Od//mfq6upy8cUXv+vr99bVZW93dwaffXbqZs1Kd3d3urq6krfFfPLfvyRwdh4AKJGgB6DmPfjg\ng+ns7MxZZ52V8ePHH/L7urq6Drpvx44d+dWvfpW6urp3PesPAFCL3EMPQM279957kyQXXXRRxWbe\nd9996ejoyNlnn/0X78kHAKhVgh6Amtbe3p6HHnooSXLhhRdWbO4dd9yRxOX2AEC5BD0ANe2xxx5L\nW1tbpk+fnkl/9uT6I7V169Y88sgjGTx4cC655JKKzAQA6G+CHoCatnz58iSVvdz+7rvvzt69ezNn\nzpwce+yxFZsLANCfBD0ANaurqyu//OUvk1T2cvtf/OIXSZJPf/rTFZsJANDfBD0ANeupp57KH//4\nx0yePDmnnHJKRWZu3LgxTz31VEaMGFHRs/4AAP1N0ANQs3qebn/hhRem7s8+Q/5I9Zydv/jiizNy\n5MiKzAQAqAZBD0BN6u7uzn333ZekcvfPd3d3Z9myZUmSpqamiswEAKgWQQ9ATVq/fn1eeeWVHHfc\ncTnjjDMqMnPVqlV55ZVXMmHChMyePbsiMwEAqkXQA1CTes7OX3DBBRk8eHBFZvacnb/88ssrNhMA\noFoEPQA16e33z1dCe3t77rrrriRvBT0AQOkEPQA155VXXsn69eszatSonHPOORWZef/992f79u2Z\nMWNGTj755IrMBACoJkEPQM1Zvnx5kmT+/PkZOnRoRWb2PN3e2XkAYKAQ9ADUnJ6gr9Tl9lu2bMlD\nDz2UwYMH57LLLqvITACAahP0ANSULVu25Mknn0x9fX3mz59fkZl33HFH9u7dm3nz5uW4446ryEwA\ngGoT9ADUlF/96lfp7u7OOeeck9GjR1dkps+eBwAGIkEPQE158MEHkyQf//jHKzJvw4YNWbduXcaM\nGZNPfOITFZkJAFALBD0ANWPv3r155JFHkiTz5s2ryMyeh+FdeumlGTZsWEVmAgDUAkEPQM1YvXp1\ntm/fnpNOOimTJ0/u9byurq59Qe9yewBgoBH0ANSMnsvtK/UwvMcffzybNm3KCSeckJkzZ1ZkJgBA\nrRD0ANSMX/3qV0kqF/Q///nPkyQLFy5MXV1dRWYCANQKQQ9ATWhpaclvfvObjBgxImeddVav5/3x\nj3/M8uXLM2jQoHzmM5+pwAoBAGqLoAegJjz00ENJkjlz5mTo0KG9nrds2bLs2bMn8+bNS2NjY6/n\nAQDUGkEPQE3oCfpKPN2+u7t73+X2n//853s9DwCgFgl6AKqus7Nz38fVVeL++VWrVuXFF1/M+PHj\n87GPfazX8wAAapGgB6DqnnzyybS1teWUU07J8ccf3+t5//7v/54kWbBgQYYMGdLreQAAtUjQA1B1\nlfy4uj/96U+5++67kySf/exnez0PAKBWCXoAqq6SQX/bbbelvb09H/3oR3PiiSf2eh4AQK0S9ABU\n1auvvpoXXngho0ePzkc+8pFezeru7t53uf3nPve5SiwPAKBmCXoAqqrn7PycOXNy1FFH9WrWunXr\nsn79+hx99NG58MILK7E8AICaVRNPClq5cmXWr1+f3/3ud9m4cWPa29szZ86cXH311Yc9a+vWrVm8\neHHWrl2bnTt3pqGhITNnzsyCBQsycuTIPlg9AL3R83F1lbjc/u0Pw6vEZ9kDANSymgj6W2+9Nb/7\n3e8ybNiwHHvssXn99dePaE5ra2u+/e1vZ/v27Zk5c2YaGxvz29/+Nvfee2/Wrl2bG264IaNGjarw\n6gE4Unv37s3KlSuTJHPnzu3VrLa2ttx+++1JXG4PAPx1qImg//KXv5xjjjkmEyZMyPr163P99dcf\n0Zyf/vSn2b59e6688spccMEF+7bffPPNueeee7J48eIsWrSoUssGoJeeeeaZ7NixIyeeeGKvP67u\nzjvvTFtbW2bOnJkPfvCDFVohAEDtqol76KdNm5YJEyb0akZra2vWrVuXcePG7RfzSbJw4cIMHTo0\njzzySDo7O3v1dQConJ77588555xez/IwPADgr01NBH0lPP/880mSGTNmHLBv2LBhOfnkk9PR0ZEN\nGzb099IAOIhKBf3zzz+fZ555JmPGjMmll15aiaUBANS8ARP0LS0tSZKJEye+4/6e7Zs2beq3NQFw\ncJ2dnXnssceSJLNnz+7VrBtvvDHJWw/DGz58eK/XBgBQggET9Lt27UqSjBgx4h3392xva2vrtzUB\ncHBr1qzJrl27MmXKlIwdO/aI52zdujW33XZbkuRLX/pSpZYHAFDzBkzQA1CWxx9/PEnvL7f/j//4\nj7S3t2f+/Pk56aSTKrE0AIAiDJig7zkD33Om/s/1bPdZ9AC1oRJBv3fv3tx0001Jkq985SsVWRcA\nQClq4mPrKqGxsTHJwe+R79l+sHvs38nSpUuzbNmyg+57+9elXI5h+RzD8uzevTurV69OXV1d5s2b\nd8T3vd999915/fXXc9JJJ+Wiiy7KoEED5vfUxdi2bZvnFhTOMSyfY1i+LVu3+XlmAFi4cOFB9zU1\nNf3F/UdqwAT99OnTkyTr1q07YF97e3uam5szdOjQTJky5ZBnLly48F3/0nsexkeZGhsbHcPCOYZl\nevTRR9PZ2ZkZM2bkM7/YmGTjEc1p/r//Z5Kkc/qFufBnayu2PgDoT79cdLqfZwrW88uYnpO+/am4\nUxldXV1paWlJa2vrftvHjx+fGTNmZPPmzVm+fPl++5YsWZKOjo7MnTs39fX1/blcAN5Bz+X2c+bM\nOeIZuza9lB0vrc2g+uE57iMXVGppAADFqIkz9KtWrcqqVauSJG+88UaSpLm5OT/60Y+SJKNHj84X\nv/jFJG89zfiaa67J2LFj88Mf/nC/OYsWLcq1116bG2+8Mc8++2yOP/74vPDCC1m/fn0aGxtzxRVX\n9ON3BcDB9AT93Llz88TvjmzG5hW3J0mO/cj5GTzM81EAgL8+NRH0GzduzMMPP7zfts2bN2fz5s1J\nknHjxu0L+h51dXUHzBk/fny+973vZcmSJVmzZk3WrFmThoaGXHLJJWlqajroR9oB0H927tyZtWvX\nZvDgwTn77LOT37142DP27tqerU8/kCQZN/uySi8RAKAINRH0CxYsyIIFCw7ptWPHjs2SJUsOuv+Y\nY47J1772tUotDYAKW7VqVbq6unL66adn9OjRRzRjy6rleXNPR8ZM+UiGjzuhwisEAChDcffQA1C2\np556Kkly5plnHtH7u9/syuYVdyRxdh4A+Osm6AHoV6tXr06SfOQjHzmi97/xm5Xp3Pb7DD1mYt5z\nypH9UgAAYCAQ9AD0m66urjz99NNJkr/5m785ohmbH78tSTJ29mWpGzS4YmsDACiNoAeg3zQ3N6et\nrS2TJk3K+PHjD/v9ba9tyI4Xn3nro+pmXtgHKwQAKIegB6Df9Fxuf6Rn53//8FsPRR171iUZMnxU\nxdYFAFAiQQ9Av+lN0Lf/sSXb1j2SukGDM35OU6WXBgBQHEEPQL9Zs2ZNkuT0008/7Pe2PnJL0v1m\njjn9Y6lvGFvppQEAFEfQA9Avdu7cmRdffDFHHXVUpk2bdljv3bNzW7asWp4kmXDeZ/pieQAAxRH0\nAPSLdevWpbu7O9OmTcvQoUMP672bH7893Xs7856pszJ8/Il9s0AAgMIIegD6Rc/l9h/+8IcP631d\n7W3ZvOL2JMmEeVdUfF0AAKUS9AD0i56gP+200w7rfZt/fWe6du/MqPd/OKNPPLUvlgYAUCRBD0C/\neO6555IkM2bMOOT3dHW2p/WRZUmSifM/1yfrAgAolaAHoM/t3r07r7zySoYMGZIPfOADh/y+LU/e\nk71tb2TEpJMz5oNH9tn1AAADlaAHoM+99NJL6e7uzuTJk3PUUUcd0nve3NuZ3z+8NEkycf7nU1dX\n15dLBAAojqAHoM+9+OKLSXKYZ+f/v+z505YMn/C+NEyd1VdLAwAolqAHoM/99re/TZJ88IMfPKTX\nd7XvSsv9/ztJ0nj+l1M3yP+uAAD+nJ+QAOhzPWfoTzrppEN6/e8fuSV7297IyMnT0jD9nL5cGgBA\nsQQ9AH3ucC6537Nja1ofeeve+fde/D/cOw8AcBCCHoA+9eabb+675P5QztC3PPC/82Zne94zdVZG\nv+/QP+IOAOCvjaAHoE+9/vrraW9vz7hx4/Ke97znL762/Q+vZcsT9yR1g/Leixb10woBAMok6AHo\nU4dz//zr992Y7je7ctxHzs/wCSf28coAAMom6AHoU62trUmS9773vX/xdW2v/le2rfvP1A2pT+Mn\nvtwPKwMAKJugB6BP7dy5M0kyatSog76mu7s7r93z/yRJxn/071LfMLZf1gYAUDJBD0Cf6gn6kSNH\nHvQ1f3xqeXa8tDaDR4zOhPOu6K+lAQAUTdAD0Kfa2tqSHPwMfce21rx614+TJCd86uoMGTG639YG\nAFAyQQ9An9qxY0eSZPToA0O9u7s7v1v2P9PV3paG6efkmNM/1t/LAwAolqAHoE/1nKF/p0vub775\n5mx/YXWGjBiTyX/3f6Wurq6/lwcAUCxBD0Cf6gn64cOH77f9tddey7XXXpskOeGyv89Ro4/p97UB\nAJRM0APQpyZMmJAkefXVV/dt2717d77xjW9k586dOfpDc3L0h+dVa3kAAMUaUu0FADCwTZs2LUmy\nfv36JG/F/Je//OU88cQTGTduXCZ++psutQcAOALO0APQp3qC/vHHH8/KlSvzhS98IY899ljGjRuX\nO+64I0eNOrrKKwQAKJOgB6BPfehDH8qpp56a1tbWXH755Vm5cmXGjx+fW265JSeffHK1lwcAUCxB\nD0CfOuqoo/KDH/wgZ5xxRhoaGvKFL3whd911Vz7wgQ9Ue2kAAEVzDz0Afe6UU07JXXfdVe1lAAAM\nKM7QAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRoSLUX8HZbt27N4sWLs3bt2uzcuTMNDQ2ZOXNmFixYkJEjRx7SjKuuuipbtmx5x30NDQ35yU9+\nUsklAwAAQFXUTNC3trbm29/+drZv356ZM2emsbExv/3tb3Pvvfdm7dq1ueGGGzJq1KhDmjVixIhc\ncsklB2wfNmxYpZcNAAAAVVEzQf/Tn/4027dvz5VXXpkLLrhg3/abb74599xzTxYvXpxFixYd0qyR\nI0emqampr5YKAAAAVVcT99C3trZm3bp1GTdu3H4xnyQLFy7M0KFD88gjj6Szs7NKKwQAAIDaUhNn\n6J9//vkkyYwZMw7YN2zYsJx88slZt25dNmzYkFNPPfVd5+3ZsyePPvpotmzZkqFDh2by5MmZOnVq\nBg2qid9fAAAAQK/VRNC3tLQkSSZOnPiO+ydOnJh169Zl06ZNhxT0b7zxRn74wx/ut23cuHH52te+\nlmnTpvV+wQAAAFBlNRH0u3btSvLWw+zeSc/2tra2d501b968TJ06NZMmTcqwYcOyefPmLF++PPff\nf3+++93v5jvf+U5OOOGEyi0eAAAAqmDAXYPe1NSU6dOnZ8yYMamvr8973/veLFq0KJ/85CfT2dmZ\npUuXVnuJAAAA0Gs1EfQ9Z+B7ztT/uZ7th/pZ9O/kE5/4RJLkN7/5zRHPAAAAgFpRE5fcNzY2Jkk2\nbdr0jvt7th/sHvtDMWbMmCRJR0fHIb9n6dKlWbZs2UH3Jf+9dsrlGJbPMSzXtm3bqr0EAKgJfp4p\n38KFCw+6r6mp6S/uP1I1EfTTp09Pkqxbt+6Afe3t7Wlubs7QoUMzZcqUI/4aGzZsSJKMHz/+kN+z\ncOHCd/1L73mgH2VqbGx0DAvnGJZt+PDh1V4CANQEP8+Uq+eXMdW4vbsmLrkfP358ZsyYse8Bdm+3\nZMmSdHR0ZO7cuamvr0+SdHV1paWlJa2trfu99vXXX3/HM/CbN2/Oz372syTJnDlz+ui7AAAAgP5T\nE2fok2TRokW59tprc+ONN+bZZ5/N8ccfnxdeeCHr169PY2Njrrjiin2v3bp1a6655pqMHTt2v4+n\nW7FiRe6+++5MnTo1xx13XIYPH57W1tY8/fTT2bNnT84444xceuml1fj2AAAAoKJqJujHjx+f733v\ne1myZEnWrFmTNWvWpKGhIZdcckmampre8SPt6urq9vvz9OnTs2nTprz88stpbm5OR0dHRo4cmalT\np2bu3LnOzgMAADBg1EzQJ8kxxxyTr33ta+/6urFjx2bJkiUHbJ82bVqmTZvWF0sDAACAmlIT99AD\nAAAAh0fQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNAD\nAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEE\nPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAU\nSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQC3eBVuAAAebklEQVQAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNAD\nAABAgYZUewFvt3Xr1ixevDhr167Nzp0709DQkJkzZ2bBggUZOXJkv88BAACAWlUzQd/a2ppvf/vb\n2b59e2bOnJnGxsb89re/zb333pu1a9fmhhtuyKhRo/ptDgAAANSymgn6n/70p9m+fXuuvPLKXHDB\nBfu233zzzbnnnnuyePHiLFq0qN/mAAAAQC2riXvoW1tbs27duowbN26/CE+ShQsXZujQoXnkkUfS\n2dnZL3MAAACg1tVE0D///PNJkhkzZhywb9iwYTn55JPT0dGRDRs29MscAAAAqHU1EfQtLS1JkokT\nJ77j/p7tmzZt6pc5AAAAUOtqIuh37dqVJBkxYsQ77u/Z3tbW1i9zAAAAoNbVRNADAAAAh6cmgr7n\nzHnPGfY/17P93T5DvlJzAAAAoNbVxMfWNTY2Jjn4ve092w92b3yl5/RYunRpli1bdtB9b/+alMsx\nLJ9jWK5t27ZVewkAUBP8PFO+hQsXHnRfU1PTX9x/pGoi6KdPn54kWbdu3QH72tvb09zcnKFDh2bK\nlCn9MqfHwoUL3/UvvedBfJSpsbHRMSycY1i24cOHV3sJAFAT/DxTrp5fxvSc9O1PNXHJ/fjx4zNj\nxoxs3rw5y5cv32/fkiVL0tHRkblz56a+vj5J0tXVlZaWlrS2tvZqDgAAAJSqJs7QJ8miRYty7bXX\n5sYbb8yzzz6b448/Pi+88ELWr1+fxsbGXHHFFfteu3Xr1lxzzTUZO3ZsfvjDHx7xHAAAAChVzQT9\n+PHj873vfS9LlizJmjVrsmbNmjQ0NOSSSy5JU1PTO34UXV1dXUXmAAAAQGnquru7u6u9iJK516Vs\n7r8un2NYtuHDh+f8nz5T7WUAQFX9ctHp2b17d7WXwRGq5gMNa+IeegAAAODwCHoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIAC\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACjQkGovoEdzc3NuvfXWvPDCC+ns7MzEiRMz\nb968XHjhhRk06NB+7/CHP/whV1999UH3z549O9/85jcrtWQAAACompoI+lWrVuX73/9+6uvrM2vW\nrIwaNSqrV6/OTTfdlObm5lxzzTWHNe/EE0/MzJkzD9g+adKkSi0ZAAAAqqrqQb979+785Cc/yaBB\ng3Ldddflfe97X5LkiiuuyPXXX5+VK1dmxYoVmT179iHPnDx5cpqamvpqyQAAAFB1Vb+H/te//nV2\n7NiRc845Z1/MJ8mQIUPymc98Jkly//33V2t5AAAAUJOqfob++eefT5KcdtppB+ybNm1a6uvr09zc\nnL1792bIkENb7rZt2/LAAw9kx44dGT16dKZMmZITTjihousGAACAaqp60Le0tCRJJk6ceMC+QYMG\nZdy4cXnttdeyefPmNDY2HtLMdevWZd26dfttmzZtWq666qocd9xxvV80AAAAVFnVg37Xrl1JkhEj\nRrzj/p7tbW1t7zpr6NChufzyy3PmmWdm3LhxSZJXXnklt9xyS5577rnccMMN+Zd/+ZfU19dXaPUA\nAABQHRUJ+quuuipbtmw55NfPmTPnL3683JEaM2ZMFi5cuN+2U045Jf/0T/+Ua6+9Ni+++GJ+9atf\n5aKLLqr41wYAAID+VJGgnzBhwmGd9T766KP3/XvPGfieM/V/rmf7yJEjj3h9gwYNysc+9rG8+OKL\n+c1vfiPoAQAAKF5Fgv7aa6894vc2NjbmpZdeyqZNm/Z7yn2SvPnmm9m8eXMGDx687xL6IzVmzJgk\nSUdHxyG/Z+nSpVm2bNlB9yU55Pv6qV2OYfkcw3Jt27at2ksAgJrg55ny/fnV4m/X1NT0F/cfqarf\nQ3/qqafmsccey5o1aw74rPn169ens7Mz06ZNO+Qn3B/Mhg0bkuSwfjGwcOHCd/1L73moH2VqbGx0\nDAvnGJZt+PDh1V4CANQEP8+Uq+eXMT0nfftT1T+H/uyzz87o0aPz+OOP56WXXtq3fc+ePVm8eHGS\n5Pzzz9/vPbt27UpLS0veeOON/ba//PLL6e7uPuBrPPvss7nnnnuSvHX/PgAAAJSu6mfohw8fnq9+\n9av5/ve/n+uuuy6zZ8/OqFGjsnr16rS0tGTWrFmZNWvWfu958skn8+Mf/zjnnntuvv71r+/bfvPN\nN2fTpk2ZMmVKjj322CRvPeX+ueeeS5JcccUVmTJlSv99cwAAANBHqh70STJz5sxcf/31ufXWW/Pk\nk09mz549mTBhQr70pS/9xQfY1dXV7ffnuXPn5sknn8xLL72UtWvXZu/evWloaMjs2bNzwQUX5JRT\nTunrbwUAAAD6RV33O12jziFzr0vZ3H9dPsewbMOHD8/5P32m2ssAgKr65aLTs3v37movgyNUzQca\nVv0eegAAAODwCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAA\ngAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoA\nAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIAC\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAA\nKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACjQkGov\noKurK/fdd182btyYjRs35rXXXktXV1e++tWvZv78+Uc0s7m5ObfeemteeOGFdHZ2ZuLEiZk3b14u\nvPDCDBrkdxgAAACUr+pB39HRkZtuuilJ0tDQkKOPPjpbtmw54nmrVq3K97///dTX12fWrFkZNWpU\nVq9enZtuuinNzc255pprKrV0AAAAqJqqB319fX2+9a1v5cQTT0xDQ0NuueWWLFu27Ihm7d69Oz/5\nyU8yaNCgXHfddXnf+96XJLniiity/fXXZ+XKlVmxYkVmz55dyW8BAAAA+l3Vrz8fMmRITjvttDQ0\nNPR61q9//evs2LEj55xzzr6Y7/kan/nMZ5Ik999/f6+/DgAAAFRb1YO+kp5//vkkyWmnnXbAvmnT\npqW+vj7Nzc3Zu3dvfy8NAAAAKmpABX1LS0uSZOLEiQfsGzRoUMaNG5eurq5s3ry5v5cGAAAAFTWg\ngn7Xrl1JkhEjRrzj/p7tbW1t/bYmAAAA6AsVeSjeVVdddVhPpp8zZ06uvvrqSnxpAAAA+KtUkaCf\nMGFC6uvrD/n1xxxzTCW+7AF6zsD3nKn/cz3bR44c2SdfHwAAAPpLRYL+2muvrcSYXmtsbMxLL72U\nTZs27feU+yR58803s3nz5gwePDjjxo07pHlLly496EfoLV26dN/XpGyOYfkcw3Jt2botv1x0erWX\nAQBV1dXt55mBYOHChQfd19TU9Bf3H6mqfw59JZ166ql57LHHsmbNmgM+a379+vXp7OzMtGnTMmTI\noX3bCxcufNe/9J4H8VGmxsZGx7BwjmHZHL/yOYblcwzL5xiWzzEsW88vY3pO+vanIh+Kt2vXrrS0\ntOSNN97Yb/vZZ5+d0aNH5/HHH89LL720b/uePXuyePHiJMn555/fr2sFAACAvlATZ+hvv/32fb+R\n2rhxY5LkoYceyn/9138lSU455ZTMnz9/3+uffPLJ/PjHP865556br3/96/u2Dx8+PF/96lfz/e9/\nP9ddd11mz56dUaNGZfXq1WlpacmsWbMya9as/vvGAAAAoI/URNCvXbs269ev32/bhg0bsmHDhn1/\nfnvQ96irqztg28yZM3P99dfn1ltvzZNPPpk9e/ZkwoQJ+dKXvpSLLrqo8osHAACAKqiJoP/nf/7n\nw3r9eeedl/POO++g+6dMmZJ//Md/7OWqAAAAoHYVeQ89AAAA/LUT9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQA\nAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBB\nDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAF\nEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAA\nUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8A\nAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAg\nQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUKAh1V5AV1dX7rvvvmzcuDEbN27Ma6+9lq6urnz1q1/N\n/PnzD2vWH/7wh1x99dUH3T979ux885vf7O2SAQAAoOqqHvQdHR256aabkiQNDQ05+uijs2XLll7N\nPPHEEzNz5swDtk+aNKlXcwEAAKBWVD3o6+vr861vfSsnnnhiGhoacsstt2TZsmW9mjl58uQ0NTVV\naIUAAABQe6oe9EOGDMlpp51W7WUAAABAUaoe9H1h27ZteeCBB7Jjx46MHj06U6ZMyQknnFDtZQH8\n/+3dX0zV9R/H8RdgHJI/OyoBkiZdhPxpzlw4xQGCM3R0UdOILlp/5tYStmrzphlLxlptLLdcy7m1\nNu0GpZgXsGrmylrJn2ieA0EgITo9J9AVYpnCIX4X/GCeQOQcPufPF56Pq/qcw4fP+bx70Xmf8/0D\nAAAAGLMgG3qn0ymn0+k1lpWVpfLyciUmJoZoVQAAAAAAmLOgGnqbzaZdu3Zp48aNSkpKkiRdunRJ\ndXV16ujoUHV1tWpqahQdHR3ilQIAAAAAMD9GGvry8nKfrkyfl5c36+3l/JWQkKDS0lKvsYyMDO3f\nv1+VlZXq7e3V6dOntXPnTuO/GwAAAACAYDLS0KekpPj0rffy5ctN/No5i4yM1LZt29Tb26uuri6j\nDX1qaqqxuRAa1ND6qKG1UT/ro4bWRw2tjxpaHzWEP4w09JWVlSamCaiEhARJE/e9n6sTJ07c9RZ6\nJ06cMLIuAAAAAID1/fdo8Tvt3r171sf9taDOoZ9NT0+PJE2dWz8XpaWls256aWkpjb3FUUPro4bW\nRv2sjxpaHzW0PmpofdTQ+kJVw8ig/0YDbt68KZfLpaGhIa/xCxcuaHx8fNrz29vb1djYKGni/H0A\nAAAAAKwuLL6hP3nypFwulySpv79fkvTNN9/o119/lTRxYbuioqKp57e0tOjw4cMqKCjQ3r17p8aP\nHTsmt9ut9PR0rVixQtLEVe47OjokSWVlZUpPTw/GSwIAAAAAIKDCoqF3OBzq7Oz0Guvp6Zk6TF6S\nV0M/KSIiwuvf8/Pz1dLSor6+PjkcDnk8HtntduXm5qq4uFgZGRmBeQEAAAAAAARZWDT0b7/9tk/P\n37p1q7Zu3TptvLCwUIWFhYZWBQAAAABA+LLkOfQAAAAAACx2NPQAAAAAAFhQ1IEDBw6EehFWNT4+\nruzs7FAvA/NADa2PGlob9bM+amh91ND6qKH1UUPrC1UNI8Znus8bAAAAAAAIaxxyDwAAAACABdHQ\nAwAAAABgQTT0AAAAAABYEA09AAAAAAAWREMPAAAAAIAF0dADAAAAAGBBNPQAAAAAAFjQklAvINz9\n/vvvampqktPplNvt1vXr1xUbG6tHHnlEJSUlys7OnvNcV69eVUVFxV0fz83N1WuvvWZi2biDyRpO\n6u7uVn19vc6fP6+RkRGtXLlShYWF2rFjhyIj+ZzMpLGxMX311Vfq7+9Xf3+/Ll++rLGxMb3yyisq\nKiryaS4yGBomaziJDIaGiX0nh4H3xx9/qLa2Vg6HQ3/99ZfsdrtycnL0zDPPKDY2NujzwHcm9r68\nvFzXrl2b8TG73a4jR46YXDL+r6mpSZ2dnbp48aL6+/t169Yt5eXlzfp3727IYGiYqmGwMkhDfw+1\ntbU6e/asVq1apQ0bNiguLk4ul0s//fST2tra9NJLL2nHjh0+zZmWlqacnJxp46tXrza1bNzBdA1b\nW1t18OBBRUdHa/PmzYqLi1NbW5uOHj2q7u5uvfHGGwF8NYvP7du3dfToUUkTf/yWLVt21z+Oc0UG\ng8t0DclgaJjed3IYGAMDA3rrrbc0PDysnJwcpaam6rffftMXX3whh8Oh6upqxcXFBW0e+M7k3i9d\nulQlJSXTxmNiYkwvG/9XX1+vixcvKiYmRitWrNCVK1f8mocMho6pGkrBySAN/T089thjeuqpp5SW\nluY13tXVperqan366afatGmT7Hb7nOdcs2aNdu/ebXiluBuTNfznn3905MgRRUZG6sCBA3r44Ycl\nSWVlZaqqqlJTU5N+/PFH5ebmBuKlLErR0dF68803lZaWJrvdrrq6On322WfzmpMMBpfJGpLB0AjE\nvpPDwPj44481PDysl19+WcXFxVPjx44dU2Njo2pra7Vnz56gzQPfmdz72NhYchZkL774opYvX66U\nlBR1dnaqqqrKr3nIYOiYqqEUnAxyXOI9FBQUTGsEJSkzM1PZ2dnyeDzq6ekJ/sIwZyZrePbsWd24\ncUNbtmyZekMrSUuWLNGzzz4rSTp16pSRdWPCkiVLtH79ep8+NEN4MVlDMhga7Ls1DAwMyOl0Kikp\nyasBkKTS0lLZbDZ99913GhkZCco88B17b31ZWVlKSUmZ1xz8dxBaJmoYTHxDPw9RUVGS5PP5mn/+\n+ae+/vpr3bhxQ/Hx8UpPT9dDDz0UiCXiHnyt4S+//CJJWr9+/bTHsrKyFB0dre7ubnk8Hi1ZQrzC\nFRm0LjIYGoHYd3Jo3mSd1q1bN+2xmJgYrV27Vk6nUz09PXr00UcDPg98Z3rvR0dH9f333+vatWuy\n2Wxas2aNMjMzudZImCODC0cwMsi7HT9dvXpV7e3tstlsysrK8ulnnU6nnE6n11hWVpbKy8uVmJho\ncpmYhT81dLlckqSVK1dOeywyMlJJSUm6fPmyBgcHlZqaanS9MIcMWhcZDI1A7Ds5NG+2Ok2OT14g\ndrYmwNQ88J3pvR8aGtKHH37oNZaUlKRXX33V5/evCB4yuHAEI4M09H7weDw6dOiQPB6PnnvuOS1d\nunROP2ez2bRr1y5t3LhRSUlJkqRLly6prq5OHR0dqq6uVk1NjaKjowO5fMj/Gt68eVOS7vr8yfG/\n//7bzEJhFBm0PjIYGib3nRwGjqk6kbPQMbn3hYWFyszM1OrVqxUTE6PBwUF9+eWXOnXqlN599129\n8847HBUTpsjgwhCsDC6Khn62WwbMZLbbEvz77786dOiQenp6tGXLFj355JNznjchIUGlpaVeYxkZ\nGdq/f78qKyvV29ur06dPa+fOnXOec7EIlxrCPybrNx9k0H/hUkP4L1xqSA6B4PjvhbhWrVqlPXv2\nyGazqaGhQSdOnNC+fftCtDpg4QtWBhdFQ5+SkuLTJ/3Lly+fcXyyEWxublZubq6xNzqRkZHatm2b\nent71dXVxZuYGYRLDSc/EZ385PS/Jse5N6g3U/ULFDJ4b+FSQzLoP19ruGzZsql/Dsa+k8P5M1Un\nchY6wdj77du3q6GhQV1dXX7PgcAigwub6Qwuioa+srJy3nOMjY3pgw8+UHNzs/Ly8lReXq6IiAgD\nq5uQkJAgaeJ+zZguXGqYmpqqvr4+ud1urys9SxMfFgwODioqKmrqMFJMMFG/QCODswuXGpJB/82n\nhsHad3I4P5PXL3C73TM+Pjl+t/NyTc8D3wVj78lZ+CODC5vpDHKJyznweDx6//331dzcrIKCAlVU\nVBht5iVN3TaNN6GBYaqGkxceOXfu3LTHOjs7NTIyorVr13J1bQsig9ZABkMjWPtODucnOztbkqZd\nbFCSbt26pe7ubtlsNqWnpwdlHvguGHs/mbPk5GS/50BgkcGFzXQGaejvwePxqKamRm1tbdq2bZv2\n7t17z5+5efOmXC6XhoaGvMYvXLig8fHxac9vb29XY2OjpIlzFmGWyRpu2rRJ8fHx+uGHH9TX1zc1\nPjo6qtraWknSE088YfYFwGdk0PrIYHjxZ9/JYfAlJydr3bp1UxdeutPx48d1+/Zt5efnT516MTY2\nJpfLpYGBgXnNA3NM1fDKlSszfvs3ODioTz75RBI5Cwdk0PrCIYMR4zP9XxVTPvroI505c0YJCQna\nvn37jN/qZmdne9124Ntvv9Xhw4dVUFDg1TxWVVXJ7XYrPT1dK1askDRxZd+Ojg5JUllZmZ5++ukA\nv6LFx2QNJam1tVUHDx7Ufffdp9zcXMXFxamtrU0ul0ubN2/W66+/HvDXtNicPHly6hYu/f39unjx\notLT06cONcvIyFBRUdHU88lg+DFVQ4kMhoqv+04OQ2NgYECVlZW6fv26Hn/8cT344IM6f/68Ojs7\nlZqaqurqasXFxUmauH1rRUWFHnjggWm3VfJlHphlooZ1dXVqaGhQZmamEhMTdf/992tgYEA///yz\nRkdHtWHDBu3bt09RUVGhepkLVmtrq1pbWyVN3LLM4XAoKSlJmZmZkqT4+Hg9//zzkshguDJRw2Bm\nkGMS7+Hq1auSpOHhYX3++eczPiciImLG+wj+t3HMz89XS0uL+vr65HA45PF4ZLfblZubq+LiYmVk\nZJh/ATBaQ0nKyclRVVWV6uvr1dLSotHRUaWkpOiFF17gIk4B4nA41NnZ6TXW09MzdciSJK9mcBIZ\nDB+maiiRwVDxd9/JYXAlJyfrvffe0/Hjx3Xu3DmdO3dOdrtdJSUl2r1794y3wZopZ/7MAzNM1DA7\nO1tut1sXLlxQd3e3bt++rdjYWGVmZio/P59v5wOov79fZ86c8RobHBzU4OCgpIlTiiabwUlkMLyY\nqGEwM8g39AAAAAAAWBDn0AMAAAAAYEE09AAAAAAAWBANPQAAAAAAFkRDDwAAAACABdHQAwAAAABg\nQTT0AAAAAABYEA09AAAAAAAWREMPAAAAAIAF0dADAAAAAGBBNPQAAAAAAFgQDT0AAAAAABZEQw8A\nAAAAgAXR0AMAAAAAYEE09AAAAAAAWBANPQAAAAAAFkRDDwAAAACABdHQAwAAAABgQf8DnS/oBimZ\nJ6sAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x105cac278>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.89334234 1.24467268] 0.0854441173131\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3X2c13Wd7//nAA6X4qRyNYDmtkGAy5obHbUjSXvMNnO3\nk8Po5rpehBqIeUhLTShc8+JsHt09sWskwU2zBCRSj6DptseLXa/4qYCKgVdkOjQT4SUXAwzz+6Pb\ncEIuHGC+M98P3u+3W7fi8/l+3vMabh+6zWM+38/nW9Hc3NwcAAAAoFA6dfQAAAAAwO4T9AAAAFBA\ngh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAA\nAApI0AMAAEABCXoAAAAoIEEPAAAABdSlowdIknfffTePP/54nn766bz66qtZs2ZNunTpkkMOOSTH\nHXdcxowZk4qKilatdf7552f16tU73FdVVZXp06e35egAAADQIcriCv2jjz6aH/7wh3nxxRfz0Y9+\nNCeeeGKOOuqo/OY3v8n06dNzww037NZ6PXr0yNixY7f7z0knndSmc8+dO7dN14PEeUXpOLcoBecV\npeLcohScV5RKR51bFc3Nzc0d8pX/yHPPPZfGxsYceeSR22x/6623ctlll+X3v/99Lrroonzyk598\n37XOP//8VFRUZNq0aaUad6va2lr/p0Cbc15RKs4tSsF5Rak4tygF5xWl0lHnVllcoR8xYsR2MZ8k\nBxxwQI4//vgkf4h+AAAA4A/K4h76XencufM2/90amzZtysMPP5zVq1ena9euOfTQQzNs2LB06lQW\nv78AAACAvVbWQb9ly5Y8+OCDSZIjjjii1ce9+eab273lvm/fvhk/fnyGDx/epjMCAABARyjroL/1\n1lvz2muv5cgjj8zIkSNbdcyYMWMybNiwDB48ON26dUtDQ0Puvffe3H///bnmmmty1VVX5ZBDDinx\n5AAAAFBaZfse9IULF2bBggUZNGhQJk6c2OrjampqMmLEiPTu3TuVlZUZNGhQxo0bly984QvZuHGj\nh2AAAACwTyiLp9y/17333ptZs2Zl8ODBmTJlSg444IC9XvO3v/1tLrzwwvTq1Ss/+tGP2mBKAAAA\n6Dhl95b7BQsW5JZbbskhhxySKVOmpHfv3m2ybss6jY2NrT5m7ty5mTdv3k73AQAAQPKHj67bmZqa\nml3u31NldYX+jjvuyG233ZbDDjsskydPTq9evdps7cWLF+eaa67JoEGD8r/+1/9qs3Xr6urabC1I\nkurqaucVJeHcohScV5SKc4tScF5RCtXV1R32tcvmHvp58+bltttuy0c+8pFMmTJllzHf1NSUurq6\n1NfXb7P99ddf3+EV+IaGhsycOTNJcuyxx7bt4AAAANAByuIt9w888EBuv/32dOrUKUOHDs3ChQu3\ne02fPn1y3HHHJUnWrFmTSZMmpU+fPtt8PN0jjzySu+++O8OGDcvBBx+c7t27p76+Pk899VQ2bdqU\nI488MieddFJ7fVsAAABQMmUR9L/73e+S/OFz53cU80kyfPjwrUHfoqKiYps/jxgxIqtWrcorr7yS\n5cuXp7GxMT179sywYcMyevRoV+cBAADYZ5TVPfRF5B4c2pp7uygV5xal4LyiVJxblILzilJwDz0A\nAACwWwQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCA\nBD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAA\nABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCg\nBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACA\nAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQA\nAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBA\ngh4AAAAKSNADAABAAQl6AAAAKKAuHT1Akrz77rt5/PHH8/TTT+fVV1/NmjVr0qVLlxxyyCE57rjj\nMmbMmFRUVLR6vTVr1mT27NlZsmRJ3n333VRVVWXUqFEZO3ZsevbsWcLvBAAAANpHWQT9o48+mhkz\nZuRDH/pQRowYkYMPPjhvvfVWHn/88UyfPj2LFy/O17/+9VatVV9fn8mTJ+ftt9/OqFGjUl1dnZde\nein33HNPlixZkiuvvDK9evUq8XcEAAAApVUWQV9dXZ1LLrkkRx555Dbb//Zv/zaXXXZZHn/88Tzx\nxBP55Cc/+b5rzZgxI2+//XbOPvvsnHDCCVu333LLLVmwYEFmz56dcePGtfn3AAAAAO2pLO6hHzFi\nxHYxnyQHHHBAjj/++CTJc889977r1NfXZ+nSpenbt+82MZ8ktbW16dq1ax566KFs3LixbQYHAACA\nDlIWV+h3pXPnztv89660RP/IkSO329etW7cMHTo0S5cuzYoVK3L44Ye37aB8YDWd89fb/LnzTXd1\n0CQAAMAHSVlcod+ZLVu25MEHH0ySHHHEEe/7+rq6uiTJgAEDdri/ZfuqVavaaEIAAADoGGUd9Lfe\nemtee+21HHnkkTu86v5e69atS5L06NFjh/tbtq9du7bthgQAAIAOULZBv3DhwixYsCCDBg3KxIkT\nO3ocAAAAKCtleQ/9vffem5tvvjmDBw/OlClTWv3Z8S1X4Fuu1L9Xy/bWrjd37tzMmzdvp/uSPzyh\nnw+237znz21xTjivKBXnFqXgvKJUnFuUgvOKUqmtrd3pvpqaml3u31NlF/QLFizILbfckkMOOSRT\npkxJ7969W31syz/Ond0j37J9Z/fYv1dtbe37/qW33LcPLfb2nKiurnZeURLOLUrBeUWpOLcoBecV\npdDSoS0XfdtTWQX9HXfckdtuuy2HHXZYJk+enF69eu3W8SNGjEiSLF26dLt9GzZsyPLly9O1a9cM\nGTKkTeYFAACAjlI299DPmzcvt912Wz7ykY9kypQpu4z5pqam1NXVpb6+fpvt/fr1y8iRI9PQ0JB7\n7713m31z5sxJY2NjRo8encrKypJ8DwAAANBeyuIK/QMPPJDbb789nTp1ytChQ7Nw4cLtXtOnT58c\nd9xxSZI1a9Zk0qRJ6dOnT6ZNm7bN68aNG5cpU6Zk1qxZeeaZZzJw4MC88MILWbZsWaqrq3Pqqae2\nx7cEAAAAJVUWQf+73/0uyR8+d35HMZ8kw4cP3xr0LSoqKrZ7Xb9+/XLttddmzpw5Wbx4cRYvXpyq\nqqqceOKJqamp2elH2gEAAECRlEXQjx07NmPHjm316/v06ZM5c+bsdP+BBx6Y8ePHt8VoAAAAUJbK\n5h56AAAAoPUEPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgB\nAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCA\nBD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAA\nABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCg\nBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACA\nAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQA\nAABQQIIeAAAACkjQAwAAQAEJegAAACigLh09QJI89thjWbZsWX79619n5cqV2bBhQ4499thMnDhx\nt9Y5//zzs3r16h3uq6qqyvTp09tiXAAAAOhwZRH08+fPz69//et069YtBx10UF5//fU9XqtHjx45\n8cQTt9verVu3vRkRAAAAykpZBP2ZZ56ZAw88MP3798+yZctyxRVX7PFaPXv2TE1NTRtOBwAAAOWn\nLIJ++PDhHT0CAAAAFEpZBH1b2rRpUx5++OGsXr06Xbt2zaGHHpphw4alUyfP/wMAAGDfsc8F/Ztv\nvplp06Zts61v374ZP368dwIAAACwz9ingn7MmDEZNmxYBg8enG7duqWhoSH33ntv7r///lxzzTW5\n6qqrcsghh3T0mAAAALDX9qn3odfU1GTEiBHp3bt3KisrM2jQoIwbNy5f+MIXsnHjxsydO7ejRwQA\nAIA2sU9dod+Z448/PnfffXeef/753Tpu7ty5mTdv3k73JUl1dfVez0ex/eY9f26Lc8J5Rak4tygF\n5xWl4tyiFJxXlEptbe1O99XU1Oxy/576QAR97969kySNjY27dVxtbe37/qXX1dXt8Vzsm/b2nKiu\nrnZeURLOLUrBeUWpOLcoBecVpdDyS6KOeEf4PvWW+51ZsWJFkqRfv34dPAkAAAC0jcIFfVNTU+rq\n6lJfX7/N9tdff32HV+AbGhoyc+bMJMmxxx7bLjMCAABAqZXFW+4XLVqURYsWJfnDx84lyfLly/Ov\n//qvSZL9998/p59+epJkzZo1mTRpUvr06bPNx9M98sgjufvuuzNs2LAcfPDB6d69e+rr6/PUU09l\n06ZNOfLII3PSSSe183cGAAAApVEWQb9y5co8+OCD22xraGhIQ0NDkj98jnxL0LeoqKjY5s8jRozI\nqlWr8sorr2T58uVpbGxMz549M2zYsIwePdrVeQAAAPYpZRH0Y8eOzdixY1v12j59+mTOnDnbbR8+\nfHiGDx/e1qMBAABAWSrcPfQAAACAoAcAAIBCEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8A\nAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk\n6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAA\noIAEPewjmpub88ILL+S5557Lpk2bOnocAACgxLp09ADA3vn973+fn/3sZ5k7d26ef/75JMmf/umf\n5u67787+++/fwdMBAAClIuihoBobGzNjxoz80z/9U9atW5ckOeCAA/LWW2/lxRdfzC9/+ct88Ytf\n7OApAQCAUvGWeyigf//3f89f/uVf5uqrr866dety3HHH5aabbsrTTz+dMWPGJEkqKio6eEoAAKCU\nXKGHAvn973+fSy+9NAsXLkySfOQjH8mVV16ZT3/600mSurq6PPTQQ+ncuXM+8YlPdOSoAABAiQl6\nKIgHHnggkyZNSkNDQ3r27Jmvf/3rOfvss1NZWbn1NTfffHOamppy0kknZeDAgR04LQAAUGqCHsrc\nhg0bcvXVV+dHP/pRkuSoo47K//7f/3u7YP/d736XH//4x0mScePGtfucAABA+xL0UMaef/75TJw4\nMb/61a/SpUuXfOMb38j48ePTuXPn7V777W9/O2+99VY+85nP5C/+4i86YFoAAKA9CXooU3Pnzs1l\nl12WDRs25E/+5E8ybdq0/Pmf//kOX/tv//Zvueuuu9K9e/dcffXVHogHAAAfAIIeykxjY2MuueSS\n3HrrrUmSU045Jd/97nfTo0ePHb5+7dq1+da3vpUk+eY3v5nBgwe326wAAEDHEfRQRn7729/mS1/6\nUh5//PF07do1V111Vf72b/92l8f8wz/8Q15//fWMHDkyZ599djtNCgAAdDRBD2XiySefzDnnnJP6\n+voMGjQoN910U0aOHLnLY/7P//k/ufXWW9O1a9dcd9116dLFP2kAAPig6NTRAwDJnDlzUlNTk/r6\n+hx33HFZuHDh+8b8q6++mm9+85tJkilTpmTEiBHtMSoAAFAmBD10oM2bN+fb3/52vv71r2fjxo05\n66yzct999+Wggw7a5XHr16/POeeck7fffjsnnHBCzjzzzPYZGAAAKBvenwsdZM2aNRk/fnz+4z/+\nI/vtt1+uvvrqfPnLX85+++23y+Oam5tz+eWX59lnn82HP/zh3HDDDZ5qDwAAH0CCHjrAypUrc9pp\np2XlypXp06dPbrrppowaNapVx/70pz/NnDlz0q1bt/zwhz/MAQccUOJpAQCAciTooZ0988wz+bu/\n+7usXr06hx9+eGbOnJmBAwe26tglS5Zk8uTJSZJrr73WffMAAPAB5h56aEcPP/xwTj755KxevTqj\nR4/Oz372s1bH/Jo1a3Luuedm48aN+fu///uMHTu2xNMCAADlTNBDO7nrrrty+umnZ+3atfniF7+Y\nm2++Ob169WrVsRs2bMhXvvKVvPbaa/n4xz+eqVOnlnZYAACg7Al6aAczZ87MhAkTsmnTpnzlK1/J\n97///VRWVrbq2KamplxwwQV54okn0r9///zwhz9M165dSzwxAABQ7txDDyXU3Nyc//k//2e+//3v\nJ0m+9a1vZcKECa1+Kn1zc3O+853vZOHChendu3d+8pOfpLq6upQjAwAABSHooUQ2b96cSy65JLNn\nz07nzp3zve99L6eccspurXHjjTdm1qxZqayszMyZM/Oxj32sRNMCAABFI+ihBNavX5/x48fn/vvv\nT7du3fKDH/wgxx9//G6tMW/evFx11VWpqKjIP//zP+foo48u0bQAAEARCXpoY2+88UbOOuusLFq0\nKFVVVbn55pvziU98YrfWeOihh3LRRRclSaZOnZq//uu/LsWoAABAgQl6aGNf+tKXsmLFigwYMCA/\n/elPM2TIkN06/umnn864ceOyefPmfPWrX824ceNKNCkAAFBknnIPbWzFihUZMmRI7rrrrt2O+Vdf\nfTWf//znt3603eWXX16iKQEAgKIT9NDGRo0alfnz5+/20+jXrFmT0047Lb/97W/zqU99Ktdff306\ndfJPFAAA2DFvuYc2dtttt6V79+67dcz69etz5pln5uWXX87IkSMzY8YMnzUPAADskst/sBfuv//+\n7bbtbsxv3rw5EyZMyJNPPpmBAwfmnnvuSe/evdtqRAAAYB8l6GEP/eIXv8g555yzV2s0Nzfn8ssv\nz3333Zeqqqr85Cc/2e236gMAAB9Mgh72wMKFC3Puuedm06ZNe7XOP//zP+fWW29N165dM2vWrHz0\nox9towkBAIB9XVncQ//YY49l2bJl+fWvf52VK1dmw4YNOfbYYzNx4sTdXmvNmjWZPXt2lixZknff\nfTdVVVUZNWpUxo4dm549e5Zgej5o7r777kyYMCFNTU0ZP3588usn9midH/7wh/ne976XioqKTJs2\nLZ/85CfbeFIAAGBfVhZX6OfPn59f/OIXWblyZQ466KA9Xqe+vj6XXHJJHnzwwXz0ox/NiSeemP79\n++eee+7J5MmT8+6777bh1HwQ3XnnnVtjfuLEiXv8sXKzZs3KFVdckST5x3/8x3z+859vyzEBAIAP\ngLK4Qn/mmWfmwAMPTP/+/bNs2bKtobO7ZsyYkbfffjtnn312TjjhhK3bb7nllixYsCCzZ8/OuHHj\n2mpsPmB+/vOf52tf+1q2bNmSCy+8MN/4xjeyX5LG97yue0VFNm3Zks0VFTtc58c//nEmT56cJLn6\n6qvz5S9/ubSDAwAA+6SyuEI/fPjw9O/ff6/WqK+vz9KlS9O3b99tYj5Jamtr07Vr1zz00EPZuHHj\nXn0dPpjmz5+/Nea//vWvb435yvr67V7b+7/8l1TW16dLc/N2+2bPnp1LL700SfIP//APOeOMM0o9\nOgAAsI8qi6BvC88991ySZOTIkdvt69atW4YOHZrGxsasWLGivUej4O68885ceOGF2bJlSy6++OJc\ndNFFqaioyH6dOmX/L35xu9d3/s1vsv8Xv5j93nOFft68ebn44ouTJFOmTMlXvvKVdpkfAADYN5XF\nW+7bQl1dXZJkwIABO9w/YMCALF26NKtWrcrhhx/eZl934MCBbbYW5e+6667Lddddt822V/+s73av\n6/yb36TzokXpfNRRaWpqyp133plJkyalubk5l112Wb761a+218gAAMA+ap8J+nXr1iVJevToscP9\nLdvXrl3bpl/3ggsuaNP1KB+vvPJKFixYkObm5nziE5/I0UcfvXVfp06dst+SJal84IGdHt952bJU\nHH107r777lxwwQVbr/Dvyac3AAAAvNc+E/QdpeV+aPYtv/zlL/ODH/wgzc3NGT9+fC6//PJU/NFb\n6Dt37pzujz6a3g88kN/sZI2m4cNzxx13bH0q/oUXXphJkya1zzcAAADs8/aZoG+5At9ypf69Wrbv\nzmfRz507N/PmzdvpviSprq7enTEpgPvuuy/nnHNONm3alAsvvDA33HDDNjGfJM3NzXnrqKPSNHjw\nDtdoGjw4t9fVZcIFF6SpqSnf+ta38t3vfne7dXZk9Zo30r179zb5XuCPvfGGc4u257yiVJxblMLq\nNW/4+Z2Sqa2t3em+mpqaXe7fU/tM0Lf8w1y1atUO97ds39k99jtSW1v7vn/pLffus2/4j//4j5xx\nxhlpbGzMGWeckW984xs7Pae6NDfnnTvuSKacu832psGD86Pzzsv4iRO3PhV/woQJO13nvbp3757P\nznh6r78XAAC2dd+4j/v5nTbX0qItF33b0z4T9CNGjEiSLF26dLt9GzZsyPLly9O1a9cMGTKkvUej\nIBYtWpQzzzwzGzZsyGmnnfa+V9Q3V1Qk/fptt/2HF1+c8//H/0hzc3Muvvhib7MHAABKonAfW9fU\n1JS6urrUv+fzv/v165eRI0emoaEh99577zb75syZk8bGxowePTqVlZXtOS4F8eKLL+bMM8/M+vXr\nU1tbm2uvvTadOr3/P4/NOwj+lpj/5je/KeYBAICSKYsr9IsWLcqiRYuSJG+++WaSZPny5fnXf/3X\nJMn++++f008/PUmyZs2aTJo0KX369Mm0adO2WWfcuHGZMmVKZs2alWeeeSYDBw7MCy+8kGXLlqW6\nujqnnnpqO35XFEV9fX1OO+20vPnmm/lv/+2/5Xvf+16rYn5nWj6aztPsAQCAUiqLoF+5cmUefPDB\nbbY1NDSkoaEhSdK3b9+tQd9iR2+F7tevX6699trMmTMnixcvzuLFi1NVVZUTTzwxNTU1O/1IOz64\n3nnnnZx++ul57bXX8vGPfzw33nhjunTZu38WkydPzvjx49toQgAAgB2raG5ubu7oIYrMQzWKa+PG\njfn7v//7PPzwwznssMNy55135qCDDtqtNZqbm7Pl3L/ZZlvnm+7aq7k8FA8AoDTuG/fxrF+/vqPH\nYB/TkZ+cULh76KEtbNmyJRdddFEefvjh9OnTJz/5yU92O+abmppy6aWXlmhCAACAXRP0fCBde+21\nmT9/fnr27Jkf//jHOfTQQ3fr+A0bNuSrX/1qbr311hJNCAAAsGtlcQ89tKeZM2fmX/7lX9KlS5fc\ndNNN+bM/+7PdOv6tt97K2WefncceeywHHHBAiaYEAADYNVfo+UBZsGBBvv3tbydJrrvuunz605/e\nreN/+9vf5uSTT85jjz2W/v37Z/78+aUYEwAA4H25Qs8HxuOPP54LLrggzc3NufTSSzN27NjdOv6l\nl17Kl7/85bz22mv5yEc+kp/+9KcZNGhQmko0LwAAwK64Qs8HwooVK3LWWWelsbExZ5xxxm5/RvzT\nTz+dL37xi1s/3u6OO+7IoEGDSjQtAADA+xP07PPq6upy2mmn5a233srnPve5XHnllamoqGj18Q88\n8EBqa2uzZs2afOYzn8ncuXNz4IEHlnBiAACA9yfo2ae99dZbOf3001NXV5dPfOITmTZtWjp37tzq\n43/2s5/ljDPOyLp161JTU5OZM2emR48eJZwYAACgdQQ9+6ympqacd955+dWvfpU//dM/zaxZs9K9\ne/dWHz99+vR87Wtfy+bNmzNhwoT80z/9U/bbb78STgwAANB6HorHPusf//Ef8/DDD+fggw/OT37y\nk1a/TX7Lli25+uqrc+ONNyZJvvOd7+Tcc88t5agAAAC7TdCzT/rFL36x9e31N954Y6sfYLdp06Zc\nfPHFmTdvXrp06ZIbbrghX/rSl0o8LQAAwO4T9OxzXn755Vx44YVJkssuuyzHHHNMq45bvXp1zjvv\nvDz22GPp0aNHbrrpphx33HElnBQAAGDPCXr2KevWrcu5556bd955J5///Ofz1a9+tVXHPfvssznr\nrLNSV1eX/v37Z+bMmfnzP//zEk8LAACw5zwUj31Gc3NzLrnkkjz//PP5kz/5k1x//fWt+ni6O++8\nM3/zN3+Turq6HHnkkVm4cKGYBwAAyp6gZ58xZ86czJ8/P927d8+MGTOy//777/L1TU1NueaaazJh\nwoRs2LAhp5xySubNm5d+/fq108QAAAB7zlvu2Se88MILmTx5cpLkmmuuydChQ3f5+rfeeisTJ07M\nv//7v6dz586ZOnVqzjrrrFZd0QcAACgHgp7C27RpUyZOnJj169fn5JNPztixY3f5+mXLluWcc87J\nypUrU1VVlenTp+e//tf/2k7TAgAAtA1vuafwZsyYkWeffTaDBw/O1VdfvcvX/uxnP8tJJ52UlStX\nZvjw4Vm4cKGYBwAACknQU2i//vWvc9111yX5w1vte/XqtcPXrV27NhdddFG+9rWvZcOGDRk7dmzu\nuuuuHHrooe05LgAAQJvxlnsKq7m5OZdddlk2bNiQ//7f/3vGjBmzw9c99dRTueCCC7Jy5cp069Yt\nU6dOzd/93d+5Xx4AACg0QU9hLVy4MA8++GCqqqoyderU7fZv3rw53//+93PDDTekqakpw4YNy7/8\ny7+87wPzAAAAikDQU1g/+MEPkiQXX3xxDj744G32vfjii7n44ouzaNGiJMl5552XSy65JF27dm33\nOQEAAEo97VupAAAgAElEQVRB0FNITz/9dJ566qkccMABOeWUU7Zuf+edd3LDDTfkRz/6UTZv3pz+\n/fvnhhtuyOjRoztwWgAAgLYn6Cmk2267LUny5S9/OT169MimTZvy85//PNdcc00aGhpSUVGR0047\nLZdeemkOPPDADp4WAACg7Ql6Cun3v/99kj9ckf/Od76Tn//851u3/cVf/EW++93vZuTIkR05IgAA\nQEkJegpp4MCBSZJbb71167YhQ4ZkwoQJOfnkk9Opk09kBAAA9m2CnkK67LLL0tzcnJdeeikf/vCH\nc8opp2TkyJE+ig4AAPjAEPQUUvfu3XPllVd29BgAAAAdxvuSAQAAoIAEPQAAABSQoAcAAIACEvQA\nAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBA\ngh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAA\nAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABRQl44e4I+tWbMms2fPzpIlS/Luu++m\nqqoqo0aNytixY9OzZ89WrXH++edn9erVO9xXVVWV6dOnt+XIAAAA0CHKJujr6+szefLkvP322xk1\nalSqq6vz0ksv5Z577smSJUty5ZVXplevXq1aq0ePHjnxxBO3296tW7e2HhsAAAA6RNkE/YwZM/L2\n22/n7LPPzgknnLB1+y233JIFCxZk9uzZGTduXKvW6tmzZ2pqako1KgAAAHS4sriHvr6+PkuXLk3f\nvn23ifkkqa2tTdeuXfPQQw9l48aNHTQhAAAAlJeyuEL/3HPPJUlGjhy53b5u3bpl6NChWbp0aVas\nWJHDDz/8fdfbtGlTHn744axevTpdu3bNoYcemmHDhqVTp7L4/QUAAADstbII+rq6uiTJgAEDdrh/\nwIABWbp0aVatWtWqoH/zzTczbdq0bbb17ds348ePz/Dhw/d+YAAAAOhgZRH069atS/KHh9ntSMv2\ntWvXvu9aY8aMybBhwzJ48OB069YtDQ0Nuffee3P//ffnmmuuyVVXXZVDDjmk7YYHAACADrDPvQe9\npqYmI0aMSO/evVNZWZlBgwZl3Lhx+cIXvpCNGzdm7ty5HT0iAAAA7LWyCPqWK/AtV+rfq2V7az+L\nfkeOP/74JMnzzz+/x2sAAABAuSiLt9xXV1cnSVatWrXD/S3bd3aPfWv07t07SdLY2NjqY+bOnZt5\n8+btdF/y/2bng+s37/nz3p4Tb7zxxl4dDwDAzvn5nVKpra3d6b6amppd7t9TZRH0I0aMSJIsXbp0\nu30bNmzI8uXL07Vr1wwZMmSPv8aKFSuSJP369Wv1MbW1te/7l97yQD9osbfnRPfu3dtoEgAA3svP\n77S1ll8SdcTt3WXxlvt+/fpl5MiRWx9g98fmzJmTxsbGjB49OpWVlUmSpqam1NXVpb6+fpvXvv76\n6zu8At/Q0JCZM2cmSY499tgSfRcAAADQfsriCn2SjBs3LlOmTMmsWbPyzDPPZODAgXnhhReybNmy\nVFdX59RTT9362jVr1mTSpEnp06fPNh9P98gjj+Tuu+/OsGHDcvDBB6d79+6pr6/PU089lU2bNuXI\nI4/MSSed1BHfHgAAALSpsgn6fv365dprr82cOXOyePHiLF68OFVVVTnxxBNTU1Ozw4+0q6io2ObP\nI0aMyKpVq/LKK69k+fLlaWxsTM+ePTNs2LCMHj3a1XkAAAD2GWUT9Ely4IEHZvz48e/7uj59+mTO\nnDnbbR8+fHiGDx9eitEAAACgrJTFPfQAAADA7hH0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEP\nAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAF\nJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEA\nAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAE\nPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAA\nFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAH\nAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIC6dPQAf2zNmjWZPXt2\nlixZknfffTdVVVUZNWpUxo4dm549e7b7OgAAAFCuyibo6+vrM3ny5Lz99tsZNWpUqqur89JLL+We\ne+7JkiVLcuWVV6ZXr17ttg4AAACUs7IJ+hkzZuTtt9/O2WefnRNOOGHr9ltuuSULFizI7NmzM27c\nuHZbBwAAAMpZWdxDX19fn6VLl6Zv377bRHiS1NbWpmvXrnnooYeycePGdlkHAAAAyl1ZBP1zzz2X\nJBk5cuR2+7p165ahQ4emsbExK1asaJd1AAAAoNyVRdDX1dUlSQYMGLDD/S3bV61a1S7rAAAAQLkr\ni6Bft25dkqRHjx473N+yfe3ate2yDgAAAJS7sgh6AAAAYPeUxVPuW66ct1xhf6+W7e/3GfJttU6L\nuXPnZt68eTvdlyTV1dWtWot92IL/r02Xe+ONN9p0PQAA/h8/v1MqtbW1O91XU1Ozy/17qiyCvuUf\n1c7ubW/ZvrN749t6nRa1tbXv+5fect8+tJXu3bt39AgAAPssP7/T1lo6tOWib3sqi7fcjxgxIkmy\ndOnS7fZt2LAhy5cvT9euXTNkyJB2WQcAAADKXVkEfb9+/TJy5Mg0NDTk3nvv3WbfnDlz0tjYmNGj\nR6eysjJJ0tTUlLq6utTX1+/VOgAAAFBUZfGW+yQZN25cpkyZklmzZuWZZ57JwIED88ILL2TZsmWp\nrq7OqaeeuvW1a9asyaRJk9KnT59MmzZtj9cBAACAoiqboO/Xr1+uvfbazJkzJ4sXL87ixYtTVVWV\nE088MTU1NTv8KLqKioo2WQcAAACKpqK5ubm5o4coMg/VoK117949n53xdEePAQCwz7lv3Mezfv36\njh6DfUxHfnJCWdxDDwAAAOweQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAK\nSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMA\nAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJ\negAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNADAABAAQl6AAAA\nKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEABCXoAAAAoIEEP\nAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAF\nJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKqEtHD9Bi+fLlmT9/fl544YVs3LgxAwYM\nyJgxY/K5z30unTq17vcOv/vd7zJx4sSd7j/mmGNy4YUXttXIAAAA0GHKIugXLVqU66+/PpWVlTn6\n6KPTq1evPPnkk7n55puzfPnyTJo0abfW+/CHP5xRo0Ztt33w4MFtNTIAAAB0qA4P+vXr12f69Onp\n1KlTpk6dmsMOOyxJcuqpp+aKK67IY489lkceeSTHHHNMq9c89NBDU1NTU6qRAQAAoMN1+D30jz76\naN5555186lOf2hrzSdKlS5eccsopSZL777+/o8YDAACAstThV+ife+65JMkRRxyx3b7hw4ensrIy\ny5cvz+bNm9OlS+vGfeONN/Jv//Zveeedd7L//vtnyJAhOeSQQ9p0bgAAAOhIHR70dXV1SZIBAwZs\nt69Tp07p27dvXnvttTQ0NKS6urpVay5dujRLly7dZtvw4cNz/vnn5+CDD977oQEAAKCDdXjQr1u3\nLknSo0ePHe5v2b527dr3Xatr1645+eST88lPfjJ9+/ZNkrz66qu5/fbb8+yzz+bKK6/M9773vVRW\nVrbR9AAAANAx2iTozz///KxevbrVrz/22GN3+fFye6p3796pra3dZtvHPvaxXH755ZkyZUpefPHF\n/PKXv8xf/dVftfnXBgAAgPbUJkHfv3//3brq/aEPfWjr/265At9ypf69Wrb37Nlzj+fr1KlT/vIv\n/zIvvvhinn/++VYH/dy5czNv3ryd7kvS6tsAoLXeeOONjh4BAGCf5ed3SuW9F5f/WE1NzS7376k2\nCfopU6bs8bHV1dV5+eWXs2rVqm2ecp8kW7ZsSUNDQzp37rz1LfR7qnfv3kmSxsbGVh9TW1v7vn/p\nLc8AgLbSvXv3jh4BAGCf5ed32lrLL4laLvq2pw7/2LrDDz88SbJ48eLt9i1btiwbN27M0KFDW/2E\n+51ZsWJFkuz1LwYAAACgHHR40B911FHZf//985//+Z95+eWXt27ftGlTZs+enST57Gc/u80x69at\nS11dXd58881ttr/yyitpbm7e7ms888wzWbBgQZI/3L8PAAAARdfhT7nv3r17zjvvvFx//fWZOnVq\njjnmmPTq1StPPvlk6urqcvTRR+foo4/e5pgnnngiN954Yz796U9nwoQJW7ffcsstWbVqVYYMGZKD\nDjooyR+ecv/ss88mSU499dQMGTKk/b45AAAAKJEOD/okGTVqVK644orMnz8/TzzxRDZt2pT+/fvn\njDPO2OUD7CoqKrb58+jRo/PEE0/k5ZdfzpIlS7J58+ZUVVXlmGOOyQknnJCPfexjpf5WAAAAoF1U\nNO/oPeq0modq0Na6d++ez854uqPHAADY59w37uNZv359R4/BPqYjPzmhw++hBwAAAHafoAcAAIAC\nEvQAAABQQIIeAAAACkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAA\nAFBAgh4AAAAKSNADAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECC\nHgAAAApI0AMAAEABCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQAAABQQIIeAAAA\nCkjQAwAAQAEJegAAACggQQ8AAAAFJOgBAACggAQ9AAAAFJCgBwAAgAIS9AAAAFBAgh4AAAAKSNAD\nAABAAQl6AAAAKCBBDwAAAAUk6AEAAKCABD0AAAAUkKAHAACAAhL0AAAAUECCHgAAAApI0AMAAEAB\nCXoAAAAoIEEPAAAABSToAQAAoIAEPQAAABSQoAcAAIACEvQAAABQQIIeAAAACkjQAwAAQAEJegAA\nACggQQ8AAAAF1KWjB2hqasovfvGLrFy5MitXrsxrr72WpqamnHfeefnMZz6zR2suX7488+fPzwsv\nvJCNGzdmwIABGTNmTD73uc+lUye/wwAAAKD4OjzoGxsbc/PNNydJqqqq8qEPfSirV6/e4/UWLVqU\n66+/PpWVlTn66KPTq1evPPnkk7n55puzfPnyTJo0qa1GBwAAgA7T4UFfWVmZyy67LB/+8IdTVVWV\n22+/PfPmzdujtdavX5/p06enU6dOmTp1ag477LAkyamnnporrrgijz32WB555JEcc8wxbfktAAAA\nQLvr8Pefd+nSJUcccUSqqqr2eq1HH30077zzTj71qU9tjfmWr3HKKackSe6///69/joAAADQ0To8\n6NvSc889lyQ54ogjtts3fPjwVFZWZvny5dm8eXN7jwYAAABtap8K+rq6uiTJgAEDttvXqVOn9O3b\nN01NTWloaGjv0QAAAKBN7VNBv27duiRJjx49dri/ZfvatWvbbSYAAAAohTZ5KN7555+/W0+mP/bY\nYzNx4sS2+NIAAADwgdQmQd+/f/9UVla2+vUHHnhgW3zZ7bRcgW+5Uv9eLdt79uzZqvXmzp270yfu\nz507N0lSXV29u2PCLq1e80buG/fxjh4DAGCf09Ts53dKp7a2dqf7ampqdrl/T7VJ0E+ZMqUtltlr\n1dXVefnll7Nq1aptnnKfJFu2bElDQ0M6d+6cvn37tmq92tra9/1Lb7lvH9pKdXW184qScG5RCs4r\nSsW5RSk4ryiFll8StVz0bU/71D30hx9+eJJk8eLF2+1btmxZNm7cmKFDh6ZLlzb5PQYAAAB0mEIG\n/bp161JXV5c333xzm+1HHXVU9t9///znf/5nXn755a3bN23alNmzZydJPvvZz7brrAAAAFAKZXGp\n+o477tj61peVK1cmSf7v//2/+dWvfpUk+djHPpbPfOYzW1//xBNP5MYbb8ynP/3pTJgwYev27t27\n57zzzsv111+fqVOn5phjjkmvXr3y5JNPpq6uLkcffXSOPvro9vvGAAAAoETKIuiXLFmSZcuWbbNt\nxYoVWbFixdY//3HQt6ioqNhu26hRo3LFFVdk/vz5eeKJJ7Jp06b0798/Z5xxRv7qr/6q7YcHAP7/\n9u4utMr7jgP41+gSN184vixNs1ndTZrEUWQsZc2orZbNlV6NusybsTEKZVXoBr0pXZgiY4NCrwal\nMAb2ypoivVC20pa9sa0oHSZ1cUmdxmITEmV1dXP1JcsuJKGp1lZzXvIkn8+V+T+H//mf+PPn+Z7z\nPP8HAKiBBRMTExO1XkSR2VSDcrNZC5WitqgEdUWlqC0qQV1RCbW8c0Ihr6EHAACA+U6gBwAAgAIS\n6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEA\nAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCA\nBHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoA\nAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAo\nIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEe\nAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAA\nCkigBwAAgAJaVOsFjI+P5+WXX87Q0FCGhoZy+vTpjI+P59FHH83mzZtvaq4zZ85kx44dH3m8s7Mz\njz/++EyXDAAAADVX80B/8eLF7NmzJ0lSKpWyYsWKnD17dkZzrlu3Lh0dHdeMr1mzZkbzAgAAwGxR\n80BfX1+fJ598MuvWrUupVEpPT09efPHFGc25du3abN26tUwrBAAAgNmn5oF+0aJF2bBhQ62XAQAA\nAIVS80BfCe+++25effXVnD9/PsuWLUtLS0vuuOOOWi8LAAAAymZOBvq+vr709fVNG2tvb8/27duz\nevXqGq0KAAAAymdOBfqGhoY8/PDDufvuu9PY2Jgkefvtt9PT05OjR49m9+7defrpp1NfX1/jlQIA\nAMDMlCXQb9++/aZ2pr/33ntveHu5W7V8+fJ0dXVNG2ttbc1TTz2V7u7uHD9+PK+99loefPDBsj83\nAAAAVFNZAn1TU9NNfeu9cuXKcjztJ1ZXV5cHHnggx48fz7Fjx8oa6Jubm8s2F0xSV1SK2qIS1BWV\noraoBHXFXFKWQN/d3V2OaSpq+fLlSa7e9/6T2rdv30feQm/fvn1lWRcAAADF9+GzxT9o69atNzx+\nq+bUNfQ3Mjg4mCRT19Z/El1dXTf8pXd1dQn2lJ26olLUFpWgrqgUtUUlqCsqpVa1VVf1ZyyDCxcu\nZHh4OOfOnZs2fvLkyUxMTFzz+DfffDMHDx5McvX6fQAAACi6WfEN/UsvvZTh4eEkydDQUJLkt7/9\nbf7+978nubqx3ebNm6cef+jQoTz77LO577778thjj02NP//88xkZGUlLS0tWrVqV5Oou90ePHk2S\nbNu2LS0tLdV4SQAAAFBRsyLQ9/b2pr+/f9rY4ODg1GnySaYF+kkLFiyY9vPGjRtz6NChnDhxIr29\nvbly5UpKpVI6OzuzZcuWtLa2VuYFAAAAQJXNikD/k5/85KYef//99+f++++/ZnzTpk3ZtGlTmVYF\nAAAAs1chr6EHAACA+U6gBwAAgAJauHPnzp21XkRRTUxMZP369bVeBnOMuqJS1BaVoK6oFLVFJagr\nKqVWtbVg4nr3eQMAAABmNafcAwAAQAEJ9AAAAFBAAj0AAAAUkEAPAAAABSTQAwAAQAEJ9AAAAFBA\nAj0AAAAU0KJaL2C2Gx8fz8svv5yhoaEMDQ3l9OnTGR8fz6OPPprNmzff1FxnzpzJjh07PvJ4Z2dn\nHn/88ZkumQIoZ11NGhgYyP79+/PWW2/l0qVLuf3227Np06Z84xvfSF2dz+7mm3LUg541P/3zn//M\n3r1709vbm3//+98plUrp6OjIt771rSxZsqTq8zA3lKMetm/fnrNnz173WKlUynPPPVfOJVMAr7/+\nevr7+3Pq1KkMDQ3l/fffz7333nvD/7s+ip7FpHLVVbV6lkD/MS5evJg9e/YkufqLX7FixUf+xXxS\n69atS0dHxzXja9asmdG8FEe56+rw4cN55plnUl9fn3vuuSdLly7NG2+8kT179mRgYCA/+tGPyrV0\nCqDc9aBnzR+jo6P58Y9/nPfeey8dHR1pbm7OP/7xj/z6179Ob29vdu/enaVLl1ZtHuaGctbDZz7z\nmTz00EPXjC9evLjcy6YA9u/fn1OnTmXx4sVZtWpV3nnnnVuaR8/ig8pVV0l1epZA/zHq6+vz5JNP\nZt26dSmVSunp6cmLL744oznXrl2brVu3lmmFFFE56+q///1vnnvuudTV1WXnzp35whe+kCTZtm1b\ndu3alddffz1//vOf09nZWc6XwCxViXrQs+aPX/7yl3nvvffy/e9/P1u2bJkaf/7553Pw4MHs3bs3\njzzySNXmYW4oZz0sWbJEP2LK9773vaxcuTJNTU3p7+/Prl27bmkePYsPKlddJdXpWc7D/RiLFi3K\nhg0bUiqVar0U5pBy1tVf/vKXnD9/Pl/96lenwtvkc3z7299Okrzyyiszfh6KQT1wq0ZHR9PX15fG\nxsZpb2iTpKurKw0NDfnDH/6QS5cuVWUe5gb1QCW1t7enqalpRnOoUT6sHHVVTb6hr4F33303r776\nas6fP59ly5alpaUld9xxR62XRUH97W9/S5Js2LDhmmPt7e2pr6/PwMBArly5kkWL/JOf6ypRD3rW\n/DBZO3fdddc1xxYvXpw777wzfX19GRwczBe/+MWKz8PcUO56uHz5cv74xz/m7NmzaWhoyNq1a9PW\n1mavGG6ZnkUlVaNneXdfA319fenr65s21t7enu3bt2f16tU1WhVFNTw8nCS5/fbbrzlWV1eXxsbG\nnD59OmNjY2lubq728qiyStSDnjU/3Kh2Jsf7+voyMjJywze15ZqHuaHc9XDu3Ln84he/mDbW2NiY\nH/zgB2lvb5/5gpl39CwqqRo9S6CvooaGhjz88MO5++6709jYmCR5++2309PTk6NHj2b37t15+umn\nU19fX+OVUiQXLlxIcnXTjeuZHP/Pf/5TtTVRO+WsBz1rfilX7ehJfFA562HTpk1pa2vLmjVrsnjx\n4oyNjeU3v/lNXnnllfzsZz/LT3/6U2cPcdP0LCqlWj1rXgT6G90y4Hpu9XYXH2f58uXp6uqaNtba\n2pqnnnoq3d3dOX78eF577bU8+OCDZX9uym+21BVzz2ypLT0LmE0+vLHU5z//+TzyyCNpaGjIgQMH\nsm/fvjzxxBM1Wh3AdNXqWfMi0Dc1Nd3UN0grV66s4GquVVdXlwceeCDHjx/PsWPHvDkuiNlSV5Of\nHE9+wvxhk+PuoVocN1tbK1asmPpzNepBz5qbylU7ehIfVI16+NrXvpYDBw7k2LFjtzwH85eeRbWV\nu2fNi0Df3d1d6yV8rOXLlye5en9yimG21FVzc3NOnDiRkZGRabuaJ8n//ve/jI2NZeHChVOnTDP7\nzaS2qlUPetbcM7mnwsjIyHWPT45/1HWm5Z6HuaEa9aAfMRN6FtVW7p5lS9BZYnBwMEmELm7a5AYt\nR44cueZYf39/Ll26lDvvvNMO9/NEtepBz5p71q9fnyTXbICYJO+//34GBgbS0NCQlpaWqszD3FCN\nepjsR7fddtstz8H8pWdRbeXuWQJ9BVy4cCHDw8M5d+7ctPGTJ09mYmLimse/+eabOXjwYJKr18LC\n9XxUXX3lK1/JsmXL8qc//SknTpyYGr98+XL27t2bJPn6179e1bVSO7dSD3oWydU3FnfdddfUpj0f\n9MILL+TixYvZuHHj1OUg4+PjGR4ezujo6IzmYW4rV12988471/02a2xsLL/61a+S6EfcmJ5FJcyG\nnrVg4nrv1pjmpZdemrqlxdDQUE6dOpWWlpapU29aW1uzefPmqcf/7ne/y7PPPpv77rsvjz322NT4\nrl27MjIykpaWlqxatSrJ1R2jjx49miTZtm1bvvnNb1brZVFj5aqrJDl8+HCeeeaZfOpTn0pnZ2eW\nLl2aN954I8PDw7nnnnvywx/+sHovjJq72XrQs5g0Ojqa7u7u/Otf/8qXv/zlfO5zn8tbb72V/v7+\nNDc3Z/fu3Vm6dGmS5MyZM9mxY0c++9nPXnNLnpuZh7mvHHXV09OTAwcOpK2tLatXr86nP/3pjI6O\n5vFvupYAAAGcSURBVK9//WsuX76cL33pS3niiSeycOHCWr1MauDw4cM5fPhwkqu3B+vt7U1jY2Pa\n2tqSJMuWLct3vvOdJHoWn1w56qqaPcs5uJ9Ab29v+vv7p40NDg5OnS6RZFrwmrRgwYJpP2/cuDGH\nDh3KiRMn0tvbmytXrqRUKqWzszNbtmxJa2trZV4As1K56ipJOjo6smvXruzfvz+HDh3K5cuX09TU\nlO9+97s2LJuHbrUe9Cxuu+22/PznP88LL7yQI0eO5MiRIymVSnnooYeydevW697W6Xo96VbmYe4q\nR12tX78+IyMjOXnyZAYGBnLx4sUsWbIkbW1t2bhxo2/n56mhoaH8/ve/nzY2NjaWsbGxJFcvC5sM\nXpP0LD5OOeqqmj3LN/QAAABQQK6hBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEA\nAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCABHoAAAAoIIEeAAAACkigBwAAgAIS6AEAAKCA\nBHoAAAAoIIEeAAAACkigBwAAgAL6P0ZFXZos0zsPAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x108e85e10>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-1.06161377 1.01498485] 0.0300050672595\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3XuMneVh7/ufB2fG9w4Gj+0Bc0mJr8SbZMshNjXE5CRA\nINVJMgxumzSBuiJgeoilSt1RsIKLOEE7Ek0rlBx2aSI4u6ptHDfdhXILjcLFgF2n9oBNxuZiEhhn\nBtf2Nvh+mfMHZ1wc2+DLWrPmGT4fKVL9vms965npk5X5rne97zugu7u7OwAAAEBR6mo9AQAAAOD4\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAA\nKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo0MBaTyBJnn322axduzavvfZaNmzYkF27dmXmzJm5\n6aabjmucuXPnZtOmTUfc19jYmLvvvrsS0wUAAICa6xNH6JcuXZpHHnkkGzZsyGmnnXZSYw0ZMiRX\nX331Yf/5/Oc/X6HZ/qfFixdXfEywrqgWa4tqsK6oFmuLarCuqJZara0+EfRf+9rX8td//de59957\nM2fOnJMaa+jQoWlpaTnsP1dddVWFZvuflixZUvExwbqiWqwtqsG6olqsLarBuqJaarW2+sRX7idP\nnlzrKQAAAEBR+kTQV9LevXvz5JNPZtOmTWloaMjZZ5+dSZMmpa6uT3wZAQAAACqi3wX91q1bc9dd\ndx2yrampKTfccINvAgAAANBv9KugnzVrViZNmpRx48Zl0KBB6erqysMPP5zHHnss3/nOd3L77bfn\nrLPOqvU0AQAA4KT1q++ht7S0ZMqUKRkxYkTq6+tz5plnZs6cObnqqquyZ88eV7UEAACg3xjQ3d3d\nXetJvNvatWuzYMGCE7oP/dH85je/yc0335xhw4bl7/7u7yoyJgAAANRSv/rK/dGMGDEiSbJ79+7j\net7ixYuPevsBR/sBAADo0draetR9LS0t77n/RH0ggn7dunVJktGjRx/X81pbW9/3l97R0XHC84Ij\naW5utq6oCmuLarCuqBZri2qwrqiG5ubmJLU56FvcOfT79+9PR0dHOjs7D9n+xhtvHPEIfFdXV374\nwx8mSWbOnNkrcwQAAIBq6xNH6FesWJEVK1Ykeee2c0nS3t6e73//+0mS4cOH5ytf+UqSZPPmzZk3\nb15GjRp1yO3pli1blgceeCCTJk3K6aefnsGDB6ezszO/+MUvsnfv3nz84x/P5z//+V7+yQAAAKA6\n+kTQb9iwIT//+c8P2dbV1ZWurq4k79xHvifoewwYMOCQf0+ZMiUbN27Mq6++mvb29uzevTtDhw7N\npEmTcvHFFzs6DwAAQL/S565yXxrn4FBpzu2iWqwtqsG6olqsLarBuqIaes6hr4XizqEHAAAABD0A\nAAAUSdADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQ\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAA\nFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRI0AMAAECBBD30A1u3bs3OnTtrPQ0AAKAXCXooUHd3d5577rn86Z/+aT7+8Y9nypQpOe+88/K5\nz30uK1eurPX0AACAXiDooTDr1q3LF77whXzxi1/Mv/zLv6SzszODBg3KwIEDs3r16nzxi1/MAw88\nUOtpAgAAVSbooRAHDhzI3/7t3+byyy/PihUr0tjYmG984xt56qmnsn79+rz44ou59tprs2/fvnz7\n29/2FXwAAOjnBtZ6AsD727VrV77xjW/kn//5n5Mkf/AHf5Bvf/vbGT58+MHHDBkyJH/5l3+ZlStX\npq2tLT/+8Y/z5S9/uVZTBgAAqqxPBP2zzz6btWvX5rXXXsuGDRuya9euzJw5MzfddNNxj7V58+Ys\nXLgwq1evzttvv53GxsZMmzYtV199dYYOHVqF2UN17dy5M9dee22efPLJDBs2LH/zN3+Tyy677IiP\nraurS0tLS9ra2rJq1SpBDwAA/VifCPqlS5fmtddey6BBg3LaaafljTfeOKFxOjs7c8stt2Tbtm2Z\nNm1ampub8/LLL+ehhx7K6tWrc9ttt2XYsGEVnj1Uz44dO/LHf/zHeeaZZzJq1Kj8/d//faZMmfKe\nzzn//POTJGvWrOmNKQIAADXSJ4L+a1/7WkaOHJkxY8Zk7dq1WbBgwQmNc88992Tbtm257rrrDjmC\ned999+XBBx/MwoULM2fOnEpNG6pq3759ufbaa/PMM89k9OjRWbx4cc4777z3fd7IkSOTJNu3b6/2\nFAEAgBrqExfFmzx5csaMGXNSY3R2dqatrS1NTU2HfR25tbU1DQ0NeeKJJ7Jnz56Teh3oLd/73vfy\n1FNPZdSoUVmyZMkxxXyS7N27N0lSX19fzekBAAA11ieCvhJ6vl48derUw/YNGjQoEyZMyO7du7Nu\n3brenhoct6effjrf+973MmDAgNx111358Ic/fMzPffPNN5MkjY2N1ZoeAADQB/SboO/o6EiSjB07\n9oj7e7Zv3Lix1+YEJ6Krqyt/9md/lu7u7tx88835vd/7veN6/i9/+cskyfjx46sxPQAAoI/oN0G/\nY8eOJO/cuutIerY7r5i+7MCBA/nqV7+azs7OXHjhhZk3b95xj9He3p4kmTBhQqWnBwAA9CH9Juih\nP7j77rvz8MMP59RTT81dd92VgQOP77qV3d3dWbZsWZLkox/9aDWmCAAA9BH9Juh7jsD3HKn/bT3b\n3Yuevmr9+vW54447kiR/9Vd/lebm5uMeY82aNfn1r3+dUaNG5YILLqj0FAEAgD6kT9y2rhJ64udo\n58j3bD/aOfZHsnjx4ixZsuSo+979unCybrzxxuzbty9f+eM/zu///u+f0BiPP/54kuRzn/ucD684\nzJYtWzJ48OBaT4N+xrqiWqwtqmHT5i3+fqdqWltbj7qvpaXlPfefqH4T9FOmTEmStLW1HbZv165d\naW9vT0NDw3FdKKy1tfV9f+k9F+ODk7F8+fL80z/9UwYPHpxv/rf/ls/e8+9Jkmsmj8yXp45K3XPP\nZVB7e3ZNmJADF16Y/9n2Zhat3XzYOGv+3x8nSZYNnHhwDAAA3vHonI/5+52K6/mQqOegb28qLuj3\n79+fzs7OnHLKKRk9evTB7aNHj87UqVPT1taWhx9+OJdffvnBfYsWLcru3bvzmc98xr256XO6u7tz\n++23J0m+/vWvZ8yYMUk25prJI/OVpv05/aLpOeXXv06SjEiyf9y4fOXH/5hk5CFRv+vNX2fnxpdT\n1zAkw3/X1+0BAKC/6xNBv2LFiqxYsSJJsnXr1iTvXKn7+9//fpJk+PDh+cpXvpIk2bx5c+bNm5dR\no0blrrvuOmScOXPmZP78+fnRj36U559/PmeccUbWr1+ftWvXprm5ObNnz+7FnwqOzbJly/Jv//Zv\nOfXUU/P1r389STL4Q3X58tRRh8R8j1N+/euc/qUv5I+eeib/tG5rdu07kCT5zc/vT5KMnHpJ6gb6\n4AoAAPq7PhH0GzZsyM9//vNDtnV1daWrqytJ0tTUdDDoewwYMOCwcUaPHp077rgjixYtyqpVq7Jq\n1ao0NjbmyiuvTEtLy1FvaQe11PPB1J/8yZ9k2LBhSZKLzm5M3XPPHRbzPU759a9Tt/y5XHTOuXn8\npS3Z87835T9WPpoMGJAxl1zTa3MHAABqp08E/dVXX52rr776mB47atSoLFq06Kj7R44cmRtuuKFS\nU4OqamtryxNPPJGhQ4fm2muvPbj91CEDM+jf2t/zuYPXtWfkf33nmhCdTy5J9/69OfWjMzOoaVxV\n5wwAAPQN/ea2dVCif/iHf0iS/NEf/VEaGxsPbt+yY192TZjwns/dOX5CNu/Ymz1bu9K17J+SJGNm\n/WH1JgsAAPQpgh5q5MCBA3n00UeTJF/4whcO2ff0a1tz4MILs3/ckY+27x83Lgc+cWGe3vC/88aj\n96Z7356cOvWSDD3z2O/iAAAAlE3QQ42sXr06v/nNbzJ27Nh89KMfPWTfzr0H8j/b3symH//jYVG/\nf9y4bPrxP+bvn38zm3/9Uv5j5aMZUHdKzrj8T3pz+gAAQI31iXPo4YPo4YcfTpJcfvnlR7zI4zu3\npBuZLz/9TAY891wGr2vPzvET0v3/34f+H9p+kw2L/3vSfSCjpv+fGXT6Gb38EwAAALUk6KFGHnnk\nkSTvBP3RLFq7Of9r/dbMOPvcjPyv47N5x948vWR9du07kNcf/B/Z8cb61I8cm+bLrj3qGAAAQP8k\n6KEGtm3blvXr16ehoSEXXnjhez52594DefylLYds27Lm6XQ9/Y8ZUHdKPvyHt2Tg4GHVnC4AANAH\nOYceaqC9/Z1b0n3kIx/Jhz70oeN67u4tndmw+LtJkjOumJNhZ02s+PwAAIC+T9BDDfQE/YT3uTXd\nb+vevz+v/sP/nf0738rvTLwwo2e2VGN6AABAAQQ91MCmTZuSJM3Nzcf8nO7u7rz+L/8jb294IR8a\ncVrOueYvMqDOf4UBAOCDSg1ADezZsydJ0tDQcEyP7+7uzhsP3ZPOJ5ckdXX58B98Kx8a+jvVnCIA\nANDHuSge1EDPefPbt29/38d2d3fn9Qf+n3Q+uSQD6k7JuX/4rQz/3f9S7SkCAAB9nKCHGug5d/7F\nF198z8ft37Mzry35q2xe9XgGnDIwH/6j+Tn1/N/rjSkCAAB9nKCHGpg6dWqSZMWKFfmP//iPnHba\naYc95u1fvZhXF34nuze9kbr6wfndr3w7vzNhWm9PFQAA6KOcQw81cOaZZ+bSSy/N9u3b8xd/8RfZ\nuXPnwX1r167Nq4vuyC+//39l96Y3MnjMuZk496/FPAAAcIgB3d3d3bWeRMk6OjpqPQUK9eKLL+aq\nq67Krl27MnLkyHzkIx/Ja6+9lt/85jfvPGBAXUbP/FLOuOy61H2ovraTBQDoBx6d87FDDqRAJRzP\nnasqzVfuoUYmTZqUBx98MDfccEPWrVuX5557LkkybNiwDJn6f2T0xS1pGDm2xrMEAAD6KkEPNTRx\n4sT867/+a15++eW88cYbGTduXCZOnJgrftRW66kBAAB9nKCHGhswYEDOO++8nHfeeUmSU045pcYz\nAgAASuCieAAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAF\nEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAA\nUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8A\nAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAg\nQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAA\nBRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUaWOsJ\nvNvmzZuzcOHCrF69Om+//XYaGxszbdq0XH311Rk6dOgxjTF37txs2rTpiPsaGxtz9913V3LKAAAA\nUBN9Jug7Oztzyy23ZNu2bZk2bVqam5vz8ssv56GHHsrq1atz2223ZdiwYcc01pAhQ3LllVcetn3Q\noEGVnjYAAADURJ8J+nvuuSfbtm3Lddddl8suu+zg9vvuuy8PPvhgFi5cmDlz5hzTWEOHDk1LS0u1\npgoAAAA11yfOoe/s7ExbW1uampoOifkkaW1tTUNDQ5544ons2bOnRjMEAACAvqVPHKFfs2ZNkmTq\n1KmH7Rs0aFAmTJiQtra2rFu3Lueff/77jrd37948+eST2bRpUxoaGnL22Wdn0qRJqavrE59fAAAA\nwEnrE0Hf0dGRJBk7duwR948dOzZtbW3ZuHHjMQX91q1bc9dddx2yrampKTfccEMmT5588hMGAACA\nGusTQb9jx44k71zM7kh6tm/fvv19x5o1a1YmTZqUcePGZdCgQenq6srDDz+cxx57LN/5zndy++23\n56yzzqrc5AEAAKAG+t130FtaWjJlypSMGDEi9fX1OfPMMzNnzpxcddVV2bNnTxYvXlzrKQIAAMBJ\n6xNB33MEvudI/W/r2X6s96I/ks985jNJkhdffPGExwAAAIC+ok985b65uTlJsnHjxiPu79l+tHPs\nj8WIESOSJLt37z7m5yxevDhLliw56r7kP+cOlbJly5ZaTwEAoN/y9zvV0traetR9LS0t77n/RPWJ\noJ8yZUqSpK2t7bB9u3btSnt7exoaGjJ+/PgTfo1169YlSUaPHn3Mz2ltbX3fX3rPBf2gUgYPHlzr\nKQAA9Fv+fqfSej4kqsXp3X3iK/ejR4/O1KlTD17A7t0WLVqU3bt35+KLL059fX2SZP/+/eno6Ehn\nZ+chj33jjTeOeAS+q6srP/zhD5MkM2fOrNJPAQAAAL2nTxyhT5I5c+Zk/vz5+dGPfpTnn38+Z5xx\nRtavX5+1a9emubk5s2fPPvjYzZs3Z968eRk1atQht6dbtmxZHnjggUyaNCmnn356Bg8enM7Ozvzi\nF7/I3r178/GPfzyf//zna/HjAQAAQEX1maAfPXp07rjjjixatCirVq3KqlWr0tjYmCuvvDItLS1H\nvKXdgAEDDvn3lClTsnHjxrz66qtpb2/P7t27M3To0EyaNCkXX3yxo/MAAAD0GwO6u7u7az2JkjkH\nh0obPHhwPnvPv9d6GgAA/c6jcz6WnTt31noa9DO1vNBinziHHgAAADg+gh4AAAAKJOgBAACgQIIe\nAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok\n6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACg\nQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAK\nJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAA\noECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4A\nAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAo0sNYTeLfNmzdn4cKFWb16dd5+++00NjZm2rRp\nufrqqzN06NBeHwcAAAD6qj4T9J2dnbnllluybdu2TJs2Lc3NzXn55Zfz0EMPZfXq1bntttsybNiw\nXhsHAAAA+rI+E/T33HNPtm3bluuuuy6XXXbZwe333XdfHnzwwSxcuDBz5szptXEAAACgL+sT59B3\ndnamra0tTU1Nh0R4krS2tqahoSFPPPFE9uzZ0yvjAAAAQF/XJ4J+zZo1SZKpU6cetm/QoEGZMGFC\ndu/enXXr1vXKOAAAANDX9Ymg7+joSJKMHTv2iPt7tm/cuLFXxgEAAIC+rk8E/Y4dO5IkQ4YMOeL+\nnu3bt2/vlXEAAACgr+sTQQ8AAAAcnz4R9D1HznuOsP+2nu3vdw/5So0DAAAAfV2fuG1dc3NzkqOf\n296z/Wjnxld6nB6LFy/OkiVLjrrv3a8JlbJly5ZaTwEAoN/y9zvV0traetR9LS0t77n/RPWJoJ8y\nZUqSpK2t7bB9u3btSnt7exoaGjJ+/PheGadHa2vr+/7Sey7EB5UyePDgWk8BAKDf8vc7ldbzIVHP\nQd/e1Ce+cj969OhMnTo1XV1defjhhw/Zt2jRouzevTsXX3xx6uvrkyT79+9PR0dHOjs7T2ocAAAA\nKFWfOEKfJHPmzMn8+fPzox/9KM8//3zOOOOMrF+/PmvXrk1zc3Nmz5598LGbN2/OvHnzMmrUqNx1\n110nPA4AAACUqs8E/ejRo3PHHXdk0aJFWbVqVVatWpXGxsZceeWVaWlpOeKt6AYMGFCRcQAAAKA0\nA7q7u7trPYmSOQeHShs8eHA+e8+/13oaAAD9zqNzPpadO3fWehr0M7W80GKfOIceAAAAOD6CHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAK\nJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAA\noECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4A\nAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiTo\nAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBA\ngh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAA\nCiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACjSw1hPo0d7enqVLl2b9+vXZ\ns2dPxo4dm1mzZuXyyy9PXd2xfe7w5ptv5qabbjrq/hkzZuTmm2+u1JQBAACgZvpE0K9YsSJ33nln\n6uvrM3369AwbNiwrV67Mvffem/b29sybN++4xjvnnHMybdq0w7aPGzeuUlMGAACAmqp50O/cuTN3\n33136urqcuutt+bcc89NksyePTsLFizIs88+m2XLlmXGjBnHPObZZ5+dlpaWak0ZAAAAaq7m59A/\n88wzeeutt3LRRRcdjPkkGThwYK655pokyWOPPVar6QEAAECfVPMj9GvWrEmSXHDBBYftmzx5curr\n69Pe3p59+/Zl4MBjm+6WLVvy05/+NG+99VaGDx+e8ePH56yzzqrovAEAAKCWah70HR0dSZKxY8ce\ntq+uri5NTU15/fXX09XVlebm5mMas62tLW1tbYdsmzx5cubOnZvTTz/95CcNAAAANVbzoN+xY0eS\nZMiQIUfc37N9+/bt7ztWQ0NDvvSlL+UTn/hEmpqakiS/+tWvcv/99+eFF17Ibbfdlu9+97upr6+v\n0OwBAACgNioS9HPnzs2mTZuO+fEzZ858z9vLnagRI0aktbX1kG0TJ07Mt771rcyfPz8vvfRSHn/8\n8VxxxRUVf20AAADoTRUJ+jFjxhzXUe9TTz314P/dcwS+50j9b+vZPnTo0BOeX11dXT796U/npZde\nyosvvijoAQAAKF5Fgn7+/Pkn/Nzm5ua88sor2bhx4yFXuU+SAwcOpKurK6eccsrBr9CfqBEjRiRJ\ndu/efczPWbx4cZYsWXLUfUmO+bx+OFZbtmyp9RQAAPotf79TLb/9bfF3a2lpec/9J6rm59Cff/75\neeqpp7Jq1arD7jW/du3a7NmzJ5MnTz7mK9wfzbp165LkuD4YaG1tfd9fes9F/aBSBg8eXOspAAD0\nW/5+p9J6PiTqOejbm2p+H/pPfvKTGT58eJ5++um88sorB7fv3bs3CxcuTJJ89rOfPeQ5O3bsSEdH\nR7Zu3XrI9ldffTXd3d2Hvcbzzz+fBx98MMk75+8DAABA6Wp+hH7w4MG5/vrrc+edd+bWW2/NjBkz\nMmzYsKxcuTIdHR2ZPn16pk+ffshzli9fnh/84Ae55JJLcuONNx7cft9992Xjxo0ZP358TjvttCTv\nXOX+hRdeSJLMnj0748eP770fDgAAAKqk5kGfJNOmTcuCBQuydOnSLF++PHv37s2YMWPy1a9+9T0v\nYDdgwIBD/n3xxRdn+fLleeWVV7J69ers27cvjY2NmTFjRi677LJMnDix2j8KAAAA9IoB3Uf6jjrH\nzDk4VNrgwYPz2Xv+vdbTAADodx6d87Hs3Lmz1tOgn6nlhRZrfg49AAAAcPwEPQAAABRI0AMAAECB\nBD0AAAADsgK3AAATqElEQVQUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAU\nSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0A\nAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQ\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAA\nFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFGhgrSewf//+PPLII9mw\nYUM2bNiQ119/Pfv378/111+fSy+99ITGbG9vz9KlS7N+/frs2bMnY8eOzaxZs3L55Zenrs5nGAAA\nAJSv5kG/e/fu3HvvvUmSxsbGnHrqqdm0adMJj7dixYrceeedqa+vz/Tp0zNs2LCsXLky9957b9rb\n2zNv3rxKTR0AAABqpuZBX19fn29+85s555xz0tjYmPvvvz9Lliw5obF27tyZu+++O3V1dbn11ltz\n7rnnJklmz56dBQsW5Nlnn82yZcsyY8aMSv4IAAAA0Otq/v3zgQMH5oILLkhjY+NJj/XMM8/krbfe\nykUXXXQw5nte45prrkmSPPbYYyf9OgAAAFBrNQ/6SlqzZk2S5IILLjhs3+TJk1NfX5/29vbs27ev\nt6cGAAAAFdWvgr6joyNJMnbs2MP21dXVpampKfv3709XV1dvTw0AAAAqql8F/Y4dO5IkQ4YMOeL+\nnu3bt2/vtTkBAABANVTkonhz5849rivTz5w5MzfddFMlXhoAAAA+kCoS9GPGjEl9ff0xP37kyJGV\neNnD9ByB7zlS/9t6tg8dOrQqrw8AAAC9pSJBP3/+/EoMc9Kam5vzyiuvZOPGjYdc5T5JDhw4kK6u\nrpxyyilpamo6pvEWL1581FvoLV68+OBrQiVt2rwlj875WK2nAQDQ7+zv9vc71dPa2nrUfS0tLe+5\n/0TV/D70lXT++efnqaeeyqpVqw671/zatWuzZ8+eTJ48OQMHHtuP3dra+r6/9J4L8UGlNDc3W1dU\nhbVFNVhXVIu1RTVYV1RDz4dEPQd9e1ORF8XbsWNHOjo6snXr1kO2f/KTn8zw4cPz9NNP55VXXjm4\nfe/evVm4cGGS5LOf/WyvzhUAAACqoU8cof/JT35y8JOyDRs2JEl+9rOf5Ze//GWSZOLEibn00ksP\nPn758uX5wQ9+kEsuuSQ33njjwe2DBw/O9ddfnzvvvDO33nprZsyYkWHDhmXlypXp6OjI9OnTM336\n9N77wQAAAKBK+kTQr169OmvXrj1k27p167Ju3bqD/3530PcYMGDAYdumTZuWBQsWZOnSpVm+fHn2\n7t2bMWPG5Ktf/WquuOKKyk8eAAAAamBAd3d3d60nUTLn4FBpzu2iWqwtqsG6olqsLarBuqIaanmh\nxSLPoQcAAIAPOkEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAg\nQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAA\nBRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAA\nAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEP\nAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS\n9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFGljr\nCezfvz+PPPJINmzYkA0bNuT111/P/v37c/311+fSSy89rrHefPPN3HTTTUfdP2PGjNx8880nO2UA\nAACouZoH/e7du3PvvfcmSRobG3Pqqadm06ZNJzXmOeeck2nTph22fdy4cSc1LgAAAPQVNQ/6+vr6\nfPOb38w555yTxsbG3H///VmyZMlJjXn22WenpaWlQjMEAACAvqfmQT9w4MBccMEFtZ4GAAAAFKXm\nQV8NW7ZsyU9/+tO89dZbGT58eMaPH5+zzjqr1tMCAACAiumXQd/W1pa2trZDtk2ePDlz587N6aef\nXqNZAQAAQOX0q6BvaGjIl770pXziE59IU1NTkuRXv/pV7r///rzwwgu57bbb8t3vfjf19fU1nikA\nAACcnIoE/dy5c4/ryvQzZ858z9vLnagRI0aktbX1kG0TJ07Mt771rcyfPz8vvfRSHn/88VxxxRUV\nf20AAADoTRUJ+jFjxhzXUe+RI0dW4mWPWV1dXT796U/npZdeyosvvljRoG9ubq7YWNDDuqJarC2q\nwbqiWqwtqsG6oj+pSNDPnz+/EsNU1YgRI5K8c9/7Y7V48eKj3kJv8eLFFZkXAAAA5fvtb4u/W0tL\ny3vuP1H96hz697Ju3bokOXhu/bFobW19z196a2ursKfirCuqxdqiGqwrqsXaohqsK6qlVmurrtdf\nsQJ27NiRjo6ObN269ZDtr776arq7uw97/PPPP58HH3wwyTvn7wMAAEDp+sQR+p/85Cfp6OhIkmzY\nsCFJ8rOf/Sy//OUvk7xzYbtLL7304OOXL1+eH/zgB7nkkkty4403Htx+3333ZePGjRk/fnxOO+20\nJO9c5f6FF15IksyePTvjx4/vjR8JAAAAqqpPBP3q1auzdu3aQ7atW7fu4NfkkxwS9D0GDBhwyL8v\nvvjiLF++PK+88kpWr16dffv2pbGxMTNmzMhll12WiRMnVucHAAAAgF7WJ4L+29/+9nE9/lOf+lQ+\n9alPHbZ91qxZmTVrVoVmBQAAAH1XkefQAwAAwAedoAcAAIACnXLrrbfeWutJlKq7uztTpkyp9TTo\nZ6wrqsXaohqsK6rF2qIarCuqpVZra0D3ke7zBgAAAPRpvnIPAAAABRL0AAAAUCBBDwAAAAUS9AAA\nAFAgQQ8AAAAFEvQAAABQIEEPAAAABRpY6wn0dfv3788jjzySDRs2ZMOGDXn99dezf//+XH/99bn0\n0kuPa6w333wzN91001H3z5gxIzfffPPJTpkCVHJd9Whvb8/SpUuzfv367NmzJ2PHjs2sWbNy+eWX\np67OZ3cfNJVYD96zPpg2b96chQsXZvXq1Xn77bfT2NiYadOm5eqrr87QoUN7fRz6h0qsh7lz52bT\npk1H3NfY2Ji77767klOmAM8++2zWrl2b1157LRs2bMiuXbsyc+bM9/zfrqPxnkWPSq2r3nrPEvTv\nY/fu3bn33nuTvPOLP/XUU4/6/5hjdc4552TatGmHbR83btxJjUs5Kr2uVqxYkTvvvDP19fWZPn16\nhg0blpUrV+bee+9Ne3t75s2bV6mpU4BKrwfvWR8cnZ2dueWWW7Jt27ZMmzYtzc3Nefnll/PQQw9l\n9erVue222zJs2LBeG4f+oZLrYciQIbnyyisP2z5o0KBKT5sCLF26NK+99loGDRqU0047LW+88cYJ\njeM9i3er1LpKeuc9S9C/j/r6+nzzm9/MOeeck8bGxtx///1ZsmTJSY159tlnp6WlpUIzpESVXFc7\nd+7M3Xffnbq6utx6660599xzkySzZ8/OggUL8uyzz2bZsmWZMWNGJX8E+qhqrAfvWR8c99xzT7Zt\n25brrrsul1122cHt9913Xx588MEsXLgwc+bM6bVx6B8quR6GDh3q/YiDvva1r2XkyJEZM2ZM1q5d\nmwULFpzQON6zeLdKraukd96zfA/3fQwcODAXXHBBGhsbaz0V+pFKrqtnnnkmb731Vi666KKD8dbz\nGtdcc02S5LHHHjvp16EM1gMnqrOzM21tbWlqajrkD9okaW1tTUNDQ5544ons2bOnV8ahf7AeqKbJ\nkydnzJgxJzWGNcpvq8S66k2O0NfAli1b8tOf/jRvvfVWhg8fnvHjx+ess86q9bQo1Jo1a5IkF1xw\nwWH7Jk+enPr6+rS3t2ffvn0ZONB/5fu7aqwH71kfDD1rZ+rUqYftGzRoUCZMmJC2trasW7cu559/\nftXHoX+o9HrYu3dvnnzyyWzatCkNDQ05++yzM2nSJNeK4YR5z6KaeuM9y1/3NdDW1pa2trZDtk2e\nPDlz587N6aefXqNZUaqOjo4kydixYw/bV1dXl6amprz++uvp6upKc3Nzb0+PXlaN9eA964PhvdZO\nz/a2trZs3LjxPf+ordQ49A+VXg9bt27NXXfddci2pqam3HDDDZk8efLJT5gPHO9ZVFNvvGcJ+l7U\n0NCQL33pS/nEJz6RpqamJMmvfvWr3H///XnhhRdy22235bvf/W7q6+trPFNKsmPHjiTvXHTjSHq2\nb9++vdfmRO1Ucj14z/pgqdTa8Z7Eu1VyPcyaNSuTJk3KuHHjMmjQoHR1deXhhx/OY489lu985zu5\n/fbbfXuI4+Y9i2rprfesD0TQv9ctA47kRG938X5GjBiR1tbWQ7ZNnDgx3/rWtzJ//vy89NJLefzx\nx3PFFVdU/LWpvL6yruh/+sra8p4F9CW/fWGpM888M3PmzElDQ0MeeOCBLF68OH/+539eo9kBHKq3\n3rM+EEE/ZsyY4zqCNHLkyCrO5nB1dXX59Kc/nZdeeikvvviiP44L0VfWVc8nxz2fMP+2/6+9+wdJ\n7Y3jOP4JiYibUfTHsN0SoSEKysEgqIamoKEl2qOhodVBWppa25qLIBpsr6ElKZTC0EBtSPG01BKV\n/fkNoVyp+7u3Oh07+n5N+igPHvjywS/nPM9THOcMVfv4aG21traWXltRD2RWdTKrdsgk/M6Kehgb\nG1M4HNbZ2dmn50DtIrNgNbMzqyYa+mAwWOmf8FfNzc2SXs8nhz38lLpyu91KpVLK5XJlu5pL0vPz\nswzDkMPhKD0yjZ/vK7VlVT2QWdWnuKdCLpd79/Pi+J/WmZo9D6qDFfVAHuEryCxYzezMYkvQHyKZ\nTEoSTRc+rLhBSzQaffNZPB7Xw8ODenp62OG+RlhVD2RW9fH5fJL0ZgNESbq7u1MikVBDQ4M8Ho8l\n86A6WFEPxTxyuVyfngO1i8yC1czOLBr6b3B7e6tsNqvr6+uy8XQ6rZeXlzffPzk50e7urqTXtbDA\ne/5UV0NDQ3I6nTo4OFAqlSqNFwoFbWxsSJLGx8ct/a2onM/UA5kF6fWPRV9fX2nTnt9tbm7q/v5e\ngUCgtBzk6elJ2WxW+Xz+S/OguplVV5eXl+/ezTIMQ+vr65LII/w/Mgvf4SdkVt3Le//WUGZnZ6d0\npEUmk9HFxYU8Hk/p0Zve3l6Njo6Wvr+3t6e1tTWNjIxofn6+NB4KhZTL5eTxeNTW1ibpdcfo09NT\nSdLMzIympqasuixUmFl1JUmRSESrq6uqr6+X3+9XU1OTjo6OlM1mNTw8rMXFResuDBX30Xogs1CU\nz+cVDAZ1c3OjgYEBdXd36/z8XPF4XG63W8vLy2pqapIkXV1daWFhQR0dHW+O5PnIPKh+ZtTV1taW\nwuGwvF6v2tvb1djYqHw+r+PjYxUKBfX392tpaUkOh6NSl4kKiEQiikQikl6PB4vFYurs7JTX65Uk\nOZ1Ozc7OSiKz8O/MqCsrM4tncP9BLBZTPB4vG0smk6XHJSSVNV5FdXV1Ze8DgYAODw+VSqUUi8X0\n+PiolpYW+f1+TUxMqLe393suAD+SWXUlSYODgwqFQtre3tbh4aEKhYK6uro0NzfHhmU16LP1QGbB\n5XJpZWVFm5ubikajikajamlp0eTkpKanp9891um9TPrMPKheZtSVz+dTLpdTOp1WIpHQ/f29fv36\nJa/Xq0AgwN35GpXJZLS/v182ZhiGDMOQ9LosrNh4FZFZ+Bsz6srKzOIOPQAAAAAANsQaegAAAAAA\nbIiGHgAAAAAAG6KhBwAAAADAhmjoAQAAAACwIRp6AAAAAABsiIYeAAAAAAAboqEHAAAAAMCGaOgB\nAAAAALAhGnoAAAAAAGyIhh4AAAAAABuioQcAAAAAwIZo6AEAAAAAsCEaegAAAAAAbIiGHgAAAAAA\nG6KhBwAAAADAhmjoAQAAAACwIRp6AAAAAABs6D9Bec6/DXgcMQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x105cbb390>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.98075454 0.9731464 ] 0.010536758873\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3X+MluWB//vPAJ3hd0aUAUZRPG1BBkOsCT2CX1A0/or2\nZLMOU3azTV3DxqOYGLL7xzaVVA5pamLWpF3Txj1+62r/ASSk37MaddXtV20VcWlhVOyMiqOVoYwE\nKCo4wDjnD3dYKaD8eJjnufD1Skyc+5655prn6m3nPfdz33ddf39/fwAAAICiDKn2BAAAAIDjJ+gB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQMOqPYEkWbt2bTZt2pR33nknXV1d+fjjjzN37tzcfvvt\nxzXO4sWLs3379iPua2xszP3331+J6QIAAEDV1cQZ+jVr1uTJJ59MV1dXzjzzzJMaa+TIkVmwYMFh\n/3zrW9+q0Gz/26pVqyo+JoPLGpbPGpbN+pXPGpbPGpbPGpbPGpavWmtYE0F/00035cc//nEeeuih\nLFq06KTGGjVqVFpbWw/754YbbqjQbP/b6tWrKz4mg8sals8als36lc8als8als8als8alq9aa1gT\nb7lvaWmp9hQAAACgKDUR9JW0f//+PP/889m+fXsaGhpy3nnnZfr06RkypCbejAAAAAAVcdoF/a5d\nu3Lfffcdsq2pqSm33nqrdwIAAABw2jitgn7+/PmZPn16Jk+enOHDh6enpydPPPFEnnrqqfzoRz/K\nD3/4w5x77rnVniYAAACctNPqfeitra2ZMWNGxo4dm/r6+pxzzjlZtGhRbrjhhuzbt8/dIwEAADht\n1PX39/dXexKftWnTpixbtuyEnkN/NH/84x9zxx13ZPTo0fmf//N/VmRMAAAAqKbT6i33RzN27Ngk\nSW9v73F93apVq476+AFn+wEAABjQ1tZ21H2tra2fu/9EfSmCvrOzM0kyYcKE4/q6tra2L3zRu7u7\nT3heVF9zc7M1LJw1LNuxrN/ZZ5+diy++OP/2b/82SLPieDgGy2cNy2cNy2cNy9bc3JykOid9i7uG\nvq+vL93d3dm2bdsh27ds2XLEM/A9PT35+c9/niSZO3fuoMwRAAAATrWaOEP/8ssv5+WXX07y6WPn\nkqSjoyM//elPkyRjxozJd77znSTJjh07smTJkowfP/6Qx9O98MILefTRRzN9+vScddZZGTFiRLZt\n25bf/va32b9/fy6++OJ861vfGuSfDAAAAE6Nmgj6rq6uPPvss4ds6+npSU9PT5JPnyM/EPQD6urq\nDvl4xowZ2bp1a95+++10dHSkt7c3o0aNyvTp0zNv3jxn5wEAADit1ETQL1iwIAsWLDimzx0/fnxW\nrlx52PaWlpa0tLRUemoAAABQk4q7hh4AAAAQ9AAAAFAkQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAA\nUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8A\nAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAg\nQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAA\nBRL0AAAAUCBBD0BR/vmf/zmtra15/vnnqz0VAICqGlbtCQDAsXrmmWdy9913J0n6+/szd+7cKs8I\nAKB6nKEHoAh79+7N0qVLD37c1dVVvckAANQAQQ9AER588MG88847GTduXJLkk08+qfKMAACqS9AD\nUPP6+/vzr//6r0mSv//7v0+SDBvmqjEA4MtN0ANQ83bv3p0tW7bk/PPPz9e//vUkSXNzc5VnBQBQ\nXYIegJq3ffv2JMnf/M3f5L333kuSnHPOOdWcEgBA1Ql6AGren/70pwwdOjQ33nhj3njjjSTJ1772\ntSrPCgCgugQ9AEW4/PLLM378+HR2diZJpk6dWuUZAQBUl6AHoAitra1JcjDop02bVs3pAABUnaAH\noGb9/ve/T5IMHTo0V199dT766KP84Q9/yFe+8pVMmTKlupMDAKgyQQ9AzXr88ceTJI2NjRk+fPjB\n6+e/+tWvemwdAPClJ+gBqFm/+tWvknwa9Emyfv36JMmFF15YtTkBANQKQQ9ATdq5c2d+97vfJUnG\njh2boUOH5sUXX0ySzJ49u5pTAwCoCYIegJr062efzSeffJIk+cr27Wn4zW/y0tq1SQQ9AECSuAAR\ngJozrL8/z/7X9fNJMuQPf8gfbrwxO5I0T5iQ/2Py5PRVb3oAADWhrr+/v7/akyhZd3d3tafASWhu\nbj7qGvb93f81yLMBgNo39P/9/6o9Bf7M5/0+QxmsYdmam5ur9r295R4AAAAKJOgBAACgQIIeAAAA\nCuSmeHAUrhEsg2vOynak9evr68uFF16Y3bt3550k5yb5f5L8IMn/neS+yZOze+3a7B386XIEjsHy\nWUOAcjlDD0BN2bRpU3bv3p0pZ5+dsydPTpIM3O/+mrPOygf/639lv/u5AgAIegBqywsvvJAkueR/\n/I/sfumldD38cF6qq8tXhg3LxS+8kH1NTTlQV1flWQIAVJ+33ANQU9auXZskuWT27Ozt78+Te/ak\nv78//+cll2TYqFE5UOX5AQDUCmfoAagZ/f39WbduXZJk9uzZSZKnn346STJ//vyqzQsAoBYJegBq\nxh//+Mfs2rUrZ5xxRs4+++z09vYKegCAoxD0ANSMzs7OJMm0adNSV1eX//iP/8iuXbsyffr0TJs2\nrcqzAwCoLYIegJrR0dGRJPn617+eJHnkkUeSJK2trVWbEwBArRL0ANSMz56h37FjR5555pkMHTo0\nf/mXf1nlmQEA1B5BD0DNGAj6qVOn5pe//GUOHDiQyy67LE1NTVWeGQBA7RH0ANSMt99+O0ny1a9+\nNStWrEiSLFiwoJpTAgCoWYIegJqwd+/e7NixI/X19Xn33Xfz2muvZdy4cbn66qurPTUAgJok6AGo\nCe+//36SZPz48fmXf/mXJMlf//VfZ/jw4dWcFgBAzRpW7QkAQJLU1dUlSbZs2ZItW7ZkxIgRuemm\nm6o7KQCAGuYMPQA14Stf+cohHy9ZsiSTJk2q0mwAAGqfoAegJkyYMCHnnntukk+fQ/93f/d3VZ4R\nAEBtq4m33K9duzabNm3KO++8k66urnz88ceZO3dubr/99uMea8eOHVmxYkU2btyYDz/8MI2NjZk1\na1YWLFiQUaNGnYLZA1AJdXV1+cUvfpEXX3wxV111Verr66s9JQCAmlYTQb9mzZq88847GT58eM48\n88xs2bLlhMbZtm1b7rzzzuzevTuzZs1Kc3Nz3nrrrTz++OPZuHFjli9fntGjR1d49gBUyte+9rV8\n7Wtfq/Y0AACKUBNBf9NNN2XcuHGZOHFiNm3alGXLlp3QOA888EB2796dm2++Oddcc83B7Q8//HAe\ne+yxrFixIosWLarUtAEAAKBqauIa+paWlkycOPGkxti2bVva29vT1NR0SMwnSVtbWxoaGvLcc89l\n3759J/V9AAAAoBbURNBXwmuvvZYkmTlz5mH7hg8fnmnTpqW3tzednZ2DPTUAAACouNMm6Lu7u5Pk\nqI84Gti+devWQZsTAAAAnCqnTdDv2bMnSTJy5Mgj7h/Y/tFHHw3anAAAAOBUOW2CHgAAAL5MTpug\nHzgDP3Cm/s8NbPcsegAAAE4HNfHYukpobm5OcvRr5Ae2H+0a+yNZtWpVVq9efdR9n/2+lMsals8a\nlmv7jp0ZMWJEtafBSdi50xqWzhqWzxqWb/uOnX6fOQ20tbUddV9ra+vn7j9Rp03Qz5gxI0nS3t5+\n2L6PP/44HR0daWhoyNSpU495zLa2ti980QduxkeZmpubrWHhrGHZRowYkasf+F21pwEAVfXvi77h\n95mCDfwxZuCk72Aq7i33fX196e7uzrZt2w7ZPmHChMycOTM9PT154oknDtm3cuXK9Pb2Zt68eamv\nrx/M6QIAAMApURNn6F9++eW8/PLLSZJdu3YlSTo6OvLTn/40STJmzJh85zvfSZLs2LEjS5Ysyfjx\n43PfffcdMs6iRYuydOnSPPjgg3nllVdy9tln54033simTZvS3NychQsXDuJPBQAAAKdOTQR9V1dX\nnn322UO29fT0pKenJ0nS1NR0MOgH1NXVHTbOhAkTcvfdd2flypXZsGFDNmzYkMbGxlx//fVpbW09\n6iPtAAAAoDR1/f39/dWeRMlc61I211+XzxqWzTX0APDpNfR79+6t9jQ4QdW8oWFx19ADAAAAgh4A\nAACKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiTo\nAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBA\ngh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAA\nCiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIe\nAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok\n6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACg\nQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAo0rNoT+KwdO3ZkxYoV2bhx\nYz788MM0NjZm1qxZWbBgQUaNGnVMYyxevDjbt28/4r7Gxsbcf//9lZwyAAAAVEXNBP22bdty5513\nZvfu3Zk1a1aam5vz1ltv5fHHH8/GjRuzfPnyjB49+pjGGjlyZK6//vrDtg8fPrzS0wYAAICqqJmg\nf+CBB7J79+7cfPPNueaaaw5uf/jhh/PYY49lxYoVWbRo0TGNNWrUqLS2tp6qqQIAAEDV1cQ19Nu2\nbUt7e3uampoOifkkaWtrS0NDQ5577rns27evSjMEAACA2lITZ+hfe+21JMnMmTMP2zd8+PBMmzYt\n7e3t6ezszIUXXviF4+3fvz/PP/98tm/fnoaGhpx33nmZPn16hgypib9fAAAAwEmriaDv7u5Okkya\nNOmI+ydNmpT29vZs3br1mIJ+165due+++w7Z1tTUlFtvvTUtLS0nP2EAAACospoI+j179iT59GZ2\nRzKw/aOPPvrCsebPn5/p06dn8uTJGT58eHp6evLEE0/kqaeeyo9+9KP88Ic/zLnnnlu5yQMAAEAV\nnHbvQW9tbc2MGTMyduzY1NfX55xzzsmiRYtyww03ZN++fVm1alW1pwgAAAAnrSaCfuAM/MCZ+j83\nsP1Yn0V/JFdddVWS5PXXXz/hMQAAAKBW1MRb7pubm5MkW7duPeL+ge1Hu8b+WIwdOzZJ0tvbe8xf\ns2rVqqxevfqo+5L/njvlsobls4bl2rlzZ7WnAAA1we8z5WtrazvqvtbW1s/df6JqIuhnzJiRJGlv\nbz9s38cff5yOjo40NDRk6tSpJ/w9Ojs7kyQTJkw45q9pa2v7whd94IZ+lKm5udkaFs4alm3EiBHV\nngIA1AS/z5Rr4I8x1bi8uybecj9hwoTMnDnz4A3sPmvlypXp7e3NvHnzUl9fnyTp6+tLd3d3tm3b\ndsjnbtmy5Yhn4Ht6evLzn/88STJ37txT9FMAAADA4KmJM/RJsmjRoixdujQPPvhgXnnllZx99tl5\n4403smnTpjQ3N2fhwoUHP3fHjh1ZsmRJxo8ff8jj6V544YU8+uijmT59es4666yMGDEi27Zty29/\n+9vs378/F198cb71rW9V48cDAACAiqqZoJ8wYULuvvvurFy5Mhs2bMiGDRvS2NiY66+/Pq2trUd8\npF1dXd0hH8+YMSNbt27N22+/nY6OjvT29mbUqFGZPn165s2b5+w8AAAAp42aCfokGTduXG699dYv\n/Lzx48dn5cqVh21vaWlJS0vLqZgaAAAA1JSauIYeAAAAOD6CHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAK\nJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAA\noECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4A\nAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiTo\nAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBA\ngh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAA\nCiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACjSs2hP4rB07dmTFihXZuHFjPvzwwzQ2NmbWrFlZsGBBRo0a\nNejjAAAAQK2qmaDftm1b7rzzzuzevTuzZs1Kc3Nz3nrrrTz++OPZuHFjli9fntGjRw/aOAAAAFDL\naiboH3jggezevTs333xzrrnmmoPbH3744Tz22GNZsWJFFi1aNGjjAAAAQC2riWvot23blvb29jQ1\nNR0S4UnS1taWhoaGPPfcc9m3b9+gjAMAAAC1riaC/rXXXkuSzJw587B9w4cPz7Rp09Lb25vOzs5B\nGQcAAABqXU0EfXd3d5Jk0qRJR9w/sH3r1q2DMg4AAADUupoI+j179iRJRo4cecT9A9s/+uijQRkH\nAAAAal1NBD0AAABwfGoi6AfOnA+cYf9zA9u/6BnylRoHAAAAal1NPLauubk5ydGvbR/YfrRr4ys9\nzoBVq1Zl9erVR9332e9Juaxh+axhuXbu3FntKQBATfD7TPna2tqOuq+1tfVz95+omgj6GTNmJEna\n29sP2/fxxx+no6MjDQ0NmTp16qCMM6Ctre0LX/SBG/FRpubmZmtYOGtYthEjRlR7CgBQE/w+U66B\nP8YMnPQdTDXxlvsJEyZk5syZ6enpyRNPPHHIvpUrV6a3tzfz5s1LfX19kqSvry/d3d3Ztm3bSY0D\nAAAApaqJM/RJsmjRoixdujQPPvhgXnnllZx99tl54403smnTpjQ3N2fhwoUHP3fHjh1ZsmRJxo8f\nn/vuu++ExwEAAIBS1UzQT5gwIXfffXdWrlyZDRs2ZMOGDWlsbMz111+f1tbWIz6Krq6uriLjAAAA\nQGnq+vv7+6s9iZK51qVsrr8unzUs24gRI3L1A7+r9jQAoKr+fdE3snfv3mpPgxNUzRsa1sQ19AAA\nAMDxEfQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAg\nQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAA\nBRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAA\nAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEP\nAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS\n9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFCgYdWewICOjo6s\nWbMmb7zxRvbt25dJkyZl/vz5ufbaazNkyLH93eH999/P7bffftT9c+bMyR133FGpKQMAAEDV1ETQ\nv/zyy7n33ntTX1+f2bNnZ/To0Vm/fn0eeuihdHR0ZMmSJcc13pQpUzJr1qzDtk+ePLlSUwYAAICq\nqnrQ7927N/fff3+GDBmSu+66K+eff36SZOHChVm2bFnWrl2bF154IXPmzDnmMc8777y0traeqikD\nAABA1VX9GvoXX3wxH3zwQS699NKDMZ8kw4YNy7e//e0kyVNPPVWt6QEAAEBNqvoZ+tdeey1JctFF\nFx22r6WlJfX19eno6MiBAwcybNixTXfnzp15+umn88EHH2TMmDGZOnVqzj333IrOGwAAAKqp6kHf\n3d2dJJk0adJh+4YMGZKmpqa899576enpSXNz8zGN2d7envb29kO2tbS0ZPHixTnrrLNOftIAAABQ\nZVUP+j179iRJRo4cecT9A9s/+uijLxyroaEhN954Y775zW+mqakpSfLuu+/mkUceyauvvprly5fn\nnnvuSX19fYVmDwAAANVRkaBfvHhxtm/ffsyfP3fu3M99vNyJGjt2bNra2g7ZdsEFF+T73/9+li5d\nmjfffDPPPPNMrrvuuop/bwAAABhMFQn6iRMnHtdZ7zPOOOPgvw+cgR84U//nBraPGjXqhOc3ZMiQ\nXHnllXnzzTfz+uuvC3oAAACKV5GgX7p06Ql/bXNzczZv3pytW7cecpf7JPnkk0/S09OToUOHHnwL\n/YkaO3ZskqS3t/eYv2bVqlVZvXr1UfclOebr+qld1rB81rBcO3furPYUAKAm+H2mfH/+bvHPam1t\n/dz9J6rq19BfeOGF+fWvf50NGzYc9qz5TZs2Zd++fWlpaTnmO9wfTWdnZ5Ic1x8G2travvBFH7ip\nH2Vqbm62hoWzhmUbMWJEtacAADXB7zPlGvhjzMBJ38FU9efQX3LJJRkzZkx+85vfZPPmzQe379+/\nPytWrEiSXH311Yd8zZ49e9Ld3Z1du3Ydsv3tt99Of3//Yd/jlVdeyWOPPZbk0+v3AQAAoHRVP0M/\nYsSI3HLLLbn33ntz1113Zc6cORk9enTWr1+f7u7uzJ49O7Nnzz7ka9atW5ef/exnueyyy3Lbbbcd\n3P7www9n69atmTp1as4888wkn97l/tVXX02SLFy4MFOnTh28Hw4AAABOkaoHfZLMmjUry5Yty5o1\na7Ju3brs378/EydOzHe/+93PvYFdXV3dIR/Pmzcv69aty+bNm7Nx48YcOHAgjY2NmTNnTq655ppc\ncMEFp/pHAQAAgEFR13+k96hzzFzrUjbXX5fPGpZtxIgRufqB31V7GgBQVf++6BvZu3dvtafBCarm\nDQ2rfg09AAAAcPwEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABA\ngQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAA\nABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNAD\nAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEE\nPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAU\nSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0A\nAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFGhY\ntSfQ19eXJ598Ml1dXenq6sp7772Xvr6+3HLLLbniiitOaMyOjo6sWbMmb7zxRvbt25dJkyZl/vz5\nufbaazNkiL9hAAAAUL6qB31vb28eeuihJEljY2POOOOMbN++/YTHe/nll3Pvvfemvr4+s2fPzujR\no7N+/fo89NBD6ejoyJIlSyo1dQAAAKiaqgd9fX19vve972XKlClpbGzMI488ktWrV5/QWHv37s39\n99+fIUOG5K677sr555+fJFm4cGGWLVuWtWvX5oUXXsicOXMq+SMAAADAoKv6+8+HDRuWiy66KI2N\njSc91osuBilGAAASyElEQVQvvpgPPvggl1566cGYH/ge3/72t5MkTz311El/HwAAAKi2qgd9Jb32\n2mtJkosuuuiwfS0tLamvr09HR0cOHDgw2FMDAACAijqtgr67uztJMmnSpMP2DRkyJE1NTenr60tP\nT89gTw0AAAAq6rQK+j179iRJRo4cecT9A9s/+uijQZsTAAAAnAoVuSne4sWLj+vO9HPnzs3tt99e\niW8NAAAAX0oVCfqJEyemvr7+mD9/3Lhxlfi2hxk4Az9wpv7PDWwfNWrUKfn+AAAAMFgqEvRLly6t\nxDAnrbm5OZs3b87WrVsPuct9knzyySfp6enJ0KFD09TUdEzjrVq16qiP0Fu1atXB70nZrGH5rGG5\ntu/YmX9f9I1qTwMAqqqv3+8zp4O2traj7mttbf3c/Seq6s+hr6QLL7wwv/71r7Nhw4bDnjW/adOm\n7Nu3Ly0tLRk27Nh+7La2ti980QduxEeZmpubrWHhrGHZrF/5rGH5rGH5rGH5rGHZBv4YM3DSdzAV\neVO8PXv2pLu7O7t27Tpk+yWXXJIxY8bkN7/5TTZv3nxw+/79+7NixYokydVXXz2ocwUAAIBToSbO\n0P/yl788+Beprq6uJMmvfvWr/P73v0+SXHDBBbniiisOfv66devys5/9LJdddlluu+22g9tHjBiR\nW265Jffee2/uuuuuzJkzJ6NHj8769evT3d2d2bNnZ/bs2YP3gwEAAMApUhNBv3HjxmzatOmQbZ2d\nnens7Dz48WeDfkBdXd1h22bNmpVly5ZlzZo1WbduXfbv35+JEyfmu9/9bq677rrKTx4AAACqoCaC\n/gc/+MFxff7ll1+eyy+//Kj7p06dmn/8x388yVkBAABA7SryGnoAAAD4shP0AAAAUCBBDwAAAAUS\n9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQA\nAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBB\nDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAF\nEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAA\nUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8A\nAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0\nAAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQoGHVnkBfX1+efPLJdHV1paurK++99176+vpy\nyy235Iorrjiusd5///3cfvvtR90/Z86c3HHHHSc7ZQAAAKi6qgd9b29vHnrooSRJY2NjzjjjjGzf\nvv2kxpwyZUpmzZp12PbJkyef1LgAAABQK6oe9PX19fne976XKVOmpLGxMY888khWr159UmOed955\naW1trdAMAQAAoPZUPeiHDRuWiy66qNrTAAAAgKJUPehPhZ07d+bpp5/OBx98kDFjxmTq1Kk599xz\nqz0tAAAAqJjTMujb29vT3t5+yLaWlpYsXrw4Z511VpVmBQAAAJVzWgV9Q0NDbrzxxnzzm99MU1NT\nkuTdd9/NI488kldffTXLly/PPffck/r6+irPFAAAAE5ORYJ+8eLFx3Vn+rlz537u4+VO1NixY9PW\n1nbItgsuuCDf//73s3Tp0rz55pt55plnct1111X8ewMAAMBgqkjQT5w48bjOeo8bN64S3/aYDRky\nJFdeeWXefPPNvP766xUN+ubm5oqNRXVYw/JZw7JZv/JZw/JZw/JZw/JZQ05ERYJ+6dKllRjmlBo7\ndmyST597f6xWrVp11EforVq1qiLzAgAAoHx//m7xz2ptbf3c/SfqtLqG/vN0dnYmycFr649FW1vb\n577obW1twr5w1rB81rBs1q981rB81rB81rB81rB81VrDIYP+HStgz5496e7uzq5duw7Z/vbbb6e/\nv/+wz3/llVfy2GOPJfn0+n0AAAAoXU2cof/lL3+Z7u7uJElXV1eS5Fe/+lV+//vfJ/n0xnZXXHHF\nwc9ft25dfvazn+Wyyy7LbbfddnD7ww8/nK1bt2bq1Kk588wzk3x6l/tXX301SbJw4cJMnTp1MH4k\nAAAAOKVqIug3btyYTZs2HbKts7Pz4NvkkxwS9APq6uoO+XjevHlZt25dNm/enI0bN+bAgQNpbGzM\nnDlzcs011+SCCy44NT8AAAAADLKaCPof/OAHx/X5l19+eS6//PLDts+fPz/z58+v0KwAAACgdhV5\nDT0AAAB82Ql6AAAAKNDQu+66665qT6JU/f39mTFjRrWnwUmwhuWzhmWzfuWzhuWzhuWzhuWzhuWr\n1hrW9R/pOW8AAABATfOWewAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACjQsGpPoNb98Y9/zNq1a9Pe3p6tW7fmT3/6U0aNGpWvf/3ruf766zNjxoxjHuv999/P7bffftT9\nc+bMyR133FGJafMZlVzDAR0dHVmzZk3eeOON7Nu3L5MmTcr8+fNz7bXXZsgQfyerpL6+vjz55JPp\n6upKV1dX3nvvvfT19eWWW27JFVdccVxjOQaro5JrOMAxWB2VeN0dh6fejh07smLFimzcuDEffvhh\nGhsbM2vWrCxYsCCjRo0a9HE4fpV47RcvXpzt27cfcV9jY2Puv//+Sk6Z/7J27dps2rQp77zzTrq6\nuvLxxx9n7ty5n/vfvaNxDFZHpdZwsI5BQf8FVqxYkRdffDHnnHNOLr744owePTrd3d35z//8z6xf\nvz5/+7d/m2uvvfa4xpwyZUpmzZp12PbJkydXatp8RqXX8OWXX869996b+vr6zJ49O6NHj8769evz\n0EMPpaOjI0uWLDmFP82XT29vbx566KEkn/7H74wzzjjqfxyPlWNwcFV6DR2D1VHp191xeGps27Yt\nd955Z3bv3p1Zs2alubk5b731Vh5//PFs3Lgxy5cvz+jRowdtHI5fJV/7kSNH5vrrrz9s+/Dhwys9\nbf7LmjVr8s4772T48OE588wzs2XLlhMaxzFYPZVaw2RwjkFB/wW+8Y1v5C/+4i8yZcqUQ7a//vrr\nWb58eX7xi1/kkksuSWNj4zGPed5556W1tbXCM+VoKrmGe/fuzf33358hQ4bkrrvuyvnnn58kWbhw\nYZYtW5a1a9fmhRdeyJw5c07Fj/KlVF9fn+9973uZMmVKGhsb88gjj2T16tUnNaZjcHBVcg0dg9Vx\nKl53x+Gp8cADD2T37t25+eabc8011xzc/vDDD+exxx7LihUrsmjRokEbh+NXydd+1KhRjrNBdtNN\nN2XcuHGZOHFiNm3alGXLlp3QOI7B6qnUGiaDcwx6X+IXuOyyyw4LwSSZPn16ZsyYkQMHDqSzs3Pw\nJ8Yxq+Qavvjii/nggw9y6aWXHvyFNkmGDRuWb3/720mSp556qiLz5lPDhg3LRRdddFx/NKO2VHIN\nHYPV4XUvw7Zt29Le3p6mpqZDAiBJ2tra0tDQkOeeey779u0blHE4fl778rW0tGTixIknNYb/HVRX\nJdZwMDlDfxKGDh2aJMd9vebOnTvz9NNP54MPPsiYMWMyderUnHvuuadiinyB413D1157LUly0UUX\nHbavpaUl9fX16ejoyIEDBzJsmMOrVjkGy+UYrI5T8bo7DitvYJ1mzpx52L7hw4dn2rRpaW9vT2dn\nZy688MJTPg7Hr9Kv/f79+/P8889n+/btaWhoyHnnnZfp06e710iNcwyePgbjGPTbzgl6//3388or\nr6ShoSEtLS3H9bXt7e1pb28/ZFtLS0sWL16cs846q5LT5HOcyBp2d3cnSSZNmnTYviFDhqSpqSnv\nvfdeenp60tzcXNH5UjmOwXI5BqvjVLzujsPK+7x1Gtg+cIPYz4uASo3D8av0a79r167cd999h2xr\namrKrbfeety/vzJ4HIOnj8E4BgX9CThw4EB+8pOf5MCBA/mrv/qrjBw58pi+rqGhITfeeGO++c1v\npqmpKUny7rvv5pFHHsmrr76a5cuX55577kl9ff2pnD458TXcs2dPkhz18we2f/TRR5WZKBXlGCyf\nY7A6Kvm6Ow5PnUqtk+Oseir52s+fPz/Tp0/P5MmTM3z48PT09OSJJ57IU089lR/96Ef54Q9/6F0x\nNcoxeHoYrGPwSxH0n/fIgCP5vMcSfPLJJ/nJT36Szs7OXHrppbnhhhuOedyxY8emra3tkG0XXHBB\nvv/972fp0qV5880388wzz+S666475jG/LGplDTkxlVy/k+EYPHG1soacuFpZQ8chDI4/vxHXOeec\nk0WLFqWhoSGPPvpoVq1alX/4h3+o0uzg9DdYx+CXIugnTpx4XH/pHzdu3BG3D4TgSy+9lDlz5lTs\nF50hQ4bkyiuvzJtvvpnXX3/dLzFHUCtrOPAX0YG/nP65ge2eDXqoSq3fqeIY/GK1soaOwRN3vGt4\nxhlnHPz3wXjdHYcnr1Lr5DirnsF47a+66qo8+uijef311094DE4tx+DprdLH4Jci6JcuXXrSY/T1\n9eXHP/5xXnrppcydOzeLFy9OXV1dBWb3qbFjxyb59HnNHK5W1rC5uTmbN2/O1q1bD7nTc/LpHwt6\nenoydOjQg28j5VOVWL9TzTH4+WplDR2DJ+5k1nCwXnfH4ckZuH/B1q1bj7h/YPvRrsut9Dgcv8F4\n7R1ntc8xeHqr9DHoFpfH4MCBA/mnf/qnvPTSS7nsssty++23VzTmkxx8bJpfQk+NSq3hwI1HNmzY\ncNi+TZs2Zd++fZk2bZq7axfIMVgGx2B1DNbr7jg8OTNmzEiSw242mCQff/xxOjo60tDQkKlTpw7K\nOBy/wXjtB46zCRMmnPAYnFqOwdNbpY9BQf8FDhw4kHvuuSfr16/PlVdemdtuu+0Lv2bPnj3p7u7O\nrl27Dtn+9ttvp7+//7DPf+WVV/LYY48l+fSaRSqrkmt4ySWXZMyYMfnNb36TzZs3H9y+f//+rFix\nIkly9dVXV/YH4Lg5BsvnGKwtJ/K6Ow4H34QJEzJz5syDN176rJUrV6a3tzfz5s07eOlFX19furu7\ns23btpMah8qp1Bpu2bLliGf/enp68vOf/zyJ46wWOAbLVwvHYF3/kf5flYN++tOf5tlnn83YsWNz\n1VVXHfGs7owZMw557MD//t//f3t3z9JIFMVh/BGxECMEfEX7kMFOtDBFBBsLK8HCRvwCFha2FsHG\nytbPIKJY+AHWNoOSAQmooLExJFbaSSy2EIXsCosyvtz1+ZXDcOHO4RR/5s6cX2xvbzM9Pd0WHkul\nEvV6nVwuR19fH/D0Z9/T01MAFhcXmZ+f/+Ad/Txp1hAgjmO2trbo6uqiUCiQyWQ4Pj7m5uaGqakp\nVldXP3xPP83BwcHLCJdarcb19TW5XO7lqFk+n2dmZublfnvw+0mrhmAPfpW3Pnf78Gs0Gg3W19e5\nu7tjYmKC0dFRLi4uqFarjIyMsLGxQSaTAZ7Gt66srDAwMPDXWKW3rKN0pVHD3d1dDg8PiaKI/v5+\nuru7aTQanJyc0Gq1GB8fZ21tjc7Ozq/a5n8rjmPiOAaeRpYlScLg4CBRFAHQ29vL0tISYA9+V2nU\n8DN70DOJ/3B7ewvA/f09e3t7r97T0dHx6hzBP4NjsVikXC5zeXlJkiQ8Pj6SzWYpFArMzs6Sz+fT\n34BSrSHA5OQkpVKJ/f19yuUyrVaL4eFhlpeX/YnTB0mShGq12nbt/Pz85cgS0BYGn9mD30daNQR7\n8Ku897nbh59raGiIzc1NdnZ2qFQqVCoVstksc3NzLCwsvDoG67U+e886SkcaNRwbG6Ner3N1dcXZ\n2RkPDw/09PQQRRHFYtG38x+oVqtxdHTUdq3ZbNJsNoGnT4qew+Aze/B7SaOGn9mDvqGXJEmSJClA\nfkMvSZIkSVKADPSSJEmSJAXIQC9JkiRJUoAM9JIkSZIkBchAL0mSJElSgAz0kiRJkiQFyEAvSZIk\nSVKADPSSJEmSJAXIQC9JkiRJUoAM9JIkSZIkBchAL0mSJElSgAz0kiRJkiQFyEAvSZIkSVKADPSS\nJEmSJAXIQC9JkiRJUoAM9JIkSZIkBchAL0mSJElSgH4D9FvpmMhz7NoAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x109125cc0>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.95825462 1.14123258] 0.00370015126405\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA/QAAAJ3CAYAAAA6dhqgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAWJQAAFiUBSVIk8AAAIABJREFUeJzs3X2M1eWB//0PyA6P0vGBp1FQt1mQwbDUO+MWGqjYWNtQ\nf7/k7jClf3TbuPxiFLKG3exu3EpXYhqbNOtmE9OG/ty6kN4RkLD+9halq02rTX3A2MIo2MEntDrs\njFOwqOiAI/cfZrg78iAP58w51/h6JU13ru+Za64zvZid93zP93uGHT58+HAAAACAogyv9QIAAACA\nUyfoAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEA\nAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoEAjar2AJHn77bfz5JNP5je/+U1effXV7N27NyNG\njMi0adNy5ZVXZuHChRk2bNhJzbVs2bL09PQc81hjY2NWr15dyaUDAABATdTFGfrHH388P/rRj/LC\nCy/kz/7sz7Jo0aJ89rOfze9+97usXr06//Iv/3JK840ZMyaLFy8+6j/XXnttRde9YcOGis4HiX1F\n9dhbVIN9RbXYW1SDfUW11GpvDTt8+PDhmnzlP7Jjx4709vbm8ssvHzD+hz/8ITfffHN+//vf52//\n9m9zxRVXfOxcy5Yty7Bhw3LnnXdWa7lHtLW1+aFAxdlXVIu9RTXYV1SLvUU12FdUS632Vl2coZ81\na9ZRMZ8kn/rUp3L11Vcn+TD6AQAAgA/VxTX0J3LWWWcN+O+TcejQofzyl79MT09PRo4cmYsuuigz\nZ87M8OF18fcLAAAAOGN1HfQffPBBHnnkkSTJnDlzTvrz3nzzzaNecj9x4sTccMMNaW5urugaAQAA\noBbqOuh/8pOf5LXXXsvll1+e2bNnn9TnLFy4MDNnzszUqVMzatSodHd3Z8uWLXnooYdy++2357vf\n/W6mTZtW5ZUDAABAddXta9AfeOCBbN68ORdeeGGWL19+0p/X2tqaWbNmZfz48WloaMiFF16YpUuX\n5itf+UoOHjzoJhgAAAAMCXVxl/uP2rJlS+6+++5MnTo1K1euzKc+9akznvO///u/c9NNN2XcuHH5\nt3/7twqsEgAAAGqn7l5yv3nz5qxduzbTpk3LypUrM378+IrM2z9Pb2/vSX/Ohg0bsnHjxuMeAwAA\ngOTDt647ntbW1hMeP111dYb+vvvuyz333JNLLrkkt9xyS8aNG1exubdt25bbb789F154Yf75n/+5\nYvN2dnZWbC5IkqamJvuKqrC3qAb7imqxt6gG+4pqaGpqqtnXrptr6Ddu3Jh77rknn/70p7Ny5coT\nxnxfX186OzvT1dU1YPz1118/5hn47u7u/PjHP06SzJ8/v7ILBwAAgBqoi5fc/+IXv8i9996b4cOH\nZ8aMGXnggQeOesyECRNy5ZVXJkn27t2bFStWZMKECQPenu6xxx7L/fffn5kzZ+b888/P6NGj09XV\nlV//+tc5dOhQLr/88lx77bWD9bQAAACgauoi6N94440kH77v/LFiPkmam5uPBH2/YcOGDfh41qxZ\n2bNnT15++eV0dHSkt7c3Y8eOzcyZM7NgwQJn5wEAABgy6uoa+hK5BodKc20X1WJvUQ32FdVib1EN\n9hXV4Bp6AAAA4JQIegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAA\nACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAH\nAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJ\negAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAo\nkKAHAACAAgl6AAAAKJCgBwAAgAKNqPUCkuTtt9/Ok08+md/85jd59dVXs3fv3owYMSLTpk3LlVde\nmYULF2bYsGEnPd/evXuzbt26bN++PW+//XYaGxvT0tKSxYsXZ+zYsVV8JnB8ff/rfwz4+Kz//Z81\nWgkAADAU1EXQP/7447nrrrtyzjnnZNasWTn//PPzhz/8IU8++WRWr16dbdu25W/+5m9Oaq6urq7c\ncsst2b9/f1paWtLU1JQXX3wxDz74YLZv357bbrst48aNq/IzAgAAgOqqi6BvamrKP/zDP+Tyyy8f\nMP71r389N998c5588sls3bo1V1xxxcfOddddd2X//v257rrrcs011xwZX7t2bTZv3px169Zl6dKl\nFX8OAAAAMJjq4hr6WbNmHRXzSfKpT30qV199dZJkx44dHztPV1dX2tvbM3HixAExnyRtbW0ZOXJk\nHn300Rw8eLAyCwcAAIAaqYugP5GzzjprwH+fSH/0z549+6hjo0aNyowZM9Lb25tdu3ZVdpEAAAAw\nyOo66D/44IM88sgjSZI5c+Z87OM7OzuTJFOmTDnm8f7xPXv2VGiFAAAAUBt1HfQ/+clP8tprr+Xy\nyy8/5ln3jzpw4ECSZMyYMcc83j/+zjvvVG6RAAAAUAN1G/QPPPBANm/enAsvvDDLly+v9XIAAACg\nrtTFXe4/asuWLVmzZk2mTp2alStXnvR7x/efge8/U/9R/eMnO9+GDRuycePG4x5LPrxDP5yM333k\n4xPtHfuKarG3qAb7imqxt6gG+4pqaWtrO+6x1tbWEx4/XXUX9Js3b87atWszbdq0rFy5MuPHjz/p\nz+3/x3m8a+T7x493jf1HtbW1few3vf+6fThVx9s7TU1N9hVVYW9RDfYV1WJvUQ32FdXQ36H9J30H\nU10F/X333Zd77rknl1xySW655ZaMGzfulD5/1qxZSZL29vajjr333nvp6OjIyJEjM3369IqsFwAA\nAGqlbq6h37hxY+655558+tOfzsqVK08Y8319fens7ExXV9eA8UmTJmX27Nnp7u7Oli1bBhxbv359\nent7s2DBgjQ0NFTlOQAAAMBgqYsz9L/4xS9y7733Zvjw4ZkxY0YeeOCBox4zYcKEXHnllUmSvXv3\nZsWKFZkwYULuvPPOAY9bunRpVq5cmbvvvjvPPPNMLrjggjz//PPZuXNnmpqasmTJksF4SgAAAFBV\ndRH0b7zxRpIP33f+WDGfJM3NzUeCvt+wYcOOetykSZPyve99L+vXr8+2bduybdu2NDY2ZtGiRWlt\nbT3uW9oBAABASeoi6BcvXpzFixef9OMnTJiQ9evXH/f4ueeemxtuuKESSwMAAIC6VDfX0AMAAAAn\nT9ADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAA\nQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0A\nAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQ\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAA\nFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUaEStF5AkTzzxRHbu3JlXXnklu3fvznvvvZf58+dn+fLlpzTPsmXL0tPTc8xjjY2N\nWb16dSWWCwAAADVXF0G/adOmvPLKKxk1alTOO++8vP7666c915gxY7Jo0aKjxkeNGnUmSwQAAIC6\nUhdB/61vfSvnnntuJk+enJ07d2bVqlWnPdfYsWPT2tpawdUBAABA/amLoG9ubq71EgAAAKAodRH0\nlXTo0KH88pe/TE9PT0aOHJmLLrooM2fOzPDh7v8HAADA0DHkgv7NN9/MnXfeOWBs4sSJueGGG7wS\nAAAAgCFjSAX9woULM3PmzEydOjWjRo1Kd3d3tmzZkoceeii33357vvvd72batGm1XiYAAACcsSH1\nOvTW1tbMmjUr48ePT0NDQy688MIsXbo0X/nKV3Lw4MFs2LCh1ksEAACAihhSZ+iP5+qrr87999+f\n55577pQ+b8OGDdm4ceNxjyVJU1PTGa+PT4bffeTjE+0d+4pqsbeoBvuKarG3qAb7imppa2s77rHW\n1tYTHj9dn4igHz9+fJKkt7f3lD6vra3tY7/pnZ2dp70uPtmOt3eamprsK6rC3qIa7Cuqxd6iGuwr\nqqH/j0S1eEX4kHrJ/fHs2rUrSTJp0qQarwQAAAAqo7ig7+vrS2dnZ7q6ugaMv/7668c8A9/d3Z0f\n//jHSZL58+cPyhoBAACg2uriJfdPPfVUnnrqqSQfvu1cknR0dOQHP/hBkuTss8/ON77xjSTJ3r17\ns2LFikyYMGHA29M99thjuf/++zNz5sycf/75GT16dLq6uvLrX/86hw4dyuWXX55rr712kJ8ZAAAA\nVEddBP3u3bvzyCOPDBjr7u5Od3d3kg/fR74/6PsNGzZswMezZs3Knj178vLLL6ejoyO9vb0ZO3Zs\nZs6cmQULFjg7DwAAwJBSF0G/ePHiLF68+KQeO2HChKxfv/6o8ebm5jQ3N1d6aQAAAFCXiruGHgAA\nABD0AAAAUCRBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAA\nAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEP\nAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS\n9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQoBG1XgDwob6+vlovAQAAKIgz9FBj+/bty3e+851cdNFFueqq\nq7Jr165aLwkAACiAM/RQQ7/61a9y4403pqenJ0nywgsvZMQI/ywBAICP5ww91Mi///u/5+tf//qR\nmE+S2bNn50//9E9ruCoAAKAUgh5q5Nvf/nb6+vryF3/xF0fGvvOd79RwRQAAQEkEPQyCEYcPHzXW\n0NCQ2269Nb/73e+SJMuWLcvcuXMHe2kAAEChBD1U2YjDh9PQ1XXU+H+MH5//9z/+I52dnfnMZz6T\nv/u7v6vB6gAAgFLVxd23nnjiiezcuTOvvPJKdu/enffeey/z58/P8uXLT3muvXv3Zt26ddm+fXve\nfvvtNDY2pqWlJYsXL87YsWOrsHo4sT8ZPjxj/uf/zFuzJw0Y/2FPT7b29OSCpqb86Ec/yp/8yZ/U\naIUAAECJ6iLoN23alFdeeSWjRo3Keeedl9dff/205unq6sott9yS/fv3p6WlJU1NTXnxxRfz4IMP\nZvv27bntttsybty4iq79ggsuqOh8DF2vfiTo709ybpL/uPnmTJ061fvQAwAAp6Qugv5b3/pWzj33\n3EyePDk7d+7MqlWrTmueu+66K/v37891112Xa6655sj42rVrs3nz5qxbty5Lly6t1LKTJK2trRWd\nj6Fl+PDhee7RR/PMf//3UcfGJHkgSfNbb+WdYcMGfW0AAEDZ6iLom5ubz3iOrq6utLe3Z+LEiQNi\nPkna2try8MMP59FHH81f/uVfpqGh4Yy/Xr9//dd/rdhcDD3r1q3Lhg0bjnmzis1J/iLJ/ubmHD7G\nTfMAAABOZMjcFG/Hjh1JPnwf748aNWpUZsyYkd7e3uzatWuwl8Yn1I4dO/KP//iPSZJ/aWw86viV\nSfqmTk1fS4uX2wMAAKdsyAR9Z2dnkmTKlCnHPN4/vmfPnkFbE59cBw4cyA033JDe3t58+Zpr8v9c\ndNFRj+mbOjVv/Z//k0POzgMAAKehLl5yXwkHDhxIkowZM+aYx/vH33nnnUFbE59c3//+9/Piiy8m\nSZ56+un09PQkF/xfAx6z/8knc+iDD/K+6+cBAIDTMGSCHurFgQMHsmbNmiMf9/T05DOf+cxRj3v3\n8OFEzAMAAKdpyAR9/xn4/jP1H9U/firvRb9hw4Zs3LjxuMeSpKmp6VSWySfApk2b0tvbmyQ566yz\n8td//de5/fbb0/1/f27A4463d3r27svo0aOrvk4+efbts7eoPPuKarG3qIaevfv8/k7VtLW1HfdY\na2vrCY+friET9P3/MI93jXz/+PGusT+Wtra2j/2m91+7D/3+/M//PDfddFN6enryV3/1V5kxY0Z+\n//vfH/W44+2d0aNH54t3/abaywQA+MT5r6Wf8fs7Fdffov0nfQfTkAn6WbNmJUna29uPOvbee++l\no6MjI0eOzPTp0wd7aXzCjB49On//939f62UAAABDXHF3ue/r60tnZ2e6uroGjE+aNCmzZ89Od3d3\ntmzZMuDY+vXr09vbmwULFlT0PegBAACgVuriDP1TTz2Vp556Kkny5ptvJkk6Ojrygx/8IEly9tln\n5xvf+EaSZO/evVmxYkUmTJiQO++8c8A8S5cuzcqVK3P33XfnmWeeyQUXXJDnn38+O3fuTFNTU5Ys\nWTKIzwoAAACqpy6Cfvfu3XnkkUcGjHV3d6e7uztJMnHixCNB32/YMe4OPmnSpHzve9/L+vXrs23b\ntmzbti2NjY1ZtGhRWltbj/uWdgAAAFCaYYcPHz5c60WUzE01OFl9/+t/DPj4rP/9n8d8nJviAQBU\nx38t/UzefffdWi+DIaaW75xQ3DX0AAAAgKAHAACAIgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIAC\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAA\nKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcA\nAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACA\nAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACjaj1Av7Y3r17s27dumzfvj1vv/12Ghsb09LSksWL\nF2fs2LEnNceyZcvS09NzzGONjY1ZvXp1JZcMAAAANVE3Qd/V1ZVbbrkl+/fvT0tLS5qamvLiiy/m\nwQcfzPbt23Pbbbdl3LhxJzXXmDFjsmjRoqPGR40aVellAwAAQE3UTdDfdddd2b9/f6677rpcc801\nR8bXrl2bzZs3Z926dVm6dOlJzTV27Ni0trZWa6kAAABQc3VxDX1XV1fa29szceLEATGfJG1tbRk5\ncmQeffTRHDx4sEYrBAAAgPpSF2fod+zYkSSZPXv2UcdGjRqVGTNmpL29Pbt27cpll132sfMdOnQo\nv/zlL9PT05ORI0fmoosuysyZMzN8eF38/QIAAADOWF0EfWdnZ5JkypQpxzw+ZcqUtLe3Z8+ePScV\n9G+++WbuvPPOAWMTJ07MDTfckObm5jNfMAAAANRYXQT9gQMHknx4M7tj6R9/5513PnauhQsXZubM\nmZk6dWpGjRqV7u7ubNmyJQ899FBuv/32fPe73820adMqt3gAAACogSH3GvTW1tbMmjUr48ePT0ND\nQy688MIsXbo0X/nKV3Lw4MFs2LCh1ksEAACAM1YXQd9/Br7/TP1H9Y+f7HvRH8vVV1+dJHnuuedO\new4AAACoF3XxkvumpqYkyZ49e455vH/8eNfYn4zx48cnSXp7e0/6czZs2JCNGzce91jy/68dPs7v\nPvLx8fbOvn37qr8YAIBPKL+/Uy1tbW3HPdba2nrC46erLoJ+1qxZSZL29vajjr333nvp6OjIyJEj\nM3369NP+Grt27UqSTJo06aQ/p62t7WO/6f039INTdby9M3r06EFeCQDAJ4ff36m0/j8S1eLy7rp4\nyf2kSZMye/bsIzew+2Pr169Pb29vFixYkIaGhiRJX19fOjs709XVNeCxr7/++jHPwHd3d+fHP/5x\nkmT+/PlVehYAAAAweOriDH2SLF26NCtXrszdd9+dZ555JhdccEGef/757Ny5M01NTVmyZMmRx+7d\nuzcrVqzIhAkTBrw93WOPPZb7778/M2fOzPnnn5/Ro0enq6srv/71r3Po0KFcfvnlufbaa2vx9AAA\nAKCi6iboJ02alO9973tZv359tm3blm3btqWxsTGLFi1Ka2vrMd/SbtiwYQM+njVrVvbs2ZOXX345\nHR0d6e3tzdixYzNz5swsWLDA2XkAAACGjLoJ+iQ599xzc8MNN3zs4yZMmJD169cfNd7c3Jzm5uZq\nLA0AAADqSl1cQw8AAACcGkEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEP\nAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS\n9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQ\nIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAA\nAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQA\nAABQIEEPAAAABRL0AAAAUCBBDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQIEEPAAAABRL0AAAAUCBB\nDwAAAAUS9AAAAFAgQQ8AAAAFEvQAAABQoBG1XsAf27t3b9atW5ft27fn7bffTmNjY1paWrJ48eKM\nHTt20OcBAACAelU3Qd/V1ZVbbrkl+/fvT0tLS5qamvLiiy/mwQcfzPbt23Pbbbdl3LhxgzYPAAAA\n1LO6Cfq77ror+/fvz3XXXZdrrrnmyPjatWuzefPmrFu3LkuXLh20eQAAAKCe1cU19F1dXWlvb8/E\niRMHRHiStLW1ZeTIkXn00Udz8ODBQZkHAAAA6l1dnKHfsWNHkmT27NlHHRs1alRmzJiR9vb27Nq1\nK5dddlnV54FqOOt//2etlwAAAAwhdXGGvrOzM0kyZcqUYx7vH9+zZ8+gzAMAAAD1ri6C/sCBA0mS\nMWPGHPN4//g777wzKPMAAABAvauLoAcAAABOTV1cQ99/5rz/DPtH9Y9/3HvIV2qefhs2bMjGjRuP\neyxJmpqaTmouOFn79u2r9RIAAIYsv79TLW1tbcc91traesLjp6sugr7/H9Xxrm3vHz/etfGVnqdf\nW1vbx37T+6/bh0oZPXp0rZcAADBk+f2dSuvv0P6TvoOpLl5yP2vWrCRJe3v7Ucfee++9dHR0ZOTI\nkZk+ffqgzAMAAAD1ri6CftKkSZk9e3a6u7uzZcuWAcfWr1+f3t7eLFiwIA0NDUmSvr6+dHZ2pqur\n64zmAQAAgFLVxUvuk2Tp0qVZuXJl7r777jzzzDO54IIL8vzzz2fnzp1pamrKkiVLjjx27969WbFi\nRSZMmJA777zztOcBAACAUtVN0E+aNCnf+973sn79+mzbti3btm1LY2NjFi1alNbW1mO+Fd2wYcMq\nMg8AAACUZtjhw4cP13oRJXNTDSpt9OjR+eJdv6n1MgAAhpz/WvqZvPvuu7VeBkNMLd85oS6uoQcA\nAABOjaAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIAC\nCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAA\nKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcA\nAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6\nAAAAKJCgBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAgl6AAAAKJCgBwAAgAIJegAAACiQ\noAcAAIACCXoAAAAo0IhaL6BfR0dHNm3alOeffz4HDx7MlClTsnDhwnzpS1/K8OEn93eHN954I8uX\nLz/u8Xnz5uWmm26q1JIBAACgZuoi6J966qnccccdaWhoyNy5czNu3Lg8/fTTWbNmTTo6OrJixYpT\nmu/iiy9OS0vLUeNTp06t1JIBAACgpmoe9O+++25Wr16d4cOH59Zbb80ll1ySJFmyZElWrVqVJ554\nIo899ljmzZt30nNedNFFaW1trdaSAQAAoOZqfg39448/nrfeeiuf+9znjsR8kowYMSJf+9rXkiQP\nPfRQrZYp1sJUAAAVo0lEQVQHAAAAdanmZ+h37NiRJJkzZ85Rx5qbm9PQ0JCOjo68//77GTHi5Ja7\nb9++PPzww3nrrbdy9tlnZ/r06Zk2bVpF1w0AAAC1VPOg7+zsTJJMmTLlqGPDhw/PxIkT89prr6W7\nuztNTU0nNWd7e3va29sHjDU3N2fZsmU5//zzz3zRAAAAUGM1D/oDBw4kScaMGXPM4/3j77zzzsfO\nNXLkyHz1q1/NFVdckYkTJyZJXn311dx777159tlnc9ttt+X73/9+GhoaKrR6AAAAqI2KBP2yZcvS\n09Nz0o+fP3/+Cd9e7nSNHz8+bW1tA8YuvfTSfPvb387KlSvzwgsv5Gc/+1m+/OUvV/xrAwAAwGCq\nSNBPnjz5lM56n3POOUf+7/4z8P1n6j+qf3zs2LGnvb7hw4fnC1/4Ql544YU899xzJx30GzZsyMaN\nG497LMlJXwYAJ2vfvn21XgIAwJDl93eq5aMnl/9Ya2vrCY+frooE/cqVK0/7c5uamvLSSy9lz549\nA+5ynyQffPBBuru7c9ZZZx15Cf3pGj9+fJKkt7f3pD+nra3tY7/p/fcAgEoZPXp0rZcAADBk+f2d\nSuv/I1H/Sd/BVPO3rbvsssuSJNu2bTvq2M6dO3Pw4MHMmDHjpO9wfzy7du1KkjP+wwAAAADUg5oH\n/Wc/+9mcffbZ+dWvfpWXXnrpyPihQ4eybt26JMkXv/jFAZ9z4MCBdHZ25s033xww/vLLL+fw4cNH\nfY1nnnkmmzdvTvLh9fsAAABQuprf5X706NG5/vrrc8cdd+TWW2/NvHnzMm7cuDz99NPp7OzM3Llz\nM3fu3AGfs3Xr1vzwhz/M5z//+dx4441HxteuXZs9e/Zk+vTpOe+885J8eJf7Z599NkmyZMmSTJ8+\nffCeHAAAAFRJzYM+SVpaWrJq1aps2rQpW7duzaFDhzJ58uR885vfPOEN7IYNGzbg4wULFmTr1q15\n6aWXsn379rz//vtpbGzMvHnzcs011+TSSy+t9lMBAACAQTHs8LFeo85Jc1MNKm306NH54l2/qfUy\nAACGnP9a+pm8++67tV4GQ0wt3zmh5tfQAwAAAKdO0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQ\nAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECB\nBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAA\nFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMA\nAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9\nAAAAFEjQAwAAQIEEPQAAABRI0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRI\n0AMAAECBBD0AAAAUSNADAABAgQQ9AAAAFEjQAwAAQIEEPQAAABRoRK0X0NfXl5/+9KfZvXt3du/e\nnddeey19fX25/vrrc9VVV53WnB0dHdm0aVOef/75HDx4MFOmTMnChQvzpS99KcOH+xsGAAAA5at5\n0Pf29mbNmjVJksbGxpxzzjnp6ek57fmeeuqp3HHHHWloaMjcuXMzbty4PP3001mzZk06OjqyYsWK\nSi0dAAAAaqbmQd/Q0JCbb745F198cRobG3Pvvfdm48aNpzXXu+++m9WrV2f48OG59dZbc8kllyRJ\nlixZklWrVuWJJ57IY489lnnz5lXyKQAAAMCgq/nrz0eMGJE5c+aksbHxjOd6/PHH89Zbb+Vzn/vc\nkZjv/xpf+9rXkiQPPfTQGX8dAAAAqLWaB30l7dixI0kyZ86co441NzenoaEhHR0def/99wd7aQAA\nAFBRQyroOzs7kyRTpkw56tjw4cMzceLE9PX1pbu7e7CXBgAAABU1pIL+wIEDSZIxY8Yc83j/+Dvv\nvDNoawIAAIBqqMhN8ZYtW3ZKd6afP39+li9fXokvDQAAAJ9IFQn6yZMnp6Gh4aQff+6551biyx6l\n/wx8/5n6j+ofHzt27EnNt2HDhuPecX/Dhg1JkqamplNdJpxQz959+a+ln6n1MgAAhpy+w35/p3ra\n2tqOe6y1tfWEx09XRYJ+5cqVlZjmjDU1NeWll17Knj17BtzlPkk++OCDdHd356yzzsrEiRNPar62\ntraP/ab3X7cPldLU1GRfURX2FtVgX1Et9hbVYF9RDf1/JOo/6TuYhtQ19JdddlmSZNu2bUcd27lz\nZw4ePJgZM2ZkxIiK/B0DAAAAaqbIoD9w4EA6Ozvz5ptvDhj/7Gc/m7PPPju/+tWv8tJLLx0ZP3To\nUNatW5ck+eIXvzioawUAAIBqqItT1ffdd9+Rl77s3r07SfLzn/88v/3tb5Mkl156aa666qojj9+6\ndWt++MMf5vOf/3xuvPHGI+OjR4/O9ddfnzvuuCO33npr5s2bl3HjxuXpp59OZ2dn5s6dm7lz5w7e\nEwMAAIAqqYug3759e3bu3DlgbNeuXdm1a9eRj/846PsNGzbsqLGWlpasWrUqmzZtytatW3Po0KFM\nnjw53/zmN/PlL3+58osHAACAGhh2+PDhw7VeRMncVINKc7MWqsXeohrsK6rF3qIa7CuqoZbvnFDk\nNfQAAADwSSfoAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAA\nAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgB\nAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECC\nHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAK\nJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAA\noECCHgAAAAok6AEAAKBAgh4AAAAKJOgBAACgQIIeAAAACiToAQAAoECCHgAAAAok6AEAAKBAgh4A\nAAAKJOgBAACgQCNqvYC+vr789Kc/ze7du7N79+689tpr6evry/XXX5+rrrrqlOZ64403snz58uMe\nnzdvXm666aYzXTIAAADUXM2Dvre3N2vWrEmSNDY25pxzzklPT88ZzXnxxRenpaXlqPGpU6ee0bwA\nAABQL2oe9A0NDbn55ptz8cUXp7GxMffee282btx4RnNedNFFaW1trdAKAQAAoP7UPOhHjBiROXPm\n1HoZAAAAUJSaB3017Nu3Lw8//HDeeuutnH322Zk+fXqmTZtW62UBAABAxQzJoG9vb097e/uAsebm\n5ixbtiznn39+jVYFAAAAlTOkgn7kyJH56le/miuuuCITJ05Mkrz66qu599578+yzz+a2227L97//\n/TQ0NNR4pQAAAHBmKhL0y5YtO6U708+fP/+Eby93usaPH5+2trYBY5deemm+/e1vZ+XKlXnhhRfy\ns5/9LF/+8pcr/rUBAABgMFUk6CdPnnxKZ73PPffcSnzZkzZ8+PB84QtfyAsvvJDnnnuuokHf1NRU\nsbmgn31FtdhbVIN9RbXYW1SDfcVQUpGgX7lyZSWmqarx48cn+fB970/Whg0bjvsWehs2bKjIugAA\nACjfR18t/sdaW1tPePx0Dalr6E9k165dSXLk2vqT0dbWdsJveltbm7Cn4uwrqsXeohrsK6rF3qIa\n7CuqpVZ7a/igf8UKOHDgQDo7O/Pmm28OGH/55Zdz+PDhox7/zDPPZPPmzUk+vH4fAAAASlcXZ+jv\nu+++dHZ2Jkl2796dJPn5z3+e3/72t0k+vLHdVVdddeTxW7duzQ9/+MN8/vOfz4033nhkfO3atdmz\nZ0+mT5+e8847L8mHd7l/9tlnkyRLlizJ9OnTB+MpAQAAQFXVRdBv3749O3fuHDC2a9euIy+TTzIg\n6PsNGzZswMcLFizI1q1b89JLL2X79u15//3309jYmHnz5uWaa67JpZdeWp0nAAAAAIOsLoL+n/7p\nn07p8VdeeWWuvPLKo8YXLlyYhQsXVmhVAAAAUL+KvIYeAAAAPukEPQAAABTorFtvvfXWWi+iVIcP\nH86sWbNqvQyGGPuKarG3qAb7imqxt6gG+4pqqdXeGnb4WO/zBgAAANQ1L7kHAACAAgl6AAAAKJCg\nBwAAgAIJegAAACiQoAcAAIACCXoAAAAokKAHAACAAo2o9QLqXV9fX376059m9+7d2b17d1577bX0\n9fXl+uuvz1VXXXVKc73xxhtZvnz5cY/PmzcvN91005kumQJUcl/16+joyKZNm/L888/n4MGDmTJl\nShYuXJgvfelLGT7c3+4+aSqxH/zM+mTau3dv1q1bl+3bt+ftt99OY2NjWlpasnjx4owdO3bQ52Fo\nqMR+WLZsWXp6eo55rLGxMatXr67kkinAE088kZ07d+aVV17J7t27895772X+/Pkn/P9dx+NnFv0q\nta8G62eWoP8Yvb29WbNmTZIPv/HnnHPOcf+HOVkXX3xxWlpajhqfOnXqGc1LOSq9r5566qnccccd\naWhoyNy5czNu3Lg8/fTTWbNmTTo6OrJixYpKLZ0CVHo/+Jn1ydHV1ZVbbrkl+/fvT0tLS5qamvLi\niy/mwQcfzPbt23Pbbbdl3LhxgzYPQ0Ml98OYMWOyaNGio8ZHjRpV6WVTgE2bNuWVV17JqFGjct55\n5+X1118/rXn8zOKPVWpfJYPzM0vQf4yGhobcfPPNufjii9PY2Jh77703GzduPKM5L7roorS2tlZo\nhZSokvvq3XffzerVqzN8+PDceuutueSSS5IkS5YsyapVq/LEE0/ksccey7x58yr5FKhT1dgPfmZ9\nctx1113Zv39/rrvuulxzzTVHxteuXZvNmzdn3bp1Wbp06aDNw9BQyf0wduxYP4844lvf+lbOPffc\nTJ48OTt37syqVatOax4/s/hjldpXyeD8zPI63I8xYsSIzJkzJ42NjbVeCkNIJffV448/nrfeeiuf\n+9znjsRb/9f42te+liR56KGHzvjrUAb7gdPV1dWV9vb2TJw4ccAvtEnS1taWkSNH5tFHH83BgwcH\nZR6GBvuBampubs7kyZPPaA57lI+qxL4aTM7Q18C+ffvy8MMP56233srZZ5+d6dOnZ9q0abVeFoXa\nsWNHkmTOnDlHHWtubk5DQ0M6Ojry/vvvZ8QI/+SHumrsBz+zPhn6987s2bOPOjZq1P/X3v2DNvHG\ncRz/tEVTsS1Va1qj4pbmWnEQFe0QUVERJ1HERVxc/DM4dJMMpYiC4CS4OVsL4hBBEEERlwYliSWl\nsaRVNEdOhzpYrFH7G0KCsbH+ml4uueT9mton4elz8OXDfXt3z7Wqt7dX8XhcyWRS27dvr/g8qA92\n10M2m9WLFy/0+fNneTwebdu2TYZhsFcMykZmoZKcyCzO7qsgHo8rHo8XjfX19enSpUvq6uqq0qrg\nVul0WpK0adOmRZ81NzfL6/Xqw4cPsixLPp/P6eXBYZWoBzKrMSxVO/nxeDwu0zSXPKm1ax7UB7vr\nYXZ2Vrdv3y4a83q9unDhgvr6+la+YDQcMguV5ERm0dA7yOPx6OTJk9qzZ4+8Xq8k6f379xodHdX4\n+LiGh4d18+ZNrV69usorhZvMzc1Jym26UUp+/OvXr46tCdVjZz2QWY3Frtohk/A7O+vhwIEDMgxD\nW7duVWtrqyzL0uPHj/XkyRNdv35d165d4+4hLBuZhUpxKrMaoqFf6pUBpZT7uot/6ejo0OnTp4vG\nAoGArl69qlAopKmpKT19+lTHjh2z/W/DfrVSV6g/tVJbZBaAWvLnxlJbtmzR+fPn5fF4FA6Hdf/+\nfQ0ODlZpdQBQzKnMaoiGvqenZ1lXkNavX1/B1SzW3NysQ4cOaWpqShMTE5wcu0St1FX+P8f5/zD/\nKT/OO1TdY7m1tW7dusLPTtQDmVWf7KodMgm/c6IeDh8+rHA4rImJibLnQOMis+A0uzOrIRr6UChU\n7SX8U0dHh6Tc+8nhDrVSVz6fT6lUSqZpFu1qLkm/fv2SZVlqaWkp3DKN2reS2nKqHsis+pPfU8E0\nzZKf58f/9pyp3fOgPjhRD+QRVoLMgtPsziy2BK0RyWRSkmi6sGz5DVqi0eiizxKJhL5//67e3l52\nuG8QTtUDmVV/+vv7JWnRBoiS9O3bN01OTsrj8cjv9zsyD+qDE/WQz6Pu7u6y50DjIrPgNLszi4a+\nAubm5pROpzU7O1s0Pj09rYWFhUXff/PmjR49eiQp9ywsUMrf6mrv3r1qb2/Xy5cvlUqlCuPZbFb3\n7t2TJB05csTRtaJ6yqkHMgtS7sRix44dhU17fjcyMqL5+XkFg8HC4yA/f/5UOp1WJpNZ0Tyob3bV\n1cePH0tezbIsS3fv3pVEHmFpZBYqoRYyq2mh1Nkaijx8+LDwSouZmRm9e/dOfr+/cOtNIBDQwYMH\nC99/9uyZ7ty5o/379+vixYuF8aGhIZmmKb/frw0bNkjK7Rg9Pj4uSTpz5oxOnDjh1GGhyuyqK0mK\nRCK6deuWVq1apYGBAbW1tenVq1dKp9Pat2+frly54tyBoeqWWw9kFvIymYxCoZC+fPmiXbt2afPm\nzXr79q0SiYR8Pp+Gh4fV1tYmSfr06ZMuX76sjRs3Lnolz3LmQf2zo65GR0cVDodlGIa6urq0Zs0a\nZTIZvX79WtlsVjt37tTg4KBaWlqqdZiogkgkokgkIin3erBYLCav1yvDMCRJ7e3tOnv2rCQyC/+f\nHXXlZGZxD+7/EIvFlEgkisaSyWThdglJRY1XXlNTU9HvwWBQY2NjSqVSisVi+vHjhzo7OzUwMKCj\nR48qEAhU5gBQk+yqK0navXu3hoaG9ODBA42NjSmbzaqnp0fnzp1jw7IGVG49kFno7u7WjRs3NDIy\nomg0qmg0qs7OTh0/flynTp0q+VqnUplUzjyoX3bUVX9/v0zT1PT0tCYnJzU/P6+1a9fKMAwFg0Gu\nzjeomZkZPX/+vGjMsixZliUp91hYvvHKI7PwL3bUlZOZxRV6AAAAAABciGfoAQAAAABwIRp6AAAA\nAABciIYeAAAAAAAXoqEHAAAAAMCFaOgBAAAAAHAhGnoAAAAAAFyIhh4AAAAAABeioQcAAAAAwIVo\n6AEAAAAAcCEaegAAAAAAXIiGHgAAAAAAF6KhBwAAAADAhWjoAQAAAABwIRp6AAAAAABciIYeAAAA\nAAAXoqEHAAAAAMCFaOgBAAAAAHCh/wBQ3m6CdAJanQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x105ca27f0>"
]
},
"metadata": {
"image/png": {
"height": 315,
"width": 506
}
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-1.0262852 1.04326517] 0.00129936724773\n"
]
}
],
"source": [
"SCORE = np.array([-2., 1.])\n",
"BALL = (np.array([0., 0.]), 2.)\n",
"solution = ellipsoid_iter(SCORE, lambda x: contained(x, SQUARE2D), BALL)\n",
"\n",
"for x, A, c in it.islice(solution, 0, 20, 2):\n",
" plot_poly(*SQUARE2D)\n",
" pl.scatter([x[0]], [x[1]], c='r')\n",
" plot_ellipse(x, A)\n",
"\n",
" if not (c is True):\n",
" plot_hyperplane(c, x)\n",
" pl.show()\n",
" print(x, np.linalg.det(A))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Ellipsis()"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
},
"latex_envs": {
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 0
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| unlicense |
basnijholt/holoviews | examples/reference/containers/plotly/Overlay.ipynb | 1 | 2816 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div class=\"contentcontainer med left\" style=\"margin-left: -50px;\">\n",
"<dl class=\"dl-horizontal\">\n",
" <dt>Title</dt> <dd>Overlay Container</dd>\n",
" <dt>Dependencies</dt> <dd>Plotly</dd>\n",
" <dt>Backends</dt> <dd><a href='./Overlay.ipynb'>Bokeh</a></dd> <dd><a href='../matplotlib/Overlay.ipynb'>Matplotlib</a></dd> <dd><a href='../plotly/Overlay.ipynb'>Plotly</a></dd>\n",
"</dl>\n",
"</div>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import holoviews as hv\n",
"hv.extension('plotly')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A Overlay is a collection of HoloViews objects that are related in some way, to be displayed simultanously, overlaid in the same space. Like [``Layout``](./Layout.ipynb) and unlike other containers such as [``HoloMap``](./HoloMap.ipynb) , [``GridSpace``](./GridSpace.ipynb) and [``NdOverlay``](./NdOverlay.ipynb) a ``Overlay`` is *not* dictionary like: it holds potentially heterogeneous types without any dimensioned keys.\n",
"\n",
"\n",
"A ``Overlay`` cannot contain any other container type other than ``NdOverlay`` but can contain any HoloViews elements. See [Building Composite Objects](../../../user_guide/06-Building_Composite_Objects.ipynb) for more details on how to compose containers. It is best to learn about ``Overlay`` and [``Layout``](./Layout.ipynb) together as they are very closely related objects that share many core concepts."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### ``Overlay`` is a heterogeneous collection"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can build a ``Overlay`` between any two HoloViews objects (which can have different types) using the ``*`` operator:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"xvals = [0.1* i for i in range(100)]\n",
"curve = hv.Curve((xvals, [np.sin(x) for x in xvals]))\n",
"scatter = hv.Scatter((xvals[::5], np.linspace(0,1,20)))\n",
"curve * scatter"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this example, we have a ``Overlay`` composed of a ``Curve`` element and a ``Scatter`` element.\n",
"\n",
"For more information about both ``Overlay`` and ``Layout``, see the [Composing_Elements](../../../user_guide/02-Composing_Elements.ipynb) user guide."
]
}
],
"metadata": {
"language_info": {
"name": "python",
"pygments_lexer": "ipython3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
Ccaccia73/semimonocoque | 01_SemiMonoCoque.ipynb | 1 | 215557 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Semi-Monocoque Theory"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/claudio/anaconda2/envs/py35/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.\n",
" warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')\n",
"/home/claudio/anaconda2/envs/py35/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.\n",
" warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')\n"
]
}
],
"source": [
"from pint import UnitRegistry\n",
"import sympy\n",
"import networkx as nx\n",
"#import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"#import sys\n",
"%matplotlib inline\n",
"#from IPython.display import display"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Import **Section** class, which contains all calculations"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from Section import Section"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Initialization of **sympy** symbolic tool and **pint** for dimension analysis (not really implemented rn as not directly compatible with sympy)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"ureg = UnitRegistry()\n",
"sympy.init_printing()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define **sympy** parameters used for geometric description of sections"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"A, A0, t, t0, a, b, h, L = sympy.symbols('A A_0 t t_0 a b h L', positive=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We also define numerical values for each **symbol** in order to plot scaled section and perform calculations"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"values = [(A, 150 * ureg.millimeter**2),(A0, 250 * ureg.millimeter**2),(a, 80 * ureg.millimeter), \\\n",
" (b, 20 * ureg.millimeter),(h, 35 * ureg.millimeter),(L, 2000 * ureg.millimeter)]\n",
"datav = [(v[0],v[1].magnitude) for v in values]"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"# First example: Closed section"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define graph describing the section:\n",
"\n",
"1) **stringers** are **nodes** with parameters:\n",
"- **x** coordinate\n",
"- **y** coordinate\n",
"- **Area**\n",
"\n",
"2) **panels** are **oriented edges** with parameters:\n",
"- **thickness**\n",
"- **lenght** which is automatically calculated"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"stringers = {1:[(sympy.Integer(0),h),A],\n",
" 2:[(a/2,h),A],\n",
" 3:[(a,h),A],\n",
" 4:[(a-b,sympy.Integer(0)),A],\n",
" 5:[(b,sympy.Integer(0)),A]}\n",
"\n",
"panels = {(1,2):t,\n",
" (2,3):t,\n",
" (3,4):t,\n",
" (4,5):t,\n",
" (5,1):t}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define section and perform first calculations"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S1 = Section(stringers, panels)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Verify that we find a simply closed section"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOgAAAAUBAMAAAB112wpAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAdt3NMolEIpm7EKvv\nVGZvmWXoAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACDElEQVRIDb2UMUgbURjH/5cYT5PLKVkqnYJW\noe3QIi5OZnQMhZSWCs3YzVCQOpVbCrFSLKUIDsI5ODmo7VJqsaWFlhb3FjoY6O6grWJQri/J8t73\n/4bg4OOW9+P7v9999949FCZgnssa4XgVf8ZwF61nfuE1eecqq8SAaWLpqz0vCCrAr6+UkKm2fG1p\ndgsPzcwZfoT9hkPak+uEgiQpE8z/ILSBzLEtzcUIPokq7xwDRcEA7zuh9IMrxDYWm8TeA3u2NCgi\n91dU9X7F5m3BgKeThHJEDPBY+hn4WLI+b7rJUpNUPm/54tKp2JUaQYpfLTtKPYQ1RXowVKJCpVNT\ncyu2OjXzWToM/p3ntNYaWNof+8dUqEp7/9l7ajI3KQfMVCUsK1JT80rWaXtqvuaWK+2LKAcE8tzn\nS7p0qSbTaqd1uNIhmYJfQ/+5oOtQpG/BP7naqRe50nyEJ0Iw0GTp752ds21Rhy/AUiyh1ukv04h9\nkMzlJv/w4CVSJ3ItgC+HCBihOkXaE8Gzpf5oZbGYPXKiYQP7g4KZglNINo/wG90jLam4Wx5X7r2x\n9zSdJEkRw7FjfVRfhmS4n+xK5j97FyN1w8n2fTjalWwqSQ5taSeQpzMIdMvw05F2Jgqz97RdlFFy\n3TLQ3WIWUxhJ1xRptyw7yGGNkbTBOXTLQiWrsY60cA3muazhDVdRGPsP/CKPSlOdREgAAAAASUVO\nRK5CYII=\n",
"text/latex": [
"$$\\left [ \\left [ 2, \\quad 3, \\quad 4, \\quad 5, \\quad 1, \\quad 2\\right ]\\right ]$$"
],
"text/plain": [
"[[2, 3, 4, 5, 1, 2]]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.cycles"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Plot of **S1** section in original reference frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define a dictionary of coordinates used by **Networkx** to plot section as a Directed graph.\n",
"Note that arrows are actually just thicker stubs"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"start_pos={ii: [float(S1.g.node[ii]['ip'][i].subs(datav)) for i in range(2)] for ii in S1.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA5EAAAJtCAYAAACv9fRpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XuclXWBP/DPDCIwisRdRUVLhUizVik1WOmmiG5plop3\n8pK6hmiUaCrglqSSRq26WZtItm1lWRm6+vrlpuSlcFu8ldc0N8vwlqHcAs7vD2JimBl4gJk5t/f7\n9ZqXnuc855zvM5z5vs5nvs88n4ZSqVQKAAAAFNBY7gEAAABQPYRIAAAAChMiAQAAKEyIBAAAoDAh\nEgAAgMKESAAAAAoTIgGS/PCHP8wBBxyQwYMHp6mpKTvvvHMOP/zw3H777Z3yerNmzcrNN9/cavv0\n6dPTrVu3TnnN9dlll13y8Y9/vMter73j7wjTp0/Pz372s1bbJ0yYkDe/+c2d8pqdbfHixTn++OMz\nePDgNDY25txzzy33kMpiwoQJaWxsbPXVrVu3rFq1qtzDA6gbDXoigXr35S9/OZMmTcopp5ySD3/4\nw9lqq63y9NNPZ+7cudl9993zhS98ocNfc5dddsno0aMzZ86cFtv/8Ic/5Pe//33e9a53dfhrrs+D\nDz6YbbbZJrvsskuXvF57x98RGhsbc+GFF+aSSy5psf2ZZ57JX/7yl+y1114d/pqd7YorrshnP/vZ\nXH/99dltt92y3XbbZccddyz3sLrchAkTctttt+WWW27Juh9fuvpnBqCebVHuAQCU2xe/+MV85CMf\nyXXXXde8bcyYMTn55JO7fCzbb799tt9++y5/3WoMVutavnx5ttxyy3bv76qAXMSGxrquX//619l+\n++1z7LHHluX1K8mWW26ZkSNHbtRjqvl4ASqR01mBuvfKK69k8ODBhfZ99tlnc+yxx2bQoEHp2bNn\n3vnOd+aHP/xhq/0efPDBHH744RkwYECampoyfPjwXHbZZUlWh5nnnnsuN954Y/PpeGtOJZ02bVoa\nG1tOzYsWLcpZZ52VIUOGpGfPnhk+fHi+9KUvtdjnrrvuSmNjY2655ZZ88pOfzMCBAzNw4MAcf/zx\n+ctf/rLB49p5551bnM46e/bsNDY25he/+EWOO+649OnTJ0OGDMnZZ5+d5cuXb/D5Zs2alREjRqSp\nqSn9+vXLyJEj86Mf/WiDx//000/nhBNOyJvf/OY0NTXlLW95S84888z8+c9/bvH8J510Unbcccfc\nf//9ec973pOtttoqn/nMZ9LY2JiGhoZ87nOfaz7Ncc2K5EknndQiSP7ud79LY2NjrrvuukydOjXb\nb799+vbtmw996EN5/vnnW7zekiVLcsYZZ2TAgAHp3bt3jjjiiNx3331pbGzc4Grqmn/TRx99NGPH\njk3v3r1z1FFHNd//gx/8IPvtt1+22mqr9O3bN0ceeWT+7//+r/n+Na/x3HPPNR/T3XffnSR56aWX\ncvrpp2eHHXZIz54989a3vjVf+9rXWrz+DTfckMbGxsybNy9HHnlk+vbtm3333bf5/rvuuisf+MAH\nss0222TrrbfO2LFj8+ijj7Z4jjFjxmT06NH56U9/mr333jtbbbVV9txzz41+7xc95s1x4YUXprGx\nMb/5zW9y4IEHpnfv3s3h+/bbb8+4ceOy3XbbNR/DrFmzWp0Ku+OOO2bChAm54YYbMmzYsDQ1NeWA\nAw7IM888kzfeeCOnnXZa+vfvn+222y7nnXdeq1XRF198MZ/4xCcyZMiQ9OjRIyNGjMg3vvGNDjk+\ngEpgJRKoe+9617sye/bs7LLLLvnwhz+c3Xbbrc391pxmuu2222bWrFkZMGBAvvOd7+SII47Ij370\noxx66KFJkl/+8pd573vfm9122y2zZs3KkCFD8uSTT+ahhx5Kktx8880ZN25c3vGOd2T69OkplUoZ\nOHBgkqShoSENDQ3Nr1kqlTJu3LgsWLAg//Iv/5I99tgjc+fOzbnnnpuXXnopn/vc51qMcdKkSTn0\n0EPz7W9/O48//ng+/elPZ4sttsj111+/3u/B2q+59u0TTjgh48ePz80335z77rsvU6dOTb9+/TJ1\n6tR2n+tb3/pWJk+enGnTpmXUqFFZsmRJHnroobzyyitJVv/96cEHH9zm8f/hD3/IkCFDctVVV6Vf\nv3555plncumll+aQQw7JPffc02J8r732WsaPH5/JkydnxowZ6dWrV4455pjsu+++mTBhQj7xiU8k\nSXbYYYc2v7drfOELX8j++++f66+/PgsXLsy5556b448/PnfeeWfzPqeeemq+//3vZ/r06dl7773z\n05/+NMcee2ybz9fe9/awww7LySefnClTpjT/ouDf/u3fcuaZZ+bkk0/O1KlTs2jRokydOjVjxozJ\nQw89lK222ir3339/pk6dmoceeig//OEPUyqVMmLEiCxatCjvec97smzZslxyySXZeeedc/vtt+eM\nM87I8uXL88///M8txnHcccdl/Pjx+f73v58VK1YkSebOnZvDDjss//RP/5Rvfetbzd+P0aNH5+GH\nH86QIUOaj+Hpp5/OpEmTcsEFF6R///6ZOXNmjjzyyDz22GPNf2u6ofd+0WPekJUrV7a4veaXB2t/\nvz/84Q/n5JNPzmc/+9nm7/dvf/vbvP/9788nP/nJNDU1Zf78+bnooovy8ssvtzr9+c4778xTTz2V\nmTNnZunSpZk4cWKOOOKI7LDDDhkxYkS++93v5mc/+1k+//nPZ7fddsspp5ySJHnttdey//77Z+XK\nlfnc5z6XoUOH5tZbb82pp56av/71r83vS4CqVgKoc0888URpr732KjU2NpYaGhpKAwYMKI0fP750\nxx13tNjv4x//eGnQoEGlV199tcX2D37wg6V3vvOdzbdHjx5d2mmnnUpLly5t9zV33nnn0vHHH99q\n+7Rp00qNjY3Nt2+55ZZSQ0NDac6cOS32O+WUU0o9e/Ysvfzyy6VSqVT62c9+VmpoaChNmDChxX5n\nnXVWqVevXhv4Dqwez9qPnT17dqmhoaE0ffr0FvsdeuihpWHDhq33uc4666zS3nvvvcHXa+v417Vi\nxYrSz3/+81JjY2NpwYIFzdtPOumkUmNjY+mWW25p9ZiGhobSRRdd1Gr7SSedVNpll12abz/77LOl\nhoaG0vve974W+82cObPU2NhY+uMf/1gqlUqlxx9/vNTY2FiaOXNmi/0mTpxYamxsLN1www3rPYY1\n/6Zf+cpXWmx//fXXS3369CmdcsopLbY/++yzpS233LI0a9as5m3HHXdci7GXSqXSJZdcUurVq1fp\n6aefbrH91FNPLQ0cOLC0cuXKUqn093/LT33qU63Gtuuuu5Y++MEPtti2aNGi0oABA0rnnHNO87Yx\nY8aUttxyyxavtXDhwlK3bt1KM2bMaN62off+xhxzW0466aRSQ0NDi6/GxsYW/94XXnhhqbGxsXTt\ntdeu97lKpdXvr+nTp5cGDhzYYvsOO+xQGjhwYOmNN95o3nbllVeWGhoaSmeeeWaLfd/+9reXDjzw\nwObbF198campqan0zDPPtNhvwoQJpW233ba0atWqDY4LoNI5nRWoe7vttlv+93//N3fddVcuvPDC\n5lNUDzrooHz+859v3m/NqXC9e/fOypUrs3LlyqxYsSIHHnhgHnzwwbz++utZsmRJ7r333hx33HHp\n0aPHZo9t3rx56datW8aPH99i+3HHHZfly5fnvvvua7F93LhxLW7vueeeWbZsWRYuXLjRr93Q0NDm\n8z333HPrfdzIkSOzYMGCTJw4MT/96U+zZMmSwq/517/+NZdeemne+ta3pqmpKd27d8/o0aOTJI8/\n/niLfbt3755DDjmk8HO35+CDD25xe88990yS5uP8xS9+kST56Ec/2mK/j370o61OY1yfww47rMXt\n++67L4sWLcoxxxzT/H5auXJlhgwZkuHDhzefstqe22+/Pe9+97szdOjQFo8/8MAD89JLL+XXv/51\n874NDQ2tXv+pp57K008/3er1e/bsmf3226/V6++2224trm47cODADBo0qPn7VOS9v7nHnCSDBw/O\n//zP/+SBBx7IAw88kPnz5+fMM89std+6x5skf/zjH3Pqqadm6NCh6d69e7p3755p06bl5Zdfbl4p\nX+M973lPmpqamm8PHz48DQ0NOfDAA1vsN3z48Ban4t5+++3Zf//9s+OOO7b6d1m4cGGr9zFANXI6\nK0BWf8geNWpURo0alSR54YUXctBBB+WSSy7JWWedlT59+mThwoWZM2dObrjhhlaPb2xszMsvv5zu\n3btn1apVzacBbq5XXnkl/fr1yxZbtJyut91225RKpVYffPv169fi9poP80uXLt2k12/r+ZYtW7be\nx5xwwglZtmxZ/v3f/z3XXntttthii4wbNy5XXnllhg4dut7HTpkyJVdffXWmTp2a/fbbL717987v\nf//7HH744a2OYeDAgYVOJ92Qto6xVCo1v94f//jHJMmgQYNa7Ff072jX2G677VrcXrhwYUqlUt7/\n/ve32rehoaHVuNa1cOHCPP300+nevXubj3/55Zc3+PpJcvLJJ7eqd2loaMhOO+3UYltb4+nRo0fz\n9+nVV1/d4Ht/c485Wf3Lg3e+850b3G/bbbdtcXvVqlU55JBD8vLLL2fatGkZNmxYevbsmZtuuimX\nXXZZq/dX3759W9xec2Getrav/diFCxdm/vz5hf9dAKqREAnQhm233TannHJKJk2alCeffDL77LNP\n+vfvn3/8x3/MlClT2lyB2n777bNixYo0Nja2ujDLpurXr19eeeWVrFixokWQfOGFF5rvr0Snnnpq\nTj311Lz22mu54447cu655+boo49utXK6ru985zs58cQTc/755zdvW7RoUZv7dkSAbM/az70mfC1c\nuLBFCP7Tn/60yc+ZJP3790+SzJkzJyNGjGi1f+/evdf7fP3798/gwYPz5S9/uc3347Bhwwq9/owZ\nM/KBD3yg1eM39mqmffv23eB7f3OPeXM88cQTWbBgQb7zne/kYx/7WPP273//+x36Ov37989OO+2U\nq666qtC/C0A1EiKBuvfCCy+0WrVIkt/85jdJ/r6iMXbs2Nx///0ZMWJEu6frde/ePaNGjcqNN96Y\niy++uN39evToUeg0zwMOOCBXXHFFvve977U4pfXGG29Mjx49st9++zVv68xQtan69OmTj33sY7n/\n/vtbVKi0d/yLFy9uter6jW98Y6OObcstt9yoU2g3ZE3/4Pe+971Mnjy5eft3v/vdzfqe77///und\nu3eefPLJHHfccRv9+LFjx+Zf//Vfs+OOO2bAgAEb/fhhw4Zl5513zqOPPprPfOYzG/34dfXq1WuD\n7/3NPebNsXjx4iRp8f5avnx5/uM//qNDX2fs2LG57rrrMnTo0Ir9JQ/A5hIigbq3xx575AMf+EDG\njRuXXXbZJX/5y18yd+7cfPWrX81RRx3VfHXPSy65JO9+97szevTonHXWWdl5553z6quv5pFHHskz\nzzyTr3/960mSmTNnZsyYMdl3333zqU99KjvssEN++9vfZsGCBfnyl7+cJBkxYkTmzZuXuXPnZttt\nt82AAQPaPNXz4IMPzqhRo3L66adn4cKFedvb3pa5c+fmG9/4Ri644IIWH1I35u/zOtMnPvGJ9O7d\nO/vtt18GDRqUxx9/PN/85jdz0EEHNe/T3vGPHTs2N9xwQ/bYY4/suuuu+cEPfrDB1ct1jRgxInPn\nzs1BBx2Uvn37Zvvtt291KueGrP29HDZsWI455phcdNFFWblyZfbee+/ceeed+clPfpIkrSpZiurd\nu3euuOKKnHXWWVm4cGEOPvjg9OnTJ88//3zuuuuuvPe9783RRx/d7uPPOeecfPe7382oUaNyzjnn\nZNiwYXnjjTfy2GOPZd68eW3Wb6zr6quvzmGHHZZly5blyCOPzIABA/KnP/0p9957b4YOHZpJkyZt\n1DFt6L2/uce8Od72trdlhx12yJQpU5Ks/qXLVVdd1eZpp+0p8jM2efLk3HTTTc3/LrvvvnsWLVqU\nxx57LPfee29+8IMfbPIxAFQKIRKoe5deemluvfXWTJ06NX/605/SrVu37L777rn88stz9tlnN++3\n44475oEHHsi0adPy2c9+Ni+++GL69++fPfbYIyeeeGLzfvvss0/uueeeXHzxxZk4cWKWLVuWoUOH\nZsKECc37zJgxI6eddlqOOuqoLFmyJCeeeGJzj9zaq1sNDQ259dZbc8EFF+Tyyy/Pyy+/nJ133jlX\nXXVVJk6c2OI4NmdVrL36i/b2XZ9Ro0bl+uuvz4033pjXXnst22+/fU444YRMmzateZ/2jv8rX/lK\nktVdf0lyyCGH5D//8z+bVwOLjOPqq6/OxIkT86EPfSjLli3L1KlTc/HFF7f5mPaeY93tX/va17LN\nNtvkiiuuyPLly/P+978/11xzTQ455JD06dNnvd+P9b3Oaaedlp122ilXXHFFvv3tb2fFihUZMmRI\nRo8enXe84x3rfY5tttkm9957by655JJcfvnlef755/OmN70pw4YNyxFHHLHBMSWrf0lx99135/Of\n/3xOPfXULFmyJNtuu2323XffVmGurWNY931T5L2/Mcfclo2pVVlbjx498uMf/zif/OQnc/zxx6d/\n//45+eSTs9122+X0009f73Ft6LXX3t6nT5/cd999mT59embMmJE//OEPedOb3pThw4e3OI0WoJo1\nlCrlV9cAUEVmzpyZKVOm5Nlnn21erQaAemAlEgA2YO7cuXnkkUfyjne8I42Njbn77rvzxS9+scXp\nzgBQL6xEAsAG3H333TnvvPPy+OOP54033siQIUNy9NFHZ9q0aRt9FVMAqHZCJAAAAIVt2iXlAAAA\nqEtCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAA\nhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAU\nJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCY\nEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFC\nJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmR\nAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQC\nAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkA\nAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAA\nAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAA\nFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQ\nmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBh\nQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJ\nkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZE\nAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJ\nAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAAABQmRAIAAFCYEAkAAEBhQiQA\nAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhQmRAAAAFCZEAgAAUJgQCQAAQGFCJAAAAIUJkQAA\nABQmRAIAAFCYEAkAAEBhQiQAAACFCZEAAAAUJkQCAABQmBAJAABAYUIkAAAAhW1R7gHAxlq4cGHm\nzJ6dJx56KK+/9lq27tMnu7/97TlxwoQMHDiw3MMDapj5BygX8w+VpKFUKpXKPQgoYv78+Zk1Y0bm\n3nZbPpJk5NKl6Z1kUZJf9uqVm0ulHHLwwTn7/PMzcuTIMo8WqCXmH6BczD9UIiGSqnDdtddm6uTJ\nOW/JkpxYKqVvG/u8mmR2Q0Mu79Ur02fOzGlnnNHVwwRqkPkHKBfzD5VKiKTiXXfttbls8uTcvnhx\ndi2w/1NJDmpqynkmUmAzmX+AcjH/UMmESCra/Pnz86ExYzJvnQn06iSzkzyc5Jgk31jncU8lGd3U\nlFvuuiv77LNP1wwWqCltzT/Lk5yZ5P9l9W//35Lk0iRj13qc+QfYXO19/jk+q+efJUm2TfLpJCev\ndb/5h67i6qxUtFkzZuS8JUta/QZuSJKL0nLiXNuuST6zZElmzZjRqeMDaldb88+KJDslmZfktST/\nkuTIJM+ttY/5B9hc7X3+OT/JM0n+nOTHSS5M8r9r3W/+oatYiaRiLVy4MMOGDs1vly5t828AktVB\n8vm0XolMkleSvKVnzzzx3HOuWgZslCLzzxp7JZmW5PC1tpl/gE1VdP55PMl7k3w5yUfX2m7+oStY\niaRizZk9O4cnG/wA155+SQ5vaMic2bM7blBQRxoaGur2a9vBgzO2QID8U5Ink7xtne3mH9g85Z4D\nKnn++eckWyV5a5Ltk4xb537zD11BiKRiPfHQQ3nX0qWb9RwjlyzJEw8/3EEjAupFzyQHbGCfFUmO\nS3JSkt3buN/8A2yKDc0/Vyd5PcnPk3wkSY829jH/0Nm2KPcAoD2vv/Zaem/mc/RO8h/f/Gau++Y3\nO2JIQJ3olqx3/illdYDskeQr7exj/gE2xYbmnyRpSLJ/km8muTbJWevc3zvJoldf7fjBwd8IkVSs\nrfv0yaLNfI5FSY45/vh8dc6cjhgS1JWGhoZyD6FsVibrnX9OTvJSkluz+gNfW8w/sOnMP8WsSPJ0\nG9sXJendd1P/IAg2zOmsVKzd3/72/LJnzzbvW5lk6d/+uyLJsr/9/7rm9+qV3ffcs9PGCLWsVCrV\n7dcll13W7vxzepLHsvrKiFuu5/tn/oFNV+45oBLnnxeTfCfJG0lWJbk9yX8m+UAb3z/zD53N1Vmp\nWOu7Otn0v32t/XvKqUkuXuu2q5MBm6q9+ee5JDtn9d8srVmBbEjy1STj19rP/ANsqvbmn5ey+iqs\nD2V1iBya5OwkH1/n8eYfuoKVSCrWoEGDcsjBB+eGNk5pmZrVE+jKtb4uXmefGxoacui4cSZQYKO1\nN//slNVzz+KsPl1sUZK/pGWATMw/wKZrb/4ZkORnWR0S/5zkwbQOkIn5h65hJZKKNn/+/HxozJjM\nW7y4VeHu+jyVZHRTU265667ss88+nTU8oIaZf4ByMf9Q6axEUtFGjhyZ6TNn5qCmpjxV8DFPJXlf\n9+6ZPnOmCRTYZJs6/xzU1GT+ATaL+YdK123atGnTyj0IWJ+9R45Mr379csJ//3e6rViR4Ul6tbHf\nK0n+Nasvu/969+659rrrsvXWW3fpWIHasjHzz7UNDTmlqSkXzpyZ0844o4tHCtSaNfPP0f/1X+le\nKpl/qChOZ6VqPPDAA5k1Y0Z+cuutObyhISOXLFndg5Tklz175jtLlyZJlvxt/9NOOy1f/epXyzVc\noIasb/6Z36tXbi6Vcui4cTn7/POtAAAd5p577slHPvKRvH/ffXPbHXeYf6gYQiRV58UXX8yc2bPz\nxMMPZ9Grr6Z3377Zfc89s2TZslx00UXN+zU2NuZXv/pV9tprrzKOFqgl7c0/J5x0kotYAB1q1apV\nefe7351Jkybl2GOPNf9QUYRIasby5cuz55575oknnmjeNmbMmNx55511XVoMAFSfOXPm5Jprrsm9\n996bxkaXMaGyCJHUlLlz5+bQQw9tse3mm2/OYYcdVqYRAQBsnNdffz3Dhw/PTTfdlH333bfcw4FW\nhEhqSqlUytixY3PHHXc0b3vLW96SRx99ND169CjjyAAAirnooovyzDPP5MYbbyz3UKBNQiQ159FH\nH81ee+2VlStXNm+7/PLL8+lPf7qMowIA2LDf/e53+Yd/+IcsWLAgO+64Y7mHA20SIqlJZ511Vq6+\n+urm2717986TTz6ZwYMHl3FUAADrN378+AwfPjxTp04t91CgXUIkNemll17Kbrvtlj//+c/N21R+\nAACV7J577snRRx+dxx9/PE1NTeUeDrTLpZ6oSQMGDGj1G7yvf/3refDBB8s0IgCA9q1atSqTJk3K\nF77wBQGSiidEUrPOPPPM7L777s2310zOFt8BgEpz4403plu3bhk/fny5hwIb5HRWaprKDwCg0qn0\noNoIkdQ0lR8AQKVT6UG1ESKpeSo/AIBKpdKDaiREUhdUfgAAlUilB9VIiKQuqPwAACqNSg+qlauz\nUhdUfgAAlUSlB9VMiKRuqPwAACqFSg+qmdNZqSsqPwCAclPpQbUTIqkrKj8AgHJT6UG1EyKpOyo/\nAIByUelBLRAiqUsqPwCAclDpQS0QIqlLKj8AgK6m0oNa4eqs1CWVHwBAV1LpQS0RIqlbKj8AgK6i\n0oNa4nRW6prKDwCgs6n0oNYIkdQ1lR8AQGdT6UGtESKpeyo/AIDOotKDWiREQlR+AACdQ6UHtUiI\nhKj8AAA6nkoPapWrs0JUfgAAHUulB7VMiIS/UfkBAHQUlR7UMqezwlpUfgAAm0ulB7VOiIS1qPwA\nADaXSg9qnRAJ61D5AQBsKpUe1AMhEtqg8gMA2BQqPagHQiS0QeUHALCxVHpQL1ydFdqg8gMA2Bgq\nPagnQiS0Q+UHAFCUSg/qidNZYT1UfgAAG6LSg3ojRMJ6qPwAADZEpQf1RoiEDVD5AQC0R6UH9UiI\nhAJUfgDu8HAAAAAVCUlEQVQAbVHpQT0SIqEAlR8AwLpUelCvXJ0VClD5AQCsTaUH9UyIhIJUfgAA\na6j0oJ45nRU2gsoPAEClB/VOiISNoPIDAFDpQb0TImEjqfwAgPql0gOESNgkKj8AoD6p9AAhEjaJ\nyg8AqD8qPWA1V2eFTaDyAwDqi0oP+DshEjaRyg8AqB8qPeDvnM4Km0HlBwDUPpUe0JIQCZuhrcqP\n4cOH59FHH01jo4V+AKgFKj2gJSESNtPalR8DBgzIvHnzMnz48HIPCwDoACo9oDVLJbCZ3va2t2XG\njBmZO3duBg4cmCeffLLcQwIAOsiUKVMyceJEARLWYiUSOtB//dd/ZeLEiXnkkUey5ZZblns4AMBm\nUOkBbbMSCR1o7Nix2XXXXXP11VeXeygAwGZQ6QHtsxIJHeyxxx7L6NGj85vf/CYDBgwo93AAgE0w\nZ86cXHPNNbn33ntdLA/WIURCJzj77LPz17/+Nddcc025hwIAbCSVHrB+QiR0gldeeSXDhw/PnXfe\nmT322KPcwwEANoJKD1g/IRI6yVe+8pX8+Mc/zh133JGGhoZyDwcAKEClB2yYE7yhk5x++ul5/vnn\n85Of/KTcQwEAClLpARtmJRI6kcoPAKgeKj2gGCuR0IlUfgBAdVDpAcVZiYROpvIDACqfSg8oToiE\nLqDyAwAql0oP2DhCJHQBlR8AULlUesDGESKhi6j8AIDKo9IDNp4TvqGLqPwAgMqj0gM2npVI6EIq\nPwCgcqj0gE1jJRK6kMoPAKgMKj1g01mJhC6m8gMAyk+lB2w6IRLKQOUHAJSPSg/YPEIklIHKDwAo\nH5UesHmESCgTlR8A0PVUesDmcwI4lInKDwDoeio9YPNZiYQyUvkBAF1HpQd0DCuRUEYqPwCga6j0\ngI5jJRLKTOUHAHQ+lR7QcYRIqAAqPwCg86j0gI4lREIFUPkBAJ1HpQd0LCESKoTKDwDoeCo9oOM5\nIRwqhMoPAOh4Kj2g41mJhAqi8gMAOo5KD+gcViKhgqj8AICOodIDOo+VSKgwKj8AYPOp9IDOI0RC\nBVL5AQCbTqUHdC4hEiqQyg8A2HQqPaBzCZFQoVR+AMDGU+kBnc8J4lChVH4AwMZT6QGdz0okVDCV\nHwBQnEoP6BpWIqGCqfwAgGJUekDXsRIJFU7lBwBsmEoP6DpCJFQBlR8A0D6VHtC1hEioAio/AKB9\nKj2gawmRUCVUfgBAayo9oOs5YRyqhMoPAGhNpQd0PSuRUEVUfgDA36n0gPKwEknV+vWvf5299npH\nuYfRpVR+AMBqKj2gfIRIqtaCBQvy0EMPlnsYXe7KK6/MpZdempdeeqncQwGAsrnxxhvTrVu3jB8/\nvtxDgbojREKVGT58eI455phcfPHF5R4KAJTF66+/ngsuuCBf+tKXdEJCGfipgyo0derU3HTTTXnk\nkUfKPRQA6HKXXXZZxowZoxMSymSLcg8A2Hj9+vXLRRddlHPOOUflBwB15Xe/+12uueaaLFiwoNxD\ngbplJRKqlMoPAOqRSg8oPyESqlT37t1z5ZVX5lOf+lSWL19e7uEAQKe755578vOf/zyf/vSnyz0U\nqGtCJFQxlR8A1AuVHlA5hEiocio/AKgHKj2gcgiRUOVUfgBQ61R6QGXxUwg1QOUHALVMpQdUFhUf\nUANUfgBQq1R6QOWxEgk1QuUHALVIpQdUHiESaoTKDwBqjUoPqExCJNQQlR8A1AqVHlC5hEioMSo/\nAKgFKj2gcgmRUGNUfgBQ7VR6QGXzUwk1SOUHANVMpQdUNhUfUINUfgBQrVR6QOWzEgk1SuUHANVI\npQdUPiESapTKDwCqjUoPqA5CJNQwlR8AVAuVHlA9hEiocSo/AKgGKj2gegiRUONUfgBQ6VR6QHXx\nUwp1QOUHAJVMpQdUFxUfUAdUfgBQqVR6QPWxEgl1QuUHAJVIpQdUHyES6oTKDwAqjUoPqE5CJNQR\nlR8AVAqVHlC9hEioMyo/AKgEKj2gegmRUGdUfgBQbio9oLr5qYU6pPIDgHJS6QHVTcUH1CGVHwCU\ni0oPqH5WIqFOqfwAoBxUekD1EyKhTqn8AKCrqfSA2iBEQh1T+QFAV1HpAbVDiIQ6p/IDgK6g0gNq\nhxAJdU7lBwCdTaUH1BY/xYDKDwA6lUoPqC0qPgCVHwB0GpUeUHusRAJJVH4A0DlUekDtESKBJCo/\nAOh4Kj2gNgmRQDOVHwB0FJUeULuESKAFlR8AdASVHlC7hEigBZUfAGwulR5Q2/xUA62o/ABgc6j0\ngNqm4gNoReUHAJtKpQfUPiuRQJtUfgCwKVR6QO0TIoE2qfwAYGOp9ID6IEQC7VL5AUBRKj2gfgiR\nwHqp/ACgCJUeUD+ESGC9VH4AsCEqPaC++CkHNkjlBwDro9ID6ouKD2CDVH4A0B6VHlB/rEQChaj8\nAKAtKj2g/giRQCEqPwBYl0oPqE9CJFCYyg8A1lDpAfVLiAQ2isoPABKVHlDPhEhgo6j8AEClB9Q3\nP/XARlP5AVDfVHpAfVPxAWw0lR8A9UulB2AlEtgkKj8A6pNKD0CIBDaJyg+A+qPSA0iESGAzqPwA\nqB8qPYA1hEhgs6j8AKgPKj2ANYRIYLOo/ACofSo9gLWZBYDNpvIDoLap9ADWpuID2GwqPwBql0oP\nYF1WIoEOofIDoDap9ADWJUQCHULlB0DtUekBtEWIBDqMyg+A2qHSA2iPEAl0KJUfALVBpQfQHiES\n6FAqPwCqn0oPYH3MCkCHU/kBUN1UegDro+ID6HAqPwCql0oPYEOsRAKdQuUHQHVS6QFsiBAJdAqV\nHwDVR6UHUIQQCXQalR8A1UOlB1CUEAl0KpUfANVBpQdQlBAJdCqVHwCVT6UHsDHMEkCnU/kBUJne\neOONJCo9gI2j4gPodCo/ACrPqlWr8o//+I8ZPHhw7r333jz88MPlHhJQJaxEAl1C5QdAZbnhhhvy\nq1/9Krfddltef/31XH311Vm1alW5hwVUASES6BIqPwAqx6JFi3LBBRc03165cmWeffZZfw8JFGKm\nALqMyg+AyjBjxoy88MILzbd79OiRyy67rIwjAqqJEAl0KZUfAOX1zDPP5Morr2yxbfLkyRk6dGiZ\nRgRUGyES6FIqPwDK67zzzsuyZcuab2+33XaZMmVKGUcEVBshEuhyKj8AymPevHn53ve+12LbjBkz\nsvXWW5dpREA1EiKBLrd25UepVCr3cADqwqpVqzJp0qQW2/bee+8cf/zxZRoRUK2ESKAsVH4AdK01\nlR5r+9KXvuSKrMBGM2sAZaHyA6DrrFvpkSRHHXVURo0aVaYRAdVMiATKRuUHQNdQ6QF0JCESKCuV\nHwCdS6UH0NGESKCsVH4AdC6VHkBHEyKBslP5AdA5VHoAnUGIBMpO5QdAx1PpAXQWIRKoCCo/ADqW\nSg+gs5hFgIqg8gOg46j0ADqTEAlUDJUfAB1DpQfQmYRIoKKo/ADYPCo9gM4mRAIVReUHwOZR6QF0\nNiESqDgqPwA2jUoPoCsIkUDFUfkBsPFUegBdRYgEKpLKD4CNo9ID6CpmFaAiqfwAKE6lB9CVhEig\nYqn8AChGpQfQlYRIoKKp/ABYP5UeQFcTIoGKpvIDYP1UegBdTYgEKp7KD4C2qfQAykGIBCqeyg+A\n1lR6AOUiRAJVQeUHQEsqPYByMcsAVUHlB8DfqfQAykmIBKqGyg+A1VR6AOUkRAJVReUHUO9UegDl\nJkQCVUXlB1DvVHoA5SZEAlVH5QdQr1R6AJVAiASqjsoPoB6p9AAqhRAJVCWVH0C9UekBVAqzDlCV\nVH4A9USlB1BJhEigaqn8AOqFSg+gkgiRQFVT+QHUOpUeQKURIoGqpvIDqHUqPYBKI0QCVU/lB1Cr\nVHoAlUiIBKqeyg+gFqn0ACqVEAnUBJUfQK1R6QFUKrMQUBNUfgC1RKUHUMmESKBmqPwAaoVKD6CS\nCZFATVH5AVQ7lR5ApRMigZqi8gOodio9gEonRAI1R+UHUK1UegDVQIgEao7KD6AaqfQAqoUQCdQk\nlR9AtVHpAVQLsxJQk1R+ANVEpQdQTYRIoGap/ACqhUoPoJoIkUBNU/kBVDqVHkC1ESKBmqbyA6h0\nKj2AarNFuQcA0NmmTp2a4cOH58wzz8ygQYMyZ/bsPPHQQ3n9tdeydZ8+2f3tb8+JEyZk4MCB5R4q\nUMMWLlzYav7ZondvlR5A1REigZrXr1+/nHDCCTn0fe/La4sW5SNJRi5dmt5JFiX55Q9+kN2nTs0h\nBx+cs88/PyNHjizziIFaMn/+/MyaMSNzb7ut1fxzd0NDeiZpSLIkKj2A6iBEAjXvumuvzbeuvTaT\nFy/Ox5P0Xef+05csyReTzP7hD/Oh22/P9Jkzc9oZZ5RhpECtue7aazN18uSct2RJvlIqtZ5/SqW8\nmuTfk/xLkvcdcIBKD6DiCZFATbvu2mtz2eTJmbd4cXZdz359k5xTKuWfFi/OQZMnJ4kgCWyWjZl/\nJic5LMlB//Zv2XXXXc0/QEXzqy6gZs2fPz9TJ0/O7et8gBuTpFeSbZL0TvLWte7bNcntixdn6uTJ\neeCBB7pusEBNaW/+WePJrJ6HTlhrm/kHqBZCJFCzZs2YkfOWLGn1Aa4hyTVJ/pLVf5P0m3Xu3zXJ\nZ5YsyawZM7pglEAtam/+WeOsJO9qY7v5B6gGQiRQkxYuXJi5t92WE0ulNu9ve+vfnVgq5Se33poX\nX3yx4wcH1LQNzT//mdWnsL6/ncebf4BKJ0QCNWnO7Nk5PK0vorPG+UkGJRmd5K427u+X5KClSzN4\n0KA0NDTU5RewadY3//wlydQkV6b9X2b1S3J4Q0PmzJ7dOQME2EwurEPVampqShIfdmlTr6z+kNaW\ny5OMSLJlkm8n+ackDybZZZ39DkjyoyRLO2mMQG164qGH8q6lbc8cFyc5Ncn2G3iOkUuWZMHDD3f0\n0AA6hBBJ1TrssMMyY8aM/Pa3vy33UKhA995+e3o/91yb963dAnlCVgfJW5P88zr79U59T5J+QQOb\nZuus/iXUuhYk+X9/+++G9E6y6NVXO3JYAB2mnj8fUQOmTJlS7iFQoU477rgs+ta3Cu3bkLZPK1uU\nZEVHDqrKlNr5ey5g/dqbf+5K8rskO2X1nPN6kpVJfp1k3WuxLkrSu297J+QDlJe/iQRq0u5vf3t+\n2bNnq+2vJbkjybKs/vD2rSTzkoxt4znm9+qVz11+eUqlUl1+AZumvfnnE0mezuqVyAeTnJ7k0Kye\nk9Y1v1ev7L7nnp05TIBN1lDySQGoQQsXLsywoUPz26VLW1zc4qUk45I8nqRbkuFJPpfkfes8/pUk\nb+nZM08891wGDhzYJWMGakN788+6pmd1qJyzznbzD1DprEQCNWnQoEE55OCDc8M6f9c3IMkvs3pF\n8pUk96Z1gEySGxoacui4cT7AARutvflnXVPTOkAm5h+g8lmJBGrW/Pnz86ExYzJv8eJ2C7/b8lSS\n0U1NueWuu7LPPvt01vCAGmb+AWqZlUigZo0cOTLTZ87MQU1NeargY55KclBTU6bPnOkDHLDJzD9A\nLes2bdq0aeUeBEBn2XvkyPTq1y8n/Pd/p9uKFRme1R2S63olybUNDTmlqSkXzpyZ0844o4tHCtQa\n8w9Qq5zOCtSFBx54ILNmzMhPbr01hzc0ZOSSJat72LL6Kog3l0o5dNy4nH3++VYAgA5l/gFqjRAJ\n1JUXX3wxc2bPzhMPP5xFr76a3n37Zvc998wJJ53kIhZApzL/ALVCiAQAAKAwF9YBAACgMCESAACA\nwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAK\nEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChM\niAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAh\nEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRI\nAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIB\nAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQA\nAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAA\ngMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAA\nChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAo\nTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAw\nIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKE\nSAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMi\nAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgE\nAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIA\nAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAA\nAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAA\nKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDChEgAAAAKEyIBAAAoTIgEAACg\nMCESAACAwoRIAAAAChMiAQAAKEyIBAAAoDAhEgAAgMKESAAAAAoTIgEAAChMiAQAAKAwIRIAAIDC\nhEgAAAAKEyIBAAAoTIgEAACgMCESAACAwoRIAAAAChMiAQAAKOz/A9vm480C/WSZAAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21aeafa940>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S1.g,with_labels=True, arrows= True, pos=start_pos)\n",
"plt.arrow(0,0,20,0)\n",
"plt.arrow(0,0,0,20)\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in starting reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **Inertial properties** wrt Center of Gravity in with original rotation"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAWQAAAAyBAMAAACZlbxNAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAiUSZq1TvELvdZiIy\nds1Wk1T5AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGM0lEQVRoBdVYXYgbVRQ+k7/J3yZb6os/bccX\nn6SbqrWL2DZCRSmuDUJFEUnQgla0DQpLQWwiFasomtpSqUVMEepTaaDqiw8b7Hs3WvFFZCO7UtB2\nTf9Ybd3Gc+7f/N3J/vjQ6XmYe873nXPnm5s7994MAJph4eUWMLOoRK5UXsidtVKfUSRvxQ9tauAM\nu4bzku4KXU9X0dlrRXn8l0BD2bzNVZkvULsPknVq01/QA4TVxktMWbKATeS6UPnN5lZY9aKueIWJ\nK9OwJrkP0JmyGBrSywGm6yBd8+dX3UdtpFpuUhtWK9McSLMpUfsDEiWMXofJTljlkq5UgS51cmtz\nEH0JWwsmCAytpedQ2qRF+vINSF8CyG7Zsq1OMbOV+6rSHdQaoxsG0UHcssrMeezuQdZlqgvpaziV\nARJdeQ+jFVO+xHTtnfCkDl4IW17ZLHa7g3Udq7BRbuJEqTAAL6lWVi59EnK33/PwKEy23MSiIiob\nWlSmM2mqBVkcW7QszuUKZEoAuR7FZCkrg3Ml2LJ1zn0CE1ZwViBDZZFiIB1ATDRhSAzkI4A7y7eY\nl3SMbJwme6Dl1ExnS3tgXiCBZXcEkgFEoqj2EOP+J2BP/xzEP/6noLJTHeVqnI0K+1x5S3KwLKUe\ne5GVyQYk6rrcPTsZGnAqPcPIjPoJDPsheWenRj8UvYqOREQNcea7DfSobMhbSinmumNtap0mMaMH\nNV0NwDSlp/Uc8MOeLfRLZ9/o41F8jSWwGS2XKyJMZZmeh6cwVzKPemGJ4VIcsNldpZK74V5vJcXi\nsMd2S4ojw5E2tcpiVUhURMQ6Iv95DnAuX5Jln4k8Z3McYLUzJl9i2XkoY7HfIvSjZ3/fvt9PAYjD\n3mRVkGe2PyNdjiQaEPuXu6wj5grJnBvBAl42KjpxNu8A+F5oiZmX4WTbmSx9o4Feot/vScDZisMe\nPje33f2+dHmbm1OSWUcMFZI5dztCvOxndymLrgCMlDy4wq4ALs0ay60/8YEGZpA87G3CKLNuI51M\n/Jaa41xu7Ky4uZCMqcjN/Lpe1NB4ewwHEkY6btDG/oY1Wsm1P2GLu8aO5GHvPYTuadk7j52B3sgw\n52rnTLHO25JHhs0b1Zq472TbVUdB5iKefIbdsI3tgs1VN8ejchtIkdbkYW8Gl4ZXIFrXJh0SHM5J\nFEBmSz4EuEXlhSbNxpnBUfZJVthO2MY77DsNAH/01zjhu6rD3kGA6BykOjJj7xGy8yyMFgS3CUyS\nvHp29vDsLD4kGnFdqEnJJQY6L/YksFEbOywl2yTzDkBGvPIewnHYQwG4D9XavgwEzkpuGiJimVOj\njFyuoN4vzSgDvmq+hUxhh/UTw7wERkUnBbEmvj+MQ8k4VGVdWrwA33HuGo02MymZuHxT3Vd3CMQ5\nebLq6VdhR/SvX7oHieGvPEU8zOAPyV+5x1FyCT6Kt/x5pwF+4dwlGG9yXkomLm/hW8BNs2LQtkHL\nkcsUtgum2i6GB7Eu5K1h5ps33Lx92MMVNddJHzLcPEWZAyseaHBuK34g4SYkMy7WTBYEzFb3WldE\nvEmVzFdBhxH9Mpy0eJrrmmyCsUogR6pOynHYw/Exx+76+kcnzf0cvssNzr1xtil4IZlzGx+SVWz3\nS30qQ9aaq35qgw4j9jKULZbFLheqp0t2JDzdD8+ohOXLHQTIieHJucDi5zwohToM19WLrmPR7r5Y\nQ50daH54Tkf5zHHmDvLf1JImfzl1XekwPPjMQ75gd/XbWMsOpPeWdLxttuJFlhGni1RkdvylOgyz\n4lch1bWzi7Zre03b9XiPeuLlhKk2VaU1pToM04zrEO3Z6UXbXYy3dzFJC+QcW4D30bEesM8vgth6\n4mFfygAAN4X/a5n6UnvADTer/jYA7F/iv/unlno/X3606oMWACZw2u9w5iQbziiMPp3vNzuFRcXh\n1omFy38f5YxYUhNu08bAz0My8Sa27DMi+2LLROAHRHnsuomiBt96iLYee8mI4rGyO7jiprOJIkl4\nUerIFOA4Tu5QW5kJtD8ZnLptQ6j1orhpJhD/1dwyFuefIAL/5YXwQcYtLurZEGoLkLRP4NFiQELo\n4HRdShqTTtjbtUpg1FJuqB3zMZL3H6SCllZ5xU8FAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\left ( \\frac{6 A}{5} h^{2}, \\quad A \\left(a^{2} - 2 a b + 2 b^{2}\\right), \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 ⎞\n",
"⎜6⋅A⋅h ⎛ 2 2⎞ ⎟\n",
"⎜──────, A⋅⎝a - 2⋅a⋅b + 2⋅b ⎠, 0, 0⎟\n",
"⎝ 5 ⎠"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.Ixx0, S1.Iyy0, S1.Ixy0, S1.α0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Plot of **S1** section in inertial reference Frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Section is plotted wrt **center of gravity** and rotated (if necessary) so that *x* and *y* are principal axes.\n",
"**Center of Gravity** and **Shear Center** are drawn"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"positions={ii: [float(S1.g.node[ii]['pos'][i].subs(datav)) for i in range(2)] for ii in S1.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA40AAAJtCAYAAACSZ5UPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xuc1WWBP/DPmRG5KCEiiKFCpUJeylwxNdmwzAtaabqm\nBZaCdtFSvKWJIl5ivUuba+ulRdTcSs0iMLddjayssNbLlopYrfszC0VDSsAYz+8PZJZh5gsDczln\nznm/Xy9eNme+55znnKGH+Zzn+30+pXK5XA4AAAC0oaHSAwAAAKB6CY0AAAAUEhoBAAAoJDQCAABQ\nSGgEAACgkNAIAABAIaERYA333HNP3vve92brrbdOv379MmLEiBxxxBG57777uuT5ZsyYkW9/+9ut\nbp82bVoaGxu75DnX5S1veUtOOOGEbn/edWloaMhFF120QffZf//98773va+LRpT8z//8TxoaGjJr\n1qwue47VXn311UyYMCFbb711Ghoacvrpp3f5c1aj448/Pg0NDa3+NDY25vXXX6/08ABq2iaVHgBA\ntfjyl7+c0047LZMmTcrZZ5+dzTbbLM8880zmzJmTBx54IAcddFCnP+e1116bMWPG5Igjjmhx+4kn\nnphDDjmk059vfe6555686U1v6vbnXZef/exn2XbbbTfoPtdff30Xjab7XXfddfnGN76Rf/3Xf82O\nO+6YbbbZptJDqpghQ4Zk9uzZWbtiuqHBZ+AAXUloBHjDVVddlY985CO54YYbmm8bO3ZsJk6c2O1j\nefOb35w3v/nN3f6873znO7v9OYu89tpr2XTTTbPXXntt8H1HjRrVBSPqHKtfV3v95je/yZvf/OZ8\n/OMfr8jzV5NNN900o0eP3qD79OTXC1AtfDQH8IaXXnopW2+9dbuO/f3vf5+Pf/zjGTJkSPr06ZN3\nvetdueeee1od9+ijj+aII47IVlttlX79+mXUqFG57LLLkqw6FfTZZ5/Nbbfd1nyq3epTQy+88MJW\nqydLly7NKaeckmHDhqVPnz4ZNWpUrr322hbHzJs3Lw0NDZk9e3Y+97nPZfDgwRk8eHAmTJiQV155\nZb2va8SIES1OT505c2YaGhry85//POPHj8+AAQMybNiwnHrqqXnttdfW+3gNDQ2ZMmVKvvSlL2W7\n7bZLv3798t73vjePPvpoi+PGjh2bMWPG5Hvf+1722GOP9O3bt3m1sK3TU9f1vq5+vDVPT139vtx9\n9905/vjjs+WWW2bAgAEZP358XnrppRaPfd1112XffffNoEGDMnDgwOyzzz6ZO3fuel9rW1b/HH/9\n61/n4IMPTv/+/fPRj360+ft333139tlnn2y22WYZOHBgjj766Pzv//5vi/dv1qxZefbZZ5tPxfzR\nj36UJHnxxRfz6U9/Ottuu2369OmTt7/97bnxxhtbPP8tt9yShoaGPPjggzn66KMzcODA7L333i3e\nlwMOOCBvetObsvnmm+fggw/Or3/96xaPsfpn85//+Z/5u7/7u2y22WbZbbfdNvjve3tfc0dMmTIl\nDQ0NeeKJJ3LggQemf//+zWH7vvvuy7hx47LNNts0v4YZM2a0OrV1u+22y/HHH59bbrklI0eObP47\n+7vf/S5//etfc9JJJ2XQoEHZZptt8oUvfKHVqucLL7yQT33qUxk2bFh69+6dnXfeOV/72tc65fUB\nVIqVRoA37LXXXpk5c2be8pa35MMf/nB23HHHNo/7f//v/2WvvfbK0KFDM2PGjGy11Vb5xje+kSOP\nPDLf+c53cthhhyVJfvGLX2T//ffPjjvumBkzZmTYsGF5+umn89hjjyVJvv3tb2fcuHHZfffdM23a\ntJTL5QwePDhJUiqVUiqVmp+zXC5n3LhxeeSRR3LxxRdn1113zZw5c3L66afnxRdfzCWXXNJijKed\ndloOO+yw3HHHHXnqqady1llnZZNNNsm//uu/rvM9WPM51/z6uOOOy7HHHptvf/vbeeihhzJ16tRs\nueWWmTp16nrf11mzZmX48OG57rrrsmLFipx//vk54IAD8vTTT2eLLbZofp4FCxbk1FNPzfnnn5+3\nvvWt2XLLLdt8vPW9r229jtUmT56cAw44IP/2b/+Wp59+Oueee26ef/75/Od//mfzMb///e9z/PHH\n521ve1uampoye/bsfPCDH8y9996bAw88cL2vd02rx3H44Ydn4sSJOeecc5o/DPjqV7+az372s5k4\ncWKmTp2apUuXZurUqRk7dmwee+yxbLbZZvnZz36WqVOn5rHHHss999yTcrmcnXfeOUuXLs173vOe\nrFixIhdddFFGjBiR++67L5/5zGfy2muv5eSTT24xjvHjx+fYY4/NXXfdlZUrVyZJ5syZk8MPPzwf\n/OAHc/vttydJ/vEf/zFjxozJ448/nmHDhjW/hmeeeSannXZavvjFL2bQoEG58sorc/TRR+fJJ5/M\nW9/61nb/XNrzmtenqampxdcNDQ3N7/Pq/374wx/OxIkTc9555zW/37/97W/z/ve/P5/73OfSr1+/\nzJ8/P+eff34WL17c6kOJ+++/PwsXLsyVV16Z5cuX5/Of/3yOPPLIbLvtttl5553zzW9+Mz/84Q9z\n6aWXZscdd8ykSZOSJEuWLMm+++6bpqamXHLJJRk+fHjmzp2bE088MX/729/yqU99ar2vD6AqlQEo\nl8vl8oIFC8rvfOc7yw0NDeVSqVTeaqutyscee2z53//931scd8IJJ5SHDBlSfvnll1vc/oEPfKD8\nrne9q/nrMWPGlLfffvvy8uXLC59zxIgR5QkTJrS6/cILLyw3NDQ0fz179uxyqVQqz5o1q8VxkyZN\nKvfp06e8ePHicrlcLv/whz8sl0ql8vHHH9/iuFNOOaXct2/f9bwDq8az5n1nzpxZLpVK5WnTprU4\n7rDDDiuPHDlyvY9XKpXKgwcPLi9btqz5tt///vflXr16lS+44ILm28aOHVtubGwsP/bYY20+xprP\n3573dezYseX999+/+evV78u4ceNaHHf77beXGxoayvfff3+bj/P666+XV65cWT7wwAPLhx9+eIvX\nUCqVyrfccss6Xv3//Rz/6Z/+qcXtf/nLX8oDBgwoT5o0qcXtv//978ubbrppecaMGc23jR8/vvyW\nt7ylxXEXXXRRuW/fvuVnnnmmxe0nnnhiefDgweWmpqZyufx/P78zzjij1dh22GGH8gc+8IEWty1d\nurS81VZblSdPntx829ixY8ubbrppi+datGhRubGxsTx9+vTm29b3c9mQ19yWT37yk+VSqdTiT0ND\nQ/n8889vPmbKlCnlhoaG8vXXX7/OxyqXy+WVK1eWp02bVh48eHCL27fddtvy4MGDy3/961+bb7v6\n6qvLpVKp/NnPfrbFse94xzvKBx54YPPXF1xwQblfv37l3/3udy2OO/7448tDhw4tv/766+sdF0A1\ncnoqwBt23HHH/Nd//VfmzZuXKVOmNJ9yetBBB+XSSy9tPm71aW79+/dPU1NTmpqasnLlyhx44IF5\n9NFH85e//CXLli3LT3/604wfPz69e/fu8NgefPDBNDY25thjj21x+/jx4/Paa6/loYceanH7uHHj\nWny92267ZcWKFVm0aNEGP3epVGrz8Z599tl23X/cuHHp06dP89fDhw/P3nvv3WrMI0aMyG677bbO\nx+ro+/oP//APrb4ulUotxvLLX/4yhx12WIYOHZpNNtkkvXr1yg9+8IM89dRTG/x8qx1++OEtvn7o\noYeydOnSfOxjH2v+O9TU1JRhw4Zl1KhRzaegFrnvvvvy7ne/O8OHD29x/wMPPDAvvvhifvOb3zQf\nWyqVWj3/woUL88wzz7R6/j59+mSfffZp9fw77rhj84pikgwePDhDhgxp/jvQnp9LR19zkmy99db5\n5S9/mYcffjgPP/xw5s+fn89+9rOtjlv79SbJ888/nxNPPDHDhw9Pr1690qtXr1x44YVZvHhxq1OU\n3/Oe96Rfv37NX48aNSqlUqnVSvOoUaNanFp73333Zd999812223X6ueyaNGiDv0dAqgkp6cCrKFU\nKmW//fbLfvvtlyT54x//mIMOOigXXXRRTjnllAwYMCCLFi3KrFmzcsstt7S6f0NDQxYvXpxevXrl\n9ddfbz7Fr6NeeumlbLnlltlkk5bT9tChQ1Mul1v90rv2qZ2rf5Ffvnz5Rj1/W4+3YsWKdt23retE\nt9566xbBJkm7dgV9+eWXO/S+rj2WXr16ZeDAgXnuueeSrDr1+IADDsguu+ySr3zlK9l+++2zySab\nZMqUKXnyySc36jmT1q9t0aJFKZfLef/739/q2FKpVHhq7pr3f+aZZ9KrV68277948eL1Pn+STJw4\nsVXFSqlUyvbbb9/itrbG07t37+a/T+35uXT0NSerfl7vete71nvc0KFDW3z9+uuv59BDD83ixYtz\n4YUXZuTIkenTp0/uvPPOXHbZZa3+fzFw4MAWX6/eSKet29e876JFizJ//vx2/1wAegqhEWAdhg4d\nmkmTJuW0007L008/nT333DODBg3K3//93+ecc85ptQlGsmrn05UrV6ahoaE5jHTUlltumZdeeikr\nV65sERz/+Mc/Nn+/Wv3pT39q87a1A0bRdYhrGjhwYIfe17XH8re//S0vv/xy81juvffevPLKK/nW\nt77VImi9+uqrG/V8q6392gYNGpRk1fWeO++8c6vj+/fvv87HGzRoULbeeut8+ctfbvPv4MiRI9v1\n/NOnT88BBxzQ6v4buttoe34uHX3NHbFgwYI88sgj+cY3vtFitfmuu+7q1OcZNGhQtt9++1xzzTXt\n+rkA9BRCI8Ab/vjHP7ZaoUiSJ554Isn/rV4cfPDB+dnPfpadd9658FS8Xr16Zb/99sttt92WCy64\noPC43r17Z9myZesd23vf+95cccUV+da3vtXiFNXbbrstvXv3zj777NN8W3vCV3eaO3duli1blr59\n+yZZtdHMz372s3zxi1/c4Mfq27dvu97XIt/85jfzyU9+ssXX5XI5++67b5I0/yzWDOYLFizIT37y\nk2y33XYbPN4i++67b/r375+nn34648eP3+D7H3zwwfnKV76S7bbbLltttdUG33/kyJEZMWJEfv3r\nX+fss8/e4PuvrT0/l46+5o5YHfrX/Lm+9tpr+frXv96pz3PwwQfnhhtuyPDhw6v6gxyADSU0Arxh\n1113zQEHHJBx48blLW95S1555ZXMmTMn//Iv/5KPfvSjzQXzF110Ud797ndnzJgxOeWUUzJixIi8\n/PLL+e///u/87ne/y0033ZQkufLKKzN27NjsvffeOeOMM7Ltttvmt7/9bR555JF8+ctfTpLsvPPO\nefDBBzNnzpwMHTo0W221VYYPH95qbIccckj222+/fPrTn86iRYuyyy67ZM6cOfna176WL37xiy1+\nQW1rhaOS+vbtmwMPPDBnnnlmli9fnqlTp2aLLbbIaaedtlGP1573tcivf/3rnHDCCTnmmGPy1FNP\nZcqUKdl///0zduzYJMkBBxyQxsbGTJgwIWeccUb+8Ic/5MILL8zw4cNbVTN0RP/+/XPFFVfklFNO\nyaJFi3LIIYdkwIABee655zJv3rzsv//+OeaYYwrvP3ny5Hzzm9/Mfvvtl8mTJ2fkyJH561//mief\nfDIPPvhgm3UYa7vuuuty+OGHZ8WKFTn66KOz1VZb5U9/+lN++tOfZvjw4Rv881nfz6Wjr7kjdtll\nl2y77bY555xzkqz6YOWaa65p8zTSIu35/9WZZ56ZO++8s/nnstNOO2Xp0qV58skn89Of/jR33333\nRr8GgEoSGgHe8KUvfSlz587N1KlT86c//SmNjY3Zaaedcvnll+fUU09tPm677bbLww8/nAsvvDDn\nnXdeXnjhhQwaNCi77rprPvGJTzQft+eee+YnP/lJLrjggnz+85/PihUrMnz48Bx//PHNx0yfPj0n\nnXRSPvrRj2bZsmX5xCc+0dzptuaKYalUyty5c/PFL34xl19+eRYvXpwRI0bkmmuuyec///kWr6Mj\nK41rV32s79j2OO6447LZZpvllFNOyeLFi7PXXnvlW9/6VnPdxvoeb+0xted9bevxSqVSZsyYke9+\n97s55phj0tTUlA996EOZMWNG8zE777xzvv71r+eCCy7Ihz/84bztbW/LZZddlnvvvTfz5s3bqNdf\ndNxJJ52U7bffPldccUXuuOOOrFy5MsOGDcuYMWOy++67r/Mx3vSmN+WnP/1pLrroolx++eV57rnn\nssUWW2TkyJE58sgj2zWuQw45JD/60Y9y6aWX5sQTT8yyZcsydOjQ7L333q3CW1uvYWN+LhvymtvS\nnve8rWN69+6d7373u/nc5z6XCRMmZNCgQZk4cWK22WabfPrTn17n61rfc695+4ABA/LQQw9l2rRp\nmT59ev7whz9kiy22yKhRo1ptwgTQk5TK1faRNAA1o6GhIVOmTGnVg9fd5s2bl/e97335wQ9+kPe9\n730VHQsA9DQqNwCoCz4jBYCNIzQC0GU25HTXrlYt4wCAnsbpqQAAABSy0ggAAEAhoREAAIBCQiMA\nAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAA\nCgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQS\nGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQC\nAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAA\noJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAh\noREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIj\nAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAA\nAAoJjQAAABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAU\nEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0\nAgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQSGgEAACgkNAIAAFBIaAQA\nAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABA\nIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJC\nIwAAAIWERgAAAAoJjQAAABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYA\nAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAA\nFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQSGgEAACgk\nNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgE\nAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAA\nQKFNKj0A2FCLFi3KrJkzs+Cxx/KXJUuy+YAB2ekd78gnjj8+gwcPrvTwgBpm/gEqxfxDJZXK5XK5\n0oOA9pg/f35mTJ+eOffem48kGb18efonWZrkF3375tvlcg495JCceu65GT16dIVHC9QS8w9QKeYf\nqoHQSI9ww/XXZ+qZZ+YLy5blE+VyBrZxzMtJZpZKubxv30y78sqc9JnPdPcwgRpk/gEqxfxDtRAa\nqXo3XH99LjvzzNz36qvZoR3HL0xyUL9++YKJE+gg8w9QKeYfqonQSFWbP39+PjR2bB5ca8K8LsnM\nJI8n+ViSr611v4VJxvTrl9nz5mXPPffsnsECNaWt+ee1JJ9N8h9Z9en+25J8KcnBa9zP/AN0VNHv\nPxOyav5ZlmRokrOSTFzj++YfuordU6lqM6ZPzxeWLWv1CduwJOen5US5ph2SnL1sWWZMn96l4wNq\nV1vzz8ok2yd5MMmSJBcnOTrJs2scY/4BOqro959zk/wuyZ+TfDfJlCT/tcb3zT90FSuNVK1FixZl\n5PDh+e3y5W2ew5+sCo7PpfVKY5K8lORtffpkwbPP2lUM2CDtmX9We2eSC5McscZt5h9gY7V3/nkq\nyf5JvpzkqDVuN//QFaw0UrVmzZyZI5L1/sJWZMskR5RKmTVzZucNCupIqVSq2z9Dt946B7cjMP4p\nydNJdlnrdvMPdEyl54Bqnn9OTrJZkrcneXOScWt93/xDVxAaqVoLHnssey1f3qHHGL1sWRY8/ngn\njQioF32SvHc9x6xMMj7JJ5Ps1Mb3zT/Axljf/HNdkr8k+XGSjyTp3cYx5h862yaVHgAU+cuSJenf\nwcfon+Trt96aG269tTOGBNSJxmSd8085qwJj7yT/VHCM+QfYGOubf5KklGTfJLcmuT7JKWt9v3+S\npS+/3PmDo24JjVStzQcMyNIOPsbSJB+bMCH/MmtWZwwJ6kqpVKr0ECqmKVnn/DMxyYtJ5mbVL3ht\nMf/AxjP/tM/KJM+0cfvSJP0HbuwFPtCa01OpWju94x35RZ8+bX6vKcnyN/67MsmKN/732ub37Zud\ndtuty8YItaxcLtftn4suu6xw/vl0kiezaufCTdfx/pl/YONVeg6oxvnnhSTfSPLXJK8nuS/JvyU5\noI33z/xDZ7N7KlVrXbuHTXvjz5qfQ05NcsEaX9s9DNhYRfPPs0lGZNU1R6tXGEtJ/iXJsWscZ/4B\nNlbR/PNiVu2S+lhWhcbhSU5NcsJa9zf/0BWsNFK1hgwZkkMPOSS3tHGKytSsmjCb1vhzwVrH3FIq\n5bBx40yYwAYrmn+2z6q559WsOv1raZJX0jIwJuYfYOMVzT9bJflhVoXCPyd5NK0DY2L+oWtYaaSq\nzZ8/Px8aOzYPvvpqq4LbdVmYZEy/fpk9b1723HPPrhoeUMPMP0ClmH+oNlYaqWqjR4/OtCuvzEH9\n+mVhO++zMMkBm26aaVdeacIENtrGzj8H9etn/gE6xPxDtWm88MILL6z0IGBd/m706PTdcssc98AD\naVy5MqOS9G3juJeSfCWrtsFv6t8/M2+9Nb169erWsQK1ZUPmn+tLpUzq1y9TrrwyJ33mM908UqDW\nrJ5/jr3vvjS+/nreHvMPleP0VHqMhx9+ODOmT8/35s7NEaVSRi9btqqHKMnP+/TJN5YvTynJsjeO\nv/jiizNlypTKDRioGeuaf+b37Ztvl8s5bNy4nHruuT7hBzrNwoULs+eee+YD++6b/3jgAfMPFSM0\n0uO88MILmTVzZhY8/niWvvxy+g8cmJ122y0Lf/vbfPWrX20+rl+/flmwYEGGDRtWwdECtaRo/jnu\nk5+06QTQ6Y444ojstddeOffcc80/VJTQSM3485//nB133DEvvvhi823HHXdcbrnllgqOCgBgw91/\n//2ZOHFinnjiifQp6I2F7mIjHGrGFltskYsvvrjFbbNmzcr8+fMrNCIAgA3X1NSUyZMn54orrhAY\nqQpCIzVl0qRJ2XXXXVvcdtppp8WCOgDQU9x8880ZMGBAjjzyyEoPBZI4PZUa9IMf/CAHHnhgi9vu\nuOOOHHPMMRUaEQBA+yxZsiQjR47M3Llzs8cee1R6OJBEaKRGfehDH8rs2bObv95uu+3y1FNPpW/f\ntjarBgCoDmeffXYWL16cm2++udJDgWZCIzXp6aefzi677JK//e1vzbep4AAAqtnChQuz99575/HH\nH88222xT6eFAM9c0UpN23HHHfO5zn2tx2/Tp0/Pcc89VaEQAAOt21lln5YwzzhAYqTpWGqlZKjgA\ngJ5CxQbVzEojNUsFBwDQE6jYoNoJjdQ0FRwAQLVTsUG1c3oqNU8FBwBQrVRs0BMIjdQFFRwAQDVS\nsUFPIDRSF1RwAADVRsUGPYVrGqkLKjgAgGqjYoOewkojdUMFBwBQLVRs0JNYaaRuqOAAAKqBig16\nGqGRuqKCAwCoNBUb9DROT6XuqOAAACpFxQY9kdBIXVLBAQBUgooNeiKhkbqkggMA6G4qNuipXNNI\nXVLBAQB0NxUb9FRWGqlbKjgAgO6iYoOezEojdUsFBwDQHVRs0NMJjdQ1FRwAQFdTsUFP5/RU6p4K\nDgCgq6jYoBYIjRAVHABA11CxQS0QGiEqOACAzqdig1rhmkaICg4AoPOp2KBWWGmEN6jgAAA6i4oN\naomVRniDCg4AoDOo2KDWCI2wBhUcAEBHqdig1jg9FdaiggMA2FgqNqhFQiO0QQUHALAxVGxQi4RG\naIMKDgBgQ6nYoFa5phHaoIIDANhQKjaoVVYaoYAKDgCgvVRsUMusNEIBFRwAQHuo2KDWCY2wDio4\nAID1UbFBrXN6KqyHCg4AoIiKDeqB0AjtoIIDAGiLig3qgdAI7aCCAwBYm4oN6oVrGqEdVHAAAGtT\nsUG9sNII7aSCAwBYTcUG9cRKI7STCg4AIFGxQf0RGmEDqOAAAFRsUG+cngobSAUHANQvFRvUI6ER\nNoIKDgCoTyo2qEdCI2wEFRwAUH9UbFCvXNMIG0EFBwDUHxUb1CsrjbCRVHAAQP1QsUE9s9IIG0kF\nBwDUBxUb1DuhETpABQcA1D4VG9Q7oRE6YJNNNsnVV1/d/PXmm2+eyZMnV3BEAEBnWrJkSS644IJc\ne+21KZVKlR4OVITQCB30gQ98IB/72McyderU9OvXL29961v9owIANeLSSy/NoYceqpORumYjHOhE\nN9xwQ25n1nG/AAAckUlEQVS77bbMmzdPcASAHk7FBqxipRE60cSJE7NkyZLcddddlR4KANBBKjZg\nFSuN0MkeeOCBnHDCCbbkBoAeTMUG/B8rjdDJ9t9//+y+++655pprKj0UAGAjqNiAlqw0QhdwDQQA\n9Fz2KICWhEboImeffXYWL16cm2++udJDAQDaacmSJRk5cmTmzp1rx1R4g9AIXcQ/OgDQ8/jQF1oT\nGqELOb0FAHoOl5dA22yEA11IBQcA9BwqNqBtVhqhi6ngAIDqp2IDillphC6mggMAqpuKDVg3K43Q\nDVwjAQDVyx4EsG5CI3QTu7EBQPWx2zmsn9AI3cQ/SgBQfXyoC+snNEI3cvoLAFQPl49A+9gIB7qR\nCg4AqB4qNqB9rDRCN1PBAQCVp2ID2s9KI3QzFRwAUFkqNmDDWGmECnANBQBUjj0GYMMIjVAhdmsD\ngO5nN3PYcEIjVIh/tACg+/nQFjac0AgV5PQYAOg+Lg+BjWMjHKggFRwA0H1UbMDGsdIIFaaCAwC6\nnooN2HhWGqHCVHAAQNdSsQEdY6URqoBrLACg69hDADpGaIQqYTc3AOh8diuHjhMaoUr4Rw0AOp8P\nZaHjhEaoIk6fAYDO4/IP6Bw2woEqooIDADqPig3oHFYaocqo4ACAjlOxAZ1HaIQqdMQRR2SvvfbK\nueeeW+mhAGtYvnx5brzxzsyd+2SWL29Mnz5NGTduVE488Si/lEIVaWpqyh577JHzzz8/Rx11VKWH\nAz2e0AhVyDUYUH1uvXV2Lr30x1m48Ng0Ne3efHtj4yPZYYc7ct55+2XChA9WcITAavYIgM4lNEKV\nstsbVI9bb52dM874U154YVLhMYMH35SrrtpacIQKsxs5dD6hEaqUf/SgOixfvjy77z41Tz112XqP\nHTny7Dz66MXp3bt3N4wMaIsPXaHz2T0VqtSAAQNy0UUX5bTTTovPdqBybrzxzixceGy7jl248GO5\n6aY7u3hEQJGFCxfma1/7Wi655JJKDwVqitAIVUwFB1Te3LlPtriGcV2amnbP9773RBePCCiiYgO6\nhtAIVayxsTHXXnttzjrrrCxfvrzSw4G6tHx54wYdv2LFhh0PdI77778/jzzySCZPnlzpoUDNERqh\nyu2///7Zfffdc80111R6KFCX+vRp2qDje/fesOOBjmtqasrkyZNzxRVXqL+BLiA0Qg9wxRVX5Kqr\nrsrzzz9f6aFA3Rk3blQaGx9p17GNjf+Vww57exePCFjbzTffnAEDBuTII4+s9FCgJtk9FXoIu8FB\nZdg9Faqb3cah61lphB7ivPPOy5w5c/KrX/2q0kOButKnT59MmTImgwfftM7jBg++KVOm/L3ACN3s\n0ksvzaGHHiowQhey0gg9yA033JDbbrst8+bNS6lUqvRwoK7ceuvsXHrpg1m48GMtdlNtbHwkO+zw\n9Zx33phMmPDBCo4Q6s/ChQuz99575/HHH7djKnQhoRF6kKampuyxxx45//zzc9RRR1V6OFB3VqxY\nkRtvvDNz5jyRFSsa07t3Uw477O2ZNOkoK4xQAUcccUT22muvnHvuuZUeCtQ0oRF6mAceeCAnnHBC\nnnjiCTvEAVC37r///kycONG/h9ANXNMIPYwKDgDqnYoN6F5WGqEHcg0HAPXMNf7QvYRG6KFUcABQ\nj1RsQPcTGqGH8o8mAPXIh6bQ/YRG6MGcngNAPXF5BlSGjXCgB5s4cWKWLFmSu+66q9JDAYAud9ZZ\nZ+WMM84QGKGbWWmEHk4FBwD1QMUGVI6VRujhVHAAUOtUbEBlWWmEGuAaDwBqmWv4obKERqgRdpMD\noBbZLRwqT2iEGuEfVQBqkQ9FofKERqghTt8BoJa4/AKqg41woIao4ACglqjYgOpgpRFqjAoOAGqB\nig2oHlYaocao4ACgp1OxAdXFSiPUINeAANCTuUYfqovQCDXKbnMA9ER2A4fqIzRCjfKPLgA9kQ89\nofoIjVDDnN4DQE/i8gqoTjbCgRqmggOAnkTFBlQnK41Q41RwANATqNiA6mWlEWqcCg4Aqp2KDahu\nVhqhDrhGBIBq5hp8qG5CI9QJu9EBUI3s9g3VT2iEOuEfZQCqkQ81ofoJjVBHnP4DQDVx+QT0DDbC\ngTqiggM6R7lczjnTzonPXaFjVGxAzyA0Qh1pbGzMtddem7POOivLly+v9HCgx7pr9l355/v/OXd/\n7+5KDwV6rPvvvz+PPPJIJk+eXOmhAOshNEKdUcEBHVMul3PlrVdm6f5Lc8WsK6w2wkZQsQE9i9AI\ndeiKK67IVVddleeff77SQ4Ee567Zd+Xx/o8npeTxzR+32ggb4eabb86AAQNy5JFHVnooQDvYCAfq\nlN3qYMOVy+Xsc/Q++fkuP09KScrJu3/97jz0zYdsLgXtZDdv6HmsNEKdOu+88zJnzpz86le/qvRQ\noMdYc5UxidVG2AiXXnppDj30UIERehArjVDHVHBA+7VaZWz+htVGaC8VG9AzWWmEOqaCA9qv1Srj\nalYbod1UbEDPZKUR6twDDzyQE044IU888YQd7KBA4Spj8wFWG2F97r///kycONG/N9ADWWmEOqeC\nA9avcJVxNauNsE4qNqBns9IIuMYE1mG9q4zNB1pthCKuoYeezUojkB122CEnnHBCpkyZUumhQNVZ\n7yrjalYboU1LlizJBRdckGuvvVZghB7KSiOQRG8WFJl8weT86n9+1a5fdsvlcvYYvkeuucjp3rCa\nXmDo+YRGoJnThwDoTC5/gNrg9FSgmQoOADqTig2oDVYagRZUcADQGVRsQO2w0gi0oIIDgI5SsQG1\nxUoj0IprUADoCNfIQ20RGoE22e0OgI1hN26oPUIj0Cb/6AOwMXzoCLVHaAQKOb0IgA3h8gaoTTbC\nAQqp4ABgQ6jYgNpkpRFYJxUcALSHig2oXVYagXVSwQHA+qjYgNpmpRFYL9eoALAuroGH2iY0Au1i\nNzwA2mK3bah9QiPQLn4pAKAtPlSE2ic0Au3m9CMA1uTyBagPNsIB2k0FBwBrUrEB9cFKI7BBVHAA\nkKjYgHpipRHYICo4AFCxAfXFSiOwwVzDAlDfXOMO9UVoBDaK3fIA6pPdtKH+CI3ARvFLA0B98qEh\n1B+hEdhoTk8CqC8uT4D6ZCMcYKOp4ACoLyo2oD5ZaQQ6RAUHQH1QsQH1y0oj0CEqOABqn4oNqG9W\nGoEOc40LQG1zDTvUN6ER6BR20wOoTXbLBoRGoFP4pQKgNvlQEBAagU7j9CWA2uLyAyCxEQ7QiVRw\nANQWFRtAYqUR6GQqOABqg4oNYDUrjUCnUsEB0POp2ADWZKUR6HSugQHo2VyjDqxJaAS6hN32AHom\nu2EDaxMagS7hlw6AnsmHfsDahEagyzi9CaBncXkB0BYb4QBdRgUHQM+iYgNoi5VGoEup4ADoGVRs\nAEWsNAJdSgUHQPVTsQGsi5VGoMu5RgagurkGHVgXoRHoFnbjA6g+H//4x7PDDjvkq1/9au699167\nXQNtEhqBbqGCA6C6/OAHP8iBBx6YJNl8883zta99LUcddZSVRqAVoRHoNk5/AqgOK1euzLve9a78\n93//d/Nt++67b3784x+bn4FWbIQDdBsVHADV4aabbmoRGJPk2muvFRiBNllpBLqVCg6Ayvrzn/+c\nHXfcMS+++GLzbccdd1xuueWWCo4KqGZWGoFupYIDoLIuvvjiFoGxX79++dKXvlTBEQHVzkoj0O1U\ncABUxoIFC7LLLrtk5cqVzbddfPHFmTJlSgVHBVQ7oRGoCBUcAN3vQx/6UGbPnt389XbbbZennnoq\nffv2reCogGonNAIVoYIDoHutWbGx2h133JFjjjmmQiMCegqhEagYFRwA3UPFBtARNsIBKkYFB0D3\nULEBdISVRqCiVHAAdC0VG0BHWWkEKkoFB0DXUrEBdJSVRqDiVHAAdA0VG0BnEBqBqqCCA6DzqdgA\nOoPQCFQFFRwAnUvFBtBZhEagaqjgAOgcKjaAzmQjHKBqqOAA6BwqNoDOZKURqCoqOAA6RsUG0Nms\nNAJVRQUHQMeo2AA6m5VGoOqo4ADYOCo2gK4gNAJVSQUHwIZTsQF0BaERqEoqOAA2jIoNoKsIjUDV\nUsEB0D4qNoCuZCMcoGqp4ABoHxUbQFey0ghUNRUcAOumYgPoalYagaqmggNg3VRsAF3NSiNQ9VRw\nALRNxQbQHYRGoEdQwQHQmooNoDsIjUCPoIIDoCUVG0B3ERqBHkMFB8AqKjaA7mQjHKDHUMEBsIqK\nDaA7WWkEehQVHEC9U7EBdDcrjUCPooIDqHcqNoDuZqUR6HFUcAD1SsUGUAlCI9AjqeAA6pGKDaAS\nhEagR1LBAdQbFRtApQiNQI+lggOoFyo2gEqyEQ7QY6ngAOqFig2gkqw0Aj2aCg6g1qnYACrNSiPQ\no6ngAGqdig2g0qw0Aj2eCg6gVqnYAKqB0AjUBBUcQC1SsQFUA6ERqAkqOIBao2IDqBZCI1AzVHAA\ntULFBlBNbIQD1AwVHECtULEBVBMrjUBNUcEB9HQqNoBqY6URqCkqOICeTsUGUG2sNAI1RwUH0FOp\n2ACqkdAI1CQVHEBPpGIDqEZCI1CTVHAAPY2KDaBaCY1AzVLBAfQUKjaAamYjHKBmqeAAegoVG0A1\ns9II1DQVHEC1U7EBVDsrjUBNU8EBVDsVG0C1s9II1Lw1KzgaGxsza+bMLHjssfxlyZJsPmBAdnrH\nO/KJ44/P4MGDKz1UoIYtWrSo1fwzcJttctU116Spqan5OBUbQLURGoG6MGHChPzyRz/K84sW5SNJ\nRi9fnv5Jlib5Rd+++Xa5nEMPOSSnnntuRo8eXeHRArVk/vz5mTF9eubce2+r+efBhobc/frrKSVZ\nFhUbQHUSGoGad8P112fqGWfkzGXLckKSgW0c83KSmaVSLu/bN9OuvDInfeYz3TxKoBbdcP31mXrm\nmfnCsmX5RLlcOP/cnOTiJEefcEJu1C8LVBmhEahpN1x/fS4788zc9+qr2aEdxy9MclC/fvmC4Ah0\nkPkHqBVCI1Cz5s+fnw+NHZsH1/qFbWySnyfplaScZNskT6zx/YVJxvTrl9nz5mXPPffstvECtaNo\n/lnt6STvSPIPSWatcbv5B6hGdk8FataM6dPzhWXLWv3CVkryz0leyaprip5Y6/s7JDl72bLMmD69\nG0YJ1KKi+We1U5Ls1cbt5h+gGllpBGrSokWLMnL48Px2+fJW1xDtn2RCkhPWcf+XkrytT58sePZZ\nu6oCG2Rd80+S/FuSe5LsnFUri7PW+r75B6g2VhqBmjRr5swckbY3vUmSc5MMSTImybw2vr9lkoOW\nL8/WQ4akVCrV5R9g46xr/nklydQkV2fV6fFt2TLJEaVSZs2c2TUDBNhAQiNQkxY89lj2Wr68ze9d\nnuS3SZ5LcmKSDyb5XRvHvTdJ764aIFCz1jX/XJBV886b1/MYo5cty4LHH+/soQFslE0qPQCArvCX\nJUvSv+B7a7YwHpfkjiRzk5y81nH9U9+TpNVG2DibZ9WHTmt7JMl/vPHf9emfZOnLL3fmsAA2Wj3/\nPgTUsM0HDMjSdh5bStuniS1NsrLzhtTjuOQdNs5J48dn6e23t7p9XpL/SbJ9Vs05f0nSlOQ3SR5e\n69ilSfoPLDrBHqB7OT0VqEk7veMd+UWfPq1uX5Lk35OsyKpf1m5P8mCSg9t4jPl9++aSyy9PuVyu\nyz/Aximafz6V5JmsWml8NMmnkxyWVXPS2ub37ZuddtutK4cJ0G52TwVqUtHuhS8mGZfkqSSNSUYl\nuSTJ+9a6v90LgY21vt1TV5uWVSHS7qlAtbPSCNSkIUOG5NBDDskta12Xt1WSX2TViuNLSX6a1oEx\nSW4plXLYuHF+YQM2WNH8s7apaR0YE/MPUH2sNAI1a/78+fnQ2LF58NVXCwu227IwyZh+/TJ73rzs\nueeeXTU8oIaZf4BaYqURqFmjR4/OtCuvzEH9+mVhO++zMMlB/fpl2pVX+oUN2GjmH6CWNF544YUX\nVnoQAF3l70aPTt8tt8xxDzyQxpUrMypJ3zaOeynJ9aVSJvXrlylXXpmTPvOZbh4pUGvMP0CtcHoq\nUBcefvjhzJg+Pd+bOzdHlEoZvWzZqh60rNql8Nvlcg4bNy6nnnuuT/iBTmX+AXo6oRGoKy+88EJm\nzZyZBY8/nqUvv5z+Awdmp912y3Gf/KRNJ4AuZf4BeiqhEQAAgEI2wgEAAKCQ0AgAAEAhoREAAIBC\nQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRG\nAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAA\nABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAo\nJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEho\nBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgA\nAEAhoREAAIBCQiMAAACFhEYAAAAKCY0AAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACA\nQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAAKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWE\nRgAAAAoJjQAAABQSGgEAACgkNAIAAFBIaAQAAKCQ0AgAAEAhoREAAIBCQiMAAACFhEYAAAAKCY0A\nAAAUEhoBAAAoJDQCAABQSGgEAACgkNAIAABAIaERAACAQkIjAAAAhYRGAAAACgmNAAAAFBIaAQAA\nKCQ0AgAAUEhoBAAAoJDQCAAAQCGhEQAAgEJCIwAAAIWERgAAAAoJjQAAABQSGgEAACgkNAIAAFBI\naAQAAGreiBEjUiqV6ubPiBEjOu29K5XL5XKnPRoAAEAVKpVKqafo05mv10ojAABADbr22mtz++23\nd/hxhEYAAIAaNGTIkLzwwgsdfhyhEQAAgEKbVHoAAAAAlbB8+fLceOOdmTv3ySxf3pg+fZoybtyo\nnHjiUenTp0+3PUa1s9IIAADUnVtvnZ3dd5+ayZN3zfe/f0l++MNp+f73L8nkybtm992n5tZbZ3fL\nY6zp61//ekaPHp3+/ftn2LBhOfTQQ/OTn/wkSfL000/n2GOPzZAhQ7LFFltk5MiROfXUU/OHP/xh\no17/hhAaAQCAunLrrbNzxhl/ylNPXZampt1bfK+pafc89dRlOeOMP60z9HXGY6zp6quvzumnn54p\nU6Zk0aJFefbZZ3PyySdn9uzZeeaZZ7L33ntn2223zSOPPJI///nP+clPfpK3ve1t+fGPf7zhb8AG\nUrkBAADUvNUVFMuXL8/uu0/NU09dtt77jBx5dh599OL07t27xe2d8RhreuWVVzJs2LDccsst+chH\nPtLq+xMmTMgrr7yS73znO+t9vtVKpVJuv/32LFq0KKeddlq779cWK40AAEDduPHGO7Nw4bHtOnbh\nwo/lppvu7JLHWNNDDz2UFStW5PDDD2/z+//xH/+RI488sl3P1xWERgAAoG7Mnftkq9NJizQ17Z7v\nfe+JLnmMNS1evDhbbbVVGhrajmcvvvhihg4d2vz1ddddl4EDB6Z///751Kc+1a5xdITQCAAA1I3l\nyxs36PgVK1of3xmPsaZBgwblxRdfzOuvv174/eeff77565NPPjkvv/xyTjvttPztb3/boLFsDKER\nAACoG336NG3Q8b17tz6+Mx5jTfvss0969+6de+65p83vv//978/dd9+9Qc/ZmYRGAACgbowbNyqN\njY+069jGxv/KYYe9vUseY01vetObMm3atJx88sn5zne+k2XLlmXlypX5/ve/n3POOSfTpk3Lgw8+\nmDPPPLO5YuPFF1/ME0+s+7TXziI0AgAAdePEE4/KDjvc0a5jd9jhjkyadFSXPMbaTj/99Fx99dW5\n5JJLMmTIkGy//fa57rrrcvjhh2eHHXbIz3/+8/zv//5v3vnOd2bAgAEZM2ZMhg0blosvvrhd4+gI\nlRsAAEDNW125kSS33fa9nH76H/PCC5MKjx88+KZcffXQjB9/WJvf74zH6EoqNwAAADbS+PGH5aqr\nts7IkWe3Os20sfGRjBx5dq66aut1hr3OeIyewkojAABQ89ZcaVxtxYoVufHGOzNnzhNZsaIxvXs3\n5bDD3p5Jk45K79692/W4nfEYXaEzVxqFRgAAoOa1FRprmdNTAQAA6BZCIwAAAIWERgAAAAoJjQAA\nABQSGgEAACgkNAIAAHWtXC7nnGnndGh31c54jGolNAIAAHXtrtl35Z/v/+fc/b27K/YYP/7xj/Oe\n97wnW2yxxf9v7/5Zo0rDMA7fR1fS7JgUGUXFTSMR3GAlhBEsFmIZEIW0sRBbg34AsTYGP4HFBhEW\ntNlGELtIGHatYgoFWYmMyoDEGIhYLLPVLPvvbJLJxBDnutoZHt5T/nhezsng4GDOnDmTp0+fJkne\nvXuXS5cu5fDhw+nv78+JEydy48aNfPr0qePzboZoBAAAelar1cr07HRWf1jNzR9vdrQp3OqM1dXV\njI+P58qVK1leXk6j0cj169fT19eX5eXl1Gq1fP78OfV6PSsrK3n06FFWVlby8uXLTZ+1E6IRAADo\nWfd/vp+FykJSJAvfLnS0KdzqjBcvXqQoikxMTKQoivT19WVsbCwjIyO5detW9u/fn9nZ2Rw9ejRJ\ncuTIkczMzGRkZGTTZ+2EaAQAAHpSe0O49t1akmRtaG3Tm8JuzBgeHs7evXtz8eLFPHz4MB8+fPjz\nt8ePH+f8+fMbnrUdRCMAANCT/rohTNLRprAbMyqVSubm5rJnz55cvnw51Wo1586dS7PZzPv373Po\n0KGNP9Q2EI0AAEDP+eeGsG0zm8JuzGg7fvx47ty5k6WlpSwuLubNmzeZmprK4OBg3r59u+E520E0\nAgAAPedfG8K2TWwKuzHjvwwPD2dycjKLi4sZGxvLgwedv9W1G0QjAADQU8o2hG0b2RR2Y0bb8+fP\nMzMzk0ajkSR5/fp17t27l1qtlqtXr+bjx4+ZnJzM0tJSkqTRaOTatWt59uzZurO7QTQCAAA9pXRD\n2LaBTWE3ZrRVKpXU6/WMjo6mUqnk9OnTOXnyZKanpzMwMJD5+fns27cvo6Oj6e/vz9mzZzMwMJBj\nx46t/7BdULQ6+RAJAADALlIURVqtVlqtVmoTtdS/r5cHX5K0ktHF0cz/NJ+i+PsfuzFjuxVFkbt3\n76bZbGZqampLs2waAQCAnrHuhrDtfzaF3Zixm3yz0wcAAAD4Up78+iSnfj+V4rf1N3+tVitzv8zl\nwviFrs/YTVxPBQAAvnrt66m9wvVUAAAAvgjRCAAAQCnRCAAAQCnRCAAAQClvTwUAAL56Q0NDX/xb\niTvp4MGDXZslGgEAgK/eq1evkiS3b9/OgQMHdvYwu4xoBAAAeka1Wk2z2dzpY3wx1Wp1yzN8pxEA\nAIBSXoQDAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABA\nKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAKdEI\nAABAKdEIAABAKdEIAABAKdEIAABAKdEIAABAqT8Adg5kSiow1DMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21aeb23b70>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_ct, y_ct = S1.ct.subs(datav)\n",
"\n",
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S1.g,with_labels=True, pos=positions)\n",
"plt.plot([0],[0],'o',ms=12,label='CG')\n",
"plt.plot([x_ct],[y_ct],'^',ms=12, label='SC')\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"#plt.text(x_ct,y_ct, 'SC', fontsize=24)\n",
"plt.legend(loc='lower right', shadow=True)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in pricipal reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **inertial properties** in *principal reference frame*"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAWQAAAAyBAMAAACZlbxNAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAiUSZq1TvELvdZiIy\nds1Wk1T5AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGM0lEQVRoBdVYXYgbVRQ+k7/J3yZb6os/bccX\nn6SbqrWL2DZCRSmuDUJFEUnQgla0DQpLQWwiFasomtpSqUVMEepTaaDqiw8b7Hs3WvFFZCO7UtB2\nTf9Ybd3Gc+7f/N3J/vjQ6XmYe873nXPnm5s7994MAJph4eUWMLOoRK5UXsidtVKfUSRvxQ9tauAM\nu4bzku4KXU9X0dlrRXn8l0BD2bzNVZkvULsPknVq01/QA4TVxktMWbKATeS6UPnN5lZY9aKueIWJ\nK9OwJrkP0JmyGBrSywGm6yBd8+dX3UdtpFpuUhtWK9McSLMpUfsDEiWMXofJTljlkq5UgS51cmtz\nEH0JWwsmCAytpedQ2qRF+vINSF8CyG7Zsq1OMbOV+6rSHdQaoxsG0UHcssrMeezuQdZlqgvpaziV\nARJdeQ+jFVO+xHTtnfCkDl4IW17ZLHa7g3Udq7BRbuJEqTAAL6lWVi59EnK33/PwKEy23MSiIiob\nWlSmM2mqBVkcW7QszuUKZEoAuR7FZCkrg3Ml2LJ1zn0CE1ZwViBDZZFiIB1ATDRhSAzkI4A7y7eY\nl3SMbJwme6Dl1ExnS3tgXiCBZXcEkgFEoqj2EOP+J2BP/xzEP/6noLJTHeVqnI0K+1x5S3KwLKUe\ne5GVyQYk6rrcPTsZGnAqPcPIjPoJDPsheWenRj8UvYqOREQNcea7DfSobMhbSinmumNtap0mMaMH\nNV0NwDSlp/Uc8MOeLfRLZ9/o41F8jSWwGS2XKyJMZZmeh6cwVzKPemGJ4VIcsNldpZK74V5vJcXi\nsMd2S4ojw5E2tcpiVUhURMQ6Iv95DnAuX5Jln4k8Z3McYLUzJl9i2XkoY7HfIvSjZ3/fvt9PAYjD\n3mRVkGe2PyNdjiQaEPuXu6wj5grJnBvBAl42KjpxNu8A+F5oiZmX4WTbmSx9o4Feot/vScDZisMe\nPje33f2+dHmbm1OSWUcMFZI5dztCvOxndymLrgCMlDy4wq4ALs0ay60/8YEGZpA87G3CKLNuI51M\n/Jaa41xu7Ky4uZCMqcjN/Lpe1NB4ewwHEkY6btDG/oY1Wsm1P2GLu8aO5GHvPYTuadk7j52B3sgw\n52rnTLHO25JHhs0b1Zq472TbVUdB5iKefIbdsI3tgs1VN8ejchtIkdbkYW8Gl4ZXIFrXJh0SHM5J\nFEBmSz4EuEXlhSbNxpnBUfZJVthO2MY77DsNAH/01zjhu6rD3kGA6BykOjJj7xGy8yyMFgS3CUyS\nvHp29vDsLD4kGnFdqEnJJQY6L/YksFEbOywl2yTzDkBGvPIewnHYQwG4D9XavgwEzkpuGiJimVOj\njFyuoN4vzSgDvmq+hUxhh/UTw7wERkUnBbEmvj+MQ8k4VGVdWrwA33HuGo02MymZuHxT3Vd3CMQ5\nebLq6VdhR/SvX7oHieGvPEU8zOAPyV+5x1FyCT6Kt/x5pwF+4dwlGG9yXkomLm/hW8BNs2LQtkHL\nkcsUtgum2i6GB7Eu5K1h5ps33Lx92MMVNddJHzLcPEWZAyseaHBuK34g4SYkMy7WTBYEzFb3WldE\nvEmVzFdBhxH9Mpy0eJrrmmyCsUogR6pOynHYw/Exx+76+kcnzf0cvssNzr1xtil4IZlzGx+SVWz3\nS30qQ9aaq35qgw4j9jKULZbFLheqp0t2JDzdD8+ohOXLHQTIieHJucDi5zwohToM19WLrmPR7r5Y\nQ50daH54Tkf5zHHmDvLf1JImfzl1XekwPPjMQ75gd/XbWMsOpPeWdLxttuJFlhGni1RkdvylOgyz\n4lch1bWzi7Zre03b9XiPeuLlhKk2VaU1pToM04zrEO3Z6UXbXYy3dzFJC+QcW4D30bEesM8vgth6\n4mFfygAAN4X/a5n6UnvADTer/jYA7F/iv/unlno/X3606oMWACZw2u9w5iQbziiMPp3vNzuFRcXh\n1omFy38f5YxYUhNu08bAz0My8Sa27DMi+2LLROAHRHnsuomiBt96iLYee8mI4rGyO7jiprOJIkl4\nUerIFOA4Tu5QW5kJtD8ZnLptQ6j1orhpJhD/1dwyFuefIAL/5YXwQcYtLurZEGoLkLRP4NFiQELo\n4HRdShqTTtjbtUpg1FJuqB3zMZL3H6SCllZ5xU8FAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\left ( \\frac{6 A}{5} h^{2}, \\quad A \\left(a^{2} - 2 a b + 2 b^{2}\\right), \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 ⎞\n",
"⎜6⋅A⋅h ⎛ 2 2⎞ ⎟\n",
"⎜──────, A⋅⎝a - 2⋅a⋅b + 2⋅b ⎠, 0, 0⎟\n",
"⎝ 5 ⎠"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.Ixx, S1.Iyy, S1.Ixy, S1.θ"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Shear center** expression "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjQAAABBBAMAAAA01SNrAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMARM1UEJmJZjLdIu+7\nq3bM4UB1AAAACXBIWXMAAA7EAAAOxAGVKw4bAAALFUlEQVR4Ae1cYYhcVxU+Mzu7OzM72V36Ixqw\nZNyi1Ai6ZX9IatMM0QhBi6vUFCTKIqY/pMZFtIVa6RA0IFaTYH5ofrQPVEKhJa0F6T/vj0ih1LKE\nUmt+lMEai9RogqtoQMfvO/fe9+57c2c3uzvLDnQO7HvnnvPdc847e999b+ZbVvZ2u00ZDqkcfbg9\nHJVIo9v9h+xdWJgdknrK85XzQ1JKaWEBrRmSYlDGd0S+MjzVvDBMrfmdyMHW0PRmqFrzX5G986PW\nRDpQ+Sda04k4dsY0TKum/i+R00s704dI1qFqDVbNqDWRX5LI6IaKtkWN2IYPjrbhaH9eEXm8FfXs\nhHGY9hq+8n1+J5oQzzlUranNV16Ml7kT1qFqTeXEtfZONCGec6haEy9xp6yj1vTt/Kg1o9b07UBf\nx2jVjFrTtwN9HaNVs02tOfVQ0jfy5hzVB1++pYm3irulYHFQfNVciIMza31ZdVM6k9k2pk0mAT7L\n15A9gb2/SpwN4UrpD92IhyF9ZdHW1M164Z6xgGZldT1kX/+VzBPkK8tnW5mjv6Y4DeFKKUKnu3Ep\n4gpjhnSVRVtTToIJoU5zm4d9PEDGslVTt5bcsZ0b5QeHsmEu3/7MTi3JD3XU5hE4DeFLUU922E21\nsKpvYUkypKus0JrpXzPit/FzUmT6xJLIBA1eSnMid2EwuegshxLvkqVUg3L8ty2PnQ3tE8ful9ua\nIiUE7qQO5KNDpZJe6sTV1wrpw7DEMURaip2OxFa5xPzBqn5nSSRYkiggEFeuq8pVVmiNnOWE8yLf\n/4PIw3IgXV0uznGR8USkhh9KBcU72ZV4DeeJZFdTHNYEdvmaXJYJ9LWBuc+lDuSjQ+W+ljc/IMcK\n6cOwxDGEL8XOUgTVsQ7zB6u6pr+idEmigEx8XFeVq6zQGt076mcwC0HOykyrupRFgHYH6lkRedoZ\nD/8idZ8KcbWketNjTeg4L6eT8ry2Rt7vHcxHB8eVL37Km4/K45JPH4S1OITwpYjswkRFMACuErWK\nrmo67BZmlyQugP5MfFwaWZWtrNAafeJML8K9Xyr/lqn5XW3omdyEipV81Vme6uKqrLzhFZ5rs/Ub\n4rAmdJyVi7Mzia2Mv1UV5qODg1r3P9bI4zHJpw/CWhxC+FJsTEVw6iPC/HZVaxv20GqXpIGWb40r\nl0ZWZSsrtGbi999tS2MZ7v2CX3xtuQb18LU7caSU/netJW+LvAQ9s6oLPQotY6sea6Ty5cttxfBw\nsLX3b69pZd/0Ns0HRw4HJ77XyqfHDZKG1ckIkZVir3bMPjON1mpXtTq+/sgbfkkazIWtt1wCWZWt\nrNCa8rnpFanNw43WrEqt8zQq/Ck0K9Pn8BvGBvSTnJU+3BQBDr/9jscaOdI+3bLzcXxS/tK6qq3B\nLWtF88GRw8H1xw5vlz5hdSpCZKXY1tQ68nM8QeaF+e2qVseHWtf8kjSY24jFJZBV2coKrZmZHV+S\nKS5tXTVTnfdh312sYkmoNDqTTYHp+ZyVrpIJcVyTHmvkC/IDOx1H7MGv4rfCIk57o+aDI8Sp7xhz\nBenDsApAiKwU25rjUvpGSz6Di2etKuq4IUftCI90KI1YXF+VrazQmh9yybjWYK+Zmb1dsOFgJd3z\nCqQ1NTu+wsc66lErk1lPaSXE8ZHqsUZekGsyxvmX9L3gefmSa40zaj48wImjeKxcnM+nD8Mq0rZG\nS7k89+G5uY4+y8tL8jkUyFoh1lF9jusLsmtu7ldzH0EBwWX5uGu25q9ysepvKH1CPYG9PWl8q6Vh\n8cSamheUiyyBlb6qyVl2y3s91lRuykuftPOltFRqr6IHLGKPs2k+OL4X4ODCTnNxOZ9egrA6GSGy\nUhiTCCmt1tEUza8oOqZN/XpbR37VhBfg4vqqbGWFVfOqPDZht+GPc/M/IEfQ/vbp97igtdZjfN3h\n3hdY6aycCS3VOxYueayRF6s3ll2Akwv3tM5NGm1NbhumI8ARfl7eaeXTh2E1oN2GXSm8MCJEPsCX\nLM2vKDpwe5klHfnWBBfg4xLYdxveJ89+Vd/JfvnUmzJx9H4kkNKb9z7gglZfR3gsVjzdAqs6z4WW\nqW73uscauf2tq741v+l25UcP8laX7N7nOyAdAY4hT/35SiF9GFaTYvvISmFMIvDnFljYovkVRUc5\nqb/e0pFvTXABPq6vyu5KhVWjk/XlxoXBVl+UZnAvZL63MjXQgDXBMFVZhH8jkDBfirBKJD0dTetl\niPS21HZbe5mvVJkwWSgGg6JN/b4qW1msNfygkIpJNaeMYQXUkqI1notY0wOFAUXoO7f1hfkKaFMY\n65BhKQyRlcILs1LteE3PmcOaDU5FmwcypKss2hp+vPTyMa/482EoeAAVxZebsxNrchY3QGUTndQR\n5kuNVulJTzPDUhgiK6Wutsih6EiA6dcahnSVRVvT4GQnY4nX3PlPPL9cMGJ4d69JiO3tIozj6Ud/\nzgrzcRxIT3r6tAScD3EQKYXmdQQF9IqrSsPyXSLyF6B10zstb3kmP9zMKLik9fPFE2iIAZQSRGdI\nV1m0NXIhAEfVrX/rOJkEgdfNF2Az1YbYeilZRGFIX1m8NQH43ava1hz6GeVOmYl/n/rus17Hihit\nmr63xfa0ZnN7R58iH+1j327ztrSm3xPn7/E7k6t3DeEHop2QbWlNOX4xpSVcYZF2PPVQHAyok0qT\nSsJDcTJtPaKgdo95w4aBtuakI2jyb7cpj9Jo3dbEa2j6qUeZHZN9gpoNq3f8h8B4AvYJ9QWTSbyo\nDTGdOCZHQXd54+bPg2xNStDkPxOlPMq9/EwfcEHK7ARUkQkuw/Mf/JzxadivqC+YnNIq/NxuxTE5\nChpPnHHzp0G2ht+pkqAJPjiuoDLPo+AqybPYb17psKywEqDKhxjYvHj+g60pz0pKuiCFlZRW0Zji\nE/kMpIS2KANujRI0JE+cGJw9jzK5LDMJGrKPPoMfeysdSqA28KM2nikpr2JwMy2mpEvGbaa0CmPa\nuZ7JUZBmoWfTMuDWKEFD8sQRJ0YLO9jiCZdPnuU+HRgYlNkJqCIT4T/Yr8kmSReNaCdjLgS0CvkS\nxvRttUyOgt5WzFYOg24NCRqSJ444MVrbk1KHCV92gWdx9CQdyuwEVJGJ8SoA4pZ72kYMuE0srI7i\nyd341iiTY0EHYNyaDLo1N2WqQ4bAESeG1eGG2L0qFejgWRw9SYcyOwFVZGK8CoDV6yRdGDHHbR63\nfAm5G9caJEozYMYWZcCtUYKGrSFx4ngN/cOLD8o4rORZIM6hzA7HjigxEf6DNxRagy97PRXj2B1+\nh6V4xAwSuQz6lx4MvQUZcGv0CYUbyhMsBqWRYJG9rWehkmexYnBSZscO7TYc4T/YGmzXT6QRLR5H\nECSKtzEB00RpBjRzizLQ1jiChtuwI04MyiOPIuVFvpmQZ7HCszI7dmhbE+E/3DZ8JI1o8VhKoFUU\nb2MynmdyFAJKaIsyyNZ4gga3vCdODMojjyKlGytQybNYMTgps2OHtjUR/oOtGV8i6VKgYkiQKN7G\nZDwmSjOAEtqiDLI1vhT7vqIj423y0SRVqZjcqPe9JnUDWG7L9HxqiCuA5aWZH25itB2tCcgak5b0\n41RTJXPo0K6aPMSOAMSTu9jKHiRgOYkSHDnEugO0ZvD/biP7eJn0K6DgqBNneCiKsR8vo6RLgE0C\nnerhwnijQ/13G58Y/L/baCQbrUTx2KJ6ZVEqTVjHkl7XWhbPx6yFWcuHf7dx91r+zfrqZrMzY/M2\n2ehYqCGwXRhkDY8OMthGYv0fi0+cuSWK+YsAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left[\\begin{matrix}0\\\\- \\frac{h \\left(10 \\left(a - b\\right) \\left(a^{2} - \\left(a - 2 b\\right) \\left|{a - 2 b}\\right|\\right) - \\left(2 a^{2} - 3 \\left(a - 2 b\\right)^{2}\\right) \\left(a + 2 \\sqrt{b^{2} + h^{2}} + \\left|{a - 2 b}\\right|\\right)\\right)}{10 \\left(a + 2 \\sqrt{b^{2} + h^{2}} + \\left|{a - 2 b}\\right|\\right) \\left(a^{2} - 2 a b + 2 b^{2}\\right)}\\end{matrix}\\right]$$"
],
"text/plain": [
"⎡ 0 \n",
"⎢ \n",
"⎢ ⎛ ⎛ _\n",
"⎢ ⎜ ⎛ 2 ⎞ ⎛ 2 2⎞ ⎜ ╱ \n",
"⎢-h⋅⎝10⋅(a - b)⋅⎝a - (a - 2⋅b)⋅│a - 2⋅b│⎠ - ⎝2⋅a - 3⋅(a - 2⋅b) ⎠⋅⎝a + 2⋅╲╱ \n",
"⎢─────────────────────────────────────────────────────────────────────────────\n",
"⎢ ⎛ _________ ⎞ \n",
"⎢ ⎜ ╱ 2 2 ⎟ ⎛ 2 2⎞\n",
"⎣ 10⋅⎝a + 2⋅╲╱ b + h + │a - 2⋅b│⎠⋅⎝a - 2⋅a⋅b + 2⋅b ⎠\n",
"\n",
" ⎤\n",
" ⎥\n",
"________ ⎞⎞ ⎥\n",
" 2 2 ⎟⎟ ⎥\n",
"b + h + │a - 2⋅b│⎠⎠ ⎥\n",
"───────────────────────⎥\n",
" ⎥\n",
" ⎥\n",
" ⎦"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.ct"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Analisys of symmetry properties of the section"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For **x** and **y** axes pair of symmetric **nodes** and **edges** are searched for"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[{'edges': [((1, 2), (2, 3)), ((3, 4), (5, 1)), (4, 5)],\n",
" 'nodes': [(1, 3), (2, 2), (4, 5)]},\n",
" {'edges': [], 'nodes': []}]"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.symmetry"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Compute axial loads in Stringers in **S1**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We first define some symbols:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Tx, Ty, Nz, Mx, My, Mz, F, ry, ry, mz = sympy.symbols('T_x T_y N_z M_x M_y M_z F r_y r_x m_z')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set **loads** on the section:\n",
"\n",
"**Example 1**: _shear_ in **y** direction and _bending moment_ in **x** direction"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S1.set_loads(_Tx=0, _Ty=Ty, _Nz=0, _Mx=Mx, _My=0, _Mz=0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Compute _axial loads_ in **stringers** and _shear flows_ in **panels**"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S1.compute_stringer_actions()\n",
"S1.compute_panel_fluxes();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Axial loads"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAe8AAAAyBAMAAACHcE67AAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHWElEQVRoBeVaTYwURRT+ZmZnd3rnr2MCMYLu\nuAYOmsDohkjAhInGgydBgUQgMKLhApFJTLyYyBhDDCa6EzAkEMnOQfwhGtYQ9QBxxpBojBqGg4cN\nIo3oAT3srEF2+ZGxuqZfT/d0V3UVN9g6bFW/977vvW+2u7re7AJs3FO0f86XcbhKSgc2Vmg5H+bs\nJtOROR72Cz/XqTJ37t9PlD6LbGPOjpveVFUK1yMnSs0kQtjBF7su4zqF+OZGgV2+fsVnE1+k/2G+\noUZJHOHz6JETVDOJCGbc6HrSMxThnY1fJtnlubbXJlkf2cyc2YYkwuvSJCeoXhJCIQBbU+G+fNMN\n8Syyh5k5u6DuMcmWU58x79lNshCPT5OckHpJCIUAbI/FfXn7VxsYicRa4P0JK+AINxRXAMYzt8Kd\nAasmOeH1khAKAdhIkftGwoXn2oB1oeLC5YviNNsJs7PyINeb0CMnnF4SQiEAcxSHCz+SmkXKVH5o\nW+MVvJlmn5XS0CMnSkMviRgmFT5lzOFeKD+0tYlqrJqsU7KIWY+cyLJ6ScQwqfAibsEylB9a5K0c\n1HcELXJSkNBLIoZFCH8+VVN/aJEs7oP6jgAd8p4CrSRimEy40cJP98N+aJc9/nf0DncEmW9bYDtC\n/NIbX1NG4axJTjx6SQiFIEwmPFvDCgvJOnLmqcGSSyJaTCGxFfaOcDHdfFkU5No1yQmnl4RQCMJk\nwgfZwbsC9qYfws8uhXhRRm4WQ2xHqGRa4ijyaJITTC8JoRCESYSnt72C9/DOtp0mcM2lEC6+vGql\nrNTRq18A+Zowihya5ATTS0IohMAkwl0Y6zzaQ54rZ2mMHRM8+HsQ4tg/KmjyQslZzmIwpdcSmiRz\ncWilNyi4Jphf+F4zGMksE/FyPOhYhHho32a0l6IQCDeKGG8FrMwQTg4M1sOiyRaeBMlOp0AhYXMP\n5hUeO9EIF77oj2UPBmnYPb0haAVi3zz5e5AnN4d8OSw8nBz4sx4WTbbwJMg8cpkiQucezOlOJgo8\nbjpYcCieGzcCjYrY3ecZWI+RZp9Ndmn8Wpe5Bb60wB405+vcdqHEJy3hZ0wd4Yw//FbniYM/4pl6\n0BhpUReeaXOyHV1KR/jOyAROwG77DhmcVAuPbedxiuRTXeGq5E4J6fOX+E0YDUv9Z0PizuuqKzy2\nxaGJmgbs75qwoBkVx/3G0kftWZE8ZnWFK5JTBcOmwTdcBVijxkBLSl2k8xsnmqg5+nP1MVAWn1Fw\nEcdt3eqM7SMBY785vR5YzDZoPnzCO/7R7kcCYx5T3h/d8bhomVxHK6AvOkD+tk/44h32+B4KSbDG\n/k3yEfvORu2qCGB7LSzkNyEL9gl34OIpVxT7Ah6jhuG5gFVkiBV8wkVhAfspYHkpYA03vFYAVlS6\nPj3hb4GpUR35GR3hqZMnG5stVe5eHNud1pi9S9kqzm51JJwvyrSEszNlTl14so5BhRN/r1QG0B9F\nYJciannFDvS9zkQbb98B5ODoQ1/ZWMEOGrtpO92RbWHcYleK5KzTqdtYAbnt4qOvpgPIvmDbo2DA\nAGsj2Zgu2T9Xb/uxZc+CV+2g82cXO4SNM53OVXsW7e07TNvrjqfGPuRrNXLEj9+waxGRE21fTcZj\nJ3jWKBgw3OYUzpGV6GjmHdV97GzaHftoET4bow9XETtadrypWngYWfXICYUDqz4GlGsiGG8le7Wx\nG6rJXc7X6xTmzE5HdZrMBVqEzwdgH4cyRccb0tB5cZrkBI1N8n1btSaCdVtJtzbA251RkDs7HRW9\nhWKW6wldTFfB7v181XE+EBrkGjXJCZc2kVwLqNZEMHZSYa2kW1uE8G5HNTDjoLPEIpifLtkb2rOm\n424JwhyzJjmRJctIz0K5JoKxx5W1km5tEcIZinVU8TKhI2f7Vl8aGeUG6JF3YZkZW7hGTV3YGd5K\nemqT3urs5cM6qszK3z51a5UvFhaA0+/+VZNHkVeTnGAYnNGpyYXtNr21yYXzjmrkB5x00dLF/pdM\nxG7W0pPSKHJqkhOMPUwFqNfkwlgr6a1NLpz3beMVHHPh8gU7BrK/Mw7X5VGul7VrGuQujJ0EbgPG\nXu3e2qKEs47qCWCrmzRiscFMNJG0IqLIrUnuwBJFaNXkwFgr6a1NKtzgHdV2GM5RngoWzIeA49XB\nAiYqggCfWZO8h73Elso1ubAc+7i8tUmF844qdgXxtS5etuiYTPhICUtkQa5Pk9zFpYo4pF6TC7Nb\nSW9tUuFJu6PKtpEsnHUJJAv2Z7PdtQvAc1lTEkWupB45wfAqcFm9JoLxVtJbm1Q476jSTeRLBSKQ\nzeeRuoVTwJWIw2qXQ5OcEhvbR1eX1WsiGG8lvbU5wp2v1ymMZrujGmZHmGVkkM4DY6tK+BwYtaRh\n5NQjJ1SGfWlVVq+JYLyV9NbmdCfJJkXMl3lPgStNX5svgknndPfVQ//hSOa7fo5ddyROW3e9Vp/A\nheucy+wNlVeQD3snX6S2uHIXTd7JQnRr/6BlI/4HdxSdee1LFdkAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ 1 : \\frac{M_{x}}{3 h}, \\quad 2 : \\frac{M_{x}}{3 h}, \\quad 3 : \\frac{M_{x}}{3 h}, \\quad 4 : - \\frac{M_{x}}{2 h}, \\quad 5 : - \\frac{M_{x}}{2 h}\\right \\}$$"
],
"text/plain": [
"⎧ Mₓ Mₓ Mₓ -Mₓ -Mₓ ⎫\n",
"⎨1: ───, 2: ───, 3: ───, 4: ────, 5: ────⎬\n",
"⎩ 3⋅h 3⋅h 3⋅h 2⋅h 2⋅h ⎭"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.N"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Shear flows"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAs8AAAAyBAMAAABRzytqAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAJu0lEQVR4Ae1ba4xbRxX+7LW9vuv12gokEiSq\nrzZqkRLRul0QVQuKBaJ/AGVT9aGGCkxAoQWkWIrgH4olBAghFNNIkaiI1oh3H4oTBBXaJGtRpBAQ\n7ELhR6S2can40fwguyV9kAfmnJlr752H765vJrtSk5Eyd+bMOd8557vjmbmzCkBlQ5nrm+X6MPBk\nvYebeqjWa958umcgv7sYgB68OaHd0xtCPPw52fEuhYSraHpvPD13aXbeX4XqalQcw83snu0+feL1\n1Xi+fjpqEN5l6Sm3NJzHpI90FSMLw1kN1HYMNwk8BHxkoLs1GdCC2CGX5kJ7OOc5YKaMfGU4q4Ha\njuFa8P4D/H2guzUZ0II40BFeC63hnH8dOFfHRHE4q4HabuFGF5B/G3hloLu1GNCDKJWF19KQRNeA\nuSJSriJ2CzcK8FJYcRVdLBw9iIDhYYkm37QKuixu4WgDWf+iBBGbaF4FHRbHcLSBrH9RgohNNK+C\nDotjONpA1r8oQcQmetgD4Qp5O4ajDWT9ixJEbKKVBejak3IM53bFj5meEkRsonkBSm1HxtHUcQsn\nVvyPthB898Yk6hrN1CBiE80LULJQ/Oo1RtMzdwsnVnx/aXS6B78eTzWI2EQfpan8/ftw3lEKbuHG\n6Bjtvbs60XQUXSwYNQiV6CODEfON8Fjyme6fOsBxnApLe+0ImLM9HeUZCectKLpKxw63bf4KxZXz\ncx1FWXYi4NQcLbb0+lYdjBaEQrTXtILj0D0/B35rGfsCHrZICcabeqqmj3iT2+rIKe9LU7HDPQk8\nMfkLTZW7o+VIuEwlbcRAVgQH7OdKKX8p7q+rOb7r/e9TNESHrMdfGb3bHCCJLbd+EArR48RCdpcB\nkmjhjgq2GHLgi6lFi5RgNiN5UR85hOxVJNq6ONS3w52BV8bBhZBe0Mw0I+EytZ2mDXCGhV8yRj7b\npWtVJcc/YBPxoRWyTne7viaVtNly6wcR3CbNCNMXgM33mhemuSLS00h2DHR84nzbFIJgjgEP6iMX\n6ngTuF0Xh/pWuHwZE2+jUA3pBc1/NSPhUqeeMW1AcMDEbmPkd6eI1XCOeUq5raux9fj213RxQJsl\nt34QhaYwOlfhx+P0b8Ikms64ubeQmGYVpSQaYwuKQHYIho6QczVt6OOVxBVgoyYNde1wmQZSD6DU\nDinKpvdiMxLuPXjWsAEIDjjyR2OkxZJwjmMtZA0u2JrudM0iaLPk1g9ifFEY7eXaq1JlIXp8iYnG\n71lHKTn/k0pfdhhmvmgSTb+vqzQfKhYTKbLDHRaDlqUjOd6MhDueaktcpRZw/gCiwznSbz1lXDOw\n9WCiLbn1g+Dc6SfzX64nylwZb5GHMiTdyg18WdSySv3ND/V6TQED7Cv2BP3nJp9csRNkWn3hcsMO\n9yorJPYsq/VaZ5noCLhP0d84zMJw+YZJ9MmXP0QjMkcRXamM1P90e7bOvfRqTZdL2izBLAcx1yCj\nWytsKdYBO9E7feBF1kk8ynVkkctJyvyT3ROfL1KSbTbeKGpurVj49+/ddqehl+gw0bHgboFJ9I8w\nUwlylNHRtjVq5MDBjBU9Y6OXREcGk3uANttjIo1MnR52onkef0sorVwJGOucTZKvbHVlBEXjMdGT\nUyE8kAQTHQvOtxBNBFaVHOlSwCRaBoOfhQMRbUFbdDDf7GCTnC/pCtlYiR4p08gBgSir7nJZDIlF\nU8BgShdz/8EiRkP6W/ZyOQ0so3VDwxKBXg6V9C7ZW66/LYi2wRVCcMv6QYvfdc1K9Aitn6EcrUuH\nDAY7GjquoC0cjBnE13zggzU2HEy0WCdDQehulL6EKSsy7vwAOFpXiDZUbALKzWtgTN+XEr5BtM3a\nkBHcBphE59ri5B/KkTbDrO4UTPQJ8GeFVgyitXHaTdh2hA4VtEPVqbLN6GyZWbqPdVZRBMw3mB21\ndItMdKqqSlfs0a+1sGQSnZ2dnft0Jxbcd2dn3zil+U23MbKk5DjWRJ4kauGlg3apHUVVHNAWmdsd\nYjKL493AzXA/8Fpvo9A9mH2Goa/jCZ1o+kjY1wh2L9NqoIT2n3QTGXEuUpVIHAuOUIwPlhGaZ20l\nx/w0RkiiFt4My8BXVCn1xPzMtw15XxCcYC5USCJOJ2xRavfHueHtmby3CtzFbdupQ1NnmMOTW3+j\nw7yELB2XRnyGiTh18FdNuGwlNhdwsKPLaaI348ER+iVocPSV/w+aGSLHILrHsLGmaYnj3yHkH9Fz\nk0RH5Ta2KJKiswzd41cp8F9fOYmMemE+TpsLDZ0mFfUcLQQ0FVR1hpnvdt805FP3VOgLo8ZWmRbX\n9rK3qMh5xfrY1E8ATY7k0csL8eCwrXtShzu0/U5yJHOU0W3493OGUw7Gu+tXRT03QVtkMIU2mdIc\nLnP9OFdcviMfSu1Vle7kP2t4L31pc9HUI2Hkh560C9UhuGwjJKd30utqcqlkhRN3h4mfVoWKZhYJ\np+VI9oOs9ZyFKyUYJQhiuCVU5OMF0abK7zVCz/CFCx29K7yAPS/H/ZAaNSNhLBcvZBKGS6poeTEH\nSKbJpZYVTt4djktDzSwSTs2RPQyytlKkBKMEoRE9FkyeREdmodRblN6PQbsy5PFHV4+CSbQVmF4n\nDHdLTxg8fxk8dTmL7XDHxN1hoS4MdbMoODVHNh9krefMumowShAa0V6T9WnzkQ+17gUopClxCEjR\nxklFV4+C6b0EYdivFLiFvlg26K5dFF3OQjscrWh0d7izaDWLglNyjLTWczaDUYLQiMYRAW6t8sFs\nl4Nj0/xMVmVPryNgzuq6oh8J59kYDmDscPPi7vA2qytEwKk5Ws0jrKEGowWhrNFWaKuwcPr2D9AJ\n4u6XzTlg1V9B6BiOvO0r4vnvnVcmxwoxXIfhcBAxiS79Gek6Smcw6yQ+x3B0Un2dDsqNXMtJdHFB\nlCDiEr2EkV04WMNTcaNQ7Epu4cQ5PfuW2K8VP2vboeP4chAxiS5Ukb+IDwOfcRK7Yzjw3SEdP9Md\nJ9HFBVGCiEl0po38VeyBJ26j4kbSt3MMh4kyTWofM7W+h3VoqEHEJDo3TTM6cRHJaScZOIYD3x2W\nKrjVSXBxQdQgYhI9SovqdH4Raf+vceMI27mG47vDc8D9+WLYy9q2xQXmchAB0XTLPVw5jo31XBuF\nij+c3QBtt3Di7vAEcFH7gB7g/PqItSDkbRLo3nu4kpx6jv+Ym1Q+74eDCGu7hRN3h88Ck52wjzVu\na0Ec8IX/nPikXuNQbih3F+TG3PsftDdU7muZbOJS4O1CZy3d3ni+Nu0Kcs5fXscN+p3Pe/bRPr2b\nhz13vPPZcZjhDxcY7P9ultTQIP9FXQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left \\{ \\left ( 1, \\quad 2\\right ) : \\frac{T_{y}}{6 h}, \\quad \\left ( 2, \\quad 3\\right ) : - \\frac{T_{y}}{6 h}, \\quad \\left ( 3, \\quad 4\\right ) : - \\frac{T_{y}}{2 h}, \\quad \\left ( 4, \\quad 5\\right ) : 0, \\quad \\left ( 5, \\quad 1\\right ) : \\frac{T_{y}}{2 h}\\right \\}$$"
],
"text/plain": [
"⎧ T_y -T_y -T_y T_y⎫\n",
"⎨(1, 2): ───, (2, 3): ─────, (3, 4): ─────, (4, 5): 0, (5, 1): ───⎬\n",
"⎩ 6⋅h 6⋅h 2⋅h 2⋅h⎭"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.q"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"**Example 2**: _twisting moment_ in **z** direction"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S1.set_loads(_Tx=0, _Ty=0, _Nz=0, _Mx=0, _My=0, _Mz=Mz)\n",
"S1.compute_stringer_actions()\n",
"S1.compute_panel_fluxes();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Axial loads**"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUgAAAAVBAMAAADWXWqdAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAZpkQ3Ynvq81UMrtE\ndiLw+n06AAAACXBIWXMAAA7EAAAOxAGVKw4bAAACuklEQVRIDc2XPWgUQRTH/7d7n8RsrjGdeBok\nos01luKCBAtRDjQqiCjYSCIksUkVXISQQoSrYucd11ooWIgfxWGRNkELOz0DtioeKlHxfDNzO5md\nezvpjnuQ3XlvfvPmn/l4ywHIHMIIW+udEOfPjLBEkrbRpEfmmy3SP7JfdCRt+/jL3QBLfJ59sQcB\ntPYgHlRbdY2oWbyIArkbIrpeFU9lxbp/Pm7Hb38R19uxA44IKmiUnQR1ntUAmwMLvR82kQspIkT6\nd+4aIieBK7uoahWqyBPYN44Y38FEGAPgCGB8XgM8sbrSsQm5iGolPxoinwMNw5Wj8iEKv/V4jth3\nG6ciJwF8uq8BcDmwuNuPPpEi8hewWTdpahe7pkiOIMjYbp6oGSJZIiFSEYMiz9BU/ncSuWWJJDfb\nFTEH0a8T6USmo0SmE0sHjsmJDUKKLEQirLbbv0XNgM7uk5oIJm1TxBxEcHFKDHAQJyFFOohn+Nq2\ncsjqs96kaF+kaCGgleREiv9OWRpxqe0makqkhNJyjIV2jnvA4zkZNC5OynZ7lXh06oHI34wRNkep\naYhkCRru/bNzFM71K7q5kqAD26jHqH6/1S2wRNDB2I5muBwnYIhkc9DRy/21c6xRgDrIjJXEK+Bg\nVQRNK1XwRfscMdE1RXLEw+XlnyvOHPkInryeklI55JnMhSJiiqRCfFRS5oM+aB+0zxH5p8jqrRKl\nejAHMK9TsIRHNSTSiMoxUILkvUO27s+ZhVmMCmZmp0N6pxOZMhpbToI6/9CfIwd9Wic7SUJ9tqXS\n6YW1shgvb7B/7X0T2dPC11bs9Xqh8FIJvDn8WuLpBK72ltw5ti9PWTkMkbIn+XiUdBlvOISx3YMa\naoMhKzIcQoqUt8eanlxfnC+nDYeAFwkVq6yUDBs1g8MhsNEWk5ZG+zfOBeA/tTTnKkhMNvoAAAAA\nSUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ 1 : 0, \\quad 2 : 0, \\quad 3 : 0, \\quad 4 : 0, \\quad 5 : 0\\right \\}$$"
],
"text/plain": [
"{1: 0, 2: 0, 3: 0, 4: 0, 5: 0}"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.N"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Panel fluxes**"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABFUAAAAyBAMAAABv8/kJAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAMDklEQVR4Ae1cb4wbRxV/a5/vvGf7zgKlKiRw\nVqIWJKTUJIoUNdBaQlTiUxIolZqG5siHiCpRMapAQnyIEWpRkMJZJIpEShRLUP5UrbhQFakKzTkK\nooqCiEsFUmgghtAP5QO5VCFJm7THe2927Z3x7NrrnZ1PGenWM29mfr+d3zzPjufZB4DpQ1W63kl3\nFAhR4GjDr5h4pO5n77zeUUCjQGlH2bMu3FlWNPrcMQUUOPJVUXDfCxgTZEtLN6n3lR2NBCCjd7VM\nB2+u0Lhm/vfL0W8xSUvLdEPUdG+JsRSuJhlToG/hHSxMLdUCpjSzlulgqYKj+c61NIcUxLZMN0TN\nB8U2ZbYdvMUE+WOPYefSUgKEWF0t07l/WcTbe3M51j2O39gyHQxRc3+XhzJLGphIF15AlNd3mIAa\nBcMyXeloG98Jq1qj3JqBNpbpYIiac1Ue05wpX6luAnC/8IEBoUaCsEyXzW4DOHy8O9K9JW9kmQ6G\nqOk5iTlfuYJ7v9KN5DqNhlC1S5edWQboXqqPdnOJW1mmgyFqGvYVt7NQh+8WUFEryTIdHMvfgHzZ\n3m7MLt0wNQ37Sql5vOE0ci0rnoJbB7t0cMG9CXeDvd2YXbphahr2lSzMdmfA3gPdLh1U4QPouvZ2\nY3bphk2ecV/JVQ+AvQc6WKVDX/lSvmlxN2aXLjtETcO+cgyKpzuAD3R330dq6T+ILNO5Hfjjx4B2\nY0dOH05/dJbpYJiahn3lAmQfB3qgZw+uT19MsExXasKmLuRaAJv/3IXUk2W6oWoa9pV5mLkBU/RA\ndxqpawlgmW4SI1114OPLuy2MzjLdUDVlXzkWrgA6+fD08vVuvpt/7voJPLEa3hpwkQ1LlunwPTU8\nFXY9CT+EH+zaWwa3Nrw5rumhyTKdGTUlX3Fb+sEduv8XAK/o60Ksbm2qHFLVNx8FYOi+hXM/Wotx\n3HToGFqhw1hnFQqjvBX6HQ/DN/qFkByridBKKv5zanNKdAyt0ImiETUlXymiYPntA2TOItxXgzUD\n9ijDs5/8W1S1qDsLAlpu6VZhoZMOnYCW6bA02QKnPWCNMLi/OdiKqBZVpCZBKym3slJJiY6hFTqA\np8tgRk0vaHi8QhRvAKzeMvjthEIZctsg06Umo6buN08PbVrCtzNDyy1nbsLsfDp0Alqmw9JbLYBY\nW/GZqZ04AUMSqimg5XbFT72NhlToBLRM57y0hLdqZPJmWwx9qUYvT+DfzKCv5OahcAOcbdTEZJps\ngoCWQScehrl2OnQCWqbDz/cXWwCrVGviMqnJ0DJSgYup0AlomQ634+grRiavuMzQe+jqzuNF4yvF\nq+Qr8HtqYzIdAfCgVVR8BqVChzwEraRMsYV3UlOsSYusJkPLSGJCU6EL9xUjaubfp5Fk3qXrTJUu\ng+sKWifRuo7awF6+GrlcZhSCVpKzGw3p0DG0QneBfCVDg4fJRaVu/CKrydAyRuHvl+sp0QlomU6s\nK2bUXGoi9j01Ipju4EXvK1srABepjbOTrmbSiwxD0HJy7/00GlKhE9AyndMlXym1ybqKr5RLnEhN\nAS1DTZdd/A5mKnQCWqbzfMWImoWHcZd8gvEnG/ii9xVaTZ7hRgYvX2Ms3UJFvpsSnXhbBEeRAfKV\n/HzQZiBPagroAbCfp0SHRAitJtqvGFLz6S7cRe9jgFwNL1pfyVaxZj/+eWnNHkqvAazESH7n3it6\nKQYDCFpNue0SnfMHottXh9kYdMsqKNMBQcvp++wrU/32ZuhITQEt02HpwSYE6MBXM9HoePIYWqVj\nXzEzed+qAGyqE0G4r/DOIkCn3s54ZZ48sWkJArhNmL4p+Uqwdvw80nnQEoZTUX1Fqh67gGp60DLE\n74BOq4K+ItePWaLJE9AqgOorav3o5QzNWJa/9Bj6DMpX4ccAD40OOlpLegYJaKn97FX2lTToPGiJ\nLn/y5NJjXZiYl6zJC6imBy1j7cQ3fzkVOhDQMp23XzGi5n28pOwhgtC97VMAb3ubTfVGkpRpbyug\nJZRcCybxc9lFyWiggHQetAqGZm+zqdYkKLOakGupEFWAfSnRCWiVkNcVE2pOUEwYfa+GF/7YSPuV\nuTaW+sndvXbLPMAGsiT5HOTc7mNSDj8VM7RiL3VgoZsOHUMrdHgjdCCZrWAm0ecgRTXxIRyhFfsh\nKD2aEh1DK3TeupJ48lCc6WWSCPiMn5bh7Mu3X4VJ75erXIXHVLijxKrXuKj72OK1w6nv9LJy5gIX\n95QlK66LAlqxf27jz7BdErpSk4gUWFqGGVqxQ+bXtzpQrFOX6POVsMCxoFNU44caQSt2d8NLKEMS\nOhEUV2CJjqEVO2zZda6TTE0xefiWapNEIH4m9ATn8XLAzwRe+RwyUBZZjhN/9BHPjoHjgeQ8Nw9Q\n4MnL87XXAs/4RVLsbNTTuRufrwMjUiMdHfDNvELVCmwkHeAh8mCS6bRh+D6dqlqkmuPSBdRUJimS\nTq9mrMlDJ1lkhcQLR7uoXGGjfNGGn7w48Rmv6Vm5iygVkcJpUz4jDP61VPVyip2tWjpYDZlr+Kb0\nOmrp4Bz2X0MYCmwknT6YJ9Nx4JhvLnjp0amqRaq5Pgjh50eh66tZ8buJ10g6rZrxJk/xlemmoHW6\n8m1wieVX7V6cGD/iUurNhih619kGZlibj0t2gF95ZdVOZi0dnAD4Mi6GDe6opwO6GdZGhY2iE87M\nsIGLREdheE3q0amqRak5Pl1PzTh0ejXjTZ7iK/4iW9JI0ptYqS7HIegJ3A9T6q3youhdt5Yxw3HV\njmTvP0NUOzXzJ1bugg+7pTowYhgd34yzDfupsP4jS7UThT+xEXQchpfrsdSnU1WLUnNsOjF2UjMO\nnV7NeJOn+ErUt/7E/k2VSsSJM/PCrn0Iw71UWayJJtLV1c2aaKGng/Nl8hVGxC/TS2B+QdyMLige\nQRfyHUqJTv/MD6eLUtPfLvo3LV5HoItQM2znjdh6NeNOnrRfke98xBLGiYub/8HLAJ3Buhse2C73\nPPffzd7ncdk+ZunrZThz8D9N7K2nK5663PCj1GNSBLv16WaqaD+07q1ysBos04FZNWNNXnJfwTjx\n3Fk4SQK+iH+fbxaXJTGd2+W5prmjrol3wLndLCyG0cHcaeddcyd5AbrpDj5xHoXz0uhs0xlWM9bk\nJfeVvfj9oTo8Twriob3zFci2JDXzV2G2Yi6Miycg+IvwaeLQ0sFCGfB/Sz0j3cP4hQDdZAO3XR24\nXwazTGdYzViTl9hXKE78GYDHSUEMLWWvwmQXs71YLWTbMFcxFyvbiBxtyBGHlg5vxkFfMRXoDNDl\nahzJeVIanRW6XiSax25QzZDJ8wPfCl1iX6FNw25wOfiIk5drwVwdTf2EhyFbG8Z8hTYNkxU4Thxa\nOjgDE/gx1pCvBOnIV3aAwyPtD88ynVk1401eUl/JYwjauQaZbaQePhTQ6Rf6QlJutmMyrvo9/F7B\nXA3uIWQtHbxPa5upoHiQDp9BuGLll4m6nyzTGVUz5uQl9ZWnMARdWoZc5XWUD/e2cw14Id/sS4m+\nUsM9jKm97VQVZpqXAL5YKofQwTXaVBiKUkt0uLd1bsJ0+0BwdLbpjKoZc/I8Xxn3fwtynLjQRoeo\noILr8BylW9orn60XOtNVfPBRffJ0ZO2639JXeq4Rh5YOXoWfYh3HVRPzSXQZHMaf4K+LFQnWMp1J\nNeNOnve/BXNtSYCRCxwnxjdcZj11eQj3tKc+8ey/pe7OA5/FcrEuGcctnF9ZuU7L19ouImjp4MOX\ncVnxotTj0vj9JLqJefyp3b++farm1/KrZTqTasadvP0VHnEBjySSJ/0ZP+Pqz1iTUUbQ6c9Yk9Hp\nz/gZ0zJdyIl1suFFqOlN3hXxfvf/f3YyuhKu0iGJ152QunHNEXSZ7rigEf3eCK2zTKcPiofe3WgV\nEWqKyXPe84CudEdDjG6lD/hhH6cd3XG82lA6fVx1PJJ+L33Aj+r1QfF+z7Fy4XSW1fTo7vJjN6Vb\n5bEGJHfyI7myFUvh4x5oGsMQSqePq8ZA1jb1A8eDleFOO9h2ZEs4nWU1BV1+Z89DVi+OPIjwhm4n\npE4fVw1pPLI5lK7UHBkjTsOwSK5lupCgeJyR6NqGqikm7yc8t/8Hw//9tfRSpxkAAAAASUVORK5C\nYII=\n",
"text/latex": [
"$$\\left \\{ \\left ( 1, \\quad 2\\right ) : - \\frac{M_{z}}{2 h \\left(a - b\\right)}, \\quad \\left ( 2, \\quad 3\\right ) : - \\frac{M_{z}}{2 h \\left(a - b\\right)}, \\quad \\left ( 3, \\quad 4\\right ) : - \\frac{M_{z}}{2 h \\left(a - b\\right)}, \\quad \\left ( 4, \\quad 5\\right ) : - \\frac{M_{z}}{2 h \\left(a - b\\right)}, \\quad \\left ( 5, \\quad 1\\right ) : - \\frac{M_{z}}{2 h \\left(a - b\\right)}\\right \\}$$"
],
"text/plain": [
"⎧ -M_z -M_z -M_z -M_\n",
"⎨(1, 2): ───────────, (2, 3): ───────────, (3, 4): ───────────, (4, 5): ──────\n",
"⎩ 2⋅h⋅(a - b) 2⋅h⋅(a - b) 2⋅h⋅(a - b) 2⋅h⋅(a\n",
"\n",
"z -M_z ⎫\n",
"─────, (5, 1): ───────────⎬\n",
" - b) 2⋅h⋅(a - b)⎭"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.q"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set **loads** on the section:\n",
"\n",
"**Example 3**: _shear_ in **x** direction and _bending moment_ in **y** direction"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S1.set_loads(_Tx=Tx, _Ty=0, _Nz=0, _Mx=0, _My=My, _Mz=0)\n",
"S1.compute_stringer_actions()\n",
"S1.compute_panel_fluxes();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Axial loads**"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA4oAAAA/BAMAAABUTCuQAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMrtUdhCZiUSr72bd\nIs25ozBRAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAN90lEQVR4Ae1cfYxcVRU/u7NvZnbn869GjdoV\nA4lgYAQ0akJ2glKFhHSi+NEK7KTWEjChIzFtSJSufxHwYzdaIBXDLkWNoND5RwhgZSGAlACdkLRq\nKnb9wKQJbpePlQKF9Z5z77n33fcx897rm900mfvH3HvPOff8zse+z/PuAog29FH8HbTTMAJ/n9JG\nbzxTDweD0ysCuf+xvdk3eTToT7sITCwok6dnTjvbBwZzBEbUwejsazBp0PeKwPtCBeqhnLiMcAzW\n5MY6XiVqQZ9aWWjQh0VgaDyMA7eEcmIyhsZ7LnBjTcgz6fCJnqsGAioCZXHacrbeJf/87ajk2vY8\n8QwxuEXAqiyRcPFVXjPoe0VgqxC4srreFWez4ikzPKURYnCLgDW2TMJj7/KaQW9HoDD7OhI27q0p\negkjtg0+qKbcOWfPi+EGnsbrH15B7SNv8zM7YbCKCFgqfTGz6EVlwDXqfZFO045RfAYbmp1inbmm\nGN0Dl/Kc+/KMGB3lWcx+tiUWvF9f1giDVUTASpZF8KAy4Fr13kinaceRe4W2wqxWOSYOG+ddOOcr\nmiIHFTycim0PNdq09MiMEHx4iaURg5sbK1OXVC9Wsix6URlxrXpvpNO0Y/+5Qtvv92qVdEG8e+iE\nN1/TDSGSHddycQaFFxfEX8pmvdi66LqwOIterGRZ9KLGsbgfst5Ip4nRvA6g9OM3tMpHcHTL5zZ4\ns/g9pI/M4W/sls3OAfzlaJ0XEgZPXFicRS9Wsix6URlwrXpvpNO0o7lRJKdg7uGvD1F+7PPfBMjL\nm8UQkVBydmQJoP5YlQXCMDiLXqyEWbRQS9ds/RXjr01vR/rwjsvw7JZOK7UnqvDJURFl1c7ggd07\n7zUmOzBksm2zu8+OZF6FTMNce0MwQGXRh5UsizbqrZ2ycbK7uf3h2pHO3w/H08MpdI7WnNrYuNZ4\nTI+sQWYZKi0o6dtMi9lrsr/0OnwZzLU3BIOz6MNKlkUL1flt0ot6L+ei8u1Ib27Dlqgre8tloVIf\nAXPJgqfFmsqKaPiXe/Vz2P4hRtkFmBRZpIfL3lo9Ek14A+olc+1FDFatsXKLi688sLg4E4CVLIsW\nanYZinWPWas7tSO9vQFPpoefhbHmRWAuWRBynJSbMF1Leiw24deZjuvaG4LBx6IPK2kWXajibDNZ\nTS9sCTTZkd4LTrKrUyDyESi/3AZxybp5Buj9GkU4t+VbHulKG8Sfz1Cid2ClNix+A8S1N38jFBtC\nsZ3FHWchDZu6LvqwEmXRRhUnkgkJsla/VqSdNyGzlJ4l+yH7S8BLVmt5aA7V/hR/vg93YedqlSlx\nZUl4j1rowHV1EEdDrtL4AOokDFae64wuqDFn0YuVKIs26mQNzs10GHMteivSzuswvHBRambMw8ir\nMPQGlL4+PzKOWi/Dn+dhvcfj0fZwUzy5zyE3biuK97RVWF+HQz+Ci3ExYbCWYkcf4SqLPqxEWbRR\ny/XCgRxDrklvR/rf8IeZVlp2/PxkPVPPnH3yNhhtjdZR63RD/DwDR6dwYpqz9dtikujdzei+J+FC\nOH/fgQbcAbtRJWGw7uKUvvNVWfRhJcmiB9XZ/Z2/fpEh16L3RHrTFz60eyp9O4pTY1XUOiZ1T2Ay\nfa1c95FiEZ6Bu1FeYfBS8WQhm8qinLiwVBYrLMcLI/YKNaI0iZW2nUHRkGucax5yzSSttPOGWhyN\nRpYjbShRRuuiCEGxOk1y2RZ1wbfBk41QXeVLhsTLnR7t8fwSSigMFi7W1cjpMEn0LqyivKmqzBH7\ns+FGuJa7hgrVRek53AQ516NxueY8711yGDLveGnR5hzpaNIs9QQPuvb53ecSX97j5JqBwg8HUok4\ntrLSCucqzi0XL+BIYigawA49cg9cWMPypnz9uOA7t8/GzaJCdSvvNb4N4D4jI9773mRmcrSxBie9\ntGhzjnQ0aSU1Im5AI7Sr4Bwp9TPsHgxe8XgwGanlGy8PZyqO0xlu05AwWLzQ5JHVu7By8jvUXXLx\nxphZ1KiW+u6T3wHMVrXIxwB8V5hbp5z3tECsgY50nFVH/hlJ+o78gpS7WnT5Vt74YJYXWmbsHY16\nCQHz0dZPJBUxdLsZfqDHZuDGKlG8HBFabHGzqFHl8ki/xxvuLL4lbshqvnVJz6g60j6NXQitaFn8\n4U6lI9ME+PAF5zcCVL4YQGNSlCzmH1J/BpkmLxOn139dcKaZ6ZGFRZ8iqPMqZ7E4o2W7DzRqdzEv\n9yBGgEAc8QXldN3LhyvJmchm6PU60prSe1DoyCwe6C2qJD4NsG9lJUjc+0LHLTP66IYqzqN5JTC4\niQvqEo9dvYVVnBecXVOSrY7FzQty2qffPJ3FCaQkhuspZW6sPz/dwGmfzVCIVwBl0XnAbUEfxsMN\n+djXF69KewGG+UIZ94yazFnXX2NJHIv+LELuN8k0J1nVkllMsjTumo/HXRBdftPzMNlW4lYWqSSC\nJZhTa35LthlSyBkV7qODkeS4QgOnZgavXjLgNMpU3Vl0XsFK0wtVWXviNUl6Lw6Cbe9ocPbqlIOs\ncPL3QOmJhlRvZVEjpjwYaboUirubiZprjsOXAM7z0jwi6U2/Bu4spqfXp+kuc+Hy8U6dsEsEjM/V\nq5LFT0Gpo80+A+Cxhp7JwUpjFbP4mT173qZ3lx4jUp+K6+52r6epgdCLlLy4PGELzaIpcUnBaL/+\nKpxYN9SEEZNF8dR/vVeZuFIfNBJeLs4DFQcJ2rQQLwReWAtZESau6IHmNQFeCF2XDAf0sokWqj5P\nRk1lkQ9NDeoqcWlahIGswk0uWKJ/27njF0iQIMWaczd4JB6FDH284DND6/GX9zSry0B64X+j8Bqu\nCbxHTdPvw1C4H4GCvEqIY5bJt2Fy69S1+461Ech1E4lTQTAlLkmI9iurcMWnLOnjKyv0fk2CON+9\ntAoeify2LVO4xGeG1uMv72lWl4Hy4rmGLXPDyp1ICHpeTNPv0jW3E3CQVwlx9LIMPbvB5JztGc1M\n9cFV4tJy4sxITW4z0WQarAOiqircRTYzYNZbAhcd3vIRtdZf3gNYp3hfUu+h1BQ7YSpSlRcxKtp+\nv40NfhzkxfObbfTjmNj740s8l0OiBnKCNKmtU6xV9u7qgy5xaZHiuBqWZzSNB0+Il79EpXekLSaH\n9r0lxFJnRr+dCHj5CgJTtmM80D2aSlTyIlZF2+O32wYvjuTF8ltbCB4ccMXeF1/JMw6JYMuahioz\nGq04clcfinWbJ74qGFeUSk0NLmQRrBJIKlbhnDrTw/reErhytAFjc6wCFVvNVCb0x4TaHjSVqOTF\nFda6HhOP324bvDiSF8dvF7YHxx17Hd9MXS6QeTEOiaryu8QJzKI4Cenqww4XIg1LfxxXpOmGGuio\nYZWAqFSFKyh2eNdbAteOzcMof9xGii2FujJhPrJne9BUSSUv2ta6HhOP3y4bfDiSF8dvF7YHB1yx\n1/HlLBLP5VD3LB431Qd/iStXHldG0NYPHHPUAKsERH1QiaTSlZdNFv2KdWUiN89obA+aSlS/Fywa\n1ntXuGzw4UheMr+9OOCKvY4vZ5F4lkPdjkXh2sEG0K4Hf4lrP2aReLT1A8PAUaMqAVJDqnAom6wV\nl4E2hfgVEybxyrs3qFM824OmEtXvRRczQvwGtsGPI+6fliG232E4OvY6vpxFYfTBhuVQ9yyK6gPt\nevCXuJy6CA3x5NYPDAdHDasERA2pwnUJXQ/WdAtoU4hfMVUmiDf5siOvEmwPmYpUvxdd4EL8FpcK\nZYMPRyibbsX2OxSHY2/ia7IoeJZD3bMonm02464Hf4krByKLxBN3V2KbCTbOIlYJiBpShSPhRD8H\nQG4K8StGTMkTt8Xy6YntIVOR6veiixEhfuNzZQiOUHYgvt+hOBx7E1+TRcGzHOqeRVF92O7a9aDf\n+AN8ArNIvCxtM4GbFhefXVzE21+qEihqlzAlYGWbYG0K4cIAY9KGketBfB0uvubR9pCpihodNMRv\n0Db4cMRjm7BPRuPUccQ/gLDia/baCN2CZznUNYtYfQje9eC0MIvEKzf5mwt1LFKVwFCjO9RTcoO4\nGwveFEKYkvcfyKtnAGmPNNVQe6JIgWC/6b9oBOOIZcK+2H6H4ejYG436WESe5VDXLIrqw6HgXQ+Z\nPXtm772EeBXaZoKuqyxSlcBQkZNOyzThpcngTSGEKXnv4PFKTdpDptYNNZotYbs9jA1Go/IbkBfX\n7zAc0LE3GnUWsSpk4IVD3bI4JKoPh0J3PYyNyx0RcpuJUMVZFKO9YKjISaetA7g8fFPIXpC8E3i5\npsbRxQPYUKPZErbbw9hgNDIO8uL6HYZjYm80chaR1zHwwqFuWaTqQ+iuh8o4EE9u/cDYsDcAr4Gh\nRotaBKnSn3ZeOx++KeQ1kLw74SylTNsjTDXUCEgoEuy3ywajUeEQL7bfwThgYm80chaJZ+CFsd2y\nSNWHsF0PufPeahNPbv1Ax3XURJXAUJGTSiuLDyfmQzeFICZtGPnqBn45w/agqYYa0ZZgv102GI0K\nR/Jo001EDBQLxgETexNJziLxDLxQ0i2LMWwhUY5a3HX9kl8te1YLh7Poj1eaWbzKr35NKatlz2rh\nWHttrMimmUVL8WCyihEYZHEVg903qIp856jKjH2DGSjuawQqS6R+8C/8+xrlfis/ukAIpZP9Bhro\n72MEdtWl8tlaH0EGqvsbAYePQbUzvL9oA+39iYC+qyk9W+0PwkBr3yNQOj7FGFn9SRdTBv1pEoHJ\n/xpDD5nhYHRaRWCIrP0/rpDiGZ2okJ8AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ 1 : \\frac{M_{y} a}{2 a^{2} - 4 a b + 4 b^{2}}, \\quad 2 : 0, \\quad 3 : - \\frac{M_{y} a}{2 a^{2} - 4 a b + 4 b^{2}}, \\quad 4 : - \\frac{M_{y} \\left(\\frac{a}{2} - b\\right)}{a^{2} - 2 a b + 2 b^{2}}, \\quad 5 : - \\frac{M_{y} \\left(- \\frac{a}{2} + b\\right)}{a^{2} - 2 a b + 2 b^{2}}\\right \\}$$"
],
"text/plain": [
"⎧ ⎛a ⎞ \n",
"⎪ -M_y⋅⎜─ - b⎟ \n",
"⎪ M_y⋅a -M_y⋅a ⎝2 ⎠ \n",
"⎨1: ─────────────────────, 2: 0, 3: ─────────────────────, 4: ────────────────\n",
"⎪ ⎛ 2 2⎞ ⎛ 2 2⎞ 2 \n",
"⎪ 2⋅⎝a - 2⋅a⋅b + 2⋅b ⎠ 2⋅⎝a - 2⋅a⋅b + 2⋅b ⎠ a - 2⋅a⋅b + 2⋅b\n",
"⎩ \n",
"\n",
" ⎛ a ⎞ ⎫\n",
" -M_y⋅⎜- ─ + b⎟ ⎪\n",
" ⎝ 2 ⎠ ⎪\n",
"─, 5: ─────────────────⎬\n",
"2 2 2⎪\n",
" a - 2⋅a⋅b + 2⋅b ⎪\n",
" ⎭"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.N"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Panel fluxes**\n",
"Not really an easy expression"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAFNIAAAA/BAMAAAB5QjxkAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMrtUdhCZiUSr72bd\nIs25ozBRAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAgAElEQVR4Ae19fWxlx3XfcMlHLpd8JFHUbtEi\nWUaFDSSOrU0cCE1dY+lAkl0FrohASCDB8bKSIsEwYDOKutokTvTyl1OjqLaNbHhhR7tRYiRxZJl/\n+KP5sM24cWy5kkUUkYrAsnedWEKV2rsruSttbEnsOWfmzJyZOzP33cf3yZ0L8N2ZMzNnzvmd35wZ\nXr73qBRcU/8KX8tVECgIFAQKAgWBgkBBoCBQEOgLAt/sWDU3vsYWS6EgUBAoCBQECgIFgYJAQaAg\nsFcE5l5gDbMvcqncCwIFgYJAQaAgUBAoCBQECgJ9QODoOaPkvpN90Da+Kto37tZc42t7sazPCJyt\nocJun+cr6iYNgeOvXZ80k4u9A0Bg7tZfaq51j+nlb+qy08XmJpURA0egpIw8xDPmoWbrk/sttf5z\nz/H5jlcdaWVtpLNfiZP7XFAfHh8MZsbHlGKJUoYoczvz54YNx9qwJyzzpRGY6ui231APpDulWvaY\nXmqHl5yRQn4U8pIyukT9wgp1XLB/Ru9y3Lh3m1r1LPymriV+8UiIPQ39q/yn/qkqmrpBYGrV69U+\nR9VE0Ht6jOHpb1I5eLJJ79J3sAhMrWr9iztTLw92pqr2khWqmIxM8k/MzI+pwztNjcinl0TWcZOY\n4Yk0hOKSMxxaIy9NrWoTSsqoC8VRvdUduFzXccLal9Y9g2+jWuJZRUIMn8f3lXgaoRJvflXYzavD\nmLktT1Iqg0Yg4MLsEZwwFfTkY4zauEbcyI9R0PzrkVFFNCIEmCiLnXY8H8ZXvLU2E+5MEw5/VckK\nFsUxKDxtbPiKOttpak42vaSyjptED1eJNETikjMcXKMujSxlTNxBYvkixWrxuVGHrM/z3+7pa21T\nNfGLR0IMp5GOpyWsxJtPhN28Oo75kicplUEj4HNBvYPmSwU9+RijPq5VP/JjFDQv5n+ZqaosksEh\n4IgyfSk6S3zF266ZcGeacDg0l6xgcRx1YXbNWnC08frMppdU1rHzmeykEmmIxCVnOLhGXRpZypi4\ng8QhnVIPDf2vRf2myNkHT+3+6AP8Cfq2v1PAL4o/9xBs65VnFSiNiI1x0Y2lfcdVK6QtPIi2fmwb\nx0X3lCdv/RFF7ajyeuxWrsEhkOWCui3BBR2/5GOM+rgKh3JccAQClTMbYlQpDhmBJFEW16KW1CSE\ngCIu0HVZAZNGyQpRyIcibH//R08/f+rCppnsrDte/lVkfrO4Iy0oSqWXxFYjSaKHk/pKGhLZqeSM\nBPTDEI9Lypi4g4Q5Yk7+SfMepeDU+G5DtrkNj3X4e+azKKk8q3iG+lXEJA2Pklp4s5q7rLWF+87S\nSewRbDc0qHVS3dtR2I5jzpKsvAwMgSwXWtspLixtkEWJxxj1cZX+pLmgHIFAZfuiHFXKw0UgSZTj\ncTvCFU+9vHjKca6hLitg0ihZQWI33PLcpjq0rWa3zKwu+sE+Ytr14o6bmE4v8a1GkgQ04nCtPkxD\nLjuVnBGHfijScUkZmIomKmXsm5PmSdWGTzX9d8O2Q0c82uE7W76HEn5W8VPcTFIrnl5jOd2jG8sH\nlfq41hY2L9OksRPJ/Lo6dEZhO45Z5IzmTVYqfUMgywV8m6zHBRt0HT9lHmNYsTGrPq7S/jQXlCMQ\nqvyfclQpDxeBFFEWNuJ2hCueevnxRJHJLq4hftJ0WQFPmiUrxDEfhnQedu0NtdAxc/2+nfMztiQL\nJlHAg4s1KaZyOr34Ww0PlCQBGQ7X6sM0JLJTyRmM3vDv45IyJu4gsV9OmlNbagGW8nWGeofXJQdb\n20odvIQS/m2VT5paasVB5ohuLPDk9PQKjQub76NJYycS+IV5/jmF7ThmdhVNKdegEMhyAd8I5XPB\nBl3Hjx9jWLExsz6u0p80F/DRuyEQqrxVjirloSKQJMr71W9FDQlXPHXy44kik11cQ/yk6bICnjRL\nVohCPhThv1TqC0fUjNk0pmirwIkPbh5ciRigFzc0hDkCRMn0Emw1rFaSRA+nfUJV0pDITiVnMHpD\nv49Nypi4g8S+OWkqNQ8JomOo92ceBWe24Ii3DSL7rIJPmiR14iBzRDeWC+twUKBxYfP7aNLYiWTp\nEp40sR3HzJyhjuVlQAhM5bigfjbkgg26jh8/xrBiY2V9XKU7aS4oRyBUeYMcVcpDRSBFlKm/f+Nr\nooaEK546+fFEkckuriF+0nRZAU+aM2dIW3kZAQJwnDy9rg6amRfOsAk//MafNKdPltBdL24ohjkC\nRMn0MreNY+0OhBW8JEmgCsNpn1CVNCSyU8kZiNxIrrFJGRN3kNgvJ02gHTwisNd7oNS+8/aPKfXb\nUFqEn6X7rz+i7LMKPmku3fap1ysntpnjyeM3QIrBaOoSKBDX4+ukLdx3nr32NugEm4aeWQyA4uIl\nhe04xvx267eXWj8RCLmgw3gQwFfbIRds0J9508/suMcYVmwYAHGNcUHEVTqQ5YIyBMKT5n2xrUxq\nKuVBIhAlyqHd3Yv+pGZF1yQEjCdenF0UB7ouK2DSKFlBgzei14fcvLPnoEwR/+Ru+P/CKAXoxQ2d\n/ByRTy/BVuOmY5LwcNon7NNUO4XITiVnCPSGXhyPlDFxB4l9dNI8u+FIdxUUP7CzdFHNPAyla+Hn\n2NOtl92zCt4Ljn1XnVJOzMv64CfUBRgD0TQlqLjr4IukjU6NTqpar6wf26E9hWYWLVi8b5PakSBT\n++0rpQJXx6AackGH8YZz8OhoLeQCB731ys78SWUfY7CYGXAiygUZV+F3ngtMIDyZHF4Rw0px2AjE\niVKxwqzomoRQOWlyoOuyAp40S1aooD5EAb7Jn68Dq1CK5XD4dQA3BrO4oZOfI/LpJdhqeDLQabYT\nHk7qK2lIZqeSMxx6wy+NR8qYuIPEPjppwjtt7AUfNG/9Cb716YkbO/QYS8FH+V50zyr4pHl0RV2l\nnJgzxy1b9P45iKYpWcVYWDxJ2sKTJnyAfXkT9xQ9szdEqUfwc+/Lm0iQxNdCBwNKdQ8IBFzQYWzf\ndFk/3/a5wEGffk7BHmMfY7CYGXAiygUZV2FvngtMIDyZnO2IYaU4bASiRKkYwSu6JiFUTpoc6Lqs\nQH8IAXKWa1QI4Jv8+cLPfnPEWWbulAzM4gaRlyNq0stRf6txig1J7HBSX0lDMjuVnOHQG35pPFLG\nxB0k9tFJE95pY6+/hnfYX6KPlB9bVQtw/lPvUa0XTfNvnj//1fPn6VuP4K/sf8CD5s6f/87D589D\nmlHvXadPIEM0TUm981G8vkV97zDaMNiiYfacOgYzneCZRRNYs6GonQgishopLC/9RiDggglj63ml\nPgtTCS6IoEN8Dq0ZQ4SYGXAiygUZVxHwChda30H+fG2F9DOB6KR5xExZbqNAIE4UbYmLmckl+Lul\noYNrg74ynkpkF9sgs4Icyeyhk2bJCqMggJkT3+TP1+KG3T20yCV/ir5Z3JUckU8vcquRHLAk4eFG\nPU4tppDZ6WzJGTowI3kdfspw/Jvgg8Q+OmmKd9rgl2ceWlXHYGOffVn/H5Zn1EGRyvmZ5pdVW/4p\ne3pNc/dB1UIxbCymJCmNX5xL2uik6VqWNtR9kAJO8MyuBUrXw7sDsZ1OmuXphYfNACoBFziM792h\nf8Xic4GDvripzgJh+GIxM+AEK+EOdJdxFQ1ZLlgC0UmzI4aV4rARSBAlMMPkkrqEgPHEi7OLDXRd\nVijPNDVwo3uVb77DZ5oc8cAiSgZmcUNTkCOy6SXYaqxiRxIz3KnHPjyFzE7lmaZFbwSF8UgZE3eQ\n2D8nTXqnzdz1//S/IvngpAnPF49CCcT4GEv9AB812svsBa3Lau6MFdplDU8/py+CeK7DJdFHXaPa\nO6QtOGkub+EDD9g0zMxyzPSG+ga145ipif+HTNK1cSyHXOAwnt2g59s+FziXH+uoXxPOGDEPVSds\nSXaScRXyHBccgfBkcnhHDCvFISOQIkpgBq/omoQQnjRtpqjLCnjSLFkhAH2oVXrz3d3/4d+twKx4\n0uSI+0boFGAWNzQFOSKXXsKtxip2JDHDnXrsE8tOJWdY9IZfGJOUMXEHif1z0qR32lw3f+4rSL7/\nBrniiHrDNGzjp9e/hJLL+DY7e5mT5sJFdWjz01bKy7r1PXXg3JvppGlKroua2lAzO6QtPGl24M09\ntKeYmcWgVyv19mVsxzHlU6YCmYEUQy5wQOcvLa7DhD4XOJd/Qak/XMBmffEuwgw4wUq4A969uIoG\ninWCC45AeDK5z80oxpficBBIESWYnXMJnDSZDq6HH0+Um+ziGhJMsOzBk2bJCg7S4ZfwzXcz6w8s\ndmDq+VW3e/iW6OibxQ1NQY7IpZdwq2HFgiRmuFOPfWLZqeQMRm8E9zFJGRN3kNg/J80D+MhyZWmL\nyAffOLa0tvDIHFQO/8oGij6iXos3c5m9YP6cWu5sstAt62+rvzgJYoimKbku6ql7jn9UawtOmvNb\nBzag3wk7sxvU/vI979qmdhyzcMa1lNIgEAi5wGGcevEanM7nAufyB+AIioQxF4uZASdYCXeAux9X\n0ZDhgiAQnjT9b34VKkpxCAikiBJMzbmkJiFgPPEy2cVlirqsgCfNkhU0eKN5vXodniqr/0uTz5xx\nu0dgDSUDs7ihKcgRufQSbjWsWJDEDHfqsQ9PIbNTyRmM3gjuY5IyJu4gsW9OmnddeOV+4N3yDpEP\nfutr3f/Lf/s2qCw9DElEqZ+/fota9IvZCw5sqbm7hZiX9c1v/aH7O3TSNCXR58Lu7ktaW3DSbN3+\nbuwGnz03M7tBS7u7u9vUjmNmV11LKQ0AgQoXFIfxH57G6XwucNBfp9Q9a84aFvPQE1aJ6+PH1clV\nhgvKEQhPJreKUaU4ZATSRPEN4RUNq5fp4Dr48US5yS6uoS4r4EmzZAUH6bBLc2/YfXYNJtVva8Kn\nyxzxwBKKvlnc0BTmiEx6CbcaVixJooc79diHp5DZqeQMRm/493FJGRN3kPBPmm15Ggui+LmgPp7V\nw2oFDTvUseZNv2CLrmD2AifQJV7WRh4cJcPe8WZ+sBH21nUcs7QWbxsz6dfT9kwqF9TRjapTQdC5\nQyiujyuPdPf8GDxfwIPSSbgyXFjYmQQHsjZWk0aie3zF284c7kh24Sbb1y9A84RkBd9uU8vQYzJS\nhfZj6uIUFf4o6mREGOaIBukloq3r7DQROSPDiZIybPQ5LzROGRN0kNDOmpPmMv7pWan/pYXha/uO\nq1bU/ATsKO2L71ObaP0svWo/vhu6A/VfjMhA1PJ9rNlY4s3MnfgMOObYerxtvKTtVUVxD6xq33PX\nkcnlwpIfYPItCDr7G4rr48oj3T0/Bk+aLb3w3JCxLCEXMO7VC95q+LtV6URJokkj7kF8xdu+HO5I\nduEm29cvQPNkZAXfbFMDesDfnjdMzd6Wrpu6bSJShbH47Ny2fvfMndaFmkKYIxqkl5jmLodPRM4A\nTlD8Y36WlGFR4bzQOGVMzkHC+Lr4MhWWz9AND2X/pnoOulnNXVatc9RlrF9a97//rWT+1Jl+2Fmz\nscSbmTtxA3DMn8abxkwKaY/iHpj1pJr+wZXIBXoAGWAhqr1wAVUunBRKxrYIXKC4Vw38InyjbFU6\nUZIGSSMeZettZulnmnA4NE9GVrC+ygKdkBZXpQjL8B8xNiciVRjDb37b3f+Riv/CCMb0NhE5AzhB\n8a9giOeLkjIYlkxeyDTB6Mk5SBhXD+ivkzy8ivWFDdX6kPxiUtPpg0p9XKm7TW0ibr/TDytrNpZ4\ncz1B/rIftg1cx2eU0nH3Z7rxiHrpSuTCgE6aiys+vONZAy7ouIfmzTwIOW8tlE5qvTZpxFe8dTez\n9DNNOByaJyMrWF9lAeih1A2rUoTlpV99O7xO1LahXZg/ou9j+joROQM4oePvg6jPFyVlMCqZvJBp\ngtGYiiYqZczpf5xz7xa6vrgDLzeuY9G7HoLvClpRt3iyMa/05bemmZWsl/Hmt9SNWdjM9hiXxseU\n0nH3DfpAp/WKugK5oGrj6uNEtfwYVEnf9RoZOV4i4IKOe2jW1/8O3gBwJpROar02acRXvHU3E+5M\nEw5/i/5HZlbTZBWAHqr9+dXQ6HkSTNS2oV0Y8z/fTUTOAE7o+IeswPNF60wondT6yFIGpKIJOUiY\n0Lbh2ACRhzMFXE/hS+SkeWEdT5pLHWyekGt6Y2wNTbwZdszsbW8rpeMeGgZ/PS9cCEHpsQ7vZpqA\nC7kAn4KFuIfXJpw01f8JpZNan94YneWTkRWi+BA95pZWw0Z90piobcO4cE3oyjjVJyJnICfSJ82S\nMvpBqAlLGac74LT5Gzr8a73oSROkj6+ruQ1sXjyJr+N//euxNfGXxtYyadjMBtUg7uH1DngmW7gQ\notJbfbYKb2+KBjpKcwHjHlwLO3jSPE7SR4K2SayOMGlMRlaIBpXo8bnISfPPr1+ZtFShHZzuRB0d\nD+FE5AzkxDzFPwTtRkx5JWWEsPRQn7CUsbgNPt7bIUdfh6/EBKqKl4PwR/aFcyi4hV6xVK79jAB8\n/xtcGPfg+t9/DamicCFAZV9XiQsU98DNmxSeND+P0tbDQVupXikIID1aa9WT5oH19uWSKq4UFvh+\nIid0/H25OV+UlBHCsv/r7QeBEn+p/fwfeIueNPFJ5vS27lVerwQEFo+gl7En2HPwdXOFC1cCB9hH\nzQWMe3Bt0knz3wbSUr2yEEB6zKnqSRNQ+PGSKq4sLrC3OmVg/MPrxnWQlJQRwnIF1G9+TB3b0n7S\nVkJMCP2+AwRTF510Gf7pTbn2EQIitjrK+rvvMe6V6+PrhQv7KPQVVxJcUBB3/5peoZPmYSd956N4\nfUupitIi2C8IROnxE/GT5nt3vFTB9Cjbx34hg/EjyglICxD/8KLzRUkZ+4wAeXc0PQ7+vmp/cZ34\nkDxp0jtx5EkzpE+p7zcE6KRJcfc9+4ZSVx/xtg+/vdT2HwLIBR1337dfUOFJ028vtSsCAaBHazNy\n0nyA3pZVto0rggSBk5gydPyDBv03U3HSDNtLfb8icO8R++bL5F/Pr1HtHXVwe79CUPyqIkB//qC4\n+22763jSLFzwUdnfNeSCjrvv50+fOvX9+5X6z7601K4wBIAe06dOnf7jtcDvh+GZ1npJFQEqV0YV\nU4aOf+jvjfhUq6SMEJb9X4f//gMf/HiBHE19ImhqQ83smE+B7H9EioeIAL6lW8fdxwPe1vt44YKP\nyX6vIRd03Cueglh/IqjSUgRXCgJID/iPQKuhvxtKfY0/ERS2lfr+RgA5oeMf+kknTfpEUNhS6vsa\ngaOb6N7VO/hK3z0ATMDv5pbXU/cc/yj/L/GBfPb8b/J/5t/dvSjNGXq5fWOdfYM36eygTTh2znMC\nv8eI4h7I/1xN/7+BcqFd52jhwii4QHEPuACEeR5+7kTiDOGz5wN3G/3Y4zUG7B18tgpooL/ybHlV\nBfIn1cInBpoqOFZjADqbErsPPiCxWX3ZwNdOEHvkBMU/kJtPHJeU4cIzBuwdCkPh30zCdfQkvuIz\n7Xd98tkt9eg6Vu11YXf3Jfi27hUUxD6NbDv2WvhwrwOHM26+M5x5crMMHKLFL3nTH9yGb27HuIfy\nO27tDJQL4wC2h4RfGQfzRsGFgxj3gAtK3bX7EaXgA0BwDf77NAfuth/pnmpjQI/BmxDQAFOFmrv6\nH7cCefvOD8E+MsBtgyM0eI95pp7u42DewNdOEHvkBMU/kOvzRUkZgkhjQI9hmDCtvzDx2Bl0nf4b\nJRamd/A1uJ4K6lC9+13+kVT2OP7adBv2m7vVfvNo+xwNFBKqm5dmYjmytlxno1HwTX1P9E6Iayev\n7yA0G4iERA5PQIRdEiPkaFN+sy97jKuBnMSD44LSYKc8iruT6s0udHPvUkeeC10q6caeoI9wvGcu\ndG9dEPMsF9rbgalBde76DwYSV621qB9uN1gDzrKwJAwJm2S9F/bK8b2WhXl5hoqO4VyZpqBrE3pE\nUgVr69P2kU8ZCYolxGxaV/cuAes5IF0Zke4kzOs5ZQgd6YmopQknxiNl5HzLtdUAYZu71HFlpAw1\ne5mAOXQJbwsbVMFvR4tcd1dks1uzqxWhEcztzJ9LtZH8N/CzafqaPRJKuAXvomNE/Copq5Snsqfd\nWhuNvtvonuidEEtT8laolAtSs4ZISuQECYigixlRYwE1b0qNSn2Gq4GcxIPjgtJgJzxKAGB6p4DU\nntRgkJiRUeB7lgsprvJguNdYkXJBOt4rF9i61BzaysZcmFsT7kWK71a3RqRaVAd6X9xusAaShkpD\nkp2goRf2Sn352HSVKrIMzfjRHUxkYJASGqYK9rdf20ce9ATF+pAyMliyi3TvNSCsZIQpoztOTGbK\nyIWvgd8cpco9p192vjJShlp6jpw+9DLdXm8QuEkiYcqtcxXh7ObCxYrQCBZ3prTOVIfH1OEd0/YO\nfRcSOSgvPiG7VspznYpICGpt1H1b23RP9E6IxTQqb4VKuSA1a4ikRE6QgAi6mBE1FmBza01qhI8E\nmeiEcuw1QC4YsBMeJQAwvVNAasdqMEjM6IOijHkJO1S9khorUi7ICXvlAluXmsPBFMY8xwX1zgCi\nsHqn+kIosvU6vPritlFSg3y+WRpira8WDD0SbnWhJB+bblKFMSExV0KMnpimPA5kQRN6RFIFw9av\n7SMPeiIWRpzHO49FBkt2Ee89B4SV5K3ohhOq15TRHSfQwCacGI+UkQtf935zkKr3nH7R29AjQdMu\nlOQp3A09emZodzBpA80R09z4f7ZvCSS4yLsN1+k+u+pVVfuOq1a0ZLED/4rs5x7ym+Fdwrf+iBF9\nRZ3tmOJtqvVj20oJiW4gaVWsG03vKM44Cw0OF6mbHk0jG40NfJva0CU9N5XhGVK8N7lXVeJAMEpC\nK0gr9SINFRfAhnDC2yoSaWYFOavcWFdjATYvaIX2tb2qi6Ecpb1wQQCqFce5MHuEOlY80lyqgk26\neuJCEKbqjPjZe7qE6Uku6D4VJcEk8JC5o3V6rzZc1bywdy4QzhLUCt/QFm/JhDHPcUHxr6eeRyK4\nKvJM89WmM+FFi8AfzcjLePeyBEhr92vAN4KNDNei7tW69njHlDB56as5e9lTw7F8bEJ6kA2BeUmG\nEswSUDbap1gXBG1Cj2iq4Jlrtg+x7swIl7/FSkuBnliSWpUZn8c7xMJNH4DODjVKGYmAjEHKsPko\nt3QmOGXUIp/z24ITyeVDSRlyEiBensJh84hSBnw3hX7waG7t2BHTrKLP2dUkCreYcyWLblb0rUlU\nnb6k1LPcYO6tk/w/1kFwdF1LW9vwvvGTWGaJloN0g0qh2DSTOIazngVVBqlCTk+moY3+tbhq6toi\nrOAvhPHez1DfUIkAQSsJrKBBSvdCvRUX0AZ/QoTIl2glKYicckXW1VgQbf46T1G998QFB6hWKIPh\nIg9g646VoMfBNsY154IJAI1PzNiIC3GujgEX3GowC6zCN8DAdWrKhYUdEwLvJoPb+j2vCStftBIM\nHDHbSrBgkdf0RVFvSwBHwvvOcZlHHXMLpdpsjYyuvFmlfoeUM2Gx0py91lPNwXxswlShbfDNa5qt\nNNhORxUH8MvBFDNQNU0VBjdVt33sMWXElyRP3jxlSFI7wFgf3YNwoqxpQMYgZbhwZ5bOJKeM+F4i\nkM/47cCpLpWhpAx/kjAnEA1dbMLmkaUM/6RJVjZ4mfl20PmDSn2cRYtrSn2PKz+lC/Pr6tAZlv2V\nKcxtKbV8BCtGMr1mWrSUxcooMY1aHMt8ehYczFyITE+moY3+dcOqqZu5ofbr8OP1tnZo90IlAgSt\nhK0wmvVN90INxgXrtUIbvAkVQuRJbGcfIhY75Yqsq7Eg2uxZW1+p5YIFNBIMG2IEW3dkdiTAtmJt\nGfXujgs+RjTcn9H62g0XWJux2jmitfTIBUf13rnAOtxqMAusO5gsCj0V5EL/92uhipkHrQQDp5cR\nHAhtR4u8pi/27m0J4Eg4S63BS5TkbqFwsyWWM9JbeagPrzcp80kUJiwKu2Uv9tWX9VRzMB+bMFVo\nG3zzwAQ/VViHNMycrXywnQ7GgQ2ku4MpZqDXtUFl0CnDZJxKJtEmNk8ZktQOMM/hIJzYVgmIRd4P\nCOsZg5Thwp1ZOi6vRCnD7nR9l+gOOmX4yHNABPIZvx047LddYUNJGcEknBM8nF1suJl9HFnK2NtJ\nU4V//nhIqdMrxufj8I3wl9h/E4xD22pevzMUMv+GacRf+u5bhxeWMCpaasW8dZphuncs8+lZUGXA\nBTG9Ng1s9K/251eNgCzCcmubHeHezCzjHovNQCVA0ErYCu5Ad+pFGowL1mu0ITAPIPIltrOZYUPr\nZrFTrr8ktcaCaLNnbReVGi6YYIKiHBcQbHKJucC9mUsMNsdAG9aECx5Gerg/o5bBt3R0wwXWFnLV\nKOmRC9brPXCBdRyiNSdc7G7JMAq93fWkZuytoY6v/x1LMHBmGYmTpkNe0xd797QEzDREmijJ3ULh\nZkssa6S/8oxKdZd+WoVVvQah0DV7WUmFY/nYhNsG2eCbhyb4EnbIwMwLyBI3oBjjYE3EgoMpZqDX\ntUllwClDx6WSSbSFPaQMQWofYuuzI67HCb83Ix8EhJUQ1rpiHOhwk7hXI8JxDuKJY7pdO5wynPLM\n9qHRQBOjlBG2dlfU+kzfwaaMAHkOCLltDBjflBHkJc4JHsguNtzMPo4sZezxpNnWvxxYLy+s25Mm\nfpB9bptbzDJYuuROmp/htp+FwvuwwhJGRUutmNeBGad7xzKfngVV8hqoTk+m2Q/bG5UwYGnVlMki\nLM9sGUdsb17T2j0rNgOVAEErYSu4A92pF2kwLliv0YbAPIDIl9jOeoYQOadcW1djQbTZs7aLSg0X\nTDBBUTUYLsQINrnEHnFvwyULNsdAG9aECwxdGCY7I/vaFRdYW8hVoyScxDKSJ6G7CxfTmd3bAxcY\nObcaDMw8hzTBdeoLF5Rc6OrsETkUPfgAABKBSURBVDkVlDftSRNBJ2ZjD4ulQ97GW/W0BFArf6dG\n1DGHPDcz8s5Iss8ZonWq+15DT6uw5qWKrthrdIDvQb7JxybcNsgG37yus5UHttDBOFgTseBgihno\ndW1SGXDK8HMjrwdjYA8pQ5BaACYdDsMJbdWAMPKkw33hC+sZg5Thwp3ZPiY4ZQTIc0AE8hm/HTi8\nVIabMmzy1F5wTmD60N3FhpvZx5GljJ5Pmk8ev2H9lpX2DzwHsfL4usI29X71W2rp/uvNJmODoRYv\nwVe63v4xdXDz4Io62IER2/Dz7LW3aQmU3Y7zzJt+Bv7fOnaki5W48fSnZ5pO97CvMAuqrHDBTk+m\noY3+9TnM/KQQh6vfhtZF+PF7sx1Lt33q9Yoc9ZU4EEgJWkEmV3uRXpO8mQsKbXATMkROgmpsZx8i\nK0YTxAjEIQaT6cQwhQZ2WUfNtVygeJBChg+glVywYHtcsPtDADYrCbgQwznggoeRi7WjGXvdFRes\nNj8QrAPuvCAsF3KR4I2c3dsDFyxyhLMAFeaIcSGASXjQW9EEt/V76iz8+iCvhR04abrAEU+x3WLp\nkKcV2vsS0I7qZd7lGmDknZFiHQkv5nc/C25VU4UAGnqztoC9Vo/zVNMDYpOhcLhtkA3OvEbZygPb\n6aCUGaOHSRVMUOtBb4WhpIxgSXIsHPNo+8jgzXnRYmUzlgBMAhCEMx4Q1pbixFikjK62j0lNGQHy\nHBCIJCfr8U0ZQV6qo/DYpIxeT5oHP6EuwPdizHxMrjMsH3xRUdvU37/xNerY0y3zVUe8yuFPTZvq\nAztLF9UPv/En19UN5+CXvjX4s9Mr68d2SII6OPKtV3bmT+qOKLZp241HnGk6ahcv922SSk4V1enR\nNLJRDAI71uCURwpp+MzD0Hot/Pi9Wdux76pTqqrEgUBK4MFFR7vsTUW9CCCTvK3XaIObkCFyElRj\nO/sQsdgqN9aBBTGYIFhkAcMUGNhllTTXcsFgAToZvoALDDZ1tFywvQOwWYnPhSjOARc8jFys3YzG\n7e64wNpCrlrseEE4LuQiwRu5cY9scJFvxAWLHOIsQe1uyVgHei3wQn9Mwe+d3nWTgpOmCxxREDtY\nLO0q1PRt5DYrcauw2RpgYjkjHf6eF/e+sh5JFRJo6M7aAvayooBjtG0QMNzB3E0Aw21DoQ3WPF5A\nTkKjEyYwTgHFMFl1Q9DAwIbVoaSMcEkyEI55dXhzXmSsXMayoHuOB+FMBIS1JTjhiDvClGF2hvzS\n4bzCMHlY9FIZVsoIkOeAOOTzfofbJhNrKCnDnwRQhi1jElJGryfNW7bgu0um7v7VnZBQiycVtR3C\nf1YOH+/T/4PIZlz8r3WtP8H3d35yd1e1b7qsnxnCh0OXN1FCF0d++jl1QHfUchNRNx7EJ/R0uoN7\nfQQ/PLa8yWuAueCmR9PIRjcGSnMKTnlkPw1/4saOfuTq92ZtR1fUVaqqBFwyIJASPGlqk72pqBcB\nFJw0yQY7oYXISkhLAiIWW+XGOsCBvEpYwDAFzV1WSXMtFwwWoJPhc8GgyDPY1NFywfYOwI5zIYpz\nwAUPI7I9mNG43R0XWFvIVYtdhQvZSAQnzb1wwSKHOEsXu1sy1oFeC7zQ/9lbfzdQsQknTbGIaRFg\nF8bSIU/03cMSoPA2WwPMTmekv/LYl+kPP/5HkVQhgYaurC1gLytxntI4TGc5CocnTbLBmscLiNKu\nS0sJEzywrQ76tZhQYxPNHWhMcWKCBs0NqzTDoFNGuCT7kTKY1AIw4XoQzkRAGPkEJyLbx/BThgl3\nfulwXtnb9iHwY3QHnTIC5DkgDvm837wW2G9eYUNJGf4kAN6EpIxeT5rvXXefsm1951G4vrZClLlD\nKdf2HtXCk+Zvnj//1fPn6Xsh1OyGmr1kP1Hael6pz0KP2XPq2CaNV3Pnz3/n4fPnT2rpoTUtlUrE\neMSZp3snWvHot6g/zoIqiQvR6Y1p2FvY/xN40iSF2qJjq2oB7RK9hbb3KPUHNJ2vRCkGwbg112GT\nxVTUi/Ri8hZekw1uQobISWRnmMFCJHQ45do+wCEGE9hJannJsDPN7qwZR4UOujaDhYAv4IIyYJuO\nZIPoLcF2YgaWep+w1EpyIcRIxJpUKDeyCy4IbTIQURCMWy4SYS/LBbFeeuaC0AGry6wG7WE3S8b0\n3MvNX+hKADu9AidNETjNbIGlQ14b0PsScPSjIxRXXZDdQglShTBSrDwRsz9VM99fF/Tpnr1CifPU\n0MNRWPRyAQxSBdngzOs+W4VgOx34TNPAJC3AlEad+nPS5EBgfMNpXJvBxK12TWW3feRThlySYj0I\n5uH2wVXJCV4wxAmBlctYAjDB7DCckYAIbTKjRUEYYcrgcOsF6DghnHV5hWDSPff0OrSUIZEXAXEb\nt3Ej4TeDQ347dg4lZVQnyVMYGO6dLkaWMno9aT6oWvwZco9cMxtKubZn1EHzkSE+9qvr4Ts84Y/D\n+lgKp9Id9SVQsLSh7jtiFU2v6eLipjrLHVFilMjxAKSbTo/CV5iFVPIaqE7vTHOjVGsTT5qkUFs0\n+7JaXIcOfm/W9mXVzoNg3JrreCabCREq0muSt/Fa2yAmNBAJCShIQMRiZZXryQCHCEy2E8NkLGt4\ni2gmDT4XXIgZvpALBmzXkbRw7wBsI/aAPeFRi70IueBhJGLN/c29Sy6wtpCrrM2CYLmQjQRv5Nq9\nPXGBl4tbDcam7pYMO9DrPVjoQs0vKDhpisBZZhssBfJmVM9LQFKzyzVgiCWMtPYJH5T6hFKHjwj6\nNGKv0SQ8NfTIU5i2DRjLpCMbnHmNspUHttOBJ02JmrHUpgomqIdF40pkBtJhVwvVDCZQ5iTQKGWE\nS7IPKcOSWgDmnK+EMx4Qjl6Q0aweC4Lxv8uI9DNl2HBro+IWVHZZ60GPBYtuZbxYjdRm4fdYLFmV\nTRkB8hwQ2jWlkrjfFhxopmuYKUMgYUCYkJTR40kTHlVOX9Qw+6/XqPYTru0H+BujDIaa3lDfgKeX\nR7VUqbMb9MxweQt/keaLI3+so36NZXg3EZXj1YmYKdMwC6kMuKCwQQ93poFivqZPnTr9x9eR/dqi\n9gv0yFX5vY0drctq7gwPlXcLgnFrruOZbLpCrx3S6580yYY1MaGBSEhAQQIiFiurXE8Gf793UbGm\n2k4Mk21pUohppvEWBqq5EBv41LQNBnVQBmzXkcQJsKNcwAfjllpaqZoOuSAx0lwNZtQDu+QCawu5\nambHQHiT1ESCN3Lt3p64wMvFIWBs6m7JsAM93qeD4Ao1P33q1PfvF5GyzDZYCuTNqF6XgEhF+Ewz\nxtTKGjDEEkZa+4QPqgXpb/7T1VQRcCnBXqNJeGrGnchSODhpkg1bzrxG2UqCLdNNDUxMUIlF43Is\nEKTErhaqOSwNjGo6YFU2ZYRL0igRzMNnml6VpqVZaG7Oi7zI3fQOdD2EXivhjAfEaGuwfcTwssTl\niGj3+pMyrHLtXZwTiIYHk4CilyLqi0QDVYnVSJot/JLF18ktLpcyQuQ5vC5Z0yRjmTIEEgaEPIXH\nJmX0etL8njpw7s0mHuI2taFmnnBtl/ENJnRxqni1Um8/dkS9YXpHy+cv0TPDZXwno7048l9Q6g8X\n3AGUt045Hk6abjqrAGchlZwqqtM70+woKhxa1QqNRafX8ZGr8nsbbfBP3w9tftofjjUHglECJ03h\nshmAvXZIr3/ShGZ43iMmNBAJCXRJQMRip1zPBqmiCpPrxDAZ05rdIppJgYOBqgYLKFeDYSbUYLuO\nJE6AbcQesLDmqjhXuCAx0lwNZjTWYBzqucDaQq4aJQ4EM0lNJPxtA5T0zgUPZ+lid0vGotBbIVzo\nvpYHZaQssxlLh7wZ1esSEKmIto1u1gCzE/82o+lk7fN8gOeJBzz6NGGv0xRwLE/hYNvA56oHdA7R\nCptkKwm2TDddEtR50ENpOCkjXJJ7TxmO1HFOOOKa9RYNiEG+wfYRwcsl7wGkDKdcBzfKCVXJrD0w\nQQ5x6Eopl3k1Ut3CL1nsoZRLGSHyrMQlazNp1G8HDm+bQ04ZjIQBYUJSRo8nTfVt9RcnN5kE7v7U\nPcc/Kto+ol5r2kww2l++513bS2sLj8wZ+dSL12BpfuvAhpHAjSP/ABzxuCO2GiVyPOTeqik0C6kM\nuCCmd6a5ebG0vKoVGosO/8oGSv3exo75c2q5kwXBKJnreCajQqUIKtJbOWmCDWJCA5GQwOgERCx2\nymku/JNYFSbXiWHSnZu+VjWThoALLsQpLigNtutIahJgx7lQxbnKBQ8jsj2Y0frfDRdYW8hVo8SB\nYLmQjURl2+idC7xcHALGpu6WjEWhp4JYabHxzysRKctsxtKtQjO25yUgqdnlGjDEgpnZSGuf58l/\nWVefiqSKgEsJ9jpNAcdOSGBMLxHAIFWQDcK8JtnKA1voqIGJCeo86KUk4yLGu9VCQoelgbHKqlzK\nCJfknlOGmF4AJux3xDWmRwNikJ/vfvsYdspwO4N2LsoJR8u9bR+Mn0CXRfLOq5FkFn6PxZJVuZQR\nIs9KAvrhL6dZ5NnvIacMRsKAMCEpo9eT5s1v/aH7O5IIunxhd/cl5dp+/vot04dX+e7u7nbr/l/+\n27fx2H94Gkut29/NArhz5F+n1D1rQm6UeONPiOm46xLNgioDLugGmt6ZxqPoPnf1P26R/caipYfX\nUe73NnYc2FJzd3ujdcWBYJTAr0bSZdGL9Abbh0Ib5IQaIilJQsTIkQliBODgosImu04ME7c0u1c1\n03gHA1VdiJNc0GC7jjQuAbYRe8DCp/AqOFe54GEkYx163RUXWFvIVaPMgWC5kI0Eb+TGvb1wgU+a\nDgFjU3dLJkSjWV2stMjAu3Y/IiJlecpYktceq3pdAlJJl2uAkVfWSGuf58nUh46bRWUi24S9VlPI\nsTyFw2eaZIMwr0m28sAWOmpgYoJaD3oqyLgIBW61kNBlAhOUKqtyoIdLcs8pQ0wvABP2O+J6nAi2\nD4N8g+1j2CnD7QzauSgnXF7Z2/bB+Al0WSTudjWSzMLvsdhjVSZlhMizkoB+dHzwdNLcDhz2e7gp\nwyJhQJiQlNHrSVNwoKuiDUbY++hGKHHHqLAlpiSf+SpcCFXW1adfiPSI2RHpZkVshRX4hfCk6bcq\n1QAiXjOhihoLappDbXusJ+FrAnZMSXdcSGFU61XUvKbaaqBmF2LuoYENuMAnzYpfPEelgQQ1BsYH\n9UeaxrKB20klNY5xcwr5Whej9GiqLR+b8KQZ2tTEhBROjEOo29RrDEyM2qs4CWMTj2NK8u4wFims\nat2KmtdUG1uRmI1diLmHQxqsnVTKqLGgpjlhd1/EaSwbuJ1UUuMYN6eQr/UwSo+m2jj+idlMc8rH\nJiakdDAOWQuW9TerL0U/Q50Y2Yv4F1ODlnaqLa2IDHvFlORxZgxiI6vzxiTfjQibamMrIqpQZFxI\nea0aQJTSUWNBTXPC7l7FafgagB1T0h0XUhjVuxMzr6m2GqjZhZh7aGADLkSXC+rgObBcvWoMrA7o\nnySNZQO3k0pqHOPmFPL1bsbo0VRbPjYcuqSPDUxI6WAcEv7WGJgYtVdxGsYGHseU5N1hLFJY1bsV\nM6+pNrYiMRu7EHMPhzRYO6mUUWNBTXPC7r6I01g2cDuppMYxbk4hX+9hjB5NtXH8E7OZ5qSPDUxI\n6WAcshYsX6Tm2RcTvcZenMe5BoMheVdjRd6FvthYY0FNc19MGIKSPJDj4WSNFXkX+oNhfo4aA/tj\nwii01DhW0zwki/Ox4ZPmII2pwaHGwEFaNgjdeXdqsBiEQRGdNVbkXYjoay6qsaCmufl84zKixrGa\n5iF5URP/muZ+GFmDg7bg7Dmaqv1SP2YchY48kDUYDMngGivyLvTFxhoLapr7YsIQlOSBHA8na6zI\nu9AfDPNz1BjYHxNGoaXGsZrmIVmcj005afY7DHm8x4MTNVbkXegLYDUW1DT3xYSRKKlxrKZ5SCbX\nxL+muR9G1uCgLbh3TU91+kg/phyBjrdk55xZyTYPqbHGirwLfbGxxoKa5r6YMAQleSDHw8kaK/Iu\n9AfD/Bw1BvbHhFFoqXGspnlIFudjo2qa+2FkDQ5DsKAfXnSrI+9ODRbdTrLHfjVW5F3Y49x6eI0F\nNc19MWEkSmocq2keksk18a9p7oeRNTiQBS1+lrn4cj+mLDoKAgWBgkBBoCBQECgIFAQKAgYB+0mg\n9lfH4ulfCUxBoCBQECgIFAQKAgWBgsA+QaB9ocOezJp/UM71ci8IFAQKAgWBgkBBoCBQECgI7AGB\nY+Ij7k/sQU8ZWhAoCBQECgIFgYJAQaAgUBDwEZii6v8HQI5WdGote2UAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ \\left ( 1, \\quad 2\\right ) : \\frac{T_{x} \\left(a \\sqrt{b^{2} + h^{2}} + a \\left|{a - 2 b}\\right| - b \\left|{a - 2 b}\\right|\\right)}{a^{3} - 2 a^{2} b + 2 a^{2} \\sqrt{b^{2} + h^{2}} + a^{2} \\left|{a - 2 b}\\right| + 2 a b^{2} - 4 a b \\sqrt{b^{2} + h^{2}} - 2 a b \\left|{a - 2 b}\\right| + 4 b^{2} \\sqrt{b^{2} + h^{2}} + 2 b^{2} \\left|{a - 2 b}\\right|}, \\quad \\left ( 2, \\quad 3\\right ) : \\frac{T_{x} \\left(a \\sqrt{b^{2} + h^{2}} + a \\left|{a - 2 b}\\right| - b \\left|{a - 2 b}\\right|\\right)}{a^{3} - 2 a^{2} b + 2 a^{2} \\sqrt{b^{2} + h^{2}} + a^{2} \\left|{a - 2 b}\\right| + 2 a b^{2} - 4 a b \\sqrt{b^{2} + h^{2}} - 2 a b \\left|{a - 2 b}\\right| + 4 b^{2} \\sqrt{b^{2} + h^{2}} + 2 b^{2} \\left|{a - 2 b}\\right|}, \\quad \\left ( 3, \\quad 4\\right ) : - \\frac{T_{x} \\left(a^{2} - a \\left|{a - 2 b}\\right| + 2 b \\left|{a - 2 b}\\right|\\right)}{2 a^{3} - 4 a^{2} b + 4 a^{2} \\sqrt{b^{2} + h^{2}} + 2 a^{2} \\left|{a - 2 b}\\right| + 4 a b^{2} - 8 a b \\sqrt{b^{2} + h^{2}} - 4 a b \\left|{a - 2 b}\\right| + 8 b^{2} \\sqrt{b^{2} + h^{2}} + 4 b^{2} \\left|{a - 2 b}\\right|}, \\quad \\left ( 4, \\quad 5\\right ) : - \\frac{T_{x} \\left(a^{2} - a b + a \\sqrt{b^{2} + h^{2}} - 2 b \\sqrt{b^{2} + h^{2}}\\right)}{a^{3} - 2 a^{2} b + 2 a^{2} \\sqrt{b^{2} + h^{2}} + a^{2} \\left|{a - 2 b}\\right| + 2 a b^{2} - 4 a b \\sqrt{b^{2} + h^{2}} - 2 a b \\left|{a - 2 b}\\right| + 4 b^{2} \\sqrt{b^{2} + h^{2}} + 2 b^{2} \\left|{a - 2 b}\\right|}, \\quad \\left ( 5, \\quad 1\\right ) : - \\frac{T_{x} \\left(a^{2} - a \\left|{a - 2 b}\\right| + 2 b \\left|{a - 2 b}\\right|\\right)}{2 a^{3} - 4 a^{2} b + 4 a^{2} \\sqrt{b^{2} + h^{2}} + 2 a^{2} \\left|{a - 2 b}\\right| + 4 a b^{2} - 8 a b \\sqrt{b^{2} + h^{2}} - 4 a b \\left|{a - 2 b}\\right| + 8 b^{2} \\sqrt{b^{2} + h^{2}} + 4 b^{2} \\left|{a - 2 b}\\right|}\\right \\}$$"
],
"text/plain": [
"⎧ ⎛ _________ \n",
"⎪ ⎜ ╱ 2 2 \n",
"⎪ Tₓ⋅⎝a⋅╲╱ b + h + a⋅│a -\n",
"⎨(1, 2): ─────────────────────────────────────────────────────────────────────\n",
"⎪ _________ __\n",
"⎪ 3 2 2 ╱ 2 2 2 2 ╱ \n",
"⎩ a - 2⋅a ⋅b + 2⋅a ⋅╲╱ b + h + a ⋅│a - 2⋅b│ + 2⋅a⋅b - 4⋅a⋅b⋅╲╱ b\n",
"\n",
" ⎞ \n",
" ⎟ \n",
" 2⋅b│ - b⋅│a - 2⋅b│⎠ \n",
"──────────────────────────────────────────────────────────────, (2, 3): ──────\n",
"_______ _________ \n",
"2 2 2 ╱ 2 2 2 3 \n",
" + h - 2⋅a⋅b⋅│a - 2⋅b│ + 4⋅b ⋅╲╱ b + h + 2⋅b ⋅│a - 2⋅b│ a - 2\n",
"\n",
" ⎛ _________ \n",
" ⎜ ╱ 2 2 \n",
" Tₓ⋅⎝a⋅╲╱ b + h + a⋅│a - 2⋅b│ - b⋅│a - \n",
"──────────────────────────────────────────────────────────────────────────────\n",
" _________ _________ \n",
" 2 2 ╱ 2 2 2 2 ╱ 2 2 \n",
"⋅a ⋅b + 2⋅a ⋅╲╱ b + h + a ⋅│a - 2⋅b│ + 2⋅a⋅b - 4⋅a⋅b⋅╲╱ b + h - 2⋅a⋅b\n",
"\n",
" ⎞ \n",
" ⎟ \n",
"2⋅b│⎠ \n",
"───────────────────────────────────────────────, (3, 4): ─────────────────────\n",
" _________ \n",
" 2 ╱ 2 2 2 3 2 2 \n",
"⋅│a - 2⋅b│ + 4⋅b ⋅╲╱ b + h + 2⋅b ⋅│a - 2⋅b│ 2⋅a - 4⋅a ⋅b + 4⋅a ⋅\n",
"\n",
" \n",
" ⎛ 2 ⎞ \n",
" -Tₓ⋅⎝a - a⋅│a - 2⋅b│ + 2⋅b⋅│a - 2⋅b│⎠ \n",
"──────────────────────────────────────────────────────────────────────────────\n",
" _________ _________ \n",
" ╱ 2 2 2 2 ╱ 2 2 \n",
"╲╱ b + h + 2⋅a ⋅│a - 2⋅b│ + 4⋅a⋅b - 8⋅a⋅b⋅╲╱ b + h - 4⋅a⋅b⋅│a - 2⋅b│ \n",
"\n",
" \n",
" \n",
" \n",
"────────────────────────────────────, (4, 5): ────────────────────────────────\n",
" _________ _________ \n",
" 2 ╱ 2 2 2 3 2 2 ╱ 2 2 \n",
"+ 8⋅b ⋅╲╱ b + h + 4⋅b ⋅│a - 2⋅b│ a - 2⋅a ⋅b + 2⋅a ⋅╲╱ b + h \n",
"\n",
" ⎛ _________ _________⎞ \n",
" ⎜ 2 ╱ 2 2 ╱ 2 2 ⎟ \n",
" -Tₓ⋅⎝a - a⋅b + a⋅╲╱ b + h - 2⋅b⋅╲╱ b + h ⎠ \n",
"──────────────────────────────────────────────────────────────────────────────\n",
" _________ _____\n",
" 2 2 ╱ 2 2 2 ╱ 2 \n",
"+ a ⋅│a - 2⋅b│ + 2⋅a⋅b - 4⋅a⋅b⋅╲╱ b + h - 2⋅a⋅b⋅│a - 2⋅b│ + 4⋅b ⋅╲╱ b +\n",
"\n",
" \n",
" \n",
" \n",
"─────────────────────, (5, 1): ───────────────────────────────────────────────\n",
"____ _________ \n",
" 2 2 3 2 2 ╱ 2 2 2 \n",
" h + 2⋅b ⋅│a - 2⋅b│ 2⋅a - 4⋅a ⋅b + 4⋅a ⋅╲╱ b + h + 2⋅a ⋅│a - 2\n",
"\n",
" \n",
" ⎛ 2 ⎞ \n",
" -Tₓ⋅⎝a - a⋅│a - 2⋅b│ + 2⋅b⋅│a - 2⋅b│⎠ \n",
"──────────────────────────────────────────────────────────────────────────────\n",
" _________ _________ \n",
" 2 ╱ 2 2 2 ╱ 2 2 2\n",
"⋅b│ + 4⋅a⋅b - 8⋅a⋅b⋅╲╱ b + h - 4⋅a⋅b⋅│a - 2⋅b│ + 8⋅b ⋅╲╱ b + h + 4⋅b \n",
"\n",
" ⎫\n",
" ⎪\n",
" ⎪\n",
"──────────⎬\n",
" ⎪\n",
" ⎪\n",
"⋅│a - 2⋅b│⎭"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.q"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Compute **Jt**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Computation of **torsional moment of inertia**:"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAKYAAAAnBAMAAAB3Si45AAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEO+Zu3ZEIlSJMmar\n3c2pvSpCAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAD4UlEQVRIDbVWT2gcVRj/bZKd3Z1kNmPjJWCM\nVijqpdFYRVSYYooHL9s/Qmm3sBSJpEY7XsSD0hWqFFRcSaEUBAfxImiT0kCRlpIepFQhJIdW8dJg\nDwlCQxZpclHW733vvZ03s/PSWPQ77Hvf7/t9v/fevGF+C2wa354OrXX37CuW2rbtj1kqAg6cBWu1\nB29l1J7e/ii2ZeAxtJRryiS93QgoY9iPmfHMqhkg/4SgFeU+S3EL4KwCHwvgMxNtz22aRdreTcF6\nmDb4B3Ct3SEmU0A34bnlBKoTm+ZgE3zq3FVqbcJt6AYeVwicAx7yE6hObJp7m+DbGXinIY7fF+kG\nHjfodxm55wYTqE4smu6HTZR+vhzhVmuh8NLtyCP+QJWeAYdzt+rjMLzW3wpIDhbNEp23vJifY3K5\njg/osL+56hVAfjE/gk+TQkZm0bxImv21bvkU+0O8Tpcy4i6oxp5K75KALJGtmauQ5tfw6tx1FJgE\nuuq07ZNjFH5XrXsO5yyKQLZmcXT0z5kDOOFyXzUXfgMMhz3n1T33+111sYwlsjWBQhN7MCvf9F0l\nDNE+o+k3lYjnzwI/WBRt+wRm/6ov4/0vuG/yEDwfzo8fvaBk3Ov0oJ/915qphnw9BQBLHYgGbGfX\ndT0GeqLH4oyedYxb1fwk3TmQBuJ8q5rFMO7h2d5UbqRb1TRa7jmVmq3/LmjF/2+fmcfpz978WibZ\nBDfZ5wTx0taYzk2p9rxTc+plX1Z3v70E0xr3NWDmtbYGTUrPPAWiwxFgh2Yp7KMaRbFSGklYo1dL\nWGUgSDrOYB5EpzUpEpp9BHihK5xBlOlbrKxRFJTxCqvkNBCYjl8wHQp6p6ZAvFphnZmXQN9iZY1M\n5T8IbJWcBsxSPzdxoibopqb0GkYgbJgiwPHXripr5MKXl35SVqk0c7vmI6aKn899QTc0lddITa+C\n9wD6Eh3x9ytr5MIdv6qsUmkORdN+W/OGoJuaymuk5hScr3w8CPooX1HWyIV1PK+sUmmO4vu2JF0Q\n0U1N9pr51d9XVyvopesrN8Qndwde5B5ZcB/Br0ZKz+ZxVFEUBrUbuCDpvJq8d+U1jEzgGJxmYQ5o\nUpcMUcgHhbUoThHkNvDqAxKA03AiQTc0ldcIxF05Rcve7qNLXOwNVIsokAEHDZlzZ4An3fUZRTh3\n6qQv6Iam8hqBdLVaa8Bx4YrfnVUdTC2Hheu+BJTm5MH9WnNnq8V0Q1P1MsLzsnzvTU09p1FpGoie\nbqbpVjSLx3ixOA0SDJV0ahayaAJLFTgNsshKc3hsT1b1nthIFqMbODBGfzPH38iq3jf27njtH0gx\nPJyQbg/8AAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\left[\\begin{matrix}\\frac{4 h^{2} t \\left(a - b\\right)^{2}}{a + 2 \\sqrt{b^{2} + h^{2}} + \\left|{a - 2 b}\\right|}\\end{matrix}\\right]$$"
],
"text/plain": [
"⎡ 2 2 ⎤\n",
"⎢ 4⋅h ⋅t⋅(a - b) ⎥\n",
"⎢──────────────────────────────⎥\n",
"⎢ _________ ⎥\n",
"⎢ ╱ 2 2 ⎥\n",
"⎣a + 2⋅╲╱ b + h + │a - 2⋅b│⎦"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S1.compute_Jt()\n",
"S1.Jt"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"# Second example: Open section"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"stringers = {1:[(sympy.Integer(0),h),A],\n",
" 2:[(sympy.Integer(0),sympy.Integer(0)),A],\n",
" 3:[(a,sympy.Integer(0)),A],\n",
" 4:[(a,h),A]}\n",
"\n",
"panels = {(1,2):t,\n",
" (2,3):t,\n",
" (3,4):t}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define section and perform first calculations"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S2 = Section(stringers, panels)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Verify that the section is open"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAAgAAAAUBAMAAABCNWFYAAAAG1BMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAB4Gco9AAAACHRSTlMAdt3NMolEZgN4ymIAAAAJcEhZcwAADsQAAA7EAZUrDhsA\nAAAXSURBVAgdYxAyKVZjCGMAIpoQQipCagCy4Q1mVUJFwQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left [ \\right ]$$"
],
"text/plain": [
"[]"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.cycles"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Plot of **S2** section in original reference frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define a dictionary of coordinates used by **Networkx** to plot section as a Directed graph.\n",
"Note that arrows are actually just thicker stubs"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"start_pos={ii: [float(S2.g.node[ii]['ip'][i].subs(datav)) for i in range(2)] for ii in S2.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA5EAAAJtCAYAAACv9fRpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xuc1XWB//H3GURgbCSuIqhgqRCp1UMpNVhpM7m5plle\nQSHE25K3WC+lckkllXKxdd1sV4Fsy8pLa9jDHj9b0U0t3McilnlDXTdvg2iIMkDg+f1BzDLMAB/l\nNqzP5+MxDz3f8z3n+/nOHI+f13y/8z2VarVaDQAAABSo2dYDAAAAYPshIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgGS3HnnnTn00EOzyy67pLa2Nn369MnRRx+de+65Z4tsb/r06bnjjjua\nLZ88eXLatGmzRba5IXvuuWe+/OUvb7XtrW//N4fJkyfnvvvua7Z8zJgx+dCHPrRFtrmlLV26NKNG\njcouu+ySmpqanH/++dt6SNvEmDFjUlNT0+yrTZs2eeedd7b18ADeNyo+JxJ4v7vuuuty7rnn5tRT\nT83nP//57LTTTlmwYEFmz56dffbZJ9/85jc3+zb33HPPDBo0KLNmzWqy/KWXXsof//jHfPKTn9zs\n29yQRx99NDvvvHP23HPPrbK99e3/5lBTU5NLLrkkU6ZMabL8ueeey5tvvpmPfexjm32bW9o111yT\nr3/967n55puz9957Z9ddd83uu+++rYe11Y0ZMya/+MUvctddd2Xd6cvW/m8G4P1sh209AIBt7Vvf\n+la+8IUv5MYbb2xcNnjw4IwdO3arj6Vnz57p2bPnVt/u9hhW61qxYkV23HHH9d6/tQK5xMbGuq7H\nH388PXv2zEknnbRNtt+a7LjjjhkwYMC7esz2vL8ArZHTWYH3vddffz277LJL0brPP/98TjrppHTv\n3j3t27fPJz7xidx5553N1nv00Udz9NFHp2vXrqmtrU2/fv1y1VVXJVkdMy+88EJuueWWxtPx1pxK\nOmnSpNTUNH1rXrJkScaPH59evXqlffv26devX/7+7/++yTpz5sxJTU1N7rrrrnzlK19Jt27d0q1b\nt4waNSpvvvnmRverT58+TU5nnTFjRmpqavKb3/wmI0eOTMeOHdOrV6+cc845WbFixUafb/r06enf\nv39qa2vTuXPnDBgwID/72c82uv8LFizIySefnA996EOpra3Nhz/84Zx11ln505/+1OT5R48end13\n3z0PP/xwPv3pT2ennXbKBRdckJqamlQqlVx++eWNpzmuOSI5evToJiH53//936mpqcmNN96YiRMn\npmfPnunUqVOOPPLIvPjii02219DQkDPPPDNdu3ZNXV1djjnmmDz00EOpqanZ6NHUNT/T3//+9xk6\ndGjq6upy3HHHNd5/++235+CDD85OO+2UTp065dhjj83//M//NN6/ZhsvvPBC4z7df//9SZLXXnst\nZ5xxRnbbbbe0b98+H/nIR/K9732vyfZnzpyZmpqaPPDAAzn22GPTqVOnHHTQQY33z5kzJ4cddlh2\n3nnnfOADH8jQoUPz+9//vslzDB48OIMGDcq9996bAw44IDvttFP222+/d/3aL93nTXHJJZekpqYm\nf/jDH3L44Yenrq6uMb7vueeeDB8+PLvuumvjPkyfPr3ZqbC77757xowZk5kzZ6Zv376pra3NoYce\nmueeey5vv/12TjvttHTp0iW77rprLrzwwmZHRRcuXJjTTz89vXr1Srt27dK/f//cdNNNm2X/AFoD\nRyKB971PfvKTmTFjRvbcc898/vOfz957793iemtOM+3Ro0emT5+erl275tZbb80xxxyTn/3sZzni\niCOSJL/97W/zmc98JnvvvXemT5+eXr165emnn878+fOTJHfccUeGDx+ej3/845k8eXKq1Wq6deuW\nJKlUKqlUKo3brFarGT58eObNm5dvfOMb2XfffTN79uycf/75ee2113L55Zc3GeO5556bI444Ij/8\n4Q/z5JNP5u/+7u+yww475Oabb97g92Dtba59++STT84JJ5yQO+64Iw899FAmTpyYzp07Z+LEiet9\nrh/84AeZMGFCJk2alIEDB6ahoSHz58/P66+/nmT1358OGzasxf1/6aWX0qtXr1x77bXp3Llznnvu\nuVx55ZUZMWJEfv3rXzcZ3+LFi3PCCSdkwoQJmTp1ajp06JATTzwxBx10UMaMGZPTTz89SbLbbru1\n+L1d45vf/GYOOeSQ3Hzzzamvr8/555+fUaNG5Ve/+lXjOuPGjcttt92WyZMn54ADDsi9996bk046\nqcXnW9/39qijjsrYsWNz0UUXNf6i4J/+6Z9y1llnZezYsZk4cWKWLFmSiRMnZvDgwZk/f3522mmn\nPPzww5k4cWLmz5+fO++8M9VqNf3798+SJUvy6U9/OsuXL8+UKVPSp0+f3HPPPTnzzDOzYsWK/O3f\n/m2TcYwcOTInnHBCbrvttqxcuTJJMnv27Bx11FH5m7/5m/zgBz9o/H4MGjQojz32WHr16tW4DwsW\nLMi5556br33ta+nSpUumTZuWY489Nk888UTj35pu7LVfus8bs2rVqia31/zyYO3v9+c///mMHTs2\nX//61xu/388++2w++9nP5itf+Upqa2szd+7cXHrppVm0aFGz059/9atf5Zlnnsm0adOybNmynH32\n2TnmmGOy2267pX///vnxj3+c++67L1dccUX23nvvnHrqqUmSxYsX55BDDsmqVaty+eWXp3fv3rn7\n7rszbty4/PnPf258XQJs16oA73NPPfVU9WMf+1i1pqamWqlUql27dq2ecMIJ1V/+8pdN1vvyl79c\n7d69e/WNN95osvxzn/tc9ROf+ETj7UGDBlX32GOP6rJly9a7zT59+lRHjRrVbPmkSZOqNTU1jbfv\nuuuuaqVSqc6aNavJeqeeemq1ffv21UWLFlWr1Wr1vvvuq1YqleqYMWOarDd+/Phqhw4dNvIdWD2e\ntR87Y8aMaqVSqU6ePLnJekcccUS1b9++G3yu8ePHVw844ICNbq+l/V/XypUrq//xH/9Rrampqc6b\nN69x+ejRo6s1NTXVu+66q9ljKpVK9dJLL222fPTo0dU999yz8fbzzz9frVQq1b/+679ust60adOq\nNTU11ZdffrlarVarTz75ZLWmpqY6bdq0JuudffbZ1ZqamurMmTM3uA9rfqbf+c53mix/6623qh07\ndqyeeuqpTZY///zz1R133LE6ffr0xmUjR45sMvZqtVqdMmVKtUOHDtUFCxY0WT5u3Lhqt27dqqtW\nrapWq//7s/zqV7/abGx77bVX9XOf+1yTZUuWLKl27dq1et555zUuGzx4cHXHHXdssq36+vpqmzZt\nqlOnTm1ctrHX/rvZ55aMHj26WqlUmnzV1NQ0+Xlfcskl1ZqamuoNN9ywweeqVle/viZPnlzt1q1b\nk+W77bZbtVu3btW33367cdm3v/3taqVSqZ511llN1t1///2rhx9+eOPtyy67rFpbW1t97rnnmqw3\nZsyYao8eParvvPPORscF0No5nRV439t7773zX//1X5kzZ04uueSSxlNUhwwZkiuuuKJxvTWnwtXV\n1WXVqlVZtWpVVq5cmcMPPzyPPvpo3nrrrTQ0NOTBBx/MyJEj065du00e2wMPPJA2bdrkhBNOaLJ8\n5MiRWbFiRR566KEmy4cPH97k9n777Zfly5envr7+XW+7Uqm0+HwvvPDCBh83YMCAzJs3L2effXbu\nvffeNDQ0FG/zz3/+c6688sp85CMfSW1tbdq2bZtBgwYlSZ588skm67Zt2zYjRowofu71GTZsWJPb\n++23X5I07udvfvObJMkXv/jFJut98YtfbHYa44YcddRRTW4/9NBDWbJkSU488cTG19OqVavSq1ev\n9OvXr/GU1fW555578qlPfSq9e/du8vjDDz88r732Wh5//PHGdSuVSrPtP/PMM1mwYEGz7bdv3z4H\nH3xws+3vvffeTa5u261bt3Tv3r3x+1Ty2t/UfU6SXXbZJf/5n/+ZRx55JI888kjmzp2bs846q9l6\n6+5vkrz88ssZN25cevfunbZt26Zt27aZNGlSFi1a1HikfI1Pf/rTqa2tbbzdr1+/VCqVHH744U3W\n69evX5NTce+5554ccsgh2X333Zv9XOrr65u9jgG2R05nBcjqSfbAgQMzcODAJMkrr7ySIUOGZMqU\nKRk/fnw6duyY+vr6zJo1KzNnzmz2+JqamixatCht27bNO++803ga4KZ6/fXX07lz5+ywQ9O36x49\neqRarTab+Hbu3LnJ7TWT+WXLlr2n7bf0fMuXL9/gY04++eQsX748//Iv/5IbbrghO+ywQ4YPH55v\nf/vb6d279wYfe9FFF+X666/PxIkTc/DBB6euri5//OMfc/TRRzfbh27duhWdTroxLe1jtVpt3N7L\nL7+cJOnevXuT9Ur/jnaNXXfdtcnt+vr6VKvVfPazn222bqVSaTauddXX12fBggVp27Zti49ftGjR\nRrefJGPHjm328S6VSiV77LFHk2Utjaddu3aN36c33nhjo6/9Td3nZPUvDz7xiU9sdL0ePXo0uf3O\nO+9kxIgRWbRoUSZNmpS+ffumffv2+elPf5qrrrqq2eurU6dOTW6vuTBPS8vXfmx9fX3mzp1b/HMB\n2B6JSIAW9OjRI6eeemrOPffcPP300znwwAPTpUuX/NVf/VUuuuiiFo9A9ezZMytXrkxNTU2zC7O8\nV507d87rr7+elStXNgnJV155pfH+1mjcuHEZN25cFi9enF/+8pc5//zzc/zxxzc7crquW2+9Naec\nckouvvjixmVLlixpcd3NEZDrs/Zzr4mv+vr6JhH86quvvufnTJIuXbokSWbNmpX+/fs3W7+urm6D\nz9elS5fssssuue6661p8Pfbt27do+1OnTs1hhx3W7PHv9mqmnTp12uhrf1P3eVM89dRTmTdvXm69\n9dZ86Utfalx+2223bdbtdOnSJXvssUeuvfbaop8LwPZIRALve6+88kqzoxZJ8oc//CHJ/x7RGDp0\naB5++OH0799/vafrtW3bNgMHDswtt9ySyy67bL3rtWvXrug0z0MPPTTXXHNNfvKTnzQ5pfWWW25J\nu3btcvDBBzcu25JR9V517NgxX/rSl/Lwww83+QiV9e3/0qVLmx11vemmm97Vvu24447v6hTajVnz\n+YM/+clPMmHChMblP/7xjzfpe37IIYekrq4uTz/9dEaOHPmuHz906ND8wz/8Q3bfffd07dr1XT++\nb9++6dOnT37/+9/nggsueNePX1eHDh02+trf1H3eFEuXLk2SJq+vFStW5F//9V8363aGDh2aG2+8\nMb179261v+QB2FQiEnjf23fffXPYYYdl+PDh2XPPPfPmm29m9uzZ+e53v5vjjjuu8eqeU6ZMyac+\n9akMGjQo48ePT58+ffLGG2/kd7/7XZ577rn88z//c5Jk2rRpGTx4cA466KB89atfzW677ZZnn302\n8+bNy3XXXZck6d+/fx544IHMnj07PXr0SNeuXVs81XPYsGEZOHBgzjjjjNTX1+ejH/1oZs+enZtu\nuilf+9rXmkxS383f521Jp59+eurq6nLwwQene/fuefLJJ/P9738/Q4YMaVxnffs/dOjQzJw5M/vu\nu2/22muv3H777Rs9ermu/v37Z/bs2RkyZEg6deqUnj17NjuVc2PW/l727ds3J554Yi699NKsWrUq\nBxxwQH71q1/l5z//eZI0+0iWUnV1dbnmmmsyfvz41NfXZ9iwYenYsWNefPHFzJkzJ5/5zGdy/PHH\nr/fx5513Xn784x9n4MCBOe+889K3b9+8/fbbeeKJJ/LAAw+0+PEb67r++utz1FFHZfny5Tn22GPT\ntWvXvPrqq3nwwQfTu3fvnHvuue9qnzb22t/Ufd4UH/3oR7PbbrvloosuSrL6ly7XXntti6edrk/J\nf2MTJkzIT3/608afyz777JMlS5bkiSeeyIMPPpjbb7/9Pe8DQGshIoH3vSuvvDJ33313Jk6cmFdf\nfTVt2rTJPvvsk6uvvjrnnHNO43q77757HnnkkUyaNClf//rXs3DhwnTp0iX77rtvTjnllMb1Djzw\nwPz617/OZZddlrPPPjvLly9P7969M2bMmMZ1pk6dmtNOOy3HHXdcGhoacsoppzR+jtzaR7cqlUru\nvvvufO1rX8vVV1+dRYsWpU+fPrn22mtz9tlnN9mPTTkqtr6Pv1jfuhsycODA3HzzzbnllluyePHi\n9OzZMyeffHImTZrUuM769v873/lOktWf9ZckI0aMyI9+9KPGo4El47j++utz9tln58gjj8zy5csz\nceLEXHbZZS0+Zn3Pse7y733ve9l5551zzTXXZMWKFfnsZz+bf/zHf8yIESPSsWPHDX4/NrSd0047\nLXvssUeuueaa/PCHP8zKlSvTq1evDBo0KB//+Mc3+Bw777xzHnzwwUyZMiVXX311XnzxxXzwgx9M\n3759c8wxx2x0TMnqX1Lcf//9ueKKKzJu3Lg0NDSkR48eOeigg5rFXEv7sO7rpuS1/272uSXv5mNV\n1tauXbv827/9W77yla9k1KhR6dKlS8aOHZtdd901Z5xxxgb3a2PbXnt5x44d89BDD2Xy5MmZOnVq\nXnrppXzwgx9Mv379mpxGC7A9q1Rby6+uAWA7Mm3atFx00UV5/vnnG49WA8D7gSORALARs2fPzu9+\n97t8/OMfT01NTe6///5861vfanK6MwC8XzgSCQAbcf/99+fCCy/Mk08+mbfffju9evXK8ccfn0mT\nJr3rq5gCwPZORAIAAFDsvV1SDgAAgPclEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAECxHbb1AODdqq+vz6wZM/LU/Pl5a/HifKBjx+yz\n//45ZcyYdOvWbVsPDwBgszP/oTWpVKvV6rYeBJSYO3dupk+dmtm/+EW+kGTAsmWpS7IkyW87dMgd\n1WpGDBuWcy6+OAMGDNjGowUA2HTmP7RGIpLtwo033JCJEybkwoaGnFKtplML67yRZEalkqs7dMjk\nadNy2plnbu1hAgBsNuY/tFYiklbvxhtuyFUTJuSepUuzV8H6zyQZUlubC72RAgDbKfMfWjMRSas2\nd+7cHDl4cB5Y5w30+iQzkjyW5MQkN63zuGeSDKqtzV1z5uTAAw/cOoMFANgM1jf/WePpJPsn+VKS\nWWstN/9ha3F1Vlq16VOn5sKGhmZvoL2SXJpk7Hoet1eSCxoaMn3q1C06PgCAzW198581xif5ZAvL\nzX/YWhyJpNWqr69P39698+yyZS3+DUCyOiRfTPMjkUnyepIPt2+fp154wVXLAIDtwsbmPz9KcmeS\n/ll95HHWOveb/7A1OBJJqzVrxowcnaw3IDemc5KjK5XMmjFj8w0KAGAL2tD8580kE5N8O8n6jgKZ\n/7A1iEharafmz88nly3bpOcY0NCQpx57bDONCABgy9rQ/OeyJOOS9NzIc5j/sKXtsK0HAOvz1uLF\nqdvE56hLsuSNNzbHcAAAtrj1zX/mJfl/f/nnxpj/sKWJSFqtD3TsmCWb+BxLktR1eq8nxAIAbF3r\nm//MSfLfSfbI6lNZ30qyKsnjSR5ZZ13zH7Y0p7PSau2z//75bfv2Ld63Ksmyv/xzZZLlf/n3dc3t\n0CH77LffFhsjAMDmtL75z+lJFmT1kchHk5yR5Igkv2zhOcx/2NJcnZVWa0NXJ5v8l6/KWssmZvXf\nCqzh6mQAwPam5Or0yep50IK4OivbhiORtFrdu3fPiGHDMrNSaXbfxCTvZPXRxzVfl62zzsxKJUcM\nH+4NFADYbmxo/rO2iWkekIn5D1uHI5G0anPnzs2RgwfngaVL1/uBuy15Jsmg2trcNWdODjzwwC01\nPACAzc78h9bOkUhatQEDBmTytGkZUlubZwof80ySIbW1mTxtmjdQAGC7Y/5Da9dm0qRJk7b1IGBD\nDhgwIB06d87J//7vabNyZfol6dDCeq8nuaFSyam1tblk2rScduaZW3mkAACbh/kPrZnTWdluPPLI\nI5k+dWp+fvfdObpSyYCGhtWfg5TVVyG7o1rNEcOH55yLL/YbOADg/4S15z9Dli3LoYn5D9uciGS7\ns3DhwsyaMSNPPfZY/vX738+Jo0Zln/32y8mjR/sjcgDg/6SFCxdml+7d0y6rP+h9ZZLLr77a/Idt\nQkSyXatUKvESBgDeDyrrXLHVHIhtxYV1AAAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAA\nKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYi\nAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAA\nKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYi\nAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAA\nKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQAAKCYiAQBgO1Ct\nVlOtVhv/HbYVEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAx\nEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkA\nAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEQkAAEAxEcl26/HHH9/WQwAAgPcdEcl2\na968edt6CAAA8L4jIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACi2w7YeALwXlUqlyb9Xq9VtOBoAAHj/\ncCQSAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiIS\nAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACA\nYiISAAAicDtOAAAJXUlEQVSAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiIS\nAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACA\nYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiIS\nAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiISAACAYiKS7U59fX0qSTok\n+cBf/jnt6quzcOHCbTswAIAtpL6+PtOuvjqnjRyZDyQ5beRI8x+2mUq1Wq1u60FAiblz52b61KmZ\n/YtfZNiyZfmrJHVJliT5bYcOuaNazYhhw3LOxRdnwIAB23i0AACbbu35zxeSDFi2zPyHbU5Esl24\n8YYbMnHChFzY0JBTqtV0amGdN5LMqFRydYcOmTxtWk4788ytPUwAgM3G/IfWSkTS6t14ww25asKE\n3LN0afYqWP+ZJENqa3OhN1IAYDtl/kNrJiJp1ebOnZsjBw/OA2u9ga5IclaS/5fVv337cJIrkwxd\n63HPJBlUW5u75szJgQceuFXHDACwKVqa/yTJqKye/zQk6ZHk75KMXet+8x+2FhfWoVWbPnVqLmxo\naPIGujLJHkkeSLI4yTeSHJvkhbXW2SvJBQ0NmT516lYbKwDA5tDS/CdJLk7yXJI/Jfm3JJck+a+1\n7jf/YWtxJJJWq76+Pn17986zy5a1+DcAa/tYkklJjl5r2etJPty+fZ564YV069ZtSw0TAGCzKZ3/\nPJnkM0muS/LFtZab/7A1OBJJqzVrxowcnWw0IF9N8nSSj66zvHOSoyuVzJoxYwuMDgDeu0ql4stX\ni189dtklQzcQkH+bZKckH0nSM8nwde43/2FrEJG0Wk/Nn59PLlu2wXVWJhmZZHSSfVq4f0BDQy65\n4IJt/j8EX63z68Mf/vDmf+ECwCZon+TQDdx/fZK3kvxHki8kadfCOgMaGvLUY49tgdHBajts6wHA\n+ry1eHHqNnB/NasDsl2S76xnnbp4kbN+zz77bCqVyrYeBgA0apNscP6TJJUkhyT5fpIbkoxf5/66\nJEveeGPzDw7+wvyaVusDHTtmyQbuH5vktSR3Z/UbbkuWJDlx1Kh8d9aszT08AHjP/AKL9VmVbHD+\ns7aVSRa0sHxJkrpOG/uDIHjvnM5Kq7XP/vvnt+3bt3jfGUmeyOork+24geeY26FD9tlvvy0wOgB4\n76rVqi9fLX5NueqqFuc/C5PcmuTtJO8kuSfJj5Ic1sLry/yHLc3VWWm11nd1sheS9MnqvxlYcwSy\nkuS7SU5Yaz1XJwMAtjfrm/+8ltVXYZ2f1RHZO8k5Sb68zuPNf9gaHImk1erevXtGDBuWmeuc8rNH\nVr95Ls3q0zWWJHkzTQMySWZWKjli+HBvoADAdmN985+uSe7L6kj8U5JH0zwgE/Mftg5HImnV5s6d\nmyMHD84DS5c2+8DdDXkmyaDa2tw1Z04OPPDALTU8AIDNzvyH1s6RSFq1AQMGZPK0aRlSW5tnCh/z\nTJIhtbWZPG2aN1AAYLtj/kNr12bSpEmTtvUgYEMOGDAgHTp3zsn//u9ps3Jl+iXp0MJ6rye5oVLJ\nqbW1uWTatJx25plbeaQAAJuH+Q+tmdNZ2W488sgjmT51an5+9905ulLJgIaG1Z+DlNVXIbujWs0R\nw4fnnIsv9hs4AOD/BPMfWiMRyXZn4cKFmTVjRp567LEseeON1HXqlH322y8njx7tj8gBgP+TzH9o\nTUQkAAAAxVxYBwAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIi\nEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAAgGIiEgAA\ngGIiEgAAgGIiEgAAgGL/HwG8ORdZUf/9AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21a663da90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S2.g,with_labels=True, arrows= True, pos=start_pos)\n",
"plt.arrow(0,0,20,0)\n",
"plt.arrow(0,0,0,20)\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in starting reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **Inertial properties** wrt Center of Gravity in with original rotation"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMQAAAAcBAMAAADM5Q0aAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMkS7zRCZdiKJ71Rm\nq90icBAQAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC3klEQVRIDaWUTWgTURDH/5tmm81HYxAPXiTr\nwYMHaUEUL5Jc/ACRLtaTIA2oiHhoToIFMSB4sIf2IOk1oqAnCQoieEguIgpWwYMHCerB+nExrV8t\nVeO89/bz7ZAIeZB9M//5zezuvMkCsVXf68S0iDAQiNCMk66NlRk5kAYCAepZmz1D7fmasRZVNG8g\nEOarwjEmwhKQt63VqKJ5A4Ewv0s4yVjnsz/CEGMPBIKcdJvss4HvWnn5djE5EAYCAYoPgOU+8haS\np+7KWD1EBKZR9u04YJ57WvDDrqG0C0C6opRJsR0Ul1xFXGMr2fUkBkg2zU9e2NuVNg9kmlLKfXVo\n3xD2TmyXknZZ8k+IAZ4B1zUeSsu3URSlgbmZGpAQVYwjj/YIRVvWA2+UOWA/0FKFgjSljU6Ie4lV\nvWxT096Rlen1urTpK5XyRpkD/gDjTS1FaakGTstAwmm1aX7PP9mncb67I/ub7Kv1Wf1hBWH+pFtU\nfVYarkad2S39YygSMX0YnSjne6Zt/KJO3oEcC192DWsdKC5EVVczVnBUBmzMV6idBfeOUVh4CVj0\npCfaOBWP0eRTLHYLpdGnYlmkGJ3O2wmIpt3mKpC2rdP5Bsw4+MgBfRplbai3SNApl4HPsFa4CqTZ\nwC3gJkweoKNtNbVUpdFbyEa16evXgLmKdEPjXDdH+xeY68h2WYBO9IWjRZRGn+1XFLDoAejPm+si\ns/BYA5U7R9skzA2MlB9yAI2+Gs1QUGk0UbMkXqPfyBrGythkL0houiw372I1yCrVcAhLL1kg3zRv\nQEuSGnINjDuY6h1AtvS3MtJGelFVzdMHMlhm6buD+71lnLy49bUt9SgAc/FSAZwG+ndnVEpQT1ls\nO8IQB3BasopR9eLhbGHzaojiAE6bdmA0Qnm+aVZ9kzc4gNPwnPLfcDXEkPZdHMBpeE9ljvctNWww\nJ5qXrQxbpl/+FRm81w8ZNnZm2AL/lf8PNIyxlBKATq4AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left ( A h^{2}, \\quad A a^{2}, \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 2 ⎞\n",
"⎝A⋅h , A⋅a , 0, 0⎠"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.Ixx0, S2.Iyy0, S2.Ixy0, S2.α0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Plot of **S2** section in inertial reference Frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Section is plotted wrt **center of gravity** and rotated (if necessary) so that *x* and *y* are principal axes.\n",
"**Center of Gravity** and **Shear Center** are drawn"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"positions={ii: [float(S2.g.node[ii]['pos'][i].subs(datav)) for i in range(2)] for ii in S2.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA4cAAAJtCAYAAACFRQXGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XuYVXWh//HPnhEZsBEQBlBUMC8QXrKTqJicsAiVsLx0\nLAtSEk3TEi/H1FDALhwVTTp5PKlPId5O5a0QzNNN8h725CVTuaTRz9sgkmIwGOP6/YHMYZgZmJHL\nDM7r9Tzz6Ky99trftfdsXe/5rlm7VBRFEQAAANq1stYeAAAAAK1PHAIAACAOAQAAEIcAAABEHAIA\nABBxCAAAQMQhQD133nlnPvrRj6ZXr17p3Llz+vXrl6OOOir33HPPJnm8qVOn5o477miwfNKkSSkv\nL98kj7kuu+yyS770pS9t9sddl7Kyslx88cUtus8hhxySj33sY5toRMlf//rXlJWVZfr06ZvsMVZb\ntmxZRo8enV69eqWsrCxnnXXWJn/MtmjMmDEpKytr8FVeXp633367tYcH8J6wVWsPAKCt+N73vpdx\n48Zl7NixOffcc7PNNttkwYIFmTlzZn7729/m0EMP3eiPeeWVV2bIkCE56qij6i0/6aSTcvjhh2/0\nx1ufO++8M9tuu+1mf9x1efjhh7Pjjju26D5XX331JhrN5nfVVVflxz/+cX70ox9l9913z/bbb9/a\nQ2o1PXv2zIwZM7L2RzSXlfldN8DGIA4B3nH55Zfn6KOPzjXXXFO3bOjQoTnxxBM3+1h22GGH7LDD\nDpv9cT/4wQ9u9sdsyltvvZWtt946+++/f4vvO2DAgE0woo1j9X4115///OfssMMO+cIXvtAqj9+W\nbL311hk0aFCL7rMl7y/A5uZXbQDveO2119KrV69mrfv888/nC1/4Qnr27JmKiop86EMfyp133tlg\nvccffzxHHXVUevTokc6dO2fAgAG55JJLkqw6hXPhwoW58cYb606RW31K58SJExvMhixdujSnn356\n+vTpk4qKigwYMCBXXnllvXVmz56dsrKyzJgxI1/96ldTVVWVqqqqjB49Om+88cZ696tfv371Tiud\nNm1aysrK8sgjj2TUqFHp0qVL+vTpkzPOOCNvvfXWerdXVlaW8ePH5zvf+U522mmndO7cOR/96Efz\n+OOP11tv6NChGTJkSO666678y7/8Szp16lQ3+9fYaaXrel5Xb2/N00pXPy+33357xowZk+222y5d\nunTJqFGj8tprr9Xb9lVXXZWDDjoo3bt3T7du3TJ48ODMmjVrvfvamNWv41NPPZXDDjsslZWV+exn\nP1t3++23357Bgwdnm222Sbdu3XLsscfmb3/7W73nb/r06Vm4cGHdKZS/+93vkiSvvvpqTjnllOy4\n446pqKjIBz7wgVx77bX1Hv/6669PWVlZ7rvvvhx77LHp1q1bDjzwwHrPy7Bhw7Ltttvmfe97Xw47\n7LA89dRT9bax+rX59a9/nQ9/+MPZZpttsvfee7f45725+7whxo8fn7Kysjz99NMZPnx4Kisr66L6\nnnvuyYgRI7L99tvX7cPUqVMbnJK60047ZcyYMbn++uvTv3//up/Z5557Lv/4xz9y8sknp3v37tl+\n++3z9a9/vcEs5qJFi/LlL385ffr0SceOHTNw4MD88Ic/3Cj7B7CpmTkEeMf++++fadOmZZdddsmn\nP/3p7L777o2u9//+3//L/vvvn969e2fq1Knp0aNHfvzjH+eYY47Jz372s4wcOTJJ8vvf/z6HHHJI\ndt9990ydOjV9+vTJvHnz8sQTTyRJ7rjjjowYMSL77rtvJk2alKIoUlVVlSQplUoplUp1j1kURUaM\nGJHHHnss3/zmN7PXXntl5syZOeuss/Lqq6/mW9/6Vr0xjhs3LiNHjswtt9ySZ599Nv/+7/+erbba\nKj/60Y/W+Rys+Zhrfv/FL34xxx13XO6444489NBDmTBhQrbbbrtMmDBhvc/r9OnT07dv31x11VVZ\nsWJFLrzwwgwbNizz5s1L165d6x5n7ty5OeOMM3LhhRfm/e9/f7bbbrtGt7e+57Wx/VjtzDPPzLBh\nw/I///M/mTdvXs4///y89NJL+fWvf123zvPPP58xY8Zk1113TW1tbWbMmJEjjjgid999d4YPH77e\n/V3T6nEceeSROfHEE3PeeefVRf9///d/5ytf+UpOPPHETJgwIUuXLs2ECRMydOjQPPHEE9lmm23y\n8MMPZ8KECXniiSdy5513piiKDBw4MEuXLs1HPvKRrFixIhdffHH69euXe+65J6eeemreeuutnHba\nafXGMWrUqBx33HG57bbbsnLlyiTJzJkzc+SRR+aII47ITTfdlCT5j//4jwwZMiRPPvlk+vTpU7cP\nCxYsyLhx43LBBReke/fumTJlSo499tg888wzef/739/s16U5+7w+tbW19b4vKyure55X//PTn/50\nTjzxxHzjG9+oe77/8pe/5OMf/3i++tWvpnPnzpkzZ04uvPDCLF68uMEvH37zm99k/vz5mTJlSmpq\navK1r30txxxzTHbccccMHDgwP/nJT3Lvvffm29/+dnbfffeMHTs2SfL666/noIMOSm1tbb71rW+l\nb9++mTVrVk466aT885//zJe//OX17h9AqyoAKIqiKObOnVt88IMfLMrKyopSqVT06NGjOO6444r/\n/d//rbfel770paJnz57FkiVL6i3/xCc+UXzoQx+q+37IkCHFzjvvXNTU1DT5mP369StGjx7dYPnE\niROLsrKyuu9nzJhRlEqlYvr06fXWGzt2bFFRUVEsXry4KIqiuPfee4tSqVSMGTOm3nqnn3560alT\np/U8A6vGs+Z9p02bVpRKpWLSpEn11hs5cmTRv3//9W6vVCoVVVVVxfLly+uWPf/880WHDh2Kiy66\nqG7Z0KFDi/Ly8uKJJ55odBtrPn5zntehQ4cWhxxySN33q5+XESNG1FvvpptuKsrKyorf/OY3jW7n\n7bffLlauXFkMHz68OPLII+vtQ6lUKq6//vp17P3/vY7/+Z//WW/5m2++WXTp0qUYO3ZsveXPP/98\nsfXWWxdTp06tWzZq1Khil112qbfexRdfXHTq1KlYsGBBveUnnXRSUVVVVdTW1hZF8X+v39lnn91g\nbLvttlvxiU98ot6ypUuXFj169CjOPPPMumVDhw4ttt5663qPVV1dXZSXlxeTJ0+uW7a+16Ul+9yY\nE044oSiVSvW+ysrKigsvvLBunfHjxxdlZWXF1Vdfvc5tFUVRrFy5spg0aVJRVVVVb/mOO+5YVFVV\nFf/4xz/qll1xxRVFqVQqvvKVr9Rbd5999imGDx9e9/1FF11UdO7cuXjuuefqrTdmzJiid+/exdtv\nv73ecQG0JqeVArxj9913zx//+MfMnj0748ePrztV9NBDD823v/3tuvVWn55WWVmZ2tra1NbWZuXK\nlRk+fHgef/zxvPnmm1m+fHkefPDBjBo1Kh07dtzgsd13330pLy/PcccdV2/5qFGj8tZbb+Whhx6q\nt3zEiBH1vt97772zYsWKVFdXt/ixS6VSo9tbuHBhs+4/YsSIVFRU1H3ft2/fHHjggQ3G3K9fv+y9\n997r3NaGPq//9m//1uD7UqlUbyx/+MMfMnLkyPTu3TtbbbVVOnTokF/+8pd59tlnW/x4qx155JH1\nvn/ooYeydOnSfP7zn6/7GaqtrU2fPn0yYMCAulNHm3LPPffkgAMOSN++fevdf/jw4Xn11Vfz5z//\nuW7dUqnU4PHnz5+fBQsWNHj8ioqKDB48uMHj77777nUzhElSVVWVnj171v0MNOd12dB9TpJevXrl\nD3/4Qx599NE8+uijmTNnTr7yla80WG/t/U2Sl156KSeddFL69u2bDh06pEOHDpk4cWIWL17c4NTi\nj3zkI+ncuXPd9wMGDEipVGowczxgwIB6p8Tec889Oeigg7LTTjs1eF2qq6s36GcIYHNwWinAGkql\nUg4++OAcfPDBSZKXX345hx56aC6++OKcfvrp6dKlS6qrqzN9+vRcf/31De5fVlaWxYsXp0OHDnn7\n7bfrTs3bUK+99lq22267bLVV/f9s9+7dO0VRNDi4XfuUzNUH7DU1Ne/q8Rvb3ooVK5p138b+jrNX\nr171AiZJs67CuWTJkg16XtceS4cOHdKtW7e88MILSVadMjxs2LDsueee+f73v5+dd945W221VcaP\nH59nnnnmXT1m0nDfqqurUxRFPv7xjzdYt1QqNXlK7Zr3X7BgQTp06NDo/RcvXrzex0+SE088scFH\nl5RKpey88871ljU2no4dO9b9PDXnddnQfU5WvV4f+tCH1rte7969633/9ttv55Of/GQWL16ciRMn\npn///qmoqMitt96aSy65pMH7olu3bvW+X31Bm8aWr3nf6urqzJkzp9mvC0BbIw4B1qF3794ZO3Zs\nxo0bl3nz5mW//fZL9+7d86//+q8577zzGlyMIll1pdGVK1emrKysLjo21HbbbZfXXnstK1eurBeI\nL7/8ct3tbdUrr7zS6LK1Q6KpvxNcU7du3TboeV17LP/85z+zZMmSurHcfffdeeONN/LTn/60XlAt\nW7bsXT3eamvvW/fu3ZOs+nvMgQMHNli/srJyndvr3r17evXqle9973uN/gz279+/WY8/efLkDBs2\nrMH9W3p1z+a8Lhu6zxti7ty5eeyxx/LjH/+43uzxbbfdtlEfp3v37tl5553z3e9+t1mvC0BbIw4B\n3vHyyy83mHFIkqeffjrJ/81GHHbYYXn44YczcODAJk+h69ChQw4++ODceOONueiii5pcr2PHjlm+\nfPl6x/bRj340l112WX7605/WO7X0xhtvTMeOHTN48OC6Zc2JrM1p1qxZWb58eTp16pRk1QVfHn74\n4VxwwQUt3lanTp2a9bw25Sc/+UlOOOGEet8XRZGDDjooSepeizUDfO7cuXnggQey0047tXi8TTno\noINSWVmZefPmZdSoUS2+/2GHHZbvf//72WmnndKjR48W379///7p169fnnrqqZx77rktvv/amvO6\nbOg+b4jVcb/m6/rWW2/l5ptv3qiPc9hhh+Waa65J37592/QvbACaIg4B3rHXXntl2LBhGTFiRHbZ\nZZe88cYbmTlzZn7wgx/ks5/9bN0HsV988cU54IADMmTIkJx++unp169flixZkj/96U957rnnct11\n1yVJpkyZkqFDh+bAAw/M2WefnR133DF/+ctf8thjj+V73/tekmTgwIG57777MnPmzPTu3Ts9evRI\n3759G4zt8MMPz8EHH5xTTjkl1dXV2XPPPTNz5sz88Ic/zAUXXFDvQLSxGYvW1KlTpwwfPjznnHNO\nampqMmHChHTt2jXjxo17V9trzvPalKeeeipf+tKX8rnPfS7PPvtsxo8fn0MOOSRDhw5NkgwbNizl\n5eUZPXp0zj777Lz44ouZOHFi+vbt2+AjDzZEZWVlLrvsspx++umprq7O4Ycfni5duuSFF17I7Nmz\nc8ghh+Rzn/tck/c/88wz85Of/CQHH3xwzjzzzPTv3z//+Mc/8swzz+S+++5r9GMm1nbVVVflyCOP\nzIoVK3LsscemR48eeeWVV/Lggw+mb9++LX591ve6bOg+b4g999wzO+64Y84777wkq36B8t3vfrfR\n0z+b0pz31TnnnJNbb7217nXZY489snTp0jzzzDN58MEHc/vtt7/rfQDYHMQhwDu+853vZNasWZkw\nYUJeeeWVlJeXZ4899sill16aM844o269nXbaKY8++mgmTpyYb3zjG1m0aFG6d++evfbaK8cff3zd\nevvtt18eeOCBXHTRRfna176WFStWpG/fvhkzZkzdOpMnT87JJ5+cz372s1m+fHmOP/74us9EW3MG\nsFQqZdasWbngggty6aWXZvHixenXr1+++93v5mtf+1q9/diQmcO1P0Jjfes2xxe/+MVss802Of30\n07N48eLsv//++elPf1r3MRbr297aY2rO89rY9kqlUqZOnZqf//zn+dznPpfa2tp86lOfytSpU+vW\nGThwYG6++eZcdNFF+fSnP51dd901l1xySe6+++7Mnj37Xe1/U+udfPLJ2XnnnXPZZZfllltuycqV\nK9OnT58MGTIk++677zq3se222+bBBx/MxRdfnEsvvTQvvPBCunbtmv79++eYY45p1rgOP/zw/O53\nv8u3v/3tnHTSSVm+fHl69+6dAw88sEGkNbYP7+Z1ack+N6Y5z3lj63Ts2DE///nP89WvfjWjR49O\n9+7dc+KJJ2b77bfPKaecss79Wt9jr7m8S5cueeihhzJp0qRMnjw5L774Yrp27ZoBAwY0uBgSQFtU\nKtrar5gBeM8oKyvL+PHjG3yO3OY2e/bsfOxjH8svf/nLfOxjH2vVsQBAW+WjLABoF/wuFADWTRwC\nsMm05DTVTa2tjAMA2iqnlQIAAGDmEAAAAHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAAR\nhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABA\nxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAA\nEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAA\nAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEA\nAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEI\nAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQc\nAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAAR\nhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABAxCEAAAARhwAAAEQcAgAAEHEIAABA\nxCEAAABJtmrtAdC2VFdXZ/q0aZn7xBN58/XX874uXbLHPvvk+DFjUlVV1drDAwCgjXIcueUrFUVR\ntPYgaH1z5szJ1MmTM/Puu3N0kkE1NalMsjTJ7zt1yh1FkU8efnjOOP/8DBo0qJVHCwBAW+E48r1D\nHJJrrr46E845J19fvjzHF0W6NbLOkiTTSqVc2qlTJk2ZkpNPPXVzDxMAgDbGceR7izhs5665+upc\ncs45uWfZsuzWjPXnJzm0c+d83RsbAKBdcxz53iMO27E5c+bkU0OH5r613tBXJZmW5Mkkn0/yw7Xu\nNz/JkM6dM2P27Oy3336bZ7AAALQZTR1HrjYvyT5J/i3J9DWWO45s21yttB2bOnlyvr58eYM3dJ8k\nFyY5sYn77Zbk3OXLM3Xy5E06PgAA2qamjiNXOz3J/o0sdxzZtpk5bKeqq6vTv2/f/KWmptFzw5NV\ngfhCGs4cJslrSXatqMjchQtdfQoAoB1Z33Hk/yS5M8nArJopnL7W7Y4j2y4zh+3U9GnTclTSZBiu\nz3ZJjiqVMn3atI03KAAA2rx1HUe+kWRCkiuSNDUD5Tiy7RKH7dTcJ57I/jU1G7SNQcuXZ+6TT26k\nEQEAsCVY13HkRUlOSrLDerbhOLJt2qq1B0DrePP111O5gduoTLJ0yZKNMRwAALYQTR1HPpbkV+/8\nc30cR7ZN4rCdel+XLlm6gdtYmqSy27s9MRUAgC1RU8eRs5P8NcnOWXVK6ZtJapP8Ocmja63rOLJt\nclppO7XHPvvk9xUVjd5Wm6TmnX+uTLLinX9f25xOnbLH3ntvsjECAND2NHUc+eUkC7Jq5vDxJKck\nGZnkfxvZhuPItsnVStupdV1latI7X6U1lk3IqnPIV3OVKQCA9qk5V71PVh1PLoirlW5JzBy2Uz17\n9swnDz8815dKDW6bkOTtrJotXP110VrrXF8qZeSIEd7QAADtzLqOI9c0IQ3DMHEc2ZaZOWzH5syZ\nk08NHZr7li1r8gNMGzM/yZDOnTNj9uzst99+m2p4AAC0UY4j35vMHLZjgwYNyqQpU3Jo586Z38z7\nzE9yaOfOmTRlijc0AEA75Tjyval84sSJE1t7ELSeDw8alE7bbZcv/va3KV+5MgOSdGpkvdeSXF0q\nZWznzhk/ZUpOPvXUzTxSAADaEseR7z1OKyVJ8uijj2bq5Mm5a9asHFUqZdDy5as+fyarriZ1R1Fk\n5IgROeP88/2mBwCAOmseRx5aU5OPJo4jt1DikHoWLVqU6dOmZe6TT+bmG27I50ePzh57750vnnCC\nPxoGAKBJixYtSq+ePdMxqz5MfWWSb116qePILYg4pEmlUil+PAAAaK7SWlcwdSy5ZXFBGgAAAMQh\nAAAA4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIO\nAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICI\nQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg\n4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAA\niDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAA\nACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAA2kqIoUhRF3b+zZRGHAAAAiEMAAADEIQAA\nABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgA\nAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwC\nAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGH\nAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDE\nIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAAAQ\ncQgAAEDEIQAAABGHAAAARBwCAAAQcQgAAEDEIQAAABGHAAAARBwCAACQZKvWHgAAbClqampy7bW3\nZtasZ1JTU56KitqMGDEgJ530mVRUVLT28ABgg5SKoihaexC0TaVSKX48AFa54YYZ+fa378/8+cel\ntnbfuuXl5Y9lt91uyTe+cXBGjz6iFUcI0HY4jtwyiUOa5E0NsMoNN8zI2We/kkWLxja5TlXVdbn8\n8l4CESCOI7dU4pAmeVMDrDqVdN99J+TZZy9Z77r9+5+bxx//Zjp27LgZRgbQdjmO3DK5IA0ArMO1\n196a+fOPa9a68+d/Ptddd+smHhEAbBriEADWYdasZ+r9jeG61Nbum7vuenoTjwgANg1xCADrUFNT\n3qL1V6xo2foA0FaIQwBYh4qK2hat37Fjy9YHgLZCHALAOowYMSDl5Y81a93y8j9m5MgPbOIRAcCm\nIQ4BYB1OOukz2W23W5q17m673ZKxYz+ziUcEAJuGOASAdaioqMj48UNSVXXdOterqrou48f/q4+x\nAGCLJQ4BYD1GjRqZyy/vlf79z21wiml5+WPp3//cXH55r4waNbKVRggAG65U+HRKmuDDSwHqW7Fi\nRa699tbMnPl0VqwoT8eOtRk58gMZO/YzZgwB1uA4csskDmmSNzUAAO+G48gtk9NKAQAAEIcAAACI\nQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg\n4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAA\niDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAA\nACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAA\nAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgE\nAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDikEaVSKaVSqe7fAQCA9z5x\nCAAAgDgEAABAHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBx\nCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABE\nHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAA\nEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAA\nQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIA\nABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHLKW6urqlJJ0SvK+d/455dJL\ns2jRotYdGAAAbVp1dXWmXHppTh41Ku9LcvKoUY4jtzCloiiK1h4ErW/OnDmZOnlyZt59dw6vqcm/\nJqlMsjTJ7zt1yh1FkU8efnjOOP/8DBo0qJVHCwBAW7HmceTRSQbV1DiO3EKJQ3LN1Vdnwjnn5OvL\nl+f4okiDuR1LAAAPNUlEQVS3RtZZkmRaqZRLO3XKpClTcvKpp27uYQIA0MY4jnxvEYft3DVXX51L\nzjkn9yxblt2asf78JId27pyve2MDALRrjiPfe8RhOzZnzpx8aujQ3LfGG/qtJF9J8qus+i3Prkm+\nk+SwNe43P8mQzp0zY/bs7Lfffpt1zAAAtL7GjiNXG51Vx5LLk/RO8u9JTnznNseRbZsL0rRjUydP\nzteXL6/3hl6ZZOck9yV5Pck3kxybZOEa6+yW5NzlyzN18uTNNlYAANqOxo4jVzs/yXNJ/p7k50nG\nJ/njO7c5jmzbzBy2U9XV1enft2/+UlPT6Lnha/pgkolJjlpj2WtJdq2oyNyFC1NVVbWphgkAQBvT\nkuPIZ5MckuR7ST7zzjLHkW2XmcN2avq0aTkqWe8b+pUk85Lsudby7ZIcVSpl+rRpm2B0AEBLlUol\nX742y1fvXr1y2HrC8LQk2yT5QJIdkoxY4zbHkW2XOGyn5j7xRPavqVnnOiuTjEpyQpI9Grl90PLl\nmfvkkxt/cAAAtFkVST66nnWuSvJmkvuTHJ2k41q3O45sm7Zq7QHQOt58/fVUruP2IqvCsGOS/2xi\nncokN99wQ6654YaNPTwAANqo8mSdx5GrlZIclOSGJFcnOX2N2yqTLF2yZOMPjg0iDtup93XpkqXr\nuP3EJK8mmZVV/wFozNIknx89Oj+YPn1jDw8AaKFSqdTaQ6CdqE3WeRy5tpVJFqy1bGmSym7r+wMn\nNjenlbZTe+yzT35fUdHobackeSarri619Tq2MadTp+yx996bYHQAQEsVReHL12b5uviSS5o8jlyU\n5MdJ/pHk7ST3JPmfJMPWWs9xZNvkaqXtVFNXmVqYpF9WnUu+esawlOQHSY5bYz1XmQIAaJ/WdbXS\nV7PqqqRPZFUc9k1yRpIvrbGO48i2y8xhO9WzZ8988vDDc/1ap6DsnFVv5GVZNd2/NMkbqR+GSXJ9\nqZSRI0Z4QwMAtDNNHUcmSY8k92ZVAP49yeOpH4aJ48i2zMxhOzZnzpx8aujQ3LdsWaMfYNqU+UmG\ndO6cGbNnZ7/99ttUwwMAoI1yHPneZOawHRs0aFAmTZmSQzt3zvxm3md+kkM7d86kKVO8oQEA2inH\nke9N5RMnTpzY2oOg9Xx40KB02m67fPG3v035ypUZkKRTI+u9luTqUiljO3fO+ClTcvKpp27mkQIA\n0JY4jnzvcVopSZJHH300UydPzl2zZuWoUimDli9f9fkzWXU1qTuKIiNHjMgZ55/vNz0AANRxHPne\nIQ6pZ9GiRZk+bVrmPvlkli5Zkspu3bLH3nvniyec4I+GAQBokuPILZ84BAAAwAVpAAAAEIcAAABE\nHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAA\nEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAA\nQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIA\nABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcA\nAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQh\nAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBx\nCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABE\nHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAA\nEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAA\nQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIA\nABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAABBxCAAAQMQhAAAAEYcA\nAABEHAIAABBxCAAAQMQhAAAAEYcAAABEHAIAAO1Av379UiqV2s1Xv379WvwciUMAaKGiKHLepPNS\nFEVrDwWAZvrrX/+aoijazddf//rXFj9H4hAAWui2Gbflv37zX7n9rttbeygA0KQrr7wyN910U7PX\nF4cA0AJFUWTKDVOy9JCluWz6ZWYPAWizevbsmUWLFjV7fXEIAC1w24zb8mTlk0kpefJ9T5o9BOA9\nY6vWHgAAbClWzxou23NZkmRZ32W5bPplOXrk0SmVSq08OgBaqqamJtdee2tmzXomNTXlqaiozYgR\nA3LSSZ9JRUXFZttGW2HmEACaac1ZwyRmDwG2YDfcMCP77jshZ565V37xi2/l3nsn5Re/+FbOPHOv\n7LvvhNxww4zNso013XzzzRk0aFAqKyvTp0+ffPKTn8wDDzyQJJk3b16OO+649OzZM127dk3//v1z\nxhln5MUXX3xX+98YcQgAzVA3a7jzsnrLV88e+ttDgC3HDTfMyNlnv5Jnn70ktbX71ruttnbfPPvs\nJTn77FfWGXcbYxtruuKKK3LWWWdl/Pjxqa6uzsKFC3PaaadlxowZWbBgQQ488MDsuOOOeeyxx/L3\nv/89DzzwQHbdddfcf//9LX8CmlAq/N8MANbr1p/fmuPvPD7L+i5rcFvn5ztn+tHTc8wRx7TCyABo\njlKplKIoUlNTk333nZBnn71kvffp3//cPP74N9OxY8d6yzfGNtb0xhtvpE+fPrn++utz9NFHN7h9\n9OjReeONN/Kzn/1svY+3WqlUyk033ZTq6uqMGzeuWfcxcwgA69HUrOFqZg8BthzXXntr5s8/rlnr\nzp//+Vx33a2bZBtreuihh7JixYoceeSRjd7+q1/9Ksccs+l/ASkOAWA9Gvyt4dr87SHAFmPWrGca\nnAbalNrafXPXXU9vkm2safHixenRo0fKyhrPs1dffTW9e/eu+/6qq65Kt27dUllZmS9/+cvNGkdz\niEMAWIf1zRquZvYQYMtQU1PeovVXrGi4/sbYxpq6d++eV199NW+//XaTt7/00kt135922mlZsmRJ\nxo0bl3/+858tGsu6iEMAWIf1zhquZvYQYItQUVHbovU7dmy4/sbYxpoGDx6cjh075s4772z09o9/\n/OO5/fZN//8Xn3MIAOvwwKMPZL/a/VJ6bv2fY1gURe6fc78L0wC0YSNGDMgvf/lYs04LLS//Y0aO\n/MAm2caatt1220yaNCmnnXZaysvLM3z48HTo0CG/+tWvcu+992bSpEnZf//9c8455+Sss87KDjvs\nkFdffTVPP/10tt122/WOoblcrRQAAHjPa8tXK13tlltuyRVXXJFnnnkmlZWV+fCHP5xvfOMbOfDA\nAzNv3ryMHz8+v/nNb/LWW29lhx12yPDhw3PuueemT58+je5vS69WKg4BAID3vNVxmCQ33nhXzjrr\n5SxaNLbJ9auqrssVV/TOqFEjG719Y2xjU/JRFgAAAOsxatTIXH55r/Tvf27Kyx+rd1t5+WPp3//c\nXH55r3VG3cbYRltj5hAAAHjPW3PmcLUVK1bk2mtvzcyZT2fFivJ07FibkSM/kLFjP9Os00A31jY2\nBaeVAgAANKKxOHwvc1opAAAA74o4BAAAQBwCAAAgDgEAAIg4BAAAIOIQAABo54qiyHmTztugq5lu\njG20NnEIAAC0a7fNuC3/9Zv/yu133d5q27j//vvzkY98JF27dk2PHj0yZMiQ/OEPf0iSvPzyyxk7\ndmx22GGHdOnSJQMHDsykSZOyfPnydz3exohDAACg3SqKIlNumJKlhyzNZdMve1czfxu6jaVLl+aI\nI47IGWeckSVLluSFF17IhAkT0rFjxyxZsiSDBw/OihUr8sgjj+T111/PL3/5y7z++utZsGBBi8e6\nLuIQAABot26bcVuerHwyKSVPvu/JdzXzt6HbmDt3bkqlUo499tiUSqV07Ngxw4YNy1577ZXLL788\n2267bW644YbstNNOSZI+ffrkiiuuyF577dXisa6LOAQAANql1TN+y3ZeliRZ1ndZi2f+NsY29thj\nj5SXl+eEE07IL37xi/z973+vu+3Xv/51jj766GZva0OIQwAAoF1ac8Yvybua+dsY26isrMz999+f\nsrKynHzyyamqqsqRRx6Z6urqLF68ONtvv33zd2oDiEMAAKDdWXvGb7WWzPxtjG2s1r9///zwhz/M\nwoUL89RTT+XFF1/MuHHj0qNHj7z00kvN3s6GEIcAAEC702DGb7UWzPxtjG00Zo899sjxxx+fp556\nKsOGDcvtt7/7q6i2hDgEAADalaZm/FZrzszfxtjGas8++2yuuOKKvPDCC0mSv/3tb7nlllsyePDg\nnHXWWXnjjTdy/PHHZ+HChUmSF154IWeffXb+9Kc/rXfbLSEOAQCAdqXJGb/VmjHztzG2sVplZWUe\neeSRHHDAAamsrMxBBx2UffbZJ1OmTEnXrl3z0EMPpUOHDjnggAPSpUuXfOITn0jXrl2z2267rX9n\nW6BUvJsP8gAAANiClEqlFEWRoigy+NjBeWTPR5oOuyQpkgOeOiAP/eShlEr1V9wY29jUSqVSbrrp\nplRXV2fcuHHNuo+ZQwAAoN1Y74zfauuY+dsY22iLtmrtAQAAAGwuDzz6QPar3S+l59Y/k1cURe6f\nc3+OOeKYjb6NtshppQAAwHve6tNK2wunlQIAAPCuiEMAAADEIQAAAOIQAACAuFopAADQDvTt23ez\nf9Zga+rVq1eL7yMOAQCA97znn38+SXLllVemZ8+erTuYNkocAgAA7UZVVVWqq6tbexibTVVVVbPX\n9TmHAAAAuCANAAAA4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAA\nAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgEAAAg4hAAAICIQwAAACIOAQAAiDgE\nAAAg4hAAAID/334dCAAAAAAI2p96kbIoOQQAAKAa5cMoPta9hYQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21a663df28>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_ct, y_ct = S2.ct.subs(datav)\n",
"\n",
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S2.g,with_labels=True, pos=positions)\n",
"plt.plot([0],[0],'o',ms=12,label='CG')\n",
"plt.plot([x_ct],[y_ct],'^',ms=12, label='SC')\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"#plt.text(x_ct,y_ct, 'SC', fontsize=24)\n",
"plt.legend(loc='lower right', shadow=True)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in pricipal reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **inertial properties** in *principal reference frame*"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMQAAAAcBAMAAADM5Q0aAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMkS7zRCZdiKJ71Rm\nq90icBAQAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC3klEQVRIDaWUTWgTURDH/5tmm81HYxAPXiTr\nwYMHaUEUL5Jc/ACRLtaTIA2oiHhoToIFMSB4sIf2IOk1oqAnCQoieEguIgpWwYMHCerB+nExrV8t\nVeO89/bz7ZAIeZB9M//5zezuvMkCsVXf68S0iDAQiNCMk66NlRk5kAYCAepZmz1D7fmasRZVNG8g\nEOarwjEmwhKQt63VqKJ5A4Ewv0s4yVjnsz/CEGMPBIKcdJvss4HvWnn5djE5EAYCAYoPgOU+8haS\np+7KWD1EBKZR9u04YJ57WvDDrqG0C0C6opRJsR0Ul1xFXGMr2fUkBkg2zU9e2NuVNg9kmlLKfXVo\n3xD2TmyXknZZ8k+IAZ4B1zUeSsu3URSlgbmZGpAQVYwjj/YIRVvWA2+UOWA/0FKFgjSljU6Ie4lV\nvWxT096Rlen1urTpK5XyRpkD/gDjTS1FaakGTstAwmm1aX7PP9mncb67I/ub7Kv1Wf1hBWH+pFtU\nfVYarkad2S39YygSMX0YnSjne6Zt/KJO3oEcC192DWsdKC5EVVczVnBUBmzMV6idBfeOUVh4CVj0\npCfaOBWP0eRTLHYLpdGnYlmkGJ3O2wmIpt3mKpC2rdP5Bsw4+MgBfRplbai3SNApl4HPsFa4CqTZ\nwC3gJkweoKNtNbVUpdFbyEa16evXgLmKdEPjXDdH+xeY68h2WYBO9IWjRZRGn+1XFLDoAejPm+si\ns/BYA5U7R9skzA2MlB9yAI2+Gs1QUGk0UbMkXqPfyBrGythkL0houiw372I1yCrVcAhLL1kg3zRv\nQEuSGnINjDuY6h1AtvS3MtJGelFVzdMHMlhm6buD+71lnLy49bUt9SgAc/FSAZwG+ndnVEpQT1ls\nO8IQB3BasopR9eLhbGHzaojiAE6bdmA0Qnm+aVZ9kzc4gNPwnPLfcDXEkPZdHMBpeE9ljvctNWww\nJ5qXrQxbpl/+FRm81w8ZNnZm2AL/lf8PNIyxlBKATq4AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left ( A h^{2}, \\quad A a^{2}, \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 2 ⎞\n",
"⎝A⋅h , A⋅a , 0, 0⎠"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.Ixx, S2.Iyy, S2.Ixy, S2.θ"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Shear center** expression "
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAACgAAAAyBAMAAADcnYSjAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMA74lUMhCZZs3dIrur\nRHbLQ9+lAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAA90lEQVQ4EWOQ//+JAQXo///IIOziiiLGEOJi\nyCCCKgTiOcIFWZOKHKDyCEEOA9ZZGIKFDAwaGIJ7GBjsAyCiCO1/GBjuG6AJsn4DCj5AE+QCesFf\nAV0QqBJDEKt2BqBF9ugWMexmYKjHcBLQ8RkQe5D8zmnACgsbhONZ9d44YKiECoAohMrhKRgtCfYX\nmjfbsAl+xiLI+xWLINMELIIcyXW7gMKoFsV3MZzBELR3AEUqRCVr50wgmOEAik45mCCQhoBJDFxf\ngCwUM1n/MjAJoAuyf2BgVChFU8nTwMB/QQFNkLuAgUkPXTuQDwYoFtFWEGvWxlYIAAAbpUDl/el8\nZwAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left[\\begin{matrix}0\\\\- h\\end{matrix}\\right]$$"
],
"text/plain": [
"⎡0 ⎤\n",
"⎢ ⎥\n",
"⎣-h⎦"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.ct"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Analisys of symmetry properties of the section"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For **x** and **y** axes pair of symmetric **nodes** and **edges** are searched for"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[{'edges': [((1, 2), (3, 4)), (2, 3)], 'nodes': [(1, 4), (2, 3)]},\n",
" {'edges': [(1, 2), (3, 4)], 'nodes': [(1, 2), (3, 4)]}]"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.symmetry"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Compute axial loads in Stringers in **S2**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set **loads** on the section:\n",
"\n",
"**Example 2**: _shear_ in **y** direction and _bending moment_ in **x** direction"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S2.set_loads(_Tx=0, _Ty=Ty, _Nz=0, _Mx=Mx, _My=0, _Mz=0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Compute _axial loads_ in **stringers** and _shear flows_ in **panels**"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S2.compute_stringer_actions()\n",
"S2.compute_panel_fluxes();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Axial loads"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAAyBAMAAABv8PuQAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAF8klEQVRoBdVaT2hcRRj/vd3sn5f9i9Aiprpr\npDmmKyEoVnDRk6cmWntIS7sGyaWiCwUvgomISAXNolKwGLIHi1oU00P1kOquFBRB6fbQQ6iYp9WD\nesimxCSa2Djvz+y+92Z23rw5JXPYmfm+7/f95rdv3rxvXwKQdlfJ/Nyz7fwMXXrfsSod7sk+M5F3\n1j3LuSSZxqbpXZmYcYLkOkXYzR2TJvv3x1IsDMm5Z22c/i8Pn7pNrIlGmecT2BRhjSLJ+fKaILHb\n5SfRt2xvatUdRcdzx8ko06BT2V4Npt9YIAQ325IsDMljVQuZa/ISLH1KrNcneC6RTQ2WOd8kX9u+\nuiizy8eQTBuWN2d+H0wrjQL6k3cYe4BBDRaNjgHvzRsByambISmULFeBr2SF3IKZDQqW7UtKsGi2\nDRjLVUkWhsSRwFWit2areDVFCEI1RdhccgPJvOxNyZKIlGRq8zPaTKweSgfZ62qwJX0Td0P2pmRJ\nREqiyBlZSO9cKlgRVsIdGLrsTcmSiJXESmchvXO7SpRgJTydrEnflFH4SURK5pD+pgWycyO3XvmS\nrjO4V4PpLfxwL8ybcvihv4Jve5ZEpGQJ0ZMwd+4vqeZzwQpohBosU8OogVgd2fyVeJnm6tmzJCIl\nFWQ3kCA7t5pu9UzJOtRgcVLgVUEebwn8yOZkLCyJQMnldSNpJC+sXwJyNSZVT4MaLHXqBbyNN0+d\nzgP/9MzdcXBIBEo6MGAanJ377iMfuUJ4Qy7sncGAajfRTvCSJUo8a3dtHiXJcW6w3h5CkfFoCzhU\nZqwuAx+mlzDbckUxw/lIJcIYiSFe51m7JG4lA4e5FTG0rx//lVx0X0vlERvz2TxTPiy7iVzFE+eb\nDPw2fL/PZE1/r/OsXRKndJwvmmFZvhJeBiBWQSp0SQb0HUWhyc8otOo/1YV+5Gz/ctkMC6Ukvaqk\nhNCId5e5EE6LpOscq8uUbluTKevTURJfcAWIhnHrGp4WhXB82qRlDAlbspX0XlvyPzNtxD74HCX7\nmhZV8MeRIonRTgQHuiP0oQfNaUiYZthKBGtr1Ejag2UzebjdReJDfq0WB/lw2OhUqo8gaHchdRQ4\ncMnO5rlPcjvexhJGS12b9u0Uac9XEQxDbLyDO2Cipr4DvFw79p7vhAFveJTwSV43sN+63qGvyS0X\nk/RQr6F/UzqaBmpFjxJq9vYvFYHRqmXzXBNvFGeWLOF9jjnAlFtVUZJcXGwcN8SpI2R3IWo/GMIp\nOQP8Ic7N88bqiNvnC88rsBGguB2yLofnFO5xPmjbnkz65ODhCrEEHUI+WKaFWUMCVmiSIHezn3w9\n1kYC++yfmytlMo5e3v7KxPY6s6fyppe2NLlJK+Yk6ATzwvDEyIdWigBY3Hk7asWSj8jnWy3S9Vob\n0N+2Qu1qhaJor49crEK7UHHmyRp1iHtFmFVb33OM5j5LB/zeR0J+eTStQOe1lw80gAh5TZsuOWZu\nieqDmFM1mFNbX6UJi3TA730kgLsWZiDkMfMMETvjOO5jAvgGNZhTW9MTWjP4yanVRxKghFzpRhVH\n8g66RbME9GqwmFVb9606yTPhSAKUXMubSoYCcjJuNZhdW0cqTDq+gSER7i6S48U8rr71p+St3uVU\ng5HaOv3wz59004hHXpIAJX23oW3XUgvilIxXEUZq68L3WGTS8Q0+kgAl5PgmL5776/xcPa2KMPKI\nma3iYs+0XoePJEDJCHleNhEzvDkCZ2ows7Z+FDgZmN4O8JGIlWRJ7ngR81XJ5E6YIsysrSehS74c\n8JOIlbwGvVYo42A4IVCDmbW1tobImBybn0SohLwsy9aWgacyebnsdpQi7AyprTNtxIrXZcgYEqGS\nc4MPfIErwJpsnWIvQQ1m1dapJnLloowShsRRwv+L6bWdnXV8BgwaMrk7MWowq7bubyEy3EkkGjAk\nTukYa4pQe8I3XbSWmVL6GberFK7YByz9X4ldtbZQi9Ho/6usGKFwuy94/7izpsxWqIN21ylJnuis\nf2Bh160uzII+aJnR/wNxXCo0lO50awAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left \\{ 1 : \\frac{M_{x}}{2 h}, \\quad 2 : - \\frac{M_{x}}{2 h}, \\quad 3 : - \\frac{M_{x}}{2 h}, \\quad 4 : \\frac{M_{x}}{2 h}\\right \\}$$"
],
"text/plain": [
"⎧ Mₓ -Mₓ -Mₓ Mₓ⎫\n",
"⎨1: ───, 2: ────, 3: ────, 4: ───⎬\n",
"⎩ 2⋅h 2⋅h 2⋅h 2⋅h⎭"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.N"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Shear flows"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAaUAAAAyBAMAAAAO6NnSAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAF1klEQVRoBd1aTWhcVRg9k8xM5mXyMkO0AWlp\nhpRWKEhHgxuLOCi4k6RSuwgFYxdBVHBAcJuA1I1IBoWARUkWiv8wVVAktRlQ1Ogis3ApZMSVLkxT\nq61tNX73u29m7nffS5x5b+gjvYv77r3fd8475/3ce98kAJWRoqpvg3JuvmkiearcbO7xozud9xws\nhLxNS9Mr2x9euBzvdZAiFp/SapzrIVWNA6eAB0OiewSTIpwbmja7FZK+CucP4MeQ6B7BLBEP6dco\nVwtHP1CHew34ORy6RyhbxFyDiXPVcPwDgLrFpXDoHqFsEWN6bhgL6YlUpWZ6JC0KjRDhmYngaUlf\nlSiKomOFiOieNuajS4rMIERE97Saj6woOoEQEd0TLU/xFyEisie1POHhKrzFOx57UkRkT2p5QmFr\nYCoeN/qsUkRkT4O0PDl3zgwvx+lJipCenPqOytxKYOjo+s2LtO4Wso2AcPd0JknnaEuE9HTO5Gy3\nX3/gXeCLdt/XSpdSZd8gQHQMtUKvjb9n0d1xz91WDnUJzZm+yAsW2ktoiZCe1ih8Nm+TJKo4VsIB\ne9jop8uTRq/VXIOGtga44RSxUJd032HU/xisQWdKNPWegUR7CS0RwpNbROJTMdVzejaP1BT6Gh42\n4JC8+FHAKNFpqIwNX0NuRtC5xF6TSQChdaYdGJ6GQDfjLRHe5nWpoCJpdbE2ffeJNlPZq0hMqZTg\nchc+DggQnYbKWPIkxmqCbrCKjO9jh9A6U6KBt76HQDfjLRG5ZR7aKKnDoqr8noa2lCd8raLB5ZNk\nLSBAdB7UDtKzZ9LRhU2qJUEUFqOeUrsUyJOJbsZbIoYu8dAs17+o2u+JBtN0GQ9xTrrKB1k9Rl+a\n/sJ0DLViiTM0oOmeVSH6OEj+a+WA0ZwpI25FeQoQ0xKR+Uch+v5mHD9AgZ4mC8BPnLOvxodOKv08\nKqgszpF7aYDpEqdViJ78Ad9PGgqtM1VKuxyE8rSrmNUKZRwuMeZpVQd6UpfzZc7pomI68J2wUOp8\nBh19Kfg9abSnzMAX2JOBNmJeM3uSZsbzukPNYE/9RQrM6SRVJ76ZpfJcGbntdmmHvRbTMdQOpU4I\nusBnj9FQmaJkyuzJEBMg4mwDo+pZoLKjJ362TRqd/z810zFUJDoVDNKMYNDRHJHxzRGE9jIFegQ+\nTyLOnRcLwP1lbu707GWKeAN41I/dfUTRaajIy22xJ4NucBnulsihDqG9TBF5ZWXlT9qNGWgR5k6f\nupr9NFVT2WmOoM3Ir83XkhM7qxSdhor81DLSNCfpt5wj7hT6ayKHOoRO6Uw7QmuuibbDwDG+RbMc\n4AmS5ojETZHnnBk/PgPcx4O7zHsWTM23DLXG3ToWGh6dnvfonuwrW1kKzZn2OHCdhOwmxlsXNktK\nsLqhx5/8oY7ZvOo2yxDNAzPAt9wPXJ+8TAlTdBpqjT8y8TYBNJ2eFUd+/xzWSVkMZ1poHN3+sokO\nFjN4ifUYeyPVz1R4VFTOjOh6HWfigzIS7+iYBaPdjS7WOA/66aysLtBCBL2GNT4DzaZUXK6p0ceD\nsgrew+5H3xW6HRpowbqkC48WImhbUmXl3uF9z8ZBaYd7BwLGgPPAE3Rl5jlow7qjC48WImxP9BnG\npe4dzUNToDnGf9RYLWMyHwjrjs4+aedo+tWoLcL25Ni8bQNupd02Wut5RXfEGDGa3dMZYHSOtkTI\nZ8+k7Lj9fB5fvfpbsOWOSaImmiKie0pepvWskq1GVRUJL0RE90RrROYqaHsTZxEionuaoK1VDalG\nnJYgRET2NFykr+AClspxepIiInt6ib4Ixko4HKclSBFRPQ3QL1aVDeBxNx+fK0tEVE+L44c+wwXg\nirWzuaUGLRGep7B/o8b69vZf6lNnvHFLXciTWSL05hWpmsza0725AsvP6h/D9rSVlvhNPQc3/5+l\nNb6HGwn1HazKZoMPt0M1esJz4d6IcS7u6ZXMnG452V/tKXN8ZG/W1bn/A8MLuevjwFCdAAAAAElF\nTkSuQmCC\n",
"text/latex": [
"$$\\left \\{ \\left ( 1, \\quad 2\\right ) : - \\frac{T_{y}}{2 h}, \\quad \\left ( 2, \\quad 3\\right ) : 0, \\quad \\left ( 3, \\quad 4\\right ) : \\frac{T_{y}}{2 h}\\right \\}$$"
],
"text/plain": [
"⎧ -T_y T_y⎫\n",
"⎨(1, 2): ─────, (2, 3): 0, (3, 4): ───⎬\n",
"⎩ 2⋅h 2⋅h⎭"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.q"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set **loads** on the section:\n",
"\n",
"**Example 2**: _shear_ in **x** direction and _bending moment_ in **y** direction"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S2.set_loads(_Tx=Tx, _Ty=0, _Nz=0, _Mx=0, _My=My, _Mz=0)\n",
"S2.compute_stringer_actions()\n",
"S2.compute_panel_fluxes();"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAAyBAMAAACAMpCuAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGQ0lEQVRoBdVZTYgcRRT+eudnpzM7PwQjSmJm\n2KCCHhwNuSSgg6IgKklQI0ZN1qARXEkGggfx4IrkEAV3YkRQWXYERZGIm0i8BHcnFwX/dhQihBzS\n+HMwl92NJlkTyVrV1a+nu7qqu9rTpg7zXr33vffVm66uftMDsLGywT+v1mF/QivPbmuRelXKkx94\nyx5XXZDTS2PMXT7vlxtbY2lmkfvnto/FwmRnOhKKlsns3VXXZV8iREjO1Nn05b9DNv2keI75Bmea\neoTSk46EUshkk1Oup7hAgKC0T3Lv6fmgLUafeII5SzMxCJUrJQmlkMkyF11PpUuAoCy9x8ylVZ2g\nLUY/dZg5f9oeg1C5UpJQCpls8IrrqYgLQyhPZjJbgLcnHcmsmzY2APb9IqEOE7WnJKEEMpn1l+up\nqQspzwPOmRYFJ8jGHDsZSuISJ0AD7kw6EoqUyazLrkddyEThIgpV001v98ZbeLXIak810pFQ6ghZ\nbCGn7EVcB9NNX2pPjlljuQ5xGcp0JJQ0QhZbSANX4Nimmz6DilOG8R1FS0pHQlERsoRCHi60jTd9\nBrnGARjfUbSkBtKQUFSELK4Qu4fvbwDb9Nlbka9SCq2cwNCJHtgddfcUntaiZEdKEgqPkMUVUmpj\ng4NcBwOV6ouUQS9PIbMD/I6qLwxu0cMkT0oSio6QxRWSZ41TC684OHgfzlIGvRxB+SLYc8m+ZqTc\n0cMkT0oSio6QxRRS3LkHb+L1naNVHMU0ZdDKYxecglP46MIRFOtFRwuTHClJKDpKFlMIBTH5DB4L\nzDzVXv+p+lGZb+YUjreGE5poJQmwL8octBBZuJD9mlv6uex8MFjoqzGg7ovzrc1RtN3AeC9qDliU\nJMDzAYhCJbJgIdYXM5pCHjjbjeY4AjwatTJLdpp3j9IoL6IyItnCUyUJygnPY59MtCiTdTfpnLoQ\nq71C8WVuA2Za4bWI2fX4LGrOPoJaN2ruW9QkmPi2D1FpPtkl13um6QpNIcX6g4ocs1VNIUezXQUc\nCVtLTYJ6QiE+2azLuVswe4WMSuvI/lyXLN50L7+C+SnJ+dCwZBBTa5cr5eSEVZOU2qKQCAmF+WTu\nHTjwj7CLQqwnCZUgs/y3LVZ1E2DCbd90O1eMk4uotRCFJJMUeQ03NkWYd0XEJPlT+zWpQ4lF7VVb\n614ham/IeqyJNewAckeokKXwmA9FuZP1AVMljF4KuEjNbSUNa3bz8Q0gRckkhVawEOtrHvVCC0qy\nwg5c6150xhIqxGfVKeWGzqOw222scF8XKXx600oEC9HjuGeQ3YMbWgKTrpDXwFZnOioL/6eQN44f\nP5/cHYk18J3rvUtJd0UGGyibF5LrIO8dKaa1C1zCA9FPNuC+LAgdv7qDRXqgvTO87kueRnOgWP/6\nHFwp9TDuMKlLzjFsSFHMIh50GhI3Rnxsdrica/LPTTu/63GpOerz4Z9Ls0tLFzhad3Z5LzE5hI97\n1n/oSk1y18c+pCjcsvQVd+lIKAz43FW9FqVvFprU4B6Q/eG5hC4Y7rtDGz8O5DGNksgAsQFqjUCu\nvio1uPW+R6VJ6AEVJmqzpnBbs282jIJEhmD3289GGnu+BBpcyyG7WobRWKtGydZiFbktfaNhFCSy\nhELCDW6pT6fUwmi4t5sSGDLmRlAMvJ00jIJEllDIrK7BDS2FJunQFDW0ECqEzElSJovfWizb3ioO\nrfujmpTX86dDU9L8Auw77txKU1MZIksqhDW42cchev1kgnRoP9/mOu5tD837czMlTJZUCDu/V/Ww\n0Sw1P+1ToP2ko7CeQqbjz82UMFlSIazBvauKPWapkQ5NSTMNZBaQd2huKMNkCYWUG/zdoRU4VeJY\n0qH9TL8BuQ5qLd9gpEhkCYWwBvfgORQMt286NC230MC7tTrGaW4oJbL4QniDe3ARK7oJzYngTof2\n17sP+LM2hsOmzYmaLL4Qt8H9Eb9M1X3aGCUdmhLZu4Y3jQw5pVHT5kQEymReIeo/Q+E2uKt/fWm6\nSbRxMh2aMg2xX7sj1vTN7/9OFiMpk3l/hua6RtHLGDTovtGB+y5lGS8zeWnsLw0+bPHmNBm/bBG1\njljanLNsl2i0MOvZqsCVLnuKUdjyA+0/QWtaPUXa1SjtH/iq/wPE2CyGmYiUrwAAAABJRU5ErkJg\ngg==\n",
"text/latex": [
"$$\\left \\{ 1 : \\frac{M_{y}}{2 a}, \\quad 2 : \\frac{M_{y}}{2 a}, \\quad 3 : - \\frac{M_{y}}{2 a}, \\quad 4 : - \\frac{M_{y}}{2 a}\\right \\}$$"
],
"text/plain": [
"⎧ M_y M_y -M_y -M_y ⎫\n",
"⎨1: ───, 2: ───, 3: ─────, 4: ─────⎬\n",
"⎩ 2⋅a 2⋅a 2⋅a 2⋅a ⎭"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.N"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAaUAAAAyBAMAAAAO6NnSAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEImZRO/dMlQiu6vN\nZnZmcXX2AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGTUlEQVRoBd1aXYgbVRT+Jn+b2SS7Qdi+bGHH\nLSr0oY0tIrRog1BfbcEWXCvEH4SyoAFB8EE3ICo+NVgo+MfmTbSFxgcV2bqbB8EH0Q1UhEKl6d+D\n+LDbqrU/W+O5d+buzL0zczOZzks8kDv3nvOd75yTuXNzkl2A5L4KG/8H8lFDFJE5XBfTEb+W5spO\nBceGu03m3ydXbi+tWvdYf0I0i3NL/ZNnrjvJnHjenpi3h8suZSFbQ7o7nJcPnRDNLHAYeMyhN+/Y\nk8I1XzytogAsVlCqakGDjQnRtGH+Cfwi4u2zH6PJjlBEu74JXGhgQuzcaE5+VDI0Y12UbgIXBf9C\nj88m20IR7UrvxEoZmWjgcFQyNGMA22dVEWemwmczQ9ZETrSDk5BkaOjhdsUpZvia2A5OQBKioYfb\nldg1sR2cgCREQw+3K7FrGvakdENKs4Ro6OF2JXZN0g52+YadJUQjPZWxa+I7eMejf9SHrULGJ0PD\nn8rU5be+4eSxa2I7eKJ8JleVcxx2lQwNfyovFjov8fCxazpNO3gMPw1bg4pPhmactUH1Ytdml2v6\nVA3prktNdw6kTvV/7JHille5OdfQnNsEsUlCNNtXN5aJbdJJUarJbLFAfjm+5zPgW78eY+v0Ge4T\nojF3f1FX9ebs9gYK0lvjQMJpmItPxirBNAuwY0o1FSlg/qCPw2hjZxVbfXospmopvxZEM43UX6rl\nOPJ3YXRUNXXDoTTcxeeQawXRmOsPwuJYqaazwPRef4deKCN7AKmej3z6yo77fUqAaL4EDqmWtQZu\nADtUNcUMpbFdVI+rrSAaY/mJS2UOdZrXRYutjtJrwl8TfYYU/oFxgEGiCNHQ58WKvRFch/1VYwOY\nchUDZkRjuyg483xLTzNJdpILVRrMGg0BNRWvsZrwPVmjCKNZLftron19FyhWo3AQhmfDXRSHVLGl\npymuc4+X2ThRYYP/PpE2R9ptDIN5PuoGTgO8WvaBtlh01LEgyLV9RlVh0zAXRc6xmnQ07K0jBD+T\nx7s0Da7pKQs4z5DGETZqhdMgI34ecLEfvEhlljpMMcVHNgsVTsNdZIjRYzVpaVaa5PJAlfnlGjQE\n18Tuzrv0iiKcJvBOpJ6m/VeLwkEYm4a5yJICq0lLUyCnrXRMkWSrNATWlK6QZYFeQvqurAuduHIa\n7BZL7/VQmT7SPAqXpe9Vc4RNA3KR5T1ek5dm0kNjY9/pYcvDLktgTZeZ3VuT7Ro82m9NxWf8EDjd\nkGvyYTwKRmO7eJS0+S1fTZKdL163gEfqbBq69/IVxv4khw8eOM3bMJsKtF9mNWVqijpsyWhsFwmR\nX1paebanp+EbNk1HNRB6RrwG/O6cERJ/8ILRUPsyodY0R2dh03m4gz0lLaOxXSQ1LbItcUbQIkh2\n1pmWn+X8fGR7b6YjIc0XZvfWgF1MGXTuKXBGc2J229cqzW/I/wukLUYTdO4F0HAXRU+9aktHA2Qo\nDMlalQa2LdJfbXyHnPPrLOmYFOkZrAE/8MU8H6VBgTOa1X7/hkqT2b2nSmT8Pcy1JQa+CKDhLooe\nqdN3uhoa2m/rnM/tjfjyfX9E53NdGHirLhYK/GiInqtPCKP/Gp9GygaTHc5t/8x3VsSxxMRzlXpY\nu1UXVgWupQnoYe+ZRs4GUl8+3rTpjZ4I47lu9cxht+qORoXraIyOl0aax6eRsqHjwN7Y9kV8JyxJ\nsZzF515llrfqjkaF62hEvV6ye6aRslFqguZLt/zd3WnVAzJjKg3NuRCXIHVkGiUb6T4FEYfqqFU3\ndz1+MNQe1XB829VyVGw4zptN/JqoVd/fdL6qhMcaaMk8g9WBoMEAbzbxa5qH8RzSrcHh9IipLvbo\nEZGs3mxi10Stevoacr1IETWgfWW8ojFHNEnZxK6JWvVsCzP1iEFDYXMweLMZCohkkLKJWxNr1Wcs\nHIsUUQMyriO/rrFHM8nZxK2JteozDZzKN6NFDUMZNzHeUZqiMGy4Xs4mZk28VS/2SvOp8EDRLD/j\n17YVDRqKUrJxahr2b9S8VTeWH/r4SmigiIbpS28sVyNiw2BKNnbzimwnDD+C+gWLJ124NYK5h6W8\nZh/G4v9ZwmCjpDfE/xmt9UYpbW2uW0QPWrpT1gJHx5g/slnJdHt00tZm+kmXmf8DdunQwP4qgtEA\nAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ \\left ( 1, \\quad 2\\right ) : \\frac{T_{x}}{2 a}, \\quad \\left ( 2, \\quad 3\\right ) : \\frac{T_{x}}{a}, \\quad \\left ( 3, \\quad 4\\right ) : \\frac{T_{x}}{2 a}\\right \\}$$"
],
"text/plain": [
"⎧ Tₓ Tₓ Tₓ⎫\n",
"⎨(1, 2): ───, (2, 3): ──, (3, 4): ───⎬\n",
"⎩ 2⋅a a 2⋅a⎭"
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2.q"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"# Second example (2): Open section"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"stringers = {1:[(a,h),A],\n",
" 2:[(sympy.Integer(0),h),A],\n",
" 3:[(sympy.Integer(0),sympy.Integer(0)),A],\n",
" 4:[(a,sympy.Integer(0)),A]}\n",
"\n",
"panels = {(1,2):t,\n",
" (2,3):t,\n",
" (3,4):t}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define section and perform first calculations"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"S2_2 = Section(stringers, panels)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Plot of **S2** section in original reference frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define a dictionary of coordinates used by **Networkx** to plot section as a Directed graph.\n",
"Note that arrows are actually just thicker stubs"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"start_pos={ii: [float(S2_2.g.node[ii]['ip'][i].subs(datav)) for i in range(2)] for ii in S2_2.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA5EAAAJtCAYAAACv9fRpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xu4VXWB//HPPojAsSNxFUEF8wKRmj2KqcFIo8nN8ZJl\naaAQ4m3wGnkplcuopFIONo6TzSiQTaNdtAx77PnliE5q4TyDWOYNdZy0PIqEqAcI3L8/GE4czjnw\nVRAO4+v1PPvRvfbae33XPtvteu+19tqVarVaDQAAABSo2doDAAAAYNshIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgGS3HnnnTnssMOy0047pba2Nv369ctxxx2Xe+655z1Z3syZM3PHHXc0\nmz516tS0a9fuPVnmhuy+++754he/uMWW19r6bw5Tp07Nfffd12z6uHHj8qEPfeg9WeZ77a233sqY\nMWOy0047paamJhdccMHWHtJWMW7cuNTU1DS7tGvXLm+//fbWHh7A+0bF70QC73fXX399zjvvvJx6\n6qk55phjssMOO2TRokWZO3du9t5773zta1/b7MvcfffdM2TIkMyZM6fJ9Jdeeim///3vc9BBB232\nZW7Io48+mh133DG77777Fllea+u/OdTU1OTSSy/NtGnTmkx/7rnn8vrrr+ejH/3oZl/me+3aa6/N\nV7/61dxyyy3Za6+9svPOO2fXXXfd2sPa4saNG5ef/exnueuuu7L+5suW/m8G4P1su609AICt7etf\n/3o+/elP56abbmqcNnTo0IwfP36Lj6V3797p3bv3Fl/uthhW61u5cmW23377Vm/fUoFcYmNjXd/j\njz+e3r175wtf+MJWWX5bsv3222fQoEHv6D7b8voCtEUOZwXe91577bXstNNORfM+//zz+cIXvpCe\nPXumY8eO+djHPpY777yz2XyPPvpojjvuuHTv3j21tbUZMGBArr766iRrYuaFF17Irbfe2ng43tpD\nSadMmZKamqZvzcuWLcvEiRPTp0+fdOzYMQMGDMjf//3fN5ln3rx5qampyV133ZWzzz47PXr0SI8e\nPTJmzJi8/vrrG12vfv36NTmcddasWampqcmvfvWrjB49Op07d06fPn1y7rnnZuXKlRt9vJkzZ2bg\nwIGpra1N165dM2jQoPz4xz/e6PovWrQoJ598cj70oQ+ltrY2e+yxR84666z86U9/avL4Y8eOza67\n7pqHH344n/jEJ7LDDjvkwgsvTE1NTSqVSq644orGwxzX7pEcO3Zsk5D87//+79TU1OSmm27K5MmT\n07t373Tp0iVHH310XnzxxSbLa2hoyJlnnpnu3bunrq4uxx9/fB566KHU1NRsdG/q2r/pb3/72wwf\nPjx1dXX53Oc+13j7j370oxxyyCHZYYcd0qVLl5xwwgn5n//5n8bb1y7jhRdeaFyn+++/P0ny6quv\n5owzzsguu+ySjh075sMf/nC+/e1vN1n+7NmzU1NTkwceeCAnnHBCunTpkoMPPrjx9nnz5uWII47I\njjvumA984AMZPnx4fvvb3zZ5jKFDh2bIkCH5xS9+kQMOOCA77LBD9t1333f82i9d501x6aWXpqam\nJr/73e9y5JFHpq6urjG+77nnnowcOTI777xz4zrMnDmz2aGwu+66a8aNG5fZs2enf//+qa2tzWGH\nHZbnnnsub775Zk477bR069YtO++8cy666KJme0VfeeWVnH766enTp086dOiQgQMH5uabb94s6wfQ\nFtgTCbzvHXTQQZk1a1Z23333HHPMMdlrr71anG/tYaa9evXKzJkz071799x22205/vjj8+Mf/zhH\nHXVUkuTXv/51PvnJT2avvfbKzJkz06dPnzz99NNZuHBhkuSOO+7IyJEjs//++2fq1KmpVqvp0aNH\nkqRSqaRSqTQus1qtZuTIkVmwYEH+7u/+Lvvss0/mzp2bCy64IK+++mquuOKKJmM877zzctRRR+V7\n3/tennzyyXz5y1/Odtttl1tuuWWDz8G6y1z3+sknn5wTTzwxd9xxRx566KFMnjw5Xbt2zeTJk1t9\nrO9+97uZNGlSpkyZksGDB6ehoSELFy7Ma6+9lmTN909HjBjR4vq/9NJL6dOnT6677rp07do1zz33\nXK666qqMGjUqv/zlL5uMb+nSpTnxxBMzadKkTJ8+PZ06dcpJJ52Ugw8+OOPGjcvpp5+eJNlll11a\nfG7X+trXvpZDDz00t9xyS+rr63PBBRdkzJgxuffeexvnmTBhQn74wx9m6tSpOeCAA/KLX/wiX/jC\nF1p8vNae22OPPTbjx4/PxRdf3PhBwT/90z/lrLPOyvjx4zN58uQsW7YskydPztChQ7Nw4cLssMMO\nefjhhzN58uQsXLgwd955Z6rVagYOHJhly5blE5/4RFasWJFp06alX79+ueeee3LmmWdm5cqV+du/\n/dsm4xg9enROPPHE/PCHP8yqVauSJHPnzs2xxx6bv/mbv8l3v/vdxudjyJAheeyxx9KnT5/GdVi0\naFHOO++8fOUrX0m3bt0yY8aMnHDCCXniiScav2u6sdd+6TpvzOrVq5tcX/vhwbrP9zHHHJPx48fn\nq1/9auPz/eyzz+bwww/P2Wefndra2syfPz+XXXZZFi9e3Ozw53vvvTfPPPNMZsyYkeXLl+ecc87J\n8ccfn1122SUDBw7M7bffnvvuuy9XXnll9tprr5x66qlJkqVLl+bQQw/N6tWrc8UVV6Rv3765++67\nM2HChPz5z39ufF0CbNOqAO9zTz31VPWjH/1otaamplqpVKrdu3evnnjiidWf//znTeb74he/WO3Z\ns2d1yZIlTaZ/6lOfqn7sYx9rvD5kyJDqbrvtVl2+fHmry+zXr191zJgxzaZPmTKlWlNT03j9rrvu\nqlYqleqcOXOazHfqqadWO3bsWF28eHG1Wq1W77vvvmqlUqmOGzeuyXwTJ06sdurUaSPPwJrxrHvf\nWbNmVSuVSnXq1KlN5jvqqKOq/fv33+BjTZw4sXrAAQdsdHktrf/6Vq1aVf2P//iPak1NTXXBggWN\n08eOHVutqamp3nXXXc3uU6lUqpdddlmz6WPHjq3uvvvujdeff/75aqVSqf71X/91k/lmzJhRramp\nqf7hD3+oVqvV6pNPPlmtqampzpgxo8l855xzTrWmpqY6e/bsDa7D2r/pN7/5zSbT33jjjWrnzp2r\np556apPpzz//fHX77bevzpw5s3Ha6NGjm4y9Wq1Wp02bVu3UqVN10aJFTaZPmDCh2qNHj+rq1aur\n1epf/pZf+tKXmo1tzz33rH7qU59qMm3ZsmXV7t27V88///zGaUOHDq1uv/32TZZVX19fbdeuXXX6\n9OmN0zb22n8n69ySsWPHViuVSpNLTU1Nk7/3pZdeWq2pqaneeOONG3ysanXN62vq1KnVHj16NJm+\nyy67VHv06FF98803G6d94xvfqFYqlepZZ53VZN799tuveuSRRzZev/zyy6u1tbXV5557rsl848aN\nq/bq1av69ttvb3RcAG2dw1mB97299tor//Vf/5V58+bl0ksvbTxEddiwYbnyyisb51t7KFxdXV1W\nr16d1atXZ9WqVTnyyCPz6KOP5o033khDQ0MefPDBjB49Oh06dNjksT3wwANp165dTjzxxCbTR48e\nnZUrV+ahhx5qMn3kyJFNru+7775ZsWJF6uvr3/GyK5VKi4/3wgsvbPB+gwYNyoIFC3LOOefkF7/4\nRRoaGoqX+ec//zlXXXVVPvzhD6e2tjbt27fPkCFDkiRPPvlkk3nbt2+fUaNGFT92a0aMGNHk+r77\n7pskjev5q1/9Kknymc98psl8n/nMZ5odxrghxx57bJPrDz30UJYtW5aTTjqp8fW0evXq9OnTJwMG\nDGg8ZLU199xzTz7+8Y+nb9++Te5/5JFH5tVXX83jjz/eOG+lUmm2/GeeeSaLFi1qtvyOHTvmkEMO\nabb8vfbaq8nZbXv06JGePXs2Pk8lr/1NXeck2WmnnfKf//mfeeSRR/LII49k/vz5Oeuss5rNt/76\nJskf/vCHTJgwIX379k379u3Tvn37TJkyJYsXL27cU77WJz7xidTW1jZeHzBgQCqVSo488sgm8w0Y\nMKDJobj33HNPDj300Oy6667N/i719fXNXscA2yKHswJkzUb24MGDM3jw4CTJH//4xwwbNizTpk3L\nxIkT07lz59TX12fOnDmZPXt2s/vX1NRk8eLFad++fd5+++3GwwA31WuvvZauXbtmu+2avl336tUr\n1Wq12YZv165dm1xfuzG/fPnyd7X8lh5vxYoVG7zPySefnBUrVuRf/uVfcuONN2a77bbLyJEj841v\nfCN9+/bd4H0vvvji3HDDDZk8eXIOOeSQ1NXV5fe//32OO+64ZuvQo0ePosNJN6aldaxWq43L+8Mf\n/pAk6dmzZ5P5Sr9Hu9bOO+/c5Hp9fX2q1WoOP/zwZvNWKpVm41pffX19Fi1alPbt27d4/8WLF290\n+Ukyfvz4Zj/vUqlUsttuuzWZ1tJ4OnTo0Pg8LVmyZKOv/U1d52TNhwcf+9jHNjpfr169mlx/++23\nM2rUqCxevDhTpkxJ//7907Fjx/zgBz/I1Vdf3ez11aVLlybX156Yp6Xp6963vr4+8+fPL/67AGyL\nRCRAC3r16pVTTz015513Xp5++ukceOCB6datW/7qr/4qF198cYt7oHr37p1Vq1alpqam2YlZ3q2u\nXbvmtddey6pVq5qE5B//+MfG29uiCRMmZMKECVm6dGl+/vOf54ILLsjnP//5ZntO13fbbbfllFNO\nySWXXNI4bdmyZS3OuzkCsjXrPvba+Kqvr28SwS+//PK7fswk6datW5Jkzpw5GThwYLP56+rqNvh4\n3bp1y0477ZTrr7++xddj//79i5Y/ffr0HHHEEc3u/07PZtqlS5eNvvY3dZ03xVNPPZUFCxbktttu\ny2c/+9nG6T/84Q8363K6deuW3XbbLdddd13R3wVgWyQigfe9P/7xj832WiTJ7373uyR/2aMxfPjw\nPPzwwxk4cGCrh+u1b98+gwcPzq233prLL7+81fk6dOhQdJjnYYcdlmuvvTbf//73mxzSeuutt6ZD\nhw455JBDGqe9l1H1bnXu3Dmf/exn8/DDDzf5CZXW1v+tt95qttf15ptvfkfrtv3227+jQ2g3Zu3v\nD37/+9/PpEmTGqfffvvtm/ScH3rooamrq8vTTz+d0aNHv+P7Dx8+PP/wD/+QXXfdNd27d3/H9+/f\nv3/69euX3/72t7nwwgvf8f3X16lTp42+9jd1nTfFW2+9lSRNXl8rV67Mv/7rv27W5QwfPjw33XRT\n+vbt22Y/5AHYVCISeN/bZ599csQRR2TkyJHZfffd8/rrr2fu3Ln51re+lc997nONZ/ecNm1aPv7x\nj2fIkCGZOHFi+vXrlyVLluQ3v/lNnnvuufzzP/9zkmTGjBkZOnRoDj744HzpS1/KLrvskmeffTYL\nFizI9ddfnyQZOHBgHnjggcydOze9evVK9+7dWzzUc8SIERk8eHDOOOOM1NfX5yMf+Ujmzp2bm2++\nOV/5yleabKS+k+/nvZdOP/301NXV5ZBDDknPnj3z5JNP5jvf+U6GDRvWOE9r6z98+PDMnj07++yz\nT/bcc8/86Ec/2ujey/UNHDgwc+fOzbBhw9KlS5f07t272aGcG7Puc9m/f/+cdNJJueyyy7J69eoc\ncMABuffee/PTn/40SZr9JEupurq6XHvttZk4cWLq6+szYsSIdO7cOS+++GLmzZuXT37yk/n85z/f\n6v3PP//83H777Rk8eHDOP//89O/fP2+++WaeeOKJPPDAAy3+/Mb6brjhhhx77LFZsWJFTjjhhHTv\n3j0vv/xyHnzwwfTt2zfnnXfeO1qnjb32N3WdN8VHPvKR7LLLLrn44ouTrPnQ5brrrmvxsNPWlPw3\nNmnSpPzgBz9o/LvsvffeWbZsWZ544ok8+OCD+dGPfvSu1wGgrRCRwPveVVddlbvvvjuTJ0/Oyy+/\nnHbt2mXvvffONddck3PPPbdxvl133TWPPPJIpkyZkq9+9at55ZVX0q1bt+yzzz455ZRTGuc78MAD\n88tf/jKXX355zjnnnKxYsSJ9+/bNuHHjGueZPn16TjvttHzuc59LQ0NDTjnllMbfkVt371alUsnd\nd9+dr3zlK7nmmmuyePHi9OvXL9ddd13OOeecJuuxKXvFWvv5i9bm3ZDBgwfnlltuya233pqlS5em\nd+/eOfnkkzNlypTGeVpb/29+85tJ1vzWX5KMGjUq//Zv/9a4N7BkHDfccEPOOeecHH300VmxYkUm\nT56cyy+/vMX7tPYY60//9re/nR133DHXXnttVq5cmcMPPzz/+I//mFGjRqVz584bfD42tJzTTjst\nu+22W6699tp873vfy6pVq9KnT58MGTIk+++//wYfY8cdd8yDDz6YadOm5ZprrsmLL76YD37wg+nf\nv3+OP/74jY4pWfMhxf33358rr7wyEyZMSENDQ3r16pWDDz64Wcy1tA7rv25KXvvvZJ1b8k5+VmVd\nHTp0yE9+8pOcffbZGTNmTLp165bx48dn5513zhlnnLHB9drYsted3rlz5zz00EOZOnVqpk+fnpde\neikf/OAHM2DAgCaH0QJsyyrVtvLRNQBsQ2bMmJGLL744zz//fOPeagB4P7AnEgA2Yu7cufnNb36T\n/fffPzU1Nbn//vvz9a9/vcnhzgDwfmFPJABsxP3335+LLrooTz75ZN5888306dMnn//85zNlypR3\nfBZTANjWiUgAAACKvbtTygEAAPC+JCIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAo\nJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIB\nAAAoJiIBAAAoJiIBAAAoJiIBAAAoJiIBAAAott3WHgC8U/X19Zkza1aeWrgwbyxdmg907py999sv\np4wblx49emzt4QEAbHa2f2hLKtVqtbq1BwEl5s+fn5nTp2fuz36WTycZtHx56pIsS/LrTp1yR7Wa\nUSNG5NxLLsmgQYO28mgBADad7R/aIhHJNuGmG2/M5EmTclFDQ06pVtOlhXmWJJlVqeSaTp0ydcaM\nnHbmmVt6mAAAm43tH9oqEUmbd9ONN+bqSZNyz1tvZc+C+Z9JMqy2Nhd5IwUAtlG2f2jLRCRt2vz5\n83P00KF5YJ030JVJzkry/7Lm07c9klyVZPg693smyZDa2tw1b14OPPDALTpmAIBN0dL2T5LckGRW\nkseSnJTk5vXuZ/uHLcXZWWnTZk6fnosaGpq8ga5KsluSB5IsTfJ3SU5I8sI68+yZ5MKGhsycPn2L\njRUAYHNoafsnSfokuSzJ+FbuZ/uHLcWeSNqs+vr69O/bN88uX97idwDW9dEkU5Ict86015Ls0bFj\nnnrhBWctAwC2CSXbP5cleTHN90Qmtn/YMvzEB23WnFmzclyy0YB8OcnTST6y3vSuSYYtX56devaM\nT0poic/QAGhrSrd/WtM1yXGVSubMmpUvffnLm3Fk8BcOZ6XNemrhwhy0fPkG51mVZHSSsUn2buH2\nw5J02OwjAwB4b5Rs/2zMoIaGPPXYY5tpRNCcPZG0WW8sXZq6DdxezZqA7JDkm63MUxcvclpXqVS2\n9hAAoIkPZM2H4JuiLsmyJUs2w2igZbavabM+0Llzlm3g9vFJXk1yd5J2rcyzLGv2VkJLHM4KQFtz\n2ujRWfbd727SYyxLUtfl3R4QCxvncFbarL332y+/7tixxdvOSPJEkp8k2X4DjzG/U6dccc01qVar\nLi7NLgDQ1mxo+2d1kuX/+89VSVb877+vb36nTtl7333fszGCs7PSZrV2drIXkvRL0jF/2QNZSfKt\nJCeuM5+zkwEA25oNnZ116v9e1v0yxuQkl69z3fYPW4I9kbRZPXv2zKgRIzJ7ve+t7Zbk7SRvZc3h\nGsuSvJ6mAZkksyuVHDVypDdQAGCb0dr2T7ImGN/Omr2Pay+XrzeP7R+2BHsiadPmz5+fo4cOzQNv\nvdXsB3c35JkkQ2prc9e8eTnwwAPfq+EBAGx2tn9o6+yJpE0bNGhQps6YkWG1tXmm8D7PJBlWW5up\nM2Z4AwUAtjm2f2jr2k2ZMmXK1h4EbMgBgwalU9euOfnf/z3tVq3KgCSdWpjvtSQ3Vio5tbY2l86Y\nkdPOPHMLjxQAYPOw/UNb5nBWthmPPPJIZk6fnp/efXeOq1QyqKFhze8gZc1ZyO6oVnPUyJE595JL\nfAIHAPyfYPuHtkhEss155ZVXMmfWrDz12GP51+98JyeNGZO99903J48d60vkAMD/Setu/yxbsiR1\nXbrY/mGrEZFs0yqVit/7AwCALciJdQAAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgm\nIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmIgEA\nACgmIgEAACgmIgEAACgmIgEAACgmIgEAACgmItlmPf7441t7CAAA8L4jItlmLViwYGsPAQAA3ndE\nJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAA\nAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVE\nJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAA\nAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVE\nJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAA\nAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVE\nJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAA\nAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMVE\nJAAAAMVEJAAAAMVEJAAAAMVEJAAAAMW229oDgHejUqk0+fdqtboVRwMAAO8f9kQCAABQTEQCAABQ\nTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQC\nAABQTERo8ce9AAAJd0lEQVQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQ\nTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQC\nAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQ\nTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQC\nAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQTEQCAABQbLutPQB4p+rr61NJ0jFJuySrk8y45pqc\nMm5cevTosXUHBwDwHqivr8+cWbPy1MKFeWPp0nygc+fsvd9+tn/YKirVarW6tQcBJebPn5+Z06dn\n7s9+lhHLl+evktQlWZbk15065Y5qNaNGjMi5l1ySQYMGbeXRAgBsunW3fz6dZNDy5bZ/2OpEJNuE\nm268MZMnTcpFDQ05pVpNlxbmWZJkVqWSazp1ytQZM3LamWdu6WECAGw2tn9oq0Qkbd5NN96YqydN\nyj1vvZU9C+Z/Jsmw2tpc5I0UANhG2f6hLRORtGnz58/P0UOH5oH13kDHJPl/SRqS9Ery5STj17n9\nmSRDamtz17x5OfDAA7fcgAEANlFr2z9rPZ1kvySfTTJnnem2f9hSnJ2VNm3m9Om5qKGh2RvoJUme\nS/KnJD9JcmmS/1rn9j2TXNjQkJnTp2+ZgQIAbCatbf+sNTHJQS1Mt/3DlmJPJG1WfX19+vftm2eX\nL2/xOwBrPZnkk0muT/KZdaa/lmSPjh3z1AsvOGsZALBN2Nj2z78luTPJwKzZ8zhnvdtt/7Al2BNJ\nmzVn1qwcl7QakH+bZIckH07SO8nI9W7vmuS4SiVzZs16z8YIAO9GpVJxcWnx0munnTK8lYB8Pcnk\nJN9I0tpeINs/bAkikjbrqYULc9Dy5a3efkOSN5L8R5JPJ+nQwjyDGhpy6YUXbvX/Ibi0zcsee+zx\n3rx4AeBd6pjksFZuuzzJhKz58HxDBjU05KnHHtus44J1bbe1BwCteWPp0tRtZJ5KkkOTfCfJjVnz\nHYF11cWLnNY9++yzqVQqW3sYANCoXdLi9s+CrDmp4IKCx6hLsmzJks05LGjC9jVt1gc6d86ywnlX\nJVnUwvRlSU4aMybfmrP+NwYAYOvxARatWZ20uP0zL8l/J9ktaw5lfeN/5308ySPrzbssSV2XDZ1R\nAjaNw1lps/beb7/8umPHZtNfSXJbkjeTvJ3knqz5kvkRLTzG/E6dsve++76XwwSAd6xarbq4tHiZ\ndvXVLW7/nJ41H5gvSPJokjOSHJXk5y28vmz/8F5zdlbarNbOTvZq1pyFdWHWRGTfJOcm+eJ693d2\nMgBgW1N6dvqpWROVzs7K1mBPJG1Wz549M2rEiMxe75Cf7knuy5o3yT9lzadx6wdkksyuVHLUyJHe\nQAGAbUZr2z/rm5zmAZnY/mHLsCeSNm3+/Pk5eujQPPDWW63+4G5LnkkypLY2d82blwMPPPC9Gh4A\nwGZn+4e2zp5I2rRBgwZl6owZGVZbm2cK7/NMkmG1tZk6Y4Y3UABgm2P7h7au3ZQpU6Zs7UHAhhww\naFA6de2ak//939Nu1aoMSNKphfleS3JjpZJTa2tz6YwZOe3MM7fwSAEANg/bP7RlDmdlm/HII49k\n5vTp+endd+e4SiWDGhrW/A5S1pyF7I5qNUeNHJlzL7nEJ3AAwP8Jtn9oi0Qk25xXXnklc2bNylOP\nPZZlS5akrkuX7L3vvjl57FhfIgcA/k+y/UNbIiIBAAAo5sQ6AAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAA\nFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBOR\nAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFBORAAAAFPv/nBPGIrFVPmwAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21a685f2b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S2_2.g,with_labels=True, arrows= True, pos=start_pos)\n",
"plt.arrow(0,0,20,0)\n",
"plt.arrow(0,0,0,20)\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in starting reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **Inertial properties** wrt Center of Gravity in with original rotation"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMQAAAAcBAMAAADM5Q0aAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMkS7zRCZdiKJ71Rm\nq90icBAQAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC3klEQVRIDaWUTWgTURDH/5tmm81HYxAPXiTr\nwYMHaUEUL5Jc/ACRLtaTIA2oiHhoToIFMSB4sIf2IOk1oqAnCQoieEguIgpWwYMHCerB+nExrV8t\nVeO89/bz7ZAIeZB9M//5zezuvMkCsVXf68S0iDAQiNCMk66NlRk5kAYCAepZmz1D7fmasRZVNG8g\nEOarwjEmwhKQt63VqKJ5A4Ewv0s4yVjnsz/CEGMPBIKcdJvss4HvWnn5djE5EAYCAYoPgOU+8haS\np+7KWD1EBKZR9u04YJ57WvDDrqG0C0C6opRJsR0Ul1xFXGMr2fUkBkg2zU9e2NuVNg9kmlLKfXVo\n3xD2TmyXknZZ8k+IAZ4B1zUeSsu3URSlgbmZGpAQVYwjj/YIRVvWA2+UOWA/0FKFgjSljU6Ie4lV\nvWxT096Rlen1urTpK5XyRpkD/gDjTS1FaakGTstAwmm1aX7PP9mncb67I/ub7Kv1Wf1hBWH+pFtU\nfVYarkad2S39YygSMX0YnSjne6Zt/KJO3oEcC192DWsdKC5EVVczVnBUBmzMV6idBfeOUVh4CVj0\npCfaOBWP0eRTLHYLpdGnYlmkGJ3O2wmIpt3mKpC2rdP5Bsw4+MgBfRplbai3SNApl4HPsFa4CqTZ\nwC3gJkweoKNtNbVUpdFbyEa16evXgLmKdEPjXDdH+xeY68h2WYBO9IWjRZRGn+1XFLDoAejPm+si\ns/BYA5U7R9skzA2MlB9yAI2+Gs1QUGk0UbMkXqPfyBrGythkL0houiw372I1yCrVcAhLL1kg3zRv\nQEuSGnINjDuY6h1AtvS3MtJGelFVzdMHMlhm6buD+71lnLy49bUt9SgAc/FSAZwG+ndnVEpQT1ls\nO8IQB3BasopR9eLhbGHzaojiAE6bdmA0Qnm+aVZ9kzc4gNPwnPLfcDXEkPZdHMBpeE9ljvctNWww\nJ5qXrQxbpl/+FRm81w8ZNnZm2AL/lf8PNIyxlBKATq4AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left ( A h^{2}, \\quad A a^{2}, \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 2 ⎞\n",
"⎝A⋅h , A⋅a , 0, 0⎠"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2_2.Ixx0, S2_2.Iyy0, S2_2.Ixy0, S2_2.α0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Plot of **S2** section in inertial reference Frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Section is plotted wrt **center of gravity** and rotated (if necessary) so that *x* and *y* are principal axes.\n",
"**Center of Gravity** and **Shear Center** are drawn"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"positions={ii: [float(S2_2.g.node[ii]['pos'][i].subs(datav)) for i in range(2)] for ii in S2_2.g.nodes() }"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA40AAAJtCAYAAACSZ5UPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XucVXWh9/HvnhEZMATkqqhgXiC8ZOeIiskJi7wQlpeO\nZUGKol20xMsxLRQwjaOiSScfz8lehZh5Km+FYJ5OF/Ie9uTlmIpYHnu8jSIpJoOB+/kDmRiYHwwC\nM8i836/XvHTvvfZav7U3uvjs35q1K9VqtRoAAABoRk1bDwAAAIBNl2gEAACgSDQCAABQJBoBAAAo\nEo0AAAAUiUYAAACKRCPASm655ZZ84AMfSJ8+fdK5c+cMGDAgRx55ZG6//faNsr1p06bl5ptvXu3+\nyZMnp7a2dqNsc0122mmnnHDCCa2+3TWpqanJBRdcsE7POeigg/LBD35wI40o+d///d/U1NRkxowZ\nG20bK7z++usZM2ZM+vTpk5qampxxxhkbfZuborFjx6ampma1n9ra2rz55pttPTyAzdoWbT0AgE3F\nN7/5zYwfPz7jxo3L2Wefna222ipPPvlkZs2alV/96lc55JBDNvg2r7jiigwbNixHHnlkk/tPOumk\nHHbYYRt8e2tzyy23ZOutt2717a7Jvffem+23336dnnPVVVdtpNG0viuvvDI//OEP873vfS+77rpr\ntt1227YeUpvp3bt3Zs6cmVW/YrqmxmfgABuTaAR4y2WXXZajjjoq3/72txvvGz58eE488cRWH8t2\n222X7bbbrtW3+973vrfVt1nyxhtvZMstt8y+++67zs8dNGjQRhjRhrFiv1rqD3/4Q7bbbrt8+tOf\nbpPtb0q23HLLDBkyZJ2e807eX4BNhY/mAN7y8ssvp0+fPi1a9qmnnsqnP/3p9O7dO3V1dXnf+96X\nW265ZbXlHnzwwRx55JHp2bNnOnfunEGDBuXiiy9OsvxU0Keffjrf//73G0+1W3Fq6KRJk1abPVm0\naFFOPfXU9OvXL3V1dRk0aFCuuOKKJsvMmTMnNTU1mTlzZr74xS+mV69e6dWrV8aMGZNXX311rfs1\nYMCAJqenTp8+PTU1NbnvvvsyevTodO3aNf369ctpp52WN954Y63rq6mpyYQJE/L1r389O+ywQzp3\n7pwPfOADefDBB5ssN3z48AwbNiy33npr/uEf/iGdOnVqnC1s7vTUNb2uK9a38umpK16Xm266KWPH\njs0222yTrl27ZvTo0Xn55ZebrPvKK6/MAQcckB49eqR79+4ZOnRoZs+evdZ9bc6K9/GRRx7JoYce\nmi5duuQTn/hE4+M33XRThg4dmq222irdu3fPMccckz//+c9NXr8ZM2bk6aefbjwV8ze/+U2S5KWX\nXsrnPve5bL/99qmrq8t73vOeXH311U22f80116SmpiZ33HFHjjnmmHTv3j37779/k9dlxIgR2Xrr\nrfOud70rhx56aB555JEm61jx3vziF7/IP/7jP2arrbbKnnvuuc5/3lu6z+tjwoQJqampyaOPPpqD\nDz44Xbp0aYzt22+/PSNHjsy2227buA/Tpk1b7dTWHXbYIWPHjs0111yTgQMHNv6Z/dOf/pS//vWv\nOfnkk9OjR49su+22+fKXv7zarOeLL76Yz372s+nXr186duyYwYMH57vf/e4G2T+AtmKmEeAt++67\nb6ZPn56ddtopH/vYx7Lrrrs2u9z/+3//L/vuu2/69u2badOmpWfPnvnhD3+Yo48+Oj/5yU8yatSo\nJMlvf/vbHHTQQdl1110zbdq09OvXL0888UQeeuihJMnNN9+ckSNHZu+9987kyZNTrVbTq1evJEml\nUkmlUmncZrVazciRI/PAAw/ka1/7WvbYY4/MmjUrZ5xxRl566aVceOGFTcY4fvz4jBo1Ktdff30e\nf/zx/Mu//Eu22GKLfO9731vja7DyNle+/ZnPfCbHHntsbr755txzzz2ZOHFittlmm0ycOHGtr+uM\nGTPSv3//XHnllVmyZEnOO++8jBgxIk888US6devWuJ158+bltNNOy3nnnZd3v/vd2WabbZpd39pe\n1+b2Y4XTTz89I0aMyH/+53/miSeeyLnnnpvnnnsuv/jFLxqXeeqppzJ27NjsvPPOWbZsWWbOnJnD\nDz88t912Ww4++OC17u/KVozjiCOOyIknnphzzjmn8cOAf//3f88XvvCFnHjiiZk4cWIWLVqUiRMn\nZvjw4XnooYey1VZb5d57783EiRPz0EMP5ZZbbkm1Ws3gwYOzaNGivP/978+SJUtywQUXZMCAAbn9\n9tvz+c9/Pm+88UZOOeWUJuMYPXp0jj322Nx4441ZunRpkmTWrFk54ogjcvjhh+e6665Lkvzrv/5r\nhg0blocffjj9+vVr3Icnn3wy48ePz1e+8pX06NEjU6dOzTHHHJPHHnss7373u1v8vrRkn9dm2bJl\nTW7X1NQ0vs4r/vmxj30sJ554Yr761a82vt5//OMf86EPfShf/OIX07lz58ydOzfnnXdeFixYsNqH\nEr/85S8zf/78TJ06NQ0NDfnSl76Uo48+Ottvv30GDx6cH/3oR/n1r3+diy66KLvuumvGjRuXJHnl\nlVdywAEHZNmyZbnwwgvTv3//zJ49OyeddFL+9re/5bOf/exa9w9gk1QFoFqtVqvz5s2rvve9763W\n1NRUK5VKtWfPntVjjz22+l//9V9NljvhhBOqvXv3ri5cuLDJ/R/+8Ier73vf+xpvDxs2rLrjjjtW\nGxoaitscMGBAdcyYMavdP2nSpGpNTU3j7ZkzZ1YrlUp1xowZTZYbN25cta6urrpgwYJqtVqt/vrX\nv65WKpXq2LFjmyx36qmnVjt16rSWV2D5eFZ+7vTp06uVSqU6efLkJsuNGjWqOnDgwLWur1KpVHv1\n6lVdvHhx431PPfVUtUOHDtXzzz+/8b7hw4dXa2trqw899FCz61h5+y15XYcPH1496KCDGm+veF1G\njhzZZLnrrruuWlNTU/3lL3/Z7HrefPPN6tKlS6sHH3xw9YgjjmiyD5VKpXrNNdesYe///j7+27/9\nW5P7X3vttWrXrl2r48aNa3L/U089Vd1yyy2r06ZNa7xv9OjR1Z122qnJchdccEG1U6dO1SeffLLJ\n/SeddFK1V69e1WXLllWr1b+/f2eeeeZqY9tll12qH/7wh5vct2jRomrPnj2rp59+euN9w4cPr265\n5ZZNtlVfX1+tra2tTpkypfG+tb0v67LPzTn++OOrlUqlyU9NTU31vPPOa1xmwoQJ1ZqamupVV121\nxnVVq9Xq0qVLq5MnT6726tWryf3bb799tVevXtW//vWvjfddfvnl1UqlUv3CF77QZNm99tqrevDB\nBzfePv/886udO3eu/ulPf2qy3NixY6t9+/atvvnmm2sdF8CmyOmpAG/Zdddd8/vf/z5z5szJhAkT\nGk85PeSQQ3LRRRc1LrfiNLcuXbpk2bJlWbZsWZYuXZqDDz44Dz74YF577bUsXrw4d999d0aPHp2O\nHTuu99juuOOO1NbW5thjj21y/+jRo/PGG2/knnvuaXL/yJEjm9zec889s2TJktTX16/ztiuVSrPr\ne/rpp1v0/JEjR6aurq7xdv/+/bP//vuvNuYBAwZkzz33XOO61vd1/ed//ufVblcqlSZj+d3vfpdR\no0alb9++2WKLLdKhQ4f8/Oc/z+OPP77O21vhiCOOaHL7nnvuyaJFi/KpT32q8c/QsmXL0q9fvwwa\nNKjxFNSS22+/Pfvtt1/69+/f5PkHH3xwXnrppfzhD39oXLZSqay2/fnz5+fJJ59cbft1dXUZOnTo\natvfddddG2cUk6RXr17p3bt345+Blrwv67vPSdKnT5/87ne/y/3335/7778/c+fOzRe+8IXVllt1\nf5Pkueeey0knnZT+/funQ4cO6dChQyZNmpQFCxasdory+9///nTu3Lnx9qBBg1KpVFabaR40aFCT\nU2tvv/32HHDAAdlhhx1We1/q6+vX688QQFtyeirASiqVSg488MAceOCBSZLnn38+hxxySC644IKc\neuqp6dq1a+rr6zNjxoxcc801qz2/pqYmCxYsSIcOHfLmm282nuK3vl5++eVss8022WKLpv/b7tu3\nb6rV6mp/6V311M4Vf5FvaGh4W9tvbn1Llixp0XOb+z3RPn36NAmbJC26KujChQvX63VddSwdOnRI\n9+7d88wzzyRZfurxiBEjsvvuu+db3/pWdtxxx2yxxRaZMGFCHnvssbe1zWT1fauvr0+1Ws2HPvSh\n1ZatVCrFU3NXfv6TTz6ZDh06NPv8BQsWrHX7SXLiiSeu9hUrlUolO+64Y5P7mhtPx44dG/88teR9\nWd99Tpa/X+973/vWulzfvn2b3H7zzTfzkY98JAsWLMikSZMycODA1NXV5YYbbsjFF1+82n8X3bt3\nb3J7xYV0mrt/5efW19dn7ty5LX5fAN4pRCPAGvTt2zfjxo3L+PHj88QTT2SfffZJjx498k//9E85\n55xzVrsIRrL8yqdLly5NTU1NY4ysr2222SYvv/xyli5d2iQcn3/++cbHN1UvvPBCs/etGhil30Nc\nWffu3dfrdV11LH/729+ycOHCxrHcdtttefXVV/PjH/+4SWi9/vrrb2t7K6y6bz169Eiy/Pc9Bw8e\nvNryXbp0WeP6evTokT59+uSb3/xms38GBw4c2KLtT5kyJSNGjFjt+et6tdGWvC/ru8/rY968eXng\ngQfywx/+sMls84033rhBt9OjR4/suOOO+cY3vtGi9wXgnUI0Arzl+eefX22GIkkeffTRJH+fvTj0\n0ENz7733ZvDgwcVT8Tp06JADDzww3//+93P++ecXl+vYsWMWL1681rF94AMfyKWXXpof//jHTU5R\n/f73v5+OHTtm6NChjfe1JL5a0+zZs7N48eJ06tQpyfILzdx77735yle+ss7r6tSpU4te15If/ehH\nOf7445vcrlarOeCAA5Kk8b1YOcznzZuXu+66KzvssMM6j7fkgAMOSJcuXfLEE09k9OjR6/z8Qw89\nNN/61reyww47pGfPnuv8/IEDB2bAgAF55JFHcvbZZ6/z81fVkvdlffd5fayI/pXf1zfeeCM/+MEP\nNuh2Dj300Hz7299O//79N+kPcgDWlWgEeMsee+yRESNGZOTIkdlpp53y6quvZtasWfmP//iPfOIT\nn2j8gvkLLrgg++23X4YNG5ZTTz01AwYMyMKFC/M///M/+dOf/pTvfOc7SZKpU6dm+PDh2X///XPm\nmWdm++23zx//+Mc88MAD+eY3v5kkGTx4cO64447MmjUrffv2Tc+ePdO/f//VxnbYYYflwAMPzOc+\n97nU19dn9913z6xZs/Ld7343X/nKV5r8BbW5GY621KlTpxx88ME566yz0tDQkIkTJ6Zbt24ZP378\n21pfS17XkkceeSQnnHBCPvnJT+bxxx/PhAkTctBBB2X48OFJkhEjRqS2tjZjxozJmWeemWeffTaT\nJk1K//79V/tqhvXRpUuXXHrppTn11FNTX1+fww47LF27ds0zzzyTOXPm5KCDDsonP/nJ4vNPP/30\n/OhHP8qBBx6Y008/PQMHDsxf//rXPPbYY7njjjua/TqMVV155ZU54ogjsmTJkhxzzDHp2bNnXnjh\nhdx9993p37//Or8/a3tf1nef18fuu++e7bffPuecc06S5R+sfOMb32j2NNKSlvx3ddZZZ+WGG25o\nfF922223LFq0KI899ljuvvvu3HTTTW97HwDakmgEeMvXv/71zJ49OxMnTswLL7yQ2tra7Lbbbrnk\nkkty2mmnNS63ww475P7778+kSZPy1a9+NS+++GJ69OiRPfbYI8cdd1zjcvvss0/uuuuunH/++fnS\nl76UJUuWpH///hk7dmzjMlOmTMnJJ5+cT3ziE1m8eHGOO+64xu90W3nGsFKpZPbs2fnKV76SSy65\nJAsWLMiAAQPyjW98I1/60pea7Mf6zDSu+lUfa1u2JT7zmc9kq622yqmnnpoFCxZk3333zY9//OPG\nr9tY2/pWHVNLXtfm1lepVDJt2rT89Kc/zSc/+cksW7YsH/3oRzNt2rTGZQYPHpwf/OAHOf/88/Ox\nj30sO++8cy6++OLcdtttmTNnztva/9JyJ598cnbcccdceumluf7667N06dL069cvw4YNy957773G\ndWy99da5++67c8EFF+SSSy7JM888k27dumXgwIE5+uijWzSuww47LL/5zW9y0UUX5aSTTsrixYvT\nt2/f7L///qvFW3P78Hbel3XZ5+a05DVvbpmOHTvmpz/9ab74xS9mzJgx6dGjR0488cRsu+22+dzn\nPrfG/Vrbtle+v2vXrrnnnnsyefLkTJkyJc8++2y6deuWQYMGrXYRJoB3kkp1U/tIGoDNRk1NTSZM\nmLDa9+C1tjlz5uSDH/xgfv7zn+eDH/xgm44FAN5pfOUGAO2Cz0gB4O0RjQBsNOtyuuvGtqmMAwDe\naZyeCgAAQJGZRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlG\nAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABF\nohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAA\nQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQC\nAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgS\njQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAA\nikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEA\nAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFo\nBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQ\nJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAA\nABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQj\nAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi\n0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAA\noEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoB\nAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJ\nRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAA\nRaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgA\nAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0\nAgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAo\nEo0AAAAUiUYAAACKtmjrAQC0Z/X19ZkxfXrmPfRQXnvllbyra9fsttdeOW7s2PTq1authwcAzXL8\nal8q1Wq12taDAGhv5s6dm2lTpmTWbbflqCRDGhrSJcmiJL/t1Ck3V6v5yGGH5bRzz82QIUPaeLQA\nsJzjV/skGgFa2bevuioTzzorX168OMdVq+nezDILk0yvVHJJp06ZPHVqTv7851t7mADQhONX+yUa\nAVrRt6+6KhefdVZuf/317NKC5ecnOaRz53zZgReANuT41b6JRoBWMnfu3Hx0+PDcsdIB940kX0jy\n31n+6ezOSb6e5NCVnjc/ybDOnTNzzpzss88+rTpmAGju+JUkVyaZnuThJJ9K8t1Vnuf4tflw9VSA\nVjJtypR8efHiJgfcpUl2THJHkleSfC3JMUmeXmmZXZKcvXhxpk2Z0mpjBYAVmjt+JUm/JOclObHw\nPMevzYeZRoBWUF9fn4H9++ePDQ3N/g7Iyt6bZFKSI1e67+UkO9fVZd7TT7sqHQCtpiXHr/OSPJPV\nZxoTx6/NhZlGgFYwY/r0HJmsNRhfSPJEkt1XuX+bJIc0NKRP796pVCp+NoEfgPagpcevkm2SHFmp\nZMb06RtuULQ60QjQCuY99FD2bWhY4zJLk4xOcnyS3Zp5/ANJOm7wkQFAWUuOX2szZPHizHv44Q00\nItrCFm09AID24LVXXkmXNTxezfJg7Jjk3wrLdIn/aW9KzDYC7cG7svxDy/XRJcmihQs3wGhoK/7+\nAdAK3tW1axat4fETk7yUZHaS2sIyi7J8NpJNg0sCAO3ByaNHZ9F1163XOhYl6dL97Z7gyqbA6akA\nrWC3vfbKb+vqmn3sc0keS/LTJFuuYR1zO3XKhZdckmq16mcT+AFoD9Z0/FqWpOGtfy5NsuStf1/V\n3E6dstuee260MbLxuXoqQCsoXX3u6SQDktTl7zOMlST/keTYlZZz9TkA2sKarp46+a2flU/Wn5jk\n/JVuO35tHsw0ArSC3r175yOHHZZrVvk9uB2TvJnk9Sw/fWdRklfTNBiT5JpKJaNGjnTABaBVlY5f\nyfJAfDPLZxdX/Jy/yjKOX5sHM40ArWTu3Ln56PDhueP111f7guQ1mZ9kWOfOmTlnTvbZZ5+NNTwA\naJbjF2YaAVrJkCFDMnnq1BzSuXPmt/A585Mc0rlzJk+d6oALQJtw/KJ20qRJk9p6EADtxT8OGZJO\n22yTz/zqV6ldujSDknRqZrmXk1xVqWRc586ZMHVqTv7851t5pADwd45f7ZvTUwHawP33359pU6bk\n1tmzc2SlkiGLFy//Hqssv8rczdVqRo0cmdPOPdcntABsMhy/2ifRCNCGXnzxxcyYPj3zHn44P7j2\n2nxqzJjstuee+czxx7toAACbrJWPX4sWLkyX7t0dvzZjohFgE1GpVHz/HwCwyXEhHAAAAIpEIwAA\nAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEI\nAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBI\nNAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAA\nKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYA\nAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWi\nEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABA\nkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIA\nAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAULRFWw+Ad45q\ntZpzLzg3U86fkkql0tbDAYA1amhoyNVX35DZsx9LQ0Nt6uqWZeTIQTnppI+nrq6urYcH8I5RqVar\n1bYeBO8MN/z0hpxw2Qn53lnfy9GHH93Ww4HNTqVSif8lw4Zx7bUzc9FFd2b+/GOzbNnejffX1j6Q\nXXa5Pl/96oEZM+bwNhwhwDuHaKRFqtVqhh4zNPftfl/2e2S/3POje8w2wgYmGmHDuPbamTnzzBfy\n4ovjisv06vWdXHZZH+EI0AJ+p5EWuXHmjXm4y8NJJXn4XQ/npltvaushAcBqGhoactFFd64xGJPk\nxRfH5aKL7siSJUtaaWQA71yikbWqVquZeu3UvL7j60mS1/u/nktnXGpGBIBNztVX35D5849t0bLz\n538q3/nODRt5RADvfKKRtVp5ljGJ2UYANlmzZz/W5HcY12TZsr1z662PbuQRAbzziUbWaNVZxhXM\nNgKwKWpoqF2n5ZcsWbflAdoj0cgarTbLuILZRgA2QXV1y9Zp+Y4d1215gPZINFJUmmVcwWwjAJua\nkSMHpbb2gRYtW1v7+4wa9Z6NPCKAdz7RSFFxlnEFs40AbGJOOunj2WWX61u07C67XJ9x4z6+kUcE\n8M4nGmnW2mYZVzDbCMCmpK6uLhMmDEuvXt9Z43K9en0nEyb8Uzp27NhKIwN45xKNNGuts4wrmG0E\nYBMzevSoXHZZnwwcePZqp6rW1j6QgQPPzmWX9cno0aPaaIQA7yyVqikimnH6+afn//7v/02lsrZq\nXD4r+Q/9/yHfuOAbrTAy2HxVKhWz9rABLVmyJFdffUNmzXo0S5bUpmPHZRk16j0ZN+7jZhgB1oFo\nBNhEiEYAYFPk9FQAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJ\nRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAA\nRaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgA\nAECRaAQSppV0AAAQuElEQVQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLR\nCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAG2sUqmkUqk0/jsAwKZENAIAAFAkGgEAACgSjQAAABSJ\nRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAA\nRaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgA\nAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0\nAgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARVu09QAA2rP6+vpUktQlqU2yLMnUSy7JcWPHplev\nXm07OAAoqK+vz4zp0zPvoYfy2iuv5F1du2a3vfZy/NpMVarVarWtBwHQ3sydOzfTpkzJrNtuy2EN\nDfmnJF2SLEry206dcnO1mo8cdlhOO/fcDBkypI1HCwDLrXz8OirJkIYGx692QDQCtLJvX3VVJp51\nVr68eHGOq1bTvZllFiaZXqnkkk6dMnnq1Jz8+c+39jABoAnHr/ZLNAK0om9fdVUuPuus3P7669ml\nBcvPT3JI5875sgMvAG3I8at9E40ArWTu3Ln56PDhuWOVA+6YJP+dZHGSvkn+JcmJKz0+P8mwzp0z\nc86c7LPPPq03YABI+fi1whNJ9kryz0lmrHS/49fmw9VTAVrJtClT8uXFi1c74J6b5E9J/pLkp0km\nJPn9So/vkuTsxYszbcqU1hkoAKykdPxa4dQk+zZzv+PX5sNMI0ArqK+vz8D+/fPHhoZmfwdkhceT\nHJTkm0k+vtL9LyfZua4u855+2lXpAGg1azt+/WeSW5IMzvKZxRmrPO74tXkw0wjQCmZMn54jk2Iw\nnpJkqyTvSbJdkpGrPL5NkiMrlcyYPn2jjRFgU1GpVPxsIj99+/TJoYVgfDXJxCSXJynNQjl+bR5E\nI0ArmPfQQ9m3oaH4+JVJXktyZ5KjknRsZpkhixdn3sMPb5wBAkAz6pJ8oPDY+UlOyvIPO9fE8eud\nb4u2HgBAe/DaK6+ky1qWqSQ5IMm1Sa7K8t8RWVmXJD+49tp8+9prN8IIAWB1tUmzx68Hsvwibg+0\nYB1dkixauHBDDotWJhoBWsG7unbNohYuuzTJk83cvyjJp8aMyX/MWPU3RgA2L5VKpa2HwFuWJc0e\nv+Yk+d8kO2b5qamvvbXsH5Lcv8qyi5J06b6m3+hnU+f0VIBWsNtee+W3dXWr3f9ikh8m+WuSN5Pc\nnuUXFRjRzDrmduqU3fbcc2MOE2CTUK1W/WwiPxdcfHGzx6/PZvkHnA8keTDJ55KMSvJfzbyfjl/v\nfK6eCtAKSlefeynLr5L6UJZHY/8kpyU5YZXnu/ocAG2hpVf/npzlEenqqZsnM40AraB37975yGGH\n5ZpVTrnqmeTXWX5Q/UuWf1q7ajAmyTWVSkaNHOmAC0CrKh2/VjUxqwdj4vi1uTDTCNBK5s6dm48O\nH547Xn+9+AXJzZmfZFjnzpk5Z0722WefjTU8AGiW4xdmGgFayZAhQzJ56tQc0rlz5rfwOfOTHNK5\ncyZPneqAC0CbcPyidtKkSZPaehAA7cU/DhmSTttsk8/86lepXbo0g5J0ama5l5NcValkXOfOmTB1\nak7+/OdbeaQA8HeOX+2b01MB2sD999+faVOm5NbZs3NkpZIhixcv/x6rLL/K3M3VakaNHJnTzj3X\nJ7QAbDIcv9on0QjQhl588cXMmD498x5+OIsWLkyX7t2z25575jPHH++iAQBsshy/2hfRCAAAQJEL\n4QAAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAA\nKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYA\nAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWi\nEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABA\nkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIA\nAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKN\nAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACK\nRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAA\ngCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgE\nAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAk\nGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLRCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAA\nFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACgSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMA\nAABFohEAAIAi0QgAAECRaAQAAKBINAIAAFAkGgEAACgSjQAAABSJRgAAAIpEIwAAAEWiEQAAgCLR\nCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAAA2\newMGDEilUmk3PwMGDNhgr12lWq1WN9jaAAAANkGVSiXtKX025P6aaQQAANgMXXHFFbnuuuvWez2i\nEQAAYDPUu3fvvPjii+u9HtEIAABA0RZtPQAAAIC20NDQkKuvviGzZz+Whoba1NUty8iRg3LSSR9P\nXV1dq61jU2emEQAAaHeuvXZm9t57Yk4/fY/87GcX5te/npyf/ezCnH76Htl774m59tqZrbKOlf3g\nBz/IkCFD0qVLl/Tr1y8f+chHctdddyVJnnjiiRx77LHp3bt3unXrloEDB+a0007Ls88++7b2f12I\nRgAAoF259tqZOfPMF/L44xdn2bK9mzy2bNneefzxi3PmmS+sMfo2xDpWdvnll+eMM87IhAkTUl9f\nn6effjqnnHJKZs6cmSeffDL7779/tt9++zzwwAP5y1/+krvuuis777xz7rzzznV/AdaRr9wAAAA2\neyu+gqKhoSF77z0xjz9+8VqfM3Dg2Xnwwa+lY8eOTe7fEOtY2auvvpp+/frlmmuuyVFHHbXa42PG\njMmrr76an/zkJ2vd3gqVSiXXXXdd6uvrM378+BY/rzlmGgEAgHbj6qtvyPz5x7Zo2fnzP5XvfOeG\njbKOld1zzz1ZsmRJjjjiiGYf/+///u8cffTRLdrexiAaAQCAdmP27MdWO520ZNmyvXPrrY9ulHWs\nbMGCBenZs2dqaprPs5deeil9+/ZtvH3llVeme/fu6dKlSz772c+2aBzrQzQCAADtRkND7Totv2TJ\n6stviHWsrEePHnnppZfy5ptvFh9/7rnnGm+fcsopWbhwYcaPH5+//e1v6zSWt0M0AgAA7UZd3bJ1\nWr5jx9WX3xDrWNnQoUPTsWPH3HLLLc0+/qEPfSg33XTTOm1zQxKNAABAuzFy5KDU1j7QomVra3+f\nUaPes1HWsbKtt946kydPzimnnJKf/OQnWbx4cZYuXZqf/exnOeecczJ58uTccccdOeussxq/YuOl\nl17Ko4+u+bTXDUU0AgAA7cZJJ308u+xyfYuW3WWX6zNu3Mc3yjpWdcYZZ+Tyyy/PhRdemN69e2fH\nHXfMlVdemSOOOCK77LJL7rvvvvz5z3/Oe9/73nTt2jXDhg1Lv3798rWvfa1F41gfvnIDAADY7K34\nyo0k+f73b80ZZzyfF18cV1y+V6/v5PLL+2b06FHNPr4h1rEx+coNAACAt2n06FG57LI+GTjw7NVO\nM62tfSADB56dyy7rs8bY2xDreKcw0wgAAGz2Vp5pXGHJkiW5+uobMmvWo1mypDYdOy7LqFHvybhx\nH0/Hjh1btN4NsY6NYUPONIpGAABgs9dcNG7OnJ4KAABAqxCNAAAAFIlGAAAAikQjAAAARaIRAACA\nItEIAAC0a9VqNedMPme9rq66IdaxqRKNAABAu3bjzBvzf375f3LTrTe12TruvPPOvP/970+3bt3S\ns2fPDBs2LL/73e+SJM8//3zGjRuX7bbbLl27ds3gwYMzefLkLF68+G2Pd12IRgAAoN2qVquZeu3U\nLDpoUS6dcenbmilc33UsWrQohx9+eE477bQsXLgwzzzzTCZOnJiOHTtm4cKFGTp0aJYsWZL77rsv\nr7zySn7+85/nlVdeyZNPPrnOY307RCMAANBu3Tjzxjzc5eGkkjz8roff1kzh+q5j3rx5qVQqOeaY\nY1KpVNKxY8eMGDEie+yxRy677LJsvfXWufbaa7PDDjskSfr165fLL788e+yxxzqP9e0QjQAAQLu0\nYobw9R1fT5K83v/1dZ4p3BDr2G233VJbW5vjjz8+P/vZz/KXv/yl8bFf/OIXOeqoo1q8ro1BNAIA\nAO3SyjOESd7WTOGGWEeXLl1y5513pqamJieffHJ69eqVI444IvX19VmwYEG23Xbblu/URiAaAQCA\ndmfVGcIV1mWmcEOsY4WBAwfmu9/9bp5++uk88sgjefbZZzN+/Pj07Nkzzz33XIvXszGIRgAAoN1Z\nbYZwhXWYKdwQ62jObrvtluOOOy6PPPJIRowYkZtuevtXdd0QRCMAANCulGYIV2jJTOGGWMcKjz/+\neC6//PI888wzSZI///nPuf766zN06NCcccYZefXVV3Pcccfl6aefTpI888wzOfPMM/M///M/a133\nhiAaAQCAdqU4Q7hCC2YKN8Q6VujSpUvuu+++7LfffunSpUsOOOCA7LXXXpk6dWq6deuWe+65Jx06\ndMh+++2Xrl275sMf/nC6deuWXXbZZe07uwFUqm/ni0gAAADeQSqVSqrVaqrVaoYeMzT37X5fOfiS\npJrs98h+uedH96RSabrghljHxlapVHLdddelvr4+48ePX691mWkEAADajbXOEK6whpnCDbGOd5It\n2noAAAAAreWu++/KPsv2SeVPa5/5q1aruXPunTn68KM3+DreSZyeCgAAbPZWnJ7aXjg9FQAAgFYh\nGgEAACgSjQAAABSJRgAAAIpcPRUAANjs9e/fv9W/K7Et9enTZ4OtSzQCAACbvaeeeipJcsUVV6R3\n795tO5h3GNEIAAC0G7169Up9fX1bD6PV9OrVa73X4XsaAQAAKHIhHAAAAIpEIwAAAEWiEQAAgCLR\nCAAAQJFoBAAAoEg0AgAAUCQaAQAAKBKNAAAAFIlGAAAAikQjAAAARaIRAACAItEIAABAkWgEAACg\nSDQCAABQJBoBAAAoEo0AAAAUiUYAAACKRCMAAABFohEAAIAi0QjA/2+/DgQAAAAABPlbT7BBWQQA\nsKQRAACAJY0AAAAsaQQAAGAFQbrZbVCPPZoAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21a685fba8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_ct, y_ct = S2_2.ct.subs(datav)\n",
"\n",
"plt.figure(figsize=(12,8),dpi=300)\n",
"nx.draw(S2_2.g,with_labels=True, pos=positions)\n",
"plt.plot([0],[0],'o',ms=12,label='CG')\n",
"plt.plot([x_ct],[y_ct],'^',ms=12, label='SC')\n",
"#plt.text(0,0, 'CG', fontsize=24)\n",
"#plt.text(x_ct,y_ct, 'SC', fontsize=24)\n",
"plt.legend(loc='lower right', shadow=True)\n",
"plt.axis('equal')\n",
"plt.title(\"Section in pricipal reference Frame\",fontsize=16);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Expression of **inertial properties** in *principal reference frame*"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMQAAAAcBAMAAADM5Q0aAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMkS7zRCZdiKJ71Rm\nq90icBAQAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC3klEQVRIDaWUTWgTURDH/5tmm81HYxAPXiTr\nwYMHaUEUL5Jc/ACRLtaTIA2oiHhoToIFMSB4sIf2IOk1oqAnCQoieEguIgpWwYMHCerB+nExrV8t\nVeO89/bz7ZAIeZB9M//5zezuvMkCsVXf68S0iDAQiNCMk66NlRk5kAYCAepZmz1D7fmasRZVNG8g\nEOarwjEmwhKQt63VqKJ5A4Ewv0s4yVjnsz/CEGMPBIKcdJvss4HvWnn5djE5EAYCAYoPgOU+8haS\np+7KWD1EBKZR9u04YJ57WvDDrqG0C0C6opRJsR0Ul1xFXGMr2fUkBkg2zU9e2NuVNg9kmlLKfXVo\n3xD2TmyXknZZ8k+IAZ4B1zUeSsu3URSlgbmZGpAQVYwjj/YIRVvWA2+UOWA/0FKFgjSljU6Ie4lV\nvWxT096Rlen1urTpK5XyRpkD/gDjTS1FaakGTstAwmm1aX7PP9mncb67I/ub7Kv1Wf1hBWH+pFtU\nfVYarkad2S39YygSMX0YnSjne6Zt/KJO3oEcC192DWsdKC5EVVczVnBUBmzMV6idBfeOUVh4CVj0\npCfaOBWP0eRTLHYLpdGnYlmkGJ3O2wmIpt3mKpC2rdP5Bsw4+MgBfRplbai3SNApl4HPsFa4CqTZ\nwC3gJkweoKNtNbVUpdFbyEa16evXgLmKdEPjXDdH+xeY68h2WYBO9IWjRZRGn+1XFLDoAejPm+si\ns/BYA5U7R9skzA2MlB9yAI2+Gs1QUGk0UbMkXqPfyBrGythkL0houiw372I1yCrVcAhLL1kg3zRv\nQEuSGnINjDuY6h1AtvS3MtJGelFVzdMHMlhm6buD+71lnLy49bUt9SgAc/FSAZwG+ndnVEpQT1ls\nO8IQB3BasopR9eLhbGHzaojiAE6bdmA0Qnm+aVZ9kzc4gNPwnPLfcDXEkPZdHMBpeE9ljvctNWww\nJ5qXrQxbpl/+FRm81w8ZNnZm2AL/lf8PNIyxlBKATq4AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left ( A h^{2}, \\quad A a^{2}, \\quad 0, \\quad 0\\right )$$"
],
"text/plain": [
"⎛ 2 2 ⎞\n",
"⎝A⋅h , A⋅a , 0, 0⎠"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2_2.Ixx, S2_2.Iyy, S2_2.Ixy, S2_2.θ"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Shear center** expression "
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAACcAAAAyBAMAAAAtlt8uAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMA74lUMhDN3SKZdkRm\nu6vv56JYAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAA40lEQVQ4EWOQ//+JARkw/f8vwCDs4oosxsDq\n4izAIIIiBOKwDJAgx6RZohi2b2xg+4AuyCrDwHkBJsiaXg4EZQ6cXxnYF8AEYX5ivMAQ74AuGK/A\nYI/hzXgDhmvMDWh+Z1vAU8eErp31lUrfanRBqIUDFXQQ62lsO+ukQw4YFrEZsFZgCB5kYFDDELzH\nwGAfABZFcuc/Bob9BmiCrD+BggvQBDmA6dlfAV0QqBJDEKt2BqBF9ugWMdxlYDiP4SSg46eB7UFO\nDOwGrNCMguR4Vq11DhgqIQIgEkklzQWxZm1shQAA8CQ2z+cQjRIAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left[\\begin{matrix}- a\\\\0\\end{matrix}\\right]$$"
],
"text/plain": [
"⎡-a⎤\n",
"⎢ ⎥\n",
"⎣0 ⎦"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"S2_2.ct"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
thammegowda/notes | usc-csci-ml/hw4/src/CSCI567_hw4_fall16.ipynb | 2 | 32928 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using Theano backend.\n"
]
}
],
"source": [
"from hw_utils import *\n",
"from copy import copy\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Variables\n",
"\n",
"data_path = '../data/MiniBooNE_PID.txt'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load Data"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Train X, Y : (104051, 50) (104051, 2)\n",
"Test X, Y : (26013, 50) (26013, 2)\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/thammegr/anaconda/lib/python2.7/site-packages/keras/utils/np_utils.py:14: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future\n",
" Y = np.zeros((len(y), nb_classes))\n",
"/Users/thammegr/anaconda/lib/python2.7/site-packages/keras/utils/np_utils.py:16: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future\n",
" Y[i, y[i]] = 1.\n"
]
}
],
"source": [
"## (c)\n",
"X_tr, Y_tr, X_te, Y_te = loaddata(data_path)\n",
"print \"Train X, Y :\", X_tr.shape, Y_tr.shape\n",
"print \"Test X, Y :\", X_te.shape, Y_te.shape\n",
"X_tr, X_te = normalize(X_tr, X_te)\n",
"d_in = X_tr.shape[1] # input features\n",
"d_out = Y_tr.shape[1] # Output predictions"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Train X, Y : (100, 50) (100, 2)\n",
"\n",
"\n",
"## (d) Linear Activation \n",
"architecture=[50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.65000000596 | time=1.86916589737\n",
"architecture=[50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.90000000596 | time=0.925344944\n",
"architecture=[50, 50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.799999982119 | time=1.17178320885\n",
"architecture=[50, 50, 50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.84999999404 | time=1.22634387016\n",
"Best Config: architecture = [50, 50, 2], lambda = 0.0, decay = 0.0, momentum = 0.0, actfn = linear, best_acc = 0.90000000596\n",
"Mean Time = 1.29815948009seconds, |Models| = 4, Total Time = 5.19263792038seconds\n",
"architecture=[50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.90000000596 | time=1.06496405602\n",
"architecture=[50, 500, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.84999999404 | time=0.992525100708\n",
"architecture=[50, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.899999976158 | time=1.31494212151\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.899999976158 | time=1.4492418766\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=linear: score=0.899999976158 | time=2.16674518585\n",
"Best Config: architecture = [50, 50, 2], lambda = 0.0, decay = 0.0, momentum = 0.0, actfn = linear, best_acc = 0.90000000596\n",
"Mean Time = 1.39768366814seconds, |Models| = 5, Total Time = 6.98841834068seconds\n"
]
}
],
"source": [
"## (d)\n",
"\n",
"# default args\n",
"args = {\n",
" 'actfn':'linear',\n",
" 'last_act':'softmax',\n",
" 'reg_coeffs': [0.0],\n",
" 'num_epoch': 30,\n",
" 'batch_size': 1000,\n",
" 'sgd_lr': 0.001,\n",
" 'sgd_decays': [0.0],\n",
" 'sgd_moms': [0.0],\n",
" 'sgd_Nesterov': False,\n",
" 'EStop': False,\n",
" 'verbose': False\n",
"}\n",
"\n",
"# FIXME: BEGIN : For quick testing.. Remove this later\n",
"args['batch_size'] = 10\n",
"X_tr, Y_tr = X_tr[0:100], Y_tr[:100]\n",
"X_te, Y_te = X_te[0:20], Y_te[:20]\n",
"print \"Train X, Y :\", X_tr.shape, Y_tr.shape\n",
"\n",
"# FIXME: END\n",
"\n",
"print(\"\\n\\n## (d) Linear Activation \")\n",
"archs = [[d_in, d_out], [d_in, 50, d_out], [d_in, 50, 50, d_out], [d_in, 50, 50, 50, d_out]]\n",
"res = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)\n",
"\n",
"archs = [[d_in, 50, d_out], [d_in, 500, d_out], [d_in, 500, 300, d_out],\n",
" [d_in, 800, 500, 300, d_out], [d_in, 800, 800, 500, 300, d_out]]\n",
"res = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (e) Sigmoid Activation\n",
"architecture=[50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=sigmoid: score=0.59999999404 | time=0.977607965469\n",
"architecture=[50, 500, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=sigmoid: score=0.59999999404 | time=1.02421379089\n",
"architecture=[50, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=sigmoid: score=0.59999999404 | time=1.30875492096\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=sigmoid: score=0.59999999404 | time=1.70223593712\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=sigmoid: score=0.59999999404 | time=2.83162212372\n",
"Best Config: architecture = [50, 50, 2], lambda = 0.0, decay = 0.0, momentum = 0.0, actfn = sigmoid, best_acc = 0.59999999404\n",
"Mean Time = 1.56888694763seconds, |Models| = 5, Total Time = 7.84443473816seconds\n"
]
}
],
"source": [
"# (e)\n",
"print(\"\\n\\n## (e) Sigmoid Activation\")\n",
"args['actfn'] = 'sigmoid'\n",
"_ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (f) ReLu Activation\n",
"architecture=[50, 50, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=relu: score=0.550000011921 | time=1.23269987106\n",
"architecture=[50, 500, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=relu: score=0.84999999404 | time=0.984317064285\n",
"architecture=[50, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=relu: score=0.800000011921 | time=1.41553783417\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=relu: score=0.700000017881 | time=1.92823719978\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=0.0, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=2.5575799942\n",
"Best Config: architecture = [50, 500, 2], lambda = 0.0, decay = 0.0, momentum = 0.0, actfn = relu, best_acc = 0.84999999404\n",
"Mean Time = 1.6236743927seconds, |Models| = 5, Total Time = 8.1183719635seconds\n"
]
}
],
"source": [
"# (f)\n",
"print(\"\\n\\n## (f) ReLu Activation\")\n",
"args['actfn'] = 'relu'\n",
"args['sgd_lr'] = 5e-4\n",
"_ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (g) Regularization Coefficients\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=0.0, momentum=0.0, actfn=relu: score=0.65000000596 | time=3.26436805725\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=3.47442913055\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-06, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=3.42006278038\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-06, decay=0.0, momentum=0.0, actfn=relu: score=0.700000017881 | time=3.3063929081\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-05, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=3.420814991\n",
"Best Config: architecture = [50, 800, 500, 300, 2], lambda = 5e-06, decay = 0.0, momentum = 0.0, actfn = relu, best_acc = 0.700000017881\n",
"Mean Time = 3.37721357346seconds, |Models| = 5, Total Time = 16.8860678673seconds\n",
"('Best Regularization Coefficient=', 5e-06)\n"
]
}
],
"source": [
"# (g)\n",
"print(\"\\n\\n## (g) Regularization Coefficients\")\n",
"archs = [[d_in, 800, 500, 300, d_out]]\n",
"args['reg_coeffs'] = [1e-7, 5e-7, 1e-6, 5e-6, 1e-5]\n",
"best, _ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)\n",
"best_lambda_noEstop = best[1]\n",
"print(\"Best Regularization Coefficient=\", best_lambda_noEstop)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (h) Regularization Coefficients -- Early stop\n",
"Epoch 00022: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=0.0, momentum=0.0, actfn=relu: score=0.800000011921 | time=2.89277601242\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=2.30634999275\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-06, decay=0.0, momentum=0.0, actfn=relu: score=0.800000011921 | time=2.31239390373\n",
"Epoch 00020: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-06, decay=0.0, momentum=0.0, actfn=relu: score=0.799999982119 | time=2.92426681519\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-05, decay=0.0, momentum=0.0, actfn=relu: score=0.59999999404 | time=2.315128088\n",
"Best Config: architecture = [50, 800, 500, 300, 2], lambda = 1e-07, decay = 0.0, momentum = 0.0, actfn = relu, best_acc = 0.800000011921\n",
"Mean Time = 2.55018296242seconds, |Models| = 5, Total Time = 12.7509148121seconds\n",
"('Best Regularization Coefficient with early stopping=', 1e-07)\n"
]
}
],
"source": [
"# (h)\n",
"print(\"\\n\\n## (h) Regularization Coefficients -- Early stop\")\n",
"args['EStop'] = True\n",
"best, _ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)\n",
"best_lambda_EStop = best[1]\n",
"print(\"Best Regularization Coefficient with early stopping=\", best_lambda_EStop)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (i) SGD Decay\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=1e-05, momentum=0.0, actfn=relu: score=0.59999999404 | time=6.84515190125\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=5e-05, momentum=0.0, actfn=relu: score=0.75 | time=8.42867708206\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0001, momentum=0.0, actfn=relu: score=0.799999982119 | time=6.8960351944\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0003, momentum=0.0, actfn=relu: score=0.350000008941 | time=6.87825584412\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0007, momentum=0.0, actfn=relu: score=0.550000011921 | time=6.68029594421\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.001, momentum=0.0, actfn=relu: score=0.45000000298 | time=6.56511807442\n",
"Best Config: architecture = [50, 800, 500, 300, 2], lambda = 5e-07, decay = 0.0001, momentum = 0.0, actfn = relu, best_acc = 0.799999982119\n",
"Mean Time = 7.04892234008seconds, |Models| = 6, Total Time = 42.2935340405seconds\n",
"('Best Decay', 0.0001)\n"
]
}
],
"source": [
"# (i)\n",
"print(\"\\n\\n## (i) SGD Decay\")\n",
"args['reg_coeffs'] = [5e-7]\n",
"args['num_epoch'] = 100\n",
"args['sgd_lr'] = 1e-5\n",
"args['sgd_decays'] = [1e-5, 5e-5, 1e-4, 3e-4, 7e-4, 1e-3]\n",
"args['EStop'] = False\n",
"best, _ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)\n",
"best_decay = best[2]\n",
"print(\"Best Decay\", best_decay)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (j) SGD Momentum\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0001, momentum=0.99, actfn=relu: score=0.65000000596 | time=3.50205802917\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0001, momentum=0.98, actfn=relu: score=0.65000000596 | time=3.60273885727\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0001, momentum=0.95, actfn=relu: score=0.59999999404 | time=3.38674712181\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0001, momentum=0.9, actfn=relu: score=0.75 | time=3.39339518547\n",
"architecture=[50, 800, 500, 300, 2], lambda=0.0, decay=0.0001, momentum=0.85, actfn=relu: score=0.550000011921 | time=3.41920590401\n",
"Best Config: architecture = [50, 800, 500, 300, 2], lambda = 0.0, decay = 0.0001, momentum = 0.9, actfn = relu, best_acc = 0.75\n",
"Mean Time = 3.46082901955seconds, |Models| = 5, Total Time = 17.3041450977seconds\n",
"('Best moemntum', 0.9)\n"
]
}
],
"source": [
"# (j)\n",
"print(\"\\n\\n## (j) SGD Momentum\")\n",
"args['reg_coeffs'] = [0.0]\n",
"args['num_epoch'] = 50\n",
"args['sgd_decays'] = [best_decay] # TODO: get this from the best value of previous step\n",
"args['sgd_Nesterov'] = True\n",
"args['sgd_moms']= [0.99, 0.98, 0.95, 0.9, 0.85]\n",
"best, _ = testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)\n",
"best_mom = best[3]\n",
"print(\"Best moemntum\", best_mom)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (k) Combining all\n",
"Epoch 00014: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=0.0001, momentum=0.9, actfn=relu: score=0.65000000596 | time=3.09857201576\n",
"Best Config: architecture = [50, 800, 500, 300, 2], lambda = 1e-07, decay = 0.0001, momentum = 0.9, actfn = relu, best_acc = 0.65000000596\n",
"Mean Time = 3.09857201576seconds, |Models| = 1, Total Time = 3.09857201576seconds\n"
]
},
{
"data": {
"text/plain": [
"([[50, 800, 500, 300, 2], 1e-07, 0.0001, 0.9, 'relu', 0.65000000596046448],\n",
" array([ 3.09857202]))"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# (k)\n",
"print(\"\\n\\n## (k) Combining all\")\n",
"args['num_epoch'] = 100\n",
"args['sgd_lr'] = 1e-5\n",
"args['sgd_Nesterov'] = True\n",
"args['EStop'] = True\n",
"\n",
"#TODO: Best values from previous steps\n",
"args['sgd_decays'] = [best_decay]\n",
"args['sgd_moms']= [best_mom]\n",
"args['reg_coeffs'] = [best_lambda_EStop]\n",
"\n",
"testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"\n",
"## (j) Grid Search \n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.899999976158 | time=1.21030306816\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.2862830162\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=1.39065003395\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.25 | time=1.21554899216\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.25 | time=1.33358192444\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.300000011921 | time=1.34109997749\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.15000000596 | time=1.25166296959\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.30975294113\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.699999988079 | time=1.35929894447\n",
"Epoch 00012: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.31907081604\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.550000011921 | time=1.33358502388\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=5e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.699999988079 | time=1.47901797295\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-05, decay=1e-05, momentum=0.99, actfn=relu: score=0.40000000596 | time=1.31222605705\n",
"Epoch 00009: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-05, decay=5e-05, momentum=0.99, actfn=relu: score=0.649999976158 | time=1.47111296654\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 50, 2], lambda=1e-05, decay=0.0001, momentum=0.99, actfn=relu: score=0.25 | time=1.27420687675\n",
"Epoch 00010: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.46441507339\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.34999999404 | time=1.4722058773\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.15000000596 | time=1.31370186806\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.300000011921 | time=1.3919467926\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.38250207901\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.37583708763\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.36326503754\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.24810910225\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.800000011921 | time=1.37515521049\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.300000011921 | time=1.38642597198\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.28251886368\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=5e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.35393500328\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-05, decay=1e-05, momentum=0.99, actfn=relu: score=0.550000011921 | time=1.23606085777\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-05, decay=5e-05, momentum=0.99, actfn=relu: score=0.699999988079 | time=1.32297897339\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 2], lambda=1e-05, decay=0.0001, momentum=0.99, actfn=relu: score=0.699999988079 | time=1.31705713272\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.72202992439\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.800000011921 | time=1.77702879906\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.85370397568\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.5 | time=1.79700708389\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.34999999404 | time=1.84643912315\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.5 | time=1.83488607407\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=1.68571710587\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.850000023842 | time=1.80838012695\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=1.81895780563\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.5 | time=1.83311510086\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.5 | time=1.68818712234\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=5e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.34999999404 | time=1.85359096527\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-05, decay=1e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=1.98514699936\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-05, decay=5e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=2.13911509514\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 500, 300, 2], lambda=1e-05, decay=0.0001, momentum=0.99, actfn=relu: score=0.15000000596 | time=1.99159502983\n",
"Epoch 00008: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=2.97883582115\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=2.65910792351\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=2.57715702057\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.40000000596 | time=2.76571798325\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=2.67143392563\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=2.74462294579\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.449999988079 | time=2.81343007088\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=2.76092219353\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.649999976158 | time=2.72733187675\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.800000011921 | time=2.41824197769\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=2.54658317566\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=5e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.550000011921 | time=2.38805699348\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-05, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=2.25120592117\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-05, decay=5e-05, momentum=0.99, actfn=relu: score=0.800000011921 | time=2.45753717422\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 500, 300, 2], lambda=1e-05, decay=0.0001, momentum=0.99, actfn=relu: score=0.34999999404 | time=2.56502890587\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.699999988079 | time=3.2302839756\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.300000011921 | time=3.14152598381\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.25892901421\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-07, decay=1e-05, momentum=0.99, actfn=relu: score=0.600000023842 | time=3.30806398392\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-07, decay=5e-05, momentum=0.99, actfn=relu: score=0.649999976158 | time=3.17942905426\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-07, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.21294498444\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.48409605026\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.06573796272\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.17743301392\n",
"Epoch 00011: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-06, decay=1e-05, momentum=0.99, actfn=relu: score=0.75 | time=3.32091283798\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-06, decay=5e-05, momentum=0.99, actfn=relu: score=0.75 | time=3.04501795769\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=5e-06, decay=0.0001, momentum=0.99, actfn=relu: score=0.550000011921 | time=3.07281899452\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-05, decay=1e-05, momentum=0.99, actfn=relu: score=0.699999988079 | time=3.09461283684\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-05, decay=5e-05, momentum=0.99, actfn=relu: score=0.649999976158 | time=3.05219483376\n",
"Epoch 00007: early stopping\n",
"architecture=[50, 800, 800, 500, 300, 2], lambda=1e-05, decay=0.0001, momentum=0.99, actfn=relu: score=0.40000000596 | time=3.06941986084\n",
"Best Config: architecture = [50, 50, 2], lambda = 1e-07, decay = 1e-05, momentum = 0.99, actfn = relu, best_acc = 0.899999976158\n",
"Mean Time = 2.0646273613seconds, |Models| = 75, Total Time = 154.847052097seconds\n"
]
},
{
"data": {
"text/plain": [
"([[50, 50, 2], 1e-07, 1e-05, 0.99, 'relu', 0.89999997615814209],\n",
" array([ 1.21030307, 1.28628302, 1.39065003, 1.21554899, 1.33358192,\n",
" 1.34109998, 1.25166297, 1.30975294, 1.35929894, 1.31907082,\n",
" 1.33358502, 1.47901797, 1.31222606, 1.47111297, 1.27420688,\n",
" 1.46441507, 1.47220588, 1.31370187, 1.39194679, 1.38250208,\n",
" 1.37583709, 1.36326504, 1.2481091 , 1.37515521, 1.38642597,\n",
" 1.28251886, 1.353935 , 1.23606086, 1.32297897, 1.31705713,\n",
" 1.72202992, 1.7770288 , 1.85370398, 1.79700708, 1.84643912,\n",
" 1.83488607, 1.68571711, 1.80838013, 1.81895781, 1.8331151 ,\n",
" 1.68818712, 1.85359097, 1.985147 , 2.1391151 , 1.99159503,\n",
" 2.97883582, 2.65910792, 2.57715702, 2.76571798, 2.67143393,\n",
" 2.74462295, 2.81343007, 2.76092219, 2.72733188, 2.41824198,\n",
" 2.54658318, 2.38805699, 2.25120592, 2.45753717, 2.56502891,\n",
" 3.23028398, 3.14152598, 3.25892901, 3.30806398, 3.17942905,\n",
" 3.21294498, 3.48409605, 3.06573796, 3.17743301, 3.32091284,\n",
" 3.04501796, 3.07281899, 3.09461284, 3.05219483, 3.06941986]))"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# (l) Grid Search\n",
"print(\"\\n\\n## (j) Grid Search \")\n",
"archs = [[d_in, 50, d_out], [d_in, 500, d_out], [d_in, 500, 300, d_out],\n",
" [d_in, 800, 500, 300, d_out], [d_in, 800, 800, 500, 300, d_out]]\n",
"args = {\n",
" 'actfn':'relu',\n",
" 'last_act':'softmax',\n",
" 'num_epoch': 100,\n",
" 'batch_size': 1000,\n",
" 'sgd_lr': 1e-5,\n",
" 'sgd_Nesterov': True,\n",
" 'sgd_moms': [0.99],\n",
" 'EStop': True,\n",
" 'verbose': False,\n",
" 'reg_coeffs': [1e-7, 5e-7, 1e-6, 5e-6, 1e-5],\n",
" 'sgd_decays': [1e-5, 5e-5, 1e-4],\n",
"}\n",
"testmodels(X_tr, Y_tr, X_te, Y_te, archs, **args)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| apache-2.0 |
tensorflow/neural-structured-learning | workshops/kdd_2020/adversarial_regularization_mnist.ipynb | 1 | 45218 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "375gw63MC9Hg"
},
"source": [
"##### Copyright 2020 Google LLC"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "6gaVU4XhC_rb"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "HxR_1l6_Oyj4"
},
"source": [
"# Adversarial Regularization for Image Classification\n",
"\n",
"The core idea of adversarial learning is to train a model with\n",
"adversarially-perturbed data (called adversarial examples) in addition to the\n",
"organic training data. The adversarial examples are constructed to intentionally\n",
"mislead the model into making wrong predictions or classifications. By training\n",
"with such examples, the model learns to be robust against adversarial\n",
"perturbation when making predictions.\n",
"\n",
"In this tutorial, we illustrate the following procedure of applying adversarial\n",
"learning to obtain robust models using the Neural Structured Learning framework:\n",
"\n",
"1. Create a neural network as a base model. In this tutorial, the base model is\n",
" created with the `tf.keras` functional API; this procedure is compatible\n",
" with models created by `tf.keras` sequential and subclassing APIs as well.\n",
"2. Wrap the base model with the **`AdversarialRegularization`** wrapper class,\n",
" which is provided by the NSL framework, to create a new `tf.keras.Model`\n",
" instance. This new model will include the adversarial loss as a\n",
" regularization term in its training objective.\n",
"3. Convert examples in the training data to feature dictionaries.\n",
"4. Train and evaluate the new model.\n",
"\n",
"Both the base and the new model will be evaluated against natural and\n",
"adversarial inputs."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "Keu58kiDPNDB"
},
"source": [
"## Setup\n",
"\n",
"Install the Neural Structured Learning package."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "plo5qfYlPKwQ"
},
"outputs": [],
"source": [
"!pip install --quiet neural-structured-learning"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "Mi_rYRjCPVuB"
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import tensorflow as tf\n",
"import tensorflow_datasets as tfds\n",
"import numpy as np\n",
"import neural_structured_learning as nsl"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "23fiFpOJP6ab"
},
"source": [
"## Hyperparameters\n",
"\n",
"We collect and explain the hyperparameters (in an `HParams` object) for model\n",
"training and evaluation.\n",
"\n",
"Input/Output:\n",
"\n",
"* **`input_shape`**: The shape of the input tensor. Each image is 28-by-28\n",
"pixels with 1 channel.\n",
"* **`num_classes`**: There are a total of 10 classes, corresponding to 10\n",
"digits [0-9].\n",
"\n",
"Model architecture:\n",
"\n",
"* **`conv_filters`**: A list of numbers, each specifying the number of\n",
"filters in a convolutional layer.\n",
"* **`kernel_size`**: The size of 2D convolution window, shared by all\n",
"convolutional layers.\n",
"* **`pool_size`**: Factors to downscale the image in each max-pooling layer.\n",
"* **`num_fc_units`**: The number of units (i.e., width) of each\n",
"fully-connected layer.\n",
"\n",
"Training and evaluation:\n",
"\n",
"* **`batch_size`**: Batch size used for training and evaluation.\n",
"* **`epochs`**: The number of training epochs.\n",
"\n",
"Adversarial learning:\n",
"\n",
"* **`adv_multiplier`**: The weight of adversarial loss in the training\n",
" objective, relative to the labeled loss.\n",
"* **`adv_step_size`**: The magnitude of adversarial perturbation.\n",
"* **`adv_grad_norm`**: The norm to measure the magnitude of adversarial\n",
" perturbation.\n",
"* **`pgd_iterations`**: The number of iterative steps to take when using PGD.\n",
"* **`pgd_epsilon`**: The bounds of the perturbation. PGD will project back to\n",
" this epsilon ball when generating the adversary.\n",
"* **`clip_value_min`**: Clips the final adversary to be at least as large as\n",
" this value. This keeps the perturbed pixel values in a valid domain.\n",
"* **`clip_value_max`**: Clips the final adversary to be no larger than this\n",
" value. This also keeps the perturbed pixel values in a valid domain.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "BVVJErI8P2SK"
},
"outputs": [],
"source": [
"class HParams(object):\n",
" def __init__(self):\n",
" self.input_shape = [28, 28, 1]\n",
" self.num_classes = 10\n",
" self.conv_filters = [32, 64, 64]\n",
" self.kernel_size = (3, 3)\n",
" self.pool_size = (2, 2)\n",
" self.num_fc_units = [64]\n",
" self.batch_size = 32\n",
" self.epochs = 5\n",
" self.adv_multiplier = 0.2\n",
" self.adv_step_size = 0.01\n",
" self.adv_grad_norm = 'infinity'\n",
" self.pgd_iterations = 40\n",
" self.pgd_epsilon = 0.2\n",
" self.clip_value_min = 0.0\n",
" self.clip_value_max = 1.0\n",
"\n",
"HPARAMS = HParams()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "FcLusOXeRGoF"
},
"source": [
"## MNIST dataset\n",
"\n",
"The [MNIST dataset](http://yann.lecun.com/exdb/mnist/) contains grayscale\n",
"images of handwritten digits (from '0' to '9'). Each image showes one digit at\n",
"low resolution (28-by-28 pixels). The task involved is to classify images into\n",
"10 categories, one per digit.\n",
"\n",
"Here we load the MNIST dataset from\n",
"[TensorFlow Datasets](https://www.tensorflow.org/datasets). It handles\n",
"downloading the data and constructing a `tf.data.Dataset`. The loaded dataset\n",
"has two subsets:\n",
"\n",
"* `train` with 60,000 examples, and\n",
"* `test` with 10,000 examples.\n",
"\n",
"Examples in both subsets are stored in feature dictionaries with the following\n",
"two keys:\n",
"\n",
"* `image`: Array of pixel values, ranging from 0 to 255.\n",
"* `label`: Groundtruth label, ranging from 0 to 9."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "Mb03tb2_RFtF"
},
"outputs": [],
"source": [
"datasets = tfds.load('mnist')\n",
"\n",
"train_dataset = datasets['train']\n",
"test_dataset = datasets['test']\n",
"\n",
"IMAGE_INPUT_NAME = 'image'\n",
"LABEL_INPUT_NAME = 'label'"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "YDXCb187RMO1"
},
"source": [
"To make the model numerically stable, we normalize the pixel values to [0, 1]\n",
"by mapping the dataset over the `normalize` function. After shuffling training\n",
"set and batching, we convert the examples to feature tuples `(image, label)`\n",
"for training the base model. We also provide a function to convert from tuples\n",
"to dictionaries for later use."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "tPWcdkhGRN-F"
},
"outputs": [],
"source": [
"def normalize(features):\n",
" features[IMAGE_INPUT_NAME] = tf.cast(\n",
" features[IMAGE_INPUT_NAME], dtype=tf.float32) / 255.0\n",
" return features\n",
"\n",
"def convert_to_tuples(features):\n",
" return features[IMAGE_INPUT_NAME], features[LABEL_INPUT_NAME]\n",
"\n",
"def convert_to_dictionaries(image, label):\n",
" return {IMAGE_INPUT_NAME: image, LABEL_INPUT_NAME: label}\n",
"\n",
"train_dataset = train_dataset.map(normalize).shuffle(10000).batch(HPARAMS.batch_size).map(convert_to_tuples)\n",
"test_dataset = test_dataset.map(normalize).batch(HPARAMS.batch_size).map(convert_to_tuples)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "489axd64RZ5l"
},
"source": [
"## Base model\n",
"\n",
"Our base model will be a neural network consisting of 3 convolutional layers\n",
"follwed by 2 fully-connected layers (as defined in `HPARAMS`). Here we define\n",
"it using the Keras functional API. Feel free to try other APIs or model\n",
"architectures."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "dcipiJgqRolw"
},
"outputs": [],
"source": [
"def build_base_model(hparams):\n",
" \"\"\"Builds a model according to the architecture defined in `hparams`.\"\"\"\n",
" inputs = tf.keras.Input(\n",
" shape=hparams.input_shape, dtype=tf.float32, name=IMAGE_INPUT_NAME)\n",
"\n",
" x = inputs\n",
" for i, num_filters in enumerate(hparams.conv_filters):\n",
" x = tf.keras.layers.Conv2D(\n",
" num_filters, hparams.kernel_size, activation='relu')(\n",
" x)\n",
" if i \u003c len(hparams.conv_filters) - 1:\n",
" # max pooling between convolutional layers\n",
" x = tf.keras.layers.MaxPooling2D(hparams.pool_size)(x)\n",
" x = tf.keras.layers.Flatten()(x)\n",
" for num_units in hparams.num_fc_units:\n",
" x = tf.keras.layers.Dense(num_units, activation='relu')(x)\n",
" pred = tf.keras.layers.Dense(hparams.num_classes, activation=None)(x)\n",
" # pred = tf.keras.layers.Dense(hparams.num_classes, activation='softmax')(x)\n",
" model = tf.keras.Model(inputs=inputs, outputs=pred)\n",
" return model"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "tJViTSlgRr_H"
},
"outputs": [],
"source": [
"base_model = build_base_model(HPARAMS)\n",
"base_model.summary()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "kUuJ1cNcRw8e"
},
"source": [
"Next we train and evaluate the base model."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "PuUwF4Y3R1iv"
},
"outputs": [],
"source": [
"base_model.compile(optimizer='adam',\n",
" loss=tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True),\n",
" metrics=['acc'])\n",
"base_model.fit(train_dataset, epochs=HPARAMS.epochs)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "VfEjXHO7R28n"
},
"outputs": [],
"source": [
"results = base_model.evaluate(test_dataset)\n",
"named_results = dict(zip(base_model.metrics_names, results))\n",
"print('\\naccuracy:', named_results['acc'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "HS5WMFrfTpdT"
},
"source": [
"## Adversarial-regularized model\n",
"\n",
"Here we show how to incorporate adversarial training into a Keras model with a\n",
"few lines of code, using the NSL framework. The base model is wrapped to create\n",
"a new `tf.Keras.Model`, whose training objective includes adversarial\n",
"regularization.\n",
"\n",
"We will train one using the FGSM adversary and one using a stronger PGD\n",
"adversary.\n",
"\n",
"First, we create config objects with relevant hyperparameters."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "DMUkmsk2TpGv"
},
"outputs": [],
"source": [
"fgsm_adv_config = nsl.configs.make_adv_reg_config(\n",
" multiplier=HPARAMS.adv_multiplier,\n",
" # With FGSM, we want to take a single step equal to the epsilon ball size,\n",
" # to get the largest allowable perturbation.\n",
" adv_step_size=HPARAMS.pgd_epsilon,\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" clip_value_min=HPARAMS.clip_value_min,\n",
" clip_value_max=HPARAMS.clip_value_max\n",
")\n",
"\n",
"pgd_adv_config = nsl.configs.make_adv_reg_config(\n",
" multiplier=HPARAMS.adv_multiplier,\n",
" adv_step_size=HPARAMS.adv_step_size,\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" pgd_iterations=HPARAMS.pgd_iterations,\n",
" pgd_epsilon=HPARAMS.pgd_epsilon,\n",
" clip_value_min=HPARAMS.clip_value_min,\n",
" clip_value_max=HPARAMS.clip_value_max\n",
")"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "aRMh8rm5UYCg"
},
"source": [
"Now we can wrap a base model with `AdversarialRegularization`. Here we create \n",
"new base models (`base_fgsm_model`, `base_pgd_model`), so that the existing one\n",
"(`base_model`) can be used in later comparison.\n",
"\n",
"The returned `adv_model` is a `tf.keras.Model` object, whose training objective\n",
"includes a regularization term for the adversarial loss. To compute that loss,\n",
"the model has to have access to the label information (feature `label`), in\n",
"addition to regular input (feature `image`). For this reason, we convert the\n",
"examples in the datasets from tuples back to dictionaries. And we tell the\n",
"model which feature contains the label information via the `label_keys`\n",
"parameter.\n",
"\n",
"We will create two adversarially regularized models: `fgsm_adv_model`\n",
"(regularized with FGSM) and `pgd_adv_model` (regularized with PGD)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "Ce676AY8UhM5"
},
"outputs": [],
"source": [
"# Create model for FGSM.\n",
"base_fgsm_model = build_base_model(HPARAMS)\n",
"# Create FGSM-regularized model.\n",
"fgsm_adv_model = nsl.keras.AdversarialRegularization(\n",
" base_fgsm_model,\n",
" label_keys=[LABEL_INPUT_NAME],\n",
" adv_config=fgsm_adv_config\n",
")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "-e7lxy80UvNP"
},
"outputs": [],
"source": [
"# Create model for PGD.\n",
"base_pgd_model = build_base_model(HPARAMS)\n",
"# Create PGD-regularized model.\n",
"pgd_adv_model = nsl.keras.AdversarialRegularization(\n",
" base_pgd_model,\n",
" label_keys=[LABEL_INPUT_NAME],\n",
" adv_config=pgd_adv_config\n",
")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "Nci891oNU_C4"
},
"outputs": [],
"source": [
"# Data for training.\n",
"train_set_for_adv_model = train_dataset.map(convert_to_dictionaries)\n",
"test_set_for_adv_model = test_dataset.map(convert_to_dictionaries)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "CTbwMW8YVCyu"
},
"source": [
"Next we compile, train, and evaluate the\n",
"adversarial-regularized model. There might be warnings like\n",
"\"Output missing from loss dictionary,\" which is fine because\n",
"the `adv_model` doesn't rely on the base implementation to\n",
"calculate the total loss."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "-SmhMHhkVEfm"
},
"outputs": [],
"source": [
"fgsm_adv_model.compile(optimizer='adam',\n",
" loss=tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True),\n",
" metrics=['acc'])\n",
"fgsm_adv_model.fit(train_set_for_adv_model, epochs=HPARAMS.epochs)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "NUrv3hwmVV0E"
},
"outputs": [],
"source": [
"results = fgsm_adv_model.evaluate(test_set_for_adv_model)\n",
"named_results = dict(zip(fgsm_adv_model.metrics_names, results))\n",
"print('\\naccuracy:', named_results['sparse_categorical_accuracy'])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "nyXwibwdVcYY"
},
"outputs": [],
"source": [
"pgd_adv_model.compile(optimizer='adam',\n",
" loss=tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True),\n",
" metrics=['acc'])\n",
"pgd_adv_model.fit(train_set_for_adv_model, epochs=HPARAMS.epochs)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "sTfLmGyc_VTJ"
},
"outputs": [],
"source": [
"results = pgd_adv_model.evaluate(test_set_for_adv_model)\n",
"named_results = dict(zip(pgd_adv_model.metrics_names, results))\n",
"print('\\naccuracy:', named_results['sparse_categorical_accuracy'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "oAwpl_IkWTsV"
},
"source": [
"Both adversarially regularized models perform well on the test set."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "iLShGGJ6WXll"
},
"source": [
"## Robustness under Adversarial Perturbations\n",
"\n",
"Now we compare the base model and the adversarial-regularized model for\n",
"robustness under adversarial perturbation.\n",
"\n",
"We will show how the base model is vulnerable to attacks from both FGSM and PGD,\n",
"the FGSM-regularized model can resist FGSM attacks but is vulnerable to PGD, and\n",
"the PGD-regularized model is able to resist both forms of attack.\n",
"\n",
"We use `gen_adv_neighbor` to generate adversaries for our models."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "DxoVVC3evZ4C"
},
"source": [
"### Attacking the Base Model"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "UyMn0wLAEWuQ"
},
"outputs": [],
"source": [
"# Set up the neighbor config for FGSM.\n",
"fgsm_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.pgd_epsilon,\n",
" clip_value_min=0.0,\n",
" clip_value_max=1.0,\n",
")\n",
"\n",
"# The labeled loss function provides the loss for each sample we pass in. This\n",
"# will be used to calculate the gradient.\n",
"labeled_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True,\n",
")\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "jpM-5en5vY59"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using FGSM on the base model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"# We want to record the accuracy.\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Record the loss calculation to get the gradient.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" base_model(batch[IMAGE_INPUT_NAME]))\n",
" \n",
" # Generate the adversarial example.\n",
" fgsm_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" fgsm_nbr_config,\n",
" gradient_tape=tape\n",
" )\n",
"\n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = base_model(fgsm_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for later use.\n",
" perturbed_images.append(fgsm_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "vQL2qWI8-h8G"
},
"source": [
"Let's examine what some of these images look like."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "MpMs1syT_p0o"
},
"outputs": [],
"source": [
"def examine_images(perturbed_images, labels, predictions, model_key):\n",
" batch_index = 0\n",
"\n",
" batch_image = perturbed_images[batch_index]\n",
" batch_label = labels[batch_index]\n",
" batch_pred = predictions[batch_index]\n",
"\n",
" batch_size = HPARAMS.batch_size\n",
" n_col = 4\n",
" n_row = (batch_size + n_col - 1) / n_col\n",
"\n",
" print('accuracy in batch %d:' % batch_index)\n",
" print('%s model: %d / %d' %\n",
" (model_key, np.sum(batch_label == batch_pred), batch_size))\n",
"\n",
" plt.figure(figsize=(15, 15))\n",
" for i, (image, y) in enumerate(zip(batch_image, batch_label)):\n",
" y_base = batch_pred[i]\n",
" plt.subplot(n_row, n_col, i+1)\n",
" plt.title('true: %d, %s: %d' % (y, model_key, y_base), color='r'\n",
" if y != y_base else 'k')\n",
" plt.imshow(tf.keras.preprocessing.image.array_to_img(image), cmap='gray')\n",
" plt.axis('off')\n",
"\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "kr_lkBtM966D"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'base')"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "y8V2ssdF-md7"
},
"source": [
"Our perturbation budget of 0.2 is quite large, but even so, the perturbed\n",
"numbers are clearly recognizable to the human eye. On the other hand, our\n",
"network is fooled into misclassifying several examples.\n",
"\n",
"As we can see, the FGSM attack is already highly effective, and quick to\n",
"execute, heavily reducing the model accuracy. We will see below, that the PGD\n",
"attack is even more effective, even with the same perturbation budget."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "qMbG-KbjGFlB"
},
"outputs": [],
"source": [
"# Set up the neighbor config for PGD.\n",
"pgd_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.adv_step_size,\n",
" pgd_iterations=HPARAMS.pgd_iterations,\n",
" pgd_epsilon=HPARAMS.pgd_epsilon,\n",
" clip_value_min=HPARAMS.clip_value_min,\n",
" clip_value_max=HPARAMS.clip_value_max,\n",
")\n",
"\n",
"# pgd_model_fn generates a prediction from which we calculate the loss, and the\n",
"# gradient for a given interation.\n",
"pgd_model_fn = base_model\n",
"\n",
"# We need to pass in the loss function for repeated calculation of the gradient.\n",
"pgd_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True, \n",
")\n",
"labeled_loss_fn = pgd_loss_fn"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "U0Og8WuKyUGt"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using PGD on the base model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"# Record the accuracy.\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Gradient tape to calculate the loss on the first iteration.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" base_model(batch[IMAGE_INPUT_NAME]))\n",
" \n",
" # Generate the adversarial examples.\n",
" pgd_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" pgd_nbr_config,\n",
" gradient_tape=tape,\n",
" pgd_model_fn=pgd_model_fn,\n",
" pgd_loss_fn=pgd_loss_fn,\n",
" pgd_labels=batch[LABEL_INPUT_NAME],\n",
" )\n",
"\n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = base_model(pgd_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for visualization.\n",
" perturbed_images.append(pgd_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "F7KJaU4f_LLx"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'base')"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "69naYIftz0Nm"
},
"source": [
"The PGD attack is much stronger, but it also takes longer to run."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "Rfj9P6fvz97d"
},
"source": [
"### Attacking the FGSM Regularized Model"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "4qgnKmh9Gy1q"
},
"outputs": [],
"source": [
"# Set up the neighbor config.\n",
"fgsm_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.pgd_epsilon,\n",
" clip_value_min=0.0,\n",
" clip_value_max=1.0,\n",
")\n",
"\n",
"# The labeled loss function provides the loss for each sample we pass in. This\n",
"# will be used to calculate the gradient.\n",
"labeled_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True,\n",
")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "XAmIbcPJ0C6d"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using FGSM on the regularized model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"# Record the accuracy.\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Record the loss calculation to get its gradients.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" # We attack the adversarially regularized model.\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" fgsm_adv_model.base_model(batch[IMAGE_INPUT_NAME]))\n",
" \n",
" # Generate the adversarial examples.\n",
" fgsm_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" fgsm_nbr_config,\n",
" gradient_tape=tape\n",
" )\n",
"\n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = fgsm_adv_model.base_model(fgsm_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for visualization.\n",
" perturbed_images.append(fgsm_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "PO8w0Gmv_XbH"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'fgsm_reg')"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "SCB48teL0O48"
},
"source": [
"As we can see, the FGSM-regularized model performs much better than the base\n",
"model on images perturbed by FGSM. How does it do against PGD?"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "fPBmdviOHmlT"
},
"outputs": [],
"source": [
"# Set up the neighbor config for PGD.\n",
"pgd_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.adv_step_size,\n",
" pgd_iterations=HPARAMS.pgd_iterations,\n",
" pgd_epsilon=HPARAMS.pgd_epsilon,\n",
" clip_value_min=HPARAMS.clip_value_min,\n",
" clip_value_max=HPARAMS.clip_value_max,\n",
")\n",
"\n",
"# pgd_model_fn generates a prediction from which we calculate the loss, and the\n",
"# gradient for a given interation.\n",
"pgd_model_fn = fgsm_adv_model.base_model\n",
"\n",
"# We need to pass in the loss function for repeated calculation of the gradient.\n",
"pgd_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True, \n",
")\n",
"labeled_loss_fn = pgd_loss_fn"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "km7Tlg_b0d5Y"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using PGD on the FGSM-regularized model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Gradient tape to calculate the loss on the first iteration.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" fgsm_adv_model.base_model(batch[IMAGE_INPUT_NAME]))\n",
" \n",
" # Generate the adversarial examples.\n",
" pgd_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" pgd_nbr_config,\n",
" gradient_tape=tape,\n",
" pgd_model_fn=pgd_model_fn,\n",
" pgd_loss_fn=pgd_loss_fn,\n",
" pgd_labels=batch[LABEL_INPUT_NAME],\n",
" )\n",
" \n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = fgsm_adv_model.base_model(pgd_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for visualization.\n",
" perturbed_images.append(pgd_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "K5i9BB1fAIQB"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'fgsm_reg')"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "XQZTIOmn2Ylt"
},
"source": [
"While the FGSM regularized model was robust to attacks via FGSM, as we can see\n",
"it is still vulnerable to attacks from PGD, which is a stronger attack mechanism\n",
"than FGSM.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "S6pb7D4E2ixj"
},
"source": [
"### Attacking the PGD Regularized Model"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "5MFkg3lsIYNt"
},
"outputs": [],
"source": [
"# Set up the neighbor config.\n",
"fgsm_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.pgd_epsilon,\n",
" clip_value_min=0.0,\n",
" clip_value_max=1.0,\n",
")\n",
"\n",
"# The labeled loss function provides the loss for each sample we pass in. This\n",
"# will be used to calculate the gradient.\n",
"labeled_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True,\n",
")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "9eee2wAM2mBL"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using FGSM on the regularized model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"# Record the accuracy.\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Record the loss calculation to get its gradients.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" # We attack the adversarially regularized model.\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" pgd_adv_model.base_model(batch[IMAGE_INPUT_NAME]))\n",
"\n",
" # Generate the adversarial examples.\n",
" fgsm_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" fgsm_nbr_config,\n",
" gradient_tape=tape\n",
" )\n",
"\n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = pgd_adv_model.base_model(fgsm_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for visualization.\n",
" perturbed_images.append(fgsm_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "wLIrI20WAbyw"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'pgd_reg')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "SAqEans_I10c"
},
"outputs": [],
"source": [
"# Set up the neighbor config for PGD.\n",
"pgd_nbr_config = nsl.configs.AdvNeighborConfig(\n",
" adv_grad_norm=HPARAMS.adv_grad_norm,\n",
" adv_step_size=HPARAMS.adv_step_size,\n",
" pgd_iterations=HPARAMS.pgd_iterations,\n",
" pgd_epsilon=HPARAMS.pgd_epsilon,\n",
" clip_value_min=HPARAMS.clip_value_min,\n",
" clip_value_max=HPARAMS.clip_value_max,\n",
")\n",
"\n",
"# pgd_model_fn generates a prediction from which we calculate the loss, and the\n",
"# gradient for a given interation.\n",
"pgd_model_fn = pgd_adv_model.base_model\n",
"\n",
"# We need to pass in the loss function for repeated calculation of the gradient.\n",
"pgd_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(\n",
" from_logits=True, \n",
")\n",
"labeled_loss_fn = pgd_loss_fn"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "Xzb9qW1K2z_8"
},
"outputs": [],
"source": [
"%%time\n",
"# Generate adversarial images using PGD on the PGD-regularized model.\n",
"perturbed_images, labels, predictions = [], [], []\n",
"\n",
"metric = tf.keras.metrics.SparseCategoricalAccuracy()\n",
"\n",
"for batch in test_set_for_adv_model:\n",
" # Gradient tape to calculate the loss on the first iteration.\n",
" with tf.GradientTape() as tape:\n",
" tape.watch(batch)\n",
" losses = labeled_loss_fn(batch[LABEL_INPUT_NAME],\n",
" pgd_adv_model.base_model(batch[IMAGE_INPUT_NAME]))\n",
" \n",
" # Generate the adversarial examples.\n",
" pgd_images, _ = nsl.lib.adversarial_neighbor.gen_adv_neighbor(\n",
" batch[IMAGE_INPUT_NAME],\n",
" losses,\n",
" pgd_nbr_config,\n",
" gradient_tape=tape,\n",
" pgd_model_fn=pgd_model_fn,\n",
" pgd_loss_fn=pgd_loss_fn,\n",
" pgd_labels=batch[LABEL_INPUT_NAME],\n",
" )\n",
" \n",
" # Update our accuracy metric.\n",
" y_true = batch['label']\n",
" y_pred = pgd_adv_model.base_model(pgd_images)\n",
" metric(y_true, y_pred)\n",
"\n",
" # Store images for visualization.\n",
" perturbed_images.append(pgd_images)\n",
" labels.append(y_true.numpy())\n",
" predictions.append(tf.argmax(y_pred, axis=-1).numpy())\n",
"\n",
"print('%s model accuracy: %f' % ('base', metric.result().numpy()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "RB2rUM4LAmMM"
},
"outputs": [],
"source": [
"examine_images(perturbed_images, labels, predictions, 'pgd_reg')"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "5P29jDqi3cgz"
},
"source": [
"The PGD-regularized model is strong against both attack types."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "luOZc_1B_oq7"
},
"source": [
"# Conclusion\n",
"\n",
"In this colab, we've explored two gradient-based attack methods, FGSM, and its\n",
"stronger variant PGD. We have seen how neural networks not trained to defend\n",
"against these attacks are vulnerable to these attacks, and also how to utilize\n",
"adversarial regularization in the Neural Structured Learning framework to\n",
"improve robustness."
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "Adversarial Regularization for MNIST Image Classification",
"private_outputs": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
elsonidoq/py-l1tf | l1tf/Quick Example.ipynb | 1 | 167463 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Using matplotlib backend: nbAgg\n",
"Populating the interactive namespace from numpy and matplotlib\n"
]
}
],
"source": [
"%matplotlib nbagg\n",
"%pylab"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"import pandas_wrapper\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"s = np.hstack([\n",
" np.arange(1, 100) + np.random.normal(0, 10, 99),\n",
" np.arange(100, 50, step=-1) + np.random.normal(0, 10, 50),\n",
" np.arange(300, 400) + np.random.normal(0, 10, 100),\n",
" ])\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox ≥ 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('<div/>');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '<div class=\"ui-dialog-titlebar ui-widget-header ui-corner-all ' +\n",
" 'ui-helper-clearfix\"/>');\n",
" var titletext = $(\n",
" '<div class=\"ui-dialog-title\" style=\"width: 100%; ' +\n",
" 'text-align: center; padding: 3px;\"/>');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('<div/>');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('<canvas/>');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('<canvas/>');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('<div/>')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('<button/>');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('<span/>');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('<span/>');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('<span/>');\n",
"\n",
" var fmt_picker = $('<select/>');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '<option/>', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('<span class=\"mpl-message\"/>');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overridden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"<div id='\" + id + \"'></div>\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html('<img src=\"' + dataURL + '\" width=\"' + width + '\">');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '<img src=\"' + dataURL + '\" width=\"' + width + '\">';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('<div/>')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('<button class=\"btn btn-default\" href=\"#\" title=\"' + name + '\"><i class=\"fa ' + image + ' fa-lg\"></i></button>');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('<span class=\"mpl-message\" style=\"text-align:right; float: right;\"/>');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('<div class=\"btn-group inline pull-right\"></div>');\n",
" var button = $('<button class=\"btn btn-mini btn-primary\" href=\"#\" title=\"Stop Interaction\"><i class=\"fa fa-power-off icon-remove icon-large\"></i></button>');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i<ncells; i++) {\n",
" var cell = cells[i];\n",
" if (cell.cell_type === 'code'){\n",
" for (var j=0; j<cell.output_area.outputs.length; j++) {\n",
" var data = cell.output_area.outputs[j];\n",
" if (data.data) {\n",
" // IPython >= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
"<IPython.core.display.Javascript object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<img src=\"data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABQAAAAPACAYAAABq3NR5AAAgAElEQVR4XuzdBXQUV9/H8d/GSXCCB0gI7u5OkbpQV1pKS0u9D22pUqPuLXVv4S2lCqUUK+7unuAWNEh833MnzSbLJsRt8p1zOA+7e/Vz55nT+XPF4XQ6neJCAAEEEEAAAQQQQAABBBBAAAEEEEAAAVsKOAgA2nJc6RQCCCCAAAIIIIAAAggggAACCCCAAAKWAAFAbgQEEEAAAQQQQAABBBBAAAEEEEAAAQRsLEAA0MaDS9cQQAABBBBAAAEEEEAAAQQQQAABBBAgAMg9gAACCCCAAAIIIIAAAggggAACCCCAgI0FCADaeHDpGgIIIIAAAggggAACCCCAAAIIIIAAAgQAuQcQQAABBBBAAAEEEEAAAQQQQAABBBCwsQABQBsPLl1DAAEEEEAAAQQQQAABBBBAAAEEEECAACD3AAIIIIAAAggggAACCCCAAAIIIIAAAjYWIABo48GlawgggAACCCCAAAIIIIAAAggggAACCBAA5B5AAAEEEEAAAQQQQAABBBBAAAEEEEDAxgIEAG08uHQNAQQQQAABBBBAAAEEEEAAAQQQQAABAoDcAwgggAACCCCAAAIIIIAAAggggAACCNhYgACgjQeXriGAAAIIIIAAAggggAACCCCAAAIIIEAAkHsAAQQQQAABBBBAAAEEEEAAAQQQQAABGwsQALTx4NI1BBBAAAEEEEAAAQQQQAABBBBAAAEECAByDyCAAAIIIIAAAggggAACCCCAAAIIIGBjAQKANh5cuoYAAggggAACCCCAAAIIIIAAAggggAABQO4BBBBAAAEEEEAAAQQQQAABBBBAAAEEbCxAANDGg0vXEEAAAQQQQAABBBBAAAEEEEAAAQQQIADIPYAAAggggAACCCCAAAIIIIAAAggggICNBQgA2nhw6RoCCCCAAAIIIIAAAggggAACCCCAAAIEALkHEEAAAQQQQAABBBBAAAEEEEAAAQQQsLEAAUAbDy5dQwABBBBAAAEEEEAAAQQQQAABBBBAgAAg9wACCCCAAAIIIIAAAggggAACCCCAAAI2FiAAaOPBpWsIIIAAAggggAACCCCAAAIIIIAAAggQAOQeQAABBBBAAAEEEEAAAQQQQAABBBBAwMYCBABtPLh0DQEEEEAAAQQQQAABBBBAAAEEEEAAAQKA3AMIIIAAAggggAACCCCAAAIIIIAAAgjYWIAAoI0Hl64hgAACCCCAAAIIIIAAAggggAACCCBAAJB7AAEEEEAAAQQQQAABBBBAAAEEEEAAARsLEAC08eDSNQQQQAABBBBAAAEEEEAAAQQQQAABBAgAcg8ggAACCCCAAAIIIIAAAggggAACCCBgYwECgDYeXLqGAAIIIIAAAggggAACCCCAAAIIIIAAAUDuAQQQQAABBBBAAAEEEEAAAQQQQAABBGwsQADQxoNL1xBAAAEEEEAAAQQQQAABBBBAAAEEECAAyD2AAAIIIIAAAggggAACCCCAAAIIIICAjQUIANp4cOkaAggggAACCCCAAAIIIIAAAggggAACBAC5BxBAAAEEEEAAAQQQQAABBBBAAAEEELCxAAFAGw8uXUMAAQQQQAABBBBAAAEEEEAAAQQQQIAAIPcAAggggAACCCCAAAIIIIAAAggggAACNhYgAGjjwaVrCCCAAAIIIIAAAggggAACCCCAAAIIEADkHkAAAQQQQAABBBBAAAEEEEAAAQQQQMDGAgQAbTy4dA0BBBBAAAEEEEAAAQQQQAABBBBAAAECgNwDCCCAAAIIIIAAAggggAACCCCAAAII2FiAAKCNB5euIYAAAggggAACCCCAAAIIIIAAAgggQACQewABBBBAAAEEEEAAAQQQQAABBBBAAAEbCxAAtPHg0jUEEEAAAQQQQAABBBBAAAEEEEAAAQQIAHIPIIAAAggggAACCCCAAAIIIIAAAgggYGMBAoA2Hly6hgACCCCAAAIIIIAAAggggAACCCCAAAFA7gEEEEAAAQQQQAABBBBAAAEEEEAAAQRsLEAA0MaDS9cQQAABBBBAAAEEEEAAAQQQQAABBBAgAMg9gAACCCCAAAIIIIAAAggggAACCCCAgI0FCADaeHDpGgIIIIAAAggggAACCCCAAAIIIIAAAgQAuQcQQAABBBBAAAEEEEAAAQQQQAABBBCwsQABQBsPLl1DAAEEEEAAAQQQQAABBBBAAAEEEECAACD3AAIIIIAAAggggAACCCCAAAIIIIAAAjYWIABo48GlawgggAACCCCAAAIIIIAAAggggAACCBAA5B5AAAEEEEAAAQQQQAABBBBAAAEEEEDAxgIEAG08uHQNAQQQQAABBBBAAAEEEEAAAQQQQAABAoDcAwgggAACCCCAAAIIIIAAAggggAACCNhYgACgjQeXriGAAAIIIIAAAggggAACCCCAAAIIIEAAkHsAAQQQQAABBBBAAAEEEEAAAQQQQAABGwsQALTx4NI1BBBAAAEEEEAAAQQQQAABBBBAAAEECAByDyCAAAIIIIAAAggggAACCCCAAAIIIGBjAQKANh5cuoYAAggggAACCCCAAAIIIIAAAggggAABQO4BBBBAAAEEEEAAAQQQQAABBBBAAAEEbCxAANDGg0vXEEAAAQQQQAABBBBAAAEEEEAAAQQQIADIPYAAAggggAACCCCAAAIIIIAAAggggICNBQgA2nhw6RoCCCCAAAIIIIAAAggggAACCCCAAAIEALkHEEAAAQQQQAABBBBAAAEEEEAAAQQQsLEAAUAbDy5dQwABBBBAAAEEEEAAAQQQQAABBBBAgAAg9wACCCCAAAIIIIAAAggggAACCCCAAAI2FiAAaOPBpWsIIIAAAggggAACCCCAAAIIIIAAAggQAOQeQAABBBBAAAEEEEAAAQQQQAABBBBAwMYCBABtPLh0DQEEEEAAAQQQQAABBBBAAAEEEEAAAQKA3AMIIIAAAggggAACCCCAAAIIIIAAAgjYWIAAoI0Hl64hgAACCCCAAAIIIIAAAggggAACCCBAAJB7AAEEEEAAAQQQQAABBBBAAAEEEEAAARsLEAC08eDSNQQQQAABBBBAAAEEEEAAAQQQQAABBAgAcg8ggAACCCCAAAIIIIAAAggggAACCCBgYwECgDYeXLqGAAIIIIAAAggggAACCCCAAAIIIIAAAUDuAQQQQAABBBBAAAEEEEAAAQQQQAABBGwsQADQxoNL1xBAAAEEEEAAAQQQQAABBBBAAAEEECAAyD2AAAIIIIAAAggggAACCCCAAAIIIICAjQUIANp4cOkaAggggAACCCCAAAIIIIAAAggggAACBAC5BxBAAAEEEEAAAQQQQAABBBBAAAEEELCxAAFAGw8uXUMAAQQQQAABBBBAAAEEEEAAAQQQQIAAIPcAAggggAACCCCAAAIIIIAAAggggAACNhYgAGjjwaVrCCCAAAIIIIAAAggggAACCCCAAAIIEADkHkAAAQQQQAABBBBAAAEEEEAAAQQQQMDGAgQAbTy4dA0BBBBAAAEEEEAAAQQQQAABBBBAAAECgNwDCCCAAAIIIIAAAggggAACCCCAAAII2FiAAKCNB5euIYAAAggggAACCCCAAAIIIIAAAgggQACQewABBBBAAAEEEEAAAQQQQAABBBBAAAEbCxAAtPHg0jUEEEAAAQQQQAABBBBAAAEEEEAAAQQIAHIPIIAAAggggAACCCCAAAIIIIAAAgggYGMBAoA2Hly6hgACCCCAAAIIIIAAAggggAACCCCAAAFA7gEEEEAAAQQQQAABBBBAAAEEEEAAAQRsLEAA0MaDS9cQQAABBBBAAAEEEEAAAQQQQAABBBAgAMg9gAACCCCAAAIIIIAAAggggAACCCCAgI0FCADaeHDpGgIIIIAAAggggAACCCCAAAIIIIAAAgQAuQcQQAABBBBAAAEEEEAAAQQQQAABBBCwsQABQBsPLl1DAAEEEEAAAQQQQAABBBBAAAEEEECAACD3AAIIIIAAAggggAACCCCAAAIIIIAAAjYWIABo48GlawgggAACCCCAAAIIIIAAAggggAACCBAA5B5AAAEEEEAAAQQQQAABBBBAAAEEEEDAxgIEAG08uHQNAQQQQAABBBBAAAEEEEAAAQQQQAABAoDcAwgggAACCCCAAAIIIIAAAggggAACCNhYgACgjQeXriGAAAIIIIAAAggggAACCCCAAAIIIEAAkHsAAQQQQAABBBBAAAEEEEAAAQQQQAABGwsQALTx4NI1BBBAAAEEEEAAAQQQQAABBBBAAAEECAByDyCAAAIIIIAAAggggAACCCCAAAIIIGBjAQKANh7coty1mJgYrV271mpi5cqV5ePjU5SbS9sQQAABBBBAAAEEEEAAAQQQKJYCCQkJOnz4sNX25s2bKyAgoFj2g0bnToAAYO78yJ1DgaVLl6pDhw45zE02BBBAAAEEEEAAAQQQQAABBBDIrsCSJUvUvn377GYjvQ0ECADaYBCLYxcIABbHUaPNCCCAAAIIIIAAAggggAACxVmAAGBxHr3ctZ0AYO78yJ1DgcjISIWFhVm5zQOoevXqOSyJbAgggAACCCCAAAIIIIAAAgggkJHA/v37XSvwIiIiFBoaClYJFCAAWAIHvSh0ec+ePapVq5bVlN27dyskJKQoNIs2IIAAAggggAACCCCAAAIIIGArAd6/bTWcOe4MAcAc05ExNwI8gHKjR14EEEAAAQQQQAABBBBAAAEEsibA+3fWnOyeigCg3Ue4iPaPB1ARHRiahQACCCCAAAIIIIAAAgggYCsB3r9tNZw57gwBwBzTkTE3AjyAcqNHXgQQQAABBBBAAAEEEEAAAQSyJsD7d9ac7J6KAKDdR7iI9o8HUBEdGJqFAAIIIIAAAggggAACCCBgKwHev201nDnuDAHAHNORMTcCPIByo0deBBBAAAEEEEAAAQQQQAABBLImwPt31pzsnooAoN1HuIj2jwdQER0YmoUAAggggAACCCCAAAIIIGArAd6/bTWcOe4MAcAc05ExNwI8gHKjR14EEEAAAQQQQAABBBBAAAEEsibA+3fWnOyeigCg3Ue4iPaPB1ARHRiahQACCCCAAAIIIIAAAgggYCsB3r9tNZw57gwBwBzTkTE3AjyAcqNHXgQQQAABBBBAAAEEEEAAAQSyJsD7d9ac7J6KAGARGOHHHntMb7zxhqsl//77r3r16nXelk2ZMkWfffaZlixZosOHD6ty5crq0KGD7rrrLg0cODBLvUpISNCXX36pH3/8URs3btSpU6dUs2ZNXXDBBXrggQfUpEmTLJWTk0Q8gHKiRh4EEEAAAQQQQAABBBBAAAEEsifA+3f2vOyamgBgIY/s6tWr1a5dO5lgXMp1vgCg0+nUsGHDrOBfRpcJAn7yySdyOBwZpjly5IguvvhiLV68ON00/v7+GjNmjO644458EeIBlC+sFIoAAggggAACCCCAAAIIlFiBfzcd0pLIo+rdsIo6hFUssQ7ndpz3b24FI0AAsBDvg6SkJHXq1ElLly5VlSpVdOjQIas15wsAPvXUUxo9erSVrnXr1jKzB8PDw7V9+3a9/vrrWrlypfWbSffSSy+l27vExET16dNHc+bMsX6/6qqrNHToUFWsWNEKCJp8pi3e3t7666+/NGDAgDxX4gGU56QUiAACCCCAAAIIIIAAAgiUWIEZGw9qyLfLXP3/fXhXtapVPk889hw7oyURR3UmLlEx8Sl/kmTm3Dzav2Ge1JGfhfD+nZ+6xadsAoCFOFbvvvuuHn74YTVq1EhXXnmlXnnllfMGALdt26bGjRtbswXNrEETwCtVqpSrB2fOnFHPnj21bNky+fj4aNOmTVZw8Nzrm2++0e233259fe+99+qjjz5yS2Lqadu2rU6ePKn69etrw4YNVnl5efEAyktNykIAAQQQQAABBBBAAAEESrbA8LEr9Nea/S6EwV1CNeqyprlGmbbhoIZ+lxpYTFtgoJ+3NryQtS24ct2QXBTA+3cu8GyUlQBgIQ3m7t27rT32zL57ZsbfrFmz9Pzzz583ADh8+HBrWa65Fi5caM0ePPdatGiROnfubH1933336YMPPvBI07RpUyuoV6FCBZkHQWBgoEeaV199VSNHjrS+nzBhggYNGpSnUjyA8pSTwhBAAAEEEEAAAQQQQACBEi0w8N052nQg2mXQvX6wvh/SMVcmZguunm/M0q6jZ9Itx8shbR990Xm338pVA/IoM+/feQRZzIshAFhIA3jppZdq0qRJuu2222Rm5I0aNeq8AUDz4KlVq5b27t1rzRg0h3ZkdJnfN2/erJCQEO3atcvtYbR161Y1aNDAymr2Evz444/TLebAgQOqXr269duNN95oHRSSlxcPoLzUpCwEEEAAAQQQQAABBBBAoOQKJCY51eTZKYpNSHIh1CxfSvOf6JMrlKWRR3XNJwvPW8bmlwbK38c7V/Xkd2bev/NbuHiUTwCwEMZp/Pjxuu6666w998wyXXOCb2YBwB07driW8959993WIR8ZXeb3lENCTL6wsDBX0q+++kpDhgyxPo8bN07XX399huU0bNhQW7ZsUe3atbVz5848leIBlKecFIYAAggggAACCCCAAAIIlFiB3UfPqPvr/3r0f8MLAxTol/PtrEb+ukbjlux2lVuulK+a1yynAF9vBfh6qZSvt168opn1uShfvH8X5dEpuLYRACw4a6um48ePW/v4mRl2n3/+ue68807r+8wCgOYwjksuucRK+8477+ihhx7KsOXm90ceecT63eS76KKLXGlHjBihN9980/psDgxp1apVhuVcfvnl+vPPP60ZhNHR0QoKCsozLR5AeUZJQQgggAACCCCAAAIIIIBAiRb4d/Mh3f71Ug+DSfd3U7Oa5XJkYw77aP/ydEXHJKS+Tw9oqOG96+WovMLMxPt3YeoXnboJABbwWNx1111W4K9Lly6aN2+ea3luZgFAM+PvnnvusVr7888/6+qrr86w5WbPvmuuucb63eQzMwJTLjPj76effrI+Hj58WMHBwRmWY/YQTDkgxMxUNDMCs3qZB8z5rv3796tDhw5WErMfolmuzIUAAggggAACCCCAAAIIIIBAdgW+nBehFydt8Mj23vWtdHmrmtktzko/ac0+3Td2pSuvOfF33uN9ZJYWF7eLAGBxG7H8aS8BwPxxTbdUE/Dr0aOHvL29tWLFCjVv3tyVLrMA4BtvvKHHHnvMSv/3339r4MCMTxoyv6fM+jOz/R599FFXPRdffLEmT55sfT579qwCAgIyFHj88cf1+uuvW7+bk4XNycBZvcyswaxeBACzKkU6BBBAAAEEEEAAAQQQQACBcwWe/G2txi7e5QHzQJ96eqR/1ieypC3gjm+WauamQ66vuoRX0tihngdxFofRIABYHEYp/9tIADD/ja0a4uLirOW25vAOsww3JbCWUn1mAcAXX3xRzz77rJV8xowZ6tMn481MZ86cqb59+1ppTb6nn37a1UvzvfndXImJifLy8spQwNRn8ptr7ty56tatW5a1CABmmYqECCCAAAIIIIAAAggggAACuRC47tOFWhxx1KOEi5tX10c3tcl2yYejY9XplRkyh4ukXG9d01KD2oZISYnSkW3SvlWSX5DUOHmrrqJ8EQAsyqNTcG0jAFhA1ikBPnOgxoYNGzz208ssAFjcZgCyBLiAbiyqQQABBBBAAAEEEEAAAQRKuEC7l6Yr6lSsh0KjamU05aEe2dZJWVLsrUTVdexXW99IvdghQb4H10gH1krxp5PLrN1FuuPvbJdf0BkIABa0eNGsjwBgAYyL2T+vZcuW1izAP/74Q5dddplHrZkFAIvbHoCZsfIAykyI3xFAAAEEEEAAAQQQQACB4iNgDs2YtfmwwoKD1LBamQJr+Imz8Wr5/NR06/Pz8dLGFwbK28tziypzcvC2w6fUKaySSvl5S4kJ0uFN0v7Vmjhlsmqc3awmjp0q5YjLuC9+paUndkvnWVlXYBDnqYj376IwCoXfBgKABTAG5hCOzz77THXr1tXLL7+cbo3m4I5ffvnF+u2ZZ55RkyZNrL9feuml1mzBSZMmWX83V25OAf7f//6nt956yyqHU4ALYPCpAgEEEEAAAQQQQAABBBCwuUBsQqIufHeudkQlz4z76MY2urhF9Sz12uR9d/pWRRw+rRs71laPBpWzlC8l0cpdx3TlmAUZ5pk9opfqVApy/W4Cf2//s16b1yxRM68IdQzYrcurHpbPofVSQky26rYSD18qVW6Q/XwFmIMAYAFiF+GqCAAWwOAMHjxY3377bY5qioiIUGhoqHbs2KHw8HCrDBNQNDMCM7pSAo7md5MvLCzMlfSrr77SkCFDrM/jxo2TORU4o8uc+rtlyxaZZcs7d+7MUfszysQDKE85KQwBBBBAAAEEEEAAAQQQKDSBP1bt1YP/t8pVf9Wy/taJub7eGe85n5L4gXEr9efqfdZHM2NvxiM9VatiYJb7MmH5Hv3v59UZpv/6lhbqXeGITkcu18YVc+R3aI0aOnbJ35GQ5TrSTVimulS9ldT3Galq09yVlc+5ef/OZ+BiUjwBwAIYqLwIADqdToWEhGjfvn1q1KiRdZhIRlfjxo1llh3XrFlT5oTdtAdymICeCeyZa9iwYfr444/TLebAgQOqXj35X2xuuOEGjR07Nk+leADlKSeFIYAAAggggAACCCCAAAJ5JpCU5JRXOstmM6rghYkb9NX8CLefP7yxtS5pUeO8bZq/LUo3fbHYLc3ICxvp7p7Jk1+ycr02ZZM+nrXdSuqvODV07FYzr0g1c+xQc68INfHeI29nLoN9ZWsmB/tqtJKqt0z+e5mqWWlekUjD+3eRGIZCbwQBwEIfguQGZLYHoElz7733ugJ2CxcuVKdOnkeQL1q0SJ07d7bKNOk/+ugjjx6a5cUmgFixYkUrQBgY6PmvK6+++qpGjhxp5R0/fryuueaaPJXiAZSnnBSGAAIIIIAAAggggAACCORaYPXu43rg/1YqKjpW13eorREDGirA1zvTcq/9dKGWnHMKb/vQCvp5WJcM88YlJOmi9+dq26FTbmkuaFxFX9zWPtM6FX9WOrheP/72h3wOrrGW8zZw7JGvIzHzvOdJsccZrHVJYVqbFKZ1zjDdd+MgtW+WPImmuF68fxfXkcvbdhMAzFvPHJeWlQCgmb3XtGlTJSQkqF27dpozZ45KlSrlqvPs2bPq0aOHli1bJh8fH+u04fr163u0Ke0y4OHDh+vDDz90S7N9+3a1adNGJ0+etJYdm9mEpry8vHgA5aUmZSGAAAIIIIAAAggggAACuRM4djpO/d+do8PRqafp1q9SWu/f0FqNq5fNsHAzW7DF81N1KtZzlt1fD3RT0xrl0s37+Zwdenmy58q2cqV8tfKZfu4zEOPOSAfXSftWSftXJf+vObDDmbtg366kylrrDNP6pDB17tZXh8o00qOT9rjaWybARyue6Zelpcy508/f3Lx/569vcSmdAGARGamsBABNU82sPDM7z1ytW7fW448/bgXpTNDutddesw72SEk3evTodHuXmJionj17av78+dbvgwYN0tChQ1WhQgUtWbJEL774og4dOiQvLy/r8JELL7wwz5V4AOU5KQUigAACCCCAAAIIIIAAAjkWuG/sCk1as98jv9mX74mBjXR711C37aVSEkZGnVavN2elW+/17Wvp1UEtPH47eDJGfd6cpdNxngG8QMVoyvXlVTtma2qwL2qz5EzKcd9MxsikqtaMPjOzb2C//vo2orx+33zWVeaFzaopPjFJ0zcecn13acsa+uCG1rmqtyhk5v27KIxC4beBAGDhj4HVgqwGAJOSkqxgnZnFl9FlDvkwpw6bAF5GV1RUlC666CItXbo03SR+fn7WzEBTV35cPIDyQ5UyEUAAAQQQQAABBBBAAIHsC0xcvU/3j0ueTJLRZZYDD+9dz+PnSWv26b6x6ecN8PXSopF9VT7Qz5XP7G//0E+r9MeqfQrSWTV1RFp79TX1ilRzR4TCHfvk5XBmvxNpcmxPqq71zlDXMt71SaE6qeSTgKuU8deCJ/ro1xV79dgva1y5gvy8leh0KiY+NdD47nWtdEXrmrlqS1HIzPt3URiFwm8DAcDCHwOrBVkNAKY0d/LkyVaQzwTwTDAvODhY7du3t04IzuqMPbOU+PPPP7cO+DB7Ap4+fVo1atRQ37599eCDD1rLjfPr4gGUX7KUiwACCCCAAAIIIIAAAnYUGLt4l75dEKnQ4EDd17u+moekv7Q2u30/dDLGWvp7/Ez8ebP6+3hp4ci+qhiUGswzGV79e5M+mZ18CEd615MXNdJdPcKlmBOK2rpUM/+dKv/Da9XMEaEwx4FcBfuS5NCOpOrWMt51SaHa5d9An4y4XY1fWqC4xPRnDA7tHqanLm5iLXXuMHq6nBnEGs0ZKMuf7qcK5/Q3u75FIT3v30VhFAq/DQQAC38MSmQLeACVyGGn0wgggAACCCCAAAIIIJADgXV7T+jSD+e5glUmOHVr51A90r+Bygb45qDE5CxmNt6Qb5dp5qbUZa/m+7euaanNB6P12ZwdbmU/0q+BHujrvs/8LV8u1tytUa503l4OBSVF/3cSb4Ta+e1UW79dqhSburdeThrslJe2uoJ9yUt5Nzrr6LRS98XvEFpR44d11oB35ljtT+/6+8Hurj0Nr/hovlbtPp5uuswOMclJHworD+/fhSVftOolAFi0xqPEtIYHUIkZajqKAAIIIIAAAggggAACuRR4fcomjZnlOcvOLGd95arm6tu4ao5qmL7hoO78bplb3otbVNdHN7axvnvkp1X6deVe1+/Bpf007/E+rpOBTQCx9wu/KiR2q7V8t6lXhLoG7lGF2NQ8OWlYgtNLzsoN5VuztVSjlVS9lW6bfEazI8+ct7gbOtTSK1e10L0/LtfktQc80prDTEwAMOwaI1UAACAASURBVOX6cOZWvTl1S7plPj6wke7pFZ6T5he5PLx/F7khKZQGEQAsFHYq5QHEPYAAAggggAACCCCAAAIIZE3gsg/nac2eE+kmNjPuxg3tpA5hFbNWWJpUj09Yo5+W7U4T4PPXtId7uJa9rt93Qhe/P8/1ewWd1Ls9pJ6l91oHdCTsXSWfk6n5s90Ak8HLR87KjfT7wcpaHh8qs1/fRmdtvXpdR9f+e5sPRGvAu3MyLf7pixvrzu519dbUzfpg5jaP9Cm/p/ywYd9JXfT+3HTLNQ71q5bJtM7ikID37+IwSvnfRgKA+W9MDekI8ADitkAAAQQQQAABBBBAAAEEMhc4djpObV6aluFedaaERtXKaNL93eTjnfFBkOnVdNF7c7Vh/0nXT679+sw3pw5J+1Zp/MRJKnd8vZp5Raim40jmDT5Pijint7Y4a+lMcDM1a9tTgaFtpSpNJd8A3fntMk3feNCV+8aOtTX6yubW56d/X6sfFu3KtO6vB7dX70ZV9PvKvdZBI2kvs2zaHEhSpWyA62szg7HrqzO170SMW9paFUtpzoje6Z56nGkjimAC3r+L4KAUQpMIABYCOlVKPIC4CxBAAAEEEEAAAQQQQACBzAX+WrNfw8eucCU0J+t2DKuk2VsOu2V+8fKmuqVzaOYF/pciJj5RzZ77RwlJTlXWMesk3hfaxyskZqsV+FP0viyXlV5Cp7efjpWurz0BDbTZK1wr4uvoWOl6uqNno3RnK342Z7tGT97kKqp+ldKa9khPnYyJV6fRM3QmLtH1W2ilQEUe8VwObIJ2tSsFyuyZeMkHqTMXTcaeDSrr2zs6eDT1md/X6ftFO92+H9wlVKMuy79DMXMFm4PMvH/nAM2GWQgA2nBQi0OXeAAVh1GijQgggAACCCCAAAIIIFDYAiN/XaNxS1KX2fZoUFlf3dbOCnBtOpB60EW5Ur6a9b9e5z+11hx5G73fCvAd2LxI65fNsWb2VXWkfxBGVvse6/S1lu0mVmupth17Je/bV7mx5ON+YvD5ylux65iuGrPALcnKZ/rpj1V7NWriBtf3Zsmz6eeQb5dqy8FTru/9fLy08YWBMr+fjk1Q0+f+cSvrvetb6fJWNT2aMGvzIQ3+eqnb99/d0UHG2S4X7992Gcnc9YMAYO78yJ1DAR5AOYQjGwIIIIAAAggggAACCJQYAbNEtfvr/2rPsbOuPj91UWMN7VFXi3Yc0fWfLXKzuLlTbb10RfKyWWvN8Ik91l592r86eVaf+ftp95mD2cU86/Szgn21m3bRmC1ltOBMLW1z1lCCfJRRkC0rdcQlJKnF8/8oJj7JlfyDG1rrnelbtOPwadd3A5tW0ye3tNWSiKO69tOFru97Naysb25PneE37PvlmrI++SCQusFB+uuB7irl5+3RlNiERPV8fZYOnExeBly9XIBmjeglfx/PtFnpR1FMw/t3URyVgm8TAcCCN6dGsQSYmwABBBBAAAEEEEAAAQRKlkBSklN/rt6nMbO26eDJWIVXDpI5ldb86RJeSXUrl/YAiYw6rV5vznL73pxia/KY676xKzRpzX4T7VOII0otvCL0fPt4VY7elBzsO5O7PfvkGyhVa6GEai304nI/LTxbS9udNZQob9UoF+Cxd96MR3sqPJ1+ZHWkb/hskRbuOH+bx97ZUV3qBVtFmr3+Pp61XZVK++mlK5q5GR49Hadv5kcoJiFJN3aordDgoAybsXznUb02ZbNh1OMXNlTbOtk/UCWrfSyMdAQAC0O96NVJALDojUmJaBEPoBIxzHQSAQQQQAABBBBAAIESL2Bm8c3ZGqVX/96kjWkO3DgXxhx6YU6pDfTzcf1k9qYze9SlXMGl/bX0yT5yHN9pBfiiI5ZpzdLZaqIIVXCkLofNCXqcd6D8arZKXr5b3fxpKQXXl7ySZ8J9OHOr3py6JcOig/y8tXbUAHmZ0zZyeL09bYven7E1w9z1zL6AD/ewzeEcOWTKdjbev7NNZssMBABtOaxFv1M8gIr+GNFCBBBAAAEEEEAAAQRKqoCZrfftwkit3XtC3eoF67KWNbJ9wq45vXfS2v36dcUerdyVtT32zOEW71zXSq1rV7Doh323RJs2rlEzR6S1V1+fsvvUIGm7FHMiV0Pj9CutJTG1tCYpTGuTwrTOGaZXh16pDnWTZ9ald5mlstd+ukird6ffl/ahFfTzsC65ate8rVG6+cvFGZbx1jUtNahtSK7qKImZef8uiaPu2WcCgNwHhSLAA6hQ2KkUAQQQQAABBBBAAAEEsiDw6ezteuXv1BNpzcyzEQMaqn+TqpnOPouIOq1X/96omZsOKT7RmYXakpM4lKQwxwG18I7UzbWOqrXvLp3ZtVxllLr/X5YLS5swoFzybD7rj5nh11orT5XXlR+n7h/ocEjrRg1QkH/q7MP06tp/4qwu/WCeok7FefycFyfnmpOJ+741W3uPp/bZTChsW6eCrmtfW4Pa1MzUP0dGNs/E+7fNBziL3SMAmEUokuWtAA+gvPWkNAQQQAABBBBAAAEEEMgbgfjEJHV+ZaaiTsV6FNiqVnl9eGNrhVQITLcyM0uu9xuzPPbGS5u4fpXSGtqtthIPb1Pc7hXW4RyNtENNHZEq7Ug+iCKn13FnkGtGX8rMvtsv7qXbu9V1K/L7hZF65o/1ru/MfoQzHu2VpWoX7ziim75YrIQk9+Dmm9e01NV5MDtv++FT+nzODpmgZOfwYPWoH6zygVk/TThLnShhiXj/LmEDnkF3CQByHxSKAA+gQmGnUgQQQAABBBBAAAEEEMhEYPqGg7rzu2UZpgoLDtKUh7qne0rs3K2HdcuXS9zyeitR4Y596ha0R9eHHFX9xO1yHFgrxaeebJujQSlVMXW/vhqtdLJiMz04OUr/bolyr9/LoR+GdFTn8Equ70f8vFo/L9/j+nxl65rW0uOsXl/Pj9DzEze4JZ/6cA81qFomq0WQrgAFeP8uQOwiXBUBwCI8OHZuGg8gO48ufUMAAQQQQAABBBBAoOgJmMM4TNBrScRR9W1URRc2r55uI+/6bpmmbjh43g68elVzXd+htkeaN/5epxlz5qq5V/KMvhbeEWrmtUt+Ts/ZhNkROuwsq+Plmqp+q26pS3nLhciaJpfmSkxy6s2pm62TcdNelYL89Of93VSzfCnr64HvztGmA9GuJM9c0kRDuoVluUnG8unf1+nHxbusPBc0rqIvbmuf5fwkLFgB3r8L1ruo1kYAsKiOjM3bxQPI5gNM9xBAAAEEEEAAAQQQyILAyZh4lQ3wzULK3Ccxh3E8Mn61qyBz4u6d3d2Xxh6OjlXnV2a4LW+9qk1NLd5x1G1fOjMLcPqDXeQdtck6jdcs4zX/G7t3rfzluT9edlp/1FFBKxNCrYM5rGW8SaE6oIr6anB79WlUNUtFvTNti9475zTd5jXL6edhna38TZ/7RyZYmHKNv7uzOoRVzFLZaROZYOrpuAT1qF9Z3rk4/TfbFZMhWwK8f2eLy7aJCQDadmiLdsd4ABXt8aF1CCCAAAIIIIAAAgjkp8CBEzG68fNF2hF1WgObVtOYm9rI6zwBpITEJG0+GK3IqDOKPHJau4+eUXBpf2vWWoWgrO0Pd/H7c7V+30lXt8zkuQ9vaKOLW6TOBPxsznaNnpx6+EeAr5eWPnWBVkYc1Ovf/aZmXpFq7jCz+iLUzGe3vJPic8dUpkbyjL4arf47oKOV4gOr6Iu5EXpn+hbFJSRZ5deqWErTHu6pAF/vLNVnTjEe+t0yzdh0yC29CWbe1LGOBn28wM0hKweAZKliEhVJAd6/i+SwFHijCAAWODkVGgEeQNwHCCCAAAIIIIAAAgiUXIHhP67QX2v3uwDMwRqXtKiRLsiGfSd19w/LtPuo52m4dSoF6vs7Oqp2JfdDOcwSVUea5bGbD0RrwLtzPMr38/HSj3d2VPvQijJ5+r0zR7sPHVVDx24194rQJZUPqXOp3XIe3CBHboN9ZUNSA30pQb/SVTK8CXYcPmUtsY2OideQbnXVsFr29tczsyuv+HC+FWRNe4VUKKU9x1ItzQnH0x/pWXJvxhLQc96/S8AgZ6GLBACzgESSvBfgAZT3ppSIAAIIIIAAAggggEBxEDgbl6jWL05VTHzy7DZzDe4SqlGXNU23+bd+tURzthzOsGtmJuC3d7RXrYqBGrd4l35aultHz8RpeK96GtojeYnvK39v1Kezd3iUYZbrtg/Yp1c6J6pU1Fod2rxY9R175OtIzBXlHmew9gQ0VKeufVKDfkHBuSozJ5m3HozWFR/N1+m4jPtzVeuaejsbB4DkpB3kKVwB3r8L17+o1E4AsKiMRAlrBw+gEjbgdBcBBBBAAAEEEEAAgf8Epq4/oLu+X+7m0b1+sL4f0tHDyCyBbT7qH8X+txQ2I8TS/j7WT6diE9ySpJx+2+XVGTpx8qSaOHZay3dTlvHWd+yVjyM1EJmjQaoQai3f/W5neU09Vt3as++4yuj+PvX0aP+GOSoyLzNN23BQ9/yw3G1fw7TlP3tJE92RjQNA8rJtlFUwArx/F4xzUa+FAGBRHyGbto8HkE0Hlm4hgAACCCCAAAIIIJCJwP9+Xq0Jy/e4papeLkALR/b1yLlmz3Fd9uF8t++71quk/SditOOw+9LWtIkCFaMmjkj1KbdPV1U7ohM7lqqeY6+8HakHX+RkoKIDa2tWdI3kwzmcyQd0fHNvf9WvUlqtXpjmdrDG2Ds7qku9gp/1l16//t10SPf8uNxt1mVKOnMwiFkCzWVfAd6/7Tu22ekZAcDsaJE2zwR4AOUZJQUhgAACCCCAAAIIIJDnAmbfOXOqa6Bf8sy6vLrMYR7tX56uY2c8D89YO6q/ypxzIvA38yM0auIGV/V1Kwdp5qO9ZPa3G/rtMi2OOKrSOmPN7DN79lmHczgiFe7YJ69cBvsSKoTLp2br1CW81Zor1reMerz+rw6ejHW1qX1oBQ3rGa4h3y5zfefn7aU1o/pn+dCOvPI9XznLIo/qjm+W6mRM6ixJc+7K2lEDFPTfDMqCaAd1FLwA798Fb14UayQAWBRHpQS0iQdQCRhkuogAAggggAACCCBQLAU+nLlV707fqlK+3nrt6ha6qHnqKbnndsgc0PHNgghVLuOvu3qEq1wp3/P2eeH2I7rh80Xppvl9eFe1qlXe7bcH/2+l/li1z/Xdza3K66WOidL+1Urcu1KHtyxWlbi9uQr2Jcmh7Uk1tM4ZqnVJYdbsvmoN2+v9wekfjPHF3B166a+Nbu00h5HsPHLG9V2HsIoaf3fnIjf+mw6c1K1fLtGh6OQA5uWtaui961sXuXbSoLwV4P07bz2La2kEAIvryBXzdvMAKuYDSPMRQAABBBBAAAEE8kXgUHSM3vxnsxWgGdq9rroW8BLSyKjT6v3WLDn/WylrAnuLRva1ZgOee5mTdc0BE2fjkw+YuKpNTb19bavzujw/cb2+nh+Zbpo3r2mpq9uGpP529pgeevdbVT216b+ZfREK8zqYK/dEp0PO4IbyCWlt7dun6i2VWLWZFu+J1a8r92r5zmMywbzXBrVQ1bIB6dZlDjExJwrvOpoa8Ds34QN96+uRfg1y1db8ynz0dJx1UEqQv7eua19L/j7e+VUV5RYRAd6/i8hAFHIzCAAW8gCU1Op5AJXUkaffCCCAAAIIIIAAAucTGPb9ck1Zf8BKEujnrbmP9Val0v4FhvbZnO0aPXmTW33THu6h+lXLuH1ngmCXfzRPWw6ecn2f2bJXp9Opbq/9q73Hz3r0p7yi9XirGN1Q86i0f5U1w0/H0g8UZhUjwemlrc4Qa5++tdZ+fWGqXK+NPh2S/sy+rJZr0s3deli3fLkkwyzjhnZS5/BK2SmStAjkmwDv3/lGW6wKJgBYrIbLPo3lAWSfsaQnCCCAAAIIIIAAAnkjEJuQqObPTVVcYuqptO9d30qXt6qZ6wq2Hoy2lvWa69H+DVS3cul0y7zmkwVaGnnM7bfXr26ha9vVcvvuyd/WauziXR5l/HhnxwxnLa7fd0IXvz9PFXXSNaPP7Ntn/oQ4onLXRy8fqUpj16y+Q2Wa6IIfo3QywX0Pww9uaK1LW9bIXV3/5X74p1X6beVej7L8fLy05rmitf9fnnSYQoqtAO/fxXbo8rThBADzlJPCsirAAyirUqRDAAEEEEAAAQQQKCkCq3cf1+UfuZ94e2e3MD19SZNcEcTEJ+qCt2drz7HkmXdVyvhr2iM9PfbrO3Iq1jqgI+mcg3Jv7Fhbo69s7mrD32v3654fV6TbpuG9wzViQKPk38w64lMHpf1rrBl921bPU6kja1XTcSRX/ZGXr1S1SXKwr0byMl5VaSr5ui/ZfWfaFr03Iznoaa4y/j5a+vQFeXYwh/Hq+/ZsHT/nQJNOdSvq/+4qevv/5Q6d3MVZgPfv4jx6edd2AoB5Z0lJ2RDgAZQNLJIigAACCCCAAAIIlAiB7xZG6tk/1rv1tWNYRf2Uy8Mkxi3ZpZG/rnUr99ygnvnx52W7NWLCGg/rJtXLavKD3a3v9xw7o4vem+t2kqz53izhbeDYo76VjujuRrHS4U3SoQ3SWffZhNkdyFinjzY5a1vLd4MbdNCACwZKVZpIPn6ZFmWWKV/32UKt2XPCSvv0xY11Z/e6mebLToIJy/fofz+vdsvy8AUN9OAF9bNTDGkRyFcB3r/zlbfYFE4AsNgMlb0aygPIXuNJbxBAAAEEEEAAAQRyL/DI+FX6dYX7ktLS/j7WclKvdA7hyEqNiUlOa/ZfRNRpj+Q/D+us9qEVXd/f9d0yTd3geciGOQBk3agBKuXnrfu/ma29m1eovtdeNXTsVgPzx2uvqjiOZ6U5500T4/SVs2ozlarTVolVW+jqP85qbXx1JSh5Ge8Xt7bTBU2qZque07EJmrctypr1aE4Ydjg8DzPJVoHnJDb7Gt785WLN35Y8q9EM05SHeqjBOXsm5qYO8iKQWwHev3MraI/8BADtMY7Frhc8gIrdkNFgBBBAAAEEEEAAgXwWMIG6bYdSD9VIqW7Goz0VnsGefZk1acq6/Rr2Q/rLdetXKa2/Hugus2edWSbc+oVprhN9AxSreg4T5Nuj+l57dH2dUyp7cqu8oj33vMusDen9flZ+CghppQn7KmlxbPIMv23OGnrnhvbWHn0p+wWmzbvs6QsUXIAHomS1Xydj4jXqz/VWkPXWznV0Zes0JxlntRDSIZCPArx/5yNuMSqaAGAxGiw7NZUHkJ1Gk74ggAACCCCAAAII5FbABJFaPj/V2jbv3CunB4GY2WlXjFkgs7dgRteIvqEa3kJat3KRZs2bbS3jNX9qOw7Jy5FOY3LSUd8grXfW0ZKYWlqbFKa1zrpq37a9Rl/dRrd8uVhzt6YeAPJg3/p6uF8D/bBop57+fZ2rtjqVAjV7RO+c1E4eBEq8AO/fJf4WsAAIAHIfFIoAD6BCYadSBBBAAAEEEEDAtgIb95/UziNn1LVeJZUJ8C1S/Tx4MsYKZu06ckY3d66jWzrV8Wjfgm1RuvGLxem2e0i3MD2Tg4NAFu04ous/W2SV6a1EhToOqKX/ftWK36kGXmb57l6FOfbLx5F66nBu4Mx+fdudNXUwIFS9u/eUKje2TubdkVBJfd6e61Z0ymnBz09cr6/nR7p+u7h5dX10Uxuduxz6ilY19O71rXPTPPIiUGIFeP8usUPv1nECgNwHhSLAA6hQ2KkUAQQQQAABBBCwpcD4pbv1+K9rrNlzFYP8NOqyprq0RfU83+8tp3jmkAhzWETK9eGNrXVJixpuxY2ZtU2vT9mcbhUdwipq/N2dFZ+YpJf/2igT2GsZUl6Du4aqcfWy7nmSkqTjO6VDGzVhyjT5HNlkBfrCHXvl70jIaRfc8iU4vRThrK6Ams1Uq2EbbVMt3f3PaUU6qylR3lbalc/0U4Wg5IM63p+xVW9P2+IqwyzjXfxkX5m9Bccu3qUnf0s9oKRh1TL65+Ee6vPmLO1Is2/h85c11W1dQvOk/RSCQEkT4P27pI14+v0lAMh9UCgCPIAKhZ1KEUAAAQQQQAAB2wmYfdcGvjtHsQnus9j6Namql69opiplAwq9z+1fnq7D0bGudlQK8tO0R3pawcqU6+7vl+mf9Z4HcJjfg/y8tXbUAJkg4ZtTUwJpTlXTUV1R84QGhUSrnmO3HIc2Soc3S/Fn8qTPSU6HdjmraIszRJudtbQ1yfxviBX8S/Ty07KnLrCCfHEJSdby5bPxia56x9zURhc1r2597v/ObG05mLq3odkn74XLm1m/LYk4qms/XejK5+ftpflP9JExS3tNvK+bmoeUy5N+UQgCJU2A9++SNuIEABnxIiTAA6gIDQZNQQABBBBAAAEEiqlAUpJT1322UEsjj6Xbg7IBPvrk5rbqUi+40Hp4/EycWr0wzaP+y1rW0Ps3pC5p7TR6hg6cjEmnnU4F66R+u6aifvrrH9WIi7BO3TWn75Z1nM2zfu1xBmtrUk0r0He8dLhG3HylOny2S0fikk/gPffqXLeSxt3VyfX1rV8t0Zwth12fb+5UWy9d0VybD0RrwLtz3LKnPX346Ok4tXnR3ed//RukCXRKAb5eVgDU19srz/pLQQiUJAHev0vSaGfcV2YAch8UigAPoEJhp1IEEEAAAQQQQMBWAl/Pj9DzEzect0+1KpbSnBG9C2058Lkz3NI29rNb2qp/02o6cCJGnV6ZoXI6lXwIh9ceNfbaY83qq+/Yo0qO6Lwbt9JVrX35EoMbafLBCvp6i7+2OkMUrUBXHcN6huuJCxvphs8WaeGOI+nWPerSJhrcNcz12yezt+vVvze5PtetHKSZj/bSm/9s1of/bnN9X71cgOY/3kdeXg7Xd21fnKYjp+Ncn81PSWnOH+kQWlHjh3XOOwNKQqCECfD+XcIGPIPuEgDkPigUAR5AhcJOpQgggAACCCCAgG0Edh4xS3/nui07NcElsxw1bTDJdNjsN1c1g6XAx07H6c/V+1SljL8GNquW54HCc0+zNe0J0lnVd+xVu8D9GtHaqejda5VwYIOqOdKfyZiTQTvmLJ28dDeplvW/d151kUIbt5MCK7oVN23DQZk9Ck+cjbe+9/Fy6K8HuqthtTJ6bcomfTxre7rVL3iij2qUL+X6bc2e47rsw/luaReN7GvN0DSHs6RcQ7uH6amLm7ilM0uATaA0o+u1Qc11XfvaOWEgDwIISOL9m9vACBAA5D4oFAEeQIXCTqUIIIAAAggggIAtBE7FJuiOr5dqSaR70Gjs0I5qVK2sur82U6fjUvej+/r29urdsIpH32PiE639AyP/C1Bd3qqG3rm2ldvstFyBxZ/VxxP+1pa1S9TQa481m6+h126FOKJyVWzazNHOUtrqrGkF+nyqNdE1F/bTP1EVdfdvu83rnpXULIVe9Wz/DPu19/hZjfl3m7YfPqWbO9VxHVDyz/oDuvv75R5tbV6znCbe383t+8Qkp1q9MFXRMakHjVQu4++296HJ8Od9XdUipLxbXnMIiDkMJL2rR4PK+mZw+7wbkzyTpyAEio8A79/FZ6zys6UEAPNTl7IzFOABxM2BAAIIIIAAAgggkBOBGRsP6pnf12nfCff98lL2nDNlDvp4gZbvTJ1N99jAhrq3Vz2P6v5YtVcP/t8qt+8HdwnVc5c2yXQmoNnb76t5EdqwP1pXtaysi6qflg5vtE7fdf05FiE53Q8nyUmfTZ6zTj8r0GeW60Z61dHw6y7V9KiKum/yIVegzxwusuzpC/TMH+v0w6LUgFqfRlX01eD22a764MkYdRw9wyOf2aPvvj71Pb4f+t0ymRmFGV21KwZq9oheHrYZLeUOLu2nvx/sIRNI5EIAgZwL8P6dczs75SQAaKfRLEZ94QFUjAaLpiKAAAIIIIAAAkVA4MSZeD35+1r9tWa/R2tqli+lfx7uodL+yQdWPP37WrcA2LkHbqQUMHzsinTLSwkY7jpyRosjjig+0alWtcqrcdVA6ViEliyepxXLFqpWwk7rMI4wxwH5OlJnHOaGK87prdjy4fKt3kwfrPWxlu+aP7udVZSk5EMwbuxYW6OvbC7Tvh5v/OtW3bSHe+i+sSu1+WDqvoFmPz+zr19Ors6vzND+c4Ktpo76Vct4FDd7y2EN/nqJnGn270ubaHjvcI0Y0Mgj39yth3XLl0s8vv/2jg7q2aByTppNHgQQSCPA+ze3gxEgAMh9UCgCPIAKhZ1KEUAAAQQQQACBQhUwS24fHb/aOliif5OqevnK5vJOcxhERo1zOp268fPF6R5IEejnre/u6KB2oal725277179KqU17ZGebsXHJiSqzQvT3JYKpyRwKEltyp5WuVNb1dCxR/W99qihY7fqee2Tv5L3ysvtleh0KNJZzTp11wryJYVYf9/prKr5Tw6w9ixML/hm6p14Xzc1Dykn49L11ZlusyEf7ddAb03b4ta8X+7porZ1KuSoyff8sFx/rzvgyhsWbA736JnhDMn526L01tTNWrHruEd9Ux7qbi3RPvdKb6bhXT3q6smLGueozWRCAAF3Ad6/uSOMAAFA7oNCEeABVCjsVIoAAggggAACCBSqwCt/b9Sns3e42vDMJU00pFvqSbIZNW7e1ijd/OVij5+71qtkzYSrUynI7Tez/NcsA065TJBx/fMDFODr7fru382HdPvXS1RVx6xTd81MPhPsM383e/UFOWLzzGpnUhUryLfdUUt3DbpEXlUba+rBsrrnp/Uye+elvaqW9dfiJy+wvkpvSW2zmmU16f7uriyP/LRKv67c6/pcIdBXx86kBikDfL205rkB8vNJnj2Y3WvC8j3WISEp1yP9GuiBvp7Lf9OWawKTiyOOWgeImFmB5rq9q1la3TTD6u/4ZqlmbjLLmaV2dSpo7NBOOW5zdvtIegTsLsD7t91HOGv9IwCYNSdS5bEAD6A8BqU4BBBAAAEEEEAgWRi8LgAAIABJREFUBwJRp2K1aX+02odVkL9PanAsB0VlmsXM/jP7yaWcNmsy1A0O0ozzzCZLKfTOb5dp+sbUveXMoRYmeHh125B0Z6Kdjk1Qs1H/uC1FnTyksZr47JEObZIObVDkxmWqcHq7yjlST6jNtBOZJDjhW0Xl6rSQKjeSqjTRXwfLacSsWJ1RgJWzSfWymvxgavDul+V79Gia4JpJ069JVX1+azsr/QcztnrM5nvpimbWQR0p1/ilu/XYL2sybFnnupU07q5OOe5aUpJTL0zaIHMgSOfwSnr1qhbZCswdjo7V2bhE1a4UeN42mPvjlxV75JBDg9rWzPf7MccgZESgGArw/l0MBy0fmkwAMB9QKTJzAR5AmRuRAgEEEEAAAQQQyE+B1buP6+pPFlj729WqWEr/PNRDgX7Je+jlx/Xbyj16+KfUmWQpdfw8rLPap1m+e27du48m73OXdl+5F69oplvSBMHc8pw9Lh3epLd++F0Vz+ywlu6aWX3BjpN51q3DzrLa6VVHR4LCNetYJesE3m3OmnIGlNPiJ/u6HJ/6ba1+THO67RWtaujd61u7teP7hZF65o/1ru8+u6Wt+jetZn02s+du+yp1b7xSvt5a8lRflQnwdaU3Pt1fd98HMG0FZraembXHhQACJVeA9++SO/Zpe04AkPugUAR4ABUKO5UigAACCCCAAAIuges/W6hFO466Pj9/WVPd1iU034Su+WSBlkamnsybUpGZxffmNS2tj4eiY6xTZEMrBalLeCVrdt8rkzfq0zmpy4bL+Pto0ZN9FaQYKWqz+6m75gTe6H151odEv7LyqtpUjqqNdTSwrpafra5FpyoruGqIbu1cR2YGZa83Z7kFJ1++splu6pg8Q+/aTxZqSWSq8YgBDTW8t+dpxAu2RcksSTaBUDMD0PTbXGZ58KUfzNOG/cnBy5EXNtLd5xzmYZbbdnvtX+09fjbdfv94Z0d1rRecZyYUhAACxU+A9+/iN2b50WICgPmhSpmZCvAAypSIBAgggAACCCCAQL4JHD0dp3YvTVPa7efSm52WVw3YejBa/d6Zk25xKbPajp+J11UfL5BZMmouc9LtUxc1VpdXZ8r/7CG18tqmFl471K9SlLVXn47vzKvm6YxKKbBmU6lK8tLdlCW8KlNN+i8Yl1FlafeuM2kaVC1tzaY0V+sXp8n0K+UyS3tNgC87l1k+a5bfmkNBOtWtmO6S50fGr9KvK1L3AUwp38fLoTWj+ufrzM7s9IW0CCBQOAK8fxeOe1GrlQBgURuREtIeHkAlZKDpJgIIIIAAAggUSYFzD3YwjQyvbPbj6+XWXjMDLSun9GbWyecnrtfX8yMzTPbC5U31y4q9MsuSS+uMmntFqJVju7qUilS9+C2q7kidRZdZXef73entL1VuqGlRFbXibPIJvFudIbq8ZweNGNgkR0Wfu0zXFDJuaCeFVwlSh5dnuJU5Z0TvTPfCy0kjxi/brccmeO4D2KpWef0+vGtOiiQPAgjYSID3bxsNZi66QgAwF3hkzbkAD6Cc25ETAQQQQAABBBDIrcBd3y3T1A2ph2qY8sxEt7WjBqi0v4/MstInf1sns29f0xrl9OwlTdSyVvnzVmvypCxdTZvQHO7Q4eXpOhmT4PrazExLSHLKVwlq5NilNj7b1Vzb1dKxXeGOffJyuJ+Mm+3+evkovny4phyuoC1JIdrirKXNzhCNe+x6nYpzesxG/GN410z7l1EbzCEZfd+erYio064kA5tW0y2d6+imL1JPLjYzHc1JxF5eyct78/LKaB/Au3rU1ZMXNc7LqigLAQSKoQDv38Vw0PKhyQQA8wGVIjMX4AGUuREpEEAAAQQQQACB/BAwS0pbvzhVMfFJHsX/dFcndaxbSX+t2a/hY1e4fvf1dliBpMFdQj2CfAmJSdbsMxNQ7FS3kj68sbUCfFNPFP51xR49Mn61HEpSqOOgFeQbGn5McTuXqokjUv6O1MBgtvvr8JIq1k1dspuyhLdiuJzevmoxaqqiY1PL/2pwO23cH603/tnsqqpa2QAtHNkn3eBlVtvz9fwIPT9xg1vyS1pU16Q1+13fNa9ZThPv75bVIrOdruurMz32AczJkuNsV0wGBBAo8gK8fxf5ISqQBhIALBBmKjlXgAcQ9wQCCCCAAAIIIFA4AlPXH9Bd3y9Pt/KnL26sO7vX1YP/t1J/rPI8TMPMbHvt6hYqVyr1FNr/W7JLT/y61lXe/X3q6dH+DaXoA9LeFZow8Q9VObleLb22q5zjTI47fUqBCgptJ0fN1lKV//brC24g+ZbKsMxzDx556IL6+nP1Pu04nDpbzxzm8cLlzXLcLpMxOiZenV+ZqVNpgo3nFnhVm5p6+9pWuarnfJkfHb9av6zY45Zk1bP9VD7QL9/qpGAEECgeArx/F49xyu9WEgDMb2HKT1eABxA3BgIIIIAAAgggUDgCI35erZ+XuweKUlpiDgJ557pW6jB6huswjnNbaQ65+GN4N5XyS57lN/zHFZq9dru1b5+Z3dcpYKd6Bu2W42T6dWSl10levlqfWFsrEutqdVK4VjvDdcOFfXRnD88TdM9X3rN/rNN3C1MPCzHLcM/GJ7pl+WFIR3Wrn/tTcj+fs0MvT96YYXOeuLCRhp1zgm9WLLKa5pfle/Toz6tdyRtVK6Mp/x1GktUySIcAAvYU4P3bnuOa3V4RAMyuGOnzRIAHUJ4wUggCCCCAAAIIIJAtAbNct/3L03Uszcm0aQswB4F8cnPbDE/sNWnNvn1fXRio7oE7rRl+EavnqE7Snlzt27c9qbpWOcOVUK21rr38CjmqNdfKfWc0YsIabTt0yjo5d8xNbeTr7ZWt/o5dvEtP/pY6O/HczE1rlNXE+7rlyb58xvbSD+dr4/6T6bbx68Ht1btRlWy1PzuJ4xKSdOkH87T5YLSVjeW/2dEjLQL2FuD9297jm9XeEQDMqlQu0p08eVKTJ0/W0qVLtWzZMu3du1eHDx/W2bNnVb58eTVp0kQXXXSRhgwZokqVKmVa08KFCzVmzBjNnTtXBw4cUIUKFdSyZUsNHjxY119/fab5UxL83//9n77++mutWbNGx44dU7Vq1dS9e3cNHz5cnTp1ynI5OUnIAygnauRBAAEEEEAAgZIkcPR0nMx5EXm5hHPxjiO67rNFGTKag0D+179hmj3ynGpZ6oiaapvqx2+2lvE2deyUvyM+50NRuqpUs51Us40+3FJOn20rp5MKUt3gIP02vKvb8mJzwMapuASVDUhdcpydilfuOqYrxyxIN4uxNSfktgg5/+Em2alv1e7junLMfDnTOcNk3uO9FVIhMDvFZTutOXBl4Y4jqle5tGpVzN+6st04MiCAQKEJ8P5daPRFqmICgAUwHNOnT1e/fv0yrSk4OFg//PCDBgwYkGHaF154Qc8//7ySkjw3bTaZLr30Uo0fP14BAQEZlhETE6NrrrlGkyZNSv8/hry8NGrUKD3zzDOZtjmnCXgA5VSOfAgggAACCCBQEgRen7JJY2Ztl7+Plx7oW1/39grP1SEVKWYvTtqgL+dFuAjNjL+dR85YJ/KaK1gn1CNop0JjN6mVY7taeO1QeUfqfnnZtT/lDNCapLrWEt5VSeG656Zr1apJk+QjhyWZA0nMvnVn4hJ0XbvaKheYs0BfRu0y5TZ97p90A3K3dw3Vc5c2zW6XMk3/3B/r9G2aZccmQ5Cft9Y9PyBPxjDTBpAAAQQQOEeA929uCSNAALAA7gMTALzjjjvUu3dvtW3bVrVq1VL16tWtIJ75P+KECRP066+/KjExUX5+ftZMwRYtWni07IsvvtDQoUOt78PDw/Xkk0+qefPm2rdvn9577z39+++/1m833XSTFUjM6DK/jx071vrZtOnBBx9UjRo1tHbtWo0ePVrbt2+3fvv8889155135osQD6B8YaVQBBBAAAEEELCBgJn51+6lafovJmf16Jq2IRp9VfNsL4FNy+F0OtXzjVnadTT1II7nuvgpceNfqn7KHNKxQyGOqBwLxju9tdFZ29qzb40zXKEteuitlU4lKXnZbtWy/lr4RN88WW6bnUb2eXOWdkS5BzHNyb/TH+2p0v4+2SkqS2lPxsSr39uzdfBkrCt9y1rl9cfwrlnKTyIEEEAgrwV4/85r0eJZHgHAAhg3E9jz9k7eJDmj6/fff9eVV15p/XzVVVfpl19+cUt6/PhxhYWFyfxv7dq1tXz5cpkZgymXqcPknzhxovXV7Nmz1aNHD4/qzPe9evWyvjezBX/77Te3tkVFRVlByl27dllLi3fs2GEtU87riwdQXotSHgIIIIAAAgjYRWDd3hO65IN5Ht3pVi9YY25uk+PlsJsOnNTAd+da5XorUQ/4/KoHfH6XQ+msV80CZmy5MK1XPf0ZVd0K+m1w1lGsUk+cNUts0wYxB3cJ1ajL8n7GXWZNvffH5Zq89oBbsk9vaasBTatlljXHv09Zt1/Dfljhyv/4wEa6p1d4jssjIwIIIJAbAd6/c6Nnn7wEAIvQWDZu3FibNm2yAntmj8C01xtvvKHHHnvM+mrcuHHp7vVn/k8dGhpqzSS85JJLXMHAtOVcfPHF1n6EJiAZGRmpkJAQDwGzN+ANN9xgff/mm2/q0UcfzXMlHkB5TkqBCCCAAAIIIGATAbOP3BUfzU+3N+Zk1wn3dMnRzLX3Z2zV29O2qKqO6n2/D9XRa1PWxYKqaF5MHS2KCbWW85plvSOv6mydsLshg0Mvzi3852Gd1T60YtbrzKOU3y+M1DN/rHeVZg4UMQdk5Pf15+p9+nPVPpmDRkzwL8D3/BMC8rs9lI8AAiVXgPfvkjv2aXtOALAI3Qft2rWzZvaVLl1a0dHJp3elXF27dtWCBQtUtmxZKzholgqndw0cOFD//POP/P39ZWbzmbJSrlOnTlnBxdjYWJl0f//9d7plxMXFqXLlyjKHl3Tp0kXz56f/H6C5oeMBlBs98iKAAAIIIICAnQWW7zyqQR8vzLCLd/esq5EXNs42wSUfzFXw/jl6y/djVXK4/7dm2sJOO/211lnX2rOvQr1Ouu6KK6RyIbpv3EpNWrPflXRQmxD9uXqv4hMzn0FYWMt/TWPNwRj3jV2pmZsOWgHIj29uq4pB6f+3dLZRyYAAAggUAwHev4vBIBVAEwkAFgByVqrYuHGjtZ+fmb1nAoFmH8CUywTkgoKClJCQYB0QMmXKlAyLfOWVV6y9Ac01c+ZMa4+/lMt87tu3r/XRpHviiScyLMfUM3XqVPn4+OjMmTPy9c3bDZl5AGXlriANAggggAACCJREgUU7juj685zUa4JpC57oK2+zxjaL174jJ/XnO/dqmE/ydjFpL6eXj8bHd9eypPrWUt5tzpquffvSLpX9fM4OvTx5oyurOdjidFyiW1nmbI/0TsAtrOW/aRuXmOTMllkWaUmGAAIIFHkB3r+L/BAVSAMJABYIc/qVmMDa3r17raW6r7/+ug4ePGgl/P7773XzzTe7Mq1fv17NmjWzPpsDO959990MW2329DN7CJrro48+0r333utKaz7fd9991meT7grzr7kZXKae999/3/rV1N/EnNaWhxcPoDzEpCgEEEAAAQQQsJXAvK1RuvnLxeft09ihHdUlPHU/6PMmPr5Lh76+WVVOrPZMVq62dPVXGvjLWW064D4r0MQXVz7T33Uy75KIo7r204xnJtauGGjNrDNLmM+9xt/dWR3CCn75r61uDDqDAAII5FCA9+8cwtksGwHAAh7Qb775RrfffnuGtf7vf/+zgoEO88+n/11mxt+FF15ofTJ7AZo0GV3Lli1T+/btrZ/NDD8z0y/lMp9fe+0166OZYWhmGmZ0mb3/RowYYf1s6jczArNzmQfM+a79+/erQ4cOVpLdu3enuxdhduojLQIIIIAAAgggYBeBfzcf0u1fp64GqV4uQOVK+boF6G7oUEuvXNXC6vLE1fv08aztqlLWXy9f2Vw1y5dKpdj0l/T7vVKMZ1BOjS6RLv9QKlVBI35erZ+Xu//3W4uQcvrzvm6uss7EJajZc/+4HeyR1nxg02pqHlJOb/yz2W0oqpTx16KRBX/6r13uB/qBAAII5FaAAGBuBe2RnwBgAY9jRgHAVq1a6ZNPPlHHjh09WvTzzz/r2muvtb7/+OOPNWzYsAxbbZYSp8zWM7P9PvjgA1fa4cOHa8yYMdZnk65Ro0YZlmPqSZk9OGHCBA0aNChbUmkDmJllJACYmRC/I4AAAggggEBJEpi+4aDu/G6Zq8shFUrpxo619fqU1MCaCQgufeoCmZN9zYEhKaftmgMnJt7XTV5J8dK0Z6XFH3vQxTm9tb3V42p8xWPSf//o/N3CSD2b5qAMk2lYz3A9caH7fy8OfHeOx0zBlAoe7ddA/ZpWdZ00nPL9bZ3r6PnLk1ezcCGAAAIIFLwAAcCCNy+KNRIALOBROX78uFJmx509e1bbt2/X+PHjrSW54eHh1vJec4Jv2sssCb711lutr7788kvdcccdGbZ6x44dVjnmGjJkiL744gtXWvP5q6++sj6beuvWrZthOSadSW+uc5ckZ4WMAGBWlEiDAAIIIIAAAgh4CkxZt1/Dfljh+iEsOEjf3dFB3V//1y3xF7e208ezt2v5zmNu339+aSX1W/+EtG+lR+E7k6rokaQH9f2zwxTo5+P6feWuY7pyzAL3/wYd0kHd61d2++6xCas1fln6Kz2+GtxOvRtWUZ+3Zisi6rQr34RhndWuEE7/5d5CAAEEEEgWIADInWAECAAWkfvABNluu+02a+mvCfINHjzY1bLiOAOQJcBF5MaiGQgggAACCCBQ7ATMkt77x6UG7+pXKa1pj/TUVWPma8Wu1KW8Zqnv3uNn3fp3oddiveH3uUrrjEe/JyV20sj4O9Wxcai+uC15y5iUy5yUawKMh6Njra8qBflp3uN9VMrP2y3dj4t36qnf1qVrapb5VisXoAXbo3Tvjyt08my8BncJ07OX5u1e0sVuQGkwAgggUMgCBAALeQCKSPUEAIvIQJhmXHfdddZsQHPir1kWW6FCBat1xXEPwMxYeQBlJsTvCCCAAAIIIFBSBX5fuVcP/bTK1f1G1cpoykM99O2CSD335/p0WfwVp6d9ftAtPtM9fo91+ur5hFs1NrGP+fd/vT6oha5tX8sj3cxNB/XCxA3WP0g/e0kT9W5UxSPNur0ndMkH8zy+NwHDZU9f4NrHOj4xSadjE1Q+0K+kDiP9RgABBIqMAO/fRWYoCrUhBAALld+98rFjx+qmm26yvvzxxx914403Wn9ft26dmjdvbv09N6cAf/jhh7r//vutcjgFuAgNPE1BAAEEEEAAAQTSCPy8bLdGTFjj+qZ5zXKaeH83a3Zex9HTPQ7hqOM4oI9931MTr50ejqfLhOnqqLu00VnH+s1s+Wf2Dgwu7Z+uudPp/C9d6oF0aROawJ45CCQ2Icktf/f6wfp+iOde1gwsAggggEDhCxAALPwxKAotIABYFEbhvzZMmzZN/fv3tz6NHj1aI0eOtP4eFxenwMBAJSYmWqfxmhmBGV3m1N8nn3zS+nnmzJnq3bu3K6n53LdvX+uzSWdOBc7oMvVMnTpVPj4+On36tPz88vZfb3kAFaEbj6YggAACCCCAQJESGLdkl0b+utbVpta1y+u3e7tan2/5crHmbo1y/WZm/v3l96Tqee3z6MPiMhfodZ+7tXx/vOu39qH/z959wFVV//8Df102blyoIA5EBPcW985c5SptWOZMTc2ZuSrNTDNLc6Rpll8z07TMvTeKe4EooDhBcCEKyrjfx+cg53LhXrnA3fd1Ho8evz/3fM5nPD/ne/593n2GG9YNaZyn9mZeiiwyG9yiIia+7penfPkwBShAAQoYRoDjb8O4WlquDACaUY9lPCF4/vz58mw9UcXGjRsjMDAQhQoVQkxMjNaAXIcOHbBjxw44OztL6QoWLCi38MmTJyhevLgUUBTptm3bprH14n6JEiUQFxeHgIAAHD2qviG0Psj4AdKHIvOgAAUoQAEKUMAaBVYFXseUDCfyNihfFH8NCZCa+tfJmxifYXZgZ7tA/OS0QI0hQemEqckfYl1KC2nJb8ZrUkc/DGyu/SA4XTy/2HQJK49eV0s6v09tdK1ZRpfHmYYCFKAABYwswPG3kcHNtDgGAM2oYzp16oStW7dKNdq3bx9atmwp12727NmYMGGC9PeaNWvQu3fvLDUX/6MuX768NFOwY8eO2LJlS5Y04ncR+BMz+65duwZPT88saf7880/06dNH+l2UO27cOL0r8QOkd1JmSAEKUIACFKCAlQj8euQavvwvWG5NQMViWDOokfT344Qk1J+xGy9S0pbgznFYgl4OB+W015XuGPBiDMKUWf8dTyz/3T+2JcoVy58nqcx7FIrM9oxpAe8SBfKULx+mAAUoQAHDCHD8bRhXS8uVAUAj9JiY2ScCdi4uLlpLmzdvHkaPHi3dF0G8q1evSkG69OvBgweoWLEiHj9+jHLlyuHUqVMoVqyYfF8E/bp164b//vtP+i3z8t/0hBmXAXft2hUbNmyAvb3qdLfY2FjUrVsXN27cQJEiRRARESEfRqJPKn6A9KnJvChAAQpQgAIUsCaBZQcj8PXWELlJmffXU83AU+KEy3CUwEM57Qb3TzA6Mm22YMbLTgGMbFMZI9v65Jnq5oNnaD5nH15uFwi3fI44Obkd7EUhvChAAQpQwOwEOP42uy4xSYUYADQCuwjoieW3PXr0QNOmTeHt7Y0CBQpIv124cEE68OPIkSNSTcRee2LmXtu2bbPU7Oeff8aQIUOk30UekyZNkg4HuXPnDn744Qdp1qC4xOw9caCItkvcF7P8xCX2CBw1ahTKlCkj1eXrr79GeHi4dG/JkiUYPHiwQYT4ATIIKzOlAAUoQAEKUMAKBBbtD8Ps7aFyS1pXKYkVH9aX/36enIK/T92GMvoi3j2dtmoj/YofdAxDtsYh6NoDlCjojADvYmhUsRgaexdDmSKuetP5ekswlh26Bkd7BWa8WQ1v1/fSW97MiAIUoAAF9CvA8bd+PS01NwYAjdBzIgAYGZn1VLbMRYvluCtWrEC7du201mratGmYPn060k9oy5xQLPH9+++/XznbMCEhAT179pSXG2fOw87ODlOmTMEXX3xhMB1+gAxGy4wpQAEKUIACFLBwgfl7ruL7XVfkVrT3d8fSvvWyturIj8Cuqarfi3gBI89LR/2Kf1dUiDW/BrxuPXwGJwc7lCyofZWLAYtn1hSgAAUooKMAx986Qll5MgYAjdDBYkbd7t27pRl6ISEhiI6Oxv3796Ugnbu7O2rVqoXOnTvjrbfekk77ze4Sh3IsXLgQhw4dkvISS3Vr1qyJfv36yXv3ZZeHuC9mCYrlyefOncOjR4+kujRr1gzDhw+XDv8w5MUPkCF1mTcFKEABClCAApYsIIJ/IgiYfnWsXgqL3q2btUm/dQGuqfb/Q72PgM7zLLnprDsFKEABChhAgONvA6BaYJYMAFpgp1lDlfkBsoZeZBsoQAEKUIACFDCEwOztl7Fof9qWLOISp+uKU3bVrufxwOwKQMoL1c9vrwb8OhuiSsyTAhSgAAUsWIDjbwvuPD1WnQFAPWIyK90F+AHS3YopKUABClCAAhSwLYGZW0Ow9GCE3OjudTzw/Vu11BFCtwNr3lb9ZucAjL8GuBSyLSy2lgIUoAAFshXg+DtbIptIwACgTXSz+TWSHyDz6xPWiAIUoAAFKEAB8xD46r9grDhyTa7MW/U8MbtnTfXKbR0HBC1V/VauCdBvq3k0gLWgAAUoQAGzEuD426y6w2SVYQDQZPS2XTA/QLbd/2w9BShAAQpQgALaBab+exG/B6oOkHunoRdmdquu/sD82sAD1SxBtJkKNBtDVgpQgAIUoEAWAY6/+VIIAQYA+R6YRIAfIJOws1AKUIACFKAABSxAYOKGC1gTdEOu6QcB5fDlG9VUNReBPxEAzHgNOgCUybRM2ALayipSgAIUoIDhBTj+NryxJZTAAKAl9JIV1pEfICvsVDaJAhSgAAUoQAG9CIxbdw7rTt2S8+rftAKmdPZX5R20DNg6VvV3/hLAmCuAnZ1eymcmFKAABShgXQIcf1tXf+a2NQwA5laOz+VJgB+gPPHxYQpQgAIUoAAFrFhg9Nqz2HDmttzCwc0rYmJHP1WL1/QBQjPs91fjbaB7hv0ArdiGTaMABShAgZwLcPydczNrfIIBQGvsVQtoEz9AFtBJrCIFKEABClCAAiYR+GTNGfx37o5c9rBW3hj3WhVVXeZUAp7GqP7uthSomeFEYJPUmoVSgAIUoIC5CnD8ba49Y9x6MQBoXG+W9lKAHyC+ChSgAAUoQAEKUECzwMf/O4VtF6PkmyPb+ODTdpXT/n4eD3zjof7gsCCghC85KUABClCAAhoFOP7miyEEGADke2ASAX6ATMLOQilAAQpQgAIUsACBAb+dxO6QaLmmY9tXxvDWPml/RwcDiwPUWzEpCnB0tYCWsYoUoAAFKGAKAY6/TaFufmUyAGh+fWITNeIHyCa6mY2kAAUoQAEKUCAXAv1+DcK+UNUS3wkdquDjlt5pOYVuA9b0VuVawB0YeyUXpfARClCAAhSwFQGOv22lp1/dTgYA+R6YRIAfIJOws1AKUIACFKAABSxA4P3lx3Hoaqxc08md/DCgWcW0v48tAbZPULXCsz4wYLcFtIpVpAAFKEABUwlw/G0qefMqlwFA8+oPm6kNP0A209VsKAUoQAEKUIACORTovTQQxyIeyE990cUfHzapkPb39onAsUWqHKv1BHouz2EJTE4BClCAArYkwPG3LfW29rYyAMj3wCQC/ACZhJ2FUoACFKAABShgAQK9lhzFiesP5ZrOeLMa3mtULu3vP98FLm9WtaLZGKDNVAtoFatIAQpQgAKmEuD421Ty5lUuA4AiKJL0AAAgAElEQVTm1R82Uxt+gGymq9lQClCAAhSgAAVyKPDmwiM4e/OR/NSs7tXRu4FX2t+LmwLRF1Q5dpkP1P0ghyUwOQUoQAEK2JIAx9+21Nva28oAIN8DkwjwA2QSdhZKAQpQgAIUoIAFCHRecAgXb8fJNf2uV030rOsJKJXALC/gueoe+v4LVGxpAa1iFSlAAQpQwFQCHH+bSt68ymUA0Lz6w2Zqww+QzXQ1G0oBClCAAhSgQA4FOvxwEJejnshP/di7Ft6o5QE8ewDMfrkXYPrdEWeBopl+y2F5TE4BClCAAtYtwPG3dfevrq1jAFBXKabTqwA/QHrlZGYUoAAFKEABCliRQNvvDyDsXrzcop/eqY3ONcoAd84ASzPM9lPYAZPvAfaOVtR6NoUCFKAABfQtwPG3vkUtMz8GAC2z3yy+1vwAWXwXsgEUoAAFKEABChhIoOWcfbh+/5mc+5L36qJDtVLApX+AdRn2+ytcFvj0ooFqwWwpQAEKUMBaBDj+tpaezFs7GADMmx+fzqUAP0C5hONjFKAABShAAQpYvUCTWXtx+1GC3M7lH9RDGz934Mh8YNcUVfvLNQX6bbF6DzaQAhSgAAXyJsDxd978rOVpBgCtpSctrB38AFlYh7G6FKAABShAAQoYTaDhzN2Ijnsul/fbRw3QonIJYMsY4MQvqnrUehd4c5HR6sWCKEABClDAMgU4/rbMftN3rRkA1Lco89NJgB8gnZiYiAIUoAAFKEABGxSoN2MXYuNfyC1fPaAhmlQqDvyvJxC2SyXS8nOg5QQbFGKTKUABClAgJwIcf+dEy3rTMgBovX1r1i3jB8isu4eVowAFKEABClDAhAI1v9yJxwlJcg3WDmqEhhWLAT/VB2KvqGrW7WegZm8T1pRFU4ACFKCAJQhw/G0JvWT4OjIAaHhjlqBBgB8gvhYUoAAFKEABClBAs0DVqdvx9EWKfPPvjxujrlcR4OtSQHKi6qF+24FyAWSkAAUoQAEKvFKA42++IEKAAUC+ByYR4AfIJOwslAIUoAAFKEABCxDwnbwNz5NT5ZpuGt4ENQonAnN91Wv/aTBQ2MMCWsQqUoACFKCAKQU4/jalvvmUzQCg+fSFTdWEHyCb6m42lgIUoAAFKECBHAh4f74VKalK+YktI5qiavJlYEV7VS72TsCkaMDOLgc5MykFKEABCtiiAMffttjrWdvMACDfA5MI8ANkEnYWSgEKUIACFKCAmQsolUpUmLhVrZY7P22OytHbgQ0DVL8X9QZGnDbz1rB6FKAABShgDgIcf5tDL5i+DgwAmr4PbLIG/ADZZLez0RSgAAUoQAEKZCPwIjkVlSdvU0u1d0wLVAxZDOydofrduzXw/kZ6UoACFKAABbIV4Pg7WyKbSMAAoE10s/k1kh8g8+sT1ogCFKAABShAAdMLJLxIgd/U7WoVOTS+FcoeGg+cWaX6vW4/oMsPpq8wa0ABClCAAmYvwPG32XeRUSrIAKBRmFlIZgF+gPhOUIACFKAABShAgawCcYlJqPHFTrUbRz9rjTL/vgVcO6j6ve0XQNNPSUgBClCAAhTIVoDj72yJbCIBA4A20c3m10h+gMyvT1gjClCAAhSgAAVML/Dg6QvUmb5LrSJBk9qg5PIGwKNI1e89VwDVepi+wqwBBShAAQqYvQDH32bfRUapIAOARmFmIZkF+AHiO0EBClCAAhSgAAWyCtyLS0SDmXvUbpyZ1Apu33sCyhTV7wP2Ap51SUgBClCAAhTIVoDj72yJbCIBA4A20c3m10h+gMyvT1gjClCAAhSgAAVML3DnUQIaz9qrVpELn/qh4OLa6pUbFw7kL276CrMGFKAABShg9gIcf5t9FxmlggwAGoWZhWQW4AeI7wQFKEABClCAAhTIKnDj/jM0n7NP7UZo/wJwXt1V9ZtjfuDz24BCQUIKUIACFKBAtgIcf2dLZBMJGAC0iW42v0byA2R+fcIaUYACFKAABShgeoHwmHi0mXtArSJhvR7A4b/hqt9K+gNDA01fWdaAAhSgAAUsQoDjb4voJoNXkgFAgxOzAE0C/ADxvaAABShAAQpQgAJZBa5EP0H7eRlO+wVwrf0ZKA7OUSWu/Drwzp/kowAFKEABCugkwPG3TkxWn4gBQKvvYvNsID9A5tkvrBUFKEABClCAAqYVuHTnMTrNPyxXwt5OgfB6/wDn16oq1mAw0HG2aSvK0ilAAQpQwGIEOP62mK4yaEUZADQoLzPXJsAPEN8NClCAAhSgAAUokFXg3M1HeGPhEfmGs4MdQiv8ANw8pkr82kwgYBj5KEABClCAAjoJcPytE5PVJ2IA0Oq72DwbyA+QefYLa0UBClCAAhSggGkFTkU+QI/Fqv39Cjg74GKhkcCTu6qKvb0a8Ots2oqydApQgAIUsBgBjr8tpqsMWlEGAA3Ky8y1CfADxHeDAhSgAAUoQAEKZBU4HnEfby9VzfYr4QqcUL6jnnDIYaBUdfJRgAIUoAAFdBLg+FsnJqtPxACg1XexeTaQHyDz7BfWigIUoAAFKEAB0wocCYvFu78clytRJ38sNqSMUK/UZzcBl0KmrShLpwAFKEABixHg+NtiusqgFWUA0KC8zFybAD9AfDcoQAEKUIACFKBAVoH9offw4a8n5BtvFAjBj8nTVQld3YAJ10lHAQpQgAIU0FmA42+dqaw6IQOAVt295ts4foDMt29YMwpQgAIUoAAFTCewOzgaA34/KVdgWMEDGJf0s6pCpWsBgw+YroIsmQIUoAAFLE6A42+L6zKDVJgBQIOwMtPsBPgByk6I9ylAAQpQgAIUsEWB7RejMOR/p+Smzyy4Du8kbVRR+HUF3l5lizRsMwUoQAEK5FKA4+9cwlnZYwwAWlmHWkpz+AGylJ5iPSlAAQpQgAIUMKbA5vN3MPyPM3KRvxVYiBbJR1RVaPwJ0H6GMavEsihAAQpQwMIFOP628A7UU/UZANQTJLPJmQA/QDnzYmoKUIACFKAABWxD4J8ztzFq7Vm5sTvyT4NvylVV4zt+BzQYaBsYbCUFKEABCuhFgONvvTBafCYMAFp8F1pmA/gBssx+Y60pQAEKUIACFDCswPpTtzB23Tm5kHOuQ1BYGacq9N31gE87w1aCuVOAAhSggFUJcPxtVd2Z68YwAJhrOj6YFwF+gPKix2cpQAEKUIACFLBWgT+DbuCzDRek5uVDIoJdPlJv6rATQInK1tp8tosCFKAABQwgwPG3AVAtMEsGAC2w06yhyvwAWUMvsg0UoAAFKEABCuhbYNWxSEz556KUra/iBnY4f6ZexKQowNFV38UyPwpQgAIUsGIBjr+tuHNz0DQGAHOAxaT6E+AHSH+WzIkCFKAABShAAesR+PXINXz5X7DUoLZ2p/CL01xV4wq4A2OvWE9j2RIKUIACFDCKAMffRmE2+0IYADRSF50+fRrbt2/HoUOHcPHiRdy7dw+Ojo4oU6YMGjdujP79+6NZs2Y610bktXTpUgQFBSEmJgYlSpRAgwYNMGjQIHTo0EGnfJKTk7F8+XKsXr0aISEhiI+Ph4eHB9q2bYsRI0bA399fp3xyk4gfoNyo8RkKUIACFKAABaxd4JdDEZixJURqZj/7bZjmuErVZM8GwIBd1k7A9lGAAhSggJ4FOP7WM6iFZscAoBE6rkWLFjh48GC2Jb3//vv45Zdf4OTkpDWtUqnEkCFDpOCftksEAZcsWQKFQqE1zf3799GpUyccP35cYxpnZ2csWrQIH32Uad+ZbFuhWwJ+gHRzYioKUIACFKAABWxLYPH+cHy7/bLU6KkOv+Mjh+0qgOq9gB6/2BYIW0sBClCAAnkW4Pg7z4RWkQEDgEboxkqVKiE8PFya7derVy9ppp+XlxdSUlIQGBiIuXPn4vbt21JN+vTpgz/++ENrrSZNmoSZM2dK92vXro3x48fD29tbyn/27Nk4c+aMdE+kmzFjhsZ8RLmtW7eWg5Ldu3fHwIEDUbRoUSkgKJ4TMxTt7e2xZcsWvPbaa3pX4gdI76TMkAIUoAAFKEABKxBYsOcq5u5KW+a71HEu2tufUrWq2VigzRQraCWbQAEKUIACxhTg+NuY2uZbFgOARuibzp07o2/fvujRo4cUVMt8xcbGokmTJrhyJe1f9sRsQU3LgcPCwuDn5wexdLdevXpSOldX1SbQz549g5htePLkSTg4OODy5ctScDDztXLlSvTr10/6eejQoVi4cKFaElFO3bp1ERcXBx8fHwQHB0v56fPiB0ifmsyLAhSgAAUoQAFrEfh+1xXM33NVas42p8/gZ3dD1bSuC4A6fa2lqWwHBShAAQoYSYDjbyNBm3kxDACaSQdt3rwZXbp0kWoj9t/78ccfs9Rs2LBh0rJccYmZg40aNcqS5tixYwgICJB+Hz58OBYsWJAlTdWqVaWgnpubG8SHIF++fFnSzJo1CxMnTpR+X79+vRS81OfFD5A+NZkXBShAAQpQgALWIjBnx2Us3BcOQIkLzgNQUJGgalrfTUDFFtbSVLaDAhSgAAWMJMDxt5GgzbwYBgDNpIPEARwFCxaUaiP25hMBwYyX2PuvbNmy0lLhKlWqSId2aLvE/dDQUHh6euLGjRtqewFevXoVlStXlh4VewkuXrxYYzZRUVEoXbq0dO+dd96RDgrR58UPkD41mRcFKEABClCAAtYi8M3WEPx8MAJF8ARnXQarN2vEWaBoBWtpKttBAQpQgAJGEuD420jQZl4MA4Bm0kEPHjxAsWLFpNqImYCbNm1Sq1lERIS8nHfw4MHSIR/aLnE//ZAQ8VyFCqp/UVyxYoV04rC41qxZg969e2vNx9fXV1qWLPYrjIyM1KsUP0B65WRmFKAABShAAQpYicBX/wVjxZFrqK6IwH/Ok1WtUtgBk+8B9o5W0lI2gwIUoAAFjCXA8bexpM27HAYAzaR/Nm7cCHEYh7jGjRsnHeiR8RKHcYi9BMU1b948jBo1SmvNxf3Ro0dL98VzHTt2lNOKvL/77jvpb3FgSK1atbTm88Ybb0iBSHGa8JMnT5A/f369afEDpDdKZkQBClCAAhSggBUJTPv3In4LjERHu2NY5DRf1bLCXsCnF6yopWwKBShAAQoYS4Djb2NJm3c5DACaQf+kpqZK+/YFBQVJtTlx4oR0yEfGS8z4+/jjj6Wf1q1bh549e2qtudizT5w2LC7xnJgRmH6JGX9r166V/oyJiUHx4sW15iP2EEw/IEQcKCJmBOp6iQ/Mq667d++iQYMGUpKbN29Ky5V5UYACFKAABShAAVsX+HzjBfxx/AYG2f+Hzx3XqDjKNwM+VN8ixtat2H4KUIACFNBNgAFA3ZysPRUDgGbQw3PnzsXYsWOlmnTr1g0bNmzIUqs5c+Zg/Pjx0u/btm1Dhw4dtNZc3E+f9Sdm+40ZM0ZOK/YX3Lp1q/R3QkICXFxctOYzYcIEeSaiOFlYnAys6yVmDep6MQCoqxTTUYACFKAABShg7QLj15/DXydvYbrDCrzvsFvV3FrvAW8utPbms30UoAAFKGAAAQYADYBqgVkyAGjiTjtw4ADatm2L5ORklCxZEufPn4e7u3uWWk2fPh1Tp06Vft+zZw9at26tteZ79+5FmzZtpPviucmTVfvHiN/FfXGlpKTAzs5Oaz6iPPG8uA4dOoSmTZvqrMUAoM5UTEgBClCAAhSgAAVkgdFrz2LDmdtY6fgtWtqfU8m0mgS0SPuPwbwoQAEKUIACORFgADAnWtablgFAE/btpUuX0KxZMzx8+BDOzs7YsWMHWrRoobFGljYDkEuATfhisWgKUIACFKAABSxWYMSaM9h07g72OI2Bt91dVTu6LQVqvm2x7WLFKUABClDAdAIMAJrO3pxKZgDQRL1x7do1aUbdnTt3YG9vL+3rJ5b/arssbQ/A7Fj5AcpOiPcpQAEKUIACFLBFgaGrT2HbhTu47NwPzookFUG/7UC5AFskYZspQAEKUCCPAhx/5xHQSh5nANAEHSmCfmLmX0REhHTC7sqVK9G3b99X1mTz5s3o0qWLlCYvpwCLvQbFnoPi4inAJuh8FkkBClCAAhSgAAVeITDw95M4F3wZQS7D1FONDgEKlaEdBShAAQpQIMcCDADmmMwqH2AA0MjdGhsbKy3zDQ4Olkr+6aefMGxYpn/B01AnESz09vaW7ohTfcWMQG2XuL906VLptniuQoUKctIVK1agf//+0t9r1qyBOBVY2yVO/b1y5Qq8vLwQGRmpVyl+gPTKycwoQAEKUIACFLASgX6/BiHuymH87fylqkX2zsCkKOAVezdbSfPZDApQgAIUMIAAx98GQLXALBkANGKnPX78WDq84/Tp01Kps2bNgjhpV5dLqVTC09NTWjJcpUoVhISEaH3Mz88Ply9fhoeHB8QJuxkP5BABPRHYE9eQIUOwePFijflERUWhdOnS0r0+ffrgjz/+0KWaOqfhB0hnKiakAAUoQAEKUMCGBN5ffhxFw//Bj06LVK0uVgn45JQNKbCpFKAABSigTwGOv/Wpabl5MQBopL579uwZ2rdvjyNHjkglTpo0CTNmzMhR6UOHDpUDdoGBgWjUqFGW548dO4aAgLT9YUT6hQsXZknj7+8vBRCLFi0qBQjz5cuXJY0ITk6cOFH6/a+//kKvXr1yVNfsEvMDlJ0Q71OAAhSgAAUoYIsCfZYeQ93IXzDWcZ2q+d5tgPc32CIH20wBClCAAnoQ4PhbD4hWkAUDgEboxBcvXkj79+3cuVMqbeTIkfjhhx9yXLKYvVe1alUkJyejXr16OHjwIFxdXeV8EhIS0Lx5c5w8eRIODg7SMmMfH58s5WRcBiyWH4tlyBmv8PBw1KlTB3FxcdKyYzGbUOSnz4sfIH1qMi8KUIACFKAABaxFoNeSo+h561u87bBf1aR6HwGd51lLE9kOClCAAhQwsgDH30YGN9PiGAA0Qsf06NEDGzak/VdbsQRYBP8yLsvNXAUnJydUrlxZY83ErDwxO09ctWvXlpYQiyCdCNp9++230sEe4hLpZs6cqTGPlJQUaR/C9NmIon4DBw6Em5sbgoKCMH36dNy7dw92dnYQh4+8/vrrelfiB0jvpMyQAhSgAAUoQAErEOi26AjG3R2LxvZp+0VLV9svgKafWkHr2AQKUIACFDCFAMffplA3vzIZADRCn7wq2Kep+HLlyuH69esaa5aamioF68QsPm2XOORDHAIiAnjaLnEYSceOHXHixAmNSUQQUswMFGUZ4uIHyBCqzJMCFKAABShAAUsX6LLgMBbFfIiydjGqpvT8FajW3dKbxvpTgAIUoICJBDj+NhG8mRXLAKAROkSfAcD06m7dulUK8okAngjmFS9eHPXr15dOCNZ1xp5YSrxs2TLpgA+xJ+DTp09RpkwZtGnTRlqmLJYbG+riB8hQssyXAhSgAAUoQAFLFug4bx82PeoOB0WqqhkD9wIedS25Waw7BShAAQqYUIDjbxPim1HRDACaUWfYUlX4AbKl3mZbKUABClCAAhTQVeDd7/7C6vhMKzDGRQD5i+maBdNRgAIUoAAF1AQ4/uYLIQQYAOR7YBIBfoBMws5CKUABClCAAhQwc4FPZ83HvMQpci2THfLBYdIdQKEw85qzehSgAAUoYK4CHH+ba88Yt14MABrXm6W9FOAHiK8CBShAAQpQgAIUyCrwzdefY2LSQvnGk8K+KPhpEKkoQAEKUIACuRbg+DvXdFb1IAOAVtWdltMYfoAsp69YUwpQgAIUoAAFjCew4qv++Ch1vVxgrEdrFB+40XgVYEkUoAAFKGB1Ahx/W12X5qpBDADmio0P5VWAH6C8CvJ5ClCAAhSgAAWsUWDrl13QUXlQbtod3w9Qps98a2wq20QBClCAAkYS4PjbSNBmXgwDgGbeQdZaPX6ArLVn2S4KUIACFKAABfIicPaLBqiFUDmLyHqTUa7zuLxkyWcpQAEKUMDGBTj+tvEX4GXzGQDke2ASAX6ATMLOQilAAQpQgAIUMHOB6Gnl4a54KNcyrPXPqNS8t5nXmtWjAAUoQAFzFuD425x7x3h1YwDQeNYsKYMAP0B8HShAAQpQgAIUoEAmgaRE4Gt3tR9Du22Hb80AUlGAAhSgAAVyLcDxd67prOpBBgCtqjstpzH8AFlOX7GmFKAABShAAQoYSSD2KvBTPbXCQj68BL/ynkaqAIuhAAUoQAFrFOD42xp7NedtYgAw52Z8Qg8C/ADpAZFZUIACFKAABShgVQLKq7ugWN1TbtNDZQHEDL2Myu4FraqdbAwFKEABChhXgONv43qba2kMAJprz1h5vfgBsvIOZvMoQAEKUIACFMixQMrxZbDfNlZ+7nxqBeT/5DC8SxTIcV58gAIUoAAFKJAuwPE33wUhwAAg3wOTCPADZBJ2FkoBClCAAhSggBkLJG2fDMdjC+QabklpgOqj/oVXsXxmXGtWjQIUoAAFzF2A429z7yHj1I8BQOM4s5RMAvwA8ZWgAAUoQAEKUIAC6gJJa96HY+gm+cclyZ3RdewvKFPElVQUoAAFKECBXAtw/J1rOqt6kAFAq+pOy2kMP0CW01esKQUoQAEKUIACxhFIXtICDlFn5cImJ/XDiAmzULKQi3EqwFIoQAEKUMAqBTj+tspuzXGjGADMMRkf0IcAP0D6UGQeFKAABShAAQpYk0DqrAqwS3wgN+mDFxMwb9JYFM3vZE3NZFsoQAEKUMDIAhx/GxncTItjANBMO8baq8UPkLX3MNtHAQpQgAIUoECOBJ4/Ab7xVHuk9fPv8M+0D1HIxTFHWTExBShAAQpQIKMAx998H4QAA4B8D0wiwA+QSdhZKAUoQAEKUIAC5ioQdRFY0kStdr6JK3H2q65wdbI311qzXhSgAAUoYAECHH9bQCcZoYoMABoBmUVkFeAHiG8FBShAAQpQgAIUyCBweQvw5zvyD9HKImj4fBGuzHgdTg52pKIABShAAQrkWoDj71zTWdWDDABaVXdaTmP4AbKcvmJNKUABClCAAhQwgkDgImDHRLmgk6mV0fPFF7j2TUcoFAojVIBFUIACFKCAtQpw/G2tPZuzdjEAmDMvptaTAD9AeoJkNhSgAAUoQAEKWIfAts+A44vltmxMaYKxKcMRPrOjdbSPraAABShAAZMJcPxtMnqzKpgBQLPqDtupDD9AttPXbCkFKEABClCAAjoIrOkDhG6VE85PfhML0RuhM17X4WEmoQAFKEABCmgX4Pibb4cQYACQ74FJBPgBMgk7C6UABShAAQpQwFwFFjUG7l2SazcuaRC22rfBpa86mGuNWS8KUIACFLAQAY6/LaSjDFxNBgANDMzsNQvwA8Q3gwIUoAAFKEABCrwUUCqBbzyBF/EySZ8XkxDsXAvnprUnEwUoQAEKUCBPAhx/54nPah5mANBqutKyGsIPkGX1F2tLAQpQgAIUoIABBZ7eB+ZUVCug6fMfkJjfEycntzNgwcyaAhSgAAVsQYDjb1vo5ezbyABg9kZMYQABfoAMgMosKUABClCAAhSwTIHbp4BlreW6Jyvt4Pv8N5QolB/HPm9jmW1irSlAAQpQwGwEOP42m64waUUYADQpv+0Wzg+Q7fY9W04BClCAAhSgQCaBixuA9f3kH2+mlkCzFz/Co4grjnymCgzSjQIUoAAFKJAbAY6/c6Nmfc8wAGh9fWoRLeIHyCK6iZWkAAUoQAEKUMAYAod/AHZPk0s6muKPd5Imo3yxfNg/rpUxasAyKEABClDAigU4/rbizs1B0xgAzAEWk+pPgB8g/VkyJwpQgAIUoAAFLFxg86fAyRVyI9Ymt8SE5EGoVLIAdo9uYeGNY/UpQAEKUMDUAhx/m7oHzKN8BgDNox9srhb8ANlcl7PBFKAABShAAQpoE1jVHQjfI9+dm9QTC1K6o0qpgtg+qjndKEABClCAAnkS4Pg7T3xW8zADgFbTlZbVEH6ALKu/WFsKUIACFKAABQwosKAucD9MLmDUi6H4J7UpqnkUwuZPmhmwYGZNAQpQgAK2IMDxty30cvZtZAAweyOmMIAAP0AGQGWWFKAABShAAQpYnkBqKvC1O5DyQq57j+fTcErpi1pli+CfYU0sr02sMQUoQAEKmJUAx99m1R0mqwwDgCajt+2C+QGy7f5n6ylAAQpQgAIUeCkQdwf43k+No0HiQtyDG+qXd8O6IY1JRQEKUIACFMiTAMffeeKzmocZALSarrSshvADZFn9xdpSgAIUoAAFKGAggRvHgBWvyZk/VzqiyvNfoYQdGlUsij8HBRioYGZLAQpQgAK2IsDxt6309KvbyQAg3wOTCPADZBJ2FkoBClCAAhSggLkJnFsLbBwk1yo8tTTavJgr/d3MpzhW9W9objVmfShAAQpQwMIEOP62sA4zUHUZADQQLLN9tQA/QHxDKEABClCAAhSgAIADs4F9X8sU+1Nq4sOkCdLfrXxL4Nd+DchEAQpQgAIUyJMAx9954rOahxkAtJqutKyG8ANkWf3F2lKAAhSgAAUoYCCBf4YBZ/8nZ/6/5DaYnNxf+rudvzuW9a1noIKZLQUoQAEK2IoAx9+20tOvbicDgHwPTCLAD5BJ2FkoBShAAQpQgALmJrCyM3D9kFyrb5L64OeULtLfr1crhcXv1TW3GrM+FKAABShgYQIcf1tYhxmougwAGgiW2b5agB8gviEUoAAFKEABClAAwLzqwOMbMsXQFyOwNbWR9HeXmmWwoE9tMlGAAhSgAAXyJMDxd574rOZhBgCtpistqyH8AFlWf7G2FKAABShAAQoYQCAlCZhRElCmypl3eT4DF5QVpb+71/bA92/XMkDBzJICFKAABWxJgONvW+pt7W1lAJDvgUkE+AEyCTsLpQAFKGA1Ao8TknAt9il83QvC1cneatrFhtiYwMPrwI811RpdK/FnPEJB6bdedT0xp5f6fRsTYnMpQAEKUEAPAhx/6wHRCrJgANH6iZUAACAASURBVNAKOtESm8APkCX2GutMAQpQwDwEwmPi8fbPxxAb/xweRVzx7/AmKF7A2Twqx1pQICcCEQeA37vKTyTa5UOVZ8sAKKTf+jTwwjfdq+ckR6alAAUoQAEKZBHg+JsvhRBgAJDvgUkE+AEyCTsLpQAFKGAVAl9suoSVR6/LbRnV1gej2la2iraxETYmcPp3YNMncqOjXLzR6NF0+e++AeXw1RvVbAyFzaUABShAAX0LcPytb1HLzI8BQMvsN4uvNT9AFt+FbAAFKEABkwm8/XMgjl97IJffvHIJ/P5RA5PVhwVTINcCe6YDh76TH79UsCk6xQyV//6oSQVM7eKf6+z5IAUoQAEKUEAIcPzN90AIMADI98AkAvwAmYSdhVKAAhSwCoGAb/bg7uNEuS1u+Rxxeko7KBRpyyZ5UcBiBP4eAFxYJ1f3YNGe6Hunu/z3oOYV8XlHP4tpDitKAQpQgALmKcDxt3n2i7FrxQCgscVZniTADxBfBApQgAIUyI1AYlIKqkzZnuXRwxNawdMtX26y5DMUMJ3AL+2AW0Fy+X+XHI4xNxrLfw9t6Y3xHaqYrn4smQIUoAAFrEKA42+r6MY8N4IBwDwTMoPcCPADlBs1PkMBClCAAlejn6DdvINZIBa/WwevVy9NIApYlsB3vkB8lFznJaVnYNa1ivLfI9r4YHQ77m9pWZ3K2lKAAhQwPwGOv82vT0xRIwYATaHOMjkDkO8ABShAAQrkSmB3cDQG/H4yy7Mft/TGBM6UypUpHzKRQFIC8HUptcK/9FyGX8Pyy7+NaVcZn7TxMVEFWSwFKEABCliLAAOA1tKTeWsHA4B58+PTuRTgByiXcHyMAhSggI0LLD98DdM3B2dRaOZTHKv6N9Sqk5ySCgd7OxvXY/PNSiDmCrCwvlqVhnptwtYr8fJv4zv4YmjLSmZVbVaGAhSgAAUsT4Djb8vrM0PUmAFAQ6gyz2wF+AHKlogJKEABClBAg8C0fy/it8DILHcKuzri7NSsB4HExj/H4FWncPH2Y3Sr7YFvulfnYSF8s8xD4OouYHVPVV1ci6JvibU4eCVG/m1SRz8MbK5aEmweFWctKEABClDA0gQ4/ra0HjNMfRkANIwrc81GgB8gviIUoAAFKJAbgQ9WBOFAhgBJxjwOjW+FskXVDwKZuOE81gTdlJMtfKcOOtXgXoG5seczehYIWgZsHavKtExtvKOYhaPh9+XfpnXxR78mFfRcMLOjAAUoQAFbE+D429Z6XHN7GQDke2ASAX6ATMLOQilAAQpYvECr7/bjWuxTje3IHNxTKpVo9M0eRMc9l9P3qOOJuW/V1MkhJVWJkLtxcHawg497QZ2eYSIK6CywczJwdIEquf+beOvBEARdfyD/Nv3Nani/UTmds2RCClCAAhSggCYBjr/5XggBBgCN9B7cu3cPQUFB0j8nTpyQ/rl/P+2/8H7wwQdYuXJljmqyfft2LF26VMovJiYGJUqUQIMGDTBo0CB06NBBp7ySk5OxfPlyrF69GiEhIYiPj4eHhwfatm2LESNGwN/fX6d8cpOIH6DcqPEZClCAArYtIPbx85u6HUkpSo0Qg1tUxMTX/eR7Nx88Q7PZ+9TSehXNh4PjW2ULKYKHY9adw4bTt6W0XIqZLRkT5FTgr75A8L+qp5qMRLerr+HMjUfyb2LJep8GXjnNmekpQAEKUIACagIcf/OFEAIMABrpPVAoFFpLykkAUAxIhgwZIgX/tF0iCLhkyZJX7nEkgo+dOnXC8ePHNWbj7OyMRYsW4aOPPjKIED9ABmFlphSgAAWsWkBTQC9jg5tUKobVAxrJP208cwufrj2XxeTYxDYoVdjllVbnbj7CGwuPyGkKujjg7NT2sLfT/v+fWzU+G6d/gZ9bAHfPqvLt9D26HvfF+VuP5d/m9KyBXvXK6r9s5kgBClCAAjYlwPG3TXW31sYyAGik9yBjALBs2bLw8/PDzp07pdJzEgCcNGkSZs6cKT1Xu3ZtjB8/Ht7e3ggPD8fs2bNx5swZ6Z5IN2PGDI2tS0lJQevWrXHw4EHpfvfu3TFw4EAULVpUCgiK58SMRXt7e2zZsgWvvfaa3pX4AdI7KTOkAAUoYPUCh6/G4r3lmv/DlWh8IRcHnJvWXv4PYJ9vvIA/jt/I4jK/T210rVnmlV7fbAvBzwci1NJo2mPQ6tHZQMMJfFseSHioyv+9v/H6Fmdp2Xn69cPbtfBmbQ/D1YE5U4ACFKCATQhw/G0T3ZxtIxkAzJZIPwmmTZuG+vXrS/+4u7vj+vXrqFAhbVNnXQOAYWFhUuBQLN2tV6+eFMBzdXWVK/js2TO0aNECJ0+ehIODAy5fviwFBzNfYrlxv379pJ+HDh2KhQsXqiUR5dStWxdxcXHw8fFBcHCwlJ8+L36A9KnJvChAAQrYhsDq45GYtPGi3NjiBZwhTvnNeB0Y1xLliuWXfmo/7wCuRMdnwXmvkRdmvFldK5qYbd/yu/2IvP9MLc2q/g3QzKeEbWCzlYYVSIwDZmWa2Tf8JNr9fgdX76ne2QV9aqNLNsFqw1aUuVOAAhSggDUIcPxtDb2Y9zYwAJh3w1zlkJsA4LBhw6RlueIKDAxEo0aqZU7plTh27BgCAgKkP4cPH44FCzJsLv0yUdWqVaWgnpubG8SHIF8+9RMTRbJZs2Zh4sSJ0hPr169Hjx49ctVObQ/xA6RXTmZGAQpQwOoE4hKTsPLIddx9nIh3G3qhmkdhfLM1BD8fVM3K61i9FIKuPUBs/Au5/ekBk0fPXqDWV7s0uvi6F8SOT5trNQu+E4eO8w9luf/VG1XRN6C81VmzQSYQiLoALGmqXvCkaLT68ZjaITdL3quDDtV4arUJeohFUoACFLAqAY6/rao7c90YBgBzTZe3B3MaABSzEcTS4du3b6NKlSrSoR3aLnE/NDQUnp6euHHjhtpegFevXkXlypWlR8VegosXL9aYTVRUFEqXTvsXznfeeUc6KESfFz9A+tRkXhSgAAWsT2DC+vNYe/Km1LDiBZyw89MWmLjhPHZcipYbO6SFNy5HxWF/aIz826DmFfF5Rz/sCYlG/99OaoU5M6Ud3PI7abz//c5QzN8bluVevyblMa1LVevDZouMLxCyGVj7rqrcgqWBMZfRbPZe3HyQIP/+S996aOvvbvz6sUQKUIACFLAqAY6/rao7c90YBgBzTZe3B3MaAIyIiJCX8w4ePFg65EPbJe6nHxIinktfaizSr1ixAv3795ceXbNmDXr37q01H19fX1y5cgVeXl6IjIzMW4MzPc0PkF45mRkFKEABqxJIeJGCml/uxIuUVLldX3atijVBN3A56on826zu1XHnUYJasC6gYjGsGdQIs7ZdxpID4VpdlvWth3ZaAittvz+AsAzLMNMzaelbAiv7NdCLdUqqEuI8kVcdEqaXgpiJeQoELgR2fK6qW9lGQP8dCPhmjzTrNf1a2a8+WvqWNM82sFYUoAAFKGAxAhx/W0xXGbSiDAAalFd75jkNAIrDODp37ixlOG/ePIwaNUpr5uL+6NGjpfviuY4dO8ppx40bh++++076WxwYUqtWLa35vPHGG9i0aZM0OHny5Any50/bU0kfFz9A+lBkHhSgAAWsU+DQ1Ri8vzxIrXH1y7vh0p04PHuRIv/+x8CGiE9MxqBVp+TfCjqnHQTy1s+BOBn5EI5Iho/iFooo4hGRWhpRKCalHdisAiZ18s8CGHbvCdp+n3ZIVuarfLF82D+uVZ7QxYx+EZz837FIaa/C6W9WQ91ybnnKkw9boMC2CcDxDP8xt8bbQPelqDdjt9q+lv/r3xBNfYpbYANZZQpQgAIUMCcBjr/NqTdMVxcGAE1kn9MAoJjx9/HHH0u1XbduHXr27Km15mLPvl69ekn3xXNiRmD6JWb8rV27VvozJiYGxYtr/5dKsYdg+gEh4kARMSNQ10t8YF513b17Fw0apM2iuHnzprRcmRcFKEABClBACGQ3ey9d6chnrWGvUKDRN3ukn4oiDn52kRhXMwnXLx2HLyJRSXEbjgpV0PCOsijOpFZCVKEa6N/7baBUDcDRRYZfsOcq5u66orEj7O0UuDy9Axzt7bLcD4+Jx77L91CioDM6VS8NBw1pxEM7L0WpBSxdHO2w+N26aFWFs7xs6u3/ozdwZZuqyc3HA60nofZXO/HwWZL8+5+DGqFRxbSgNS8KUIACFKBAbgUYAMytnHU9xwCgifozpwHAOXPmYPz48VJtt23bhg4dOmitubifPutPzPYbM2aMnLZTp07YunWr9HdCQgJcXFSDnswZTpgwAbNnz5Z+FicLi5OBdb1ysqSJAUBdVZmOAhSgQM4E/jp5Uwqm5Xe2x7c9aqCxt2XMJHrjp8M4d+ux1sbaIRWV7aOxtbcbFNEXERR4AOWSI1BK8TBnQCK1vVNaENCzPlC2Pj7YBRyIdgag0JjX3jEtULFEAfne2ZuPsGR/OHYER0GpTPs5fR9CTRm8s+wYjobfV7slAovf9aqBbrX5H8Ny3oEW+sSiAOBesKryXX8C6ryP6tN24MnzZPn3vz8OQN1yRS20kaw2BShAAQqYiwADgObSE6atBwOAJvLPaQBw+vTpmDp1qlTbPXv2oHXr1lprvnfvXrRp00a6L56bPHmynFb8Lu6LKyUlBXZ2WWcxpCcW5YnnxXXo0CE0bZrptLpX2DEAaKIXi8VSgAIUeCkgTsFtOHMPnien7aPn6eaKg+NawU5sPGfG1+OEJGkWVOrLYFp+JKCK4gb87SLhp4iEv90N+CpuwlWhOvlX382JVhbB6VQfaaag+L8XlBXxHGkHhqz4sB5aV3GX9h4cv/48DofFZine0V6Bo5+1kWYDZryuRj9Bu3malxeLdNO6+KNfkwr6bg7zMzcBESme6QEkPVXV7IP/gArNUWXKNiQmqfa+/HdYE9QsW8TcWsD6UIACFKCAhQkwAGhhHWag6jIAaCDY7LLNaQDQ0mYAcglwdm8A71OAAhQwrMDhq7F4b/lxtUK2jGiKqmUKG6xgsb/dupO3sPhAOBQK4J0GXvigcXmNS2azVEIERR7dwOkTh7D/wD5pKa+/IhLl7O7pp76O+dUDLjnINUlpj2BlOSkYWL5mC7Rq2wl9N0Tj4NWswb/0bMe0q4xP2violTLln4tYdezVh2qtGxKA+uU54ysH3WN5SZ/GAnO81es98jzgVg6VPt+K5PToN4DNnzRFNQ/D/W/W8vBYYwpQgAIUyI0AA4C5UbO+ZxgANFGf5jQAaGl7AGbHyg9QdkK8TwEKUCBvAqsCr2PKv5fUMvns9SoY0iJT4CFvxchPxz9PxqSNF/Dv2TtqOXqXyI8vulZFM58Sqt+TEoGYECDqIhB1AYi+mPZPovZlv7pWM1HpiMvKsghJLYcQpReCU8uhf48ueL1OJfy8cQfCTu9FbUUYattdha/iFuwUL6ca6lrAy3QxysLyDMEzqT44r6yABKi21XAv5IzDE1rLwc8niUloNHMPnmY4xKRC8fy4FpthFhiANlVKYvmH9XNYGya3KIFbp4BfMqzkUNgDk+9BaWePChPTtmlJv3aMag7fUgUtqnmsLAUoQAEKmJ8Ax9/m1yemqBEDgKZQB5DTAODmzZvRpUsXqbZ5OQV47NixmDt3rpQPTwE2UeezWApQwGoFtl24i10h0dJeez3qeEinqBviEsGklFQliuRLW5aq6fpi0yWsPHpd7VaTSsWwekAjvVcp5G4chq0+jYhMwSxRUHE8lmbz9SjzAF3cH8D+3iUg9gqgVB3MkesKFSgFlKoGlKoOuFfDv9HFMHr3E6TAXi3LwImtUbqwK/aERKP/byflewXwDDXsIlBHcRW17cJQx+4q3BTxuapOKuwRnFpWmiUoLR9WVsK43h3QuaaHlN9vR69j2iZVQFasxBYBQjEjcPH+cLlM8crsG9MS5Yvnz1U9+JAFCFzcAKzvp6pokXLAqPNITklFpUkZDgYR276MaQHvDHtOWkDrWEUKUIACFDBDAQYAzbBTTFAlBgBNgC6KzGkAMCIiAt7eabM2xKm+YkagtkvcX7p0qXRbPFehgmo/oRUrVqB///7SvTVr1kCcCqztEqf+XrlyBV5eXoiMfPWSpZwy8gOUUzGmpwAFzF3g4JUY9F0RJFdzQZ/a6FKzjN6rLQJJ0zcHw06hwKROftISW03XByuCcOBKjNotJ3s7nJvWHq5O6gGyjIkSk1Kk57ZfjJICem2rlMTw1pWyBDPFjL8dF6Pwz9nbOBIWC4UyBRUVd+V9+vwV1+FndwMlFHmf1SeW4IYpyyBEWQ4hqV7SctyP33oDTWv5qbUvNVWJt34OxMlI1WEgYu9DEWgT1+NnSaj/9W68SFHtsaZup0QFRRQaO0egd+koVFdegTLqEhTQlv7V3RunKIxCPgFQetbHmEAnbH/ogWcvZwm+VtUdP79fD0+fJ0unGD9JVB388GHj8tKsSV5WKnB4HrD7C1XjKjQHPvgP4n97VaZsV2u02LfTq1g+K4VgsyhAAQpQwFgCHH8bS9q8y2EA0ET9k9MAoNhXydPTE3fu3EGVKlUQEhKiteZ+fn64fPkyPDw8IE7YzTgDRQT0RGBPXEOGDMHixYs15hMVFYXSpUtL9/r06YM//vhDr1L8AOmVk5lRgAJmIPD+8uM4lGFPuIYVimLt4AC91uzek0Q0/mavvEeYk4MdTnzeFoXzOWYpp/nsfbjx4FmW33/tVx+tfEtm+V0sRZ2364o0Sy7jMlWRcHaPGnirfln5mZ93nMbhw/vhnXoNfoob0gw/sZzWWZGU5/Y+UuaXl+9G2FfElAFvocnyO4hNVM9a28yosHtP0G3hUfkk1XGv+WJYq0qquh8Ix7fbL0uHjJQs6IwA72IIqFgMPu4F4JbPCcXyO6Ogi4N8WErw9TuYvvR/8rJhMUuwmOJJrtqZolQgVOklLR1u0Ow1+NRtAxTzxsxtl7H0YIScZwFnB4hZiwVdsvZrrgoGcPPBM6w/dQslCznj7Xpl4WCv/RCw3JbB53QU+G8UcOpXVeLa7wFvLISY2Vv9i51qmRz5rDU8irjqmDGTUYACFKAABTQLcPzNN0MIMABoovcgpwFAUc2hQ4fKAbvAwEA0apR1GdexY8cQEJA24BTpFy5cmKWF/v7+UgCxaNGiUoAwX76s/2V51qxZmDhxovTsX3/9hV69eulVih8gvXIyMwpQwMQCdx8noPGsvRDnWKRf9nYKnJ7cTmNwLrfVXX74mjT7L+O15L266FCtlNpvz5NT4Ddlu3ySbsabHzWpgKld/NXSi9l8ImD44Kn6ybpi5punIgYtC0Xhy4ZK2EVfQsLNs3B9dju3TcjwnAIoWuHl8t3q0lLer0/ZY9l5UYe0pdNt/Urilw/qY8L681h78qb8rFgme3l6Bzg7aJ7JeCX6Cf49exvliuZH9zoeWYJdIpD6IjlVCqxkt0xb2FSbtiNDvZXwUtx7uWz4qrRsuJr9TWkGZK4uVzckuNfB4jA3nEr1wblUb8QjH6Z29sdHTXN2IvD12Kc4cf0B6pUvCrG/YPol2vDavIO4/ShB+kkEAL/tWSNX1eVDehBY1Q0I36vKqNVkoMU4iJO7a321S62AoM/boGQh1d6SeiidWVCAAhSggA0KcPxtg52uockMAJroPchNAFDM3qtatSqSk5NRr149HDx4EK6uqv8qnJCQgObNm+PkyZNwcHBAcHAwfHzUTyAUzc24DHjYsGH46aef1BTCw8NRp04dxMXFScuOxWxCkZ8+L36A9KnJvChAAVMLLNwXhjk7QrNU41XLgI+Gx+LEtYdo6VsCNcsW0akJXX86jPO31JfUvt+oHKa/WU3teTELru33BzXm6VOyAHaNbqF2b+uFuxi9OhC+ipvSsl1x+q6Y1VdFcRMFFWlBo7xcz5TO8sEct5wrYUzf7nAQe/c5F5CzFTPdm367Tw5SiRvpQbBDV2Pw/nLV8mpf94LY8WnzvFQpR882+Ho37j15rvEZsaz6/OdN4BJzAbgVhLDT+1H4/plcL31OVSpwRemJK45V0LljV9h5NQSK+QB22mfsPXz6AnN3heKP4zekoK+DnQLrP26MWi/fq3Unb2Lc+vNq9f/74wDULcfThnP0Iugr8fw6wAPVvo/ovgyo8RZinjyXlqhnvE5PaYei+bXv9amvKjEfClCAAhSwbgGOv627f3VtHQOAukrlMd3hw4cRFhYm5xIbG4tx48ZJfzdp0gQDBgxQK+HDDz/UWKKYlSdm54mrdu3amDBhghSkE0G7b7/9VjrYQ1wi3cyZMzXmkZKSghYtWuDIkSPS/R49emDgwIFwc3NDUFAQpk+fjnv37sHOzg7i8JHXX389j63P+jg/QHonZYYUoICJBETgqs33BxARo36aq6hOt9oemPd2LbWaiX3qZu8IxZIDaQEAMZtt07CmqO5Z+JUtCLsXj7bfH8iSpmKJ/Ng7pqXa7zsvRWHQqlNa8lPi+CdV4f4sDIg6L53EGxt+Cm4JN2CfyxNx1Qoq5CEdyCEdzFGqGi6jHDquuo1UqAJYP/auhTdqpR2OkX7duP8MzefsU/tt+6hmqFKqEITx6L/OYeOZ23B1tMcPvWvhtarqsx4N2f1iX8Ggaw80FpF5qfe9uEQ0nrUHpZRilmDaacPin6qKSDgqcjlL0KUw4FEPKNsA8KyX9v92LSIdGvFH0A3M3XkFjxPUl1+38i2BX/s1kOo84LcT2B1yT63+Iui88ePG8lJnffnFxj/HnUcJqFamsN7z1lcdTZpPairwtTuQkmG27Uc7Aa+GEDOJA77JMDMQkPbsLOyqv6XgJm07C6cABShAAZMJcPxtMnqzKpgBQCN1hwjo/fbbbzqXJgY7mq7U1FQpWCdm8Wm7xCEf4hAQEcDTdokAZMeOHXHixAmNSZycnKSZgaIsQ1z8ABlClXlSgAKmEDhz4yG6LTqqsWi3fI44ObkdxHJgcYmluePXn8e/Z++ope9dvyxm9Xj1ksy5O0OxYK/qPyRlzCD9lNv030Rwcda2y3BAMrwVd17O6BMz+9IO5sjtHnYZy3yhtMcNey9UrN4IdlKwL+0kXuTLOqus15KjOHFddTBHDc/C+HdYE3n5rTj8YNSfZ7H9UpRcRPECTjgxqa3aEl2xj53YH8/NyDOiPvv7PP48oVqCnNFhZBsffNquslp/jlhzBpvOqfexM17gnbIPMKTifbjHnQdungDiVe3N6bubWtwXB5+Vx7bHaXsKXlV6QJkhyCreueOft4GLoz3qTN8lLXnOfP3wdi28WVs9EJvTemRMLw6PGfj7Sams+uXd8OegAPndz0u+VvXs49vAPPUl+BgTChQsJe3T2Gy2ehA8+KvXkM9Jv6swrMqTjaEABShAAZ0EOP7WicnqEzEAaKQu1lcAML26W7dulYJ8IoAngnnFixdH/fr1pROCdZ2xJ5YSL1u2TDrgQ+wJ+PTpU5QpUwZt2rTByJEjpeXGhrr4ATKULPOlAAWMLTBp4wWsPn5Da7HpSy3jEpMw+PdTCIy4nyWt2Ivu8IRWWvejE/9RSMyOu/lA83Lc73rVRM+qBaXZfIi6gBPHDsDlQTAqSwdzqE6Xza3NfWVB6fRdcQpvcGo56f+GK8vgx3cboGP1tAOjXnVtu3AXH68+rZZk/ZAAaa86MWNMBI3O3Hikdl+coCyWUJvDlR5Q1VSXPwc1QqOKxdRuiZlcvZYE4tbDBBTL74Se9TzRp74XymfYl0/aMPLxLeDWibR/bgYh9c5Z2Clz119xSlecTa2EM8pKOJPqIwUFR3dtiGIFnDD8j7TVAZmv0oVdpNmjrzoVWlf/hBcpaDFnn9pS6UXv1tHp/dC1DKtIFxkI/NpB1RQHF2BSlDQVWBzE0+q7/WrNvDLjdYjDfnhRgAIUoAAF8iLA8Xde9KznWQYAracvLaol/ABZVHexshSggBYBMXNN7A8Xl6g9aDOslTc+ae0jBYQu3Fbfvy9jtvvGtlQ7uCHjvVORD9BjceDLn5Qog/vwt4uUZvaJ/1vf5RaKJd3Ncz+J/eeuKUvB078hnD1qYNf9Eph0zA73IPYoTJvFmH75ly6EzZ801WmZZ0qqUgoOiYBY+lWlVEFU8yiMwPD7avv+iftiD7vNI5pKy3/N4dp+MQpD/pd1SbWzg520RFPMsst8ieW5dx4lonQRFzjqeOLu88SnGDnvN3jEX5KWDYsDRsooNC891sXllr0nbuWvik33PXE61UfaWzDjUmyRx5h2lfFJm6z7BeuSf8Y0mvbB1LQ/ZU7ztbr05/4ENg5WNUvs7/jJSenvq9FP0G6e+t6dETM76vS/MatzYoMoQAEKUECvAhx/65XTYjNjANBiu86yK84PkGX3H2tPAVMJiBkyxyLuo0GFovAuoTpAQp/1ESdxrgqMlLLsG1D+laf4bj5/J8vsKjFz7b8Myz9FoKteeTf875j2WYKirOlvVMX7AeXVm5L8Aoi9gvVbt+JRxGk54FdEkXW/wZwapDgWgH2paghVlMOv4Wkz/EKVZeFezA0HxrWSsnv6PFk63Tjz/nLi3vIP6qGNn7vOxf5yKAIztoRkm76gswMWvVcHzXxKZJvWWAnEqcLtMwVmRNkBFYthzaBGeq1GeEw8Bq86BbHno7hK4T5q24VJwUDxf6srrsFZob7fn64ViFe64CIq4WSKtxQQFLMEnzu5QQSf3fNw0qz434xYuvokUyBcvPvbRxnvsBZdHUyabv+3wP4MezRXagu897dUpeA7ceg4/5BcPbFzQMQ3nUxaXRZOAQpQgALWIcDxt3X0Y15bwQBgXgX5fK4E+AHKFRsfooBNC1yOikPPxYGIf54sHZwh9pCr4anb6bm6wonDC95eGigvtRX7mP01OEDr0tx+vwZhX2iMnL0ICIn94MShEa+6xP52FYrnV9sXr6tvfsxv5SAt4U375zwQE6p+WICumEaIugAAIABJREFUDcmULqmgJ4KelcHJ554IfrmU9622TTC8jS/GrjuH9aduyU+8UasMfuytWnqrae/B2l5FsOHjxlpdNFVTLIEOmLkHT19oPwhDLIVe8WF9+JYqmMuWGuYxMdPTb+p2adVuxmt0u8oYoYfZc5lrLfbQW3n0Gn7cfTWLlxOS4KeIlAKCaf+Ew0OhegdzKnAt1R3xJeugeoM2aYeMlKwK2Odsz7lvtobg54MRGos+O7UdiuTL+Sm2/569jWMRD9DOvyRaV9E90JzT9hs9/T9DgbOrVcXW6w90/l76+8Ktx+jy02H5nlj6K5YA86IABShAAQrkVYDj77wKWsfzDABaRz9aXCv4AbK4LmOFKWBygcwnmXaqXhoL362jt3pFPU6Ugn+R95+p5bl3TAtU1DDb8H78czSYuQdieWv6Jfbie7NWGdSdsVvjrDmRztXRDls/KI+o0BM4dnS/vJS3rF3ugzhyBewckeDmg83RxREs7ddXHqEoi6DpvfD1lmD89nJmo0ifPjtLnCycPttM/D6tiz/6NakgZxnz5DmafLtX7RCJ1QMaokml4jm2X7Q/DLO3h2p8ThwM8ssH9VCyoEuO8zXGA01m7c2yVFkEh8VsVENd4p2ctS1EOlAkw2smFycORPm9fwPUcXsu7yN4/dx+lIoPgUsuZwnCMR9Qpg5Qtj7gKf5pABTQPhtT7HfYcs5+PNdwyIio6C9966Gtf84CeP+cuY1Ra8/K7Vw3JAD1yxvO2VD9pzHfXzsBkaogH9p9BTQZKSU9feMhumc4UCi/kz0ufZVhv0CjVpSFUYACFKCANQlw/G1NvZn7tjAAmHs7PpkHAX6A8oDHRylggwIiQCUCVRkvcbjCycnqp8RqoxGzBpcfuoanL5Ih9iUrWzSfWtLouET0XnpM2oQ/8zWre3X0buCV5fcNp29h9F/n5N9dHe2l+uR3dkD6KbCOSIaP4hb8FDfkQF9d51twSo7Lcy8+syuAc0leLwN95VCoQh1M69cN/16Mwcg/VcGTcsXySUt6j4bH4p1lx9XKXTuoEXovO6Y2s23j0Mao7eWmlm7VsUhM/feilE74ffVG1RzN/kvPTBxmsvn8XSnQIS57hUI6JdarWD70qOOpcS+9PEPpKYP3fjmOw2Gxcm4ujmn7/zk7ZN3/T09FytmI02F/D7wunUScvsw2n5M9fvuoQZbA2KnIh3h78UHpnUvfR7CO4iq88hJgdiuvCgZ61ks78dneUarfhPXnsfak5hOSxf3BzStiYke/LCRiWfnSg+EQAWax1F7sBymu1FQlWs/dj+sZAvHdantg3tu19M1qmvzmVQMeZ/Dq9RtQ9U2pLkHXHqjNHi7s6ii9Y7woQAEKUIACeRXg+DuvgtbxPAOA1tGPFtcKfoAsrstYYQqYVGDihvNYE5Q1yLDr0+bwcX/1clERdHpv+XEcCUs7fVcExLaPbC6ffCpm8vX6ORARMZr31etexwPfv5U1+PDJmjNqe/296ZsPP7RMW8J7I/g44iPPoJLiFpwU2pe86op6I7UEgpXlpRN46zZshhbNW2NDuAKj152Xsyjo4oAzU9ph/t4wzN9zVf69pW8JrOzXQAqsNP12L+48TpTvVS1TCJfuqIKRTvZ2uPCl5qDWvSeJSHyRKgXrbPGa/M8FtX0cm1Yqjv8NaGhUCrEn445LUYiKS8SbtTxQpohrlvLF+95izn7ceKA+k7U4HmN7TxcUf3QeuHkCiZEn4ILnuaq/0sEVj92q4lBCBWx+IA4YqYQYpAWNxaxEEXBPv2qVLYJ/hjXJUs6Yv87h79NpS8/Fvo9bRzaTAvN7QqLR/7e0QzHSrxIFnRH0eZtcBZ1z1UBDPZSSBMwoCShTVSUM2g+USVtyfzQsFu/8ogrSi//IcWpKO0PVhvlSgAIUoIANCXD8bUOd/YqmMgDI98AkAvwAmYSdhVLAIgU0LUFNb4iYiSZmD73q2nbhLj5efVotyYw3q+G9RuWk30avPYsNZ25rzaJsUVccGt9adV+pRPKDSIxd8D+UTw6XD+bwVKhmh+UWOgkOCE0V+/SVk2f2XVZ6IQ75pSzb+7tj0bt14GBvBzFrseHMPWpFiUDL8sPX1AKT/ZqUx7QuVaV0326/jMX7w7VWr2bZItLeiryyChy8EoO+K4LkG3N71USPup5mSaVp38bqHoXx3ydN5fquD7qGXzdulWYJSjMFFVdRwS461+25pSyOc8rKKFujBaaccpUC1uJ9Fic6n/+iPfI5qfYVTHiRgppf7sSLFFUgrHON0vjpnTrIPNMyvUI7RjU3u70hc4x15yywtIX6YxOuA65pwdPM75h7IWcc/7xtjovhAxSgAAUoQIHMAhx/850QAgwA8j0wiQA/QCZhZ6EUsEiB73eGSrPaNF0dq5fConfram2XOEyh/bwDassJRWJxAMee0S1w/f5TaWlxxv3VihdwRmx82swoceCCj+I2VndxRZHHoUDUxbQDOp4/zrulSxE8LFQFf99xexnwK49wZRkpaJJ+ueVzxORO/vB0c0W5YvlRqrD6/niZ9+8b274ytl+KwsXbqll9GU8Xvhr9BO00nGabXt6Hjcvji65pwUJe6gJiZt3GM7ex9/I9ad+/9xqWg504ptUML01L5se95othrSrJtX32IhkNv96DJxlm601sURyDKz7Es4hAPAkLRLHHF+CQrD6TUNfmPlc64oKygnTScLNWHVGlfhugUBnp8cyBrvQ8v+leHRM3XNBYxOROfhjQrKKuxZtnumNLgO0TVHUr6g2MUP3Hib2Xo/HRStXsR3EozpHPMvzHB/NsFWtFAQpQgAIWIMDxtwV0khGqyACgEZBZRFYBfoD4VlCAAroIiCBF41l78ehZksbkRcUSuVfsA/jb0euYtumSxmeXvl9XCpZtOJ02+68w4lHH6SbmtXTAwYN74JN6HZUUt+GohyW8iQW84FK2JlCqRtr+aeKfQh5ISErNMhMqY2W/6OKPDzMcyJG5IdP+vah2sIc4XfjZixTpn/Qr84EdXRYcxoXbmgOYP/auhTdqeejSNUxj5gJvLQlE0PUHUi3F0u5do5tLQeSM16SNF7D6+A35pzKFXTCmvS++2HRJCgzaIRV+9rfQpehteMZfgF9KKLzt7ua+5YU8pL0Ed8d7YdHVoriorIAXSNtLMLurlW8J/NqvQXbJzPv+Xx8Awf+o6ljrPSR3WSDtPepe2AWB4fcxeNUp+X76/p3m3SjWjgIUoAAFLEGA429L6CXD15EBQMMbswQNAvwA8bWgAAW0CYiTT8VBBiL4d/rGI6wJUgUoND2z89PmqKxhH8C4xCTpdNIHT19kekwJT0UM2haJRtH4UPghEn52kdDHEl7YOwEl/V4G+V4G+9yrAi5pBxxouvosPYbAiLT9CTNeFYvnx45Pm8PR3k7rs5oO9sic+OhnrdX2iltx+Bq+2hysMc8D41pmCRLxTbVMAXFwiDi45e7jRAxtVQlda6bNvst4Xbz9GJ0XZDiRVoemFsET1LILQ227MDRzuYbquArHZM37Z2aX3XOlg7RU+HSqjzRTUPzfOygmFqhkeVQcenJ2ans4OWj/34N46EhYLL7eEiKdbO1gr5CWILs42qOpT3F8/WZ1ee/P7Oqm9/viBJ3v/YAnqgBqUqf56H7MWwrIi/3+ejcoi4X7VEv0vUvkx54xLfVeFWZIAQpQgAK2J8Dxt+31uaYWMwDI98AkAvwAmYSdhVLALATEstyY+OfSgFcMzDNe4gCAAb+fVDuVNuN9MQvoSnQ8bj9KkH/Wtg/gnB2XsWzfZekUXn+7SHmvPj9FJAopVM/nFuWhsgAupZZDiLIcWrVog0o1AoDileXTUXXNd+G+MMzZEZoluZih2L5qqVdmI5alDlp1CruCNe/dJk6qDf6yg9pSVbG8WewdmJJx3TOA7GZT6toeprMsgc4LDqktGdel9uLAmSmd/dGrricU4kCLmFDgVhBw64R0wAhis77PuuQr0kQp3aRg4FllZZxO9cb51Ip4DifpcXFqdcOKxaTg3qazt1G+eH5pxqo4SVpciUkpaPrtPnkJf+YyxQnW09+spmtV9Jvu4XXgx5pqeW5tsRlDd2g/EbxKqYLYPqq5fuvB3ChAAQpQwCYFOP62yW7P0mgGAPkemESAHyCTsLNQCuhV4PDVWByLuI+2/u4QJ31qu0TATxxMIZbb3nmUIA3OxWQYMWgXwbt3G6YdxpGckiqdXpoxuJc5zzUDG2H9qVvy6aHivrwP4LMHafvzRV3Ao2unEX3lBCpCP0t4r6e6o0yV+nDyqIVD8aUw7pASUSgqzVQSJ5ientrulTP1XgV//tYjdP3piFqShhWK4s9BjXQ69fTu4wS0nXsATzMs+03PTFsAod+vQdgXGqNWplUssdTrG24bma06Fokp/1zU2FhHewWSUpRZ3pOZ3aujdOGsJxCnJ3x0PwYj5i5DHXHAiCJttmAhRe72EkxS2uOSshzOpPqgpF9TVGvUFp1X3cCTxLRl7hn3Nsy8h17mRomA+PGJbVE4n27LjvX6Bpz7E9g4WJVlvuKYVGkjVms43Tw9UTWPQtj8STO9VoOZUYACFKCAbQpw/G2b/Z651QwA8j0wiQA/QCZhZ6EU0JvAvtB7+GjlCSmQJybfbB3ZDFVKFdKY/9KD4Zi59bLGeyIIuHt0C+lQji3n72LYH+qn9WZ8KD0otv7kDSzYsEea0SeW7tZyuInmhaKgiLuV9/bZO0tLeFPcq2PmaXucS/KCOIU3HvmwrG89tPN3x7DVp7HlgmoZ3+vVSmHxe9oPIsmuUmImXrNv9+LO40Q56X/Dm6K6p/Zlw5nz1LbXYafqpbHw3TpZqrDp3B2MWHNG7fdP21bGyLY+2VWX961MQCyVF4eBJCSp9o0sks8RM7tVRyvfktI+goeuxCAqLhGvVS0FcVqvQpH94SevzTuI0OgnkpYCqfimuQt6l4rCycM7UCD2LCorbsFOoR5c1JU2RllYXjYc5uyPJeP7w8GlAD7feAF/ZNjTUFN+YuZi/6YVdCpK/AcLcQp5NY/C8ixDnR7UlOi/kcCplao7VTrjrUfD5X0aNT3CU7lzrc0HKUABClAgkwDH33wlpH8n+z979wEeVZnvcfw3qYQmvSWUkACht9CbVMG6FnTtXVlxLXhFsSCuLLJgd0EWG6uuuta1oIB0pIXee+i9txAgydznnMgkQyYkk5lkzpx8z/PweJlzzls+73vPve+ftziN9UNcCBSxAB+gIgYnOwT8LHDje/PMffouXJc6PbbvW7O1fl9mIMDTdX3LaL15SwtdnKaxJDWhUrjitFPtS+5Rj3L7FXV4rTL2rlLI+VM+1+iIuYS3jrmEt0q9RP2pb1+pUj3XEt6L9+Z7qGtdc7ZRq1d+08nUNFf+o25sppvb1PSpPHM2HdTgb1bq1Nk0DenXULe1q+VVekYQ0fBbvvOY23uPdo/X/13RIEdaxlLJxOFTzfwuXJ/e31Zd6lX2Kl8etofAV4t26tnvVpqnYfdIqKKRNzRVlbLuJ057W9MX/rdKny3I2r+zZ0IVfXhPG/V4faaSD55WGaWoWcgWPV7/mBqlr1fajiSVcxRsL0GnI1Sq1kTf7K+huamxWuqspx3OKrq/c11tO3Ra09YfcBX/wgngeZ3g/N3SXRr01QrzvcsbVNYHdyUq7BL7cebpM6addDDrH0KcvV9Ry2kJuR5wZKSXWLu8vvlLxzyT5gEEEEAAAQTyEmD8nZdQ8bhPALB4tLPlaskHyHJNQoEQyLfAjsMp6jp6htvzxuy8/z7cIUcaRoCp2bDJZmAht8uYTPTaTc01/Os5ahiyw7VXX6/y+1X2ZLLkzJqZlO9CXvRgevlYhVbPPJTjP9sv0ztrorRf5c25SZFhIZozuHuOgMcbv23UO9M2uVIyljkP6ZegW8YvcEt94XM9VdXHYImRoBHEM2ZT5md2lSeHdXtPyDjhNy0b9pu3NNf1LWM8sn06f5te/CHzhORWtcrpmwEd3fYKLKg17wWnwNHT55RyPl3R5XJf2utNzX5YvluPf7nc9YpxeMfH97TR7R8sdEvmx0c7qVlMOU1bu08/zpitxNAturHKHpXcv1TOA2sz9xgswHXIWVZRse10pHwzDV5YQisy4pSizKBmXsHu02fT1OHVaTqRLdCf1wnZxhYGqWkZKh0ZlrO0xvYEo9xnHR657Re1+sg9YH/xi+3rGlsB5PyuFoCDVxBAAAEEirkA4+9i3gH+qD4BQPpBQAT4AAWEnUwR8IvA21M36c2pG93SKlsiTCte6pMjeGWcyJl9wG+cyPn5A2310oSfVSct2e1wjuqOIz6X76wzXOudNbU2o7bWO2urXouOuqnfFSpROmuPQmOPwavemeOaefNYz3oa1Lt+jryNPQ7v+DArWGGUvU2dCm4n9jaqXtZc/myVa+zMzRo1KfMAhkqlIzTr6e4q5SkgIclYALBmzwnzlNhu9SvnebqqVepIOYJD4MDJVHV4dbrbYTPGSb4p2faqNL4by4b2yX157dmTGvH+fxS2d4m5n6Dxp4KjYLN/050ObXDW0tKMeJ2v3lr33nKLVDHOiLjnAPW0pN7YT/PXx7t4DNBPXbtfT361XMZ+p0/1qa+Husa5p7lhkvTFLVm/hUVpXv+luu1j92X4FxekS71K+vT+dsHR4JQSAQQQQMDSAoy/Ld08RVY4AoBFRk1G2QX4ANEfECg6gZOp52UE4upVLaO4yqV9ytgIGnV/baa2Hc65of+8Z3uoxkWzh8ZOWaVfZ8z8I9C3TW1K7FajkB3SuYIN4rMX/rCzjLmEd62zttZl1NJaZx0lO6srXaGKr1Jar/VvnuvhJBv3n5QxQym2Umnd0DLa48y3lHPG7MUpbjPqLsYb2D1OT1+R4JOpv1829mc0lj1e07yGKpWO9HfypIdAvgVe/mmNPp67Ldfn+zSqqvF3JV4yvfdmbtE/Jl1YOutUbcd+tXJsMg8WMQKCCY4dCnMUbJagospLMW2kmLZSTKIU3VrpEWXU83XP3zhjBmP3hCpu5TWW0xunah8/c9783djXdNbTlyumfMms5357SZr7Vtbf63TRx/Xe1cs/rb1k3Y2lxxPubZtvbx5EAAEEEEAgNwHG3/QNQ4AAIP0gIAJ8gALCTqaXEDCWby3cekRGsMwY4EWGhdrC63jKefV+c5YOnDxr1ueqZtX1bN8E1ayQbXDqRU2X7Tiq68fO8/jGp3+uqy5l9rlO4jVO400/uEGhKuDgPHsuFeLM5buZf5ppd4l4dRprDJ5zzt65r1OsBvdtoBLhvrfhdWPmasVF++plL9bPf+1sHhDAhQACOQWM4NiV78wx9/zzdL18bWPd3bHOJelW7z6uq9/93e2ZWhVKmktt1+49oSilqplja+aJw3/8qew4UcDmcOjkZfX00+FoLXPWMw8aMf5RwakQM702dcrr6wHue/JdvNTZeG74n5rojvaZp5ub14dXSDuzbR3Q9WkNOXadvkjK2iPRU4F7NayqD+6+dIC0gBXlNQQQQACBYibA+LuYNXgu1SUASD8IiAAfoICwk+klBF79dZ3+NSvZfMJYDjnh3jYF3outMKCNkzo/nb9dxt5UxoEb+d2gf8yMzRo9OXNJ6IUrIjRE93auI+OAiDIlwr0q7tAfVuvT+VvNWTjGKbyNQra7/lvNkXUoiFeJZns41RmuQyXjFdOwrSvYp6qNpMgyOZLs8dpMJR/KCixULBVhzvq7eIZOQctivPf3iWv1/pytOZIoExmmZ/oluA/yfcmIdxGwqYBxMI1xQI2xx+XF19RBXRVfJef/bmd/LiPDqc4XnZL9xYPttWbPcQ2fuM6DmlMNI4/op+sjFbZnsbRrUeY/SmRkHXjjDfVxZ0kty6inZRnx5uEiT959q1o1yApa3vnhQs3ZdMgtSeO0cOPUcPM6nyqNrCmln8t65o5vddNvJbU420FKnsrk6wnj3tSTZxFAAAEE7C3A+Nve7Zvf2hEAzK8Uz/lVgA+QXzlJzEeBI6fPqc3fp7oNUC9sTO9j0n57fcCnSzRpzT4zvRqXldDEx7qofKmIPNP/8/j5WpDseW+9JtFlzQ3mPW5afyHl82ekA2vNAXT63pVatfh31XNuUylH5oxCX66MkpW0ICVaK9NqmXv2rXHW1jZnNU0e1MNcwpvXNXvjQQ38z1KdPJvmt5NLL87TCDIYB2tciF0Ye5gZAVjjROByJfP2z6sO3EegOAhcfKCOUecqZSJlHKCTn0NvPJ2Sbezl2WnkdI98VzWtrjG3t8q6dy5FO9bM02fffKNWfywdruK49AEcubVLhhwKqdzAXDp8tGIL3fJLujZl1HDNEjTeM76py4b2VrhxavD2+dLHfbOSc4TI+cw2NR+5wO2QEU/5Gcv43721ZXHoItQRAQQQQKCQBRh/FzJwkCRPADBIGspuxeQDZLcWDe76fJm0Q89+t8qtEs/2S9CAbhdt5B6gahoBylav/OaW+7XNa+idPAaGxmzBFn+bovPpuR/B+2Sv+nq8V73MtE8dlPatzJwts3+10vasVMjhTQrxcQlvhtOhrc5qSg6NVa/uveT44zRela6qMTO3uM1Q9HbPK2OJ4cnUNFUuU3h73U1bt1//W75H8ZVL6/b2tdhXL0D/e0C2wStwPj1D14+dq9W7s5bm3tAqWm/c3CLflTJmAoYYx2Rnu24YO1dLd+QM5L3ev7lubJ3z9Otbxy/44xAfp6J16I9lw5l7CTZybFOEo2Anjp9wRml5Rry5bNiYKWj8Gf9gT7UL26TTU4ar1O6sJcwZVZro4B3TzH0D87qubxmtN2/Jv1Fe6XEfAQQQQKD4CjD+Lr5tn73mBADpBwER4AMUEHYyzUXA0xIuYxnwv++zxubrk1bv1YDPluYo/ZjbWpl7+uV2zVh/QPdOWOS6bYydQxwOpWekq84fS3hbhO/QPXEnFX5gjXQqc4ahL5czLEoOY8lutab6YV9F/Tu5jNY7aylFJXRF46r6153u+1mdTUvXo58v029r96tupVL69IF2ir7oIBFfysO7CCBgDYHNB07pjg8Wat+JVHOG3P8GdsrXTN9Llf7D37fqlZ/dD9IwDvVd8kJvVfAwQzr54Ck98p+lWr/vZI5kI3VOjR3bXHsJGjMFfTmZ/HR4eZU6n3NbhDXRt+jo5SPcThjPrY79W8dodP/m1mhASoEAAgggENQCjL+Duvn8VngCgH6jJCFvBPgAeaPFs4UpcPT0OSVetPzXyM9Y6rnipT6ZS7gCfA37cY0mzMt5kmb5kuGa8mQ3RYSFmAG0XUdTdEXjampYvaxZYuMEzi/mblADx05zr77Ly+5X5zJ7pP1r/LKENyW8ghadjTGX75p/nLX19iM3qUnNCmb+fd+a7TbQHtIvQQ/nMqvSOHzFCArkZzlggJuD7BFAoIACx1LOac2eE2pco6xfltDvO56q9q+6z6RrXbu8vv2L+0Ed2YtrnGRuBACNmb1T1x2QsUehpysyLEQLByao3JHlWjp3ipy7FqmJY6siHQXbS/BCHsPKvqxaba/T3y4KXHoqw61ta+nVG5oWUJvXEEAAAQQQyBJg/E1vMAQIANIPAiLABygg7GTqQeCrRTs1+NuVHm2MQaQxmAz0dXEgLXt5YspH6cCJszqXnqFKOi5jRt/ITlKlUxu1fW2SYtJ3KdSR+xLg/NTtwhJeI8C3NqOOGejb6KijX567yVzWt+1wiiuZ0Tc1U//Emjp1Nk3Nhk127Z1nPPD1gA5qUyczOMiFAAII+EOg/7h5WrQta6adcQL4I5fH5ztpY5/PUZM2aNbGg27v3NaulkZcnxl8MwKX3V+bqdMpKeYswZZ/7CPYImSzYhzuB4DklrFxwNG/0q/Rm2k3qlN8Jc3dfDjPMt7ZvrZe+VOTPJ/jAQQQQAABBPISYPydl1DxuE8AsHi0s+VqyQfIck1SbAt0z8dJmrnBfeB3AePpKxpoYPf8DyQLA9EYeLZ85Tc5s8XwjD356jj25TiFt6Cb2ruVO7ykVKWRklKjzSW8xsy+9c6aOqMSbo9dmJmS/XAS44H7OsVq6DWNNHfzId3+wULXO2EhDq1++QqVCA8tDCbSRACBYiqwdMdR3TxuvtIynKpZIUq/PNbF69PNDbp5mw/JOKxk2c5j5j/8fHB3ospmOyV9YfJh3flRks6lZbhJV9FRtQzZpIdiD0u7ktRYySrhOO96ZltGVX2a3kvfpHfTcXk+3MhYrmzs9XrxdW+nOnrpmsbFtGWpNgIIIICAPwUYf/tTM3jTIgAYvG0X1CXnAxTUzWebwh9POa/Ev/+W6yEZneMr6bMH2gW0vr+t2KoxX/5oLuE1NqlvHLpDCY4dipLvp/AecJZzLd01ZvS9eP8tqliroRQSqm6jZ2h7tpl9xmEhxqnBSVuPmAdu3NG+thnMe2vqRr01dZPLqGNcRX3+YHu9O22TXv9to+v35jGX6YdHOwfUkswRQMCeAgdOpmrd3pNqF1vB539kMA4syW3rh19X7dUjny91+wcZQ9TYX3X+kJ567rtVmr1+jxo6tpv7rO5xVtASZ323E4I9tcDNiTH6avGuHLeM08afu7KhPRuNWiGAAAIIFKkA4+8i5bZsZgQALds09i4YHyB7t2+w1O6bJbv0f1+vyLW4JcJDzH0AI8MKZ9baur0n9P6cZB06dc48IOPG+uEqcWht1km8+1Yp4/AWv5zCuz+ipqo3aGMezmH82RkRp+7j1pmzZi5c93Sso2HXNtb2w6fVbfRMN5ef/9pZTaIvy2E1afU+Dfhsiet3Y1/CpS/21n0TFmlGtpmVF9IOlr5BORFAAAFPAv+et00v/bjG7daF08s/mb9NQ39wv5cfxQ/vTtT9/16c49FHLo/T4L4J+UmCZxBAAAEEELikAONvOoghQACQfhAQAT5AAWEn04sEjCDV9PUHXL8cZMVbAAAgAElEQVS2rVNBi7YfcZvd8dXDHdQ21r/71u09ekqfTJyuXesWZi7jNf6EbFdlx3Gf2yjFGal1zlrmzL515p59tbXBGaMXrk/U7e1qu6U/5LuV+iJpp+s34zCR35/prsmr9+nFbIPYSqUjlPRcL4UY01wuujwFCxc+11NXvDVbx1KylsG9c2tLXdu8hs/1IwEEEEAg0AKjJq3X2JlbXMX4zwPtzH39th06rctfc//HE/P/2XbIXE58/EzWN/HCy6UiQrXohV5qNHRyjmo91iNeg/o0CHR1yR8BBBBAwAYCjL9t0Ih+qAIBQD8gkoT3AnyAvDfjjfwJGCc6Tl+3X7GVS5kn4paMCPP44onU82r9ivvy37duaaF/zU6WMTPvwmUsfX28V738Ze7pqbOnpAPGrL5Vcu5bpf0bF+myExsV5ci535PXmZSu5prRd7JcQ938wyltOF9ZGcp5cvHsp7urVsWSblnsPnZGl4+e4bYE+uFudZV88LR5qvCF6/qW0XrzlhYei5eR4VSTYZOVci7ddf+Zvgn6x6T1bs8bgcWY8u75e11fXkAAAQQsIGCcJPzD8j1auPWIeiRUUe9GVV2l6jpqhnYcyToYybjRp1FV1SgX5fE09+Y1y+mHgZ3U4dVp2ns81a12g3rX12M9ffi/PxawoggIIIAAAtYQYPxtjXYIdCkIAAa6BYpp/nyAimnDF3K1V+8+rqvf/d2VizGz4prmNdQ/MUYta5Z3zWA7ePKsXv5pjX5eudf1bERoiBa/2Etv/bZJH83d6vq9Q92K+uKh9kpLzzAHZ8apuw5jOsfFl3FKx6n9ZqBP+1b+8d9V0mFjlohvp/CmOx1KdtbQetVW3159FF6jWWbgr3QVt1L87ae1bmW/cLN2xZKa9XR3j/rPfrtSXy7KmgVYOjJMxuD2dLaA3hs3N9cNrWJybT3jJOBlO4657hs82Q8tqVImUsasQI9uhdwnSB4BBBAoSoEX/rdKny3Y4ZalMZPcmEB907j5OYrSv3WMRvdvrtveX6B5W9xPBvb2ROOirCd5IYAAAggElwDj7+Bqr8IqLQHAwpIl3UsK8AEKng6y+cApM6hkBNOME3HLlYywbOGH/bjG4wwLo8DlSobLWOJbp1IpfbFwh06eTXOrR8+EKvrwnjaasmafHvo0a087Y1mssQxr3KxknTqbpsTa5TX21uaqcn5XzmDfac+nCXsDdtpcwpu5dNcI+K1Or62NzhilKlLt61bQlw91yDW5vcfPyJh9cj7dPeB4e7ta+vv1TT2+t/XQafV8faaybQWY47mk53uqShn3U4CzPzTku1X6Isl9wJv9PidZetMDeBYBBIJZYPbGg7rroyRXFZoZByAN7GT+o0inf0zPMcvv+Ssb6kHjsI/vV+nzhe7f0Qv3gtmDsiOAAAIIWEOA8bc12iHQpSAAGOgWKKb58wEKjoZPOZem3m/MlrFU1Lha1y6vr42ZDB72giusGhlLTEf8sk4/rNijxjXK6pXrmqhmBc9LSW/513xzSVZBrnF3tFLfJtVlnAzc4pUprhlsJZVqnrp74RTeRiE7lBCyUyXk+xLeE2GVFFmzhSJjmmt7eJzeWBWpH3dG5npi5OM96+nJ3vUvWb2L9/UzHh53R2v1bVIt1/cGfr5UE7PNhsz+YMPqZfXr410umeelNr433v/vw+3N/a+4EEAAAbsLGDOojYNAjH8UqV6uhCbc21ZxlUub1R7+81p98HvWDHPjtwn3ttHlDarogznJGj5xnRvP0Ksb6b7OsXYno34IIIAAAkUgwPi7CJCDIAsCgEHQSHYsIh+g4GjVrxbv1OBvVroV9u0/t9B1LaL9XoGdR1K05eApJdapIGMZ6oVr+vr9um9C1umIlUpH6uN72qhpjPuJtMagq+Urv7kdPJGfQhp5PX1FA93VvpYcfyzh/ff3P6niqQ3m4Rx1HPsV4vB9Ce8WZw2t/WNm35aQunqg/7Xq0Mz9dEcj+Nj37dk5ZohcqMcXD7ZXh7iKl6zWjsMp6v76TKX/MaXPOMl44XO9dFlU7gG4NXuO66p3spZOZ8/A2BNwSL+Gl8wzaesR3fyvnEvbalaI0rcDOqpK2dxnD+anjXgGAQQQCDaB1PPpKhHufoL8ip3HdN2YuW5VmfdsD3N/wGnr9uc4CfiV6xrrzg51gq3qlBcBBBBAwIICjL8t2CgBKBIBwACgk6XEByg4esFN783T4u1H3QprBHWmDuqmyDD3gY0vNVqQfNhcMnUuLUPR5aL0y+NdXAErY/bf+NnJbslHhYdqzO0t1SMha+P1/SdS1W7ENLfnHuwSq2nrD5iHWrhfTsU4Durhukd1Q/VDKnUk85AOpRzypRqZ70aUlqo2MffoW5QarVcWh2qDs6bOKnPpdNkSYfr43jZqXdvzycLzthzS7R8sdNtDz0w2NEQrh/XJMaD0VOBPF2zXyz+uUWiIQy9e3Uh3tHc//dfTO/d8nKSZG3IuYf78gXbqGF/pki7GgSrNhk1xe8Y4OfibAR3NJddcCCCAAALG3qhO8//WzdmU+X9rjANEPrqnjfk/G/8A1vP1WW5Mz/ZL0IBucdAhgAACCCDgswDjb58JbZEAAUBbNGPwVYIPkPXbbPOBk+r1xmyPBS3IsiRjRtrEVXuVcjbNnEEYFZEVQLxvwiJNX3/AldfL1zbW3R0zZz3kFpgyViGPvKGZbm5T03xu1saDujvbvkslI0K1etgV5nLlvfv2KnnFLJ3ekqTLjq5Uw/RNKpuRdWhFQVtjr7OCtoTEqkJcazVo0Umh1ZtK5WOlkBBzv8DLR8/UoVNnXckbsxc/vb+tjGWxl7o8BT2N/Qu/GpD7/n8Xp2fMPjmblnHJmX/Z3/E0i88ItC5/qXe+gr13frjQNag1ZlV++VB7NYl2n6VZUGfeQwABBOwiYMz0/mHFbqWlO3VTYoxrewTjH8Dqv/CrWzXvaF9Lw//kef9Wu3hQDwQQQACBohFg/F00zlbPhQCg1VvIpuXjA2T9hvUUhLpQ6vIlwzVrcHev9nXLflBEy1rl9N1fOpqnwnpauntT6xi91r+5mV2nkdNdexBerGbMivttUFfVrlhK42dv0Yhf1itC59XQsV1XV9yjB+selXYtlo4YJ/EW/MpwhMpRqb5OV2iojzaX1sIz0VqXUVtHlBXIq1+1tLlUtntC5sm8oyat19iZ7vkawb8u9SrnWZCzaem6fsw8rd17wvXsoN719VjPenm+68sDF8/47N6gsj6+t22+kjQCnf+cvlmnz6bp4W5xiq+SuecVFwIIIIBA/gTqPDvR7cEh/RLM7ykXAggggAACvgow/vZV0B7vEwC0RzsGXS34AFm7yYyZCB1HTtOhU7kfdDGwe5yevsJ9D7vcanXmXLqaDpustGxHzRqnIjavWU7G3n9dRs1we7VJdFn9/Ncu5iy6Ji9NzhXLoQz9vWsp3RZ9UHNm/qoyh1eawb9Ih/sJv15pR5SRqmUu4c2o2kQh1ZtJlRtK4Zn72BmnIv95/Pxcba5rUUMPdqmrG96bZy5pvnBlX+qVn/IkHzylez5epB1HUmQEF78e0DHfs/nyk76nZxZtO6Lb3l/gOkX4k/vaqmv9vAOWBc2P9xBAAAEEsgRe/XWd/jUrc8sLYwsHY3/AquyhShdBAAEEEPCDAONvPyDaIAkCgDZoxGCsAh8ga7fapNV7NeCzpW6FNIJ1xgbmFy7jcImZ/9dd1S7L+4CHJduP6sb35rmlZ+xNd3/nWP28co8e/XyZ272IsBCtffkKrdp9XNePzXqvsuO47q59WBm7FquFY4uah2zRZY6UgmNGVZCiW0s1WpgBP/NPuTrmEt5LXdsOndbz/1uluZsPe3zM4TD2esq6FRbi0KQnuno9K85YxmvsbRhTvqQ5GCyKa8n2I5q14aDa162Y595/RVEe8kAAAQSKi4Dxj2X/mr1F2w+n6M9taqpd3Usf+lRcXKgnAggggIDvAoy/fTe0QwoEAO3QikFYBz5A1m60ez9O0oxsB0K0qVNeI29spj5vznadLmvUIL/7E308d6te/mmtW6WvbFpNY29vrdyWGk99tI12rJ2vubMmq2XIFjV3bFHNkJyHVORbMjRSqt5ciknMDPoZf8rXkYxoXQEuY+ny7E2HNPLX9VqXbamup6Tu6VhHw65tXIBceAUBBBBAAAEEEEAAAQQQ8E2A8bdvfnZ5mwCgXVoyyOrBB8i6Dbb3+Blz371sq3U1+qZm6p9YU899v0qfL9zhKrwxU2/O4O55LlEa9N/l+m7ZbrdKVykTqYXP9dSt7y9QUvIhxTn2qEXIZnNmn/HfhqG7FOJMLzBUesX6CjWCfTF/BPuqNJbCMk/i9eeVkeHUN0t3afjPa3UiNefS48uiwjXr6ctVrqT/8/ZnPUgLAQQQQAABBBBAAAEE7CnA+Nue7eptrQgAeivG834R4APkF8ZCSeTtqZv05tSNrrSNE12Tnu+pkhFh2nc8VV1HzdC59Ky97R7oHKsXrm50ybL0emOWuXfehauqjqhFyBaNan9e65fMUCMlq4zjTIHrczSkvBadr6vlGXFa7ozXnpIJmvnCdQVOryAvGjbPfLvSPI04+zXsmka6p1NsQZLkHQQQQAABBBBAAAEEEEDAZwHG3z4T2iIBAoC2aMbgqwQfIGu22Y7DKer79mylnMuaeXdr21p69YamrgJfPAswKjxUc5/toQqlImTsWTdj/QFzX8AWNcuZp/yeOnFUD45831zCawT9jH37qjuOFBwgvKSSI+ppyvGaWmEE/DLitVcVJGUt5e1Sr5I+vb9dwfMo4JvGsuAvF+3U6MkbdOT0OV3drLreuqWFwkIvvadgAbPjNQQQQAABBBBAAAEEEEAgTwHG33kSFYsHCAAWi2a2XiX5AFmvTYylrMZy3IVb3YNzP/+1s5pEX+YqsHFq7+WvzXTbC/DR7vHq26Sa/vLvhSp7cpMZ5Lun9iHVP79RzoPr5VC2EzG8qHq606GNzppalhGnFc54Dbitv2ITWuv7lfv05H9X5JpSfmYlelEMrx9NS88wlwMbQVEuBBBAAAEEEEAAAQQQQCCQAoy/A6lvnbwJAFqnLYpVSfgAWa+5J8zdqmEXHdRxW7taGnF91uy/C6Ue9NVyfbd0l2Ich9TCsVmJ4clqqs1qpK2KcpwrcOV2OStpRYaxlDfenN23yhmrM8o8Zdg4BXft365QZFio9hw7o44jp+eaz4U9CwtcEF5EAAEEEEAAAQQQQAABBGwiwPjbJg3pYzUIAPoIyOsFE+ADVDC3wnpr26HT5tLf1PNZe/tFl4vS5Ce7ytgD0LzOHJV2L5F2L9Xp5IU6sy1JlRwnClykE84oM8i3wpm5jNcI/B1U+VzTq1u5lKY/dbnrfud/TNeuo573Dfzp0c5qGpM1a7HAheRFBBBAAAEEEEAAAQQQQCDIBRh/B3kD+qn4BAD9BEky3gnwAcryWrnrmN6dvlllSoTp2b4JqlI2c8ZbUV3pGU79efx8Ldp21JVlhM7rmz+VUTPH5syg367F0pEtBS7SeWeo1jlruWb2LXfGKdlZXU65740X4pDb6cPZM+zbuJrG3dna9dNTX63Qt0t35SiTkcbav/VVifDQApeXFxFAAAEEEEAAAQQQQAABuwgw/rZLS/pWDwKAvvnxdgEF+ABlws3fclh3f5ykc2mZM++aRl+mHwZ2UogRxfLy2rT/pF78YbVOpqbpqT711SOhap4pGIdWDPthtWYvXPjHIR2bzYM6moTuUJjzfJ7v5/bAtoyq5sy+NY56Wnw+VmucdXRWmfvhlSsZrmMpntPukVBF09cf8JjsYz3iNahPA9e9rxbv1OBvVuZ4tm6lUpr+f1kzBQtcCV5EAAEEEEAAAQQQQAABBGwgwPjbBo3ohyoQAPQDIkl4L8AHSFq9+7j+PH6BTp1NcwP8+J426p5QxStUYxZfz9dnatvhFPO9y6LCNXtwd/O/Oa5TB/9YyrtEO1fPVpnDq1TOcdqr/LI/fMRZ2lzKu1Lxqtu8m15aEqkjzjIe04sIC9FtbWtpwrxtOe7XrBCluzvU0fCJ6zy+++6tLXVN8xque9sPn1a30TNzPNuvSTW9d0fWTMECV4wXEUAAAQQQQAABBBBAAAEbCDD+tkEj+qEKBAD9gEgS3gsE8wfImDV3NOW8Tye8Gnvu3TRung6dynlgRuf4SvrsgXYeUX9YvlvvzdyiymUiNfLGZjL26TOu39bu14OfLHZ75/27EtU7voy0b2XmEl5z/77F0rEd3jfYhTdCI6XqzaXo1lJMos5WbaEPVju1/+RZ3dKmphrXuEy3jl+g+cmHPebRvGY5/aVbnAZ8tiTH/auaVdetbWrpjg8Xenx30hNdlFCtrOue0Q4dXp2ufSdS3Z5/olc9PdGrfsHryJsIIIAAAggggAACCCCAgI0Egnn8baNmCHhVCAAGvAmKZwGC7QO080iKPk/aoVW7jmvV7uMqXzJcM5/unu/G23v8jH5esVe7jqZo/4mzWrLjqA6ePJvr+xcHu4wHjRlvvd+YrXPpmcuFG1Yvq4l/7WwuF777oyTN2bhfcY49ahGyWS0cW9Sr7E5VPbNFcqbnu5w5HqxUX4pOlKJbmQE/VWkshWUu5c3t+s/C7Xr++9Ueb9/Vobb+2qOe2vx9ao77Q/ol6MbWMUocnvNe9hOAs7/42BfL9OOKPW5pjbujlfo2qV7wOvMmAggggAACCCCAAAIIIGAjgWAbf9uI3lJVIQBoqeYoPoUJtg+QsVz36nd/d2ugFS/18bzE9qJm3HPsjK58Z06u+955avWbE2M06qbmbrfenbZJr/+20fVbVR3RO10ylJC+UWsWT1dTx1aVcXg+FTc/PSsloqJKxrbLnN1n/mkllfD+JN3Dp86q7YhpMpYlX3yNvqmZ+ifW1OWjZ7iWK1945osH26tDXEUzAHjolHtwNK5yKU3LdgLwhXc8BRtn/N/liq1UKj9V5hkEEEAAAQQQQAABBBBAwPYCwTb+tn2DBKiCBAADBG+lbHfs2KF33nlHEydOlPE/R0ZGKj4+XjfffLMeeeQRlSxZ0u/FDbYPkHFIR5OXJrtm3xkgnz/QTh3jK+Vp87ef1uqjuVtzfa5xjbJqX7eiPvw96xljr7y5z/Qwl/qa19mTeubdT1T+6ErzkI7mIVtU3XEkz7xzeyDFGalVzlgty4g39++Lb9lVg27sIUeI+6m8Bc3gzg8Xas6mQzlen/xEVzWoVkaDvlqu75budt13OKSVL/VRmRLh8vRubvv6JR88pR6vz3KlY+x5uPTF3jJmDHIhgAACCCCAAAIIIIAAAghIwTb+ps0KR4AAYOG4Bk2qRtDv9ttv1/Hjxz2WuUGDBvrll19Ut25dv9YpGD9A1/7zd63cleX0bL8EDegWd0kXI3DYbsRUc89AT1e9KqX1+YPtzVudRk43A4yhSlcDx04NanTSXMarXUvkPLheDuWcUZefRnE6QrQ+PVrLjWCfM8787yZntNIVar5+VdPqeufWln4Nmv130Q498+0qt+JFhYdq9ctXmPl8kbRDQ77Lup99ht+IX9Zp/Oxkt3cf61lPg3p73tdv6A+r9cn87TJifi9f10R3tq+dHxaeQQABBBBAAAEEEEAAAQSKhUAwjr+LRcMUcSUJABYxuJWyW7FihTp27KiUlBSVLl1aQ4YMUffu3XXmzBl9+eWXev/9983iJiQkaNGiReYz/rqC8QP03Per9PnCrAM0jEMrxtzW6pIkv6zaq0f+s9TtGSNoGF0+SjHlo9QhtoJKnN5tHs4xa8YkRR1cYS7ljXLkPBwkv/a7nRW1PCPOnNnXumMvna7QVIN+2Ox6vUyJMDOYVjIiVDXLlzRnHxr7CPrzOpZyzlzKm5ZtGXCbOuX19YCOZjYnUs+rx2szXYeg/O26xrqrQx3z3ndLd2nQVyvcivPP21rq6mZZJwBfXNYtB0+pRHio61AUf9aFtBBAAAEEEEAAAQQQQACBYBYIxvF3MHtbtewEAK3aMkVQLiPYN3PmTIWFhWn27Nnq0KGDW66jR4/W4MGDzd9efvllDR061G+lCsYP0JdJO/RstllrtSqU1OzBlz4IxDicY9bGgy637rXD9XHv0D9O5DVO5V0inc667y3wCWeUVmbU1XJn5lJeI/B3UOVdyfypRQ2dz3Bq4sq9rt+ubFpNY29v7W1WXj9/z8dJmrkhq24PdI7VC1c3cqVz4GSqWS5jv77LG1Rx/b52zwlzz8Ts14Wlw14XghcQQAABBBBAAAEEEEAAgWIuEIzj72LeZIVSfQKAhcJq/USNGX1t27Y1C/rwww9r3LhxOQqdkZGhJk2aaN26dSpfvrz279+v8PBwv1QuGD9AHg8CGdpHl5X0bLLn0DE98sa/1cyxJXPfPscWxYVkBeK8hTzvDNU6Zy0z0Lc1sqFmpdRSsrO6nMrat69TfEXN3XzYlXR0uSidOpum42eyliD/48amuqVNLW+z9/r5FTuPqf+4+eay5siwEE0d1E01K+S9n+T59Ax1+ccM7TuRauZZ/bISZqA1PNQ/+xN6XRFeQAABBBBAAAEEEEAAAQSCWCAYx99BzG3ZohMAtGzTFG7Bnn/+eY0YMcLMZMGCBWrXrp3HDEeOHGkuDTauKVOmqHfv3n4pWDB+gMyDQIZNlvHfC9dn97dT53qVJKdTOrzlj5l9i83/pu9ZqVCn573/8oO4PaOKObNvc3gDzT1TW2ucdXRWESpbIkz/vq+trh87zy0Z48CQD+9O1LX/nHvJ5OcP6aHql0Xlpwg+P7P5wCkt2X5EXetX9irPBcmH9feJ68z8X7iqodrVrehzWUgAAQQQQAABBBBAAAEEECiOAsE4/i6O7VTYdSYAWNjCFk2/a9eumjNnjkqVKqVjx46Zy4A9XfPnzzf3CTQuYwmwsRTYH1ewfoCu++fvWrHruCrohFqEbNYj9Y4rMcwI/C2VUo8VnCaqvBTdWopO1NhNl+n95PI6qrIe07uhVbTeuLmFBn6+1G1p72M94vV4r/pqNmyyTp9L9/hu/aqlNeXJbgUvJ28igAACCCCAAAIIIIAAAggElUCwjr+DCjkICksAMAgaqTCKWLlyZR06dEjNmzfX8uXLc83i6NGjqlChgnm/f//++uqrr/xSnKD7AJ3YI63+TiuTpqv8kZWqGVLwffsUGilVb2YG+8ygX0xrqXys5Mg8iGP/iVT1fH2WuXTX0/X+XYnq3aiqDp86q/smLDIDksbS3w/uaqOoiFDd/sECt2XA2dN4sEusnr8qax8+vzQmiSCAAAIIIIAAAggggAACCFhWIOjG35aVDO6CEQAM7vYrUOlTU1MVFZW5BPSqq67Szz//fMl0jNN/T58+rfbt28uYEZify/jAXOrau3evaw/CnTt3KiYmJj/JBu6ZnUnShwVb/rw5o4a2RjZQr95XyWEE/Ko2kcIiLlmXCXO3athPa3M8UyoiVEte7G2eeHvhOn02TaUis2Zwvj5lg96dnnXqb/ZEPr2/rbrUqxw4R3JGAAEEEEAAAQQQQAABBBAoUgECgEXKbdnMCABatmkKr2AHDx5UlSqZp67ecsst+vLLLy+ZWdWqVXXgwAHzQJBVq1blq2COP2az5efhoAgAnk+VXo2WMjzPynPVs1QVpdVopXfXX6bF6XW1KqOuTqiUuY/dA13q5ofDfCY9w6k/jZmrVbuPu71zTfMaevfWlpdMZ8b6A7p3wqIcz5QID9HyoX3cgof5LhAPIoAAAggggAACCCCAAAIIBKUAAcCgbDa/F5oAoN9JrZ+gEXCrVSvzFNg777xTn3zyySULbTxrvBMXF6fNmz3PLLs4AdsFAI0K/qubtDdruXSKM1KrnLGKbtxZMU06Zy7pvSxGk9bs14DPlrhIwkIcWvhcT1UsHelV51i167iuG/O7MpxZr429vZWubFr9kukcSzmnFn/7LcczlzeorAn3Zp78zIUAAggggAACCCCAAAIIIFA8BAgAFo92zquWBADzErLh/aKYAWi7JcBGP5jzhnQkWWM2ldfPh6trozNG6QrV01c00MDu8a6e8tRXK/Tt0qwl0J3jK+mzBzyfspxX93pr6ka9NXWT+Vij6mX1v4GdFBEWktdr6vn6TG05eNrtuZeuaaR7O8Xm+S4PIIAAAggggAACCCCAAAII2EeAAKB92tKXmhAA9EUvSN8tij0A86IJ5g/Qi/9brU8XbHdVsV+Tanrvjtbm342lu4nDf9PRlPOu+8OuaaR7fAi8zd9yWAdOppoHf5SM8Hxa88XeT3+9Ql8vcd+HcdpT3RRXuXReTcN9BBBAAAEEEEAAAQQQQAABGwkE8/jbRs0Q8KoQAAx4EwSmAJwCXHD3rxbt1OBvV7oSiC4XpbnP9jD/nrT1iG7+l/tBKb8/010x5UsWPMMCvPll0g49+13Wfo1GGY1yeLM0uwDZ8goCCCCAAAIIIIAAAggggIDFBAgAWqxBAlQcAoABgg90tl27dtWcOXNUqlQpHTt2TGFhnmeWGaf+duzY0Szu0KFD9fLLL/ul6MH8AVq394T6vT3HzWHpi71VoVSERvyyTuNnJ7vuNaxeVr8+3sUvZt4kYpwM3OuNWdp7PNV8bdSNzXRzm5reJMGzCCCAAAIIIIAAAggggAACNhAI5vG3DfgtUwUCgJZpiqItyHPPPadXX33VzHTBggVq187zHnUjR47UkCFDzOcmT56sPn36+KWgwfwBSkvPUOOXJutsWobL4t/3tVW3+pXV47WZSj6UtffeYz3iNahPA7+YeZvIwZNnNWnNPsVXLq32dSsw+89bQJ5HAAEEEEAAAQQQQAABBGwgEMzjbxvwW6YKBAAt0xRFW5CkpCRX0O/hhx/WuHHjchQgIyNDTZo00bp161SuXDkdOHBA4eHhfilosH+Arh87V8t2HHNZGAeBXNG4mjnrLvv106Od1TTmMnDAWLoAACAASURBVL+YkQgCCCCAAAIIIIAAAggggAAC3goE+/jb2/ryvGcBAoDFuGdcWAZsLP+dPXu2OnTo4KYxevRoDR482PztpZde0rBhw/ymFewfoKE/rNYn87MOAjGW+vZMqKJ/ztjsMqpaNlILhvRk5p3feg0JIYAAAggggAACCCCAAAIIeCsQ7ONvb+vL8wQA6QMXCSxbtkydOnXSmTNnVLp0aRnLgrt3727+/csvv9T48ePNN+rXr6/FixerTJkyfjMM9g/Qt0t26amvV1zS4/Z2tfT365v6zYyEEEAAAQQQQAABBBBAAAEEEPBWINjH397Wl+cJANIHPAj89NNPuuOOO3TixAmPPkbwb+LEiYqPj/erX7B/gM6cS1eP12e6DtnwhDPh3ja6vEEVv7qRGAIIIIAAAggggAACCCCAAALeCAT7+NubuvJs7gIsAaZ3aPv27Xr77bfNQJ/xYYiIiDADfv3799ejjz6qkiVL+l3JDh+gDftO6vYPFujQqXM5fEpFhGrp0N6KDAv1ux0JIoAAAggggAACCCCAAAIIIJBfATuMv/NbV54jAEgfsJiAXT5Amw+c0m3vL9CBk2fdhPs1qab37mhtMXWKgwACCCCAAAIIIIAAAgggUNwE7DL+Lm7t5u/6MgPQ36Kkly8BO32Ath46rVvHL9C+E6muuo+5rZWualY9XxY8hAACCCCAAAIIIIAAAggggEBhCdhp/F1YRsUhXQKAxaGVLVhHu32AdhxO0eBvV2jN7hO6vlW0Xr62Maf/WrDfUSQEEEAAAQQQQAABBBBAoLgJ2G38Xdzaz1/1JQDoL0nS8UqAD5BXXDyMAAIIIIAAAggggAACCCCAQIEEGH8XiM12LxEAtF2TBkeF+AAFRztRSgQQQAABBBBAAAEEEEAAgeAWYPwd3O3nr9ITAPSXJOl4JcAHyCsuHkYAAQQQQAABBBBAAAEEEECgQAKMvwvEZruXCADarkmDo0J8gIKjnSglAggggAACCCCAAAIIIIBAcAsw/g7u9vNX6QkA+kuSdLwS4APkFRcPI4AAAggggAACCCCAAAIIIFAgAcbfBWKz3UsEAG3XpMFRIT5AwdFOlBIBBBBAAAEEEEAAAQQQQCC4BRh/B3f7+av0BAD9JUk6XgnwAfKKi4cRQAABBBBAAAEEEEAAAQQQKJAA4+8CsdnuJQKAtmvS4KgQH6DgaCdKiQACCCCAAAIIIIAAAgggENwCjL+Du/38VXoCgP6SJB2vBPgAecXFwwgggAACCCCAAAIIIIAAAggUSIDxd4HYbPcSAUDbNWlwVIgPUHC0E6VEAAEEEEAAAQQQQAABBBAIbgHG38Hdfv4qPQFAf0mSjlcCfIC84uJhBBBAAAEEEEAAAQQQQAABBAokwPi7QGy2e4kAoO2aNDgqtG3bNsXGxpqFTUpKUvXq1YOj4JQSAQQQQAABBBBAAAEEEEAAgSAS2Lt3r9q2bWuWeOvWrapTp04QlZ6i+kuAAKC/JEnHK4FFixa5PkBevcjDCCCAAAIIIIAAAggggAACCCBQIAFjAk6bNm0K9C4vBbcAAcDgbr+gLT0BwKBtOgqOAAIIIIAAAggggAACCCAQpAIEAIO04fxQbAKAfkAkCe8FUlNTtWrVKvPFypUrKywszPtEiviN7NOmWbZcxPhkV2gC9OtCoyXhAArQrwOIT9aFJkC/LjRaEg6QAH06QPBkW6gCVu3XaWlpOnjwoFn3pk2bqkSJEoXqQOLWFCAAaM12oVQWFGDjVAs2CkXyWYB+7TMhCVhQgH5twUahSD4L0K99JiQBiwnQpy3WIBTHLwL0a78wkkghCRAALCRYkrWfAB9z+7UpNZLo1/QCOwrQr+3YqtSJfk0fsJsAfdpuLUp9DAH6Nf3AygIEAK3cOpTNUgJ8zC3VHBTGTwL0az9BkoylBOjXlmoOCuMnAfq1nyBJxjIC9GnLNAUF8aMA/dqPmCTldwECgH4nJUG7CvAxt2vLFu960a+Ld/vbtfb0a7u2bPGuF/26eLe/HWtPn7Zjq1In+jV9wMoCBACt3DqUzVICfMwt1RwUxk8C9Gs/QZKMpQTo15ZqDgrjJwH6tZ8gScYyAvRpyzQFBfGjAP3aj5gk5XcBAoB+JyVBuwrwMbdryxbvetGvi3f727X29Gu7tmzxrhf9uni3vx1rT5+2Y6tSJ/o1fcDKAgQArdw6lM1SAnzMLdUcFMZPAvRrP0GSjKUE6NeWag4K4ycB+rWfIEnGMgL0acs0BQXxowD92o+YJOV3AQKAficlQbsK8DG3a8sW73rRr4t3+9u19vRru7Zs8a4X/bp4t78da0+ftmOrUif6NX3AygIEAK3cOpQNAQQQQAABBBBAAAEEEEAAAQQQQAABHwUIAPoIyOsIIIAAAggggAACCCCAAAIIIIAAAghYWYAAoJVbh7IhgAACCCCAAAIIIIAAAggggAACCCDgowABQB8BeR0BBBBAAAEEEEAAAQQQQAABBBBAAAErCxAAtHLrUDYEEEAAAQQQQAABBBBAAAEEEEAAAQR8FCAA6CMgryOAAAIIIIAAAggggAACCCCAAAIIIGBlAQKAVm4dyoYAAggggAACCCCAAAIIIIAAAggggICPAgQAfQTkdQQQQAABBBBAAAEEEEAAAQQQQAABBKwsQADQyq1D2RBAAAEEEEAAAQQQQAABBBBAAAEEEPBRgACgj4C8jgACCCCAAAIIIIAAAggggAACCCCAgJUFCABauXUoGwIIIIAAAggggAACCCCAAAIIIIAAAj4KEAD0EZDXEUAAAQQQQAABBBBAAAEEEEAAAQQQsLIAAUArtw5lQwABBBBAAAEEEEAAAQQQQAABBBBAwEcBAoA+AvI6AggggAACCCCAAAIIIIAAAggggAACVhYgAGjl1qFsCCCAAAIIIIAAAggggAACCCCAAAII+ChAANBHQF5HAAEEEEAAAQQQQAABBBBAAAEEEEDAygIEAK3cOpQNAQQQQAABBBBAAAEEEEAAAQQQQAABHwUIAPoIyOsIIIAAAggggAACCCCAAAIIIIAAAghYWYAAoJVbh7IhgAACCCCAAAIIIIAAAggggAACCCDgowABQB8BeR0BBBBAAAEEEEAAAQQQQAABBBBAAAErCxAAtHLrUDYEEEAAAQQQQAABBBBAAAEEEEAAAQR8FCAA6CMgryOAAAIIIIAAAggggAACCCCAAAIIIGBlAQKAVm4dyoYAAggggAACCCCAAAIIIIAAAggggICPAgQAfQTkdQQQQAABBBBAAAEEEEAAAQQQQAABBKwsQADQyq1D2RBAAAEEEEAAAQQQQAABBBBAAAEEEPBRgACgj4C8jgACCCCAAAIIIIAAAggggAACCCCAgJUFCABauXUoGwIIIIAAAggggAACCCCAAAIIIIAAAj4KEAD0EZDXEUAAAQQQQAABBBBAAAEEEEAAAQQQsLIAAUArtw5lQwABBBBAAAEEEEAAAQQQQAABBBBAwEcBAoA+AvI6AggggAACCCCAAAIIIIAAAggggAACVhYgAGjl1qFsCCCAAAIIIIAAAggggAACCCCAAAII+ChAANBHQF5HAAEEEEAAAQQQQAABBBBAAAEEEEDAygIEAK3cOpQNAQQQQAABBBBAAAEEEEAAAQQQQAABHwUIAPoIyOsIIIAAAggggAACCCCAAAIIIIAAAghYWYAAoJVbh7IhgAACCCCAAAIIIIAAAggggAACCCDgowABQB8BeR0BBBBAAAEEEEAAAQQQQAABBBBAAAErCxAAtHLrUDYEEEAAAQQQQAABBBBAAAEEEEAAAQR8FCAA6CMgryOAAAIIIIAAAggggAACCCCAAAIIIGBlAQKAVm4dyoYAAggggAACCCCAAAIIIIAAAggggICPAgQAfQTkdQQQQAABBBBAAAEEEEAAAQQQQAABBKwsQADQyq1D2RBAAAEEEEAAAQQQQAABBBBAAAEEEPBRgACgj4C8jgACCCCAAAIIIIAAAggggAACCCCAgJUFCABauXUoGwIIIIAAAggggAACCCCAAAIIIIAAAj4KEAD0EZDXEUAAAQQQQAABBBBAAAEEEEAAAQQQsLIAAUArtw5lQwABBBBAAAEEEEAAAQQQQAABBBBAwEcBAoA+AvI6AggggAACCCCAAAIIIIAAAggggAACVhYgAGjl1qFsCCCAAAIIIIAAAggggAACCCCAAAII+ChAANBHQF5HAAEEEEAAAQQQQAABBBBAAAEEEEDAygIEAK3cOpQNAQQQQAABBBBAAAEEEEAAAQQQQAABHwUIAPoIyOsIIIAAAggggAACCCCAAAIIIIAAAghYWYAAoJVbh7IhgAACCCCAAAIIIIAAAggggAACCCDgowABQB8BeR0BBBBAAAEEEEAAAQQQQAABBBBAAAErCxAAtHLrUDYEEEAAAQQQQAABBBBAAAEEEEAAAQR8FCAA6CMgryOAAAIIIIAAAggggAACCCCAAAIIIGBlAQKAVm4dyoYAAggggAACCCCAAAIIIIAAAggggICPAgQAfQTk9YIJpKamatWqVebLlStXVlhYWMES4i0EEEAAAQQQQAABBBBAAAEEEMhVIC0tTQcPHjTvN23aVCVKlECrGAoQACyGjW6FKi9atEht27a1QlEoAwIIIIAAAggggAACCCCAAALFQiApKUlt2rQpFnWlku4CBADpEQERIAAYEHYyRQABBBBAAAEEEEAAAQQQKMYCBACLb+MTACy+bR/Qmm/btk2xsbFmGYwPUPXq1QNaHjJHAAEEEEAAAQQQQAABBBBAwI4Ce/fuda3A27p1q+rUqWPHalKnPAQIANJFAiKwa9cu1axZ08x7586diomJCUg5yBQBBBBAAAEEEEAAAQQQQAABOwsw/rZz6+a/bgQA829liSeXLl2qSZMmac6cOVq9erUOHDig8PBw1ahRQx07dtT999+vLl265LusRlrjx483Z+EZm4IaB3IYe/M99NBD6tu3b77T8fZBPkDeivE8AggggAACCCCAAAIIIIAAAt4LMP723syObxAADKJW7datm2bPnp1nie+880598MEHioiIyPVZp9OpAQMGmMG/3C4jCDhu3Dg5HI488/T2AT5A3orxPAIIIIAAAggggAACCCCAAALeCzD+9t7Mjm8QAAyiVo2Pj9eWLVvM2X79+/c3Z/rVqlVL6enpmj9/vl5//XXt3r3brNGtt96qzz//PNfaPf/88xoxYoR5v2XLlho8eLDi4uLM9EeNGqVly5aZ94znhg8f7nclPkB+JyVBBBBAAAEEEEAAAQQQQAABBHIIMP6mUxgCBACDqB9cffXVuuuuu3TjjTcqNDQ0R8kPHTqkTp06aePGjeY9Y7agp+XAmzdvVsOGDZWWlqbExETzuaioKFd6KSkpMmYbLl68WGFhYVq/fr0ZHPTnxQfIn5qkhQACCCCAAAIIIIAAAggggIBnAcbf9AwCgDbsAz///LOuueYas2aPPfaY3n777Ry1HDhwoMaOHWv+bswcbN++fY5nFixYoA4dOpi/P/roo3r33Xf9qsUHyK+cJIYAAggggAACCCCAAAIIIICARwHG33QMAoA27AOnTp1SmTJlzJpdddVVMgKC2S9j7z/j9F1jqXBCQoLWrVuXq4Jxf8OGDeYJvTt27PDrXoB8gGzY+agSAggggAACCCCAAAIIIICA5QQYf1uuSQJSIJYAB4S98DI9cuSIKlasaGZgzAT88ccf3TJLTk52Led9+OGHzUM+cruM+xcOCTHei42N9VvB+QD5jZKEEEAAAQQQQAABBBBAAAEEEMhVgPE3ncMQIABos37w/fff64YbbjBr9fTTT5sHemS/Jk6cKGMvQeN688039cQTT+QqYNwfNGiQed9478orr/SbFh8gv1GSEAIIIIAAAggggAACCCCAAAIEAOkDlxQgAGijDpKRkWHu25eUlGTWatGiReYhH9kvY8bfX/7yF/Onr7/+WjfddFOuAt9884152rBxGe8ZMwLzexkBvktde/fuVdu2bc1Hdu7caS4z5kIAAQQQQAABBBBAAAEEEEAAAf8KMAHHv57BmhoBwGBtOQ/lfv311/V///d/5p3rr79e3333XY6nRo8ercGDB5u///rrr+rbt2+uAsb9C7P+XnvtNT311FP51nI4HPl+lgBgvql4EAEEEEAAAQQQQAABBBBAAAGvBAgAesVl24cJANqkaWfNmqVevXopLS1NVapU0cqVK1W1atUctXvllVc0dOhQ8/dp06apR48euQpMnz5dPXv2NO8b773wwgv51iIAmG8qHkQAAQQQQAABGwkcP3Ne87ccUu2KpdSwelkb1YyqIIAAAggEqwABwGBtOf+WmwCgfz0DktqaNWvUpUsXHT16VJGRkZo8ebK6devmsSxFNQOQJcAB6QpkigACCCCAAAIBFEg5l6ar3/ldyYdOm6V4+88tdF2L6ACWiKwRQAABBBCQCADSCwwBAoBB3g+2bt2qzp07a8+ePQoNDTX39TOW/+Z2FdUegHmx8gHKS4j7CCCAAAIIIBBsAlPX7tcDnyx2K/a2kVcFWzUoLwIIIICAzQQYf9usQQtYHQKABYSzwmtG0M+Y+ZecnCxjye2ECRN01113XbJoP//8s6655hrzGU4BtkIrUgYEEEAAAQQQsIvA6MnrNWbGFrfqzBncXTUrlLRLFakHAggggEAQChAADMJGK4QiEwAsBNSiSPLQoUPmMt+1a9ea2f3zn//UwIED88zaCBbGxcWZzxmn+hozAnO7jPvjx483bxvvxcbG5pl+fh/gA5RfKZ5DAAEEEEAAgWAR+Pe8bXrpxzVuxR3+pya6o33tYKkC5UQAAQQQsKEA428bNmoBqkQAsABogX7l+PHj5uEdS5cuNYsycuRIPfPMM/kqltPpVExMjLlkOCEhQevWrcv1vYYNG2r9+vWKjo6WcVKvNwd75FUYPkB5CXEfAQQQQAABBIJN4IM5yRo+0f3/t+rdqKrevysx2KpCeRFAAAEEbCTA+NtGjelDVQgA+oAXiFdTUlLUp08fzZ0718z++eef1/Dhw70qyiOPPKL33nvPfGf+/Plq3759jvcXLFigDh06mL8bz48ZM8arPPJ6mA9QXkLcRwABBBBAAIFgExgzY7NGT97gVuxSEaFaNrSPIsJCgq06lBcBBBBAwCYCjL9t0pA+VoMAoI+ARfn6uXPnzP37pkyZYmb7+OOP66233vK6CBs3blTjxo2VlpamxMREzZ49W1FRUa50zpw5o65du2rx4sUKCwszlxnXq1fP63wu9QIfIL9ykhgCCCCAAAIIWEDgjd826p1pm3KU5PMH26ljXCULlJAiIIAAAggURwHG38Wx1XPWmQBgEPWDG2+8Ud99951ZYmMJsBH8u9Sy3IiICNWvX99jDYcMGWIuHTauli1bmkuIjb0Bt2zZon/84x9atmyZec94bsSIEX5X4gPkd1ISRAABBBBAAIEAC7z66zr9a1ZyjlI83K2uhvRrGODSkT0CCCCAQHEVYPxdXFvevd4EAIOoH3i7B1/t2rW1bds2jzXMyMjQgw8+qI8++ihXgfvvv988BCQkxP9LVvgABVHHo6gIIIAAAgggkC+Bl39ao4/n5vz/vRKqldGkJ7rmKw0eQgABBBBAwN8CjL/9LRqc6READKJ282cA8EK1f/nlFzPIt2jRIhknC1eqVElt2rQxTwju169foenwASo0WhJGAAEEEEAAgQAJPPf9Kn2+cIfH3BcM6alql5UIUMnIFgEEEECgOAsw/i7OrZ9VdwKA9IOACPABCgg7mSKAAAIIIIBAIQo89dUKfbt0l8ccRt3YTDe3qVmIuZM0AggggAACngUYf9MzDAECgPSDgAjwAQoIO5kigAACCCCAQCEK/PWLZfppxR6POVzVtLrG3N6qEHMnaQQQQAABBAgA0gdyFyAASO8IiAABwICwkykCCCCAAAIIFKLAQ58s1pS1+z3mULZEmJa+2Fthof7fW7kQq0TSCCCAAAI2EGD8bYNG9EMVCAD6AZEkvBfgA+S9GW8ggAACCCCAgLUF7v4oSbM2Hsy1kF8P6KA2dSpYuxKUDgEEEEDAdgKMv23XpAWqEAHAArHxkq8CfIB8FeR9BBBAAAEEELCawK3jF2h+8uFci/XSNY10b6dYqxWb8iCAAAII2FyA8bfNGzif1SMAmE8oHvOvAB8g/3qSGgIIIIAAAggEXuCGsXO1dMexXAvy9BUNNLB7fOALSgkQQAABBIqVAOPvYtXcuVaWACD9ICACfIACwk6mCCCAAAIIIFCIAle/O0erd5/INYfHe9bTk73rF2IJSBoBBBBAAIGcAoy/6RWGAAFA+kFABPgABYSdTBFAAAEEEECgEAV6vzFLmw6ccuUQFuJQWobT9fe/XB6nZ/omFGIJSBoBBBBAAAECgPQBzwIEAOkZAREgABgQdjJFAAEEEEAAgUIU6DpqhnYcSXHlUL5kuI6mnHf9/f7OsXrx6kaFWAKSRgABBBBAgAAgfYAAIH3AQgIEAC3UGBQFAQQQQAABBPwi0H7ENO07kepKq2aFKO08csb19zvb19Yrf2ril7xIBAEEEEAAgfwKMP7Or5S9n2MGoL3b17K14wNk2aahYAgggAACCCBQQIGWf5viNuOvUfWyWrs3a0/AWxJr6h83NStg6ryGAAIIIIBAwQQYfxfMzW5vEQC0W4sGSX34AAVJQ1FMBBBAAAEEEMi3QKOhk5RyLt31fLvYClq49Yjr79e3jNabt7TId3o8iAACCCCAgD8EGH/7QzH40yAAGPxtGJQ14AMUlM1GoRFAAAEEEEDgEgLxz/3iduhHr4ZVNHXdAdcbVzWtrjG3t8IQAQQQQACBIhVg/F2k3JbNjACgZZvG3gXjA2Tv9qV2CCCAAAIIFDeBtPQMxT//q1u1jRl/3y/b7fqtV8Oq+uDuxOJGQ30RQAABBAIswPg7wA1gkewJAFqkIYpbMfgAFbcWp74IIIAAAgjYWyDlXJoaDZ3sVsm7OtTWJ/O3u37rWr+yPrmvrb0hqB0CCCCAgOUEGH9brkkCUiACgAFhJ1M+QPQBBBBAAAEEELCTwLGUc2rxt9/cqvTI5XEaO3OL67f2dSvoy4c62Kna1AUBBBBAIAgEGH8HQSMVQREJABYBMlnkFOADRK9AAAEEEEAAATsJ7D+RqnYjprlV6Zm+CfrHpPWu31rVKqfvHulkp2pTFwQQQACBIBBg/B0EjVQERSQAWATIZEEAkD6AAAIIIIAAAvYW2HkkRV1GzXCr5PA/NdEL/1vt+q1JdFn9/Ncu9oagdggggAAClhMgAGi5JglIgQgABoSdTPkA0QcQQAABBBBAwE4Cmw+cVK83ZrtV6e0/t9DjXy53/Va/amlNebKbnapNXRBAAAEEgkCA8XcQNFIRFJEAYBEgk0VOAT5A9AoEEEAAAQQQsJPA6t3HdfW7v7uqFBbi0D9va6UBny1x/VanYknNfLq7napNXRBAAAEEgkCA8XcQNFIRFJEAYBEgkwUBQPoAAggggAACCNhbYOmOo7ph7DxXJUtFhJoBwHsnLHL9VuOyEpo3pKe9IagdAggggIDlBAgAWq5JAlIgAoABYSdTPkD0AQQQQAABBBCwk8D8LYd16/sLXFWqUCpC797aUrd/sND1W6XSEVr8Qm87VZu6IIAAAggEgQDj7yBopCIoIgHAIkAmi5wCfIDoFQgggAACCCBgJ4GZGw7ono+zZvtVK1tC797WUv3HzXdVs0yJMK0adoWdqk1dEEAAAQSCQIDxdxA0UhEUkQBgESCTBQFA+gACCCCAAAII2Ftgypp9eujTrP3+alcsqXf+3FLXjZnrqnhkWIg2DO9nbwhqhwACCCBgOQECgJZrkoAUiABgQNjJlA8QfQABBBBAAAEE7CTw04o9+usXy1xVMk78ffvPLdXv7Tmu3xwOKXnElXIY/wMXAggggAACRSTA+LuIoC2eDQFAizeQXYvHB8iuLUu9EEAAAQQQKJ4C3yzZpf/7eoWr8k2iy5oBwJ6vz3ID2fT3fgoPDSmeSNQaAQQQQCAgAoy/A8JuuUwJAFquSYpHgfgAFY92ppYIIIAAAggUF4HPF+7Qc9+vclW3de3yeuuWFuoyaoYbwZqXr1CpyLDiwkI9EUAAAQQsIMD42wKNYIEiEAC0QCMUxyLwASqOrU6dEUAAAQQQsK/Ax3O36uWf1roq2DGuohkAbDtimlull73YW+VLRdgXgpohgAACCFhOgPG35ZokIAUiABgQdjLlA0QfQAABBBBAAAE7Cfxr1ha9+ut6V5Uub1DZDAC2+NtvbtVc+FxPVS1bwk5Vpy4IIIAAAhYXYPxt8QYqouIRACwiaLJxF+ADRI9AAAEEEEAAATsJvDNtk974baOrSlc0rqo3b2mhRkMnu1VzzuDuqlmhpJ2qTl0QQAABBCwuwPjb4g1URMUjAFhE0GRDAJA+gAACCCCAAAL2FRg9eb3GzNjiquA1zWvozZubK/75X90qPXVQN8VXKW1fCGqGAAIIIGA5AQKAlmuSgBSIAGBA2MmUDxB9AAEEEEAAAQTsJPD3iWv1/pytrird1DpGr/VvrrpDJirDmVXTXx7rokY1ytqp6tQFAQQQQMDiAoy/Ld5ARVQ8AoBFBE027gJ8gOgRCCCAAAIIIGAngaE/rNYn87e7qnR7u1r6+/VNlfDir0o9n+H6/X8DO6lFzXJ2qjp1QQABBBCwuADjb4s3UBEVjwBgEUGTDQFA+gACCCCAAAII2FfgmW9W6r+Ld7oqeG+nOnrpmsZqNmyyTqSmuX7/6uEOahtbwb4Q1AwBBBBAwHICBAAt1yQBKRABwICwkykfIPoAAggggAACCNhJ4Mn/Ltf3y3a7qjSgW5ye7ZegxOFTdejUWdfvn93fTp3rVbJT1akLAggggIDFBRh/W7yBiqh4BACLc0OKUAAAIABJREFUCJps3AX4ANEjEEAAAQQQQMBOAo/8Z4l+WbXPVaXHe9bTk73rq9PI6dp97Izr94/uSVSPhKp2qjp1QQABBBCwuADjb4s3UBEVjwBgEUGTDQFA+gACCCCAAAII2Ffg/gmLNG39AVcFn76igQZ2j1f312Zq66HTrt/H3dFKfZtUty8ENUMAAQQQsJwAAUDLNUlACkQAMCDsZMoHiD6AAAIIIIAAAnYSuPPDhZqz6ZCrSi9c1VAPdKmrK96crQ37T7p+f/vPLXRdi2g7VZ26IIAAAghYXIDxt8UbqIiKRwCwiKDJxl2ADxA9AgEEEEAAAQTsJHDzuPlK2nbEVaVX/tREd7avrWve/V2rdh93/T76pmbqn1jTTlWnLggggAACFhdg/G3xBiqi4hEALCJosiEASB9AAAEEEEAAAfsKXDdmrlbsPOaq4Kgbm+nmNjV143vztGT7Udfvf7++iW5vV9u+ENQMAQQQQMByAgQALdckASkQAcCAsJMpHyD6AAIIIIAAAgjYSaDvW7O1fl/Opb63jl+g+cmHXVV96ZpGurdTrJ2qTl0QQAABBCwuwPjb4g1URMUjAFhE0GTjLsAHiB6BAAIIIIAAAnYS6PHaTCVnO+zjvdtbqV/T6rr7oyTN2njQVdUh/RL0cLc4O1WduiCAAAIIWFyA8bfFG6iIikcAsIigyYYAIH0AAQQQQAABBOwr0GnkdO0+dsZVwY/uSVSPhKp68JPF+m3tftfvT/Wur7/2rGdfCGqGAAIIIGA5AQKAlmuSgBSIAGBA2MmUDxB9AAEEEEAAAQTsJJA4fKoOnTrrqtJ/HminTvGVNPDzpZq4cq/r97/2iNdTfRrYqerUBQEEEEDA4gKMvy3eQEVUPAKARQRNNu4CfIDoEQgggAACCCBgJ4GmwybrZGqaq0pfD+igNnUqaNB/l+u7Zbtdvz/cta6GXNnQTlWnLggggAACFhdg/G3xBiqi4hEALCJosiEASB9AAAEEEEAAAfsKNHjhV51Ny3BV8MdHO6lZTDk9++1Kfblop+v3ezrW0bBrG9sXgpohgAACCFhOgACg5ZokIAUiABgQdjLlA0QfQAABBBBAAAG7CDidTsUO+cWtOpOf6KoG1cpo6A+r9cn87a57t7WrpRHXN7VL1akHAggggEAQCDD+DoJGKoIiEgAsAmSyyCnAB4hegQACCCCAAAJ2ETiblq4GL0xyq86M/7tcsZVKafjPa/XB71td925qHaPX+je3S9WpBwIIIIBAEAgw/g6CRiqCIhIALAJksiAASB9AAAEEEEAAAfsKnEw9r6bDprhVcN6zPVSjXJRGTVqvsTO3uO5d27yG3rm1pX0xqBkCCCCAgOUECABarkkCUiACgAFhJ1M+QPQBBBBAAAEEELCLgHH6r3EKcPZryQu9VLF0pN6aulFvTd3kutW3cTWNu7O1XapOPRBAAAEEgkCA8XcQNFIRFJEAYBEgk0VOAT5A9AoEEEAAAQQQsIvA7mNn1GnkdLfqrBrWR2VKhGvszM0aNWmD616PhCr66J42dqk69UAAAQQQCAIBxt9B0EhFUEQCgEWATBYEAOkDCCCAAAIIIGBfga2HTqv7azPdKrhxeD9FhIXogznJGj5xnete5/hK+uyBdvbFoGYIIIAAApYTIABouSYJSIEIAAaEnUz5ANEHEEAAAQQQQMAuAuv3nVDft+a4quNwSMkjrpTD4dCn87fpxR/WuO61rVNBXw3oYJeqUw8EEEAAgSAQYPwdBI1UBEUkAFgEyP7M4sCBA0pKSjL/LFq0yPxz+PBhM4u7775bEyZM8Cq7SZMmafz48WZ6Bw8eVOXKldW2bVs99NBD6tu3r1dpefMwHyBvtHgWAQQQQAABBKwssHLXMV37z7muIkaGhWjD8H7m3/+7aIee+XaV617zmuX0w8BOVq4OZUMAAQQQsJkA42+bNWgBq0MAsIBwgXrN+Jfk3C5vAoBOp1MDBgwwg3+5XUYQcNy4cea/Xvv74gPkb1HSQwABBBBAAIFACSzadkT9x813ZV+2RJhWDrvC/Pv3y3bpyf+ucN1rWL2sfn28S6CKSr4IIIAAAsVQgPF3MWx0D1UmABhk/SB7MK5mzZpq2LChpkyZYtbCmwDg888/rxEjRpjvtWzZUoMHD1ZcXJy2bNmiUaNGadmyZeY947nhw4f7XYkPkN9JSRABBBBAAAEEAiTw+6ZDuuPDha7cK5WO1OIXepl/n7hyrwZ+vtR1L65yKU176vIAlZRsEUAAAQSKowDj7+LY6jnrTAAwyPrBSy+9pDZt2ph/qlatqm3btik2NtarAODmzZvNwGFaWpoSExM1e/ZsRUVFuSRSUlLUrVs3LV68WGFhYVq/fr0ZHPTnxQfIn5qkhQACCCCAAAKBFJi+fr/um7DYVYToclGa+2wP8++/rd2vBz/JulezQpTmDM68x4UAAggggEBRCDD+Lgpl6+dBAND6bXTJEhYkADhw4ECNHTvWTHf+/Plq3759jjwWLFigDh0yN6h+9NFH9e677/pVig+QXzlJDAEEEEAAAQQCKPDrqr36y3+yZvnVrVxK0/+Y5Tdr40Hd/VGSq3RVy0Zq4XOZswO5EEAAAQQQKAoBxt9FoWz9PAgAWr+N/BoANPb+M5YO7969WwkJCVq3bl2u6Rv3N2zYoJiYGO3YscOvewHyAQryjkfxEUAAAQQQQMAl8L9lu/XEf5e7/p5QrYwmPdHV/Pv8LYd16/sLXPfKlwzXsqF90EMAAQQQQKDIBBh/Fxm1pTMiAGjp5sm7cN7OAExOTnYt53344YfNQz5yu4z7Fw4JMd67sNQ471Ll/QQfoLyNeAIBBBBAAAEEgkPgq0U7Nfjbla7CZj/pd8n2o7rxvXmue6UiQrXmb32Do2KUEgEEEEDAFgKMv23RjD5XggCgz4SBTcDbAODEiRN19dVXm4V+88039cQTT+RaAeP+oEGDzPv/z959gMl09Q8c/y2rRI/ee+9lrb7KIki80pQQCYmEhCRvJESLaMGLFIQEIdIQIk1dlsXqq7fVO6uszurr/9zJP5fJ7tqZ3Zlbznzned7nNXfuPef3+5zjPM4vM/dq17Vo0cJjybIAeYyShhBAAAEEEEDAZIEf1x2Vj//crUcRWCSrzO76961Udp26Is+MX61/liqlnxz41HP/pjI5dbpHAAEEELCBAPtvGwySASFSADQA2ZtduFsA1L7x99ZbbzlCmjNnjrz44osJhvfrr79K69atHZ9r12nfCHT1pS0wj3tFRUVJYGCg45QTJ044fmbMCwEEEEAAAQQQsKPAt+GHZdiCh7dVqVciu/z4eg1HKvvPXpOmX6xySuvw8BaSIoWfHVMlZgQQQAABGwpQALThoHkhZAqAXkA1skl3C4CjR4+W3r17O0JctGiRNGuW8E9QtM//+dbfmDFj5IMPPnA5NT8/1/9RSwHQZVZORAABBBBAAAELCkwIOyijQ/bpkTUuk1O+fbW64/3R6BvSYMwKp6j3Dm0maVOltGAmhIQAAgggoKIABUAVR9X9nCgAum9mqSvcLQAOHTpUBg4c6Mhh2bJl0qhRowTzWb58uQQHBzs+164bMGCAy7lTAHSZihMRQAABBBBAwOYCny/dL+OWHdCzeLpCHpnQoarj/enLN6X2yOVOGe4Y1FQypU1l86wJHwEEEEDALgIUAO0yUt6NkwKgd3293rq7BUCjvgHIT4C9PvR0gAACCCCAAAIWERi5aK98s/KQHs1zVfLJF20rO95HX78tAcNCnSLdNKCxZM+QxiLREwYCCCCAgOoCFABVH2HX8qMA6JqTZc9ytwBo1D0AEwNjAUpMiM8RQAABBBBAwC4Cg+ftlu/WHNXDbVe9gIx8oaLj/dVbd6XioCVOqazt00jyZnnCLukRJwIIIICAzQXYf9t8AD0UPgVAD0Ga1Yy7BcD58+dLy5YtHeHyFGCzRo1+EUAAAQQQQEAlgX6/75QZG47rKb1Sq5AMaVXe8f7W3ftS+uPFTumu+LCBFM6eXiUCckEAAQQQsLAABUALD46BoVEANBDbG125WwA8fPiwFCtWzBGK9lRf7RuBCb20zydPnuz4WLuuSJEiHkuBBchjlDSEAAIIIIAAAiYLfDhnu/y6+aQexRv1ikj/p8s63sfGPpCi/RY6Rbjk/SApmSujyVHTPQIIIICArwiw//aVkX58nhQAbT4P3C0APnjwQPLnzy+nT5+W0qVLS2RkZIICZcqUkb1790q+fPlEe1KvOw/2SIyVBSgxIT5HAAEEEEAAAbsIvDNzq8zbfloPt0fD4vLhU6X09yX6L5S79x/o7+e/U1fK58tsl/SIEwEEEEDA5gLsv20+gB4KnwKghyDNasbdAqAW59tvvy1ff/21I+R169ZJzZo144S/fv16qVWrluO4dv6ECRM8miILkEc5aQwBBBBAAAEETBR484dNsmTPWT2Cnk1KyrvBJfT35QYulht37uvv575VW6oVetLEiOkaAQQQQMCXBNh/+9JoJ5wrBUCbz4OkFAD3798v5cqVk3v37klAQICsWrVKnnji4Y2ob968KUFBQbJp0ybx9/eXPXv2SIkSD/8R6wkyFiBPKNIGAggggAACCFhBoNN3G2XFvvN6KH2bl5au9f++5Yr2qjJkiVyKuau/n/lGTalVLJsVQicGBBBAAAEfEGD/7QOD7EKKFABdQLLSKatXr5aDBw/qIUVHR0uvXr0c7+vUqSNdunRxCrdTp07xht+3b18ZOXLk3/8orVJFPvroI8e9AQ8dOiT/+9//ZOvWrY7PtPOGDx/ucQIWII+T0iACCCCAAAIImCTw0uT1su7wBb33QS3LSqc6D++dXGN4qJy9elv//PvXAqV+yRwmRUu3CCCAAAK+JsD+29dGPP58KQDabB5oBb3vv//e5ai1e/7F94qNjZU33nhDpk2blmBbr7/+uuMhIClSpHC5P1dPZAFyVYrzEEAAAQQQQMDqAs9PXCNbjl/Wwxz+XAVpX6Og/r7eqOVy4uJN/f2UVwKkSdlcVk+L+BBAAAEEFBFg/63IQCYzDQqAyQQ0+nJPFQD/iXvhwoWOIl9ERIRo3ybMnj27VK9e3fGE4ObNm3stPRYgr9HSMAIIIIAAAggYLPDM+HDZdeqq3utnrSvJC9Xy6++DP1shh87f0N9PaF9Vnq6Yx+Ao6Q4BBBBAwFcF2H/76sg7500BkHlgigALkCnsdIoAAggggAACXhBo8vlKOXDuut7yV+2ryDMV8+rvm48Nl8iohwXCL9pWkueqPCwQeiEkmkQAAQQQQEAXYP/NZNAEKAAyD0wRYAEyhZ1OEUAAAQQQQMALAvVHh8mxCzF6y5M7VpOm5XLr71tNWCPbTzz8ifD/Xqggbas//ImwF0KiSQQQQAABBCgAMgecBCgAMiFMEaAAaAo7nSKAAAIIIICAFwRqDl8mZ67e0lv+90M+2nyzTjYevah/PrRVOelYq7AXIqFJBBBAAAEE4gqw/2ZWaAIUAJkHpgiwAJnCTqcIIIAAAggg4AWBKkOWyKWYu3rLM9+oKbWKZdPfv/ztBll9MFp/P+DpMtKlXlEvREKTCCCAAAIIUABkDsQvQAGQmWGKAAVAU9jpFAEEEEAAAQS8IFBu4GK5cee+3vJvb9eWqgWf1N+/Nj1Clu89p7/v3ayUvN2guBcioUkEEEAAAQQoADIHKAAyBywkQAHQQoNBKAgggAACCCCQLIHi/RbKvdgHehsL3q0r5fJm1t93+3GzLN59Rn//38Yl5L+NSyarTy5GAAEEEEDAVQH2365KqX0e3wBUe3wtmx0LkGWHhsAQQAABBBBAwA2B+7EPpFi/hU5XhPYMkuI5M+rH3p25Vf7aflp//3aDYtK7WWk3euFUBBBAAAEEki7A/jvpdipdSQFQpdG0US4sQDYaLEJFAAEEEEAAgQQFbt65L2UGLnb6PLx3QymQNZ1+7MM52+XXzSf1913qFpEBz5RFFQEEEEAAAUME2H8bwmz5TigAWn6I1AyQBUjNcSUrBBBAAAEEfE3gcswdqTxkqVPaG/sFS85MafVj/X7fKTM2HNffv1KrkAxpVd7XqMgXAQQQQMAkAfbfJsFbrFsKgBYbEF8JhwXIV0aaPBFAAAEEEFBb4OzVW1Jj+DKnJLcNbCJZ0qXWjw36a7dMX3tUf9+uegEZ+UJFtWHIDgEEEEDAMgLsvy0zFKYGQgHQVH7f7ZwFyHfHnswRQAABBBBQSeDExRipNyrMKaXIIc3kidQp9WMjFkbKpFWH9ffPV8knn7etrBIDuSCAAAIIWFiA/beFB8fA0CgAGohNVw8FWICYDQgggAACCCCggsDBc9ek8eernFI5NLyFpEzhpx/7bMk+Gb/8oP7+6Yp5ZEL7qiqkTw4IIIAAAjYQYP9tg0EyIEQKgAYg00VcARYgZgUCCCCAAAIIqCCw+/QVeXrcaj0V/xR+cnB4C6fUxi87IJ8t3a8fa1I2l0x5JUCF9MkBAQQQQMAGAuy/bTBIBoRIAdAAZLqgAMgcQAABBBBAAAE1BbYcvyTPT1yrJ5c+dUrZPaSZU7KTVh6SEYv26sfql8wh378WqCYIWSGAAAIIWE6AAqDlhsSUgCgAmsJOpyxAzAEEEEAAAQQQUEFg3aEL8tKU9XoqWdOnli0fN3FK7bs1R2TwvD36sVpFs8nMN2uqkD45IIAAAgjYQID9tw0GyYAQKQAagEwXcQVYgJgVCCCAAAIIIKCCwMr95+XVaRv1VHJnSivr+wU7pfbzhmPS//dd+rFqhZ6UuW/VViF9ckAAAQQQsIEA+28bDJIBIVIANACZLigAMgcQQAABBBBAQE2BJbvPyJs/btaTK5Qtnazs1dAp2TmbTkivX3foxyrkyyzz3qmrJghZIYAAAghYToACoOWGxJSAKACawk6nLEDMAQQQQAABBBBQQWDe9tPyzsyteiolcmaQpT3rO6X257ZT8t6sbfqxUrkySsj7QSqkTw4IIIAAAjYQYP9tg0EyIEQKgAYg00VcARYgZgUCCCCAAAIIqCAwd/NJ+WDOdj2V8vkyyfx36jmltnhXlHT7aYt+rEj29BL2YQMV0icHBBBAAAEbCLD/tsEgGRAiBUADkOmCAiBzAAEEEEAAAQTUFJix4bj0+32nnlx89/dbvvesvDZ9k35OvixPyJo+jdQEISsEEEAAAcsJUAC03JCYEhAFQFPY6ZQFiDmAAAIIIIAAAioIuPKE39UHouXlqRv0dLNnSCObBjRWIX1yQAABBBCwgQD7bxsMkgEhUgA0AJku4gqwADErEEAAAQQQQEAFgUkrD8mIRXv1VBqUyiHTOwc6pbbxyEVpM2mdfixTWn/ZMegpFdInBwQQQAABGwiw/7bBIBkQIgVAA5DpggIgcwABBBBAAAEE1BQYt+yAfL50v57cU+VyyaSOAU7JbjtxWZ6dsEY/ljZVCtk7tLmaIGSFAAIIIGA5AQqAlhsSUwKiAGgKO52yADEHEEAAAQQQQEAFgdEhe2VC2CE9lZaV8sr4l6o4pbbn9FVpMS5cP5bCT+TwiKdVSJ8cEEAAAQRsIMD+2waDZECIFAANQKaLuAIsQMwKBBBAAAEEEFBB4NMFe2RK+BE9lRer5ZcxrSs5pXbw3HVp/PlK52OfNhf/lClUICAHBBBAAAGLC7D/tvgAGRQeBUCDoOnGWYAFiBmBAAIIIIAAAioIDPxzl/yw7pieSocaBeXT5yo4pXbiYozUGxXmdGzPkKckXWp/FQjIAQEEEEDA4gLsvy0+QAaFRwHQIGi6oQDIHEAAAQQQQAAB9QT6zN0hsyJO6Il1rlNYPmlZzinRs1dvSY3hy5yObRvYRLKkS60eCBkhgAACCFhOgAKg5YbElIAoAJrCTqcsQMwBBBBAAAEEEFBB4P1ftsnvW0/pqXSrX0z6NC/tlNqlG3ekytClTsc29guWnJnSqkBADggggAACFhdg/23xATIoPAqABkHTjbMACxAzAgEEEEAAAQRUEHj7582ycOcZPZV3g0tIzyYlnVK7cfuelPskxOlYeO+GUiBrOhUIyAEBBBBAwOIC7L8tPkAGhUcB0CBouqEAyBxAAAEEEEAAAfUEunwfIaGR5/TEej1VSro3LO6U6N37sVKi/yKnY8s+qC/FcmRQD4SMEEAAAQQsJ0AB0HJDYkpAFABNYadTFiDmAAIIIIAAAgioINBx6gYJPxCtpzLg6TLSpV5Rp9QePHggRfstlAcPHh5e9F49KZMnkwoE5IAAAgggYHEB9t8WHyCDwqMAaBA03TgLsAAxIxBAAAEEEEBABYE236yTjUcv6qkMbVVOOtYqHCe1UgMWye17sfrxP7vXkUoFsqhAQA4IIIAAAhYXYP9t8QEyKDwKgAZB0w0FQOYAAggggAACCKgn0GrCGtl+4rKe2KgXKkqb6gXiJFphUIhcu3VPPz6nWy2pXjireiBkhAACCCBgOQEKgJYbElMCogBoCjudsgAxBxBAAAEEEEBABYFmX66SvWeu6amMbVdZWlXOFye1gGFLJfr6Hf34z11qSJ3i2VUgIAcEEEAAAYsLsP+2+AAZFB4FQIOg6cZZgAWIGYEAAggggAACKgg0GrNCDkff0FP5ukNVaV4hT5zUao9YJqev3NKPf9epujQsnVMFAnJAAAEEELC4APtviw+QQeFRADQImm4oADIHEEAAAQQQQEA9gTojl8upyzf1xKZ1CpBGpXPFSbTB6DA5eiFGP/7Ny9WkWfnc6oGQEQIIIICA5QQoAFpuSEwJiAKgKex0ygLEHEAAAQQQQAABFQQChoVK9PXbeioJ/bS36RcrZf/Z6/p5416qIv+plFcFAnJAAAEEELC4APtviw+QQeFRADQImm6cBViAmBEIIIAAAgggoIJAxUEhctWFh3s8Mz5cdp26qqc8pnUlebFafhUIyAEBBBBAwOIC7L8tPkAGhUcB0CBouqEAyBxAAAEEEEAAAfUESg1YJLfvxeqJ/dWjjlTMnyVOos9PXCNbjj98WvDw5ypI+xoF1QMhIwQQQAABywlQALTckJgSEAVAU9jplAWIOYAAAggggAACdhe4fe++lBqw2CmNkP8GSancGeOk1m7yOll/+KJ+fFDLstKpThG7ExA/AggggIANBNh/22CQDAiRAqAByHQRV4AFiFmBAAIIIIAAAnYXOHD2mjT5YpVTGjsHNZWMaVPFSe2VaRtl1f7z+vF+LUrLm0HF7E5A/AgggAACNhBg/22DQTIgRAqABiDTBQVA5gACCCCAAAIIqCcQsvuMdP1xs55YjoxpJKJ/43gT7fL9JgmNPKt/9mHTktKjUQn1UMgIAQQQQMByAhQALTckpgREAdAUdjplAWIOIIAAAggggIDdBb5ecUj+t3ivnkZgkawyu2uteNPq/vMWWbAzSv/s3eAS0rNJSbsTED8CCCCAgA0E2H/bYJAMCJECoAHIdBFXgAWIWYEAAggggAACdhfoNWe7zNl8Uk/jpcACMuL5ivGm9f4v2+T3raf0z7rVLyZ9mpe2OwHxI4AAAgjYQID9tw0GyYAQKQAagEwXFACZAwgggAACCCCgnsCLX6+VTccu6Yk97r5+H/26Q37ZdEI/97U6RWRgy7LqoZARAggggIDlBCgAWm5ITAmIAqAp7HTKAsQcQAABBBBAAAG7C1QdulQu3rijp/HtKwHSuGyueNP6+I9d8uP6Y/pnL9csKMOerWB3AuJHAAEEELCBAPtvGwySASFSADQAmS7iCrAAMSsQQAABBBBAwM4Cl2PuSOUhS51SWP5BfSmaI0O8aQ2dv0emrj6if9YmIL+MerGSnQmIHQEEEEDAJgLsv20yUF4OkwKgl4FpPn4BFiBmBgIIIIAAAgjYWWDL8Uvy/MS1egr+KfwkcmgzSZUyRbxpaQ8L0R4a8s/r2cp55ct2VexMQOwIIIAAAjYRYP9tk4HycpgUAL0MTPMUAJkDCCCAAAIIIKCewK+bT8qHc7briRXNnl6Wf9ggwUS/WLpfxi47oH/eokJumdihmnowZIQAAgggYDkBCoCWGxJTAqIAaAo7nbIAMQcQQAABBBBAwM4Co0P2yoSwh9/oCy6dU6Z2qp5gShPCDsrokH36543L5JRvX034fDvbEDsCCCCAgLUE2H9bazzMioYCoFnyPt4vC5CPTwDSRwABBBBAwOYCb/20WRbtOqNn8Ua9ItL/6YSf6vtt+GEZtiBSP79eiezy4+s1bK5A+AgggAACdhBg/22HUfJ+jBQAvW9MD/EIsAAxLRBAAAEEEEDAzgLNvlwle89c01MY/lwFaV+jYIIp/bDuqAz8c7f+eY0iWeWXrrXsTEDsCCCAAAI2EWD/bZOB8nKYFAC9DEzz8QuwADEzEEAAAQQQQMCuArGxD6TMwMVy+16snsKsN2tKzaLZEkxp1sbj0ue3nfrnVQpmkd/frmNXAuJGAAEEELCRAPtvGw2WF0OlAOhFXJpOWIAFiNmBAAIIIIAAAnYVOHExRuqNCnMKf2P/YMmZMW2CKc3dfFI+eOShIeXyZpIF79azKwFxI4AAAgjYSID9t40Gy4uhUgD0Iq5dmj5+/LiMGzdOFixYINqf06RJI8WLF5c2bdrI22+/LenSpfN4KixAHielQQQQQAABBBAwSGDV/vPyyrSNem8Z0vjLzkFNxc/PL8EI5m0/Le/M3Kp/XiJnBlnas75BEdMNAggggIAvC7D/9uXRf5g7BUAfnwda0a9Dhw5y5cqVeCVKlSolCxculKJFi3pUigXIo5w0hgACCCCAAAIGCkxfc0QGzduj91gxf2b5q0fdx0YQsvuMdP1xs35OoWzpZGWvhgZGTVcIIIAAAr4qwP7bV0feOW8KgD48D7Zv3y61a9eWmJgYyZAhg/Tt21caNmwoN2/elFmzZsmUKVMcOqVLl5aIiAjHOZ56sQB5SpJ2EEAAAQQQQMBogU/+3CXukYxoAAAgAElEQVTfrzumd9uqcl4Z267KY8MI23dOOn8XoZ+TJ3NaWdc32OjQ6Q8BBBBAwAcF2H/74KDHkzIFQB+eB1qxb8WKFeLv7y+rVq2SWrWcn0Q3evRo6d27t0No8ODBMnDgQI9psQB5jJKGEEAAAQQQQMBggY5TN0j4gWi91/cbl5T3Gpd4bBRrD0ZL+2836OdkS59aNn/cxODI6Q4BBBBAwBcF2H/74qjHzZkCoI/OA+0bfYGBgY7su3btKt98800cidjYWClfvrxERkbKk08+KWfPnpVUqVJ5RIwFyCOMNIIAAggggAACJgjUGblcTl2+qfc8/qUq0rJS3sdGsunoRXnxm3X6ORm1+wYOfsqE6OkSAQQQQMDXBNh/+9qIx58vBUAfnQf9+/eX4cOHO7Jfv3691KhRI16JkSNHOn4arL2WLFkiTZp45r9UswD56MQjbQQQQAABBGwucOvufSn98WKnLOa/U1fK58v82Mx2nLws//lqjX5Oav8Usn9Yc5trED4CCCCAgB0E2H/bYZS8HyMFQO8bW7KHoKAgCQ8Pl/Tp08vly5cdPwOO77Vu3TrHfQK1l/YTYO2nwJ54sQB5QpE2EEAAAQQQQMBogcioq9J8bLhTt7sHPyXp08T/b6l/Ttx75qo0+9L5uiMjWjz2ycFG50Z/CLgrEBv7QHadviLbT16RdKlSSr0S2SVnprTuNsP5CCDgZQH2314GtknzFABtMlCeDjNHjhwSHR0tlSpVkm3btiXY/KVLlyRr1qyOz1u3bi2zZ8/2SCh2XIB+XHfUI7nTiPcFUqTwk1K5MkqlAlkkVcoUeofHLtyQTUcvScyde94Pgh7UFvDzkzT+KSRtqpSO/3/w4IHcvhcrt+/Gyu37sSIPHqidv0WzK5QtvdQulk38H/l7r4V68lKM435t97Sx4YVAMgX2nrkmP284rreSO1NaWd8v8Yd5HD5/XRp9ttKp90Ety0rKFH6PjahYjgxSq1i2xxYKb9y+Jyv3n5cL128n2FaOjGmlYekcksY/pdM5+85ck03HLopWyLHMy89PSufOKAGFnnTKW/v25ar95+Xs1VuWCdVXA9Fmy57TV2X53nNy7przvNOeit2gVE7JkSG1r/KQt2ICeTI/IY3L5rJ1Vnbcf9sa3KLBUwC06MB4M6xbt27JE0884eji6aeflvnz5z+2O+3pvzdu3JCaNWuK9o1AV17aAvO4V1RUlH4PwhMnTkj+/PldadbUc4r0XcCe3tQRcL/zDGn8pWbRrJItfRpZezhaTlx8eL8m91vjCgQQsINAs3K55ZuO1fRQI45elDaT1rF+22HwbBqjVnSe8UbNRKPXCtF1/xeW6HnxndC1flHp27xMvNdqhe3nJq6VnaeuJNq29u2sH14L1ItqYXvPSZcfNsl9KxX/HsmiRM4M0qlOYalVNJv8uvmkzNx4XC7F3E00T05AAAEEPCkQVDKHY+2084sCoJ1Hz3OxUwD0nKVtWjp//rzkzJnTEW/btm1l1qxZj409V65ccu7cOccDQXbu3OlSnn5+j/+v2Y82QgHQJVJOQgABBBBwUWDhu/WkbN5MjrM7fLte1hy84OKVnIaA+wIdahSUT5+rkOiF2rfzqg0LTfS8+E7ImNZfdg6K/4EhW49fchQAXX0teT9ISubK6Dj91WkbHd8c5IUAAgggkLAABUBmhyoCFABVGUk38tAKbgULFnRc0bFjR/nhhx8ee7V2rnZNsWLF5ODBgy71RAHQJSZOQgABBBDwgoD2s8pOdYrI3fuxUmFQiNy6y09/vcBMk/8vMPXVAAkuk/hPw7RbBTT5YpUcPHc9SXaHhreI9+fCoXvOOr7F5+rry7aV5dkq+RynBwwLlejH/GzY1TY5D4FC2dLJxet35NptbrPCbFBPgAKgemPqqxlRAPTBkTfiG4Aq/gS4rfYTMh+cL3ZM+XLMHdl/Nv4NVvYMqaVo9gwirn9J1Y4ExOxlAe1eWXfu/33Pv1v37kuK/78nYJpUKSV1Sj9u6u9l/383f+JijERdeXhPsKcr5JEJHapKfN+MCiyclb//Bo+Pqt1p9wBtUT63tK1ewOW/88cvxMi45Qfk+MWYx7Jo9xTdfuKy0zl7hzZz3Hf0368FO6Kk+4wt+uG0qVJIxfxZ9PfavQejr9/R3//zc+Lz125L9U+dv5FYpaDzvXPNGjvtHn/HLiRsVCFfZnkidVwLs+L11X61W61oP88OLpNTiubIIHfuxYp224XQyLOyN+qa3Od+uL46NZTLu3KBLNKvRfy3YbBLsvwE2C4j5d04KQB619eSrRtxD8DEEmcBSkyIz5MroG1s1h6KlnWHLsiNO/elYr7MUqd4dsdNxbWHhPBCAAF1BGZHnJDec3foCeXMmEY29AuWb8OPyKcLI/XjxXNmkNCe9dVJnEyUFTh9+abUHrncKb+dg5pKxrSp4uQ8d/NJ+WDOdv14ubyZZMG79fT3Y0L2yVdhD3/BUb9kDvn+tUBZfSBaXp66walwuHtws0QfSmIEuvZtSe3BPdPXHnU8ZEJ7PZEqpbxQLZ90ql1Yiuf8+yfMvBBAAAEEXBNg/+2ak+pnUQBUfYQTyI+nAPvowJM2AgggoKDAkegb0nDMCqfMVvZqIMMWRMrSPWf14y8FFpQRzyd+rzYFiUjJZgLxfTtvy8dNJGv6uE9V/XnDMen/+y49w6oFs8hvb9fR38/fcVp6zNiqv8+VSSuQN5Zvww87/o7886qUP7P82aOu5aS0h6dof8e1bzVmfiJuAdRyARMQAgggYEEBCoAWHBQTQqIAaAK6FboMCgqS8PBwSZ8+vVy+fFn8/f3jDUt76m/t2rUdnw0cOFAGDx7skfBZgDzCSCMIIIAAAiKifVuo+qfLnO5lNurFijJiYaTTE0O/aFtJnqti/afOM6gIaLeyqDxkqROE9q3WXJnSxsGZtvqIDJm/Rz/+76cSa/ccbPz5SqfrtGLisAV75Lctp/TjbQMKyP9erAg+AggggICCAuy/FRzUJKREATAJaCpc0q9fPxkxYoQjlfXr10uNGjXiTWvkyJHSt29fx2chISHStGlTj6TPAuQRRhpBAAEEEPh/gbd+2iyLdp3RPbRvQW057nwPtfDeDaVA1nSYIWB5gRu370m5T0Kc4kxo/k5ccVBGLd6nn9uodE6Z1qm6/v7e/VhHW9p9Bf95zehSw/Htvz1RV/Vjn7QsK53rFLG8DQEigAACCLgvwP7bfTMVr6AAqOKoupDTxo0b9aJf165d5ZtvvolzVWxsrJQvX14iIyMlS5Yscu7cOUmVyjM/vWABcmGQOAUBBBBAwGWBf38L6t8X5smcVtb2aeTywxpc7pgTEfCCgPYwhZIDFjm1vPyD+o4HLfz79fnS/TJu2QH9cPPyueXrl6s5ndZy/GrZeeqKfqxv89Ly2ZL9jocZ/fOa9WZNqVk0mxeyoUkEEEAAAbMF2H+bPQLW6J8CoDXGwZQo/vkZsPbz31WrVkmtWrWc4hg9erT07t3bceyTTz6RQYMGeSxOFiCPUdIQAggggICI7Dx5RVp+tTpBi/9UyivjXqqCFQK2ENB+1l6k70KnWEP+GySlcsd9+MWIRZEyaeVh/dznquSTL9pWdrq296/bZfamk/qxSgWyxHnK8LaBTSRLurj3GLQFGEEigAACCDxWgP03E0QToADow/Ng69atUqdOHbl586ZkyJBBtJ8FN2zY0PF+1qxZMnnyZIdOyZIlZdOmTZIxo+eeuMYC5MMTj9QRQAABLwhoP3OsNHiJ46nf8b2GtionHWsV9kLPNImAdwRK9F8od+8/0Buf/05dKZ8vc5zOBv212/G03H9eLwUWkBHPO9/Lz5VvyK7rG+ydRGgVAQQQQMB0Afbfpg+BJQKgAGiJYTAviHnz5snLL78sV68+vAfMo9Foxb8FCxZI8eLFPRokC5BHOWkMAQQQQEBEOk7dIOEHouO1WPzfelI6dyacELCNQNmBiyXmkYL272/XlioFn4wTf5+5O2RWxAn9eKfahWXQf8o5nbf2ULS0n7Ihwdwblsoh33UOtI0NgSKAAAIIuCfA/ts9L1XPpgCo6si6kdexY8dk7NixjkKftjCkTp3aUfBr3bq19OjRQ9Kl8/wN01mA3BggTkUAAQQQcElAuw+adj+0f78ypfWXbQObSooUfi61w0kIWEGg4qAQuXrrnh7K7K61JLBI1jihvf/LNvl968On+XatX1T6Ni/jdN7FG3ek6lDnpwo/esJbDYrJR81KWyFtYkAAAQQQ8IIA+28voNqwSQqANhw0FUJmAVJhFMkBAQQQsJbAukMX5KUp6+ME9e+noloraqJBIH6BgGFLJfr6Hf3Dn7vUkDrFs8c5+d9PwH4vuIS836RknPNqDA+Vs1dvx9uZdn9M7T6ZvBBAAAEE1BRg/63muLqbFQVAd8U43yMCLEAeYaQRBBBAAIFHBG7euS8VB4c43TdN+1j7ZpP2DSdeCNhJoNaIZRJ15ZYe8nedq0vDUjnjpND5u40Stu+8frx3s1LydoO4t255ddpGWbn/4XmPNrT0/SApkctz93q2kzOxIoAAAr4gwP7bF0Y58RwpACZuxBleEGAB8gIqTSKAAAIIyHMT18jW45edJOa+VUuqFYr700m4ELCyQNCoMDl+MUYPcXLHatK0XO44Ibefsl7WHrqgHx/4TFl5rW6ROOf9+2nB/5yQOmUK2TPkKfFPmcLKHMSGAAIIIJAMAfbfycBT6FIKgAoNpp1SYQGy02gRKwIIIGAfgeELI2XyqsN6wKn9U8jOQU0ljX9K+yRBpAiISPBnK+TQ+Ru6xcQOVaVFhTxxbJ6fuEa2PFL0Hv5cBWlfo2Cc8/7cdkrem7UtzvFyeTPJgnfrYY4AAgggoLAA+2+FB9eN1CgAuoHFqZ4TYAHynCUtIYAAAgg8FPj30055uimzw64Czb5cJXvPXNPDH9uusrSqnC9OOi3GhsueqKv68c9aV5IXquWPc96+M9fkqS9XxTn+QtX88lmbSnZlIm4EEEAAARcE2H+7gOQDp1AA9IFBtmKKLEBWHBViQgABBNQQGPTXbpmx8bgUzJpOJnWsJsVyZFAjMbLwKYH/fLVadpy8ouc8+sWK0jqgQByDf39TcEL7qvJ0xbjfFLx7P1bKDlwc5x6ZA54uI13qFfUpW5JFAAEEfE2A/bevjXj8+VIAZB6YIsACZAo7nSKAAAI+I3Dr7n1J459C/Pz8fCZnElVLwNWf9tYZuVxOXb6pJz/11QAJLpMrXozmY8Ml8pFvC2onJfR0YbU0yQYBBBDwbQH23749/v9kTwGQeWCKAAuQKex0igACCCCAAAI2EWg7aZ1sOHJRj3bwf8rJq7ULx4k+YNhSib5+Rz/+0+s1pG6J7PFm2fOXbfLb1lNOn20e0FiyZUhjExXCRAABBBBIigD776SoqXcNBUD1xtQWGbEA2WKYCBIBBBBAAAEETBLoOHWDhB+I1ntP6Ke6FT4JkWu37+nn/dqtlgQUjv+p15NXHZLhC/fq5+bImEYi+jc2KUO6RQABBBAwSoD9t1HS1u6HAqC1x0fZ6FiAlB1aEkMAAQQQQAABDwi8Nj1Clu89p7f0UbPS8laDYnFaLtF/odN9/ea/U1fK58scbwR7z1yVZl+G65+9WC2/jGnNA0A8MFw0gQACCFhagP23pYfHsOAoABpGTUePCrAAMR8QQAABBBBAAIGEBbr+uElCdp/VT+jZpKS8G1zC6YL7sQ+kWL+FTsdCewZJ8ZwZE2z45w3H5Ie1x6RI9vQypFU5yZkpLcOAAAIIIKC4APtvxQfYxfQoALoIxWmeFWAB8qwnrSGAAAIIIICAWgI9ZmyR+Tui9KTeaVRcPmhayinJmDv3pOzAEKdj4b0bSoGs6dTCIBsEEEAAgWQJsP9OFp8yF1MAVGYo7ZUIC5C9xotoEUAAAQQQQMBYgfd/2Sa/P/LAjq71i0rf5mWcgrh4445UHbrU6djG/sGSMyPf6jN2tOgNAQQQsLYA+29rj49R0VEANEqafpwEWICYEAgggAACCCCAQMICvX/dLrM3ndRPeK1OERnYsqzTBacv35TaI5c7HdsxqKlkSpsKWgQQQAABBHQB9t9MBk2AAiDzwBQBFiBT2OkUAQQQQAABBGwi0P/3nfLzhuN6tB1rFpKhz5Z3iv5I9A1pOGaF07F9w5pJGv+UNsmSMBFAAAEEjBBg/22EsvX7oABo/TFSMkIWICWHlaQQQAABBBBAwEMCg/7aLdPXHtVba1e9gIx8oaJT65FRV6X52IdP9fXzEzk8vIX4aX/ghQACCCCAwP8LsP9mKmgCFACZB6YIsACZwk6nCCCAAAIIIGATgeELI2XyqsN6tC9UzS+ftankFP3W45fkuYlr9WNPpEopkUOb2SRDwkQAAQQQMEqA/bdR0tbuhwKgtcdH2ehYgJQdWhJDAAEEEEAAAQ8IjA7ZKxPCDukt/adSXhn3UhWnltcfviDtJq/Xj2VJl0q2DWzqgd5pAgEEEEBAJQH23yqNZtJzoQCYdDuuTIYAC1Ay8LgUAQQQQAABBJQX+GLpfhm77ICeZ/PyueXrl6s55b1i3znp9F2Efix3prSyvl+w8jYkiAACCCDgngD7b/e8VD2bAqCqI2vxvFiALD5AhIcAAggggAACpgpMCDsoo0P26TE0LpNTvn21ulNMi3edkW4/bdaPFc6WTlb0amhq3HSOAAIIIGA9Afbf1hsTMyKiAGiGOn0KCxCTAAEEEEAAAQQQSFhg8qpDMnzhXv2EoJI55IfXAp0u+HPbKXlv1jb9WKlcGSXk/SBYEUAAAQQQcBJg/82E0AQoADIPTBFgATKFnU4RQAABBBBAwCYC3605IoPn7dGjrVU0m8x8s6ZT9LMjTkjvuTv0Y5XyZ5Y/e9S1SYaEiQACCCBglAD7b6Okrd0PBUBrj4+y0bEAKTu0JIYAAggggAACHhD4af0xGfDHLr2l6oWflDndaju1/MO6ozLwz936scAiWWV211oe6J0mEEAAAQRUEmD/rdJoJj0XCoBJt+PKZAiwACUDj0sRQAABBBBAQHmBON/uK5BF/uxexynvKasOy6cLI/Vj9Upklx9fr6G8DQkigAACCLgnwP7bPS9Vz6YAqOrIWjwvFiCLDxDhIYAAAggggICpAr9tOSk9Z2/XYyibJ5MsfK+eU0zjlx2Qz5bu1481KZtLprwSYGrcdI4AAgggYD0B9t/WGxMzIqIAaIY6ffIQEOYAAggggAACCCDwGIF520/LOzO36meUyJlBlvas73TF6JC9MiHskH6sZaW8Mv6lKrgigAACCCDgJEABkAmhCVAAZB6YIsACZAo7nSKAAAIIIICATQQW7zoj3X7arEdbOFs6WdGroVP0w+bvkW9XH9GPvVgtv4xpXckmGRImAggggIBRAuy/jZK2dj8UAK09PspGxwKk7NCSGAIIIIAAAgh4QGD53rPy2vRNekv5sjwha/o0cmp5wB875af1x/VjL9csKMOereCB3mkCAQQQQEAlAfbfKo1m0nOhAJh0O65MhgALUDLwuBQBBBBAAAEElBcIP3BeOk7dqOeZM2Ma2di/sVPeH87ZLr9uPqkf61K3iAx4pqzyNiSIAAIIIOCeAPtv97xUPZsCoKoja/G8WIAsPkCEhwACCCCAAAKmCqw/fEHaTV6vx/BkulSydWBTp5i0ewRq9wr859W9YTHp9VRpU+OmcwQQQAAB6wmw/7bemJgREQVAM9Tpk4eAMAcQQAABBBBAAIHHCGw+dlFe+HqdfkaGNP6ya/BTTle88cMmWbrnrH7sgyYl5Z3gErgigAACCCDgJEABkAmhCVAAZB6YIsACZAo7nSKAAAIIIICATQR2nLws//lqjR5tav8Usn9Yc6foO07dIOEHovVj/VuUkTeCitokQ8JEAAEEEDBKgP23UdLW7ocCoLXHR9noWICUHVoSQwABBBBAAAEPCERGXZXmY8P1lvz8RA4PbyF+2h/+/9Vm0jrZeOSi/n5Iq3LySq3CHuidJhBAAAEEVBJg/63SaCY9FwqASbfjymQIsAAlA49LEUAAAQQQQEB5gYPnrkvjz1c65Xnw0+binzKFfqzVV6tl+8kr+vtRL1SUNtULKG9DgggggAAC7gmw/3bPS9WzKQCqOrIWz4sFyOIDRHgIIIAAAgggYKrA8QsxEjQ6zCmGvUObSdpUKfVjT32xSvadvaa/H9uusrSqnM/UuOkcAQQQQMB6Auy/rTcmZkREAdAMdfrkISDMAQQQQAABBBBA4DECUVduSq0Ry53O2DGoqWRKm0o/1mB0mBy9EKO//+blatKsfG5cEUAAAQQQcBKgAMiE0AQoADIPTBFgATKFnU4RQAABBBBAwCYC56/dluqfhjpFu3lAY8mWIY1+rObwZXLm6i39/fTO1aVBqZw2yZAwEUAAAQSMEmD/bZS0tfuhAGjt8VE2OhYgZYeWxBBAAAEEEEDAAwJXYu5KpSFLnFpa3zdYcmdOqx+rPGSJXI65q7+f9WZNqVk0mwd6pwkEEEAAAZUE2H+rNJpJz4UCYNLtuDIZAixAycDjUgQQQAABBBBQXiDmzj0pOzDEKc/w3g2lQNZ0+rHSHy+SW3dj9fd/dK8jlQtkUd6GBBFAAAEE3BNg/+2el6pnUwBUdWQtnhcLkMUHiPAQQAABBBBAwFSBu/djpUT/RU4xLPugvhTLkcFx7MGDB1K030J58ODhKYveqydl8mQyNW46RwABBBCwngD7b+uNiRkRUQA0Q50+eQgIcwABBBBAAAEEEHiMgFbgK9J3odMZIf8NklK5MzqO3b53X0oNWOz0ediHDaRI9vS4IoAAAggg4CRAAZAJoQlQAGQemCLAAmQKO50igAACCCCAgI0ESvZfJHfuP/yJ7/x36kr5fJkdGVy5eVcqDXa+R+C6vo0kT+YnbJQhoSKAAAIIGCHA/tsIZev3QQHQ+mOkZIQsQEoOK0khgAACCCCAgAcFyg1cLDfu3Ndb/O3t2lK14JOO9+eu3ZLAT5c59bbl4yaSNX1qD0ZAUwgggAACKgiw/1ZhFJOfAwXA5BvSQhIEWICSgMYlCCCAAAIIIOBTAto3/LRv+v3z+uXNmlLj/5/ye+JijNQbFebksWfIU5Iutb9PGZEsAggggEDiAuy/EzfyhTMoAPrCKFswRxYgCw4KISGAAAIIIICApQQChoVK9PXbekw/vV5D6pbI7nh/4Ow1afLFKqd4Dw1vISlT+FkqB4JBAAEEEDBfgP23+WNghQgoAFphFHwwBhYgHxx0UkYAAQQQQAABtwRqj1gmp6/c0q/5rlN1aVg6p+P9rlNX5Jnxq/XPUqX0kwOftnCrfU5GAAEEEPANAfbfvjHOiWVJATAxIT73igALkFdYaRQBBBBAAAEEFBKoPzpMjl2I0TOa1LGaPFUut+P9pqMX5cVv1umfZUzjLzsHP6VQ9qSCAAIIIOApAfbfnpK0dzsUAO09fraNngXItkNH4AgggAACCCBgkEDjz1fKwXPX9d4mtK8qT1fM43i/+kC0vDx1g/5Z9gxpZNOAxgZFRjcIIIAAAnYSYP9tp9HyXqwUAL1nS8uPEWABYnoggAACCCCAAAKPF2g+Nlwio67qJ33ZtrI8WyWf4/2yyLPy+veb9M/yZXlC1vRpBCkCCCCAAAJxBNh/Myk0AQqAzANTBFiATGGnUwQQQAABBBCwkcB/vlotO05e0SMe9WJFaRNQwPF+wY4o6T5ji/5ZsRzpZdkHDWyUHaEigAACCBglwP7bKGlr90MB0Nrjo2x0LEDKDi2JIYAAAggggICHBF74eq1sPnZJb+3T58pLhxqFHO/nbj4pH8zZrn9WLm8mWfBuPQ/1TDMIIIAAAioJsP9WaTSTngsFwKTbcWUyBFiAkoHHpQgggAACCCDgEwLtJq+T9Ycv6rkOallWOtUp4ng/Y8Nx6ff7Tv2zqgWzyG9v1/EJF5JEAAEEEHBPgP23e16qnk0BUNWRtXheLEAWHyDCQwABBBBAAAHTBTpO3SDhB6L1OPq3KCNvBBV1vJ+2+ogMmb9H/6x2sWwy442apsdMAAgggAAC1hNg/229MTEjIgqAZqgno8/r16/Lli1bZOPGjY7/RUREyNGjRx0tFipUSP+zq13s3r1bxo8fL6GhoXLq1CnJkCGDlClTRjp06CCvv/66+Pv7u9qUW+exALnFxckIIIAAAggg4IMCr0+PkGV7z+mZ925WSt5uUNzxfuKKgzJq8T79s0alc8q0TtV9UImUEUAAAQQSE2D/nZiQb3xOAdBm49ywYUNZsWJFvFG7WwCcOnWqdO/eXW7fvh1vezVr1pT58+dLtmzZPK7EAuRxUhpEAAEEEEAAAcUEuv24WRbvPqNn9X7jkvJe4xKO918s3S9jlx3QP2tePrd8/XI1xQRIBwEEEEDAEwLsvz2haP82KADabAwbNGggK1eudET95JNPSkBAgKxbt060bwa6UwAMCQmRFi1aSGxsrOTKlUv69+8vNWrUkIsXL8qUKVPkt99+c/QRFBQkYWFhkiJFCo9KsQB5lJPGEEAAAQQQQEBBgR4ztsj8HVF6Zj0aFpcPnyrleD9iUaRMWnlY/+y5Kvnki7aVFVQgJQQQQACB5Aqw/06uoBrXUwC02ThOnjzZ8TPdwMBAKV7875+AFC5cWI4dO+ZyAfDevXuOn/kePHhQMmXK5PhJcbFixZwktG8GTpw40XHs+++/l1deecWjUixAHuWkMQQQQAABBBBQUKDnL9vkt62n9My6BhWVvi3KON4P+mu3TF/7921gtNdLgQVkxPMVFVQgJQQQQACB5Aqw/06uoBrXUwBUYBzdLQDOmTNH2rRp48h8xIgR0qdPnzgKMTExkj9/frl06ZKUL19edu58+JQ5T5CxAHlCkTYQQAABBBBAQGWBj37dIb9sOqGn2LlOYfmkZTnH+wq3NfcAACAASURBVL6/7ZCZGx9+1ql2YRn0n78/44UAAggggMCjAuy/mQ+aAAVABeaBuwVA7QEfM2bMcGQeFRUluXPnjlehW7duMmnSJMdn+/fvlxIl/r7njCdeLECeUKQNBBBAAAEEEFBZYMAfO+Wn9cf1FF+uWVCGPVvB8f79X7bJ749+O7B+Uenb/O9vB/JCAAEEEEDgUQH238wHTYACoALzwN0CYMGCBeXEiRNSqlQp2bt3b4ICM2fOlPbt2zs+nzZtmnTu3NljWixAHqOkIQQQQAABBBBQVGDwvN3y3ZqHP/NtV72AjHzh75/5vvXTZlm06+EDQt4LLiHvNympqARpIYAAAggkR4D9d3L01LmWAqACY+lOAVB7WIh2378HDx5Iq1at5I8//khQYOvWrVK1alXH57169ZJRo0Z5TIsFyGOUNIQAAggggAACigqMWBgpk1Y9fNDH81Xzyedt/n7Qx2vTI2T53nN65r2blZK3G/x9f2heCCCAAAIIPCrA/pv5oAlQAFRgHrhTANS+8ac9AER7aQ/6+OqrrxIUiI6Olhw5cjg+b9eunWjfCHT1pS0wj3tpPz3WHmSivbRvI2r3G+SFAAIIIIAAAggg8FBgdMhemRB2SD/QslJeGf9SFcf79lPWy9pDF/TPBj5TVl6rWwQ+BBBAAAEE4ghQAGRSaAIUABWYB+4UACMiIvTC20cffSQjR45MUODmzZuSLl06x+fPPPOMzJs3z2UtPz8/l8+lAOgyFScigAACCCCAgA8JfBm6X74MPaBn3KxcbvmmYzXH++cnrpEtxy/rnw1/roK0r1HQh3RIFQEEEEDAVQEKgK5KqX0eBUAFxtedAmB4eLgEBQU5sv74449lyJAhCQrExsZKypQpHZ8HBwdLaGioy1oUAF2m4kQEEEAAAQQQQCBegQlhB2V0yD79s+DSOWVqp+qO90+PC5fdp6/qn33WupK8UI1fVDCVEEAAAQTiClAAZFZoAhQAvTAP7t27J6lSpUp2y99995106tQp0XbcKQAa9Q1AfgKc6LBxAgIIIIAAAggg8FiBKasOy6cLI/Vz6pXILj++XsPxPvizFXLo/A39swntq8rTFfMgigACCCCAQBwBCoBMCgqAXpoDVi4AGnUPwMRoWYASE+JzBBBAAAEEEPB1gelrjsigeXt0hlpFs8nMN2s63tcZuVxOXb6pfzb11QAJLpPL18nIHwEEEEAgHgH230wLCoBenANaoS25rzx58kjmzJkTbcadbwBqTwHOmDGjo02eApwoLScggAACCCCAAAKmCfy84Zj0/32X3n9AoSfl17dqO94HDAuV6Ou39c9+7lJD6hTPblqsdIwAAgggYF0BCoDWHRsjI+MnwEZqe6kvdwqAWggFCxZ0PHm3VKlS8rhCpfbU3/bt2zuinjZtmnTu3NljGbAAeYyShhBAAAEEEEBAUYHZESek99wdenaV8meWP3vUdbyv8EmIXLt9T//s1261JKBwVkUlSAsBBBBAIDkC7L+To6fOtRQAFRhLdwuAWlFPK+5pr6ioKMmdO3e8Ct26dZNJkyY5Ptu3b5+ULFnSY1osQB6jpCEEEEAAAQQQUFTg960n5f1ftuvZlcmTSRa9V8/xvkT/hXL3/gP9s/nv1JXy+RL/5YiiVKSFAAIIIPAYAfbfTA9NgAKgAvPA3QLg7NmzpW3bto7MR4wYIX369ImjEBMTI/nz55dLly5J2bJlZffu3R6VYgHyKCeNIYAAAggggICCAvN3nJYeM7bqmRXPmUFCe9aX+7EPpFi/hU4Zh/YMkuI5/77NCy8EEEAAAQQeFWD/zXygAKjIHHC3AHj37l0pU6aMHDp0SDJlyiRbtmyRYsWKOWl0795dJk6c6Djm6tOI3eFkAXJHi3MRQAABBBBAwBcFQnafka4/btZTL5Qtnazs1VBi7tyTsgNDnEjCezeUAlnT+SITOSOAAAIIJCLA/pspQgHQhnPg4MGDsnr1aqfIP/zwQ7lw4YJky5ZNxowZ4/RZs2bN4v2J78KFC6Vly5YSGxsruXLlkgEDBkhgYKDjG39TpkyRuXPnOtqpW7eurFixQlKmTOlRLRYgj3LSGAIIIIAAAggoKBC295x0nh6hZ5YvyxOypk8juXjjjlQdutQp4439gyVnxrQKKpASAggggEByBdh/J1dQjev5CbDNxnH69OluPYwjLCxMGjRoEG+WWqGvR48ecufOnXg/1wqCCxYskOzZPf9EORYgm008wkUAAQQQQAABwwVWH4iWl6du0PvNkTGNRPRvLFFXbkqtEcud4tkxqKlkSpvK8BjpEAEEEEDA+gLsv60/RkZESAHQCGUP9uHJAqAW1q5du2TcuHGybNkyOX36tKRPn97x8+AOHTpIly5dxN/f34PRP2yKBcgrrDSKAAIIIIAAAgoJrD98QdpNXq9nlCVdKtk2sKkcib4hDcescMp037Bmksbfs7/YUIiSVBBAAAGfFmD/7dPDrydPAZB5YIoAC5Ap7HSKAAIIIIAAAjYS2Hzskrzw9Vo94vSpU8ruIc0kMuqqNB8b/vAf9H4ih4e3ED8/PxtlR6gIIIAAAkYJsP82Stra/VAAtPb4KBsdC5CyQ0tiCCCAAAIIIOAhgZ0nr0jLrx7e+zl1yhSy/9Pmsu3EZXl2whq9lydSpZTIoc081CvNIIAAAgioJsD+W7URTVo+FACT5sZVyRRgAUomIJcjgAACCCCAgPICe89clWZfPvymn5bwkREtZMORi/H+NFh5EBJEAAEEEEiSAPvvJLEpdxEFQOWG1B4JsQDZY5yIEgEEEEAAAQTMEzh0/roEf7bSKYADnzaXNQejpdN3D58OnDtTWlnfL9i8QOkZAQQQQMDSAuy/LT08hgVHAdAwajp6VIAFiPmAAAIIIIAAAgg8XuDExRipNyrM6aTIIc1k1YHz0vXHzfrxwtnSyYpeDeFEAAEEEEAgXgH230wMTYACIPPAFAEWIFPY6RQBBBBAAAEEbCRw5sotqTlimVPE2z9pKiv2nZP3Zm3Tj5fKlVFC3g+yUWaEigACCCBgpAD7byO1rdsXBUDrjo3SkbEAKT28JIcAAggggAACHhCIvn5bAoaFOrW0aUBjWR55TnrP3aEfr5Q/s/zZo64HeqQJBBBAAAEVBdh/qziq7udEAdB9M67wgAALkAcQaQIBBBBAAAEElBa4cvOuVBq8xCnHdX0bSeies/Lxn7v144FFssrsrrWUtiA5BBBAAIGkC7D/TrqdSldSAFRpNG2UCwuQjQaLUBFAAAEEEEDAFIGbd+5LmYGLnfpe1auhhOw+I58ujNSP1yuRXX58vYYpMdIpAggggID1Bdh/W3+MjIiQAqARyvQRR4AFiEmBAAIIIIAAAgg8XuDe/Vgp3n+R00mhPevLop1R8tnS/frxJmVzyZRXAuBEAAEEEEAgXgH230wMTYACIPPAFAEWIFPY6RQBBBBAAAEEbCTw4MEDKdpvoTx48DDoxf+tJ/O3R8lXYQf1gy0r5ZXxL1WxUWaEigACCCBgpAD7byO1rdsXBUDrjo3SkbEAKT28JIcAAggggAACHhIoOWCR3LkXq7c2r0dd+XPbKfl29RH92IvV8suY1pU81CPNIIAAAgioJsD+W7URTVo+FACT5sZVyRRgAUomIJcjgAACCCCAgE8IlBu4WG7cua/nOvet2vL71pPy0/rj+rGXaxaUYc9W8AkPkkQAAQQQcF+A/bf7ZipeQQFQxVG1QU4sQDYYJEJEAAEEEEAAAdMFKg9ZIpdj7upxzHqzpszdfFLmbD6pH+tSt4gMeKas6bESAAIIIICANQXYf1tzXIyOigKg0eL05xBgAWIiIIAAAggggAACiQtU/zRUzl+7rZ/44+uBMnvTSZm3/bR+rHvDYtLrqdKJN8YZCCCAAAI+KcD+2yeHPU7SFACZB6YIsACZwk6nCCCAAAIIIGAzgTojl8upyzf1qKd1CpCZG0/I0j1n9WMfNCkp7wSXsFlmhIsAAgggYJQA+2+jpK3dDwVAa4+PstGxACk7tCSGAAIIIIAAAh4UaDA6TI5eiNFbnNSxmvy84bis2n9eP9a/RRl5I6ioB3ulKQQQQAABlQTYf6s0mknPhQJg0u24MhkCLEDJwONSBBBAAAEEEPAZgSafr5QD567r+X7Vvor8sO6YbDxyUT82pFU5eaVWYZ8xIVEEEEAAAfcE2H+756Xq2RQAVR1Zi+fFAmTxASI8BBBAAAEEELCEQPOx4RIZdVWP5Yu2lWT6mqOy/eQV/dioFypKm+oFLBEvQSCAAAIIWE+A/bf1xsSMiCgAmqFOnzwEhDmAAAIIIIAAAgi4INDqq9Vxin3T1hyRvWeu6VePbVdZWlXO50JrnIIAAggg4IsCFAB9cdTj5kwBkHlgigALkCnsdIoAAggggAACNhN48eu1sunYJT3qYc+Wl2/DD8e5L+BT5XLbLDPCRQABBBAwSoD9t1HS1u6HAqC1x0fZ6FiAlB1aEkMAAQQQQAABDwq8NHm9rDt8QW/xk5ZlZdLKw3Lm6i392PTO1aVBqZwe7JWmEEAAAQRUEmD/rdJoJj0XCoBJt+PKZAiwACUDj0sRQAABBBBAwGcEXpm2Mc4Tf8cuOyDXb9/TDeZ0qyXVC2f1GRMSRQABBBBwT4D9t3teqp5NAVDVkbV4XixAFh8gwkMAAQQQQAABSwh0+T5CQiPP6bG837ikfBG63ym20J5BUjxnRkvESxAIIIAAAtYTYP9tvTExIyIKgGao0ycPAWEOIIAAAggggAACLgh0+3GzLN59Rj+zY81C8uP6Y05XRvRvLDkypnGhNU5BAAEEEPBFAQqAvjjqcXOmAMg8MEWABcgUdjpFAAEEEEAAAZsJvDNzq8zbflqPulm53E4FQe2D/cOaS2r/FDbLjHARQAABBIwSYP9tlLS1+6EAaO3xUTY6FiBlh5bEEEAAAQQQQMCDAj1nb5PftpzSWwwo9KTTU4HTpU4pe4Y082CPNIUAAgggoJoA+2/VRjRp+VAATJobVyVTgAUomYBcjgACCCCAAAI+IdBn7g6ZFXFCz7VQtnRy7EKM/j5v5rSytm+wT1iQJAIIIIBA0gTYfyfNTbWrKACqNqI2yYcFyCYDRZgIIIAAAgggYKrAx3/scrrnn/aNv5g79/WYyuTJJIveq2dqjHSOAAIIIGBtAfbf1h4fo6KjAGiUNP04CbAAMSEQQAABBBBAAIHEBYbM2yPT1hxJ8MRaRbPJzDdrJt4QZyCAAAII+KwA+2+fHXqnxCkAMg9MEWABMoWdThFAAAEEEEDAZgIjFkbKpFWHE4y6efnc8vXL1WyWFeEigAACCBgpwP7bSG3r9kUB0Lpjo3RkLEBKDy/JIYAAAggggICHBMaE7JOvwg4m2NpLgQVkxPMVPdQbzSCAAAIIqCjA/lvFUXU/JwqA7ptxhQcEWIA8gEgTCCCAAAIIIKC8wNjQA/JF6P4E8+xav6j0bV5GeQcSRAABBBBIugD776TbqXQlBUCVRtNGubAA2WiwCBUBBBBAAAEETBOYuOKgjFq8L8H+P2pWWt5qUMy0+OgYAQQQQMD6Auy/rT9GRkRIAdAIZfqII8ACxKRAAAEEEEAAAQQSF/g2/LAMWxCZ4Ikjnq8gLwUWTLwhzkAAAQQQ8FkB9t8+O/ROiVMAZB6YIsACZAo7nSKAAAIIIICAzQS+X3tUPvlrd4JRf92hqjSvkMdmWREuAggggICRAuy/jdS2bl8UAK07NkpHxgKk9PCSHAIIIIAAAgh4SODnDcek/++7Emxtxhs1pHax7B7qjWYQQAABBFQUYP+t4qi6nxMFQPfNuMIDAixAHkCkCQQQQAABBBBQXmD2phPS+9cdCea58N16UjZvJuUdSBABBBBAIOkC7L+TbqfSlRQAVRpNG+XCAmSjwSJUBBBAAAEEEDBN4I+tp+S/v2xLsP81fRpJvixPmBYfHSOAAAIIWF+A/bf1x8iICCkAGqFMH3EEWICYFAgggAACCCCAQOICC3ZESfcZWxI8cffgpyR9Gv/EG+IMBBBAAAGfFWD/7bND75Q4BUDmgSkCLECmsNMpAggggAACCNhMYMnuM/Lmj5vjjTpVSj/ZP6y5+Pn52SwrwkUAAQQQMFKA/beR2tbtiwKgdcdG6chYgJQeXpJDAAEEEEAAAQ8JhO07J52/i4i3tewZ0simAY091BPNIIAAAgioKsD+W9WRdS8vCoDueXG2hwRYgDwESTMIIIAAAgggoLTAmoPR0uHbDfHmWDxnBgntWV/p/EkOAQQQQCD5Auy/k2+oQgsUAFUYRRvmwAJkw0EjZAQQQAABBBAwXGDD4QvSdvL6ePsNKPSk/PpWbcNjokMEEEAAAXsJsP+213h5K1oKgN6Spd3HCrAAMUEQQAABBBBAAIHEBbYcvyTPT1wb74nBpXPK1E7VE2+EMxBAAAEEfFqA/bdPD7+ePAVA5oEpAixAprDTKQIIIIAAAgjYTGDXqSvyzPjV8Ub9fNV88nmbyjbLiHARQAABBIwWYP9ttLg1+6MAaM1xUT4qFiDlh5gEEUAAAQQQQMADAvvOXJOnvlwVb0uv1SkiA1uW9UAvNIEAAgggoLIA+2+VR9f13CgAum7FmR4UYAHyICZNIYAAAggggICyAofPX5dGn62MN7+eTUrKu8EllM2dxBBAAAEEPCPA/tszjnZvhQKg3UfQpvGzANl04AgbAQQQQAABBAwVOHExRuqNCou3zyGtyskrtQobGg+dIYAAAgjYT4D9t/3GzBsRUwD0hiptJirAApQoEScggAACCCCAAAJy5sotqTliWbwSY9tVllaV86GEAAIIIIDAYwXYfzNBNAEKgMwDUwRYgExhp1MEEEAAAQQQsJnAheu3pdqw0Hijnt65ujQoldNmGREuAggggIDRAuy/jRa3Zn8UAK05LspHxQKk/BCTIAIIIIAAAgh4QODqrbtScdCSeFv6o3sdqVwgiwd6oQkEEEAAAZUF2H+rPLqu50YB0HUrzvSgAAuQBzFpCgEEEEAAAQSUFbh1976U/nhxvPmt+LCBFM6eXtncSQwBBBBAwDMC7L8942j3VigA2mwEjx8/LgsWLJAVK1bItm3bRPuLfP/+fcmePbtUq1ZN2rVrJ61btxZ/f3+XMtu9e7eMHz9eQkND5dSpU5IhQwYpU6aMdOjQQV5//XWX23Gps0dOYgFyV4zzEUAAAQQQQMAXBe7HPpBi/RbGm/q2gU0kS7rUvshCzggggAACbgiw/3YDS+FTKQDaaHAHDhwow4YNkwcPHjw26oCAAJk7d64ULFjwsedNnTpVunfvLrdv3473vJo1a8r8+fMlW7ZsHldiAfI4KQ0igAACCCCAgKICRfsukNh//fPPz0/k4KctJGUKP0WzJi0EEEAAAU8JsP/2lKS926EAaKPx69Kli2hFu/Tp08tzzz0nwcHBUqJECUmbNq1ERkbKuHHjJCIiwpGRdnzLli2Ob/TF9woJCZEWLVpIbGys5MqVS/r37y81atSQixcvypQpU+S3335zXBYUFCRhYWGSIkUKj0qxAHmUk8YQQAABBBBAQGGBkgMWyZ17sU4ZZn4ilWz/pKnCWZMaAggggICnBNh/e0rS3u1QALTR+H300UeOb+O99dZbkjFjxjiRaz8Fbt++vcyePdvx2ZAhQ+Tjjz+Oc969e/ccP/M9ePCgZMqUyVEoLFasmNN52jcDJ06c6Dj2/fffyyuvvOJRKRYgj3LSGAIIIIAAAggoLFD+kxC5fvueU4YFs6aTVb0bKpw1qSGAAAIIeEqA/benJO3dDgVAe49fnOgvXLggefPmlTt37kjFihVl+/btcc6ZM2eOtGnTxnF8xIgR0qdPnzjnxMTESP78+eXSpUtSvnx52blzp0elWIA8ykljCCCAAAIIIKCwQJUhS+RSzF2nDCvmzyx/9aircNakhgACCCDgKQH2356StHc7FADtPX7xRl+9enXZtGmT46fC169fj3OO9oCPGTNmOI5HRUVJ7ty5422nW7duMmnSJMdn+/fvd/ys2FMvFiBPSdIOAggggAACCKguEPhpqJy75nzP5nolssuPr9dQPXXyQwABBBDwgAD7bw8gKtAEBUAFBvHfKWjf/NO+saf9TPjq1atxMtQeDnLixAkpVaqU7N27N0GBmTNnOn5SrL2mTZsmnTt39pgWC5DHKGkIAQQQQAABBBQXqDNyuZy6fNMpy5aV8sr4l6oonjnpIYAAAgh4QoD9tycU7d8GBUD7j6FTBufOnZN8+fKJdp8/7ZuAGzdudPpc+0agdt8/7UnCrVq1kj/++CNBga1bt0rVqlUdn/fq1UtGjRrlMS0WII9R0hACCCCAAAIIKC7QcMwKORJ9wynLjjULydBnyyueOekhgAACCHhCgP23JxTt3wYFQPuPoVMGWqFuzJgxjmOjR4+WDz/80Olz7Rt/2gNAtJf2oI+vvvoqQYHo6GjJkSOH4/N27dqJ9o1AV1/aAvO4l/bT48DAQMcp2rcRtfsN8kIAAQQQQAABBBCIK9Dk85Vy4JzzbV3eaVRcPmhaCi4EEEAAAQQSFaAAmCiRT5xAAVChYd6wYYPUrVvX8e0/raC2b98+SZcunVOGEREReuFNe6rwyJEjExS4efOmfv0zzzwj8+bNc1nLz8/P5XMpALpMxYkIIIAAAggg4IMCLcaGy54o59u6DHi6jHSpV9QHNUgZAQQQQMBdAQqA7oqpeT4FQEXG9ezZsxIQECDaX2yt+BYaGiqNGjWKk114eLgEBQU5jn/88ccyZMiQBAViY2MlZcqUjs+Dg4Mdbbr6ogDoqhTnIYAAAggggAACjxdoNWGNbD9x2emk0S9WlNYBBaBDAAEEEEAgUQEKgIkS+cQJFAC9MMzaN/BSpUqV7Ja/++476dSpU6LtXLt2TRo2bCibN292nDtixAjp06dPvNcZ9Q1AfgKc6LBxAgIIIIAAAggg4JJA62/WSsTRS07nTnklQJqUzeXS9ZyEAAIIIODbAhQAfXv8/8meAqAX5oGRBcBbt25JixYtJCwszJFJz5495bPPPkswK6PuAZgYKwtQYkJ8jgACCCCAAAII/C3Qfsp6WXvoghPHnG61pHrhrBAhgAACCCCQqAD770SJfOIECoBeGmat0JbcV548eSRz5swJNqMVGp9//nn93nxdunSRKVOmPLZb7SnAGTNmdJzDU4CTO0JcjwACCCCAAAIIeF/g1WkbZeX+804dLX0/SErk+vvfdLwQQAABBBB4nAAFQOaHJkAB0KbzQLs/X4cOHWTWrFmODNq2bSszZsyQFClSJJpRwYIFHU/eLVWqlDyuUKk99bd9+/aO9qZNmyadO3dOtG1XT2ABclWK8xBAAAEEEEDA1wW6fB8hoZHnnBg29g+WnBnT+joN+SOAAAIIuCDA/tsFJB84hQKgTQf5jTfekG+//dYRvfaE3t9++83l+w5qRT2tuKe9oqKiJHfu3PEqdOvWTSZNmuT4THuicMmSJT2mxQLkMUoaQgABBBBAAAHFBd76abMs2nXGKct9w5pJGv+/H9bGCwEEEEAAgccJsP9mfmgCFABtOA+0+/x98cUXjsi1p/MuWLBA0qRJ43Ims2fPdnxjUHsl9MCQmJgYyZ8/v1y6dEnKli0ru3fvdrl9V05kAXJFiXMQQAABBBBAAAGRd2dulb+2n9YpnkiVUiKHNoMGAQQQQAABlwTYf7vEpPxJFABtNsSDBg2SwYMHO6KuXbu2LFmyRNKnT+9WFnfv3pUyZcrIoUOHJFOmTLJlyxYpVqyYUxvdu3eXiRMnOo65+jRid4JgAXJHi3MRQAABBBBAwJcFPpi9XeZuOakT5MmcVtb1DfZlEnJHAAEEEHBDgP23G1gKn0oB0EaDO378eHn33XcdEefLl09++eWXxz4kRDtPu89fqlSp4mS5cOFCadmypWj3EsyVK5cMGDBAAgMDHd/40x4kMnfuXMc1devWlRUrVkjKlJ79iQkLkI0mHqEigAACCCCAgKkCfX/bITM3ntBjKJ07oyz+b5CpMdE5AggggIB9BNh/22esvBkpBUBv6nq47QYNGsjKlSvdavXIkSNSuHDheK/RCn09evSQO3fuxPu5VhDUfl6cPXt2t/p05WQWIFeUOAcBBBBAAAEEEBAZ+Ocu+WHdMZ2iZtGsMuvNWtAggAACCCDgkgD7b5eYlD+JAqCNhtjTBUAt9V27dsm4ceNk2bJlcvr0acfPibWfB2tPGO7SpYv4+/t7RYgFyCusNIoAAggggAACCgoMmbdHpq05omfWrFxu+aZjNQUzJSUEEEAAAW8IsP/2hqr92qQAaL8xUyJiFiAlhpEkEEAAAQQQQMAAgelrjsigeXv0nt5uUEx6NyttQM90gQACCCCgggD7bxVGMfk5UABMviEtJEGABSgJaFyCAAIIIIAAAj4pcPHGHXll2gbZdeqqFM2eXn54PVDyP5nOJy1IGgEEEEDAfQH23+6bqXgFBUAVR9UGObEA2WCQCBEBBBBAAAEELCNw936snL92W7KmTy1pU3n24WyWSZJAEEAAAQS8IsD+2yustmuUAqDthkyNgFmA1BhHskAAAQQQQAABBBBAAAEEELC2APtva4+PUdFRADRKmn6cBFiAmBAIIIAAAggggAACCCCAAAIIeF+A/bf3je3QAwVAO4ySgjGyACk4qKSEAAIIIIAAAggggAACCCBgOQH235YbElMCogBoCjudsgAxBxBAAAEEEEAAAQQQQAABBBDwvgD7b+8b26EHCoB2GCUFY2QBUnBQSQkBBBBAAAEEEEAAAQQQQMByAuy/LTckpgREAdAUdjplAWIOIIAAAggggAACCCCAAAIIIOB9Afbf3je2Qw8UAO0wSgrGyAKk4KCSEgIIIIAAAggggAACCCCAgOUE2H9bbkhMCYgCoCnsdMoCxBxAAAEEEEAAAQQQ5G9eJAAAHdpJREFUQAABBBBAwPsC7L+9b2yHHigA2mGUFIyRBUjBQSUlBBBAAAEEEEAAAQQQQAABywmw/7bckJgSEAVAU9jplAWIOYAAAggggAACCCCAAAIIIICA9wXYf3vf2A49UAC0wygpGOPRo0elSJEijsw2btwoefLkUTBLUkIAAQQQQAABBBBAAAEEEEDAXIGoqCgJDAx0BHHkyBEpXLiwuQHRuykCFABNYafTiIgIfQFCAwEEEEAAAQQQQAABBBBAAAEEvC+gfQGnevXq3u+IHiwnQAHQckPiGwFRAPSNcSZLBBBAAAEEEEAAAQQQQAAB6whQALTOWBgdCQVAo8XpzyFw69Yt2blzp+PPOXLkEH9/f8vLPPq1aX62bPnhIkAXBZjXLkJxmq0EmNe2Gi6CdVGAee0iFKfZRoA5bZuhIlA3BKw6r+/duyfnz593ZFKhQgVJmzatG1lxqioCFABVGUny8LoAN071OjEdmCDAvDYBnS69LsC89joxHZggwLw2AZ0uvSrAnPYqL42bJMC8Ngmebl0SoADoEhMnISDCYs4sUFGAea3iqJIT85o5oKIA81rFUfXtnJjTvj3+qmbPvFZ1ZNXIiwKgGuNIFgYIsJgbgEwXhgswrw0np0MDBJjXBiDTheECzGvDyenQywLMaS8D07wpAsxrU9jp1EUBCoAuQnEaAizmzAEVBZjXKo4qOTGvmQMqCjCvVRxV386JOe3b469q9sxrVUdWjbwoAKoxjmRhgACLuQHIdGG4APPacHI6NECAeW0AMl0YLsC8NpycDr0swJz2MjDNmyLAvDaFnU5dFKAA6CIUpyHAYs4cUFGAea3iqJIT85o5oKIA81rFUfXtnJjTvj3+qmbPvFZ1ZNXIiwKgGuNIFgYIsJgbgEwXhgswrw0np0MDBJjXBiDTheECzGvDyenQywLMaS8D07wpAsxrU9jp1EUBCoAuQnEaAizmzAEVBZjXKo4qOTGvmQMqCjCvVRxV386JOe3b469q9sxrVUdWjbwoAKoxjmSBAAIIIIAAAggggAACCCCAAAIIIIBAvAIUAJkYCCCAAAIIIIAAAggggAACCCCAAAIIKCxAAVDhwSU1BBBAAAEEEEAAAQQQQAABBBBAAAEEKAAyBxBAAAEEEEAAAQQQQAABBBBAAAEEEFBYgAKgwoNLaggggAACCCCAAAIIIIAAAggggAACCFAAZA4ggAACCCCAAAIIIIAAAggggAACCCCgsAAFQIUHl9QQQAABBBBAAAEEEEAAAQQQQAABBBCgAMgcQAABBBBAAAEEEEAAAQQQQAABBBBAQGEBCoAKDy6pIYAAAggggAACCCCAAAIIIIAAAgggQAGQOYAAAggggAACCCCAAAIIIIAAAggggIDCAhQAFR5cUkMAAQQQQAABBBBAAAEEEEAAAQQQQIACIHMAARcEjh8/LuPGjZMFCxaI9uc0adJI8eLF5f/auxPgnao/juMnO1kiKqQsUWSKIkU09iXapFJZSiRMNYoGFSYhZWJKsqRtLCHNqBQV0iaMdmRJJipJZW8U/edz5v+Yx8/z/M69P/f5/X7ned5nxkx173PvOa9znO793rPcdNNNpl+/fqZEiRIBrsIpCKRW4JRTTgl0g6uuusosX74823PfffddM3XqVLNq1Sqza9cuU6FCBXPZZZeZPn36mHbt2gW6Dych4BL47bffbBvTn9WrV9s/u3fvtj/r0aOHeemll1yXOO54FO3233//NS+88IKZOXOmWb9+vdm/f7+pXLmyadWqlbn33ntNnTp1QuWJkzNPIIp2rbZ/xx13BMJ78cUXTc+ePbM99+DBg2bSpElm3rx5ZvPmzebw4cOmSpUq5uqrr7bt+pxzzgl0L07KXIG1a9ca9bEfffSR+fbbb43aeeHChU2lSpVM48aNTa9evUzTpk0DA9FfB6bixBQKRNGu6a9TWEFcOnIBAoCRk3LBdBNQ0O+2224ze/bsSVi0888/3yxatMhUr1493YpOeTwTiCIA+N9//5m+ffva4F+ypCDg888/b4LezzNGspuLAtm1oTABwKjarYKPCoh8/vnnCRX08ee5554zd955Zy4qcSvfBKJo11G+UG7ZssW26++//z4hZZkyZcysWbNMhw4dfKMmv7kkoA+HK1ascN6tW7duZvr06aZIkSJJz6W/djJyQi4JRNWu6a9zqcK4TSQCBAAjYeQi6Srw1Vdf2a+a+nJesmRJM2TIENO8eXNz6NAhM2fOHDNt2jRb9AsuuMCOXNE5JATySiD20nnPPffYkanJ0qmnnmqqVauW8PCwYcPM6NGj7bH69eubwYMHmxo1ahi9QI4bN8588cUX9pjOGzVqVF4VlfumiUB8oESjkWrXrm2WLFliSxcmABhFuz1y5Ihp0aLFsZfcG264wfTu3duUK1fOBgTV3jXipWDBgnY0eNu2bdOkFihG1AJRtOv4F8rFixfbUVbJ0tlnn21OO+20hIc1grVhw4Zmw4YN9rja9C233GKKFy9uli1bZsaMGWNHuWomw2effWYuuuiiqDm4XhoIaNaLngPUDrt06WJH+mnUqPpNtZvx48ebHTt22JJ27drVBpSTJfrrNGgQaVKEqNo1/XWaNIgMKQYBwAypaIqZMwEF+zRVslChQval8IorrjjuQk8++aQNkCiNHDnSPProozm7Eb9CIAKB2Evn8OHDzYgRI0JfUdPCFIDRFMgGDRrYNq+XxFhSIFxfS9esWWP/TuiFUsFBEgI5FVBbVXBCf84880zz448/HgtOBw0ARtVu4x/gFUDXdMn4pPtceumlZu/evaZmzZpm3bp19u8BCYGsAlG06/j2uHXrVlO1atUcQev/BXo+UdJHnEGDBh13HQVvmjVrZvt9PfMsXbo0R/fhR+kt0LFjR9O9e3fTuXNn+xEka/r9999NkyZNzMaNG+0hPT8kmg5Mf53e7cS30kXVrumvfav5zM4vAcDMrn9Kn42ARvRpzTOlu+++2055zJqOHj1q6tata9eJKlu2rNm5c6ddD4WEQF4InGwAsH///nZ6o5JeCi+//PITirFy5cpjgfABAwaYZ555Ji+Kyj3TVCAnAcCo2u2FF15og3rqy7dv355wbdexY8fakeBK8+fPty/DJARcAjlp11G8UP7zzz/mjDPOMH/99Zf9uKN12woUKHBCdrXsw5QpU+x/1wceBbpJCIQVeOutt0ynTp3sz7Su5MSJE0+4BP11WFXOz2uBIO2a/jqva4n7hxEgABhGi3MzSiB+ioKCHo0aNUpY/vgXQk1da926dUY5Udj8I3AyAUCtyaMpmJrCoyntCmonSzqutaQ07Uyb4rAWYP5pA77nJGygJKp2u2nTJlOrVi3Lp2DI5MmTE1L++uuvpmLFivbYrbfeajcKISHgEgjbrnW9KF4o33vvPdOmTRubPT2rPPTQQwmzGv9hZ+jQoebxxx93FYnjCJwgoKnkpUqVsv9da04qcBKf6K9pND4KuNo1/bWPtZrZeSYAmNn1T+mzEdCUGO10pvXS9PU82VQvjZTSOoFKmgIcm2oDLgK5LXAyAcAffvjh2HTeZCNeY+XR8dgmIfpdsvUEc7v83M9/gbCBkqja7YwZM+wOlkqzZ8+2a6QlS9r4SdPctP7Vtm3b/EenBCkXCNuuo3qh1DPJY489ZsuXbFS3jmn6r9YQPHDggJ0O/OGHH6bchBukn8Aff/xhTj/9dFswjQRcuHDhcYWkv06/Os+EErnaNf11JrSC9CojAcD0qk9KE6FAhQoVjNY0ufjii82XX36Z9Mp//vmnXSReSQsjz507N8JccCkEggvEAoB16tSxL3QanafA9VlnnWWD1D179rRrPCVK2tRAa6EoPf300+b+++9PemMdHzhwoD2u37FzZPA64szsBcIGSqJqt1oX7amnnrKZ00Y39erVS5rRa6+91r7Y6u/bvn377EciEgLZCYRt11lfKLX2qkZl63mjdOnSRgvXt2rVymjDp8qVKye9tZ5JNFVdSb9NtlGIjutZ5+uvvzZ69tFmNyQEwgq88cYbRpsnKalP1ZqT8Yn+Oqwo5+cHAVe7pr/OD7VEHsIIEAAMo8W5GSPw999/H9v8INE0hqwQ2v1XX861Zpq+spMQyAuBIFNxr7vuOju1rEyZMsdlUWtc6mVSad68eebGG29MWgS9UOrFUkm/04hAEgJRCIQNlETVbjXi77XXXrNF2LVrlylfvnzS4mjty9gGIdoIRyMCSQhkJxC2XWd9oUx27WLFipkJEyYk7YP1TKIdrBWk1jS27JI+AClAo6RnoKJFi1KpCAQW0JrY2ihv1apV9jdaR1ubicUn+uvAnJyYTwSCtGv663xSWWQjsAABwMBUnJhJAnoB1MLZSjfffLOZM2dOtsXX7pX6Yq4NQb755ptMoqKs+UhAL3nXXHONadmypV3HT4FptWVN59KD9+7du21uNZpEa0PFb1gTv6P1O++8Y9q1a5e0ZDoeG/WnUVMPPPBAPlIgKz4LhA2URNVu9aFn0aJFlu7QoUNGgZVkSeuoxUa2sGGCz60t9/Ietl3HXig1fVcjqhRY0RqtSppG+frrr9uRfVpTTUkbePTp0+eEAsU2ttEzitavzC7pWSc2g0GzH2JTOXNPiTv5LDB+/Hjz4IMP2iJcf/31ZsGCBScUh/7a5xrOzLwHadf015nZNnwuNQFAn2uPvKdM4KeffrLrOyl169bNvPLKK9neS+fqNzVq1DCbN29OWb64MALZCWitymRTvLRDdfv27e30RiXtzqdd+mJJL5paL0rpgw8+MC1atEh6q6VLl9ogo5J+9/DDD1MxCEQiEDZQElW7VXtWu1Y6cuRIwp1SYwWMX1dN68ReeeWVkZSdi6SvQNh2LYk9e/bY6b7JRnZrgwUFB7XTb4kSJcyWLVvscg/xSc8kChgqeKglIbJL3bt3N6+++qo9Rc8z2uSJhEAQAX1k1JR0LT2ij+eaSq6gc9ZEfx1Ek3Pyi0DQdk1/nV9qjHwEFSAAGFSK8zJKgBGAGVXdGVNYvQjWrl3bHD582K4hpZ1PYymqL/MZg0lBUyIQNlASVbtlBGBKqpOL/l8gbLsOCqfdemMfYEaNGmWGDRt23E8ZARhUkvNyKvDdd9+Zpk2b2jUmNW188eLFdpZBokR/nVNlfpfbAmHaddC80V8HleK8VAsQAEy1MNf3UoA1AL2sNjIdQCB+nacdO3aYSpUq2V9FtTZPgCxwCgJJBcIGSqJqt6wBSKNMpUDYdh00L1p6RKP+NBW4devWZsmSJcf9lDUAg0pyXk4Etm7dakdA//zzz6ZgwYJ2/WBN/02W6K9zosxvclsgbLsOmj/666BSnJdqAQKAqRbm+t4KsAuwt1VHxrMRGDx4sNFXeCUt1t2wYUP7z5pO1qlTJ/vP7AJME8orgbCBkqjardau0lo/SuwCnFe1n773Dduuw0hoyqVmLWj3d41aiU/azEnrBSqxC3AYVc51CSjop5F/mlmgaeraXEzTyLNL9NcuVY7ntUBO2nWYPNNfh9Hi3FQJEABMlSzX9V6gWbNmRus7aWMFra1WqFChhGXSrr+NGze2x7Q21MiRI70vOwVIX4FBgwYZbdyhFB8A1EO81otS0q6++lKfLOn41KlT7WH9rlq1aukLRslyVSBsoCSqdjtjxgzTq1cvW9bZs2cbjQhMlrTr78aNG+06sdu2bctVH27mp0DYdh2mlLGPlYkCgPHrVepZRSMCEyWt3ab1Yw8cOGD07KO1r0gIJBPQJjGa5rtu3Tp7yrPPPmv69+/vBKO/dhJxQh4K5LRdh8ky/XUYLc5NlQABwFTJcl3vBYYOHWrGjBljy7Fy5UrTqFGjhGUaO3asGTJkiD2mtU/atGnjfdkpQPoKxK91tn37dlO5cmVbWE0h06Lv+vqpHYTXr1+fFEHrCG7YsMH+VovFJ1ukPn0VKVmqBMIGSqJqtwroKbCn1LdvXzN58uSERdROqhUrVrTHunbtambNmpUqCq6bRgJh23XQosdPKdMmDNrdPT5pSnDbtm3tf9KzinawTpT0jKOdhpX0PDN69OigWeC8DBPQ5jTaJGzt2rXOdpWVhv46wxqLR8U9mXYdtJj010GlOC/VAgQAUy3M9b0V0OioWNAv2Yioo0ePmrp169pgib6eq3MvXLiwt2Um4+ktoK/vCu5p18jq1avbXSPjU79+/Y4FPpKNFol/UdT5kyZNSm80SperAjkJlETVbjWCSn15uXLlbGBbO6tmTfEffObOnWu6dOmSqz7czE+BnLTrICXVxh+PPPKIPTXRjuza8ElTzvRyqw83miKc6IONgt5Tpkyx14kfGR4kD5yTOQIHDx60H7k/+eQTW2htOqM2GCbRX4fR4tzcEIiiXQfJJ/11ECXOyQ0BAoC5ocw9vBWITQPW9N8VK1Yc+0IeK1D8jmbDhw83I0aM8LasZNxvgTfffNO0b98+6VT1nTt32uNa30xJ650NHDjwuEJrFJR2jdR0sAYNGtg2X7x48WPnHDp0yE4PW7Nmjb2Ppv/UrFnTbzhyn68EchIoiardxk8D1nQ2TWuLTwqYX3LJJWbv3r12urxGwSZbGiJfoZKZPBcI2651vtbsq1+/ftK8az21zp07213dixUrZjZv3nxsRHf8j+KnAY8bN85oGYj4pI896tfV72ta5/Lly/PciwzkPwG1M60THNto5r777jMTJkwInVH669Bk/CCFAlG0a/rrFFYQl06JAAHAlLBy0XQRULCkSZMmRoGPkiVLGk0Lbt68uf33OXPmHFsHrVatWjYoUqpUqXQpOuXwTKBq1ap2ZJ9eCDWVS/+u4J3WNNELndb02717ty2Vdu17//33TdGiRU8opaZ/aZSTkl4+NWVMwQ4FP5544oljAUSmiXnWQPJpdj/++GMbuIgltddYgEJ971133XVcznv27JmwJFG02yNHjtgASGx0i/4u9e7d25QtW9aOitIIK43yLlCggN00RwF1EgKJBE62XavP1rOG+nIFXerVq2dH8mkKpUZyz58/3/7Rvytltwbbvn377AcdBV6U+vTpY9e41P8fli1bZqf77t+/3/77p59+au9FQiCrgPrDBQsW2P+sKcAK/mW3/EeRIkWMno0TJfpr2ld+EYiiXdNf55faJB9BBQgABpXivIwV0Miq22+/3Y76SJT0gPP222+b8847L2ONKHjeCyjgF2RDAj3sTJ8+3U5ZT5Q0rV1BD42GSpa0WYI2AVEghITAyQgooPfyyy8HvkQs4JH1B1G1WwUgO3ToYFavXp0wT3qpVbBFf0dICCQTONl2HXuhdAlrmrp2bVdQL7ukILva9aZNmxKeVrp0aTNz5kzTsWNH1y05nqECYdf6Pffcc41GRqXyOYP+OkMbY4TFjqJd019HWCFcKlcECADmCjM38V1AgZWJEyfaQJ82TtBLoAJ+Wv9pwIABCdeK8r3M5N8vAe3aqD+azqURInowVtBaI1erVKlid6ru0aPHCdPYk5Vy0aJFNsinQIiuVb58edOwYUO7QzAjn/xqG/k5tycbKMlatijaraZCTps2zW7woTUBtTNqpUqVTMuWLY2mvWmaPAmB7AROtl1r1N7ChQttf67ZBb/88ovth9U2NSJVbVDtUSNkNTIwSFI71pqt8+bNs6NuNfVN/29QYFDtWgEbEgLJBKIIlNBf077ym0AU7Zr+Or/VKvlxCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCRAAdAlxHAEEEEAAAQQQQAABBBBAAAEEEEAAAY8FCAB6XHlkHQEEEEAAAQQQQAABBBBAAAEEEEAAAZcAAUCXEMcRQAABBBBAAAEEEEAAAQQQQAABBBDwWIAAoMeVR9YRQAABBBBAAAEEEEAAAQQQQAABBBBwCfwP72LWQOJV09UAAAAASUVORK5CYII=\" width=\"640\">"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x11dba8ba8>]"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"fig, axs= subplots(2,1,sharex=True)\n",
"axs[0].plot(s)\n",
"tf = pandas_wrapper.l1tf(s, 0.5)\n",
"axs[0].plot(tf)\n",
"\n",
"d1 = tf[1:] - tf[:-1]\n",
"d2 = d1[1:] - d1[:-1]\n",
"axs[1].plot(d2)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
taroplus/sparkling-notebook | notebooks/Matplotlib Example.ipynb | 2 | 18884 | {
"cells" : [ {
"metadata" : {
"trusted" : true,
"collapsed" : false,
"editable" : true,
"deletable" : true
},
"cell_type" : "code",
"source" : [ "import matplotlib.pyplot as plt\n", "import numpy as np\n", "\n", "t = np.arange(0.0, 2.0, 0.01)\n", "s = 1 + np.sin(2*np.pi*t)\n", "plt.plot(t, s)\n", "\n", "plt.xlabel('time (s)')\n", "plt.ylabel('voltage (mV)')\n", "plt.title('About as simple as it gets, folks')\n", "plt.grid(True)\n", "plt.savefig(\"test.png\")\n", "plt.show()" ],
"execution_count" : 4,
"outputs" : [ {
"output_type" : "display_data",
"data" : {
"image/svg+xml" : "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?><!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\"><!-- Created with matplotlib (http://matplotlib.org/) --><svg height=\"280pt\" version=\"1.1\" viewBox=\"0 0 391 280\" width=\"391pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\"> <defs> <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;} </style> </defs> <g id=\"figure_1\"> <g id=\"patch_1\"> <path d=\"M 0 280.960381 L 391.349969 280.960381 L 391.349969 0 L 0 0 z\" style=\"fill:#f0f0f0;\"/> </g> <g id=\"axes_1\"> <g id=\"patch_2\"> <path d=\"M 45.849969 244.394475 L 380.649969 244.394475 L 380.649969 22.634475 L 45.849969 22.634475 z\" style=\"fill:#e5e5e5;\"/> </g> <g id=\"matplotlib.axis_1\"> <g id=\"xtick_1\"> <g id=\"line2d_1\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 61.068151 244.394475 L 61.068151 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_2\"> <defs> <path d=\"M 0 0 L 0 3.5 \" id=\"ma1eda46f12\" style=\"stroke:#555555;stroke-width:0.8;\"/> </defs> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"61.068151\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_1\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 61.068151, 257.836506)\" x=\"61.068151\" y=\"257.836506\">0.00</text> </g> </g> <g id=\"xtick_2\"> <g id=\"line2d_3\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 99.304788 244.394475 L 99.304788 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_4\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"99.304788\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_2\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 99.304788, 257.836506)\" x=\"99.304788\" y=\"257.836506\">0.25</text> </g> </g> <g id=\"xtick_3\"> <g id=\"line2d_5\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 137.541426 244.394475 L 137.541426 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_6\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"137.541426\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_3\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 137.541426, 257.836506)\" x=\"137.541426\" y=\"257.836506\">0.50</text> </g> </g> <g id=\"xtick_4\"> <g id=\"line2d_7\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 175.778064 244.394475 L 175.778064 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_8\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"175.778064\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_4\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 175.778064, 257.836506)\" x=\"175.778064\" y=\"257.836506\">0.75</text> </g> </g> <g id=\"xtick_5\"> <g id=\"line2d_9\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 214.014702 244.394475 L 214.014702 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_10\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"214.014702\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_5\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 214.014702, 257.836506)\" x=\"214.014702\" y=\"257.836506\">1.00</text> </g> </g> <g id=\"xtick_6\"> <g id=\"line2d_11\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 252.251339 244.394475 L 252.251339 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_12\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"252.251339\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_6\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 252.251339, 257.836506)\" x=\"252.251339\" y=\"257.836506\">1.25</text> </g> </g> <g id=\"xtick_7\"> <g id=\"line2d_13\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 290.487977 244.394475 L 290.487977 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_14\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"290.487977\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_7\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 290.487977, 257.836506)\" x=\"290.487977\" y=\"257.836506\">1.50</text> </g> </g> <g id=\"xtick_8\"> <g id=\"line2d_15\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 328.724615 244.394475 L 328.724615 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_16\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"328.724615\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_8\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 328.724615, 257.836506)\" x=\"328.724615\" y=\"257.836506\">1.75</text> </g> </g> <g id=\"xtick_9\"> <g id=\"line2d_17\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 366.961252 244.394475 L 366.961252 22.634475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_18\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"366.961252\" xlink:href=\"#ma1eda46f12\" y=\"244.394475\"/> </g> </g> <g id=\"text_9\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 366.961252, 257.836506)\" x=\"366.961252\" y=\"257.836506\">2.00</text> </g> </g> <g id=\"text_10\"> <text style=\"fill:#555555;font-family:Arial;font-size:10.8px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 213.249969, 271.487319)\" x=\"213.249969\" y=\"271.487319\">time (s)</text> </g> </g> <g id=\"matplotlib.axis_2\"> <g id=\"ytick_1\"> <g id=\"line2d_19\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 234.314475 L 380.649969 234.314475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_20\"> <defs> <path d=\"M 0 0 L -3.5 0 \" id=\"m65f7a5d176\" style=\"stroke:#555555;stroke-width:0.8;\"/> </defs> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"234.314475\"/> </g> </g> <g id=\"text_11\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 237.535491)\" x=\"38.849969\" y=\"237.535491\">0.00</text> </g> </g> <g id=\"ytick_2\"> <g id=\"line2d_21\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 209.114475 L 380.649969 209.114475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_22\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"209.114475\"/> </g> </g> <g id=\"text_12\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 212.335491)\" x=\"38.849969\" y=\"212.335491\">0.25</text> </g> </g> <g id=\"ytick_3\"> <g id=\"line2d_23\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 183.914475 L 380.649969 183.914475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_24\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"183.914475\"/> </g> </g> <g id=\"text_13\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 187.135491)\" x=\"38.849969\" y=\"187.135491\">0.50</text> </g> </g> <g id=\"ytick_4\"> <g id=\"line2d_25\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 158.714475 L 380.649969 158.714475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_26\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"158.714475\"/> </g> </g> <g id=\"text_14\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 161.935491)\" x=\"38.849969\" y=\"161.935491\">0.75</text> </g> </g> <g id=\"ytick_5\"> <g id=\"line2d_27\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 133.514475 L 380.649969 133.514475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_28\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"133.514475\"/> </g> </g> <g id=\"text_15\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 136.735491)\" x=\"38.849969\" y=\"136.735491\">1.00</text> </g> </g> <g id=\"ytick_6\"> <g id=\"line2d_29\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 108.314475 L 380.649969 108.314475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_30\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"108.314475\"/> </g> </g> <g id=\"text_16\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 111.535491)\" x=\"38.849969\" y=\"111.535491\">1.25</text> </g> </g> <g id=\"ytick_7\"> <g id=\"line2d_31\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 83.114475 L 380.649969 83.114475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_32\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"83.114475\"/> </g> </g> <g id=\"text_17\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 86.335491)\" x=\"38.849969\" y=\"86.335491\">1.50</text> </g> </g> <g id=\"ytick_8\"> <g id=\"line2d_33\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 57.914475 L 380.649969 57.914475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_34\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"57.914475\"/> </g> </g> <g id=\"text_18\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 61.135491)\" x=\"38.849969\" y=\"61.135491\">1.75</text> </g> </g> <g id=\"ytick_9\"> <g id=\"line2d_35\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 45.849969 32.714475 L 380.649969 32.714475 \" style=\"fill:none;stroke:#ffffff;stroke-linecap:square;stroke-width:0.8;\"/> </g> <g id=\"line2d_36\"> <g> <use style=\"fill:#555555;stroke:#555555;stroke-width:0.8;\" x=\"45.849969\" xlink:href=\"#m65f7a5d176\" y=\"32.714475\"/> </g> </g> <g id=\"text_19\"> <text style=\"fill:#555555;font-family:Arial;font-size:9px;font-style:normal;font-weight:normal;text-anchor:end;\" transform=\"rotate(-0, 38.849969, 35.935491)\" x=\"38.849969\" y=\"35.935491\">2.00</text> </g> </g> <g id=\"text_20\"> <text style=\"fill:#555555;font-family:Arial;font-size:10.8px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-90, 15.062063, 133.514475)\" x=\"15.062063\" y=\"133.514475\">voltage (mV)</text> </g> </g> <g id=\"line2d_37\"> <path clip-path=\"url(#pc09e0e0faa)\" d=\"M 61.068151 133.514475 L 67.186013 108.446534 L 71.774409 90.595922 L 74.83334 79.503134 L 77.892271 69.262137 L 80.951202 60.034437 L 84.010133 51.965562 L 85.539599 48.40622 L 87.069064 45.182762 L 88.59853 42.307908 L 90.127995 39.793005 L 91.657461 37.647978 L 93.186926 35.881292 L 94.716392 34.49992 L 96.245857 33.509313 L 97.775323 32.913381 L 99.304788 32.714475 L 100.834254 32.913381 L 102.363719 33.509313 L 103.893185 34.49992 L 105.42265 35.881292 L 106.952116 37.647978 L 108.481581 39.793005 L 110.011047 42.307908 L 111.540512 45.182762 L 113.069978 48.40622 L 114.599443 51.965562 L 116.128909 55.84674 L 119.18784 64.512127 L 122.246771 74.265722 L 125.305702 84.953705 L 128.364633 96.40752 L 132.95303 114.626438 L 146.718219 170.62143 L 149.77715 182.075245 L 152.836081 192.763228 L 155.895012 202.516823 L 158.953943 211.18221 L 160.483409 215.063388 L 162.012874 218.62273 L 163.54234 221.846188 L 165.071805 224.721042 L 166.601271 227.235945 L 168.130736 229.380972 L 169.660202 231.147658 L 171.189667 232.52903 L 172.719133 233.519637 L 174.248598 234.115569 L 175.778064 234.314475 L 177.307529 234.115569 L 178.836995 233.519637 L 180.36646 232.52903 L 181.895926 231.147658 L 183.425391 229.380972 L 184.954857 227.235945 L 186.484322 224.721042 L 188.013788 221.846188 L 189.543253 218.62273 L 191.072719 215.063388 L 192.602184 211.18221 L 195.661115 202.516823 L 198.720046 192.763228 L 201.778977 182.075245 L 204.837908 170.62143 L 209.426305 152.402512 L 223.191495 96.40752 L 226.250426 84.953705 L 229.309357 74.265722 L 232.368288 64.512127 L 235.427219 55.84674 L 236.956684 51.965562 L 238.48615 48.40622 L 240.015615 45.182762 L 241.545081 42.307908 L 243.074546 39.793005 L 244.604012 37.647978 L 246.133477 35.881292 L 247.662943 34.49992 L 249.192408 33.509313 L 250.721874 32.913381 L 252.251339 32.714475 L 253.780805 32.913381 L 255.31027 33.509313 L 256.839736 34.49992 L 258.369201 35.881292 L 259.898667 37.647978 L 261.428132 39.793005 L 262.957598 42.307908 L 264.487063 45.182762 L 266.016529 48.40622 L 267.545994 51.965562 L 269.07546 55.84674 L 272.134391 64.512127 L 275.193322 74.265722 L 278.252253 84.953705 L 281.311184 96.40752 L 285.89958 114.626438 L 299.66477 170.62143 L 302.723701 182.075245 L 305.782632 192.763228 L 308.841563 202.516823 L 311.900494 211.18221 L 313.42996 215.063388 L 314.959425 218.62273 L 316.488891 221.846188 L 318.018356 224.721042 L 319.547822 227.235945 L 321.077287 229.380972 L 322.606753 231.147658 L 324.136218 232.52903 L 325.665684 233.519637 L 327.195149 234.115569 L 328.724615 234.314475 L 330.25408 234.115569 L 331.783546 233.519637 L 333.313011 232.52903 L 334.842477 231.147658 L 336.371942 229.380972 L 337.901408 227.235945 L 339.430873 224.721042 L 340.960339 221.846188 L 342.489804 218.62273 L 344.01927 215.063388 L 345.548735 211.18221 L 348.607666 202.516823 L 351.666597 192.763228 L 354.725528 182.075245 L 357.784459 170.62143 L 362.372856 152.402512 L 365.431787 139.843759 L 365.431787 139.843759 \" style=\"fill:none;stroke:#1f77b4;stroke-linecap:square;stroke-width:1.5;\"/> </g> <g id=\"patch_3\"> <path d=\"M 45.849969 244.394475 L 45.849969 22.634475 \" style=\"fill:none;\"/> </g> <g id=\"patch_4\"> <path d=\"M 380.649969 244.394475 L 380.649969 22.634475 \" style=\"fill:none;\"/> </g> <g id=\"patch_5\"> <path d=\"M 45.849969 244.394475 L 380.649969 244.394475 \" style=\"fill:none;\"/> </g> <g id=\"patch_6\"> <path d=\"M 45.849969 22.634475 L 380.649969 22.634475 \" style=\"fill:none;\"/> </g> <g id=\"text_21\"> <text style=\"font-family:Arial;font-size:12.96px;font-style:normal;font-weight:normal;text-anchor:middle;\" transform=\"rotate(-0, 213.249969, 16.634475)\" x=\"213.249969\" y=\"16.634475\">About as simple as it gets, folks</text> </g> </g> </g> <defs> <clipPath id=\"pc09e0e0faa\"> <rect height=\"221.76\" width=\"334.8\" x=\"45.849969\" y=\"22.634475\"/> </clipPath> </defs></svg>"
},
"metadata" : { }
} ]
}, {
"metadata" : {
"trusted" : true,
"collapsed" : true
},
"cell_type" : "code",
"source" : [ "" ],
"execution_count" : null,
"outputs" : [ ]
} ],
"metadata" : {
"kernelspec" : {
"name" : "python",
"display_name" : "PySpark",
"language" : "python"
},
"language_info" : {
"name" : "python",
"codemirror_mode" : {
"version" : 2,
"name" : "ipython"
}
}
},
"nbformat" : 4,
"nbformat_minor" : 0
} | apache-2.0 |
olafplacha/OpenCV-intro | feature matching.ipynb | 1 | 1851179 | null | mit |
wcmckee/garrison-wow-track | Untitled.ipynb | 1 | 556 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
bgruening/galaxy-ipython | templates/notebook.ipynb | 1 | 1083 | {
"metadata": {
"name": "",
"signature": "sha256:%s"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Welcome to the interactive Galaxy IPython Notebook."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can access your data via the dataset number. For example, ``handle = get(42)``.",
"To save data, write your data to a file, and then call ``put('filename.txt')``. The dataset will then be available in your galaxy history.",
"Notebooks can be saved to Galaxy by clicking the large green button at the top right of the IPython interface.<br>",
"More help and informations can be found on the project [website](https://github.com/bgruening/galaxy-ipython)."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
}
],
"metadata": {}
}
]
}
| mit |
4DGenome/Chromosomal-Conformation-Course | Participants/deo/00_fastq_QC.ipynb | 1 | 240339 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"00_fastq_QC.ipynb learning_python.ipynb\r\n"
]
}
],
"source": [
"!ls"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/media/storage/Notebooks2/deo\r\n"
]
}
],
"source": [
"!pwd"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"head: cannot open ‘/media/storage/FASTQs/K562_HindIII_1.fasta’ for reading: No such file or directory\r\n"
]
}
],
"source": [
"!head /media/storage/FASTQs/K562_HindIII_1.fasta"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"@NS500645:59:HCL32BGXY:1:11101:14163:1054 1:N:0:GCCAAT\r\n",
"CATTCNTAAAGAAAAGAATTTTCAACNCAGAATTTCATATCCAGCCAACTAAGCTAGCTTCAAGGAAATACATTT\r\n",
"+\r\n",
"AAAAA#EEAEEEEEEEEEEAE/EEEE#EEEEEEEEEEEEEEEEAE</EE/EEEEAEEEEEEEEEEEAAEE</EEE\r\n",
"@NS500645:59:HCL32BGXY:1:11101:4416:1054 1:N:0:GCCAAT\r\n",
"CGAGTNAGGGAAGCTAGCTTCCATTCNTTTGCTTCTGTTGTGTGTTTTTTCTTTTGTTTTTTTTTTGTTTTGGTT\r\n",
"+\r\n",
"AAAAA#EEEEEEEEEEEEEEAEEEE/#EEEEEEEEEEEEEEEEEAEEEEEEEEEEEEEEEEEEEEE/<EEEEEAE\r\n",
"@NS500645:59:HCL32BGXY:1:11101:14193:1055 1:N:0:GCCAAT\r\n",
"AAAGTNCCCTGCATGATAGCATTTGTATAAAGTTCAAAACAGACCAAATGGATCTCTAATTTGTAGAAGGTCAGG\r\n"
]
}
],
"source": [
"!head /media/storage/FASTQs/K562_HindIII_1.fastq"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"40000000 /media/storage/FASTQs/K562_HindIII_1.fastq\r\n"
]
}
],
"source": [
"!wc -l /media/storage/FASTQs/K562_HindIII_1.fastq"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "SyntaxError",
"evalue": "invalid syntax (<ipython-input-6-7a5b333cb00e>, line 1)",
"output_type": "error",
"traceback": [
"\u001b[0;36m File \u001b[0;32m\"<ipython-input-6-7a5b333cb00e>\"\u001b[0;36m, line \u001b[0;32m1\u001b[0m\n\u001b[0;31m (!wc -l /media/storage/FASTQs/K562_HindIII_1.fastq)/4\u001b[0m\n\u001b[0m ^\u001b[0m\n\u001b[0;31mSyntaxError\u001b[0m\u001b[0;31m:\u001b[0m invalid syntax\n"
]
}
],
"source": [
"(!wc -l /media/storage/FASTQs/K562_HindIII_1.fastq)/4\n"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "SyntaxError",
"evalue": "invalid syntax (<ipython-input-7-ee1d8fffead7>, line 1)",
"output_type": "error",
"traceback": [
"\u001b[0;36m File \u001b[0;32m\"<ipython-input-7-ee1d8fffead7>\"\u001b[0;36m, line \u001b[0;32m1\u001b[0m\n\u001b[0;31m count=(!wc -l /media/storage/FASTQs/K562_HindIII_1.fastq)\u001b[0m\n\u001b[0m ^\u001b[0m\n\u001b[0;31mSyntaxError\u001b[0m\u001b[0;31m:\u001b[0m invalid syntax\n"
]
}
],
"source": [
"count=(!wc -l /media/storage/FASTQs/K562_HindIII_1.fastq)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from pytadbit.utils.fastq_utils import quality_plot\n"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6sAAALJCAYAAABSqbVgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XecXHX1//HXmbK7KZsCCRCSJXQUwlIEggQkoigQOvxA\nVKRJtzsqigiKX1QcxALSBCkqgoAYmlJDLwGETagSSEhCIL2TLTPn98e9k9wsW2brndl9Px+Peczc\nez/3c8/MnU3m3E+55u6IiIiIiIiIlJJE3AGIiIiIiIiINKdkVUREREREREqOklUREREREREpOUpW\nRUREREREpOQoWRUREREREZGSo2RVRERERERESo6SVREpO2a2j5m9EXccnWFmE81sTmT5FTObGGNI\nLTKzE83siQ6Un2lmn+3JmHpCR99nC/tfaWbndWdMkbq3N7Pnzcw6sE+nv09mdr2Z/bwz+0r3MrML\nzOwvRZS73cwO7I2YRETioGRVpJ8ws73N7CkzW2Zmi83sSTPbPe64OsPdH3f37XqqfjM72MyeM7NV\nZrbIzP5iZqN74ljuvoO7TwmPW9QPVIlHS4mtu5/h7hf20CEvBLIe3hC9pQsCzWOKfp+6ooWLKlPM\n7KstbWth36+FSXa9mV3fwvbPmNnrZrbazB4xs7GRbWZmvwr/7haFry2yffNwn9VhHc0/jy+a2azw\nb/dOM9sgsq3SzK4zs+Vm9r6ZfafZvjub2Qth3S+Y2c4d/Nji8CtAFxhEpM9SsirSD5jZEOBu4A/A\nBsBo4KdAfZxxlSIzOxr4G/BbYASwA9AAPG5mw+KMTfoPMxsFfBq4M+5YOuE9ggTquuYbzGwEcAdw\nHsG/Rc8Dt0SKnAYcDuwE1AKHAKdHtt8M/BfYEDgXuM3MRoZ17wBcBRwPbAysBv4Y2fcCYBtgLMFn\n+30zOyDctwL4F/AXYDhwA/CvcH27zCxZTLnu5u7PAUPMbLc4ji8i0tOUrIr0D9sCuPvN7p5z9w/d\n/X53rysUMLOTzew1M1tiZv9p1tqxf9iKsczMLjOzRyOtLOu1BoYtH25mqXB5qJlda2bzzGyumf28\n8MOu0CpkZtnwuO9Eu7SZ2QZm9mczey/cfme4vnmrz0wzy5hZXRjjLWZWFdn+/fD475nZV8P4tm7+\nIYUtOJcAP3f3v4Wf0/vAVwl++H6zyPd8UvhZrjCzt83s9ObHahb7Z8MfzT8CjjWzlWb2spn9PzN7\noVn575jZv1qpq9XjFj4zM/uumc0PP4+TIts3NLPJYavTc8BWrcUclj8+bMFaZGbnNtuWMLNzzGxG\nuP3WZi1chVb+pWY228xODNcPNbMbzWxBWPePzSwRbmv1u2Jmx5rZ881i+LaZTW6v3mb7rHcew3VT\nwu/Mx4ErgU+G52dpuH29rrNmdqqZvWVB74XJZrZpZJub2Rlm9r/wvV8efudasj/woruvaes8tPAe\n1ra+ht/TW8P3vsKCLsK7RcruYmYvhttuAaparbgD3P0Od78TWNTC5iOBV9z9H+F7uwDYycw+Fm4/\nAbjE3ee4+1wgC5wYxrstsCtwfvi3eTtQBxwV7vsl4C53f8zdVxIkxEeaWXWk7gvdfYm7vwZcXagb\nmAikgN+6e727/x4wYL+W3mN43q8ws3vNbBXwaQtabrNm9q6ZfWBBF/EBYfnhZnZ3+B1cEr4eE6lv\nCwv+XV1hZg8QXCgrbKuyoHfHovB7M9XMNo6EMwWY1OLJEBEpc0pWRfqHN4Gcmd1gZgea2fDoRjM7\njCBROhIYCTxO0IIRbQn5McEPqBnAhA4c+3qgCdga2AX4HEHyVzAeeCOs+2Lg2sgP+JuAgQStmxsB\nl7ZxnGOAA4AtCFpkTgzjPwD4DvDZMIaJbdSxHbAZ8I/oSnfPA7eHsRdjPnAwMAQ4CbjUzHZtawd3\n/zdwEXCLuw92952AycAWYaJUcDxwYyePuwkwlKBl/RTg8sh34XJgDTAKODl8tMjMtgeuCGPZlKCV\na0ykyNcJWsf2DbcvCevHgosg9xG08o8EdgZeCvf7QxjfluG+XwnfR0Fr35W7gO3MbJtI2S8StJAX\nU2+7wuTmDODp8Px8pJXdzPYDfkHwXRwFzAL+3qzYwcDuBN/RY4DPt3LIHcP32lWHhjEMI/g+XRbG\nWkHQansTQQvnP1iX9PWkHYCXCwvuvgp4K1z/ke3h6+i2t919RRvbo3XPIOg9sm34PR/VTt11hS7X\nLWxvyReB/wOqgSeAXxJcGNyZ4N+a0cBPwrIJ4M8ErbqbAR8SnovQ34AXCL7bFxIk1gUnEHx/awj+\n1s4I9y94jaAlWkSkz1GyKtIPuPtyYG/AgWuABWGrT+Hq/BnAL9z9NXdvIkiadg4Ti4MIWkJuc/dG\ngu6x7xdz3LD+g4Bvufsqd59PkHB+IVJslrtf4+45gq53o4CNLegGeSBwRtgS0ujuj7ZxuN+7+3vu\nvpggeSmMNzsG+LO7v+LuqwlaclpTaM2Y18K2eQTJVbvc/R53n+GBR4H7gX2K2bdZPfUEXSS/DGu7\nOW5O0KW7M8dtBH4Wfpb3AisJkrwkQaLyk/A8TSc4F605Grg7bMGqJ2jByke2nwGcG7aO1RN85keH\nLZZfBB4MW/kb3X2Ru78UxvAF4IfuvsLdZxK0ch8fqbfF70p4Xv8FHBd+TtsAHwMmF1lvd/kScJ27\nvxi+7x8StMRuHinzS3df6u7vAo+w7nva3DBgRQvr7wxb15aGrbt/bKFM1BPufm/4md3EuqRmTyBN\n0JLY6O63AVOLeI9dNRhY1mzdcoKEr6Xty4HB4UWJju4b3T44XG5edzH7tuZf7v5keDGrnqAL87fd\nfXGYUF9E+G9d+D2/3d1Xh9v+j+DCCWa2GcEFjPPCVt3HCP4NK2gkSFK3DnvGvBD+m16wguD7IiLS\n5yhZFeknwkT0RHcfA4wjaPH6bbh5LPC7yA/gxQRd4EaH5WZH6vHocjvGEvwgnhep+yqCVtKCtYlv\nmHRA8MOxBljs7kuKPFY0gV7Nuh+n68XfTuwLw+dRLWwbFdneprD1+pmwK+hSgoR9RHv7teIG4Ivh\nj/XjgVvDRKgzx10UXowoKHxOIwm6QEY/m1ltxNT8O7GK9bt8jgX+GTnnrwE5gnGENQSt882NIPiu\nRI87i+A7WNDadwWClqnjwtdfBO4MyxRTb3fZNHqcsCvqIlp5D6z/PW1uCS0nSoe7+7DCAzirnZia\nH68qvGiwKTC3WUtiW+e8u6wkaPmPGsq6xLz59qHAyjDOju4b3b4yXG5edzH7tib69zKSoBfIC5Hv\n/b/D9ZjZQDO7yoJu6MuBx4Bh4cWUTYEl4d9RQfRc3AT8B/i7BUMZLjazdGR7NbC0jThFRMqWklWR\nfsjdXyfonjsuXDUbOD36I9jdB7j7UwQtijWFfcOkqSZS3SqCH2kFm0RezyZocRgRqXeIu7fVtS66\n7wbW9UmN5rF+F9Wa1goSdLucA/y/6EoLxjceRTA2DNp4z2ZWSdBlOEvQ6jcMuJcg+W+Pf2SF+zME\nEzztQ5CE3dTSjl087gKCrtrRz2azNso3/04MJGj5KZgNHNjs+1TlwRjE2bQ8HnYhQQvS2Mi6zYC5\nRcQP8AAw0oIZXI9jXRfgjtRbSBZa+z5/5Pw08170OGY2iOBzKfY9RNURjjXvIfOA0c3GzLZ1zrvL\nK0S6rIaf0Vbh+o9sD19Ht20ZGYPa0vZo3VsBFcCb4UWvee3UXdvs86iNbG9J9PuwkKBr7g6R7/xQ\ndy9cjPguwTCD8e4+BPhUIcwwruHhZ1Gw9lyELd8/dfftgb0IupJ/JVL246zfvVlEpM9QsirSD5jZ\nxyyYWGdMuFxD8IP+mbDIlcAPw26mhQlpCgnbPcAOZnZk2CLzDdb/Af8S8Ckz28zMhhJ0fQTA3ecR\ndEW9xMyGWDDxzlZmtm97MYf73gf8MZycJG1mn2pvvxbcCpxkZh8Pk6pW74kZtt5kgB9bcAuMKjPb\nBPgTQQvdH9p7zwQ/jisJE0ALJgEqdqzrB8Dm9tHJf24kGN/W6O6t3RO008cNu4jeAVwQtgBtz/pj\n5pq7DTjYgomSKoCfsf7/J1cC/xd2I8fMRobjogH+CnzWzI4xs5QFEzvtHMZwa7hfdbjvdwhmZy3m\nPTQSjLv8NcEYzAci762oet19AUFi+WUzS5rZyayfWH8AjLHWZ4i9meC7tnN48eAi4Nmw63FHPQDs\napGJwrrZ0wQXKL4R/m0dCezRHRWH57UKSALJ8O+oMGnVP4FxZnZUWOZ84OXwAhoE3/XvmNloC24X\n9V2CC2u4+5sEf3vnh3UeSTC29/Zw378Ch1hwH+ZBBGM/7/B1Y1xvJPjbHm7BOPBTC3UTXIjKhZ9H\npZl9gyAZfbiY9xx2Bb6GYJz4RuHnMNrMCmOSqwmS2aUWTDZ2fmTfWQSzIv/UzCrMbG+CWZALn+en\nzWzHsBV2OcHFl2i3+30J/q0UEelzlKyK9A8rCCanedaCmSufAaYT/BDE3f9JcL++v4dd1KYTjBfF\n3RcStDT+kqBL4zbAk4WK3f0BgnGVdQQThDQfT/kVgkTqVYKujbfRcjfblhxP8MPsdYLJg77Vgfdc\niO8+4PcE4wPfYl2C3mJXWne/JTzutwm6Q88DdgP2DRPoNt9z+MP4GwQJ0hKC1tDJRYZbmNhpkZm9\nGFl/E0EreKuJWxePC/A1gi6p7xP8gP9zG8d6BTiboPVyXni86H03fxce+34zW0HwmY8P932XoHvy\ndwk+35dY19r1dYLWzbcJJqz5Gy3c/qQNfyOYSOsfzbo7d6TeU4HvEXzXdwCeimx7mKCl7X0z+0iX\ncHd/kOBiyO0En8tWrD8+u2ju/kF4vMPaK9vJ+hsIJlQ7keA8HEtwwaI7/JggMTuHYLz1h+G6wgWB\nowjGbC4hSJCjn9FVBOM1p4WPu8N1BV8g+HtcQjCZ1dFhnYXv5RkESet8YBDrd5M+n6AL+iyC5PRi\nDyY2K3wehxP8e7WU4HM5PFxfrB8Q/hsT/jv6IEFrKgRDLgYQtMA+Q9BFOOqLBH8ji8M4o5OobULw\n7+Zygi71jxL2sLDgXtkrPbiFjYhIn2PrD1cREWmfmU0B/uLuf4o7lo4KW1SmA5XNEprWyn+OMAly\n95faK98TLLj9xXxgV3f/XxwxSO8LW7hvAPZw/WctLTCz24FrPZgwTUSkz1HLqoj0eWZ2RNi1bzhB\nC/JdxSSqAO5+P8FtTvbsyRjbcSYwVYlq/+Lur7r77kpUpTXufpQSVRHpy1LtF+kZZtkkwRiNue6Z\ng82yGxB0q9scmAkc454pdhZQEZG2nE7QtTVH0IWuvRlU1+Pud7VfqmeY2UyCSVgOjysGERERkTjE\n2bL6TYKxFwXnAA+5Z7YBHgqXRaQEufvEcuoC7O4HhDNzbuDuRxTGnpYDd9/c3ce6+3/jjkVERESk\nN8WSrJplxwCTCGbYLDiMdTehvwG1IoiIiIiIiPRbcXUD/i3wfda/4fnG7plCa8f7BDeP/wiz7JT1\nl7+/bzqdzvVEkNJ5iUTCAPL5vMZalRidm9Klc1O6dG5Kl85N6dK5KV39+dw0NDQk3F3z9pSJXk9W\nzbIHA/PdMy+YZSe2VMY942bZov54Kisr8++///4/uzNG6bqqqqptAdasWfNm3LHI+nRuSpfOTenS\nuSldOjelS+emdPXnczNs2LCDurO+8N7oFwJDgOfd/YZ2dpEOiKNldQJwqFn2IKAKGGKW/QvwgVl2\nlHtmnll2FMFtGj7CPTMxulxZeW7T7NmzH+jpoKVjampqANC5KT06N6VL56Z06dyULp2b0qVzU7r6\n+blpN1k1s+uAsIHNx0XWH0BwL/Ek8Cd3/yXBUMYxBPfnntNCddIFvd4E7p75oXtmjHtmc4Kbez/s\nnvkywQ3kTwiLnQD8q7djExERERGRfu964IDoCjNLApcDBwLbA8eF98PeDnjK3b9DcKs56Uax3bqm\nBb8EbjXLngLMAo6JOR4REREREelbqsxsSmHB3Sc2L+Duj5nZ5s1W7wG85e5vA5jZ3wlaVWcDDWGZ\nfPeH27/FOrjYPTPFPXNw+HqRe+Yz7plt3DOfdc8sjjM2EREREZFSMPadMw/p7rJV0761fXcfu1jF\n1tkTx+6C0QSJacGccN0dwOfN7A8E93KXbqSZsERERER6WE/8OO/uOsslIYrrfccZY/WKJw4u9tjF\nlq189/qizk1Hjt3d76cjx+6ANeH94ie21KraUe6+2t1Pcfevu/vl3RCfRChZFRERkVaVww/+ckiI\neuLHeXfXWS4JUVzvO84Yy0Vfez/NzAVqIstjwnXSg5SsiohI7JQQlWY5KI8f/OWQEIlI2ZsKbGNm\nW5hZBcFEsZNjjqnPU7IqItILlBC1TQlRaZYTEemDkmZ2tZm1+n+Umd0MPA1sZ2ZzzOwUd28Cvgb8\nB3gNuNXdX+mdkPsvJasiUpLKYQxRTyRjSohERER6VM7dT3P3u1or4O7Hufsod0+7+xh3vzZcf6+7\nb+vuW7n7//VeyP2XktUSotnWuk9fej/l0J2xJ2IshzFESsZEREREeo6S1RJSLrOtlUNCVOz7KYfW\nu3LoztgTMYqIiIhI/6ZktUzF+YO/HBKiYpVD652IiIiISH+kZFVERERERERKjpJVERERERERKTlK\nVkVEREREpL9o99Y1UjpScQcgIiIiIiLSS3LuflrcQUhx1LIqIiIiIiIiJUfJqoiIiIiIiJQcJasi\nIiIiIiJScpSsioiIiIiISMlRsioiIiIiIiIlR8mqiIiIiIiIlBwlqyIiIiIi0l/oPqtlRPdZFRER\nERGR/kL3WS0jalkVERERERGRkqNkVUREREREREqOklUREREREREpOUpWRUREREREpOQoWRURERER\nEZGSo2RVRERERERESo6SVRERERERESk5SlZFRERERESk5KR6+4Bm2SrgMaAyPP5t7pnzzbIXAKcC\nC8KiP3LP3Nvb8cVl6dKG1KX37cOdV70wKZ/3RD7vls+z9tndE8F6Eu5u+2x8OE8ueObYRMI8kSCf\nSFj4IB+sC15/duR+/OfK5yfl8yRyOU9G68vl1taX2HPEUTy94OkvFxPrniOO5ukFTx3vDoC5Y4Vt\n7m4Ao0cP3XR0w7E8t+DJE83MzXDAEwlzADPyZsHu4Xv5AuC2tiZzMyjsBzBx44N59NLnjoquD16v\nrTM8jvHpkZ/nwd8/d0Th82rps3THxo/8fzy38KnjwxjziUTwbBZ8ruGz77fxgUz5w9TDmx8nfE0Y\ni5sZnxn5WR644vmD3YPPxt2jz7iTcIdPbzyJx37/3BGJhOWTyXXnL5m0XOEcJpOWm7TRJ7nv5rp9\nC8c1s8L7Z108wed16MhPcO/kV8YX6gufPZm0fDIZvKedd16z8VYzt+buqW9vF2wLzkv4HfJEAgqv\nG1Ob8u9Z741JpYL9k0nzVGpdnel0wpNJy2+wYgjTpy8bkkgE8YXH8rCcJxJGIoEnkwnfqiHFqlVN\nyaqqZC6ZXHvCRURERETW0+vJKlAP7OeeWWmWTQNPmGXvC7dd6p7JxhBT7H7zmzfGz/zvrlSNyqcK\nSUo6bY2RZNQjCal/bMR8ZiSrFhQSznUJbrDc2JhP5fOeWFVfQS7nyUTC8hUViYagbqKJTD6ZtPxu\nG81h/pDBs9qL093ZfeTsfRYOq36nsC6aLBWWd9hhVGrzeTPGrtro8DfdIZ/3RLA/ls+vn7xtN2IB\nM5JV89cdgzCpc4MgEXaHjYeuYGh9asW6JBBgbQJogLk77lhlOseAAck1hc/MDF+XEFr4mvyEETMn\nLBle/U7ks1v7HCS1wXL1gHoqKxP1zY8TvA4SUHDc3RpzSdwxM0gkyJkl1ibnhcTdDN+wehUDViXX\nhBcS1p6zyPlM5PMkptWPYtb8VWMKFwUKn1vh44+uHzhiG/47f8m4QnIeJsZWSM7dPfHUU0tHbti0\nH68tfndSNKEGEpHzYoDdMehYZi1/7eTCcdwL9az3OjG08pssXfPsedHPJKjPozGaO5ZO/Iz6pgcv\ncycRfi75RMJy4UWCXHiRIL/x4B+yuP7BnyaTiaZk0hqTSWtKpawpmbTGVCp4nUolGj816kienP/0\nlwrfnch3db3PCWDvTY7iucXPHJtKWS6VShTqaEqnrSmdTjRVVCSa0ulE7pANd+WuO1/5ZPi9sML3\ndt1Fj+C9HzBybx7828sT0+lgv0I96XQiV1GRyFVUJJoqK4PX9ZWjuT9M/FMpy1dUJPKpVCJ8tnw6\nncibDa9oWjGQN99cMTj87Ai/i2tf5/PBBaERS6t5660VgwYMSOYGDUo1DRiQzFVWJte9YxEREZEy\n1+vJqnvGgZXhYjp89PsfWE8+uXDva778AFue9NV/FVN+XN1Tx02sverh9sudcsD02l9Pbr/cs1/a\nq3bHx4s79rNf3qt2xyfaKlNTUzN46D3P775b7bin2q/vyeM+XXtlEe/l0aMPrL3s/uJiPOmQI2ov\nva/9clO/Mr6d9xKUO+GIQ2t/1259QdmTD5pem72riDqPmlT7hyJiPHXi9Nqf/rW4Y5/xyem1517b\nVpmampr9h95z8tHTa6f9pv36drxqeu20nxVZ7nvFxbjjVdNrp52ZyzkNDflEfX0usWZNPllfn0vU\n1+eTDQ35RENDPrH34sN/9S+/5YoPP8ylVq/OpdesyaXq6/NrnxsacqmGhnxqx6HzJswZMGhOobW5\n0PpceB099i7D5054t6JqQWOjp5qa8snGRk+vXt00IJfzVGOjp3K5fKqpyVOVI7Zl2qKl20UvLhRa\n36Ot7u+wAbPnrd40l/NkLufJpiZP5XKeCpdT+XywPpfz9N3VRzNz2Wsn5fMkw0Q6EXmdzOc9kU4/\nX1nB91nZ8PTPWK+nwfot6YAPqfg2S9c8/fN83pPBgyQEF0gSCQsfNCUSlttwwI9YvOaBiwq9AcK6\nPVqfmfmY6u/y3qqHzjMLLvAULiIUehyEF37ytSNOZvrix84uXAiKfD5rPyMz/JMbH8NzC586PtoD\nxGzdBbNob5DPbfJZHrr6hQMLvRkiz/nCshk+aaNP8p9b6vaJ9D5Ye0EvmbS8mXkySf6w4Ttw98Nv\n7BTGvrZHQuH1uvX4EdVb8p9ps7ZKpy1fUZHIFS42VFYmcxUVlq+sTOby+aGVo5YP4rXXllevPSmR\niwjBc3AhYcMl1bz22vLqyspELp1OeDqdyFdVBa8rKhL5dDrR7//PExERKUYcLauYZZPAC8DWwOXu\nmWfNsgcCXzfLfgV4Hviue2ZJC/tOiS5XVSWspqZm/14Iu8c899wH1Q0NvulBO7/OqmLfS12QdPR6\nuSLLVlVVbQulHWN/PXa5nJuh9yzm5Em779h+uS/ypUn3VRRz6KH3fJHjJv07SZD8NYWPFsqdwbJJ\nV85tv76vsmzSjQvaKxeUHTZ22aSlz7RVpqqqatvK26tql01a2u5FjKH3DDt62aSl6w2VaGzMEyT/\nTYnwQoDV1+cSmzyzy6S5u7/4bNBK7OTzQctzPu9rW27zebdN/ztx1MwdHn6tqSlvuZxbY2M+kcsF\nrwvrcjm3mhmXM6Pm1BWFlt6gHl/vdS7nic3eu5ZN995mQHTfXC4oF12Xz7s1LEsyZszwj+XzzrqW\n7KCucJl83m3a7FE0VqQm5PNEj7neI5dzW9ywO++nVh1R6KUR9oBYr8U9rJuXGj/HfOad0tTkifC9\nJoLYCs+egJdSyaYM9Uy9aP2LIGsvjBSevdK/zer81IsKsRTeQ+E1EHaVN09yEXm7/4/BvutfZIl2\n+R+QuICm5MO/j3Tt92QysbZ7fiFxH8HZLEk+c1EkrujwirXLI3Knsyg19cKgB0gwlCJM4In0AsHM\nfFTuBOZXvPSTwtCNRGL97YV9xjQey7yqV35Y2L6uvnVDARIJ880/PJj3h7/97crKRL6yMpmrrEzl\nKisT+aqqVK6yMpmvqkrmqqqS+aqqVG7xO1swh9wXUqlEOAxh/ed0OuG53OrNhy0YxurVgw9NJNZu\nI5VKeLBsnkwG69Y0pNhww00+X4ipcO7CiyNrz0EiYfH9W67/b7rl2LGWK4Nj97lzI31WLMmqeyYH\n7GyWHQb80yw7DrgCuJDgR+SFwCXAyXHE19uuueaVLQ44YOysVDK/XdyxiEj5SqcTpNOJ/ODB6Xx0\n/dAZSxm2wwar29t/6KL32exTmy5rt9w9r7Fs0sfntV9u6u7LJu36TnvlgrKHbL9s0i3T2y/3/7Za\nNum6F9ov95Wjl0367ZPFHfvko5dNWvpIW2UiFxLa7akSXkhotVwul6epya2hIWcbPDD6yAX7zZlc\nSKALFxEKiXV4YYERj25z2Jzxr9/f2JhPNDbmLXwkmprWfz36lYv2m7ntqXWFuiL1Fi4CADD2rYv2\nfWfLU1+PXrgobHd3y+XWLW8+++JN3x592ruF5D4c2mHROt2xse/N2OztjTdeWLgIUrjgEL3YkM+7\njVq4ghWDUk319bnkkiX1FQ0NHybr63OJhoZc2LNi3fOwxgNYwNTaaOIfdslf+zqRsIpU/Vms9Lv2\nCy++FC4QrD1m4QKI+YXk/IYjCuciMuQEb9bebfYrzP60dp6Eda3z6z9XJS6gKXH9IWFr/9pH4YJE\n4bGhfZNVP/vHp9PpRH7dI5mrqAiGAxReb91wELPvnjIuSPCDhD94XnehoJD8b7F0IjOfeHq7dTFH\ne2Gs65qx1bJ9mPvi1K0qKpL54HjJfGVlMl9Zue51RUUyv+07o1n83AfVgwenc9XVFU3V1elcdXU6\nl0xqPk4RiUcsyWqBe2apWfYR4IDoWFWz7DXA3a3sMzG6XFl5btPs2bMf6NFAe9DKlY3JyZPf+fwl\nl+x8MXBhse9lKBxdTNnuLlds2ZqaGiqhtpRj7K/H1rkp3WP3xLnpSNlS/3ziPHZPnZsxlY1Hrlgx\n/9/tlRtRvfqw91PL7k6lYMCA1koZ45pm7je0Nvn39uobVzlj3+m1lUUOL5i+1/TaIde3X+753afX\njrim/XKPXjW99rI/FHfsU66aXjvtR22VCYY2DDt6eu20b7Vf345XTa+ddkZ75XI5Z8dpO131wnb/\nPSuXy1tqW2sMAAAgAElEQVQ+jzU1FZ7dCusaG/O217zPXPrw8PvPbWz0RHjRILHutSeamvKJpia3\n/XM/P++O1ftfGwxlCIYx1NfnUw0N+VRDQz7d2NiUWrnSk8OHf7jNc/OWvbZuuEAwf0MhES/MLZDP\nk6jeaNCOz894bx40T7Z9vdnrUiOG80jdzGWFoQ7hcIWKZsMWUqMHHs2Mi+/bqakpX9HU5BVhmXQ4\nb0BDKlV4JBo2H/JNZn79hvGReQ/C+RvWzTkxcGDFoGq+z/yzrp9QmJ8gMiQg8pr8ziNPYtqP/rpN\ndKhFdGhBdN0+mxzJs7/+x4bJpOWij3AuglzhccjG4/n3bfeujgwbWDvxYDihoSeTlj982Me47+kp\nc1Mpy4WTB+aDZ8unUol8Om35dDqRO9hHHP3kP19+vro61ThkSLpx2LCKxgEDkutdHCzor/+mxfm+\nO+AQM7sauMvd2x22JfGKYzbgkUBjmKgOAPYHfmWWHeWeKVypPwJo9wp7X3DllTNqhw+veH/ffTea\nT13c0YiIiEgyaSQSTpCIJNssO2LlarbffuiK9uocVzeHAbVjZ7Rf7pFjDq79fbsXMIKyp3xueu0v\nb2+/3Ff3n177fze3X+4bV02vnXZ+dF1jY96WLWtML17cULFsWWPF0qUNFStWNFVMSl587n3+pxvD\nxJNkMhhbnkwGCWUyab7jjmP32vSFvQ64J/G3q8JeAclIUp9sbPREU5Mnm5ryiQMH/nGHycsmPRlO\nHBntPr92wsDCEIOdhs+bMKuian44V0BhzoBkOAdBYa6A5NSVNbwxf8VW4aR4690VIDL5YGL2sAlM\nWzRn/3D8f3jXgLXPycLy5QNOYd6KF37Q1OTpfN7TTU1eEb7XxuaPsUO+zbsrHj6vvc98i6HfZM7q\nR76fSiUaUylrTKWsIZyoryGVssaKikRjOp1onDT60zx03X8/Fybm+WSSfDgUIBcm3blwtv78YRuM\n464HXt8lcrcEwufCEAMfN27lqG3nbsdDL76zzeDBqYYhQ9INQ4akGoYOrWgYPryiYfjwdEMfnrQv\n5+6nxR2EFCeOltVRwA3huNUEcKt75m6z7E1m2Z0JugHPBE4vprIEubLum/Lww/P33mefke1O8CMi\nIiLS29LphI8YUdkwYkRlQ3T9uLq5VNaOebetfWtqRq4cOm8BjbWbtDtsYFzdq2xZu93LxcQ0ru7p\n4/epvbqIiRlP23d67fk3tl/u7Kum1077Xfvldrxqeu20c6LrVq1qSi5f3phavrwxvXx5U8XKlU2p\nlSubKg70i8+7l+v+3F6dn8v/+rzbVl5xx4cf5lIffpirWLMmn16zJpeur8+lGxry6fr6fEVjYz69\n7MMqli1rGFK4Y0AuFyTa4W0J195BIJ/35IoNd+W/CxfsGT1OofWbcED7yy+vHLlB/T689MGswwot\n6dEW9aYmr0gkyKVSiYYRg37MsoYHLgomvLNcs4n8coW7WCQSlhs/6su8suKpEyorE/WVlYn6qqrk\nmqqqZMOAAcn6QYNSawYNStYPHpyu/8nHq9r7aESAeGYDrgN2aWH98Z2pL0GubG/U+OKLS4Z98MGa\nLc86a+ur4o5FRERERDpm0KBUbtCgVG7UqAH10fXj6t4jVTt6Tnv7j6ubQ1Xt5m+1X+6kg6fXXnxb\nMTGNqzvrqum137uirTJB9/kTjp5eO63FW0bmcs6KFY2phQvrK3ebfeBv/j3gzkvq6/PJ+vp8srEx\nX5i9P9nUFDw3NnqysTGf/Exl3bhb5k763+rVucoPP8xVrlmTq1q+vHFIfX2+sqEheNTX5wbcsOoc\nPr7z84ecc87HHxw7dtCHxbwv6Z9iHbPa31177dt7bbdd9fPNr1aKiIiIiMQlmTSGDatoGjasomnM\n6mXsWTtiUTH7jaur4+NF3LZwwAMTrzrkmos2OPLIJ3++xx4bTFHSKq0p6y605ayxMW8vvrhkwlFH\njVEXYBERERHpN7baeBG33rrXDb/97S6/XLSoYYMjj3zy52ec8fwhM2euGhh3bFJa+k2yOvadMw+J\nO4aoG26YuV06bWsOP3zMrLhjERERERHpbfvsM3JBIWldsqRh+FFHPXmhklaJ6jfJavWKJw4uplxv\nJbX33vvehPHjN3wymSzbIbciIiIiIl22zz4jF9xyy143/v73u/6ikLSefvrzhy5Z1eq9uqSf6DfJ\narGKTWqh+MS2ebmZM1cNnDlz1Y6nn77Vsx2NT0RERESkL5owYcTCQtK6dGnD0FOvOTrukCRmSla7\noNjEtnm5K654a4+xYwdN33rr6lU9E5mIiIiISHkKk9abbvnGX+IORWKmZDUGzzyzaO+DDhqliZVE\nRERERFqRTHjcIUjMlKz2sjvvnLNZfX1+4IknbvFG3LGIiIiIiEjnmdlEM3vczK40s4lxx9PXKFnt\nZf/4x+y9d9112JPptC4ViYiIiIiUGjO7zszmm9n0ZusPMLM3zOwtMzsnXO3ASqAKmNPbsfZ1SlZ7\n0eLF9enXX1+x20knbfl03LGIiIiIiPRDVWY2pfBopcz1wAHRFWaWBC4HDgS2B44zs+2Bx939QOAH\nwE97LOp+SslqL/rjH9/adaONKmfuvvsGi+OORUREREREPsrdHwOa/17fA3jL3d929wbg78Bh7p4P\nty8BKnsxzH4hFXcA/cljjy2YsP/+m0yJOw4RERERkX5qjbtP7MR+o4HZkeU5wHgzOxL4PDAMuKzr\n4UmUktVe8vjjC0YuXtyw6ZlnbvVy3LGIiIiIiEjXufsdwB1xx9FXqRtwL7nxxpkTxo0b+uzgwelc\n3LGIiIiIiEiHzAVqIstjwnXSg5Ss9oKmXIKXX176yeOO20z3VhURERERKT9TgW3MbAszqwC+AEyO\nOaY+T8lqL/j3y9sxeHBq8ec/P2ped9W5onrvu7urro7WV2zZ+s1OfLU76+vu91wuxxYRERGRbpM0\ns6vN7JDWCpjZzcDTwHZmNsfMTnH3JuBrwH+A14Bb3f2V3gm5/9KY1V5w7aN7MGHCiCfbK9eR5GXW\nFlfcVUy5Yusstr6OlF2z429fZfbsdssVW19HYuzu9x3nseO8kCAiIiLSx+Tc/bS2Crj7ca2svxe4\nt0eikhapZbWHvfrqsuopr27JWWdtPbW9sh1JiIrVE3WWgzjfd3cfu8cuJBShJ1qe1aIsIiIiIsXo\nVy2rjY15mzv3wwFz53448IMP1gxcuLB+0JIlDQOXL28cuHx506BVq5oG7VJ9FI/Pe+qEfN4TwYNk\n+DqZz5NY99qTWw45m/8teeQcd0+4B9vcSbi7Bc9YY2O+6oQJdYwadWR93O9fpKN6ouW5J1qURURE\nRKTv6bPJ6osvLhn24IMfbPXqq8u2fPfd1Vs2rf4pS1ff/8dUyuorKpKrKysTq6qqkqurqhKrBg5M\nrR44MLm6ujq1cpexc1k4bMj/kknLp1KWTyYtl0pZPpVKFJ7zqZTl0mnLHzbgN5n7cgfdEqw3TyYT\n+fB1oZwnk5Y/ecD3LnqdC+L+SETKSpzdpOOqT0RERETW6RPJ6vLljal7751XM3Xq4i1nzFi51bx5\nH26Zy3l6k02q3t5ii8Ezjj9+83/+cNtzvjtrt6fOqqxMelt1jat75si9a695qpjjjqubydDazd5p\nr1yqLl/sWxGRDoqzVbcnxjLHVZ+IiIhIqSn7ZHVNY4pPferhS4cMSc8fM2bAjF13HV43ceJ2/5ww\nYcSCZNLWlhtRt5r320lURUQg3vHjxU5+1ROJshJgERHpB5JmdjVwl7v3y7ldyknZJ6vpZI677v1U\nZtSoARoTKiJlr9hZtDuiu8ceK/kVEZEy1u5swFI6yn424GTCUaIqItJ74rzlkxJlERGR/qPsk1UR\nESl/3Z0A90SiXGwX7Z6Y9EvJt4iI9EdKVkVEpF/r7vsT98SkX3F20VZCLSIicVGyKiIi0kfEeW/k\ncrjdlIiIlBclqyIiItJreiJRjrOLtoiI9Jxenw3YLFsFPAZUhse/zT1zvll2A+AWYHNgJnCMe2ZJ\nb8cnIiIi5aXYWbTjvC+zulOLiHRcHC2r9cB+7pmdgJ2BA8yyewLnAA+5Z7YBHgqXRUREREpWOUwO\npgRYRMpVryer7hl3z6wMF9Phw4HDgBvC9TcAh/d2bCIiIiLlIs7xxCJlLGlmV5vZIXEHIu3r9W7A\nAGbZJPACsDVwuXvmWbPsxu6ZeWGR94GNW9l3SnR5YAXU1NTs3+5B67q5XE/V2UdUVVVtC1BTUxN3\nKNKMzk3p0rkpXTo3pUvnpvvka+5eUwNF/V6pX3riq+39tqmqqtq2aZtvflDMb6Bi6uto2aLrLIff\niN187MjfTd9538XLuftp3Vyn9JBYJlhyz+TcMzsDY4A9zLLjmm13gtZWERERESkxxd7KKVf7qw+6\ns76OlC22XLETdBVbTkS6TywtqwXumaVm2UeAA4APzLKj3DPzzLKjgPmt7DMxujyo8ns+e/bsB9o7\n1lA4ujvLdaRsonrvqmLr7CsKV7j72/suBzo3pUvnpnTp3JQunZvSVTbnZth3Hyhmgq6iy1H8b79i\ny3X379OamhoqoTau38Y98bu8Aw7q5vqkB/V6y6pZdqRZdlj4egBBd5PXgcnACWGxE4B/9XZsHVXs\n2I6OTJYgIiIiIuWtHO5PrJZiKQdxdAMeBTxilq0DpgIPuGfuBn4J7G+W/R/w2XC513XkHwMloSIi\nIiLS03ritkvFdpPW/YklTr3eDdg9Uwfs0sL6RcBnejue5pSAioiIiIgE4rw/sUgsEyyJiIiIiEj/\npMYhKVa/SVZ1BUdERERERKR89JtkVVdwREREREREykest64RERERERHpL8xsNDCWSB7m7o/FF1Fp\nU7IqIiIiIiLSw8zsV8CxwKtALlztgJLVVihZFRERERER6XmHA9u5e33cgZSLfjNmVUREREREJEZv\nA+m4gygnalkVEREREZH+ImlmVwN3uXtvT8C6GnjJzB4C1rauuvs3ejmOsqFkVURERERE+oucu58W\n07Enhw8pUtknq3mSHncMIiIiIiIibXH3G8ysAtg2XPWGuzfGGVOp6wvJaj7uGEREREREpHutqN77\n7rhj6E5mNhG4AZgJGFBjZifo1jWtK/tkVURERERE+p5ZW1zR22NKe9olwOfc/Q0AM9sWuBn4RKxR\nlTDNBiwiIiIiItLz0oVEFcDd30SzA7dJLasiIiIiIiI973kz+xPwl3D5S8DzMcZT8pSsioiIiIiI\n9LwzgbOBwq1qHgf+GF84pU/JqoiIiIiISA9z93rgN+FDiqBkVUREREREpIeY2a3ufoyZTQM+cttN\nd6+NIayyoGRVRERERESk53wzfD441ijKkGYDFhERERER6SHuPi98eZa7z4o+gLPijK3UKVkVERER\nERHpJDMbZGbPm1l7Laf7t7DuwJ6Iqa9QsioiIiIiIhIys+vMbL6ZTW+2/gAze8PM3jKzcyKbfgDc\n2kZ9Z4bjVbczs7rI4x2grmfeRd+gMasiIiIiItJfVJnZlMKCu09socz1wGXAjYUVZpYELidoHZ0D\nTDWzycBo4FWgqo1j/g24D/gFEE1yV7j74s68if5CyaqIiIiIiEjI3R8zs82brd4DeMvd3wYws78D\nhwGDgUHA9sCHZnavu+c/WqXPNLOzmx/LzDZQwto6JasiIiIiItJfrGmlNbU9o4HZkeU5wHh3/xqA\nmZ0ILGwhUYWgZfVg4AWCW9dYZJsDW3Yinn5ByaqIiIiIiEgXuPv1bWw7OHzeotcC6iM0wZKIiIiI\niEjb5gI1keUx4bqimdkEMxsUvv6ymf3GzDbrxhj7HCWrIiIiIiIibZsKbGNmW5hZBfAFYHIH67gC\nWG1mOwHfBWYAN3VvmH2LklUREREREekvkmZ2tZkd0loBM7sZeJrgVjNzzOwUd28Cvgb8B3gNuNXd\nX+ngsZvc3QkmZrrM3S8Hqjv3NvqHXh+zapatIZgGemOCAcVXu2d+Z5a9ADgVWBAW/ZF75t7ejk9E\nRERERPqsnLuf1lYBdz+ulfX3Al3JT1aY2Q+B44F9zCwBpLtQX58XxwRLTcB33TMvmmWrgRfMsg+E\n2y51z2RjiElERERERKQnHQt8ETjZ3d8Px6v+OuaYSlqvdwN2z8xzz7wYvl5B0Iw+urfjEBERERER\n6S3u/j7wV2ComR1McBudG2MOq6RZ0G06poNbdnPgMWAc8B3gJGAZ8DxB6+uSFvaZEl2uqjpvn/ff\nf/+OHg9WOqSqqmpbgDVr1rwZdyyyPp2b0qVzU7p0bkqXzk3p0rkpXf353AwbNuwgdx8Ux7HN7BiC\nltQpBPda3Qf4nrvfFkc85SC2CZbMsoOB24FvuWeWE8yOtSWwMzAPuCSu2ERERERERLrZucDu7n6C\nu38F2AM4L+aYSlocY1Yxy6YJEtW/umfuAHDPfBDZfg1wd0v7umcmRpcrK89tmj179gMtlZX41NQE\nt6HSuSk9OjelS+emdOnclC6dm9Klc1O6+vm5OcTMrgbucve7evnYCXefH1lehO7O0qY4ZgM24Frg\nNffMbyLrR7ln5oWLRwDTezs2ERERERHp09qdDbgH/dvM/gPcHC4fS9dmF+7z4mhZnUAwXfM0s+xL\n4bofAceZZXcmuJ3NTOD0GGITERERERHpdu7+PTM7Etg7XHW1u/8zzphKXa8nq+6ZJwgGFDenqwoi\nIiIiItKXPQXkgDwwNeZYSp76SIuIiIiIiPQwM/sq8BzBkMejgWfM7OR4oyptsUywJCIiIiIi0s98\nD9jF3RcBmNmGBC2t18UaVQnrUsuqWXZbs+xDZtnp4XKtWfbH3ROaiIiIiIhIn7EIWBFZXhGuk1Z0\ntRvwNcAPgUYA90wd8IWuBiUiIiIiItLHvAU8a2YXmNn5wDPAm2b2HTP7TsyxlaSuJqsD3TPPNVvX\n1MU6RURERERE+poZwJ0Edz8B+BfwDlAdPqSZro5ZXWiW3YrwAzfLHg3Ma3sXERERERGRWCTN7Grg\nLne/qzcP7O4/7c3j9QVdTVbPBq4GPmaWnUtwZeBLXY5KRERERESk++Xc/bS4g5DidDpZNcsmgN3c\nM581yw4CEu6ZFe3tJyIiIiIiItKeTo9Zdc/kge+Hr1cpURUREREREfkoM0ua2bfjjqPcdLUb8INm\n2QxwC7CqsNI9s7iL9YqIiIiIiPQJ7p4zs+OAS+OOpZx0NVk9Nnw+O7LOgS27WK+IiIiIiEhf8qSZ\nXcZHGvr8xfhCKm1dSlbdM1t0VyAiIiIiIiJ92M7h888i6xzYL4ZYykKXklWzbBo4E/hUuGoKcJV7\nprGLcYmIiIiIiPQZ7v7puGMoN52eYCl0BfAJ4I/h4xPhOhEREREREQmZ2cZmdq2Z3Rcub29mp8Qd\nVynr6pjV3d0zO0WWHzbLvtzFOkVERERERPqa64E/A+eGy28SjF+9Nq6ASl1XW1ZzZtmtCgtm2S2B\nXBfrFBERERER6WtGuPutQB7A3ZtQ7tSmrrasfg94xCz7NmDAWOCkLkclIiIiIiLSt6wysw0JJlXC\nzPYElsUbUmnr6mzAD5lltwG2C1e94Z6p73pYIiIiIiIifcp3gMnAVmb2JDASODrekEpbl7oBm2XP\nBga4Z+rcM3XAQLPsWd0TmoiIiIiISN8Q3k91X2Av4HRgB3evizeq0tbVMaunumeWFhbcM0uAU7tY\np4iIiIiISE9ImtnVZnZIbx/YzKqAbwAXAj8Fzg7XSSu6mqwmzbJWWDDLJoGKLtYpIiIiIiLSE3Lu\nfpq73xXDsW8EdgD+AFwWvr4phjjKRlcnWPo3cItZ9qpw+fRwnYiIiIiIiKwzzt23jyw/YmavxhZN\nGehqsvoD4DTgzHD5AeBPXaxTRERERESkr3nRzPZ092cAzGw88HzMMZW0rs4GnAeuBK40y24AjHHP\n6F5BIiIiIiIi6/sE8JSZvRsubwa8YWbTAHf32vhCK01dSlbNslOAQ8N6XgDmm2Wfcs98uxtiExER\nERER6SsOiDuActPVCZaGumeWA0cCN7pnxgOf6XpYIiIiIiIifYe7z2rrEXd8pairyWrKLDsKOAa4\nuxviEREREREREelysvoz4D/AW+6ZqWbZLYH/dT0sERERERER6c+6OsHSP4B/RJbfBo5qax+zbA3B\nPYY2Bhy42j3zu3CCpluAzYGZwDHumSVdiU9ERERERETKU1dbVjujCfiue2Z7YE/gbLPs9sA5wEPu\nmW2Ah8JlERERERGRsmVm74SPZ+OOpdx09T6rHeaemQfMC1+vMMu+BowGDgMmhsVuAKYQ3MdVRERE\nRESk5JjZx4FvAiOAh9z9iuZl3H2LXg+sj+j1ZDXKLLs5sAvwLLBxmMgCvE/QTbilfaZEl6uqElZT\nU7N/D4YpnVBVVbUtQE1NTdyhSDM6N6VL56Z06dyULp2b0qVzU7p0btpmZtcBBwPz3X1cZP0BwO+A\nJPAnd/+lu78GnGFmCYKhjh9JVs3sHYLhjwvcfXxvvIe+otPJqll2O+A04GPhqteAa9wzbxS5/2Dg\nduBb7pnlZtm129wzbpb1zsYmIiIiIiLSSdcDlxEknwCYWRK4HNgfmANMNbPJ7v6qmR0KnAnc1FJl\nalntvE4lq2bZTwJ3AFcBVwNG0EL6iFn2SPfMM+3snyZIVP/qnrkjXP2BWXaUe2ZeeDuc+S3t656Z\nGF2urDy3afbs2Q905n1IzylcqdO5KT06N6VL56Z06dyULp2b0qVzU7r6+bk50symFBbcfWLzAu7+\nmJlt3mz1HsBb7v42gJn9nWAY46vuPhmYbGb3AH9rXp+ZbdZWQO7+bsfeQv/R2ZbVnwDHuWemRNbd\naZZ9GDgfOLC1Hc2yBlwLvOae+U1k02TgBOCX4fO/OhmbiIiIiIhIdxoNzI4szwHGm9lE4EigEri3\nlX3vIegGbJF1DowENiLoViwt6GyyulWzRBUA98yjZtmr29l3AnA8MM0s+1K47kcESeqtZtlTgFnA\nMZ2MTUREREREpCVrWmpN7Sx3n0IwMWxbZXaMLoettj8APgtc1F2x9EWdTVZXtLFtVVs7umeeYP2r\nClGf6WQ8Za+urm7oj3/84+MmT558ZdyxiIiIiIjIeuYC0RmpxoTrimZm2wDnAuOBS4BvuHtjt0XY\nB3U2Wa0xy/6+hfVG0EQuHXT//fdv+c477+wSdxwiIiIiIvIRU4FtzGwLgiT1C8AXi9nRzMYRJKk7\nABcDp7h7rqcC7Us6m6x+r41tz3eyThERERERkViZ2c3ARGCEmc0Bznf3a83sa8B/CMaYXufurxRZ\n5csE413vIZioaQ+zdR1N3f0b3Rh+n9KpZNU9c0Nr28yysd67tVzttNNO84YMGfJ+3HGIiIiIiPRh\nSTO7GrjL3e9qqYC7H9fK+ntpfRKltpxCMKGSdFBnb13zhHtm7/D1Te6Z4yObnwN27Y7g+pPx48cv\n/PWvf91S12oREREREekeOXc/rTcP6O7X9+bx+pJEJ/cbFHm9Q7NtrU2eJG145513Bt144417xR2H\niIiIiIh0HzP7s5ldZ2aXxh1Luelsl922mrHVxN0JdXV1I5988smDgRa7I4iIiIiISFm6niBHaog5\njrLT2WR1mFn2CIKW2WFm2SPD9QYM7ZbI+pkPPvigOu4YRERERESk211AkKwuBo6ON5Ty0tlk9VHg\n0MjrQyLbHutSRCIiIiIiIn3HieGzblfTQZ2dDfik7g5ERERERESkh7U7G3B3c/dZvXGcvqjTt5kx\nyyaB4e6ZheFyBcFVg2+7Zz7ePeGJiIiIiIh0m16fDVg6r1OzAZtlv0DQ57rOLPuoWfZzwNvAgcCX\nujG+fmOXXXbRfVZFRERERERCnb11zY+BT7hnNgW+TTCD7ZnumSPcMy92W3T9yO677677rIqIiIiI\n9DFm9lD4/Ku4Yyk3nU1WG9wzbwGEyen/3DO65UoXzJgxY/BNN930ybjjEBERERGRbjXKzPYCDjWz\nXcxs1+gj7uBKWWfHrG5klv1OZHlYdNk985uuhdX/vPzyyyOfeOKJQ4C7445FRERERES6zU+A84Ax\nQPM8yYH9ej2iMtHZZPUaoLqNZemgBQsW6PMTEREREelj3P024DYzO8/dL4w7nnLS2VvX/LS7AxER\nEREREemr3P1CMzsU+FS4aoq7q1dlGzqVrJpl25wIyD3zjc6FIyIiIiIi0mN6/T6rBWb2C2AP4K/h\nqm+a2V7u/qPejKOcdLYb8AuR1z8Fzu+GWERERERERHpSnPdZnQTs7O55ADO7AfgvoGS1FZ3tBnxD\n4bVZ9lvRZemcT3ziE3PvvPPOD+KOQ0REREREeswwYHH4emicgZSDzrasRnk31NHv7bHHHgsvvvhi\n3WdVRERERKRv+gXwXzN7BDCCsavnxBtSaevsfValm7355pvVf/nLX/aMOw4REREREel+7n4zsCdw\nB3A78El3vyXeqEpbZydYWkHQomrAALPs8sImwN0zQ7opvn7j5Zdf3kj3WRURERER6bvcfR4wOe44\nykVnx6zqnqDdbOHChYPjjkFERERERKRUdLZltQo4A9gaqAOuc880dWdgIiIiIiIi0n91dszqDcBu\nwDTgIOCSbotIRERERESkDzGzpJm9Hncc5aazswFv757ZEcAsey3wXPeFJCIiIiIi0ne4e87M3jCz\nzdz93bjjKRedbVltLLxQ99/usdtuu82prq6eH3ccIiIiIiLSI4YDr5jZQ2Y2ufCIO6hS1tmW1Z2a\nzQBcmBFYswF30u67777o17/+9e/ijkNERERERHrEeXEHUG46OxtwsrsD6e9ef/31IX/961/HT5gw\n4Z64YxERERERke7l7o+a2VhgG3d/0MwGAsqr2tDZltUuMcteBxwMzHfPjAvXXQCcCiwIi/3IPXNv\nHPHFoa6ubqPHH3/8UEDJqoiIiIhIH2NmpwKnARsAWwGjgSuBz8QZVymLJVkFrgcuA25stv5S90y2\n94HQ/54AACAASURBVMOJ36JFiwbFHYOIiIiIiPSYs4E9gGcB3P1/ZrZRvCGVtliSVffMY2bZzTuz\nr1l2SnS5qiphNTU1+3dHXHEaN27caIC+8F4AqqqqtgWoqamJOxRpRuemdOnclC6dm9Klc1O6dG5K\nVz8/N0kzuxq4y93v6uVj17t7g5kBYGYpwHs5hrISV8tqa75ulv0K8DzwXffMkrgDEhERERGRPiPn\n7qfFdOxHzexHwAAz2x84C+jthLmslFKyegVwIcHVhQuBS4CTmxdyz0yMLldWnts0e/bsB3ojwJ40\nffr0XYFP9oX3Auuu1PWV99OX6NyULp2b0qVzU7p0bkqXzk3p6ufn5qAYj30OcAowDTgduBf4U4zx\nlLySSVbdMx8UXptlrwHujjGcXjd+/PjZd9xxx4L2S4qIiIiISLlx97yZ3UAwZtWBN9xd3YD/P3v3\nHR9Fnf4B/POwhCSEGpJQwiaEKhxFEMVCEwQBKZ4VpCh6KneHiooVf8rdWSFYONthF0WkCSioFI/Q\niwUkgEioSSCEThJTNsnz+2Mm57JmUzeZ2eTzfr14mZ35zneenZmsefbbilDD6gAKiMQ2dXv5ZwDx\nVsVihW7dup2OjY191eo4iIiIiIjI90TkOgD7AcyEMdlsgogMtjYqe7Nq6ZrPAPQFECYSmwTgGQB9\nRWIvhvEtwyEYTePVxp49e+rPmTOH66wSEREREVVNMwBcraoJACAirWAsW/m1pVHZmFWzAY8qZPN7\nlR6IjezcuTN87dq1XGeViIiIiKhqSitIVE0HAKRZFYw/sM2Y1eqO66wSEREREVU9InKD+eP3IrIc\nwDwYvUlvBrDNssD8AJNVIiIiIiKiijPM7efjAPqYP58AEFz54fgPJqtEREREREQVRFXHWx2Dv2Ky\nSkREREREVMFEJAbAfQBawC0PU9XhVsVkd0xWbeLyyy/nOqtERERERH5ERK4HcB2AegDeU9UVRRRf\nDGNS2S8B5FdCeH6PyapNdO3aleusEhERERFZTETeBzAUQKqqdnTbPgjAawAcAN5V1RdVdTGAxSLS\nEEAsgKKS1SxVnVmBoVc5NawOgAzmOquXWR0HEREREVE19yGAQe4bRMQB4A0AgwF0ADBKRDq4FXnK\n3F+U10TkGRG5QkS6FfzzYdxVDltWbcJcZ3UEgOVWx0JEREREVEUFiciagheq2tezgKquFZEWHpsv\nA5CgqgcAQETmAhghInsAvAjga1X9sZhzdwIwFkA//N4NWM3XVAgmqzZx+vTp2lbHQEREREREhYoE\nkOj2OglADxgTJl0DoL6ItFbVt4uo42YALVU1p+LCrFqYrBIRERERUXWRVVhralmZY1BLOg41HkAD\nAKm+On9Vx2SViIiIiIioaMkAnG6vm5vbSqMBgF9EZBuA7IKNXLrGOyarRERERERERdsGoI25Vmoy\ngJEAbitlHc/4PKoqjrMB28SVV155JCQk5JTVcRARERERVWEOEZklIsO8FRCRzwBsAtBORJJE5C5V\nzQUwEcC3APYAmKequ0pzYlWNK+xfed5MVceWVZvo0qXL2enTp79idRxERERERFVYnqreU1QBVR3l\nZftylGPlDhFJgzH7LwDUAhAAIENV65W1zqqOLas2ER8fX//zzz/vbnUcRERERETke6paV1Xrmclp\nMIAbAbxpcVi2xmTVJnbu3BkRFxd3vdVxEBERERFRxVLDYgDXWh2LnbEbsE2cOXOG66wSEREREVVR\nInKD28saALoDyLIoHL/AZJWIiIiIiKjiuU/qlAvgEIAR1oTiH5isEhERERFRdeEQkVkAvlTVLyvz\nxKo6vjLPVxUwWSUiIiIiouqi2NmAfU1Eni5it6rqvyotGD/DCZZsolevXoe5zioRERERUZWTUcg/\nALgLwGNWBeUP2LJqE506deI6q0REREREVYyqzij4WUTqAngAwHgAcwHM8HYcsWXVNnbu3NmA66wS\nEREREVU9IhIqIs8C+BlGg2E3VX1MVVMtDs3WmKzaRHx8fDjXWSWqONdee+2Dy5Yti7Q6DiIiIqpe\nRGQ6gG0A0gB0UtWpqnrG4rD8ApNVmzh79myw1TEQVVXff/99w6NHj17kcrkcVsdCRERE1c7DAJoB\neArAURE5b/5LE5HzFsdmaxyzSkRV3vLlyy+yOgYiIiKqnlSVDYRlxAtHRFVeQkKC0+oYiIiIiKh0\nmKwSUZV39OjRKKtjICIiIltwiMgsERlmdSBUPEu6AYvEvg9gKIBU1ckdzW2hAD4H0ALAIQC3qE6u\nNgOP+/Tpc3j+/PmnrY6DqKpxuVxy6tQpZ/v27Tc2atQo0+p4iIiIyFJ5qnqP1UFQyVjVsvohgEEe\n2x4HsFp1chsAq83X1UaHDh3OxcbGvmx1HERVzfr168MDAwMz5s2b91GvXr1OWB0PEREREZWMJS2r\nqpPXisS28Ng8AkBf8+ePAKwB8JjnsSKxa9xfBwXVEKfTOcDnQVay+Pj42tu3b4+67bbbfrE6Fl8I\nCgpqCwBOJ4cK2k11uzejR49G3759N/rD50R1uzf+hPfGvnhv7Iv3xr54b8hf2GnMamPVycfMn1MA\nNLYymMq2e/fuOrNmzepodRxEVY3D4UBUVFR27969e69bt66+1fEQERERUcnYcuka1ckqEqte9vV1\nfx0YOCU3MTFxZaUEVoHWr1/fDUDvqvBegN+/qasq76cqqW735qGHHhowatSoH5KTky/78ccft7Zo\n0eKI1TF5U93ujT/hvbEv3hv74r2xr2p+b4ZYHQCVnJ1aVo+LxDYFAPO/qRbHQ0R+Li8vD3FxcYOD\ng4NzrY6FiIiIiErHTsnqUgC3mz/fDmCJhbEQURXw/fffhzocjtyOHTuetzoWIiIiIiodq5au+QzG\nZEphIrFJAJ4B8CKAeSKxdwE4DOAWK2Ijoqpjw4YNUWFhYbbt9ktERERE3lk1G/AoL7v6V2ogNnL1\n1VcfXLBgQbVZV5aoMuzduzfK6XQeAYCYmJi9YWFhXGeViIiIyE/YqRtwtda+ffvzsbGxM6yOg6gq\nOXnyZFi7du2OAMAHH3ywoHfv3tVundXly5dHHj58ONjqOIiIiIhKi8mqTWzfvr3hvHnzLrE6DiI7\nmDlzZueHHnromvLWs3Dhwvfvu+++Hb6IyV899thjT3/++ecdrI6DiIiIqLSYrNrErl27wtesWfNn\nq+MgsoO1a9desmXLll6+qCsgIEABYNCgQZOWLl3a3Bd1+pt9+/Zx1XciIiLyO0xWbeLcuXPspkdk\nSkpKapORkRH6888/1y9rHbNnz2593333DS54nZWVVdvlcjl8E6F/SUpKirI6BiIiIqLSYrJKRLaS\nmppaKzQ09NiKFSse7ty587my1rNly5Y2GRkZtX0Zm786ceIEk1UiIiLyO0xWichWIiIicpYvX/7v\niIiInPLUc+TIkei2bdse9lVc/kxVa5SnlZqIiKgKcYjILBEZZnUgVDwmq0RkKy6XSwAgIyPDMXz4\n8AkZGRll6rqbmpoa1aNHD66xCmDSpElvNmnShMv2EBERAXmqeo+qfml1IFQ8Jqs20b9//wPBwcFn\nrY6DyGoDBgx4cuXKlU1CQkLyzp07F/bFF1/ElLaOAwcO1M7Ozq7Ts2fP/y1VExMT82t4ePhvvo3W\n/nbu3Hnv2LFjE8rbUk1ERERU2Zis2kS7du3SZsyYEWt1HERWSkhICDl37lxEz549UwGgdevWu9at\nW1fqZVf27t3boGXLljsKZgIGqu86qwCwZ8+eujNnzuxsdRxEREREpcFk1SZ+/PHH0Pnz53OdVarW\nli1b1qpx48YHgoOD8wGgZ8+eu/bu3duxtPUMHjz46MKFC9/zfYT+Z9SoUWOOHTtWe86cOSOtjoWI\niIioNJis2sTu3bvD//vf/3KdVarWtm/f3qZVq1YJBa9vvvnm/efPn4/49ddf65S37kGDBj2wePHi\najcrbnx8fK9evXqlZmdnhxw6dIizIxMREZHfYLJqE+fPnw+yOgYiqx0+fLhN9+7d9xW8rlOnTl7n\nzp03/PLLLw1KU8/AgQMf2rx5cyP3bdnZ2bVdLle1/MwLCAjQ0NDQpO+++85pdSxEREREJVXT6gCI\niAq0a9cufsSIEQfdt3344YfzS1NHSkpKYGpqakynTp04YZmbZs2aJcbHx0cB2Gt1LEREREQlUS1b\nGYjInt56662vQkNDXZ7b09PTHXl5eSWqY/Xq1c0bNmx4NCQkpGQHVBOtWrU6cvjwYbasEhERkd9g\nskpEtrB58+ZGJ0+erFXYvuuuu+6Jb775JrIk9ezYsSOqadOmXF/Vw9133/3jSy+99LnVcRARERGV\nFJNVmxg4cOD+4ODgc1bHQWSVZ555ZtzcuXPbFbbP6XTuX7ly5Z9KUs+hQ4eiYmJi/pCsxsTE/BoW\nFlYt11kFgMjIyKzWrVtnWB0PERERUUkxWbWJtm3bpsXGxk63Og4iK6SnpztSU1Njhg0bllDY/ssu\nu2zXnj17SpSshoWFnezZs+d+z+3vv//+wquvvjq1vLH6s6lTp165evXqJlbHQUREVFWISEsReU9E\nFlgdS1XEZNUmtm3b1mjhwoXdrI6DyApfffVVVN26dU9ER0dnFrb/lltu2ZuamhqTkpISWFxdb775\n5rLBgwcf9X2U/icvLw+jRo0aU/B6z549rVatWlVo6zUREREZROR9EUkVkXiP7YNEZK+IJIjI4wCg\nqgdU9S5rIq36mKzaxO7du8O/++67G6yOg8gKmzdvbhMdHb3P2/4mTZpkh4eHH5o/f37bourJyMjw\nOhHT4MGD71+0aFG1Wmc1Pz9f4uPjexa8jomJSTx48GC1ugZEREQegkRkTcE/L2U+BDDIfYOIOAC8\nAWAwgA4ARolIh4oMlJis2kZaWhrXWaUy27NnT92xY8eOtDqOskpISGjTsWNHr8kqANx8883LW7du\nfaqoMi+++OIVY8aMGVPYvqysrNq5ubmO8sTp77p06XIkJSWFMwITEREVQVXXAjjtsfkyAAlmS2oO\ngLkARlR6cNUMk1WiKuDtt9++Mjs7u9gusnZ16623fnvrrbfuKarM3Xff/Utx3Xv3798f1bx5c3YB\n9qJ///5JZ8+ebZqRkVGtk3YiIqrWslS1b8G/UhwXCSDR7XUSgEgRaSQibwPoKiJP+DJQYrJK5Pdc\nLpds3bq1V35+fo3Tp08HWB1PWYwdOzahRYsWxc7Uu2jRoqg9e/bU9bb/2LFjUV26dOGyNV5ERETk\n1K1b98TGjRvDrY6FiIioKlDVU6o6QVVbqeoLVsdT1TBZJfJzH3zwwUW1atXKOnjwYKeTJ0/6Xevq\n/PnzWyxfvrxEa6jOmTOn/8cff1zoRGSZmZk1zpw5E9m/f//EwvaTYcWKFc8OGDAgxeo4iIiI/Ewy\nAPehNM3NbVSBmKzaxLXXXrs/KCiI66xSqX311Vd9rrrqqrUA1OpYymLOnDnXbN26NbokZbt167Yr\nPj6+0MkM1qxZ0yQkJOR006ZNswvbHxMTsy88PNySdUZfeOGFS3/66acGlX3egIAA3blz5wT3bcHB\nwfmVHQcREVEVsA1AGxGJEZFaAEYCWGpxTFUek1WbaNOmTdqMGTO4ziqVSl5eHurVq3fuvvvu22J1\nLGWRl5eH5OTkNv369StycqUCN9544+7k5OR26enpfxhzGRIS4ho4cOA33o61cp3VzMzMWnfdddcz\nDzzwwLXnz5+vaUUMBTZs2BB2xx133GRlDERERBZyiMgsERnmrYCIfAZgE4B2IpIkInepai6AiQC+\nBbAHwDxV3VU5IVdfTFZtYtu2bY0WLVrU1eo4yL84HA588sknn3lrTbS7zZs3h6mqXHXVVSdKUr5d\nu3bp9erVS12wYEFLz329e/c+8cwzz2zyfZTl989//nPDq6+++nxCQkKbQYMGPfPWW2/9qTLO63K5\nxH2dVQBo2rTpbzt27OjtcrmkMmIgIiKymTxVvUdVv/RWQFVHqWpTVQ1Q1eaq+p65fbmqtjXHpz5X\neSFXX0xWbWL37t3hq1evvtHqOMh/ZGdny+LFi/16zczVq1e3iYyM3OdwlHxy2jZt2uzesGHDH5K9\ndevWhWdnZ3tNwIYMGXLfggULStTd2JdmzpzZefHixVG9e/c+sWzZstdvu+22ebNnzx75+uuvd6ro\nc+fn58N9nVUAaNmy5W+BgYHp69ev5yRLREREZGtMVm0iPT3d7ybGIWu98847HV977bXRBa9fffXV\nF51OZ7Ez6trJ7t27W7dr165EXYALPPLII6umTp16QXdfl8sl999//1PJycnB3o7Lysqq7XK5Kn3J\nlmXLlvVPSkqqX/B64sSJO7/55pt/3H333fEAsGDBguiTJ0/WqsyYIiIijmzdutWvv+ggIiKiqs/S\nsVOFEYk9BCANQB6AXNXJ3a2NiMievv766969e/eOK3jdq1evEnWltZPXX3/989zc3FJ1R23btm26\n57aNGzeGBwYGZrRs2dJWyXpGRoYjNTU1ZujQofvdt9erVy+34OfFixdfOX369M433XTT/FdffRU1\nalT8d4hOp/PIr7/+GgXg+wo/GREREVEZ2bVl9WrVyRczUSUq3LZt20JTUlJa/f3vf/9fsvHEE0/0\nqewWuvIKCwvLadKkSanH286YMaPrrFmz2he83rx5c1RERITt1lf95ptvmtepU+dkUWvIfvLJJ59N\nmDDhg6VLlw7t06dP7wMHDgRVdFydO3c+lJ2dzd4cREREZGu2a1ktjkjsGvfXQUE1xOl0DrAoHJ/p\n2LFjJABUhfcCAEFBQW0BwOl0FleUymD69Ol/Gjx48LFLLrmkT8G2uLi44S+88EIdp9OZU9Sxdrk3\nS5YsCTt48GDIpEmTDpf22MaNG7fctm1bmNPp3AoAubm5nfr165db1O9Pw4YNG3Tq1OlSp9PZqjxx\nl8bp06fb9OzZM7u43+unn34ajz/++OZbbrllwLfffnvxX//61yxfnN/lckFE/vAZ+eyzzwLASQBV\n4vOmMtjl94b+iPfGvnhv7Kua3xuHiMwC8GVRkyyRPdixZVUBrBKJ/UEk9h6rg6ksAwcOPFmvXj2/\nnNGVKld+fj6+/fbbqAkTJhywOpbyWLx4cfOUlJQytSIOHz485fvvv2+cl5cHANizZ0/Drl27ninq\nmG7dup0ICwtzleV8ZbVr164GPXr0OFmSsrVq1dJx48ad7tatm08SVQAICAjAmTNnFviqPiIioiqg\n2NmAyT7s2LLaU3VyskhsBICVIrG/qE5eW7BTdXJf98KBgVNyExMTV1Z2kL6WnZ1d44UXXtiSmJjo\nd+MOC1PwTV1VuDd29NFHH62LjIzMSkxM/N+2nJycQXv37o0D8Icxne7scm/i4uIuu/feexcmJiaW\nOumuV68eAFzy1ltv/TJixIjEHj16pDidzv2JiYleu9tOmTJlJQC4X7OKNmPGjJU5OTk1EhMT80tS\n/oYbbgBQOfdm/PjxN/Xo0WP3hAkTdlf0uaoCu/ze0B/x3tgX7419VfN7M8TqAKjkbNeyqjo52fxv\nKoAvAFxmbUSVY+vWrWFcZ5VKKjIy0metb1ZITk4OOn/+fOPhw4eXugtwgVatWu1atWrVnwDgvvvu\n22m3yZUAYx3c4ODgEiWqAHDmzBlHenq6zz6Xs7Oz5bbbbrutsH01a9bM3bFjxx/WqyUiIiKyC1sl\nqyKxISKxdQt+BjAQQLy1UVUOrrNKJbFhw4awIUOGTLQ6jvJaunRpq7CwsMN16tTJK2sdV1555c7T\np0+HbtiwIWzFihVNiys/ZMiQifPnz29R1vOV1quvvtplypQpvUpzzMSJE7vMnDmzha9iyM3NreG5\nzmqBNm3aJCYmJnL5GiIiIrItWyWrABoDWC8SuwPAVgDLVCd/U8wxVQLXWaWSeP/993tFRESkFLbv\nlVdeeTEqKsp2rYuFSU5ODm3Xrl25up9OmDBh96effjrn448/vnLhwoWXFlc+Ozs7xOVyVdpn3qZN\nmzrn5eVV+rquJXXFFVccOXHiRLWcWYOIiIj8g63GrKpOPgCgi9VxENlRenq6Y8eOHVdNmzZtemH7\n/Wmd1WeffXadr+pKSkpy9uvXb6Ov6vOVpKSk1mPGjPmv1XF4c/nll590uVzBv/76a53C1q4lIiIi\nsprdWlaJyIs33nija2ho6NF+/fodL2y/P66zWl4vvfTSJUeOHOl81VVX2WqN1b1799bJzMysP3Dg\nwGSrY/EmICBAO3XqtDE5Obm21bEQERERFYbJKpGfWL16de/+/fvHedu/cuXKYSdOnLB9d/I5c+a0\nvPXWW8f6oq6LLrooFQAuvfTSU76oz1eWL1/eunHjxgcCAwPV6liK8tFHH827+uqrU62Og4iIiKgw\nTFZtYujQofsCAwPTrI6D7CkvLw8XX3zxT3//+9+3Wx1LeW3atKldcHCwT2YzHjFiROJXX301yeEo\nfmhoixYtfm3cuHGljOlNS0sL6tKly8+lPa5///4p3bt3P+urOEJCQvJ+/vnnvxVVxuVyia/OR0RE\n5AccIjJLRIZZHQgVz1ZjVquzFi1aZLz88ssvWR0H2ZPD4cC0adNsO/6xNBISEtoMGDBgbfElSyY6\nOjqzJOXee++9L3x1zuI8/fTTm8ty3J133nkUqLy1YNeuXRs+ZcqUv65bt+6flXJCIiIi6+Wp6j1W\nB0Elw5ZVm9i8eTPXWaVCnT59OuC5556rEusNZ2dny/Hjx1ted911CVbHUlHy8sq8Go/P11nNzMys\n4W2dVcDoPp2WlhaekpJi++7jREREVP0wWbWJX375heusUqHeeOONbuvWrbvC6jh84euvv3YGBwef\na9euXaXPPnvddddNnDdvXkxFn2f27Nlthg8fPqEsx953332dX331VZ/FmJeXJ97WWQWA4ODg/IYN\nGx5dvXp1c1+dk4iIiMhXmKzaREZGRrWaxZVKbs2aNb0HDhzodWKlAq+88spLLVq0yKiMmMoqKyvL\ncfnll/usC3Apzx2ck5NT4euefv/9960bNWrkN8sINW3a9MiOHTuirI6DiIiIyBPHrBLZWFxcXMT5\n8+fD77333p3FlfX1OqvLly+PfOWVV0YCEADo0aPHlmeffXZdcnJy0B133DHRs3xJ948cOfKgL+O0\nm/3797e59tpri/1ywS5iYmKO7Nu3r2VJy0+dOvVKh8OR93//939bfBXD8OHDJ0yaNOkLb8syERER\nUfXEZJXIxpKSkurWq1fvZEhISLEDIZ944ok+Dz744KaIiIgcX5x7z549EapaY8yYMYsBoE2bNmcA\noEGDBq7Ro0cv8Sxf0v1VWcGY3MGDB79vdSwl1b9//19LUi4zM7PGvffee9P27dv7tm/ffjMAnyWr\nBw8e7Lp8+fJ9TFaJiIjIHZNVoipi1apVQ0ePHv2Tr5JVAKhdu3baHXfcsc99W0hISJ7nttLsr8pW\nrFgRadWY3LLq16/f8ZIkicuXL3eePHky4pprrvkiOTm5aWXERkRERNUbx6zaxPDhw/fVqlXLb/7A\npcoxevTo/atXr55mxbkffvjhn5YuXfq2FeeuCC1bttwXERFRoWN6HQ6H9uvXb2VZj+/fv//xSy+9\n1Gct0HXq1Cl2nVUASE5ODvI2I3BycnIQANx4442Hv/zyy9cHDRoUP3DgQJ+1qgJAeHj4we7dux/w\nZZ1ERETk/9iyahPR0dFcZ5WoAr3zzjuLK/ocQ4YMSR4yZEhyWY8fP358pa6zWuCBBx4Y1b59+33/\n+te/1rtvf//999u99dZbd73++usv9ujR47TD4cDAgQOPATjmy/PPmjXr302aNMnyZZ1ERETk/9iy\nahMbNmyIWLJkSRer4yB7Wbt2bfikSZMGWnHuRYsWRT355JO9rTi3P8rLy8O2bdtC7bTOakZGhmP0\n6NFe11ktEB0dfeTAgQNO921Tpkzp9eabb949YcKE93r06HG6YPuBAwdqb9u2LdRXMQLAa6+91vvn\nn39u4Ms6iYiIyP8xWbWJPXv2hK9cufImq+Mgezly5Ej9nTt3WvIlxv79+8N27drV3opzV4Trrrvu\n73Pnzq2wdVa///770L/97W9PlKeO+++/v/Mrr7zisxhdLpfEx8dfVVy5Tp06HTl27FgUYEykNHbs\n2FvXrFlzzYwZM6bddddde93LfvTRRxdPnz59mK9iBIA1a9Zcv3HjRi6fQ0RERBdgsmoTv/32G9dZ\npXJ5+eWXp7Vq1Yrjnr3Izs6u7XK5Kmyd1VWrVrVu1qxZgsNR4Uu5+lz//v2Tzpw5E5mdnS0zZsy4\n9MSJE03mzJnzYp8+fVIrK4bjx483rKxzERERkX/gmFWiKsLX66xS6ezatat1mzZtEqyOoyycTmdm\nUFBQWlxcXJMnnnhiS05Ozrbg4OB8q+MiIiKi6o0tq0RVxJNPPtnb24yuVPESExNbX3HFFX6ZrAJA\nz549V0dHR6c5HA4wUSUioirMISKzRMSnQ1qoYjBZJaoiVq5cOTQ1NTXI6jiqo0OHDtVOT08PGzJk\nSOVO4+tD06dP/86f1oclIiIqozxVvUdVv7Q6ECoek1Wb+POf/7y3Vq1aFboGJPmfMWPGJKxevXq6\nFed+5JFHflyyZMl/rDh3RYiJiamwdVYDAgLyx48f/255WyT79et3vHv37j5bZ7VBgwa5O3bs+Luv\n6gOAnj17HqiAdVYPdOvW7ZAv6yQiIiL/xzGrNuF0On97+eWXX7Q6DqKqqiLXWY2MjMy6//77fy5v\nPVats1oaAwYMSAGQ4ss6Z82a9TrXWSUiIiJPbFm1ifXr1zfmOqvkKS4uLsLKdVanTJnSy4pz+5s3\n3nijY2pqarln9D579qwjLS3NZ5/L6enpjtGjR4/yVX0A11klIiKiysNk1Sa4zioV5vDhw/Xj4+M7\nW3HuhISE8Pj4+CqzzurQoUP/NmfOnJa+rvfs2bM133333Xvy8vKkvHX5ep3VnJycGrt27Sp2H+tI\n5wAAIABJREFUndXSmD17dpdp06YN92WdXGeViIiICsNk1SYyMzMDrI6B/NvLL788vU2bNmlWx2FX\n2dnZtXNycny+COqyZcui69evn9K0adNsX9ddnaSkpPi0tZaIiIj8H8esElURXGfVGlu3bm0dFRXl\nt0vWEBEREdkVW1aJqogpU6b0OnbsGNdZrWQJCQmtO3XqxGSViIiIyMeYrBJVEStXrhyakpISbHUc\n1YnL5ZKUlJTW11577X6rYyEiIiKqatgN2CZuvPHGX+bOnfub1XGQvYwbN27fuHHjYq0496OPPvoD\ngB+sOHdFiImJ2de4cWOfrrNao0YNnTlz5nOdO3c+54v6+vXrl9K4cWOfjX0NDQ11bd++faKv6gOA\nnj17HmzWrJnP1oIFgIiIiP1du3Y95Ms6iYiIyP8xWbWJyMjIzJdffvkFq+MgqqpmzZq1xNd1OhwO\nXHXVVSd9Vd8dd9xxDLD3Oqv9+/dP6d+/v0/XWf3Pf/7zBtdZJSIiIk+26wYsEjtIJHavSGyCSOzj\nVsdTWdauXdt4yZIllixRQvb13//+17J1VhcuXBj91FNPcZ3VIvzf//1fz9WrVzfxVX0Vsc7qmDFj\nbL/O6quvvto7Pj6e66wSEZHfEZEQEflIRN4RkdFWx1PV2CpZFYl1AHgDwGAAHQCMEontYG1UlWPv\n3r3hK1euvNnqOMheEhMTrVxnNawqrbM6bNiwv3766aetfFnnqlWrBvuyvkmTJnWaMWOGz9aCzcrK\ncsTHx1/pq/oA4JNPPvH5OqtxcXHXr1+/nuusEhGRLYjI+yKSKiLxHtsHicheEUkQkYJGtRsALFDV\nuwH49P+PZL9uwJcBSFCdfAAARGLnAhgBYHdBAZHYNe4HBAXVEKfTOaAyg6wIrVu3jgSAqvBeACAo\nKKgtADidTqtDqVTvvvtu5MiRI4/VqVMn3xf1derUKaxRo0YNS/JcrFixYlPbtm0vCwwM1KLKlfTe\ndOzYsfmhQ4caV5VnMiQkJPKiiy7q4XQ6fZIM7t+/PwhAvXHjxnWqUaNGJ1/UWa9evQYNGjSo7atr\nXr9+fYfD4XD48h526NAh+vTp0xG+fi7q169/hdPpDPNlnb5UXT/T/AHvjX3x3thXNb83QSKypuCF\nqvYtpMyHAF4H8HHBBhEpaFQbACAJwDYRWQqgOYCdZrG8Com4GhPVIv+urVQisTcBGKQ6+S/m67EA\neqhOnuhWZs2FRz3SG0Bm5UVJRERERER+qjaAuIIXXpJViEgLAF+pakfz9RUApqrqtebrJ8yiSQDO\nqOpXIjJXVUdWXOjVj91aVoulOrnvhVsmWxIHERERERFVG5EA3GdATALQA8BMAK+LyHUAvrQisKrM\nbslqMgD3/gjNzW1ERERERES2oqoZAMZbHUdVZbdkdRuANiKxMTCS1JEAbrM2JCIiIiIiqubYqGYB\nW80GrDo5F8BEAN8C2ANgnurkXdZGRURERERE1ZzZqCYxIlILRqPaUotjqvJsNcESERERERGRlUTk\nMwB9AYQBOA7gGVV9T0SGAHgVgAPA+6r6nHVRVg9MVomIiIiIiMh2bNUNmIiIiIiIiAhgskpERERE\nREQ2xGSViIiIiIiIbIfJKhEREREREdkOk1UiIiIiIiKyHSarREREREREZDtMVomIiIiIiMh2mKwS\nERERERGR7TBZJSIiIiIiItthskpERERERES2w2SViIiIiIiIbIfJKhEREREREdkOk1UiIiIiIiKy\nHSarREREREREZDtMVomIiIiIiMh2mKwSERERERGR7TBZJSIiIiIiItthskpERERERES2w2SViIiI\niIiIbIfJKhEREREREdkOk1UiIiIiIiKyHSarREREREREZDtMVomIKokYPhCRMyKytQTlW4iIikhN\n8/XXInJ7xUdadiLyoYg8W4bj0kWkZUXE5O9EpLGIrBWRNBGZUYLyd4jI+kqIq6+IJLm93iUifSv6\nvOVV1meUiIgqH5NVIioVETkkIplmcnHc/MOvjtVxuTNjvMbqOArRE8AAAM1V9bLSHqyqg1X1I9+H\n9TszOW5dkecojKrWUdUDZgyVlkyIyF9EJMF8nr8RkWZu+6aKiMvcV/CvpbmvpojMFZGz5nH13I57\nUkQe8mGY9wA4CaCeqj7sw3p9SlX/pKprrI6jsojIv0Rkp4jkishUj31dzOT9pPuzICIBIrJFRJyV\nHjARkR9iskpEZTFMVesA6AagO4CnSltBQWthNRMN4JCqZlgdCBktgwCeBzACQCiAgwA+8yj2uZlI\n13FPqAHcAEABhAE4ByOhhIjEABgOYKYPQ40GsFtV1Yd1UvklAHgUwLJC9r0AYDKALgCmiEgTc/tD\nABaqamLlhEhE5N+YrBJRmalqMoCvAXQEABGpLyLvicgxEUkWkWdFxGHuu0NENojIKyJyCsBUc/vd\nIrLH7OK4W0S6mdubichCETkhIgdF5P6C85otXvNE5GPzuF0i0t3cNxtAFIAvzZawR83t80UkRUTO\nmV0q/+RWXyMR+VJEzovINjPu9W77LxKRlSJyWkT2isgt3q6JGfdSs2yCiNxtbr8LwLsArjDj+kch\nxzpEJNZsjTkA4DqP/WtE5C9uZWeYZQ+KyES5sMtwUfeitYjEmdfipIh8bm5fa55qhxnjreb2oSKy\n3WxF3Cgind1i6ioiP5r34XMAQUVcm0LPa+5Tc/89AEYDeNSM4Uu36+rtebhMRL43799xEXnZWwwe\nhgJYoKq7VDUHwL8A9BaRViU4NgbAGlXNBfBfAAVdmGcCeNjcXmIicqX57J0z/3uluf1DALfj9+vx\nhx4D5vO71Hz/WwG08tj/mogkmvt/EJFebvu8/i6Z+7uJyE/mvvki8rl4afUWtx4NvqzXLF+mzwNz\nv9dnVETCROQr89k+LSLrRKREfxup6keq+jWAtEJ2xwD4zvyM3AcgSkSiAdwI4JWS1E9ERExWiagc\nxOjKNgTAT+amDwHkAmgNoCuAgQD+4nZIDwAHADQG8JyI3AwjaR0HoB6MFqlT5h+LXwLYASASQH8A\nk0TkWre6hgOYC6ABgKUAXgcAVR0L4AjM1l9VnWaW/xpAGwARAH4E8KlbXW8AyADQBEZi8L9xoSIS\nAmAlgDnmsSMBvCkiHbxclrkAkgA0A3ATgOdFpJ+qvgdgAoBNZlzPFHLs3TASqK4wWqxv8nKOgrKD\nAVwMo4X7eo/9H8L7vfgXgBUAGgJoDuDfAKCqvc39XcwYPxeRrgDeB3AvgEYA/gNgqYgEikgtAIsB\nzIbRMjkfxh/j3hR6XneqOgvGvZlmxjCsBM/DawBeU9V6MBK1eQX1icjPInJbETG5E/O/Hd22DTOT\nmF0i8le37fEA+olIIICrAewSkT8DOKmqG0p4voIYQ2G0zs2EcY1fBrBMRBqp6h248HqsKqSKNwBk\nAWgK4E7zn7ttMJ6TUBjP8XwRcf9SodDfJfP+fgHjWQqF0er851K8NZ/UW57PgxI8ow/D+H0Nh/G5\n9CSMFnOIyJsi8mYp3q+7eAADRaQ5gBYA9sN4Th9RVVcZ6yQiqnaYrBJRWSwWkbMA1gOIg5GQNYaR\nuE5S1QxVTYXRgjDS7bijqvpvVc1V1UwYydM0Vd2mhgRVPQzgUgDhqvpPVc0xu16+41HXelVdrqp5\nMP4Q7VJUwKr6vqqmqWo2jAS5ixitjw4Yf7w+o6q/qepuAO7jQofC6Lr7gRn3TwAWArjZ8xxm8n4V\ngMdUNUtVt8NoTR1XgmsKALcAeFVVE1X1NIyuhEWVfU1Vk1T1DIAX3eIo7l64YHQtbWbGWdRkPPcA\n+I+qblHVPHPMbDaAy81/AWbMLlVdACMx8qY053VX3PPgAtBaRMJUNV1VNxccqKqdVXWOl3q/AXCz\niHQWkWAAT8NIVGqb++cBaA8jkbkbwNMiMsrctxxGt+FtMLoBzwXwDIwW0OfEaL1/00yWinMdgH2q\nOtt8xj4D8AuAYcUd6Pb8Pm3e63hc+PxCVT9R1VNm3TMABAJo51bE2+/S5QBqAphp3t9FAIqdGKwC\n6i3P50Fxz6gLRpIfbe5fV9DdWlX/pqp/K8X7dTcZwF9hJM4PwvhcSANwUESWiNHD4A+fIUREdCEm\nq0RUFteragNVjTb/oMuEkYQEADhmdqk7C6MVLsLtOM9xWk4YLQ6eogE0K6jHrOtJGC0fBVLcfv4N\nQJB4GQcrRpfZF0Vkv4icB3DI3BUGIxGp6RGb+8/RAHp4xDIaRiusp2YATquqe7fAwzBag0qimce5\nD5eirGfMRd2LR2G0Im41Www9W+LcRQN42OP9O83zNwOQ7DGWsqiYS3NezxiKeh7uAtAWwC9idKEd\nWpJKzVbKqTC+fDhk/kuD0dIGVd2tqkfNJH0jjJaxm8x9qqqPm8nwPQAeB/A2jMSqO4A+AGrhj62c\nhWmGP163kj43hT2/F9QlIpPF6Gp/zrx29WE8+wW8/S4Vdn9LM9ayTPWKMet1wYRWo1G+z4PintHp\nMMaerhCRAyLyeCnen1eqelhVh6hqNwBLYPQqmAwgFsDnMFqCXzZb1YmIyIvqOMEJEVWMRBgtbmHq\nfbye5wQxifAYX+e2/aCqtiljLJ7nuQ3GJDrXwEhI6gM4AyNxOgGju2xzAL+a5d1n6kwEEKeqA0pw\n3qMAQkWkrlvCGgUguYRxH/M4d1QxZZu7vfaM2eu9UNUUGC2FEJGeAFaJyFpVTSjkPIkAnlPV5zx3\niEgfAJEiIm7JQBQK/wKiNOct7Dnx+jyo6j4Ao8zuojcAWGB2oS12IitVfQNGN1qISFsYk4XFeyuO\n37sK/4+IdAJwJYDHADwC4AdVVRHZhmJa/E1HYSRk7qJgtPwWp+D5dcJojS04tiC2XjC+JOgPYJeq\n5otIwbNfnGP44/319gVTaRRZr6oOdi8sIleg7J8HhZ3rf8+o+Xv6MIwvZDoC+E5Etqnq6jKcy5un\nAbyjqsfNZ+UpVT0nxrI/rVG61moiomqFLatE5BOqegzGeMQZIlJPRGqISCszofHmXQCTReQSMbQW\nYxKSrQDSROQxEQk2W0Y7isilJQznOH6f8AYA6sJI3k7B6OL5vFvceQAWAZgqIrVF5CJc2G33KwBt\nRWSsGMtOBIjIpSLSvpBrkAhgI4AXRCRIjImI7gLwSQnjngfgfhFpLiINYbTWFVX2ARGJFJEGMBKl\ngjiKvBcicrM5lg4wknYFkG++9rx27wCYICI9zHsUIiLXiUhdAJtgJEr3m9flBgBel+Qp5rzuPGMo\n8nkQkTEiEq6q+QDOmscUVq9nPEFmPSIiUQBmwehafcbcP0JEGpr7LwPwAIxWMvc6BMb4yPvN8x8E\n0FOM7r99YIzRLphg7JCXUJbDeMZuE2NJnFsBdIDx7BWpkOe3A9zGXMN49nNhJLU1ReRpGOPDS2IT\ngDwAE824RqCI+1sKpa23PJ8HRT6jYkwe1tq8j+fMuIp9dsxjA8QY+1sDxrUNEnMSM7cyHQD0BfCW\nuekgjLHOjWGMoT9SknMREVVXTFaJyJfGwej6uBtGMrIAxniwQqnqfADPwZj0JQ3GRCih5h/gQ2FM\nCnMQxhqT78JoES2JFwA8JUaXwckAPobR9S/ZjG2zR/mJZt0pMMa7fQYjuS1oeRkIY3zcUbPMSzDG\n/RVmFIwJVY7CmETmGS18UpzCvAPgWxgTyfwIIwkpquwKAD/DmOBqOYw/yvPM/UXdi0sBbBGRdBhj\n6h7Q35dkmQrgI/Pa3aKq38NoDX3drCcBwB0AoMYMujeYr08DuLWYmIs6r7v3AHQwY1hcgudhEIwJ\njtJhdNUdaXZNhxjdjUd7iScIxrOXDiMh2gTg/9z2jzTfbxqMZ+hF/eM6t+MBxKvqD+brRTDu/QkY\nkyXNMrc7ARQ68ZKqnjLf38MwvlB5FMBQVT3pJW5PEwHUgfFsfgjgA7d938Joof0Vxu9AFkrYldft\n/t4F40uAMTAS6OwSxuWTesvzeVCCZ7QNgFUwnoFNAN5U1f8CgIi8LSJvF1H9OwAyYfzOTzF/HutR\n5g0Yz3nB7+UTAO4HsAvA82ZvAyIi8kKUy7YREV1ARF4C0ERVby+2sE2IyGAAb6uqZ3dSsgERWQEj\nadljdSzlISJbYDxnHxRb2Ab1EhGRf2PLKhFVe2Kso9rZrbvnXTBaRW3L7A45xOxGGQljJlpbx1yd\nqepAf0xURaSPiDQxn7PbAXRGycbSWlIvERFVLZxgiYjIGNf3GYyZQ48DmAGPsYk2JAD+AWNm0UwY\n63Q+bWlEVBW1gzE+OgTG+NubzDHRdq2XiIiqEHYDJiIiIiIiItthN2AiIiIiIiKyHSarRET0P+a4\n3Q9E5IyIVPr6jyLSV4z1Jyuq/q/NMZLe9n8oIs+WsK4WIqIiUrMkdZeHiDwpIu9WRN1FnDNdRFoW\nX5KIiKhiMFkloipHRA6JSKb5x/ZxMwGpY3Vc7swYr7E6jkL0BDAAQHNV9cWamraiqoMLlp8x1z5d\nXxF1l0dhCbuqPq+qfylv3aWhqnUKlhYqTRJfEiLyiIjEi0iaiBwUkUc89l8pIlvN/T+LSE+3fV3M\nJYlOishDbtsDRGSLiDh9FScREVmLySoRVVXDVLUOgG4AugN4qrQVFLSYVTPRAA6pakZJClfTa0Tl\nJzDWAm4IY53ciSIyEgBEJBTAlwCmA2gAYBqAL0WkoXnsCwAmA+gCYIqINDG3PwRgoaqWaB1ZIiKy\nPyarRFSlqWoygK8BdAQAEakvIu+JyDERSRaRZ0XEYe67Q0Q2iMgrInIKwFRz+90issds5dktIt3M\n7c1EZKGInDBbh+4vOK+ITBWReSLysXncLhHpbu6bDSAKxh/g6SLyqLl9voikiMg5EVkrIn9yq6+R\niHwpIudFZJsZ93q3/ReJyEoROS0ie0XkFm/XxIx7qVk2QUTuNrffBeBdAFeYcf2jkGO9XaM7zWt0\nRkS+FZFot2NeE5FEM/YfRKSX275gs9XujIjsBnCpx/keM+9Tmvm++hcSU4yInBWRGubrd0Qk1W3/\nbBGZZP68RkT+IiLtAbzt9l7PulXZUESWmefcIiKtvF1LjzjWiMhfzJ8dIjLDbP07KCIT5cIuw+Pd\nnqkDInKvuT0ExvPazIwr3bxfU0XkE7dzDTefqbPmedu77TskIpPFaJE8JyKfi0iQl5hbi0icWe6k\niHzutk/N/fcAGA3gUTOeL839Xp//4qjqNFX9UVVzVXUvjNm3rzJ3XwnguKrOV9U8Vf0EwAkAN5j7\nYwB8Z/5u7wMQZT5vNwJ4paQxEBGR/TFZJaIqTYwugUMA/GRu+hBALoDWALoCGAjAvXtlDxhLaTQG\n8JyI3AwjIRsHoB6A4QBOmYnRlwB2AIgE0B/AJBG51q2u4QDmwmgdWgrgdQBQ1bEAjsBs/VXVaWb5\nrwG0ARAB4EcAn7rV9QaADABNANxu/it4jyEAVgKYYx47EsCbItLBy2WZCyAJxlI9NwF4XkT6qep7\nACYA2GTG9YyX4z2v0QgAT8JIJsIBrIOxFFCBbQAuBhBqxjjfLXl6BkAr89+1Hu+rHYCJAC5V1brm\n/kOewajqQQDnYdxPAOgNIN0tgesDIM7jmD0e77WB2+6RMJYFagggAcBzXq5DUe4GMNh8390AXO+x\nPxXAUBjP1HgAr4hIN7NFezCAo2ZcdVT1qPuBItIWxvWdBON6L4fxxUctt2K3wGixjIGxhukdXuL8\nF4AV5nttDuDfngVUdRaMZ3GaGc+w4p5/Eenp8QWAVyIiAHoB2FVUMZhfOAGIBzBQRJoDaAFgP4DX\nADyiqq6SnJOIiPwDk1UiqqoWm38sr4eRqDwvIo1hJK6TVDVDVVNhtMSMdDvuqKr+22zxyYSRyE5T\n1W1qSFDVwzBaAMNV9Z+qmmOO7XvHo671qrpcVfMAzIbRbdErVX1fVdNUNRtGgtxFjJZgB4xWo2dU\n9TdV3Q3AfWzkUBhddz8w4/4JwEIAN3uew0zerwLwmKpmqep2GK2p40pwTb1dowkAXlDVPaqaC+B5\nABcXtK6q6ieqesosPwNAIIx1NgEjqXpOVU+b3Tdnup0nzyzbQUQCVPWQqu73ElMcgD7ye5fQBebr\nGBgJ4Y5SvL8vVHWr+V4+hZFwltYtAF5T1SRVPQPgRfedqrpMVfebz1QcjISxV2EVFeJWAMtUdaWZ\nnMUCCIbRIllgpqoeVdXTMJJKb+/BBaPrdzPzeSjpGN4in39VXe/xBUBRpsL4e+QD8/UmAE1FZKQY\n41Bvh/FlRm1z/2QAf4XxBdCDMJ7nNAAHRWSJ2VL8h2efiIj8D8caEVFVdb2qrnLfICKdAAQAOGY0\n5gAw/kh2H+PmOd7NCaPlxlM0jK6a7q1HDhitigVS3H7+DUCQiNQ0k6ALmAnpczASzHAA+eauMBiJ\nSM0i4owG0MMjlpowEmRPzQCcVtU0t22HYYzrLSnPaxQN4DURmeG2TWC0uB0WkckA7jLPrTCSxzC3\neNzrO1zwg6ommN13pwL4k4h8C+Ahz5ZGUxyMluwkAGsBrAEwFkAWgHWqml/IMd543reyTM7l+b4u\nuGYiMhhGq3JbGM9gbQA7S1G3+3XKF5FEGNe7gOd7aOalrkdhtK5uFZEzAGao6vsliKEkz3+xRGQi\njC9Keplf0kBVT4nI9TCS8DcBfAtgFYx7C/PLoiHm8bVhJLcDYbQKfw5gGYB4EVltJutEROSnmKwS\nUXWSCCAbQFhhCaNJCzmmsDGLiQAOqmqbMsbieZ7bAIwAcA2Mrq71AZyBkfSdgNF1uTmAX83y7jOe\nJgKIU9UBJTjvUQChIlLXLWGNApBcjtgTYbSOfupZUIzxqY/C6Ca6y0ysCt4XAByD8V4KuoBGXXAi\n1TkA5ohIPQD/AfASjCTUUxyMCXmSzJ/XwxiTmgWPLsBFvA9fOgbjfhX43/0SkUAYLd/jACxRVZeI\nLMbv16S4uI4C6ORWn5j1l+YeGidSTYHRZRlizLi7SkTWqmqCZ1GP1+V9/iEidwJ4HEBvVfWc/TgO\n5vhlc5zvAQAz/lAJ8DSAd1T1uPll1FOqek6M2ZRbA6j05ZeIiMh32A2YiKoNVT0Go7vlDBGpJyI1\nRKSViPQp4rB3AUwWkUvE0Nrs3roVQJoYEwAFizGhTkcRubSIutwdB+C+hmVdGIn0KRitbM+7xZ0H\nYBGAqSJSW0QuwoXddr8C0FZExprdJgNE5FL3SXfc6koEsBHACyISJCKdYbR6fuJZthTeBvCEmBNC\nmV2XC7ph1oWRaJ8AUFNEnobRslpgnnlsQ3MM4n0FO0SknYj0M5O7LACZ+L3F2fN97TP3j4GRuJ+H\ncY1vhPdk9TiA5h5jPX1lHoAHRCRSRBoAeMxtXy0Y3ZtPAMg1W1kHesTVSETqF1H3dSLSX0QCADwM\n49nZWNogReRm87oDxpcjisKvsefzWq7nX0RGw3jGB5hdiD33dzWf43owWlgTVfVbjzIdAPQF8Ja5\n6SCAfmZ3/zYwxoUTEZEfY7JKRNXNOBjJwm4Yf5wvANDUW2FVnQ+je+4cGOPiFgMINRPIoTDGAh4E\ncBJGYustwfD0AoCnxJjNdTKAj2F07Uw2Y9vsUX6iWXcKjO69n8FIUGC2kA6EMV7wqFnmJRgJUWFG\nwZiY5iiAL2CMhV3lpWyxVPUL83xzReQ8jAlwBpu7vwXwDYwW4cMwkk73LrH/MLcfhPFFgnvX5UAY\nYz1Pmu8pAsATRYQSB+CU/r50SRyM1sofvZT/DkaLboqInCz2jZbOOzDez88wJvdaDiNpzzPv1/0w\nks4zMFrVlxYcqKq/wLi/B8zn44IuvGrMnjsGRrfXkwCGwZisK6cMcV4KYIuIpJsxPFBY8gjgPRhj\nh8+KyOLinn8R6WXW6c2zABoB2Ca/z3r8ttv+R806E2H8fv65kDreMOPNM18/AeO67gLwvNlqTERE\nfkxUK7IXFBERVQQReQlAE1W9vdjCZDmz9fRtVY0utjAREREBYMsqEZFfEGMd1c5mV+TLYHTd/cLq\nuKhwZtfYISJSU0QiYUymxPtFRERUCkxWiYj8Q10Y41YzYMx4OgPAEksjoqIIjC7OZ2B0A94DYzIg\nIiIiKiF2AyYiIiIiIiLbYcsqERERERER2Y7fr7MqIupwOMoyAyJVIIfD4QCAvLy8vOLKUuXivbEv\n3hv74r2xL94b++K9sa/qfG/y8vICVLVKNtiJyDeqOsjqOHzJ75PVWrVq5f3www/3FV+SKpPT6RwA\nAImJiSutjoUuxHtjX7w39sV7Y1+8N/bFe2Nf1fnedOrU6RWrY6hAYVYH4GtV8lsFIiIiIiIi8m9M\nVomIiIiIiMh2mKwSERERERGR7TBZJSIiIiIiItthskpERERERES2w2SViIiIiIiIbIfJKhERERER\nEdkOk1UiIiIiIiKyHSarREREREREZDtMVomIiIiIiMh2alodQHldEplvdQhE1Zrm5eHUli2NGvXo\ncUocDqvD8RsuV76cOZMTcOpUTuDp0zmB587lBLZooaE1a9bQpKTjjcPCArMiIoKywsMDsx0OsTpc\nIiIiokrn98nqWzfk8a9jIgvtePTR/ikrVtwSNXLkex2mTNlqdTx2s2zZ0cjXX993Y3p6bgOXS4Ny\nc/Nr5eZqYF6e1vpj6Z8LfujvtlEDAiQrIKBGVkBAjaxatWpk1apVIzM8PPD4s892WhIdHZJZCW+D\niIiIqNL5fbJaO0CRbXUQRNVUbkaG48S6dQMB4Pzu3a0AMFl1s3RpcvN//GPXgzk5+XUK2+9wSE7N\nmpJTs6Zk16xZIyc8vHZQfr7KiRO/5bhc+UEulwbl5Wktl0uDXa68YCDvf8cmJ2d2GD1680XTpnX5\n95VXhp2qtDdFREREVEmqQLIKJqtUJj89+OCA7JMnQy95660FAXXq5BV/BHlKePPNLnmZmQ0AIOfM\nmTCr47GTJUuSnf/8564Hc3LyQ6Kiau/8299af1GvXkBOo0a1skJDA3MaNaqVExBQQ93W6ZWyAAAg\nAElEQVSPcTqdAwAgMTFxZcG2zMy8GsePZwUdP54VdPp0TtCZMzlBp0/nhHz++ZEbzp51Nbv//h+f\nePjhdm+OGhV9oLLfIxEREVFF8vtkNSjA6gjIH52Lj693fNWqGwHIlrFj610xd+67jsBALfZAukDK\nypV9C352nT/fyMJQbGXx4qSof/1r94M5Ofm1o6Nr/zxnzhX/qVcvILcsdQUHO/JbtAj5rUWLkN/c\nt48YEZlw993b7klOzuzw4ot7Hj5y5LcPHnus/fe+eQdERERE1vP72YBrM1mlMjj06addAQgApCck\ndN86fvwozWPjammkrFjRNOvYsXbicLgAIDc9vRGvIbBo0QWJ6o7yJKpFcTprZ37xRc9/d+pUPy4/\nHzU/+eTw3RMn/jA4L4/fuRAREVHV4PfJanAAgHwXp8qkUjnzww+XAED9Tp3ixOFwndu5s8/3f/3r\nCKvj8ieHZs/uAwD1OnTYVKNWrd80L6/W+b1761odl5UWLkyMfvbZXQ/m5OTXbtEiZPvcuRWTqBYI\nDnbkz559+ZwBAxrPB6BxcSeuHzly4x3p6S5OPEdERER+r8KS1ViRoFiRrbEiO2JFdsWK/MPcHhor\nsjJWZJ/534ZuxzwRK5IQK7I3VuTakp6rZs4Ztq9SiZ2Lj6+XdexYW9SokdvlpZe+iLnzzlkQyT+1\nadOQ7Q8/3L/4Gijz2LHAc/HxVwBA9OjRa2rWqXMSAM7Fx1fbcasLFiRGP/fc7kkul9Zu0SJk+2ef\nXT6rTp2ACm9qdjgEL7/cddWdd8a87XBIzi+/pF3x5z9vmHTgQHrtij43ERERUUWqyJbVbAD9Jqt2\nAXAxgEGxIpcDeBzA6smqbQCsNl8jVqQDgJEA/gRgEIA3Y0VK1DpQM+dMIUtAEBWuoAtwbadzd22n\nM7Pt/ff/7Lz55g8BIGXFilt2/fOfV1gbof3tmznzcs3NDQps3Dih2XXXJQfUr38KADIOHqyW41bn\nz09s8fzzux90ubR2TEzIT3PnXlEpiaq7Bx9st/3pp/80PTjYcS4lJavt2LGbH1+79kR4ZcZARERE\n5EsVNsHSZFUFkG6+DDD/KYARAPqa2z8CsAbAY+b2uZNVswEcjBVJAHAZgE3u9caKrLngPLFA42bN\n++U3dHKtQRsJCgpqCwBOp9PqUP5g66FDfQCg4513ZhXMvuqcNQtbmzbdvuO11y5OWrjw9ugrr2zb\nfvz4o9ZGWjHKe280Px/rd+wYCABdH3jglNPpHNDkkktC9h88iDp16lzudDobFldHVbJixZHQ6dP3\n9na5tOZVVzVJXrRoyIHAQEe/stRV3nvzwANODB7cfv0tt3zT89ChtMaPPfbz02+91WfjsGExJ8tU\nIf2PnT/TqjveG/vivbEv3hvyFxU6ZjVWxBErsh1AKoCVk1W3AGg8WfWYWSQFQGPz50gAiW6HJ5nb\niiWuNL+f1Zgqx/mDBwNP79oVLjVr5re97bYLktHL/vGPhHbjxu3R/HzZ+Oijlx9YvJitUoU49NVX\nYemJifVq1a+f3X78+CQAqON0/gYA6YmJIdZGV7m+/fZI6O23r+6dmZlb86qrmiYtWjRkc2Cgw9IZ\njtq2bZD53XfX/7d794hj6emuWuPHr+792GMb26Wnu/x+jgIiIiKqXio0yZusmgfg4liRBgC+iBXp\n6LFfY0VK9YfdZNW+/8/eeUc1kb19/JkUINTQe28KSG8WLCj23nvvXbG7uu66rq6CvWPFirpr7wWU\nIh3pHQIBEkIIIYXUybx/CPuyClIEUX/5nMMhmdx7504mmdzvPO0/G4IRjF0Um8gWGZR+7XzldBwN\nd+oa14v8HkjdsaMfYBiQjI0zmELhU6BS//O6xfr1LytTU6exU1P7v1m40KeypCTYZPz4n+qz1dpz\nExPD1E5OrjGaO9ciq7FLa+zvvy8CAFBzdHxFYzJfAABwebxKAHBlpKYKvrdz3hlIJDLk+PF8l9BQ\nykipFCNYW6smBQc7nmcwKr7K9bcjvzcnT7o8X7IkYVJKCtv/zJnMHteu5RpMmWJ6e9Uqu1Q8Xp6T\nri2gKAYXL9Jt9PRIotGjyR3y+eZwJITLl4u7jx9vkm9srCzsiDH/V/lef2/kyM/N98z/+LkZ3tUT\n6FKCkXUAsBA+erymA8A8AFAGgDAAsAAACgBMhkCspr79VgBYAAAoAKyGQOx5/XYPALgEACQAeAIA\nayAQ6/Ab9t/kTvsGDGMDQDh8jEWtDEIQQwCA+v+M+mblANDYF8GkfluL4KU8ecyqnFbRkAVY28en\nyXqUCB4P3hcv3lS1tY3HpFKlrD//XFP5+rXBt51l1xMTw9RevTp565kzhSsHDAjft2RJ4uiUlBoy\nOy1Ng1dY6AYIIrNZsuRdQ3s1W1smwM9fa5VGEyhu2pQ6oF+/N79fuFC8TCrFlKytVRNv3Oh5TkWF\n8F3V7SGR8LLQUN+wVatsD2toEGk8nlT3/Pni5SNGvFv7/DnNsKvn9yOxYkXSqCNHUl23b4/1+f33\nTN+vHU8kQpEZM2IXnT1btHLSpJjtDx6Um3TEPOXIkSNHjpwvEowYA8BqAPCEQMwJAPDwMWfQFgB4\nDYH/zSkEwZ/nFILgf3MKnQKARQBgW/83tDOm3JnZgHXrLaoQhCAkAAgAgBwAeAAAc+qbzQGA+/WP\nHwDA1CAEUQxCEEv4eNDxrdkXTsqXi1U5LdI4C7Dl3LlpzbXDEYmY75Url5RNTTNkIpFq2rZta1gJ\nCVrfcq5dCZVaR9q0KXWVSCRTIxAQoVAoU4+JYY6YMydu76LlaWsLMUu8srlFqqa7O7uhD9nVtRoA\nQMrj6cgkP18pqehops7cuXGTRox499fTp7SpXK5UT1kZzwoI0L9z40bP8yQSXtbVc2yOxYuts1++\n7P/78OGGNxQUcHXl5YLuGzem7pw1K3aqPGNwy+zZk+UdHc0c2fD8zh3q7CtXKDZfM+aiRYmTKBS+\nKwAAlyvV27EjfeuOHel95DVy5ciRI0fO19BND+whGIn4969pCABAgmCEAB8tqhXwMXfQ5frXLwPA\n2PrHYwDgJgRiIgjEigHgY06hYMQQANQhEIutt6aGNurToXSmZdUQAMKDECQNABLgY8zqIwDYBwAB\nQQiSDwCD6p/DBgzLBIBbAJAFAM8AYEW9G3GL4FCBvHSNnBb5NAvwl9oSVFRQn9DQM4p6egVoXZ1W\n8tq1a/gUyk+/sBcIUNyiRQmLa2slhhoaRNqDB35bAgPtg6ytVZMAAHJqdYxOwzLYUbXEbOvWtH50\nulARAIBkaCjCKSjwQCYjcLKz1bv2KDqGj66fxXajRkUuW7o08Y+kpJpBEglG0tdXLJg92+JMRIT/\n9oMH3V5+z0K1ARIJL/vrL5eIsLCev7i4kCMwDJAPH9gDJk2K+WPLltT+AgEqj2dtguvXS6xu3Sqd\nAwCwdq3Lh3HjrAowDPCHD+cta2+m5Y0bP/inpNQMxOFAumKFzREnJ41ImQwI9+6Vz5o6NWYugyGU\n33yVI0eOHDmdQyBWDgBBAFAKADQAqIVA7AUA6ENgm3IKGdc//nR7h9OZ2YDTAMCtie3VANBkLcsN\nGLYHAPa0dV84VCD/cZfTIi25AH+Koo6O2PvCheOxs2ZtkNTUmOQcONDf48SJJ507y65l0aKEKeXl\nAgdFRRx3/36XY6amyoK5cy3z5861zH/5y7E+T+5TZsUivWQsvor2o0cV058/p41zdNR4P3eu5VuC\nmlq1uLpatTYzU5vs7Fzb1cfSXthsMeHQoTzv8PDKgTU1EhMAABwOpHZ2agkzZpi/GTvW5IeNYbax\nUeNfvep748mTineHD+dNodGE9o8f06ZFRzP7zp1rGbZggVVuV8/xeyEmhql98GDucpkMCM7OGm93\n7vSqQlEMkpLogtLSuh5bt6auunat5z4LC5W61o55+HCuy7Nn9MkAAFOmmF1eutQma+lSm6zff88s\n+Oefshk5OdyeEyZEm+/a5XRm4EB9eucdnRw5cuTI+RnJYUAuBH6S36cxwYgmfLSWWgIAGwBuQzAy\n8z9tAjEMgtuWU6gz+SnupiNysSqnBVrrAvwpKubmAvPp0/8GAKhJTu6Fod9VWGKHsmlT6oDUVHZ/\nHA6k69fbn+zVS6e68evE+IfeQ+AFHBkU//eMGeYhenqKBRIJRvrwge2/dm3Kb8/RQXgAAH5xsU7X\nHEH7YLPFhNDQYtsVK5JGDBnydl3//uGH/vmnbE5NjcREURHH7dNH59G1az233r7d+9KPLFQbM3y4\nUfnTp/0OzptneUpVlcBksyXGhw/nrR84MHzjunUpAeHhDL2unmNX0tgV3tiYlHXunPdNHA4BIhEH\n5855hWhqEss4HKn+4sUJS3k8Savqgd+5QzW/dImyEACQfv10723b5vBvmMvOnY6xe/c671VXJ9DZ\nbInRhg0ftu3bl+3ZaQcoR44cOXL+VxkEAMUQiFVBICYBgH8AoBcAVNa79kL9/5ZyCpXXP/50e4fz\nU5R8waFytyk5X6YtLsCfYjlvXnbxhQtsKY+nS7l2zdZy9uz8Tppml3HyZL7j06e0KQAfLT7Tp5sX\nNX6d/vKlgZBGs0fweLHTupXR3qamgi1buic+eFBucu1ayYCsLE6fJ2xPE0UoBV0a7btOssRkihTu\n3y+3TEhg2RUW8uwYDKGVTPbfa6G2tkKJv7/+m7Vr7RLV1YnSrpprZ4LHI7B+vf2H+fMtM3bsyBgU\nFVU1nMEQ2bx6VWnz6lXlRHV1At3eXj1twAC91MmTTQu7uiTPt0IgQHGLFycsanCFDwnxOtvY1dvQ\nkCQKDnY7sXx54lYaTWi/YEHC9OvXe175UoblmBim9r592atQFFNwcFCPPnLE/emnbYYNM6xwdSX/\nuXx50qyCAp7XtWsli9LTa21PnfK4/bN+BuXIkSNHzjenFAB8IRhRBgABfPR2TQQAPnzMJbQPPs8p\ndB2CkYMAYAQNOYUCMRSCEQ4EI74AEAcAswHgWGdM+OcQqzKRXKz+oPzxR6ZPZibHdtIk03fjx3ee\n1aqtLsCNwSsqYmQXl/fVsbHDaI8e9frZxOrTpzSjkJCixQCA9O6t86ixxacBSmhofwAA9e7d4xqL\n/dGjjctGjza+snVrWumjRxXT78J4IObEO3gAfLYY70rKy+uU/vgja1BeHrd7VZXIEsPgP9YwMplY\nbmGhkufsTM4bOdIov3t3dW5XzfVbQyYrSI8dc39Gpda9vX69xCE+nuVCofB7cDhSg4QElkFCAmvw\n4cN5PCsrlXQfH+3UGTPMswwNSaKunndnsWhRwpSyMoGjoiKO99dfLsdNTZU/u7nl5aXF2ry5+/E/\n/sjakJXF6RMY+KHy8GG3F02NR6HwlRtZabMvXPC+1pywNTQkie7c6X3ul1/S8p88oU1OS2P3Hz06\n0nLfPuczvr7/9XSQI0eOHDly2kwgFgfByB0ASAYAKQCkAMBZAFAFgFsQjCwAgBIAmFzfPhOCkYac\nQlIAWAGB/+YUWg7/X7rmKXTS2u+nEKuITCwXqz8gFApf+c6dslkoihEzMmr9QkIKM6dNM3s6e7Zl\nh4rB9roAN8Z8+vSY6tjYYdz8fA8hnX5TycDgp1isZ2XVqv32W8ZKqRRTsrFRTThxwuPhp22EdLpi\nbUZGTwAA85kzw5saZ+9e57fiomyzF1kafW7TPe0U9+d4bNrULamz598aLlwosj9zpnBuXR3akNEZ\n09JSKLWwUMl3dSXnjRpllG9jo8bv0kl+B5iaKgs2b+6eBABJAgGKCwsrtY6IYLjk5nJdeTypbk4O\nt2dODrfnlSsUqaWlaurBg65XraxUWx2v+SOweXNq/wZX+HXr7E/27q3DbK7txImmJcXF/IuhoZQl\nr19Xjj94MJexfr39h8ZteDwJfvHihKW1tRJDMplYERLidaalEkd4PAJ797q89fTUohw4kLOkulps\nvnx50i/z5lleWLXKLr2jjlWOHDly5PyPEoj9CgC/frJVBM3kFILAZnIKBWKJAODUwbP7jJ9ErMot\nqz8iR4/m9UJRjKiigq8WiWSqZWUCxwMHch1DQykF48ebPFmyxCbzS651reVrXIAb0BswgKGop1cg\nYjBsCk6f9nDatSvmqyfWxbBYIuLKlcnL+XxUW1dXsej8ea/LTb3feUeP+mBSqZKivn6B0YgRzcYj\nbFyg+QoLfNbnJQyGq1cpC0gknLgrF9csloi4du2HcSkpNQMBPrr2jh9v8mjMGON8c3OVdn0O/lcg\nkfCyhsRaKIrdefOm0uDRowqXjIxaFwZDZFVYyPOYNSvWZO9el2N9++pWfc2+IiOrdA8fzhvl4KCe\nt2uXU1RHfOfbw8mT+Y5PntCmAgBMnmx2ecYM88KW+mzc2C25tLTubkQEY1xoKGWBhYXKgQYPERTF\nYO7c+Nk0mtBeSQlXe/Cg27GmrLTNMWGCaYmbm+Yfq1YlzystrXM+e7ZoZUZG7eOjR90f/q+4ZHck\nKIpBSQlfWSKR4ezt1XldPR85cuR83yBIEAUAuACAAoAUwzZ4IkiQFgCEAYAFAFAAYDKGbaipb78V\nABbUt1+NYRue12/3gP+3Pj4BgDUYtkF+DW8DP4VYxaFyy+qPhkQiQ2Jjq/sBAEydahY2cqRRQXBw\nrn98PMu/slJkc+pU4eqwMCp1xAijp2vW2CYTcTJgJSVp6fj6ttkV7mtcgBuj07t3TPnduzbMqKhe\nAPBDi1WZDIMFCxLmVFWJrJSV8azjx91PamkpSj5th6EoVEVG9gcA0B84MOJLY2q6u1cHQCCIQBF7\nh/XDnztXtJREIhxbuNAqp3OOonnu3KGaHzqUN5/DkRggCMh699Z5HBTk+rQlq1ZbQAUCXG1mpoaW\np2dNR435PYLHIxAQYEAPCDCgA8Dz2Fim9qZNqctraiQm69albFm/3v5ka4RdUwQH57hdu1YyRyLB\nSHl5XJ/UVLbT4cNuod/aYtvYFb5XL53H27d/7grfHIcPuz2bNu29fnY2p9e+fdkrLSxU/nR312Sv\nXJk0KjeX60sgIKLt2x2Oe3lpsdo6Lysr1bp79/qcDAz8MCQ8nDE2JqZ6xJgxUZbHj7ufk3sD/D8y\nGQaVlXXEhw8rTEpK+JoVFQJNJlOkWVMj1uRwJJo8nlSTz0c1URRTAADQ01Ms9PLSip8zxzLpf8nl\nX44cOW1mAIZtaOxhswUAXmPYhn0IErSl/vlmBAlyAICpAOAIH+M6XyFIkB2GbUAB4BQALIKPcZ1P\nAGAofGehUt87P4VYRTC5WP3RuHChuDuXK9VTVsazli2zSVNUxGOnTnk+pNEEL/bvz+kbFVUVwGKJ\nTa9coSy+f7+MPkQvm+pRcM5Lr5fvY68zZx60dj8d4QLcgM2yZYkVDx5MFVZW2la9e6er27fvV1mU\nupL166McCgp4DgQCIvz1V8fjDg4aTS7YSq5ft5Gw2cY4RUWu7apVyV8aU1FHR4xXVOSOFD1S43Qb\n9P5DjqTn8eP5K0gk/OH2ipm2wudL8evXfxjx/j1zGIYBTkODSFu3zu7ihAmmJR25HxGTqfB+6tTV\nwspKG8edO/eZTppE6cjxv2d8fXWqw8J67V+wIGExlVrntH9/9vrSUv6lrVsdElo7Bo8nwS9fnjyh\nweptbEzKZjCEFsXFfLdp095brFhhc76jwwGa4xNX+MSTJz1afX0B+CjmL1zwujpuXLQOnS60W7s2\nZVWvXtqRUVHMkQCAzZ9vGfI1WaSJRBx29Kj7s5CQQsqZM4WLyssFDjNnxm7ftKn76c6M8/9RSEmp\nIY8aFT2IQuGS4WM5hmYhEhGBTAZ4BkNk/fgxzfrJE9oUY2NSdu/eOnELFlh9+JljseXIkdMYXSUE\nCYpoeIZhG/q3suMYAGhoexkAIgBgc/32mxi2QQQAxQgSVAAA3vXWWXUM2xALAIAgQaEAMBbkYrVN\n/Byla2QSYlfPQU7bePSooh8AgLe31rvGLm2GhiTRoUNuL1++7L9t5Eij6yoqhGoOR2pwu8DWax9s\ngVcxdSMy/tjj3dr9dIQLcAMkQ0ORqq1tEgAA5erVXl8zVlchEqHIwYMfzC9dynEAAGzhQquQ4cON\nmnXtLfvnnwEAAJru7pFEVdUWrZJENTUmAgC7RtGiunVTe4+imEJwcM6qf/4pM+u4o2ia589phiNG\nvNsSE8McgWGAeHhovnzwoM+ejhaqUj4fHzd79mJhZaUtACAVjx//8CVGKh4/Nn7Vu/dvEYMHry84\nfdqhpRJNhoYk0d9/9z7h7KzxViYDwvXrpQtXrkwahqItezbFxVVrjRoVtTElpWYgggA6dKhB2OPH\nfQ8fP+6xW1dXsaiuDtU8cCA3cNmyxFECAdqpv1E0mkCxkSt88fnzXpfa44asqkpET53yOK2mRmDU\n1IhNHj+mTQMAGDnS8EZzrvAFp087vPTx2Zd39Khza/axaJF1zqlTnnt0dBQofD6q/dtvGZt//TXj\nh7wOdRQpKTXkFSuSAikULllREY9qaBBpJiakTAcH9ag+fXQejhtnHLpype2R4GDXXc+e9V2TnDxk\n7YsX/QKnTzc7Z2amnA4AWFmZwDEsjDp/2LB3QePGRS06ciTPubXliOTIkfNTg8FHC2kSggQtrt+m\nj2EbaPWP6QCgX//YGACojfqW1W8zrn/86XY5beDnsKzKJHLL6g9EQgJLi0LhuyAIoMuW2UQ11YZM\nVpDu3ev8ls+XRh3cHu4f8bpiIgP04TrMgPiwgvnzCXfQUVsmtpjAp6NcgBswGj48Jjcnpyc7NbUn\nKhI9wCsqfrdxBwyGUOHNG4ZxairbjELhm9LpQpOaGrFxgyvc0KEGt1assM1orn9tRoY6r7DQDQAw\n68WL37Vmn0QNjWoRk2kpLKVoh4ZOC5027b1CYSHPY8+erLUkEj5o2DDDig46vH8RiVBk69a0Qa9f\nV46VyYCgokKoXrrU+uLcuR1vmZNJJEjs7Nlz66jUHggeL8FQlMjNy3MBgDsdva9vBfXvv82z//xz\nrUwsVpZyOAYFJ07Yl968WWI8evQT21WrUnFEYpOfcRIJLwsN9b2+aVNq5YsX9Elv31aNnTbtvd6F\nC15XVVWJTardY8fyely6RJkvFsuUlZXxrHXr7M9OnWpWDADQq5dO9cOHfkFr16aMio2tHhoVxRw5\nalSk/b59zuc9PbXa5GpddP68Pe3Zs54ex47daCoZGopicPhwrltYGHWqQICS613hTzTlCt9abGzU\n+Hv2OB/bsOHDVrFYpuzpqfly716Xt0215ZeUkIovXJiLCgQa5ffuDbdbvbpVXh9eXlqs+/f9Dixd\nmjglPb227z//lM3Jy+NanTrlcZNMVmixvA2PJ8FfuVLSLSKC4c5kigz8/HSjd+xwjOmqOOGvoUGo\ncrlSPUtLdfaTJyPfSqWsJy3109NTEtd7ASTk5XFVL10qdo+PZ3lXVgptCwp4ngUFPM/QUEqdra1q\nsomJcoW2tgJHX1+JY2KizLGxUa01N1ep+xHfLzly5DSmStgKa2ofDNtQjiBBegDwEkGC/hPShGEb\nMAQJ+m7XgD8TP4dYxaRysfoDcfZsYV8AQGxtVZOacz9tQEWFgI7AHuE8IBzidScUPa52MyuQ2RB2\nXJMufpL1+s2ew33+aW6B2ZwLMJ8vxR8/nu/26lVlfxwOQc+e9Tzd2oQ75jNn5heePcuU8ng6lMuX\nu1kvXpzdpoPvBFAUg7Q0Njk2tto4O5tjSqXWmTIYQhMOR6oPAJ+tqnR0lOrGjbMqWrHC9M2Xxi04\ndcoPMAyvYmmZ0tq4TAVtbSYUFoKQRtMmkfCyq1d9zk+Z8p5YWlrnvHNn+jplZfyBfv30GC2P1Dpe\nvqQb7N+fM5NOF9oCADg6qkcdOuR2qzPc+TAUhfh586by8vK8EQJB1H3r1kM5f/21Wsrl6jHCw/X0\nBgzosOP6VpRcu2adExy8CpNISMrm5qmq1taFzOjoAHF1tXnxxYvLyu7erTAcOvSp/fr1iXgSSfZp\nfzwegeBg19eHDuVWX75MWZCdzek1fny09tmzXqctLFT+jTsVCFDcypVJY+LjWUMBAMzMlNOPHHG7\n+GncpYoKAQ0J8bp37lxRztmzhfMrK4W2S5Yk7pwxw/zyp5l2m4NXVKRccPLkYplYrFp49myu486d\n7xu/HhdXrbV7d+a0kpI6ZwAAHR3F4h07HC62dC1qDQMG6DGCglz3xsVVmwUG2jd7My1ty5YJqECg\nAQAgqqqypL98aWAQEEBvzT7U1YnS69d7Xtu1K6P47t2yGRkZtX5jx0aZ/fWXy2kfH+3P4mLZbDEh\nNJTiEBlZ5V5YyHORSDDlhtf+/rvM5v17ps/27Y5XvzZR1rckNZWt0SBUtbQUSp88GZliaKgioVLb\nFhZsZ6fG+/NP53cA8C4hgaV19SrFKyWlxrumRmKSmcnpk5nJ+awPggCqpITnKivja5WVCRw1NQLH\nyIhE8/bWKhwxwqhUXhNXjpyfAwzbUF7/n4EgQXcBwBsAKhEkyBDDNtAQJMgQABp+98sBwLRRd5P6\nbeX1jz/dLqcN/BxiVW5Z/WHgcCSElJSaPgAA48ebRrSmT21amhsOMJg2Sv35ZH/f4r8W3tieLLTX\niEqR+I8Y/s551myL68uX22Z+2u9TF+DsbI7a8eP5fgkJrH4CAUpuaLdwYcLyv//ufaQ1iwwckYiR\n3dximJGRo2nPnvX61mKVQuErR0VVGWVmcoxLS+uMKiuFxjU1YmOxWKb8aVsEAZRMJtL09ZWo5uYq\nVEdHDeqAAXplfn7degMAUKnUz3dQj4TDIbASEvoBABiNGhXR2vkp6etXAwCImEwdgI/ukdeu+Z6Z\nMuX9qooKQbdNm1LXBQW5HvTz+7qF8evXlQYnT+aPyMvjeQEAoqSE48yZYxm6cqVtp2UfTlqxYhQ7\nNbU/4HBS21WrTphNnlxcGhaWwcvL8y5/+NBZb8CAV521786g6Px5+/xjx1ZiKDrFrGUAACAASURB\nVKqgam2d6Hvt2gWCigoqYjLDc/bv7814+3aIhM02Kr15c0HFo0ej9QcNetZt48ZYorr6Z9+Tdevs\nP5iZKQft25e9gkYT2s+YEbt5/36XY7176zBTUmrIGzemLqysFNoiCMj8/fXuHjjg+pJIxDV7R3rh\nQqscPz+d39et+zCXSq3rcfFi8bKkJNbbY8fcb7dk/czYuXOMTCxWBQDgl5QYNGzn86X4X35J9w8P\nZ4xGUUyBSEQEQ4YY3N21y+ldR2bXHTBAjzFgQPM3ZIovXbKtzcjwAwRBSYaG+YKKim6lN270NggI\n+Lst+9m1yynG1ZVctm9fztL68jbblyyxPrd4sXU2iyUiXrpEcYyOrvIoKuI7S6WYUkM/MplY3qOH\nRpKmpgLn+XP62IoKYbfVq5N/7dtX99Hevc4vOzIJWWeQmsrWWL48sUGoUi9e9D5kaKjS+2vH9fLS\nYnl5aT0HgOdPn9KMnj2j9WCxxGQuV6rB50vV6+qk6gIBqi6RYCSBACULBCi5uloMAABZWRx49aoS\n9u3LlurqKlIsLFQKXFzIBSNGGBX+bOWd5Mj5XwBBglQAAIdhG7j1jwcDwO8A8AAA5gDAvvr/9+u7\nPACA6wgSdBA+JliyBYB4DNuAIkgQB0GCfOFjgqXZAHDs2x7Nj8/PIVblltUfhuPH891FIpmapiax\nbOpUsxaT7rASEzVFTKYlgseLLWbNylLU0RGfCBu16+rU7Tv/FgzWpPMNdU6dKlz9/Dk9+ddfncLc\n3TXZDX0bXICpZoOLJ02KnpuXx/WSyT5+5jU0iDQfH+3IyMiqIXS60G727Lh5t2/3OvelBXQDlnPm\nvGdGRo7iFxW58UtKSCrm5p1WBuXduyrdS5eK+9JoAuPqarFxY5HdGAUFXJ2WlkK5gYES1dpalerm\npkkdMECP1t67/DlBQT6oQKBB1NQss5o/v9XZfJVNTasBAMRstnbDNjJZQXrlis+JadPer2EwRDYr\nViT9bmamnDFokH7UokXWGW1ZHL95U6l/4kTBiLw8rjcAIAgCqJOTRtSuXU4P7OzUOq0cxYeNG/2Z\n0dEjAQCznDs3xGr+/FwAAG0vr1ReXp53bUaGMwD8MGI1/8QJp8KzZ5eBTEZQ69btve/Vq5cbXNoV\ndXTELvv3h0t4vHc5+/f7Vr56NVTK5eqV37s3i/78+Sjdfv2ed9+8OUpRR0fceMwJE0xLzMxU9q1f\nn7KSzZYYr1mTvMXfX//xmzeVI0QimRqJhGevWmUbMmuWRUFr5mhvr857+NDv+JYtqf4vXtAnpKXV\n9hszJspm9Wq70LFjjUua+q6WP3hgwk5N7dfwXMRgGAAA3LxZannyZP7MmhqJCQCAtbVq4m+/Od1y\ncSHXfs372FZELBax8OzZ2QAAOr17P9Ht2zcr+88/u7HT031QgeBuU9brLzF2rEmpk5PGnlWrkheU\nlQkcjx3LX3P3blkWnS60kUoxxYZ2WloKpc7OGsnjxpkk+/vrVzZsnzPHMmX79rSJOTncnuHhjHHD\nhr3zWr3aNnTixI6N8+4oGoQqhyPV19JSoJ4/73WoM8TgsGGGFc2FLLDZYkJuLle9pISvQaMJ1Sor\nheTiYr4ZlVpnU1srMaysFNlUVops4uJYcPZsEWhoEGmmpsoF3burFw4ZYpDblPVbjhw53x36AHAX\nQYIAPmql6xi24RmCBCUAwC0ECVoAACUAMBkAAMM2ZCJI0C0AyAIAKQCsqM8EDACwHP6/dM1TkCdX\najMIhv3g7tbBCCYlqNNzBkZ/WtxWThdiamoaAABApVJfNt4+cGD4RgZDZDNmjPHVP/7oEdnSOKmb\nNg2gPX06VcXKKtnv/v0zDdsrX782SNqwecs7qS/pBTIMlWB4PIGAiAYM0HuwZ4/zm9rMTPXL8/7a\nFwV+QAGLBldYzNxcOW3sWJM38+ZZ5uDxCDx8WGGyc2f6RqkUU/Lw0Hx56ZJPq2IP3w4Zsk5QUdHN\naNSoa85//tmqeM62kpxcQ16yJGG7UChTb9iGxyNiMplI09NTKjcxIVXY26uX+/pqlyvH3jIqOnN6\nidHIkbd7/P579JfGbe7cNCCTSJA3/fvvknI4BmZTp5532L691WU8Kt+80U9Zs+Z3gqpq1aD3739p\n/BqVWkdavTp5ZmEhzw3DAA8AoKSEq3V2JsfOmGEe3XgR/Snh4Qy9EyfyR+bm/kekRq9bZ/+0PSVB\n2kLm7t0+1Fu35gMAmEyYcLlxjV0+haIcOXp0MABgfg8fBn7tjYuWzk1HkBMU5EYJDV0EGIbXcHZ+\n63Pp0o3m4lIBPpboyT182IP25MkwCZttDABAUFNj9P777z9IhoafuVuXl9cpLViQsKS8XODQsM3Y\nmJR96JDb+faWCbl/v9x0//7sRfWu7UAkIgJdXaUSMzPlYkdH9WJ/f31KD0e12ojBgzeJGAxrkrFx\ntqC8vLtYTa8yzPKPnLS02r4AgKioEKpnzza/1pQnRkt0xLlJWLRobHVs7DAimVzR9+nTPwgkEvq6\nb9/fpByOgdXixcftVq1ql2eASIQia9akjIyOZo5s2Kajo0BxcSEnTZhgmtKSJ8PZs4XdL14snsnj\nSXUAAPPw0Hy9b5/LAwMDpQ51p09JqSGHhlK8KioEhj4+2mlLllint/ZmVVoaW2PZso9CVVNToezC\nBa+DDW7k3+J70xqKinjKjx9XWKemsm0olDrrqiqhZcMN0gZ0dRWLvL214ubNs0z8X6j3+r2cGzmf\n8798bnr06HEIwzCVrp5HZ4AgSCKGYT984sfG/BRiFcUrs7IHxW3t6qnI+X+augg+fFhhsm1b2g4i\nERE8edJvc2sWQhGDB68X0mj2ZtOmnXfYtu0/oqnwzBmH/BMnVrExddwt7bWU/GpVCwAAMplYIeXX\nafIkRBLAx4WtszM5atEi64jevXWYn+7j3LmibkeP5q3GMMAHBOjfPnjQrUULWdaePd6lN28uUNTR\nKR4QHr6vxTekjbBYIuL48dEbq6vF5vr6igXDhxu99PDQrPD11a761GVRyufjIwICdkm5XD2cggK/\nz4MH25SNjYXNjd3SD1TuoUOuxRcuLMMrK7MGvHnzC0FFpdWWTxGLRQzv1+84IAgakJCwoqkEVFlZ\ntWohIUW+8fGsPhyO5F83TX19xQI/P92oZctskvT0lMQA/4rUEbm5XB9oJFLXrLF7+i0sFHlHjzoX\nnTu3DDAMpx8QcMft4MHP3rOIgIBAIZ1uZz5zZkj3zZu/KpFXZy8esvbs8S4NC5sHGIbT9PB46X3+\n/B0E37rEpzKJBCk4ebJH6c2bk6U8nq7xmDFXe/zxR5M3nPh8KX7x4sTJmZm1vXv21H52+LDb4691\ntaXThYobN34Ym5fHdaurQzU/fV1VQcq3FGepmBAqhd1mTb5QefH4socwCuGCOiAIoN7eWi/37XN5\nrKOjKG5q/Jb42nNT8fChSdr27dsBw5Du27btN582rQgAIHnNmiGMN2/Gq1hapvg9eHC6PWM3cP58\nkX1eHtdw3DjjdF9fnTbVpGYwhAqbN6eNSkxkBQAAoqKCr54zx/LasmU2bRb2jaFS60jnzxe5vX/P\n9KmoENpDozh6JSUcx9mZ/H72bIuoL8Wy1wvV9RyO1EBTk1h27pz3ocaeFN/ropvDkRAeP64wi49n\nWRcU8GzKyuq6N1i8EQRQU1PlrD59dOIWLbJObe/n8nvnez03cv63z41crP5Y/BRiVYZT4GUFJAV2\n9VTk/D9NXQSnTXs/MyOj1s/VlfzmyhXfsJbG4OTmqsZMnBgECCLr+/hxYFOlZ1I3b+5Pe/JkGuBw\n0jz/XXevv1fz5/Ol2gAAelAJvt1kMauOTbvZkjDesyfL++bN0gUAADNmmIds2dL9i6JDxGQqRAwe\nvB+TSEiuwcG7DAYPpn2pfVtAUQwmT46Zn5fH9VFRIVSHhvr8+SUX13/fg3p0+vR56Hnq1KPm2n/p\nBwpDUYgICNgsqqqyMhg6NMz1wIEvJmFqihdeXvtlQqGG94ULW7W8vJoVlCiKQVhYqdX9++V98vK4\nng2LOAIBEdnbqyVIpRihsUh1dNSIWbvW7kl7RKqYzSZk7NrlT1RTq9MbMCBfr1+/ypZEWnFoqG3e\nwYNrMBQlavv6PvUKCbnXVLuUdesCKl+9mqhmbx/X+86dC22dW2M6c/GQvmNHn/J792YCAKLTq9dj\nj5MnH7RWqDYm848/fKhhYfMVtLVL/CMi/vxSW5EIRToyHrSB1FS2xps3lZZZWRyL0tI6yyqG0ELS\nKC6zMQZaQF2/xeXC12ai/ppzgwoEuLfDhm0RV1ebk11d3/heufLv9Y+dmqoRO3PmX4Agst537mxS\ns7PrUmvbvXtlZocO5c1iscRmAAB2dqrxkyaZvXF21mDa26tzW5MJl8eT4M+dK3KKiKjyKS7muTRY\nF3E4kJqbq6SbmiqXpqayvWtrJYYNfQwMlPL69dONWr7cJrlxXHJGRq36kiWJgRyOpEmhCvDjLLoZ\nDKHC+fNFLpGRTJ+ysjpHDPtYPpBAQETW1qopAQEGcbNnW+SQSPg2uYN/z/wo5+Z/kf/lcyMXqz8W\nP0nMKiqPWf3OoVLrSNnZHB8AgNmzLZos5/ApJdeuuQAAomxikt1cjVTnP/+MqKNSjWrT0/t1i/pz\nyPW/jgeduyd2NQg/NM4WKUT7HXx0S7kVFtzt2x3iq6pE5NevKyfcuFEyT19fiTNvnmVec+0VdXTE\n6vb2ibUZGX6lN270Mhg8uE3JUb5EYOCHwXl5XB8CARHt3Olw4ktCtY5KJVW+ejUKAEDT0/NlTWJi\nQHVsbAC3oCBczcaG31y/5ii5ft1GVFVlhVNQ4HfbuLHJskItQVRXrxYJhRq12dnaXxKreDwC06eb\nF02fbl5EownCTp8u9IiKqurDYIisMzM5fQA+Wh8cHTVi1qyxfdpWS1FjklevnsBOSfEHACi/dw9w\niopckrFxvpqdXb5unz75BkOHljW2Apffv2+ad/jwCgxFiRo9erzzPH26SaEKAGA0cmR65atXE/nF\nxU6oSIR8j+WMPmzc6E9/9mwKAIBe//533Y8de9besWyWL08uv3t3qri62rzs3j0zk7FjS5tr2xlC\nFQDAxYVc6+JC/gAAHwAA3s+ZOykvmTqoVM2FkWMxMbu8QmiBsZmG/uhzhUmjHB85DBva4SWT2kLa\n9u3+4upqc7yyMstl//7/fJbILi61yqamGXVUao/CkBDv9twgaoCTna1WV1am0trMwk0xdqxJ6ZAh\nhnu3bUsbGB7OGJ2Xx/PesyfLGwAAj0ckKiqEanV1QrWmpgJTV1ex2siIVG1pqVLt5KTBTE6u0X/y\nhOaTm8v1EItl/y4EDQ2Vcn18tOMXLLBKbsgSjaLYk1u3Sq3u3Svvk5vL9aLThXZhYVS7f/4pm+bg\noBE3ebJppJWVKqdBqJLJxPKmhOqPREPZnK1bISE7m6N26VKxR0ICy6eqSmSVm8v1zc3l+p47V8hx\ncNBI2Ly529OOyFAtR44cOT86P49YxVAARF7H+3vl2LF8XxTFFIyMlHICAgxatZCqSUx0AwDQ9PBI\naa4NgseDV0hIWNT48frCiopulN82LZrk5hZfCfmIspl5VnMitymCg11fzJ0bp/nhA9v/2LG85fr6\nigeGDzdqNsW40ejRMbUZGX7sjAxfKZ9/ry3uss1x8mS+4+vXleMBAGbNsrjwpf0DAGTs2jVUJhar\nKunr53ufO3fn3ciRRoKyMsfsP/8c6n3hQpsFdOnNm0MBALS8vMKV9PTa5ZZG1NBgihgMqzoKRQcA\nWlXr1NCQJPrtN6cYAIh5+ZJuEBZW2hNFAbdokVVEr17tF6kAAIUhId3YKSn+gCCoioVFmoBGs5YJ\nher8oiJ3flGRO/3ZM8j47TcBycCgUNXaOl/F2ppWcvXqLEwiIalaWyd6X7x4/UsWSL3+/ekENTWG\nlMvVK7tzx8p8xowWE4d9SxrcTAEA2mstb4yilpZE3dExlp2S4k+9dauPydix1792jl8j8mnPnxvW\npiT76wOGDdrc76zxmF5UAIC4uXMn1SQlDRKWKBu0NEZnwoyO1mG8eTMGAMBi1qzrTcX56g0YEEMJ\nDe3BiovrDQDtOj9iNpsQP3/+Zmldnab3+fO/tLbcVFOQSHjZoUNuL6OjmSmHD+eOrKoSGXG5Um2x\nWKbK4UgMOByJQVnZly+tmprEMnd3zbiZMy0SmqqTi8cjMG2aedG0aeZF5eV1t06dKvSKjq7qw2SK\nLVJT2f1TU9n9CQREJJViih+FqtfBH1mofkr37urcv/5yiQCAiHfvqnRv3izx/vCB7cvlSvWSk2sG\nzpkT57lsmc35+fOtcrt6rt8bUj4f3xG/t3LkyPkx+OHFqkACQCIC4CW1RFRBq90F3eV0HiiKQXQ0\nsz8AQECAQURr+tRRqaS68vLuAICZT5+e+qW2BBUV1PPUqTOxM2duFbNYppWvX5sAAGj7+LQpfhCP\nR+DcOa9bkyfHkIuK+O67dmWu1tNT2tfUQgsAwGzy5KL848fpUg7HoOj8eUe71avTmmrXWt68qdQ/\nd65oEQAgffroPGypriQzNlablZg4CADAesmSOwgeD9aLFt3L+PVXx5rk5P7s1NRXZBeXVmc7pT19\nalRXWtoDwePFduvWhbf3OBS1tat5+fkgoNG0W279OQEBBvSAAIO77d1/Y/gUinJRSMg8AABdP79H\nHidOPMFQFKrevdOrDA+35WRn2wrKymylPJ5OHZXqVEelOkFEBAAAkIyNs3yuXr3QkohC8HhQs7VN\nr0lOHlgZHu78PYnV9B07+tQLVcx47NirPXbvbpe1/FPMp02LZKek+HOys32EDMad9t7YAACoePLE\nOGPHjvVKhoZFnqdOXWjLDSYMRSE3OHgaYBiO7OwcYTxmzL/1mJRNTWk1SUkgoNO7TKxiKAqZu3fP\nwFBUQdXWNt525comEyhZL1mSVnrzJl9cU2NSfv++aePjaC0Zu3b5S3k8XQCA8vv3HbU8Pb/6XPfu\nrcPs3VvnUsNzGk2g+OEDW7uggKtdVibQrqwU6rBYYh0OR6LN5Up1iEScwNFRPWHCBJP4lm60NcbY\nWFlYn3Av8uHDCpNbt0p7Z2bW+kokmHKDUP2ZkxH17atb1bev7mMUxR7fvVtmfuZM4UQ6XWh36FDe\nusRE1sNDh9yedJaXwo9G+s6dvcvv359uNHz4Lee9e1vlpSVHjpwfG1xXT+BrqauXpwQxS+4K/J1y\n6VKxPYcjMSCR8Oxly2xaJegoV686gUxGUDIwyFfv3r1FVyhVK6u6Hrt3n0CIRAEAIIDDSS3nzm2z\neFRUxGOXL/uc19dXyhcIUPK6dSmrKRT+ZzVMAT6KFC1PzxgAgMpXr3q1dV+NKSnhk3bsSF8hkWAk\nKyuV5KNH3R+31CfnwIGxIJMRVG1t400nTaIAAJiMH1+qYmmZgqGoQs7+/cPbMoeiCxcGAwBoODnF\nqNvbt3thqGRgwAQAEFdXt0usdiQp69dPQwUCsqKubpFrUNAzgI/nTW/AAEaP33+P7n379qVB799v\n97l8ebPZ9OnnNJyd3xLJ5HJlM7N0n9DQU0RV1Vbdvdf180sDAODm5vbozONpCzXJyeSKR48mAQAY\njxt3paOEKgCA4bBhFYp6eoWYVKpUcOLEV8XGFJ46NVomFqvWlZQ4v582bXNVZKRua/vmBAV5Cmk0\ne5yCAs9p9+77jV9Ts7OjAwCImEzDpnt3Pll79vgKyssdcAoKfOc9e241146ori5Vd3CIAwCg3rnT\n5msJNy9Pterdu3+/77Xp6Q5fat9eDA1JomHDDCtWrbJL/+svl4hLl3zuPHjgdzoiwn9PUtLgdbGx\ng7adP+99ty1C9VNGjTIqu3LFN+zVq/6bVq2yPXzzZs/9P7NQbQwej8DEiaYlDx74HerVS/sxAEBk\nJHP06NFRazMyatVb6v+zk3PggHv53buzQCYjVMfG9uzq+ciRI+fb8MOLVWG9WMWL2XKx+p3y4EF5\nfwAAT0/Nd60tU1AdG+sGAEB2dW3WBfhT9AcOpNssXXoGweMlara2iW2x0DSGTFaQnj3reVJDg0hj\nsyVGixYlLGezxU16IVjNnx8LABifQnHm5Oaqtmd/IhGKLF2auIjDkeqTycTyM2e8LrVU75V65445\nLy/PG3A4abdNm/4TA2ezYsV9AMDY6el+zNjYVglGVmKiJjc31xsAMJtly74q2cK/tVZranS+Zpyv\nJWvvXi9efr43gseLnXbtuvClGpaa7u5sh61bE3peu3Z9YGTk730fPz7eFmuh6dSp+QiBIJSw2cat\nfc87EwxFIX3HjhmYVKqkYmmZ0lI5o/ag27dvJABAVWSkX3vHqHj82JhPobgieLyEqKFBk9TWGqas\nXbuFcuWKTUt9hXS6Ytnff08CADAcPvyuqpXVf+ptanl70wEAJGy2AYZ+e49BTna2Wvn9+5MBAIzH\njLnV0k0304kTYwAAOFlZPhIOp01eT5m7d4/AJBKSgqZmGQBAHZXaDRWJWs6E9B2jpaUoWbzYOtvY\nWLnZzOY/KyQSXnbmjNeDVatsjygq4rgVFYJu8+bF7Th/vsi+rWOhKAYPHpSbnD5d4PD2LUOPz5f+\nkPFShWfPdqdcubIQ6rNJi5hMC25eXrt+c+XIkfNj8cOL1QbLKl7CkYvV75CUlBpycTHfFUEAXbLE\nplWWHRGLRawrKekBAGA2ZUqrxSoAgPXixdl+Dx9u9L127VKbJ9sIKyvVukOH3I6SSHg2nS60nTMn\nbsHbtww9iUT2nwVgQ3IUwDB8UUiIT3v2tXx50riyMoGjggKO99dfLidaylyMoSgUnjkzCQBAy9Pz\ntY6v739iOg2HDKGp2dvHA4bh8w4eHNn0KP8l//jxQYBheFUbm0Sd3r0/K+/TFtTs7asBACRcbpeJ\ntprkZDL19u3pAABGI0fe0u3b94t1Jr8WoqoqqmxmlgkAUH73bpdbV3OCgjzqSkudESJR0GP37hud\nsQ/bFSuSECJRIKqqsqp48sS4PWMUhYSMAADQcHaO7BkWtk/Z1DRDJhar5hw4sD7jt9++aDlJ++WX\n4ahAQFbQ1i5x+OWXz8S4mo0ND6egwMekUqXajAyN9szva0jbtm2KTCxWIRkbZzls3x7bUnvjMWOo\nCpqaZTKxWKXwzBnn1u6HER6ux05N7QcAWPetW88TVFSqZWKxCu3xY9OvOgA5Xc7ixdbZ58977zY0\nVMoVCmXqhw/nrVu2LHGUSIS2eCPi+XOa4ZIlCaP9/F7v3r49fceJEwVrVq5M3t2z56vjPXu++mPo\n0LdrZsyInRYY+GHgkSN5zi9e0A2buyn7LQgJKew2b17cxL17s7xyczn/EaGlt25ZFpw6tQwwDK/p\n7v6aZGSUAwBI2T//dOui6cqRI+cb8sPHrNZJEADAAC/lEbt6LnI+58yZQj8MA5y1tWqSiwu5VfGT\nlNBQBwxFFRR0dCjtSRLSXovqp3h5abF+/dXx6I4d6RuLivjuK1cmuxMIiEhLS4FqaEgqs7RUobq6\nkqlWfQbG1d241KM6Pr4XhqKvW1MORMhgKCAEAhZ0iu4WH88agiAgW7HC5mxrkgnlHTvmIqTTbXEK\nCjzHnTufNtXGbs2ah0krVnhysrN70l++fP6l7KB8CkWZnZrqBwBgOXfu8xYn3wKabm4sAMDQujpN\nVCDAfcmi2RnIJBIkbdu2OZhEoqxsZpbu9NtvTdYC7Wi0PDzS+EVFHuy0NGcAiPgW+2wKXlGRMvX2\n7WkAAEbDh//dlrjltqCooyPW6N49jp2W1r/0xo0+RsOHt1iOqjH0Fy8MeYWF7oDDSe3XrXuubGws\n7P333ycSly6dWJOcPLDszp25daWlhp6nT9/FEYn/8TSofPNGnxUfHwAAYLtixfWm4ooRPB6IZDJN\nxGDYsBITDTrrfWiKvGPHevAKCrwQPF7suHPn1daWCNLy8YmmP3s2hREe3qvbxo3JremTe/DgBMAw\nvLqjY5ThsGEVlNDQrNqMDD9GRISDyfjxzWZqlvNj4OJCrn340O/QmjUpI6OjmSOiopgjR42KtD14\n0O2ck5MGp3Hbd++qdG/dKvVMTWV7sdmSf28gKSriuFpaChUcjkSHz0e1eDypLo8n1S0vFzik/TdY\nBlNVJTB79NBIWLDAKvJb1LKWSGTImjXJwyMjmaMBABITa+D69VLQ0lKg2tioZnkZsSpNHwdPxEul\nimrdur33OnfudurGjQGCiopuNcnJjgDwVbWt5ciR8/3zw4tVQb1lFSflyS2r3xkiEYokJbH8AADG\njjVudcIeZnT0RxfgHj3aZFXtDEaMMCrn86VHLl+mDK+qEpkJBCiZwRDZMBgim9RUNty7Vw4I4ijT\nQzbIjGvKTJ7MfzrJ2sc+q0cPMsPbW4vZOCmGhMMhFJ0/78SIiPDhUyjOZUQrwW3JYhIAAsOHG4a1\nJuujlM/HU2/fngAAoD9w4CMVc/Mmhbmun1+VhpNTdG16et+CEydGGwQEnG1uzJygoH6YVKpIMjbO\nak9il08hqqtL8SRSLSoQkGtSUzU/tfx2Nunbt/evjxPkufz1V2h7aom2B9MpUzKot29jgooKeyGd\nrqhkYNBiyaTOIG3LlkkykUhNycAg3/HXXzssTrUpzKZOjWSnpfWvzcz0FTGZdxV1dFrtOl1w5sxw\nAEA0nJyiNd3c2AAAeBJJ5nP58q207dtpFQ8fTmfFxw+JHj9e3ysk5ELD+4mhKOTs3z8VMAyv7uAQ\n1RCv3RSKOjp0EYNhw83PNwSAb5JVVUCjKZZcvToDAEDP3/++Tq9erf78Wy9aFE9//nxiHZXqxE5N\n1WhJYBeHhtrWu1GLHbZtewAAoOnmll2bkeHHyc3tDgDtLlEk5/tBURGPnT7t+TAkpDD/zJnChTSa\n0H7u3LidS5ZYn3N11WRcv17ikZJS41VdLTZv6KOggKuztVVNHjTIIGHGmgDGHQAAIABJREFUDPO8\nhtqtHI6EkJDA0snKqtUtLa3TpdOFekymSK+2VqLL40m1eTyp7vv31cPfv68eZmamnDF0qMHbxYut\nMzojwVN5eZ3S0qVJ8ygUvisAYE5OGlE1NWJtOl1oy2KJTePjWabxAECAX8BMsYpraehMq37KMHbz\nD8isfP16Ap9CccBQFL7VNV6OHDldww8vVuvEgAEAgkP5crH6nXHpUraxUCjT0NAg0mbNsmhVCRMp\nn4/nFRa6AACYjBvXKstCZzN5slnx5MlmJwAAcnM5qm/fVplmZXFMqVS+aWWlyLS2VmJQCfpIJegD\nJMMgSC4cBACAw4FUTY1QpaMk5BuKixUNOBn6uihNQReqAAMVuCSaooYCAq5G3Ow9e4ZEtGYumbt3\n+0k5HH2CmhrDYefOd19q223Dhsdx8+b14hUWejSXYVTEYhGrY2MHAgCYTJjw1VbVBghqakxUICBz\nsrJ0vqVYpb98aUB/8WICAIDZ9OlXNZycOC316SjU7e15inp6xSIGw6rkxo3u9uvWfTGbc2dQGBLS\njZOd3QtwOGn3rVuvfGqR7GiMRo0qyz14sFjEZFoWnDzp7rhzZ4vurgAfXVd5eXlegCCo3erVnwkq\n5z17IlUtLavyT55cwqdQXGMmT97kevDgcS1Pz5q8o0ddBeXlDgiRWOf0++9fzBpNMjKic7KyQFBe\n/k0yApc/eGBScPLkBLSuTlNBW7vEec+eNpWhUbOz46lYWKTxi4vdii5c8HU/cqTZ76RMIkGKL16c\nCACg3bPnc7Kzcy0AgPH48TmUK1cwIZ1uI2IyFdpyA0HO982iRdY5Pj7auzds+LCARhPaHz2avxbq\nYzgBAAgERGhtrfphwAC9hDlzLLJVVYmfBWurqxOlAwfq0wcO1P/M20YgQHF37lCt7t0r71tQwPUo\nLa3rcfZsUY+rV0tYnp5aUYsXW0e11kOqJd68qdTfsSNjOYcjMSASkbqFC63OLV9umwkAwGKJiLdC\nUpzTw57NLJCYKleAMRSJjNSKwpnjX4czxysoEHnqyBYZTiAl7+7z4g8gKogQBMEQBDAEAVn9YxmC\nAIZhABgGeJkMw2EY4Br9xzd+TiTihObmynkuLuScsWONc/9XknrJkfMj8MOLVYH043+8tE4uVr8z\nQkNzrQEA+vTRicDjW5fro+TaNTtMIlEmkskVegMGMDp1gu3A3l6dZ2+vng0A2Q3bWCwR8dnJF275\nYfcWlOPMJCX6fYtqa0QGfCFo1NZKDWtrCVAItgBg++84CAIyDAOcJRTBlIqz3T+seTvM/ciRp1+6\nQ1xHpZIqX70aBQBgOnHi3y1lqtV0d2drurmF1yQlBRSeOTPGeMyY45+2yQ0K6ikTidQUtLVLrebP\nz2n7O9I0Cpqa1SIGw6autPSbxa1K+Xx81p498zEUJap37x7TLTDwm1vm1R0c0qoYDKvq2NgeAPBN\nxaqIyVQovnBhJgCAbt++j/T9/Su/xX51+vSJKr93z5Lx7p2fI0CrxGr+yZPDAQBRd3B4r+3j06Sr\nodXChTkqVlb70n/5ZaW4psYkcdmyrbYrVoSUhoVNBgAwGDz4fktZq1WsrD5mBK6q6lSxWnLjhlXJ\n1avD60pLewAAIASCqFtgYGh7XOD1AwKii86edWMlJvbCUPR5c9eEnKAgTzGTaYEnkWqdfvvtRcN2\nNRsbvoK2dqm4utqceueOjc3SpVntPjA53x3Ozh/dgteuTRkZFcUcgccjYgsLlTQ/P53EefMsM7S0\nFNtdwo9EwstmzbIomDXLoiAvj3vr1KmCnnFx1X25XKneu3dVoyMjq0ZaWKikjhhh9G7+fMvslhIB\nNsexY3k9Ll4sXiCRYCQymVixZ4/zyb59df/NK6DIpRPsHm8abiGpUVbQ1i7V3n3uzJMosWVKCtuB\nQuE7CAQomQn1Py080AX4+qqFAgEK6em1BunptX2vXi0BTU2FMisrlRxPT62cCRNM8gwNSV3iKSNH\njpyfQayKP8asIqhALla/I2Jj6eqZmSxdAgERrVpl26oFLAAAIyLCHQBAw8Ghy12AW4uWlqJk+i+j\n4t+8ODBEXBNvQuA+05IKeRpiIAITdIChYMana7pUVCjaCKrqlNRqa8UGEglGUlHBV690ob6XxaAj\nqt6+HRszZYqh17lzoQpksrSp/WTs2jVUJhKpKunr59utWdMqIdR969Zn76dO7VtHpfYouX7dynz6\n9KKG11CRCGGEhw8GADAcNqzZRXF7UNDWZgIACOn0byZWP6xfP0JcXW2OV1Gpdj10qE3xkx2F4dCh\naVUREWN5RUXOMokE6WzLZmNSN24cJeXxdIlkcrnLvn0vWu7RMdiuWJFQ8ejRZFFlpQ39xQtDg8GD\naV9qz4yO1uHm5voAgsjsVq1qMua6AX1//0qVq1f3Ji5dulRIo9nnBgdvAABQ0NQsc/r11y96FgAA\naLq60gEAxDU1HS5WMRSF4osXu5XeujVcSKPZAwAgeLyY7OISabd27YsG1+a2Yr1wYSYlNLRWyuEY\nlN66ZWU+bVrRp23EbDah/P79cQAAhsOG3fs0c7WqjU02q7ranBUX1x3kYvWnQ1ERj5065fkwObkm\n0siIJGgpKV97sLNT4x065PZSIpG9unyZYv/wYXnf4mK+a3Ex3+348Xy3S5eKq1xdyXEjRxolDx1q\nWN6aG9ISiQxZuzZl+Lt3VaMAALG0VEk5c8bzYmMhKGIyFeIXLFgprqkxIairV3qeOnVUvbsN18UP\nmACQgKIYJCaytMpvXnPnvro/CdE1LtJct+8aispwKIohMhkgUqkMJ5MBgqIyHA6HYHg8IiMScSiB\ngGBEIg4lEnEyAgGREYk4mYLCx+cFBVzNyEimfV4et3tlpdC6pkZskpQkNklKqhl09myhTFdXkWJj\no5rt46OdO368SSGZrNDk77QcOXI6nh9erDZkA8bJhHKx+h1x8mSGNQCAg4N6bGtLD6AiEcLNz3cF\nADAcMeK7cAFuCw3JUaQ8ni5CJAp0bG2TnYYMibOYNSuvsWhBUQwKCriqurqKIi2tAEnuYf1SyuXL\nC7i5uT7REyboeBw/furTMhfVcXFarMTEQQAA1kuW3GmtsFS3t+dpeXu/qo6JGVF86dJYsylTDja8\nln/kiLuUx9MlqKpW2a1e3aHvt5K+fjUAgIjJ/Cbla0pv3rRkxsQMBwDMZvnyi8rGxl1S7sJw6NDy\nzN9/Z6F1dVrl9++bmU6cWPIt9lv2zz9mrMTEAADA7NasuUxQUflmtVqUDAxE6t26xddmZPiVXL/e\nx2Dw4Ntfap937NgwwDCcWrdu71uTeVrVyqqu9z//HElYuHA6JzOzDwCA1eLFN1pjtdTy9mYCDidF\n6+o0BTSaIsnQ8KsX9RiKQv6JE87l9+4NF1VVWQIAIESiQMvDI8J+w4ZXX1OjGOBj3C65R484VkLC\n4IoHD3o1JVYzdu3yR/l8bSKZXN5927b3n76u07NnFisubiivsNABAP7+mvl0Jdy8PFVlc3N+Uwm0\n5AC4u2u264ZIWyAScdjChVY5Cxda5aSlsTXOni3slZDA6svjSXWjopgj/4+9Mw9r6kr/+PdkJQEC\nhH0JO7KoKO57calWrbZq7djWaq21ztTa6QxMNzuLnel0mdDp8mvt1HbsMq2dVu2i1bF11yKIC6Ig\nIPuWAAmEsISs5/dHEooIkSUBgvfzPHkI995z7ptAlu993/N9z5xR3P3yy3l18fGii4sXB15csSKk\nvDvhKpNp+I8/fv5R6/rU5GTfb998c8KhzscaWlvZmevXP66trY1mC4WNE958882un4VsNsHUqd4N\nzV53Zfx8ZOd9UCpC507n1Q203H3CBC/V/feHlgL4n0ql4+zbVxWVkaGMKypqiVMotOF1ddrIujpt\nZHq6cumRI7Wnvvhi+ucDOR8DA0PvGTGta1hGRqwOF+Tydv6PP1aEAcBDD4Wd7O24yq+/jjK1t4s4\nbm6KoKVLqxwXoWMY/ec/n/SbP39v2Nq1HyQfOfKHGf/976eRjz5a0DW7xmYTxMaKWqzlWrFPP315\nzPbtr7OFwgZtXV1U5oYNz8sOHQrqPCb/9dfvhcnEcYuJOWfLUKY7El544ScWj9fWLpPFlvz733EA\nQE0m1Bw8uAgA/JKTf7K3Y69rWJgCAPQqlcMzq+1yOb/w7bcfBUDEkyf/FLFuXa/WRzsCwmbDPTo6\nBwBqjxzpdfuRgWBobWUXvvXWOgDEa+LEI4MlkDsjWb36FAA0XbkyXadS9XgRVJmZKVbn5U0HQGOe\neOJgb+fnurkZp3/++WfhDz/8Qfi6df8KX7u2qDfj2Hw+5YpEtQCgSE8fUHbVpNfj6o4dIcfmzv1j\nyc6dW7T19REsHq/F9447vp31zTfPT96589uBClUroWvWmHuu5udP1ioUN3y2NRcWutWfOrUEAMLX\nrt3TnZCTrF5dTNhsna6xMaQpL8/dHjENNiUffRT78333/ePSU08tG+pYGMwkJno2/d//TTx06tS8\nF558MuatMWM8TvP5rObmZoPfuXMNd23fnvvCjBlHXlm3LvP+zz4ri7a22Ll4sd5t9er058vKWsdz\nuUTz619H/d8770y8Qaia9HqSsW7dI20VFWNZPF7L2L/97U3x5Mk9uhG7jxrVwvP2roDJxKn46quY\nno7rD56ePMOjj0YWfPDB5O+OHZv72qFDc373+OOR/zdhgtdRLy9u1bhxnnZbMsPAwHBrnD6zanUD\nJoxYHTZ8+GHx+PZ2IycuzlO5ZElQdW/H1R45kgQA7nFxl5zR3Y/r5mac8Oab/Sq/DF6+vMotMvKV\ni1u3PqFVKCJyXnjh2ZaSkp0xW7Zcrdy7N6y5sHAqWCxD3DPPfNvXuV3DwjQ+M2cerjt+fEX5F1+s\noH/5y/mSb77x1SmVYSw+vzn2D39I70/MthDFxQ1ar9VLv//9fYbmZj+up2d10ptvfufo890K75kz\nc1Q5Ocnq/PxEAPsdfb6cF15YoGtokHBcXZXjXn/9e0efrztCVq6sKHz77QqdUhlatGNHUsLzz2d1\nd1zh22/fBUrZbqNGnevrmnTCZiPumWcu9DU2nlgs16tUwepr1wIA9EvIGzUa1jd33JHckJfnAwBs\ngUDlO3v2j3HPPnu6awmuPQhYuFDG9/ExG1e9/37S6BdfzLTuy/3rX5dSvV4gCAnJjdq8udsSX65I\nZHAJDLyuqaoaXf3tt/EeCQnn7B2jo6nat28BKGU1X78eD2BI/q8ZuofPZ9PNm6PyNm+OytNqjZ9/\n8UVFzLFjtRMKCpqT2tqM4kuXGudfutQ4/+23C9WzZwc3/PyzLLitzcD18ODKXn557Ht33OF302v/\n4tatd7cUFk4hHI42/oUX3rbVbs2Ke2zsVWV6elhDRsZoPPFErmMeLRAcLGzfunXUFQBXAHN1FAMD\nw+Dh9JnVjtY1Ji0jVocJ6enKKQCwbFlEr78YUqMR6vz8JAAIuPNOpysBtgceY8aoZ+zdm+YWHX2e\nGgwuxe+//2R2Ssr84vffvw8AxBMnHuuvs27Ciy8eY7m4qHUKRXj+J58E5bzzThwAeE+deowvFg/c\nnaILnuPHN8LSa1Xf0uKwKw+Fb72V2HTlyhywWIb45577iCsSDfk6orAHHywgbLZOp1SGNl665OnI\nc9WdPOlXf/LkMgCI2LDhP44QTr3FZ8aM0wBQd/z47O72N1665Nl09epMADR68+ZeZ1UHiiAgQA4A\nbRUV/c6s1hw8KGnIy/PhCIX6oOXL/5N85Mi28WlpRx35fHtPn54OAPWnT8+wbqs7ftxPdfnyHQDo\nqKee2mNrvCgu7hoAqLKz4x0VY2euvPji7Atbty6mxoFXoDdevOhpNavSqVSB9piTwTHw+Wy6YUNE\n4WefTfvy55/nP7dtW8KrkyaJf3Rz4yja202in36qDG9rM3AjIlwvff31jFe6E6rtcjlfmZm5AACi\nf/ObHZJVq3r13cF39uw8AGguLh5t30dlm94aRjIwMNgHpxerbXpCAYCYdIxYHQYUFKjdqqraEths\nQtevj+t1KW/1/v2hxtZWb5aLS5Nk9epSR8Y4nOGLxfqZe/bs9Jk16wAAIv/xx/vb5fJRLB6vZfSf\n/9zvL/gufn46/7lzDwJA1l//mqTIzvYnHI42NiXlhL1i7wzH1dXIFgobARDVpUtiR5yj/IsvIkt3\n7doEAP5z534XtHRpr7P4joTn6WkQhIRcA4CqvXvHOuo81GhE3ssvr6VGI9c9Lu5sT1m2wSJ6y5Zz\nhM3WtctksXXHj/t13V/wz38ugsnEcYuKungrEyZ7IgwLkwNAu1we2N85GjIzIwEgYPr0msSXXz49\nGBdFojZvziJstr69piZOkZHhDQAF//znSlDKFo0e/XPg4sU1tsb7z5t3DQBay8vjHS329C0t7Orv\nv3+g/sSJe8t3744e6HzFH344E5aWLFSvF6hychx60YfBPnC5LLpmTWjprl1T9p45M3/b3/429m+P\nPBKXl5Iy/tLevTP/1ZOjbuHbb0+lBoML39+/KOrxx691d0x3hKxYUUq4XI1BrQ5QZmY65HOGgWHE\nkUZikUayO93USCNPI42IkUZ+Qhq5bvnp1WnM80gjRUgjBUgjizptn4g0csWy722kEYdcyRkBYtX8\nk5h03KGNhAEAPv64bCKlYCUl+dSGhLj1OusgO3jQXAI8alT2YDqoDkcIm41JO3bsD3vooZ2EzdYD\ngP/8+Qdcw8I0A5k34cUXT7OFwgZtQ4MAADwTE8+4RUa22SPm7uCKREoAaC4osHspcM3Bg8H5UulW\najTyRPHx6ePT0gbN/bY3eCUl5QBAY3a2w9atXt2+fWa7TBbL4vObE195xaap0WAgDA5ud4+NzQKA\nss8+uyG72nT1qqgpJ2c2AERu2vTDYMYlSkgwOwI3NPQ7s9p8/XoUAPhNmjRoPYNdw8I0rpGRlwCg\n7JNPppd99ll0a2lpEmGzdQkvvHDLstiAu+6qZvH5zca2Nq+6Eycc2rpHcfq0PyhlA0DlV18tGMhc\nRq2WNF64MAswG1cBQENWVr8vNDAMDWw2wT33BFe++ebsvD/+cXJxT21uqNGI+tOnkwHAf/78E305\nB8fV1SgMCckHgJr9+wc1u8rA4LSk0AKk0PFIoeMBTATQBuAbAM8BOIoUGgPgqOV3II0kAFgDYDSA\nuwC8hzRirZjbAWAT0NGf8S5HhOz0YlVjkUMsJrM6LMjKMpcAL18eUdGXceq8vCQA8EtOvi1LgLsj\n/rnnzie+8srfJatX7xrz17+eGOh8XJHIELBo0QEAIGw2jXnyySMDDtLW+Tw9FQDQWl5uV0dgxc8/\n+1z9859/S/V6oWt4ePbUTz75bLitcZbcd98VANBUVcVpGxrsfiFNlZPjUXPgwGoACFm16r/u0dGt\n9j5HfwhZteo0AKhycqZ3Lv/OT0tbSI1Grmt4ePZgZ8B9ZsyQA4BerfYzajT9+szT1NREAUDQnDm3\ndC+2J4F33ZUOAKpLl2aU/PvfqwHAe/r0w56JiU23GsvicqkwLOwaAMgPH3ZoKbAqJ6fDEK61tHS8\nIj293xeoSj76KMHY1ibmuLnVi2JjzwNA8/XrjFgdoZR/8UW0XqUKZrm4qGO2bu3z57/H2LG5AKDK\nyWHEKgMDgDg/xCKNnOi42WY+gGKk0HIA9wD4xLL9EwD3Wu7fA+BLpFAtUmgpgCIAU5BGAgGIkEIz\nkEIpgE87jbErzi9WLcVYxKRnxOoQk5XVIK6t1Uaz2US3dm2szRK1zsh/+ilA39QUyOLx2sIefHDI\nnFyHI4GLF9eM/tOfMuzVuiHh+efPRq5YUTT+97+/ZMtp0R7wvb2VANBeW2u3zKoqJ8cjOzX1aVN7\nu4dLYGDB1M8+22lvJ2N74DluXBPP27ucGo28it27Y+01b+PFi54Xn3564flf/zqV6vUCoURyJf6Z\nZ7o1MxoKJKtWlXK9vKpMWq178XvvjQcAdUGBm+rSpTsAIGLDhkHNqgLmEni2UNgAStnKc+f6fOGk\n8dIlT2Nbm5jt4mLwnzJF7YgYeyJ8/fp8tlDYYGht9dYpFOFsgaBpzPbtva4i8ExMzAOApry8BMdF\nCbSWlprFJCEmAKT4gw/m9ncu+aFDcwBAPGnSGUFISA0AaKqrGbE6Qqnat28uAHhNmHCa6+bW53r1\noGXL8gCgraoqrr8XoxgYbmPWANhtue+PFGpdoiMH4G+5HwygstOYKsu2YMv9rtvtjtO/sNt05vJo\nRqwOPZ9/XjYJACIiXHPEYpder+mq/v77JABwjYy8PJj9IW9H2AKBaf6uXdmTtm27qXejvXEJDFQA\ngE6ptItYbS0rE17YsuW3hpYWX563d/mUXbve43l6DrmhUk+I4uOvAIAiPX1ApcBtlZWCq3/+84wT\nCxf+PnP9+lfrjh5dZWhu9mMLhQ1jtm//YjhllQmbDZ/p008DQO2xY7MBIP8f/7iTGo08oURyJWTl\nyj5VXNgLnpeXHABUly/3uRy29siRSADwiotTsriDu9qEzedTz/HjO/qoBi5e/G1fTJ2Cly27BgCa\n6upRhtZWh/2jaGSyIADwSko6DgCqnJxZGpmM39d5VDk5Hq3l5YkgxBi1eXO6e0yMDAC0dXVOL1Zz\ntm2bffaBB9Y60nDO2VDl5Hi0FBcnAaBRmzad7s8cPtOmKTkiUS3V6wVV+/ZF2DlEBganI78OBUih\nyR23nkgjPADLAdy8jMicKR02S/KcX6xa16xSRqwONRcvqqYCQHKyX+atju1M05UrSQDgO2sWUwI8\ngnANDVUCgE6lGnAZcHtdHe/cxo1P6lWqYI5IJJ/0r3+9LQwObh94lI7Df8GCHABoKSoa21eDG31L\nC7vw7bcTz9x776bTy5b9o2rfvvXtMlksWCyja2TkhYiNG99LPnr0RUdnx/tD9BNPZBI2W6+pro6v\n3Ls3rPHChbkAEL5u3aBnVa3w/fzkANBSUtJnsdqUmxsFAD7jxw/aetXORKxf/zNhs3U8b+/y+Bde\nOHvrEb/gNWGCiisSyanB4FL97bfhDgoROoUiCACCV6zIcPH3v071ekHBG2/M7Os8xTt3zgClLNfw\n8ByPMWPU4smTZQCga2wMcmZH4Joffgiu+f77h5quXp1dsnOnw0zXnI3if/1rFihlu0ZEZIsnTWrs\n7zxukZG5AFB/6hRTCszA0HsWA7iIFFpr+b3WUtoLy0+rc3c1AEmncSGWbdWW+1232x2nF6saPSxu\nwAZGrA4hhw/LAhsbdSFcLmnbsCEiry4ry73swAHvhvPnvYxabY/uYMrMTLFOqQwjHI42fP36IXUz\nZbAv7vHxSgAwDLDXqr6lhZ25fv2vtXV1UWyhsGHCW2+9KYqNbbFPlI4jePnyCrZA0GRsaxPLDh4M\nudXx1GhE+aFD4p8efjjp+B13vF6yc+eWluLiSdRo5LoEBhYEr1jx6ezvv0+d/d13H8Q+/fTl/pTM\nDQauYWEat5iY8wBw7dVXn6QGA18QHJwXumbNkLl8C0NCZADQXlPT5wxdW0WF2Qm4n22jBorPjBnK\nqZ9++uKML79M689yANfIyDwAqD9zxiGlwPqWFra+udkPAPWdNUseuGTJEQBQnDkzz9Z7f1dMej1p\nPH9+FgAELl58GgA8ExNVhMvVmHQ61+bCQndHxO9oqNGIwn/+8wFY3I3rz5yZOMQhDQuMGg2rIStr\nDgAEL19+YiBzeU+dam5hU1jo0HJ3BoYRxgP4pQQYMPezXm+5vx7Ad522r0Ea4SONRMBspHTOUjKs\nRhqZZnEBXtdpjF3hOGLSweSXzCojVoeSvXurpgDAqFHuF02lea7fP/LIndRgYAGYC0KMHKFQxXF3\nV3I9PBp43t5KFz+/BqFEomw4f34UALiGhV0ZziWdDH3Ha9y4RhBiMmo0nnq1mtOfdh9GrZZkPvzw\nBk1V1WgWn9+S+Morbw7kCvxgwuJyqWtk5BV1bu4s2eHDY4OWLeu2lVPdyZN+FV9+OVWVnT3V0NLi\na93O9fSs8ZowISN87dqs4ZhBtUXIvfeevvbqq9NN7e0iAAhbu3bIsqoA4B4TIwcArVLZp8yqTqXi\naBWKMAA0eN68Ifsb9MZQqSfEkydfU2Vnz2suLIwHsN+OYQHocAJmcdzc6vk+PrroLVsuV371ldLQ\n0uJb/P77Y0f99rc5vZmndNeuOENLiw/b1VUZ8eijeYC5rJzn6SnT1tdHKjMyAkXx8c32jt/RXHvt\ntSnttbUxhMvVUL1e0FpSMk7b0MB1RH9rZ+L6u++OM2o0nhyRSB6xYUP+QOaS3H9/QfHOnQatQhHe\nXFTkOlwM5xgYhi1pxBXAnQA2d9r6KoCvkEY2AigHcD8AIIXmIo18BSAPgAHAFqRQ68XyJwB8DEAA\n4JDlZnecXqxq9JYLt0wZ8JBhNFJcudI0GQAWLgw4Jz/yTSQ1GFgcoVBvMpk0pvZ2kaG11dvQ2urd\nLpd3O4f39OmXBjVoBofDFghMHKGw0dDa6t146ZLY7447bmoGbwtqNCLr0UfXtBQVTSYcTnvCCy+8\n5T9vXu2tRw4fvKdNy1Hn5s5S5+UlotObuLqgwK303/+e1JCVNU1bX9+xzorv6dkecuedFcLx4/8b\ntHRp1XBaj9oXQtesKS7asUOmb2oKdAkMLAhfu7ZoKOMRT55sdgRWqQKo0YjePq+ygwdDQSmb6+lZ\nLfTzc0pxIVm9uqDkww+N2vr6iLbKSoFQIhlQC6yuWJ2Aed7eMsC8ztZn5syj8h9/vL/mhx8W9Fas\n1vzww2wAEE+c+HPnDDLf11emra+PVBcWBgIotGfsjkYjk/Grv/32PgAIXrbsq7qTJ5N1SmVY2Sef\njI793e+yhzq+oUT+449zAcBnxoyTA32fc/Hz07kEBBS119TEVe3dGx//7LPn7RIkA8NIJYW2AvDu\nsk0Jsztwd8e/DODlbrafBzDG7vF1wenFapvFaoIpAx469u6tjGgVxXCjAAAgAElEQVRpMfgKBGzV\nQw+FFeY8VbgMACLuuac46oUX/qlTqTiqy5fFzYWF4rbKSm9tXZ1Yq1R665uaxIbmZjFbKGyO2LCh\nV19oGJwLjkikMLS2ejfn5/v0VaxeeOKJ5aqcnGSwWIZRTz317lCZ8wyEsDVr8kt37TJo6+sjlJmZ\n4roTJyLrT52a1lZZmWDtS0k4HK1bdPTFgIULM+b88Y8SFpeLysrKbrOwzgJhsxGyatW3lXv2rIj+\n9a/3DHU8ovh4taWcVKguKHD3SEjoVYauISsrCgCEISEONyRzFILAQC3fz69UW1sbXbl376jYp5++\nbM/5rU7ALgEBHQ7wo55+Or322LF72mWy2Orvvw8JXr7c5v9zU16ee2tp6XgANPKxx36+If6gIJk6\nLw+aqiqnM1m68sILdxs1Gg++r29pwosvntWpVO51x46F1Z85M/F2Fqvyn34KaJfJYgmbrRv11FN9\nWofdE6L4+Nz2mpq4xgsXRgNgxCoDwwjC+cVqRxmwcXBtGhk6OHCgZgoAJCSIzvP5bKqpqpIAgE9i\nogoAeJ6eBr877qjrq1hhcH54np7KdpkMbZWVfVq3evmZZ+Yq0tOXghBTxIYNH0Rs2OBUGRUrLgEB\nWkFQUIGmqmp01qZNL4NSs08AISahRHLFZ/bszKhNmy7zfXx0AMDiciU2J3QiYn/3u+zh8oW8czlp\nw7lzAb0Vqy3FxVEA4B4XVwzAzaFBOhD3mJhr2tra6MYLF+IB2FWsWp2AXcPDO8SqUCLReI4de6bx\n0qX55f/5z/zg5cs/6XkGoPiDD6aDUrYwLCzHKylJ1XmfW3S0rPbIEbQ7mSOw/KefAhouXJgPgEZv\n2bKbxeXS0Pvvv1B37NjK270UuOzTT5MBQBQfn2mvTH/A/Pl5dUePrmotK0voS/UEAwPD8MfpDZY6\niVUmszoEaDRG1rVr6kkAsGxZ0DkA0NbXhwKA/9SpKltjGUY+PB8fBdC3Xqut5eUC+Y8/rgQAyX33\nfWrvTNBgI540yexyTSmL7+NTGrh48Zcz/vvfZ+YcPPh/Cc8/n2UVqgyOhe/jIweA5uvXe7VulRqN\n0MhkkQDgN2dOsSNjczS+s2fnAUBLSUm8vee2OgF7jBkj67w9ctOm4wCouqBgSlNeXo/mSNRoRMO5\nc7MBIGDRolNd93tNnGh2BG5ocBqxSo1GFKSlrQGlbI8xY85IVq0qBwCfmTMVPG/vcmow8Ms++eS2\ndK7VyGT8pqtXpwNA2Nq1x+01b+CSJVUsF5cmo0bjKTt82CG9HhkYGIYGpxerGut1SWrggQ5Lc8wR\nzWeflcW2t5tE7u6cunvvDSlXFxS4GTUaTzafb/QeN27YO7YyOBZBQIASALQKRa/b1xS9995UajTy\nBMHB10b/6U92KREbSkb/6U8/Rzz66I4Jb7/9x7nHj7867vXXjzujUYyz4xIYKAfQ63JSZWamt6m9\n3YPF47X4zpnj1FUhIStWlBEuV2NQqwMazp/3ste8XZ2AO+/znT273jU8/DJMJs71d965o6c5Sj/5\nJNbSN7gx6rHHcrvuF0+c2EDYbJ2pvd2jpaREaK/YHUnBG29M0FRXx7N4vNYx27d/23mf57hxF4Db\n1xX4+jvvTKUGgwvf378oaOlSu7W5IGw2XMPD8wCg9qefGFdgBoYRhNOLVRMloGAZCEDY+manL2t2\nNo4cqZ0CAOPGeZ5jswnqT56UAIB7RISKxZTh3Pa4RkQoAEDf1NSrzCo1GqFIT58DAH5z5/arSfxw\ng8Xl0tjf/S7bb+5cpxY8zo5rRIQcANrr6nqVWa07fjwKAFwCAkqcvaSQLRCYhMHBBQBQs3+/3bKr\nnZyAFd1VCISsXHkUABqyspJ1KlW3n881+/fPBgCvpKSf2QKBqet+FpdLuZ6eMgBQnj077LOr7XV1\nvMo9e1YDQMCiRd+6jxp1w0Xb0PvvvwAA1lLgoYhxqKBGI+pPn04GAP/580/Ye36vCRNyAUB97dpt\nmbVmYBipOL1YBQBK2DoA4OgamFLgQUSl0nGKipqTAGD1ask5AFDn5UkAwDMmhikBZoDI0mtV38te\nq5V790boVapgFp/fHL1ly7BY78gwMvAaN85cTtrY2Cuxqr52LQoA3CIjnboE2Ipo9OhrAKDKybFb\n1qmrE3BXwtetK+SJxZUmrda98K23Jnfd31xY6NZSUpIEgEZu3PhzN1MA+KWEW52fP+zF6pUXX1xs\nbGsT87y9K0b/+c83XXC7nUuByz7/PEavUgWzXFzUMVu3XrT3/JJVq64BoBqZLEarUDDfBxkYRggj\nQqyCxdEBAFvfxLw5DSIffVQyVq+nAm9vXsW8ef61ANBaUSEBAO+xYxmxygCPsWNVIMRoam/36E0W\noWrv3tkA4JmYeJbr5sbU9TPYDfGUKUoQYjS2tnr35otsW2VlJAB4TZjgtE7AnQlYuPAaALRVVsaZ\n9NaebwOjOyfgzhA2G/7z5x8FgLqjRxdQ440v6aL3358Gk4kjlEhybfUSFgQG1lhiH9Zite7kST9l\nZuZCAIjavHl35xY8nXH2UmCtQsHL3LDhvqL33+/ThY/qb75JBgCvCRNOO+L93X3UqBaet3cFTCZO\nxVdfxdh7fgYGhqFhRIhVSqxiVc2I1UHk1Kn6KQAwYYLXOes2bV2dBAD8Jk5kxCoD2Hw+5bi6NgCA\n6tIlm9nVtupql+aCgskAEP7wwyOiBJhh+MBxdTVyRaI6AFCkp/vZOrZdLufrGhokIMQUuHRp2aAE\n6GD87rijli0UNpi0WnfZoUN2MaDpzgm4K6OefjqLxec36xobQ8o+/XSUdTs1GtGQmTkbAPzvvNPm\n6901KkoGAO21tcNWrFKjEfmvvfYrmEwcUXx8etgDD/R4kcPZS4EL3357cuP583cWvfvubzMefvhX\nPZV4d0aVk+PRUlycBIBGbdrksPd391GjcgGgISPjtspaMzCMZEaIWGXrAYBlYMTqYFFZ2SYoK2tN\nBEDXrg3PAsxXW/VNTQEgxOQ/dWrTEIfIMEzgikRKAGguLLQpVovefXcKNRp5LoGBBcz6TgZHwBOL\n5QDQlJtrU/TUHDwYDoDwxOJKFz+/EeHWbDGguQYAdceO2aUUuCcn4M5wRSKDePLkEwBQuXfvAuv2\n8i++iNar1QEsF5emqMcfv2LrPF5JScPeEfj6u+8mtlVWjiFcrmb0X/6yz9axzl4KrM7NjbXeV2Vn\nzzu9bNkLssOHbf5tit5/fxYoZbtGRGSLJ01qdFRsvrNn5wJAS3Gx0z2vDAwM3TMyxCqLa86sGloY\nsTpI7NpVOt5kAicgwOX6hAleKgCoPXYsGADhenjIuG5uNxllMNyecD09FQDQVlFh0xFYkZ4+GwD8\nkpPPDEZcDLcfLv7+cgBoKy+3uW618eLFSAAQSiQjogTYildSUh4AqPPzB2yyZMsJuCsxW7eeBItl\naCsvT6w/dcoXAKq/+24OAHiNH5/OcXW1WRLqPWWKAiyWwdjWJm6rrnYZaOz2RtvQwK3YvftXAOA/\nf/73venj66ylwNRoRFtlZSwASFav/pjj7l6nV6mCc559dlvO88/f0bXUGwCMWi1pPH9+DgAEL19+\nwpHxhaxcWUo4nHa9Wh2gzMwUO/JcDAwMg0OvxaqUEFcpIcPSEtFaBswytDJidZBIT1dMAYCpU707\nSoBV2dkSAHDx968cqrgYhh98X19zr9W6uh4zq1X79oXqlMpQFo/XGv3EE3Y33mBgAABhaKi5nFQu\ntylWW0tKogBAlJAwIsyVrASvWJEPAO1yeUxvSjdtcSsn4M54JCQ0i2JjzwEgxR9+OK+lpETYfP36\nRACI2LDhliWhbIHAxPXwkAOAMj29VwZZ3XHp979fcHTWrL8U7dhh16zblRdfXGhoafHhenpWj33p\npRO9GeOspcD1p075GTUaTxaf35ywbdvZWfv2/U0UH59OjUZuzYEDD565997fNBcVuXYek//pp0FG\njcaTIxLJIzZsyHdkfBxXV6MwJCQfAGr272eyqwwMI4AexaqUEJaUkAelhPwgJaQOQD4AmZSQPCkh\n/5ASEj14YdrGmlllGTVO84bvzOTlNblXV2viCYHxkUfCO4RFa1mZBACEoaGMWGXoQBAYqAQAnVLZ\no1it/PrrOQDgMWZMBs/T0zBYsTHcXoji4+UAoG1o6FHwmPR60l5bGwkA/vPmjSixKoqNbeGJxRXU\naORW7dkzoM/wWzkBdyX84YePAkDTlSszC9LS5sJk4giCg/N8ZsxQ9mY839vbXMKdl9evUmBqNELx\n888L9E1NgUXvvfdU5iOPrNar1QNud6fIyPBWpqcvBoDITZt2d9d+pzuctRS49ujRWAAQhoQUEjYb\nLgEB2hlfffVJ2EMP7SRcrqa1rGx8xoMP/qnko486SoULPv00GgB8Zsw4ORhtoDzGjs0FAFVOjtM8\nrwwMDD1jK7N6HEAUgOcBBKRSKkml1A/ALAAZAF6TErJ2EGK8JZRYxWobk1kdBD7+uGwSABIaKsyN\njnZvtW5vl8kkAOAxZgwjVhk6cA0PN7ev6aHXartczlfn508BgLCHHmKMlRgchvf06bUAoG9qCjBq\ntd064tafOuVv0ulc2QJBk3jSpB4dap0Vt6iofABQnD07oFLgWzkBdyVo2bIql8DAAmow8OtPnVoG\nAP7z5/f69e5idQSuqOiXWFWkp/sa29q8CJutByGmxgsXFpxetuy52qNH+52p1avVnLy//W0NNRq5\nbqNGnYtYt+56X8Y7Yylwk2W9qig+vqDz9vjnnjs/8b33/sr38ys2ajSehW+++btzjz22QnbmjIfy\nyhVfwmbrYp588uxgxBh09925ANBWVRVn1GhGxHI3BobbGVsv4gWplP41ldKcVEo7rhSmUtqQSune\nVEpXAfiv40O8Nb9kVtsZsToIXLjQMAUAZs706SgBNmo0LF1jYwgA+CUnM2KVoQOPMWMUAKBvbu52\nzer1d9+dTA0GPt/fvyhg4cJeZWkYGPqDMDi4nS0QqGAycRrPn+/24kn96dORAOASGFg8GFmgwcZ7\n2rQ8AGgpLh6QyVJvnIC7ErR06RHLXcLi85ujfvOby70d6xYRYS3h7pdYlf/4ozkjGBp6NeHFF1/n\nuLnV6xoaJNkpKduu/PGPs7pba9kT7XV1vOzU1PknFix4ua28PJFwONoxf/rTnr7G5GylwNRoRFtV\nVSwA+M2bV9B1v8+0aco5Bw5IfWbNOgAADZmZdx1cuXIeAIji4zNdw8I0gxGnz4wZSo67ex3V6wVV\n+/ZFDMY5GRgYHIctsZp5q8GplOp72iclRCIl5LilbDhXSshvLdv/IiWkWkpItuW2pNOY56WEFEkJ\nKZASsqi3D4IRq4PHzz8rfOrqtJFsNtFt3BjZ8UWj/vRpf2o0ctmurkq3yMi2oYyRYXghSkhQg8Uy\nmLRa9/a6upteo/VnzpiNlebMYbKqDA6H5+UlB4DG7OxuM2rq/PwoAHCLihpRJcBWQu67rwgslkGn\nVEqaCwvd+jtPb5yAuxL9xBNXOG5u9QDgOW5cel96bXqOGzcgR+CmvDxrRjA/9P77S2fs2fM399jY\nDGo08qq//fbhMytXbm4pKRHamqOtslJwYevWxaeWLHlFfvjw/UaNxpPr6Vkd8+ST73qOG9dnB3xn\nKwWuO3EiwNTeLmK5uDT5z5vXrakWWyAwTdqxY3/cs89K2UJhg0mnYwNA2IMPnhjMWN2ionIBoP7U\nqWH/vDIMXwiRsgmRXiJEesDyu5gQ6U+ESK9bfnp1OvZ5QqRFhEgLCJEu6rR9IiHSK5Z9bxMitUuf\n69sJW2J1oE+mAUBKKqUJAKYB2CIlxHol95+plI633A4CgGXfGgCjAdwF4L3eGjpRFk8HAMSkZcSq\ng/nyy/LJABAV5Zrt5+fSYarRcP682VzJ15fJqjLcAIvL/aXXanb2Ddms6u+/D9EpFOGEy22LfvLJ\nC0MTIcPtBN/XVw4ALcXF3YpVTVVVFACIJ08eUU7AVvhisV4QGHgdAKn65pu4/szRFyfgzrC4XBq5\nceN/3KKiLsSlpv7Ul3N6z5hRB0KMhpYWH61C0afPemo0QlNZOQr4JSMoDA5un7lnz67QNWs+IhxO\ne2tJyYSzDzzwp9KPP47pOl5dUOCWtWnTvafvueeV+hMn7jVptW58H5/SyMcee3fusWN/jdy48aYs\nY29xplLg2iNHblivaovwtWuLZnz11UuRK1deT3jssatBy5ZVDUqQFrynTs0FAPW1a+NMej0jDhj6\ny28BXOv0+3MAjlKaGgPgqOV3ECK9ScMQIrW+SHYA2AQgxnK7a3BCHznYMhfwlRLy+552plL6hq2J\nUymVAZBZ7jdLCbkGwFYj8nsAfJlKqRZAqZSQIgBTANywxkFKyInOv7NcXAjXNyEEjRfgIpbESyQS\nW2ExDACTiaKo6Mw8AHjqqQk6iURyp3VfkdGYCACSuXN5EonkThcXl1EAwPw9hh9D8bfxjIqiiuxs\niPj8BRKJpOPLbX5GRhIAhC9ZUhM9blzyoAU0TGFeN45HPn++R/bly+Cz2ZMkEskNX2Lb6uq4+qam\nQMLhmKY++WQMVyiMsu4bSX+bqOXLDVd37ICpvv5OiUTidesRNyI/e1YESlkCf//W6KSkO/oyVrJ9\nO7B9eynMF7H7REZQUFtrdbW7QK2+JzgpSWXdfqu/Tf3Fi25GjcaTKxJpJz/66BjCYo3piOf996Hc\nsuX40Ucfndp0/bq44I03UlFXd22mVJrXXFHBv/DKK7FlBw5EWjOE3mPH1if+9rfXolaurCMslj8A\n/74+js4It28X7Dt2DJqKigkBXl5Vw7nt22WVahoAjFq1it35879HJBKMX7BAAwDt7e23Pt6O+G/b\nxq7YvVura2wMUe7Zs2nCM8+UDub5nYGR9J7mCAiRhgBYCuBlAFY9dA+AZMv9TwCcAPCsZfuXlKZq\nAZQSIi0CMIUQaRkAEaWpGZY5PwVwL4BDg/MoRga2MqtsAG4A3Hu49RopIeEAkvBLafFWKSE5UkL+\nLSXE+kEZDKBzVq4KtsVtB5TjYgQAYtCMvAVGw4j0dLlHVVWLyM2Nq1u1Kqq2877GggJPAPBJTFR1\nP5rhdsY1KKgVANSlpR0tDXRqNbvqyJEwABj9+OMjMovFMPzwsvTAbC4vv+lzrOroUTEAeERHN3KF\nwmErGgZK2JIlcgCoy8ryp6a+P0xFdrYIANzDwtR2Ds0m1vMpc3JEfRlX8eOPvgDgk5hYT1g3f+3x\nHju2ddWZM8dHrV17DQAKPvss/r9JSQv3TJ++pGTfvhiTTsf2mzRJtnD37mMrT58+GX3ffXXdzdMf\nvMeObRVFRjYa29s5RV9/3W+zJ0dDTSYocnJ8ASB00aK6oY7nVvBEIuPE557LBoDLb76Z2FRSMuz6\n8zIMJb4uhEhPWG89HPQmgGcAdH6T9Kc01br0QY5fLlb1pGGCLfe7bmfoA7Yyq/JUSl8a6AmkhLgB\n2Avg6VRK1VJCdgD4KwBq+ZkG4NHezpdKaXLn37fx+Yb2hoo8PjBGX59fU1lZ2afSIobe89JL51YA\nQHi4MFOhkP1o3U6NRjReu3YXAOg8PPZXVlY2WK/UMX+P4cdQ/G00bW1sAJEVJ0/WBzzyyE8AcHX7\n9ukGjYbD9/UtMYSG7q2sZCrImdeN42nj8TwBzGkqKXHp+jznfvbZcgAgbm4Xu+4bSX8bKpGA5eIy\nRdvQ4JH1739fDVy0qE/GZtcPHFgGAAZCLg/m86EHBACCiw4eVHjde2/HeW/1tyncs+cxACCenqcq\nKytP9jR/5LPP/kj8/WOKduzY2FpT4wWAukVFXYh49NGDwcuXV1nOYcdHZMYlPJylLilZmb1jB8dt\nwYJh+f8lO3w4UK9W38cWCJo0YvE3vX0ehvJ147FkCYTvvy9sq6gY+8N99wXN/u67fw12DMOZkfSe\n1g9W2tpJiPRuAHWUpl4gRJrc3TGUplJCpNQRwTHciK1LgwN2ppMSwoVZqH6eSuk+AEiltDaVUqPF\nYXgnzKW+AFANoHMtQohl2y0xsVwsa1Z1zJpVB6HXm8jVq01TAGDJksCMzvtUly97mnQ6NxaP1+Y1\nYcKIa/XAMHBcgoKUAKBtaOhwBK4/dWoOAPjOns0YKzEMGp6JiSrC4WhNWq1bV4Oh1vLySADwGDNm\nRJorWSFsNlzDw/MAQH748JhbHd+V/jgB2wPX8PA+OwLfysG2KxGPPHJ9+u7dLwXeffcXSW+++ZdZ\n3377gVWoOopOrsCJOpVqwL1fHUHd8eOxACCQSAqcxSWbsNkY85e/fEE4HG1rScmEgjfeGD/UMTEM\nF+rbKU1Ntt66OWAmgOWWMt4vAcwjRPofALWESAMBwPLTWmXQk4apttzvup2hD9gSqwMqgZISQgB8\nBOBa5/WtUkI6f8isAHDVcv97AGukhPClhETAvAj5HHqBiW0Vq/phb/3urHz+eXl0W5tRLBSyG9as\nCb3hi1z9mTOhAMDz8alwlg8xhsHFLSLC3L7G0mtVduhQkLauLpJwOO3RW7acH9roGG4nCJsNroeH\nHAAasrI61hsatVrSXlsbCQABd9454svSvZKS8gBAnZfX5xY2/XECtgeelvNplcpei9VODrbqnhxs\nu+IWGdk27pVXTvrPn99r86iB0MkV2KX044+HpXut+tq1WADwSEjot5nUUCCePLkhYOHCfQBQ8eWX\nD7aWlwuGOiaG4Q+lqc9TmhpCaWo4zMZJxyhNXQuzVllvOWw9gO8s978HsIYQKZ8QaYeGsZQMqwmR\nTrO4AK/rNOYmCJFOIkT6O0Kk/yBE+hIh0vs7Ow7frtgSq4YBzj0TwMMA5nVpU/O6lJArUkJyAMwF\n8DsASKU0F8BXAPIA/A/AllRKe2Vrb2ILzK1rqJ7JrDqIw4flUwEgMdEzk8tl3VD20FxQIAEAQWAg\nU8fJ0C0eY8YoAcDQ3OwNAOW7d88GzL33XPz8dLbGMjDYG76PjwwA1Pn5HaKn9scfg6nBwOe4uio9\nExP73IbE2QhZtSoPANXIZKP64q7bXydge+A9c2YtAGpobvbTq9W9ykD2xcF2KOlwBT59etJQx9IV\nk15PNFVVowAg4M47nUqsAsCYl146yffzKzFqNB45zz9vs/yTgeEWvArgTkKk1wEssPwOSlNv0jCU\nplo1zBMAPgRQBKAY3ZgrESLdQIj0IoDnYV7uUABz1nYWgCOESD8hRBrqyAc2nLH1Zu83QDfgM+i+\n/c1BG2Nehtl1q09Qi1glJkasOgK1Ws8pKFBPBID77gu5qf9uW2WlBADcoqMZscrQLaL4eDVhs/Um\nnc5Nfe2ae9PVq9MAIPRXv2JKgBkGHZfAQHlzQQHaqqo6DG0UZ89GAoBLcPCILgG2IoqNbeF5e1fo\nlMqwyq+/jon+zW9yezNOcfq0Pyhlcdzc6vk+PoN6oYkvFus5bm4KQ0uLr+Lnn/0CFy++ZRmyNSMo\nSkjId3yE/Sf0/vsv1B07ttJaCszz9BxowqCD4p0743RKpVv8c8/1q4pF/tNPQSadzo0tFDb6zJxZ\nb6+4Bgs2n0/jnnnm08t/+MMfm65cmVP66afnItatuz7UcTE4B5SmnoDZ9ReUpioBzO/huG41DKWp\n5wHcarmFEMBMSlM13e0kRDoe5mxtRW/jHkkMihuwozFyhGaxymRWHcKHH5aM0eupUCzmVS5aFHhT\n2Ze2vl4CAOKJExmxytAthM0Gx9VVCQD5UumdVK8X8ry9y4PvuYf5n2EYdFzDw+UAoK2r6xCrzYWF\nUQDgHhNzW4hVAHAfNSoXAJQZGb0uPVXl5AQBAM/be1BLgK1Yz9t05cotS4Et61XNGcEFC4Z1RtBR\npcBGrZYU7djx6/LPP99U/d13/epRYl2vKnSi9apdCVy0SOYzc+ZBACj+178eHq5rgxluW0hPQhUA\nKE3NpjT16GAGNJywJVZlqZS+lErp9u5ugxZhLzCx3cxXd00GRqw6gBMn6qYBwIQJXjdlVVvLywWG\nlhYfsFgGv+TkQS0JY3AuOCKREgAaL1yYCwC+s2YxWVWGIcFz7Fg5AOgaGjrEqqa6OgoAvKdNG/Hr\nVa34zp6dCwAtxcW9XrfaWloaCAAuAQGDaq5kxcXfvwYAWixx2EJ+5EigSat1ZwsETb5z5gz7diuO\nKAWuPXIkiOr1AgAo3707uT9zNOfnm9erjh49rAX/rRj32mv/43p4yAxqtf/lZ55ZOtTxMDB0otdd\nUW5HbInV7kp4hyVGrrsls8qIVXtTXt4qKC9vHQuArlsXntV1f93x4yEAwPPyqmYLBCO2LyHDwOF5\neSkAgBqNPMLhaKO3bOmVgRoDg73xnjGjDoSYDC0tPjqViqO+ds3d0NLiS9hsXeCiRQ51fh1OhKxc\nWUo4nHZ9U1Ngw/nzvTLx6HACDgsbErHqGhZmdgSWyW4pVp3NwdYRrsDKjIwI6/3m/PwpfTUYMun1\nRFNTY85OL1rk1GKVKxIZords+RQAVWZkLKr54Qem3yUDw2CRRvyQRlYgjWxBGnkUaWQK0kivGlbb\nejPcLCVkcSqlNywEtpgk1aZSemEgMdsTI8ciVpnMqt358MOSiSYTOEFBLvlJSV6qrvubcnOt5kq3\nZR09Q+/h+/kprPfdY2OzBIGB2qGMh+H2hevmZuS4u9cb1Gp/RXq6f3NhoQ8A8P38Sm+ni24cV1ej\nMCQkv7WsbHz1d9+NFk+adOZWYzqcgMeOHZIyYNHo0TJ8/XWvHIGdzcHWWgqsUyrDSj/+eHTs009f\nHuiczdevm8UqISZqNPKuv/POjPFSaa/LCWWHDgWbdDohWyhs8J46VTnQeIaasAceKJEdPHhClZ09\nN18qXee/YMGrbD6f6ZXJMNQkEiJVd7OdAKCUporserY04gmz6dMYABTmzG4BgP8CCAdQBuB+pNBG\ny/HPA9gIwAjgKaTQw5btEwF8DLMp1EEAv0UKvfH1lEbmAvjvgJ4AACAASURBVHgOgBjAJZiNo1wA\n3AsgCmlkD4A0pNDuHj8A25nVV2F2tepKLoB/2Bg36Ji4Ij3AZFYdQWamcgoATJ/uc1MJMAC0lpWF\nAoAwPJxZe8hgE0FgYMcXHcl9950aylgYGHheXnIAUF+9GtB05UoUALiGhd02JcBWPMaOzQUAVU7O\nLUuBh9IJ2IrvzJlyANA3NQUYNZoev8M4q4Otx+jR2QDQmJXV55ZC3aGpro4AAPHEiUcAQJGenmzS\n63tdOVd/8qR5vWpoqFNkp3vDuNdf/4YtFDbqFIrwK9u2zRvqeBgYAFyhNFXUzc3d7kLVzFsA/ocU\nGgdgHIBrMAvKo0ihMQCOWn4H0kgCzO17RgO4C8B7SCPWN4MdADbBbP4UY9nflSUANiGFTkYKfRwp\n9EWk0FSk0OWWc18CcKetYG2JVfdUSsu7brRs87E16WBj4HpZyoCNjFi1I+fPN3jJZO2xLBYMGzdG\nXuruGG1trQQAPBMTGbHKYBPxpEnVACjP27s8ZMWKm95bGBgGExd/fzkAtJaXB7SVl0cCgOe4cbeN\nuZKVoLvvzgWAtsrKBFviD7jBCVgx2E7AVlwCArRsobABlLIVZ8/69nScszrYiqdOvQ4AbZWV0QOd\nq10u5+tVqiAQYkx85ZUDbKGw0dDc7Fe6a1dcb+dQFxTEAoDn2LFOI/hvhSAwUBu2du3nAFB75Mi9\niowM76GOiYHBXsT5IRZp5ETHrStpxAPAHAAfAQBSqA4pVAXgHgCfWI76BObMJyzbv0QK1SKFlsLc\ngmcK0kggABFSaIYlm/pppzGdOYsU2n31ZQo1IIV+ixS619ZjsvXBZGv9itDWpIONkeepBwBQIxe9\na83K0Av+85+yyQAQEeF2WSIR3uRSplerOTqVKhAA9Z87t3rQA2RwKvznz5cnbNv22sT33ntnpFyh\nZ3BehKGhMgBoq6oK1ioU4QAQcNddt11m1WfGDCXH3b2O6vWCqm++Cbd17FA7AVvhicUyAFBdvtxj\nKbCzOtgG3X13GQgx6hobg9uqq10GMpfsf/8LBUB4YnG1S0CAVjxp0ikAqNm/P7k3441a7YhZr9qV\nUVu3XnGLjs6iRiMvd/v2h6iR+e7IMKTsG8RzRQCoB7ALaeQS0siHSCOuAPyRQq3v7XIA/pb7wQA6\nJ6SqLNuCLfe7bu/KiwMN2JZYPSIl5GUpIR3lIlJCiJSQlwAcG+iJ7YmJ42qkIEYCymIZNM7zqTTM\nuXChcRoAJCf7dlsCXHf8eCAoZXNEolqXgABm/SHDLQlds6bUIyGheajjYGAQxcbKAaCtvHwsNRq5\nHJFI7h4d3TrUcQ0FblFRuQBQf+qUzZYpQ+0EbKXDEbikpEex6qwOtnyxWM/38akAQGQHDkQOZK7G\n7OwIABAEB5cCQPRvfnMGhBhby8rGNWRliW81XvbDDxKq1ws4bm4K76lTGwYSy3Ak8e9//y+Lx2vV\nVFWNzvv736cOdTwMtzUr7DVRfh0KkEKTO243wwEwAcAOpNAkAK2wlvxaMWdKh81abltiNQVAJIAi\nKSF7pYTsBXAdwCgAvx+M4PoCJRwdAHB0SqYU2A788ENNsEqlD+bxWK2PPRZ5tbtjGi9elACAi5/f\nbeOeycDAMDLwnj5dDpjdqQFAGBx822VVrYinTMkFgObCQptidaidgK1Ys+LtNTXdilVnd7AVhoYW\nAUDjxYsDKgVuLSmJBABRbGwpAHiMGaN2i4q6CIAUf/DBnFuNrz9zpmO96kDiGK6I4uObg++552sA\nqPrmmwfOb968vO74cb+hjouBwcFUAahCCrUmovbALF5rLaW9sPy0tvuqBtC5R3OIZVu15X7X7V2J\nQxrJ6eZ2BWkkpzcB9+gGnEppK4AHpIREwryoFgByUykdnh/ohK0D1QvYehUPCOuxsS5D79i3r2oq\nAMTGul9wc+N2Wx/TUlIiAQBhaCjjBMzAwOBUuIaFaVguLk2m9nYPAHCPjb3t1qtaCV29urBk506j\ntr4+vKWkROgWGdnW3XFD7QRsRRQfL6v+5htoFYpuxaqzO9h6JiYWNV64cGdLWVnUQOZpr60NBwDv\n6dNLrdtCVq06kf/aa5MbL12apVerD3BFIkNP45st61U9xowZkWIVABK2bTvbkJU1vrWsbLwiPX2p\nIj19Kd/Hp1Q8eXJmxIYN50Xx8UwlEMNgMHhuwClUjjRSiTQSixRaAGA+zIa6eQDWw2ywux7Ad5YR\n3wP4AmnkDQBBMBspnUMKNSKNqJFGpgHIBLAOwDvdnLEUwLKBhNyjWJUSwgYgsIjTEikh0wCESAkJ\nAXApldJh9QKmLI4OJoCtb2IyqwNErzeRq1ebJgPAkiWB3ZYAA4BGJgsFAFF8PGOuxMDA4HTwvLzk\n7TKZBwD4zJp124pVl4AArUtAQFG7TBZb+fXX8fHPPntTa7rh4ARsxWfGDBkA6JuaAo1a7U3OtvWn\nTjm1g23AXXcVl+7aBW1dXYRRo2H1p52S6vJlD2NbmxfhcjV+ycm11u1hDzxQVPzBB1X6xsaQ6++8\nMyFh27Zu+10bNRqWRiaLBoDAxYsL+/9ohjeEzcaMPXveL//Pf0bJDx+e1nz9+gStQhEhO3QoQva/\n/90vDAnJ9Zk9OzNq06bLQ2UqxnBbcIXS1KRBPN9WAJ8jjfAAlADYAHO17VdIIxsBlAO4HwCQQnOR\nRr6CWcwaAGxBSodB0BP4pXXNIcutK1qk3GzY2xds9Vl9DeYU8OuW37+AuW2NC4CLAJ4dyIntjbUM\nmG1oYcTqAPn88/Lotjaj2NWVrfzVr0K7/QJn0uuJTqkMAQDfOXMYscrAwOB08H185O0yWSzhcjX+\n8+YNqQAbakTx8bntMlls48WLowHcJFY7OQHXD/WXdtewMA1bIGgyajQejefPe4dH31gtq7asV3VW\nB1uPhIRmjrt7naG52U926FBIyMqVfa5eqj16NAIAXPz8ylhcbsfaM8Jmw3f27BM133+/tvbYseSe\nxGrNL+tV68WTJjX2/9EMf9h8Po3cuLEgcuPGAq1Csbvko48S60+dmtpWWTm6rbJybMUXX4yt/Oor\nrVt09MWAhQszwtetK2B6szI4NSk0G8CkbvbM7+H4lwG83M328zD3arUFt4/R3YStNavzAbzR6fem\nVEqXAVgIYOZAT2xvrGKVxYjVAfO//8mmAcDYsZ7nuFxWt2/IyrNnfajB4MIWCJoYwxwGBgZnRBAc\nLAcAF3//ks5f6G9HAhYsyAWA1tLS0d05ow4XJ2ArPC8vGQA0Xrp0QynwSHGwFQQHFwOA4uzZfq1b\nbcrLiwAAoURS1nXfqK1bzxEuV6Otq4uq/v77kJsGo9N61bAwp30O+wPfx0cX/+yz5+f88MO7M77+\n+pnApUt38319S6jBwG/Oz59+/e23f5e5bt3aoY6TYcTx9VAH4EB6XGrQW2yJVVYqpZ1P8CwApFJK\nAbgN9MT2hrI4eoDJrA4UlUrHKSxsnggAq1dLeiwBVmZmSgDA4lrIwMDA4HREbd6c6RoZeTHsoYcO\nDnUsQ03gkiVVLBeXJqNG4yk/cuSmtaDDxQnYCt/Pz+wIXFR0Q6yyQ4dGhIOtKC6uCABarl/vl1ht\nq6iIAACPMWNu8hlxCQjQeowefRYAKnbvTu5ufEthoTk7nZh4W4nVzohiY1vGvfrqibnHjr028d13\nX/SZNWs/x82t3mfGjMtDHRvDiENMiHRz142ESDcTIn11KAKyIwO+EGyrDJgnJcTdujY1ldIfAUBK\niAfMpcDDCkq4lsxqGyNWB8BHH5WM1eupQCzmVSxcGNDjFfTmwsJQABAEBzNOwAwMDE6Je3R06+zv\nvvvXUMcxHCBsNlzDw/Oa8/Onyw8fHhO4aNEN7//DxQnYilAikamys6ExOwJ3xNR5veqQBWcHfOfM\nKar+9ltoamqiqNGIvqy9NWq1RFtfHw4A/vPnl3V3TMQjj5y89PTT89TXrk1tLS/f6xr2izGlobWV\nrZHJYgAgaOlSp34e7YXvnDn1vnPmHKBG4wFqMt20TpqBYYDMBfCHbrbvBJCDrq1lnIu4Hlx/CQCK\nFJp4qwlsZVZ3AvivlJBQ6wYpIWEAdgP4sK+ROhrKsohVIyNWB8LJk/VTAWDiRK9u17FY0VRXhwCA\ne0wMs16VgYGBYQTglZSUBwDqvLyErvuGixOwFfe4OBkAaOvrb8isjhQHW7/k5FoWj9dq1Gg8lVlZ\n3n0ZW3fiRAA1GPhsobDBY8yY7hxG4T9/vlwQFJRPjUbe9XfemdF5X83+/aHUYOBzRKJaz3Hjmgby\nOEYahM3G7b5kgMEh8ClNven/itJUE8yizpmxugF3vd2NXroE9yhWUyl9A2a74jNSQpRSQpQATgHY\nn0qpdICB251fxGr7gBfy3q6UlbUKy8tbxwKg69dH2BSrWoUiFAC8p01jyoAZGBgYRgAhq1blAaAa\nmWyUVqHouPA7nJyArXhPnSoDAJ1KFURNZrPczg62zp4RZHG51CUgoBgAao8c6VMpsDI9PQIABIGB\npbaO81+48AQAKNLTk016fccXYkV6eiwAuN5m61UZGIYQDSHSmK4bLducvR2nDim0vMdbL7CVWUUq\npe+nUhoKIBxAeCqlYamU7pAS4m+H4O0KZfF0AEBM7UxmtZ989FHJBJMJnKAgQcG4cZ49Xk1tystz\nN2o0HoTDafeePl0xmDEyMDAwMDgGUWxsC8/buwImE6fy6687vjh1cgJWDLUTsBVRbGwLi89voQYD\nX3X9ugDo5GDr7l7nNWGCaqhjHChuUVHFAKDOy+tTv9XmwsJIAHCNjLQpVmOeeOIyWyhsNDQ3+5Xu\n2hXXafxtv16VgWGQ+ROAQ4RIHyFEOtZy2wDgB8s+Z+bngU5gU6xasaxbZUsJ2Sgl5CiASwM9sb2h\nLK4eAFhGRqz2l4wM5VQAmDHDO8PWcfWnTkkAgOftXcWUwzAwMDCMHNxjYvIAQJmRMdq6bbg5AVux\nOgIrsrNFAKCwOtiGho6IvqDiKVOKAKCtsrJPmVVNTU04AHhNmGBTrLIFApN40qRTAFCzf38yYM6i\nt8vl5uz03XePiOeRgWG4Q2nqIQD3wrx29WPLbS6AVZSmOrsBYKmld+uNpJGNSCNP92YCWwZLkBIi\nAHAPgAcBJAFwh/nJPNXnUB3ML5lVLSNW+0FWVoNYLm8fxWYT/WOPRdq8GKG+dk0CAILAQGa9KgMD\nA8MIwmf27FxlRsbiluLijnWrw80J2Arf17emXS6PacjNFQGoHWkZwaC77y7L/8c/DHqVKqi1vFzQ\n2QSpJ7QKBU/X2BgMQkyBd911y2U60b/5zZn606fvbi0rG9eQlSVuvn7d8//Zu/PwuM7y/v/vW6PR\nZkne5EW25V12bJw9mGyFJDQQSAiUQAilkLb50oW0LJ3zLdD+2lD6y/fi155h+bK1QEsSIIWwlWxO\nIGlCCCQEO3Gc2M7iRY4X2fImS5ZlaTS6f3+cI0d2tIyk0erP67rmmnOec54zz3gullv389yPZ7NF\nycrKvb2tdxWR/HMPngduHO1xDIM/BC7sof07wFrgi/09oNfMamh2J/AScCXwZaKpwIcD90cD987B\njHY4dRYUtwEUdLYrWB2E73637vUACxdOenbu3LLjfd177JVX5gOUL16s9aoiIhNIzXXXbbPCwuOZ\nI0eqD61dOxXGXiXgLmXz5tUDNL78cmW2rc0mWgXboilTOuLt4WzPffctzqVP/Zo183EvKJo6dXcu\nU7Ynr1rVVL5kydOAbf3GN97YtV61bOHCCfFvKDIemIWXmoUf6nb+I7Pwf+LXFaM5tjwoJOWZ17Sm\nvJ0ci0f1NQ14JXAY2AxsDtyz5GGvnOHiBcVxZlXB6mA8/fThNwBcfvnMXvdW7XK8oWEewJRzz9W2\nNSIiE0jhpEnZsnnzXgDY/bOfvQ7GXiXgLuW1tfUAzdu3V+7+5S+nTsQKtpPmz98C0Lh+fU5TgQ8/\n/XRUXGnu3D6nAHc377rrHgU4/Mwzlza/8MLrAKaefbaCVZGR809EWcYuy4m2svkM8LejMaA8KiDd\nQ62jntp6fUAvAvdzgOuJpv4+FJo9DlSMxeJKAJ2J4gwoWB2M++7bM7exMTO3qKig5aabFm3s697j\ne/cWdzQ1zcIsO+uKK8bUX9lFRGToJq9atQmgccOGlWOxEnCX6atXR8Hqzp2Vux5+eAZMvAq2k88+\newtAS11dTkWWWrZvXwRQUVubc7C64P3v35KcMmV3Z1tbxfF9+6Ls9DveofWqIiOn0j3Y1O38Zfdg\nnXvwGFEcNp79K3AfaXsTaauIX5cB9wI57S7TXzXgFwL3WwL3M4CPAXcAvwvNfjPEgeedF5TEmdWM\ngtUB+slPdr0BYPnyirXl5clsX/fue+SRuYAlp0ypT1ZWdozIAEVEZMTMueaajQDHdu5cuf+RR6rH\nWiXgLpNXrTpiyWRrR0tL8pUHH5wPE2e9apfqt71tK0BbQ8OijpaWRH/3t9bXLwKYfvHFOQerlkgw\n441vfKTrPDllyp7KFSuaBzNeERmUKd1P3IN3dzsdk0nCnKX8DuAfgM8CdfHrn4B/JOW35/KInKoB\nAwTu6wL3FLAA+NRAxzrcOhOlmgY8SC++2HwWwFVXzf5df/c2bthQA1Aya5aKK4mITEBVl1xyoLCi\nosEzmdKdP/zhxTD2KgFDFGR1VQRurqubDBOvgm3l8uVHCysr93k2W1R///01fd175PnnK7PHjk2z\nwsLjMy+7bEBZ8GV//ddPWTLZCjBJ61VFRtoLZuHVpzaahdcA4/8/jylfQ8rfRMqnx683kfI1uXbv\nsxpwd6HZSuD9wA3AEeCCgY92+HQWlsXBakdytMcynmzadKTiyJFMdSJh7dddV7Otv/uP1dXVAExa\nsEDBqojIBFW+ZMnGxvXrZzY+99ylMPYqAXcprqra09bQsBggOXly/USsYFs2d+7WpqamWQeffHJJ\nzXvfW9fbffsefnghQPGMGTsSxcUDqjFSMnt22/TVqx8+8OtfXz37LW9Z238PEcmjTwD3mYXvAZ6O\n284HLgauGbVR5UPaXgcsIeV3x+dfACbHV79Cyp/urWuXPjOrodnC0OzTodkGohLDfwlcGbiPqUAV\noDMRB6uuacADcc89e5YBzJ5dsmXSpMI+pwADtNbXzweYvGqVKgGLiExQ01av3gjgHR3FMPYqAXcp\nnTv3RMa3bMGCCZVV7VK5YsXLAM1btvRZZOnI888vBiibPz/nKcDdnf/Vr97ze/fe+4mFH/zglsH0\nF5HBcQ+2AGcBvyLafWUh0TahZ7kH4/2/1z4HHOh2/lbgPuAR4B9zeUBfW9c8ET+sELgucD8faA7c\n6wY72uGULZwUF1jqULA6ABs2NC4HqK2t6HeaQba1taD98OG5ADMvv1yVgEVEJqj5733vS5id+APm\nWKsE3KV86dIT45qoFWxnvOlNWwFa9+xZ4tne/6Z87JVXFgFMft3rBhWsWiJBLnu5ikj+uQdt7sF/\nugep+PWfwAVm4VdHe2xDVE3Ku9c6aiLlPybl3wGqcnlAX5nVfUQVqGYBM+K2Mbt1TWdheZxZVbA6\nEDt2HFsGcPHF0/v9y03DY4/NorOzsLC8/ID+B01EZOIqmT27rWT27K4M25irBNxl2vnnnwhWJ2oF\n25lvetO+guLio53Hj08+8JvfzOjpns5Mxo7v378AYNYVVwwqWBWR0WcWnmsW/otZWAf8M/DCKA9p\nqE6uZpzyC7udzczlAX1tXfMu4ExgHfCZ0Gw7MDU0Wz3wcQ6/bGGFgtUB6r5e9dpr5+7o7/5Dv/vd\nfIDiGTO0XlVEZIKrXLFiI8BYrATcZdoFFxxacPXV25a+730vTtQKtpZIUDJ79laAhkce6XELm4ZH\nH53lmUxpoqzs8ETaZ1bkdGAWLjMLbzELXwC+DOwEzD243D348igPb6j2kLY3vKY1bRcCOS0v6bPA\nUuB+BPg28O3QbCbRvqtfCM3mB+59VqUbadnkZBVYGqCBrlc9tnPnLIDS6uoxuXZJRETyZ/773rd2\n/69+9baK5cvXj/ZYemOJBG/53veeBti5c+L+HbV86dItx3bsOLtp8+alwJOnXj/wm98sAiiZPVtZ\nVZHx5wWi9arXxOtXMQs/MbpDyptPAj8gbbdxcvGoG4H35fKAnKsBB+4NwFeAr4RmCwY2zuHXUTQ1\n+quvZ5VZzdFA1qsCtB84UAVQUl19oL97RURkfKu6+OKDV/72t58oSCbH7BKg08X01au3NDz8MMd2\n7eoxs9r80kuLAMoXLVKwKjL+vJtot5VHzMIHgO8DNrpDypOUPxVnVv8K+OO4dSNwISnfl8sj+iqw\n9M3Q7MxeLh8Izf40NPvAQMY7nLLJqZoGPEADWa8K0N7YOB1g0oIFClZFRE4DClTHhjnXXPMKBQUd\nmcbGOUe3bSs79Xrr7t2LAKacc46CVZFxxj34b/fgBuAMoiq5HwdmmoVfNwvfMrqjy4OUN5DyfyTl\n18WvfwSKSNv/zqV7X5nVrwL/EAeszwP7gRKgFqgE/hP43tBGnz+dhaVZxzoNTxR0tCQ6Cyf1O631\ndDbQ9aoAHc3NVQAVK1YcHN7RiYiISJdkZWVHcVVVXVtDw9L6++9fUvtXf/Vc17W2Q4eS7YcOzQW8\n+qqrtK2cyDhjFha6Bx3uQQtwJ3CnWTgVeC/RNNqfj+oA8yVtM4i+0/uBOcBPc+nWa7AauK8Hrg/N\nyoELgGqgFdgcuI+98vCWAEu04x0lifbGpILVvt17b/2A1qtmmpoKs62tkzHrnHr22YeHf4QiIiLS\nZdLChVvbGhqWNj777BLgRLC6d82a+bgnklOn7iqZPbttFIcoIoPzFHBe9wb34DDwjfg1fqWtgmia\n8x8Cy4CfAItI+bxcH9HvmtXA/Sjw6CCHOKLcCtvNO0oKM4eLMsw9PtrjGcuefbZxGUBtbXlOU4AP\nP/PMNMAKy8oOJUpLO4d1cCIiInKSKWefveXQU0+9taWubmn39sNPP70QoHTOnLrRGJeIDNnEWJ/a\nswaiYPz/AR4n5U7a/mAgD8i5wNJ44JbIACQyR7RutR87drQsB7jooqqcsuTNL744HaCwslLrVUVE\nREZY9dvfvnXbN79J2/79CzNHjyaS5eVZgKPbti0GqKit1XpVkfFphln4N71ddA8+P5KDybNPExWP\n+hrwX6TtBwN9QK8FlsYjLyhsB0hkmhSs9mHz5qZu61Xn5LRe9dgrr1QBFE2ZovWqIiIiI6xi6dKW\nZGXlXs9mk/X33ju/q/14ff0igOkXXaRgVWR8SgDlQEUvr/Er5V8k5RcC74xb/huYQ9o+SdqW5fKI\nnDOroVlZ4H5sEMMcMW5RsFrQcVTBah+6769aXp7MaW3v8X37pgMUVVUpsyoiIjIKSufN25LZtGn2\nwaeeWjr/hhu2N23eXNHR0jLdCgvbZr35zdoDXWR8qncPPjtin5a2OqAZyAIdpPwC0jYN+AGwEKgD\nriflh+P7Pw3cFN//UVL+YNx+PnAbUArcD3yMlPdcQT7l24D/A/wf0raKqMjS/cDSHu/vpt/Mamh2\ncWi2iWjDWkKzs0Ozr/XXbzR4QTIKVrMtydEey1g20PWqAG0HD04HKJ09W5lVERGRUVC5cuUWgKNb\ntiwB2PvQQwsBiquqdiSKi7XNkMj4NBprVi8n5eeQ8gvi808BD5PyWuDh+BzStpJoGu/rgKuAr5G2\nRNzn68CHiXaKqY2vnyxtr/1uKX+elP89KV/a6z3d5DIN+AvAW4GDAIH7s8Abc+g34royq4mOY8qs\n9mGg61UBMo2NVQBlCxcqWBURERkFMy+7bCtA6549Sz2b5cjzzy8CKJs/X1OARcavPzcL33Zqo1n4\ndrPw/IE86IyZLCdtj5545e6dwO3x8e3Au7q1f5+Ut5Hy7cAWYDVpqwYqSfmTcTb1jm59unuEtP01\naZt/UmvaikjbFaTtduDGvgaW0zTgwH1neHLQOza3hTmRWVWw2pvBrFcFyDQ3TweYrD1WRURERsWM\nSy9tKCgubu5sa6vY//jjM4/t2LEIoHLFCgWrInliFpYAjwHFRLHSj9yDW8zC10yVjbeYwSw8aaqs\ne/Bg3P6aqbLuwamzID4H/EkPQ9kIfBu4Io9fD8CBh0hbFvh3Uv4NYBYpr4+v7wVmxcdzgSe79d0V\nt2Xi41PbT3UV8KdExZUWAY1ACdE63Z8DXyTlz/Q12FyC1Z2h2cWAh2ZJ4GPA5hz6jbhOi4JVy7Yq\nWO3FYNarth06lOw8fnwyZtnJZ52lPVZFRERGgSUSlFZXb22pqzun4ZFHlh5vaFgIMOuKKxSsiuRP\nG3CFe3DULEwCj5uFa4j2C33YPficWfgpoqmynzQLu0+VnQM8ZBYucw+yvDpV9rdEwepVwJpTPq/C\nPXhNAsk92GEWVg1k4C808CIpv6yf2y4l5btJ20zgF6TthZOuRtvL5GdZQcqPE1UC/hppSwJVQCsp\nb8z1EblMA/4L4GaiaHk3cA7wkYGPdvh5QVGcWT2uYLUXg1mv2vjMM9G2NZMmHdKaGBERkdFTXlu7\nBeDAr399sWcyZYnS0sap552X8//xE5EZJWbho12vU6+6B+4eHI1Pk/HL6WeqrHvQ5h6cmCprFlYD\nle7Bk3E2tbepslP7GGzZAL9c/1K+O35vAH4KrAb2xVN7id8b4rt3AzXdes+L23bHx6e29/W5GVJe\nP5BAFXILVpcH7h8I3GcF7jMD9z8CVgzkQ0bKiQJLnW0KVnsxmPWqzS+91LXHqqYAi4iIjKLpq1dv\nATi+d28tQMns2cqqiuSZWZgwC9cTBW2/cA9+C8xyD3qbKruzW/euKbFzyW2q7ENm4a1m4Yk1l2ah\nmYWfBf4nL1+oS9omkbaKE8fwFuB54G5eXTt6I/Cz+Phu4AbSVhxP460FnoqnDDeRtgvjAkkf6tYn\nr3IJVr+cY9uo84LieBqwgtWeDHa96rGdO6Nta6ZMDjEx3wAAIABJREFU0bY1IiIio6j6mmtesUQi\n03U+aeHCulEcjsg4tP+4e3BZ16unO9yDrHtwDlHGcLVZuOqU606Ubc2HFLAY2GIW/tgs/DHwMrAM\n+Js8fUaXWcDjpO1Z4CngPlL+ANG62StJ28vA78fnkPKNwF3AJuAB4GZS3rWM8CPAt4gyyVt57fTm\nvOh1zWpodhFwMTAjNOv+D1VJtCh2zPGCogwos9qbbutVt+a6XhXg+L59VQDFVVXKrIqIiIyiZHl5\ntriqqu74vn21AFPOOUeZVZFh4h40moWPEK013WcWVrsH9fEU37xMlXUPWoD3m4WLida9Amx0D7bl\n99vQtd/p2T20HwTe3EufW4Fbe2hfC6x6TXtPoixuKynvJG3LgDOANaQ800/PPjOrRUA5UUBb0e3V\nBLwnp4GNsM5EnFntbFew2oMNG6L1qkuXluc8BRigPd5jtaS6WsGqiIjIKCtbuHBrfOjVb3tb3WiO\nRWSiMQtnmIVT4uNS4ErgBfqZKmsWFpuFJ6bKxlOGm8zCC+Mpvj1OlY2nHJe7B9vcg3uA/cA8s/CN\nZmHFMH7VkfQYUELa5hJVAf4gUZXkfvWaWQ3cfwn8MjS7LXDPecroaOosULDalx07WpYBXHRRVc7F\nlQAyR45MByhftEjTgEVEREbZ1HPPffnQb397VXLKlD2l1dVtoz0ekQmmGrjdLEwQJfbucg/uNQuf\nAO4yC28CdgDXA7gHG83CrqmyHcDNcSVgiKbK3ka0dc0aep4q+/8RZWn/JT6/k2jbmhLgaeCTef+G\nI89I+THSdhPwNVL+L6RtfS4d+5oG/MXA/ePAV0J7bfniwP3awY93eHiiNA5WM8nRHstYs3lzU0Vj\nY2ZOImHt73znnLqB9M00N1cBVK5cqcyqiIjIKFvyZ3+2sWnTpp9Nv/DCAf3xWUT65x5sAM7tob3X\nqbLuQY9TZd2DXKbKvhl4fbfzI+7BO+Js7K9yHfcYZ6TtIuADRPvRQo7LSvvaZ/U78Xs4hIGNKE0D\n7t299+6phUGsV21oKOpsa6ugoKBj8qpVR4ZvhCIiIpKLgmTSz//qV+8f7XGISF4UuAcd3c4/CVER\nJ7OwfJTGlG8fBz4N/JSUbyRti4FHcunY1zTgdfH7L7vaQrOpQE3gvmFo4x0enYmyKFj1jILVUzz7\nbONyGPh61cb160/ssVqQTGqPVRERERGR/CkyCyvcg2YA9+DnAGbhZKKpwONfKlpe2u18G/DRXLr2\nlVkFIDR7FLg2vncd0BCa/Tpwz3cp5SE7Eax2dihYPcVg16s2v/zydIBkZaXWq4qIiIiI5Nc3gR+Y\nhX/hHrwCYBYuAL5OtDXM+JW2e+hri59U/8tK+w1WgcmBe1No9r+AOwL3W0KzfjOroVkNcAfRfj4O\nfCNw/1JoNg34AbAQqAOuD9wPx30+TTSPOQt8NHB/MIfxndBZOCnOrCpY7W4o61WP7dxZBVA0darW\nq4qIiIiI5JF78Hmz8BjwuFk4KW4+CnzOPfj6KA4tH7qWk74bmA18Nz5/P7AvlwfkEqwWhmbVRBWv\n/n4Ag+sAUoH706FZBbAuNPsF8MfAw4H750KzTwGfAj4Zmq0EbiDaX2gO8FBotixwz3l9ZbawoqvA\nkoLVbga7XhWgbd++6QDFVVXKrIqIiIiI5Jl78G/Av3VtVdM1JdgsnOUe5BTUjUmpeDlp2tKk/IJu\nV+4hbWtzeUQuwepngQeBxwP334Vmi4GX++sUuNcD9fFxc2i2GZgLvBO4LL7tduBRooXE7wS+H7i3\nAdtDsy3AauCJ7s+NpyWfUFBSYjU1NVcCJEreUM5zUFBYPKWrTaCx8cVzAd72tkXZgf67PFtcvBJg\n8ZVXzhlI35KSkmUANTU1/d0qI0y/zdil32bs0m8zdum3Gbv024xd+m3GJveg2SycEm+P84fACqIk\n3ng3ibQtjteqQtoWAZP67hLpN1gN3H8I/LDb+TbguoGMLjRbSFQC+rfArDiQBdhLNE0YokD2yW7d\ndsVtOfNkeVRJq7Mtp1LIp4tnntk/A+Dyy+fuH2jflvr6SQCVixe35HtcIiIiIiKnO7OwlChx94dE\nMVMF8C7gsdEcVx59AniUtG0DDFgA/HkuHXPJrA5JaFYO/Bj4eLz29cS1wN172sO1L4H7Zd3P/764\nuGPnzp2/AChq2VtWAdfQ3uJdbae7zZubKnbuPPqeRMLaFy/u/OHOnTsHNA346K5dVwE0dXY+sHPn\nzpy3run6S51+h7FHv83Ypd9m7NJvM3bptxm79NuMXaf5b/P20R5Ad2bhncDvAT8Hvgz8D7DFPXh0\nNMeVVyl/gLTVAmfELS+Q8rZcuhYM36ggNEsSBarfC9x/Ejfvi9fAEr83xO27ge5zEebFbTnrKJoW\nF1jKJocy7olkKOtVW+vrizvb28stkchMft3rtMeqiIiIiEh+rQQOA5uBze5Blr4q6I5f5xPVJjob\neB9p+1AunYYtWA3NDPgPYHPg/vlul+4GboyPbwR+1q39htCsODRbBNQCTw3kMzsLJ3U4uNFZaNnW\nYQ3Ex4sNGxqXASxZUj6gLWsADj/zTBVAYtKkg5bQzGoRERERkXxyD84hKmRbATxkFj4OVJiFs/ru\nOY6k7TtElYEvBV4fvy7os0+s12nAodkXA/ePx8cfC9y/1O3abYH7H/fz7EuADwLPhWbr47a/Az4H\n3BWa3QTsIPpxCNw3hmZ3AZuIKgnfPJBKwABYAqywHe8oLmxvTGZKS3NKL09kdXVd+6tOH3CwenTL\nlq49VrVtjYiIiIjIMHAPXgBuAW4xC88nWrv6O7Nwl3tw8eiOLi8uAFaS8gFnjPtas/rGbsc3Al/q\ndn5Wfw8O3B8nWkDbkzf30udW4Nb+nt0Xt0S7eUdxov1wUaa0+rQOVl98sam8sTEzN5Gw9muvnVs3\n0P6tu3ZNByiaOlXb1oiIiIiIDDP3YB2wziwMiNayTgTPE+2zWt/fjafqK1i1Xo7HNLfCdmgjkWk8\n7fdaveeeaL3qrFkl2yorkx0D7X+8oaEKoHjGDGVWRURERESGmVm4Eng/cANwhByny45xVcAm0vYU\n8GoyMeXX9texr2C1IDSbSrSuteu4K2gdswsYvaCwnSwkOo6e9sHqs882LgdYurT8xcH0bz90aDpA\n6Zw5ClZFRERERIaBWbiQKEB9P5Ah2trlAvegbhSHlU+fGWzHvooQTQbWAWuBSuDp+HxdfD42WWEG\nINHRfNoHq0NZrwqQOXJkOkD54sWaBiwiIiIikmdm4RPAfURJxOvcg/OB5gkUqELKfwnUAcn4+HdE\nsWW/es2sBu4L8zG2kRZNA4aCjpbTOlh96aXmrvWqmcGsVwXINDdXAUxetUqZVRERERGR/NsHzAVm\nATOAl5loW9ek7cPAnwHTgCVE3/ff6KWOUXcD3t4lNFsWmn1zoP1GihcoWAVYs6Z+McDMmcWDWq/a\nsmNHqWcyZZZItFcsW9ac/xGKiIiIiJze3IN3AWcSzV79jFm4HZhqFq4e3ZHl1c1EO8U0AZDyl4GZ\nuXTsa+uas4j2w5kD/DfwVeArwBuA9JCGO4y8IBkFq9nW5GiPZTStX99YC7Bo0aQtg+l/ZMOG6QCF\n5eXaY1VEREREZJi4B0eAbwPfNgtnEm3t+QWzcL57UDO6o8uLNlLeTjouf5S2QnLMHvdVYOmbwNeB\nJ4CrgPXA7cAHAvfjQxntcHIr6gpWT+vM6o4dLUsBzj136qCC1eatW7v2WNV6VRERERGREeAeNBAl\nCL9iFi4Y7fHkyS9J298BpaTtSuAjwD25dOwrWC0O3G+Lj18MzT4WuP/t0MY5/E5MA84eP22D1QMH\n2ooOHGhbAPg73jFn22Ce0bprVxVA0dSpWq8qIiIiIjIMzMJvAv/XPXiuh8sHzMI/Bdrcg++N8NDy\n6VPATcBzwJ8D9wPfyqVjX8FqSWh2Lq9uV9PW/Txwz6mC00jrLIgyq9Z5+gar9967Z4E7iWnTinbO\nnVs2qCx4W0PDdIDimTOVWRURERERGR5fBf7BLDwTeB7YD5QAtUQ7sPwnMJ4DVUh5J9Gs3W+StvNI\n5R5H9hWs1gOf73a+t9u5A1cMdJwjwQuKTvvM6tq1h5YCzJ9f9vJgn9F++LD2WBURERERGUbuwXrg\nerOwHLgAqAZagc3uwYujOrjh8S3gvFxv7mvrmsvzMpwR5gXFcWa1/bQNVrduPVoLsGrV5EGtVwVo\nP3KkCmDS4sUKVkVEREREhpF7cBR4dLTHMQKs/1te1VdmdVzqTETBasFpGqy2tWVt377jiwHe8pbZ\nWwfzDM9m6Th6dDrAlDPPVLAqIiIiIjJRpC0BrAV2k/JrSNs04AfAQqAOuJ6UH47v/TTRetMs8FFS\n/mDcfj5wG1BKtAb1Y6Q8lwq//zSQoQ54n9WxzguKM3D6ZlZ//vN9czMZLy0vLzxw7rlTGwfzjGM7\nd5Z5JlNqhYVt5UuWHM33GEVEREREZNR8DNjc7fxTwMOkvBZ4OD6HtK0EbgBeR7Q7zNfiQBeiXWM+\nTLS2tja+3rO0nXfiBa/Ex0viLWz6NOGC1c5EyWk9DfjXv96/FGDu3NJBTwE+vH59FUBhefkB7bEq\nIiIiIjL2nTGT5aTt0ROvnqRtHnA1J1fjfSfRFqXE7+/q1v59Ut5GyrcDW4DVpK0aqCTlT8bZ1Du6\n9enJ14AngW8QFVp6Avgh8CJpe0tf36nXaDY063Ph69itBlwaB6uZ0zJYffHF5qUAZ5xROehg9eir\ne6xqCrCIiIiIyDAxC+8hKl7bI/fg2jx/5BeBvwUqurXNIuX18fFeYFZ8PJcoyOyyK27LxMentvdm\nD3ATKd8IdGVsPxuP4yfAz3vr2FfqNR2/lxBVpnqWaEHsWURznC/qo++o6SyMg1XPJEd7LCMtm3V2\n726tBXjjG2cMOlht3b17OkDRtGnatkZEREREZPiE8fu7gdnAd+Pz9wP7BvKgFxp4kZRf1usNabsG\naCDl60hbz/el3ElbLmtPB2LZiUA1+oxNpO0MUr6NdN/1lvqtBhya/QQ4L3B/Lj5fBXwmD4MeFp2J\nrsxqx2mXWV279tC01tbslKKigpbLL5+5d7DPadu/vwqgeMYMZVZFRERERIaJe/BLALMw7R5c0O3S\nPWbh2jx/3CXAtaTt7UQJyUrS9l1gH2mrJuX18RTfhvj+3UBNt/7z4rbd8fGp7b3ZSNq+Dnw/Pn8f\nsIm0FRNlaXuVy5rV5V2BKkDg/jywIod+o6IzMakrs3raBau/+MXeWoDq6pKtyWTBoP8i0n7oULTH\n6ty5ClZFRERERIbfJLNwcdeJWbgImJTXT0j5p0n5PFK+kKhw0v+Q8j8C7gZujO+6EfhZfHw3cANp\nKyZti4gKKT0VTxluIm0XkjYDPtStT0/+mGi968fj17a4LQP0uV1qLlvXbAjNvsWrKekPABty6Dcq\nOgvLT9vM6qZNTUsBli4tf3koz8k0NU0HqFi6VNOARURERESG3yeAR83CbURLLxcAfz5Cn/054C7S\ndhOwA7gegJRvJG13AZuADuBmUp6N+3yEV7euWRO/epbyVqIlpukerva580guweqfAH9JVOIY4DGi\nUsVjUjZZEWdWT79gdefOY0sBVq+ePuj1qvEeq1UAU84+W5lVEREREZFh5h48YBbWAmfETS+4B23D\n9oEpfxR4ND4+CLy5l/tuBW7toX0tsCqnz0rbJUTLSBfQPf5M+eJeepzQb7AauB8Pzf4NuD9wfzGn\nAY2ibHJyOwCnWbC6bdvRssbGzJyCAjquuWbOK4N9ztGtW8u9o6PYksnWspqaY/kco4iIiIiIvJZZ\nWAb8DbDAPfiwWVhrFi53D+4d7bHlwX8QZY7XAdl+7j1Jv8FqaHYt8K9AEbAoNDsH+Gzgnu8yynmR\nTVZmAMyzp1Wwet99e5YAzJxZsr2yMtkx2Oc0PvdctG1NeflB7bEqIiIiIjIivk0UzHXtuLKbaC/S\niRCsHiHlvU8T7kMuBZZuAVYDjQCB+3pg0WA+bCR0FE07Ldesrl/fuBRg4cJJg54CDNCydWsVQHLy\nZK1XFREREREZGUvcg38hro7rHhwjWrs6ETxC2v6VtF1E2s478cpBLmtWM4H7kdBO+rfK9947eZNN\nTo4yq3QWWrbNPFE8ZseaT3V1LUsBzj13ypCKK7Xu2RPtsTp1qtarioiIiIiMjHazsJQ4zjILlwDD\nt2Z1ZL0hfu++NY8DV/TXMZdgdWNo9odAIjSrBT4K/GbAQxwplsAt0W6eLUpkjiQ7EjPbR3tIw62x\nsb3wwIG2hYBfffWcbUN5Vtv+/dMBimfNUmZVRERERGRkfAZ4AKgxC79HtCfqn4zqiPIl5X1uT9OX\nXILVvwb+niiyvxN4EPjnwX7gSHArbDfPFhW2Hy7qKJn4weq99+5Z2NlJ4dSpyV0LFkxqHcqz2g8f\n1h6rIiIiIiIjyD34uVm4DriQaPrvx9yD8Z08StsfkfLvkra/6fF6yj/f3yNyCVavDtz/nihgBSA0\ney/Rgt8xyS3RDpDINJ4W61afeurQUoCamqGtVwXINDVVAVQsWaJgVURERERkBJiFD7sHbwbu66Ft\nvJoUv1cM9gG5BKuf5rWBaU9tY4ZbYRSsdjSdFsHq1q1HlwKsWlU5pGA13mN1OsCUc85RsCoiIiIi\nMozMwhKgDKgyC6fyalGlSmDuqA0sH1L+7/H7Pw32Eb0Gq6HZ24C3A3NDs//b7VIlMOitUUZEQRSs\nFmSaJ3ywmsl0Wn196xKAK6+cPaRgtfmllyo8my0qKCo6VlZTM6TpxCIiIiIi0q8/Bz4OzCHauqYr\nWG0CvjJag8qL9Ekx5Gul/KP9PaKvzOoeYC1wLdE/XJdmok1dx6wTmdXssQkfrP7iF3vnZDJeVlaW\nOHTBBdMOD+VZjc89VwVQWF4+vufHi4iIiIgMgllYA9wBzCKqWPsN9+BLZuE04AfAQqAOuN49OBz3\n+TRwE5AFPuoePBi3nw/cBpQC9xOtQz1ppxL34EvAl8zCv3YPvjzsX3Bkrev/lr71GqwG7s8Cz4Zm\ndwbuGYDQbCpQE7gPKSgabl6QzAAUdLRM+GD1V786sBRg3rzSIa9Xbdm+fTpAcvJkTQEWERERkdNR\nB5ByD542CyuAdWbhL4A/Bh52Dz5nFn4K+BTwSbNwJXAD8Dqi7OhDZuEy9yALfB34MPBbomD1KmBN\nTx/qHnzZLFwFrARKurXfMUzfc/il/PahPiKXNau/CM2uje9dBzSEZr8J3MdsdrUrs1pwGmRWX3qp\naSnAsmVDW68K3fZYnTZNmVURERERmYBmlJiFj3aduQeXdb/qHtQD9fFxs1m4mWjt6DuBrntvBx4F\nPhm3f989aAO2m4VbgNVmYR1Q6R48CWAW3gG8i16CVbPwlvj5K4kC27cBjxNlece3tN1DvH9sN0eI\nZvH+Oyk/3lvXghwePzlwbwLeDdwRuL8BGNNVqbwgGQerrRM+WN21q3UpwO/9XtWQg9W2/furAEpm\nzlRmVUREREROa2bhQuBcoszorDiQBdhLNE0YokB2Z7duu+K2ufHxqe29eQ9RjLXXPfgT4Gxg8hC/\nwlixDTgKfDN+NREtLV0Wn/cql8xqYWhWDVxPt+1rxjIvKGoHsOzx5GiPZTj97neHph07lp2WTNqx\nK6+cvWeozzuxx+q8eQpWRURERGQC2n/81GxqT8zCcuDHwMfdgyaz8MQ198DNwlMzhUPV6h50moUd\nZmEl0ADU5PkzRsvFpPz13c7vIW2/I+WvJ20b++qYS2b1s8CDwNbA/Xeh2WLg5SEMdth1xsFqQfb4\nhM6sPvTQ3iUA1dWlW5PJgiH/BybT1DQdoKK2VtOARUREROS0ZBYmiQLV77kHP4mb95mF1fH1aqJg\nEmA3JweV8+K23fHxqe29WWsWTiHKNK4DngaeGOJXGSvKSdv8E2fRcXl81t5Xx34zq4H7D+m2p2rg\nvg24blDDHCEnCix1tk3oYPX556P1qkuWlA95CnBnJmMdR49WgfZYFREREZHTk1lowH8Am92Dz3e7\ndDdwI/C5+P1n3drvNAs/T1RgqRZ4yj3ImoVNZuGFRNOIPwT0Wu3XPfhIfPhvZuEDROtdN+Txq42m\nFPA4adtKtDXPIuAjpG0S0frfXvUbrIZmy4gqWc0K3FeFZmcB1wbu/+/Qxz08vKA4mgY8wYPVnTtb\nlgKsXj1tyMFq0+bNlXR2FhYUFR0tra5uG/roRERERETGnUuADwLPmYXr47a/IwpS7zILbwJ2EC2R\nxD3YaBbeBWwiqiR8c1wJGOAjvLp1zRp6Ka4EYBae10PbEmCHe9CRh+81elJ+P2mrBc6IW17sVlTp\ni311zWXN6jeB/w38O0DgviE0uxMYy8FqG4BlJ26wumNHS+nhw5m5BQV0XHPNnLqhPu/Ixo3TAQor\nKpRVFREREZHTknvwOFH2ryc9Fpl1D24Fbu2hfS2wKseP/hpwHrAh/vxVwEZgsln4l+7Bz3N8zlh1\nPtEetYXA2aQNUt5vpeNc1qyWBe5PndI2pqP7zkSUWS3ozEzYYPW++/YsBqyqqrhuypSiIf8eLdu3\nVwEkJ0/WelURERERkZG1BzjXPbjAPTifqArxNuBK4F9GdWRDlbbvACFwKfD6+HVBLl1zyaweCM2W\nEO+NE5q9h3jvobGqs6Akmgbs7RM2WH3mmcZagIULJw15CjBAa339dIDiadOUWRURERERGVnL3IMT\nlXHdg01m4RnuwbbulYjHqQuAlaR8wAVhcwlWbwa+AZwRmu0GtgN/NNAPGkmeKMkA2ATOrNbVRetV\nzzlnSl6C1fYDB6JgdfZsZVZFREREREbWRrPw68D34/P3AZvMwmIgM3rDyovngdkMIuGZSzXgbcDv\nh2aTgILAvXng4xtZnYnSuMDSxAxWm5oyhQ0NxxcBXH31nK35eGb74cNVAGXaY1VEREREZKT9MVFB\npo/H578GAqJA9fJRGlO+VAGbSNtTwKuFXFN+bX8dc6kG/DennAMcAdYF7ut77DTKOhNlEzpYvffe\nPfM7OymcMiW5Z/Hi8mP5eGa3PVYVrIqIiIiIjCD3oBVIx69THR3h4eTbZwbbMZdpwBfEr3vi82uI\nqlT9RWj2w8B9zC34zRZOitesdiRHeyzD4amnDi4FqKkpy8sU4HiP1emgPVZFREREREaKWXiXe3C9\nWfgccY2g7tyDs0ZhWPmV8l8Otmsuweo84LzA/ShAaHYLcB/wRmAdY7A6VWfhpGjNqndMyMzqli1H\nawFWrqzMS7B65PnnJ+OeKCgubi6ZObM9H88UEREREZF+fSx+v2ZURzGc0nYh8GVgBVAEJIAWUl7Z\nX9dcgtWZdJ9bHM2bnhW4t4Zmbb30GVXZwop4GvDEC1YzmU6rrz++BOD3f39WfoLVjRujbWsqKlRc\nSURERERkhLgH9fH7jtEeyzD6CnAD8EOiGbsfApbl0jGXYPV7wG9Ds5/F5+8A7owLLm0a+FiHXzZZ\nGWUHJ2Bm9ZFHGma3t3dOKi1NNL7+9dPzMmW3pa5uOkBy8mRNARYRERERGSFmYTOvTv+1+N3jY3cP\n+s0+5ixtJcBjQDFRHPgjUn4LaZsG/ABYCNQB15Pyw3GfTwM3AVngo6T8wbj9fOA2oBS4H/hYn1vT\npHwLaUuQ8izwbdL2DPDp/oacSzXgfw7N1gCXxE1/EbivjY8/0F//0ZBNTu5aszrhgtXf/ObAIoA5\nc0q3JBLW3+05OR7vsVo0fboyqyIiIiIiI8Q9qBjBj2sDriDlR0lbEnictK0B3g08TMo/R9o+BXwK\n+CRpW0mUEX0dMAd4iLQtiwPOrwMfBn5LFKxeBazp5XOPkbYiYD1p+xeiLWwKchlwrzeFZpXx+zRg\nG/Cd+LUtbhuzskXT4mA1O+EKLO3Y0TIHYN680l35embbgQNVACWzZimzKiIiIiIyCszCS83CP4mP\nq8zCRQPpf8ZMlpO2R0+8TpVyJ+VdlYWT8cuBdwK3x+23A++Kj98JfJ+Ut5Hy7cAWYDVpqwYqSfmT\ncTb1jm59evJBorjzr4AWoAa4Lpfv1Fdm9U6ihb7rOLkylcXni3P5gNHQkZwcF1jKFtGZMQqSvaek\nx5l9+9qqARYvLh/wprq9aT94cCZAWU2NglURERERkRFmFt5CtJ5zOfBtokJE3+XV2a35kbYEUXy3\nFPgqKf8taZtFyrtii73ArPh4LvBkt9674rZMfHxqe89SvoO0zYiP/2kgw+01WA3cr4nfBxTRjwkF\nSXdLZMyzycLMkWRHcdWEqXB76FAUrJ577tQ9+Xhe24EDRcf3718E+Kw3v3kiL+wWERERERmr/gA4\nF3gawD3YYxYOaIrwCw28SMov6/OmaArvOaRtCvBT0rbqlOtO2vKT6EubAbcQZVQLACNtHcCXSfln\nc3lEr8FqaHZeXx0D96cHMNQR55ZoN88mE+2HiiZKsLp37/Hilpbs9IICOi68MD/rS3f9+MdL6ews\nLJo+/ZWKZcvG+4bDIiIiIiLjUbt74GahA5iFk4b101LeSNoeIVpruo+0VZPy+niKb0N8126iKbtd\n5sVtu+PjU9tP9QmizPDr42nEkLbFwNdJ2ydI+Rf6G2ZfC1vT8eurRAtnvwF8Mz7+an8PHm1uhe0A\niUzThFm3+vjj+2cDVFYm95WWJjrz8cyDTz65AqB8yZIxWdlZREREROQ0cJdZ+O/AFLPww8BDwLfy\n+glpmxFnVCFtpcCVwAvA3cCN8V03Al27wNwN3EDaiknbIqAWeCqeMtxE2i6Ms6cf6tanuw8C7z8R\nqAKkfBvwR3GffvU1DfhygNDsJ8B5gftz8fkq4DP9PTg0+0+iNa8NgfuquO0zRFWj9se3/V3gfn98\n7aSyyIHHZZEH69VgdcJUBN60qWkOQFVVcd7Wqx7dunUlQNVFF23O1zNFRERERCR37kFoFl4JNBGt\nW/1H9+AXef6YauD2eN1qAXAXKb+XtD0B3EX+4b/1AAAgAElEQVTabgJ2ANcDkPKNpO0uou1KO4Cb\n42nEAB/h1a1r1tBzJeAkKX/tbNCU74+rEfcrl31Wl3cFqgCB+/Oh2Yoc+t1GtAHsHae0fyFwD7s3\nhPbassih2bLAT/xjDJhbIgOQ6GieMMHqjh0t1QDV1SV5Wa96ZNOmivbDh+dZIpGZ9573bMnHM0VE\nREREZODi4PQXAGZhgVn4Affge3n7gJRvIFoXe2r7QeDNvfS5Fbi1h/a1wKrXtJ+sr6WYOS3TzCVY\n3RCafYuoGhVEe6tu6K9T4P5YaLYwl0EQl0UO3NuA7aFZVBYZnjj1xtBOLsNcUFJiNTU1V556n02a\nWUrjYaZWL7qkYoJUuXV/+iyAa69dNqOn7zxQjXffXQMw/cwzDy0588zLh/q87kpKSpYB1NTU9Her\njDD9NmOXfpuxS7/N2KXfZuzSbzN26bcZO8zCSuBmomq6dxMFqzcDAfAskL9gdeSdTdqaemg3oCSX\nB+QSrP4J8JfAx+Lzx4g2gR2svw7NPgSsBVKB+2F6L4s8eIniLIBlWhJDes4YsmNHcyXA2WdX9fSj\nD9juX/5yFsDsiy/el4/niYiIiIjIgHwHOEyUpPtfwN8RBXPvcg/Wj+bAhizlQ47D+g1WA/fjwBfi\n11B9Hfhnon1a/5mogNOfDuQBgZ9cjvnvi4s7du7c+Zr53LWtR5YlYGbLjqee21d8Ub+Z4LHuwIG2\nooaG1uvMyFZWHvvZzp07Bz1FGsCzWfY8/vibAWzu3J/t3LlzV399BqLrL3U9/TYyuvTbjF36bcYu\n/TZjl36bsUu/zdh1mv82bx/tAZxisXtwJoBZ+C2gHpjvHhwf3WGNDf0Gq6HZJUQFlRZ0vz9wXzzQ\nDwvcT2TwQrNvAvfGp72VRR40L4gKLFm2dUKsWY0rAVtlZbJh0qTCIQWqAA2PPjo7e+zY1ILi4ubq\nt71tSP/WIiIiIiIyKJmuA/cgaxbuUqD6qlymAf8H0R4564gq9Q5aaFYduHdVsv0D4Pn4+G7gztDs\n80QFlqKyyEPgVtQOUDBBgtXnnz9SDTB9elFeiivtffDBFQBl8+dvLkgm87Pxr4iIiIiIDMTZZmHX\nEj8DSuNzA9w9qBy9oY2+XILVI4F7T6WI+xSa/RdwGVAVmu0CbgEuC83OIZoGXAf8OUDgvjG0k8si\nD6USMIAXJKNgtfP4hAhWd+w4FlcCLs3LtjVHNm1aATDlzDO1ZY2IiIiIyChwDyZMfZ3hkEuw+kho\n9q/AT4C2rsbA/em+OgXu7++h+T/6uL/nssiD1FnQlVltmxDB6t69x6sBFi2aNOTMakdLS6J19+7l\nAHPe8Q4FqyIiIiIiMubkEqy+IX6/oFubA1fkfzj544niaM1q58QIVg8ebJsDcNZZU4acWd393/+9\n0Ds6SgorK/dOu+CCw0MfnYiIiIiISH7lUg04r/tvjhQvKMoAWGf7uA9WGxvbC5ubO2aY0XnJJVUN\nQ33e/scfXwlQvnixsqoiIiIiIjIm9RqshmZ/c0qTAweAxwP37cM6qjzoLOjKrI7/YPVXvzowG7CK\nisJ9lZXJjqE+r/mll1YATLvggk1DHpyIiIiIiMgwKOjjWsUpr0qiqcBrQrMbRmBsQ+KJkrjA0vgP\nVp9/vjGuBFw85CnAx3bvLmnbv38RZp3z3v3ul4c+OhERERERkfzrNbMauP9TT+2h2TTgIeD7wzWo\nfOhMlMaZ1UxytMcyVHV1LdUAs2eXDDlY3fWjHy3DvaB45sytZTU1rUMfnYiIiIiISP71lVntUeB+\niGjfnzGtW7A67jOr9fXH50B+KgEfWrt2JUDFsmVaryoiIiIiImPWgIPV0OxyYMxXkD0RrPr4D1YP\nHmyrBli1auiVgI9u27YCYMall2q9qoiIiIiIjFl9FVh6jqioUnfTgD3Ah4ZzUPnQmZg0ITKrTU2Z\nwubmjpmAX3LJ9H1DedahtWundjQ1zbbCwuNz3/WuuvyMUEREREREJP/62rrmmlPOHTgYuLcM43jy\nJlsYB6veMa6D1V//+sBMdwoqKgobpk0rzgzlWXvuvXcFQOncuS8VTpqUzc8IRURERERE8q+vAks7\nRnIg+daZrGgHYJwHqxs2RJWAp00rGvIU4MYNG1YATF65UlOARURERERkTBvwmtXxIltYkQGwzvEd\nrNbVtcyBoVcC7sxk7Ngrr6wAmP3Wt6q4koiIiIiIjGkTN1hNTo6nAWfHdbBaX3+8GmDhwqFVAq5f\ns2ZuZ1tbRaKs7PDMyy7bm5/RiYiIiIiIDI8JG6x2FE2dEGtWDxxomwOwatXkIWVWG/7nf1YCTFqw\nYLMlEvkYmoiIiIiIyLCZsMFqNjn11cyqj89aQi0tHYmmpsxMwC+9dMaQsqFNL7ywAmDKOedoCrCI\niIiIiIx5EzZY9USxOwUdAIlMc19Vj8es3/zmwAx3EuXlhQerqorbB/uc9sbGwuN799YCzPuDP1Cw\nKiIiIiIiY96EDVYB3BLtAIXth8blVOBnn81PJeBdP/rRUs9mk0VTp+6qXLGiOT+jExERERERGT4T\nOliloLAdIJFpHJfB6vbtUSXgWbOGVgn4wBNPrAAoX7JEW9aIiIiIiMi4MC6nx+bKrStYPTIug9U9\ne1rzUgn46NatKwGmveENmgIsIiIiItILs/A/gWuABvdgVdw2DfgBsBCoA653Dw7H1z4N3ARkgY+6\nBw/G7ecDtwGlwP3Ax9wDH8nvMhFM6MxqV7Ba0HF0XAarXZWAV66sHHSw2vzSS+XtBw/WUFDQUfOe\n92zJ3+hERERERCac24CrTmn7FPCwe1ALPByfYxauBG4AXhf3+ZpZ2LXtxteBDwO18evUZ0oOJnZm\ntWsa8DgMVltbswVNTZlZAJdcUjXoSsC7fvrT5YCVzJ69pbiqatBFmkRERERExr8ZJWbho11n7sFl\n3a+6B4+ZhQtP6fROoOu+24FHgU/G7d93D9qA7WbhFmC1WVgHVLoHTwKYhXcA7wLW5Pe7DFDaaoA7\ngFmAA98g5V8iba/JHJPyw3GfkzLHpPzBuP01mWNSnvfM8UTPrGYACjpaxl2w+uSTB6s6OyksK0sc\nqq4ubRvscw4/88xKgMrlyzUFWERERERk4Ga5B101ZPYSBXsAc4Gd3e7bFbfNjY9PbR9tHUCKlK8E\nLgRuJm0riTPHpPykzHF87aTMMWkb0czxBM+sJqNpwNlj4y5YXb/+8BwYWiVgz2ZpqatbATDzsstU\nXElERERETnP7j5+aTR0I98DNwjG59vSMmSwnbY+eaEj5ZSfdkPJ6oD4+biZtm4mC6D4zx6S8DdhO\n2rYAq0lbHVBJyp8EIG3Dljme4JnVOFjtaB13weq2bUerAWbNKhn0etX9jz8+M9vSMr2gqKil+uqr\nd/bfQ0RERERETrHPLKwGiN8b4vbdQE23++bFbbvj41Pbx460LQTOBX4LzIoDWRhjmeOJHax2ZVY7\njydHeywDtWdP6xyABQsGXwm4/oEHVgCU1dS8kCguHpN/ARIRERERGePuBm6Mj28Eftat/QazsNgs\nXEQ0HfapeMpwk1l4oVlowIe69Rk2LzTwIim/7MSrN2krB34MfJyUN510LVp3OmbihtMjWM0eH3eZ\n1QMH2qsBVqyoHPQ04KaNG1cATD7zTE0BFhERERHph1n4X8ATwHKzcJdZeBPwOeBKs/Bl4Pfjc9yD\njcBdwCbgAeBm9yAbP+ojwLeALcBWRru4Upe0JYkC1e+R8p/ErftIW3V8fUxljif4mtWidgDrHF/B\naltb1o4cycyGwVcCzra2FhzbtesMgOqrr1ZxJRERERGRfrgH7+/l0pt7uf9W4NYe2tcCq/I4tKFL\nmwH/AWwm5Z/vdqUrc/w5Xps5vpO0fR6YQ5w5JuVZ0tZE2i4kmkb8IeDLwzHkCR2sdhYUx5nVtnEV\nrD711KGqbNaTpaWJxpqastbBPKN+zZp5nsmUFpaXH6i68MKD+R6jiIiIiIiMK5cAHwSeI23r47a/\nIwpS7yJtNwE7gOsBSPlG0taVOe4Abibl3TPHtxFtXbOGYcocT+hg9dXM6vgKVp955nA1wLRpRYNe\nr3rgiSeWApTOm/dyvsYlIiIiIiLjVMofB6yXqz1mjkl5j5ljUj4imeMJvWa1M1ESB6uZcRWsbt0a\nVQKeObNk0OtVm196qRagcsUKBasiIiIiIjLuTOhg1QuKMwDW2T6ugtXdu7sqAZcNKrPq2Sytu3fX\nAsy6/HIFqyIiIiIiMu5M6GC1K7NaMM4yqwcOtFUDnHHG4CoB73/ssZmdbW0VBcXFzTPe+MaG/nuI\niIiIiIiMLRM8WC2NpgH7+MmsZjKd1tiYqQa46KLpgwpW9z3ySC1A6dy5L1sikc/hiYiIiIiIjIgJ\nHqyWxWtWO5KjPZZcrVt3aFo260UlJQVHFi8uPzaYZzRt3lwLULFsmaYAi4iIiIjIuDSxg9XCrszq\n+JkGvG7diUrAgy6u1Lpr11KAqksu2ZKvcYmIiIiIiIykiR2sJsrbo4OOcROsvvzy0TkAM2eWDKq4\nUuOzz07uOHp0hhUWtlW/9a278js6ERERERGRkTGhg9VssiLOrI6fYHXPntZqgJqaskFlVusfeKAW\noGTWrK2J0tLOfI5NRERERERkpEzsYLWwomvN6rgJVvfv76oEXDGoYPXIc8/VApQvWaL1qiIiIiIi\nMm5N7GA1OWVcZVazWaexsX0OwIUXVg0qWG155ZWlANNe/3oFqyIiIiIiMm5N8GB1cgbAPJtTsJo5\nejSx/bbbajtaWkZlv5dnnjk8taPDi4uLC5qXLas4OtD+LTt2lGYOH56LWfb/b+++w+Oqr7yBf8+t\n0zXq1bYsy93GNtimBmJYEloCBkIIIW0T8m4SXpKsvQupJNl1CthZNgmb5E2hhBDCsqGEhVASIGAw\nboBtLFsuki3JaiNp+sytv/ePGYEQFpbcNLLP53n06M6dmXvP1ZFG99xfuTUf/nDrMQiRMcYYY4wx\nxo6LE7tY1cIWAEDYGoRzyNe/ev31/7hzzZqVLy1f/uXk3r2+Yx3fcBs39lcDQHHx4c0EfODPf24E\nQHp5eateUmId1eAYY4wxxhhj7Dg6oYtVV/E7AuQQQJKdUt7rtTvvuGNBcs+exQCQ7eycue7667/W\n89xzFccn0pzm5sQRzQQ88NprjQDgr6/nLsCMMcYYY4yxCe2ELlYBQJBiAoBi9o/YFTjd1ubdf//9\n1wFA6RlnPKkVF7fbiUTFaytWfG3vr38963jF2tExOBOw9/DGq7a2NgJA8aJFfH9VxhhjjDHG2IR2\nwherkHLFqmzF1JFe8sbNNy93MpmwXl6+99Sf/ezRsx588DZ/ff3rwrJ8zT/5yZe3fOMb7zseoUYi\nRg0AzJgx9pmAzWhUMSKRegCi5kMf4mKVMcYYY4wxNqGd8MWqIHmwWD1oy2rr737XGNu69TwQObNu\nvvleWdeFp6rKOPtPf/pFydKlT0EI6cBjj13/6ic/eY1jGHSs4nQcgYEBsxoAzjijdMzdgDsee2wq\nXFdRi4s7/FOmZI5+hIwxxhhjjDF2/JwExepgy2riXcWqGY0qu3/xi08AQNlZZz1Z/cEPvtWiKamq\nWPqb3/yp7uqr7waRM/DaaxesXb78xnRHh+dYxLltW6zIsoRX06TUzJmhxFjf379+fW686uTJ3KrK\nGGOMMcYYm/BOnmLVfnex+sbNN19ix+NVaijUteC225482Pvn3XrrK7P+5V9+LGlaMt3WNu+Va6+9\nOfLyy6VHO8716/vyMwGrnbI89gbc5J490wGgaP58nlyJMcYmAMken9ukscIiWXEl2P3XqopdP51f\n98a/nD9l0xc+FOz+a9V4x8UYY4XgPWfIPREISTUBQLJT7yhWDzzxRG3fK69cBACNX/zivWooZI+0\njfpPfGJ3oKHhB2/cfPONVjRas/mmm74+86tf/a8pH//4nqMV55HMBOwYBmW7uqYBQPVFF3Gxyhg7\nbORkJMWMqrIV1WQrpslWXJPspCrbKU1y0prkpDUIAVcJGI4aNBy1yLC1kqytlRi2XpF11KANencN\nRk5GUrPdHjXb7VHMPq9sDngUK+aR7IRHslMe21MVTZYsPZAuXjRwsPefKLyxbaHS1ntP8w9sWqIa\nPdMcJRAxvXW7sqFZu+Ply3YlKs7rPhGP3xNvCpa13nOav3/jEtnsr7X1sv1GYFpzqmRp80Dt8r2O\nFh7xf/CE51qkp/f5PPGmYk+iuVxPt5UrRneFYvSXy1a0QnLSxQS84yp1ILL2kkzR3LWds275cya8\nIDZeoTPG2Hg78YtVUiwAkJzMW8WqYxi08/bbPwEh5PAppzw/mqKz7OyzI2f+4Q8/2nDDDZ/PdHTM\nabrttn/uevrpF8KLFu2sueyy3cHGxtSRxNnSkqoHgNrasc8E3Pnkk5OEbXuUQKA3vID/qR1taqZT\nD0TWVmVDswYyodnx43YiKRyo2R6dXEM2/fXp47NTdixoqVafo4bNQjshl81+tXTf/bMCfWsX6Mm9\ncyUnU0QQR/QLLkCuIMUQkmKAZItcWydheUg4I87IPqhiz8/hkppxtHCnpVccsHx1BzLBmR2pktM7\nM0VzYxO1iNOTu/1lLXef6u9fv0TNds4YWpjIdrLMm9hR5k3sOLO44xG4kp6wvDW7s4Hpu5JlZ+2O\nVl/SJmSvO57xHy413eYtb/ntwkDfK0vVzIFZBPFWby4t2zlTy3bODEZeQmXzHbblqWgxAtN2poqX\nNA/ULd/raIV9r3DFiGh6ojmop/eH1Gx3UDEjIdmMBmUrFpTtZFBy0kHJTgclJxMk1wgOPfbhBMh1\nFH/EUYt6ba20l1xL9SR2nOGLbXtfw/pPnZ4qWfpsx5xvPW35JvF8FIyxk86JX6wOtqw66bdOlLZ+\n85vLjEhkquz1Rk+57baHR7st36RJmXMefvinGz7/+Wuir7++bGDz5gsGNm++oOU3v4EaDh/wTZ68\nq2jevF3VF120q3jRouhot3vffa2NO3cmlgIQ559fuWNMBwggsnZtIwB46+p4vOpRohgRrazlt/MD\nkbWL9fS++SQcFQAEKYajhnpsNdxj6xU9premxwg09qTDC3pHOpkmxyDFiOiKGdEVs1+XrZhHtqK6\nYg74FaM/IFvRoGzHg5KVDMhOKig5mQA52aDkZIMEVwEAV/LEbL20w/RUtxuBhvZ0+NT2RPl5Xa4a\ncN7rONR0hyfQ93KVN95UraX3VanZ7mqVrAYhe5xpQq8xfZPaM6HZHYnyc9uN4Izk4fysyDFIT+4J\nSE5KlZyMLDlZRXKyMrmGIjlZhVxDkVxTJtdUyDUVCJcIrgQhALhEQkiASxAC+fWUX0+59a5EwiXA\nlUgIgnCkt5bhSiRciVxTJdfSSFgquZZKrq2SsFUIWxtcJuGojhIYsPXyTtM3qTMbnNGZLDnjQDY0\nM3G0iyDZjColbQ9OD/S9PE9P7p6rWLFqAHBJzQjZG3cUX9yV/XFHDcYctShuayVxWy+PK/TBYqd4\n9hFd+DoUT2x7sKTtgVP8A6+domXa5gwvIgUgQIopSDYFKaaQZAuk5h5Lqpm7AEiCXNNDwtLJzX8J\nSyfX9hBchYTlhWN5h29XkJoRkpoVkjb4lXElPSsk1ZStWIli9tdIrhGUjN4G1ehtQPxNFHU9BQBw\nJS3laMUHbKWoH5JiC1JskftuCUm1Bam2kFRbSKolSLNdWbccNZy2tZKU5alMW57qlOmbnD7U38zR\nkivU7lrg71u3RMu0zx68CCAg2YZv8rZE2dkb+qZ8Ypt/YGN5IPLSdE+iuVHLHJguudmQnmpZpKda\nFhV1P42a7f9uWJ7KPZanqsPWywYsT1W/4ZsczQZn9meDs+JC1sUhgxEO9NQ+n57cXaSl9xep2e6Q\nZCe9RnB6V6zywv1HswjKfXb+Zn4w8tJSLbV/3uBnmAA5hm/ylmTpWRtiVR/YHex9cbIv+voMPdU6\nU7EG6rRs13Qt2zU9GFmLyl0/sW1PeUvWP605HV64J171wRYj0HDsLti5FqnZHl3NHvCp2R6vYvZ7\nFbPfpxiRkGz1hxQzViTZiaBsp4okJx2SnEyIhD2m+StcUjOu4o05arjH1st6LU9Vj+Gr780Uze1J\nF5/W7yr+d/xeBrv/+lTVrv+8Qk+1LAr0vXLJ9LVXnJuoWPZEx5xvv+CqI/cEOxzkZCRfdEvYk9hZ\nqpj9vmxgeiRVenqvrZeZR3M/BSl/UVhyMrLprc5O1AtDjJ3ISIhD/58rZLqu25s2bfriSM9Pe/nq\nz3gTO8/or/vI3QfmfvuVyLp1pZu+8IVbhW3rDZ/73J0zvvzlLYez35Z7750eWbt2dmrv3hnZnp6p\ncN13FP5KIBDx1tXtCs2evWvyNddsLZo3L36w7XR1ZfXly1/6VjJpl59xRumTv/rVkkfGGsuLl1/+\nf1J7955au3z5vfO/9721h3M8R9ukSZMuBIC2trZnxjuW0ZLNqFLWete8YO/fF+up1lNI2Prgc7Za\n1Ck5mZDkmv6R3i9IMRwlEAFI5E/iPSRsfTQtSiNvMzeb9cG2IUCOoxZ1WXpFu+Wb1G7467uVbHdY\ny7RXqUZvtWz2V8tOJjzafbmyN2Zrpe2mt7rD8De0p8OL2o1AQ1xP7g1p6f1hNdtVpBqRYtkaKJKt\neFiyk2HZSReRkyka3oVtInElLe2o4QOWXtFp+Wo7s4HGzkxoTm82OCtmeypGfbIW7Hmhoqjzf+d6\n49vmapkDM4fmTJBsQrjyaFstXckTt7WSA5an8oDpm9KRKZpzIFF2TudhFRXCQVHXU7VFnU+e4o2/\nuUAxeuuH5svSSvdlQ3PeiFV9cEu8Ylmnq/gP2o13tCQrKStmRFeMiC7bKdXWig3LU5Wx9VJzNNv1\nxJuCgb5XajyJndVauq1WzXbXyOZAjSQs32EHNYQgxXAlLS0kLe3KnpSQvSlbK4mY3tpuIzCtJ1V8\nWlemaN67Ljy912eaYkQ0f/+GMk9iZ7mWbivzJHdN11L75g8p1FzLW9uULD1jQ6T+06+b/hFmbBcO\ngr0vVQR7/tbojTdN1zJt02U7WT7isYAcV/bGXCXQ76ihAVsrHhCSZspWrEi2EiHJToUkJ10kOdnQ\nYCwH4yjBHstT1Wr46/enw6e0xisubLN8tdn3/kHmCmBPYmc49/nQGfZGt87ypPYuHPzsFICwPNXN\nqZLT10emfmbzSAWnntzrCx94bLov+tpMPdU6Qzb764Z/pthKqMvy1rRkA40tqdIz9saqPtAxWFiM\nlBvJTsn+/o2l3vi2Ci3VWqFmuyoUM1pMbtYnuaaXHMNHruklYXnH+hkmINmu7Im7sjfhKv64q/gT\njhKMO2pRwtZKErZelrA81QnTNzmRDUxLHm6BWbL/Dw3le39zlWp0NwKAI/v7ojUfeqRz1r9ugKSO\n6gROTXd4vPFtxZ7k7lI101GiZntKFXOgRLaiJZKdLDlYN+Tcvnz9jlbcbWul3aa3ptv0T+1Ohxd0\np4oX9711kSRf7OnJ3SEt3RZUs10hxewLKuZASLbiIc0baIRryk6qt1tAckHkArIriFyQ5ObWSQ4g\nCUGSA5KEQO65/DoXRAKQXEGSC5AAye5oDpwAkGvokpP2SnbGK7kZHzmGV3INL7lmLveu6Rt67LnP\nBzUjJD3/GaFnhOTNuLIn48q+tKv408mSpbv7p1y3d1QJLGAT8TztaJk/f/5/CCFGPJ+byIhooxBi\n8XjHcTSd8MVqw7rrPu6LbT13oPqy+9vn/vsLf7/sspsy7e1zA9OmbTznkUd+dTRisOJxpeOxx+r7\nX321MbF794xsV9c0Yb991ZVUNX3qHXd8v/zcc3uHv/e66165buvW2HnFxVr7E0+87/uBgDqmq/7C\ncfDM6aevdg0jeOpPfvKtimXLeo7GMR2pifIhKFlJuWzfPbODPc8v1pN7Fkri7dYgSytrSRcv2tg3\n+bpN6ZLFA0DupMo3sKnCk2iu0DLtFUq2p0KxBipkK1ZxqEJWkJIVkmrkWpZUw5U8mdwJTiDhqEVJ\nRw0nbb00YemVCdNXlzT8DQnbU2HCtSjQv77U37++zpPYVatmOupUo7dOshPlhzrBEpBsRy3qsvXS\nLstT1WX46js98z5aT2ZMsd58oFNL76tTs911itlfO7Q4HytX0lKCFBMk2YJkG5AcQbKdf+yAZFuQ\nPLjOBSByJyIkAMpdyc4vC0gid1SUP1khFyTlT1ZyJy25kxwSoNwJjJB0S0ia5Uq6KWTddiWP6cpe\nS8gey1H8lit7LSHpjie5u0RP7q7RMh1VihGpkc2B6qE5P1jecsWAL+bIgbijhmKOWhSz9bKYpVfE\nJdeU/f0b5uqpPXOHFxW2VtKWDczYlih/35sDdVftdWWP81brVqY9pGa7Q4rZF5LNgVCusEgUKYpS\nK6U7g+QYB63qHNnXb2slnYOtbJJrquQaGjmGJrmmTq6pkWtqJCwt1+Jpa5KTLpKddPHQ3wnTV9eU\nDi98Y6Du6q3p4tH3Ahk3woEvuiXs73+1RjF6g7njtpRca72lkLDV/HdlyHeNnKxPcrN+yTF85Br+\n3InpyN0x39pdrgdFt62VdFueym7TO6nbM/cj9XBtyu54pEVLd5QrRk+5Yg6Uy3a8XHIyRe/aBiAs\nT9WuVMmSDX1TPrU5G5p5WD0XvNEtRUVdT03TMu3litFXIlvRYtlOFkt2slhyjeBot+OSmsn/Lsdd\nJRATkmop2Z5axRyoPVgh6yihbstTtc/wT9kP4ZJiDYRzRXAyLDmpIsnJhAd7nAxn6eUtqeLT1vdN\n+cSmTPiUMQ9N0VKtvuKORxt90ddmaOm2BsWITBkeoyDZtPWyfYZvcos866NBofgcs/mxDjXbVaEY\nkQrFilZIdqp0NPnObe/dRYqrBBKOEorbWnHM1krjtqcybvrq4tnA9Ljpm5Q+nkNCKnbfeUpJ24NX\nDvbSsLWStr7J1/0pXnnBPk+8qVhP7S0Jp9AAAB92SURBVCtWs51hxYgUK9ZAcf6CYrFsp4oP1Qos\nACFkb8xRAv2upGdkK14q24nykS6uCUi2owQiJBxVcrPBI7kgWwgEyaaA5JCwPKO5aJEoO+fxfaf9\n/M/HI7ZjaaKcpx0LXKxOLCd8sTp1/ac/4h/Y9A+xygv/+y+PlyTa/vjHf5Q0LX3673737aI5c8Z8\ni5jRcAyDOp98clJk7drGgU2blhq9vVO1kpK2cx599Ida+O0xa7/4xe45d965+8tEcH7wg1NWXXpp\nTcdY99Xz3HMVm2+66d8kXU9c+OqrK0kujDFd4/kh6Ik3BT2JncWKOeCRrZhXtuJeyU56JSftkZy0\nT3IyXsnJesnJelWjZ6rkmm+12Nhayf50eOHGvkkf3ZgqO6tvLPvVk3t93ujrZSDFtbWw4WglhqVX\nZG2t2BrtFfCxULI9WrD3hRpfbEudlmqtVY1IpaMGY6anptMITOtMhxd2pUqWRoZ3EzxobkYoiMk1\nAvmWm6ijBKOOGo7aeknU0itilrc2mg1Mi2WDs2PHq2vlUScceGPbivz9G6o9ieZqLdNerRi9NbKV\nKMmN3xy5NWo4V9LSpm/y9nR40baB2iu2H85J+qRJky6E66B/y582+/s31HiSu2vUTEdtrqU8WjOW\neN4Zm54wAtO2JEvPfKNv8nVNY2kxPqEIB2qmy6Nl2n1qttunGL1+xYwEtHR7uZrtqlLM/krZilZI\nrhkY02ZBjqsE+my1qNfRSntN36QD/ZOueeNYXwiQzajijW0p9iT3FKuZ9mI121NCrqk6WknM0svi\nlrcmZvimxIzgjMRIXTolKymHep6t9fdvmqyn9kxRMwemKGZ/3Wh6AQx2bXXlQNRRg1HLW9PZP+mj\nG5NlZ0eO5nFKVlIu6n6qzt+/fqqe2N2gZTunynai4lDvE4BwZd9AruttaY/lqeqxvDURWy1O23pp\nxtbL05anMmN6azMTofsnOQZVN33/zKKuJy8fS68ZQbLpyr6oo4b6HLWoz9ZK+y1PVb/pq+vPBmf2\npYvmR4e3/JKTkQJ968u8sa2VeqqlQs12VipGpEq2opXD9y1INl3Jk3Blb76FORB31WDCVsNxvf7c\neqH47FT7G1tIOBKEI1HuS4ZwiIQjD10PiLeGfUC8NUxEenv4SG5oyKiPXdIsV/GnHSWYdtVgxlbD\nGVsrSdt6WcbyVGUsb23mrS7Yb3UH7/SqRo9PMfq8shX1ylbMJ9sJr2SnvJKd8iXLznoz0nDDmIds\nFRouVrlYnSiOWbG6mui3AC4D0LNSiHn5dSUA/gigHkArgGtWCjGQf+5rAD4LwAFw00ohnhrNfg5V\nrNZvvOGKQN+6i/t8pz95z1dee59rmoG6q666Z953vvPyERzeqKXb2rwvX3PNN+xksrxo/vy/n3n/\n/b8HgNbWlO+aa16+NZNxwsuWVTz8k5+c+pfD2f7Wb3/77I6HH/6kv6Fh8/seffSXRzf6w3fcPwSF\ng5L9D0wrbfvjhVqqZeFYunTZargjHT5l40Dd1RsTFYXRMn0sncz/oMZEONDS7V49ubtIT+8rUrPd\nodwYtoGwbMVDsp0sgnBkI9DYnCg/b9tA7fLWUY0ffA/vlRtyDAr0rSv3DWyq0VN7ahQzWuRKmilk\njykk3XBlj5n78hqu7DNdxW86SsB0tOJMvPz93cfigsmJSk/u9vv7N1R6ErsqtUxbpZLtqdTIniZI\nFpZLe3JjDmt6DX99b6ZobiQdXtR/pLkvJJIVV0Ldz9b4BzZP0VMtdUJSbVsridp6edT0VkdN39RY\nJjQzZnuqjPGKUU80B4q6np7qjW2d6qX0YhIOGTZ2WJ6qHtM3pTsTmt2bKlnaW2iTmh0Nstmv1r75\nvWWByEsfhHBlV/EPuIo/6qhFA7ZWPGBr5QOWt3rA8NdHs8FZA4Z/ylFtBVayXbp/YHOZowRNI9AY\ntzwVxkjb5/83hetkzg0XqxPLsZxg6W4APwNw75B1twD460ohfria6Jb845tXE80BcC2AuQBqADy7\nmmjGSiGOuLXGlXQDALo27FjgmmbAU1OzY+63vnVcClUgNynT7Ftu+eXWb3/7ltjWreduX7Vq15xv\nfGP9ihWvX5vJOOGKCn3v7bcvGFVhfjDxpqbpABCcMeOkvGUNORmpctdPFhV1PXWhavROBXJdlGy1\nqCs31kTPuLIn/92XcRVfxlH8GVcJZB0llMmEZvcmKi/oGu/jYAWIZJj+KRnTPyWTAMb9d0TIukhU\nnNeTqDivB8Dr4x3PicwINKaMQONeAG+NSzuZTuxcNWRH667cH627cv94xzISIzgj2ROcsRXA1kmT\ncmO5T4bcAICjlVj7F93xNITz9HjMkG17qoxY9SVj7gnGGGOH45gVqyuF+Ptqovphqy8H8P788j0A\nngdwc379AyuFMAC0rCbaDWApgFeONA4h6SYAZPtiNSTL5txvfvO+491Vtvbyy9v6N2x4oOPRR69v\ne+ih6x8fWBxobhanyzKZ3/723Lt0XT7sK/KZ9vZGACg788yTaiZgNdOpVzWvOSfQ+9IFspMqBXLj\nJlPFi5/vmf5/n88UHXxCK8YYY+yEMEFv5cQYG0dr3u75ihW5nq9Y8+6er1iR6/mKNe/s+YoV+Z6v\na+g05BomvQCeAPBlrDg23XWP961rKlcKMXgf0S4AlfnlWgDrhryuPb/uXVYTPT/0seTx0OAV76HS\nXV1q091318V3bZl51pmAogHz/umfdpx63XULj/goDkPdXXfhyauu2t/03MbJf3omfQ3gxVe/uvDN\n668/bcHhbjO2Z4/HTibLZY/HXvqFL8ySNW3m0Yz5SHg8nhkAMGnSpKO6XSna7NVfX9Ootv65gey0\nCgCurzppzri+2Tjl/+6DFnLKgNOP6k5PMMcqN+zIcW4KF+emcHFuChfnpnBxbk5ad2OEnq9YIX6I\nNW/3fMWad/d8xRqagRXCAfBzADcAeBW5YvUiAE8ei4DH7T6rK4UQq4mOagVupdPSrvvvr97zP/8z\nuXvDhmph29KcUwGcCZQ2VCcmrbz1qHWVpXSXKjylFqSDTob47tdLEpb9+jebVs1ZXZMyvMrscH/2\na7cs2nMkMbQ980wZABTPmtUna1rhj5cyorLSuzko9W8LyQM7QlJ8T0hK7A+RGdeFrNuQdSf33eMI\nxWND1p3cstcWsteRsn263LW2joRDAOAUz4mYc25oNmd+8gAkvsLMGGOMMcZOXrMqMBNrhjTsrRDv\nf8cLVoi/Yw3VD3vbe/Z8xYpcz1esyfd8XUOtAEJYIXINjWvoXgBX4AQpVrtXE1WvFKJzNVE1gMHJ\nbDoADL20U5df9y4rxTt/6N/QdfvF73+/pfOJJ86I79x5mrDeuhef8NbWbq8+u6wbeGNZ2VTP7t3d\n3U8f6QF4YtuDNU3/drk3tu0cVwn2Rms+9FjnzJUbRzN5yXe+s+2sN42pigcZXBn9L8/Tn9+Zmvfd\n7x72+NmmBx64FgAoFFpXSGN1yMlI9Up7WI68Fpb3PBlSje5qxeivGeyue9D32KlRVf0C5GYDjZv6\nJn/86YFJV+8DAHQcOEqRnxwGr6IW0u8My+HcFC7OTeHi3BQuzk3hOslzc8l4B1BgKrFiTD1frfzy\n8PXHxPEuVh8D8CkAP8x/f3TI+vtXE/0YuWbm6QDWj2aDwjTlHbfd9i+Dj7WSkrbi005bN/VTn9oQ\nXrAgVrH7znnY88Yycq0jug+YYkS0mje/c0EwsvbiwftRynaionT//Z8r6nzi4oG6qx/pnn7jlpHG\nkLz6al/Jo492fBQALp8XeTG8Lfa+jkcfva5k6dJ9NZdeelgTFaT37ZsOACVLlozr5ErkZKTwgccn\nByNrZ+jJ5hlapnP6we7rJkCOo4Z6bK30gOWt7jR8Uzsz4fmd2UBjTLbiqmzFNdmO67Kd1CQ7qUl2\nWpOcjCY5GV1ysxoA9Nd95LVU6en9x/8oGWOMMcYYK1w7erDzXa2pY7FCCKw5uj1fj9QxK1ZXE/0B\nuSblstVE7QBuRa5IfXA10WcB7ANwDQCsFOLN1UQPAtgOwAbwpbHMBCz7fP1F8+evn3TVVa9WX3zx\nO5rZXNlnAgAJ+/CKVdei6h0/XBo+8Phy2UkXA4Dhm7Klp/GLjwT6Xpka6nr6UsWK1pa3/PpL4Y5H\nWvqmfPyRSMPn3nH/Lcty6Vvf2vpp2xaeqVP9r33tvs/d9+p1z0rx7dvP3r5q1T+FFy5c5autzY4l\nrNS+fV5zYKAWRE7Nhz/celjHdpgkOyWHD/x5cqDvlRl6onmmlu1qHCzgB7neypRbPKs/bYnNhr+h\nMx1e2JkqPaP3rfuZMcYYY4wxxsZbN9ZQNVaITqwZVc/Xjvzy8PXHxLGcDfhjIzx1wQivXwVg1Vj3\nQ4riXvDSS1+X1IN3w3WUQK5YPYyW1bKWu2aUtd7zEcXsmwwAtlayPzLlkw9FGj67EwBi1Zd0dM1Y\nsa66adW5oZ7nLlHNyNSqXf/51ZK2B3dGpn7mkf7JH9sLAF//+pZlnZ3ZmbouJW6/fcF9skw47c47\nH3hp+fJ6Kxqt3XzjjZ84+6GHfjWWWYoPPP74NACkl5e36iUl1liPbaw88Z2B0n33LvIPbF6kHqQ4\ndZRgj+GbsjNTNK85Vn1xc+kply8BTtruJYwxxhhjjE0E79nzFWuG9XxdIRysoTjW0BnITbD0SQA/\nPVbBjdsES0eNJImRClUAcBW/BQAknNHNhAQg2P23yqrmH1+lp/ctAABH9kZj1Zc9cmD219YNH5vq\naGG7fcHtf1OyXWtrtq9aFois/aCW7ZxZ0/T9m0v33bf1WeMzLz7zTPBKALj++im/mzkzlAQAvazM\nnPfd7/7y9RUrvpHcvXvxlm9+s3nBD37wwmhjHHjttekA4K+vP2ZdgPXkXl9p692LAv3rF6uZA7MI\nQhp8zlZCXaZ/SnOmaH5ztPqS5kx4QWzoe0ccnMoYY4wxxhg7/ta83fMVa97Z8xVr3tnzFSvEm1jz\nzp6v+ZmAAeCLePvWNU/iGE2uBJwIxeohOEpw1N2A9URzoGb7v13mi75xLkHIghQjUXbWXw7M/e6z\ntl5mvtd7bU+Vsf/Un/5FS+17oaZp1Qd8/Rsu0NP751+K785/5oZpyFBx9zlnBqvNplrVCDRE0uEF\nkcpl53VPvvbae/fdd98NnU88cU3pkiUtdVeO7ibsqZaWRgAoXrToqN5fVU23ectb7lrg71+3WEu3\nzyEIGciNNzW8k7alSk/fOFB31Zt8H1PGGGOMMcYmkBVj6/mKFSP0fF0hNgKYd9Tieg8nfrGqFuW7\nAY9crMpmVKl989YLAr0vXiwJyysAkQ7Ne7FzzjceG2tR1p6qdL7y4JfiOzbtSd14+rP6F896Bcsa\n9wBAJXqwfOhrBSnGrCWBSG+VP3KgOVVmrFv1lRLPw68GKwMpErYC15ZJ2AoJR8k9dmQSjiJcR44v\n6mlo3QFRe+kH9h7Oz2UoLdXqK93/h7mByMuLtfT+eQRXAQABCNNb25QqWbIxUv+p14xAY+pI98UY\nY4wxxhhjo3HCF6u2Vjxyy6prUfWO25aEDzy2XHbSJQBgeOve7Jl+00Ox6ovHdD+UpqZ48I47mpdt\n3Nj/ftN0/YAP33n+yp4d3uV//8YVTZEitz2sGj1litlXJpuxMslOlkrC8ipWtLa6CqiuAgDTD7x+\nPiKH3t9ZF+a+3F3XrrLaa3dmiuY2xSo/0JSoOK97pBmJAYAcg0I9f60JRF5u8CSaG9RsR4NixasG\nnxeAMD1VzanixRv76j+5ORuanRjLz4ExxhhjjDHGjoYTvlh1tJJc991hY1bLWu6aUdp6z9Wq2TcF\nAGy1uL1vyvUP9U77fNNYtv/CCz0Vv/zlngu3b4+f6ThCBYDycr3l0kurn7rxxumv67osErgQ76r4\nhAM9tc/njb5e5knuKUNkT03/lqYF0baBWscSsm0DejjQUz6/4c1w46ROIWu2kFRbkOa0PPnKIiW6\nZ/H0hWom4Le8erp1oZ5uXRju/F84sq/f9Nc3pcKLtkdrl+8QkiyKOv/S4IttadBS+xpUo6d++G1l\nBCTb9pS3pMKLNvdNuX7T8PGnjDHGGGOMMXa8nfDFqqv4HQFyCUKW7JTs71tXXtX8H1cOTp7kyt5o\ntPrSRzpn3bJOyPqo7ivU2ZnRn3qqa/Kf/tR+QUtLaiEAAoApU3xbPvrRyU9dd92U3bJM770RkmEE\nGtJGoGE/gP0ANuMcPG43NQV3/vjHF/Rv2vR+YSUr8D9bKvTyzr21V1zx5PQvfWkLyTLW//PFZ2Xa\ngd3+j9532g3n7w0f+PNsX2zrHC3dNkt20iXe+PazvfHtZ5ft//1Bd+3I/j7LW703G2jcmypZujdW\ndXGbqwb4ljKMMcYYY+ykR7T6IgD/CUAG8GshVv5wnEM6aZ3wxSoAgGQTwvZM3fCZ6z3xHWcQhHSo\nyZNSKVtev76/dOvWaFVra6qyszNbGYkYlbGYVZnJOEWDr5Mk2LNmhV793Ocanr7wwqquIw01NHt2\nYsmvfvVIat++p3bcdtuyvnXrLjB6exv2/upXX2p76KH2mksueTLb1TUNAKovumhXumRBLF2yZC2A\ntXAtCnc+URfqeW62J7FjjprpnA4i19bL9hm+KXszobl745X/0JIJn8Itp4wxxhhjjA1DtFoGcCeA\nCwG0A9hAtPoxIVZuH9/ITk4Tvli1rLB00UUvfJkIgogEAEG5Rk0xuG7TZ3WlxGvDG286y3EJj+9e\nErntlcs7O5Mlk4Gmfxy6PdsWajRqViSTdpkQkA62T0mCHQqp3TNmBLfedNOMvy1YED7qxZ9/ypTM\naXfe+US2q+uvO26//ZzeF1/8gDUwULfv97+/AQCUQKA3vGBYd11JFdHay9uitZe3AXhaspKykGQh\nZK97tONjjDHGGGPsBLQUwG4hVu4FAKLVDwC4HLlbuLDjbMIXq0Jo1NGRmfNer9kTKUbJpBQe3z4b\n//q/l6Kpu7IMQBnwnpPbCr9f7guHte7ycr27utrbPW1aoHvBgqLuRYuK+3VdHlWX4SPlqaoyFq5Z\n81crHn+h6Uc/OrPnb3+7yE4mywKNjVsP9V7u2ssYY4wxxthQ5R6i1c8PPhJi5fuHvaAWQNuQx+0A\nTj/2cbGDmfDFqqJE3c9/vvFnQggIAXJdQUKAhACEEOS6oIezK/wvtPR6tzmL+pZelLtcMhJVlZwZ\nM4KR008v6S0p0a3jdiCHoIZC9imrVr3oZDJrO/785ymV55/fMd4xMcYYY4wxxtixMuGLVUkyxRe+\n0Pjme79qJgDgouMQz7Eme73u5GuuaRnvOBhjjDHGGJt4erMHaU0dqgPApCGP6/Lr2DiY8MUqY4wx\nxhhjjB0lGwBMJ1o9Fbki9VoA141vSCevg04gxBhjjDHGGGMnGyFW2gBuBPAUgCYADwqx8hC9ONmx\nwi2rjDHGGGOMMZYnxMonADwx3nEwbllljDHGGGOMMVaAuFhljDHGGGOMMVZwuFhljDHGGGOMMVZw\nuFhljDHGGGOMMVZwuFhljDHGGGOMMVZwuFhljDHGGGOMMVZwuFhljDHGGGOMMVZwuFhljDHGGGOM\nMVZwSAgx3jEcESJyAWTGOw52UAoAe7yDYAfFuSlcnJvCxbkpXJybwsW5KVwna268QogTssGOiP4i\nhLhovOM4mk6EYnWjEGLxeMfB3o1zU7g4N4WLc1O4ODeFi3NTuDg3hYtzwyaCE/KqAmOMMcYYY4yx\niY2LVcYYY4wxxhhjBedEKFb/33gHwEbEuSlcnJvCxbkpXJybwsW5KVycm8LFuWEFb8KPWWWMMcYY\nY4wxduI5EVpWGWOMMcYYY4ydYLhYZYwxxhhjjDFWcCZssUpEFxHRTiLaTUS3jHc8Jzsi+i0R9RDR\ntiHrSojoGSLalf9ePJ4xnoyIaBIRPUdE24noTSL6cn4952acEZGHiNYT0Rv53Hw3v55zUyCISCai\n14jo8fxjzk0BIKJWItpKRK8T0cb8Os5NASCiMBE9REQ7iKiJiM7k3Iw/IpqZ/3sZ/IoT0Vc4N2wi\nmJDFKhHJAO4EcDGAOQA+RkRzxjeqk97dAIbfhPgWAH8VQkwH8Nf8Y3Z82QBWCCHmADgDwJfyfyuc\nm/FnADhfCLEAwEIAFxHRGeDcFJIvA2ga8phzUziWCSEWDrlHJOemMPwngL8IIWYBWIDc3w/nZpwJ\nIXbm/14WAjgNQBrAw+DcsAlgQharAJYC2C2E2CuEMAE8AODycY7ppCaE+DuA/mGrLwdwT375HgBX\nHNegGIQQnUKIzfnlBHInDrXg3Iw7kZPMP1TzXwKcm4JARHUALgXw6yGrOTeFi3MzzoioCMC5AH4D\nAEIIUwgRBeem0FwAYI8QYh84N2wCmKjFai2AtiGP2/PrWGGpFEJ05pe7AFSOZzAnOyKqB7AIwKvg\n3BSEfDfT1wH0AHhGCMG5KRx3APhXAO6QdZybwiAAPEtEm4jo8/l1nJvxNxVAL4C78t3nf01EfnBu\nCs21AP6QX+bcsII3UYtVNsGI3D2S+D5J44SIAgD+B8BXhBDxoc9xbsaPEMLJd8uqA7CUiOYNe55z\nMw6I6DIAPUKITSO9hnMzrs7J/91cjNzQhnOHPsm5GTcKgFMB/FwIsQhACsO6lXJuxhcRaQA+DOC/\nhz/HuWGFaqIWqx0AJg15XJdfxwpLNxFVA0D+e884x3NSIiIVuUL190KIP+VXc24KSL6r3HPIjfvm\n3Iy/swF8mIhakRtmcj4R3QfOTUEQQnTkv/cgN+5uKTg3haAdQHu+hwgAPIRc8cq5KRwXA9gshOjO\nP+bcsII3UYvVDQCmE9HU/FWiawE8Ns4xsXd7DMCn8sufAvDoOMZyUiIiQm78UJMQ4sdDnuLcjDMi\nKieicH7ZC+BCADvAuRl3QoivCSHqhBD1yP1/+ZsQ4npwbsYdEfmJKDi4DOADALaBczPuhBBdANqI\naGZ+1QUAtoNzU0g+hre7AAOcGzYBUK7Vf+IhokuQG1MkA/itEGLVOId0UiOiPwB4P4AyAN0AbgXw\nCIAHAUwGsA/ANUKI4ZMwsWOIiM4B8CKArXh77N3XkRu3yrkZR0R0CnITWsjIXTh8UAjxPSIqBeem\nYBDR+wGsFEJcxrkZf0TUgFxrKpDrdnq/EGIV56YwENFC5CYl0wDsBfAZ5D/fwLkZV/mLO/sBNAgh\nYvl1/HfDCt6ELVYZY4wxxhhjjJ24Jmo3YMYYY4wxxhhjJzAuVhljjDHGGGOMFRwuVhljjDHGGGOM\nFRwuVhljjDHGGGOMFRwuVhljjDHGGGOMFRwuVhljjL0LEQkiWjPk8Uoi+s5hbutuIrr6MN/7aSKq\nGfL410Q0Z4TX/Sy//E9E9MnD2d/hGrrP0cbMGGOMsfemjHcAjDHGCpIB4Eoi+oEQIjKOcXwawDYA\nBwBACPG5Q71BCPGLYxzTofb5aYwxZsYYY4y9G7esMsYYOxgbwP8D8NXhTwxvKSWi5JDlm4loKxG9\nQUQ/PMh7TyOiF4hoExE9RUTV+fULiWgdEW0hooeJqDi/j8UAfk9ErxORl4ieJ6LF+fd8hoiaiWg9\ngLOH7OM7RLQyv9xIRM/m49lMRNOGxVNPRDuI6PdE1EREDxGRL//cBUT0Wv54fktEen79D4loez7W\n1UP3OYqYP5bf3jYi+tHQnyERrcrHuY6IKseYL8YYY+yEw8UqY4yxkdwJ4ONEVDSaFxPRxQAuB3C6\nEGIBgNuGPa8C+CmAq4UQpwH4LYBV+afvBXCzEOIUAFsB3CqEeAjARgAfF0IsFEJkhmyrGsB3kStS\nzwEwUjfb3wO4Mx/PWQA6D/KamQD+SwgxG0AcwBeJyAPgbgAfFULMR64n0heIqBTAcgBz87H++9AN\nHSLmGgA/AnA+gIUAlhDRFfmn/QDW5eP8O4AbRjgexhhj7KTBxSpjjLGDEkLEkSsibxrlW/4BwF1C\niHT+/f3Dnp8JYB6AZ4jodQDfBFCXL4bDQogX8q+7B8C5h9jX6QCeF0L0CiFMAH8c/gIiCgKoFUI8\nnI8nOxjbMG1CiLX55fuQK35nAmgRQjQPiykGIAvgN0R0JYCDbW8kS4bEbCNXSA8epwng8fzyJgD1\nY9guY4wxdkLiMauMMcbeyx0ANgO4a8g6G/mLnUQkAdBGuS0C8KYQ4sx3rBxly+0xJA7x+O0nhLCJ\naCmACwBcDeBG5FpKj5QlhBjcrwP+/8wYY4xxyypjjLGR5VtHHwTw2SGrWwGcll/+MAA1v/wMgM8M\nGfNZMmxzOwGUE9GZ+edVIporhIgBGCCi9+Vf9wkAg62sCQDBg4T2KoDziKg03734IweJPQGgfbCr\nLRHpg7ENM3kwJgDXAXgpH2s9ETUOjYmIAgCKhBBPIDeed8FBtjdSzOvzMZcRkQzgY0OOkzHGGGPD\ncLHKGGPsUNYAKBvy+FfIFV1vADgTQAoAhBB/AfAYgI35br4rh24k3133agA/yr/3deTGkQLApwDc\nTkRbkBvP+b38+rsB/GJwsqIh2+oE8B0ArwBYC6BphNg/AeCm/HZfBlB1kNfsBPAlImoCUAzg50KI\nLIDPAPhvItoKwAXwC+SK0Mfz23sJwD8fZHvvFfMtAJ4D8AaATUKIR0eImzHGGDvp0du9jhhjjLGT\nCxHVA3hcCDFvnENhjDHG2DDcssoYY4wxxhhjrOBwyypjjDHGGGOMsYLDLauMMcYYY4wxxgoOF6uM\nMcYYY4wxxgoOF6uMMcYYY4wxxgoOF6uMMcYYY4wxxgoOF6uMMcYYY4wxxgrO/wfVFUVL0p0HpwAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f35f23dfe90>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"(0.8355, 28.7747)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"quality_plot('/media/storage/FASTQs/K562_HindIII_1.fastq', \n",
" r_enz='HindIII', nreads=1000000)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3UAAALJCAYAAAATcQqaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XecHGX9B/DPZ2bb9UsjhOQgBAII4QClqBQjiAKhKPKj\nqAiKoIiCwvIDQQXlh6KuWBGIghQVQWxUIZTQpCOGmAgESEhCSELq5cqWme/vj5lNNseVvdxudu/y\neb9e+9opT9udzWW+8zzzDM0MIiIiIiIiMjQ5lW6AiIiIiIiIbDoFdSIiIiIiIkOYgjoREREREZEh\nTEGdiIiIiIjIEKagTkREREREZAhTUCciIiIiIjKEKagTkS0KyQNJvlzpdmwKklNJLipY/w/JqRVs\nUo9Inkry8QGkn0/yI+VsUzkM9HP2kP8akt8qZZsKyt6V5HMkOcB8N5D8v3K0SfpX7PdP8hmSu22O\nNonI0KCgTkT6RfIAkv8kuYbkSpJPkNyn0u3aFGb2mJntXK7ySR4ZnnC1k1xB8nckx5ejLjPbzcxm\nhvVeSvJ35ahHBq+nANDMvmRml5WpyssApCx8GG0YOGdIju7Wrn+RNJITB1shyZkkv9DLvnEk7yD5\nVk/1kYyTvJ7kWpJvkzy32/49ST5PsiN837Pb/q+H+daG5cQL9o0k+dfw3+QCkp/qlvcQkv8Ny36Y\n5HaD/S42gxSA71a6ESJSPRTUiUifSDYCuAvALwCMBDAewHcApCvZrmpE8jgAfwDwUwCjAewGIAPg\nMZLNlWybbDlIjgPwYQB/67brDQAnFaTbHUDtZmqWD+AfAD7Zy/5LAUwGsB2Ctv8vycMAgGQMwN8B\n/A7ACAA3Avh7uB0kPwbgQgCHhPknIfgblXcVgn+HYwF8GsDV+V6uMMj9C4BvIfj79hyAW4v5QAxU\n6jzqDgAfJrl1heoXkSqjoE5E+rMTAJjZLWbmmVmnmd1vZrPyCUh+nuRckqtI3ld4pZvkoeFV8DUk\nf0nykfzV/O69SyQnhlfxI+F6E8nrSC4huZjk/5F0w32nknycZCqs9w2ShxeUNZLkb8OegVUk/xZu\n7z6EcT7JJMlZYRtvJZko2P+/Yf1vkfxC2L4du39JJAngxwD+z8z+EH5PbwP4AoAOAOcU+Zk/F36X\nbSRfJ/nF3g5M2PaPhCe/FwE4geQ6kv8m+T8kn++W/lySf++lrF7rzX9nJM8juSz8Pj5XsH8Ug16Y\ntSSfAbBDb20O058c9pisIHlxt30OyQtJvhbuv43kyIL9+V7j1SQXkjw13N5E8iaSy8Oyv5k/4e7r\nt0LyBJLPdWvD10ne0V+53fJsdBzDbTPD38x7AFwD4APh8Vkd7t9oqB3J00nOY9AbfgfJbQr2Gckv\nkXw1/OxXhb+5nhwK4AUz6+q2/WYAny1YPwXATT3kH01yRvhbeIQb/3v+IMlnw38rz5L8YC9t2IiZ\nLTWzXwF4tpckpwC4zMxWmdlcANMBnBrumwogAuCnZpY2s58DIICDC/JeZ2b/MbNVCHqwTg3bW4cg\nkPyWma0zs8cRBIgnh3mPBfAfM/tT+H1dCmAPkrv01MjwmF5O8gkE/64nse+/UzuQfCj8Lb9D8vcs\nuMBDci+SL4Tf9a0ACv/2jCZ5V3i8V5J8LP/bC9v6PICP9fPVi8gWQkGdiPTnFQAeyRtJHk5yROFO\nkscgCCiOBTAGwGMAbgn35a+CfxNBz9VrAPYfQN03AMgB2BHAXgA+iiBIytsPwMth2T8EcF3Bie7N\nCHohdgOwFYCf9FHP8QAOA7A9gFZsOCE8DMC5AD4StmFqH2XsDGBbAH8q3GhmPoA/h20vxjIARwJo\nBPA5AD8h+d6+MpjZPwB8D8CtZlZvZnsguJK/fRhQ5J2Mnk/ii6l3awBNCHpqTwNwVcFv4SoAXQDG\nAfh8+OoRyV0BXB22ZRsAowBMKEjyVQAfB/ChcP+qsHyEwcW9CHqNxwDYE8CLYb5fhO2bFOb9bPg5\n8nr7rdwJYGeSkwvSfgpBj2sx5fYrDFK+BODJ8Pi8q9eW5MEAvo/gtzgOwAIAf+yW7EgA+yD4jR6P\n3k/odw8/a3dPAWgk+Z4w6DgRQe9Xd59GMHxzNILv9/dhG0cCuBvAzxEctysB3E1yVC/tKEr4OxoH\n4N8Fm/+N4N8uwvdZ+aGkvezvnnds2K6dAOTM7JVi8ppZO4B5Bft7cjKAMwA0IDhON6D3v1NEcFy3\nAfAeAC0IAsd8D+TfEPytGongb0dhT+Z5ABYh+K2PRfB3tvA7mAtgjz7aKSJbEAV1ItInM1sL4AAE\nJxO/BrA87EUYGyb5EoDvm9lcM8shCC72DE/Aj0BwFfx2M8siGJb4djH1huUfAeBrZtZuZssQBGYn\nFiRbYGa/NjMPwZCscQhO5sYBOBzAl8Ir/1kze6SP6n5uZm+Z2UoEJ/n5+3WOB/DbsAegA+HJWC/y\n9yot6WHfEgQnZv0ys7vN7DULPALgfgAHFpO3WzlpBMPIPgMADIabTUQwlHZT6s0C+G74Xd4DYB2C\nYMhFcCL67fA4zUZwLHpzHIC7zOzRsI3fQjA0L+9LAC42s0Xh/ksBHBf2gH0KwANhr3HWzFaY2YsF\nAco3zKzNzOYj6DU9uaDcHn8r4XH9O8JhiWFwtwuAO4ost1Q+DeB6M3sh/NzfQNCzN7EgzRVmttrM\n3gTwMDb8TrtrBtDWy758b92hCIKCxT2kubvg+FwctqMFwDQAr5rZzWaWM7NbAPwXwFED+aA9qA/f\n1xRsW4sgaMrvX4ON9bV/bfjeEO5bi40NpOye3BD+TcghCMZ6/TtlZvPMbEbYw7gcQSD8obCc9wOI\nIuiBzJrZ7di4JzOL4He6Xbj/sW6BbRuCYy0ioqBORPoXBmynmtkEAFMQXHX+abh7OwA/C4cIrQaw\nEsHV6fFhuoUF5Vjhej+2Q3DCs6Sg7GsR9LrlrQ8Qw5NzIDhJawGwMhyKVYzCQLMDG04yN2p/P21/\nJ3wf18O+cQX7+xT2hj4VDrdajeCEcXR/+XpxI4BPhT1SJwO4LTxR35R6V4QnsXn572kMgqFxhd/N\ngj7a1P030Q5gRcH+7QD8teCYzwXgIeipaEHQ29vdaAS/lcJ6FyD4Deb19lsBgl65/L1mnwLwtzBN\nMeWWyjaF9ZjZOgTfS4+fARv/Trtbhd6DkpsRfMZT0XuvbeHxWYfg3/Q23dsYKsX3sS58byzY1oQN\ngem6bvv6298UvrdtQt7u+3tS+Fvv8+8UybEk/xgOy1yLoGc0/+9qGwCLuwVqhd/vjxD0Gt7PYEj0\nhd3a0QBgdR/tFJEtiII6ERkQM/svguFGU8JNCwF80cyaC141ZvZPBD1ULfm8YXDRUlBcOzaeqKHw\npv+FCCZjGV1QbqOZFTON90IAIzn4yUmWYOOhgS29JUQw3G0RgP8p3BjeA/NJADPDTb1+ZgYz9v0Z\nwcx2Y8NhevcgCJL7Y+/aYPYUggkiDkRwIn9zTxkHWe9yBEPPCr+bbftI3/03UYtgKF/eQgCHd/s9\nJcxscbivp/v13kHQq1E4a+G26LkXqiczAIxhMKPiSdgw9HIg5baH7739nt91fLp5q7Ce8F6wUb3U\n1Z9ZCO+F7c7MFiCYMOUIBEOje1J4fOoR9Ea91b2NoYF8zz0KL74swcZDCfcA8J9w+T8AWrvdQ9ja\nbX/3vEvNbAWC4eORbsNru5e9Pm/4ve9QsL/HJhcs9/d36nth+t3NrBFBz3n+cywBML7b51r/byfs\nHT7PzCYBOBrAuSQPKUj7Hmw87FREtmAK6kSkTyR3YTBBxoRwvQXBie9TYZJrAHyDG2aTayKZD2zu\nBrAbyWPD4XNnY+MT3RcBHERyW5JNCIacAQDMbAmCIYA/JtnIYAKNHUh+CP0I894L4FckR5CMkjxo\nEz7+bQA+F96DVItgqGBvdRqAJIBvkvwUyQSDmel+g+DK/C/6+8wAYgDiCAMlBpN5FHsv3lIAE/nu\nSTxuAvBLAFkLJonoySbXGw5n/AuAS0nWhvfMndJHltsBHMlgwpMYgkktCtt8DYDLw+G7IDkmvG8T\nCO7t+gjJ40lGGEzQsmfYhtvCfA1h3nPR8/1iPX2GLIL7mX6EIICZUfDZiio3HFq3GMBnSLokP4+N\nA9ClACaEn7kntyD4re0ZBtnfA/B0OORzoGYAeC8LJvzp5jQAB4e9pD05ouD4XAbgKTNbiCDQ3yn8\nfUdIngBgV/QypLe7sD35Rw3Eu7XvJgT/dkYwuA/0dAQXj4DggogH4GwGjz44G0Gg9FBB3tMYPJtv\nBIJ/pzcA63uC/wLguyTrSB6AIEDKX+D4K4ApJD8ZtucSAP8OL171q4i/Uw0IegPXMHi0yfkF2Z9E\ncEHk7PBv1LEA9i34vo4kuWMY9K0JvwO/4Lt8H8LfqoiIgjoR6U8bgkkmnibZjiCYm43gJn6Y2V8B\n/ADAH8PhRbMR3M8GM3sHQc/VFQiGkk0G8ES+YDObgeC+r1kIZnLrfnL4WQQBxxwEQ8puR8/DG3ty\nMoJelv8imATkawP4zPn23YtgUoiHEQyDygeyPQ5hNLNbw3q/jmDI2hIAewP4UHjy1+dnNrM2BIHv\nbQg+76cQTHhSjPwELStIvlCw/WYEvaq9BjiDrBcAvoJgKODbCE6mf9tHXf8BcBaC3rAlYX2LCpL8\nLKz7fpJtCL7z/cK8byLoYToPwff7Ijb0snwVQW/Z6wAeD8u/fgCf4Q8IJsT5U7dhpgMp93QEJ+0r\nEEy08c+CfQ8h6P15m+S7huKa2QMIgpE/I/hedsDG948WzcyWhvUd08v+18zsuZ72hf6AILhZiSBw\n+EyYbwWCyVrOQ/AZ/xfAkeG/82J0YsNQy/+G63mXIBhauwBBEPdDCyYAgpllEEye81kEww1PBfDx\ncHt+oqAfIvh3mu+JvKSg7C8DqEHwd+APAM4Mf4f5YPyTAC5H8FvcFwP/3vv6O/UdAO9FEJTdjYLe\n0bD9x4afZyWAE7Bx7+lkAA8g+M6eBPArM3s43HcUgJlm9tYA2yoiwxQ3HsotIlJeJGcC+J2Z/abS\nbRmosAdhNoB4txP/3tJ/FGGwYGYv9pe+HEjmT2bfa2avVqINsvmFPaY3AtjX9B/9sEPyaQCnWTAx\nkYiIeupERPpC8hPhkK8RCHok7ywmoAMAM7sfwfT37y9nG/txJoBnFdBtWcxsjpnto4BueDKz/RTQ\niUihSP9JRES2aF9EMKTQA/AIgqFcRTOzO8vQpqKQnI9gUoaPV6oNIiIiUn5VN/ySTLkAngOw2Cx5\nJJkaieD+k4kA5gM43ixZ7DTlIiIiIiIiw1o1Dr88B8FzifIuBPCgWXIygAfDdREREREREUGVDb8k\nUxMATEMwC9W54eZjAEwNl29EMCvWBf2XRXNdN1P6VspguK7rAoDneV6l2yIb07GpXjo21UvHpnrp\n2FQvHZvqtSUfG8/zomZWjR1eRamqoA7ATxFMkdxQsG2sWXJJuPw2gLE9ZSRTMwvXE4mE//bbbw9k\nSm7ZDBKJxE4A0NXV9Uql2yIb07GpXjo21UvHpnrp2FQvHZvqtSUfm+bm5iMq3YbBqJpolEwdCWCZ\nWfL53tKYJQ3BA0dFRERERESqFsmpJB8jeQ3JqeWsq5p66vYHcDSZOgJAAkAjmfodgKVkapxZcgmZ\nGofgeUvvYpacWrgej1+cW7hw4YxyN1oGpqWlBQCgY1N9dGyql45N9dKxqV46NtVLx6Z6beHHpqie\nOpLXAwg7o2xKwfbDAPwMgAvgN2Z2BYLOqHUIYptFJW9xgarpqTNLfsMsOcEsORHAiQAeMkt+BsAd\nAE4Jk50C4O8VaqKIiIiIiGzZbgBwWOEGki6AqwAcDmBXACeR3BXAY2Z2OIL5QL5TzkZVTVDXhysA\nHEqmXgXwkXBdRERERKSstnvjzKMq3YbNLfHS13YtNm2x30+p0w00bZESJGfmX70lMrNHAazstnlf\nAPPM7HUzywD4I4BjzMwP968CEC9xezdSlUGdWXKmWfLIcHmFWfIQs+Rks+RHzJLdv0QRERGRqlKO\nk9OhcAJdbLqhEjg0tD1+ZCXqruSxib95Q9HHptjvp9TpBpp2MxgPYGHB+iIA40keS/JaADcD+GU5\nG1CVQZ2IiIhUt3L0YAynwKEcJ6dD4QS62HRDJXAo1nA6NluwLjObmn+VokAz+4uZfdHMTjCzmaUo\nszcK6kREZIsynAKHSl7NL3UPxkDKHAqBg4gMOS7J6SQ35YLVYgAtBesTwm2bjYI6EZFhZkscyrWl\nBg5D4Wq+giARGSI8MzvDzO7chLzPAphMcnuSMQSTPm7W52UrqBORIWWoBA6V7A3aEodyKXAQEZHN\ngeQtAJ4EsDPJRSRPM7McgK8AuA/AXAC3mdl/Nme7FNSJyHpDYRjZUAkcKtkbJCIiIgNW1PBLMzvJ\nzMaZWdTMJpjZdeH2e8xsJzPbwcwu3zxN3kBB3RCxJU6pK/3bUme8EhERESmxwQy/rDgFdUNEpabU\nLUeZQ6E3aKgM8VPAJCIiIiIK6oaZ4TaMTPcGiYiIiIj0TUGdiIiIiIhs6QbzSIOKi1S6ASIiIiIi\nIhXmmdkZlW7EplJPnYiIiIiIyBCmoE5ERERERLZ0Gn4pIiIiIiIyhGn4pYiIiIiIiFSGgjoRERER\nEZEhTEGdiIiIiIjIEKagTkREREREtnSaKEVERERERGQI00QpIiIiIiIiUhkK6kRERERERIYwBXUi\nIiIiIiJDmII6ERERERGRIUxBnYiIiIiIbOk0+6WIiIiIiMgQptkvRUREREREpDIU1ImIiIiIiAxh\nCupERERERESGMAV1IiIiIiIiQ1hVTZRCphIAHgUQR9C2282Sl5CpSwGcDmB5mPQis+Q9lWnl5nfl\nlS/vOWb5Ebj/R0+dmE778WzWj2UyfiyX82PZrMWyWT+ey1nM8yxWH70EbZn7f+g49En4JH3HCd5J\n+I5Dj4Tt0PxVvLb6oYvM4Pi+OWZwzIzB+4ZtADi69iKsSj/wf44Dz3HouS49x6FXsJ5zHHq7j/wc\nXlz+yDm+b27wgut5+eVgPR6P1Me8b2JV1/0/BEAzMPyYBACz9csEgKbEJViXnfGDfNvz9XZvwy4j\nvoj/rpp5bth+mBmB/DIIGM3AiY1nY0HbQ98gaSQMgJ9fJmGOQx+ATRn1Bcxe8cg5YZscwGC2vr0M\n2mk0A3YZ+SXMWzvz62H7/IJ2+WE7fdeld8DYY/H40ic/E5RpzH/W/HcQthn7jjkBzyx/4tTCdhW0\nN78MEv7B447EEyuf+UQk4uQiEeYiEceLRje8R6NOLhZzvE+O2Q0PPvnarrW1bqauLpKpr49kGxsj\nmcbGaGbEiFimuTmWLffvWERERETKo6qCOgBpAAebJdeRqSiAx8nUveG+n5glUxVsW0UsWNBe87vf\nzT/10k90YeutE8tqatx0TY2bqa2NpPMn6A0N0UxjYyTT3BxLf2Tt4T98oPHey7NZ38lkfCeXMyeb\n9d1czmcmY67n+U42a87hzo+/8Q+75veRCM11HT8SYfhy/EiEFo0Gy65LO2jl0T+4O/qXn6XTnpvJ\n+G467bvptBfJZn03kzE3ePfdo5ueav1H59EPRKOOF4vRi8XcXCzmePG44wXvrrfXXhM/uO3zex4x\nc8Tdl5OA49AcB0YSjgMDgMLlDyz56JX31d3z/UzGC+sNXplM0JZczpxMxnePrPnZznd3HXE3SXNd\nmOPQyPVlm+sGQdE090cX3ZWbfovnGX3f6Pvm+L7R80DPC5Z93zit9he73tU+7YGgnPUBXxhMBdtc\nlwYAR8R+ev5f1h52by4XfBe5nDm5nLm5XH7Zdz3PnN1HLjlwcW3dm2GQhjBIQ0HQBhL24ZGvfaB9\nq4+/Ygb4vjkA4PtBUBoGg/R90PfNGTeiDTWdkc5czo+k0368vd1zPc+P5HLmep65nmeRXM4ibc17\n47m3Fx2ay/mxXM5i2azFPM+P5i8G5HIWc12iNnoZ0v79PyHhhYF0wQWBIFDNXyyY2HgO5q996GJs\nCMjDAD2IVvPr2zefg8UdD1/gusxGIk42EmH4cnKRCLPRqJOLRpn96DYfxYNXPXd0Pn9hGQXBPw4Z\n+zE8es1z02IxJxuNOrl43M3GYk4uHney8biTTSTc/Ct3VKwFf5+9YJLvm5PLBcc7OPYIj3twzI9u\nfA9mPP3aLomEm6upcbM1NW6utjaSra11cw0NkWxdXSTX1BTNej7R3p5zs1mf4b8tZjK+k836jucZ\ns1lbvzymsx6LF3ckmptj2bq6iFfWPxQiIiIyWC7J6QDuNLM7K92YgaqqoM4saQDWhavR8GW95xj+\nrrnmtX1bWmrnXHTMQ++b3fqzh/pLP3bWOuzR2rymv3RTZr2J+taWBcW0YbtZq3FQ65jl/aWbMmsu\ntm/d8T99pWlpGdnR9MbaotoIAGM71uG9rSNW91/3PIxtnfRy/+kWoaa1ZX7/6V5GSz+fZUPa1zGq\ndYf/9p/uyc8c1Dr90f7TPXfq3q1T/llc3Y8cf1jrL//Rf7oz957dmvxZb/s9z7DVVuM+Vnt3y7GP\nbPXwxUHgHAQr4Xs+gHay2eBiwTT3hxff7f3mZiccxE1yfZAarsPM8FE/9a0/t19ze2enF+3q8qJd\nXV4kk/Gj6bQfyWS8aDrtR7NZP+rS4LrwAIJkYfM2Kjce9eB55q5dm0tks34kl7NoNutHczmL5nLB\nuudZNJezyIymj2N+2+v/g7BHNui1hoWBaj6Y9heN+AD+vXzh4bmcRTzPop638bvvB+9mVwB44Jf5\nwDYM+PO9vT6wobe3PnoeVnU89kPPsygAuC6z4SvjusxFIsxEIk52cvNZmLfm4QsKg/bw5YS9t6yr\nizU04Tws7XroYtdlJgyIM9Gok41G8+9ONhplNhZzMkds82E8dMO/DnVdepGI40Ui9KLRjXpxvWjU\n8T7etBPuevK1XQsuWqy/cOG6Gy42HFOzHe5/deF2sZjrJRJOLh53vZoa14vHHS+RcL26OjdXU+N6\n2ZyD1aszka4u302nPSf/OwpenpvJBBeZMhnfoY3FwyuWbRWLOX544cfPlxePu34i4Xg1Na7n+cQ7\n76Rj69blIh0dObe93Yt2dOQiXV2eG/ymfLery4tMi++AJ+cvnjBhQu26iRNr20eOjKv3WUREBmJI\nP9KgqoI6ACBTLoDnAewI4Cqz5NNk6nAAXyVTnwXwHIDzzJKruuWbWbieSDhsaWk5dDM1u2zmzPnn\nIeefv/dsACjq88wqcboSl5lIJHYCKlN3WdINo7oTicSO8doufOhD79m/mKqb7l6MHad9YOf+0y3C\n5GkHTOonWa7p7lPxtWl/yvRf3qk4e9rtnQA6+0/bvP2aaatf6D/dWa1rpq2eXUR5x62Ztvov/aUr\nSHsnAGQyHtety7r5V2dnzmlvz7nt7Vm3Ze6V27+5yxkLXJcW9FwT3Zebm2u3q39kn51fmfzgq52d\nOaejI+d2dGTdzk7P7erKRTo7c/Fw2e3q8tzVqxNoaqpvzeWCALyz03Pa2oy5nOfkcusDc76W+RCW\nuStPCocprx8WHA5Zhu8H7zOzR2G5LfxyLhf0UOZyvuN569+ZX/e978FxZ/7CcWiuSz9877bs+I5D\n+61/Mlbbfy/I5czxPJ++b8zlbH0Pquf59DxzgCsQiTzys2jU8cKRBH406vjRqOttWHb85+xQzO+Y\nf/batZl4W1sm5ji0hoZYprExlm5sjGaam+PppqZ4ZsSIeHrH9kPwxoMLzi4cRg1s/B0AwKT2Q7Hk\nkYVfDUca+EGw6eaXvUQi4m+99dvbjHllOyyK2AmFx2zDSASa6xLBRQXCWbQVFo2MfjKXW/+Z6fuG\nYDnY5nnGFfMmYaGfO8lxaJGIs/73EIms/21YJOKYu3grvL1V/FgAG412CN4RvgcXXF5bOgqrVtV8\nvFua9RdO89sWLG9Ge3v90WGAjzDoRz7gd5xg+/K1dfD9piM9z+h5wRB13zfkR0KYBcuvvj0a7TvU\nH11bG/FrayNeXV3Ui8ddc5yNLt4EtsT/bypZt84FqrduHZvS1b2FqLqgzizpAdiTTDUD+CuZmgLg\nagCXIbhifxmAHwP4fOVauXk8+uhbTWvWZBLHHbfjUtxf6daIyKaKxVwbOdLNjRyZyHXf1+TPx5Qj\ntlvRV/5EIpGOv74ULYdMWNVXuvVl3n30e9ZMu2VW/+lOPW7NtB/123vcdPfpx62ZtvqB/tMNOOjt\nt5e52DKb7v7CcWumrZ4BAL5vWLMm4771Vnt86dKO2LJlnfF33umMvfNOV3zVqnSsKxtBNus7ANYH\nKuHwZzgODQjWzYi1azPRTMaLB73Unruh1zEIjiMRpz6y+iis4FN75oOagl7X/NBpmAWBThM/i3b3\n4ffne0cdh8j3kuaDNZIY7X8Uy/n8lPyQ8LDs9eXnt9f7p6CND3wwf09u3oZA1dbfr1yP07EO/zio\nIA03LG8YFFNjX0a73XlwPk0Y/L5rOWbnI+v89aNBMBkMm88HgQXBoNXZaVidu+vgbNZzMhnfzWZ9\n1/eNQe9xEKDHYo4Xi7neVpFz0HHZ7R/OD9nPv8JgOlyOeLulD8LyWc9PamiIZuvro7nGxliusTGW\na2qK55qaYrnm5lhu3Lgo4gA8z0dnp+d0duaczs6c29mZc9Jpz+ns9JzwQoiTTnvOtq9MwpveG6ML\ng+GeAtv3LBwLf8Ha+LhxdZlYzN2iRxOJSPWouqAuzyy5mkw9DOCwwnvpyNSvAdzVQ/qphevx+MW5\nhQsXzih7Q8vo299+6sRddql/8O23F88YDRxXzOdpKnG6UpfZ0tKCONBaibrLkW441a1jU71169hs\nWrrGxuA1eXICQGL99imz7rt2dmvqp/2VOWXW/dfObv3xlX2laWlpObTp7lOOm9360jf6Ky8o86xr\nZ7e+dH7/6U67dnbrSxf3n+7L185ufSlZXN27Xzu79aVzi0z3tSLTnb0p5QW9x9nI2rXZaFtbLrpu\nXfD6cPryS/7U9pHrOzq8WFeXF+nq8mLBsO1srK2tK7piRTBcu7mpabcZs15r7+ryEpmM35DN+vFM\nxk9ks37l5s+gAAAgAElEQVQ8m7VELufHczmrcZ0rkPOuO85xkHMc5sKJvXKuy2x+oq9gWDS8nZo/\nhldWPzYB2HjSroJJrQAYx8ROxuuX/OnDmYxfG406nYmE01ZT466rrY201dVF1jU0RNoaG6Pr/mfb\nffCX39+VTae9WDodTHAWvqLZ7PqJzmKeZ9F9tzkV8y6/deuGhsi6xsZoW3NzbN3o0bG2sWMT6yZM\nqG3bYYf6daNHxzPD4d9sOu1xm23GO6NybtX/Tatk3fr/pnR1D8ARJSxrs6uqoI5MjQGQDQO6GgCH\nAvgBmRpnllwSJvsEgH6HSQ11q1dnInPmrN3nqqve+71Kt0VERKSUampcv6bGzWy1VWKjIddTZi1C\nonXivP7yT5n1+WmzW7/3u77SjB8/4dC6O0cfN3ePf33RdXsY6vmuMs++dnbrSz/qP93u185ufem8\ndNrj/PntdQsWdDS89VZn/fLl6YaVKzMNa9dm65cu7Rr9eOf2WLS6c1wsxmws5mbq6iIdI0c6qxMJ\nN1NT42YSCTdTW+tmYjHHO9CuPffGNz46f/XqTP2KFZmRCxZ0bNvenmvo7PTqu7q8hq4ur4GkP7Iu\nmBE6CEjXB6rhbNDBsusyt8foz+Hf7zz61YL7dAtmuN5w7+72jV/F62sevrDgNmYrXMaGe5qxQ+NZ\neHX1wxfmy/H9d5XpmIEj4xdheceMH/i+ueFs2hu9A0AkQoNdDvC+n8diTntNjbsukXDX1dS47fX1\nkXX19ZH2ILiNto8cGW8/ZewEPLN6+Zitt050trTUdtTUuH6/B1RkC1NVQR2AcQBuDO+rcwDcZpa8\ni0zdTKb2RPDHZT6AL1awjZvF1VfP22vMmPib73//6D6HZYmIiMi7OQ4Ri3goJqDbFPG4azvv3Lhu\n550b1/W0f8qs0w+e3fqtW4opa8qs2Zh82u6P9bbf8wzLl6fju7/64Z/fV3fP9zs7vUhXlxdJpz03\nnJgokk77+dmoI4fXPj3lnvajZubvZ3Uc5O9r9Tfcsws7Kpa64K7s1bcCG99Pmh9CHC7DzHh0zZXJ\ne3OH3xaJOL7jwPL3uAb3d26YPfvwzCf/77GRf//+hgmQXL+mxvUSieDe1GjUsZaWlkMb72o+7sGx\nz54/f/66+rfe6qpbtqyrfuXKTP2qVZn6trZc3eLFneNeeaWtvqPDq38yfixeXv7vczIZvzab9Wtc\nl9lYzGmPxZzORMLtiMedjpoat+ND2xyLfy5/8lOFj/4pnLU6uIeUNnXsNDzwo6dOyE+w5XnmhpNs\nRcKZo6OeZxHfN3enkWdhQfsjX49GmYlEnEws5mSiUSeTD9bjcScTjzuZT07YFzPvmbt3ba2bqa+P\npBsaoummpuA1alQsPXp0PN3QEM3lj2dnZ85ta8tF2tpy0fb2XKSjw4u0t+einZ1epLPTi3zM2R73\nzl4wacNQZKfgFQxJrqlxvdpaN2caBCyosqDOLDkLwF49bD95oGU58Ib0g9Vnzlx+wMEHb9XrH3gR\nERHZMrgusfXWifTYZcXOCD0Hk1onv9R/ujdR37rtG8W0Ycqs+Whu3e71/tJNnLUK64poIwlsvXUi\nvfXWiTSAPi9gT5n1lWtnt770TQDIZn0uW9YVX7Sos3bZsnTtihXpmlWrMnVr1mRr92hc8oHFtbWL\n84/+KeiVhJmtf47tmIZ2bL11Ynn4LNf8M11z8biTi8fdXCzm5BKJ4DmvH/F/ctFtqw+9t6PDi3V2\nerFwSHAsnfaj6bQXa2/P1axa5Tc91bUtnl60Yq9MZv3zhBPBI4T8eC5niVzOj/k+3ET0e+jK3ndN\neJ9mOCQYWdd1cq6LbDgkOPfwiCPw6urXj/d9C5/5i/XP/TULngNsFmyHXQE3cv+VsZjTEY87HYmE\n255IuB21tcGrvj7S3tAQ7Th6q71x600vHtLenqvp7PQSnZ1eTVeXV5NO+zWZjF+TTvs1juM0++nv\nosu7/8dBLzByBc8kzvcMr+8Vbh31Ocxe9ehZ2PAc3Xc9VxeAHTj+fzBr3dPH1dVFOurrIx2NjdGO\n5uZox4gRsY4xY+Id48bVdEyYUNNRzG9RelZVQV0pOfDKc2luM3jiiXdGr1iRnnDmmTu+WOm2iIiI\niFSLaNSx8eNru8aPr+0CsLJw35RZT55yYOv0R/orY8qsUz55ROsv+n1MVJB2PpqKemzR6QfPbr3k\n132lWbcu6+4+Z79fzdn92S/3N4R0yqxzrp3d+tIVxbRx5xf2uPaOuse+/dZbXbXLl3fVrViRqV29\nOlO7dm22tq0tV7tmTbZxyZKurR9ZsQOWresaXVPjdo4YEVvT0hJ5u74+0tnUFO1saop2jRoV7zzo\noMl77/ivXY58aNRDl3R2em5nZy7S2Rk8Oiad9iJdXb6byQQ9w+m0H51W/9SUO9Yc+ZjvB0Fz4cRO\nQH5SJ/CD9Qv2WTg/tmbdulzdokUdzZ2dXk1np1eXTvu16bRXk077dZmMXzuu+Zt4z3v/9dELLtjl\nkXHjatLFfH4JDNugbiC2e+PMoxZsf3XVPGTwppve+OCuuzY93dgYfddMeSIiIiIy9NTXR726RBal\nvicwGvHR11DgvCmzvrj/7NZv3tpXmpaW5q6mV7qw004NfZa1ocy52L51p35nW54y65nT3t+6V5+T\nmnieAfd87Nrjrv/2tkcd9dj33ve+kY+cd97ODxXbli3dkB6iWCoNbY8fWek25KXTHv/1r9X7n3hi\nyxOVbouIiIiIyObgusQe2y3BX/96wG+uvHKvK9auzTaedNKTl51yytPHv/DCqubN0QSS00ketRnq\nKjkFdQOw3RtnFnWQi03Xk9/85vXd6urc1Uccsc3iTS1DRERERGSoOuigMctvueUDv/vNb/b5Dgn/\n9NOfveSEE/558iOPLNuqjNV6ZnaGmVXN6L2BUFA3AMX26BWbrqfg77773j5g//3HPD7QtomIiIiI\nDCd77TVi9Q037Hf7rbd+4JsjR8ZWn3feixd8/OOPn37HHYsnVLpt1UZBXQV1D/7mzl3bsGhRxy5n\nnrnDs5Vqk4iIiIhINdlxx4b2q6/e+8477zzwokmT6uZffvmcs5auqa90s6qKgroqMn36a+/fYYf6\nF8MZnUREREREJDRuXE36yiv3mvHoowdfNLZJ86cUUlBXJTzP8MwzKw845pjxGnopIiIiItKLeNzV\nI9e7UVBXJW699c1JgOGkk7abV+m2iIiIiIjI0KGgrkr87W+LD9xnn1FPuO6QfWa6iIiIiIhUgIK6\nKrBkSWd83ry2Pc84Y9KTlW6LiIiIiIgMLQrqqsCvfjVvn/Hja1/Zddemtkq3RUREREREhhYFdVXg\niSfe2f9jH9taE6SIiIiIiMiAKairsPvuWzJu3brcyNNOm/SfSrdFRERERESGHgV1FXbLLW8esMce\nzU/W1Lh+KcprazjgrlKUU84y09ueOqdSdYuIiIiIDDcK6ioonXUxe/aa/T772YlPlKrMBdtffWcx\n6QYSLJW6zK7df1p0UFfqukudbqjULSIiIiLDl4K6Crrjhd0wcmTsrQMPHLO8v7SlPnkvNliqdJml\nrrvU6YZK3SIiIiKy+ZGsI/kcySPLWY+Cugq6bua+mDp1q6ImSNHJuwyGevREREREBo/k9SSXkZzd\nbfthJF8mOY/khQW7LgBwW7nbFSl3BdVu5cp0dPHKRtx775Jtli/vqlu5MlO7Zk22ds2abF17e662\nvd2r6+jI1XZ1+bWTG8/A3JUzzwUAMxAAzQDAwvdg2/YNX8G81Q9d7Pvm+D5cM3N8H47vm2sG1/fN\nMYM7pm4s/vCLHf5VsQ8vW4xiLwqU435HBZQiIiIyjNwA4JcAbspvIOkCuArAoQAWAXiW5B0AxgOY\nAyBR7kYN+6Bu2bKu2Isvrh716qttoxYt6hi1dGl69MqVmVFr1mRGtbXlRmWzfs3YxrPRYXPOiMed\n9poat6Omxm2vqYl01Ne77dtsU/N2Y2Oko7k51nHcyJ9Ouatj2j0kjARIGglznPXLIGlHJ378v/fj\n6t/FYq4Xi9GLRh0/GnX8RML1YjHHi8UcPx53vI+tOuAnr448MVvp70gkr2v3n87BwoVFpS31cFIF\nfyIiIlJBCZIz8ytmNrWnRGb2KMmJ3TbvC2Cemb0OACT/COAYAPUA6gDsCqCT5D1mVpLJEbsbtkFd\nVzaCvfe+P5XLWaKuzl3R2BhdMWJEbMXo0fEVO+3UsGDixLoVU6Y0rdh554a2vebucc3s1pcu7a/M\nKbNexdatk/7bf7oFaGhtWdBfuvgsr8hPIzL8lSP4q2RvooJUERGRLcZ4AIVXxRcB2M/MvgIAJE8F\n8E65AjpgGAd1sYiH396w33d33rmhLRp1rNLtEZHSqOQkNuWYNVZERESqQldvvXODZWY3lKPcQsN2\nohSHhilTmtYqoBORUilHoFZsoDiQ+x1FRERkwFyS00ketQl5FwNoKVifEG7bbIZtUCciMhQUGygO\n5PmOmsRGRERkwDwzO8PMNuUC7rMAJpPcnmQMwIkA7iht8/qmoE5EZJip1LDTSt7vqABVREQ2B5K3\nAHgSwM4kF5E8zcxyAL4C4D4AcwHcZmb/2ZztGrb31ImISGmUOkgsR5m6h1FERAbJJTkdwJ199daZ\n2Um9bL8HwD3lalx/FNSJiMgWRb1/IiLSA8/Mzqh0IzaVhl+KiMgWpdS9fwOZxKaSw04rVbeCYxGR\n8quqnjoylQDwKIA4grbdbpa8hEyNBHArgIkA5gM43iy5qlLtFBERyeva/adzsHBh/wlR2WGnlap7\nIG1UACgismmqracuDeBgs+QeAPYEcBiZej+ACwE8aJacDODBcF1ERESGkXI8M1JEpEiDeaRBxVVV\nT51Z0gCsC1ej4csAHANgarj9RgAzAVxQmJdMzSxcr40BLS0thxZV8awi01Yq3TCSSCR2AoCWlpb+\nkspmpmNTvXRsqpeOTWX4LXd1tQB9/v+ZSCR2yk0+Z2mx/8+mV586p5i0xaYb0P/xQ+E8pIRlFvy7\nqe7vp5J169iUru7i6Z66UiJTLpl6EcAyADPMkk8DGGuWXBImeRvA2Io1UERERIYEr/UHS4tNW+yz\nIAfyzMhiDeS+TBGRnlRVTx0AmCU9AHuSqWYAfyVTU7rtNzJlPeSbWrheFz/fFi5cOKOYOpuA44pJ\nW6l0w0n+avaW9rmHAh2b6qVjU710bKpXpY+N03BAoui6m8+bUcx9mZU8DyllmS0tLYgDrdV+nlbJ\nunVsSlf3ABxRwrI2u6rrqcszS64G8DCAwwAsJVPjACB8X1bJtpWK7gkQEREZnsrx7MRSnzdU8jxE\nvZNShYb0PXVVFdSRqTFhDx3IVA2C8fL/BXAHgFPCZKcA+Hsl2lfq6Zv1sFwREREpVqknkinHzKTF\npivHMFaRQfLM7Iy+HjxezaoqqAMwDsDDZGoWgGcR3FN3F4ArABxKpl4F8JFwfbMrx/TNIiIiIqVU\njvOQSp4DaWSTSP+q6p46s+QsAHv1sH0FgEM2f4tEREREpJJK3UM5kCCxHGWKlEO19dSJiIiIiAxY\nOXoTS11mJQNP6deQvqeuqnrqKkX/GERERESk3CoZeBZ7vjuQSWyGWU/mkH5OnYI66B44ERERERne\nij3f7dr9p3OKecTGQMrUuXZxSI4HsB0KYjQze7SYvArqRERERESk4oZIj15ZkPwBgBMAzAHghZsN\ngII6EREREREZGrbwHr2PA9jZzNKbknnYTpTiw7VKt0FERERERKQIrwOIbmrmYdtT58P1K90GERER\nEREZElyS0wHcWaEHkHcAeJHkgwDW99aZ2dnFZB62QZ2IiIiIiEiRKj375R3ha5MoqBMREREREakg\nM7uRZAzATuGml80sW2x+BXUiIiIiIiIVRHIqgBsBzAdAAC0kT9EjDURERERERIaGHwP4qJm9DAAk\ndwJwC4D3FZN52M5+KSIiIiIiMkRE8wEdAJjZKxjAbJjqqRMREREREams50j+BsDvwvVPA3iu2Mzq\nqRMRERERkSGlreGAu0pcpEtyOsmjSlxusc4EMAfA2eFrTritKOqpExERERGRIWXB9leX+llyFX2k\ngZmlAVwZvgZMQZ2IiIiIiEgFkLzNzI4n+RIA677fzFqLKUdBnYiIiIiISGWcE74fOZhCdE+diIiI\niIhIBZjZknDxy2a2oPAF4MvFlqOgTkREREREpLIO7WHb4cVm1vBLERERERGRCiB5JoIeuUkkZxXs\nagDwRLHlKKgTERERERGpjD8AuBfA9wFcWLC9zcxWFluIgjoREREREZHKMDObT/Ks7jtIjiw2sFNQ\nJyIiIiIiUhl/QDDz5fMIHmnAgn0GYFIxhSioExERERERqQAzOzJ8334w5Wj2SxERERER2dK5JKeT\nPKoSlZPcn2RduPwZkleS3LbY/ArqRERERERkS+eZ2RlmdmeF6r8aQAfJPQCcB+A1ADcXm1lBnYiI\niIiISGXlzMwAHAPgl2Z2FYLHGhRF99SJiIiIiIhUVhvJbwA4GcCBJB0A0WIzV1VQR6ZaANwEYCyC\n2V6mmyV/RqYuBXA6gOVh0ovMkvdUppUiIiIiIiIldQKATwH4vJm9Hd5P96NiM1dVUAcgB+A8s+QL\nZKoBwPNkaka47ydmyVQF2yYiIiIiIlJyYSD3ewD7kDwSwDNmdlOx+asqqDNLLgGwJFxuI1NzAYwv\nJi+Zmlm4nkg4bGlpObTkjZRBSSQSOwFAS0tLpZsi3ejYVC8dm+qlY1O9dGyql45N9dKxqRySxyPo\nmZuJ4Fl1vyB5vpndXkz+qgrqCpGpiQD2AvA0gP0BfJVMfRbAcwh681ZVsHkiIiIiIiKlcjGAfcxs\nGQCQHAPgAQBDN6gjU/UA/gzga2bJtWTqagCXIbjP7jIAPwbw+cI8Zsmphevx+MW5hQsXzoBUlfyV\nHx2b6qNjU710bKqXjk310rGpXjo21WsLPzZHVLh+Jx/QhVZgAE8qqLqgjkxFEQR0vzdL/gUAzJJL\nC/b/GsBdFWqeiIiIiIhIqf2D5H0AbgnXTwBQ9MSQVfWcOjJFANcBmGuWvLJg+7iCZJ8AMHtzt01E\nRERERKQczOx8ANcCaA1f083sgmLzV1tP3f4Ins3wEpl6Mdx2EYCTyNSeCIZfzgfwxco0T0RERERE\npCz+CcAD4AN4diAZqyqoM0s+jmC2l+70TDoRERERERmWSH4BwLcBPIQNs19+18yuLyZ/VQV1IiIi\nIiIiW6DzAexlZisAgOQoBD13RQV1ZbmnjkztRKYeJFOzw/VWMvXNctQlIiIiIiJSbUi+h+Q1JG8n\neWY/yVcAaCtYbwu3FaVcE6X8GsA3AGQBwCw5C8CJZapLRERERESk7EheT3IZydndth9G8mWS80he\nCABmNtfMvgTgeARzh/RlHoCnSV5K8hIATwF4heS5JM/tr13lCupqzZLPdNuWK1NdIiIiIiIig5Eg\nOTP/6iPdDQAOK9xA0gVwFYDDAewK4CSSu4b7jgZwN/qfI+Q1AH9DMDEkAPwdwBsAGsJXn8p1T907\nZGqHfKPI1HEAlpSpLhERERERkbIzs0dJTuy2eV8A88zsdQAg+UcAxwCYY2Z3ALiD5N0A/tBHud8Z\nTLvKFdSdBWA6gF3I1GIEUeany1SXiIiIiIjIYHSZ2dRNzDsewMKC9UUA9iM5FcCxAOIo82z+JQ/q\nyJQDYG+z5EfIVB0AxyzZ1l8+ERERERGR4cLMZgKYuTnqKvk9dWZJH8D/hsvtCuhERERERKTKuSSn\nkzxqE/IuBtBSsD4h3FYUki7Jr29CveuVa/jlA2QqCeBWAO35jWbJlWWqT0REREREZFN5ZnbGJuZ9\nFsBkktsjCOZOBPCpYjObmUfyJAA/2cT6yxbUnRC+n1WwzQBMKlN9IiIiIiIiZUXyFgBTAYwmuQjA\nJWZ2HcmvALgPgAvgejP7zwCLfoLkL/GuTjF7oZjMZQnqzJLbl6NcERERERGRMnBJTgdwp5nd2Vsi\nMzupl+33YHCToewZvn+3sFgABxeTuSxBHZmKAjgTwEHhppkArjVLZstRn4iIiIiIyCAMZvjloJnZ\nhweTv1wPH78awPsA/Cp8vS/cJiIiIiIiIgVIjiV5Hcl7w/VdSZ5WbP5y3VO3j1lyj4L1h8jUv8tU\nl4iIiIiIyGAUNfyyjG4A8FsAF4frryC4v+66YjKXq6fOI1M75FfI1CQAXpnqEhERERERGQzPzM6o\nUEAHAKPN7DYAPgCYWQ4DiJ/K1VN3PoCHydTrAAhgOwCfK1NdIiIiIiIiQ1k7yVEIJkcByfcDWFNs\n5nLNfvkgmZoMYOdw08tmyXQ56hIRERERERnizgVwB4AdSD4BYAyA44rNXJbhl2TqLAA1ZslZZslZ\nAGrJ1JfLUZeIiIiIiMgguSSnkzyqEpWHz6P7EIAPAvgigN3MbFax+ct1T93pZsnV+RWz5CoAp5ep\nLhERERERkcGo6D11JBMAzgZwGYDvADgr3FaUcgV1LplifoVMuQBiZapLRERERERkKLsJwG4AfgHg\nl+HyzcVmLtdEKf8AcCuZujZc/2K4TURERERERDY2xcx2LVh/mOScYjOXK6i7AMAZAM4M12cA+E2Z\n6hIRERERERnKXiD5fjN7CgBI7gfguWIzl2v2Sx/ANQCuIVMjAUwwS+o5dSIiIiIiUo0q/fDx9wH4\nJ8k3w/VtAbxM8iUAZmatfWUuS1BHpmYCODos/3kAy8jUP82SXy9HfSIiIiIiIoPgmdkZFaz/sMFk\nLtdEKU1mybUAjgVwk1lyPwCHlKkuERERERGRIcvMFvT16i9/uYK6CJkaB+B4AHeVqQ4REREREZEt\nXrmCuu8CuA/APLPks2RqEoBXy1SXiIiIiIjIFqtcE6X8CcCfCtZfB/DJctQlIiIiIiIySJWeKGVQ\nyvVIg01CploQPHhvLAADMN0s+bNwBs1bAUwEMB/A8WbJVZVqp4iIiIiIDCsVmSiF5Bvh4jIz229T\nyynX8MtNlQNwnllyVwDvB3AWmdoVwIUAHjRLTgbwYLguIiIiIiIyZJnZ9uFrkwM6oMp66sySSwAs\nCZfbyNRcAOMBHANgapjsRgAzETzgfL3wMQrrJRIOW1paDi1vi2WgEonETgDQ0tJS6aZINzo21UvH\npnrp2FQvHZvqpWNTvXRsNr+wp84ALB9MYFfyoI5M7QzgDAC7hJvmAvi1WfLlAZYzEcBeAJ4GMDYM\n+ADgbQTDM0VERERERIYsM9u+FOWUNKgjUx8A8BcA1wKYDoAIArOHydSxZsmniiynHsCfAXzNLLmW\nTK3fZ5Y0MmXd85glpxaux+MX5xYuXDhjUz+LlEf+yo+OTfXRsaleOjbVS8emeunYVC8dm+q1hR+b\nIypRKclt+9pvZm8WU06pe+q+DeAks+TMgm1/I1MPAbgEwOH9FUCmoggCut+bJf8Sbl5KpsaZJZeE\nz79bVuJ2i4iIiIiIbG53Ixh+yYJtBmAMgK0AuMUUUuqJUnboFtABAMySjwCY1F9mMkUA1wGYa5a8\nsmDXHQBOCZdPAfD3wTdVRERERESkcsxsdzNrDd93B3AUgCcArAPwtWLLKXVPXVsf+9qLyL8/gJMB\nvESmXgy3XQTgCgC3kanTACwAcPygWikiIiIiIrJBRZ9TR3IygIsB7AfgxwDONrNssflLHdS1kKmf\n97CdCGax7JNZ8nFs3PVY6JDBNExERERERKQXlXpO3RQEwdxuAH4I4DQz8wZaTqmDuvP72PdciesS\nEREREREZyv4NYCGCe+v2BbAvuaGPy8zOLqaQkgZ1Zskbe9tHpqrqmXgiIiIiIiIVdhqCiVEGpdSP\nNHjcLHlAuHyzWfLkgt3PAHhvKesTEREREREZqszshlKUU+res7qC5d267evtXjkREREREZEtDsnf\nIuipW2NmX9/Uckod1PXVdTjobkUREREREZFh5AYEcVJmMIWUOqhrJlOfQPD8u2YydWy4nQCaSlyX\niIiIiIjIUHYpgqBuJYDjNrWQUgd1jwA4umD5qIJ9j5a4LhERERERkaHs1PB9wI8xKFTq2S8/V8ry\nREREREREhiszW1CKcpxSFFKITLlkanTBeoxMnUGm5pa6LhERERERkRJwSU4neVT/SatPqR9pcCKA\nawG0k6lXAVwO4HoAzwL4dCnrEhERERERKRHPzM6odCM2Val76r4J4H1myW0AfB3AnQDONEt+wiz5\nQonrEhERERERGbJIPhi+/2Aw5ZR6opSMWXIeAJglXyBTr5ol7yxxHSIiIiIiIsPBOJIfBHA0yT+i\n27O9zayojrFSB3VbkalzC9abC9fNkleWuD4REREREZGh6tsAvgVgAoDusZIBOLiYQkod1P0aQEMf\n6yIiIiIiIgLAzG4HcDvJb5nZZZtaTqkfafCdUpYnIiIiIiIy3JnZZSSPBnBQuGmmmd1VbP5Sz375\n8772myXPLmV9IiIiIiIiQx3J7wPYF8Dvw03nkPygmV1UTP5SD798vmD5OwAuKXH5IiIiIiIiw800\nAHuamQ8AJG8E8C8Amz+oM0vemF8mU18rXBcREREREZFeNQNYGS43DSRjqXvqClkZyxYRERERERku\nvg/gXyQfRvBYg4MAXFhs5nIGdSIiIiIiItIPM7uF5EwA+4SbLjCzt4vNX+qJUtoQ9NARQA2ZWpvf\nFbQ12VjK+kRERERERIYDM1sC4I5NyVvqe+r0TDoREREREZHNqNQ9dQkAXwKwI4BZAK43S+ZKWYeI\niIiIiEi1I/lxBLNaNgK4zszuL1ddTonLuxHA3gBeAnAEgB+XuHwREREREZGKIHk9yWUkZ3fbfhjJ\nl0nOI3khAJjZ38zsdASdXif0UaZL8r+DaVepJ0rZ1Sy5OwCQqesAPFPi8kVEREREREotEU5UAgAw\ns6m9pLsBwC8B3JTfQNIFcBWAQwEsAvAsyTvMbE6Y5Jvh/h6ZmRcGhNua2Zub0vhS99Rl8wsadvn/\n7H6+LcQAACAASURBVN13fFX1/cfx1ycJJOyNCAQRWTLcouLCvcfPumsddXVotRqr1lr9tc72qq22\nVlzV/to66y7WOoqWgoKbPQxgCGEGCBAIJPn8/jjn1mvMuJnn3uT9fDzug3vP+J7PPd+TcD75fs/3\nKyIiIiIirYm7v8dXc8nFjQMWuXu+u28DngZOscDdwOvu/nEdRfcAZpvZ22b2SvyVbFxN3VK3e5UR\nL+MjYGr0SxERERERSVVba2mdq8sAoCDh8zJgP+BK4Eigm5kNdfeHainj5gYeG2j60S8zm7I8CYwd\nO3biFVdc8dvLL798Tt1bi4iIiIhI1Nz9fuD+JLd918x2Aoa5+1tm1hFIOrdKqcnHzWKPAycCq9zz\nxoTLbgUuBVaHm/3UPW9SNBFG54svvtgBUFInIiIiItL0Ms3sYeBVd3+1nvsWArkJnweGy5JmZpcC\nlwE9gV0IWv8eAo5IZv+USuqo5sHD0H3uebGWD0dERERERNqACne/rIH7zgCGmdnOBMnc2cC59Szj\nhwTP5n0A4O4LzaxvsjunVFLnnveeWWxwQ/Y1i01O/JyTk2G5ublHNUVcqWDkyJEjc3NzU6q+GiIn\nJ2c4QG5ubl2bSgtT3aQu1U3qUt2kLtVN6lLdpC7VTd3M7ClgAtDbzJYBt7j7Y2Z2BfAGQZfJx919\ndj2LLnP3bWYWP04W4MnunC5JwpVmsfOBD4Fr3fPWRR2QiIiIiIi0Gkl1v3T3c2pYPglozCNi75rZ\nT4EOZnYU8AMg6W6g6ZDU/QH4JUGm+kuCCc2/W3Uj97wJiZ+zs28qLygoeLMlAmwBpy9cuHBOQUHB\nu1EH0ljxv/y0orppNVQ3qUt1k7pUN6lLdZO6VDepq43XzfGN6H7ZFG4ALgZmApcTJIiPJrtzyid1\n7nkr4+/NYo8Ar0UYTiRmzpx5edQxiIiIiIhI83D3SjN7kuCZOgfmu3vS3S+bevLxJmcW2zHh4/8A\ns6KKRUREREREWqVMM3vYzE6K4uBmdgLwBcEUCL8DFpnZccnun1ItdWaxhAcPY8uAW4AJZrE9CDLW\nJQTNkW2K5qkTEREREWlWjRn9sincAxzm7osAzGwX4O/A68nsnFJJnXtedQ8ePtbigaSg/Pz8vmie\nOhERERGR1mhjPKEL5QMbk905pZI6ERERERGRtsLMTgvffmhmk4BnCXoonkEw/11SlNSJiIiIiEhb\nl9SUBs0g8Rm+lcCh4fvVQIdkC1FSJyIiIiIibV0kz9S5+0VNUY6SujSRkZGR9JCmIiIiIiKSPsxs\nZ+BKYDAJOZq7n5zM/krq0oDmqRMRERERadVeIhgg8lWgsr47K6kTERERERGJ1lZ3v7+hO6f85OMS\nzFM3ceLEUVHHISIiIiLSSkU6+TjwWzO7xcwOMLO94q9kd1ZLXZrQPHUiIiIiIs0m6snHxwLfAQ7n\nq+6XHn6uk5I6ERERERGRaJ0BDHH3bQ3ZWd0vRUREREREojUL6N7QndVSJyIiIiIiEq3uwDwzmwGU\nxRdqSoNWRvPUiYiIiIi0Wrc0ZmcldWlA89SJiIiIiDSrTDN7GHjV3V9t6YO7+7uN2V9JnYiIiIiI\ntHWRjn5pZhsJRrsEaA+0Aza7e9dk9tdAKWlA89SJiIiIiLRe7t7F3buGSVwH4FvAg8nur6QuTYTz\n1ImIiIiISCvmgZeAY5LdR90vRUREREREImRmpyV8zAD2AbYmu7+SOhERERERkWidlPC+HFgCnJLs\nzkrqREREREREIuTuFzVmfyV1aULz1ImIiIiINJtIpjQws5/Xstrd/ZfJlKOkLg1onjoRERERkWYV\n1ZQGm6tZ1gm4GOgFKKkTERERERFJVe5+T/y9mXUBrgIuAp4G7qlpv6o0pUEaGDt27MSHHnpI89SJ\niIiIiLQyZtbTzG4DPidodNvL3a9391XJlqGkLk3k5+fvEHUMIiIiIiLSdMzs18AMYCMw1t1vdfd1\n9S1HSZ2IiIiIiEg0rgX6Az8DlptZSfjaaGYlyRaiZ+pEREREREQi4O5N0simljoREREREZE0pqQu\nTWRmZlZGHYOIiIiIiKSelOp+aRZ7HDgRWOWeNyZc1hN4BhgMLAHOdM+r98OD6Uzz1ImIiIiISE1S\nraXuCeDYKstuAN52zxsGvB1+FhERERERaSqZZvawmZ0UdSANkVItde5575nFBldZfAowIXz/JDAZ\nuL7qvmaxyYmfc3IyLDc396gmDzIC3bt3P33ixIn/Puuss1ZGHUtj5eTkDAfIzc2NOhSpQnWTulQ3\nqUt1k7pUN6lLdZO62njdVLj7ZVEH0VCp1lJXnR3c84rC9yuANjlf27x587pEHYOIiIiIiKSelGqp\nq4t7npvFvIZ1ExI/Z2ffVF5QUPBmiwTW/E6fN2/evIKCgn9FHUhjxf/y04rqptVQ3aQu1U3qUt2k\nLtVN6lLdpK42XjfHRx1AY6RDS91Ks9iOAOG/qyKOR0REREREJGWkQ1L3CnBB+P4C4OUIYxERERER\nEUkpKdX90iz2FMGgKL3NYsuAW4C7gGfNYhcDS4Ezo4swOpqnTkREREREqpNSSZ173jk1rDqiRQNJ\nMZqnTkREREREapIO3S9FRERERESkBkrq0sDYsWMnTpw4cVTUcYiIiIiISOpRUpcm8vPz+0Ydg4iI\niIiIpB4ldSIiIiIiImlMSZ2IiIiIiEgaU1InIiIiIiKSxpTUpYmMjAyPOgYREREREUmOmQ0xs8fM\n7PnmPlZKzVMn1dM8dSIiIiIi0TOzx4ETgVXuPiZh+bHAb4FM4FF3v8vd84GLWyKpU0udiIiIiIhI\ncp4Ajk1cYGaZwO+B44BRwDlm1qLTkSmpSwOap05EREREpFnlmNnk+Kumjdz9PaC4yuJxwCJ3z3f3\nbcDTwCnNF+o3KalLE5qnTkREREQkJQ0AChI+LwMGmFkvM3sI2NPMbmzOAPRMnYiIiIiItHVb3X1C\nUxbo7muB7zVlmTVRS52IiIiIiLR1mWb2sJmd1IB9C4HchM8Dw2UtRi11IiIiIiLS1lW4+2UN3HcG\nMMzMdiZI5s4Gzm2yyJKglro0oXnqRERERESiZWZPAdOAEWa2zMwudvdy4ArgDWAu8Ky7z27JuNRS\nlwY0T52IiIiISLPKNLOHgVfd/dWaNnL3c2pYPgmY1FzB1UVJnYiIiIiItHWN6X4ZOXW/TAOap05E\nRERERGqipC5NaJ46ERERERGpjpI6ERERERFp6xozpUHk9EydiIiIiIi0dXqmTkRERERERKKhpC5N\nZGZmVkYdg4i0HieffPL3brrppoOjjkNEREQaT90v04DmqRORppaTk7MlKyurIuo4REREUkRS89Sl\nKiV1IiIiIiLS1umZOmleY8eOnfjQQw9pnjoRaTJz5849YN68eUOjjkNEREQaT0ldmsjPz98h6hgk\nPeXn53csKirKjjoOSTm2du1a/V4RERFpBZTUibRy3/rWt+4677zzro46Dkk97du33xJ1DCIiIilC\n89S1BLPYEmAjUAGUu+ftE21EIumhvLw8e+PGjb2ijkNSy6677jp11KhRC6OOQ0REJEWk9TN1aZPU\nhQ5zz1sTdRAi6WTMmDH/7tmz57qo4xARERGR5pFuSV2NzGKTEz/n5GRYbm7uURGF0+TGjBkzPDc3\nN+3rKycnZzhAbm5u1KG0GSNHjtyhX79+3er6eVDdpK7mqJu5c+eO79mz5065ubmdmqzQNkg/N6lL\ndZO6VDepS3WTvtIpSXDgLbNYBTDRPe/hqANqKevXr38+6hgkfR1++OGrunTpUh51HJJajjnmmMV7\n7713cdRxiIiISOOlU1J3kHteoVmsL/CmWWyee9578ZXueRMSN87Ovqm8oKDgzZYOUmoX/8uP6qbl\nPP7446d37959wx577FHrOVfdpK7mqJuCgoJ+HTp0WFxQUDClqcpsi/Rzk7pUN6lLdZO62njdHB91\nAI2RNqNfuucVhv+uAl4ExkUbUcvRPHXSGHPmzNl77ty5un5q8Oijj46866672tzAS3Pnzh0/f/78\nXaKOQ0REJEVo9MvmZhbrBGS4520M3x8N/CLisFpUOE/dnKjjkPRTWlra093T5g84LW3atGm7rly5\nckfgw6hjaUnunrF27dq+UcchIiKSIjT6ZQvYAXjRLAZBzH91z/tHtCGJSGswZ86cvTdt2tQn6jii\nkJ2drXnqREREWoG0SOrc8/KB3aOOQ0SktRg5cuS0MWPGzI86DhEREWm8tEjqRKThRo8ePaV3796a\n31FERESklVJSlyYyMzMro45B0lN2dnZZdnb2tqjjkNQyb968A7Zt25YNTIs6FhEREWkcJXVpYObM\nmZdHHYOkr/322292ly5dyqKOI1UddNBB76xYsaLNPVM3evToKcOGDVscdRwiIiLSeBoRT6SVmzFj\nxsiPPvpoSNRxpKqjjjpq7gknnDA96jhEREQkUmk9pYGSujSgeeqkMebMmbPPvHnzdo06jlS1dOnS\nbkuXLu0VdRwtbc6cOZqnTkRE5CsV7n6Zu78adSANoaQuTSxevFjzSUmDlJaW9iwuLu4fdRyp6v33\n3x81ZcqUfaOOo6VpnjoREZHWQ8/UiUibFs5T1zvqOKKQnZ29NeoYREREpPGU1ImItEEjR46cNnbs\nWM1TJyIi0gooqRNp5UaNGjWlb9++mqdOREREpJVSUpcmNE+dNJTmqZPqaJ46ERGR1kNJXRrQPHXS\nGAcccMDsTp06KamrwcEHH/xWUVHRDlHH0dLGjBnz71122WVp1HGIiIhI4ympE2nlZsyYMbJr164b\nzz///IVRx5KKjjzyyHnFxcVLoo5DREREpKE0pUEa0Dx10hizZ8/WPHW1WLJkSfelS5f2jDqOljZ7\n9uwDFyxYoEnpRUREWgEldWlC89RJQ2meutqF89SNi+LYRx555HUnnXTS96M4trtnFBcX6/eKiIhI\nINPMHjazk6IOpCHU/VJE2rS5c+fuFdU8dZWVlZmVlZWZURwbIDs7e0tUxxYREUkxFe5+WdRBNJSS\nOhGRiAwZMmR+hw4dIkmsRowY8cHuu+8+O4pji4iISNNSUifSyo0aNeo/ffv2XRV1HPJNpaWlHd09\n6jBEREQkzSmpSxOap04aKjs7uywnJ0dTGqSgmTNnHpKVlVUGvNjSx54/f/5+27dvzwI+aOlji4iI\nSNNSUpcGNE+dNMYBBxwwS/PU1eyQQw55s7CwcMcojr3//vu/npOTUxbFsceMGfPvIUOGaJ46ERGR\nVkBJnUgr9+GHH47o3LnzZs1TV70jjzxy3po1a76MOg4RERGRhtKUBmlA89RJY8yaNWvf+fPnj4w6\njlS1ePHiHl9++WWPKI49Z86cPefOnTsmimPPnj37wIULF2qeOhERkVZALXVpIpynbk7UcUj6KS0t\n7enu+gNODaZNmzZq7dq1fYCPWvrYJSUl/UpLS7e29HFB89SJiIi0JkrqRKRNmzdvXmTz1PXu3Xtx\nx44dN0ZxbNA8dSIiIq2FkjoRkYgMGTJkfqdOnSJJrIYPH/7BnnvuqXnqREREWgEldSKt3K677jq1\nX79+K6OOQ75py5YtHaOOQURERNKfkro0oXnqpKGys7O3Zmdna0qDFBTlPHULFizYr6KiQvPUiYiI\ntAJK6tKA5qmTxjjwwANn5uTkbI86jlR16KGHvllQUBDJPHUHHHDApHbt2kVSN2PHjn1v8ODBBVEc\nW0RERJqWkjqRVu7DDz8c0aFDhy0XXnih5qmrxhFHHKF56kRERCStpc0w52axY81i881ii8xiN0Qd\nT0vSPHXSGLNmzdp34cKFmqeuBvn5+T0LCgoimadu9uzZe82bN290FMeeNWuW5qkTERFpRmbWycye\nNLNHzOzbzXmstEjqzGKZwO+B44BRwDlmsTaV5OTn5+8QdQySnjZv3tyruLi4f9RxpKr3339/1ylT\npuwbxbFLSkr6FRcX50ZxbHfPLC4u7hPFsUVERNKVmT1uZqvMbFaV5cea2XwzW2Rm8Qao04Dn3f1S\n4OTmjCtdul+OAxa55+UDmMWeBk4hYTJus9jkxB1ycjIsNzf3qJYMsjmNHDlyZG5ubrrUV41ycnKG\nA+TmRnIf22ZlZ2dn1/Xz0Fbr5ssvvzxw1apVnaL4fTFs2LDi7t27l0VVN4MGDeqcyr8nZ86c2Wn5\n8uXZxxxzTHHUsdSkrf7cpAPVTepS3aSuNl43OWY2Of7B3SfUsN0TwO+AP8UXmFm8AeooYBkww8xe\nAQYCM8PNKpo84gTm7s1ZfpMwi50OHOued0n4+TvAfu55VyRsM/nre113CKCJdUVEREREpC4dgXfj\nH2pJ6jCzwcBr7j4m/HwAcKu7HxN+vjHcdBmwzt1fM7On3f3s5gk9fVrq6uSeN+HrS/IiiUNERERE\nRNqUAUDiiNLLgP2A+4HfmdkJwKvNGUC6JHWFQGI78MBwmYiIiIiISMpx983ARS1xrHRJ6mYAw8xi\nOxMkc2cD50YbkoiIiIiISPQNUGkx+qV7XjlwBfAGMBd41j1vdrRRiYiIiIiIxBugbGcza0/QAPVK\nSwaQFgOliIiIiIiIRM3MngImAL2BlcAt7v6YmR0P/AbIBB5399tbNC4ldSIiIiIiIukrLbpfioiI\niIiISPWU1ImIiIiIiKQxJXUiIiIiIiJpTEmdiIiIiIhIGlNSJyIiIiIiksaU1ImIiIiIiKQxJXUi\nIiIiIiJpTEmdiIiIiIhIGlNSJyIiIiIiksaU1ImIiIiIiKQxJXUiIiIiIiJpTEmdiIiIiIhIGlNS\nJyIiIiIiksaU1ImIiIiIiKQxJXUiIiIiIiJpTEmdiIiIiIhIGlNSJyIiIiIiksaU1ImIiIiIiKQx\nJXUiIiIiIiJpTEmdiIiIiIhIGlNSJyIiIiIiksaU1ImIiIiIiKQxJXUiIinAAn80s3VmNj2J7Qeb\nmZtZVvj5dTO7oPkjbTgze8LMbmvAfpvMbEhzxJTuzGwHM3vPzDaa2T1JbH+hmU1pgbgmmNmyhM+z\nzWxCcx+3sRp6jYqIRE1JnYg0GTNbYmZbwpvwleENUueo40oUxnhk1HFU4yDgKGCgu4+r787ufpy7\nP9n0YX0lTCKHNucxquPund09P4yhRW66zezb4XUcf5WG33/vcP2PzSzfzErMbLmZ3ZeQYGeZ2dNm\ntt7M/mFmXRPK/amZXdOEoV4GrAG6uvu1TVhuk3L30e4+Oeo4WoqZ/cvMVofXx2dmdkrCut3DJHdN\n4rVgZu3M7AMzy40mahFJZ0rqRKSpneTunYG9gH2An9W3gPjNcRuzE7DE3TdHHYiAu/8lTCY7h9fz\nD4B84ONwk1eAfd29KzAG2B34UbjuNMCB3sAGgsQLM9sZOBm4vwlD3QmY4+7ehGVK411N8AeargT1\n/2cz2zFcdyeQR3DN3GRm/cLl1wB/c/eCFo9WRNKekjoRaRbuXgi8TnDDi5l1M7PHzKzIzArN7DYz\nywzXXWhm/wlbO9YCt4bLLzWzuWHXsjlmtle4vL+Z/S38S/hiM4vfTGNmt5rZs2b2p3C/2Wa2T7ju\n/4BBwKth68tPwuXPmdkKM9sQdmUbnVBeLzN7NfyL+4ww7ikJ60ea2ZtmVmxm883szJrOSRj3K+G2\ni8zs0nD5xcCjwAFhXP9bzb6ZZhYL/7qfD5xQZf1kM7skYdt7wm0Xm9kV9vWumrXVxVAzezc8F2vM\n7Jlw+XvhoT4LYzwrXH6imX0atkpNNbPdEmLa08w+DuvhGSCnlnNT7XHDdR6uvwz4NvCTMIZXE85r\nTdfDODP7MKy/lWZ2b00x1OEC4E/x5Mndv3D3tfHDAJVAvBVzZ2Cyu5cD/wLiXUfvB64NlyfNzMaH\n196G8N/x4fInwrji5+MbLdDh9ftK+P2nA7tUWf9bMysI139kZgcnrKvxZylcv5eZfRKue87MnrEa\nWlEtoYW8KcsNt2/Q74NwfY3XqJn1NrPXwmu72Mz+bWZJ3Te5+2fuXhb/CLQD4i1wOwPvhL8jFwKD\nzGwn4FvAfcmULyLyDe6ul1566dUkL2AJcGT4PheYDfwy/PwiMBHoBPQFpgOXh+suBMqBK4EsoANw\nBlAI7Etw0zyUoFUiA/gI+DnQnuCGOR84JizrVmArcDyQSfBX8ferizFh2XeBLkA28Bvg04R1T4ev\njsAooACYEq7rFH6+KIx7T4KucKNqOD/vAQ8S3DjuAawGDk84B1NqObffA+aF57UnQbLgQFa4fjJw\nScK2c4CBQA/grSrb1lYXTwE3hec5BzgoIQYHhiZ83hNYBewXnusLwvObHdbNUuDHBDe0pwPbgdtq\n+H5JHRd4IrGMJK6HacB3wvedgf0T9v0cODeJ63onoALYucryc4GSML7VwO7h8hOAZ8Lz8AzwQ+B/\ngD824GeqJ7AO+E54jZ0Tfu5V3fmoZv+ngWfDuh5D8DM1JWH9eUCvsOxrgRVATl0/Swn1e1VYv6cB\n2+KxABOAZTX8bmhwudV8vwb/PqCOazTc9qFwXTvgYMDCdQ8CD9ZRd6+Fx3bgH0BGuPw54CSCn88V\n4fl/CTi0OX8/66WXXq37FXkAeumlV+t5hTdum4D14c3SgwQJ2g5AGdAhYdtzgH+F7y8EvqxS1hvA\nVdUcY79qtr2R8IY5vIl7K2HdKGBLlRiPrOU7dA9vwrqFN4HbgREJ62/jq6TuLODfVfafCNxSTbm5\nBIlBl4RldwJPJJyD2pK6d4DvJXw+mpqTuncIk7Tw85HxbZOoiz8BDxN0HasaQ9Wk7g+ESXvCsvnA\nocAhwPL4TXC4bio135wndVy+mdTVdT28B/wv0LsR1/XNBC1vNa0fBvwS6Bd+NuAugqTxYYKb9k+B\nPsDtfJXct0/i2N8BpldZNg24sLrzUWW7+PU7MmHZHXVcZ+v4Kjm9lRp+lsL6LaxSv1NIPqlrULnV\nxNvg3wd1XaPAL4CXSbjmG3DttAOOA65JWLYTMImgK+85BF1y470IXgbeBc5o6DH10kuvtvlS90sR\naWqnunt3d9/J3X/g7lsIbmLaAUVhV6b1BMlP34T9qj5Hkgt8UU35OwH94+WEZf2UIFmJW5HwvhTI\nsRqe0wu7Kt5lZl+YWQnBzScEz0P1IUiEEmNLfL8TsF+VWL4N9OOb+gPF7r4xYdlSYEB1cdWwf+Kx\nl9Zj26ox11YXPyFISqaHXdW+W8txdgKurfL9c8Pj9wcK3d2TjLk+x60aQ23Xw8XAcGBe2HXxxCTL\nTXQ+UOMgNO6+kKBV+sHws7v7De6+m7tfBtxA0OKzL8FzpocStBIl8x37883zlux1U931+7WyzCzP\ngi7OG8Jz143g2o+r6Wepuvqtz7NgDSrXglFe44PXfJvG/T6o6xr9NbAI+KcFg+LcUI/vB4C7b3f3\n14GjzezkcNlSdz/e3fciSOJ+SfCMXYygZfdk4F4z61nf44lI29UWByMQkZZXQNA61Ntrfp7Iq3wu\noMrzPwnLF7v7sAbGUvU45wKnELRmLSG4qV1HkGCsJugWOhBYEG6fODJdAfCuux+VxHGXAz3NrEtC\nYjeIoFUiGUVVjj2ojm0HJnyuGnONdeHuK4D4s34HAW+Z2Xvuvqia4xQAt7v77VVXmNmhwAAzs4Sb\n5kFUn6jX57jVXSc1Xg9hwnVO+CzUacDzZtbLkxyQxswOJLj5f76OTbOo5no1s7HAeOB64DrgI3d3\nM5tBMFBGXZYTJC6JBhF056tL/PrNJei6G983HtvBBMn0EcBsd680s/i1X5civlm/Nf0hpj5qLdfd\nj0vc2MwOoOG/D6o71n+v0fDn9FqCP1yMAd4xsxnu/nYDjlXt9UHQbfQRd18ZXis/c/cNFkwHMZSg\na7SISJ3UUicizc7di4B/AveYWVczyzCzXcIb/5o8CuSZ2d4WGBoOJjAd2Ghm15tZh7ClbYyZ7Ztk\nOCv5auAKCJ6lKwPWEjw3d0dC3BXAC8CtZtbRzEYStNrEvQYMN7PvWDAceTsz29fMdq3mHBQQdO26\n08xyLBhQ5GLgz0nG/SzwIzMbaGY9CFp/atv2KjMbYGbdCRKKeBy11oWZnWFm8YRwHUESVRl+rnru\nHgG+Z2b7hXXUycxOMLMuBF0Ey8OY25nZaUCNUzXUcdxEVWOo9Xows/PMrI+7VxJ0C6aGcmtyAcGI\nhIktrJjZJWbWN3w/iqDL39tVtjHgd8CPwuMvBg4ys/YErXXxaRouNLMlNRx/EsE1dq4FUyWcRdCF\n8LW6Aq/m+h0Vfp+4LgR1tBrIMrOfA12/WVK1phF0J74ijOsUaqnfeqhvuY35fVDrNWrBIEBDw3rc\nEMZV57VjweBJx4XxtDOz8wi6er5bZbtRBN1U/xAuWgwcbmY7EHTp/TKJ7yAiAiipE5GWcz5Bl7M5\nBDftzwM71rSxuz9H8PzRX4GNBAMJ9AxvVE8kGGhkMcHAJI8StLAl407gZ2FXrTyCZ7mWErSYzQHe\nr7L9FWHZKwiee3mKIAmM/yX/aOBsghaVFcDdBANkVOccYHC47YsEz969lWTcjxA8Z/gZwbM4L9Sx\n7T8Jnun6hCAxKCe4KYXa62Jf4AMz20QwbP9VHs4RR/B80pPhuTvT3T8kaF37XVjOIoJnA3H3bQQt\nYxcCxQTPH9YWc23HTfQYMCqM4aUkrodjgdlhub8Fzg67BMcnxP52TQGZWQ5wJtV3vTwQmGlmmwnO\n7ySCbn+JLgJmuftH4ecXCOp+NcFzdg+Hy3OB/1QXgwcjbJ5I0GK0lqBl7UR3X1NT3FVcQTBAzAqC\n5+/+mLDuDYIWvwUEPwNbSbILZUL9XkyQLJ9HkGiW1bZfU5fbmN8HSVyjwwgGGdpEkAA+6O7/AjCz\nh8zsoRqKNoKflVUEdX0VcJa7f1xlu98TXOfxn8sbCabFmA3cEbZei4gkJT6Kk4iIJMHM7iYYEOOC\nOjdOEWZ2HPCQu1ftxicpwMz+SXBzPzfqWBrDzD4guM7+WOfGKVCuiEhropY6EZFahF2pdgu7mIQj\nXAAAIABJREFUF44jaEF4Meq4ahN2+zo+7L42ALiFFI+5LXP3o9MxoTOzQ82sX3idXQDsRnLP+kVS\nrohIa6aBUkREateFoMtlf4Lnue4hGLEulRnBMP7PAFuAvxMMyCDSlEbw1Rx4+cDp4TObqVquiEir\npe6XIiIiIiIiaUzdL0VERERERNKYkjoREUlK+FzhH81snZm1+PxZZjbBgvm7mqv818NnuGpa/4SZ\n3ZZkWYPNzC2c9L6ushvDzH5qZo82R9m1HHOTmQ2pe0sREWkJSupEpE0xsyVmtiW8KV0Z3qh3jjqu\nRGGMR0YdRzUOAo4CBrp7U8xJllLc/Th3fxL+O3fclOYouzGqS2zd/Q53v6SxZdeHu3eOTzlRn2Q3\nGWb2YzPLN7MSM1tuZvfFk+OEba4ys8VmttnM5prZ8HD57uFUFWvM7JqE7duZ2QdmlttUcYqIpBIl\ndSLSFp3k7p2BvYB9gJ/Vt4CqN5ltxE7AEnffnMzGbfQcSeO9Auzr7l2BMcDuBPO3AcHE7wSj0J5A\nMAffiQTz00EwD2VeuM9NZtYvXH4NwSTySc3DJyKSbpTUiUib5e6FwOsEN46YWTcze8zMisys0Mxu\nM7PMcN2FZvafsNVgLcHkwpjZpWFLwUYzm2Nme4XL+5vZ38xsddiikHhTequZPWtmfwr3m21m+4Tr\n/g8YBLwatib+JFz+nJmtMLMNZvaemY1OKK+Xmb0atmzMCOOekrB+pJm9aWbFZjbfzM6s6ZyEcb8S\nbrvIzC4Nl19MMKnzAWFc/1vNvjWdo++G52idmb1hZjsl7PNbMysIY//IzA5OWNchbAVaZ2ZzCCYo\nTzze9WE9bQy/1xHVxLSzBROVZ4SfHzGzVQnr/8/Mrg7fTzazS8xsV+ChhO+6PqHIHmb29/CYH5jZ\nLjWdyypxTA6TEcws08zuCVuTFpvZFfb1rpoXJVxT+WZ2ebi8E8H12j+Ma1NYX7ea2Z8TjnVyeE2t\nD4+7a8K6JWaWZ2afh9fSMxZMsl5dzEPN7N1wuzVm9kzCOg/XXwZ8G/hJGM+r4foar/+6uPsX4aTr\nEIzkWgkMDcvNIJii48fuPscDX7h7cbj9zsA74c/2QmBQeL19C7gv2RhERNKNkjoRabMs6Ip1PPBJ\nuOgJoJzgBnJP4GggsVvbfgRDrO8A3G5mZxAkLucDXYGTgbXhjeerwGfAAOAI4GozOyahrJOBp4Hu\nBC0TvwNw9+8AXxK2Jrr7r8LtXweGAX2Bj4G/JJT1e2Az0A+4IHzFv2Mn4E3gr+G+ZwMPmtmoGk7L\n08AygikcTgfuMLPD3f0x4HvAtDCuW2rYv+o5OgX4KXAa0Af4N8EUEXEzgD2AnmGMzyUkGbcAu4Sv\nY6p8rxHAFQQtOl3C9UuqBuPui4ESgvoEOATYlJDoHAq8W2WfuVW+a/eE1WcTTBfRA1gE3F7DeajN\npcBx4ffeCzi1yvpVBK1PXYGLgPvMbK+whfQ4YHkYV2d3X564owXdEJ8CriY435MI/kDQPmGzM4Fj\nCRKg3YALa4jzl8A/w+86EHig6gbu/jDBtfirMJ6T6rr+zeygKonyN5jZuWZWQtACtzswMVw1MHyN\nCf8YsNjM/jeetAOzgKPNbCAwGPgC+C1wnbtvr+2YIiLpTEmdiLRFL4U3lVMIbujvMLMdCBK8q919\ns7uvIvjL/tkJ+y139wfcvdzdtxAkfL9y9xlhi8Eid19K0KLUx91/4e7bwmePHqlS1hR3n+TuFcD/\nEdy41sjdH3f3je5eRpBI7m5By2ImQSvELe5e6u5zgMRnt04k6DL5xzDuT4C/AWdUPUaY5B4IXO/u\nW939U4LWufOTOKc1naPvAXe6+1x3LwfuAPaIt9a5+5/dfW24/T1ANsE8ZRAkH7e7e3HYbe7+hONU\nhNuOMrN27r7E3b+oIaZ3gUPtq654z4efdyZInD6rx/d70d2nh9/lLwSJWX2dCfzW3Ze5+zrgrsSV\n7v73sPXJ3f1dgsTq4OoKqsZZwN/d/c0wiYkBHYDxCdvc7+7Lw9atV2v5DtsJutz2D6+HZJ8xrPX6\nd/cpVRLlb3D3v4bdL4cTtJquDFcNDP89GhgLHAacQ9AdE4Kul98n+EPJjwmu543AYjN7OWx5/Ma1\nLyKS7vS8g4i0Rae6+1uJC8xsLNAOKDKz+OIMIPEZnKrP4+QStARUtRNBF7nE1ohMglaquBUJ70uB\nHDPLCpOFrwkTt9sJErE+BN3RAHoT3LBn1RLnTsB+VWLJIkgkq+oPFLv7xoRlSwmeO0xW1XO0E/Bb\nM7snYZkRtOAsNbM8ghvy/oATJFm9E+JJLG9p/I27Lwq7Td4KjDazN4BrqrZchd4laBldBrwHTAa+\nA2wF/u3uldXsU5Oq9daQQXaqfq+vnTMzO46glXI4wTXYEZhZj7ITz1OlmRUQnO+4qt+hfw1l/YSg\ntW66ma0D7nH3x5OIIZnrPynuvtDMZgMPErT2bglX/crd1wPrzWwiwR9kHgn/qHI8gJl1BKYRJIAP\nAM8AfwdmmdnbCV02RUTSnlrqREQCBUAZ0Nvdu4evru4+OmEbr2af6p6pKgAWJ5TT3d27uPvxScZS\n9TjnAqcARwLdCLqVQZAcrSboMjowYfvEEf4KgHerxNLZ3b9fzXGXAz3NrEvCskFAYZJxVxd7AXB5\nleN3cPepFjw/9xOClqseYevNhvB7ARRV+S6DvnagoDXnIIIkwoG7a4jpXYKWrgnh+ykELTjf6HpZ\ny/doSkXUUF9mlk3QkhoDdgjPySS+Oid1xbWc4HzEy7Ow/PrUYXAg9xXufqm79wcuJ+i2O7S6Tat8\nbuz1X1UWX/2czQe2VTlmTefk5wSJ3kqCVr0P3X0DQXJf3fcQEUlbSupERAB3LyLo5naPmXU1swwz\n28XMDq1lt0eBPDPb2wJDw26F04GNFgzk0SEcGGOMme1bS1mJVgKJc4B1IUg41xK02tyREHcF8AJw\nq5l1NLORfL275GvAcDP7jgXDurczs30TB89IKKsAmArcaWY5ZrYbQSvan6tuWw8PATdaOLBL2GU0\n3v2tC0FCuhrIMrOfE7TUxT0b7tsjfEbqyvgKMxthZoeHSdBWghacalvc3H1huP48ggS3hOAcf4ua\nk7qVwMAqz6I1lWeBq8xsgJl1B65PWNeeoFvpaqA8bLU7ukpcvcysWy1ln2BmR5hZO+Bagmtnan2D\nNLMzwvMOsI4gearuHFe9Xht1/VswWE3f8P0o4EbgbQB3LyVocfuJmXUJ47uM4DpPLGMUQRL/h3DR\nYuDwsJv1MILnVkVEWg0ldSIiXzmf4KZ6DsFN7PPAjjVt7O7PEXSL/CvBczsvAT3DROtEgmeVFhMM\n9vAoQStbMu4EfmbB6IV5wJ8IutQVhrG9X2X7K8KyVxB0q3yK4EaesCvl0QTPMy0Pt7mbIHGozjkE\nLYHLgRcJntV7q4Zt6+TuL4bHezoc+GIWwWAfAG8A/wAWhN9vK1/vivi/4fLFBAl3YpfRbIJn0daE\n36kvwc1/Td4F1vpXQ9q/S9D69XEN278DzAZWmNmaGrZpqEcIvs/nBIP0TCJIbivC+voRQXK2jqCV\n9pX4ju4+j6B+88Pr42tdJ919PkHy+gDBuTmJYNCdbQ2Ic1/gAzPbFMZwVfh8XFWPETzbuN7MXqrr\n+jezg8Mya3IgMNPMNhOcm0kEg+3EXQFsIrhGpxH8/FXtFvr7MN6K8PONBOd1NnCHu69ARKQVMffm\n7GEiIiItzczuBvq5+wV1biyRC1vjHnL3nercWEREpBpqqRMRSXMWzEO3W9gFdBxBl8kXo45Lqhd2\nSTzezLLMbADBoCiqLxERaTAldSIi6a8LwXN1mwmeN7oHeDnSiKQ2RtC1dB1B98u5BIN6iIiINIi6\nX4qIiIiIiKQxtdSJiIiIiIiksVY7+biZeWZmZkNG+5JmlJmZmQlQUVFRUde20rJUN6lLdZO6VDep\nS3WTulQ3qast101FRUU7d0/bBq9Wm9S1b9++4qOPPrqy7i2lJeXm5h4FUFBQ8GbUscjXqW5Sl+om\ndaluUpfqJnWpblJXW66bsWPH3lfXNmaxHwOXEMzbORO4iGD+2GcIpgNaApzpnrcu3P5GgsHLKoAf\nuee90Ryxg7pfioiIiIiI1MosNoBgvst93PPGAJkEc8DeALztnjcMeDv8jFlsVLh+NHAs8KBZLLO5\n4mu1LXUiIiIiIiLJ6ZNjFpsc/+SeN6GajbKADmax7QQtdMuBG4H4tk8Ck4HrgVOAp93zyoDFZrFF\nwDhgWnNEr5Y6ERERERGRWrjnFQIx4EugCNjgnvdPYAf3vKJwsxXADuH7AUBBQhHLwmXNQi11IiIi\nIiLSxq3eWkPrHABmsR4ErW87A+uB58xi5yVu457nZrFI5otTS52IiIiIiEjtjgQWu+etds/bDrwA\njAdWmsV2BAj/XRVuXwjkJuw/MFzWLNRSJyIiIiIiUrsvgf3NYh2BLcARwIfAZuAC4K7w35fD7V8B\n/moWuxfoDwwDpjdXcGqpExERERERqYV73gfA88DHBNMZZAAPEyRzR5nFFhK05t0Vbj8beBaYA/wD\n+KF7XrPN/6eWOhERERERkTq4590C3FJlcRlBq111298O3N7ccYFa6kRERERERNKakjoREREREZE0\n1nqTuspK27piRXbUYYiI1CQ/f1PHpUs3d4g6DhEREUlvrTap8/LyjLXTp/eJOg4RkeqsX78t65xz\npv383HOn3VBREcmUNiIiItJKtNqkDqB806b2UccgIlKdZ54pGF5aWtGjpKS832efre/eFGVOnbqm\n1zHHTP7xo4/mj2yK8kRERCQ9tO6kbvNmJXUikpKmTl0zJv5++vS1/ZuizD//ecn+y5dvHfnww198\nt7CwNKcpyhQREZHU16qTuorSUiV1IpKSFi3aNDr+fsGCjU2S1C1fvrU/wJYtFd1uumnmSU1RpoiI\niKS+1p3UbdmipE5EUs7776/pVVKyvV/8c2Hhlh2botw1a8oGxN9//PG6wydNWj6gtu1FRESkdVBS\nJyLSwl5+efkYgA4dMjcArF5d1uiWupKS7VklJdv7Aj5qVNf/uJNx770LztEgLCIiIq1f607qtm5V\nUiciKWfmzPVjAPbfv9c7AOvXb9uxscnXlCmrd3Ans0uXrNV3373789nZGRtXrtw67I475uzXBCGL\niIhICmvdSV1ZmZI6EUkpJSXbswoLt4wAuOiind/Pzs7YtH27d/jkk3U9GlPu559v2BGgV6/s5YMH\ndyo9+eQBfwN4+eXCMzQXnoiISOvWqpO6yrIyTT4uIinl2WcLhpaXe3b37u0K99yzx/oePdovB/jw\nw+JGPVeXn79pAED//jmFADfeuOv7fftmLyorq+zys5/NPLnxkYuIiEiqau1JnVrqRCSl/Oc/q8cA\nDB/eZRZA3745y6HxI2AWFQUjXw4Z0nk5QLt2GX711SOeAvzTT9cf9sorhQMbFbiIiIikrNad1G3b\npqRORFLKwoWbxgAcdFCfWQC5uR2KAAoLtzQqqYuPfLnbbt2Xx5eddFL/ZXvu2eMdwH772wXnbt9e\naY05hoiIiKQmJXUiIi1kxozinhs2bN8xK8vKzjhj4BcAI0Z0XQ6wenVZg7tfrllT1n7TpvLeZlQc\nfHDvlYnrbr997Ks5ORkbVq0q2+X22+cc0LhvICIiIqmodSd127crqRORlPHyy4WjAQYO7Di3c+d2\nFQDjx/daDo0bAfO991b3A6xbt3Yr4+XG5eZ23HLqqQOfB3jtteXfWrJkc8fGfAcRERFJPUrqRERa\nyGefBVMZ7L5791nxZSNGdN2UnZ2xsTEjYM6atWEAQO/e2curW3/DDbtO79cvZ2FZWWXnm276/NSG\nHENERERSV6tO6ry8vF3UMYiIAGzatD1z2bLSXQFOOWXA7MR1PXq0LwKYMaO4Qc/VLVmyuT9A//4d\nqk3qMjONa64Z8VczKj//fMMhL7ywbFBDjiMiIiKpqVUndWqpE5FU8dxzy3YpL/fsbt3aFe27b8/i\nxHXxETAXLtzYoOfqVqwIRr7cZZfOhTVtc9xxOy7fe+8ebwP2wAMLNWiKiIhIK9KqkzovL1dSJyIp\nYcqUYCqDYcM6z6q6btCgoIWtoSNgrl1b1h9g7717VNtSF3fHHbu92qFD5vo1a8p2/sUvZh/YkGOJ\niIhI6mnVSV2lkjoRSRELFmwcA3DggX2+kdQljIBZ76SuoKC0Q2lpRc/MTNu+//69Vte27Y47dig7\n7bSBzwFMmlR02qJFGzvV93giIiKSelp1UqeWOhFJBR9/vK77+vXbB2RlWdmZZ+Yuqrr+gAN6FQGs\nW1f/ETCnTFm9I0C3bu2KsrMz69z5uutGfti/f868bdsqO91886z/qdfBWti7767q+9RTS4dEHYeI\niEiqU1InItLMXnpp2WiAAQM6zO/atV151fXxETDLyz2nviNgzplT0h+gT5/qR76sKjPTyMsb+RTg\nc+ZsOKCgoLRDfY7XUt57b3Wfq6/+5KY77ph7/fe//+FJDZ3uQUREpC1o3UldRYWSOhGJXHwqg7Fj\nu3+j62Vcz57tl0P9R8BcunTzAICBAzvUOEhKVUcd1W/FjjvmLKisJOvxx/P3qM/xWkJJyfasn/98\n5qXl5Z4DMGXKmhPPOWfaBZs3l2dGHVsqWbp0c4dJk5YPiDoOERGJXmtP6tpVbt+uEd5EJDKbN5dn\nFhQEUxmcdFL/GpO6vn1zigAWLtxYr6Ru5cpg5MuhQ7sU1We/ceN6zQCYNm3tuPrs1xKuvPLj09au\n3bZTp05Za888M/fxzEzbNnduyfjTT//PD4uKtmRHHV8qKCnZnnXeee9fd/31n9/8xhtFDRo1VURE\nWo9WndQBbFu3TnPViUhk/va3giHbt3uHrl2zVowf33ttTdvl5gYjYC5bVr8RMIuLt/UH2Hffnkm3\n1AFceOHgj82oWL58y8i5c0u61Gff5nT//Qt2+/jjdUeYUXHNNcMfufnm0R/89Ke73pudnbFx2bIt\no88+e9p1n322vlvUcUbt+us/O3b9+u0DAPvHP1aMiToeERGJVltI6tQFU0Qi8+9/rxkNMHRol9m1\nbRcfAXPNmrKkW13mzy/pvHVrZdesLCvbZ5+vz31Xl6FDu2zOze04x52MJ59cvHd99q1JY5/P+/DD\n4h5PPrnkQoDDD9/hpTPPHLQY4MwzBy2+77497+7SJWtVcfG23Msum3FDW26deuONoh3/8581x8c/\nz5+/cWSU8YiItBVmsRFmsU8TXiVmsavNYj3NYm+axRaG//ZI2OdGs9gis9h8s9gxzRVbq0/qtq9f\nr6RORCITn8pg/PjeNXa9DNfXewTMqVPX9gfo0aP98szM+vc0Hz++93SAGTOK9633zlXcfPPMg44/\n/r3fnHnm1AtKSrZn1Xf/LVsqMm644bNLtm2r7JSb23HWr3+9+5uJ6w8+uM/qP/5x3N19+mTnl5ZW\n9Lzxxs+v/+MfFw9vbNzppqyswu6+e9757mQOHtzpU4Cioi3D9LyhiEjzc8+b7563h3veHsDeQCnw\nInAD8LZ73jDg7fAzZrFRwNnAaOBY4EGzWLP8vm69SZ0FNzjbS0qU1IlIJD7/fH234uJtuZmZtu2s\ns3IX1Lbt8OFd/jsC5scfr+uZTPnz5v135Mt6db2Mu/jiIZ9lZtq2VavKhs6YUZzUMauzZUtFxj//\nueIEgLlzS8afdtp/rl6wYGPn+pRx9dUfn7hyZdnQDh0yN9x33x5/bNcu4xuZ7YgRXTc9++z4+wYP\n7vTp9u3e4Te/mX/VXXfN3aehcaejm2+eNWH16rIhHTpkbnjwwb2f6No1a0V5uWe//HLhTlHHJiKS\n3vrkmMUmx19J7HAE8IV73lLgFODJcPmTwKnh+1OAp93zytzzFgOLgGZ5lr31JnWh8o0bldSJSCRe\neCGYyqB//w7zu3dv/42pDKqKj4D54YfFSXUtLCgo7Q+Qm9sxqekMqurXL6ds8OBOnwP85S9LGpwc\n/eEPi3YrLa3o2bFjZnGHDpnrV67cOuyCCz644e23V/ZLZv9HH80fOXXq2uMB//73hz46YkTXTTVt\n27t39rbnnx//0B57dH+nspKsv/xl6aVXX/3x0W1hyoMZM4p7vvnmiv8BOOecQX/Nze24ZfDgTvMB\npk5dMyLa6ERE2pyzgafC9zu458UHLFsB7BC+HwAUJOyzLFzW5FpzUucA5Zs3K6kTkUh8+un60QBj\nx3artetlXH1HwFy1ausAgBEjujSopQ7g0EP7zAD45JP1Df7L4T/+UXQ4wCGH9Hlz4sR97uzZs/2X\nmzaV97nuuk+vf/TR/Fqf95ozZ0OXiRMXfRewgw7q/feLLtq51hZNgOzsTH/iif2eOeqoHZ4DePvt\nVd86//wPzikrq2i1ox1XVDi33DLr2+Xlnj1kSKePfvzjEZ8C7LFHj3kACxfquToRkcZZvdU9b0L8\nVduWZrH2wMnAc1XXuec5YR7SkpotqYuZ5cbM/hUzmxMzmx0zuypcfmvMrDBm9mn4Oj5hnxtjZoti\nZvNjZsckLN87ZjYzXHd/zCzp/7iV1IlIFLZsqcj48svNowBOPLF/rYOkxMVb3JIZAbOiwv878uV+\n+/Wq13QGiS6+eMisdu1sS3HxttxkW9YSTZq0fEBR0dYRWVlW9qMfDZ+255491j/33Phfh10kO95/\n/4If3XzzzIOq23f79kq75ppPv7t1a2W3fv1yFvzmN3u+luxxMzONe+/d863zztvp4YwMyj//fP2E\nq6765MT6xp8u7r577riCgtIx7dpZ6e237/Z0fPkppwxYALBixdah69dvq/ezjCIi0iDHAR+7560M\nP680i+0IEP67KlxeCOQm7DcwXNbkmrOlrhy4Ns99FLA/8MOY2ahw3X157nuEr0kA4bqvPUgYM4s/\nSPgH4FJgWPg6NtkgKkpLldSJSIt74YVlO2/f7h27dMladfDBfVYns8+IEV2WA6xeXfcImLNmbei2\nfbt3bN8+Y/Po0d02NDTOrl3blQ8d2uUTgOeeK6j3gCn/939LDwMYM6bb1NzcjlsA+vbN2fbCCwc+\nNG5czzfcyXzppcLvXHjhB6dXbUm79tpPjyks3DIqOztj069+tftj2dmZ9f7L5vXX7/rRD34w7PeA\nT5265vinnlo6pL5lpLoFCzZ2fuGFZWcBnHhi/+fHjOlWEl83fHiXTT16tF9WWUnWCy8s2yW6KEVE\n2pRz+KrrJcArwAXh+wuAlxOWn20WyzaL7UyQx0xvjoCa7a96ee5FQFH4fmPMbC619yE9BXg6z70M\nWBwzWwSMi5ktAbrmub8PEDP7E8HDh68n7hwzm5z42TIyDHf6Dhmyd25ubp8m+lrSSDk5OcMBcnNz\n69pUWpjqpmktW5Y/GuCII3JLcnNzj0pmn4su6tH+nnvms2lTee6AAQOPysgIcqDq6mbq1K07AAwd\n2n3L4MGDkiq/Jj/+8d7ll132L/LzSycMGDBwa/y4dSkq2txuwYKN4wHuuefQstzcvl+L45//3Gnj\nr3/98Yd33fXx3h99tO6oH/7w89FPP33MBz16ZFdMmrS017vvrp4AcO+9B3168skjGjwC52235bJm\nDQuefnrhiEcfXXLFJZfs82bPnjl1PsPYFJL9uamsdBYt2tBh5527bmnXrn5/T73qqknjysoqO48d\n22vVY48d1zEjw752ng87bOCWF17IZ+1aOy43N3dQfb9Da6XfaalLdZO6VDd1M4t1Ao4CLk9YfBfw\nrFnsYmApcCaAe95ss9izwByCBq8fuudVNEdcLfJMXcxsMLAn8EG46MqY2ecxs8djZvF5HGp6kHBA\n+L7q8tqFPTTLS0s1zLOItLipU1f0Azj66EErkt1n4MDO27p2bV+2dWtF1oIF62ud823mzLVdAYYM\n6drgVrq4U0/deXXXru3LiopKO0+eXNg92f0eeODznbdtq8zcc8/eK/feu2+1g5tcd91eSx555LD3\nOnXK2v7BByv7H3bYi4dPmVLU7Uc/em+/ykq3M87YZcG3vz0i6XNUk3vvPXD24MFd1q9ataXT978/\neY/GltcUKiudt99e1uOyy/612/Dhfz5+3LjnTthrr2eOfv75RX2TLeOppxbs8M47hYPatcuofOCB\nQz6qLuE+9NABqwCmT1+VdLkiItIw7nmb3fN6uedtSFi21j3vCPe8Ye55R7rnFSesu909bxf3vBHu\nea9XX2rjNXv/+5hZZ+BvwNV57iUxsz8AvyR4gPCXwD3Adxt7nDz3CYmff5qZWQlY4SefLOpTUPBO\nY8uXphH/y09BQcGbdWwqLUx103TmzNnQJT+/5PSMDMp33TXjmYKCgm3J7tupU8bYkhJGPPnkJ1/8\n4AfDZkP1dfP220vD5+7KPigoKHi3sTEPGdKx56efbjvsjjve92HD9qvzGigrq7Ann5x7GMC4cd2e\nKygomFnTtvvu254779ztrZtu+vzKJUs29j3xxNeOBKx37+zF11wz+DcFBQVN8lfLK6/c5fOf/OSz\nm954o2Dw1Ve/+Y9rrx35SVOUW5uqdVNR4fz978sHvvJK4b6zZ5fsvWlT+X97iphRUVCwqesll/zr\nkNtum/7pddeNfP6QQ2rumrtixdbsa6+dcivAIYf0ebFXry3/LCgo+MZ2w4ZZB2D8/Pnrus+YsfC9\nfv1yypr0S6Yp/U5LXaqb1NXG6+b4ujdJXc3aUhcza0eQ0P0lz/0FgDz3lXnuFXnulcAjfDVXQ00P\nEhaG76sur1X8b5mVW7fqmTqRCFRUOH/60+Jh77+/plfUsbS055//aiqD3r2zk07oIHEEzE21DpYS\nf+5u1127Nmg6g6qOO27H6QBz5pTss317ZZ39Lx98cNHumzdX9OrcOWv15ZfvUufonocd1nfVn/60\n3139+uUsAKxdO9ty221jH+3cuV2TdUM5+uh+RUcf3e9vAH/965ff+eyz9d2aquzaVFYZpH3FAAAg\nAElEQVQ6r79e1P/yy2ecfMghb//ipptm3vzBB8XHbtpU3icnJ2PDHnt0f+eGG3b91TvvHHb1hAl9\nX8zKsrIlSzbvceWVH9168cXTTyssLM2prtyf/OSzU0pLK3r26tX+yzvv3O2tmo6fm9txS+/e2Uvc\nyXzxxWVDm++biohIqmq2lrpwhMrHgLl57vcmLN8xfN4O4H+A+M3AK8BfY2b3Av0JHyTMc6+ImZXE\nzPYn6L55PvBAnQGE3S8rtm1TUifSwoqKtmRfccVH5y1YsGlchw6ZG1577eCf9e2bU6/kJp198sm6\nMQBjxiQ3lUGi3NyOyz/7bD2FhTWPgLl9e6WtXx+MfDl+fO8mSerOOmtQ/v33L1i7eXNFr6eeWjr0\n/PN3Xljb9q+/HkxjcNBBvd+pbqLw6gwd2mXziy8e+Jvbb5970H779Vx84IG91zRF7Iluv33s5Jkz\n149dtmzL6Ouv/+zCV189+P5k46uvigrn/vs/GzRx4uxdCws3nx5fnp2dsXHEiC4fH3lkvw/PPXfQ\nwsQBYB54YK9/fP75+mm33Tbn1LlzS8ZPn158zKmnTjnguON2fOmmm0ZNjW/7/+zdd1xTVxsH8N8h\nCSEhrLA3IiIgMtyKe7VSZ7W22rq1rdpqbWNdtX1bRx3RqtVSq9bZWm217ln3BhRFEVGm7GkYScji\nvn9A+lJeRoAwe76fjx/h5t5zDyIkT55znue33162iYh4NZAQlCxY0H4fj8cqqW4u7u7GMTk5ijbh\n4XntAehUbZWiKIpqPRoyUxcEYBKAgRXaF6wra08QCWAAgAUAIGKYKADajYTnAMwVMYz2Hdw5AHai\ntAt7HCoUSakCAwAlNKijqEZ14kSq09ixt754/ryoGwDI5RqzFSuiBjX1vBqLQqEhL1/KfAAgONih\n1kGdt3fNFTDDwvKEajXDNTIyyPfwMJHWfbb/w2IRdOhgFgYA585lVFu05OzZdIfybQxqcx+BgKP5\n9lu/a6NHO72sz3yrwuEYMGvW+O81NDQoSk2V+yxb9rh/Q9wnMVHKHzfu1qwvvwztlpoqNTE0NJD6\n+prdmDev3Xc3bgz6/Jdfev46bVqb55VV9PTzM88/fLjX3q++6rDaxoYbV1xcYvrnn6mTX3vt2tL9\n+xM9iopUrG3bXkwGQLp2FV4YNcrx/9dcVtCtm2UMAMTFFdF+dRRFUf9CDVn98ib+twqyvDPVXLMK\nwKpKjocD8K3LPGhQR1GNQ6Nh8MUXj/udOZM2vqQEbHNzTmrfvtZXTpxIe+/WrZzXYmMLr+srAGnO\n/vgjxV2pLDEWCNg5fftaZ9V8xT/16GGVDsRAIlE6aDQMWKz//zUaHp7nCACWlly9ZOm0Ro92CgsN\nzXs9Jqaws1SqPmRszK50aeS+fYkDAaBDB7M72jYGzYm/v3n+xIkuB/bsSfzwwoWMsYMG2Tx77TX7\nOvfyq2jPnoR2ISGx02UyjZDLZWk++yzg4ciRFruq+veqyrhxzkljxjitW7cuuuuxY6ljc3OVLuvW\nPVv4009xqRKJysHEhJ21fr2/Tr37xoxxjN227YUmN1fpkpgo5bu5Gcvq9tVRFEVRLVGjVL9sEmXL\nL2lQR1ENLzlZxhs79tb7p06lTSwpAbtjR7Prx4/3/nbVKr8bTk68KJWK4a1c+XRYU8+zMRw+/HIQ\nAHh5mURUFpDVxNPTpIjLNShUqxlueHiesLJzYmNL99vZ2hrpNagLDrZPMTPjpCuVJYK9exMqzfgk\nJkr50dEF3QFg2rQ2V/R5f3367DOvCB8f01saDcNZvTp6RkGBqt5vYhYVqVizZoWN3rAh5jOZTCO0\nsuImnD8/8sLnn3dKqG1Ap8ViESxZ4hN2+nTfL3v3tjrFYhGlRKJyBIBZs9ruFwq5Kl3GsbExUtrY\nGMUDIMeOpbSry1woiqKolqv1BnVlGJWKBnUU1YCOHEl2HT/+9rK4uKLObDYpfvdd1x2//trzF+2L\n0dmzPY4CQETEqwH37uVWGqS0FhcuZNjHx0s7GRhAPW+eZ5WFLWoiFBqmAcD9+3mVLsHU7rdzceHr\nNahjsQj8/c3DAODy5axulZ2zefPzII2GMXR05D0dNMi23q0IGtLmzZ0OCQTs7Lw8pfOCBREj6zPW\nlStZNsOH31h0927uMADo1cvq9KlTfdYHBFjpJftsZcVVhoR0OblzZ9cvAwLMrwQH2x+cNq3N89qM\n4eEhiAGABw8k7fUxJ4qiKKrlaPVBXQkN6iiqQWg0DBYufDjw66+jFhUVqa0tLQ1fbt7caeXixd7h\n5c8bOdIxxdNTEFpSArZY/KxeL6ybu59+ihsGgHToYHYrMNBCUtdxtBm4qipgZmcrHAGgQwezGisB\n19bbb7uEAkBcXFFgXp6CU/4xhUJD7tzJHQAAw4c7NPtWMXZ2Ror58z13EYKS0NC8obt3J3jWdgyN\nhsHy5Y97L1gQsTw3V+lqbMzKXbTIS7x9e5cTdc3OVadLF+Gr/ft7/LZ2rf/V2l7bo4flMwBISKD7\n6iiKov5taFBHUVStxccX8UePvjn73LmMtxkGrIAA88snTvRZW1XPrU8/9TpOCDTPnhX2OHMmzbGx\n59sYbtzIto6JKexGCErmzWt3vj5jOTnx0wFUWgFTLtcY5Ocr7QCgTx8rve0T0+rb1zrb0tIwSa1m\nuLt2JXQs/1hISKyfVKrWuY1Bc/DOOy4JQUFWZwCQH3+MnZaUJK22qXt5sbGFxmPG3Pzw2LHUSRoN\nY+jpKQj9/fegFe+95xbbgFOuszffdEpgsYhKIlE5RkcXmDT1fCiKoqjG03qDurI9dYxaTYM6itKj\n27dzLCdMuLM8MVEawOEQ+dSpbj/u39/jkKkpR13VNUFBVjn+/ubXAJBt22JHN+J0G80PP8S+BoB4\neZne7dHDKrc+Y/2vAmbx/wV1d+7kWJeUgM3ns/IcHfnF9blPVTp1sggFgBs3sv+xBFPbxiAoyOpK\nQ7UJaAhiccAZa2tugkymES5YEDGx4uNSqZoVHV1gcvlypu3Bg0nu27a98F2+/HHviRPvfpmQIA3k\ncIj8nXdcdh050ntXcywMo2VqylHb2RnFAsCJE6m1zkpSFEVRLVeDVb9sBkpbGtBMHUXp1datL14r\na4ictHq13/ZevXQLYJYu9TkzceKdoJcvZX779yd6TJrUPLMddREenmcRFZXfCwAze7aHLi1XqlXa\ney4GEonKXqP5Z+z04MErBwCwtOTqfeml1qRJbuEXL2aOS0qSdkxOlvGcnfny8+fT7dPSir3YbKKY\nP9/zdkPduyEYG7M1X33V4edPPon44sWLom6DBl2xUqkYQ4VCw1cqS4zVaoZb1bU2NtzYVas6/lzf\nQL2xtGsniElNlXs/eiRpD+B+U8+HoiiKahytN1NXhmbqKEp/pFI1KyamsDMAfPaZ1z5dAzoA8PY2\nLezRw/ICAOzZkzC2YrDSkm3e/Hwow4Dl4SEIHzDAptZtDCry8DCRGhkZFFRWATMursgRAOzt9Vv5\nsrzAQAuJnZ3Ri5ISsHfvTggAgL17S9sY+Pg0zzYGNenXzyZr+HCHwwCQlaVwf/VK6SSTaYRlAR1j\naGhQZGLCzrKy4iY4OfGiPDwEYa+/bnfo1Km+G1pKQAcAQUHWzwAgKUlK99VRFEX9i7TmTB0AgNFo\naFBHUXqyd2+Cl1JZIjAz46QHB9un1Pb6L7/scHHEiBv9s7IU7lu2PA9YsKD9w4aYZ2N68iTf9PHj\n/D4AMGuWe72zdFoWFobp6enFpuHheQ7jxv3veFpa6T47NzfjBsvUAUC3bsLQEyfSPO/cyemamCh9\n9PRpQQ8AmDrVrdm2MajJihUdb3p5maYXF2vYVlZcma0tV+bszJfa2fGK69J+ojkaNcoxae3a6OKC\nArXtgwevzDt1qnvBHoqiKKrlaL2ZOm2fOpqpoyi90Za59/c3D6vLi2B7e55i0CDbUwBw5EjKaLlc\n0+J/B23cGDNEo2E4bm7GD4ODHfQWaGkrYMbGFv2jrUFurtIBADp2NNN7kZTypk1r84AQaFJT5d4r\nVkS9pm1jMGSIXbNuY1CTd991jZsxwz1m1CjH5B49rHIdHfmtJqADAB6PVeLgwHsBAKdPp9W6tcHT\np/kmOTkK+rxJURTVwrT4F1Q1ocsvKUo/8vIUnLi4okDgf2Xv62L5cp8bAgE7Oz9fZf/tt0976m+G\njS82ttA4IuJVPwCYOtXtjD7HdnYu7UFXvgJmQYGKXVCgsgXA9O1r3aBBnYeHidTJif+UYWAQGpr3\nOgC88YZ9s29jQAHt25vEAMDjx/m1WoL5++/JbhMm3FkzfvztT/X1hotGwyA2ttBYH2NRFEVRVWvt\nQR0DhmGppVJWU0+Eolq6XbsSOqrVDNfS0jCpqtYFuhAIOJqRIx2OA8C5cxkjK/ZCa0nWr48ZpFYz\nXCcnXtTYsc5J+hzby8skHfhnBcwbN7JtGQYGJibsbG1z94bUq5dlmPZjgYCd/eGHHi2ijcG/Xb9+\nNn/vq9N172pOjsJw06aYaSUlYGdnK9osWRI5WB9zef/9sDFjxtza+N13MQH6GI+iKIqqXKsO6gib\nrQQApUTSYl80UlRzoS1vry13Xx8ikVe4UGj4Ui7XmH/zTdSA+s+u8SUny3hhYbkDAeC999xO63v8\n0gqYKKuAWQIAiIyUaCtfNliRlPJmzHB/yGIRVdl8WlQbg3+z4GD7FENDA5lMphHevZtrpcs1n34a\nMaagQG3H47HyAeDq1ayR169nW9dnHj//HN9em+U9dSrttfqMRVEURVWvdQd1LJYSAFSvXtElmBRV\nD8nJMl5SkrQjAGbSJLfw+o7H4Rgw777rehQArl/PHpaYKOXXe5KNbN266P4qFcOztzeKefdd1zh9\nj1++AmZMjIQPAPHxUkcAcHAwatAiKVr29jxFv37WJ52ceFGffup5qzHuSdUfh2PAODryYgDg3Ln0\nGpdg7twZ7xURIRlICDRLl3pv9fQ0uafRMJxVq6Leq2uV2tRUmdH27XFTtZ9nZSncT55Mc6rTYBRF\nUVSNWnVQZ1CWqVPl59OgjqLqYffuhICSErDt7IxeBAbqp5re+++3jXZw4D1TqRj+ihVRr+tjzMaS\nlVVsePt27mAAGD/eRa976coTCg3TACAiItsUANLTS/fXubsLGiVTBwCbN3c6f/Zsvy0N1eicahje\n3qbPAODp0/xqi6UkJ8t4O3bETQGAPn2sT40e7fTy22/9DnO5BkVpacVe33wT1asu91+w4OHb2n6W\nHTuaXQOAgweT+tVlLIqiKKpmrTqo0y6/VBUU0KCOourhzp2crkBpmXt9jvv+++5HAeD+/VcDHzx4\nZa7PsRvSmjXRfZXKEoG1NTd+2rQ2zxrqPjY2RukAEBWVZwr8r/JlQIB5o2TqqJZr0CDbGAB4+VLW\nvrps26efRrwtk2mEVlbcBLE44BwAeHqaFI0Z43QIAE6eTH0rMlJiVpt7b9oU4x8dXdCLxSKqZct8\nfp46tc0VAIiOLuiemiozqvMXRVEURVXpXxHUqYuKaFBHUXUUE1MgSE2VexMCzbRpbR7oc+yxY52T\n2rYVhGs0DGf16qdvRkZKzBQKTbOuLy+RKNk3bmQPBYA333Q605Dl8LUVMJ8/l5hJJApWUZHaihBo\ngoKs6t3gnGrdBg2yTTcyMigoLi4xu3w5066yczZujAl49qywJ4tFlMuX++zm8Vgl2scWL/YOdXbm\nP1GpGP7y5Y/f1vW+0dEFJgcOJE0CgCFDbI8OGWKXMXSoXbqdndFztZrhbt36onv9vzqKoiiqolbd\nfNyAw6FBHUXV0549CZ0ZBgbOzvzHHh4mUn2Pv2CB5/GPP34QGBNT2P3dd+92B8DweKx8Pp+VLxCw\nJaamHImFhWG+paWhxM7OSOLtbZY9YIBNkwU1a9dGBxUXl5gJhYbJs2d7PG7Ie3l7m6adPJmGxMRC\n0/v3s00BEDMzTqZAwNE05H2plo/FInB25j978aKo26VLmV4V+wtGRxeY/Ppr0nsAMHSo3dGBA20z\nK17/1Vcdfvnww/D/xMdLO3/3XUzAggXtH1Z3T42GwaJFj95VKEpM7O2NYlav9vu7Uf3gwbbXDhxI\n8rx5M6efRsNca029ASmKopqDf0emTiajQV0rVVCgYo8de2v6kiWRdK9GAwkLe9UV+Gd5e33q188m\na9gw+8MWFoYpXK5BIQAil2vMc3OVrklJMv/Hj/P7Xb+ePfLPP1Mnh4TEzZs378GKOXPC32iIudSk\nqEjFunw563UAGDHC4XRDvzDt2dMyHQCSk4tMIyKyzQDAyqpxKl9SLV+HDmYxABAdXfCPfXUaDYPP\nP3/0nkJRYuLgwHu2alXHq5Vd3727Zd6QIXZ/AsDBgy8nJCfLeNXdb9Wqpz0SEqSBbDYpXrGi457y\n1VLnzvWIMDIyKJBIVI4HDyZ51PuLoyiKov7hX5Gp08jltKVBK7VnT4LP8+eF3RMTpb7ffON7nZZc\n16/w8DyLzMzidiwWUc2Y4V7tu/T1sXat/1UAV4HSwOnZs0LT+Pgi85QUuVlWVrF5bq7SPD9fZVZQ\noDJPTZV737iRM3L16qfZS5f66HWPX03Wr4/pLpNphGZmnPT58z0b7N9DS1sBs7hYY3rlSqodADg4\n8GhQR+lk6FC7mGPHUpGSIm+vUpUQ7e/HlSujeiYmSgM4HCJfteqfwVdFK1b4Xg0Pz+uWna1wX7To\n0Zu//trzl8rOCwvLEx47lvIOAIwe7fhb9+6WeeUfFwg4moAAi1t37+YO+/PPlH7vvecWq8+vtaEp\nFBqya1e8z8WLmT3t7Y3Sf/ihi97bmFAURdWHzkGdmBBjAMUihmkxy34MDA21QR3N1LVSoaF5HQBA\nqSwxvno1y7biEiOqfn75JakLALi5GUfa2/MUjXFPgYCj6dJF+KpLF+Gryh5fuPDhwHPnMt4+dOjl\nFDc345yJE13jG2NecrnG4OLFjGEAMGyY/ZnGegNBKDRMS0srNg0Ly7QHgLZtBbRICqWTXr2ssvl8\nVp5MphGePZvuOHKkY8q9e7nCY8dS3wGAMWOcDlb1c6bF5bKYRYu89i1c+Gj548f5fffsSQidOrXN\ni/LnqFQl5IsvIqeoVAzPzc344RdfdLhT2VgzZ7pfv3s39/XY2KJO0dEFh729TQv199U2jKdP801C\nQuKCwsLy+kqlaksAiI0twq5d8bEzZrjHNPX8KIqitKpcfikmxEBMyEQxIafFhGQBeAYgXUzIUzEh\n68WENPvlE39n6oqLaVDXSsXHF/loP75+PbvZ/59saSIiXnUDgL59rRs1I1adNWv8L/v5mV8tKQF7\n48aYOXfv5lg21L00Gga3buVYrV0b3XnKlHuTCgvVNgIBO/vTT9vXu1efrmxsjNIAQKksYQFA584W\nNFNH6YTFInB1NX4GAFevZnmpVCVk+fLHU9VqxqhNG+OIpUt97ukyzmuv2acHBVmdBYCffoqbLJEo\n//GG8LJlj/unpRV7cbkGhevW+R+oally9+6WeS4u/MclJWCHhMQG1fPLazAaDYOff45vP3r0zVnv\nvHNn7dWrWWOkUrWlsTE718WF/xgA9uxJeFsu17TqLSwURbUs1WXqrgD4C8ASAE9EDFMCAGJChAAG\nAFgrJuRPEcMcaPhp1o02U1dCg7pW6fbtHMvCQrWN9vOYmMK2AG425hzOnk138PMzy2uNPbyuXMmy\nyc1VunA4RD59epsnTT0fLRaLYOfOrofGjLlpk5oq91m48NFHv/3Wc219vwcaDYMHD14Jr1/Pcn32\nrNA1OVnmmp2tcFMqS/7RGD042P5k+SqBDc3FhZ/28GFpa0AWi6h69LDMbqx7Uy2fr69ZTHR0Qa+Y\nmEKvJUsimfT04vZcrkHh+vVVB1+VWbvW/2xw8PXO+fkq+4ULHw3fsaPrMQC4dCnT7sKFjLEAMHGi\n64Gasm/BwfbXfvwxzi80NK+vQqE5z+Wyms2S+fj4Iv62bbE9797N6VtQoNZWDGXc3IwfBgfbX585\n0/2pVKpmDRt2/WuJROX4zTdP+nz7rf+1Jp00RVGNihCxOYCdAHwBMACmA4gBcAiAG4BEAOMZRvSq\n7PwlAGYA0ACYxzCi8w01t+qCusEihlFVPChimDwARwAcERPSrPeq/b38UqGgQV0rdOpUWgcAEAjY\n2UVFauvUVFnbxrz/jh1xXlu2vFjg7Mx/cuZM3+8b896N4fDhl90AwMPDJMLc3FDd1PMpj8djlWzf\n3uWnd9+9u0giUTnMmhU+68iRoG21DbYUCg1ZseJp7wcPXgVkZRW7KhQlJhXP4XINCm1tjRJdXPhJ\n3bpZxkyb1ua5/r6Smnl5maafOFGanDMz46Q3pxfBVPMXHGwf8/vvyUhNlbdPSZF5A8CkSW772rc3\nLarNOKamHPXcuR77Vq+O/vzevdzXTp5MCx882DZt5cqoaRoNw/HyMrnz6afVV8cEgJkz3aP270/K\nlUrVljt3xneYO7ddk79hFBtbaLx06eNxMTEF3UpKSl8X8XgsSefOFjdnzWp7o1MnC4n2XHNzQ/Vb\nbzn/vnt3wuwLFzJHzZpVFObuLpA13ewpimpkmwGcYxjROELEhgD4AJYCuMQwojWEiBcDWAxgESFi\nHwDvAOgAwAHAX4SIPRlG1CBb2aoL6gLEhFiJGOZs+YNiQoIBZIoY5n5lQV9zYsDlKgCgRKHgNvVc\nKP178iTfBwD697e+ePZsxriCArVtTEyBoLYvVupCo2Hw228vRwFAcrLM9+LFDLvWtJ9Po2EQGSnp\nCgCDBtk2SNXL+nJ1NZavXeu/dd68B0uSk2W+H3wQ9ta+fT0O6Xr9+fPp9mvXPpucna1w1x4zNDQo\nsrHhJjk785O8vU2T+vWzSfT3N5c0Zfn1oCCrv5dbWlvTypdU7XTpInxlYsLO0q5q8PY2vT1/vmdk\nXcaaMME1/syZ9CsPH0oGbtjwbPLp02mPc3KUbnw+K2/jxkCdfva4XBbTrZvw+pUrWWPOnEnv19RB\nXXx8EX/GjLAFeXlKZwBwcuJFDR1qd/3DDz0iq3qTaP58z4fnz6c/S0sr9vrqqycj9+/v8Vvjzpqi\nqIZhbUSI+Kr2M4YR9S//KCFiMwB9AUwte1wJQEmIeBQA7bl7UVr4bRGAUQB+YxiRAkACIeJYAN0A\nVLrvuL6qWw++FsDTSo5HAVjfEJPRNxaXW7r8UqmkmbpWRipVs1JSZF4AMHq002MbG24CAJw7l+Fe\n/ZX6sXt3gldW1v+CgX37EltVS4VTp9KcCwrUdlyuQeHkyW7Pmno+VQkKsspZsMAzxMAA6ogIycAl\nSx7V+H0oKFCxZ88OH7Fw4aPl2dkKdx6PJRk3zmnPjh1dloaGDvns7Nl+W376qevxBQvaP+zUyaJJ\nAzoAcHcXyMzNDYsBwMmJR4ukULXm5la6r87YmJX73XcBOr/xUZl16/yP8fmsvNxcpeutWznDAWDW\nrLZ7nZ35cl3HmD3b4xYh0Lx8Ket4716usD7zqY/ERCl/+vTQT/LylM4mJuysLVs6LT97tt+WBQva\nP6wu689iEcyf73kYAPPokaTf2bPpDo04bYqimk4bANkAdhMijiBEvJMQsTEAW4YRpZedkwHAtuxj\nRwDJ5a5PKTvWIKoL6kxEDJNU8WDZMauGmpA+GRgZ0aCulfrzz5Q2KhXDMzVlZ3Tvbpnn5mYcBwCR\nkZJGKZZy6NDL4QDg4SEIA4CoqPyeGRnFrSYjfPx4ajcA8PIyvd+Y+8fq4r333GLHjnXeDwCnT6e/\ns317nE9V5x48mOQeHHz9i5s3c4YzDFgdO5pdP3Ik6D9ffeV7p0cPq9ymDuCq4uFh/goAfH3NXzb1\nXKiWZ9q0NpdcXPiPRSKv7fXde2pvz1NMmeL29176wEDzyzNnutfqjR9vb9NCDw/BfQBk5874vvWZ\nT10lJ8t406bdm5+bq3QVCNjZ27Z13jBggE2WrtcHBzuk+vubX2MYGGza9PxtjYauiqaoli+7mGFE\n/bV/KjmBDaATgBCGEQUCkKJ0qeXfGEbEoHSvXaOrbvmlRTWP8at5rNlgaYM6lYoGda3MjRvZPgDg\n7i54CgD+/uZxd+7kIjFR2uD76vbsSWiXkVHcjsMhsq1bOx2YPPmeRVaWwuP77593W7XK70ZD37+h\nqVQlJCoqvwsADBtm32yqXlbnyy873E1OltndvZs7bPv22PfbtDFeO3SonfZdM6Sny7mff/5o9MOH\nkgEAiIkJO+v999vuq1iavbnasqVPxPXraUmvv27abLOmVPM1ZIhdxpAhdlv1Nd6cOe2iHj3KP52R\nIbfbuDHwz7qMMWaM07V16551i4h41buoSHVSIOA0Wruk1FSZ0ZQp9+bl5CjdBAJ2zvffd9oQGPi/\nfXO6+s9/Opx4++073dLS5F5btjwPWLCg5j2FdXXrVo7Vxo0xI6VStamREUvK57NkxsZsqbExW2Zi\nwpaZm3OkFhaGMisrrtTenifz9jbJb8x/U4r6l0gBkMIwIm3l4D9QGtRlEiK2ZxhROiFiewDaN4hS\nATiXu96p7FiDqC6o+0tMyCoAX4gYhgEAMSEEwNcALjfUhPSJxePRTF0r9fx5aSuD7t0tnwLAG284\nxP/4YxxychRuBQUqtqkpp8EKexw8mDQcAHr0sPzL0ZFfPHiw7dVff33pcf169gCNhrnRXLM9ujp0\n6GVbmUwj5PNZeePHOzdKDzh9+OGHzsfHjbtlGx8v7fTVV08+cnXlf9u+vWnRDz+86LB3b+J7MplG\nSAhKune3PLd+vf+p5lb8pTo+PkKZj49QlpycXPPJFNUItm/vcqI+10+c6Br7009xaRKJymHbttjA\nRYu8G6VNSHq6nDt58r152dkKd2NjVu6mTYEbaurVVxUPDxPp4MG2x8+cSZ9w+HDyuGnT2jzR9+8V\nuVxjsGxZ5KDLl7NGajSMzq9l+HzWqzVr/DfWJvtIUVT1GEaUQYg4mRBxe4YRxf76+TgAACAASURB\nVAAYhNKtak8BTAGwpuzv42WXnADwKyHijSgtlNIOQIO9WV5dUPcZSkt2xooJ0b775A8gHMDMhpqQ\nPrH4fJqpa4ViYwuNc3IUboRAM368cwwAuLkZy8zMOOn5+Sr706fTXCZMaJiG1AcOJHqkpRV7cThE\nvmiR92UAmDu3XcSRIymFEonK8eDBJI/33nOLbYh7N5azZzO6AoCvr1lYYzXY1gcOx4DZtavb7nHj\nblnm5ipd58y5P9vc3DD3+fPC7gBgaWmY9NlnXvtGjHBIaeq5UtS/HYtFEBRkde306fQJf/2V2a8x\ngrqsrGLDSZPufZyVpWjL57PyNmwI3Ni9u2Vefcb8z398r9++ndNPIlE5LF/+ZPD333c6p6/5njyZ\n5rRhw7PJublKVwDw9DS5N2iQzb38fBW/oEDFLyhQG0ular5MpjGWyzX84mKNcXGxhi+Xa8xkMo3F\n8uWP5/z+e69v7e15Cn3NiaIofAzgl7LKl/EApqF0O9thQsQzACQBGA8ADCOKIkR8GKVBnxrA3Iaq\nfAlUH9RZihhmgpgQd5SW4gSAKBHDtJh37tllQR2jVtOgrhU5ciTFGwCxszOKtbEpXWILAM7O/Nj8\n/Hz7sLC8tg0X1CW9AQDdullecnU1lgOlpb47dbK4cedObvCRIyn9W3JQp1RqSExMQWcAGDXKsUUs\nvSzPyoqr3Ly507ZZs8KWZmUpPLKyFB4sFlEOGGBzYvVqv0vNfX8gRf2bfPxxu7vnz2e8mZFR7Hnh\nQoZ9+SXT+paTozB87727H2VmFrfj8ViS9esDNgYFWeXUd1wej1UyZUqbQ5s3P19w82Z28KNHkjv+\n/ub59RlTIlGyFy58NPzevdyhDAMWn8/KmzLF7cCcOe2idLk+PV3Ofeut20vy81X2H3wQPu3PP3v/\nWJ8VJMeOpbiIxTHTfX3N7v/4Y5eTdR6ohcjKKjbcvTuh4+3bOV0yM4tdfXzM7m/aFHi8IVcAUS0H\nw4geAuhSyUODqjh/FYBVDTqpMtUVSjkGACKGiRcxzMmyPy0moAMAtkBAM3Wt0IMHr3wAwNvb9B9P\ncN7epnEAEBtb1CD76g4eTHJPTZX7sNmk+PPPvS6Vf2zWrLY3ADBxcUWdnjzJN22I+zeGo0fjbRSK\nEhNTU07GG2+0zIyWv795/rJlPlt5PJbEyYkX9f33nb757rvAizSgo6jmxdGRX+zlZRoKAPv3JzZY\nwZS8PAXn3Xfvzk1PL27P47Hy167139C3r3W2vsafOdP9mZub8UO1muGuXBk1pj5j7duX0O6NN65/\nefdu7jCGgUFAgPnlY8d6/0fXgA4oLWazalXHHzgcIk9IkAZ+8smDYXWdz/nz6fYrVjydn5+vsr91\nK2f4jh1xXnUdqznLy1NwNmx4Fjh69M1ZQ4de23DgQNL78fHSTlKpxjIsLG/oiBE3Fl+8mGFX80gU\n1XSqC+pa9sYgAGxjYxVAM3WtiUbDICFB2gEABg2y/ceTXL9+1nEAkJYm92iISmT795dm6bp0EV6p\n2Gy2a1dhnpub8SOGASskJLa33m/eSP74I9YFAPz9zUJb8t7AUaMck+/cGbzo7Nl+W/r00d+LN4qi\n9GvCBJerQMNVEC4qUhlMnHh3Tlqa3MvIyKDg22/9GmSf2eefe/1hYAD1s2eFPQ8fftmmttcnJ8t4\nEyfembh+fYyooEBta2bGSV+61Hvd/v09DtVl+WS/fjZZ06e77wLAXL2aPeqHH150qPGiCq5fz7b+\n4ovHC5TKEgGfz3oFALt2xU/Wx/cpKiqPv3JleNusrOIme31WUKBib9783G/s2JszBg26umHPnsQP\n4+KKumg0jKG1NTf+tdfsDn/4YdvvBQJ2dl6e0nnhwkdfLFkS2Y9WOqWaq+qWXzqKCdlS1YMihpnX\nAPPRK46pKV1+2cr89VeGvVyuMTcyMigYNsz+HxWEeve2zuJyDQoVihKT27dzrPX5Yv6PP5Jdk5Nl\nvmw2USxc6PVXZeeMGOFw9fvvXwSEh+f1lcs15+qaGcrJURhaWXGVNZ+pX0VFKoNbtzIcAeDtt12a\nZcPx2mjJQSlF/VuMHOmYsmnT8/jsbIX7tm0vuq5Y0fGmvsaWyVQGo0ad7pWaKrfjcg0KV63y2zho\nkG2GvsYvr08f6+xu3Swv3r2bOywkJO7tMWOc1uqyJ1mjYbB16wu/X35Jelcu15gTAk1QkNXZtWv9\nz9Z3ud9HH7V7HB1dcPL69eyRO3fGz/T1NV+ta4YyLCxPuHDhw0+Li0vM7O2NYvbu7b5twoQ7otxc\npcvChQ/H1Kfhenx8EX/mzGv9s7Pl/IMHeXMOH+61taGXNsrlGoOIiFcWUVH51klJMuuYmIK2cXFF\nASoVw9OeY2lpmBQYaBH2zjsu98vvtXzzTacV8+dHvBMdXdDr1Km0iZGREl+xOGCft7dpYUPOmaJq\nq7qgTg7gfmNNpCFwzMxKl1/SoK7VuHAh0wcAXF2Noys+YbJYBPb2vLjERGnAlStZbfUZ1O3ZkzAc\nADp1srjq6WlSVNk506a1ebZ3b0JmQYHaNiQk1u/TT2tX3lqjYfDee3ffi44u6DFtWpuf5s/3jNTH\n3HX1228v7OVyNdvS0jCpXz9aMY2iqMYxYIDN1cOHk92vX8/up9EwN+vzhkx6upz7yy9JPvfu5fqn\npBR3LipSGXK5BkUrVnTc2JB79gDgm298z44adbNXTo6izbffRnf/8ssOdys7TypVsw4efNnu+vUs\n/+fPi/ylUrUlAFhbc+MXLfLa99pr9nqb56ZNgWfefPOWS2KiNGDZssg5v/8etMbOzqjazF9kpMRs\n/vwHC2QyjdDGhhu/b1+PbXZ2RorPPvPau2xZ5NKHDyUD9u9PDJ80qfb7x1WqEvLRRw+mZ2fL+QCQ\nmir3njTp7vTDh3vt4HJZ9UqBFRSo2DduZNvGxBRaJyfLrLOyiq1zc5XW+fkqa6lULWQYsCpeIxQa\nJvv7m4e//bZLeFV7LO3teYrDh3vtXbs2+smhQy/fe/lS5jdp0t2vpk9vs7s2y2IpqqFVF9Tlihhm\nb6PNpAFwLCxKM3UaDQ3qWomnT/M7AEBAgHmlv0jbthXEJSZKA6KjCzwAVPqEWlvHj6c6JyXJ/Fgs\nohSJvC5WdR6HY8D07Gl17fz5jPEXLmT0r21Q99VXT/o8eZLfBwD27UucMmCAzTd+fvXbcF8ZlaqE\n3L2ba/XgwSv72NhCx7Q0uUN2ttKhsFDlAACdOlm0+CwdRVEtx8cft7t/7Fjq+Lw8pcuRI8ltxo93\nSajN9Q8evDL//fdk/4cPX/mnpcnbl5T877WNk5Og4KOP3DcNG2afpv+Z/5O9PU8xfLjD0d9/T552\n8mTqm7NmuUdol04mJUl5v/6a5BsamueflCT1LZ8h4nINCgcMsDmzcmXHK/UNbCricAyYH3/svHv8\n+DtLJBKVwwcfhE05erT3T1UFzrGxhcZz597/pLBQbSMUGib//HO3LdogcMQIh5TTp9PO3rqVMzwk\nJHbKsGH2K2q7qmT+/AfBycmyjgIBR7lyZfewhQtvdYqPl3aeOjVUduBAjwN1Deh//z3Zbf36Z7Pl\nco15VefweCyJqSknWyg0zHZwMEofNcrpYW2W4i5a5H1/0CDb+CVLIqdnZBR7hoTEzbtzJ/fy5s2B\nR4VCrqpOE6coPaouqGv05V/6Zmhu/veeOkajAWH935s0VAuSl6fgpKcXewLAm286Pa3snG7dhLGX\nLmUiJUXmrq/77toV/wYABASYX6tpucXHH7e7/ddfmaNTU+Xely9n2g4caJupyz2OH091Pnky9R0A\nMDFhZxUWqm0WLXo05dSpvlvqu4zw9Ok0x4sXMzqkpsodsrMVjhKJyq6qfkfOzoKCWbPa6iUYpiiK\n0oW5uaHaz8/8dnh43tCVK58u3LAhJl8gYEsEArbE1JQjsbAwzLey4krs7Y0krq7G+e3bm0gePpRY\nnTuX7h8dXeCfm6t0KTccY2PDje3Y0ezR4sU9BZ07WxempqY0WLPfipYs8b539WpW/+xsRZvPPns4\n1tGRlxEZKfFPTy9uVz5TZG7OSfPyMn00aJDto7FjnRIbsn2MoyO/eMUK3x9EoodL4uOlnRcsiHh9\ny5b/b72QnCzjzZwZNl8iUTmYmXHSf/qpyyZtlWctsdj/zLBh1wMlEpXjwoWPRuze3e2IrvMICYnt\ncONGzggAzIYNQffefrtdZmpq9raNG5/Pf/Ikv8+HH4YX7djR9Vhtv7516551/vXXpGkaDcPh81l5\nlpbcVEtLw2xbW6McFxd+tpeXaXaXLhY5+gi8unQRvjp1qs/Gzz9/NPTKlaxRDx9KBo4adbP9kiXe\nu4KDHf7+f5aXp+BERxeaJSQUmaemys2ysxXmeXlK8/x8lRmfz5Ju29b5CK2mSelblUGdiGF6VDwm\nJqQtgIkA3hExTK033TY2trGxBoRowDAstVTK5pia0h+gFuyPP1I8NBqGIxQaJvv4mFUaXAUH279c\nuzZaLZGoHJKSpLyKT0i1dfp0mmNCgjSQxSKqTz9tX2WWTsvV1Vju5WUSGhVV0HvPnsR+AwfaHq7p\nmuRkGW/NmugPSkrA9vU1u7F4sffJ6dNDv0xJkXdYujSy/9q1/lfrOv+fforz3rr1xccVl53weCyJ\nUGiYZmdnlOrqapzWoYNp+rRpnb2EQiN1cnIy3SdAUVSjmjPH48rHHz/oLJWqLWUyjVAm0wizsnSr\nD8JiEaWLCz+qc2eLR++84/K4fXvTIgBwdrYZ0qCTrgSHY8B8+GHbQytWPF38+HF+v8ePSxdbEIIS\ne3ujGD8/80ejRjlGNnYBp4EDbTOnTm3z844d8XOvXMkaHRISmzx7tsffK16ysooNp06991FurtJV\nIGBnb9vW+Tvtv2N5AgFHM3++596vv45aEh6eN+Tw4ZcPdMms3r2bY7lzZ/wMAKRvX+vjb7/dTgUA\nkye3eSGRqH7auTN+9t27ucM+/TSiaOPGwEr3rVek0TCYP//BsGvXskcDgI+P6c1du7r+KhBwGqwP\nGABwuSxm8+ZO548eTYnesOHZTIlE5bhkSeTSzZtfxMpkalOZTGOuVJbwqxvjo48eMPv2da/x9QFF\n1UZ1mToAgJgQBwBvozSY6wjgWwDvNPC89Iaw2UpGpeIp8/IMaVDXst25k9MBADw8BFWuYTc3N1Rb\nWXGTsrIUbU+fTnOv73r3HTtKs3R+fmY3dF0KOXGi65Vlyx73fvJE0isrq/hY+V56FWk0DD766P7k\noiK1tVBomBwS0vk3c3ND9cSJLgf27En88Pz5jHGDBtnG1GUvyJkzaY4hIbEfMgxY7u7GDzp2NH/q\n7W2a1ru3VVplwa5QaORR23tQFEXpQ9euwry7dwcvrS7DUVioMpdK1WYymcbC0NBA1rat4HFQkNWj\nd991fWZubthsnt/Hj3dJOHMm/eKTJ/k9nJ35MV27Ch9NnOj6xM3NWFbz1Q1n3jzPyOjogpM3b+aM\n2LEjbqavr9nqPn2ssyUSJXvy5HtzsrIUHnw+69V33wV8V12vvXHjnJPOnk2/EBqa99qWLS+mvP66\n/crqsk4SiZK9eHHkB0plibGLCz9y06bAswAGl59Xfr5qz+HDydMvXsx86+uvn0i/+sr3TnVfS0GB\nij19euikmJjCHgCYwYNtj4jFARcbs0DWm286vezd22rlJ59EvPX4cX7ftDT53+0eCIGGx2PlGxuz\nJQIBO9/MjCMxNzeUcLkGqgsXMsZGRLwatHnz82eNvXeeat2qDOrEhLwPYAIARwCHAcwAcFzEMF83\n0tz0woDNVmpUKp4qP5/T1HOh6ic2tsgHAIKCrCpdeqnl6mocl5WlaPvokaQtgDoHdefPp9vHxRV1\nMjCAesGC9ud1vW7kSMeUzZufx2dlKdy3bHnRfeXKjjeqOnfx4kcD4+OlndhsUrxiRcft2hcmn33m\nFREamnfr6dOCoFWrns7o1cvy29q8+/jokcTs66+jPlarGSMPD0H44cO9djbk8h6Koih9EAq5qqAg\nbo4+GoM3pT17uv8B4I+mnkdFW7Z0Oj1mzE2XpCSZ/9KlkbMPHOixfu7c+9NSU+XeRkYGBWvW+G/s\n0cMqt6Zx1q/3PzlixI2A/HyV/cKFD4O3b+96oqpzZ8++/065DODuyp6Lli/vcK+gQGV87lzG20eO\npEw2M+PIPvmk/aPKxnv+vFAwZ0747MxMhQeLRZRTprjtWrCgdnvY9cXGxkj56689fzl6NOVGRobc\nxNnZON/TUyBxdxdIq3rO/fTTCIOLFzPH7duXODUoyGpFly7CV409b6p1qq5P3dayxyeKGOYLEcNE\nAmhxLwoJi6UEAFV+Pi2W0oI9eiQxk0hUjiwWUY4b5xxX3bkdO5rFAUBCgrRemaft2+OCARBfX/Ob\ngYEWktpcO3Cg7RUAuH49q39VPW1+/z3Z7fz5jHEAMHGi696KpaY3bQo8pO2PM39+xChd752eLufO\nm/fgY5lMY2Fjw43dvbtbpU+iFEVR1L8Lh2PAbN/e5WdTU3aGRKJyHDv21oqkJJm/oaGB7OuvfTfp\nWjhEKOSq5sxptxcAc+dO7rDjx1OdKzvvP/950uvJk/w+LBZRLVni/WN12cr16wMu9+pldZphYLB7\nd8L7u3cneFY859KlTLspU+4tzsxUePB4LMnXX/uua6qArrw333R6OWdOu6gRIxxS2rc3LaruOXft\nWv+/nJ35j5XKEuNFix7NlMs11b0WpyidVfcfyR7AQQAbxITEiAlZAUDnbJeYEGcxIVfEhDwVExIl\nJmR+2XGhmJCLYkJelP1tUe6aJWJCYsvu91q5453FhDwue2yLmBCd8+uEzS4N6goLaVDXgh07luID\nAI6OvJiaNhe//rp9HABkZSnaSKXqOlXHuXQp0+7Fi6KuhEDzySeeOmfptD7+uN0DLteg8NUrldNv\nv71sW/Hx+Pgi/oYNz95nGLACA80vL1zo9aDiOfb2PMW8ee1+BsCEhuYNrewJriK5XGMwY0bY+3l5\nSmcTE3ZWSEiXkOa0LImiKIpqWo6O/OJvvukYwmaTYoWixITNJsVLlnhvKl/oQxfvvusaFxhofoVh\nYLBxY8yUis+3x4+nOh87ljoRAMaMcfxl5EjHlJrG/OGHzif8/MyulZSAvWXL87nHjqX8XQRnx444\nr4ULHy4uKlJbW1oaJu3Y0XX1qFGOybWZc3PA4RgwmzYF7uHxWJKsLIXH/PkPRjT1nKjWocqgTsQw\nuSKG+VHEMP0ADAIgAZApJiRaTMhqHcZWA/hMxDA+AHoAmCsmxAfAYgCXRAzTDsClss9R9tg7ADoA\neB3AD2JCtL8gQgDMAtCu7M/rOn+BHI4SANQ0qGvRHj6UdACADh3MalxO6e1tWmhiws7SaBjD8+dL\nm2nXVkhI7DAApEMHs9tduwrzarygAlNTjjow0OImABw9mty//GMqVQn5+OMH06RSjaWVFTfhhx86\nV7lEZ8IE1/igIKvTAMiPP8ZOS0qS8qo6V6NhMGNG6ITkZJkvl2tQtGaN/5aqeupRFEVR/16DBtlm\nzJnjEeLoyHsqEnltGTfOOaku44jFAX8KBOycvDyl86JFj4ZqjycmSvlr1kR/qNEwHF9fsxs17ZHT\nYrEIfv6520EPD0G4Ws0YrVz5dN6VK1k2y5ZF9vn++xfzVSqG16aNccThw73E1e37a+48PU2K5szx\n2ImyTOeOHXFeNV5EUTWosVAKAIgYJgXABpRm7dqhdK9dTdekA0gv+7hQTEg0SvfnjQLQv+y0vQCu\nAlhUdvw3EcMoACSICYkF0E1MSCIAUxHD3AUAMSH7AIwGcLb8/cSEXC3/uYGREXF2dh4isLMTKLKz\nYefu3tPZ2ZkWgmhiRkZGngDg7FzpSo1KaTQlyMhQ+AOASNTNXJeKZt2728n/+isFr16x3nB2dq5V\ng9SHD3OMnz8v7MFiEWb79sGFzs7COlVQ27jRmAkKOoK4OGnXkhKzTFdXUwUALF16x/PlS5mfsTFb\ndfz48Ghvb+HA6sY5etRB0bv3kbwXL/KFYnH8p8eOBYdWdt6SJXfaP36c35HDMSjZs2dw6LBhrgG1\nmW9dvjdU46Dfm+aLfm+aL/q9qd433zjjm2/wFIB72Z9ac3YGNm0iT2fOvNL31q2ckampHH7XrjYF\n06ad6F1UpLZq29b01blzY7IFAs4/nkdr+t7cuOGUFBx80jkiIsd20aLIr+RyNRsAJkxo92zr1r5x\nLJZBv7rMtzlZvtwZeXkkevfuZz579ybNmTGj0wXt64SmRH9uWq4qM3ViQkzLAjjt52+JCZkMoCeA\n7bW5iZgQNwCBAO4BsC0L+AAgA4Bt2ceOAMqn0VPKjjmWfVzxuE5YXK4aAFQymU4BLNX8XL2aZlFU\npDK0sjKSBQZa65R56trVNgcA7t/Psqrt/VasCPNhGGDwYOfEDh2Eda5W5uMjlHXrZpum0TBk69bH\nbQDg1KlEyx9/jOoIAGvW9AzVZXwul8X89NOAUENDA83Vq6kuW7dG/t9v2h9/fOIUEvKkIyHAqlU9\n7g0b5lrr7CJFURRF1da4cR5ZwcGu8Wo1Y/Dxx9e7fPbZLZ/w8Gw7gYCj3L9/yB2BgFNS2zF5PDbz\n55/Btz09zfPkcjWbxSLM8uVdwkNC+j9hsVrPFrR164Ke+voKs/PzldwpUy5102hq/U9FUX+rLtAR\nA7gN4EXZ59+iNDvGA9ALwIe63EBMiADAEQCfiBimQFxuO5yIYRgxIXop4CBimP7lP1/G5aqTk5Mv\nyl69agPA/uW9e1HG/fvf18e9qLrTvvOTnJxcY883rS1b7g8DADs77v3U1BSdrrOy0tgD6Hz/fpZx\nbe519my6w6VLKWMJgebNN212JCcn11gFrDpdupik3ruXOf+XX2Ic+vc33TdrVtjSkhKGdOsmPN+/\nv/HR5GTdtgNYWQHBwfbZx46lTvr661A/BwfmmHZZ6C+/JLVdty56NAAMHmz7x7Bhphd1Hbe8unxv\nqMZBvzfNF/3eNF/0e9N4PvrI9ebVqylfvXiRL3zxIl8IgJk61S3ExET6NDlZ+n/n6/q92bCh4/Vv\nv306uH9/myfjx1vF1+W5rblbvNgzdMaM0C8fPsyxHTv2JOv77/+/MXxj+pf/3AQ31Y0JERsBGA6g\nDwAHAHIATwCcZhiRTpXcq3u7oytKl0dqFYoY5mMRw8wE4KvL4GJCOCgN6H4RMczRssOZYkLsyx63\nB6CttJQKoHwGwqnsWGrZxxWP64SU7anTFBfTPXUtVExMYQcA6NLFQuf2BAMG2GRwOEQmk2kswsLy\nhLpe98MPsaMAED8/8xu9etVc1rkmM2a4R5uYsLNkMo3w/ffDFsnlGnMbG27sli2djtd2rP/8x/em\nqyv/kUrF8JYujZymUGjItWtZNhs3xswtKQHbz8/86vr1Af/GX8IURVFUE3J25ssnT3Y7oP28b1/r\nkx980Lba9kO6cHMzlm3f3vXEhAmu8fUdq7ny9zfPnzHD/WcAuHYta9QvvyT9X3E1qnUjRPw1ShNp\nPVG6qnE7StvJqQGsIUR8kRCxX03jVJepY4sYpnwWbVK5j81rGrisQuUuANEihtlY7qETAKYAWFP2\n9/Fyx38VE7IRpRFqOwChIobRiAkpEBPSA6Vf6GQA39d0fy0DQ0Ma1LVgqakyo8zMYndCUDJunPMz\nXa/jcAwYOzteXHKyrOOlS5nuuhQ7+e23l20SE6UBLBZRLl7sfbp+M//fPHr0sLx28WLmW1KpxpLL\nNShavz5gh7ExW+eec1osFsGGDQH73nvv7lcZGcWec+feHx0VVdBZ29B1586uhxqz8SpFURRFac2d\n2+5JWpr8QH6+SvDdd4FNmm1qaWbP9ogKC8u7EBaWN3TLlucze/a0XOHuLmjSZvVUowplGNFXVTy2\nkRCxDQCXKh7/W3WZuhIxIXbaT0QM8wQAxIQ4AtBl0W8QSgPBgWJCHpb9CUZpMDdETMgLAIPLPoeI\nYaJQGpU+BXAOwFwRw2hf+M4BsBNALIA4VCiSUu0XWBbUldCgrkX6/ffk9gwDlrU1N8HV1Vhem2vd\n3Y3jACAqKr/GAjkaDYOff44fAwBduwov+fqaFdRtxv9v3jzP2ywWUQJgZs1qu6tTp9r1vCuvfXvT\noqlT2+wFgHv38l4vK+38cteubjt5PBZdjE9RFEU1mVWr/G5s3dr5LO2NWnvff9/pmLU1N0Em0wjn\nz4+YUlWPW6pVukSI2LriQULE1oSIjRhGlMUwovCaBqkuU7cewEkxIZ8BiCg71gmle+3W1zSwiGFu\nAqgqbTCoimtWAVhVyfFw6LjksyKWNlOnUNCgrgUKC3vlAwDt25vovPRSq3NnYdy1a9l4+VJW41KG\nXbvivdPTi9tzOES2bJnPhbrMtSpubsaypUu9NxYVqQ2nT3ePqe94c+e2e3L7du7VyEhJfz6flbdl\nS6etdnZGTV4xi6IoiqKoujE2ZmtWr+64Y86c+8sTE6UBS5ZEDli3zv9KU8+LahRbUJrQOlrheG8A\nQwHM1mWQ6vrUHQCwHMBKAIkAEgB8A+BLEcPsr/18m4YBl1uaqaNBXYsUH1/UAQD69rWp9dr8ESMc\nEglBSV6e0jkjo5hb1XkaDYNff00aAwC9e1ufd3Mz1vuSh/HjXRL0EdBphYR0/n3cOKc927Z1Xufn\n13J79VAURVEUVapHD6vciRNd9wLA+fPp48o3X6datc4MI6oY0IFhRH8C6KvrINWW+RcxzDmURo4t\n1t9BnVJJg7oW5saNbOuiIrW1oaGBbMwYx8TaXm9lxVUKhYbJublK11On0trMnOle6Z68776LCczN\nVboaGRnkf/llh8v1nngjMDXlqHVt5kpRFEVRVMsgEnlFRES8uhYZmd/v0KHkvqNHOx2o+SqqheNX\n85jOPTyq61P3hZiQKqsGigkZKCZkuK43aiosIyMa1LVQZ86k+QCAszM/wsnBdQAAIABJREFUmstl\n1WlxuYuLcSwAPHiQV+kSTLlcY/Dnn6nadgCnraxK3wSgKIqiKIpqCtu2dT48cqTDgX37uv/S1HOh\nGkUWIeJuFQ8SIu4KIFvXQarL1D1G6Z66YgAPygY1QmlVygAAfwFYXZsZN4W/gzqVigZ1LcyTJwU+\nANCxo1mdyyL7+prFRUS8GpSQIK00qFu7NrpHQYHKTiBgZy9b5nOzrvehKIqiKIrSB3NzQ/WqVX43\nmnoeVKNZCOAwIeI9ALQ9tbugtOL/O7oOUt2euuMihglCaZPxKAAsAAUADgDoJmKYBSKG0Tl6bCos\nHk8JAAwN6loUqVTNSkmReQHAqFGOtS6SojVkiG0cAGRmFrsrFJp/FO6RSJTss2fTRwDA8OEOJwQC\nTq3bDFAURVEURVFUXTGMKBRAN5QWmJxa9ocA6M4wonu6jlPtnjoAEDHMCwAv6jTLZoDF59NMXQt0\n5Eiyu1rNGJmZcdK7dBG+qus4gYEWEmNjVq5UqrH8669MhzfecPi7cf3KlU/7yWQaobk5J/Xzz73C\n9DNziqIoiqIoitINIeI9DCOaCqCqXnU60XnzXUvFNjamQV0LdPduricAuLsbR9d3LAcHXhwA3LqV\n8/cSzPR0Offq1axgAHjrLedjtKcORVEURVEU1QT89DFIjZm6lk4b1DFqNQ3qWpDkZLkLAHh5mSbU\ndyxPT5O4Fy+Kuj1/XugB4DoArFgRNVihKBHY2HDj585tF1nfe1AURVEURVGtHyHiRACFADQA1Awj\n6kKIWAjgEAA3lLaCG88woldl5y8BMKPs/HkMIzpfYUg+IeJAVNHfm2FED3SZV+sP6kxMSjN1NKhr\nUbKzFc4A0KWLMLm+Y/XqZRV7+nQ6UlPlbQHg+fNCwZ07uUMBYNIkt6MsVqU/QxRFURRFURRVmQEM\nI8op9/liAJcYRrSGEPHiss8XESL2QWmxkw4AHAD8RYjYk2FE5es4OALYgMqDOgbAQF0m1OqDOo6p\nKc3UtTBJSVKeVKq2ZLGIqk8f68z6jjdkiF3aV189URQVqa0iIyVm330XM0StZoycnHhRU6e2abH7\nRSmKoiiKoih9sTYiRHxV+xnDiPrX4uJRALTn7wVwFcCisuO/MYxIASCBEHEsSouilO81HMswIp0C\nt+q0+j11HHPz0qBOo6FBXQtx5UqWEwBYWHBSeTxWSX3H4/FYJba2RvEAsH9/YucHD14NAIAPPmh7\nrL5jUxRFURRFUf8qDEozbvcJEb9fdsyWYUTpZR9nALAt+9gRQPlVZyllx/Su1WfqDC0saKauhYmK\nyncGADs7Xr2XXmq1aWMcl5oq975wIWNsSQnYbdsK7o8e7fRSX+NTFEVRFEVRLVl2sY7Zud4MI0ol\nRGwD4CIh4mflH2QYEUOIuDYF+BZVdpAQsTOAdxhGtF6XQWoM6sSEzAewG6UbAncCCASwWMQwF3Sf\na9MxtLBQAaWZOkajAWGxmnpKVA2SkmTOAODmxtdbUBcQYBF382YOSkrAJgQl8+a1O66vsSmKoiiK\noqh/B4YRpZb9nUWI+E+ULqfMJERszzCidELE9gCyyk5PBeBc7nKnsmPlx/s7piJEbA3gLQATULoH\n709d56XL8svpIoYpADAUgAWASQDW6HqDpmbA4TCExVIBgDI/n9PU86FqlpFR7AIAfn7megvqhg+3\nj0dpuhze3qa3Bw60rfdePYqiKIqiKOrfgxCxMSFiE+3HKI2PngA4AWBK2WlTAGiTBycAvEOImEuI\nuA2AdgBCK4xpQoh4CiHi82WPtQXQhmFEbRlGJNJ1broEddpKLMEA9osYJgpVlNxsrgiLpQQAZV4e\nXYLZzBUVqVgSidIeADNggG1qjRfoyNGRX+zkxHvK5RoULVzodUpf41IURVEURVH/GrYAbhIifoTS\nAOw0w4jOoTThNYQQ8QsAg8s+B8OIogAcBvAUwDkAcytUvgRKs3rTAawE4M4wos8AKGs7MV321N0X\nE3IBQBsAS8SEmACod/GKxkTYbCWUSmOVRGIIQNrU86Gqdvlylj3DgGVqys60szNS6HPso0d7by0s\nVLFtbIxq/YNCURRFURRF/bsxjCgegH8lx3MBDKrimlUAVlUz7BKUtj34AcBBQsSH6jI3XTJ1M1Da\na6GriGFkAAwBTKvLzZoKYbOVAKAqKKCZumYuIuKVMwBYWxvpbemlFo/HKqEBHUVRFEVRFNVcMIxo\nE8OIeqC0/QEAHAPgQIh4ESFiT13HqTJTJyakU4VD7mLSolZd/s2gLKhTFxbSoK6Zi4uTOgOAs7P+\niqRQFEVRFEVRVHNWlgVcDWA1IWJfABMBnAHgocv11S2/3FD2txGAzgAiUbqXzg9AOICedZxzo9Nm\n6tRFRTSoa+bS0+X/Ze/O4+Oq7rOBP2f2TaN9Gckj27ItbzI2eCMYCISQkECAEGKgaZI2hNCGNMlL\nblOSpk3bhLc0vUnbJE3SQtKQQEId4A1LWAwmBgzGGBnbWDa2Ze2y9mU0+3LnvH/MHTMYSR7Jkmds\nPd/PR5+5985dfva15Hl0zj2nFgCWLy9gqCMiIiKiOUdK5QCAb+pfWZkw1ClSXg4AqhCPAlirSPmW\nvt4A4B9Oq9IzzGA2p0JdMMhQl8c0TWJoKDoPAC69tIKhjoiIiIjOaUKotwIoSc9HJ4TaDaAAqca0\nv5ZS+Vk258nmmbql6UAHAIqUBwAsn3rJuXOipS4UYqjLY7t2DZXG49JusxnGGhoKx3JdDxERERHR\nLPsLAL/IWO+XUnEDKEdqvrqsZDP65X5ViPsAPKCvfwqprphnjXRLnRYOM9TlsddeG/ICQFmZla10\nRERERDQXCH30zLTfAYCUSkQI1Z7tSbIJdX8O4C8BfEVffwnAT7O9QD4wWCwMdWeBI0f8XgCorrYz\n1BERERHRXFCUuSKl8n8BQAjVAKAs25OcMtQpUkYA/Jv+dVYymM1xAEhGIgx1eayrK+QFgCVLOEgK\nEREREc0JW4VQvyul8q2Ttv8TgK3ZnuSUoU4VYhNSA6PMz9xfkbIu24vk2omWumiUoS6PDQxEvQCw\nfn1JV65rISIiIiI6A/4awH1CqM0A9unbViM128Dnsz1JNt0vfw7g/wBoBKBNsci8YLBaYwCQZKjL\nW83NfmcopJUYjSJ28cVlfbmuh4iIiIhotkmpBAHcIoRaB2ClvvmglMqxqZwnm1DnU6R8eqoF5hOD\n1RoFGOry2YsvDswDgJISS5fVapS5roeIiIiIaLYJoX4YQIGUysMAWjK23wjAJ6XyXDbnySbU/VEV\n4l8BPAogmt6oSLlnaiXnjjHdUheLMdTlqaYmnxcAqqpsfJ6OiIiIiOaKvwdw/TjbtwN4AsCMhbqN\n+uu6jG0SwAeyuUA+MNpsqVAXjzPU5amOjtQgKQsXOhnqiIiIiGiusEqpDJy8UUplUAjVme1Jshn9\n8vKpVpZvjHY7W+ryXF9fxAsAq1cXcZAUIiIiIpor3EKoJimVROZGIVQzgKznqTOcagdViEpViJ+r\nQjytr69Qhbh1yuXm0IlQl0gw1OWh0dGYyeeLewDID3ygsjvX9RARERERnSGPArg3s1VOCNUF4Gf6\ne1k5ZagD8EsAzwKo1tePAPhq1mXmAaPDEQMAye6XeemFF/qrpYShsNDcW1aWev6RiIiIiGgO+BaA\nPgDtQqiNQqiNAFoBDOjvZSWbUFemSLkFQBIAFCkTOMumNjA5nWypy2N79454AaCiwsrn6YiIiIho\nLlknpXIXAC+AP9O/aqVU7pJSiWd7kmwGSgmqQpQiNTgKVCEuBOCbcrk5ZHK52FKXx1pbg14AqK11\nMNQRERER0VzyEwAXSKmEAbw13ZNkE+ruBPA4gEWqEK8AKAdw43QvmAvmggK21OWxnp6wFwCWLy/k\nIClERERERFOUzeiXe1Qh3g9gKQAB4LAiZdZNgfnAXFiYaqljqMs78XhSDA3F5gHAJZeUsaWOiIiI\niOaSOiHUxyd6U0rl2mxOkk1LXfo5uiZViP9WpPxClgXmDXNRUSrUaRpDXZ7ZuXOoLJGQNrvd6Fux\notCf63qIiIiIiM6gAQDfP92TZBXqMqw79S75x1JSwu6XeWrXriEvAJSVWTtyXQsRERER0Rnml1J5\n8XRPks3ol5n6T/eCuWAuKEgAkEgmTVo0KnJdD73j6FG/FwBqaux8no6IiIiI5pq2id7QJyDPypRa\n6hQpr5rK/vlCGI0QJlNMJhLW+MiIxVhVFc11TZTS3Z0aJGXJkgI+T0dEREREc4qUyg2Z60KoAsAH\nAPwJgGsAVGZznlOGOlWIJ6BPZ5DBB+ANAP+lSBmZ4Lhf6IX0K1I26Nv+AcBtSPUdBYBvKlI+pb/3\nDQC3IjUH3pcVKZ/Vt69FagJ0O4CnAHxFkfLkek5JGI0xmUhYYyMjFhtDXd4YGIh6AWDjxhKGOiIi\nIiKak4RQL0QqyF0PoATAHQCUbI/PpqWuBalpDH6rr98EwA+gHsC9AD49wXG/BPBjAL86afu/KVKq\nmRtUIVYAuBnASgDVAJ5XhahXpNQA/BSpILgLqVB3FYCns6j7XYTJFEM0ipjPx+fq8sThw2OucFgr\nMplE9KKLygZOfQQRERER0blDCPX/AvgkgA6k8tY/AnhDSuX+qZwnm1B3kSLl+oz1J1QhditSrleF\naJroIEXKl1QhFmRZx3UAHlKkjAJoVYVoBrBBFaINgFuR8jUAUIX4FVLp9T2hThVie+a6wWYTXq/3\nyvS6rajIEgwGUV1b+/5Kr5ejLOaIzWarBwCv14udO5srAGDx4sJAXd38D+a2Msq8N5RfeG/yF+9N\n/uK9yV+8N/mL9+bUhFCNSPVY7JZSuUYItQTA/wJYgNTzcZulVEb0fd/VE1FK5dlxTvl5AEeQash6\nQkolKoQ65V6J2QyU4lKFqE2v6MsufTU21QsC+CtViP2qEL9QhSjWt9UAyOx+16Vvq9GXT94+ZUar\nVQOAeCAw1RE/aZbs3TtQBAD19cWjua6FiIiIiCgLXwFwKGP9LgDbpFSWANimr0MINbMn4lUAfqIH\nwpN5AHwXwMcAHBNC/TUAuxDqlDJLNjt/DcAOVYhjSE0+vhDAF1UhnACm1CyIVAL9DlLP6H0HqTkZ\nPjfFc4xLkfKyzPW/tVoTnZ2dz6XXo8HgGgBFLa+99qasrz86E9ekqUv/5qezs/O5559vqwUAgyH2\namdn546cFkbvujc5LoVOwnuTv3hv8hfvTf7ivclfc/velN8ghLo9vSalctnJewihzgNwNYC7Adyp\nb74OQHrf+wFsB/A3+vaHpFSiAFqFUJsBbACwM/OcUioagGcAPCOEakVqTBI7gG4h1G1SKn+STfWn\nDHWKlE+pQiwBsEzfdDhjcJR/z+YiGefqSy+rQtwL4El9tRtAZjvvPH1bt7588vYpM5hMMQDQgkE+\nU5cn+vpSg6SsWVPEQVKIiIiIKN/9O4CvAyjI2FYppdKjL/findEqawC8lrHfKXsc6gHwEQCPCKEW\nAPh4toVl26y3Fql+oiYAq1UhoEh58gAop6QK4VGkTP+hPw7ggL78OIDfqEL8AKmBUpYAeF2RUlOF\nGFOFuBCpgVI+A+BHU70uABjM5hgAJEIhhro8MDwcNft88SohkLz88orjua6HiIiIiOaygch4rXNp\nQqjXAOiXUmkUQh13PykVOdXn4fTWvwVSKjv09TvxzqNuv8n2PNlMafBrAIsA7EXqIT8g1X1y0lCn\nCvFbpJoiy1QhugB8G8BlqhBr9OPbANwOAIqUTaoQWwAcBJAAcIc+8iUAfBHvTGnwNKYx8iUACIsl\n1VIXDjPU5YFt2/prAIjCQnNPSYk1nut6iIiIiIgmsQnAtUKoHwVgA+AWQn0AQJ8QqkdKpUcI1QOg\nX99/op6IJ/tXAA9mrN8O4L8BOJAaCfNT2RSXTUvdOgArpjo3nCLlLeNs/vkk+9+NVP/Uk7e/AaBh\nKtceT7qlLhmJMNTlgX37Rr0AUFFhY9dLIiIiIsprUirfAPANANBb6hQplT8VQv1XAJ8FcI/++ph+\nyOMAfiOE+q6eiOOceqmUypMZ6yEple/r13k52/qyGf3yAICqbE+YrwzpljqGurzQ2hrwAsD8+Q6G\nOiIiIiI6W90D4Eoh1KMAPqivQ0qlCUC6J+IzAO7QB0U5me2k9SsylsuyLSKblroyAAdVIV4HEE1v\nVKS8NtuL5IN0qEtGo+Zc10JAb2/ECwArVhQy1BERERHRWUNKZTtSo1xCSmUI7w5imfuN2xPxJH4h\n1HoplSP6McMAIIS6DEDWc2tnE+r+IduT5TOj1ZpqqYvF2FKXY/F4EsPDsRoAuPTS8q5T7U9ERERE\ndI76NoAnhVDvBrBH37YWwDeRmhMvK9lMafDitMrLMwY91CWjUYa6HHvrrSFXIiGtDodxpL6+IJDr\neoiIiIiIckFK5Rkh1BuQmirhy/rmAwBukFI5MPGR7zZhqFOF2KFIebEqhB+p0SrTBACpSOmeRt05\nk26pS7KlLud27eorAoCyMiu7XhIRERHRnKaHt8+czjkmDHWKlBfrrwUT7XM2MdrtqVAXjzPU5dj+\n/YNFADBvnp2hjoiIiIjmLCHUewH8UErlrXHecwK4CUBUSuXB9xycYbKWupLJDlSkHM6y1rxgtNnY\nUpcnDh8eLQKA+voChjoiIiIimsv+E8DfCaGuQqrb5QBSI2IuAeAG8Au8ex67cU32TF0jUt0uxTjv\nSQB1Uyw4p4wORwwAJFvqcq6lxVcEABdeWMZQR0RERERzlpTKXgCbhVBdSM0P7gEQBnBISuVwtueZ\nrPvlwtOuMo+kQ10ykWCoy6HW1jHr6GjMZjaL8IYNJUO5roeIiIiIKNekVALQp0mYjlOOfqkKccE4\nm30A2hUpE9O98JlmcrnYUpcH0oOklJRYu8xmgzzV/kRERERENLls5qn7CYALAOxHqitmur9noSrE\nXypSbp3F+mZMOtSxpS633nxzoAgAPB4bu14SEREREc0AQxb7HAdwviLlOkXKtQDWAGgBcCWA781m\ncTPJXFCQaqljqMsZTZNobOwvB4C6OhdDHRERERHRDMimpa5ekbIpvaJIeVAVYpkiZYsqxhtDJT+Z\nCwvZUpdD/f0Ry+23v/HZ5uZAlcEg5BVXVB7NdU1ERERERLkkhPoE3j0n+LtIqVybzXmyCXVNqhA/\nBfCQvn4TgIOqEFYA8Wwukg8sxcWpljpNY6g7w3btGir5+tf3fXF4OOa12YyJf/mXi3ZdeqlzINd1\nERERERHlmKq/3gCgCsAD+votAPqyPUk2oe7PAHwRwFf19VcAKEgFusuzvVCumdOhji11Z9Qvf9m6\n5Mc/PvoX0WjSVVBg6n/kkY++uWFDpb+zk70viYiIiGhuk1J5EQCEUL8vpbIu460nhFDfyPY8pwx1\nipRhAN/Xv04WyPZCuWay2zUIkYSUxkQwaDQ5nVquazqXaZrEt7711vv/8IfjN0kJ47x59qaf/nTd\nfRs2VG7KdW1ERERERHnGKYRaJ6XSAgBCqAsBOLM9OJspDTYB+AcA8zP3V6Q8qyYfF0YjhNEYk4mE\nLTY8bDE5neFc13SuCgTixttue+OWAwd8lwDA+vUlW3/607WPWq1GTmFARERERPRe/wfAdiHUFqRm\nHJgP4PZsD86m++XP9Ys0AjirW7eEyZQKdSMjFofXy1A3Cw4e9BX81V/t+Yv+/uhio1HEP/lJ76/+\n9m9XvJ7ruoiIiIiI8pWUyjNCqEsALNM3vS2lEs32+GxCnU+R8ulpVZdnDCZTLAkg7vPxubpZ8Mgj\nnfO/9723/zIU0oodDuPI17++7Kef+IS3Pdd1ERERERHlMyFUB4A7AcyXUrlNCHWJEOpSKZUnszk+\nm1D3R1WIfwXwKIATaVGRcs+0Ks4hYTLFACDu9zPUzbB77jm07qGHOv5M06S5osJ67D/+44KfNTQU\njuW6LiIiIiKis8D/INUz8n36ejeA3wGYsVC3UX/NHI1FAvhAlgXmjXSoSwQCDHUzqKUl4Pjtb9v/\nPJmEqaGh8OX/+q91D7nd5kSu6yIiIiIiOkssklK5SQj1FgCQUgkJoWY9KXg2o1+eNdMWnIpBD3Va\nMGjOdS3nkpdeGqhJJmEqLbW0P/DAhQ8YjWfPpPRERERERHkgJoRqhz4RuRDqImT0kjyVbFrqoApx\nNYCVAGzpbYqU/zS1OnPPYDanWupCIbbUzaDDh8eqAaCiwtbNQEdERERENGX/AOAZAF4h1AcBbALw\n59kenM2UBj8D4EBqovH7ANwI4KwczVDooU5jqJtRHR2hGgCYN89+PNe1EBERERGdbaRUtgqhNgK4\nEKkpDb4ipTKY7fGGLPa5SJHyMwBGFCn/EamH9+qnVW2OpVvqtHCYoW4G9fdHqwGgvr6gO9e1EBER\nERGdbYRQt0mpDEmp/EFK5UkplUEh1G3ZHp9N98v0fG4hVYhqAEMAPNMpNtcMFksq1EUiDHUzRNMk\nhodjHgDYsKGULXVERERERFkSQrUh1SuyTAi1GKlWOgBwA6jJ9jzZhLonVSGKAPwrgD1IPbx379TK\nzQ8MdTPv8OGxglgs6TKbRXj16qLRXNdDRERERHQWuR3AVwFUIzWlQTrUjQH4cbYnyWb0y+/oi4+o\nQjwJwKZI6ZtarfkhHeqS0ShD3QzZuXOoGgCKiy09HCSFiIiIiM5FeovaSwCsSGWoh6VUvi2EWgLg\nfwEsANAGYLOUyoh+zDcA3ApAA/BlKZVnTz6vlMp/APgPIdS/klL50XTrmzTUqUKUAvgTAMv0TYcA\n/Ga6F8s1g9WaCnWxGEPdDHn77bEaIDXyZa5rISIiIiKaJVEAH5BSCQihmgHsEEJ9GsANALZJqdwj\nhHoXgLsA/I0Q6goANyM1g0A1gOeFUOulVLTxTi6l8iMh1AYAK5Ax44CUyq+yKW7CgVJUIZYDOABg\nLYAjAI4CWA/ggCrEsomOy2fGdKhjS92M6eoKVwMc+ZKIiIiIzl1SKlJKJaCvmvUvCeA6APfr2+8H\ncL2+fB2Ah6RUolIqrQCaAWyY6PxCqN8G8CP963IA3wNwbbb1TdZS9x0AX1Gk3JK5URXiEwDuBvCJ\nbC+SL4w2WyrUxeMMdTOkvz/iAYD6+gKGOiIiIiI6S5XbhFC3p9ekVC47eQ8hVCNSz70tBvCfUiq7\nhFArpVR69F16AVTqyzUAXss4vAuTD3xyI4DVAN6UUvlzIdRKAA9kW/1kUxqsOjnQAYAi5SMAGrK9\nQD4xpEMdu1/OCE2TGBmJVQPAxo2lPafan4iIiIjobCWlokmprAEwD8AGvbtk5vsSqda76QhLqSQB\nJIRQ3QD6AXizPXiylrrgNN/LW0a7nS11M2j//tGieFw6LBZDaOXKwrNy8BwiIiIiImAgMl7r3Hik\nVEaFUP8I4CoAfUKoHimVHiFUD1JhDAC68e5QNk/fNpE3hFCLkJploBFAAMDObKufLNRVqELcOc52\nAaA82wvkE5PDwVA3g15/fTg98mU3R74kIiIionOVEGo5gLge6OwArgTwLwAeB/BZAPfor4/phzwO\n4DdCqD9AaqCUJQBen+j8Uipf1Bd/JoT6DAC3lMr+bOubLNTdC6Bggvfuy/YC+cTodMYAQDLUzYgj\nR/weAKiosPJ5OiIiIiI6l3kA3K8/V2cAsEVK5Ukh1J0Atgih3gqgHcBmAJBSaRJC3QLgIIAEgDsm\nGvkSAIRQLxhn2yIA7VIqiVMVN2GoU6T8x1MdfLY50VKXSDDUzYCurlA1AHi9DoY6IiIiIjpn6a1m\n54+zfQjAFRMcczdSA0xm4ycALgCwH6mekQ0AmgAUCqH+pZTK1skOnmyglHOOqaAg1VLHUDcjBgai\n1QCwdGkBB0khIiIiIpq+4wDOl1JZJ6WyFqkA2YJUN8/vnergORXqzHqoY0vd6csc+XLTpjJOPE5E\nRERENH31UipN6RUplYMAlkmptGRz8GTP1J1zzEVFbKmbIXv2jJQkEtJmtRr8S5e6A6c+goiIiIiI\nJtAkhPpTAA/p6zcBOCiEagUQP9XBWbfUqUJ8TxVirb78b9OpNNcsxcWpUKdpDHWnaffuIQ8AlJRY\n+DwdEREREdHp+TMAzQC+qn+16NviAC4/1cFTaal7HcBfq0KsBLD7VDurQvwCwDUA+hUpG/RtJQD+\nF8ACAG0ANitSjujvfQPArQA0AF9WpHxW374WwC8B2AE8BeAripTTmtTPUlQUB1ItdVLTIIzG6ZyG\nABw9GqgGgIoKG5+nIyIiIiI6DVIqYQDf179OdspecRO21KlC/IUqROaEeX8A4AIwDOBoFrX9EqkJ\n+TLdBWCbIuUSANv0dahCrABwM4CV+jE/UYVIJ66fArgNqbkdloxzzqwZ7fYkDIYEABH3++dU19OZ\n1tUVqgGA2loHn6cjIiIiIpoGfdoDCKG+JYS6/+SvbM8zWbC5Q5HyZwCgClGM1AR6/w/AvwHYBeCf\nJzuxIuVLqhALTtp8HYDL9OX7AWwH8Df69ocUKaMAWlUhmgFsUIVoA+BWpHxNr+NXAK4H8PTJ11OF\n2J65brDZhNfrvfLk/Uw2m0yEQvCUl3/IUVV1yv6pNL54XCwDgM2bV9SM9/c8EZvNVg8AXq/3VLvS\nGcZ7k794b/IX703+4r3JX7w3+Yv3Jie+or9eczonmSzUmVUhnADKAPwewPcVKR8AAFUIxzSvV6lI\nme6u1wugUl+uAfBaxn5d+ra4vnzy9mkzWq1aIhQyx/x+I0Pd9GhaEp2dATcArFtX4ct1PURERERE\nZyMplR79tf10zjNZqPs+Ug/oGZGaBA+qELUAPgvg8OlcFAAUKaUqxLSejZvgfJdlrv+t1Zro7Ox8\n7uT9tETiUgC2Y7t27aqw2fpn6vpzyauvDpbGYskbbTaDL5EYfqqzczjrY9O/+Rnv3lBu8d7kL96b\n/MV7k794b/IX703+muP35qO5uKgQqh9AOhMJ/VXqy1JKxZ3NeSb7yddAAAAgAElEQVQMdYqU9+qD\nnaT3+2cA3wCwB8Dt0ykaQJ8qhEeRskcVwgMgHaq6AWS2887Tt3XryydvnzZhMsUAIDE2xhEwp6mx\ncbgaAEpKrBwkhYiIiIhomqRUCmbiPJMOFqJIqemLGoA7Z+B6jyPV0neP/vpYxvbfqEL8AEA1UgOi\nvK5IqalCjKlCXIjUc3yfAfCj0ynAoIe6eCDAUDdNR48GagCgstLGQVKIiIiIiGaAEOrFAJZIqfyP\nEGoZgAIpldZsjp21ESBVIX6L1KAoZaoQXQC+jVSY26IKcSuAdgCbAUCRskkVYguAgwASSA3Skg6U\nX8Q7Uxo8jXEGSZkKYTbHAEALBhnqpun48XA1AMyf7+AcdUREREREp0kI9dsA1gFYCuB/AFgAPABg\nUzbHz1qoU6S8ZYK3rphg/7sB3D3O9jcANMxUXemWukQoxFA3TQMDUQ8ALF/uZqgjIiIiIjp9Hwdw\nPlKPukFK5bgQatZdMyecp+5cZUi31IXDDHXTEI1qwueLewBg06YyPlNHRERERHT6YlIqEvqgKUKo\nzqkcfMpQpwpRqQrxc1WIp/X1FXr3ybOSwWJhqDsNu3YNl2maNDscxpH5853hXNdDRERERHQO2CKE\n+l8AioRQbwPwPID7sj04m5a6XwJ4FqkBTADgCICvTrHIvHGipS4SYaibhsbG4RoAKCmxsOslERER\nEdEMkFJRATwM4BGknqv7eymVH2Z7fDahrkyRcguAJAAoUiaQGg3zrJRuqUsy1E3LsWMBDwBUVtoY\n6oiIiIiIZoiUynNSKn8tpaIA2CaE+qlsj81moJSgKkQp9P6d+vQCvumVmnsGqzXVUheNMtRNwzsj\nXzoZ6oiIiIiIToMQqhvAHQBqkJrm7Tl9XQGwD8CD2Zwnm1B3p36BRaoQrwAoB/DJadScF9KhLhmL\nMdRNw+BgtBoAVq50c5AUIiIiIqLT82sAIwB2Avg8gG8CEACul1LZm+1Jsgl1TQDej1TfTgHgMM7i\nUTMNFkscYKibjnBYM/h88SoAuOSScrbUERERERGdnjoplVUAIIR6H4AeALVSKpGpnCSbULdTkfIC\npMIdAEAVYg+AC6ZyoXxhtNnYUjdNr746WJFMwuR0Goc8Hns01/UQEREREZ3l4ukFKRVNCLVrqoEO\nmCTUqUJUIdW3064KcT5SrXQA4AbgmOqF8oXRbmeom6Y33xzxAEBJiZWtdEREREREp2+1EOqYviwA\n2PV1AUBKqbizOclkLXUfBvBnAOYB+EHGdj9SfT3PSidCXTzOUDdFLS2BagCoqrLxeToiIiIiotMk\npWKcifNMGOoUKe8HcL8qxCcUKR+ZiYvlA5PDEQMAmUgw1E3R8eORagBYsMDZnetaiIiIiIgoZbLu\nl3+qSPkAgAWqEHee/L4i5Q/GOSzvGZ1OttRN0+BgtAYAGhoK2f2SiIiIiChPTNb90qm/us5EIWeK\nyeViS900BAJx49hYvAKAvPTS8t5c10NERERERCmTdb/8L/31H89cObPPXFCQaqlLJMy5ruVs8sor\ngxVSwuhymQbKylJz/RERERERzQVCqF4AvwJQCUAC+G8plf8QQi0B8L8AFgBoA7BZSmVEP+YbAG4F\noAH4spTKs7NV3ynnm1OF+J4qhFsVwqwKsU0VYkAV4k9nq6DZZna72VI3DXv3jlYDQGmphV0viYiI\niGiuSQD4mpTKCgAXArhDCHUFgLsAbJNSWQJgm74O/b2bAawEcBWAnwihzsigKOPJZhLxDylSjgG4\nBqn0uRjAX89WQbPNXFjIUDcNLS3BGgDweOwMdUREREQ0p0ip9Eip7NGX/QAOITX923UA7td3ux/A\n9frydQAeklKJSqm0AmgGsGG26stm8vH0PlcD+J0ipU8VYrL985qlpCQV6jSNoW4KenrC6ZEvGeqI\niIiI6BxTbhNC3Z5ek1K5bKI9hVAXADgfwC4AlVIq6em+epHqngmkAt9rGYd16dtmRTYtdU+qQrwN\nYC2AbaoQ5QCmPMt5vjAXFsaBVKhLxuNnbzo9w4aGoh4AWLWKI18SERER0dwkhOoC8AiAr0qpjGW+\nJ6UikXre7ow7ZahTpLwLwEUA1ilSxgGEkGpOPCsZzGYpjMYYAMR9Pg6WkoWxsbjJ709w5EsiIiIi\nOkcNRKRULkt/jbeHEKoZqUD3oJTKo/rmPiFUj/6+B0C/vr0bgDfj8Hn6tlmRTfdLKFIOZywHAQRn\nq6AzQRiNMalpltjwsMVaVsaRHE/h5ZcHKqWEwe029RUVWRK5roeIiIiI6EwSQhUAfg7gkJRK5nzd\njwP4LIB79NfHMrb/Rgj1BwCqASwB8Pps1ZdVqDvXCJMphlgMcZ+Pz9VlYd++0RoAKC21suslERER\nEc1FmwB8GsBbQqh79W3fRCrMbRFCvRVAO4DNACCl0iSEugXAQaRGzrxDSkWbreLmbqgDEB8bY6jL\nQmtrsBoAPB4bQx0RERERzTlSKjsATDQexxUTHHM3gLtnragMEz5TlzkXnSrEppPe+9JsFjXbDOlQ\n5/cz1GWhtzfiAYCFC10MdUREREREeWaygVLuzFj+0UnvfW4Wajlj0i11iUCAoS4LQ0PRagBYvbqI\noY6IiIiIKM9MFurEBMvjrZ9VDGZzDAC0YJCh7hQGB6MWvz9RLgS0Sy4p68t1PURERERE9G6ThTo5\nwfJ462eVdKhLhEIMdaewY8dAFQDhdpv7XS7zrD3cSURERERE0zPZQCnLVCH2I9Uqt0hfhr5eN+uV\nzSKRbqkLhxnqTuGtt3weACgttbDrJRERERFRHpos1C0/Y1WcYQazOQ4w1GWjrS018mV1tb0n17UQ\nEREREdF7TRjqFCnbx9uuCmEAcAtS8zCclQwWS6qlLhJhqDuF3t5INQDU1bm6c10LERERERG914Sh\nThXCDeAOADVIzYj+HIAvAfgagH0AHjwTBc6GdKhLRqMMdacwNBSrAYA1azjyJRERERFRPpqs++Wv\nAYwA2Ang80jNmC4AXK9IuXeS4/IeQ112ensj1mAwUSoEtIsuKhvIdT1ERERERPRek4W6OkXKVQCg\nCnEfgB4AtYqUkTNS2SwyWq2p7pexGEPdJPSRL1FYaO51Ok0c+ZKIiIiIKA9NNqVBPL2gSKkB6DoX\nAh0AGGy2VEsdQ92k9u4drQWAsjIrB0khIiIiIspTk7XUrVaFGNOXBQC7vi4ASEVK96xXN0uMeqiT\n8bg517Xks/37R1cCwLJl7iO5roWIiIiIiMY32eiXxjNZyJlktNvZUncKwWDC2NkZWg4A111XfSDX\n9RARERER0fgm6355zjoR6uJxhroJbNnSuSiRkLbCQnPPhReWDeW6HiIiIiIiGt+cDHUmhyMV6hIJ\nhroJ7Ngx0AAAS5a42EpHRERERJTH5mSoMzqd6WfqGOomcOSIvwEANm0qZ6gjIiIiIspjczLUmV0u\nttRN4o03hotHR+M1JpOIbt7sbc51PURERERENLE5GepMbneqpY6hblyPPda9EgDmzXMccrvNiVzX\nQ0REREREE5tsSoNZowrRBsAPQAOQUKRcpwpRAuB/ASwA0AZgsyLliL7/NwDcqu//ZUXKZ0/n+maG\nuknt3Tu6CgDOO6+QXS+JiIiIiPJcLlvqLlekXKNIuU5fvwvANkXKJQC26etQhVgB4GYAKwFcBeAn\nqhCnNd2CpbiY3S8nEAjEjV1dqakMrr9+XlOu6yEiIiIiosnlpKVuAtcBuExfvh/AdgB/o29/SJEy\nCqBVFaIZwAYAOzMPVoXYnrlusNmE1+u9crwLxUtLDS8DgJS2ifaZqx599Fh5IiGtXq9r7IYbVq+d\n6fPbbLZ6APB6vTN9ajpNvDf5i/cmf/He5C/em/zFe5O/eG/OXrlqqZMAnleFaFSF+IK+rVKRskdf\n7gVQqS/XAOjMOLZL3zZtJpstCSEgEwmDFouJ0znXueaZZzo8AHDRRVU9p9qXiIiIiIhyL1ctdRcr\nUnarQlQAeE4V4u3MNxUppSqEnMoJFSkvy1z/W6s10dnZ+dxE+wuj8WMykbAe27v3RbvHE53Ktc5l\nW7e2XwQA1dWGP3R2dh6e6fOnf/Mz2b2h3OC9yV+8N/mL9yZ/8d7kL96b/DXH781Hc13A6chJS50i\nZbf+2g/g/yHVnbJPFcIDAPprv757N4DMNuB5+rbTIozGGADERkb4XJ1u9+7hktHReDWnMiAiIiIi\nOnuc8VCnCuFUhShILwP4EIADAB4H8Fl9t88CeExffhzAzaoQVlWIhQCWAHj9dOswmEwxAIiPjjLU\n6X7/+66VAOD1Og66XGYt1/UQEREREdGp5aKlrhLADlWIfUiFsz8oUj4D4B4AV6pCHAXwQX0dipRN\nALYAOAjgGQB3KFKeduAQ6VDn9zPU6fbtS01lsHp1EacyICIiIiI6S5zxZ+oUKVsArB5n+xCAKyY4\n5m4Ad89kHelQl2CoAwCMjcVN3d3hZQDw8Y/PY6gjIiIiIsoghPoLANcA6JdSadC3vWeubSmVEf29\nd821LaVyWnNtTyaX89TlVLr7ZSIQYKgDsGVL5+JEQlqLiszdF1xQPJrreoiIiIiI8swvkZo3O9Nd\nALZJqbxrrm0h1PfMtS2EelpzbU9mzoY6YTanQl0oxFAHYMeOgQYAqK8veCvXtRARERERnVnlNiHU\n7emv8faQUnkJwPBJm69Dao5t6K/XZ2x/SEolKqXSCiA91/asmLOhzqCHOo2hDgDQ3BxoAIBLLiln\n10siIiIiouxUSqmckbm2J5Oreepy7kSoC4fnfKh77bXBUp8v7jGbRfiTn/S25LoeIiIiIqIzayAi\npXLZ6ZxBSkUKoU5pru2ZMndb6iyWGAAko9E5H+oee+x4AwB4vY5DTqeJUxkQEREREWWnTwjVAwD6\n66zOtT2RuRvq0i11kcicD3X79482AJzKgIiIiIhoiiada1sI1SqEOmNzbU9k7na/tFpToW6Ot9SN\njsZOTGXwiU94GeqIiIiIiMYhhPpbAJcBKBNC7QLwbaTm1t4ihHorgHYAmwFASqVJCDU913YCwB1S\nKrPWI27uhjp2vwQAbNnSuUTTpKW42NK1enWRL9f1EBEREc1VgZYWx/Enn1w8um/fYs9HPtLovfHG\n9lzXRO+QUrllgrfGnWtbSmXG59qeyNwNdXpLXTIWm9Oh7pVXBlcBwNKlnMqAiIiI6EwafuON4t6t\nW5f4mpoWhzo6FsdHR0+Mjmgwm+MMdZStORvqjDYbQx2A5mb/SgC49FJOZUBERESUrXQgGzt4cFEy\nHjcZ7faI0W4PmxyOsMnlCptcroi5sDBsKS4OW0pKItby8nCkt9fR/+KLi/1vv70k1N29WAsGS991\nUoMhYSsvb3UuXNhc8YEP8LMZZY2hbg6HuldeGSwbG0tUmc0ifOONnMqAiIiIaDxS09C3bZun/8UX\nF/sPH14S6up6byCbBmE2h+1VVc2uRYuaSzZubK6+5po2S1FRYiZqprll7oY6uz0V6uLxORvqnnii\nuwEAamudB+12YzLX9RARERHlmhaNCv/hw27fgQOlw7t3Lwo0Ny8OHz++OBmLuTL3ywxk5qKiQCIY\ntGvBoF0Lh21aJGLXIhF7Mhq1a9GoPRmP25KxmF0YDAl7dXVLQX390fKLL26u/NCHuo1Wa07mNaNz\ny9wNdQ5HDADkHA51+/f7GgBgzRpOZUBERESnT2oahNGY6zImlAgGjYOvvloebGsrivT0FEUHBopi\nIyPF8bGxwoTfX5QIBou1SMQNKd8z7ZfRbh+119Q0M5BRPpqzoc6kh7q52lI3OhozHT8eXgoAN9ww\nrynX9RAREdHZJx4IGNsfeGDpwEsvrQk0N69OxuN2S2lpp6O6ut21ZEl76caNHeXvf39vrsKPv7nZ\n2fP003Wj+/YtDrW3L4oODMyXmnbKz34Gq9VvcjpHbR5Pe+GKFc2VV1xxtPTCCwfzObDS3DZ3Q53L\nlQp1icScDHUPPdRRr2nSUlJi6TjvPE5lQERERNkJdXfb2h94oGHotdfWBNvbG2Q8bs98P9rXtzja\n17d45M030bllC4TJFLWUlHTaa2o6ChYvbjffequ7Yu3asZmuKxmPi/7t2ysHXn55kf/w4UWhrq5F\nibGxqpP3M7lcgyaXa9jkdo9a3O5RS2npqK2iYtQ+b96Is67OV7hihc/sdvO5NjqrzPlQJ+doqHv1\n1RNTGbDrJRER0Tki1N1tG92zp8xgsyVMDkfC6HAkTAUFcbPLlTAVFCSMNps2ndYm34ED7o6HHlo9\nsmfPmlB39zIkkyc+Q5qLiroLV6580/ORj+wtqK8f7d++vdbX1FQb6uiYH+nrm6+FQiXR/v7F0f7+\nxaNvvonO3/0ORqtVs5SWNjjr6ppL1q49Wn3ttS22iorYlP6snZ32nqefXjC6b19dsLV1YaSvry4Z\nizkz9xFGY9xaXt7mmD//WNF55x3zXHVVS0F9fWDKfwFEeW7Ohjqz2z2nQ11zc6ABAN7//gqGOiI6\no5LxuAAAg9nMZ1HonBTq7LQP7NjhSUajxmQ8bkzG40aZftW01GsiYZSJhBEAStavb/N89KNd0/2e\niA4Pm1t//vNVAy+/vCHY3r4qM3CNQwqjMQ6DISGMxoQQIgkhJIRICv0VQsjM7UgmjXGfrwqASJ/D\nVll5tPC88/bO+/jH95VfcslA5gXcy5c3ATjxaIf/yBFX3wsv1I41NdUGOzrmJ/3+ZeGBAUf4+PFl\n4ePHlw3u2IEjP/yhZi0t7XDMn99ctHp1c/XVVzdnhi8tGhV9zz9fPbRzZ53/yJG68PHjC0+qCYD+\n3Ft19THX4sXHSjduPFb1kY90ml0ubTp/r0Rnk7kb6goL52z3y5deGij3+xMVZrMI3XDDvNZc10NE\nc4P/yBHXwe9+96Mje/deZnQ4Risuu2zrsq9//RVrSUk817XR3KVFo6Jv69YaV339qHvp0mm34Iy8\n+WZR55Ytq0fefHNN+PjxpZAy6+aw7sceQ9N3vuN3zp9/sGjNmqZ5H//4ocKGhkm7J2rhsKHtV79a\n1vv88xsCzc3ny0TCpr8lzYWFPVJKAU0zy2TSJDXNLDXNJJNJE6Q0SE2zQNMsMj6Fbz2DIeHweg+W\nrF37Zu3NN7/lXr7cn+2hBfX1gYL6+oMADgKA1+u90t/RYX3tBz/o9u3fvyTY3r44NjzsjQ4OLowO\nDi4caWy8svUXv4DZ7e61VVe3xn2+kujAwAKZSFhPrslaWtrh8Hpb3cuXt5Rfdllr6fr1Q3zujeai\nuRvqiovnbEvdk08ebwCA+fM5lQERzb5If7+l6Z/+6YrBV165Kv3BUwsGS3v+8Idb+p5//pqy973v\n+WVf//qLDq83nOtaaW7QwmFD+29+s6Rv27a1/iNHLkhGowUAYHK5BuzV1S2uxYtbStavb6266qqu\niVp5pKah74UXqo4//vga34EDa6KDgwsz37aUlHQIszkmDAZNGAyaMBpPvCJjWcbj5lBXV70WChX7\njxzZ6D9yZGPnli2wFBd3uRYvPlh20UVN8268sdlSVJSQmoaOLVvqep56av3YoUPr03UDgKWsrK3k\nggteX/CZz7xRtHr1hM/Ka+GwIe73mxKBgCkRCJilpgmZSBiSmiZkPG6QyaRIbzvxKiVKN2wYsFVV\nRWfqHhTU1kaXfe1rbwJ4EwDCPT3W4088UTfS2Lgk0Nq6ONrfvzA+NlYVz3gmzuRyDdo8nhbXokWt\nJevXt3quuqqTz74RpczZUGcpKooDgNQ0S74PvzuTDh70Fbz0Uv+VAHD++cVv5boeIjp3aeGwoem7\n393Uu3Xrx5KRSCEAOLzeA4tuv/33/ubmsuNPPPGR2NDQ/P7t2z8+8MorV5WsXbt96Z13bptKCwBR\ntrRw2ND+4IP1fS+8sNZ/5Mj5mYHI6HAMJ6NRVyIQKPcfOVLuP3JkY89TT6HpO99JWMvK2h1eb0vh\nihWtFZdf3ho4dqyw97nnzh97++01ibGxyvQ5hNEYd3i9TcXr1u2df8stb03lua10QOx99tmVYwcP\nrggfP14fGxmZN7x797zh3bs/dPTHP47Zqqqa4z5fRSIQKEsfZ3K7e4tWr3699qabdle8//392VzL\naLcnjXZ7DFN8fm222T2e6KIvfOEQgENAalTNnqeeqh3Zs2e+3eMZrrzyytbCFSv4s4FoAnM21Jmc\nTg1CaJDSmAiHjXOhv/XoaMz0pS/t+WIwqJWWl1tbv/zlJW/kuiaiqQh1dtp7nnlmvnPBgtGyiy4a\nMDmd5/z37dlIahoO//u/n9/16KPXp0ees5SVtS349Kcfrfvc5w7ru3Uu/epX32z5+c+Xdz788Eci\nPT1Lh1577SM7b7nlg4WrVu1Y8qUvbS3duHE4h3+MnJFa6p/16f6yUWoaRvftK+rfvn1BoLXVY3a5\nQtbKylGH1ztasGTJaMHSpWMzPcx8dHDQEmxtdYWPH3dG+vpcseFhZ2x01KUFg7ZEKGQ/MSFzalJm\nmxaL2WUsZk/G4/ZkPG41OZ0j1vLyTofX21mwdGln+cUXdxStXj063b8LLRYTx+69d1n/Cy+s8x89\nen4yGj0xebSpoKC/cOXKxuqPfeyN6quv7krGYobe556rHnrttTr/0aN14ePHFybGxqqi/f2Lov39\ni0YaG9H261+/6/wGiyXorKvbX3bRRXvnf+pTB6c60EeaMBpRdeWVvVVXXtkLYFtsdNTU9fDDiwd3\n7lwROHp0ZWxkZF64u3sFkHpmzL1y5e6a6657veZjH+s4V38pbXa5tNrNm1trN2/mYyJEWZizoQ4A\nhMkUk/G4PTY0ZDG7XOd0tx9Nk/jc517/7MBAtM7hMA7/8IcX/KSoyMIuC5T3tHDY0PrLXy7v3br1\nfcHW1jVS08wAACE0s9vdbykp6bVVVfU4FyzoKVy5sqds06Y+a1lZXv0GOt/4m5udXY88shyALFm3\nrrvsoov6jXb7jHTFbvv1rxe3/s//fCI6MFAHpD44z7v++t8v/drXGk/+8CmMRiz6whcOLfrCFw51\nPPTQwrYHHvhIqL199ejevZfvvu22SwuWLn194Wc+87znox/tmokPrlo0KnqffbYmGYsZTU5n3Ox2\nx8yFhTFzcXHMUlQUz9UvCcYOH3b1bt260PfWW3Wh9va6SH//AgghLUVFPdby8h57dXWPa9Gi3uLz\nz+8p2bBhaKLBNAItLY6+555bMLp//4Jge/uCaH//Ai0cLpzwwkIkjTbbmMnpHDEVFIyaCwtHLcXF\no8JkSkhNSw3koWnGE8vJ5DvrmmZMxmKWRDjsSobDLi0adSajUdeJ789pSgQCZYlAoCzY2nr+wEsv\noeXee2GwWgPWsrJOe3V1p2vx4s6S9es7HLW1gXBXlyvc0+OKDg464yMjzpjP50r4/a5EIODSQiGn\nxWbzBrq6CuKBwInHLExud1/hypWNNR/7WOPJ/66Mdnuy5tpru2quvbYLwEsAEGxrc/Q880xqdMW2\ntrpof/8Cg9kcKaiv31tx+eV7a2++uXmmvncyWYqKEnWf//zbdZ///NsAHvUdOOA+/oc/LLFVVo7N\n/9SnmjnIEBGdTEh5bv5csFqticbGxi9Ots/W9eu/l4xECi984IGvT9b//FzwxS++cfXLLw9eazKJ\n6He/u+pfrr66ujsXdXi93isBoLOz87lcXH+2SE1D+Phxe6i72xHt63NEBwcdsZERR9zncyb8fkci\nGHQYHY5w6caNR6uvvbY9H1uG8+3e9Dz9dHXnli3v8zU1bcz8YGopLW1PRiKuRDBYOsGh0uR0DltK\nSo676uuP1G7e3Fh20UVDZ6jsWTET96b/j3+s6H7iidW+t95aHentXYyMEeOE0Rg3FxUdt1VUdDtq\na7vcy5d3lV9ySfdE3ceS8bgINDe7Ai0t7nBXV2Gkr68wOjTkDhw9uiTU2bkKSE3cW3nllU+s/Na3\ndkwlLPU8/XR1y333XeU/enQ9pDQAqa5xrkWLDpSsX99Ue/PNh+weT9bP9fgOHizoevjhlSNvvtkQ\n6uhYcfJw5+8ihCZMppgwGuMG/VX/So0SaDLFhdGYMJhMCZH6ipcuWuQx2u2Jsf7+g+bCwoCluDhg\nLS8P2Corgw6vN+BcsCCY+aE/HggYe595Zt7w66/X+Y8dq4scP74wEQiUZ/vnEUZjzFxY2GcpLe2x\nezw9Bqs1Fmxrmx/p7V2Q8Psr3rO/2RyyVVS02Tye7mQkYov7fEWJYLAoEQwWZXY/nDEGQ8JotQYM\nNlvAaLcHTHZ70OhwBI12e8jocERMTmfY5HKFzQUFYXNhYdhSXByxlpWFreXlEUtZWXR4167y4cZG\nb6C52Rvu6fHGBgdrk7GY43RKMrndvYUNDY01117b6Lnqqu5ztWXrbJJv/9/QO+byvVm1atW/SSkn\n/j8iz83pUPf8+9733UQgUL72P//zW+WXXjow2b5ns3vuObTuwQfbbwMgb7990X9+6UtLcvYsXb7/\nsJCahpE9e0qGdu/2xH0+R8LvtydCIZsWDDq0SMSmhcOpLkPRqD0ZjdqTsZg9GYs59A8d4pQXQOpD\nma2yssW1ePHh0gsvPFJz3XVt2TzoHRsdNQ2+/HKVr6mpKtjW5okMDFQYLZaoubDQZykuHrNWVPjs\nHo/PsWDBmHvZMp+lqGhKLbHTuTdS0xDq7HSM7ttXGmhpKQ13d5dG+/tLYyMjpfGxsdJEIFAiTKao\nubBwwFpa2m+rrOx31Nb2u5cv7y9Zv37w5Ba1scOHXS333bdhePfu98WGhmrT200FBf3FF1zw6oJP\nf3pXuktedHDQMvjKK5W+piZPsK3NE+nt9cSGh6viY2MVJ486ZyktbS9avbqxdvPmxrJNmwan8vcy\nHcH2dnvg2DF3RG9FiA0Pu+I+nyvu9zv1VgRXIhx2JSMRpzCZ4paion5refmAvaam37V4cX/xmjX9\n7uXLx9IfPqdzb7Rw2ND58MN1/X/84+qxw4fPe9cEvEJodtIeBPUAABtkSURBVI/nqDCbY9HBwRpt\ngoBstNtHLaWl3eaCAl8iEChIhEKFWijk1iIRdzpwnUyYTNHSCy/c2vDtbz93OoMqDL7ySlnzT35y\n5djhw2vfFT6E0GxVVc2FK1YcqPrwhw9UfehDxzM/pGvhsKHr0UcX9r/4YoP/yJGGzH9HQGqgBYPV\nGpSJhEUmEpZkImGRmmbWR9XL6nt4qoTZHDJarUGD2RyN+XxVJw83L4zGmLWiotXh9bYWNjS0Vl5x\nRaswmZLDu3Z5xo4c8YS7ujzR/n5PbGTEM1nLmzAa45bS0g5HTU1bwbJlbWWbNrWVX3xx/0QhJj42\nZho7dMgdOHasKNzVVRwZGCiMDQ0VS00zCqMxNbCHyaTpoTYpjEbNYDKltplMmtFuj1lLSoLWysqA\n3eMJOBcuDFhLS2MzGZrSP5MHXnnF6z982Bvu6vJGBga8Mh63GazWoNFuDxhttoDJ6QwYnc6g2eUK\nmIuKAuaiouDiD3xgWUFtbThUVPR7Brn8ku+fBeayuXxvGOryVDahbtsll/x9fHS05rx77vmn6quv\nzknL1Wx76KGOhf/8zweVZBKmD3+4aouqrtmWy3ry6YeF1DQMv/FGycCOHfP9b789P9TVVRsdGJif\n+czFVAiTKWqwWEIGiyVktNlCRpst/dvpkMnpDMVGRgpD7e1LM0fyAvSJUSsqWlyLFh0tWb/+SNmm\nTd2j+/aVjx06VBXq6EiHFY/+cHzWHzqF2Rwy2e1jRqfTZ7Raw+mWBUPmq8USN5hMCYPZnKg677xF\nBqNR9uzffzQZj5uT8bgpGY+bZSJhkvG4KZlImGQiYU6m1i1xv78kEQiUZgyjPWVGu33UXFTUZykp\nGUgEAu5QR8fKdCATZnPIvWzZ7pprr93p/eQnW7P9UJYIBo2Dr75aPrJnz7yhXbtWB1tbV2cOg20p\nKekoOu+8Ru8nP9k4E7/MSc+/5Gtqmh9qb58f6e+vnSgkTYUwmaJmt7vfXFTUX71xo9M1b16o/+jR\nJmEwJGEwSGEwJIXBIDOXhdGY1MJhy8jevSuCLS2rkrHYiX/LBosl5Fyw4K2SDRv2zf+TPzmYOdJk\nsL3dPvDSSzW+pqZ5ofb2eZG+vprYyEjNe4YPz2CwWIJGu33M5HT6TC6Xz+R2j1lLS0cWfu5zr8/k\nYAbJeFx0P/54bf8LLzSMvf12Q7S/fyEyvg+MDsewq66uyVFb2+U/fHhJsKNjhYzHT7TsCKMxbvN4\njhQ2NByovuaaAxMNJiE1DYlw2BgbGrLEfT5LfHTUkggGzVo4bNIiEZMWDpu1aNSUjEbNyVjsxGtZ\nXV1DIhQy9jQ29iSCQVciFHJp4bBTi0ScyUjEpbcMvuv71ux299pralpcS5a0lF14YWvlBz94PNsu\nfMH2dvvQzp1VY4cOeUIdHR4tGrW56uo6SjZsaK284ooePmf6jnz6/4bejfcmf83le8NQl6eyCXV/\nvPzyu6KDgwtX/N3f3XMuPoi7a9dQyR13NH4zGk0WrFpV+NKvf33hg0bjrPwiOmu5+mERDwSMw6+/\nXjayZ0+1//Dh+aHOzvnRgYHazA+9aQaLJWgpLe0yORx+g80WMdrtYZPDETY6HGGTyxU2uVwRS2Fh\n2FxUFLaUlETsHk/I7vWGsu1S6Tt4sKDnySfrR/fvrw+2ty+Jj47WZPWHECJpKigYsJaU9FgrK3sd\n8+b1adGoOT48XBgfG3PH/f7CRCBQqIXDbi0cdk9ljqTTIUymqMnlGjS73UOW4uJha3n5oN3jGXbW\n1Q26V6wYjg0N2XxNTeXB1taKSE9PRXRoqCI2OlqR8PvL3lOjEEmH13ug4rLLdtbddtv+qbY2jic6\nPGxuu//+lQM7dqwNtrSclxlCLSUlnYXnnddYunHjUaPNFjdYLJrBatWM6VebTTNYLEmDzaYZ7XYt\n7vOZB158sdbX1FQb6uiYH+nrm6+FQiXv+TsxGmNGh2PUqHdBMzocQZPTGTAXFATMhYVBc3FxwFpa\nGrBVVgbjfr/Vf+RIRbi7uyLS318RHx4uj4+NVZ5ulzMg1cJZUF+/r+Kyy/bV3nTTsak8+5OMx8XQ\na6+VDe/eXRMbHi6wlpf77NXVY84FC8YKli4dy9Uw4oGWFkfn7363YviNNxqCbW0rk5GI++R9TAUF\n/a7Fiw+Uve99B7w33XRkNufBO9XPtGQ8LkKdnfZQe7srOjRkL1m3bsC5YEFotuqhd8zlD6f5jvcm\nf83le3O2h7q5PVCK2RwDgETGQ9Tnip6esFVR9n4pGk0WVFfb37733vUP5TrQzbb42JhpePfuMt/B\ng+WhtraKSG9vRXRoqEIfAroU47RyGSyWgLW8vMPh9bYXLF3aXnbxxR2zPXFp4YoV/sIVKxoBNAKp\nlp7uJ55YMrpvX32ora0+7veXmwoKBqylpT02j6fHtWBBb+GqVT1lmzb1Z/tBOhmPi2BrqzNw7Jg7\n1NlZGPf7bSdaGGIxk94KZ0rGYmYZj5uTiYSpqKZmodQ0g+//t3fn0XHV1x3Av3dWzYz21bYkW5Yl\nywiwjVccLziGpKy2k9AGQkigDU3S5MTQ6JS06SlpTjmFVulJTuMCKSG4DU0KJATHoeSw2OCQYGwL\nb3iTLNmSJdlarMWjkTTb7R/zFAZZsiyB/N5ovp9z5sx7v7fMnbke69z5/X7vNTc3iNMZtjmdIeM5\nbHM6QzaXK2xzuUI2lyts93hC3pkzuzPnz+/wzZoVGOPzOp+3enU7jJvODon099u6amqyew4dyvc3\nNOSLiM66++6aj/qS1e7s7FDFAw/sq3jggX3B7m5Hw9NPX9mxc+dif339guC5c8XtO3YUt+/YMeHz\ni8Mx6MrJafLMmNGYVlZ2Knv58lP5a9eeGedVBS/4UclfX+89t2dPgb+2Ns+bkrKiv60tpevkyRao\n2lRV/vgcjdqgKmo8Q0R9paX1hbfddiB/7dozE/23bHM6NW/16nYjd5aRWloauOLBB/cA2BMNhaTl\nN78pPvvaa1cOtLRMTy0rq59x663vWSlmm9OpqaWlgdTSUhZyREQ0aZK6qLM5HEEAiAQCU6qoGxyM\nyJe+tPu+7u5QYXq648wTTyx5wudzTIkhOX0nT3q7ampy/XV1eYHm5tzBtra8YFdXbqi7Oz/c15eN\n0YcnqsPn63RmZZ3xFhU1ps2bdypv1apT2UuWnDN7rkXa3Ln++BuwfhRsTqemzZ3rNy500XIpx1zu\nX+fsHk80d+XKDmOO2+ExD/gIuDIzwxX337+/4v779we7ux0nt2ypbN+5c3Hw3Ll8jUbtGo3aMexZ\no1E7VGPPIhF3dnazp7CwMbW8/FTO8uWn8tasOftRXxYeiBUvqaWlDQAaiouLM4Dk/OX0YmxOpxZt\n3NhYtHFjo9mxEBERmSmpi7qhnrqpVtR9+ct7bm9sDFztctn8jzyy4IclJb6E+4W4c9eu7JZt2yr7\nW1ryBzs6ckM9PXmh3t7c+LkyI1BHamqHMyOjzZ2T05YyfXqbd9astozKyvbspUs7zBouRtbkyswM\nz9206cDcTZsOmB0LERER0YeR1EWdzeWKFXUDA1OmqPv2tw+s3ru36wYRRDZtKn989eo8ywxDGsvZ\n118vaH7hhWu6Dx5cFOzsnDXSPuJwDDrS0tpdGRkdrpyc9pRp0zq8xcUdGZWVbVlLl3Za8VYBRERE\nRESTKbmLuqGeuv7+hC/qIhHF5s2183/965bPAcBnPlP031/4wuxas+O6GI1E0PrSS0Ut27Yt6jl8\n+JpQd/eMoW3icAx6Z8485C0ubvIUFnakzpnTkblgQXtaWZnf7OGSRERERERWktxF3VBP3eBgwhV1\nfn/Ivm1b68xduzrLamvPl7e2DswJBqOpALB8efbLDz101R/Mik0jEUSDQVs0EhENhyUaDNo0EpFo\nMGjrczicnQcOpO2urv5M75Ej18TfdFeczkDqnDn781atqpl1991HJvOKdUREREREU0VyF3VudxAA\n2rZvv+3Nm2+el1pefjx3xYrjM267rdFq9/o5c2bAvXVrc+nevV3lDQ3+sra2wdmRiH6gGPV47N1X\nX52x67HHlvzqcsXVc+hQet0TT6zs2rNnZbivL2e0GxKPxuZ2n08rL9+Xv3Ztzcy77jrG4ZNERERE\nROOT1EXdjJtvfrfn0KEl4d7egkBT01WBpqar2l5/HUcefXQwpaDgRGpZ2fGca6+tLVy//uR4LiUP\nxK7K9mFi6+0NOZ7dcmTenlePfuxEi5afHUhPU8gHruyYnu48M3Omt7ayMr32+usL6pYvz+m8HLct\n0EgEDVu2VLRs3Xqdv75+4Sj3Q1OIRCGiYjxDJGp3Oh3O1NSgu7BwV8ENN9TM/Oxn6ybjyoFERERE\nRMkiqYu6wg0bmgo3bPiHrpqazNaXX57bc/Dg3L7Gxrnh3t6C/ubmyv7m5sr2N97AserqkDs/v97h\n9Z6PhkKuaDjs0lDIpeFwbDkcdmkk4tJIxKmRiFMcjsGUgoJ6X0nJicyFC0/MuOWWBm9xcf/FYolE\nFC//X3Ph9l8eWl57rGdBU6+3IASnALH76toQQRGaMRsNsYejuT/LaR90DWR53E1507yvFtlON8xp\n88yYcR62sTvL7Ckp4cz587vHczNif329t27z5hUdb799Xbi3t8BoVl9Jyb7pt9zyxqzPf/6Y3e2O\nis2mo817S+abWhIRERFR4hKpvhHADwDYATypWvWIySH9UVIXdUOyFi3qzlq06B0A7wBA6+59Wcde\n3H7lmffq5/W2dszu6wvn9rd6KuyIwIN+eBGBF2F40A83BmHDBzuaNBx29zc3X9Hf3HxFx1tvoW7z\nZnVmZrZ4i4tPpM+bdyJ/7doTWdd+rP3wUX/Gi8/Wzn9vV+OyU+32En8kxRhOmQEAmI4WzPGc7aks\njhydn9naZT/XkhPs6soP9fbmayjkCXZiVrCzc5a/rg6dE3njIlGHz9fpzMjocGVldbjz89u9hYUd\nqWVl7VmLFnX4SkoCGomg6Re/mN303HPX+Wtrl2gk4gQAu8fTnbV48e/m3HffzqxFi7on/OETERER\nEVmcSLUdwGYAnwBwGsBukeqtqlWX5V67Y5myRV0olGFbv37nV8baTxUyMBDxDg5GvIODUW8wGPWF\nw+oGrkDscXECqNOJfrfLFnC77QG3x+53IoxowJ8eHehPjQZDnnBE3eFuR2G421EYOuhcE3quB2G8\nGncWHwAgHT0oszWE5uYFTq5YlrVr6Z/fVpNWVtZ3QcyRCM7X1aV21dTk+2tr8/ubm/MH2tryg11d\n+dFg0HMpn4+Gw65If39G2O/PC/v9ef3NzRe+N6czYHe5+sN9fTlDbZ7CwsPTPvnJN8q++tUD4+nl\nIyIiIiKyrrwUkeodQ2uqVWuH7bAMQJ1qVT0AiFT/HMAGACzqJpOqWxoa+q6ZyLEiiLpctoArVqj1\npaTYAikp9kAkoo5YARj1DgxEfMFg1BsOa0owBG8wFPWe74sCGLpgY4rxGJ0bAyjBSZT52jsWlMmB\nlZ9a9Iei9d9sGms+ntjtSK+o8KdXVPgB1E/kPQJAsLvb0VVTk9N79GhuoLExb+DMmdxgZ2desKcn\nN3z+fJ6GQt5wKOS1uVz+zAULfj/7nnvezFuzJmHue0dERERE9BEpBNAUt34awHKTYrnAlC3qHI6e\n6F13lfxorP1sNtGMDGd/bq47MG1aSl9RkScwbZpn4FIvONLXF7afPh3wtLQMeNvbB3wdHYPeYDDq\n8HgcIa/XHvR47CGfzxHy+RyhtDRHKCPDGUzz2cLhw7szA8dP5U77k40nfSUlgQ/9hifAlZkZLli3\n7mzBunVnh28b6g30Hz+embt69RlXZuYlXSiGiIiIiCjxtA+M0DuXMBKmqKsW+cDExCrVi05MtNkG\ntapq3ruTHZfP54hUVKT7KyrS/eM6sOC6Nnz8urZJCutDG9YbSERERESUzJoBFMetFxltljCue4qZ\npVpkaGLiTQAqAdxZLVJpblRERERERJQkdgMoF6meLVLtAnAHgK0mx/RHCVHUwZiYWKVaX6UaBDA0\nMZGIiIiIiGhSqVaFAXwdwG8BHAHwrGrVe+ZG9b5EGX455sTEapEd8eu2lBQZuicaWUdKSspcACgu\nLh5rV7rMmBvrYm6si7mxLubGupgb62JuLk616iUAL5kdx0gSpaeOiIiIiIiIRpAoPXVjTkysUl0b\nv/5ttzvc1NT0yuSHRuMx9MsPc2M9zI11MTfWxdxYF3NjXcyNdSV5bm42O4API1GKut0AyqtFZiNW\nzN0B4HPmhkRERERERGS+hBh+WaV6wcTEKlXLTEwkIiIiIiIyS6L01KFK1bITE4mIiIiIiMySED11\nRERERERENDIWdURERERERAmMRR0REREREVECE1U1O4ZJISJRAP1mx0EjcgAImx0EjYi5sS7mxrqY\nG+tibqyLubGuZM2NR1UTtsMrYS6UMgE1qrrE7CDoQiKyh7mxJubGupgb62JurIu5sS7mxrqYm8SU\nsNUoERERERERsagjIiIiIiJKaFO5qPuR2QHQqJgb62JurIu5sS7mxrqYG+tibqyLuUlAU/ZCKURE\nRERERMlgKvfUERERERERTXks6oiIiIiIiBLYlCzqRORGETkmInUi8i2z40lmIvKUiLSJyKG4tmwR\neUVEao3nLDNjTFYiUiwi20XksIi8JyKbjHbmx2QikiIi74jIfiM3/2i0MzcWICJ2EXlXRLYZ68yL\nRYjISRE5KCL7RGSP0cb8WICIZIrI8yJyVESOiMgK5sZ8IlJhfF+GHr0icj9zk3imXFEnInYAmwHc\nBKASwJ0iUmluVEntaQA3Dmv7FoDXVLUcwGvGOl1+YQDfVNVKANcC+JrxXWF+zDcIYJ2qLgCwEMCN\nInItmBur2ATgSNw682ItH1fVhXH32WJ+rOEHAF5W1XkAFiD2HWJuTKaqx4zvy0IAiwEEALwA5ibh\nTLmiDsAyAHWqWq+qQQA/B7DB5JiSlqq+CeDcsOYNALYYy1sAbLysQREAQFVbVbXGWD6P2B/YQjA/\nptMYv7HqNB4K5sZ0IlIE4BYAT8Y1My/WxvyYTEQyAKwB8GMAUNWgqnaDubGa6wGcUNVTYG4SzlQs\n6goBNMWtnzbayDoKVLXVWD4DoMDMYAgQkRIA1wDYBebHEowhfvsAtAF4RVWZG2v4PoC/ARCNa2Ne\nrEMBvCoie0XkL4025sd8swG0A/iJMXT5SRHxgbmxmjsA/MxYZm4SzFQs6iiBaOyeGryvholEJBXA\nLwDcr6q98duYH/OoasQYDlMEYJmIXDVsO3NzmYnIrQDaVHXvaPswL6ZbZXxvbkJsSPma+I3Mj2kc\nABYBeExVrwHQh2HD+Zgbc4mIC8B6AM8N38bcJIapWNQ1AyiOWy8y2sg6zorIdAAwnttMjidpiYgT\nsYLuGVX9pdHM/FiIMURpO2JzU5kbc60EsF5ETiI2tH+diPwUzItlqGqz8dyG2LygZWB+rOA0gNPG\niAMAeB6xIo+5sY6bANSo6lljnblJMFOxqNsNoFxEZhu/OtwBYKvJMdEHbQXwRWP5iwBeNDGWpCUi\ngtj8hiOq+m9xm5gfk4lInohkGsseAJ8AcBTMjalU9W9VtUhVSxD72/K6qn4ezIsliIhPRNKGlgF8\nEsAhMD+mU9UzAJpEpMJouh7AYTA3VnIn3h96CTA3CUdiPapTi4jcjNi8BzuAp1T1YZNDSloi8jMA\nawHkAjgL4CEAvwLwLICZAE4B+DNVHX4xFZpkIrIKwE4AB/H+/KC/Q2xeHfNjIhGZj9jEdDtiP749\nq6rfFZEcMDeWICJrAVSp6q3MizWISClivXNAbLjf/6jqw8yPNYjIQsQuMOQCUA/gXhj/v4G5MZXx\nI0gjgFJV7THa+L1JMFOyqCMiIiIiIkoWU3H4JRERERERUdJgUUdERERERJTAWNQRERERERElMBZ1\nRERERERECYxFHRERERERUQJjUUdERJdMRFREvhe3XiUi35nguZ4WkdsneOw9IjIjbv1JEakcZb8f\nGstfEZEvTOT1Jir+NS81ZiIiovFymB0AEREllEEAnxaRf1bVDhPjuAexG0u3AICqfmmsA1T18UmO\naazXvAfjjJmIiOhSsKeOiIjGIwzgRwAeGL5heM+biPjjlh8UkYMisl9EHhnh2MUi8oaI7BWR34rI\ndKN9oYi8LSIHROQFEckyXmMJgGdEZJ+IeERkh4gsMY65V0SOi8g7AFbGvcZ3RKTKWC4TkVeNeGpE\nZM6weEpE5KiIPCMiR0TkeRHxGtuuF5F3jffzlIi4jfZHROSwEWt1/GteQsx3Guc7JCKPxn+GIvKw\nEefbIlIwznwREVESYFFHRETjtRnAXSKScSk7i8hNADYAWK6qCwD8y7DtTgD/DuB2VV0M4CkADxub\n/wvAg6o6H8BBAA+p6vMA9gC4S1UXqmp/3LmmA/hHxIq5VQBGG974DIDNRjwfA9A6wj4VAP5DVa8A\n0Avgr0QkBcDTAD6rqlcjNuLlqyKSA+BTAK40Yv2n+BONEfMMAI8CWAdgIYClIrLR2OwD8LYR55sA\n7hvl/RARURJjUUdEROOiqr2IFVvfuMRDbgDwE1UNGMefG7a9AsBVAF4RkX0A/h5AkVE0ZqrqG8Z+\nWwCsGeO1lgPYoartqhoE8L/DdxCRNACFqvqCEc/AUGzDNKnqW8byTxErEisANKjq8WEx9QAYAPBj\nEfk0gJHON5qlcTGHESs4h95nEMA2Y3kvgJJxnJeIiJIE59QREdFEfB9ADYCfxLWFYfxYKCI2AK5L\nPJcAeE9VV3yg8RJ7AieRjrH+/gbVsIgsA3A9gNsBfB2xnrcPK6SqQ68bAf9uExHRCNhTR0RE42b0\ntj0L4C/imk8CWGwsrwfgNJZfAXBv3Jy07GGnOwYgT0RWGNudInKlqvYA6BKR1cZ+dwMY6rU7DyBt\nhNB2AbhORHKMYZ1/OkLs5wGcHhriKCLuodiGmTkUE4DPAfidEWuJiJTFxyQiqQAyVPUlxOYbLhjh\nfKPF/I4Rc66I2AHcGfc+iYiIxsSijoiIJup7AHLj1v8TseJkP4AVAPoAQFVfBrAVwB5jeGVV/EmM\nYZK3A3jUOHYfYvPcAOCLAP5VRA4gNt/su0b70wAeH7roSNy5WgF8B8AfALwF4Mgosd8N4BvGeX8P\nYNoI+xwD8DUROQIgC8BjqjoA4F4Az4nIQQBRAI8jVqxtM873OwB/PcL5LhbztwBsB7AfwF5VfXGU\nuImIiC4g74/qICIiIiB29UsA21T1KpNDISIiGhN76oiIiIiIiBIYe+qIiIiIiIgSGHvqiIiIiIiI\nEhiLOiIiIiIiogTGoo6IiIiIiCiBsagjIiIiIiJKYCzqiIiIiIiIEtj/AxIIa/1V64uGAAAAAElF\nTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f3627cf0c90>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"(2.814, 35.674)"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"quality_plot('/media/storage/FASTQs/K562_MboI_1.fastq', \n",
" r_enz='MboI', nreads=100000)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from pytadbit.mapping.restriction_enzymes import RESTRICTION_ENZYMES"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
ehsteve/ipython-notebooks | RHESSI Workshope 13 - SunPy.ipynb | 2 | 1006964 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src=\"https://raw.github.com/sunpy/sunpy-logo/master/generated/sunpy_logo_compact_192x239.png\">\n",
"# SunPy Demo RHESSI Workshop 13\n",
"## Author: Steven Christe\n",
"Email: [email protected]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What is SunPy?\n",
"### A community-developed, free and open-source solar data analysis environment for Python."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"website: [http://www.sunpy.org](http://www.sunpy.org)<br>\n",
"docs: [http://docs.sunpy.org](http://docs.sunpy.org)<br>\n",
"code (version control!): [https://github.com/sunpy/sunpy](https://github.com/sunpy/sunpy)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"SunPy is built upon foundational libraries which enable scientific computing in Python which includes\n",
"\n",
"+ [NumPy](http://numpy.org)\n",
"+ [SciPy](http://scipy.org)\n",
"+ [matplotlib](http://matplotlib.org)\n",
"\n",
"and also (increasingly)\n",
"\n",
"+ [AstroPy](http://astropy.org)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This ipython notebook file can be found at\n",
"\n",
"* [ipython notebook file](https://raw.githubusercontent.com/ehsteve/ipython-notebooks/master/RHESSI%20Workshope%2013%20-%20SunPy.ipynb)\n",
"\n",
"or can be viewed (if you don't have ipython installed) here\n",
"\n",
"* [ipython notebook viewer](http://nbviewer.ipython.org/urls/raw.githubusercontent.com/ehsteve/ipython-notebooks/master/RHESSI%20Workshope%2013%20-%20SunPy.ipynb?create=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Setting up the notebook for inline plots"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import numpy as np"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import sunpy"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"sunpy.system_info()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"==========================================================\n",
" SunPy Installation Information\n",
"\n",
"==========================================================\n",
"\n",
"###########\n",
" General\n",
"###########\n",
"Time : Friday, 04. April 2014 07:22AM UT\n",
"System : Darwin\n",
"Processor : i386\n",
"Arch : 64bit\n",
"SunPy : 0.3.2\n",
"SunPy_git : v0.3.1-878-g5d3d14a\n",
"OS: Mac OS X 10.9.2 (i386)\n",
"\n",
"\n",
"###########\n",
" Required Libraries \n",
"###########\n",
"Python: 2.7.6\n",
"NumPy: 1.8.1\n",
"SciPy: 0.13.3\n",
"matplotlib: 1.3.1\n",
"Astropy: 0.3\n",
"Pandas: 0.13.1\n",
"\n",
"\n",
"###########\n",
" Recommended Libraries \n",
"###########\n",
"beautifulsoup: 4.3.1\n",
"PyQt: 4.9.4\n",
"SUDS: 0.4\n",
"Sqlalchemy: 0.8.3\n",
"Requests: 1.2.3\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/Users/schriste/anaconda/lib/python2.7/site-packages/pytz/__init__.py:29: UserWarning: Module _imaging was already imported from /Users/schriste/anaconda/lib/python2.7/site-packages/PIL/_imaging.so, but /Users/schriste/.local/lib/python2.7/site-packages is being added to sys.path\n",
" from pkg_resources import resource_stream\n"
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#1. Solar Images in SunPy"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"SunPy has a `Map` type that supports 2D images, it makes it simple to read data in from any filetype supported in `sunpy.io` which is currently FITS, JPEG2000 and ANA files. You can also create maps from any `(data, metadata)` pair.\n",
"\n",
"SunPy contains a few test data files, under the `sunpy` namespace:\n",
"\n",
"* `sunpy.AIA_171_IMAGE`\n",
"* `sunpy.CALLISTO_IMAGE`\n",
"* `sunpy.EIT_195_IMAGE`\n",
"* `sunpy.RHESSI_EVENT_LIST`\n",
"* `sunpy.RHESSI_IMAGE`\n",
"\n",
"These are all just links to FITS files contained in the SunPy distribution."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print sunpy.AIA_171_IMAGE"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"/Users/schriste/Dropbox/Developer/python/sunpy/sunpy/data/sample/AIA20110319_105400_0171.fits\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import sunpy.map\n",
"\n",
"aiamap = sunpy.map.Map(sunpy.AIA_171_IMAGE)\n",
"aiamap"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 7,
"text": [
"SunPy AIAMap\n",
"---------\n",
"Observatory:\t SDO\n",
"Instrument:\t AIA_3\n",
"Detector:\t AIA\n",
"Measurement:\t 171\n",
"Obs Date:\t 2011-03-19T10:54:00.34\n",
"dt:\t\t 1.999601\n",
"Dimension:\t [1024, 1024]\n",
"[dx, dy] =\t [2.400000, 2.400000]\n",
"\n",
"array([[ 0.3125, -0.0625, -0.125 , ..., 0.625 , -0.625 , 0. ],\n",
" [ 1. , 0.1875, -0.8125, ..., 0.625 , -0.625 , 0. ],\n",
" [-1.1875, 0.375 , -0.5 , ..., -0.125 , -0.625 , -1.1875],\n",
" ..., \n",
" [-0.625 , 0.0625, -0.3125, ..., 0.125 , 0.125 , 0.125 ],\n",
" [ 0.5625, 0.0625, 0.5625, ..., -0.0625, -0.0625, 0. ],\n",
" [ 0.5 , -0.125 , 0.4375, ..., 0.6875, 0.6875, 0.6875]])"
]
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Maps contain both the image data and the metadata associated with the image, this metadata currently does not deviate much from the standard FITS WCS keywords, but presented in a instrument-independant manner.\n",
"\n",
"[Documentation on the Map Object](http://docs.sunpy.org/en/stable/api/sunpy.map.mapbase.GenericMap.html#sunpy.map.mapbase.GenericMap)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The data (stored in a numpy array)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.data"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 8,
"text": [
"array([[ 0.3125, -0.0625, -0.125 , ..., 0.625 , -0.625 , 0. ],\n",
" [ 1. , 0.1875, -0.8125, ..., 0.625 , -0.625 , 0. ],\n",
" [-1.1875, 0.375 , -0.5 , ..., -0.125 , -0.625 , -1.1875],\n",
" ..., \n",
" [-0.625 , 0.0625, -0.3125, ..., 0.125 , 0.125 , 0.125 ],\n",
" [ 0.5625, 0.0625, 0.5625, ..., -0.0625, -0.0625, 0. ],\n",
" [ 0.5 , -0.125 , 0.4375, ..., 0.6875, 0.6875, 0.6875]])"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.data.max()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 9,
"text": [
"9429.125"
]
}
],
"prompt_number": 9
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The standard deviation"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.data.std()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 10,
"text": [
"292.43424704678557"
]
}
],
"prompt_number": 10
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.data.min()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 11,
"text": [
"-2.0"
]
}
],
"prompt_number": 11
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The original metadata (stored in a dictionary)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.meta"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 12,
"text": [
"MapMeta([('dsun_obs', 148940609626.98), ('t_obs', '2011-03-19T10:54:01.34Z'), ('tobsepoc', '1977.01.01_00:00:00_TAI'), ('simple', True), ('datavals', 16777216), ('aimgshen', 4), ('aiagp2', 0), ('aiftsid', 40960), ('comment', \"FITS (Flexible Image Transport System) format is defined in 'Astronomy and Astrophysics', volume 376, page 359; bibcode: 2001A&A...376..359H\"), ('aihis348', 8388262), ('roi_llx2', -2147483648), ('extend', True), ('aivnmst', 453), ('aicfgdl4', 236), ('crlt_obs', -7.064078), ('aicfgdl1', 0), ('aicfgdl2', 137), ('aicfgdl3', 201), ('totvals', 16777216), ('acs_mode', 'SCIENCE'), ('isppktvn', '001.197'), ('aimshobe', 26.076), ('aimshobc', 41.099998), ('aihis860', 8388603), ('r_sun', 1608.94397), ('orb_rec', 'sdo.fds_orbit_vectors[2011.03.19_10:54:00_UTC]'), ('fid', 0), ('wave_str', '171_THIN'), ('aecdelay', 1540), ('int_time', 2.273438), ('aimshcbc', 2040.791992), ('crval1', 0.0), ('lvl_num', 1.5), ('acs_safe', 'NO'), ('aimshcbe', 2025.864014), ('aifoenfl', 1), ('y0_lf', 'nan'), ('aifdbid', 241), ('ctype2', 'HPLT-TAN'), ('ctype1', 'HPLN-TAN'), ('exptime', 1.999601), ('quallev0', 0), ('obs_vn', 2177.6711), ('aiasen', 0), ('aifcps', 10), ('cdelt1', 2.4), ('cdelt2', 2.4), ('rsun_ref', 696000000.0), ('naxis', 2), ('date-obs', '2011-03-19T10:54:00.34'), ('rsun_lf', 'nan'), ('aistate', 'CLOSED'), ('obs_vw', 30775.731671), ('datamean', 236.57), ('datarms', 294.02), ('obs_vr', -2132.568376), ('rsun_obs', 963.879683), ('aiawvlen', 7), ('instrume', 'AIA_3'), ('camera', 3), ('blank', -2147483648), ('oscnrms', 'nan'), ('oscnmean', 'nan'), ('aimgots', 1679223275), ('roi_llx1', -2147483648), ('naxis1', 1024), ('naxis2', 1024), ('datakurt', 49.56), ('aifiltyp', 0), ('acs_eclp', 'NO'), ('agt1svy', 18), ('roi_nwin', -2147483648), ('agt1svz', 10), ('aiaecenf', 1), ('checksum', 'J7qAL7o6J7oAJ7o5'), ('inst_rot', 0.102488), ('percentd', 100.0), ('acs_cgt', 'GT3'), ('bitpix', 32), ('asd_rec', 'sdo.lev0_asd_0004[:#8948067]'), ('aimgfsn', 5), ('quality', 1073741824), ('roi_sum', -2147483648), ('dataskew', 4.63), ('mpo_rec', 'sdo.master_pointing[:#116]'), ('roi_nax2', -2147483648), ('fsn', 22642033), ('roi_nax1', -2147483648), ('dsun_ref', 149597870691.0), ('aihismxb', 7), ('expsdev', 0.00016), ('aiahfsn', 22642025), ('car_rot', 2108), ('gciec_y', 'nan'), ('gciec_x', 'nan'), ('gciec_z', 'nan'), ('aimgtyp', 0), ('datasum', '3958014355'), ('cunit1', 'arcsec'), ('asqtnum', 2), ('cunit2', 'arcsec'), ('crln_obs', 315.285065), ('origin', 'SDO/JSOC-SDP'), ('roi_nay2', -2147483648), ('aihis604', 8388597), ('agt3svz', 0), ('datamin', -7), ('imscl_mp', 0.599076), ('aifrmlid', 3024), ('crval2', 0.0), ('crpix1', 512.5), ('crpix2', 512.5), ('sat_z0', 14.820671), ('telescop', 'SDO/AIA'), ('wavelnth', 171), ('isppktim', '2011-03-19T10:53:57.50Z'), ('keycomments', {'DATASUM': 'data unit checksum updated 2011-03-19T11:08:18', 'EXTEND': 'FITS dataset may contain extensions', 'NAXIS1': 'length of data axis 1', 'CHECKSUM': 'HDU checksum updated 2011-03-19T11:08:18', 'NAXIS2': 'length of data axis 2', 'NAXIS': 'number of data axes', 'SIMPLE': 'file does conform to FITS standard', 'BITPIX': 'number of bits per data pixel'}), ('datamax', 16228), ('asqfsn', 22642033), ('y0_mp', 2046.589966), ('roi_nay1', -2147483648), ('aimgshce', 2000), ('aimgotss', 5339), ('agt3svy', 2), ('aecmode', 'ON'), ('date', '2011-03-19T11:08:25'), ('aihis192', 8381297), ('img_type', 'LIGHT'), ('aiagp8', 393), ('aiagp9', 457), ('aimshcte', 2068.676025), ('aiagp5', 0), ('aiagp6', 0), ('aiagp7', 0), ('aiagp1', 0), ('aimshctc', 2054.875977), ('aiagp3', 0), ('sat_rot', -8.8e-05), ('agt4svz', 0), ('crota2', 0.0), ('aiftswth', 0), ('agt4svy', 14), ('x0_lf', 'nan'), ('recnum', 76202), ('aifwen', 204), ('hciec_z', 'nan'), ('aiagp10', 748), ('hciec_x', 'nan'), ('hciec_y', 'nan'), ('datamedn', 192), ('missvals', 0), ('aiaecti', 0), ('tobsstep', 90.0), ('asqhdr', 2170125681), ('acs_sunp', 'YES'), ('history', ''), ('waveunit', 'angstrom'), ('flat_rec', 'aia.flatfield[:#7]'), ('bzero', 0.0), ('roi_lly2', -2147483648), ('x0_mp', 2052.399902), ('roi_lly1', -2147483648), ('aiagp4', 0), ('aimshotc', 55.312), ('agt2svy', 10), ('aimshote', 69.316002), ('agt2svz', 8), ('ispsname', 'aia.lev0_isp_0011'), ('bscale', 0.0625), ('aectype', 0), ('sat_y0', -0.365593), ('detector', 'AIA')])"
]
}
],
"prompt_number": 12
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.meta.keys()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 13,
"text": [
"['dsun_obs',\n",
" 't_obs',\n",
" 'tobsepoc',\n",
" 'simple',\n",
" 'datavals',\n",
" 'aimgshen',\n",
" 'aiagp2',\n",
" 'aiftsid',\n",
" 'comment',\n",
" 'aihis348',\n",
" 'roi_llx2',\n",
" 'extend',\n",
" 'aivnmst',\n",
" 'aicfgdl4',\n",
" 'crlt_obs',\n",
" 'aicfgdl1',\n",
" 'aicfgdl2',\n",
" 'aicfgdl3',\n",
" 'totvals',\n",
" 'acs_mode',\n",
" 'isppktvn',\n",
" 'aimshobe',\n",
" 'aimshobc',\n",
" 'aihis860',\n",
" 'r_sun',\n",
" 'orb_rec',\n",
" 'fid',\n",
" 'wave_str',\n",
" 'aecdelay',\n",
" 'int_time',\n",
" 'aimshcbc',\n",
" 'crval1',\n",
" 'lvl_num',\n",
" 'acs_safe',\n",
" 'aimshcbe',\n",
" 'aifoenfl',\n",
" 'y0_lf',\n",
" 'aifdbid',\n",
" 'ctype2',\n",
" 'ctype1',\n",
" 'exptime',\n",
" 'quallev0',\n",
" 'obs_vn',\n",
" 'aiasen',\n",
" 'aifcps',\n",
" 'cdelt1',\n",
" 'cdelt2',\n",
" 'rsun_ref',\n",
" 'naxis',\n",
" 'date-obs',\n",
" 'rsun_lf',\n",
" 'aistate',\n",
" 'obs_vw',\n",
" 'datamean',\n",
" 'datarms',\n",
" 'obs_vr',\n",
" 'rsun_obs',\n",
" 'aiawvlen',\n",
" 'instrume',\n",
" 'camera',\n",
" 'blank',\n",
" 'oscnrms',\n",
" 'oscnmean',\n",
" 'aimgots',\n",
" 'roi_llx1',\n",
" 'naxis1',\n",
" 'naxis2',\n",
" 'datakurt',\n",
" 'aifiltyp',\n",
" 'acs_eclp',\n",
" 'agt1svy',\n",
" 'roi_nwin',\n",
" 'agt1svz',\n",
" 'aiaecenf',\n",
" 'checksum',\n",
" 'inst_rot',\n",
" 'percentd',\n",
" 'acs_cgt',\n",
" 'bitpix',\n",
" 'asd_rec',\n",
" 'aimgfsn',\n",
" 'quality',\n",
" 'roi_sum',\n",
" 'dataskew',\n",
" 'mpo_rec',\n",
" 'roi_nax2',\n",
" 'fsn',\n",
" 'roi_nax1',\n",
" 'dsun_ref',\n",
" 'aihismxb',\n",
" 'expsdev',\n",
" 'aiahfsn',\n",
" 'car_rot',\n",
" 'gciec_y',\n",
" 'gciec_x',\n",
" 'gciec_z',\n",
" 'aimgtyp',\n",
" 'datasum',\n",
" 'cunit1',\n",
" 'asqtnum',\n",
" 'cunit2',\n",
" 'crln_obs',\n",
" 'origin',\n",
" 'roi_nay2',\n",
" 'aihis604',\n",
" 'agt3svz',\n",
" 'datamin',\n",
" 'imscl_mp',\n",
" 'aifrmlid',\n",
" 'crval2',\n",
" 'crpix1',\n",
" 'crpix2',\n",
" 'sat_z0',\n",
" 'telescop',\n",
" 'wavelnth',\n",
" 'isppktim',\n",
" 'keycomments',\n",
" 'datamax',\n",
" 'asqfsn',\n",
" 'y0_mp',\n",
" 'roi_nay1',\n",
" 'aimgshce',\n",
" 'aimgotss',\n",
" 'agt3svy',\n",
" 'aecmode',\n",
" 'date',\n",
" 'aihis192',\n",
" 'img_type',\n",
" 'aiagp8',\n",
" 'aiagp9',\n",
" 'aimshcte',\n",
" 'aiagp5',\n",
" 'aiagp6',\n",
" 'aiagp7',\n",
" 'aiagp1',\n",
" 'aimshctc',\n",
" 'aiagp3',\n",
" 'sat_rot',\n",
" 'agt4svz',\n",
" 'crota2',\n",
" 'aiftswth',\n",
" 'agt4svy',\n",
" 'x0_lf',\n",
" 'recnum',\n",
" 'aifwen',\n",
" 'hciec_z',\n",
" 'aiagp10',\n",
" 'hciec_x',\n",
" 'hciec_y',\n",
" 'datamedn',\n",
" 'missvals',\n",
" 'aiaecti',\n",
" 'tobsstep',\n",
" 'asqhdr',\n",
" 'acs_sunp',\n",
" 'history',\n",
" 'waveunit',\n",
" 'flat_rec',\n",
" 'bzero',\n",
" 'roi_lly2',\n",
" 'x0_mp',\n",
" 'roi_lly1',\n",
" 'aiagp4',\n",
" 'aimshotc',\n",
" 'agt2svy',\n",
" 'aimshote',\n",
" 'agt2svz',\n",
" 'ispsname',\n",
" 'bscale',\n",
" 'aectype',\n",
" 'sat_y0',\n",
" 'detector']"
]
}
],
"prompt_number": 13
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.meta.get('rsun_obs')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 14,
"text": [
"963.879683"
]
}
],
"prompt_number": 14
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We also provide quick access to some key metadata values as object variables"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(aiamap.date, aiamap.coordinate_system, aiamap.detector, aiamap.dsun)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('2011-03-19T10:54:00.34', {'y': 'HPLT-TAN', 'x': 'HPLN-TAN'}, 'AIA', 148940609626.98)\n"
]
}
],
"prompt_number": 15
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The properties of the map provide a standard way of reading meta data. For instance the pixel scale can be accessed with the `.scale` attribute:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.scale"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 16,
"text": [
"{'x': 2.4, 'y': 2.4}"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.yrange"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 17,
"text": [
"[-1228.8, 1228.8]"
]
}
],
"prompt_number": 17
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiamap.xrange"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 18,
"text": [
"[-1228.8, 1228.8]"
]
}
],
"prompt_number": 18
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Map provides some useful functions such as \n",
"\n",
"+ submap\n",
"+ plotting\n",
"+ resampling"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Playing with a map"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiasub = aiamap.submap([-250,50],[-550,-250])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 19
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"aiasub.xrange, aiasub.yrange"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 20,
"text": [
"([-249.59999999999999, 50.400000000000006],\n",
" [-549.60000000000002, -249.60000000000002])"
]
}
],
"prompt_number": 20
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"fig, ax = plt.subplots(1, figsize=(7,7))\n",
"im = aiasub.plot(axes=ax, vmin=100, vmax=aiasub.data.max())\n",
"ax = aiasub.draw_grid(grid_spacing=5)\n",
"cbar = plt.colorbar()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAbYAAAGVCAYAAACSMdToAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4FEX6x789kwk5CCQhAUIihCMYwhnRACusgAQhioKu\n7IIuoosHKIL8VhFdVl3lUFZFdFFQPGA9V+VyEWG5FOXQyB2OyBGScCXkhJwz078/JtVTPfNOdydM\nmGRSn+eZJ5k+qt6u7umq96233leSZVmGQCAQCAR+gsnXAggEAoFA4E1ExyYQCAQCv0J0bAKBQCDw\nK0THJhAIBAK/QnRsAoFAIPArRMcmEAgEAr9CdGwCgUDQRImMjIQkSV75REZG+vpyFETHJhAIBE2U\nwsJCyLLslU9hYaFb+fHx8ejVqxeSk5ORkpKi2vfqq6/CZDKhoKBA2TZv3jwkJCQgMTERGzZsULan\np6ejZ8+eSEhIwLRp03SvK+AK2kQgEAgEjR3ZWm9FS5KErVu3umlz2dnZ2LhxIzp06KBsy8jIwOef\nf46MjAzk5uZi2LBhyMzMhCRJmDx5MpYtW4aUlBSkpaVh/fr1GDFihMd6hcYmEAgEgnqDCm41Y8YM\nvPLKK6ptq1evxrhx42CxWBAfH48uXbpg165dOHv2LEpLSxWNb8KECVi1apVmnaJjEwgEgqaMbPXO\nh0CSJAwbNgzXX3893n33XQCODiwuLg69evVSHXvmzBnExcUp3+Pi4pCbm+u2PTY2Frm5uZqXJEyR\nAoFA0JSpR1Pkjz/+iJiYGOTl5SE1NRWJiYmYN2+eav6sPsIVi45NIBAIBLVm69YfsHXbD5rHxMTE\nAACio6MxZswYbNu2DSdPnkTv3r0BADk5Oejbty927dqF2NhYZGdnK+fm5OQgLi4OsbGxyMnJUW2P\njY3VrFcS0f0FAoGgaSJJEuRqd2/GOpVliVBpX2VlZbDZbAgLC8Ply5cxfPhwPPfccxg+fLhyTMeO\nHZGeno7IyEhkZGRg/Pjx2L17t+I88ttvv0GSJPTr1w+LFi1CSkoKbr31Vjz++OOaziNCYxMIBIKm\nTD2ZIs+fP48xY8YAAKxWK+655x5VpwY4OlZGUlISxo4di6SkJAQEBGDx4sXK/sWLF2PixIkoLy9H\nWlqaZqcGCI1NIBAImiySJEGuyvNOWYHR9TJfVheExiYQCARNmXp0HvEVomMTCASCpowfdmxiHZtA\nIBAI/AqhsQkEAkFTxg81NtGxCQQCQVPGDzs2YYoUCAQCgV8hNDaBQCBoyvihxiY6NoFAIGjK+GHH\nJkyRAoFAIPArhMYmEAgETRmhsQkEAoFA0LARGptAIBA0ZWSbryXwOqJjEwgEgqaMMEUKBAKBQNCw\nERqbQCAQNGWExiaoLwYPHozIyEhUVVWptk+cOBGzZ89Wbbt06RKaN2+OtLQ03XJnz56Nnj17wmKx\n4IUXXlDtmzt3LsLCwpRPSEgIzGYzCgoKAABffPEFfve73yE0NBRDhgzRrGfnzp1ITU1Fq1at0Lp1\na4wdOxbnzp1THTNz5kxERUUhKioKTz/9tGE5z507h9tvvx2xsbEwmUw4ffq07nV/8skn6NChA5o3\nb44xY8agsNCZJfipp55C+/bt0aJFC8TFxWHGjBmwWj3/uPXaYe3atejRowfCwsJw44034vDhwx7L\n2rJlC4YMGYLw8HB07NjRbf+pU6cwZMgQhIaGolu3bti0aZPHsrZu3QqTyaS6hytWrHA7rqCgANHR\n0Rg0aJDHsgBg79696Nu3L0JDQ3H99ddj3759qv2vv/46YmJi0LJlS/zlL39xe1YZFy9exI033oio\nqCi0bNkSycnJWLVqFXnszTffDJPJBLvdrpJ3zJgxaN68OeLj4/Hpp5+qztm0aRMSExMRGhqKoUOH\nuj0PWs9Zbdq3ySBbvfNpQIiOrQFw6tQp7N69G61bt8aaNWtU+yRJUmWZBYCvvvoK7du3x9atW3H+\n/HnNshMSErBgwQLceuutbuU888wzKC0tVT4zZ87EkCFDEBkZCQBo1aoVZsyY4fZyoCgqKsIjjzyC\nrKwsZGVlISwsDPfff7+yf8mSJVi9ejX279+P/fv3Y+3atViyZIkhOU0mE9LS0vDVV1/pygEAhw4d\nwiOPPIKPP/4Y58+fR0hICKZMmaLs/8tf/oKMjAyUlJRg9+7d2LBhA9577z2P5Wm1Q2ZmJu69914s\nXboUxcXFGDVqFG6//XbYbPSEfPPmzTFp0iQsWLCA3D9u3Dj07dsXBQUFmDNnDv7whz8gPz/fo2yx\nsbGqe/jnP//Z7ZiZM2ciKSnJrV15qqqqcMcdd2DChAkoKirCfffdhzvuuAPV1dUAgO+++w4vv/wy\nNm/ejKysLJw4cQLPPfecx2t8//33ceHCBRQXF+P555/H2LFjcenSJdVxH3/8MaxWq5tcjz76KIKC\ngnDhwgV8/PHHmDx5MjIyMgAA+fn5uOuuuzBnzhwUFhbi+uuvxx//+EflXL3nrLbtK2ikyAKf88IL\nL8ijRo2SX3rpJfm2225T7Zs4caL8t7/9TbVtyJAh8quvvioPGzZM/uc//2mojnvvvVd+/vnnPe63\n2+1yx44d5eXLl7vte/fdd+XBgwcbqoeRnp4uh4WFKd8HDBggv/vuu8r3999/X+7fv3+t5KyurpYl\nSZKzsrI06541a5Z8zz33KN+PHz8uBwYGypcuXXI7NicnR+7Zs6e8atUq3Wui2uHNN9+Ub731VuW7\n3W6Xg4OD5U2bNmmWtXHjRjk+Pl617ejRo3KzZs1Ucv7+97+X33nnHbKMLVu2yHFxcZr1/Pjjj/KA\nAQPkDz74QB44cKDH47777js5NjZWta19+/byd999J8uyLI8bN05+9tlnlX2bN2+W27Ztq1m3LMuy\nzWaT16xZI8fExMiVlZXK9qKiIrlr167yzp07ZUmSZJvNJsuyLF+6dEkODAyUMzMzlWMnTJggP/30\n07Isy/KSJUvkG2+8Udl3+fJlOTg4WD569Kgsy9rPWW3btykAQJYL/ueVT0PqToTG1gBYvnw5/vjH\nP2Ls2LH47rvvcOHCBY/HZmVl4fvvv8fYsWMxduxYLF++3Csy/PDDD8jLy8Ndd93llfK+//579OjR\nQ/mekZGB3r17K9979eqFQ4cOeaUuV1zr6tSpE5o1a4Zjx44p2+bPn4+wsDBcc801uO2223DHHXfU\nqS5JkiDLsvLdbrdDluU6XduhQ4fQqVMnhIaGKtt69+6tlHX69GlEREQgJydH2X/hwgW0bdsWnTp1\nwowZM1BWVqbss9lsmDp1Kv71r3+R9fXu3RufffaZUnevXr3c9rO6qft3/vx5lYnXlV69eiE4OBgT\nJ07EypUrERgYqOx75plnMGXKFLRp00Z1zrFjxxAQEIAuXbqQchw6dEglR0hICLp06aIpJ3+uVvs2\nWYQpUuBttm/fjtzcXNx+++1ISEhAUlISPvnkE4/Hr1ixAikpKYiLi8Odd96JjIwM7N2794rl+Oij\nj3D33XcjJCTkisvav38/XnzxRZW57dKlS2jZsqXyvUWLFm6mKW/hWherr7S0VPn+9NNPo7S0FOnp\n6fj444/x9ddf16muYcOGYdu2bdi2bRuqqqowd+5cVFVVqToYb8ndvn17FBYWIi4uDgDQrVs37Nu3\nD+fOncPmzZuRnp6OGTNmKOcuWrQI/fv3R3JyMlnfvn378Kc//clQ3dT9A6BqU1f279+P0tJSPP/8\n87jrrruU+/3LL79gx44dmDp1KtkGrGxGWFiYSg7X/XpysnqNPBcC/0B0bD7mo48+wvDhwxEWFgYA\nuPvuu/HRRx95PH758uW4++67ATjmfgYPHqx5vBHKysrw5Zdf4r777ruicgDgt99+Q1paGhYtWoQb\nb7xR2d68eXOUlJQo34uLi9G8efMrru+HH35QHCd69uyp1FVcXKw6rri4WGljnuTkZEyZMkVxunjk\nkUeU8ubPn69b/7XXXouPPvoIjz32GNq1a4eLFy8iKSlJ6Xxqg2sbAY65S9cXOaNNmzZITEwEAMTH\nx+OVV15R5iHPnDmDN998Ey+99JKhusPCwsi6WZtR94+dp0VgYCCmTp2KsLAwbN68GXa7HVOmTMHC\nhQthMjlfP0zrpdqguLhYaQNKTv7eaj1ntW3fJoPQ2ATepLy8HF988QU2b96MmJgYxMTE4NVXX8W+\nffuwf/9+5Tg2uf7TTz/ht99+w0svvaQcv2PHDnzyyScenRV4PDkPrFy5Eq1atcJNN91Uq/NcycrK\nQmpqKv7+97/jnnvuUe3r3r27SrPct2+fylRZl/oAYNCgQYrjxIEDB5S6eI++48ePo6qqCl27diXL\nqK6uVsxT77zzjlKeq7OIJ7nuuusuHDhwAPn5+Xj++edx6tQp3HDDDYavgdG9e3ecOHFCpcnu27cP\n3bt3N1wG8y7cvXs3zp49i6SkJMTExGD69OnYvXs32rVrpzKd8nXzzxwAHDhwQKmbun9t2rRBRESE\nIbmsVitCQkJQUlKC9PR0/PGPf0RMTAxSUlIAAHFxcfjxxx/RtWtXWK1W/Pbbb2QbuN7by5cv4/jx\n45pysufMG+3rl4iOTeBNVq1ahYCAABw+fBj79u3Dvn37cPjwYQwaNEiZO5NlWXkRMe2OP/7gwYMo\nLy/Ht99+S9ZhtVpRUVEBm82G6upqVFRUqFyrWbkTJkxwO9dut6OiogLV1dWw2+2orKxUvORcyc3N\nxdChQ/HYY4/hoYcects/YcIEvPbaazhz5gxyc3Px2muvYeLEiYblrKioQEVFhdv/FPfccw/Wrl2L\n7du34/Lly5g9ezbuuusuhIaGQpZlLFmyBEVFRZBlGbt378bixYtx5513eixPrx3S09Nhs9mQl5eH\nhx56CHfccYfHTlSWZaUsWZZRWVmpuM137doVffr0wQsvvICKigp8/fXXOHjwoMd5z61btyIrKwuy\nLCM7OxszZ87E6NGjAQBpaWnIyspSnpN//OMfSE5Oxt69e8kOevDgwTCbzVi0aBEqKyuxaNEimEwm\nDB06FIDj/i1btgyHDx9GYWEhXnzxRZXXK8+uXbuwfft2VFVVoby8HC+//DIqKirQv39/hIeH4+zZ\ns4pc69atAwD8+uuvSElJQWhoKO688078/e9/R1lZGbZv3461a9cq3p5jxozBwYMH8fXXX6OiogIv\nvPAC+vTpo7S31nNW2/YVNGJ85LQikGV5xIgR8l//+le37V988YUcExMjW61WeeLEifLs2bPliooK\nOSIiQv7mm2/cjp8yZYp89913k3Xcd999siRJqs9HH32k7M/JyZEtFot8/Phxt3M/+OADt3Pvv/9+\nsp7nn39eliRJbt68ufLhvSJlWZafeuopOTIyUo6MjJRnzpxZKznZNpPJpPzV4pNPPpHbt28vh4aG\nyqNHj5YLCwtlWXZ4LY4YMUKOjIyUw8LC5B49esjLli3TLEuvHQYOHCiHhYXJkZGR8iOPPCKXlZV5\nLGvLli1u1zJkyBBl/6lTp+TBgwfLwcHBcmJiosq7MisrS27evLmcnZ0ty7Isv/baa3JsbKwcEhIi\nX3PNNfK0adNIz09ZluUPP/xQHjRokGpb9+7d5U8++UT5vmfPHrlv375ycHCw3LdvX3nv3r2q4197\n7TW5TZs2cosWLeQHHnhArqqqUvaNHDlSnjdvnizLsrxt2za5d+/eclhYmBwVFSWnpaXJBw8eJOU6\nefKkbDKZFK9IWZblgoICefTo0XJoaKjcoUMH+dNPP1Wd87///U9OTEyUg4OD5SFDhrh5yWo9Z1rt\n2xQBIMsXvvTKpyF1J5IsE3YJgUAgEPg9kiRBPv+Zd8pq8yfSzO0LfGKKfPLJJ9GtWzf07t0bd955\npzIRferUKQQHByM5OVmZ1Gekp6ejZ8+eSEhIwLRp03whtkAgEAgaAT7p2IYPH45Dhw5h37596Nq1\nK+bNm6fs69KlC/bs2YM9e/Zg8eLFyvbJkydj2bJlyMzMRGZmJtavX+8L0QUCgcC/EM4j3iE1NVVx\n9e3Xr59qwSnF2bNnUVpaqnhQTZgwwWPsOYFAIBDUAtGxeZ/3339fFcz35MmTSE5OxuDBg7F9+3YA\nDo87fl1QbGwscnNzr7qsAoFAIGj41FvamtTUVLfo7oAjovyoUaMAAHPmzEFgYCDGjx8PAGjXrh2y\ns7MRERGBX3/9FaNHj651uBuzSYK9YcxfCgR1pqqqCsuWLcPkyZN9LYqgASEBsHvbQaOBaVveoN46\nto0bN2ru//DDD7Fu3TpV2ojAwEAlntx1112Hzp07IzMzE7GxsSpzZU5ODmJjY8ly7TIQyF2V2QRw\nAQ5gMrD2t7DUEXE8vLmZ3G+zu28LIA7lj2PPInWuFlabs2y9dcusDuo46rdgNrn/T53Lb2PHUe3I\njjt70Qq7zYZ20c1U90KSgJIyoJnFuY0NQij5+HpZfdXcOnR2jlnH7lDbgY7WtfH1ShJQVgmENHOe\nQ7UVj9XmLhM7l382oiMcv4OWzrCGSr18W2nd67o8LxVVQFCg+ji2X++3Qz1D1HPP/td7rqj7plUe\n3y7s3Gor/dt0hXrWeFh5evJ5A1Uddsf1saqs+nEYao9cH4X6Fp8kGl2/fj0WLFiAbdu2ISgoSNme\nn5+PiIgImM1mnDhxApmZmejUqRPCw8PRokUL7Nq1CykpKVixYgUef/xxj+VbXK5K70Xl+gI4fToL\nUVFRqg4RoF8E1MuGQXVs1AtND+rFwrapfszEuVovOdUPk3jZUPIp9REvJf56JZMJkgRUcYNBu+zo\nmKgXDdUu/LXZNF7q/LlMFqODWr17oNfRa5WnJYNqH9UparQBVQ7/rFLPBoXWdRi9bqozocYZeh0+\nNTCgytEaF7p2NMWllTCbzQgNDnAr21P9PHqyGC2H6hSNYnIZmNdLx+aH+KRjmzp1KqqqqpCamgoA\nGDBgABYvXoxt27bhueeeg8VigclkwpIlSxAeHg4AWLx4MSZOnIjy8nKkpaVhxIgR9SZfcs/O9VZ2\nU6BtZICutiDQJr/YDpvNhtYRFv2DBSR2uw1mswF1ranjh6ZIv1ugLUkSWoS4bnP+rzWi4jHaKpRp\nUcs0wmNkdGe3O0dseqNehp7sWiYUSivkt1HaFqk9EqNUSXKYhniNmtJktdAzwzH0Rsee5HPdpnUc\n4NBIeXOrhWsfdi6luVPwx+VeKMOhg/sxbEh/t3P1zLZGTdHU8VZCo6a0KS2MmutMxPOs9xywNrIS\nJmm+/fi2d/2t6GlnFN54S1KWHh4jv4GKKmfAaG8gSRLk7De8U9Y105r2Au2GTlRUFIou2ZXI6b7E\n1RzaGMg5fwkFJbTNxNVM3NgJrKfriW0dguFD++sf6GWMzEc1JvTmXwX+ibjtBPn5+Yai5QsEgoZL\ncWklLpX5n5nN69TzOjabzYbk5GTFG3737t1ISUlBcnIybrjhBvz888/KsfPmzUNCQgISExOxYcMG\nZXttI0/52fjZgdYojTKbKWY/blurlhbV8YDTzESZHynTCIVRUyhPbT3f9ExRtZ3E5uVj10mZvli5\ncW2aK+eonEII+SivSKNefUq5Om1K7TfaBqRTg8a5Rk2qnrwsGXlFjoaObOGuQumZtKjyqOdea5se\ndXGEcIX0yiWeA7029WTmd51jq4sJ0vU4ow45em1KbdPSMup1CVM9z7G98cYbSEpKUhK6PvXUU3jx\nxRdxyy234Ntvv8VTTz2FLVu2ICMjA59//jkyMjKQm5uLYcOGITMzE5IkKZGnUlJSkJaWhvXr12v6\nWQiNTSBogJSUFJPrQAXGaRUeguYhfjl2bzTk5ORg3bp1mDRpkjL/FhMTo8QHLioqUpZurV69GuPG\njYPFYkF8fDy6dOmCXbt21SnyVJO463qjMkprKCx1HzEzTY1aQ+OtEZXRiXpWn7mWI07gyjQirZEr\na5bJj07HnHmvIjrcTLYVj1GnBkpmStNm2/QcQKg6aguvcVAOQwyj23j5OrePdNvGmq8ubvxKW+kc\nr6WJ6T0HlAOI1sjZTCxRgE67MMMIJTO1HIKH1OyI8qh67cTzZ9RqonUcdX8pjP7O60Q9amxPPPEE\nFixYoMpcPn/+fAwcOBB//etfYbfbsWPHDgCOrO/9+zvnlePi4pCbmwuLxVLryFNCY/NAQcFF7N+/\nx9diNEr27vnF1yIIBCgsEXNsvuSbb75B69atkZycrPKW/Mtf/oJFixbh9OnTeP311/HAAw94ve4m\nobHVhc4dWgO4shF9U2XHT9sRHe5n7nVXmQuFjug3US1FO9YVsY7NIHXU2LbuPImtO0953P/TTz9h\nzZo1WLduHSoqKlBSUoI///nP2L17N/73v/8BAP7whz9g0qRJAByaWHZ2tnJ+Tk4O4uLiahV5iuGX\nGpskGTPlKR+74yPLzo+tJpSN1eb+Yfv4j14dWnKauI9R2PG8zAxqG1WvVrn8R5Lcz5Ek9w91rtnk\n/FAyUeVQ8rFtQRbnhzqOau/atq3etVGwa9S6Hr1r4z/Zp7NQWlpKyqBXnut18zJT94g6Tq9sreM8\nPTtG2oN6dvTw9BurzRyb3m9G63ehh9HjtGTRku2KqaMX5OB+1+D5aYOUjytz585FdnY2Tp48ic8+\n+wxDhw7FihUr0KVLF2zbtg0AsHnzZnTt2hUAcPvtt+Ozzz5DVVUVTp48iczMTKSkpKBt27ZK5ClZ\nlrFixQqMHj1a85KExuaBM+eLERYWhrAQv+z7653zhTbkXTiPpK7tfC1Ko+SGPiL6jcC/kGp696VL\nl+LRRx9FZWUlgoODsXTpUgBAUlISxo4di6SkJAQEBGDx4sXKObWNPOWXkUciwxz/a8VvpKJk8Nse\nmzods597EW2iwgzVqxe9xGjkEYbeRLOWE0ddJq61oNzGKfjRdV6RDefOnUNSV6fJQCvWJlUuNVoP\nIgIo6wXEre1yCb1oJJrOGQbd1fXK04umoYW3nWQY/P0w+uxqvV2oxfp24tr4wNdUEGk74dQFOObY\nzGazm9ZWl+fe6BIP6jmoLVptVlZZD5FHjs/yTlmd54nIIw2df721EG2jjXVqAneiWprR41ptO7jA\nMzl51ThbUMtUEAIVdrsIsmAIkWhUIBBcDbZv24TKygpfi9GoEevYmi5+edcpBwUGlWJF6d1dzA3F\nl+2wWa0Ib+FIUEWZI1g55L6roJXrmX28YYKizHp6k/p5RY4RXHS48xGj2kPLrEcFyVVdL6HQsOgw\nvPmKNCNdQbtoRTrRMz8r5kluG7VGadzdGlEVNOrn8XYUEW+l+DERzxCVo01rbSAPtcZMqUv7VAVe\nlisxIxoN+lzbc+uVBqZteQO/7Ni8RUHBRfzrzYW+FqNR0lBs7YKmS0GxY46tRah4zWkiOrbGgRKV\nw0DMSC06tY9WlWM02gLpmGDwPU8la5SICekrSXxIYXR0bzR1Skwr91ibtXVg4a+XxRCkHCeoMiw6\ny5e0HDqoe0lpeKrMC8yBoQ5RQajnZWf6cbSP74jW4c5KtKKH6EWmuJLnwKgzilGHEk3nG+JcPccs\nTw4bbB0bZaVxlUXlKELIcCUYbRdWLy+mlkVI4BkxxyYQNECWvfumyDBxhURFhCAizC/H7t5FOI80\nLQpKrCi6JDzT6sL+w7k4XyhezHVl6dsLERctsmcLrgKyzTufBoRfD2dkwiSpBJIl+itX0+Wqr7/A\ntYndDa0Z401BivmAl4Uwl1DBea/E5ECZMdllGk24WBdnE2qt16VLJWiDtqp6jTq3aLWByumHMiNp\nmBNVTkTEPaXupdZUod40opYsZABgDup+UfdXiytxHKqL+ZGZZvXuM2UmthEm7tpO07oGLWZzbK5a\nG+VMRu03uhbSaMZ1X6UHaor4dcd2pTz4wHjfeSo1cn53QzcA3vHKbKrk5Nsx5HdJOHLkiK9FaZSI\nWJEGaWBmRG/glx2b6yjnSlyhKaiRF6k1cOcoTiZ10NipUT4FNbqjIlhQmo7WaFwvAoPRtiTTmtSy\nDqoNKFdtldZKuJJrOYXw1HbJBlUH5dZuBJvNhsKCfLcknHWJPGKU2mrQvAONpnMLoaHy10FpNVcy\nqDRJQOvIEFWcRmrJiJa2rBedSEtOo8tw9NIXXZWJED/s2MQcmw6FpXZs3LLT12I0Ss4X2vHM7Jd8\nLUajpUMbC/Lz830thkDQ6PBLjc2bnDmTg6mTJ/pajEaJLMsICg7xtRiCJkp+kWOOLbKFeM1p4oca\nm1/ecS2THTW5q5Udt2die+fx1HoyykzjYjriy6OC2hoNkEyZbrw9uUy1HRUBhMeT+eqaaDPssvs5\nlPmFMlVR5kk9pwt2HB95hJKZWh9EmZu0zKy6kS40nEd4EydlIgMcc2wFF/PRp1tNbkANcxjFlUTT\n0AvSrBUcmvr5mXRMc95ez28yOefYAsz6dVDXGMBNz7Hnxco9V8o5BmXXM08ys66dmDaoV0THJhAI\nrhbW6mp8vGKpr8VotLSNCjHsDSzwL/yyY2MjI8qtuJpw3iBHcjVlsLVYsVHOwihHDJU2pTHJX5do\nJFrojcSvJA6g1rmkw4bL8dl5NtjtdnSMUa/H0nPppkbYgcSTWlUz0AwOdJeFSm9TxQ1Mr6RdWHkB\nxCQ/f3/thFZoNJ4iAMTHNDOc4oeHdMghjjPqhm7UsYiCPSd6DjRsm97zTO0nnTc0nKao4wO5d4WW\nRYHfZzQqiFabUr8Fo2l/vIbQ2Joeq1d+jtOnTvhajEaJLMuorq72tRiCJkpeoWOOrVVL8ZrTRHRs\nTY8pD473tQiNlvatA9TxFAW1IiffDpvNhvi2IgJJXZDtdkCsY2uS+GXHpqQ9oRwhCJMHFSSVmcPI\nyBncNsrUwsydvBnB6uUFKUajeJDRKjTWsVFmM73MyZTzA+Xs4SoTwKVx0dlWUaP48eZlVjaVooZ3\nzqCCYpPrkWzu18HOseqsP6SeIaNrpBiubVteXoa96bvc2sOo6Yu6v0bXYFLYiXOpNuUfdS1TJWWG\n0zO9GY0EY7UBkeHBavl0HES0MHp/teS86iZGowiNremx9IOvMPK2MbgmWqgeteW3nEqYAwLQpZ0Y\nNdeFhGtNQ5LWAAAgAElEQVSa+1oEQVNAdGyNEzsV4UA1rKw5jhhFTX3oLnzw6Xo0szidDySd0Rg1\nutOKXMBzJZE9jDp7ME2WilFpdPROacNmF022sqoCweZQzbQ/Wgk6LYSDil47ux7Pl60XcYI5qOg6\nHGilziE0GLI84lyteIT8cXrmXSqGoQLRfnrLTRSNl3g2+ONsRL1aDht1iSyiFbHDlcISdT42rfa1\n6lgvqKSnRp15jGqZWuWI0H61o0l0bFfK/eM8ZzMWeKZ3QksRxPUKOH3BYf+8JlpovHXBbreLWJFG\nEBqbQCC4WhQWXMSl0lJfi9FoaRUe7GsRGgeiY2scWGquimkLVh3TIVPz+bVSyrk24NR5O2RZRvvW\njtEfFf2iosq5jTJbMFTOFBoOJZRJUC9ArVagYL06tCKZqMyErF5uP1WfLANTpj2L/3v6RVwbZ1Id\nR5l4qHVO1NpA3aCxGmsIKVMaj1YbkFm1iXMtxHWQ5RhwJuqd2Fr3eknzrss+13Ncz9XNvk1sMxqN\nhFGX4MZaDiVkBm1if12CnVNOMFQbaf0eeeclynSsZR4nzZPCFFkrhEeEAd5bshA39GjjazEaHZu/\n+wpyg3L/EjQlCksqUXzJ/7QRr+OHGbQl2c/ePJIkoU24439PMfgA/clnNtrmz2UaXUgz5zbmLlzA\nWYwuV7rXYSVcyakRfW3TuFDOFGT8Ph0tRAuqPMpNmloWwG+jllBoOTDwTj+UFqcV2YWKEEHVq5cG\nh6qXLT3g24Vdm572qBWjkkeWgazzVkiSpMyxURq51nIKvWUaDKO/D2qJDKWJUe3HH0cth6Ecbai2\nV+KrGtB48wrKEWCxoGVzxw/XaLomCi0nGKPHGV2iQ53D2uByBbw6WJQkCXL677xTVt+fGsxA1i9N\nkfVBVFQUSopEChHB1SMz8whi2rbztRiNlujIYOFNaIQGpm15A9GxGeBkbhmaBQUhvo2w3NaWozk2\nlJWVIblrmK9FaXQMG9ijYS3kFfgnch2yHzdw/LJjczVvBehEnKBMHnxZI4Zeh9hrOirl8sF0K5lZ\nSmOCmEe1xsesltMTRifqldQaxOSznnnSaHZrytxJOmwopioZpSWFNf+7H8dMeEHck8jKo1KEUMGX\nKfOVRJgJKWcUfk0ii2rCn8sckQIIk5un58V5YM1f4vlTtamGAwiP0Ygi1BozLZO0XmZxKnoN6SSh\nscbMaOZwO9HOPFomUtfrZbEiWT622g4S9JxgqHupdZlGnb881Scwjl92bN7myJEjOHLkiGpuTWCM\nxGvEI1ZXjudWwmKxiKg3dUTEijSIMEU2LmRi5E+lmaki7qviJFHzNyoqCu3aRuHIkSOkhlDOuftX\nazwnlCbBy0c5OlDnKtemkxqHcl1mrsNU7DweNhrXSzlCaQPUJDp7xVBONZRDBF8eczigtC4yXiFX\nB7u/VL08zDmIWs5BpdCh0uBQ2i3f+Fr3VTU6twPfrv0Kw9NGuzlB6TnBaLWpHkxU6j4HEKldKC2D\nP1dLQ6WOq4uG4skxpnWrYEgSrekagUyHY9Dtn3LZp6wcKgsJIUNdZa8VomNruuw/egF2ux2dYkST\n1YZjOQ7PvoRYMXKuLY9PFpklBIK6IN7SBhl6YxJO/HbE12I0OqzWapjN4jETXH1EPjaDCI2tccDM\nVqTZkTlYEI4JvPmAZWVmf7NOHNFcI6U3Ua9lSqDWhOmZZCgThVYGXr1gq5QJlIqSQQUeVs4hTC09\nOjrCGlGOKjz8/WD7m3FpyJjM/HFUAGXKDEcFN9ZaN6W3to3JpZt6hjDHaj0brvfoy3U70adPCrq0\nUwtEZYbnz6XMk2QKJ+L3YXL7R3v9FV8stT7NVSbX+jyV6yjI834jJksjc2y1jVBi1FSqZ7alzI7U\n82zUhHxF+GHH5pNZ6dmzZ6N3797o06cPbr75ZmRnZyv75s2bh4SEBCQmJmLDhg3K9vT0dPTs2RMJ\nCQmYNm2aL8TGXx6a7pN6BU2Tf736AqxWkYG8rrRuFSy0tSaKTyKPlJaWIizMsa7pzTffxL59+/De\ne+8hIyMD48ePx88//4zc3FwMGzYMmZmZkCQJKSkpeOutt5CSkoK0tDQ8/vjjGDHCPeq+JEmIauH4\nn3IDphwJGPwoy9UDMuu8FSaTCa1amFQjcKbRVXLvH616KShtSm+kVtvJZKNRD4xqmUajjGz+6TA6\ndb4WXWNNbvv4cygNi/JCLSdicvIwjY1vb1ZeWaVzG4seQtXL7qkn+dj95e+51sifclQxGnGCilHJ\nt59WHFHKCUYvJQ+L6FHbeI6AOuErtV+pg3DqYlCOVHrRZoymJTL6pjOqFWr9fqjIQXybasWTpWDH\nlZbXQ+SRnzp4p6zfZZGy2Ww2XH/99YiLi8PatWvx5JNP4ptvvkFgYCA6d+6MDz74AC1btgTgUGze\nf/99mM1mLFq0CMOHDwfgUGwmTpyIiooKpKWl4Y033tCUxScaG+vUAODSpUuIiooCAKxevRrjxo2D\nxWJBfHw8unTpgl27duHs2bMoLS1FSkoKAGDChAlYtWrVVZW5Q5sAtGoh3K5ry970nQ0mzI6gaXGh\noBIXi/3PzOZ16jlW5BtvvIGkpCRINb398OHDcejQIezbtw9du3bFvHnzAAAZGRn4/PPPkZGRgfXr\n12PKlCnKu2Py5MlYtmwZMjMzkZmZifXr12teks/e1M8++yzat2+PDz/8ELNmzQIAnDlzBnFxccox\ncXFxyM3NddseGxuL3Nzcqy6zoPY8/cT9uDZOeETWlaM5dsx//QNfi9EokY0ElBTUKzk5OVi3bh0m\nTZqkdFKpqakw1Uz69uvXDzk5OQC8q9jUmwE6NTUV586dc9s+d+5cjBo1CnPmzMGcOXMwf/58TJ8+\nHR984L0fr6u5ooowb6jWXNV073zamksVjr/8b+O551/CF5//G0ePOr0jedMYg3Kw0Ey4adCsSJk3\nqEl5ynxlVGkigoeQMqgcMTRMLVSUEf445ghBmWN501ZYsHof4DQ3Uu8vyszFO6MwUyTlCERBRWTh\nnxcluzpxj64k+K3VWo2vPl+GwABtRyVy/RwHleHbWZm2LNSzq/Ws8WiZ9fQcn4yu+aNM/wAQEx1M\nOu7oRQ+5kpQ3WmvW9FLtuNYP1N5kWSfq0XnkiSeewIIFC1BSUkLuf//99zFu3DgADsWmf//+yj6m\n2FgsllorNvXWsW3cuNHQcePHj0daWhoAh8C8I0lOTg7i4uIQGxur9Opse2xsrMcyy7m5lAAz7RFW\nF2Y8+QwenjINcW1F3MPakJ1nR3bWSfy+X2dfi9LoSO4iwt00ZWw2R+dWr8b8eurYvvnmG7Ru3RrJ\nycnYunWr2/45c+YgMDAQ48d7f72mT1yGMjMzkZCQAMChfiYnJwMAbr/9dowfPx4zZsxAbm4uMjMz\nkZKSAkmS0KJFC+zatQspKSlYsWIFHn/8cY/lB9aMzCkXcQbf2bGRIa99Uec0DzapygXoyWKtyCPU\nyF+v45WJESmVkofSkrTS1ZiobfzIVSPKgl5kBUa1DbDb7cg6fQqXK9Sy8//zbcC0ON45g20L45Ii\ns/vFX6+FWM7BtCneGYWVx2uFVKSaAEKjZBo25XhCpXYhYzFyUOleKGrrrECdy1dBaQOe4i7yx7v+\n73ocpRHxUClvbBpvbr2oJVSsTUkCzuY71rG1jgjQlZnappdaiKFpjeHkorRbPa3QbHZ8qGfT12zd\nU42tezx77f70009Ys2YN1q1bh4qKCpSUlGDChAlYvnw5PvzwQ6xbtw6bNm1SjveWYgP4qGObNWsW\njh49CrPZjM6dO+Ptt98GACQlJWHs2LFISkpCQEAAFi9erEw4Ll68GBMnTkR5eTnS0tJIj0hBw4S9\nWPReAAJ39hy3o6qyAv2SQnwtSqNDlu1wBnITeKSOGtvgPhIG93G6EL/wQblq/9y5czF37lwAwLZt\n2/DPf/4Ty5cvx/r167FgwQJs27YNQUFByvHeUmwAH3VsX375pcd9zzzzDJ555hm37X379sWBAwfq\nUyxdbrllJCY9/CjG3nWbT+UQNB0qKyqw5quPfC1Go6RddLD+QYKrskBblmVFSZk6dSqqqqqQmpoK\nABgwYAAWL17sVcXGLzNoh7k8z1SUDH4tENtPrTXjW6eswgZJkhAS5G4zogLxGl0nRpnmyEDGOo4O\nzASql3rGKFqm0tqsi8srcgjWNtJ9HEVdL1VvUI15uV0kt41bb+YqF2/GvFDs+Ms7j7D9zEkIcJoT\n+cgers8SLzMvn9b6L730NloRT/TWiVFORFpmM6OZrPVM3FpOF9T16rUL5eSklbZGz2mFgnLiqK2J\nkfpt8WhF9aGcnPSuw1W+iqp6WMe2LdQ7Zd10ucEs7RHL8mtBSJDjjVevkbb9EJvNBru9AU0OCJoE\nuXmOOTZqQCXg8MOQWn59x6nRGJV0UisaCTVCoxwnjDpTUNERVHJqjOr48pgGw4/Ui1mMTKK+K5nf\notpFb5tybQBaR6o9+6hJeZXGS8jKHEWY9gUA4TUDzeZOM72SGJQvjx1Xyk0BMO2NdxjSaiMqigfl\nPKIVYYaHXypAJUdlZW87YIMsy7gxif6pkoMsjSUeRpPa1iXqBrUEgPrNUJqTbtxNdq5ygrZ8jjId\nc2xujjN8uRpLPIxGblHJRy09oJxlNBx3eK6KAuSHHZsIpVFLDh89rkRKEQjqm9KSQmQc+MXXYjRK\n4loHI6aVX4/dBR4Qd72WxMd3xHcbt6Jvcg9fi9JoOJVTgJYtwxERJsZRteWWfmIQJahnZP+bJvDL\njs1VpddLk1KbyedmgerClIwtBt/ZesFRlcy6lEmSKId3KKDSs1DmIdf6jexn1NY0IsvA/v17cOON\nN5H7NSfo+WzZNcfx5kRq/WGrmrXzvKNIRHP345iDSBB3HKtXItpF4s1r7iIr8CZGdm3VRMBoHmYe\n1wtAbdKKjEJFguH2G41Ao7Wfel74Z416htjzqec4oeXkpGeyZLiem3PBMccWG+W4Kew3aiOeK8qM\nTkaRMbiWlMdMXJNWCixKvnqlYfh7eBW/7NgEDYtRI28GIJxu6sK2A46e4aaeYj1WbRHr2Jouft2x\nKRE7uGebaWrUSFMvvpskAe8t+wB9+lyHlOt7A6BH2wyTzkjdVU6eAEJm6hxq1EstPSBdsHlZKUcW\nDfn0RtvUiLTWUVB03klMA+PTzDCNjq+LaW+twtyP45cMsOUS1H3T1aaItmfl8Noj2085mVCWhTM5\nx2GxBCHIQo/oKQ2fijKiFQ5Y775R0T5kjRiGKvkMWgwoqGecwtOymc6xjrUartFjeK2L/bT4NmBa\nvN5yDi1HG72lG5RWzbjqgQyExia4994JvhahUVJ0yY7dO3/CyOEDfS1Ko+L+27v6WgSBvyM6NkFQ\nM7MIDVUH7HY70n/d7WsxBE2IE2ccc2wd2ojXXFOjSdxxKtoCZd6gtlFri6hgxNQ5VAdIRZzgzY5G\nswFryW80IgKFUYcSvc5dMU/WXG/riADDgV9Jsy5hbrISkTOYeZKKxMGbLCmzntWg2VHrfgRw+6hI\nJq77eBmoZ2PtrmqYzWakXU9nIGfXq3J0YGUQThfUPaXaVO8eaUUS0XNQ0Qv2rIVidiQinrg+N67r\n2ChnDwpmgqSyxFPw7UwFeGboRSLSSmWj3PNKYueV4ocam/C/rgN5BZd9LYKgibDn5024fInOZSXQ\npnNsMOLbNomxu8AFv7zrrpqBXroN1/N4qFFbcHAwZj79LF55eY6yT0+rojQO9j9/nBIFRcfl10yM\nKtm5WtfIy0ItM6C0UaOjTy1X7fxiRwSNtpEBuglTTRqaMRUNgr8OpjHxMSDZObwTB4tWQjlx6Gnk\nlOu8ViQWC/cro7R+Sntk57w03RHsNTDAOWqnnIkol3NK66eujYqlyp9LacasnCqDS6Co+0ZBRvDh\n9lPLDJw7jclApayi4NtZ6/dNWXUoN36950qr3ivRcnXxQ43NLzu2+iYsRCi6tcVqtaK8vFz/QIHA\nS5w+r17HJvCA6NgEgrrRtlWz+h11+invf3MGkVFtMbq/aLzaItaxNV38smOj1ka5YtS8FkD8Lnbu\n2oewli3Rs1u8YbMKs5Lwx7PUKfw2KnoI6xAsRKodPvII1XEoa7N0HFkomRm86Uar3fg6qPV9bBvV\nppTDhtG1Y3qBZMtqJtx5UyTLps0HUGbw7WIhgmZrpRui4E1LzIElkPjl8al2WH1fvPccHpjxBppx\n69h48ylrAythJqTSwlCOSpTTip4DiFYKHWiY7VTHEVDRUvTSNVF1AMA1bYJJky+VKoZvF2rNGtVW\n1D03GtyYQnnur/YYRmhsAgBI6iHiRNaWk2fKEBQUhGuiheZRG7b8911s+e+7vhZD4M+Ijq1xoIz0\nXL67/u/pPMA5gqNGZRFhzrxsWpPFPJQmRmHRiBtITVLrxqkLdN+n5XZPlaEaYdf8z49wmcxa8h3c\n/yuS+/ZDgNm4pkPJQEV+UC1RqJGf186YrLxG5LoPcEYmKeNcqhVtmXAA4TVoyhHIVXaAXuJBLQeg\n0vlopVfSc+YhLQFmdbl65VFaml7sU6Uug1FG9GInutblCUkCss6p59gUuQj3fL3fh4V4U2rF36SW\nX6gPILYxGYgThBm/dojmElwV7r59ILrEWvQPFLjx4SY7ut8w0tdiNDpkWWcUKXAge+nTgBAdWx2I\niorCxWJi+C8Q1ANWazXOn/zZ12I0OuJjgoVHpBFEx+bfSJLzYza5q/+q/WYzht/iHEXbZeeHwcow\nmxwOBFabw8zFPja742MxOz+sDL4udlyV1flh2/gPVS8rl4ftk2XnxyQ5Pvy5gQHun5Bmjk8zi/sn\nwOz88OWwz8lzdrz9wVeqepns/DZXmVzX/7jeG75eS4Djw7cfJWvzIMenT0fnJyYCeGXpJmVffFwU\nvth8QamvTesorN1RrrRpbNdEfPVjNQJr6oxJSMRXP1oRFgyEBQNduiXi659sCAp0BFvu1WsgPtpk\nQ2CAo7yOSQPx1jc2ReZeKSPxzrc2pa17pYzEh5vsmHxrMxQX5aP7DSPxyTbnjb5p+J+w9YDju8UM\n3JL2J/yYYVeu+9ZRf8Kuo3YEBzra5o6xD2L3MbtyD0f94UHsOOI8fvQfH8TeE3bl2Rg99kHsOW5X\n7tH9D03Hb2fsynMy6ZHpOHnOrrTHAw9Px/GzduWePTb9WZw8Z1fab+oTju9s/6PTHN/Zc/Do9GeR\nnWdX7v9Dk6fjzEXn+ZMfnY7zhXbleXho8nScLXDK/+Ajju/2mvImPez4znhkiuN8Ju+URx3ls2fn\nkSnq+tj3ALND3gcfmY7TF5zyTXpkOrLznOU/+Ij6+Idr5GfyMXnZ+4KX1y4Df574IC4UOeu/7/4H\nkV9sV36/9973oN4rTFCD6NjqQH5+PiLCTNi44Vtfi+JzPvz3N8r/UVFROHi8VPX9aLZTs7Xb7Rh+\nyx3K98TERGTmOidurrthII7mOL8n3zAQh7O5F/nQkcg47fw+YtSfVN+H3/Yn7Dnu/H7H2AfxS6bz\n+8gxD+J/e53fbxs7HfO/dH4fcMuDSOw9RPneZ8AYtAx3JvrsljwMlsBmyvfOHfvAbHaOGjp16gMT\n59LWpnVHSNxkS2BYmOo7ANX38rJS1b6KslLI3AROVan6+/GsvarvJ7L2ws6F+Xf9nnHoB9X3HVtX\nwmZztvePm9Xff9i0EtXVziR2/135b5SXlSnf1379bxQXFSjfP1i6EOfPn1W+L35jDk6d/E31/UjG\nAeX7WwvnYMdPW5Tvi16bg1Vff6Z8X/r2Qiz/YInq+9K3F6q+L3ptrvJ9ydsLMe+l2cr32S+8rLre\npW8vxPw5zv3vvrMQ773jLO+9JQux4qMlqu9rOHmWLVmIb79Z6dz/zkLs2O6U/913FuLo0QzV99yc\n08r3r//zb+TnX1C+f/Wff6OkxBlVZv1/V6rWeq7/70pUV1ervtcLfqixSbKs5U7R+JAkSUlFQk1m\nU+64lBMCcz7Qi+/mWi5/Dq8psZh+qnQgRCQEV7fiyY9Ox7s1Pz6zCThysgiJHcMBODqOvYfPoW2k\nw9wSHR2Fg8fOIzbKUXFiYiI2bT+Edq3MsMuO79t2ZCAm0lH4Df0HYs2679EmwgSTBKT0H4jV675X\nPBf7DRiIL9d8j/g2ju9Dh43E+x//Fx3bmmA2AUNuHol3V/wXXdo59v9+iGN/fBsTJAnom+I4n+2/\nLmUgvlj1PTrHmBT5/rslA11jTQgwO75/vSEDPTo49se0jcKGnedxXRczzCbH9X7703nc0NWsXP+6\nH89hYPcA5fvXW3IxpLdzzdyaH/MxdoijcwoPBWYtWI95T45A13aO/UnXONv+dJ7j70Hnu0hJb0O5\nb/Mu++x/3mmFufbzMSrZufxx7Fw+ESof7WPhGjsqyi/jgREO75biMvfj+CUFzDGFWjLCO8ZQkWqo\ntE5GlwAYTf9UTdShFblFL5WSp/iXp86WIyDAogRBZr9LKk4nj9H3hlZ7UEsFqP21ffvmlwDefGVL\nkgR5jZfKut27sl0JomODdsf215nP4tVXnKGzzuaVIbZ1CI6dvABJkhAeHoHo8ACl3MJSGyJbON4s\nFjNwociO1uEmlFc5XrwnT19A82DHW6ZN6ygcz7qAiDDH96ioKGSevIDw5iblRX70xAW0iXAev//o\nBbRr5Tx+/9ELaB3u+B4dHYVDmc79AHDmoh0xkSalDc4V2NCulVlpl7MXrYhpFaBce05eNeLbOi7e\nbAJ+OXQO13dvq5Q36eHpWLZ0oW5Wcq1QQFTnznsJMlkoT0SKQOI4/nj2PISHOrc1po7t5S8u4bsv\n5uGzZY7nUHRsxjo2/i8gOjYKf+3Y/M4UabWqfZdLy2yIinKakyqr7KrvVdV2JCYmKt/LK9Xf/zb7\nRdX3oKAgJCYmIjKyFSIiImEymVT7JUlSlS/LsvI9Pz9fZRrJz8+HjZM3Pz8fhw4eUH1v1cKk+s53\nWvn5+Uqnxr6zTpDBtDNG20j1hFtMK/XkOuvUGHynBgDLli5EXcnMteFYDuFbLtBk5tjm2PzlHP0D\nBYK64IemSL9zGTKZTBh+y0h8t/5b2OHoaLpem4i8vO0AnB1Nfn4+AMBms6HgYr4yIX7q1ElkHjui\naAtMm2JEhDnMdlEtnVoPT3hzkyo4b3S44zg2cowIC1CZIKMiAlXZj2/s78jMrRcomI0g+QzQ1HFs\nVE6taeJH+WybXmZsrYzcVEQRfnRcVVmJkpIihAU7t1GjbWbC5c9l5lp+QMj28/KxiCKRzZ3bolq4\nn1tSo/WkH3cvLybCuS265lxemyq67C47+59fE0aZs0Nq7hcf8YTt5+8HawN+7R2TTy/9DpUGh0pv\n43o8v58MNq3nPU9E7NBat6nS7NhfIjs4hWrNpIdINSwfm2uEf73s5axe/n5opZOitEc9xaUuaW3q\njQbWKXkDv+zYVKGTgkyqhyiomfrtGxJsUT08Pbp1rmcJmy7XJ4YAEItNa8urq+yw2+14INXvfq71\nSkMxiwmuPn75S3Ed+ai+GxwFUvC29wG/G4hvvt2KyBaem1BPq1HmJHTmoagYd1T0C9d9fH3UfAav\nOWmNynn5jCai1IrKQM398FDphihNgg1gWMQQwHm9fL1Mw+IHPNQ8HjuH14hYeVFcvWyujr8fbO7q\nMpcuh8Xp5LUuJmsop7EFWdRl8FRWA5dK8pH926+K/JRWXcHVwcqp4LRMBq+FKG1APEOqGKSERqQV\nFYSHdLTSOp7XFA32S57SJXWODdLVnCgrA3VNRhP1Gj2eek6paDNXQ2MzGsuyMeGXHdvVoLAgHyaT\nSWXWFGjza2YlLBYLesYLla02PDehta9FEPgx/qjYijdMHTly5AgiwkyiU6sFe3/ZDptNOI8Irg4n\nzlTi9AXxvDVF/FpjMzoSodz9tQK66k38MtMO5fJLBUelJuqpQMGUOZEy10mEqUomzEiUGdBMuM5T\nk+iUiYQKUMybtO69+2b3+gh3f9cyeJl5h5LWLR1/Q5xrpslAwc0IU1/LEHX9vPwtuWUBzHmEz8jN\nTJu8fHGt3OU/W+j4y7cfky+Wq4M9L7xDCXP2sAQA8/7jKOCx28xuxzGzaa5znbSm6zz1XPH3iMnK\nmye1gh/z5SnPuI6bvPLb4sqjgiRrBevWM3FLknOOTXNqgiiPko86jkzxRLw3tAKl671fJOK3722E\nKVKg4mzeZdjtdsS2CdM/WCCoI+ezD0MyEz2/QJMucfpzbAL/NEX6ZcfmOkqsixutosVpHBMUFARZ\nliFJ6hEuNTFMJQalkhxSC0sphw1Km2Ku/xbCQYVyB6dGlVS9vPMD2887YrD/eVmopJhVVuBojh3f\nb16HRx+4zWO97N5QqV14RxH2P7UMol2kc1vBJbhBOagwDZBpcwAQ0dy9DErDZ+W04M7t2cHx9/g5\n5zbWlkFc+zEnHv7ZYAvDzxUC/3rSkf+PaWd8u7DyKO3bRDjaGE2AWc3dN2V5CrHwmm+/asLqpyQ9\nJZ41PecQrd8vdRyPnTjXqCMGuyZqmQsV2IGqn9JkbQaXMvD7qFRLAn38smO7WkSEmWvtLdXUsdls\n2LRxta/FEDQBjufS69gEaoQpUiC4QpI6WFTzZAJ9XvjUCpPJhL+OEb5etUGsYzOGPzaTX79irkSb\noiaQXU0jqcNH4rP/rEWrlgGkKc3ET8ATa5SoSWUq2ofWmhceaqKeyrTN9vNmDuaQwF8Hc7ZQ1UWs\nX2IdFe/Ewcop5Ex4rA7ejMnMb1TGcJ5QQj62dot3pmDm2DOcMwXVLuza+fiRrJ15J5NjZxx/WRxJ\n/lwqSzffBsws2TveuW3fKcdf3hmFHcdMoYCzTc8XAYd2r0Z8txuV+vi2p0xVvAwMdg5/PHUutb6P\noVrjSGR7tplc9nH/UqbSAB1nLS0HET2znkkCul4TRGa513Me0cqGbhS936qWAxo1bSCoHWIIeAXs\n+fqWRAgAACAASURBVPVnt1iRAm1+OmzD5n3CBbs2/GfhXVjwcFv9AwWCOsDnkrySjysVFRXo168f\n+vTpg6SkJMyaNUvZ9+abb6Jbt27o0aMHZs6cqWyfN28eEhISkJiYiA0bNijb09PT0bNnTyQkJGDa\ntGm61+TXGhsFNYFMaTVG4IMUU6N3KiYdpZnoxZ+jRm2UzFbCLZsaKTMtiY9/SDkmUPVbCbdx9lDz\n51LaWUkZUF52CUUF+W5RFqgRM695UNExztW407ePdm5jWoir04or7Hr5NjDVuPHz8TfZcXyUFuZc\nwjt7MM2UvwfsHOZEAjivKYvTAFn7Uu7+vEbJtuUVO7cx7ZJ3RjHV1MFrWOxcvi2oe61lCaDa0U7E\nt7TrDJdNhGai1MtrKzXbqgmnJMqJw9VR5MhpxxxbQiwLKupZJsoyQ8WypCwfemg50FBxNanfcX1S\nX6bIoKAgbNmyBSEhIbBarRg4cCC2b9+O6upqrFmzBvv374fFYkFenuPHkJGRgc8//xwZGRnIzc3F\nsGHDkJmZCUmSMHnyZCxbtgwpKSlIS0vD+vXrMWLECI91C41NcFVJ698Sfxop4nHWhgf/mYsZy4RN\nqtb44+RRIyMkxDEKrKqqgs1mQ0REBN555x3MmjULFotjNBYd7RiZrl69GuPGjYPFYkF8fDy6dOmC\nXbt24ezZsygtLUVKSgoAYMKECVi1apVmvaJju0LOXazEuYvEBJpA4CU2f/p/qKos0z9QoCKxQ5BT\nWxN4pL5MkQBgt9vRp08ftGnTBkOGDEH37t1x7NgxfP/99+jfvz8GDx6MX375BQBw5swZxMXFKefG\nxcUhNzfXbXtsbCxyc3M1r8kv77qrqYM3H1CBRrUGdrw5oopaT2ZWp6Xh91PJM6koDibCvEGtv/E0\nSe6s2PHHSkSSoNbK8aYqZmbiAwBTCTAZvCzMBMWbzdj/fFBgswn44vtyWCzNcHNvhxDMAYS/DlYv\nv40dx5sJmVmPrfkCnKZI3gGkmTrFnOqaeCcOdh3UekHeLMpMjLzpkO3nr/fUBff6mVmSvx/selWB\nh1mao+ZAwdHP8PFTn5HPM1vLx5sJKYccaq1hNRH1he3ny2PlUN6szQgnCb3EpVrbKLMjBfV7ozC6\ndo13ZKHq1Qr6bDQyChVJh4omZLQ8b1GfZZtMJuzduxfFxcW45ZZbsHXrVlitVhQWFmLnzp34+eef\nMXbsWJw4ccKr9fplx3Y1aR3haEK+QxB4ZseWleh/02hfiyFoAhzOcsyxJV4jXnP1wQ8ZwPYMY8e2\nbNkSt956K3755RfExcXhzjvvBADccMMNMJkcMXdjY2ORnZ2tnJOTk4O4uDjExsYiJydHtT02Nlaz\nPr+841TUAYbiiq/jXk6hFWmA0rBU7v41f5vxThca8eLIeonRol48SmpkSGmATIOhEmDqpdFgo3sq\nJQqvDZRVAnOeHq9aAkDVQTmAMG2BiqPHa2xMU+M1NqZNUele+EghrF5ei2NOGbz7e36J4y+vibEI\nJXz0DXZtmWec25is8VzAfnbtwVwdzEGFpZ4Z+4odGz+egb3/Wwgr58hCOXRQSWMpzZ1B3VNKi7MR\nGr7eNqMam1bCWeq+eZJVRc3D4upopRWphK+D2sbHXGXiU/Ejqd8ltY2yuIBol/oMBFFXjW1gN8eH\n8fLX6v35+fkICAhAeHg4ysvLsXHjRjz33HMICwvD5s2bcdNNN+HYsWOoqqpCVFQUbr/9dowfPx4z\nZsxAbm4uMjMzkZKSAkmS0KJFC+zatQspKSlYsWIFHn/8cU3ZfDLHNnv2bPTu3Rt9+vTBzTffrPTS\np06dQnBwMJKTk5GcnIwpU6Yo59TW3fNqkZiYiLyiq+zGJGhyWKsrkLN3va/FaFT07hKE7h38cuze\nKDh79iyGDh2KPn36oF+/fhg1ahRuvvlmPPDAAzhx4gR69uyJcePGYfny5QCApKQkjB07FklJSRg5\nciQWL14MqaZHX7x4MSZNmoSEhAR06dJF0yMSACTZB8vzS0tLERbmmBx48803sW/fPrz33ns4deoU\nRo0ahQMHDridk5KSgrfeektx93z88cfJi5MkiVxcyjARGgKlNVDzCcz+z7dYgBnIL7Zj4vhbsfl/\n3wLQT9zIoDQ2aoE2g9eIAoj5IK0FrdScIl8v0z5YNHteZl4jojQxNs/TJty5jS025ufn2KLp7361\n43hmBsbd2kOz7flrY9uoBdWVRJLNumhsrF30NDZ2f41qbHzsybYRjr+8xsbM2Pwzx67t5HnnNrZE\ngL8fTEui4jTy11tS43vC3w9Kc6KeUy2Njcpc4C2NTUtz4vGoscF4bEejGhYl85VobBRa7VJ82bsR\nVSRJwsV/e6esVvc2nGgvPhnOsE4NAC5duoSoqCjN4z25e3rqtV1/EEbNjnpOJtR6FJsdiAgzqToz\na83/RkNHqSaQNSI/8D9g9vxQk/w81I9Z6UwIkyX/4mPy89dBrblibcRMdPxxfEfEZLBWV+Pzj96A\n2eS8TpVTg01dLn8u32GxzrOEcxhknVI1sY6Nv7+sA2cpaACn2Y/vsEqt7ttc5QScnQ3leMLLx87h\nBwF9Ojr+8u188LTjL7XWkMpAzt97dg7f4bN6qXbmnyEqKo1WAG++POpFr5Uh3axjWtca5Okhy8De\n3yphMpvRI179Y6IGg6qA1sR1aHa8LvW6lkcEaVHMjlRnpxp0UyZLL9NA+iKv4jM9/dlnn8WKFSsQ\nEhKCnTt3KttPnjyJ5ORktGzZEi+99BIGDhyI3NzcWrt7Choug3oSMZ8Emty30A6rtRLvPBqsf7AA\nQMPRHgRXn3qbY0tNTUXPnj3dPmvXrgUAzJkzB6dPn8bEiRPxxBNPAADatWuH7Oxs7NmzB6+99hrG\njx+P0tLS+hLRa+QXVePsRZFfQlB/VFwuwM61L/lajEZFckKQm7YmcKc+17H5inq76xs3bjR03Pjx\n45GWlgYACAwMRGCgw95y3XXXoXPnzsjMzKy1u6fbPAdvTmTbdTz9tPIvuWfkdWygTGgMKnQUE8as\n81BoZeDVM7NSsmitl+FNX2w/b4Zj9fHryYprTG2UWYo3WbL8YD8ddhw4sLtZuVf8OjG2Zk2V383s\nLl/ORcdfyjOQN9uy6+DDTrFyeNMmk/mSy9o7QL2cQyvEGZ8vjsnP/+iZrPx6N7aNl5ntZ+d++kyU\n4k1awbXB5Ur3bRXEWj5mWqTMk9R6RirUEwVlHtczr2lhdG6KMidSclI55Cio34Jqm4bHsV1nrpC6\nDko+yjxptTreZ/XZb/ijYusTr8jMzEzl/9WrVyM5ORmAwz3UZnP82k6cOIHMzEx06tQJMTExirun\nLMtYsWIFRo/2vBbKbHZ+TFfhClu1DECrlmJkaJS887k4efywr8UQ+Dl7j1di/8nGHXA7MMCR2SKk\nGZ21QUDjk7fxrFmzcPToUZjNZnTu3Blvv/02AOD777/H3//+d1gsFphMJixZsgTh4Y5Z9sWLF2Pi\nxIkoLy9HWlqaprun66hOT6uhjmPojT61tDPVCI0YFVET/5qjTp0JZCafhXD24LUfUnusgXJG4QMA\nsx8XP/Jn2gJ/vbxThqsso25qr2xjmhBfL9M0qMzYlDcrP2IOIhbKs3N4bY/Vx7dBBWFNpu4R02D5\ndmFekWHEGjN+3R5zeOG14ANZjr+8AxJrP9a2k9+2w263Y959AarrYBqvKvII4SlJBdbVClpcFy9B\n6lzX4/XKI++5jnZGOa0AgGyXAZMxMxlfnvKOIJxgVFYTjfIoxxPSa1njvQB4cDzxMg3NjOgNfNKx\nffnll+T2O++8U1mR7krfvn3JZQANhXMFNvTo2gb5+fm+FkXghxTlncT5bKHl1obkhCC/fGl7G2GK\nFGhy730P+1qERsGWX4ux66iIVl8bPv17Z3z5+m2+FkMgaBQ0iYkhftRm1jHnuZ2jsyaHjXbaRDjt\nSNS6KQa/VomZh6iFyNRIkwqSSy1O5UdgrA6tNW6eYNfBmx2ZCY1yQtAKHgsAMTWLkz9Z8hzueeRF\nxEQ4r5M3XbJr489l9fJmR3advPmPWhfHTJvUYmIqizRlDqPuUSjnGMOcZC5yTrxsbRtfL8ugzedj\no8yTjDDCu5+/50w+Kng1fxy7Tr0QWAw9U5rRhcjKtRPmdv7nRIWn0pKF+n24Ps97fquEyWRG707q\n15yqPGWje3nUOkrKdEiVrdcuWtiu8rSgP2q1QmMTXHW++WIhxg0N0z9QoDD73zbM/rcI3VYbZH98\nY9cDsuydT0PCo8Y2depU3ZPZIuqGDq+tUEGQtc7RC4PDlg2cya+GJEloGxlAansMyjmDH1lT0VKo\nrMHsfypoMa+FUM4Z1AicqpfBO1UEaYwm+REuc0wo5jQxpkl0buvcxjQcXpNlru68MwVzhGBOGoBT\nw+HP1Qodxbvxs22UlkSl5KHuPd/2VKoYprHxGhErL8+qfRyrj92/w/t3oEWLcGSeUXvHMfkpawLf\nLqy8amJJBhldR8c5Q2sbr1VT2je1TU9rdD1Oz9ELAFK6OW5QgMs9pIJ1U0N8qg2upK806pzGoxUG\nTOAZjx3bmjVr8I9//AOyLCvrtHhkWcb8+fMbRccmaHi8t8GO8rLLGH+z0NyM8MzDA0mzpEBwpfhj\np+mxY5s+fTruu+8+zZMLCwu9LlBjJaYVMfQXeOTypSKsXv4PX4sh8GN+PuqYY+ub0CRcCeqMP1ps\nfRLdvz6RJMkt8j21jo1ai6ZaP6IRJUAvwgdlVqEi/muZgqggyFS5fOR4av0ctX6JylasFfGcl52Z\nt3j5qMjyVOBcZlbr2s65LbrGcSKbWyXBzJe8+TSqJmgxb8ZkQZcLuHVizATJXzczT/LtopUYlr8f\nLPo/H7SYel5Yeby581zNuI+PAKKV3Zo3i7qa675Lr4bZbMaQXuqA28yBhdfmqOj51DPLTIaUyU0v\nszO1DrC2UfF5qCgeWuitlbPLwI6MCpjNAbiha4DqHOpZV0W5IbJuUFFktCKPUO2nF+BZy/TKzq2P\n6P6n3vVOWfEPNpz4nLrOIxMmTFBpZgUFBXjggQfqVajGyvlCO1557W1fiyHwQ1Z++iby8875WoxG\nxYCkIKVTE3imSTmPMPbv34+IiAjle2RkJH799dd6FepKURwh2HduH+XuT90UynnEdZ9rGbIsI6xF\nS3Iin2k4qhEp4RQSUHMcpcXpZbJmsvKjdxa5gh9BUtqFVjxAPe3WquGIw8vJzim6DGzZ7xgC3/k7\nh/oRyjlEMA2Ld6phDhN8LjKmqfEaEdvPO4+w9qUcRVoQGi/vdMEcRGKcPwFl9M4ihvBl88sWqOzl\nVDszLY53+mHPC4tv+faCGXh7wQyYJFqT4NuAcuM36gxFyawVW5SH0kyMOoUw9GI2yi6/bfWB3L+E\ndsa26WlnWpodWS0RU5KiLumzFOeRelz26Y+mSN2OTZZlFBQUIDIyEoBDY2PxHAVq2Fq2+kzj7i8c\n2LvD1yII/JwfDznm2PonCq2tqaF7x//v//4PAwYMwNixYyHLMv7zn//g2WefvRqyCfyYxycMBKB2\n3xd45qU3v8GA36fh5t5i6alRGsp8T0PHH5tJt2ObMGEC+vbtiy1btgAAVq5ciaSkpHoX7GqipWEZ\nTQtjswNnL1bDZDKhbaTZ7VzKwYIRSmSjpib+LUQAYJUZs8Z0x5u02DberMf+5+tgpjvKxEkFHuah\noqVQ2cOpKCmsXj7dC4vEwcvHTG18uhd2nXyGat4E6SoLfx3MtNnNmb8W7aPdjxtU86gPHNRG2fbt\nhvMAgPNFzuOOnXH85c1cVFsppjQqqgV/z5mDT81x7yz6K3r3HQS7rDanU/eXwbeFVlQYKjWTytRM\nZNrWWk/GQwYJ13CkorJ565VHZu6WgJt6BUGWuXOIQNpkXTX7Kccrj+e4QGXQNtqBUKbr+ux8/NEU\naWj4V1BQgNDQUDz22GOIjo7GyZMn61uuRklFRYUYJRrkg5UHsfWAiBdplJNHjuDWAS19LYZA0CjQ\n1dief/55pKen4+jRo7j//vtRVVWFe++9Fz/++OPVkM/raK3u50fYWrEVqX0BZiChvUPtoLQuLU2I\nd9/Wit9nItzuqfJ4JwnSpdvufhzlzkyNbCm5mCyqGHeSu5xMqwgMAF762x/w2tvfK9feIdp5HHNq\nOVPg3MY0tktEgk5e+2GOMfy9ZM40vNmzU40C1q+rcxvTGn+X6NwWHl+T0Da4s7Itv8ShsfGOJ2Rk\nCmI5BxUpRCvaDK/pW5qpy+DL4Z8hysGHtR+vEVHPPSuHiktKuasbdUahNEoqSakqLQz17LoX4zGt\n05Z9jjm2QT0cDyGljVKxQKlnnO2nnGq0jnccSGwjUNqZ0BTrc97eH8fiuhrbypUrsXr1aoSGhgIA\nYmNjUVpaqnOWQKBN9tEjuHtoa1+L0ajYtM+OFeuO+1qMRoOwnhjDLnvn05DQ1diaNWsGEzckvnyZ\nyCApUDhz0Y6cnNNI6R3va1EEfkZpSQEWzXvM12I0Gob2EfnYmiq6Hdvdd9+Nhx9+GEVFRVi6dCne\nf/99TJo06WrIdsW4rmcD6IlcygzCghvrpXtxjSBgt9tx5kwOAP1JanYOb/ZhjiS8aYkyg1Br27TW\nAPGBc6m1O6xe3uHAQjgmUE4DvInR9Tgq9QwbJ61Pt8Nms+HWFIsqegirl5+8ZyZI3pTG1ujxJsF2\njlUpKjMmM0VeE+XcxhxF+PKurbE6Zp51bgvMywUArNmdq2w7dUH9F3CadynnEb7tWbvxDkPMfMqf\nyzKB8+38h8HcBbhgJh5yfhurrxlXB5XKhnK+0XLiCCCeOZXjRM25/DNEBVp2LRegTYe1XWOmMu9q\nmASpFDX8ubKk/suXQ70P6mS2Ja5Naat67KD9UbHV7diefPJJbNiwAWFhYTh27BhefPFFpKamXg3Z\nGiUd2gRoLnYWODn1WwZWfvKGr8UQ+Clsju2mnmIdmxb+qNXq3vHLly/j5ptvxvDhw3H06FEcPXoU\n1dXVsFj8L+ivXvJCLe2NGmXxMC2Fj7DBRvJ8R0i5pjONjq+jSiNJKT86ZtpANTEhzcvC9lMaB6/V\nsEgYerEsbYSDCrteJufj9/RAYIAjukcQdxw1EmZaF7+UoU9Hx9+B3Zzbfjri+MtH4ohr5fjLp5lh\n18S387ZD6roA4O7fO/4Wchrl8XPusrD2oKJk8O3HymaaJeCMakLFe+TPffkrO+x2Ox67zdn4TJPl\nNS1Kg6buP6uD0pL4a6M0fFYcpelQlgqVE4zGW4dvPzPx22LaKDV2dEuhQ0QaAfRT8lCyaGlnvBZn\ndExLWWEo7BpapsAzus4jgwYNQmVlJXJzc3HLLbdgxYoVmDhx4lUQrXFy4kw5svNEZBaB97l4/jS+\nX7vI12I0Gm7q3Qw3JgltTY8mGStSlmWEhIRg2bJlmDJlCp566in07t37asjWKDl58jgSEhL1DxRg\n1Q4rTCYT/nCjiKZhhLkPx/taBIGgUWBoOLNjxw58/PHHWLZsGQCHg0RDxkjQVqPBjVX7qSgKLlEK\nhg3soZgXeFMQS7vCO4UwMxKVDoRaa1NFRC/hj2PmI370xEx8/LVdqjHT8c4UsTXmul3HnNuoYMTM\npBXEpX2xEqZStp8KoMzWi234ehGi2nRARHPaQYBvK2bS5E03zEHk653ObazN23Pr4lh9fKoaZpY8\ny6UUZKlpbuji3IYQdRkAMLiH4y8feYS1EW8CpYICs/vBm14p5xZ2nXx5bBtvdmQmPj74MstKzp/L\nnl0qqzYV5YZ0YCBMzdS6Lt7sSaVrMhOvD60M7nqOE5SDhUlyX8fGXltGgxbzUA5mFErZOu8X6np9\nNdfV0LQtb6DbsS1cuBDz5s3DmDFj0L17dxw/fhxDhgy5GrIJ/JzP35lBLtwV0DzxnqPHmDtBNJoh\n/PCFXR/4o/OIXycapUZFlAsx5bBBTcC7Hs//z2tTx8/aYa2uxo09nN4ZzHHiIre2nYpFR7nTM+2H\nGh3zUKNtdg7vmMC0Rz5O4oPD3euY/5Xj72+c+zsrm4/iwbQffqROOcaw9uUTjTKtgro2Xpti5RUS\nSUV5d3p2P8JDndvYtfNtcKHY8Zdv58Sa9mDtAzg1Kz7iCUtXw2tsLFEqryVRkWq6xDj+8holaxc+\naWzbGocS/hm5afJOVJQV4b9vjlC2MS2dT+fD2qWYi6HJYmzyTiEMfnDBfjP8cVTyVur5o5yctDQx\nrWUzns6hnD20HEC0YmTy5/DPLhWfkdJQqYS9WsYsqg69WLSuSWNLyryfaHTvQu+U1Wd6w1kUrzu5\nkZqaiqIi5y+4oKAAt9xyS70K1dix2Ww4lnnE12I0eKSoKLz8lR1de4/0tSiNgq9e7q/q1AQCb9Ak\nnUfy8vIQHh6ufI+MjMT58+frVajGTscYxzCfT04pcEfOz0fWsd04tu9bX4si8EPYHNvA7sIzUgt/\nNEXq3nGz2YysrCx06NABAHDq1ClViK2GiKv5w2jmX6Nr1iiHCN4xgVm8+HVTzJTAm3OY+ZKKRmIi\non1QGbSpbMWU+ZRfN8XWdfFmM+Z80D/Zue2FcY6//1zl3MZMqbxTADMFdnRmdlFMX7yZi5kRebPt\nqgX90S5SbeJhZjA+oggztfFtwMrhHTvYNj69DZVpm1pPxtan8SbGzm0df3mzKJOBtSMPfy67Dt5s\nO6FmeroT11Ys0klesXMbe574Z2jsyw4v0g+mORtB0ngOeHMsW7PImydZe6iyRxPPGjPHVhFOTjzs\nmVCZ/4g1cAz+LVJFmDHZa4ZyQFGV4yk6h8u6OrvLd4Bey6c41ehFJyLeB64yqerVMZUq2XV01tQJ\n9NHtoebMmYNBgwbhz3/+M+699178/ve/x9y5c6+GbI2W7XvzcDCrYXuOChofx3e9i8JzGb4Wo9Ew\npE8zEXXEAPVliqyoqEC/fv3Qp08fJCUlYdasWQAc01mpqano2rUrhg8frprqmjdvHhISEpCYmIgN\nGzYo29PT09GzZ08kJCRg2rRputekedftdjuKi4uRnp6OnTt3QpIkvP7664iOjtY6zedoaWomYkJf\nC724cmxUyZe3+osluHfSTNVxbAKe0rqqeTdqKsqIRpJSHsoJhm3jXclZIs9YTuM4V6ORrPveuY1p\nZyzCBwDkXnT85TUxVt7D912rbDt7+CgAYOtB53FMY+PPffAtO2RZxmdPOjdS7upM++FHs0wj4duK\nOYXwyUeZ9tOaS2fGlg/wx7GyeQcVtp+PoNIr3vF3TH/ntqM1oSTfWOvclluzHIFPg3PTgJp/OCci\n5qzyEzctyzRUfkSfvWkysqF2MmHwlgAWF5JvPyqVEns2eKeGy0RMTi2HK5UDlNZvioj2oWcCU1Ip\nUSmciN+RqjpCwzIa6o6KMkJGHnH7h7akMM1RL/akso9wjKlP6quOoKAgbNmyBSEhIbBarRg4cCC2\nb9+ONWvWIDU1FU899RRefvllzJ8/H/Pnz0dGRgY+//xzZGRkIDc3F8OGDUNmZiYkScLkyZOxbNky\npKSkIC0tDevXr8eIEZ7nmzU1NpPJhFdeeQXR0dEYNWoUbrvttgbfqTUE3nn9bxjY3f9CjtUHGduX\n4JvXbvK1GAI/ZNv+Smw/ZHBUKKgXQkIco7Cq/2fvy+OrqM73n7lLQghhCYEACasEwy6LURSr1rKF\nioiWKirgLvor2qi11bpWxK/7UsENXGitS61gtaBIEYvFqGxlEYgQJAkECEsIkITk3vv7Y3LmvjP3\nvedMwg335maez+d+kpk5c847Z5Zz3ve87/OeOAGfz4d27drh448/xrRp0wAA06ZNw8KF+lrHokWL\ncOWVV8Lr9aJHjx7o3bs38vPzsWfPHlRUVCAnJwcAMHXqVOOccLDlFfnUU0+hqKgIBw8eNH4OHEQC\n+R/MQNmuldEWo0lgxMwS/PyPjonbNuLQKaIx0JhekX6/H2eccQbS09Nx4YUXon///ti7dy/S0/VF\n5vT0dMMZcffu3cjMDMYgZWZmoqSkJGR/RkYGSkpKIIPSAP3uu+9C0zS89NJLpv2FhYWqU6MGq/lQ\nFSsiwC0Mh6tHgMtg7PUAKzb4EAgEMG643sUcQbH4n7YrzC+0HBfv5mFSuwgnDup0kVrnuEDTwwlT\nGnVqECweVJYOdaY76sCwbbf+V8RtAUFTxuqvtxr7BIsHzYwtZGlDnBoOVpjbB4KOLJRhY/8R/S+X\nZbqCmNyEmY5j2KCxXsLcSeO1OGcecR0/6x/cJ/qvlDiUUJOrgHC6oHF2xse268+MXUlVemBc0o6f\njH0ibo7e3x8+vgF9J7xucgoxzHoMKwg9V5glExWGBC4DuUgPxJnmuOeUi4vj0upwWavtxqJxaWGs\nOG9gIn9AUTdXr/E/wwjEpsWyGXPKMe6Y9jFLE5FGY5o7XS4X1q1bh/LycowZMwbLly83Hdc0DVoj\neMYoB7adO3dGvNHmgGPHKrC76MdoixHzGP1ADdxuN+b9JrY9bWMBh3cuxqoXMqIthgMHAIA12/Wf\nHbRp0wbjx4/H6tWrkZ6ejtLSUnTq1Al79uxBx44dAeiaWFFRkXFOcXExMjMzkZGRgeLiYtP+jAz5\ne2DLZWjjxo3YvHkzqqqCPtRTp061d0UxCm72ySUCNGlxrtBzBawhABef09akxYlZLGW/EFoFnTVy\ns2OhSbRkUt5QbUrEzaUHww4Nh4nBxAFEuJpT12/hJPHzQcF9yV1075KdPxww9gltgXJKChlWBRU2\no9/6dQ3uE4k5qdaw+5kL0Sa9L44xrvhU6+KcGoSGwDmZVDFpV6gGI/6njCJiVk5ZQQRTCNWSRF9t\nDCpYRn30/op7TkMKDAeLVEJysOsJAGZNVjjBmFzxmRm9cOPnrA1cAlHaBxydmehfk4u90OIYNhL6\nnFoZf2g9nDOKKlWM0G6595KWq2X2uV3A15v0OLazs82fOWs5QM3qYzirUA3PwhMbDhxnqNFXqb4L\noAAAIABJREFUlKczYD4GAAkMP2ik0VBtcEgv/Scw7wvz8bKyMng8HrRt2xaVlZVYunQpHnzwQUyY\nMAFvvfUW7rnnHrz11luYOHEiAGDChAmYMmUK8vLyUFJSgoKCAuTk5EDTNLRu3Rr5+fnIycnBggUL\nMHPmTKlsyoHtoYcewooVK7Bp0yaMHz8eixcvxsiRI5v8wOYgNlD200qU/eSssdnFL+73o/h/76Lg\nn1OiLUrsw1ljs4XGMnPu2bMH06ZNg9+v5xG85pprcNFFF2HIkCGYPHky5s2bhx49euD9998HAPTr\n1w+TJ09Gv3794PF4MGfOHMNMOWfOHEyfPh2VlZXIzc2VekQCNga2v//971i/fj2GDh2KN954A3v3\n7sVVV10VgcuOb1x143244Td/wughjonNQeRQeaQUBaseibYYTQLnDkiMOaqn5oSBAwdizZo1IftT\nU1PxxRdfMGcA9957L+69996Q/cOGDcOGDRtst60c2JKSkuB2u+HxeFBeXo6OHTua7KCxCKu5QsUo\nwqGGYSTgzuXMDLU+4K2XZ2HazX8MySTNsZbQfUkM4bEwydG4M+GIQU1fgiyZi2miGYwFE0dJ0MJo\ntJFM4t02rSMFLODYFqhzhiA65sxh+wjDRq0PeOhvflRXHcftl+oXxaVTOcqQ+HLmNWEWpeWE6ZDG\na4l7SdPvCJaRgd1D6xNmVABYV+c3Ney04D5x31IJC4poI5U46UCrszN5iL34hN4h9CMsro32QasW\nwH+e7WKK4RLyU1OfIQtpV/QH7SuOEFk8pzKHJYAn/+bgYp5x4RDBMZ5wYOO6FEwmQn5u2YA6dnDf\niJC2aBs02zhzXPSHykQrronW52GWRFpa/F8OIfJolpRaZ555Jg4dOoQbb7wRw4cPR3JyMs4555xT\nIVuTx9gzk9SFHOCTt/LwybsRohh34KAO+Vv0Nbac0x32ERniUatV3vE5c+YAAG655RaMGTMGR44c\nifkM2lZtwnTjGOYRzvWWYxCQzWw4hgPqwMC6PdeB8kyK2R3d14KZgXMzdeEMQpNYUucSAeGqT2fl\nwmFiX9D5yHDK6EDSuOyq20f5GYWrPmU3ETN6ER4ABF3sqVPIwaPA539/DmVHgvuEXLT/xDnUUUSU\no33AaSaiT6l21qlOYaL8lkJboZqs4Iik2o249h+KQ/dRlhZxH4YSzQ5pl+h/K4Mes/66fjnCOPPQ\nGbvHDUx41A+fz4elfzL77atYMgS7Ced8wznaUAcfoenSPuWsDYbLviLUzuB2JPtk6WgoOG3ecACx\nOtAwZWn73DHjXMCkFQqNUiYTlUWVKJj75oh66Psr2nO4IuuHsAPbnj170LlzZ9O+nj17Kss4CGLl\nJv3VHdnfSQypQlpaGsrKytQFmznK923Fzm9fibYYTQJnZqvj2Bw0M1Pk+PHj2YW/+pZpztiwdhUq\nK4+qCzZzPP+xD5qm4fJzHUcbFVa80JfN3uDAQUPRrEyR69evR0pKSrjDAIDWrVtLj0cLsqy9AnZT\n1FBwZhCBGmaxfcbVI43/rZlwgaAZgsaTCRMQV47GsohrpOYrwTjSieSBE9dBHTbEPpp2RbSx7H/B\nfSJ2i5pFC+tS8QlHCyB4bfSDK8x/VURmIYPXwkzx1F3nY/P6lYYjDLfwL0yQXGZx2q7XEyqzMBPS\n+D7Rv4LlBAg6iND7IZBMJv9Crh2lwX3i2RjQLbjvguF1/5z22+DOlGH6333vG7u4dD41jJlV9Avt\nA44cmovbE6BsM1xsFMcAIkxj1AGJcxoRz5BdAm8ZeTGtx8+Y+rhM1lZz7JoCfY1taG/zZy4kvQ3U\nJkZun5EOhxwXUzMqH5ctm5uc1DDvEWcGdqBG2IHN53N60sGpwc4tThybXVz6mP5efvqAY95WIR41\nkcZAszJFngo8/fTTuPvuu1FWVobUVJ2eYfbs2Zg/fz7cbjdeeOEFjB49GoCej2f69OmoqqpCbm4u\nnn/+edvtcAvrFIZjB6PFcQkDuWShnFOIzw+s/tGPPSW7cMmFPQCYHRgCjGbJtSvaoOlUxCwwmTiH\ncLNA4bBB6xNsJNR9e/1O/e9qQpGTW6dcbCeaidBm2hMnDsHOQV8Q4frfi2h2pXVpl6hzhri2M88d\nh43fLTadSx0nxLXRj5Vg6qDalDWpJBDU9ii/pdB0KfMIx3UonG8o/6bQktKIwUKwvlCnGgx6ve7g\n9cF9J+o6s/BBY5e4R1RTPMaEN7hdwJ6CL3Hs0C6jLJc+hksgKuqhz4G4tmMM+0otY5Wgz67QJAKM\nZkIh7kc140jF8T3SNC41jPZYI3FMMSXt1IAhvROhyonMMQyJc7hvhcZ8D7jjnPOIRvZxz6kAtf5w\nlp5IIx4nAFFb1CgqKsLSpUuNzNwATPl4lixZgltvvRWBul4X+XgKCgpQUFCAJUuWREv0euHHgs2Y\nftlwdcFmjPueWYJ7nvg02mI0CSydcxG+ff/aaIvhwEFMI2oDW15eHp544gnTvkjm44kV/HrcAMfb\nT4FZeWPx2191jLYYDuIM67ZXY912Jx+bCv5AZH6xBFumSJ/Ph71796K2NviQdOvWTXKGHIsWLUJm\nZiYGDRpk2r97926cfXYwLbHIx+P1euuVj0eWQVtW3m56G26hnsIgoUVoOS/pcS57rihHF/YFQTA1\nbwjHDs7kwcV6UWcKYX6jDiUiBQs9V/QHjYXrW3cbqFlPmORo6hlxDnVkycnS/24gsggzXKC6zDDj\niWuijgeiPtrfQlbKeCLMKtQsK8xgR0g5zhFDmBtTmLh6akoTpMbUGUWcM3AgOan1Wfrfo+uC+45t\nAgAc3B60+QoHFuoIZJivLCbp61+ohcvlwsu36p3EpZmh5lUB4fhBn11xDo1Zo/ffOJdJnSLOofeI\nczxhTXNMeiAOXIZ5GUOJVWZRv7jXnHOLUS+VWUXOXAdxvSozoYchghYOOYnE7C2ul5bjzMqRRjya\nIpUD24svvoiHH34YHTt2hNsdvAsq3q5Ro0ahtLQ0ZP+sWbMwe/ZsfP7558a+QDz2bB3Wbdc/RGf0\nclzZZeiaPRLJSSnYsnZxtEWJafxv+QtonxnbBAmxggE9E9m1bwfxD+XA9txzz2Hr1q1o3769qqgJ\nS5cuZfdv3LgRhYWFBntJcXExhg0bhvz8/Ijl46Huv26X2RmA0+ZkfHFcWICKP5Ie+9N9M9AyOTmY\nGocucNfJRbUzblFZzMqTGMcTzh2cahfi2uksXtTN8S5SLcTaPsAn6BT/U41NXC/VpoT2RkMFxPXe\n+cRX8Pv9uHeyByn+UJk57k4RNsCxN9B9QrtozyQfpRDn0HsqNGPqKCI0S5qOZtQZ4mBucOfhr+ou\nZH1w3773AABbicGB49AU/Uy1x5aJwNcf5IU4SQDm51RcG9W+OG1KPAdcYlCV271ol2rGnAbjYzRj\na3kKlp+RSVGjYigxyhOzCZfyxnqMysVpnqpyHIOKAH0mxbNNZalheCaPV/OhRJFEPOoVyvlMt27d\nIhqvNmDAAOzduxeFhYUoLCxEZmYm1qxZg/T0dEyYMAHvvvsuTpw4gcLCQiMfT6dOnYx8PIFAAAsW\nLDBy+HDwuPVfgof3VjyV+Oi91/DX+Q4Pogq/v9yFeyc338jjNt3HYfBFdxjbF0y6D9Pv/cTYnnjb\nO/j1/cE03ZfkLcO1TwT5yi65+3tMfeKwsT39sW24Z17QjfaOF3bhvreDI91dr+zDg38Nzk4efvsg\nHv8guD3n43K8/llw+7V/HcWCfwdnUW98dgx/WR7cfm/Fcfzru+D24m8r8fma4PZnq6uxdG1we/n6\naqz6Ibj99Sbzdv6WE/i+IPhFX11wAmu3B7c37jyBzbuC25t/qsGWotDtLUV6nT/sqjGV31BYg00/\nha9vQ6F5+387qrFxZy05Xo1txcHtLbuqUVAS3N5WVIUde4LbmwqPm8v/dNx0fHPhUezaR47vLMdP\ne2vh9egTmtJ9h1FxjGGtdsBC+SXp2bMnLrzwQowfPx4JCfrUXdM05OXlRUQAmhY8kvl4Yg2nZ2dj\n65Yt0RajyWDwyCvQq9/5WPDCDADALfe9g57Zw3HvtD4AgAfmfI9OmVmYcbEeu/D8eyVIaZeGa0fp\nvv9zPj6MxBbJuH60rq7NW3IcHm8Crvm5/si/vUwP3r36Qn17wb9r4HK5MPXnuvoy73N9+7eX6Nv3\nvl0LTdMw6xp9++aX9O2P/6hvt7hMNzljwy/1C+j/se43vnuuvp01V5+K12lsZ92ls61886Q+8xpy\n1SfQNA3rl+mToPFXPwJN0/BhXX8MHDEZLpcL1z1VhqRWqfD7/Xp7dUjreobpXWrboZdpOyW1i2m7\nZatU03ZiUoqpvoTElqZtb0KiqbzHm2Dadrs9pm1N6Wdv3tSvJ6g6+mproXmDddTW1sIr2a6pqTG+\nT3a2a2tr4PXSbXn9VvkC/oBULXBZ1EKPx9w/Xq/XtJ1g6d8WLVqatpOTk033I5KINcePSEALKBa4\nHnroIb1gXScHAgFomoYHH3xQclb0oGmaEf8k09ZcjDmRlhfmGWqmEaYvjmGDy0YssHa7nmjvzD78\nPII+WAkMc4a4Ho4YmTp2CFYJuo8uXKelZaOsbAtaeIGf/foZdM/+Gf72qB6KcOUfv0dqpyw8eaM+\nUMz8824kp3TAske9SEkCht9xFG5PC7z+G13A656vhtvtwVPXuZGSBNz4oj4Q3DZeb/DPn+gffrrt\ncrnw5LUutE0OOkG89v/0Tr/hRf1DP3uqCzU+4P6/6NszL9aPP7dIL3/9KH37tc/0+m8aq9f/ymJz\ney/+MyiPzw/M+fQEXC63UX7uJ5Vwub24dbx+Pc/9owIJiUm4e5IH7VoBv527Hy1atsXcW/WBcepj\nO9GyTToW3JmEXunAGdeuR9v23YEldbbbEcuAVlnAuhH6dpcHgJQBwLYpQHUxkPZrQOuE0u+fAQB8\n/UPwHglT5K79wX3COYfGKaYkAT0HjsO4qc9g/r19jX2A+dkV5l/KqsI5gHAxZsJRiZ4ryzJNTX2C\nTJmyzYhzONMmPZeTT5zjY5xHOGYPzlQqi62j/9tlHlGZaGVmWy5NDzUzcgwlVrkOVkTWJ0HTNHx6\nf2TqGv+n2PGXsJVBGwAqKnSjv4pmy0Eo7pk5BZWV5fjDI3Mx+wFdA3nu1U8w4Iwc/CJHd3P/11c7\n0bFTBs7pp39I//VNOVokJePng/Vb9PE3+kBy+bn6h/ntZfqH+5ZxdR/qf+kf/t9frr+p976tbz8+\nTd8WA8UjV+nbOWNmmmaA6d3PMG0np3Qwbbvc5hkl/D4EyAy2pqoC3hbBZ+PA/mK0Sw0upu344Rt0\n7tbH2F7z2ePo0D0Y3ycmTAJ/utptYvy/aaz5Ub1xjMc0Obl5nH5cTD5+c7GZ/f7W8Qmmj8SMX+oj\ngviw3TEpxRTo/ewMPd2BWGP78JEepvrWvTEYFwwgO7ZN1v+66kai3Y8AGpG57D1EAoUbFmP+vY6D\njQMHMig1tg0bNmDq1Kk4cECni+jQoQPeeustDBgwQHZa1KBpGuuubcVtv7kDvxg9FpddMhZuF/DZ\nsm/Qr/9A9MrQv2Sbf9yPNm3boUcn/eNUUHQcCQmJyMpwI8Gj2+hdLheGnKZ/Sdf8qA8kOX1c8AeA\nb7fq28Oz9C+n2B7WW9/+bltw2+MG/rtZr09kAljxP30g+/lgN1omAh9+dRQJiS0w+TxdnlcXlqBN\nakfjA37XM9+gc9dsPDytLZISgPN/9Si69BqONx8NNdmK8aMlw9hBZ9E96kLLqEOJYCGhLCiiHqpx\nCJYROnsX94WGAIhzM4gjhnD2oJqESB9jcihhQpRk6U8oR6Vow6oRAWYmE6EZ05Q8gmklg+wTLuxU\nGxCzcerGLxheCnaHlhM8nECwf2niUi9jHRD9JwZgIOg0QicGnNs45/4utC6qsXEu9lw4grhfnNNK\nDePEwWldnFbI7VNxY/oDQEGxbm7OyvCElZlzGJJpb5x2RsE9f5zjGKeNcixGVm2vMTS2f/4xMnVd\n/GgT0thuuukmPPPMM7jwwgsBAF9++SVuuukm/Pe//2104U4Ghyr0gaNNsovdfvSxp0wayRlDhpnC\nGVJSWps0CJ/Pb7ppZWX7kJYWDCpe+90K9Ok7xNiedf8M9Bsw1Nh++fkHMX/OLGPbapYUmpr4aI0a\nak65cdnPWplMkbdP1r1Cxcf4qbyzTbRPKz6I0NPqIObwyLt+fL/8LXz8isNAIkOMfGNjHvHYT8qB\n7fjx48agBgAXXHABjh07JjkjNvDl8i8wbHiOsf3ryy/GoMHBgaZ9G/Olp6d6TTP6Hp31gUWMfdk9\nWpnW1i48Ux9YxL4Z11xkqm/R+69hUR2B++KVJeiQ3tk0sDkIxUU3f4LvP7wLVeWOk40M+0q24l8f\n3h1tMWIefbomSsNxHMQvlKbIiRMnYtiwYbjmmmsQCATw17/+FatXr8ZHH310qmSsFzRNM2ku4UDV\nfaGY0YFNaE5cOTrACZMWdy4Xb6SSRQykNIuuMIdRE6s4Ts2JyUy2bC7diyjHZdemMovjGSSEcW+d\niZHGp4k+EGlf6HFTKpa6/2nqFGE+apEAvLzYj4ryMjxyra4JU/MfZzbjMhNzpLHivqliqcR9a0Oe\nH5FZnMastWTyVwptmksvcpCYbTf8pP+lZkIhA+0/YdajWdNFOUpGLPqFyiz20XaFaZNzaqAQfUnN\nwOJe0ueUM9eJa6dxmVxanVqJo4iJ8JgpZ9dkKYsn48yxqgGwvhm+G+J4wqXfscpVdiTypsiF90am\nromPNSFT5Pz58/Hggw9i0qRJAIDzzjsP8+fPb3TBHDQ/3DJO/8rYWSN14EAFscbWq3PzjY+0gxgZ\niyIK5R1PTU3Fiy++eCpkiRiszAKqRKLccW5GJWJv6KxcaGp+ZsHXQ7Suiy+7EYOGnoM//SG4LsIt\nIHMsKKINTk66KC/Sj3D8fZyWQSFkobNtoe1RLkExA6dtiLqpfMJphNOIuFn5UaLBCA2BaoXCOYL2\nvYpBwgqqcQitm16buA7aV+I69wZjn43rTDQ7XgIwa1OiD4TjC62HXhuXekbs45wuHv+7Hz6fD7+d\nGDSfU4uB4CPlnhdrGhwrxPVy2gi955xVQoBNIGpTw6KQOY+oEAiEvsOcNiXk4sJ1ZCmu6iMLB1nK\nG7vlHYRH2IHt9ttvx/PPP4+LL7445Jimafj4448bVbB4w+//9AoCgYBpYHNgxqVT78Nppw/Fiw9d\nFm1RYhrbN/0XX37y52iLEfPIykx0BgQbiMc+CjuwTZ06FQBw5513hhzTZFMLByzO7eewsaow5aZH\nAABNyz5w6vH870dGWwQHcYRmZYocNkxPn7xu3TrccccdpmPPPfcczj///MaV7CRgJTtVjcNcfIuR\nuoI6gDAsBca5lIGh7i81D3FmRzDlhHmIOqjYNRlxJKqG7GSfzOniMOPw2rIi+L8wv3ExSDR7tDC1\n0bgzYdqk59Jzrr5Q7whx/7g0LrSvRBZpjkmCmgmFow3tF2F6SmIcMWifChlov4i+pOcKhxzqsCH6\nYD8hNxZOI9TsWMvE7QlzKJd5mqK27jqoCVRc5wkmzs/ULuPowj2nXCyakZpJkUGbOyZjI1ExgNgl\nTta04BqbiEW1yk7ro31hRAEpHG1k4NoIMPWpnHmsdTiwB6Ua8dZbb4Xse/PNNxtDlrjH4pXhc8g5\ncGAXry7x4dUljUz5HgeIR02kMdCsEo3+7W9/wzvvvIPCwkLTOltFRUW9U9icaljdu+uz4BzyP2Uk\nYLjcuJQSYvZXY+Ge7JDeGa/+ZRluvOoiYx9gnm0LLSCBuTN09i6ukZtpUg1G1EcXx8U51IFBaFaU\nNUKcS1lGhGZC2xVaDWW/EC793EydOqiIdqtrgLS0NDzy8ve4eVIPAGbtTDjG0FAO4QpvSo5q031b\naDPlRCuUaYDUoUT8T6+NC28Q9VHXfqH50VCLSsbRRvQvZx1Y9e/3ULZnB2pqg8/pMaIZnxCOJzTU\nwhcqn4DGPOMmXkPGaYpLAcOda62D/q9KASODSnNzaUB2t0T4/IQ3kqmb1ZzAyKfQJAVk1hIqMpde\nieOKFHASjdYPYQe2c845B507d8b+/ftx1113GfEJKSkpRi41B/WDk2xUjonT/4SOnRuemb254NXH\npkRbBAcOYhphB7bu3buje/fu+Oabb06lPA6aMV5/agZef2pGtMVwECfYWuTEsdlBs9LYzj33XHz9\n9ddo1apViBekpmk4cuRImDOjDyP+hTGXWMuYjisWaIU5j1v05mJ8vBbWkjvvewa5E6Zg1Nk6670w\n9VEzF2eCFKYqjrzVZDYLhNYh/qflhEmTc+ygZkLO3CSOczFhtF+EqY22IdqlfS/2UUcMYcIzmZtq\nzOWBYFZrLnasmpxrZN8m53LZt2XMMnSfMPtVMKa0Y0yfUscTUc6UTbnuelXmP3HuX5brvKdXXeAy\n9tH+Q92zSJ9JLoZL9AvnWETBmQk5sxnnFCL6lDO5UciYOrh+UTld+AP2PtjGsgU9V/IdUDm3cJm2\nuXdVls2bq7sxEybH2vpYJBB2YPv6668BAEePHg1XxEE9MWW6OVWMg1A88sr3+GnnNjxzv2NuC4e/\nvnQXevXLURds5ujTNTEutREHaih19O3btyMjIwMtWrTA8uXLjTQ2bdu2VZ0aNVhnk6x2RmDV8Ci4\nWRaF3dmOS9MZ/RO9QS1A/KW8kEI+qplwjgQc+4X4n85gaaJRAaF1Ue3iCHEksZbj+ow6dghZqSON\ni9F+hEOJLPVMzz5D0b33GXj+wSmmmT036xWaHaXgEtovdSgRbfglYRO0btp/4tqpzOJ4FblHog+o\nhiUcSmi5VMapRpSjz1ct4+whjv/zveeCsjBJQIXMNYxrP+fMU8toRBRcck8ZVIwiMnDOMpxTF5dm\nRjWIcdqUTGOyq1lyx018lJJzOVYV6uhl9EEjuvvH4+CvVB8mTZoEj8eDH3/8ETfffDOKioowZYoz\nm3bQOLjmQhcuO9dZE3Fw8vixpBo79jBuoA5MiEd3f+XA5nK54PF48I9//AO/+c1v8OSTT2LPnj2n\nQra4xBffl+PPby+LthgOmjDm/GMX3l/pROyqEI+aiAN7UE6NExIS8M477+Dtt9/GP//5TwBATU2N\n4qzYADuLkCzGqkhP3Uw5bnFXmEk4k2DL5BQMHvozJHotC/514EiGRRvUtCTa41LVUPOkOJfGrFUx\nziPCLMmRL9Ms2B7JPs4ExTkNeBnCWVF+7GV3YOI19+LWSzuazInWOug55cQ5o5pxyGlZ1x53fzni\nYZO5ru466fXK0qnQfhb3kppKxf0qJcTIwuTbgiGb5q73j3mjcVveS6jxAQmM2dFgCmHIsLlYOc7k\nxjFncOZOu+Y1VRZs6zEVOAcu63uZlckzf6ucyezKxZXj3n1Z/3FtcOWaYhxbUVERpk6din379kHT\nNNx0002YOXOmcfzpp5/G3XffjbKyMqSm6nmhZs+ejfnz58PtduOFF17A6NGjAQCrV6/G9OnTUVVV\nhdzcXDz//PPStpUa2/z587Fq1Srcd9996NmzJ3bs2IFrrrnmZK63WePCQS78YghDC+8AAHDljP9D\nSts0dcFmjL3bt+CB2y5SF3TgwAYayxTp9Xrx7LPPYtOmTfjmm2/w0ksv4YcffgCgD3pLly5F9+7d\njfKbN2/Ge++9h82bN2PJkiW49dZbjfjpGTNmYN68eSgoKEBBQQGWLFkivSalxta/f3889dRT2LZt\nGzZu3IjTTz8d99xzT336LWqw61LLuSRzjiccp6SYXHlUrvh1/1NtRZM4IVBwnH5cKhsx46ftCm2A\naoBC+6DahShH5RP7TFqrL1RO0R5tQ2g/dhM9ir9TL0pEUoJ+vioJI9fPnOYk+sVLnnaOcYJzluFm\n0dby1vYEBBOLCEsAgq7/lPGEa4NznbfKDpBQC6rZ1f217TzCcECq3PiF5YNz7OC0KVVSUZlGwrn7\nc7A6hYTjirQrM4VMQ+XKcc8k91yZviWc9tuEmdM6deqETp300KZWrVqhb9++2L17N/r27Yu8vDw8\n8cQTuOSSS4zyixYtwpVXXgmv14sePXqgd+/eyM/PR/fu3VFRUYGcHN0TeOrUqVi4cCHGjh0btm2l\nxvbll1+iT58+uO2223DrrbciKysLK1asONlrbrYYe+mNWPx90zDlOohdLPzGj2cXrI+2GDENZ43N\nHkTuupP9ybBz506sXbsWZ511FhYtWoTMzEwMGjTIVGb37t3IzMw0tjMzM1FSUhKyPyMjAyUlct5d\npcaWl5eHzz//HKeffjoAYNu2bbjiiiuwZs0a1akOGGT1HQq3m1lkcmDgz4vKsfhvT+DDBbOiLUrM\n4n9rluOFB34dbTFiGn26Jjqs+DbQ2B6NR48exeWXX47nn38eLpcLjz32GJYuXWocDzTCDEQ5sNXW\n1hqDGgD06dMHtbWx7UIrM0HaTT/BmWSEeYEzh1ETHkdGLExGLz0+Ay89PgMuV9AkyGVJpvuEmYky\nbAjnCOoowjlxcKZNUTc1pQkzosmcI3HeoP1ygmG6EI4xnPlFla4kqWUKxl91r2lgY1Os1PVvteK9\nsMbKhQOX5kjIR9sX/WbKpF53fzu2Ce4TpkhKIn2gIvRccd8402E4xo7f36SvsVFSaAFRD9dnKvOk\nzOnHRLjNpK2x1gHwM3nOPMk9B7JBScX2YdSncHiRfdS599wkk+TaaDnDoYSJTzOdK+nTWMSWYmCr\nImFJTU0NLrvsMlx99dWYOHEiNmzYgJ07dxp8w8XFxRg2bBjy8/ORkZGBoqIi49zi4mJkZmYiIyMD\nxcXFpv0ZGRnSdpUD27Bhw3DDDTfg6quvRiAQwF//+lcMHz5cdZoDBw3GpSP0r0hL3qnNgQNb2L77\nBDTNhW4dnbhIGRqqMJ2eof8EPv7WWm8A119/Pfr162fk9Bw4cCD27t1rlOnZsydWr17uJYqsAAAg\nAElEQVSN1NRUTJgwAVOmTEFeXh5KSkpQUFCAnJwcaJqG1q1bIz8/Hzk5OViwYIHJu5KD8o7PnTsX\nL730El544QUAwHnnnYdbb73V7rVHBVZNjdPSuBkfV86UfNSmFieOUwYBI4mlH/joP4fh9SZg9PDQ\n6bbQeuisTdTDuY23YBwsTzBu3nYdIrhzKbhknNxs1pilKphbDHdmcq4IPeAcd2gIgJCBS8rKOe5w\nmrHK0YGDuB80TU9qSmg5ka6GOopwTjCcRsTJJ/rI6wE+/c4Pv9+PK36mX/wJxtGGc77huCe51Esc\nCwqXxoXT9lRpV+rrOq8KFRC32vq8+v0BUKs/1y7nRGQ9Fg7cuUYfkHI1DD+oXdQ3wWks4euvv8Zf\n/vIXDBo0CEOGDAEAPPbYYxg3bpxRhvIQ9+vXD5MnT0a/fv3g8XgwZ84c4/icOXMwffp0VFZWIjc3\nV+o4AgBawIaBs7q6Glu2bIGmacjOzkZCAhOAFSPQNC0ktkv5gEo8FrkPJN0nPnIc8TDVOIRpzu0C\nlqyuhaZpuHBQ6FqbbGCj2abFIMfRcXGmSPohFaaxPSSWiqMv4nKRyQY2CiFXQwa2Z+avRLeep2Pq\n2A4h8sXSwEZzqnEDmxigVQOb9RiVgfYfHdjunvUOln2yAFvXLA6pTzawUfOzkTeQGdhcTH0ygmTa\nnmpg40zDssFV5S0qM4ueTFwcR5BtNx6Po/xS0fNx8W5WHDoa2TUpTdPw2m2RqevGlxpnvawhUGps\nn376KW655Rb06tULALBjxw688soryM3NbXTh4hVjhzmmERn6DT47JKOEAzOevE+ntUt2zLUOThKx\nRocVCdjyily+fDl69+4NQCdFzs3NjcuBjd5gLzPz55wLBDgNgavbp5itcjN6oZ1RphKhXXKEqZzT\nAJdORQWhPVJZhHZkmpEKhxJy3VymZpm2R+sbPdRjOgYEnWTo9Yo2qIMMNzsWMlNHG5lWoTqXu78i\njq2GIZvmMp+rMk8L+TjTIdWgxTknSBvcpJmzBBjaD+NgQQnBZcwZnLMHF3rFmZW54yqTJXfMz+zT\nNGBnqb7GltnB/JlTWXC4a3NLzuFIsym4c2WEzKoUPw7UUFp9W7dubQxqANCrVy+0bt1acoYDO/j3\n+lo88uyH0RbDQRPFR6t8+GhVE47ePQXwx6Mq0gg4FXFspxq2vCJzc3MxefJkAMAHH3yA4cOH4x//\n+AcAnf0/1mB19+eeb27WrdLOOB44jveQg9V92+VyYcCQc1HjM8/yhawtiXYmNDUP0xbH/cdpS5QX\nkq6zyOozQg8k2hf9n9NGKYRcbkazs9b3xdoaE/UYN5sV2hS9Xs6RgOPfFPctUbFGKfqKS8DaEIcI\nbt2IdShh6qVrhW/NfQDlB/exoRZcuItdrkhO4+DWtdxMXwnNTxXiIUszY5fZw46lulcXPR+bdQ2O\nU4K4EABOc+LKcSwtKkc02XWe6vE4Hsd/5cBWVVWF9PR0g22kQ4cOqKqqMgiRY3Fgawq4YKCLXTB3\noMPtduO3f5yLZx+dEW1RYhIfvKHH+DVmZmUHDpoqlAPbm2++eQrEcODAjAsHOV9sBycHscbmxLHJ\nEWtmxEigXnd86NChcUmlJWa9sjgXgDeHceAWhq2LwK+//z369BuCc/qa7YvCNNaGhLjJnFGoCYpj\nGeFMaVxKFM5UJa79BGMqTVA8OcLMpXJu4fpKxrpBHWgCnClIElJA6+P6z9p+uHOtMlFZONM1dw6X\nbVxFuJ0gTJG1wOLva+B2uzF2mCtEZg5S5xEmJszknu8LvR7O8YSL4eLAmWNVKaOs57LvqsWd3hrH\nJjNfco47XLtshm/mGyFLmRUOds3ZkUY8miLDPoPjxo1DYWGhaV+sxCjEA1qmOA44Mvzrv/vwz5X7\noi1GzOL+2yfgnfmPRVuMmEavLomOttZMEfauX3fddRgzZgymTZuG3/3ud/B6vRg/fvyplK1R4GJm\n4C6bC9IyF3Fups6l+RCzvMtH9WEXmmUci9SJo5aRhQvGPlIXHFzFBOayrtp0Rh/ahHEu1xe0TzmN\nTcDkdMG063YBbdq2N9VjlCfncn1lyKDQRu2uTcmChDnHDgpOI5Ixj3DOKFQzptfx3xWL8d8Vi1mZ\nOScYTlvmnDhYRhHxP9WIJG7odhOSqpxMONRXi1NBFijdEGcPt+R6T0amxtQp4lFfCft6/+pXv8Ka\nNWtQXl6O4cOH46mnnkK7du3w9NNP45lnnjmVMjpohjg72x1ipnXgoD74ae8J7NoX24TtsYDGSjQa\nTUjnrV6vF61atUJVVRUqKipw9OhRHD16FBUVFadKvrjGt1trkb/Fyc3moP747R/n4ssNTvSuDE4c\nW/NFWFPkkiVLkJeXh4svvhhr165Fy5ZMfowYhYwEWSwwm555xvTAsWSIchy5scp8EC52R9M0U32c\nU4Y41884HHD8h9QUxMU5iXM4ZwVuEZ0zs9UwDhYc2FQn5LjRLxaz2ZTr7kDe75/EWdlekwy0vmN1\nDCocEbTJNEzqheV/jvlBRv5Mz1E5lMhin2SmPFq3yVxM7uFTj8yAN6GFNGSEc8hRpYXh0vQY5zCO\nIiqHBzdjlpdlB+dg1zRnra97JzPfWH1NbqqYNZkZk6tHtVxxqk2Qp7KNU42wA9usWbPwwQcfoH//\n/qdSnmaFM/vo3Z/IfJibO4YOO89JyKrA7D9eG20RHMQB4lGxDTuwffXVV3FJRCubbbuYGZXJQcAd\nWo6DmLWp2LzFcQ/jkswmTaQzcOFQQpNd1tVDuSA51g2pJkH3ib9MGxTcYru1fcDsqm+F1aHkjlsu\nYzVok9MPMzsW2hsXKsAxy6hmqzInE05b4sIlOC2OCyPh+s9uklQKP6N1cfJZy4fbZzx/TFsqLkPu\nWbNrHZA51diRoXi/HsfWuX14z0hOm6pvChtVuAQbzlFP1/541KoaE2Ff23gc1GIR+Vt9uPrm+6It\nhoMmiFVb/Phy/XF1wWYKZ43NHuKRKzKq9A5PP/00XC4XDh48CADYuXMnkpKSMGTIEAwZMsSU0HT1\n6tUYOHAgsrKycPvtt0dL5EbB6dlDoy1CTGLNtmp8tnJntMWIWbz75nO4/KJu0RYjZtEtPVGqrTnQ\nEY8DW9TuelFREZYuXYru3bub9vfu3Rtr164NKT9jxgzMmzcPOTk5yM3NxZIlS5RZVO3Gp7GEx0zy\nUWEyVLFLcClqxLlWst9z+7mRlBBsx3hASL2cyYszUVXXmWSo+U+cy5mlVI4EHFOCzCTDmdeoyaWG\nYRQxmqJmVmE69HiQ3jkTgYB9Zw/RLx7mvpkbDF8f53Shis1i2WYYZx4BF9MHlMWjhjHvWj8ezzyW\nx5qvZCwysjiwcOcGC4aew5kJTe+bzQ+eLDUOZ5bnEpxS2GUPMY7ZZEGxa77nzuWSjzblDNmxjKhp\nbHl5eXjiiSdsld2zZw8qKiqQk5MDAJg6dSoWLlzYmOI5iAEM6unG4F7OjNtBw1C8/wT2HHDi2FRo\ndnFsjYVFixYhMzMTgwYNCjlWWFiIIUOG4IILLsDKlSsBACUlJcjMzDTKZGRkoKSk5JTJ25hY+n05\nvljn0Pw7qD++3ebHd9ucZyccnDU2e3BMkfXAqFGjUFpaGrJ/1qxZmD17Nj7//HNjn+Cg7NKlC4qK\nitCuXTusWbMGEydOxKZNm+rdtpE3jcnOLHvWqdmRy1DNeTeBMSVwJL6cV5/bBRw8sBdJScnBnGaM\nCUpKOEvKcTFrfpsmHi6XFgeOEJfrUy9jthVycXFnHEHxy28twdkjf4HBvTy8Z54wBTGycJ6I9F7K\nXkTVS8od56iyOA9cI46SuZcq85/1+JOz8rD6v0vg8/MmMgqZKZczvarAycrts0MIHq4OLkZU2lcE\nfgCZHRNZc6wyBu4kPtJc3Rwxsl3TcH3yzzkIotEGtqVLl7L7N27ciMLCQgwePBgAUFxcjGHDhuHb\nb79Fx44dkZCg+4QPHToUp512GgoKCpCRkYHi4mKjjuLiYmRkZIRtm3ImetxqJvpoYsq4PlI3+OaM\nAYOGw8UtRjkAALwz/7loi+CgkVHrsz/ZaCjiUbE95Z/8AQMGYO/evcZ2z549sXr1aqSmpqKsrAzt\n2rWD2+3Gjh07UFBQgF69eqFt27Zo3bo18vPzkZOTgwULFmDmzJlh22hRN1CIGR/HQkH3Ce3CxWgN\nFNw+TexjZmOqWZbQILhZKuccwrJMEJm5dDTcDFfIxS1ccy8RF//F1WfKZM3EJYmZKC0nJh01TB+M\nHJJmqp/WQUEn7wbLCKMh0HbdjHMQB7svPfesGTN1IiB3jzjNjiUolmhEKm1elkaF0265Z1flOMGd\ny7G+yJw4KDgtk0O4a9t7UI9j69jOE7acjEHFruZkV5viHIvsEK8neILluNRUJ4tYMyNGAlHXZWi8\n3FdffYUHHngAXq8XLpcLr7zyCtq2bQsAmDNnDqZPn47Kykrk5uYqPSKbEr5Y50MgEMCoIVG/HQ6a\nEP5X6IOmaRjU09FqOVjzsTloPoj6l3THjh3G/5MmTcKkSZPYcsOGDcOGDRtOlVinFH6/HydOVKsL\nNkOs216Lgq2b8KvcwdEWJeZw2/W/RMURh5A8HDqnJaoLOXBMkU0FVkcNzpTFmYwCjDlRZTJiCXM9\noeWsbVFcdIZXepyLpeJIgWuYcjKnAdu5ryQmMFo3R77M8WBScwrnVGM2c2ro0TNLus5gMrmJfZwS\nw8RDcdmyaX0cGTGbGdtmPJks5oozNXPXLcp/tWwxa0rj7q8s7oyVT/Eu2DXhiZhElSxcn9b3Ouzm\nT1NBdU1W+Shkca2q+rhj4ly3TXNnQ+CYIh04OMUY3MuxJTloGPYd0tfYOrR1PnPNDXF5x1mmCcsx\njiWD0xpULCNitsOlslG5LtP/v9zgx/sLnsOcJ/JC2jghiTHltDNOy6Sw69rPtSFmkNTpgnNW8NX9\nTzUOjrmlsi6zN+cZymlOLLEvp60oPMlkDj50HxfewEGmwahQK9HsuOdUyLRmSzmSW6Xg9EyLempT\nQ/BLtB8Kn6Sc0nVe1CFJ50LbULGW2O1nTQtdY7NrcpOVU61mclEIhsZr00GFgyq84WTgmCIdNBr8\nfj/KDx+Ithgxh89XlSCtQ7rDQMJg9MjTMGDwmdEWI2bROS0xLs1sDtRwvhYxgp8Pdm4Fh9TUNCfT\nRBiUlZXhy2WLoy2GgyaOeBz84/Jras15Zfe7yC7sk/81xg7BOT/IZKLlZGYuanrgWC0E7OZZoxD7\nPEyMmWqhHoyJzKiX/C9k4TJtc31FHUqEw4kfwJnZiaZzaB+wMT2SGC6TqbSezgAqS5DUfKW4v7L8\nZLRdLuu2LK+cXcLjcHJZzzFlxuYyzDOor8nSLuuHKt8ZELrGZpftg9vHsodI5OOc01TOLTIS6cYc\nfOJxYHMCYGIEy9dX4z+bGtGQ7iAusbXYj/c/+SbaYsQkHK7I5ou41NjsaGoqZgXZLItqbizvotAQ\nmHbDMWeszl+OYWddaMyYqZME54ItYHI4sOk8ws2i68vKoNJuZTN/SnEm/ue4MYVW8H2BD5/98z38\n4bdTTG2Ic6nWapd+SPZsyFzPKVTpd0QfnVA4Tth1GuA0jhuvGY/lyxbbZudQsYfY1dw57YLLDm7X\nQYWD3Szn4UIoOrVPZMspXfftuuIzxzlmI3EO7ZeA5Noa01GEQzyO/3E5sDVF5N0YP0wqkYamaeg/\naHi0xYhJLHfW2BycJOLRFOkMbA5iHsN6u+JyVumgcbHvUA00TXPi2Joh4vKOW01EKpYMAS5miKuH\nlrProCLapc4U1nO/2aIfPLOPWzmL4thIrHLS/zXGPMS1wZlLfArzlTW+itbDmbmoLEZcIZFBXBvn\nrEAh9lF2E44lg3POkJqbmP4zORExMXrWtkLak4BjlZDFgtFjhaV++P1+nNYl+CrLmDhUsWgcaTb7\nLEqYebjnhULGvqK6R7L3wvqM+/1+uG2SRbKsQ4yjjckBiXEIE/JrtA8s9VJZ2SUMm8w2kUI8Thod\n55EYQvmhA9j4v++iLUbM4dvNx7C6wMmEzGHyJT9DVkZczk9PGh1TEx1tzQbsJhJV/ay47rrrkJ6e\njoEDBxr7vv32W+Tk5GDIkCE488wz8d13we/d7NmzkZWVhezsbFO+ztWrV2PgwIHIysrC7bffbuua\ntEBApRs0LWiahoz2+v8ypwfuGMcewiUa5dK4UHAhAJy2x50rS9XBMaOomEe4lC1cShwjXQ7RQmTh\nAxwrCAeNKUfLi/6lTCbWsIANhTVwuVwY2MPNc0Ay18GFS9A+kKVOodcr4xu1u8jPsddw+1SysGmL\nLHVQ0Pr8EllpOdnzp0wfZNfpwqbGxmnfkYaMt1IZ+mIpD4Sx6jAJj7n0T3bu0bEqIJKfbE3T8PvL\nIlPX4x+aZfvPf/6DVq1aYerUqQaB/QUXXIA//OEPGDNmDBYvXownnngCy5cvx+bNmzFlyhR89913\nKCkpwS9+8QsUFBRA0zTk5OTgz3/+M3JycpCbm4uZM2cqs7s4GpuDmMfAnl4M7OFwRoZDWlpatEWI\nSRwor8HBI46mr4I/EJmfFeeddx7atWtn2te5c2eUl5cDAA4fPmwkjF60aBGuvPJKeL1e9OjRA717\n90Z+fj727NmDiooK5OTkAACmTp2KhQsXKq/J0dNjDGu3+/FjwWZcPmZAtEVx0ATw0149J1uPdGeO\nakV91tiaM06lze7xxx/HyJEjcdddd8Hv92PVqlUAgN27d+Pss882ymVmZqKkpARerxeZmZnG/oyM\nDJSUlCjbicu3wefXf9ysgrMHa5r+c7uCP7HPRX5iH1cf9xNy+PzBfdy5tNyRwwfx8B9uMVLC1/qC\n5Wk5cYxrg0LsU12HgEsL/VGIfbKZGqCbGD1uc59yMot9NeTH9eWGnT5M/PWN5n7xh5pvamr1Hz03\nwaP/WiYGf0kJ+k8cS/AEr43KbO1Hq9OM7EfrkT1Xdp9hDmPO749uHfnXmJOZ9r3sZxdUPutzSH+q\nd4Y7164sok+t6NAuEe1SPMq1oHDXxLXB3Tfu2kzfnbrnlOsrCpdL/9FnKN5w/fXX44UXXsCuXbvw\n7LPP4rrrrmuUdhyNLcYwcohjVuKgaRpGnHsh/vHua9EWJaawZcuWaIvgoImjoV6RRfuBorL6nfPt\nt9/iiy++AABcfvnluOGGGwDomlhRUZFRrri4GJmZmcjIyEBxcbFpvzBfyhDXA5ts8ZlzaqDgnAZk\nqUs4d3pVckDOfdvP7BOuw5z7MQX3gLIcd6JfmHPtctxxjiycEwInC+cmr5pJ9+3qCpHFcE1nllFU\nyWUFKAuKl7FasaECDGRtcI4TnJMOB9rPQj6rLGlpadi/P/iFkaUvsvvcqJhl7LLSyN4ZJQMIA1n/\nWu/5gXI9jq1disd0nGV9CZjPBexfBwXHEhRgzuXeLQ6cfJFGQ02RmWn6T2DVVvU5vXv3xooVK3D+\n+efj3//+N/r06QMAmDBhAqZMmYK8vDyUlJSgoKAAOTk50DQNrVu3Rn5+PnJycrBgwQLMnDlT2U5c\nD2xNEWsLquBNSEC/bnFpJXYQYfxYUgO32+2ssTFw1tiiiyuvvBIrVqxAWVkZunbtikceeQSvvvoq\nbrvtNlRXVyMpKQmvvvoqAKBfv36YPHky+vXrB4/Hgzlz5hhZPebMmYPp06ejsrISubm5So9IIE7d\n/TvVOeLUV2Pj3NDpPrsam7Ve+r8qaHb0+CswZvyvcPvNl4WcS8FpPbKgXurqLrRCqjVwbchm/qrr\nkPEt0mNc4ldv3XSLalA/7NJn3wN6hM7FVDN/zsVedh0UjaWxcSEZHLjnj8qSlpaGsrKykHU0a731\n1dg4cByQDXHj5wLDBSKpsVnbkGlsXF+pnuf69hsX/qN6XgSEfI3h7v/bCZGp69mPIyvbySAuNTbj\nwWSOcalTuIHNLhGurDyFGIi4OCz6LHy66F18uuhd03G76WhkH1eOUYQDW44xO6pkkU0mOGYPk0y1\noW0YMjEfJRpryH2UuPRARrs2BxjbA5Yv9LgqPo3bxxIAMxMDYYK0yyhCIbtH3CDWEFYVq0zW/2Xl\nuHeFGyhlLEEcVAMgh5Nh56jvYHyq4TCPODhlcGKTzDi9qxd9MuNyHnbSyM7OjrYIMYmyw04cW3NF\nXH4prLNdlVlKpsVxM2HWDEfa57Q3T5iFf1qHOL6lSJ/29+tmXh9QmZHsml45OY1zOLYUKqtoQ2Gm\n4bjtuL4SmqyJ9aXuL+eMwpkxObMydy7tF64/ahj+Tc5ZRoB7NlSQOVuoTNdcuwCwZMVmTPrlz/Bd\n/krTcdNzyvSBgKoNTvOUXa+Kl1SmIbiYd0uVxDcc7Kyxce++wa6D0H0cImVS5Y7Z1ShPBjFiPYwo\nHI0tBjH7kTtDBrXmjuzsbOzYYzPZWjPD8P4d8V3+SmRnZ+PMs0Ya+2+acQduz7vP2H7y2bl4bf47\nxvYHC5dg4afLjO1lX32Pr/M3Gturvv8B6zbsNLY3bd2FLQW7je2CwlLs2LXf2N5ZXIaiPeXG9k8l\nh1FcWmFsl+wtR2nZMWN7b9lR7D943Njed+AY9h+sNLZLy45j/6Hq4Pn7jqP0QHB7z/7j2Hew2lSe\nbvv9PviIbXjvAXN91vr3HjiOssPB7bJDx3GwvMrYPnDoGA6VB+UrO3gUBw8H5d9/oBwHDx8N1r/v\nMPYfCF7/T8VlKC4N9k9BYSkKib/85m27sPXHYP9+u/oHrNu43dj+etX3aAw0FvNINBHXziMyjc3F\nzI69DFckpxGpnBC4clx9AjTIWLYepHIYkXEOctyJXDJTVfJMTvvhYHe9SshMNTZxH6z3aMceH26e\n9kt8WZeDTJwj/l56xY3okNYRr780C/4A8PJbS5DSui0u/6XOaPDv/J3wehMwckgXaBrw3eaD8HoS\ncEafVgCA/20/DpfLjdMy9ASVhXtOANDQo5MXbhewfbfuwNKrs27o2LFHN3P16KQHAf+0V9/unq4f\n/2lvLTRNQ7eOuoC79ukd3rWDvl20X9/OSNO3S8r07W4d3XC7gMJSfbtXZ3dde6HbgnXE59fr1zQN\nXdq7TPVlpLlR6wP2HtK309ro55eV69sd2urb+w/z29byqa317BOHKvTtdin6cbGd2lrfPngkuO33\nA4cq9P5onawfLz/Kb7dtJerTt0X7+w8Ht/0B4EC5vi3a47b19j118tTWuf+7Q7b16+HlSWmpt3f0\nuL6dnKQfF9stW+jbx6v0623Zwg1NA45V6tuiviPH9O22rfTjsv6i2+1S9PtXcdwHt9sdceeR/zc+\nMnX9+VPHeeSUgFsI5whJZR5PJhOKKE/KiQ+4ybTgCi0nG5S4AWbazXcg/z9L9ABcifmKk8+u2cck\nM1PfWSNGonOXTCz8UHdmefvdT9A+NQ1jf3E2NA3YsKUESUmJOK2bvh5YvPcoPB4vOqYmQtP0NQ4A\n6NhOzyuz/7D+oWnfRn/sxIdIfEhLD+od0aW9+cPftUMwjc8rb32Cnp3041uL9Q/56Zl6Tz/02MsA\ngJdfmAWPGxhx3igAwbQ2Xbp0BaDHrvn8QEpKGwDBe+j1Jhguxnr/BO8gZ9oUL7GYmNTW1tR9ePTt\nqqoquF0u4/4eOnQQHo8X/oD+zBX9tBPeBK8xmVi/9jt4PB64Xfpg/cmi9+BNSDSez2f+7wFT+2PO\n74/9+8uQ1ScbPn9wgBTtd0o1a/3p7fQPtLhE0e+ivBhAxPWKD6yAGBDEOWIAsh4X15PWxm2a4Ih4\nMoE2rUK36bsoBiRRn5WpXzxH4bYDgYDpflqPp7b2GIwwPn+wPSGDkE/T9JjUNq08BosPALRqaa5P\nDHB628FtIYIY4PQC+ja9XtF/oryYEAiktGwcK06MjEURRVxrbAKqgU3Gxs95qnFrU5x2pvKUlA1s\nP+72o7a2Fks++Tvu/H9TAACfrdyGlFatMWJwJ/gDwPqCCiQkJCC7m65hbCvWNQqRxqSgRB9IRK6u\n7bt5DSIjTf8AlR7UB4rOqfoF7D4Qug0EP5DWGb2YUVtnzOKDJBI/ig9MaZmuIXVOS4TbBWwtLIPX\nm4jeXVMAACvzf4DXm4Bzhp8GTQOeeeENJCYmYuYMvT8G9NedJgq2Bdk3hLZHNUDRp/QjIe4bFyht\nN7xB9ebY9Trk1nmE/FwbVOZAACja74fP50PXjl7TOap1MusxClU52boSF7zfkDU2rj47dQjsO1gN\nt9ttDFjcO81lg7DbV7IgdQrZdXDXa1qjtDyTx6sj7+4/Y1xk6pq7OHY0trgc2NLb6v9zC/Dch8Uu\ny8gzL72DLhndcMVEfR1j5drdSGnVGoOzdFPWpsIquNxuDOihf2A27tQ/5P276y/Wpp/0D79YP9u8\nS/9C9e6ib/+4Wx9IendxoWOHNHy9bq+xDQAFJcHy/kBwoBKmqR9L9PbEQLatqBoulwunddHl2VBw\nGN6EBGR1bQkA+OI/G5HUIglnDzsNtT7g3gceRYsWLfHAvXmmfqHg4rq4GCnZ4jg3WZCxvwD6/Sgp\n0wfKbh3165M5j6jCOQQ4E6114ADsx2FRcOZdDzPp5syxom4afygbJOwygKji5xoSmmAFvY76yqwy\nU8uculT3yO4zaXfAspYH+D6VpSpSfXOssjgDmz3EnSmytLQUg7M7AQC2/lSOFi1aokcn/cO+s1T/\n8PfoFFwj0QcO/c0RA0dWhtnU1SdDf5vGX/Jrk2kjLa2jadvtsZpC/NC04Ft57OgRJCS2MLY3bVqL\nVq1aG9u3z7gKlcf0xeWysjKcnmn+Cgo5BWjWZADoneE1bffpmmh6OQdmtTUdv/BccwaBxx75I2IZ\nsfLSOHAQT4jH1yruBrYOHToY/yclJZsGHiuOHT2KFklJxvba71YhtUNHY/vKS8/H8Yqg11J2V/PA\nkt3Vw26LWeXAnomm4zn9U03bl40dbtr+dNG7phncp//eiPE/d9LXCGR28LJaV3a6j7wAACAASURB\nVHNHWloaBp1xJpYtXRxtUWIKVq5IBzxizaMxEohLU6SVUoszRVJ4GZNWfSl0OKYGu6DmC/HhXv7N\ndnTt1hOndXaxphGWmcJyjB5XmWmE+c3umqLd9RsOKmoma/uAnB2GK6c6l1uL4yDLSq7qKy7jNfdc\nJSXof2n/CRMkl/XbajbbfcCPQCAQ4jzCPVe0DWF6PZl4PNU9t+uYJYuzpPeIu1/iOqzPfekB8xob\nt54myxjOgZOTW59rSD0yj2TRZ1UnIm+KvGlMZOp69bPYsao4898YxQVnnYbTOju3h+KWW+/A3kP1\nSBbWTNClvcsY1BwE0al9ojGoOQiPQCAyv1hCXGpswnnErmOCzKHErmai0kK4GZpdZgXZIn+902mQ\ndrkFcy4sQZWihtMQOMhm5XadMw4f9Rlelxy5rMwRyGVT21NpdjIHC5UzirU8lcGa2NR6LsfSwrVr\nlylExgqichhpiHYua0OmwdDr5Z4XGa8rZ5VQpU2yS+Zs992rb0wnh8bU2K4fFZm65i11NDYHNvDs\n3Hfw1Xc7oy1GTMEaW+VAx00z7oi2CDGH3WU1KD3ocEU2Rzh6egzjYosXpgMHHH7aWwuXy4VX5z4X\nbVFiCgG/H5qTj02JGFGyIoq4Htg4k5Y0bYxi4V+AmhaE+aDG5gIyR7aKMPFfIj5NFujbEI8mzkzD\nmeaM4HPOZGTTaYUL6pWlI9ErMrdPQWmSjMNMOhXOrMw5U1DUMn1wwmWWnYIzZ9cqAr5lpleu/9jg\nZEu/iLg+o25RB9MvVD7W0YZ5NjjTnew6TGDMwEZGeEnMF5WLM9Fx5merObZLB7NXMteGEbzfgPdI\nZrLk3nPuOaB95mOeAwcNQ1wPbA7iD4FAAH7rl92BAwcNhqOxNRHIHCvENzHAzOgbwrrgYzQTDhqj\nhRjn0NmnZSa3aUcF/rf2W0y+9CLbTA0Usmuy63LMaTqcQ4mJQ1PSH6pZqmzW276NOQg9XN20fe55\n4KjQuHZljiwc0wpXzi4FG0uQzWjVnMv+fQ88isf+9MeQ9qxgNXKmD1SOQHZDUDirhEyD0RgHH5XD\nBudA4/PrXKU0jo2zcti1rhjthy9uqpsaQN0Srd8uGnPwicc4Nsd5JMaRnJyMnBE/i7YYDmIYEy+7\nArfn3RttMWIOjmbffOEMbDGOHukugxLMATD35Tdw+KjzwaJY+OG7SG/nvMpWdExNdFhHbCAe49ia\nxV3nTBkmc1jdd9JuPJksJigcRNV2zSrcPnout8gvzG8cO4dKPtmDyTmAsOYrRVwSZ9ZjzVcSOZ97\n9v9wxVVTTS8TLS9beFeaXo2bJBGA1GPKLC5xAFGyxDP7BDhnD1qf8T+9R/WMDaSKTa3MjK8w4UnN\ntYpYUlnGcFYG0tYJLs7TZt5A2XtB+z6h7kuZmBDcx7H1CKYYFSG4zHTNvR+N6VDimCIdnHKkpaVh\n1z4nFkdgy5YtIXnAHOisLGePGKku2Ixw8EgNjhxz3p3miLjU2KyzTaWzQt1flQs2B7uzHa6cjPFE\nzPjKysrgcrnwu3sfxeOzguz74ngCuYOysAAotCROC/FZjtE2OFd3tk9JfXbNFTInGaVGZLMNjnPQ\ncM8n+2QODFwdAYVDicyRxVQPc201et5W1nHn0dnPwOfzIa2tF1ykimy5KdIzdu454MBpbJw2anf2\nbe1nv98Pt9sdch/svueqfeIe1jJOMBy4c7nbonJAijRizYwYCURFY3vooYeQmZmJIUOGYMiQIVi8\nOMhKPnv2bGRlZSE7Oxuff/65sX/16tUYOHAgsrKycPvtt0dD7KihS3uXaVBr7jhU4cPBI85MnKJd\nigtpbZ21WIrUNokhWbodhMIfiMwvlhCVgU3TNOTl5WHt2rVYu3Ytxo3TM91t3rwZ7733HjZv3owl\nS5bg1ltvNbjHZsyYgXnz5qGgoAAFBQVYsmRJNER3EAOora3F8ePHoi2GAwcOYhRRm85wZJmLFi3C\nlVdeCa/Xix49eqB3797Iz89H9+7dUVFRgZycHADA1KlTsXDhQowdO1bahnQWQc2TdX9dTLxWg5wB\nGHOTzKxhSgXP1P3Ff9YjO7s/MjuE3i5VSh7V4rmsPsPRhsrHyOmylKflOBMohV2TL+3fDu3MjBJ2\n0+DI0oLQc1l2GAKZyZczGdHyor4TCvOVzLmAYwKZdPkVSE/vhDl/DtJqncwsuiHncuZEjuCZi5/j\nwMUkymCNES0/qsextWppfm84lhsKjslEOIr4q8PUI6qTXJMqLi5aWo9jiowgXnzxRQwePBjXX389\nDh8+DADYvXs3MjMzjTKZmZkoKSkJ2Z+RkYGSkpJTLnO00K1rD7g4HioHDuow/8138NjjT0dbjJiC\nE8dmD/Foimw0jW3UqFEoLS0N2T9r1izMmDEDDzzwAADg/vvvx5133ol58+ZFXAaZq7vKpVa28K9K\n48LxLsqgShuS1b1NSH1c2IJVJqusVtDXnvsGsK7GjHyyzwerxTFgF8wZBhAAWPC3D3HxxZeibStX\nyDGjPYW7uuArpEwXbkbr4u5vsEJyritkl3TWyDk0ceAsBlw9oi80rf4zcFX6GFn7FDLHIu4eeZlU\nQBx7jardcFp6u9aJDXovZfec05a591LVBhciIyvnoH5otIFt6dKltsrdcMMNuPjiiwHomlhRUZFx\nrLi4GJmZmcjIyEBxcbFpf0ZGRtg6j1YG/0/wAB5n/TiuMOvh+zB+/CXRFsOBg0aHz1//5YT6wjFF\nRgh79uwx/v/oo48wcOBAAMCECRPw7rvv4sSJEygsLERBQQFycnLQqVMntG7dGvn5+QgEAliwYAEm\nTpwYtv5WScFfQpw4ihXvr0HRvppoixET2LJli5MZ2YLs7GzMffmNaIsRUyg/WoOjx5u296zbpU/O\nxa8x4DCPRAj33HMP1q1bB03T0LNnT7zyyisAgH79+mHy5Mno168fPB4P5syZY+QjmzNnDqZPn47K\nykrk5uZKHUesi7+ccwGbYVmxGMyRmbKMDjbNmOJ4rSL2SdMQNi8bNY3IluFUJi2rnOHALaxz9Upj\n25hyKicJu/FBsuMcUwjXbg3j2KEyCXGMGEJ8u44sdplCOPz3241wuVy45eZrpeVkMYL0uOp54Z4T\nGYE27T/uOZU9VyqEM+uJODbrvVO1IWMEshvXmkDMrOI5NvUZQybu94W2ISN0dxAeWiBWcnlHCJqm\noUuq/j/3ANvNoSQLCObouFTrWtzAxg2UUoZ0RmbTPqY+u96dfsm6AtePdgc27jjLYq+4V9brPXzU\nh0AggHYpHtsDGyeLaoCx+0E5mbUprt2TCWbn6pOVj/TAxk0kuYGNrrFx2S9qGcoqGewOikr6O2Zt\n3u7AJkC1K25g4/pKlgNSlDtezXuUNxSapmHSiMjU9Y9VkZXtZBCX9hw7HjqchqVM9Mi8fLK2IsUL\nyaUS4Rad68snZ5fvj5VdoQVzMFy/GecMNmxBMthVV1ejouII/AGzJuZiPhhSRhYGqsSWnLOCbNBW\ntSEYTKxpV6yIxCDGQTWxkrXB1WNKPcOcK9tHIZuQqOSSyarSoGUDpGpiIHCCsYByKasSyVIJp7We\nCk0tRsaiiMLxIW9C2H3Ah9Ubd0VbjJhAh9SW6NW9U7TFiCks+qdDWkBRcazpr7E5aBicga2JoUVi\ni2iL4CAGMXrMOPz8otHRFiOm4MSx2UNjxbFdd911SE9PN5wDAeDuu+9G3759MXjwYEyaNAnl5eXG\nsUjSKcblwGbHS0d3yDD/OA8f4W7r8wdvIC3nduk/Wo8MLi34E/Wp2hDHOqW60bd3xxCiWO4c8RPH\naLvctQuI67Ga3mRBmKJe2b0Idz/EubRdsc/jDv68Hv0nvMM+/OgTVBz3m8p43LwstG5rGxy4/uH6\nmStH+1kGWp+4vy4t9GcXn3+2GCktg3F99TEvce8AJ6tdcPe8IdfGPa+y9qxok5KI5CRPyHtEIerl\n3kG7P5W3oMxln7bL9ZWQz/pORhKN5RV57bXXhlAfjh49Gps2bcL69evRp08fzJ49G0Dk6RTjcmBz\nEP94+P674PNJVtsdOHAQVZx33nlo166dad+oUaMMFqWzzjrLiE8OR6e4Z88elk5Rhbgc2KwzYTq7\nks0c6ezJ5Qp1S/b7637MbJtrn9OcVNqPrPzVU2/E3kN+03HaRo0vvGcVvTajX8jPzoyYtsvNolWz\ncTuzPApOExIz14JtW9C5vRdet1wDVdWtklP0FSdzfa9H1Ya4fzU+/v6qru2dv32Iy391Rcg1hvtx\nsnDg3hnZfVY96zJLhaqvuHKcVg3oa2zHKoNrbDINkPtGqGTh3lWuPq5vOU2Rg1XmxkBjmSJVmD9/\nPnJzcwFEnk4xLge2eMWCt15DIBDAWU5CSQcMLr7kUrw+f0G0xYgZxIrreayjsUyRMsyaNQsJCQmY\nMmVKo1xTXLr7xzPS2+m+4Y01e2tK2HtIV087tHUyagMw1tgc6GjdKiEuXdljBQeOAAcq6n/em2++\niX/9619YtmyZsS9SdIoCcT2wCfXY9LrXDQjcwEDV6Zra0HKyQGUuKJVCyKB60bhzuXPEPlV8kJ8x\nTXJErVx9siB1Lu6Mk9Mu4wl3jooJ5tChgzh4oExZH2smCdiTSbRH6xCBxXSfLO6Me9ZUqXE4BBiZ\nuXMjPemRBbGrhlKDucUVuo9j/+ECtLn6TNcYMB+j8lFwz5WMxMHu89qQmEnZO8gxj7gbcSLbEDMi\nALRL0X8CBXvClxVYsmQJnnzySaxYsQItWgQ9vCdMmIApU6YgLy8PJSUlBp2ipmkGnWJOTg4WLFiA\nmTNnKtuJ64EtHrGr9DgSExMNza05I7tXh2iLEFN48KFH0alzBmYoaLWaCyqO6fnYkpOcz5wMjaXV\nXnnllVixYgXKysrQtWtXPPzww5g9ezZOnDiBUaNGAQBGjBiBOXPmRIxOUSAuKbXSWuv/czMvjmKK\nmz1xNDicdsbLEP6Ym5m5UshmkG4XsHzlemT37Y9OqZ6Q8qJulVvwydA/CVnssiPY1UApDIYShlez\nvtpNQ2UIJxMQpEvimCRoW1wbKgovK2TauvXcI8f0h7Z1cvhJj93r5ujlPKRaI7ULw8LDncs9Ix5G\nTKql2U1IKmSgjlOBAFBx7ARcLpcxsNmlq2OtIRJLDwX3jeCeZ9k7KuurQ0cju3aoaRrGDo1MXUvW\nxM66pmOUb2K4cORgdG7vzEAB4Kln56Ks3AnCFWid7JYOas0NKckJjrZmA9HyimxMOAObgyaLu347\nAzU1TiofBw4cmBGX0xnZ4i+36C0IhblFW64OaoKSmVoouPQn9SWcFe3uPxz0BuScOFQOG3ZNqrJZ\nmNJZhrleP9PPMjntoHNaorIMx6QuM/ly98jF9CmV2ShH6uOIqmV9xZVT9Qtloh89Zhzu/t19GPOL\nkWHbUjkrcOXYZ1xkDCf9KMxlKhJpa/u0DWqelGZ/p+bEMEr70eP6GlurluE/c7L+5Z4D1bmyd8qU\n4YBxSuL2NRbbCEWMWA8jirgc2OIdx48dhS/WdH8HUcf7f/8YbrdjihQIBAIIl8fQQRDOwNZEIHM0\nMFzimfIUdh0OZIvKpvLMbIxzOedm6tYZc8/MNgZ/XH2cC04lOO2Hm5EKqPovnDZVelDXXru01z/o\nhlMDI5OVE9MKj+QbqHIUSWBSz4g2OIcSu99blYZF+6htSv3SxXMWA5lzlSqtDgfDoUTSPgXXfw15\nxjVNj2OjLCLGs3ESmix3Tn20auNcxtFGdZ0O7CMuBzYHzQfbtv6AXbt2RlsMBw6aLOLR+OMMbE0U\new/54fP50Ll9/Wbp8YafjRhwSpIxNhVs2LwdA/udFm0xYgIijq11svOZkyEetcK4vOOyGYhxTHEz\nZQwbFDLnEc5a05D4KmMfaaOyshKLFr7PlvMxbaji5zizCmeCqi+4xXEVuHLSmD/GrMiVTyBPu7hO\na+yTFZxpWHbfvEyslxYI3ad0CpCYy2Qm8R49emLs2HH4/LPFtmfids3oYY/bgMrEaDeeTFaewqWF\nX2NTmfwisSzHxfJx7dmNG41HraoxEZcDW3NAjy7J0RYhJjBq9Dj87YNPcf6IftiyZUu0xYk62iQ7\nETwCbVMSoi1Ck0A8DppxPbDJuAsbwgPHgWP7EC7LlEWBYzKRycAtZqscE2TOGfQ6ZOwXHDemKnxA\n1i7XhipUgCvHwaUBy5Yuxr69pfjhhy1KGTgHEJmctJxKuxaaH8uhKeGRNJWz6dQQ7ri1nKqfZbDj\nuBMOJscT5rgslIFq1aKcl1Qi+lnlas+1YdfyUF/TtspRiT1HyMUwt3D93JjJwOPRFOlM75oo0tLS\nsO+wH3l33RdtUaKOAad3ibYIMYMvvvwGDz74aLTFiAlY87E5aD5wBrYmirKyMhw+fBBvv/lKtEVx\nEEMYPjwHd9z1+2iLEROIFd7CWEc8UmrFpSlS9jzLWCO4fVw8DzXleT2h+0Q5Lu0GB1laFQprqpPe\n3dPY+lTpXmSxclxMk8qEY9fEaOeYqhx3bSIvW6dUt5HegzOlnWjA5N0gsGVMglwsJEcObXIksGl+\nZq+DKWd1cmqX4kIgoG/b/a7bdRSh13syRNoyJx3VPbLDKiSOpyQn1DuNjJ3jAlzd9WUK4ViMVPF9\nkUY8jv9xObA5aF746KP3sHXzpmiL4cCBgxhBXKatSUmq7zn6X06D4VJNJHpD93Epb6jGJlv0Vrlb\nc04cLg0o3nsMSUlJSGvjMvZZy3EzSNlMk+NTVGlYdh0suNCIk3FqsJvAUUDlPGLXzbu+b4zdpKKq\nfrHTz3NffgM9e2dh7C9G2ma0CSdDyDHGKhEpE5QdKwuFn3k/rNd7vFKPY2uRaJ6/q1JWcWEu9dXE\nGvIu2EmrU3Ui8mlrRmRHpq5VW2LH/OtobE0Yl186BldPvT7aYjiIIVxx1dRoixAzcLgi7SFGxqKI\nwnEeacL45r8r8ZsZ10ZbjJhAWbkfL859I9piRB3tUtxol+IQIQNAcsuEEG3NQfNAXN91u2YfuzFN\nYuGfLnB7mW8IFxPmZUhy7S4SczFrFNOm34i33nyNPcaZr7i0NYYTAseYwMTKUUgIQEwsKJwTggwq\nZx6Kv73zlmmQp7JwZh8uVZFKBoH6xnXZNUupzHoyR5Za6rQiIQ9WmeFOxkQrg12HkoaYvWX7KOxe\nhyy9kt1z6XdB7OPebR8Tx8ahMWnjHI3NQcxh/2Efnn7ecfl3NFcdl/3qCmzauivaYsQEKqtqUFXt\nxLGp4Lj7NxFYNQ27sx0VL6SAyrFDwOQMwNRb3xQmnIZw8bjz8c2qlXobdfXRGT3nAMJxT1rLm9pT\ncDEKTZZb9LaboDESWkF2djZLq3UybtlCs1PyFUqeNbt8maoEpzVM+Ij12l6a+zqSklqG9LEsBIRl\nS7H5obKbrNYUbiJJ8hop6OEO+hqb9dmyq2mrkqPKUjOZ3vO667XLfMPCWSqsF+JyYGtOEINac8f+\nwz5ommZ4iDZXdEprFZFJQjwguaXDFWkHjinSQUzi3gcfxVPPzo22GFHFlMm/bPaDmgMHDUE8miLj\nMo6tjYT43s+Y5mRmGi79hMxhhNbHxS+pGAR8jNlCZu7RNN0jMBAIIK2N2yQnlYFjQeFi9DiZT+YJ\n4ZxWuD6wax6yC5VJkDMDc7FZMqcGLvux6gWXPWsqsx7Xb1x723/aj9zR5xnE0OEge8ZV98guuGfI\nrrMWB47hJdy5Io4tqYVumFK9R1ZwbELUHCyLmeSWK+w6ilBYvyXVNZGPYxsaofR9a7bHThybM8WN\nA6S1caFDW8fFe9r0G5GWxtOMNSekprbHvDffi7YYUUesfGRjHYFAZH6xhLjU2Nq1Mu/jZuDcjE/F\nDCDS0XjIGCLSbFSeCO7jEinaYRUIJ4vdNC7c7FiwsByvDi3PaSv02uy6UcvqoxB9zjlBUNidWVvL\n7Tvsx769pRhwehfbM2K76WMaAhnXpV0NX8UUwmmehsOQIrSE09hkjCINSaujes9k4J57mTNUfbWg\ncLDLCiIL11GxvliPqeQTbdXURl5jG9wzMnWtL4ydyYSjscUJCosPY9q1N0ZbjKiiX++OTgobBw4c\nOANbvKB169Z47PFnoy1GVFFWVhZtEWIC367+AW+/82G0xYg6jlfWoLLKiWNTIR5NkXHp7m9V/bk4\nHW7hn8aK+BnzBmcGEWYDFdOA3UV5IVeNTXoO0ZZIVwKYHzJhIuVkobMacZiTT5V+h6tPxH9R06as\n72mf2mX2sJpx0tLS8OCfnsRvZlxrm1CYNW0qzuUgM4fZJX1uSGoSjpUmq8/pOK13lqnvZXJxpi9O\n5voyd1Bw7+DJZIW2a9IHIsPawX24Zfsi7SXYmANHrHk0RgJxObA5aJ7YXFAKl8vV7FlI2qWYsz00\nV7RM8jb7PmiuiMuBzTq7US34Cth1NaaoqtH/cgvwqhmumLEGmNkxu9AsqWPEuSPx6eLlaJviNR3n\nmFE4zkaXpbypnGpGzMjHhRnIXOZpAk7ZTFjmrNChrYflXZQ5Pag+fJwjkEwjMWnBNp1H7DoHWetQ\nHbfLPWnXgYHT4rh3i2O+kbVPQevjEt3WV7uwq0FzvKmNmNtTes9PdYB9rJkRIwFnjS1OcOhAGdxu\nNy7/1RXRFsVBlPHa/HewfuPOaIsRdThrbM0XcamxNUds2bIFKS2decrCT5bho7+/GzbbQXPAxEmT\n4XI5z4IDe4hHjS0qcWwPPfQQXn/9dXTo0AEAMHv2bIwdOxY7d+5E3759kZ2tp3QdMWIE5syZAwBY\nvXo1pk+fjqqqKuTm5uL5559n6w4EAmiTbH6pTyY1CQfOqUEVw8WBi3nhYDe+ijMPCQcCzpTGMU5Q\nRIKk2a75KlKsFgeO+FFTU4POaYnGvvrG3qlYaRoSIydDfU2RKhOe3X6WxWHVN2O0ChyTjooJRuzj\nzNn1cR6pL+prHmxIfBpnopURqYv6GiOOLTszMnVtKY6dOLaoaGyapiEvLw95eXkhx3r37o21a9eG\n7J8xYwbmzZuHnJwc5ObmYsmSJRg7dmxIOZ9P4cLXxFDrA7w279K/PluGc889H62TY1cRr6k1e0pG\nGu1b61/kU7VOUVNr//40BdT6Gvf+nGr4/cH8dA6aD6J2y+szsu/ZswcVFRXIyckBAEydOhULFy5k\ny3q9XikpZ33jL1xa8Od2hc5k7dYnZPL5gz875Wt9wfIqEtKsrL5wuVzQNBg/0QYtJ/ZRWfx1P+56\n/Mxxmcz0Omt8wZ/Pb07SSvuPI1Ol18H9xP2g+7j7wsnH3Q/uuVE9S/oM+uTiesTzZReqtkacMxLF\npRVsv6ja9fn0fQ15P7j6uDq4PrU+r/T55J5dO+S7xytrUE0euPrSrdH+k90j7tkM1x/Wcyi48qeC\nYDge49iiNrC9+OKLGDx4MK6//nocPnzY2F9YWIghQ4bgggsuwMqVekqWkpISZGYG9eWMjAyUlJSc\ncpljHVm9ujT7dbZp196IDVsin2jzmmk34uZb7zC23/zLh1j46TJj+5vvf8Dq/203trcV7kNhcfC5\n3rWnAiX7jhvbe8oqUXogyHO271AN9h2qMW3vPxz8KO8/XGt7+47f/h7Jyck4eCRovTh4xGfaLiv3\nYe8hHznfh/2HzcfLysMft27vPSSvz9r+wSM+HKrwh90+VOFDxfHg9rFKH45XBberqn2oPiHfdrvd\npu2S3ftsn3+8ytxexXEfjlaGl+dYpQ/HKn2W84PbVdWh21XVwe3qE/LjVdU+vD7vDTQGVBNmuz8O\nhw8fxuWXX46+ffuiX79+yM/Px8GDBzFq1Cj06dMHo0ePNn3/Z8+ejaysLGRnZ+Pzzz9v8DU1mhFl\n1KhRKC0tDdk/a9YszJgxAw888AAA4P7778edd96JefPmoUuXLigqKkK7du2wZs0aTJw4EZs2bapX\nu+vXr8fAgQOb/Qc+1pCWloasPtlY/qU+WXlt/jvokJ6OieMvAgCs27ATLZJaILt3JwBAYXE5PB4v\nunVuCQAo3lcNl8uFLml6OMPuMp25vXN7/RHed0j/qAcCAbjdbuw/XFuXn03/uImPdGprfVt8ZK3b\ngkzamt/tqedehqZpeGXOcwCA8b+caLq+3ll9TNupqe1N20lJSdDIFN3jMYdlaOHUqjpYLRyBgB80\nkry2tgaapsv661/9EiV7j5ocSCoqKkwf+oMHD8BNzA8lRUVISAzmL9u69Qe4XcHy3+WvQmJSC2N7\n+fKlJnneffdtJCYE1zWffXY2WrZoaWzf94c7TeVvuO4q0/b4seebtrN6ppvWoZKTzPbRFon2tn0+\nwO22X16gW2a6SaM6c2j//9/evQdVVe1xAP8eEMQERRsD9OAFDgqJ58XDssbk4RmFLnQhaCo1NS3B\nbpomYI01OCXCiAlzs0Kn1JhMR5IwRwlxNCpRBAWZIEGBkacl8SjCyxz83T+4bAEPPo4Hzz6H32dm\nz7jPfpz1cwFr1t6/tdaA4xHh/xyw/+9/R2PsI7eWFdmU8D4eGTtG2P/4P2kYM+bW/sGDB2BrO07Y\n/zH/FB4Ze+v60tILsLa+9f9dXX0FKVuTYWrWrFmDkJAQZGZmQqvVorOzE5s3b4ZGo0FcXBySk5OR\nlJSEpKQklJeX48CBAygvL0dDQwPmzZuHyspK/RKhyMhqampo5syZOo/5+/tTcXExNTY2kqenp/D5\nvn37aOXKlTqvmTt3LgHgjTfeeDO7TalUGvTvLwBydzLMBgxsTtra2sjV1fW27/Tw8KDm5mYiImpq\naiIPDw8iIkpMTKSkpCThvPnz51NBQYFecRnltXdTUxOcnJwAAFlZWZDL5QB65/qbMGECLC0tUV1d\njaqqKri5ucHe3h7jxo3D2bNnMWvWLGRkZGD16tU6733q1KmHFQZjjJm84XqHV1NTg0mTJmHZsmUo\nLS2Fj48PUlNTce3aNTg4OAAAHBwccO3aNQBAY2MjnnzySeF6qVSq9ysnkox2vwAADHhJREFUozRs\n8fHxKCkpgUQigaurK9LT0wEA+fn5eP/992FlZQULCwukp6fD3t4eAPDJJ59g6dKl6OrqQkhIiM6M\nSMYYY+Kg1Wpx/vx5fPzxx/Dz88Nbb72FpKSkAedIJJI7Poa/2yP6oRilYfvyyy91fh4REYGIiAid\nx3x8fFBWVjacxWKMsRFH34zGrm7gRvfQx6VSKaRSKfz8/AAAkZGR2LJlCxwdHdHc3AxHR0c0NTXh\nscceA9CbFFhXVydcX19fjylTpuhVNpPNsIiNjcXjjz8OpVKJiIgItLe3AwBqa2sxZswYqNVqqNVq\nrFq1SrimuLgYcrkc06ZNw5o1a4xVdJ2GigcYOlNIzPEcPHgQXl5esLS0xPnz54XPTbV+hooHMM36\n6S8hIQFSqVSok2PHjgnHDJWl9rDl5OTA09MT06ZNQ3Ky6SVdAICLiwsUCgXUarUw1OlOGYX60jcL\ncrQVMH7srW0wR0dHODs7o7KyEgCQl5cHLy8vhIaGYu/evQCAvXv34l//6k3ECgsLw/79+9Hd3Y2a\nmhpUVVUJcd83vd7MiUBubi719PQQEVF8fDzFx8cT0Z2TUfz8/Ojs2bNERBQcHEzHjh17OIW9B0PF\n88svv5BSqaTu7m6qqakhmUxGN2/eJCJxx1NRUUGXLl0SEoD6mGr9DBWPqdZPfwkJCbRt27bbPtcV\nW9/PqJhptVqSyWRUU1ND3d3dpFQqqby83NjFum8uLi7U0tIy4LPY2FhKTk4mIqKkpCTh74S+ANA/\nHjPMpqs5KSkpIV9fX1IoFBQeHk5tbW3U0tJCQUFBNG3aNNJoNNTa2iqcv3nzZpLJZOTh4UE5OTl6\nx2WyPTaNRiOkgT7xxBOor6+/4/n3M8jbGIaKJzs7Gy+99BKsrKzg4uICd3d3nD17VvTxeHp6Yvr0\n6Xc/8f9MNR5TrZ/BSMfzKF2xFRYWGqF096ewsBDu7u5wcXGBlZUVXnzxRWRnZxu7WHoZXC+HDx/G\nkiVLAABLliwxyM/UcA7QViqVOHfuHEpLS3Ho0CGMHz8eEydORF5eHiorK5GbmyvkUQDAu+++i8uX\nL+PXX3/F/Pnz9Y7JZBu2/r744guEhIQI+6Y+yLt/PI2NjQPK3ZcpNPhzMcczmKnXT3/mUj+6JkwY\nKjaxa2hogLOzs7BvKuUeTCKRYN68efD19cWuXb2Teg+VUfgghnOAtrGIepa7oQZ5JyYmIjQ0FEDv\ngG9ra2u8/PLLAGCQQd7DRZ94xOxe4hnM1OvHVOkzYYIu+mapPUymUMZ78fPPP8PJyQm///47NBqN\nMDl8n7tlFI5kom7Yjh8/fsfje/bswdGjR3HixK2pjaytrWFt3TuDgre3N2QyGaqqqjBlypQBjysf\nJONGX/rEoytTSCqVmkQ8uphy/egi5vrp715jW7FihdCIGzJL7WEaXO66uroBPU9T0TfWd9KkSQgP\nD0dhYSEcHBx0ZhQ+CLHN82gIJvsoMicnB1u3bkV2djZsbG5NPXP9+nVhhv/+g7ydnJyEQd5EhIyM\nDCEbRwyGimeoTCFHR0dRx9Nf//cEplo//fWPxxzqp6mpSfh3/wkTDJql9hD5+vqiqqoKtbW16O7u\nxoEDBxAWFmbsYt2Xv//+G3/++ScAoLOzE7m5uZDL5QgLC9OZUfggzHESZJPNinR3d6epU6eSSqUi\nlUpFMTExRESUmZlJXl5epFKpyNvbm44cOSJcU1RURDNnziSZTEZvvvmmsYqu01DxEA2dKSTmeA4d\nOkRSqZRsbGzIwcGBFixYQESmWz9DxUNkmvXT3+LFi0kul5NCoaDnnntOmO6IyHBZag/b0aNHafr0\n6SSTySgxMdHYxblv1dXVpFQqSalUkpeXlxDDnTIK9QGAJk80zCam5sQoC40yxhgzPolEAscJhrlX\nc6vu7FpjEPU7NsYYY8NLJG2RQZnsOzbGGGNMF+6xMcbYCCa2MWiGwA0bY4yNYPwokjHGGBM57rEx\nxtgIZo6PIrnHxkShrq4Obm5uaG1tBQC0trbCzc0NV69eHZbvS09PR0ZGBoDeGV/6D1J+7bXXUFFR\n8cDf0bccTEJCwgPfyxBu3LgBlUqF0aNH448//jB2cZhImOMAbR7HxkRj69atuHz5MtLT07Fy5Uq4\nubkhPj5+2L83ICAAKSkp8PHxMeh9N23aBDs7O6xbt+6er9FqtRg1angfpLi6uqK4uBgTJ04c1u9h\n4ieRSDDB1jD3av1LPOPYuMfGRGPt2rU4c+YMUlNTcfr0aaxfv/62c2pra+Hp6YlFixZhxowZiIqK\nQldXFwDgxIkT8Pb2hkKhwPLly9Hd3bu874YNG+Dl5QWlUom4uDgAvb2pbdu24ZtvvkFRUREWLlwI\nb29v3LhxA/7+/iguLgYAfP3111AoFJDL5diwYYNQDltbW2zcuBEqlQqzZ8/Gb7/9pjOm/r/ohYWF\neOqpp+Dt7Y2nn35aWIBxz549CAsLQ1BQEDQaDTo7O7Fs2TIoFAoolUpkZWXh5s2bWLp0KeRyORQK\nBVJTUwEAV65cQXBwMHx9ffHMM8/g0qVLAHpngQ8PD4dKpYJKpUJBQcED1Q0zX+Y4u7945kBhjIhy\ncnJIIpFQXl6ezuM1NTUkkUjo9OnTRET06quvUkpKCnV1dZGzszNVVVUREdErr7xCqamp1NLSQh4e\nHsL17e3tRDRwcc3Bi4f27Tc0NNDUqVPp+vXrpNVqKTAwkL799lsiIpJIJMJ0YHFxcfThhx/eVtaE\nhARKSUkR9js6Okir1RIR0fHjx+n5558nIqLdu3eTVCoVpkeKi4ujtWvXCte1trZSUVERaTSa2+II\nDAwUYj5z5gwFBgYSEdELL7xAaWlpRETU09MjnE+kewFLNjIBoPFjDbOJqTnhHhsTlWPHjmHy5Mko\nKysb8hxnZ2fMnj0bALBo0SL89NNPqKyshKurK9zd3QH0LsKYn5+P8ePHw8bGBsuXL0dWVhbGjBmj\n85406BEKEeHcuXPw9/fHo48+CktLSyxcuBD5+fkAelcpePbZZwEAPj4+qK2tvWtsbW1tiIyMhFwu\nx7p161BeXi4c02g0woKLJ06cwBtvvCEcs7e3h0wmQ3V1NVavXo3vv/8ednZ2+Ouvv1BQUICoqCio\n1WpER0cLS9OcPHkSMTExAAALCwuMGzfuruVjI5M5vmPjho2JRklJCfLy8lBQUIDt27ejubkZ9fX1\nUKvVUKvV2LlzJ4CB620Rkc41qfoaKktLSxQWFiIyMhJHjhzBggULdH63rnsM/qz/d1lZWQmfW1hY\nQKvV3jW+9957D0FBQSgrK8N3330nPEIFgLFjx+osfx97e3tcvHgR/v7++Oyzz7BixQoQEezt7XHh\nwgVh67+23eB7MKYLN2yMDRMiQkxMDNLS0uDs7IzY2FisX78eUqlU+KP9+uuvAwCuXr2KM2fOAAD2\n7duHOXPmwMPDA7W1tbhy5QoAICMjA/7+/ujs7ERbWxuCg4Px0UcfobS0VPi+vj/8dnZ26OjoGFAe\niUSCWbNm4YcffkBLSwt6enqwf/9+zJ07V+8YOzo6MHnyZADA7t27hzxPo9Fgx44dwn5bWxtaWlqg\n1WoRERGBDz74ABcuXICdnR1cXV2RmZkpxHTx4kUAQFBQED799FMAQE9Pz23xMWbOuGFjorBr1y64\nuLggKCgIALBq1SpUVFTgxx9/vO1cDw8P7NixAzNmzEB7eztiYmIwevRo7N69G1FRUVAoFBg1ahSi\no6PR0dGB0NBQKJVKzJkzB9u3bwcwcPXhpUuXIjo6Wkge6ePo6IikpCQEBARApVLB19dXWISzf2/u\nXlcyjouLwzvvvANvb2/09PQI1wy+fuPGjWhtbYVcLodKpcKpU6fQ0NCAgIAAqNVqLF68GFu2bAEA\nfPXVV/j888+hUqkwc+ZMHD58GACQlpaGkydPQqFQwNfX1yDDF5h5MsfkEU73ZyaltrYWoaGhd3wH\nJxabNm2Cra0t3n77bWMXZQBO92d9JBIJHhltmHv9/V/xPP7mHhszOffSOxIDW1tb7Ny5U3QDtLVa\nLSws+FefmS/usTHG2AglkUhgY22Ye93oFk+PjeeKZIyxEUwkbZFB8fMIxhhjZoV7bIwxNoKJLaPR\nELhhY4yxEYwfRTLGGGMixz02xhgbwfhRJGOMMbPCjyIZY4wxkeMeG2OMjWDcY2OMMcZ0mDBhgrGL\nIOAeG2OMjVBimQLL0LjHxhhjzKxww8YYY8yscMPGGGPMrHDDxhhjzKxww8YYY8ys/A8uuwOwOzHB\nDAAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x10ab322d0>"
]
}
],
"prompt_number": 21
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Composite Maps\n",
"Composite maps inherits from genericMap and can handle multiple maps and lets you plot them together."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"compmap = sunpy.map.Map(sunpy.AIA_171_IMAGE, sunpy.RHESSI_IMAGE, composite=True)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 22
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"levels = np.arange(0,50,5)\n",
"print(levels)\n",
"compmap.set_levels(1, levels, percent=True)\n",
"compmap.set_alpha(1,0.5)\n",
"compmap.set_colors(1, 'Reds_r')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[ 0 5 10 15 20 25 30 35 40 45]\n"
]
}
],
"prompt_number": 23
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = plt.subplot()\n",
"compmap.plot()\n",
"ax.axis([200, 600, -600, -200])\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAASMAAAEZCAYAAADcwUPmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXuQZ1V1P/rZ5/V9d3+7e949MwzM8FQTFRgEtSA/fxAl\n4iVVySQQhElueX3yiJpUIlImBlDLJAatGvUmPAxahni9iok4yjWCSiqgYCAyCA0CzvvRPdPd3+d5\nrfvHPuvstU/P8Ji3zXdVTfWc7/d8z9lnn73XXuuzPmttRUSEgQxkIAM5xuIc6wYMZCADGQgwUEYD\nGchAjhMZKKOBDGQgx4UMlNFABjKQ40IGymggAxnIcSEDZTSQgQzkuJCBMhrIK0q+8pWv4Ld/+7eP\nyr1WrVqF73//+0flXvNBBsroOJIf//jHOO+889BsNjE2NoY3velN+OlPf3rI133uuefgOA4ajQYa\njQZOPPFEfOpTnzqoaxERPvvZz+I1r3kN6vU6VqxYgXXr1uHnP//5IbfzaMgf/dEf4bvf/W5+7DgO\nfvnLXx709RzHQb1eR6PRwPLly/GhD30IaZoCAJRSUEq96DXuu+8+rFix4qDbMF/EO9YNGIiWmZkZ\nvP3tb8cXv/hFrFu3Dv1+Hz/60Y9QKpUO2z2mp6fhOA7+67/+C295y1vw2te+9mVbCddeey3uuece\n/NM//RPe+MY3Io5jfOMb38C3v/1tvPrVrz5sbT2acqi838ceewwnnXQSnnzySVxwwQU45ZRT8O53\nv/swte4VJDSQ40J+8pOfULPZPOD3H/vYx+iKK67Ij5999llSSlGSJEREdP7559MNN9xAb3zjG6nR\naNBFF11Ee/bs2e+5RERnn302/e3f/i29//3vpw996EPWvS655BL6zGc+M6cNTz31FLmuSz/5yU8O\n2M59+/bRO9/5Tlq4cCGdcMIJdOONN1KapkREdPvtt9N5551Hf/qnf0rNZpNWr15NDzzwAN122220\nYsUKWrRoEX3pS1/Kr3XVVVfRu9/9brrwwgup0WjQ+eefT88//3z+/QMPPEBnnXUWDQ8P09lnn03/\n+Z//mX93++2300knnUSNRoNOPPFE+spXvpJ//qY3vYmIiN785jeTUopqtRrV63X613/9VyIi+rd/\n+zf6zd/8TWo2m3TeeefRY489dsDnVUrRM888kx///u//Pl199dVERLRq1Sr6/ve/T0REvV6Prr32\nWlq2bBktW7aMrrvuOur3+9RqtahcLpPjOFSv16nRaND27dsPeL/5LANldJzIzMwMjY2N0VVXXUXf\n+c53aGpqyvr+r/7qr15UGa1Zs4YmJiao2+3SBRdcQH/xF39hnRvHMaVpSj/+8Y+pWq3Sf/zHf9BD\nDz1Ey5YtyxXG7t27qVqt0q5du+a08fOf/zytWrXqBZ/jne98J1166aXUarXoueeeo1NOOYVuvfVW\nItKKwPM8uuOOOyhNU/roRz9K4+Pj9IEPfIDCMKTvfe971Gg0qN1uE5FWRo1Gg370ox9Rv9+na6+9\nNlckk5OT1Gw26ctf/jIlSUJf/epXaWRkhKampqjVatHQ0BA99dRTRES0Y8cOevzxx/M28DWI5iqT\nRx55hBYtWkQPPfQQpWlKX/rSl2jVqlXU7/f3+7xKKXr66aeJiOjxxx+nJUuW0G233UZEtjK64YYb\n6Nxzz6Xdu3fT7t276bzzzqMbbriBiIjuu+8+Wr58+Qv26ytBBsroOJInnniC1q9fT8uXLyfP8+gd\n73gH7dy5k4he3DK64IIL6Kabbsq/37BhA731rW+1zm02mzQyMkKnn346fe5zn8vPPf300+nee+8l\nIqLPfe5z9Du/8zv7bd+NN95Ib3jDGw7Y/jiOKQgCeuKJJ/LPvvjFL9IFF1xARFoRnHzyyfl3jz32\nGCmlLMU3NjZGjz76KBFpZXTZZZfl37VaLXJdlzZv3kz//M//TOecc451/3PPPZfuuOMOarfb1Gw2\n6etf/zp1Oh3rnBdTRu95z3tyJcFy6qmn0v3337/fZ1ZK0dDQEI2MjNDq1aut30pltHr1avrOd76T\nf/fd7343V+w/+MEPBsqIiAYA9nEkp512Gm6//XZs3rwZP//5z7Ft2zZcd911L/n3S5Ysyf9fqVTQ\narWs7ycnJzE1NYVNmzbhAx/4QP75lVdeiS9/+csAgC9/+ct45zvfud/rj42NYfv27Qe8/549exBF\nEU444YT8s5UrV2Lr1q358eLFi602AsDChQv3226lFJYvX55/V6vVMDo6im3btmH79u1YuXKldf8T\nTjgB27ZtQ7VaxV133YUvfOELWLZsGd7+9rfjySefPGC7pTz//PP4u7/7O4yMjOT/tmzZ8oLP/bOf\n/QxTU1N4+umn8fGPf3y/52zbtm1Ov2zbtu0ltemVIgNldJzKqaeeiquuuiqPUtVqNXQ6nfz7HTt2\nHLZ7XXHFFbj77rvx6KOP4he/+AUuvfTS/Z73lre8BVu2bMHDDz+83+8XLFgA3/fx3HPP5Z/96le/\nshTKyxEiwubNm/PjVquFqakpjI+PY9myZXj++eet859//nmMj48DAC666CJ873vfw44dO3Daaafh\nXe9610u658qVK3H99ddj7969+b9Wq4U/+IM/OKhnYFm2bNmcflm2bBkAvKSI2ytBBsroOJEnn3wS\nf//3f59bEZs3b8ZXv/pVnHvuuQCA1772tfjhD3+IzZs3Y3p6Gp/4xCfmXIMOMiq0fPlynHXWWbjy\nyivxe7/3eweM4J188sl43/veh8suuwz3338/wjBEr9fDv/zLv+BTn/oUXNfFunXrcP3116PVauH5\n55/HZz7zGVxxxRUH1S4AuOeee/DAAw8gDEPccMMNOPfcczE+Po63ve1teOqpp/DVr34VcRzjrrvu\nwi9+8Qu8/e1vx65du3D33Xej3W7D933UajW4rrvf6y9evBjPPPNMfvyud70LX/jCF/DQQw+BiNBu\nt/Htb397jpX5cuWyyy7DjTfeiD179mDPnj34+Mc/nlugixcvxuTkJGZmZg7pHr/2cozdxIFksnXr\nVlq3bh2Nj49TrVaj8fFxes973kOzs7P5Oe9///up2WzSySefTP/4j/9IjuNYmBEDxUREd9xxB735\nzW8mIo0ZyXP3J3feeScppei+++570bbecsst9KpXvYqq1SqNj4/TH/7hH9KmTZuIiGjv3r10xRVX\n0MKFC2nFihX0N3/zNzk4LttERDQxMUGO41jXXr58OT3wwANERLR+/Xp6z3veQxdeeCHV63U6//zz\n6bnnnsvP/fGPf0xnnnkmDQ8P01lnnZX/bvv27XT++efT8PAwNZtN+q3f+q0cxyq24Qtf+AItXbqU\nms0mfe1rXyMioo0bN9LZZ59NzWaTli5dSuvWrbPegxTHcSzMSUoxmnbNNdfQ0qVLaenSpXTttdda\noPif/Mmf0NjYGI2MjAyiaUdTPvzhD9Npp51Gv/Ebv0G/+7u/S/v27cu/u/nmm2nNmjV06qmn0ne/\n+93885/+9Kf06le/mtasWUPXXHPNsWj2vJYf/vCHtHLlymPdDEvWr19PH/3oR491MwZylOSYuGkX\nXXQRHn/8cTz66KM45ZRTcpdj06ZNuOuuu7Bp0yZs3LgR73vf+3LX473vfS9uvfVWTExMYGJiAhs3\nbjwWTZ+XEkUR/uEf/uEl4ypHS2hQhPQVJcdEGV144YVwHH3rc845B1u2bAEA3H333bjsssvg+z5W\nrVqFNWvW4MEHH8T27dsxOzuLtWvXAtDRn29+85vHounzTp544gmMjIxg586dLytydzTkpaZTDGR+\nyDFPB7nttttw2WWXAdDhzze84Q35d8uXL8fWrVvh+74VkRkfH7fCxQM5eDn99NMPGZw9UnL77bcf\n6yYM5CjKEVNGF1544X7DzzfffDMuueQSAMBNN92EIAhw+eWXH6lmDGQgA/k1kSOmjO69994X/P6O\nO+7APffcY5VYGB8ft3glW7ZswfLlyzE+Pp67cvw580mKMlxVmOkeYuMHMpCBvGxZvXo1nn766YP+\n/TFx0zZu3IhPf/rTuP/++1Eul/PP3/GOd+Dyyy/HBz/4QWzduhUTExNYu3YtlFIYGhrCgw8+iLVr\n1+LOO+/ENddcs99rz3SBD10KEAFxoj9TCgg8IM3w0H4EdEMgivWx7+nzg6w3klT/1hfHWVUIdEN9\nneVj+vi/ngTeeLq5VxgDUWKOKwFQKwNOBn24DtDq6fP42q5j7k0EtPv6L18vjM39f/48cMZK/TsW\nR5ln813Accz5/H9P0GwqAVAOzPmuo89jkef/15PAW37T7htuJ/eH/DyKdX/PZgtC4OnrA/qejvgu\njHW7ua0/mQBev9pcqxsCjQpQLZnn7EXm/EYFGKoC26b0catnzuN7V0v6eQHdrn5knvOnTwNnn6z7\nANBtCWOglz3TbFe/S35XLLWsPSVf/+Vrlnz9j4+rJaBZ020EgB88BrztTNPXZV/fg68fJ/Z7HaoC\ny0bN8UzH3DPw9G87/azfE6BeNn3lOsD/85/Ab73G9HWSmuvzO+C+Kvn6NwzR+a6+h5wDlcD8vh/p\nc8tZe8oB8H9+zvC1DkaOiTK6+uqrEYYhLrzwQgDAueeeiw0bNuCMM87AunXrcMYZZ8DzPGzYsCEH\nMDds2ID169ej2+3i4osvxlvf+tYDXp8VgTwOY/Oi+IXyJPFdPZB5YlUCexK1+/Yg4fMBPSlbPfN9\nnOjPWDmkpI9L2YTwXDOAWGTQyHX0P76eo0w7ADOQ+Rn4HL6fKwY6349IT2J5LvcRKxmeQET6N3wc\nxUC7B6RZ++WABvQkAIyCSFJbGfNCAOh+VQrY1zZt40HO58pn4LbPdMznSWqedXFTX0sqIal0PVe/\n01rZ/L4f2e+KlT3/XinzPf+fj7ld/My9SI8pbneU2L+PE90G7oskte+XlvX5/H27by+QtdR+9lbP\n3Kvk6//L9+655nvPBYYqwMos02a6DUx3zPVqJfv8JM3Gbdb21NHPI/uCyPRBkhpFdrjkmCijiYmJ\nA373kY98BB/5yEfmfH7mmWfif/7nf17S9XkV4I5jq4cnPXcsr4CRY6+Y/JK8rLNH62YCJam9wnZD\nfR++Nk8gnoBppph4wsj7AMBwdW7bfddcr6icXEevgKmwnADbspKDNEmNEub2SOVWbI8cfHx9qWyT\nVN9L/o4VLv9OrvBOahRhNdGTiNvTj4B+YtruufpaUtFGiXlPrpNN/uxeu6aByVlj2bieUSjclrox\nvOG7RgFyu6Vi7QulwRJ4tjKpBHb7YqF4+d3LPgxje7Hh3wDA7hndJm6vXMRIvD9A92G9bN5dL9T9\nx++fsnfQqJj7sIIBjNXGlg4rbkcoo07ffF8v6zHPv6+W9L34/o7SC6O08A9VBukghyhLRo7u/RY3\nj+79lo6++DmH7V5HuS+P9v1WLTq693vVyhc/53iSYx7aPxLC5re0jDzXXm2ixDa3A09YMxlmxKt/\ns2ZWwzBzW3g1a9b0Ci1xCrYe+HxpRbDlwqsjr2Z8Pn/ObVdKm+58vHBYX5PPk1YJH0sXUz4HX9dz\nzffcTxKjUsI1XDaqV0xp+RRdNdcRK7qwOvj5+Nww1itvLPq95JvjlQvtZ+tF9rM5jv6MMZuZjnGL\nAf1cvche7bnNgH6vJd98Pz6m+0a6OtKSUeKdcnvixB5XKdmWDbtm3PftnnFDT1ikfytxmNmubany\n/wMPWDRs7s3u6Gjd9K9SxirsRfpabIGXfN1fT2WFARYO2RY2Ze+4x26ha3BEwEAJPO6jDEMtueZz\naTFXxG8PVuatMioC2HJStAuYTdm3j9nNadbs6wHGvJXX9sVLbvX0S56cNb/tReYeRWyn5Ovf8iAK\nYz0Q+PqMcUjzuxvak1S6jfysElwtB7Zykq5B2df3kxNX4irs9vD12c2RbqRUTvydBLolIC05jK6j\nBzFjdUWgOE2NcuTjtHC9RIDtSgFpoicat8V1tEIANHbkezY2Je/J57NbKNsJ6H5LyUxU1zHvb3/t\n9z19bkmAvFFilOFQ1eBagF50+D3zoiPdcA6O8L2S1OBhi5t6DPG44zHIMEAkFj8AmO0ZYJ3PL3um\nr7qhHis5YO7qsSIDMWXftF2Oz4OVeamMin5sraxfOg9aJxvErCDYMuJB6mSTbzoD+3wxYPqRjSN0\n+rYlwlEJ/l5aX4AZDNJy4EnF9wpjcz+2pHLQk2xloBQAAkLx+6I1EcX2qtcNbeBaDvKyb4PESXbN\npIC3MZCeZpNLKh8JfHLfyvci2ycVa5RF11gZMN6WCMzGdTTWwud7rpkI9TIw1bIDGN3QrNr9yAZd\n+X0XrcwcF3E0PiWVjwsbvyMy1ol8R/y9VL69UCsoT1gXo3UzzrZNmd/OdPRzMeZVLRnchmVf2ywS\n+9rGI+BnkvgWLwoSC+yF5lnr5bnYVpKadzFUtcF6XoQOJ0F+gBkNZCADOS5k3lpGbFEAJiIlrZeu\nMMVlhADIcJrEWDOjdbOaMe5Ry85t92w3rhjl4r8cspWhX8BYVpI/EsbGanMK0TSOCkqej+R7MN7D\n7ZVhfUCvbv1IhO4TfQ0+n1c7xn7YauC+iTI3z7IOBMbEfU/C8pPcFEcZ10Jlx5GwTFzHfN/u2e42\n4zG8WktshttWCYwlQ2SsXJaUbHxDutwc+s+jcdkYknih787tKz7md8fP3unb747HQjv7y+4zX78S\nzKV5cORxcVO3ja1Cvu7eLJOHKRRyHDqFsVbEKpXo+z0ztvXMXLycKtC3I6Fs/bPlJsfYwcq8VEa5\nGyLMf2lSsknKioMHEbsTPOEkp4IHtKNsTIe5I1IkCAvYoXaQPUGZ8yMHoe8akDNOTPsBDd5Kt9Fz\nbWIfA7L8LDzB+HrdAh7iZG5XJMx76YZy+yTIKt24IvVAPjP/lcpE8qa436ViKwLIzPmSfcvPwhgS\nPxMDupI35Di24pa4h+SCAQDIxtdY5LtJUjNpOSjC92NwPHd5Pbs9/Hzc3gVD2r1iQH6oavqqVtb/\nGLcca+jf7Zo27XCUcVE7fd0eSTvoR0Z5VEs2uM6uvy+OO33TN/3IHhfdEEhnbexQUlgOR4GFeamM\nmOfC1kI7408wmMcs2XwQZSAqD6J+ZGv6Xjh3wEdCGUnh6xYBYH7pABAmYiKkABxzP7acpFXHBDfA\n4DG8+tfKNs7BGJJUlhKAZsXBz172504+XtH5elJZ8iDO+S4A3MS2KqVwJBPQ10nJnhCuY/qSwfWo\noMgZaOX3yt8rpfuP3w2v1jwBO33DCOd3IZWx59qWTi/Uz8YTfH8TTeKBOR/Ntc/nvmlUMtA8+36q\npfub28dRTX4etlq5rYAZF8zS59/umbG5dOXAYGh878Az46QfacUmAxcp2Vajo0xwh9sl+WpM8OVn\ndcW4re6/OOjLkgFmNJCBDOS4kHlpGRWtCyJ7tWdMhbU6R1w4qsGYh8QiZOi6yBuS6RNzombQEScW\nzntjcZSxCLht8t4c5eO2s4vI5rijACj7fL4P/5WuRKNiTHDAMJ6LoV/JG2JmNB9LXhK7nDKax3iF\nfBf8bDLXjPEddrvYHeVnrZb0dWSUSkY9ORLHbWn19PeSqiGvF+6HwyV/z9fntjM+VcTrilYv4ybc\nj/z7Zs22kgPPWLKAxsQ6feNic0SMry2tjS2T+jr83mtlzSuSaTy+mM1xorFOzm3jSBvnpLkOADFH\n5mCD6VzsT7rrYazPPRz8IpZ5qYyKSZwS+wF0RzZrpiOnO/YELf6uWjIvkX11OcE6fdu1AA7MjUlT\nO5dMTlxum8wZAvQEZ/OZJyDfj3GQYopCJAaXdCWZuyLJailsBZmSAbCLeBC33RGDWKYV9CM75UKS\nGqFs8JvBV5mkqxRQEYBuV4SfWfFz33GiqfwttwkQofAC+ZEnMONrRU4UX58ne5E0KnPnqiVzXAmA\nmlDUKxfqZ2TuDx/3xMIlFwqJjY0M6bbs2Gu+k/QUwA7Hs+ssFXGnr7EmAFixQN+b3bZ2X98/Eoqe\nn4+fDTB9w/fOFTEOryIC5qky4o7NQVllr7C9UA80xpB4pedBxyuAxAIkQ1pO5igxE5ClyPNxYOMy\naWpPMMexvy9G52RSYiUwoDSgJ9hwzVhWs117QsGxeUm80ss2yvvxd5HARSQmxefL3Dul5ipUSYqU\nijVJgeQA0TDHAaq+AYgZIJVtKeZ6yWgYr+TMier0M8ssO5cz0Vkkh0n2NechsuKV7ZSKuVrSILTM\n0q+VTbSPrRv+DQPEDFhz9E+Jd8vKgxOqObGV28TWEmNCDHB3Q3uMc78zxsNMcE4n8lxg97TGsQCD\nl8nAA5/HfQvYi4xcGA6HDDCjgQxkIMeFzEvLqBhmZNTfYi2LlBAOv8rIgcSJ2pjL6ua/cWJbBbw6\ns+tRK9luTRgDEeamGEhmLEc6AG1FyagGR1WkZSKjJlEy15LJn3k/fcNlLyRmlJKxtJJ0bma5TKNg\nTIjEilqsMsASeDYjul7W1+HVOYq1tSrxMxk9K3KsirlnRXecv5Pvx2LiKz0uZARL5jByyQ75+5Q0\nCxswlIqgMIv43TNPSEb3hqs2S1rmJS4Yskt69ATPh9nhsn7USN1E/pg/JWtFSSsySrTVtmBIH5d8\n3f8cqdzb0taXHGfyudkalx6AfLeDdJAXkGLyqEw2ZWxgT0YgqwR2jR8OGbdEWFWGc4sAtOSyAHa+\nFKBflPwNu3aA4TNJUFRiKE52b2k2Sx6R5ATxs0gcojhhlQJ82BiXBHmTVOfa8aDMMSJzumWeM4Yi\nFUgPRuHIpFzOYWOglZOIJQFTcrZYcfCzSnoEYPNmABts5ev7LvLGs9JnxV0J7PQZIq04ZLqGTALm\n4AW790xW5Yk4OWu/C9+zXWpAu1Vy4aiWjOtEZFzUyVmzsHC/chv42ds9u08kr4jxI3m+pLvUy3qh\nlLWmmjVz/nRHKyhVWGglTYL7AJib33kwMi+VEVsmMqLTJyDJBnq1pF90kL3IYr5XsSpecWW0AFzS\n0TJZk0daLuXAjsB1Q1PACtDtKIKiMmLD7XcKg0CCsFxBEdArPVszgGYRM3GSr+84gFuwkHLLLeM9\nycx3CVwWFQNbQgygc7a4rCBY5MxIgmWSmmuypcQKabhq88GKysj37PcEFPC6TJEqoUx6oa1c5GSr\nlmzAnScotzuMbVynXjYkWEBP7jA292OcRgLqMtAw1dKWirTYGW9q9+yKAmydSqyQqz0Cup1yQa2W\njCUKAL/arQmTHF1rVLJMAhEJlAtDkYPFOCJ/nwcRMuU5VKjLdTAywIwGMpCBHBcyLy2jIobAq7dM\nSxitG60eZRT9rmAtS0spKVgRRKYqIKBXEHZLeOWz8CeRFa8ybopbMH/l/yVjmzGSgNuazGVESyat\nzIAHTP0g2R5p6RWPc5dR4B6y79hl4+csso99F2iL3xMBtcyNqZVtrsqCrMYOr957Zua6j8USwtKN\n812AfMFDwlxGfBHPkxEj5srIshxjDTsVx3EMj6jTBxpDZtz0Qv3/Unb+WEP3e15VIAGqytxvwZAu\nBbs9C9c3azYel6Smnvfk7NzyJsXKEt3QRNO8gtUI2PW1lbJL5yxu2ilPYw3dP0xDaPftXDVAH3Nf\n8Bhlt5BLjxyKzEtlBGhXyMs6k0P3bNLmeTmeOZYhyiQ1/CAWHtTlwMZwAP1CfOGmJalRNsyNKaaP\nFGn50geXOIscqIBxbeQkle1h4L1IapQ1qtuh8fFZ+UheiZz/TAyUysz15rptkjvDvwG0AmKMhesm\nseLcOqknRUdwqOSzMslPutvSjeJQdt5XZPcFu+tFxc3uAD+LBKC7om+cjEMm87vY1QPMux6qmOux\n28N9USzVGsbmnOm2vh9XC312pyHeFgFodsEkzaDkG/B/tqv7kpUFKyI5ThYOG3yL3/t4trHEwiH9\nG54jtZI9jjp9Uz6Hn0WScUu/rpjRn/3Zn+Hf//3fEQQBVq9ejdtvvx3Dw8N47rnncPrpp+O0004D\nYAr1A8DDDz+M9evXo9fr4eKLL8Ytt9zyovfhjmRejOSv9CN7FeZaOoDuaN+3v5eWiuTOMAtVAofF\nLHH27wGjSCT+IZUP+/rF2sZFbo303SXrt2gV8mTgY8nZ4fbI84skRxm14/ZI5d0NswJjBcB8pG6u\nwfdkzEEy27dMmr5gzIiVUjfUn+XKKclA2ez8In5RbD+TMRPxXiXJkXP+uG8ZvGbFzcEAVpacTM0T\nmrE9qTyl1crJqfx9N9QROqncZKa+fE+cJMzCC5ZUnHIXmEpFX5t5RWzt8/lDVW39nLRYH9fK+voV\njoKlgB+ZOVLy9YYAsi/7ka18uHAgP/uhyjHBjC666CI8/vjjePTRR3HKKafgE5/4RP7dmjVr8LOf\n/Qw/+9nPckUEAO9973tx6623YmJiAhMTE9i4ceOxaPpABjKQIyTHxDLiLYoA4JxzzsHXv/71Fzx/\n+/btmJ2dxdq1awEAV155Jb75zW++4HZFSWq0duBpbog0pwGzYs8WNn0sWgP7Y7bKFADApgXI6JIs\noQFkq6mITnGkTIZYi7lwMtzPlpk0163M6yySFRTuL6NxZZHzxOkZso0Sm6CC5eUXzPE4mZvlzyFy\nvj6nfQSezYWJE+3y8Llc85ktEW57brV5Nh9Mhr75epL7UgyLs0iekaxawLllMq1Euh+8Iwe7cX5G\n82B2NF87pzUULKdeqC0UtgSjWO/zJ61OxoAAkxok+64isMN62bw3jgDzON3XNixpQF93uGpcQiIg\nKCE3R8KM7S2rWnIkGAC8rG8lZiT7+3BYRsccM7rttttw2WWX5cfPPvssXve612F4eBg33ngj3vSm\nN2Hr1q1Yvnx5fs74+Di2bt16wGsyRnQgchxjJDL8LP1hDqHy7/sFILESmJfMoeM89yyyN7tjLopU\nbN3QmMMy6RQwfr7Ml0phE/Nk+kheu8cx94sT4+qUfDtcXtwzLm+3wFXkdj85RnUAV4hJmHJCFdNV\n+NxmzZA4+TvZllZPTyKpPGRJDwbSJX4mFaV0c1iKJL1irl5KyHPXuHQMT7hGRf+GXZ8iftbqwdqU\nktM/+iWPUO/pAAAgAElEQVTzvLNd0+c96O2aJBFxumN+L1NDGFtjYDglm+TI7ZHgu3RxOXAhE6o9\nF/DZ9StDKyJemFs2JaQcAH5hkaoENnyQCuzwcIT2j5gyuvDCC7Fjx445n99888245JJLAAA33XQT\ngiDA5ZdfDgBYtmwZNm/ejJGRETzyyCO49NJL8fjjj7/sezN/ROIgPGkA89Ik2U365wwcygnKg4R3\nUSjmchUtGUnskzt4SBIfny+Jd0wElJaJBMtdb//WkASkZeZ5lNisYo6AyIqUDLIDZrLKekgyGhcl\nNkNcYi58vuQlSSxutmuDsGyVFBNc+b0V85448BAJfEpu3Lg//CtKbNCVr5P3nRgnXFGArydxPCCz\nnAqF9HoCA+O8RclLkknLbBVKvFFaVjLnrxva0bAiFskLnmTOx8nc6KO0nDp9mOiEA6B2KkD6BrX0\nGXT6dr0nia9xrSWJPUqybHEROBg5Ysro3nvvfcHv77jjDtxzzz34/ve/n38WBAGCLIb9+te/HqtX\nr8bExATGx8exZcuW/LwtW7ZgfHz8gNd+Zrv+qxQw2jj6e40NZCCvBHnkGeDhZ/T/veNZGb2QbNy4\nEZ/+9Kdx//33o1w2sdA9e/ZgZGQEruvil7/8JSYmJnDSSSeh2WxiaGgIDz74INauXYs777wT11xz\nzQGvv2aZ/iu3eJa1kIsZysUaQGzOyxVSrpIyR0jyb+Q9ZfhZrvDsxsgSH3wPbkOxhIcMV7OfLiN9\n7N8DplIiR1l8V7sdxcx5fjYu0yGje9KqZH6LrMZYE3u6R7FdikLiWcDckrzSimJ+lmSTS0uGSFfh\n5PfCuIh8b5KnlNMqhGVVfC7pojmOKQMi28u4SXHnl/2NF+n2RYm2ZuTWQ9JK7Ec2VYC3A+Kx0g1N\nfxV3Kubnk3yefmTcMMaLZM11uZtIp68tsF/u1McnKQDRkzo3CEDaKWBADtAVe74V2+46epPI16/W\nx8NV4P/+Hg5JjokyuvrqqxGGYQ5kcwj//vvvx8c+9jH4vg/HcfDFL34RzaY2azZs2ID169ej2+3i\n4osvfkHwmic8KwE2nyXZTU5IPl8OVFnqVbphRayF3YyKUAaSNySxFMCUKZUhU6nsipsJFF0Vzt+S\nSoxz6QCdhOso5MBkOdvSWLqVkvvC+VtWIq7Iv8tdCgHY+2JSMEArw+UykVYm7XKf87V7ERAV6hEV\ni/1LrotMGGYp0iSk21XseyLbhS4LPIX7Qrop7GYVcSfuk5I/d2GS6S2AXSQ/jHW/SQC/WAer6KpK\neEAKu0xS2RPZbmRKtnKb7Zoa2iVfK5Ci25W/m9DGpACbI8bBB8bXmK90KKKIinncv96ilMJbX2/X\nQmbeDvvy7Z6trMq+jQuxNcMDoKhcfNesnr5nT2ZgbpZ7URnInCHGoHgCtns2xlRUgoDZMEB+LxNn\n5UrPyZiyHhMziwFTI1piTFI5Mp4krYJKAGzeY/pDgso82eW+bLLtsp8YbC/Wji4qahnhKVp4zBnj\nY4mP8aIj8wal5cQ5hNxfPNkkqC8jo2yhclSW96TjccXF2ByhwGsCnytiTsUNMSX+xgqTCaNFhnW9\nbN4Vt11u3MDPx3wvxsKWZJDFyoU6T01aUlFi76wigwNhrMF2HneTsxqgf+Pp+rg8Cqi3AIeiTo4J\nz2ggAxnIQIpyzEP7R0KSVK9KxRAu71Pe5jo14jdWeH0/eI68luR/FFm4jOfwiuW79o4XbHXJTHXH\nMSkGTDPg2xXL0vJqKqkFMvLXy7Yl4tWe3TDJRo+SHCrIaQckVu80NSFkz9UrPlcn5F1WOG2BV9Kc\nVZ3aKRsSpylGXNjSkHvSAabt/H2ROyRdF1kLqsjI5vQR2X/SheLonCwZIp+Jo13W9tmpzfni6Cdf\nW1qJSQx01YFdcCqUNwZs/liRIiExIt5Gnd9LLwI6id0W2ad8H04fGalr/hef1+rpdrcEJiWtuDDO\nKqRm73WsAbzuJKDMVANSAA7eKgLmsTKSUsk+4wlUNNd5QHrCfC/mqsnSCpKjxAOaxRPuGaAHriQR\nhrFWQHLbJOar8L2UMgC2rBPEx9IV4AkreUlssgOmXAr/vhwASlAHXEe3mZUhuzWyaL7cZHLRsP7L\nyZ5RAVfh++fgvyB9pqQnM7sgSaq/L7qaUuTW3JxqITEbxgP5XRQxKiJAickuXSGmLEiAXOKDxfLF\njcpc5SNdXC7gJ9+FpJDwuZJzBsztO8C4h3KLLMmd48CGxPqky8dbpstrc9leQCuiJDVuHJdC4d/z\nmOTfM92EF6k1S+0FHK4LoBCteJkyb5WRIybBvrY9YR2l+Tr5INkPUY6vwdfjAc51XiS+JC0n/l0p\nMN87DuBk3zcq2tdmpq2s3wyYQm9yNS+KUvYgdcSESKEnj7TqZESIazrL5E0ZoXJgiJIsHHEDNFbQ\nEyAvY22yb4u4jry3UnZFAck+l3WggKySQjgXTJd9bxX8z6S4uYA8X7LTpRLiYxkd48nO1+NiaTLa\nJkFoXhgk1igxMyaPFpWRJOXyd6wEZERX9g9bfFwju9Wby6KXJErGv3icTc5qK4nZ8QuH7XpGHBXl\nQMVUK2NwN833zTEAHA0/ZxOAk3AoMsCMBjKQgRwXMm8tIyowc+WqsL8VtsiHkVXuVGG1L3JpJGYk\na8QAZmVl16RWApaOmFrEu6f1vWUdJOkicvRLWmaBZ9cvChMTYk1ie4WVO9UCJtQso4NyBwyiudse\nTXds/EAydfuRXdKXLUdpeVkRH+HSOQWrijGeIvM9x4JSu4Y1W3TOfixb/n5/OVP8LnzYeBtH5iTr\n2RORRcYaZZi9FwlaRYGVzP2QY1yOrhNkUQ0c21Iq0hBYuP605BWVfDsvrizqcfMuMpLekqSmXhFg\n/373jO2WccUBtrwaFW09sUXfrAEY/U1g/H3ZzU+c29EvU+atMooL/rcEQovKhcPRcuBK5UVkEyh5\nwrHIUg2lggvAvj//fsEQcNYaw/fwMzxG4gyyDAV/x+3le/cLSkZ+LxNjATtEy66ILGdadK3k/SXO\nABisIRUKhPsQ0J/3BS4kCZtSMfGzyWcv7g2WpvbmmhIjYZETmN1RSSJ0HfOuuAyGxPtkX3BJWonl\nVEvmWXuR3a+MH0kahgwGMM7Cz9xP7DpZTK7NsZeCa54UzpUE0SQFEBjMp93TfS7TmpLUJs9yOg5g\n6l1LbDFODAdqRuCrgL5Ps2Zy0Cqv+1Ngzd/NbfQhyLxURgxySuWTpIAjLB2JTXC2NFfoK2btS54O\nf19UAiyMHxVxEJ6cK+oKrS0OpiYVekN6JFQiB27XQbsa52CztB44L0gRMLY3QOIR9sYpUkXop0CX\nCJ0eAcpYSHLPdMZW+NglQHUVUNMPKHc5LUa+eIWWxeGK+7OXAxsAl7iQpfT7Ck5A+airBDZIy8RU\nWcxfEbAgctFvJLmV53QcJB4h9chk7hOg2g7c4dR6hnwhmXW0BRyk+bP4LqwqnjxmSFgHclGql4Bk\nxkHHTwE1N6mZAWSpQIg0mxnQikgpmCqfMUCJQlrKfpACC7o+JssxVJnmZMXLe3EmAL9X7kuJdxWx\nTrmopaQDFy4Xxwvnfg+YQMuCIY0XDb/2Sv3BYVZEwDxVRsejDO0M4HddqEkFv+LCrWltUZr10Nxe\nxpbGS6jbSUC3lCCIHTRCFw4ppDHgxgoeFGb8BC0/Qlystl+UFMBOH1gZmhj/URB32gWGE5D38kLA\npWkPKlHo1WKoFBjeHWB6YYhUXocAb48HDIf2j1NA7fD0M48VkO6XKx0FtdcFFu3H9zsIcWOFSttF\nq6Q1tyJgrOdjNkiQHGKY/NdR5qUyKmaSsy8sozLSWhipmyqDLHGidzcFbF89zXAImQsmSyuwZcQr\nEueFLaw5KLkOmiWF7ngf0wgRzLoY3V3Gc0s62B2mQJjxRgoMaslSno0TBF6CONuhgneQpVgP5PE9\nZUzWIkQV8zCy3pDnAl4ZoOEEmHZRWqo7RYa7k9SURiXS/cN91+rtP9eO3Zeco+OY/mBLqgRtFSgR\nbZJWKueCyUxz1wGipSGGtpSwaK+PRBHCaoq0miJN7HvFBIQiz06lQLDLR1RNkSxMUAqAuljM2SKU\nFQocYZlxZK3k6/6Nd3sIR+LcIODaRWzZMfdHutzSMmQLPcfIHEI9cvTlFBAR8MRoB6QAFdt4k1La\nXeVx2A01zYJdSFI2NUC67YC2VIeqJjTP2KG0SqPEWEJM12Bs86TFQPOM/wWcfgc/DQ63zEtlxMS0\nHAiluROyJ7g2Yw3tc0tXRhLMinulSW4K4yBMqMzrDol71ctAp9xHN1VIq8DoohSLeoCnFNJ9KWZU\nmt+rUbFdIQZUmffjKENQA0w5EwqAbjXCzjTGsj1ldLwUPS+F6+hn5UHXqGRFughAavSeBI0ldjZU\n1efLvcZkfhe7JTJXTaarSHBc94mCyvby4fdRxNlkvW0iIE4J3aU9OImCihRCPwXSgiJ09OR2Wg6S\nRgokQGWPj6iSIhxJADILELuyzCeTxdxkQbIw1mMp7AJqu4+wliIYIoyWzbuR2/e4jkmvYdlfeRk5\nduIghTfroFdL89QhJX4ry5Owy86/lX3FUBz3aZzYoX3XsQvJ8bOx4uU2SQ5VswaclpURa65cALz2\n/8ORUEIs81IZARlQyKuGa9cRYlCVJ9DENsPDAIx/LTPvZZEqyaBmgiC/VM6U5hWI+SBRooGNMEtQ\ndBSAcoz+r0pYnHroN/SK62SKMBWDQ+ZHLRvVIDID4LunteVioiaEqaEQJ7QDbB7tQbn2hNvXBmY7\nwOiUg+5YjGbL7BHP7Q88o0xmOmYPLxaprHhyWBNSAM1EZvL7JcD1AV/0jQSYOUmWf5tqnZPfL1IE\n8kkfp2bRyDGaFTG8bR6SREF1HKhGCm80QV3cr+zbhe06fTNh+R12+vr6SVvBablIWg6SkRjeSIol\nTaOsZjpASShi1wFiMVdzAquIlslx5jpAq5ZgaK+HXjnNa1XxdymQU/GT1B5nKsMHRxvmfCuwUNg4\nYrRuMu8BPT6Hq6LCQGKD/9WSXqTHl2UXOO2fcCQVETDgGR1bUcDsoj6Gp0pY8mwdw7tK8LvOobLq\n0SoniFzCcGf/a43fVyAXSP2jjEt4BIqO4IAOCOmyCGrGRTqUgEaTlz1/0pYCtvjAcwGcKQ8IUkTL\nQ6SNw4MTFSXxCGGJUOq6L37yPJd5aRnJXROAuSFXIFsxMlU83bHZrRzNaoia2Ryar5b0ysrHjGvk\nq3lmCbA14Ll6PzDGlPo+8OBTZsWqVmP0Tonh9h2UZzws2l3BUATsLUVo1WK4TmqtiEM+sHDEQS0B\nolKKva1sVYzN/UYaACohlu8qY0sGjubh5QgIZly0gwRhZPbn4hWzWbNLm7KbKMPztbJxE6olmyUN\nFHawkKFwP4U/6+af8U4bMhQvGc9MK5C8IcloZndZZroHdSA9LYTKonyuY94FR8eKZTdcR2NC/m4P\n3VmFeCgBKinCDC8qZ+0dqsxllMtqjFwlQKa/FKNrRWa9UjooUZ/10K8Z2Jp3IilyqiQ2ya4WYNcd\n4r9sPbEkqcGAhrIdZfn6+9r2/Zo14IwVAIZO0B8s+D9wpGVeKiMuGSLzeIpAokyhAGzzmXOxZE1s\nJnsx4CpxDVkfiCcY8zFmOvrckVkfiUdAOUZPpGsQZbVjnBSdZoip4RBoOwimfYzvrGJBKQEtCVF1\nFMpTPvxtLrqKMDyjsGu0h0YltrhAtaxURDckhOUEw20PYSXOXaHAA3xSmK5Q/ju5lxdPMHZlFg7b\nNbUBDZzyhOv0NYaVE/s8W+lLVyFoEJy9DlSkoEqUu7/SjZH1jNiNY56RTEBlKb5bGQ7nuuYymVfW\nqWKwvuEqtDd7iEopaEWMNLSvlxeSS2zOFuNFTBws5rbx/4t1sWSSc5ICvkcAAWFXAYHuDE5uln3D\nSc98remOrayKeFfgGdKro/SYZOXEC4xUPjLnshwAi9YsB17/QxwtmZfKiAexxDlkfhZHCuTOC5LE\nyBEPCf7x5GOAWeYj8TX43tWSAbTDWPMzqj6hNBnA317G5rEO9mZsNPb1I3GdpJyiX+qjtaCP8oyP\nJXvK8HxCfyTCE5Uu9naBUupiyWQZjWUxprvm2XoRgIwVvasaYenuMqrVBGHmkpV8IPY0Gzh1TUSl\nlE1Y3qdsz4zpj+GqDZjvmjYTPPBsXhUDtBIz4tU7VEB5NEa0w4W3Is77mcHwUmon9fL/eQJxRnnR\nCitWA5DKifPH+L22eoX6SS0Heza78BYl6FdSlFyTq8gkR1b0rKRlPuG+tk1ElFwgxou4PWxVSaud\nsaHEIZQd5HvCsZKVu8xIRcebkLKyYotSWn1KAbE4HqmbZ2crUZIguWIEYBKiUVqBoyXzUhkdjxIN\nx4iGY5RaLkafrqI30kW39sK8F1JAr5ygUw1R8oDUJQShi1KUKZbYQSlyYAqO2JJ4hNl6hObeALtG\n+wY/OfBPjrioZgrMuqCWo7XPERDqKVBHgSIFSoG0TlDlFMQRwFSfE026cBIFf0UMp0JA/4WveyQl\nVYBKFQ4ZMPw1lnmpjJo1rfHltskcqgRMmF+auGzWAub/xVowgFktGTMi0qutzOnZNW1vP5OSYSTv\nUwmihV0s3VXBtNuDOxTD9+wdIuIECFouxibLoEShX43RUYCbKFQ6CrVUwXEJuxd2EQYpIMqlMqeK\n3ayZRoz6Hg+VrotuNdGVEKspyrGDuKaPO33DoGYMyqpOKHhOSWpSQgBDiZDb+/QFlaBYdTIlwFkU\nI9zmwamkiKsG7yDfdi2Usld7jkZJy6dYC9wlINrqwWmkcEoExArRlAP0PIQEOB4hhoIKCMFoAnck\nRUJ2XSpZMjcRrhL3FVsPXMpVumEy1chRAJSde8ZVHOSYcp25nxVrMXGumWRgV0sG36uW9DvkvquV\nbBpBvWxXSBhtaOuH58jkrL2n3anjClj2LhxNmZfKiCcEC+M/OWhcsnOQODzM7gJjQpyfUxOb5c10\nzH5agElf4AG8c59NCmSXzarHXE/QG+5g0fNVJJU+ogWRbksKJHs81Gd8uB0HzzR7aJUSVEoCNB21\nTf+osDEAg5A8wXshsKMaYulsgB21RJ9XTVGa9OD6SQ4Ky/22ygJ7iDIchMPXXIJW5kDJNAQmYUqy\nHn83Ws8+rxGiOEW4zUN/OLbcZfmeGITd39ZOgJl47L4FHuDucUGVFGokyUFelYG20FkcoABaSXhA\nP7R5P/LZisnTMx27VEc3tFNlVMGwYWxSCWUkQ/0MbvuubpevgDh7z2XfBpQ5+bmUHTcqwMIhA0jH\nid6Xjcc0u1wyGCAxonpZ44EcxBmu6u+HeSed5kpg9zeAJVn6R3kVjrQcE2V0ww034Fvf+haUUhgb\nG8Mdd9yBFSu0b/qJT3wCt912G1zXxWc/+1lcdNFFAICHH34Y69evR6/Xw8UXX4xbbrnlRe/DqzVj\nSDzoeBDJQV/17Z0P2oJY2OmbinpsUbEls6+trRDGAYoMWCCzyjwNToaJPr+LFOHyDpZNlVHeUULY\n1oNWOSn2eBF2j0RIHUAlQLcFjI/qa/lZxj7XocnrJwmCpqw44LlAXE3RbxHclouwkiD0CKVIAbHO\nTZJZ/vvaejLKKExPKHY3G9xsGfLKzCssZ67L4IDEOThB01+SIJn10Z10oBboE3j15/fAVmcx875X\nwGhyIt+MgjPjIB2PAAFCy7bEyrCwud9kPXJZK4rr+8ikZMla5kRT+a5lfSXGs1ipeQngkgI5hNQF\noIw11iknGGl5mA0IqU+5BShxTln0btmovfsHB10WDptnm+6Y8+tlu/BcswZgwTjQeL0+3vlvQKSA\n192WvdAngf/5JDC9Wh//70NMpXkJckx4Rn/+53+ORx99FP/93/+NSy+9FH/9138NANi0aRPuuusu\nbNq0CRs3bsT73ve+vMD3e9/7Xtx6662YmJjAxMQENm7ceCyaftDibPfh/LKkUdxMkiBFZ00H+05r\nYet4G5tXtLB5UQeTNa2IDqe0qzFqzGVRQFpJ4XSOHc1MKcBbFCPc6eaZ5QcSIiCdcZDuc0DTDtBT\nc6GVUMHd7SEdi4HjjLLjRQrD0x6a+3zUZz0M7/MxusdHteXmzxEFhE4jQWOvB+fQCib+2soxsYwa\njUb+/1arhQULFgAA7r77blx22WXwfR+rVq3CmjVr8OCDD+KEE07A7Ows1q5dCwC48sor8c1vfvMF\ntytKUiA8gLWSpBoclhEwGZUJPCD27ZAwr4ZDVf05M6B5pxFegRgfkrlBUQx0GiFK+zw0niojWd2D\nX9ejsB/rnKrpbP/oXmhHgBi/YkusWZu77ZLcbptZthIv089LqIROzgmiUgq34yCqpXMsD4m3cbqJ\nrN9EgtHNzGAWuU0Sf89uVRhrbCJ3ccsEeEDcUvAaZLGhAY2juJFC/Lx+UWmQIo6VLixN+vfKS5Em\nCs6Mi2gkRlwisAcpS4XwuyhGVff3V1YskH0jI2V8nJLe2onvI0vwBh6gQoVGy0enFiMcTkHIIIIY\nqE/7UCkhreiLUjlFDIV620OvHFs7lTD2yH3JVhG/h8VN3W7G/nbPzKU9yO2xh5co4MS/ApIMi6is\nBn71D0B7U/bwMTB+JrDtERwtOWaY0fXXX48777wTlUoFDz30EABg27ZteMMb3pCfs3z5cmzduhW+\n72P58uX55+Pj49i6desBr80gMJvX7dROqWB/urgRY7EoF38vJ/ds1wCZgCl6JXN+4sQAyOzS9SIA\nXoxamTC6qYxoVQ9pibBoOOOvZKvhVMveEponhMR0GhUb7+qGtnKSmFLO84kU+irNJ1Topih3XfQK\nhEUiAK7tokraA/OxuD29zI0ppr+wK+UWFJOkASQpUKqk6E47CMoJSr6eTPybzpRC63kf/oIYblMr\nzTTM3muokHQU0p5CmihEi0Kd9gPTds+3J6jkngH6uSRHjF1MmSMnJzO/B6m0rOJshedLU6A54yEc\njpFWU/jcFykAH6BGgnrooOfpG3ou4C1MUNrmwyOF0CGLQOm7hg8209HvRrppnjuX/lCkrOTud2lc\nF0RLsmpre7+va+x4GWhUexVQPRVQt2cN6AGO8N2PgBwxZXThhRdix44dcz6/+eabcckll+Cmm27C\nTTfdhE9+8pO47rrrcPvttx+2ez/6rCmUtWBIrwhRYcLJQcc7gfILZPKYZGDL/dNlcbUosasTMhBe\nTMZkALjvJYjqIUafKaPdDPGrboJ6PZuEiYLXVUhCza6G0isgc38AYOukAS0Bgyvkq3+sUI8d9HsK\nCkBVAYGjUJ31sLce5XhOJwH8SKHTAyAjQFkkjYmFPOFkfSVpXTBDm4mJ9bJJDi4K79dm7chaI6gZ\nB+XAnjiUAp0tHrzxCJFPeXvy9+YRkjqhJ4B0FFj2XLiMAxNRbO/aOly1Gd58jmRU8+LCx9wn3PeS\ntFmsbd2IHKiA0C+nQGZNyuCHpwilCIB4BtfRFRWctpOD8IC2jEbqoiJBdm9e9Lj6J1dy5GeXFu6I\nsOAxuxWI9wEj/0sfT34HWH4NMPrb+rh6CrD5M0CwJLvg3Bd633334b777pvz+cHKEVNG995770s6\n7/LLL8fFF18MQFs8mzdvzr/bsmULli9fjvHxcWzZssX6fHx8/IDXfN1J2hqR2dLHk3SrCaa9Pqqz\nHuqzAYIAWDareUTliBDFCl4b2FuNEQYvEUAgoNp2sWAyQFhJkKQEgo7SKAVsG+lp4iMzchOF1KUj\nnfv4EmT/bYhmFZwAQNW0+ddNgo6L7lB8wD5WkQLtJz+QPOYcHd9ywQUX4IILLsiPGfs9WDkmbtrE\nxAROPvlkABonet3rXgcAeMc73oHLL78cH/zgB7F161ZMTExg7dq1UEphaGgIDz74INauXYs777wT\n11xzzQGvzyuGdJ3kzp8y9QOYuwWOUnoFk9E2WT9b7oPGFfZYiruF8A4Y0YwCqpTv2tl3UkwOhYhC\noFlWmCnrSck7yg6TgwWzPtptYDIx4W+mGfBxJQDCCBjaE8CPHOxc1EMLlLt9XDrVTfWWTWnGcvZD\nhdQnOI797Fy2QlYw4GgkkHF5HMPZ2tc2OVnc11JkBIj7RZZqSUih39XPwTWhO32gt9dFXE2gxELC\n0SCJ+XCVA8DsoybTeKR1wLWn2MWUVhJgmPCSRySFc8uKJU7k+0/SrHRHAlSVQlwj9EXVzcAT5WU6\nCm5gqARsPRMIbmbBVkVEmDE3wJRmyflrbbtOuePYfVUJNK7Ebh7KJSCaBLwRfVx7lcaLgsX6uPWY\n/mzVDThackyU0V/+5V/iySefhOu6WL16NT7/+c8DAM444wysW7cOZ5xxBjzPw4YNG6CyWbJhwwas\nX78e3W4XF1988QuC15xMKfkccsJwzg8POpmCAAjMQpRbkFsc9yNjLjN+E4rJLxVUvs/ZlAfHidFz\nybLUIgJ2d3WeGDKlMFwBfC9FpxJi6VQZ5SUxQjL3rwRmgndDoNFz4fUd7FjUQ5gCjgCVo8TOaRqq\nAv0O4HQ99BdHKMNgJdx+2RdcdlYW7JcF0HiCyWcqluWV7m8lMHl7I3VgWxdAlgjc6gFp1r9hD1DD\nZNeIhp0ewsfF9krQtxfNdaOKRe1lgENSPriUjPxeJsrKgnSAUTK9SL/LKghRRyHJiEaVbBvzXBlB\nIVIpSswtympcU6IAx05IBrLaSoKCIbE5LgonNyeQRQGXjgAnLASCVWuzzlkD9LcA0w9kF+/pfypT\nCf4YMPxGHE1RdCibYx+HopTCH77ZxjXaff0iJT+FFRSL65gqd7WyvS96NzSTsZiLxgOGmatMGuRB\nwIXO21MKyU4P3ZEYXUV57WUGUGUERloeI3sCdN0UMw3TWCJhbUQKI9vL2NLsIQ4InVmFdNpBKVFA\nqq0fVUlBPoE80qVvp12EQzHSRpoXlc8tOYFJAAYfk+C/ZPZyDWqpAGplg7dxwTHAVBqUWfSTv3Kw\nd0xUmiQAACAASURBVFphaGWCTl9jT3ECdJ/2oRbH8GtkRbtkYbt+ASSXzGnA3vxR/pWWjVQ+DO5L\njEgysvl8XyzhSaqJk36kkLiaP8TnD/VclEIHyVCCuJSiVLItRbXDQ1xJ4Q6neV8mKeDOOHAiB+4S\nYxGXfE0aza08zyae8rtaPmaesRcCqxbp43NOAcbO/r+M5ePWgT3fAsYuzjotBmYfAV7zTRysKKVw\nKOpkXjKwj0dRNYIzlsDZ4SGIgTggwCGoWMGFocY4NQLqaV4svz0SobGljHYl0Vn/8poJMLSzhPZI\nhNgnoK3g7/DRryVI64kuLN9XcPoO1KyukqhqKWhZhFQdH2uQGwCJ4F4BWYQqVPCC46ONBxQCqvs8\n1DoOEpfgJgphKcV0KUbiamyQHEKt66A67UFVU6CZ6IpsANJGAm+3DxWmSJuxpkTEgDfjIlwYH290\nqSMu81oZ8YpX9u3thHj1k65Ho2LvLy9FugKMW8hQurSEXMcu1dDp6/uVAwALU0TVFN0ZgLIiarFD\nUB7glUkftxw0dntwSgmcRooQhO5whMbOAHsW9NHNVud+F1g8WUZnKMFeP4bXckCTLtTKCF5AwnUh\nKJVa0b84AVwRGfJFFUzGbVh810T0uG9kzSGl5tYYkqF+yeZeNGzX5JlqAUGFkPSUhUnNthQSh+ZU\nAOBytqFwCQHT94FndkUBtGUgLQiOisrIXC+2LaVQlHcpbotEBPiMnxEQ7PXgOMDM4hDkAGFfu8zD\nbQ/TzRiBD/jVFMrXtASv48Df40F1CcmCGH6DEAYh1IwLd2uAAECSEqJGCipR7tZyP0einEmrZ+/s\n63ualc0ucC/Uv2VG9thSaNcryaj7U98FkraOqAE6anaEQ/cvJvNWGUlQkSeLDEfLMrQcJmVQurgR\nYXFQFvc5k3wUrgkjAWzOCwI0SEk+0M/S5uMECEpAOZu8rXKCcjkFbffhVSKkDmGyEsNrKYxtrWCm\nFKOiFMqhi9lajLARwekp9Ha4iJdGSKHD+VLR9iIzcH3PLjTH+WAyGVS6Xdx2iZvIvuMaRCxc0Is/\nWzRsJhAnH+cuXgy0UkIYAzue9OAuiJF0FGibh8qCBJQpyqLbVNzuOs/HCrQyktybONE5aIAZA1wa\nloMaxe2xWdc5yq6dzu+rFwJBz0EpVOgujlDJrl8JAK+RoLw9gNcw18gXqkqKeChFaZcPJEon8roA\njSSImwmQAlE/i7BlCl+WlpGBBsbY5CLpuwYu4L5fmuHTKI0BrUc1KA1oN82tA+FOfdzfCjglYPZh\nfdw4E0db5qUyYiJhMXlU7k8P2AqlF5pVJQdxs+9lnReOCAWFnuNBwfiKrCW8c5+xNnhjQZnQKPOh\nKgEQuoTSghid5zx0FkVIFRCPRUgaMcp9F24txba+5t+gBagtHrpjMdJEg9cS9CxWFmRCqFQ2o3W7\n4Bdbc9w3cWKyWFhZsTDIKzGvcgAsGbGfD9CfSwymnCUYl0+K0NvpYvqJAL5PqKyI4WUM9SLJUALI\ngMan+Lgc2EXzuK0yt0yy6XuRzSPyXI0tsvIo7hCrMuXkEDA07WJmNAbFQJT1VbMGNEpAd5vpO09g\nl9USELmACgguCQa3sEpV5oqz9S2zBJo18yyNir2DLPe93K9OLsjoTQL1nk1qpFhbR4DORUv7wN7/\nyG4wUEYDycQZSkF9BbXNBxZHgK/zl6IgBip6oqiWA3evi14zMRsB/hqK4wLVZQnUSKJ3IjnOc7PK\nPQdhQIh9movrKOh8sxd6HQ6ARL3ISa88mZfKqN3ff4iWhVdO3k2TI1qOMPtltrUv+By92HBJgKzW\nj2uvximZ1Xf3jNkPjL/nEC+QpY745l7sEoUxQM0E1AfUNh/ewgTwCJ4DRHsceJN6ue2PxWgRgSJz\nfb6ufDbGbXoFAiFbG2wV8urPIsP0fF2Z/S3L8wIGo+GsfsaUuF/7hftL2kBQ0jmD8n5l31yLy5NI\nt1lumb172na5HAWEydwse0mGlZZUmpoIHB8DxlXKXduei1Y1BqWZ25r93s8y8cklqESD8xIemBH7\nnnFysKRJADa/S6Y0MdNbjqNGxRz3I7sKJZeGySPGIYD246YUSLAYmHnQLg3SndBpIQCw8s9wtGVe\nKqNOXw86HliMGUlzvBKYQcbJnRIzAsTA2Q+xTdbQCWNTYoRp+TxhOgXFmBePd81fWSqC28qDMKwl\n8EBwWxrsCKEJk1E9QVpJNZWgsI1Qp2/n2XkFkmZxz/tWz0zYkm+4USyyLjUXD5PF5PaHMbHS6/RN\n33EuFT87P6fkDcltkTgXS9Z1lm4Vg+FyAkpFNt0xNA7+ntvIx2FifqOUXToGyJJazSGSBHBjBZUo\n9COy8LRd09qVChzAVQq9iPLyroChgSQOQZFOkOZ+4O9lbSUZKJmc1WO6uKWUdO+Lib3d0CR0nzQO\nINpjlE3jTK2cWo/q4/6kZrpH38OxkgMqo6uvvvpFfzw8PIwbb7zxsDbocAgXwefICpHJegZMcTUr\nm5/MJGFrQJLa8rwjxwwEwFRB5AG+Zinw7E7DlO2GuggWD7hWT08SvvZQVU8AmbQrGc/VEkBBijSj\nIkexqLETA7M9G2znFVUyoiuBrVykZVbkGbV6evJ50H0SK13BgI0RBvcl10fm8TFPiouypV2FVk+X\nf3VcICgThocJrm/aKnk+EjBmsFpytvhzwFh1rGiZWc9tYXa43P8uTGzekIweygRl7hsFwI8VCEDk\nEzwPmBmJUG95GOt5SIIUcUCIghSlOiGJgDhS6KQE19VYJCtbvna5TqCugxipvWtNAiyaCdAaCeEU\nqiXsa+sxIjlOHCzg9yKjnJx0vDtTRrsmgUWVBJh9Xn8w8zwg3OFeZnXWstrt2PaPx0+lx29961v4\n+Mc/DiLKWdBSiAif/OQnj0tlNJCXLypScDoO3J6CEzl6gjqkoz4OIW2koKHkRWsFJX2g33LQn3EQ\nzij4JQ3YKke7Jt1YYTZW8CuE+liK0sIk3+76eJNax0Wt5yLxUihScBOF2aEIYYmwbyRCoIBSrOCF\nDmozHsozCo4Cun76wjl/JQL2zT1heG+AStdDv5IgCZL9/HB+ywGV0XXXXYerrrrqBX+8d+/ew96g\nwyGMufAqUc5SELg6IpvWcu8vGbkIPG0OM3ZSTCWRJT0AzdzmnT3jRP+WcQ5OlWC+h+sAM12DOXWz\nusUdkb8ko1OOAmLhfhRZxoDtlrFpL10hwLaMJD7mOoA/6yKZcpBUU/RqCZxKnGcFAFpR+S0Hzq8C\nUJmAZoqkQoACeqnCUAmoVhT6LQUFBfJTVJspmitTeCUbD/Nd7cr0ZhT2/MrFvikP/ngM5ZicuGLZ\nV35Wxr/YUprp2LQDxrO49hNbkJJHJDEndo+lpYU0i44RUOu62DsaZomrwNjeACqg3BqJEyAJCO5Q\nghAJHA8ISIFAqChTSkZaW64DuBWdElQihVZKphxMWwGUYraNPEWmaAVKusls1/QNW9MyUuwLtvfk\nLFDdbeYERwojYSXqcZGlrmzdAIy9DSiZ0j1HWuZlOsjvnGXXK/JcTQiTKQtyj6gFQ3qSyCLySpka\n2N3Qxh3ixKRrsA8v96NyBf60t6X/rdD14zDa0Mfsxs10xHY3BFRThUrkwFmgrRDf1YMqB9A5ny47\nbvfn1j/iEDeLxC24PGnO0Zl04fQcpEsiwLNr5PD5XDyOUiBIlN5wMgub1yrAyBChMQSU6ilS10wU\nFkkilGBtPwQmJzwoB6isjPOcOy5HwjWw+feTs/aE7Ia2W8cLBSv24iaPnIMo32URnOfkUy9UqMx6\n6CzUZVcqLRc+KXRHYgyJTS4B4zo1Kto14mfnetocHHCUAZmTXS7iFJiuJHl7Fk+W4MUK09UYrUaM\noapZ1FxHv2teMBc3dTtlUT/G7wBzX+k+j9TNuOUSO1LZSZLlCeMKeM0tWiEBOpftReSIp4NceeWV\nuOWWWzAyookjU1NT+PCHP4zbbrvtoG96pEWuhoDBRfJdKMjslgAYjEgmUErcpbhaO8oMgjjRL50n\nEO/asGVSH8929XWf26WPt0zaBbmmOxmzOFY6ZUABTongTXqIF8b5BPYLGBWTGBkw52fh3SxiAWRK\nRrQs2E8xELVd7FsYYjh7Pu4DiavIROGST4iTBAuymtyeq1nJPRiu1kzbKM162VyLJwArpH4ElFbE\n6D3jI2krdEFzrIiWALRZUUortXgsLSVWNnJHV6mcWNHx98wzUgo6jy9VqE97gE8IQgfOygiLRS0p\nvqbcQ25vSyTkZopfRhZZnGait9AuJzmjPFYEP3WQZpGwKBY8I9cGrPe27GfjSCU/26xrE0SjRI89\nJkGONQznjX9P4t1s30lYuuA2PUgAYMWf4kiL82InPPbYY7kiAoDR0VE88sjRK0X5ShC/56C+10ev\nkaC1IEJ/QQwVKzitF309hyTUcXS+1JG9zQuKcgB/JEW07xg2Yj+SusC+sRBRKYUioDMaH9bYswoA\n1FK40wYwi9wU7q9BHaMjJS/avUSEqakpjI7qpXBqagpJcnyDa1waNg+np2arYwB52VTGVWY6hh3M\nIs3/4ap28wDtUk0JN0uycwFtcUx3jOXiuTpaJkuM5Ks9afMfLQed0UjjD07GjakmOt+snuZYCGB4\nKbmbld0zLzMq2LyA2auM79+omFURMzrT3HWMa8H5XzJVRrpKnGsmrUhZunVvy97OZ7hqqiEkqe4X\nubVPnABxKUU46SHtJ2j1bAs2iu1Sqt3Qxr9k9QXefoqtBe437pM0ncuoLta1tvIQFZCUUrhljdtX\nS4aKAWT1zwNjdbJlku9NVtcQgIxc+q7hLwWjCeItHqJsy5U4w/K8DPsp7skmS+hGsX4ufm/FUi78\nTrlt7DL2ClFbiU06DlCTFRC2/zfgZWDn+HuPfdnZD33oQzj33HOxbt06EBG+9rWv4frrrz+ijTpU\n4T3RZWEpWTQrJduNa1RsYiSTzWT9m6mW+Y5rCgGGXMYDfvMeO50CMNgHoBVft69LTpSnPZBP6CyM\nQK4OwORJvD2FCAQvMQXHuC0yFC9THQCzVTeb88Wtg7htvgOUpxyESyKkoR3eJjI4B5dhlds+WZiU\nM7e4WrsHDNdMe4pbLst+6UdAEhOSHkCRXX9IKUPDAEwxNFkyxCoBEtv5Wzz5ZYqE5FelBQIlu3V8\nyv5qO1VLps9b2SLDfLZKoMcBL3LNmj5fkkgZWAaA2NeuoAMAmcInAEjVnJzBXgQMVQw8MN3R7ZNb\na0tskDlZkoc00zHjNiXtskmOkxsDiXDTp9vAcOdJ/cHu/xdYfDmOpLwkzOjMM8/ED37wAwDAN77x\nDZxxxhlHtFGHS+Rme64DQOxiIVnR7Z6d3FqMxs105uIUMhet3QeiLILDg0DykEo+4E67UJHSFlpH\nIXWAXiNBv5RatZcYJ3F6Cv1aAocARXO5NDIaJjlRvqsVieTqSC4NZ9WrnoM+NDHXEYrT92yCqCQE\n8vVZIesOAZKWA7/v6Ex2B6g2Uriedv/2tefWhpaYESsUSlXeNpm3JxNNk9ROwmUsUCo4ybDmfuXf\n9zKlW0yM5fOrJTv3TipYQD8LA8CA/r/nmkAHW9+yggNb4UCGFQIos/VaBtpKY0twzOaZZRfYm9oL\nZBQBqmquzYmysv6UXHS44J98FvleeRzxOG31NB+OLan8HU9libTtx3Gk5SV5wVNTU6jVavjjP/5j\n7N69G88++yxOPPHEI922eSVUTkGeQuoCnWqKhKGCdO65bqTgJApRiaT+PGyiEqA046IzFh8SXOTM\nuPD3+EhigBoJ4AAqBtztAdxI6T3MRqMX5SYhUnmC6CtKYmhzmN1GAl7J+Wovqoz+f/bePdiypK73\n/GTmeu3n2eecOvU61d003Y1eBLFt6WEcGCQQnWkGR4lQAkMZvaEY+ocoPiLUUCEIxGv4QAkxNGy8\nDoNKSFzBibgieCeAUKRHm4bhIW3T76quqlPnsc/Zr/XMnD9y5V65dnV1NV3dgBcz4kTVfq2VK1eu\nX/7y9/t+v783velN3H333dx777388A//MHme8wM/8AP8wz/8w5ejf0+puWyV7x3Ms8addlgTnw3u\nbyV81xesS7zkVzkPw0Nv+zB8txq5vXyla9xRxwAGWUI1b3syvgxHpSGZKtKOrbG1qq3kth6+5+X3\n322Z3Aq6OWgyfWDtwtokQI80Sd/SGVrbFd32EpdZOo+npQ2IfYXaDTk6lqP7mp5Ld0vIKTCZINgN\n0f/SobhlsTRIPuQiryU8klo2w8Wa/Pia7/k4L9D3PHyFBLct8TmF4Ol1e9fh7qHzhlwrK5aARbdV\n9/sz80o3ubiiX6poo9/e2vkQB9fnpZc9k0RdbYPZgFKQhIIqsWl4PzsWKns+dy1uO7/0mHWt9eRB\nPKCNbvflkUlh96iJhbrP/GvVBnYO7IGOz++1dJLwGM9Uu6ox+qu/+ivuuecebrvNSgpsb28zmUye\nsQ49Hc0ZIv+GaNO4007mwnGD/NQsNOlz99o3VM7wrJav8QONgbo8qJqX2EWvEES1YcuUWbr1S/d5\nKggLwXStOan2HiAXlHUPZC9u+gtNDMu1QNnvTFML3OsfhoR9jd6sCGsOmeuju/bLArpeOnyWQqcS\ndC9GTK9LSYamtR1Ia4leERrykznRfoe5F9+apo3wvGvzQwuULPImqAxeMNrHUIXtbZi/qLgClw70\nGIftGnNOTsRP5fvFFdw5XcDcbel8CIiDUrjrWZXqiMPm92DjYNXDEaKjEX1NFmurwHmgkBNJfH25\n1FeKNiqYQBFqOlET/4NGg8q/9m68QvqV7e2+MW2SsF/PzxGY/ZjSIm/6PurZe7kkDp//L7aM0bFX\n1R04ydPdruqlx3GM9KT/ZrPZNZ/0l3/5l3nBC17AN33TN/Hyl798WZ7ooYceotPpcOutt3Lrrbfy\nEz/xE8vf3H333Tz/+c/nlltu4Q1veMM19+HL3TaPQm7Y6XBmP+HMNOa6acyNR3Gr+gUGksOA+Vr5\nxHSCp9BkIejvhlSxNURP+fgGOo/FpMfzq8uWlHU0+CqzTCykRXb/d9iq3QA5qpBDjZ5I9KMh5v4I\nM5EE1xdI77qryLC/lZF2v7qz1c9Uu6pn9L3f+7382I/9GOPxmD/6oz/iXe96Fz/yIz9yTSf9+Z//\ned7ylrcA8I53vIM3v/nN/PEf/zEAN998M/fcc89lv/nxH/9x7rzzTm6//XbuuOMOPvjBD16xQkg/\naZNbXaDOD8b66FUXsHafF3Xw2vc2nKfjpBx8kq0fEHVBR5+4mpcw7ZYc9kvm2lhyqYTrDmOGpSKN\nK7uy5QIjQCcGJ1FdlG20uFudEy/9LWXjPTnPwKeHMBPEewGH/Yqwr6lWszvqcsrCarGCZTo8s32U\nG1Utk1oz3ev+uNLcgYLoSNIJqmU62WWf/LELpUXuyjWzrE4rPC/ND7r6KHJortspOY56tcBY/f3D\nWTuD5o7nAJlpDoW3zYqCWpbWS4/7W7iNvoUpuK3XtPZcfFWBqQfjMAbUXBDdUCFjwzzSFi3vYkVA\niOf9aKj61dJ2+4hqPxAObeCtu49+YsM1P0Dt+uh+H6i2AqgUzTZQG+tVjuptHNrA7gesGiTA6H9u\ne0fGmzBPsV3VGP3cz/0cH/rQhxgMBvzrv/4rb3nLW3jFK15xTScdDAbL/0+nU44de+J96Pnz55lM\nJtx+uy2z8rrXvY73v//9VzRGcdhkYqDZ/8oVY7Sa5XE33jmC7sb5etku3evSs44f5G9tOlE7+3Q4\nhwNhwGP4S2ElZvuZ4iC0xihaCHRsK3YMPMqB8Cae25r4WBlRtLMk3djL4BxJuhPFeK2kDA3zeUOH\ncdfuY2OkasMg3NgtDXsmqeo+uvNvDNoZJce+X99X7PcrikXTN3+sKg0UILShnDcPpS8J4n5n/2Pf\nW8VADWrYgaNP+FKt/qK05Kp58S8/85nV8rx+ds7fridRW27Fp6G4787SFaR1JZChafEFw/peOtqR\n66+PH1s9t6ua4u6Lkwzx6+c52o5r41mzaA06bUPZjW1qf71m6Z9at2Pr13CbZSDHzdiy+1+bmFG4\nafWz3WsnX3sN7arGaDab8fKXv5zv+I7v4N577+Xee++lKArCMLzaT5+w/dIv/RLvfve76Xa7fOIT\nn1i+/+CDD3Lrrbcu5Ule/OIXc+7cOc6caQh729vbnDt37orH7sbtlcMBD93kTiIrrbCMc5TtOI8z\nVv4Kjbe3jgKWou4uWO4/OKvSrE5LGRovwxiYhxWjWUA0qleuXFJGetl/dy2+RMmql+C+s3zA503g\nU1TQmwQcjApyaaA2yH5qfgmGK5rrWY2huGsGiGMIF4KxNx4H0zbvz8WnokxxaZRj6mv3iZnudVVB\nD4HQNvjqX9cspVX7y/c43Rj0PByeezhdX9zvlvpIKzHASreD9w6/5Y+9H59zMZil1lTZ7o9PRVn2\nB0M+F8iOWQrR+TAL7QFatbGe4vIzz9hs9NtemwNzukUrCa3BcADTC2PoerE8JwXsl21a78OzTzSv\ns6Ihk5/esO+5+F5Rwro2SPN/1hcb2PhRsde8vsZ21SO85CUv4e///u85ODjgO7/zO3nhC1/Ie9/7\nXt7znvc84e9e8YpXcOHChcve/7Vf+zVe9apX8da3vpW3vvWt/Pqv/zo//dM/zZ/8yZ9w+vRpHn30\nUdbX1/nkJz/Jd3/3d/O5z33p+IZ7z9U6NIHVw97e/JIP8WVppTIE2iHdrPEw6umLnSQzRZbUJY4e\nB0LwVFrZrxC7IcFcUnavfFB3bnO1tL4CMyqROyEcL67y5X+DbU2jxwrZeRLbGANmIazEyL8BVshH\n/uEzfOTj/2pfiGun8zwpOki32+XOO+/kJ37iJ/j5n/95XvCCF1z1wB/+8IefVAe+//u/nzvusIXk\noigiiqyf+M3f/M3cdNNN3HfffWxvb3P27Nnlb86ePcv29vYVj/mc0yzLOkOdlei1MwvQZvWvZsx8\nCoRPMZimbdi9T7x0r336hmP8+4L8Lotj3LHruE1oBIVqi6VtDtoSI2td21c/g+MImq7vlYaygHCm\nODiW222lB45bbgeMJejqqSQoBUWooWuzPcHK95fpdAUXejmbF2MWmwW7YYlSjddRAWjoTEKO1nKK\nsi3b6kt4LEF3axoySXwhpDpWUtX10lY9Iefh+ix5P/vlzuHG2gEm/dXdqRpArQhagbP/LSkRmut2\n82ietbdRq30MZRtkmZeQdyrCnRA9F8RD04rpVNrKlSwhKGNFcKSQo4pys2KyaAv++Vuwo7mdC355\nrc1B4/n04jalaXNgXzskvcu6Xjpq34tjNRHYVbf1WQs7h7BVT2zV+yjfdutz+LZveVH9hZQ3/yeu\nqT0p3+of//Efec973sOdd95pz6uvbZm97777uOWWWwD4wAc+wK233grA7u4u6+vrKKV44IEHuO++\n+3j2s5/NaDRiOBxy1113cfvtt/Pud7+bn/zJn7zi8V2g0rGl+wmtChxK2sH2eTo+FGD5sHuT2rVZ\napUPfenSVgynTjX72x4fIZ2VTR+CSmBUU11CaOsZLbxKJU42wk3wadquY+bUAdwkdK58XAl0qDES\nlGge0F5cP8wVRHsBRSqYCE0ZacJCEl4KyNZKGNhOuRiVa1kB00hjTqQMLkVslAH5ekGwaUGPaWYL\nS6ZojpRGyia2ucjb26DSf7A3S4KFhPMB9DTlWkUUtTWp87JdO8xPY0OdivZS/64ijDMgk0V7XvQS\n+97qQrTKnfNRzH41D9fcPMrl5QsVEoJTJdX5gCIqiDvNNR05xQYF+kgiJhJ5Q0H5SMgiqSg9TJKj\n4PjyJD5dxW3/j9dUMhfb8g2sC9C7++i2dG5sQ9WWU/Zjh24Ous/XDr4I/bsgucG+4bZr19Cuaoze\n/va387a3vY3v+Z7v4Ru+4Ru4//77ednLXnZNJ/2FX/gF7r33XpRS3HTTTfzBH/wBAB/72Mf4lV/5\nFcIwRErJH/7hHzIa2dIq73znO/mhH/ohFosFd9xxxxWD12AHbtiFF1p7Rz+Bzz/aGJC0JslWjiO0\nEodxQd3lpKIdDPcnqMs8+XrGlWmCpM6YbNYxe98g9nJpmdoSytxSItLKEmWd8dHaXovruysYucoF\n88FtlYa4lEvirTYss3PaQJUKBvsBuq+RJ0qMI/Z2NKoUrI9DsmEOokkG+NggbawE6/7JDDORDCch\nyW5EFRriUnAYVJxfy0GD8QLIUkDmBWmTcIWoGmrCbY3YDYjOh4iTJSRmaTwcrcfnX7njgh23edaW\nSzmaN2PuFiAfq+OXoXLX5pwxZ5jGHtXH99Rc8+OFqwBWKeBIGkS3ovNoSHBjASsGtsyA8wH9mwvC\njq08nE8UxbBaPvyVtjEe36v0iyH0kiYg7o7rcFdg9Y8c1QisJ52XTeJhVQLYYZB8srg/5hRYPe3+\n1XdJT7Zd1Ri99KUv5aUvfeny9U033cTv/d7vXdNJ3/e+9z3u+69+9at59atf/bif3XbbbXzmM5+5\npvN+NTWh4dg0ZHfNPinhXFF2rgH/s9KCQpAnj+PBaoh3A6qNCj3Ql7EPqsAGujFcvS8Cso5m3M9Q\nAoJMgoCx1nayPpWmoNwqkTNJcjHAlBpzvLosJGFKqDJJGRlMYJDR4x/uq6WZNY0MBPkjId3nFG2p\n3YWERNuijljAKLN/A0Gjp7ld1Ri94hWv4C//8i+XHsr+/j6vfe1r+du//dtnvHNPtTnypVvN17rW\nuzhRe0AujuHiMOf22uJrjmjqu9stpOtK1sRH8brfuW1RWGfWuqWkkBoZg0kFm+OQidSkibZ8rplk\nMSpbW0X376okrq/GmOaXx0wwFg+06GjQTQocIDhU6MgghxqBLbPU82IRhVMBkIBoqCer7HC3XXDu\nvAggj/Vy2+NXde3Uno1beVeJqD5MwQn8657GDDTqKMA8GhJcV9BLGgKzeTQkjQylApELwq2KhT6l\nwQAAIABJREFUeNOWkfa3WZVurs/RdFZLHbltX1bQCvQ7dLe/NerFbanWx5GHX3rkH/9Ce56Uo4pB\nCPMHQ5JnFeRlnc2bSExsMUilsBk2jD2wG8esjhs6D7us+9b1YAKDTjOWzuN51nGWx/FLTDnROz8+\n5peSWhKYPY/a9zrzAqL0EMqP1TfRYxA/xXZVY3Tp0qWlIQIrrnbx4rVjCp7JluY2tenc8+deB9dv\nNe78oAMPXGyCvuv99v4a2vrDPkdo1Z1d5cH54En/+/1MMVzEVNKQpYLdoORiUrBeQTxWZKGhCg26\nbHA60MSy3LbNGUK/b/5rY2zp5YWGaWkZ+ct0t4G1maQ4ZcXk/bbUKyolVaTJvfS+n9p3D7p7wF1M\nZu6l71OPH1ZWXvC8hGSsUKUgXS+XhnupYllaI76sBpJAPCrRY0n2UIg6bTk1em47q86UxJGlXOQP\nhwgjiLaqVn36Y8M2r3CRN1pULla4NNSqnZ5fNZZOscEd3yU+fIDroNOuPuzTT6YpjI5XzB8WLL4Q\nko1KOkagKwG1Ie3Glj9bBIZwZRFwx4AG2OtDPvwabM6Q+jikhy81C3S4IlEy6Nhtnb/9T8Km784Q\nLaVqQtAzkM6CBNfOzLiqMVJK8fDDD3PDDTZQ9dBDD7XoIV+tzQ86703s326dOXDkSGflfY1raCak\nm2SrEra+9AK0A9YO3Lb8bX2cs3GBiArWhOSxUC9jTGIiCXLJZL2wx6WdoVslMDoe26p3seThYYXk\np96WbxlkLwWlhlRD6B3PBzUmM0ne0y2AqH/9PjIdGilUXwDNJ5OCNWDySJLsByySCplohnsh5kTJ\nRJgWFsZdMzSGWA+05ZU9EhKulehUQk/b4K+2xR/ljQXZQyFR1yDq4Lv/YII1kr5hddeyysXzy0b5\n88ih+Fe9YJ+nKAX8y9nmOg7nTcCcyC6SYq2EQFKdCzBSED+rQNTfOZwDc4GoY2NuHJ0krBtnJ4zm\n8y99MTat7Y7gRO1HHM2bOnRgF+KJaRaVblxfr+cpTau2sWrNe4HdGjtT8DQwWK5qjN761rfykpe8\nhJe+9KUYY/jYxz7GH/3RH137mb8GmxGQRRqTYnloC0lUKvJT5dOGA+otrEpbGl5+QKWhUlfGsARZ\nLV2S6KuqfnxJrQI1DkhPFuQWCYiODZ1LIWIjbwV0r9TkUGOSHP1YCBgYtGe/DCE8UZHvSTj5NA3m\nl9DiQ2UfzCdTYkgAfU0RWKMvVnViUgGjL/81fKXbExojrTWHh4fcfffdfOITn0AIwe/8zu+wtbX1\n5erfU2qOU+S8EydD6yN5V1HO07TZtuVFU9kV2vymaoW35tzgNU903ZdCzWvayXxujVGlgRK6c0Wc\nSaanCgLRXoE7UbMVSFfc9FVpCL+oX7KQdDPJ7vDy6LExbcUBH3MVh1Z9MjkMWAwrIq96iENrO+b9\nanlsJ8/iewdu++PGR+814Evp6BeBIV9UBBNFXj/ALkPUiP/bsVvCJCSY7WI59s4DXZbHHmnmFwMr\ng6IaiIYbu0HHesc+59CXW9GmwSK5a/dZ+UXtKa3SQMKFFZdTXUNyMWSaVuhuWy4Y7LHd9gog11BJ\nKL1iDukCgrkkWy9RK9SUSoOTfXIKnMttc9KWFBGiXSx0srDj6OJfblu9VeOKnEqlm4eTRVu29tjQ\nwgY2HIBYABmWXAfPvGckpeQ3fuM3eM1rXsOrXvWqaz/bl6m5QKcP+3cVMcDedL/CrNZtHlBW2PS8\newgSL4XqJGzdw9z3yi9DG6QGtT6PALUfEBYSGRniTFAkFUfrBYkE6U1Yp+GzTOVTbw29B9Anm2pT\nP5RTSW+uOBiWGNUA+VwqXBu7v5dz0YqLLK9rLu1M72qSqG1spWjGwm1VloHSRZtIvNSddv1XUE0U\n85M5umgImgBpTxNcCNC1BrS7R2kKYSEJurrlxbkFwp171GtzDgFkTzO5oOierFqBd7DzYurRggIF\nRQ5pLhAVLFLIvQolPvbMNSGaa12CHeeSbFhhehpjBL39EN3PGZftLe1SrsUzZn6sstIQzyV0NVqw\nTD64++w3X+fb/StjCxFxr/cm8A//UvcxaGtFJZGlfLhnIqwTIy7w7cZpo9+M9fENmvuRxCA8xrVH\n4n2q7Ull037zN3+T17zmNfR6TcTcCfR/NTan87wkf65kvxw+Y5mRKu0q4Acs/e/73oBDT/uGy5FT\nwf5ub9KAFpcliYYlsoLICBY9WybZfd/3JFyde2fs3MO/ivh2COoRgvAoYF7A7FhJFBiUvvyBASgD\nY6tPVBDVsYOigigXdOYB6fF8qeHsQJVO5MvhTFww3HmRboX2ya3+AzubSeJEo0KWD9dSwCvyAl31\nbxcLWz9MVYLuHIr1krRjJVWcHpFPHtVeAFwK0Bslh49E5JFmODItRHRWNKL6xoC8JFk8piwmTBmG\nM0EkDUfdEq0aD9cPSBvV9oyUxG7Paq9zLg10S9S5kO52QVq070VWtDWKoL7XBoKJRE8CypPF0pD6\n2DffEPugW3eMzYG3wJpGDA5AFe04nruHpn6k55nFUzlMlZI26XPaK0k1nTXzXJoMemugXRALrKv0\n1NtVjdFf/MVfIITg93//91vvP/jgg9d04q/FphUU0lyzSytKSOaKcKEIE0M5rJhofcVYUPNDK9wV\n1gFgAJkKgv2A6WaBqcMxT2cLFrZS7eM2XXeqblLD8XFMHhoOtjJORJLBOGR0qJhu5ORPgrcnIwi3\nSxYPhpieQXU1UdcgI0NlLE0mn0jKiUQXwKmSsnZ/ZlNgrBjthxyul5RPkieopUF697QaaFQqUfsK\n+k/uZkdThSolxam82fp8jbWrGqOHHnroy9CNp7flZZvHU1TtzIMT4Pcrj/qtqNrMdh8W343tts2t\nxknUzno4V3zmIWf9rIzL0vmrlPC2Lk7Ow/0+lY03ITQM54puqaj6FfnJHNWzcayeF7PRXjpZGC+b\ng8W6rB0GVH2DzATiSDHfKpdCaev9NiXCeWF+LOLxSkb7W5/lCq4hLiRpr0TKZnvprrU7UzZGVY/l\nqaMIHRvSYzkdAXmkeWw9Q40Va+cSFt2Cebdk4XkLPobKbas6kcZs54QIKCR6ISnGWO+lAhEZkpMl\nQWyYHUFQX1sSw+GgYmEMg4OA/bWCwNNHctfry8kUFehQE88UVU8v582sX7I1CRHaLA2/G89VrahK\n2+RBsV7aVHntZfnwEseV9GNIPgTEwQxmXlbT9/4dU8DHq6112+W7dg4bj3hzYDmeN9asflcyynns\ngxKSbtlUmg03gY9xLe1JcdM++9nP8vnPf540bdB1r3vd667pxM9kiwI7qD6vJvC2Vr3E/jmXdNht\nkwJD1Z50SjYTMivsw+0Lffm6MrNJDfTz9LanHl3Dl4gACERD8YDmZi8f9tLx2GA4DikTjbght8BK\nGipI6RkP+0DWx1/ZVoquQQlNdDGk6FcUtSHqe1IcfvmdedYO/rsguONjLXL756fjpairjEwsZinT\ngG6MfFyCmkvEQtG7PgcF8ULSLxXZLQvK+j4UJcQRzIYVe92UtYsxQS7ZH+ZoaRMC/rUHqk16rroG\n1a8wgR2rOKyvx1Ee6uoa7gF2xnIRaUQpGByGS4Pk7qUvdAd1CCAxBGNpY38Ot6RgvlEQXQjREsqu\nXhoe4S1Mxtg5EZYS3S0vAyH6SRcf/Kq1HXd33xytZhWm4GI+Ls63DPYH7eB8oCxAcrWyybKUt4Lx\n0QoGy5S1EXp62lWN0Zve9CY++tGP8rnPfY5XvvKV/M3f/A0vfvGLv6qNkRQ2EOczz33gYBK2+VxH\n87YBcXrAvnC87zkXFYzqNwYduy9f4nQilsUCwU4WY9q1u3wVgDi0AU0/XuVnAqWw+KDeOGDRq6gG\nmp6EjveA+MbOgfh8wS+fjyUEyLWKcs3ikJKw7aU5r8fhTwLVEI2hKUDpj407LzRFDouZ3f6N1wuy\n+mHXxsqkJPMAUQqq0wVJBMNCMZxElDdkNlA/F6zNQ7qVpCsEY1kxS0pmZ1Ki3ZAz+wk7mxm5sCx4\nX/kRGq84VG0v5GBqv+Nzx3w0uzOWUtgimlEqCQtBWWcY/N+5ZuqHvAw1IhfIbuNmpwaKzZJkL0Dm\nAnGsWoJg3fG0gagQiNiggkZp0cUwfSKsbzx0bciWSZayfS3uXvvZVl/Rs6pxSG7OuwROx4NZ+J5V\nYNqGPgqA+Az0vsG+Mb42rwiehAb2+973Pv7u7/6OU6dO8Sd/8id8+tOfZjweX/OJ/709uRbPJYP9\nkHm/InsC/aArNgNBLi6PBV0tvnQtrYRkPyAblejQLPsRzyWjvQgdGrITBUSG3iRgsBsxPpFRJZr+\nJOTZOz3iUrKIKw6HBdIITu93OHPQIe9pJt2Sk5cS4vwZBN8KWMQVnfTJIa6qwKCKy/uj6yKdshBE\nl4LHjRfKhUQ/Ho/wa6xd1TPqdDoopQiCgMPDQ44fP74U0P9qbWHQVmp00Hafd+N7So7f5XsXfpPC\n4lagUXX0vS4/WxcqyxFdeEhZf4Vz51ir3V8n++nHp8qq3r5NFVEmmR7L0YG9WU6/x1/B8rLxvBwN\nQBroLhRJISnrWMmsUxFt6KWSANi+bQ7a7rfwU/mmDZNw2BY3dpOFJ0sC9BQU50PGgSaVmsopQs4U\n4UKyP8rZXLPyKZs7EXEAh6dSIiM5fbaHjA1nt+aESjEqQ9YqxTw25IlmpAzDccIs0OydzDmzG3MU\n5aSdanntvrxKXtY61zmEmSQIDQsMmYeh8tUU+4kdx6XMRkfT3w9YaJt88DWu3PlcKWqJwEhNYS6H\nTagQiuMl8VzR2QlJ1ywMoNI2GRHOFfnJfDn+0EBI/FCBjxaPwzb0wJi2ZzRN25gmJduVjpVs482c\nF+Tu60bfev0u6zqdtncLx9cFnPqPlosDcHjtRR6vaoxe+MIXcnBwwI/+6I/yLd/yLfR6Pb71W7/1\nmk/8TDZ/rw3WlU6Ldgp4lcfj44zcA+0H93zJED9o6m6gn9pe5I2xkKJNYFwGsD1ogJ+6NxrCI8Xa\nWFJEhtlmQSXs+2AJkj62xpWz8QPkIhX0DwPy0LA3KCEyBLlg7ShgsTCkoVkaL6dRk3jbTvAAfbUm\nkC8w5oP5XDmgrTUbQjj4QshRVDGPtfXKFFZYbC7ZWytQIYRTxclpxHRUsNMvuWkcs5aG7B5P6XYk\nNx4MqYQhS0ryxJAgGFQhw1JSblaEqWFj0eHi6ZRoJ2JCQTosl/11wL68hKgUDC7GICASMCwEh8cz\n8o5mnrVBjG4Bc9uxAlgkFclMMelX9p7LdnysrOyWqZMKyp5p5oiBY0Iyx1DJGvW+WdENNfrhAGaS\nItQEqUQMK8Kkqebr7qODIECzdfc5irEHTnXVeP1FY5q25Vv8mJILD/ipfF8v3CWB3Fgqae/zMrYY\nDCE7azVi3MBfY5pYGLMK67pye/DBBzk6OnpSSo9fqSaE4H//Hy4nswrRDKQDAfp7/37S9g6csDy0\ntYddyeQzddzOxYiO6ps2SxskLzSoVn8v72tau+yKy4qYEoY7EZNjxXKLk6XW0zHSZsMH3bbQepp7\nv88FwfmQca8gj83S0CoBg72QxaCkiEyrGGXPKxkdrgTkXQZnuUJrOH4YcSEuySO9xLdUGthV7Ixh\n3G0yZACd/YAi0mRdzaZWnElDHhvmdIXg5jQh71RMuyVfZ/oMOgaGkp6KWY9iSqVs9RAjKLISrVPk\nXHNkUiZ7hvP9lOpAkQ1KJsOynW0qYfBwwnRQMuuXdCKQc8noUszO6QVHWcMng4ZX58ayrCzcYO0g\npAgM6VqJCtteMEA3lcQzxfR4gQE6EraPYkIEAYJIwf4oZ5ZUDLv1wjKTZPsSkwv0dmFF2FYSBT7p\nup/Ye+0rO/ptnrW1mVyw3B3PCaf5iZdhty0o6Ae4T47gumOwX+PJurH1lq6vyRfh132flWq48GcA\nVIcQvBq+BHNyWbuiZ3T+/HlOnTrVeu/GlZLWj/edf2/X2IT9kxWoUhKkks7MwrSFEbbKbF/bOlyd\ndpxBFIJkN+BwUJKH7UmhSit6X0ZPfbIIDcd2Ywjh+H7MhWM1yQ6slZwo0n5+Gc8uKATzvibQglOz\niMfWM9argNNZyKODjJvihO2yQ943DNb6qE6I7MSoXo9KOrdPEOcGUcwI5jlMBaJboCeC84OUeBqg\nS8F8o1jGw7pHAVVgmPWalaBINFmnon8UchRfXXRJS9gdFfTnivX9kGxQsYisgibGbv+SqWK6ac8b\nloLrj2KmccVjgwKlYCQkxw4iklRRJLmVZxloTKy5RtHU/67aFY3RK1/5Sj75yU8+4Y+fzHe+Es25\nmy6NHkcNcx2sXoyPI0oiu4I4VLG/l4YG+wN25fHdY4eSXeI3+naV8vfyQrZXNH/xcJmpJZbFQBFp\noqmyqeuuZjoo7eTHqgIOtCQ5kKhLislQU3Yqwgji/cDGIyJN5LnrSkJ8pMhrekXgx8TqWILbVh56\nVXeh0VWOQxhOQmRsmJ3IkTshxxYhaiNHG7h4ThKWelle2a3AiwXoSpAauDENOUpKulpyMgu5sJny\n4nhAGmn6vZBu0CEcdekNRsj+kKg/JIg7hHGAEJJsMkWmOfpgj0iG9PQExIxqGrG7ntGdSPqXYs72\nc6JMIndCdo6nVKYe16qWme0WnNxJmPXsFtjdS1c5xbUlP0/DOKkoEk0/VWxOArQ0KCNQgeFoVFIp\nu4BcP43Zj0v2OyWigjyDaKh5dCPl1CQi2Y1IT7lAjR37VXkWaOKS/va/EzUsfKeF5Ktd+qqZ7n76\nyhMb/XZW1dexcjpUzpMSdWzSQTi6sX1Owq1a1/bgv4FMqA7tS+dBXUu7ojH69Kc/3apv9nhtOBxe\new+egeYefJ+i4YtkOZkIfyuS5m3X1w8WduO2e5uXjbFa67ZLBc0zG39x+A4n3enXUZtlTV/cJPCx\nMvv9Bm+yMbAlZ5aTLgEVawpsKrnaVwQHIWEAeWIQa5qkbAdag0KgMsGkXxKIRn9JaugXkrHRpPX3\nRZ3ud2M3TZsJ2pkrZidykrgmrQa2DPPZPRsXmgd6GT9b4qgqgVYGJWCzUpztZbxg0eWhbsr/aIZc\nUiXXJUPyMCDZ2EKtraOOnyAcnUD2h3QGI5QsEQii0pAd7BBunUad+yJJvEdRnaebG0Z7gounZ+SH\nks3HEow0nNtKmWEovXr3ZWW9wzSqWCsUl4Kq0dBeESBb5cKVynAYlUyoPc3QELutv7GGKI80h70S\nJZqtkjaAgOnxnOMXEw52FPNOxXq/zZmMPC9pteyRM1iOO+Y+d/f52LCZU+46Y6+GnNZNQVCw2z7t\nATDjsB2zcs+HP283B1BcstbH/c7FnFJv8X6q7YrGqKqeBhruV6gNu/ZG+TW6XCUIsBbeB5/lNTfN\nab2E9d7dDXgnah7ORW5vgF9v/Zhnkx3nx1+ZfE/KxXd8MTLjcducbo0f+9gYNN8f9ZoaWmCYHCt5\nZAcWlUAHhq26eOWSlV9B/zAg7Ve2QGNZx7GAZ01itBacLARlpHl4mBFF7ZiWm5yzKeiFZDqHQwPP\nKhSz9ZzxzHLx1gtJ1ilRNHgfAFVZDM2GUSyUZtuEHHYKnhv22AkLnhWtMUtiRqMtzOYJopPXkZze\nplSKNDvg0c/9N/J0CsawduIbOHndNyI3ThGHEZl6iGGmyfPzFHrO8GyHz23MSLY0VWALTXZUM3b+\n/SgHFRtjxUVVLWvguZiJ7x2t8sGcmJ72Kph0EJyYhQQSdtZzYu/ehRqSABAw6MNOmrN5KWbRWSwf\n5FUvxjU/qeIUPv2++J+DNTBL4+Ch5KGt4e5fi78IuiC260uaNwvRyXX7PLi4ayeCi2N4eMe+Hnri\n/k+1PYNAjau33/qt30JKyf7+/vK9t73tbdxyyy18/dd/PR/60IeW79999908//nP55ZbbuENb3jD\nV6K7X71NWDzLKnZIFoK1/ZBKGfKV+NLGIkALuH+Y8rm1BVrAKLtyclUruDjKOHYQcfJiYh9275jC\nYJnmKy3KJWWoGZSSaVCxWQQUkSFAsNXtM00ko9EWwcYW3eufQ3DyBo7yGXd95E4+/jf/iXP3fYyd\nRz7JzqP38LlP/F984oO/xqWDR+D4GaLrbkYc32IwWqOfxIgYrjvqUEQafRV4UNqpSHKF+lJjNsYG\n8TulYJQrTs5Cnj1OyJXh3Fq2vAdrueLWgz4vGg94/m6fsLIf5LGmCPWTxi99LbUnRQd5Jtqjjz7K\nhz/84aWCJMDnP/953vve9/L5z3+ec+fO8e3f/u3cd999CCH48R//ce68805uv/127rjjDj74wQ9e\nsUJIqGp8iSev4KsPus/81L2PIXHZNL+518799WEAad6wo93KmXrfT4u26+9n6lzqfzVlu1Q/DO1W\n0O3vXcmlm+oy5w6X5BQAs6lAHigGuUBUgnGnpOzpFkp5oAQn8pBH1lOUBqVg0Ss4M464X5TL6wC7\n4qW5vYZZp+L+sKK/CFD9EpM2GRopLDbKqQVqDbKEMJek6yXDScS0VxBWcFrGlDHEQUR3uIVYO060\nfQty8zq++MA/88Cn/gt5NmNY17X3M0R5Oeaej/4hL/if/g9OnX4+nXlKOZ3TnWf0FjnTRcZwGrLX\nLZYZR+e5rnUbyVkjoRxWnMoDdpJyea98r8hheeKaQLw9iehmilJbwnOmNLkyfHEtpVSGxG3ljeCm\nWYcHhwumQcWz85itecRiLbNZ22HFeqYQcWXVA+p510sskVeohnbjI7D9arlONtbPAKdFW3t95m2x\nXczJNbeV9pHzYdDW1D617nnGKXzxfHtH4OADADc8DRJnXzHP6I1vfCO/8Ru/0XrvAx/4AK997WsJ\nw5BnPetZ3Hzzzdx1112cP3+eyWTC7bffDlhe3Pvf//4rHtttyRxPyz0svsvdixs3V8km7uP+wqD5\nc0C/orJbvE0vlGaMDfruHtk/h8OZpfZvmjb6PqFqNGUcjyoK2vEdd0yXxu0l9mFKomZ76UCIeQkX\nDtolfNKxJK/goFuyO8oxA70syROH9ZYTQRZoysBy0pIQMqVRlaATNVKzbrJqr/8ygHRYMk7tdS/y\nOo7W0XQnCkHdF2O5dPlayXokiULoodiTJSMdkkQRZRySRwkMNxFrWzzw4Gf5fz/yHop8tiQHu/Fy\nae5Bx5Zc/6eP/Gcm6SFsbCHWj1F1O/TDmKNQs34UkeWNjIyv6eTwOFkBh72CrSxEVg38I4masR/1\n6liKgo1SERrBvWsLvrCx4P5RyqP9nIudYsnud/yvURZwGJaknYp+z7L6EXa8lITBsYp1JVuLkKmg\nuKDI74vgUBIF9t67++5KWQ/r4hKO6uL+FnnbkBZVQ7B2Y+fPb228LadpQhUuhDBZwPkDa5BOrdtz\nP7rbjJ0DCbtn7N5zT8kMtNqT8oyqquLixYuUZROEuf7665/yST/wgQ9w5swZvvEbv7H1/mOPPcaL\nXvSi5eszZ85w7tw5wjDkzJkzy/e3t7c5d+7KV6+NfcD8gnWdqI31ycsmRpTUALBDT1O8G3txHdN8\ntxfbCeT2zk5fx1/B/CqkbtK4vbw29rf+CgTNuQ6mjcKh6+fepAnKOwDmI5fsayFsDMkdXxjIA4NI\nDIrGAPlxiX4OnVqjyAWoe0IgI0MUWhVYB8rsRLVRrfsXBfbhWHjZk7KCql/RPwjYOAgRsUFkgmKt\nQvU1vUnEflSyVYQcyYpFCQMT0UmGDDZOEm5soZXi0//014RKt1Qt86oZo35i+xIoMNWce/+/D/GC\nb3kNerhJZ22T2fiI6+cdxianmyqKmo7vY2ncAwhwpA0qLtmexTy2lqHqxcHxw/anjSHbmgRc6pc2\nLe+h3d1C58+rQRYwDkqrtVQKtqqAC8NsqWeUx4ZOLpaEa11B9kCE2KgY3FSweDgkHBSUgVneNyd4\n5/MIfeVGp+PujJsD9bp5udZtgx4dK8G1aWbH2V37Rt8e++NfaM4Vh0221TX/eNfarmqM3vGOd/Dm\nN7+Z48ePo1QzElerYfaKV7yCCxcuXPb+W9/6Vt72tre14kHXApR6vPapBxo29/FRM8BfC80ImyV7\nolYGhrBs89XiXJI/jm72k24CZqMSoyWBhKpv0JEhLASDXPHQqODGacxhUmECQSkFQZxQhCFrmye5\n5zMf5+jgYks94Grt7AP/xHNe8N1Ea5uMQ8Wg1+PiwYRZUnFqEfNIf37VY+wPCrZ2YzZnIePHket1\nLdCC4moDW7epqjiTxnSKBBkask7FPK6WAGUjQepm/E0BKEOybTN74UZFMZaoY1/dSaTPPAz/fJ/9\nf/E0dPWqxujtb3879957L5ubX5pUwIc//OHHff+zn/0sDz744BLFffbsWW677Tbuuusutre3W7y3\ns2fPcubMGba3tzl79mzr/e3t7Sue+7abrVV3GSUno+HiOkloXV1fWtWPEYVBIzcB9Wpaz8Oisl6S\ns5/OHfb34/4K5KgnzrNyWwff/vqZvV69+vvMbl8CpKysF+Q8JVdPa7lixZroMEDVal8+vcC1MjSo\nyLBuJKnSNm07D5ivW90hX9Jk0IFE2liUKQWpNOzn5rLxWqa/0QQhDBMbvB4cRixGBYMudFNBLxZ0\nu9DtKlQo6K9tUOmS/Z2HlttYX8bCVyA4nNtrd+fqRBMmsxnCSILOkIU8T9xVMJUkhUTkgoU0Db2j\naqOMy8qCGi+tZ1y3l1DkFSLR3vGb+5X2KjbLgHlcXCbTsSzfU2/7D6KcA5MTAP2eLbmUAH2XsSpA\nC6v2KTTkQiBloyRRYVCZXDItwM4/p58Edn4b067K4mdgXV+WulbCej6+TI6/O/i6bTtXHcL64tiO\ntYu79WK7e3Ap/KKyKpB3fEszD//r3VxTu6oxuv76659WPNHznve8Vt21G2+8kbvvvpuNjQ2+67u+\ni+///u/njW98I+fOneO+++7j9ttvRwjBcDjkrrvu4vbbb+fd7343P/mTP3nFc/gSF2DU3i8UAAAg\nAElEQVTdez/Y52p5+QCwQMFa7UG5tKZbpVfF16SwQV+w8aNubGM3YG/wsNOc39V3X7rPUdMHsLiR\nWdaW7Nhaa87t+uiO77YF7nVa2EnsJpkRhiQXrWv1jeNa117PoleRzAK6aznxTBEUgrRTEdXX64xb\nOhXI84FlzAYwPxBoaYg3SqhjbekKaLNXSLYWAUmmOFzPKfsV67liEWgU0sbiQoGQkt5gwEKXpPO9\nVrkn13e/ZLMbSx/TMp8d0lEBcdLhAEEYSdalYtwpSOYBl3RjNQMJ3YDlrHeJAh3A0bGcU4cRD3XS\ntkRITUAtVMmZowQRFS3j08IJ1VtYv/BhEjcPvIuvJEKggmZrpesYjqrvL7HBTNqLmOM3+vX0DqbN\nPHJG24cHFFUT33QyML4Er49lcnCUTz3Yfu0vSn5A3WlmO0P/pXi0V2pXNUY33ngjL3vZy3jlK19J\nVD9JQgje+MY3XvvZ62O59tznPpfv+77v47nPfS5BEPDOd75z+fk73/lOfuiHfojFYsEdd9xxxUwa\neLXVvf3zKhE2LZq9vlM2dJPI1S13N2qaNoOeFfa3S7xFHeB0nsrh/PIsCDTHKipaFAAnfO6D0bbW\n2g/cuf3mtTN+btgOdxvvDCza26ycz/fEippvVXYrBtOATiUYjSN2T2QWqUw7GKrHkirUzLs1M34L\neuMAFpJqqJdZlUBBN5OcmkdIBeOk5LGNnEVpeUtbmcTkGtkzmAp0pa3ImS6QUhIG4VIHyiHhT4za\nsYjVOmYAvcEG1d55jM6psMUnRSXJjCEQwiYPSsHxSURSSqslFRrmScWkV6DrLFLZ1Yh9QagFRb1/\ncqBHYyBXhllYMZoH7HbK5fzqJe04jTHWEwL7sKZ5O86Tl5BMLMxhWQBSGvCC7TIArcQyeA52zvQ9\nj3w8ay+SLj7kDHq4ok2U1URx90z0E3hsvzn+wRR2dVvh08/eXTqy4Q4X8pimjXcGba/sqbYn5Rld\nf/315HlOnucYY1oG5FrbAw880Hr9i7/4i/ziL/7iZd+77bbbrhqn+vdmA9jmKrcnKAWdPECVgo29\nmP1hThk/fjxEZBI98BW7bGo62A2ohs1vepnk+CRmdz2j6mqKlcPFRlBIgxEVUoPShhBBlS+Igoik\n+8Ro/8drg7UTKBUghSDL52ijrdgZ1iC7YTg2DUlDzc4ogwD6laS3UGzvdBgPCtI1K/ifhZq4kBTx\n4wdAxknJsUm0NEZfUjOgckHvMCCZBBwdb5CYQtLm8wmedi3yfwvtqsboTW96EwCTiQVoXI0i8tXQ\nlLQehI9OrXSz/3USIb4nsBoH0EGzSqyubEfzxlNZ79e6OW6bVGeA/C2gj3SV9erlV4RdzXKMZ009\nq26tFXSx1rMLlL2OZcnmmsriPLAks4Fo3+srK2ukRmnA8SNFWEmqUcn5EymDnZgs0La+uzdWrmVJ\nhTwIEFuWWR4pSCqB6BgC5z1qOD2J2N3MyGNNVTXbCYfaFYHhRE9wMKqIJgZlKgK9QE8PCKqSZ938\nQr74hU+iZBPbmyzaVBxXYsrhhm6+7X8jNprZZIdiPsaUJeNFSaE1KpfMewU9IwlzyblBarNNWFnZ\nRaQ56JZsHUYMM8X+ek5YCuZCL8fWScy6e5WGmkSLJaLaxcp8HqK/JTcGxFQSnQ8JC4lKDIukYryd\nokOz3HLb+SKWeDRdWPWGRd7M2cN5m8Xva0y5e+bTmYra6/JxQd24YSUoaT1P5+HvTewc26m5Zr3E\nnt9J8sahfaZcKONoYb0s1wcf5f5U21WN0Wc+8xle97rXsbe3B8DW1hZ/+qd/yvOe97xrP/sz1Lqx\n/XPGaJFbLWl3s+KwLcjvit+5ST9NL9/auPRyErbBcc7YuEnj9IF8eU+/5XlbBtYVBnScIyWhmjeT\nxE1Q9wA6Um7mxVe0YUlpiBaCwkuP92I4mQesL0LSsOJwrWCqNFFdOqiDIRRtadWiZOnZVD1NlEmi\nSwH5yIL0qonEDKwBM7WRS5VmFmqyrL0F3hzUWBll6OWKw8AwExVZkWH2J2yuz0nHe5y+7j8QdI8T\nlDvLsXKyGL4Er8O53HDLi7j++q9H756D2SEyX5DoEiszWXEsl1wQmmPTkMN+uRTH843HQhjOrWes\nZYqt8wkCQaHMMnDsC/Rhh4tCGaJKkNfVFJdlo1gpK2VguBcRziWzYwWzjqXjxKEVoHO/dXPFxabK\nCkhBz+Bo3KZnrMroJh4EZJVK4gLb/oI8S9sl3YfddsHMXgKdGirg4qoOOtCrNeUf3bWv9yZtKMHT\nQQe5qjF6/etfz2//9m/zspe9DICPfOQjvP71r+fjH//4tZ/9GWqOFHsl9Co0D7FrPvPevXbBw5nH\nXnbZnuVeuRasL+qb5seW/H+X2abq8vMq2Xhh45k9/u6Rfe08A7dXd+xpF8B2k849AGEqWazbkwoD\n100jIil4aJiSB4bjAxjJZpLJsjFEYM+dFh6iu4BJpyQqFfFjIVWomUSGeaXhqO7bXPFYVDKd17gr\nCS8qejzWyZir0q6gqiQsIzb3Yx4JUm6cSmSQkx+MCYeX6Gyc5Dte+R/5f/7v3yEM7CrRrT0TF4S1\nWUfJiVv+F577jS8nymYUR5eoxhcw2ZxMppwk4NJayloV0QshOhJMBiUCK3sbzhVpoqn6FVm9EMhO\nxSJMUblsoZKLyqKCfZRzjkHW5F9niFwM0AWzKw3JOECWgv3tFLxFENqZ2VDVhTW7mrV+/ZBLW202\n9xDUDiHtI/etwmTdZMPkh0ZXvaVZTdtj70QNPs2BS0Pve65/YPWNDueNh766yK4aw6fSrmqM5vP5\n0hABfNu3fRuz2ewJfvHv7SvVokKgFVSBRUDfMIsghgvr2eOC0mQFSgvKwDzxRBCQDSqyQdXQZtxk\nNJCUkkW32ecdL0JKYdiex0yUZJrYah6PHpuzfbHLvCxZBBV6NqXa3aGfJJB0OXXd1/HyV/4Yn/jo\nX3A03rmsGxsnbuY5L/hfWdt4Dvmls6QHZ5k8di/Z9AgxW7CfzghkgEolk15J7yDgqFdCCfGlEBEZ\n9HqJPFQEj4UUoxISa4jLwJDJBgt0pWaENfJP1GQp6IxDdk+lGHl1ufFqIlH9r8Eg0Up7Utm0t7zl\nLfzgD/4gxhje85738OxnP/vL0ben3CYLlhQIaCQ3nZfiMES+eqOvhezQq35NKl/vx1UTAetBuNI8\n0KwQfjbMp5DMs3a2yr32VxY/brKa7k4Le2yXMXTnEQKSTLGIK7SBUa6QWvDFKGOgm21mWdWZrxj6\nRwFpp0KtyJtqLxvoy6yA7VfmxcSiOkY2r4B6q9sBSqkRRtKTkqP62NMSPtNZcPNelwe7Kc/JA0w4\nx+zvIbo9dBhz+vizeNX3/gL3f/EeDi49RJbNOX7iJKevey7Hj58hNjnFzoPonUeZXzwL0wnxfMEl\nJpxIEz4XTNjaj3lwY8YoTzjcKjg5CRCnNGqrYucQ8qBEzSSqLl7pl+72NYECZW2T7wVUwlCVgly1\nY4nQ0Cy6+yHZsJb79eaE4yT60q/poaA8kMjrCwJde92lrSwiReO59BPr7fhyv/59gTa6XJi2Z+Rk\nbN08yAo4t9d87pRQ3Twdz+zcOrluX4dBG7vn8978eXIt7arG6F3vehe/+qu/yqtf/WoAXvKSl/Cu\nd73r2s/8DLZA2Ru31GKpYfSuBpTwYjTAUqDeDehaty0+XlbtbZojJUJDMViCFIN2sT2figENPcNt\nk5wh9OVO/JiQ06yZeyLzR/Pm90lN16CCKJPMB6UV2S8CduOS0ljX303CXmzd704I/VnA4Vbewpuk\neVM/zPXXpyFo0xZ+LytBVplWyaILYckti4TduGCvn9IPm9/mkeGRjQU3j7s83J8RjCUVu6RVxbAo\nmezv0j95HV934wuI/sPtBAGEAvLZIWr3LProHOXeHuX+JarDI6azKfuzOZ1M8rnOIYOdmLNJhp4o\njsKKSBn6WjK6KefS1NOiCjRhqdBzgemY5b111wDNg+8eeG2sMVJaLOEgUjRbbCWtdlSyUBzdsCCq\n+XBZCmYhyGYWcuDkhDWCalehj1vxPMfFM5bK1k4kFG3xMyfyt1pXzfXVhSGW86p+0v3EgjsGWP4Z\nNKDHm07a1P/9NYlirSYtu+Mv8na44ssSwN7Y2OAd73jHtZ/py9h8gCM0q0LheSMdLyNljH2gndFw\ntcHcjcpXApmrwuZZcfnK4JMWjfFq01f2xrqAtIs7uO/PamyKHxTtxm3FP+0FDjcH9vtJKaliDcpq\n6KwjudCv6NXs7YkXmKw0bAuFig2ipyFvZ+d8cJx7z489+J6cqUAascylRwGoxPDp/gQtQGeQeRmX\nQMEMzb92Um4cJ1zopWweQLcy5IuSaLRPMBtTRhFxRxLHEZHOCI1hcbiLTOcsDvcxi4zdbEq+Z5iX\nhk9HY0Y7MWkJFzsFpw86jE+mmP2AWVKRTZrMENi+zuKKYK4ovFS9f29drHHptdZ4o00jyT0smjPU\n6zEkj8ak6wWmTgSYHIoHI0SiKYxB5xJRlycpBwZ1omSuDKwoi2KasYbLM4vQRqfLOnPmF47AI2Er\n3cYhufvtFxv1QZX//EX7XecpuWq1DgzrPGw3L3xht6farmiM3vCGN/C7v/u7vOpVr7rsMyEEf/3X\nf33tZ/9aaiVPWbDFIXevCO8ykCwUaXcl4HGF7wsD/YOQw60VeT4NZN4MfxKtkIZSGLqVZB40K4D2\nHuDHa4dRyX3DObdMulwMUo5XhiAt6c4XMBvT7Q2QHUEVgEAzy+bofAF5zjxPKRc5QQH3JzMmE7hx\nr8ehKnlgOGf9MGKelJTSoKYSdSp/3D5UgSHObBWQJ9vGScnJSUKSS/CwWVJD52xC0a/IRo0MS3Ex\nQK1XqGMVizloH7IV1xijyx7kr8340RUfD1cx9md+5mcu++zpBD0+U23Vm1GycVkdzsftr90WzaeQ\naNNeSf0shI/mdlkLtwItq5LKph+LDNTFAJ0Y1k5XLeVHB9N32auNsOmHw6mIHUUkBCIy7GSaYlhh\n6tV4kUNvqogTgx5pCygUoDIYSoGODLPUS2dncHIacamj2Uk1XQMiF6hzAVSCIjBEWpDGFeWwoler\nSroVU4rmD+y4HQYVJ6qAs3FOJ2rkOtz3/a2BX/boSGm+uDnj2YcdDsoFUVag05yqnDKb7LHeiemG\nkvNVRmoKYlORLOBIlux1F0wy2DiIkabi4fU5lyrN6CAk0pILmynxgYJBRSVYBqYTb2tRxIZgKlow\nDR89b0wbwxUoQMF0o+CGcUxhKqpE060k8UJxNCwphgVOJDU/kASlQJ8ql+f0uXeDToPyduNTaaCw\nC4bPe6u0HTs3rmHtsfkKB/73HRTANVnP/8P6GXCZOefRn6+zs07L+rpjTZkq13YOm3CFk1fxVQOu\ntV3RGN12220AfOpTn+KnfuqnWp+9/e1v56Uvfem1n/0Zak5Xxk+rj2dtGobTEoKmpPNqENl3EByO\nyAHV3IRyYl1+vSolG9xPUdqbmpwoiS6EFHuGfE0vA5NxaGNZ7vhO/L86lFR7itLA+vUl+4WBQlBl\nEvNIRBZpqkijS2G3aNsFkbQZskUO47WCM5OYx/oZaVFLURg4NYuIKsEjowydgapAnQ+Y9irKjiYt\nYRRBMFPEF0OysqTqNAPhrtPHUe0kBc9bJKxXCiMrDufNgzDoNMF9R1upKujmkt4iQPQrHtqYcyyN\nOJVKduMZoyxgLQ0Zz1N2A02gJbGWXAxz9voL0qlgaycmFIYHRnMulpqwEBzbjSmBC8dTTCEwE0ny\nnILAS1cnkR+0tQRVv968v9VxW2IfEBoo2A8qJqOUDaMYaUkeaaZrBbJjKLJ6+7QQiN0AcX1DrHVz\nzA8+++W5W6EB0V7kHPTEjWscXi6R62Pl3PccJKSo2teWFvYznwzuyLRg45InRo1x2j2yxsjd90Gn\nlunJm/5da7tq3bRbb72Ve+65p/XeN33TN/GpT33q2s/+DDQhBD/8cmux/QoeDkAHl2OKXJzAfT7q\n2b2xH0dZrezpx5+cjjU06G4/AO0IlKKEzb2IaqtE93XdX4sViQSQC8RCEmcSGRrERkVvwyzRt1Cz\n9o/ATCSqkIgSzLGKzsB2wMWHkhBGmeLEImK/0ojAEFcCFcL9nQxVqxeOdkPyYV10kTaYU9WFH4tB\nRVqX1nbG1vXHxctORZLThzGXNjOORAO69KuazjJbs/2meYw0goO4pK8lG0aRdiryXskoD9nMQzKl\nmUa2LFDQ02SyIl4ojh3GFIXgfD9j3rF10uSFkMEi4GJcsJ+UGA2d3ZBoo2JjW7f6OvW8xHwiiA8D\nuM7eLIcRcgvFzAOvunvfT9oLk5+c6MaWjGuOJNUlRedMSRaZ1vnTogEeDjr2ofcTJb3EzoPqXIC6\nsWihu5Oo/dBnRdtj9+vdOQH91binn3297ljj/S9y2x93vVtD+1u32O4e2WfC3ctBp8m8unv7W++/\nNjmgK3pGf/7nf86f/dmf8eCDD7biRpPJ5EuWE/n3BioTRHNlq2qEBnUkkalEVAJZCmQAhBrTMYhT\nJbJjWpVr2weDrGd5GMbYzNhlTdjyOrN4QTVRxArGkaHqanRpcXhhKtGBoezppWCY36rIMDtW0N8N\nKaWhTK480Rah5uIgZ3scE4UlO53icTlyJ+YReWDYGVhi7iyAvAP9ScDaXsy8WzE+NqNTKgaTkPVJ\niJoZdC2yfXGYcVFYLpkC1vYjikLw6NaCeWkNfrIXoEOzNPhXvCe5pIz006O9XIHel5QThQgMwZkS\nNTDgFecU+7XmttAQP8FDq/kKq9N/ZdoV78O3fuu3curUKS5dusTP/uzPLi3eYDD4qq4oC9ZKuz02\nNNkht6q4DJjzjuKwnSGKgkbpDtqa1S6F6lYYKSwQzm0FXHVY7XlKRWUJp7nSyGMlvaPA4kCGmkwY\nTGA4tdmcG5rzLepMl8tiBMqunm5FdBAE19fVTNi8gpmqmnLbZZO9S6aSedfSOvztgK/ltDBQDkv6\n+yHZZkGJuSzj5OIXi07FznDBYC/iWQcJ+52SqS7J6rHop4pBKbm/l6JrpUElIQgh3SjJ1kr6RyGj\nxxJm/ZJHNhYsFrAeSQItmAYVFZA5XuAkpFoIHhtlVlQuF8R7AWmiyQcVWWqr7/qehxRYKoyBMpPk\no5K1msrg1EB9ZcjCgzk4+eGuZ2TzAsRYoY4U045m7VRJUJe53pvUnNdLCqYK062ghPxcwP/P3rvG\napZV5b+/uW7vbd/r1nWB6hvgH2w9TXP6i3wEDaWI6eQQJSJESbSJQNIk8sFIiAFJjJgIEe1EjEJi\nYkgQNJoWPqAk5IjnNPA/ICoN1U3Xrbuu+/q+612XOc+HucZaY65dm75UVV/Kmkmneu/33esy11xj\njvGMZzzDpY76qDeqC4q2Mcq84SozR9WzV7qtuJaOlc8EnoBOrlZTLlYXlBqD816ZrFORmtWe1SgL\n8b6+xz8edOFgX03h+Yw9jdHx48c5fvw4//Zv/3btZ3mBx07eudTgJ3yUdSCx1sKG7iHKg5JSEq3d\nIiJ/ZRUCf3pxQMfBkYcUN8WUeeYPPk79xmcdXlnRhOJuR9b8MYQHJS+AbggQR90LJi9MFAEO9uUx\nkzLGxA4bgRlaEufYLv25BKOwzmO6Ivyux+IobFYwnTuqumJxK6ZaqsjV/ZkovP55CvlaQbwTsTxL\nOLIxaue1ihynFoq215jgdmI8pxYuLJREo4r9lzIGRcp8tWQT6z0FFZJEFoYbCSdXZ36DmEN2ISFf\nrXFjS0pH+tP3Nx5AXUJ0OYbUMdnfSbte3u7qy6C7x1raPimj5B8+jDdjKA35bQV1BIPY1xaCX2+T\n2hDtRNijBTtVo3ke10RnUuJZhFuwgVDeMIM6N7jMl4Vo4i10xuNqdBJZH+BDTV3LNkjh9nH3nE4+\n3Wle06yDVGFSLfap1v1Oj0ukJV1uKOnxZ37mZ/j617/OwsLCruyZMYbNzc1rP/sNGmJc2kaCPWAS\nwg4f8sA2Z93P+xa7Ca4tgSSGNCqEjoymjYPWxBZAusUWDNiDFdG5lDSPMIuWYRYypHWH2ek8BMxn\nTd81WVStJo6Dxe0Y4wxbBwsWBmBqw8RFVBcjJvOE+ahmZ+h1dIYZVAs1g/WEadYUzuKPtTntcI39\nS35hX6wtySxmOPOAreZZCS4m17sw9AW2lycFF+q2NIvLU3//k+besgQG84jZ2diXnMSO+bjGjByn\nl+YcujAkrh0bC1U7N8L7WdpJ2EhqZg7qOUwupuQLtW/5rVjKWvtpcwcW5hHDjRgzcXC0YlZ1uIjU\nYrVFxo3qZkMLaj05+TzNI5hF2GOlfwY9byWNIboU41b9JEzibr44UBFdTEiXu7lcmTT6VnPD3DlS\nVR8p/fb0GtQ8ozYLqDxc67p1lcTwxPlu3QibWs49L8OOOf2qgP6GJZ/3PflrGXsao69//esAbG9f\nh761t0Y4DNhJTTT11e/X5ZDOl4OsHyiYxOAScInDDWt2nG+LPdqJWdxMWF9uXu7MkUaOyWZCuVb9\n+CIqA7PVkuHTGTtLJXXSiyGcD5OS0hCVXnHSZg4i1U/NhN+P12PII8wRD2K5dUN6IaU6WmBjeGpt\nzuELQ2aDmiJ1wd8u7yT8aOx3gKSxFuXEsucGbSG7mEAG8bEKM3B+s3oe0kQykmlEuViH7cL1qIEi\nwk2uchLB3yoDaW8ua9j7Rm7e8YzY3Q9/+EOOHj3KcDjkq1/9aispsrKy8kJc3/Maoman5RGquksx\nDxuMSHAY6R6rPaeZYkFrr0qyZdoT0piShHe6pkv/LPhKObFk64n3bBQGJEqRGgsQ3Ai6HmbyubDN\nxaTVeJdavL2y8SbmEWwv1CxcSFlwhqJxG3dWfUHp4ErCzlJFolqCy2h3wASqlYrlzYTpmmcZpwaW\nipjkSoSLIE8s89LgKoiKiChy1KmjGlhGqcMZGMwN6UZMOnS4oyUzAziwi4648t6aO1RR4Li8ULC2\nnnFqZc6soWBMyoitAi5lHowfTyOmqW05QTLXK5MmZAY4l8LIMrm9DsIy7UELS1/zc6zrQhHBSFpJ\nk4blrL8rErIAA2MwiQvkS2aNnLHLvfTskdtcl72bd2suiT02pzEeXe4hsjcaqzmy1t37+o7/T1L7\nV7bDbJh47/r4OjsnHr3mi6VJx9XTdA05/rWOZzRGDzzwAI8++ig/+MEP+M3f/E3e9ra38Y53vIN/\n+qd/uvaz36AxzEKpDonF5cFIH3EBLtMk1A8uKgKuTBJ3k29tV9wKYTpVhhgg2K1BPWquIxmBWbDY\neQQLnRjaTt6B4OAX1KwIU/t6iBEdNNT/mLCEITJhGcG8qBlsx1T7G5awgepgxeBCyqAB2SXFLefT\nRcXF0LLsDKMrGTa1pDbCjizT/RWu2eF3ii50XEp9qYrJI0wBdWVIU4e9rcKNHEnmMRx5Dna1Jj2b\nek8rg+lCzeIsYXWeUGcV0xyWt1OeSjx25ZwPvaaTqg2RdYlDXUN9LsFlltGRut08ZG50iCkhlDx3\n2Ri0DpbGEo2DyhEI5wfNCSo/v61kiOBXFXAhIVmxrfYW+HXxxHnIh+AKQ246nKbFcppzSfG2lGtM\nhmHrIaljE9xUCJGSypckhk5EaGM0SL2h0cZJ+udB2KpLjnet4xmNURRFJEnCF77wBd73vvfxvve9\nj3vvvffaz3wDh+5jD91utt0Dm2UCIwN3HILHmz4BYmhkovUCF8xAGyDN2i0qL7qv+SG69/zOvNsd\n08oRVY23U3TXro1RXoZZlH5zAGi6i6ZA6lhKDMOha88p19Z6OgNLsh2HxaARRPsrltcT8lUbXO/Z\ny7TNEwGKFOpRTb5YE88NeVx1np3rjKXMV2VgecXTEIrKZ7Wz5uXLi66nHTT64BHUqcPNItzEY1mX\nVwuOXRySlRF57Rg4w8awIjUdkVI4P9ozqi0ks4gsNqTHq6ArCHjcRKs5LI4a5UxVvxVHcICIKna4\n1IPdQd1h4iibZ2JMx+8B2EwcW2cNtgAa7zvNI+qnYlixsFpT2647sGTTGHqmvGa6ayMBIfAv97RV\nhVX5cdR5LEK4PNQENMK3avGyqtHlUpwovdGKwR723oOrqQc83/GMbIYsy/ibv/kbPvvZz/ILv/AL\n/sLL51LNs/f4xCc+QRRFXL58GYAnnniC0WjEvffey7333st73/ve9ruPPvoo99xzD6961av4wAc+\ncF3O/6KPJjy5XqNOHFH141eFjcOeXe3vB85n2+bPclVFUI8c7mocp2sdqWebyyhTx6kDOUViMQ5O\njechh8m4q2sMWeBiTHJb9fx3bgdH1occXh/s/qw2PxbbMQbcpCa+kBBdiUmfToivxHCkwqzVe15T\nlDjcMzzHm3E8KwmRP//zP+d3f/d3ueOOOzh58iTvfOc7r/nEp06d4itf+QrHjx8Pfn/33XfvYnwD\nPPjgg3zmM5/h/vvv58SJEzzyyCN7dgiRtKfOeAkvAjoZDPk86KmuhpZHkN1zMgxZt5LGl9hZatf0\n7qzDtKpx1asaFrYNxcSSX+o+16lUGRq/6XtGqcIjXOoYWsNU1Qm12ZtmxDGQ+SaOdeYorS93GA/A\npI5JapiajjUsu7N4i6OsoRo07n4Sh1ibzIGEFzpkFblffT2SfZO/8981mKHFZN3cucyxZSrmA99M\nY9LMS1JDObZMpjF2paJ2XYg43kwoUsdw4FoulaZF9LXP++lsKR9JYyDp+tfVFigMsQEzcpjm+wIF\njBXuNjtUU1/2D8msWphYXxfbKEfozKu02Kpc00FFQQcyN/LzeBBmdaeNDM7BZf/zZOhVGSUskyyf\nDlExXbZuYyfEVfMiXGuSmdTZO11SdT3GMx7qda97HX/0R3/E97//fb773e/ymte8hg996EPXfOKH\nHnqIP/zDP+Rtb3vbM3733LlzbG1tcf/99wO+iPeLX/zinsZIuDmpcjHbFDhdeCNLgp4AACAASURB\nVFYqY6XrgpZGHaAnn8vL1ecoQUOLVyCoJiU6xeeBjiRZVmCKiHKlamvjjIPDs5SVKubJUcFWYtuX\nUa5ZeEH9RWodlIllkMfMept4lkDa3FteQpVazNxgU9e+oHJ8Aeh1WCrSH9D9/+pCd+zadmGmc964\ntS+54srI3BXqBbGuI2wOUs8mN9YwWHNUcXivl7c77hB04evCAcvgXExExDSzrE6A8wnGQnmwap/j\n5jSUH5YXWY6XF2HBdJb40O3cYIYzjiT2nw9SYD0iXrNkC933pWxIy2wMBjBd8yeqG4xLQl7RSxdd\n6RakTsE2npGuLcuL3WtP7kHaX0stmTRCEGMkDSK19pIOA4X4a5VhlcaR8v3a0nqkkQk35evRFPoZ\njdG//Mu/8K53vav1YJ588kn++q//+poKZb/0pS9x7NgxfuqnfmrXZ48//jj33nsvy8vLfPSjH+WN\nb3wjZ86c4dixY+13jh49ypkzZ/Y8vkhu1Cretg4KJXov8T10chdCNLTOg9sy2ZqtLbuVLm6sFD9D\nGMl6d9WekYhejYoIm1oK4ULVhrtnA+ax5eyo5PhswIW05ExS+eybYoADvucYIVhdpg67HmFHPhyT\nz6UBH3hjVIws4/WE+dgTIY0BZ32IVsWu9Rwh7L8OHYlQG+os6XZUKWHRHocuRNWeUb9J4zQHdy5h\nNHBUsWufk8budKaxfdbAfK1ifCFlJYbREMzIkh+qyNT5pKOGfjbaIxZhPLlfeY5F5DB0a8ZsRth5\nxOhoSUm3joaNprTW9jm4HOpmQfgsdQNOmT8a8uRtBzrDtjXr8BqZu1EWKowWFUiXpSzxx9ZkyVhF\nfs4Bam6k3jJVHn2ahozrOOqE9/MyJLu+IEqPDz30EF/+8pd5zWteA8D3v/99fvmXf5lvfvObP/bv\n3vzmN/PUU0/t+v3HPvYxPv7xj/PlL3+5/Z2Umhw5coRTp06xurrKN7/5TX7pl36J//iP/3hONwSd\nOl1kYG2xAxRfKiOqYLwds7PUxWL7yphpZDk9KrDAlsm5K89wznA2e5YYXQTFoPbekTALrzLqzGFj\nRzaNKCZ+NUaFaevmtNDXCzYcxOcTHw4dfe4Yjxs4ylcUpBlkIyBpFBavIyYHYDcj7KWY+BUlJuGa\neEp7DWMc7vrQz27oePJCl/SJoh//3WczntEYVVXVGiKAV7/61VTVMz+Br3zlK1f9/Xe/+10ef/zx\ntr7t9OnT3Hffffz7v/87Bw8ebLvWvv71r+euu+7iscce4+jRo5w+fbo9xunTpzl69Oie5z66z1t4\nsdZSVyNDdjiZQKt2Suh4R6VygeUFlZ1afzfuhVFJ7A0OdLH6oDIYB7Y2LG/EFMs10cS1hZQjInbS\n2peKWLCR4wfDOa/ZGXHJ1ZSNcJm41Ror0mNrYNm3lTAaO8qxbUsCNC/KOSiWa8aXE6rmO1yJKIaW\nqglndemMeDAyF7pFjebC6OvRUq26/bMx7Mr0VTUwN9iZwdxRBtIvUtunjy+mWXAP3WxgdQB1w4YW\nj1Vjgec3dtcZDhMYlRGH4ogkc6ysWtzQcWGj01P3kxsRb8Skt1dETXdXregwGYTXAn4j1DWSRRVm\nnkS+FbwnU9bgyq6OVs7dT6WLR6T5aJq2IM9Lh8hyz37yQuy9tv76dapfvwMSzuuq/8kQ7n91d75/\n+2+uaTyjMbrvvvt4z3vew6/+6q+2gvxveMMbnvcJf/Inf5Knn366/fmOO+7g0UcfZW1tjYsXL7K6\nukocx5w8eZLHHnuMO++8k5WVFZaWlvjGN77B/fffz+c+9zne//7373mOstrd8wpCHMeYMB7Wn8sL\nolPBIhObJb7Vb98IyEPXIRF0tWDpLCKZG8oS6kMVuXFgu8VcGUfiOm3lOPKaNj9M57yqyPjfUU5t\nOuKb7kevr72KHNP9FWubCYk12OWaLQVGyr25gaMaW/ZvpVQ7jrSImB8uWkBaFn9tQwxoYHw9mpzX\n9V4a4bcIAD9R/dqlfEG7/tLQwDRp6bjht7ga2I6I88infGNHlFhc7AJ8SwPk8q82foKFQPfit+vA\nwoFpyqE6oYwtg7FjwcDgiYzi1bM2hIsjqDci7HrM5O6KsmntVNRdE0+5d5HWkJ+HWYi/DdX1iJSs\nzM/WrAnxyk6XSr4r61k/B61fJOu1DzALQJ30mgFAry26CQFrwfP05mJddz0CD4jRe0Ewoz/7sz/j\nT//0T/nkJz8JeEF+nXK/1qHr3r72ta/x4Q9/mDRNiaKIhx9+uGV6f/rTn+bd7343s9mMEydO7Ale\nQ6dip3cpPVmmSan3jYYsImG2ysNZmYRgpwbupHOnzp4JIC7nqi3kkxom3UOMBfRsFucMx1IV4ZQQ\nGMBOZpliOVannM7KgIWrr0cbmzp2rK+WjDYSsq0Ml1rs0FJlju3atSTPfLFmFDmGCUzGNWbU4R07\nvR1VF2zWtrsGYenKohRt8bp5weRlkDkuqm53FeXCUQbGObK5gTMJdW0wpcENLfWi9UJ1lcFtJKRz\nQzWsKRZ9V5M0Dl+o6TwEiPV8aeIpDm67MsAYx/yuHJs4Joe812ZPDmAasTiyHgObG2aXY4Z3VMRD\nx6h5Rk+v+/uRex8PQtbzwtDfv8yhwAcaI4oMXFHezXjgC2SlU4l47dZ1mVh5Du290GUqdRdk/ZzS\nOPxcmj6MlGKAXre19eduDbcJa9eEod0vFL+W8YzGaDgc8tu//du86U1vwhjDT/zET7Sh1PUYJ0+e\nbP//gQceaLuQ9Md9993Hd77znet23pfauJxWHClGDGtD2SMBnctKXr095FxadnVezzBcDNO1ihJw\nOxFZach2YrLCYIcWM7ZUA4ubWCgi7GZElF6HasfnOVwC5aGSGAOJJxgSA1HHcK6Wa+YziC4ljM+n\nzNcqGD+/LXn/dkrl4NRiwV39t6A2ONUxtjibMLitxvwYPafrOtz1YTS/3MYzGqN//Md/5Ld+67fa\nXmknT57k4Ycf5sSJEzf84q5l7KooVqFNP7UbR11tl3yutWR0yCYelHgQo6biPle7XRyF5SP969Kh\nhWSHrIGn05JjZcr3B0XwfRc78mHNcZPw9CAEJdrUvqox0vdmI3Ajy04NjGuKHNbiiHQeMd5MiK+A\nGVvMosP+KGNhbDFrNVEjNSt1buJlru80oYVSGZC209CVzgwVw1vLWPS1yUWSBaBIHUXqGMSAhaII\na8fiphbMHapwM8PilYRqWLWtf4QPJp7K2kIXBsqziiPYXjcszBL+93iGtb1QxeLlfSPH6gLUW4an\nS6gGFlN0TG/weNBk2K2FtQU4fqDTk7bOz9eFjW7unKIy1NZ7oFKWJGGPc8YL9dOtVVl3mumvOVML\nQ7+Gg5bulqDbrRbrk/BQwmnJXAbRQdTU9TX3ggs9Mi238oK0KnrooYf46le/yt133w34wtkTJ068\npI2R1ADpRaaLAiGsXTPO81tafeAmfJBYfjvvFjjAQtwtyCgKDV8c0fZNh44YprWFTRTSBuQ6zmcV\nB3aGLNUR26rTRlXD2UHJa7aHbI1qbOLav+kLsVc9o1RXHXcIIBtCumCJI68SSQI2hR2AYU00i4ie\nSFk4XBGt2LZZgCxCoTLoUMPpRVyFhFNtyER0TjcWtI5WwF74SmLIBW/TBcvyUtqRo7Q18fmE6nDZ\najXpxocSwi02L/tiE4bGZxI2RhVREqa7p3MoNyIWnWO7go2LsHMugoW6TUxI+CTXM1XFracu+nsT\n8P/ipn/u0hJawHD5HDpQG7xRSmJPy3DN3Ojyi4ub4SYWRx22lybd9ci8O/X3sulpMF8nA9IYikjx\njHoE4KIK5VH6QP0NFeSXsbS01BoigDvvvJOlpaVrP/MNHNKxQ+8qGryT7rH9rIZugOfUxDsX8i+2\n85A7onlGskh03zP9MsuLpr22lvVr4Myg5BVFxn/GeSu5UVuYGsfTScXBacrZxSI4n2R1oMl4lEAN\nR/OMkTNEzvD0qGArtaRJqF1sm6xKKlX5mWU7LinOJdhNQ7q/DjJmV1uMGsxPk5AwqjlJ8oJo763P\nxtaM3iT296KPX1iIZVNJLJMogssx5XLtvc5IbSolHNvXvfzzEuoCFucJT+6bUc38tZz11Uis78DB\nzZjttGLrssdo7PmIwfES5pDVXZNLGX3RMS2aL/VhUg8mVf16bWgWeFukWzriHRjOO/xJ5q1q5nKY\n+Wcuxmba9NuTTKWQYwWf01gP+GtK444kKZtArrKufVE/2TzkeNejHk2PZ5VNO3HiBG9/+9sB+Pzn\nP88b3vAGvvCFLwDsifHcGs9vXElqbitSluuIDeUdATyVlfx0PmRcRVS9z/rjtnlK4uCpYYmxhttn\nA54wc+rsmZFGlzrq1Yp44yUuqmOgWKwZXUkol58d3jXeStgc1NRXubW0NIzzhAurEkfhGZU3ov7u\nmcYLBE+9lMYzGqM8zzl06BD/+q//CsCBAwfI85x/+Id/AF6axqiVA1E7jo6H9e4so5+q17jG/qWQ\np6OzDMLolayRKAQENUB0sbmUE/RZxO3/A+fSkoPzlMtRt+XWzr8bTyQlhzczftR4TjqLJ/cRWzhQ\nJfzXQk7dMKqfjOfcMR1wfpJTVq4NG+OoIWHaiGhkqRvd4+3aMZoZqtluLlF/frTsxkRlZ2Q+dClM\nUYcdSPrH1JyiVnFApe6F/9LObewYVgZbwnjBn18rLUo7cPDp8snllAvjvA3TF0dNCO3gwOWMc4OS\npxqMJ5lFDIzDNc9SMoWtxo+DfCNqMElHvOBr+iaqBtKYrnV0Evu5HaoQXRQWoSvZMDWMS3DKCxtl\n3msRD+fwql9Ha01ZzpnLvRrEKPRkBE6Q79x5yFNU5HhabhZ8Nb/W0ZJ+gH3tJ618ca3jGY3RX/3V\nX137WV7gsdRo/Wrtlr7krH4RWhdYAdpLY9+uBeDuw/D/PeH/X4yP7htWVF2qnqa4s60BajAUcZ+l\nVXWuwhipnQN/3EtxzVGbMbS+qeJQCaNfSWoOVAnLOwnnB1WLA2gqwdAaKuMoI0dEs3AGlrqypNaQ\npI6lMbi5YWkjoa5gtOSon46ZljDMfUjihs43wlUEUsFsdIsbPdpGBb3aOZnXPhdG1/qVtTccMndC\nI2jD7TQ0ivMSbOILfBMMtXWB+FlZ+xBsXkJSGQ5cHPBUVlI2mbK1hab9j4N96xl5BWfTqvVKotxg\nh24XHlduRLAZUW77luLSDGA+qzErNghpnetS+qIhpCVujOmMVy4hpoEkMkEZkkgRiyHbzsOC5KwJ\nsXTqP03C8D2Ju0Ja2TB1GUdedCGtyNJqfE80lMAb/bzonuXgOiTYn1PN7etf//pnLAN5KYylEWzS\nvRjjXhZH8CJZtBoMlp+dg9e+wv8sgCg0D1FxlIQsJi/QwHMZA4xJv5DSn7xUD1mOq8fmsOI2l3Ah\nK4MdDwOnRgU/MR2ymXgwWwOiOMiN7wprmoVtHcSlIasiZpllEvlMUH455sgdNcXEtljL7Jwh2vGZ\nLJf5mqws6YBSraIIXi/n/EZIKNX1XtN5eG+ZMhbGeOOj50arVMpOrLE+XdsmJMLYQZy69llI3d4o\na2q68oj96wO2lkq2soqJ8pBdCSsXB+Sx44mRb58UNfM4mEeUa838W6gvxyRbngsWrdZwW4Vp8DG3\nHRFtRbgVG+Bqwn2CDv/qg/u6WDWJ/TMzzfXJsxUsSitJrEy6uVhuNk8xTmUV1siV6pzy877F7nhb\nM7i81Rkb+VdXJwzSkMBpHW30cT0A7D0rSt7ylrfw+OOPB7+7lgZtt8ZzG5fTin1lQnSVKZ9HjrOD\ngmP51bcjZ2A7sRyfZQxrQ2oNr9wZcGlQtVXX9Y7Bzg0Lh2yQdTQDB0OHG7ofszpeQsOCcYa9dIUW\nNhP2rWdcXJmzvRCmgJLKcPTSkGlmeWqpCDSShpsxdeY8CdVC8lQKuSE+WpG8siRasm36HYDUYf4H\nahBdz7GnZ/Trv/7r/NzP/Rzvete7+J3f+R3SNOXnf/7nX8hre95DOBgHGpdUMlbaA7J0O+ggCevN\nJD2v67O0Ro3GhATDsDb8rtYOrno4ic4YlU3Ipn9nHUwrx0Zcs7qdcmZQtt6D7AcX4pqDeUqUR9Rx\n5zpFxuNLjw/nHCxSbt8ZMHCGzeWSzVHFKIFxBuZSwsorasZDj+NIRqm2vsRhuTmkZAJ126fNadgv\n/vJ2GOLKnMv99stsNM9LS3qIJ6HT1xrbE09J5no8gEUM0cgrQqYNI1uubbiewCzhqdvm1EknwFZb\nD1YfWR+wvlhxMa7a30cGsp2IpIgobisZGHBnE4rE4lZrTEyLIemKd3IDI4dReKDOeMr9a7xSPE59\nj201vXOBNy8ZW13yonGao/tCqRcJ3S82TXyk6l+8fSnbkWs0pmnj1Fzr/qXOGwIflmv5FgnD+x7X\ntYwf2956e3ub3//93+ef//mfeec739mWbhhjeOihh6797DdgGGN4U9NjshUNr3YLaSVx2A++rLtw\nTGqafvKV/ufpvPvMOu/OirSD8E/a2Dn1eJO4s5LO1oW023kY1syK7vuCCeQFJBbu3hxxajRnp2k/\nLUbTGLitSBg6w6lRR/rRwm7geTQLma/5kjGsDCuzhOT2kiz19yaLcnnshd2FGyOtkbSeuBZqzwsf\npslLIrVgVysPmAxCgPnSVojn9cNleXHF8Fvnn6U811EGB+cx6QjssldOXGjE74yFw+dGnFzJ2WwY\nrK1WkzUcvjxkfaVge1h3ekczj/0srSdsHygZDL1nlcRg91ckyW46ghhpdzH2bPHVOigX0vrhYmg1\n5UQTF9sedhUk51JmR7rnKtha26/O+Gf1ygP+51fs9//KsaUkRkJEkZkVBQsB02Udp3EYaj15IcSM\nRJtdvrM87mguMr7wf19b9PRjMaM0TVlYWCDPc7a2toiuh07ACzBEcF9eyiNrfvcWDGnYYAkahNY9\n4YVV/P2z3c+aRawXo+zeqdqRNAmyXz19aQvKEvbNEnZiy3Zqg+Pplxrg6bU5d20OeDIq2MjqoEvE\ndmLZl2cY03lOYozkvFnSkPlUNfeCjVg8YMkmnm+yNetlbcpOtyZqvMB6D+VJ8QR1MSqEVfsyN1Js\nLLu1dEFtdZbj3dpR2hCKIZAuSWUB1WbMzqTATT0gfX6jwQQtrJWNFpHUZ0UQV4ZDlwacXyjYTmpM\nr4ZxNI+oJhaTgC2h3oqwxwuwMIjCTjHyrK3D90/bV7Ey6V74UxfDZyFsdOkWIhpC2ustazC1wZkQ\n3BdDpZnuet5XFwj0uZfGfq3pbiD7FrtnNy+9IRHsMi/CjSFNQkMqhbPyXOUdkxHgls9z7GmMHnnk\nER566CHe+ta38q1vfYvxeHztZ7s1ALhrZ0Dp4ECZ8rQrOW329nFnieVHC3OObmWM64gfmrIlQ+aR\nZXQVPetnHNsR8bEbIMTzAo/hPKLKLO4qeJEzgIPxTkwd+YzXQh4z3kq4Mq7YHl2dl5TmEbN9fm7S\nnZhqaIPWRVcbrsTrGl2v2jXri2X/p409jdHHPvYxPv/5z/O6173uhbye6zLEndWyFrosQf6/nyHS\nLWukKlmOp70oTYvX4Rb4kEerCerULDSs3CriB2O/lfyv6ZDtgaVuhJSl2lrXIO1Yy5Vhzp2zAT9h\nBjyRFeQ4lsuYncT6ynfliel+WtJtRGRijx+AtQzWDsBgwV/3Xbd1ntsPznV4Anh8RtfdSalHX7pE\na3Zrb2B5HM7ddt5leURio1XcbL4nu6x4CjIk8zRIAQejKzHryxWJ8sp0qPFdU3DwSsL+2rPQdwY1\n50YFW5mFqptnHR5WiSOdR5gpxLOI8lBJqUosdH2YPPM4j3ATD/g7B2cu+d/v5KHomHg3WgJF5gv8\nvFQ1xIXBRK4L2/BZQy2dLPWAQrF47Cy8/q4Q25RQDfz/65Bw1qTl5fvbufek9PG1Lpdu/6TvR9b3\nRJVLPd+xpzH62te+Rr+t9ctl3LYaEsTiyPMrdPwsDwf8y6DrraImZaxJki13pYcB6Row+VlzSZLY\nu8eyaIoKrHFkBmax48yw4HCR8v15R3DULWKE31EbeHxhzr484X9Nh2zGNSMb8dSw7FLCdOljWXTb\necMzqrqfR8Zx5aJhEjvmpccNnlLFnVe2w5IFPTeCefRDVQ2cQvci1MqY2R7G0G+AkBcd1wiuXrku\nocJgFmFTR5W6tqp/Ou/KcwDWk5qLpg6EyIyhVWdswyZ9r8s1S5dSqknN9FAJMS3wLeUqumX0MIM8\n94RR28yvBnlTxc3pt4wW/E/WigjyD6aG2DlqtYZLRYeQMcq6+XzivD/2bQ3BcnMKrznqfw9+410Y\nduUf6zshmXVedsYQ/D1qPSR5NlrnSp4H7KamPJ+x5yFerobo5TA2kppDhX8Tt2PL0D27uXYGnh5U\n/Nc4J48cl9KK9eS5y34M9tXsnIsppy/TZ+x8q+7pj5HWfb7DZo7pkYJird6TLtAfJnG44vrNZVwY\n6n7L6/8B4zmRHl8uQ2j7GpgcDzqrLi1XNLtU2960KdDUu7+uhtdAXltc20tpa7lOXeEOcDopee1s\nyNE640LD+NVEOe2VCWlQvIh5CTPjONPoYi9kXUdc6Fi+mqZf1mEl+bx0xEnNU/+ekN1eUkdd6CQZ\nHzn/rKBtpQzeA0zWY5J5hCkNNrOYSU3SvDx9tUVNGC1VeAddswDxDMq6SyHL5/2240kM2SyiSpyX\nOSnDdj3aKxQvTj9nfW/SsrlPUowzwNIy3yvl9UrLHvDnvbgJ8agmOpVhK6gKiDGYGuLIwNiyM3SY\nBduGebqJpG7YKaJ/8TyiWPU0DH2tFlp88NDK7mxWUXWa1HEE/3m6C4FFXUDOffby1QmYmnYh7bwB\nqli1aWqGLiB/QZQeX45Dsgp6kUOY2SrUSyH8D/lcOBq6ZY2WEFnf8Sxs+Vut5reT+0Wr8ap+LVya\nwn+Oco4VKUfLFAPstzHrac2kcY/lJZ6XuxncfbVHvUhEZkPfW0xnnIrK6+3U1pIB+x5L4XCFyVw7\nR2m8m71bNUWjg4sJhYF6scIlDrMTMbycsL6/s7jjQYgLyTyKxnNbD5X0pEjc7tCgr9Zpa8h2YjYW\nK4ZNJk/LZsgcyNDZPM3vkX9NHdIudO0bhAqg8nOrwjmnbecTLVfY3GAjR5Q6iHxpSlpEcDqhur0g\nb3BKuV4pudAbyVLhQflsGJb51Jag7bhkHfWm+INzXar+jkN+bkRbSSRuNRiv6+ykDk3TDjT/TXSc\nNO9JG9LxjcSMXs5jceQtv5QsyG6m+Sp9Mp7W+xWylxixWRHKqmoagGjuaOA0jUOAN4463Rw5Vw38\nKC15fT7i7MKc26cDfpjM2cptywEBf51pFL4QVQ3D3sNv9ZVMCLDLfelCSOea72cWh8OcS8j217Bk\nWylRAbyFEzUvIVv3B8lXKsqmRCIeW5LNmDL3OjxyfA3AtzrOPeJebcN5M70XX+6nVi/rOI+YGcc2\nDoqQL6aF7/WcaIBav4C28nV8IxsRlcbLgQxrtoyDhrOkPRl5duKNiCFKYmDRUgxCzetZAfPaYRPL\nvGlXvZ2HG43mLQ1jmEwTpgcKinlIYpQh93ph0xt3Mdz9jfc7P/JAuibuigwudBiQBuO1dpQ8R7nW\nlYk/h26vvTi6Ph6RjJvSGL1chjWwGdfEzvDksODO6YAnBgU7cf3Mf3y9xthRHS6JL6ZQGThy9XPH\ns4goj8gPlSGVwECdOpIyolBM8BsxjIOleczGyt60BGNhMosZlIYRhsgaauNwkQ9zCutIjSGykBhD\nPLYwclQTSzH3EiODCnbGNQyu8X4cxFsR5fDZHWeQR9SZxSb43ep/2HhRjNFHPvIR/uIv/oIDBzx9\n9A/+4A94y1veAsDHP/5x/vIv/5I4jvnkJz/Jz/7szwLw6KOP8u53v5s8zzlx4gR/8id/sufxs8Tv\nULJLLI0JBM8k46KLDiEk1+nQSP4G/O/2LXbua1523UhkaDXDq6lMarXA1BkuWcdsYHkimnN8lnG5\njMhTzyeS69aYlW6eJ8Q4LdClaf1yL/re4igUkqtj4GgJZ1JGU8fwoA2utyphtBlT7q9IUk/+0wWW\nVF11e1V3IYFcjw4NdBgk4mM6FOiLsWmMYjKPmEWOKQ6qkI2O817TaDumGjjycU09dqwswWzq69eq\nwpM/p/iM5mAIicJlXOwbIMSFYbIVE1+IqVYqaEJYwXxk7vISxsrrjIchVaC6GFPPYbpgoQm3JYyX\nuYHm/A4m85iLo4pyp3tG8l2ReW2za3UoPyLKjBr7vLgZ0gfk2chIk92ekX5OElZDl2HVrZAWRx05\n9mqM++c6XhRjJOUk/ZKS733ve/zt3/4t3/ve9zhz5gxvetObeOyxxzDG8OCDD/KZz3yG+++/nxMn\nTvDII4/s2SEkL/1E6bbGadIZDB0bQ/gi++vbrTdkVJilU9mp7Zjd0IRI6nNxfTVrt2015GDsIszI\nkRooYst/Rzmv2B7wijLl9KBsdYvlBdY8ELk2cffBL1oB8OVz0S+Oah8uamO5OW26uibAkZL6ckpV\nG4ZHakzUyOSux9SJoxp0zQUlFDF4wLZoeDaCPWggv5VHEZqCMpQQYnP6Oej5jqz3is5PqqDbhzHN\nZ9sJ1IZLi1WbiRrhQ7zJBMCRl7ClWMmJ855UW5/VGEY7cNQLFXYWMdlMGKW+rVOdOOIaoqnBVIbU\nOPLCMS98WCfhaV1Duh0RbUZs7y8DyRCNH1rr12UaQ1IYInxXYD20NlOsNoHlsQ+hZE0vDDtKBHQy\nLxJWxVHItE9ib8B0t189qrpjmINS3FQh9vpO93fXI7X/ooVpV6th+dKXvsSv/MqvkKYpt99+O3ff\nfTff+MY3OH78OFtbW9x///0A/Nqv/Rpf/OIX9zRGW7PupQRv1fNZV2ApeFGrgW1Cb0Vi9WDnaoYA\nyvIC6UwTNNkr60sbwD/QSunQiOBXbWHUdALZqV1QLPr9bM5PzUZcjCvy9BeOrgAAIABJREFUxAWL\nUHhMfY0g2RmXxiGYmBeQXErI5hHOOGJjKEc15cRiU9e2KU4TIIbySMlwOyE/mZIuWdwFg90yzPf5\n8Ey0kFutqAr2Ja4V6Bf8rC2gnIeGURtywbbkOQipTxNJBThfmSVMU0uduhZ/K2sYFIbVacJsYNmc\nVD6CVMfLy64842pyLbrkQrxYwRrnE0ty0OI2IoZ5hJsarIV57KhTh5tFxFcMdezYWawwTUPPdCOh\nrA35Wsm07DYrwe90gqGqvfFa3UjYXvDtl+Raa8Jry5LOs9HeuRxHN4roN6+UudC8oqKCoSpz0vw2\nfUzwzqH21MSrbbHTG8kzutHjU5/6FD/90z/Nb/zGb7C+7qsyz549y7Fjx9rvHDt2jDNnzuz6/dGj\nRzlz5swLfs3Xe6xUCRtX4QlVBs5kXgv7WkeSR0SVYetAwdahkp0DBS6C8cWE0aWEqMePMTGMX1kx\nOlQTxRCv1dRHyj05N1FlfFuhGzUcLM9jUmtYH3ZzZRysTGOWpwnrixXbk7otk7muw4BdstQHK4oj\nJfMjJfO1inKxZrpSsb6vpMwsy1cyVs5nLF5OsZFjY7XEPkueUlYaIgfzZ4kt3azjhnlGb37zm3nq\nqad2/f5jH/sYDz74IB/+8IcB+L3f+z0++MEP8pnPfOa6nfv/eayL7Y/tg4WRT3lqxnVf2VHLhAhX\npVS4Tz9s09mioVIgFBkKGZKZk98Jl8UAa1XMD7NiV1M/6zywfVuZtJ6PDk2uVlirQxzZtQDSwpAP\na98FooYkg2hfTbVWE29HLFxJYOaoDlWQdozpxTV/kmwD0q2u9ZDMxWazAw8qz4TW86GzMkN17/3w\nWDAQ8aLyIpQ2TQzsL2KSKuL8uPTFowbSuWF1llAmjqcXS5K0ey6aQlFU3oMTxU5pumDV+aXjB3S0\nCQllxMvT4aTmPdXWe8F2bJkNC+/5SZa2hsqGuI5U6eu/NxYmm75ejl52S2N9knmUa5UqfL0udEeb\nVvGg14yzxbuq3dI3pc7sZd7bkXuXtkZt6j+GH13o1B2uxz5ww4zRV77ylWf1vfe85z289a1vBbzH\nc+rUqfaz06dPc+zYMY4ePcrp06eD3x89enTPY/4fd/iJbEHmIgSsnfMvyQV5oRShUP7VVcmxIQAG\n9f9b272A0AHMMsaDkB8iL3NSR14XKfX+uO4EmsYwcQYS1xlChVnpdLMx/l40R0qn9qPaUKnWRlXt\nAethBqxazIol2oyJz2bY/SV56ji/EXbU0CGs3NttTccLUxgqlXWSVLzcr8Yd5Px6foIQuEntx/iM\n2GQeMYsdFxY9mJ862DdNiErD5WFFOXBkKpwWQ61LaWrbaTVJiKmfo+5IO8rCDhkCEks5i6ThAw3u\nZjhV0d/2EitC42OiDjcCH54t7yRME8s0cYwJAWcN7gu/SXxDubegqt6G4XufzCtlTuBT/FrjOi/9\nGtJda3RtnPCh5Gfp3KvLfr77JNc0XhTM6Ny5cxw+fBiAv/u7v+Oee+4B4Bd/8Rd5xzvewUMPPcSZ\nM2d47LHHuP/++zHGsLS0xDe+8Q3uv/9+Pve5z/H+979/z+P3+5wZ4xfajuJi6GJUa/2O1geJ9QvV\nb5Gsd7eiUpIbDZekxXBG/kHKopBGhgdszNawIo47Vrccr7awXCZsmO4l73sUmu8xGYb4wGSgMocD\nmAFS+SYvlHh9wwzSAzWjfRZ7NsGt+tWp2+1EJpQkiSPPALYlXH4qolyp2m4bVe0xOp3ty9X/T4Yh\n50kXMDsHaWXYP00oUsfFpZIcnxAwDg5ME+bA+mLnJfWLlrVOs8yrfq462zVIGw1sZSy1gRE2uGYZ\n9z1fp/AzAXn78jFa77zFXZowM7OGK0sViQnZ4RB6bVqbS+4NQhKiCPnJver7SRO/LtKesdHk3K1Z\naFy04dZJCeiMk8a0rnW8KMboQx/6EN/+9rcxxnDHHXfw8MMPA/Da176Wt7/97bz2ta8lSRI+/elP\ntzVyn/70p3n3u9/NbDbjxIkTe4LXL4exVMQsFwknF3OCVrbNWKliFuqI743zq4J6xkJsn139khtZ\n4nXzjE/ajBwmc7jtCBafHXZRPJ1glmrfyuc6wB3jecTSLGZroSYfNFrSDYC9b5pQRXB5UF2Xhf9i\njqQ2rG4nVJH3+nQjyciCfdGQ3Bd3/Filx5fjMMbwf/2M3x1bGQznrb5OwWsXd16GnRSkvEJCJy3x\nqTM/0El0SIviUeZTnnLu1QW/c0r27VCZcHCe8vgkJ09c2wSwqiG1hsNVwmqR8IPRnJ3YtjyjqKEC\nTGYxC/OYJHZUmaNeq1hc7Ha0URZiJ/m2YetkwsVVH+oIrUC8h5VGYG1egt2MKC7GzA+VQSdTXVNW\nVN5TWZjFuO2I4R0lm/POe9ia+fuf9rxQmdfFUdisYGvWeBSVYXU95cJS0XpxLX6RRywUMecXygCc\nkMyUZg2vTLrdWrCzlobReKH63odZuC4mw7CKvqg6L6+vYCmf69/pkDlLPFZZ1d7IZFXEaB4xrCO2\nRhWzoSWOO28ljWF1HrOR1r65ZtR53Mtjv050I4e+1KuW5E3isIZSvHsth1zW3bNIm0ydbjml6ztr\n23Valr/XVQtZAo988wYqPb5ch7jf4oJuzRqcqFmEC8Ow9qyoGq5H8yBGWVekCY0Knri9+Aegw5BU\n4RbCC9IFo/Iir00TlubeI6oSRwxkxrBaxwznMeM64kJc8d+TnKJpMwTKgMxiRpXh8krB6hKkWzEr\n6xlpUhGNvEC8lDu0uEbqSAdwIImwY9sWCMvn4ponMURLlvhKRLoTkYxsOzdaWsIA5nzCZm0oDpRM\nZt1ChU4mQ4xxbemaADQbgAb7JQyaTCOKSY1rFBahCcFqWMljLowrX8ZDGBJoCkbWW81iiLRUa2zC\nMh9dV1g2IaYOxfULKVIq+gXVQ3CeogIc2K2IhblhUEVE1jCPLcXQUixWYKCpzGivL4nhUuYvLo12\nJz60vpNsONqwp3HXrrotQ1JJG+kSC11ZU1siZX0YJyl6CefFtogh0iHqIO3giOG1J35vTmMkLV10\na17oqvZHPZxAAGEtriYxuPzc4hIuBAZF1FxXyWeJIgU2oGy1GbG0k/Kj1ZytyhHVcGSWslwmbKYV\n66OKs2lN3nghuk1xm+0rI6bjGpPCdgEMaoZrlngzpliPYbkmW7PMq+6eF0dQL9ckeddGR6Rowf+/\nFthPD9SYJ1PsoCJatCHOUUF6KcEB8wMlRJ1n0Bdba4l9LjQWVxNmMxaGeczFlSLwpJyD5SJmljiK\nxGGt3ww0Gz4ytNm0/nPtN8usbajfLT/Lc764GXKkBC+Tn8UL1tfXr6cTL2//TkJlHLPUsjWuKGNH\nHHsPR7zYouopIig8So6rdbP6c6fxLzGCQacX5TWK0db4nDGdEZFMX2toexww0XnXnpGcB26wuNqt\ncX1HEVuMA9sw8g7mKaMq5rGVGTUhOLjnMYY1w2nEtq6Zyhwcrnx3io0Y+3iCGViY1L6JG0DZpKKe\nxTADhzlSYs8nuPUIBv66062IaBZRLdSUi3XYpucax2gWMx9Yz8vpzcO4jLg02rsW7aU2BqVhbSdl\nfVix3bQSvx7s5P8J46Y0Rn0VRqlVE29FxMgltEjisCGepFF1OrztEBuF/0p2SQuZaxkM27jPJoV8\nUJPtxCwaw0oZ8/jinEKlpeVatKKAxkOK1LI2ixhPY+oVf0HrOx6XijMHByqsBbcRE19MwME0dcRF\nhDtS7to15byXtzvMa16CiR0cKmEWwXaEKcEOLOVyhYt9StpW3XXp+XDOewda2kLPWZ+nY4BRHrGx\nUu3qvJFaTwYsG4qDeDX97iGpOn5fXgUTejL9ppJPnA/VC/Xfi5SKbnwYeC9Rr4axgtXthAvjknnq\nWu9D4zJp0jG8peuMLu0RT8W5UHNLMnl6XVjXqUEIpUTLkUjjR/kZOi9O88BkiJqFnE+HeTlhtEFD\nKdHRxLWOm9IYCeajXdp+XzII9X+LqjNWuj2xfF+/UBKKQWeMNNdF6oDk88nQL0Ab19x9fsCWs5xd\nnRPHjrhkF+nRma6DRJ+GsLFYcWg7pZg7qpFlmIU8p8jA8GDN8GgNhWE2hQhLNfSAi+AeOszUGJMQ\nLMsaSC2uadecxD5EkrICHSrp9khBWEeoGa0Nify8MovJY8e80XbVXVOz2lCmjkptEkkMmUpM9NPZ\ntaX9vk6NQ9P1JLuKRpK6Vm0Md+YdHUSGfkH1MXCwf5awmVnyxIHrDIK8qPsWw1BINgUBsK0KdwWz\n1JuGNuTaaMDuFkp9DKeqQ0MYRR3YDX6N6r+XDVmuZ5h2XCToNL5kLnQB7vMdN6Ux6ivSiaehxcN1\nFgZ8xksmdpD6hyUTXNWdoRIei2A6o0ZQvi8cLzow8nJnCdSTmkuLBRfimjnOM6LjcAfUCxV272yk\nMF2tWN5I2Zl49vbyOATUx4PmBUgdZgDTeQeGyw6ryW2aRyTGRO5H1+tBp8bY58No1YI4ImhtFGRw\nlGcxqA2jecTltZKkwT/KWhUlWyhwAWlQPE45nsaF5Dzycvc9pTT29ykv5E7ujY2wiPtcGtmE+oZX\n6yMJ431hHkFt2BhWbcJPGkpKbdwrD8DtB+E/GnLghc1wrVauq89qvXS656AJleJxynPSnCBo+sup\nJEzfc3Eu1JKaDHfXNAbHq/28aaHCOw95FrYc71rHrWj2hRwG1icV1dV6Vj+HUWcOFzmil3E7ZWNh\naTNhZ7Hesy2PwfAs5cFf1JFYWJknHtt6GVzvS3XclJ6RKNi10hW9lKS4l7oGaahkN8Q9lb9ZHIWu\nvG7kKJXmmvVb1d3uC6r6nC6212HfMA09EZ2x6YcEEoqUxlEVvqh2Yxrenz4+7ObH6OxfX9bWmNDL\nMaarg9LH0jo6uoWO3GOfxQ7dc6lrb4jy1HqW+R78LwdErvPCpLSkf6+aA6Y9Dfmu9jrXd0JdaM3d\nkfuV48X0mPounMvaes7VoWnCpbRiHnlFAc3APrwKd/tiA55e9+dfazylrVkjXau4a1oiV9fR9ctD\npExI36vGnIaNdy8ejoTamr6yfwkubHTn1rK08TBkaFvnm6FqtdRXHek8Lq11/nzHTWmMBBcJeCAm\ndFWNCfuB6dS+AHW6e6ceWuNaGyX517ou1SkSslLrFRkgUuJqDeZkmnP1SYvCNdGLYDqHYrmG2LXF\npgLCyrVp8F1fZ1+PScJELQUhgnHgDYj+vN9cQATt5QWW7+uwQQPWIpmxFVs2IwtliOsERjStcc4E\n2lD6c7kuea7DJMQKnfNa52I4JVzv31t/rmTo5IFcfz+9bR1sJJadxGJ6eNl4ENZ7iTErFT5X2w67\n0TyiNPbpdb0OFke7y0PEmIihl1BLJHOnqj5Tt1U/sua/I89tfcffvxZL0wXXcRSe/+xl+K/T3Rzd\n0sDeY8gik5eg7ynIotCKgqn6Tr++x7kQh9APqbYdniLHkqp/OZcGF0VbW3d96L+MGgcRjRlZJJ3m\nj2uvVfNHyjrEAgRw7QuSOf1C0QG1aeNpiKF2vetvAU3FT1kcKaA1h1kZGkEtJmYbA1E07HINCFfq\nRQQwCSSxCzAb3flEvFvtKQ2zTr97OvfeR6S+b0znLQi7Wm8o2jNr56dnfPoYVRVbcJAJIK3q+rRm\n9r5F30TzdNPk0ZgQRNaZQTEuLZjfcNfEqxplYdNF02y2mkCpKwemc3/fmgSpayaXxuGGLKqd2kDr\nxMzG1POyBDsVXOxaxi3M6Na4NW6Nl8S4KT2j5bHfjXSadDzodqG+xRfXu5/R0up12hMSLWT5W628\nKK687Gg78zDTIF6LlgPdyTtPQ2qrtBSrc92OJDu3rqPre0NyXeDLA0TaVH6vQy2Nf0GHIbUaRL3S\nhzjy16pVA+TvoGNca2Zwv9uujMiEIaAxMFLXI1hWn+2rmfVjVcKQNfIf4qnKc7Y9z0qX+fTr7nQJ\nhD4n7OJjtiUY2lPrY3yR8kKXJ35dSkgtYVnLQ1LHEqa5XidJDGsL3bHjKPTYU1XnpjWa5DrKugun\ntPaR/L3obIP/7lSpdMo8yToT71KelXQkvpZxUxojecF0+JTGUCgQVqdxg5oi/ETXNhRb0wC0tWEY\npf8WfKx/tUJROZYegt/oUGWUdSUDm1NYn4YlDCPFIZGwTZ+/n462trt3OcZVuTLN/WVxuCh1KBH1\nXjgxPn1xOV2P1v5tY1yMOld/TvraULq2TY6njelcYU5lFRo8MSxirGRe9LPUxqmfntblFnq0YZ8y\nBDK0XpMkPqSX2eYMXrE/NH7aOA/SUBJEPycB7w81OlKC8ejaMG0MxQiK8RhmPpTSRkTLzB5ZC5sF\nCGFSGyxN0BwPQjrLLZ7RHqOo/ELQE3l5uwMOBWTWO5qA3tBhTrp+Sy84jSuIeqD+TGfD9IsK/poW\nlKbPMAu7Z0itmxY614s2isCqTJ+Ax33Cpmgp9+U2xIvTno3W9I4IAXvZEeU44oXJ7i7zpo1ZmkDZ\n67gi/983hNaFXpUuWNZ4DXTZILl2qRXThliz14U5r7laGiQWz0kboch0pEoBmPv4V2tEze5npf8V\nw6k9v1MXu3U4nYfGUwPQQubUDOfxoDuXFPSKRy34kPYeteLA8tgbHDEaV7b9sQVfEyOl1/ziqPO0\natspXcrQDUOj3jp7PuMWZnRr3Bq3xkti3JSe0YUNb9V1T3S9u0tV/l7eh3g+soMGLZmb3XmmdpJ+\nNkyHSX3SnlD85djJVThJuu1z2mRRxNW3jWcjJQ/9MKlfgiDyuYHnorCJrVnoCfVrmMQr1Lt3Xvid\nVb6nq+WjJkPU1+SWz7TmdWTC3VyzjeVzYzrcSkoaxNORtLlOvfer/uX38q9eB1dL5fdr6fTxxdPS\nGS7N2dIeLnT4m+5ppnuRre90WTA5n8bmtCKAMXBwGU42svKXtnZnz7QsTl9CRNaFxpI2puG61oqh\nl7d6SpMpkHbXc3GTQA65L6fyfMZNaYxmRShdIcZBJloMghSHTpqeU1r+YmumCm5V6nxehkQ7CWO0\ngJc2ZBIW9UFU/ULocpNZ0aVhoZGwzUIujA4T494i03Vj0BkivQirupNKFWOla9ucC8tfxGhA2HxA\nhnWe4yPzo3Effa9XW7Aad5AQq89R0nOnuWHDNDSkMi992ZAWzO/xiqKe4RUjrQ2xvu6qvnpIrTcC\nDQ3kzVzk6i0zJsS8+kRGTeCU8hXwwHVe+hIS+VwD2GIo9TrRz+niZtcjT+45L7qwrahgnIcb9Hau\ninpn3RzqoQ31tY6b0hhN5+ELK7u7nsix0ole3/HfFRykFWRXFen97Fs/46N3Y81FEbEx6VAhTQ37\nnUg0qCqZE7nO2naLQjASMSaCYbSgaULbLBHC48rPgTGLuqJI8PVRGmeaDBpcrNlhJ8Pw/uQFipRx\nLRX3xxiYCx5lQkVNeeG0YBjsBr31vGs2fV7imyqq4+nRGid1jKsB0n3vQQzKKAuzToKR6LpE/XN/\noxEOk1Y20IbfOv98F1S9nV5n2qtc3wlBYjGCelPsrwt9rKrJjgkmlDZMdWFOjwfhtcvfPKWULbTY\n2+LIG8brKQH8omBGH/nIRzh27Bj33nsv9957L4888ggATzzxBKPRqP39e9/73vZvHn30Ue655x5e\n9apX8YEPfODFuOxb49a4NW7geFE8o73aWwPcfffdfOtb39r1++fS3loYzrqSHcISCK12qPEZ6NLX\nshPpsMxff5g6v1p2SHYl4cK0HVar0NUXCkI/va2zbYujzjOqLWzsdDta2/Gk6u5hmIWhA9C2pYZO\nikPOpTNc8v+CPUg/dTleWe3GyIqqm0vhYLUp6Z6Ui2aziweU9kI8TZsI0vouDLv6VfWS/dL4VeX8\n38n39RC29NUyfu3cqRBXWNA65NUMbrkemXPxeHTNow7j0oZZr5+9zKNkaeVYFzf9PMkxxRuX/nVl\nFWa7+llc8eAlzM177wbsVizoz7XmMYGHOeR6p1fxOJ/reNHCtOci3H3u3Lnn1N5aNHEkFErjsLWv\nhG1aaF2nhOdlKKqljYO45LqgUZckCF4kxmGQ+rBJE/X0ubWchwxduCov2+Wt7vy6/5ekpnXPdC01\nocsf5F70vcoLrEMjvZAFI5NrHGb+BdI1TRvT3S+cxh7kb6cNAVQAXTH6fT0iDTjjdpeLyHC9udfS\nHjJ0yCscKI0ZaQMh62Ko8DL5HvjvBRLEPXwrMoC5OgYkx9PGTwB4ncDQmxh0HC/ZYOXcsgHIXEkI\npkNCMSBybt20sR9eyTrUvKaRKh4ve0ZM68vL9VzreNGM0ac+9Sk++9nP8oY3vIFPfOITrKx4Ntfj\njz/Ovffey/LyMh/96Ed54xvfyJkzZ55Te+s+XiLsVBkSx+uJTOLu583p7q4P7S7e7PqCQUa93VVe\nqL4olowo2r1rae8qjjxOIz9P5+F3JeunGwladtdr6YyPc119lPR00+Cs5t7o+ZPj6bHQdM+Q72/n\nuzNQWg9ZeyqCF2lSoHTQgI65LtcqmIj2VPovt969+wC4XJf2iPvHW8p2Ky7Iz2Io+0XFuu5Q37t4\nWgOVPYNQvVH/XvApPR/ytz841+E40IHl4pkMG1E8KZSVigOtp62xzD7wLGRdvU416C1rSDO25z1x\nNV2z+JLWM3rzm9/MPffcs+u/v//7v+fBBx/k8ccf59vf/jaHDx/mgx/8IABHjhzh1KlTfOtb3+KP\n//iPecc73sHW1taNusRb49a4NV5C44Z5Rs+nvXWWZWSZ30Ze//rXc9ddd/HYY4895/bW/9V8NYk9\nN+O21dDqT4ZhDyhhFYtLKuldnYnSoYBxXUlDkoT6PbLbye5eVBATus9OYVCS6pW/H2VhGAXeY5Pd\neqHJZu0oT0dnXdI4ZES3rGPlnfVZ38IEhjAzBrtr3qQjrhz/lQf89V3e2v0dCEsOhuwOm3QmUVqS\nSxgnczBQ39dem4SomjGgr112/r3UG6RmUdfXxVGHy0hvey2Poa9XPGqtX6RLdfqeXBx3UiBy/TrM\n01X2+5dCLFHCLvHepRxEh6ZJD//S4X4+D69l0JtjUe9sGdWNh61rJPX8DlJfjybv2suWZ7RXe+uL\nFy+yurpKHMecPHmSxx57jDvvvJOVlZXn1N76ta/w/7YPogiJi2KI+gCfuNN5Dzx0Vi14FxY/yksn\noYksfg1wQ8hd0YL4/XKOqxVaLgzD0ELjKH2cRbgtGpBOk06uNW1ern5Dy5aLY3cbX31dxvj6Ks27\n0oZd8DC5X/1yyAuldZv1XGRxiH+196v+X9Mq5Noj9bkOTeRnMSajLCwfkTBPg/malKkNp5xLhyZC\nBdCcrOB+e9fziv2+WFY2gqfX/bXtb2gfm9MwcdBPDMg1QQPMKwjAOn8+fS1CUIWOvKnX10BxxoQ2\nocM63Q9w2NTNiTEcD+D4we755CWcfJprGi+KMdqrvfXXvvY1PvzhD5OmKVEU8fDDD7dY0nNpb60X\nG4T6MtBUd6u6GnkZ+1kaLbamWcMaEyqK0BOQz/oa0XINZe0JgrIoRK9a4xJ9gTDoQE7RmZkrwp6+\nPtE+1lrJaezrksD/rearCP7T17zWYzzoCKKCrcn1i3egO69oT3GUdKCnMLO1aF1fu0kbACn+1AXP\neu4hxD36JEb5nTxH6coq53cubAAghkOepWg79XEUDc5rA1RWYNX1iN62zM1PHvceyOXt7v6016U9\nKSGe6nWQKsO3vhOSJ8Xb0gC0xvZkbvXmqPGu2npjprFHja/JMWTDliSNTmxc63hRjNFnP/vZq/7+\ngQce4IEHHrjqZ/fddx/f+c53buRl3Rq3xq3xIo6bkoENYTV4X8mxrV9SaXphsEK3Y+jQROMYeueV\n1L7eUfrpep1BEle4H4roeF5361gYek9Ec1l0+Qd03pB8rmUyRH1AvJODy13nVJkLnR4XDWkdhm6q\nGibJ+Oi5jaNuZxYvUasr9lPtWg5FlygII1nzePTOLMxu7cloiV3tzcqwrrs2wXeWlbSqzIG+Pu0h\nl0qCV+61nymV74sEiGBOaez/X/dJEyxRzlXb7ne6m63MocaXsiRsyd5vEdXPhulQ3JgubLza6HPp\n+sqPojypuzIX8e7w8VrGTWmM4sgXlO6Vduy/zPJQ++UI/TAPduMWQgTTPc/7WIPGLdYWwthd954C\n/5IfWunKRwSglhdgcxpiNGK4xNgURShKL7VzIhUxHnT9u8Cn1WsbkiY1CNs3bluzsFg0ajAkLbq1\nNQvT2X1MZkvVOaXqhVoe767r089O7lkbfh3SCtlUjrdvsWlw2dyrgL7ygovWtw7bdIipQxg5r3Ud\nRiW4Sl8ATY4/K/zzkvncnIbH37fofyfGSOtG1TY0zKI1JH+7MPTHl0SGzEO/9ESGhPJ6k9D/Cn6k\n8bUk7o4fR96oasObl92165KW5ztuSmPUF5FPFWYAuzEGCL0VASk1DhQcXxmTKPJek164unutHE8e\n4mQISRlm7qzzi1LGygQOLHf3omuKtKi6vnZZyHEUFkxKXzW5t6fXQ8ExwTQubXXHEmYw+JfhwmY3\nF+s7ECvMad+iX4jyAp674u+/LaxVXBkBh3XdnfweQhwPOqOvNXNypa4gu70MzTyHTs/HqbnQhl0Y\n33oeoTPMURSSJIXb054vDTN0kk2TdZaX4bOwrnvJwT/TJO6enRRJy9CblPCn5FiLI3+v8lylGNr2\nNlRtzLW6ggx5zuNB6KVKVncedz/raxJPTLy+6+EZ3TCe0a1xa9wat8ZzGTenZ1T1MjrNbqXbWesw\nra9FLLiOuKja80hi7x3oUgGtTySpeM3q1WFZUYXZM8FnZCcrKt9xVLqcbs26yn8I9XDk3owJvTjN\nO9KYBPiwZWHYpZO3c3+OQKaj6HZc6SjRfk43DzLEg5C5FLawnl/5V7g7+tolxBOcTr4vPBs5t4R0\nOv3dv1dp9QRdRkl3VdXHl2uW5y7h+q6wTdEcNP4nc71Xdm3fYiiBKe9ZAAAbfUlEQVQ7khe7aRCa\naqCfw9qCv5c2tZ75Zy/H2s793GnNLim3Ab9etb65YEJ9XpM8CwnDxMM9stZVIsjQNZfbufem+2Hf\ntYyb0hgJyCsPamXiX0ApLhVXWAyGGAvh4mSJ/65TMh86FteuvrTfaXt3paEMhS6HkKGPJ8ZIvj9I\nPY4j16h5ORDWvUFXhyaL5Mq2Nw5lbxHJNfyfh/19y/mWxvDY2XBRl7UvxgU/J9pQCzFR3PM09oZT\nFuXS2L808rMG9/tgp2BpmtMk1ADwn+lyGLlPCYPK2r8w+njOdaGHGHG9MeiXMU1CUqSE83vVHcrx\n+/pFOiTfnIbGajzo1p3gYZo4qMtftISxaHKJcZAEjE6E6BpEweZ0nZ2mnMjfSiKmXygr4bnMxamL\n/rpkHchc6KJn4UIBQTvz5ztuSmO0MAwXofwsHoW8jBp7GQ+6B69rcmB3/RSEOIgwefX35SEvjrr6\nLTk3KB0aG2aNpB5KqvG1MBp0xZF6UcjfQIOXqbo68RDFm7i46Q2MKDWOMnjifPd9wSEihav0+SaR\nUdXajbFYboyTFNJq7EPuWTwJ/QLkqt5Jqs41CziNwwRCZLoXqaw6zM3fbHjtMn8jJSimcaJ+ZrTs\nvVByrZqPprk5AjD370fmdnEUMtiXx/78uhuvVvXsN8hcHHWGVwynHK/PQxMvSeZSDId0E5F71Ryt\nvnGZLIbZus3p7nUvWOMg9ZnZc01XEP28n++4hRndGrfGrfGSGDelZwRhaCQMYx2WSXgl39UpWmtD\nT0d2PPAxv9SHQZcO1bH3LtaqwogkJNRhXF/dT7cH0nwpOZ/u+qDbIcvo83Ogw7/+3x/4ejLZ6Z6c\ndVkd6GQ9csVD0mHkeBDynibDELeB3XpO+lo0F0Zq8CSTKJiRZmj3eUkQymCIKoFcm3VhN9xElXeI\nuqHmj2kqQKRkiaHDAzX1QORawYeq2lsRpQf5Wegi2uPWGt26lEP+DThOdRfiSd3aXpwtmbt+ql5+\nXpl4b1toFaLlriVBtGyOXGPf05KRxh4z0njdtY6b0hjpdCp0pMe+lKs8KKG5a1dTxKrAL369gAEW\nmockYK18bhuSYRuORbsxHKHmQ1erprWV+twcCMO2foEkdH8vhMR+ard9wSJ48sJuHpAmEpYKVNVF\noOCPq43RIPVhmVzvTr47jNQ8II3RCGaiZTIS9ZxkzjSRT0ujJj2So2A68hyF5NinbPQFzvSzE9Ba\n/h66MG1huJuH1W9Lpf8VeEDOV6p5kLnXNZKxWieb0zCxsZ3vNgiRCY+taR+Tgd8oNCVE95jTQL1c\ns9Y7kiROS45VSQB9vuuhfS3jpjRGfcC4rLoMG/jFNB6EJEfhbUBHjuszuKHT4NGaSdZ1WaZh2tUR\ngV+QVQ2oTJ4GnPvqg4L/9HuBpco46b/pEzVFYF+uTxa89uS2VS2aNOuT6+0XTAqbXDf/S9T3NWcH\nvKHSwKpVXiWEIGqLnSgcTTJg+t5lSNGvXJtgf/KCXdluBMWU5s/iKAS4R1lYx4fZbXz6xqk1jnV3\nDfL3ep3INWoCYP/69VyKF6i9Cu0FljWM1fxKxkzmbGHc/a0W75Nr1exwwdaWFRtda5VD6AELZqS1\nm/rkXI3D9jujPJ9xCzO6NW6NW+MlMW5Kzwj8rihWPk1C9UGpote7luZ0yG6ld3StnKgzNvJ72d0l\n7NJhjC6BkNqmVIUAeRnuOq7n+UhlPOyW94yi3SleHZJWtffadFinvQkpHdkld9p8Py9DvSPpiKs9\nn5081EYOQqlezZOWZhkPwvBVlCC1CqUOw2SexPNYGvt7FVxFs5GhY4L3y3pyhbdp3tHC0ONCZy43\n34/C44mHXCglSl3H10+/9zWAhME96GFTOpMp62B5HJbKSCZS6CeybnTdXFmF61DP3cLQn1/KgnR/\nNflXz5XgR/pz3dY9iX3JlZa1vdZxUxoj0V5ptVYKP5GSllyKQtxAh13ysxDorja0Doxo5ghIuTz2\nf79v0f/8owuhUROjt61qfrQhFEC2NQp4nR8Ndmq5k8iAUS9UknRkQOgA80y9IBpwB298tbyKLvaU\n0EcTFaHj8miwGrrFqVPPlboW67ow7f9v78pjorq+/2dghkUW0daVsWVRUZRZELHa8C2KNFGL1bok\nLrjbik1stYLa2FTTWm3FhRq1aoxNTLekjZYal2qFauuOWP2KURT4Cbgju9Bx4Pz+eJyZ+4bBflvm\nKdD3SYzMvHn33PPufeeec+455zpOYDYBxdKp4jiwr0/87Kaxbz/zIiP6y2QvVMOixKYOhyyIJUa6\nBNgFK8eD8VZ9VW3jYnOOxcy8dXJhIy4yGo1kioimmBg6wH0GJB+h+2O5YBbDGjy0gEUovsYhEGKR\nPc4FBOwhG9x+rQMf3AdOC2K/II8Rp7GI5VU4RYV5ay7apDBiiCukuALyS8EDVVUrjwWqb9A0xBo9\n/HJ5e0kTmgepqlaK5eCX01MnrdS8urJDlweRM/Qd43oYouYANC6E5gie8GL8hzhpWPsQg+HEeBPe\n4RHjpkRBJWbUA3afVoUgAMTEXO6PmH8lnu0l+sNYS+PnzGPgJrzAnOsHAP7e0jXRAVzz2C4AeVdU\ndBSLAarubpKg6SKVyEJJpTyAs8fz0mfWHqwNu1niDlWtxb6ZYKs0KQgXdtJz/8TAQN79EnPtxKBO\nWdxTvXxRAuy7h4DdX+YvJOWKkfiP/gTqagFvfzkvrKHz6bPiIiRWruBaTmIOphgUyc9DnFfNheoz\nUqFCRYtAm9SM3Nzk2dGOYGkuqsdi9UPe6hdjKHTCitTB1756sj+If9u+nVxz4FQKsS6M6Gfganzi\nLoio/vL2rrhjI+6OOWZTs99B3B4XM9/56CTRjOJyrIDdT8H0eAV23N0TayOzOST2w0vw37BZxHzz\nvW4auRnFJ3NwGxxn5OMQ3c5tsy+LeXU0obg8i2hq+HnbNU3OzwtrKKfOpimbfY61o7jyoo8QMe5Y\nk7vGYjelnvOTtD1yMOXEvx2j78XTcsUYLX4WYrqIp04+Dx7X2Z8NII29WOKDTXC+X3w2FqtEUzyR\nVpYXCMBC8sqRYsS3m2qmOQermI4lQlid12jkZUDYZ8KTmV9wnlRikSne0uS2qx38CFp3yWzjSfTo\nT3msS2kVUCnco9FI6rOYrOmmASwa+3VZPpW73PHLyZ9iIq543A6HHrBAYAc694+TJ8WzzaprHZzM\ngmOVnd3cPvshRIe9zt1Or1bINeOXiycwO3RZONRYpJdH9AmJqTZcx5l3wnkjgGmzn4Tv9/OWhCsL\nXi7xwf49L53EGwshcVHg/oq1m5g/0fkrLhQcQ8XPShTCDNEM52JpYqCjmNQs9sUxMLe6IcGZ5wEH\nn7LJ2Ucv5QyKZldVrRSbBQDBXaRF6cYd6XNlTeOkYrHkLm+KiEGU4rzTuUCStElh5HhuFdveYua7\nY7CWY7VFnVaeTKgRNAut8LKVVUsDyBOcV3be9aisAe6VS4GGgH0C86Cz8BBz2UqEkzZ4svMLwCuc\nm4Ow4tNKePVzzIznYLZ2nlL7YtClY2Svn7d9xeTDAMQgSLFAmaVh9RX9XhygJ/IL2HfZxNWdX3i+\nzm3yc+/kb98M8POWnqUoWEXotPKdR0+dfRwYYk1qD630LPjZcrtPOhBTjDnjjHtR2LgLgZgs6EVh\n8+ixXBtxjL4X29Jp5eMkJhVzJDwLLx8ve8wYIAnabh3k/jOd1i68OvpK0fh8Pws20WEOYaNHp21c\nz0l0/rfqekabNm1C37590b9/fyxZssT2/erVq9GrVy/06dMHP//8s+37rKwsREREoFevXnjnnXee\nRZdVqFChIJ6JZpSRkYH09HRcvHgROp0O9+9LakNOTg6+++475OTkoLi4GMOHD0dubi40Gg2SkpKw\nc+dOREdHY+TIkTh48GCTJ4SIqxlgt41tfpqG0qjsJ+JrvGL5eNl9LYD9BA9AWgmKS+xq6d0y6Wgk\nPn0jwAcoKpGH8d8plaolAvZYFF79WSvilaX8kXz1qbXIt4hLKqVsaTHPDpBHNYvnd2ndAXdBU/Fu\nqELZVMpEQIM2waZLwT1pl4nxsEp6tqw1ijsugD2FQNwhEmNTxAoDom8MkMajo599dSeSdq74WRY+\nkLQjjitik4i1PsdUDT4JhbU4PlaIn8XlQqCDcLT04zr70ebcnixavl7uk/FoMOvErH5x3omxWoBU\nMSHAR+4jsljlZqhoDovmsVgpgZ+lWGmCz71nX6afN3C1GAh8zn5PaZW9f38USBn3/CxqLQ2+RSG2\nSpbf2TAHuYoAm8O1gonaXDwTYbR161YsW7YMOp00sp06dQIA/Pjjj5g0aRJ0Oh2CgoLQs2dPnD59\nGi+++CIqKysRHR0NAJg2bRr27t3bpDBi250nEb9wjpNGNJXEQMbqWumF7CjUNuYJ5N/Obi8DQOYl\nYHCY3VbnCSQGj4k+GabPLxDX73Fm1gD2Ym082DfvSxNNdFyLk8ajIc6IeeE0F1vxNzfJOS+WohBN\nF/FIZUAyiwb2EkIbPOymKX8WfVKeOumFFVwfNn4CfOShCjUWeQ2fyhrJqcz8dPCV2uKjfdisckwX\n4b4wT2yaVdVK48VmHm82cPs5N4E4o134OG4UaCx2oQA0BBYKfiVOX3HMWxSLyYlm6cNKyTxyDEAV\nj7HSauzP1VOYF5zoLc4NsbwxhxRwH17oBHx/Ql70z1MnCSgAuPVQXhuLfXmiP0ssict13kXBKaaI\ntNqgx9zcXBw7dgzvv/8+vLy8kJqaiqioKNy6dQsvvfSS7Xd6vR7FxcXQ6XTQ6/W27wMDA1FcXNxk\n+wE+8qp5nDkvOufEgmOcIEiCb0DMBhdztbw9gN7d7StQ1nXAHGIfpJxCqW2OjWnfzl6ADJAG9dZD\n+4rCuy0Ni72sT9xX0WdVXy93JHLQJV/nWBBtw8hyZUVbEXqLPMHSzeF+jh3h/nNgnui70Lrbd5w8\ntEBFjbw4m7gDJr7Mvl72wEXm0U0j1XTivmjd7YKd/y+4Z29b3BFyzIdy1Ez820laJAsvsUoi0xc1\nZEdeucKAGIUsat2sOYm+Ri8PILBBS+YdsXvl9t+LmuDjOsCdgBohhstNaLvWIvdviXWieM5yX8of\nSbyy4OUd0QcNGnlZtSTImVfedGAh4uct9Z2vu2nkWuDz/pL2z7xwLJt4ik1zoZgwio+Px507dxp9\nv2rVKlitVpSWluLUqVM4e/YsJk6ciLy8PKW6okKFilYAxYTR4cOHm7y2detW22GNAwcOhJubGx48\neIDAwEAUFhbafldUVAS9Xo/AwEAUFRXJvg8MDHTadmhoKNb/eMNFXPxv2HrwqZJr9jHCfxe//vfp\n0fq/+0+PFgAcyn669HJvPV16TxOhoaHNuv+ZmGljxozB0aNH8corr+DatWuwWCx4/vnnMXr0aEye\nPBmLFi1CcXExcnNzER0dDY1GA39/f5w+fRrR0dHYvXs3FixY4LTt69evP2VuVKhQ4Qo8E2E0a9Ys\nzJo1CxEREfDw8LAddx0eHo6JEyciPDwcWq0WW7ZsgabBKN6yZQtmzJiBmpoajBw5sknntQoVKlon\nNERiuJsKFSpUPBu0qkTZwsJCDB06FP369UP//v3x+eefAwAePnyI+Ph49O7dG6+++irKysps9zQV\nRNkceitWrIBer4fZbIbZbMaBAwdcQq+2thaDBg2CyWRCeHg4li1bpih/TdFTij8AqKurg9lsRkJC\ngqK8NUVPSd6CgoJgMBhgNpttYShK8ueMnpL8lZWVYfz48ejbty/Cw8Nx+vRp1/JHrQi3b9+m7Oxs\nIiKqrKyk3r17U05ODiUnJ9Onn35KRERr1qyhJUuWEBHR5cuXyWg0ksViofz8fAoNDaW6urpm01ux\nYgWtW7eu0e+bS4+IqLq6moiIHj9+TIMGDaLjx48rxl9T9JTkb926dTR58mRKSEggIlKUN2f0lOQt\nKCiISkpKZN8pyZ8zekryN23aNNq5cycRSfOlrKzMpfy1Ks2oa9euMJlMAABfX1/07dsXxcXFSE9P\nx/Tp0wEA06dPx969ewE4D6I8c+ZMs+kBADmxbptLDwDatZNCXC0WC+rq6tChQwfF+GuKnlL8FRUV\nYf/+/ZgzZ46tfSV5c0aPiBQbO25fhJL8OaPX1HfNpVdeXo7jx49j1qxZAACtVov27du7lL9WJYxE\nFBQUIDs7G4MGDcLdu3fRpUsXAECXLl1w9660933r1i1ZsCQHUTaHHgdlbtq0CUajEbNnz7appq6g\nV19fD5PJhC5duthMRCX5c0ZPKf4WLlyItWvXwk2onqYkb87oaTQaxcZOo9Fg+PDhiIqKwo4dOxTn\nzxk9QJmxy8/PR6dOnTBz5kxERkZi7ty5qK6udil/rVIYVVVVYdy4cUhLS4Ofn5/smkajse3AOcOT\nrj2J3vjx45GWlgZfX18kJSUhPz8fFy5cQLdu3fDee++5jJ6bmxsuXLiAoqIiHDt2DBkZGY3acyV/\njvQyMzMV4W/fvn3o3LkzzGaz05Wb23IVb03RU3Lsfv/9d2RnZ+PAgQPYvHkzjh8/3qg9V46dM3pK\n8We1WnH+/HnMnz8f58+fh4+PD9asWdOovebw1+qE0ePHjzFu3DgkJiZizJgxACSJzNHet2/fRufO\nnQHAaRBlU8GSf0Vv6tSpNnqdO3e2Pfg5c+bY1E9X0GO0b98eo0aNQlZWlqL8OdI7d+6cIvydOHEC\n6enpCA4OxqRJk3D06FEkJiYqxpszetOmTVN07Lp16wZAyrUcO3Yszpw5o+jYOaOnFH96vR56vR4D\nBw4EAIwfPx7nz59H165dXcff3/JgPWPU19dTYmIivfvuu7Lvk5OTac2aNUREtHr16kZOtD///JPy\n8vIoJCSE6uvrm03v1q1btr/Xr19PkyZNcgm9+/fvU2lpKRERPXr0iGJiYujIkSOK8dcUvdu3byvC\nHyMzM5Nee+01IlJu7Jqip9TYVVdXU0VFBRERVVVV0ZAhQ+jQoUOK8dcUPSXHLiYmhq5evUpERB9+\n+CElJye7lL9WJYyOHz9OGo2GjEYjmUwmMplMdODAASopKaG4uDjq1asXxcfH214wIqJVq1ZRaGgo\nhYWF0cGDB5tNb//+/ZSYmEgRERFkMBjo9ddfpzt37riE3sWLF8lsNpPRaKSIiAj67LPPiIgU468p\nekrxx8jMzLTtbinFm4iMjAwbvalTpyrCW15eHhmNRjIajdSvXz/65JNPFOWvKXpKjt2FCxcoKiqK\nDAYDjR07lsrKylzKnxr0qEKFihaBVuczUqFCRduEKoxUqFDRIqAKIxUqVLQIqMJIhQoVLQKqMFKh\nQkWLgCqMVKhQ0SKgCqM2iMLCQoSEhKC0tBQAUFpaipCQENy8eVMRetu2bcPu3bsBAF9++SVu375t\nuzZ37lxcuXKl2TS4NMaKFSua3ZYrUFtbC5PJBE9PTzx8+PBZd6dNQI0zaqNYu3Ytrl+/jm3btuGt\nt95CSEiI7LBMpTB06FCkpqZiwIABLm135cqV8PPzw6JFi/7ne6xWK7RaZYuZBgcHIysrCx07dlSU\nzr8BqmbURrFw4UKcOnUKGzduxIkTJ7B48eJGvykoKECfPn0wdepUhIeHY8KECaipkc6q+eWXXxAZ\nGQmDwYDZs2fDYpEOJVu6dCn69esHo9GIlJQUAJLWsm7dOvzwww84d+4cpkyZgsjISNTW1iI2NhZZ\nWVkAgG+++QYGgwERERFYunSprR++vr5Yvnw5TCYTBg8ejHv37jnlSVw3z5w5gyFDhiAyMhIvv/wy\nrl27BkDSzEaPHo24uDjEx8ejuroaM2fOhMFggNFoxJ49e1BfX48ZM2YgIiICBoMBGzduBADcuHED\nI0aMQFRUFP7zn//g6tWrAKTM+7Fjx8JkMsFkMuHkyZPNGhsVTeBvx4SraDU4ePAgaTQaOnLkiNPr\n+fn5pNFo6MSJE0RENGvWLEpNTaWamhrq0aMH5ebmEpFUVGvjxo1UUlJCYWFhtvvLy8uJSF7QKzY2\nlrKysmy/4c/FxcX0wgsv0IMHD8hqtdKwYcNo7969RESk0Who3759RESUkpJCH3/8caO+rlixglJT\nU22fKyoqyGq1EhHR4cOHady4cUREtGvXLtLr9ba0hJSUFFq4cKHtvtLSUjp37hzFx8c34mPYsGE2\nnk+dOkXDhg0jIqKJEydSWloaERHV1dXZfk/kvMCZin8GVTNqwzhw4AC6d++OS5cuNfmbHj16YPDg\nwQCAqVOn4rfffsO1a9cQHByMnj17ApCKZh07dgzt27eHl5cXZs+ejT179sDb29tpm+Rg+RMRzp49\ni9jYWDz33HNwd3fHlClTcOzYMQCAh4cHRo0aBQAYMGAACgoK/pI3LoEaERGBRYsWIScnx3YtPj4e\nAQEBACQN7+2337ZdCwgIQGhoKPLy8rBgwQIcOnQIfn5+qKqqwsmTJzFhwgSYzWbMmzfPlo2ekZGB\npKQkAFLJFX9//7/sn4q/D1UYtVFcuHABR44cwcmTJ7FhwwbcuXMHRUVFttrI27dvByCvMUNETmvO\nsHBxd3fHmTNnMH78eOzbt+8Jx4s3bsPxO5EWH3MOSC+71Wr9S/4++OADxMXF4dKlS/jpp59s5iUA\n+Pj4OO0/IyAgABcvXkRsbCy++OILWyXIgIAAZGdn2/5dvny5yTZUuB6qMGqDICIkJSUhLS0NPXr0\nQHJyMhYvXgy9Xm970d58800AwM2bN3Hq1CkAwNdff42YmBiEhYWhoKAAN25Ih2Hu3r0bsbGxqK6u\nRllZGUaMGIH169fjjz/+sNHjl9XPzw8VFRWy/mg0GkRHR+PXX39FSUkJ6urq8O233+KVV175xzxW\nVFSge/fuAIBdu3Y1+bv4+Hhs3rzZ9rmsrAwlJSWwWq1444038NFHHyE7Oxt+fn4IDg7G999/b+Pp\n4sWLAIC4uDhs3boVgFTg35E/Fa6BKozaIHbs2IGgoCDExcUBAObPn48rV640qjwIAGFhYdi8eTPC\nw8NRXl6OpKQkeHp6YteuXZgwYQIMBgO0Wi3mzZuHiooKJCQkwGg0IiYmBhs2bAAgr/A3Y8YMzJs3\nz+bAZnTt2hVr1qzB0KFDYTKZEBUVZTuxQ9Sa/qpaICMlJQXLli1DZGQk6urqbPc43r98+XKUlpYi\nIiICJpMJmZmZKC4uxtChQ2E2m5GYmIjVq1cDAL766ivs3LkTJpMJ/fv3R3p6OgAgLS0NGRkZMBgM\niIqKckmogorGULf2/8UoKChAQkLCE31KLQUrV66Er6/vE8uoPguoW/uug6oZ/cvxT2qCPwv4+vpi\n+/btLS7o0Wq1ygr+q/jnUDUjFSpUtAioIl2FChUtAqowUqFCRYuAKoxUqFDRIqAKIxUqVLQIqMJI\nhQoVLQKqMFKhQkWLwP8D22A3x4clj6oAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x10c1e9b90>"
]
}
],
"prompt_number": 24
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Spectrograms"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy.spectra.sources.callisto import CallistoSpectrogram\n",
"tstart, tend = \"2011-06-07T06:00:00\", \"2011-06-07T07:45:00\"\n",
"callisto = CallistoSpectrogram.from_range(\"BIR\", tstart, tend)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 25
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"callisto.peek(vmin = 0)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWwAAAEgCAYAAACQBUmuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXt8VNXV8P8dIMkQkjBISBASGDSQgFwSQNBfQUPFS4tS\nvNRb+1RFbLUPWqt9ay9ao+KjfavtY+tja723toq2VVArWtRQ7VO5KEGshkthgITrgAOEZBIu8/vj\nnDVnnT17QoC0KO+sz2c+c87ea6+99m3ttddeZ+9AIpFIkIEMZCADGfjUQ5ejzUAGMpCBDGSgY5AR\n2BnIQAYy8BmBjMDOQAYykIHPCGQEdgYykIEMfEYgI7AzkIEMZOAzAhmBnYEMZCADnxHICOyjBPPm\nzaOiooLBgwfz4x//OBl+6aWXUlVVRVVVFYMGDaKqqiolbSQSYcSIEZ3Cx+9+9ztGjRrFyJEj+dzn\nPscHH3xwUB6ff/55TjrpJLp27cr777+fDN+xYweTJk0iPz+f66+/Pm2e1dXVVFRUUFlZyamnnspH\nH310SDzX1NRw//33A3D77bfzxhtvdDhtfX09lZWVjBkzhjVr1pCXl3dIeXcEamtrOe+88zqV5u23\n386bb74JwH//93/T0tJyyDQmT57M7t27AejatStVVVXJuvj73/8O+PtWbW0tPXv2pKqqimHDhnHr\nrbcmac2dO5e77rrrSIuVgUOFRAb+7bBv377EiSeemFi7dm2ira0tMWrUqMRHH32UgnfzzTcn7rrr\nrpTwtWvXJoYPH94pvPzv//5vIhaLJRKJROLVV19NjB8//qA8fvzxx4kVK1YkqqurE++9916S1p49\nexLvvPNO4le/+lVi5syZafPU6Z544onEueeee0g819TUJO67775DSiNwzz33JGbNmpV8z8vLOyw6\n7cFbb711yGU6FAiHw4loNHpIad54443EN7/5zeS7Lvdrr72WOP300xOJhL9v6XK0tLQkKioqEkuW\nLEkkEonEgQMHEqNGjUq0tbUdSVEycIiQ0bCPAixatIiysjLC4TBZWVlceumlzJkzx4eTSCR47rnn\nuOyyy9ql9eSTT/q02XPPPZe//vWvAOTl5XHrrbcmNdmtW7empD/11FPp2bMnAOPHj6ehoeGgPFZU\nVDBkyJAUWrm5uXzuc58jJyenw3Vxyimn8M9//hOApqYmJk+ezJgxYxg5ciRz585N4t19992Ul5cz\nceJEVqxYQSAQAODKK6/kj3/8IwBvvPEGo0ePZuTIkVx99dW0tbX58vrzn//MAw88wC9/+UvOOOMM\nX5ypFc+cOZOnnnqKXbt2UVFRwcqVKwG47LLLeOyxx1LKMW/ePIYOHcqYMWN44YUXkuF79uxh+vTp\njB8/ntGjRyfL9OSTT3LBBRfwhS98gSFDhnDLLbcAsH//fq688kpGjBjByJEjeeCBB3zl/MUvfsHG\njRuZNGkSn//853niiSf49re/nczvkUce4aabbkrh7/e//z1f+tKXrG2wc+dOjjvuOGucQDAYpLKy\nMtlWgUCAU089lddff73ddBnoXMgI7KMAjY2NlJaWJt9LSkpobGz04bz99tsUFxdz4oknHhJtEWQA\nzc3NnHrqqdTV1XHaaafxyCOPtJv2scce44tf/GKHeewID+kg4X5gO2/ePIYPHw5A9+7deeGFF3jv\nvfd48803ufnmmwF47733mD17NsuWLePPf/4zixcv9uUVCASIx+NcddVVPPfcc3zwwQfs27ePX/7y\nl748v/jFL3Lttddy0003HdSMInQLCgp48MEHufLKK3n22WfZuXMnV199tQ83Ho/z9a9/nZdffpn3\n3nuPzZs3J+vg7rvv5owzzmDhwoW8+eab/J//839obm4GYNmyZTz33HMsX76c2bNn09DQQF1dHRs3\nbmT58uV88MEHXHXVVT5+rr/+evr160dtbS1vvvkmF198MS+99BL79+8HnInA5A/gb3/7G2PHjk2+\nt7S0UFVVxdChQ7nmmmt85g4b7Nixg0WLFnHSSSclw8aNG5dUDjLw74GMwD4K0BGB9swzz3D55Zcf\nUT7Z2dlMmTIFgDFjxhCJRNLivvXWWzz++ONJW3VHeDxcSCQSfOUrX+GEE07gjjvu4Kc//SkABw4c\n4Pvf/z6jRo3izDPPZOPGjWzZsoW3336bCy64gGAwSH5+PlOnTk2ht2LFCgYNGkRZWRkAV1xxRVph\nkujgaQyCN3nyZIYPH87MmTN59NFHU/Dq6+sZNGhQcnL96le/mkz7+uuvc++991JVVcWkSZNobW1l\n/fr1BAIBzjjjDPLz88nJyWHYsGGsX7+eE088kTVr1nDDDTfw2muvkZ+f3y6PPXr04POf/zwvvfQS\n9fX17N271ydUBTZu3OjTort3787SpUv5+OOPmTdvHl/72tes9N9++20qKyspLS1l2rRpPtr9+vVr\nt09loPMhI7CPAvTv358NGzYk3zds2EBJSUnyfd++fbzwwgtccsklB6XVrVs3Dhw4kHyPx+PJ56ys\nrORzly5d2Ldvn5XGBx98wDXXXMPcuXPp1atXh3g8EggEAvz+979nzZo1zJgxg5/85CeAswEajUZ5\n//33Wbp0KUVFRcTjcQKBgE/I2gSuOcF0VCgLtFePBw4c4OOPP6ZHjx7s2LHjkPP+05/+xNKlS1m6\ndCmRSISKigoAn+moa9eu7Nu3j1AoxLJly6iuruZXv/oVM2bMOCjvM2bM4IknnuDJJ59k+vTpHSuw\nglNOOYVoNEo0Gk2JmzhxInV1dfzjH//gT3/6k69PHDhw4F86sWcgFTIC+yjA2LFjWbVqFZFIhLa2\nNmbPnu3TGufPn8/QoUPp16/fQWmFw2Hq6upIJBJs2LCBRYsWHRIv69ev54ILLuDpp59Oaqcd4VHA\nJhg7IiwF56677uLFF19k/fr17Nq1i6KiIrp27cpbb73FunXrCAQCnHbaabz44ovE43F2797Nyy+/\n7KMVCAQoLy8nEokkbay//e1vqa6u7nA9DBw4kI8++oi2tjZisRhvvPFGUhj97Gc/46STTuJ3v/sd\nV111VcrEJ3mvWbMGcFZHAmeffTY///nPk+9Lly5NW0eJRILt27ezf/9+LrjgAu66664kvob8/Hx2\n7dqVfB83bhwNDQ38/ve/T7vn0a9fP7Zv326Nq6+vZ//+/fTu3dsaD04/+9a3vuXzDNm0aRMDBw5M\nmyYDnQ/djjYD/y9Ct27dePDBBzn77LPZv38/V199NUOHDk3Gz549u93Nxn379iW1swkTJjBo0CCG\nDRuW3PQS0NqP2EBNuOuuu/jkk0+47rrrAEcrX7RoUbs8vvDCC9xwww1Eo1GmTJlCVVUVr776KuAM\n7N27d9PW1sacOXN4/fXXkxqlBuElGAzyrW99i3vuuYdZs2Zx3nnnMXLkSMaOHZvMr6qqiksuuYRR\no0ZRVFTEuHHjUujl5OTwxBNP8OUvf5l9+/Yxbtw4rr32Wmv9mfUCUFpaysUXX8zw4cMZNGgQo0eP\nBmDlypU89thjLF68mB49enDaaacxa9YsampqkjSCwSC//vWvmTJlCrm5uUycOJE9e/YAcNttt3Hj\njTcycuRIDhw4wAknnMDcuXOt7REIBGhsbOSqq65Kavv33ntvCv9f//rXOeecc+jfv3/SFn/xxRez\nbNmy5AayCRMmTGDJkiWcffbZgGfDBmei+M1vfpPkx1Y/ANdeey1DhgyhoaGBkpISFi1a1Onuixlo\nHwKJQ107ZuCow5w5c3jmmWd49tlnjzYrGfiUwHnnncdNN93EpEmTrPG1tbXMnj07ZSP2cOHAgQOM\nHj2aJUuW0K1bRu/7d0HGJPIZgx/96EfcfvvtfP/73z/arGTgUwCxWIzy8nJyc3PTCmtwPlZatWpV\n8sOZI4WXX36Ziy66KCOs/82Q0bAzkIEMZOAzAhkNOwMZyEAGPiOQEdgZyEAGMvAZgYzAzkAGMpCB\nzwhkBHYGMpCBDHxGICOwM5CBDGTgMwIZgZ2BDGQgA58RyAjsDGQgAxn4jEBGYGcgAxnIgIINGzYw\nadIkTjrpJIYPH548CybdTUsA99xzD4MHD6aiouJfekZ45sOZDGQgAxlQsHnzZjZv3kxlZSVNTU2M\nGTOGF198kUAgQJcuXfjGN77B/fffnzxv5qOPPuLyyy9n8eLFNDY2MnnyZFauXEmXLp2vD2c07Axk\nIAMZUNC3b18qKysB59amoUOHsnHjxrQ3Lc2ZM4fLLruMrKwswuEwZWVlh3xqZkchI7AzkIEMZCAN\nRCIRli5dyvjx49PibNy40XdW/KHcznSokBHYGchABjJggaamJi666CIeeOAB8vLyDintv+pih2Py\nqK2iomFs2/bx0WYjAxnIwBHA6aefTm1t7WGn7x4IED84Gnl5eSmnGO7du5cLL7yQr371q0ybNq3d\n9ObtTA0NDfTv3/9wWD4oHJMCe9u2j+HM22F0NUyshneAMBACYkATUAIUAg1AFJAz9uWWpEIXrxCo\nc/HjRjhu+qBBNwxEAHNSjrq4cZX+pRqoqnF4E8hz6YZcvLjKp1DRyXOf6xX/wm+hyqvJ/Q8qPvLc\n8KjKo1DxXQFUQlbZLvbOL4Df1sCkGievPMV/k6KHkafkIWWKqnq08VKo4mwjTWgGFZ60l+S/uAaG\n1nj1FFZl0rxI/rpNNZ+6nsPus60sDe6/yYfganypnzxgQQ2MqfGXx+QvrtJIWTQfZl1JmTTovAWk\n7XQdCB0pexCoBOYDC2tgfE0qX3JBkfR9qeO4Gyd4Uj+Sz2rgFDeuDpiAM0bzcPr8P2rhg1oWzLnD\nUqCOQxyY1QG8W5uafO+JRIKrr76aYcOGceONN1rTaF+NqVOncvnll3PTTTfR2NjIqlWrrJdsdAYc\n2yaRATBwSr3XEQpxOk8eUAnDz3Bv357s4A2cUu/El8BZU+bAhDgXnvE0VMDwSxZz7hXPc+6U5720\nJdDnivWMu2SBQ78Esibv4qzxczjrkjlcOOVpsk7ZxfApix16hTD4kmVwiks/CD37RiEE4y5ZQM9p\nmz3BG8I/gGQAyCQD3sDLwxkAMgk14QnAiIsjgkIGkQhKPXi1QCxxhDW4+bXhH8xCI6poaChUP0Uz\nRciEFb6Oa3KfhS+hJeUF/8Qn+NmKlggrLaD1RCblF3yhIxOvm0fPKzc79Rt2fzJxQnJio9B91jwK\nvtCSNgAoUHlX4LRv2H2e7OJdpPKSMggNtw8ny1SowgtdWtLfSxQd+a90fllX7vJP3IX4+0oYaMYT\nxrrPVLr8Nqk8ShQeLt3VeIqRpJX6lnLp8DY6DbI68DPhb3/7G08//TRvvfUWVVVVyRuVXnzxRUpL\nS3n33XeZMmUKX/jCFwAYNmwYF198McOGDeMLX/gCDz300L/MJHJMuvUFAgFHwz6xGiqr/doO+LUt\neQd/R4PUdAKmVqbDBUxtx6QruAtq4MIaf34mf0LbpKkFXLAdXJv5TeiLJmlqoKJdv1vghIuGLfTB\nL3hN0HG6XrUmpgUpB8HXPKcrE8CrNXB+jV8DT9e+Nl7T8W/Wk7yDvzxmG5p4Qu/tGvhCjYfTgNen\nND1d7oPViYaO9un26lZWGK/VwEk19j5l0jfrXINeueiJVugJrZW1sKEWlt9xyJcpawgEAtzfAbyb\nOfRLm48WHBWTSDwe5/TTT6e1tZW2tja+9KUvcc8991BTU8Ojjz5Knz59AMcZ/ZxzzklJP2/ePG68\n8Ub279/PjBkzuOWWW1JwTvj/6smtziNcvY02ssk2pu02sslnN63kJOPbyAbwPTeTS4iY7z2XZmu5\nbHkImHQEdnyuG32rnyeHVgBace5qzKE1+ZwOBEf4z6GV3eQn+Rd+hLbQN/Myec6mjXJWsIViWqZ0\nZzf5xIv3EqyeY6Uteer0mj+TL6l3s5wmrY6AbrMcWmn8HPSvfjoZ350WWnDKYOZr1oHm1wSz3kLE\niLl2LF0mk0Z3WthKEUVsBaCF7gBsq91LgdvuZjqzXXSYrf40jyako2/Wta0+pL2iZ0NB9RwABrOS\nVQyhmdwkP7pP6PbPpTmJlw43RMxHC6C5dgk7a//JhuUpxTlk6H7kJD5VcNQ07ObmZnJzc9m3bx8T\nJkzgvvvu44033iA/P5+bbropbbr9+/dTXl7O/Pnz6d+/PyeffDLPPPOM7xLbQCAAl90OZdUwvtpL\nrLU6m00wjGdCSKd5QnrN0qYBi50zneZhapqivZt2VJOu5iOd5i2aWxRv6aptmrL8Ff5Wk7Sln3XJ\nHN7aPom9DQUevraH6xWG1iJ1XDrNTpsypHzptFSpN222wAiH9jV9Ha/50vWn+da0StpJH7WktWnH\n6drcNCfpPpJOY9d2ZLNsJn2TpllmeY+pZ/d9yPg6Vq6ohLw4NAVT6z4GlMQhanQ+TV/SCsTcVVs8\n2wvPU4SF1srX4e9/hZ/dfcQa9iMdwLuGjIZ9UMjNdWfVtjb2799Pr169gINX3KJFiygrKyMcDgNw\n6aWXMmfOHJ/ABmB5DSwHXsVvCxbBUoEjqGRJCumFn4COK8Hb3LPh6YEQUjjSoeNGnCyJ9Yadjpf0\npk02iLdpo5fWDTh2VylzhQp36ScHz7tBZ6KKu3QqYNYlt3Jm3l/YOb/ACT8FuA/H1tpA6hJeTywx\no65kE0rXkynUdNuAX1jF1X8JzsanrndzM1nqWfiQd82fhmCaZ92mJn82PJ2XbntzghJ6pjA2bfIa\nzAnF1k/NCT6Gv/9oXMHRbafCV9ZUOvReDvondlAb4EFvM1HnLc/xoJ/nQtj7ToG/D4RVQZJ8nAX9\nzwLutjB/aHCseVUctfLIrcv//Oc/ue666zjppJP4wx/+wC9+8Qt+85vfMHbsWO6//35CIX+Pa2xs\npLS0NPleUlLCwoULUzM4vsaxYZ9S7XU0c1BIJ6zAPxBE2DXgdOh6/F4iIvwrSdVY9cAW4QaegJfB\nKZuL2tYqQlBvvGnhrAWG1qLjwAycwbla0Qs7+Wad4mwelvdeQeuobFY1lkM0SG5eM83A3lOC/pVA\nGO7kR+yMhpzJoM6ldy7eRpSpJUbxe05UuvUmQkOErV51SJ1F8CZQeUflI5OUtJtstolmrldJpk22\nUOHIxBXBr6lq0HRMT50KnAmtEm/yFDAFuJm/lKmS1MlKyqkFqakVg9dXtWCUNmvPY0TXn0x2uh/X\n49WlTIgPAjPxPJBkpZHnliGqwgTkXdpfe4k0GHgNeBu4KNw40FALm2rpDDjWTCJHTWB36dKFuro6\ndu7cydlnn01tbS3XXXcdP/rRjwC47bbbuPnmm3nsscd86Tq8+7oZZwv4FByBA6meF9JZZWCOxfM2\nCONpo7qzleEMPu22pE0OQTyNUQbJOzg7/+IeWKdoh3Fcp3Tnj7s4QZduHp4GrU0IuPxfCryLJyTq\n8LwggL2/KoAS+LDkZIfGfCd8Z11fb4IS00nceY59IwTzgw598IRODG/AyVwqQkDoSBmEHxFQMmHp\nlY1MhvNVnKTRmvBq/Bp9CK9tRKPVE7JMXqvd9JL2HewmFqlb00UvpuLmuzSkroWGtClAPpBQfMqE\nJdq+nsBFIXjHfV+t4gTy8PfZerxVhZiwtNA2J1IJb1D0dL+WSRT3Xfpog8vXu/hXZoV4SkEcb2Wm\n61D6vC6DnijexZsYpI8LrTxgPbCJTgGbF8hnGY76iqFnz55MmTKFJUuWUF1dnQyfMWMG5513Xgq+\n6aS+YcMG32ehSdhdC+sj8EAt5FfDkGq/v6g2Z5ThdCKtNUXxhFPIfa/EG6zz8QaraF55eJ05z8UR\nes/iuTeBp2Evwa9ViaAucfMXQR3EE57gCa0KHFNFpYoX4SRmgIsgq3AXk3q/xRBW8HDJteyNZzOh\n/9ssbx3Bzvl9HTr1JAdWOSt4p+JMh54M7AjeykMmP8lP/rWpBvza5AS8ya0ez4QRM/5NzVUEaaFK\nJ3TL8CYo3Z51eJpgOpu0uKKJMNICVfLV6bQmL2WQfyljf7w21BO37hdaCZAJWOoY/Jqz/GPwpicC\nqQ9JqyctmRREMEsfl8lWBHhU4UQVrvAi5Zdn0yQj7rKFbvlPwT+WzL4hba/LtbHW8Q5piUBrhM6A\nY01gHxU/7Gg0SizmqE8tLS385S9/oaqqis2bNydxXnjhBUaMGJGSduzYsaxatYpIJEJbWxuzZ89m\n6tSpqZl0r4bjroTiGsit9paM0tmCOANbmwIEtKYng0M0LG3HA6dz1itcESwRPOEkHV0L5iV4GmtM\n0ZuMt+QvU/iiMZs2ThEaemNTlpuVOD7f5XMI917Lf/BbpvIS4d5rOav/a1TzFuNzFnp855H0i35s\n2Uz/SkR/aCTLcalHiRMhIOUsMfAieH66kp+JD6kmBfnXKx0RfHUqXngRAa7xhV7crRf90UceXt1q\nrVT6SEjRknit8YpABE/wiY8yblpZkUmdSNm1oNOmCj15CN9Sjgr8IOlFedBmBj1BFLp8SD5inhHB\nHFf0yvDv75gmEL1ykYkxgqc16wnJLIOsYEVBkcnyuGrnA53wlVBYTWdAtw78PktwVPjdtGkTV1xx\nBQcOHODAgQP8x3/8B2eccQZf+9rXqKurIxAIMGjQIB5++GHAOVzlmmuu4ZVXXqFbt248+OCDnH32\n2ezfv5+rr746dcMRPG1mpPuuO450QtEiRIjLM/g3A4PqXQSHCGL5r8TT1EQoxHE6sJhDwBtQooXp\nQaP5lKWwFmLCgwxyvQyW8lYoOiXQp3w9ZzCfDZQydf9csuN7Ke6xlREsZyzvAfBW5ST21hU4WtHL\neINJaIqQCqu6lTKK5ijCK4xn5tBLbj3Ypa5ME4TgNeF9CSf1J7T0pqNuUw1inhLQphQRJnoigNQJ\nQttdtTYoeCII9T5GGd7kKnZjqZsmFV+oeJQJV7R3acMIXh+SMoMnHCe7OIV47VKPf5KV+jUFf0jx\nLOWV8kh4FLg9DtcEvZVcA84qaQn+dpOyCh29twJef4qoPCJuXIUKq3TL9QMwvF8PG441G/ax++HM\nr9xiieABvxeFFpJaq5GOJwNTd+o4/sFv+5cBKwMrirephAVfwgREQwnj2fQkT+FTBoXwppesLs7g\nm5dRzFbOYy7f3fAgy0oHM+r/roLTYdb4mxnPQs7c8A5zSs/iPr7DO40T6VkYc8wj4AiXvDh9+m9l\nW2MRWcE2z8VP14O2r0p9adDaqvAtwk9vkJomAymr1J/koU0sWOowQuqmaFDhSBuFVd5mnJRF2kM0\naMHV8QJ6wzgPT8DKhCVlqsfZK9F8aRrgTeqiLOi+IjyJ3ReDTjr6cRUmAl3s1VJ+8CaBCXiaueQ3\nH28yKVQ0hWfdNrqOdJ+QcumJJeLybMbdGjhit753Do7GBD47bn3HrsD+0u1QUQ1V1faOrW2eTUa4\n4GpBo00OhQpHQDaVJJ05KWgQLUe7nYnWA6mDTU8ipqDXA1vx/vElYX7H5YxkOV++5mXHi+THwOkw\n51tn8aW612EtbD6/J48yg5c4j2Zy2dBays5oiMH9VwDQixhbKCabViLbBwGwt6GAnhWb2Rnpm1r2\nBguPAiGSk0BbazY7691NT1lea5OR1JOAtq/qetTlNl0gdZwO0+8hI1wEr+4HJh3w9w/TjdEMs9Gy\n9UmTrl51FRrP8i94MpFLeYSGacoQfmTy0LR0vP6cvkHxYiopus30qkeEcRP+zWOzLvXKRtKurnVs\n2a8c+ZeO73YA7xQ+OwL7s2bC6ThsBvYCplOJOWgFpBPqziQdPqzibAJSdzbdkU1aOn9zUJoaiXT2\ndDzLoDI1XDf//+Gb3td4wyH5AdsA2EqR8zwINlBKK9msxRHGO+v6QhNsLSwmO6eNra3FNDc5PvN7\nowWOcG2CnfT1NMfVeMt9PThNoV0CBINsaxrg4InAqCd1EJv1JBqrbQJU5bZq4HkWXBHKJo+m7RgV\nLkLRpKk1db0KMtNpfnR/aLLEmyYfWdmAp/XXW9LpZ/k3Nzh1/6zHr5AIT0vwf6ugVyu2fp2ncMHv\nZWWuumygJ/mNwIZ2cA8BjrVNx2NXYK/H6VhbjXBTe4qSOngFZABo/2kBLURNgSCQjp5NU9ZCpD1I\nJ5iMgVT7w0lM4wVCxGAE0BsYDPSEMBHYAZTCRvrR4n4avK2xKGlbbG7Kpbkp1xHSUt4ofsEpGmo9\nnvlGzBh6wpEyRvDsrVGcepWltoB2d4uqMGkfbV7QgtCsH1OTNuvJ1OrTTYq2ibYQv2ubhgZSJ5t0\ndDRPEleIt8mthbRNybDxbApWWzrBS7ey1JNBEL9ZSO/TmHxppUfaEAu+XrlKe2m3zE8gzekPhwzH\nmg37qAnscDhMQUEBXbt2JSsri0WLFnXqWSLk4mxcDHTftZnBtIXmkTrwtUlDCwDboNZakaQpxC/Q\noxYa5qASHrTWrQW0nlh0h6/As327UM1bxAg5wnkJ0ANHYPfAEeJxiPdzcEPECPEJbYXZjuacB6He\nMXJpJpbX7HxAI8SlLkytEvzLWx0mz9qEI+WwrUjkXZuepB30e5jUSdEmRCXcbGNtOtBhWMJ0m0WN\n8LgRbubRHn+67XU/Caowm23dnARM3nRewTQ42syh2yiK49tvKhGyUS5pdH/VdHV+EmebGM0VbZ56\n30enwLGmkR618gQCAWpraznuuON8YTfddNNBzxKZOXOm7yyRqVOn2j1Ferr/Qfy+o+YAFChTz7qj\nxQx8U1vQdMTLAZU+jufWJVqpafeEVLt3EM8uGzLCZFKI4h9wLr+vcTaXMJuT6z6EBcAer0wjhn8I\nGyG4A8b3WMgGShlEBHJgZ0VfCDp+2DFCjinFFcA+M0gh3jJYe7Jo7boCv7YnXh6a90L89lKpB6HX\nhP/MF22nljRCqz1tGTzhZ9IwJ01zEjAhHf3CNOEmvjmB64nEtDcLv3pz0FyhadDhpiar87DxpPOL\n4rVXOhu49GUJg/T927bKsEEZsJJOO2I1YxLpRLAZ+jvtLJGpNc5/b/wdPIDTYXLc5wTQ6saJNr4d\nv6eBCDtwOloPN6yHi9vbfRfQ2qXkgZuP0OjjPvfAr60UGrQEZw+pA68HnnDUtPNhJyFGshxed3lf\n48Y1QrCJ31elAAAgAElEQVTJ5bvF4a00sIFy6tlJT/qMWs/e1iwqWcpOQkQIU5DjfNq+orA7bXHH\nRBJwB1yi0N0kiOANwhD+CUYLpsIEgSAUhLc4m5bhBMRdGtrGagodEezSDtvxa5AVql62q7zBaR8J\n0/WbcPParvD24K2jzXrvofLYA/RIwPaAl4/EB1x8nW8PnQ6/50/cTdMbvyBvxb+mF34KjX8d10Ol\n6Y1XX0If9S79UtLp+kngfcw0Gc88o1cqks6m6W/H69tCB1KFtrECCAQTJCZUQ7QavnNkFxhAxiTS\naRAIBJg8eTJdu3blG9/4Btdccw1A550lsqYGRlZDSbUXprVm27JUtALLh5NWm6RozkJb52FLa+Zn\ns62a7zYtRuLNz54V7WK2MIQV8ChwHN4gKoN4HgQDQDPkHmgmt2szJTSwlNHk0kx+zm6K2UoLufRk\nJ5/QixAxju+9iXXxHLKCbYR6x2hrzSY7p82xfZuFliWyYU/OKlFXMYWBklaSp8FpTxkB02YvgrwM\nu2DXbaJptaeV6jbUmr+5x6BxAJoCfj5svJeoeDFdCU2bOUV/E2DL35aXLW8baDzbSlGHCb/fBu7B\n3s/S9d8g+E7qs5mdbO95cRJNQXi7Fhr1xsbhQ1ZHJFwnmV/+HXDUBPbf/vY3jj/+eLZt28aZZ55J\nRUVF554lkoszvWqtDLxOaw4C1LMWNjaw2Ty1xmQOeFMzET5sy8J09lob2LRYFwayjpWUMyq+CvoB\n44GFDl5wI47faw/4pKtjwd5NvntOsXNOcpgIEcK0ke3YsgkRa/Umz9j2kHPSH0BD0L7RZS79gb0U\nQGGcnavl2NagJ5xiKp2uO9w4oa2PGJDyR1U6aQMBbWvV7WoKbx2vPR5MYVZP6gax5se0/Ura1Wlo\nnoJ3ZoeYImy0Nb96g89marBNTjrsYPxXuDxtwDsXpD1Thgl5CtGkbX7Mk4Sgg7cC+LBzRFO3jMDu\nHDj++OMB6NOnD+effz6LFi1i4sSJyfgjPktkZa1zlsh7tc652FXV/i/sNGjBrQ/yEUgnMGXAmfbY\nKKlCI65+poA17eBa4xKQJX+E1ONB5eAgNXCTB9uLCUeWw4NxPER6OJuOWykmRijpKZJDGzF6JQ/J\n30g/Wt3rAZqbcp0PaPR5xjGcc5GblOCVMgXxJia9AqkPpnpAFOKd7id0RfCJx4FpI5dn3Qbg/5BI\n6kaD1vq1UBO6pmAUHiReBI6cWQKenb0Sz6tIzp7RtKUuwngfoKzGs39Lecw6i+P/OKUeT7Dqj02i\n+PuZ5C3nv4iWLK6Yut9oN9Gwi1+N5yWihb3QxJKPKCdR7BuR5rjALcdfap2T+nZFnF8nQFbXTiHz\nqYGjIrCbm5vZv38/+fn57Nmzh9dff53bb7+dzZs307dvX6BjZ4n069eP2bNn88wzz6RmEqyGvtVQ\nWu3YAue7P61ZmJtV5hI+naC2LUkxwuoMPJumLOlk0NniZKC8o96lw8sgrzPSAN2/0eLccnIcjoad\ngyOsg/hsltnuDSRFbCGbtuTtHyFitNA9Kaw3bu/nfOkodbMaTyi+E0w1FwnI4BeoV/UQwf/FoQgd\nrZmLNiumBFOYmaC1YK1163YwcU2wLddtJq138PqLCL56hWf7zE7oyGJF8yhgmkvA+yJQJif5ybvG\n05Oa3hvRmnoQ/4mLcVJP/dO2Z22DbsCuIa82cORZ152e1KWsUg97qp3xGquFbrXQuMCSyaFB946s\nCMw9o08xHBWBvWXLFs4//3wA9u3bx1e+8hXOOuuszj1LJBcYgHN6WpzU40v1gBCbpKndFKZJY7Nx\npwMbPTN/EU46XoShaHjmKsDMo0mlD8IIPnC8PFpxtOsdCn8ncBwE90CoR4wcWh1XP5xrnUJ8krwG\nLcfdrg/1jrGtoYDkDSHBoLdSMJfwPlumKps2m6DKZda/FkCoeL2sNs0aeiLTKxXDhm4T0uf+9Hle\nvunL6QW1Nl9p4ao1Xm2eaM8cYYu/EnjSfRZhK2VrUs8aJF+9GivELvg1hI1ypbPrF+Kcf94N+A5+\nv3edTitAHVFQZNVjKkvgrSL/Aey38HQ4cIxp2Mfup+nPJlKXhunAXH7qMDOtDtM4NjcmOHjetg0Y\nkycbrzJYbBpMEMZdsYAZPMo1Nz7taNeuzzWD8bwXxkJ90UDexjFFPcoMPiFEGzl8h/t4jbOJEGY3\n+TST63xOHg155g8pN3jLe22mMHnTgigP72MbLTBsdW5+5q3pmsLHBNtqKB3ewey6WNLahJ05sYhg\nsu2PaOFnCkEpmynYbJCuXswwsww6D90+hThHAoN3i7vJu1kuU3DrthFIV3+2ieM7R36WSKJfB/A2\n+r3Tpk+fziuvvEJRURHLlzsXSy5btoxrr72WPXv2EA6H+d3vfkd+fj6RSIShQ4dSUeHMNqeeeioP\nPfTQYfN8MDjW/Mo9+EsNjK6GMdX+cDkqUzqnaCfmkjlO6oUHWlBKvAgsmyAwB00QP932hLMZZhvI\npvDGe/+EkKM1r8e5OWQ5ngvWdqAfxHtAK9l8QohJ1AIwiAgb6Ze8MFhfONxGNj0LY45PdjTkHBYl\nAly0I5v2L3UqglfKX4GnUdu0M1PYREltJ7NttNBLZxLRdEywCW7JRws8vVrQKzHbBGF6rWhBbq6e\nzOd0pjfbJGdOXKYGbdO4BSoVnphHojjmthoVV6GexUMGI62t30ucbYIyzZD1tc7eU2fAYUi4q666\niuuvv56vfe1rybAZM2bw05/+lIkTJ/LEE0/wk5/8hDvvvBOAsrIyli5d2jn8HgSOXYEdS8DOBIFo\nInXZLMtX8OK04JZOJPZTWcpJ59PnLmgwNSdNT4PZiTWtdINN07fR0/zFYHXhSFpH5UBvWDepDwNb\ntnnmiyDEj4NYbk9iiV6sCgyhijoihClnBQ2tJSzLGcVK93bs2PaQ84m6WrEE4rArWkwgCsRd7aSQ\nVDuoWaeCJ/Wty2pqY2Z9AIkGCGgh5wqXBO6xMVqQm/+qrhNRpwy+dpDJ1NhMS0g8rv+5SzPh9qOA\n9Ce3XEldza0noZ8QE1LcO+JGaIgdPKBs24m44ywdkLRxJ/+EpI4DQdePXf71hCN7FT6B7fjBC7+J\nqFFvQCIPeCOAe/ougbpEsh4EN4FXfwklnAMqLuHSTOJtDzj8+OziLt9SvyRIrE7AFjoHUi+SPyhM\nnDiRSCTiC1u1alXSKWLy5Mmcc845SYH974RjV2C7HT9R6A4yrRVpjUhrd9KxlWBLzv42TUdAa4nS\neSWfBpIeBImg2+FtGoaNhzh+IddkCCZXQ0u4+Qe0LTMODzKT/F/v5o9cyLgvLmInIRI4H9W0kkWM\nXmwNFLGUKpYzgm1vDGBb4QCIw2/Gf83xr24Keh4bYLdjilCSTSzTI0H9J4JKwOEInwAJEnF3YJdA\noiGQFCwJJTwdMRUgETWWya5gSwTdgR9P1pIjyACCnlDw8jZxSb08V8Ld/4Q+YdFt54Se/I1JIKEE\nodbaE2aYm2/CdFkkgC6tCO5kPiIE5eMjmfjA/1GWKB17AiR64/McSZimQ/GAGQPshETIc6VN5AEN\nCSgJOJON1I/Lr0xACXUcbfJZf7iTrD81+eBORj0D0IvOgU6ScCeddBJz5szhS1/6Es8//7zPU23t\n2rVUVVXRs2dPZs2axYQJEzonUwscFYG9YsUKLr300uT7mjVruPPOO/nkk0867yyRNQHICsA7gaRA\nA1J30LV2pJfL+hAf87zpuMLVtj9ziSfaZj3OUrIO3+Dz2QVF69TXJullfb2XLFmeEJ4LmWh2om2f\nC/WtFXwr5wHGsoRaqhmH8xn6S0xlLEsIEeMTerG1sZit0YHe7n8cWitzSDR19y9jI3g35Mjny+DX\nlqUsuv5Q9VyiBISUJ+oM2kQQ5VKpBJVo18n6DfjNEVGgSQmsJk/AEA/YJ2Wpq6BKB/4+INqqOTGB\nX5NNt98AfuGeznShtXwNesUiK8MwnvAN490faTMdmXUPrnB3fxH8iojggtNfR7l4Mfw36hDwXP1k\ngtYKkYCeyE2Tkk4nm9Z6hZWuPg8VLBKutglqD9Ez5PHHH+eGG27grrvuYurUqWRnO98g9OvXjw0b\nNtCrVy/ef/99pk2bxj/+8Q/y8/M7gflUOCoCu7y8PGnzOXDgAP379+eCCy7g8ccf77yzRNbg7BBH\n6Ngu/qGCngTeVeEiQIIGnny4ZRv86Wx+4B+INlOKaU9Vm0gzfvYo9224jUdKv8p/7Hma4B7Hbj2j\nx6PJo1cjDOJb/R9gRv9Hua3+PnpO28zOur6U56xgUayvk5e4a9XjDS55rsfTwMUNzLRZmiD+8GJy\nEmhv0EP79tmDgdAxzSmQWqe2vDWe8Gmm1aYeTSudTd5sTzMfM/90fcSMw3g2adrsx9okCLA6gXN2\nwXLoO95uU7eBDcc0kdn6sYZWOu0sEZtJpDoHqpW2f4d5oqcFysvLee211wBYuXIlr7zyCgDZ2dlJ\n4T169GhOPPFEVq1axejRo4+YdRscdZPI/PnzKSsro7S0lEQi0XlniVxe43QG8YjIwekIsgJuUnHm\nOQ+N+L/GGgUsc/8FD5VOBLCcz1Di4le67404t2mPMtJKB5azTCTvJjetXtLKgNrj8tUHONENK3PL\nIVp5OXAKvMS5/CL3espZwfLcERTlbmUrfXiJqUxOzKc1kMNrnM22ZQP47aivQhx2vVMM0QSLg6fB\nG24eTapOwPkSTbSvCjyNTs5g2YP3YUajqufeeIc7VLhh7sqDUTgDN+Dm09utw1K3TPo8FonriacB\n/82N7+/WNfgnhKgb1+qG5ag2y8H5CnQi/o9EpN716kfaocp9NvuG2I610DLt6OPxzn6R/ig4vfE2\nhnu4tMVEJ2fXxEk12fRwaazAfxtNCEfuFrpp64GLgH/iTbINOJ4gy3DaLAZUBmBdLiTGwyC37gpd\nnBPx2jXg0iw3+O7ulk36htSzCG4500eXRcoer4ZgNdx75GeJdJaE27ZtG3369OHAgQPMmjWL6667\nDoBoNEqvXr3o2rUra9asYdWqVZxwwgmdk6kFjrrAfvbZZ7nssssAxw2n084SueeHOCPwNBUo0qLF\nfXYP1KAF5wuTFhwH7mY33n1/3k32fMKSVmgGcHprd+fXLQBvJTwa3SR9IJV+0hNDHVXzaouFZwMn\nbXgL1OeycmElF45/mg2UsjHQj57EGMIqhvMhiUCAbNqYyNv8cf5X+WTUcfAgJL4TgPmu7fhtYCme\n6Ud717yEpzmJ3Vd6k+9TX2Uj7gbsS0DI3RzbB7zqxr9l4ut/s7xS/xjxKp3kJWm65Tr5dQP2NePU\nu2pPX3tp+s1uWrOtXdqvuniv6rQGL4LbLeDw9JZ5vIKqI1u4lEXSW3EV/mJLevDKvxSvjSTuL25Y\nsh1wvnKsbYYlualtK+8yuf0lDUt6RSQmJLCvdAV3Uy24XktHDIfhh33ZZZexYMECotEopaWl3HHH\nHTQ1NfE///M/AFx44YVceeWVAPz1r3/lRz/6EVlZWXTp0oWHH344RWZ1JhxVgd3W1sZLL73Ej3/8\nY4DOPUvkxCw4LggDcy12y1z1nguF7rt7swp5kkbhObl7YXlANNfoeL29OLG1Nil8GWhNuS6O0Ff5\nJNMKT4pPqzknN9XrojCX4eWLCRMhRIwwESqpo5wVjNjzITk9Wp1zsoEtFPPXm09jKnN5bMZMBl5S\nz7q8Cu/QojI823aE1DOoxTwCfpt7cskbMLxFAoZLZcBIG1B1p/6T+eX68YMBwyyk+4d4TeQa5oVc\nL97XxgGnb4gWWIhX75Jv0iShNjGFT3INU4RZFrf8KXbjgN9vOWlCULjJ54DfTp3MX+EkTR3+Db0k\npDPN6HLLl7rgnDsD/npOZxoxTVSmwDY9rEIGHjga+lY65wvEw5Bw1i+ngRtuuCEl7IILLuCCCy44\n9EwOE46qwH711VcZM2ZMcpOxqKgoGXfEZ4nsr4W9EdhbC72qYWB16iaPLMf15pKALBX15qG7aebb\naNQ2QR2uNQp5jhr/pt1RCzZZzou3ir7hRHf4KH6zhBv24eyT+TB8sn8AFUJ2yU7aXu7pz381PLZn\nJnwM65oqHFqTVb5NXnrfXoDkqc9XlvILr3KWc4OiIfHCt5RHN2MQ7/Q+n8BXz/qLOa3UtGfrlXhd\nHh2uNygx8EwhWWik1eXTfII3oQptoWlOtuns07ruIXXy1s+ahtkvbc+mTb8QOAPHbDMt17tQWnBN\nTxrhX98WpO3i4L/1Xt9GE3LpvgusqXXucuwZgf0R2MSRg639P8NwVAX2M888kzSHAGzatCl5KNQR\nnyWSqIZYNYSqHXub2fjtaQL6XcK0sJeBa9sEk45tbrRo7VPjH2zTzNwwtQmjdw0c4OrFDwLwh9aL\nuD7n5xSzlYn8lVFbV/HgJVdTygZyaWYF5Tx8xjfIpZlFd5/O4JuXsWrhKG8iq8A7E6MO78OJIN4J\nejIwRYOSetKTmflubi6adaGXz2Yd2TwI9MQn9SBh6QS3Thsz3m3eH+ZGme1f45n8pttMPFi4GWfS\n1xuGpgC39WtzQpJ4Xeer1wIFwBYYOyyVfjqebGH6GGDzo7GQwqHasV13rYXGWpybN44QjrFP04+a\nwN6zZw/z58/nkUceSYbdcsstnXeWSDnOxtBQ0n/ZpjuPKQS1NqG1KVMIpNuVlw0dm3DRmrZtKWwu\neYVeXpo4i7B4gzOYwDvU51Q4Z4rgHOhU32dgUlg3k0sL3SlnBa3kkHXtLudm9BCc+43nWc4I59Cn\nSvd0PhHGktcEvBWIhKebVDSvAmITNz0XNOhVjRluapE2k7cp9ITfQgOnvXY0J488A9e2mjLbXZfP\nbNd0qy0dLvzbNGqdt7kK1H1M95tgO3GFQHSQe4BWb5iWpl7Q+KS2icaLG7iQ2jcEpwEoIr1d/FDg\nqO/SdS4cu2eJcIB2N3Ksm1N6c8zET0fHDPNxYuSnNiBTNpFUPAkjvUnPlod/s+zqxIN0p5kHF36X\nX4yfwULGM5W5jGMhjzKDAWwgRIy/MpEIg3h54ZfhUej54GZ2fq+vdx60Pm52NY6ppB6/mUNs2HK0\nqBYUTajNPhcv+azKIhuRqLopBDbrujY39lDvLZYweT4O5/Qrd0OYHXibzCZ0J5VmiyXOhi+4kqdO\nq3FNmhp03ibtLUBxO/TMekhXNp1vOj6W49zeDIzNddp1Go57agw8tx/ztlxbPchzd7xNdslX6kmf\nTiZpehz5WSIdMC8H/nTwm64+LXCMzT8abgXGAWfidPQCO9q+43B204pJdqJ9MsA16LBdBj3zXcA2\nwJthn+TTXfEmNFrcZ8VPMo9iha8Hn07rvG+glIm8DU3O2djOUak5tJBLjBDFbGULxcToRRvZjtkj\n7tyWntxgjEHyy7kgjkAVLU4+hojjTToxHEG8Wd7FG6PZLasutwhQVwglTRJufe0DNufied7oeomo\nOkj3DfMu979A4be4+EKrwPKv8zFp7zL+2wONYwpt4WsXnhDW+Fvw95kIfqEt6dPxJ3maE5vkr9Oa\ndISXHV6aJRHn/w+SfiuO7+RqPB9Kqa/dKkzzK6AFejGwyMXX/fklHFeWToDD+DT90wzHsMAGp7W6\n47g2pNPQUPGm5mTiSZhoANLJxAtfu+ulu01O0w3gdFpN08Qx6RWTyqfJz3HEWE8r2cmlf4gYpWyg\nlWxyaKPYHEju0jjUO8a2YIF/6SwbXIVGmDzLp8sh9yfeEeKBsU9WFe4KIATERLMqxlt1NJPUuLq5\nHg+x3iptb5w2DKu6smmcZv1rLU/qL6DidNtLfdpog6edazdOM38UDzpdbyONVgIKVJip9WotVMLk\nSiWbFtui6OlVBTjC2OxbYcUz0G0Q7Fvnhq3G0bR1OQ38JA+2CUKvboyVSN/esFkUpgK8SXg9nSZp\njzEJd4wVR8GILOgVhAHuwCwBGlzXK/EOEcGT3BQJKHthrt/GFgRiygWsKdf9ss/FqwTedeNPyVVf\nP7ph+mwN7VHRoPPJNTbA3LSVuf6D8XFpkKs2bcTtzHFLW9FaTnOOE/YaZ7OC8uSZ128zkS0U00J3\nljDWubTA9drY1ljklKUE/y0qcfdfeyuIjT7i8pDn0EjxfKjAvbhA1W9U3NS0u1yufyKQckaBQteN\nLuRq8iW5/qMBkhufuY67pZhjxBMlmuu4SmpvnwaUK1xuqgdIYa7nrSPt0tRb0TTcOHHLo+lJftHe\nbt2pT+xKcCYkvQEbR7mZYkBvh+a5OOdnB3Nhci687D6T6/ULMLx6hFfJT7mUJu3nqi+/XO2G9fZO\nYkzZY1E0mtz00ieaVBvk9fYm8GRbueOwIQAM8tvm1wWd9B+b5T8MOMY2HbscjUwfeOABRowYwfDh\nw3nggQcAqKmpoaSkhKqqKqqqqpg3b5417bx586ioqGDw4MFJ/20r7MKb5KM4ioIs4SN4blp6I0fC\n9HPUwDN3yQWvHu+8h/l4nhSSpoHUfKIqTGiYBy01Kdr6F1R0Y6k0S3McGzVBGMpH9GMj41nIeBYy\nhJWUs4JK1zgd4pPkhk/PwphHZ4niI2qUAZxJL+LWg0wyevNLhK2+eUULJ13XppdBTOFoQSr06xW+\nbUNScOtUuFnX5uaXbus4/ttx9MZqvcKPq3/Z/ItY8pN8BBf8V5eZ3iwmTfmP4h1zEMcR1uCZrnSf\nEhwzXujrzVH9Px/4cC0sWQsfvurgRvCOE5C60H0urujqcpv9oUHF1aVJD6mm8cOFbh34fYbg387u\nhx9+yKOPPsrixYvJysrinHPO4dxzzyUQCHTeOSJA7hU7CXxuB91O20x2Tptzkax7iWxRzhbnjkJy\nk+c9N6sPKHRYW2s2oZwYzeQS4hPayCHWGiI7xzErbFHLZrlFXCC2PURuXnMyf6E5iLXJdM3kUswW\ndiu7XzatxOiV5Fn4Ff4lb51GeBJ+L2E2EcKEymPk0EYpju+68yHNWkI4N82cx0ts4nhyvu7wWBrY\nwAf/NYI2d0maTSs5tCWvCtM8bm0tpihnS5JXgHWNYQb2j5DP7uTFB+KRIvXT1pqdLIeuc7O+dXiI\nT8ihLVlmwQWS+Jq+GabbJ7Y95L/1fcUAeoY3O2d740xaoZwYG7f3IzevmeamXPr13pg8ahZc01Fj\nET0LY47dHwj3XkuMXskLigf2j6T0rbbWbJqbctkbzyYr2JZMI2WRvHQd76zrS1bZLl++WcE2+vXe\nSKw15NCLFtAzvDlJIzfPaY+d0RAD+0eItYbYGQ3Rp/9WtjUWMbz/cj5sHMG4/gtZur0qhd8Qu1g1\nexQ9p3UHNidpyvnnWYW7fLyEe69lVWM5PQtjyToGqOq9lLUMStbJuP4LWdQ4nqyg0ya5ec2EcmLJ\n8pazilfndqfb4iZa7+bI4Rjzw/63e4n84Q9/YN68eTz66KMAzJo1i5ycHJqbm8nLy+Pmm29Om/bv\nf/87d9xxR1L7vvfeewH43ve+58MLBAIMTtSlpAd8ggi8K7BEIImA2k1+EidGL0cLddM7F9RmJ98F\nT57NPLSgy2c3Wyj20RNcM3060BON0ANvogH4b27k7D2vE3wdxxy4CgLvuecanxbwTJqDYcH546ja\nv5Sbu97PubzMO0ygkmUs5GRCxNhEP7ZQzFaKnHsik3WZ7Qgx5Ta4haJknUq9isCXcBHCus5tbZOu\nPnT5Y62h5IC3Cfz2wDY5SH5CV+LMyRicCVmEqwjzUO8YJpiThm0ykTggJcyccLTykQ5fpxPFQYOm\nKROO5n3bwgFJLXjgD+ut9WnyL+1qvgu/Zjna4xlgW2DgkXuJfKsDeA9kvETSwvDhw/nhD3/Ijh07\nCAaD/PnPf2bs2LH07t27884RAbbWPMLODy+Cu6sZWF7PuoUVdj/nd3Bsdnk4y706GPjTetb9ugLq\nYfDPlrHt2wOI3Rpi7yxnI6fPz9YnNYu9DQVklexi72p3k6cO/+fc4vfr2nF73rvZOQmvcTxEg54G\n8CsgAFk/3EXouBjbvj7A4elKoDDu3DQuNsFngXzoec9m1tVXeEvdN5z0e1cX8Nj4q/ljjwspP38F\ns7mEs3mN8SxkLlP5Gr9hIeMpZgtxgixjFJNq36XnhM08Vj/TqYMr6ilmC4sePp2si3ZR3nsFH37/\nZAjA8P9azIrt5ez9QwETvvEXPlx4smuTjzua27KT6TNyPds+GEDPCuf0v+R1U7h1EXHb4lLgUZx7\nA590w66ErBJHg1u3sAJCMLjc+aAnq2xXUmvb9v0BcCk0l+Sy93tu/c+A5jJHgyXqVm5hnKycNvYu\nLPDs2m74zvq+DD9jMR9+/WS4GrLKdrE3WkCf8vWsaww7GumKAfQpX8+2uwc4fM9w+009rKPA4d39\nem9bncuHtJX2Ua6MQ1OQovItrHujwn+o17Mk/aeHP7LYqdOo25dmuf1AzAtiErnUDXsRx+UOl8Z9\nOHbu1W7fBnYGC5Kbxn1GrWfbtwfAtS7fTzr1v+3GAse56j4c982wk/+6xjDUBZP8J/d89G3vUo6X\nnbx7TtjMtncGOGFRvD2dII7/fiEMHr+MVd8e5eQlcXnAT2oht5ZOgc+YyeNgcFT8sB9//HEeeugh\nevTowUknnUROTg4/+MEPKCx0etRtt93Gpk2bUs4R+eMf/8i8efOSH9s8/fTTLFy4kF/84hc+PMcP\n+3bgdJwTbPRBQdo32nLokkPBeNc+17Zn2yE/ZnpNO93BRgJ6t180FtPvu9mI07SBsepcibAbLZ96\n6/McxC4dwxFGFfhtlBq0P7XPV90CSf92s7y2urNBuoOfwPNVNw+Asvm967a1+bvbfN1tNDUPNk8g\ns83SHVrVEUiXpzy356svOKTB0+lth1VJvNbIbXVo5pfOdzwdmH1bQy3OrPRfR65h/6ADeP+V0bDb\nhenTpzN9+nQAfvCDHzBgwIDkeSLQCeeIAPAqjrr7B+BkHJ9sAd35dxvpbAePm76lGiwfK+wzP0po\nL8dVHmoAACAASURBVL0NTHx513nZaKr4Jd1J+nIvSfehh/zvIOnD+6H45ZofWYgPNerfLKfKY1+a\ncCu+Lo8u126cT97EDCPhZp3b6sKkY9KWcEjNrz3+2ns306Yrk86zvfQ2sJXL7BcCmp7to5r26s02\nLmxxuk22Wspg43eri6/bFhy3kMU4Z0k00ilwjGnYR6U4W7dupaioiPXr1/PCCy+wcOHCzj1HBHB8\nR4cDp7rvurNAeg0gXfxu/JpDvoGv48yObRuE5kAy85NOnU/qAJD0No1mt/rXg6G9gan/xf+2iNQy\nm+XUtGw82MBGU5cH/OXdajx3T0NfhIXgCD05UEzy1QLDpCt56zrWeO2Vs8XgVfB0e+RbwnUb6vRm\n/ro/6TKCv8+mqzuT1+4Gju5rtolWl0PT2Gr5t4HUnW7jreq9O845EmHgI+B9PDelI4CMwD5yuOii\ni9i+fTtZWVk89NBDFBQUMHPmzM47RwTwr9fNQSJhAt0NPBPHppXuNsJI8y4gH1yYdDWYS18zToM5\nOHWeWnAJiEDTdWAKPjMunbZny1eeLR9IJPnpiPBPl48Nz6xHmyA322k3qXVnCmX9gUo6PFtb6TAb\nvzaBbOaRbjKzPdvysPHdUVNFOmFr9uuO8ie46SYUm/bfHee6mfbsbYcAx5jAPobPEnnLEpNuEOrO\nogWrHrjtQRrzQbsDpCPCSr5gM5eOHck7HY4pVGx1kY6OjW9bObSGe7jl1zi6LmzQkTo4WB6HmjZd\nXdmE9qHwo2l3pI50vjrPg7WhiZNOoB9szLRH00yfLi4dr5OO3IZ9fwfwbs7YsD8F8AiO7bqc9gfV\nDuNZ4tNpOmYHlnMnNI7g2bR1DTJB2Aa/xEHq0jEdPU1L52HmKXml0yT10vVgZbDFpdPuND3bqqU9\n7bI9Lc4UFukEkpnGLNvBJitNp4WO8WSDLfjPijmYNi9x+swaG586jals2Camg7Vne6tHzW93Us+z\nSbfSxBJv0luB/2urI4BjTMIdY8VRkDMYWiuhb3Xqucri5YB6DwGxhN/Doxuph7Hn4X6FZ1y/pGlp\nTwpJU4h3sWm3XD++3snXfIDnadEX5+Q6+cS9G557Whz/HX+2MNvZzuYRoO2dv2we/5mOhgm2DxfM\nI0NteYuL1zt4p/bpei3EOWRKXzfm80zBKb/EyXOeykfaJMWrR9PCOyulCe+Ks5iRj7SJ9I++eH1m\nn3qX9FLmKP68xZNVe+jsA59XUF/sfVqXF1Uu3+mIgdR6SuLqfrfdjevu9VfzFEaMZw37dF6qbppw\nzowRmuaVY4XA1u5wIAb80UL4EOEY+zT92BXY7tEK5OH3iQX7JQXgnFeRDjRuEPdKKAPSnXksgq2v\ne5ZJnplGHS1aqPiQOIEyN0z+C/GDWR4JM4Wm+P/KRGJ+2q2FqfCuz8UQHCmrTQBrOiatwjThZhrw\nLpTtq3hP5h9IrYemgAVPPQuu5FsW8LebTmulJcI2kEpX6KRrlzzwXeNVaMRrMGno6+h0fel89TuB\nVLq6POZznptGYLV79ohWDDSv+iAw66RtjA+ZnArdsvjaDH9ddgF2ctSuCPs0w7+0ONOnT+eVV16h\nqKiI5cuXA/D8889TU1NDfX09ixcvTl4HH4lEGDp0KBUVTu849dRTeeihh1Jo7tixg0suuYR169YR\nDod57rnn7JdetoH7MaL/gCCtLWrNwNQUDqZFiKAC/zVLWvhJOt0h4ypcn5EhcabmpJ/NAaiv5jIH\nza1451pI2cOKRwmTczHkw6H2LgtIJ1TjacLMctjATCsCXdLVGe+63m00bMJDzrcwfdBtdazP9NDn\na+gzPpIHOrlhul1sYSafEbz6ljM+TD503xDhps/cMPuPzlfizHLoMmp+87DQdU8V3LfFucxA07XR\nSTc5m+fG6A/XMJ4lbivp3fMPFQ7j0D+b3Fq0aBEzZ85k7969dOvWjYceeoiTTz4ZgHvuuYfHH3+c\nrl278vOf/5yzzjqrk5hPhX/p4U9XXXVVyiFOI0aM4IUXXuC0005LwS8rK2Pp0qUsXbrUKqzB+Rz9\nzDPPZOXKlZxxxhnJz9MzkIEMZCAFDuPwJ5vc+u53v8tdd93F0qVLufPOO/nud78LwEcffcTs2bP5\n6KOPmDdvHt/85jc5cODAv7Q4/zKYOHEikUjEFyYa9OHC3LlzWbBgAQBXXHEF1dXVdqE9tMb5j+Nd\n1moq4qbGaMbroz7FHmwzFwRVWlMbD1roC09Nljxt6UTrDapfCE9bNLXOIM6nzmL6kPR1pF4R1aDS\n6ZPVwK7NocLAr+Wle9ag69CmtQmOrAJEu5TVRDoTjhxdK+nN9hKIWcJstvuO2PPNOwrNNOa+goB8\nzm3TUNPtCQi+XtWJ7Vy+HbOVV/NjfmMmYTbeY73dC3IH+ftdEHsetvLo+tG0bSY6HVZYDfFqWH1H\nmsIcAhyGhLPJreOPP56dO3cCEIvF6N+/PwBz5szhsssuIysri3A4TFlZGYsWLeKUU045Us6t8Kmy\n8Kxdu5aqqip69uzJrFmzmDBhQgrOli1bKC52vDKKi4vZsmWLndiSGuhS7fw02K6rArvZw9wsscXp\ntCZtGVA6HzNdDHsrmBuj6cLSCUYR0iKgRFjry1Ab8F/pJekasAtR0yxiEy564JmCVfi12YxN+7+5\n6RZSYWbbSVg3Ix5S670jeChcWxtq0FfJJS9dsOAdFNJsfmqwbh6acaQvCyqtLU9dZtZC0yCIrXUu\nNBA4WN2nezfLofH0hnG3AByodX6dAZ10D8K9997LhAkT+M53vsOBAwf4+9//DjjfiWjhXFJSQmNj\nJ32laYFPjcDu168fGzZsoFevXrz//vtMmzaNf/zjH+Tnp/+kOxAIuD7XFugF9MQrobmxESdVczQ3\ncHQ6vcki2t/BhJce7AcTcDYN1sZHOk8NzXsTMBPvPOcKVQatlTWocuhy6XzS2c/bA1kNmBt8tn+M\nZ60Fin1Vl9VWJzawrQDk3ZzczHo1J42QKks6OnrjWDZITXu8hNk8ZPTlDrZ0GgTXNtHJJKknYV9d\nB5SWHkjNQ/KW6+FieH0i3aRqawNbfdriffm7Y/lTuOl49dVX8/Of/5zzzz+f559/nunTp/OXv9hv\nCU4rkzoBPjUCOzs7m+xsZ5dw9OjRnHjiiaxatSq5KSlQXFzM5s2b6du3L5s2baKoqMhGDqiFAxHI\nqoW8aiir7viy3qbltSdQbYNYhEAUu5AQHBFuOkxv6qRb4tp4VnHnjnqehaPGE9seck7aC51Mn/L1\nhPiEVY3lDOwfcU5hC7oZBPFOd6tTtIUPSN2QtNVVlOQJcb7NJAHbJpikFyEjk4g828oo0J6Hijkh\ntPdvo3kwk4VNCbBtzpoT9cHCTYWgPZA6KVP5myY4W92loy9lWi1pCpwJXyYI3SbtTbwax6wnLHkH\ngU21EKuFeAS6RdKV+NDAIuFqP3B+hwKLFi1i/nznmMSLLrqIGTNmAKnnGzU0NCTNJf8KOKoCW39d\nFI1G6dWrF127dmXNmjWsWrWKE044ISXN1KlTeeqpp7jlllt46qmnmDZtWgoOAEOqoaQaSqtT48zB\n1Z6mZksjcDB7o83eqkFs2DbN2eRJBoqOa8fuGWYtWymC3jCElewuz2csS+hOCzn92wgTIb//bj6s\ndI5GzSrcxV4K/Edolhm0pTw2jwABbQ7QZdflERq2ui/Bb3s3wTaJdmSCE3w9SQgf6bRuLZTS0W9v\nX8OGZ5tETDp6ZaL3PUy7eBy/oDbt1Dq8TNEw7dBWG3PY1bB3QZm61kxWTuZkayuzbc/IVgdSrsJq\nCFZDpBa21MLyBRwxWPywq6ucn8Advz84mbKyMhYsWMDpp5/Om2++yZAhQwBHHl1++eXcdNNNNDY2\nsmrVKsaNG3cQaocP/1KBfdlll7FgwQKi0SilpaXccccdHHfccVx//fVEo1GmTJlCVVUVr776KgsW\nLOD2228nKyuLLl268PDDDyfd9a655hquvfZaxowZw/e+9z0uvvhiHnvssaRbnxUKgAFAfzq+LLbF\ni5BKt6FmLl/NTTVzg80Gksam1cu7bcNIBrYpRIFitjKElcQIkUMrpWxIXgm2lSLCrAVgQ0Vp8tD4\nbeEC5/znygGpdlhTmJgCV7/bNEydTk88NiFXSHrBq/PQG5Emr9o0oDV6jau19xL8gkvHCxxkVZME\nW98yw80Jo73JwwRt+pC6i+LdNWlCuglWC1sTPyQmmmLHHdRcGem6s5mLNOj6ipO6yWjy9gntnx92\nKNDeBJ4GTLl155138utf/5r//M//pLW1le7du/PrX/8agGHDhnHxxRczbNiwpLvfv9IkkvYskR07\ndtiCfdClSxe7D/RRhkAgALPcYtk6kR64WuhoLVbjaRvvwcwgGsw0ks4c+Ga+FgHso28Tknn+8Jk3\n/19yaCNCmO7uJ79n8xoRwrzNRIawgk30Y37r5OQNKNveGMDAM+pZt6LCuyeyEMfWrc0h7S3XBacJ\nvwcK+Cc3036p6zGMXfDoelmNozWmA13vHTU12MwgZvuB33xjW5mZ/UHTtfUxSC9ItZnI1nfkuQ7n\nYgDTjJVOMKbTkiX8D27azc3wvVw/nqavwdSe9cRyOPDfgSM/S6QDX7gHJhwDZ4kcf/zx9OvXr93E\n+/bt89lvPlXwxxqoqIbiaqfzmNqcCBO9LGsywszBJHi2dHkKV+KbjDSCp991x9cCybQVa9q2pbqk\nccNbyKWYrUlhDc51YvLfQi7daaG5KZdQjnO/IXF1/6Aue4mfdvIWGY1naoZx419wBacS/y0kTdiF\nWRx1QwzeRydRPHNSCf5LeYMqvfxLvUdxBJt88i6ukVq4SFl0+4i3jdZoO+INostsaScfaO8dsw+a\nfUXXbxxnAgsbPJq46cxSmo4eF1GFq+lofky7ddDAN/EKLWFmPWyshQ21dAp8anbpOgfSFmfo0KHU\n1dnvRRSorKxsN/6oQgjHS0QvdfNwriOS25rBb2fWy3aBON5AiMLAm+tZd3dF6iaMKTxttkktkEwz\ngeCF8b5ORMVLmibsfEr53LAtFDOehaygHIAW9+CfGCG600IrObTQ3bkkmFbHLFLo3KAeKwwRKo85\n9/oFneu69sYLktrp+JyFvFU2ib0NBX5/ZxE2Ju8iGKUMsnyPkepOCJ4Ln7RNE2Rd6VywsPdXBR7d\nsIOTddEu9t5nXM2Vh6OBr8YTTq5ZafgVi/mw/mTPz1s0ZS1UdFuYy3it+ZrCXtPQdYBKm27vQfiu\nwC+0tdmhDKf/mv1Klc9XD7by2QSlnhyEB9FOC9W/lPM7cbgv2L4NXq8+wi79yTjXiIUVXwJSl3tw\nPrTsDPh/RWC/++676aIOCeeoQTdSBTY4wkCsOLqT25bDqLASJyyf3f6BIRqDFsSi5eThDTx51x9a\nmPkE8Z8TYtM+pJM34WipIgANbWkrRUmh3Oo6o26lKHlhbwvdfdq38NJGDrl5zc4lt2497Y1ne2UI\nwgrKnRuz3Zu/9zYUQF7c2awUYafrSISx/khDNGTNt6QpxHM9dOP3vlvg0RWt250k9tYV+AWqbpMG\nF1eZjT5842TPVQ31r80EhXgfN5n9QsogOOaqS9OWcPAL/nSTQBDPFi2CWq9yZJIBv8CTujLz1ROH\nlEvCtZCOGmnm4/lP6zzlvS5o3xQG/2QhvEl5V6s8TBOKQE+w3Pl7eNBJftifFkgrsIOuu9f06dO5\n/vrrqarytlVvv/127rjjjiROOrB9k3/bbbcxd+5cAoEAvXv35sknn6S0tLTzzxIB5zwRscVKx6gj\n9c5CrSnpZT0Kr8HB+/CVk+1LRN35xddZhCn4l+mikQVVGhmwDXgC3caXXsJG1b9hU91CMSsYwgZK\nyca5aXsLxckbzmOECLlr+jZy2NZYBA2wsaQfe+PZ7Iz2VeYe1c5x91LWpqAjSAm6PAQ9viRdVD2b\n/AaNMFNYSp03KRq63ipwtF/w2rgMT2sXu26U1PbS4WFFRwsx+Z+M/wLhJuNZeNSTs+5vEbwzXASi\n+PuOngSa8PznNb7kZ64OJc8JeHUvE6KesEyTkTbPCG1x64wqfFogqqSntJn89IpG6Ei4tIOE67qN\nGLzqOtqG/0rJI4FjTMM+6Fkir732GldccQVPPfVUMmzu3LkdIp7um/xly5ZRV1fHtGnTuOMO7/PT\nTj1LZB+O870ePPKshaKAKVDMX9xIqzu6/ARPfyyjbZhCK6Le40acFuKoOOFRd/z/n713j5OrqvK+\nv0VId6WpJAUpEkg60AiSAEET7uPDpXm5yDjglYvwMAiYQeBVPii84IwOBkGJCjLKPPggBFHwQUDl\noqKOoI1EHyRoEkRJIEBBQoCkklRI2anuBPv945x1zu+s2tXVSRoEJ+vzqc+ps8/aa699W3vttfde\nuyo0bBAqR2HLV03kJaI1CBPSrzCeftroj71iVSmytlJM7dZJevnGLXkqfGv5SKO2sLKUifJeJ7Uz\na3gh/h1dz3ZaLVcV+vbU/49J2ZiAWwBjz3w5W+c6oFlerC5LZLe7BQaXBe/cs5EvbSueN21XFXkq\nnppQQmXs61kHa037x4K3SOi4AX/ax+Zl26kKU6XfI/ETl66D5En59nyGykW/1V248rKeSNkaDtgM\nXyJvZmgpsMePH8/DDz/MXXfdxfnnn8+GDRuGTPywww5j++23z4TpycVarZbclD5UuO+++/jIRz4C\nRL5E7rnnnjDiwbPg8O70/cx60lBHfja+cNa00tgUcdBn4n2fNlXNx/EShuOfTr27SDWzgtA0gWr0\n7LvFE61k7MdfjmieSKP2rw1dJzQlCS81fttQj4RykSpFqoxnBYfzMJNZShv9iXZ9/KQfReYPhTjN\nQw/+Rcp7CaYdPI9jj7qPXacs4kuT/r90Sjwd6Kwz7ah5Mq2vpxpvaGpeI5pWax7VlJCH0y+6MSrf\nAo1Tcjs+r3VVgrVX75TQOP6iu+AQUnupDBrTrp0XhS2I4k67dl5wbWD6T55KTQI6wBsfHybNs/Ce\ntBNvdrG8d8p/bRtm+lDTibapCnCA48HidTo6saB94poDs2mU46cfNE4UnoDMJRw2qOrgWpInNCpA\nVj8G58ZPy1uB1M+PxtmzG66YxbDAiCH83kIwJG99Y8eO5Uc/+hE77rgjRx55ZOIEZXPhM5/5DLvs\nsgvf/va3+fSnP52Emy+R7u5u5s4N78cZsi+Rh2fBkz1bxOdWCMFbY/vTVngLw9Ie+O6s4aGVH8Lv\nLQQtJwQnnHACEO1pvPzyyznggAO49tprtyjRL3zhC3zhC19g9uzZfPKTn+Rb3/rW8PsSMZNIjnj6\nlU805A31tlRbMI22AIv7pmS3HBmIbbjBDlcQHLVTG45pRzr1MzqaTh3Gdr0c2Y5V81GtxTQR+25a\nyiL5b/bAZXnWTRqd2KpXkB7hX8F4ilSTb9W+YmQGqREtIMa8d9CbmQK/wgSeeHFfRub7YZyURVx+\nCX6BaDGyLoWoWmONyFSyiKz93fDi9YIVjE9NSAWHZ7MUi+/NFhVopy/aOujrsgLrGJ0xa3TQG+bn\nAVKtUutETVeartWLx/XarM7ulpEuhFcEV/e+m7atJrujSbVlyNq+dY3AmXkyfKm5Q09VJgPzqNRW\nb/xZ2asZBrJbJ5Fv9l13BandviLxK0T9dkeGB95iJo9W0FLD/vznP595P+GEE/jlL385LImfdtpp\nzJs3D4h8iZj5RH2JeDBfIsDgvkSW9cBDt8AfZ8FTPZF9zhrU9/LZhlID9oC139spS6MAPJDPCl2b\nYkNj4ywIngmzqfG3vOAo1ON087D2lp2yHcp406cKC+3caquNO8lyJrKGIpNZSpUi9/HexJ69nIn0\n0cbvOJi1lWKjTR/4r8Xvi/7E0/eVL47HFhdv5YzU1FGEHSet4Dl2S8wDGypjUkI6HVczge+wNVI/\nJMB/3fG+1HRkeba4x5O1e3sBBfzgjtOjPxXSm2vi3/PXWMVE748+eER20bNZGXuzSLOdr35AtjB7\n+vqESKDZGkmJ7E0vGt/4OYR0cVvt8tr+LF7omLjFhch89X3C7mchXVw1rTRUFgZ5eRreATSaYswZ\np+E80QMPzYJnboG5PU2IbxoMjGj9eytBU4FdKBQYPXo0o0ePZsyYMcl/e99cUCF87733JrtPKpUK\nr732GsCQfIkAg/sS6eyGvc+Et8+KbGKLSBuMX3QsEWlSugJvnd/vef0xqWZhjVc1Ld9B55LtvNaI\nxZ6apGGastqkzX6qC1XeHq6avWhSfbRRXhW5xjQtu4921sgOkZUvjk/jKu086RYshTwUx1VZ2jeZ\nsV2x7b0QFWR/X7T9b2Tnqxn8hL4uMunuHZ2aWhnU4/R1gFOBZ9+sbKxMdWB4QPI1l+xtM6odGi40\nnmBUAWhp6y6LuTQXXJZP1XrzZL04atvSaXqJqK1ZXOXd/n9P0rGBJZ6dJLxbGtbmvRnA8r+EdBsj\nRG5Oi7no6fO3RPg1+qr5e6XDZqOPCF/W3vU07E7dcMQs2OtMKHYzHNCfb/17K0HTCUOtlkqUGTNm\nMH/+/E0mHvIlcv/997N48WJGjBjB7rvvzje+8Q0Afv3rX3PZZZcNny8RzVmNVCvWRubBawahygyF\nqcbo8VSLtI5oC2bNePHTWpq8m7C2DtpFRiOvsj0blo1h8bgp9NPG4r4p7Nv+R6psTzv9VNmexNGT\ndjpLyzpzshCah3okmHtrsrOklqe6qhiZmqqwodCWFcg6OHnNT2cQXWR3XxgffpDTwQuy9FSg+nos\nunBoFIKeV3/CUdtIMwf9Cp4XD5pPzUMzc4OvF22PBRrLVsM0n94MVSDdAliVeJqunzXoSc9Qmavw\n1oNThqNbIg1shiRj/pbAxhFDWaZ7/W6IGW5o6ktEYXMF9t8KcrkcXD2QNSuo5mQNzt7te919C4Vp\n47KGp43f0rN01CZaoFFYtOrMPo5O2729VXkrEU2ZF8HIo19lw5LYNj21HglegyVkNXcI37ZunbwA\ndNbJ7Luuke56sE6s2pa3UyI4KtS75LmI7FY8jePL1peNpeNnPF57DoEKkFoTHG0TXiBqexhMexts\nIPbCuxkdjaNtWGk2a29KwzT+Mqli8wDRzfDFXGR+MlObgS8jFfChMGgsk2ZlZ23iti33JbJ2Y1tL\nvLHb9r/1fYm85eEns2C3bnhbdxqmwk8bknZg38ggXcjzQlk1Zx/HviPxNEzx9H/B/a8FvkG2s/p0\nC0AxPVLeNe45VhQmsLa8E2+ftJgVfRNoa++nv6+NtdWdstqQTYvzkr4J61ggjC1VWWtG0Uo+YxbB\nFhq144XATCTNykK1Xa8NW1iBsLC2dy8c6rQWgha3QPgglZ/u238Vsl4I+dmWxleBat+rNApxn6aC\npzlY2XqN3vOawc81noj0M0bImnf80/OsZxTsXfmvAC/0wMoehgNeG/EWM1K3gKYC+wc/+EHk7Wpg\ngLVr1/LDH/4wGYVyuRwf/OAH3zAmNwv6ITl57Ruy1w6aacn2VFOBCiGvwTQTqqGpqtLygiH03adZ\nIztD8EJoGZFWvQhWTJ8QOWuqwNOFKamQNdsipCYM7xTLBIjlo0K0SGkadlJmeSjVU54qQlPLQvNg\n8b1JyWvUWjehMtX4Xqh7aKX1Kl9eELbSdr2gCpm8Qjx6oa3g24XOEtRk4cvCvjebJWhaIWWjBLw8\nAJVcmE9ITUIePF5o9mDhfgAZZuijtYaNd9HwJoamAvtHP/pRsmXu8MMP50c/+lHm+5teYG+FrbAV\n/tvDa39nRoSmubnlllu2mHjIl8isWbO46aab2HHHaKPlVVddxXHHHTf8vkRKpM6fSqQjeElwTHtb\nRrStKS/fvYaknuhUYyg5PK9dmFOe0N2OITusX7SBxpN+hrco5tsWMU1Tcpr32vJOqU14WT5dsPIm\nIbNdq+1YcfJRfsaWqqyt7ZQNL8W2ccNXftU8oWVVkPjN+Cg5vDyprVvL29uNrRzU1o/891ql8WlQ\nbxInZL/2WrO3n3uTjs6qmpnpmoG2UePZ59W6g5aj5a1T4tTIasjTSeo42m2SS51wGQ1rq76ctX9p\nXmoSXhkkTNv7a0Bfi3IYIrz2VjvK2AKaCuyvfvWrQNaxt5lIcrkcn/rUp1oSP+uss/jEJz7BGWec\nkaHxqU99KhjffIkMBuZL5JJLLuFLX/oSs2fPDvsTsdPWuvClpg0Viiq41Vzip6M63YessAh1Zo+n\ndlkD5Qn5XgngKehKu+JbZ9G8WRqWvuW1k+y2M3vaQQ5vjonTSPZtK2/xDpIEz9tIQ/bZiqNhzyLZ\nqXKFtD7UhGLpeFOKf2o9aBw/VVfBWiMrSJWe8pwPfPd2bAMvsCxOyN7sFQYdPIxPHejr7pvGV4+R\n3twWMtsYnY0uTAcU7T9qalS3sL4cfH1XBE/Lv59h8yXy9yawm+55ufjii7n11ltZtWoVtVqNWq3G\nunXrkudQIORLBLbsdoch+xJ596x0L6c2UhNA2thD9uOKe/oGaMKjJjhq7y6T7cD6RPAMKjQKbqNv\n8YxmzcXxfCjtMun+3CrZXRyaH/vvefZaq0LI7mgDgmrOJdKbx82lqu/IXtiopz6fJxXe9g6Ndnh9\nb0ZL4yPf9Wk8aphvJ9q2tFxqZMtV09JtcaG2qIOK3wJn9WXlVqaxfUJjHdXdT/loWDgdiH5a/37Q\ns7pGaDSz9YdmDzr7MpjcHe3HHgboi7y9D/p7K0FTDfsPf/gDt99+O/fffz/77bcfp556KkcddRTb\nbDMk9yODwnXXXcd3vvMdDjjgAK655prEpGG+RMaOHcuVV17JoYce2hB3yL5E5syC9d1wQHdWCNnJ\nNJlG3nnXCZx80o+456538/6Tfp6dnpVIDwosIutgx/BUKy9JXJ326jRQBUHN4Sl/ZdIOYYJHfBBf\n99OZfOKkm5LtWB+/88v853suSXkqwHU3zuQTd9zER6/9T+Z88uPceu2J/PM13+e/LjqMY7/wmJwz\ntwAAIABJREFUMLnnBxio59IOb5qcPlUzLJBq016DUi1JNXuv/alQReiUUtzTb72R2/75X7La16IY\nPy6Di356Jdf842eTerzupzP5xIE38fF5X+Y/j7yEY391L/914Pu4Yt7F/Ps/Xh05xbf1JZtlGN8L\nyGqxml8dtBS03g1sIc7XvdesITWx5eW/th/jzcpI3+OZyrF/vJf/2vd9HP/Hu/jxvidFz7efxLSn\n5/HEvgdGpgX1CW0zGK88mAZu9VohOjSzcSA98BLn9fR5N3Lbkf/S2oSj+Q4pSFYHZuaxfG/oiW5P\nHwb4e7NhN5W+06dP50tf+hLz589n5syZ3Hfffeyzzz5Ddq3aDM477zyee+45FixYwM4778xFF10E\nkPgSmT9/Pl/96lc57bTTWmryg/oSATiHdHsawP+OnzfV0/d8dAow0yEtjjUy0wpvI2s/NDy/8l2Q\ncHuOdnGRePrUDnCTC79NaENyWpFZ0WPf3BNRGhcDt0V5nEA0oE1nAeRhMtGVbm30R3QvCuTJfgYF\nOOhjD6V4hXqKo3nVvJTI5r/kvvv1AfftcH6d1dSKREenb0t5msLitFzqcV4LMIWnADiMh6ErLYPc\n5wYi3M64jAg8/aCVBz4r+ZTyz5STtZfvy3d95t17AbhH4tt///NpGW+3Re8H8TvIw8H8DkrxsxPe\nz91x/cpstkT2kgijZ7Mf49MGHBxujL8vj0f/L46/nevKImknpP3GwNI0+hfLfw0fJjn7GiNa/t5I\nWLVqy67Saakur1y5kvnz5/P444/T2dmZLBZuLowfPz4RtDNnzuTRRx8FXgdfIqt64NZb4E+z4Pme\nbGf6z7hlfT96vHvxryEPH1j8s0bhq1rj98hqOt6uPJi2MRDA9524ImF50qPHFu/HErcEZyy+K/of\nH6s+93ffjnAfAW7JQw1OefFOKMAFv7sR6vD+vnugDseu+i+ow8BDuUZNSafLcXk8uvAIsS/nG7Ul\nw7UBS/kerFxU4El5f2zhd7JCoA7cEpdJTO9jv/tOlP4tUXmc8rv7IA8XLLwRgMse/ArUYjxg4MFc\nhFsnEpDEz3pchs0ErB1bV5698DUe/9PlC5qbJ74n/21w1vJT7Rz3jMvhyp98IcrrT6K8XvaTrwBp\nOA/mGgdghI6aUNRstAex4F3fYE769INfT8usFj+1zXjT2v+m0V5u3x+QsJd6YPEsePkWWN0TYHjT\nYXNMImeffTYTJkxg3333zYRfd9117LXXXkybNo1LL70UgHK5zKhRo5gxYwYzZszg/PPPH5SfQw45\nhJNOOon7779/s0zDTcexOXPmcOedd9LX18eJJ57InXfemZgitgReeukldt55ZwDuvvvupFAqlQrb\nb789I0aMGJIvkUsvvXRwXyITuiMfItt3N97e7WCAXOb5VgHPb4h/n7eGvL5JD3gNpS6a5f+tltct\ngyZ5fR3z/Lr1k+27YWR3ZBKp9cCah7aY5OaYREKbJX71q19x33338fjjjzNy5EhWrlyZfBvKZgmD\nxYsX88ADD3DzzTfziU98gpNPPpmzzjqLPffcc0jxm+bmX/7lX5g2bRq77rorP//5z/n5z3+efMvl\nckMyjYR8ifT09LBgwQJyuRy77bYbN9xwA/A6+BKpEM0ftiddnDmeSDM5kUhbPTF+X0Jkw7RfSBup\nE7mzVI3AnvnAf297zBF1Hr8oo/+nkrrIrBNNF38sOMfH382m+EjMbznGeY7URei1wDVElwR8j8jR\n/oJ4i99c2HB0fEfib4BJMT1LezrpgRrT8Er11HNhKf4+ldS+X4zfF5C9Zd3KvpOs+0+zR4fKrCD5\n1Lo4Osb/fpxeOU7//RJmdbgo/rYkxltAZMM+hag8KqR+M2xtYgHh3R3LSG3Mqjkqz1pH35e4h5Be\nS+dnWMeTlt+H43h+5hZ6r5BeJr0splGTfJsTsyXAi0R2e9XUa0R1vMCFmca9kci7XgVgVIpneV9C\n6rip4srFbNG2DpAncZGQyYetDRm+5jPH33SXyGGHHUa5XM6EfeMb3+Bf//VfGTlyJMBmWxq22WYb\njj32WI499lh++ctfcvrpp3P99dczffp0rrrqKt71rncNGr+pL5Genp6Mfdhv7zviiCM2i+E3AnK5\nHHTH/GpDsD3LJaIGNJVsR1SzRF3C/iOKPrLz1chftIEu0viOGzKZXBg/bRHG8M8lbdxXkzZ2a8zW\nGbrIbm37D+GzHufvXMmr0Vdep5K9lX0ZkZvLuaSdbyrZDkh6a3lxXGQ3r64q0lHoTZxAbVgwJqVn\nfOvU14SwdnoVfqH1AKNlZdYVf7fOb+l0kt5HWCbdXtbpnnmJY2Wi6dfdf28eo0k8/a63v9dI21g3\nqb8OrXsrJxvQoNEUAlmBanVtHva0DPx73tE0Pkvu3YP1lZfj/7bOUJW0fd69omMmNKsPHF4obc33\nki33JfLQwEEt8Y7IPdqQTrlc5oQTTkjOj8yYMYP3ve99/OxnPyOfz3P11VdzwAEHUC6XmTZtGm9/\n+9sH3SxhUKlU+O53v8t3vvMdJkyYwMyZMznhhBNYuHAhJ554YsNA4aGpht3d3d0yo29qWDwLxndH\n0ywD0wjq8g5pJzdBaGCLjnGcxMezCpgaYYFt/6GxIVsaPr1mdkAD49PSXSR8I/g1UkFlaXhBqjsU\nfMdV4RDDhmVjGNn5anKdWJUivbWOyENfzWXQD1iD2bAN39u9LdznS4VtLX6aMC7H3youvCK0LL5B\nvcl/FdrN6lHj6ICv/KmXOl/OulVvkYR7bRj3v0R2P7vVp/IaMgP6/BiE2muB9Jox3fVSlDDIthOt\n5wrZQznqKVHT9WWbJzKH9PUEMrDpELJRL+ypsrBn027N2rhxI2vWrOGRRx5h3rx5nHzyyTz77LOb\nfPHKu971Lk4//XTuvfdeOjvTLV8HHHAA5557bjCOQlOBfc455/DNb35z0MhDwfmbwUaiqeBIGrdm\nWafyWodfSDO8W+Sb+jLW/yGtQTub8WCajQqh79PY4T9OpG0rbS9c/zfZ2cGZZAckFdgm3PT7YMLL\neIVk+9UGxvB8vY1DJz3M80umZukZHxrPaFq+NG0d6KpkhYlqf17A+fK1QUgHXD/QWd2r5uqfdRqF\noxcw9v1Mojah4NuOfx5KtJvH8qRtTGdzKoQVVLgpvg7WJcKDN2Tr2tpfIfDfymIRkXatoPhKy+AQ\nGhdoDadA4+UIdRpNSAYbA2GbASEb9rTuEtO600Z62+VLW9Lp7OxM3HEceOCBbLPNNqxatYpx48bR\n1hYNCrpZYr/99gvSufLKKzn55JMzYXfeeScnn3xy5rrEZtBUYN99993k8/lBpyTDdfPM6wJHA/sC\n79iEONbovaYVEgKbA82m2aGwThJTTIIT0oLVftgJzBZ8FWYqEEyoxprSjlNeYOXCXRL6I/dInRGb\nCaTIGiawAoi2yR10cLQgNH/VDLrGPcf2VOmlg6WHTmZ8+yv00061L9LCi+Oqkb/sZTJD8YOFapWD\n2XG1HtQsogPmIjI31wRnQK1MHF64KB9TSc0zrcDWJaYS1U2z9AdrG83MFlaX0DiL8UI49C30bunZ\nNspOIvu65yXEV5FoPSHEpw0y5nNb83y05KFGZDN/EpgToLWJMFzb9t7//vfzy1/+kiOOOIKnnnqK\n/v5+xo0bN+TNEgazZ89uENhXXXVVQ1gzaCqwv/KVrwy+x5nIOD8YhHyJfPjDH2bx4sUAVKtVisUi\n8+fPH35fIlthK2yF//awOQLbNkusWrWKyZMn8/nPf56zzz6bs88+m3333Ze2tja+851oq+hgmyUU\nfvrTn3L//fezbNkyLrjggkQRXrduXbKQORQY0gUGmwsPP/wwhUKBM844IxHYChdffDHFYpHPfvaz\nDUb+ZnDJJZdQKpUSXyJr1qxp8CWSy+Vg389FW/t26o4CQwuEBs0WmjSex/X/m+EP9RtktRd9x4Ur\nvs0K/JTZDkPorSS6kKlhR5PuRy4JPXsWInpju16mrb2fImt4+sUp2f3YeaIDNYvyqe3TzCBmo1U7\nrmmGvuwtPa+Ba36baY5qcvIaJDSaQhC80PtgM6vB2oF/93RCMyUFLQ9fFoOtlYTAl5dquz6vmvYi\nIveq2+Yi81wIT2dq9u7zGqqrEB3jDeDxnugcxe8u3+JFxzsHTmiJd3LuR6/7BQYLFy5k/vz5XHbZ\nZVxxxRVJemPGjOHII48MuvAIwesqsKFxtdVgYGCAXXfdlV/96lfsvvvuQxbYU6dO5aGHHkoO0HR3\nd7No0aIMTi6Xgz1ctnwjavbNvocasTYuaOwMoU7gbYuDTU+bNezQok4ovg8zG3tooUefNm3XNMzE\nVwyElwRfbb0lot0DuqPAoCx01JbdLB8hgRl6V/xmgnOwQdr+W95CAjoUX8ONLy/AhkLH8ziUwd7n\nqRldj6vC37dpbwqsARt7gVEwLZdNw9YdPF+2sDiYqc/nSb/7+hiGXSK3DzQ5pyFwau6eN+zGmQ0b\nNmySRu3hb3bQ/uGHH2bChAnsvvvuSdiw+hJZMotoL1V347dtCSxqWIXl0v/bOpPQRsPLyVPib5uL\ntJKETgwVIp8MFmbp+2eIv6bfYnrbGn3lLQZdFLW4tvijNW9b7HSAguaDkNpOYXBtTwWv5RWGsKjk\ny9fCIFiOEJexfM/EaRaeS9+r7l3bQlNeyOL5hbqGND1NLyh8WG6QeIOFtcJ39F8OhAGwHp4YFcjP\nYDxq/TQrPwjXMUAP8KtA+KbDm8Vb30knncRdd90VXIzM5XI8/vjjQ6LTUmD/8Y9/bDiiORxw++23\nc9pppyXvm7o9Blr5EhmQn4ON0NAoARiVxU+EIILXQeS7dVT87EhxNio9aeQbXRobc1HcjaPku6Sx\nUWn6uMZ7zFtDXqQTVF2n2kgslCxtw4vjVXORkNddF9BoEjJQwW//k7zIgGL0G/JqeRvlA4VGCNeV\njZVjph5DYPWWC+DqrSOjHL7/b5Bz4f7mEuPV+PZ57XW40Nje9Pt693+wMMun9QGP79PV9AxP+XVl\nH+TNLmaO09vo+QvBAI3p1hmubSJ9Gc9Xfzv42te+BtBwEcymQkuBfd5559HX18dZZ53F//yf/5Ox\nY8duUYIQ7Wm8++67+cMf/pCEtbW1DWl7jJlCdtppp8F9ifBL4BmifUZHAwe77806mTZUe2rD8w02\n1CF95wk1/JCQ8Wkrn8pfM941b75DKZ8h4RG/12QA9PbJBhiIBx/97zqgH4yCMJhgUpxmQsfTCAml\n9e6brw9Pq5lAtP+rA7yEynR9E3xfB62uqVrt4vl0fTqQDgijAnihuKH2qrw149Hz5uMZjrZ7T3cU\n8HPgYeD5+Lfl8GbRsCdOnAhEJyTz+TwjRoxg8eLFLF68mH/8x38cMp2WAnvu3Lk89dRT3Hzzzey3\n334cdNBBnHXWWRx77LGbzfwDDzzAXnvtlWQCXgdfIjsfBe3dUOpO7a56As1stJVYK7AFuXIHFDri\nqXyH2DQ7ZN92R7RtLNlb3BGfLOuQxb44rN4BtY6sHVHtibUO2X7XEcUrSnoVoNQhpoVAOGTt0cvi\nfFk6xPjEfC+L6SDfl3WkpyOtvGxxUm28IPbunJhCYidS5KI8I3HN5p3vSC8zNr67yO4pzgOdHeme\n6+RbRxS/DhzSkR5rzsf5KcX5tcVNzXst/u63BhZinoy+fZsKLOrI7gk/FJjbITyPi+l1pKcCrc6t\nrPLAIzFfmr59XzQu2rtsB7qsLDyf9Th+0maF31L83xZ6rX0geSsT1UmJtAx1YVjbYFeH1HtH9gQm\npCcd6zHf04EFHalrgmUxX3YJRnIy0sohptMZ810HpsfteMFxUDgOlvfAiB54ci5bCm8WgW1w2GGH\nMXfuXNasWcO73/1uDjzwQO644w6++93vDin+kGzYe+65J1deeSUHHHAAF1xwAQsWLOCvf/0rX/zi\nF/nQhz7UNF5oe8xZZ53FHXfcwamnnprBHXZfIqvj3NktMn4vr+6YMPA4qmF626ztvniZ1IygC4u2\nCBUSEpYWpA3fzBDmT7nZbgilY/SVP72BJrSY2cwRlvGrh238QpWlp0LFwOcTwdVyXuLClB9b/FpA\nVlib/dvKpS64Fi8zCEo8q8OQLw9cPN1JtMzRqQptT8vqD8JtAOFVF+SsPCsxffMr4qFGJMw1HUjb\nSlXCQzuLrCyND9sFAtly1rwkSkSAH0vL8mfxtVy0HVv+bA0FUr/vlqYNtiVgBTAukO5mwJtNYA8M\nDNDR0cGcOXM4//zzueSSS3jnO9855Pgtd4ksXLiQW265hR//+Mccc8wxzJw5k/3224/ly5dzyCGH\n8MILL2xxJoYbIru22nQhuDDSzObqzWfBRUqJM+hiTwg/QGfbXHjh0C8yhmjZ4o5fJPU7WDz4hc1t\nSbXrEo2DBaQC0+8oUKgHwqD5wmvoewJDKTOP12zxsYWXuYZF4E3hpxmE6s0gN4SFuTiO1W1DfpvE\nDbXthjIKLbA2W1QM5afJInBDfMMZZKHSLkvIvG/5LpFrBgZ3dwpwUe76N2yXyIwZM7j++uv55Cc/\nyZw5c9hnn33Yd999W+6OM2jpD/uCCy5gxowZLFy4kOuvvz6xKU+cOJErr7xyy7h/XeFzpCvN60lt\nq1YxvXED0YoakLDe9FsSpvhNdglkbLghfE9L0zCbo6XdhEdPyzr8Rv1JHNNQC/HPcAz8YOS1NNOi\n/Ha8GlkBrvurlbZPL+G5N8xvcMHYl9l6Vy+QqbOkrq1cte5DddCb8phZbB6IBxXPi39q/Tk+fXtq\nKAfjN5SOtI+Nnk4It1fo+rayPhDHoJfsIqXy1Etjfnw7J8Cf2rAHAu/2tIHXaPfAxlkMB7zZLjD4\nj//4D6666io+8IEPsM8++/DMM89w5JFHDjl+Sw27VqsxatQoRoyIMvbaa69Rr9fZbrvttozz1xGS\ngzPbd8M23Y1+LhK7Hqn3ui5Sk4BN0cxGZ0JKp+E2pSw1wYXsFV/QaC4w84PSbrbXegmRLVCn+nat\nlTcJdLo0jUdITRLGq017bWpte2nNFmtOpLzpxQS1lZWmrXlMbMyOzwVE9ls1syTrCKRHy9X8UY/5\nU9OBzgQWSd4tv+qlz+hB47Fum44bnpptNG0bmHQKX5D3Lomv4HmCrPnJePJ7mC0tq+sSYfOej498\ntzhLBM/yqR4R1UzTEwvYYkfkhlhnVdpW9Kl8+zUQ3butjqCsfq2N1YEVPbCmB/645Qdnrhq4sCXe\nv+b+4w3TsLcUWtqwjz76aB544AEKhahV9Pb28u53v5vf/va3rztzWwQbgTaiDqQN2jrwoaQddipR\ngzFhbYsq6q2sLuF5UoFinW6q0DaYTlYAm/1zKqnA65SnHXJRG2Ip/qYd1TqI8WDf8qSLWCp0VXhM\nJ+3khZgXJK0usldE+QMZVmZVeVehoSYYK4/pRMLMFjWXxHwqj7qX28rSaKpA0XwbL52ki4X23wTR\nHnEcG3isLpG4Vi4qZIwnXXjU/zZA60Dlha2W3TLSurEFa6Nn+TIcc11qPC+RPC8iHWzVRl8hbZ+Q\n+gbXNYi84Fs7srI1HonDjsuli+jGpxfAXaTKTtmVmeXPDmV1kbWblyQ9a4OlOK+TiO6iHAbY+Caz\nYS9evJirr76acrnMxo3RlC6Xyw3ZL1NLgV2v1xNhDTB69Gh6e3sHiZFCyJfIwoULOffcc/nLX/5C\nV1cX3/3udxk9evTw+xLpB8aSas7WWK2hHE96RdOhpBqMakFHE3llsw5mtCAVJocSXQt1NNmFnQJR\nBzK6C+I0H5B0THibpmYdVBt7svpPurAzldT3sQl00xIhK/x00cs6iNq0bWdJTeJZhzLNu1Bnx0mR\n46eVi3dhZCn2C76I7CAC2ZnALZJenaxQN8GiZhT7brRs8NKZDaQLYypYK4KvNHV2ZULdvuvsAdKF\nMEurTHZx2teP1asJ7EWCa3RsQDBN2tqDhRl/kA6CC1w6tgBqfJaIzpYUHR0b5BYRtTVrK7boZ7MT\nq7PjiS6JsEGBOB1rTzZwa9lqHS5AdtBI3q2+a6SOr6wcysKr0T2ayDOl9aHh2YINQP+bZB+2wUkn\nncR5553HzJkzE6vFpkBLG/Z2223H73//++T9scceY9SoZpvgs3DWWWfxs5/9LBM2c+ZMvvzlL/P4\n44/zgQ98gK985SvJN7tqZ/78+UFhDZG3q2OOOYannnqKo446qsGPyFbYClthKxi82WzYI0eO5Lzz\nzuPggw/mgAMOSH5DhZY27Hnz5vHhD384uYfxpZde4o477hhyIt5HSLFYpFqNVImlS5dy3HHH8ac/\n/Wn4fYlcOZBq1TY91ne1re5BpGnY9BkazRI1F1dNHaZFaJxOSQNSjebHZLW+6aTaTZmsFl8iq4Gp\nvU+nr3vIN9OwakTXPJkWDFk7qsWtO3qx1j5yj1fpKPRSbK8ymnUUqdJBL4uZwmjW8QoTWLl4l0bb\npZVPnVTrsnDTZheR1Zih0RarZenNSjpD0HzoN9MoLd/ebqwzCa/pGg3VaL3GrmsQ3lZv73mJq2YA\n+1YleyZAzV3eHq1lUiItQ28jtroskjUr4XDrQlPtx4anM1JfB5A1x3h6BYfjTVpqu4b06j1ftmdu\n+S6RSwdmtcT7Um7WG2bDnjVrFjvuuCMf/OAHaW9Ptf8ddthhSPFbmkQOPPBAnnzySRYvXkwul2PK\nlClb5Lxkn3324d577+V973sfd911F0uXps7Dh9WXyJ9mRZ76OrvT6Zg1KGuQKujUPm32ashOaafS\nuHhSEHqdEscGAf2udtwi6b18exAJbRsDjYdOIoH+iOTLeDCbN0RCfi6poFG7eMXR0QUfSKftNdIF\nszxMHLec0awDYCLLaaOfftqYzNL01plSkQ312Md1qQ61fETP7KddZBfvTKjaFHkB2cFPF+HMJGSC\n1jqylacJZ10krslT7fAqcHXwQ+Lk5ZsOOvYO2UVfE9BWlpZWnWwadUenRnZgUMFlcf1AYt8NJ7TX\nvkJqmiiQXZhVwX8I6V2ZRldNZcR07iEd/FU3U3OK7qW2NKx+KoJjcdR0BlHdHULaB6wsn+yBu3sY\nDniz2bBvueUWcrkcV199dSb8ueeeG1L8IR2ceeyxx3juuefYuHFjcpxcbxTeFLj55pu54IILuOKK\nK3jve9+bHEcfbl8i7W+r0bcn8cJQLEwgq0VoeDMwnD3i/51AJZ/VopLTbTHxWj7CPUTS1PRitJGd\nr7KBWOB1kdUy1W5rC05eC9W8HEoqCKwj6qk7o+Pj2XNq+n/HKS/QRh/FeERoi29EHc06qhQTbTvJ\ns5VhQUYCs/3q4KAaVp7sJQM2Iym5d11IU75NWOnswd413NK3/HlQWiEtUmkYdEkcG5Bs8LAwnQWU\nJEyFr5UDZPk1UAXAa7++2eZJF/40TZ++zjZ1cLEyKwGPkQ7yC4Djpd1q+zk6+jMy3x+taSR1EeGP\nLL3Khrzcgarh9ajfjy1V6S3F94LGYXT0Q//wGLLfbDbsVnc2toKWAvv000/n2WefZfr06Rkj+eYK\n7ClTpiQ3sD/11FP85Cc/AYbfl8jGX/8W/lSBR3vgiHfBOzb/KP1W2Apb4Q2A3/4a/u+vYenzsOzv\ny5eIwV/+8he++tWv8sILL3DjjTfy9NNPs3jxYo4//vghxW8psH//+9/z5z//ueXtM0OFlStXsuOO\nO/LXv/6VK6+8kvPOOw9g2H2JTPx/dmds9zQ6ug+klw5gXvKtSJUqRfpoS0bgCbxCLx100Bvjp6Bh\nHfTSOyn93kcb7bEG6uPaezOcDnpZM66YfOujjSrbU2QNAO30s47RCV9t9FFl+0S79fx20JvYl/v7\n2qKrut7ZTlu8R6qf9sTMYTytY3QSZjTa6GcCrzCK9axnFEWq9NFOO3300Z5o3jPGzU/SXsfohL8i\na1jRNYG29n466KXaF82D7Yb1pB7GVenvSy9J7a110FFIdyC1tffT39eWCVcaGmY3uCeXAhe85j8I\n6CxLtcDKmOy+awVvu1W7rJ8FqTardnF9V1wDnUVYfN1hAo32fE/PQ+h7mXSGYOlXiWYlJTh20s+p\nUkxmWgb9tKVh49Iwgzb6k3Brp9p2LZz2uC2ftJ7qScfQ2zOP3p4NPKumwM2EN5tJ5KyzzmL//fdP\ntkVPnDiRE088ccgCu+UukWnTpvHSSy9tFnOnnnoq73rXu1i8eDGTJ0/m5ptv5vbbb2fKlCnstdde\ndHZ2cuaZZwKRL5F3vvOdzJgxg5NOOqnBl4jtVPn0pz/NL37xC/bcc09++ctfDuniyq2wFbbCf0/o\np73l742EZ555hksvvTSxJmzqAcSWGvbKlSvZe++9Oeigg5JVzVwux3333deS+O233x4Mv+CCCxrC\nPvjBDya3Enu48cYbk/877LADDzzwQMu0x866gD7aWBdXiGqZqg0amCbcF2sI/aSa6TpGJzT0u2kM\nprn20pHQbqefNbLCYvFMq2+jL8G1p4I1JNXYNcw0lTb6Eg22o7035bW9P8E3Dd7eTbtWntpFezLa\n7YHTC2bD7m8R17Rr+w+pdqyatWrhE8ctb8hzW3t/Ej/JVxy32B5d/Ftsr6bfY9qqnfs0Layj0Etb\nez/VVcXkHUi12EIvaytFRuazmqXChnobI/P9qYafH5No9CPz/Wyot0V2WtX+IdX6K/l0HaBQT+IA\nWVz/3+zQkNWkdWGv7r759Qv7b4upak+/mmSBuo1+2uhPZl+mWevTwHCABjwgeVdNW9dKilQZ370r\n/d1v59nL72ha7kOFN5tJpL29nfXr0yP6zzzzTGa3SCtoKbBnzZoFRELatr4Ml3nk9YQ/X/JDcv/j\nUF474CggWtwAWFveCSCz8AGwkvFZPNdRdaquU/AqxaRTrq0UM08VDAYmfJavmtiSpgkCiBq/dfqx\npWry3l9I82A0Ld3kW3tWCIZMPyFNw0wi7fSxgvGMZh39tLGC8VQpsoZixkRjA2AvHfQs6YCVAAAg\nAElEQVT3tWWnx3G+i+OqrHxxfJSHvjaK7dWU7zieCVHLuwppL/wtf/bdhLQ3r/hyVjDBDWTS7a11\nZOrRxwEgLu8EJxa6Vg/ahsaWqqylmBXwpUiwI3WdDBSlV5O01sZS2HAVtB0bThSWjxa2daDQhUGI\nwjvrjfEXjEl2DamA7afNtRsxaSUKjJhKHJ4X8snitdBe3fNH1vYsZDhgcwR26MDfrFmzuOmmm9hx\nxx0B+OIXv5j4sb7qqqu4+eabGTFiBF//+tcHdT09a9YsjjvuOJYtW8Zpp53Gb37zG2655ZYh8zak\nOx3L5TJLlizh6KOPpre3l40bNzJmzJhW0f5mkMvl4J8/B4d3w27dUaDffaF7b+tkV9Jt54DfspUX\nGrobQEH3tkLjnlq/ewF5h7C9Ur/7tPzeVo0f7y7QTusHKmp5xna9DEQCqjgu2gEymaVM4JVY+++n\nTBdFqrzC+IxtvbqqGBYYlbR9JGma0NCdIn4HT8OuEwHTRiv5bFy/22ew8Jg/IKzxajzPjweNY5DY\nqANasY/r45UCGrYvH89KiFfV3r0tO6Rlh9pkN9G2POCgGx+ijX6qmT15zddvVAhDKsjXUMzMxgz8\nmsyKnifp73mE5Zd/e4v3YZ88cEtLvDtzZ2bSCV0efvnllzN69Gg+9alPZeL++c9/5rTTTmPevHm8\n+OKLHH300Tz11FNss01za3OlUuGRRyID/cEHH5wMAkOBlhr2N7/5TW688UZWr17NM888w7Jlyzjv\nvPN48MEHh5zI3wSeIDriOiF+ty1L3mGSHWaA7EGBqUTbmwoSZjh26EUXfAruu+8kocUoHSR0S54e\npLABw+8j1sUo7XAl0u1dMZ0NhTEJnQ35Mdm9v3lYW9gpYXVl5xjohOdLXclsA2Dtop3SvcdWjloG\nljawQW9Th3TrouXPyqBAYLulCu98Gic53JNP82amgWV5Zx6wd9liWIvpVWBDIZ/dZlcDuvJyoEbo\nIdvZrG6UV1/+SFrJNyeYfVgSnmdDXfMX86LQYAbJS3uO81CS8rf24BcvfdvNS5jlcwGwDB598Agy\nDtP8IGBmGOtL1n79nvc8Wb8j9s1vOxwxAE+9zHDA5tioDzvssOD2u9Dgce+993LqqacycuRIurq6\n2GOPPXj00Uc55JBDgrSPOuooHnzwwcwio4UNBVouOv6v//W/mDt3bqJR77nnnqxYsaIl4aVLl3Lk\nkUeyzz77MG3aNL7+9a8DcNddd7HPPvswYsSIzBVh5XKZUaNGMWPGDGbMmMH554f92K5evZpjjjmG\nPffck2OPPTY5NdkAto3TDiqYxuzBH3iwTmvf7JCECswQLWt0fu+r0bGGqQJL07d9wF1khbvSVdq6\nn1fBGn6Xy0NoL7N69TONFxJNLTFjmI24UA8f9FAe9cBKTWkK/7pfWfm2/cza4S0tv7dcefD5mkq2\njnQHR7MNI8a/7ubQWZbF8+VuuPXAu+bPaFXku77XXJwyqR8VrX+lrW2i5mgrHeVLFYOCi2s/SAcm\nE6JzSQ8KVUl9qxh/y4gE/KL4vz3NqdUyF76M6HBPXd7NN8kS4FWGBYbzaPp1113HO9/5Tj760Y8m\ncmf58uV0dqYuKjs7O3nxxRcb4q5fv55Vq1axcuVKVq9enfzK5XIQvxm01LDb29szRvGNGzcOyYY9\ncuRIrr32WqZPn06tVmP//ffnmGOOYd999+Xuu+/mYx/7WEMc8yUyGJgvkUsuuYQvfelLzJ49O+xP\n5FVgJbAr2aPf2nEgPc5rjQVSAbtI6Jl2qVpKqEMvkzjWKaxxmyaiJ+TUxapq0otID0xYgzbhZ0eO\n1dtZmeyhiEVkPQia1mR58rMNE3IAi/JQgJUvRnb9tkn9cWfOZ4/1l0lPw5mgUCGwgNQrYllwTHh3\nkR6jr5I9bm35n0p60lPrQPPUSfYUp6+DiqRlcY0X4928AM6N4yVaefxudW6Owgy8tgrRCVbjuSp4\nRoc4LVs7V/Oa0jlUcLzZwp6alh/cDP94si4R/OBTj+nYKUkTwlYfNpuyk7mh/Bh/B5DtN5aOV4J8\nPJ0RPAVs3sa0BhiubX3nnXcel112GQD//u//zkUXXcScOXOCuCH5eMMNN/C1r32N5cuXs//++yfh\no0eP5uMf//iQ+WgpsI844gi+8IUv0Nvbyy9+8Quuv/56TjjhhJaEd9ppJ3baKZpqFwoF9tprL5Yv\nX85RRx01ZOZCcN999/HQQw8B8JGPfITu7u6wwB49K8rdIzRqpl77MQ1BvZ9BoxBWLQrSxmcNUKeV\nRkc1mTKNdxoanmrgqhGqEPd+THznM2Fl2lHN0THhqOl6jQ6y/h8qear5YqPrWC0P1Vofk7SMrvKo\nAt7KVY+Wq0AyDU1NLqa1q1C2I9/QOOia0LUB2cI1HaNpwlrz5bVfFVgh7b5Oehx7mYRrO6iQClnV\nzu3d8jDX8ZyX+Eb3AbKmDMjOUEoxTt7FMzpdkpa2tTqpJ0kL80qN0VdFxtqYCmY/I/T5NcVlSYw3\nsTv6zb+cLYXXAiJudc8fWd3zxCbR0QN6M2fOTGTgpEmTMu41li1bxqRJkxriX3jhhVx44YV8/etf\nD+6SGyq0FNizZ89mzpw57Lvvvtxwww285z3vYebMmZuUSLlcZv78+Rx8sL+5PAvD6kvklVnQ3w1j\nuhtH9ZrDrZDdCmXCwxqehWtjJfCuHdx3MvteJjV/mOatfHjBow3dm100nhcIKox8vlXQ5Em1QNUG\n7Zh9nnQB0YS/acGqqVqZVeNfXWiGpuMqQIymCmyfnglVFfSaN9WENW/eRKBPo6l01BGW4uflXc1I\nqpEaVMhe5ACNdmLjeRmDQ8G9G7/WhrROvWOrUFzIClvjQ4W9DnIbA3yHBmoDLV+rAx0EbJbpByoV\n+i/3wKqeAPFNB93FYlDo3p9Cd6rlPnv591rSeemllxIHeHfffTf77rsvEB3kO+200/jUpz7Fiy++\nyNNPP81BBx3UlM4FF1zAb3/724w/bBj6yfGWAnvEiBGcc845nHPOOUMi6KFWq3HiiSfyta99LeNX\n28Nw+xLhbUQNeDKNGo41SN/gPJ6FGeg3P0VVCNFVQa5hqu2EOpjX3oz/Alka/glZTRtSfyUKfjo+\nNYq346QVmZX/lfVdInyzP1fIdmI/iNUdXQ+qMWt5+QEuVM46MFmaJRqFis5YQnm2/x6nU77hcJuV\nn6VpeSiQ3eUTggKNt/loW/F5apam5dPqr1nbVG2YQHwVzD8m9eNyKOnAbnH9wqNCM/ONn9lAY5sF\neJJIUx/cOjok2ByTiF0eXqlUmDx5Mpdffjk9PT0sWLCAXC7Hbrvtxg033ADA3nvvzcknn8zee+/N\ntttuy/XXXz+oyXhLXX20FNi77bZbQ1gul+PZZ59tSXzDhg186EMf4vTTT296hNxguH2JsLIH+spQ\n74E9u2FqdxRuUz1t8Gpm0E4W6rAmZEJ2R8XX7x5CjV3T953HgwoZ63AGqr1ZJ1MnUN68ANmFwk4Y\nO/VlduM51lCMDzasodoZTUE2MCbbuTw99QZotnb1wqfxdEAJlVczoaCd3MqiJN90UOyU78aDNy3Y\nDS4hMC3ca9WaBx28lD4Buj6PqtHqgKxlY2mqtuovRtB2icPVwd0uvdCZm49vbUfbZJ7wANSsfvSb\nn/0ongrrBT2wsAdeLMNL5QDhTYeQSaQVhA78nX322U3x/+3f/o1/+7d/GxLtLXX10TI38+alPjjq\n9Trf//73WbVqVUvCAwMDfPSjH2XvvffmwgsvbIpjMNy+RMh1R3awUd3R4uOT8s0LVtx7SAD7DuU1\nZf2v+CFtQ3HVXu2FdLMBwGvboc4OWY3KC/UuUvOMvdeAQ2FtqcgrkyZQ7SuytlKMDhUtiDOySOio\naUKn2RWynVO1fOPVzAYqsDUMGu9QhKxwNvxlhAW34SB0m81qfFw/g9Ay9vWsW9k8+Lq0MF/Pfnbn\nBys/OHj6KuD97CVPo5C2dCsOVwdys8WrxcBMGrqX3nyPNxv0FNQk0jAgd0O+G9b1EF2p89AQCA4O\nIZPI3xLM1cfEiRM3K35LgV0qZVvihRdeyH777ccVV1wxaLzf/OY33HbbbbzjHe9gxowZQHQ6qK+v\nj0984hNUKhX+6Z/+iRkzZvDTn/6Uhx56iM997nOMHDmSbbbZpsGXyLnnnsv+++/Ppz/9aU4++WTm\nzJmTXBHWFGqkF1n7abE1ShWUBt5G57Vcta0aqBZnOBbPC4+C0NZpfd69h4SeHwQ0LITj8wnZbVkq\n/Gr2ixB7ax3RzhDlUzu959G+66UGWg5WbhbmF+V01qC22jLpgKLC2fJi9trQbAQX7oVuqI5VCFse\nNU3jV+3jzcxXkC0nayPaFjQtbUdaFtqu/CDn8QpCS00e3vRkeS5LHC2XKpGEqJNe7WVgfFqdWvvR\ngU2hmTITGkBXwnCdKH+zHU3fElcfMISTjr///e8T9f2vf/0rjz32GN/4xjdYuHB4jo6+HpDL5eA4\nyVZI46jQeLuLCmFr8KGpbr1JWInsIQWv9amw0+/NOpzXnA1U8/a2XdXaTPv0WqfXkuxbnWgL2PTI\nJ3bmRplFZBc37b92PKWpAsl4VXyF0EyiK1BeNhh0ki1/FR7NNFoVLpBO87V81cyiu4Y0TaOtwttr\npgZKT+OGdtwovqel7URnBAbafkzb9W2rRHawsDS6iDRpy6uW0xOkF20sEt40PyqcVSnwA6iWmfYx\n+6bvVSL7+c+2/MaZaQOPtsR7InfQG3bjTE9PTzC8u7t7SPFbatgXXXRRIrC33Xbb1lrtmwWenAXF\nbti+O3pXzRXSRqmNyv8PaY/aEE0j1U4UitNMMKgmX3NxQuFe87T4xpPyojx64eA1X68RFurRcWE/\nCwiB0vczk2ZP3Lvxrxqvry8/W9HyrDoaHlRQe43O86LhOqBpu7FfMRDHa451F25tzjtoMvOCT8vT\nHGq4f6pWD+nspuxwdebAAJDL5k3buG9vvm5USCu0yt/GnsiWPQywOTbs1xOGKpibQcvcNBsR3vSw\nA7AzMJFGIQbpVV3QqKUqrtcIVTj7xS8Nt/eSPEPCV0GFjk6Lm8XZIxCmA0qX8JK1bIVtphVganwL\nCB0pXY2ruxosT6oVlx0Pqmk3M1kMVhbN4jarPzVLePCacTNoNqXXtEI8+3g+Tkgzt+9m19V24tPQ\ndzU7KT2jGbIphwYSP1iblj4XIBe9TyfbLg1UYNs7ZGc7Vk+hOtTZq8YvA6sYlsMzbxYbdqFQaLrQ\nmMvlePXVoR3tbCmwr7nmmoaE1Gufd4bypoGNgL/c3RqGTnehcdqquPqu2l5oCgxhwRj6HjIZqBbp\nzR3N/vspaC3w33dq1YbUFgqwDNbWd8raaVX7Vc1c07I8habLvmMaaJh28gKNtEOCQcPt6YWKBxto\nvMAK8acDqJqpvKmh2SBrcUIzHJ8WpGYaFXzKl6Wh/Gh+fRv2bc3S1v+DKSQMQD2XhpcYXOBrWyMQ\nFuovWg5Gvy3+DQO8WS4wqNWaaSubBkO6cWbevHm8973vZWBggB//+McceOCB7LnnnoPGW7p0KWec\ncQYrVqwgl8txzjnncMEFF/Dv//7v3HfffeRyOcaNG8ctt9zC5MmTKZfL7LXXXkydOhWAf/iHf+D6\n669voLt69WpOOeUUnn/++cQ8Y4uTGagAfcAYso3aCxPfuVRwILgqoLWz+M7nBY1CgfSYvBc6Gs/s\nkK2gRNjZjnZwm/rq7gtIj8dDdjfGVGAPGNv1Mmsf2CmlY1NqbzrQcszTeFO3pQXNhWSeqFy8BjiY\nJghhIZsnPVKtA4iVUZ3sBbWDCWyfh9CAWZH3ivvWTPMPaedLaJw1QOPhmpDpRXkLtU0V7F4R0PRK\npAedpgMLchFP/iCRCm6tN4My2UFEQRWE0MBaI9ooMJgZbhPgzWYS2VJoueh42GGHcf/99ycHWNat\nW8d73vMeHn744UEJv/zyy7z88ssZXyL33HMPnZ2dCa3rrruOhQsXctNNN1EulznhhBMSd4bN4JJL\nLqFUKiW+RNasWdNwND2Xy8HOn4PR3dDWHQX6KamBNnQ/XdatSxDugEMxdYSmkn4QUB68fbQZrtEK\naVuQvVFcNR2dgtfJdsozYcejXgBg5e92Sena8W/1TaL2V+XVCz9vx4esoFRhGoLBOnezwdKXTwj8\nN2/bV3ORgQreUJtpZhbxce1dha4KbD+IW1qhdJqZxELvHpQH1ehrRIuR0x1eq7L0A4INnAoqsEMD\nyKoeWN0Dz1y+xYuOOw+0Pi/yUu5tb9ii45ZCy+FnxYoVjBw5MnkfOXLkkLz1NfMlstdeeyU4tVqt\nYdtgKxiyL5Fxs9L/Op3XMLPXeWFSdXjQ2BHt3Ws8EHW+kEbr09FtbSFhpnRrLkw7v/Kg5guLpyYM\nD4oPiWDs72tLBYRp13524mcinkeDZoLGIHQ82+P7aX2oTo1X0/QVdzBt3eh4u6/NdGo08m1p6aDe\nDMdr1aEBzMINzw+Mzej5vBme8q+Lp4oTSt++2bH0JTTumw61o9DMwmZmzQY5pWP5qiKbBbbcl0j/\nX98cNuzhgpYC+4wzzuCggw7igx/8IAMDA9xzzz185CMf2aREvC+Rz3zmM9x66610dHQkjrzhdfAl\nsl03FLo3idetsBW2wt8YXu2JD89sOWzc+OawYQ8XDOnGmd///vfMnRu5Mjv88MOTgzBDgVqtRnd3\nN5/97GcbTiXOnj2bxYsX861vfYv+/n7+8pe/tPQlsv3227NmzZrkfYcddmD16tXZTOVysN3nInNI\ne3fYzhnS9JqFQ+M0udm0MzRl9BqJx1dbbt3FC5k+dKo+WD68Qyu1PeoUWx0ezY6Opq8t75S65DRX\nql4r9VPdZqYhr3WHtO1m5gl91/RCdQrZnS+6SOjXKDYHQuaVZiYXX3fGc8iMg3z3NDRc20kzG6+3\nXft0aw4PwkfVl9iJsw6YRuOZBOWFwPfBQOs2pK339QA9sGbLTSKFv6xsiVfbbse/H5MIQG9vL6NH\nj+bss89m5cqVPPfcc0EfIx5a+RI57bTTeM973gO8Dr5EXuuBDWXo74G+bpjUPXhH9dNWj+sbYat3\npQvhHRvWSZoJKg0vtMD1/Ptpsee1SLjT5+N7E+tkBwZNo1k5hgYzP3W3MM1DKD+hNPxAZWUYGuwU\n3z8HM0F5npR/TaeZiUFt8p6XZsLMl7Oas0JlqoOSQi3A12Dt1P7XA3iMAtan322g87i+LHRAKQCH\nEC0Ch8yMHrbpgbU9kCtHfoCGAV77O9OwW944M2vWLL785S8nduL+/n5OP/30loSb+RJ5+umnk//3\n3ntvoq1XKhVee+01gCH5EgEG9yUyuhvGnAk7z4Jx3VEjMsGlAii0QKjfiu7pBWLoGQrzHSIkEBWM\nTqgTqjD2nVzjmmA2sM7kBap9K0Tv1VXFVJirDVI7XTO7uL37MggNJn7AUci7HwE8LUMvcP3g0Gzh\nbbBZlX73fJjw8hprIcALNLYBC/fCTwcsqy+LGxq0Pa0QXrPFWVyYPWsQCWvZF+v7habthbjPa6h8\nVfu3AW6H7qi/jjlz2EyZfevbWv7eStBSw7777ruZP39+ckvCpEmTWLduXUvCzXyJzJkzh8WLFzNi\nxAh23313vvGNbwDw61//mssuu2z4fIlsS7SX03dcW9jQjqiLKgqhMKPRTEPLk91q5zu7voeEGO6b\n19aa4Slty1/BfbeFwwLZ7YXqs3oZbFg2Jj2KbqYP05gsTE0Lg5mDFPxhD81D6D3v4jRzMOTLSzVQ\nL1B8naoGbQt0ocXDwTRyyA4I3mRh5dZKiIXo66DQbIYQmmVonJCwVvOQCvBMHcZCO59rbGetZnoG\nCwjn1ZfFlpiqBoG/vvbfbFvfQQcdxKOPPsqMGTOYP38+f/nLX/iHf/gHHn/88TeKx02GXC4Hpw80\n1948hPD89Da0Gm8QGhRC9BU/ZMoINXoV6H6gGYxXyO4QMIHUbAprND4e/7ebVSru2cyuHgKfby/E\nWtk7m9n2B8MNrRcYhATpYFsDPagWXSE8e/B24mZb15opA8pzZRAco90Mz7efUPv1edH/P4PkaPpx\ngbx5fpWGX2epDBLX86z89my5LxGe39AacdeRbxkbdkuTyEknncTHPvYxqtUq3/zmNznqqKM2+caZ\nvwksnAUrev7WXGyFrbAVNhVW9cBzs4aHVn3b1r+3EAzK7cDAAKeccgqLFi1i9OjRPPXUU1xxxRUc\nc8wxbxR/mw+7EN02sweD2++aTef9arjXkkyr8CaLZppGKJ3BtMIQHdWkbOrvV/j13ZsHQhqtmmeA\n5GqwWj4KMy91nYKvWppfVNQyaWY2GMpsRcvXl49qus1o+kVeg0ogPGRW8uBNB2pSaDbDqhA2OygM\ntttosB0kFjfUvnw8P7NQvNBsqUB052R1PWzbEd0404x/K3Nrm779QWOdhED71wrgOeD5JribAhtb\no7yVoOXw8p73vIcnnniCY4899o3gZ/igP/5pQ7VppApDC9dnJ6kTo4r7FhIkIROGX5RT4eTpemGu\n/Hje7Gnb8CpkO4Th5AkfCfd510M+NWBuPjsIeXt7hfQWF7MvVwS3ILR8upbHZGFLwOhrHgwvNKjV\nHE3jw5etN/8Ynt6CYwu7etjGCzoVuvb0dYF8szLTA1O+jfhBX/PuhbwOvAbGny8jXy7lQFyjF2o7\ndeLTrx0pvh9MLP1koA98twF/EY0DryoheiWbH1i2FP7OBPagJpFcLsf+++/Po4+29inrYenSpRx5\n5JHss88+TJs2ja9//etAtOuks7OTGTNmMGPGDH72s58B0eGaUaNGJeHnn39+kO7q1as55phj2HPP\nPTn22GOpVqtBvK2wFbbCVmDjEH5vIWipYT/yyCPcdttt7Lrrrmy33XZAJMhbLTqOHDmSa6+9NuNL\n5Jhjjkk8/IW8/O2xxx7Mnz/4zZuzZ8/mmGOOSXyJzJ49O3w0HVKPX6oFlMmaExYR+UswTdOcItk0\nz0+BvRbjYbDFMdMYVasO4Rjo9FK1NsOZSqq91OW9S3BMk+wk0oinEy0o+ssNjC8b/yy9gtAxnrxZ\nRnezmCdEW/DUMvSad8m9G04+Tm8u6UUGyouVieZ/WfxeJtXqDiC9rcbwLA3TfqeTrUutX28Sg1Rb\nVQ1YTVWhGZjWaWjxMbQopzMa1dB9Ol2S90VxuLVl40MdfRkobVuY9u4TppKdDWlb0OvhumjUng2M\nx4p8U23f3y6fB4bmaXRo8DrsPPlbQlOB/cILL7DLLrvw85//nFxu01drQ75EXnzxRYAtWpEdsi+R\nd8/KOmm3DmEdFaIGXiN1bFQhnWLazwSUCk41AZTJChWDkC00NO33uz5UwJm5QwW34ZtQqgue8aD2\nQPtmW/e8t0BL1zphd3TbTAe9LF+V3ju3oTImTcN4rwldA+PBytR4D5mGVKBZng3fhI+ZK7y5o0ZU\n9lZ/xO9qIirH/8vCk6atfNq3gnvaYKhmIqPfRdYznQ5keXlXs4Pi2KCotI2O5df46HL8atmp35qK\nvPvBpIu0LqycNQ0VvhVSwa/lAVlTW0Hw1cSi/c3y5NNF6Fj6AOO7YUw3/GrLfYlsjgZ99tln85Of\n/ITx48cnzui21MvocEHTbX22jQ/gQx/6ED/4wQ82O5FyucwRRxzBn/70J6655hq+9a1vMXbsWA44\n4ACuueYaisUi5XKZadOm8fa3v31QXyJ6NH1gYIAddtghc1Qd4u08//w5OLobDu6GQtwiKvloUc0W\n1PKk32p5RpaioX1DvS2LvywfX7tUT/A2VMZEOOr8R2gBEd6CMWmjj08dZuKHhLbyFtOKrqmK35WP\nZTGdUj3iN443Mt/PhnobI/P9SZ7GliL1eW15J3adsojnF09lbNfLSbn11joojqtSZA3t9PMKE5jA\nK7zChASnI74ks9pXjO58tPBCL2vLOyVlqGn21jqiMrVyN17rpOW6LOZd68dA8xaot4QmwLI8I/d4\nNU2PGNfiG8RxRub708FI7c6dMc1FcSSboRiNPFn7v4XpydJCHL+TtG0tkVvnLa82q2nw0CiFsCyf\n4nhnTiqklQc/c7HBbrq0owX5eGFe2vky4ErSGchnyZT52FKVtZVi2gYXjGHk9LhNF1xdWRkvG5Pt\nS3F7tvZpsKHeBg8+wjZP/Jy/fmX2lm/re3AI8Y/KKqQPP/wwhUKBM844IxHY69at2yIvo8MFQ9rT\n8uyzrV0UNoNarcaJJ57I1772NQqFAueddx6XXXYZEI1aF110EXPmzGHixIksXbq0pS8RhVwu1/QW\nh8lve4bddtnALlOepp0+qhRhEoxiPU+xJ5NZyjpGM5mlvMIEqhSZwuIIz2BS9Oib1E47fUnwziyn\nPG43JvAKi5kCQBdlVjCe0ayjSJVXmBDddnEUjGYdo+Jjvuvj02PrxkX5aqOfIlXWM4o+onTWMZrx\nrGA9o3iFCRTjHm14AH1EF3gyLmW3fVIffbQn+IZbpEqVYsrDlFHszHKqU1IXuVWKFNurtNOX0G6n\nj1H0sp6OJP56RkXP9lHQHpVnUr5TSHCsDIpUqbYXE3rGX3VSFNZPG6NZR9+kNM11pGXTT1tUFpNG\nOb7WJ3wn+aePVyZNoCu+9ypTVnFd+rIBWDpucqYdFN9ZpYNe2uiHSVEa9m7tYB2jYUpUt5n6iNOw\ntrBu0ugkXh/tVMcVKVKln7Yk/BUmJAOh5bmhbcTlY/Es35Yff7NKLx2Zuu+gN4kznhWU6WI6C1gx\naXyUZ6pJGS2fMpEnrj4wErpFOPad90Z5YXTSltdPGpXUwVNHRf2JcWlZr2A8bfQzgVeitjAu7g+T\nIt6sDMazghWMT/hazyhe3GUJK559js2XOgKboWEfdthhlMvlTJjKoc3xMjpc8LpuQgz5ElHfHzNn\nzuSEE04Aht+XyLqe+TxZfpmVPU+yW/dktulOtXVrzMuZmHS4ftroo71BWLSRanmdVJIAACAASURB\nVADWKV9iYoLfkVzLHnXsNvrpo51+2pKGaTQh6uht9NNGPysYz2SWsp5RGRyDpUyml45Uq3VOQZKO\nFvNvwkSFfx/tVClmBMo6RlOkIyPQrNP4wcPiGX/2bt+rFBMh20Y/6xid8NlPW/LfC1Z7Wjma4Nb6\nsbxXKaaCnfZMXlS4rWM0HfSygvGMZ0WCpzjKT5FqwovhFqlm6hTIvGvaobB2+tJBOS4zrZsOehN+\nLNwGg/64ZVj+R7MuaRvaDi2u1b2BbysmFI2+DgY2qPj4SZsym3khzWMb/YmQ7qM9+W9lXaSa1GUb\n/XTQm9SXKjyWfpmuTNov9JRZ2fMkfymvpFZe1VDOmwXDaMPeEi+jwwVNTSIjRoygoyNqOOvXr2fU\nqFQjGcodZAMDA3zkIx9h3LhxXHvttUn4Sy+9xM477wzAtddey7x58/g//+f/UKlU2H777RkxYgTP\nPvsshx9+OE888UTDbTKXXHIJ48aN49JLL2X27NlUq9XwBQb/7+fgoG446pB02mtgU0ZbdCvVM6aG\nBhOKQU3noTLN9VNBS0Om+CNLryYmiuRZGZOEZ9JSMwg0OG9KTCrJ4l09y1vMfzIVFTMJZM0jZtaw\nKaviGI2OQm9i1tD3TN5r+eiWmniqnDHnGDhzRoM5AhrNTZL35JuYfJK04qm24TTUzbJ8ZFIyCJW3\n8ajtoRJ/ExNVA22loflWU4kPTxYPA2Y2X6+h9RBvIgNYlI9ME2omC9WFN1sYj1rmJ5KafL6fln9H\noTeqY8iYMxrK3OVN41ncpP3H+IZX+9nvee2h/wvXfmHLTSI/CMR/ogf+1JO+39noFXAwU8fmeBkd\nLhiSe9XNgblz53L44Yfzjne8IzFbfPGLX+T2229nwYIF5HI5dtttN2644QYmTJjAD3/4w4wvkc9/\n/vP80z/9E5D1JbJ69WpOPvlkXnjhhaZXhOVyOTjmczC5G97Wne4OKdB475422ESgkN0t4BdKvK3Z\nQG/oeITIU5lPo0C0+0EHYVvstJ0FJRfPL8qFFvAWEa3q+/2utkAZuj1EF1J1N0QpjvMI6cEjK7MF\ncTpmwzW+HgOOJl2E1EUnS8vypYuoRs8WUbskzwTwHyESKFPjd93p4net+EsMjC+/iAvZAzUF0tvE\nLX9WvpDai3X3ii6slkh9aFiZezzjYUmMo+3OdmuEFjo1L2ZjNj79bhfdWbQoxrUFVF0cLpFtYwBX\nkwrvi4W/PFH7tbJYRLQbx+rX0rM2Xo6/GY7SsXwY/4/FcX7dA6/0wE+23L0q3xtC/A83bqoYTGC/\n8MILyfkUD0ceeSTXXHNNg2VguOB1E9h/S8jlcvDAQHYbmTYoBWvAukXLgzbwKunpPxOGkG34Brrb\nQ3cShLY6LRH+9Gov5dF3ihqNHTCjvZEVDiX5bmE+XPNs5aYLWn7nig2GkO4wMOGiZWll5fmpyLfM\nQiONdeIX+rxQUqFofNVJhUuZtB5MKKsAt10SynvevXe5cggJfH23eP5wiMcLDbRW13rNm5avwh6k\ng6W1L20fmgetz0VkBbXxcSLpwP1ZYGo9uwhvs0fiRcjyTnH+Um1+ZOnVaJG1lk0zqIlD46xm+jD4\nEvn2EOJ/pLXAfvrpp3n7298ORIuOjz76KLfeeuuQLQPDBW+tg/SbAnNmwR7dkR9s69hml9OVdtXC\nrBOWSRt8gXQrVcHFgex2phrZFXzfWTRuWXAUTEiaoLS4+g1SDVI7sfFgwlbjKI/L5H+daLDQfbt1\nia9amIabYEDy7LVHi6/fzS5aFZ6MT505WBkav9bhtQxs/7G9V0j3DiuUyQriAtn2oLMN3S4XGsC1\njHQgNlwdeLwANjyjY+81Gs0TypOWhQnjMtmZn+6f1wEzNGu079YO/IyuTlpnSRvMx/zkU9r5yFzT\nm++QuLEJp7MeCWRVAnRwypSLmADrefhND/yhh2GBzVh0PPXUU3nooYeoVCpMnjyZyy+/nPvvv3+T\nvYy+HvD3q2H/j8/BlG7Ypjus+WiH1AZkeKE7ASEVlBauQlUFVZeEG65qo6U4/UVkp4nKn9eMtHNp\nuB5kMJ6VnpoPvPZtdP1BC5tqWzomaKzcyhLXa/j2rpqwmhA0TcVXYd9FVmgZX14omrlnKo2HoioB\neqZRmiap9WI8+XqpkR5MMV50gIF0xmR0VeNWbd63p5BJTgcENe9ovWr7hMb2401eSNlp+9W6MrPP\nMuA/iYSdmURqjpamrTMlD75tWJjVtZqarG6e7Rk+k8gNQ4j/sS3T5N9I+PvVsDuAsaTb3kJar3UG\n7Zhe2/ACrkvevWAITS1NAJRjWl1CxwSB14p9usaPDjyWhjZ+3HfDUUFREpyKhHnNx6evYUWyBzm0\nHFXImCbrtUfNT8HFV35NW1TBYOGaNxs0u9x3pWPPLomrA2IX2VmUnuy0GYbhWF3pwGG86bvxpKAC\nTDV4H1fbgvLv09ETq76t+vbSSbaeLR0riy4JN6g2oW3/fb40zGYOxru2BatbzY/V5ypgLcMDb7Gj\n563gdRPYS5cu5YwzzmDFihXkcjnOOeccLrjgAk455RSeeuopAKrVKsVikfnz5w/5xNDq1as55ZRT\neP7555suOgIwhrQzmxkEGoWWgQoODbOGD2lHVgFSJNsxTPPKk93d0UV6mMFr5hZPO6Z2Cq+NGY/G\nm9cWNW5NePRx7TBIJ9kObgMLEsfPSFRr0nwpv6o1hqbmpSZ4SLjVieVPBbg9pwbKKETT6kt5gWzb\nsLh+IO4kSxMpD6Vl9Wn01MuhPZODNWTboc7a6gG8vItTknCDTuFdQfMcStMPBAXSRUebfemArYJZ\nafk20km23m2QsMHd8qh9cscA/5sLIa3/LQyvm8Bu5kvkjjvuSHAuvvjijLAdVl8ieo5ABac1DJ1+\nFyQMsg3bhK8JIwTHN3yvMalw6nS4SsM3Kku3EPOug4Z2CD8b8HE9TeskqlHbNN8LAs+r/feavGrr\n+s1sqip4rCz9IKjaVp1G/lUY6wk+FQLmw8TzHDJf+AFFByCf12Z1pBAqaxXmPq4KLW0nOpuyp848\nlHZIsVDNPKTp2n/jwWvEBPBUS1a+lU/tH5pWiWy/6SJbD8qnpttGtv9uCQzh/oK3ErxuAjvkS2T5\n8uXstddeQLRP+8477+RXv/rVJtEdsi+R983KLlLp9Dcv4WYWUMGjglYXkAqC7zth1YXrtE9NBQb2\nboJN0/Np2H/TMpWe8qpaqO+MSk8HppCg8p2+7p41svn3vOL+2+Jo3f1UCCjfofjKl9ZRiA8tI58n\nPbat5Vx0cXXg0HpSWp5fTdPytUzCTXv2i9ZqWvFtS9uJzgS0DkNudH2ZWLjxr3xZufhZJ0QmBS33\n5HyB8GZPfzWe9isF7YOGo3XZ2Q1Tu2HOMPgSeW3LSbyZ4A2xYZfLZebPn8/BBx+chD388MNMmDCB\n3XffPQkbyomhV155hQkTIt8WEyZM4JVXXgkneuss2LM7uoBXtZcaWcGnGiukjcd7PDPwQks7t2mu\n1pm8AySd9vlOGaJp8fzgAVlNRTu75k+/e4GqHSakPYbS8mEmhE2rsnwYz34G4HkruW82gBrdkLnB\naJZJd4hYmatZqCI0vAarBwQNRwdkHbw1/5q+1rPSCSkIOnCbcNXvFl9NGWp2MTwdQJBwPzB1SpjR\ntu+aR8+/N6dZOfkBRv/roN7MDKPloYONtgMt8xd74IUehgW22rA3DbwvEYPbb7+d0047LXkfbl8i\nVIjs2AM0aq8GNpXWRqUC2ATuIrICyWhlMkpWo1Ct0AsPw1cINXgVHqqNmMZlZhalZTsprOMa/37q\na3nXfJowUKEQ0pK00zXrpKbFKVgc09JMyFq5VFx8i2P86F531fp0eq+CX4W9gearJPjQKNj1m0HI\njGDlp2WwIJD30GzI4ls+VGB6UN68hqtxKjTmw75bOeqAUHPxDLYlEniPBWhpGvoMnUcw/FCevEJU\nA5YzfIuOIWXkLQxvuC8RgI0bN3L33Xfzhz/8IQkbbl8iPNMDL5Vhux4odMOu3VG41xAgPNX24IWY\ngXYG3a/sO4zFr7unCiscfisIaX7Kn592Kqg2rAKyJM9QOYT49mYCz5+F64zByqNKWEh5Aad8+7Sq\nZAc3jefzrmnYQFam+e6gZmYGKx8VWH5A13wZTpm0rfh6UkHq8+HBC0rjCbJ14jVczZOmDdl6rZFq\np0sCeEZHy9zqVmdOmoZ/2jfL96oeWN0DtTLUy00yvomw1YY9NBgYGOCjH/0oe++9NxdeeGHm2wMP\nPMBee+3FxImpv2V/Yujpp5/mbW97WwPd9773vXz729/m0ksv5dvf/nZmIMjAdt3Q3h09B8juG9aG\no2AN3wshbciG5+H/b+/Ko6Mqsv6vQ4ghJhogKOu4IfsWRRkXMGzKIsggi2GGVfEDB/gOCsgiEnFB\nB2fGI5/OgMoijIoji44LyBYiCiMgAVwARQKGTcImIYmkyf3+6K6X++6r6jTQ6aTj+53Tp9+rd6vq\n1vJu3bpVdZ8SJFL7TGLhClKD5HHA6DmPuheGa6y8XAUo9pWiIGcPfGCR4LyZnhWgWFBy4SXrjqeT\nK+LLWYscMKV2q+JxuycXWNyUxHnnJgM+SHMThQzn8bndW7YdH/hkf5GmFd5HpFlDQQpaxRNEHNV2\ncqDXpSnLx/PKFWGKRppE5DqHzFOlr/qiDrr3jucfmwJUSQEqpQNR6cDp9YaELgAVzIZd4lfTLxaf\nf/45Fi1ahHXr1jk+B7Z48WKkpqba6DMyMtCyZUskJyejb9++thNDw4cPx9atWwEAEydOxKpVq9Cg\nQQOsXbsWEydOLK0iuHDhItJREMQvglBxTzp2If3ij9SWOeQUl4eZpshKs1DTfTkd5JD2V5UOnypL\nfhQCmUikCUXao3lefMeB3TtnMY36l1NeqdECdvuptKdyDVZOlfkCGIesIzn9luYmRSPzlXya0g9k\nM5Yw8awg+4rim+dbUh/hZeFmGt7fZNk5uGkiXtDIdDgfsq+l+6+j4XPIxPsDt5XrTDiSBzmbSBLX\nOtMKAKSHwJfIQ0HEf9096Vj22J/ms13HpziFrbQnK6iXik+p5Wo9v5YCsQD6F593WpU+YO+8suOq\n9GWYbsovy5cEfRl1/9yMwvOUwpWXTf2rMJUOfyZ5M02pA8XjZVDlyobz9KBEkiaMm1ri4dx7rbMF\nc8HO05SLZDJvPrBJgabCVRp8EFI0Mh9pg1Z0JsVD5WmqB5mPjBeP4gHdi+K2kIoLP1ug+lmsuOZ8\n6N4P1Q68H/2c7tspEgpUMJNIxRXYp+Bbac5nYYEWQhR0miDvgHK/qkxD7ozgafBDHyouty3qNGUF\nHs7tpZKW06mXjp/GVHFN5eeaoEqPCzK+mCcX1VS4HCh0+UjoBitpd1X1xW3S/LnKg+9LlmmaPN/x\ngUunQZu0agmVps7uzBFM3eTA7rtd0fD1CdWe8rSmqgfTeg2nBex9VMVTu0TUoqMJkn9eJs677HN8\nBsbTyoF7NN2Aiiuwf4HvtBR/0fiimM40oSAXkOS0VgownQDRLczIhUVdHMWfEoi6RUvALtCk1sLT\n5guT/MCI0mx4fEWr0+ZUvFhBy22B6pkytSjNidNK6Bag5PRY1YccqEwDJy8bEFho8fiKlpsuTHQy\nbWmCkO0p8+A8m/jg5gqery5NnRlJ0UKElzRIAHbHXbo0eNvy2SHnhw+Kqi7kIC/NOwXw7ewIlaDN\nL5kkklBqi44//fQT2rdvj6ZNm6JZs2Z4+eWXAQDbt2/HbbfdhhYtWqBnz544c8b3WaisrCxUqVLF\nWqB85JFHtOmeOHECnTt3RoMGDXD33Xfj1CmdIRa+Bj8H+4vONTbesfgpRZ15QCFHE5f/qzy4liU1\nNil8+T2PKzVZ+VMvDBeI8uUq0KQly6ji5Yp7GO55XJmWrmw6YZ0LJ09cGOvqTZZN1jHPQw4sUkOX\n9aCro3jxPIfRSf45TzxMVy+qHKosvG/y9KUglm0i880R9Lo2lvnyLZW54lrl6RVl5vUDFNcTj6Pr\nj3Jw4Cd8edqynJeK80H8Igiltuh45MgRHDlyxOZLZPny5Rg0aBD+9re/oW3btpg3bx727duH6dOn\nB/314QkTJiApKcnyJXLy5En9J8KumQZcleLb1ifNHBzSbimf6TQBCZ1gl25XpeZhguywXMsEirUV\nlQZ/xuPkwunyU6an0/CSxL/SjKQWzgVdvOG/QKTBeVPXYHGktiq1SE4LTRhPV+YZSBPWpRtM219s\nHMDOr7rXQVcHurKocNlWprJLflQeqq/8AJ9QVYuOMi3OB8/XVM9g4VIjl2U8lA78mg7sD4F71R5B\nxP9P5Cw6hm2XSK9evTBq1Cj06dPH0op/+ukndOnSBd98803QArtRo0ZYv369dYAmJSUFu3btstF4\nPB5gItk7rhTYOsGSxJ4B9o4phRHgfDEU+HQ6V9CpePwFkC8Z78SKVgr+QNPsJNh50C2syRdLxeF+\nLZRdVNntuQ1fzjLkCyhfREnHIetR1plpwOOmEj4o8bLGI3B76AQu4NxH3Qh2M4AUWkkwtzW/N9WB\nDrqBkPNaAPsxdF0fD5Smji/VDz5Ecb0N0aQj20HWDVcqdPFMAyeneSIEu0S6BhH/k8gR2GH3JdK0\naVO8//77uO+++/Dvf/8bP/30k0UXUl8ib6QBVVOAK1LMJg4JaROVz0xCSQqnAtgXgXS2Q3XNedK9\nyLoFHbl4qV4yyYt8gZVQ0QlsThML504IJfg4TzpBrCtvjngORsM/NBxI6zLZfXXaHgRtgeaZep5o\niCfpfoBdUCuoQcyUjk5D1vErF7N1fJv6nC4vSSvT1aXH+VTtmgPgnSDiK/By6NI3tSvvX+fSgZPp\nCAkCve8RiLD6EklISMDcuXMxZswYPP300+jZs6d1HL1UfIl44Vt81HVmsHuOCxHqMr5O85SQz6UW\nYhoQ+HMuOAH9zg9ug1VQeZ4StPLDuVwzV2lwm6N6ubhmy9PimrmCzqwj68PUTio/XX1wcG03R/Ms\nR0OrE8KSRvEvw3SaYTBp6aAzb8h0TX0vkKDWCUvdbE3Hm+ov8mtGgcrIZ4vyWaB3j6cbyuPk7i6R\n4KHzJdKwYUOsXLkSALBnzx589NFHAErBlwilAyezgMvSgcIUACn2xRA5JfTCVxvSbKE+k6Ro5fRP\nmkI4dNM/ZRdU+cl7FU9qtRKKpqRwJSjj4VzokTS5sLsZldNcJcx5fK7ZK3ouqOWUm4epsks6fs/z\nVve8TXRxVZ2pwUPX7lIQc3Czl4kvyUsOnG2phCKvr3jYy837WaC8SgpXaco65X1QtjnnXQcl7Djv\nvE9IOlV2aTrkacj3iz+/LB3ISwcoC8W+JC4RFUxgl9ouEZMvkWPHjgEAioqK8Mwzz2DkyJEAgJyc\nHJw/71uyDcaXCIDAvkQ8KUDUEOB8mu+7jrKDyQ4czZ4Bzs7Ep/78uXx5ZHz+n+vPJx5OIQ0UCxMv\n9C+wLr946DUaJSiURqPiSQ0pR8ThAkZOk7mmK386myWn1dWXTl0wDUSA/eULJFBzNc/5ICFpTCjp\nOR/kZbmUH2n1sWGI54HykG3P+4MS7pLPaEEvn8u0TPl7xb+Cro+pMJ43Hyx0wtIb4PnZFKBSmu+9\n9aRoIl8ECoP4CQwbNgxXX301mjdvboWNHz8ejRs3RsuWLdG7d2+cPl28UXzGjBm48cYb0ahRI3z6\n6aeh4duAUlt03LBhA9q1a4cWLVpYZovnnnsO33//PV555RUAwP3334/nnnsOALB06VLb14enT5+O\n7t27A/D5EhkxYgRuvvlmnDhxAv369cOBAweMnwjzeDzAZdOA6BTg1xTn6raE0pqVRsSnb3KKV5IN\nTzcl1OXN0w7Em9JqdeYA/kzHT5Kgl4uIKn+uhatDNvKjvDoedWYCnQnGxJ9p6i5nLoFQkqmhJNqS\nwgLxJetfl16wZdGZRHTl0tnETWGmPgcDT4oHaT7ifTSQWSaQzbykeJz+TDqAdOBsCHaJNA8i/k77\nouNnn32G+Ph4DBo0yNoEsWrVKnTs2BFRUVGW/6Lnn38e3377LQYMGIDNmzfj4MGD6NSpE/bs2YOo\nqNLRhSuuL5FEMtvzgl0MkbQQNDo6/uLpOqlpoShQ3jIveS35lzZoLsCBYgEt7dJA8Tf4klg8SSfN\nFLwsgQQ3pzNBN4iZBD1PEzCnq7OZKwRKx9RHZNrBQJZBmgR06Zr6pEzXxJOpD5vKYxqYguVZpsXX\nFKQpRPKjaHgeR0KwS6RxEPG/c+YTaNfasmXLsGTJEixatAgzZsxAVFQUHn/8cQBAly5dkJaWht//\n/vcXzXcgVNyTjvlpwC8pxbtEdFNoKXQgaJRJQZpHdPZrGY/b++Rz3b3J1qizB3Le+bNYOGcLgFN4\n6oSpLh++4s/pTPWmy0uF8QEN0AsfGU/RyHLkQh8/kPCU9RUvnoGFF4hrBal16njmayP8mi/4yXRL\n4ovnLwcz3XqKLAfnT6bHIddreJjUunXgAwPPL0fwJAcO+U4WpqPY+9QlohT8Yc+dO9fyNnro0CGb\ncK5bty4OHjwY+kz9qLgCOxDky6XCdItNBYJOvqg64eVltNJ+GEzeunw4ZBpyIS1QHB2/fHAxabc6\ngSJfNE7Pw6WwloMEDPcmXiV0wlLS6uq4pIFRV8/BPI8XtKp+A/EdSCnQ5akT0KZy8DyS4Bx4FC1f\noLXWVwiAx7z7g4MPrJLWNEBy8HKEarHw1xCl48ezzz6LmJgY29eyJIw710KAii2wq7BrKdx0wpFr\nk4Gmf1wDzGFhKo6pVtWCo44n3curm+7qhBF/xl9Mk/1Q8qArp05oJ7F/Xm7AvjecC3mwcCn05eDA\nZwWAUxBxngvEvaQ3pRFo8JXtXxJ0MyKVjhRwOtu3rAuTAA8kgGXaMj+ZTg675rwb+4THbGoqqZ5U\nOaWpUPLJeYj1ZRkyga1L59d0317vC8T8+fPx8ccfY82aNVZYnTp1bGdJsrOzUadOnQvnM0iU2i6R\ngoICtGnTBq1atUKTJk0wadIkAMC///1vNG3aFJUqVbJ9IizkvkTO+f9zxU+FecU/YDYV6K4B8zY+\n071pl4NJ6zNpIpyW/0yaoC4ejy+n/Vzw6l4ynSZfIH48n0AvfIG4Ns0yuADSaeoyTOYj20UXJ0fQ\n6NIJ5jk3U8j8THlJXnRaejz0W+10fSgQr17NtYojd6hEw9kugWYGMj85WEvIAbUAxe9uKKDbFRKV\nAsSmFf+CwIoVKzBz5ky8//77iI0t7tA9e/bEO++8g3PnzmHfvn34/vvvceutt4awAHaUmsCOjY3F\nunXrkJmZiR07dmDdunXYsGEDmjdvjmXLlqFdu3aOOPXr18e2bduwbds2vPrqq9p0n3/+eXTu3Bl7\n9uxBx44dHX5ELMT4/02adSKK7XNJhkKol4Tf8/8k/3WS4blMR005uSYs09dpiDItFa7LT/eycJgW\nrnQvU0k2UC7QuZBX6fHy8IUrfp8r0omHWcCD0ejCStKKS6prlbcuHRXOf4F4UdANQDINE3QDDd+/\nrfiS9Drtml8rO3U8nLNBtUsI0GunchCSAwbPx2sI12n1vKxnETqhfRHOn1JTU3H77bdj9+7dqFev\nHubOnYvRo0cjNzcXnTt3timUTZo0Qb9+/dCkSRN07doVr776aqmaRMKySyQvLw933XUXFixYgCZN\nmgAA2rdvj7/+9a/WwZiQ+xJJ1BSLd4pAuyxMMO3e4M9zUPIXRUw7PwLRBeLDVBb5Uieh+ISiHDDU\ntXphk6D3sczz52YReSTZdHiGQ7crQ5ZP0oLR6J6ZdgDxMgdqH0nP01FxVZ5cYAGBTTPBhAfqC9A8\nk7wpHuSagWlg4HUlTThK21ZmPKlV6xYoeZ+Saeq0ct3Axp97Q7BLpEoQ8fNdXyIAfIdjbrrpJuzd\nuxcjR460hLUJIfUlcjrNf3gmxXmKkN9zLYKHmQ518H8FSZ/D0pUn2nLhzFPyo06syfgyjL848oSb\n7mWQgpebP1S4Eg71YXb0pOLmsHiBpsOSDwkZzssiP2emBEigxV51mEXVzRGWluJdF4fzIw+qqOcy\nrm5g8gI4RUC0x9nWvBxe9q/LS5cujyf7kqKVVkJen5Ken46U2jEI8HrsfJkGYlUX8vQu51HmIfuz\nStObDnjSERK4X00PHlFRUcjMzMTp06dxzz33ID09HSkpKVrakPsSIQBEQJH/3qtGUI+4V2H+zqlW\nxfnLYSXI85L38HdA/4uq4OXPVDyWr+NkGecD/msRn/MJAnI1+UlhxoV2oJdGaUU/+O9N2+eUsOfp\nyu1xOgGtXUwSbaPoFG+8Xrlg8GraAOTPw183NuHF21f2B8kLAG8+gDiWJuxxeBvoymbjT7Yr7Hx4\nNW1oS5/3UZ621Ax5mAdAnp8+zvdv1ZvKHz4abxVNfMG3VzzzaurB67Gnp+vLtjiqvKI9QqXxRpi/\n65JQajZsjiuvvBLdu3fHli1bjDQxMTGoWrUqALsvEQllCgEQ2JcI0gHMBzxpANbB1xF4hyvpUxTy\nJWXhAOwvLTQLOeT/5Rni6V42CZ6H+slnnF//c9MwLDVhvnWL8y9tyCZbqFok0k3jtcJa8S//edvI\ncnIBwe4toZwXIJ6mjiwhyZ/lset88a9oS7JLKnodXZ6419FI3nkdSUHnD4vmaUlBrmir+H/+eF5d\nPnw7lY7PQLzoymFKT7aT/F8PYBqA+f7rEICC+EUQSk1g5+TkWDs48vPzsWrVKiQnJ9touN0o5L5E\nkAJgKEBp/mvA3uH8GodNg2GIlp1VvBiO9CTUSy41Fx7HI4SrFO7BwMOEl0gv1vCvYNGyMij7Yyyc\ntnAJRZsk0tYt1nKt1wb50orwaF7vOoHB21H958M8IOvyq8LuVXvFwS54eD/QzAi0PKp/lY6pXXUD\ngscQzvLxivuAPJjygaDjCk0gfhV0Gr7/ua3tTOXj8e8C8BSAwf5rFxKlgS2s0gAAIABJREFUJrAP\nHz6MDh06oFWrVmjTpg169OiBjh07YtmyZahXrx42bdqE7t27o2vXrgCA9evXo2XLlkhOTkbfvn0x\ne/Zsy0fI8OHDsXXrVgDAxIkTsWrVKjRo0ABr1661zvXroRGQNhg0F+tlYBqrVmvlQliGQfzrXnKp\nxUvNRDdYyIFF0Ho1MwO1J9q0M0GWj9u6lVaufoHs1ab93tbuBqat6gYLiDBF43AuFEiT5lqlSksK\nLR6uEzgyDw4Vngdn+5g0UcmHSVOV/dUw0wg4oLM+bHwO2GcEkl4pGpxnHb+m98oUxp8FKkMwM5rf\nJiquL5FoIbgsezQvbj6KX2x+rbsHHPZEbUdHABqddqarfmm6qWJ4JnmC/ZqfXAPsAlS3+AQUb1WU\nDvn5tW7xTqWrQ4nrAKY2kXXIbMpael1d5cHZjrq2VWGBhIkuf1P7wm9zl7yqGYEql44/RQvo+6Sp\n/wXDq8qPpwXo+5uij2P/uj4NTXi+oOflDKbNASDq0neJBLU/MCZidomExYZdJvBOg892re51mhTv\nsHxqLTUMroVw4aH+FaQWJKeVKn6+hh4aOkAvrE1ao0jPtH1K7kTgi6tKg5bCWv10PrX5NYdDm+cz\nEpM2Gld8Gc3jqDbhdajCFHSCr6QwKRjljIzzpkvLZELID7AGwstusveWxCP/h4E2UP/kyBN0nF7l\nyc1GCnKGqRPWck0gUH4qjXQAaYbnF4r8IH6Rgwp8NJ29aNFgK9Sm6bH/3xJeHnvteDkdUCzQmdC3\ntk6pdITwsQYNNjhod6LozCeacunyVfd8Py63YfPj9FJo80NA6j8Xdnu2zutcEoqFPIc6QGPbsugx\nCDLeXqLt1DOvEOzqmWOHR0l1yOmr2Ol4+zv48wsnS3PmA2UV6IW7HIx05hIYwlWaQcSz+Bb90SsH\nfJUWF/5x4lr2w0CmHw4VJ47xo66rsfhxIh6fCXAFKRSoWF8wqLgatg7SJqo75WVB2YShMR8I257c\n4xotrq1nQsA6EMgmqIHOtq5Lmx8PhuZaQi44qp886CLTkIuVOidAvF4c9miIASxIWO3pbxclyG11\nQXZ6ayBgQkjuiY8W14qeD+i6+rbt3pDlk3yJNGzPOK0YxGR4oI8FGPuTQTBGG/qh5M3xM+SlHQAD\nIZTmiYv4gkE5Rth9iUydOhUtW7ZEq1at0LFjR8txSsh9iXDIvc46kwAgbLtMuOo0UZPA0UHRBXIK\npVtYCygQGNSgIoWd9I1iOuaurpU2zZ9J96oSMlxu8+NmGblACsChycntkfwn4dj3rAv3py13/TjS\nCyRQxKyAD8K6HTq6Pd18QJDgAk0uduvWGrQDmtph5IG9rzG+bELeNKCY+Pcw3nSKh0hHCmkHLTel\nSJ6kjftS4ArsoGDyJTJhwgRs374dmZmZ6NWrF5566ikrTkh9iXgARDEtyKRVm7Qq+WJEQ2jgKp7h\nRXfk49H7blDp8LxVAZTQTNTwpeji4SwfF7Y6bbgkHxbcLMJ9e6gtfOqn/Guo4+zxcG7xU1CCOxFA\nosfuyEjVYbQQBLLcukFWCnOtcOJhOuHL25D0AzpPV3c60pavzhzDrkvcqSOErMM0p4mrTA+OQUOT\nv60+TSY2vlbiEWFg9cDKKtuNp6XqlM9UHKYv6NvtklCxbNilahKJi/PZqs6dO4fz58+jWrVqtpOL\nubm5SEpKMkXX4oMPPsDgwYMBAIMHD8by5cv1hJXSfMfSXbhwEWFIAZAWorTkNE33ixyUqsAuKipC\nq1atcPXVV6N9+/aWL5EpU6bgd7/7HRYsWGDbR618iaSkpGDDhg3aNIP2JXI+zfcVZqBYo+Hapy6c\nL7rJcMC5RU56PeP0/LmEpOd8ca1a3UurT6Kg1XmRU9owL5N8Hgt7ebl2nMhoZN3wAzNq+18inAuR\nAHAtijVyeVyd14GKx2cOYNfx0Neb1L7lLCZR3HP6RNjTAWBpiiYtWPKtrm16B9eQha07GsULsXK2\nFWgGFmiW6AgLMLPUzRy16Xk0cXSmEE35FM+A0zQi85R5ewFEpSN0Ats1iQSfuN+XSHZ2NjIyMpCe\nng7A99WGAwcOYMiQIRg7diyAYl8i27Ztw9/+9jcMGDAAZ86cCZh+QF8iyr2qdEBj2n7GD4ZwAaGj\n5wdJdDTyOc9D3UsfI4HyUfFlGUzOqADnoRcdTMfKlXBVNMq2zYWYyUMe55u7WVUweatTgozT6Ewr\nOu9vCmrfue6AkFSk1ECoc8ZlSl/HtwLfk64TxOqftyOn5f00WtBJIavSksI2PgA9RBgXqHJA4OFy\nXSEaTsWU33vhVDB06wa6NFT6QOgsIq6GfeEw+RJRXxsGSsGXyK/pwNn5ANKAonTzSwQUvyjqpVG/\nU3B2QNm+0mNZrqDLFeEQNPzl4nTSyxn/N+XPFw35M53nPh248yZ5KEYH7vhJ/cvTj5yO163iyyTA\n+TbBXPHTLS7KuuNp6QQD326oq1fFl2r7YBY9eRi3g8vyyzbXrU1wOt2Csmxb3k9L4gs8PSVMScgv\nw6Kfzn6vE8i2uhULsjwPHicqHfBOA4rmAZSuz/+C4dqwg4LJl8gPP/xg0bz//vuWf5HS8SUyBD6B\nnQLHkW3+8vMXhXcorcYBe+c2aQoQLwAfEBTki+v4V2mQnVcdrRSe/N50lFw3iEgXrFxDVkI0h9Gf\nMsTjkJo8HxjVoCghZy46Ic3zl894feme69Lk9XsKztmQFGqy/XQDsCm+FMCmuDrede1uojMpkF65\na8ljf2aEf3eHV+7y4M9hL7MUzKY98kV3wedLZCiK/f9cKiqWSUSnW4QEhw8fxuDBg1FUVISioiIM\nHDgQHTt2RJ8+fbB7925UqlQJN9xwA/7xj38AADIyMvDkk0+icuXKiIqKcvgSGTFiBG6++WZMnDgR\n/fr1wxtvvIFrr70W7777roGDQvikhDh95ZXagH8Lkc1VJEQHk9uMNEebeXyHG0kWR7mfRJxdw7Hx\noq4lGK1X8K0OcnBfxEpL5lNtWTbp31jFqQsgy3/NtW3pPzsHTtOFbpCwaW7q4Il0X6q2pHmKXapC\nhbMyOrb/sfaR7Wq71sWV/DFod4z6+bYOpPBrlQ7rH15dmxIcrnw5jamPcgTi28pf9TnBk5WG7oQi\nP+avYDqNyenzGC3BmZbJT46EbsvfpSCyTB4loeL6ErEcYVuhcHYkR0yUKJhtNOLFMKKkzmuKL48k\n614oQ7pqyxQX1PzepEXV9DgXTJWGrPvKixLm/ASlbqHU8iURTDtwGPYLSyGs9b2BAPmogVPFCaYt\nTe0YjB+aQOC8m/jg4WD0EicAVAvAB/chIv2KmOglb6ZnOp5MPlEk8v18c/pQ+BL5OAjKbhHjS6TU\nNOyyxxMA2gJwfjvS16l/AXCF/577S+B2LfmCqE51As4OnC/iS8Fq0l4kdL4X+DOT0BYvsvxAg81U\nE+DFkwI4Cc4PxvKj6Fx7V3k4tGMlGDm/RwFcrefBVKaAZVbIMqQbSMDy9pTtHajNZFvphGqwgp23\nbb7mPlDf4qiiKU8gYanuT2jSAoKvz5Ke8Wtd23H6DQC+NPBzoYgsG3VJqLgC+/LKQEwscJnfb4FN\nQ4wDcqoXf9vP5pEuDk5fByweAKA6owVQEMd2SsQV38cDyGVpxcNsQuC8qTQ5YkVYLICcOLadrHqx\n1qsEqrIDyy1nMp2CuGL6uv44jQBkwy6wk+B7f/mhGS7M1bccYwEUcJNOnN1GHgug4Drx/UVeZ/5/\nxNnzzvWHqTjx/nLY7OzX+f7jGb1KCyLMsv/yuo6z86TKn8TKoMqt6jUnTvDD0uBp29JjdEBxX7J4\nFzzFs2urHHDa+jmNqlOO+DgNvQgvAHBKDbLXAvV19RznXMy20mD1a0s3ztnPHWWoDvx6JYDKwEkN\nnxeMyLJRl4SKK7CVQzC1rKpbKDrCwtQ0/kJqRNpno1kayh4szQN8+5ouLQWutao4MkzZqaXZQyEe\nvpcv23+vXhbFl8yba9f846ySP+65j7/EchuhPKLOt0/KsiiaHBaX7/DgAkp+F1GBf9vyCAvXmYSO\nwPktTEmjFvW8gu4IABBwymPnQbdGIPnUpefV8C7bWdYVz4e70ZU7NWTf4/1Fl66Nd7/Wm8WC+DuT\nA3vZ5T3g7J+6GZnkBQjxtr4Lw7Bhw/DRRx/hqquusj4KfuLECfTv3x/79++31s4SExORlZWFxo0b\no1GjRgCA2267zXhKOxQIuy+RtLQ01K1b1/IZsmLFCgCl4EuECCiSW5XyxOKX/98L30dT4afliz6O\nn26HCF8JJ0bj393BP2NlTEtcA870+IKZ7V7wqwSp2s2Ry+6lED3F4qmwAvheUh5f9x1HiPscRiO3\n5Kk65nVm7SDQ1OkpXjZZn6oO+AIViW1t5Iwr68yizxM0cP7b2oGHcR7JyZPcUeEVcb063g11pMrM\n46m4vHzRIi5Ymo70NLxY8JtUvLxsefqy8vyRJ+LIvi3rjaWp6iZkJuWStvQ5TSZDhw615JJCIJcY\nwbjUCBXC7kvE4/Hg0UcftQrYpUsXK05IfYkAcC4imnxLK7Bv79kEu1xNh+ZeNbxutwn3rc1fZg98\nvn95+uRMQ/q6cOx+YPxyDUxq7XzqKZ/xeErDVho6AJxLt5tCVBpKa88S6RnTl/ybHBF5xL//2vHx\nZP5PKK5P3U4dFc7/AaevZ1N7qzDuz1nSBFINebrpcLYv7xslxQ8Q7lAqdfFK4rMK+60Xz3mb8X6v\n6lW+Z7q8ZRl4fYZMvcbFbOtr27atdSZEIWiXGKWMsPoSUZVwKSuywVfcU/Dt5dR1GCmEeUeT4XwE\n5h2Vp8Xj6l4mXQdUnXYdHEJJCm6lMVnPZRkYTOYRwLlzw6Htwb4jRAnkAgBn0ovj6Q7kcOi29DmE\niGwXOVDx8Hxoy6oVROsM9PlwCgq59a+ktDmNzt+1pOfxZHnTNXE5nzI+/5daoQd6wSmVCM6L7D+m\ndzIf9j4qBzf54Qf17xHhprLwNBTuQuiOpmunyeJXMgK5xAjGpUaoEFZfIk2bNgUAzJo1Cy1btsSD\nDz5oM2mE1JcIpqH4izPBdBoO3tEDfWVEvRTBDEDKLMI1iXw4O4xKi6Wr3YIXQFDIfsgFq5xyB9Qm\n/Yj10ys7NDd3SPOHIw+eNteo+aAkB0lNmSyUVN9eBL+lTrWBFHY6OrkNUKaheDPtn5d0gP6jy0og\n5pVAZ9plocqhy5+nxZ/pINPn7ltNGrJOCdK1r2xnuZNlJcqzLxHuEuNiXGpcCsLuS2TkyJHYt28f\nMjMzUatWLTz22GMASsGXSEkCOlqnDSga2fl5PJ4OwefWktFE69ID7F8PUTRV/AlKPiQdS8eWv0f8\nOI9w+kORjpBkfOnACew6joVxp1CKPonlp/ZwW8eTPcIkwvPmZffA8XEIq55kPeoGYY8/Uxk/H+av\ntqhpP+dV9heWd7Sos2jVVrx8unaRdLyf6fLjfMn+WAX2/mGaJVSBo06j5afwdHxq0gBQLJRlG0o6\n/n5IWp3WH6cJu/hZuB06m/U3AD5kv5JhcokRrEuNkIHChOnTp9PMmTNtYfv27aNmzZpp6VNSUmjr\n1q2O8IYNG9Lhw4eJiOjQoUPUsGFDB03t2rXlUO7+3J/7i7DfDTfccEkyJ9h8qlat6ogrZdP48ePp\n+eefJyKiGTNm0OOPP05ERMeOHSOv10tERHv37qU6derQyZMnL4nvQCi1bX05OTmIjo5GYmKi5Utk\n2rRpOHLkCGrWrAkAWLZsGZo3b27RV61aFZUqVQrKl8jjjz9u9CVy8ODB0iqWCxcuIgR0kWtlqamp\nWL9+PXJyclCvXj1Mnz7d6BIjkEuN0kCpHU3fuXOnw5fI+PHjMWjQIGRmZsLj8eC6667D7NmzcfXV\nV2Pp0qW2gk+fPh3du3cHYPclcuLECfTr1w8HDhyw7Yd04cKFi4qOCulLxIULFy4qIn5bX00PEkVF\n0nFU+USk8AlEDq8un6FFpPAZKXAFth+5ubmYNWsW9u7di4IC3z618jj5iBQ+gcjh1eUztIgUPiMR\nrkkEwNq1azFy5Eg0a9YMSUlJiImJwaxZs8qaLQcihU8gcnh1+QwtIoXPSEWltLS0tLJmoqzx+eef\no06dOvjHP/6BNm3aYMaMGYiOjsZNN92EoqKiAHu9w4tI4ROIHF43bNgQEXyW9/okIng8nnLPZ6Tj\nN2kSOXDgAL766ivrfteuXbj88ssBAFdddRVeeOEFTJ06FYDv8E9Z4fvvv7ecZgHAd999h/h43+mV\n8sQn4HPe9cYbb1j333zzTbnkdf/+/UhPT7dsq7t37y6XbZ+dnY2vv/7aui+vffTECbsf7fLcRysE\nSm2HdznFlClTqG7dutSpUycaN24cnTx5kjZs2EDXXXedja5Hjx40ffr0MuGxsLCQJk+eTLfccgul\npaVZ4Z988onjMEFZ8snRpUsXqlWrFr3//vtERPThhx+WK14LCwtp0qRJ1KhRI+rWrRuNGjWKiIhW\nrlxZ7vicMGECNWjQgDp37kxjx44lIqLVq1fT9ddfb6MtSz69Xi/97//+LyUlJdG6deus8BUrVpSr\n+qxo+E0NeTk5OdizZw9++OEHvPvuu4iOjsZTTz2FO+64A40bN8bkyZMt2mHDhuHo0aMoLAy/A/Sn\nn34ar7/+OjIyMjBt2jQrvEuXLqhTpw6mTJlSLvgEAK/X5zCkdevWePjhhzFv3jycOXMG3bt3R82a\nNS3tqqx5nTFjBrKysrB9+3YsX74cGRkZyM7Oxt13311u6pSI8MILLyArKwu7du3C/PnzsWfPHmRk\nZKBjx46oXbs2nnjiiTLnEwCWLl2Kw4cPY/To0XjmmWes8HvuuQd169YtN3xWNPymBHblypWxadMm\nHDt2DFWrVkW/fv0AAAsXLsScOXPwr3/9CxkZGQB8U+U6deqgcuXKYeNPTdNHjRqFqlWr4uTJk9i4\ncSOmT5+OxYsXAwDmzZuHRYsWlSmfHNHRvsOyO3bswC233II6depg3rx5Fq8LFiwoU17Jv6Y+YcIE\nvPXWW4iJicH69etRvXp1y8FYealTj8eD/v3745VXXoHH40Ht2rVRq1YtrFy5EgDw2muvYeHCheWi\nPnv27IkZM2ZYSs7s2bMtmtmzZ5c5nxUVv4lFx/Pnz8Pj8SA2NhYHDx7E3r17ceedd6JGjRrIzc3F\nhg0b0LdvX1StWhUrVqzAX/7yF2zevBnDhg3THo8vLSiBHR8fj9OnT6Nfv37YsWMHWrdujddffx1Z\nWVno0aMHatSogY8//hgzZ84MK5+FhYWoVKkSAF+dRkVF4dy5cygqKsLWrVsxbNgw1KxZE6+88goy\nMjLQu3dvXH311Vi5cmVY6/Ts2bOIiYkB4KvTqKgoREVFwePx4KuvvsKAAQOQmpqKd999F7t370bP\nnj3LpE5PnTqF2Fif9yyv14uoqCjEx8cjISHBqt/33nsP3bp1Q/369VGjRg3ExcVh9erVZdZHFV/R\n0dGoWrUqoqKiUKNGDbzwwgsYOHAgYmJikJSUhLi4OKxatarM+KywKGOTTKlg6tSptHLlSiIiKioq\nsj1bvnw5DRs2jHbs2EFERJs3b6b77rvPctiSl5dHH374YZnxyfn9+9//Tnl5eURE9OWXX1Lfvn1p\n586dYeeTiCgtLY1effVVys/P1z4fPHgw7d69myZNmkQJCQl0xx13EJGvPOHk9cknn6SBAwfSgQMH\njDSqjrds2UL9+/enb7/9lojCW6czZsyg2rVrU3p6uvb5r7/+SkRE3bp1oy+//NL2rKCgIGx8Pv/8\n87R48WLatWuX9rmqyz/96U80btw427Nw8vlbQYUT2Hv37qWEhAS6++676fz580TkW8gZPHgwffnl\nl5SdnU3PPvssDRs2zIpz55130nfffVcu+BwyZIhtEYejU6dO9PXXX4eRS6IPPviAWrRoQYMGDaKD\nBw9a4YWFhTR06FBav349nT59mh588EFKSkqiPn360H/+8x/q0qULZWRkhI3PM2fO0MCBA6l///70\n/fff2/gcMmSIjRc+KHbp0sUS2OHAO++8Q7///e+pV69e1L9/f1q9erXF59ChQ218Hj58mHr06EFE\nRG+//Ta98MILdPz48bDw+cUXX1BycjL17duXnnjiCbrzzjuJyFd3sj6JiA4ePEg33XQTTZs2jcaN\nG0fZ2dlh4fO3hgojsAsLC4mIKDc3lx5++GFq1aoVzZo1y3p+7Ngx6/rIkSPUtm1bGj58ON16663U\nt29fOnXqVFj5NfGZk5NjXSvBkpGRQffeey898MADpeq6UeLw4cM0YMAAevjhh62ws2fPWtdHjx61\nrhcuXEibN2+27t98803avXt3eBgln6vdjh07WvcnTpywro8cOWJdq8FR1emAAQPC1va7d++mBx54\ngD7//HMiIurTpw+99NJL1nPe9kS+XUEtW7akbt260Z133kn//e9/w8InEdHLL79s8fbzzz/TmDFj\n6Ny5c0Rkb3eFr776ihITE6lFixZhHah/a4hogX38+HEaP348FRQUWGFr166lZ599ljZv3kw33nij\nMe7PP/9Mn376KS1YsKDU+eRCTgnhYPnctGkTtWjRgt54441S55OI6OTJk7Rq1SrLFPPuu+/Sk08+\nSe+99x499thj9Mgjj9DcuXOtgUP5AlYoKiqyhGJpQrb9nj176M9//jPt37+fhg4dSt27d6dBgwbR\nTz/9ZItXWFhIq1evpuTkZJo7d26p88nbXmLevHnUtWtX4/N33nmH4uPj6Z133ikN1myQ7T5y5Ega\nMWIEbdq0if7whz9YisXPP/9MRPZZyrFjx+j++++nV199tdT5/K0jYgX2iy++SG3atKFHHnmEvF6v\nNfpnZWXRQw89RERE/fr1o1atWtH//M//WPFee+01x0tcmnjuueeoevXqlsC9ED7VtDIcApCIaObM\nmdSwYUNL8zx58iSdPHmSxo4dS9dddx1NmTKF3nrrLUpNTaXhw4dreQ0HeNurmdXBgwfpjjvuoKlT\np1JaWhqdPXuWRowYQX/4wx9sfCqzTjjq1NT2apD75JNPaMSIEbbZgOLz0KFDVFBQ4BgQSwO83VNT\nUykvL48OHjxI//rXv6hx48Y0YsQI2rFjBw0ZMoS6detm41OtFci1Ihelg4gU2IsWLaLKlSvTvn37\nHM9Wr15Njz32GG3ZsoUaNWpECQkJ1mEOIqIFCxbYpsilic8++4zuu+8+evHFF6l169aW9kJEtGbN\nGho3blyJfIbrRXjzzTepa9eu1guYnJxsTcEzMzOtxU4iou+++47at29vffknnHWqa3tVR8888wxd\nc801tGLFCutZrVq1LLv//Pnzy7ztz58/b/GbmZlJ119/vaWFq/AFCxZozQ6lAV27q0XOnJwcGjBg\ngEVbWFhI9evXt9YIwt1HXUSYwOYdo1WrVrRx40bau3cvPfnkk7Ro0SLKzc2lw4cPU3x8PDVu3Jg2\nbtxI06ZNs9k2ww21uj5gwADrs0JEPptrXFwcNW3atFzwyTXO7777jtq1a0evv/661mb+9ttvWycF\nw4VAbb9w4ULKy8ujwsJC6tSpE7322mt0+vRpysrKor59+zpsw+GCru1VPavydO3alRYuXGgLCyd0\n7f7GG2/QL7/8QufOnaOrrrrKsrl/8cUXlJqaGtDM46J0Ue4FNu/EXq/XmiIuXryYYmNjqXXr1jRz\n5kzq0KEDPfroo/Tf//7Xpg2eP3+eFi1aVOp8qqm54lNi+/bt1KxZM+slzs/Pty0ihYtPIj2v6sXN\nzs6mBg0a0OTJk+nee++lsWPH0rZt24iI6Mcff6THHnuMWrVqFRa7quTT1PYdO3akMWPGUHZ2Nm3d\nupWefvpp6tmzJ7Vo0cK2oFta4GsonGcF2fZer5eKioro7NmzNHToUJo/f35YTDScT2WeMbX7qFGj\n6Pjx4/TPf/6T2rZtS/3796fk5GSaPXt2qfPpwoxyLbBffvlleuaZZ+j06dO2cCXEZ82aZdlOf/jh\nBxo0aJC1r5nI3kFLE3//+9+pT58+tH37du1z9VJMmjSJ+vbt63hu2ttcGiiJVyKypu8//vgjDR48\n2Np6prZsnTlzpsz4NLX9wIEDbW2/cePGsGiCc+bMoXr16hkXr3nb9+vXzwpXg8+KFSusPddlySeR\nvd0HDhxIa9asISLf7hY1g3VRtiiXAnvTpk3Upk0buu+++6wDLgqTJ0+m+fPna+P16tWLPv3003Cw\nSES+ww0TJ06kTp060ZYtW2zPJk2aZE11iXyCpqCggNq2bUuTJk2i0aNHh3Xb24XyqtCnTx+rTsMx\nAJbEZ3lp+zVr1lCHDh2oS5cu1K9fP3rrrbeIyFd3kydPLrHtw7Xv/0L5VOjTpw+tWrUqLDy6CB7l\nSmAXFhaS1+ulMWPGUO/eva1wrinpDg7s3LmTBg4cSB06dAh4wi1UUNPJvLw86t69u2Uj5ft5dfup\ns7Oz6YYbbqBrr72WFi9eXOp8XgqvO3fupEGDBlGnTp3CsqvmQvlUCHfbe71eOnPmDKWmptKyZcuI\nyDeQPPLIIxYN3/VRVm1/sXyGu91dXBjKhS+R8+fPY8KECfjwww9Ro0YN/O53v8P58+dx6NAhLFmy\nBG+//TaOHTuGxMRE1K5d2/JnAAB79+7F4MGDcdddd2HOnDm48sorS53PTz75BNHR0ahWrRq+/fZb\nNGnSBC+++CL++te/IiMjAzVq1EDDhg0tp+4ejweFhYV49NFHkZKSgqVLl6Jp06alxuel8EpE2L59\nOx5++GHcddddmD17Nq644opyxydQNm2v+ujYsWPRqFEjAEBMTAwWLFiABx54ADExMahSpYoVL9xt\nf7F8hrvdXVwcylxgFxUVYdSoUTh+/DhSUlLwf//3f7jiiivwyy+/4PXXX0diYiK6du2KjRs34u23\n38Yf//hHREVFYdmyZcjNzUWzZs3wxz/+Ee3btw8rn3PmzEFubi7wuKFaAAAGLUlEQVTWrl2L3Nxc\n/Prrr3jllVdw4MABvPTSS3jooYfg8XiwbNkynD59Gtdccw26du2KDh06lCqfl8Lr0qVLkZ+fj5tu\nugmpqanltk6XLl1aZm3fvn17vPTSSzhz5gyaNm2KmJgYHD16FPv378ett96KxMREK97y5ctx6tSp\nsLX9xfK5bNmysLa7i4tHdFkzcObMGWRmZuLTTz9FQkICqlWrhi+++AKVK1fGkiVL0KBBAwBA+/bt\n0adPH+zcuRPNmzeHx+OxvmwRFxcXdj4TExOxY8cOXH755Vi2bBlGjx6NqlWrYsKECXjzzTfxwQcf\noGfPnvB4PJamojzIlWdeVV2qr5uUVz7Lsu2TkpLwySefYMmSJRg0aBCuueYarF+/3vrgrPIQCCCs\nbX+xfIa73V1cPMpcw46NjcWaNWuQk5ODNm3aoFatWjh69Cj27NmDTp06ISEhAQCwbds27Nq1C8OH\nD0dUVBQaNWqEGjVqlBmfNWvWxKFDh1BUVIRjx47hxhtvRL169RATE4PPPvsMqampqFatWtj5vBRe\nGzduHBF1Wh74PHHiBL788ku0aNECtWvXxo4dO3Do0CG0a9fOMtmUhz5aHvl0cfEoFx8w6N27NzIz\nM3H48GEkJCSgefPmuOyyy3D06FH8/PPPePbZZzFy5EjceuutlsP8subziiuuQMOGDZGYmIg///nP\nKCwsxNixY9GmTRs0aNAA9evXLzM+I4nXSOQzPj4eLVq0wGWXXYZjx46hqKgI1atXR+XKlXHu3Lky\n4zGS+HRxkSjTJU8/Dh06ROPHj6fnnnvOCrv99ttpy5YttGDBAnrwwQfDsgOgJOj4vO2222jTpk1E\n5POvrI5rlzUihddI5vP222+3PNOtW7cubK5PAyFS+HRxcShzGzYA1KpVC7169cLjjz+OG264Abfc\ncgtiYmIQHR2NgQMHYtCgQWXNIgA9n1WqVLG+FHPzzTeXMYfFiBReI5nP2NhYa8aXkpJStgz6ESl8\nurhIlPWIwfHRRx/RkCFDqGHDhmE5UnyxiBQ+iSKHV5fP0CJS+HRxYfAQ+b+qWU5w7tw5VKpUyfp2\nYHlFpPAJRA6vLp+hRaTw6SJ4lDuB7cKFCxcu9CgXu0RcuHDhwkXJcAW2CxcuXEQIXIHtwoULFxEC\nV2C7cOHCRYTAFdguXLhwESFwBbYLFy5cRAhcge3ChQsXEQJXYLsoFRw/fhzJyclITk5GrVq1ULdu\nXSQnJyMhIQGjRo0KeX5DhgzB9ddfjzlz5lj3S5YssdHEx8fj66+/tviqXr06rr/+eiQnJ+Puu+/G\njz/+iFatWlkeIl24KG8oF75EXFQ8VK9eHdu2bQMAPPXUU0hISMCjjz5aavl5PB68+OKL6N27t3Wv\n3IdymmbNmll8DR06FD169LDiAEBmZqYrsF2UW7gatouwQB2oTU9PR48ePQAAaWlpGDx4MNq1a4dr\nr70WS5cuxbhx49CiRQt07doVXq8XALB161akpKSgdevW6NKlC44cORIwD9N9MHFcuCjPcAW2izLF\nvn37sG7dOnzwwQf405/+hM6dO2PHjh2oUqUKPvroIxQWFmL06NFYsmQJtmzZgqFDh2LKlCllzbYL\nF2UC1yTioszg8XjQtWtXVKpUCc2aNUNRURHuueceAEDz5s2RlZWFPXv24JtvvkGnTp0A+D4yW7t2\n7aDSDibMhYtIgiuwXZQp1LcOo6KiULlyZSs8KioKXq8XRISmTZviiy++uKB0q1evjpMnT1r3J06c\nQFJSUmiYduGijOCaRFyUGYKxHzds2BDHjh3Dpk2bAACFhYX49ttvS4yXkpKCxYsXo7CwEAAwf/78\nsHyx3oWL0oSrYbsIC5Q5gu/ekDs5dLs6KleujPfeew9jxozB6dOn4fV6MXbsWDRp0sSYBwB0794d\nW7duxc0334xKlSqhfv36+Oc//xkwjgsX5R2uP2wXFQJDhw7Fvffei/vvv/+S00pISMCZM2dCwJUL\nF6GFaxJxUSFw5ZVXYurUqdbBmYuBOjhTs2bNEHLmwkXo4GrYLly4cBEhcDVsFy5cuIgQuALbhQsX\nLiIErsB24cKFiwiBK7BduHDhIkLgCmwXLly4iBD8P9zhz4VQLhGAAAAAAElFTkSuQmCC\n",
"text": [
"<sunpy.spectra.spectrogram.SpectroFigure at 0x10d04ec50>"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 26,
"text": [
"<matplotlib.axes.AxesSubplot at 0x112f440d0>"
]
}
],
"prompt_number": 26
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"callisto_nobg = callisto.subtract_bg()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 27
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"callisto_nobg.peek(vmin = 0)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWYAAAEgCAYAAACHJ9lnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl8VNX5/98DiRAkQQMkQIIMEoSwByKLoMQC7rhQd9uq\ngP2KX1otWpe2lvhVf2LrUqtVW3frhlZRoEgFNAgohC2AAgqVAYISCSmEJUgmzO+Pc5+55565d2ay\nYIKdz+s1r3vvOc95zjLnPve5z3nOc32hUChEAgkkkEACTQbNGrsBCSSQQAIJOJEQzAkkkEACTQwJ\nwZxAAgkk0MSQEMwJJJBAAk0MCcGcQAIJJNDEkBDMCSSQQAJNDAnB3EiYO3cuPXv2pHv37jz44IPh\n9CuvvJK8vDzy8vLo2rUreXl5EWUDgQB9+/ZtkHa8+uqr9O/fn379+jF8+HDWrl0bs41vvfUWvXv3\npnnz5qxatSqcXlFRwZlnnklqaiq/+MUvPOssKCigZ8+eDBgwgGHDhrF+/fpatbmwsJCHH34YgKlT\np7JgwYK4y27cuJEBAwYwaNAgvvrqK1q3bl2ruuNBUVERY8eObVCeU6dO5cMPPwTgT3/6E1VVVbXm\nMXr0aPbt2wdA8+bNycvLC4/Fp59+CjjnVlFREW3atCEvL49evXrxu9/9Lsxr5syZ3HvvvfXtVgJe\nCCXwvSMYDIa6desW2rJlS+jw4cOh/v37h9avXx9Bd+utt4buvffeiPQtW7aE+vTp0yBt+eSTT0J7\n9uwJhUKh0Pvvvx8aMmRIzDZu2LAh9MUXX4QKCgpCK1euDPM6cOBAaPHixaGnn346NHnyZM869XIv\nvPBC6IILLqhVmwsLC0MPPfRQrcoIHnjggdB9990Xvm7dunWd+ETDRx99VOs+1QZ+vz9UXl5eqzIL\nFiwI3XTTTeFrvd//+te/QiNHjgyFQs65pfejqqoq1LNnz9CKFStCoVAodOTIkVD//v1Dhw8frk9X\nEvBAQmNuBBQXF5OTk4Pf7yc5OZkrr7yS9957z0ETCoV48803ueqqq6LyevHFFx3a6QUXXMDHH38M\nQOvWrfnd734X1ky//fbbiPLDhg2jTZs2AAwZMoTS0tKYbezZsyennHJKBK9WrVoxfPhwWrRoEfdY\nDB06lH//+98A7N+/n9GjRzNo0CD69evHzJkzw3T3338/PXr04PTTT+eLL77A5/MBcN111/H2228D\nsGDBAgYOHEi/fv2YMGEChw8fdtQ1Z84cHnvsMZ566ilGjRrlyDO13MmTJ/PSSy9RWVlJz549+fLL\nLwG46qqreO655yL6MXfuXHJzcxk0aBAzZswIpx84cIDx48czZMgQBg4cGO7Tiy++yLhx4zj33HM5\n5ZRTuOOOOwCoqanhuuuuo2/fvvTr14/HHnvM0c/HH3+cr7/+mjPPPJMf/ehHvPDCC/zqV78K1/fM\nM88wZcqUiPa99tprXHTRRa7/wd69e0lPT3fNE7Rs2ZIBAwaE/yufz8ewYcP44IMPopZLoG5ICOZG\nwI4dO+jcuXP4Ojs7mx07djhoFi1aRGZmJt26dasVbxFYAAcPHmTYsGGUlJRwxhln8Mwzz0Qt+9xz\nz3HeeefF3cZ42uCFkLXhdO7cufTp0weAlJQUZsyYwcqVK/nwww+59dZbAVi5ciXTp09nzZo1zJkz\nh+XLlzvq8vl8HDp0iOuvv54333yTtWvXEgwGeeqppxx1nnfeedx4441MmTIlpvlD+KalpfHEE09w\n3XXX8cYbb7B3714mTJjgoD106BA///nPmT17NitXrmTnzp3hMbj//vsZNWoUy5Yt48MPP+TXv/41\nBw8eBGDNmjW8+eabrFu3junTp1NaWkpJSQlff/0169atY+3atVx//fWO9vziF7+gU6dOFBUV8eGH\nH3L55Zcza9YsampqACXwzfYBLFmyhPz8/PB1VVUVeXl55ObmcsMNNzjMFG6oqKiguLiY3r17h9MG\nDx4cVgISaFgkBHMjIB7B9frrr3P11VfXq57jjjuO888/H4BBgwYRCAQ8aT/66COef/75sC05njbW\nFaFQiGuuuYaTTz6Ze+65h0ceeQSAI0eOcNddd9G/f3/GjBnD119/TVlZGYsWLWLcuHG0bNmS1NRU\nLrzwwgh+X3zxBV27diUnJweAa6+91lNohOKMQiB0o0ePpk+fPkyePJlnn302gm7jxo107do1/BD9\nyU9+Ei77wQcfMG3aNPLy8jjzzDP57rvv2LZtGz6fj1GjRpGamkqLFi3o1asX27Zto1u3bnz11Vf8\n8pe/5F//+hepqalR23j88cfzox/9iFmzZrFx40aqq6sdwlPw9ddfO7TilJQUVq9ezYYNG5g7dy4/\n+9nPXPkvWrSIAQMG0LlzZy6++GIH706dOkWdUwnUHQnB3AjIyspi+/bt4evt27eTnZ0dvg4Gg8yY\nMYMrrrgiJq+kpCSOHDkSvj506FD4PDk5OXzerFkzgsGgK4+1a9dyww03MHPmTE488cS42lgf+Hw+\nXnvtNb766ismTpzIH//4R0AtRJaXl7Nq1SpWr15NRkYGhw4dwufzOYSpm2A1HyTxCl9BtHE8cuQI\nGzZs4Pjjj6eioqLWdb/zzjusXr2a1atXEwgE6NmzJ4DD5NO8eXOCwSAnnHACa9asoaCggKeffpqJ\nEyfGbPvEiRN54YUXePHFFxk/fnx8HdYwdOhQysvLKS8vj8g7/fTTKSkp4fPPP+edd95xzIkjR44c\n1Qf4fzMSgrkRkJ+fz6ZNmwgEAhw+fJjp06c7tMD58+eTm5tLp06dYvLy+/2UlJQQCoXYvn07xcXF\ntWrLtm3bGDduHK+88kpY24ynjQI3ARiPUBSae++9l3fffZdt27ZRWVlJRkYGzZs356OPPmLr1q34\nfD7OOOMM3n33XQ4dOsS+ffuYPXu2g5fP56NHjx4EAoGwDfTvf/87BQUFcY9Dly5dWL9+PYcPH2bP\nnj0sWLAgLHQeffRRevfuzauvvsr1118f8YCTur/66itAve0Izj77bP785z+Hr1evXu05RqFQiN27\nd1NTU8O4ceO49957w/Q6UlNTqaysDF8PHjyY0tJSXnvtNc81iU6dOrF7927XvI0bN1JTU0Pbtm1d\n80HNs5tvvtnhifHNN9/QpUsXzzIJ1B1Jjd2A/0YkJSXxxBNPcPbZZ1NTU8OECRPIzc0N50+fPj3q\nol8wGAxrWyNGjKBr16706tUrvPgk0LUZsVGauPfee/nPf/7DpEmTAKVlFxcXR23jjBkz+OUvf0l5\neTnnn38+eXl5vP/++4C6gfft28fhw4d57733+OCDD8Iaog5pS8uWLbn55pt54IEHuO+++xg7diz9\n+vUjPz8/XF9eXh5XXHEF/fv3JyMjg8GDB0fwa9GiBS+88AKXXXYZwWCQwYMHc+ONN7qOnzkuAJ07\nd+byyy+nT58+dO3alYEDBwLw5Zdf8txzz7F8+XKOP/54zjjjDO677z4KCwvDPFq2bMnf/vY3zj//\nfFq1asXpp5/OgQMHALj77ru55ZZb6NevH0eOHOHkk09m5syZrv+Hz+djx44dXH/99WHtfdq0aRHt\n//nPf84555xDVlZW2FZ++eWXs2bNmvBCrokRI0awYsUKzj77bMC2MYN6ILz88svh9riND8CNN97I\nKaecQmlpKdnZ2RQXFze4W2ACCr5Qbd/5Emh0vPfee7z++uu88cYbjd2UBJoIxo4dy5QpUzjzzDNd\n84uKipg+fXrEgmhdceTIEQYOHMiKFStISkrodw2NhCnjGMPvf/97pk6dyl133dXYTUmgCWDPnj30\n6NGDVq1aeQplUJt6Nm3aFN5gUl/Mnj2bSy+9NCGUjxISGnMCCSSQQBNDQmNOIIEEEmhiSAjmBBJI\nIIEmhoRgTiCBBBJoYkgI5gQSSCCBJoaEYE4ggQQSaGJICOYEEkgggSaGhGBOIIEEEmhiSAjmBBJI\nIIEmhoRgTiCBBBJoYkgI5gQSSCCBJoaEYE4ggQQSaGJICOYEEkgggSaGH2RoqIyMHuza9WVjNyOB\nBBKoB0aOHElRUVGdy6f4fByKTcaJJ57o+mWaxsQPMrqcCu59HnAGMBZ4E8gFsoAdQAXQF/AD64AA\nMNIqvdU6drHo/MAsi36fkY5VPtXg2w9YC5hfHt5q0QofjLYJ0i2+WVY9ldZ1mlVO+KRb58uAIVq7\nZ1nl0qyyFdYxzaIpA1KAKqN9eloucC5kp0HpYuBPwCirrNDiwqOxUQQUaNdu/TSh08i5ORYBF5pM\n1HjIUfIw6jTbkAJ8DJxqncv/pPOXNKzzMpd2xAOv/1n4gj03pA1S/1jgWWAxMMKlXcOto8z9dOy5\nNhw1z0HdEwHrOhVYAlxj5c2yzl+1ymcBq4GlwGu1/kSYDp/Px31x0P2O2n+K7GjjB2zKOAL0hIJe\nQDLq5slCTe5UYARcmQ1UAzcquoJeqgw9obAXtBwBz2YDw+HKEfCnc+FPvbSy2TDgXLhxhMU/FzqM\ngMI0KBwBz/aCDr3gyl6KH1lwwQjgXOs6xZLPmYpHzghVF0GLXwWw2TofDOy2zldpNNVW/8612p6J\nurnKrP5usGhSrH6LZlBlldOh38C50CFNVcMq4AC28MGqP5aAMPnXlcaki1bGnNLR2phs/fSHoi6M\nLeRcAVwO5Fi/FKtctXV9DkqoDLR4Ba18odd4kWzlt8cWRMNRD9Yci8dE1H91h1VXllUuRas72aLV\n+yG/dItXulV3ukaHxe9c1e4Ok3DOF6lH5kqO1p8qK136KPNVHhop1rEKJcCrgU2oh+Uq61zKVlj5\nqRrPamzBbn9/sT4wR8bt1xTxA9aYzwK6oQSa+ZqSbqTJxK3AqeV6vd5UojRSM79SO08z8ky+Qvsp\ncJWW7tY+4W3y1DWdtCi0puau1yUauF5nOnAutMuE8pVW+l9QbyDCH5zak4loeSad3u76ogi4EOfY\nxNMGk85Mi3VdG97SzoJa8mosFOF8CznaCFi/hfXWmB+Og+5Wmp7G3Cg25kOHDjFy5Ei+++47Dh8+\nzEUXXcQDDzxAYWEhzz77LO3btwfggQce4JxzzokoP3fuXG655RZqamqYOHEid9xxh0st3wEHUX+w\nCbkJ5DWv0iUvFtz4utURi29Hi5f+ClyJ+yuoySNFSzPL6LTV2rm8qsr5Ohf6SmATlL+D/Xqb4dEn\nL1OBnuf2Ki/X1USaCOqKFNQDU94QqlFvEPorul4XOP9/vb3VGo3eHzQafTzMvqZo6ZVWO9DKnGLk\ne40VLmlu/QD3sXNrl9d/YvIQGr917UMpOstc6mmaSIlN0iTRaBrzwYMHadWqFcFgkBEjRvDQQw+x\nYMECUlNTmTJlime5mpoaevTowfz588nKyuLUU0/l9ddfd3zMVGnMI1ETyu/CRTQUsTkL9Ou6aINu\nGm0uypwQSyvS7X3SDjm68dXb4aVJiykD61xsfDu0tDT39g0thKXrUYJb6OurHdcFeh/dNFZ93LzK\ne+WbvGWMdFqZV5ImYwj2f6OXTTVo9HOMNPmP9fbsMHiInVZPi9V3vU6dp9lnUG9HAS3Puk66AYLz\nNHrzDTOAWksJ4IS8eaUT+Z8FsG3P+hzW80GZ7FYBz9VbY34mDrobSGjMYbRq1QqAw4cPU1NTw4kn\nngjEHqDi4mJycnLw+/0AXHnllbz33nsOwaxQYB29NM9MnEIZ4zqaoKlE2d42u6QL5Fm9AVsDc2uP\n0Olld2hHvaxbP1KAy4DXUDe52KTLUNrNcCAAF4+A1sBGYD/q/GLr/Algf6XF71VgOAs+PY1Rj30C\nt/QCQlDgg6KnLH5rtXqkDaZGaSLHOoqgMQWL+ZCUm7pao0Hrm/mmIDA1Qrf/xHyrkKOMt04nDzZ9\nga9So6s2yupHtHPRmPVFwhSUEJO+Cl0Q294qkLwKrQ49X1+MlLwqjUY/mulSRvgCA4DsMfAu0AE4\nATV3AChF2cTTUA8u/f9L0/pTiZqDIohHo7Ruucf3QWtNMO8frOX7gOeoL45Vt7NGa7d8Zfff//43\nkyZNonfv3vzjH//g8ccf5+WXXyY/P5+HH36YE044wVFux44ddO7cOXydnZ3NsmVur1ZrUZNmNM7X\ndZnAYAvXIaintGgam4FxFo+2qFe3HCvfj3qyt8WeiHKzZWr5oBZY1lrn/YD3sYWRrGhLnQFsYSfa\nkQgvXUMTiPDJAmZb/HWtrZKwEOw5Qt1UBaj1wfnYN9l+68de4LNwm0Y9+wlMA3WTzIWiLOwVdXAK\nrzTtXNLNB9dmbGGZgxoz+S+qtPKZRp4uWDNxQrwE9EXJKuOo05j1uT20vcwBZah5os+FMoPGi2em\nQYtx7WZnNx/e0ga9/fIgNh/uVUQ+YMx2yJikGTQWzxWFsGIi8CzszIGd4mnUFnu+SpqJzaj7bh+2\n15Lcg+JZtA7ww379zSJgnZcC37jwrT2OVVNGo3llNGvWjJKSEkpLS/n4448pKipi0qRJbNmyhZKS\nEjp27Mitt94aUU6ZKeJBJcrG3A81AWUSinaXim3mWIaaGGMt+iHQoR+2sBOkolbg/dZR3NlSUBPR\nr6UNt8pfqHjnCL9rNJ77UK5ES1ATPgfbjU9uoL4oiaq/9qZZtP0Uj9aTsIV3X4u2yk7buBg2VsIr\nKC+knWuBtbCiEjaG1DkLrWOVOp4I7KwE5mrjKcIolcib3RQC5tuEW54ubCRNF1hlOAVUGc6HoGhm\npsBGS6sikqfZHh1ut3I/K10UgM04+5xj8aqCCM9Zt7cjvX3SJlNAplg0Odj/ew5OE4A8yN1sxlVE\n9s98OOiQtumCXoRpW9TckLed+ag5JnNiB863vBxsN1T5yVtOyCqfavEUN1CZv6mo+zZaW+NHXbwy\nvvjiC/Ly8sK/Nm3a8Nhjj/HrX/+a3Nxc+vfvz7hx49i7d2+DtNENTcIr49577yUlJYXbbrstnBYI\nBBg7dizr1q1z0C5dupTCwkLmzlUC44EHHqBZs2aOBUAlvAegpEsKyjVpCN5/9kCUTUtcoMAWOKId\nVaAEtz5BK1CCMB012QTJKBt3ANsvuq9WB8DVqEks/cuyzs36hV+6S/szUQ+Ad6w+CK8uVhuHA37I\nT1Ovo5OhTcFO9l7aQWnJk1Gvqq8Iv7Woh0QWyeUFVPdJs4TzWpRwehXblCFjokNc9/Bo72hsO+MS\n7HEU4SzjvVUbB/lPkq1+mQJf/ju3NJMXxDeubjB5yRuB+WZgXnu12w0ydkIvbZV0c0zcNHG3OSzn\nFS55env1snpfklHzV59fYo9eh/M+AHUvjMPWgHU/51RsLyB54MjDZiWwBiWY9wOf19vGPDMOugvx\nNqEeOXKErKwsiouL2bhxI6NGjaJZs2bceeedAEybNq3O7YuGRtGYy8vL2bNnDwBVVVXMmzePvLw8\ndu7cGaaZMWMGffv2jSibn5/Ppk2bCAQCHD58mOnTp3PhhRe61NIGOAnlxO/H+Qon6Gtdy42tT0rd\nFlhm5b2DmqhVWtoqnELZj5pwxRbtYI1O6qgGZlg0ogWustKHW+2qso5Sxk14VFl1+63yYvO0BEZS\nP+iTpjzoB8DlZ7/E/7T4q3pm3QIn//hzuBRl0PJLX3OAaqrz02CnjFcmJKWhPDOkngzs1+We2AuJ\n4s2gr+YLilHmpQpsv1fd9ODHtq8KsrSjm3AzhbL+f242eIEaR/nfvcbV5Cfaqc5rs3H0G9fy5iP/\nR5pB54YsnP2UtsmcEQy2jqZGnKbl6eXlPAt7TmVY599qNOZYfaulb0b9z9Wo/2gVtrfOOVZ+Mfa9\nsEorV4U91kHsebbZovvWSmsDXIA9n+qPpDh+0TB//ny6detG586dGTNmDM2aKZE5ZMgQSktLG6SN\nbmgUwfzNN9/wox/9iAEDBjBkyBDGjh3LqFGjuP322+nXrx/9+/dn4cKFPProowB8/fXXnH/++QAk\nJSXxxBNPcPbZZ9OrVy+uuOIKl4U/HbqtDZw2y3VELh6ZWGdciynErR6wX93kJluCc4OBbHKRxZEs\no/4lWrvMuk1UW3QB61pv1xJoCXSALhdthCvhUv7B6Xys0vMPkcdqWhZUqHskUAl0t3i1sq6FX3dr\no0krlKaVbZ2fg9KAglafqlFvJtKvgNa3XGyh090qI8JCHigmfa6VJkdJB+//LJZ3SAr2+EaD1KOP\ngxc/s69gv8qb7ZK0IVodWVpeQLvWxwKNdolVXh6CQ7DHfYlGZ5YNYM+pCpxvaC7I/pVR7zqrHumD\nzNX5OMdJ7jnR0OW/lzZIO/XFV3lYT7HSvvNuVy2QEscvGt544w2uvvrqiPTnn3+e8847r0Ha6IYm\nYcpoaChThrxi6FqFbg+N5RfqZn/Uab2OZl1u/E16fXq4LUzJud5+WbzJdD/mFyrF475q3uwyjplc\nyN8/+znL+/Rh8OfrGNF7Hr/kz0zjDlb9dIQyZ7QG9r9v1Tlc1dEBS3MGtSgTwLk1XRZt/BZNwBgv\n030qFWUWAXVzituYeD+YfXUbM6/xwoUu2v+sLxyatPVBLF7x5NenbfHQm2YQc95fji28y1zo42mD\nIJ62m30GuKfepozFcdCNwN2UcfjwYbKysli/fn14bwXA/fffz6pVq3j77bfr3LZYOFa9SeLA+0T6\nMcufLhPFzQ/UbRLp/pjmqr95dOPjdu6Wloay51Ua+bJMUaa1pQp7MRPsvqnjBcvfYvarl9G63R4u\nWzib5iNrYAN067OZDr2/4n/4K934N3mUsOrKEVCC5aFh2YHbWWPTDihHuUuVJ6O03bXaMQVlE0zC\nttfq/rdJqNddrKOYBqqtvBRs7xaxUQZw3qBi5hBXL7f/KNYYu9F4/Uf1RSxe8eTXp23x0EcbG7AX\nfeU/qY1QFn6mH3MsemlDgNgbuOKDm4BbSaQBzA3vv/8+gwYNcgjlF198kTlz5rBgwYIGaZ8XfsCC\nOR7ok6Y2k8iEW9na8kpzuTb9bM1zPfaF/pBJY/bKy2g2+gD+4wOQBL1YDwshfeQh2mXsJp8VAKRw\nkGb5BzjS+nilMQeqCWvKrVHCOttivScTgpuwHyC52BpzP+uor65X4NzmbgnlJCBYraWJIDcXE3UE\nouT9EFGf+RgPYvHWzVF1gTmfGwduXhdDrZ/Ay1v69ddf56qrrgpfz507lz/+8Y8sXLiQli1bNmAr\nI/EDDmJUW8TaUFLXsrWpX7fTxcNTXJb08tb5RsjPXMF5zAHAf2CrikO0Ca7nBXou2UrPb7fSjt30\nylyvHCaygaRWkJQJ+ShTSLZ17GCdk4bjLSRJ3NYC2OaKCmwNWBfKFUCqXQ9gb0yQ9nfR6NFomsaN\nrnA02yJvFOZuwdqUry+dvlB5rpY2PM5y4L6zz4s+LQZd3VFXG/OBAweYP38+48aNC6f94he/YP/+\n/YwZM4a8vDxuuummo9JmaESN2e/3k5aWRvPmzUlOTqa4uLiBY2UITFcjSas2jl40tYFexus83vJu\n7UxHaZYm30iXsQ7XfMU2OpPDZlgALdui1IS2kMo++A42ZWTzHS3UdTvUL4haHGyH0phbokzLLbFc\ndMVkAVAGQctrA7D9pzOx/WsrsVVu61YIhLB3nJVZ/RCtucq6TsL+X1JQK/de4xMv3P7nuuBoaLLS\nNuGt97827Y23bV50Ykobh/qPMjT6JR5lvHjGq9DIsS73XHTUVcAdf/zxlJeXO9I2bdpU/wbFiUYT\nzD6fj6KiItLT0x1pU6ZMiRkrY/LkyY5YGRdeeGEUzwy3P7ra4xirXCzoQrTaSK8LzPZ5vepHWsx2\nTjqZNn/aydgWs2AFSk5au/z81uvpQVLoy1rmcJ4SwqAE8AkoWVoK7LHKORDAjve8Dmf0OhHEAZxb\ncys1ugrUpgWwbdGyY9HSqiPGwDzXr2tzQ8eia3jhELuOZJdzGRezLebDOhZvrzS3cnp9EoP8+0TD\nj3tTDesZC41qY3ZbCW34WBnfN+ozuWpbNgr9UujVYj0dFu5VMnA3cDxwAPaRCs3V8Rs60ZZy5TK3\nFGW22IPydRYNOmjxDIL92ulDMZabd51OhP1qmqKVER/YttbO9Wxst0JwmkNkd6bYqeWNwe3hFGvc\npFw849uQwiGe9uo0fuwxIEZZr3a68a5Lv621BhZi7ybVvWsgMmSAHnBJD/Ak6w8YtF7BmqS+hXG0\nOzpiucM1VTSajdnn8zF69Gjy8/N55plnwumPP/44/fv3Z8KECeFNKDrcYmXs2GEGIwIVQzbQ4O0+\nZrATmlOjwmjkoj4+chIcGNqMTziNA0Ob8SU9+IIefEkPZaYosX6HUJ4Yn6GGcLF1LAfl1laG2lor\nWvAOlHpdinrWl2IHAKrSft9aZUstP+lSbPOH7jFThnOV3svLItZtJ1ZEN7fEaGVMWrOcaZ1MMdJ1\nP149f4hRRsw9YgoKWOnJOPsaqy63unWXQTe6TJfzTIO2CvuLKQNRT+/u2FvF5Vz82/VfAXbg/yrs\njwYIfY7Gp5VGm4nydRf3yfohOSn2rymi0Zq1ZMkSOnbsyK5duxgzZgw9e/Zk0qRJ/P73vwfg7rvv\n5tZbb+W555xrpvHHypAtnwNx2rp0L4EKjVbP0xezdJgazD7tXPx601FbTrto9KIV6PzctCFdezDL\nm9Bf911CS14MAfzwBZADlfnJpP2zmuMOHWFQixWsa9GXFA46y7RWtOyHNhfsZG9pBzUMokUDakyl\nH9XYGi04Q0qmoJ4IpTi1sQqLxyrtOhU7LnMKTi1SdopVWed6nggvL9uzKciDxEY0d8ZY115uapK+\nzEjz8mOPx/UyVpu8EK1/poumtHczkTsd6wOvNwlBgAZzl4tHwsUzLb5nNJrG3LFjRwDat2/PJZdc\nQnFxMRkZGfh8Pnw+HxMnTqS4uDiiXFZWFtu3bw9fb9++nezs7Ag62Ibyxfwr6vtq+1BP8e7W+T5s\n/2C5Tke9dommJ+kSpKXK+KWjnm1drHwpL3uchS7JOu5ATewdWt3JBj+J37DDKD/S+qVjCx35DcTp\n41th24xbA8dDefO2UANftjmZTL7lIK0I0JUAfsp2Z9p25BOA/ZDRokylbUZtMNkJSkuWBUhp3war\n/rbYQW0vpnAeAAAgAElEQVREG5YxlAUl+RVb5UTTbmvxEC1TXOcqrL7LTSwPAlODrTbS9OtMI11Q\nm5dcN43Z5C3I0c6HuOS7IZqQaixU496/hoBXfwOoN90SGkowJzeP/WuKaBSN+eDBg9TU1JCamsqB\nAwf44IMPmDp1Kjt37qRDhw5AfLEyOnXqxPTp03n99dddaskGOqMEMajJ8BL2t8XAtumJzWyrRScT\nUt9iqkM0VBEAEqioAjWxUrC/y2cGKBde1dia8HDUZg1dcMhjXDTohdo12II8DfUtNRGYAMnwE/gp\nf1em355w8sadsBt6f/0VvfmK6uPhuDbf0YqD7GubysEft2LNnqFKTubApbzNAwX9laa8BxUmNOhT\ngps02JwC7ZKhPBO1Wl+NGnPRmAUpqJV9Wd0Xr5IsbLe6FNQTIIj6T+Thk4YS3n7s6GVipzbhpUF6\nbYyozaaN2vDWNcplLvkCfVlKt7HKtf72UYm9wUbOTehvfwGN3nxLk4cnuHskydtGAWpe3h+lD/Gg\nNoupfux7MoB9X9UdKfG4Gx+odzUNjkYRzGVlZVxyySUABINBrrnmGs466yx+9rOfUVJSgs/no2vX\nrvz1r38FVKyMG264gX/+85+OWBk1NTVMmDDBwyPjO9RqFzhf9Su1azNWgH6DmOYBt69T6OXcoNPv\nIHLhQ2iKrPN0I1+0R7R27sN5s0l/9JsslTY9d7KMwdAJpWinAd1hR6d0MvZWsK5NLt+SyT5SKSNT\nucx9htKS98C3ZKhr3TOjvBr2Sx0BKJfYGnpb0NKknTtwBsIXISIbGPzYi336ekEldjwQ6Z+Xi2M9\nvCn+WAi/Lqxb2TpDb+sknAJQNw+ZR/PcRMA66h8kQEvLwinkvTayVBptEvODlwsnmHPQoSiE89HS\n3LxHBA30Mt9ENeJY+AHHyngSe0U6ltOMbvMyb3SzrJ4m5dJxhmc0+USDWUcsQWP6R5v2OotfwW9J\n/kclh9e0gTSotl4c1rfpzrdkkkEZRZzJCvKZvvsKVfLSNCWI9wNLq2FashW/GSWcD4Fy79AfbqLV\nbMD5SSy3m15MTpK3gUht0dTyIDL0ZV18xONBY7jKRaNpzPZIuv7FkWjtqaubXjTUP1ZGqFMcdF8n\nPi31PWI69quRPjlEeOguP/orqZ6ehfNLIrppoxI1fNVaeXMSmq+jctT56vx0pMTBL0WrW9pt+VAX\nHaR6cxpkwFN9riWflRykFevJpRVVfMJprKcXyxhC9RtptP/fbewqSlOycyewOVl5dIQjG4oHhSCA\nHU61EvV6vxklaHUPC/3toAjbvcotML5ANqa4jbn00XTZMsfPSxP0She+sWjqi9q4rh1toRytDkkP\nuaTFy6eu7Q/QYB5Vx6iE+4FvyW6F096ZhruHgwm52c3XavPczU1P315qCg29nBs/vbxpq43GT871\n6yWQfQj2QhFncpBWVFn27TIyOEgrUjioTBg7oZV4aGQDHFQ25XBUuTKtzQGjft1mmYXTFLRDy9cf\nhuZ/ovdb71clzvHQy1TiPg5ESYuWXlsaN5j/V1OHV3uPtX5EQYs4fk0QP2BTxtVAR5QDr9zgpbjv\ny3fTuuSLDW5C0rxxK7EXvnRaP2pRT7bR6ULITZM222CaAUyBFcC2z0odwj8Nhp2L/5MNBH6Ti+/a\nEJRCCJ9trtiBEsAzgGHAp/KWUYGKkVBq8d6q1R3AacIRbxCB7j/rtcAWLU+3RUejqy1qy8v0f/bq\nkxudmU8t6463XQ3Nz6ut+uK3eAzJ4q2eDvZ80P9H/dytfrPOAGruLai/KcNrQ7BOt6HpmTIaRWP2\n+qZWYWEh2dnZ4XT5fJSJuXPn0rNnT7p3786DDz7oUYtoa2tRtkwRWnK+Vjvq+QGrnARTr7TyhZeu\nqQWsvAotr8LIz8b+NFPA+q3Fnnxgf9ByLfaDI4Ad+AetTEDrm/AE5wNhAzAStkPg1FzIgtB8Hy3y\n/6Oyn7DIBmGvj34qPs1Wu7Kx2u5HuQMOxxmasx92QCNzU4Ps5MPIA+Xb7Mfe8WfS6jdwNAEk/LKi\n0OiIV5iZgkL8qqMJ5VjCV6dxc9MzN6xIWq52LkjH2XevzS46X7c6ZdxMf2a5zsUO5p+O8tIoQP3n\nIpTTsWNrg/OBKnRucyHL4i1jW4AdTD8F9eWh2rgzRkF9P2HSSGh0jVn/ptbzzz9PampqzFgZPXr0\ncMTKeP311x2eGUpjHgmcifrun2iiMpkawoZYgXtweD+R22r9Wn16WwSmBqovflW40ICzLwEXHmMZ\nFtrLJ1+P4hedHuQeppK69xD72rRkJfm0ZTe7acs6+nLrX5/kgv95i9ntL1PfAZwP3If6JBVgRxtf\niboRxaTRD+UqF8D5oNC9T9zG+VzsD3HqfdX7YvY/gf8eBKzfwvprzPlx0K2I1Jj37NnDxIkT+fzz\nz/H5fDz//PMMHaqChT788MP8+te/pry83BHrpyHR6M+L+fPnk5OTQ+fOnQmFQg0YK+MKlFDIxNY+\nRcORXyaRX3h2e23NRWmhUkcF9vZVrHMRQMKvAltDCGh8xOVIztHKSn3CPx3b8yKg8RXI5hTph5TN\nBQby6SQfzVYdITTKx1/+5xayuwQo3eqHu5PhDmA/hB70wXyYXXIZlK+Fe/pCaAdckA373wROQwnQ\ndSjzznzUBpHBqG8gpmltWIZ6CMnW60xtHGRM0yweMqGrtLxkLc2PvS1X3+hQ6ZKXjnMLbywNVtqh\nPyzlf6utmUDGXvd91zVkt3bo88Wkkba5taeu5iEzX58vtSnvR42z132jt1ve3nQ6GfNY/0sKSqOu\nf6yMukq4m2++mfPOO49//OMfBINBDhxQzs7bt29n3rx5dOnSJQaH+qHRBfMbb7wRDkbt8/l4/PHH\nefnll8nPz+fhhx/mhBNOcNC7xcpYtszNkV/spW7bTQWmQNSh3ygB62je/GXGtc5Hn/wy4TZodGUu\n5fTyZRqNm+dCtPQNMNcHO+Gap55lPbn0YgNDWIa/yxZefPn6cIS5sncyeeWSG2g5rYJDT6fDHT54\nMVuFCH33cotfGsqcsQ71ujkKZ5Aa3bYuphzdi0IfgzLsh5JpCtDp3cbKzDPHSR/LNCL/D2mj0Ovj\nbgqrlBh5Ulb66vZfmAJa+LgJZZ1OeJoCL82F1oT5QNCFJNp5inHthknAIxoP+c9E4YFId039IQpO\nZcaP82HotrEG4ANs8149UQc/5r1797Jo0SJeeuklQH1ntE2bNgBMmTKFP/zhD1x00UUN0z4PNKpg\nPnz4MLNmzQrbiRs2VoYgmtlCv4nBfprrZbye7nqgGTevgTKcGkKyVk8V3tqDudhott2tP34izCnl\nwFD4F2eTSRkn8B9OYA95lPAue+jE1wB8x3HQB1Lb7OcQHdXOviBWwKJq8CdDIA07RrIIONl6nIRT\new3gtEXrNnddI9aFmWjIUjbagqggGedNro+lbisVuAljt3xc8qPlRbMre/GJpgi4pUtetPJefMyx\ncMv3wiMePPRyXsoBLvmxaAXb8F4srCXqIOG2bNlC+/btuf7661mzZg2DBg3iscceY968eWRnZ9Ov\nX7/YTOqJRhXM5je1MjIywnkTJ05k7NixEWXij5XxNWr3XxJwHEqQyBNZhMYIYCZ20CBde+iHvRi3\nFlsz6IdatNM3S5heEpKue2pka+VKcW5f1r0tsNKWoLTT4VbdRVob9NeorSitRLbxotrxk03g686u\nUDt2+drxGb15IqmVCkj02SZgPGEf49A8dt1nLXje2VfxXHyjug5I+yssevHQcBOYAWNMTFQadF5l\n3Y5evKKt+DcUTL9zgZunjix26WEsIbKNwrMLzq3H+kNZTzPbYGqc+rnOQ3ZTSrvczs1dghKoSjTh\nC3F6AAWsdL9FI4vY+j2TpqWDbQrTaYRHFvAqKuLWNpT/82EaBHX4AlQwGGTVqlU88cQTnHrqqdxy\nyy1MnTqVRYsW8cEHH4TpjubyXKMu/l155ZWce+65XHvttQB888034eBGjz76KMuXL+e1115zlAkG\ng/To0YMFCxbQqVMnBg8e7LH4dw5KgxuI+zZq05/ZLaasTqvHvJDt1fuI3GZtLjDqPr5u27Jj+VUL\njb4TzNyVaNJA/9AoANY8PJSLbn2drgT4Mf9gxNer+FWn/0cv1pNCFSsZxJ8W3qU05QHVMDsZnkaZ\ngQ+h4jKX7LbqmYVaVJXX0iXYDySw3QNlnKT/qS7XYms3+ymQ3YMQOUaxdkRGS3PD97HD7liG2zZr\ncA/275XmtZvRrdxulCBvgMW/8yLTi3arn+CezU4hu3PnToYNG8aWLVsAWLx4MYWFhXz22WekpCgT\nUGlpadhpQVcoGwqNJpgPHDhAly5d2LJlC6mpSli5xcrIzMx0xMoApWnLp6UmTJjAXXfd5eBte2Xk\nAz1wbm7QIaE13eJg+HH68IqWke5SBiInbSVKQ3DzKtBjR+iajxlbw9TI0jzyzHYAfW+A/4XC/7mT\ncusNoR272U06yxhKClVUkULxjiHwSkvl1zwNtQO3+iD8rhW8ixW8CNSXsCUYvmm2EWHsFvzcfCDq\nq9his3bbXakjllbcEF42CdhwM825zW+B2/9TG1OciQAN5pVxYRx0MyO13zPOOINnn32WU045hcLC\nQqqqqhyuuV27dmXlypVHzSuj0d3ljgaUYJ6KuzA27Zd64Bz99c/ttdCNj5mmw81OqtepC2fTXmqe\nu1170cDtoX204iCFrz7I+9cUMJML+SV/pueSrTw1/Fp6sYFMypjOFaynF2++ei3cCSw9BOe0tAVy\nNlAqtsEiSLoCguuBXsB6K32JdbwQZRry47QXez3E9HbnatcyNn5sf/KE8G08TAJmQtINEJyO7Udf\nl/+kNmUaIFbGuDjo3okUzGvWrGHixIkcPnyYbt268cILL4QXAAFOPvlkVqxY8cN1lzt6+BS1868f\nkRNBt1+aYTmx0ioNejetoDaTUhfiwsctApiXUHbj52bLVddlZHIl06G1+sZfKvtI4WA4xGErDqpP\nTIFKXwq0hpatD3JoT0tLSxY3sFTU9vZ0Fd95T1sIB9mXPqRpxwC2yUe3YZrt1B9cO4x0icns9mCL\nd4zqg8SDwMZT6hAsNNLrMj7xlAnQYLEy6rjlun///ixfvtwz/6uvvqpjg+LDDzhWxnfWUb+J3eD2\nihxvmkAWO0zoDwD9Fw+iLZ555dvYQC+2WAuRZZYLU+aBXdAVqmhFKvtIZR/ltGU37ZQp4xAkJdVY\nQfMtwbsflJC0rvdI3XosjHTsZ7x8RVseem5tTjeuMWilbBL2GwZE37JeW+j/WbT/Llr5utTZUGhI\nXibi3U1ZXww/+lUcozv/mmizGgLSNfHXzMW2hQ5HrW6ZTvGVOP1XdZ9QodMhfqnVqN1s71jp47Rz\nk1b3T80w6vSqZzSRn47XNwuA6ctb/LORFA8aCU/AmTlLCc338frNV0F32P7cKdw2+jDsTyb0ok9p\n0S+q1fb9F/SDPWtRQrcv7FlstWmTVcdilFDejf02IpHi5uEeR2G41v5qIj9PVIm9+CNjEURtVKm2\neOr+s2UoL5sd2ljqfue6a5dOp+dnaO1wE8IpVj8245wnOs94YPo863Db6BEHfFMgZLmy+cZByJxr\n9YQvW20yioA+dxtio0sd+l5bHKPxmBtFY37sscfo27cvffr04bHHHgNo4DgZYH/lQibCKusYxH5N\nqsIWCPqXQXThXGXQQeRKchVOh3i5UXT7ky44pUyFllZlpOkeC6twtqVK412GUwhak34kSn5kQ7/e\nyyAffszb/Ji3Sb64kqFdFjO090fKNNFD+pKq3OnCgdqLsDcWVKBcmeQbfGnYH7ytxv4aif5J7aDV\nHnkIiu+3rpFJP7Osc+FfodoT9gGXcZMx34xzLAXm5ovNRlqKli5wsxMGNRrxuZa2mjyj8UmJkq/z\n1KGnpRtHIPSidi5zLRYft3wP+2jIbcMWRN+sZdLEk98Q3w+MgWNUY/7eF/8+++wzrrrqKpYvX05y\ncjLnnHMOTz/9NK+88kqDxMkA3SvDj+1XrL8Gm54A4NRmzDQpa/qS5hL/13x1nsNxejjk4tTAzM+/\nu/nRmmWM9g+dokJbVJfBsExYgVrcy0S5w+WihPIMYM9BlCtcutW2V3Eu1Jmuf3ob3eJbp2np8S4S\nxbIjZxFpi3YrGy2tNohn4dWEuQ7h5ZkQrYxezvyiS6w21oZO5q7+NqO3t7b+4V70On+3a73eVGAs\naqIGaBCvjMlx0D3R9KLLfe/Pi40bNzJkyBBatlSe3yNHjuSdd9RTv+HiZIDyEDAhE1QESRqRn2mS\ntACRwkaEox+l0ZneHG4LVZIuaX5s/1/BBq2cm/Bxm/DyQPATuVBSCaOh9bxdXHH8W+wjlb6sYyRF\n4IPZN11IhqXBb3gul+f+OplmF1/AkY7Hq8BFT98AFwMvorwyAqBMGWtxRhOrxOmPnIUdmEjX6s2j\neGXoi3smTGGyw2McwF041VUoR19UjY66LA679anSOHqhPusVMn+WeNDVdtOOF70phM1rvd5KlNbg\nt34NECsjYcqID3369GHRokVUVFRw8OBB5syZE97J9/jjj9O/f38mTJjAnj17Isq6xcnYscNrQuxC\nCZIsYCL2h1NTsLcVV2OvAMsrciXKRiznosEPxp5Ao1Eax2CL12CNfyXKGVjKmzfFYGhdaJVPsY66\nq9hgq72CTOyvLZuvz5cTaQsfra7nwv6ftue5v0zmzWbXcvdvHuKM9Ss445IV/LlyMrc9+RduW/AX\nnnt7MiyBIx0fAtbDfU9BeSE8W6l2TQUKUXbl7iih+5p1XgbMguwx1rmYiaZY56Ot4znY8SFkrNdh\nR6STMTPDQ8o4VFvjU2ilj7bGT8Yo06pLLzvaGrNMbfx0Gj0di7deb67Ff4h1lGu9Dh25LulyrseO\nGKL1xY2PoFDLc1M6osGMVWHmZWL3JdfIM9OkDUO0oz5vhcatzstd0nSkYI+DmR7A/g5mPZEwZcSP\n559/nieffJLjjz+e3r1706JFC37zm9/Qrl07QMXJ+OabbyLiZLz99tvMnTuXZ555BoBXXnmFZcuW\n8fjjjzvolCljFHY8YXNBL54FDB2m3TkWP3Pxy7SBxqrfrS2mADbbofMGdfOlW+2wto9no8wXG7G+\ndo1lxhDtfy2RZhYdFRpPOXohHXvRzhwniO8/iJXn1X+vsm6LhCZttDGNF3UpU5vy0RY746FzK1MX\nnvWF2xoBNOgGk9/EQff/EqYMAMaPH8/48eMB+M1vfsNJJ50UjpcBDREnA2ALKhJPAKetuQr71dlr\ngrmlV3mcy4KWnrYPZ5AdNz7xTm6zrkqPPL0tAG+idjZqu+9KIfyqvsc0nYiQLca5OQTjfId29LKh\nitlHb2OVC308i0hu9lG3MTfrisYzGm2sMY4GaWtdBVe85c1+eNma9fmgn9dmfkej06HPp3hNLOZY\nB6zfHuvXAGiiGnEsNEqzv/32WzIyMti2bRszZsxg2bJljjgZM2bMoG/fvhHl8vPz2bRpE4FAgE6d\nOjF9+nRef/11j1o64xTIYGt59VkU0nmBu9ZYieeKd53qkTpi/V16fiW25it8wBasYguWo7Q54MEr\nVn06otFH07Lj5eXF302LN9Niafr1uSVizatYdUcrH62sV7nKOGjirSMWotnFvfiatH7sNZMAzuBO\ndURCMMePSy+9lN27d5OcnMyTTz5JWloakydPjoiTATjiZCQlJfHEE09w9tlnh+NkuC/86dCDp3gF\nDDKDraBdmzx0Xl5BWao96jLd7LyCvOg0Op99RLYv2YU2k0hXrArswPVSt/BLJnJ89HO3MREar8BB\nej+kPRW4j6XJ1w0mvV7GHHO3MdFp3P4zDPpYbfBqu5tbmsB0hYxn7Lza7TUOeprX/HJrezLRhbJZ\nd7S5b5ariJLvxrsBcYwK5h94rAwTXq5x5it7PG5OJl+31/76QncV81rkjKfueNPr8joaq00NhWg8\nG2r8a1M2nrGq7TyqSzuOJg/hA973TEPAi18DxMp4OA66WxM25u8RRUA3lElDnsimvRbUhNDPwd5Q\nYj69vbSkKi1dt+mZZU3IK56bBqLb3751abe+ucXsi6nFJOGuTel9l/HRbZFmP6JpZnqdbjbhWGWj\nacTg7Kc5llKfW9u9NDG3ut3Gz4T5P0u73DTHaHPBrW36f5qOd4hNvQ63toHzv9XrjMXP1LLdxtPs\ns1db3Prpdm7y2w78mwbBMSrhjtFmx4MkoAbbNS4J5ySrNs5TtLRqIz0Ne+eeycfk5ZaWglqIM3c6\nVRi0Ul8Vke0Tc4Bev7gx7UbZ5vQb2Uxz+4yPV0xqPGjj4WHCDPspvOOJf52G2kUpfdchabqXgPk/\nJGlpMm4p2nUW6j8xx9qE7j2g/0cQOXckz2yzfi380rG39Jt1RTMreM3paHPc7dotL9pYSHv1ery8\nNNz4JXmk6+eZNFgAI6izH7Pf7yctLY3mzZuTnJxMcXExoFx6n3zySZo3b875558fY/dx3fEDFsyy\nNdi8ob0QbSU/3hXraKjv9lPph16/Fu076ldB2hIpUCXPr53v1ujluq3B26TR6cw26fUKzW6PdL2t\nWPn78P6eXm08O9zoqoh/E4WX90c0WrPNZS408dTlBi/PjYZyYzMhD4t4xjwaj3j71oCoo4Tz+XwU\nFRU5wnp+9NFHzJw5k7Vr15KcnMyuXbsaqJGROKqCefz48fzzn/8kIyODdeuUh8Bbb71FYWEhGzdu\nZPny5QwcOBCAQCBAbm4uPXv2BGDYsGE8+eSTETwrKiq44oor2Lp1K36/nzfffDPig61ND7WZyLWh\nHYKnnfOWQSoy3EagA7ATKw4G1petRqjjCoARyr85UA3tkq3v/enwevU28800iL3Kr9v05dqvlVvm\n3r86C6GGeMhG49mUy9UV9X2QHA26OFHHsJ8QaXd+6qmnuOuuu0hOVnNdd/FtaBzVnX/XX399RDCi\nvn37MmPGDM4444wI+pycHFavXs3q1atdhTLAtGnTGDNmDF9++SWjRo1i2rRpR6XtCSSQwA8Addz5\n5/P5GD16NPn5+eENbZs2beLjjz9m6NChFBQUsGLFiqPa7KOG008/nUAg4EgTjbiumDlzJgsXqj30\n1157LQUFBR7CucC4ro+PZm0Qbz21aY8X7ft4rpr/KRvbL7k7UKZ2Vof9mZNVmsRMKAfYDeV+nGYG\niP7NRPMbhm7nOnQN2ct2vRbnR0P1vn1f/2MCjQc/DRYro44SbsmSJXTs2JFdu3YxZswYevbsSTAY\n5D//+Q9Lly5l+fLlXH755UctYH6TsjFv2bKFvLw82rRpw3333ceIESMiaMrKysjMzAQgMzOTsjIv\nG3IRzg0msW7maDd8PNuPJT/ezQzxbGvWaWOlG+ct1RhxyG+Zka2g8y2T4VC1ioNxKAl7Z2RAKx8g\nUljuwN0tzdzEIEJ3H+52b3lY6JtZzG3ecnQby+9bKNf2QfBDeHA0dh8CHM0vmBR9pn7RIJvd2rdv\nzyWXXEJxcTHZ2dmMGzcOgFNPPZVmzZqxe/du2rZtG41VndBkBHOnTp3Yvn07J554IqtWreLiiy/m\n888/D3+o1Q0+n8/yWfaCV1m3iRdtIroJiHgmb5pGU9s6vRAnnxtR9uP9yeqbtK+0VbbmbKA0Wdmb\nN7aFwHCUQB2O8+Ow+iIc2NqrPqZe4yt89N2R8YyX0OFCf7QFhVf7alvvsS6UoWH6UBtl5ijCRcIV\nDFA/wT1vOvMPHjxITU0NqampHDhwgA8++ICpU6fSunVrPvzwQ0aOHMmXX37J4cOHj4pQ9mh24+C4\n447juOOOA2DgwIF069aNTZs2hRcHBZmZmezcuZMOHTrwzTffRPl0eAD1aY501Lf//NjaXBDv8Jxe\nGwfMshVaWoVGo/Os1s7dJqHbolYs5329Lrl2aeuNwCuoBb4C1HAMRQnnIpSwbg0EuqsiSVbXTuiu\nhSkwV+P74dRk3B5SpdiRx/T+y7ilaNcCOZeNNFk4vyXYEJteYuGHIFCPNmrzXwRj5LuNd4CmECuj\nrKyMSy65BIBgMMg111zDWWedRXV1NePHj6dv374cd9xxvPzyyw3TRhc0qmDWVz3Ly8s58cQTad68\nOV999RWbNm3i5JNPjihz4YUX8tJLL3HHHXfw0ksvcfHFF3twPxnoah0FsuIrr+nixC/O+OJQrx8F\nSThtp/oGAH3TQbLGP8ODl0DfGCFldGf7aFtsq6wy0g6dtgqSQpDks6057VCC+QRs60U5yqRxAkpg\nlyQpuj1JqDgFEgRJ9/1Nwakpp1jp8oCsMvLkqGvD31o8zA0L31o0Kda52//htv051nZunT7WZgc3\n2gQU3NzlvMapLg9RPw0eK6MOfsxdu3alpKQkIj05OZm///3v9W9THDiqXhlXXXUVp512Gl988QWd\nO3fm+eef591336Vz584sXbqU888/n3PPPReAhQsX0r9/f/Ly8rjsssv461//GnaDu+GGG1i5ciUA\nd955J/PmzeOUU07hww8/5M4774zSAtEq03EGFZIbWheser5+3sWg0eNLgJqUOr0es0G30eo0ejv0\nWAhmG93aDE7B7XFjJAWV2SIJ5Sp3AtCnGrIt2hO0X2usj64K/Nj9TrV+fuwHCDj9mPXrdCKXu2XM\n9mk0Xu51sTasmPCKveB27rWpIZq7XwIK8YxjE0TLOH5NEJ6xMioqYr/aNWvWrEn6ECu7s2ySN80V\nkiY2U/0TU24+tfJarX/uyeTrVgcuZaScl+lEp3GDWU60bJNPKqy4QQncFagjMPiihaw/0Iv9T7RX\nceM3AtNQ2vJ+YGkZjM5Upo7gQYt3JurrJZZnB1hpBz3aKJs2KnB+BxGLXxcrz/xUlj6OfXHXlo6m\nKSOB2KitOam+5qcGiJWxOA66EcdQrIyOHTvSqVOnqIWDwaAjPnLTwkygF+oV2xRo4P5ZKJ1Grk0B\nEuG57nIAACAASURBVM0rwczfZ6SZNPq5eCmYwj1WOW+a9j22sWvnSeFrPwG2HN+V/eKxKKGsT8DW\nmJNQgnwPhLXjpO6WoLbShgJLW1nXkt7KOtfHUzf3CETgjkV9WxCcfU7DXjiswF6YFEiY0oCW1hdn\niNNYGIv6xuHRtlv/0BDPWOljWtexDdBgXhlNZhWtdvA0ZeTm5rJly5aov6O1Itlw+A47WI9Mkktw\nmgjc/jmxZ0rZdML24gGFGo1pajB3lelBbJJdzvWygSjtcSuj16HXbZ3PhuYE1U7wzcAK2E5ndi05\nSdmWS1Qa5ShTRznAQSWgDwE5rVAa8m6raomRUAYjsF4Bd2NvtQ1hb58We7yM0UBsO3QS9pjK+FVi\n26grsbdLy1gUQ8sx6kclEQuQLX/sMjZY9brggkHa+LmNq8a7URCtTR59+l6gt6vQgyaWMB7XME2J\nF8fop6U8m7V06dKYheOhaXxEC7STjL39V7fVmjbHCosuVStHDL6yMCcxMlItPmZ7zJvQbI+bbVnQ\nF3UjbDX4VkMR7PxJV2WusBa4V+zOh/kWyX6UZrzTOpZa/dmMEsxhm3OlJfO1Nr9i9neHTRs+pltM\nK622bbXaK7yWGH3aSqQdUzTuajj0Ckobc7GpH5ppNig6Zgt9LPtoPC5dR2OR0C3gVUPXU1t+5jyM\nmARx1vFOLepsANRjS3ZjwlNjlq9Yjx8/ntWrVzvypk6d6qDxwvjx48nMzHR8jeTuu++mf//+DBgw\ngFGjRoVNIYFAgJSUFPLy8sjLy+Omm25y5VlRUcGYMWM45ZRTOOuss1w/2mpDXrertd8qnFHd9HNd\nQ5JFL90XtwJKigx+Or1ci61AXIb0ekQ4o+VJOV0QpGr5qUTWJ3lB65im0aYrDXijz1YuW0P1nlRF\nHkQJ6yDKC6MlShhTYcfJ2LnbIpBNHZqb207UJpVwf8T7QtzhpE1SfpXWB8nT26yPn6QLb8nfjPOj\nufr/Ip3si/M/XIU79PRoWvFm4BdR8qHhhbLU61WPV5+iwa2PtW23Pv+qiS8oVxNYGDxGNeaYXhn/\n+te/uPbaa3nppZfCaTNnxqehuMXKuP3221mzZg0lJSVcfPHF3HPPPeG8ho+VsY/Y/pS6kDQ3NFQQ\nqTEFPPjo9exDCZcsLU23o5o8dUGUZaSZPtM69mm8AhpthRKepSj78R4srVjbjCOeGPJcSwJItT7S\nKg8SsfeC0ny1PiYlWzRBq24RwhjlclFvAeLHLB4efki6zuijQP4T878z/x/zfB34f6mlm7ZrE2nA\nuS7pNiaHnouaf0zg0l/GpokLacbxGMAPVTBnZGSwaNEi3nrrLW666Saqq+N/Cp5++umceOKJjjR9\nJ9/+/fvDX8aOFzNnzuTaa68FVKyMd99914OyAHXTSXsLreNmaC3nmeqaFGAIXFNoFycF5yfW9XCO\n+qfpM63rSi0tYNHpWoVuezO+wp09RWujaETiAaEvQurlxLZbqbVB+pqpNF/RiDsAOTBw5GIYgNKQ\n21n5hdZ10OrjIam7GiYL3zLF8+JMuKM75EPLXRUoT41qYIyV311rS3dgMPb4ZmGr61XAtxCUJXN9\n7Kx2kAIvTNHSzL67IQUChfblvVOwY1Ybts+LC620d7TrTEw80ew0j7oEU2Lk1xZefdMR2c6oZf8h\nMYOj7ZKNBX2OV2pptUGhB18TfuC+WvL2QPM4fk0Qcfkxt2nThlmzZtG+fXvOPPNM9u7dW69Kf/vb\n33LSSSfx0ksvOfyQJVZGQUEBixe7+7nULlbG57VrWH3m7X8LfMbx+6irscqDWtNM4HtGAHi+YVgd\no37MMQXz2LFjAeUTeM8993DHHXfg9/vrVen999/Ptm3buO666/jVr34F2LEyVq9ezSOPPMLVV1/N\nvn3RNxvEjpVRQ/h1uCWoxYhg2K9XvTKLZ0M1fCY0ENbuOgitLMSJDRVsG6g89fUFO7Gl5hC5wKe/\noicr7RWUNhvOC7qUS9HSqrB305VZ9NKOLCBkK6g5wB5ox27VHzFtBFHX4eakWYt+1ttCjvQ7Sx33\nAC9avNpI5LkUVZellYft3DmSl4XS8MRGmanyycIZxEjKQthEskdP071gpMHJxtEYsxxQ8ZyTtZ/B\nQt6EcsA9IP98Iv8HHQ39Wm/MDVeYdnZBtI891BcNEZjf7SnnZWr0jpFTK/xQTRn/93//57geO3Ys\nH374YYNUfvXVV7N8+XJAxcoQs4ceK8OExMoA4oiV8U+UtA1YK/fpQDXsfAU16fVNDAVQYmrp6bBz\nsUUrQvg6bO8CscUm2/RhOtnNJz64UW6yEquOkpm4f3oH1KQ2PTXMxUtpS6WqeyPKzpyvjh/86yLL\n+wLbW+MVlD2aEM4t4sDvpO6udhk19JRO6m494NpCa59a71xhXeML0yno/uPp2rnsCKzQrkfbxW5Z\ni3N3pv6gHkekF42xQHrlWi1/pDNvtuFV8JBu6jBNBdHMd3HsYKgV9LpGetDIeF1XS97R1P9oD5+6\n0up0A4n0NTdd/wKoN90S1D6E+iPUPPavKcJTMLdu3ZrU1FRSU1NJS0sLn8t1XaEL2/fee4+8vDxA\nxcqoqakBiCtWBhAjVoYfpYL2sM5XYWtE8p03uQnSgGdR2pF+s5dpadLnR7DtwLLIpduf9bGpBmZo\ndQm9eaNLHas0GvFw0BcRpf16+SyXOr8lbC8uQWkFfmxXuHLruqWVlgROn940IBP2W7blJIBW6niC\nVbYE6IO9rTvJ4n0CSkhLGTKtY5X2E7u1fENP728xtoa9DNu/2fwm4zJjDN2Ep+6aNd/IM70KntXO\n4/0cmRvfhkJWHLwfacD6auNBES+tTreZSFe5VQaNH7U2NAA7JED9cLhl7F9ThKciv3+/HTwhLy8v\nwmUuHlx11VUsXLiQ8vJyOnfuzD333MOcOXP44osvaN68Od26deOpp54C4OOPP+b3v/89ycnJNGvW\nLCJWxo033sigQYO48847ufzyy3nuuefCn5ZyRwrKsi+alB/lb+sWwF2GQfxm9QDuOpJd0kAJFdlU\nkWTQSQyMCmwJKZqDV1vMD6jqPM1v92ViB/zJwtZ6DyoBHEApdftR9/nFODeViKAOC00xUaQpHqRD\ncLdqwyGcP2mu8BAvj3bWkYMWz4M4P2hapZ3LUf+PJF2CHZk7CCXgUW2DGEVDU9sBuCM2yTGFxhnf\nYPN4ltGOuKbW1NSQn59PdnY2s2bNori4mMmTJ1NdXU1SUhJPPvkkp556asM22IJnrAwddRXMjQVl\nd34B+5WvEjtqlWz3RbuW/Aojzy1N105F4HbBaRaRV3fZOmzWXWGU99rIUOlSRia48JQjRtu6AD8G\nVoJ/kPqeHxXQLtMZUTG4SSuv83Zro/VVFMd3AS2+Sdbrf1CEZMD6SR9E0OgPtq04b1j5L2SLte6q\nl8B/H+ofK2Nv8LiYdG2SDrvW88gjj7By5Ur27dvHzJkzKSgo4K677uLss8/m/fff5w9/+AMfffRR\nndsXDUc1ulzj4i1gO7bbWwpKu8xCaWTWa3o4PcU419PKjGt5rRYXoqB2beZLeTNNp6tyyZeFMsk3\ny1bhbHOmwSPX2ucyUG2hzk+G1plwDupNcYR1JAflUpaFMjkMwV60y9XOxRUuScntDtaPZJXeDmsR\nUxbZcjSeertbWT99zATVGo30RdeGa+uelcCxiQDK1lx/1DRvHvPnhtLSUubMmcPEiRPDQrtjx45h\nj7Q9e/aQlZXlWrYh4GnKePvtt1V0plCIvXv38s4774Qb6PP5wp9YaboIomJl6PEbJAZDOs5X6kqc\nAhScNlER5BKTolKjERuz5KXjfEWX8J0VBl+wX9szsRfuUrTzKi1frz+NyPaJZio8NsDGXsAqCAyy\nFubKYHGmc+NJ2Na6A2Vy2GBdp2t1BSy+acC3UJ5paMxAebIVFEkW4r7VeMrYgzOutSxUCoTmILaZ\nQvpVqeUnkEB8+I7YGrPbvPrVr37FH//4Ryor7fk5bdo0RowYwW233caRI0f49NNPG7ClTngK5lmz\nZoVd0c444wxmzZrlyG/6gjmBBBL4b0dNHfzhZs+eTUZGBnl5eRQVFYXTJ0yYwJ///GcuueQS3nrr\nLcaPH8+8efMasLU2PFv94osv1pv5+PHj+ec//0lGRgbr1qkFr8LCQp599lnat28PwAMPPMA555xD\nIBAgNzc3/BXtYcOGuW7Lrqio4IorrmDr1q3hxT/3mNAp2CEp07DDd/qtNN3+K4F23CD25VSNPtwa\ng860E4ttNtUlT8p42U+lfcLH3A4rZaVdolWmadcrgYWwuB8qxGYWBPwqr7zUolmrlQX7004VOLVV\n4Yla5HPYktMgmGnZsaXNAp23wCuwlG4jrzSuY/FMIIFI1Lhs7fu06DBLiw57lvnkk0+YOXMmc+bM\n4dChQ1RWVvLTn/6U4uJi5s9XnjKXXnopEydOPGrt9lz8e+QR5YqjZ4tpw+fzMWVK7K2oixYtonXr\n1vzsZz8LC+Z77rmH1NTUiPKBQICxY8eG6bxw++23065dO26//XYefPBB/vOf/0TEy1Ca/jkoO2d3\n3D0t9PMKi3azdZQ0E0InC33CUw/+rn96yqQzhb/QuD0UTO8LU5CJsE93oa+20vuhorj9BnjcusZq\n7zrUItsS3BfZsolcNLVcmFp2hUMyL2Sc2qL8ZCuwvV/0WB7yINCFvdv4iO93EU5PFN3W3JDeGAk0\nPQSs38J6L/59FeoYk+5k3zee9SxcuJCHHnqIWbNmMXDgQB599FFGjhzJggULuPPOO8P7MBoanhrz\nbbfdRv/+/Tn33HNp0aJusfNOP/10AoFARHp9BnvmzJksXLgQULEyCgoKPAIZjUMJCLHZyjHTSs/B\n6T6n76iToDpZRH4cVBbdKrGFjrh1WTvWHHlp2LvygjgfDN9iL4qJ14IsKOgPBinvFm/DfICIn7T0\nWfyaK7D9c3Ot8xycNu4qg4e+8Il13GdFo/NZH3C12pEEBH3YWw3B9l/2Y38rUMZRt+dLH6Sfur+y\nmQYJgdyUcDTeXvzWb2G9OcVnY44OMen+7W9/43//93/57rvvSElJ4W9/+1u9eXvB0ytj1apVnHXW\nWcyZM4etW7dy2mmncffddzN16tRw2M+64vHHH6d///5MmDDBEbazYWNlTEc9deWmF8G3AfvVXAnQ\nW0NJQIDCkGxzdnutr9bSRGiJENV34JkfKq208is1vvruQF2Ii4CWB4qgmsjJv4Mfh3I0uhS6HLnS\noEu1aDJJD94ApDEppNr/YMjaFefTN7CA0pQlLQulvWYBfSG7FfTMVDsJe6Lkb3Yr9cvB+vJ2proO\nby7J0o7m+Eho1RTtWgnjlnt+SXgruIPGRm7oQse16it0CV2pEpYWAjAyNNTqawSLYx9WH/nMOL5o\nHaOGLKgb1H8jOBompQAN5pVBUsxfNIwcOTIcTTM/P59ly5ZRUlLCp59+Gt4cdzTgKZgHDBjAgw8+\nyOrVq5k4cSIzZ86kd+/ecYf89MKkSZPYsmULJSUldOzYkVtvvRU4GrEygkRsWc0vVMeCQqAqfJ1i\n2aL3hWNnyP59EZTWq37PQmxXNZ0OnJ4Wrq3F1tp1zwwvVFn1aTCuU8J8VH/yWWHVMdXqYwVt2Q2E\nyG++AoDObAcqrAkZhPwrcIQLDSPoTHu2lf3JqaBBJteyJ0licYS3AIe0OoLGURvfcOQ5OL/NHJzf\nD0xT/5c2Br1Yr06s/7GttTmmB18AMHCIeri3C7uQ6OXNYzRloxaKiPmfRUOHQvfzWpTtPmQNAAN7\nL3Ycu1+7xiKcUDu+cSC/zUrrbKpx9CpQGCWzoaPzOVFD85i/o4Hdu3fHJoqCmH7Mu3btYvXq1axd\nu5bs7Ozwol1dkZGRERaoEydOpLi4GDgasTK2oybMYsI20hXWNt4iayV1hQpwc99p9wPpPHza77B3\n8UGEO9zGeThf9+XcK3aAHmQnZPMJI92gk/os/hvnaenARn0bchqvnHaDdT4dgLe7XGPRvglFy4Aq\n/nbWzYCPD066CKjkt+MfAar47Th1ZHkZ9hdHkrE//aS7+iXDQyjB68f5hZND2nDJtwNli3aYhw97\n96IePUZc8MzxruTtXj/B3lxjuQmumKeNCbx90k/UyQqV9reTbgbgg14XAbAqfYSTLvQmbJxulX7G\nOOpbsk1EyzOw8ZnYNIKd07XzWpTTym5q1h+AVc1GOI6SzlGIJ704fYx19qxx9MCK6VEy9bIB7FgZ\ngbo0LQLfcVzM39HA0P/P3ruHSVVc68PvwDQyyDTSoIPMoK1cZMDhMqDE++QAXoNJVDAQo4kSj+Qx\nxmgCGpNIDCp4ifH4occoojEeoh6D+DMCwchFTDjKdRAREOkII45CQ2ZGGplh+vuj9upae3XV3rt7\nei7ovM/Tz967atWqVbVrV1etWrXqa1/D+PHj8dprr2WlurV2zHPmzMEFF1yACRMmIJlM4oUXXsCS\nJUtwxhlnNEng3bt3p+7nz5+fOt0k974y+kE5gbkUbksKA5LOqPtIc/Eo5U0aZg9J9zXp0CRNtG0J\nQd5FWvl9rkfcCw4A3zI3Y545RxTaV0Y0JxybqsrIFlu2bMEPf/hD/PGPf0S/fv1w++23Y+vWrYHT\nWzvmH/7wh9i9ezcKCwuxePFiTJ48GePGjcO4ceNw6aWX2pK5MHHiRJx55pnYsmUL+vTpg6eeegrT\npk3DkCFDMHToUCxfvhwPPfQQAOUrY+jQoRg+fDjGjx+f5itjzRo1fbrtttuwZMkSDBgwAG+88YbL\nn3N60Q5Bj/rygWGj1POwsc51FICEHt0ddK6pjSJOOtog0W8sC5c+H/jomOWZ2hTSCXrEGGI8KCwC\ndXozxdcAPce6+fYb5dBAxac2eTibT1I77xLAdaMUz4OA2pbtyNnToe8MoPMoKGuJ/lBe3SjvK6Gc\nBzkH0KJIBXWGdvfRE2r3IPnK6Azl1AhgR1V1QWpW0K+LQ0w+LhxHS6hhYayuO4PFJXT996TRWkS7\nS6UwR7WcUq3QN5c6i+FToPOV+h4VTtkB70NOP/WIE+j8QxHgwTcliymdHyaoi8tlLLR/4X7wQST7\n+FRfViWugHn26LXnoXnNHltLldGhQwecf/75+POf/4wnnngCzzzzDE477TScd955+Mc//uGb3mou\nt2zZMpf+VprNnXeezSVh60PJ/aDzxC0BzoKy241CmYmdBWU2RuZu3HyN7J7DwBWOHmwglOtLAh3P\nRAebgt1THMf//s65qYFeDKsForfoNKuegNa7kg8OarxlcOllr7hFOw6qg1p8e5ryIHejlJZWz6nM\nUSe8EsgfCzQsgbbTPovVmWORQS5AS5zrLlFGcoT2vkOzy4njnWTDNmg99ltI/yjDcC8Ocv0z+dAI\nQx/kSmUi6xnuY6PGcAWax4qAQ/Kn54ugKmUjXO++xeTKJai+gyLbsjXdV8by5Om+dOflvd2kfEzY\ns2cPnnvuOfzxj39EUVFRamC7YcMGXHHFFUZrNQ7rOL6ioiKngrY8XgEwCO6hw2aoBkWdzkZ2JUc7\ntK0ZSDnz+QSq8yMfw/uh9Kj83LxjRBzdgz2nQHnE4NpEUQcmWw3S/deSnE5DXw190jXAFrJrnLKW\nQZsE0h9QlRNPf1ARp/OsYeXmHvEcvA/1x9RVB6X+lOqgWxK5BqVwQLQyW5OjejAt+NawOOksCtCd\nxEYRLq/yvjkg+XMZuG9pSdvWOmXbHwzgfkfyT4/QlPLEkEsdc2vgzDPPxFVXXYUFCxagpKQkFT5y\n5EjccMMNvumtHfP111/va6cXhKb10AHK7Wc+dKdLi1zkoJ12z3EVAy1+5SP1wa9cA90Y+WiB35tc\neMqGnYB2zUmyAIgtgx7ZOeqNnncAe6Y7aelD5nmEgNjT0DsXw8DACiDG/X/QRxN15CTfFKJj6Azg\nYA/oDpnqpUjF9YLq/J1FvQ43fI7GV492DniF6oBLoEfugO6c9zj3eyg/qh/uypQsVWimQnVEaiCS\nl0wV86AVnSE0za6Z8wqKOwDcnVmSnmPZ+4xlmF9rgLfdCPRCbA0Lg7ifAuAx557eLSEKVW6erhbA\nVKi65CqQjsiVf7Xm0iH7YcaMGZgwYYIr7IUXXsCECRM81K8aVlXGsccei4kTJ3oO8RcuXIgPPghy\njHnLQqkyvg518kb6AqId5NGNm41FYN9CnCn4Tj16hiWMpuVcDi4XOQs6kclWBm2UH4H+4+A76+hP\nijq/KJTq4v9Bf3SkBgFSKg86pQRQ11XO/Qc7gK4nqc67DsAnNUDXsNNB10D5d45CfZR8RMtHvrw8\nprLyZ9kJN7Vjzga0SzQT2kzStDXQrNNPJRSF+U+HaGuhNzZxNRMf3NQC2ArVPuY3WZXxanK0L903\n8v6ec1VGeXk51q5d6wrLxH2y9e/k/vvv9zlPT+3s84LJV8Z3vvMdbNmi7Ez379+PY445BuvWrWsG\nXxntaEc7vuporsU9GxYuXIjXXnsNu3btwk033ZTq8GtraxEK2cxq02HtmL///e83Wcgf/OAH+PGP\nf4yrr746FfbnP/85df+zn/3M1an269fP9x9l5syZGDt2bMpXxsyZMy1bsrkqA9CjLtpSzcH9IdfA\nXS1MpeGilfcEOdrjOE7EUT408iA1hOO20zUS5FuYKW0CahRW4OT7Fgtn1h0uu+EiaPVAD3UtyQN2\nkTVJFFrN00Xr0kugdcwlUKqNOgD5znmAdOTUwbCi2w/gkzCwn/SO0r0pt12muifrFDkaozKYNuW0\nxvbsTEa+H4jrkQjqUPjRaaRmIp8qYag2a9JNUzquJguxH6kbw1Btcjtypcr4Atm5k8gWvXv3xogR\nI7BgwQKMGDEi1TGHw+GUBVoQBDrBpCmwOSdKJpM48cQTsXTpUvTt2zewE6OBAwdi+fLlqY0mFRUV\neP/99100aqQvO2v+UZs6Zoh43unyaZf02VxguMo48qdsy9vW0XMeprSmNDwsCvupK/x6FtyWDoA+\nc63EHU4dc6rKSV9OH9Z7cJtuEOi9hqG3w3uVQ5YdlmdO31RI/s2drqWRrZxFcHv7i8B9ag69yyjc\nLg38FgNlfFjQ3tZkVca8pG2fg8bEvJdzrsqor6/PaIQs0TqacSjPc0VFRejbt28qjHxldOvWDTNm\nzMDZZ5+dli64r4yF0M5QJGhrtA2yI+QOfXg8vyfb57ghrl6E8U6ROqC4IZ5k8MqD9NOyPAnxI9qE\nUw6SqRrK1o0vPhZCjX56sCsA7AXqegDvk6tRgvTa9zaL44uQXMdu6iBkmN8z1VsE/u80CLLtXI+E\nThnIXk7Z7vk3x3luFumCfmfyOYZcLZC2tCpj/PjxePHFF1FeXp4Wl5eXh8rKykB8fDvmjRs3pnbn\n5RLz5s3DpEmTUs/kK6N79+5Yu3YtvvWtb2HTpk0oLLT5SfbzleEFPmIMQsvhtTBl4+cX7iWHjJOy\nywVFsOeYIYxGI3ERRvzIk57sfAl7oQ9s5XbGdC/5807ZVJ6mIFueQd99S/FpLrS0fDK/1q+bpqgy\n5GGsQda3Hn74YQBIO1gkU/gqcqZMmYLTTjsNjz76aOq8q6aioaEB8+fPx5VX6p1PufeVEYPac78M\nwMeGeJMKQD7HDeG2f/kCdi0QYba8ebwtDxONlN00WuZhBSxMqk7kDkZys9kFyj1oEZRqosHwS0B7\nyUuwKx/9Vxvk9YIsr1c9eYV5xccR7D15yUV8skXQ+mgKf1P79Utjug+KICNy0zslxJBrXxlN2fn3\n8MMPY9CgQanBH61vbd26FaNHjzaubfXu3RuAsmrr06cPotEovvjiC1RWVmZ0RqBvx7xy5Uo899xz\n+Oijj1BeXo6JEyfib3/7W+AMTHj99ddRWlqaKgTQHL4yolD7VCsA9IXqZPwQtoSbVBelMOvsgk4X\nSW0AAx+/+wTs+ZRaZKKwqIEPp485Vz5ipiu5Ao1B6675z9RRJeAua5GIL4I+UJYwCm4vfrIORrG0\nVF66N8Gmh6dw+d5NfLgJYVjwGwV3J1/g8BjFaGT+lCdPW2Sg4yhCev3Z+FPZaLFX0tGfLg9PIJ2/\nqS54Xpw+GkA2qvcoCx8DVQ9RaF8Zgy28MkO2HbPpMNZXXnkF11xzDQDlC/7ll1+25nvOOefgiy++\nQFVVFS644AI8++yzGRlUBFr6HDBgAGbMmIFZs2Zh+fLl+MlPfoJTTjkFL730kmc68pWxdetW9OnT\nB3PnzgUAPP/885g4caKLNve+MjgSSP8HJn0th1yg8BpRSX2a5O0nT42FbyYwyRfz4esndxR6Z2KZ\n84sitUsQIaiTUOiZkM+eqXOieuD1KhdBTbvzKuFdh7SoSJuBKL1pgSlIHZNGL2i91Qj5diFd3hqo\ncthkIVl52mrYy13syGlbU5H8Ad3OTIiJONO7AszthcvI5YlZ8jKVaTML38zyzWQW449sO2Y6jLVD\nB91FBl/fUsYNXbp0wV/+8hf86Ec/wosvvoh33303sNy+OuYNGzbg6aefxquvvoqxY8fi1VdfRXl5\nOT7++GN87Wtfw+WXX25NO2/ePGM4ddAcl112mfWA1yee0C4RI5FI6twtb1SIZ1PjkJtGaHQnzddC\nMKe3jWy9wmxpTQb78Ag3ycdHfrTzih/ZJCE3C/BV9yiULplM6CR404mztHwzAV+VJtM9/pwQNF4z\nAQ4yX+S+JhIw+29IiKspntKFYOcjTSb94iQP28wq6MYlPzrJn96DLV+v+vCK94LtO/EDd5PABwfe\nA78gyEbHbDuMlSPI+tY///lPPPfcc5gzR7lebWxsDCyDb8d800034brrrsPdd9+NLl26pMJ79+6N\nGTNmBM6o5bEMdqsMAv+Xto0YCixhUrfs1SCDmCnZOl8ebuNDNNL6g+u06qHrIsb4UVwB9M5AQJ8m\nIg97pTjArLrgHbyJhsogZbapdWxhlFem8HoXVA/SNpp2UMr3nkA6v0xN0kzv19SmMi2rF72pb4G8\nKAAAIABJREFUHPI+U5i+k0zS8jqPwW1qmT1MI+Lty3Zh+zK7EybbYay0vtWrVy+f9S3g97//Pe69\n9158+9vfxuDBg7F9+3Z8/etfDyy3rx1zXV0dCgoK0LGjKuDhw4dx8OBBHH300YEzaWmof7KLoT6o\n3vD+eOQHVgT39KwI7lGZV0fMaTmNLY3Mi9NymGQ3pTXxIVrqTGmjQz/oLbIFSD/fkCxx6NBWOfLe\ny9JLuQjS9lvWua38CehtwJQH1W0x3Js1TB0k1xsTf5KLzxKk7HQPIR/Pm3kddKU32bjLcplk4mnk\nlmeS15SXqU2aZlf8/fN6o/qQ+ZvaFLUV4s3bCr9yuaNQHSyftXEfM7w9VYs8tju02TmZJ+Tl5eHe\n5M2+dLfn/T7QYaxTp05Fjx49MG3aNMycORP79++3bG5rOnxHzGPGjMHrr7+Orl2VW7EDBw7gggsu\nCORTtHXxOZQ/5gJo3SftTgJ0Y6IPKArVKPjIqADuTkWOaAC1OBJz8pD/wjxvQFtF0DmCJt6mDl+O\n2EguiQKnHKS/4we78o+K5MiHXqDa5aQlnTLNjqQt+QHnGnOu5JZUdiQ1TEYuP1gZZUfG61XulKtm\n4VQuen9UJl4+2enKZ9kRm+SkNPSZ8LxJdnrvUXjriGmKvpnlUy3iE1DtaTMLk+/apGow3fM/m2qk\ntxfTn4hNdio3yUPvpodTDroSX36NOvRRuHdB8j9Y4h1x0vUCoA/UaAoacmDHTCqL2267DRMmTMCc\nOXNS5nI2bNmyBQ888ABisRgaGhpSfN54441Aefp2zAcPHkx1ygBQWFiIAwcOeKTQMPnK2LBhA264\n4QZ8/vnniEajeO6551BYWNhMvjJOgNI1x6Cd+jjOgY65EthPuuvvQjnxoUUtKBrcAnUmXLnDYwjS\nFziudGj47rkoVOc0CsASJ99FAKZBHWU0BNqt54VOuqhz5R9mKfRoFdB/LFHo7a9Uph5Q6hv+JxSG\n9ipXzPhGoTvqfCZ7XJefb8XuCu3AaHUX9d28P8jZ/Rd15KMR2P9Bd/bToY+Pos4LcC8ocd0zdQzU\ncdn06/IPkD/Xwt3BSL2nfI5A68OJj+yghkDVD3WulEc59DuXC8kE/ocVhXY9yyHl4WGmzpLna+Nj\no+EgeTIBz+P/nOt5zn0Y6fJuhvJFXQZVtkonX77D94dQbWWIQ78HyNFW6kNN5HPeeeelfM8HX99S\nG02mTJmCyZMnp7QNmcDXKuPoo49OWUQAwOrVq1FQEGzF9Ac/+AEWLVrkCps8eTLuu+8+VFZW4tvf\n/jbuv//+VBz5yli3bp2xUwaC2RK2ox3taAfQeieYhEIhTJkyBaNGjcLIkSNTv6DwHTH//ve/x4QJ\nE3D88ccDUJs6nn/++UDMzznnnDRP/du2bUt5pRszZgwuvPBC3HXXXYEFfuWVV7B8uXJtec0116Ci\nosLSOX8X7p1tNDKKqvv99G8fFTR8gYtGuzDwopEQHQ5Ko6Ao9Oh6G7QZVyHoYGq3aRdZJcQYf7B7\n7keapuvc+VEhtNP9fJG2DHpkTbpAKkcE2gFNLQtzRr80Ui5xfr2gRtGfOM8Hnfv9XQB00Vk3RKHU\nHbXQp7AQ8pG+GGgaEWfqYpWPrCU/v+cgJ3EsZPd8FLrREi5BeS70oAnCJ9c0fqNlen/kopUvJtdC\nn/yzELpt0QlAnAZQdUXWPmGothlj/MgNLZ3SMwS5sMpo6S3ZhHHjxmH27Nm47LLLcNRRetQeidhm\nVm74dsynnXYaNm/ejC1btiAvLw+nnHJKk5xzDB48GAsWLMA3v/lNvPjii9i5c2cqLre+MiqhDkSL\nQp/rlg/VGMmjVTlU49ns3NO0fy/0WW1R51rlhOVD24BGoW1+CxltFMjvDzQsc557qLCGNYxvBMDl\nUOoHmnbSghtN7/tDqWJeYuGkthgH3bCjTnpaYInCPXUewvhE4fZtEYVSQ0QcOgfUIdM9ndYyEO7T\nsPkpLfudcuWHgIbN0L6ieR3SVu0h0Eeu0J9OFO4/mHJoW2DbLjtK4wX+p9ZUcF5BrBCytVTIBrkq\nJ/kCJ3Ubd8nQA+r7+CHU++sh0p7ohMWgVIHLoN5nLdT7p44pBKA/kF/BvotaJ+1OaIf7TUMudMzZ\n4Omnn0ZeXh4eeOABV/iOHTsCpQ/kxGj16tXYsWMHGhoaUs6fuSvPTPDUU0/hpptuwm9/+1tceuml\n6NRJHf2Se18ZPQAMgGoI/aH9O9CfSiF0IyNQo+GjPKI5EUp/1h/uk0D4xgrSs+4FGmqcNNQ58fxo\nRJhkacuhO60i6A6qkvENwd2wKXwz1Ko2pac/GFpQ4XxI5gS0TnCHE75Zydn1JLUuw4+LAlTnvBqq\nc/4AQCzplGUvsIc5OmogmcLQm0DIxSOg/wz5M7drpmeiicPtEJ/fBxnxNod/jraIXMlGMwGq57HQ\n7bYQWldMgww6uoy+1R5Q7T4J/S1FoNt/FKlvoAGMD30Xn8Pb4ig4mqpjzhZ+Z/r5wbdjvuqqq/Dh\nhx9i2LBhLiV2th3zKaecgsWLFwMAtm7dir/+9a8AlK8M6qS5rwzppSm4LeEyqMayCsD5UOf/taMd\n7Wi7eBPASih1yEc54dhaqozPP/8cv/vd7/DRRx/hiSeewLZt27BlyxZ84xvfCJTet2Nes2YN3nvv\nvSy9uKXjs88+w7HHHovGxkbMmDEDU6ZMAaB8ZXTv3h0dO3YM5Ctj2rRpPr4yygGcAeAUaF0tIQo1\nIn0fesRMlhLSEoBbB0hLAQqjkUKMxXFabsfJ028U6UPQJ1jTCLQS7hE3H5lI22JSp5Bemu+Qc0a2\nKbUCpYmxMAd1u4APSrQzfDo2qiuAT5LA6jygLgk93QWUKqUH40e7uciFKN9OXA+3fTCBm3ARaqA3\nftBIn0bLcoOMzdyrHdmBb/qg8yDBrjHodRkKi0O3LZq5Abrd09mSJt3/OQD6ANgCYC2C6cm90Vqq\njB/84AcYMWJEyqy4d+/euOKKKwJ3zL5WGaeeeip2787OppB8ZWzZsgV9+vTBU089hXnz5uGUU05B\naWkpSkpKUo49mtdXRjva0Y6vIg7hKN9fc2D79u2YNm1aSguQ6YY83xHzZ599hkGDBuH0009PrS7m\n5eXhlVde8WVu85Vx0003pYXl3lfGWVD/zMucZ25Puhb6JA1CAdJPuOZpOA8KI50uoFaVq6FHxXKn\nVbVIy/1TbGO8adRIcSRjvZMfbZ6ghR6+AYHTwOFLZQOjp5FstZNPA/QonNx+1gMNzmhnP5QVRgMA\nrAXqRjhli0Pv7oo7BDQaps0ItJnFBJKbysJHXYB9EwWB+Evb33bkFty1K39XBdDvgMA3VcXhbqcJ\nA301tMdD4vcfUB7mmm4K21qqjKOOOgqJhG6P27dvd1ln+MG3Y54+fToA1RnTtsVcqTWaF4/A7StD\nLozIZ9ORVn5peFjch45AHXDMI72M85IlFoCG/+nQVLOehdUz2jBSTokanMXFzgAOVgMHi6A632qH\nZq9zJVWCLAuXh/8R8Wks387bYKHhz/w+LtJ5wbZZhcuFAHy+imiANtFpYNcwuwK6HumPPgy9hZzT\n05ZsGGgAddK73jvRFLRWxzx9+nRceOGF2LVrFyZNmoS33noLTz/9dOD0vh1zRUUFYrEYPvjgA4wZ\nMwYHDhxIbTFsRzZozQ+f7J4B/WHUQNunctmKlG75E8mDW8nQzEDaHRcivfPl+XGYZimmGYqpYw3S\n2fL1AOLH68ArvVceXL5seNjCeH2a/qSC5JPrP5lCqC36NMMh/nuh10IKBb0pLAatYzblUQvVVrzP\n/cwEraVjPv/881FeXo5Vq1YBUE73jz322MDpfTvmP/zhD3jiiScQj8exfft27Nq1C1OmTMHf//73\n7KVuNUThb/NKjZtsOXmYvPdKHwS2UWQueHLQws2JLJ42DUThPkk8CqC/MgE/xvkBwP4iZ4NMD6hF\nu0pou1QyaSPTKNpcwvM3yWaS1VTOGmjbbPkeokh/pzXiSrQRRss7MFs6mzyZxtnKZAqTf0p+7523\nH5P8TW07gDZf3IX0o81ooTkKNaquhHvTFhhtBNrUDiwuysqxEqrzzs2fSmuZy40ePRp///vfXYt9\nFBYEvot/s2fPxsqVKxEOq4YyYMAAfPrpp76Md+7cia9//esYPHgwTj31VPzXf/0XAODFF1/E4MGD\n0bFjx5RNNKDs/goKCjB8+HAMHz4cP/rRj4x84/E4xo4diwEDBuD888/H/v37jXRmmF52JEMaW4OJ\niPiIIU7mRTbQdI0YaKMeeZog84/A/NFGoCxXuO2pM/rpCb2BJB96FnsMpSc/zTXQG0j4fSG0/TKV\n70SWd5TJxUHljzJZiSbG0vJymOpGnlFJdUE8pIG2jU9rIhN5vMZX2bQdic0AnoO2wolBdcjvQ1vf\nbITaAfgWVMf7lhMWc9Jvdp4pnO5rHHpKXwt1tFRu7Jhbekt2IpHA3r178dlnnyEej6d+sVgMVVVB\nbO4VfDvmo446yqW0bmhoCKRjDoVCeOihh7Bp0yasWrUKs2fPxubNm1FWVob58+fj3HPPTUvTPL4y\nStm9aXEoDvdWUx5OMJlxedHLZ65zLRDhRdCexaSethT2o4Q4Rgm+xIc8rdHCSyn04mAR1OJgF+f5\nOC3DHqhv/aBz7emw3QPoRSD61UM7syFdM5e7CG6PZBRWBGC8I6NcnKTnAignTxwxFidpKGyjeK6G\ndqxU4OTN8yWMgj+C0EiZs6UJmpfXmkYu8toGVe+j4V6APgB9zBh5sBsPve7AF6PJw9825xpzwj9w\nfjGW7r0AZQqGBnT0/UkcPHgQo0aNwrBhwzBo0CDcfvvtAICf//znKC0txdChQ3HZZZcZz0B9/PHH\nMXLkSGzZsgUjRoxI/S699FLceOONgeX27ZjPO+883H333Thw4ACWLFmC8ePHY9y4cb6Me/XqhWHD\nhgEAunbtitLSUnz88ccYOHAgBgwYEFhAieDnblUg3XuWbdXe9E/G9WDcTaQf5PRYQm5nr2H8pe6N\nRhp+kEcbcdvRMPSOuioWxv1thKH1rTVqZHwq1Eg5H2JAFnUiToT2GRKB6uii0LbZJLccwYcdeasA\nkOtYLjvX+yYYDaUFtJtIAtGEBC09R5g8fKQv8X+GMPk+NxvCJDbC/GfPEcRtrkkeiUUB5FnkEUdp\n/w/efIqhRsjUfsqh3vdZznMUqp4/Zs/E7yzo2RBvL+RfIwrlgY7oR0Nt+W46DiPf9yfRuXNnLF26\nFOvXr0dlZSWWLl2KlStX4vzzz8emTZuwYcMGDBgwAPfee29a2ptvvhk7duzA/fffjx07dqR+lZWV\nGXXMvjrmmTNnYs6cOSgrK8Pjjz+Oiy++GJMnTw6cAaDUFOvWrcOoUd4jgNz6ylgG/xNMvMCN6zPZ\nvBBEJ8hR5REXhB9gdgzEN1/QlVbGa6BXwKmjjCPVSTdA+6nvBe0PI5VXF6h6JV/MxIesI6R+lUZM\nJAf5PDb9IdbAXfdUFr6xhKeje7mAyeuA8i2Auz74bIJAbld5ntxvcT1UZ0J8IoZyxKE2LFE4NxUj\n/Wwh3K5YOZ3XM1gYzYhosZXnkxBpOLiOmOSIOfdk+sjzLWFpZPvhFhj0zC0sSkS6GmjnWbydxKAd\nGW2CcpbfdBxCp6zS0WlNhw4dwuHDhxGJRDBokN49PGrUKM8zT2+66Sb84x//cPljBoLvmPbtmDt2\n7Ijrr78e119/fSCGEnV1dbjiiivw8MMPu/w6S+TeV0ZT4WdD25Zgko+rR+ievL5RfMgJ49cEUFcP\nxELacZEL1LlVOWmITz7jAegPWc42uJ9h3kF4lSchrjT65mm5gxwuawJm/8ecF89vM6OR+ZC8nJ+t\n7rcZaLgsVYa0pmdeR1xmLoesH1vbjULrhwkkB8km6wPQuy4PQK1DFEB1xtTp92d0gF634HRkdbHX\neT4At/8Msu4ogvKVkZst2dlaZTQ2NqK8vBzbt2/HlClTXJ0yoHz+yAOlOZrqysK3Yz7ppJPSwvLy\n8vDhhx/6Mq+vr8fll1+Oq666ymPrtELufWXEoIZ6MTRt5NwcyGSlvCl5AO6DUsHCyLkSn9I7H1S+\n0ynvcn4lMm0D0nXo3MyLr9zz0ZKEn9mlVzpTuOzk+QyB8+LhXvJ5rRvwPExy8zxs4PxsFismGv5O\nJY0Xv5glzrQewrEX6s84DD1TIDpT+epZ3F5o23iiJTcIYRZfD2CD89sJg51mVjCpKoKgQ4cOWL9+\nPf7973/jggsuwLJly1BRUQEAuPvuu9GpUydMmjTJmr6prix8pX7nnXdS9wcPHsT//u//Yu/evR4p\nFJLJJK677joMGjQIN99sPneLn7OVe18ZUQAjoXqYXHSENh483HTPPyA+nTN1GNnKYnoG0o9Nol19\nhdCmTZTWmV7m91fq+ZFQaoxeTvL3nWtDPdTHVCj40a6/KLSagJfdJqtX2WjkJeuR0/ENKpIPpy8U\nzxwyzCSj7T2b0BIWHn4y51K+f7F7XudhaB8w3FbdC5Re+nkB1JLXudA+MrZkKGc6TKqM2mVrUbts\nXaD03bp1wyWXXILVq1ejoqICTz/9NF577TVfszdyZdG7d++s5PY9jNWE8vJyl6mbCStXrsS5556L\nIUOGpP417rnnHnzxxRf48Y9/jD179qBbt24YPnw4Fi5ciJdeegl33nknQqEQOnTogLvuuguXXHIJ\nAOUr44YbbsCIESMQj8cxYcIEfPTRR9ajpVR+o6HMpro5obyT4o2Ypvu8ozTprXl6rr+jDoCc8lBa\nctBDjZcvavERrJQjiNpE6hopTD7LD4imizGounkLWjcbVTJ2vQgYA9U5vw/dIS8jvpUsjyro0Q/3\nyxtzrrLctjJKnSjRAfp9UH0mkF7Psu5NkHXmVdcmXjwsaBmC8jbJmvC4+qUzyeCnr7bRcZlN7wRw\nl8cmo+0d83dN8TGoqdrfm3wY67DkP33p1uedkTZIzM/PxzHHHINEIoELLrgAd955J+rr63Hrrbdi\n+fLl6NmzpwdHtTFv/fr1WbmyAAJ0zGvWrEl1rI2NjVi9ejUee+wxbNiwIVAGrQEl78MshJ+2QP/U\ncagVLhoN0EkNtEmCpuHkk5ac4RM/U9iJUKY/FB4RPPnIg8fzk4R5nhG4t00TQoYwCuc+i2mTDOXP\nR5ElUI0/zOJqgF6X6hHzaugZ5SoAB5NQH00YqlOOwT3q5zxjTkKupzVNk2V5qAz83QC6bng5Qyyc\n6oqXn1BviecjNlm/fnXrFW8qn1daL3pTeilvUB7UxmU9c1NGWU8QNGRdQe+Cj3i96tCrDKYyRQD8\npMkd86nJt33p3s073ZXPxo0bcc0116CxsRGNjY343ve+h5///Ofo378/Dh06lDqFxHYuKQAsW7bM\nGE7qED/4qjJuvfXWVMecn5/vezps28FCqAbVH+6Pmr/8OHum+zh75vS8A5Ar+xFLHjS9J50op+Gr\n4lIu2z0P4x8H3VM48SfdXQNLB7j9HtRDj3bDyi9GL4dkNdTzJ1AaoYN50OZScXHlrjhJH0mr935T\nZ1PdxWGuL05fL8K96k3+KRQawmxp/XjbwoKm9eOVaXobjw8M8fI0clOd2HTQ1PZN6WQb9SqDfI6B\nTdGahGx0zGVlZUaNwLZt2wzUZgTtgG3wldrW87d9kF2wSddp+tjp3rYgxeNNiydhQc8XyGKGNDJ/\nmXfYEG9Ly+95R7iXxfNTWWjBRT5XKSuM96EGvquhnvfD0S1TOWJw+56m0y2i0GZXgHvkLOvHVhZT\nObwWq7zCJDifIPS5RpD1hFysh+Qasl02GOK43FGkz5C89PamtYjcIFtzuWzRtWtX64JfXl4eamqC\nldG3Y37wwQfTMuJe5m655ZZAGbUO6KXw0RzgrQOz0fJ4k75PprONCqRejucTdPHGBJKH27N+Cr2T\nLgH9IfCjnBJQHamzzX5PDbAo7JjKsaOjUrriaugP7lN32pRDfHqmMhQwuTh4PXIdMqeXtsSUTpab\n16PJdhdwvwPZ6Zt0nV56UZm/vDc9+9nG07uqETRcLi67yVY5iB7ZCya5qP5NC9ZS3jDSvyNbxytt\ny3nZsrOmkGhpJ0Z1dWn2pVnBd+ffmjVr8Nhjj6Gqqgq7du3Cf//3f2Pt2rWoq6tDba19FdbmK+NX\nv/oVhg4dimHDhmH06NGpw1ibx1fGIeeaED8TKDxkofWyFTXlYUtfDfdiiZdMfuCjUFNetM2aFm6q\nned8qI+BtvUVObT5QH4YuALAzQCieUA0DOSfBKUWKoI+a7CI8c937ougOmXiG4FaXAxBf7AJ6Dom\nWWkxiXSN8srTmOodLC5soKdn4lcN83uyvTMup9xVyZ9NOy7pnvOgsoVFfEjQJKDrj9ehiY5oigW/\nCHvmcWGk518s6AmkV853eB7nPJc5Yf0EDb3LMAvLZ/kXC76Sf08gRx1qNjv/2gJ8F//OOeccvPba\na6mNHrW1tbj44ovx5ptvejL+5JNP8Mknn2DYsGGoq6vDiBEj8PLLL6OkpCTF65FHHsGGDRvw5JNP\nIhaLYdy4cdi40dvl39SpU9GzZ09MnToVs2bNwr59+9L8ZagR/nloe/bLLQ1a/KMPhC9U0i6rWqgt\ns461xamXA1c5ZC9DqTLq4Ggk6qFN7GIsPd8EROqjCAuLwdvEr/mmspnBpkbgHRWXOYJ0VY1pum5K\nS8+megDcDunpGrPkY0pne5bgMkRFnlLNQGU2wZaOFhw5qCxRAz2g9N7bAfytyYt/xyf991vszju5\nSfk0B3z/Lj799FOEQnqFOxQKBfIu16tXL/TqpYxgua+M0tLSFE1dXZ2v2YnEK6+8guXLlwNQvjIq\nKiosjowqMuKbewQ1fQuaJogZknxmp5GgAFofSPddGI3agpqyX6YZWS9okznUQ6tiyC66QadNbacu\nhFmVw2XzU9sEUTvZwjMxZ+P3poU1qj/T9L5aPJvy5CoZKlONuJc8CqA6Lj7LoTQ8rVSvSd4yTsom\n30XMUBbOrx7pC64Err7gPD6Au64jcM/gKJzXE50u/zdDPpnhUGPL6phzBd+O+eqrr8bpp5+Oyy67\nDMlkEi+//HLKiVBQSF8Zd9xxB5599ll06dIl5UgaaGu+MtrRjna0DrYD8B/pBkFDQ+s4ym8qAm0w\nWbNmDVauXAkAOPfcczF8+PDAGdTV1aGiogK//OUv03bpzZw5E1u2bMHcuXNx6NAhfP75576+Mrp3\n7459+/alniORCOJx9z+4vyrDa8ramtPpTPP3Kwfp8kjdEIWeNoahbY6HIKXKuHmsGjW/D+D/gzKb\nex9AQ7XIK+6khwgjcBWHPL0kiOrCS/VhozfxzJTPkYBclyFI3dris1FD+eUXc37Lm6zK6Pr5Z750\ndUcf2+ZUGb6LfwBw4MABFBYW4ic/+QlKSkqwY8eOQMz9fGVMmjQpteW7U6dO6N69OwC3rwwJ8pUB\nIICvjPVQI+cY3CvXtikrTadsq/rZQPIqgD0PaX2QCW8+veWqiyp2T78CuFUR9fq+M9Rvj3NtcK6u\nFfRqd5rUjzp8zjMuZKJ65iv5XHaCaQXfVFYeFsS+2FTHfu/IVs+mcBO/oLDlKZHrPxY/fiaLGh4n\n65jTTkC6T3FbfjGo73U9/E8aCobDDR19f20Rvh3z9OnTcd9996X0uIcOHcJVV13lk8ruK4N3tgsW\nLEiNvvfs2YPDhw8DQCBfGQB8fGWcDHXSbgXUSJH0W4BuOHylnvSvCeee4iLiarMc4Fd+38CeKZ8G\nuPV+IRFn4gMDPbdkoJV56ngLoHcXkm6QwuMsbK87bj+08yJAfR91gN6gQDISj2rGiz8XiCvpTnl9\nkHUBhXH72JD48Xrh74oQt9Sd1K/yOuYymGgaWLyUw2TBYcrT7x1ySAsRWRYb/OJzAVOZ6N6kWydI\nh1cmEL/+UN/rMORKBflFopPvry3CV8c8f/58rFu3DiNGjAAAFBcXe5rJEd566y386U9/wpAhQ1Kd\n7z333IM5c+Zgy5Yt6NixI/r27YvHHnsMALBixQr8+te/TvnKePzxx1M+MLivjNtuuw0TJkzAnDlz\nfHYhFkCZ3NBLJ5lDSN9qXcTCOOph/rC8tpvS4obcZmx69uNv+ihtdJw3lSUCfd4foHpbUjG85YTV\nQvtVrtH+MVJbsOPQ26+5NQb51A1B122hQV4O+kAzrUsKp/ckIevLxg9w1xd/poXNaqSPAP14cl4y\nXl4lrQmm9F7ymPINgqD0vH7pD9jGh7cHAPh/AfLgvHOLxsNt0xzOD7465tNPPx1vv/02hg8fjnXr\n1uHzzz/HGWecgcrKypaSMWMoHfODMJshmWCi8zNt4pB6Npmfl97TZLRvMqHi5lLSvMimu42KNFGk\nm7IVsvha4NTvO+Zx1CHyoTOQrjs2nZJNkJ1otlPwXOlUvwz65SMNTanz3zRZx4x/BejsTwy1OR2z\n79/J+PHj8Z//+Z/Yv38//vCHP+Cpp57K+AST1sFiAMej3SqjHe040hBDrnTMOHhkjpg9dczJZBJX\nXnklLr/8clx++eXYunUrfvvb3+Kmm25qKfmaAF60fParMTwD7h1K+Syshj3zf/6IIV2E0fG8IiId\nDzPxzhf3fLGMy1sjeMtnzoNG3JyfM0pOXQG865BhF9QW61ongJzqF7J7QPtClrawlK+s06Dg9Wsb\ncdk2O9jQPlpuebRyncv1adNPwLZrmfDggw+iQ4cOadZguYTv13LxxRfj3Xffxfnnn99sQjQPOkD7\nyiCdYg3UmW4x6F1MIWhdKTWiIVCHU3LdMy1oRJ30/R0a2hpLafkKNL/nC47USZo2hwBm3w88DNBG\n+pKWnsOChuSRO7hiTjgt0qx0yljE+PRj6WJQJyrHoC0+qI4oDeA+N45koTIG2XhDNGTVYUpDH4ap\nrkyQdcHrh545bRjpvpNN7yLbLfVB66K1ITf70LNUU1A98jD+LVXD/K54mgTUd5ujka5eZKkdAAAg\nAElEQVTfITkGhEIhPPTQQ65dy2PHjkVpaSl27tyJJUuW4MQTT/Rn1AR4jpjz8vIwYsQIvP22v09T\nCdu/zvTp01FSUpLyibFokTrBt3l8ZbSjHe34SiOLEXOvXr0wbNgwAO5dywBwyy234L777mt2sX3N\n5VatWoUzzjgDJ598MsrKylBWVoYhQ4b4MqZ/nU2bNmHVqlWYPXs2Nm/enPJIt27dOqxbtw4XXnhh\nKk2/fv1S4TYH1DNnzsTYsWOxdetWjB492rIdGwCOAnAs3CvwpVAmX8VQo61iqH/xs5z4s+D2LRyH\n+jeno5OKoX0N74V21EILaF6LjGTfG4c27eImWSFGQz9ua0zOXzjNWawcYaijR+JOOUmms5z4i5zr\nFCfudKgRC9HyMpMpXAlSx8x3HQR0LQFwtnMd4vAshfLJcSGAgYznWc6V5CYnSPxLKEK6hQZdz2I0\nZIpWBPcspNy5Fjs05XAf8V3upON00qaWNuHIQ38TMJ80Ih0eNWXEm8VwLg1Unn7iOSSemwJqb1T/\n9J3Qd1EKXbeFcLfhvdD1T+aGYej23g/u7ycE4Gio7zcHOBjg5wG+a3nBggUoKSkJ1P81Fdb5wkcf\nfYQTTjgBixcvRl5eXsarliZfGVVVSh/ZlBXQ4L4yroR2Q0kfGBnDk3NwMhnb6MRVObQ0raKpF9kC\nV0FPb+V+fz5NA9Knu4C26yXds0lNwVeRq+A246I86qE+hreYXAm4p+ZkJlfl3BPNW3Db5lKHVK7q\noeulwNeg3H6mfGRAqZzrnDqka6rO+NS1ysmX6jQqaHj5qB4ojHTh1dDvhjY3UAfIO8vNzvUD9lxv\neN7s8OBO4WtEWukwnuClujCpP+BBL/lydROnM6k4iqDqZrMIp3KQzl+qr7h8XF6bGoXUCjwuH+5B\nBzkaozaWgP42ahk9rV2Q+o7aQwxalUbmnVSWfCgHLd0AvGaQL0M04b+vrq4OV1xxBR5++GF06NAB\n99xzD5YsWZKKb05LDqu5HJnHAcDll1+Ol156KetMYrEYzjvvPGzatAkPPvgg5s6di27dumHkyJF4\n8MEHccwxxyAWi+HUU09F//79PX1l8C3ZyWQSkUjEtUUbMG3J9jJ543FR5z5uoedmZzFDSW3mahK2\ncBM/KSuXifORckaQfsIE6cU2AhgHZWNaxviT17mow6MSru3aANy6aXnC9ka4rWAoT/I4ZzIHNMnu\nZV7IwyDS0XPUJz/Og/T9JjTVvI6njzrXmCXelp6Qy0U0PxNNP3nIYxxvg3Q1vVtp6injOOJQ7W0/\ngAVNN5f7uyH9+mXAhmX6+Y/pZnn19fX4xje+gYsuugg333wzNm7ciDFjxqBLF+Wwa9euXSguLsbb\nb7/tsfs4ewTqmPl9ppC+Mj799FMce+yxAJRv5t27d2POnDnN5CujL5Tjh0Jo14M0IiODdn6emTxn\njiA3JZQBWCvS0mgkBH32H4FGDID5qB1aZJSbHeIWOpme50NpeV70IXEZyuA+XboaeirKN4zQx0Tp\n4+wKaHeivH6pQ/4A7lGa3Mgh5Zb3stychspi4iPLL+uQx1F8JpstOE/5THnwNgbY+fvla2oHuYJ8\nD17gm0zkn77cUCXTye/BJgOVdRty5SsDiwOkv8CtEUgmk7jmmmvQo0cPPPTQQ8YkJ510EtasWZM6\n/y/XCOQrI1uYfGUcd9xxyMvLQ15eHiZPnpxaWGweXxlrALwCd2dLDYc6fLIoALSPB7nrik/5iTfR\nE+Q2VALfLcV5U54REc75yTDemXB9LN3Tzrt66DPzeDopQz2jJboGFhYXYbJeChkNhVUjnaf8aPkH\nzkGdvATxJysaLjuBd3BSrcRppLym/Di9SQfOUSho6X0CbvlsuyJ5egneNrgsUiav3ZacTt4H7ZR5\numKk+wshfsUWWRqQ7tIgyngQ3oOyCnoP5gFSFshCx0y7lpcuXZoyRli4cKGLxnZ8VK5g1TFXVlam\nRquJRMI1cg1ydpXNV8bu3btx/PHHA1DbvcvK1FR6z5496N69Ozp27BjIV8a0adN8fGVEnR8tQFEj\njBuu1Aly/RucMKqiBNwLZBTG9b+UJsbkIB0qmeNxk7VqFi7z5TzAwgH3KIP01rwzTECfBkHh/AMi\nPXcEWk9YDa33Don7QiY3dZ68gyR95InQuuwEi5fg8nEaWmy1lZvKQ2Xh9Sb1vglWLornzZ3erUlO\nTi91rfTOwfLhdLYFQd5+ZDiYrDLOJB/dc/03l03qkaU+mev1g4JmIvlQ75iXmWTndc7zp3Cil/VF\nGARlirkGSi0Wy1BGA7LQMZ999tlobGz0pPnww9y4JbXB2jGTQ6FsYfOVMW/ePKxfvx55eXk46aST\n8PjjjwNoDl8ZNBlIwK2r49NMQHcsfEEsDD3SozA5OgPjQ6vNPK5ehPM8SaYi9syvtmkhyU+yUXzC\nEA92JZVLMdzg6gde7hOhVt7/AvXHRjrCYigVTqFzv1GUgRZ/aOWdRtp8Ggwn7b/gngFItRCPO1HQ\nJ+D+4mSnTH8mxE86PSqC7jDo/fHOPwxzB0vPXN1Do0H+Dk3qCbJqkGodSkd/Snw0zx0+mVQilBeX\ngXfuvF3ztGHY5bSBj4QpLcnK/0xpAFfN8qkW6fjMKM7Cqp3wfciZVUZzaIBaAIH8MR9pUNOMmWgZ\n4325oh6EPgHVOVX50PjxCAo5ciqAXqyR4YQotNVFKdwbTLj8vBzFcG8sCSqPqUzEiyxLbOlkONFL\nuQC9IQaCr40WSH+/xXDXg8migj9DhFO+Jr78z4jqOAxtVUK6XVP9joIynYmztPyel4m/z82Cj+kd\nFkB5fYtBtYtKJ22UpSFLDb7+cCKUdU0cahGZ8qRFaD4wANxHaAHAd5quY34mQPprMrc6a240q465\ndfEGcrbf3hM0CrAhLJ6pwds6ZU7jFS/5BqHnI3ZSOfB4mnISXRi606L8QnDnXSvueUdgg01XKsF1\n0FJ+Hi7LIeXi8vNZkR9MI2fupZCunB+vPw5Ox/mGDTQRqDokM8di6LpIQHWsgK5nbmURFXnwssiy\n8T+jYpZOyk+mbvTj1hU10Kovvt2frHGizo/z6OH8InBP2il+E4AXkRNkscGkLeBL3DEfBtCdPdNC\nhR/86GQcX6TjcUXQetkCFsbTSX2qibdNlhpB5yVrKfThqwWGH6AXdeijo4+V0tJHS2Gktya9OeCe\nglO+RQb5agR9EdL17KQOoXyKDTQkN/EA3OfWcdo4dIdWw/hyeYmugdEReNoY3B0Tf8ekviHQe64R\naanuiU8c2s6e1ED8uQrpOngaefP1hRiThfLgPpFLoUbJJEcR9B8XLxNHA5QKKw6lHqI6ikFbUVAc\nxS930lDeMXa/Fsohfr1zTwucMSd9LXKmymjvmNsaOsJ9BHomq9dedNKSgOvwTAtFYbhHO5yPbeRH\nsC0kSdhoKJx/aBHoEQzJTh9lVMjCZwM1SHfMRPRSN54QaWz1aao3zqOGyVBlSMc7E667tcnE64HK\nUIx0vazXSJPz5HG0qYIWwQhyVEhtQVqlSLn5onMNu5fLQlERTqNXmhHRO+bvGexZLjiaZnL0Dvmi\nMMlVw9KQHPmMroZdqc53Oc+bmXxVjH9H5Kxrau+Y3bD5yrjyyitTJignnXRSamGweXxlHMhCcmps\nTQVv4DZ/xdxUKxd52kAe5HheXL5CAw2nDWqrKUdcNBUPWjY5auP21DYQDY3oa9izSTaTqiMMcwfM\n00meYSYXhXvJyeU15VVjCJdyyXiuyqC65nSc3vZuw+Le9q74OwXS2y5PV8XCOWSd0/NGpPPP0fpQ\nE7dktxaazVmpzUPT888/n6L52c9+lrK8ALSvDC+Qr4ypU6di1qxZmDlzpmVLdge4O+ZcdXyywcjR\nKF/AyWfPsnPLVE/cFPDOtQp6FEeLNjTSodEL6QMBpQsEi6c4PlPw+5j9wN2sUp3J0aSpqXLauIij\nvDlPPvqkOqFrzEfuaqT/8eSzq2wXJBM366O0Ueg65LTEr5rR0syGj7Rp5Jlgz3HGV46sqW54Byrz\nlDMKDi6n7MwB3aHTSJ34ReA2wyS9M8nN2yUvRz5yNmY8Qq0ymm3E7OWhCVB2zi+88AImTpyYEd9X\nXnkF11xzDQDlK+Pll1+2UF4KrRcEguuYTeDpvP7J5Up2BFrHSI2xCG5zrZZAEVRj5xsCQgC6OPF8\nmkq0XaD9M/DwIicuX/CE4RoE3MKC+w8JsXtuash5hxitjKP7agMd6b3pHcTg1oWbdP1xdl8At9xS\n7QMWVy3CqTwJuNUvBexK/Pg9dfLcvpzaE8lWDbcs/M+T8iYdNenYKR96Nn0n9N5JDt7ZhlgZOQ+i\nTYgfV4UUMB487ESo7zcHOBzg1wbRIjpm7qGJ8Oabb6KoqAh9+/ZNhe3YsQPDhw9HRUUFVq5caeRV\nXV2NoiLVuIqKilBdLXVkhJfh3j0UVMdsAtcpeq3o81FwCMCncDfAAgDHOT/6CFti1EwLQEUs3+Og\nR0v8g+SdsFwk5B9XAeMndcWZ/OHw99KA9A+VngsYPS8X/4PjumfZaXI9K+dJ/HgHatL183suI6Dr\ngbfFIpaXLT3PW8ppKns1VJtqgH4nfFbIO7dqpOu7bbJQWMhAA+h2zOu0Aea6kDz5cwPjJcvMBzAb\noXbs5gBHqI652VQZBO6hqWvXrqnwefPmYdKkSann3r17Y+fOnb6+Mjhoa7cZX8C9+MfVCl6wTYuD\n6llpmsmn46bVbrmQFkS2bMGnnyRTDyiXjFJGiqN6r2L3RFvL0sgTWmyqBRv4e6kxhPF8pJxSpSDD\n5TN/jySnNNcKCk4bM8TzMBNfU3u06YFlmUkdEoO5XZrk4fnakIlKKuYRZ0PMEi7LeAD2dZkM0UZ1\nyH5ocV8ZANDQ0ID58+fjyiuvTIXl3lfGTqijnv8JbaoTZHRq+wvloxTiZVqYoXgwurhzpSljPePH\nzbNyDTJzM5nI1RviKIy2PTewK/3icNcBjXSIRxj2ujaFNYj7MAvj9KaOXtJ75cPTULqYIW1QyAU2\n08KdjRYI9sflVQ5Kz+X3WsTMJN9skIuZXwzKjG490je+ZIn6AL82iGbrmG2+MgDg9ddfR2lpKXr3\n7p0K27NnT2obeBBfGQB8fGUMADAYwBnQiyJB/t1tIwpaVKFFEtNIBiyewiLQIzNSA3BdoVeeTQXX\n6XEVBU0/+SJeiP0oPN/wCzF+fKGJFqjyxZWP6GwjQn6fD3f9eUHSE/xGhfzdZbsoLEfwtlG6F40f\nvOhtM4hcLXJnilzkG4XaYTgMOTtEuV3H7IbJQxMdI/X888+nLfqtWLECQ4cOxfDhwzF+/Pg0Xxlr\n1qwBANx2221YsmQJBgwYgDfeeAO33XZbcxWhHe1ox5GOLMzlrr32WhQVFaUcrBEeeeQRlJaW4tRT\nT8W0adOaVeyvgK8MWjih0SlfTc8EJj4mvl78bX4IIvDeop0tiDeBprq7oI6N2mVIw6fdXDdNts7S\n5jnmXCPQ6gH+zKekvG5s5ZZ1xOvZVrcynHjLujbxzwRB35XJiofn69VGZB0RD9neTHnBIp+NTybf\nAm/f1KZo5yHPm3T3VSItwSYDhfG06Q7sM0FeXh4wOUD6J92+Mt5880107doVV199NTZuVD5Ali5d\ninvuuQevvfYaQqEQPvvss5Rf+ebAl3jn3xK4T/cgeDXEoOZeFM91tH70RdAr2TyNSUfqhyDmaKTv\nJR02bRXeC30WG9chx6H133FoJ/mA25saXfk2YKoHrrCLI12fKS0CeDzVieyUbXp8m2kX0ck6JTrK\ns8gSz/nb0nvlLc3oCHERT+lJP28C1xlL/bEtjalOTfBqQ15pqG7j0JYnJBdfU+HgNJK3fL8FAD6G\n0jXnAFmoMs4555zUehfhsccew+23345QSFnSNGenDLSAVUbrw2T+40XLrzJOjlpsdDYZTKMem7mf\nF4KUR8pIGxVi0HpwfuXpauDeRUa790pg1qXLjQVy1Gcbncl8OaiuuHz5gtY2azHVqRyd5cMsk0kW\nW5gXvMrKUQ3zCBvQZSfzN4Kp8ze1rWzK4VcnJv7SbFHy82rjFMfXbw75yJgBcrSuvm3bNqxYsQK/\n+MUv0LlzZzzwwAMYOXJkbpgb8CXumBuhzOW43SvtRKIwk49liLgQu+cjMfJDGxe0FGeymbb51+Vp\n+FXmzxEknPwek9wFLIyuZN8M6NHgKOjpKpnKkU04bQOOwe18KMxoadsxTWu9DEZN9R6C9jFM76se\nygaWg/vArmfPRTAfOUX1T/a0PP+EeLa9Q1nn8j0kkP4eTe+c+6q2tQuSSdZdwkDPnSdxuU1tXLYx\nyRtw+8fmMH078j0gYJyJdzYqJg/kiF1DQwP27duHVatW4Z133sGECROa1Vl+i/vK2LBhA8444wwM\nGTIEl156KWpr1dQ4974yGqHmKdwuhj5Wk52MyYYmIuiqRXw93D4DZBz/FTo/mbdMA0O8CUHC+ZFQ\npGpoYFcpUyHc6hw+dZW0YcZHmtVx87t6ls4mr6x3+b4KWbgtLY+vhlu3bnsnJpspr3doKoNXmOQT\nJA8TX1sesu1J/rb6svHksP2R2vh6yRkkv6A0GcKkuvhkGfDudP0LgJKSElx22WUAgNNOOw0dOnTA\n3r17cy+vg2brmMlXxqZNm7Bq1SrMnj0bmzdvxuTJk3HfffehsrIS3/72t3H//fen0pCvjHXr1uHR\nRx818iVfGVu3bsXo0aMtfjIIvOEG3SDC4WfzSXpUE29uKhaBWefaUqCFPL4gUwO7PHuhTa/iSHfI\nVOvQ8EVA2zWTMst6pDrMRb3Z3lFbhzQ5BHuW9WIrTzbljAXgFfEIk2m80pnKmCOYdvp1rwD6T9e/\nAPjWt76FN954AwCwdetWHDp0CD169PBJlT1a1FdGVVUVtm3bhnPOOQcAMGbMGLz00ksZ8Q3uK6MC\nSidKI0Da2soXREwLPH6LJaZFItOCENe5JQzp6FrE7m2LSZmC0pD+kqa+ESYL1QcttlFcF+e6GVpf\nuwt6K+0uVjZu12z6FUFvs/WTl9cjhdECYRHS35tcOJP15GXZ4PXebO+BvydbGUzpgywO22BaDJU6\nYL6IaWrjQPqCoJdctjCet6xT7qvEtPhoW2Ph6fmCaBTARQY5skAWW7InTpyIM888E1u3bkWfPn0w\nd+5cXHvttfjwww9RVlaGiRMn4o9//GNu5LOgRXTM3FfG4MGDsWDBAnzzm9/Eiy++iJ07d6boyFdG\nt27dMGPGDJx99tlpvIL7ylgGtcmEfHHwTooQxGTJBtlI/XiaeAeRxY8HoHWqctGtGO6trfwfns8m\nwnC7o4zCbeAfhvbAFoXWJ8tts4Xsys3raPQs5QPSP1oT5AIZQS5cwkJH+Zju6Vn+qZpgahe2tuLX\nhkydnC29lJ13rjWMtsZCY1vMM9H4LRjaviGveje9dx5HZpn0LX8MYKuFX4bIYkv2vHnzjOHPPvts\nE4UJjmY3l+O+MgoLC/HUU0/h0UcfxciRI1FXV4dOnToB0L4y1q1bh9/97neYNGlSSv9sg7evDAnT\nKMbWqQZpnHT1SmPK12+13jYCNPGgMph2Xdm2yMrpFy3mcR5k3lQMt6P/qHje64SRbw3i3YPdS//D\nQUaPsow0KuQfubQC4HFhpL8X0+yIw8ST01TD3ZlJOcMwy2b745HxJpjaqWx70jLCC35tMVP4lcE2\nY+SyUFre/g4hZ2PGdidG6TD5yjjllFOwePFiAEpX89e//hWA8pVBnTT3lVFeXu7iSb4yevXq5eMr\nIwZgP4APoVQapfBuKGBxgH10R//sphGzbSTmNyK0yeE3GrN9WCQnba+mzpQ3fn52ndxIQqhi4XFo\n5zmEHnCPimMiH64fNpU/yIxBdrC2kRdYOB9FyjoM0jl5dVq20aJp9F7Ewm0daNC8/MJtAwT5Z2aS\nPWgHbatTk1y2kbXtjzIBPVLe7/xygDba8fqhxX1lfPbZZwCAxsZGzJgxA1OmTAHQHL4yolB77s+G\nPn6Hw6tjA9Ibla2DSMDsUtREx0dXJlBnapKBh3Eabrwv05KvDu5PgnTJ5PuiCulHBvFRjPSCRzbN\nFE/3pgWcKsGPm0PZXLAmDDQmWskPSNd3w3I1jY45bO4/bfAaMdKfpOTNaWw8M8lHwq8dBYnj4G2T\nu8HNlq8pvjdy7ivDyxDHZmjTBtCivjIWLlyIefPm4ZRTTkFpaSlKSkrw/e9/H0BL+MrwGrFK9YGX\nOoG/yQIWVg97HjK8BukjNwo3qSWkPJymnj3XMzoyaeNzNm7PTHbGNNqjezKno7xolxfg3hnI5Zc0\nfBehl3ymsnH4Of+R9ejnSMeUR9B3HJSnSR6TQyM/eLUlU54yzNTjBJ212eqE6pubX8o0tvooED9b\nXvSco8n8FwF+bRBfYl8Zd8Js6G+6AmYDf0kLQWOig4jjMPEx8bXx9Np4wuWnkav0dxF1rjG4j1Mi\ndQQADHHuoywd+dQg08A40s8I5HGAWW1C8tlGyxRP5THVh4mHfIcmnqaNETKNqS2Y2ohJXj/IMpgW\nTyVfW5uUfG0yBdnoYkpnkj2IzJIX5RuB+6zAWoM8RMPz+GXTfWWUBki/Oa9J+TQHvsQ7/5ZBWxeY\nDP75Vd7zZxoZ2BqtbQRh4umVjynMi9YURwtQcbhPvCYUQnecRM9HynxDDd+51wW6g+c7H/lop1A8\nc58JlFeN5dkETmOqD9Oip1cn6fX+vPj4bfQICtmOgthm296/rEu/9EHak58cJh8YEnwgYCtr3BDP\naeJQA4bdAWXzQRtVVfjhS9wxk5bGaxuq3zOQrtMlED/bootthCbz8hodS7n9Rjxe+luTjwtANQHy\nhwFoXTHplUn/TGFh6GbDR0+10LbS9JHlO+ERpI+0TLLKkbBNd1rPZKN08HjmvOVoMgH7O+B5cj6A\nmZfXe+J17jUS9msXgLvu/Eb5Mk5u2PGahXGaGpjblZQrBPs3I+lsM8+OFjmyQBtVVfjhS9wxNzrX\nIKNiAh9R2mhs9JmORoKMZugjynbEw22JeRrp0YuPSgGtj64RNCXsSiNn6nCjUOZzPF9u0SFRz2gp\nPsguP68Rp1/9mNoCDzO9fxMfP16Sj9e79eMVdEYVtJ17tW9be6LyZNNZBt25yeuuC/T320S0W2W4\ncfDgQYwaNQrDhg3DoEGDcPvttwMAXnzxRQwePBgdO3bE2rVrU/S595UBuM/8I9j+yUPQoz5bfJo0\nHnQ2i4KQR5yfPLZ7yZuPWvLFleK4FUYto6li8RGgKww8EiKMn2aSEPxD0IeV8nLTfa24l+UICXpZ\nfr869KPnz3FDGlv+XnlzPl40tniZp+nZJINX2WQZ/Ea/HPK9+N3za62F1iZbLdSZfznqmuoD/Nog\nmq1j7ty5M5YuXYr169ejsrISS5cuxcqVK1FWVob58+fj3HPPTUuTW18ZUpVhm+bS9NsEW2Oma0Sk\n9+uMabpmmvaa8uPyShl4WtNUux7u8wTJ2iLMwkkWcjLE9ceOpUUdpd0r0gBar9zAeIbh1l0XsDy4\nrNwxUaEoi/0A3vTy8jC/zsavrilvEx8K9+okTfmYVApenT2HbB8mXnI2xPnaRsN+snvJxdsXb8d+\nszqTLLJs9HwYORsxtx8tlY4uXboAAA4dOoTDhw8jEolg4MCBGDBgQNY8g/vKOBdAH9gbTD4Lj0OP\n/GQD4unzRVpuPkbh9XDzkX/P3MSO85L5SVl4vDQp4mWh5wSjp00BDVCbY/JFOO9AQ4yuB+NbBPfu\ntxCU/4wGlhdtKgjBvdjFR9H0k3bi+YK+XtDL90L+lHnZed1Ikzz5DkxDJt4WeD4UzmXyGnJ5hfN4\nSSfNL7kMpnZCC70yD5uGUuZPdAWCJkjnKuMkpLw2GUxhUSh75hwgi6Ol2gKatWNubGzEsGHDUFRU\nhK9//esYNGiQJz35yqioqMDKlSuNNJn5yoh55JbphhOexkZX4BEfscQF3WAQMcR57aKizpNUDwko\ns7d8FsdVD3xXVz6QXwL3yEb+eNoD0GqNBLQPZc5bble2beCR5aL0si5sux9l3UQ8aGwwyWKTNZfw\nagtBN5Z4hdvomqM8TeEZQ85OMGlXZRiYd+iA9evXY9euXVixYgWWLVtmpc29rwyuyggyhZVXUlH4\n6fo4LckbQXpHZtJfmzo8wCxvrSFe0kl5OWhVndcpyVwr6GqBBnL9WQ+98YXrk/nmCa4fBOxmcKZ6\nMZVVllnWa61HGh4OpFsgEB+/9DKNDPNSBwSl9Sq77V375S3LJvmbym6TSYbZ2q8fjaT3UumEYF4b\nyhJZqjLuvfdeDB48GGVlZZg0aRK++KJlzTta5My/bt264ZJLLsHq1autNJ06dUqds8V9ZUiQrwwA\nAXxlrAfwDwDb4J6uy6meVAnwqX6+IZxPo+k5wei4GqHekA5CFv7jcvA8pJqDT+NJz0fTcOrAON8Q\n9AIdH82S7TI3ceIdKHXEIcaD38tOmy8Qyo6G5DPViVQv5AsaXq9U3zKNnDKbdsPR9J+rg0zqApmG\n8zK9K4LMk6thpOpATvelmoTnb1LZ0MyB8+RlM6nlpLWIHDJymSQfWacm9Z4XP/meeDsAlK+MJVDf\n7UfICZIBfgKxWAxPPPEE1q5di40bN+Lw4cP485//nBt5AqLZOuY9e/akLCYSiQSWLFmC4cOHu2j4\nbpvm8ZUxAsCZzj3pQkmHyv+1eTigN1tQmgaRrsHAr0Gk5yMBek4gXYYCwQ/sanN/xfOjDo/y450V\nbQgJs2eTrpXkIRpa1CsQ6aUukBb6SlhephNMqDOkOqAyUFl52SHC6T3I98TrH4Yrz0Py5VcpB0Hy\n4bbDsk1AxHFZeLzMkx+7xMvFw2Q4z4cWXHm9mmTg6WwjfAr3UuOQzCEDjZQbcL8722ib59EbwFgA\nZQBOsMjZ/AiHwwiFQjhw4AAaGhpw4MABFBcXt6gMzdYx7969G//xH/+BYcOGYYnPJXkAACAASURB\nVNSoURg3bhxGjx6N+fPno0+fPli1ahUuueQSXHTRRQCA5cuXN4OvDDpaKsg0q57R1kNvGwW0f2GJ\nENJHHSG4OzAIGpmn37ZcnsbUwOWxS7RdmoN2W3GHR5JHoaAH3CNi+pGXOcCtsqBdghxhRkeWH1QG\naaXBQWGF4kr3ciQo61TyMqk4KNxEb+Ij+ZveKY/zmvbbZK4XcaZFMy/ZOG8/+aVcsg1LmU3yeqlU\nbH8AFOdVho5oocm8EZFIBLfeeitOOOEE9O7dG8cccwzGjBnTojJ8iX1l/AHuaRsZujdlUYIvRvEr\nj4cHjbwHzPJIvl5xcoGM30eR7mcZMB8rRZ1qCbSvjBqRhu5jzrVK8LDplikvuZBnqkMOvzr0Qya0\nQdPY6t8UV4z0OjK1kUxha3+ZyGqSxy8f2/uAIdxLzqDt+zdN95UR6MTtTq58tm/fjnHjxuHNN99E\nt27dMH78eFxxxRX47ne/m7UsmeJLvPPvOajOpdR5rkK6VytbowPSOxEgvZGZpt+yocupoVd6G51J\nZp7e9nGZdtTRiFfu7IuLMD4CpjQNLL6W0dh2dsk4U5m8Ot6wgcbrjzEXsLUFL3rTPWCuFz9VQRAE\ntaYw1XUQuqDpZf0H7Xz96jMGb4uqTGDK600AZqsvAFi9ejXOPPPM1Jl+l112Gf7xj3+0aMfcevOF\nFgPXt5kakbxKfZ3UhXk1qjDLS6oMeCfDrybVgi0fnpbfm6br5PNCLs7Qwh5PR/f5LE0R9AIfD48I\n/hGoo+4pXi5kynxM5ZXvhVQulJbXK6enOBuy6fgoX0pv6py88mxq/tnCJFMQOYPIaOugvdKa1Eet\nAdORJWcA+Dn7uTFw4ECsWrUKiUQCyWQSr7/+uq+pb67xFeiYAa3PkivYckRchHRdHjcNI8h09Ezm\nZQUsDY8zpW+KIaVcZAN7bmBXvitPLvzxn2nxjuum4yyeLy5yH8580TCOdPl4vch6pPAapMtmqide\nFnhcTXl45V1goOP0QcpggymNnMn58TLxMKmRgvp+NvHPJNwE/r6ylSMXMLUj73Y1dOhQXH311Rg5\nciSGDBkCALj++utbSmAAreAr41e/+hWGDh2KYcOGYfTo0anDWJvHVwbBNDo2fQw1SB8FyI+gANq9\nZtCGmmlHYeoYTPwIcopPkPbJ0kOYyZmRXHDjOmYg3ayMwmlUbLKLJj5B6kuOnvnPi5Y/2/SlXmkz\nkYurOGzhJtim95moA4Kqb2ztKUi6oCoIL36Z0DYnMu+YAWDq1KnYtGkTNm7ciGeeeQahUMuO+pt1\n8e/AgQPo0qULGhoacPbZZ+OBBx7A0KFDUVioPvpHHnkEGzZswJNPPolYLIZx48Zh48aNnjynTp2K\nnj17YurUqZg1axb27duX5i9DKf3PQ/ppz00F6UyDesyypc9lfqY40g3LTlU+A+l66LOQXm9xaGf5\nJYxHDPocwBij5070bbKZ4iSyree2ji9ruQhNLV/M+S3PweJfkNO2B7Q5R/kt7iuDOmVAnaDds2fP\njHgG95VRgdx2yu1oRztaBlHkzFfGEXpMdqv4yrjjjjtwwgkn4JlnnnHZIefeV8ZO5962EGEyvi8S\nfPjCGo0CTK4MJb3J5rjWQm+7Uj5y9GGi4T/utJ4W7Gqh1RA8DZW31rmnqWyI0RcwfgecZ1ogLIKy\neKHFwoTIsx+jo7JIdYetHk1uQGUaCS9bdRNtUD5+NLLdeME2mmzNRbJcIujxUzbEkDNfGVmqMlob\nreIr4+6778ZHH32E73//+/jpT38KoDl8ZeRD77m3GefzLbL0kmjxhy+ASatC0+45zlPG8zyoU5Py\n1LP0kg+lN6WRW4q5P4sEdCdIW6WpwwXcC5tcpqjjhzkPWi0RgfI2xy1cuKUHnVTC9cw8nPKg8nvV\nAdHwdPxPQtKC3fNFSFkuGGj9NmJ46UZ5WtsAgfPwW5fg/Px0spkuOrYk2lJn1z5itsLmK2PSpEl4\n5513ADSHr4wPALwNu5c5boLlt+AU1I7V69lkjufFT9LYRlOSL/dzwU3dKD0tAPKOmqd3rnXEX3bo\nvGOvZenIfwX3m0HhNew5wfKx7UQ01b9tEdBkRmczkZR5eEGaNzYFXuZ3fmn84sOGsCMVMajvdT1y\na8fs92t7aHFfGR988EGKZsGCBSn/Gc3jK2MY0nXN/INNGML5cyZTy6B2m7zTyGQabeuQeHlkJ0lq\nCT6yLoC7k8w3pMuH9u6SAHAcizsANToks7lqpHXqqZEhjXB5ZyzrX1p10C9iSGOqY2lpIu3OTTDx\nlHVOs4RMeJj42PgHVWd55Q+425MfbdDw1kIU6nsdhtytDx2Zqoxm2/m3e/duXHPNNWhsbERjYyO+\n973vYfTo0bjiiiuwZcsWdOzYEX379sVjjz0GAFixYgV+/etfIxQKoUOHDmm+Mm644QaMGDECt912\nGyZMmIA5c+YgGo3ihRdeyEAqbgpUL8L4KI/Hy3Q2yFEidYIyHe80bfnwtHSNwD1dlioMThuGW5dc\nC63WAJNJesWjDq3KyY8sMapYvjYTPBpJRxgd13fzUTOvF1OZi+A+h7DAkNakPoJII9+xKa1Mx+Fl\nWRDUjwVXSXFzunwRxmlsbdSUf5COxU9d82VG21RV+OFL7CvjThHKtxvbkCuatoCoc5XOheg5Zkl3\nlhNfwsKoAw6LMDA+YegOvBDAvwRfbrKXSf2ZTPw4n2zfx5HyHpsLR0L5c+Er47UAlBd/tczlWhfL\n4O58mqsRyk0aTeGTbXrT9u849IhPesaLsfxMm0wINGLmYbyD5lYqnEY647el9wLvkCmNKV2277Wt\nd0rNjbZYfu4ka1mOeLbrmL8ECNJYJY3sdDhs/jJsfHPZydSwaxx6qlwo5JDPYeg/tDhLT51wDG4n\nM8Q7DvMx9+QcyU9enr/pXqaTnbXpTwYiLps/0bC4yjBTPpnys9HIsKaUw4/eTx5TmaU8tjoKKhN/\nv0cFSBcE7TrmIxzNsRuLFpDi7LklQLreYij1glzB5wtbfAGO/hx6OPHlULJHGU0U2tHPXij9MR+R\nR9hVljdIHXPzvbgh3FafcrHO6w+T0weVx8TP6086E36Afzux8Q5ajiB8gqTxqtcgdRQ071wd5XRk\n6phb3FfG9OnTUVJSkvKJsWjRIgDN6StDbk6wrcjHRVxEpDXx8Nr04LUS7iWP6V7KaioDl1cu8hG4\n+ZxcpAvBbVa3i9HL46KIRw8W1wPp5nK8ozTVMUQ8/8XhXbcmHnLjj0wrr7ZzFG3v3ZR3ppY7NmsO\n00YhU3pTnnLjkrQmsfEMalkSFH5WJEG/DyB3XVO7KsOFzp07Y+nSpVi/fj0qKyuxdOlSrFy5Enl5\nebjllluwbt06rFu3DhdeeGEqTb9+/VLhjz76qJHvzJkzMXbsWGzduhWjR49O85PhRkfYpyohJ443\nEE5by8JsK+Am3iERJ3ev8SlUCMCHgn+9gYeUkYfLfCIsTn7sEaRbS4Cl4x92LVRnS3w3QY2WC51w\nwK0v3ixkleUmuaT8/IPl9WnrMOIeNPXQ9Wl6rxTOr5JG0kvI6a+k8eqcON8Y0t+v3/Tarx3KtuCV\nLoichJ3i2dbJy3rn+ci8vcqYw8NYs1RlLFq0CAMHDkT//v0xa9asHMoTDC3qK4M2kDRlBTS4r4yL\nAAyANrWiF2A67FKaLQHpL40fGsp3rplMnjjqDWkAbc61naXn4ZxvhPG15cV3/Nnsb6vEM41u66HV\nGPSLsGstgHecNCG41Qqmj7RWXE36c/5epI11vQgHe+ZlNXU42w1hPE/eDqRJHYXz9DzfILvtbPnK\n9hUTecq2YToUNYg7Tr770cSP72jlZfPStco2ytPxMNPOSy4L3/nptUuxD4ALPOIzQeY7/w4fPowb\nb7wRixYtwnvvvYd58+Zh8+bNaXTNiRb1lTF48GAAyqvc0KFDcd1117lUEbn1lbEQehTH7YYB/4Yu\n6SQSIj7IdEhOm4LsSKN7Uxm93FhSR8hVCnwbNt+ynRDpTR1tBErnxztsspPmecmdfjycZKYf5c1t\ndLOpo6ZA8vFyyxnEZSfxMNF4pZVxtnoIWm6bW1hbXkEg36FfeRIG2qAqhBjUadm5QOYj5rfffhv9\n+vVDNBpFKBTCd77zHSxYsCBH8gRDi/vKmDJlCnbs2IH169fj+OOPx6233gqgOXxlEGSDpEYRgbnx\nm9LydAXiGXCPUE2jVb/Gn0lH4/VnIDs76mSroTdu8E5RogjpGzno/mgDX77xg4+eiwSPiODnVe+2\n0b6kzaZz9krP24XXO5Rx8jnbP42m/NmY2ikPk+2zqXll0plnm1euFu0y1zFXVVWhT58+qeeSkhJU\nVcnZZvOiRawyuK+MioqKVPjkyZMxbtw4AMpXRqdOnQC4fWWUl5e7eJGvjF69ell9ZfTu3Rsff7wc\nwPJmK1NucaTIeX9rCxAQR0p9HilyAq0ha9++fXPA5Ze+FF27dnU9+w/2mh/N1jHv2bMH+fn5OOaY\nY1K+Mu68885UpwoA8+fPR1lZWYq+e/fu6NixYyBfGdOmTbP6ymjpf7d2tKMdbQ/ZrmUVFxenTlYC\ngJ07d6KkpMQjRTMg2UyorKxMDh8+PDl06NBkWVlZ8r777ksmk8nk9773vWRZWVlyyJAhyW9+85vJ\nTz75JJlMJpMvvfRScvDgwclhw4Yly8vLk6+++mqK1+TJk5OrV69OJpPJ5N69e5OjR49O9u/fPzl2\n7Njkvn37mqsI7WhHO76CqK+vT5588snJHTt2JL/44ovk0KFDk++9916LyvCl9JXRjna0ox1NwcKF\nC3HzzTfj8OHDuO6661L7MFoK7R2zAY2NjejQoe3vVj9S5ASOHFnb5cwtjhQ52xraa8xBXV0dHnnk\nEWzfvh0HDx4E0DR76+bCkSIncOTI2i5nbnGkyNmW0T5iBvDGG29gypQpOPXUU9GzZ0906tQJjzzy\nSGuLlYYjRU7gyJG1Xc7c4kiRs62j4/Tp06e3thCtjbfeegvFxcV47LHHMGrUKNx7773Iz89HeXk5\nGhsb24T5DHDkyAkcObKuXLnyiJCzrddnMplEXl5em5fzSMFXUpXx0UcfYe3atann999/H0cffTQA\n4LjjjsOsWbPwq1/9CgBaVT+2bds216LD5s2bUzaXbUlOQDmhmjNnTup506ZNbVLWf/3rX1i2bBka\nGxsBAFu2bGmT737Xrl149913U89ttY3G426vdm25jR5RaFEbkDaAO+64I1lSUpIcM2ZM8mc/+1ly\n3759yZUrVyZPOukkF924ceOSd911V6vIWF9fn/zFL36RPO2005LTp09PhS9cuDDZt29fF21ryslx\n4YUXJo8//vjkggULkslkMvnqq6+2KVnr6+uTt99+e3LgwIHJiy++OHnjjTcmk8lkcvHixW1OzqlT\npyYHDBiQHDt2bPKnP/1pMplMJl9//fXkySef7KJtTTkbGhqSP/nJT5I9e/ZMLl26NBW+aNGiNlWf\nRyq+Un9he/bswdatW/HBBx/ghRdeQH5+Pn7zm9/grLPOQmlpKX7xi1+kaK+99lpUV1ejvr7lHWn/\n9re/xZNPPokVK1bgzjv1EVkXXnghiouLcccdd7QJOQGgoUFtnR05ciSuv/56zJ07F7W1tbjkkkvQ\nq1ev1GiptWW99957EYvFsGHDBrz88stYsWIFdu3ahfPPP7/N1GkymcSsWbMQi8Xw/vvv4+mnn8bW\nrVuxYsUKjB49Gr1798Yvf6l3srVmff7lL3/B7t278eMf/xgzZsxIhV9wwQUoKSlpM3IeqfhKdcyh\nUAirVq3CZ599hu7du2PChAkAgGeffRZ/+MMf8Nxzz2HFihUA1BS3uLgYoVC2vmkzB02vb7zxRnTv\n3h379u3DP//5T9x11114/vnnAQBz587Fn/70p1aVkyM/X20eraysxGmnnYbi4mLMnTs3JeszzzzT\nqrImnbXtqVOn4n/+53/QqVMnLF++HD169Eg5ymordZqXl4crr7wSs2fPRl5eHnr37o3jjz8eixcv\nBgA88cQTePbZZ9tEfV566aW49957U4OZxx9/PEXz+OOPt7qcRzq+Eot/hw8fRl5eHjp37oyqqips\n374dZ599No499ljU1dVh5cqVGD9+PLp3745FixbhvvvuwzvvvINrr73WuC28uUAdc9euXfHvf/8b\nEyZMQGVlJUaOHIknn3wSsVgM48aNw7HHHovXXnsN999/f4vKWV9fj44dla/cw4cPo0OHDjh06BAa\nGxuxZs0aXHvttejVqxdmz56NFStW4LLLLkNRUREWL17conX6+eefp/yukB1thw4dkJeXh7Vr12LS\npEn/f3tnGhTF8YbxBxREwioKpISK0SiKChJQI4knIDGAt4IIyuUVvKhCUYPGIxU1sSSlpYmleATU\niFgClomlUfCsACJGBKNi4hkOARERRGQXnv8HsvNnFTUezC6mf592Z3bYH/3OvtPd090DX19f7N27\nFzk5ORg5cqRWyvT+/fswMjICUNfy0NfXh4mJCRQKhVS++/btg6enJ6ytrWFhYQFjY2MkJSVp7RxV\nezVv3hxt2rSBvr4+LCwssHr1avj7+8PQ0BDm5uYwNjbG0aNHtebZ5NFyV0qjsGTJEv76668kydra\nWo19+/fv5+TJk5mVlUWSPHv2LEeNGiVN7a6srNSYDi63Z33ftWvXsrKykiSZnp5Ob29vZmdny+5J\nksuXL+fGjRv56NGjBvcHBgYyJyeHERERVCgU7N+/P8m6/0dO16VLl9Lf35+3b99+5mfUZZyRkUEf\nHx9puq2cnt988w2trKx44sSJBvc/fvyYJOnp6cn09HSNfVVVVbJ5fvvtt4yLi+OVK1ca3K8uy0mT\nJjE8PFxjn5yebxtvXWK+du0aFQoFhw4dypqaGpJ1N1QCAwOZnp7O3Nxcrly5kpMnT5aOGTBgAC9f\nvqwTnkFBQRo3U+rj5ubGixcvymhJHjhwgPb29gwICGBeXp60XalUMjg4mCdPnmRZWRmnTJlCc3Nz\nenl58eeff6a7uztPnTolm2d5eTn9/f3p4+PDP//8U8MzKChIw6X+xc/d3V3WdRD27NnDjz/+mKNH\nj6aPjw+TkpIkz+DgYA3PgoICjhgxgiQZGxvL1atXs6SkRBbPlJQUOjo60tvbm19++SUHDBhAsq7s\nnixPkszLy2OvXr24bNkyhoeHMzc3VxbPt5W3JjErlUqSZEVFBadPn04HBwdu2LBB2l9cXCy9vnPn\nDgcOHMhp06axb9++9Pb25v3792X1fZbn3bt3pdfqBHLq1CkOHz6cEyZMkHXRpoKCAvr5+XH69OnS\ntocPH0qvCwsLpdc7d+7k2bNnpfc7duxgTk6OPKIk8/PzOWTIEOn9vXv3pNfqhbJIShdBdZn6+fnJ\nFvucnBxOmDCBv/32G0nSy8uL69atk/bXjz1ZNwrnww8/pKenJwcMGMAzZ87I4kmS69evl9yKiooY\nGhrK6upqkppxV/P777/T1NSU9vb2sl6Q31aadGIuKSnh/PnzWVVVJW07duwYV65cybNnz7JLly7P\nPLaoqIhHjhxhTExMo3vWT2bqZPtvPdPS0mhvb89t27Y1uidJlpaW8ujRo1IXyt69e7l06VLu27eP\n8+bN48yZM7l9+3bpAqFSqTSOr62tlZJfY/Jk7K9evcpZs2bx1q1bDA4O5rBhwxgQEMC///5b4zil\nUsmkpCQ6Ojpy+/btje5ZP/ZP8uOPP9LDw+OZ+/fs2UMTExPu2bOnMdQ0eDLuM2bMYEhICNPS0jhm\nzBipAlFUVERSs9VRXFzMcePGcePGjY3u+V+hySbmyMhIOjk5cebMmVSpVNLV/ObNm5w6dSpJcvz4\n8XRwcODnn38uHbdly5anfqyNyapVq2hmZiYl1pfxVDcH5Uh0JLlmzRra2NhINcnS0lKWlpYyLCyM\nH3zwARcvXszdu3fT19eX06ZNa9BVDurHXt1SysvLY//+/blkyRIuX76cDx8+ZEhICMeMGaPhqe6O\nkaNMnxV79cXs0KFDDAkJ0ajdqz3z8/NZVVX11IWvMagfd19fX1ZWVjIvL48//fQTu3fvzpCQEGZl\nZTEoKIienp4anuq+/Cfv5QhejyaZmHft2kUDAwPeuHHjqX1JSUmcN28eMzIy2K1bNyoUCmnSA0nG\nxMRoNG0bk9OnT3PUqFGMjIxknz59pNoISSYnJzM8PPyFnnKd8Dt27KCHh4f0Q3N0dJSazpmZmdJN\nR5K8fPkyXVxcWFBQoOEqBw3FXl1GK1asYIcOHXj48GFpn6WlpdQvHx0drfXY19TUSL6ZmZns1KmT\nVKtWb4+JiWmwu6AxaCju6puNd+/epZ+fn/RZpVJJa2trqQ9f7nP0v0STSsz1TwAHBwempqby2rVr\nXLp0KXft2sWKigoWFBTQxMSE3bt3Z2pqKpctW6bR9yg36rvZfn5+XLhwobQ9Pz+fxsbGtLW11QnP\n+jXIy5cvc9CgQdy6dWuDfdqxsbHSzDm5eF7sd+7cycrKSiqVSrq5uXHLli0sKyvjzZs36e3t/VTf\nrVw0FHt1Oav/Hw8PD+7cuVNjm5w0FPdt27bxwYMHrK6u5rvvviv1iaekpNDX1/e53TOCN4POJ+b6\nJ6tKpZKadnFxcTQyMmKfPn24Zs0aurq6cu7cuTxz5oxG7a6mpoa7du1qdE91k1rt+SQXLlygnZ2d\n9GN99OiRxs0cuTzJhl3VP9Dc3Fx27dqVixYt4vDhwxkWFsbz58+TJK9fv8558+bRwcFBln7PJz2f\nFfshQ4YwNDSUubm5PHfuHL/++muOHDmS9vb2GjdWG4v69zjqO6t5MvYqlYq1tbV8+PAhg4ODGR0d\nLUvXSn1PdbfKs+I+e/ZslpSUcNOmTRw4cCB9fHzo6OjIzZs3N7qnQMcT8/r167lixQqWlZVpbFcn\n6w0bNkh9m3/99RcDAgKkccGk5onYmKxdu5ZeXl68cOFCg/vVJ39ERAS9vb2f2v+sscGNwYtcSUrN\n7uvXrzMwMFAa0qUeClVeXq41z2fF3t/fXyP2qampstTsoqKi2L59+2feRK4f+/Hjx0vb1ReZw4cP\nS2OWtelJasbd39+fycnJJOtGk6hbpAJ50MnEnJaWRicnJ44aNUqaCKJm0aJFjI6ObvC40aNH88iR\nI3IokqybBPDFF1/Qzc1NeiahmoiICKmJStYllKqqKg4cOJARERGcM2eOrMPJXtZVjZeXl1Smclzo\nXuSpK7FPTk6mq6sr3d3dOX78eO7evZtkXdktWrTohbGXa9z8y3qq8fLy4tGjR2VxFDyNTiVmpVJJ\nlUrF0NBQjh07Vtpev+bT0AD77Oxs+vv709XV9bkzvt4U6mZgZWUlhw0bJvVh1h8P29B45NzcXHbu\n3JkdO3ZkXFxco3u+jmt2djYDAgLo5uYmyyiWl/VUI3fsVSoVy8vL6evry8TERJJ1F4yZM2dKn6k/\nykJbsX9VT7njLmgYnVgro6amBgsWLMAvv/wCCwsLvP/++6ipqUF+fj7i4+MRGxuL4uJimJqawsrK\nSpqvDwDXrl1DYGAgBg8ejKioKLRu3brRPQ8dOoTmzZujbdu2uHTpEnr06IHIyEh89913OHXqFCws\nLGBjYyMtHq6npwelUom5c+fC2dkZCQkJsLW1bTTP13EliQsXLmD69OkYPHgwNm/ejFatWumcJ6Cd\n2KvP0bCwMHTr1g0AYGhoiJiYGEyYMAGGhoZo2bKldJzcsX9VT7njLng+Wk/MtbW1mD17NkpKSuDs\n7Izvv/8erVq1woMHD7B161aYmprCw8MDqampiI2NxcSJE6Gvr4/ExERUVFTAzs4OEydOhIuLi6ye\nUVFRqKiowLFjx1BRUYHHjx/jhx9+wO3bt7Fu3TpMnToVenp6SExMRFlZGTp06AAPDw+4uro2qufr\nuCYkJODRo0fo1asXfH19dbZMExIStBZ7FxcXrFu3DuXl5bC1tYWhoSEKCwtx69Yt9O3bF6amptJx\n+/fvx/3792WL/at6JiYmyhp3wYtprm2B8vJyZGZm4siRI1AoFGjbti1SUlJgYGCA+Ph4dO3aFQDg\n4uICLy8vZGdno2fPntDT05OelGBsbCy7p6mpKbKysvDOO+8gMTERc+bMQZs2bbBgwQLs2LEDBw4c\nwMiRI6GnpyfVPNQrnumyq7os1U/L0FVPbcbe3Nwchw4dQnx8PAICAtChQwecPHlSevBo/SdDyxn7\nV/WUO+6CF6P1GrORkRGSk5Nx9+5dODk5wdLSEoWFhbh69Src3NygUCgAAOfPn8eVK1cwbdo06Ovr\no1u3brCwsNCaZ7t27ZCfn4/a2loUFxejS5cuaN++PQwNDXH69Gn4+vqibdu2snu+jmv37t2bRJnq\ngue9e/eQnp4Oe3t7WFlZISsrC/n5+Rg0aJDU1aIL56guegpejE4slD927FhkZmaioKAACoUCPXv2\nRIsWLVBYWIiioiKsXLkSM2bMQN++faWF2bXt2apVK9jY2MDU1BSzZs2CUqlEWFgYnJyc0LVrV1hb\nW2vNsym5NkVPExMT2Nvbo0WLFiguLkZtbS3MzMxgYGCA6upqrTk2JU/BC9Dqrcd/yM/P5/z587lq\n1SppW79+/ZiRkcGYmBhOmTJFljvuL6Ihz08++YRpaWkk69b3VU9T1jZNxbUpe/br109aSe348eOy\nLcn5PJqKp+D5aL2PGQAsLS0xevRoLFy4EJ07d8ZHH30EQ0NDNG/eHP7+/ggICNC2IoCGPVu2bCk9\neaR3795aNvw/TcW1KXsaGRlJLThnZ2ftCv5DU/EUvABtXxnqc/DgQQYFBdHGxkaWqbSvSlPxJJuO\nq/B8szQVT0HD6JH/PF1RR6iurkazZs2kZ8vpKk3FE2g6rsLzzdJUPAVPo3OJWSAQCP7r6MSoDIFA\nIBD8H5GYBQKBQMcQiVkgEAh0DJGYBQKBQMcQiVkgEAh0DJGYBQKBQMcQDi+/eAAAApRJREFUiVkg\nEAh0DJGYBY1CSUkJHB0d4ejoCEtLS7z33ntwdHSEQqHA7Nmz3/j3BQUFoVOnToiKipLex8fHa3zG\nxMQEFy9elLzMzMzQqVMnODo6YujQobh+/TocHBykFQ0FAm2hE2tlCN4+zMzMcP78eQDAV199BYVC\ngblz5zba9+np6SEyMhJjx46V3quXtaz/GTs7O8krODgYI0aMkI4BgMzMTJGYBVpH1JgFsqCeYHri\nxAmMGDECALB8+XIEBgZi0KBB6NixIxISEhAeHg57e3t4eHhApVIBAM6dOwdnZ2f06dMH7u7uuHPn\nznO/41nv/80xAoEuIBKzQKvcuHEDx48fx4EDBzBp0iR8+umnyMrKQsuWLXHw4EEolUrMmTMH8fHx\nyMjIQHBwMBYvXqxtbYGgURFdGQKtoaenBw8PDzRr1gx2dnaora3FZ599BgDo2bMnbt68iatXr+KP\nP/6Am5sbgLqHjVpZWf2rv/1vtgkEuohIzAKton4Wnr6+PgwMDKTt+vr6UKlUIAlbW1ukpKS81N81\nMzNDaWmp9P7evXswNzd/M9ICQSMjujIEWuPf9O/a2NiguLgYaWlpAAClUolLly698DhnZ2fExcVB\nqVQCAKKjo2V5QrlA8CYQNWaBLKi7EeqPlnhy5ERDoygMDAywb98+hIaGoqysDCqVCmFhYejRo8cz\nvwMAhg0bhnPnzqF3795o1qwZrK2tsWnTpuceIxDoCmI9ZsFbQXBwMIYPH45x48a99t9SKBQoLy9/\nA1YCwashujIEbwWtW7fGkiVLpAkmr4J6gkm7du3eoJlA8PKIGrNAIBDoGKLGLBAIBDqGSMwCgUCg\nY4jELBAIBDqGSMwCgUCgY4jELBAIBDrG/wBIeS59O2JcnQAAAABJRU5ErkJggg==\n",
"text": [
"<sunpy.spectra.spectrogram.SpectroFigure at 0x1129d2b90>"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 28,
"text": [
"<matplotlib.axes.AxesSubplot at 0x1129c0250>"
]
}
],
"prompt_number": 28
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"callisto_nobg.peek(vmin = 0, vmax = 40)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWYAAAEgCAYAAACHJ9lnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4VEX29z8NBAIkAQMmSKI2GpZAgASQ6IASZFdwQcVl\ndECEEWbQUdxwG8KIo/Mbl0F9xV2cwQVcQGQAlSUIqIQlYRlAQWwhwURDBsKSmK3fP6qqb3Xl3k4n\nNAad/j7PfW4tp06dqlv33LpVp6pcXq/XSxhhhBFGGKcMGjW0AGGEEUYYYfgjrJjDCCOMME4xhBVz\nGGGEEcYphrBiDiOMMMI4xRBWzGGEEUYYpxjCijmMMMII4xRDWDE3EJYtW0aXLl3o2LEjf/vb33zh\n1113HWlpaaSlpdGhQwfS0tJqpPV4PHTv3j0kcrz55pv07NmTHj160K9fP7Zu3VqrjO+++y7dunWj\ncePGbN682RdeXFzMwIEDiY6O5rbbbnPMMyMjgy5dupCamsoFF1zAjh076iRzZmYmTz75JADTp09n\nxYoVQafdtWsXqamp9O7dm7179xIVFVWnvINBVlYWo0aNCinP6dOns3LlSgD+8Y9/UFpaWmcegwcP\n5siRIwA0btyYtLQ0X1188cUXgH/bysrKolWrVqSlpdG1a1ceeughH69FixbxyCOPnGixwnCCN4yf\nHZWVld5zzz3X++2333rLy8u9PXv29O7YsaMG3V133eV95JFHaoR/++233pSUlJDI8vnnn3sPHTrk\n9Xq93qVLl3rT09NrlXHnzp3er776ypuRkeHdtGmTj9exY8e8a9eu9b7wwgveKVOmOOapp3v99de9\nI0eOrJPMmZmZ3ieeeKJOaRQee+wx78yZM33+qKioevEJhFWrVtW5THWB2+32FhUV1SnNihUrvH/4\nwx98fr3cH3/8sXfAgAFer9e/benlKC0t9Xbp0sW7ceNGr9fr9VZXV3t79uzpLS8vP5GihOGAcI+5\nAZCdnU1SUhJut5uIiAiuu+46PvzwQz8ar9fL/Pnzuf766wPymjNnjl/vdOTIkXz22WcAREVF8dBD\nD/l6pj/88EON9BdccAGtWrUCID09nby8vFpl7NKlC506darBq0WLFvTr149mzZoFXRfnn38+33zz\nDQBHjx5l8ODB9O7dmx49erBo0SIf3aOPPkrnzp258MIL+eqrr3C5XACMGzeO999/H4AVK1bQq1cv\nevTowS233EJ5eblfXkuWLGHWrFnMnj2bQYMG+cWZvdwpU6bwxhtvUFJSQpcuXfj6668BuP7663n1\n1VdrlGPZsmUkJyfTu3dvFixY4As/duwY48ePJz09nV69evnKNGfOHEaPHs2IESPo1KkT9913HwBV\nVVWMGzeO7t2706NHD2bNmuVXzmeffZYDBw4wcOBALr74Yl5//XXuvPNOX34vv/wyU6dOrSHfW2+9\nxeWXX277DA4fPkxsbKxtnEJkZCSpqam+Z+Vyubjgggv45JNPAqYLo34IK+YGQH5+PmeeeabPn5iY\nSH5+vh/NmjVriI+P59xzz60Tb6WwAI4fP84FF1xAbm4uF110ES+//HLAtK+++iqXXHJJ0DIGI4MT\nvHLB6bJly0hJSQGgefPmLFiwgE2bNrFy5UruuusuADZt2sS8efPYsmULS5YsYcOGDX55uVwuysrK\nuPnmm5k/fz5bt26lsrKS2bNn++V5ySWXMGnSJKZOnVrr8IfiGxMTw3PPPce4ceN45513OHz4MLfc\ncosfbVlZGb///e9ZvHgxmzZtoqCgwFcHjz76KIMGDWL9+vWsXLmSe+65h+PHjwOwZcsW5s+fz7Zt\n25g3bx55eXnk5uZy4MABtm3bxtatW7n55pv95Lntttto3749WVlZrFy5kjFjxvDRRx9RVVUFCIVv\nygewbt06+vTp4/OXlpaSlpZGcnIyEydO9BumsENxcTHZ2dl069bNF9a3b19fJyCM0CKsmBsAwSiu\nt99+mxtuuOGE8mnatCmXXnopAL1798bj8TjSrlq1itdee803lhyMjPWF1+vlt7/9Leeccw4zZszg\nqaeeAqC6upr777+fnj17MmTIEA4cOEBhYSFr1qxh9OjRREZGEh0dzWWXXVaD31dffUWHDh1ISkoC\nYOzYsY5KwxvkLgSKbvDgwaSkpDBlyhReeeWVGnS7du2iQ4cOvo/ojTfe6Ev7ySef8Pjjj5OWlsbA\ngQP56aef2LdvHy6Xi0GDBhEdHU2zZs3o2rUr+/bt49xzz2Xv3r3cfvvtfPzxx0RHRweUsWXLllx8\n8cV89NFH7Nq1i4qKCj/lqXDgwAG/XnHz5s3Jyclh586dLFu2jN/97ne2/NesWUNqaipnnnkmV1xx\nhR/v9u3bB2xTYdQfYcXcAEhISGD//v0+//79+0lMTPT5KysrWbBgAddee22tvJo0aUJ1dbXPX1ZW\n5nNHRET43I0aNaKystKWx9atW5k4cSKLFi3itNNOC0rGE4HL5eKtt95i7969TJgwgb///e+AmIgs\nKipi8+bN5OTkEBcXR1lZGS6Xy0+Z2ilW80MSrPJVCFSP1dXV7Ny5k5YtW1JcXFznvD/44ANycnLI\nycnB4/HQpUsXAL8hn8aNG1NZWUnr1q3ZsmULGRkZvPDCC0yYMKFW2SdMmMDrr7/OnDlzGD9+fHAF\n1nD++edTVFREUVFRjbgLL7yQ3Nxc/vOf//DBBx/4tYnq6uqT+gH/X0ZYMTcA+vTpw+7du/F4PJSX\nlzNv3jy/XuDy5ctJTk6mffv2tfJyu93k5ubi9XrZv38/2dnZdZJl3759jB49mrlz5/p6m8HIqGCn\nAINRiormkUceYeHChezbt4+SkhLi4uJo3Lgxq1at4rvvvsPlcnHRRRexcOFCysrKOHLkCIsXL/bj\n5XK56Ny5Mx6PxzcG+q9//YuMjIyg6+Hss89mx44dlJeXc+jQIVasWOFTOk8//TTdunXjzTff5Oab\nb67xgVN57927FxB/OwrDhg3jmWee8flzcnIc68jr9XLw4EGqqqoYPXo0jzzyiI9eR3R0NCUlJT5/\n3759ycvL46233nKck2jfvj0HDx60jdu1axdVVVW0adPGNh5EO/vTn/7kZ4nx/fffc/bZZzumCaP+\naNLQAvwvokmTJjz33HMMGzaMqqoqbrnlFpKTk33x8+bNCzjpV1lZ6ett9e/fnw4dOtC1a1ff5JOC\n3ptRY5QmHnnkEf773/8yefJkQPSys7OzA8q4YMECbr/9doqKirj00ktJS0tj6dKlgHiBjxw5Qnl5\nOR9++CGffPKJr4eoQ8kSGRnJn/70Jx577DFmzpzJqFGj6NGjB3369PHll5aWxrXXXkvPnj2Ji4uj\nb9++Nfg1a9aM119/nWuuuYbKykr69u3LpEmTbOvPrBeAM888kzFjxpCSkkKHDh3o1asXAF9//TWv\nvvoqGzZsoGXLllx00UXMnDmTzMxMH4/IyEheeuklLr30Ulq0aMGFF17IsWPHAHj44Ye544476NGj\nB9XV1ZxzzjksWrTI9nm4XC7y8/O5+eabfb33xx9/vIb8v//97xk+fDgJCQm+sfIxY8awZcsW30Su\nif79+7Nx40aGDRsGWGPMID4I//znP33y2NUPwKRJk+jUqRN5eXkkJiaSnZ0dcrPAMARc3rr+84XR\n4Pjwww95++23eeeddxpalDBOEYwaNYqpU6cycOBA2/isrCzmzZtXY0K0vqiurqZXr15s3LiRJk3C\n/btQIzyU8QvDn//8Z6ZPn87999/f0KKEcQrg0KFDdO7cmRYtWjgqZRCLenbv3u1bYHKiWLx4MVdf\nfXVYKZ8khHvMYYQRRhinGMI95jDCCCOMUwxhxRxGGGGEcYohrJjDCCOMME4xhBVzGGGEEcYphrBi\nDiOMMMI4xRBWzGGEEUYYpxjCijmMMMII4xRDWDGHEUYYYdigqqqKtLQ037Lz4uJihgwZQqdOnRg6\ndCiHDh06aXmHFXMYYYQRhg1mzZpF165dffuFPP744wwZMoSvv/6aQYMG2e5jEiqEFXMYYYQRhoG8\nvDyWLFnChAkTfDsBLlq0iLFjxwJiv++FCxeetPzDijmMMMIIw8Cdd97J3//+dxo1slRkYWEh8fHx\nAMTHx1NYWHjS8g8r5jDCCCMMDYsXLyYuLo60tDTHvcWdttENFX6VW0PFxXXjxx93NLQYYYQRxglg\nwIABZGVl1Tt9c5eLstrJiIqK8tt17/PPP2fRokUsWbKEsrIySkpKuOmmm4iPj6egoIB27drx/fff\nExcXV2/ZasOvcnc58SW7TlxtL4eiTGAU0BvYBOQDl0EKsP0gsA7aytM5iuQpD23bQBGSZpGg56B/\nOCp9G3++g4HlQFtDsCJFK/kAJGTCFiWbRFugaJMISwEKlN8t85d82iqezwK3aXLPBvoKejxSrnwg\nQWawGYgHzF8xPWwUDO4Nk4CrAX4PjJRpFS02PBoaWUCG5rcrpwmdRrmNuiDbhqYXoj7UXcVh5GnK\nEA98BnSW7gTE89H5qzCke7ONHMHA6TkrvmC1DSWDzD/lMtieCWwAzrORa7K8bzJ45Ms4+S6ltIHt\nSH8bYDakyLTbF8Hgy2D5Ipm+N+IZLgH+XucjwnS4XC5mBkH3EM6n7qxevZonnniCjz76iHvvvZc2\nbdpw33338fjjj3Po0KGTNgH4Kx7KqICUVkTuKQZigF6QBET1BmLhDui1bS1QCtddRuSeYkGb1AaS\n2nDHj4/BE/DStpsg6jJ6edfyV+9M/vrjnVbawcCuNgz1fij4Mwrmwh2fPsYd3sd46ceb4B/Q68e1\ngl9UG8727oI7JP/W0Hh4KdBL8FiO+J6UIfnlwXYvdAGSegM7hZs3ABlOqSjfHUJuEVYI7IGoNsBH\nkiZWXntk/RTKetGhvcBRvWGckmUeUIylfFS+tSkIk399aUy6QGmaGf5AMsbIq7sNvXYyx/LekDQZ\n8cAHI+oxBlEHgyHpMiAZmCB5yWfio9dP+VDpOsk03SHqMsQXcLDg0X+yyOMOeaeXTBev5R0j89PL\noa5kyStZ5p2s0SHznCzknnuZLPNmKXsMvrbiQfI5JsMLZZws4x2I9soemU+8vBdCFLKcy2H7WkQb\nWi7eQUoF7zIEv7bIMpYCecCPgP35lHVFRBBXbVBDFtOmTePTTz+lU6dOrFy5kmnTpoVERts8f709\n5ssRWmoQ1hdeIcEIM3sOaH47eIB+NvEeze22yVPnq2hzgT8a+ZnyKd4mTxVmxpl+PW9dBhDlWEeN\nHlqfIUJXTAA4DtyKqEvFHy1vOwSKM+l0uU8UWYgviqeOMph0Zlht/rrwBv+efbC8GgpZ+P+FnGx4\n5LX6hHvMTwZBdxd1P7z3ZKNBFHNZWRkDBgzgp59+ory8nMsvv5zHHnuMzMxMXnnlFU4//XQAHnvs\nMYYPH14j/bJly7jjjjuoqqpiwoQJ3HfffX7xQjEPQDR4dwBJYhE9wYaEByGjOlpeyROMbCaNU5pY\nzV1sk5cNXJngXSTlK8b6Da1NBru4QHI6ueuDWKyhBQU3VhnMvHCQS68vNDo9jT58YabVad2GTB55\n342oT7t0Zh3UVn+6jCac+NvxNHkoGo8oh8sF3luBF2zyCSU8hEoxPx8E3R8IK2Yfjh8/TosWLais\nrKR///488cQTrFixgujoaKZOneqYrqqqis6dO7N8+XISEhI477zzePvtt/0OM61dMaveYTqwXgvX\n/Xa9VjO9XbiOfOBKYEEt/PS0ulzqbsdXl8MuPkGm/0CGpSN+ExOxypgu6T6oKV/eNOgTCQVbNfq6\n1kcooJfR/MvRyx5INqd4k7eqI512tJFe1SFYz0ZPm2jQ6G6MMPWMdXnWGzzyZJweVlvZ9Tx1nmaZ\nQbwf67Q46X94BDxSghjCKKHm38I6YASw1cjbjdXZUGkV1kG7EWLOxBeuD0spXsWIXvqME1bMLwdB\nN5GwYq6B48ePM2DAAObMmcN7771HVFQUd911lyP9F198wYwZM1i2bBlgnSKsj/cIxTxd+px6Yd2B\nbScg+SjE+K0TnHpnwfRUTD4EoImFLrfBrmeB3wCLscqWKUZzdsE53v/QliKyv7kIClwQ7+XepL9Q\nSBxvzJoskuUBu54BbicTF829U7jv/mchD1q9XMDh5uug9VVwaJMse3esl3xbLWVR46weeTcVixpS\nUdAVsc7P7rnZ9bqdep5O8pk0teVrR2eXt3KrcWzFQ9UdWGXV6UxlW6ylsevVq3jzOdTW+9efnRa+\n5zbOOXcHe6d1gzRJ9m+ZZCFCz6u59DygD7BRhiu3Ci/Q3Pq3pgAxn6ywEf/vz+OuE1bMrwdBdzOn\nnmJuMHM5dcruN998w+TJk+nWrRvvvfcezz77LP/85z/p06cPTz75JK1bt/ZLl5+fz5lnnunzJyYm\nsn79epM94un2QvyovA+4ZJje+EcASxEzyB6sFrEMWk+Hw+sBN3hng2sEePOA/sBaSRcr7+plS9Hi\ngda3wyEp22np8N9nsJTR7fKuZsHXi3xJwWqdSnmp3k42oBrQf4HTgHTYtQC4FlrHw6HvJL02w74K\n9mZ1o/OAD+h7zmdkbxgAC138361/Ftnsl9ntKpC8C0isvoEJ7wilzNxCDi9uJ/geel/S6C9/guZW\n4apuFT7CevlHyDpTz6IYMdmjKxddESnok3RKBqVYFIqNu06j56fiTCXtNBywDdFOZgPDpVx2itqO\np93HRPfbzWuYH28lgy5/OqKOY23SxuL/jFyItqXyTUCYSujPTuOZNIO9XTJh1wxR3tbpsi27gXjY\ntR42plvtexfWffkyRMeoUIbHA+9Ld6LM432gP6yQFiLeQnzvDYXAD4QCzUPC5edHg1llNGrUiNzc\nXPLy8vjss8/Iyspi8uTJfPvtt+Tm5nLGGWfY9pyDN+reD/wo5yy2IX6TEhC/Tkp5qd/I2UAedLkK\notKBSWIYrWU6tFQNB5Hmxnigv7ynI3p60YiG2B+iZHzUVWLiLEP+4i4AuBYyrtLyLYQu8cBTiAY/\nHFDx2xDK6iroko7oTfaVYQmS9lrB+4nRQLycyL5K0hbjM4saCMyApU+NJvuzAeLf7QVgogtedcGL\niBeNt2S6t2jrKhLhc6WVwiFEXmyTdadeZKV01C+pCteVMg5xMVjKRoXpCmsb/gpqG/49zgTEszQV\nNlpYsQ1PUx4ddhYf18rw2dK/DP8yj5C8isEVSNHrvHWZt+GvICuxrEVGINpDpXR/J+kSEHWmFHWM\nkVexxgtEAzY/DnovUcm21HLvKpQ0bqmAVVc3E1intYl1WH876xBt832Eol2L6HRs02TPRLShN8H7\nPrQEy4QvEWGVEZp1CKGwymgINPgCk1atWnHppZeyceNGMjIyfOETJkzw7eqkIyEhgf379/v8+/fv\nJzHRHMMD+AnYDllXI2x3VC9NYSmWMpgAvAK7vsM39nVdMrBTpksG1kHUVJi7HvDAXLB6tFMRjQ04\nChADR6fCE+vxNdiMPJFHlmz0SemwJx52zZM8KiStkknlnwm7YrBeRLAUVDJEXQt3Z4oyHJ0v4/sJ\nGaOAdsBCOLvzLubyW/p/shn3kZ0cPNaGuS1v5C88zOZ7+gPp8EI6HJ0H9OPy3LukRUa8NSmfVQlR\nmXB0vZRPvWi6wlHuBCm/jkxgvSy7rEdfb1av73X4j0Gqsc5+1FTg8tn5QYWZvPR6VbxNOXVahdk2\nvNQfgfFn4DX/FGKw/qp03nY9aFV3qpyV+CnKGh+0ZI2PWV9mWZMR7VXFKYWty6bSKhqPvL8JjJHl\n/06WOcHgMwars5Mp24lS5Ouw6lrJ6JFpkO0JYAvwEsKOrpxQ4FRVvLWhQXrMRUVFvi3zSktL+fTT\nT0lLS6OgoMBHs2DBArp3r9kT6tOnD7t378bj8VBeXs68efO47LLLHHJqifh9c2M1ULcW/1vpVy+2\n/uIo+ljpLoGjmYiXo1SGHZFpMyWtC/FSdQfmSNpbJV89jxLYM0fS7JTXKzLuXilXqbyrNKaSQ9Ac\nnSPzfEXKWiLzHQV3A/+AFZ1/wyUsof/Zm1k0HC5hCR+2vJzL/98n/J17hQLPAFoj0lGKK98rOjtd\nEO9bBkAvOPoplm2t+l0eJcvslvnHSvn7GfLOAdKlKXW6RodGrysGsHqWeq9ah6mU3VrYUmoq2p3A\nDZqsdvVq8nPb8Fpq3Ptpfhfi2anyLMVqd2ad6OiOfzmVbGad3CrvpfjDrcXp6ZW7O1ab6oWoh0Af\nJT3/5YjnrGR5BWFG2Qu4U8bPweqgfIrPjplSrLpW7WOUjHtFhsci1NH1QAesHvSJoUkQ16mIBpn8\n27ZtG2PHjqW6uprq6mpuuukm7rnnHn73u9+Rm5uLy+WiQ4cOvPjii8THx3PgwAEmTpzIv/8tZh+W\nLl3qM5e75ZZbuP/++/0L5WeVoQ0bOCK+lvhgaM3w0YhewWYsywwQDdmNZS3RC/9VX3VBPGIszuER\nPpdJqwkFHPrXGRy7qRF/j6wGoNSbyd/2Zwqz5H+BC694n1KBxxcB/WBEG8G2neTVDnhcruRS46ht\n20DRIuBsoCeiZzkGsRJxtCyjqhdl3QAM7yFGA5iN/6RfoZZO0X+ghWHDt66wS+eiZh3qedbGT63M\nq4tMU4ADMo9e+JveKb/iZ7afzTL9uzJsjJT/ORseTuUw87DBu9PhmhnSo/hMMfLBhkc8vr828rF6\n25txhnwvpnWHx28mVOZyq4KgG8ipN/nX4FYZJwNCMc+SPn3cTTVGO8sIOwsKO5gz705WAPrLVpvV\nQKAZft2ty+/Gfzmwcd8znQvOXcXn+weReRY82AoePSy4Ta2MIOb6CjLfhcw/wm+eW8EXN10sZs3v\nkC/Y4HihjK/AmoVfjFxaWygnGqXbz+zLnIjVzbMSgXixmAxguZr4VFYedmW1qzOn+sKGLtBzVnVo\nxp0oauMVTLyb+ssWDL35MTDafetM+XwXUXPZebAyKAQju1lmCIW53NrayejPqaeYT9WefAjwAeJB\nd0SM34IYS4tADEGA9XuZjzUapRpRhEwXgVAqHiO+WOMVYZOu2HBjpD9ihKl81Pib4gvWUtttUuZ8\nza3GH9VY42YgAu91jXh3w0jYK0KVUgaI+UAoZYCDL8DM5x5i0N2fC/OlK+KF2dJ1kjgJMZzRDjHk\ncT7wZbQY2lgMYtIxGYiGJi2gUo0lKgsBJTvQRCr7JKQta7RogZWqLG6ZZh01J+kysBaK2L3oqg71\n53vEhkZ368/oiOY2YReutw8zzszXTBdIUal4s30Eoq8w/Ca9OdJqtkmbPA7NkQ63vNdFKSt+boK3\nb9efq4dQrYT8pSq4X/FeGQoVhrtCC/PIqwJrAs5MZ/eimvwSjDDFu7a0OsxFIkqeCkNOD/75ejR6\nt8+dvyGWa3Yvhk9sss61nPlVcPHuL2jU7hiNUo+JuZx2QCo0Gin9qTJsOHJivoXlT5Vl6dNCzgPF\nSdnUXZO3Hdal5oza6WX3+NP7IYvaX1bz+Qaqfz2NnjYQjVO6YOiDidPjzfYQLD8neezafiB4pAxZ\nQcphwh1Anp8Pv1SrjP8BxRwsPPWMCyY+2PzVFSzPdQa95f6MC+H/YOlfa6bK1MLWAcyBW+NfpGv8\nDjGcMRIG9F7GhfFrOL33Pk6/dB+N+hwTce0Qd4WRAG5rcYCvl+RGvNjaCrM8Lb3ikaqXw4MwCVR8\nFPoZ/oaG+yTzdhO8YrZLf6J0Kq4f1sS2GzExHUw68N9PpTZ6dy109UfzIC4TZWVlpKenk5qaSteu\nXf3msJ599lmSk5NJSUmpsRVEKNFgPX23201MTAyNGzcmIiKC7OzskO2V4Q/1q19ihJUYdyeaukBP\n4+QONr2dnKbJkwqvaTJ2/dwPYQCsN40WDMQC7IMz2U97DrD9EJAo/G0pohk/8RWdORIZRdmhlhAp\n4olELBg4BES1EMzyvIjf0WQRdlQNy0hLhCh5zUX2vDfDrv5YplRqVVsM4pVRz6W5Fn4iz8juOdcH\nnhNMbwclm+Ktl78u8npqpQhMJ59ZVCYc9Yphpz2K/v/qyLM2WTzGvT7vXGDUR8FFRkayatUqvy0j\n1q5dS0VFBYsWLWLr1q1ERETw448/hlRWHQ3WY3a5XGRlZZGTk0N2drYvbOrUqeTk5JCTk2OrlKuq\nqpgyZQrLli1jx44dvP322+zcGcjkyTQ1QvOXBEFTFzgp+fo2NlPOndjzqql9L7nxfTGaUAt2AsRD\nW4poTJVQuu2gKzsooi1FtKHwsMaoCaJ3XICgXWtOmsiJvqN54k6EDMu2SAqQPeYIOdaspaux90cJ\n1g+n0zOKIXjU9izqwqu+MPOIMdwxWGOzprwxxr023oFoTRpNMR59iuDHh0OF0CplqP9QRosWorNR\nXl5OVVUVp512Gi+88AL3338/EREilepAngw06Ni43UxobbOj2dnZJCUl4Xa7Abjuuuv48MMP/TYx\nEsiQ90CTNCbUY9Lpg5n40Wl0RRLM+JrOozTI/BSc6GHpltHwdhDZA+yE3/A573CtsJgogMtYRBJ7\nKKcp5a3EHsfby2KFrXNrxB66bYEyuRLzSyVDKWIAOV7eY6U7XqwbKEOYlg8H/tFLuL/sJdOuwxor\n92DZOe+UdzeWstDLrNe5GYfGT9GZk2UVmrvEJk6/63nY8dLjVb56XAX+z00vkzIdVB8mUzEq+fS7\nLrviraB4l2o0dqgwaCok/3jYk4WwfV6H9dF0S1oP/sMuSt4ESe+WNDcAn2txijbBuAOuBGm5uA5Y\n7SBv8Kjvkmy7LSO+/vprPvvsMx544AEiIyN54okn6NOnT+3M6oEGU8wul4vBgwfTuHFjbr31ViZO\nnAgQwr0ysvAfu6rLRJDuDmbiJ5gJmNryDGbCqA757ELsb26DDKwpnbEAV8IRoln5zaXwDpAK3+Lm\n31zCRvqwd1436OMVv7RZWBYaBYhf3cVg7QwWLd2JiBUqbnyz7ZXArngh2y6ZZldvxJai+VgKQfFC\nC9PvCrpZmF1dKJOtEs1vWiOYz9zO1C5auhWtaVKpaKMN3h4jfhJiLbzKRymkLggrlCwZHo1VH3p6\nUz4Fu7xHuDwQAAAgAElEQVRVuaMNOpVOU4a2O/gpK4ksxGKQsQjLjASE3Xcc1gb8SL/qmcdD647S\n3A6ESWWGdHsRtvcdpb+jjO8oPviHAD6AZh6xePcEERGMhrPZk19tGXH48GGGDRtGVlYWlZWV/Pe/\n/+XLL79kw4YNjBkzhr179564kDZoMMW8bt06zjjjDH788UeGDBlCly5dmDx5Mn/+858BePjhh7nr\nrrt49dVX/dIFv1fGOYhtsa7AWjoM9tslml9xN/49Fwx6O39fLX225tf5JjikNWXLt0lvwuTlL+vQ\naz8U7/G71ECW5o4AiIRKGhPZ9r+UDY6FAhj5yUq2De3BNroTObyYsoJYq7ebiGjMZQjdc8iL1aP1\nyHscYlHCOvyUXx5iwm+5THPIi9W7Lqbm8UWq910s3foyY6UYncaeTSUczKkYxcbddAfyO5m1qfAX\njDAVHu8QbpefU17B2jkHKp8eFoO1N8hHBN5J0QaHAkXqz9AujQd+8tQtPwc0sdFwa6pgbXVw6fUt\nIxITExk9ejQA5513Ho0aNeLgwYO0aWO3T/mJocHGmM844wxAjNNceeWVZGdnExcX5zt9dsKECb6x\nZx1B75XR+BvgX4jzCeYhNgzqj/hyF8pLLcpUfje07o+wgS7Urs3yKjSus2X6fjLeDa37aWF6PorP\ncnlvYpO/4ne2kV8TxLLXO2VciSGHWlqr/Ds5gwO16qHmQOIAIAUO0pYmTarA7RVnGm6Eg7Rh8zf9\nKMuNFSZ2RaKIFCD8BxGd4gwXoueTL/NXY8o/SL8aZ84Xe4msLUSsZNss6ToiVofFauVQS9Wb4L80\nWC3f1VFihOn+7ka4gskjEExa6XfZbZ40QnNPCpJ/bcvCGwIl2G8OFQo4ldeD6DbkEqoJ1ojGNa+L\nm8KfI63LhNOWEVdccQUrV64E4Ouvv6a8vPykKGVooJV/x48fp6qqiujoaI4dO8bQoUOZPn06PXr0\noF07sQb46aefZsOGDbz11lt+aSsrK+ncuTMrVqygffv29O3b12Gj/JuBM7B+t/RxPI/mVmNh4D/G\nCc6Nw+yhmj1vOzq3DT+V7l7ERjF2cXrvUfnVuX1JBl+L7gfvTD5zHQ1qx+nMG4H2MPtvY/mazqxi\nIA+7LqCb92z+wp85SBs+O3whZQtjrR1IX0CYyi0G3vPifMzVOojsb3nLFC3AfIRCdmPtUNYP/zFK\nFbZOpilFfFLMfSJ+adBHP+2esRv/Ou2HdSRZPxt+5viuojfbqUejVXWp3EquUmA6XO2C9zKDLpE9\n6vOsPIRqSbY3CL3pOug/t+W0ZURFRQXjx48nNzeXpk2b8uSTT/ptvBZKNMhQRmFhIVdeeSUgFO1v\nf/tbhg4dartXBuC3V0aTJk147rnnGDZsmG+vjJoTfyD+i3pI93eIniaIB678b+E/xpiANeyhp9H9\nZrhKZwfF72zERIZKp8Iq5V3tR5BkxO/R5KnQ4hSdXh59cupsTl95lKuGwja7BSYaYkFYSByANVxE\nIXEUEof4b8hgB10pJI6yvFihhFNlwo2IseaNYHXNPfKuJm1kGcu+hSYdoPJbrQwglnGv09ImyLT9\ntLBS7a7m0ZVbr5dgJnftkVldSmajn3vnXk1ZXX2joQD3YH18zbvpdoKqY7MN95PXd9Q8JUWHB957\nQ/MruzlzQjQJ/zZqtUERXknNZwX2z0ufnAzRz3zjuifp3r07mzfXXOkYERHBv/71rxAIVTt+xXtl\nvINl81ubuZDeYzFthM20epg+abLToA3WlMvMozbbZ9M+2uxtCX6Rh8ZR+m0bMtMC5z49FlwrhLt5\nh4Ni2CIPvENcXBL3Pku/Gm2Zx+Uh/jLzpL8dsEc1n/lYPVu9t2aOw6PFzafmn0TN8XL/utXtus36\nOFGE3o62fnmY9usNIY8K1zd4CiSPXdyJyn/ie2V42wdBd+DU2yvjV6yYnc78S0dstKMmXMydtfTw\ndITSUJvtFGo0Kt7OIgSDzrzrfHU6u7TB8DPlBoZn4lkax+sueyP4BGBiB+A+eOrWyUxdMBvXZq/o\nPS+GTS93pfeHOyylvBG/pdzCcqKHvKtfZHA+yRusendr9IF26rOrc50GGzqThxPvQKjvznVhhAYe\nQjaUcVYQdPtOPcX8K1+S3Rb/3lcC1m+b026sajIuAaFIFI3+oiq3nVLWrS8Un0LNr9LZ8dPTq7QY\ndHb8lFvzLyvh7G+FUs7sYAUrm5ZEoOQAcAC+orOYpysA+pRBAazhQhulXII4WaIEUS8lCKWcJ/0D\nsOo3DzGxVyjd66XsanJT1b8qo1lvenn1MqP57eqBAGGBwutKYwenIa1TFYGG4H4laBbEdQriV9xj\nvgdxPPwE/M3YTLM1sP3tbtsDirbiP1yh05vplXmbTtsDsel5Xy1vDJ76vT1ij167fOzM7/Rhg/OA\nDRr/BFyeaKqXNWPi75/h6Z/uYGezroBQxD8Qx06S+cx1IV//ORXXLeV43bvA1QO8B+HhNsJCKg8o\nOqjlrS8cUHezJ+vUizVp7KD/hYSy51pXXna99dp65k7x1DHvYOUKNb/a/iJBPPP1WH99ejhY7UF/\njoH+LO3y9CCOl1py4j1mu+knk25nuMcMwFdffUVaWprvatWqFbNmzSIzM5PExERfuDoJ28SyZcvo\n0qULHTt25G9/+5tDLtmI7t58hPmbsqdV7vnaXYWBb0Odoq1YM9gfyPt8/H/b18k4j4zzaBeI3/y+\nMm4EluXBfM2N9IMwOlYfDmUh4pFy62nWYx3No8p1AGtHug9geBu8G5viGl5OsmsnL0XeynnZ28EF\nN+17G1xwlet92lAMFeCd1FSI4N0qePZETPT1QWyIn9JDk61C5p2A+DDEa1chYu9eBT0OhG1zP0nT\ny4ZWf4EDKSDFr1cAGh3BKjNTUSi76tqGlgLlodPE28TH24THYx0WoMcl4F92M63ptuOt0poy638h\no4Hb5D0BcRDtZOnuhTVZK4+HogL/D6qi64U1yadk6SV5K7rJMh9VngsJ2dL4X+gRJg3eY66uriYh\nIYHs7Gxee+01oqOjmTp1qiN9VVUVnTt3Zvny5SQkJHDeeec5mMsNBMbLEDXzrKwdnGai6wI1ww2W\nggVrAuxsg07lp8uioFt72FmDmDTgX5Z1NXk0eRDvjS4y54h1W4GWB8R7xzI57Q1cd3iZMvb/ePHg\nJHLapJF2MAeAikz5kigTOTW8MRJYWCHzz0McWqovzFHDHAbcN4JnN8JEULcw0ctilh/8Z/11y4C6\noP7WG7XzCAXvMEI6xhzEimnXxlOvx9zg34vly5eTlJTEmWeeidfrDeFeGX9EKAalKBOwltaqS53w\nrC+xtVuSq1TbSMQorQexjFYtd+2C9au/VYbvwVpem6Xx8SBsO4fjb39cgbXsdg/WGXrNEYrqc42v\nQnPEKg+1pBcZPxKug8ten8fiB6/iu3Nf5LUDf8S1FBgB57dfxcdVQznYuA1D+ZRvnklhac6lcBo8\nt+Je2Ajdb92D987N0Lm3PC1Z2hwvBKGhJ8FCZW51EGEvPlvW91bEUScpWj2oOk0Az/tYv77FWlxz\nrR76YX1O9IUO+cBvELZ7FTLubOlXMJdM66jAfzk0WAfC2i3ZtoOufFUbUjLma+VRMHl2p+ZwmL68\n20meQPLVJrser2Sua3r1TJzeG11u9XHW6VSdBypDAtaZgCe+V0bDa7j6ocHFfuedd7j++usB8YUL\n3V4Zz+K3T4NtY8gPEKe/KOvk3Xz5txl+nU8v/I8GciMataLbZpNOT79No3FaJuIUvpgv/jWBr+jM\ne32upemNUD4X/ipPMfmy40CydgMUsLNVd7oc2s6ijWNwJXoZ+8/ZvPH+ZDpctYO9G3sLvbsxHjbe\nBoc2Ab2B6YjjoFTvX42tuzX3afgrH1UHmxEvXT7+ChuD3q6urPJZafR60uvSTc3n4dFkAP9615+X\n4hUoTqVV5bB7FqaCVnzslLJOZ9aNktltQ2vC/CCo9Apug06PMzD4dlieqfFQcuVjDYWYJpHm0JI6\n6T4fMdas/zk6Wdq8CHzhLFddUA875lMBDaqYy8vL+eijj3zjxKHdK0PBjfMKPv0lBuvoIj2N09c9\nxkiv5+HGepEUzxj8e4l6nJ28ukx28Tr0lXHC/y253HB4PhEvA7mwSzta6uBeqw8fexiG8TF8CySJ\nfZg5BJ5Ct1g+3R+xVmcXcChGGwXqLTlEY/Vsk7EmB/XhDCWvGjcsxtpjWfn7YT+xaFdexUuFKxqd\nn1mvdsrYLh6b+EBxTu3DLh9TBieeZriKC5TeiY9ZF3bxDlg+Q6NxSmfWjYnNDu5A8BCyPa8bvOtZ\nPzSo2EuXLqV3796+fU3j4qx9fydMmMCoUaNqpAl6rwwOIornQWiYzljrieUYZmpXyF2K0DT98DvJ\nOTUGcpWR/1KsMdwRCJOxrpKwRKYfjWUlgQzrqsV31dLtQCixI/gb4avexGjgKUQPY5xYyFGgy6AW\naiDzHIJQhIm+sBvaL+S3I714C1ziFOxRCF16KfzlMsSkXh78JRG8jY4wm+HgzWRmoxvB+zLVIyeK\njulCJb9cKZaXhf3iESULOL9YHoPOKa3d3YlXbbbkoYDq6ZnltbPUSZd3vWcINWVUPM2Pqt0CG723\nqQ+/6HMlulvnkUjNw3JNt55OyXYWsE94U0cIc8lUxPxCQQnghXat5H7aOwRdu65QsEPmGWOFA76h\nMD8ayaMPsHgpYghsnziEoTGOuyPWCTZ7YfwS0KCTf9dddx0jRoxg7NixAHz//fe+zY1OfK+MKxGN\nYzDOjV1HghFuvnRmQzfN6JR7D2JCS//NB0uBmPSmHCYUjb5HhH63owHvvdMAmPm3u3go7Uk25Vr9\nWn0ycBQQ6T2HOH4g7pojZL2bzo3MJe9vHYX4kxAWhwBfZoE7Q7yMqcCX32JN2IFQMvO0elLlT7Dx\n7yHwfhF2CkPBbu+F5jbhdmF2CJbufxVmO1MotaFxCjPbbqB0akI5BJN/lwRBtyQ8+efDsWPHWL58\nOS+//LIv7L777gvhXhnFiEmieIQSMF88NZmhfrXj5V2NkSm74XUyrRr/isMar1R38DchKkUMFozR\n0lVovFXPWk1Kuqn5+75O46XG9WKNOIV4rXxuABqNqeYfvW8lvtFTbPVaZ3CnAz0mQG9lwXUPPMy1\n/EA8pMDAGV/i3eTi9x/O4qVNf4L3EHN4BQAZsrgl8CUIO3HdEuENRK/eg7X5uipzBZaplKovtYzb\ng3hG+oufpZXP7FWaUOnUMJd6yYJVtieilPUly6HGyeJdG19TAat258F+PsDu+ZgdHVXHsTgrd4Xa\nOit1wC90KKPBzeVOBkSPeTr2K5jMhR2qBwz+vWK730I7PmaYDnMBiQrTfy/X28Tbue38TjSwhN+T\nBzT3XsUe1/uMwbKWNlNP7ABz917FTR++h7eHC1exV1hfFCAMUTIlce4OeKirOMlK7SwHcpgF+cu7\nFH+TQbvNcsy/CYBr8P06++rmN1i248H8XYRxUpCaKZ7rQyNg5g78TzOp6zOpi6lqCPbKGB0E3Qf+\nPeaysjIGDBjATz/9RHl5OZdffjmPPfYY99xzD4sXL6Zp06ace+65vP7667Rq1are8gXCr3hJ9gZE\nA6rEshRQjci8g+jNmTS6O9GBjxmmo1K7K+P6SqwPgcdGDuWOpyZPfYNl1RM3aYQsA1oKV1uKbKl0\nHP8B3uMqMZb9A9YmRRslge9k7EThbidpKtHO7EvQ7qpHv1re9XpQ7nytDPHAZ4j6UPtpeBBKXdHp\n9WLWwcnAyeT9C0NuJrAeZmZifSihfh/KYJSyB/8/phNAPZZkq8NYc3Nz2bp1K6tWrWLt2rUMHTqU\n//znP2zZsoVOnTrx2GOPhUZGG/yKFbOaOVDmOHa9XrCUZBObMDs6O6gVcSb0vRz0SyHQf1Zt+z8E\nXsnWQlggigNWcd4zPx1okQyHOE1shK+UbYEUrwARXiDl3a6FFR0HjuPb+6KJKtPZUr4kah5IEIG1\ngESVoYlGi5ZW7aWhFqEk1KkOAkN/ZoGeXaD09ckzVAglLxP9HMLrahFVG+4NMT8b1HPln3kYa2xs\nLEOGDKFRI6Ey09PTycs70UVqzvgVK2b1KYyR12WW25WpxamFAbEGve7W6XSosKMQPdEKjs4MQKvz\n7hFcPq5MgyZGi+xupBFx57+8isjqPzF09Rpur44kt/oOMl+DzNfgrOrrycyD26sjebr6eS7d8B6r\nLx4O10FMaqHYZmRxofi2TQK+Av4NsE2sLSkohI3rIboF0ALfaSMb1wPLENYm26zLNRHLzrdE0ujI\n1+JV+Uok3yOIHniMpJNldY0w6hIbt0mnxbt6ELjnFyPTqjRaHbtGSLmCgZ63mU/9TghxZUz38XJF\nT68Xj8AZ9HCIUAuqYhzia4sz4l3BHONwgmgcxGWD6upqUlNTiY+PZ+DAgXTt2tUv/rXXXuOSS4KY\nWawnGkQxz5o1i+7du5OSksKsWbMAQrxPBlgnOSYgXvI5+A7z9K6VcSVYfcl4LSxBc5cYdGDNJKuw\nw3BkrRV9JFM69ElJ1Qh13h5DxhKslX2axYJ3niFLicZ7G/6rAYXp3Xheo79rDc1TDxJ7TxlXuhaw\nfjysHw/j//M2TIPY35XR2nWIC/hCFKUdXNDyCzjiBddu2LVWmBsd8YI3DzE04UVMgCbAkfmIs6Uq\nsSbvKoyrBLyZMq45QqHp5n6qnOdhrfxTVhvxsjzNtXqTde5datSlgtGT9KPT4r1LtTC7yeMKjUat\naGvuwDMQn4QA8RpPP+hhycYdvFnWbIH3iLI1ro2PXbzDDj/e2fbhvnoucYivLc6I93sGJwk2PeSs\nHyBzi3XZQR3GmpeXx2effUZWVpYv7tFHH6Vp06bccMMNJ03sn33yb/v27Vx//fVs2LCBiIgIhg8f\nzgsvvMDcuXNDsk8GOO3HrE9U6Dah5uwxNmEqrWlLeg22p53aQud5J9ZUXD7WZkQKpkmenR3tNVhH\nwteU35V3I7wYifcjF67FpXhfjOTWGbNIZid3bn6B5N6bacNB1rw4VPSGP5K2paNi4CNl261k0Sfx\nTBmdzADVBGBdzQKd3Mq2VpW5rpOidUUwE68mTJtqu7ZVWxo9XaJNnEl3gNotN+xkV9PBdwJP28hb\nV/twJ3qdv51fzzcRUodD7s2EbK+MKUHQPRfYXO6RRx6hefPm3H333cyZM4eXX36ZFStWEBl58oyk\nf3bF/N5777Fs2TJeeeUVAGbOnEmzZs04fvw4UVFR3HXXXY5pv/jiC2bMmOHrTT/++OMATJs2zY9O\nKObXHbiYdsp6Y1RKJAH/bTo9WAo+H/stOHW3mYf+UvTF/5xBUwEFowAqsDbzUfxAP5pncnVz/t9n\nd3NwMLSJh9kHxLweiLPDc6R7SmN4u/wWpux+lUZPVzP5+aeY/epUBtyyjNV/HS52mfs3wgIjbzck\ndrTEKAAqj+NvxzxfK7dZJyrcjbVzn93H0ak+7cpvulU9VBAcdNoILb8KguNj5l3XPOuDE00fDHST\numDzM+mUv77yhsAq409B0M3yV8xFRUU0adKE1q1bU1payrBhw5g+fToVFRXcddddrF69mrZt29Zb\nrmDwsw9lpKSksGbNGoqLizl+/DhLlizxreR79tln6dmzJ7fccovvlFoddvtk5Oc7KLEOHsTMbncY\nPA7LHjhWhPnOkfscy1a5UoQPHmK5x42TDMfhs89NGYJYmjFO8tL5e2TaCqwVcNqvfdsh8GymTB+L\n2MxouJZuHKQ8qKXpjhjorZD0qoFXQtsH8bexrgQeBGKZve82Ol+Uwxvlk2l0UzWbq5/hnlIXb1Xn\ncHm2l5jqSVxSncIX5Rfztut6GnWZDu/D7MZJMHEGq4cOh1bAqBli64IbAd6C/BnCnQdUzoB3W2DZ\niZfCNFkXKUPE/fRxMt6DtW3pm/i2V/XVWXetzLFaPZSK+hn3oAx/UNSfr456yTKreomX/tuwtp28\nDWHzpyav9PAKmJYpw2W+DIeUTFHvKfJZpSgalYdChXx+Zri+NafCbYLXuAdt6DVMy9Tiaq5+Dazk\nzL0qzLheWllGGXF6mFeTQZ32LeUnXqPTbdMr8NVx20xNTjt542Fcpn14KK0y6jH59/3333PxxReT\nmppKeno6o0aNYtCgQdx2220cPXqUIUOGkJaWxh/+8IfQyGiDBrFjfu2113j++edp2bIl3bp1o1mz\nZjzwwAO+r9DDDz/M999/X2OfjPfff59ly5b5FqXMnTuX9evX8+yzz/rRiR7zJcDpiN6ZamBqVYV+\nt4P5wph77tbGrxf+vTxzo5ba8reTRc/XTg6dN+LlUyajV8joVETYYoTJG9Kdh7C2YBG0vUzuRQ01\nl0Obvd9APfsExN4IZnnt6s4OwcQ5ld8pbXwQtAHqNGjUJ01d0tuVoy50dmnqw/NEYda1goeQDWU8\nEATdX8Mr/wAYP34848eLvZIfeOABzjrrLN9+GRCKfTIAvsFa1efGGjoo1NxOqIupWnObMLVJjycA\nn2Abt5mXxyFOlwXYPge2yyGX7frQghv7VYZSyRZ9iv9mQhhuXX63dOsyKfpijc6JPlAdqDg9bwW7\nOjfzCsQzEG1tdRwIbmqe6FIXBJveLIdKZ8Jp8u9ETDGd4pQMTrLYwaxrj7wOySsE+IWu/GsQsX/4\n4Qfi4uLYt28fCxYsYP369X77ZCxYsIDu3WuaEvXp04fdu3fj8Xho37498+bN4+2333bIpT1iskgb\nEyUB6+FH4H9cuoI+3mgXp8L1cdAII071KO3GQe3ycYpXY54eLd5pPNWMzwcWaPyUvNnyvkCGqbuS\nWZ+EVLxVGZ3KYld+bOgCxTn9ntvlrYfp6d1YdaX4ubU8TRo9re6v7bk5tY3a6sl8ljqdmd7kof+h\n6GkisJSbOZar83OSzRxfV7x0BHoXdBmcno0+bq9D/+OKQLyrbmA/YrvD7zhhhBVz8Lj66qs5ePAg\nERERPP/888TExDBlypQQ7pMBUC3vzbGOgte3LtQbibKtLMHfDrNEiy8x7sVGmOKp/MVGHirO5Kvi\ndDlVWIUms3Krno+ib27QqnHpbUZZPDL8Oy294het+RV0+fXeVoUWrurALKNejhJNHo8MdyqvHVS4\nnk6hxIhT8jfHX8YKg0Z/Zio9Br2ZvymDWUZFq8LszNM8RpyeToWbdaLCijW3om1uk17nrbv151Lh\nkFbJZ0J/rhg89Pagy4dG69HcZnsxw2OAKqz39wTxC1XMv/K9MkzovVw9zM4ywqQLBDseoYDiFch0\nKZi8gw0Pdvy4NoSyDoLhGar6r0vaYOqqru2oPnKcTB6KDzi/M6GAE78QWGU8GQTdXafeGPOvWDEP\nADohhjSa479NZiA3NvQEoKUWOj3MRDJidZuenymDnduU1czXlM2Nf29Ip7Orh0D8g8nThJ38dnI4\nyeAkh10+ppx2+TrlbaYJlIfOw05WuzZgl7eT3G5qPjNTDrswO9mc/Hb8ArUHO5pAstS3TR8AviYk\nk3+zgqD706mnmH+hHf1g0BwoxzpfzfxVLzXcsVpYqRGegLVyz+Rj8rILi0XsC20eibrTIb9iG/nU\ncICe/2R5z0Psgq9PzJhhdtYH5kSOafVh0gbDw4SdSVgh9tYPRnxr4FAm9mfU6efOqfoIpLxUvcVq\n/n6IZ2LWtQn9mCn9GUHNtqPiTJl1v+KXJMPMtgJW27CDU5sO1Mbt/HZxgepCyavno9dFbfyaO4Tr\nbmXKGiL8Qo+W+pX3mN3UboHxc8Cp8Z4orZ2Nqx1My5V4xJl9IJT3JiNe0Ttt16ncSjHnGWns8tV5\nOYXbyToP+/qoSz2Z6aDmgbsnghOR5edMV1/Eam4z32BlqQvdZkJmLvdCEHST/sd6zOPHj+ff//43\ncXFxbNsmegvvvvsumZmZ7Nq1iw0bNtCrlzBO93g8JCcn06VLFwAuuOACnn/++Ro8i4uLufbaa/nu\nu+9wu93Mnz+/xoGt/gh29ZHTqiW7uNrSmuHFDvzs0h0JkLeRLrG3WH3XDm37TYExFW9QRBuyCgfS\nNX4HOwq7khG/CoAd3q50dX3PDrpS8CpAb/FT8CJin2W13afqxRbEa3nEWzbQiqZAD1Np8L/7bfGp\nIS9e6mIZnofYYlSl+7IYexOs+iomc4IzFAiFLD9HuvpCb79mmw1WllDTBQmbbT1/CTipK/9uvvnm\nGpsRde/enQULFnDRRRfVoE9KSiInJ4ecnBxbpQxiGfaQIUP4+uuvGTRokG9Zdhh1gN3ujaHe0TGM\nME4F1HPbz4bGSRXrwgsvxOPx+IWpHnF9sWjRIlavXg3A2LFjycjIcFDOQ+Rdfd3tZn5Nm2U7e020\nONP+0+zNOuVjZ4Psxt7m0y6dm5o9xgjImyPi8jDi3cy/YKzoxW6E7SPPg1xYyUhfz7ag3TnigM0v\nj2vp8mFxR7n/BVo5dEsVjLgEG5pAli0eamwslWfUWZ6yp+6npVF17ca2Lmr8eZjPS8Hpz8aMtwsz\n+db2J1aXONOuOBhetf3J/Zxw+uOsj4xuea0+cbFOUcVbG04psb/99lvS0tJo1aoVM2fOpH///jVo\nCgsLiY8Xv73x8fEUFjpNPn0KnAucI/12xvlgvRBqBzUTEVqcnRLV4yvwN6RPQuwTYafQ82W6PQ58\ndSgFbiqafKxHmO8fPjLD8l6BUMLqJJKNiOGDXBALTvphLSzpiLWBk85zPfbjzfqYsj5+nI/9OX1n\nYx07tU4L+8645yM2RFLlVnHmogRs/LptLVqY3QfSjDPTqGeop9PvpjI6W6MPpJACyedEH6yiN8tX\nl3R6mc02Z5eHmY+d3y5PRWf3oduLWLkbAoSHMk4M7du3Z//+/eTk5PDUU09xww03cORI4M3IXS6X\nnOizQyPEXhkKemNJoGaj+c6gU7QV+CvsBKyem0KlRq/uEQglpdwJBo1Tnk5QjdbsuVba8KlgzINv\nEBLG18cAACAASURBVDGpBDLh4mGLxdjxJETYJGj34F6xr09iBjSJEHf6yR51giyfnle69KfbuNON\ncI9Mk6DxUPdK4667v5N0lVj1jCz3d4bfqcdpunXoCsBMa/d8oKZS1tPatRV9b+xAsjjJFyhdbcrV\nqdcdbC9cuWu2J+tuKmS7D4pdO43QLrDeQbs8Qoh6DGXs37+fgQMH0q1bN1JSUnjmmWcAyM7Opm/f\nvqSlpXHeeeexYcOG0MpqiH1KoGnTpjRt2hSAXr16ce6557J7927f5KBCfHw8BQUFtGvXju+//564\nuDgHjnsRZjhtEac5uxEbvIN4+HFYvVvzF1y/Y9Aot0cL88i7niZB5q/TmzDzcApD8+t5qbxryvrG\nsXG0bnOIHW26cjNz2PZgD65kAV3ZwYvDbuUq3uP9YVezc7is30TghQh4CMjsKMIKOiJ60HJVVmqM\n7GVLqAlBv8nHHYA6AVOZQakXOA4xyVdBTQVXgbWQJh2rJ66ekypjsErHKd6OXq/XYNMFK0d9FU2w\nH2u7e13TBxOu2rH5bgSiDySPxyaNh1Nhr4yIiAiefvppUlNTOXr0KL1792bIkCHce++9PPLIIwwb\nNoylS5dy7733smrVqtDIaaBBe8zmHqhVVeJ8ur1797J7927OOeecGmkuu+wy3njjDQDeeOMNrrji\niho0AkkIm8j+iIUcyvZSLckt1sLzsZa8mnd1xWhpY2TaYoNOuVVctAOv5lq+aGl0WgxaDLeSJZma\n/IuJPAYtOE4fNtKHjZzJPm7inwzjY3qziTRy6c0mUU0ZwHVAlKy2KKDAK9yRQGSMuKKkP0mji9TS\nJSHliTauZE3WaE12vSzNga0Gjd3z0NHcJiwQmgfhDhT2vw7VXk3b6UC0dYEb0RhTCZmZaz2OlmrX\nrh2pqakAREVFkZycTH5+PmeccQaHDx8G4NChQyQkmH8FocNJ7TFff/31rF69mqKiIs4880xmzJhB\nbGwst912G0VFRVx66aWkpaWxdOlSVq9ezfTp04mIiKBRo0a8+OKLPjO4iRMnMmnSJHr37s20adMY\nM2YMr776qs9czh6NsX6X1OGf6hetCf4brujjxBjufoixUHVg6HcavwisvSAUfYnGt5DAY9gRRpok\njcaUyfxVL8F6fKXUOGutErqzjR105Ss6E88P9D+wWdRM+0rac4B4CkX7Vz1e9Wt3PtBEDhG5JT9l\nDqf79TTKH+WCo2b58rAOY03EOlw1QsquyhMj68GN8xCAvhhBpTNh7r2g3E6LGkqpuY9DoMUY/4sI\nph5PQZzgISMej4ecnBzOP/98OnbsSP/+/bn77ruprq7miy++CI2MNnBcYFJcXLs9YaNGjWqxIW4Y\niHHnl6RPH1pAC0uXbv2IqXwHOjWptR7/YQ+oOXyhw0yj0jkNneg0djDTqQk4k08ied4baXOsmPda\nXiUUMDBk0lq4CR7udz+TeJFVDOSmTe9xeu99/JgfByMjOT1nHz/OOEtMECqb4sX42zfrdsYmFE0B\nwFIjMg/xoVPHVOnl1OvRPGqrtnoJ4+eBOYQRanoTIdgrY23N8KzNkJVj+We8br/A5OjRo2RkZPDQ\nQw9xxRVXMHjwYP74xz9y5ZVX8u677/LSSy/x6aef1lu+gLI7KeZmzZrRvn37gIkrKyv99kc+VWCt\n/Dsf8cl0yxgPNc2tTL8Zptz1SYcNjRNUz9yOrxP0PPzzzvPeRcK7xWy5pqOPuudZu+FJ+PSa/nRl\nB0W0IXXT16T03sCOwq5Uj2zJ6Rv28eOrZ8FCmSgRn9mdGk9u9MoxqjNbinjTSEMp7I0gxpv1F1Nz\nJ46DvEyHcijFnC/D9GPu1dFVuuJW59cFi0x5uQnp8t8wCE2degjZyr8vg6A7v6ZirqioYOTIkYwY\nMYI77rgDgJiYGEpKxF+D1+uldevWvqGNUMNxjDk5OZlvv/024NWmTZuTIlTooMYlPfgaS9I4/E8H\nthsjK8Qav/RI+iTh356p0Zh8dNO9Qs3vNE6sp12nuU04jaWqPPS8hfsJ7oafIJt0sknnIy6DAbDr\nmrPx4GYJl4iwXbDn8LlUb28Jh+DI4SgoAu4AdgHbwRXpFe5IEXZt/Dzx/m2XYYcQaSK1MLyI+k+C\nyCFSriSrTjug1Z8Ha3jDI8uyWSvzs/B4C3H5jqhSSIbH/Y+WtzDWNjTRu1urv0BjyUq+n3v1TSCZ\n7Mv080CT645MBxpPYBaRTulOEuphleH1ernlllvo2rWrTymDWACn1lCsXLmSTp06nVSxbfHll7V/\naoKhaXi4cW4saiObndTcYEV/OXZKunxZYyouEF83ome3XJNjp4085ktoymNOUuljer/FUlQ631Je\nOHw7Tw99gM+4iB+UNcp9T/IitwJQRFvaUgQboaxdrG/oomxxrOj1akuqvYtdfubKb7853vI0QaTt\n45+GSBeUAeRDYgfYs07Ki5BzjWKoyrROK6sae1bWLKUwba0so1kHwLQ87GE/Tp3nUvnUNj6aQODN\nhLCX54TRD6vdmPnUxfwuEOoqt9EO/2EzRhBMHmWZdcgzBKiHHfO6deuYO3cuPXr0IC0tDYC//vWv\nvPTSS/zxj3/kp59+onnz5rz00ku1cKo/HHvM6mju8ePHk5OT4xc3ffp0PxonjB8/nvj4eL/TSB5+\n+GF69uxJamoqgwYN8g2FeDwemjdvTlpaWsCDDouLixkyZAidOnVi6NChtoe2WkVTu35V4jssdM9u\nLOP5Siy700qsSacIhFlXvBa2R1xdKiSt4qkQL8MiEOZiKl+ke4/GR+0XEaHxQual5FE0lRpv0166\nVAuP1+5uyjyxrIy7gFxSqaQxrTlExZlQSWMqacwBzqCSxpCCsCjMA8oqrDNhn0MoVo+82sqrDPhS\nXpVaXKVBU6lk3yPrPN6Qt1STWa8/VQZVVyp+NUJZKeXkluF7sJTYb7VwgDewhx6u05tKbzWcn4l1\nWrQdTsbkl92KN5WPLnuwStodgF+w0NtfJcGtyqusneRkox495v79+1NdXU1ubq5vi4gRI0bQp08f\n1q9fT25uLl988YVPaZ8M1Gou9/HHHzN27FifiRqIZdHBwG6vjHvvvZctW7aQm5vLFVdcwYwZM3xx\nod8r40fNbRrGKyRocbotcL526TaZWRqN+WIoGo/k29fIR/Hx4G9cr0/q9dXClKG+OTmo4MHqJa/D\n6mHmw0bYQVfacJAfiKcNB9nRqiNVNKGKJrSV4b5ebjvEQpN2WAv62mFZYxTg/172kTSVQN5xedd4\ntVP1MQaaqHHuBKtemnSEmRky3I1f3Texe1YV/jS+cuvuN2HxOC2tXmduaj4vtxjrDoAtX9Z3GCOQ\n0qxPr7cuC078keLtFoL8wX+x0InYSf+M+IXulVGrYo6Li2PNmjW8++67/OEPf6CiIvjKvvDCCznt\ntNP8wqKjo33uo0eP+k7GDhaLFi1i7FgxzjZ27FgWLlzoQHkR8AeEiU8FTHtQhi+FpzNFGN2Fn2jg\nVi6ovgCrMUkbXF86tVhkp4xDpu+F6Jl7tLB1kk7/HfVo7lj8FM5744Rz3IPAKzJ8J5bSqUBYMkRb\naXx/Ax6ZZzSWOVN32APHaU4Se3DjIZ319Jyym0v4N9EcwY2H47Tg3gdnQOsKYeJWibjvEfeRG94V\neyLnAV3gnA3/Yfy+/wfTKqge1khsMV0GjGsBg+Gc/f+BLog0NwKth4g6iFL1UiplLIXKg2Ixi18Z\n5Z9Vpaj/173LZP2adaZvQ6kjFkZm+nz3VO8DbtPq36rzc6qvEWF5YlWX8JvnTFaQ6qrliKPBmQ4R\ngd6TQHGxDvH6B6qXTbxKWxPbXcqsS31k6qMwo7HasLo7PQcHjMu0CbTj4QZCtHCjHnbMpwKCWmDS\nqlUrPvroI04//XQGDhx4wjORDz74IGeddRZvvPEG06ZN84WrvTIyMjJYu9Z+DCv4vTKy0Pav9Idt\nJ8gV3mEtCLhc4rfeFfD3PkR5nWAeSlYH5oH9El5vuFH8/PAAM2ojCg6RQVynIGpVzKNGic3YXS4X\nM2bM4L777sPtdp9Qpo8++ij79u1j3Lhx3HnnncDJ2CsDxAkm8v+7LQgj+UrpBmvzbnEyxRdfXYy1\nUEOOqaUoWrUIQR8X3YM1Vqr4Kzo1jjqYGos//MbeYqw8pulxlTbp4rWwYpl/MsKCQY3NAvQCD1TR\nhJ9oxm/4nAO0h52QxDccoD2tOUQ5TUliD5RFiJ5vFOKdaC3q6zd8LsKTgDL4/nA7Xn1zCuyJEFYa\nreVVBqRo9G1lsdtKWVJU/ZXi+8OIagOoj6+yflDjnmKM5ADttbBijU7VUYxx96+zdNYDz2Kt1rTi\nqnxdJWGv/xs+l/VoIpOaz0FDinNU/WC0DVuoOkk2wp3WHsjwE/rG2PGu497JZXaBDuPQp9kH1xm/\n1qGMv/zlL37+UaNGsXLlypBkfsMNN/g2AmnatKlv2EPfK8OE2isDqGWvDA/wKuIl98DdeYixsRK4\ncT2i0Wdb5BmJ4jfcDwnil5wYxNDCEci4FmE3i+DlN2uvZvFL8K3mS1I75Dm9ZCUy3xjokoc1HGGu\naPNq4frpzDsNt1w9VwBruJAdJHM177GDrqxd0Yuv6AyIuCLaMPXYU5aN8lH8GusDTz4tHHLVe+ni\nNmKvjCZwyY3vC9vl84E+EHXFjyw8doXw+3aukygA3wRUlMtyk49Vt8qf6Uv2QPTTWOPKMfjZQUdl\nGnWlVqZZ9XZV9BItfqpf3Hcu/7++uQMnaj5T4dmtLpT4h3NU/aDnNdWBRtZXxrV1Yx3QJjjAx6fe\ntDrdBLFQyQ8TDL8H8aebC//9Vx3kcYa3ce3XqQhHxRwVFUV0dDTR0dHExMT43MpfX+jK9sMPP/TN\nbIZ+rww3Ys19zP9n793Dqyquxv9PIEGDJIWABEkoxwoCItcoCKjEV6FqhSpeKNbXW6nV/pT6qtX2\n2xttbb211kvVWq9v1a9aX+8X9MVqUPFBRa4qBFAOkihBEjGJBEkgvz9m1tlrz5l9zklyuPgt63n2\ns+eyZq01s2fPnr1mzRobvptgAJhD+CUuhoo7MIOCftlXqLRioBUqZhPogcVyQ2YOKwif0FEPa+5Q\nvATffdGFx90KpxhjblRMsEtRD8ICY5N5ssjYJFPAoreOpAtfMYrFvM1YGiggToyRLKErTTS+vL+Z\nKYtxy2YCvxcPEvjL6GavGBQdWc2c6hPhe1tN0w6ALvtuo3FzgYmfpspQau/2z6QRoBAa622abpd8\n4A5ThnponEMwSOYTejaN7q5Cz+DZONtpYw1O+Yo7VCSdiZwGl262YGx62hXZ5J3i49NuXI33rPM8\nwPR3jRMj8JXRrw3yRMO2fdNfeyJETuQbGxMODxg1alSSyVwm4POV8cILL1BZWUnnzp056KCDuOMO\n80K89tpr/PrXv86ir4wioAuBLeVxBJYLEN6RVqDuUdukwXQin3VETJUtcPDEB8YamzceeMzmRcni\nbveutfVwt7iWYKbbywhssuMmazPEiUEFPDD2bGrozd9rf8Svev6eODH6sd7kb8bMmBsBmmGlXbHv\nQzBIVxAM3o3QsLkANtsebdPrVpaYmfFKK9JKi08zbM4jvHBZq9pT7voZyeLUMlvHAU69xeFRpvbI\nmUDUWsXugrd2twBZht3Tvi2dM1lGS7PAuxsgo8NY2zsw7y4weuf/JXwCxxgCB/AyIGqH8GMID8Zv\nR6TpgVnKynZqASlTouho3u7AG+VToNpTRu5CU+5CT2ACXDjQTEqewtyrgAsJ+7n4G8bcTdPOHRic\nYpLb1YRzu5qJTClhvxkbLF35cVmo7lVbVB2kfWKKuWy7blZ51RhV0UOEVR4CgivmhtrsMB20BXcv\n7H7ouK+ML1q6pMX7Ru62f6/DWHcv3AUMxazOFGBm0IMJdshVEyiVB9v8emA4CfuwRNoKYDphU7lq\nAtO4YYRnyTJrFjO2FU6azBSLVJ6erQv9wSTPwoV/vVMvVLkS6D7Q6McbYcx35vH24KPhuRzG/GAe\nb394NN8oreGLqmJYmQMbupqBdHMhDBbb5q7Kz3JXY7cstsvlrVZXjNElDybYUS0/Wt2A57oamnQl\nMIsSNZjo08XFp65ToWp7CJvJ1TlpbRlo9w7KXw+Iky0fJts776FK5DQQOTA//vjjxglIaytffPEF\nTzzxROKrkpOTw7Rp06KK7iGwjcBCYqW9NwDLMQNcg70gWIQSPGxencJbpmjIDE5OcK5TeSWKrqSX\nOGUkf7kNy8JWoRNuUPkrVVx41Cl6MqhbGptXw4MD4RFY+KfD4M858A68PWAiLIEv+vQxg26FFWXz\nFqAeVtqBP7er0b70wcx8V3Y1g+9KzGAuGxRX2ns3zIx6pS2zUtEMDb6FBM6KJCwzWWkXvcApuHGV\nD+HZ796Z8F7ww1eknzHvia5LIwfmZ599NmGKdvTRR/Pss8+G8vf8gXkvhGDP+lPbC3thl8D2r6lS\nIFLq+++/v8PEzz//fJ5//nl69+7N8uXLAZg9ezZ33303++9vzuO75pprOP7444nH4wwZMiRxiva4\nceO827Lr6uqYPn0669atSyz++X1CFxAoU2Wrcpzg5GXRe8qCWQy/D2BRLcQIn9wM0f6EdX4J4S3H\nLu24J13Lp+ng3LXcMSdeDX8bCNzPjgvPhafmGtkv7Bq48SwFqlY7sts6tlj9sJxgXVUCC7salA2E\ndcmyBXshnj09vnYRWQXcremouuDBiyq/F/ZCGLa3Y2vf+vXrOfvss9m4cSM5OTlccMEFzJo1K5H/\n5z//mZ/+9Kds2rSJoqI27n7MECIH5htvvBEI+ykV1UZOTg6XXRZlYxnAeeedxyWXXMLZZ58donHZ\nZZd5y4uvjFQgvjKuvPJKrrvuOq699toIfxlNwCGYX2jtxlN+qeMExzJB2G0mDm4+weYD7WIzRuCy\nstrhIwNrjZIhhv/oKJ0m4UUOXtypn+QtsvWIO7LlY6bJNXZ3k6Vb1Wo8v1EF+5aS7OJUeE8w4X27\nwlabLyZ14uJTmgCCXVQxgkF/366wtdW2j9Q/TuAlTnhLusggCmtxrerWXcrteb+ge2HPgvYMzFFn\n/g0ZMoT169czd+5c+vfvn55QByDSluSKK67ggQceoLa2lsbGRhobG2loaEjcMwGfrwzwnxaQKWTu\nK+MHmOrp3XhNBItvUwjrMuXL10CwKFeo7vVOfpPNa1I44gtC/GQ0ESxiyb1Q0Vth04XPCpXfpK56\nxVMukVvKNSl+kp5j0lZqvBXWrni5XagTHXY9gQ67KEjfWo8ZZXPMIl83zG4/Oeevu4p3w9A8DoM7\nGFNuZA5wJPQpNXdKFR9pa11P6V86TYPUdS/sfvCZj3YUYhh75o7DV3RJe7ngO/Pvk08+AeCyyy7j\n+uuvz4psqSByYF60aBGTJ0/mhRdeYN26dYwfP55f/epX/OY3v0m4/Wwv3HrrrYwYMYIf/OAHIbed\n2fWV8VfCq7tiF/pPzOx2HnJCxv/yW2Ae9/Fbi79GlRlN4AtT0mT7sziTEf+XEN7sUWx5tBD2VCf0\nJF2Xfctemo7gaXiL1oG/VXjF7Pj7b8N4vTA4x0Pr0wZ3FUOhBa7mRGiBHPpCL9lC3owxvys2ab0K\n4Xi7Zfx44Fzgb/CNczeYTVsn2bRzbfiXzSb9XEyZkc5dXIOC5aU300j9jRytC35r27fFwQmgVXkm\nBFtXoPUuc/+w9U4TP8XEU+7e/5qC1LFx6+9D9/tbzSaZnVFn82wEfCq6jkKcYFW6YyDeFFNdKSWx\nZ/6NHTuWp59+mtLSUoYPH54V2VJB5MA8cuRIrrvuOhYvXszMmTN55plnGDp0aMYuP6PgoosuYu3a\ntSxZsoQDDjiAyy+/HNgZvjK+hDPOJaR/XGM+KN0a/z+gxsab7c9/s/2BriFsnrUI6G3SKmbbtBoH\nr5lAhaD9Laj8HKEXjyiv71aOxM4um+7s9GreaPGumG3uN+YYHmfNNnXcBGtXYyzTbgRo4QlMPNdE\nYfUwO1iuJvTBaMGoLGzSPXPONHhx2N7S2fg92BqgG9/NeYH7zz4qTwbkTTacqHtcta9uxxYzuLNI\n4fU2z0u3wcP2bp/rWtlU+qC5fetSu8YgG/kuV+WvcO5nhds2BKnyXGjLbrxHZvvDbSj7rT+aOu53\n1Y7Q/Zw/2o1Xgzo2ifLCzfYu7ZJon4h3cU0KGcpnR+dlAbbTOelaUPEVf539eeKKgsbGRk477TRu\nvvlmOnXqxB//+MeQm+JUf/61tbWReZlA2m0xn332GYsXL2bZsmWUlpYmFu3aC717904MqDNnzuTt\nt83miOz7yqiGf96ImX3GgWIYaDpOY4E91mBgDpDH2eu3AAM5ev0Wg4dd5KLOxjcCeXCMbCNGpUO0\nf9u84N6aY8tq3IEOnvCz9I+pV+nAMZp2Mfu8ZzeB/GkZAJ2v2W5wH1xGY8H+QD2HN6+HGHT6rx1A\nDc/teAk2wz07FsNmaD2jkxkwGWjlsLpf+ZGJAfvCzLceMmlHbjVbrzeb9IS+eV9gwFYTj2FGfsmz\nNAB1AkxXggMJpL032ngNne7bYcMi10YY2KDaBDpdY3dsDTQf8IOeNPFO19r7wB0hvNY/L4djltk2\nmxO+P+hu8VaQKs+FY9qAO2OZCrehnCrbqcnWscC52/TWyt95CncMOk2w7f6g23YRA9XA5dHEKv6m\nInESvjKyZMfsU10ML+/O+bP7Ji4fNDc3c+qpp3LWWWdx8skn8+GHHxKPxxkxYgQHHnggVVVVlJWV\nsXHjRm/5I444gtNPP50XXnihXarbyIH5nnvu4dvf/jZnnHEGra2t/POf/2Tu3LmMGzeuzUw0fPrp\np4nwk08+mTjdJPu+Mg4GvovZZREzSdI+zr3Vzrpb0/337WqTM5efE3flbdUzFrdukpfj3DMWZdfq\nAbzPopVQGyRwIp6jyByitbOfYVvot0aE21A2UceI+86ob5v7QkoZdGaMwFdGrG08IqA9qgzfmX/D\nhg2jpqYmcd5paWkpixYtipwYVlZW8sMf/pB//OMfDBgwgJ///OesWrUqY7kjB+Yf/vCHfPrppxQU\nFPDSSy8xc+ZMpkyZwpQpU5g6dWpGxGfMmMH48eOprKykX79+3HvvvVx11VUMHz6cESNGMG/ePP7y\nF+PB7LXXXmPEiBGMGjWK008/PclXxrvvvgvAz372M+bOncvBBx/MK6+8EvLnHIZ9gC0Ys7kB5r4c\nIB+WF9o7QD377rcFqLX+H+pNOOHJR3bl1cPcQpWunSDVk2xpIWWt850cSS9Q+bUqbYA9qFLya+C+\nwjDduajDLGtgpUxDrd+IAcK/nkk7noF9C9nSmA9/gn0nGodB/VgPrKUrTXAtZmGwHDhyeFDXS4eb\n9yKGWdArh5+MuRa6QX63LxlRsgQGwOSxTwc+NLrB5JKXzOKfLALKjsBG4ArsDLvV8llm260mkF+3\ndTdUXn3Q/vfJoucAOMgGbdqM795r4qIB62bvgsdyuFb0g8uAX2OU58C+JxANKWZ8Llzr0klxeOq1\nSld5TSr+HviJLSsGLOJoTuo80d4jx9ABURnp8/eTgLgC0H493DMsgdNS6WR3rg8NnyrDvVyQM/9e\nffXVxFF3c+aE/2hSuxuGTp06MXnyZB555BHuuusu/vu//5vDDz+ciRMn8uabb6aVO9JXRkVFRYi5\nazY3ceJEX7E9AozcclBijOC36IeY0W0CcD1wJcYnwwTCPh2kjEkb0loGQDkVVKjV4t5sZCO9g4NN\nCQ45lTwNK3LetSHxr4Hh89wPoQ90Kv2SHX3eJHC2JD44ZIHlDBuen5BrE72orenJjqr9mFj2IvNy\n1qu6gvk4gVEXbIGTuhr3i4fZ5IVbYHZXmL2FhA3zSV0DE3CLd9EdxnxyEJUAVDKInmyi1q7m3Vlj\nDnnd8dR+poy4EtVHV/1NxbmL5IUjsfkWcJ1OnWHzr1f42lfJGZjFXdcHic8/yc4Cn6OpaoynuA+s\nfOrZ7zK5sgmub5h00N66ddxXxrzWMWnxJua8nXVfGZs2beKhhx7iH//4B8XFxYmJ7dKlSznttNOI\nx+Mpy0cuSZaXl2dV0F0PD2MsDPIIdLhzMV/5apv2T3t/ksDhkAwEeciAXVkziB0b9qOyj/FlvGPD\nfnTq8yWfF3dnY00xOzbsR22fnom82j49qcSUAejU50tLU3SKMXtX/HKx+CLbRiuXyIKSMwZUs+L5\n0cbyzG7qmLfheOB+S2Mu5E6CFvnQ2EF3yUBgi7U17mq2Xm+A0IuzAbv5JEh6naM4itfpbWc4lQyi\nll7U0pMabTGRaz8wG/azumtLy+YlelyLfi4QHoAFBKda3d9W5azuPzFIPKnw8Nx99LO9rdu3yQjM\nBzIqz1dud0OMwIooj2RHWvIM3I+eQJzQGkvI6ZQG3f4SjwMfd0x8C5ltyc4+jB8/nrPOOithySFw\n2GGHceGFF6YtH6nKuOCCC9IWzgRn90EnzIFeuZhOJpYQ/e1d0n1HGkj+IqCGHbH9YGQzO/p0Yce4\nILzhwG+xo08XE4/tF8br0wVGroWRa9lxwEYTT2yyyFWy5MJJzRa3OeB9/y8IDm8VufqH5TupwpSZ\nuRZmNpM3VlQDlk4pDs9cO1jaF2WTagZiJm3fria4AeP0PgacDJW1g6jkYN5kPDNWPs2bjE/E36wd\nz7Di5fQt/gQ2Qefc7aZcqaVfaultAlqazRWqk6q3K28iXZ5HnMC0T+gISHqm0Ey7zsE7bXYbeFi4\nryvBB2Q+bZtx7g6IE7RJf8wzmUDQB/snh087l+BZ5Ts4ExQtlZ5oS12uCxmeepcWOmou1164+uqr\n+fWvfx0alMVFcbT6NYBIVcb+++/PjBkzUk7x58yZw5o1ayLzdxcYVcZkjHIxnS5Ng3h/W6fS+pM0\nfWw3rLP0dJyINPkt13JouWSzygQl26lYuziLPxaj/xP5SzGzmrdsXrW5fw94pIrEzGewOObHlDu4\nfwAAIABJREFUrMOAUU+cZIJjBs3j7XlWlXURZi/PYZjB928WT7Ztb7A0lgArRU5Rx2jQm33cuuq4\n66S90JO2s+EEkhztp8VtS5k9DUT/nU4lJP3NBcGtwujrTyCsZpIy0k/fA9YD93RYlfFc67Fp8U7K\n+VfWVRmjR49m0aLwUWVtcZ8c+bm44YYb0iq4jzrqqJT5Pl8Z3/ve96isNHrKzZs30717dxYvXrwT\nfGXshb2wF/7doT1bsjsCc+bM4YUXXqCqqopZs2YlBvyGhgby8qLMapMhcmA+99xzOyykz1fGI488\nkghfccUVoUE1u74ycjGWGbJKLF/oGpJ3kUlaPUZvqVeW8whvGtHlfbRSLXT4TuKAwB5aVqiLgWcJ\nzwSXO7zE18Qcm16COZZJ0sUmWfSwEi8l8Mdh/yZOAx4Rq5HhgfrhMAIHRYc1M66/0TEfwgrWHDmA\nuqrecJ/tbH2aKTpyI3WbSoxqZkNe2G/Gy9iAWKJI3XXb5xPo0LV9qDwT3wr+rp4tQ9tmvnOc+9cR\ntF+WmEqrIbxw/gzJDqZiqtxAe8UJ+kA+pm/GCE6rWUn03oC2wVfskxU6mULfvn0pKyvj6aefpqys\nLDEwFxYWJizQMoGMTjDpCMTjcaZMmZKYMQu0trbSv39/Xn31VQ466KBIPBcGDx7MvHnzEhtNysvL\nWblyZQjHzPRvdkrqE31d3wt1TlwcsgtejMD5ziKVXufg1kXkjSYY3H283TJunsjn82TlltFpsnoe\nU3kei4VDy+A9sRixOrHu9iMg1ht9COKHYVQWEFhe9FHpCYsPxXazpi+bflLVw607EXGN31Fw6e/s\ncrsa2iunuCWI2bj2fBgjeJYySMdVnkCcZHDzYyoM8JMOqzIebo3a5xDAjJynsq7KaG5ubtMM2YXd\n5qz09ddfp7i4mIMOShiZJnxlfOMb3+Dqq6/myCOPTCqXua+Mp4ADAdmkohupiLAO012ddwdCcaQj\nH40GghXmBlVGzvbDyat30kRn2p/Amc86T34eYac+Ok/4iw5dpwkduUTu/hid7HJCNtjvNRDooFcA\nJbC5HojBy3FCL8xDMcjNg2a9K7Ma3iuxs+JqexcQulWEdezudvs8T5q0n0CdwoWg3frb8BonH8KL\ner50bQ1Q58TdfqFB003lOsDlmc4SxE3LS1EuVZovzydnJjLIpELaZ7nKr1P4LyreYPqY75loujpd\n+ulHwIce/LbDrlZlnH766Tz22GOMHj06KS8nJ4dly5Z5SiVD2oF5+fLlid152YSHH36YM888MxEX\nXxk9evRg0aJFnHzyybz//vsUFBRE0kjtKyMVrCOscnBfPrm7zoOaCWYIeSou5kPr8Hf0dap8HoH1\nwDonX3BaVFwGXJHLlV3iWm6J6wW2EgJnS81OuTiBsyXXptuB1riqnp6NSzhu40JD0rS8GnwmVESk\nuenSNi7NKHxt+hX3Yoc/blo2V06XTtQAF1VW0n1y6vyOmPDFyMwMzyePmx/1nDS471Sq5+LjK3y2\npymXOexqVcbNN5s/dfdgkbZCWpuUiy66iMMPP5zbb7+dL774okPMBFpaWnjyySeZPn16Ii37vjI+\nAt7F2C5vIujkcomLTN0ZixycuL1rPHE3qeMapwijM2126KHKNVkcne/y0OmufE1O2TjJdYs7NCRN\neAueXDou7jjLMVYqAx1c1yVpvQpr3to1qtu2ul103G2TIsJt49KB5Ofo8tD50l7isc5tY11eh4tJ\nphf34Keio9OieLp10/luOFWaOMzSvFLJKHXECftkj5KtCX+ddVn3mWqc1WTbV0Z7dv51BPr2Nb43\n9t9/f/r160csFuOrr75i2bJllJSUpCkdQNqB+Y033uChhx7i448/ZvTo0cyYMYP//d//bb/kwMsv\nv8yQIUMSlYCd4SsjhrHTKsf4zZiSgWRRDVfjCU9BHO5E46bjpRf7fDyiwjVE85kSIZOkjfHQ0fjz\nMS9LT8yHDXtvxhxUO5zADrfEuXyzsxrCdXV/8UYTdqEKcAlBm7jy1dh8KSv1lbAPohZ8Jd197j46\nF6lwiUPvEkLOpyi2NC5ROL5FYrfsaA+ehtEkt18UfanbaMLtJ3hTHFrS3i59X1toXho/apedxpd2\nH6PSZ2PaIUbgK6NjPnkEdvXALHDUUUfx1VdfUV1dzbe//W0eeOCBNhlUZGTFffDBB3P11Vdz3XXX\nMW/ePH7yk58waNAgHn/88ZTlxFfGqlWr6NevH/fddx8Ajz76KDNmzAjhZt9XhoYagn39Oi3mpLkD\nS7Fz15DqVyXd4FxjeaV6CTMBn3xvp6GbTu4JJNqlVxmM7AmUmSvhS/kMhZenrpiSR39sdLsuUjg6\nT+P8k9RtKM8yj8B6o5qwJYdAJm0sv9TFTlyDtqoQ6x4tjyvvRsJ26K4sUl9ddpGHjsBYki2EXPAN\nzlGqjLedPN+zAn9/0TJqedx3zIev6Ur6HMVX6pAdE9jdNTC3trbStWtXnnjiCX784x/z2GOP8d57\n72VcPq1VxtKlS7n//vt57rnnmDRpEjNnzmT06NF88sknHHHEEXz8cXa2TmYTjN45Ez+0vllepmnZ\nhigemfAWHHfmpzeW+DbICF1dfgJwiJm0iLWFhoT/C22m5tJel4ZflMxtbeNsPxct085+3i7PTPDI\nELctdLMJHeHpli0BLuiwVcafW3+cFu/ynNtDfKLO/GvLHopRo0Zx++2381//9V/cc889DB06lGHD\nhqW1OhNIO2OeNWsWo0aNYunSpdx+++2J1ca+ffty9dVXZ8Rk90AF6fVU7ldap6HyombSEk43K8tk\n1hbVoXV6FB3B0Z7pZYAR3WgLZtY1VuGI7DpsefTBzJD7YMbYFnXvBca6o1nRlmuN4lvs5Ok6uDL7\nnkWm9W4LpHoW0g4tTrr8rrvP3UevrX9Bvufr61PVtK2+qXB99XDDbQXfe9KWsrrN4xirqo5De2bM\ncubf+++/z4IFC7jttttYsWJFYg/FqlWrOPbYYyP2Txi46aabuOaaazjllFMYOnQoH374Icccc0wk\nvgtpZ8yNjY3k5+fTubOpwPbt29m6dSv77bdfqmK7FcyM+XTMA+9JantY1w55GGE3j8MIOpxrc+yC\nxtU4UWVcXhpXg092X1kfHcGN2bj8mk7BvADLCds8T7Dpp1q8x21YdJby+1mlyrtyCcjHYTn+No+q\nfx2BblN4SNtOIPx77T4/SZMZptAXufRfgiu7hHHk07zjTr00v+VEP+somXQZPWvUM2QfL1+f9M1Y\n9fPX7Sbt4fL39SnpK0Jb9xV913IfCbxB8untUj6u8pY7PFZj+tljHZ4xX9N6aVq8n+fclJLPySef\nzMUXX8zFF1+cdg9FtiDtwHzEEUfw8ssv062bcfTa0NDAt7/97Yx8iu4uMAPzRMyDH0vQWWLAEwQL\nPlo/dgrmF3wRwQCU7g4wjWAhbBHGKY40qbuwJLrJ0Srso+mCbFDRuBtJ9kBeDIwn8EonM71UKoTx\nVuY3gf7Qa3iw4w8Cz3BYdrIeKJtHNtU69LQqwG1rmZH5FqPcHZWpQOq1SMV9bSv0XX5R/N121vyi\nnp3UbZqtbyo4BfNs9IYjVybBSdUvovqKTk/Vn9LR8YGvbS4GHsNMgh6zaS69izHnb8rdpZcDjLJp\nMUwb9sMYwz/S4YH5962Xp8X7Vc6fI/nE43EmTpzIe++9xze/+U0+/9wcRdXa2kpRUVEi7kJlZSV/\n+tOfiMfjtLS0JOR55ZVXMpI9rSpj69atiUEZoKCggC1btqQoEcD5559PcXFxyA566dKljBs3juHD\nhzN16tTEuX7xeJz8/PyEY+of/9ivG6qrq2PSpEkcfPDBTJ48OXSYazIchVlNjwHlZtDpNRuYALdO\nJfFrf/xsTAeZClwGfB8ohpmyEv99i3sR5gWcYO/T4JfDgRroJfTGWBqzbflym1dt42MtH8ujl6R9\n3/KapuSfZuUV2hNsutyLA5yRtl4cqPJihGc5slV7AsGCXRc4vicJz+qya+8w4GTgwq0Uza7mu79/\nmO9e/TDcvZWBc5Yan84nY8qOHA4ze5oLG/7lcALPbTElg8iuwbUSGavq4INFhAc2vWimB+VMbNxF\ntmJF0x1c9MEQ5Sr8fVUmhh+0WmKEkleD5negk+YbOL/vSXNxo3A0+J5FFMiCqObxVxM/vhfRA/xj\nwGyLMxvzbC8j6Jet8MupmDYRh/rvka3Fv23sk/aKgsbGRk499VRuvvnmpP0U6fZQnH766YwePZqr\nr76aG264gRtuuKFNp2unHZj322+/hEUEwMKFC8nPz09RIoDzzjuPF198MZQ2c+ZMrr/+epYtW8Yp\np5zCDTfckMgTXxmLFy/2OjAC2qTn2Qt7YS/8e4NPp/xRxXpenf1G4vKBnPn3n//5nwmT3Mz3UBg9\n9UUXXcTYsWM57LDDElemkHbn30033cQZZ5zBAQcckBDo0UcfzYj4UUcdleSpf/Xq1QmvdMcddxzH\nH388v/td5gdGPvPMM8ybNw+Ac845h/Ly8ojB+RcEv9fWNG4TZia4KWZNTHOBsbYVaszve+KEjQFw\ndz1hP7JCq4TEP/7V1jphU31Aj7eASWZWSZX1gTzAFsnFWDRUmXCupL2l6BOENwluf4JZRq7CrTHR\nJTpd1ZknCFwrTlBt0h84xMgiDu2ljUZifDH32cqQkg84hA8Ywgf0opZVJYM4hA/YPLYHny35pilW\nGjRHwv3nEoC+hGdluSTrQH0zLbHoyNRjgNatanqtHvpu/C3Sw2wVvlGF9XsQ5aBG13l2BI6GG9Oj\nZA0nnepFrHTmE/apDEYfPAGohhc/IOhb8wn7vLBlXsS+XxMwC8ffJ9H2G7B49QSn9EwicMjSfvAt\n7pWWH0RpeeAK4o3fvhbK9535B8EeiquuuirNHgqYMmUKt912G9OmTWOffYJZeVGRbw0pGTJyYrRt\n2zYqKyvJyclh0KBBbXLO4TonmjBhAldeeSXf/e53ufHGG5k9ezb19fXE43EOPfRQBg4cmNJXRo8e\nPdLqeXJycqDgN9AwAHLPso7Zgbw8aLbhXFuHluZwOAez7Th3oEkTXWtVM5ycZwbb7avNO5870Fot\nWBratOxHwK+aSSxy5Hra7ELgr7Zsy/0EHb/alvs+XJwHf12t0ksCei02/eSB8FQF4QEqDqXnQtX9\nYTq5A8N17oNRSYgfZYBS6HPrRxzCBwAczev0pJZaerKJnvSiltc4ildeOsl+fAjM6xZiBufZWPlk\n0ex6wvrt7wN/ILy1uZxAXx/HfFwfUnVvwTR8HsGOsXKMBY6k6TyBGOktdHzlfDgi254IMbJTz+8T\ntLvEHR4XDzR9NwFxB2c+XFyu+rfnvQP4fR78lnAa8+x1dYd1zJe3/j4t3p9zfhXi88Ybb3D00Ucz\nfPjwhLrimmuuYcyYMZxxxhl8/PHHac3lYrGYV9Wxdu3azGTPZGB+8803Wbt2LS0tLQlm2pVnKnAH\n5srKSmbNmkVtbS1Tp07llltuYdOmTWzbto0vv/wyra8MPTCD+QLV1YVXwHNycmDcb6CqHPYrD8+E\nZTJWijNDjgCNIwPvQoJDR7WJsPypbCCZp+Yn+CcRDGyNGhESzuzlYFOcfJ3eTZeXskC3U6HRoeOW\nw6lDKTDT1KX/RLPiLAN0T2p56suTOWq/13n9y6NonLl/2Luc1B1g5VuEB+J/YmbpyzEzJtcZPp40\n+UtxneQXRoT3QnbBtm357KDf+vp7MfA8QdeVfi4HJOBJ12dKCj1J+7wCNlfAuo6f+XdJa3q97q05\nV2bdu1xHIe2/4llnncVHH33EyJEjEyZzkPnA7MKgQYN46aWXAFi1ahXPP/88YHxldOlizufSvjJc\nL02i5+nTp09qPc/6CqiPw5YK2Kec8KLNXtgLeyFr0B4/Yj6QAXlr3FxZgF3tXU7gyy+/5MYbb+Tj\njz/mrrvuYvXq1VRWVnLSSSelL0wGA/O7777LBx980E4vbsnw2Wefsf/++7Njxw6uvvpqLrrIWD5s\n2rSJHj160Llz54x8ZaTV8zSVwzfKoaEcljp5gzG+uFfWkPhcdy+DzZjFYG3osVKlSVhmnI1Cw666\nL1FldTlqYGVxcvkXgUZtJpaHsRs+koServFdApvPUpsfszRsemPclo9htk+/BVRb2vbcPJlRN5ZZ\n3BpoLAbehZWShpm13A1sgnVLBsMGWDdycDArfg7mHDbN/DW8qOv7rpXvDSu/zJhjGF1mLoGNbD1h\n+2ABbVMrUE3gdlXsjWWG7Dp4+jr4RP46gW3nXIIDelH3JQSzYEnTJ6Pr2bLehLrJg1MFlJbDunIo\nqICuFfDFvA7XoGU3DcznnXceZWVlCbPivn37ctppp2U8MKe1yjj00EP59NNP2yWc+MqorKykX79+\n3HvvvTz88MMMGjSIIUOGUFpamnDssXN9ZeyFvbAX/h2hI+ZyHYEPP/yQq666KqEFaOuGvLQz5s8+\n+4xDDjmEMWPGJFYXc3JyeOaZZ9ISf/jhh73ps2bNSkqbNm0a06ZN82DDXXfdlQgXFRXx8ssve/FC\nUHsO1K4DHrQJ8kmvMjNXSgn5G95sna4nZstKn7tZKWBD+drx+wSbN9+W6w+btb50haWlaG8WHnOV\nfCsxuxUlT2RssjTWWRzRx/YkmIlqHCxdCGaWKwg7l6+wfMQBP7C5FLrnmZ3Voo9eg5nhNAKPYGb9\nbwCbm618/S3tBiWDG9YgC1Cya6q/ZaKd/qPy8xQNvXgldZFy2mm7u8gVteiVyWLYvzk02msrwQy5\nj413J7xO053weoPgS/lGB78Co2eWvO5An3LYUE6wKth+2F2qjH322YempqZE/MMPPwxZZ6SDtAPz\n7NmzATMYi4I8W2qNnQvnYX6jYzbunubtxv/bQyNdGZ22Jg2egJirVaQo7+alkqUiA5xiglXzNQR+\neiWtOYwbzzP+MA4l8I3xFOYFagEWSNHV9mq2PMR6ZLVDE/wOgpoJb+dt8uDgxHV4jVNOaOq7QG+S\nTfV0ut65uBdC0EJwWnoLZhCVfpHwnUIwl2jBDMgaR4cPJRicezk4W4G6CsiryIrou2tgnj17Nscf\nfzxVVVWceeaZzJ8/n/vvvz/j8mkH5vLycuLxOGvWrOG4445jy5YtiS2Ge6E9sDtefHle1QQz87hK\nEzO9dQHuSHvJ1mt5cfqg/M2IAbPQ0um6nmMJlt7d+uuy7qCst7O7g3VUmk7X+XrwVX9PaT36RfHQ\n8rWHRlSaNnvwfaQy4ZPlj4wcyLtQxVsIW+PIgNxC2DoDlbaQwCmWj0cV5uO/ggwdEqeH3aVjnjx5\nMqNHj2bBggWAOdlk//33z7h82oH573//O3fddRd1dXV8+OGHVFVVcdFFF/Gvf/2r/VLvMtAPJQ+z\nXXq+g+P+ysYwg8WZwP910iRcTfTvry8/6rdacN1ZZJ4TjrKdzfPga1n1NtoYxjJFeEk7TFB4A6C0\n0JjxHUb4h2MJwTh8GLBkC2aBbwDBJgoZ4OOEtyjLVnBXNpFFt89GkusVJzjyStoppnjOd9pAaAot\n4RPD+AzOI9nlaB7BkWHVit5Gle+qSDaS3P54ym0k+ZnqNEnf6NQvj+TB1eUl9YornhtVvuTpOvhA\nt5ODswHziN8DWrZAbldzlzyq4b2B9kO+BTZ1VXm2zBJMubEY0zpU3qauwSC/ZLXxZ1QRIWYbYWfp\nkNPBsccey7/+9a/QYp+kZQJpv0u33XYbb7zxBoWFhYBxmr9xo88heRjWr1/PMcccw9ChQzn00EO5\n5ZZbAHjssccYOnQonTt3ZtGiwGfAzvGVoaEZ/y6z/k48jumkWl0TU+GoQXmAytdxzUOn5WF6e391\n729xmgnpriNfTh+4/GXHoOsIPYbZOBBT8f5GlCOADZBXalbl+4z4yKTLivoSkUEcsU8kMWjmDrC0\nZLCWsK5HOeGdjAIDbLq70QYCJ+zl9i7pUi95JnmYj2ozwdQ+ZuNv27vMR/S8xKcKkSvPSXeh2ZPu\ni/tou+kC8TbwylV5PjpRMrl0I3gubDYbmFoqgGq7cehtjLMl63C/pQIWVgA3QdVqqLL4Last3pMm\n/nSzTa+AlgdN2arVJl71kIk/2wINtSlkzRx2taP8pqYmamtr+eyzz6irq0tc8Xic6urM/2DSDsz7\n7LNPSGmtN5mkgiifpsOGDePJJ5/k6KOPTiqTfV8Z2zHeugQaSDa6XEPycTotJBbrwIbFpE06ro+O\n5DdjTvnNcfLWED47bg3GcYucZl3o4E4jUPRqcF/AHxE+163Ylh9m70WGfq+Bti4rbN6LNm8F9LIL\nbN1ImPU1N+ZD92YOJB6kNwJfgjGlarD3eyzfeuieY/kMt2mH2nq9rOQ91OT3+j9WDpF9jcWVeBHB\ngQdStsLepR0LFY6cIyd/Or1tfAXGu5m0zXDLt9Bp04vxgx6sLo5I1/AbB8eHl8lBDlHyuHRSrWlk\ng9ccoAIOnUjQf1Zgnn2FvWxar5+rvHobXq3CczAdqcLK/bK9KhTe80BmO+TSQQud017ZhDvvvJPD\nDjuMyspKysrKEtfUqVO5+OJMnqeBtKqMiRMn8oc//IEtW7Ywd+5cbr/9dqZMSX9+Xp8+fejTxyiZ\nunXrxpAhQ/jkk0849thjMxbOB5n7yii39ydVWpQHLNfbVyvh2ZyvXNROIXGLmOlOIj2bdUHcZqaj\n9U4EjZiiX2z9bsRsnszY7ax2k5VlQ08zMz55KwNLKlldPYjObDf5fTBqjFLg057G5wglBGqKCbBp\nGYHtMsAnKl9stt8B4rBJVAZadq1GqCHsL0HaVvyRSD18PhW0Z7oYgVtK4SGzeQ1/JRlc15iPedJc\neNGR0QeZ+IHwyePCbzOQJ5V1g5T9awo6ecBYeK+BoM3KCVRWD5H4I9okODEC/8qXEfbXnEf4T7UE\n87G8w+adZ9O1zqN9sD1jfyvZgUsvvZRLL72UW265xWt9limklfraa6/lnnvuYdiwYdx5552ceOKJ\nzJw5s01M4vE4ixcvZuzYsSnx1q5dy6hRo1L6yqipqaG42Lx0xcXF1NREdcgKwkrSjkBb/Namw0vl\nRMdXNhO+cU8Zn8vMZsJ6RInPJ6HH7mNcL44rsf62SyqpoXewcl5FMEC/OEbRihH8Dmt54iR/fN6y\n8vkGLp/TIbf93/KERyt8XU7qjSce99AWv8qub2NNW+umS0j+sMcxznhENu1bWS/QTSDsSKgtvqMh\n8A1dQridfLJrcBcMRU9fovI03zEYs8xakvXQzaqcjjersnGCdZI4gVorrngsI3Cg/w5Q6ZG77bCN\nLlmh01aYNWsWb775ZsgfM2S+YzrtwNy5c2cuuOACLrjggnYJ2NjYyGmnncbNN98c8uvsQt++fVm/\nfn1aXxka0vlEDcC36JEurUal1Xnw3cUcDW3h5Vs48pVLRaPOiYvMdUCBCtcRPvmiMPneCLwMC793\nGD17bqK21tpCaf8asgsyQbMQyFdhMPridZhfU2k/VLhG4bjt6toj1zllZbalf+GX23TdngWWj3sq\nh7QJtkyNKves4unaVYu8eodhAcnPsA7zy+7WuY5wXeqdetYQfs4iwzoV13IsV/WEoM/q9tOyTsBM\nWHRajZWjxqb3d/IBCs1I0VKH+QAXWsdE8qxPCPBAOSpSeLl50DIEM/BKfxtC+IQTbNo8suUoqj2q\nivPPP5/nn3+e3r17h87ou/XWW7n99tvp3Lkz3/nOd7juuusiaXTUlUXagfnAAw9MSsvJyeGjjz5K\nS1x8mp511lkpXeTBTvCVQRwzgsTxz5yjFlYySXPTUy2q+PJjhG2IMymXSjbfPUagx46p9GbM4Cyz\nXS1H74TNaveem9nw7rfMQt9IAjW3nPsXd+lpO2GZxa1R/IWPhhZPvXTcLSd5LSTTk7q69IWGptVC\nMINLJV8mduy+OpQ4PKLAtfOOK1oik8bRaTGb5uJA2DpH06tweLly+NoQYDW0xAjNhBOe4OLJ6C1K\nthbLu6VZ4a5WMq0m6KuvAa8D7wPpx5dMoD2qjPPOO49LLrkkNIi++uqrPPPMMyxbtoy8vDw+++yz\nlDQ66soirdTvvPNOIrx161b+53/+h9ra9CumUT5NXRyBrPvKIIb5kjeRnRODo2i4v4VuWH7xqlVa\n3Mlvq2xuGV9cfimx4QkqrwXji1l2AK4j4Zv5XCj6ZTWn8CQflB3CByMPAaCul6Wl1RkbND3JlN9i\nqSOEX14tq+9jo/Nlgc9tR62SidLllqiyLi2Xb9yJ+55J1HP21cGllwmk+kD50lwersxufqqy6WA+\ngY5Yt3kJZsHBejBMGCjP95QXqFa46+xd5x9pcTLzW5wO2qPK8PmRv+OOO/j5z3+ecHmcziZZXFn0\n7du3zfwhA6uMXr16Ja7S0lIuvfTShEe4VDB//nwefPBBXn311YQJ3Jw5c3jqqafo168fCxYs4Dvf\n+Q4nnGB+g+bNm5dlXxn5mG1EEDxouYapME7aMPzQ5JSBMD0i8oowusBhiobm1URYjkxAl9H10/Em\nR+YmjJ6wJyBHg6226fLX0QS9oHvnzRzEGrqzmW1bu7BtaxfTlO5FT1W+p61nk6Uv9dbtILJrOd16\nN6m01YTbRudJWamL+9yqCQ9UUlfdPlHgew4+GYWWm5/qOUb1Ly2r1M/tF6lkdvuAK4Nb1u3LUeW0\nPNKftqh0Cb+lcKo9l96dudqGVxPuq9UEH9nMTklKB9kyl1u9ejWvvfYaRxxxBOXl5SxcuDAlvriy\nmDx5MlOmTGHKlClMnTo1ZRkNGXmXk+n4jh07WLhwIdu3b09L+Mgjj2THjh3ePN8s99RTT+XUU0/1\nYLfTVwbnqnCcYKEkjpnZ1QHHYb7WTQQmZnJGWzXGvCefoOPELL0mdclsMd+WW27DLZbnfEVTm8LF\nCH73Y0qGOsVTdHLCE09YQJcTnGLnLrMmsfQYTbA41Grye0F3Pmcb+/AJB9DSYjtuL4zQxncjAAAg\nAElEQVRaoxdqF1izapfVBLPlsfa+xtZR2lPrWDU0EW5nCNpuDUF7SllpR0nH3nX99YstbRB30qLa\nN9XWexfXl+bWUcuVzrRN06rzxPOdNA2ar5vfRLi/N6k0/T4VE34OkracQC9cTLDNL+7IJDLkE91n\n5Xm79ROIYf52X6SjkC1zuJaWFj7//HMWLFjAO++8wxlnnJFSnSuuLNoLaQfmyy+/PDEw5+bmJjz3\n7/nwKKYTDSGsU9M6wTjBiy1hwVun8PMIBtH+Kq1Fpfl4tBAM3lUWRxa71hBewZYyeQQdVdIhvEjU\nQuD4B4LFoBbCC1b6BRJ6YAZOSW8m2E9bDL1gEKsYRCXbyaX7Nzaz4f1vmcFY/BrIFt24/piJrFKf\nYgKFtLsH110sk3ZB1T3upK9RbSDPQtrfbSucMCQPiCWeNJHNN+jJM29W+boeqWaz+hn6yqbihS0j\ncZ9OOxVPgSbCA7DI4brWlH6pIR6Rr514rSNcJ+mL0sapno3UT/N7jWyAT8f8ZcVCtlSknvG6UFpa\nmnCydvjhh9OpUydqa2vp2bOnF7+8vLzNsmpIOzBXVFR0iMHug80YJWhXkn0HSCeSl76Z8EAsoAdD\nnS+DcJ4qW0IY9CBfQfjEal3OLSMQIxiMfCB1cOm0KD5xdZ+g6McJfxAkPh+qJvEq5SxnGO89f3jg\nX3chga+DBUDVFgJ9bdxcuQdCi/wByOAs+sMST10kLvXU+boeWn8qz8Kl5balj4/+eLr4Ue0cRa/Z\niUPygKbT5eMeV/kuDVm0q3bS0/GPSosqlwmuBv2h0GsKqLB+RhNsWD8nn94+xk7x7aHAp2POKx/P\nN8rHJ+Kbfvv3tHROPvlkXnnlFSZOnMiqVavYtm2bd1Du1q1b5IJfTk4O9fWZnbaTdmD+85//nMRI\ne5m77LLLMmK062EHsA9hkyH55fI1Tj6BaZfGbbZXocqvJ3ykkeYhJkTu72ydxRMdo5g6CX49yfa/\nQltD1KKQyBNX4WW2HmIeFrP5VQ5Oqb0DD8KGld9iQx9rkVFFcKxQo70nzLKcsi1vWbo2nvg7KFRy\naZB2bMacXrBOpel66F94KScg5fXzcvkIyDMZRjAwy+Kn8BUaQlt45eN/7qmOucrH30ckTz9LoVXg\n4a/lknbStCXf5af7lq6Xy1eDKxcE7S+8pc2arbzrVNn+BM9MZJBZdRRdaRehD237UEZDe1QZM2bM\nYN68edTW1tKvXz9+97vfcf7553P++eczbNgwunTpwj/+8Q9v2cbGRm96WyEjHfM777zD1KlTaW1t\n5bnnnuPwww/n4IMPTllu/fr1nH322WzcuJGcnBwuuOACZs2axa9+9SueeeYZcnJy6NmzJ/fffz/9\n+vUjHo8zZMgQBg8eDMC4ceO827Lr6uqYPn0669atS3sgYrAwkclXSnAK8H+56yPubn46+q5NbWZf\nUD/oWYimI+Ehlt9yG5YBsxCzWaBQ4dl6l8OQ3yziKF7n78//xGQvVNcGCPTSQyz/QoIV+kcJdPHy\nEYoTbldX7hIrY4mNFzj3evwzLl1XuQuei1+i8PQzkA+tpuHS1nK64VR57mxQ16OAwP4YlVancOoJ\nNl2g8qUtSxy6YNo8rujFVHyCCrt/eJKPwhHQC5YFmOcuz7waON7Bn2/zhL+A8I9ZHN9CaAFmy362\nfGW03Vwuyo/8Aw880FFxMoa0h7EeddRRvPDCC4mNHg0NDZx44om8/vrrKQlv2LCBDRs2MHLkSBob\nGykrK+Opp56itLQ0QevWW29l6dKl3H333UmHtkbBlVdeSa9evbjyyiu57rrr+Pzzz5O2ZJsZ/kSy\nt/Pv6wpnYA5BjRHeneW8pKWToMocuMrCQ/hl2f8B4I81v2BH1X5mMH4OM1t+DuuZcgv+l7zakzaf\nZFthHY/Zu87fHRCLkCGmwnGVZtU/IRy3fFRZicc86ZD8gRFePj6+clFxF7QMooKQMpKn8dwBXSCq\n3BgCB1RapvmEdwDqOqy019MdPoz1gNb09tCf5nzr63cY68aNGxO2e2CcE2XiXS7KV8aQIUMSOI2N\njfTq1SuKhBfa7itjd0FbtnFnUiYqL9U2Xrugl7BKaFE4Kq0XUGVmwUeWzWUQq9hIb3Zs7ULRyGrq\nnisJnKOLw/StXWFTseIB5iVrcXgJCD+RLa7y4iSD0Mykzm66L1+nRYV9C3jSVi69JpItNXw8445c\nqDQJuzRENy+LqzWqjC4rdDVvne/mubK5z0I+MlH0ZCFbyywgvNy6aFrFBGsn2krJbSfxtPi0h0/b\nYNuO3bMlu6OQdmA+++yzGTNmDNOmTaO1tZWnnnqKc845p01MXF8Zv/jFL3jggQfo2rVrwpE07Mm+\nMvbCXtgLuw5W2avjkDD3/JpBWlUGGD3zG2+8AcDRRx/NqFGjMmbQ2NhIeXk5v/zlL5Psl6+99loq\nKyu577772LZtG19++WVaXxk9evTg888/T8SLioqoqwsvtKVXZUT93qX77dvZ0Fb+6eqhdYYxwjq+\nrsAHJnxYV+PgHDi19QlO5X94naO5487LjLOi5whUGQIbsOU1aFmEj4R1fiar8G39JY+i2VY6XwfI\ndh0yaduo/PZYVGSiXokD8zqsyuj2Zeqt0wCN++2/x6kyMjrAZcuWLRQUFPCTn/yE0tJS1q7NzFdq\nOl8ZZ555ZmLLd5cuXejRowcQ9pXhgvjKADLwlbEEM3OOE71zS0DvtsrOdtCArhuP4tHURt6+nV6y\nQ64Isyg0X4XlgNSuZgGcJpPWCOITuhsNFNDAevqZgzHlwE05KHMr6jDNJucqUryaCHzwFjn5oofW\n7eHWx31x9TPz4Rfhf66+jRa+Z+LGo+QqcnB8NNrbf6J4upDtD0s6evJeROW5baxwu8/GvyvTB3HM\n+7qEbK03bG/pnPbaEyHtwDx79myuv/76hB5327ZtnHXWWWkJR/nK0IPt008/nZh9b9q0KbGjMBNf\nGUAaXxkDMArRcszMrRizmgyBziyf5J1UdQQ7k/JtGX3PV2Wj7jrcRNjUSwYx13RK5/no4MFfrsJ6\n51+xuoYQbCbpTWLjR4vwW23DvYHefEpfljCKJYw06W8Q7L1Z2Wq3YrcaGgk9qx6cZeNHsXOvI9DX\n6nrp9tYveL5z6XbRz0pgDf62c80W3V1t+Slw9A41Vw53F6M26fM926hnqMH1PufWJQqys305Nfjq\nJGG3/YqD4FZIv9tR6A3BvK8jyZYK8qumLmmvPRHSqjJGjBjB4sWLKSsrY/HixQAMHz6cZcuWpSrG\nG2+8wdFHH83w4cMTdtB//OMfueeee6isrKRz584cdNBB3HHHHfTu3ZsnnniCX//61+Tl5dGpUyd+\n97vf8Z3vfAcwvjIuvPBCysrKqKur44wzzuDjjz+ONJcz/E7FDDYDSAZtj6rNfnx4YhLm4rg2pNpE\nbYWTXuiUi8rzyZiKn2vn6qZNIDBdgmQXixD4Djaz2H03DwRg691FgXncQqBRdi7KbFdW2+OKVozo\nmc4KFfbJ7csrUeXc5xRVJiqPFGkSl2fnQhR+FKTLTwftpd9Wvpni6/b1tSVEvw9t5QHZVGVQvTU9\nYsm+e5wqI+3APGbMGN5++21GjRrF4sWL+fLLLxk3blzagXl3ghmY78NvhuQDH56bFie9OVUUP7eM\npiNhX5qmpc2l4qSXFYKBWcpocygtizJzWjLJTIZn2+zEzlX509G84wSbDXzgfuziPqQMINaBsjuD\nzl7IHGK0v81/2/GBeV0GOxz75+1xA3Naq4zTTz+dH/3oR2zevJm///3v3HvvvW0+wWT3wFMYpWhs\nN8vx/zq0z9/sXtgL0RAnax/Qrbv2aKlsQUqpW1tbmT59OitXrqSgoIBVq1bx+9//nkmTJu0q+ToI\nnUne2unbEJFHsuG8pAl+HoF/DAj8HsRUmRjhTRdyj5FskaDT8pQcrgwQnnkKXoywkb7k6XieohHD\nqB5clYzmkQd32+gSHGfoUsaV253Fi0w+EF6p/DX42tdtGymv6xJFU5fz1VuXdcM4OD5Z3bKQWT13\nJexMGVzaOi79ejeCa07/NYGUqozW1laGDRvGe++9tytl6jAYVcb3MDsnxE8wBL/zMpi4O5XiFm86\n5mDIKZijhkaTrB44A3OgZhF+1YMLOl/vGINg8aQ9q/mad52SVae7uCIDVo7pGP1FNTDV7IjFJpU6\n4fcw+e8BvGsz5eUbS2BTJ+0qfBfZcBF+158uaLx0ZaTd6tLg6rzRViZJk7jGjZF8np/g62eVSX3S\nybMng25fHY8R7mO6/wnIe6LbW3CLPGXqMNux1wAvdlyVsTSD8iNy9jhVRkqrjJycHMrKynj7bXdL\nZXpYv349xxxzDEOHDuXQQw/llltuAYyVR2lpacJ5/osvGp+r8Xic/Pz8RPqPf/xjL926ujomTZrE\nwQcfzOTJk9m8eXObZcsO7P2F3wt7IT3s5vekJYPLgfPPP5/i4mKGDQvM/H76058yZMgQRowYwbRp\n0/jiiy92qthpzeUWLFjAuHHj+Na3vsWwYcMYNmwYw4cPT0s4Ly+Pv/zlL7z//vssWLCA2267jRUr\nViQ80i1evJjFixdz/PHHJ8oMGDAgke5zYARmU8qkSZNYtWoVxx57bMR2bID9CJytiOnTNIz/2bGY\nL3IZ5is+y+bPIvAtjMXRjsHHEpiAxS3tYudybXvlEhprCEzK5CpUtHT6WBUutnGNM8vSkvTZNj5N\nyTPL5HebBYyGclvHAWU2f5qi2QRUmaptxVgtHWqvX2LOHrjC3suB8jLoVgZMhQFTYYDl2a0Muk1V\ntEdjHJ+L6Z6APB+BQnWfpXDqbJr41xaQtY6xFmempX+Cyi908KR8k0qD5NOk60ieLUu63F2TubZC\nNv6zpT4nOPFCJ94RkP4m7S/vifSbaQRt6/bhOKb9m6xM0pelv59A+P0pBHpg3t8sgO/knaSTeMJw\n3nnnJSaMApMnT+b9999n6dKlHHzwwVxzzTXZkS8CInXMH3/8Md/85jd56aWXyMlp+1Tf5yujutr8\n8nbktyFzXxkXYdQQRQQmUDUYk5w5Nn6LULV571pc2eYtmyMG2HJvYX7fVqi8FRg7TIkLuL+7WBpF\nln4u4d+5IsJuG7H86gl+A4VHPUbNcouSqw4zMAv9Giv3uybcWGvuFfmG9yYsP+tTtvtY2JwLN5Xy\njQs30HOfWj6aPzQQRUznltj4Jqwr0FogDmvKbMYiaCy1bRrHqH4WEfyq6vpJOwjkqrreonCkjQYQ\nHiyfsPc5Kl7viT9hacxRZWucsjpPQyrVhU/9QQp8l26M5N97zVPDaIz66Vknvca5Sx+pU3FNI51K\nSdQKOi+XsIruGUzfkT5WQ/Bu1Cj8uIoLnqgCxYw1F6P2yrf4uRgV5KHA4x752gjt+Pb5zvzT62pj\nx47l8cezIFsKiJwxf/e73wUgFotx2WWXEYvFQldbQHxlHHHEEYDxKjdixAh+8IMfhFQR4iujvLw8\nsQXchcx9ZVxO0MFi9pKwQJ1Kl2sC5qsteIUEL0MhpmNPUOUh6Owy85V0me3pmVWdSse5uzM0mfVI\nuq7DswSzIV2vOoKNJ3IcUL7FF9meNecIcCvGDG41bF5t8i7dwhcD+vDR4UPhyC1wKfa+Ba7dYg7B\neBl4bzVsnmtlq7N0Zltec+1d2iOfcLtoWV3Zfe3itoPQKIyIT1BthcNbQPhGLVQKzVQzZPd5ufJr\nvhMcXi5unZMn/OVaRPKgrHEXedJc8PUjVJrg+NpK0nX/XUTQt4Y4ODps+1ziXXLz9WYuecc+jKhD\nG6Edqox0cO+993LiiSdmR74IyGhLdqqzrdJBY2Mjp512GjfffDPdunXjoosuYu3atSxZsoQDDjiA\nyy+/HIC+ffuyfv16Fi9ezI033siZZ55JQ0NDSto5OTlpjgfvitkOqn+HxfeG/tWLqzQZzNwXq1Cl\nub+PEPjBrVPp81XZYfYSHjhlCxWupLkvSIEjk15AjKuy4sdYBmkps8xehZjp7jCV9hAJX8VVj8PC\nx014YZWl8TfMrPJGzEzmWZsuGw/kxatXPOOW9nyPfBp8g5Kv3gLyHDWduCpbr8qIHAL6OUj7CE0X\n4p40oRkVFx4Qrstykk+Pjkfw1fnigzmbELd3t/1SgbSj9KM6TD3lD0g/cw36w+rmxQncBswnfFDF\n+jTyZAhZHpj/8Ic/0KVLF84888zsyBcBO9XIz+crQ/u2mDlzJlOmTAGMr4wuXcz2SO0rY/To0SGa\n4iujT58+GfjKkOOlTid8fhqYXYH1mJmebLUV/w6oNPma9yawPqhwaEFCJZB0/puoJyStnvD23gEO\nX5GzJ8kDuN7a6m73brIyCn9tsrfakaveiUu91hCcfC0+EHSZJlWumeDcPJFfZukQbEhZo2SVOorc\nUl7qLL+37k4x4TGA4DirJgdHq4GWY5Tg7lbgfJWmZZD2cEG3rcRdPOkXgltCuM00nk9u6YfulnQI\n9w0ti7tFXcsYBb5t7al9n4eh2ZaT91H6itBrxuiZ33JkkTrLsxNZyzHvkT6eaRFG9fIZWTOz8238\nW14B71W0mdT999/PCy+8wL/+9a+OSpUWImfMy5Yto6CggIKCApYvX54IFxQUUFiY6itvIMpXxqef\nfpoIP/nkk4mVz+z7yogR+MroQtiXA85dOrfsZixSaTKI1nlo1BLMjqRsE8HALeXlLrOMfIJBSPsa\n0Hw1DQHhLy+spEkZGcD076HIm6+uImAjMNAjS61TZ4nLDH6ALTdA0Rf5y0nWl+rBHZWnfUBIvn4W\nbr1FPv2x1O0mOPI8agnaqUiV13w1DS2jxnc/stL+elasP+x1+H1DSP/xpYPfdYCmpdtR7lJveaYQ\ndhhU5ODperQVpN75BEeW1RJuZwlr/pIufU1klRNK9Eklo4GrMCd3D2qHjB7wzZCHlMPps4MrA3jx\nxRe54YYbePrpp9l3332zI1sKiByYt2/fTkNDAw0NDbS0tCTCDQ0NGR0oOH/+fB588EFeffXVhAnc\nnDlzuOqqqxg+fDgjRoxg3rx5/OUvfwHgtddeY8SIEYwaNYrTTz+dO++8M+ED44c//CHvvmtsZn/2\ns58xd+5cDj74YF555RV+9rOfRUiwj727v4HScfUvqFZbFBIcOClp4oQHp+xyzHbkQoJ/Ik1Xpy9X\nYaHl/vJqFUrUx0/Oq9P5dU6+9EDZKn2CxSm1l7ZhFhyp9zqD020W8DlmFjTWlpuGNWC2aessP6FX\nYq9Cdce5FxJYm+it3K5aqFBdJ9i74NcRnAqu6z+M4Je6lGBGqPHqlLzybF3VhM7XIPFSldZCeHOS\n/nXHwdODpu57ELRloVPGpzpxeWkZ3GOzXHUcCjf9BCuarzw/d9ZdSlBPLVOVKlei8KQvy7MDWEuy\nuqud0JzB5cCMGTMYP348lZWV9OvXj3vvvZdLLrmExsZGJk2alNKcN1uQkT/mrxsYvfPttP0EkfaA\nmFllyqvY4ror+j6cdDQyBcHXd1kdd9MFJmDUQYswA3KcYGefll/XYzTmFzSdbK48vjoJrRJF31fO\nTRd8Vy5sXOpY4uT7cCH5+Y4m3A5uflR/cPn66Orfd2njGMaqROoW1b6XWJmqVVkd1nXSz/MJh47v\nGRZjrJyWAcMxVhkxG8ZuOJKZb08Ss+BePWHTM5aeOMoqMekAm3QZbLmeBH+fIzq+weS/Myh/ztds\ng8nXG55j1zisyWQQ8uFHDcqZ0HQH0XTg4tcQDCw6v4bklfqxhM+aw+JGbRevIbAN7gjItnPh48qv\nZdH1EDm1XItUuuDGVH6eE9Y8axx+UbpPkS8WkY/K13SlXJ6DM9bymm/DMYtTgxlYIWyDXU1gZVJM\nYLomtF25YgSLkfJXVOzBE9x6goNfY4S8/OUKj7wAr1dPa5JZbmXqScIzofy40ZPkLfP1wDuYnbdZ\ngJ1glbEr4P/hgRmMXkugmMwGs3R4bl5xRHi0vfTLN9rBDS9s+mlHyeIOTqlknYJx0ymyyOxL0x9j\nw70t3nB7nWDzRE0xBjP7iROe/WuQ/8OTbF7Ux0lgtEoT3GYri/A53IMjcgsNSLZ8ENw4ph2Ef5ww\nLxRes8IT0GXdj1oNwW+7+28sz7nGKSttL3TiKiwLhTr+lsUZrXi85dSvmcDNa7Pi0UwwSZmCmSXr\nP5+3CJ675ivQDPxfAkf2wutdYLW1bV9t82z+pmcwM2vh/W4QXlILS2Q7/0OKz3xbfgNZU2XsHZj3\nRNgZRicxT1qNc4fAgYuehejZVsyJ+9QT7mwtCqJwJH0jYWdGYucrOMUWZ4LFK8bMXGQtQeqSp2gJ\nHUieRUr8M/wOgVz5fLPQastLcN7xlBO5IfkPxG2TaoULQR3GOmVrSH4ugu+C/kBIuy1yeMdIng37\nwpq/nrXXKLndPDDPwE3Pwzis0u0rfVHTEnlRZX3uF/IwhyNIWOhttNcywn0kz8ETXGnzt218jqVZ\nT6C+yMO8t1k6WWTvwByGKF8Z06dPTywGHnjggYkTTLLvK6MTZmAQyCWzgTrTwVDT9cFbimdVBG7M\n4buzQBwUCVQTyCdyCI7bTvLr6qtnrnN3P1BVlk+6ukn5EoeGtFsq/oIjM/oaFffJJun6AMMSwgt4\nmleNSitxwjGHZoz0IAcOuPXRs27dHlouN3+skkXaOhfjI1vS5XnWpOEp+vxUH3lpb3cnoAy+Qv8t\np4ykV6lwfxV/VJWX55LewCAjaMeW7D0Bdpods/jKGDlyJI2NjZSVlTFp0iQeffTRBM4VV1wROn1E\nfGWkAvGVceWVV3Lddddx7bXXRmzJ7oyxKuhGMNPLWHqi3SRqvR2Kbh6Bq0qJy6wBgo6sZ0KxNLzS\nyZIpiGlcHsHW2TzMbOshghlXvsJ1dbGSL1trBReS21ZkrnbiPtAzPZFRBgnNV88Gm1VYdKtxB0dk\n0jRl9in5A225gZjfaP1MhY+eSbr11fzcvyXpC/mE1zrkz0TyBFfPNmXWKnXLJ3gOUiZG8BykfkJX\n/yEJHamzyB4jaDORX5fTz0t4SHuJLFIvTWuRohezdZF4OcFzkP4jz1nXYz+yNmfs6Kuzm2CnzZj7\n9OnDyJEjgcBXxieffJLIb21t5Z///CczZsxoE91nnnmGc845BzC+Mp566qkIzP8ExNeDGMfnZ8jF\nfZo+0zTX3qaZsHlVPsE5gYNtXoENS7zWwyudLO2BwQT1LyTYNSf1kriWuRAYCN3kxR2o7oUOPWlX\noee2c6o65BO0m4TzCXa85WNe9gKFI1CgcHVeswovcvCaVXvUWh4VKq1Z3TWtuA3rurtmjgWqjORp\n2UXGRQTbkpsd+fIJm01KP4k7+fLMhijZFil8ya8j6KfSFyHYdShtHFf1cp+flBM5FjlySB01jTqC\nnYL6krxah0atyu8HnEVWYHsG1x4Iu0THLL4yxo4NVutff/11iouLOeiggxJp2fWV8QDhmVwRHTu9\nGMwMQJzP+KBe5RVhdjHJlmW5y6JaEWGfHDsThP8wxXc44e3phTavwOLZvNBxilvsVWBxhZ78drr3\nTEA/F9FrF2FO7dbxQoXv1qtBlYfAigCVL/eYvQtNobfckUNDvRMWmSRd2kHb9A5TcjRElNe8tZz1\n+Ou+nHCfkvq7tAst7nJPvk8WwSly4gIrkFPUk8tJW/ry3Hi9kn+5Q0NsmcUq40GyAl9THfNOP3fF\n9ZUh8PDDD4f2m4uvjB49erBo0SJOPvlk3n//fQoKoldnU/vKqCc4waQZU9V1Do77i51HcIZds8qv\nJnlnlrsYJPjiSWudpSW/cfoOYb2f4Ld1duz77XR/9WWVXTZFxNS9yvLOs2GRvxRyLe2q5iBMV3Nr\nkfbU8gtIvd22duUUyMXsbtPtI89Kt790Va0r1/pfHHxUWrW691dyxgi/Alr1EiWvSxPM77qL+7aD\nq+UTmaWOwsuVW2SqJlw3UVvMJ1mF4vLW9ZC2desi+dX4IU5yf9fqlmYnP0p15colskmdBDaQVR3z\n1xB26ozZ5ysDoKWlhSeffJLp06cn0rp06UKPHj2AsK8MF8RXBpDGV8Z64F/Am5iOJV/2kISeeINK\nb3bSe9pLaBUR/CaKWVJPRUPw1th7T8yMoUnRW+PwbAtoVYqvTmKq1lPJK1eTqo/I1hTcu2NnE3nO\nDKPepIXaY7hDS+rd7Fw+sz6Zaen2kvYoUnlrVFiXLXZoQPg5uzLIzK8Io8JocHB1mSgQ2fTdrZuu\nf5FKE1hDWC63bpq2i9OM6UdSH82zyIOrabrbxd38KPDR0ne3zVPRiKrTaswzWUJqO/82gI+lT4Q9\nDHbawBzlKwPg5ZdfZsiQIfTt2zeRln1fGUPtNR6jFxUdF4QXbdwr38GRcB2BxYbWmeWpfFS+pA0h\nWMCRRY98FdeLW3ohzAVXHh++GxZ+chdfB3UEM16t180P0vclWFDXF7kYdYbQ1XUS+qKnjhEsNOo2\n0jK6bZhPuP2i6oqDr+sf1Z5CU56lXrTTuD6e7l14aFk1nxrC9fLh+Oqk+dSRLL/up772c8u4ZdOl\nZQK+9yaKr1vOV15gIGaBsAxIfvfbBXt1zGHw+cqQUwEeffTRpEW/7PvK2At7YS/828PX1Fzu38BX\nhs+XQdSCYSpI5xMhyo+DhtH4/RCUkLVftxAIbYESwidZz/eUEfwYYdMo8YEg97hNf1uVK/HEtXN3\n1zeGr95uG+l2jmpbn++MEpLb2ke/LZDps/JtH9d8U/URt42ERjofHAI++aLotOVdcP2RQNjnh/Cu\n9sjgtodPBp8Pk9923FfGzAzK373XV8YuhKcwg0cTZrupQKqOWOjcNTQRuE4sVHQLVRz8rh1lxVkW\n4qQMBNtv2wI++Xw4vQnrMltUXO7FKr6G4Jy2npgFwxYbrrFhuQuetEMxwbmBTZZW3JGpxglrfae0\nyRqFJ3WQNu3t4Lptj8JrdtKlzcQ16jCnTKETdttY+KxxeLtQaOVvIlxf4Sv5Uj1pHYYAACAASURB\nVN71KKdl7k1QZx3W8jY5l69Ndd+VsK/dXNoapIy07Roru8jVZNOlz2nQOK48Uifdjzbid3vbDmin\nKuOaa65h6NChDBs2jDPPPJOvvvoqO/JkCP8Pz5hPBPYnu+Zo7Z1tZ6t8e/nJLCeG36OclklmdhNs\nXGZBcZsmq+dxFS5RYd8sqK2zM5FdQM86fTOxTP+G3PZwZ+bZeDaZ0mnLn4DvjyBq5tzROrSnHTL9\nA8iU1luY/jWv4zPm/8yg/APhGXM8Huc//uM/WLFiBfvssw/Tp0/nxBNPTOyf2BWw083ldh+0YMy7\n9Ne/BLOaLWnaJMedJdSrdG3n2aTyhxB4xNI06kk963Dp6zL67vLXkEn6aMxALHIXqTS5NxEclVWN\neTGmQDdrhtgHoCessTPMbtZFY6PQkgG5ifCOsCKC31o9Q/LJq0Hq30T4edWTPBPTfzD1Kj6E8CGk\nOl/PfDX/Gice9QzdNnefQw3Jz9H3zJucuvpwRCa37Wo8+E0k9ylXXl9fc0F4noD/gFrfu+M+BzLM\n89HO8sQlqtulkqKwkLy8PLZs2ULnzp3ZsmULJSUl6QtmEXa5r4ylS5cybtw4hg8fztSpUxPn+mXf\nV0Yz8BVBh5WXMY9goNArwu4vYR5moJFwHsHvaJOiI2ZCEq/30NMbCpocmjquy+IJaxCzNddaQKdr\nGYo9dXRlkniLMZfrjjmweCuQm2OuxIKJS6/YCRc7dHWdBbSM9YTbVT8vaWO3zu7zkvsaws6DdH49\nye0gbew+D/cZus9C8/SluXT0M5K6CF2XvsbX8ulnW0Tyc/e1SxRfLbMbjup3Lt08hesrU4+/naJo\ng9l/kKWhqR2qjKKiIi6//HK++c1v0rdvX7p3785xxx2XHXkyhJ02MIuvjPfff58FCxZw2223sWLF\nCmbOnMn111/PsmXLOOWUU7jhhhsSZcRXxuLFi7n99tu9dMVXxqpVqzj22GMj/GQI7K/C7fnixe09\nSgdcTeDPQEA6nyx+NRN4kqtOQUuXzUTn7OKmsmeOYeqiF/vipNxQsAFzVWE2mQi0NNsNJlI+ruj5\n7sIjldFoM6Y+JSoOQRtWEwwCkpfnlPfx0GHf80/VJ9x29Zl6afo+eVKBLi/11/QFYlZOnSZyx50y\nbn10O7ofcM3HJ2+FI6vc3cVknLSYh0dJBI6+x1SZLNqw+Xb6baiA92cHlwMffvghN910E/F4nE8+\n+YTGxkYeeuih7MmUAexSXxnV1dWsXr2ao446CoDjjjuOxx9/vE10M/eVcTTQl2DbcYFzNRP2YdDs\n5Lkvpi7T7ODHHdqQvC21IILWYIeWC1E7H1MNdFJmGYEfAtlqrf0oiOz1BNth7S9ny7umE1dZOi01\ndsPJMozNar2iUWvj7l38gujZmTtwNhNsBY8Tfl71Nm0w4faR8GAnTdPV6ieJu+XjKix4mo/uA/o5\n+TZHaNpFJPeRVB8NTafZKRu3smta9ar8YAe/iOQ6xBV+AW3vb5qu7su6Dwiey0vK6Pav95TX4RgQ\ntT+hjeAbmLuXw0Gzg8uBhQsXMn78eHr27Elubi7Tpk3jzTffzI48GcIu95UxdOhQnn76aQAee+wx\n1q8PjinPrq+MCoKTmiHwY6A3mrgbHgSKItJdHF/5KJq+cnUEM0otVya8NQzzpBdh3ELqmYo+80/u\nRQSe0AS3DAaXBeNq9zIYXBzkdS829wQ9l2Ypweka+nw8Vz6Jp6t31GnO1Z6ymq4G97nXOXlavlT9\nwscvCjcVFKm7D9ftJ3jCoseX8tUROD6Iwonq01HvjfThdHykvI+XrEUITi3JR161E9phxzx48GAW\nLFhAU1MTra2tvPzyyxxyyCHZkSdD+P/bu/LwqIps/0tIR5IhEUKQJXGIEDbZEkSZN6Ky6bCIOsoi\naNhEBhz0PZRBgUFxxmUYeTO+YXRGRAVxRPwE1FEBRYGIgqwhOGyCNJoAYSdEgnSS8/64XbfPPV23\nuxOS7g7e3/fdr+6tOnXqV0tX163l3BrvmLmtjKSkJLz66qt48cUX0bVrV5SUlCA+Ph6Az1bGtm3b\n8Je//AXDhw8355/tENhWhoSuU5CNKVCHrWvIdj+eQOlKObsfeqAfPO9I1I9Twu41PUM8qw6U6agP\nY9Gvq9dt4vVvy8IAGJ15N6/OdFjtcKh7ZX+Y8w8GmUf1x3OShek6VxWWBv96kenq6l7q5DI74N+x\ncJ5p0HPTdUjQhOuga6ey7Z0Uz4EQrC1WFsHywMPtyl/F5W34LKr2JW8NqmDEqHPnzhgxYgS6du2K\nTp06AQDGjRtXPXxCRI3uytDZymjTpg1WrlwJANi7dy8+/PBDAIatDNVJc1sZXbp0sehUtjKaNGkS\nxFaGG8BpGAtBjeHfiQb7h5edgwpLg88Smd0IgD/r5EIBjyshf5S6uGkwqleNRjJgNQ7PjfcrGcDc\ndhUHYDN8A94jMIqzLRgy4NvOVQBgnUgnA755ULtRrO5eJxOoo7UbRerKMJTOKVCnZTfS1o3eOzJ/\nuw401LSC+dsNEOSfmY57Zd7UArXLQPkK9kepRso7YDQ0u0X9SqKK1uOmTJmCKVOmVA+HKiDstjKO\nHTO+KlJRUYGnnnoKEyZMAFATtjIyAGTBN6LTNdhADVI2KrsO4iT0Nmx1cnx0pUOa0GPX+LkMX1iR\ncZUx+ET4jKC38oYleq+t3niJXv9i4zdxHIYb53Xrwhgp7/Y+oxg+WxnFXr2tYF0c28ryrXirPNmN\niE5qZHSyUh/Yc7D60o2OORKYbCgINGJUf5JSN5ex01mZdCSCtaNQwjh420xgflXVqwtvCMNWRhaq\n7fyBbupeXlGIsNrKWL58ORYtWoQ2bdqgXbt2SE9Px6hRowCEw1ZGoBGrnD4INJ3AtwSlMD++dS5Y\n2nJOjs8R6qYlJB8uUwrrXmIlVwrfKS11qV0ijb1h38D3hWV1722paptcGYzR8nmvC+UmC93fwLfQ\npC5VLnb8dHnjKBSuLjxFPAeC3VyuhK6OQ9Wp41Oo8QuGQG1Jl6b0021dC/Wtza5MVHnzLZAyjl15\npIjLLi31XE1TGT+GcEUhLuGTf0/AqNzSEFzA1xD4s5SFkNHJQYRx6PTo9NrplHxlmNKh7CNnwGrv\n4nqv+wWMTlptn+NTGfcAdWN888uAMaUBGB1yE697nmA9cq10qI5HhvE8BvrR6fIn6yBQudnplPWr\nEEiPXRvR8Q0GmQdeVjroOIfSxnTyuvLTxbXLS6icpS6VbiaLp3RIPkqGp/HYxZ/8axdC/F2OrYww\nIhfG6S8XfBNN3OX+yk/5c9nGIpxvlHd5w11MDiysFP6rDHbPugMFSoZzUtMEurDGMDrhg/Ad8FBu\nqXFAxBzFKnnplhq3qTD6VnXP3TIw3fIqZWE8r+oZ4tluJaYMvn2uvL54vfA6c9no43Fl3bmEHmhk\nuX5+cEOmDaFX3jeGtU0cZDpKhSvzy9Pn+39dNnF5PiBcu/yUsngSqr44Z93F25GK5/LG4/lWZcH5\nHmThewGs1/CoAmrpVMYlfCRb/eeoLHq897w2Eti9B9YRifIvgnVkIfUVwWecCEIujukDi8fTVjJ2\nI2DOW6UtRzzyS9Bx8B8NuQ3vMjUvrObF1RePvwCQCdRNNEbFx2HMK2d47zNgrOmle6McSfSOmhWK\n4PuaiRrxqIXF5rAerlHlpcpcQY6Ei+D/y+HlZlceuhGhLGNV7kWwrwNeVzyOvFec+MhUhruZXh1v\nqdfurUmWnQfWctTF4W0xE9aj7YHewnh8N/zblIQqS/mbUTqknOSouNcBUBIkrRARpVMVwXAJj5gr\nYFSwHIHwUQwfXfDRL4SMvFSDaszu+WiMx5PgozvuyhGLGnnIkQ+X0/HiLh/BpHvVlMFnNU7d7/M9\nK28+Olb3WcxNhXcEroS6sfvGTDcfafGyVc98xJqhyY8ckfJRmG4EKEfd3I/rsxuFy9GuLGfJQ+kF\nrHp0aXGealTpErpke+BhMm1dW+Dhsg274OuUJXfdW5iCHOHK9mZ38TcnnSxPi7eHFBi/32pAIHp2\nP9EoQI11zOfPn0e3bt2QlZWFq6++GlOnTgVgHCpp37496tSpg61bt5ry1W8rowLAZfB/b5GjZDB/\nvuNBnuzioxOTtUjTA+uXovkzmD8fYdmdCON85MiN6+dXstc/GcbWI/6cYIyAzbAEr8u/TpxgjKhP\nA6gHY3CV4b2vy9zT7N7sAORuB6VfndBT+ZZlcFLce1h4srhX5cPLTpYhL0tel7JedO3BLeIkiEvW\nkxwVcj3J8OfnETKSD9ebLHSoZx4HsC7Ccu7ymZc/oOeuK0PAv144J50/T/ukjaysG94GiqGfUqkC\naulURo11zHXr1sXq1auRl5eH/Px8rF69GuvWrUPHjh2xbNky3HjjjX5xqtdWRhyMv0PeGQC+o7rc\nPxP6mpINSOrKZPGVv67z542x2HslMNcuPQ/8jzPzfEg+St4DY4Syy+uegzl3jBRYjTGVwtihUeyT\nLYOxC2MfjP7jPHP5lQpv5+xhaSnbu9/A9x1A5c/LRu0/L/be87KTu0l09SI7Ednx8DBedlJe6lVc\nVBx1XQFrPcoOiIPrLRb+PG2ZPueq6jIB/m2Bp8v38St52dbVPc97IO525cg5yHbM/XmcYvhzV36y\n3Spe51BtcxDOp6X8kZhofFX5woULKC8vR0pKCtq2bYvWrVtXWWfotjK6w7CVwacaOJKZ/z7oja7z\nRZFSFke5+1h85V8Kqx65wNKY+XNdMj3JhYc3ZjIyL+r5LJP3fnz0POAzo6n8VeepXr+TfZ1yWxhT\nfSXe+30wwpTlObf32ezUU+D7FL3qkFU6yl9d/FSnCuPypUJe1kuylzPPOy8bPs3UGP51wJ+5XtUW\neDrKn3PSxed67Px5uJRrLMI5B107aQy9KVT5lmaXvpJrLGR07Q4afzs/aPjacdD5ZcDYz1wNqKWf\nlqrRjrmiogJZWVlo3LgxevbsGfS8efXaysiF8aVs3ZwhYLwy8delIuHn0lwnhStX4BNYOISeDE0Y\n2LPUVST8M0QcritByPJDL2pK5CSMUaz0L4LfR1vjAAyC72CJ7joOGCObcyK9kzBObyUI3ZyHuuQ0\niHouYuWp4vPyzBD6eNkVwVo2GfBfmJVxeNnxuPJecpXQ6ZTh8p67Mi2Zpp28TEP3m5DcAOsHaWWa\nOt46f7s8S75SPpC/G8bvtxrgTGVolMfGIi8vDwUFBcjNzcWaNWtsZavfVkYsjPcUtUNB1YJ8Bnw/\nfLX7IcF73xy+FW0Pu5fPCV7ZIq9/c/g6IyVTxOIpJLD4fJcBX8Hm8SVPLq84WD5pzVAA3y4JFaY4\nF8GSTpkH+ADGfuXj8JkAVVD+5o9a6StkaXHu6pL8eFnK8uR5Vh1NJvzLMk7EgygbNyOuwpuzNGU9\nyblWvgtH8uQ6Af9fupzbjdOEeViYbAse4YLJeIQ+heaa/HL9mSJc5k+2Uc5bpsd5yjx6NHFknfOy\n5+nHo9oW/5ypDHtcfvnlGDBgADZv3mwrEx8fjwYNGgCw2sqQULYyAASxlXEAQB6ALfC9vqtX0GAj\nArXirY4xS3+XVxd/PsrkjsL6qirjQXDRjb6VjEvoAqzpA0bjVq/bLvjmvuV1FNaFv6NeWZXXBACJ\nQD2XdXR8WnMfB/iOfR/VpHVC46f46cpETg+4hAwvV1XeMo5uugMaPz5dwdPQjYJ1Uwm6ulKQaSr9\nXDZZPKt0eJ7lVIaLPSu/TFjbE+A/FQMRb5/GT/KVedFN53HOPF4gfbKeeDsAjDpdDmAbjLfdagCF\ncNmgvLwc2dnZGDhwYPVwqQRqrGM+fvy4uWOitLQUn3zyCbKzsy0y/LRN9dvKuArAdTDMU2bAf4GB\nL8Rwf3jdTBZHrjbbLc7oFvz4czH8OVwh9AHWhZJAi0NKxz6WnvroZSm7l64MV3y888Sp8F1qTlnO\ny5kLiVfA+MQU180X/dSz4hhscQjCX9WDrCde/tC4PA2pl7uSh4LUwxeNZZuACONceLhMU7cQKf2k\nP09nH6xlY8eBx+PPEGGco7xXkIuGMk88DV53Ml3lx9O4AsYnrdoDuNKGZ/jwf//3f7j66qsrYcGy\n+lBjHfPhw4fRq1cvZGVloVu3bhg4cCB69+6NZcuW4corr8SGDRswYMAA9OvXDwCwdu3aGrCVcQG+\njgfQNw6FUiZbCt+xUcD/Cww8vhx1JMA6IoCQkWkWwh4yjq6BpwnZfUKnmr7IgNUcp9SR5pPnNjHs\nLgD+FurkVEUGk0uDr3wToDe8BOGXJlx1L0eCskylLtk5cX+dvE6P1K+rUx5m1xEF4lwqwnSLZoG4\ncd3B+Etesg1Lzjq+dr8rOz8eFigP8Yj02beCggJ89NFHGDt2bESOa1/CtjLeg7WDSoP1q8hVQWME\n/sK0Wt22k5H3gJ6P1BsojKcDcX8d/MsA0BtLUmHXA2gIdIDPNgbE/dcqzhahw+5PRvlzbvw5WF7t\nyjAYKiMbahy78teFdYH1q95KBqjal8NlmhfDVccnWDp29QGNfyCeobbvJy/eVgYuhCAZ75fO4MGD\nMW3aNBQXF2P27Nn497//XWUeVUFk/5ZqFH+BMWLr4n3eCr0tXp0Lca9Q5PUrYs+6cNjIqHC1YV+3\nqi7lOFJgTUPpSRH61Gul2+tmsHs3/I3FpMH3BRM3gDKgoLHREZfBZ4u5DMxMbhF8BpKUbgkVpvjw\nsrPLK79X0zxcht/b2QVWqMqSu9QPkYbUKeuXw22j304+VNi1v0Bp2ckHa4dKRvcs65Pfp2jkA/Hg\nYW7Yt6nKQjcy/xyG7XA9PvjgA1xxxRXIzs4OuGGhJnEJj5hvgu/VvaqjLDm6CyWukg11lFDVUZNd\nuuo5A77Ol7uA9aOsHBkwLdBleRd5CjRix9VNPnzTFW7oR+E8rVBHiY1t/Csz2qsqQuVXnWlWB+xG\nw5HiWdW3HMDXMa+thhHziRAkG1rSmTZtGhYuXIi4uDicP38excXFuOuuu/D6669XmUtlcQnbyuDg\n//A6V6EjrP/uarQmG5WdDdki+EawRZowXfyL2UipbNvyxSH1fI6533jdxkxWd7rOe0IQyb6FP74Q\neBzGqLm+Sr8xfPOiSqe6VLo8HcBaLnb2kYvgzy3QIqhdvVbGpjFPW9oQlrpCyYMddHFCsU8cTIeu\n46tqpxyo3EIFr69I/onp2lHgdvXMM8/g+++/x4EDB/DWW2+hV69eYe2UgQjYypgxYwY6d+6MrKws\n9O7d2/wYa/XbyrDE0ri6H0Mh9NMHUjZD4x8Ile0odB2DTp+COoDAX+1dMPLjYvd8+KsOaihkeGW8\no9AmMCa60r0u38dsgRxSq/lrnq7SH0p5nRT3/Aoky591sroyqwy4PJ/isPPXwW7qReY5kHyw6RvJ\nhd+HUv6B9Ou42KEysjWJynfMEpHYlVGjUxnnzp1DYmIiysrK0L17d8yePRudO3dGUpLxGfM5c+Zg\n+/btmDdvHtxuNwYOHIgdO+y+iGxgypQpSE1NxZQpUzBr1iycOnXKz16GUZA9YWyZ41vuPDA6C+VK\nfwnpL6cGeLiq4EB6+bwul9el74Gvs+TxpF4ZpvwA6zSD7hmwzjMXApgEpCcahvIVjsBnLF/5FwAo\nOGfEiWsFlH0jdLrZvY4b58HLIFjeZLlJSB2yXmQcF/Q6A7WHYPJ2P3YlnwH/OdRA7ShU3sHyaNf2\nA/HQpad75n4ZsP4+7OrALg/foPqmMvaGINn6p2UoX2crQ3XKgPEF7dTU1ErpDN1WRm9YO2UHDhzU\nDmSg2mxl1FK7nxGxlTF9+nT8/Oc/x4IFCyz7kKvXVsYn8P1rJ8C6AR42/gkwrPV4NP4e+HYYKNsQ\nyUwPhDwP97B4Onnlck7JLB230MPTlXYxlF8SfCcA2wk5Fa5McipubQEkGjsvMuFvHyMTvpN/9QDU\nSwTQCigrMFwLH5VmH69eZfrTDf8pgATh8ryp+wToy02C61BlxZ85koUeHq7qQb7yShkF2W50UGFu\nmzDJJdj8urwPJivlAs3bB0pP98z9TkJfXlK3XR7cANZo9FcFFz+VEQlExFbG008/je+++w6jRo3C\npEmTANSErYwEGIbyAfvTTGq3YAp8p/IKYf1oZDH8dxUWs0vJcJ0ynKeRIvTJk2jcLkEx80+xiRPH\nXH6pPdvqkuFq/ldNFSg/AL+Ab275OHxfMEln0Y/wbKR701ACKs1Mr5vh1R3H8h+oDJSMsuvAeado\nZMHuVRmnsLg68DrXQaffTgYwDDfZIdiagU5fsDnZyi46hhN2ZRoJOCNmW9jZyhg+fDg2bdoEoCZs\nZeyCsV9xDfQjlDT4RijBFpwCLbbYLUDJZ+UmaGQCySvYjRClXjVyTYDPfkem8Evw+vNRaALM1fPj\nMA6RqJGy6hPrMlfZzQBgtcvL7YsUwWpHhJdrAuxPVCqZIvGsWwRMEPGUq6tbmUYgKF6VXSQMlJbd\nImagOMHC0zR+tRVuGL/XPFTvPuZgV/Qh7LYy9u3zGVF57733TPsZ1W8rIwPGN5B6wLr7QL3aKhvB\n0p8/S79ASLa5lzgLf8MzgXTxeDoZnp9kGJ1jMkwbzChmYcovWfgns3sytsOVwJiuULaYlV8JgN0s\nHAUwpkSKmZvC0uEjU16mqvzViD1ZXO0EP1ku6r5Q46/yYwedTlnmhV4OldGh02OnXxcnGCdd/LNB\n5ALpqUz7DgcyYPxes6A3HVAV1M6pjBo7+Xf48GGMHDkSFRUVqKioQE5ODnr37o1BgwZhz549qFOn\nDlq2bIl//OMfAIDc3Fw8/vjjcLlciI2N9bOVMX78eFxzzTV47LHHMGTIELzyyivIyMjA22+/XQlW\nfCtQsfCLswmX8ezA4/MpEhkvDvpThVy+mN0rtzmsr8t8yoPLFsEYRcXBZ+qzAFbznEUsbpHQdRTI\nawzcCmCF15tvlTvORE8D1q1xMbDax+AcCkXeVbno8tzRK8/rSJaHbkoKsJ/isIsrp1E4dmn8ZLxA\n95wbn9aSbQRCxq6N6tIPZdog2HTNpYzonKoIhkv45N8TwjcDwV+PqksmGnC91+Un/viz3em/KQA0\n2+UKYEwhK5jbl9V0E9eZodHvZmFuhI4MEZ/7u6ugT8b/qSID0Z//6rCV8VEIkv1/WtvlIos1sDY8\nt1bq4pFhc18VPVWNL+NlwLqwJ8O/YOnxMBXPC7UkwM+QFMBnzAjnvK7bGs9S1mnwrwfJRwcl42Zx\ndPHcGr9QUNV4lwrckSagQYbXdaP6dmU4c8yXANxVkHEHCJMLW7qFLh43lPTt4nLwrX1Sr1pwU/Nr\nfAHOA+Pk307vc7G3U/bOEZfBCNvsdVHGdLth7YSVfuUfiC8H58LjKV1cB+cuFxLlfaDwQEgTrvTT\npVNZfXYy0u9i8hFMPhgfXZ4lH7syCpWTm/klaeSqgto5x3wJT2XIk3+qAuxOLDWH7wsblYXUzXUo\nvTytUHXqTnTpTnHp0gSM6Qw+paDmIr6A9RNEB9n9cENukMvolNX8sprKUK7b4304GEBXgfBvzsLt\nuPM8HIT/qTFenrIuM+GrQ+6vO43pEfKwkQl0ck1yqOrpQskl1HpWejJhLVddujI9O726jkqXZrCT\nlYFOwOrKlfu5AXwHYHU1TGW8EYLkvT+dqQw7WxkzZ85Eenq6aRNjxQpjhan6bWVUwPfNP/WdNIh7\n7qe+sKG+P5YJ6/5Z/q0y6QemB0xG1+nY6ZL3CRp9nD9/huCrFuT4wpzavqb2B2cwmTjm79WZB2Oh\nj9M9wu7rurw6VPoZ8O2dVkIqDbWHeZ8oMw9zZZnuY3Iqn6o8+aEfjkJRNjKuLDMl7xEyCRoXIhxC\nlwrXdWzKT+qLY2GF8E+Xx1VtwiPiqbg8f+1EXFVePJ5sY3FCXvKXedM968pCyfC2DY0s5wRUX9fk\nTGVYULduXaxevRp5eXnIz8/H6tWrsW7dOsTExODhhx/Gtm3bsG3bNvTt29eMk5mZafq/+OKLWr1/\n+tOfcPPNN2Pv3r3o3bu3n50MKxLh/z03dZ8M/ffU1L3q1EqZf6nQweWVv9qCpGTldjDeIJJhjHTk\nFywUp1IW1yVkeB4430z4OkJ5sCSD+SnXxeJ5n+vFGJ1wOnydcaM1xsGTDPjOkZhfRnEBWMrS5XuY\nZafPfwx8exwvTxfzU+Wp7ncJGcBa5qo8+VYwXr7JwnUJGc5Dth3JH+Kec9GB63XDv35529C9RZQK\n186/UBPO2xNPk/8upD6Fo+JZt5WUl6v05xy4rA6lMH63dWzCK4uqTWWsWLECbdu2RatWrTBr1qxq\n4hI6wmorQx0guZjXhtBtZdwJYwOuOkXGT9bxE1/yhJ70B4untm3xUZ+MK7cgFWviAL79vTvhv7VL\ncmoO/21gOn5qtMynFji+Es9qtFwM32JhkbFHWXXKyj23xkffPPWXDuuPWwkUCJcvRPJ8qrSVy/24\nP9gzz6tuy9hOjR9Pk7cD/ixPCurSDeW0nV26sn25RZqybchnu/Slv8qT9ON54G1M5lcH2UZ5PO7H\n004R/oCvzONgnxfAMBU7IEB4ZVD5k3/l5eWYOHEiVqxYgZ07d2LRokXYtSvQ1snqR1htZbRv3x6A\nYVWuc+fOuO+++yxTEdVrK2MpjK+WuGDsAVVG1V3snhtk141QZLi6Tgo9wfY4qzhc7qQI1/mr+x0a\nWWlMXnFywffl6kTv1crrupj/UcGJx4fVRkYGjA0Y6mi2muLACfiOXycK3dzl5aUulba6BwKXEc/7\nSejrKxjk242sg8bQ16XkKcM4dEb+Zb5kXJkfu3Kwa2cyX40D6NOlFQqUHK8/Oxlet7r6tSsPBTeA\nlSHyCobKj5g3btyIzMxMZGRkwOVy4e6778Z7771XTXxCQ9htZUyYMAEHDhxAXl4emjZtikceeQRA\nTdjKUFlTDZG7J+Gz48A7W8C/0bpEvCT2rOJnsniZsO8AXOJSKBJ+OjnlICToiQAAFrJJREFU8vSl\nHOd4Er65xXwYnWg7b9gJm/jtYM5jqiPXymhRCnx+9byXaQRIladKr503DZVWJuNUJNLmeZdlKfPP\ny7EI/uUsy0r68TiyY+DtIpPFkWkrfjq+0ORHxwWw/vR4fULISejaSBHzkx2frn3q6j5Q2pyr+iPW\n5UnqCEVWFw8AftDwqAoqP8dcWFiIK6/0faU7PT0dhYXyja9mId9HagTcVkaPHj1M/7Fjx2LgwIEA\nDFsZ8fHxAKy2Mrp06WLRpWxlNGnSxNZWRrNmzXDo0Oqay1C1Y22kCfhjA7t3e93CJyNApCqIwvLU\noja10fBzbdmyZTVo+X1QiXr16lmeI2EYX6LGOubjx48jLi4O9evXN21lPPHEE2anCgDLli1Dx44d\nTfkGDRqgTp06IdnKePTRR21tZYT7382BAwfRh6quZaWlpZlfVgKA77//Hunp6QFi1ACohpCfn0/Z\n2dnUuXNn6tixI/35z38mIqKcnBzq2LEjderUiW6//XY6cuQIEREtWbKE2rdvT1lZWdSlSxf64IMP\nTF1jx46lzZs3ExHRiRMnqHfv3tSqVSu6+eab6dSpUzWVBQcOHPwE4fF4qEWLFnTgwAH68ccfqXPn\nzrRz586wcrgkD5g4cODAwcVg+fLl+J//+R+Ul5fjvvvuM89hhAtOx6xBRUUFYmOj/7R6beEJ1B6u\nDs/qRW3hGW1wSsyLkpISzJkzB/v378f58+cBXNx+65pCbeEJ1B6uDs/qRW3hGc1wRswAPvvsM0yY\nMAEdOnRAamoq4uPjMWfOnEjT8kNt4QnUHq4Oz+pFbeEZ7agzc+bMmZEmEWl88cUXSEtLwz/+8Q90\n69YNzz77LOLi4tClSxdUVFRExfYZoPbwBGoP13Xr1tUKntFenkSEmJiYqOdZW/CTnMr47rvvsHXr\nVvN59+7d+NnPfgYAuOKKKzBr1izMmDEDACI6P/bNN99YFh127dpl7rmMJp6AYYTqlVdeMZ//85//\nRCXXgwcPYs2aNaioqAAA7NmzJyrrvqCgAF9//bX5HK1t9ORJ60GdaG6jtQph3QMSBZg+fTqlp6dT\nnz59aPLkyXTq1Clat24dXXXVVRa5gQMH0h/+8IeIcPR4PDRt2jS69tpraebMmab/8uXLqWXLlhbZ\nSPLk6Nu3LzVt2pTee+89IiL64IMPooqrx+OhqVOnUtu2bal///40ceJEIiJauXJl1PGcMmUKtW7d\nmm6++WaaNGkSERGtWrWKWrRoYZGNJM+ysjL67//+b0pNTaXVq1eb/itWrIiq8qyt+En9hR0/fhx7\n9+7Fvn378PbbbyMuLg5PPvkkrr/+erRr1w7Tpk0zZceMGYOioiJ4POE3pP3HP/4R8+bNQ25uLp54\nwveJrL59+yItLQ3Tp0+PCp4AUFZmGIHp2rUrxo0bh9deew1nz57FgAED0KRJE3O0FGmuzz77LNxu\nN7Zv3453330Xubm5KCgowC233BI1ZUpEmDVrFtxuN3bv3o358+dj7969yM3NRe/evdGsWTP8/ve+\nk2yRLM+lS5fi8OHDePDBB/HUU0+Z/r/61a+Qnp4eNTxrK35SHbPL5cKGDRtw7NgxNGjQAEOGDAEA\nLFy4EHPnzsW//vUv5ObmAjBecdPS0uByVcVYTtWgXq8nTpyIBg0a4NSpU1i/fj3+8Ic/YPHixQCA\n1157DW+88UZEeXLExRmHR/Pz83HttdciLS0Nr732msl1wYIFEeVK3rXtKVOm4M0330R8fDzWrl2L\nhg0bmoayoqVMY2JiMHToULzwwguIiYlBs2bN0LRpU6xcaRj0efnll7Fw4cKoKM/bbrsNzz77rDmY\neemll0yZl156KeI8azt+Eot/5eXliImJQd26dVFYWIj9+/eje/fuaNSoEUpKSrBu3ToMHjwYDRo0\nwIoVK/DnP/8ZmzZtwpgxY7THwmsKqmOuV68ezpw5gyFDhiA/Px9du3bFvHnz4Ha7MXDgQDRq1Agf\nffQRnnvuubDy9Hg8qFPHsJNbXl6O2NhYXLhwARUVFdiyZQvGjBmDJk2a4IUXXkBubi7uvPNONG7c\nGCtXrgxrmf7www+m3RW1jzY2NhYxMTHYunUrhg8fjmHDhuHtt9/Gnj17cNttt0WkTE+fPo26desC\nMN48YmNjUa9ePSQlJZnl+84776B///7IzMxEo0aNkJiYiFWrVkWsjSpecXFxaNCgAWJjY9GoUSPM\nmjULOTk5iI+PR2pqKhITE/HJJ59EjGetR4SnUmoEM2bMoJUrVxIRUUVFhSXs3XffpTFjxlB+fj4R\nEW3atIluv/1282j3uXPnLMfBw82T8/3rX/9K586dIyKijRs30uDBg2nHjh1h50lENHPmTHrxxRep\ntLRUGz5y5Ejas2cPTZ06lZKSkuj6668nIiM/4eT6+OOPU05ODn333Xe2MqqMN2/eTEOHDjWP24aT\n57PPPkvNmjWjNWvWaMN//PFHIiLq378/bdy40RJ2/vz5sPH805/+RIsXL6bdu3drw1VZ3nvvvTR5\n8mRLWDh5Xmq45Drm/fv3U1JSEt1yyy1UXl5ORMaCysiRI2njxo1UUFBATz/9NI0ZM8aM0717d9q1\na1dU8Bw1apRlMYWjT58+9PXXX4eRJdH7779PnTp1ohEjRlBhYaHp7/F4aPTo0bR27Vo6c+YM3Xff\nfZSamkqDBg2if//739S3b1/Kzc0NG8+zZ89STk4ODR06lL755hsLz1GjRlm48D+/vn37htUOwltv\nvUW/+MUv6I477qChQ4fSqlWrTJ6jR4+28Dx8+DANHDiQiIgWLVpEs2bNohMnToSF55dffknZ2dk0\nePBg+v3vf0/du3cnIqPsZHkSERUWFlKXLl3oiSeeoMmTJ1NBQUFYeF6quGQ6Zo/HQ0REJSUlNG7c\nOMrKyqI5c+aY4ceOHTPvjxw5QjfccAPdf//9dN1119HgwYPp9OnTYeVrx/P48ePmvepAcnNz6dZb\nb6W77747rEabDh8+TMOHD6dx48aZfj/88IN5X1RUZN4vXLiQNm3aZD6//vrrtGfPnvAQJaJDhw5R\n7969zeeTJ0+a98pQFhGZf4KqTIcPHx62ut+zZw/dfffd9MUXXxAR0aBBg+j55583w3ndExm7cDp3\n7kz9+/en7t2701dffRUWnkREf/vb30xuR48epYceeoguXLhARNZ6V9i6dSvVr1+fOnXqFNY/5EsV\ntbpjPnHiBP3ud7+j8+fPm36fffYZPf3007Rp0yZq1aqVbdyjR4/Sxx9/TAsWLKhxnrwzU51tqDw3\nbNhAnTp1oldeeaXGeRIRnTp1ij755BNzCuXtt9+mxx9/nN555x165JFH6IEHHqBXX33V/IMoKyuz\nxK+oqDA7v5qErPu9e/fSb3/7Wzp48CCNHj2aBgwYQCNGjKDvv//eEs/j8dCqVasoOzubXn311Rrn\nyete4rXXXqN+/frZhr/11ltUr149euutt2qCmgWy3idMmEDjx4+nDRs20K9//WtzAHH06FEisr51\nHDt2jO666y568cUXa5znTwW1tmOePXs2devWjR544AEqKysz/83dbjeNHTuWiIiGDBlCWVlZ9Jvf\n/MaM9/LLL/v9WGsSzzzzDDVs2NDsWCvDU70OhqOjIyJ67rnnqE2bNuZI8tSpU3Tq1CmaNGkSXXXV\nVTR9+nR68803adiwYXT//fdruYYDvO7Vm1JhYSFdf/31NGPGDJo5cyb98MMPNH78ePr1r39t4amm\nY8JRpnZ1r/7Mli9fTuPHj7eM7hXPQ4cO0fnz5/3++GoCvN6HDRtG586do8LCQvrXv/5F7dq1o/Hj\nx1N+fj6NGjWK+vfvb+Gp5vLlWo6Di0Ot7JjfeOMNcrlcdODAAb+wVatW0SOPPEKbN2+mtm3bUlJS\nknnogYhowYIFllfbmsTnn39Ot99+O82ePZu6du1qjkaIiD799FOaPHlyUJ7havCvv/469evXz/yh\nZWdnm6/OeXl55qIjEdGuXbuoZ8+edPjwYQvXcEBX96qMnnrqKWrevDmtWLHCDGvatKk5Lz9//vyI\n1315ebnJNy8vj1q0aGGOqpX/ggULtNMFNQFdvavFxuPHj9Pw4cNNWY/HQ5mZmeYcfrjb6E8Jtapj\n5g0gKyuL1q9fT/v376fHH3+c3njjDSopKaHDhw9TvXr1qF27drR+/Xp64oknLHOP4YZazR4+fDg9\n+uijpv+hQ4coMTGR2rdvHxU8+Qhy165ddOONN9K8efO0c9qLFi0yT86FC4HqfuHChXTu3DnyeDzU\np08fevnll+nMmTPkdrtp8ODBfnO34YKu7lU5q/z069ePFi5caPELJ3T1/sorr1BxcTFduHCBrrji\nCnNO/Msvv6Rhw4YFnJ5xUD2I+o6ZN9aysjLz1W7x4sVUt25d6tq1Kz333HPUq1cvevjhh+mrr76y\njO7Ky8vpjTfeqHGe6pVa8ZTYvn07dejQwfyxlpaWWhZzwsWTSM9V/UALCgqodevWNG3aNLr11ltp\n0qRJtG3bNiIi+vbbb+mRRx6hrKyssMx7Sp52dd+7d2966KGHqKCggLZs2UJ//OMf6bbbbqNOnTpZ\nFlZrCnyNg3NWkHVfVlZGFRUV9MMPP9Do0aNp/vz5YZla4TzVtIpdvU+cOJFOnDhB//znP+mGG26g\noUOHUnZ2Nr300ks1ztNBlHfMf/vb3+ipp56iM2fOWPxVZz1nzhxzbnPfvn00YsQIc18wkbUh1iT+\n+te/0qBBg2j79u3acNX4p06dSoMHD/YLt9sbXBMIxpWIzNfub7/9lkaOHGlu6VJboc6ePRsxnnZ1\nn5OTY6n79evXh2VkN3fuXLryyittF5F53Q8ZMsT0V38yK1asMPcsR5InkbXec3Jy6NNPPyUiYzeJ\neiN1EB5EZce8YcMG6tatG91+++3mQRCFadOm0fz587Xx7rjjDvr444/DQZGIjEMAjz32GPXp08f8\nJqHC1KlTzVdUIqNDOX/+PN1www00depUevDBB8O6nayyXBUGDRpklmk4/uiC8YyWuv/000+pV69e\n1LdvXxoyZAi9+eabRGSU3bRp04LWfbj2zVeWp8KgQYPok08+CQtHB/6Iqo7Z4/FQWVkZPfTQQ3Tn\nnXea/nzko9tgv2PHDsrJyaFevXoFPPFVXVCvgefOnaMBAwaYc5h8P6xuP3JBQQG1bNmSMjIyaPHi\nxTXO82K47tixg0aMGEF9+vQJyy6WyvJUCHfdl5WV0dmzZ2nYsGG0bNkyIjL+MB544AFThu+yiFTd\nV5VnuOvdgR5RYSujvLwcU6ZMwQcffIBGjRrh5z//OcrLy3Ho0CEsWbIEixYtwrFjx1C/fn00a9bM\nPK8PAPv378fIkSNx0003Ye7cubj88strnOfy5csRFxeHlJQU7Ny5E1dffTVmz56N//3f/0Vubi4a\nNWqENm3amMbDY2Ji4PF48PDDD6NHjx5YunQp2rdvX2M8L4YrEWH79u0YN24cbrrpJrz00ktITk6O\nOp5AZOpetdFJkyahbdu2AID4+HgsWLAAd999N+Lj45GQkGDGC3fdV5VnuOvdQWBEvGOuqKjAxIkT\nceLECfTo0QN///vfkZycjOLiYsybNw/169dHv379sH79eixatAj33HMPYmNjsWzZMpSUlKBDhw64\n55570LNnz7DynDt3LkpKSvDZZ5+hpKQEP/74I1544QV89913eP755zF27FjExMRg2bJlOHPmDJo3\nb45+/fqhV69eNcrzYrguXboUpaWl6NKlC4YNGxa1Zbp06dKI1X3Pnj3x/PPP4+zZs2jfvj3i4+NR\nVFSEgwcP4rrrrkP9+vXNeO+++y5Onz4dtrqvKs9ly5aFtd4dBEdcpAmcPXsWeXl5+Pjjj5GUlISU\nlBR8+eWXcLlcWLJkCVq3bg0A6NmzJwYNGoQdO3agY8eOiImJMb+UkJiYGHae9evXR35+Pn72s59h\n2bJlePDBB9GgQQNMmTIFr7/+Ot5//33cdtttiImJMUceyuJZNHNVZam+lhGtPCNZ96mpqVi+fDmW\nLFmCESNGoHnz5li7dq354VH+Zehw1n1VeYa73h0ER8RHzHXr1sWnn36K48ePo1u3bmjatCmKioqw\nd+9e9OnTB0lJSQCAbdu2Yffu3bj//vsRGxuLtm3bolGjRhHj2aRJExw6dAgVFRU4duwYWrVqhSuv\nvBLx8fH4/PPPMWzYMKSkpISd58VwbdeuXa0o02jgefLkSWzcuBGdOnVCs2bNkJ+fj0OHDuHGG280\np1qioY1GI08HwREVhvLvvPNO5OXl4fDhw0hKSkLHjh1x2WWXoaioCEePHsXTTz+NCRMm4LrrrjMN\ns0eaZ3JyMtq0aYP69evjt7/9LTweDyZNmoRu3bqhdevWyMzMjBjP2sS1NvKsV68eOnXqhMsuuwzH\njh1DRUUFGjZsCJfLhQsXLkSMY23i6SAIIrr06MWhQ4fod7/7HT3zzDOm3y9/+UvavHkzLViwgO67\n776wrLgHg47nf/3Xf9GGDRuIyLDvq44pRxq1hWtt5vnLX/7StKS2evXqsJnkDITawtNBYER8jhkA\nmjZtijvuuAOPPvooWrZsiWuvvRbx8fGIi4tDTk4ORowYEWmKAPQ8ExISzC+PXHPNNRFm6ENt4Vqb\nedatW9d8g+vRo0dkCXpRW3g6CIJI/zNwfPjhhzRq1Chq06ZNWI7SVhW1hSdR7eHq8Kxe1BaeDvSI\nIfJ+XTFKcOHCBdSpU8f8tly0orbwBGoPV4dn9aK28HTgj6jrmB04cODgp46o2JXhwIEDBw58cDpm\nBw4cOIgyOB2zAwcOHEQZnI7ZgQMHDqIMTsfswIEDB1EGp2N24MCBgyiD0zE7cODAQZTB6Zgd1AhO\nnDiB7OxsZGdno2nTpkhPT0d2djaSkpIwceLEak9v1KhRaNGiBebOnWs+L1myxCJTr149fP311yav\nhg0bokWLFsjOzsYtt9yCb7/9FllZWaZFQwcOIoWosJXh4NJDw4YNsW3bNgDAk08+iaSkJDz88MM1\nll5MTAxmz56NO++803xWZi25TIcOHUxeo0ePxsCBA804AJCXl+d0zA4iDmfE7CAsUAdM16xZg4ED\nBwIAZs6ciZEjR+LGG29ERkYGli5dismTJ6NTp07o168fysrKAABbtmxBjx490LVrV/Tt2xdHjhwJ\nmIbdcyhxHDiIBjgds4OI4sCBA1i9ejXef/993Hvvvbj55puRn5+PhIQEfPjhh/B4PHjwwQexZMkS\nbN68GaNHj8b06dMjTduBgxqFM5XhIGKIiYlBv379UKdOHXTo0AEVFRX41a9+BQDo2LEj3G439u7d\ni//85z/o06cPAONjo82aNQtJdyh+DhxEI5yO2UFEob6FFxsbC5fLZfrHxsairKwMRIT27dvjyy+/\nrJTehg0b4tSpU+bzyZMnkZqaWj2kHTioYThTGQ4ihlDmd9u0aYNjx45hw4YNAACPx4OdO3cGjdej\nRw8sXrwYHo8HADB//vywfKHcgYPqgDNidhAWqGkEvltC7pzQ7aJwuVx455138NBDD+HMmTMoKyvD\npEmTcPXVV9umAQADBgzAli1bcM0116BOnTrIzMzEP//5z4BxHDiIFjj2mB1cEhg9ejRuvfVW3HXX\nXRetKykpCWfPnq0GVg4cVA3OVIaDSwKXX345ZsyYYR4wqQrUAZMmTZpUIzMHDioPZ8TswIEDB1EG\nZ8TswIEDB1EGp2N24MCBgyiD0zE7cODAQZTB6ZgdOHDgIMrgdMwOHDhwEGX4f1ojjHqwAZWcAAAA\nAElFTkSuQmCC\n",
"text": [
"<sunpy.spectra.spectrogram.SpectroFigure at 0x1083e6c90>"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 29,
"text": [
"<matplotlib.axes.AxesSubplot at 0x11299ac10>"
]
}
],
"prompt_number": 29
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"callisto.data"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 30,
"text": [
"array([[117, 117, 117, ..., 117, 116, 117],\n",
" [117, 116, 117, ..., 116, 116, 116],\n",
" [117, 116, 116, ..., 116, 116, 116],\n",
" ..., \n",
" [128, 128, 128, ..., 125, 124, 126],\n",
" [127, 128, 127, ..., 123, 123, 125],\n",
" [145, 146, 142, ..., 143, 137, 140]], dtype=uint8)"
]
}
],
"prompt_number": 30
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Lightcurves"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import sunpy.lightcurve\n",
"evelc = sunpy.lightcurve.EVELightCurve.create('2014/01/01')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/Users/schriste/Dropbox/Developer/python/sunpy/sunpy/lightcurve/lightcurve.py:223: RuntimeWarning: Using existing file rather than downloading, use overwrite=True to override.\n",
" warnings.warn(\"Using existing file rather than downloading, use overwrite=True to override.\", RuntimeWarning)\n"
]
}
],
"prompt_number": 31
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"evelc.data"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>XRS-B proxy</th>\n",
" <th>XRS-A proxy</th>\n",
" <th>SEM proxy</th>\n",
" <th>0.1-7ESPquad</th>\n",
" <th>17.1ESP</th>\n",
" <th>25.7ESP</th>\n",
" <th>30.4ESP</th>\n",
" <th>36.6ESP</th>\n",
" <th>darkESP</th>\n",
" <th>121.6MEGS-P</th>\n",
" <th>darkMEGS-P</th>\n",
" <th>q0ESP</th>\n",
" <th>q1ESP</th>\n",
" <th>q2ESP</th>\n",
" <th>q3ESP</th>\n",
" <th>CMLat</th>\n",
" <th>CMLon</th>\n",
" <th>x_cool proxy</th>\n",
" <th>oldXRSB proxy</th>\n",
" </tr>\n",
" <tr>\n",
" <th>HHMM</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2014-01-01 00:00:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00196</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000958</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.9</td>\n",
" <td> -0.9</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:01:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000959</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -0.9</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:02:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000957</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.2</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:03:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000956</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -1.0</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:04:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.0</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:05:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.157</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:06:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.158</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:07:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.158</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:08:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.158</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.8</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:09:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.158</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -2.0</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:10:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00196</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.159</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.6</td>\n",
" <td> -2.1</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:11:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00197</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td>-1.000000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.159</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.6</td>\n",
" <td> -2.4</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:12:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00199</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.000445</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.336</td>\n",
" <td> 0.159</td>\n",
" <td> 0.348</td>\n",
" <td> 0.157</td>\n",
" <td>-28.6</td>\n",
" <td> -3.0</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:13:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00203</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.007550</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.338</td>\n",
" <td> 0.160</td>\n",
" <td> 0.345</td>\n",
" <td> 0.156</td>\n",
" <td>-28.6</td>\n",
" <td> -4.7</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:14:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00208</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.013800</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.341</td>\n",
" <td> 0.161</td>\n",
" <td> 0.343</td>\n",
" <td> 0.156</td>\n",
" <td>-28.5</td>\n",
" <td> -6.7</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:15:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00212</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.242000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.341</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.155</td>\n",
" <td>-28.5</td>\n",
" <td> -7.6</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:16:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00215</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.537000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.342</td>\n",
" <td> 0.163</td>\n",
" <td> 0.340</td>\n",
" <td> 0.155</td>\n",
" <td>-28.3</td>\n",
" <td> -8.3</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:17:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.597000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.155</td>\n",
" <td>-28.2</td>\n",
" <td> -9.5</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:18:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.998000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.1</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:19:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000957</td>\n",
" <td> 0.934000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:20:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.870000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.166</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.6</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:21:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.808000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:22:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.746000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:23:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.687000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:24:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.629000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:25:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.574000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.344</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.5</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:26:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.520000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.5</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:27:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.470000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.2</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:28:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.421000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.3</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:29:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00219</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.376000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.338</td>\n",
" <td> 0.154</td>\n",
" <td>-28.1</td>\n",
" <td>-10.2</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:30:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00220</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.332000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.154</td>\n",
" <td>-28.2</td>\n",
" <td>-10.4</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:31:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00221</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.292000</td>\n",
" <td> 49.6</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.164</td>\n",
" <td> 0.337</td>\n",
" <td> 0.154</td>\n",
" <td>-28.3</td>\n",
" <td>-10.6</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:32:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00222</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.254000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.154</td>\n",
" <td>-28.4</td>\n",
" <td>-10.6</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:33:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00224</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.219000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.153</td>\n",
" <td>-28.5</td>\n",
" <td>-10.9</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:34:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00226</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.186000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.347</td>\n",
" <td> 0.164</td>\n",
" <td> 0.337</td>\n",
" <td> 0.152</td>\n",
" <td>-28.6</td>\n",
" <td>-12.0</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:35:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00229</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.156000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.336</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.0</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:36:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00231</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.218000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.4</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:37:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00233</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.361000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.351</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-14.1</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:38:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00236</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.320000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.165</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.6</td>\n",
" <td>-14.3</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:39:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00237</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.283000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.351</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-14.1</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:40:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.247000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.9</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:41:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00240</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000957</td>\n",
" <td> 0.214000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.5</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:42:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00241</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.183000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.152</td>\n",
" <td>-28.7</td>\n",
" <td>-13.0</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:43:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000860</td>\n",
" <td> 0.00242</td>\n",
" <td> 0.000908</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000960</td>\n",
" <td> 0.155000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.336</td>\n",
" <td> 0.151</td>\n",
" <td>-28.8</td>\n",
" <td>-12.8</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:44:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000861</td>\n",
" <td> 0.00243</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000960</td>\n",
" <td> 0.307000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.163</td>\n",
" <td> 0.337</td>\n",
" <td> 0.151</td>\n",
" <td>-28.9</td>\n",
" <td>-12.6</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:45:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000861</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.620000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.151</td>\n",
" <td>-29.0</td>\n",
" <td>-12.1</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:46:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.742000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.348</td>\n",
" <td> 0.162</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-11.6</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:47:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.763000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.348</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-11.6</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:48:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.695000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.347</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.8</td>\n",
" <td>-11.1</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:49:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000863</td>\n",
" <td> 0.00243</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000962</td>\n",
" <td> 0.675000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.2</td>\n",
" <td> 0.346</td>\n",
" <td> 0.163</td>\n",
" <td> 0.339</td>\n",
" <td> 0.152</td>\n",
" <td>-28.8</td>\n",
" <td>-10.8</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:50:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00242</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.140000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:51:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000866</td>\n",
" <td> 0.00241</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.260000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:52:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00239</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.470000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.0</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:53:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.820000</td>\n",
" <td> 49.5</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td> -9.8</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:54:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.890000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td> -9.4</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:55:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00236</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.880000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.153</td>\n",
" <td>-28.9</td>\n",
" <td> -9.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:56:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00235</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000964</td>\n",
" <td> 2.040000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.153</td>\n",
" <td>-28.8</td>\n",
" <td> -9.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:57:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00233</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000553</td>\n",
" <td> 0.000964</td>\n",
" <td> 2.250000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.154</td>\n",
" <td>-28.8</td>\n",
" <td> -8.6</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:58:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00232</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000553</td>\n",
" <td> 0.000963</td>\n",
" <td> 2.060000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.154</td>\n",
" <td>-28.7</td>\n",
" <td> -8.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:59:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000863</td>\n",
" <td> 0.00230</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000554</td>\n",
" <td> 0.000962</td>\n",
" <td> 1.870000</td>\n",
" <td> 49.4</td>\n",
" <td>-1</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.154</td>\n",
" <td>-28.7</td>\n",
" <td> -8.2</td>\n",
" <td> 2430</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th></th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1440 rows \u00d7 19 columns</p>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 32,
"text": [
" XRS-B proxy XRS-A proxy SEM proxy 0.1-7ESPquad \\\n",
"HHMM \n",
"2014-01-01 00:00:00 0.000006 0.000000 0.000858 0.00196 \n",
"2014-01-01 00:01:00 0.000006 0.000000 0.000858 0.00195 \n",
"2014-01-01 00:02:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:03:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:04:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:05:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:06:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:07:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:08:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:09:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:10:00 0.000006 0.000000 0.000857 0.00196 \n",
"2014-01-01 00:11:00 0.000006 0.000000 0.000856 0.00197 \n",
"2014-01-01 00:12:00 0.000006 0.000000 0.000856 0.00199 \n",
"2014-01-01 00:13:00 0.000006 0.000000 0.000855 0.00203 \n",
"2014-01-01 00:14:00 0.000006 0.000000 0.000855 0.00208 \n",
"2014-01-01 00:15:00 0.000007 0.000000 0.000855 0.00212 \n",
"2014-01-01 00:16:00 0.000007 0.000001 0.000855 0.00215 \n",
"2014-01-01 00:17:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:18:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:19:00 0.000007 0.000001 0.000857 0.00217 \n",
"2014-01-01 00:20:00 0.000007 0.000001 0.000857 0.00217 \n",
"2014-01-01 00:21:00 0.000007 0.000001 0.000856 0.00216 \n",
"2014-01-01 00:22:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:23:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:24:00 0.000007 0.000001 0.000855 0.00216 \n",
"2014-01-01 00:25:00 0.000007 0.000001 0.000856 0.00216 \n",
"2014-01-01 00:26:00 0.000007 0.000001 0.000856 0.00217 \n",
"2014-01-01 00:27:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:28:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:29:00 0.000007 0.000001 0.000856 0.00219 \n",
"2014-01-01 00:30:00 0.000007 0.000001 0.000856 0.00220 \n",
"2014-01-01 00:31:00 0.000007 0.000001 0.000856 0.00221 \n",
"2014-01-01 00:32:00 0.000007 0.000001 0.000856 0.00222 \n",
"2014-01-01 00:33:00 0.000007 0.000001 0.000856 0.00224 \n",
"2014-01-01 00:34:00 0.000007 0.000001 0.000855 0.00226 \n",
"2014-01-01 00:35:00 0.000007 0.000001 0.000856 0.00229 \n",
"2014-01-01 00:36:00 0.000008 0.000001 0.000856 0.00231 \n",
"2014-01-01 00:37:00 0.000008 0.000001 0.000857 0.00233 \n",
"2014-01-01 00:38:00 0.000008 0.000001 0.000858 0.00236 \n",
"2014-01-01 00:39:00 0.000008 0.000001 0.000859 0.00237 \n",
"2014-01-01 00:40:00 0.000008 0.000001 0.000859 0.00238 \n",
"2014-01-01 00:41:00 0.000008 0.000001 0.000859 0.00240 \n",
"2014-01-01 00:42:00 0.000008 0.000001 0.000859 0.00241 \n",
"2014-01-01 00:43:00 0.000008 0.000001 0.000860 0.00242 \n",
"2014-01-01 00:44:00 0.000008 0.000001 0.000861 0.00243 \n",
"2014-01-01 00:45:00 0.000008 0.000001 0.000861 0.00244 \n",
"2014-01-01 00:46:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:47:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:48:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:49:00 0.000008 0.000001 0.000863 0.00243 \n",
"2014-01-01 00:50:00 0.000008 0.000001 0.000864 0.00242 \n",
"2014-01-01 00:51:00 0.000008 0.000001 0.000866 0.00241 \n",
"2014-01-01 00:52:00 0.000008 0.000001 0.000865 0.00239 \n",
"2014-01-01 00:53:00 0.000008 0.000001 0.000865 0.00238 \n",
"2014-01-01 00:54:00 0.000008 0.000001 0.000865 0.00238 \n",
"2014-01-01 00:55:00 0.000008 0.000001 0.000865 0.00236 \n",
"2014-01-01 00:56:00 0.000008 0.000001 0.000864 0.00235 \n",
"2014-01-01 00:57:00 0.000008 0.000001 0.000864 0.00233 \n",
"2014-01-01 00:58:00 0.000008 0.000001 0.000864 0.00232 \n",
"2014-01-01 00:59:00 0.000007 0.000001 0.000863 0.00230 \n",
" ... ... ... ... \n",
"\n",
" 17.1ESP 25.7ESP 30.4ESP 36.6ESP darkESP \\\n",
"HHMM \n",
"2014-01-01 00:00:00 0.000904 0.000547 0.000958 -1.000000 49.4 \n",
"2014-01-01 00:01:00 0.000904 0.000547 0.000959 -1.000000 49.4 \n",
"2014-01-01 00:02:00 0.000903 0.000547 0.000957 -1.000000 49.4 \n",
"2014-01-01 00:03:00 0.000903 0.000547 0.000956 -1.000000 49.4 \n",
"2014-01-01 00:04:00 0.000903 0.000547 0.000955 -1.000000 49.4 \n",
"2014-01-01 00:05:00 0.000903 0.000547 0.000955 -1.000000 49.5 \n",
"2014-01-01 00:06:00 0.000903 0.000546 0.000955 -1.000000 49.5 \n",
"2014-01-01 00:07:00 0.000903 0.000546 0.000955 -1.000000 49.5 \n",
"2014-01-01 00:08:00 0.000903 0.000546 0.000956 -1.000000 49.5 \n",
"2014-01-01 00:09:00 0.000904 0.000546 0.000956 -1.000000 49.5 \n",
"2014-01-01 00:10:00 0.000904 0.000546 0.000956 -1.000000 49.5 \n",
"2014-01-01 00:11:00 0.000903 0.000546 0.000956 -1.000000 49.5 \n",
"2014-01-01 00:12:00 0.000903 0.000546 0.000955 0.000445 49.5 \n",
"2014-01-01 00:13:00 0.000903 0.000546 0.000954 0.007550 49.5 \n",
"2014-01-01 00:14:00 0.000903 0.000546 0.000954 0.013800 49.5 \n",
"2014-01-01 00:15:00 0.000904 0.000545 0.000954 0.242000 49.5 \n",
"2014-01-01 00:16:00 0.000904 0.000545 0.000954 0.537000 49.5 \n",
"2014-01-01 00:17:00 0.000904 0.000545 0.000954 0.597000 49.6 \n",
"2014-01-01 00:18:00 0.000904 0.000545 0.000956 0.998000 49.6 \n",
"2014-01-01 00:19:00 0.000905 0.000545 0.000957 0.934000 49.6 \n",
"2014-01-01 00:20:00 0.000905 0.000545 0.000956 0.870000 49.6 \n",
"2014-01-01 00:21:00 0.000905 0.000545 0.000955 0.808000 49.6 \n",
"2014-01-01 00:22:00 0.000905 0.000545 0.000953 0.746000 49.6 \n",
"2014-01-01 00:23:00 0.000905 0.000546 0.000953 0.687000 49.6 \n",
"2014-01-01 00:24:00 0.000906 0.000546 0.000953 0.629000 49.6 \n",
"2014-01-01 00:25:00 0.000906 0.000547 0.000954 0.574000 49.6 \n",
"2014-01-01 00:26:00 0.000906 0.000547 0.000954 0.520000 49.5 \n",
"2014-01-01 00:27:00 0.000906 0.000547 0.000955 0.470000 49.5 \n",
"2014-01-01 00:28:00 0.000906 0.000547 0.000955 0.421000 49.5 \n",
"2014-01-01 00:29:00 0.000906 0.000548 0.000954 0.376000 49.5 \n",
"2014-01-01 00:30:00 0.000906 0.000548 0.000954 0.332000 49.6 \n",
"2014-01-01 00:31:00 0.000906 0.000548 0.000954 0.292000 49.6 \n",
"2014-01-01 00:32:00 0.000906 0.000548 0.000953 0.254000 49.5 \n",
"2014-01-01 00:33:00 0.000906 0.000549 0.000953 0.219000 49.5 \n",
"2014-01-01 00:34:00 0.000906 0.000549 0.000953 0.186000 49.5 \n",
"2014-01-01 00:35:00 0.000906 0.000549 0.000954 0.156000 49.5 \n",
"2014-01-01 00:36:00 0.000906 0.000549 0.000954 0.218000 49.5 \n",
"2014-01-01 00:37:00 0.000907 0.000549 0.000955 0.361000 49.5 \n",
"2014-01-01 00:38:00 0.000907 0.000549 0.000956 0.320000 49.5 \n",
"2014-01-01 00:39:00 0.000907 0.000549 0.000958 0.283000 49.5 \n",
"2014-01-01 00:40:00 0.000907 0.000550 0.000958 0.247000 49.5 \n",
"2014-01-01 00:41:00 0.000907 0.000549 0.000957 0.214000 49.5 \n",
"2014-01-01 00:42:00 0.000907 0.000549 0.000958 0.183000 49.5 \n",
"2014-01-01 00:43:00 0.000908 0.000549 0.000960 0.155000 49.5 \n",
"2014-01-01 00:44:00 0.000909 0.000550 0.000960 0.307000 49.5 \n",
"2014-01-01 00:45:00 0.000909 0.000550 0.000961 0.620000 49.5 \n",
"2014-01-01 00:46:00 0.000909 0.000550 0.000961 0.742000 49.5 \n",
"2014-01-01 00:47:00 0.000909 0.000551 0.000961 0.763000 49.5 \n",
"2014-01-01 00:48:00 0.000909 0.000551 0.000961 0.695000 49.5 \n",
"2014-01-01 00:49:00 0.000909 0.000551 0.000962 0.675000 49.5 \n",
"2014-01-01 00:50:00 0.000910 0.000552 0.000965 1.140000 49.5 \n",
"2014-01-01 00:51:00 0.000910 0.000552 0.000966 1.260000 49.5 \n",
"2014-01-01 00:52:00 0.000910 0.000551 0.000966 1.470000 49.5 \n",
"2014-01-01 00:53:00 0.000911 0.000551 0.000965 1.820000 49.5 \n",
"2014-01-01 00:54:00 0.000911 0.000552 0.000966 1.890000 49.4 \n",
"2014-01-01 00:55:00 0.000911 0.000552 0.000965 1.880000 49.4 \n",
"2014-01-01 00:56:00 0.000911 0.000552 0.000964 2.040000 49.4 \n",
"2014-01-01 00:57:00 0.000911 0.000553 0.000964 2.250000 49.4 \n",
"2014-01-01 00:58:00 0.000910 0.000553 0.000963 2.060000 49.4 \n",
"2014-01-01 00:59:00 0.000910 0.000554 0.000962 1.870000 49.4 \n",
" ... ... ... ... ... \n",
"\n",
" 121.6MEGS-P darkMEGS-P q0ESP q1ESP q2ESP q3ESP \\\n",
"HHMM \n",
"2014-01-01 00:00:00 -1 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:01:00 -1 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:02:00 -1 39.2 0.334 0.157 0.350 0.158 \n",
"2014-01-01 00:03:00 -1 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:04:00 -1 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:05:00 -1 39.2 0.335 0.157 0.350 0.158 \n",
"2014-01-01 00:06:00 -1 39.2 0.334 0.158 0.351 0.158 \n",
"2014-01-01 00:07:00 -1 39.2 0.334 0.158 0.350 0.158 \n",
"2014-01-01 00:08:00 -1 39.2 0.335 0.158 0.350 0.158 \n",
"2014-01-01 00:09:00 -1 39.2 0.335 0.158 0.349 0.158 \n",
"2014-01-01 00:10:00 -1 39.2 0.335 0.159 0.349 0.158 \n",
"2014-01-01 00:11:00 -1 39.2 0.335 0.159 0.349 0.158 \n",
"2014-01-01 00:12:00 -1 39.2 0.336 0.159 0.348 0.157 \n",
"2014-01-01 00:13:00 -1 39.3 0.338 0.160 0.345 0.156 \n",
"2014-01-01 00:14:00 -1 39.3 0.341 0.161 0.343 0.156 \n",
"2014-01-01 00:15:00 -1 39.3 0.341 0.162 0.342 0.155 \n",
"2014-01-01 00:16:00 -1 39.2 0.342 0.163 0.340 0.155 \n",
"2014-01-01 00:17:00 -1 39.2 0.343 0.164 0.338 0.155 \n",
"2014-01-01 00:18:00 -1 39.2 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:19:00 -1 39.3 0.343 0.165 0.336 0.155 \n",
"2014-01-01 00:20:00 -1 39.3 0.343 0.166 0.336 0.155 \n",
"2014-01-01 00:21:00 -1 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:22:00 -1 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:23:00 -1 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:24:00 -1 39.2 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:25:00 -1 39.2 0.344 0.165 0.336 0.155 \n",
"2014-01-01 00:26:00 -1 39.3 0.343 0.165 0.336 0.155 \n",
"2014-01-01 00:27:00 -1 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:28:00 -1 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:29:00 -1 39.3 0.343 0.165 0.338 0.154 \n",
"2014-01-01 00:30:00 -1 39.3 0.344 0.165 0.337 0.154 \n",
"2014-01-01 00:31:00 -1 39.3 0.345 0.164 0.337 0.154 \n",
"2014-01-01 00:32:00 -1 39.3 0.345 0.164 0.338 0.154 \n",
"2014-01-01 00:33:00 -1 39.3 0.346 0.164 0.338 0.153 \n",
"2014-01-01 00:34:00 -1 39.3 0.347 0.164 0.337 0.152 \n",
"2014-01-01 00:35:00 -1 39.3 0.349 0.164 0.336 0.151 \n",
"2014-01-01 00:36:00 -1 39.3 0.349 0.164 0.335 0.151 \n",
"2014-01-01 00:37:00 -1 39.3 0.351 0.164 0.334 0.151 \n",
"2014-01-01 00:38:00 -1 39.3 0.350 0.165 0.334 0.151 \n",
"2014-01-01 00:39:00 -1 39.3 0.351 0.164 0.334 0.151 \n",
"2014-01-01 00:40:00 -1 39.3 0.350 0.164 0.334 0.151 \n",
"2014-01-01 00:41:00 -1 39.3 0.350 0.164 0.335 0.151 \n",
"2014-01-01 00:42:00 -1 39.3 0.349 0.164 0.335 0.152 \n",
"2014-01-01 00:43:00 -1 39.3 0.349 0.164 0.336 0.151 \n",
"2014-01-01 00:44:00 -1 39.3 0.349 0.163 0.337 0.151 \n",
"2014-01-01 00:45:00 -1 39.3 0.349 0.163 0.338 0.151 \n",
"2014-01-01 00:46:00 -1 39.3 0.348 0.162 0.338 0.152 \n",
"2014-01-01 00:47:00 -1 39.3 0.348 0.163 0.338 0.152 \n",
"2014-01-01 00:48:00 -1 39.3 0.347 0.163 0.338 0.152 \n",
"2014-01-01 00:49:00 -1 39.2 0.346 0.163 0.339 0.152 \n",
"2014-01-01 00:50:00 -1 39.3 0.346 0.162 0.340 0.152 \n",
"2014-01-01 00:51:00 -1 39.3 0.346 0.162 0.340 0.152 \n",
"2014-01-01 00:52:00 -1 39.3 0.345 0.162 0.340 0.152 \n",
"2014-01-01 00:53:00 -1 39.3 0.345 0.162 0.340 0.152 \n",
"2014-01-01 00:54:00 -1 39.3 0.344 0.162 0.341 0.152 \n",
"2014-01-01 00:55:00 -1 39.3 0.345 0.162 0.341 0.153 \n",
"2014-01-01 00:56:00 -1 39.3 0.344 0.162 0.341 0.153 \n",
"2014-01-01 00:57:00 -1 39.3 0.343 0.162 0.341 0.154 \n",
"2014-01-01 00:58:00 -1 39.3 0.343 0.162 0.342 0.154 \n",
"2014-01-01 00:59:00 -1 39.3 0.343 0.162 0.342 0.154 \n",
" ... ... ... ... ... ... \n",
"\n",
" CMLat CMLon x_cool proxy oldXRSB proxy \n",
"HHMM \n",
"2014-01-01 00:00:00 -28.9 -0.9 2320 0.000005 \n",
"2014-01-01 00:01:00 -28.8 -0.9 2320 0.000005 \n",
"2014-01-01 00:02:00 -28.7 -1.2 2320 0.000005 \n",
"2014-01-01 00:03:00 -28.8 -1.0 2330 0.000005 \n",
"2014-01-01 00:04:00 -28.7 -1.0 2330 0.000005 \n",
"2014-01-01 00:05:00 -28.8 -1.3 2330 0.000005 \n",
"2014-01-01 00:06:00 -28.8 -1.3 2330 0.000005 \n",
"2014-01-01 00:07:00 -28.7 -1.3 2330 0.000005 \n",
"2014-01-01 00:08:00 -28.7 -1.8 2330 0.000005 \n",
"2014-01-01 00:09:00 -28.7 -2.0 2330 0.000005 \n",
"2014-01-01 00:10:00 -28.6 -2.1 2340 0.000005 \n",
"2014-01-01 00:11:00 -28.6 -2.4 2340 0.000005 \n",
"2014-01-01 00:12:00 -28.6 -3.0 2340 0.000005 \n",
"2014-01-01 00:13:00 -28.6 -4.7 2340 0.000006 \n",
"2014-01-01 00:14:00 -28.5 -6.7 2340 0.000006 \n",
"2014-01-01 00:15:00 -28.5 -7.6 2340 0.000006 \n",
"2014-01-01 00:16:00 -28.3 -8.3 2350 0.000006 \n",
"2014-01-01 00:17:00 -28.2 -9.5 2350 0.000006 \n",
"2014-01-01 00:18:00 -28.0 -10.1 2350 0.000006 \n",
"2014-01-01 00:19:00 -27.9 -10.3 2350 0.000006 \n",
"2014-01-01 00:20:00 -27.9 -10.6 2350 0.000006 \n",
"2014-01-01 00:21:00 -27.9 -10.2 2350 0.000006 \n",
"2014-01-01 00:22:00 -27.9 -10.2 2360 0.000006 \n",
"2014-01-01 00:23:00 -27.9 -10.2 2360 0.000006 \n",
"2014-01-01 00:24:00 -28.0 -10.2 2360 0.000006 \n",
"2014-01-01 00:25:00 -28.0 -10.5 2360 0.000006 \n",
"2014-01-01 00:26:00 -27.9 -10.5 2360 0.000006 \n",
"2014-01-01 00:27:00 -28.0 -10.2 2370 0.000006 \n",
"2014-01-01 00:28:00 -28.0 -10.3 2370 0.000006 \n",
"2014-01-01 00:29:00 -28.1 -10.2 2370 0.000006 \n",
"2014-01-01 00:30:00 -28.2 -10.4 2370 0.000006 \n",
"2014-01-01 00:31:00 -28.3 -10.6 2370 0.000006 \n",
"2014-01-01 00:32:00 -28.4 -10.6 2370 0.000006 \n",
"2014-01-01 00:33:00 -28.5 -10.9 2380 0.000007 \n",
"2014-01-01 00:34:00 -28.6 -12.0 2380 0.000007 \n",
"2014-01-01 00:35:00 -28.7 -13.0 2380 0.000007 \n",
"2014-01-01 00:36:00 -28.7 -13.4 2380 0.000007 \n",
"2014-01-01 00:37:00 -28.7 -14.1 2380 0.000007 \n",
"2014-01-01 00:38:00 -28.6 -14.3 2380 0.000007 \n",
"2014-01-01 00:39:00 -28.7 -14.1 2390 0.000007 \n",
"2014-01-01 00:40:00 -28.7 -13.9 2390 0.000007 \n",
"2014-01-01 00:41:00 -28.7 -13.5 2390 0.000007 \n",
"2014-01-01 00:42:00 -28.7 -13.0 2390 0.000007 \n",
"2014-01-01 00:43:00 -28.8 -12.8 2390 0.000007 \n",
"2014-01-01 00:44:00 -28.9 -12.6 2390 0.000007 \n",
"2014-01-01 00:45:00 -29.0 -12.1 2400 0.000007 \n",
"2014-01-01 00:46:00 -28.9 -11.6 2400 0.000007 \n",
"2014-01-01 00:47:00 -28.9 -11.6 2400 0.000007 \n",
"2014-01-01 00:48:00 -28.8 -11.1 2400 0.000007 \n",
"2014-01-01 00:49:00 -28.8 -10.8 2400 0.000007 \n",
"2014-01-01 00:50:00 -28.9 -10.3 2400 0.000007 \n",
"2014-01-01 00:51:00 -28.9 -10.3 2410 0.000007 \n",
"2014-01-01 00:52:00 -28.9 -10.0 2410 0.000007 \n",
"2014-01-01 00:53:00 -28.9 -9.8 2410 0.000007 \n",
"2014-01-01 00:54:00 -28.9 -9.4 2410 0.000007 \n",
"2014-01-01 00:55:00 -28.9 -9.3 2420 0.000007 \n",
"2014-01-01 00:56:00 -28.8 -9.3 2420 0.000007 \n",
"2014-01-01 00:57:00 -28.8 -8.6 2420 0.000007 \n",
"2014-01-01 00:58:00 -28.7 -8.3 2420 0.000007 \n",
"2014-01-01 00:59:00 -28.7 -8.2 2430 0.000007 \n",
" ... ... ... ... \n",
"\n",
"[1440 rows x 19 columns]"
]
}
],
"prompt_number": 32
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"fig = plt.figure()\n",
"ax = evelc.data['XRS-B proxy'].plot()\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEmCAYAAACXl2yGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8VNXdLvBnIEEuouEiI2TAgclkkhCYoJBYc9DQGCKg\ngUrF4C1UeopUBGuJyFFb31ZyedWXgtSifbnEtzVCT5HQQ0ix0qi0hAiCVYIlSiJhclESwkUuQ5Lf\n+WOZIQlzSyZkJjvP9/PJB/bMXnt+eyD7mbXW3nt0IiIgIiJyope/CyAiosDFkCAiIpcYEkRE5BJD\ngoiIXGJIEBGRSwwJIiJyyauQKCgoQEREBMxmM7Kzs52us3jxYpjNZlitVhw4cMBj27q6OiQlJSE8\nPBxTp05FfX294/EpU6Zg4MCBeOKJJxzrnz9/HjNmzEBkZCSio6OxfPnyDu0wERG1g3jQ0NAgJpNJ\nysrKxG63i9VqlZKSklbrbN++XaZNmyYiIkVFRRIXF+exbXp6umRnZ4uISFZWlixbtkxERL799lvZ\nvXu3rF27VhYtWuR4jXPnzklhYaGIiNjtdpk8ebLs2LHDU/lEROQDjz2J4uJihIWFwWg0Ijg4GKmp\nqcjLy2u1zrZt25CWlgYAiIuLQ319Paqrq922bdkmLS0NW7duBQD0798f8fHxuOaaa1q9Rr9+/XDH\nHXcAAIKDg3HzzTfDZrP5GJFEROSOx5Cw2WwYOXKkY9lgMFxxcHa1TmVlpcu2NTU10Ov1AAC9Xo+a\nmppW29TpdC5rqq+vx1/+8hckJiZ6Kp+IiHwQ5GkFdwfrlsSLu3uIiNPt6XQ6r1+noaEBc+fOxZIl\nS2A0Gls9N3ToUNTW1nq1HSIiUkwmE7744gunz3nsSYSGhqKiosKxXFFRAYPB4Had48ePw2AwOH08\nNDQUgOo9VFdXAwCqqqowbNgwr3bmJz/5CSwWCxYvXnzFc7W1tRCRgP/55S9/6fcaWCfrZJ2ss/nn\nyy+/dHnM9RgSEydORGlpKcrLy2G327Fp0yakpKS0WiclJQVvvvkmAKCoqAghISHQ6/Vu26akpCAn\nJwcAkJOTg1mzZrXapsiVPZPnnnsOp0+fxsqVKz2VHdASEhL8XYJXWGfnYp2di3V2EfFCfn6+hIeH\ni8lkkoyMDBERWbt2raxdu9axzuOPPy4mk0nGjx8v+/fvd9tWRKS2tlYSExPFbDZLUlKSnDx50vHc\nTTfdJIMHD5Zrr71WDAaDHD58WCoqKkSn00lUVJTExMRITEyMrFu3rlWdXu4OEfUwn30mcuqUv6sI\nXO6OnbrvVtAEnU7ntAdCRD2bTgc8+CDwhz/4u5LA5O7YySuuiahHcDEvSx4wJIioRzh92t8VdE8M\nCSLqES5c8HcF3RNDgoh6BIZExzAkiKhHYEh0DEOCiHoEL2/qQG0wJIioR+jd298VdE8MCSIicokh\nQUQ9QlOTvyvonhgSRNQjMCQ6hiFBRD0C79jTMQwJIuoR2JPoGIYEEfUIDImOYUgQUY/A4aaOYUgQ\nkaY19yAaGvxbR3fFkCAiTWtsVH8yJDqGIUFEmtbYCPTpo/7kkFP7MSSISNMaG9UtOYKCgEuX/F1N\n98OQICJNaw6J4GAOOXVEkL8LICK6mhobgV691F1g2ZNoP4YEEWlaU5PqSTAkOoYhQUSa1jzc1Ls3\nh5s6gnMSRKRpnLj2DUOCiDSt5cQ1Q6L9GBJEpGk8u8k3DAki0jQON/mGIUFEmsbhJt8wJIhI0zjc\n5BuPIVFQUICIiAiYzWZkZ2c7XWfx4sUwm82wWq04cOCAx7Z1dXVISkpCeHg4pk6divr6esfjU6ZM\nwcCBA/HEE0+0eo39+/dj3LhxMJvNWLJkSYd2loh6Hg43+cZtSDQ2NmLRokUoKChASUkJcnNzcfjw\n4Vbr5Ofn44svvkBpaSneeOMNLFy40GPbrKwsJCUl4ciRI0hMTERWVhYAoG/fvnjxxRfx8ssvX1HL\nwoULsW7dOpSWlqK0tBQFBQWd8gYQkbZxuMk3bkOiuLgYYWFhMBqNCA4ORmpqKvLy8lqts23bNqSl\npQEA4uLiUF9fj+rqardtW7ZJS0vD1q1bAQD9+/dHfHw8rrnmmlavUVVVhTNnziA2NhYA8Mgjjzja\nEBG5w+Em37gNCZvNhpEjRzqWDQYDbDabV+tUVla6bFtTUwO9Xg8A0Ov1qKmpabVNnU53xWsYDAbH\ncmho6BV1EBE5w+Em37gNibYHa1fEi5u0i4jT7el0Oq9fh4iovTjc5Bu3924KDQ1FRUWFY7mioqLV\nJ3pn6xw/fhwGgwGXLl264vHQ0FAAqvdQXV2NG2+8EVVVVRg2bJjbIkNDQ3H8+HGn22pr3rx5MBqN\nAICQkBDExMQgISEBAFBYWAgAXOYyl3vQcp8+CejdGzh1qhAHDwJ33x1Y9fljubCwEBs3bgQAx/HS\nJXHj0qVLMmbMGCkrK5OLFy+K1WqVkpKSVuts375dpk2bJiIie/bskbi4OI9t09PTJSsrS0REMjMz\nZdmyZa22uWHDBlm0aFGrx2JjY6WoqEiamppk2rRpsmPHjivq9bA7RNQDffCBSHy8yOzZIps3+7ua\nwOTu2Om2JxEUFIQ1a9YgOTkZjY2NmD9/PiIjI/H6668DABYsWIDp06cjPz8fYWFhGDBgADZs2OC2\nLQA888wzmDNnDtatWwej0YjNmzc7XtNoNOLMmTOw2+3YunUr3n33XUREROC1117DvHnzcP78eUyf\nPh133XWX+/QjIgKHm3yl+y5FNEGn03k1P0JEPcd77wErVgAGA3DnncAjj/i7osDj7tjJK66JSNN4\ndpNvGBJEpGkcbvINQ4KINI0X0/mGIUFEmsbhJt8wJIhI0zjc5BuGBBFpGkPCNwwJItK0lsNNnJNo\nP4YEEWkaexK+YUgQkaYxJHzDkCAiTWtqAnr1Ykh0FEOCiDStqYk9CV8wJIhI09iT8A1Dgog0rakJ\n0OkYEh3FkCAiTRNhT8IXDAki0jQON/mGIUFEmsbhJt8wJIhI09iT8A1Dgog0jXMSvmFIEJGmsSfh\nG4YEEWka5yR8w5AgIk1rHm7ilw51DEOCiDSt5XATbxXefgwJItI0Djf5hiFBRJrGs5t8w5AgIk3j\n2U2+YUgQkaYxJHzDkCAiTeOchG8YEkSkaZyT8A1Dgog0jcNNvvEYEgUFBYiIiIDZbEZ2drbTdRYv\nXgyz2Qyr1YoDBw54bFtXV4ekpCSEh4dj6tSpqK+vdzyXmZkJs9mMiIgI7Ny50/H4hg0bMG7cOFit\nVkybNg21tbUd2mEi6lk43OQjcaOhoUFMJpOUlZWJ3W4Xq9UqJSUlrdbZvn27TJs2TUREioqKJC4u\nzmPb9PR0yc7OFhGRrKwsWbZsmYiIHDp0SKxWq9jtdikrKxOTySRNTU1y8eJFGTx4sNTW1oqIyNNP\nPy0vvPDCFfV62B0i6oGefVbk178WOXtWpF8/f1cTmNwdO932JIqLixEWFgaj0Yjg4GCkpqYiLy+v\n1Trbtm1DWloaACAuLg719fWorq5227Zlm7S0NGzduhUAkJeXh7lz5yI4OBhGoxFhYWEoLi5GUFAQ\nBg0ahLNnz0JEcPr0aYSGhnZyXBKRFnG4yTduQ8Jms2HkyJGOZYPBAJvN5tU6lZWVLtvW1NRAr9cD\nAPR6PWpqagAAlZWVMBgMrdocP34cvXr1wqpVqxAdHY3Q0FAcPnwYjz76aEf3mYh6kLa35RDxd0Xd\nS5C7J3U6nVcbES/edRFxuj2dTuf2dXQ6HU6fPo3Fixfjk08+wejRo/HEE08gMzMTzz777BXrz5s3\nD0ajEQAQEhKCmJgYJCQkAAAKCwsBgMtc5nIPWm5qSoBOB7z/fiF69QIaGhIQHBw49fljubCwEBs3\nbgQAx/HSJXfjVHv27JHk5GTHckZGhmRlZbVaZ8GCBZKbm+tYtlgsUl1d7batxWKRqqoqERGprKwU\ni8UiIiKZmZmSmZnpaJOcnCxFRUVSVFQkiYmJjsfff/99mT59ervG1YioZ1q6VOQ//1P9vW9fkW+/\n9W89gcjdsdPtcNPEiRNRWlqK8vJy2O12bNq0CSkpKa3WSUlJwZtvvgkAKCoqQkhICPR6vdu2KSkp\nyMnJAQDk5ORg1qxZjsfffvtt2O12lJWVobS0FLGxsRgzZgw+//xznDhxAgDw7rvvIioqyn36ERHh\n8nATwHmJjnA73BQUFIQ1a9YgOTkZjY2NmD9/PiIjI/H6668DABYsWIDp06cjPz8fYWFhGDBgADZs\n2OC2LQA888wzmDNnDtatWwej0YjNmzcDAKKiojBnzhxERUUhKCgIr732GnQ6HW644QZkZGRgypQp\n6NWrF4xGo6OrRETkTvMpsABDoiN033U1NEGn03k1P0JEPceTTwJGo/pTrwcOHgSGD/d3VYHF3bGT\nV1wTkaa1HW7iFw+1D0OCiDSNw02+YUgQkaY13+APYEh0BEOCiDSNZzf5hiFBRJrGkPANQ4KINI1z\nEr5hSBCRpnFOwjcMCSLSNA43+YYhQUSaxuEm3zAkiEjTONzkG4YEEWkah5t8w5AgIk1jSPiGIUFE\nmsY5Cd8wJIhI0zgn4RuGBBFpGoebfMOQICJN43CTbxgSRKRpLYeb+vQB7Hb/1tPdMCSISNNaDjf1\n7QtcuODferobhgQRaVrL4aZ+/RgS7cWQICJNazncxJ5E+zEkiEjT2g43nT/v33q6G4YEEWlay5Dg\ncFP7MSSISNNazkmwJ9F+DAki0jTOSfiGIUFEmsbhJt8wJIhI0zjc5BuGBBFpGoebfMOQICJN43CT\nbzyGREFBASIiImA2m5Gdne10ncWLF8NsNsNqteLAgQMe29bV1SEpKQnh4eGYOnUq6uvrHc9lZmbC\nbDYjIiICO3fudDxut9vxk5/8BBaLBZGRkdiyZUuHdpiIehZeJ+EjcaOhoUFMJpOUlZWJ3W4Xq9Uq\nJSUlrdbZvn27TJs2TUREioqKJC4uzmPb9PR0yc7OFhGRrKwsWbZsmYiIHDp0SKxWq9jtdikrKxOT\nySRNTU0iIvKLX/xCnn/+ecfrnjhx4op6PewOEfVA8fEiH3yg/v755yJms3/rCUTujp1uexLFxcUI\nCwuD0WhEcHAwUlNTkZeX12qdbdu2IS0tDQAQFxeH+vp6VFdXu23bsk1aWhq2bt0KAMjLy8PcuXMR\nHBwMo9GIsLAwFBcXAwA2bNiA5cuXO153yJAhnRKSRKRtLeckONzUfm5DwmazYeTIkY5lg8EAm83m\n1TqVlZUu29bU1ECv1wMA9Ho9ampqAACVlZUwGAxXtGkejnruuedwyy23YM6cOfj66687tMNE1LNw\nuMk3Qe6e1DWfN+aB6q14XsfZ9nQ6ncfXaWhowPHjxxEfH49XXnkFK1euxNKlS/Hmm29ese68efNg\nNBoBACEhIYiJiUFCQgIAoLCwEAC4zGUu96DlpqYE6HRq+dw54MKFwKrPH8uFhYXYuHEjADiOly65\nG6fas2ePJCcnO5YzMjIkKyur1ToLFiyQ3Nxcx7LFYpHq6mq3bS0Wi1RVVYmISGVlpVgsFhERyczM\nlMzMTEeb5ORkKSoqkqamJhkwYIDj8WPHjsnYsWPbNa5GRD3TpEkie/eqv9vtIr17+7eeQOTu2Ol2\nuGnixIkoLS1FeXk57HY7Nm3ahJSUlFbrpKSkOD7RFxUVISQkBHq93m3blJQU5OTkAABycnIwa9Ys\nx+Nvv/027HY7ysrKUFpaitjYWOh0Otxzzz34+9//DgB47733MHbsWPfpR0SE1sNNQUFqjqKhwb81\ndSueEiY/P1/Cw8PFZDJJRkaGiIisXbtW1q5d61jn8ccfF5PJJOPHj5f9+/e7bSsiUltbK4mJiWI2\nmyUpKUlOnjzpeG7FihViMpnEYrFIQUGB4/GvvvpKbr/9dhk/frzceeedUlFR0a40JKKeacIEkX37\nLi8PGCBy5oz/6glE7o6duu9W0ASdTufV/AgR9RwTJgDr16s/AWDoUODwYeCGG/xbVyBxd+zkFddE\npGkth5sA3pqjvRgSRKRpbUOC10q0D0OCiDSt5V1gAV4r0V4MCSLStJZXXAMcbmovhgQRaZqz4Sb2\nJLzHkCAiTXM23MSehPcYEkSkaW2Hmzhx3T4MCSLSNGenwHK4yXsMCSLStLYhce21wNmz/qunu2FI\nEJGmtZ2TGDgQOHPGf/V0NwwJItK0tnMSAwcCp0/7r57uhiFBRJrWdriJPYn2YUgQkaZxuMk3DAki\n0jRnw00MCe8xJIhI0zjc5BuGBBFpGoebfMOQICJNazvcdN11PLupPRgSRKRpbYebBg8GTp70Xz3d\nDUOCiDStbUgMHQqcOOG/erobhgQRaZqzOYmLF3mTP28xJIhI09rOSeh0qjdRW+u/mroThgQRaVrb\n4SaAQ07twZAgIk1rO9wEMCTagyFBRJrWdrgJYEi0B0OCiDSNw02+YUgQkaa5ColvvvFPPd0NQ4KI\nNM3ZnMSwYcDXX/unnu6GIUFEmuZsTuLGG4GaGv/U0914DImCggJERETAbDYjOzvb6TqLFy+G2WyG\n1WrFgQMHPLatq6tDUlISwsPDMXXqVNTX1zuey8zMhNlsRkREBHbu3HnFa6WkpGDcuHHt2kki6plE\n1J9texJ6PVBd3fX1dEduQ6KxsRGLFi1CQUEBSkpKkJubi8OHD7daJz8/H1988QVKS0vxxhtvYOHC\nhR7bZmVlISkpCUeOHEFiYiKysrIAACUlJdi0aRNKSkpQUFCAn/70p2hqanK81pYtWzBw4EDo2v6L\nExE54WyoCWBPoj3chkRxcTHCwsJgNBoRHByM1NRU5OXltVpn27ZtSEtLAwDExcWhvr4e1dXVbtu2\nbJOWloatW7cCAPLy8jB37lwEBwfDaDQiLCwMxcXFAICzZ89i5cqVeO655yDNHw+IiNxwNtQEsCfR\nHm5DwmazYeTIkY5lg8EAm83m1TqVlZUu29bU1ECv1wMA9Ho9ar6L9MrKShgMhlZtKisrAQDPP/88\nli5div79+3doR4mo53F2ZhOg7t/U1AScPdv1NXU3Qe6e9HZYx5tP9iLidHs6nc7t64gIDh48iKNH\nj2LlypUoLy93+zrz5s2D0WgEAISEhCAmJgYJCQkAgMLCQgDgMpe53EOW7XZAp7vyeZ0OuO66QuTl\nAQ8+GDj1dtVyYWEhNm7cCACO46VL4saePXskOTnZsZyRkSFZWVmt1lmwYIHk5uY6li0Wi1RXV7tt\na7FYpKqqSkREKisrxWKxiIhIZmamZGZmOtokJydLUVGR/O53v5MRI0aI0WgUg8Egffr0kSlTplxR\nr4fdIaIe5tw5kb59nT8XFyfyz392bT2Byt2x0+1w08SJE1FaWory8nLY7XZs2rQJKSkprdZJSUnB\nm2++CQAoKipCSEgI9Hq927YpKSnIyckBAOTk5GDWrFmOx99++23Y7XaUlZWhtLQUsbGxeOyxx2Cz\n2VBWVobdu3cjPDwcu3btcp9+RNTjuRpuAoAhQ3gnWG+4HW4KCgrCmjVrkJycjMbGRsyfPx+RkZF4\n/fXXAQALFizA9OnTkZ+fj7CwMAwYMAAbNmxw2xYAnnnmGcyZMwfr1q2D0WjE5s2bAQBRUVGYM2cO\noqKiEBQUhNdee+2KoShxMWxFRNSWu5AYPJgh4Q3dd10NTdDpdDzziYgcTp0CRo50/p3WTz4JjBoF\nPPVU19cVaNwdO3nFNRFplqtTYAEON3mLIUFEmuVpTqKurmvr6Y4YEkSkWa6uuAbYk/AWQ4KINKup\nCejd2/lzDAnvMCSISLN4CqzvGBJEpFk8BdZ3DAki0qzGRvYkfMWQICLNcjcnMWCACpHz57u2pu6G\nIUFEmuVuuEmn42mw3mBIEJFmuQsJgENO3mBIEJFmuZuTABgS3mBIEJFmuZuTAHiGkzcYEkSkWRxu\n8h1Dgog0y5uQ4MS1ewwJItIszkn4jiFBRJrlaU6CIeEZQ4KINItzEr5jSBCRZnkKCZ7d5BlDgog0\ny9OcxNChwIkTXVdPd8SQICLN8jQnceONQHV119XTHTEkiEizPA03hYQAFy8C5851XU3dDUOCiDTL\nU0jodOxNeMKQICLN8jQnAQDDhzMk3GFIEJFmeZqTAFRPoqqqa+rpjhgSRKRZnoabANWTYEi4xpAg\nIs3yNiQqK7umnu6IIUFEmuXNnMTo0cDRo11TT3fEkCAizfJmTsJsBkpLu6ae7sirkCgoKEBERATM\nZjOys7OdrrN48WKYzWZYrVYcOHDAY9u6ujokJSUhPDwcU6dORX19veO5zMxMmM1mREREYOfOnQCA\n8+fPY8aMGYiMjER0dDSWL1/eoR0mop7Dm+Gm5pAQ6Zqauh3xoKGhQUwmk5SVlYndbher1SolJSWt\n1tm+fbtMmzZNRESKiookLi7OY9v09HTJzs4WEZGsrCxZtmyZiIgcOnRIrFar2O12KSsrE5PJJE1N\nTXLu3DkpLCwUERG73S6TJ0+WHTt2tKrDi90hoh7knXdEZs70vN7gwSLV1Ve/nkDl7tjpsSdRXFyM\nsLAwGI1GBAcHIzU1FXl5ea3W2bZtG9LS0gAAcXFxqK+vR3V1tdu2LdukpaVh69atAIC8vDzMnTsX\nwcHBMBqNCAsLw969e9GvXz/ccccdAIDg4GDcfPPNsNlsnZWVRKRB3sxJAIDFAhw+fPXr6Y48vn02\nmw0jR450LBsMhisOzq7WqaysdNm2pqYGer0eAKDX61FTUwMAqKyshMFgcPt69fX1+Mtf/oLExESv\nd5SIeh5vhpsAID4e+PDDq19PdxTkaQWdTufVhsSLAT0Rcbo9nU7n9nVaPtfQ0IC5c+diyZIlMBqN\nV6w7b948x+MhISGIiYlBQkICAKCwsBAAuMxlLveQ5U8/BXr39rz+978PpKcXYvLkK5+Pj0/AunXA\nW28V4tw5QK9PQK9ewH33FWLUqMvr79pViPp64N57A2f/XS0XFhZi48aNAOD0ONqKp7GqPXv2SHJy\nsmM5IyNDsrKyWq2zYMECyc3NdSxbLBaprq5229ZisUhVVZWIiFRWVorFYhERkczMTMnMzHS0SU5O\nlqKiIsfyj370I1myZInTWr3YHSLqQd56SyQ11fN6Fy+KDB0qkpcn0tgo8vXXIr/9rUhyskj//iKT\nJ4u8/rrIX/4isnatSGamSL9+IsuWidTVqW0sXSoCiFRWXt19uhrcHTs9HlUvXbokY8aMkbKyMrl4\n8aLHies9e/Y4Jq7dtU1PT3cERmZm5hUT1xcvXpSjR4/KmDFjpKmpSUREnn32WZk9e7ZjuT07SkQ9\nz//8j8gDD3i37htvqIP8ddeJ9O0rkpIi8txzIi0+o7ZSUqK2PXSoCojhw0XmzhVJT++8+ruKTyEh\nIpKfny/h4eFiMpkkIyNDRETWrl0ra9eudazz+OOPi8lkkvHjx8v+/fvdthURqa2tlcTERDGbzZKU\nlCQnT550PLdixQoxmUxisVikoKBAREQqKipEp9NJVFSUxMTESExMjKxbt87rHSWinicnR+Shh7xf\n324XKSsTcfE51KkPPhC5+WaR7dtV28GDRU6dam+l/uXu2Kn7bgVN0Ol0Xs2NEFHPsHEjUFio/uwq\njzyibvXh4pKygOTu2MkrrolIs7w9u6kzvfwykJMD7NvXta97tTAkiEiz/BESw4YBr7wCPPooYLd3\n7WtfDQwJItIsby+m62wPPACMGgVkZXX9a3c2j9dJEBF1V97c4O9q0OmAtWuBm28Gvvc9ICmp62vo\nLOxJEJFm+WO4qZnBAPz5z6pXceiQf2roDAwJItIsf4YEAEyeDGRmAg89BFy44L86fMGQICLN8tec\nREvz5wPjxgHf/z7w7bf+raUjGBJEpFn+mpNoSadTp8RGRgKpqd3veysYEkSkWf4ebmqm0wG/+x1g\nswHr1/u7mvYJgLePiOjqCJSQAIA+fYA33wSWLete310RIG8fEVHnC4Q5iZaio4HnnlO37mho8Hc1\n3gmgt4+IqHMFwpxEW0uWAIMHA//5n/6uxDsMCSLSrEAabmqm0wG//z2wciXw6af+rsazAHv7iIg6\nTyCGBKBu2bFyJXD33cCJE/6uxr0AfPuIiDpHoM1JtPTQQ8CDD6pbdnz++ZXPf/YZUF/f9XW1FaBv\nHxGR7wJxTqKlFSvUxXbx8eoU2ebJ7BMn1AV4M2eqffCnHhkSR48Cu3apTxlE1HE2m/p9OncuMC8S\nC9ThpmY6HbBokToe/elP6oaAJSXAr38NPPaYutX46tX+rbFH3QX2xAngySeBggJg5EjgzBngt78F\nkpP9XRlR9/Pxx2qopLEROHUKmD4d+L//F+jXz9+VXRboIdHMagXee09daPe97wH9+wOffKKOUfHx\nwIgRwJw5vr/O2bPAv/8NjB0L9O3rXZtu8PZ1jtpa9R968GDgyy+BAweANWuAhQvVKWn+7tIRdTe/\n+hXw4ovAV18BX38NXH89cP/9gXX+fyDPSbSl06mhp08/BQ4eVF9eZDIBf/0rsHgxsGGDb701EWDW\nLPUTE+N8HsSZbvL2tV99vfoP/PzzwM9+pi5imT4dWLVK/WcGgLvuUmHxySdqAsnZt0gdPQr8/OfA\npUtdWz9RIDt/Xg2RzJ2rfp9uuEF9j/SlS8D//t+BM/R0/rz6VN6djBoF6PWXl61W4N13gd/8Bvhf\n/wvYvl0NR335Zfu2+9Zb6sNyWRmQng7cfrvqDXqi2ZBYuhT46CP1KWLECDXEtGKFSuuWrr9ePXfh\ngjod7ezZ1s//7nfAf/2XNr5hiqiz7NmjPniFhFx+rE8fNdz0+efq1hOB4Ny5wBr+6qhx49QB/bHH\n1Hv7j3+oYahNm5wH8rFjqjfSbM8eNdT+xhtAUJDqsaxdC8yYoYaf3NHcnMTu3eo/6f/7f2rnm3sN\n7vTtqyaNFi4EbrtN3bFxwgTg4kXgj38EduwAHn4YmD0biIq6+vtAFOj27gVuvfXKxwcMUJ90J08G\nBg0CnnhCHaT9dYZRd+xJuNK7tzoOPfywWi4qUgf7//5vwGhUB//x49Ww+qJFaphKBCguVvMZ//3f\nwKRJl7fwAk/LAAAVv0lEQVR3771qLmnqVPevq7mQWLoUuPFGYMsW7wKiWVCQStn/+R81kf2Tn6j/\n3OPHq2GpX/8auO8+YOdOIDT06tVPFEgaG9VPnz6tH9+7Vw01OTN4sPo9uece4P/8HyAxUQXHNddc\n/XrbOndOOyHR1q23qt7F5s1qBKSxUY2e/PKXwDffqHXuuw8oLFS9hpkzr9zGj36kgvTxx12/jk4k\nUEYPfafT6dAZu1NZqbp0JSXqzZ00SSXySy8Br72m7uR4++2dUDBRAKuvVz2CL75QX5gzYwYQHKwm\nqV96CfjXv9T4uSsialJ76VJg/35g9Gh1AdnMmcCQIV2zD0lJwNNPd+/vmG6vr78GXn0VmDhRzUHc\ndhsQEeG+jbtjJ0Oinf78ZzXpc8MNapjqwgVgzBg1DDV2rPozLEz1TIi6o4oK4J131Dzcww8Dy5er\nnkF+vprTGzJEzfM99ZR32xNRJ4d88YUa8iguBl55BZg378o5ws52220q0OLjr+7rdHcMiU526ZLq\nwvXpo36+/FJ90fmhQ6r3YbOpsJg6VX2CiY/3T1c7kPz+9+oEgM8+C+wrYHuif/5TzckVFADHj6sP\nP1OnqrMCJ07s/Nf77DPVoxgyRAVRy3Fy4PJpq50RIDfdpH5XR4/2fVtaxpDoYufOqe71zp3A3/6m\nwuO221Rg3Hyz+mnPfIkW/OAHwNataq7oBz/wdzXaJaImNG02dYAcNUqdgdSnjzronjypTl398ku1\nnJ+vhoTmzVNn95lMwMCBV//agoYG1at48UUgPFx98AoOVr8nK1aoEElKUusNGqQe79NHjbHrdCq8\nrr8eePRRdT1B221fvKh+DAY1ORscfHX3p7tjSPhZfT3w97+rwPjkE3VqmsGgwuL0aWDoUDXHcccd\naujqanfBu0LbK12NRmDBAiAvT52OdzX2cfNm1Wvr6hMLVq1S81S//736N3VGRM112WzqoDdsGFBX\nB5SWqj8nTfLu3760VJ2519ioruu5cEEdDGtrL/dmhw9XPdljx9TP6dPqINy3r+rFTZ6svm+5sVFd\n3Xvvvf47iJ4/r87C0elUDbt3A5mZ6rk5c9Sk89dfq97OxYvqy3ruvvtyEP75zyoMhwxRv2dVVeq9\nEFH/B+fNUxehkXs+hURBQQGefPJJNDY24sc//jGWOTkBevHixdixYwf69++PjRs3YsKECW7b1tXV\n4f7778dXX30Fo9GIzZs3I+S7E64zMzOxfv169O7dG6tXr8bU787P2r9/P+bNm4cLFy5g+vTpWLVq\nVbt2NJA0NKhf5oMHgeuuA2pqgPffVz+9eqlPf+PGqYPGqFFqfuPaa9XBr6kJsFhcn/tdU6N+Ybpy\nTkQEyM5Wp+MNGaI+IS5YoH6ZL1xQNZeWqk+vUVFq2OmeezrntW024IEH1AH4iy/U7VZ+/3tgypQr\nz8hxpfkAa7Op923AABXco0erP2tr1afx3r3VgapXL7XeqVPq7JJ771WTo7/5japl/Hj12rt3q7NO\nTp5UF202NKiw/OYb9dh116kPC0OGqA8P58+rkBkyRB0c+/ZV6zTX89FHwLZt6tN0v37qoNqvnxrK\nDAlR1y2MHatCqK3GRvVvERzs/fviL88+C2RktL5aurFRhenQoa2D9Px59VWgp06pnsXw4SqAdToV\nGoMGaeND19XW4ZBobGyExWLB3/72N4SGhmLSpEnIzc1FZGSkY538/HysWbMG+fn52Lt3L5YsWYKi\noiK3bZ9++mkMHToUTz/9NLKzs3Hy5ElkZWWhpKQEDzzwAD766CPYbDbceeedKC0thU6nQ2xsLNas\nWYPY2FhMnz4dixcvxl133eX1jnYHIupAun375bmOigr1C3LmjBovbj5j5Prr1QT5qFHqYNLYqD4t\n/vGPasggMVEdOPR6dcC57jr1c/68+mR2003qNZpPcWxsVAexkyeBb79V27rhhssT9Ndcow4wNTVq\nGyNGqANgZaUKu1dfVTU1NqqaVq9Wv6QDB6pPvBERqt4PP1QH1SlTVBB++60Kv0GDWv+IAOXlqqbR\no9V2muu4dEkFwgcfqLPPfvxjdcbM8OFq+ytWqFCKj1cH5ZCQy7eKOHNGXYjUr5/6hF1Tczl4R49W\n6337rTqQHz16OeRE1HNBQervly6p9/OGG9T3Atxzj/p3yclR7ex2dcC+6SZVe0yMel/cHbCa38tT\np1QN58+res+cUfcdGzsWSE1Vp3hr2fLlaq6iG/8qdzvujp1uP28WFxcjLCwMRqMRAJCamoq8vLxW\nIbFt2zakpaUBAOLi4lBfX4/q6mqUlZW5bLtt2za8//77AIC0tDQkJCQgKysLeXl5mDt3LoKDg2E0\nGhEWFoa9e/fipptuwpkzZxAbGwsAeOSRR7B169YrQqK70+nUgXTJEvfrffutOgAfOgRUV6tPt717\nq09dy5erg8wnn6gD/rFj6mBz+rT66dNHfdJqHrLo1Uu1bf4ZPFh9cg0KUtuorb08pGG3q4Niv36q\nWz9woDowDxqkahky5PKnWlcmT1YXOW7dqg7kAwaoix9Pnrz8U1+vDhA33aTq+OqrywdNu109ZjCo\nWxS0PR35Bz9QPydOqE/yNpvaXnPPKjRUjWM3D9Xo9erg6+rgfeaM2t/m4bPm7Yhc2eamm4Bf/ML9\nv507I0aon57OYlE9ZwoMbkPCZrNh5MiRjmWDwYC9e/d6XMdms6GystJl25qaGui/uzmJXq9HTU0N\nAKCyshK3triMs3lbwcHBMBgMjsdDQ0Nhs9navbOBorCwEAkJCR1uP2CA+nE39n7bbR3evIOvdboy\neLA6UHcWZ3UOHapuZOargQOdP96RIYyr9X52Nn/XOW+e+vHE33V6q7vU6Yrbcxh0Xv4meDPEIyJO\nt6fT6bx+Ha0oLCz0dwleYZ2di3V2LtbZNdz2JEJDQ1FRUeFYrqioaPWJ3tk6x48fh8FgwKVLl654\nPPS7j756vR7V1dW48cYbUVVVhWHfncPmaluhoaE4fvy40221NGLEiG4TOP/xH//h7xK8wjo7F+vs\nXKyzc5hMJtdPihuXLl2SMWPGSFlZmVy8eFGsVquUlJS0Wmf79u0ybdo0ERHZs2ePxMXFeWybnp4u\nWVlZIiKSmZkpy5YtExGRQ4cOidVqlYsXL8rRo0dlzJgx0tTUJCIisbGxUlRUJE1NTTJt2jTZsWOH\nu9KJiKgTuA0JEZH8/HwJDw8Xk8kkGRkZIiKydu1aWbt2rWOdxx9/XEwmk4wfP17279/vtq2ISG1t\nrSQmJorZbJakpCQ5efKk47kVK1aIyWQSi8UiBQUFjsf37dsn0dHRYjKZ5IknnvBtr4mIyCuaupiO\niIg6V0B/6VBBQQEiIiJgNpuRnZ0NQF2Il5SUhPDwcEydOhX19fVet21Pe1/rfP7552G1WhETE4PE\nxMRWcy2BVCcAvPrqq4iMjER0dLTTiyW7sk5nr/PJJ5/ge9/7HsaPH4+UlBScOXPGrzUCwKOPPgq9\nXo9x48Y5HktPT0dkZCSsVivuvfdenDp1yq91OqvxhRdegMFgwIQJEzBhwgQUFBT4tUZXdRYXFyM2\nNhYTJkzApEmT8NFHH/m9zoqKCkyZMgVjx45FdHQ0Vq9eDQD405/+hLFjx6J379742M1XvXVlrZ3K\n310ZVxoaGsRkMklZWZnY7XbHnEZ6erpkZ2eLiEhWVpZjPsObtiLiVfvOqPP06dOOdVavXi3z588P\nyDp37dold955p9jtdhER+frrr/1Wp6vXmThxonzwwQciIrJ+/Xp5/vnn/VZjsw8++EA+/vhjiY6O\ndjy2c+dOaWxsFBGRZcuW+f3/prMaX3jhBXnllVfctguE9/KOO+5wDDfn5+dLQkKC3+usqqqSAwcO\niIjImTNnJDw8XEpKSuTw4cPy73//WxISEloNt/uz1s4UsCHxz3/+U5KTkx3LmZmZkpGRIRaLRaqr\nq0VE/aNZLBav2mZmZoqIeNXe1zqbX6tZRkaG03/4QKhzzpw58t5773WobWfX6erf/Prrr3c8duzY\nMYmKivJbjS2VlZW1OrC1tGXLFnnwwQf9XmfbGl944QV5+eWX3bYJhPcyNTVVNm3aJCIib731VkC8\nl23NnDlT/va3vzmW3YWEv2v1RcAON7m6SM/dhXgzZsxw2xZwfSFfZ9cJAM8++yxGjRqFnJwcPPPM\nMwFZ55EjR/DBBx/g1ltvRUJCAvbt2+e3Op29TmVlJaKjo5GXlwdAde2bh+789V56Y/369Zg+fXpA\n1vnqq6/CarVi/vz5jqGNQKsxKysLP//5zzFq1Cikp6cj87u7/gVKneXl5Thw4ADi4uJcrhMotfoq\nYEPC1YV3bZebHxsxYgS2b9/udD25ihfyuWu/YsUKHDt2DPPmzcPPfvazgKyzoaEBJ0+eRFFREV56\n6SXMmTPHb3W6artu3Tq89tprmDhxIs6ePYs+392hzl/vpScrVqxAnz598MADDwRcnQsXLkRZWRkO\nHjyI4cOH4+c//3nA1QgA8+fPx+rVq3Hs2DGsXLkSj353iX4g1Hn27Fn88Ic/xKpVq3Ctm/uHBEKt\nnSFgQ8LZhXyhoaGOC/EAtLoQz11bZxfyuWvva51tLzhsvmlhoNUZGhoKg8GAe++9FwAwadIk9OrV\nC7W1tX6p09V7abFY8Ne//hX79u1Damqq0wt/uvK9dGfjxo3Iz8/HH//4R6fP+7vOYcOGOQ5EP/7x\nj1FcXBxwNQJq4voH333xyA9/+MOAqfPSpUuYPXs2HnroIcxqx31fAuE97aiADYmJEyeitLQU5eXl\nsNvt2LRpE2bOnImUlBTk5OQAAHJycpz+Qzlrm5KSAgBetfe1zpSUFJSWljrWycvLc9w+PZDqnDlz\nJmbNmoVdu3YBAI4cOQK73Y4hbb6AuKvqdPU633z3re5NTU148cUXsXDhQq/bdnaN7hQUFOCll15C\nXl4e+vbt26597Ko6q6qqHH9/5513Wp1RFCg1AkBYWJjjJqC7du1CeHi43+sUEcyfPx9RUVF48skn\nXa7jTCC8px3mr8kQbzi7GM/VhXg2m02mT5/utq279p1d5+zZsyU6OlqsVqvce++9UlNTE5B12u12\neeihhyQ6Olpuvvlm+fvf/+7XOp29zm9+8xsJDw+X8PBwWb58uWNdf76XqampMnz4cAkODhaDwSDr\n1q2TsLAwGTVqlMTExEhMTIwsXLjQr3U6q/Hhhx+WcePGyfjx42XmzJmOCdNAei/Xr18vH330kcTG\nxorVapVbb71VPv74Y7/X+eGHH4pOpxOr1er4N87Pz5d33nlHDAaD9O3bV/R6vdx1111+r7Uz8WI6\nIiJyKWCHm4iIyP8YEkRE5BJDgoiIXArIkHB2jxNv749SXl7u9IwNIiJqv4ALicbGRixatAgFBQUo\nKSlBbm4uDh8+jHHjxuGdd97B7S2/0JiIiK6qgAuJ4uJihIWFwWg0Ijg4GKmpqcjLy0NERITTc6Xd\nKS8vx+23345bbrkFt9xyC/bs2QPg8nfO3nfffYiMjMRDDz10NXaFiKjbc/v1pf7g7B4ne/fu7dC2\n9Ho93n33XVxzzTUoLS1tdeXzwYMHUVJSguHDhyM+Ph7/+Mc/EB8f3yn7QESkFQEXEp153xK73Y5F\nixbhk08+Qe/evVtdBR0bG4sRI0YAAGJiYlBeXs6QICJqI+CGm7y5F1JLjz76KCZMmIC77777iudW\nrlyJ4cOH41//+hf27duHixcvOp675pprHH/v3bs3GhoaOmkPiIi0I+B6Ei3vcTJixAhs2rQJubm5\nrdZpeZH4+vXrXW7r9OnTjoB588030djYeHWKJiLSqIDrSQQFBWHNmjVITk5GVFQU7r//fkRGRuKd\nd97ByJEjUVRUhBkzZmDatGlO2zc0NDh6CT/96U+Rk5ODmJgY/Pvf/251W19ntx0nIqLWNHfvpry8\nPOTm5uLtt9/2dylERN1ewA03+eIXv/gFtm3b5rjtLhER+UZzPQkiIuo8ATcnQUREgSOgQ6KiogJT\npkzB2LFjER0djdWrVwMA6urqkJSUhPDwcEydOtXxZe51dXWYMmUKBg4ciCeeeMLpNlNSUnhvJyIi\nLwV0SAQHB2PlypU4dOgQioqK8Nvf/haHDx9GVlYWkpKScOTIESQmJiIrKwsA0LdvX7z44ot4+eWX\nnW5vy5YtGDhwIM9kIiLyUkCHxI033oiYmBgAwLXXXovIyEjYbDZs27YNaWlpAIC0tDRs3boVANC/\nf3/Ex8e3ulCu2dmzZ7Fy5Uo899xzLr+HloiIWgvokGipvLwcBw4cQFxcHGpqaqDX6wGo+zPV1NS0\nWtdZT+H555/H0qVL0b9//y6pl4hIC7pFSJw9exazZ8/GqlWrMHDgwFbP6XQ6j8NHBw8exNGjRzFz\n5kz2IoiI2iHgQ+LSpUuYPXs2Hn74YcyaNQuA6j1UV1cDAKqqqjBs2DC32ygqKsK+ffswevRoTJ48\nGUeOHMH3v//9q147EVF3F9AhISKYP38+oqKi8OSTTzoeT0lJcVwwl5OT4wiPlu1aeuyxx2Cz2VBW\nVobdu3cjPDwcu3btuvo7QETUzQX0xXS7d+/G7bffjvHjxzuGlDIzMxEbG4s5c+bg2LFjMBqN2Lx5\nM0JCQgAARqMRZ86cgd1ux6BBg7Bz505EREQ4tlleXo6UlBT861//8ss+ERF1JwEdEkRE5F8BPdxE\nRET+xZAgIiKXGBJEROQSQ4KIiFxiSBARkUsMCSIicokhQdQOLb8nHQA2btzouC39Cy+8gFdeeaXV\n80ajEXV1dQCAXr164eGHH3Y819DQgBtuuAH33HOPY1u9evXCe++951hn69at6NWrF7Zs2XJV9ofI\nE4YEUTu0vU9Yy2Vn9xFruTxgwAAcOnQIFy5cAAC8++67MBgMrdYZN25cq+9nz83NddwJmcgfGBJE\nPmh7Laqna1OnT5+O7du3A1ABMHfuXEcbnU6HyZMno7i4GA0NDTh79iy+/PJLWK1W3piS/CbI3wUQ\ndSfnz5/HhAkTHMt1dXWYOXMmABUQK1euxB/+8AfH85WVla3a33///fjVr36Fu+++G59++inmz5+P\nDz/80PG8TqdDUlIS/vrXv+LUqVNISUlBWVnZVd4rItcYEkTt0K9fPxw4cMCxnJOTg3379gFQB/in\nnnoKTz31lOP50aNHt2o/btw4lJeXIzc3FzNmzGj1XHNv4f7778eqVatw+vRpvPLKK8jIyLhau0Pk\nEUOCyAftHW4C1F2Mly5divfffx/ffPPNFc9PmjQJn332GQYMGACz2dxptRJ1BEOCqJN4O2/w6KOP\nYtCgQRg7diwKCwudrpOVlYV+/fp1YnVEHcOQIGoHZ2cvNT/m6VsSm58LDQ3FokWL3La/66673L4u\nUVfhrcKJiMglngJLREQuMSSIiMglhgQREbnEkCAiIpcYEkRE5BJDgoiIXGJIEBGRS/8faDPmpyi0\n0wAAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x105eaaf90>"
]
}
],
"prompt_number": 33
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = evelc.data['17.1ESP'].plot()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEmCAYAAACZEtCsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHOhJREFUeJzt3XtwVOXBx/HfIvEGlNhWNpDAxJew5EoS5aLDq02Miwq6\npIBIvTSUYC0d2uJtjG1teR0Jy6iDIHbGtmLipRE7I5BqGgXjeo+RAmIFDGoyhFy2DjECgxqSPu8f\nvOxrmk2Iuyfk5PD9zGTGZ89z9vwSnB8PT/bsuowxRgAARxky0AEAANaj3AHAgSh3AHAgyh0AHIhy\nBwAHotwBwIGiLvfKykolJydrwoQJWrVqVbfjzzzzjDIzMzVp0iRNnz5du3btivaSAICTcEXzOvfO\nzk5NnDhRW7duVXx8vKZMmaKysjKlpKSE5rzzzjtKTU3VyJEjVVlZqeXLl6u6utqS8ACA8KJaudfU\n1CgpKUmJiYmKiYnRggULtHnz5i5zLrnkEo0cOVKSNG3aNB04cCCaSwIA+iCqcm9sbNTYsWND44SE\nBDU2NvY4//HHH9fMmTOjuSQAoA+GRnOyy+Xq89xXX31V69ev11tvvRX2+Pe//30dPHgwmjgAcNoZ\nP368Pv74426PR7Vyj4+PV0NDQ2jc0NCghISEbvN27dqlW265ReXl5TrvvPPCPtfBgwdljLH91+9/\n//sBz+CUnIMhIznJafevTz75JGynRlXukydP1r59+1RfX6/29nZt2LBBPp+vy5z9+/drzpw5evrp\np5WUlBTN5WwhJydnoCP0yWDIORgySuS0GjlPjaheLSNJf//737Vs2TJ1dnaqsLBQ99xzjx577DFJ\n0q233qrFixdr48aNGjdunCQpJiZGNTU13YO4XIoyCgCcdnrqzqjL3SqUOwB8ez11J3eoAoADUe4A\n4ECUOwA4EOUOAA5EuQOAA1HuAOBAlDsAOBDlDgAORLkDgANR7gDgQJQ7ADgQ5Q4ADkS5A4ADUe4A\n4ECUOwA4EOUOAA5EuQOAA1HuAOBAlDsAOBDlDgAORLkDgANR7gDgQJQ7ADgQ5Q4ADkS5A4ADUe4A\n4ECUOwA4EOUOAA4UdblXVlYqOTlZEyZM0KpVq8LO+eUvf6kJEyYoMzNTO3bsiPaSAICTiKrcOzs7\ntXTpUlVWVmr37t0qKyvTnj17usypqKjQxx9/rH379umPf/yjlixZElVgAMDJRVXuNTU1SkpKUmJi\nomJiYrRgwQJt3ry5y5zy8nIVFBRIkqZNm6a2tjYFg8FoLgsAOImh0Zzc2NiosWPHhsYJCQl69913\nTzrnwIEDcrvd3Z6vtTWaNAAGWkyM1N4+0CkgRVnuLperT/OMMX06LykpmjQABtKxY9KRI9KIEcdL\nHgMrqnKPj49XQ0NDaNzQ0KCEhIRe5xw4cEDx8fFhn8/nW6jExERJUmxsrLKyspSTkyNJCgQCksSY\nMWObjv/5T+kXv8hRRYXU0THweZw6DgQCKikpkSQlJibqf/5HYbnMfy6rv4WOjg5NnDhRr7zyisaM\nGaOpU6eqrKxMKSkpoTkVFRVat26dKioqVF1drWXLlqm6urp7EJer2wofwODx9tvS9OnSG29I//3f\nA53m9NFTd0a1ch86dKjWrVunK6+8Up2dnSosLFRKSooee+wxSdKtt96qmTNnqqKiQklJSRo2bJie\neOKJaC4JAOiDqFbuVmLlDgxurNwHRk/dyR2qACxx4nUSfXydBfoZ5Q4ADkS5A4ADUe4ALMG2jL1Q\n7gDgQJQ7ADgQ5Q7AEmzL2AvlDgAORLkDgANR7gAswbaMvVDuAOBAlDsAOBDlDsASbMvYC+UOAA5E\nuQOAA1HuACzBtoy9UO4A4ECUOwA4EOUOwBJsy9gL5Q4ADkS5A4ADUe4ALMF2jL1Q7gAsRcnbA+UO\nAA5EuQOwBCt2e6HcAViKkrcHyh0AHIhyB2AJVuz2QrkDsBQlbw9RlXtra6u8Xq88Ho9mzJihtra2\nbnMaGhqUm5urtLQ0paena+3atdFcEgDQB1GVu9/vl9frVW1trfLy8uT3+7vNiYmJ0erVq/Xhhx+q\nurpajz76qPbs2RPNZQHYECt2e4mq3MvLy1VQUCBJKigo0KZNm7rNiYuLU1ZWliRp+PDhSklJUVNT\nUzSXBWBjlLw9RFXuwWBQbrdbkuR2uxUMBnudX19frx07dmjatGnRXBYAcBJDTzbB6/WqpaWl2+Mr\nVqzoMna5XHL18lf2kSNHNG/ePK1Zs0bDhw8PO2fhwoVKTEyUJMXGxiorK0s5OTmSpEAgIEmMGTO2\n6fjjjyXJPnmcOg4EAiopKZGkUF+G4zLGmB6PnkRycrICgYDi4uLU3Nys3Nxc7d27t9u8Y8eO6Zpr\nrtHVV1+tZcuWhQ/icimKKAAG2K5dUmamtGOH9H87sTgFeurOqLZlfD6fSktLJUmlpaXKz8/vNscY\no8LCQqWmpvZY7AAAa0VV7kVFRdqyZYs8Ho+qqqpUVFQkSWpqatKsWbMkSW+99Zaefvppvfrqq8rO\nzlZ2drYqKyujTw4A6FFU2zJWYlsGGNw++ECaNEnaufP49gxOjX7ZlgEA2BPlDgAORLkDsMSJV0Jz\nE5M9UO4A4ECUOwA4EOUOwBJsx9gL5Q7AUpS8PVDuAOBAlDsAS7BitxfKHYClKHl7oNwBwIEodwCW\nYMVuL5Q7AEtR8vZAuQOAA1HuACzBit1eKHcAlqLk7YFyBwAHotwBWIIVu71Q7gAsRcnbA+UOAA5E\nuQOwBCt2e6HcAViKkrcHyh0AHIhyB2AJVuz2QrkDgANR7gAsxQreHih3AHAgyh2AJVix20vE5d7a\n2iqv1yuPx6MZM2aora2tx7mdnZ3Kzs7WtddeG+nlAAwSlLw9RFzufr9fXq9XtbW1ysvLk9/v73Hu\nmjVrlJqaKhd/6gBwSkRc7uXl5SooKJAkFRQUaNOmTWHnHThwQBUVFVq8eLGMMZFeDoDNsXazl4jL\nPRgMyu12S5LcbreCwWDYebfddpseeOABDRnC9j5wOqDk7WFobwe9Xq9aWlq6Pb5ixYouY5fLFXbL\n5YUXXtCoUaOUnZ2tQCBw0jALFy5UYmKiJCk2NlZZWVnKycmRpND5jBkztue4sVGS7JPHqeNAIKCS\nkhJJCvVlOC4T4V5JcnKyAoGA4uLi1NzcrNzcXO3du7fLnF//+td66qmnNHToUH311Vc6dOiQ5s6d\nqyeffLJ7EJeLbRtgEPv0U2n8eKm2VpowYaDTnD566s6I90p8Pp9KS0slSaWlpcrPz+82p7i4WA0N\nDaqrq9Ozzz6ryy+/PGyxA3AOtmXsIeJyLyoq0pYtW+TxeFRVVaWioiJJUlNTk2bNmhX2HF4tAwCn\nRsTbMlZjWwYY3OrqpP/6L2nfPikpaaDTnD4s35YBgHD4B7o9UO4A4ECUOwBLsGK3F8odgKUoeXug\n3AHAgSh3AJZgxW4vlDsAS1Hy9kC5A4ADUe4ALMGK3V4odwBwIModgKVYwdsD5Q7AEpS6vVDuAOBA\nlDsAS7GCtwfKHYAlKHV7odwBwIEodwCWYgVvD5Q7AEtQ6vZCuQOAA1HuACzFCt4eKHcAlqDU7YVy\nBwAHotwBWIoVvD1Q7gDgQJQ7AEuwYrcXyh2ApSh5e6DcAcCBKHcAlmDFbi8Rl3tra6u8Xq88Ho9m\nzJihtra2sPPa2to0b948paSkKDU1VdXV1RGHBWB/lLw9RFzufr9fXq9XtbW1ysvLk9/vDzvvV7/6\nlWbOnKk9e/Zo165dSklJiTgsAKBvXMYYE8mJycnJeu211+R2u9XS0qKcnBzt3bu3y5wvvvhC2dnZ\n+vTTT08exOVShFEA2EAwKMXFSY2N0pgxA53m9NFTd0a8cg8Gg3K73ZIkt9utYDDYbU5dXZ3OP/98\n/eQnP9GFF16oW265RUePHo30kgCAPhra20Gv16uWlpZuj69YsaLL2OVyyRVmo62jo0Pbt2/XunXr\nNGXKFC1btkx+v1/33Xdf2OstXLhQiYmJkqTY2FhlZWUpJydHkhQIBCSJMWPGNh23tkpSjlwue+Rx\n6jgQCKikpESSQn0ZTlTbMoFAQHFxcWpublZubm63bZmWlhZdcsklqqurkyS9+eab8vv9euGFF7oH\nYVsGGNT+9S/J7ZaamqTRowc6zenD8m0Zn8+n0tJSSVJpaany8/O7zYmLi9PYsWNVW1srSdq6davS\n0tIivSQAoI8iXrm3trZq/vz52r9/vxITE/Xcc88pNjZWTU1NuuWWW/Tiiy9Kkt5//30tXrxY7e3t\nGj9+vJ544gmNHDmyexBW7sCgdmLl3tx8/BerODV66s6Iy91qlDswuH32mTRqFOV+qlm+LQMAsC/K\nHYCluEPVHih3AJag1O2FcgcAB6LcAViKFbw9UO4ALEGp2wvlDgAORLkDsBQreHug3AFYglK3F8od\nAByIcgdgKVbw9kC5A7AEpW4vlDsAOBDlDsBSrODtgXIHYAlK3V4odwBwIModAByIcgdgiRPbMmzP\n2APlDgAORLkDgANR7gAsxbaMPVDuACxBqdsL5Q4ADkS5A7AUK3h7oNwBWIJStxfKHQAciHIHYClW\n8PZAuQOwBKVuLxGXe2trq7xerzwej2bMmKG2traw81auXKm0tDRlZGTohhtu0Ndffx1xWABA30Rc\n7n6/X16vV7W1tcrLy5Pf7+82p76+Xn/605+0fft2ffDBB+rs7NSzzz4bVWAA9sYK3h4iLvfy8nIV\nFBRIkgoKCrRp06Zuc77zne8oJiZGR48eVUdHh44ePar4+PjI0wKwLUrdXiIu92AwKLfbLUlyu90K\nBoPd5nz3u9/VHXfcoXHjxmnMmDGKjY3VFVdcEXlaAECfDO3toNfrVUtLS7fHV6xY0WXscrnkCvPX\n9ieffKKHH35Y9fX1GjlypK677jo988wzuvHGG8Neb+HChUpMTJQkxcbGKisrSzk5OZKkQCAgSYwZ\nM7bp+MsvJSlHLpc98jh1HAgEVFJSIkmhvgzHZYwxPR7tRXJysgKBgOLi4tTc3Kzc3Fzt3bu3y5wN\nGzZoy5Yt+vOf/yxJeuqpp1RdXa1HH320exCXSxFGAWADR49Kw4ZJhw5JI0YMdJrTR0/dGfG2jM/n\nU2lpqSSptLRU+fn53eYkJyerurpaX375pYwx2rp1q1JTUyO9JACgjyIu96KiIm3ZskUej0dVVVUq\nKiqSJDU1NWnWrFmSpMzMTP34xz/W5MmTNWnSJEnST3/6UwtiA7ArfrFqDxFvy1iNbRlgcPvyS+nc\nc6XDh6Xhwwc6zenD8m0ZAIB9Ue4A4ECUOwBLnNhrZ8/dHih3AHAgyh0AHIhyB2AJtmXshXIHAAei\n3AHAgSh3AJZgW8ZeKHcAcCDKHQAciHIHYAm2ZeyFcgcAB6LcAcCBKHcAlmJbxh4odwCWoNTthXIH\nAAei3AFYihW8PVDuACxBqdsL5Q4ADkS5A4ADUe4ALMEdqvZCuQOAA1HuAOBAlDsAS7AtYy+UOwA4\nEOUOAA5EuQOwBNsy9hJxuf/1r39VWlqazjjjDG3fvr3HeZWVlUpOTtaECRO0atWqSC8HAPgWIi73\njIwMbdy4UZdddlmPczo7O7V06VJVVlZq9+7dKisr0549eyK9JACgj4ZGemJycvJJ59TU1CgpKUmJ\niYmSpAULFmjz5s1KSUmJ9LIAgD7o1z33xsZGjR07NjROSEhQY2Njf16y3wUCgYGO0CeDIedgyCiR\n02rkPDV6LXev16uMjIxuX3/729/69OQuB/5mZbD8gQ+GnIMho0ROq5HzFDFRysnJMf/4xz/CHnvn\nnXfMlVdeGRoXFxcbv98fdu6YMWOMJL744osvvr7F1/jx48N2asR77t9kjAn7+OTJk7Vv3z7V19dr\nzJgx2rBhg8rKysLOHezbNQBgJxHvuW/cuFFjx45VdXW1Zs2apauvvlqS1NTUpFmzZkmShg4dqnXr\n1unKK69Uamqqrr/+en6ZCgCngMv0tOwGAAxa/fJqmXA3LrW2tsrr9crj8WjGjBlqa2vr87nf5vxo\nc957773KzMxUVlaW8vLy1NDQYMuckvTII48oJSVF6enpuvvuu22Z8/3339cll1yiSZMmyefz6fDh\nwwOac9GiRXK73crIyAg9dtdddyklJUWZmZmaM2eOvvjiiwHN2FPO5cuXKyEhQdnZ2crOzlZlZaUt\nc9bU1Gjq1KnKzs7WlClT9N577w1ozoaGBuXm5iotLU3p6elau3atpOhvxOyPn6elovx9ajcdHR1m\n/Pjxpq6uzrS3t5vMzEyze/duc9ddd5lVq1YZY4zx+/3m7rvv7vO5xpg+nW9FzkOHDoXmrF271hQW\nFtoyZ1VVlbniiitMe3u7McaYf/3rX7bMOXnyZPP6668bY4xZv369uffeewc05+uvv262b99u0tPT\nQ4+9/PLLprOz0xhjzN133z3g/2/2lHP58uXmoYce6vU8O+T8wQ9+YCorK40xxlRUVJicnJwBzdnc\n3Gx27NhhjDHm8OHDxuPxmN27d5s9e/aYjz76qNcXhZzqn6eVLC/3t99+u8srZFauXGmKi4vNxIkT\nTUtLizHm+A974sSJfTp35cqVxhjTp/OjzXniWicUFxeH/QOzQ8758+ebV155JaJzT1XO4uJiM3Lk\nyNBj+/fvN6mpqQOa0xhj6urqupTRNz3//PPmxhtvHPCM4XIuX77cPPjgg72eY4ecCxYsMBs2bDDG\nGPOXv/zFNj/PE2bPnm22bt0aGvdW7gOZM1qWb8v0dONSMBiU2+2WJLndbgWDQUldfwHb201PPZ1v\ndU5J+s1vfqNx48aptLRURUVFtsxZW1ur119/XRdffLFycnK0bds22+VsampSenq6Nm/eLOn4P4NP\nbHMNVM6TWb9+vWbOnGnbjI888ogyMzNVWFgY2gawW06/36877rhD48aN01133aWVK1faJmd9fb12\n7NihadOm9TjHDjmtYHm5h7tx6T8fc7lcocfGjBmjF198Mew8Y0yPzxftDVK9nb9ixQrt379fCxcu\n1G233WbLnB0dHfr8889VXV2tBx54QPPnz7dlzscff1x/+MMfNHnyZB05ckRnnnnmgObszYoVK3Tm\nmWfqhhtusGXGJUuWqK6uTjt37tTo0aN1xx132DJnYWGh1q5dq/3792v16tVatGiRLXIeOXJE8+bN\n05o1azR8+PAe5w10TqtYXu7x8fFdfgnZ0NCg+Ph4ud1utbS0SJKam5s1atSok5574MABxcfHS1Kf\nzo82Z0JCQpc5N9xwQ9hfBg10zvj4eCUkJGjOnDmSpClTpmjIkCE6ePCgrXImJCRo4sSJeumll7Rt\n2zYtWLBA48ePP+m5/ZmzJyUlJaqoqNAzzzwT9rgdMo4aNSpUIosXL1ZNTY0tc9bU1OiHP/yhJGne\nvHm2yHns2DHNnTtXN910k/Lz8/t8nh1+npGyvNy/eeNSe3u7NmzYoNmzZ8vn86m0tFSSVFpaGvYH\nHO5cn88nSX06P9qcPp9P+/btC83ZvHmzsrOzbZdz9uzZys/PV1VVlSSptrZW7e3t+t73vmernD6f\nT5999pkk6d///rfuv/9+LVmypM/n9kfOcCorK/XAAw9o8+bNOvvss7/V93eqMkrHC+SEjRs3dnmF\nip1yJiUl6bXXXpMkVVVVyePxDGhOY4wKCwuVmpqqZcuW9TgnHDv8PCPWHxv5FRUVxuPxmPHjx5vi\n4mJjjDEHDx40eXl5ZsKECcbr9ZrPP//cGGNMY2OjmTlzZq/n9na+1Tnnzp1r0tPTTWZmppkzZ44J\nBoO2zNne3m5uuukmk56ebi688ELz6quv2jLnww8/bDwej/F4POaee+4JzR2onAsWLDCjR482MTEx\nJiEhwTz++OMmKSnJjBs3zmRlZZmsrCyzZMmSAc3YU86bb77ZZGRkmEmTJpnZs2eHfplnp5zr1683\n7733npk6darJzMw0F198sdm+ffuA5nzjjTeMy+UymZmZoT/jiooKs3HjRpOQkGDOPvts43a7zVVX\nXTWgOa3GTUwA4EB8zB4AOBDlDgAORLkDgANZWu7h3oOhr+/fUF9fH/a3/wCAb8+ycu/pw7D78kHa\nAABrWVbu3/ww7JiYmNCHYScnJ4d9nWtv6uvrddlll+miiy7SRRddpHfeeUfS8Y+9ysnJ0XXXXaeU\nlBTddNNNVsUHAEex5JOYpPDvwfDuu+9G9Fxut1tbtmzRWWedpX379nW5U3Tnzp3avXu3Ro8erenT\np+utt97S9OnTLfkeAMApLCt3K99Xob29XUuXLtX777+vM844o8tdo1OnTtWYMWMkSVlZWaqvr6fc\nAeA/WLYt05f3avmmRYsWKTs7W9dcc023Y6tXr9bo0aO1a9cubdu2TV9//XXo2FlnnRX67zPOOEMd\nHR0WfQcA4ByWrdz78mHY37wZdv369T0+16FDh0J/MTz55JPq7Oy0KiYAnBYsW7n39GHYPX2Q9n/q\n6OgIrcp//vOfq7S0VFlZWfroo4+6vD1nuLcPBgB0ZZv3ltm8ebPKysr07LPPDnQUABj0LNuWicbv\nfvc7lZeXh94+EwAQHdus3AEA1uG9ZQDAgfqt3BsaGpSbm6u0tDSlp6dr7dq1kqTW1lZ5vV55PB7N\nmDEj9CG/ra2tys3N1YgRI/SLX/wi7HP6fD7efwYA+qDfyj0mJkarV6/Whx9+qOrqaj366KPas2eP\n/H6/vF6vamtrlZeXJ7/fL0k6++yzdf/99+vBBx8M+3zPP/+8RowYwatjAKAP+q3c4+LilJWVJUka\nPny4UlJS1NjYqPLychUUFEiSCgoKtGnTJknSueeeq+nTp3e5SemEI0eOaPXq1frtb3/b42cdAgD+\n3ynZc6+vr9eOHTs0bdo0BYNBud1uScffQyYYDHaZG25lfu+99+rOO+/UueeeeyriAsCg1+/lfuTI\nEc2dO1dr1qzRiBEjuhxzuVwn3WbZuXOnPv30U82ePZtVOwD0Ub+W+7FjxzR37lzdfPPNys/Pl3R8\ntd7S0iJJam5u1qhRo3p9jurqam3btk0XXHCBLr30UtXW1uryyy/vz9gAMOj1W7kbY1RYWKjU1FQt\nW7Ys9LjP5wvdrFRaWhoq/W+e900/+9nP1NjYqLq6Or355pvyeDyqqqrqr9gA4Aj9dhPTm2++qcsu\nu0yTJk0Kbb2sXLlSU6dO1fz587V//34lJibqueeeU2xsrCQpMTFRhw8fVnt7u8477zy9/PLLSk5O\nDj1nfX29fD6fdu3a1R+RAcAxuEMVAByIO1QBwIEodwBwIModAByIcgcAB6LcAcCBKHcAcCDKHaeF\nb34OrySVlJSE3lp6+fLleuihh7ocT0xMVGtrqyRpyJAhuvnmm0PHOjo6dP755+vaa68NPdeQIUP0\nyiuvhOZs2rRJQ4YM0fPPP98v3w9wMpQ7Tgu9fbB6uPc4+uZ42LBh+vDDD/XVV19JkrZs2aKEhIQu\nczIyMrp8/m9ZWVnoXVGBgUC547T0n/funexevpkzZ+rFF1+UdLy4f/SjH4XOcblcuvTSS1VTU6OO\njg4dOXJEn3zyiTIzM3mzOwwYW3xANtDfvvzyS2VnZ4fGra2tmj17tqTjxb569Wo9/fTToeNNTU1d\nzr/++ut133336ZprrtEHH3ygwsJCvfHGG6HjLpdLXq9XL730kr744gv5fD7V1dX183cF9Ixyx2nh\nnHPO0Y4dO0Lj0tJSbdu2TdLxYr799tt1++23h45fcMEFXc7PyMhQfX29ysrKNGvWrC7HTqzOr7/+\neq1Zs0aHDh3SQw89pOLi4v76doCTotxxWvq22zLS8Xc0vfPOO/Xaa6/ps88+63Z8ypQp+uc//6lh\nw4ZpwoQJlmUFIkG547TX133xRYsW6bzzzlNaWpoCgUDYOX6/X+ecc46F6YDIUO44LYR7NcyJx072\niWAnjsXHx2vp0qW9nn/VVVf1el3gVOEtfwHAgXgpJAA4EOUOAA5EuQOAA1HuAOBAlDsAOBDlDgAO\nRLkDgAP9L3J2N9Nb/IAcAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x1083e6390>"
]
}
],
"prompt_number": 34
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can see that the missing data in this file hasn't been properly removed. (This is probably a bug in `EVELightCurve`). We can check the header:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"evelc.meta"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 35,
"text": [
"['; DATA_list: 20140101_EVE_L0CS_DIODES_1m.txt\\n',\n",
" '; DATA_list: 20140101_EVE_L0CS_DIODES_1m.txt\\n',\n",
" '; Created: Wed Jan 1 23:59:12 2014 UTC\\n',\n",
" '; Origin: SDO/EVE Science Processing and Operations Center, LASP/CU\\n',\n",
" '; Units: W/m^2 for irradiance, dark is counts/(0.25s sample), quadrants are unitless, solar lat & lon are deg\\n',\n",
" '; Source: SDO-EVE ESP and MEGS-P instruments, http://lasp.colorado.edu/eve\\n',\n",
" '; Product: Level 0CS, 1-minute averaged SDO-EVE Solar Indices from broadband photometers\\n',\n",
" '; Version: 3.0, code updated 2013-Feb-02\\n',\n",
" '; Missing data: -1.00e+00\\n',\n",
" '; Column descriptions:\\n',\n",
" '; HHMM: hour and minute in UT\\n',\n",
" '; XRS-B proxy: a model of the expected XRS-B 0.1-0.8 nm value, calculated using two-component method\\n',\n",
" '; XRS-A proxy: a model of the expected XRS-A value\\n',\n",
" '; SEM proxy: a model of the expected SEM 26-34 nm value\\n',\n",
" '; 0.1-7ESPquad: the total irradiance over the ESP quadrant diode 0.1-7 nm\\n',\n",
" '; 17.1ESP: ESP irradiance measurement near 17.1 nm\\n',\n",
" '; 25.7ESP: ESP irradiance measurement near 25.7 nm\\n',\n",
" '; 30.4ESP: ESP irradiance measurement near 30.4 nm\\n',\n",
" '; 36.6ESP: ESP irradiance measurement near 36.6 nm\\n',\n",
" '; darkESP: ESP dark diode count rates (background)\\n',\n",
" '; 121.6MEGS-P: MEGS-P irradiance measurement at H I Lyman-alpha 121.6 nm\\n',\n",
" '; darkMEGS-P: MEGS-P dark diode count rates (background)\\n',\n",
" '; q0ESP: ESP quadrant 0 fraction (q0ESP to q3ESP add up to 1.0)\\n',\n",
" '; q1ESP: ESP quadrant 1 fraction\\n',\n",
" '; q2ESP: ESP quadrant 2 fraction\\n',\n",
" '; q3ESP: ESP quadrant 3 fraction\\n',\n",
" '; CMLat: Latitude centroid of ESP quad diode irradiance at the sun in degrees\\n',\n",
" '; CMLon: Longitude centroid of ESP quad diode irradiance at the sun in degrees\\n',\n",
" '; x_cool proxy: Cool component for calculating XRS-B proxy\\n',\n",
" '; oldXRSB proxy: XRS-B calculated using the version 2 method\\n',\n",
" '; Format:\\n',\n",
" '; YYYY DOY MO DD\\n',\n",
" '; HHMM XRS-B XRS-A SEM 0.1-7 17.1 25.7 30.4 36.6 dark 121.6 dark q0 q1 q2 q3 CM CM x_cool oldXRSB\\n',\n",
" '; proxy proxy proxy ESPquad ESP ESP ESP ESP ESP MEGS-P MEGS-P ESP ESP ESP ESP Lat Lon proxy proxy\\n',\n",
" ';---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------\\n',\n",
" ';END_OF_HEADER\\n']"
]
}
],
"prompt_number": 35
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from pandas import isnull\n",
"evelc.data['17.1ESP'][evelc.data['17.1ESP'] == -1]"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 36,
"text": [
"HHMM\n",
"2014-01-01 17:23:00 -1\n",
"Name: 17.1ESP, dtype: float64"
]
}
],
"prompt_number": 36
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"evelc.data['17.1ESP'][evelc.data['17.1ESP'] == -1] = np.nan"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 37
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"evelc.data.replace(-1, np.nan)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>XRS-B proxy</th>\n",
" <th>XRS-A proxy</th>\n",
" <th>SEM proxy</th>\n",
" <th>0.1-7ESPquad</th>\n",
" <th>17.1ESP</th>\n",
" <th>25.7ESP</th>\n",
" <th>30.4ESP</th>\n",
" <th>36.6ESP</th>\n",
" <th>darkESP</th>\n",
" <th>121.6MEGS-P</th>\n",
" <th>darkMEGS-P</th>\n",
" <th>q0ESP</th>\n",
" <th>q1ESP</th>\n",
" <th>q2ESP</th>\n",
" <th>q3ESP</th>\n",
" <th>CMLat</th>\n",
" <th>CMLon</th>\n",
" <th>x_cool proxy</th>\n",
" <th>oldXRSB proxy</th>\n",
" </tr>\n",
" <tr>\n",
" <th>HHMM</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2014-01-01 00:00:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00196</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000958</td>\n",
" <td> NaN</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.9</td>\n",
" <td> -0.9</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:01:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000959</td>\n",
" <td> NaN</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -0.9</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:02:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000957</td>\n",
" <td> NaN</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.2</td>\n",
" <td> 2320</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:03:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000956</td>\n",
" <td> NaN</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> NaN</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:04:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> NaN</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.157</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> NaN</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:05:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.157</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:06:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.158</td>\n",
" <td> 0.351</td>\n",
" <td> 0.158</td>\n",
" <td>-28.8</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:07:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.334</td>\n",
" <td> 0.158</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.3</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:08:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00194</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.158</td>\n",
" <td> 0.350</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -1.8</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:09:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00195</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.158</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.7</td>\n",
" <td> -2.0</td>\n",
" <td> 2330</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:10:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00196</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.159</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.6</td>\n",
" <td> -2.1</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:11:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00197</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000956</td>\n",
" <td> NaN</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.335</td>\n",
" <td> 0.159</td>\n",
" <td> 0.349</td>\n",
" <td> 0.158</td>\n",
" <td>-28.6</td>\n",
" <td> -2.4</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:12:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00199</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.000445</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.336</td>\n",
" <td> 0.159</td>\n",
" <td> 0.348</td>\n",
" <td> 0.157</td>\n",
" <td>-28.6</td>\n",
" <td> -3.0</td>\n",
" <td> 2340</td>\n",
" <td> 0.000005</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:13:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00203</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.007550</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.338</td>\n",
" <td> 0.160</td>\n",
" <td> 0.345</td>\n",
" <td> 0.156</td>\n",
" <td>-28.6</td>\n",
" <td> -4.7</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:14:00</th>\n",
" <td> 0.000006</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00208</td>\n",
" <td> 0.000903</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.013800</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.341</td>\n",
" <td> 0.161</td>\n",
" <td> 0.343</td>\n",
" <td> 0.156</td>\n",
" <td>-28.5</td>\n",
" <td> -6.7</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:15:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00212</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.242000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.341</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.155</td>\n",
" <td>-28.5</td>\n",
" <td> -7.6</td>\n",
" <td> 2340</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:16:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00215</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.537000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.342</td>\n",
" <td> 0.163</td>\n",
" <td> 0.340</td>\n",
" <td> 0.155</td>\n",
" <td>-28.3</td>\n",
" <td> -8.3</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:17:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.597000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.155</td>\n",
" <td>-28.2</td>\n",
" <td> -9.5</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:18:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000904</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.998000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.1</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:19:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000957</td>\n",
" <td> 0.934000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:20:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.870000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.166</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.6</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:21:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.808000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2350</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:22:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000545</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.746000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:23:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000905</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.687000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:24:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000546</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.629000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.2</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:25:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00216</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.574000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.344</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.5</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:26:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00217</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.520000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.336</td>\n",
" <td> 0.155</td>\n",
" <td>-27.9</td>\n",
" <td>-10.5</td>\n",
" <td> 2360</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:27:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.470000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.2</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:28:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00218</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000547</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.421000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.155</td>\n",
" <td>-28.0</td>\n",
" <td>-10.3</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:29:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00219</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.376000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.165</td>\n",
" <td> 0.338</td>\n",
" <td> 0.154</td>\n",
" <td>-28.1</td>\n",
" <td>-10.2</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:30:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00220</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.332000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.165</td>\n",
" <td> 0.337</td>\n",
" <td> 0.154</td>\n",
" <td>-28.2</td>\n",
" <td>-10.4</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:31:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00221</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.292000</td>\n",
" <td> 49.6</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.164</td>\n",
" <td> 0.337</td>\n",
" <td> 0.154</td>\n",
" <td>-28.3</td>\n",
" <td>-10.6</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:32:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00222</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000548</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.254000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.154</td>\n",
" <td>-28.4</td>\n",
" <td>-10.6</td>\n",
" <td> 2370</td>\n",
" <td> 0.000006</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:33:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00224</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.219000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.164</td>\n",
" <td> 0.338</td>\n",
" <td> 0.153</td>\n",
" <td>-28.5</td>\n",
" <td>-10.9</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:34:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000855</td>\n",
" <td> 0.00226</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000953</td>\n",
" <td> 0.186000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.347</td>\n",
" <td> 0.164</td>\n",
" <td> 0.337</td>\n",
" <td> 0.152</td>\n",
" <td>-28.6</td>\n",
" <td>-12.0</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:35:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00229</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.156000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.336</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.0</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:36:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000856</td>\n",
" <td> 0.00231</td>\n",
" <td> 0.000906</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000954</td>\n",
" <td> 0.218000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.4</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:37:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000857</td>\n",
" <td> 0.00233</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000955</td>\n",
" <td> 0.361000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.351</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-14.1</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:38:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000858</td>\n",
" <td> 0.00236</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000956</td>\n",
" <td> 0.320000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.165</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.6</td>\n",
" <td>-14.3</td>\n",
" <td> 2380</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:39:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00237</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.283000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.351</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-14.1</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:40:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.247000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.164</td>\n",
" <td> 0.334</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.9</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:41:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00240</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000957</td>\n",
" <td> 0.214000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.350</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.151</td>\n",
" <td>-28.7</td>\n",
" <td>-13.5</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:42:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000859</td>\n",
" <td> 0.00241</td>\n",
" <td> 0.000907</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000958</td>\n",
" <td> 0.183000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.335</td>\n",
" <td> 0.152</td>\n",
" <td>-28.7</td>\n",
" <td>-13.0</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:43:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000860</td>\n",
" <td> 0.00242</td>\n",
" <td> 0.000908</td>\n",
" <td> 0.000549</td>\n",
" <td> 0.000960</td>\n",
" <td> 0.155000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.164</td>\n",
" <td> 0.336</td>\n",
" <td> 0.151</td>\n",
" <td>-28.8</td>\n",
" <td>-12.8</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:44:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000861</td>\n",
" <td> 0.00243</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000960</td>\n",
" <td> 0.307000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.163</td>\n",
" <td> 0.337</td>\n",
" <td> 0.151</td>\n",
" <td>-28.9</td>\n",
" <td>-12.6</td>\n",
" <td> 2390</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:45:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000861</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.620000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.349</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.151</td>\n",
" <td>-29.0</td>\n",
" <td>-12.1</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:46:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000550</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.742000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.348</td>\n",
" <td> 0.162</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-11.6</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:47:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.763000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.348</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-11.6</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:48:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000862</td>\n",
" <td> 0.00244</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000961</td>\n",
" <td> 0.695000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.347</td>\n",
" <td> 0.163</td>\n",
" <td> 0.338</td>\n",
" <td> 0.152</td>\n",
" <td>-28.8</td>\n",
" <td>-11.1</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:49:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000863</td>\n",
" <td> 0.00243</td>\n",
" <td> 0.000909</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000962</td>\n",
" <td> 0.675000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.2</td>\n",
" <td> 0.346</td>\n",
" <td> 0.163</td>\n",
" <td> 0.339</td>\n",
" <td> 0.152</td>\n",
" <td>-28.8</td>\n",
" <td>-10.8</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:50:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00242</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.140000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2400</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:51:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000866</td>\n",
" <td> 0.00241</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.260000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.346</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.3</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:52:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00239</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.470000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td>-10.0</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:53:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000551</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.820000</td>\n",
" <td> 49.5</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.340</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td> -9.8</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:54:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00238</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000966</td>\n",
" <td> 1.890000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.152</td>\n",
" <td>-28.9</td>\n",
" <td> -9.4</td>\n",
" <td> 2410</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:55:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000865</td>\n",
" <td> 0.00236</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000965</td>\n",
" <td> 1.880000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.345</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.153</td>\n",
" <td>-28.9</td>\n",
" <td> -9.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:56:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00235</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000552</td>\n",
" <td> 0.000964</td>\n",
" <td> 2.040000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.344</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.153</td>\n",
" <td>-28.8</td>\n",
" <td> -9.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:57:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00233</td>\n",
" <td> 0.000911</td>\n",
" <td> 0.000553</td>\n",
" <td> 0.000964</td>\n",
" <td> 2.250000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.341</td>\n",
" <td> 0.154</td>\n",
" <td>-28.8</td>\n",
" <td> -8.6</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:58:00</th>\n",
" <td> 0.000008</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000864</td>\n",
" <td> 0.00232</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000553</td>\n",
" <td> 0.000963</td>\n",
" <td> 2.060000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.154</td>\n",
" <td>-28.7</td>\n",
" <td> -8.3</td>\n",
" <td> 2420</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2014-01-01 00:59:00</th>\n",
" <td> 0.000007</td>\n",
" <td> 0.000001</td>\n",
" <td> 0.000863</td>\n",
" <td> 0.00230</td>\n",
" <td> 0.000910</td>\n",
" <td> 0.000554</td>\n",
" <td> 0.000962</td>\n",
" <td> 1.870000</td>\n",
" <td> 49.4</td>\n",
" <td>NaN</td>\n",
" <td> 39.3</td>\n",
" <td> 0.343</td>\n",
" <td> 0.162</td>\n",
" <td> 0.342</td>\n",
" <td> 0.154</td>\n",
" <td>-28.7</td>\n",
" <td> -8.2</td>\n",
" <td> 2430</td>\n",
" <td> 0.000007</td>\n",
" </tr>\n",
" <tr>\n",
" <th></th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1440 rows \u00d7 19 columns</p>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 38,
"text": [
" XRS-B proxy XRS-A proxy SEM proxy 0.1-7ESPquad \\\n",
"HHMM \n",
"2014-01-01 00:00:00 0.000006 0.000000 0.000858 0.00196 \n",
"2014-01-01 00:01:00 0.000006 0.000000 0.000858 0.00195 \n",
"2014-01-01 00:02:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:03:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:04:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:05:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:06:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:07:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:08:00 0.000006 0.000000 0.000856 0.00194 \n",
"2014-01-01 00:09:00 0.000006 0.000000 0.000857 0.00195 \n",
"2014-01-01 00:10:00 0.000006 0.000000 0.000857 0.00196 \n",
"2014-01-01 00:11:00 0.000006 0.000000 0.000856 0.00197 \n",
"2014-01-01 00:12:00 0.000006 0.000000 0.000856 0.00199 \n",
"2014-01-01 00:13:00 0.000006 0.000000 0.000855 0.00203 \n",
"2014-01-01 00:14:00 0.000006 0.000000 0.000855 0.00208 \n",
"2014-01-01 00:15:00 0.000007 0.000000 0.000855 0.00212 \n",
"2014-01-01 00:16:00 0.000007 0.000001 0.000855 0.00215 \n",
"2014-01-01 00:17:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:18:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:19:00 0.000007 0.000001 0.000857 0.00217 \n",
"2014-01-01 00:20:00 0.000007 0.000001 0.000857 0.00217 \n",
"2014-01-01 00:21:00 0.000007 0.000001 0.000856 0.00216 \n",
"2014-01-01 00:22:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:23:00 0.000007 0.000001 0.000855 0.00217 \n",
"2014-01-01 00:24:00 0.000007 0.000001 0.000855 0.00216 \n",
"2014-01-01 00:25:00 0.000007 0.000001 0.000856 0.00216 \n",
"2014-01-01 00:26:00 0.000007 0.000001 0.000856 0.00217 \n",
"2014-01-01 00:27:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:28:00 0.000007 0.000001 0.000856 0.00218 \n",
"2014-01-01 00:29:00 0.000007 0.000001 0.000856 0.00219 \n",
"2014-01-01 00:30:00 0.000007 0.000001 0.000856 0.00220 \n",
"2014-01-01 00:31:00 0.000007 0.000001 0.000856 0.00221 \n",
"2014-01-01 00:32:00 0.000007 0.000001 0.000856 0.00222 \n",
"2014-01-01 00:33:00 0.000007 0.000001 0.000856 0.00224 \n",
"2014-01-01 00:34:00 0.000007 0.000001 0.000855 0.00226 \n",
"2014-01-01 00:35:00 0.000007 0.000001 0.000856 0.00229 \n",
"2014-01-01 00:36:00 0.000008 0.000001 0.000856 0.00231 \n",
"2014-01-01 00:37:00 0.000008 0.000001 0.000857 0.00233 \n",
"2014-01-01 00:38:00 0.000008 0.000001 0.000858 0.00236 \n",
"2014-01-01 00:39:00 0.000008 0.000001 0.000859 0.00237 \n",
"2014-01-01 00:40:00 0.000008 0.000001 0.000859 0.00238 \n",
"2014-01-01 00:41:00 0.000008 0.000001 0.000859 0.00240 \n",
"2014-01-01 00:42:00 0.000008 0.000001 0.000859 0.00241 \n",
"2014-01-01 00:43:00 0.000008 0.000001 0.000860 0.00242 \n",
"2014-01-01 00:44:00 0.000008 0.000001 0.000861 0.00243 \n",
"2014-01-01 00:45:00 0.000008 0.000001 0.000861 0.00244 \n",
"2014-01-01 00:46:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:47:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:48:00 0.000008 0.000001 0.000862 0.00244 \n",
"2014-01-01 00:49:00 0.000008 0.000001 0.000863 0.00243 \n",
"2014-01-01 00:50:00 0.000008 0.000001 0.000864 0.00242 \n",
"2014-01-01 00:51:00 0.000008 0.000001 0.000866 0.00241 \n",
"2014-01-01 00:52:00 0.000008 0.000001 0.000865 0.00239 \n",
"2014-01-01 00:53:00 0.000008 0.000001 0.000865 0.00238 \n",
"2014-01-01 00:54:00 0.000008 0.000001 0.000865 0.00238 \n",
"2014-01-01 00:55:00 0.000008 0.000001 0.000865 0.00236 \n",
"2014-01-01 00:56:00 0.000008 0.000001 0.000864 0.00235 \n",
"2014-01-01 00:57:00 0.000008 0.000001 0.000864 0.00233 \n",
"2014-01-01 00:58:00 0.000008 0.000001 0.000864 0.00232 \n",
"2014-01-01 00:59:00 0.000007 0.000001 0.000863 0.00230 \n",
" ... ... ... ... \n",
"\n",
" 17.1ESP 25.7ESP 30.4ESP 36.6ESP darkESP \\\n",
"HHMM \n",
"2014-01-01 00:00:00 0.000904 0.000547 0.000958 NaN 49.4 \n",
"2014-01-01 00:01:00 0.000904 0.000547 0.000959 NaN 49.4 \n",
"2014-01-01 00:02:00 0.000903 0.000547 0.000957 NaN 49.4 \n",
"2014-01-01 00:03:00 0.000903 0.000547 0.000956 NaN 49.4 \n",
"2014-01-01 00:04:00 0.000903 0.000547 0.000955 NaN 49.4 \n",
"2014-01-01 00:05:00 0.000903 0.000547 0.000955 NaN 49.5 \n",
"2014-01-01 00:06:00 0.000903 0.000546 0.000955 NaN 49.5 \n",
"2014-01-01 00:07:00 0.000903 0.000546 0.000955 NaN 49.5 \n",
"2014-01-01 00:08:00 0.000903 0.000546 0.000956 NaN 49.5 \n",
"2014-01-01 00:09:00 0.000904 0.000546 0.000956 NaN 49.5 \n",
"2014-01-01 00:10:00 0.000904 0.000546 0.000956 NaN 49.5 \n",
"2014-01-01 00:11:00 0.000903 0.000546 0.000956 NaN 49.5 \n",
"2014-01-01 00:12:00 0.000903 0.000546 0.000955 0.000445 49.5 \n",
"2014-01-01 00:13:00 0.000903 0.000546 0.000954 0.007550 49.5 \n",
"2014-01-01 00:14:00 0.000903 0.000546 0.000954 0.013800 49.5 \n",
"2014-01-01 00:15:00 0.000904 0.000545 0.000954 0.242000 49.5 \n",
"2014-01-01 00:16:00 0.000904 0.000545 0.000954 0.537000 49.5 \n",
"2014-01-01 00:17:00 0.000904 0.000545 0.000954 0.597000 49.6 \n",
"2014-01-01 00:18:00 0.000904 0.000545 0.000956 0.998000 49.6 \n",
"2014-01-01 00:19:00 0.000905 0.000545 0.000957 0.934000 49.6 \n",
"2014-01-01 00:20:00 0.000905 0.000545 0.000956 0.870000 49.6 \n",
"2014-01-01 00:21:00 0.000905 0.000545 0.000955 0.808000 49.6 \n",
"2014-01-01 00:22:00 0.000905 0.000545 0.000953 0.746000 49.6 \n",
"2014-01-01 00:23:00 0.000905 0.000546 0.000953 0.687000 49.6 \n",
"2014-01-01 00:24:00 0.000906 0.000546 0.000953 0.629000 49.6 \n",
"2014-01-01 00:25:00 0.000906 0.000547 0.000954 0.574000 49.6 \n",
"2014-01-01 00:26:00 0.000906 0.000547 0.000954 0.520000 49.5 \n",
"2014-01-01 00:27:00 0.000906 0.000547 0.000955 0.470000 49.5 \n",
"2014-01-01 00:28:00 0.000906 0.000547 0.000955 0.421000 49.5 \n",
"2014-01-01 00:29:00 0.000906 0.000548 0.000954 0.376000 49.5 \n",
"2014-01-01 00:30:00 0.000906 0.000548 0.000954 0.332000 49.6 \n",
"2014-01-01 00:31:00 0.000906 0.000548 0.000954 0.292000 49.6 \n",
"2014-01-01 00:32:00 0.000906 0.000548 0.000953 0.254000 49.5 \n",
"2014-01-01 00:33:00 0.000906 0.000549 0.000953 0.219000 49.5 \n",
"2014-01-01 00:34:00 0.000906 0.000549 0.000953 0.186000 49.5 \n",
"2014-01-01 00:35:00 0.000906 0.000549 0.000954 0.156000 49.5 \n",
"2014-01-01 00:36:00 0.000906 0.000549 0.000954 0.218000 49.5 \n",
"2014-01-01 00:37:00 0.000907 0.000549 0.000955 0.361000 49.5 \n",
"2014-01-01 00:38:00 0.000907 0.000549 0.000956 0.320000 49.5 \n",
"2014-01-01 00:39:00 0.000907 0.000549 0.000958 0.283000 49.5 \n",
"2014-01-01 00:40:00 0.000907 0.000550 0.000958 0.247000 49.5 \n",
"2014-01-01 00:41:00 0.000907 0.000549 0.000957 0.214000 49.5 \n",
"2014-01-01 00:42:00 0.000907 0.000549 0.000958 0.183000 49.5 \n",
"2014-01-01 00:43:00 0.000908 0.000549 0.000960 0.155000 49.5 \n",
"2014-01-01 00:44:00 0.000909 0.000550 0.000960 0.307000 49.5 \n",
"2014-01-01 00:45:00 0.000909 0.000550 0.000961 0.620000 49.5 \n",
"2014-01-01 00:46:00 0.000909 0.000550 0.000961 0.742000 49.5 \n",
"2014-01-01 00:47:00 0.000909 0.000551 0.000961 0.763000 49.5 \n",
"2014-01-01 00:48:00 0.000909 0.000551 0.000961 0.695000 49.5 \n",
"2014-01-01 00:49:00 0.000909 0.000551 0.000962 0.675000 49.5 \n",
"2014-01-01 00:50:00 0.000910 0.000552 0.000965 1.140000 49.5 \n",
"2014-01-01 00:51:00 0.000910 0.000552 0.000966 1.260000 49.5 \n",
"2014-01-01 00:52:00 0.000910 0.000551 0.000966 1.470000 49.5 \n",
"2014-01-01 00:53:00 0.000911 0.000551 0.000965 1.820000 49.5 \n",
"2014-01-01 00:54:00 0.000911 0.000552 0.000966 1.890000 49.4 \n",
"2014-01-01 00:55:00 0.000911 0.000552 0.000965 1.880000 49.4 \n",
"2014-01-01 00:56:00 0.000911 0.000552 0.000964 2.040000 49.4 \n",
"2014-01-01 00:57:00 0.000911 0.000553 0.000964 2.250000 49.4 \n",
"2014-01-01 00:58:00 0.000910 0.000553 0.000963 2.060000 49.4 \n",
"2014-01-01 00:59:00 0.000910 0.000554 0.000962 1.870000 49.4 \n",
" ... ... ... ... ... \n",
"\n",
" 121.6MEGS-P darkMEGS-P q0ESP q1ESP q2ESP q3ESP \\\n",
"HHMM \n",
"2014-01-01 00:00:00 NaN 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:01:00 NaN 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:02:00 NaN 39.2 0.334 0.157 0.350 0.158 \n",
"2014-01-01 00:03:00 NaN 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:04:00 NaN 39.2 0.334 0.157 0.351 0.158 \n",
"2014-01-01 00:05:00 NaN 39.2 0.335 0.157 0.350 0.158 \n",
"2014-01-01 00:06:00 NaN 39.2 0.334 0.158 0.351 0.158 \n",
"2014-01-01 00:07:00 NaN 39.2 0.334 0.158 0.350 0.158 \n",
"2014-01-01 00:08:00 NaN 39.2 0.335 0.158 0.350 0.158 \n",
"2014-01-01 00:09:00 NaN 39.2 0.335 0.158 0.349 0.158 \n",
"2014-01-01 00:10:00 NaN 39.2 0.335 0.159 0.349 0.158 \n",
"2014-01-01 00:11:00 NaN 39.2 0.335 0.159 0.349 0.158 \n",
"2014-01-01 00:12:00 NaN 39.2 0.336 0.159 0.348 0.157 \n",
"2014-01-01 00:13:00 NaN 39.3 0.338 0.160 0.345 0.156 \n",
"2014-01-01 00:14:00 NaN 39.3 0.341 0.161 0.343 0.156 \n",
"2014-01-01 00:15:00 NaN 39.3 0.341 0.162 0.342 0.155 \n",
"2014-01-01 00:16:00 NaN 39.2 0.342 0.163 0.340 0.155 \n",
"2014-01-01 00:17:00 NaN 39.2 0.343 0.164 0.338 0.155 \n",
"2014-01-01 00:18:00 NaN 39.2 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:19:00 NaN 39.3 0.343 0.165 0.336 0.155 \n",
"2014-01-01 00:20:00 NaN 39.3 0.343 0.166 0.336 0.155 \n",
"2014-01-01 00:21:00 NaN 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:22:00 NaN 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:23:00 NaN 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:24:00 NaN 39.2 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:25:00 NaN 39.2 0.344 0.165 0.336 0.155 \n",
"2014-01-01 00:26:00 NaN 39.3 0.343 0.165 0.336 0.155 \n",
"2014-01-01 00:27:00 NaN 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:28:00 NaN 39.3 0.343 0.165 0.337 0.155 \n",
"2014-01-01 00:29:00 NaN 39.3 0.343 0.165 0.338 0.154 \n",
"2014-01-01 00:30:00 NaN 39.3 0.344 0.165 0.337 0.154 \n",
"2014-01-01 00:31:00 NaN 39.3 0.345 0.164 0.337 0.154 \n",
"2014-01-01 00:32:00 NaN 39.3 0.345 0.164 0.338 0.154 \n",
"2014-01-01 00:33:00 NaN 39.3 0.346 0.164 0.338 0.153 \n",
"2014-01-01 00:34:00 NaN 39.3 0.347 0.164 0.337 0.152 \n",
"2014-01-01 00:35:00 NaN 39.3 0.349 0.164 0.336 0.151 \n",
"2014-01-01 00:36:00 NaN 39.3 0.349 0.164 0.335 0.151 \n",
"2014-01-01 00:37:00 NaN 39.3 0.351 0.164 0.334 0.151 \n",
"2014-01-01 00:38:00 NaN 39.3 0.350 0.165 0.334 0.151 \n",
"2014-01-01 00:39:00 NaN 39.3 0.351 0.164 0.334 0.151 \n",
"2014-01-01 00:40:00 NaN 39.3 0.350 0.164 0.334 0.151 \n",
"2014-01-01 00:41:00 NaN 39.3 0.350 0.164 0.335 0.151 \n",
"2014-01-01 00:42:00 NaN 39.3 0.349 0.164 0.335 0.152 \n",
"2014-01-01 00:43:00 NaN 39.3 0.349 0.164 0.336 0.151 \n",
"2014-01-01 00:44:00 NaN 39.3 0.349 0.163 0.337 0.151 \n",
"2014-01-01 00:45:00 NaN 39.3 0.349 0.163 0.338 0.151 \n",
"2014-01-01 00:46:00 NaN 39.3 0.348 0.162 0.338 0.152 \n",
"2014-01-01 00:47:00 NaN 39.3 0.348 0.163 0.338 0.152 \n",
"2014-01-01 00:48:00 NaN 39.3 0.347 0.163 0.338 0.152 \n",
"2014-01-01 00:49:00 NaN 39.2 0.346 0.163 0.339 0.152 \n",
"2014-01-01 00:50:00 NaN 39.3 0.346 0.162 0.340 0.152 \n",
"2014-01-01 00:51:00 NaN 39.3 0.346 0.162 0.340 0.152 \n",
"2014-01-01 00:52:00 NaN 39.3 0.345 0.162 0.340 0.152 \n",
"2014-01-01 00:53:00 NaN 39.3 0.345 0.162 0.340 0.152 \n",
"2014-01-01 00:54:00 NaN 39.3 0.344 0.162 0.341 0.152 \n",
"2014-01-01 00:55:00 NaN 39.3 0.345 0.162 0.341 0.153 \n",
"2014-01-01 00:56:00 NaN 39.3 0.344 0.162 0.341 0.153 \n",
"2014-01-01 00:57:00 NaN 39.3 0.343 0.162 0.341 0.154 \n",
"2014-01-01 00:58:00 NaN 39.3 0.343 0.162 0.342 0.154 \n",
"2014-01-01 00:59:00 NaN 39.3 0.343 0.162 0.342 0.154 \n",
" ... ... ... ... ... ... \n",
"\n",
" CMLat CMLon x_cool proxy oldXRSB proxy \n",
"HHMM \n",
"2014-01-01 00:00:00 -28.9 -0.9 2320 0.000005 \n",
"2014-01-01 00:01:00 -28.8 -0.9 2320 0.000005 \n",
"2014-01-01 00:02:00 -28.7 -1.2 2320 0.000005 \n",
"2014-01-01 00:03:00 -28.8 NaN 2330 0.000005 \n",
"2014-01-01 00:04:00 -28.7 NaN 2330 0.000005 \n",
"2014-01-01 00:05:00 -28.8 -1.3 2330 0.000005 \n",
"2014-01-01 00:06:00 -28.8 -1.3 2330 0.000005 \n",
"2014-01-01 00:07:00 -28.7 -1.3 2330 0.000005 \n",
"2014-01-01 00:08:00 -28.7 -1.8 2330 0.000005 \n",
"2014-01-01 00:09:00 -28.7 -2.0 2330 0.000005 \n",
"2014-01-01 00:10:00 -28.6 -2.1 2340 0.000005 \n",
"2014-01-01 00:11:00 -28.6 -2.4 2340 0.000005 \n",
"2014-01-01 00:12:00 -28.6 -3.0 2340 0.000005 \n",
"2014-01-01 00:13:00 -28.6 -4.7 2340 0.000006 \n",
"2014-01-01 00:14:00 -28.5 -6.7 2340 0.000006 \n",
"2014-01-01 00:15:00 -28.5 -7.6 2340 0.000006 \n",
"2014-01-01 00:16:00 -28.3 -8.3 2350 0.000006 \n",
"2014-01-01 00:17:00 -28.2 -9.5 2350 0.000006 \n",
"2014-01-01 00:18:00 -28.0 -10.1 2350 0.000006 \n",
"2014-01-01 00:19:00 -27.9 -10.3 2350 0.000006 \n",
"2014-01-01 00:20:00 -27.9 -10.6 2350 0.000006 \n",
"2014-01-01 00:21:00 -27.9 -10.2 2350 0.000006 \n",
"2014-01-01 00:22:00 -27.9 -10.2 2360 0.000006 \n",
"2014-01-01 00:23:00 -27.9 -10.2 2360 0.000006 \n",
"2014-01-01 00:24:00 -28.0 -10.2 2360 0.000006 \n",
"2014-01-01 00:25:00 -28.0 -10.5 2360 0.000006 \n",
"2014-01-01 00:26:00 -27.9 -10.5 2360 0.000006 \n",
"2014-01-01 00:27:00 -28.0 -10.2 2370 0.000006 \n",
"2014-01-01 00:28:00 -28.0 -10.3 2370 0.000006 \n",
"2014-01-01 00:29:00 -28.1 -10.2 2370 0.000006 \n",
"2014-01-01 00:30:00 -28.2 -10.4 2370 0.000006 \n",
"2014-01-01 00:31:00 -28.3 -10.6 2370 0.000006 \n",
"2014-01-01 00:32:00 -28.4 -10.6 2370 0.000006 \n",
"2014-01-01 00:33:00 -28.5 -10.9 2380 0.000007 \n",
"2014-01-01 00:34:00 -28.6 -12.0 2380 0.000007 \n",
"2014-01-01 00:35:00 -28.7 -13.0 2380 0.000007 \n",
"2014-01-01 00:36:00 -28.7 -13.4 2380 0.000007 \n",
"2014-01-01 00:37:00 -28.7 -14.1 2380 0.000007 \n",
"2014-01-01 00:38:00 -28.6 -14.3 2380 0.000007 \n",
"2014-01-01 00:39:00 -28.7 -14.1 2390 0.000007 \n",
"2014-01-01 00:40:00 -28.7 -13.9 2390 0.000007 \n",
"2014-01-01 00:41:00 -28.7 -13.5 2390 0.000007 \n",
"2014-01-01 00:42:00 -28.7 -13.0 2390 0.000007 \n",
"2014-01-01 00:43:00 -28.8 -12.8 2390 0.000007 \n",
"2014-01-01 00:44:00 -28.9 -12.6 2390 0.000007 \n",
"2014-01-01 00:45:00 -29.0 -12.1 2400 0.000007 \n",
"2014-01-01 00:46:00 -28.9 -11.6 2400 0.000007 \n",
"2014-01-01 00:47:00 -28.9 -11.6 2400 0.000007 \n",
"2014-01-01 00:48:00 -28.8 -11.1 2400 0.000007 \n",
"2014-01-01 00:49:00 -28.8 -10.8 2400 0.000007 \n",
"2014-01-01 00:50:00 -28.9 -10.3 2400 0.000007 \n",
"2014-01-01 00:51:00 -28.9 -10.3 2410 0.000007 \n",
"2014-01-01 00:52:00 -28.9 -10.0 2410 0.000007 \n",
"2014-01-01 00:53:00 -28.9 -9.8 2410 0.000007 \n",
"2014-01-01 00:54:00 -28.9 -9.4 2410 0.000007 \n",
"2014-01-01 00:55:00 -28.9 -9.3 2420 0.000007 \n",
"2014-01-01 00:56:00 -28.8 -9.3 2420 0.000007 \n",
"2014-01-01 00:57:00 -28.8 -8.6 2420 0.000007 \n",
"2014-01-01 00:58:00 -28.7 -8.3 2420 0.000007 \n",
"2014-01-01 00:59:00 -28.7 -8.2 2430 0.000007 \n",
" ... ... ... ... \n",
"\n",
"[1440 rows x 19 columns]"
]
}
],
"prompt_number": 38
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"evelc.data['17.1ESP'][evelc.data['17.1ESP'] == -1]"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 39,
"text": [
"Series([], name: 17.1ESP, dtype: float64)"
]
}
],
"prompt_number": 39
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import pandas as pd\n",
"pd.__version__"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 40,
"text": [
"'0.13.1'"
]
}
],
"prompt_number": 40
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = evelc.data['17.1ESP'].plot()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEmCAYAAACXl2yGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtcVNX6P/DPgJjXxExRGXQMhpvIYKIUpkGE90bLUqwM\nxTpmGVbq0X7VyTqJeMr8ap7SOprYhcyOCiWSpoGnAhHUrJgUa0jkZomkKDoCz++P5QwMzI1hYIbh\neb9evGDPrLX3MwPsZ9baa60tISICY4wxZoCLvQNgjDHmuDhJMMYYM4qTBGOMMaM4STDGGDOKkwRj\njDGjOEkwxhgzyqIkkZ6eDn9/f8jlcqxevdpgmfj4eMjlcigUChw7dsxs3R07dmDo0KFwdXXF0aNH\n9fa1atUqyOVy+Pv7Y9++fQCA6upqTJ48GQEBAQgKCsILL7zQ7BfLGGOsmciMmpoa8vb2JrVaTRqN\nhhQKBeXn5+uV2bNnD02cOJGIiLKzsyksLMxsXZVKRSdPnqSIiAjKy8vT7evnn38mhUJBGo2G1Go1\neXt7U11dHV25coUyMjKIiEij0dCYMWNo79695sJnjDHWAmZbEjk5OfDx8YFMJoObmxtiYmKQkpKi\nVyY1NRWxsbEAgLCwMFRWVqKsrMxkXX9/f/j6+jY5XkpKCmbNmgU3NzfIZDL4+Pjg8OHD6Nq1K+6+\n+24AgJubG26//XYUFxe3OEkyxhgzzmySKC4uhpeXl25bKpU2OTkbK1NSUmK2bmMlJSWQSqUm61RW\nVuKLL75AVFSUufAZY4y1QCdzBSQSiUU7olZc3aNhDDU1NZg1axYWLVoEmUymV+7WW2/F+fPnWy0O\nxhhzRt7e3jh9+rTB58y2JDw9PVFUVKTbLioq0vukb6jM2bNnIZVKLapr7nhnz56Fp6enbvtvf/sb\n/Pz8EB8f36Tu+fPnQUQO//XKK6/YPQaOk+PkODlO7devv/5q9JxsNkmEhoaioKAAhYWF0Gg02L59\nO5RKpV4ZpVKJbdu2AQCys7Ph7u4ODw8Pi+oC+q0QpVKJTz/9FBqNBmq1GgUFBRg1ahQA4KWXXsLF\nixexdu1ac2E7tIiICHuHYBGO07Y4TtviONsIWSAtLY18fX3J29ubEhISiIho48aNtHHjRl2Zp59+\nmry9vSk4OFhvtJKhukREO3fuJKlUSl26dCEPDw+aMGGC7rmVK1eSt7c3+fn5UXp6OhERFRUVkUQi\nocDAQAoJCaGQkBDavHmzXpwWvhzGGGMNmDp3Sm4UcAoSiQRO9HIYY6xNmDp38oxrxhhjRnGSYIwx\nZhQnCcYYY0ZxkmCMMWYUJwnGGGNGcZJgjDFmFCcJxhhjRnGSYIwxZhQnCcYYY0ZxkmCMMWYUJwnG\nGGNGcZJgjDFmFCcJxhhjRnGSYIw5va+/BlasAH76yd6RtD9mb1/KGGPt3YYNQFYW4OoKBAXZO5r2\nhVsSjDGnV1sLSKXiO2seThKMMadXWwt07sxJwhqcJBhjTq+2FrjpJk4S1uAkwRhzetySsB4nCcaY\n06up4SRhLU4SjDGnV1sLuLlxkrAGJwnGmNPj7ibrcZJgjDk9vnBtPU4SjDGnx9ckrMdJgjHm9Li7\nyXqcJBhjTo+ThPU4STDGnB4nCetxkmCMOT2+cG09s0kiPT0d/v7+kMvlWL16tcEy8fHxkMvlUCgU\nOHbsmNm6O3bswNChQ+Hq6oqjR4/q7WvVqlWQy+Xw9/fHvn37dI/n5eVh2LBhkMvlWLRoUbNfKGOs\n4+IL1y1AJtTU1JC3tzep1WrSaDSkUCgoPz9fr8yePXto4sSJRESUnZ1NYWFhZuuqVCo6efIkRURE\nUF5enm5fP//8MykUCtJoNKRWq8nb25vq6uqIiGjkyJF0+PBhIiKaOHEi7d27t0m8Zl4OY6yDGjyY\nKDGRaMYMe0fimEydO022JHJycuDj4wOZTAY3NzfExMQgJSVFr0xqaipiY2MBAGFhYaisrERZWZnJ\nuv7+/vD19W1yvJSUFMyaNQtubm6QyWTw8fHB4cOHUVpaikuXLmHUqFEAgMceewy7d++2QYpkjHUE\nfE3CeiaTRHFxMby8vHTbUqkUxcXFFpUpKSkxW7exkpISSKVSg/tq+Linp6fZfTHGmBYnCeuZTBIS\nicSinYjWCmOMOSa+JmE9k7cv9fT0RFFRkW67qKhI7xO9oTJnz56FVCrF9evXzdY1dzztvjw9PXH2\n7Fm9xz09PQ3uY86cOZDJZAAAd3d3hISEICIiAgCQkZEBALzN27zdwbZraoDffsvAuXMAYP947L2d\nkZGBrVu3AoDufGmUqYsZ169fp9tuu43UajVdu3bN7IXrrKws3YVrS+pGRERQbm6ublt74fratWv0\n22+/0W233aa7cD1q1CjKzs6muro6vnDNGGuWnj2JPv2UaPx4e0fimEydO022JDp16oQNGzZg/Pjx\nqK2txbx58xAQEIBNmzYBAObPn49JkyYhLS0NPj4+6N69Oz744AOTdQFg165diI+Px59//onJkydj\n+PDh2Lt3LwIDAzFjxgwEBgaiU6dOeOedd3RdXu+88w7mzJmD6upqTJo0CRMmTDCd/Rhj7IaaGp4n\nYS3JjSziFCQSCV8fYYw14eYGfPEF8K9/AQcP2jsax2Pq3MkzrhljTo2IWxItwUmCMebUamsBFxeg\nUydOEtbgJMEYc2o1NSJBuLpykrAGJwnGmFOrqRHXJDhJWIeTBGPMqV2/zi2JluAkwRhzatySaBlO\nEowxp9bwmkRdnb2jaX84STDGnBp3N7UMJwnGmFPj7qaW4STBGHNq2paEiwsnCWtwkmCMOTWeJ9Ey\nnCQYY06Nu5tahpMEY8yp8YXrluEkwRhzatySaBlOEowxp8bXJFqGkwRjzKlxd1PLcJJgjDk17m5q\nGU4SjDGnxi2JluEkwRhzatprEnzTIetwkmCMOTVtd1OnTuJn1jycJBhjTk3b3cRJwjqcJBhjTk3b\nknC5cbbj5cKbh5MEY8ypaa9JANyasAYnCcaYU9N2NwGcJKzBSYIx5tS03U0AJwlrcJJgjDk1bkm0\nDCcJxphT42sSLcNJgjHm1Li7qWU4STDGnBp3N7WM2SSRnp4Of39/yOVyrF692mCZ+Ph4yOVyKBQK\nHDt2zGzdiooKREdHw9fXF+PGjUNlZSUAQKPRYO7cuQgODkZISAgyMzN1dT744AMMGzYMCoUCEydO\nxPnz561+0YyxjoNbEi1jMknU1tZi4cKFSE9PR35+PpKTk6FSqfTKpKWl4fTp0ygoKMB7772HBQsW\nmK2bmJiI6OhonDp1ClFRUUhMTAQAvP/++3BxccGJEyewf/9+LF68GIBIHkuWLEFmZiZ++OEHBAcH\nY8OGDTZ/MxhjzoevSbSMySSRk5MDHx8fyGQyuLm5ISYmBikpKXplUlNTERsbCwAICwtDZWUlysrK\nTNZtWCc2Nha7d+8GAKhUKkRGRgIA+vbtC3d3d+Tm5qJTp07o3bs3qqqqQES4ePEiPD09bftOMMac\nEnc3tYzJJFFcXAwvLy/dtlQqRXFxsUVlSkpKjNYtLy+Hh4cHAMDDwwPl5eUAAIVCgdTUVNTW1kKt\nViMvLw9FRUVwcXHBunXrEBQUBE9PT6hUKsTFxbXwpTPGOgLubmqZTqaelEgkFu2EiCwqY2h/EolE\n93hcXBxUKhVCQ0MxePBghIeHw9XVFRcvXkR8fDx++OEHDBkyBM888wxWrVqFF198scn+5syZA5lM\nBgBwd3dHSEgIIiIiAAAZGRkAwNu8zdsdaPv69Qh06iS2q6uBmhrHis8e2xkZGdi6dSsA6M6XRpEJ\nWVlZNH78eN12QkICJSYm6pWZP38+JScn67b9/PyorKzMZF0/Pz8qLS0lIqKSkhLy8/MzePzw8HBS\nqVSUnZ1NUVFRusczMzNp0qRJTcqbeTmMsQ7o6aeJ1q8XP48cSXT4sH3jcUSmzp0mu5tCQ0NRUFCA\nwsJCaDQabN++HUqlUq+MUqnEtm3bAADZ2dlwd3eHh4eHybpKpRJJSUkAgKSkJEybNg0AUF1djcuX\nLwMA9u/fDzc3N/j7++O2227DL7/8gj///FP3XGBgoOnsxxhj4O6mljLZ3dSpUyds2LAB48ePR21t\nLebNm4eAgABs2rQJADB//nxMmjQJaWlp8PHxQffu3fHBBx+YrAsAy5cvx4wZM7B582bIZDJ89tln\nAMS1igkTJsDFxQVSqRQffvghAHEROyEhAZGRkXBxcYFMJtM1lRhjzJSaGnHrUoCThDUkN5oaTkEi\nkVh0fYQx1nHMnQuMHSu+33MP8NJL4jurZ+rcyTOuGWNOrba2/oZD3JJoPk4SjDGnVlvL3U0twUmC\nMebU6urqk4SrKyeJ5uIkwRhzatzd1DKcJBhjTo27m1qGkwRjzKk17G7iJNF8nCQYY06Nu5tahpME\nY8ypcXdTy3CSYIw5tcbdTbW19o2nveEkwRhzatzd1DKcJBhjTo27m1qGkwRjzKm1l9FN0dFAVFTT\nx+vqAIkEeOedto8JMLMKLGOMtXftpbvp668NP15aKr4fO9Z2sTTELQnGmFNrD91NdXX1Pze+sF5Y\nqP+9rXGSYIw5tfbQ3VRaCvTvDwwYUN9y0CosBIYP5yTBGGOtoj10NxUWAjKZ+GqcDAoLxf0wior0\nWxxthZMEY8yptYfupm++AQYPNp4kAgKA3r2btjLaAicJxphTaw/dTYcOAQqF4SRRWgoMHGj4ubbA\nSYIx5tTaQ3dTURGgVIpEoFbrP3fhgmhFcJJgjLFW4OjdTUTA77+L7qb+/YFz5/Sfr6wE3N05STDG\nWKtw9O6mrCzg+nWgRw+RDCor9Z9vmCQatzLaAicJxphTc/Tupuxs4L77xM+Nk0RNDfDnn0C/fuLr\nzz/bPj5OEowxp+bo3U3aIa5A0yRx9izg4QF07my4ldEWOEkwxpyao3c3aedIAE0TQcPnevfmJMEY\nYzbXuLvp+nX7xtNYw0TQowdw5Up9ImucJM6fb/v4eIE/xphTa9jddNNNwLVr9o2nISL9RODiAvTq\nJYa9SiSASlX/3IABYuRTTY1Idm2FWxKMMafWsLvJ0ZLEhQsiMbi71z92yy3ACy8AgwYBmzcDoaHi\n8c6dgVtvbftZ15wkGGNOrWF3k6MliYatCK3Bg4GPPwbWrROjmZTK+uduuUUklrZkNkmkp6fD398f\ncrkcq1evNlgmPj4ecrkcCoUCxxosem6sbkVFBaKjo+Hr64tx48ah8sbVGI1Gg7lz5yI4OBghISHI\nzMzU1dFoNPjb3/4GPz8/BAQEYOfOnVa/aMZYx+HI3U3GksTVq/UtiIbsMcLJZJKora3FwoULkZ6e\njvz8fCQnJ0OlUumVSUtLw+nTp1FQUID33nsPCxYsMFs3MTER0dHROHXqFKKiopCYmAgAeP/99+Hi\n4oITJ05g//79WLx4se44K1euRP/+/XHy5EmoVCrcfffdNn0jGGPOyZG7mwwlia5dxffhw5uWd7gk\nkZOTAx8fH8hkMri5uSEmJgYpKSl6ZVJTUxEbGwsACAsLQ2VlJcrKykzWbVgnNjYWu3fvBgCoVCpE\nRkYCAPr27Qt3d3fk5uYCAD744AO88MILuuP26dPHFq+fMebk2lt3U1wcsGqV4fIOlySKi4vh5eWl\n25ZKpSguLraoTElJidG65eXl8PDwAAB4eHigvLwcAKBQKJCamora2lqo1Wrk5eWhqKhI1x310ksv\nYcSIEZgxYwbONV7ghDHGDGhv3U0jRgDLlxsub48kYXIglUQisWgnRGRRGUP7k0gkusfj4uKgUqkQ\nGhqKwYMHIzw8HK6urqipqcHZs2cxevRorFmzBmvXrsWSJUuwbdu2JvubM2cOZDfedXd3d4SEhCAi\nIgIAkJGRAQC8zdu83YG26+oi4OoqtouLgWvXHCe+n34CZDLLy1dWApWVLT9+RkYGtm7dCgC686VR\nZEJWVhaNHz9et52QkECJiYl6ZebPn0/Jycm6bT8/PyorKzNZ18/Pj0pLS4mIqKSkhPz8/AwePzw8\nnFQqFdXV1VH37t11j585c4aGDh3apLyZl8MY64Dc3IiuXhU/FxURDRhg33ga6tmTqKLC8vJvvkn0\n3HO2j8PUudNkd1NoaCgKCgpQWFgIjUaD7du3Q9lwPBYApVKp+0SfnZ0Nd3d3eHh4mKyrVCqRlJQE\nAEhKSsK0adMAANXV1bh8+TIAYP/+/XBzc4O/vz8kEgnuu+8+fPPNNwCAAwcOYOjQoaazH2OMQb+7\nqUsXx+luunpVxNJwjoQ5dlm/yVyGSUtLI19fX/L29qaEhAQiItq4cSNt3LhRV+bpp58mb29vCg4O\npry8PJN1iYjOnz9PUVFRJJfLKTo6mi5cuEBERGq1mvz8/CggIICio6PpzJkzujq///47jR07loKD\ng+nee++loqKiZmVDxljHBBDV1YmfL14katApYVelpUT9+jWvzuefE91/v+1jMXXulNwo4BQkEolF\n10cYYx2Ddvir9rSg0QDduzvG+k2//AJMnQqcPGl5nQMHgJUrgYMHbRuLqXMnz7hmjDmthl1NAODm\nJh6rq7NfTFramwk1h8MNgWWMsfas4UQ6QCya17mzY1yX4CTBGGN21nAinZajzJXgJMEYY3bWuLsJ\naN9Jolcv4K+/2ra7jJMEY8xpNe5uAsTaSNXV9omnIWuSRKdOQLduQFVV68RkCCcJxpjTMtTd1KMH\ncOmSfeJpyJokAbR9lxMnCcaY0zLU3dSzZ9t+EjeGkwRjjNmZoe6mnj25JdEcnCQYY07LUHcTJ4nm\n4STBGHNaxrqbOElYjpMEY8xpcXdTy3GSYIw5LWPdTR3twnVdHRAdDXz5ZfOPx0mCMea0uLtJKC8H\nvv4a2L+/+cfjJMEYc1rGupsuXrRPPFpXr4qVabt0aX5da5JEYaH4/v77QGpq8+pykmCMOS1D3U3a\npS3sSduKsPAO0XoMJYm6OtOzyH/9FXjoISA+HsjKat7xOEkwxpyWoe6m3r3tcHe3Rs6fF3FY45Zb\nRP2G4uPFch3Grjls3AhIpYBCAaxd27zjcZJgjDktQ91NdrkFaCNnzgCDB1tXd9AgUV+rqgrIzQWC\ng4FDh8RrJhI3M6qtFT+r1cDcucD06WJxw6tXLT8eJwnGmNMy1N3Upw/wxx/2iUfr7Fnxyd4aXl5A\nSQlQUyO2X3lFXJheuBDYtEncve7oUcDfH0hPB376SZT39hb30vDwAD7/3PLjdbIuTMYYc3yGupu0\nn8SJrLsmYAuVlaLbyBqdOwP9+gHFxWJF2++/B9asAR54AMjJATIyRLcSIH4ePBiYMkV0RwHAnDlA\nSgpw++0ikTROoo1xS4Ix5rQMdTf16CFuY2rPLidrh79qyWRixNLbb4sL1mFh4nGFAti3Tzx3883A\nV1+JlsXQofV1p0wRLYmhQy1rUXCSYIw5LUPdTYD9L15fuNCyJDF4sEgAX30FPPcc4OkpHr/vPuC3\n34AvvhDdT2fOAMeOiVaG1l131bc0cnPNH4u7mxhjTstQdxNg/4vXZWVAZKT19UeOFK2AI0f09+Pl\nBSxaBFy+DDz+uOhiqq4Ghg3Tr//ii6Lc8ePmj8VJgjHmtAx1NwEiSVy40PbxaP3+u+gystaECcDy\n5aIFMWhQ/eMuLsA//lG//eKLhus/9BAQGAg8+KD5Y3GSYIw5LWPdTQMGAKWlbR+P1rlzYpSRteRy\n4L33xOuw1uDBIlkRmS7HSYIx5rSMdTdpL/zaS0svXLu4ALNntyyGHj3E1333mTlWyw7DGGOOy1h3\nkz2TRE2NuE7Qs6d9jt/QwYPADz+YLsNJgjHmtIx1N8nlwH/+Y76rxRa2bBET2X79VWxfuCDWj7LX\nHI2GgoIAX1/TZThJMMaclrHupshIMfLn3LnWj+Hbb8Ww1B9/FNtnzlg/27o1pKSYft5skkhPT4e/\nvz/kcjlWr15tsEx8fDzkcjkUCgWOHTtmtm5FRQWio6Ph6+uLcePGofLGWDSNRoO5c+ciODgYISEh\nyMzMbHIspVKJYY3HczHGmAHGupskEjG6py26nAoLgYCA+mNt3gzcemvrH9dSPXqYft5kkqitrcXC\nhQuRnp6O/Px8JCcnQ6VS6ZVJS0vD6dOnUVBQgPfeew8LFiwwWzcxMRHR0dE4deoUoqKikJiYCAB4\n//334eLighMnTmD//v1YvHgxqEF7cOfOnejZsyckjtBOY4w5PGPdTYB11yWuXAFUqubdj6KwEIiI\nqO/7LysDbpwm2wWTSSInJwc+Pj6QyWRwc3NDTEwMUhq1TVJTUxEbGwsACAsLQ2VlJcrKykzWbVgn\nNjYWu3fvBgCoVCpE3pgZ0rdvX7i7uyP3xpTAqqoqrF27Fi+99JJe4mCMMWOMdTcB1iWJV14RE9ks\nPcnX1Ig1lqZMAbZuFY8VFrZsjkRbM5kkiouL4eXlpduWSqUoLi62qExJSYnRuuXl5fC4MUjYw8MD\n5eXlAACFQoHU1FTU1tZCrVYjLy8PZ8+eBQC8/PLLWLJkCbppV6lijDEzjHU3AdYlidOngfnzxZLc\nlnxWLSkB+vYFJk4U2z/+KJbJaE9JwuQ8CUu7dSz5ZE9EBvcnkUh0j8fFxUGlUiE0NBSDBw9GeHg4\nXF1dcfz4cfz2229Yu3YtCs38VufMmQPZjd+Au7s7QkJCEBERAQDIyMgAAN7mbd7uINs//gi4uBh+\n/uLFDOTlAYDl+/vlF2DBggi89RbwyScZ8PQ0XT4/H/D0jIBEAnh7Z+Cuu4AhQyLQp49935+MjAxs\nvdG0kZnLWGRCVlYWjR8/XredkJBAiYmJemXmz59PycnJum0/Pz8qKyszWdfPz49KS0uJiKikpIT8\n/PwMHj88PJxUKhW9++67NHDgQJLJZCSVSqlz584UGRnZpLyZl8MY62C2bSN65BHDz/30E5G/P1FW\nFlFFhWX78/Ul+uUXojFjiDZtMl9+714i7Wnwn/8kAkRMjsbUudNkd1NoaCgKCgpQWFgIjUaD7du3\nQ6lU6pVRKpXYtm0bACA7Oxvu7u7w8PAwWVepVCIpKQkAkJSUhGnTpgEAqqurcfnyZQDA/v374ebm\nBn9/fzz55JMoLi6GWq3Gt99+C19fXxw8eNB09mOMdXimupu0y1LceSfw8suW7U87U3rECOC77ywv\nD4i7wj3/PHDPPZYdy1GY7G7q1KkTNmzYgPHjx6O2thbz5s1DQEAANm3aBACYP38+Jk2ahLS0NPj4\n+KB79+744IMPTNYFgOXLl2PGjBnYvHkzZDIZPvvsMwDiWsWECRPg4uICqVSKDz/8sElMZKTbijHG\nGjM1uqlHDzHzGRCjlswhEif9Xr3Eheh//tN8He3EOUAMg12zxrK4HYnkRlPDKUgkEh75xBjTef99\n4PBhMbvakJtvBi5dEvd/3rLF9L6qq8Xd5KqrxezpqCjzF77/8Q/RknnlFavCbzOmzp0845ox5rRM\ndTcBwL33iu+//25+Xw27jhrfZ9qY9jbc1RBOEowxp2WquwkAtm0DMjMtGwrbMEl07iyW+r4xQt8o\nThKMMebATE2mA8R1iVGjxMm+ttb0vhov762dZ7F8ubhGYYgzJAm+nwRjzGmZ624CgC5dgD59RPdR\ng/m/TRhLErt2AadONS2v0QDl5fX3n26vuCXBGHNa5rqbtCyZfW0oSRw+XJ8gvvlGv/znn4vvndr5\nR3FOEowxp2Wuu0nL2iSxezcQFla/VIdWaSlw5AiwdKkVQTsYThKMMadlSXcTILqZzF2ENpQkysqA\nIUOAMWOAFSuA69eBa9eA224DvvhCTNRr7zhJOKDSUnFbwYbDlo8eBfLz7RcTY+2Rpd1Nt9wikoAp\nhpIEADz2GPDII2Ihvx9/BE6cEOVOnwYmT7Y6dIfBScIBvfKKmKjz889im0iMwJgxw75xMdbeWNrd\n5O7e/CQxaBDwwAPA8OFiW6EQrYcvvwSCg62P2dG080sqzufiRTFawsUFePddMZX/2jXxx65WAzt2\nAA89ZO8oGWsfLO1usiZJuLkB//1v/faMGcCNJekwd27zY3VUnCQczNdfi1mcW7eKkRO//CIeX7cO\nqKgQzdqpU8VkHsaYaZa2JPr2FdcXTCkvF+WMiY4WXU1A/UxuZ8BJwsF8+aXo45w9W3w1tmGDGEXh\nTH+EjLWW2lrLPlDJZOaX5jA3MU4mA95+2/LY2gu+JuFgjhwB7rrL+PP33ANkZbVdPIy1Z5Z2N0ml\nYsCIsbWYamrE81KpbeNrDzhJOJBvvwV++kncNN2YqChxXYIxZp6lo5vMrcX09ddiZnZH7OblJOFA\n0tOBBx803e95//1imF1dXdvFxVh7df265Sf2fv2AP/4w/FxurrgW2BFxknAgW7aYH1fdrx8wcKAY\nEnv1atvExVh7de2a5UnC1AinrVudY2KcNThJOAhtn+fMmebL5uYC589btgY+Yx2ZRtPyJEEkbjI0\na5ZtY2svOEk4iCVLRN9p167myw4YANx6K3DjTrGMMSM0GuCmmywr27u3+PDV2Llz4v+t4RyJjoST\nhAWI6u+F21r7z8oSk+gs9dRT4iI3362VdVQajfl7QDSnu2nQIODMGf3HqqqA777rmKOatDhJWODj\nj4Fu3Vpv/3v3Ajk5Ylq/pUaMAPbsEUNmGeuIBgwAnn3WdJnmdDcNGdJ0JdiwMGD69PqlNzoinkxn\nAe0SwI2n5bdEQUH9p5b0dGDhQmDwYMvrBweL6xdffCFu5K7RAN27izkWlgz5Y6y9q6gAdu4EXn5Z\nDOgwpDndTTIZkJ1dv33pUv2imm+80aJQ2zU+nVjg2DHx/d//tt0+Z8wAXnwRSEgQC/lNmND8fSiV\nwPffi3ViJk0C7rsPOH7cdjEy5qiKisT32lrg1VeNl2tOd1NQkFgfTduaeO89cXvTO+8Uq8R2VJwk\nLHDuHLBsGfDpp8ZnZDbH5cviZJ6WBhw4IL6sWVL44YdF3SefFNv33ANs3ly/3hNjziozUwwD/89/\nxEQ3Y5o7umnsWNG9nJ8vuoFXrhQfxCQS28TdHnGSMINIDE2NjRUXim3xSf2bb0R/au/eLd8XADz+\nOLBpEzB5dujcAAAgAElEQVRvnvjj/te/bLNfxhzVoUPiOsEdd4jbh1ZUGC5XUdG8LuKnnhKJYfFi\nsW1NC9/ZSIicZ3yMRCKBrV/OlSviJunV1WLG5a23ik/rLbFggfj+7rstj6+x/fvFwoClpR370w9z\nbuPHi4vWEyeK5fRffbXp/VaIgJtvFktt9Opl+b6HDxfXDL/80vQSOc7E1LmTWxJmNLxY/fjjoina\nUjk5QHh4y/djSHi4WNLY3LLHjLVnDVdkvesusax+YxUV4p4PzUkQAJCYCLz2mujOYtySMCs/XwyB\nU6nEJ5Nu3YA//xQjiazxwgvA+vWiiezpadNQdYKDxVLib73VOvtnzJ4OHhQLXV6+LP4fP/8ceO45\ncZG64QrKly6JyXFHj9ov1vbC1LmTh8Ca0bAlIZGIYaq//w4EBjZ/X0QiQXz6aeslCABYuhRYtYqT\nBHNOKSmiS1U7d2nSJDFCcMUKsXRGw6XBfXzsEqJTsai7KT09Hf7+/pDL5Vi9erXBMvHx8ZDL5VAo\nFDimHTNqom5FRQWio6Ph6+uLcePGofLGoikajQZz585FcHAwQkJCkJmZCQCorq7G5MmTERAQgKCg\nILzwwgtWv+jmaDw3wttb/IGam+lpSEaGuMZx3302C8+gKVPEWjMJCa17nOY4fhwYPdreUTBHsGiR\naO0qFPrzEiwxZYr4oDV9ev1j3boB06aJnx96SNx3WvvlTPeathsyo6amhry9vUmtVpNGoyGFQkH5\n+fl6Zfbs2UMTJ04kIqLs7GwKCwszW3fp0qW0evVqIiJKTEykZcuWERHRhg0bKC4ujoiIzp07RyNG\njKC6ujq6cuUKZWRkEBGRRqOhMWPG0N69e/XisODlNNvHHxPFxNRv//knkYcH0Zkzzd/XmjVEjz1m\nu9hM+ewzorvuaptjWeK994gAospKe0fC7E0mI9qzh+jRR4neeqt5dUV7nKimpulz58/bJr6OyNS5\n02xLIicnBz4+PpDJZHBzc0NMTAxSUlL0yqSmpiI2NhYAEBYWhsrKSpSVlZms27BObGwsdu/eDQBQ\nqVSIjIwEAPTt2xfu7u7Izc1F165dcffddwMA3NzccPvtt6O4uNgmidKUxi2JPn1Ea6Lx9H1zqqvF\nsLq2Wm549GhxE6O0tLY5njnaFWt55dqO7cQJ8b8TFSX+RpcutfyWn6+9Jr736mX4bnMdecJbazKb\nJIqLi+Hl5aXblkqlTU7OxsqUlJQYrVteXg4PDw8AgIeHB8rLywEACoUCqampqK2thVqtRl5eHs42\nul1UZWUlvvjiC0RFRTX39TaboaU4Bg9u3oS1q1fF8t4yGTB/vk3DM2rgQHEx7/vvHWMRQG1S5Yl+\nHdv334sba910k/hfePtt8VhDGk3TepWVotyOHcbv+cBah9kL1xILB9uTBWciIjK4P4lEons8Li4O\nKpUKoaGhGDx4MMLDw+Ha4GNDTU0NZs2ahUWLFkFm4K7kc+bM0T3u7u6OkJAQRNwY7JyRkQEAzdo+\ncQIYPlz/+SFDIrBlCyCXW7a/jRsjsG8fcOedGcjMbN7xW7Ldu3cG/vlPYMyYCIwf3/rHM7V99izg\n5ZWBNWuAGTPa/vi8bf/tb77JwIIFwJtviu3MzAy4uACffhqBjz8GDh0S5SMjI3DkCFBVJbbHjo2A\nlxfQtWsGrl0DAMd4Pe15OyMjA1u3bgUAg+dRPeb6qrKysmj8+PG67YSEBEpMTNQrM3/+fEpOTtZt\n+/n5UVlZmcm6fn5+VFpaSkREJSUl5OfnZ/D44eHhpFKpdNtz586lRYsWGSxrwctptieeINq0Sf+x\n/HwiX1/zda9dI/r2WyJ/f6IjR2wemkUWLCB6++3WP84vvxBVVxt/fsQIovXriQYMMF3OHoqLiQ4d\nEl8XL9o7GtsoKxOv59gxoitXiE6eFI9XVBAdOCCurR0/Xv+6tV+//NJ6MWVmEt18M1Fdnf7jPXqI\n/4/r18X/C0D03HP1Me3eTdS/f+vFxUyfO82eVa9fv0633XYbqdVqunbtmtkL11lZWboL16bqLl26\nVJcwVq1apbtwfeXKFaqqqiIion379tHdd9+tO86LL75I06dPp7rGf2UWvFBrTZtGtGOH/mNVVURd\nujT9Y29s506ivn2J7r3Xfief1auJFi9u/eMARBs3Gn/e35/o+++JJBKiDz5o/XiaY+pUoqFDiby8\nxPvlDB55RLznnTsTvf66+P0Q1V/4BcRzd91V/3XnnWJQRms4c0b8zzz1VNPnJk8mGj+e6KuviG65\npT6+hrE9/3zrxMWEFiUJIqK0tDTy9fUlb29vSkhIICKijRs30sYGZ4Wnn36avL29KTg4mPLy8kzW\nJSI6f/48RUVFkVwup+joaLpw4QIREanVavLz86OAgACKjo6mMzeGERUVFZFEIqHAwEAKCQmhkJAQ\n2rx5s8Uv1FrDhxtuBfTtS3SjIWRQdbUYyfTsszYPqVm2bxevoTUdPiz+qU2N3PLyIiosJHr5ZaLZ\ns1s3nuaoqSHq2VN84t6wgej22w2PnHEEBQVEH30kPnHX1Ynf7f79Tcv99pv4ffzvf0QBAUSjRont\n99/XTxKNG++1teLxo0dtG3damvi9Gxttd/Qo0eDBRHPnipY7a3stThLtRWskif79RXdEYyNHEmVl\nGa/31VdEUqloPttTcbH4x798ufWOMWuWaCEMGGC8TJ8+ROfOEX35JVG/fq0XS3P98AORi4tI6idP\nivfq+HF7R2XYE0+I+HJz6z+Z9+nTtJw2CVy8KFp3c+YQPfCA+H7XXaKFcccdRO++27TupEliaKqt\naDT18Xz0keEy1dVETz4p4jtwwHbHZpYzde7kZTnM6NpVrAHT+N7TDz4oluZISjJc77nngIsXW74Y\noC1IpcBLL9UvKW4rP/8MfPKJWM9q0yZxf4slS4BHHxWLrjXUtatYIsHFRQxhvHLF8DBGAPjvf8Xq\nm9YufWKpt94Sd/a7dEks5gaIyVq9egFr1gD9+7fu8S1VVSVuevPJJ2KxuvvuE8M98/LE7yA+XqzZ\nlZMjTsfaSZTW/Ct88414D9Rq4zfyMeSnn4DkZPFzly7A8uXAZ5+JmNavtz4e1jZ4gT8rXb0K1NWJ\nP/rGnngC2LbNeN3Dh8Uyxo5g7lzbLEzY2CefiKG9Tz0FjBkDbNggTgrbt+uXu3hRJIeuXcV72aeP\nWKXWmAcfFEMdW1NlpUicQUHA3/9e//iyZWKdLlP3KGhrubni9zdvnrgPel2dSMp33im+5+eL9+zr\nr8Xs48WL65Nec40aJZawP3iwefU++kiskdStm7g5V0GBWKesSxexQqu18TAH0EatmTZh65dTVma8\na6SuTvRlP/gg0YwZ4uvECaIvvhA/9+gh+oYdwenTorn/11+23a+fH1FSkv5j//kPUVCQ/mMnThAF\nBtZv33mn6C//6COiV18Vs27nzRPXNB5+WMQaGirex6eeMj9AwBrHjzeNU2v5cjFgQUujIYqLI/rw\nQ9vHYc7ly0SRkfrXcfbtE+/Rnj1ie9cusb1ypW2OuWSJ+Ls25Pp18V40/L1fuCD+3j/+WGxHRdVf\nGNdobBMTa12mzp2cJEz45RfTQ10zM4k+/VR8TZkilt149FGihQuJUlJa5+Rmjbo6ooEDbXt9RNvX\nXFGh//i5c02XTUhNFX3dWrNmiRNucLAo6+1d3289YoS4wKp9X3v0aHoMW9i9W/zODDl4UFxI1Soo\nELHde6/t4zAnN5fotttEote6elWMnNMOJb5yRSzDcu6cbY751VdEPj6Gn9N+4LjnnvrHvvlGfJi6\ndEls79kjyjT+AMEcFycJK2Vni5Ehlli/Xgwf7NlTjO12NNOnE4WH225/r71G1L274ec6dxYjWh57\nTJwsBg0SiVNryRL9oY6dO9f//Pjj+vsKDrbtaJv4eHGxd/Bg8bMhVVUill9/Fa3BwEAxCMHHR8yR\nCQ213ad2Y1auFCOtfHyI7r+/dY/VWGWl+J00fo11deLC9+DB4qL5u++KxBAYSBQbW19O+wGC1+lq\nPzhJWCk9nWjcOMvKVleLT33HjomhhI7m9GkxAslWrZvoaOPzIuLiiFatqj/x5+bqnzC0Q2aVShHX\nyZNEv/8uhho3PrEoleJTs614eopjz55t+iQ2dqyYH/P556K7R60muukmMcfDy0t0mbWmO+4g2rJF\nvHe2aiE0x2efiRgaOneOyN1dDP1++20xvyQ3V3Q7Nl5czx4xM+txkrDSp5+KfnFnoW3p3Hyz+HJ3\nb/5M8GvXRMugUyfRDWPI5s1Ebm71SaIx7Sf1DRvMH+/vfxefWv/f/2tenIZs2lQf0zvvmC67dGl9\n2RvzPEkmE5+wn35aPG5oaHRzXb0qks6CBaK/X3tMNzfT83BaW1mZiEH7t/LEE0QzZ4r3gIjop5+I\nXF2JunUTj7P2zdS5k4fAmrBpkxixsWmTzXZpV1ev4sbaN8JTTwFhYcDDD4tFDDuZWcnr+nXgxx+B\n++8XI2qMDVElEiOaOncWo1sMLf9VXW38uYbq6oDdu8VCcDt2iKGfLmbG5BGJYcuN/xQWLxb3L37q\nKXFbS1PHrq2tfz9qa8Uxte9fz55iNNff/w5ERgI9ejSN6do1MbS2a1fTQ3l//lmMsFIoxHDqkBDx\neFVV6w8BNufyZaCmRqzcumCBGLL8zjv19wWpqhLvTffu5v92mGPjIbBWMrQCbHvWpYuYA6D9uusu\nsfzykCHipvLmPPGEuDH8XXeZPoFJJGL/XbsaPxGbeq4hFxdg5EixeuygQWL+gjlffSVWwfX31//a\nu1cMS+7c2fyxtXM4brutPgFo3z8XF2DsWDEktVcvMfy0sfvvF0vK+/oaPwaReC+nTBFzSLSLGj/0\nkP0TBCBi6NVLJLBLl0TibXhHxh49xPOcIJwbtyRMmDlTfLJro5vg2U16uhjLvnat2O7aVXxiLy4W\nn+Q7dRJzGx54QP+TZFvbtEnEummT6Ylezz4rPuFaep+CltAmm6ws8d3LCxgwQLx/OTni7yczUyS6\nP/8ESkrEifboUXHSnT0b+OOP1o+TMVNMnTs5SRhRUSFOjPv3A/fea5NdOqzSUmDGDNGdBIhbjfbr\nJ1pRP/5YX27UKHGS7t3bPnGeOFGfuLWzexu7elUkud27galTWz8mHx9xkg8IEN0v/foBiYmiG+/a\nNdFN8/HHYgbztGkicaxZA6xcCcjlQGiomITImD1xkjDi6FHg5EnxCfmmm+of12iAdevEjOIGt+vu\nMMLDxSfj0lLxqVjr4kXRH29PWVnAxIniDne9ejV9PjMTeOQRsXxFW/vtN/HezZwp3rvPPhOP33EH\nMGkS8MorYjs8HLj99rZp6TBmCVPnzg7dm/jMM2L9Gw8P4J576h//7jvR9bJihd1Cs6u//U2cxPr1\nA95/X6yzpFbbP0EAwLBh4prArl3AnDlNn//6a2DEiDYPC4C4ZjJtmri+8Mgj9Y/Pnw8cOCA+jBw8\nKK4BTZ9unxgZa64O25IoKBAXFe+5R3SrrFkDpKYCZWXiH9nPz/jifcy+/vEPce/uJUuAmBixDYjk\n8cUXIvkbSiCMMcO4u8mA118HUlJEf/Dzz4uRJWvWiBEn1dVAdrboV2aO5+RJMVoJENcgunQR2zNn\nigvJ8+c7zgqujLUH3N3UyBtvAB9+KMbNh4WJIYxvvSUuQvr6Ap9/zgnCkfn51f88a5b4Pn16x+0e\nZKw1dciWxMCBYpnoWbPESJ0//xSjdnx9xdcff4iRJ8xxFReL7sGePcU1k0cfFctUM8aaj7ubGrh6\n1fxNbxhjrCPhGdcNnDkjJjxxgmCMMfM6VJL45BMx87VhnzZjjDHjnD5JEAF//SW+vv1WDJvcudPe\nUTHGWPvg9Eli7VoxKWzQINGSGD1af3Y1Y4wx45w6SZw/L2ZPr1snWhKVlfozqxljjJnm1EnimWfE\nonB33GHvSBhjrH1yusl0NTXi2kO/fmJdpm3b6m/kwhhjrHmcLkl89524W5i7u1gMLijI3hExxlj7\n5XTdTW++Kb5XVgIvvugYK5cyxlh75XQtieBgcQOYrl35WgRjjLWU2ZZEeno6/P39IZfLsXr1aoNl\n4uPjIZfLoVAocKzBXXqM1a2oqEB0dDR8fX0xbtw4VFZWAgA0Gg3mzp2L4OBghISEIDMzU1cnLy8P\nw4YNg1wux6JFi4zGu3Il8K9/idtxGropDWOMsWYgE2pqasjb25vUajVpNBpSKBSUn5+vV2bPnj00\nceJEIiLKzs6msLAws3WXLl1Kq1evJiKixMREWrZsGRERbdiwgeLi4oiI6Ny5czRixAjdcUaOHEmH\nDx8mIqKJEyfS3r17m8Rr5uUwxhgzwNS502RLIicnBz4+PpDJZHBzc0NMTAxSUlL0yqSmpiI2NhYA\nEBYWhsrKSpSVlZms27BObGwsdu/eDQBQqVSIjIwEAPTt2xfu7u44cuQISktLcenSJYwaNQoA8Nhj\nj+nqMMYYaz0mk0RxcTG8vLx021KpFMXFxRaVKSkpMVq3vLwcHh4eAAAPDw+Ul5cDABQKBVJTU1Fb\nWwu1Wo28vDycPXsWxcXFkEqlun15eno2iaM9ycjIsHcIFuE4bYvjtC2Os22YTBISicSinZAFq40T\nkcH9SSQS3eNxcXGQSqUIDQ3Fc889h/DwcLi6ulocR3vRXv5oOE7b4jhti+NsGyZHN3l6eqKoqEi3\nXVRUpPeJ3lCZs2fPQiqV4vr1600e9/T0BCBaD2VlZejfvz9KS0vRr18/AICrqyveeustXZ3Ro0fD\n19cXvXr1wtmzZw3uq6GBAwe2m4Ty6quv2jsEi3CctsVx2hbHaRve3t5GnzOZJEJDQ1FQUIDCwkIM\nHDgQ27dvR3Jysl4ZpVKJDRs2ICYmBtnZ2XB3d4eHhwf69OljtK5SqURSUhKWLVuGpKQkTJs2DQBQ\nXV2Nuro6dO/eHfv374ebmxv8b9zM+Oabb8bhw4cxatQofPjhh4iPj28Sb3vugmKMMYdk7qp3Wloa\n+fr6kre3NyUkJBAR0caNG2njxo26Mk8//TR5e3tTcHAw5eXlmaxLRHT+/HmKiooiuVxO0dHRdOHC\nBSIiUqvV5OfnRwEBARQdHU1nzpzR1cnNzaWgoCDy9vamZ555xuKr9owxxqznVLcvZYwxZlsOvSyH\nocl4xibiWVK3OfVbGufLL78MhUKBkJAQREVF6V2fcaQ4AeDtt99GQEAAgoKCsGzZMrvGaeg4P/zw\nA+68804EBwdDqVTi0qVLdo0REIMsPDw8MGzYMN1jS5cuRUBAABQKBR544AH89ddfdo3TUIwrVqyA\nVCrF8OHDMXz4cKSnp9s1RmNx5uTkYNSoURg+fDhGjhyJI0eO2D3OoqIiREZGYujQoQgKCsL69esB\nADt27MDQoUPh6uqKo0ePGq3flrHalL2bMsYYm4xnbCKeJXWJjE/ks3WcFy9e1JVZv349zZs3zyHj\nPHjwIN17772k0WiISExitFecxo4TGhpKhw4dIiKiLVu20Msvv2y3GLUOHTpER48epaCgIN1j+/bt\no9raWiIiWrZsmd3/Ng3FuGLFClqzZo3Jeo7wXt59992Unp5ORKLbOiIiwu5xlpaW0rFjx4iI6NKl\nS+Tr60v5+fmkUqno5MmTFBERodfdbs9Ybclhk8T3339P48eP122vWrWKEhISyM/Pj8rKyohI/NL8\n/Pwsqrtq1SoiIovqtzRO7bG0EhISDP7iHSHOGTNm0IEDB6yqa+s4jf3Oe/XqpXvszJkzFBgYaLcY\nG1Kr1XontoZ27txJjzzyiN3jbBzjihUr6M033zRZxxHey5iYGNq+fTsREX3yyScO8V42NnXqVPr6\n669126aShL1jbQmH7W4yNknP2ES8kpISTJ482WRdwPhEPlvHCQAvvvgiBg0ahKSkJCxfvtwh4zx1\n6hQOHTqEO+64AxEREcjNzbVbnIaOU1JSgqCgIN1s/R07dui67uz1Xlpiy5YtmDRpkkPG+fbbb0Oh\nUGDevHm6rg1HizExMRGLFy/GoEGDsHTpUqxatcqh4iwsLMSxY8cQFhZmtIyjxNpSDpskjE28a7yt\nfWzgwIHYs2ePwXJkwUQ+W8aptXLlSpw5cwZz5szBc88955Bx1tTU4MKFC8jOzsYbb7yBGTNm2C1O\nY3U3b96Md955B6GhoaiqqkLnzp3tFqMlVq5cic6dO+Phhx92uDgXLFgAtVqN48ePY8CAAVi8eLHD\nxQgA8+bNw/r163HmzBmsXbsWcXFxDhNnVVUVHnzwQaxbtw49evQwWs4RYrUFh00ShibyeXp66ibi\nAdCbiGeqrqGJfKbqtzTOxhMOH374YYMX3uwdp6enJ6RSKR544AEAwMiRI+Hi4oLz58/bJU5j76Wf\nnx+++uor5ObmIiYmxuDEn7Z8L03ZunUr0tLS8PHHHxt83t5x9uvXT3cievzxx5GTk+NwMQLiwvX9\n998PAHjwwQcdJs7r169j+vTpePTRR3XzuyzhCO+ptRw2STScyKfRaLB9+3ZMnTpVNxEPgN5EPHN1\nlUolAFhUv6VxKpVKFBQU6MqkpKRg+PDhDhfn1KlTMW3aNBw8eBAAcOrUKWg0GvTp08cucRo7zh9/\n/AEAqKurw+uvv44FCxZYXNfWMZqSnp6ON954AykpKejSpUuzXmNbxVlaWqr7edeuXXojihwlRgDw\n8fHR3Srg4MGD8PX1tXucRIR58+YhMDAQzz77rNEyhjjCe2o1e10MsYShyXjGJuIVFxfTpEmTTNY1\nVd/WcU6fPp2CgoJIoVDQAw88QOXl5Q4Zp0ajoUcffZSCgoLo9ttvp2+++caucRo6zv/93/+Rr68v\n+fr60gsvvKAra8/3MiYmhgYMGEBubm4klUpp8+bN5OPjQ4MGDaKQkBAKCQmhBQsW2DVOQzHOnj2b\nhg0bRsHBwTR16lTdBVNHei+3bNlCR44coVGjRpFCoaA77riDjh49avc4//e//5FEIiGFQqH7Hael\npdGuXbtIKpVSly5dyMPDgyZMmGD3WG2JJ9MxxhgzymG7mxhjjNkfJwnGGGNGcZJgjDFmlEMmCUNr\nnFi6PkphYaHBERuMMcaaz+GSRG1tLRYuXIj09HTk5+cjOTkZKpUKw4YNw65duzB27Fh7h8gYYx2G\nwyWJnJwc+Pj4QCaTwc3NDTExMUhJSYG/v7/BsdKmFBYWYuzYsRgxYgRGjBiBrKwsAOJ2ghEREXjo\noYcQEBCARx99tDVeCmOMtXsm70xnD4bWODl8+LBV+/Lw8MD+/ftx0003oaCgQG/m8/Hjx5Gfn48B\nAwZg9OjR+O677zB69GibvAbGGHMWDpckbLluiUajwcKFC/HDDz/A1dVVbxb0qFGjMHDgQABASEgI\nCgsLOUkwxlgjDtfdZMlaSA3FxcVh+PDhmDJlSpPn1q5diwEDBuDEiRPIzc3FtWvXdM/ddNNNup9d\nXV1RU1Njo1fAGGPOw+FaEg3XOBk4cCC2b9+O5ORkvTINJ4lv2bLF6L4uXryoSzDbtm1DbW1t6wTN\nGGNOyuFaEp06dcKGDRswfvx4BAYGYubMmQgICMCuXbvg5eWF7OxsTJ48GRMnTjRYv6amRtdKeOqp\np5CUlISQkBCcPHlSb1lfQ8uOM8YY0+d0azelpKQgOTkZn376qb1DYYyxds/hupta4h//+AdSU1N1\ny+4yxhhrGadrSTDGGLMdh7smwRhjzHE4dJIoKipCZGQkhg4diqCgIKxfvx4AUFFRgejoaPj6+mLc\nuHG6m7lXVFQgMjISPXv2xDPPPGNwn0qlktd2YowxCzl0knBzc8PatWvx888/Izs7G//+97+hUqmQ\nmJiI6OhonDp1ClFRUUhMTAQAdOnSBa+//jrefPNNg/vbuXMnevbsySOZGGPMQg6dJPr374+QkBAA\nQI8ePRAQEIDi4mKkpqYiNjYWABAbG4vdu3cDALp164bRo0frTZTTqqqqwtq1a/HSSy8ZvQ8tY4wx\nfQ6dJBoqLCzEsWPHEBYWhvLycnh4eAAQ6zOVl5frlTXUUnj55ZexZMkSdOvWrU3iZYwxZ9AukkRV\nVRWmT5+OdevWoWfPnnrPSSQSs91Hx48fx2+//YapU6dyK4IxxprB4ZPE9evXMX36dMyePRvTpk0D\nIFoPZWVlAIDS0lL069fP5D6ys7ORm5uLIUOGYMyYMTh16hTuueeeVo+dMcbaO4dOEkSEefPmITAw\nEM8++6zucaVSqZswl5SUpEseDes19OSTT6K4uBhqtRrffvstfH19cfDgwdZ/AYwx1s459GS6b7/9\nFmPHjkVwcLCuS2nVqlUYNWoUZsyYgTNnzkAmk+Gzzz6Du7s7AEAmk+HSpUvQaDTo3bs39u3bB39/\nf90+CwsLoVQqceLECbu8JsYYa08cOkkwxhizL4fubmKMMWZfnCQYY4wZxUmCMcaYUZwkGGOMGcVJ\ngjHGmFGcJBhjjBnFSYKxZmh4n3QA2Lp1q25Z+hUrVmDNmjV6z8tkMlRUVAAAXFxcMHv2bN1zNTU1\n6Nu3L+677z7dvlxcXHDgwAFdmd27d8PFxQU7d+5sldfDmDmcJBhrhsbrhDXcNrSOWMPt7t274+ef\nf8bVq1cBAPv374dUKtUrM2zYML37sycnJ+tWQmbMHjhJMNYCjeeimpubOmnSJOzZsweASACzZs3S\n1ZFIJBgzZgxycnJQU1ODqqoq/Prrr1AoFLwwJbObTvYOgLH2pLq6GsOHD9dtV1RUYOrUqQBEgli7\ndi0++ugj3fMlJSV69WfOnInXXnsNU6ZMwY8//oh58+bhf//7n+55iUSC6OhofPXVV/jrr7+gVCqh\nVqtb+VUxZhwnCcaaoWvXrjh27JhuOykpCbm5uQDECf7555/H888/r3t+yJAhevWHDRuGwsJCJCcn\nY/LkyXrPaVsLM2fOxLp163Dx4kWsWbMGCQkJrfVyGDOLkwRjLdDc7iZArGK8ZMkSZGZm4o8//mjy\n/E14HmEAAACUSURBVMiRI/HTTz+he/fukMvlNouVMWtwkmDMRiy9bhAXF4fevXtj6NChyMjIMFgm\nMTERXbt2tWF0jFmHkwRjzWBo9JL2MXN3SdQ+5+npiYULF5qsP2HCBJPHZayt8FLhjDHGjOIhsIwx\nxoziJMEYY8woThKMMcaM4iTBGGPMKE4SjDHGjOIkwRhjzChOEowxxoz6/21Q43sBtspoAAAAAElF\nTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x10c1b3e90>"
]
}
],
"prompt_number": 41
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Solar Constants"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy.sun import constants as sun"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 42
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"sun.mass"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$1.9891\\times 10^{+30} \\; \\mathrm{kg}$"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 43,
"text": [
"<Constant name=u'Solar mass' value=1.9891e+30 error=5e+25 units='kg' reference=u\"Allen's Astrophysical Quantities 4th Ed.\">"
]
}
],
"prompt_number": 43
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"type(sun.mass)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 44,
"text": [
"astropy.constants.constant.Constant"
]
}
],
"prompt_number": 44
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(sun.mass)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
" Name = Solar mass\n",
" Value = 1.9891e+30\n",
" Error = 5e+25\n",
" Units = kg\n",
" Reference = Allen's Astrophysical Quantities 4th Ed.\n"
]
}
],
"prompt_number": 45
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"(sun.mass/sun.volume).cgs"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$1.40851 \\; \\mathrm{\\frac{g}{cm^{3}}}$"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 46,
"text": [
"<Quantity 1.4085115422744656 g / cm3>"
]
}
],
"prompt_number": 46
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"sun.find('age')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 47,
"text": [
"['age', 'average angular size', 'average density', 'average intensity']"
]
}
],
"prompt_number": 47
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"sun.value('age'), sun.unit('age')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 48,
"text": [
"(4600000000.0, Unit(\"yr\"))"
]
}
],
"prompt_number": 48
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Searching the VSO"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy.net import vso\n",
"client = vso.VSOClient()\n",
"tstart, tend = '2011/6/7 05:30', '2011/6/7 6:30'"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 49
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"lasco_query = client.query(vso.attrs.Time(tstart, tend), vso.attrs.Instrument('lasco'))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 50
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"lasco_query.num_records()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 51,
"text": [
"8"
]
}
],
"prompt_number": 51
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"lasco_query.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Start time End time Source Instrument Type \n",
"---------- -------- ------ ---------- ---- \n",
"2011-06-07 05:35:23 2011-06-07 05:35:48 SOHO LASCO CORONA\n",
"2011-06-07 05:43:09 2011-06-07 05:43:29 SOHO LASCO CORONA\n",
"2011-06-07 05:50:13 2011-06-07 05:50:38 SOHO LASCO CORONA\n",
"2011-06-07 05:57:59 2011-06-07 05:58:18 SOHO LASCO CORONA\n",
"2011-06-07 06:04:58 2011-06-07 06:05:23 SOHO LASCO CORONA\n",
"2011-06-07 06:12:45 2011-06-07 06:13:04 SOHO LASCO CORONA\n",
"2011-06-07 06:19:43 2011-06-07 06:20:08 SOHO LASCO CORONA\n",
"2011-06-07 06:27:29 2011-06-07 06:27:48 SOHO LASCO CORONA\n"
]
}
],
"prompt_number": 52
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"now download the data"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"pathformat = '/Users/schriste/sunpy/data/{file}.fits'\n",
"results = client.get(lasco_query, path = pathformat)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 53
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"instrument_condition = ( vso.attrs.Instrument('lasco') | vso.attrs.Detector('cor1') )\n",
"coronagraphs = client.query(vso.attrs.Time(tstart, tend), instrument_condition)\n",
"coronagraphs.num_records()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 54,
"text": [
"117"
]
}
],
"prompt_number": 54
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"coronagraphs.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Start time End time Source Instrument Type \n",
"---------- -------- ------ ---------- ---- \n",
"2011-06-07 05:35:23 2011-06-07 05:35:48 SOHO LASCO CORONA\n",
"2011-06-07 05:43:09 2011-06-07 05:43:29 SOHO LASCO CORONA\n",
"2011-06-07 05:50:13 2011-06-07 05:50:38 SOHO LASCO CORONA\n",
"2011-06-07 05:57:59 2011-06-07 05:58:18 SOHO LASCO CORONA\n",
"2011-06-07 06:04:58 2011-06-07 06:05:23 SOHO LASCO CORONA\n",
"2011-06-07 06:12:45 2011-06-07 06:13:04 SOHO LASCO CORONA\n",
"2011-06-07 06:19:43 2011-06-07 06:20:08 SOHO LASCO CORONA\n",
"2011-06-07 06:27:29 2011-06-07 06:27:48 SOHO LASCO CORONA\n",
"2011-06-07 05:30:00 2011-06-07 05:30:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:30:09 2011-06-07 05:30:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:30:18 2011-06-07 05:30:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:30:25 2011-06-07 05:30:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:30:34 2011-06-07 05:30:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:30:43 2011-06-07 05:30:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:32:55 2011-06-07 05:32:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:33:04 2011-06-07 05:33:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:33:13 2011-06-07 05:33:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:35:00 2011-06-07 05:35:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:35:09 2011-06-07 05:35:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:35:18 2011-06-07 05:35:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:35:25 2011-06-07 05:35:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:35:34 2011-06-07 05:35:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:35:43 2011-06-07 05:35:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:37:56 2011-06-07 05:37:58 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:38:04 2011-06-07 05:38:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:38:13 2011-06-07 05:38:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:40:00 2011-06-07 05:40:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:40:09 2011-06-07 05:40:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:40:18 2011-06-07 05:40:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:40:25 2011-06-07 05:40:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:40:34 2011-06-07 05:40:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:40:43 2011-06-07 05:40:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:42:55 2011-06-07 05:42:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:43:04 2011-06-07 05:43:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:43:13 2011-06-07 05:43:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:45:00 2011-06-07 05:45:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:45:09 2011-06-07 05:45:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:45:18 2011-06-07 05:45:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:45:25 2011-06-07 05:45:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:45:34 2011-06-07 05:45:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:45:43 2011-06-07 05:45:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:47:55 2011-06-07 05:47:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:48:04 2011-06-07 05:48:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:48:13 2011-06-07 05:48:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:50:00 2011-06-07 05:50:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:50:09 2011-06-07 05:50:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:50:18 2011-06-07 05:50:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:50:25 2011-06-07 05:50:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:50:34 2011-06-07 05:50:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:50:43 2011-06-07 05:50:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:52:55 2011-06-07 05:52:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:53:04 2011-06-07 05:53:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:53:13 2011-06-07 05:53:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:55:00 2011-06-07 05:55:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:55:09 2011-06-07 05:55:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:55:18 2011-06-07 05:55:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 05:55:25 2011-06-07 05:55:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:55:34 2011-06-07 05:55:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:55:43 2011-06-07 05:55:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:57:55 2011-06-07 05:57:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:58:04 2011-06-07 05:58:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 05:58:13 2011-06-07 05:58:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:00:00 2011-06-07 06:00:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:00:09 2011-06-07 06:00:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:00:18 2011-06-07 06:00:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:00:25 2011-06-07 06:00:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:00:34 2011-06-07 06:00:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:00:43 2011-06-07 06:00:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:02:55 2011-06-07 06:02:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:03:04 2011-06-07 06:03:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:03:13 2011-06-07 06:03:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:05:00 2011-06-07 06:05:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:05:09 2011-06-07 06:05:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:05:18 2011-06-07 06:05:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:05:25 2011-06-07 06:05:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:05:34 2011-06-07 06:05:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:05:43 2011-06-07 06:05:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:07:55 2011-06-07 06:07:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:08:04 2011-06-07 06:08:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:08:13 2011-06-07 06:08:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:10:00 2011-06-07 06:10:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:10:09 2011-06-07 06:10:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:10:18 2011-06-07 06:10:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:10:25 2011-06-07 06:10:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:10:34 2011-06-07 06:10:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:10:43 2011-06-07 06:10:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:12:55 2011-06-07 06:12:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:13:04 2011-06-07 06:13:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:13:13 2011-06-07 06:13:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:15:00 2011-06-07 06:15:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:15:09 2011-06-07 06:15:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:15:18 2011-06-07 06:15:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:15:25 2011-06-07 06:15:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:15:34 2011-06-07 06:15:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:15:43 2011-06-07 06:15:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:17:55 2011-06-07 06:17:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:18:04 2011-06-07 06:18:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:18:13 2011-06-07 06:18:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:20:00 2011-06-07 06:20:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:20:09 2011-06-07 06:20:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:20:18 2011-06-07 06:20:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:20:25 2011-06-07 06:20:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:20:34 2011-06-07 06:20:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:20:43 2011-06-07 06:20:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:22:55 2011-06-07 06:22:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:23:04 2011-06-07 06:23:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:23:13 2011-06-07 06:23:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:25:00 2011-06-07 06:25:01 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:25:09 2011-06-07 06:25:10 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:25:18 2011-06-07 06:25:19 STEREO_A SECCHI CORONA\n",
"2011-06-07 06:25:25 2011-06-07 06:25:27 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:25:34 2011-06-07 06:25:36 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:25:43 2011-06-07 06:25:45 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:27:55 2011-06-07 06:27:57 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:28:04 2011-06-07 06:28:06 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:28:13 2011-06-07 06:28:15 STEREO_B SECCHI CORONA\n",
"2011-06-07 06:30:00 2011-06-07 06:30:01 STEREO_A SECCHI CORONA\n"
]
}
],
"prompt_number": 55
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Searching for events in the HEK"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy.net import hek\n",
"client = hek.HEKClient()\n",
"tstart, tend = '2011/08/09 00:00:00', '2011/08/10 00:00:00'\n",
"result = client.query(hek.attrs.Time(tstart,tend), hek.attrs.EventType('FL')) # \u2019FL\u2019 indicates flare\n",
"len(result)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 56,
"text": [
"52"
]
}
],
"prompt_number": 56
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"result"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 57,
"text": [
"[{u'SOL_standard': u'SOL2011-08-08T01:30:04L247C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -470,\n",
" u'boundbox_c1ur': 573,\n",
" u'boundbox_c2ll': -174,\n",
" u'boundbox_c2ur': 476,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 521.5,\n",
" u'event_c2error': 324.9,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 51,\n",
" u'event_coord2': 151,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Small flare in the lower pat of the AR. Few instants before, a coronal shock wave appears from the right part of the image.',\n",
" u'event_endtime': u'2011-08-10T00:00:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T11:55:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T01:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small flare in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:26:01',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:26:07.457',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A07.457/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A07.457/thumb/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-146.807764 -5.167838,-79.64706 -5.630367,-69.862234 34.479115,-154.290862 35.148002,-146.807764 -5.167838))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-113.8074292 15.364686)',\n",
" u'hgc_x': -113.8074292,\n",
" u'hgc_y': 15.364686,\n",
" u'hgs_bbox': u'POLYGON((-29.808574 -5.167838,37.35213 -5.630367,47.136956 34.479115,-37.291672 35.148002,-29.808574 -5.167838))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(3.1917608 15.364686)',\n",
" u'hgs_x': 3.1917608,\n",
" u'hgs_y': 15.364686,\n",
" u'hpc_bbox': u'POLYGON((-470 -174,573 -174,573 476,-470 476,-470 -174))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(51 151)',\n",
" u'hpc_x': 51,\n",
" u'hpc_y': 151,\n",
" u'hrc_a': 341.337688166087,\n",
" u'hrc_bbox': u'POLYGON((0.529988 110.315196,0.633264 253.108304,0.787746 309.716939,0.707395 44.636607,0.529988 110.315196))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.168543050299641 341.337688166087)',\n",
" u'hrc_r': 0.168543050299641,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:26:13',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL211_AlbertoSainzDalda_20110811_172601',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T013004-20110810T000004_SDO_211-6173_300.0_20110811_172601.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL6173_AlbertoSainzDalda_20110811_172601'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T01:30:04L247C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -470,\n",
" u'boundbox_c1ur': 573,\n",
" u'boundbox_c2ll': -174,\n",
" u'boundbox_c2ur': 476,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 521.5,\n",
" u'event_c2error': 324.9,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 51,\n",
" u'event_coord2': 151,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Small flare in the lower pat of the AR. Few instants before, a coronal shock wave appears from the right part of the image.',\n",
" u'event_endtime': u'2011-08-10T00:00:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T11:55:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T01:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small flare in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:26:01',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:26:07.457',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A07.457/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A07.457/thumb/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-146.807764 -5.167838,-79.64706 -5.630367,-69.862234 34.479115,-154.290862 35.148002,-146.807764 -5.167838))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-113.8074292 15.364686)',\n",
" u'hgc_x': -113.8074292,\n",
" u'hgc_y': 15.364686,\n",
" u'hgs_bbox': u'POLYGON((-29.808574 -5.167838,37.35213 -5.630367,47.136956 34.479115,-37.291672 35.148002,-29.808574 -5.167838))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(3.1917608 15.364686)',\n",
" u'hgs_x': 3.1917608,\n",
" u'hgs_y': 15.364686,\n",
" u'hpc_bbox': u'POLYGON((-470 -174,573 -174,573 476,-470 476,-470 -174))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(51 151)',\n",
" u'hpc_x': 51,\n",
" u'hpc_y': 151,\n",
" u'hrc_a': 341.337688166087,\n",
" u'hrc_bbox': u'POLYGON((0.529988 110.315196,0.633264 253.108304,0.787746 309.716939,0.707395 44.636607,0.529988 110.315196))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.168543050299641 341.337688166087)',\n",
" u'hrc_r': 0.168543050299641,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:26:24',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL6173_AlbertoSainzDalda_20110811_172601',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'6173',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'HMI',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 6.173e-05,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T013004-20110810T000004_SDO_211-6173_300.0_20110811_172601.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL211_AlbertoSainzDalda_20110811_172601'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T01:30:04L247C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -470,\n",
" u'boundbox_c1ur': 573,\n",
" u'boundbox_c2ll': -174,\n",
" u'boundbox_c2ur': 476,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 521.5,\n",
" u'event_c2error': 324.9,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 51,\n",
" u'event_coord2': 151,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Small flare in the lower pat of the AR. Few instants before, a coronal shock wave appears from the right part of the image.',\n",
" u'event_endtime': u'2011-08-10T00:00:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T11:55:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T01:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small flare in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:26:01',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'MetaEventCreator',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:26:26.640',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A26.640/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A26%3A26.640/thumb/panorama_asainz_AIA-211_HMI-6173_20110808T222504_at_20110811T172017.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-146.807764 -5.167838,-79.64706 -5.630367,-69.862234 34.479115,-154.290862 35.148002,-146.807764 -5.167838))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-113.8074292 15.364686)',\n",
" u'hgc_x': -113.8074292,\n",
" u'hgc_y': 15.364686,\n",
" u'hgs_bbox': u'POLYGON((-29.808574 -5.167838,37.35213 -5.630367,47.136956 34.479115,-37.291672 35.148002,-29.808574 -5.167838))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(3.1917608 15.364686)',\n",
" u'hgs_x': 3.1917608,\n",
" u'hgs_y': 15.364686,\n",
" u'hpc_bbox': u'POLYGON((-470 -174,573 -174,573 476,-470 476,-470 -174))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(51 151)',\n",
" u'hpc_x': 51,\n",
" u'hpc_y': 151,\n",
" u'hrc_a': 341.337688166087,\n",
" u'hrc_bbox': u'POLYGON((0.529988 110.315196,0.633264 253.108304,0.787746 309.716939,0.707395 44.636607,0.529988 110.315196))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.168543050299641 341.337688166087)',\n",
" u'hrc_r': 0.168543050299641,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:26:36',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FLMET_AlbertoSainzDalda_20110811_172601',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'FL',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'HEK',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 0,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T013004-20110810T000004_SDO_211-6173_300.0_20110811_172601.mov'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T02:50:04L318C074',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 586,\n",
" u'boundbox_c1ur': 1171,\n",
" u'boundbox_c2ll': -71,\n",
" u'boundbox_c2ur': 552,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 292.75,\n",
" u'event_c2error': 311.55,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 879,\n",
" u'event_coord2': 240,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Coronal loop In the lower part of the AR. Later, a small flare in the same part of teh AR. Finally, in the upper part of AR there is a small CME.',\n",
" u'event_endtime': u'2011-08-09T04:30:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-08T19:20:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T02:50:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small Flare and small CME in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T01:28:12',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'MetaEventCreator',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T01:28:36.980',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A36.980/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A36.980/thumb/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.600542 0.608558,-28.372415 -3.420548,-30.374693 25.110375,-64.485948 39.507605,-79.600542 0.608558))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-42.384257 16.348716)',\n",
" u'hgc_x': -42.384257,\n",
" u'hgc_y': 16.348716,\n",
" u'hgs_bbox': u'POLYGON((38.133228 0.608558,89.361355 -3.420548,87.359077 25.110375,53.247822 39.507605,38.133228 0.608558))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(75.349513 16.348716)',\n",
" u'hgs_x': 75.349513,\n",
" u'hgs_y': 16.348716,\n",
" u'hpc_bbox': u'POLYGON((586 -71,1171 -71,1171 552,586 552,586 -71))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(879 240)',\n",
" u'hpc_x': 879,\n",
" u'hpc_y': 240,\n",
" u'hrc_a': 285.271663830959,\n",
" u'hrc_bbox': u'POLYGON((0.624217 263.091693,1.240586 266.530293,1.368999 295.238814,0.851323 313.288684,0.624217 263.091693))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.963552110051466 285.271663830959)',\n",
" u'hrc_r': 0.963552110051466,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T01:28:50',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FLMET_AlbertoSainzDalda_20110811_012812',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'FL',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'HEK',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 0,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T025004-20110809T043004_SDO_304-171_300.0_20110811_012812.mov'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T02:50:04L318C074',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 586,\n",
" u'boundbox_c1ur': 1171,\n",
" u'boundbox_c2ll': -71,\n",
" u'boundbox_c2ur': 552,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 292.75,\n",
" u'event_c2error': 311.55,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 879,\n",
" u'event_coord2': 240,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Coronal loop In the lower part of the AR. Later, a small flare in the same part of teh AR. Finally, in the upper part of AR there is a small CME.',\n",
" u'event_endtime': u'2011-08-09T04:30:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-08T19:20:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T02:50:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small Flare and small CME in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T01:28:12',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T01:28:19.388',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A19.388/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A19.388/thumb/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.600542 0.608558,-28.372415 -3.420548,-30.374693 25.110375,-64.485948 39.507605,-79.600542 0.608558))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-42.384257 16.348716)',\n",
" u'hgc_x': -42.384257,\n",
" u'hgc_y': 16.348716,\n",
" u'hgs_bbox': u'POLYGON((38.133228 0.608558,89.361355 -3.420548,87.359077 25.110375,53.247822 39.507605,38.133228 0.608558))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(75.349513 16.348716)',\n",
" u'hgs_x': 75.349513,\n",
" u'hgs_y': 16.348716,\n",
" u'hpc_bbox': u'POLYGON((586 -71,1171 -71,1171 552,586 552,586 -71))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(879 240)',\n",
" u'hpc_x': 879,\n",
" u'hpc_y': 240,\n",
" u'hrc_a': 285.271663830959,\n",
" u'hrc_bbox': u'POLYGON((0.624217 263.091693,1.240586 266.530293,1.368999 295.238814,0.851323 313.288684,0.624217 263.091693))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.963552110051466 285.271663830959)',\n",
" u'hrc_r': 0.963552110051466,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T01:28:25',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL171_AlbertoSainzDalda_20110811_012812',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'171',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.71e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T025004-20110809T043004_SDO_304-171_300.0_20110811_012812.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL304_AlbertoSainzDalda_20110811_012812'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T02:50:04L318C074',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 586,\n",
" u'boundbox_c1ur': 1171,\n",
" u'boundbox_c2ll': -71,\n",
" u'boundbox_c2ur': 552,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 292.75,\n",
" u'event_c2error': 311.55,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 879,\n",
" u'event_coord2': 240,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Coronal loop In the lower part of the AR. Later, a small flare in the same part of teh AR. Finally, in the upper part of AR there is a small CME.',\n",
" u'event_endtime': u'2011-08-09T04:30:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'0.80000000000000004',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-08T19:20:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T02:50:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Small Flare and small CME in AR',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T01:28:12',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T01:28:19.388',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A19.388/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T01%3A28%3A19.388/thumb/panorama_asainz_AIA-304_AIA-171_20110808T114004_at_20110811T012120.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.600542 0.608558,-28.372415 -3.420548,-30.374693 25.110375,-64.485948 39.507605,-79.600542 0.608558))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-42.384257 16.348716)',\n",
" u'hgc_x': -42.384257,\n",
" u'hgc_y': 16.348716,\n",
" u'hgs_bbox': u'POLYGON((38.133228 0.608558,89.361355 -3.420548,87.359077 25.110375,53.247822 39.507605,38.133228 0.608558))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(75.349513 16.348716)',\n",
" u'hgs_x': 75.349513,\n",
" u'hgs_y': 16.348716,\n",
" u'hpc_bbox': u'POLYGON((586 -71,1171 -71,1171 552,586 552,586 -71))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(879 240)',\n",
" u'hpc_x': 879,\n",
" u'hpc_y': 240,\n",
" u'hrc_a': 285.271663830959,\n",
" u'hrc_bbox': u'POLYGON((0.624217 263.091693,1.240586 266.530293,1.368999 295.238814,0.851323 313.288684,0.624217 263.091693))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.963552110051466 285.271663830959)',\n",
" u'hrc_r': 0.963552110051466,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T01:28:34',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL304_AlbertoSainzDalda_20110811_012812',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'304',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 3.04e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/AVC_AlbertoSainzDalda_20110808T025004-20110809T043004_SDO_304-171_300.0_20110811_012812.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL171_AlbertoSainzDalda_20110811_012812'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-08T23:06:35L310C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T00:13:35',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-08T23:20:11',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-08T23:06:35',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 308.391,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T17:19:34',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_183646_73279/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/EDS_FlareDetective-TriggerModule_20110808T215935-20110809T012035_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_183646_73279/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-70.85253 17.450746,-40.194181 13.98048,-40.710058 18.351142,-68.029544 22.053859,-70.85253 17.450746))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-50.557306 17.854422)',\n",
" u'hgc_x': -50.557306,\n",
" u'hgc_y': 17.854422,\n",
" u'hgs_bbox': u'POLYGON((58.05139 17.450746,88.709739 13.98048,88.193862 18.351142,60.874376 22.053859,58.05139 17.450746))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.346614 17.854422)',\n",
" u'hgs_x': 78.346614,\n",
" u'hgs_y': 17.854422,\n",
" u'hpc_bbox': u'POLYGON((768 230.4,921.6 230.4,921.6 307.2,768 307.2,768 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.847191 286.699244,1.003723 284.036243,1.026428 288.434949,0.873972 291.801409,0.847191 286.699244))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975443813355769 286.927513064147)',\n",
" u'hrc_r': 0.975443813355769,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T00:30:50',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_001945_2011-08-08T23:06:35.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_183646_73279/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_183646_73279/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/08/EDS_FlareDetective-TriggerModule_20110808T215935-20110809T012035_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T01:40:04L230C084',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -1224,\n",
" u'boundbox_c1ur': 1231,\n",
" u'boundbox_c2ll': -1137,\n",
" u'boundbox_c2ur': 1130,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1227.05,\n",
" u'event_c2error': 1133.7,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 3,\n",
" u'event_coord2': -3,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Large flare taking place in the right part of the image and propagating to the left. Several small flares and small CMEs (previously submitted) are seen few instants later in the center of the solar disc and in lower left part of the image.',\n",
" u'event_endtime': u'2011-08-10T00:00:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'1',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T01:40:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Large Flare',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:47:46',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:47:52.315',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A47%3A52.315/panorama_asainz_AIA-211_20110809T081004_at_20110811T174052.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A47%3A52.315/thumb/panorama_asainz_AIA-211_20110809T081004_at_20110811T174052.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((145.862964 -42.529021,-46.455608 -42.368037,-45.691509 42.274393,145.096836 42.435508,145.862964 -42.529021))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-130.13125087 6.108429)',\n",
" u'hgc_x': -130.13125087,\n",
" u'hgc_y': 6.108429,\n",
" u'hgs_bbox': u'POLYGON((-83.823846 -42.529021,83.857582 -42.368037,84.621681 42.274393,-84.589974 42.435508,-83.823846 -42.529021))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(0.18193913 6.108429)',\n",
" u'hgs_x': 0.18193913,\n",
" u'hgs_y': 6.108429,\n",
" u'hpc_bbox': u'POLYGON((-1224 -1137,1231 -1137,1231 1130,-1224 1130,-1224 -1137))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(3 -3)',\n",
" u'hpc_x': 3,\n",
" u'hpc_y': -3,\n",
" u'hrc_a': 225,\n",
" u'hrc_bbox': u'POLYGON((1.766377 132.889674,1.771806 227.273217,1.766793 312.550467,1.761348 47.286722,1.766377 132.889674))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.00448584148013299 225)',\n",
" u'hrc_r': 0.00448584148013299,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:47:59',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL211_AlbertoSainzDalda_20110811_174746',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/AVC_AlbertoSainzDalda_20110809T014004-20110810T000004_SDO_211_150.0_20110811_174746.mov'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T02:30:04L319C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 666,\n",
" u'boundbox_c1ur': 1182,\n",
" u'boundbox_c2ll': -62,\n",
" u'boundbox_c2ur': 496,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 257.9,\n",
" u'event_c2error': 279.05,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 924,\n",
" u'event_coord2': 217,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Large flare and post-flare loop activity.',\n",
" u'event_endtime': u'2011-08-11T00:40:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'1',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T02:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Large flare (zoom)',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:59:36',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:59:42.190',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A42.190/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A42.190/thumb/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-86.189597 0.732381,-41.363108 -2.95562,-43.122506 22.650306,-71.759645 34.956826,-86.189597 0.732381))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-41.978419 13.164641)',\n",
" u'hgc_x': -41.978419,\n",
" u'hgc_y': 13.164641,\n",
" u'hgs_bbox': u'POLYGON((44.582683 0.732381,89.409172 -2.95562,87.649774 22.650306,59.012635 34.956826,44.582683 0.732381))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(88.793861 13.164641)',\n",
" u'hgs_x': 88.793861,\n",
" u'hgs_y': 13.164641,\n",
" u'hpc_bbox': u'POLYGON((666 -62,1182 -62,1182 496,666 496,666 -62))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(924 217)',\n",
" u'hpc_x': 924,\n",
" u'hpc_y': 217,\n",
" u'hrc_a': 283.216324063791,\n",
" u'hrc_bbox': u'POLYGON((0.707218 264.681487,1.251467 266.997389,1.355322 292.764273,0.878001 306.676705,0.707218 264.681487))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(1.00354097989888 283.216324063791)',\n",
" u'hrc_r': 1.00354097989888,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:59:47',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL171_AlbertoSainzDalda_20110811_175936',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'171',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.71e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/AVC_AlbertoSainzDalda_20110809T023004-20110811T004004_SDO_211-171_300.0_20110811_175936.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL211_AlbertoSainzDalda_20110811_175936'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T02:30:04L319C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 666,\n",
" u'boundbox_c1ur': 1182,\n",
" u'boundbox_c2ll': -62,\n",
" u'boundbox_c2ur': 496,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 257.9,\n",
" u'event_c2error': 279.05,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 924,\n",
" u'event_coord2': 217,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Large flare and post-flare loop activity.',\n",
" u'event_endtime': u'2011-08-11T00:40:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'1',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T02:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Large flare (zoom)',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:59:36',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'Annotator-build_20110621-avc',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:59:42.190',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A42.190/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A42.190/thumb/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-86.189597 0.732381,-41.363108 -2.95562,-43.122506 22.650306,-71.759645 34.956826,-86.189597 0.732381))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-41.978419 13.164641)',\n",
" u'hgc_x': -41.978419,\n",
" u'hgc_y': 13.164641,\n",
" u'hgs_bbox': u'POLYGON((44.582683 0.732381,89.409172 -2.95562,87.649774 22.650306,59.012635 34.956826,44.582683 0.732381))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(88.793861 13.164641)',\n",
" u'hgs_x': 88.793861,\n",
" u'hgs_y': 13.164641,\n",
" u'hpc_bbox': u'POLYGON((666 -62,1182 -62,1182 496,666 496,666 -62))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(924 217)',\n",
" u'hpc_x': 924,\n",
" u'hpc_y': 217,\n",
" u'hrc_a': 283.216324063791,\n",
" u'hrc_bbox': u'POLYGON((0.707218 264.681487,1.251467 266.997389,1.355322 292.764273,0.878001 306.676705,0.707218 264.681487))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(1.00354097989888 283.216324063791)',\n",
" u'hrc_r': 1.00354097989888,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T17:59:51',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL211_AlbertoSainzDalda_20110811_175936',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/AVC_AlbertoSainzDalda_20110809T023004-20110811T004004_SDO_211-171_300.0_20110811_175936.mov'},\n",
" {u'ref_name': u'FL: HER Entry',\n",
" u'ref_type': u'ivorn',\n",
" u'ref_url': u'ivo://helio-informatics.org/FL171_AlbertoSainzDalda_20110811_175936'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T02:30:04L319C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 666,\n",
" u'boundbox_c1ur': 1182,\n",
" u'boundbox_c2ll': -62,\n",
" u'boundbox_c2ur': 496,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 257.9,\n",
" u'event_c2error': 279.05,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 924,\n",
" u'event_coord2': 217,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcsec',\n",
" u'event_description': u'Large flare and post-flare loop activity.',\n",
" u'event_endtime': u'2011-08-11T00:40:04',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'1',\n",
" u'event_importance_num_ratings': u'1',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T02:30:04',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'Large flare (zoom)',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Scott Green',\n",
" u'frm_daterun': u'2011-08-11T17:59:36',\n",
" u'frm_humanflag': u'true',\n",
" u'frm_identifier': u'MetaEventCreator',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'asainz',\n",
" u'frm_paramset': u'n/a',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'n/a',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'pod_sainz+dalda_alberto_2011-08-11T17:59:55.697',\n",
" u'gs_imageurl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A55.697/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'http://www.lmsal.com/hek/gallery/podimages/2011/08/11/pod_sainz%2Bdalda_alberto_2011-08-11T17%3A59%3A55.697/thumb/panorama_asainz_AIA-211_AIA-171_20110809T145004_at_20110811T175740.jpg',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-86.189597 0.732381,-41.363108 -2.95562,-43.122506 22.650306,-71.759645 34.956826,-86.189597 0.732381))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-41.978419 13.164641)',\n",
" u'hgc_x': -41.978419,\n",
" u'hgc_y': 13.164641,\n",
" u'hgs_bbox': u'POLYGON((44.582683 0.732381,89.409172 -2.95562,87.649774 22.650306,59.012635 34.956826,44.582683 0.732381))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(88.793861 13.164641)',\n",
" u'hgs_x': 88.793861,\n",
" u'hgs_y': 13.164641,\n",
" u'hpc_bbox': u'POLYGON((666 -62,1182 -62,1182 496,666 496,666 -62))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(924 217)',\n",
" u'hpc_x': 924,\n",
" u'hpc_y': 217,\n",
" u'hrc_a': 283.216324063791,\n",
" u'hrc_bbox': u'POLYGON((0.707218 264.681487,1.251467 266.997389,1.355322 292.764273,0.878001 306.676705,0.707218 264.681487))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(1.00354097989888 283.216324063791)',\n",
" u'hrc_r': 1.00354097989888,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-11T18:00:05',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FLMET_AlbertoSainzDalda_20110811_175936',\n",
" u'kb_archivist': u'sainzdalda_alberto',\n",
" u'obs_channelid': u'FL',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'HEK',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 0,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'n/a'},\n",
" {u'ref_name': u'Event_MapURL', u'ref_type': u'unknown', u'ref_url': u''},\n",
" {u'ref_name': u'Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/AVC_AlbertoSainzDalda_20110809T023004-20110811T004004_SDO_211-171_300.0_20110811_175936.mov'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:19:00L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 1263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 69,\n",
" u'event_coord2': 17,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T03:54:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T03:45:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T03:19:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'M2.5',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_031903_0094.fits,AIA20110809_034303_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.22158 17)',\n",
" u'hgc_x': -62.22158,\n",
" u'hgc_y': 17,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(69 17)',\n",
" u'hgs_x': 69,\n",
" u'hgs_y': 17,\n",
" u'hpc_bbox': u'POLYGON((16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(845.838 239.7366)',\n",
" u'hpc_x': 845.838,\n",
" u'hpc_y': 239.7366,\n",
" u'hrc_a': 285.824366951751,\n",
" u'hrc_bbox': u'POLYGON((0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.929541790218704 285.824366951751)',\n",
" u'hrc_r': 0.929541790218704,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:38:00',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110808_213442_412',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0319.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0319.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'16',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:19:00L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 1263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 69,\n",
" u'event_coord2': 17,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T03:54:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T03:45:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T03:19:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'M2.5',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_031903_0094.fits,AIA20110809_034303_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.22158 17)',\n",
" u'hgc_x': -62.22158,\n",
" u'hgc_y': 17,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(69 17)',\n",
" u'hgs_x': 69,\n",
" u'hgs_y': 17,\n",
" u'hpc_bbox': u'POLYGON((16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(845.838 239.7366)',\n",
" u'hpc_x': 845.838,\n",
" u'hpc_y': 239.7366,\n",
" u'hrc_a': 285.824366951751,\n",
" u'hrc_bbox': u'POLYGON((0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.929541790218704 285.824366951751)',\n",
" u'hrc_r': 0.929541790218704,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T17:29:07',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110808_213442_412',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_212102_87513/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0319.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0319.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'58',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:19:00L297C072',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1,\n",
" u'event_c2error': 1,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 68,\n",
" u'event_coord2': 18,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T04:08:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T03:54:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T03:19:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'M2.5',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1,-130.22158 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-63.22158 18)',\n",
" u'hgc_x': -63.22158,\n",
" u'hgc_y': 18,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(68 18)',\n",
" u'hgs_x': 68,\n",
" u'hgs_y': 18,\n",
" u'hpc_bbox': u'POLYGON((16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642,16.57968 -87.642))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(835.494 254.0208)',\n",
" u'hpc_x': 835.494,\n",
" u'hpc_y': 254.0208,\n",
" u'hrc_a': 286.911194232554,\n",
" u'hrc_bbox': u'POLYGON((0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341,0.094308 190.712341))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.923303934134074 286.911194232554)',\n",
" u'hrc_r': 0.923303934134074,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:13',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163057_20110809031900',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:24:11L308C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T04:21:59',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T04:01:59',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T03:24:11',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1026.21,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T20:43:16',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_223735_93850/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T022623-20110809T051947_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_223735_93850/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-75.149901 12.872694,-49.774896 10.322956,-43.086788 18.349944,-70.394145 22.05885,-75.149901 12.872694))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-52.926774 17.856924)',\n",
" u'hgc_x': -52.926774,\n",
" u'hgc_y': 17.856924,\n",
" u'hgs_bbox': u'POLYGON((56.119279 12.872694,81.494284 10.322956,88.182392 18.349944,60.875035 22.05885,56.119279 12.872694))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.342406 17.856924)',\n",
" u'hgs_x': 78.342406,\n",
" u'hgs_y': 17.856924,\n",
" u'hpc_bbox': u'POLYGON((768 153.6,921.6 153.6,921.6 307.2,768 307.2,768 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.827509 281.309932,0.987158 279.462322,1.026398 288.434949,0.873947 291.801409,0.827509 281.309932))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975415893964311 286.927513064147)',\n",
" u'hrc_r': 0.975415893964311,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T04:39:37',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_034429_2011-08-09T03:24:11.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_223735_93850/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_223735_93850/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T022623-20110809T051947_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:48:50L307C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T04:27:38',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T04:13:14',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T03:48:50',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1365.71,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T21:06:21',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.30000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_222228_92586/www/ssw_cutout_211_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T031002-20110809T050626_AIA_211_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_222228_92586/www/ssw_cutout_211_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-65.897717 11.977829,-50.002024 10.323189,-43.303245 18.351022,-58.917951 20.911084,-65.897717 11.977829))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-53.153509 17.857163)',\n",
" u'hgc_x': -53.153509,\n",
" u'hgc_y': 17.857163,\n",
" u'hgs_bbox': u'POLYGON((65.597793 11.977829,81.493486 10.323189,88.192265 18.351022,72.577559 20.911084,65.597793 11.977829))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.342001 17.857163)',\n",
" u'hgs_x': 78.342001,\n",
" u'hgs_y': 17.857163,\n",
" u'hpc_bbox': u'POLYGON((844.8 153.6,921.6 153.6,921.6 307.2,844.8 307.2,844.8 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.907214 280.304846,0.987155 279.462322,1.026395 288.434949,0.949762 289.983107,0.907214 280.304846))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975413214446382 286.927513064147)',\n",
" u'hrc_r': 0.975413214446382,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T04:45:28',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_040808_2011-08-09T03:48:50.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_222228_92586/www/ssw_cutout_211_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_222228_92586/www/ssw_cutout_211_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T031002-20110809T050626_AIA_211_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T03:53:15L307C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T04:18:51',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T04:07:15',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T03:53:15',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 346.522,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T21:11:08',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 3.00000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220423_90897/www/ssw_cutout_94_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T032739-20110809T044427_AIA_94_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220423_90897/www/ssw_cutout_94_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-63.23307 16.474154,-42.822368 13.980967,-43.339086 18.351536,-58.958525 20.911139,-63.23307 16.474154))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-53.194132 17.857206)',\n",
" u'hgc_x': -53.194132,\n",
" u'hgc_y': 17.857206,\n",
" u'hgs_bbox': u'POLYGON((68.30299 16.474154,88.713692 13.980967,88.196974 18.351536,72.577535 20.911139,68.30299 16.474154))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.341928 17.857206)',\n",
" u'hgs_x': 78.341928,\n",
" u'hgs_y': 17.857206,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.92518 285.255119,1.003691 284.036243,1.026395 288.434949,0.949762 289.983107,0.92518 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975412740379358 286.927513064147)',\n",
" u'hrc_r': 0.975412740379358,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T04:37:13',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_041312_2011-08-09T03:53:15.570_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'94',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220423_90897/www/ssw_cutout_94_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220423_90897/www/ssw_cutout_94_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T032739-20110809T044427_AIA_94_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T04:03:29L307C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T04:22:17',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T04:12:41',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T04:03:29',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 276.237,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T21:21:12',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220120_90813/www/ssw_cutout_335_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T034441-20110809T044105_AIA_335_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220120_90813/www/ssw_cutout_335_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-63.327078 16.474312,-42.931095 13.979357,-43.448172 18.349892,-59.052541 20.911266,-63.327078 16.474312))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-53.28826 17.857305)',\n",
" u'hgc_x': -53.28826,\n",
" u'hgc_y': 17.857305,\n",
" u'hgs_bbox': u'POLYGON((68.302942 16.474312,88.698925 13.979357,88.181848 18.349892,72.577479 20.911266,68.302942 16.474312))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.34176 17.857305)',\n",
" u'hgs_x': 78.34176,\n",
" u'hgs_y': 17.857305,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925179 285.255119,1.00369 284.036243,1.026394 288.434949,0.949761 289.983107,0.925179 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975411627354244 286.927513064147)',\n",
" u'hrc_r': 0.975411627354244,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T04:40:18',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_042312_2011-08-09T04:03:29.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'335',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 3.35e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220120_90813/www/ssw_cutout_335_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_220120_90813/www/ssw_cutout_335_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T034441-20110809T044105_AIA_335_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T06:13:49L240C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 153.6,\n",
" u'boundbox_c1ur': 230.4,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 230.4,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 192,\n",
" u'event_coord2': 192,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T06:17:25',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T06:14:37',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T06:13:49',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 556.588,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T23:31:31',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_054300_31220/www/ssw_cutout_171_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061013-20110809T062101_AIA_171_XCEN192.0YCEN192.0.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_054300_31220/www/ssw_cutout_171_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-123.174613 15.51129,-118.26725 15.401713,-117.867524 20.121487,-122.910976 20.235683,-123.174613 15.51129))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-120.579358 17.813479)',\n",
" u'hgc_x': -120.579358,\n",
" u'hgc_y': 17.813479,\n",
" u'hgs_bbox': u'POLYGON((9.652107 15.51129,14.55947 15.401713,14.959196 20.121487,9.915744 20.235683,9.652107 15.51129))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(12.247362 17.813479)',\n",
" u'hgs_x': 12.247362,\n",
" u'hgs_y': 17.813479,\n",
" u'hpc_bbox': u'POLYGON((153.6 153.6,230.4 153.6,230.4 230.4,153.6 230.4,153.6 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(192 192)',\n",
" u'hpc_x': 192,\n",
" u'hpc_y': 192,\n",
" u'hrc_a': 315,\n",
" u'hrc_bbox': u'POLYGON((0.229505 315,0.292563 303.690068,0.344258 315,0.292563 326.309932,0.229505 315))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.286881605034599 315)',\n",
" u'hrc_r': 0.286881605034599,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T06:35:22',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_063330_2011-08-09T06:13:49.340_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'171',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.71e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_054300_31220/www/ssw_cutout_171_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_054300_31220/www/ssw_cutout_171_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061013-20110809T062101_AIA_171_XCEN192.0YCEN192.0.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T06:13:50L240C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 153.6,\n",
" u'boundbox_c1ur': 230.4,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 230.4,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 192,\n",
" u'event_coord2': 192,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T06:16:14',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T06:14:26',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T06:13:50',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 305.103,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-08T23:31:31',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.30000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_233738_99110/www/ssw_cutout_211_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061126-20110809T061838_AIA_211_XCEN192.0YCEN192.0.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_233738_99110/www/ssw_cutout_211_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-123.174773 15.511291,-118.26741 15.401714,-117.867684 20.121487,-122.911136 20.235683,-123.174773 15.511291))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-120.579518 17.813479)',\n",
" u'hgc_x': -120.579518,\n",
" u'hgc_y': 17.813479,\n",
" u'hgs_bbox': u'POLYGON((9.652107 15.511291,14.55947 15.401714,14.959196 20.121487,9.915744 20.235683,9.652107 15.511291))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(12.247362 17.813479)',\n",
" u'hgs_x': 12.247362,\n",
" u'hgs_y': 17.813479,\n",
" u'hpc_bbox': u'POLYGON((153.6 153.6,230.4 153.6,230.4 230.4,153.6 230.4,153.6 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(192 192)',\n",
" u'hpc_x': 192,\n",
" u'hpc_y': 192,\n",
" u'hrc_a': 315,\n",
" u'hrc_bbox': u'POLYGON((0.229505 315,0.292563 303.690068,0.344258 315,0.292563 326.309932,0.229505 315))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.286881605034599 315)',\n",
" u'hrc_r': 0.286881605034599,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T06:34:07',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_063330_2011-08-09T06:13:50.080_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_233738_99110/www/ssw_cutout_211_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110808_233738_99110/www/ssw_cutout_211_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061126-20110809T061838_AIA_211_XCEN192.0YCEN192.0.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:19:00L227C090',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -90,\n",
" u'boundbox_c1ur': 90,\n",
" u'boundbox_c2ll': -90,\n",
" u'boundbox_c2ur': 90,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 90,\n",
" u'event_c2error': 90,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 0,\n",
" u'event_coord2': 0,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T07:27:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T07:23:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:19:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C1.4',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((136.57478 -90,-43.42522 -90,-43.42522 90,136.57478 90,136.57478 -90))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-133.42522 0)',\n",
" u'hgc_x': -133.42522,\n",
" u'hgc_y': 0,\n",
" u'hgs_bbox': u'POLYGON((-90 -90,90 -90,90 90,-90 90,-90 -90))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(0 0)',\n",
" u'hgs_x': 0,\n",
" u'hgs_y': 0,\n",
" u'hpc_bbox': u'POLYGON((8.3e-05 -939.63,-8.3e-05 -939.63,0 940.578,-0 940.578,8.3e-05 -939.63))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(0 -104.3232)',\n",
" u'hpc_x': 0,\n",
" u'hpc_y': -104.3232,\n",
" u'hrc_a': 180,\n",
" u'hrc_bbox': u'POLYGON((0.993455 180.000005,0.993455 179.999995,0.994457 0,0.994457 0,0.993455 180.000005))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.110299150625322 180)',\n",
" u'hrc_r': 0.110299150625322,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:14',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163058_20110809071900',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:19:00L296C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 69,\n",
" u'event_coord2': 15,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T07:27:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T07:23:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T07:19:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C1.4',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_071903_0094.fits,AIA20110809_072103_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-132.42522 1,-132.42522 1,-132.42522 1,-132.42522 1,-132.42522 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.42522 15)',\n",
" u'hgc_x': -64.42522,\n",
" u'hgc_y': 15,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(69 15)',\n",
" u'hgs_x': 69,\n",
" u'hgs_y': 15,\n",
" u'hpc_bbox': u'POLYGON((16.58016 -87.81,16.58016 -87.81,16.58016 -87.81,16.58016 -87.81,16.58016 -87.81))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(854.37 207.7254)',\n",
" u'hpc_x': 854.37,\n",
" u'hpc_y': 207.7254,\n",
" u'hrc_a': 283.665334418618,\n",
" u'hrc_bbox': u'POLYGON((0.094481 190.692621,0.094481 190.692621,0.094481 190.692621,0.094481 190.692621,0.094481 190.692621))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.929626565101221 283.665334418618)',\n",
" u'hrc_r': 0.929626565101221,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T13:04:26',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_011036_207',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005128_5991/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0719.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0719.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'3',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:22:38L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 0,\n",
" u'boundbox_c2ur': 537.6,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:32:02',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:38',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:22:38',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 2326.86,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:42:15',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.30000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_030038_16962/www/ssw_cutout_211_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061314-20110809T094126_AIA_211_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_030038_16962/www/ssw_cutout_211_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.272961 3.698481,-56.808186 1.461054,-46.821891 30.087467,-49.037247 35.437909,-79.272961 3.698481))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.120106 17.859233)',\n",
" u'hgc_x': -55.120106,\n",
" u'hgc_y': 17.859233,\n",
" u'hgs_bbox': u'POLYGON((54.185619 3.698481,76.650394 1.461054,86.636689 30.087467,84.421333 35.437909,54.185619 3.698481))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.338474 17.859233)',\n",
" u'hgs_x': 78.338474,\n",
" u'hgs_y': 17.859233,\n",
" u'hpc_bbox': u'POLYGON((768 0,921.6 0,921.6 537.6,768 537.6,768 0))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.811417 270,0.973701 270,1.127257 300.256437,0.990461 304.99202,0.811417 270))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975389965093471 286.927513064147)',\n",
" u'hrc_r': 0.975389965093471,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:50:15',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_074225_2011-08-09T07:22:38.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_030038_16962/www/ssw_cutout_211_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_030038_16962/www/ssw_cutout_211_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T061314-20110809T094126_AIA_211_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:22:44L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T07:28:56',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T07:23:08',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:22:44',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1698.83,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:42:16',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 3.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005303_6027/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T071632-20110809T073508_AIA_193_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005303_6027/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-65.157509 16.477391,-44.762639 13.979168,-45.280403 18.349626,-60.883125 20.913741,-65.157509 16.477391))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.121028 17.859234)',\n",
" u'hgc_x': -55.121028,\n",
" u'hgc_y': 17.859234,\n",
" u'hgs_bbox': u'POLYGON((68.301991 16.477391,88.696861 13.979168,88.179097 18.349626,72.576375 20.913741,68.301991 16.477391))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.338472 17.859234)',\n",
" u'hgs_x': 78.338472,\n",
" u'hgs_y': 17.859234,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925158 285.255119,1.003668 284.036243,1.026371 288.434949,0.94974 289.983107,0.925158 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975389954788153 286.927513064147)',\n",
" u'hrc_r': 0.975389954788153,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T07:45:18',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_074226_2011-08-09T07:22:44.840_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'193',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.93e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005303_6027/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_005303_6027/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T071632-20110809T073508_AIA_193_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:48:00L296C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1,\n",
" u'event_c2error': 1,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 69,\n",
" u'event_coord2': 17,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:08:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:05:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:48:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'X6.9',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((-132.69149 1,-132.69149 1,-132.69149 1,-132.69149 1,-132.69149 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.69149 17)',\n",
" u'hgc_x': -64.69149,\n",
" u'hgc_y': 17,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(69 17)',\n",
" u'hgs_x': 69,\n",
" u'hgs_y': 17,\n",
" u'hpc_bbox': u'POLYGON((16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(845.868 239.6748)',\n",
" u'hpc_x': 845.868,\n",
" u'hpc_y': 239.6748,\n",
" u'hrc_a': 285.819958914644,\n",
" u'hrc_bbox': u'POLYGON((0.094501 190.690233,0.094501 190.690233,0.094501 190.690233,0.094501 190.690233,0.094501 190.690233))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.929526600347797 285.819958914644)',\n",
" u'hrc_r': 0.929526600347797,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:14',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163058_20110809074800',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:48:00L296C076',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 69,\n",
" u'event_coord2': 14,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:08:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:05:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T07:48:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'X6.9',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_074803_0094.fits,AIA20110809_080305_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-132.69149 1,-132.69149 1,-132.69149 1,-132.69149 1,-132.69149 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.69149 14)',\n",
" u'hgc_x': -64.69149,\n",
" u'hgc_y': 14,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(69 14)',\n",
" u'hgs_x': 69,\n",
" u'hgs_y': 14,\n",
" u'hpc_bbox': u'POLYGON((16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304,16.58022 -87.8304))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(858.24 191.643)',\n",
" u'hpc_x': 858.24,\n",
" u'hpc_y': 191.643,\n",
" u'hrc_a': 282.587513727527,\n",
" u'hrc_bbox': u'POLYGON((0.094501 190.690233,0.094501 190.690233,0.094501 190.690233,0.094501 190.690233,0.094501 190.690233))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.929746801046064 282.587513727527)',\n",
" u'hrc_r': 0.929746801046064,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:05:36',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_013817_504',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_012104_8601/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0748.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_0748.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'25',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:55:59L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 614.4,\n",
" u'boundbox_c1ur': 1075.2,\n",
" u'boundbox_c2ll': -76.8,\n",
" u'boundbox_c2ur': 460.8,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:28:47',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:06:23',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:55:59',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 2360.49,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:13:10',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021824_13328/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T072311-20110809T090135_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021824_13328/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-93.458557 0.166674,-44.489903 -4.030322,-46.160931 23.082726,-83.104613 33.16948,-93.458557 0.166674))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.426879 17.859555)',\n",
" u'hgc_x': -55.426879,\n",
" u'hgc_y': 17.859555,\n",
" u'hgs_bbox': u'POLYGON((40.306243 0.166674,89.274897 -4.030322,87.603869 23.082726,50.660187 33.16948,40.306243 0.166674))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.337921 17.859555)',\n",
" u'hgs_x': 78.337921,\n",
" u'hgs_y': 17.859555,\n",
" u'hpc_bbox': u'POLYGON((614.4 -76.8,1075.2 -76.8,1075.2 460.8,614.4 460.8,614.4 -76.8))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.654183 262.874984,1.138874 265.914383,1.23591 293.198591,0.811414 306.869898,0.654183 262.874984))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975386327329574 286.927513064147)',\n",
" u'hrc_r': 0.975386327329574,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:47:16',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_081511_2011-08-09T07:55:59.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021824_13328/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021824_13328/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T072311-20110809T090135_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T07:59:49L300C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 0,\n",
" u'boundbox_c2ur': 460.8,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 192,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:25:37',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:37',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T07:59:49',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 3242.64,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:17:23',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021217_12865/www/ssw_cutout_171_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T073401-20110809T085125_AIA_171_XCEN883.2YCEN192.0.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021217_12865/www/ssw_cutout_171_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.61462 3.699417,-57.15057 1.46152,-46.63743 26.425263,-62.368798 31.274942,-79.61462 3.699417))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-60.355569 13.556974)',\n",
" u'hgc_x': -60.355569,\n",
" u'hgc_y': 13.556974,\n",
" u'hgs_bbox': u'POLYGON((54.18537 3.699417,76.64942 1.46152,87.16256 26.425263,71.431192 31.274942,54.18537 3.699417))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(73.444421 13.556974)',\n",
" u'hgs_x': 73.444421,\n",
" u'hgs_y': 13.556974,\n",
" u'hpc_bbox': u'POLYGON((768 0,921.6 0,921.6 460.8,768 460.8,768 0))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 192)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 192,\n",
" u'hrc_a': 282.264773727892,\n",
" u'hrc_bbox': u'POLYGON((0.811414 270,0.973697 270,1.088626 296.565051,0.946263 300.963757,0.811414 270))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.954920987577787 282.264773727892)',\n",
" u'hrc_r': 0.954920987577787,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:43:26',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_081923_2011-08-09T07:59:49.340_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'171',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.71e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021217_12865/www/ssw_cutout_171_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021217_12865/www/ssw_cutout_171_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T073401-20110809T085125_AIA_171_XCEN883.2YCEN192.0.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T08:00:03L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 76.8,\n",
" u'boundbox_c2ur': 384,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:15:15',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:06:51',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T08:00:03',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1375.93,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:18:12',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 3.00000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015102_11187/www/ssw_cutout_94_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074451-20110809T083027_AIA_94_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015102_11187/www/ssw_cutout_94_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-78.936028 8.298989,-55.822356 5.994814,-46.131754 22.507276,-68.793517 26.685187,-78.936028 8.298989))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.464287 17.859595)',\n",
" u'hgc_x': -55.464287,\n",
" u'hgc_y': 17.859595,\n",
" u'hgs_bbox': u'POLYGON((54.866112 8.298989,77.979784 5.994814,87.670386 22.507276,65.008623 26.685187,54.866112 8.298989))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.337853 17.859595)',\n",
" u'hgs_x': 78.337853,\n",
" u'hgs_y': 17.859595,\n",
" u'hpc_bbox': u'POLYGON((768 76.8,921.6 76.8,921.6 384,768 384,768 76.8))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.815461 275.710593,0.977072 274.763642,1.054838 292.619865,0.907189 296.565051,0.815461 275.710593))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975385884204381 286.927513064147)',\n",
" u'hrc_r': 0.975385884204381,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:33:15',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_082012_2011-08-09T08:00:03.570_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'94',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015102_11187/www/ssw_cutout_94_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015102_11187/www/ssw_cutout_94_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074451-20110809T083027_AIA_94_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T08:00:20L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 0,\n",
" u'boundbox_c2ur': 537.6,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:28:44',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:05:08',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T08:00:20',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 6275.98,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:18:12',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 3.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021520_13176/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T073156-20110809T085708_AIA_193_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021520_13176/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-79.619373 3.69943,-57.155333 1.461526,-47.168958 30.087377,-49.384421 35.438121,-79.619373 3.69943))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.466891 17.859597)',\n",
" u'hgc_x': -55.466891,\n",
" u'hgc_y': 17.859597,\n",
" u'hgs_bbox': u'POLYGON((54.185367 3.69943,76.649407 1.461526,86.635782 30.087377,84.420319 35.438121,54.185367 3.69943))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.337849 17.859597)',\n",
" u'hgs_x': 78.337849,\n",
" u'hgs_y': 17.859597,\n",
" u'hpc_bbox': u'POLYGON((768 0,921.6 0,921.6 537.6,768 537.6,768 0))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.811414 270,0.973697 270,1.127252 300.256437,0.990457 304.99202,0.811414 270))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975385853288685 286.927513064147)',\n",
" u'hrc_r': 0.975385853288685,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:47:21',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_082011_2011-08-09T08:00:20.840_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'193',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.93e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021520_13176/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_021520_13176/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T073156-20110809T085708_AIA_193_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T08:00:53L305C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 384,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:15:53',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:07:05',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T08:00:53',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 923.984,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:19:12',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015056_11154/www/ssw_cutout_335_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074553-20110809T083053_AIA_335_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015056_11154/www/ssw_cutout_335_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-77.690992 12.879081,-52.324483 10.325568,-46.136646 22.507576,-68.801164 26.685201,-77.690992 12.879081))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-55.47195 17.859603)',\n",
" u'hgc_x': -55.47195,\n",
" u'hgc_y': 17.859603,\n",
" u'hgs_bbox': u'POLYGON((56.118798 12.879081,81.485307 10.325568,87.673144 22.507576,65.008626 26.685201,56.118798 12.879081))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.33784 17.859603)',\n",
" u'hgs_x': 78.33784,\n",
" u'hgs_y': 17.859603,\n",
" u'hpc_bbox': u'POLYGON((768 153.6,921.6 153.6,921.6 384,768 384,768 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.827483 281.309932,0.987128 279.462322,1.054838 292.619865,0.907188 296.565051,0.827483 281.309932))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975385791457299 286.927513064147)',\n",
" u'hrc_r': 0.975385791457299,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:33:25',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_082023_2011-08-09T08:00:53.080_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'335',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 3.35e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015056_11154/www/ssw_cutout_335_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015056_11154/www/ssw_cutout_335_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074553-20110809T083053_AIA_335_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T08:01:21L300C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 768,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 76.8,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 192,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T08:16:45',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T08:05:57',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T08:01:21',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1019.83,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T01:19:13',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015407_11260/www/ssw_cutout_304_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074557-20110809T083209_AIA_304_XCEN883.2YCEN192.0.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015407_11260/www/ssw_cutout_304_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-78.947964 8.299021,-55.834319 5.994829,-45.635505 18.349576,-72.938361 22.064189,-78.947964 8.299021))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-60.369667 13.556994)',\n",
" u'hgc_x': -60.369667,\n",
" u'hgc_y': 13.556994,\n",
" u'hgs_bbox': u'POLYGON((54.866106 8.299021,77.979751 5.994829,88.178565 18.349576,60.875709 22.064189,54.866106 8.299021))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(73.444403 13.556994)',\n",
" u'hgs_x': 73.444403,\n",
" u'hgs_y': 13.556994,\n",
" u'hpc_bbox': u'POLYGON((768 76.8,921.6 76.8,921.6 307.2,768 307.2,768 76.8))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 192)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 192,\n",
" u'hrc_a': 282.264773727892,\n",
" u'hrc_bbox': u'POLYGON((0.815461 275.710593,0.977072 274.763642,1.026367 288.434949,0.87392 291.801409,0.815461 275.710593))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.954920826153573 282.264773727892)',\n",
" u'hrc_r': 0.954920826153573,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T08:35:14',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_082035_2011-08-09T08:01:21.580_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'304',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 3.04e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015407_11260/www/ssw_cutout_304_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_015407_11260/www/ssw_cutout_304_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T074557-20110809T083209_AIA_304_XCEN883.2YCEN192.0.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T13:29:00L302C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 78,\n",
" u'event_coord2': 17,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T13:45:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T13:45:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T13:29:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.2',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_132903_0094.fits,AIA20110809_134303_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-135.82247 1,-135.82247 1,-135.82247 1,-135.82247 1,-135.82247 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-58.82247 17)',\n",
" u'hgc_x': -58.82247,\n",
" u'hgc_y': 17,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78 17)',\n",
" u'hgs_x': 78,\n",
" u'hgs_y': 17,\n",
" u'hpc_bbox': u'POLYGON((16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(885.696 254.4336)',\n",
" u'hpc_x': 885.696,\n",
" u'hpc_y': 254.4336,\n",
" u'hrc_a': 286.027753295361,\n",
" u'hrc_bbox': u'POLYGON((0.094744 190.662502,0.094744 190.662502,0.094744 190.662502,0.094744 190.662502,0.094744 190.662502))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.974264092387068 286.027753295361)',\n",
" u'hrc_r': 0.974264092387068,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T07:44:31',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_073454_155',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_072113_40045/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1329.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1329.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'58',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T13:29:00L303C074',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1,\n",
" u'event_c2error': 1,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 79,\n",
" u'event_coord2': 16,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T13:57:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T13:45:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T13:29:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.2',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((-135.82247 1,-135.82247 1,-135.82247 1,-135.82247 1,-135.82247 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-57.82247 16)',\n",
" u'hgc_x': -57.82247,\n",
" u'hgc_y': 16,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(79 16)',\n",
" u'hgs_x': 79,\n",
" u'hgs_y': 16,\n",
" u'hpc_bbox': u'POLYGON((16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674,16.58082 -88.0674))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(893.388 240.2718)',\n",
" u'hpc_x': 893.388,\n",
" u'hpc_y': 240.2718,\n",
" u'hrc_a': 285.053194252152,\n",
" u'hrc_bbox': u'POLYGON((0.094744 190.662502,0.094744 190.662502,0.094744 190.662502,0.094744 190.662502,0.094744 190.662502))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.978087816690325 285.053194252152)',\n",
" u'hrc_r': 0.978087816690325,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:15',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163059_20110809132900',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T13:34:35L241C068',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 230.4,\n",
" u'boundbox_c1ur': 307.2,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 268.8,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T13:41:23',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T13:37:35',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T13:34:35',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 42.0628,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T06:51:21',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_071004_39147/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T132747-20110809T134811_AIA_131_XCEN268.8YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_071004_39147/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-121.913638 20.138485,-116.760598 19.974601,-116.01836 24.781359,-121.366967 24.955231,-121.913638 20.138485))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-119.056178 22.454571)',\n",
" u'hgc_x': -119.056178,\n",
" u'hgc_y': 22.454571,\n",
" u'hgs_bbox': u'POLYGON((14.960102 20.138485,20.113142 19.974601,20.85538 24.781359,15.506773 24.955231,14.960102 20.138485))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(17.817562 22.454571)',\n",
" u'hgs_x': 17.817562,\n",
" u'hgs_y': 22.454571,\n",
" u'hpc_bbox': u'POLYGON((230.4 230.4,307.2 230.4,307.2 307.2,230.4 307.2,230.4 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(268.8 268.8)',\n",
" u'hpc_x': 268.8,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 315,\n",
" u'hrc_bbox': u'POLYGON((0.344241 315,0.405692 306.869898,0.458988 315,0.405692 323.130102,0.344241 315))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.401614431200272 315)',\n",
" u'hrc_r': 0.401614431200272,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T13:58:13',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_135322_2011-08-09T13:34:35.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_071004_39147/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_071004_39147/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T132747-20110809T134811_AIA_131_XCEN268.8YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T15:43:00L298C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 76,\n",
" u'event_coord2': 15,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T15:54:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T15:45:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T15:43:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.4',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_154303_0094.fits,AIA20110809_154303_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-137.05282 1,-137.05282 1,-137.05282 1,-137.05282 1,-137.05282 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.05282 15)',\n",
" u'hgc_x': -62.05282,\n",
" u'hgc_y': 15,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(76 15)',\n",
" u'hgs_x': 76,\n",
" u'hgs_y': 15,\n",
" u'hpc_bbox': u'POLYGON((16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(887.568 219.2358)',\n",
" u'hpc_x': 887.568,\n",
" u'hpc_y': 219.2358,\n",
" u'hrc_a': 283.874749018686,\n",
" u'hrc_bbox': u'POLYGON((0.094839 190.651733,0.094839 190.651733,0.094839 190.651733,0.094839 190.651733,0.094839 190.651733))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.966559616090556 283.874749018686)',\n",
" u'hrc_r': 0.966559616090556,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T14:53:59',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_093355_285',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_092030_50113/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1543.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1543.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'38',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T15:43:00L297C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1,\n",
" u'event_c2error': 1,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 75,\n",
" u'event_coord2': 15,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T16:04:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T15:54:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T15:43:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.4',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((-137.05282 1,-137.05282 1,-137.05282 1,-137.05282 1,-137.05282 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-63.05282 15)',\n",
" u'hgc_x': -63.05282,\n",
" u'hgc_y': 15,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(75 15)',\n",
" u'hgs_x': 75,\n",
" u'hgs_y': 15,\n",
" u'hpc_bbox': u'POLYGON((16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598,16.58106 -88.1598))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.638 217.5492)',\n",
" u'hpc_x': 883.638,\n",
" u'hpc_y': 217.5492,\n",
" u'hrc_a': 283.830992943956,\n",
" u'hrc_bbox': u'POLYGON((0.094839 190.651733,0.094839 190.651733,0.094839 190.651733,0.094839 190.651733,0.094839 190.651733))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.962098648386101 283.830992943956)',\n",
" u'hrc_r': 0.962098648386101,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:16',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163100_20110809154300',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T16:58:00L222C090',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -90,\n",
" u'boundbox_c1ur': 90,\n",
" u'boundbox_c2ll': -90,\n",
" u'boundbox_c2ur': 90,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 90,\n",
" u'event_c2error': 90,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 0,\n",
" u'event_coord2': 0,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T17:05:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T17:02:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T16:58:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'B8.6',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((131.25856 -90,-48.74144 -90,-48.74144 90,131.25856 90,131.25856 -90))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-138.74144 0)',\n",
" u'hgc_x': -138.74144,\n",
" u'hgc_y': 0,\n",
" u'hgs_bbox': u'POLYGON((-90 -90,90 -90,90 90,-90 90,-90 -90))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(0 0)',\n",
" u'hgs_x': 0,\n",
" u'hgs_y': 0,\n",
" u'hpc_bbox': u'POLYGON((8.3e-05 -939.642,-8.3e-05 -939.642,0 940.596,-0 940.596,8.3e-05 -939.642))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(0 -104.7252)',\n",
" u'hpc_x': 0,\n",
" u'hpc_y': -104.7252,\n",
" u'hrc_a': 180,\n",
" u'hrc_bbox': u'POLYGON((0.993403 180.000005,0.993403 179.999995,0.994412 0,0.994412 0,0.993403 180.000005))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.110716988633909 180)',\n",
" u'hrc_r': 0.110716988633909,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:17',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163100_20110809165800',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T16:58:00L298C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 1265,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 76,\n",
" u'event_coord2': 15,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T17:05:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T17:02:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T16:58:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'B8.6',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_165803_0094.fits,AIA20110809_170003_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-137.74144 1,-137.74144 1,-137.74144 1,-137.74144 1,-137.74144 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.74144 15)',\n",
" u'hgc_x': -62.74144,\n",
" u'hgc_y': 15,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(76 15)',\n",
" u'hgs_x': 76,\n",
" u'hgs_y': 15,\n",
" u'hpc_bbox': u'POLYGON((16.58124 -88.2114,16.58124 -88.2114,16.58124 -88.2114,16.58124 -88.2114,16.58124 -88.2114))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(887.574 219.2238)',\n",
" u'hpc_x': 887.574,\n",
" u'hpc_y': 219.2238,\n",
" u'hrc_a': 283.873928752543,\n",
" u'hrc_bbox': u'POLYGON((0.094892 190.645757,0.094892 190.645757,0.094892 190.645757,0.094892 190.645757,0.094892 190.645757))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.966554567483081 283.873928752543)',\n",
" u'hrc_r': 0.966554567483081,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T14:54:41',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_103259_656',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_102039_55122/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1658.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1658.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'79',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T18:04:00L296C074',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 1263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 75,\n",
" u'event_coord2': 16,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T18:11:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T18:11:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T18:04:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.0',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_180403_0094.fits,AIA20110809_180903_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-138.34743 1,-138.34743 1,-138.34743 1,-138.34743 1,-138.34743 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.34743 16)',\n",
" u'hgc_x': -64.34743,\n",
" u'hgc_y': 16,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(75 16)',\n",
" u'hgs_x': 75,\n",
" u'hgs_y': 16,\n",
" u'hpc_bbox': u'POLYGON((16.58136 -88.257,16.58136 -88.257,16.58136 -88.257,16.58136 -88.257,16.58136 -88.257))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(879.384 233.484)',\n",
" u'hpc_x': 879.384,\n",
" u'hpc_y': 233.484,\n",
" u'hrc_a': 284.869451243678,\n",
" u'hrc_bbox': u'POLYGON((0.094938 190.640458,0.094938 190.640458,0.094938 190.640458,0.094938 190.640458,0.094938 190.640458))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.961901674929019 284.869451243678)',\n",
" u'hrc_r': 0.961901674929019,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:49:55',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_120755_850',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_115101_62850/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1804.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_1804.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'4',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T18:04:00L221C090',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 0,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': -90,\n",
" u'boundbox_c1ur': 90,\n",
" u'boundbox_c2ll': -90,\n",
" u'boundbox_c2ur': 90,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 90,\n",
" u'event_c2error': 90,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 0,\n",
" u'event_coord2': 0,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T18:42:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T18:11:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T18:04:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C2.0',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((130.65257 -90,-49.34743 -90,-49.34743 90,130.65257 90,130.65257 -90))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-139.34743 0)',\n",
" u'hgc_x': -139.34743,\n",
" u'hgc_y': 0,\n",
" u'hgs_bbox': u'POLYGON((-90 -90,90 -90,90 90,-90 90,-90 -90))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(0 0)',\n",
" u'hgs_x': 0,\n",
" u'hgs_y': 0,\n",
" u'hpc_bbox': u'POLYGON((8.3e-05 -939.648,-8.3e-05 -939.648,0 940.596,-0 940.596,8.3e-05 -939.648))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(0 -104.7708)',\n",
" u'hpc_x': 0,\n",
" u'hpc_y': -104.7708,\n",
" u'hrc_a': 180,\n",
" u'hrc_bbox': u'POLYGON((0.993402 180.000005,0.993402 179.999995,0.994404 0,0.994404 0,0.993402 180.000005))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.110764374385294 180)',\n",
" u'hrc_r': 0.110764374385294,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:17',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163101_20110809180400',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T20:17:35L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T20:19:35',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T20:17:59',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T20:17:35',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 73.1711,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T13:33:19',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_134015_72906/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T201535-20110809T202135_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_134015_72906/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-72.275814 16.489249,-51.885026 13.97844,-52.405436 18.348609,-68.002071 20.923277,-72.275814 16.489249))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.248487 17.866686)',\n",
" u'hgc_x': -62.248487,\n",
" u'hgc_y': 17.866686,\n",
" u'hgs_bbox': u'POLYGON((68.298126 16.489249,88.688914 13.97844,88.168504 18.348609,72.571869 20.923277,68.298126 16.489249))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.325453 17.866686)',\n",
" u'hgs_x': 78.325453,\n",
" u'hgs_y': 17.866686,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925078 285.255119,1.003581 284.036243,1.026282 288.434949,0.949657 289.983107,0.925078 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975305066963748 286.927513064147)',\n",
" u'hrc_r': 0.975305066963748,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T20:35:20',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_203518_2011-08-09T20:17:35.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_134015_72906/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_134015_72906/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T201535-20110809T202135_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T20:35:11L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T20:38:23',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T20:35:35',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T20:35:11',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 74.4124,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T13:51:19',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_135823_74342/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T203159-20110809T204135_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_135823_74342/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-72.437504 16.489517,-52.046805 13.978424,-52.567275 18.348587,-68.163777 20.923492,-72.437504 16.489517))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.410386 17.866854)',\n",
" u'hgc_x': -62.410386,\n",
" u'hgc_y': 17.866854,\n",
" u'hgs_bbox': u'POLYGON((68.298036 16.489517,88.688735 13.978424,88.168265 18.348587,72.571763 20.923492,68.298036 16.489517))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.325154 17.866854)',\n",
" u'hgs_x': 78.325154,\n",
" u'hgs_y': 17.866854,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925076 285.255119,1.003579 284.036243,1.02628 288.434949,0.949655 289.983107,0.925076 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975303129904948 286.927513064147)',\n",
" u'hrc_r': 0.975303129904948,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T20:54:33',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_205321_2011-08-09T20:35:11.080_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_135823_74342/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_135823_74342/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T203159-20110809T204135_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T20:39:23L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T20:42:23',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T20:40:59',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T20:39:23',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 77.0096,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T13:56:09',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_140429_74728/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T203623-20110809T204523_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_140429_74728/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-72.476086 16.48958,-52.085408 13.978421,-52.605892 18.348582,-68.202363 20.923543,-72.476086 16.48958))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.449018 17.866894)',\n",
" u'hgc_x': -62.449018,\n",
" u'hgc_y': 17.866894,\n",
" u'hgs_bbox': u'POLYGON((68.298014 16.48958,88.688692 13.978421,88.168208 18.348582,72.571737 20.923543,68.298014 16.48958))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.325082 17.866894)',\n",
" u'hgs_x': 78.325082,\n",
" u'hgs_y': 17.866894,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925075 285.255119,1.003578 284.036243,1.026279 288.434949,0.949655 289.983107,0.925075 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975302666248398 286.927513064147)',\n",
" u'hrc_r': 0.975302666248398,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T20:59:11',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_205734_2011-08-09T20:39:23.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_140429_74728/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_140429_74728/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T203623-20110809T204523_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T20:59:11L298C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T21:11:35',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T21:04:47',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T20:59:11',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 108.128,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T14:16:14',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_144339_78137/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T204647-20110809T212359_AIA_131_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_144339_78137/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-72.657988 16.489881,-52.255523 13.979708,-52.775812 18.349886,-68.384283 20.923785,-72.657988 16.489881))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.631156 17.867084)',\n",
" u'hgc_x': -62.631156,\n",
" u'hgc_y': 17.867084,\n",
" u'hgs_bbox': u'POLYGON((68.297912 16.489881,88.700377 13.979708,88.180088 18.349886,72.571617 20.923785,68.297912 16.489881))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.324744 17.867084)',\n",
" u'hgs_x': 78.324744,\n",
" u'hgs_y': 17.867084,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925073 285.255119,1.003576 284.036243,1.026277 288.434949,0.949653 289.983107,0.925073 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975300492220231 286.927513064147)',\n",
" u'hrc_r': 0.975300492220231,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T21:28:27',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_212153_2011-08-09T20:59:11.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_144339_78137/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_144339_78137/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T204647-20110809T212359_AIA_131_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T21:57:59L242C068',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 307.2,\n",
" u'boundbox_c1ur': 384,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 345.6,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T21:59:59',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T21:58:59',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T21:57:59',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 39.3408,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T15:18:50',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_151945_81166/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T215559-20110809T220159_AIA_131_XCEN345.6YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_151945_81166/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-121.381348 19.993275,-116.069837 19.775267,-115.117461 24.568,-120.638427 24.799646,-121.381348 19.993275))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-118.358093 22.277434)',\n",
" u'hgc_x': -118.358093,\n",
" u'hgc_y': 22.277434,\n",
" u'hgs_bbox': u'POLYGON((20.114432 19.993275,25.425943 19.775267,26.378319 24.568,20.857353 24.799646,20.114432 19.993275))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(23.137687 22.277434)',\n",
" u'hgs_x': 23.137687,\n",
" u'hgs_y': 22.277434,\n",
" u'hpc_bbox': u'POLYGON((307.2 230.4,384 230.4,384 307.2,307.2 307.2,307.2 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(345.6 268.8)',\n",
" u'hpc_x': 345.6,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 307.874983651098,\n",
" u'hrc_bbox': u'POLYGON((0.405669 306.869898,0.473087 300.963757,0.51951 308.659808,0.458962 315,0.405669 306.869898))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.462533624545167 307.874983651098)',\n",
" u'hrc_r': 0.462533624545167,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-09T22:19:03',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110809_221901_2011-08-09T21:57:59.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_151945_81166/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_151945_81166/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T215559-20110809T220159_AIA_131_XCEN345.6YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'1',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:33:00L297C072',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 11263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 1,\n",
" u'event_c2error': 1,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 79,\n",
" u'event_coord2': 18,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T23:49:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:43:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T23:33:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C3.9',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'[email protected]',\n",
" u'frm_daterun': u'2011-08-09T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SWPC',\n",
" u'frm_institute': u'U.S. Dept. of Commerce, NOAA, Space Weather Prediction Center',\n",
" u'frm_name': u'SWPC',\n",
" u'frm_paramset': u'-',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.swpc.noaa.gov/',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'',\n",
" u'gs_movieurl': u'',\n",
" u'gs_thumburl': u'',\n",
" u'hcr_checked': u'false',\n",
" u'hgc_bbox': u'POLYGON((-141.36818 1,-141.36818 1,-141.36818 1,-141.36818 1,-141.36818 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-63.36818 18)',\n",
" u'hgc_x': -63.36818,\n",
" u'hgc_y': 18,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(79 18)',\n",
" u'hgs_x': 79,\n",
" u'hgs_y': 18,\n",
" u'hpc_bbox': u'POLYGON((16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.968 271.8192)',\n",
" u'hpc_x': 883.968,\n",
" u'hpc_y': 271.8192,\n",
" u'hrc_a': 287.09260610172,\n",
" u'hrc_bbox': u'POLYGON((0.09517 190.614251,0.09517 190.614251,0.09517 190.614251,0.09517 190.614251,0.09517 190.614251))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.977685454704634 287.09260610172)',\n",
" u'hrc_r': 0.977685454704634,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2014-01-09T23:11:18',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SECstandard_20110907_163102_20110809233300',\n",
" u'kb_archivist': u'cheung_mark',\n",
" u'obs_channelid': u'XRA',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'GOES',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 5e-08,\n",
" u'obs_observatory': u'GOES',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.swpc.noaa.gov/'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:33:00L298C075',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': 1263,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 1,\n",
" u'boundbox_c1ur': 1,\n",
" u'boundbox_c2ll': 1,\n",
" u'boundbox_c2ur': 1,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 0,\n",
" u'event_c2error': 0,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 80,\n",
" u'event_coord2': 15,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HGS-TOPO',\n",
" u'event_coordunit': u'degrees',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T23:49:00',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:43:00',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': 1,\n",
" u'event_starttime': u'2011-08-09T23:33:00',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'C3.9',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': None,\n",
" u'fl_peakfluxunit': u'',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Samuel L. Freeland',\n",
" u'frm_daterun': u'2011-08-10T00:00:00',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'SolarSoft',\n",
" u'frm_institute': u'LMSAL',\n",
" u'frm_name': u'SSW Latest Events',\n",
" u'frm_paramset': u'AIA20110809_233303_0094.fits,AIA20110809_234103_0094.fits',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro',\n",
" u'frm_versionnumber': None,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-141.36818 1,-141.36818 1,-141.36818 1,-141.36818 1,-141.36818 1))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-62.36818 15)',\n",
" u'hgc_x': -62.36818,\n",
" u'hgc_y': 15,\n",
" u'hgs_bbox': u'POLYGON((1 1,1 1,1 1,1 1,1 1))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(80 15)',\n",
" u'hgs_x': 80,\n",
" u'hgs_y': 15,\n",
" u'hpc_bbox': u'POLYGON((16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832,16.58196 -88.4832))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(900.618 225.9972)',\n",
" u'hpc_x': 900.618,\n",
" u'hpc_y': 225.9972,\n",
" u'hrc_a': 284.086689887523,\n",
" u'hrc_bbox': u'POLYGON((0.09517 190.614251,0.09517 190.614251,0.09517 190.614251,0.09517 190.614251,0.09517 190.614251))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.981622638249268 284.086689887523)',\n",
" u'hrc_r': 0.981622638249268,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T16:52:15',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_SSWLatestEvents_20110809_174046_847',\n",
" u'kb_archivist': u'freeland_samuel',\n",
" u'obs_channelid': u'EUV',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 9.4e-07,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO/AIA Movies',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_172144_91907/www/'},\n",
" {u'ref_name': u'Event-Context',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/'},\n",
" {u'ref_name': u'Event-Detection(diff)',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_2333.png'},\n",
" {u'ref_name': u'Event-Summary',\n",
" u'ref_type': u'html',\n",
" u'ref_url': u'http://www.lmsal.com/solarsoft/latest_events/gev_20110809_2333.html'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://sohowww.nascom.nasa.gov/solarsoft/packages/gevloc/idl/ssw_flare_locator.pro'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'42',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:37:38L296C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-10T00:26:26',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:51:14',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T23:37:38',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1103.52,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T17:03:14',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.30000e-01 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183326_98814/www/ssw_cutout_211_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T224850-20110810T011514_AIA_211_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183326_98814/www/ssw_cutout_211_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-76.820276 11.998542,-60.956108 10.334385,-54.233063 18.34965,-69.84007 20.925716,-76.820276 11.998542))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.088686 17.868597)',\n",
" u'hgc_x': -64.088686,\n",
" u'hgc_y': 17.868597,\n",
" u'hgs_bbox': u'POLYGON((65.590444 11.998542,81.454612 10.334385,88.177657 18.34965,72.57065 20.925716,65.590444 11.998542))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.322034 17.868597)',\n",
" u'hgs_x': 78.322034,\n",
" u'hgs_y': 17.868597,\n",
" u'hpc_bbox': u'POLYGON((844.8 153.6,921.6 153.6,921.6 307.2,844.8 307.2,844.8 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.907093 280.304846,0.987024 279.462322,1.026258 288.434949,0.949636 289.983107,0.907093 280.304846))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975283007616269 286.927513064147)',\n",
" u'hrc_r': 0.975283007616269,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:44:29',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110810_000411_2011-08-09T23:37:38.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'211',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 2.11e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183326_98814/www/ssw_cutout_211_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183326_98814/www/ssw_cutout_211_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T224850-20110810T011514_AIA_211_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:37:47L292C077',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 153.6,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 192,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-10T00:04:47',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:43:59',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T23:37:47',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 267.613,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T17:03:14',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 8.00000e-02 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_175258_94550/www/ssw_cutout_131_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T231047-20110810T003147_AIA_131_XCEN883.2YCEN192.0.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_175258_94550/www/ssw_cutout_131_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-76.821657 11.998545,-60.957493 10.334387,-54.246306 18.348348,-69.84145 20.925718,-76.821657 11.998545))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-68.978709 13.568826)',\n",
" u'hgc_x': -68.978709,\n",
" u'hgc_y': 13.568826,\n",
" u'hgs_bbox': u'POLYGON((65.590443 11.998545,81.454607 10.334387,88.165794 18.348348,72.57065 20.925718,65.590443 11.998545))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(73.433391 13.568826)',\n",
" u'hgs_x': 73.433391,\n",
" u'hgs_y': 13.568826,\n",
" u'hpc_bbox': u'POLYGON((844.8 153.6,921.6 153.6,921.6 307.2,844.8 307.2,844.8 153.6))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 192)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 192,\n",
" u'hrc_a': 282.264773727892,\n",
" u'hrc_bbox': u'POLYGON((0.907093 280.304846,0.987024 279.462322,1.026258 288.434949,0.949636 289.983107,0.907093 280.304846))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.954820239214902 282.264773727892)',\n",
" u'hrc_r': 0.954820239214902,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:22:38',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110810_000522_2011-08-09T23:37:47.070_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'131',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.31e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_175258_94550/www/ssw_cutout_131_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_175258_94550/www/ssw_cutout_131_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T231047-20110810T003147_AIA_131_XCEN883.2YCEN192.0.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:38:20L296C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-09T23:55:56',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:51:08',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T23:38:20',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 2144.81,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T17:03:16',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 3.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_173152_92738/www/ssw_cutout_193_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T232044-20110810T001332_AIA_193_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_173152_92738/www/ssw_cutout_193_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-74.120067 16.492292,-53.721017 13.979272,-54.241902 18.349386,-69.846504 20.925724,-74.120067 16.492292))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.095128 17.868604)',\n",
" u'hgc_x': -64.095128,\n",
" u'hgc_y': 17.868604,\n",
" u'hgs_bbox': u'POLYGON((68.297083 16.492292,88.696133 13.979272,88.175248 18.349386,72.570646 20.925724,68.297083 16.492292))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.322022 17.868604)',\n",
" u'hgs_x': 78.322022,\n",
" u'hgs_y': 17.868604,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925057 285.255119,1.003558 284.036243,1.026258 288.434949,0.949636 289.983107,0.925057 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975282935494864 286.927513064147)',\n",
" u'hrc_r': 0.975282935494864,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:13:25',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110810_000523_2011-08-09T23:38:20.840_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'193',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.93e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_173152_92738/www/ssw_cutout_193_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_173152_92738/www/ssw_cutout_193_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T232044-20110810T001332_AIA_193_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None},\n",
" {u'SOL_standard': u'SOL2011-08-09T23:38:25L296C073',\n",
" u'active': u'true',\n",
" u'ar_compactnesscls': u'',\n",
" u'ar_mcintoshcls': u'',\n",
" u'ar_mtwilsoncls': u'',\n",
" u'ar_noaaclass': u'',\n",
" u'ar_noaanum': None,\n",
" u'ar_numspots': None,\n",
" u'ar_penumbracls': u'',\n",
" u'ar_polarity': None,\n",
" u'ar_zurichcls': u'',\n",
" u'area_atdiskcenter': None,\n",
" u'area_atdiskcenteruncert': None,\n",
" u'area_raw': None,\n",
" u'area_uncert': None,\n",
" u'area_unit': u'',\n",
" u'bound_ccnsteps': None,\n",
" u'bound_ccstartc1': None,\n",
" u'bound_ccstartc2': None,\n",
" u'bound_chaincode': u'',\n",
" u'boundbox_c1ll': 844.8,\n",
" u'boundbox_c1ur': 921.6,\n",
" u'boundbox_c2ll': 230.4,\n",
" u'boundbox_c2ur': 307.2,\n",
" u'chaincodetype': u'',\n",
" u'comment_count': u'0',\n",
" u'concept': u'Flare ',\n",
" u'event_c1error': 2,\n",
" u'event_c2error': 2,\n",
" u'event_clippedspatial': u'',\n",
" u'event_clippedtemporal': u'',\n",
" u'event_coord1': 883.2,\n",
" u'event_coord2': 268.8,\n",
" u'event_coord3': None,\n",
" u'event_coordsys': u'UTC-HPC-TOPO',\n",
" u'event_coordunit': u'arcseconds',\n",
" u'event_description': u'',\n",
" u'event_endtime': u'2011-08-10T00:26:25',\n",
" u'event_expires': u'',\n",
" u'event_importance': u'',\n",
" u'event_importance_num_ratings': u'',\n",
" u'event_mapurl': u'',\n",
" u'event_maskurl': u'',\n",
" u'event_npixels': None,\n",
" u'event_peaktime': u'2011-08-09T23:39:25',\n",
" u'event_pixelunit': u'',\n",
" u'event_probability': None,\n",
" u'event_starttime': u'2011-08-09T23:38:25',\n",
" u'event_testflag': u'false',\n",
" u'event_title': u'',\n",
" u'event_type': u'FL',\n",
" u'eventtype': u'9',\n",
" u'fl_efoldtime': None,\n",
" u'fl_efoldtimeunit': u'',\n",
" u'fl_fluence': None,\n",
" u'fl_fluenceunit': u'',\n",
" u'fl_goescls': u'',\n",
" u'fl_peakem': None,\n",
" u'fl_peakemunit': u'',\n",
" u'fl_peakflux': 1286.45,\n",
" u'fl_peakfluxunit': u'erg/cm/cm/s',\n",
" u'fl_peaktemp': None,\n",
" u'fl_peaktempunit': u'',\n",
" u'frm_contact': u'Paolo C. Grigis - [email protected]',\n",
" u'frm_daterun': u'2011-08-09T17:03:15',\n",
" u'frm_humanflag': u'false',\n",
" u'frm_identifier': u'Feature Finding Team',\n",
" u'frm_institute': u'SAO',\n",
" u'frm_name': u'Flare Detective - Trigger Module',\n",
" u'frm_paramset': u'DerivativeThreshold= 2.00000e+00 EndFraction= 2.50000e-01',\n",
" u'frm_specificid': u'',\n",
" u'frm_url': u'http://www.cfa.harvard.edu',\n",
" u'frm_versionnumber': 0.51,\n",
" u'gs_galleryid': u'',\n",
" u'gs_imageurl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183329_98818/www/ssw_cutout_171_context_full.gif',\n",
" u'gs_movieurl': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T225025-20110810T011425_AIA_171_XCEN883.2YCEN268.8.mov',\n",
" u'gs_thumburl': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183329_98818/www/ssw_cutout_171_context_thumb.gif',\n",
" u'hcr_checked': u'true',\n",
" u'hgc_bbox': u'POLYGON((-74.120828 16.492294,-53.718762 13.979604,-54.239579 18.349724,-69.847264 20.925725,-74.120828 16.492294))',\n",
" u'hgc_boundcc': u'',\n",
" u'hgc_coord': u'POINT(-64.09589 17.868605)',\n",
" u'hgc_x': -64.09589,\n",
" u'hgc_y': 17.868605,\n",
" u'hgs_bbox': u'POLYGON((68.297082 16.492294,88.699148 13.979604,88.178331 18.349724,72.570646 20.925725,68.297082 16.492294))',\n",
" u'hgs_boundcc': u'',\n",
" u'hgs_coord': u'POINT(78.32202 17.868605)',\n",
" u'hgs_x': 78.32202,\n",
" u'hgs_y': 17.868605,\n",
" u'hpc_bbox': u'POLYGON((844.8 230.4,921.6 230.4,921.6 307.2,844.8 307.2,844.8 230.4))',\n",
" u'hpc_boundcc': u'',\n",
" u'hpc_coord': u'POINT(883.2 268.8)',\n",
" u'hpc_x': 883.2,\n",
" u'hpc_y': 268.8,\n",
" u'hrc_a': 286.927513064147,\n",
" u'hrc_bbox': u'POLYGON((0.925057 285.255119,1.003558 284.036243,1.026258 288.434949,0.949636 289.983107,0.925057 285.255119))',\n",
" u'hrc_boundcc': u'',\n",
" u'hrc_coord': u'POINT(0.975282925191807 286.927513064147)',\n",
" u'hrc_r': 0.975282925191807,\n",
" u'intenskurt': None,\n",
" u'intensmax': None,\n",
" u'intensmean': None,\n",
" u'intensmedian': None,\n",
" u'intensmin': None,\n",
" u'intensskew': None,\n",
" u'intenstotal': None,\n",
" u'intensunit': u'',\n",
" u'intensvar': None,\n",
" u'kb_archivdate': u'2011-08-10T00:44:34',\n",
" u'kb_archivid': u'ivo://helio-informatics.org/FL_FlareDetective-TriggerModule_20110810_000523_2011-08-09T23:38:25.350_1',\n",
" u'kb_archivist': u'flare_detective',\n",
" u'obs_channelid': u'171',\n",
" u'obs_dataprepurl': u'',\n",
" u'obs_firstprocessingdate': u'',\n",
" u'obs_includesnrt': u'',\n",
" u'obs_instrument': u'AIA',\n",
" u'obs_lastprocessingdate': u'',\n",
" u'obs_levelnum': None,\n",
" u'obs_meanwavel': 1.71e-06,\n",
" u'obs_observatory': u'SDO',\n",
" u'obs_title': u'',\n",
" u'obs_wavelunit': u'cm',\n",
" u'rasterscan': u'',\n",
" u'rasterscantype': u'',\n",
" u'refs': [{u'ref_name': u'SSW Context Thumbnail',\n",
" u'ref_type': u'thumbnail',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183329_98818/www/ssw_cutout_171_context_thumb.gif'},\n",
" {u'ref_name': u'SSW Context Image',\n",
" u'ref_type': u'image',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/ssw/media/ssw/ssw_client/data/ssw_service_110809_183329_98818/www/ssw_cutout_171_context_full.gif'},\n",
" {u'ref_name': u'SDO Movie',\n",
" u'ref_type': u'movie',\n",
" u'ref_url': u'http://sdowww.lmsal.com/sdomedia/h264/2011/08/09/EDS_FlareDetective-TriggerModule_20110809T225025-20110810T011425_AIA_171_XCEN883.2YCEN268.8.mov'},\n",
" {u'ref_name': u'FRM_URL',\n",
" u'ref_type': u'unknown',\n",
" u'ref_url': u'http://www.cfa.harvard.edu'}],\n",
" u'refs_orig': u'',\n",
" u'revision': u'2',\n",
" u'skel_chaincode': u'',\n",
" u'skel_curvature': None,\n",
" u'skel_nsteps': None,\n",
" u'skel_startc1': None,\n",
" u'skel_startc2': None}]"
]
}
],
"prompt_number": 57
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Filter the results of the previous result to return only those events that have the FRM \u2018SSW Latest Events\u2019"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"result = client.query(hek.attrs.Time(tstart, tend), hek.attrs.EventType('FL'), hek.attrs.FRM.Name=='SSW Latest Events')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 58
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"len(result)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 59,
"text": [
"9"
]
}
],
"prompt_number": 59
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following returns flares west of 50 arcseconds or those that have a peak flux above 1000.0 (the units of the flux are FRM- dependent and are described at the HEK website)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"result = client.query(hek.attrs.Time(tstart, tend), hek.attrs.EventType('FL'), (hek.attrs.Event.Coord1>50) or (hek.attrs.FL.PeakFlux>1000.0))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 60
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"len(result)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 61,
"text": [
"48"
]
}
],
"prompt_number": 61
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Downloading the VSO files associated with events"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy.net import hek2vso"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 62
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"h2v = hek2vso.H2VClient()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 63
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"vso_results = h2v.translate_and_query(result[0])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 64
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"h2v.vso_client.get(vso_results[0]).wait()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "KeyboardInterrupt",
"evalue": "",
"output_type": "pyerr",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[0;31mKeyboardInterrupt\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-65-72e4e3caeaa5>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mh2v\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mvso_client\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mvso_results\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mwait\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/Users/schriste/Dropbox/Developer/python/sunpy/sunpy/net/vso/vso.pyc\u001b[0m in \u001b[0;36mwait\u001b[0;34m(self, timeout, progress)\u001b[0m\n\u001b[1;32m 123\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mprogress\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdraw\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 124\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 125\u001b[0;31m \u001b[0;32mwhile\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mevt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mwait\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mtimeout\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 126\u001b[0m \u001b[0;32mpass\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 127\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mprogress\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/Users/schriste/anaconda/python.app/Contents/lib/python2.7/threading.pyc\u001b[0m in \u001b[0;36mwait\u001b[0;34m(self, timeout)\u001b[0m\n\u001b[1;32m 618\u001b[0m \u001b[0;32mtry\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 619\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m__flag\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 620\u001b[0;31m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m__cond\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mwait\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mtimeout\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 621\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m__flag\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 622\u001b[0m \u001b[0;32mfinally\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/Users/schriste/anaconda/python.app/Contents/lib/python2.7/threading.pyc\u001b[0m in \u001b[0;36mwait\u001b[0;34m(self, timeout)\u001b[0m\n\u001b[1;32m 356\u001b[0m \u001b[0;32mbreak\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 357\u001b[0m \u001b[0mdelay\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mmin\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdelay\u001b[0m \u001b[0;34m*\u001b[0m \u001b[0;36m2\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mremaining\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m.05\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 358\u001b[0;31m \u001b[0m_sleep\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdelay\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 359\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mgotit\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 360\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0m__debug__\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mKeyboardInterrupt\u001b[0m: "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"ERROR: KeyboardInterrupt [threading]\n"
]
}
],
"prompt_number": 65
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## WCS"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sunpy import wcs"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 66
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"wcs.convert_hg_hpc(10, 53)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 67,
"text": [
"(100.49244115330731, 767.97438321917502)"
]
}
],
"prompt_number": 67
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Convert that position back to heliographic coordinates"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"wcs.convert_hpc_hg(100.49, 767.97)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 68,
"text": [
"(9.9996521808465175, 52.999563684874893)"
]
}
],
"prompt_number": 68
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Try to convert a position which is not on the Sun to HG"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"wcs.convert_hpc_hg(-1500, 0)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 69,
"text": [
"(nan, nan)"
]
}
],
"prompt_number": 69
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Convert sky coordinate to a position in HCC"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"wcs.convert_hpc_hcc(-300, 400, z=True)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 70,
"text": [
"(-216716967.63331246, 288956420.9477042, 594364636.2208252)"
]
}
],
"prompt_number": 70
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## More References\n",
"\n",
"+ [Python for Data Analysis](http://shop.oreilly.com/product/0636920023784.do) by Wes McKinney is great\n",
"+ [Lectures on scientific computing with Python](http://jrjohansson.github.io) Great lectures on scientific computing in Python"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Consider [contributing](http://sunpy.org/contribute/) to SunPy!\n",
"\n",
"+ Provide feedback on the [mailing list](https://groups.google.com/forum/#!forum/sunpy)\n",
"+ Report [bugs](https://github.com/sunpy/sunpy/issues)\n",
"+ Provide Code (see our [developer guide](http://sunpy.readthedocs.org/en/stable/dev.html))"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | bsd-3-clause |
di-br/CalMAdju | doc/metric_tests/Gradients.ipynb | 1 | 541682 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### Import required modules"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# manipulate arrays and have math\n",
"import numpy as np\n",
"# plot results\n",
"import matplotlib.pyplot as plt\n",
"# plot them inline in jupyter\n",
"%matplotlib inline\n",
"# make matplotlib load images\n",
"import matplotlib.image as mpimg"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"## Load test images"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"sharp_image = mpimg.imread('picture.png')\n",
"soft_image = mpimg.imread('picture_gaussian_10.png')"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### Display the raw images"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"sharp image\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAADzCAYAAACPBsFkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXecE9X6/z9nkmyhS/0J7KZttsAiKggIoiBwLYgFv3aR\nooIoxXuvqAiiKAgq94pcG6B09aLeqyhgR0QQKUpZyu6mbAO5ghQRlt0kM+f3R/bMTupMkklZNu/X\nK6/dTKacTOY8z3Oe8zzPIZRSpEiRIkWKxgeX6AakSJEiRYrEkFIAKVKkSNFISSmAFClSpGikpBRA\nihQpUjRSUgogRYoUKRopKQWQIkWKFI2UuCsAQsi1hJASQoiNEPJkvK+fIkWKFCk8kHjmARBCNABK\nAQwBcAjADgB3UUoPxK0RKVKkSJECQPxHAL0A2CilDkqpE8C/AdwU5zakSJEiRQrEXwF0AlAleX+o\nbluKFClSpIgz2kQ3wBdCyFgAY+v+75Gm0yW4RSniTWG3bn7bioqK0C3AdgCoqalBRkYGqiqrcOqP\nU+jWrRuKiopAfM61f98+dC0sRFFREVq0aIE/T59G+/btkZaejkNVh1DYrVC8zr6iIlBAvGZNTQ0A\nwFpaisJu3UAIAQDwbjc0Wi1KS0qQrdcjIyMDf5w6hZatWgEAzlVXw2az4cKOHdGmTRvxOPF8Vqt4\nDbfLjVpnLY7/fhztO7RHRkaG2PZfDx/GiRMnkGOxiNtLiksAUOTl5wMA9hUVIcdiAaUUmZmZ4rYU\njY9ap/N3Smk7uf3iPQdwOYBnKaXX1L2fCgCU0jmB9s9IT6edL+wYt/alSA5s5WUAgAJLLjp27Ihv\nv98IQRBACAEBAQhAKQUhBJRS5JjMsJc5YMrW46ZbbsErr86HUW+AhhAIggBbeRk4znuwa87Sw15V\ngRyDUbweAJiNJtjLHMjJNoASIC0tDQetpTAbTWjRogV27d6NfIsFxTYrACDHZIbNYUdBXj6cTifs\nZQ50bN8Bh/53BBzHIddkBqUUU5+ejjnPz4K1zOHVDpPBCHuZA4QQFOYXYF/xQTw0dhy+/vpr2Ov2\nNRtNqD13DmkZGSCEiNsBIM+cgxK7DWajCek6HQ6UlnidP8dgVO+HSdFgsFeU/0wp7Sm3X7xdQDsA\nWAghRkJIGoA7AXwa5zakaCDsLT6Az7/+Ct9/txEcx8Gcpcfkhx/BpAkTUWC2QJ+VDUIIhg4dCgD4\n6IMPsW7dOgAAX+sEOA6OygpwxPOYT/nr3zBpwkQYOmfhyRnT0dWShyXLlgHwCFIA0BCCSRMmghAC\np9OJvQf2w+VyYejQoejfvz9yzGbwPC+20eawAwCaZWRi6NChoLyAX4/+BsoLAIB1n38Oa52At5Y5\n4Kp1en1HSikcNjucTif27N8Hi9EEuHnxO7ndbtjLHBgxciS0HOe5BgAX74ZZbwDRaEAB2MscqKk+\nB54KSJV3TKGUuI4AAIAQcj2A+QA0AJZQSmcH2zc1AmicSC3yFNGRGgE0TpSOAOI+B0ApXQ9gfbyv\nm6LhkBJaKVLEh1QmcIoUKVI0UlIKIEWKFCkaKUkXBno+89P27X7b+vTqlYCWKGfrju0gPtNEffv0\ngSAIiWlQgmmIv2Gs0Gg02LJ1q9c2SoDLL0vu+5H6DetJKYA40rp9W3Ag4nuXy5XA1ihj8ICB2LN/\nn9e2xir8AaBte9nQ6kYDz/N+9+OiLl0T1BrltLygFXSS/KLGHDeVcgHFkXxTjtd7DUn+23/27NlE\nNyGpuPv2O7ze33Xb7QlqSXJSXV2d6CbI4tvv8ozmBLUk8SS/BDqP8LWczcaGF+1iNpoS3YSEsm3b\nNq/32wO4ExoTRr0h0U0IG99+F+9Q+GQipQASiEajSXQTwqYxdxYAYimHYO8bG74Z1g2BhtjvYkXD\n+/UaOE89ORVAw/KjG7OyPf/Q1AMD1CvBxq4MAYBQCgie+2BuQKMB1v+mPtG4lyRJ9ec488G//w3A\nU+emocAspjdefz3BLUkOck1mr7+NnbfffhtAwxoNsf734erVCW5JYkkpgAThdrsT3YSwoJTin/Pm\nJboZSQHP8xAEwasmUGNm7gsvNLjRUEPrf7EipQASAKtk2ZAwZOsT3YSkgeM4EI5rkP7vWNG5Y8Na\n1oNVkm3sNOg8gJ+2b0fb9u1gNpo8vsgABCssJggCuuTm4aC1NGxhTCmFxWjCq//6F4YOu8Hvc57n\nYTHngAtw/RyDERajKWi78sw5EATBr2xwpLC6OoGux/M83luxErNnz8ZBmxWh7oIgCCmB50OqaF09\nbrcbWm1wcUIBFORYMG3aNNx934iAE7GhntVIsBhN4DgOJXZbwM+DXS/HYIQAwGq3BWznus/WYvLE\niWKV13CglKLAkosDpSVB+1PQWlgcB5vDjiOHf0X/fv3Cum4wGrQCYEjro2/45luMfeABr8/Zw9m1\noAtqz52LSRvcbjfyzDniA6FEVLKRgMVoios1wq5nyNZDG6YwtxhNsFeUx6ZhKRo8BZZcWaPF7XZj\n5syZmDlzpue9IKC8siJmI2JKKXieFwUqx3EoddgVXY9DfYlwSilK7LaQCi4c3G631/xRemYm9h88\nEFCJLnr7bVw9eJAq1w3EeaEApFw9eJCo0aurq9ElNw81NTUxsV41Gg1yTWYxokDxQ6zViA9AvKKB\njHW18zmOC1v4A57vtnr1atxxxx3yO6doVKxcuTIiA0bLcR5rWxBAKY15eKYgCMgxGEVZQDQaUAXz\nOIQQ5OdYAHiUyILXXlO1XbXnzon3ISMjA3sP7EeTzCYIOSRXifNOAQDeQyimDHwtdDXgeR6ldQuC\nbNy4EaPuHaHMSnDzKC0v81giIMgzmcHT2CqCsqpK8DwPDeFgMZsj6rAzpz2dUgAp/HjhuecBhD+3\nRQiB1W6HAAquThnEEg3hUOKwg8LTTqXXc7vdWLZqJQYMGADA4wJSE0oprGUOUTGxdlFKYz7qbvAK\nwOVyYeXyFXhh1qyQ+2m1WvFmCoKAbt26wVmtnjtowIABKD9Uv959YX6BuO5rMFhnKSmzi9uyO3aK\nmTuIWVjSobopWy+rtIxZ2dBoNHC6Y1e76JabbsbHaz6J2fkbO2a9AfaKclx99dXYsGGDqudmNa1M\n2XqUVVUG3Y/jOLjdbjgqK7y3x8jUra2tBSEElb8e9tpOFFwvIyMD+4oPxqRdAJDetAmKiopCeiZ8\nldTTzzyDe+8boWo7GrQCUFrBz2I0odRhByFE9LN9sXYdsowGVdrhdrtBCIFGo4E+KxsVVZWKHh6L\n0SQKY7a2rO/DqjoUcLldeHflKowaM9qvMwbC6yEVKMDFdmwayjKzlZdhyt8fw8f/+U/Az4ttVmi1\nWlj0wc9hrShDl9y8oJ/7rqt7PsCMnw0bNvitgxwNbOlLIHRWMAHE0TKjwJKLg9ZSPP63v+Olf/5D\nlfZIqTryq9d79r2l/S4QgSaFbeVlKMzNh1vg8Y9XXom4TYQQ2MrLIAgCCswWHLCVIsdghL2iHLk5\nFlh97pGU52fOxPN18ydq0aAVQDi89NJLePzxx6HVapGfY4HT6VQk/JSg1WrBu9yApn6NWCVYyxzi\nsPnCCy9UpS2ykPDT96XD+hxT8AimiBEoivbsUbz7y/+Yh5f/ETonwVoRuo3no5APxaoVK8FpNVix\nbDlsZer9fhZz/WRmuO7Vg9ZSAIiJ8PejblD98EPj4QwzB4BoNAAFikoOwtCxsyrN4TgOP+/ZDY7j\nMOfFF/HQ2HEotVlhztbHNdquUcT1WcsceOyxx7Dlh80ABV59/TXVhD8A/Pe//4VG59GlkQxneZ7H\nD1s2q9aekFCPK2jUmNGKdj94MHbDYBGOeCkVW3lZ0FeKyLj3vhG4++678cVXX8Z0crG4uFj5zjTI\n/zFAIJ6SFRu++QZlYfrVS21WAJ4RS8URdUbolFLUOGsBAHfefRc21rnl9hQVqXJ+pTSaEYBGo8EV\nV/YHAFxzzTWqnnv48OH119GFd0uZ6yhuhNn5jxz+FW8sWhibtqRo8Pg+G78eOoz8/HxlB5Mg/8cA\nDgS2yvKIjmUjm+I6RaAGhBC0bdtWfM/cY81btlDtGkpoNAogRWTEMgY5RcPnL3/5S8jPWUADy7wV\n3UQUotCX/JsizpBkTofOSE+nnS/sGNU5YuI2qHtieZ5PlZZNcd5CeQGVlZVYunQpVq5cCZ7noat7\n3imloJRCp9PB6XSC4zhQSj3zYTwfdqmFSLJqE4XY72OkudQIh7VXlP9MKe0pt19KAaRIkUBYLohA\nBVFosknANWvW4P1338OOHTtE4cvzvCh4AY+QpkR5bRtKKTSE8yRf1QkvJnj7X3UVRowYgasHDRJj\n5QFv9zyBJ4yaENJgBHZDI54KoFG6gELdYAHAvHnzMPzWW1Pj0vMEZq0yK5UQIko1XvAfxTGhDACr\n//1vvPfee9i3bx84KF8DgF2H4zzClmV8cxznEeY6nVhNVKPRwO12gxKCgQMHYuTIkbhq4ADcdNNN\nuOmmm9S5CWEijZX37QapmlDBCVXWheM4WPLysG79eoAkR32tRjcCYIXcwjpHWVlKGcQZu92OFStW\n4N2Vq4A64cmEKqEQrVcOxCNc63IT+Lp9NISEVaKjVatWGD16NO689x60adNG3O47yhdQpxwoBaGI\neU5EioaFoXNW2DWDAuUdREtqBBAEGkl/bSR9nFkk6z5bi/feew9bt24V44SZBc3qtrCHnFLq5YaQ\ng1IKcJxHQMOTRTpw4EDcfffd+Mu19dFZZrPZq3AYE/7sb7ysJz/rF6LfpNE8FymUo9PpGlSZ6Uan\nAGKRdi71vxJCsHnzZvTr16/ehyqJfvCNiogH0mqIlFLQOgHapEkTjBw5EiNHj0K7du1EAX/9DUMx\ndOhQxUI9HrB2iNVWEzx0zjV4jyJLy9Up350iPrBnnf2v1WrhdDqh0WhAKYUgCNi9ezcuvfRScVJb\nekwwGpLwB6JUAISQcgB/AuABuCmlPQkhrQGsBmAAUA7gdkrpSeLpua8CuB5ANYBRlNJforl+RMTg\n93G5XNDUTdAtWrQI/fv3FyfKpIKqtrYWPM9Dq9XG9UEJZyJcbG8jNHBfmvsiHnvycUVGglKBL4Bi\n3tyX8PiTT0TbvBQqwvonE/ZSA431zZ49e+Lll18GIQQ6na5BreOtFDXMqIGU0osl/qYnAXxLKbUA\n+LbuPQBcB8BS9xoL4E0Vrh024x96SPVzSkPfHnzwQa9JxSFDhogPTlpamrhvosjJNiTs2inOXwyd\ns5BjMIqvWGf2qoFv9VJKKW6++WYAEJf8nDRpErRaLWpraxPVzJgSi3H0TQCW1/2/HMDNku0rqIef\nALQihMSpAE49G775JmbnZg+TdL3RdevWoW/fvujTp4/XkDMRePzvjc2uTxEPtFzDzocZMGAALrnk\nEvynrsgg66MsWitWfTbRaxNHOwdAAXxFCKEAFlJKFwHoQCk9Uvf5/wB0qPu/E4AqybGH6rYdQRyJ\npfUtCAK0Wq1XnDTHcdi2bVtCXD++EEI81TxTiDhs9cX7/vzjD0XHyEVppHJPAIvJOxySUPkCfbHE\n6XSKbhzpCJ0FNNTW1kKr1Yr9lhACl8sV8z7LqbTKWMTXj/L4Kyill8Lj3nmEEHKl9EPquXNh3T1C\nyFhCyE5CyM5YCOtY+/GYKwgA3njjDXE7m4AF4PWQMbLjsKi21NcZT1YsWw6z3hD36yrBlGMWX8/P\neUH1IAEOBAvffBNmvUF8pYg/GsLh0UcfhUaj8et/0ox+SinmzfNUmo2Hu/bHH3+M6fnliEoBUEoP\n1/09CuBjAL0A/MZcO3V/j9btfhhAluTwznXbfM+5iFLak1LaMxZlFmLtfhk8eLD4/7hx47ysB/Y/\nm2iSfrby3Xe9VKXFaIJZb4AhW4+nnpyqiuLiOC6yMNgo2bNnD15/MyFTPqrz+r/CXw7QXlHu9UoR\nPrkmM0zZeuSYzJ6qvmFSXlmBe+66G06n06//eY1UCMHf/vY38X3fvn2jb3wI/l/HuHvBvYg4EYwQ\n0hQARyn9s+7/rwE8B2AQgOOU0rmEkCcBtKaUPk4IGQpgAjxRQL0BLKCUhlzRJRaJYJEkWYQ7pK+u\nrkbTpk29IoF8Bb4ckSwUr6Sdpmy9qqWwlXDubDW6de16XrhGjHoDNDKjqPPhe4ZLTrbBa35J7eTJ\ncPttuMspMtetNHnQ5XKB47iwjMZw2xnoWYlnIlg05nAHAJsJIXsAbAewjlL6BYC5AIYQQqwABte9\nB4D1ABwAbAAWA3g4imsnNU2bNgXgH7seFjHy1bNRlZqTT3IREplNm5w3QlEnMypNlrwJxVBg9fv/\n9tv82WefhXUat8CDUIivRMcQh+s9YDWWpG5anU4XlvCPZJQuJDhcKuIZCEqpA0D3ANuPwzMK8N1O\nATwS6fXUghXCIoSAJwCRsbIj8QHqdDq4XC4xzEw6LxAItmC91GKJlatGm5YGAH7XixSe55Genh70\n80AZu6tWrMS8l17C7n3xXfxCDc67WHACXDngKr/Nw4YNU5T4xJCuh50MjBg5Mqz9WY0mAGK2e7hK\n5B//8KxsRiggcHWF/eQOisMSq6FodJnA0gXYpfhm67L/P/7Pf8O+htvtxpdffukXYwwg4DaO40IK\nUTUZ88D9ftsCKac5c+Z4vaeUYurUqX77saiKwsJC7Nu3z++YQBbUvfeNwJthzgkEaiOL0pg7d67Y\nvhdeeAEcx+HJJz3pJ3PnzhX/nz17NrRaLZ544gnMnesZmLLP1CKSEcDevXtRVFSEG264AW+88Qam\nTp2K2bNnY9q0aV7nkwopteB5Hhd2+H8BP2toWa1Snn5mht82aXSebz+U3leO47BmzZqwC/FNmTIF\nU6ZMkd2PGUWUF0BSxeCCcz6Ug5arXUMpRX6OBSV2m9f2WM1VHDt2DO3atcOObdtxWe/6KRjFdXwC\nIAgCvvjiC9xwww2qW8idO3ZCRlpayO/mdDqRkZHh5b8NVHKD/e92u8VRWriFu+R+l2E33YRXXp0f\n1jmlbXvppZfwxBNPxF34smeUPQdpaWnihKk0gi0Y6enpcDqdQT9nFU8jIaICjgGel/WffoZx48b5\nLRYf7JqJcuc1lDmAFEGQWhRyyV+EED/hH+k15RAEAe3atQMAL+HPjpd7SdFqtejcuTMqKjwTymyZ\nzYyMjKDXd7vdYQu2Q78ellVsaWlpoJRiZIhhv9TC69XL893DFf5K+Of8VyI6jrkbHn/8cQDKXE3G\nrOyIrhUI39EaE9ZKfeC1tbXicyKNhAMgukEj5cCBAxEfK+X6G4fJCn9239mcwPlOSgHEAGnnlfMj\nqjWkV2KtRGPR+HYGnudx5MgRGI1GzJ49GxqNBqdPnw46ISwIAiZMmBCwDZ07dop6UppSihUrVojv\nfYfiUhfbrl27Yta5I7nHkVSQfP/d9zB12rSwryXF95rS90zwsyJp4VjEX3/9tZfhwHzqkXLj9UMj\nPjZcpGtGnHfzPQFIKYAYoNFoxKqC0voigbjjttvj1q5QykbqGw308rUEKaVo1aoVKKWYOXMmTCYT\nmjVrhltvvTWgxTd27Fi89dZbAa/dunVrlJeXR/XdmIBhnfaf//yn1+c8z2PdunVRXSNWuN1utGvX\nTvwOBw8eDCps2X29/c47MPahcRFf0+l0ei36IkWj0aCmpgZNmjSBy+USo2FCjZh8nxVCCDQaDWbP\nnh1xG6XtUYstW7YEjbsZMmSI2GdZHz7fSSmAGEMIwaeffgoA+OCDD7wmoJw1tfjgow9VCcm86557\nZPdZsWx50M/CdQEBwPHjx0Epxdq1a1FVVYX09HR89NFHAIAffvjBa9+333476LV/+eUXDOx/ZdDP\nAxFMSc2ePVu0On25/vrrMXRo/KxJpQwYMAD79+8X5wHy8/ODKgAmlKIVTvk5FpyrOee3ned50WI/\nd+6caA3X1NTA5XKFzCZnRoJUGU+fPt1v0tUUpo9bTUu8X79+EKhQv7gQIWLG/jfffBPQ2FGLZBxR\npBRAHZdddpmq5xs7dqxoCbMOcfvtt3sJ07SMdLEWSbTMfP452X1WrlwZ9DO5EUCo4f+QIUNQW1sL\np9OJO+64A06nE4MGeSKBQw392Tm1aTpFE3NSAiknnucxY8aMoNeklGL9+vVwuVxhXYvx2ZpPIzpO\nju+++w5t2rSJ68Sjo7ICmZmZ4trCjMzMTLjdbnFehY1k2TPAFI+vMGPzXuEYEEpR212nIZyobCml\nePjh+pSkU6dOQRCEgBFvSklGQR+MlAKo48q+/bzeGwwGv0U/wmHx4sUAgGXLloXcT61hphKrJVo3\nSzA0Go3oO/3444/RpUsXuN1u0RUQ7JhgHbumpgb5OZaI2xPMimPXi1ThPjppUsRtkkMq/MeOHQvA\nM6EufUVLoDpEtbW1Xs9gTU2NWACN+cFra2uRmZnpJcx976+ckSAl3PIK8XTFLFmyBBzHiWHCkUBo\n4AJo/3ol/OiwWJNSAPCUR1izZo3XtvLycriovya/8YZhis9LKcWiRYvCtuqOHz8e1v6Asop7oZQE\nc5sEeym1wk6fPo2JEyeiVatWYphlVZV/klCo+YiLCruFVX+dUuoXghjICkv0KmLBkLpVnnvuOdF4\nqKmp8XpFS6DEP2lugVarRdOmTUXh73a7QQhBRkYGeJ7HgAED/Pz8vs+2khHkqvfeDavd8Vw/gwUS\nBOqzJoMR+4v2+W3Xd+rsvYHzrFstbTfvcmOypMZQspCcPSLO2CvK/UMNKVDmYzGb9QY/ISIIAjZu\n+C7geSml2L59O4YMGRLw8/tHjwm4vU2bNrCVl4kva5lD/P+bDRsgwLP4uSAIgOCxyBSpmBBDU2bF\nB3sptZozMjKwYsUKHD9+HFqtFm63G126dEFaXQayoma63SirqvTb/tprrwUUhIQQxedPxok9Qgi+\n/fZbAMCCBQsUGQy5ORbkmXNUawOL06+urhbdI1qtVvT7cxyHjRs3+kX2MMOA/c8y4Cml4m8SrVuL\n9c9AfeLRv/0NRKPxlKAgnnLnoVwwXfILglpLd9xxB/bs2RPUZeUoK8OQQd5FDtw1ntGRlP1F+3D/\nmDFez5pGpwVNwlVyGmUimLT8aygCJW8Nv/kW/PeTj8X3zPfpKyBZGr00EYnFylNK8dVXX0EQBJw6\ncRKt27YJ+3tFgsVogrUs8FKGcn5LttaBUlgxrSZNmsDpdGLu3Ll46qmnUFNTE1BYS+9TKIxZ2Sir\nqhTvpZQvv/wSAGC325GTk+OXhBdtaJ9cgT6O41DqCJxpLkfz5s3x559/ghCCe+65B6tWrcKQIUP8\nnj/2Hc1GEzIyMrD/YPgx8r73+tFHH8X8+fMxZ84cPPPMM6itrUWzZs1w5swZpKWloba2Vnb05HQ6\nw1LyiSTXZEapw45rr71WvA/svgbqt4xnnp6BFcuW+RknvnM3wZI+fQkmh+KZCNYoFYBOp/OEwclY\nJkom5QRB8NSQ5/yHwuz4YPfYkK2HhpC4lQjOMRiDJlVFkwkcjHbt2uHYsWNip/rzzz/RokULv/Mo\nFf5jxozBj5u3oLi0JOR+bLKSuTAopfjoo49w2223RTWhKKcALuvdG++v9i+spgQ2WlJyLyilyM2x\nQBAE2IModAAw6g2eUWyAn1Z6HUEQkJmZ6RXlI/fsBjof4L3YOlA/4lqzZk1SRGBdM+QvKLPbgypq\nFrgRao5KDiVyg42QAgUkpDKBYwwr86qGxcJxXMBiTosWLZJ9EMorKxJSH14QBD+fuW+ddDWiOI4d\nO4bTp09j6dKl0Gg0aNasGSilmDx5std+Ss+9ZMkSWeEPeBT89u3bvbb93//9n/KGB0DJPYhU+AP1\nBciUWI6EEFjttpDCHwBsDjuWLlsasN3MjfP7779Do9GIwv/3338Xn9lwfnN2jO8Ii+d58DyPG264\nIeTxkyZMVHytaPjy669kR2kcx4mF3WJBWloaOI6LOBpNTRqlApD6KwkhuPzyy4P6liPlgQceSNp0\nco7jkGMyA6i3Vpo0aaIo5DNcWrRogREjRqB58+bQaDQ4c+YMXn31VVXvC7vPTPi4XC5ceuml4ufs\nWlFlQsc4OlPqrlILs9GE56bPCCpoNBoNOnTo4HXddu3aRdSGP/74wysMVBAEVFVViSMAOcVmMBjC\nvmYs+VsUE7aBnjOn04nevXuLrtFoQ2PVolEqAOYPZv77rVu3omnTpl5hi4IgRBV9QCnFF198oVaT\nZQm306bXxX9LC6RJCScPQA6O43Dy5ElQStG+fXscPuxZCC6cSJ9QsGX+mJDxbavd7rH4oulwai8V\n6QurAdS8eXPVzlleWYGyw1VIS0vD999/7/UZc5MJgoDKSo9Pu3Xr1hHfI992z5s3D1lZWarlNsQz\ntn7Tpk1RHc+S6YD6kOQmTZpg27Zt4kgvlgln4ZD4FiQAqUXIhMeGDRu8wh737t3rtUh0uD8Wx3HY\nu3dvdFYnpRg6dKiXEJ4zZ45XJ92zZw+0Wm3Y0S2+k8HsoQ32ijZbmSma2tpamEwmtG7dGrfffntM\nOravdTVp0iSvqJRIiPXCHSzx6M4774zJ+fv1q89zYc+kTqcDz/Po3NkTxnjixImIz+90OsFxHF57\n7TVwHIepU6eCECLWOfr5559DHv+3x/4e8lnQaDTQarXYs2ePuI1Sijlz5nj1DzXmGX755Zewj5GG\nxWq1Wuzdu9er/2zYsAFarRY6nS4iF1usaJQKAPDPJL3qKs+iGJMmTYJOp8Mll1wi7iudFOvVqxes\nViuAwKOEo0ePYuLEicjIyMC0adO8tD0hBB07dsR9992Hjz76CNXV1WJbpH9//vlnPPnkk8jIyMD6\n9eu9zv/UU09Bo9HgwQcfRHFxMbp37w632x21IFUrDFQOnufhdDpx6tQpbNiwISZhmZMnTwYhBMeO\nHQPgifBgCU2R8tPm2C7e3aJFCwCeUEQlmPUGFOYXwFUbvASzFPb7VVZW4qKLLkLHjh0xa9Ys1azQ\ntLQ0DB48GBMnenz5zB3EqoRefPHFsucI1RZmhHTv3h3FxcV48MEHodFo8NRTT3ntt379eqSnp+PJ\nJ58UlY7ZtLLfAAAgAElEQVRv/6qursZHH32EkSNHomPHjl79EwD++te/IiMjAxMnTsTRo0e9zi+1\n7q1WK3r16hVw9HnJJZdAp9NhUl3yYP/+/eF2u8WKuMkg/IFGGgUkZ5UHimTged5ve7AoCTayYL4+\nZmmF2l86KpHuw6wK34dGuh9rl9xvGSoKiAnJYKSnp+Pqq68OeX6lsFXEeJ4XIyFiMRIYP348Fi5c\nCACiJRapwFMSmRHN2hNut1scjTICtZXdpxyDEYIgwFZeFlbJ5uPHj2PgwIE4ceIEJk2ahKeffjri\nNkthQlD6O/bq1Qvbtm3zcwNF4hbyPX8k/USu/7E+y0YuwebwfM/D2sXkhO/2UAQ6fyoKKMb4Wv/S\npJaioiK/H8XXyp8wYYLfcezF8zwcDoco8KWZln369MHMmTPx008/eR0vzbbdtWsXJk2ahJYtW4pt\nlfoNAY+VyDoWG4VEq8ivueYaXHfddUFfagl/oD7pqHPnzmjevLkqowvpPAWLPHnrrbe8fptk8LkG\no6amxk8oBnLFARATmRyVFWEVVktPT8ddd90Fq9WKEydOqCb8gfoFZRjz5s0Tfd5s4lOOHIMxqPBj\nfYv1hW3btomjJSaQpUZQixYtMHnyZLH0t7SPsb8//fQTZs6ciT59+gCAaOSxUFDWj337OXs/YcIE\nrzb6ygmpPAkmLxJNoxwBAP6jgNtuuw0ffPCBVzQGE0zMoj969KhYAtnXsvClV69euP7669G/f3+x\nMBpDXBJOxhJaunQpxoypzxZu06YNysvL0axZM/Ec48aNw+LFixU9UPHOA5DD5XJh2bJlGD16dFhK\ngCWDySH9TjabDWazOaJ2ArEfAUybNk2V0snBEAQB48ePx6JFiwB4RgNqJm5JVw07evQo2rZtK1rF\nSkde7B4HG7UTQvDggw9i4cKF4jnPnDkDg8HgVT5lyZIlGD16dNDrSPu4b7t+/PFHfPHFF9i0aRM2\nbtwY9Fjp/6dOnUL79u29DDFWC4vtM3r0aL+6YMH6UyoRrI5Yu4BYrRppJi+rhR6tVcpxHO666y68\n8cYbojWfaEJlAidCAUQKU2SBFCirX+9yufwEXDTtj7UCIISguroaGRkZqobhMhYtWoSHHnpItG7V\nJi0tTRx5+fLVV1/hmmuuUWSgAIldxvXs2bMYO3Ys3nvvvaifd7fbLdZRAupHGFJ5k3IBJQBmLaen\np0Or1WLnzp3iNrfbrYpLglIKh8ORNMIfACgf3B/pOzQN9EoWbOVl0HfqHFBQsvLGHTtGZziEi8kU\neeVYxm+//YZTp06p0Bp/xo0bJ7pRYkGPHj288gAAjwDs378/rrnmGlWqmcaDpk2bwuEInWCnFJbd\nze7Jjh07oNPpxMioZCgb3SgVAOCxuMaNGwe3243evXuHdaxSYVhSUhK0wwXyiQbaN9iDEsnDE41l\nqTQMlNL6klexVBoVhw+F/Pz333+P2bUD8dWGb6M6nuM4nD59WlHuiMvlCjuLNNZK/Mcf66OkmHsl\nLS0NmzdvBiFElWqmUoL1iUDfMVylV1paGpNRWO/eveFyuTB+/HjVEy4jpVEqAOa/ZysBhX28wqSg\nkydPguM4sbyvlED+11ALxyvdNxShslkDJX5JX74Lh/giCAJM2XqYsvUwZ+tRfeYszHoDKsrKkWMw\nItdkhllviJkQiiSyRClKlG2036qwsBAnTpzA2rVrZfdlViQATHj4kSivrA5s8pSFDbNaOtK5AbWv\n50uw31/pvv/6179AKcWJEydk28zzPHKyDcoa68Prr78e0+c1HNQJ7m5gRP1AknqLqri4WHzA8vPz\nxV3GjBmDJUuWiMlbDz74YHTXVIFQ3ztYiJwSuuTmeaImKiu8r0cI9EaD6NPleR5dcvPgdDpVr4EU\nLDRPDZQoW4EK0JDI7akJEybg+PHjogKglKKkxLvuESEEeXl54ntTtt7vnicK6f2W/g7J4OZQyty5\nczFx4kQQQjBq1Civz4qLiwF4vltBQYFnzWBddOJTjaVgo6VRKgA1YJZxly5dAn4+evRoLFmyBIIg\noKzMf1JLWmedUVtbC61W6zUHEdRKEGjAInShkJYzYCVxGSNHjgypAAJ1ZJ7nUWDJVVwCWaPR4KC1\nFG63G7kmMw5aS2NWnz/egica4Q94akctXrwYp0+fBuD53aUGRSCSRfgDnuSqI0eOwGj0TGBKw58B\n4J133pE9R7STv8H6SqDtgZ71I0eOiG4kafQdgIC/RYndFmFLPSTD2hQpBRAjrrjiipAlJLRaLUyd\ns+E4VB/O2K1rIabPeBojR4702jfXYEJpef3EVKhwzlAQTX1bfCe6ly5dGta5BEFAnjkH1gjaodVq\nUWK3waw3wFrmiEtHiGa4zWoJxRJCCE6ePBnz6wQiVHSYUpo3b46bbrrJLwmLwRLyVIXCq9T170eP\n4dixYyjo6m2UuZ0uaNPqXZis3LMA6mUUSXNFrrjiCvXbm4TImi2EkCWEkKOEkH2Sba0JIV8TQqx1\nfy+o204IIQsIITZCyF5CyKWSY0bW7W8lhIwMdK3zCblJt4//8180v6CV17bc3FzccsstfucpKffu\nnJFGckiHnAfqyipHainnmsywlZchz2SOyHVk1hvgqKxQJeQtENJJtmgn3K675lq1mhUUnudx7Ngx\nsZ2fffYZZs6ciZkzZ+K5556LyTVdLhdyDEZQSqP+Hc6dO4fu3bt7zRtJI2DYUouhCKcNhs5Zftva\ntm+HGwOUnZa6zYA6l55AQxb4a0iuq2hQMm5dBsC3BzwJ4FtKqQXAt3XvAeA6AJa611gAbwIehQHg\nGQC9AfQC8AxTGg2VcB4QvV7vt+2WW4djT9Fer23rPl+PpplN/Pb1fUyVJEEFItBohG2TUyrS72vK\n1qPY5qmHVOqww6w3hKWUcgxG0X1RVlUJY1a24mNDkZmZ6ZWkI1VMn3zySeQnlvmt1ZjM02g0OHHi\nBLKzPfdi2LBheOaZZ/DMM89gxowZUZ/fl9raWhRYcr22RfM7aLVadOnSRQwFdTgcojuTEOK15rYa\nhfVs5WUos9n8jA/fkYzb7YbdJ6yTEILSOp++FKmikPtNKaUwdVbnuU0ksgqAUroJgG+ZwJsALK/7\nfzmAmyXbV1APPwFoRQi5EMA1AL6mlJ6glJ4E8DX8lUqDguM48FTwsnikSN0/r7zyiuLz+k4sxStS\nQM4NIy2zQAjxciE5KivQJTcv2KFemPUGP/eVWhmp586dEwUCK9LFGDZsWMTnVbJcphocO3YMf/nL\nX2T327vXYzgcPxZ5qGvXPH+ftkajgVlviCikye124+mnnxbrGbEKrOfOnYPb7Ubbtm3FfdUora3V\namG05Mj2D61WG3BFtNwuBX7bWD8N1p/9RpWahh9EGek36EApPVL3//8AdKj7vxOAKsl+h+q2Bdvu\nByFkLCFkJyFkZ6ySVqKFAlixbDk0hAuaKLVx40ZxhSVft06iiCb6iT34FqMJtgARPCV2G0zZ+pDX\nsBhNsFb4zxkcKC2BJcwFzl186AiKdevWiW3p0KFDTIf0aoU5/vnnn4pyUm4ddhMAoE27tjJ7Bsas\nNwT9jBACY3b4li0r1cwmUZkCTktLEwurJTvXXXcdqqqqQCnFli1bvD7z7edn/zwTsB80NKKeBKaU\nUkKIaoG+lNJFABYBnlIQap1XTQiA+0aFnsZg9d13796Nq6++OuGFyARBAB9CUH322Wchk4syMzNx\n3XXXgQuRBeGorIAxKxuOygo/C8qsNwQN/dRoNKBhCoi/TpyMa6+9FjfcGNiyv+CCC8TQxHvuuSem\n97/lBep4M2tqatC3b9+gn0ujxh5+aDw4AK+99abi87tcLhRYcmWtZjYSCCdUV5pBz3EcVq1aJQrL\n6upqMS+AvRLdHwIhCAJ2794NAHjiiSewefPmoPs2bd4sXs2KKZEqgN8IIRdSSo/UuXhY0ezDAKSz\nM53rth0GMMBn+8YIr90g2LZtGwgh2L17NwYPHpzo5oAQEnJd3HPnzoW00sQJZJnQU+bTl7p5cgxG\n1eP+X3vj9ZCfS+PSb7vtNlWv7cuuPbtVO1eo0E8mNAONouSora0N6PYJBiFEcdE9AGJNLeYm6dq1\nK+69914IgoDevXuLa1AnSwZsINgiTgD8RgDnK5EqgE8BjAQwt+7vGsn2CYSQf8Mz4ftHnZL4EsAL\nkonfvwCYGnmzE49cJh+zcvbu3ZsUWX+EEIwaE7xC4hVXXCG7IAcAPDdrluy1yqoqUWDJhZbjlFuS\nKliELOuU3W+WHBZuqY9Ecfr06Zg9K+EIf4ZGo0Ge0Yw9+/cho0lmyH0rKyu95pHOnTuH9PR0EEKw\nfPlypKeny7rhEt1HpCMAJfsm4ygmXGQVACHkfXis97aEkEPwRPPMBfABIeR+ABUAbq/bfT2A6wHY\nAFQDGA0AlNIThJDnAeyo2+85Smnk688lAfqsbFQeqvKa7GUWNBv6CoKAoqIivPPOO3jggQcS1lZG\n165dg342f/78kBPBlFLMnTsX06ZOxYzp08O6rpLwPjX86FIBIwgCrrzySvzwww9RnTOeRfBOnToV\ncF1jVlsnUizGyAvV8VRAYX4BbJXlIffr1KmTWPu/V69eaNKkCSilGDRoEL755hu/3JZARJuLEC1L\nlizBvn37Aioi1jfYHAfHcWLl2YZMoywHHS1K/Ji+D1Ey3Gclo5ZgMGv6vVXv4p4R98peK8dgFGPB\n7RXlstZSuD5nJSxYsACTJ08WBVOkyCkwtZ4xrVYLu90eMGw4UtTKs6ipqcGh/x0J+nl6erro5mEj\nMbbwD0NJOehEloKWuqdYEcZgz01ujgWldaHQapMqB53khMrwZUjdDoke2jJCFbFzOp0hi8E5nU4Q\nEDwjs4qU0+kUQz3dgoCyqkqY9YaYDv+DCZbhw4dH7XM+8ftx+Z1UQhAEbN++PeQ+BRJXjm8cvy9q\nJtllZGSEjB6SBhAwKzncWjeJ7ifSelIsqS0YsRL+8SalACJEzpp5++230b59+zi1Rp4v1n8eMB6a\nIReLn5aW5imCJ9NJu+bl+1nyZVWVyDPnxCwUMFhH7dSpU9Qjrx49ekR1fDgQQrBt27agnwuCgIMl\nngSmZ6c/HVLAxiLDmhACc5Y+YJ4As/4BYMWKFaCU4syZM0hLSwMhJGRETbLAnqMWLVpg0aJFss9O\nMozqoyWlACKAZTKGEmiFhYXo3r07gOR4UJYsWRJ2sTcpTNhoaPDvY9YbUBrEj3vQWhrSF62GcnC5\nXF7zL2pYlGlc/Ap2sUVD2P++SEedq1evxrna2oDnicbnLwfRcMgJMBLQarUYNmwYCCGYOXMmAE/o\ncFpaGiilmDZtWszapBasD/To0cMvkdCXD1d/EK9mxZSUAogADh63AleX9RjIzSAIgqgApEPLRLFz\n586gDzTz17Ja7oFebLKrtNwRsGQAC/UM1mW0Wq1nEfNsvZ+yMWXrIy5vIUWn04nfUSoso7n3cgln\nENT7XSml+OWXXwDIu0MOWktx6NfDAT+rkVjjsSDYhPCMGTOg0+lgt9tFBTx9+nRwHIdNmzbFtE1q\nwJ6ZSy65xO8z335+2x23y7rgGgIpBRABFECeOQcE/hmCQH3n7du3Lwgh+P777xPu35Ra2HmWXJiy\nPRONLJxNrhREZmZ9GGB6err4faU+fyU4Kiv85gQiCafLz7HIjlrYRH009162bWGW5A4FIQRnzpyJ\n+jxVhw/FrMJqsN/Z7XajZ8+eYmTMiy++CEIInnjiiQYTMslWL+vdu7ffCNK3n0vrYTVkUlFAMYBF\nv5w8eRLt2rUDpRS7du0KaFnEC9/6/77odLqQPuX09HSvZf1YxEaoUsJGvQFlQSJ7WNRPNJEfFMCS\nd97xE3ZsMQ82sokmhFLOl+4WBJSrVJefZcsKgoBly5Z5fea7QIkS9FnZ0KmoCEL9Ti6XC1qtFo8+\n+igWLFgAjUYDp9MJSiluuOEGbNy4EefOnQMAvPDc83hqhn8wgRplqSPll19+wcUXXwydToeqqip0\n7NhR1UWFwiGeUUApBRADCCH44Ycf0K9fPzEkLtFuoJxsg2wsdzhQSj0dtrwsqNsnlAJgxx+0lkYc\nS63Esoz2vst1xlKHXTXrlhCC7t27K05GUoKhc5bf2g+RIPc9ly1bhlGjRuHUqVO4oK40xuHDh3Hh\nhRdi+/bt6NOnj/g7lNkdMJpjN08RCew5YTkXu3btQs+ePc97BdDoF4SRu9kCAEeYSmTevHkYNGiQ\nl8UcrZBY9NZCvDR3bsh9Qim7UOsBA/KTpoIgeFnahBBxBHDQWhqekKH16wFEgxqC1/f3Ly13hFWt\nUq4NAihyDd7CLtTvdNlll4U83+KFi/DguLE4cvhX9L7sMlQGmQdglB+qQlanzkiPImFJiRE1ffp0\njBo1Cq1atUKzZs1w5swZzJw5EwsXLvTLxI5W+Juy9bI5ONGMJAghuOKKK1RZhyFeOSSR0ugVgByh\nsmeD8eijj2LKlCkgxLOYOhvWR4Oc8JdDTlClpaXJRuIEsqStZQ50/n8XepKYKsplfc+GzllIS0uL\ny3KGrDZNKKQd8KW5L/p9rsaobexDD+HxJ5+Q3Y8QgosvvhgA8Omnn/qF5l577bV4cNxYAMCAK69U\nvMpW1eFDMGZlRzQvoFRAvfzyywCAkydPoqamBhzHidFA27ZtU6SslboD5c4VzW/GRqPnzp3DU089\nFfF5AKgaIBArUgpAhjWffRr2MVK/M4uPjlaQROuPjGUi1qH/HfFY9QYDwHEglOKzz9cDADZt2oT7\nR46CAEBwu1F+qCrkudSEDevZEoCRoHZ2cih0Oh0KCjx16m+88caA+1x6UXcQjQY1NTV45JFH4Bjm\nvwJWIMqqKmExmsJ6Dg9aSxXvO336dNx1111o2bIl0tLSUF1djenTp+Ptt98WJ1XjRSR9TRrUEOk5\nfNHr9arOwcSClAKQQb1C14lF7nuEKgWt7AL+wrKkzjVU6rDHPApKahUyy59tO3LkCDp37qz6NdUu\nXdC6dWt06dIl5D6/7N0T8fmtZQ7FCXnhfq///e9/ADy/w/Tp0zFt2jS88847WLhwITQaDe67776I\n2hwJm3/8MW7XCkWaVpvw8G85UgpAhmRZ9SfqrESZcMVp06aF9OO7XC688MILoa/hg1orfSkhkIXJ\n7skPP/yAu+66S/Ycjz0+JaT/PzeC9Y/DmU9o0aIFOnToIL9jFJTYbSiw5IZU+JEoterqajHgAagv\nl5KWlib+NsuXLw91CtW4sFN0gSNqkezCH0gpgAaD3MPUQ2byUI6XX345ZBgopTRsBZAIpAXv2F+l\nCkDOt+wbRqs0WkOJ/x/wXtM4lhy0lgadE4h0ROProvTNjYlVXkJDJhkWnk8O8zZRJL+CVswHH30Y\n1fFnz56FIAhBXw1hST8g8FzG1q1bE9CS8OE4Lm73uayq0u9eRePOOnv2rJh0xwrBcRyHLl26QBCE\nuGYCJ4vlLSfgpyZBeYxGrQBGKahR3lCI9pFnRbuCvZLNgnv11VcV76tmXL0UtUP4mjZtqug+F1hy\nIQgCOnX4f1Fdz1rmEK8X7XfJzMxEXl4eBEHAypUrodVq8cwzz2D//v146KGHcOWVV8qeg6j0jCU6\n654hN6J8YOyDcWpJcBq1C+iHJCjRoBbRfotksZqU8q9X5mPy5MkBf79x48bhrbfegsvlQlFRkVel\nSqVcMyj6ZTy//PabsPZ/9913xf8DfS/2G+09sB8cx6FJkybRNRCeOQE1whVfeuklTJkyBTfeeCPW\nrl2LsrIyGAwGr/r6cljtNtl9nDWBC+AlHQpuaTKsFNioFYB00qqxwkIkH3jgAa+MXN/7Ul1djRUr\nVoQ8V1FREbp16xaTdvpS6rDDLBPWqNPpUFhYGNH57fYAZTMEiqKDB9ClSxd0794de/fuRVFREQrz\nC6DRRd+VsrPri+wF+1533XEneJ7HPSPuVa9sggr1jKZMmeK1JCfg6V8FBQU4cOAAfvzxR/Tt2xeU\nUuRZcgPW0x808Gp8+92GkNcplImSShoU3NJkqI/UqBWAXJmAZJikARCTWupM8GvqKpoqQU4BXHTR\nRXHzY3McB3sc68aUWK3Iy8tDYWEhbA47+vTpA5vDjhyTGdqMdJSWlsJiNse8He+v/nfMrxEJOp1O\n7C8cx6FNmzYQBAHffvstNBoNbr/9dvTt2zfqDPBEW8xqkgxLSiZeBSUQOUHFcRxM2XrkmszIs+Ti\n96PHwPN83CdER49QP4b6rxMnif9TSuF0OkNOAitZ3Um6jN751FF79uoFfVYWiktLYHPYkWsyY/Xq\n1Z48AIcdB0uKkdWpE/r07ZvopiaMs2fP4rvvvoNOp8Ojjz6KY8eOYcyYMRg8eDA+/PBDvP/++wAQ\ndQa4kucwx2CEWW+AUW/A999tjOp6sYJSmnDhD6RGALL7iOFtgoA+vXrJ7usWBHz1zdfIyckBoKxg\nWSJY8MbrXu/T09ND7s9xnGIlAHhqqrP7y9aGTdZ7EQpCCP79wWpkdeoMnuc9Rezy8mAymVDQtavH\nGBAoiEaDocNuwI4dO8BHm1TXAHn44YfxzjvvYMeOHejZsyeaNm2K6upq1NbWIi0tDWlpaRHNxfii\n1G9OCIEGwP2jR8vu63S7MWvWLIwYeZ9XUbhouLgwtCtUbmW9eNGoFYDaCIIADsC1g4co2n/R22/j\n6sGDPMeCBk0aIjT2EatquLtYp/nzzz+xa9cur88uuOAC/PHHH+J7VqJB6jdORuVQYrehML8AlYcP\n4dFHJuDvU6agtLhYXBTnyOFfMXvOC7j1llvwt0f/ilKbFT0uuRRCmOvhNnTeeecdcfTHcRwuuOAC\nnD17Fl988QWuu+463HrrrapcJxYjyzStFs89+yyee/ZZ2X2fe+453DXiXtYYcU0Q33bJretA+ORw\nLzdoBbB161ZcfvnliW5GxIx94AG/bcyHLp2f4LRaIEq3k9xk9+WXX46MjIygn/M8LxvL3a9fP2zZ\nsgXNmzcHAC/h/vnnn+Paa68F4BnGs7kHSim6d++OoqIiaLVauN1ur7UJHA4HDAZDGN9UXQzZepRY\nS2HsnAVrmQM6nQ6zXngBd959Fz5c/QGyDXosXLgQpmw9WrRqiYKCAgy/+RasX7s2YW1WCybUli9f\nLlvKgVKKb7/9FkOGDMGUKVMwZ84cjBkzBkuXLsV//vMfDB8+XNU2JYoZM2ZgxowZfttZGWmtVqvI\nkImmwsCmTZsUhdUqIflMrjAgGg1s5WWwlZehxG5Tpe55opGWZWa+dCoj/DsqqHMj91Du3LkTP/30\nU9DXli1bZK+xefNmr5WTXC6X6DZZv3691/KSLGmI4zgUFRUBqFdSbdu2xa5duyAIgp/wD6TI5s6d\nixYtWojVV0PlMlx99dX46KOP/M4hnddh17CVlyFdp/OsbavVQafTwWI0Ydq0aaAEePzxx73O4ayp\nxa5du/DJJ58kzRAfALZs2SKGZOp0OlxzzTWolawnvHr1avG+cRyHWbNmib+hIAhYq0CZjRw5EkOG\nDMHu3bvx4osvomXLlli6dCkopRg+fHjCBXesYaMAnucV1dUKJ/pQp9Oh1GEXZZ1a+RJAA18Q5qft\n29G2fTu/7TzPIz/HAo7jPHHOQVBj4YVkQEkSj0VvhLUi8mQft9stq2CDdXJCCO6++26MGzcO/fv3\nD7gPm2xm1wi0xKYS32ygfdi2w4cPw2azwWq14uDBgzh58iSOHj2KiooKFBcXe81xsGUuLUYTim1W\nPPzww3jttddQYMn1ut/GrGxkZGTg6+82oHPnzl4rpeV2KUDr1q2RnZ0Nk8mE1q1b48ILL0R+fj5a\ntGgBwKOYT58+DavVit9++01sT1lZGQ4ePAiHw4Hjx4/7CYxOnTrBZDIhr24+orCwEH379hWjb3yL\n4wHAzz//jG3btmHXrl3YsmULSktLQ1aZzcjIwIgRI3D33XdjwIABIe+7EgGvhqw5X/rs/ePGYurU\nqQE/y8+xgOd5FNusARMDjxz+Ff379Qt5/ka7IAxbBpD5mIPx+GNT4tiq2KJEMAoyswiZmZleC9j4\nwiZyQyEduUjjwWfMmIH7778fWVlZQY9lowP2XXzXY1UqYHz3O3DgAPbt2weHwwG73Q6bzQabzYZD\nhw55udmkx0kVDnue/jh+wk+oajQagOPgdDpx7mw1QOtq3tT9Xb9+vXi+Dh06oEOHDujYsSMsFgvM\nZjOMRiNyc3NhsVhwySWXeJ3fbrfDarWirKxMVFrFxcWwWq2iMvv111/xww8/ID09HV27dsXll1+O\niy++GD169ED37t3F82k0GvA8j169eqFXr16w2+344Ycf8Pnnn+Orr77CqVOnvL47c0PW1NRg8eLF\nKC4ulnX/MbddNEJeLkhAcDeMciRKCCb8gfpIJybHYjl6Om8UAO9yo0t+vrgerxz/+fDD82ZYqsb3\nYOu1RkOoiWTWsX0LhAmC4Cc0lixZgtGjR/spA9/vKQgC3nzzTfz1r3/1G3YHEu533nknnn32WVx1\n1VXi8b4VLNn2XJPZ6/vs2LFDtMbY2rX5ORbYHHbwPI/CfE8d/52//AKjwRB1kqHZbIY5SF4BUz6B\nhIOvEGXvV65cidF1ETGEEMyaNQurV68G4PlN+vbti59++qle4f3xB5o2bQoA2L9/v2x7TSYTrFYr\nBEHAqlWrMGLECOzcuROXXnopNBoNLBaL7Dk4EtpN6buy2PlOjsEIrVYLQRBwsKRElWRDXxr0HMDy\n5cthMZqQYzAiz+IZNikR/kphnSzZUdLGeCg7Qgi0Wq2f7525GZiwZ75ll8sVUGmMGTMGHMdh+PDh\nXqM43305jsMjjzwiLj4uffleSxAEvPfee6LwZ8ezdkvvD9ueZ85Bi1at6udlKLC/xOMqyjEYxfZr\ndJ6JP6fbjW7duqFLly4gPr+JtDT20qVLFd1P3+/L7gVTRIF+U18Lmr0fNWqU1/2QrnZFCMHWrVvF\nz7ZI55UAACAASURBVM+dO4fMzEzce++90Gq14uR9KGw2G1q2bAnAkxGu0WjQpUsX8ZwXXXSRou8c\nipPHj4f8nFDPEq7JUGJBLVj4dJ7FghyDERajCcuWLVPt/LIKgBCyhBBylBCyT7LtWULIYULI7rrX\n9ZLPphJCbISQEkLINZLt19ZtsxFCnlSj8W++/nrEAlrJQi8ldhvsFeXi5EugV+u2bQO6D+KF0uvJ\n7Zeenq5KMTie5zF//nwvYczzPGbPnu11Pq1WKxZ08xXeTEh9/PHHXtf1FW6h4sqlI5qbb75Z0f0I\ntG3HzzuRZ86BrbwMhqwsbN70AxyVFeLvv2nj9zB1zkbTpk3RNDMTaz77FMUHDvidRzpCCfVbBFJE\njOnTpwf9LNg5fPuHkv7C3HGrVq2C2+1GVZX8Km48z+Po0aNYv3495s2bh7Vr1yIzMxMajQatW7fG\ne++9J3sONXCUl8FeUQ5rmSNon82t8xT4lqxuCFBK8c7ixaqdT8mYYhmA1wD41gF4hVI6T7qBENIF\nwJ0AugLoCOAbQkhu3cevAxgC4BCAHYSQTyml/j0lTggcUWX4s33njqCfiY8WpejdoydOnDihwhX9\nUaIELpMZPtfU1IQ8j5KOwixUjuOwdu1aDBs2TOxo69evV9zZmNuC+a6lSCctmVU9depUzJkzx2u/\njIwMVSzBPHMOrOVlsOiNcFRWoGtePpxOp9iOtLQ0lFVVwpylx9afd6B/vysajPUZagI40L0PRXp6\nOrRaLXbv3g1KKS655BLxd7z44ovBcRxcLhfyzDnifdxfUqzWVwEAUIW3ff0XnwfcLggCCMeJsf0P\nPzQeX3/5pXoNTEJkFQCldBMhxKDwfDcB+DeltBZAGSHEBoClz9oopQ4AIIT8u27fhCkALUjIidFQ\n0UNKEZ9HQrD9l5+D7sfi4gVBwP8NvxXFBw4oXqJRqVC9//77vd77rpMrt24uz/OKooB8J0qVJnd5\n5T3UHSOXnOZ0OhWtOvbJJ5/4bQt034LdS33HTrBXVcBiNIHnea91jQ2ds2AxmlBaWYYuOZ6Vts6X\ncORwYEX3bDYbKKXo0KEDjh07JuZ5CIIAnU4HDeGQazL7La6jBtEqXumzSgjBmwvfUnTcjOlPeyq5\nSkK4GwrRGMETCCF761xEF9Rt6wRAOl48VLct2HY/CCFjCSE7CSE7Y1lzRy4qJp5LQTK/uUajwcdr\nPsFBa6k4XFWLQYMl5Y1pfeIKADE+nA39mfUtfSkpPcw6UG1trV9mr1S4qpXxG0r4+/r1o71OYW4+\n7BXlKD9UhX17i2A2mrBvbxHKD1XBXlGOwtx8UEqDCn+1XQ2hBHSoa8VKQBUUFEAQBPzyyy8APC6v\nnTt3iqMB8b5wBK1at46J6+XNxYtUP6cSnpv1POxlDtFd7JKTWyqU31aLSE2VNwE8D4+X43kA/wAw\nRo0GUUoXAVgEePIA1DinL7xLfqKYRF1hP04oEKZ+rhACdMkrQHFpifi5b9SKbwdVMiJhk6W+Mfxq\ndvZEVWjled4rBp0AuPnGGxPSlmSksLAQHMdhz549aNq0KXQ6Hfbu3QvAEyHEnr+QJayj7HKDB0e/\nhoMa6OTmy1Qov60WESkASulv7H9CyGIALFXwMABpsHfnum0IsT3uKAqnohRoAMM5W6C69QHwVQJM\n+DOWLFkS8nglliPbZ82aNX4Tr7J5CklSepsx/7V/xeS8+TkWFNusmDD2IXz59VdeAtGUrfcUm6sL\nM5Vi1BtQVlGO5UuXYeToUV6fOZ3OkCUI4lGEr7CwULyOxWKBIAjYs2cPCCG49NJLZV2MjYlkchNF\npAAIIRdSSo/Uvb0FAIsQ+hTAe4SQf8IzCWwBsB0e3W4hhBjhEfx3Arg7mobHmoYSSkZBZUcrP+/Y\niZ69Qi8aP2rUqJCfK60ESggRK6GGQ6B7rXTkMGfOHLz//vuyC7+Hkw19ww03KNovXIrrFkL57PP1\nfus4s1LJzVq08IytJbckPz8fAHDHXXf6nbNLbp7Hp+5zTHbnLFQeqkKX3DwAnsXgpWzdujWocgh3\n1Mb8/ADQo0cPcBwnJq1lZmZiz5496N69e1jn9GpPxEcmH0OHDUt0E0SUhIG+D2ArgDxCyCFCyP0A\nXiKEFBFC9gIYCOCvAEAp3Q/gA3gmd78A8AillKeUugFMAPAlgIMAPqjbNyHM/+crsvskQ2VKteL7\nly1bJtuBpPHygV5KrDfWFukqXIG+g1JLcPFCZT5dk8GoKEvUWlEGV230JYmjoeelPXBVvyvQsmkz\n3HZLgAJpFPhlz25M91kwPK3Oh56RHrhgH8dxfi6UyrrJ6oOlpSg66B9vcfrUHzDqDQHPl2fOCSsK\nqFOnTvjtt98gCIKY9MXmAwRBQElJSajD5Wlg4ZqhmL9A+XrWsaZB1wJSQqCJVCX1RNRe8DsSKACL\nTFuVtNNkMMJaZocmRKZlaWlpyGzgjIwM5OXlyV5LTQK5QoLx7spVuIeV6Q2CoXMW0jIyAi5H2FBh\no65AI9ZhQ2/A//73P5z4/XePRe5zLyml6Ni+A44cO+p33lMnTqJV6wv8tgdDSeZzNLLmpmE3Yn9d\n0cBgJEOfBeTli1w71ah31GhrAalBQ3D9hIOW42TT7PPy8mTzANQyFlh4aKjrsWJYkydOwqv/WiB7\nTjnhD8ArfPN8IViZDAD4bF3oKp6EkIDCHwBaXtAKn36yBjfefJOidsTakNy3d2/UeSop/Em8nyMJ\nSZaH6ezpP1U7l5xK0+l0ATNy2UtNl5ihc5askmXhp0qEfyAoLzRox7G0XHMiIIQoFv6A9xxRRUUF\nKKXiPMrUqVOjnuSXe16SwWULoME9c6kRQAC4JEnkuSSKSTMpSny5cvuoGaVT+WvsA8AIIVGHFSaS\n9LTQS3QmG+PHjwelFFu3boVer0ebNm1w7JhnDW2dToe5c+fGNNIraaLIGtgzlyRqM7k4UHww6nMw\ni4X5RiNZAFqtwnZKJl3lRj1KLCylxs/55mJLASxevBiEEPTq1QuUUrRv3x4cx+Hrr78GpRTz58+P\n6fWjfaZ851Eizea++87QkWjJRkoBBCDaVP4ZM2bgggsuEN0nhJCwIiqUtkOpq0rJtaWllwO9lFhY\nOUEiSlKc/7Ay0Glpaejbty8OHDiAU6dO4frrrwchBOPHjxf37RRlYEcgZr3wgqrna926NZ544omw\nj9u6dauq7Yg1yeHriDOxjhaYNWsWduzYEbIqoxKURsDIodQ6Spa5j0hgCVRSkiUqJFJ8o0GS+fuw\nke4999wjVpY9cOAAKKV47LHHkJaWJj5f6RGMhmP93aXGDgB89913KCwsxIsvvhjWecoqymPQutjR\nKBWAWgTLbqSUokePHjh6tD7C4tChQ/FsmheBRgDhhFgqvYY9gQ8/ISSpBWTYkOQW+L7MmjULhBCM\nHDkStbW1OHDgAC666CI0adIEJ0+exLx5nsLBr732mpjwlkyUlnqS5CilqKioQNeuXRuFqzLlAooQ\nfVZ26OXrBAHbtm0DAHz++efo1Clg7bu4EKidvS+/XPxfyYMuN4+QSvNv3EybNg2UUixfvhyEEGRn\nZ8PpdKKgoAAajQYLFniiuSZMmJDglgYmJycH3333HQBgy5Ytsi7PhjxalpJSABHSqVMnQKBiPHsg\nd8+WLVtACMH1118f7DRxIZCAf+ONNwB4x/f7DoOlxLIya4qGDyEEjz32GGpra/HRRx+hZcuWsFgs\n4jKTkydPTnQTQ0IpxaBBg0AIwebNmwF4RxaxfiFdRe6qflckpK1qknIBRciPP20VyycEghAiLo6R\n6KFkIGulRSvP8n3RzlMkI3lGM3gqQABgtdv81ilIoT5sLeF//vOf4nKfbdq0EdcjTvZni1WylRax\nk+Lbfp7n8f2WzfFsYkxIKYAoCCXYS0tLsW+fp0Zesj/85xs89ShlDp6aNqGglOLTtWvRtVthyLIK\nKeT5448/0Lx5c/Eenjx5EoQQ3HvvvejXrx8MBkOimxgUtiATIQR79uzB3r17QxavO19cnikFECPG\njRuHX3/9VdWFSSJFifU7fvz4kH7P82GVq0AQQnBTgOqMlFJQQsDVufl4KmDNurVehe5S1OP7jPu+\nNxqNSW8Isb569uxZPPzww9iyZUuimxRzGmUxOLUozC/AviBJYzqdTqykCSR2FKA04ieUAkhmF4pv\nSWM1immFS0ZaOmpdnrWC//XmGxg8eHBS3zO1kSsGx3Fc0s8jse/AFEGo9saiRAojVQyugbCv+KCX\nhS8VoG63G4QQFBYWYsqUKYlqIgDlyqehCizCceKCKYmixump3cPzPB4eOy7kvpQXoNFpsXDxYgwc\ndDUEUHANrYaAD6dPn0azZs0A1AvSFi1a4NSpUyCE4KeffkpwC+V5/fXX8corr8Bqtfr1GdY3pMmd\n5wMpBRAhVqsVFosl5OLilFL07NkT9913X7ybFzZdu3YNucbuuXPnUFxcHMcWnb8QDQdBEPDg/ffL\n7ttQcgHS09PhcDiQk5MDSinGjh2LN998E4QQ/P3vf8eCBQsULSuaSMaPH49NmzbBavWUC5cKet/R\ncZ8+fRqEUpMjpQAihC16EQipddC1a9cGYTEcOOC/YEiKxBNoTYhkVAqvvPKKmAuwadMm9O/fH4C3\n5dwQkM7xhOqz54PwB1IKICZQStG/f39s3rwZPXr0SHrhDwBff/11SAstWSeBjXoDtFotqs+cgVFv\ngM2hbI3khgKBR+Ab9QY4KsqT1lE0bdo08DzvJejZc28wGLxWBBPcPDhtckbRXHrppeA4DoMHD24Q\nhlu0JGevbgAU5hfgTHU1ygOktRNCMHPmTFx99dXo1q1bAlpXj1LLa+DAgQ0ytM3X799QLM3zDWlO\nzCeffILhw4eD4zgsWLAADz30kPhs5ZlzUGK3JbKpIbnoootAKcWzzz4bVPifT4ohpQAipLqmBhzH\neUU/SIXPwIEDAQBt27bFhx9+iNtuu83reJ7nAyYoud1uVa1tpQ+qkms2BOEqWxOIAia9HkB97Dc7\nLkXk1NTUAABGjBiBVatWgRCCX3/9Fe3btwfgiYpzuVwosdvw/XcbcdXAAXFrm9I+9dlnn2HYsGGg\nlKJPnz5en0nLu9fU1ECn08Et8NByDc9oktIwwz6SAMrzoDwPQRACLpcotRKeeuopv+M5jkOe0ey1\nzZCtx5NPPum1TRAEGDpneW1r3bq16isPyXWQhhoh5AcBHJUVcFRWwFrmgL2iHLbyMs+rrAylDjts\nDgeatWiR6JY2KB577DFoNBq8++67sNvtEAQB7dq1g1arBcdxXmtbqCH8KaUBwzQDhTL7rYVNPce7\nnd4uz6eeeiqokcP6OM/z0Gq1MOsN50WfSOUBxBCWWh4oRjrflIMBgwfhrUULxW2GbD10Oh2skiGy\nIAgQQL0sjXAreeYYjF73gWU8SrNe1R55nM+weyYIAm64fiisJSXiPVWbZJzwDQR7xtl9+OOPP9Cq\nVSsAQK9evcTCiGphMhhhLbP7CXdjVjbKqiq9tlF4L9QlCAJyTWa/eyvtD4mUi6k8gPMAJviDZQK7\neDfmL3jVa9vcuXPx+bp1Ac8jxVrmgKFzlqJFzgM9xmyZPsb8+fOxadMmrzmAwYMH+x3z8MMPy16v\nMSB1B6z/4vOQ+7KS4f83/Fbs2bULgpsHOI/yaIhzLsHQ6/Ww///2zjzOiSL9/59KJzMD6E9lYeWY\nyZ2Z4fArCguDuuoXRREQdFXEXdcD/KoIiid4ooigqyuXCHgsyIoiKoqKqyzXKiqgqKAgc2QuDhFF\nUFzmSNL9/P5IV093jkknk0wypN+vV15Jqqu7q6ur6ql66qmnKoMT8AsWLMCECRNgMpmwcuVKXBxh\npXVLKasoR6HdqXFBLopiWOMPAEVOF8pVxgEmkwlmeX+CbFf9GSOABCl0uiASoTJKT3zbtm3o27ev\nouvXk8+RGvuWFlIigtNqi1gx1Oi5RyaXlWOFG2+8EWs/XB2cXwJDeU3y9mxoDc466yzFC6667Mda\nKZwsItWXSPUqEuq0btq0CQMGDIgYTxTF4PUYS4lVljECaAuYTBAkCaNGjVJ6csuWLVMOz58/X3EF\nUVxcHHZ6JKGQKqsDPT1Nn8/X7L7FPp8v4fsb6Of5559PdxISIpL3zNbWkUcTMJHqTqT6Z7fbFV3/\nM888oxEAV10V3OtXFEUsW7YMgUAATz/1d9x7/30tSm+6RyBZKQB476QlBTTXYsFZ556DBQsWRDzO\nN8k2mUxhE7utCWMMrmYWrXHy8vKyZhMMA4NITJ48WVHZvvLKK1i6dKlyTN25A4Dp06dHNO7QSyAQ\ngMViSXudavvT2AlARDCbzcjNzU34Gt/u+i5q4885/vjjQUS49tprI6YhFLWlhDqsJU60JES+fyg+\nn08ZsUT6GCMAg+Zo3749VqxYofSgiQhLly5VRp+tMd8himLUOhRKpPp38803g4jQuXPnmPeaMmVK\nwkYTxx13HNq1a5f2xh/I8jkAbsc/cOBAbNy4sUX3iXTt008/HVu3bk3qdRMi1AwiAsfCHEBb2kQ9\nJgS4HW3nedRWZaHlxOl0orq6OuPLD+ess87C5s2bIwqOlsC9A3ALsmi05hxAzBEAY6yAMbaBMfYd\nY2wnY2yiHN6RMbaGMVYhf58khzPG2FzGmJcx9g1j7HTVta6V41cwxmJ3S1MEY0xx19zY2IiNGzcq\nwiCZekuHw4Gff/45addLGB1qxkAgoOm9hX4y3ZUvgCZ7/gxuKONB/TyZ/kzc5YkgCDCZTJgyZYrS\nI6+oqMiMeqCD//73v3A4HDHVoXrhamBBELBx40b4/X5IkgSLxZJ2/T+gTwUUAHAXEfUEUAJgPGOs\nJ4B7AawjIg+AdfJ/ALgIgEf+3AhgARAUGAAeBjAAQH8AD3Oh0doEAgHk5ORAEASYzWaNxz+1D3+T\nyaQsZGGM4eabb1auEauAnHHGGXA6nfjmm290p0l97YqKCnTt2lWzT+/8+fMhiqLSGG/cuDFsr9JE\n4c8Z7XMsmSwaJJ8vvvgCR44cUToM06ZNQ15enlKu/p9qYR2J8TeuapNqPlrndWH+/PmaetK1a1d4\nvd4w9+x6+Oabb+ByuXDeeec1G089mrnpppuUe1ssFqUu8kWi/JsfFwQBOTk5SR9hJELMVoOI9hPR\nV/Lv3wDsAtAdwEgAS+RoSwBcIv8eCeCfFGQzgBMZY10BXAhgDREdIqLDANYAGJLUp9EJ3/VH3evl\nhWXs2LFKLwbQumx47rnnUFJSgr1790Z1E7t3717cfPPN2LJlC5588kkMGjRIOZ/3kIYNG4b58+ej\nqqpKI2w4R44cwbvvvosOHTpo0jxhwgSYzWaYzWaMGDECJpNJU8gi8cMPP+jKk/Xr12PdunVRPx9/\n/LHO3DXIRhhj6NChgzKaBpr2xGCMKfryI0eOgCXQWVGXc5PJhBEjRih1YcKECZredPv27fHuu+/i\nt99+U8LUjXJVVRXmz5+PYcOGQRAETf0888wzMXXqVKxduxbjxo3D3r17w9LBn3fPnj0oKSnB888/\nr3SUeKPOO01jZZffao8BPp8PR48ezYgRQFxzAIwxO4CPAfQGsJuITpTDGYDDRHQiY2wVgCeI6BP5\n2DoAkwGcCyCPiB6Twx8CUE9Efw+5x40IjhxgFoS+thA3CPESaeiszviWrvqLdj7X8xGRom4C9OnR\no5mIRlulGE33CgB/mz4Dkx+Iba0QqzCazeaM9+eu5opL/4TlK95su8v1dczbZBrqzkzPnj1RWlqq\nlMmJEydi9uzZwTIMBkJ8JpDR1hHoqRexUC/s8/v9URdvxnPNaOnj143kP4yTUXMAHMbYcQBWALid\niI6oj1HwKZIyw0NEzxNRPyLqlyq1g1oaq38TEbxeradC3mtXc8MNN4Sdz13hiqKIAwcOKHbQfCu8\n3NxcjBgxAgsXLoTX69Xck1+jrq4OS5cuxYgRI5R7RfKnPm7cOOUakiRBlH0SRWLx4sW68iTWHEBd\nXZ2u60Si0B3bDJXTs7AIvYt76I7vsNnhcjjDwt94+62Ijb/H4YSjwKr7+qF+mJpNi3zdQqcrRkwd\n14/SNsbbOBTHkfcumx1jrklsas5iseAvf/mLop789ttvcfjwYeUdzJs3D4Dc2LL4ne/xMs7ritfr\nxbhx45TjvH7w+zHGMHLkSCxduhR1dXVR6/rChQsxYsQI5ObmKqbh/HPgwAFNvQ69xg033KBJIx9N\nqOG7i6lHMLFG7a1Kc5Ve1au0AFgN4E5VWBmArvLvrgDK5N/PAbgqNB6AqwA8pwrXxIv0yc3JIZfN\n3qJPNAAQY4wAkMlkoquuuiosDmNMiQOADh48GPV6kZg2bRoxxnTFFUUxLOypp57S3N/tdofFGzly\npBInEs3lgRqz2azcJ9JH73O0JA0cp92hO273rt3IUWCNL0FSfNELnS59l5Uk5dINdfW6zil2e3Sn\nY+TFI6iHp1B3fCIiu9UWV3yXwxlXfI66nBw9elQJF0WRJk+eHLV8EhEtWfxSMK4/QI89MjXq9Rlj\nNHLkSE24KIrkdrs193/qqafCzo9Uv6LdZ+bMmbricg4ePKipKyaTifx+vybO1VdfrUljc/nR0jbP\nZbMTgK2ko22PqQKS1TtLABwiottV4U8B+JmInmCM3QugIxFNYowNAzABwFAEJ3znElF/eRL4SwDc\nKugrAH2J6FC0e6fKDJT36vmMPBEhR+UbJBmSmYjw3nvv4ZJLLkmrpA91BAcAVd5KON3BXip/5jVr\n1jSbTiLCkCGJTdkUOVwoq9a3UYsoihBMQlzqD1uBFbUxXF20hK+//Aqn9T09dsQ44XmvO74ogQnx\nqbTi2SvZ5XCi3FuR0IT/7NmzcccddyjPU1RUhF27dsV1jdGjrsRrry+P+97JxGQy4aOPPlJ2NGsp\nfFQgiiL8fr8yF5KTkwO/3592FZAeAXAWgI0AvgXAW4j7AWwB8DoAK4BaAKOI6JAsMOYhOMFbB+B6\nItoqX2uMfC4ATCeiZvUTqRIA/Jn5RM1nn32G/v37t+g+ke4hSRJycnLSakLptjtQUV2laWhEUcSd\nt03EnGdVw/IQQstFvI1VosTdKGZYfEC/7xmgyVlcphBP2tX4fD6YTCbk5uYqHkGJtNtDxsJutcHh\ncmLDhg1x3z9ZCIKQsvr68ccf45xzzgEQVLlGe+8ZNQdARJ8QESOi/yGiPvLnX0T0MxGdR0QeIjqf\n9+TlUcx4InIR0Sm88ZePLSIit/zRp5xOAUTBlcDXXXcdAoEA+vfvj8bGxojxEmXu3LmKlU66CX0O\nQRCUxj/ScaBpYQ//NLdhvBr1WorQyTTGmGKVxI9JkoSTTjpJ+S8IQnC/AxXbt2/XpIVbZgUCAeVe\nhYWFWL58OR5//HFcfvnlStzHH38ceXl5YdYe/ON0OrFkyRJNWj/77DNl0vE///mPco/169crcRhj\n2L17N1avXo0ZM2ZgzJgxOO2003DccceF3YubGvMJRgAYNWqU8rxvv/22Et6uXbuwfHM4HGAsuLk6\nH7Wq30mkfGaM4ayzzgIQFDI2my3snfK0ql1ZC4IAQRCiTqxGIy8vL6Kxw9lnn93spKqamt21aW38\ngaaJ7GnTpiV8jWh5dvbZZ4OIcOmll8JsNmdE25CVK4F5I5JITyeSb3G33YGqkK0heeNmNpuj9ijG\nXHc9Xlz0j5RaqkQaAURi6tSpzR43m8144IEHYt6PN5zqnjP/r7bkCLWGUDdAoijixhtvxHPPNe2V\noLbU4A0/V901NjYqFhzcv4o6vtp0jzfMDz30EB544AEl700mE0pKSrB582YQEW655RYsXLgQkiRh\n3LhxWLhwIYgIEyZMwLPPPgugad2IemcxIlJ6dgcOHEBFRQWeeOIJvP/++2CM4YUXXsDYsWOVdN13\n333429/+hiNHjqC0tBT9+/fXNCDqvBMEAZs3b0a/fv3w5ptvRtxl7oQTTsDRo0c1VmEHDhxAly5d\nwBjDhg0bcO655yrp50YKvNGfN28eJk6cqAhZvfscxHJvnZubq+walm6cdgeqoiys4++lJdaBekaN\nofVBTUapgNJJOt1BDx86DJ9//jl+PPiTJvziYcPx3vurNGHFbg+++W6nppfMK4+6cdi8eTOAoMVE\n3759AUDRC6ZKvaJXACRLxRPa4PJr8wKv3oyGH+OECoFPP/0UJSUlSk+aH+Ob13BBwFdW8h62+lkY\nY7juuuswbdo0dOvWDQcPHkTnzp01aTp8+DA6duyImTNn4tFHH0VeXh727duHTp06QZIk/PLLLzjx\nxBORm5uLffv24eSTT8ahQ01TV8cffzw8Hg8KCwvRr18/nHLKKSgqKkJBQQFMJhOefPJJTJ48WZPP\njz76KB566CEIgoBevXph27ZtsFgsKC0tRWFhoZKXgwYNwpo1a5T/fOTDGMOwYcPwwQcfRGxEduzY\ngZ49e2qEHtC0rkWdFvW3umGKRwDwODfffLOyMCvT4fURgLIFJJ8b5AJRjcfmQFl1ZViHzWm1aTqA\nvGOQqK+g1hQAuqyA0vVJpRWQHv7Qt5/mv8tmp97FPSLGbaxv0PyHrA0DQMOHD49+kygWKYVOl+Y5\n3E4X/fD9fv2JV6U5IMW2gFBbG0X76IExRj6fj4hIc96f//xnzTXUxyRJIkmSaMWKFZp0mEwm5TgP\nE0WRANBPP/1EgwYNojlz5tCCBQuoX79+9MsvvxAACgQCmuuLokiBQCAsrUuWLCGn06nEHTJkiHLu\nww8/rKRz+vTpShqmTZumpOGiiy6ibt26aSw7uOUYY4wsFgsJgkDHHXeckpbFixcraTSZTDRixAgi\nIho2bBhZLBZN3gAgs9lM77zzDomiSOvWrdPkiyiKmvwSBIFMJhOZTCaSpGDBuv7668OsTtR5w627\n1HFCv/WgtnpRW7zEW36i4bY7NPXhyitGKc+YEBFO5ekmivzsvoCf/nLVnzVh990zKaydaVG6v/A2\nAAAAIABJREFUKMOsgNJJa44AKKQHzDMoUfUM7z0NGDAAX375ZdwTSx6HM+4haKRn1TsCGDx4cLML\nvdq1a4cPPmh+9ysg+ghA/VutLuDPyNURl112Gd555x1NfqnPV2+xyXut6pFF6CQmV/Vt2bIFDz30\nEB5++GFMnToV69evV9Kipra2Ft26dUNOTg5qamrQrVs3WCwW1NTUoHv37rBYLKiqqoLT6dSknev4\nKyoqsG3bNuzcuRPbt2/Htm3bNPbkjDE0Njbi448/xuDBg5VrCIKAhoYG3H333Zg7d67mWdWWaWPG\njMHixYvRp08ffPXVV2H6da7S4WnieXHfffdhxowZShylAZDz8IILLsCaNWvC8vOmm27CwoULY773\n0DSE7pXd0hFBvL1iItLsFqYHPhrbvn27ZuTOcdjsKC0vC/MiHGppR0Q4sP8HnNy1S5NVlMsNItLs\nTBYNY0OYNBAqAPROXDUHYwxjxozB119/3Wy8iDuBiRJgavkwWu9zrFq1qkXusdWo/SnFwuPxoKKi\nQknjihUrlMlRdQPCifQs6rwLPX7TTTfhxRdfVP6r1SkAMHToUDz44IM444wzcPXVV8PhcMDv92PZ\nsmWw2WwgIixbtgx2ux2BQABvvPEGnM7gwrMhQ4bg1FNPRe/evRW1T69evdCrVy9NGp566ilMmjQJ\nZrMZAwcOhMViweDBg/H9999jz549sFqtmDNnDhhjeOaZZzT5uGfPHhQUFChCYNGiRXjttdewfft2\nTJ8+PWxeZu7cuUojrs6XGTNmQBRFvPLKKxE7Fh9++GGYUAaCG9ToEQCRVEVEhJkzZ2LSpEmKQPjl\nl1/QoUOHZjcfSgaJdNwkSWrWdXo0c9rQjpetwAqzyaRRC5VVeuGy2eNOU6oxBIBMsidir7nmGgBB\nnej48eOjxou6GXsSGn8gttM6Tiwrn3jMFdWNz4MPPqiEqydm+f/KykpMmTIFjzzyiGaUoBYA6obl\n/PPPx7PPPoslS5Zg4MCBaGhoCBtdqSfwFi1apDgks9vtKC8vR48ePTBlyhRceeWVmmsPGDAAR48e\nVe69bNky5VrLly9XbLdHjRqF119/HatXr8bq1as1ecgbus6dO6NPnz5wOp3Yv3+/8tyffPIJnE4n\nunXrhq5duyp5etttt4ExhltvvVURAocOHUKXLl3w9NNP46677lIMCurq6hSPm1dffbVy/82bN2PA\ngAEgIsyZM0fJA54/giBEbOA6d+6MAwcOaMLiHQGHxgu1gOOjyxNPPBH2bvmo+V7rYyfZ3DnpnqjH\ndu/eDas18mrw66+/Howx3HbbbQnfe3eEvboH/+8gVNbUJHzNVGGogFoB3oi8/PLLimCQJAkl/Qdg\nyxefK9YrahIZBkZTAenJgxkzZjSrAsrNzdW1s1moCihUBUBE6NChA+rq6jQTkLt27UJRUZFyHZ/P\nh7y8POUc9fX5pvaNjY1KY202m3HgwAFcdtlluPTSS3H77cE1i8cffzweeeQR3H777RqVEYeIsHXr\nVvTv3x9dunTB/v37kZeXB7fbjR07dih+bXbs2IGcnBx4PB7s3LlTuVZDQwN27NiB8vJyfPvtt/j6\n669RWlqK2tqm3h+PW1pais6dO6NTp04IBAI4//zz8cknn6CxsRHPP/88xo8fD7/fH5Y+ICicPv/8\nc4waNQrLly9X8kKtHlI3uFywXHzxxXjnnXcAACeccAKOHGny4hIIBOB2u1FbW6v04LmgnzVrFiZO\nnBhRFRIJxhhqa2ujNqycgoICtLPk6FKFqIm3PkQr8zU1NejWpSty8nKVMjlv3jyMHz8+zPIntPPR\nWhhWQDJtWQCoe8yjR4/Ga6+9FjWeWlfLSZYAcDmcUTeuV6OnoMcqK4wF3d36fL6IliZcOIR+8+N+\nv19Zke3z+RSVFLfKGDhwIL788kvFCmbMmDGKeqexsRFmsxmCIODHH3/EySefHDXtfMTFFy9ZLBbU\n1dWhrKwMp556Knw+n2JlxO21ee+bp/WRRx7Bpk2bsHr1as2zVldXKyoiPsdARFi8eDFuueUWxeor\nEAggLy8PDQ0NMJlMyuhi6NCheOutoB+jgwcPoqCgQNmtjTGG3NxcXHPNNXjhhReQk5ODrVu34tCh\nQxg8eDDq6uqU/LNYLKivr0eHDh1w9OhRdO7cGUVFRdi8eTMYY7DZbKiqqsLKlSsxatQoJT4A7Nu3\nD/n5+WCMwe1244ILLlB8+USDz7Xs3btXUZ2Flo2W2L0nSwAA0Rv2Sy65RFmTkay5i0TIqIVgBvET\nqg9dtmxZ1MZT7Xq6JUS7frIEvN40NjeKUFsfqP9z1JtkqFVSahUZd7fLe/3qc3ka1Y7rQif2gSY/\n8vwYH1Fwh3ih2xhGaryICO3atQu7R+iCQm6/z80L+f0AKHbxfGMiURQV4cOFI9+Kk9/D5/Mp11Fv\nF8qFFY/H/3PhyUdT6vTzuRZRFDXHeb5yoa1H9cfTbLVaQRR0g0JECAQCcc0JReKjDf9J+NxIRGvU\nV65cqTEfzoSFWqnGmANIAaGLlWL1IpLhDiBqYdVZiGMtfGmzbpUNWgUuaELLOhcmLWlQ/0/2qd/a\nZJKLjlRhCIAUUF9fr3EuFwuTyQRrt+7Y/f2+hO8ZrYGOVIjddgfKKiogWJpef5cuXZq1AsqE3YsM\nMhc+h8VHLmqfOrfccouyejqdiKIIgZnQ9eSTsf+nH8OPhVhB1dfXo3379q2eztYkKwXAohf/gTE3\njE3Y8VUsOnTogFdffRWjR49WhAAvYJFUEowxHH/88S265x133RUxPNr2e4WFhcrcQCQhFUnlYWAQ\njVSWj2RdmxsMtG/fPqwehrYDS5YswdixY+Nev3PB+YPx4b9Xa1xsZDJZKQBmPPYYZjz2mO74148d\niwceejB2RBkiwlVXXYXRo0crBc1sNke0aweCi76+Ky3Vff1IjL91QsTw0ILtF4N648raGmWCWE8F\nS9VkWGuplhJRQZSUlLTaJGAijVwi5yTyPHPnzsWcOXPiPi9ZJEsABAIBFDpdYX67AO2OY9zAIJG8\n8paWxbUhEJBeS8WsEwCJFKX774+9paKa0JWWsQpShQ4rnVhEu0do5bEIZlTLvvP1WAcZGKSbWPNT\nejGbzREb/0j3SdQE1GTO7B5/KFk3s0cJiIB4N+HYvXt3i2yI491IAwCkCM9FRKDM98llYNAsraV+\nDPUE8NNPPx3zc19ZNwIwpXin7TvuuAOzZs3SWABxq6Dm8Pv9MJsEMMGEHj16RN3IhrGgN8hJd98T\nNFvj/mgCIkwhK4oZY2CJ1h0C3A6VPbJE8O6uiesSkQRgNKHo8/mQk5MT0aeM2o8On1wUBEEx9wxd\nTa2+BvceysPVro+5fpeI0NjYiPbt2yuTmTk5OfD5fIoOl0/qq+/B1y7w8IaGBo35qiRJypoF9Wpc\n/gzqMP5bkiTFoobPGanvG0mnrFZdRMtztXkqX0BGFHSnzfXV/FqCIGjWP6Sb5jZ14nn7h779UPff\n/4YtpNMgBd15z5sfPiHNTYHVdOzYEWPGjMGiRYta/hAZStYtBNu3Zy/OiXO7t3h0dNz22mQyYf78\n+Rg3bpxS2fgCoEgTwbwBTCaSJKHI4UJFbez0i/6AZqTDCPC4VLpMHQIgkaF6Jp/D9weIByLCoEGD\n4t7YJJPzIVkqmEwhtP5xYc+fc9asWbjzzjshSRLy8vIibhYVjWQ4rTNWAsukQgDYCqywxDkzH48A\n4D3OvLw8+Hw+Ta+dTwRHwm21o7TKm/Qel15XEB6bQ6MuCqv0CYwAYtHaS+3jtfqK6qcpyaTKGs1A\ni617Psxmc1iDGzoyZIwhLy9P4xdKL21NAGRdqRNS2ODwobTJZFKW1QPAFVdcAZfLpWxcEgnv7pqU\nNDattZrR7/fH7e2QrxCNtwtCRPA4nHHf6+0Vb8V1TrHbE1d8APjt1yPKBuB6ac3Gv76+HsVOt+74\nvPz4G31xW7dkGrX79oY1trxTVlxcjKFDhyrh9fX1GoGQKtK92jjrBIBFSE2PjrsR4PBKfeaZZ2L5\n8uWora1VRgKthdqtQapJxL2vIAhwWm1xz8owxuJqYAFg187vsHf37rjO8dZUx32f008/HQBgjjM/\nnFZbXPGB4Pt96aWX4jpnyoMPxdXo8HJszrEAx+Aohc99VFRUYNWqVRg+fLhGIKv3mUgFwy6+OCXX\n1UvWqYAKna64X6YeFQpXmXD9r7rnwBea8MZEvXl2xhLnJHAkj6ax4MPueFUtP/90EL/r3Cmue7Um\nv/76K0444YS4zkmkp3nw4EF06hRfPjTWNyC3XV7siMc4dXV16NChgzLRz3v7ap9QjDGcd955WLt2\nre55kHjVN+VV4VtMGiqgFJLshlft7RIANmzYgCeeeCJiPIvForjXTYeXwVSS6AgAQNyqr0xu/AHE\n3fgDiS3QirfxB2A0/jIdOnTQ1EmOeuXv7NmzsW7dOgCpm69K99xP+m282jiRfIjH+h3pf8bBMmMv\nBQODVBCtbqo7iBMnTsTEiRMjxksWEijlpunNkXUjgHjJ+IbawMAgM0igqUhn4x+8f5bhralWPo8/\n9SQAuZGXSHGcRoyB9wOONVWNgYFBimDa9qVLfncACC7wJCiLMkm1MDDdHcysmwQ2MDAwyASizStk\n1CQwY6yAMbaBMfYdY2wnY2yiHP4IY2wfY2yb/BmqOuc+xpiXMVbGGLtQFT5EDvMyxmJvMGtgYGBw\njJIJ2gU9KqAAgLuIqCeAEgDjGWM95WOziKiP/PkXAMjHRgPoBWAIgPmMMYExJgB4FsBFAHoCuEp1\nnZQS6tO7pZZARAS33YH331ulub4eG3+33aFIeHX8eO3N9aK+X7bCbew9DmdwEZnLDZfNDiKCy2ZX\n3t+TT/xNySv+jvl/9W9+jKPJYwrP8yKXWwlr9mO1pzorMprWLquJ3u/991bBbXekXX2TDGJaARHR\nfgD75d+/McZ2AejezCkjAbxGRI0AqhljXgD95WNeIqoCAMbYa3Lc71qQfl0UOl2orK0BIaiHM5lM\nuOLSP+GNt+NbGRoNk8qc0Wm1NetyVk2RpxAV1ZWAROhd3ANlld6kpEcPb77+Bi4fdUXMeMOHXBTW\nU3nr3XcSMvtMF71OOQWlpaUoLCxEaWkpehQVAQDKy8vRq1cvlJWV4d6778F5gwdj1YcfYMTQYfCL\nIt5c+TYsFguuuPRP+m8m64HtVpvihqOs0gu3240VK1Y022hk+uYhofh8Plw28pKw8Pc++FcaUmOQ\nCHGZgTLG7ABOA7AFwJkAJjDGrgGwFcFRwmEEhYPag9ZeNAmMPSHhAxJKdQJs2rQJAwcOBJ90r6mp\nSd7FiQB5la/exh8AIEkYP+4WLFiwAC9mqMfBl195BX/o21cT1pYafwB4+52V6OEpREV1Fdx2B8qr\nKsEYQw+XB7sqK+C2O8AYw7CLL0ZxcTG++y7YJ+nTpw8A4Ouvv9Z1H7XfpZrdtXDbHbB1z0ftvr3w\ner2t5luotbBYLGGuy7/UmVdA0AGhL+BHu7x2EFthhfwpRT3wbVkwvbW1cdRTAIsWLcK/P1yN3//+\n97jwwgtjn6AHiQATU3xBFbo9wb3Ek3N1XegujYyx4wCsAHA7ER1hjC0AMA1B46dpAJ4GMKalCWKM\n3QjgRgAwJ6lH5K2tAYjgFwOwCGYEJBFffP1VUq4dCARALDiyEMxmiCRBYPpeYWVtjdIjPOOsM5OS\nnuYgKPIPl+no/QPASb/rmLL0tBbFTje8u2vgstnhralW/Ah5a6rhtjsU/zBcBeStqdaoeXg8Pbjt\nDpRVeiEIArzV1XA7HLDnF6CytgZFLnfzet8UONxLJZGe5YSTTtR9vmAxI88sACzyfhbJ5MwBJfjt\nt9+Cfwiw5hfoP5kAj8uNa5ddi57FPZInAExNngL8fj8YESwq1+Ctga6WijFmQbDxf4WI3gIAIjpA\nRCIRSQBeQJOaZx8Ade7my2HRwjUQ0fNE1I+I+sUaEut108qCz6D4ATKbkjfUNpvNsAhmmM1mMEB3\n46+kTa5ErTH8Z1F+A+HzJJrzVBW9og1aVYU2/txMj4c5CqxKXMXPPIIL/OrjcAXMBUeRyx1szhjg\nra6G2WxGkcsNgTXtFBfp0yi2vc1H1OWhuVWtkcqXx+FUHMz1LCxKfuJUfLplM/Lat0Oh04UehYVx\nbZTkstvxx3PORi9PEaQkjlSKXG78Z/0G9C7ugVUr3wEAXWrgeNxTxyLmCIAFa/8/AOwiopmq8K7y\n/AAAXApgh/z7XQCvMsZmAugGwAPgcwTbHA9jzIFgwz8awJ9bkvjPt25Fpy6/xx8HDMTBgwfjOnf2\n7NlYMOcZ7KqsSPpybEmS0MNTiIAkxb3toq1rd+Tk5Ojy4Z8MnFYbGAHePdGHxIFAoM3pp9W4rXZU\nqoQA781X1tbAbXeges9uuO0O3DN5shLGjwPxmeXx8z1cHcSAcq8XhW43ymuOvS041e1oc8YVJkGA\nx+ZAQBKVLUnVW6Fy9Vwy8dgc8Pl8qN0f7GeWeit0nedyOGE2mbCrohwmk0kpB6VVwcaZG38kSpHD\nhf8bP05p7HdVlAMALr3i8mbP69SpEzZu2YSDP/yIP56ZHI2BHhXQmQD+CuBbxtg2Oex+BK14+iCo\nWagBcBMAENFOxtjrCE7uBgCMJyIRABhjEwCsBiAAWEREO1v6ABbBjM1bv9CERStIvKenbsySZYrl\na2hE7549NZVAz5UlSYLTalN0w5bcnBQPhoP5wHcq0yP8eAPp9/vTvG4xMby1wcafN86l5eUw51jg\ndrqUkQAAZUMeIoIY4ipATznhzu3KKr2K5Y+3phoms6BvPYpaR9eG4PkT6xmJBeue2+4IugEnUoRB\nStLFgvVJbXVXtbs2Zpln8m5xfHRiMpmw47vvkJOX2/I0EUEkCQvnPYuF855VXKLX7N0TMX6q1zHp\nsQL6BJGLZdSpfiKaDmB6hPB/NXdeslBnmtNqU154snuxgUBAc329CIKg8UraGhODLpu9xeqmm8aN\nS2aSWg9VAy5JkuKqmat7BIsF5d4KZQ6Az82EjhRiUeRyw1tdHdT/yyMN9cSw+h1EpI3NAXCuvuYa\nvPLyy3Gdw+sMz9fW2BTHbDZrGnW+Q18sJElCz+Ji5fesOXOSlibeCVPnQ1yGJC3k2DFJQDDzhg65\nCN7yciVMnZl333kX3l25MmkeQc1ms+b69vwC5OTkxLy+KIoaIWXNL0C73NyUTv6oN8KwFViRl5MT\n1/0kScL9Dz6QgpS1Aqam3qn6fXH1XLmsGph072RMuncyAIT1aNW/mzumJjQ8dDOSY4Wp0x7FP+Pc\nl4AxBpEIVao8SuUaAEEQUN/YiN2qnrae+5lMJvh8Pk0PvaUqoNDrXzxyJJ6epWjXtWtMCgvxrw8/\nSJlwPCYEQKHTpUykNcffZz6Nv898GiBAIinpOxzV7N2j9GTiGRnwQkkAbrj2Onz00UdJTVcotfKw\nmwAwUYLbFTsfquI0mzPILqp1brbjraoCmVirabrOOeccvLjkpbjvx3viqRqZlFV6YQLT7MMdCW95\nOQqdLjDGwBhDeVVlUtNxzPsCykTiMSvMFMwmAQGp9czTMp3yqso2v0ViUpFt2tsSbbEe6sXYECaD\nyWShG41dlfosKLKFdG/kkWm0ltVaMmmL9TDZGKU4DTDG2pxZJWMMs+c9k+5kZAR80v5YWtXbEp5d\nsCAjHJvFgyAIbS7NqcAQAK1M//7B9XK7ysrSnJL4GT58eLqTkBFwe3K9duXHOhdeNCTdSYgbXv94\nfcxWDAHQyrz6+nIAgMncdkYA6gU7ojFsNlChLg+t6cywpfD6x+tjtmIIgDTSVvTIal2pkOXD5tB3\n1lbeYapgzex7nalk+ztTY+REK9Lg82n+J9ukK1WoK0y277B2YseOzf7PNtTrKtrKnEhovQutl9mE\nIQBakdoULntPFQ7HsWkmlyifbtnU7P9sx6VjTUmm0RbrZbJoGyL7GGHqw4+kOwlx07+kBFMefEgT\nJrSyy9pMYtrDU9OdhIxBEISwstGvf39UVmb2yDY0zdmMsRDMwMDA4BjDWAhmYGBgYNAshgAwMDAw\nyFIMAWBgYGCQpRgCwMDAwCBLMQSAgYGBQZZiCAADAwODLMUQAAYGBgZZSkYvBOt9yinYunVrupNh\nYGBg0KbQ6+raGAG0kI0bN6Y7CWE88cQTcNsdEXesSmThX319PQDAbrW1OG3RVhAXOl3w+/3wOJxK\nmMPhwKxZs+BxufHHgWdg6UtL4HG5AUCJR0To4SkMe9YDBw7oSk+h2xMxnG8KH+14vITuE53MfWUj\nQUSavIxGY2NjStMRDUmSUOz2wNa1e9ixH3/8EQDw0ov/iPoMvByn2lWJzWbDueeeCwBwW+1KOK8T\nnIvOG5zSdKQMvpduJn769u1LRERup4skIiKJ6Nyzz6ELzh9MvYqKKb9LV7LmF5A9v4DuueceIiK6\n7pprSc3oUVcSEVHfvn2p0Okiu9VGHoeTdldVk8Nmp2WvvEoOm52kgEgl/QeQJEl0YP8PREQ07qab\nleu8/PLLZM0vIJfDSZIk0V133Elnn3Emue0O+nj9BvI4nE03lYgcNjuFIREFAgFtkCTRX//6VyIi\namxsDD+HiERRjHhuc/D7+wJ+CkgiFTlcJEkSSZKkXMdutSlp0NxLlV5XgY1WvvW2cs2XFi2mhrp6\nWrdmLbntDiIicsn34t+j/nQZUdMlyWm10a3jbiG31U4+n0+5tjW/IPjc9Q3k8/mo0OlS4qu/+bU8\nDid9//33dOedd9Lc2XOUcFEUqdjtocbGRk1aPvl4I0mSRP/7x7NJkiS6bcKtSpr4+7KH3kvF7Jmz\nqLiwiGwFVtrxzbdUXlqmOf7i8y9QQddu1Ltnr7Dzy0vLIr5Pt9NF1vwC+uD9f4Udmzb1UeV57PkF\nmudzWm0UCASoR1Gxku9SoOld9S7uEXY9kogaGhqCzynnNWfTpk1ERLRuzVoiIlr17ntEkrb+dPv9\nyXTlZZcTEVGRw0Vvvv4GBQIB8rjcFAgE6Jk5c+nB+x8gW/d8chRYiSSi/G7dg++ivoFEf4Dyf9+F\nJEmi007toylnAweUBPPDaieSgmXfVmClObNmK+XAI9c1oqb3w//zb7vVRqIo0qGDP1PA5w/Pgxbi\nstlJkiQqdLrIabVRsdtDjgIrrV27VnlHAweUkL1bvnKOU34/P//8c9LToxcAW0lHG5v2Rr65j1oA\nEBH5G4ONhyRJVFVVRURE906aTJIkkccWzPRAIEBer1fJCL+/qVCI/oBScFwFNiIKFizeMPJrhwoA\nW/d8kiRJ+SZqaqx5g8NfuiRJNHvmLNq18zvlvmrh4HI46bNPPiU1w4cOU84liejXw7/Qlk2byVFg\npaNHj5LD4SBJksIqcXOECiC/30/2/AJNJZQkiUjViCiNMxE5CqxUX19PLpud/v3vf5MoiuSw2cnv\n91MPTyGtX7uOCp0u8vl8Sh7YuucrAsRRYFV+Hz58OGIaeUPG47lsdkXYNTQ0kD2/gBrrG0giogF/\n6E8SBd9v95O7kN/vJ2u37mHPW9C1GwUCAXLbHdS7Zy8iIsrv0pWIiG6bcCtJkkQNDQ1U5HITkUoI\nEtEdE2/XpE+iYNmLJMwlSSLRH6BeRcVEFC5AJEkKNoohjBh+MbmdLkUAqMsnFwCcGY9NV36r3z0v\nTz6fT3mfgUAgYgN4zdV/VX47Vc/a2NhIkiTRZ598SqIoUqHbQ0RE1197nRLfpXpu/q54eH19PQ0c\nUEK27vm08q23Ne9CiSs1CSm71UZ1dXVhaXFbgw3sGSUDydY9X3MsEuryy6/rKLDS5bzTIUqRT0wQ\nngdL//kyua12uv22iTR/3rP00qLFZM8vCJZXUQoKMgqW5YKu3bQdwjSgVwBktC+gfv36UaJzAL17\n98aOHTuSnKL08vRTf8dd99yd7mS0PQhwu1yoqPQqutFCuxPlNU0b3bz26jKM/vNVrZIWZPeWCimH\niFq03aMoihAEoUWvylFgRbXsZTQQCGhcZYf+j4QkSTH3LWguDmNMly+gjBYAjLHfALS9vRNbj04A\nDqY7ERmMkT/RMfKmedp6/tiIqHOsSBltBQSgTI8Uy1YYY1uN/ImOkT/RMfKmebIlfwwrIAMDA4Ms\nxRAABgYGBllKpguA59OdgAzHyJ/mMfInOkbeNE9W5E9GTwIbGBgYGKSOTB8BGBgYGBikiIwVAIyx\nIYyxMsaYlzF2b7rT01owxhYxxn5kjO1QhXVkjK1hjFXI3yfJ4YwxNlfOo28YY6erzrlWjl/BGLs2\nHc+SbBhjBYyxDYyx7xhjOxljE+VwI38AMMbyGGOfM8a2y/kzVQ53MMa2yPmwnDGWI4fnyv+98nG7\n6lr3yeFljLEL0/NEyYcxJjDGvmaMrZL/Z3fe6Fkt1tofAAKASgBOADkAtgPome50tdKznw3gdAA7\nVGFPArhX/n0vgL/Jv4cC+ADB9SolALbI4R0BVMnfJ8m/T0r3syUhb7oCOF3+fTyAcgA9jfxR8ocB\nOE7+bQGwRX7u1wGMlsMXAhgn/74FwEL592gAy+XfPeU6lwvAIddFId3Pl6Q8uhPAqwBWyf+zOm8y\ndQTQH4CXiKqIyAfgNQAj05ymVoGIPgZwKCR4JIAl8u8lAC5Rhf+TgmwGcCJjrCuACwGsIaJDRHQY\nwBoAQ1Kf+tRCRPuJ6Cv5928AdgHoDiN/AADyc/5X/muRPwRgEIA35fDQ/OH59iaA81hwCe1IAK8R\nUSMRVQPwIlgn2zSMsXwAwwC8KP9nyPK8yVQB0B3AHtX/vXJYtnIyEe2Xf/8A4GT5d7R8OubzTx6S\nn4ZgL9fIHxlZxbENwI8ICrZKAL8QUUCOon5WJR/k478C+B2O3fyZDWASAO6a9XfI8rzJVAFgEAUK\njkOz2nSLMXYcgBUAbieiI+pj2Z4/RCQSUR8A+Qj2TIvTnKSMgDE2HMCPRPRlutOSSWSb/y9EAAAB\nsElEQVSqANgHoED1P18Oy1YOyKoLyN8/yuHR8umYzT/GmAXBxv8VInpLDjbyJwQi+gXABgADEVR9\ncbcv6mdV8kE+fgKAn3Fs5s+ZAEYwxmoQVCkPAjAHWZ43mSoAvgDgkWfocxCchHk3zWlKJ+8C4JYq\n1wJ4RxV+jWztUgLgV1kVshrABYyxk2SLmAvksDaNrIP9B4BdRDRTdcjIHwCMsc6MsRPl3+0ADEZw\nnmQDgMvlaKH5w/PtcgDr5RHUuwBGy5YwDgAeAJ+3zlOkBiK6j4jyiciOYHuynoj+gmzPm3TPQkf7\nIGjBUY6gDvOBdKenFZ97GYD9APwI6hfHIqh7XAegAsBaAB3luAzAs3IefQugn+o6YxCcoPICuD7d\nz5WkvDkLQfXONwC2yZ+hRv4oz/Q/AL6W82cHgClyuBPBRsoL4A0AuXJ4nvzfKx93qq71gJxvZQAu\nSvezJTmfzkWTFVBW542xEtjAwMAgS8lUFZCBgYGBQYoxBICBgYFBlmIIAAMDA4MsxRAABgYGBlmK\nIQAMDAwMshRDABgYGBhkKYYAMDAwMMhSDAFgYGBgkKX8f0rkkfyXJjthAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb64e825ed0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"soft image\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAADzCAYAAACPBsFkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4FNX6xz+zJdnspodUQid0BQQRkC5YAEFQ4Eq1IEVQ\nKSJ4vXgV9V4FC9JEpeNFQEUFUQERpSgIAUR6CD2kkEo2m+3z+yOZcTfZJLtJSOCX/T7PPsnOnDlz\nZuec933PWwVRFPHCCy+88KLmQVHdA/DCCy+88KJ64GUAXnjhhRc1FF4G4IUXXnhRQ+FlAF544YUX\nNRReBuCFF154UUPhZQBeeOGFFzUUVc4ABEF4UBCEM4IgnBMEYVZV398LL7zwwosCCFUZByAIghI4\nC/QBrgIHgcdFUTxZZYPwwgsvvPACqPodQAfgnCiK50VRNAPrgYFVPAYvvPDCCy+oegZQG7ji8P1q\n4TEvvPDCCy+qGKrqHkBRCIIwDhhX+H87H7W6mkfkRVVCEARatmoFQE5ODjqdDpvNxvXr16lduzY5\nOTkEBweTm5uLWq3GbrdjMpkICAggKzMTjZ8fAQEBpKenY7VaCQ8PJz8/H39/f1KSU4iMiuT69euo\nVCqsVisqVcESsNlshIeHk5aWRkREBGlpaVgsFqKjo8nPz8dgMKDVatHr9fj6+hIcHIzVauVGzg00\nfhqys7PR6XSIoojVaiUkJASlUknytWsICgW+vr74+vpiNptRqVTk5eXh6+OLxWqhVq1aGI1G8vLy\nUCqV2Gw2VEoVQcFBiKKI3W7nxo0bWK1W1Go1AQEBiKJITk4OCoVCPpaWloZSqUQQBEJDQwE4cfw4\n3nQvNQ8mszldFMXwstpVNQNIAuo4fI8tPCZDFMVPgE8ANL6+Ymx0TNWNzotqh6+vL3/88QcKhYKl\nSz5CpVLx2NAhnDx5Ep2fltNnzzBkyBC2bdtGbGwser2ek8dPMOjRwXzxxRdotVpGjRrFhx/MRxCE\nAobSsiW9et9HfHw8jRs35urVq3z1xZcM/ccwvvvmWxo1bcIdd9xB48aNmffOXGbMfIl578xFoVCg\n0+loeUcr9u3ZS/eePcjL1fPHH38w658vk5qaytdfbaLnfb34aPESunbtitVu48yp08z658v4+voy\nY/qL1G/YgMDAQK5cuswrs/8FwG+//cY999zDogULGTdhPGfOnGHrlu9o3+Fuzp1NQKfTMXL0KAwG\nA6tWrCQxMZHo6Giio6Pp278fx44do0uXLqxYtpy6deuSlpZGUlISE56diFKpJCQkBLvdzh3NW2Ay\nmar5rXpR1Ui8dPGSO+2qWgV0EIgTBKGBIAg+wD+AzVU8Bi9uEzw2dAhBQUHs2bOHVq1asWffXk6f\nPMXWrVs5ffIUu3b+TEBAABqNBoPBQFBQEOlp1wEICApEF+DPwwMHoFApAdi3bx/79u1j546faNq8\nGdt/3EadevWIiIhg3759ACiVStatW4fWX0dAUCBdunVFrVaj1Wox5RtJz8xAo9HIbUeOHkXz5s0J\nCgoCICgoiFdm/0vur0u3rkyePBmtVsuARwayYcMGjhw5go+PDwAarR9fffElMTExjBw9iosXL+Lv\n749arcZqtQLwj+GP0+nezgQEBODj44PdbqdVq1asWLYck8WMRuvHE089SXTtGJnpeeGFO6hSLyAA\nQRD6AvMBJbBCFMW3Smrr3QHUPPj6+nLs5AkUir9lE1EUXRI16XhJ5121VygUbqtEHPt1/F+6pyME\nQcButxcbR9Gxufvd3eOOYyl6zm63c2eLlt4dQA1E4qWL8aIoti+rXZXbAERR/B74vqrv68XtAbPZ\nTNs77vRKsZUAURQxm83VPQwvbmHcckZgL2o2RFHEYDBU9zC88KJGwJsKwgsvvPCihsK7A6giCILA\n9BkzZOOfhPfmzbuldbRPPv000dHRTseWLFpEdnZ2NY2o+qBUKnnxpZdQKpXyMZvNxrtz52Kz2apx\nZNWDkJAQJk6a5HQsOTmZlcuXV9OIyoaPjw8vvvSS0zGz2cx78+bVSHdZLwOoIoiiSJu72tKxY0f5\nWGZmJv99q0Qb+C0BURR5auzT8nez2czct9+uxhFVH2w2G73v70ODBg3kYxcuXOCd//63GkdVfcjN\nzWXk6FFOQs2bc96oxhGVDYvFwiODB8lxEgD79++vkcQfvCqgKsX/1n7m9H3Htu23/MT7/rvvnL6f\nPn1adk+sifhiw8ZSv9ckWK1WTp8+7XSs6Hy51SCKItt/3OZ0rOi6rEnwMoAqxK+//ordbpe/r1q1\nqvoG4yauX7/OjRs35O/LP11WjaOpfnz11VdObpebNm2q5hFVL1Ys+1vdo9fruX79ejWOxj2sXr1a\n/t9ut/PLL79U32CqGV4GUIUw6PWkpKQABdvni+fPV/OIyoYoivz0009AwWLZXYMXC0BWRgZ6vR4o\nIHgZtwHBu5n45eefZfvH9u23/o4W4OL58+Tm5gKQkpJCfl5eNY+o+uBlAFWMjes3ALBz504sFks1\nj8Y9rFy+AihYLI67gZoIu93OT9t3ALeHCu9mQ6/Xk5aWBjjvBm5lWCwWdu7cCfy9HmsqvAygivHF\nhg2IoigT1dsBZ0+fxmw28+XGL7wBWsCKZQVqsFvZ26Uq8eXGLzCbzZw7e7a6h+I2Vi5fgSiKfLmx\n5tpwwMsAqhypqank5ORwtojx7FaGzWbj+PHjbNhQs6UlCQkJCWRmZpKQkFDdQ7klsH79eo4dO3bb\n7GihQKjJzs6WVbI1Fbe1G6irnCxFIaXHLQnu5pEpCpvNhiAITjlr3OnbZrOxZNFi7Ha7nIq4ssbk\nqh/J6Ozou16e+y1asJCsjIwSx1yTIIoiS5cuRRRF7+9BgV1kyaLFqMtI3V7WPJNsCQqFotLmf0n9\n2O12Plq8RF7DpeVncnWtKIqlrqnyjEk6X1ZMiTt0z13c1rN3xsyZdO5yLyuWLWfXzp2yYUeCVqvl\n8LE/i73c7OxsfvjhB1atWMmkSZMYOOgRj+6blpZGt8738sLUqUx4dqLTOavVysmTJ1mxbDkHfv+d\nfQf2y0wiJyeHu9u1x2g0cvLsGafr7HY7Fy5cYO3qNXz//ffs2bcXX19fj8ZVFKIocnfbu/D19WXv\n/t+dEptBwW5k4/oNbNy4kc/W/Y/69euX2NeuXbtY+snH5Zr0/18xc+bM6h7CLQGbzcbu3bv5dHnJ\nHmIXL15k5PARDB06lKH/GEZkZCSA05zs0rETRqORQ0ePVJgBmEwmut7bhYceeojRT4yhQYMGxYS1\n1//9GnZg/x8HCA4Olsdx7z0d6dCxI0+NfZoWLVoUY/JLl3zE/Pff5+fdv8rP4S42f/MtixcvZvQT\nY+jbty/BwcHF6NNdd7Yulg4lICCAHr168fQzY9m3Zy/z3nnHo/uWhNuaASiVSlq1asX78z/AbreT\nmprKpi+/4osNG7h27RqCIKBUKrFarVy5coXP1qzlu82byc7OliVjqY0nkDJKStfm5uaye/duVi5f\nwcnjx+UEXH5+fqhUKvkFO95HoVBgNBqJj4/n048/If7gQYxGo3xOpVJVmNiKoigTe6VSicVi4dSp\nU6xcvoJffv6ZvLw8p/Ol3W/JosU0a9aM2NjYCo3Ji/9/SE5OZsmixfTu3bvENkqlkuupqSxeuJAl\nixah0+no0asXTz79FM2bN5d3DwqFosxduztQKpXk5uSwft061q9bh0aj4a727Xlm/Djat2+PRqOR\n7+G41qRcVD9s3coPW7fi4+NDi1ateGrs03Tt2pWAgACn9VyeNXrx/HnmvPpv3nztdYKDg+k/YAAj\nR4+iTp068rMrFApiYmIY+o9/MOjRwURGRsoMbP9vv1fot3HEbc0AHKFQKIiOjmbSc5N5dvIkUlNT\nWfjhAua//wFrV6++Kd4r6enp/GPoMI7Ex8vbQneQfSOHMaNGE3/wIGaz+aZ7ktjtdt54fQ6bvvzS\niei7C6vVyplTp9i0aRPPP//8TRqlF7crNm3axKlTp5wqrJUGURTR6/V8t3kzW7dsQafTMfixx25q\nOg2j0chve/fy+759qNVq2nfoQEhISJnXmc1mjh4+zAuTjqBQKGjbrh0tW7aslDHZ7XYyMzNZs2oV\na1atIjAwkFFjxtB/wAAmP/8cUVFRN93p4v+NEdhut6PX69m65TsGPzKInl27seXbb5kybSq//XGA\ntZ+vo0evXnIxj8pArVq1WLf+c37dt5epM14kJja2VJuAhODAINZ8tpa9+3/n9TfeoFFc3E3VJSsU\nCmb/+1X2HdjPwsWLaXPXXWXqax2RkJCAyWTii8/X3zRmVdPdKW9nfPH5eiwmE+fOnXP7GrVaTdt2\n7Vi4eDH7Duxn9r9fvanqRZVKRaO4OF5/4w32HdjPms/Wymqf0iAIAjGxsUyd8SK/7tvLuvWfExYW\nVmnj0mg09OjVi7Wfr+O3Pw7wwtQpbPn2W3p1686jgwazdct36PV6pwDSysRtvwNISUlhw4YNbFy/\ngeupqU4/lFQz1sfHh06dOnH33XejUChITExk4/oNbP7mmwpzWIVCQVhYGBMnTmT8+PHk5+ezb89e\nPv30U86dPevS6CN9Dw4OZvjIEfxj+OOYTCYOHz7Myk+XceDAgQqNyRUEQcDPz48H+z7E/Q8+gM1m\nI+HMWZYvX87OHTtKvXbVipVAge1Dr9cTEBBQqWM7f/4823/cVsyeUhIqy0heXrhjyHN3fJXxLKUx\nT8lg+PZ//sv0GS/yySef0KBBA/r161ehe0owGAxyHMDK5St4Z97cEtv6+/tzX58+PDX2aZo1a3ZT\nCb4gCGg0Gjp06MCTz4zl7rvvLpaIsSQolUra3HUXzzzzDF27d8PPz6/S5ptELwY88ggjRo2kbt26\nLoVGi8XCsaNHeeG551AoFIRHRjJk2FCGDRtWqcLSbc0A5r3zTpnJ1KxWK+/Ne5fuPXug0+kIDg4m\nJSWF5s2b88rsf1V422m327l06RIpKSmEh4fzzTffMHPmTB546EGsVmuJOwJRFFm+fDl9+/bFYrHw\nxYaNvPjSDO69917sdrtbOwlPIIoiP/74Iz169CA9PZ1fd/3CqDGjee+D90uVLkRR5Kft24ECY9/e\nvXt56KGHKnVsDRs2lImBxWKhw13tXI4pPDycn37ZxUeLl5Tog//Vt98QFRXFuLHPuFwoERERzHvv\nXbb/uI2TJ0+67GP8xAmo1Wq2bNni8nxUVBQdO3bk1KlTZGRkFDsvCAKdOnWS3WddISwsjHr16nHh\nwoUSi7Y0bdpUtl+5QkhICCEhIVy7ds3lPFYoFMTGxiIIAg/2fQiDwcCAAQNY99n/Ko0B/PLzLvne\nO7Zt4+2577gklnXr1uXwsT/leS2KIgvmf8ik5yZz6NChSt2ZQ0HWz6PH/3K636IFCxk/cQIrV67k\nwQcfdHmdIAgcOnpE3pHbbDaWL1/Offfdx19//UVmevH37Qn6D3iYgYMewWazMf/9Dxg/cQLr169n\nzJgxrF69mjvuuKPYNXa7ndTkZBbN/5BF8z+sVG3Bbc0A3ElK5uPjg39gAKdOnaJnz55oNBoSExPJ\nysgESnePdAeSC5ndbicwMJD77rtPPleam2dCQgL+Wh3JyclORjCpz8qGIAg0bdpUNi453qO0+6Wn\np5OdnS0v6k+WflzpDODcuXNcvXpVfp+BgYEu362/vz8AE56dyMRJz7rsSxrnytWrSr3n/Q8+wP0P\nPlBqm0GDBpV6vkWLFqWeVyqV3HXXXaW2adiwYann1Wp1mW1q165d6nmA3/bu48aNG5w6cZI727Qu\ns727WLbsb8+fnJwc0tPTCQ8PL9au6BwTBIE2d7UlLy+P1q1b88f+yt/1Ot5z27ZtGAwGjhw5gq+v\nr5zOwxUc161SqSQ8PJyrV6/ywAMP8OnHn1RofUr0RqlUUrduXbZu+Q4flZrdu3ejVqpY99n/yuyj\nMpMx3tYMwB1YLBZiY2Np3749f/15jNp1YgkLC2PIkCGV1v9ff/1Fu3btiI+Pd0uSEQSBJk2aULdu\nXTIyMti/fz8dO3eqlPGUhsTERDIyMggNDUUX4I/NZiuTAW7atMlJojt14oTbxj530bhxY15/Y478\n/Ze9e0pt784C9EYsO2PSc5MB6NatW6X9NlarlVMnTsjfBUFg06ZNjB8/3q3rTx4/gU6nQ6PRcOzY\nsZtqB2rVqhV/HjlKRkYGUVFRLndurmC1WtFqtaSlpTF//nxat27N+XOJFR6P3W4nISGBLt26kpGR\ngdFopHadWIJDQ9hVmKaiKvD/ngGo1WoGDx4MFGxDAdq0aVOp/T/ySEEcQZ06dTy6VqPRULt2bbck\nuMrA/fffL//fuHFjt64JDg5m+owZTsfy8vIICgqq1LE5wku8bx4q87c1GAw8P2WK0zF3DKsSHG0+\nLVq04LM1ayptbEURGxvLzJdnAX/bXaScTqVBpVLRu3dvp99tyaLFFR6PQqHgn/96xWk8EgOc/fI/\nK9y/u/h/zwBuBipiuFNQtQTOMdCmPPcdNmxYZQ/Ji/8nCAwMLFEV5yjNSxHpjh+r1Sp/LBYLoaGh\nsir1ZkNaB4IguOUG6WrdOMbYVOZ4qtobTriV3e80vr5ibHRMua/XarX8eeJ4pRNcm81GVlYWWq0W\nrVbr9nWiKJKRkYGfnx86na5Sx1QSMjMzEUVRXmBe/P9D0TUsfZeIqSMBttlsToTXbDZjNpsxGo0Y\njUby8/PJz8/HYDBg0OeRl/f3x2AwoNfrMRgMcjuTyYTJZMJisWCxWLDb7VgsFpSFxFwKalIqlSgU\nCtRqNT4+Pvj6+uLr64tGq8XPz4/pM16kVq1aCILgVK3rZiIvL4/8/HzCwsI8WhsGgwGDwUBISEil\nezKJokjrlq2KRQJ7isRLF+NFUWxfVrsatwMQRZH8/HzUajUKhaJceUeUSiW1atXy+N6CIJTruoqg\nqhZTTYdE7ByLxUgE2GazOX0kwmuxWDAajZiNJoxGo0xYpI9EbB2JsER4JeJrKSS+VqsVi80GhfeU\n5Gi1UgkKBRofH9RqNUq1Gl9fX7SFhFcSRop+tFotwaEh1K4Ti1arLSDWGg2+vr74FPalVqtRqVTy\nOnJcT9JHwq0ofEjP6ilKE/wMBoMcye8qz9CthhrHADIyMujSsROCIODj41OwCHQ6QkJCqFWrFpGR\nkURHRxMVFUV4ZARhYWHUrl37puq8vXAfEoEtaVsuQYrMLqp+kCRgSWK1WCyYTCYnCdhgMJCfV0B4\n9Xq9THwlgmwwGDAVEmCD0YjZbMZW2JcoilitVuyAIIpQSAwUCgU+KlUB4ZSkX40GrVaLRqNBp9Ph\n7+8vEyU/nZaIqEiZGEtEWLpOkqRVKpWcysCRABclPCXFonhRuXh82D84c+oUKpUKX1/fgvcaGEho\naCgRERFERUURHR1NRFQk4eHhhISEONWYrmrUOAag1+tlNyqLxUJeXh6kp3Pl0qUSr3ll9myefPqp\nqhribQlHnaj0f1HVgyT9SgRYUh84El5HiVev12PQ58nHSlI9mM1mrFYrgihilTI1OqoeComkxsdH\nJr46P78C4ltIXP39/fH39y+QjHVa/LUFMSMabYGUrNFo0Gg0+Pj4kJOTg81mo379+jJxd8zh4igB\nV3fQmhdVi8zMTFnFZjQaycnJgWvX5POOBl9BEPD19eWvUydviuu3O6hxDCA7O9vjayKiPMv4d6tB\nYnpWq9VJ9WAymf4mqnnOqgdHna8j8ZUItkR87XY7tkLJ11Y4qRUAhUTRV61GoVLJ6gNJ/SBLR/7+\naP3/Vj34+/sTEhJCTEyMrKaQrpNUD45SryT5OqbmLqp+qGycOXOGy5cv07p12f70XuJfcyCKIsYy\ndPeOBl8oiFOqzjlS4xhAeYpWuwpskbB//36mTZvGggULaNq0KQ888AAjR45kwoQJ3HfffURFRfH5\n558zYcIEzpw5w44dO9i4cSMfffQRn3zyCc2bN6/I45QJi8XCiMeHo1Kp8CuUeiW1gvRXUj34+fkR\nFRUlt/PRFNf7KpVK2X4iZUN1JLiOmVJvN+In2YbciXFYsWw5m7/5Vv7+n7f/W2JgmHcXcGvh1KlT\nTJgwgfHjxzNs2DD69OlDkyZNWLp0KcOHDyc5OZmff/6ZpUuXsnbtWn744QcSEhJ44YUXeO+99+jY\nsaPLfkVRxGQyeTQWjVZ7+zIAQRAuArmADbCKotheEIRQYANQH7gIDBVFMUsoeMoPgb6AAXhCFMXD\nFbl/eXA9Nc3ja0ozpHbs2JH333+fHj16cPr0ae6//35mz57NhAkTuHLlCmFhYRiNRlauXMmmTZvY\nv38/48aN4+TJk3Jcws2EWq3m2y2b5e/uBH9VFLcrsfv4o6V07NypxAXuiOEjRzB8+HD5e0nGxIMH\nD3L4UDzjJ06otHHeirDZbE4unNLO7FZE8+bN+eyzz2jevDl16tThxRdfZNCgQcyfPx+LxcLly5cR\nRZF//etfTJo0Cb1eT48ePdi+fXupc0MUxRLTepSEys6r5Skq4w31FEWxjYPL0SxgpyiKccDOwu8A\nDwFxhZ9xwEeVcG+PkZyc7FF7QRDKfEkdO3Zk6dKl9OrVi5kzZ5KXl0dmZiYxMTHExcVx7NixgkRY\n991H//792bNnT5UQ/6LIz8+n74OVm8ahJkKlUhEcHOz0KSm7qs1mIz8/v4pHWPV4sHcf7mjeQv58\ntmZtdQ+pVNSpU4e9e/fy8MMPc9999xEQEMDRo0dp0qQJtWvXJjMzE71ez8svv0yvXr1YunQpnTt3\nLrXPokzQHXgSOHczcDNUQAOBHoX/rwZ+AWYWHl8jFlgK9wuCECwIQrQoip5R5ArCUwYABYVdysKI\nESN4//33+fPPP+nUqRMHDhwgNjaWevXqyeHxK1asYODAgbRt29bpWqmYzc3O/22z2bwlDCsIi8VC\nYGAgwcHBHD16tNh5URRp1qyZW3Pm/xMkG5OEq1evOv0+vr6+N13dWRpMJhO5ublObtht2rThkUce\nYdmyZYwbN46vv/6aRo0acf78eQ4cOEDnzp05duwYOp2OkSNHlnkPs9nsMQOIiIjw+FkqExWlBiKw\nXRAEEfhYFMVPgEgHop4CSBbU2oBjWsOrhceqlAFIqWvdheQu6k67devW8dRTT/Hiiy+yfft2IiIi\niIyMZOXKlaxdu5bu3bu7LCRus9nQarXEx8fTvn2ZsRvlhtVqrXCZyf9vWLVipVzM/PDhw2XmZDp5\n8iRDBz9a4nlBENjz+29ODMBoNJKVlSV/d6cQye2OlcuXs8IhUVz9+vX56Zdd1TYes9lMUlJSsSDM\nRYsWERcXx549exg+fDidO3cmIiKC7du389xzzzFt2jTWrVvn9j08jeaNiory+FkqExVlAF1EUUwS\nBCEC2CEIwmnHk6IoioXMwW0IgjCOAhURqpugq87MzPSovSAIbkvNTZs25erVq3Ts2JH58+fTu3dv\ngoODSUpKIjAwkObNm+Pv78+aNWs4evQogiDwzjvvoFKp+Oyzz5g40b18+OWFxWKpFsl006ZNaDQa\n+vbtW+X3LgsNGjWU0xk3imtMs2bNSm1/5dLlUs+LoihnLYUCHe+hQ4c49PRYoCCIaPXaNbetneR2\nhUql4tixY7Rs2ZIZM2Zgs9lo06YNo0ePpnnz5uh0Oq5du0ZQUBBhYWH89NNPzJo1i6tXr9K0aVO3\n7qHX6z1O5XBbMwBRFJMK/6YJgvA10AFIlVQ7giBEA5LInQQ4ZkuLLTxWtM9PgE+gIBVERcbnCjk5\nOR61d6zpWxYEQWDEiBFkZGRw7do1goOD0RZa+Xft2sW0adMAGD16NKNHj5avy87OplZoGMnJyXJi\nuJkzXiI1NZXIyEiioqKIiooiMjqKsLAwgoOD8ff3l/3Si7pBloTqYABWq5X4g4e4q327Kr2vu+je\nvbtH7c+fP1/qeaVS6ZQRtmXLlny56atyje12RmUGnplMJkY8Ppzw8HA5mCoyOoqIiIJAzaCgINm1\nWK1WuwyEO3nyJBqNBlEUmTdvnlP/06dPZ9euXSgUCrlmSHJyMpmZmQwfPtztsZfHxdzTovKVjXIz\nAEEQdIBCFMXcwv/vB+YAm4ExwNuFfyVfuc3AZEEQ1gP3ADlVrf+XCj57AonAuounn36aLVu2IAgC\nOp0OHx8f6tevz1dffcWqVatcXhMcHMywx//hdOxIfHypxEYURafwe19fXw4eOVxqqUeLxeJR7qLK\ngEKhoGHDhpw7W1z1dTuirLKHns6XWxUVLUo0fcYMho8cIX+vKAP488iREqVrSe0ijVelUtG9Z08+\n+nip3KZdu3a0a+daCOnevTtjxoyhfv36qNVqdDpdQSGkn37iqafcDwB1N8W0I2pFlOxiXhWoyA4g\nEvi68MWqgHWiKP4oCMJBYKMgCE8Dl4Chhe2/p8AF9BwFbqBPVuDe5YbFQz9dTwlmvXr12LFjBxER\nEfj7+xcUvmjThl9//bVEV0GTyVQsIKSsIvbSpJcibN3ZARiNRvz9/bHb7ZjN5kqrwmQymUq0LYii\nyOgnxpTb9dRqtcqxBrcCLpUSMQ7I7/x2wZ49e0hNTeWxxx5zOv7pp5/y+OOPExgY6FY/oaGhTsJV\ncGhIpbk4GgyGUlUrRZPfmc1ml6lbpCykRW16Op2OhIQEevbsiSiK6HQ6IiMj2b59O88+6zrbqSuk\npKS43VZCZdYXLg/KzeJFUTwvimLrwk9LURTfKjyeIYrifaIoxomi2FsUxczC46IoipNEUWwkiuId\noigeqqyH8GDMNGnWjNi6dQkJC0On08lbxpKg9XBBq9VqMjMziYuLw8fHB6vVyh133EHDhg1LzF+T\nmprK4oWLnI4ZjUaPnk3hhqrKaDSi0+kwGo3Me+fv2q2OqRpsNptHesz09HQ++ugjlwF2+/fvZ8eO\nHXLgmIRjx46x/NNlZbpHiqLI5s2bS2xX1ZlsRVEko4xAwrDw8NuKAXTp0oX8PEMx75XAwEC3PF8k\nfPXtNxyIPyR/KjONeFnCkCtER0cXO5adnc2ePXuKrS1BEGjUqBF33HEHNpsNHx8fGjVqRHp6ukde\ncyqViriygI4zAAAgAElEQVSmTQmPjCQwMBCNRiOrkAVBQBCd56wgCE72oupAjfIJVCgUTvpYKVeN\nY4bGvLw8bty4QXp6OtdT0xCUnvFIURRp1KgRTZo0QaFQFFT6qV2b3r17I4oizz77LPn5+cTFxfHK\nK6/I1znepzwBJRqNpswdQH5+PrqAgnw3kqpozZo1TJ061WlRREZGMmbMGKdrQ0JCeP75552OZWRk\nsHbtWiwWC0uXLuWll16SdwIHDx4kLS2Nhx9+uNg47rzzTn7//fcydyCCIMjlECdMmOA0RlEUWbBg\nAf7+/rz99tvExsYyZswYli1bRnJyMq+88grnzp1j3bp1TJgwgfDwcN566y1iY2N56qmnWLVqFVev\nXuXll1/2aHeSm5tb6nlPiwLduHGDo0ePyjsdi8UiJ3nr3Lkzs2bNkiXLNm3aMKVIAZaKYtu2bbS7\nu30xpmUwGNDpdGRkZODj41OtAUvlUa24Mq4GBwdjNOQjiiJvvfUWCQkJ+Pn5sWTJEnr37k1MTAxG\noxGlUinXY/aEmQ8ZMoQhQ4Y45cSShCqz2Ux+fj56vZ7MzEyZvlR3tt4axQCKQkploFQq8fHxQVeY\nFbSifXbu3FleMHl5efj6+tK5c2cEQeCjj5zj3+x2O9u3b6dLly5OxzwtVu9OWluDwYC/vz85OTnE\nxMSQl5fHqFGjGDlyJE2bNpX12xcuXOC1115zurZx48ZODCA1NZWVK1fKqR9EUeS///0vs2fPRqlU\n0r59caLi+Hzu1ic4dOgQVy5dZunSpSW28fPz45lnnmHQoEEEBwczbtw4Jk2aRFZWFq+//jpPPPEE\nly5d4t///jdff/012dnZjB07lg8++MAj4m+z2coM9Xe30poElUrFgQMHyMjIIDAwUE5sd/fddwPw\n9ttve9Sfp+jZsyd2u52PP/6YRx99VE578vvvv9OzZ0927tzJ1KlTuXLlSqkCxqhRo0hKSirxndau\nXZs15az4VZ7o/fDI4v71Bw4cIDk1BV9fXyfhC6BTp05kZmaSn1/AIGJjY8sdpOVUcKawBoJGoyEw\nMJDIyEgaNWpUrn5vBmo0A7hZaN++PcnJyXLtAVEUS0wcplQqGTt2rNMxq9XqcUCJO7ra/Px8dDod\nQUFBjH7ibwlfEAR+//33UpmO41Y4NTWVxYsXI4qinCdIqVRiNptZsmQJzz33nEtCkJycTK1atVCr\n1cV0ziUZHYv+No64fv06SqWSF154gTfffJN58+Yxa9YsBEHg2LFj1K5dWzbG//DDD6jVau6//37m\nzJlDUFCQR/pdKLB1lMWYPWUAfn5+cp+iKKJSqTCZTGUGTWVlZbF+3eeMHfdMqYb/kmCxWFAX1gYA\nGD9+PP/617+YPn06wcHB/PDDD7z55pv079+fLl26IAhCqbaeuXPncunSJc6dO8fJkyc5ffo058+f\nJzU1ldzcXGJjYz0eo4Ty6NZd5e/q1KkTnTq5jvOoW7cuFy5cQKlUIooigYGBNGnSxOP73m7wMoCb\ngLp163Lt2jXsdrucUbMkAu2K8Hmq/gHcKjSTm5tbos7xypUrpUq3vr6+ssEqODhYDnuXIkB9fHzQ\naDQkJyezadMmuQ6zhKSkJFavXs0//1lQ79SRQSxasJCIqEgGDx7sts5VFEVyc3PRaDSEhoby4Ycf\n8txzzzFnzhxiYmL4+eefZQLv6+vLjh07aNWqFRqNhsWLF7Ns2TKPDdN6vb7MNvUa1PeoTyh43yqV\nCrvdLifci4iIwGg0cuiQs6lMpVLRsWNHvv5qE2q1Wk5g5wnsdjuXLl3i9MlT9B9QoKITBIE333wT\nURRJTExEp9Nht9s5duwY27dv54svvmDy5MkkJia6VAcFBgbSvn17OnToUCwRoFSbobzwNHpfFMUS\npfeS6kkEBgaSmppKQEAAfn5+qFQq6tWrV74B30bwMoCbgODgYPR6PSqVCoPBQHJysstFKoois1/5\nF2+89aYTE8jLy/N4wbjjT5yXl1cio3j88cdLdXFs1KgRZ86cAQoI6pw5c1i8eDGpqakyw5Iyjh49\nepSYmBinxFkHDx7k5Zdfdtl3QEBAuQL0JPsAFNQuHjt2LJcvX+bBBx/kwIEDTJkyBUEQUKvVHD16\nlMcff5wLFy5gNpuLMSh3kJaWVuZ78TS0X4o0l4zv0i5AstPcddddTu2l+7dtdxc5OTnk5+e77akj\nQaFQYDAYXPrqC4LAxIkTWbFiBUOGDOHDDz8kKSmJESNG8Nhjj+Hn5+cyu2mbNm24dOmSrOqIioqi\nUaNGNG/enKZNm9KsWTPatm0r68M9iUfxdAcg7fpcYdOmTbRq1apYcJdKpSI5OVmu5mU0Gqs9T09V\nwMsAQDb2VFaWTLVaTUZGBmFhYRgMBpm4bd26la+//hpBEFiyZAk7d+6k5R2tyMvLc5Kqbty44XEK\nYXciCvNy9SW6tf7111+lEreiY1EqlTz//PNs2bKF+Ph4eUcg+cFv27aNgIAAWrZsCcAjjzxSYt+R\nkZEkJCR49Lxz587l7NmzAMTGxvLaa6/xwAMPsHr1agYPHszzzz8vex+pVCquXbtGv379WLlyJf37\n9y+X2uTy5dKjgAVB8JgYQ8HuTZJy7Xa7bJcSBKHE99W2bdty++rn5+ezb98+unfvjtFodDLGX7p0\nCaVSKRvcBw0aROPGjXn33XeZNGkSn3/+Of/5z384cOCA07P269ePAwcOcO3aNbKyskhLS+Pw4cPy\nnIqLi+Ps2bMYDAZWLFvOC1PdN2aX5XlVFIIguGQwOTk56Py0pKSk0LBhQyZPnozNZmPQoEH07duX\nzMxMQkJC0Gq1ZGVluZUCxl1IRY6qO/dPUXgZABAfH8/uX37lxZdmVIoLn1KpJDMzk8DAQLmAikKh\noG/fvnI6BEEQ6N27N8eOHSvmDZOTk+PxONyZWHn5hhIlr2effZakpGKB2TJiYmJY5pDbRcLDDz9M\nWFgYO3bskL0elEolVquVjRs38vzzz7v0dTaZTLz66qu88847PNj3IR7k7yylZrO5zMU3Y8aMYsem\nTZvGc889x9NPP01GRoZcNEayxdSrV4+vv/66mCHeXVxILD0K2N28UUURERFBUlKSPFZAJuxF3QYd\n4SnxlxiGn58fEydOxGq18vTTT7Ns2TLUajWiKDJq1ChWrVpFt27dOHz4MHfffTeLFy+mV69etGrV\nisuXL9O9e3d2795N//795b7nz58vj1cqu5mXl0dGRgaXL1+Wc3AFBASgUHkmaHkaYVuSMBcYGEjn\nLveSlpaGWq12ciwQBEGuUmexWMjMzCy3QGixWLDZbE7r2mg0cvz4cbp06VKpjKWi8DIAoHXr1iSc\nOeu0wHbs2MHxY38xdfo0p7bu5NMXBEGuwuUYcFV0AatUKtq2bVvseGpqqsfP4E7VsrxcfYmul/Xq\n1SvVk6g0d7XOnTtTu3Zt1q5dK6sy1Go1ZrOZxYsXM336dKe+LRYLEyZM4JNPPinWl8lkYs+ePVy6\ndImnn366xHtKv5nkMqtSqejUqRMXL14kNDQUo9EoR4dKY9JoNFy8eJF77rmnxH5LgiiKZUYBS6kI\nPEVMTAxHjhwB/p5fgiCwefNm4uPjgYIAM1dMzxMs/3QZgx4dLKsBVSoVy5YtY9GiRUydOpUff/yR\nJ554gmHDhrF161Z69uzJxx9/TFJSEi1btuTdd99l1KhRZGRk8Oeff7Jq1SqGDx+Oj48PTzzxBDqd\njpYtW9KkSRPq1q1LrVq1qFevHo0aNZLXTFJSEmqlSjZCu4OyXG+LQqlUurQlSTs0aedSdN35+PjI\nxNsde48EvV7vZFvLzc3l112/8PDAAfI4/Pz8SE5OvqWIP3gZAFBghCwaOdi5c2d27fzZSRVjNBp5\ncdp0Fi1ZLLdLT0/n1KlTsqeEBFEU5fq3nqoF0tLSnAicO3DHCJyXl1ciA+jevXtBfeQSUJabab16\n9Xj22WdZvHixXAdYrVZjs9mYP38+M2fOlBeDSqVi+fLlLiVYtVrNyeMnSoy4LaoaMxgM7Nq1i1at\nWlG/fn1CQkLIz89HpVLJ+nSz2SzndwkPDy9XRlRBEMqMAnbHFdcVwsLC5Mhuu90uq30GDBjAgAED\nytVnUVy+fJm4pk24ceOG01xRq9VMmTIFvV7PkiVLaNSoEfPmzZPtAB988AGCIHDhwgXee+89YmJi\n0Ol0NGvWDH9/f7Zt28Znn33Gb7/9JjNIR0OrZINp2bIl8fHx1K5dmwnPup/0UKqy5UmWzdKCO0tT\nrQYEBMi7AFcxAHNee50u3brSq1cv+djly5dZ+OEC5r33rnwsMDBQfpcS4uPj0Wq1VVKQyRPUSAZQ\ndBIMe/wfxdzGEhMTad68uayTBViyaDExMTFO0ktiYqJLLwWFQiH7dJcU7r1q1SqioqJ48MEHnY4/\n+eSTjBgxQq7Zm5OTQ1ZGJtevXyc1NZVr166RkpLC9evXuZGdjV6vdyuk3GAwlCiBLFiwgKtXr5Z4\nbWxsLF27di21/9DQUGbMmMG8efNk10aFQoHJZOKDDz5g2rRpxUpISpAYpkqlQqP1K7bzgoJ0zX8e\nOcrwkSNkIq7T6ZxUEb169eL06dOEhIRgsVhQKpXo9XpiY2M5ePAg999/f6nPUBrSy0glHlqrVrlU\niJL0KBG4sqJDRVHkvffeQ7TZmTHzJbfuUadOHfz9/V1GVYuiyJAhQxg5ciRGo5HZs2ezcOFCxo4d\ny9tvv83p06dp3bo1c+bMkVMqF33O48ePk5eXR1ZWFleuXOHs2bOyO+iVK1fKLfkKgsD+QwdlwqzX\n68nOziYzPYO0tDRSUlLkT0ZGBjeys0v1JHtzzhv07d/PZV6g8PBw0tPTsVqtLncn3Xv2YN+evU4M\nYOXyFeTk5GC1WuX77t27F7PV4vTM7du3Jz093Yn43wqlQmscA8jOzmbv3r1ORCMzM5OgoCAn6Tgu\nLo4mTZo4vbDnp7wgpzaQ0KZNG6Kjo0lPT3diIn5+frI/f61atRBFkXfffReTyUTdunUZPXo0HTt2\nZPfu3cWkAoVCgUajQaPREBQU5DKs3RHuTqTSXAb/+c9/luoG6u4C1mg0zJo1i4ULF5KXlyc/W15e\nHosXL3YZI2Cz2Zg4cSILFixAoVAwbtw4l323adOGP/74A4C33nrLSSJUKpXMnDmTwYMHs2/fPurW\nrUt+fj5KpZLc3Fzi4uLYtWsXAwcOdOs5XKGyo4AlaLVap2eRdowffPBBsV3Z5MmTCQ4OJj/P4NHO\nUhAEQkND0ev1TJkyhffff1/egf3nP//hhRde4LfffuPQoUO89957TJgwgTVr1jBy5EhmzZrF5cuX\nS7U5XLp0Sfb+qVu3Ll27dnVi9BVxA/Xx8ZEDNUNDQ8usplfaeujzwP3s2Laddu3asWbNGi5fvoyP\njw8zZsygVq1apKWlYbFY8PX1LdZPenp6sfXz6mv/5siRI05Mp3PnzsWeV7IrSHPEbrezdetWunbt\nWq3eRjWOAahUKoYOHcp3330nc3JXkyUlJUUuki4hNze3mG+wxWIhLy+v2KQMDAyUKyTVKpQMX3zx\nRac258+fJzs7u8LZI92VIhx3AEU9SBYvXsy1a9dKvDY6Oprly5e7dR+1Ws3UqVNZsWIFSUlJ8lY4\nMzOTZcuW8cwzzzi1nz9/Ph9++GGZqSGkLKuCIMjxBI4QBIG7776blStXEhcXJ7viZmZm0rJlS775\n5hteffVVt56hKNyJAnZ0S/UEarVa/o1EUZTVkS+88EKJaZX9/PywiaUHC3700Uc0bNiQBx54QD7m\n7+/PnDlz+PLLLxk6dCi7d++mcePGbN68meTkZKZMmcLChQuZPHky//3vfzlw4IBbSQP79u3L+fPn\nUSgUKJVK/Pz8CA0NJSYmhoYNG9KxY8ebXu9CQmnrISEhQY72HzVqlNM1kqBms9lcxjr07t2boEed\niwGdOnWq2HuXIoobNGhQ4rh27drFsGHDXObQqkrUOAbg7+9PfHw8HTt2ZMyYMbz77rvceeedxdq5\nmkR2u72YFOjr68u5c+eKRW4GBQWRnp6OIAgyhy/ap6NXUFXAXJjnJCEhgePHj9OnTx9Z3dCrV69S\nffE9TZEhCAJPPfUU33zzDceOHZN93K9cucKGDRsYOnSo/HtMnz7drT5Lkt6lvqFAn3727FlGjRrF\njRs3UKvVXL9+nSZNmpCamlru7IuSXrg0xDUtX+RoUZ2w9FuXJhi8+FLZBuFu3brxyy+/0KdPH6e+\nAgMDGTp0KMnJyezbt4/Tp09jMpkYOnQohw8fxmAwUKdOHbcrYcHfebWk4ECTyUR2djbnz59n7969\n/PbbbyUyAKvVyvp1nzNi1MibrhIpSvQdERISItsagoODi53/9ddfeeihh5x2Abm5uS6jw10Fmt15\n552YzWamT5/OmjVriI+PL7fdqLJQ4xiAXq8nJSWF1NRUpk+fTmRkJBMnTmTatGmyMQ4KtvNFt3Ge\nxAoEBgZy/fp1BKHsovJVBZPJhFKppHHjxvzyyy9otVq+/PJL5syZQ0JCgizh1qtXj9mzZztdW17D\n6aBBgwgKCuKXX36Rj588eZLvv/+efv36Veh5JGRmZrJlyxZ69OhB3bp10ev1NGrUiKysLFQqFRkZ\nGbRo0UJOslYeuOMVUr9+/XL1Lc0rm82GQqGQVTuS+6OUmsBT4+G5c+cw6PP4448/6NChgxMTMBqN\nvPPOO/IOtGvXrtjtdv744w/Wrl3rMWF68sknCQ0NpV69emi1WjIyMkhISOD06dNcuHChVBWiUqnE\nYiuduVYFpFTejruwsuAqVXlRe6IoiqSnp/P++++zdOlSRowYQWpqKr///rtsm6ku1DgGYLFY6NOn\nDy1atODDDz/knXfeYe/evQwfPpzExES6du3KsGHDaNeunSyJSbrA0NDQYu6QKpXKySgkISgoSN7W\nV8YLlsYgSbtSTn8p0CwpKYnu3buXKjUazWYUCgW7d+/GlG/EaDQyYMAA7r//fgYOHCh7uSiVShYs\nWOB0bWxsbLH8Pe6iV69eBAUFsXnzZpmpHjp0CH9/f48rcrlCWFgYTzzxhPxd0kVLRresrCyCgoKo\nW7duudVt6enpZeqxy1vdqWj1KqkgiWPgWaNGjTwmygMHDoSBBfr5999/n+nTpyMIAjabjWnTpmG1\nWvHz86NevXqEhYXx119/8cUXX5TLS+Xee+9FoVBgtVpJSkoiMTGRc+fOyTmxysoFlJ9nwGg0uoxT\nsdvt7N69m5iYGEJDQ9FqtU6V8KR1UdHdg7RObTabSwZw3333FRMgHGt4S2Ow2+1kZWURHx/P+vXr\n2bt3L40aNWLatGm88sorHDx4kA4dOnDy5EnS09MrNOaKosYxgODgYI4cOcJ//vMfHn30UWw2Gy1a\ntGDAgAG89tprhISEkJyczKpVq/jzzz/JzMwkODiY+vXr07RpU+rVq0d0dDQhISFyPQGNRiNLb/B3\nsRaDwYDJZMJsNsvbRGmbLBFxyVXUaCwgyFLuIL1eT05ODjdu3CAvL4/8/HzMZrM8yaSPpJs2m810\n7dq1VAInecV0796dbt26yQvGx8eHzz//vNREZxV1XWvXrh0KhYLNmzfLv8Hu3buJiIgoM/FZaThw\n4IAcZKTT6ejVqxeNGzcmICCAM2fOyPUZ1Go1bdq0Kfd9rly5Uup5QRDclhpdQQqeA+Qyoq5Uk/C3\nukV6/2X509erV4++ffuSlZVFSEgIb7zxhpzvJiwsjFq1apGfn89bb71V7vGrVCquXLnCuXPnOHfu\nHNeuXcNkMuHv70+9evXk7KYl4fERw0ucY3a7ne+//x4fHx98fX3lgDnpIwXgaTQa/P39CQwMJCgo\nCH9/f/z9C9KfS04VKpVKjhAvWkrVbDZjMpmc3DcdUzv7+vpiNptlu19WVhbJyclcunSJs2fPcuHC\nBbKzswkNDaV169a0b9+eWbNmkZWVxa+//srrr7/OiRMn5KSE//vf/yo0ZyoDNY4B2Gw2tFotS5cu\nRaPRyNxaeonnz5/n8uXLZGRkYDQaEQQBo9FIcnIy+fn5JCQkyPV4pVTIUuSjlPvbbrezaNEi4uLi\nsFgsbN++nSFDhjhJKAqFwintc1HmAc66bUePiqLpZv39/cssbCM9e9E+JIwaNarUVAd16tThp59+\ncvt3doW2bdui0+lYv369rCvesGEDTzzxRLnVJ+3atZMXrPRMrVu3xtfXl5ycHFQqFVlZWRgMhgox\ngLJqAQuCUC41meP10vjL6icrK4tPln5McHAwMTEx9O3fr0zVVosWLYCCSl9WqxWNRoOvry++vr60\naNHCKW9TeXDt2jWOHz9OYmIiaWlp2Gw2QkNDqV+/Po0aNZJTIJvNZrKzs50i1wVBKNXGJAgCkZGR\nsrBktVqd1ggUCDd6vV62uznOc6mNNE+USqW8/iSIosiXX36JVqtFpVKxYsUKJk+eLBu1lUqlzDgk\nKT8/P19O8ZCTkyMzj+vXr7N3715OnTpF3bp1adiwIT169GD06NFyGnSTyUR6ejo2m63casnKQI1j\nAJJLICBLA5Jk4efnh0ajkf9KqY6tVit6vR6z2Sxna5SkCUkHKEUfOkoxP/30E6mpqbLLqST5SxPI\nEZJEJ8GVr7wkORet2uXqWFGIoghF7uGIRx99lKysrBKvryxXtSZNmvDkk0+yatUqmfmtXr2aZ599\n1mUK37IgLR7HZ2/ZsiUmk4mcnBzUajW5ublkZWXRrFmzco874czZUs+r1eoKLWSJKEnBazk5OUyZ\nMsXpuaTiJaGhobJq674+veX4ibLw448/kpqa6hQd/dhjj1G7du1yj1vC6dOnOXHiBFlZWSiVSqKi\nomjYsCFxcXHExMTI80fKNipl3XQHoiiSkpIiS+0SpHVX9LjjdY4fCdI6kto4qpE2bNggu7KazWZ5\nlyW5dEtrTdq1OxaTslgswN+egVevXmX//v3y7t5oNMrtpN2epGGoLtQ4BhAQEMDx48eJjIyUpfjc\n3FyuXr3KhQsXSExM5MqVK1y/fp3c3FxEUZQLxkjbSp1Oh5+fn7z1FgRBlkwcifwjjzwipySA4lK+\n5IopEX9H4iz1I6UzkK6TmJajGkitVpe5AyhLT9qrVy95ArtCeVIclIQ6deowceJEPv74YywWC+Hh\n4RUuxLNkyRIuXrzI22+/TVxcHNnZ2bIXkF6vJzk5ucxAttJw+eLFUs9XtBawWq2WM3RKWVVXrlzp\nsm1qaip2u50HHnqQ3377rVj1Nlc4ePAghw8flomP3W5n+vTplWaAvHjxIhkZGWg0GqKjo2ncuDFx\ncXFERkaiUqnkADSp6LrFYnFiAKIo8sJzz2O3Wln40ZJiwlB0dHSxNeb4kQi6o5TveL10D4nJSpK8\n4+7AbrczZswYNBoNgiDIAW9SQkHHPi0WCwaDAYPBQG5uLrm5uXJVN61WS2RkJOHh4dSpU4dGjRrR\noEEDYmNj8ff3l6ObU1JSvCUhqxoqlQofHx9mzpzJ999/T05ODo0bN6Z///706tWLhx9+WM51cuTI\nEVnyCA8PJy4uTn6RYYU1hTUajdPWUIKU4dJut9O3b1+6d+8uT1bHXPoWi0WOcpS2lHq9ntzcXG7c\nuEFubi4Gg0EuLFM0n7nNZiMvL89pW+wKZRWYefXVV8uMBF6/fr0nP3WpqFWrFs899xzr1q1j7Nix\nHtUBWLFsOZHRUU7BfJMmTZL/j4iI4MyZMxgMBjkS+fLly+XK1CkhrYwoYHdScZQGRwm2LEN1ZGQk\nM1+eBVAsXbQrJCYm8tNPP8lzTRAE5syZU6l5afLz8wkICKBOnTryOpF+k8zMTHJzc+natSvnz5/n\nemoarVq1crpeEAT+KJSWi0LaAahUKjQajbzrLqoe9fPzQ6fTyXaAgIAAJ4FNytUk7dYk9Y50fffu\n3fn+++8RBIGhQ4c65aJytNkZjUa5tKMkOJ47d478/HwEQSAmJobWrVvTpk0bwsLCuHbtGps2bWLL\nli2cO3eOoKAg+vbty6xZs6pV/QM1kAHk5OTQtGlTOnTowJYtW2jSpAlbt25l4cKFbNy4kX79+vHY\nY48xYsQIxo8fX+4X5OvrK3N7yXAloTKkaYmB5Ofnk5OTI+cyLwslSalBQUGlujreDFfWwMBAJkyY\n4NE1giDQKK4xKSkpHDp0qJjh+s477yQgIICkpCQMBoOclC4pKcmtgCZXEEWxzMLkMRWoeCUlz5OI\nmpS+4sSJE0DBM7dv375cHkx2u52vv/5aJlwajYZXXnml0glPUFAQERERxMXFUb9+fYKCgrBYLKSm\npnLhwgU5fqZx48alVk1z9YwKhYJHH32U6OhogoKCZAN2RQMoi8LHx0eWyIvuqB13An5+foSEhFCn\nTh2Xlf4klfHx48f5+OOP2bp1KxEREbz88sv069ePM2fOMHnyZJo2bSpnIagu1DgGoFAo+P3332nZ\nsiXjx4/nxx9/ZMaMGfzwww8VkhAdIW3xJAnFVf6VikKhUMgh8pKLY2koamMoiqJF14uiIgbOyoTd\nbsff35/k5GQGDBhQbNej0WiwWq2kpKTIWUJFUSQtLa3cnkyiKJb62wiCUKE6r5IaD/72K/fz83OS\nkstL7BQKBRMnTuT9998nIiKCF154odIJJxS4qYaGhhIbG4tWqyU/P5+rV6+SmJjI+fPnKyT0KBSK\ncmVw9RTSO5byUpXXtVSlUhEcHEyXLl3o0qUL8+fP58aNGyxZsoQGDRrwwAMPsHPnTk6cOHFT3oUn\nqN67VwMCAgJQqVRERUVRv359kpOTmTlzpkfE32q1cuLEiVJVLo66SlcpBByLZUi4ePFiMVWN5FHh\niMzMzDLTEhSFZFwsaUJLSbZK+ribHtdisXD+/Hl27tzJN998w65du7h06VKp9gVPoFAoaNu2LVOn\nTkWr1aLT6eSP5D6pVCpJS0uTA9+gwPhfXh29oxuvK4iiWO4oYAmSPlwiOkql0unZHHHt2jUsFgvH\nj+xAoNcAACAASURBVB9363fV6XRMnz6dKVOm3DSC07RpUxo0aIBWqyU7O5vExET++usvTp48SXJy\ncplR1J7CZDKRkZHhdMxmsxVT1dntdi4Wsd+Iosjhw4eL9Sm5WYuiWOp4RVHk9OnTpQoFRREYGMis\nWbNITk6mQYMGsm2kuoNEa9wOIDc3l3vvvZeff/65xALRZWHrlu+4t2sXzp49K3sUgbOR13Fhupoo\nX3/9NXfeeafTVjw+Pp6YmBgn3ezJkye55557nAxm165do3bt2h5J5WWlof3yyy9Lrb0aGRlJt27d\nXJ6z2+3s2bOHt//zX7IzM+nQoQMt77iDxQsXMvn559nw+XqOxMcTFRPD62/MoXXr1hUymLp6jtTU\nVGbPns3o0aO59957nYxygOzRUR5IzgAlQRTFcruxSpDUU46FYFzdUzJi5uXlERcXx8b1GxgxamSZ\n/ZdUWayy8M0333D8+HEuX74sBzdptVoCAwMrHOvhClKpVcfUHmazmZMnTzq5mNpsNuLj453ejyiK\nfPvtt8XsJ9JOXXLqKOqUIV1rMpmw2WzMnTuX2bNnezSv1Go1b775Jv369aNz585cv369WplAjWMA\nNpuNzZs3l5v4Q0FGwV27dtG8eXM2bdpEcnIyvr6+PPPMM07GWUCOIygKxwAUCa4WvCtiVx5CJopi\nqUa/K1eulBrsVJKkeenSJUYOH0H79u1Z+7/P5HQaVquVjz/6iGfGj+OZwvunpqbyr3++QlJSEmv/\n91mFDaeOiIyMlAvMSBKc9PtWNIitrIRdCoWi3FHAEiRmLu0Azpw5w44dO5za1K1bl4EDB8pBYyuW\nLWfsuGdcdVfl+PXXXzl//rzT3JScGZKSktwq6uLpvHbV3tW7djcTqRT3I4qiXOdaun7ZsmWYTCZi\nYmIYPHgwWVlZqJUl76jLQqdOnfjuu+9K3VlWBWocAwgKCqJPnz4V6kNKFtWwYcMSM0BKL7YkFdC4\nceOcqoUB9OjRA6PR6GSAatasGQaDcynHxo0be1wmz2azyQzg0qVLbN68mfHjx8vHunbtWmoyOFcV\nwX777TdemDSZNev+R7Nmzcp0Q42KimLZiuXs37+fB3v3Yd3GDTRpUjHVCRQQaOn31mg0Tsn3JD/x\niuigS9sZSfepqP2o6G6uWbNmJcYtXLlyBUEQaHlHK65evVos66SnqIw0CtOmTePChQtkZmbKuYvC\nw8Px8fGRC7qUhe+3b3MKViwNQUFBxVRjGo2mWECbSqUqlnNKEASX1dUc7XaOqlhBEJxSlEs2ginT\nppY5ztLQu3fvCqXJrgzUOBtARSc6FOhU77333lLbOOoTixqBbTYbJ/46LtdRlbBy5UpWr1xVLC/M\nkkWLndrNnz/fYwZgtVrxKWQ2derUIT8/H5vNxp9//smCBQswmUyyvrlWrVrcc889Tp+i3g779u3j\nyVGj+erbb2jevLlHv2vHjh1ZvnoVAx/qJxd2rwjy8/PljyS5Se6CkutgRTwtyioFKRltKwKJ6Rd1\nJ3aFu+++m/bt29OtW7cKE/+zZ88y9LEhFdbR37hxA51OR/PmzbnjjjuIjIzEYDCQkpKCXq93i0H6\n+Pi4na31xIkTfPfdd06E+vTp0yxd8hEGg0E+dvToUTZ/863Tejl9+jTfbd5SjLEXNQKXBEEQ6Nmz\nZ4XfudRXdaJMBiAIwgpBENIEQTjucCxUEIQdgiAkFP4NKTwuCIKwQBCEc4IgHBME4S6Ha8YUtk8Q\nBKHsyJVbGKIoFjNAFYXjxHTcTkLBNlVvyCMzPcNJAvBRqeVCFBIUCkWximEZ19PJysryyBAshf9D\ngb68e/fu3LhxQ/YgkiQqyZgaFBTk9HHUU6anpzPt+Rf4dut3DB4w0OOEVomJiYx94km+2/4jw4cO\nq7CXVN26dWnQoAENGjSQ9b9+fn74+PjIgTkVUTeVFQVcNEioPPDx8XGSxHfv3s3cuXOZO3cuH374\nYYX6LgkJCQkM6NuPI/HxPDb40TJjRUpDrVq1UCgUXL9+natXr2IwFBSsqVOnjpxnvyz06dnLbUb0\nxYaNcr4tCc2bNy+WUE6r1XL58mWn9yMJOwcP/OHUpyS0QdlxMzdu3Kh29U1lwB0V0CpgEbDG4dgs\nYKcoim8LgjCr8PtM4CEgrvBzD/ARcI8gCKHAv4H2gAjEC4KwWRTFknMP3MKIj48nMDBQzpteEqQA\nk6KTWhRFtFotz09xLvjRqVMnTBZnY2Vubi5t2zkbq6ZOn8bJ4yc8MgI7Rl5GRUVRq1YtWS1Sv359\nfv31V6fFVNTrxzH3yojHh/PZ+s+Ji4vji6838UCf+9m2Y7tbRDYxMZF/PDaEH3/aQVhYGPMXLWTC\nuPGsXrumzGtLg91uZ+LEiYSEhPD222/LJSGljJflSTMh4cKFC6We1+l0FfauKWqf6datm7zLvBlS\n4tmzZxnYr788N48fO8aggY/w1debyhUjkJmZiSAIREREIAgC+fn5ZGdny+VTpWygmZmZJCcn07Jl\ny2J92HH/Wfv378/x48edCLvVaqVbj+5OfWRnZ1OnTh2MRqMsxNSvX5+//jxG3/7OqiFHw29JDEAK\nCNu3bx9nT5/hhalT3BrvrYoy37QoirsFQahf5PBAoEfh/6uBXyhgAAOBNWIBtdgvCEKwIAjRhW13\niKKYCSAIwg7gQeDzCj9BNcBoyEen02E0Gnn33Xc5f/48Op2OuXPnykYkR2muKAMQBIGHHnqoWL8d\nOhb3dXZFuKKjo8ssE1kUZrNZ1pk6+p1L+D/2rjs8imp9v2d2s5tNNr33Hjp4USkiAtJEERQRUEBE\nEAWxoKJcy7ViR4WfXBSUa2+oWBAERIqIXhUFIiLppG5CymZ7ye75/ZGccbbOZrMhyYX3efIkmTk7\nOzt7zvd95yvv19jY6DVQxxbP0aNHkZKSwmc/ZWVl4ZPPPsWUiZOwQ0QJlJaXOQh/oI1G+NnVT6Gq\nqkqUMliIk0WFyMrI5AUnx3F49dVX+fNRUVFQq9U8SZu7GIavEKsCjvKzyYwQ7HMIBZq7XYXFYsHX\nX23D1dfMwL59+zBmzJgOK4jCwkJcNfVKFzfH8YICzJxxDT7d+lmHdzSRkZGorq6GSqUCIQQhISGI\niYmBRCKB2Wzm3+vnn39GcHBwp+MOw0YMd1kvUqnUpV5g+PDhGDZsmMN7RUZGYv6CG1yuyeIPzkyj\nlFKsXLkSBoMBOTk5uP322x26uPVm+BsETqCUMgeaCgBLgUgBIEwlqWo/5um4CwghSwAsAQBpJ7fV\nXYV/nD8Uu77ZicunXuHS5lEI4QTqbrBtryeo1Wq0tLR4PM+2u4898ij+/eoGh3NZWVn4WEQJlJaW\nYs7Ma7H9210Ofl5CCJ586ik8/+xzWPt/61xe5w4WiwUnCo4jMT7BJcOKkLYGPNHR0aiqquL7u/rb\nCYxSCo1IvCUQZGoymQx2u51XzAaDwcVwCA4OhkwmQ3V1dZurpaKyw4K0sLAQ06dc4bEByx/HjmHm\njGvw4ccfdWiHqdVqIZfLERkZydOTsBqWkJAQPjA/YcIElJeXQ6vVBqzwUgy+PB8hn5DzawgheOGF\nFxzGmgxGTJs2LbA32g3odBYQpZQSQgIm4SilGwFsBIBgubz7JacbhIaG4uprZng8L6QnZtw/gci0\n6AxMJpNX4inGQ+QJjAu9pqrK7e4jKysLH336Ce8OEjIclpSUYPY1M7Fzz7duBXH/gQNw6OBBlz7F\nnlBRUYEaVS0KCgpclBrHcRgyZAiio6Mhl8thNpshl8v9Jpuz2+2isZbOVAEzMLcL+/wqlcpFIScn\nJyM+Ph4GgwG//PILCgsL0dDQ4JD37g3M598q0n2r4OhRTL1sCnbs3uWzOygkJATNzc1oamqCRCKB\nUqnk+2kbjUbevahWqz323O1usMJN4f+e0rCnTrvyTN5al8FfBVBHCEmilNa2u3jYHrkagNApntp+\nrBp/u4zY8X1+vne3g/U8VSgUbgWWkG62p+wATAajVwUgppwYncKgQYM8jsnOzsYnn32KSRMmYvs3\nOwC0Cf/rrp3lUfgDbRkwMXFx0Ov1PgmG3Nxc5OTkeL3niIgIPrOG8TL5A7EqYADIzc/zet4XOHPb\neEovppTittuXIzg4GJMmTfJZQDv7/MVQVlaGyydNxrZvdvhEGscMjJiYGJ4OWaVSgVKK0NBQXknF\nxsYGtP4jkGB0KWw34EkBAOCJBv3ll+op8Ddy9SUAlsmzAMAXguM3tGcDjQDQ0u4q2glgEiEkqj1j\naFL7sV4Jlj4ptJiFQp7RQLAgsPP2sjtgNHpXAKwvgrefiooKDPnHP/jF4e4nIyMDn279DJdPmgyD\nwYBZM67B9l07ERUV5fV1OTk5oplVQrgT/s899xzuuusu2O12REZG8m0DGa2CP9Dr9aIKvLNVwAD4\nLleedkBC5svQ0FA+xdUXePL5i6G0tBRTL5viU7ZZUFAQ1Go1qquroVarIZfLkZSUhMTERHAc57XX\nBEMg2oP6CyGNO+uXIFSWznNArVbjqy++PNO3GXCIziBCyAdos95jCSFVaMvmeQbAx4SQRQBOAZjV\nPnw7gMsBFAMwAFgIAJTSJkLIEwB+aR/3OAsI90bI5XIcOvgDRo4ciaeeegonT55EWFgY1q1bB47j\nHFo3AhClaj4TMBgMXukAWDtKT5DJZNBqtdj46qt4c/Nmn96PsZVOHj9BdLzRaMTyO24XHecNK1eu\n5IUoa9fJ+if4m7MtppQopbyrozMQksEBwDPPPIMTJ04AaGvp+Pjjj/t13aqqKlx95TSXVGRfUVpa\niuuunYWPP/vUq8KRSqVISEhAa2sr9Ho9zyGlUCigVCp9svqfee7ZbnOTsupxRh7IagEUCgXsdjvu\nuOMOaLVa5Ofn48EHH4RGo8Fll7smcvQ2+JIFdJ2HU+PdjKUAbnMzFpTSzQDEJUcvgN1ux6TLJoMQ\nggceeMDFv88qH4VCv7tbvxkMBq9WsFKp9LpLCQ8Ph1KpxM233CIqqJnPnymd7bt2igqA5ctu81tI\nO5N3OSsAQojfW/Waqmqv5zmO63QzG+DvlGE2R1atWuXS+6GjqK6uxpSJkzpMHOiMY8eOYdaMa7wq\ngY8++ghmsxkhISFoaWnB6dOn0djYyGdgDR06FDfddJPX93numWf5PgdnGsIMIOBvCpfw8HBwHIdX\nXnnFYZ2Xl5d3qsNcT8FZRwURCHAc59Cw23mB6nQ6h3QyAHw2SndBp9N5zVaJjIz0mvoXGhqK9PR0\n/GfT617dFKWlpbh+1mx88+1uTJk4CZ98vhWXT5qMb77d7VUJlJWU+O0bbmpqwo4dO/j/58yZw3PG\ns36u/irfkpISr+dZjKGzYG0Nhem57gT/nj17EBYWhoaGtmLAuXPnur1edXU1Jl06vtPCn+HYsWO4\n9uoZ2OKhTqC6uhqlpaW8EcHmiMFg8EoxIsThw4cDcq/+QFi5D7Q9e+ekCOH34Vyc2VtxTgH4AebT\n9yQwW1paHPquMj6g7mz/ptfrERzi2cJmMQBPCA4ORkJCAo4dO+ZxTGl5Ga67dha++XY3T72QmZmJ\nTz7fiikTJ/E7AWfBZrVaUV9f7zdjZUxMDObNa2PEZFYa69Im7LPrD4qKiryeZx2mOgt2r0yZHD9+\n3KVCOi8vD+PGjcOePXvwxdbPvXIFXTZhYsCEP0NBQYFHJbB06VKo1WoXIcoMoUDskroSzEVms9n4\nuJG3tOjO7s56Cs46LqBAoKKiAj/++KPHBdbY2MhPDLYgvKVYngnodDoHF1BBQYGDy4e1n/T0wxqs\np6SloaamxuX6paWlmDNjpkueP9CmBD7+7FNcPmmyW9qIgoICjB4zptPVtD/99BM2bNgAo9Ho0Kaz\nMwpArAqY9SDoLCQSiUMabEZGBvr06ePwo1QqUVlZibKyMuTl5bmljG5qagqI28cTCgoKMGvGNS7v\ny7KYWNcsphiFx3oydDqdS7aXJ4oTu92OjRs3emXP7S3o2d9KD8XR348gJy8XJSUl2L59O0pKShAS\nEoIXXngBhBCcPn2an/jMt6hWq0W7dnUl9Ho9b13qdDr89uth9O/fH83NzVCpVCgoKODbHrJMEyGi\no6NBCMGjjz+Ghx54EJvf/LthuQO9Q7T7VM+srCxsac8OElYCU0rxwKp/OlzPF1RUVIBSioyMDP7Y\nsGHDcOGFF/J0yew7YJkd/kClUnk9z55LZ8FxnEOWjqfdYkZGBhYvXsy/p/N7R0dH4/KpU/HZJ590\n+p7cgUgkuO+Bf7r9zEKjR3h/wrTongpWNc6SCDiOc1AA99xzDwwGA3Jzc3HbbbchLCwMH7z3frfF\nLAKFcwrAD4y9dBzeeust3HDDDS6VwJRSXgGwCRUUFASVSuUQNzjT0Ov1fCD0wIEDKCoqQlVVFcrL\ny7F582YUFBTwVbUhISHo37+/w+uZdTR48GCoampQXFiE3Pw8Xvjv3POtKN0C2wlMHj+Bjwl8//33\nflFbvPv2O7jm2pkugoU9c9ZaEYDPBWbOoJRC68UNAABJAagCBv52lzC3onNVqlDgin2WZ59/DgAC\nrgQkEgne+eB9DBs2zOUcE5rO980EKrv/wsJCFBcXY+LEiQFxnQUKKpWK7x/NnreQAmTNmjUO4zXq\nFheOrt6IcwrAD4SHh+P2291nwjBrn1mdzP3gzm1yJqHT6Xgf/+WXX44JEyYgKCgIGRkZGDNmDFav\nXu015VHIsf/2++/hismX4c1338EN18/Fjt27fObaycrKwqdffI7JEyfhgy0f4e477sSBQz902Iq+\n976V+OCDD7B3714X99qiRYt4vhmO41y6O/kKu90u2vYvEFXAgGPTcQB44403+B1Znz59MHXq1A5d\niymBT7dsCZiL6s1333Er/AHHDmZCHh3nbLj8/HwcOviDW5dQd/rTa2tr+VoMtmvxFgO4ddnSM3h3\nXYezXgGIFccIU/N8BXM/MIpfqVSKurq6ztwmbDab6Dbam0VlMBgcslWcA75ZWVle+XKEFbqxsbFY\nu/4VTL9iKvbs39fh7J2MjAy88Z/NmD7lCny1Y7tfwd/i4mKMHz/eI4EcC+oxAeROuDinjwLgG8iw\na4g9c2FLUHew2+0uvmV33xOzntm5m2923+lLKKCcdwZCEEL4vPpPt2zxeo9ikEgkePv997w2Zndn\n+QuVgHA3JpfL3d73f95606f7Eaur8WfN1tXVISgoiN89+vLdi8Hd/HKGtz7dZwJnvQIYPepiNHnh\ns58waZIL+ZkYgoKCeA4atgi8WRO+YMP6f2OdUwMZIaRSKY79edzjxDcajV4XhdVq9aoMnYXYiBEj\n8M5772HGVVfj7bffRr8B/T280hU/HfoRy5ctw+fbvvLbgnZ2UQFti/jgwYMYM2aMQwMYJiydoVar\nceWUy3lhotfrsXHzG7yVazAYRIWAWBXwL7/8glsWLeZjKorQUOze863L/bD/xVg4t23bhgEDBmDn\njm+g1+tx732una0YOI7Ds88/B0qp3+4gX4Q/4JgVIyRBFMYF2PnZ181xew1f+fXnXT8Xv/36q8fz\naRkZ2LP3O5+uxaDRaBAeHs7PldbWVp8oMLzh0KFDWDjflXWUgeM4/F5wLCCNZfzFWa0AKKUw6HRe\nF7kwyOgL7HY7UlJS0NzcjKioKL4bVWdzxUtKSrzeJxFYru5gNpu9Cpf6+nqvvW/dNW0ZPnIEPvt8\nK264fi7OGzoUDzz0oAt9NfO/U0pRW1uLB1b9E00NDdj13Z5OUTS7Q0xMDC677DLewmQuIE/PLSoq\nCt//eIj//+UXX3IYazQakSNi4aekeaewppRiwcKFDu0D3SkjYcAaADZu3Oji2rrpppswYcIEVFdX\no+50PZITfYubPPPcs2hsbMT+vXt9Gi+8z7XrXxEV/mws4Or+cTfOk8X7/LPP4fEnnxB9L5VK5XUt\n+FNPEh8fD6VSCZlMhoiICKjVap6+xN8EgoryU17vk3kJuhNntQKw2WyiJfJiW3xncBwnWvHoD06d\nOuX1vFKp9DpRTSaT1x2AXq/3mqrqyUpJS0vDdwf249ChQ7jphgU43diIoUOHYuDgQbBarfj3K+tx\n9OhRHDtyBBkZGXjwkX9h8ODBXbLtlUql/GdkLjNhJpY7ONP+CpGamopvdrmnrGptbcX27du9NgQS\nXtfXz8uU9OLFi13OcRyHr7/+GpWVlYgIC/c51ZPjOLy++Q3cvGgx9n3nm2VMCMG6f6/3ueDJOSvJ\nORMoUPCFntufNpl33nmnv7fkEWKtRIODgzud+txZnNUKwGw2i247A0H0FQicFokhiFk9VpEdQE5O\njldaYTEm0VGjRuGrHdthsVhQXV2N8vJyrH72GURERGD61VchMTGxy7I+bDYb7rjjDv67vOWWWzB4\n8GB+O98VKYhmsxnPPfNswDjhnbOAPAkG1uC8o/TihBBsfH0Tbl60WHQnwHFch4Q/ux8hmZoYm6a/\nsNvtoi1Ec3NzA/qe/kKsirw7C0MZzmoFoNFoREna4hMTvJ4/E6CU8hkhnuDNEmXEVt6sDcbl7gm+\nkonJZDK+P++ZgkQiwfr16x2OsWpt5ywUb1iw8EaPnEGUUlw19UoYBFlBvvis4+PjMXCwZwptBib8\nmZJkdCKA+yptf6xqjuOw6Y3XsWTxzR53AizbZ+TIkR269nvvvYeCggJIpVJERERAIpHwu0q5XI5B\ngwYFxMq2Wq2iCj07NzCZWZ1FdbV3HqnY9vaZ3YmzWgGItfoD4BBM7C4EoimJRSQboaWlxStlb6At\nua6AxWJBSUkJEhMT+e+tIwvMG10BIQTvf/wRr0S1Wi2unn6V6DWzs7M9cvs7X1+4AygsLOQzSJKS\nknxyNfkCjuM87gQ4jsMbb73ZYeEPgO//a7fb+U5gLK6h1+u9xpc6AqPRKKp4O9JatCuhFuFA6mh8\nsStwViuA8lLvZf4SiaRbCdwYfHFViW17WXqbJ2RmZjp08XKGt3PdAUqpC8OpRCJBYmJil2VVCN/L\nbrcjISGwu0NGSAYAQ4e6LzIym82QSqWw2Ww80V1H4S4mwHEc3nrvXb+EPwDcdttt/A7SXeZPoLiA\nfOkZ0RMazthsNq+uKkppj3BVndUKwBeir57AYeJTU5JsEZeLyLa5srLSI/cJAL976nYVPvzwQwwd\nOhR9+vThj0kkEl7QCIuSOhKE9RWhoaH47POtAbuer2mgdXV1eOs/b6Jv376oqKjAPSs996QWez+2\nE/h+/368/f57GDFihF/XEl5TKPzZbsmXeAWlFDl5uaJjq6qqvF6H47huTatksNvtXtOqOY5DTt45\nBdCtEIvSK0JDuz1KD8Cn7bO3AC6lFHb8LWSsVivUarUDM6eYhdbT2Bz//OM4hgwZgvXr1+NXp5zw\nK6+8EjNmzMD48W10yB0NPtvtdqx5/oVOBY85jsO99630WfFwHIcJEyYgIyMDlFIsXbrUwe1HKcUr\nr7wCQggmTJoIqVQqmhnmy3u+vvkNFP51En36dY7b3lnJCusAfHkGhBAsWLBAdFxpsffAqkQi6fbU\nSkC8hsRut3crNxjDWa0AqioqvJ7vKVZvhch9EkK8xioopQ60r8ePHwfQ9vlsNhtsNhs0Gg1frEaI\nawMVsYppSinPj3QmlOZtty/Hrl27sGzZMo8Cxl+LllKKza+/7vCZCSGIjY3F8JEjkZSUBKlUitbW\nVtTW1uK/P/6IhoYGh11aUFAQ7r73Hp9dNBzH4eKLL+b/f/XVV92Oe++99xATEwOJRILJUzrPSU8I\n6bTwB1xbJrJrO/9dXl6O/Xv3Yf4Cx3lCKcWXX36J6dOne30fsV27XC7vEUYbo8b2BELhUjPTHTir\nFYCYPzE5OfkM3Yl3iFESi8UqKKWAYFEMGjQItbW1qK+vx+7du7Fy5UoYDAZ+wsbFxeGaa65xuIYv\nHbUefPBBrFmzBp988gny8/O7NMMhMTERN9zgucoykJDJZJgxc2bbguUIYKewgyJYKkV2djYys7PQ\nUH8an27Z0uG+ux3FLbfc0qXX7wyc3TfuKoG3bduG8ePHo7Gx0UEAEkJQrxKnSxHb9fSEpA2gzVXn\nzZ1FJNy5NNDuBKUUOp3O65ifDh3CJRePRmJiIjIzM9GnTx9kZGQgNT0NsbGxfNtBIfNkV6CkyLur\nit2DJ1BKIRVUmZ46dQr//fEnzL5uDubPn4958+bh9ddfd8gCcv48YkFgQgh2796N6667Dv3790ef\nPn3w+OOPY+rUqX63Y+wpWLhoEeRyOeygkIAAHHHYUVG7HfHx8bj5lluw+fXXRQnk/hchJH7zVgC2\nYMECHDp0yC/3B6sm9waVSoVLLhqF2Ph4ZGVlIT8/H9nZ2UhNT0NcXBxf7Susuu4KlJWVeb1+T0kw\nOWsVgM1mE7XWLBYLaqqqUFNV5ZZ7hKXtBQcHQxkeziuKvD75yMnJQWpqKq8onLemHSnkKS8v93pe\noVB4vRalFJwgmO2cmkgIQXNzs9cdkS/+8LS0NPz+++9oaGjASy+9hBUrVmDevHno06cPbr75Zkyf\nPp13n/QWZGVlYcy4sfj+++8h5SQgXBtPjLCBCwcCIuEgIVLccOON2PTaa91922ccrBCM0X546pgV\nEhKC0aNH+0UA6EsVsM1mQ21tLWpra1Fw9KjLebZmpTIZwsLCkJCQgIyMDOTm5yEnJwfp6emIj49H\nWFiY34qCUoriwt7hquo9KzHAMJvNokx9YmBsfzqdDjqdDqqaGhz57TeXcSwfOjg4GOHh4YhvVxTZ\nuTn8pIuJieEnnZCWllIqyiQa7abNohA2m03U2ggLC/P6PMLDw72+HgD69esHhUKBZcuWYfny5Xj0\n0UfR2tqKI0eO4LPPPsMVV1yB6upqhIeHY8iQIRg3bhyGDRuG7OxsREZG8j18ewoIIXj9zf/g+lmz\n8fHnn+GDd96DVCqFwWDgFUBEREQb46e1lf+Oh40Y4ZWs7H8VzkV3QlZQBolE4nfrT7HUSl/AWM0f\nlgAAIABJREFU1mxraytMBgNO19XhDzdtToUtOsPCwhAfH4+0jAzk5eUhO9dVUbAKaKDtc4tVASuc\nGi51F3qtAmD0A1U1Nag8dcpnJkEGMfdPIMHK4pmiqHFSFMKts1Qq5SddXLt14o2tFPBeBQy0KwCR\nTBiz2ezVdSHm1qCUYsmSJfj444/x0EMPYeXKlZBIJIiPj8egQYMwZswYrF27FllZWVAqlTAYDKit\nrUVhYSG2bt2KwsJC1NfXw2g0IjQ0FHFxcUhLS0NmZiZSUlKQkpKCmJgYREREQKFQQC6X820IhYsP\nCBz3zHlDh+LtN9/C/61fj5sXLsLSpUv5VNm0tDRUVlbyViITTHa7HRdeeCF+78YG576CCWZGWW02\nm6HValFXV8e3nmxsbERUVBRWrFghcjXHawq/g0BZukajsdNGm69ga7a1tRV6vR4qlcqlHzb7jKwF\nZlhYGKJjY5Genu5WqQiRkJDQ4ecikUiQmp6O9NRUHDx40OcKd2/otQqAUorRY8bgpsWLYDKZ8PNP\n/8WmTZvw++HDPpFkibX6O5MQ5qwzWmadTofa2locO3JE9PViBSV2ux0yET+8u/6yHQEhBP/617/w\n8MMPg1IKs9mM5uZmVFZWoqSkBCdPnsTmzZtRU1ODhoYGaLVavm9CSEgIwsPDERMTgz59+iAuLg6x\nsbGIiopCWFgY5HI5Wlpa0NLSgtbWVlgsFhiNRp5qQK/Xw2QywWKxOFAFcBzH96YNDg7mfxQKBUJC\nQiCTySCXyxEcHAyZTIbg4GBesVBKMe+G+Xj+6Wdw0+JFMBqNuHTCeIwedTHGjRuH4SNHYP/+/Rg3\n/lKoamp53humjKTtVqEYnOsVhH+z78S52QojumM/bM5YrVZYLBZemZtMJhgMBuj1ehgMBhiNRpjN\nZuj1elitVodrt7a28i4t3k0ilSI4ONgn95/Q+neeR4EQVEBbtXqgrhUIsHthz95gMKCurg4n2rPs\nvMHXym65XI7zhg7FkiVLMGzEcAQHB+ONTa/j+++/79S9M/RaBcBACIFCocCYcWMxZtxY2Gw2lJaW\n4s3N/8H+vXs9LkIxv3pvgpgCaG1tFXUBMaHo7bwYBg4cCL1ej8jISERFRSEiIgLh4eEIDw9HREQE\nBgwYgAsuuIC34JkQZq4fYWNxZ+HEhJ4w7iKVSqFUKnnhxbb2QoHG0lzZ36zBvVDg2u12FwVos9mQ\nn5+PkJAQ/Pbbb5gyZQp27doFoK3lIsdxGDp0KBYuuJFv2M7umxACpVKJF1980aE9pSceGyFXEyNS\ns9lsLnEiRmznXHDF7lvoPmOfyXn+C487KxyW2srex2q1+uyy2bhxI06dOgWr1QqbzcYnJjBjrG/f\nvrjjjju8XuOGG73XATAa6O7mzwkEPBWBsZTuK6dPx403LUR2dnaXukV7vQJwht1uh8FggE6nc7uI\nGMQKSnoTMrIyvZ63WCwuTd6dodPpvBLO+TIJWRtGpVLJC36mDJRKJZRKJW+BM2ubCQphJy4GYTNx\nRu7GBBgT7K2trbzQYQJWKPSZImCvZwJTyPPuznLlBbHATcJxHKjNBqlUyl+L3bfzHKOUQiaTOVjV\nQuHtbNkzJSF8zuyckM7a2cXizucuPM/GiLGiCt2QQmZPq9Xqk9uF4zhYLBZIpVIoFAqYzWZYrVYo\nFApeIYtBzLoXo27pTfBEMy+MKxqNxi5hVBWi1ysASin0ej32792HzZs348Tx4zxzpTfLRawKuLeA\nEILExESvYywWi6gVFxwc7DUv2ZcdwC+//AJCCGw2GwwGA06fPo2ysjL8+eefKCwsRHl5Oerr69Hc\n3MxP7uDgYISGhiImJgbx8fFISEhAXFwcYmJiEB0dDYVC4VDZabPZYDKZHNw/Op0OJpOJd2sAf7t/\nnF0/7O/Q0FBeCQndQMxl9OlHH+PkyZMwGo244IIL8MJzz+OOu+7EA/fdj5sX3oQFCxfizc2bMWHC\nBD62I0wH1uv1WL58udvML6GQdve3cLw7d5DQ/SPcIQndQCaTCWazGUajETqdDnq9nnebGQwGnl+K\nXU/YcpQQwj8H9rcYFi9ejObmZo+fR6z5D6UUu3bt8kqvXVJS8j9h/QPwmgar1+vx9VdfYfu2bQgK\nCkKffv2wePFijBk3VtSQ6yh6rQKglGL3zp14c/Nm1NXVdbhsX6y6NjY2FuPGj0d5eTlqa2vR3NwM\ni8nkU2/eMwmxKmCgLcArNnGY+8ITfLFC7r33XnzxxReoqqqC1WqFTCZDamoqhg0bhosvvhjz589H\namoqZDIZWlpaeOVw4sQJFBUVobi4GMXFxQgPD0dSUhJycnKQmZmJ5ORkJCUlITIyEmFhYQgODuaF\nk3MnLW8QS71lBGvM4n7nrbcxbdo0lJWVITIyEjt37sTOPd9iyeKbsezWW5GSloaLLh6F3TvbXEOE\nENioHbTVDqvZ7PA8P/zwQ8yZ09YKcd++fRg7diyANv9xZWUlcnJyQAhxONfS0gKlUslnhdXW1vLF\niazjHACH3QjQ5vLzNdVWuMuwWq3Q6/VoaGhAdXU1iouLUVNT49O1nF1ozjsTMRBCQETc+2KZNcHB\nwZgxcybKy8tRU1MDdVMTHzhmz6inwBt1CwOlFBaLBQVHj+LO228Hx3FISEhAUkpKh9LIvUH0myWE\nbAYwFUA9pXRg+7FHAdwMgJHUPEAp3d5+7p8AFgGwAbiDUrqz/fhlANYCkAB4nVL6TGdunBDiwgHj\nKyilXonPAKD/wIF4+tln+PHCTAm1Wo3a2lqUlZWhpKgYRUVF/ITT6/W8RSa03txZeIEAC9R5g8Vi\nEbXgmXXoCb4Uc3388ccAgFWrVmHevHlIT0+HzWbDiRMn8PXXX+OOO+5ASUkJZDIZ+vbti0suuQSj\nRo3CtGnTEBcXB7lc7rGojj1DYa9lvV4PpVKJ0tJSZGVlgVKKP/74A4MHD8b333+PUaNGgeM4vPPO\nO5g/fz4OHDiA888/H0qlEvfccw/WrFmD0tJSREREIDo6Grfeeis2bdrEv+fxggK8vG4t5l0/F1u/\n+ByXT5qMG25aiI+2fAy5XA6z2Yy33noLH733Pq6bO7eNAplw+O233x0+g91ux5EjR3gFcPjwYYwZ\nMwaEEFgsFvz11188nfdbb73FK4CysjLk5OQgPDwclFK8/fbbWLVqFQBgzZo1eOKJJ0AIQWNjIzQa\nDX+NpUuX8p/j+++/x7Bhw9oK2ex27Nixg28qs3fvXowdO5a/V7lcDoVCgdjYWPTp0wfjx4/nn70Y\nnDl/nJVBIOa+GL9+eGQkHnvicYcdE9sxtrS0oK6uDuWlZSguLkZ5eTkqKirQ1NAAnU4Hi8Xi1tXW\nFSCEICwsrMOvs9vtfI1DoHZCvpgJbwJ4BcDbTsdfopS+IDxACOkPYA6AAQCSAXxLCMlvP70ewEQA\nVQB+IYR8SSn9sxP37jcopdBrtV7HOBdKMT+1rL2AJC0tDcOGDXPRxGxLbjKZoFaroVKp+ElXXFyM\nmqoqNDQ0wGg08r7rziA4OFjUOjeZTC7uHedep2IuIF8UQEFBASIiItDc3IzXXnsNmzdvRmVlJTIy\nMrBgwQK8++67SE9Pd0vW1djYiNDQUDQ3N0MqlSIsLAwPPfQQnnzySRgMBhw7dgwjRozAww8/jGef\nfRYWiwXfffcdpk2bhi1btmDlypWglOLnn3/G4MGDUVxcjJEjR4LjOFRWVgJoi3MIMzcAx8YxztXO\ndrsdy5bcgufXvIB518/Fjt27sGnDq5gwdhyviK6++mp8vu0r3HjDAkyePBkWowmHDh7s8mI3b5k2\nwgJHi8XiEEcRVtJ+8sknvLKpqamBRCJBSkoKgLYWievWrePPJScnexU6zha281iO41BXV4cvvvgC\nY8aMwd69e3HLLbd0SJA1ipAiJiYmOlQhsx0iS9FMTU3F+eef7/I6oaLQaDSoq6tDRUVF2660sAhV\nVVVoqK+HXq/nFUVnwOoLegJEZyml9AAhJNPH600H8CGl1AygjBBSDGBY+7liSmkpABBCPmwf2y0K\nwG63i3a48pWq1XkCC/2nTFFceOGFbu+B7ShaWlqgUqn4HUVJSQlPz6xRq71OuMjISNFFZDAYHCyO\n8vJyFBYWYuzYsQ7C2NsC9mWhNjc3Y8qUKfjvf/+LzMxMPPzww5g1axZCQ0MdFOXevXsxbtw4HDt2\nDBkZGYiIiMB9992HN954A2q1GsHBwQgLC+Opf4V+aHaPUqkUgwYNcjgmkUh4K1t4z8xqFmLt2rUu\nx55//nmXYydPnsQrL6/Fy+vWYuZVV+Oiiy/Gxs1vIDo6Gk1NTfjogw9xzfSr8Orrm/D0E0/i199+\nc2s9elrwQtdNRxAIC9BdoJj9LSy4OnToEK666iqvsQBPbjhhgD0hIQHqpmZ8/tlWzJ0/DxqNpkPc\nPQaDwet5f7vQsQwolqiQnJyMf/zjHy7jmLHAdhT19fUoKytDaWkpiguLUFlZidOnT0Pd1OR1zbJi\nz56AzpgpywkhNwD4FcA9lNJmACkAfhKMqWo/BgCVTseHu7soIWQJgCUAIO2ihyTWYIVS6lMXp86A\n+a6DgoKgVCqRkpLiYp1QSnHJxaNR62Xrm5CU5JMCEMYAfvzhEHLz81BdXY0ff/wR9913n0MA1R0Z\nnC8tIVmJ/++//44hQ4YAaOucBQD79+/HiBEjIJfL8emnn2LcuHEOcQf2211wTKFQuDwbiUTidsGz\nXUxISIhDQNgZ7JlFR0eL7m5++uknXD/nOjz99NPIzM7C/r37eKt4wcIbMXbsWFw/5zqPNAUcx+HR\nRx91ey4sLAyTJ092e27IkCEev9t77rnH4zl3DeWBtmfsKRjrbQ754g5x5+YRuoWY+66pqQl5eXk4\nevQoJk6cKHpdBpbt5Q1dza/PPAGhoaEIDQ1FcnIyzjvvPJdxixbe5LXvslKp7DHBbH8VwAYATwCg\n7b/XALgpEDdEKd0IYCMABMvlXeKI02q1Xic1IQRJSUld8dYdhpiryherR6/XO2QBjZ84AZ9u+QTX\nz5uLOXPmYObMmVi3bp1DT2BnBelL4PvFF1/EzJkzeeuRUornnnsOTzzxBF8uL8TAgQP5v5mQFrOM\n7r77bp8Wz6xZs3wa52ufA41ajduWLkVQUBCio6OhDA+HTqPBS2vW+MQAKryXfv36OWT4CM8J2wQ6\nKy6hEhfeNzMmGIS00kJIpVLMmDHD7bmUlBSPz8vXilVvOwC73Q6ZTIYnn1rNB9qd3WTRsZ7p103t\nCRjeINYW9UxBrGlNT6CBZvBLAVBKeXIaQsgmANva/60GICxxS20/Bi/HzzgaGhq8BmUJCVwLu87A\neSvuDp7yiYXQ6XQOky4+Ph5Lb1vG/y+TyfiqWE/wJRVw1qxZAIDXXnsNd911l4NAuOiiiwB4tiZf\nfvll0esDcKuY3aXBuhNGF154oU++V47jcOeKFZ3y9Xpq1/jBBx9g+PDhWLduXdv7tDdKp5RizZo1\nWLVqFTas/zfGjb8Uffu28fRbLBZsem0jbr/9dmzduhXTp0/nhXJraytkMhliY2PR0tLi4lIZNWqU\nx+9O2HbSm+KdMWOGqBLwFOh19skzoe8uRsLmiDuIVQETQgLWN7kzoJSK0syn9ID7ZPBLARBCkiil\nLJp0NYA/2v/+EsD7hJAX0RYEzgPwMwACII8QkoU2wT8HwPWdufHOoLy8XHQy9QQKY18CTtm54laP\nQadHaGam1zFSqdRr4FLMMm9tbcXBgwcxduxYvxqxuAtA//Of//Tptddccw22bt3q4rZyxqbXNmLm\nrGsd2ki6AyEEty5b6tN7dxRXXXUVVCoVdBotEpL+VlyEEEybNg319fUwWy2ora3lFQBT0IwUUBjA\nt1gseGPT67jxpoXY9uVXuG7u9fx3tWfPHgBtwXlKqQOfD3MH/fnnnxgwYIDL5xfGQ3zZAfgSAxDD\nb7/95jZIC4hTt1BKfUqtPBMwesmmA4D8/Hyv588kRL9ZQsgHAH4E0IcQUkUIWQTgOUJIASHkGIBx\nAFYAAKX0OICP0Rbc/QbAbZRSG6W0FcByADsBnADwcfvYboFYFTCjJ+hu6HQ6UdcLy9oQu45YGqiw\n0MjdjxiEqbUXXXQRLxDuv/9+l7HuAmzOsNvtOHz4MPbv3y/6vlu3boW2xXMVM8NNixdh/9593ZoP\nvmfPHuzeuQtKpRIWk2PLx7/+PIHa2lpkZWU5CDybzYbm5maUlpaiurLKwVXHqMBNJhMys7MchPW4\nceNAKUVKUlsdhXNqZlVFJf77ozBk14bW1la89867KC0t9flzsaQGRsfhXKwm5o6jlELtheq5otx7\nIxhCSMCLpPwBK8bzhp7iqgJ8ywK6zs3hN7yMXw1gtZvj2wFs79DddRHEqoBDQkJ6RJBGbCtJCPGp\nbaVerxdVAELaBXfw1x3iLv107NixLmmozuA4DsEyuU/ZEhdccAF2fbNTdNw333zT7el3U6dOdXuc\nEIKp067k/xc+G47jcNfdKyCVSjF8+HCHc01NTcjrk8+3+RRSB/z+++/4+af/8m4h59qEgQMH4tCh\nQy73UlhYiCC5DGVlZT4nQ6xfvx5lZWXgOI7Pp2duVrvdjvz8fFEuIG8QawXZU3oBm0wmUQNDjLrl\nTKL7zdxugFgVcLhI96szBbHCF8C3/Hy9Xi8q+MSyLAJV/Wy32xEdHY3Dhw+7TY9lMJvNSE5NQVlJ\nKeA+pgmgTaj1798f/fv3F7U0Fy5c2Jlb73J4UoiEEI/CLSYmBpdffrnbc0OHDuVdKs5CSSqVYsCg\ngRg2wjUZLzk5GRkZGVA3Nbuc84Tg4GBER0eDEAKDwQCbzYaQkBBIpVIYjUafYkjeILYbYbTc3Q2x\nBBPAtyrgM4WzTgFQStFQX+91jC9ulTOBshLvk14qlfpk9RgMBtFxztkoXQWpVIoPPvgAt956q9dx\ncrkcw4YNw/DhbrOF3UJ4/xUVFZDL5UhISPD7XrsTp06dgkKh6JSwED4Pd9+tp2yUyMhITJw4sUMC\nlXEBeaotEOMCEoNYZk1YWFiP2LWL9TX2twq4q9D9KrMb4I3yAOg5Pjqxba9CofBpkfqiAIC/lYC7\nHzGrRiKRYPDgwaLvodVqkZWRidMiVZ2A58CiL9i75zscO+LaErC34Ltv96DgqPemIl2JjlrTrOrW\nk9LpbNxFbL7E9RBFL9a0vidVAQNn4Q7AbreLplZ2tqDknXfeQUtLC8LDw6HRaBAWFgadTofbbrut\nQ9cpK/NOf6sMD/dJQPq6A+gMbDYblEqlqBsmPDwcU65w77I4h94L57oGJvCd54K3+eHpOKVUNLMm\nUyTLTQzr16+HUqmEVqvl1214eDjmz5/fobVRWFjo9XxPqgIGzkIFYLFY2jo2ecjyIYR0egdQXl4O\ns9kMjUYDjUaD6OhotLS0dPg6p0+f9pqNlJqa6tN1TCaTaFaT2CT3ZRG8+/Y7uG+Va9bPmQJrqgIA\nrfbO8bX0BLTabQ7B954kOJzhiUTN+f9ffvkFh3/5FYuX3OwQFyCEYPTo0W6vzRh4vc1hsdReMVRX\nVyMiIgJNTU2IiIiA0Wh0yLbyFeXl5V7vMyIiokfEKhjOOgWgUChw9PgfHs+zcu/OwGq1IigoiLd2\nWPPwjmLXt7u9bp19nUi+KACxLbqYAmCfN1A0tR2FVqvFpEvHO+SdP/OCK7dPb4FMJsMjDz6ERx58\nCEDbd73v4Pc9ItPFHZy5hAD3c4bjODQ0NLhNKvA0b6RSKY78UeB1jnY2bTsqKqqNzbWdnkTYHa0j\n+L/1r4g23ulJOOsUAOBbVasYLBYLNBoNYmNjXc6xRcoWhc1m84taIlC1CGzXw3DixAns3PENbrhx\ngUNwrjN8MEajEeMnTuD7AJxphIWF4cdffj7j79tVuH7eXMydP6+7b6NDEAp+T8ZAcXExzr/wAhiN\nRgdfOKUUhw8f9hj07+q6nISEBFRWVvLrleM4r4ZgY2MjwsLCXOa6pwrwnoqzUgF0FpRSvPziS5g1\nZ7ZbBRAREQGNRsPnQ1ut1m7NLGq1WBwmZb9+/XDo4A+IiorCt99+i/Xr16OlpYW3XEJDQ3HBBRd0\n6D0UCkWHX3MOntHTLEUxCK1/592A0HiYM2eOaA1IdyApKQmlpaX8DkAikSA8PNzt2KamJhw5cgQj\nR47ssTsyX3FOAfgBZuHs+24vWrQalJWVISQkBKtXrwYhBPHx8Xx/XVYY053piMyiYbDb7Xza3LBh\nw5CdnY3//Oc/aG5uy/vuTRbMOfQMOPcDcKcIGHqa8AfadgAs3sLuna1ZSikefPBBGAwGZGdnY8aM\nGejTpw8+/PBD3HRTQDgwuw3nFICfmH71VTAajW5pDWJjY3Hy5EmHRhz+xAACBWGnI6BtAc6aMxsA\n+ObtMTExAU3b6y7Y7XZMm3oloqOjkZOTg9zcXGRlZSE5NQWRkZEICQnx2Mj9HPxHb3+WERERvMJi\n1cusyp4Qgqeeeoofa7fbsWfPHlx77bXddbsBwzkF4CcYUZc7ML+60ALqTp4SZwXgDs6Uws7oLQuc\n4ziUl5fjrz//xKGDB13OSSQSyOVyhEdGIiEhAZmZmcjNzUVOXi7S0tLaqJ6VSgQFBfHtKbsrsN2b\nYLfb+Upy9tyEbVF7OpRKpcv891S8xnFch3oZ9GScUwB+gk12dwHliIgIBz4Uu93ebeyizJrxxaLv\nDQu1M2B8R1arFTqdDjVVVfj98GH+OwIACeFACXhFERYRgYSEBGRnZyM3Pw85OTlIS0tDTEwMQkJC\n+Lzu//VnJ4YNGzaguLjYbS0A0EZbzqiveyIYqR77Hu12u8cYgN1uR2trq9d08t6C3n333QiVSoVN\nr23E408+4XJO2AKRTajumijsPnqi3zVQMBgMqKurQ2Zmpl+CWGil2kEBCp7VUq/XQ1VTg6O//+7y\nOpYyzFpYxiUkICsrC7m5ucjNzUVaRjpiY2OhVCp7DFdNVyEvLw96vR4ajQZyuRyxsbEIDQ2FXq9H\nY2OjQ0MiT/AkcM8EJBKJS8zCU49su92O8vJymEwmn6rfezLOKQA/ERkZidnXzcHq1atRXFwMpVKJ\ndevWgRAChULhoAACUVvgLyilIAF4755s4ZaVleGjDz50q4y7EpRStLa2QqfTQafToba2FseOHHEZ\nx1xPQXI5IiIiEBcXxyuKnLxcpKamIjY2lk8r7I3xicmTJ+Oiiy7irWObzdb2mYOCQAgRFe6EEPTr\n1+8M3a0r2C6O/VitVgcG3eXLl0Ov1yMvLw8PPPAAjhw5gpkzZ3bb/QYK5xSAnygtLcWgQYNcmmkA\nbda+0JLoTheBu7aD/l7nHPyD0PVk0OlQW13tUVEwrpjw8HCkpqfjg48+dBjTU33qLNuttbUVlFI+\nhgK0uUtbW1tFr1FWVuZ3Y/fOgilpYfaSMMXzlVdecRgfFRX1P7GjO6cA/ARreu4ObPILm5J312Sx\n2+0I8nEH4K2C8ZwC6HowRcFcT80tLaiqqsLsa/62NIOCgrBn/74el6rb2toKi8XCC06WT2+xWGC3\n2z2yhAqPsdTp7oJDLEikoOt/JQjc+1VYN4Hxk7gDSzNk1kR3WgqsGbcY2H16+umJVqfdbsfqJ57E\n6xs34bdff8UTjz3OdyX7X0FycjL2/3AQYy+9FBs2bcTuvd/1OOEP/N2mkgl/u93OtzRlriAAOHny\nJL78/ItO9VvuCrA4mXDNenvOYl2/egvO7QD8xIsvrIHNZsOqB1z71jqzIZ4prn13sNvtkPpIBd2Z\n890BQgimX32Vw+4kNDQUKSkpOF1XB5PJxLcn7K1gClgikUAqlQaExqQrQAhBUFAQOI7jA+iUUr69\nKps/n3/+OQYPHASNRoOoqKhuvuu/0ZE12tzcjJMnT0Kr1fb6ncA5BeAnmFX/7LPPoqioCKGhoVi7\ndi1/XjihnC0JSimMRqNLQxfWTk4YfDIYDLDb7Q4ZCXa7HVqt1qfistbWVih85B/35ubpiUKUEIKB\nAwe6HN+5excopbxP2mAwoLGxEVVVVagoP4XCwkKUlpZCpVJBo1bDaDTyisKX3gfn4AoW7GX+fo7j\neFeosEZg6tSp+OmnnzrNie9uDVgsFlgsFoSGhjrE4Bi1s1DAM7p24TFh3Qfw9xqnlOKuu+6CXq9H\nbm4ubr31Vqhqajvd5KYn4JwC8BNBQUHgpBK3HP9CMizAtfSdUoodX29HaWkpVt5/H3/85ZdfhjxI\nhhX33M0f02g02LD+33j08cf4ybphwwZMnDjRJwXgrgZBr9fjwIEDmDRpks/uhJ64A/AGQgikUimk\nUinfrjAvL89hDPt+LBYLT9+tUqlQXlqGoqIilJSUoLq6Gk0NDdDr9bBarT7XVAQazLruqbDZbDCZ\nTPxOICgoCDabDWaz2eGZDRgwAP379+/0fNq+fTuys7Md1oDRaMS3336LK6+8kjesvv/+e0RFRCIx\nOYnvgHZg334kJiehoqICgwYN4l/vrSXnyy+/zP9vMBhQW1vrc7/knoxzCsBP3HGX96IWthVmC8L5\nXH19PcrLyx0CYix2IER0dDTGjh3rsGAK/zqJ/n37ITs7W7S+wGKxINgpB7u4uBhBEilaWlpgMpnw\n559/ora2FlqtFkCbsInsIX2RuxLsmcrl8r8zb1JT3ZLasQCt0WiEWq2GSqVCVUUlioqKUFpaioqK\nCjQ0NMDYrihYFWyg8NC/Hu7RSri1tZV3U7G5zxRmUFCQw043EJ/jyG+/Izc3Fy0tLbwSiIiIQGlx\nict7NTQ1Ii7h79aaffr1xWeffIqsrCwHBeCN0lz4f2hoKJbetqzTn6En4JwC6CIILWt3QdjgEAVu\nvmWJw8TKycqGyWJ2GHf69GlcfIljo4xblt6Kn3/6L8b5UFxmsVhcdgBlZWUYNWoUGtot2x9//BE/\n/PADrwAiIiIwduxY0WufTWC++LCwMISFhSEtLc2lqT0T+MwabmlpgUqlQkX5KRQXF6Pz10MfAAAg\nAElEQVSoqAjVlZX8c2cZMr6gJwt/AA45/84xAF/iFoQQtynVnrDo5sXYtm0bFi1axB+zWq24bu71\nDuNycnLw9VfbMHLkSP6YXC6HJEiK8RMnOIwVGlMsINzTn3tncU4B+Innn30OMpkMd664y+35oKAg\nfkvsjgZizpw5Dr5+AJg67UoXZZGYmOiyK+jTpw/69+/v030yn6gQ06ZNQ21tLfLy8kAIwT/+8Q++\nG5InnPOLi0NY9a1UKqFUKpGSkoLzzz/fZazdbucVhUajQX19PU6dalMUxYVFqKiogF6v75HUye4g\ntPjNZrNDdzbmChJDR4RtUlISbrrpJodnI5VKXfpuJCUlYcHCGx3WVWRkJObPn++imFi1snMNgDOa\nm5uxb98+5Ofnd0hp9UScdQpArVbjwIEDmDZtWqeuQynF8ePH8dZbb6G6uhrBwcG4++67+XNCa8Kd\nAnj66afx6KOPOkzgr776ysF/CQCHDh3C+eef71BKf+LECaSkpPiURWEymVwUAMdxbvsTeFuAvUEI\n9SawHUVQUBDCwsKQkpLiwCzrratWT8SGDRtQVlbmUHgoDKrn5+djxYoVHl9PKUVRUZFXkkUhmpub\nUV1d7ZAEYDQacfjwYYfWkq2trdi2bRtmzJjBH7Pb7XjmmWfw2GOPOVwzODiYv1/n4s0XX3wRJpMJ\naWlpuOKKK2AxmfHD9wf9VgCUUnz11VcYPXp0t2ZDnXUKQCqVYvbs2di2bRvGjx/v1zUopcjOzUFG\nRgZmzZntYh2zACQb604BMJI2McHqC5OnN5hMJoSFhfk09lwhWM9BbxH8DNHR0YiMjERycjKioqIQ\nFBSEiooKVFRUoKmpyedalM6AMZD6e93g4GB+rHNs7a677uLfw2q1wmg2YdpV0/2+171792L27Nk4\nffq039cIBM46BaBUKvHbb79h+PDhWLBgAdasWdPhrj6EEAceEHeLlW0vCSFuU97mzJnjkoEzfPhw\nl2MDBgxwmYxpaWku7iNPcLcDcAcxwrjeJpDO4cziiiuuAMdxSExMhEKhgF6vR1ZWFlQqFbRarV8t\nUb0hNDQUaWlpDseCgoJcLHKO41zaTHIch9mzZ7tcU7hOnWWCcG3IZDLceOONft23xWLBvffeizff\nfBOHDx/2SDh3pnDW7eu1Wi3q6upQX1/Pd/25//77A66JmSD3pAAGDBjgIlRTU1NdFEBcXJyLrzIi\nIsJnpaXT6XzaAbBUPW8/PRmff/45xl4yBpdeMgbjxozFpZeMgclk6u7b8hsfffAhxo2+BJe2f6Z5\n18/t7lvyCp1Oh/LychQXF6OhoQFyuRxpaWnIy8tDampqwF2IMpnMJQ1aKpXyqZ4MEokEqampLq93\nF0OTy+Uea3c6i9OnT+P+++9HYmIi7HY76uvrUV9fzydedBdEdwCEkDQAbwNIAEABbKSUriWERAP4\nCEAmgHIAsyilzaTtCa4FcDkAA4AbKaW/tV9rAYCH2i/9JKX0rcB+HHHYbDZMmDABAwcOxMsvv4xn\nnnkGBw8exNy5c1FaWoqLL74Ys2fPxvnnn4/o6Gi/idxYRoRzYVdnwQQxy7QQFjldcsklLrsFg8Hg\n8w7A2+fs6TuAK664ApMnT+b/v3zS5B6vtLzBYDDgvlWrMPbScQB6/vNPSkrijSutVovExETExcUh\nKiqKp0dn6Ghgu7W1FQcOHEBKSgpiY2MREhLC13gAgXs2zFXryWjzBawAsampCYcPH8aHH36IgwcP\nIicnBytWrMDDDz+MX3/9FSNGjEBBQQEaGxsDcu/+whcXUCuAeyilvxFCwgAcJoTsBnAjgD2U0mcI\nIasArAJwP4ApAPLaf4YD2ABgeLvCeATABWhTJIcJIV9SSpsD/aG8ISIiAuXl5Xj55ZexcOFC1NfX\nIy0tDePHj8fSpUuRm5sLo9GIHTt24MiRI6ioqIDNZkNsbCxyctr8/unp6YiPj0dkZCQUCgXPf8I4\ncwghMBgMUKvVoJTyRUTM788IvxiBlsVigdFohMlkgk6ng0aj4X8bjUYYDAb+9cDfE55VWLJ0QmHw\ni0Gv1wckp7+nCyBWfMRAu5F+I1CQyWQBNR66EqmpqbBarVCpVFCr1Th16hRaWlqQlJSE6Ohovr2i\nzWbD3XetwMvr1nbo+/nmm294riFhURwLNLN6m5CQECgUCoSHh0OpVPK/g4OD+bXK6ClYzQJbtwaD\nAc3NzSCEQKfTOex+2bpla1WtVqO+vh6VlZUoLy9HaWkpGhoawHEc0tPTcd5556Ffv3645557cPXV\nV2PXrl1YsWIFKisrkZCQgBkzZmDbtm3d2ioW8EEBUEprAdS2/60lhJwAkAJgOoCx7cPeArAPbQpg\nOoC3aZu0+okQEkkISWofu5tS2gQA7UrkMgAfBPDziIIxFD788MN44oknQClFc3Mzn4K3ZcsWnDp1\nCs3NzTCbzTy/v81mg0qlgk6nQ0VFBeRyOZ8rzCgH2G+gjT42JycHVqsVe/bswaxZs3gBzrIMhIRy\nQuXBxrCJ52ydCzMtZDIZbxG5W1BmowkhyeLNONh1PaEnUkGIoTfvAHobgoKCEB0dza8BrVYLjUbD\nC2sm6L766isMGTIENpvNYbfqKV2aIT4+njeabDab23aTFosFer3eYb0Iq/KFTJ+MvpqN4zgOH330\nEYKDgyGTyfDuu+/ybmGmLBhDKMtwMpvN0Gq10Ol0fNGnXq/H8ePHUVJSgqioKGRkZCA3Nxfz5s3D\ngw8+yNNIm0wmNDU1dXutQYeCwISQTAD/APBfAAntygEAVGhzEQFtyqFS8LKq9mOejju/xxIASwBA\n2gWshxqNhqcEYBYF+1EoFFAoFAgJCeGrQ2UyGWw2G7RaLSwWC1paWiCVStuKSdonBCPrEnKKs8bR\n9fX1uPzyyx0qQ1mxjPO2WEghLfRFsknCriEsrWf/e6o81el0vcaKDCTmzJnTq9v1yeVySGU9k/jN\nHZqbmyGVSpGSkoLw8HCoVCqcPn0atbW10Gg0vE99ypQp2L17t1sXUGZmpttrU0pRX1/PJyoIhTv7\nXxhzY7+dLXgGoeEl/G232/HJJ58gPj4e6enpfB0P4+Nir2MKyGw28/UP7G9KKd9ytKqqCj///DNM\nJhOMRiPMZjMsFguvyACgoaGhd6SBEkKUAD4FcBelVONkkVJCSEDMLUrpRgAbASBYLg+4CRcWFoZj\nx44hKSmJD/potVrU1taipKQEpaWlqKqqQl1dHXQ6HWw2GziO49v+hYSEQKlUOljdbBfAJggT2Fdf\nfTVfAONMqSzkSGc+UaE14E6gs0XD3lfIEumORgIADB1QAF2RBVRVVYXt27djyZIlPo3fvXs3/vrz\nBJbfcbtP7/nvf/8bsbGxmDVrlsPxW5ctdRlLKcWbm/+Duro6tyyuzrDZbHj11Vcxbtw40cI7Sile\nWvMili2/DW9seh1z588Tdb01NTXhw/c/wLWzZ7kEL6+be73L59doNHj37Xew5NZbfFZuL6150YFb\nyhs2b94MuVyOuXM7HnAuLy8HIQQJCQkIDw9HSEgIwsPDUVdXh+bmZtTU1ABoU2xTp051ew1P3zfL\nLhLutIVJCwBc0j+d1xujqBbOceHf7DoLFy7kEyxYn2Bm6AlTu1n8TafTwWAwQKvV8iR4oaGhSEhI\nQHx8PNLS0pCdnY2cnBwkJSUhLCyM3z2oVCqfU7S7Cj7NIkJIENqE/3uU0s/aD9cRQpIopbXtLp76\n9uPVAIT5Wantx6rxt8uIHd/n/637B2b133///di+fTtaWlqQl5eHKVOmYNy4cZg6dSoaGxtx9OhR\nHDlyBLW1teA4DtHR0cjPz0dGRoZLCz8mgIXbySFDhuDAgQOwWq1YsmQJ8vPzXfyJjDnRYrHAZDLB\nYDDwk0qj0fDbS4PBAJPJ5OAuYteyWCzQaDQedwBardZla22329HQ0ID4+HiX457grzslJSUFzc2+\nh3lGjBiBA/v2+zyeA0FD/WmfttKEENxw4wLs+Hq7T9e2WCwYMmQI3tj0Ota89KLotS8cPgx//fVX\nG03Bl19h5qxrvb6GWYTuspXcfZb33nmXz0P3RQEcOHCgQ4r7xhtvxEsvveTzeCGsVitvNCUmJiIm\nJoYXePX19V5fu337dgwYMAAlRcVobm7GNdc6tlqklEKlUvH9l51dMQB4Iy00NBShoaEICwvj/f8h\nISEICQnh3TuMVts5bnfttddi48aNCAoKwrJlyzB9+nT++mzdspibVqtFQ0MDqqqqcOpUG8MsY/hN\nSkrCeeedh8GDByM6OhrV1dXYsmULvv76axQVFSEyMhJTp07Fvffe2+29HXzJAiIA3gBwglIqXAVf\nAlgA4Jn2318Iji8nhHyItiBwS7uS2AngKUII2+9MAiBuhgUYLS0t6Nu3L4YNG4atW7eif//+2LFj\nB1566SVs2bIFU6ZMwbXXXou5c+filltucRDsjN8lISGBv57VasXevXsxadIkh/fhOA5KpRJms7lt\nOx8gd4TQ4mFUAmq1GjU1NW4Xu85gcMlo2PrpZ7jo4lGorq5GdHQ0r2CEuxXnNFN/dwAmkwnqpma0\ntrb69AxqamowcOBA3iUmhkvGjsH27b4JdAA4cuQIJk6eJD4QbVkh4eHhGDnqItGxlFJUnqpA3/79\ncPToUWTn5oi+pqysDJdOGI+ysjKXnHZ36Nu/H5RKpc9uPYVCgfqG0z4/+6eeXI3pV18lOs4dEhMT\nodVq0dTUBL1eD7VajeTkZISFhSE9Pd2rATFhwgQUFhaiqKgIaRnpLpY6200nJycjMjLSQQmw84EA\nCxQrFAr+eQnvw2g0IjQ0FCEhIYiMjERaWppD9Tbwt6LQarUoKCjAa6+9hq+//hpxcXF48MEHMWXK\nFPz1119Yvnw5+vbti8bGxm4lXvRFKo0CMB9AASGENTJ9AG2C/2NCyCIApwCwPfh2tKWAFqMtDXQh\nAFBKmwghTwD4pX3c4ywgfCYhlUrx448/YuDAgbj11lvx9ddf47777sM333zj0Li6uroaFovFwUrW\n6/UoLy93UAAA3FpwLFZgNpthMBgCdv9CvhkWi4iIiEBGRobb8Ua93kWYj584Adu+/AqjRl+MnTt3\n4umnn0ZFRQUsFguAttqDOXPmOLzG1yDwyZMnERwcjIyMDKhUKjQ3N/NU1n/99RdiYmIQFxeH0tJS\n/vkajUZ+Cx8aGopLJ4yHwWDgA+VGo5HnKYqJieG384QQxMTEYN68eWhqauLddXa7HY2NjeA4js8+\nYUhLS4NWq3XIv2bjFQqFS2FOXFwckpKSHDqNWa1WqNVqhIWFOeyuLp0wng8uBgUF8a8xGo3Q6XR8\nWjFDfn4+LBaLy/U1Gg0sFgtiYmIchNugQYP4wKVwfGNjIyilSEpKcsgwS09Pxz333AO9Xs/7qhk/\nPqUUYWFhkEqlCA8PR2VlJe69byVqamrQ2NgIqVSKpqYmZGRk+JSymZCQgJqaGtTV1aG0tBQ2mw0Z\nGRnIy8tDUlISYmNjPb5WpVKhuroaGp0WJSUlLu8nkUgcyNy6Cnq9HkDb2mppaXE5/9133+Gyyy5z\nWE+//PILsrOz+XnGXMKhoaEYPXo0Ro8ejbVr10KtVmPDhg1IT0/H1KlTsWfPHhw/frzb41S+ZAEd\nBOBJxbpwKbRn/7iS5Led2wxgc0duMNBQKpUICgpCfHw87rzzTtTV1UGlUrkUW1mtVp8sUEKI21Qu\n1t/Ubrd77HV6+vRpaLXaLuUV1xkMbq35pJRkZGRkICsrC1dddRXWrVvnlQzOFyvLbrdj8ODBuOSS\nS7B7926sWLECH3/8MTQaDerq6tCvXz+sWbMGK1aswPDhw9HQ0IA333wTf/zxB/766y+o1WpERUUh\nPz8fgwYNQmZmJux2O37++Wc88sgjsFqtuPvuuxEfH4+mpiZERETwjT0MBgOkUinvGnviiSeQnJyM\nm2++2WshG8dxsFqtWL16NS655BJceumlAFxdXsLsrNLSUrzzzjuYM2cO+vTpw59nbijn3wcOHMB3\n332He++9FyEhIQ5cOc6WLqUUn3zyCf744w/861//QlBQEE8vzVwXLB2R0Yw899xz0Gq1eOONN6DT\n6XDy5EnodDqkp6fzhkFpaSmqq6sRHh6OV199Fa2trbj77rtRVFSEtWvX4qKLLsIPP/yARx55BBER\nEZg5cyYWLVqEgoICl8Yp7vDQQw+htLTU4dihQ4f4v/Py8hyq54VISUlBcnIyJk2adEYyt+rq6qDX\n613WnVar5d/fnQJw9wzcGUYNDQ0wmUwOQe3IyEisWrUKK1euxMMPP4z4+Hj88MMP5yqBzzS0Wi1G\njhyJ3bt3Y/Xq1ZBKpWhsbHTp8cl8hUJER0e7BOsKCwtx8uRJl4nQ0tLCL261Wg3g70wDNvbLz7/o\nkH/cH5hMJpfPERERgfHjxwe8OpNZ5SzeUVJSAolEArlczgcB+/btC0opvytKSUlBXl4eMjMzERIS\ngpaWFpSXl6OkpAR1dXWQSqXIzs5Ga2srL/wkEgksFgvkcjksFgtkMhlf8GYwGBASEgJKKWJjYx0y\nppyzR5j/l+3g3G3FhYKf/c++MybMxcB2GzKZzOF6wo5TTPgDbQJE+L9MJoNEIuEDoBzH8d8piyGw\n+6qpqYFOp0NUVBTi4uIgk8nQ0NCA06dPQyaTISkpid9t9evXD+Xl5byfvKqqCgMGDEBhYSHS0tJg\nNBqh1+t9EsoPPfQQli1bhvHjxyMvLw/R0dF8fQx73p7AAqxi4wKFD9//AA0NDS7rkdXtcBznVgEM\nGzbMRU5ERET4ZMVrNBoUFBRAKpXi6aefxu7duzFixIhurwQ+6xSAzWbDtm2O/ODuJl1xcTG+/PwL\nh8lfWVmJ9999z2WsUW9wobvVaDT8pD59ui1I+dprr2HdunX47LO2OPr8BTfwgUBnBMoSsphMHer6\n5emnI2AZM7W1tbzwKioqAgBkZGTAarXyC0mhUCAtLQ25ublISUmBVCpFQ0MDn5HV1NSEuLg42O12\nKBQKBAcHw2w2QyaTwWKxOGRPCVNlgbbdnvAzODe6B9qeM/vudDodf4y9RhhcZtdl/nem2MXA0vyE\n37MwTdH5+TLFwpIEgL8zvxjlsnA3ALTN4bq6Op54jRUqsgw3s9nMGzDsc+Tl5fHuo9jYWBQWFqJf\nv36orq7mCd3q6up8motffvkl6uvrcdFFF+Gxxx7Djh07UFRUhPr6eqhUqv9v77zDo6ryBvyeKZmU\nSe8hQEJHqgIBEaRKkUWaCIioiKKiq65t1y6W3W/V3bWuSBWwgVKVpksRIQJiIXQSQkJJSC8kM5lM\nud8fM/c6E1JmICHBzPs882Ry5pZzz733lF/l22+/daut6qK21Zy7PPjQHIQQfPbZZ7z77rt89NFH\nSJJEXl6eYlnnvBqQWbRg4UUDQ/v27fnPv1wNBEJCQi6aKMp1l+nfvz/ffPNNtcHrriRXr6H0JRIS\nEsLw4a6JIEJDQ7lw4YKLDiApKYm9P+5x2e7jxUs4d+4cRqNR6QSioqLo1/96KioqXBRz8sxbCEFB\nQQFCCB580NU08cSJE9UqXAFm33sfGRkZysMUExNDbGws0bF2F/vw8HDFLFVWMlc3E6msrHRrAHCe\nCVWHJy9d+/btkSSJkpISZVZ94sQJwC5Tl+2qhcPjUlYUlpWVYTQaycrKIjc3l/T0dPR6PaGhoUiS\nPbmIXq/nwoUL6PV6ysvLlb9+fn5UVFTg6+uLwWBACEFxcfFFIhbn65GvSW43Z1FddasGmZCQEJcZ\nel3I7W8ymeoMyyGEICIigoyMDADFwUju8CsrKzGbzWi1WjQaDVarFV9fXywWC4WFhVgsFiIjI4mM\njMRisZCbm0tJSQmBgYHExMS4PGtxcXFUVlZSVlZGYmIix44do0+fPsrkJTg4mPT0dJesWTXx3nvv\nkZWVRXp6OocPH2bVqlWkp6eTl5eH0WikQ4cOLiIhT6ioqGDE8JvQ6/WEhYURFRVFbGwsMTExRMfG\nEBERQUhICEFBQYqlj7OSuCpHjhzBbDZzxx13uJTLYRnUarWyqnLmoT8/zJJFi3ns8d/DWq9evfoi\nK7ucnBySd+3mtqlTlDrIuhZnqvZDjUGzGwCqIzIykuVLlzHrvnuVm15WVka3bt1crFFefPklMjMz\nXTr68PBwgoKCLurEZUWgLGKqjuoSmstkpKdz6tSpOuvurBQ+ePTIRYNAhZsDgPOsuLbzuEPr1q0V\n0USHDh0QQnDkyBGEEOj1es6fPw/YX7QzZ86QmJhIeHg4bdu2xWCwr6ZkEzt5hQC/h9YuKCggPDyc\noqIiYmJiyM3NJTw8nOLiYoKCghQRiuzJ6ew05/xdRr6fsk12Vfl81VWAwWBAkqQ6rTfkfWTdSnX3\noepKQ7Yxh99t2c1ms2KPrtFolP/lVIs6nU7Zz8/Pj7i4OHx9fcnJyVFmtXJcHllXYrVaCQkJwcfH\nh3PnztGhQwd+/fVXoqOjsdlsVFRUEB8fz9GjRxk/vm7LoPHjx3P27FlCQ0Np2bIlHTt2ZOjQoXTq\n1IkWLVooM2LZZ8YT5afJZCLr7Fm3t1epVAweOpT5CxdU+3vPnj2rLZeV3z4+PtUO7hs3bqRzF1d/\nkJYtW7L3xz1YrVbl/spxkZyPkZyczMEDKTzy2KONbvrpjHcAwK4gGzjoRpdOTq/XM3jokItuVlVr\nGyGqzx4kp8iTrSlqoqKiwiUKoYy7skHnmWp1HbjVKTOTu8e6XCIiIigvL8dqtdKuXTsATp48qXRY\nZx0vs1arJS0tDV9fX+Lj44mOjsZkMlFRUaH4N2RkZJCRkYFKpVK8KJ1tt2VLIVkkJIuI4Pf47rWJ\nDZzbTZ6hyXLg6kRB8spCCHGR6M55teA8aMgGBs4zReffqw42sshQjlUji4LkBDKyN6qzLgDsA1hU\nVBShoaGUlZVx/vx5ysvLiYiIUCzX8vLy0Gg0LlZUqampdOnShfXr1yue8OfPn6djx44cOXLErXu+\ncuVKJdaO0WgkNzeXtLQ0fvjhB1JTU6msrGTlypWkpaVx9OhRRo4c6XbANU+t6Gw2W61WRxUVFYp+\nwpmSkhKioqJcYg05M23atIvK+vXrR1JSksv23377rZIjWWb48OGkpaU1ucRK3gGA30MzOFNbXJK6\nkM3A5NmEbLFRnQjinf+8zVN/ffqi3zwNZVzTjEruKK4UarUavV7PqVOnsNlsij4gJydHiZ90/Phx\nwN7uqamp+Pr64uvrq4i5jEYjRqORtDS7Y9CJEyfQ6XSUl5e7iH/8/PwUcVxFRQVarVaZBQshiIqK\nUsRaVTtl579GoxG4WKbvLOZxvj9BQUFIklTtIF3dfZatxKobhKquSqqKluSosnLQQDk8iSwKUqlU\nGAwGxVtWNkfMzc2lsLAQX19fYmNj0ev1FBQUkJ2draweysrKaN26NYcPH2by5MkUFBRgtVqJjo7m\n1KlTdOnShY8//titicH777/Pnj17yM7OVuLxBAUFER8fT9u2bZUc0wkJCWzevNmjaJvVKWTrIi4u\nrtpym83G++++xwNzHnSxwJGdKmXjD71e73bU0qrbVOfp/MVnnxMeGua2f8uVwjsAgNtp6NzFarUS\nHh7uEk8I7BEN161bhxCCd955h7Vr16LSqDl//rzLAys/jJ7g4+tb/QrAAyVTbWIedwcReeVz+vRp\nhBCK1U9paSmRkZGKOEg+X35+Pmlpafj5+aHT6QgJCaFVq1YYDAaMRiOZmZlkZGS4+FTExsaSl5dH\nWFgYxcXFyoAQGBioDBA2m02xupGvyznWEvzeIcsKadkOXP6tanvI28srBXcjOcrKZaPRqKxKqoYk\ncK5XVFQU586dU8QlsjzbarViNpuViJjyoGAymZRY+LKILDc3F5vNRnR0NGFhYRiNRqVzBvsKNzs7\nm44dO3L06FHFOqioqIh27dpx5MgR+vfvX6cXr4xOp2PSpEl06tSJhIQEwsLC0Ol0SoRN2W9hy5Yt\n+Gi0bjunAbWuoGsiJiam2vJvv/0WnU7HsWPHWLJkCTabjVtuuUWx79fpdGi1WkJCQurVJHXKtKn1\n5rBWn4grYXd7qfjqdFJ8bPUjuTv4+/tz4PChK97wBoOBVatWodVqKS0t5dy5c7z00kvVdqLnz58n\nMjLSZVZgsVjo0rGTR513i5Yt+f6HnS5lkiTR69rr2P/Lz3V24HX5AYSGhvLoo4/Weoz+/ftz+PBh\nSkpKmD59Olu3biU1NZW+ffsyb948nnnmGV599VXeeecdpk+fzrPPPsvq1au59dZbefHFF9Hr9fzj\nH//gySefJDo6mjfffBODwcBDDz2E2Wxmx44dijgoKiqKhIQEgoODlRm5bL1hMBhIS0ujvLwcrVZL\nUFCQsm1FRQUnT55UxFNGo5HTp08THByMEAKTyUR8fDxnz54lOjqa/Px8wsLCKCwsJDw8nMLCQvz9\n/cnPzycoKIiAgADKy8sVc1dncY3sRS6H+AgMDKxRKe08UMkroJCQEMWxTR68qlo8AYpjlyxnlwcK\nWXksO6fJq9wLFy4obShH7oyJieHs2bPExMQoyegDAwPJysqie/fuzJw5s9Z7f/z4cdLS0jh27BiH\nDx8mNTWVrKwsRbHetWtXtm/fXusxamLt6jU8+bh78YxkFi9byo033ljtbwUFBUoYFxmbzcbcuXOJ\ni4sjODgYq9XKxIkTr3ggRUmS6NGl62U7j57MzPhZkqTedW3nXQE0ALKXqMViwd/fn5iYGEU+XZXq\nZioWi8Xj8MsNHfPfnUE0IyNDmTWVlZUpgbHS09Np3bo1arVa0Q20aNECIQRxcXEuepCcnBwsFosi\nS5ZXUyqVipCQEEwmE1arVQk9rNVqXWbIsrw9ODhY0RnIg4Mcs0luX1nxbbPZCA8PV3IyyJ2tcyRW\n+H0FIYc+lnEW48gKZGcRkxyHxtknwRnnMiGEEo6g6m/V7SO3i7PyGFCc4uSQIXVOldAAACAASURB\nVHL9AcWqSg53LvtfBAUFuXjDlpeXExwc7JY+asaMGeTl5RETE6PE1urcubPiJetOUqKayM7Ornuj\nKlT1AK/rN7PZTExMjBLk0dfXl8LCQlq0uChg8R8K7wDQAGRmZgIossSAgIBqg7LJGAwGfJ1EOCaT\nyePlZ3VKL5vNhqaamb98bGdrDLmzqImmvFL00visW7cOrVarZMM6e/YsR44cYcuWLaSlpaHVatm0\nadMlHdvTAcBZ71KVsrIy/P39L1oRl5aWEhUV5SImzMzM9A4AXjxn//79BAUFKRnDhBCcOnWqWucQ\nsCu5Fi5cyCOPPAK4yqLdpWpkT5mqjlwGg4F/vP53Btw4EJ1OR+/evfHz83NZcVyK85eX5s3LL7+s\nmJzKQfRatGjBoEGDmDVrFp07d77kY+fk5Hi0vWxuXBVZF/XZZ59dFJ781KlTBAUFYbPZlIxfp0+f\npn//ugMBXs00uwGgoqKCBR/NJzY21u5QFRlBcHAwer1eUQA5hwm4FJKTk+natSuhoaHK8vrHH38k\nKSmJhx56iPLyctq3b89zzz2n7OOcTaG+rB4kSUJVRdHm7+9PcHAwJ1PTuOPOGbz33nv861//cpn9\nd+rUiUWLFrnsV5fVxqWuEK7UQONdwTQsH330UYMd2znwnTsIUX1OX1k8h03i9ddfJzU1lYCAAD74\n4AP27NlDu3btCAoKoqKigrNnz3Lo0CFlUuYunyxbjsViUfIBBIeGKA6bsoNa1ex/jUmzGwCKi4t5\np0rMc/lGyHbVGo3Gbg/t8EK9a+bd3HLLLW6f49SpU+h0Orp06YKvry/Hjh1j586dPProo3zwwQcu\n21qtVtavXUff6/u51NFTqlsB2Gy2i4LcGQwGsrKymHjrJD755BOeeOIJnn76aZdtLiUmS25uLsXF\nxR45+NhsNh544AGPziNJEufOnfN4ab506VIee+wxj86zdetW/Pz8arUpr0pRURHZ2dl06NDBo3Nt\n27aNm266ye19bDYbq1evZtKkSW53JJIksWHDBsaMGeNR5/PNN98wZcqUi6LgXilKPXwfZOV3VSwW\nCxu+/oakfn0vCuO8c+dOAgICFNPhtLQ0xRvbEz5dvlwJe+JcH/mdkiP4+gUEEBQURFRUFEuWftxo\ng0GzGwBqst2G32Psm0wmuxgmP5/TGRkYJtee2MMZs9lMaGgoaWlpVFZWotFoSElJUUIhVEWtVjP7\ngftdHgDZg9UTomIufjnlAcD52P7+/vz7bfsAOGDAAI/PUxOyAtWT6IZCCHbs2OGRpYUcPsJTJbm7\nDk3OyAm8PcFgMHg8gEuSxJkzZ6o1Pa2NtLQ0j/dxx7u8KhkZGYqvRGPgacA0WdlfXXnVd00mNTWV\nuLg4evXqRWVlJWlpaYSEhChhN9ylusi/spGAHKpbzityPiuLs6dPe3Rt9U3Tcku7AtQUlqE2qutc\na+LMmTMMGzaMvLw8ysrKkCSJgwcP0r59+xpNu5xN+sC+5JXN99x9uauzbLBYLJfs0CYnm3H+XM00\nheW2F8+RO07ZpNad+yi/O1VxTgLvjMFgIDExkYMHDwJ2RXFOTg7Dhw/ntAcdtBwmxBO01UQBuJI0\nuxVAfq7ns2tPRAAff/wxkydPZt68eZSXl2M2m0lPT+fvf/87u3btuihzGNgfuGPHjuHro6Nr927M\nnDmTu+66S7HnNplMlJaWUlxcTGF+ATk5OWRlZSmJtwsKCqqto9lsvuQB4NPln/Dq3LnK/61bt+Z/\nO2q34w4ICKBNmzZIkkRcXByJiYkAtG3bVkmV5+/vT2xsrJI05uDBgyQkJKDX6/Hx8SExMVFJtNKi\nRQssFoviQRweHq7Ep5EdnGRbfNmZSnbxl52tKisrCQkJQavV4u/vj1arVaKLyuVy5EzZEiskJISI\niAj8/f0JCwtTzCaDgoKwWq2Kial8Prl+Op2OoqIidDodYWFhLjmj5Y4MLg40J3v0yqalznGH5L/O\nzmLOsYrkpDFVvYirehQ7l4eGhrrIoZ39C6rbv7pQJ1cKIQR79v+kzJ4rKysxGo3296GwiLy8POV9\nyMnJURzgqq6MrFYrKb8d4NixY0ybfrvLOXbv3s2tt97K888/T2VlpeLJPGrUKJYsWcJrr73mVl0l\nSbooXHRdXI55bH3Q7AYAORCZJ7jr8SlJEh9//DH3338/cXFxFBcXK+KKIUOGMHnyZEaMGMGiRYvY\nv38/arWat99+G71ez5kzZxg9ejSAEuNGrVbj4+NDQECAi925u3iyAti6dSsm4++z/IMHD7p0IO44\npQ0bNoy1a9cC8OGHHyrlhw8fBmDFihXKdgCbNm0iMTGR77//XnlZ5d/ALrd3JikpCbD7Trz11lse\nLc3Xrl3LqFGjLorIWBslJSWMGzfOI0uQ3bt38/XXX3ukbygtLeWTTz7xSOFoNpv5xz/+4dE+kiTx\nz3/+kzlz5njUqW/bts3tbRsC2ShDts8PCgryWDSnVqtBJbhh4AAefvhhrFYrvXv3ZtasWbzyyius\nWLECi8VCeXm5EmQwNDSUZcuW8eqrr7o1S5dzBnuCJ89jQ9DsBoBLcSqRo0TWxZEjR2jdujXJyclc\nd911FBQUUFxcTIsWLSgtLSUzM5OSkhJmzZrFrFmzlP1ycnI4dTKd8+fPk+CURehyMZvN+Pv7u7Xt\nP159zUXp5emyNDQ0lBkzZni0j1qt5vHHH/c4PspTTz3l0XkAnnvuOY+v6aabbvJo9QfQpk0bBgwY\n4JFsXqPRMGfOHI/kzSqViqeeesolCqU7/PWvf3V7W7Drdu677z78/PyU/NZXI2azma/XrWfQkMG8\n//77SnlJSQmnTp2irKyM+Ph4SkpKKCwspHfv3iQnJ5OQkMDhw4drjdwrcykOnLU5rF0Jmp0OwNMV\nQE0mZVWRJImpU6fy9ttv8/777zNy5EhlSTps2DCWLFnCSy+9VK3VS3R0NI8/+US9dv5gzwVwpZaY\nPj4+nDh23KN9bDYb99xzDz///LNH+82cOZMFH833aJ/IyEhWffmVR/v8/NN+j0VocqfhidmpTqdj\nwIABSswgdygpKWH06NFs3rzZ7X3MZjN9+vS5KIFJbcgOUlu2bHHpOK82tFotL778EoMGDXIpf/DB\nB3nhhRdYtGgRw4YN4/z585w/f54RI0bw3nvv8fbbbzNt2jS3OnZP43dBzf47V4pmNwB4amEjR06s\ni8WLFyNJEh07duTHH3+kT58+nDt3jszMTCZMmMD8+fO588472bJlC/v27bvU6nuEyWRye4kpB3GT\nP55GLPTz87soqFldaDQaPv/8c3r16uXRueSUkO5is9n49edfqk3dWRt/eeJxknft9uiazmSeJjw8\n3KPnTKVSsWnDRo/CecgJ3o3l7isdtVot586c9chKKTw8XNGX+OkuPUJuU+Snn35i8+bN3H333SxY\nsIDx48dz+vRpsrKySEpKYs+ePXTu3BlJki7yi6kOo9Hosb9JbGzspVa/Xmh2A4CnJnqy40ZtbN++\nnUceeYStW7fy+uuvExwcTGhoKFlZWZw4cYLu3btjNBrZuHEjW7ZsYfDgwaSlpV3OZbhFhw4dePmV\nuXVvCGz8dguHjh1VPn995hmPzlVaWkqnazp7ZC104cIFEhISPOosrVYrO7ZtZ/KU29zeR6VS8djj\nf+Gee2d55N+QnJxMQptEj0RH990/m19++aVGr+/qEEIwYdJEj84THh7OyZMnGXaT+1mlhBD46wN4\n5rln3d7n8OHDFBUVERcXx/AR7vspNHVOnjzJoEGD2Lx5M5s2baK8vJwePXpw4sQJsrKylHd47ty5\nbN26lccee6xOXcil5PetKWrplaLZ6QDqy6ZYZt++fTz22GNs3LiRgIAANm3axDPPPKNEW5QtRaZO\nncobb7zB7t27effdd5k6dSqffPJJvYeidsYTb8Oq1xgWFkb7jh2V/+PqeFCDgoIYN26cRzOgoKAg\nbr75Zre3l+s5bkLdGaqqIoSgffv2Hu0jx7D3hICAAMaMGePxfm3atPFoe41G45FzooyndevRowc9\nevTw+DxNmePHj3P77bfzzjvv0Lt3bwYMGMDUqVPx8fHBZrMpMYH+9re/sWzZMp5//nk2bdrEww8/\nzIIFC+jbt2+1xy0qKvK4LpHRjSsCalbhoCVJ4toePSmrxlmjJkJDQ9n3y8/1aqvrqfOOFy9e6p/6\nfg83btzII3Me8mifL9esdvFKvtLhoJudCMjioaLG19+/3jtrb+fvxUvjU9/vYU625ybm9RHG/XJo\ndiKglatXKRmTsrOzOZ+VTU5ODvn5+RQVFWEoK6OiogKLxYLFYiE0NLSxq+zFi5ergLHjbqFbj+7k\n5+dz/vx5ss/ZnTXz8/MpKCigtLSUCoNByWlhtVrdNjFvKJrVACCEUHLU1oQsErPZbErybS9evHip\ni4iIiFr9Rpz7FjmBT2P7VdQ5AAghWgLLgGhAAuZLkvSOEOJl4D5ANuF4VpKkjY59ngFmAVbgEUmS\ntjjKRwHvAGpgoSRJ/1e/l3P5OGd/kk0jq2K1WsnNzUWv13s0gkuSxPnz5/Hz87tiS7/s7GxUKlWj\nRXJsCuTl5RESEkJRURGhoaGUlZUpmbeKi4uVl7asrIzy8nJFeZ+fn694nhYUFCgKQjmYV1BQEH5+\nfuTk5KBWqwkPDyc3NxdJkpQQwDabjfz8fLeU43KYiuZKTk4ONpvtiplGFhcXYzQaiYmJ8UgcdOHC\nBcrKyhRlsbs49y2AR5FzGwp3dAAW4AlJkq4B+gEPCSHkafR/JEnq6fjInf81wFSgCzAK+K8QQi2E\nUAMfAKOBa4BpTsdpMKxWq2L6Kb+cBQUFlzWzz8/PZ+D1/Vm+dJnLceV8tDVRWlrKjf1vUBxxzGYz\nNpuN0tLSS0oCUxeSJDH6phGMG/MnACU4ncViuWwl09XEhx/8l61bt/LKy3PZuHEjH7z3Pv99/wM2\nbNjA3JdeJjk5GbVazceLl3Bj/xsoLi6moqKCQTcM4F9vvoVareb226YwfPAQJEkiOTmZgdf3Jzk5\nGYARQ4cxbfJtqNVqUlJSGDxgIDf07aeEx5733w+5sf8NDB4wkBv731Dj5957ZtVxJX9sxo35EzeP\nGHnFcje8/e//MKD/DR5bBi5fuowb+9/gcZ6CpkidQ5AkSdlAtuP7BSHEUaC2YOzjgC8kSTIBp4QQ\naUCS47c0SZLSAYQQXzi29TxOrwdIksSiBQvp2LkT0dHRpKamEhISwtfr1nPXzLvrRRFkMpn47rvv\nSEpK4qMP5/Hk0zWHKpDdkOS4QUOGDCEyMpJ5//2QJ5568rLrUhvHjx+nU6dOlJWV8b9vv2P6jDvq\n3GfJosUX2enf/+ADbsdHagq0atWKjIwMEhISyMrKQq/Xo1KpyMnJIbFtGw4ePMje3clodTqefvYZ\nFi9chBCCvzz1JJZKM2/83z8pLCys9Rxnzpxhz549jBw5kvc++IA/PziHoTcOYuv3O3j5lblIwq7w\nqy00R2OHBfCU4uJi5s9zTQQTERHBPfe6P5DJljiyg15DGkhUtfrxdKBxzvVcn3VxDsR3pa0yPVqD\nCCESgGuBvcANwMNCiDuB/dhXCUXYB4c9Trud5fcB40yV8uoNausR2Y6/uLiYnj17otFoOHToUL3K\n9mUxUHp6OrfeVnfuAEmSOHHiBCajPfNQq1atPIqJf6nIsfrDw8OxSu55xAohmD9vnvK/j48Pjz/5\nRIPUr6Ho0zeJN/7vn9xz7yw+Xf4JAwfdSGVlJfv3/cT0GXfw7zfe5OCBFB55/C/Mnj2bpN59MJtM\n/HzgN1Z+sYLnn7U7TtUWFkKSJO68fTpLP/2EkaNH8e68//LnB+cwbNBgvtu+jblz59YZ88g5qfvV\nQGBgIB8vXuzilf3cCy+4vf/ihYu4484ZpKenk5KS0hBVVLBarTzxl8d59fXXOHgghbwC92bvkiSx\ne/dusrKyaNWqFfv3/eRxsqSaePvf/2Ha9Nv57bff6NevH8uWLau3Y7uL22cTQuiBVcBjkiSVAh8C\nbYGe2FcI/6qPCgkhZgsh9gsh9tdHJ221Whk95mbGjh2rhHmNj49n5qx76mU0t1qtZGVl0a9fP4KD\ng90KNSCEoGPHjjww50F69epFVlYWkybfetl1qQu1Wk1RURGlpaX07dvXrdnG2HG3uLTTNV27NgnZ\npSe8+c83eP7FF/i/v/+Dh/78MAcPpHA6I5O775nJKy/P5cMF8/npwK9YrVZ6XXsdK75cyYYtm+mX\n1JejR4/y06+/EB8fX+s5goOD0Wq13DX9Dvbs2cOoUaN4f96HGAwGRgwdRmF+AWNG30zv63rV+Jl5\n191XpkHqCbVaTZdu3ZT/hRDcMn6c2/tff0N/rFYrbdq0QUXDmkZ//ulnREVFYTQaUWvdz7UhhCAs\nLAybzUaPHj3QB9WP1Y4Qgp7XXcuxI0dp0aIFGRkZqIWKwwcP1cvx3cWtAUAIocXe+X8qSdJqAEmS\nciRJskqSZAMW8LuY5xzQ0mn3eEdZTeUuSJI0X5Kk3pIk9a5LweKOAkatVtOxY0eCg4Pp2LEj0dHR\ndOrUSYlb42n0vuqOf8011xAUFETbtm1dPDrrGsA0Gg2BgYEkJCS4KGkvt0410a5dO+Lj4wkLC6Nj\nx44uS9CaBoPQ0FCXLF933n1Xg9StIXnr3//iwfsf4L0P3uelF16k7/X96NCpI2/+8w0+WjCfO++Y\nga+vL5IkUVlRga+vLxqNhgqDAZvNhp+fX53PWnBwMKvXr0OtVnP3HTM4cuQII0aM4JXXXqO8vJxR\nI0ZQXFyMyWis8VN5FSbdmXHXncp3vV5fY9jy6p6xH77fyY4dOzh48CCpqan1/tw7H2/KtKl07d6N\n5ORkDh88RFxcXI3PvPN7a7Va2fvjHqKjo1m6dOlli2gsFotyjJ9//hm1VkPyrt3k5uYSFhHO1Nun\n1XkMT+N01YY7VkACWAQclSTp307lsQ79AMAEQB661gOfCSH+DcQB7YF9gADaCyESsXf8UwHXzAwe\n8uTTTzNy9Cg+WbacdWvWUFhYWOcNstls5OTksHLlSlZ+sYKn/vo048d7HlqgJkwmE/v27WPBR/M5\nePAgP//6i1vLOrPZzKFDh1i8cBE//PADe3/a16AmYlarlYyMDJZ9vJQNGzbw1epV1UYjValUDB0+\nnHVr1ti/Dx3aYHVqKJ5/9jneee9dnvjL4zz77LOsWbMGPz8/HnnsUR798yP83xv/pFvna/jzo4+S\ncuQw/ZL6UllRwS8pB/hyxUq6dbbbKtR1Pzp27Miar9cz/k9jmTRuPKvWrWXq7dMQahUvPPMsu/b8\nWKuVz9Vocjxs2DBUKhU2m42hw4fXOKvOzMzk1omTGDNmDHfefRcJCQnMfuB+5fdevXqxbs2aequX\nyWSib58kBg4cyD33zqJr166MHTsW+F3PsH7tuov2s9ls9L6uF926deO++2fTp08fZs66B4AhQ4YA\n8N/3P7hoP3f5+uuveeuNN5k85TamTZtGTExMnalZ5VXIuAkTmHHXnWzeuIn/+/vf60WC4c5a/gZg\nBnBQCPGbo+xZ7FY8PbGbhmYA9wNIknRYCLESu3LXAjwkSZLVcSEPA1uwm4EuliTp8OVUXghBq1at\nePb553jmuWcpKSlh8+bNLFm0mJMnTyrbmUwmjh8/zsL5C9ixbRsGg+F3pYv18mcdxcXFfL1uPcuX\nLiUzM1N5kf38/Gq8SZIkUVZWxo5t25k/fz6px48rMmBPUkF6QkVFBfv3/cRHH33EL/v3YzKZ3Npv\n5qx7WLdmDVFRUY2ewehSmDFjBvPnfcS9997LV199RefOnbFarWz4+hvuv/9+Fs5fwNDh9qBq3235\nluuvvx6bzcb2rdsoKytj+IgR7P7hh1pnqKdPn+bT5Z8wfcYdrP3ma8aN+RMTxt7C2m++ZurUqdhs\nNnb/sKvWnMn++oB6zdN8JQgICCA6Oprs7Ow6lb/FhYV8unw5ny5fjk6n47revZk9ezZ9+iZdcua6\n2jCUlbFpwwY2bdhglwR07sy9997LkGFD0ev11b5jQggslZUk79pF8q5dqNVqWrduzZ13382YsX+6\nfMdQm0ROdjYfvPMu77/9Dv7+/gweOpR7Z99Hp06dfjc7V6lo27Yt99w7i5EjRxIcHKzU15MYX3Xh\njhXQLqhWQLexln1eB16vpnxjbftdDkIIQkJCmDp1KlOmTCE/P5/3332Pt954k0+XL78o1np9aNvz\n8vK4deIkDqWkeKTAKyopZsb0O9i/b98VUfxZrVZeeO551q1Zc0nmn507d0an0zFp8uSrMoxFYWEh\nkZGR5OfnExoaqnhiBgcHk5eXR0JCAk/99Wne/vd/mPPAA+zZ/xM6nY5ePXpy29SpfPjRPIYPHqLk\nkqjp2XnphReQBNxxxx18vWkjY0ffzPg/jWX1+nXcfvvtXN8nqdbIp126dbvqBgCACZMmsWjBAo8C\nG5pMJn7cvZsfd+/Gz8+P8RMnNpjoE+zvwJFDh3j8scfQaDT0TkoiLKJuqyur1Up6ejovv/gir73y\nCt169KCbk97jUpGfIYPBwMZvvmHjN9+g1+uZPmMG4yZM4JHHHiUiIqLB37erS5tXCxaLhXPnzrHy\nixWsWbVKceI5cPgQTzz1JOfOnePLFStZ9eWX5OXl1Zgg2hMiIyP5ctVXVFZWkpyczOKFi/j155/r\nDIkcGhzCu+++i9ls5sCBAyycv4Afd+9uEF8AsMsMX339Nea++gonT55k6ZKP2bJpEyUlJW69dGq1\nmmu6duW2qVMapH4NzegxN9OuQ3sSExPJzMxUcgIXFhbSunVr0tPTsVgs3DZ1CsNuGq6YiX61dg2h\noaFYLBben/ehIr/t06cPq9evo2XLlthsNj7/cqWLGaPJZKJNmzZs/2En+fn59lmlxcKS5ctqzWNw\nJSzBGoIp06ayZ88et2XTKpWK4OBgRo4ezV0z76Zt27aoVCq+27KlQeonhMDf35/+AwYw67576d69\nOz4+Prz0wot17uvr68u1vXoxc9Y93HDDDfj4+PDhB/+tl3qpVCoiIyOZNHkyk6fcRosWLRBC0KNL\nV1Z8/jkRERGMnziRKdOmEh8fX6+yf5mregCwWCzs37+f+fM+InnXrmo7XlkcExsbyyOPPcqfH32E\nCxcusH37dpYsWKg4RnmCfEw5VIRarWbgwIEMHDgQs9lMRkYGS5d8zI5t27BYLMpAI59HTnAthKBn\nz568/98PsFqtygC2dvVqLBZLvZmEyR0QQGJiIi/NfZmX5r5MQUEBX69bz6fLl2O1Wmtthzlz5hAV\nFXXVmSrKyKGg27Ztq5TJ3tjyb1FRUS4ZmpzDhrRr1075rtfr6dy5s3Jfa5r5Vj2e8zFq4mps36io\nKObMmVNr3S0WC/Hx8UyfMYM/3TLWZXYrh10BlPfxcidnFouFsLAwxk+cyG1TpygdqDzzdlbGynG/\n5PMHBAQwZuxY7pp5NwkJCS7RAKxWq1JX5/3cRZIkOnXqxMz77mXw4MEEBQW5tIOMzWYjNzeX+fPm\nMX/ePHx9fek/YACzH7jf47zDtfGHDgcNtWvMLyccrOwUUpuMv7rfbDYb9z5wP4s+ml/t787343Jf\nAvlYkiTVOpjI29V2vkFDhvDD99836DL9amL2Aw+4+Ec0Z1QqFQMHDeL77dtr3Mad59rZ0aq+nv2a\njiVJErPun83CeR9V+27U1jfIFk2XOkGrq9+pD2MAd8NB/+EHgKaGEIK9P++nf1Lfq2q2t3L1Kv7y\n50c4d+4iy91mh0ajYc/+n+jXu89VdQ8bihYtWvCf997ltomTGrsqbuPj48PuvXtIuq7XFfe+vRJ4\n8wE0UaJiYggLC+Oarl0buypuo9Zq6d69O1Nvv/2qVALXNx06dSIkJIQODZjN7WpBpVIx9fbb6dat\nm1u5s5sKna65htDQ0EbPydvYeAeAK8yECRMAu6XI1UK7du3sKQjHe5by8Y/KHXfcgSRJV9U9bChs\nNhtjx92CVqsl0Um/0tSZMWMGAGPHue+5/EfEOwBcYWRPv5tGjrjicT8ulbvvmQnYE1hfjX4A9c3I\n0aMQQjDq5tHNfkUUEBCgzKJlh6mmjkqlYthNdr+PadMvyxf1qufq6IH+IPgFBBAXZ9dp6PV6EjxM\nBN4YCCEYOXIkYFeoD7jxxkauUeMSFhFBUFAQYA+GFnqVRfCsbwbceKNiaDFy5MirYkBMaNNGCeAY\nFxeHfy3OeX90vAPAFWTAgAHKrF8IwV0z727cCrlBZGSkS9Kbe2ff14i1aXwmTJjgYqkyceLERq5R\n4+L8PAQGBtaaEaup4BwGXqVS0b9//0auUePhHQCuIFVd5W+++eYmP2O6pUqcpKtN2Vff3H7HdJf/\n3Qne9UdFo9HQpUsXl7LxTXxAFEJw8803u5TNuu/eRqpN43NVO4JdTQgh2LFtOz98v1MpkyQJjUZT\nr44d9Ymc5UzOYCbj5+fXZOvckKhUKr5csdJFdyPH+L8aA7ldLv7+/rz/7nsuZSUlJY1UG/fQarVK\nwh8ZOSpAczRw8PoBePHixcsfDK8fgBcvXrx4qRXvAODFixcvzRTvAODFixcvzRTvAODFixcvzRTv\nAODFixcvzRTvAODFixcvzZSm7QcgBBpN066iFy9evFytNOnetWvXruzdu7fBjm+z2S47IFt9HKO+\ncU5PKIRwSV5Ttb7ytnJZbclhnBNhVN3P3XrJDjfO9al6PncS1MjbOR/vUpJ01Ja4R8bdY1Z3LLnN\nnMNH1HY/6ovaEhZVTWhSV3KjhsD5Wah6/XKbVH0OnJ85+RpkGqr+zklqqj63zvV2rk9T6A/cnTg3\nfk3rQK1W89NPP5GWloZKpUKtVtf4KS0tVfaRP8ePH+e3336jsrLSpVwIQXFxcbXHyc3NRa1Wk5WV\nhdlsxmazcfz4ccXLUd7OYDBw6NChi/aX6ymEqLGuzr/J29d0fbUdp7pPCwOwdgAAD35JREFUSkoK\n7/znbd566y0Ajhw5ohz/7NmzqFQq5ZiSJFFWVqac58cff3Spj0ql4tixYwghSE5ORqPRoFKpSElJ\n4cSJEwghlONV3U8+h/P/p06dwmQycfr0adRqNSUlJWRmZrJw4UJSU1NZvHgxBoOB3Nxc1qxZw7ff\nfsvHi5ewZs0a1qxZw2effcbWrVtZvHgxqampHDhwgE+WLeerr75yaa/ffvvNpe2c6+Bc5w0bNlz0\nzKjVavLy8li6dCkLFixwua4LFy4oL79zOcDx48dd7lVBQQEVFRUcPXqUHTt2KNtqtVr279+PSqUi\nNzcXoNr6yfWveg1yufP2VZ+T9PR0ln28lMrKSmVbeXs5ub1arebEiRPk5uZe1C413ceatqn6qVpv\nm81GWVmZUv8TJ06wZMkSli1bdtGzk5KSglqtZt26daxcudLl+tLT0xFCkJKSgkqlYuHChZjNZoxG\nY539w6V8Vq5cyeeff45KpWL79u1KHVNTU13uz6ZNmwA4f/58ne/zlfi4S5NeAcj8+vMvTJt+O2/+\n8w3iW7WkrKwMrVbLmTNn6NCuPfn5+UTFRJOUlMS6desICQpm5OhRZGZmsm7NWiZNvpUPP/ivknTb\nKtmIjY0lI/0ULVu3oqCggAA/f6ySjcGDB/Pj7mR6XNuT5F27ufPuuzhw4IASwsEvwB8fjRYfXx3H\njx4jsW0bvtvyLYGBgTz40ByMRiPr16+nrKyM66+/HoPBQExMDGfPnkUIQYcOHUhLS6OwsJBBgwax\na9cu8vLy6NChA+Hh4cqM6OzZs+j1esrKyrDZbJxMTWPCpIlcuHCB+Pj4WturV69e7NzxPR07d2Ln\nju/Jzc1ly6bN3PynMaT8doDTp09TWVnJxm82MPHWSRgMBvr378+ePXtIS0vDZDIRFxfH3r17OZRy\nkMjoKCIiIkhPT2fv3r1MnDiR3T/sAuyDy/Gjx5hx151s+Pobruvdix3bttPj2p6oVCrCQkL55bdf\nOXr4CG3atKFt+3YUFBRw9PAR/vftd4wYNZJjx44REhLCqi+/4vkXX+CtN97kyaef4kzmaR5/8glW\nrFjBxIkTee+ddxk5ehTb/reVjp07cfb0GUwmE4lt2/D1uvVoNBqyzp4jNDyM40ePcfDgQSIjI8nO\nziYyPILMzEz6Xt+PnJwcftydzIAbB3L86DEkSeJ0RiZt2rVl1KhR2Gw2SktL8fX1pbiwiLfeegs/\nnS9+Af5EREQQHx/PiRMnKC4sotxosM/+rDa6du3KmTNnuP7661m0aBHR0dF06tQJo9FIQUEBAK/O\nfQV9UCBRUVGcOXMGQ1k513TtQtu2bVn5xQpi4mIpLS3FaDQSHx9PXFwc5eXlfP/993Tr1o3U1FRK\ni0tI6teX/ft+YuToUZQUFbNz504mT7mNbt26IUkSubm5xMfHs3TJx8S3asneH/fQf8AN6PV6ioqK\nKC8vZ+TIkaz+ahUDbhzIzp07CQwMJD3tJIlt2zBkyBD+/trrhIWF0aVbV37+aT/BoSF069aNrd/9\nj1E3jybzVAY2JI4dOYpOpyMyMpLi0hKKi4tpm9hGqUfb9u3Iy8ml0zWdyc/NY+ToUWzfuo2HH/kz\nf3v6ryxatIgePXqw9bv/ERgYSHZ2Nl26dOHIocMMGTKETz75hMxTGST164tOp+PcuXOk/HaAnj17\nUlxYxMGDB0lJSSEuLo5Bgwahr8fonidT04iPj+e5Z54lLCyMnTu+JzAwEI1Gw4YNGwgODMJsNnPq\n1ClGjBjB9q3bKCgoYNyE8aSkpDC+SiytpkaTXwEAygsJ0Lp1a3pdex2F+QUk9e5DWVkZNwwcQPa5\nLIQQjB07lsrKSt75z9u0a9eORx57lM0bN9Gnjz19X8+ePenduzdpJ1IZMWok6WkniY+PJyommilT\npnDqZDqo7B21PJv5/NPP+NMtY+0DTocO9LzuWgwGA927d+dCSSkdO3dCqO1NWV5ebq+zxUq7du04\nefIkX331FXFxcSQmJvLvt/5F1tlzSnJpo9FIRUUFGo2G/337HUePHmXVqlUUFRXx4+5kSkpK2Lnj\ne1q0jOfLL790OxCbPNNM6tcXg8HAxFsnsX7tOmJjYxFCEBsby8xZ95C8azcBAQFUVlYSGxtLcHAw\nffr0Yd2atURGRtKyZUvatWuHn58fVrOFcePGsX7tOqKjo1Gr1URGRuIX4E/r1q0xmio4fvw4EyZN\n5IvPPic6OpqENono/QO4/Y7pJLRJJDQ0lMDAQPpe34+KShNgT8p+7bXXkp+fT2ZmJh06daSiooLi\n4mI+++wz2rVrx4KP5jPq5tH4+/tTXFxMx44dOXHiBCqVigEDBtC2fTt69+6NwWAgPDycsIhwKisr\niYmJwVBWjl6vR6fTYTabadmyJRcuXCAqKgp/f3/69OnD8BE3kZeXB6DMJnv16oWvry82i5XBQ4cQ\nERZOq1at0Ov19O/fn9DwMCSrjR49euDv76+cT6fTMWbMGHb/sEvpjORVgr+/fQJhqTQTGRlJQptE\ngoKCSE9Px2g00rdvX8LCwhg2bBhlpReIjo7m7Nmz5GSfp2/fvrRNbIMQgvDwcLp3705QUBCxLeJI\n6teXbf/bSmVlJUajESEE/QfcwL59+2jfvj3Tpt/Ois+/ICYmhsoKExqNhpMnTxIbG4uvry9lpfb2\n0Gq1JCUlUVFRQWxsLJ2u6az8P3jwYCoqKrBYLJiMFZw5c4bMUxl07d4NH18dg4YMpkePHrSIjaNz\n5874+/szcvQo+vXrhyRJBAYG0vO6a9m/fz9Go5EzZ84QFBREt27d2LnjeyorK0nq15fQ0FBUKhW3\nTZ3CgQMHCAkJYciwofTt25fiwiLCw8PJzs5GCEFQUBC7dv5A+YUy4mJiOXHiRP11PIBOp+Pue2bS\ntXs3dDodna7pTHyrlgQEBGCpNDNw0I0EBgbi7++PJElERESgUqlYtGAhN910U73WpSFo0rGAevfu\nLe3fv5+srCz8/f3RaDT4+vqSk5NDWFgYPj4+mM1mhBAYDAb0ej05OTmEhISwYsUKZs2aRVZWFj4+\nPthsNrRaLWVlZWRnZ9O9e3dUKhUGg4GKigq0Wi1hYWFUVFRgs9kICAigpKQEf39/SktLCQsLw2g0\nUlRUhI+PDyaTCV9fX7RaLRqNBovFQnBwMGAPiOXn50dOTg4BAQH4+fmh1WpRqVRUVlZSWFhIcHAw\n/v7+FBUVKddlNBqVhCvnz58nKCiI8vJye+drtbJl02amTXcvLaMc4EqlUimDjbyUtlqtWCwWRQQE\n9hyplZWVqFQqNBqNyz6yzFUIgcViQaPRKCsVi8WCcCjrbTab8lGr1VgsFnx8fC6SjcvHlbez2WyY\nzWZ0Oh2VlZXodDpsNlu1Adbk++i8nXxNcj2d62i1Wjl79iybN27ivvtno9FoqKysZMWKFUyZMkUR\naX333XcMGDAAf39/AOU4gHItclvYbDblnsviDlksZLFY0Gq1mM1mpR3lJbkQgi1btjB8+HCEEFit\nVmUbq9WqPCPycVUqFSaTyUX0Y7PZlOtSq9VoNBpMJpMiipAnCM71MZvNimjAbDbj4+ODEAKz2YxW\nq1XaS66zs8zdWeZtsViUAIbOMnD5OZKPJ/8my+zlesv3VKfTAVBRUaHURX5e5W3lusvIz5gkSZhM\n9gFMbju5vvIzffToUYxGo3IN4KrjctYbOV+H3Kbys92lSxfl/bZardXqeJyfO/m+AyxevJjZs2fz\nyy+/KHWQ93c+j7NOSK6vcxvUpFcSQtCuXTtCQ0Orff+FEFd/UnghxAXgeGPXowkTAeQ3diWaMN72\nqRlv29TO1d4+rSVJiqxro6auAzjuzijWXBFC7Pe2T81426dmvG1TO82lfa4KHYAXL168eKl/vAOA\nFy9evDRTmvoAML+xK9DE8bZP7Xjbp2a8bVM7zaJ9mrQS2IsXL168NBxNfQXgxYsXL14aiCY7AAgh\nRgkhjgsh0oQQf2vs+lwphBCLhRC5QohDTmVhQojvhBCpjr+hjnIhhHjX0UYpQojrnPa5y7F9qhDi\nrsa4lvpGCNFSCLFdCHFECHFYCPGoo9zbPoAQwlcIsU8IccDRPnMd5YlCiL2OdlghhPBxlOsc/6c5\nfk9wOtYzjvLjQoiRjXNF9Y8QQi2E+FUI8Y3j/+bdNnIQo6b0AdTASaAN4AMcAK5p7HpdoWu/EbgO\nOORU9gbwN8f3vwH/dHy/GdgECKAfsNdRHgakO/6GOr6HNva11UPbxALXOb4HAieAa7zto7SPAPSO\n71pgr+O6VwJTHeXzgAcd3+cA8xzfpwIrHN+vcbxzOiDR8S6qG/v66qmNHgc+A75x/N+s26aprgCS\ngDRJktIlSaoEvgDGNXKdrgiSJO0ECqsUjwOWOr4vBcY7lS+T7OwBQoQQscBI4DtJkgolSSoCvgNG\nNXztGxZJkrIlSfrF8f0CcBRogbd9AHBcZ5njX63jIwFDga8c5VXbR263r4Bhwu52Og74QpIkkyRJ\np4A07O/kVY0QIh4YAyx0/C9o5m3TVAeAFsAZp//POsqaK9GSJGU7vp8Hoh3fa2qnP3z7OZbk12Kf\n5Xrbx4FDxPEbkIt9YDsJFEuSJMdVcL5WpR0cv5cA4fxx2+dt4GlAjvUdTjNvm6Y6AHipAcm+Dm3W\npltCCD2wCnhMkqRS59+ae/tIkmSVJKknEI99ZtqpkavUJBBC/AnIlSTp58auS1OiqQ4A54CWTv/H\nO8qaKzkO0QWOv7mO8pra6Q/bfkIILfbO/1NJklY7ir3tUwVJkoqB7cD12EVfctgX52tV2sHxezBQ\nwB+zfW4AbhFCZGAXKQ8F3qGZt01THQB+Ato7NPQ+2JUw6xu5To3JekC2VLkLWOdUfqfD2qUfUOIQ\nhWwBRgghQh0WMSMcZVc1DhnsIuCoJEn/dvrJ2z6AECJSCBHi+O4H3IRdT7IduNWxWdX2kdvtVmCb\nYwW1HpjqsIRJBNoD+67MVTQMkiQ9I0lSvCRJCdj7k22SJE2nubdNY2uha/pgt+A4gV2G+Vxj1+cK\nXvfnQDZgxi5fnIVd9rgVSAX+B4Q5thXAB442Ogj0djrOPdgVVGnAzMa+rnpqmwHYxTspwG+Oz83e\n9lGuqTvwq6N9DgEvOsrbYO+k0oAvAZ2j3Nfxf5rj9zZOx3rO0W7HgdGNfW313E6D+d0KqFm3jdcT\n2IsXL16aKU1VBOTFixcvXhoY7wDgxYsXL80U7wDgxYsXL80U7wDgxYsXL80U7wDgxYsXL80U7wDg\nxYsXL80U7wDgxYsXL80U7wDgxYsXL82U/wcs9XawMomRZwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb62f2aa710>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(sharp_image)\n",
"print 'sharp image'\n",
"plt.show()\n",
"plt.imshow(soft_image)\n",
"print 'soft image'\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### Extract smaller region from images"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"sharp_test = sharp_image[1000:1400,2000:2400].copy()\n",
"soft_test = soft_image[1000:1400,2000:2400].copy()"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### Display said regions"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"sharp image\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQsAAAD8CAYAAABgtYFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXec1GT6wL9vMm0rHUSKdJAOYjlQUUHEdojeKVY8sZ1Y\nzt7wxHp2T/HUs/w87GLnOBUV8U5UpAlIb9J73zozSd7fH5k3m5mdhQXc3SyT7+ezn51JMjOZTPLk\n6Y+QUuLj4+OzN7Sa3gEfH5/agS8sfHx8KoUvLHx8fCqFLyx8fHwqhS8sfHx8KoUvLHx8fCpFlQkL\nIcRgIcRiIcQyIcQdVfU5Pj4+1YOoijwLIYQOLAFOBtYC04HzpZQLfvMP8/HxqRaqSrM4ClgmpVwh\npYwB7wJDquizfHx8qoFAFb1vM2CN6/la4OiKNm7YsKHctm2b8/yII45wHhcUFLBkyRIAsrKy6Ny5\ns7Nu5syZaV+Tuq579+4Eg0EAFi5cSHFxcYWv86k9mIbBggULEaKm96QmEEgkXbt2RVTyAMycOXOr\nlLLR/n5iVQmLvSKEuBK4EqBly5bs2LEDy7IAmD59unMApk2bxjHHHIOUktatWzNjxgz3ezj/3cul\nlGhamdL0008/EYlEAGjRokWSsHC/zqd2EI/G0AI6P0z5nssuvZRMLFmQUiKlZObMmUgpKyUwhBCr\nDuQzq8oMWQe0cD1vnljmIKV8SUrZR0rZp1GjRliWlfSF1QlQr14952CUlJQkfUi67YGk7XRddwSF\nlBKlwVRWGvt4j2AohK7rzJ8/37nBZBrq/DVNs9rO5aoSFtOB9kKI1kKIEDAMGL/HHXFpAu4vX7du\nXWdZaWlp0muEEAghkgSFlDJJWNSpUydpe/UeUkry8vKcxz61j9mzZ2es0Ffac3V+/yoxQ6SUhhDi\nWmAioAP/J6Wcv5fXJKlTSgjk5+cDYFmWIwTUduqu4j5gqUJFCQS35qL+N23atNzrfbyPRCItydyE\nsMhEYS+EIG6a1frdq8xnIaX8DPissts3aNCAbdu2OZpBVlaWvYOBsl10+xqACk+UWCzmrM/JyXEe\nq+11XceyLA455JB9/l4+NY8S7lu2bMlIQQG2Jh5OXBuWZSVp5lX2mVX+CZVEaQCQLBTUQRBCEI/H\ngfJmQ+pz93ZK6KTzb7g/06d2IYQgFotlrLAwTZPs7OxqNUU8IyyaN2/u/PCbN292lqeaJZAsQNJJ\nVLewUQ5SsCVwIBBwTBJfs6jdaJqWscLCsiw6d+7saMzVgWeERaNGZeHf7du3J63TdR0pZZJJokg9\nUFJKR7MAyMnJcbbRNA3DMBwBo3wWPrUP5beqDvXbi2RnZ9OpUycsy6o2gVljeRap7ElYmKYJgGEY\nQJmNls5pKYQgGo06r83OznYeuzUMwNcsajECW1AICTID/dMxw6Bbj+6gCagm5cozYtl9l1fCoiL1\nKt1yt3RV0RAhhBNNSfc6X1jUXkzDqNa7qteIxWIceeSRlU7I+i3wnLAQQjjCItVHoUinTbhRIVYh\nBLm5uU5Y1p3ZqWkaDRs2rKJv41OVSCn59ddfgfLnRqZQv359mjRpgia0aktM88yRzs3NdR67L/ZU\n9hYJgTJzRQhBOBxOEiru3Az3Z/rUHoQQrFmzZu8bHsQ0btzYqXfKOM3ikEMOcb70zp07AVsQmKaZ\nJDndF7wSFG5VzLIsR1iYpkl+fn65VPJAIICU0jdDajELFy50HN+ZyBFHHOE48jNOs6hXr54THi0o\nKHCWp1Mz9yZJ3dEQVRcCZcLFMAyEEDRo0OBAd9unhpg7d25N70KN0rZtW4LBIJa00HW9Wj7TM8Ki\nSZMmjoTcunWrszxdaLSyPguwa0uUEHKH2rKzs5MEiU/t4pdffgEy12fRvXt3oHrrmjxzpJs0aeI8\nTg2dQvqisYpwR0NS/RJKIDVr1uxAdtenhtmyZUtN70KNcvjhhwOga9WjVYCHhIU7SrFt27a0Jesq\nmqEu+EAgUC6LT9O0pHTv7OzscuElTdM49NBDM9bePRiQpokuNKzqSjLwGNm5ds2TrMYSfc8IC3Ux\nSykdB2XqunSku+DdDp9gMOgIIpXcBRAKhfxq01qKZVnOX6b+hunKIKoazwgLKPviO3furLCxjdrO\n/T+VdCXqkBxlcZs9PrULpWVmclKWigpWp7D0lLBQP/yOHTuSNI1UUg9QqnR1Ozjz8vKcdUoIqbBp\npp5otR1d151qS7e2mGmkljxU+edVy6dUEhUCcleNpouGVLROoXwWmqYlFZLt3r07qV1fpqqwtR3D\nMDBNM6koMBNR3z/j8ixUApb7AlZqZmonLHVwVFKO2kY9dvs8lGah+m+q92rcuHE1fTOf35rVK1cR\nDAYRukamdeDUdZ28vDyn3QJkYAZnOrPDXauf+nhP/1P7bCoBs337duf9/fL02svPP/+ckSakOo+7\ndu1aYc/aquSAStSFECuBAsAEDCllHyFEfeA9oBWwEjhXSrljb++VzrzYl6pTN+7QqbsHRqovw6d2\nsmnTJqdNgSklZIg5qa4Rt1Zc26pOT5RS9pRS9kk8vwOYJKVsD0xKPN8rlfnC6Ryb6r86kO6GvW5t\nRNf1pGQvX7OovSjNIlN9Tr169SrX4Lo6qAozZAgwNvF4LHBWZV6kGumqx0BShagKlYGdL5Hqq3Cb\nMar5TeqIAHefjGbNmpXL5/CpHcyZM8fpiBYgMwSGpmlI0/ZTdOxSve30nH04wNdL4EshxExhTxgD\naCKl3JB4vBGoVEKDCoOlOjOhfFWdu01eOtyFZO7X7Nq1y95pKQkGg2nb9Pl4n+3btyOEqLYCKi+g\nHJqxWCxphGd1cqBXy7FSynVCiMbAV0KIRe6VUkophEjriRIp4wvdZkS6JKx0jk9Vap5Kaj8MpXns\n2LEj6T18aifRaJSIysC1JDIDUr41TcMy7QpTNd6i2vfhQF4spVyX+L8Z+Bh7evomIURTgMT/zRW8\nNml8oRCCSCRSznQwTbPcwXH7IVJx+yxSNQ+lWajtMtGjfjCgQuaZlMGZ2umtJtjvTxZC5Agh8tRj\nYBAwD3tM4fDEZsOBTyv7nqrzD5QdHBXRSGejVaQdpE4qU/99H8XBg/v8yARUpmZNft8DMUOaAB8n\nLsQA8LaU8gshxHRgnBBiBLAKOLeyb1ivXr2kxjdKc8jLy3PqOqCsu7cSIqkds5SDM1U4pJa++6ZI\n7UL9vkF3h6wM+QkDgYDdtKkm92F/XyilXAH0SLN8GzBgf96zUaNGrF69Gki+kN0dut3r0vkspJTl\nBigr3ALHp/ahnODKEa7qQzJhkrr6jkaiq3lNmCOeCQdYluVUgqbe8fPz89NGSdxmi1oupaS4uLhc\n1aoQIklYZHKcvjazbNkyR+NMF0E7WDFNE13Xyc/PrzG/hWfSvTVNo27dukByI15IPygI0js4IbmQ\nDMqEy+7du53nmWLrHiyoxs3z5s3DsizC4XBGFZKpYd4dOnSosXPXU0e6SZMmaWtAVGs8dxIWVBwN\nUUlbqnxZbR+NRp3XZ8pJdrCgazpCwsL5C5yIV6bNOhVC0KNHjxpLb/fUFaM0iFQvdygUStpub0lZ\nFfU4SM329KldCE1j3bp1Nb0bNYI6Z5s0aVJjeSWeERZSygrLxitKQkn1WSjc/TDcQsc0zYy7Gx1s\nzJ49u6Z3ocaQUjpdvWsCzwgLsKvpUlO83WXm6rnCna7tXu4ejAzJPop0NSg+3sWtZW7dsoXNm9Pm\n+B30WJadvdm5c2dEDQVQPSMshLCH/ighoVKzhRBOsw/13N38RnX4dgsZ5Ztwb+8WNqm+DB9vI4QA\nAfPmzfPOCVvNBAIBYoZBdm5OjeVaeOrY16tXD7BPjqKiIudiTp394U73TvVvpIt0KNMj1dfhOzm9\nj3JYAyxatChje26WlpbWeBTPM1eL22eR2uG7otqQYDBYrj4gNUkntdZE07QkTcXH27jNxp9//jmj\nKk3dhMPhGo/ieUZYQLJQcGdhhsPhtNtX5sClk8T+9PTag9vXtHHjxoyNZHnhe3tGWAghnI7bQggK\nCwudE8UtRFKTsipSy9wl74CT6WdZFo0aNfKjIrUEtwm5aNGijNUIo9FojZvNnhEWKt9d2WVbtmxx\nHrv7ZbrtNk3TyqmlFXUDV3UkypGq1vl4HOkS+GmaGmUKgUCA/Px82+yuoX3wjLBQUlMJAnfvCbew\ncAsD5bNIpSIHp6JRo0a/3Y77VBuZnFBnWRbdunWzz+VMT8pSpCv6UmZIqvPSXXVakUnh3l4JDX90\nYe1BJhzYKqEuU6MhmqY5CVl+bUgKKnQqhEgSFm4qqg1J99ydp5FasObjXUTCNNV13am8zERM06Rj\nx44AaCLDq06hrFmNO3RqWZZTG2JZVlJDm9RBK6rVmnKSBoPBpHoQFWbNycnJmNLm2o4UCUEvy2Z7\nZiKaptG02aG2llVDHd88Iyzc7fPA1izUieEuUY/FYs7jii52pTFUFHKtU6fOb7LPPlWPxBb027dt\nq+ldqVGklHTp0gWgxrrSe0ZYpNZ+7Nixw4mOuIWFe6pYOpPD/T5u88W9rWoQ7ON9BPZvt2DBgowe\n3WCaJtnZ2TXad9QzwiI1C3PXrl3lfBZAhS3zUvMqIFkjcS9v2LChLyxqGbNmzcpo01FF/mry++9V\nWAgh/k8IsVkIMc+1rL4Q4ishxNLE/3qJ5UII8awQYpkQYq4Qondld0QIkeSzUINkINmccJshyieh\nXu98qYRGkpWVlfxlEz6O+vXrZ+xJV9sQ2OfD/Pnz7YhIpnToTUHounNe19S5WxnN4l/A4JRlFc0z\nPRVon/i7EnhhX3YmEAg43m4VDUnVGNzTxvbms8jOzk7b6FQlZfnUDoQQzJs3j0AgkLEOTrdj37Nm\niJTyf8D2lMUVzTMdArwubaYCdUVi4FBlUXF0pVmk+jLcmkXKfiY9llKSm5vrLFf9Ny3Lol69en7Y\ntJaxYcOGGi+kqknc14GXNYt0VDTPtBmwxrXd2sSycgghrhRCzBBCzNiyZUu59W5Hpus1SUk5ezto\noVDIOblUiS9U3OjXx7vUdHl2TaMieLW6RF3ae7/P30CmjC9U6qW6uN2t8dxds2KxWLkDVtGJFA6H\nHQFRWFjoLFde9Uw++WoLKjcm07ubdejQwclirSn295Mrmme6Dmjh2q55YtnedySRiu1Ws1RExH2A\n3F2wgsGg8xp3bYmmaWialjScaPv27UnvXZOOIp/Ko84L5XPKVGHRo0ePGteI91dYVDTPdDxwSSIq\ncgywy2Wu7BF1IatuWUDS1HNFRT4LhdIypJRJoVN/GlntxV2NnKk+i27dutX0LlQqdPoO8CPQUQix\nVtgzTB8BThZCLAUGJp4DfAasAJYBLwPX7OsONWjQwBEcO3bsKBcSdZsh6cKmQFphoQSPKkrK1DtU\nbcOyLGKxmFMXkqm/m1tY1NQx2GtKnJTy/ApWlZtnmvBfjNyfHVEXvCpHl1ImDUmGshMn9TVq+1Sh\nofIzpJQUFRU5yzP17lQb0TSN1atXO0I+FAhiyswLnx522GFAzUZDPJM/q7LT3C3vVETEPW7eHdVQ\nBWbuA6geu99LCMHu3bsr1ER8vIuFZO3qNQSFZheV1Vjrl5rFQqIlUt9rajCyp26x7vJxgIKCgqQq\nUtg3n4U781O16XMf5ExVaWsTArudnqo4zVSt0P29M34wsrrI3VPJ3MVkKnxamapTRarPIrV5jq9h\neB+JZO7cuYAd8jZqqDzbS3g2g7O6UBduw4YNnWU7d+4sd2DSOTih/AGUUjq1Iao/hk/tQyCYPXu2\nH+p2UdsyOKsEIUSSsHBHQ9TJ4vZZuAvJoCwKorZV80FEok2fWm9ZVsbWGNQ2BLB582biZqLIMEME\nhspUVv9rRW1IdeNuzuueSqbMlHg8nlazSOe8jEQizmN3Rqh73KGPt7Esi3g87pggmeCzUHNN1f+2\nbdt6opdHze9BCllZWc6F7M7WVALC3dNgbxe8W/NIHZbsUzsQQiTNDpFSHvRF6u7zO12Dad8MwRYI\nKoNT0zQnz8JtXrjVsT2VqKtOWWobVXUK1HgTEZ/KI4QgFAo5SVmZYD6mCscePXrU9C4BHhMWYJsh\n6iC5E6kAxwxR7E3DcJshKmdD3al8ag+ZaIaoyF0wGHS6eis8m8FZnag8C3X3KC0tTXJYSimTzInU\n4UHu0KimaUQiESc2r6IhvkZRuzDjyQJCl3Cw6xaapiUSsMCwLA7v1jVpvW+GJHB33k5N94b0nbLc\nfg139am7RF05ON0p4D7eZ/ny5QAZNVxI9W0RQpCfn0/btm1repcAjwkLKSV169ZNKlFPdXC6hcWe\nVFIpZbloiDr4NZlf77NvqIQsyJymRapvhWr/75Ubm6eEhRDCucCFEGlTu/flDuMONxmG4TTxVYIi\nE5xltZ3169cnDc3OhN/MnYDWtOk+daWsUjwjLFQEIxQKlfNPuKMXSoC4hxK5Ja8SJpqmJUVD1Pu4\nfSKZ4CyrbajzQP2OC+bNg8TvZVkWMgMUQlNKTGmhBXQ6derkGS3Yc1eL22mpwp1uSbu30KnbbIlE\nIk7Gplqnoi1qGx/vIYRwele4u3q72+sdzCiBaRgG3bt398x56hlh4Y54KEflrl27nHXqgt/TKIBU\nB2e6dPD69etX+Hqfmic1uqW6eqvlmWCGBAIBpzVk165dPXOeekZYKPZUHAbpHZwVHUx1F3KvVw5U\nr0hrn2SUYFC/j6ZpjjaZKb+bWyBmuSqnaxrPCIuK8iVU0Ze64FVLPCEEgUAg6cRy0oH3UKHoR0O8\nja7rxONxBAJplpkee7sxHExo2Oe9aZoYpuGZdj/7O75wtBBinRBiduLvNNe6O4U9vnCxEOKU32In\nU52U6QrJ9oR7+2Aw+Fvskk8Vkgl+icqgaZqnjsX+ji8EeFpK2TPx9xmAEKIzMAzoknjN80KIff62\nqVqG+/HexhfuzXlZr169jLg71VZUpSWAyNBoVerICukR3WJ/xxdWxBDgXSllVEr5K3aX76Mq88KK\nLuBUx2c8Ht9rTYgSFG67V72HKlTLBNu3NuKEs6XEcN0YMo1U340XOBDRfa2wJ6X/n0hMUec3HF9Y\nkdZQmarT1PXKdFGhUx/v4lwcQrBmzZo9b3yQovqNuhMIvcD+CosXgLZAT2AD8OS+voFMM77QXYqu\nwqDq5FHTx9xt9VIbgqgDm9rcxm2a+A5Ob2Or3YCAOXPm1PTu1AhC2ud2z969AdA80sFjv4SFlHKT\nlNKUUlrYw4SUqXFA4wuh4lkgqp9mLBartBmS+hjKfBZeUu980jN79uya3oUaxSt9LBT7JSxEYs5p\ngqGAipSMB4YJIcJCiNZAe2Davrx3RXaaimLsrVNWagJPahhVCR0f76Icehs2VGry5UGH0rLr16/v\nqZvaXvtZCHt84QlAQyHEWuBe4AQhRE/s6ekrgasApJTzhRDjgAWAAYyUUu5TbXFFgiA7O5tt27al\nHQXgzq9IzfBLNTncs1R9vIuUMmM1C2WK9ezZ01Mm8/6OL3x1D9s/BDy0rzvijmCkXvzualHDMJKi\nHO7XmKbpOEBTU78Vql+GV34AnxQkaIlw4c7tlQ3CHVyY0gIJXbt3s52diWlkNY3nAtluf4L7IldN\nayrq7q2epxtC4y4kc0888/EepmE4N4hManjjRjnow+FwokFxzQsK8JCwcOdTuFEHLicnB7AdnBWl\n/gphzxVJxa1hqPmoPt5ETxRRuTXDTEX1YKk1SVnVTUU+C3c0JN16tWxv6xWZUL3oUztRN04vpXqD\nB4VFRagDt7dZpemEQKqPw73Mx5ukc1ZnCuUc974ZUjEqAcstDJT54HZw6rqetsgs1ZxRQkJVrGby\nNG7PI2xBbhlmxgp0aVpYuCJ5HjkOnrxiVMTCnTOhJqLvaYq6MkMqOsmUeudHQryNEIJly5Z5Tg2v\nLoQQ1KlTJykq6AU8LSzcByk7O9tJ9071a7gPqnuuSKrJktr7wsd7qN9nzpw5Gf0bdevWDfCWOeZJ\nYaGKvdz9MyORSIWhUfdJlVpolpq/4dYsMlXN9TKq6cuiRYuS2hFkEpZl0a5dOwBPRYW8sRcpqPoN\n5RFWzXcVym+h1qm4vPsxlJkdqSed27fhZdzdzWs658Adkq7KO52u6+iazpw5czLWDJECevbuhcRb\nGrAnhYUSDO47v7vDlbpw0h1I5cRUKNPFvb2XfoA9oZJyUsc01gQBrfouXGlZrF+/3jN31OpG13Wa\nNWuGJW2hXNO/vcKTv0bdunXLdctSbf1T/RJuUtep7QsLC4GyO2Jt0CoUsViM4sIiLKNmNQtd10Ha\n2k5VdrCSUlJQUMCGDRs8Y6tXN5Zl0bFjRzSheepc9dRgZIV73qk6WO5q0XSagtoudYqZlNIRFqma\nhZd+iHQYhkG7Nm0JeKAXo2ma/Lp6ta3tVOHnCCGYMWOG3Yw5Q9O9pZTk5ORgSQshvaMJe1KzULM9\n3Cng7q5BKiKiLiB3boWaE+l+vRqwrHwatSUiEggEiIRCNS4oANA0VG5QVR811fQmU80Qy7IwDANN\neOv7e2tvErijISUlJU5RjVqmHJYVFZKl2nhqgroQolwXLR9vYVkWS5YswTTNtLNuM4FAIGAnJuKd\nSAh4VFjk5+c7j9UIw6ysLMfZl3oSuS/+aDRaTlgoMyS1sY5XHEc+ZWiaxowZM9B1PWPHNigHfrrq\n65rEk8LCHSZVgkGdOO5ci9QWfJB+ynqm3qFqK+oG4aW7anXiVc3Xkw7O3Nxc57EyIVRtiNsMUbgd\nnKlJW5ZlJZkhFfX49PEGhmEQj8dt3xOZOXBImeHKZ+GVc9STwsLd+q6oqAgoqw1R4wzBFiDublpg\nn2zuO5I7dKpQQsLrdy4pJfMXLyIUClFcXEx2VtXPvXzyscd44YUXqvxzKkLTNISUhDQdw8rMaMjh\n3braD6T0VGJWZcYXthBCTBZCLBBCzBdC3JBYXl8I8ZUQYmnif73EciGEeFbYIwznCiF67+tOuWd7\nqAvd3bQmnRniXpfqm1ACxx0F8YoduCeEsMctFhcX28JSUDV/UjqP06XTVyfucRBeuUiqmx49eiTd\nAL1CZW6tBnCzlLIzcAwwUthjCu8AJkkp2wOTEs8BTsXu6t0euBJ7xsg+obpiQXlhoWlaUgZnahjU\nLSzUAS8qKvLc3MjKYhgG2dnZVet30cpOSr2GnYruIcipc2Eyhc6dOzuDhmpVIZmUcoOUclbicQGw\nEHvK2BBgbGKzscBZicdDgNelzVSgrkgeHbBX3MKipKQEsB2cboFQEW4HpzrgymeRk5NTYc8LLyKl\ndBy7Vd0OUKq/Gj4mhmE4uTI1vS81RZcuXRxz2ku9V/ZJdAshWgG9gJ+AJlJKNdhhI9Ak8biiEYZJ\nQyCEEFdiax60bNky6XMikYhzoKLRKJZlOSXqbhMj9c7j7u6t0DTNSQFXPg6vqXcVUZ37KRMnZU1f\noDt37kQPBrGQxKOxjAifplZCt2zZ0hEQ6jfxwjlbaWEhhMgFPgT+IqXcnRJVkEKIfTrLpJQvAS8B\n9OnTJ+m1eXl5jgpWWlqKlNIRDHtSy9wnu3v/iouLkVKSnZ3tR0M8zvz585FSYkgJmkBmwM9jJVr/\na5qGpmtJArKmhbebSgkLIUQQW1C8JaX8KLF4kxCiqZRyQ8LM2JxYvt8jDBXKDFGRDF3XCYfDzoW9\npwxOZYa41XYlLFLnnHpFvfMpo6SkhMGDB6PrOqZp1ko/076izK5056OXbmaVmUgmsIcKLZRSPuVa\nNR4YDjyS+P+pa/m1Qoh3gaOBXS5zpVKolGzLshyfhbr43QIhnZagzBB3erh6j7y8vLROUR/vMHjw\nYAYPHpx29OTBjGEYBAIBT/daqYxm0Q+4GPhFCKHmyd2FLSTGCSFGAKuAcxPrPgNOA5YBxcCf9nWn\n3A5IFQ1R6d7u7lnK6elW1ZTWoYSFKiQTwp494tUfwieZTNP6lJnt5e9dmfGFU6i40HBAmu0lMPJA\ndsp9MZeWlmJZVpIz0z1hLBWldbjtPuXg9H0WPj77j2fFmNIWVDl6OmHhRl30ap3aXqWHSykdbcPH\nx2ff8bywKCwsTCpRT1dI5tYO1Mg3t9miMjiVg9P3Wfj47DueFRZQNrs01QzZU/Na5RhTg4qklOXM\nELffw8fHp3J4Mp/W7eAsLS11wkqpodNQKFQuDh2Px7Esi3A47DiLdu/ejRDCKUZzD0r2tQuf6qJb\nl64UpxQ1Agw4+WReeuVlu2is+ner0nhSs3BfwMqEUOxNK1Bah9s/UVJSgpQyqUDNi4U6Pgcf6mYW\nj8fZunWrEw52/6mO9F6Zll4RntQsoGy4Smp5OZQ5MVPDTMqZqWlaks9CvYe7XZ8vKHyqA+VjE0KQ\nl5dXYRNiy7KwkAhN9+y56VlhoUg3lWpPKbBKELgz/5RD1J3V6QsMn+pAJVtBolQhzbnrZHAKr8xL\nT48nzRCFZVlJMz9S54a4K1HdGZymaTp5FvF4PMnB6W5846W8e5+DE7djfk/V0kIIJNLT56SnhQWU\nJVS5tYB9Scpy94FwR0PAW0U6Pj5ex5PCwp0HkTogCNJ3ynJHSlSehRDC6WUBZXkWCi+n1vr4eA1P\nXi1uYaEqRtVzIG2nLIVyJqkO4aqITDmY1Gt8rcLHZ9/wpINT5VWoLlfKF5HqswgEAuVMEdM0sSyL\nUCiEZVlJ/TdVIZmvUfj47Duev2rcWoXbmVkRqWFVd06GW7j4moWPz77hWWGR6oR0awPKaZlOQ1Dr\nVAu90tJSZ507KcsXFj4++4YnzZB0PgW3RpAuQqLWKeEQiUTKOTjz8vJ8IeHjs594VrOAiud77K3q\nFEjKs1Db+IVkPj77jyc1C+WfUIJC1XGkmia6rju9LpTzU20biUSSytMhefaI7+Qsw53Neuvtt3Hr\n7bel3SZ129rMlClTGDH8UizDTJqbUhVYlmWfq7Vcq60VV0xqL0ZlaqTTPJTPQhWSuc0Qn/S4hXNF\nZlo6La42o6Jl1dHnU9f1g0KTPZDxhaOFEOuEELMTf6e5XnOnsMcXLhZCnLKvO+U+YVO1DEhvhqjH\nap1Ks1WoxZeyAAAgAElEQVR5F76vomLcESfVCiDd38GEaZpOvo6an1sVf6qi9GCgMmaIGl84SwiR\nB8wUQnyVWPe0lPIJ98bCHm04DOgCHAp8LYToIKWs9JRbt4BIvaOpCIc7X8Lt/FRt+NyahS8s9oxb\nq6hIMKj1B4v55v6eVTn1S+UL7enY1hYOZHxhRQwB3pVSRqWUv2J3+T5qX3bKHS5V6pvbZnYXgwFO\nVyzls1BJWe5OWz57xq1V7Gn9wYIw7Qs4bhp2aYCkSv7cpk5tn662T7++SB5fCPZ8kLlCiP8TiSnq\nVDy+cF8+x+lqlQ7ll6hMNET5Nw6mE93ntyESiaDrum2q6loV/elY2OdfunYLtYkDGV/4AvAA9jzd\nB4Angcv24f0qnHUKUKdOHadZb8rrnHoP9xxItZ07zwLs2hC3huLjA3B0v74sWLK4zNStIitVUvb+\nndq332OZutep1O1WpBlfKKXcJKU0pZQW8DJlpkalxhdKKV+SUvaRUvZp1KhRuc90Z1um7MtefRZQ\nFg1RgsXHx40ya52LV1TNnyktYrGYM3i6NlOZaEja8YXCnm+qGArMSzweDwwTQoSFEK2B9sC0fd2x\nimZcKr9ERaT2unAXoPn4OAiBBALBIHGz6u72mqYRDIUQmlaun2xt40DGF54vhOiJrcCtBK4CkFLO\nF0KMAxZgR1JG7kskRJGXl5fWfDBN0zE7lEMu3YR11YNTNev18XHjvnUE9arLTdTUJwkIhEJQi8/F\nAxlf+NkeXvMQ8NAB7Bd5eXlJgiJdUla61niqbsRthvihUx+fA8ezRlSdOnWA8hmDysFZkc8itZBM\nOTh9fHwODM9eRRWFToUQtsMoTcKWlDIpg1MJD1+r8PE5cDwrLLKystKaGe5MQnfyVuqycDiMEMKZ\nUObj43NgeFZYpM74cJNOU3Cn7kJZNCVdc18fH599x7PCok6dOmmrAvfWi0IJh6ysLKAsz8I3RXx8\nDgzPCguVlOX2Ryj2Jiw0TStXSObj43NgeLL5jZSS7OzschV7UObgTEVVDqqyY3e6t69V+NQUViKP\nXJMCLCttVrkpEzc/SyI8HLnz5J6JxJAghftir8gMSdUeVKKWu1GOj091Y1mWk5gVTGi7qajQvtdH\nanpSs4AynwWUrxjdk7BQCViptSFe/hF8Dl4CWqJsQcCcOXMIZ0XKbaOqUb1eluBJzQLKMjDTUZkL\nX0VD1DhDH5+aJhwpLyigrJ2C189TzwoLd1JWZUKnarm7bgTwk7J8ahRpWk75u2mZWMhyf27T2ss9\nLzxphkgpnaSs1M7eqkQ93WvSVaTuaSCRj09VI/Sy866iSmpEmVbh5W5anryChBDk5+en9U1U1sGp\nUMLC1y58fA4Mz2oWqYVklc2zSIemaU4o1cfHZ//wrGbhDp2mUllh4W7yW1HnLR8fn8rhSWEBZUlV\n7m7eUPnGp6m5GXsSPj4+PnvHs8IiKyur3BAh5eisyJfhxu3D2Fu3cB8fn73jWWGh6zrBYDApiqFy\nL9J1SE51cKYmuOTn51fRnvr4ZAaVadgbEUJME0LMEfb4wvsSy1sLIX4S9pjC94QQocTycOL5ssT6\nVvu7c6q1njI7QqFQUoObVCqa+iSE8H0WPj4HSGWiIVHgJCllYWIkwBQhxOfATdjjC98VQrwIjABe\nSPzfIaVsJ4QYBjwKnLc/OxeJRAgGg0SjUTRNQ9f1JJ+FMj2i0SimaTrrVVNf9d+yLF9Y1AQSux1+\n4rdJX0blU1uoTMNeCRQmngYTfxI4CbggsXwsMBpbWAxJPAb4AHhOCCHkPiY6WJZFVlYWuq4TjUbJ\nzc0lJyeH3bt3A/YJGAqFnEQX9d897lAt8zWLmsMyTDQhMGJxp7jPp3ZSqV9PCKEDM4F2wD+A5cBO\nKaWyB9wjCp3xhVJKQwixC2gAbN2XHdM0jaVLl2IYhnOSrV69OikcWr9+fUfLiMfjBINBR1io0nbL\nspLew6f62LhhAyeeeCKWYaDretrWAj61h0o5OBOTx3piTxc7Cuh0oB8shLhSCDFDCDFjy5YtSevU\nBS6ldC5ylfatZoUIIdB13TEzgsFgUkhVbZ/4rAPdXZ/9QIoyEzFaUj5F36d2sU/RECnlTmAy8Dug\nrhBC3a7dIwqd8YWJ9XWAbWneq8LxhZZlEQgEkkKk6UKjapmu647AADta4l7vN+ytOYLBIELuoS7C\np9ZQmWhIIyFE3cTjLOBkYCG20PhDYrPhwKeJx+MTz0ms/2Zf/RVKm3CfYO7H7rwL54u4QqyBQMBx\ndoK3i3MOZsy4gRmPgybKukHVYlRzGtVJPhAIYBgGpmkSCAScG1RqVC51udpWmcfqfVVLSK9SGUO+\nKTA24bfQgHFSyglCiAXAu0KIB4Gfseehkvj/hhBiGbAdGFYF++3jU+0ooWCaJoZhYBgG2dnZzsgJ\nTdOciz01g9g9EEtF6SKRCMXFxY7ACIfDntaCKxMNmQv0SrN8BWWT093LS4E//iZ75+PjJTSNWOLu\nHzMMQqEQcdMkGAzSum1bmjdvTsOGDWncuDGNGzcmOzubcDjMjh072Lx5M5s3b2br1q0UFRWxYsUK\nduzYQSAUIhaL2YICiJsmAY9qF36IwMenkuTm5nL99dfTv39/2rVvnzQBWEqJaZps2rSJDRs2sGHD\nBgoKCijYXkijRo3o0q0rTZs2pUmTJo5zvuzFsGzpUlavXs0777zD5EmTqv/LVQJfWPhkJCqqFiuN\nOmUFym8QDodtUwNJLBZjwIAB3HjjjXTr1QORkBAWkiXzFvDll1+yYsUKpk6dyubNm9OaIZA8BCsY\nDNK1a1f69+/PwIED6ditC206tKN1+7acOHAA8+bM5dFHH+W7775zIn6aJR3Hv/KBGIZBMBwiGo1W\niwPZFxY+GYkKuUuRCPGadqheaAICOq/+36v069fPviBDIV54/nkefvBBpk+fjqZpdqjeNOnduzft\n27fnwYcfJi8vjxaHtaRp06blqqUBNm7cyIZ167Esi3nz5jFhwgSe+vvfCSXm8kajUZo3b87Fw4fz\n5ltvEY/FnEjfTTfdxPjx4zHNxBCtoJ2QWJ1t+IQXOkj16dNHzpgxo6Z3w+c3Zu3qNZxw/PHOhemp\nfBdLogft8LwFtGx1GGPHjqVZs2bous7kyZO5/dbb2LRpE7qu06ZNG04aOIBrrrmG3NxcZ/C2avM4\nbdo0VqxYwe7tO9iwYQNbt25l586dFBYW0qJFCxo2bEjTpk2p37gR2dnZ9OnThxYtWhCLxZJGdf7n\nP//hicceZ9WqVcRiMVq0aEHv3r15ZsyzCCFYt24dl1xyCWtXrnLyjvY2pU+xfNXKmVLKPvt7yHzN\nwicjicfjxE2Dv44ezYgrLseMG7z00ks89dRTGIZBbm4u9957L0OGDCEYClFaUkIgFOSZZ57h9ddf\np6CgAGlajiBU3diaNWtGs2bNqF+/Ps1atCA7O5uNGzeybsMGps2YwaZNm4jH40mT8qSAQw45hA4d\nOnDzzTfz1VdfEQgGsUyT999/n6+//ppWLQ8jKyuLm266iUlffY0eCLBzxw4GDx5MUUGBM/KiKvGF\nhc9BSVZWFsWFRXZyX9wgnJtNNBolFovRunVrLr/6Ki644AIKdu2mT89ebNmxnWbNmjF+wr85/PDD\nAVi7chUj//xnJk6caJcSaIJ69erx5z//mUGDBtGqTWsEAklZCYIQwvFrpCKxNQBd07GkhSY0LGmx\n6teVfPXVV8yaNYshQ4YQSswaGThwIPfccw/nDbOzD5YsXszll1/OY489Rv26dbl4+HCm/vQThmnQ\nv9+xrF27lpycHIqKitB1nVDAzmrOzs2hsLAw7T7tC76w8DnosCzLzl8IBTHjBjJR+Vq3bl2mTp2K\nHgqxZfNmDu/YCV3XufLqq7jhuusxDIPJkyfzxGOPM2nSJKSUHHvssYyfMIFu3brZzkshKNi9m8mT\nJ/Pic//giy++oKSkxMkaVmaB8jUop6Qaq6miJsFgkOzsbE499VSO69+fC8+/gCsvvwKhaZiGwdy5\nc3n88cfpd9xxBINBwuEwzz33HP/73/8wDIN/vPA8r776Ks8++yxXXXUV30+dCqbJkUceiWVZlJaW\nEjPi6IHfribH91n4VBk15bNQbQ1UJME0TaQQzJkzh9zcXO6++24+/fhjTCkZOXIk191wPUh4+IEH\n+Oc//4mu64TDYR598gl+//vfOxpDtKiYF154gddee43CwkLb+RkMOpmcDRo0oEmTJjRt2pSmTZuS\nl5dHJBJhy5YtbNiwgfXr17N582aKioqIRqNIKZ1krtzcXNq3b8+oUaPofdSRTmHkhAkTePvtt/nu\nv7aQGDlyJKPuuQcEFBUVcfyxx7Fl0yYuuuQSHnzwQUpKSnjiiSd4/fXX0ShLJBMSlqxccUA+C19Y\n+FQZNeng1DSN4tJS8vPzue+++xg6dCjvvPMODzzwAA0bNuSaa67hoosvprSkhNPPPIOF8xfQuHFj\n3njjDbp1704scTGPGDGCqVOnJrVEGD58OBdccAFNmjUlGLBLCUzLRNfKhy8lMskskcgkcyUai7Jx\n7Xreeecdpk+fzrRp05xyhX79+vHqq68STDhAZ//8M5dddhnbt2+nfccO9n4MO9/RgHbu3Mndd9/N\nRRdfjLQsjjiyD5s3biIUCKALjWWrD8zB6QsLnyqjpoSFlJJgMMibb79Nnz592Ll7F8cccwyFhYUs\nWLCA/Px8CgsLOfHEE9m6eQvHHHUUb777DpqmsWTJEj799FOeeeYZciNZNGzYkLvvvptTTz0VqZdV\nPM+fP5+vv5jIxIkTWbVqlVNdq+qa3EOx3CFUpY1Eo1G6du3KoEGDGDj4FLp06eI4SjEtvvj8c+69\n9162bt2Kpmk0a9GCF198kU4Jf8qwP/6RaYlr5rY7bueKK66gqKiIHj16oGkaF1xwAffffz/Tpv7E\n8IsvRpqWr1n4eJfqEhZBPUBJtNTp2xrOymL69OmsWbOGe+65hx9//JH777+fiy+5hKk//si5555L\nTlYWAwcN4umnnyYQCvLSi/9k9OjRBAIBIpEIjzzyCGcO+T3BYBDTNBkzZgzTpv7ElClTCIVCTvev\nunXr0qpVKwYMGEDfvn1p1MRO9XY3XlJ+is2bN7Nty1bWr1/PpEmT+Prrr9mxYweAYzLl5ORw6WV/\n4rrrrkPXdQzDIBaLcc3VtqMV4IEHHuDyK68AYMG8+Zx++umYpsm7775L3379KC0p4ZhjjqG4uJgv\nvviCFi1a0KtXL+YvXOALCx9vUl3CQt25NU1jxBVXcPsdd3DXnXfywQcfUK9ePX6aNg1pWfTu3ZuC\nggJefvlljj+hPxqCJ598kjFjxhAIBXn55Zfp16+f0xj63rtH8eabb2JZlj2aIqBz8cUXc8MNNxAO\nhx1fhbrQCwoKnHTvzZs3U1hYSElJCY0aNaJx48YceuihNG7cmHA4nCRwDMOgtLSUGTNm8MQTT7B8\n8RJKS0sRQnDRRRdx3nnn0aVHd2KxGD/88AMjRozAjMZo2LgxX3zxBQ0bN2LSV18zcuRI6taty1/+\n8heGnX8+30+ZwqWXXsrQoUN57PHHEZrwhYWPN6kuYWEkirom//e/NGvenG5duxKNRlm8eDFC07hn\nlH3Rn3jiifzfa68B8MH773PttdeSk5PDW2+9xZFHHokeCHDJxRczc+ZMioqKsCyLyy+/nFGjRqEl\nNAXTMFi2bBlPP/00U779L7FYzEkRLy0tJRQJJ3VnCwaDlJSUOGna8WjMERSaphEKhTj2hP7ceOON\ndOzUCWlZCE1DWhYPPvggr7zyCrquo+s6v/vd7xg7diymaTJjxgxefPFFpkyZQoNGDflp6k8AXH3V\nVUyePBlN05gxYwaRSITOnTsTCoWYt2C+Lyx8vEl1CYtQKMQJJ53EmDFjuGvU3bz3zrtMmDCBrt26\nsWjhQk455RQOPfRQpkyZgh4I8IdzzmHu7NnowSAffvghHQ/vhK7pnD10KLNnzyYajRIOh3n51VcY\nMGAAYIdjly9dxrPPPsunn35KXl4eBQUFzoUciUQYOHAgDRo0oHnz5jRq1IicnByn6nTLli2sWbOG\nzZs3s3z5chYuXOhkXubn57N7926aNWvGLbfcwpChZzm+j0mTJvH+++/z+X8+IxAI0L17dz7+5BM7\nT0PT+NPwS/n66685+uij+eDDDzENg88//5yrrrqKPn368On48SxcsIBTTjmFNevW+sLCx5tUlbDQ\nEOjBALFYDMuy+HWN3Zv16COPomDXLn6ZP59YLEbnzp3RdZ1nn32W0888g/GffMr1119PdiTCtX+5\ngSuuuIKApnNcv35s2bKFmGHw9ttvc0zf3wEgJDz1xBM89+yYJJPjrLOHctsdd1C/YQMnn8IpIEvZ\n19RoiHqkTCcpJVs2bebRv/2NmTNnsn7tOmf91df8mb/cdBN6IAACfpjyPRdeeCGhQICGDRty3Q03\ncO655yIFdO10ONF4nL///e+cfuYZCCHo3bMXhYWFLFy4EIBQJOwLCx9vUpWaRTwRylyybCkfffAh\nt912G61atWLS5G947513ueuuu7j00ku58847CQSDdO3SxUlmGjBgAEi4fMQIvvnmGyLZWXz88cd0\n7NgRJMycMYNhw4Y5xV3Dhg3jb48+ghbQEQgM08AyTKZN/YmJEyeyevVqvv/+e1toJPbPXX2qvj+A\nSDQuPuyww+jfvz+DBg2i77H9MKVVNsoibnDbLbfy4YcfkpWVhWVZnHTSSfzzpZdAwKJFizj77LPZ\nuXMn4WCI7777juYtW/D5559z3chrCYVCjBkzhuOPP55HHnmEf/3rXzz99NMMGXqWLyx8vEmVCQtN\no06dOsz8eRZPPfUUr7z4T7r37Mm7773H1X++msmTvmHixIm0aNGCtWvXcuqpp1K/bl2m/PADFpKT\nTz6ZDWvWEo3HeeWVVziu//EEAgHOPfdcfvpxKoZh0LVzZ9546y0aN25M3DQwLJOZP03n4YcfZt7c\nuQT1AIFQ0GmFV6dOHU477TQOad6MQw89tMKkrPWr17BkyRLmzJnjJF7FozFMaRGKRBg+fDi33HEb\noUAQDcHGjRuZOHEiDz/4IKWxGEcdczTvv/++kzF68oCBLFm0iE5du/DVV18hTYv//ve/XHzhhRx5\ntL3thg0bOOmkk1i2YrkvLHy8SVUJi2g0ihCCvscey6xZs1iybCkApw0+lRUrVrBo8WIA2rVtSzwe\n57rrruOW225l5vQZnH322QCcevppvPjiiyDhrCFDmD17NkII3nzzzSQz5IUXXuCxRx4hHA4jhKCw\nuJiBAwdy++23c3iXzmnzKNzNbdQ60zSTutW7mTf3F5566ilmzZpFYWEhuhBEo1Fuu+MOrrrqKjuF\nPGGGXHzxxViWRa9evXjsscdo06YNa9ev44Tj+xOJRPj4449p064tmqbRoV17gsEgixYtQtP1qo+G\nCCEiwP+AMHYtyQdSynuFEP8C+gO7EpteKqWcLeyj9gxwGlCcWD5rT5/hC4uDk6oSFiqUGY1GeeON\nN6jXqCEXXnghhYWFLFmyhO2bt9DnqKPo378/Dz78EM2aNePyS//Ed99/z4CTB/Lss88S0AN8OXEi\nV1xxBcFgkA/Gf0KPrt0Q2I2GB5x4Ihs3bqQkGqV169a8/OortGvfHkta6EIDCQsWLuCzCf9h5cqV\nfPvNN5SUlDihUNVcR0U9LCthZpj29dauYwcGDjqZM844g/adOjnODAvJimXLGfGny1i5ciXhYJBY\nLMZDf/sbF1x0IQjB7DmzOffsP2BZFo0aNXKKyW644QYmfv4Fpmkye9Ys6jSoz/CLL+H7779n6g8/\n0KjpIVUuLASQ4x5fCNwAXA1MkFJ+kLL9acB12MLiaOAZKeXRe/oMX1gcnFSVsMjOzmbXrl0Eg0FC\noRDBrAhbt25lzJgxDBkyhFNOHsSKFSuYP38+WTnZ/Pjjj1x6yXCklCxashhN01i54lcn0nHfA/fz\nx/POJRwMMfa1fzFmzBi2bt6MKSXDhg3j/vvvJysnG7A1h/Vr1/H888/z708/paCggFAohEaiexUy\n7fdUxyCAQAo7Cau4uJj8/HxOO+MMrrvuOlq2OgywtZHiwiLuu+8+xo0b5+R9jBo1iosuuRjDMHhj\n7OuMGTOGXbt2cdRRR/HuuPeIx+N079qNgoIC2rVpw7dTvqOkqJguXbrQpk0bJk3+pvrMECFENraw\n+HPiL52w+CfwrZTyncTzxcAJUsoNFb2vLywOTqrSwSmEwJSSWbNmEQyH+Pbbbzn11FM5/PDDKSoq\nYtWqVViGye23384nH33EGb//Pc+OGcOO7dvp06cPQko6dOrEfz7/DCEEEz76hJtvvYV4QhN45JFH\nGPrHc9CFhjQtHn74YcaPH8+OHTuIlpSQlZVFaWkpp512GocddhgDBw3iiCP7lHNoQtkoTSklCMGW\nrVuY9NXXTJ70DV989pmToxGJRLCAP/3pT9x5553owYATXRk8YCArV64kbpo899xznHbG6UgpmfrD\nj1x26aXEDINZs2ZRp25dYtEonTp1Iicri5/nzEHoGq1atWLt2moInaaOL5RS3p4wQ36HPTh5EnCH\nlDIqhJgAPCKlnJJ47STgdillhdLAFxYHJ1UlLKSUoGlMmvwNLVq0cPwDF110ET///DPz589n69at\nHH2k3Xz+vffe44gj+/DKSy/z5JNP0qRJE5555hl69upFUWEh/fr1o2DXLtq1a8fEr76yoxoBnQXz\n5nPmmWfayVOBAMXFxQw4+WRGjRpFixYtMIV0CskALEBPXE67du6koKCA0tJSGjduTH6dOvYK4aob\nQRCPxQiGQqxZvZoff/yR++69F9M0KY3FiEQiTJgwgVatWtm+DiHof/zxbFy/nkh2NhdccAG33nor\nmq5z3LHHsmXLFm6//Xb+NOIyAI7o1Zvt27czY9ZMGjRogBDVmMGZGDb0MbaZsQ3YCISAl4DlUsr7\nKysshBBXAlcCtGzZ8ohVq1bt73fw8ShVJSwMw+D1N9/kd/36EggGMRPZkpZl2aZHMMTJp5xC27Zt\nefvdd2jYsCEDBw5k+dJl3HPPPVx26aWIUJBbb7mF8Z98SlBoTJw8iebNmwMwefJkRowYQXx3EVm5\nOVx2+QjuuPtukBIpbK2mNBblmy+/5vnnnmP16tWUFpcgDRNLt7+j6muhcD8OBALEDINOnTox8rpr\nOeXUwQT1hOMzsdkjDz3EKy+9TLS4hDp16nDE8X0Z+9q/nON68oknURqLgqaxePlSQmi89MorPPzw\nw2gBnf/+97+0aNGCQQNPZvHixUyeNIm2HTtUbzRECPFXoFhK+YRr2QnALVLKM3wzxEfxWwgL1fg2\nEAhgxu207ksuv4w77rgjyYGo3nvzxk387sijOO7EE3jt9bFIJL169KRo125mzP6ZunXr8p9/T+DO\n22+nNBZj6NCh/O3RRzBidkLTP/7xD2SiZuOZMWP4/VlDnBoOLMmNN97Ie++9R15eHvFo1BkspHpp\n9j32WNq1a0f9+vWTQqfbtm1j2bJlTP3hB+LxeNK0Mj0YpKCggEMOOYRnn32WY48/zvnM8Z98yvPP\nP8/6tWvZVVDAyJEjuemmm9CDAeLRGO3atSMUCPDMmDGcdsbp7Nq1i8svG8H8X37hg48+ol2H9lxz\n9Z+ZPGkSv65ZXeUOzkZAXEq5MzG+8EvgUWCmlHJDwgH6NFAqpbxDCHE6cC1lDs5npZTlhhG58YXF\nwclvISzMuIGFJBQKUVRURPv27Zn83f/Kja+Mx+MENJ22bdui6zqvvfYaixcv5plnnqGooIClv65A\n0zQGnjSApYsXY0rJ//73P1q3bs26desYcOKJdjet+vW5+dZbOP/885107EsvGc70n37CiMURukZp\nLEbPnj255tqRnHrqqc4+uJvvqqljKrSqkrRSG/R+9tlnvPCP55k9ezZBXSeoBxC6xpFHH82/Xh/r\ndOeKx2Ic27cfO7dvB3DqYJCSc845hxnTptGuQwcmTf4G0zQZNWoUn3zwIfc/+CDn/PEPXHXVVbzy\nyitVLiy6A2MB9/jC+4UQ3wCNsIM+s4GrExETATwHDMYOnf5pT/4K8IXFwcpvISx0oWFYdo6CYVk8\n//zznPH7M23hkCjOUnfhq6+8igkTJpCbmwtAaXExuq5zzbXXctMtN7NsyVIGDx5MQNO45NJLuXvU\nKAB6dO9O4e7daIEAM2bNpE6dOpjSQkPw+zPOZN7cufZsU01H6Bp/HT2aCy66sCypKvEfcARM6hwP\ntwak9tfRWIC333yLjz/8kFmz7CwDy7Lo2r074yf82zluu3fvpk/vIzBiMfLq1OHxxx/npJNOIhaL\n0btnT2KGwZdffkmrNq3RAwHaHdaKopIS1m/cQMyIkxWO+ElZPt7ktxAWsdIocdMgJy+PxUuXOKXo\nqq9kKBTCjBs8/vjjvPzyy+jqYkwImWuuvZYbb76JL7+YyPXXXkudevX4YdpUQoEga9as4aQTTqS0\ntJS/jr6XK66we0RYlsXgQaewdPFitIRAGjduHL36HIF01YEg4fWxY5kzZw7jx4+3v2fCf2IY9nwP\npVmoZRa2P6Nly5ZcccUVDBs2DKFrzueiCWbPmGXXfEjpvN97779PryN6I4TglVde4cHR9xEMBjms\ndWu+mvQ1hmXyuyOPZvfOnQRCIRYssutB2rQ8DDSNZSuWo+u6Lyx8vMn+CAun5ZxqGhM3CISC/D1R\nDBY3DTSEM9lLAj27dHVa6wshwJJoiUa1wXCYm2++mUcfepgOnQ/nsy8+x0LyxMOP8Oprr1FUVMTC\nxYvIy8tDmha9e/akuLAIIxojkJPF5MmTObR5M6yE57G0uITrRl7LN19+lZh1ag8nUjNL1TwRsAVZ\nKBRyOmsLIZL6X0jTJKjbBXEnDTqZYcOGMfCUQfa2wPq16zjhhBOQpklACiJ5OcyaPRuha5SUlHDX\nXU8TtLgAABkVSURBVHfxyUcfowvBspW/YiEZPOgUFsybT14owsKVyzGlRce27ckOhfll8UJfWPh4\nk/0RFkpIKCzLIisnh/kLFkCiS7dS3ePxOPfeey8fvjfOcYSq3hZFRUXk5ufz0EMPcc4f/sB9o0dz\n7+jRlJaU0LFjR3Rdp3nz5vzvu++IG3G+/WYyV111lTMd7IUXXuCkQSfbs0E0jQvOP59pU6cmmRla\nIMCQIUPo168fZ5091Nln1cvCTeqyDRs28NQTT/Lpp59iGQamaWKaJllZWfTu04d33n3X7m2h29mf\nx/ftx9atW4kZBv/85z859vjjyMrKYuniJQwePBjTNFm4eBHBYBAhoVOnTmiaxi/z5xGPx+nZvYdf\nG+LjXQ5Es1CPtUCAxYsXYyGd8KhKclJZmGbCZxCNRsnLy6O0tBQpBCt+/dXOYwjbDsUpU6Zw8YUX\nEdR1junbl9ffeAPTMDj77LOZ/8svGIbBV5Mm0b5jB6eBzbBzz2Pu7NmAXSsSCAS44647ueiSS+yk\nqUTLPHfvTff+A0nP3cfAqRuJG7z5+ut88skn/DJnLkK3w67de/bknffeJRwOI6Vk2ZKlnDxgAIFA\ngC7duvHyyy/TuEkTigoL6dm9O4FAgC++/JLDWrdi+84d9Onek5y8PH6ZP4/i0hJysrJ9YeHjTQ5E\ns1ARhN+fPZTHHnvM6a6tekcYsTidO3UCcOZ95ubmUlhYiBSCZcuWgSaci9iy7KE+F5x/Pm+/8w6m\nZd/Je3TrTlFREQ0aNODnn38mGo8RDod5/fXXeei++zEMg+LSUq6//nouv/xyGjVpnOTQXL92HdOn\nT+fRv/2NdevWOUOW1T4pR6bq5WkYBtnZ2fQ/8UT++te/cmjzZs53UM7Sxx99jDFjxpAdiRAIBMjK\nymLmnNl2R65giF69erFz505isRhjx45l4KCTiUajtGp5GHXz82nTrh0f//tTdu/cxZG9etO8ZUu+\n+37KASdlaXvfxMen+lCCAuwL7bY7brena7kEhWmaLF26lHg8jjQTvgspKSgoICcnh/r16xNIzPNQ\naMIe3vPWW29BQjN59913icfjhAIBPhn/KRaScDjM0sVLGP3Xe7EM2+S5/vrrueOOO2jYpLHTObyw\nsJBRd91N3759ufHGG9m4cSOhQNCJdqh5Imp7FUoNBezHX37xBX379mXUXXdTWFhIMGiXuweCQe66\n+25uuOEGp7dFUUEh5583jHA4jIW099UwyMvL4/LLL8eyLELhMCNHjkRKyeLFi9GFRm5+Ho0bN2bL\npk1gHbhS4GsWPlXG/mgWlmESioQxTZNGjRrxw7SfktYr1b1t6zaY8bhTZFVQUEBubi6mafLLwgUE\ng8GkcCbY/o54NMYRRxxB186dmTt3LkZionkkO4tYaZS2bdsiEtGL+g0bMmPmzLKKUMtiwYIFnPX7\nIezatYu8nBzHNHI+R9MIh8N06NDBGYj8888/s2TJEru0PiGo3JpEaSxGMBikf//+vDb2X2VhVwl9\njjiCHTt2oAGlsRjLly8nFAkTj8f566h7+GDcOISuO5GiSy66mO+++w4hJb8sXEBOdg5tDjuMYDDI\nEt9n4eNV9jd0GkyUZS//9VdMaTnhUiUobrnpZsaNG0dudrYz2Uu9//SZM8mvW8fRRKCsaxVAj27d\nKSkpIZbwa6xasxoJLJq/gAEDBji9KN58802OPf44p7z8vvvu490333LKz8GuBenbty9nnXUW5/zh\nD45DEsr7JxSWYaLpOps3beLmm2+2O2wZhlNyn5eXx9A//oF7773X+WzDMDjmqKPZtGkTUkq+/vpr\nOnTqCNj5Gffdey+GZbFq9WoAdmzfzjHHHIOmaSxctIitW7bQv39/Fiw6sGiIb4b4eIpgMMjuwkIa\nH3JIUphRCYPS0lI++egjsiMRiouLAZwu2YMGD3YEBeAIGQCk3RyncPduSEQz4vE4P/04lU8+/pg/\nnH02gUCAW2+9leXLl3PcccchpeSDce9zeMdOvPryK44g6d2nD0uWLWPx0iW88dabnPPHP4AgKV8i\nNaLjCK6ATjQWpfEhTXjjrTdZsmwpK1aupFuPHuTm5rJ7925effkVDu/YiQ/GvY+Udvbq9OnTufXW\nWwkEAvzxnHOYMP7fBPQAl1w6nOtuuAEhBJ062gKkTr26PP7kExixGDffdBP16tXjmmuuOeDfxtcs\nfKqM/dEs9GCQSCTCDz/8QE5ebtI6wzA47bTTWLV8BYFAwNEqwL4gl6381e4Ildje3Uj3k48+5rbb\nbsOMxx2fQjQaJRQKOfkZL730EsefcAKariORDBp4MiuWLSM7kkUsFqNuwwZ8//33BEJBovEYoWBZ\n2vbiJYu56667+HXxUrZt20Z2drajFahxAA0bNqRNpw4MGDCAESNGJI8+FHZ255uvv8ED944mFApR\nXFpCm3bteO6552jTri260Pjft9/ayWOWJGaZrFxjaxN/GXktEz77jBYtWvDl11+haRrn//Fcps+c\nyX/+8x+6dOtavVWnVYUvLA5O9kdYxAyDn+fMpn6DBhjxOIFg0K72lJIzTz+DJUuWIBL5FMqBWFpa\nyjvvvMOxxx8Pmv0Z7nyMWCxGm5aHEQgECIVCTus7KJsEdtdf72H48OH2BR6L21PTLQma4JzzzuXB\nBx8EcHI5gsEgt996G+PGjSMSiRB3jS9Uqd3KWeuuDxESp/lNUUkJF154IY8+/pgzIFnt86hRo/jw\nvXFgSUpKSrj97ru4/MorkFKydvUaBg8ahGmaZOfm8sv8eQD06tGTwt27CYfDzF0wH03TaN+6DaZp\nsmL1Kj8a4nNwEQ6HadCgAbF4zNYKEnkMmqYxa9YsR8VX1Z5CCM477zyO7d8/yZGp2ttJKbnnnnvI\nyclxwpihUIhAIOCEOKWUTtcsM25w9513YsbjFBQVEjdNRo8ebQuRRI1KMBDknKFn89FHHxEKBDAT\n7xEKhZzUbnXhB4N2hET5UIQQBDSd0tJSsiMRPhg3jnOGnk0wELT3T9omy+jRo4mbJgVFheTk5fLU\nE084UaHWbdsQDofREj02Vv26EsOym+JYlkVxcTFLFtjp3icOGACaxsb1FRZ9Vxpfs/CpMvZHs2je\nsiXf/u+/SMC99bffTObqq68m7jI99ERb/VVr1wJgJZyhzudIiEWjdOvWjWhiKpg7y1NKSTQe54sv\nvqBLt67EozG6du5MPGqnbXfs0pl/T5hA3Ig7r73zzjt5+/U3CAdDaAFbIKmMzrZt2zL0nHPo06cP\n7du3Jz8/H03X2Z4oT585cybvvv02q1evJisry5lmFtB0O78jK4tJk7+hZcuWtvYSCHLmGWewcOFC\nYsUlhCJhvv52Moe1aoUZizNx4kRGjhyJEIJfV63EsizOGXo2s2fNAkvy67o19jE9tBnhYJAVq1f5\nZoiPN9kfYfH5xIkc1roVwVAIyzTRNR2kpGXLloQT+RRutf60007j78+NoSTR6g7s/jHxWIz1a9dx\n5umn24laiXwHd8KXEII7776b/2/v3IOsqO48/vn17bnvmQEmyLKLA4MMIg8dlxBeJjyqJEhWWCm2\nkhhFF5V1JQYWosaNZULloVC10YgpGfCxhmUxqyui7lImI0ogxgwJEkBgYEZQgWQtA3MHhpn76D77\nR5/u6bnMMBOHOI/qb9Wt2+f06e7z68fvnPN73rTwZi9nx7lz5/jG1+9mwoQJ/NM/3wk40cSvv/56\njhw85NluhMNhzjQ28vDDDzN95gwGDx7sear6fVv87unQenn0s03Pcc8991CYSJDJZEin08TjcUqH\nl/HKK694auFcLkfZpaUUJpJYyqamthbE0awsWbKEbVVVhEIhDtTUgEDlE2tZ9dBDjJ8wgf98bhO/\n2rGTOxcvpqauNmAWAXomOmIWympRNeZs21lbHzvquZ67yKYzjLniCgzDoCmdJqwjTWEIF4qwVjZ0\nmJYTtMgZPBWsgr/668FUbdvmmYP7BaKHDx/msvIRhDAYVV7uZD/TNiBZy+LfHvkRN8yf72Ucs7Tm\nhnwa8zKS4UsNICEDQXhp82aWL/sXZ+kiQjabJRaL8a5OcegKXIeVDiWklzE1R+tABIVi1IiRZJua\n+fqypay455sAjBx+GbZts2f/PpLJJJeVDee9Y0cDmUWA3gm/QVM4HGbWrFneGt8/iC1fvhzbtslm\ns4RCIS/h8OjRo9s9d9XPHY2AsiwAYrEY6XTay02asy2279xJgVazujMAS7cfOXIkb7/1ay4fMcJJ\neBwOY4YLmD1nDjU1NcyfP590Jg228liBlc1x6N0DrF9byd13LeHvr5/L5ydP5e67lrB+bSWH3j2A\nlc2B0rYftiKdSXPDDTdQU1PDoUOHvDyrtm0zdOhQx5BMu+O/954TwMdGMXniJP708ccYCAcOHURC\nBmvWrAEcpvd2dTVKKWbMmIFSiueff77LzyuYWQT4i6GjmYWBkLMt7eptUV1dTcnAz3gCTXB8Jq64\nfJTnLKZEyDQ3UxCJ8Nbbv+aSSy45f3mjnARDpmF4cSVcwWY2myWXy1G5fj2zZs0iVNBiEu6fWbjb\nI4aVYds2yaIiVq1axbXXXosZ9gW8sRXV1dXcfvvtTgAdhIKCAhobGzFNE9M0aW5uJpFIkM1msVFk\nMhnmL1jAY489Boa08ki1cxYVFRVOFnednf3GG2/kge9+BwOhrq7OEcbaNhIKcfTYMRSKB//122za\ntIkhpaW89tprhApMJk74HKdOneLQ4RonXYFhBDOLAL0TrtzA1XAMGDAAwFvzux+4q96EljW/ZVkM\nGjSo3XO79hSgTci1QDORSDB//nyu+9IcDDPUKmS/X91pGAYH3z3gebhu2PgffPG62ZjhAs9OA1ux\naNEiFixYwJlUypMxWJZFYWEhkYhjll1YWOj1JRKJkEwm2bJ5M4sWLQJbeerWTCaDYYbYtGkTOe22\n3tTUxDPPPOMFxhk+4jJEhEgkgmkY/OH4cUSEbyxbhmEYnDx+nA0bNmCaJgsXLsQ0DF56cfN5y6NP\n9Ly6fIYAAT4h0um0F0FKKYXoUd01czZNk61bt5JOp4HWI39JSYkXLSsf31+50hvVXbdyl8E0NDTw\n6Jo1Xj4Ov/DRH3gnk8kwb948AMLRKFdddRXiyyy2evVqSktL2VZV5QT4FcOLF4ohpLMZcrblWGxm\nM2AINk4wn2za8WzdVlVFaWkpq1ev9tSiChgzdiz79u3zaAiFQlRUVHjOaIdrj3j2INOmTfP8aC65\nxHF0W7VqFTaKpcuWYVkW9957L+q8/O5/PnoEs/jwww9ZuXIllZWVbN68me3bt7N3717q6upIpVLe\ny+SHW/b/59f9OWjvGP/I015dR2X/NdxR1FW5udd1y/66tsyG2zMjbu9a+WV3hOvo+I7O4y+3de/c\nZYcbHcr/UbpwP2AJhRg9dowj4c/z53j80R8T1lN0wzAwcOQba37yuGN9SUtCHztngYKNGzd67uBK\n8Kb+hmly0623aKEjrYWoVouhFrZi9KgraGpsdOwjcjkqxo7jze1vYhgG078wjfVPrPXMxqPRKFll\nk3OEEWRyOQYOGsT4CRO4ft48Bg4apAWyBpghMEMts6dslifXVvLFa2dx8vgJbMtCCRT1K+aJykrA\neTfO1qdYunSpEyEsZFJWPoKCSBhRsGvXLjJ2jp9XVRGNRmk8c4ZXtrwMAjNnziRsmpz6+E8XfM6d\nQadlFuIkGvotcEI5If/LgOeAEpwERDcrpTIiEgF+CozHyS3yZaXUsQ7OrXzb57187kiTj/bq/YjF\nYoTDYQoLCykpKSGRSNC/f3+Ki4sxTZP+/fvTr18/+vfv77k3RyIRBgwYQHFxMUVFRZSUlHhqOfd6\nfn2+/8Nwy/kfh9+xyH8Of31+kJS2gqfknzO/Ly78QWLctm77tj7ctvrpv8aFrpV/jHvtk8dPMEMb\nS+Xn0QBHZmEpGxt4dsNPmTp1qtc393wjhpUBOtdGJuMtXQ6/V+e0Q1oMMhTUnz7N+KuvJhQKtTLg\nUsoJ+Hvsg/a1J27Mi39YsIA9e/ZgalWqiJBIJGg410giFudMKkVxcTEp/V/f0EAsFmPDhg1MmjLZ\nE5S6997dtm2bnb/cwQsvvMDWrVsxDYMzZ85gmiZNTU3Ek0nWr1/P1M9f47xvtmLFihVs2bIFZVkY\npsmR2lo04dz8tZvY/sYbSCjE+9rs+/LykV54vyN1tZxJNTBu3DjGjRvHq//7P5+O6lRElgOfBYo0\ns/gv4EWl1HMishb4vVLqCRG5C7hSKXWniHwFuEEp9eUOzt2qE/6Ap+3Bv74EvPRw+XX+0bitjy7/\nPJ1p4+u3t+buqK9uG9eqr7i4mFgsRmFhIYlEgqKiIqLRqMfYYrEYRUVF3r6CggKvjb8+FAq1Oj4a\njZ53/fwPvj1m0d498E/PAc/BK79tPhP54Nj7fOGaazAMw9NGtIKtCBU4atCj7x9zqvJmJKNGlKOU\nIpvNkkwmOXfuHLZt88HJE07/bEVzJu0YOTWnWbx4Mb/asaPVDMVlGCUDB/LLnTs81/XzbwDMnDGD\nP548SSaT8SKI27ZNJBLxmJWbER3DoLy8nAceeIBpM6a3kNXGYJFfl2lOM2fOHGpra7F8Wh7TNKne\n/Tvi8bj3HezcuZNFt/4jyrK4sqKCF1/a7N1/l5k+8+yzTJoymerqam65eSHKsqipq8U0TYYPKyNS\nUMCh2iNdYhbn539vAyIyBPgS8ANguThvxUzgRt3kWeC7wBPAPL0N8ALwuIiIugBXGj9+PLt27Trv\nZbMsi7Nnz9LQ0EAqleLUqVPU19fT1NREY2MjqVSK06dPc+rUKc6ePUsmk+H06dPU19eTSqW8Ns3N\nzee/qBrtjdY+2lu9wP6Por0puHucfznhlt1Yi83Nze3djvOOb29mcTHQ1kyuPZimSTKZJB6PE4vF\niEajFBcXk0wmSSQSxONxIpEIhYWFxONxChNJx7zZNL0AL36498PPbP3CzbfeesvrnxtwJh6PM3Hi\nxJaR2xBv1heORHjzzTcJae9Q96N2mc26desuyChy2SzvHz3qMfdIJOJpZrJaYBqJRJxIXbkcd951\nF/fedx+WHthchtAWM86XjYSjEapef53vf+97PP3kk61mH2PGjKG21vnQQ6bJtOnTHa1KJsPu3btJ\nZzPEQzFs2+bKigr27n6HO+64g0OHa5gyZQqLFi3i6XXreegHP+SB7zzI3LlzefWlLZ16xhdCZ3Od\nvgA8BBQC3wRuBd5WSo3Q+y8FtiqlxorIfmC2Uuq43lcHTFRKfZx3Ti99ITAW2N9lanomPgN83GGr\n3oe+Shf0XdouV0oVftKDO5xZiMjfAR8ppX4nTprCiwKl1DqcHKmIyG+7Mj3qyeirtPVVuqDv0iYi\nXTJm6swyZCowV0TmAFGgCPgx0E9ETKVUDhgCnNDtTwCXAsdFxASKcQSdAQIE6MXoUHWqlLpfKTVE\nKTUM+AqwTSn1NeANYIFudgvgLope1mX0/m0XklcECBCgd6Ardhb34Qg7a3HUp0/p+qeAEl2/HPhW\nJ861rgv96Onoq7T1Vbqg79LWJbp6hG9IgAABej56hAVngAABej66nVmIyGwRqRGRWhHpzJKlR0FE\nnhaRj7TK2K0bICK/EJEj+r+/rhcReUzTuldE/rb7en5hiMilIvKGiBwQkXdFZKmu79W0iUhURKpF\n5PearpW6vkxEfqP7/zMRCev6iC7X6v3DurP/HUFEQiLyjoi8qssXja5uZRbimJD/BLgOGA18VUTa\nD1LQM/HvwOy8um8BryulyoHXaZHbXAeU699iHCO2noocsEIpNRqYBCzRz6a305YGZiqlrgIqgNki\nMglYBTyibYdOA7fp9rcBp3X9I7pdT8ZS4KCvfPHo8ptIf9o/YDLwmq98P3B/d/bpE9IxDNjvK9cA\ng/X2YKBGb1cCX22rXU//4Wi7ru1LtAFxYDcwEccIy9T13nsJvAZM1tumbifd3fd26BmCw8BnAq/i\neM1cNLq6exnyN8CHvvJxXdfbMUgp5YZT/iPgBl7olfTqKerVwG/oA7Tpqfoe4CPgF0AdUK8cmyFo\n3XePLr0/haP964l4FLgXJ1kaOP28aHR1N7Po81AO6+61KicRSQL/DSxTSjX49/VW2pRSllKqAmck\n/hwwqpu71GX4La3/UtfobmbhWnu68FuC9mb8n4gMBtD/H+n6XkWviBTgMIqNSqkXdXWfoA1AKVWP\nY1w4GW2RrHe1ZZFMD7dIdi2tj+GEjpiJz9Jat+kSXd3NLHYB5VpiG8axEH25m/t0MeC3Ys23bl2o\nNQeTgJRvSt+jII6r61PAQaXUj3y7ejVtIjJQRPrp7RiOHOYgvdwiWX0altY9QCgzBziMs278dnf3\n5xP0fxPwByCLsya8DWft9zpwBKgCBui2gqP9qQP2AZ/t7v5fgK5rcJYYe4E9+jent9MGXAm8o+na\nDzyo64cD1UAt8DwQ0fVRXa7V+4d3Nw2doHE68OrFpiuw4AwQIECn0N3LkAABAvQSBMwiQIAAnULA\nLAIECNApBMwiQIAAnULALAIECNApBMwiQIAAnULALAIECNApBMwiQIAAncL/A9bdPrCg5va8AAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb62569cb50>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"soft image\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQsAAAD8CAYAAABgtYFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXmMbNl5H/b7ar219r6+Zd4MOYlBE/JQnpAS5D8UGkpI\nxsjYgCORDkRKIUIHoBAbchKRDhDLcYjIQCxGgh05NKSIDGyPGNqCBgQdhaYUGAZMURxpTHMJR284\nb+Yt/bpfb7XvdfLHvd95X50+t6q6u7rrVtX5AYXuuvu9dc7vfvtHSik4ODg4jEJs2hfg4OAwG3Bk\n4eDgMBYcWTg4OIwFRxYODg5jwZGFg4PDWHBk4eDgMBaujCyI6ANE9H0iuktEn7qq8zg4OFwP6Cri\nLIgoDuB1AD8B4AGAPwTwEaXUdyd+MgcHh2vBVUkW7wVwVyn1A6VUG8DLAF66onM5ODhcAxJXdNwb\nAO6L7w8AvC9s40KhoHK5HDqdDuLxODzPQyKRgFIK7XYbrVYLSimkUimk02nEYjH0ej20Wi10Oh3E\nYjGk02nE43HE43G9T7/fRzKZRCKRQCqVQr/f1/sQERKJBLLZLDzPQyqVQiwWAxFd0SNxmASUUuj1\nemi326jX66jXamg2m+j1+uj3e5j3iGQiQjweRzKVQjKRRDaXRTabRSqVQjweHzp+X3311UOl1MZF\nz31VZDESRPQJAJ8AgPX1dXz0ox/F3t4eisUinn/+eWxubqLX6+HBgwd444030Gq1cPv2bTz33HPw\nPA/VahWvv/469vf3kc/n8Y53vANLS0vI5XJ49OgR7t69i3q9jhs3bmBlZQU3b95Es9nEG2+8gYcP\nHyKdTmNjYwPvec978O53vxs3b95EJpNxhBFRMEn0ej2cnJzg3r17eO2P/hivvvoq7r7+OqrVKiqV\nCnq9+SQMItIvzKWlJdy+cwdbW1t48b3/AX7oh34IzzzzDPL5PBKJROj4JaK3LnMNV6WGPARwS3y/\nGSzTUEp9Tin1olLqxWKxqFmx3+8P/NhEpD9KKf0xwQ/Ito25Th7XkcNsQSmFfr+PTqejP0wiAOb+\nt2TJgqVllpyvYxxfFVn8IYDniehZIkoB+DCAV8I25gfAhCAJgyd12H7mOhtR8Db9fh/9fh8AEIvF\ntNriCGM2wL9tr9dDp9NBu93WZGG+ZOYN8uUWi8WQTCaRTCaRSqWujSyuRA1RSnWJ6OcA/C6AOIDf\nUEp9Z9g+fLOSLEwykETA6wEMSB28jpdLqUQegx8wkwVv7xBt8Pjodbpot9vodrsDv32v15vL35HH\nu1LKt1kERMGShZwLcvtJ4spsFkqprwD4yrjbm6Qg/8oHYFtunHfgmHJfqc8yUUhCcYg2mBS63e7A\nZ96lCgmWLhKJhCYKadi8CpJgRCKCU9oOhqkRAM4MijBVxNzGXOdsFrMHaY9iOwUTxaKRhU2FnlWb\nxbnBuhhgtzvwcnOZCdOIKR+m3J/Pxx9HGNGHVkECm0Wn00G329WkMe8wpQr+SFVabjtpRIIs+CEA\nZ70ZwySLUWqICWngZIuyI4rZgZQqut2uJotFlCwkYfAYXhjJQhpppGhpE7FsA0MagBjyIZqGUdO6\nbDKzQ7TA46Hf72ui6HQ6A/aKfr8/18TPY5aNm+wJYcniKu0VQITIwlQXRsVJyHVhrGoul14WJohR\nUW8O0QFLht1uV7tNF8XAyWOZJWKWKlg6vg5Egiz4ITA7mpLFMCIxYZNITInFNBI5j0j0weNiUcmC\nYSMLOYavEpEgC+CsmzNM1bjIMcMMpI4kZgtSFWFD56KQBDDoweMX3XVKxpEgC5sLU8ZD2AJO5L78\nV0oUpnXcNJyGRW864ogemCCISNsqWLKQRut5/u20TY4IccMTcl0vvEiQBTAYwTksKMtcJxGWF2Ie\n14yxmOdBNk9gdUMGZHFOyLx7RKREIQOyrtOjFzmyAGDNDRll5GSMcrsyQ7NU4QhjNmDGWHCo96IF\nZUm3qZmWvhA2C+mdAOyxFrx8FMLsEsAgCcm8EEcU0ceikwWPY0kU15lxCkSELICzaogt/8O2niHV\nk36/r48nj2uey7SVONKINpgsuu0gxqLbhTKiN+eZNPgFl0wmkUynkEynrjVGKDJkIaWA87wpzjPB\nbSqKI4jZgPSCmP8vCmSsxTTGbyTIQtoQgHBVIkyqGHVshiQKF2MxWzDDvLmOxaKQhRnmzWqILS/k\nqhAJsgDC1RBgdKi3bbkZ1m0jIDOJbFEG3qxBhnP3+3202+0ztSzm3W4RFsF5nWkKkSAL28QFwif8\nuN4QE/wmcpLF7MFMHlukbFMGSxbSuLlwkoWZryFDvoGzgVe8j4RtssuHaBo4TQOoQ3TBvx0Thiyn\nZxsj8wYpCXNsBRNFPB7X21w1IkEWpmQhxUpbuHaYisLrzP3kcjM3xGWbzgY4J8Qki0UxckqymIbb\nFLhkWT0iugegAqAHoKuUepGIVgH8FoA7AO4B+Eml1MmoY42yHYyyK4Q9sDADpwvImg1Ikmebhc0T\nskiEMa0X3STO9h8qpV5QSr0YfP8UgK8ppZ4H8LXg+1CESRZyPXBWOrBN8mEGUJs3RBbrdaQRXZgB\nWYvoDWHDZjqdnopkcRXU9BKAzwf/fx7AXxxnJ6l/AYNVrWww3yzyuy2WwkY0UhdclEE3a5DRt9Jt\nKgvfzPNvJ1+ksgWAzDrl7a4alyULBeD/IaJXye8wBgBbSqm94P/HALbGuhBDspCY9IOQhk0nTUQb\nTAZs3DQ9IYviDZHRmzKR7DpVkcu2AvhzSqmHRLQJ4KtE9P/JlUopRURW2ifRvnB3d9dq3LS5TsOi\nME1VxVzPOq9N73OEEW3wb8fGTZkXskiQ/UKm0e/mUrSklHoY/D0A8Nvwu6fvE9EOAAR/D0L21e0L\nV1dXh9osLPueyRmR63hZGImYVb2dhBFdSOOmrGWxaBWyBvJCphBjAVyCLIgoR0QF/h/AfwTg2/Db\nFH4s2OxjAH5nzONZoy15HeO8KsooL4kjiejD5hFZhKhNEzI2aBpFpi+jhmwB+O1gsiUA/BOl1P9N\nRH8I4ItE9HEAbwH4yXEOZtoQpBoC2OMpbOvk/ubDlJKFGcFpHtNhOrD9BkqpM8ZNGb05z4TBzyIe\nj4PicT/GIp0aUKEjH2ehlPoBgD9jWX4E4M+f93i2PA1TpTBhWx4W0WeqIbboTUcU00dYkJ1sLGSS\nxTxDeuymVceCEYnwRTlxbYlBtoAtc5KHkQzDNJi6TmTRh1Q9bGQxrxKFbWzLOAtbj9PrQCTIAhg0\nOtq8HsB4fU5N2OwgNi+KQzTBvx2rIWzcXKROZPxyM12m1z12I0MW/EAY7OaUE9pGGrZJP4pkpNvU\nSRfRBqsg/a5fIUtXyRI9YOYN5viVNjazC9l1vvAiRRbD7A9hNovzIMyt6hBdmF4Qs3P6IkgWwCBh\nXGeR3oFruLYzjYCZHGOTHszlcp1tG7nMLNZrBmU54oguzIAslizmGeYYNtUQMz3iOhAJsjANjmaO\nByNsOR9DrpPMKw2nfC5HFLMBs2XhIgRkma58IhoIyJLl9BZWsjB7h8iu2DbbxahALjaWyvVmUAuv\nc4QRPfBvJr0hvV7P94SwN6Q/f4RhS3akeNzPNjViLK4TkSMLmxoiMSoMXMLmOuVzOY/IbMBMIuOy\nejb3+LyCJQtZJWsa9x0psjBjJcIMnKY9Q8KmqpjHsuWGOEQPZl4IqyHSyDnvtgsep7YYi1ksfjMx\nhE3aUdGb4+5nEoYjidkAqyH8WYQ6FhLSbmHa2hbOZmG+7YHwKt0XHSQ274ojjOjCdJlKFYQJYxGk\nQkkUUg1ZeJuF9B+bpGAaMcN0VjOs2/SGyLwQ2/4O04f8bTl6c8BeITqn9zF/0oVpW5MqSCqVskYk\nXwciRRbDIjGHBWbZCCNsH2ezmB2wZCErei+S61SOVRljsfAGTlMtCGPOUWrIsP3keVyod3RhSpcy\nL0QmkS0C0cuiN2bLwoVVQ2w2hEnYJmzrnMt0dsBGTbMT2SKEe8txakZvTgORIQupEsRiMW3AkhPc\nrOBtm/Qm2Uh7hbRb8AMfFhXqMB2YtilWRaRhU/6W8w6ZEyKreS+kNwQYVA8Yw4yYNtiMomHncUFZ\n0YckCvmZZ3uFhGmzmKYnBIgYWciJG5YwNmqQ2OpgyOVhNotxju1wvbAZOBeFLEyXKdssJFlc95iN\nBFnY4iyAs3U45fJxjhlm/3DekNkAB2PZmgstAmQgliQLs3bsdWEkWRDRbxDRARF9WyxbJaKvEtGf\nBH9XguVERL9KRHeJ6FtE9MPjXgg/GGZLWxd1CSklDAvg4r+mZCHtI4uUZzArMEO9zdqbc21r6oti\n1PE44iLbVLpNrzsBchzJ4jcBfMBYFtbP9IMAng8+nwDwa+NeiM1+cN7AkzCbhS3PxEkU0YeZRKYz\nTufcC8KQEreZExJJm4VS6l8BODYWh/UzfQnAF5SPrwNYpqDh0MgLCanubbLnuHEWwwK8XIOh2YBM\nTW+1WgMekUWAmUDGMRbTGq8XtVmE9TO9AeC+2O5BsOwMiOgTRPRNIvrm0dHRyIl7ngc0TCXhYzmS\niDakGrKICWRSTbbVjI2kzWIUlP/LnfvXU6J94fr6+rmCssaVLOQyp4bMHkw1ZFGressqWdNITWdc\n9Kxh/UwfArgltrsZLBt9IQFRSCOnzYhlLjMDcyQJmMfh85hJa440ogMpUQB+BKd0my4EUcSC8WgQ\nRTKZnKoH76JkEdbP9BUAHw28Ij8CoCTUlaEwbQmmzeIiBk5zHZ/HSRbRB0sVZk7IPDcXYkgVxIyx\nmKbNYmT7QiL6pwB+HMA6ET0A8LcA/BLs/Uy/AuBDAO4CqAP42XEvRJIFML6B0xaDYRKMqYa4RLLo\nQwZkhblN5xVyrIYZOKfxshtJFkqpj4SsOtPPNLBffPIiF2J7448ihbB1o85jinKOMKIJGeptShbz\nTBg8NmXBG9mJbFqIRAQncLZit61Dts0GIbdhiSLMG8L2DdPGMc8Db5bB0kW/65MEKQUKieqdJ0jJ\nWDcXSiZA8elGHEeKLCaZoj5MQnE2i+hCE4QR6r1IMRZSsjDtFdNUnUeqIdcF08DJCHOFhmGU1BF2\nHodoQP4mMtTbTCCbZ2nQNHBKNWSaYzZykoUtRV1iXKIYV7JwEkY0IaM3pTdkEQycAAYkC1vG6TQQ\nCbKwTV4zmYwL4gA4k2Rme3jmetNmMYqUHKYD+buzcXMR6m4ypO3ODPc2x+11IxJkAQzv5XGRUO9x\nIzidZBEtSGmQJYtFkyqAp27TVCoVGZtFZMgCGJ15Oi7C9nGu0uhDxtewKsIGT7luniHngZSEp11C\nMDJkMSpQKswGwTANX2GkE6WH73AWJlHI8v/zThIMm3FTBmRN6zlEarZcVqq4SOq6kzKiCbZZmG7T\nRck8ZQOnTQ2ZtUSyiUOKXbbgqzCpYtycEYkwCWbeB+AsgIjOdE2XNgs2cs8zyctgLHaZyiQy3ua6\nESmymHRGnXkc8xzzPOBmFTIoiz0h3Dl9kchcBmRJt+k0ESmyMD0io5LCbBhmzzDP4cgiepA2C9lY\naGHS0wNwKT0mC7N7+lSuaSpnteAqHoLNGORIIvowpYtFkyrO5IUEn2mP28iRhbRZAIMVjE3j57CH\nx8cwbR3DGgxN+8dYdPBvNEAUHV+qIFEQZ56JQ5KEDvNOJacevQlEiCyAi9fGHHd7F2cRfZhJZDJ6\nc1EgyWLaXcgGrmuqZxew2SzM9Yzz1LmwFb5x0ZvRhjRu2pohzzN4PLLbVPYLcQZOAXMC2yplmdtL\nDKuuJfdxxW+iCw7zNpPI5j3U2zTCm7U3px3qDUSILIa96W22h3G9IsOIwnZMh+lBJpGpXh/ddke7\nTedZDeEERx6PMoEsnU7rgCxgui+2i7Yv/EUiekhErwWfD4l1nya/feH3ieg/Ps/FTFI1GCZZOEki\n2pDu00WK2mSYKvm0JQrGRdsXAsBnlVIvBJ+vAAARvQvAhwH86WCf/42I4uNciGlHCIvYHGeZjShk\nvIazV0QXMszbVsdi3gmDyUHmhMhQ72niou0Lw/ASgJeVUi2l1Jvwq3y/d9yL4Qc17KGcNyBLLpfH\nd0QRTdg6p/d6vWlf1pXDfNlFqW0h4zJU9XPkd0r/DQq6qOOC7QsPDw+v7G1vexs5ySLaCKu9Oa+S\nhZSi2bgp80Kk6zTSNosQ/BqAdwB4AcAegL933gMoo30hMJjgZXN72oKohnlKYrGY/gH6/f7IUG9H\nHtODmZouVRG2W8zr72OqyIjFEOdSeqlouE2BC5KFUmpfKdVTSvUB/CM8VTUu3L4QGDTsDDn3Ra5X\nH99UQ+Z1AM4imCykCrII4d7mC1BGb8oYi2mP1QuRBQV9TgP8JQDsKXkFwIeJKE1EzwJ4HsA3xjzm\nwF/GuINklL3iPMdymB6kF8RUP+ZVDZGQL0yzc/q0cdH2hT9ORC/A755+D8BfBQCl1HeI6IsAvgug\nC+CTSqmR1ilJFGGekDBX6LBjmsFdZjUuZ7uIDqQaIiULNnDOO0kwZEAWp6ZHRbK4aPvCXx+y/WcA\nfOa8FxLmqQh7o4TZMuRym2HTLKtnS1hzuF5Iu5IkCzMvRCkFUgDm9GeS49M0bgIY6AM8jbE6fauJ\nwLA3/XkezjCjpyOEaMPmNjUN3fMM02067c7pEpEhCzNqLSwoaxzbhDymXDdOHIfD9CCL3pgGTmC+\niUKOf7NIr0kW03oOkZk1Uqq46GS22TiGRXA6RAPyt2Ky4OjNRWkuBJyN3pQ2iyiM18iQBWOch7II\nA2cRYHqqzM88B2INg2lbiwJRABEjC/nWNzNBbQFZtv/DksZMFceUMKLygywSbKpmt9vV2aadTgf9\noEoW4Nsz1Bz+TOYYZG9IPPnUXjFMNb8uRKqLus0jMsp9avN6yG1txW+czWI0bJ6kq4ZsLOTcpqmB\nOhZyzE7rxRYZsgAm4w0ZJimESRVRg0mE054s7Na8ymcmQ71tGafzDn62USx6w4gMWdgm8qgM02Eu\nUnNb23miCFMkn0Y9B/PZ2HToq3h+KqiSJcv/L4pxE7Cnp0elsjcQIbIAxu/rcZ7KVuY2snp4FH4A\nhnk9XIOy2WzqalEsko8i0klASmjxeBzpdFp/5NtuUs9xWF4IgLlOJAPESyzIC+FeIdPubyoRKbIA\nhqsb5x0sNiNolKUKBr9hO50O6vU6arXawJv2qiGfEUcT5nI5EJF+20lX9KTA982fRVA/TPDLUhJF\nVMZsZMgiLM7ivIw6LNIviu4oEzxhms0mTk5OsLe3h6OjIzSbTTTrjWsTy+WgLRQKWFlbxfb2tv5t\nksnkRKWzRc04BewBWbJlIT/zaY/ZyJAFYK+8LdcN22/YMvkWjDpRAL6LsN1uo1Qq4f79+3jrrbdQ\nrVZRPi1di3TBz4fDjdfX13HrmdtIpVLI5/PwPG/iE9jW33SRbBaSnG0VsqIwZiNHFuM+GFvquTQC\n2nR7swBqVH4E4Kyrt9lsolQq4fDgCd6+9xbK5TJKJydotVr6LXzZa+f9JfX4yVpK961IJBJo1uvI\nZDLY2thEc7OJQqGAXq+HROLyw0f+ZixNSMlCdk2fV9LQYzUYm6YnJCqu/siQxShviC3GYhRMD8Is\nuE0ZSim0223U63VUKhWUSiWcCLKYxMQxY1lkLYlYLIZ0Oo1UKgXP81Aul9FsNq9MLQjLC1mEOhbS\n28TGzajU3ZSIDFkA9qApc7KHBWANCyKyqSFRJwybDptMJifa71MeQxab4aY+bGhsNpt64k7q3CbM\ncnpSBZlnopDg39vWtjAKYzVSZMEwJQvbYLEZMoctk8eV36MISRTpdBqZTMZ/2xYKSKfTl55AJrky\nSXS7XTSbTQC+61YO1OuwHcjArLB2hfOsjgAY8IRExbDJiBRZnPeNf95BE3U1RJJdIpFAoVDA1tYW\nms0mqtUqapUKWq2W3nZS8Q3twC1bq9VwfHyMk6OjASOqtI9clQri1JCnzZBtakgUxmtkyEL69fnh\nmZKCOWBtQUFhdgrze1QHH997JpPB2toa2u02vGwGzWYTrcbkbQb9fh/NdgvtdhtP9g+QyWSghKQB\nDFZouqrnxufrdbo61FuJWAuWbvj/WUWYGm16QmTRm6jc7zg1OG8B+AKALfg1Nz+nlPoVIloF8FsA\n7sCvw/mTSqkT8u/sVwB8CEAdwM8opf5onIuxvfUvOjjD1JMoSxZMYrFYDJ7noVgsIhaLYXV1VU+k\nSbpN+W1ebzbQbDZxP5dHt9tF+fQU1WoVvV7vyp+TlCo4EI0D0GwqSJSJ/qLgF55p4IxaTNA4kkUX\nwN9QSv0RERUAvEpEXwXwMwC+ppT6JSL6FIBPAfgFAB+EX9X7eQDvg99j5H3jXExYUNawrNJxYix4\n/1loA8D3n0wmkc1mkUqlzlS5vux1m96PWq2GRqOBVqOJx48f61Dj65qckizMnBA5HqIWoj8pyFyQ\nVCqlyYKL3kTlnscp2LsHv5EQlFIVIvoe/C5jL8Gv+g0Anwfw/8Ini5cAfEH5I+zrRLRMRDvBcUIh\nJ/AkHhAP8jD3a1R+AIZtIvCknbSRT+7P0kMsFkM2m9Vdu8PKBEwa8rfm87Dunk6nkc1mdTzHvJIF\nh9Nncznkcjl4njdA2FHBuWwWRHQHwHsA/AGALUEAj+GrKUB4C8MBsiCiTwD4BADcvn2bl53LuDlq\n8IRJHTYimTZsdhWOd7gq8DM4058iFkNPKSgi9AGoaxqw/rkJ6XQanufB8zy0u13EA5dxlCbOJJFM\nJuFls8hms8hkMn4XslRyYD5E4d7HJgsiygP4ZwD+ulKqbIj6iojONfOUUp8D8DkAePHFF0P3lZN6\nEtJGFB76uLjqyD1JuNO25RD5SWr5fB5ra2uavOr1+tznh7DKmc1msb29jdXVVWSzWW23iMqYHYss\niCgJnyj+sVLqnweL91m9IL9D2UGw/MItDIcN2os8MOl2M489a8RxlZjmM2GDbiKRQD6fx9bWFrrd\nLtYq69jZ2UGr1Row6s6jKsIlADzPw/r6Ora3t5HL5ZBMJiM1TsfxhhD8pkLfU0r9slj1CoCPAfil\n4O/viOU/R0QvwzdslkbZK8S5rKLXpN4qjiSGY1pvbzbo5vN5bGxtwvM8tFqtgcbIcizM2+8nu6Zn\ns1msrKzMJlkA+DEAPw3g3xHRa8GyvwmfJL5IRB8H8BaAnwzWfQW+2/QufNfpz45zIZIgZGEVKRXw\nev5fRrjx9qMGlfnwo/JDRAHTcEtyPE0ikUA2m0UsFkM+m9MeoFmvaWHayKQnipfH43EATyUMGZQl\nt502xvGG/GsgtGHcn7dsrwB88qIXZCOFix4jTA1xiBakezSXy/mBYXMQuWnm3iildKAbg4gGCt1E\nueZKZCI4geGxE1d1LofpQb4xeaKwB2hSMSXXDSkxAIORp91u94wnju816kQBRIwsgKfh3qZ0EIYw\naWGYChIld9Qiw2bEZtEbiI74fRHwmGWJgkskNhqNgTodHEsiJYyoIlJkMYmBYZKHU0NmF/PwWyml\ndNWzJ0+e4Pj4WOe+EBFyuRzW19exubmJdDoNItJ/eX8gGs8iUmQBXLy0HrvgmLHDYhTksWdZH3aI\nPjiMvdls4uToGA/vP8Dbb7+NWq2GZrOJVCqF1dVVtNttJBIJFIvFM8bNKJAEI1JkcZm3/zj7hHlV\nHByuAmzQbLVaKJVKePjwIX7wgx+gVCqhWq3C8zxsb28j5aWxurqKdDo90RygSSNSZAFMNvOU941K\nlKLD4oEJQ9dUPTzE8fExyuUyPM9DMplEqVTS/WGi7CqODFmMa6Sc9DkcHK4K0shp9nBtt9uIxWID\n/VxlDEYUERmyAAZT1G02BZvRR37YbiG3sR3fkcZ4sA1g9+zGg6nycoCZrALGn16ni363N5CWH0VE\no8a4gC26chJM69QQh+tE2Jhl0pCfWUGkyGLYhB4Voh1W88HMWnUxFuPDEev5IcehlMpmPRoViJga\nAgwfoKMG7rAfZJhL1uEs5j1/ZtYn7jQQSbKQIa9hdgvzuxlia1tm+zgMeoy4cKz8HRKJBBDzC9NI\nz9JVF+e5Ctje/GG4yPiQUgTHWQyMy34fMcDv+kYEmiHSihxZOEwHpiRh610hcxdmFTbVQOZvTPI8\nsgcKf84TaBg1RIosbG9+k/3PIz7apJKoJulME/xcEokEPM9DJpNBPp/XyzKZDDzP0wVke72errUw\nS2BykJ3XeBLbCHAS8T31el1HbHKnt6i7SMMQGbKQBDHKtjDuQ5bbOaI4C/m8uRFyoVDAxsYGOp0O\nGo2G7qLOpd64WfKsPUd+0/N9dTodVKtVtFotTRiTOg+j3++j3W7j9PQUh4eHqFarA8FXUXaT2hAZ\nsjBxFQ/ReULsYKIoFovY3d1Fr9fD8vIyWq2WzlnY3t3BysoK0ul05NrqjQvO0yiVSiiXyzg8PMTJ\nyQkajYZVDbnom58lYianWq2Gx4/2cHh4OBORmmGIDFnIiWwme9l+tPOoJ+axHXxwEFsymQQALK0s\no9vvwctmsBM0GQKAbDaLYrGI9fV1eJ6nbRmz9GZk9aPZbOLw8BBHR0f4wd038PjxY9SrVbQCFQG4\nXMUwuS+P3WaziUql4ksXlYpWg3pKoTdDqkhkyAIIj7AchyxGLXdJZOGQDYUSiQSWlpbQbrf1eu6S\nlclkdD8LYLYkC37Tt1otlMtlHB8f49GjR3jzzTdRKZXQCAoDy0DAy94fH4OjNhuNBtrN5pnyj7OC\ny7Qv/EUA/yWAJ8Gmf1Mp9ZVgn08D+DiAHoD/Win1u+Ne0Hndm3L9uNKFbd9FhM0DkkqlQOTXVGCw\noVM2652lQQ4MekF6vR7a7bY2PlYqFWth4MsoCvyM4oFBuNvtottu6zwQbh41S2PwMu0LAeCzSqn/\nRW5MRO8C8GEAfxrALoB/SUT/nlJqpAXpMjEQ4/jMXXyFHWZMRTqdDi0axJNgFp8h31O327Umdk2q\nW7x8Nj1gwIU6yzk2l2lfGIaXALyslGoBeJOI7gJ4L4B/M84FmaqC6dEIrsO6j+k7N7dxRBGOUSra\nrD83WUWl7pMSAAAgAElEQVQ8lUohl/HtMCsrKyAitFqtiYRkm2NWJ5C1Wtq4ySpeIhaLVr7FCFym\nfeGPwe8P8lEA34QvfZzAJ5Kvi924feF5zhMab3FZxneEMRrz+nyk16ff7eHGjRuIx+Oo1WrodDoT\nz99glafVaqFSKuH4+BiVSmVmx+Bl2hf+GoC/A9+O8XcA/D0A/8U5jhfa63RScRbG+Wb2R3K4PNgm\nk06nsba2Bs/zQPEY1jc3/K5n3cm3SOz3+2h12qhVqnjy5AmS9+5pTwi3BJil8Xjh9oVKqX2x/h8B\n+HLwdaz2hSqk1+mwSX0Zd5Y8tsNiIh6Pw/M8rK6uIhd0LK/X61oCmCSk9+X4+Bi5XA6VSgWlUgnd\nbheNRmOi57sOXLh9IQV9ToOvfwnAt4P/XwHwT4jol+EbOJ8H8I2LXNwkCSPseA6LA9PjQ0Q6bN1m\nfJxEUBZHiJ7kjpFOp5FIJLRHadZwmfaFHyGiF+CrIfcA/FUAUEp9h4i+COC78D0pnxzHE8IwVZHg\nmGeMlmHZg2GWelO6cFLGYsH8vZPJ5ECB3EkF68mx2Ov1dHTo4cET5PN5xJNJUDyOPgBFNF9BWSq8\nfeFXhuzzGQCfuehF2SbyJNjekYSDfAklEokrS+piyYKIdGHeKDcQGgeRjOCUBk6bC9XmOh0VuWlK\nKw6LBSlxmsFoV3U+Pr4ZpzKrYzCybt7LBmYNi7OY1R/L4eIwf/PriEC1hQCEXc8sIHJkYZMsbJDM\nLSMNzWPJ7Uy9dNZClh0mh+uarLJpkDlOTRtc1MdjJMnC9v+wZWGI+sN3WDxI4jAl4WHqdBQQKbII\n0+vCJAeJUczs1BCHaUBKypx7Y37MbaKKSBk4gclU4Q5TSRxROFwXTAmZXbWe58HzPHQ6HXieh3Q6\njXQ6PVDvNKqIDFmYetww9yljXD3PdkxHHg5XCR6XnM3rZTPIFwu6AXI+n0cqlcLa2hryxQJSXloX\nSY4qIkMWElcxgZ0a4nDdYCk5nU6jWCxiZ2cH/a4fqFWr1ZBMJrG+vo7NzU0UCgVkMhlHFuPCFhNh\nsxzbYJMy5D6uwZDDdUKOW8/zsLKygtu3b6NQKOg09Xg8jnw+j7W1NV3fNJFIRDYeKFJkwRjnQbnM\nU4dZgGyxUCwWQUS6+A4TCaskUW+vEBmyGCd3Y1TMxbBtHUk4TANEfolC/ru8vDwgBcfjcW38ZJtF\nVMdpZMjCzPgbRxQzQ8BHZQ3OS9itw2yAiHStzWQyqRs22UoWjhOIOG1EhiwkhtkXLvIgh4XdOjhc\nJaQEIb/LXJWou0wZkSIL26S+7MQOc5WG1ep0cJgkxlGlZ2UcRpLSRhHFeR+skygcpoVxYoFmZVxG\nhiykBGDGz3OnKFtMvflDmPH2ttLrjjwcrgvzNM4iQxYS8gFz017+33z4o/JFJDGYluYoJ+3ME2Yh\no9JhNCJlswCekgN/OFxWkoa5nD/cF6Lf7+tt5N/zEI3DxcHEINOzHWYf4xTs9QD8KwDpYPsvKaX+\nFhE9C+BlAGsAXgXw00qpNhGl4bc7/LMAjgD8lFLq3jgXI91IMvGGyQDw6xrGYrGBnpvcOAbwyabf\n7+touG63q33csv2ew9WBG+twF/Fut+tIYw4wjmTRAvB+pVSV/JYA/5qI/gWAn4ffvvBlIvqH8Hub\n/lrw90Qp9U4i+jCAvwvgp0adhIumcix9oVA4E3PRbrf1dvF4HP1+X4fNcidwbhbDFZx5kC4tLSGb\nzQ5IGLNihZ4V9Pt9LeE1m03Umw3UqzW/L0fQK4OfuSOO2cM4BXsVgGrwNRl8FID3A/grwfLPA/hF\n+GTxUvA/AHwJwN8nIlJjjA62K3C8fDabRS6X01IFEwGThVJKk0Ui4d8KD0gmDzaOFotFFAoFHSnn\nSGLyYBLodDqo1+s4OHyCJ/sHODk5Qa/TRavztJ/oLJJFzKhb3cdk7uGqjjtpjNtkKA5f1XgngH8A\n4A0Ap0qpbrCJbFF4A8B9AFBKdYmoBF9VORxxDhCR34cyl8PGxgba7TZarZYmC9aBpWTAagmTB5OD\nGQHKMfgcejurAzbK4Off6XRQqVSwv/cYb775Jh49eIhWq4V6va5/w3nAJDwds6SejUUWQd+PF4ho\nGcBvA/hTlz0xWdoXAtD2imw2q+0W/IPYyILfVJJQbGpGKpXSdg7ppnWYPJgw6vU6yqclHB0dodls\nolarDTTzmTWQobb2efk5jOY2t3/MWK8iOi7P5Q1RSp0S0e8D+FEAy0SUCKQL2aKQ2xc+IKIEgCX4\nhk7zWGfaF7IakkqltFfDFFvD8j9YV7bZIZg8uIyZw9VAEnir1UKlUsHBwQHu37+PZr2OcrWqe33O\nIlHzpNYvIyPXSP4NgzmOlVIgIV0opTQJRQ3jeEM2AHQCosgA+An4RsvfB/CX4XtEPgbgd4JdXgm+\n/5tg/e+NY68Q5xto/sJqxSTCvucpQCaKkMFzvV4P7aavetSrVdRqNVTK5chIFuY4MA2vZr6GrJGp\nx5IwlvOLTu5rvtCkK5mfVb/fB4KXIn83K4LbrtPEdTzTcV6zOwA+H9gtYgC+qJT6MhF9F8DLRPQ/\nAfhj+P1QEfz9P4noLoBjAB8e92Js7Gwm4FwUjiSuB2bkbbfbRafTQbvd1nUczLfrdcBGDvxXet3k\ntkwAMuaHjemJRAIIalXI7cJeSvKZ8N9er+dLWsFz4efV7XY1afDzkiQirz/s/mzbXBbjeEO+BeA9\nluU/APBey/ImgP9sIlcn4Cb77MF8O5oD/jrBb26GJAQmCRnsxw2M2daVSCQQSySQTCYHPlzZSgYA\njkMWTBRMDu12W9t6Oq2W/zcgWaXUAIlw4RxbSoTtHieFyCvwVzGwHPFcPcaJYZmmZCEDAKW0wK71\nVCqlq297nucbxwNy4KpWvJ8kiFFkIT+SADqdDnq9niaLdruNZrOpu7C3Wi00m01NICxxsERiw7VL\nFtOGm9izCy1RBB/bhL2q8w47tjR4E/ll+pPptCYILlLDZftTqZQmEZYmZM+PM7YMQ52WqoNNyuoK\nNaTdbqPjeWi1Wkh5HhqNBrrdLuLJJGKJBFqtFigeRzcgDCLSUsow1WQSxBF5snBwOC/CiEKqCxzT\nk06nkcvlkM5kkMlktMteShWJQP0wVY1hiY1hNhL53VQjpHrCYfIsWTSbTdTrddRqNTQaDbQaDXQ6\nHTSbTW0PYinFZhidBDE7snCYS8h4HJ7YUtVIpFKaHAqFArLZLDIBYbCqwZKETc0ABg2icnIOkyyG\nqSf8XebWcEQyByg2Gg1NHK1WC9Vq1f+/0UArsHWwtCKJw5GFg4MF5sTmSe95HjKZDPL5PBKpFPL5\nPPL5fCBZeE8NmWzgpKcShB8s9TSeBzjrbpXn5v+HQbppZewJq0j9fh/JZNLPdfLS8LoZZPM5tFot\ntBpNdLtd3yVdqaBeraJaraLRaGhJRHtbQmwa54UjC4e5gZyostRBKpWCl81iaWkJ+Xxe5wjlcjmt\nbiTTKU0sNvcngXQGh57UsKgbBKggt4PX8HcQQEI7kPvKuA6Kx4JlTxsOxXt9JOMJpJMpZL0M2hnf\nZsGEV61WkSmXUavV0G63US6X0Q2MpCxlXBaOLBzmDlKS4FyjwtISlpeXkcvlkMvldCoBezXiyYtN\nBVOqkBHGttDusByxAZXFIpBwvBGrFpwLxUZYSRrNZhOZTAa1SgWVSgWtwLtyWTiycJgbyJD+dDqN\nTCajJQj54TaBTBSTqq4tJ/qk3ZZmmoNUh1KpFJRSus0AqzAIbB5s/7gsHFk4zCykjs+2hXQ6jVTQ\n/atYLMLzPCwtLaFQKCCXyw10/pJFlZRxTGD0hLetH0kRlg3O2D0s2yiS6g8BSoEAxBBHLBHXBMkd\n2rPZLMrZrO8SLpdRqVRGXdlIOLJwmHmwUZKLJuWLRSwvL2NpaQmpVErbKNjDIcswmrioRKD3o/DS\nB2EGT+mtGOa5CPOqxGIxxBKkg8T6/b6OE2EJiyvJXQaOLBxmDkop7engN2oqlUKuUMDy8rL+sCRh\naw3YhwLFaKgkwG/4cQhET14FYQr1JYJx78n8f8DAKg2jGLxuIvKNp0JFkfkq/HwuC0cWDjMHGTeR\nyWS0HWJpZQWrq6soFou62bBZsPnpQUafZxRJjBO7QDFjm374MW2BW6POabppbUWtWfW6LBxZOEQa\nUuSWf9nbUSwWsbKyglwuh+XVVSwtLWnDJk8YpRQwQooYNokZFwpXN7cJ2cVURcIg1R35naUZuS+r\nZyxhXBaOLBxmDixVpNNpZLNZHVjFJME5G4BoUzlElFCBsTAM4wZZ2bYxp30YIZhuV9s25jWHXZO5\nPz+vy8KRhUOkYeZdaDtFJoPi8jJWNtaxsrKq1RHP85BIJQf2jVHsjP1B0Vk7gS3Hw/zf9l3CLLZL\npsfS8OAM7MNCQwhHDCSkmetCrpslq3Q6HXrN48KRhcNMgRPAOKdjaWlJu0hZqlCwuECN2WUSRcwi\nPYwiCWtymMkjQ86rJYAQ7jHvgaUPItJRoZpAgIH1Ydd8GTiycJgZmLkT7OmQ9SXYMxCGp5Nr0BYi\n1ZRxXJe27WznPsMdIe7aUZP6DBEMOY55fZMiDEcWDjMBa74GPS1eM5AubomiDEvZHnB5Gsc2ySEM\nA+c5szL8fmznkvuESQjW7NW+OkMow+waF8HIOFci8ojoG0T0b4noO0T0t4Plv0lEbxLRa8HnhWA5\nEdGvEtFdIvoWEf3wRK7UYSFhTqRYLKarX8cSfsh2yksj5aWRSCURS5wN37ZJBDH4H1K+jcCcUDJN\nPIwsZB0KnWbeH/wowsCHCU3uo6/BuBaz1oV8Jnz9+j4MMun3++jDPz//vSwu074QAP5bpdSXjO0/\nCOD54PM++F3K3nf5S3VYVJiTh12BssQd152QNSDOe/xxlw879ihvyDixFHwcMynNJmkM3X/Max4X\nl2lfGIaXAHwh2O/rRLRMRDtKqb1LX63DwoEnCTefSiQSyGazKBaLWF9fx+bmJlZXV5FIJNDr9XQj\nIyKyFukdpscPc2faJpstAe0MWZin6Y9/DlNasEZ2jmF0vTY1JLigOBG9BuAAwFeVUn8QrPpMoGp8\nlvzu6YBoXxhAtjZ0cLgQ2AuSyWSwurqKGzdu4Pbt27h16xa2trawvr6OYrGIdDqt3YWmGjFMUrBN\nMrNEHZONjAg1P1J9MVUUnrjmR0ZbymsMU4Vs12s77rDtL4ILtS8koncD+DSAxwBS8DuL/QKA/3Hc\nE1NI+0IHBwmeTJ7nYXl5GdlsFrdu3cKzzz6LZ599Fjs7O0ilUgM9SbiMPnd15+jFM+5UC8ImITDY\n9U42VBo2GZURZ8FNkOW1yPJ8pnoxLBbE5oYdpZ5cBudK5FdKncLvRPYBpdSe8tEC8H/gaQ8Rbl/I\nkK0N5bE+p5R6USn14sbGxsWu3mFuod+65Oc25PN5rK2tYXt3F7eeuY1n3/Ecbty4geXlZcTjcfT7\nfdRqNVSrVZRPS6iUymg1mmg3W+h3ewOGvrAu5WeMiMbbXjYGMitqS6lDfhKxOBKxOOIU02X6TAMn\nE52sm2key3aNA9duGFIRs0sZl8GF2xeyHYL8K/mLAL4d7PIKgJ8jopfhGzZLzl7hcF6wITMWjyOT\nyWBtbQ03bt3C+vo67ty5g52dHRSLRSilUKvVUC6Xsb+/j0ePHuH48AhKKWSzWZ0jQvGYri6lgvBv\nmx3AJsLbPCKmyjBqQkqSkMc2YyNku85hUo0pSciG4HL5JN2nl2lf+HsBkRCA1wD8V8H2XwHwIQB3\nAdQB/Oylr9JhIUH0NAU9m89jKSiNVywWdRXuRqOBWqWKSqmM8mkJpZNTVKtVvS97SOQxh3kQ5GSz\nVZga9bY2t5eqg+2vOamlehN2befBsPs9Ly7TvvD9IdsrAJ+8/KU5LCp4YiSTSWSzWSyvruLmzZu4\nfecZbGxsYGdnB7lcDp1OB0dHR3jw4AEODw/x5ptvYm9vD/V6/UxSGRMHMBj+bU5cnli9Xu/M9cjt\nz2O3kMcxj2mSj5R+TMnHlGb0vQAA2QnGlFwuAxfB6TB1mHo/T+5EIoF8sYjd3V3cuHUTt27dwsrK\nCvL5PACgfFrCw/sP8NZbb2kV5PDwELFYTBfr9TzPTzDLZEBEOgZD9c6K+6bngcmFJylPXi6vLych\nT2Z5THlvAAb2keqG3F9GokrC4OuS1zKwf3AOnareVwCdXX4ZOLJwiARM70AikUChUMDGxoYvVdy+\njc3NTeRyOSQSCVSrVTx+/Bj379/HvXv3cHR0hOPjY3S7XeRyOR2Hsby8jK2tLaS8NDqdDmq1mj/5\nMNjNXQZymW98SRDyGsNaFoaRhZQUJBGwobTb7QLAgFuWz8HXx4QjjZ7SKHqVcGThMHXIicatAjOZ\nDFZWVrCzs4MbN25ga2sLhUIBqVQKjUYDR0dHmij29/d1yft0Oo21tTXcunULzzzzDJaXl7G2toZY\nIo5qtaonZVdhoPK19EDwRGUPhSk9yLgIhhnXMSoOQhajkfuylwXAwDm4tqa0o0hCMbuP2aSPy8KR\nhUMkIAmD+2Bsbm7ixo0b2N3dxcrKCuLxOHq9HkqlEh488NWPvb09nJyc+I2EUymsr6/j5s2beO65\n53Dnzh0Ui0UUCgX0lP9GrtfrAKCJoNfrDdSsBHBGkpAVpxjc+VxO8jDPibxHqdrI48pu7nxuSRy8\nj/SK8HlkRTBbHsmkpA5HFg6RgfR+sK2Bm+dw8RYO6S4H5e3r9boW35PJJHK53IDXJJ/PI5vNotFq\n6onKE1F26jLf9DxJOQ9FvuVlH1I5sXlfU52Rb3w+H09uPi9XspJqh5z4HGAmJQb5N6xa+SThyMJh\najDfetxqsFgsYnV1FZvb29i5sYullWUkk0k0m02Uy2UcPN7HowcPcfD4MSqlEmIAEskk1tbWsLu7\nizvPPYvdmzewsuZX0CIiqKbfULhSKuP48Eg3EWYjaCwW0xOfr0k2RgaeShPdbldLFQzZoT3MayFJ\nhTult9ttLVHw+VgVi8fjutExk5PZxkBes2mINeNFLgtHFg6RAEsVmaBc3ur6Ora3t7G2toZsNgul\nFMrlMo6Pj/Ho0SOtfvR6Pd11bHd3F3fu3MGtW7ewubmJfD6PeDyOer2OUqmEJ0+eYG9vD3t7e2g0\nGiAi5PN59Pt9eJ53piI2u105fFyqLlxinyc5qxRhcRimV0MSD5MP/89ZtHxMtrPwNQCDnhrpwpXu\n4UlLGo4sHKYGU7dOJpPIBR6Qra0tbGxtYmlpSU/4J0+e4ODgAI8ePcLR0RFqtRoAaLVjd3cXN2/e\n1MZQnuinp6fY33uMt++9hbcDg2i720UikUCn09HXwH1G2J7AE7rVaqHb7WppQ1bnsrk6pQTB0OHf\nonBuOp3W52i321ra4L+pVAqpVEo/G1ZPWJqQdhQ+70ARIEw269SRhcPUIA10XNp/ZWUFGxsbWN/c\n0CX+AaBSqWB/fx97e3s4ODjA6emp7iK+sbGBzc1N3L59G9vb2ygWi0gkEqjX66jX69jf38dbb72F\ne/fu4cGDBzg+PkYf0MTAKe+skgC+ytFut9FqtaCU0m96z/P0xJVGSCkZSNUAGPSisFuUiSAej+uw\n9H6/j1arpTufNxoN9Pt9rZ5x7492u63tKnxsaZA11SBn4HSYecg3YCyRQDafx8rKCjY3N7G5+VSq\nqNVqOHpyiP29x3iyf4CjoyM0m00kUiksraxgc3sb29vb2NrZxsraKjzPQ7fbRenkFJVKBfffehtv\nvvkmHj58iMPDQzQaDX/yigCwfD6PQqGgJx7bNAAMRIPG43F0u100m000m00tETBRSKOjbYLy5Ga7\nBBtzJXGwe7jdbqPdbmtVREoabDPpBhISEwQbX82mSs5m4TDzkG9drleRy+WQzWb1G5yDqWq1Gur1\nOprNJvr9vg4HLxQKfo/ToAtZLBZDq9VCrVZDpVJBqVTC6ekparUaWq3WQGATx3TIt7s0GPJ1cafy\nbrerj91sNvWkNd2YwwycLBVISUQppQkklUrpY7ZaLS25sGTCLmSp9sg0fKmS8LknAUcWDlMHESGd\nTmsvyMrKCpaWlpBO+1GXpVIJh4eHODw8xMnJiZYMWAXZ2dnB1tYWlpeXkU6n0W63USqVcHBwgMPD\nQ7z99tvY399HqVRCq9XSE3J5eRmbm5u4efMmdnd34XkeGo2GVj36/b5+a7OaUa1WByQKqUKx9MFS\nggQbKJlcms2mVjn4bzKZ1G7idDqtbSK8L6slrArxddlsFWYWqpngdhE4snCYGuTbPZvNYmVlBevr\n61haWkIulwMRodls4uTkBE+ePMHx8TFKpRI6nQ5yuRxWVlawu7urK2Xl83kQEdrtNo6Pj7G3t/c0\nbf34GM1mU5NMNpvFzs4OnnnmGdy+fRtbO9tIJpNaYvCyGbSb/iSu1+sol8tot9t6wiaTSV2Mh6WT\nVCqFZDo1GN0pqm6zhMBkwZJSrVZDo9FAvV5Ho9HQUhJ7ebrdLur1urahsBrDxlI2irJUIz0utsI/\nF0VkyGLc0FTbdtcRF79IGEdsHfW8w9abWZBEhDirE0tFLK+uIF8s6NiHSqWC0+MTHB8fo16totVo\n6Dqcy6srWN/cwNrGOopLS1pVYGPow4cPsb+/j6OjI7SbTfS7XR1Gni8WcfP2bdx57lncuHUTa2tr\n2ijaarVwcnKC0+MTrcawCpNKpXRzI26byJNXqhrdbm/gftmTwnaPfD6PYrGIer3u3+Ppqfa8lEol\ndLtdnYrPAWlKKbTbbZ/MPE+rLbwcwIC7Vaojc2OzkBFzQHhBUvm/mbVnuuHMZcPgiGYQl30e4/r4\n2SbAKsja2trA27rT6aBcLuPw8BBHR0eo1+vodDpIJJNYWlryvSZCEonFYqhWqzg8PMTjx4+xv7+P\nw8NDLRVI1WU98J7s7u7qmAyWCJLJJOr1Onq9HiqVCiqVCrrdrlZduFM72zh6vZ72vLDhUwZt8TGl\nqsKGTJYestksms0mjo+PUalUUC6XtV1C2kyYGKTRk42ZbG/h+5B2DVtx4fMiEmTR7/dRqVTOZO4N\n+59h+24jmHEmwLBtwtaNk7BjWz5OhJ3NSCaXj3NP4xx30rD9TrZt+E2byWRQLBb1pGd9vNFooFQq\n4eTkBNVqVU/AfCaDpaUlrK+vY3V1VRfC6ff7qFarOD0+wcHjfTx58gSlkxO0m00A0KrOzs4ONre3\ncePGDWxsbKBYLCKZTGo9n9WE09NTHB8fo9FoIJvNatWnWCwOBHu1222Uy2WUy2Vt8zAnKpNiNptF\nIpHQsSH5fF4XIWZCSqVSKJfLqNfr2p7DSXTsAeFnwaoHx4zIMHVbKvxlEAmy4Hh/00gjE2/MyLhx\nCcU2scJcWsP2Cftum4zmpB4l9QwT2Ydd50WJYNRbfxIDa9i1SdGcXZf8lpXVuaWLkicHb+953oBL\nU7o82XPSDgyRfD7ZI5XzRnTZPWFX4POypMDJZmwYZQ8Nqw/NZlOrKhwjIbNA+U3P98LJYnxdnA/D\ntptms4lGo6E9L0opLW2xrYKJga9NHtOU7CYVzRkJsmi1Wnj99dfPtKFjsuC3kG251Afld9sHGE06\nkpxs68f5azuGibB9bdvYvo8rxYxz3IvAJtaaZfCHgZ81SxY8gTmXo9fr+cV3y2WUSiU0Gg098XK5\nnPaa8CRSSulJe3R0hKOjI51o1u/2kM54WFpawtbWFm7evInV9XWsr6/rNz27KdnN+uDBAzx8+BBH\nR0cgImQyGbRaLa1uVCoVHB0d4fT0FO12W9fJ4LHIAVQMSXwAUC6XcXR0hNXVVT9adWNDqyRsuDw6\nOtL3XalUdBh6NptFpVIZcKlKArHZKuaGLOr1Ol577bUz/RNMMjDX8XcZRmvbhpfbiEYewzynbdmk\nP8BwG42N5PhjZjea/5vHHFfiGrbMlA7kOflN1263B2IIYvCLt5rXS/E4ElzNquAbC9mYxx6ARqWK\nZr2OfhDwlMlkkM/nsby8jKWlJZ03AgDVcmAMPTxENVAJut0uKB5DOsg5Wd/ewtrWJtbW1pArPI3L\naDQavmF07zGOj49x/623dVg5jy0mil6vh3K5rFUjKbWw/YElJAA6MrNer+t9mNhYimg2m8jn89ja\n2kIyncL65oYm3Xa7jWq1qqUKdg+3221NFlK60ERBAGKEXr+PeGzQlXsRjE0W5Bfs/SaAh0qpv0BE\nzwJ4GcAagFcB/LRSqk1+s6EvAPizAI4A/JRS6t6wY7fbbbz99ttDJ5Kc2GETWm43auJLEgkjFxvB\n8DpzmY14Lnqttm0k5PHN4/D3sPOI3zP0uLbnHyYtyW35jcbiObv7bAVhpFjP0ZNsr2DCqVarWrzn\nSEXW39kbwVIFx0CwVMFGzX6/j1QqhVwuh7W1NWxu+kSxurqKbDarIzIbjYZ2tx4cHODBgwd4/Pgx\nSqUS4vE4ms2mjraUbslcLgfP8/Qxuewfe3MAaBtItVrF6ekpWq0Wnjx5omNGnjx5glarhUKhAADY\n3N5CNpvF2sY6Op2Odq9Wq1X9vDzPAxHpZ8ykxwFbvV4P8dj04iz+GoDvASgG3/8ugM8qpV4mon8I\n4OPw+5p+HMCJUuqdRPThYLufGnZgItKiIGAvgGq+Lc39RyHsTS6/j3qjmmRhTqxxJRFzW9v12Sa+\nKSWZ60d9TPuP7Ti2ZbbrtdmSiHzjIOdjsHGQA5qkNMIDm/V0WbafA5XY9sBRl57nwfM8TSyZTEZP\nDo5bKJVKqFQqWqoA/DoXXGZvfX0dhULhTIRotVrVJMEJa2xYZcmDjY+e56FYLGJ5eRk3btxAoVDA\nzs6O781ZXdGeDkkW7XbbN4ie+GSxt7eHR48e4fHjxzg5OdGqFkdobm9va/dwIpXUAV31el3badgz\n0u12NWGwYZPVEf7drk0NIaKbAP4TAJ8B8PPk/+LvB/BXgk0+D+AX4ZPFS8H/APAlAH+fiEgNudpk\nMqTZ/9QAAAUcSURBVInt7e0zJCH/l28nOehk/QG53vTnm6e3nUMe19wv7PL5HGEEJP8fh9TkPrbt\nbSRm/h0mYYQtDyMf27Jhy1nkPjo6wsHBAarVqrVRMRFpyYLDrTOZjI5YZDtArVbTRsp0Oq3VkEKh\noL0gTChMFvy25RDqdDqNpaUlrKysYGVlRXsW+FwsVezv72N/f1+/9fk4bDxlY2I6ncbm5ibu3LmD\nO3f8alybm5tYXl7Wqo3MzeDJ2263UVtZRafTwdLSklaj3n77bZ3v8uTJE01Iy6v+tcaTCTRqdX1N\nHBLPMRusjrAXia/XliNyGdCYAThfAvA/AygA+G8A/AyAryul3hmsvwXgXyil3k1E34bfsexBsO4N\nAO9TSh0ax9TtCwG8G0+bFM0b1gEcjtxq9jCv9wXM7739+0qpwkV3Hqcj2V8AcKCUepWIfvyiJzKh\nlPoc/B6pIKJvKqVenNSxo4R5vbd5vS9gfu+NiL55mf3HUUN+DMB/SkQfAuDBt1n8CoBlIkoopboY\n7GfKvU4fEFECwBJ8Q6eDg8MMY2QMqFLq00qpm0qpOwA+DOD3lFL/OfwGyX852OxjAH4n+P+V4DuC\n9b83zF7h4OAwG7hMwPgvwDd23oXvPv31YPmvA1gLlv88gE+NcazPXeI6oo55vbd5vS9gfu/tUvc1\nloHTwcHB4fKpaA4ODguBqZMFEX2AiL5PRHeJaByVJVIgot8gooPAZczLVonoq0T0J8HflWA5EdGv\nBvf6LSL64eld+XAQ0S0i+n0i+i4RfYeI/lqwfKbvjYg8IvoGEf3b4L7+drD8WSL6g+D6f4uIUsHy\ndPD9brD+zjSvfxSIKE5Ef0xEXw6+T+y+pkoW5IeQ/wMAHwTwLgAfIaJ3TfOaLoDfBPABY9mnAHxN\nKfU8gK/hqd3mgwCeDz6fgB/EFlV0AfwNpdS7APwIgE8Gv82s31sLwPuVUn8GwAsAPkBEP4KnEcnv\nBHACPxIZEBHJAD4bbBdlcKQ1Y3L3ZUY9XucHwI8C+F3x/dMAPj3Na7rgfdwB8G3x/fsAdoL/dwB8\nP/j/fwfwEdt2Uf/A93b9xDzdG4AsgD8C8D74QViJYLkelwB+F8CPBv8ngu1o2tcecj834RP4+wF8\nGQBN8r6mrYbcAHBffH8QLJt1bCml9oL/HwPYCv6fyfsNRNT3APgDzMG9BaL6awAOAHwVwBsATpUf\nMwQMXru+r2B9Cb73L4r4XwH8dwA4a2wNE7yvaZPF3EP51D2zLiciygP4ZwD+ulKqLNfN6r0ppXpK\nqRfgv4nfC+BPTfmSLg0ZaX1V55g2WXC0J0NGgs4y9oloBwCCvwfB8pm6XyJKwieKf6yU+ufB4rm4\nNwBQSp3CDy78UQQRycEqW0QyIh6RzJHW9+CXjng/RKR1sM2l7mvaZPGHAJ4PLLYp+BGir0z5miYB\nGcVqRrd+NPAc/AiAkhDpIwXyUxV/HcD3lFK/LFbN9L0R0QYRLQf/Z+DbYb6HGY9IVtcRaR0Bo8yH\nALwOX2/876d9PRe4/n8KYA9AB75O+HH4ut/XAPwJgH8JYDXYluB7f94A8O8AvDjt6x9yX38Ovorx\nLQCvBZ8Pzfq9AfghAH8c3Ne3AfwPwfLnAHwDwF0A/xeAdLDcC77fDdY/N+17GOMefxzAlyd9Xy6C\n08HBYSxMWw1xcHCYETiycHBwGAuOLBwcHMaCIwsHB4ex4MjCwcFhLDiycHBwGAuOLBwcHMaCIwsH\nB4ex8P8DoKfFHvy9mFAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb62406ef50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(sharp_test)\n",
"print 'sharp image'\n",
"plt.show()\n",
"plt.imshow(soft_test)\n",
"print 'soft image'\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### Again extract smaller region from image, now adding noise and small shift\n",
"(hoping to mimick some differences when taking pictures)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"sharp_test_noise = sharp_image[1000:1400,2000:2400].copy()\n",
"soft_test_noise = soft_image[1005:1405,2012:2412].copy()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# add noise\n",
"def noise(data, noise_value):\n",
" noisy_data = data + noise_value * np.random.random([400,400,3]) - noise_value/2\n",
" # shift values to be within bounds\n",
" tmp_data = noisy_data.copy()\n",
" noisy_data[tmp_data < 0] = np.abs(tmp_data[tmp_data < 0])\n",
" noisy_data[tmp_data > 1] = -tmp_data[tmp_data > 1] + 2\n",
" \n",
" return noisy_data"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### Display those images"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQsAAAD8CAYAAABgtYFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3NmuZUmC5vW/ma152vM5x2cPjzkiMyOzKGhKNIIugeAK\nJJoLuEQt9RUPwAvwEjwBAoQEEkhAI0FVdVWjKsjKzMiIyAgP9/D5DHtc82ADF9mguik6ISqrE8l/\nd2vLtGytJX2fbO9l2sI5x1tvvfXWP4v8530Bb7311v8/vC2Lt9566zfytizeeuut38jbsnjrrbd+\nI2/L4q233vqNvC2Lt9566zfyWysLIcS/LYT4lRDisRDiP/ltzfPWW2/97RC/jX0WQggFfA38m8BL\n4M+B/9A598Xf+GRvvfXW34rf1sriXwIeO+eeOOdG4D8H/t3f0lxvvfXW3wLvt3TeO8CLv3L8Evg7\nf93g9WrlTuUBawTOwU9+78c4CzjD0E588fRrJJCEAe998DFOOKSDX/z0p2gUQjl+/KNPwUiMFAgJ\nP/v5TxEOpJP8+KOfQDjhpOSLz79lshVGK6Q0/OSzz7AIhLU4JEJZrFM4K0A5hAVhDUYqfCdBObTR\nKDwEhslKlJIYpxFO4JRFGQWexTqHcgKsBARaCrAOJQ1OejBNoAQAzkikBIRDCIm2GqEUShuc8rFu\nQggPaQ3WCZx0OKFQRmCURWhQEpASayxWOZQGqxRC2l/fgxUoIZHi189ZWLAKjPi/7hNQFukUAod2\nvz6fswbpCYQWWOHwnGASBqEUngYnLVaAdQIpLc55SCacFgipsAikM0ghmKTAQyOEh7EOYQxGCqSQ\nOGdRViJ8g7Y+iAnpFNZYhPr13D5gtcRJkNbwxedf4HxQo0IHEl8apt4iI5+x14TC/tNnIiBUWOfw\nlED3PSqQqEEweT5ajgQuROuRIAixukOYCMHAIDxE4BFgEW4EJ+mVh5sESINAEGqL9T2s1XjGQ3gj\nvWcR2iewHoMcECLEup7AOGwgkdahDPS+JMBndBP+4JgURJ5kGAXOTQRKogkwvsMbQSkY1YQThs8+\n/DFYgXQO64HF4jmJtQaLQgmHwSGF46c//fnWObf5/xrq31ZZ/DMJIf4h8A8B7t6/h6cMNTGy3PHH\n//hPqJXGKsHP/6cdf/8/+hcJqi3BOzP+/L/7EyZv4BjCo3sLfH/JzPT8b3/255SnI0tvyWnR8uHt\n21SlBG35x3/8X3IsIuS14+6/8/fwvh0JZIJQAX/6F/+IdhpJjgVu2dNUK9x8JGtOHKMMr/RJ5yPN\npEmbCJFoMD6V1XiNwctiptgwHxuOXoYtFZqebNAEuaHJDHYfIYMYITuMCognx7GfKIKEJtoS1Su0\nm0hzRXX0MNbip5Ykb5nakMhV1OWc2WaALmTv1VjPEZQFZIaw9fCMYpodkWKGUhVWe1gXUPY71qFg\nCBKG0Wc6gJ8FuLpBXRiKm4kRie8C+kLTacnYBvhZhBRXFJ7iZptAWBGZDVkwMSUtfWuZkpz4VJHM\nI4zXoSaLHZd4VUe3agjHc8p6wASaBQ0OxTEpCGWHK2d4wQ1lUzAvNFPr4eUh0l5yEGt8VZJ7E7aF\ncFTcqAWZmSDsiHuP7TLl9Gd/xD/4B/8e2/A96lcvWK4TktMbDhfvoZonRIecODnn6ixi+sVXLNY/\npBS/5Jb/KUaUvGg1YqwZHs6oX2451++w6Vpe6ZxbP4abYSD8qmP8xKP6akL/pOKjny+5/IHHHfuK\nJ28GgvMYrwsonoQ8jXre9SKq+Z43rz7hh+YxL5Zz3j/PEddbposlj/cei/w7LpOQn/zyIW/Of8lq\nf8bNpxJ13JG8mvNtofnh7SOPn92ntwXLR3surl9gh5DLw0C9vE9wC9570vCP/uJ/YTAetB1ebEkb\nj8Y3hP6KyrdcDIZxbDmJkfPZ+bPvk9nf1teQV8C9v3J8959+9n9zzv1nzrnfd879/nq5pBYOr2+I\nx4hBH0l2Nf6u4sEPFPra45hFdF7JdgatmJj1AfPmAjPe0FlFHyiUKRiN46BrBhEikohxPnKYNuQH\nQRgvmL5qSAJYSInwavo6xW9myNRSCYXr90SnlmZKyY8RTmqONkb1EV7U4+REWylmvkNGPX1ckx/3\n9EOGvx1YRIZo4ajWCftgwWwryfOenAGLIZU+YTvizSL6tsaXAp3viKxGWocIKoL8BHHJ6WqgFT2n\negOi5GA0lVRYX+BOAdockfsQN+tozJGmiRHGIXcDqu05GcfZsMHVGaeTplAdmR8y9RCGEfEh5CQt\nY5zQJC1+MCGUzzw4YZM9TkccvYggDPCLlFiCUwYfw8II4n3FaGaYJmXfeWzHNeNQcX2ukIdzTHKN\nR8li0JxmMWOokR3krUL5WxqzJBATwZiSJgdEMzJGa1bdHtPOMdrnGKzRUUo0GiLREiYzGk9hyyv+\nq58f6K7fYYcmfDAnLXd82XzC1VeP+S7foMc1owf7rwzZO59R759yfW55Mf8Fv7DP6VfXlLVmelLz\n6G5OeVfxTAtM1vJSvOHer77h8NnE7dfPmT42LK8j3thv8UTPr7Tm1vIR7dWSodng309gXXIwCe1h\nzt1iz9MwIy86ntY9PQ1PmmtiP0Ltz3iw7bn8+BXxZUT16TnezqPqPqC82xKtBddXF3x0MbJ5/+f0\nLmPrPuXxvYlD+iNs/5QPfxVz8hS5GIi1R9b7LEoDvmYZp5imIh63bE3JwQ+JXfi9Q/3bKos/B94X\nQrwjhAiA/wD4b/+6wU4JjPHBg5siQIYz+rVglq/gtMQzlyTbjnvfeiysIxOKLvMp1SWBWRN6NcPV\nERNrNA0PTwWlrjDasvE1uWuRixWjcmSJxmznXOsTi6MgCRtcF6OaGHXKgCWDnJP6DpY3ZIPEHhsS\nf0LGKYcqIJj3NKqh60GUGXiKo7TIeYvodtgmIfNqlmpEM+OmdJxcSK8UgdxxfTYRtxDhYaRHMK7o\nQkVdHjFBweCnxL0jTgPCFgr2uEiBr+h1TeAsZzNQmU/sO/o2JaQgGh2t2zPpGZWvOO8a9lHLELRE\ng0/XGjyjYdbieVtkaJGZT9JCX8+oDzkikPguhOscqSyxqXBOkOoJk4wMTcOuy2iSAC9YEuQV1axn\noUZiZYi0x3kdUa0d+rRiSC39ecpMaOpxzkyDs5ZRW0LVMc0FVtdUssAbK1JbMWQSTwhEaZk1Bs8Y\nnJ4Yep+6rkntwNqt+Ccv/4haf8vty6cszAua3PHJB6+QDwWfbe+wHzKe1o71g1dc7y7Rn3bkN++w\nfebzQfIO6yBG3LVkdwO+qwreUS9Js5RUtJys4/IiRXYhl927iMd7UhER/egDtvZA/Grgie8wWUkW\nJ5zcjruJZZdZFl1K//AN9+5CdtVxsVpybR9wXjrux8+p9ktyk3J4PqdZSo7f9pynhm79jG6WsAnX\n2FahX7xgdv0pm/E7VOOxuYn4Qb0jW32MLxx1Lzlda4bRUc5aGhEjdIyuBwyW3lMEacQ5R2Siv3eo\nfytl4ZzTwH8M/A/Al8B/4Zz75V87XktMc6AWilUsmKqIeFK0leTBxxF6fsakBJ/fTujrHiE1wt/R\nJgljq+j6OdlKsBwMSW4Zb67YbEMy3eH0j9DxBtk5TBox1AarJgrtoWa3OE4R4QU085E875iiEa/f\notoAMzmCUHARGOp44HB9JAhbxirEneZ4nmSWSI7dCvwBQmjthnliGEfBjaionSWK5sS+I+89Bpkg\n2oQ6H6mLmFzHBAbypCOZJSBr4uZAO4QEUcpMjTQzyP0ZyzpFtAKJoB8aVOK4yStUImC1Ryw0bvKo\nwwbft9QqJPehEhmJavGikXHTEOwlBxNi4x7TLegTDy0NhaqhDWmyiE1wYGgUYVOQ2pGoDeiEpF45\nRKboKh8TCGozEQ4NprQMU8c+z5iikUAaRjOyms5R1wpRZ+SeTxX6XE8G1Bmh9ok6QWc1wTFBe4rJ\npPQ7TZK1dETUwcixnuiVpFx7BFKznxv2/g7+8r9B9pLvZu8wfLNC14Jpusd9nfHdXFCdH9CZIAh6\n7p+9QW8zztOOu63PtX+gK2vuv/E5+T2f2YjTzQ3ew1cU73Z8eN2hswqd3jAuXnHnnfcIxy3iVclH\np9vcXt9h86uQTRZgZp+Tpw+5rALe71PcJx6bn7/P82BF0edkv4BpbgjuptjnBVXYoMod2UNL3Ppk\n0xNeP5nx4JcV8deG5W5ifzFx/d5tXk3PKJ8u2a4fIwLH1w8rhtNrnnzyhKZ4zcIkuHygUI5IJBDF\nVFIzGJhVEmliWn+BPw3fO9e/tX0Wzrn/3jn3gXPuXefcf/r/eBFKcOe9D4hsw9j7LBZvmGxI4B8Z\njw1jpFmIDcvLK6TwOE1Lpt5RNB7C3xOZimDUNEXEQS14fedIGQYcM8VH0Zqsadm1isgdWE4QKw9n\nc4p/4X3U2OGZFu/QshUR60giXcwuGWi7M0zuU/Uj0z5HLwSFjInlgEqgSANwFT7XMCV4u5hqbsF4\nBJ0lcwJv5hMnB0Q94okOY0vOhpLVrierLmlcSyvh2BaU0mNtJd64IRYDw2nCjBG9UozdgZPsKTaS\nYRtQ+oqgzDnrLO10wh9X+M4g+jkzkWPLAX8UuEqw7CeUXIJXYMuJSTUkseFYa4SpiOIKz3aYeEk8\nNXRlz2Hw8BYt16Yh8gOurWHWdyx1gr22KO9ANg0ULZh2gTet8LyMhS6pDgq7V0xTQrvYcSgOyHTA\nDyy0PTM5IbyKyj+S5g2oHo8T6AkpG5bhGYPQeEGNCQJGAuKZxVYjgfYpmoA0Tvif/+gWT5N7/ODN\nNfl7ATengeA7eHJd43s17+Utd7w3uC+XmOcpet7xZJiwq5B9lHDI30F+GPNRF/Lk1RcUwwXLcsk3\nP7/F4/OE5ZOMD64M60GTRF9xOR/J8iUnp/hcCk7iS5JXdxiqjMeXgmmV8WK+Z7iK2dmAj48eL7OR\n8qMbLtI9T8WKYV1ydhcmdZuTGdl2PdPiI+6aF0y+YH7/NleJJDi2eK8jhsrhv7/B1LfYMCfaL9hY\nwftfGu6Pv0d3URAOE3aMGKVjrByhdRShwbchptshncehj753pn8ndnA6q+kUjCKiqY58Uw+oakQE\n4M8E5+XANE605YogzZDrEqs8xCIhLeBgJnY6ou400a5j/FlC1pfkx5T6XcP1RnI+P9GPCy59n707\n0ngnlpd75qHH/ibBqJDcjlybERVbZnFD0e7YuxOmiIizEohwnWAcIiZ/oBo9+mkkTRVBDnbesUEx\njhOeJ2m2Brc/4oaERmu8bsZkQo7pkiOK0ctxFtxkWZiSeTUy9j3TUuAvFuTOol3Cwg1UfkLUBwSu\nRfoeZ/4SFRpUPwPjODR76gaUukKIkiSN8HzFaRVjohqtJcEpok9WxB4MtSNUGd0M9oSEiaXEYueK\nZQxinmP6OQUzjsPEat2wDWKmXiMXE8wjmkgSMKefDQyrE5E9oBtNGpZkakTNj0xEnLdz3tgG0x8Y\nKKlcAoli5a8QN3OySDKsBU2R0OxSSs9QtDPCKWExatyFRLQDOaBNTtt1VC5ELT5ndb9idyvmp7+6\n5FGQ8d2qZu4t2V6NiBfvUNoQLzPosOdedY+7C8Ob6wuCw5qP5RPooesGzu449uuIoSg5f3DD3W9j\nhDrnmb7gxQNJ93jBWTRj554TB9/ysYTb85AX/Y7Vk1t8Ej7l4xe3uPMmwQ3PGdxLruwvEasO882O\nvrzLo2HgxRo2HjAl/OikebQoCPRLqg8fsQ1u8c2LkWJ4THR+5M2FQXpn8KLGb2um1yfu5Qdy3fIX\nj1LCDwpOpx2MlmHs6MY9o7+n7AxGhWzFiEklIVtmYfK9c/o7URZYyZl3C9D4m560F3hZQO805iCo\nAw8jGsLCY6eukZVBuTm+foM+GYosZOGPrHWPS0O67jvc2YJmOvBoyMhbzZVfIEZIspplmJK3Hovf\n+7t0J8nifE9HgGob5vVE7QVMQ4G4yFjuJvwxZ5okqtY00sNEFlMJ/LFjUmuqyiPtDP1QYMSBIfJQ\ng0+OxVc+WvrYc4ta70kPE7PqhFmMMOtI1BySI0oJygKsWTK2Fj2WiLlPc9YznEJmrscrDlxXc0Te\ncLmrcdOBm+URTxVYsWQgQhdzttmCk+o4+iNRX6ODDOGXTGIira/RgUaGCcOYsK4U4cGRDwJzHPEb\nDys7nKhZGolOGuaiYjIJF/0BNxvZmARFjxJbjmeCzUkiDylDX9DKCZkHiNQSR46JmutQs57OmLyC\nwjmcC0mqgJvQsVvsuQkFzT4l7jus85Fdz0EbmiW0ZcnFVuM7aOMAq3e0y5C0H0lv3oFfvSRdwmc/\nDBlu3UNcbknPjnxwqNhqjd+PfJNEXI63+fr5Dr95wMMPeu4OX/O0eRcnb3h+fUHUbrj1uKY+XmGC\nE8YK+sUV5/uJO/0jeDDHihuoHvH86j1eHmLEdiLXJ9688yvedCem+IifjjR5THOnQuzv037nWIyP\nyMUNgbzi3THnhZ4oVzmnk6FfBly1R7578ksCOfLBnZ4nPRB8yPz5iUebl1zZiY/OE6aPH/LqMPHq\n1j1mB8FPPjtjOVvSDiF2FqCzhCkoSJjR6Zps9FDXkgMrBlN+75j+c3t1+lc5IXj4L8c8/98ThsDw\nxf+657N/bc3ZtMFsDkyuJooCdkbghxv8qCGzE9tK4LsVRejgNKMKNa5z2LWHOQ4kviX6ELzRUjQt\nKhrwRsdWWFZ5xzvnI92FwN1kuEjS9DmTdyIYJxLrsz1NzCONT4tfSYSXg3/AJhGTixmNAl2TBzkj\nmiCxePUKv9cgHSrYMCU3BHZFRsGugjw6MfaSMxViRoU9WIZ5iBAxdqtQfs3SDGx7idUB2oRo74BX\nGHbOYzV5HMeUJJKYVjOvC7Q6MGyWWKuRlcSPjwiTEdqINm8RfQjpgW6cyKMlE5qgGpiGPfv5gnU3\nMU4layfo44bqMKOIHYdsIrMzrt2BaIoYXEzgBqqxRpceKs9IDlBmAqF8ZsmIcGeUpwpvChlUQp5D\nlNaYPqCLJC7xWR0mqqSG1ofqjGxVYWYlpXGE7Incki6/xjtGjEmCwyIKj6R31J7iVh9g2onyoufj\n6FOuXj+jTD7CvRaweZe7r0vehCGb2Z5pBR+9fMXu/BHqNPLyyc+wZHx4FnB8fcmTi4lHxRXuwvE4\n71lfS1K95E03J53tkMERMTR43x15LSWdGvng/ae89N7Fn3s0TJxffcaz5f+BP21w3XewuM0t6/FK\nFvzgg4EX8RP6lxPj6znaPIMHZ9xSM27OtoyvPD6SH/N5cSDKNKeT5WzxiNObgThPqaZz3rnj6F+/\n5mbvkWzeIxueE1xk3E/epeJI5M8Z2hPOtijh4+UVcZsTRZbWB9EBxv/eOf2dWFl4TvDBzS1c2kFs\nkPIJ/sxSrQW7CUTps4sGVrIiHi360ocbD7Ge4WYHZH9ilyh6NZKrA09fFfjByClYMXv+EGsEXhxT\nBxrhQnwJ7rTk4oMZiy3Y1UgUVywXAdKXJFHMIY0IFh6Nyyhbn/BC0q6uMYWlPCXIQ00c+EgRM2pD\nP0x4N4Ky3zKEI6MSyPBIWmWIQDLtBcgWG+YEgeG6DumOJ/bLA5EZuekn4lijV5YytszGECcg3lwi\np5HKxPilpEkrAiXIAoknCry4JBIjyhhMpzFRiPRzhJcyeluSOmDRS8JWEHdzvEEhRx96w0Z45A4a\npanWObugod5JZnlDFcWsex81VsxijWaPXQWAJo07pB8zBB1mYSm8nlleoT1HD5AONHnDwlzijVfY\nY8QuqggmTXFTcJgbhFxS9B6zs5Zh1xJXE1mYY42HdFeMWhCZAT/yOVhBuJfEfk2aayYRcQoTHniW\n5vFLVrIgGyw/GAc+WTxhO3sN9jvGyze82j3geLZh+d1TSN+Hzz5EfmLYR5o7tuTDFxtaAd7Xd5gN\nEbl2ON3hPTLMr0pe3ZtTzk6kmcQWcz66HdHIBL/3uf72AT0b9ieHLT/myhvIb/VMLyt40aOnX/Ey\nHsj+0nC/V/iLFHUrx1Vz6mvH7esPcPc1Iu85L3N8c83xoOh1zx29JfRe4UTLs+MzTFGzj2uKl1+T\niI79l/CHv/8+fe9jaaC2iNQR9yGiTkjSAOGlxM4nUY68sN87p78TZWGkYfbAQ/cRanC83p4InM8w\naLJqQS8CkmGDZqR0kqjQyHDH2U6THOcMLsTzNGmao+cpG3WAOCJoGo5/d8Hgt4zbEVcFxK1PMSnM\npuGzsz9Eu5j2OsYBxuxJ2zOQFX5zYJh6JhzEHTdjSsoM22jWGUQXAeFxItUTdlOR2oQx63/945Jr\n6dMOoRJcCKOYmMQNi3hiGA9YAqy9pEsXzA7gtEdqIkS+g+1ESEyzqvH8axgWLJcrJBVmzLFZT659\nbK3wko5T6NjqGK12kEx44xHRHQmrPYvOw0YVwh6ZxjWxHWnZosWJUaUckpFjB3nSE9oENS9YSZ9A\nzElaOIYH/FgT2hTXJWQ3W6LRQ5mALKhJVUzgjsiTpCwVJZKSawazYNn5DKsC2S8wc4c/tKgwxreG\neDuR7zzGpOZUVYxehjIhSRuQCYmnIVUL9qNDH2KS1OeAz7idUw4zVLijyEaCNwP+BwFleJtbJ0db\nHHH9HO0+ouzOyYoUESqa54LHt87wL1/QH54we/OQQa05zBQy6lFiTulKrpKBy/hjnp4F5LNnND/5\nCC8euPXVDzHJHOPfY+sczXHF6lizxuc9+4rq0wZvNlEcdqRewmSPHJORH/uP2PYSzjMeR+8z6Iap\nm/OwfcNNXvNlVrI4/oT9ZYVZGOat4F3Rs/dTvKHgVReyZM+j9D2myafYOazfcmkiXncNiz/490la\nAYwkZ5aNhTq+YkxHetlhxZ6p9enCkkPzO/w25P8NJR32/r/FLJR4uaR/4/APE6rrIRP4yiNJDvhk\nnA1bmtpQR3OGWJLkB/oJ5uLINB0YrUSojLJsWZ9NOPOSxLekUpDpiT5rGemxx4j7Q8JW95yd9bRe\nwk21phIH0CljNMeTIUUA8z4mKhsad6L2FZPuwPXI3CKTmmxco2TFOELopdxEjqKcY11JGYaMW40v\nC6YxI+tm9HHAzESsekMUKAY/xC8E8XFGH8UM40ikM7oxpCslvRTIVjDLBUPlgwPjl/TG4pcO60vM\n5JDNHJNYBj/FLjwOcUEsBdafYdITNqvRjcKdLHpREfcSbwanyhJyjawb+uLE0Er8fo+uZ2htKYXD\nzQU6g9YJRjtnSi3BtqQNfW7mLakOKJqAbOdY2Yld3jO1EzpzqF3DIlwjTwPlpsOba6TssGXG3MX4\nRtOKmIYjodey3ZzRH3aYec7cXlOrkj6bMKJjxYHykNBe3nBYWp5vTxTFnr0qiR/u+aKMuWgg+/FT\nyvAus/4x8tyilpb9g3PePT3ExA1XiULzMU+aDV32lC7O8fyR3fEFDAPReEFY/YpzM+fZxc94ucn4\ntP8Z3cuefsoR+oovP3mOfG1IuyveH0oOheX57jZ3P50zzVrKzY77b0bS456Pbr1gfuvEh2PB1XrF\nPKnIY8fO/SXbDdxaJdi8oIqvWRxjSp3w/q37PJt3xM9DjFvx7ntzrsYNcnrIjz79jA/uamxgUQrE\ntWS/3RDqM9wQEI8x+zZDmJZ8CiHKv3dOfyfKAjz+1fgJ03girHy+Xl8Teg67nrBDTzz1jNWAayp2\nzpJkmnb08aaEwayZOnDeipkUOKlQL48UNsHpFT88fEY1rGjjE32xQY2KvoOsiHi5XJPIhENj2NQH\nCmWwK0vpxcyikYXn44893ZllSA3FaU3cLqgbj3YvuMRy6BcMbUepEobep4sFojJUxRHnCYRfkTHg\njQFTYtjPD7QeTCnUOXTFAlU3DGHJoWgosoG0SOiPECc9c9vihpoxWCHURJpGnHxos4k2yEjjBUUs\nCaoVYz8ithZ11Iw3IbPoyL4KcO2OsZtzEh6hDVkEMUo7xkWKZWQK1pzEksnNCZoMUzR06Qzskb0o\nCG2Mv43pojVJlSGiBtnE7OIlUzMhxQKiI8fmhMwjrPMRpUcjBqTnc0wjro5HRG5IzEC9m3Odn/Bz\nyTFJQGXEC4nnZljPJ5ItmTtjHRvGWYTdJSypGWYaZRSDdDz7k3/CcV1wvo5xz2sOt3d8BfzAwLYV\n7LtPMYuR+fI+Oodhctw/fkPSfMMoct5r3nA2fU1+9h3ni4BZ9QTvOidiSarmYJ8SfrMg2D/lwTNI\nnoU8v/MeD+JveLgveby+z+0xR8wUF8/nNMfZr18HB1vsdcIHq4ErT6EezBAR/PJXd4iPt6nSx9xd\nb0lfzFFuxf3rCK9MeH19Rfts5EY5vP4p+bIj/8Vz3n0d8ua9E4fgjCffHFlcCK6Xf0nzcYXUAVL2\naC8mnPnExRYT9fR+z5DCJj9SZzMm4WBf/w2k9HeAQRPd/QNG52O8nOtvvsIVM2xp0KOjXGocijRa\nYtwMD0E8nZCdRsYtZ4uMqrwmcwlh3PAqK9CzFmMM2WzGMLdI1sykYRAKITqG2vLJDzRtCDOT0AQ+\noy9ITxNxpvAvfbabkYQQeRXgpxKRjvSTQ4mAyCqEEtTpCXmYCMMY4QIoJ2bnAd52pM0cURVS+wmx\nhrrz8WJJUrbkY8gUKdoBVmeS695jHnQcTgGZ31IEPnUgGIqOWCcsi5q6VYR9TZKs2W9jVnNwtkUE\nEuf7RPaAJWLpS3bK0u4jMjxOmWQdlBz2BUOxo26XbHrHODWM1iDSmEQ1+J6lnzx6leCNB+IcvLbh\nECUUXkSv34D0KYVGJ+fIxpCS4VRHqxS50Ngxps8lMizYTB1vaksYtSx9jd85dJ0zIXCHMyK/g1mL\n9ENsXyNkgQhCRgSN3eEPBVHSQxsyHWpCodkGa86M479+KthUz7jWHzJ7+IR4lCQ3t5kefoNu4dF2\ng7exNI9TfHng7MOMsvqE4JORh18PvBjgtXiES07kzz2iT18yPr1NTMnmakNTSpofCd7p7vGzd17h\nxpFZ3dM8iHhzKTl/8yW7O/dputs0+cA6EtwpHhDk37H7Lub0XcjGaxnb98imLe/OXpNdn3P07uKW\nl7ywGfdnY63+AAAgAElEQVT7z7l5qFAq5XYtuL7dMe7vcCdqYZmwm43krxx+V5Bd7bmZ1virFfnO\n8a+8+/cp3Q1h7KHGkOpQky9jpApRnSEwO8p+iY47/GbAZup75/R3oiykc9x6cEYwG3CTQI1w3A+E\neUChd8yOoDPDaGAVtbSDgSmlciWuTbHihlwt2Q0e1p447ib6agH2yO7+RHYayXWLOUuJcwhlTBCl\nOHfGamzYdyGZaNHCYHxJfJqoZhMFCl1MaKA71IRtiFecmNQZQRCgbhrSswClF9j2xGzU6NWEvoqw\nqaPWI+Hc4q4azDxiHUxovaa1NTZ0lOENuRdTdh7nYsAOKaEVnCJBrB1qUPiDYBgtZggIQ4iDiFNt\nic4a9mVHQkZ5CEnWO2QZYlaa7XWML/bIsxV9PZFMPlf+QJB1LMIUW0ts0eA8j6SMqHchwzLE9RaD\nIzUKT2o6E9IZwfI04Kkeq2ZsY5iVAYTXNCamXQwE9ZxkCDGTwV/ENM0VSznHRAFi3BL7c4ZTxD5V\n2PkJv/WZTRVD6hj3EenKoJxhJwMWXU/Uj7jzlNmpZO/PSWeWup1zLgP6SXPISv7i+D9SbO8TPnjD\nVWmJ4nfp5ZeIb0LWtieSG754XlG813DnxuI/jjHikl/8UnBxLyC8VLRRRP6wI3hR0hzuMInncO8u\nvXrCza1zvB52345slIeKJ2rrURzusZ0nXN9/n7ttw+LM8vPnEbcON3xxtkF/pdnkRxbyLlcXPcV3\nluHDc15NjqZ9zJ35DPO1wyy/wBs/wnMvKXefc3hnTtz7vG9e83iIKF63nOYrdvIW0cs39KsLovPv\nePPNVzyw7/D79yRqCGnqAk8NREvF8TTghyHhmeXSnJMnlwi7pstGsr+JnP4NnOP7E4rmgWGvMiYT\nEgwtMqgpgiN7App1QOilMFq800gWBGTnoKKAYVUjulvorMfMJOssYwh7RnHAi2b8ncLgexNXYYHb\nag7ScWpbjrOGlYwIhpyEBr0KmBETyAAZlvRBAULTbUfkduI8mBiFhxsikqqGridKFvhCclwYJpui\nREI/SoZYMUUFa3WLeIgRKqTzJJW2NLZjmfp0diLUF/imwzgLxxl6tBg94awhUB5+lTLOJzbCZzHz\ncX1HZSR9MhE0AaKwhKpHrfaYXUigCnwdkZxrxFlItG9Y6BCbjvhViBkvsCqlzmtkmdKWMXU8IGYw\nCY9kmjDrjmYC1fVErUe2rGiCGJsnTEaTuQChO1y7xtmGUDtcM7FPSrzMQTmixIybZGTbd4Qiw+57\n3KwiVB6+NyeJSlo7o/I9gk3IeKyp65zz6wGv/vVemcwOyHDGajhAqcjFiUN3QHk14Snjz/70T3ll\nO5LIMNYW+8s99w85l4+WnB5+xOdOcLZc4PUXfD0GXJUznt2e82kGaurQU4flK3wbo7c+s23HB9pH\n5idGvSY6lYg3r3l19xWBges6o75f8ov3XrAqXnOuD2z7PY+nFcv3M17kM6IXGR9+4lPUA30A1WtJ\n8M4rXjlQ1TVr+ZCzcsbik4Af3L9Pq7+lmtfcGz6mfXKHRZTx6k5Ee9bz5rTn/quRzZnkdqYopopZ\no6jSgKv3cn7wb3xAECRs/GviKUb1C9zSoEdJU1mK3TXTac5GVsh2TjlM3zumvxNlIYTjE+8uM+MT\n+JI/ftIjVMy+9FjJHF/HyGZkzHbcnKecYkdZ9zTjxHwS5IsbgjagCK6QlSHadpg4xjMjz04fMYmY\nxdgwBB7uWBEEK6LEg3jgctbAYkFadXRmjxgGDqEg2Tf4J4sqJGFaUQYLvOxEKGa0c0vWDwxqpL42\nLMYao0q6wEIiyQeL13aUwTVN1+LpCr8+MC8Vi5Pi4IPLgP5ERUqoU8p1x85TjEVKdBOjUkelWlKR\nIc4UW7lHzjMaP2B27KiDiXRn2IczzEkzzWNC2dPSM5kS70pysgWDsdQ2wtcDdjRMlycyf2CIFGZW\no4YV0pTMdnva1URxmRNMli5ZMHoVni4wKeynPYEnKZXBhRZWE7PpDEdKPqvJxYpyUjTGJ5GSgBFp\nFNNsQPo9MQmJPRLpHadpTTjfIW4qhqanns7wheImtFRzj7GWlMw5lQ1Tu0SrDhVdkIc5IjP0acn+\n5ycWtxLKZx6JfsTq3p6bWcJFmbO/UiynHaV7jVd9SxbPKd73sN9+zReLE+lwzS2z4fbtgejzb3j9\nUcqbYUG9ipg3Ne7S574IsPOPMU1MYc+I46/4sEuRB59qUiyPPd1pxaOr5+hholpv8MxT1Fbz6m5B\n2lbc6TxevT5w8dWMu8m7jNk1x3WDUrf55fGG5N5d6D9Cec+4P12hG8G9pwb/5jaPXMi4Ocf/7nO+\nnAzP1k95Ng5E4Zo137Be/OsY59F0t5ChQ5trNvsFs5klMpqgSOkTn6byGCPLWfD91xa/E2VhnWN/\nE+PXB9ypZd+/QStLPgqYDKbdMaJRBwWtI+s9/FiT5BtKlYLv4UzE0J6x9zrc6uckB4XLSz5NJobC\nUvkKIXpckDHpPX/w4A+xZULRhnj6SMsZ/SIkLDxW3cjo9exyRV4t0cmcqNqTTHOyqee8DxliibKK\nYp0hWkOcL3BBg1c5VKxxWYA+hiwmiYwMbr5C25SdHdGdj9n15JHA6pg+OaEOAYXXkBxqjBowLiFT\nBuEM7mpgLRdUjWZxDFCJx4olrVrgNz2qiFhpy1H6RM4jr5Z0IsdXIMUR1c/oREFeHLHnMdvpDJlI\nFgfJ3FjE5HN0E+FuZPQNgdgT25HRxbRDhxtrlj30vUHFgl1mCCbHca3odxHakySdI4sG4vk1cuiw\n9ZzISOzREHvAKeEQZjR9wMVQM8mAILxAlo4z1xJELcnUwCFAeyGRtsRy4KT3yNzQHTXSq5htC+ZB\nTjZMxC8iJO+wXj2jUTPC0w3jQnDPerizlnQzY1el3B1Tvt11eMt7XFx9yLfVe3ztMpL9OW2sudNE\n3PqBo2l3RHqFzZ9zuLzFR/pr5vkDniUnJiWZXr/mPWeIug3PixDOn3O41TLsHfJ4w/m9B/TFjyjq\nA7uLCO7GeHGE/NRyUl8SjnNuGsHL3YGIBdvOoq9fklwEvDq/x5V6RVvcJV/ATo48sUe2i4BH7TXF\nq4zlSnAuX/LFV3dIw4C63qL9S/buimCRcpUdEbuSIbM0HWTTiUG1pPsBO3z/HZy/E2UhnceYnCid\nQqwt8SHGRJpKNphVR7Q4o8mXmHlMELY0cUBXrvDKFofGswOtrFhOl3ix5enre6jsSHXw0LOB9Vgx\nm1lMCYnYkxvIkgHfN1RO4mKJLCaiQ4BSATcFTMIRW0N/pulGhV6l6GlA+z3HTuEFmik+Io6GNp3h\nTyUJKaM0XHWOphfM4xBHjK8Fg1UYYB7kBElNUCRUrf31btHOoG1JcLKMm5hFkDJdXSG1hztJxCzm\ncOxhKrFJR+k0/b4mE47CnQi7ESU7ZkLiHwts5mAGY2A4SUckHNEiIC4XeNWAHCyBadiPhlJp3CgI\n05AqnxNbRZctqOYNmYYg9bC+/vU/ewURwQR5bbHNkay1FEmPcTEEAqdGdHlOnwjiccAEA0EUYfv/\nk7s329XsWPL7frlyzeM3771rriKL5CHP1G0DBiwZgtCyL3xjv4Few4/g19ATGL4wIHRDF4b7Spb7\nnMOZrCJrrr33N695zExfkBZsQFbDTRg66LjJyMyVcfcPRMbKiH/AOFMI60Q02BRBRd/V9PGAyjTG\nUhxsh0G72K5DZhpkLiiVS7iReIOFWpSMOuU2OHFwHE53Rlz/HdP5c26se0QvBK9LwfPCp1oe8N61\n3NwY1pngWlfcm96QX0jsh5rIfo01O/DsnLAJP+T6tuXzLwfmp9/iBiDMr5myW77UgvMbl+nRGd07\nVJ/Oaa01a3HLQ9twp/zPKKIZq3rLnQcb+uNrXn73Dakz4+K7iut2z6Kted5+wfZFBkvFk0OL01Rc\nzVPSlw0fXnm87u9SNzcU2UC51BzfnEnvWtxf9Cx0T/DgLrV/yfFrj/fikk8jC+wOO4mQcxc/9rBz\n8GyPU+TgHyRxZ+HpBVEyw0Qdtbv55Tj95VD/5WIsxSId0VPIvh24Lf9ESECyyGiUoc8n/KbB63Li\nKSDd5SwygzuvcFyH87QiyBxqe43dgH0YaQfJzA45L57S2z6HeoRhS2cvaDKPoP+UOjGk40SXjyQn\nlzEZONmGdPSwnRlj3mMdNJM/4Tc2duoyNiND4pJXIeF+AlMz2BVSJ6haMxHgxyHeJDi3NVvPZnRD\nbN3Qyh39rCLcRbSOhAWUsaZ017jeAltLnDpnmAzqckmbwJQm3AwjC8smDVYEYYfvSSZtGNOKnYgI\n4hDddkhH4BmFsGsmUxJ5OSpaYewKS7aoixbTaIwlOAwu9iwjczxm7sDgSIJ+YC8nwskh7ELKUHLS\nAVbv04UJ8cJj0pIpWFJGVwi3YsDFjBXbZqSRHirRqGkg0AMqsokHh1M8UJUOTn9BIGyCEuaWYKk9\nYu1TLgTi3DHzFMovKTqBijoib4FX+ZSWZrkbQDbMh0uCbmT0Wo75gpUN1ovXHMxI4j9g+eMXlGmP\nq++xCW5gW7G9stitn/LJC4+bl1+waR7iT/ex1xHfb0bKjwYexEucRc1NfsPhruKy8UiPEZIvSb97\nwicXIXe+bFly4O2ywylnLPgW8/mJahmTfdmR5x/wof2U72cxlb/g0cpDzz7jM3mX+w8nknIFuqW6\nt+H264byg3fkRUidlbQb6N+79PuRX8k14pXkpr5H6yxR1++Y1key5ZFV43OKnxFWDqn2ka0g1SFD\nFDG6Eysx0q0M2g84xXvM4UwTDrjOP5LIQo2a836Fvc5ZNy7jcYko4XyGTvWkVo1rK2bpCqMShmCO\nmnpOts9Ya/RxQJ1cqkExBUt2j/+OLIshFMQPt9hthN+ntHvBqqyglzz8Jy3+3kZZhlj6FLJjjkN2\njjjpCI8B27HQyuKylRwsh9uDTet7+E2F3XXsswi5gHmhodlz0LCeHKyyovZKFnpOqM80do2oKxI7\nwx4Mx2UHucLsEtaNwLXVT7mSwMbpU0RaQmehiWGCjI7aOGgK2rNFrxP6tUd1DljHNae2Y+trtgdN\n6VnIfk7gJTRVgjwUNEVLpCXDNiJfJiy5ActHlgG2qjFmjqckjYqYOS0FmrJLmNsF7rjFND6+7zEM\nE0HRwLGgP7ach4QhqhnKBaFl0W81preI9YKj3xOXFqVTsfBXLOSEbwv62Ma1EqSdoq2cSdaYpiKM\nY7ZhhtMsCYOapDRUEvajh3XScGUzFB6Ts0edfZziL4g+e0Wx+pTJdXj4+5BxETPLBE/e38PcH1Cv\nW2r/Pr85rwiPz3juFnw0SoZNQ/x04IPFl3Qv5lx0Bfvljnrzmm7/a+48e8b3k2Y9i1ksVhx+U/Fm\nd4cpi6m2DuvyMdwKXk41V1cG6+2cP/xGc7r7Ff1s5Pc3LbfZkbf4TOYVSh85vYh4ucx5+eQBwzBy\n+fFL1jcJN9XIo9dLNtcBS9eG3mb7wSsWjx4QpDX1aNE9Ely+OjL2Vzjjln76mNrx6FuDfR4Z8x63\nPqHPMV0UYIsVKjUEWuPNZ9RnB3Wb/WKc/lk4C9t2WIqctF1TuBPzYKC3BZE4s7Q1RqXkzOjOJaaf\nqPqO07HnUobMugaFh+UIEtdGNwey6QIpS/rR8OniKQenZFja/JB1jCYFBOJ2xmQJrEhQRx2OaTnq\nAS8pmLmaydO0rgCnpvQKUnHgYlMx9wYmJbAtSWQrqgNcrzVmEaMiwW1ioaKR1TSC2JOpAUvOCOwY\n1XUoCXrwCCaBHR050GH6M54psAYfL7YRVc/Mk6S9zaAbtDPiiAOqNchsga1G5N5lhs9tbhOGikCs\nsDYj3uzEcBoJbw/Etiabj6wWKQfhEWQ3uKbDEjEMCmtRoYVi6hssb0DqjhJBmrc405mDEfQ6JJ51\n6HyH0x+Q8YiPRlxYGOcW0Qj8iwGXM7PliK1H9taRzFxQOh6RWTEOBadQMbYVfeNydC3KxsIyLVbr\n4LUOQVWQKQsT7gidDbdxhKduuYx6gsBAF9JENr5Y08trHqj3BMVHdGLkk6sNeW2oki95r57STC1N\neeaO/JTq4i3fXO+YXTp8cG9Hnq1onTOnd9/xcnoMoeK4v8vD7QK8z7D0gepJQMqOV8f33O3mLF6W\nFKv3XN8fkU/u4739gvbxLfqc0HkWIr7ld9cOjw73uLm9oRbwwf6S4e2B7ibhdX3B3Ar54OvXyPzE\nx6+u6W8/5bn2+eTpgnz2FfV8h7ta8nFww/jdR1hWjXsr6Us4vF0wyxbc7za49YbHd96RdiU63KHD\nGOV0FH0A7YTTD1g7gZBHxmlG2XaIYaSI/5FEFpOaGFX4Uz2FTpiaE7E+YA0uB5Ow7w6kWDhOhkAS\nLXvccMZOV4yWx2ohaHWDrDQyimmrnlEF+EWD935JeF6wuD3w4nVNHdUEYYTzV3MsndOKM64x2KGP\nKxWFMNTSIZU9yzGkH0amIsJtPYaD5mgCIl8SLl3yQ49jOuJ9xql38N0WdwuTTjlOASZ0KB2J6SZc\nM+GEIXqCjdNTXmgcX6O8Eel6nGch06qhaxzcUHDOz/S657JxifqI0t6gZcTBFESOJtlobNcgxpG4\ndFFOzeKkqaYIG8n5ckXrnnGnmFpB2I905YyoNHRWhG3neMeRofTxLlq6McZybPxWMaoJfIU7CLKz\nh9tpXNdnsuYctcBbCoLKsCDEczT1YKjjOU5voUYFU8pZnLFliehb6tpFnx1iv2PwCsK4hqymOYRU\nWUDHgsleYtSZovKpleHCzXF0yFlO1FnCtvNJHaisI92PI+9sw3b7DO/oYYIQ3sZkbsbjey85zJ9z\nES34wXmGrxWPPna5vhZ813zG0LtcbEMy7ze47UjQKZ7YGnXnS97dWIybM/m1obyymQKfm1mLs4LL\nfcXuZUIuX1L+6jO+fzUjuYIp/xSGO7ya78iaGeITyXt2/HjV81HnU9Y3fPSqwLlwiOP76IsQ0T1F\ndi8x2nBoTjTLu2RuT5hbbLNHFJuCyUyc9AueXChKa8V+3+NcvOTdb2eo5xt84SHaObljY6wZyUKA\n7aIqhZ9UVFPAWELvdsw3PnL8RxJZOEYwRC4jAzLxIUnprYQu0aRdBYsRR2razsaJOsZckAU9qkkI\nrJADE6QD+VwjbzuOJqeyQhqZMZ8PaOdIyYz6/ANZ3jLlB/5L+zMCE5DaC9QxQJket5wzHeak0xFx\nHLh1R3QsiKOOKoxwHIPdRkydwZxL1pZPELoEQU7gnvB7j/Fyx0KdmXkhBwUmDpAypAwEZmgwSqGN\nw7rtqHcGJ98g7Aa3mAjPCZXuGboFKIndCxBHjl2L0iN6mpij2VsW09AzNQdc54LRGvFyw36pcO2C\nKbQwzUh4sqjaM3gdynM5+wMqU0y2JnY8lOvShGByG22fCcVElWQ4S02LIg48lGM4CA+MTy96NlbP\n/mxIZM5BRPh2xLIWiErRjzMGqwOnQhiBa0ZOMczTEeSWbsyIIg/VZbAz1J5HKCus2Ykci0HF+MKh\ntSZOVsrka0YrxGwL5naL1Tdk3Zy/3v1vzCuFuHfJy6fvsd6Cc7UjkZJpuCCPIv6kz2RiIN8Lumc3\n1EvFZ8UPVE8jbh613Nwc2YgFd7rveFO/Jugkcf1HLr37bK4u2cQr1GXETbAnOGS0VxmXzXtGObK7\nfcls1pMun6IXHfriDUN/ZGh/pNt6VPklj7TDV+6Zzx7/hrMwfPsm5KW7Z/F+5Hb2Ct+3+bSq8d2a\nzj4jug3V9TXe8IZgfc3bds5vFyE3XU48lVQf3mV8d5eH5TX3/tlfQebSWTZhf6TzFbkGdzFhkoC2\nmRjtEhHauNqCsscM6hfj9Bc5CyHESyHEF0KIPwoh/t3PawshxN8IIZ79PM7/PjvGMvTBFns/0dlH\nCnFARRGmhaNcsZnuUFUTwypH1JpGz6lUjtQ+u67HKwzjlCAal2Ke4H8z4e1HAkuznUpcBnq/56pb\nstUOoxtxFk+5ESXVoWSUhjGf8Ja3SO+W9hhzjiOCyWMW2OSiQuWKtjPECmTqc3TX9IlL4wYc/InA\nLPCqkkxsKIWk9krSpGfaCma6Q9Ueh7Elqh3GQrKtFlibGOVO6G1I4Hd4cc1M+7hui6cMUyzRak64\n8FjaAiMTRulxcSrpholRWDh2hfFd/CAibkLE2eLk3bAeGvapSzUGxJYm2oFPjCkNbTNQjIIyCYjC\nA0aMxMahTT2cqUVK8CMf65Sj9ZmZY2iqM65v0LWFmbucQsO8ErRacewVM2xad8TXKanQJHrA8xIk\nDkdtE8gr+janMqAmRbSYs7Y8VDERDSkELd2wxw5ykqIhbY5MtU9U5cx9MLVLrRLKrObdvoblQ9bt\nwNK6pemP3LwtSfY79i88Pnzb8vSQYD16zOOPDNaTS6JWsG1dzLN3eNcJH25c7Dc/8Mo2hP6Gnb/k\nw+VTVqtr3NuA8kVEUrdcoIisgXuzM93HAfuXKwLOdF3F99+8QZqOcXZiVinKzMXYNpFSvHnTkvKQ\nQTYcQs1H05b6qDjNNDIPCI1F/7TjrbXA/Fgi94bg4RU3h5r4x7vcHd5R1x9yb3/B2pM8CAyV49A/\nq7j6VYjqdiTRGTO4yPzM2CiCUjKZGD3ZZN0Cr28RvkD4S5zkz6NE/Z8bY35vjPnPf57/D8C/McY8\nBf7Nz/P/qAhp4csEaRTWKJFThB53TMolcQyFn+OMLYqOPIELWxOYC+40OzI6PO9E2BuCbMu823HK\nJK1psKwaIh8zc9jMLL6erjELjedM/Bcf5FwuFX4mSRNFGmmGk0MjMrSf05YNylgIFeGVgtR2EHFE\n7W8RPoxRQ2Ea/GLClx5iUtRMHNuGYVoSlx5ec4FtO6hhghiyKKFMLHwliSaHsChJrBZDQ215nM8j\nXTJywMJdOXT+HuHUMKb0vcDNGqai47DZoH2NcD36TmHRkQtF6Cnq2Cc9euzsDHsSbNKesVeMpqZt\nD/QmIVIVenDA9JjhgkoF1KNhUBUzOXI4C8LapnfnaNuh6zSdHcK2pV5KIkuS7gJkdqRtOha2gFTj\nCwdBTeOk1IOg304EB5u0GHCEYphp4snH1RKr3jIkB4S0qPwTq2FgFVlUzgJ36dC4DqOo8AcLEzuc\nLZtF1KHGke/++m8JTgU/3p1x548LvA8GLqwV7ekKtGAoV/TeGncIOTzbUPghKrSw9IGN1+KFM+zt\nia/cu3wwBlQXCe9vZxwjj/d/HOiikfsXe0rZkR9cfrjr8s3fPcTXPvPlkbYUaG/JU12Qs2f8fkNa\n/IqiETjzgrt2T/iXO8TiyPT2lurxfcS9is9+Z1jmMdX6RFVc8Tb8DPmVjf3Y540MEN2RcPqA9R3N\nqyqmf/0l7bjG3wQ4715zuvec4+JD/vnyIw5CMuQuvjsj8Fx8JMFU09cHuk2I8h3kusYb50jXJvOP\nvxjo/39cQ/474F/9rP8r4L//+w5Mk6Y7KTy5Yel2zNoKqUKshaFrFe6tR58lrOolkejY2zm1teX6\nYkG+iSl0St7t8Yo52o5oX9T4i4TR89i4AbWxqHeavvoTAov63DHwG4YiJRAxk3I4djYm9LkwPZGK\nEdonbRWyLsCzKUyF9CZcYzHe7kH1XEwJuyHEVhkm10Qzj6AZ2IiS1vKQZocbNZxCRTrYGNfB9nOI\nRtrNjtZ30E1NupqTuAl2GJG4ClUMWLuBoFtw4/c0g8DN9ownBzVGBNsRMQT4fUuWaKwxxUhBV07E\noqRhIhNnosGl7jYUwwq5EayTOarXNJ7FMujZSBc97LEyjQzmJHXGLnRxdcK+rih9j24WYuKWWWSh\nLiUuiqmESVkIuWSTjDROw25vsPwzfiRQrWBmNGXgo9Y5Ym7BlBPKDaK+ZcChFDacBC0pSi8Y3RkT\na3xzotuO+MZjvvQYlY+NSyq2tL1FGjj84X//Er97x+nHE42V80auaVY1iZux3pzZOjXa+ROvX49c\nZA2zz6F37uNnC05rhXK2VE4F9Tu+/1hi72oeZjva5wJrc4+seM7Xb23u5h3p3Ed1Hp980iG+irBL\nReM+5qPaY/pghRM8QD/eUqx+5FK6LG4UcqxoD/e4v+sp+wHx8hVOOePt9gk3F++oNOStZPzhHReR\nJGCOv97TzDxO4h2WsjCJRb16Qvy777n+YcdzHjLPB1L1Dv+//WfMpEUvJ2pZ43QjkVtQWxJbS9xq\nQJUTQ7HA70ZGc4T+P32nLAP8tRDi//iZYQzgwhhz/bN+A1z8vUYsm83MovbOHI4zCssmaEpCJYn9\nAbPscUaLPDogMCgd0VcWafEWd1uxtEc8taBzJE2rWH1gIUVO4VtMJ4VGE6wn+nJLVkWsozUPs47z\nGFBXNZOReHKBKgW3xBx7j3kgmOyRoTW4UjGmIdZU0TcOlZeSVT5bLNbrI25es0dw8AKcQXPjCdJh\nYNQJruexGRyUJzjbJ+qDyyEsEFubvo/o8DkNmhuR41gavWu5CB36yNC7NRdiQxh1FLcXTEGOmQRT\nMpIJyFVEWQtUpUmNoclGjE5YZQoXhyaxmJY1li5ohaJUPbN5je8knJqUYnukDSFsB0yeo21NdjY4\nQ4mzWiHzW8S5xzQB/QT0IU5lQWBxXtucVcW2SbGDFOeqoS9c+tYwMyf28xCMTa87unPPeekQHnOq\nYI69NERKoOYaq9/ia0U/gOhPeMZQ0iFVzmAiOhRKuAglcaeB22HCmhrGxx9gpQ7WrxOab99i3ZZY\n4Q6WG+xYs0g/Qy5b9KHC//QlD4Mjye0M9AdEhwvqzmMhMh5bd5CRItP3KT6qMPLAzb0L0iuBebJk\ncS64G3WM1z3WQwd5yIhrhynxubYzZgcXf/9bNuYu5tHAfBGjrzIugldsLyf6WcQ8WtPJHP1ekTif\nsDr5nO//gVV7wbJ7Q73N6OuGeXXgt47k1WuX8m5BPrziD9Mj9K98PpENZbCGK8m/yFY0Omb059DV\nGP0g8fYAACAASURBVJmwQxDRY0URo62x7AnCI+ehxm4CRvnLE5y/tOr0nxpj3gkhNsDfCCG+/b9v\nGmOMEOI/SNP+/6AvvP+AcudD5OOIETm69LOMqfYxQuPKAakMwXbN0K7wVM187nAUPms7Zag00dzD\nMVuCaMl37w3lKeQqNhRpT8JPbwq++y5Hq5Z6qthZMLNukVHEzquQ7si6GfGdgWFwKNMOr1phpyNG\nWKyKDitLaGclgfbo3QYOkqoLIXB+Ii/aSTqREI4O2t9xUBvSvKCLLLzhzCUJ+7XDrBmpFjni5OP7\nCZ5z5KQVExN6luG2I55JkG1PtyqQBwclemZ+wmBruq7jPEqEI0n9nmEMqZyJ7BRQio7z4DCzWqLE\n5tx4eLZPqxoi22YqBcOqZD7N6K0FgegRCiCkmzSuY9NdBEz7GkcuEDRYVkQX1yxuHXof+nPHhddy\njlYshxyY4R9ybmIXXwh6C5w+QA019hBTpjGumZicniR3kKakygLkyeC5FU3jYhYTkTXDxaIJbxmN\nxLEmgosIc3tmWiyp8xvcg8vr/Qv8+V/y8SFHBlf4d0vK4mOs8jvO3TMWd+7yot7zUXNmuP8A+ezI\nD3HAY9mz2eVUjyLKrx9jlobmy7dki/t8ZX3FkxtFV/2aQrxnGd7Hf73kpTEE3Z+o3TmB/5bjJzOE\nyrHajHR8y02kEfGMaW84nn28VcLOrXDdjOX3S9KPa17sb4nXAy/uPcHNP8dbfEJaOxSXOxrTsN7u\n2F84vPXvkG4i7osDP36b0jl7fvv9kRefDLw/aGR3B/3oNb3fM/oNgZFk64RG+Sythr4NCJqK2p2j\nUo0xGmfuIEqPIfrl/Sx+UWRhjHn387gF/id+Yk+/FUJcAfw8bv9fzv57+sLNYo6KT7R5S28rLDdl\nPDm0Vs2s7zhuA8q0p/N7Kl3im4htOXA5ZLT2gG1NmGagLgVTeUA/P+HMPcagJPUi3JPHwdbcFDGt\nmVNkAV4tsE3G+QxhkZGcYYhnnExHlVREzZxxNOz7jvZ05BiW1MVAgsEeLMSwghjwW4LagJDEmcZe\nukSDIp8SLuQOyzbEY8kwDlQiwNQVY+2g2guyjUOtLfJ9ij2EuHWEozr6RDJGCtt16aoUuVAs05L2\n5CFzh1Ta6KXF6AuaSaLcM4t2YogVzAM8fG7nMf0YceGVxNURz/JoG4FlLMTtkhMWujtRFCFd6hFz\ngzZHHGzsYiCVFk5gI4WD8DXT3mJcCtwOrKXmpp2TtCO1NLTtxOHygnnn4kQe/rBGTGdWGOzEITzf\n4Jxr8lTiRh0jPa7RyFgw9R6GCascufWP6EYz6yNMZSFvJdvtxHmd4Fg3pMsV+IKnH6bcOXxD/2RJ\n8L3kSrqsb19zXNisjg8Yph1XVsnx3oZJab6PT9gPX1JKn9PkEpRHHs2+xSkki88eoerP0fbHTBcp\ns3tfkAnF8eVL/pR/S375PZv3LpVs0NZTPutXXPQ50rnl8Cxklnjc+8FljDzuriqabwbEUOOIkuOd\nHV+82eKWitd2SpLDQ/cJob2ntyZWgcXm+inFuODxxufO64Dq1Y+4zYwPlw1XVyF2cKT64szVWLMI\nn3EWM+osIDt4qNNItRuwh5bjCYpFx07FLIMRUe7I9ga9t+j8kSn/JUj/Sf7BzkIIEQkhkv9LB/4b\n4Et+oin8lz9/9i+B//nvtyYRYYz2R2LbxlQFna6ZBYLbsUd+1DEVAuUPzCdFHlg4OuA0cwnGBpOe\nkUzIpUXhGhayQhVb5E1ELRRTcCCsCnpdsTAVlqgJMp9+1SLikaEf6JMQ0dXMuw2zcoY3SUItSW1F\n5MwRxYIaC9O7qKSlbwuSqUQ5HlaqcNRIrmsidWCPYe52TCIm1x0iWmAHc4a+wZcddnbCDHtUYZHO\nc2J7pGo0o29wu5DKNDRG0bcHgqnlrByOniR0z7ScQY+MB8PC+NRqjZpSjjLDPrlEGCanYJ1PJJ3F\npH2s6IpeuEx9yGEZY6c3ZPSUK4WYDFE5kg+SzjIcaoc4AXsqidsTYubRSbBWhrEfKAKDj4uzadBC\n0loTgdeQbRu6SdD0PZ2skJlPRYmuBoxZomeK4NzQBhbhZk4+uVRNiBMojLsnniT+rc1ufqZOS1rL\nQQZblrpD9jl96WIri6UN+2+W2NuA9s0tJAXvBwu5ususyGgCBd9f8swWzP5gEPntTzyo+Ry5cjCX\nK6xhzvNQEZtv8X4YuR0vWdyOvBYj18Wc7P2MK5PB7x/y4ctLns8c7heaB9df8OLdD+z9gLfP1nz0\nscL6ccnzBw69Gui+tNFXBVd2xoNRoev7PInvMkvuw+dHlvuC3ZuG0/uChw8GXh0Ez+a3PI1f8INa\n8EP9kge/v6S7Y2jWOc6LGX8IL/nsd0v+9JtPednbxM0R9+SRrzzU4oIqNTR2R7JaoW8XyFlDVVb0\nvkexEoTeT7/PI/Gflr7wAvhbIcSfgH8L/C/GmH8N/I/Afy2EeAb8i5/n/1FRgNvaPMhmFKpEuhaR\nM6CqmPlFzIfJFaG2aKyRXTrHKd8RRjFBnnLrufTTml1rk08RG2nh379lLUIKu2A42Th9QGnPGE8D\nt7HGLQJaNdCcLSJXoCKBY++wHJ8ittDSpozO9DTASKdK4nnNhW8xypT43LNybEJxAXrgjEW7Dwjt\nBWdvxCwVVTOiRUvo2hRa4A8tQdjiTyGnbsbcmahFxbkdGBKH+SJBhx3tJFhbirld0m5meJGNnfck\neYY1xIxLxckzrFcBhSNgZkjFSHAGOT9S7xrGwKOd9TTBAXNokfKI2J2wLyvsQ0toe5xi8OWMhduS\nRwVz6ZMpg4PivId8YyP6GdkoiGqN1hNl5RFGHtMoiYSgsI+oQXKIDbYs0baFMgqhFGrXYWVLEmPD\ncsI+jIyziRjNSRi07JknHRYhsXuBnue4yxnLE3R4uEJQ+g7dhSIJBLGzoJhKhmqOmy0JgwVXdwO+\nqSNWhxBz55ZivWAZK9JU4AZzzCOP0HH48EvFQy9m3VrceVNiHxqsZEEbT+Tx12SLE8tsgusaL1xx\nvdzx/adbkuMr7EzysXpAbCb+eGdO2wrG4Q6984biJcwWirtWy23f0Fl3uZ/NuHEyirdPeVj9kXL7\nkr5u6eKQrO04Lk58cOcB+R+e8ReT4dPyHiq7wHyj+ThcYl5pTtPA4flvmNwFWVezax0+/bamfWRj\nLlvSqGTTtATqTODE2CdFd92CV6PP0U9Xj9OApWf0dkw0bMjTX96D8x+cszDG/Aj87j+wfgD+6v+b\nMYVbdoTyL1g0f4vRA44OmbqGoSsIAwtP2USjjZ/nzD2XU3vLPSGoHbD6M9HSJdINU2PIn2sKVzLa\nC9au5qYfuFgeiL7YkvUtzBZ0bkFmNohC4QQTrclwm4b5qDlrg9ERetHg53PKrMM5SXoakmVFPs0Q\no4/Jtrh1SMtAf5GDsfBJiJoS4zqM7gTKQlc9thei6zNlr1m7gia7wDtskZmPNTlM+4qMmHNsYxUp\nMvWZVS153JIGNmLqOEUxF/2S666ls0/EnQVFyG7lE7c5qrYJdIY9VFSlIV0pcnWBavZYS5jONuuo\ngjbANT7x6UzuxFDPOYqehRcSWQKV1Fg3a8arLVYZUbgFolmwWVcc8hgZVYzFhBlDbFcwHUbqOCRp\nekY3o+lOWGlAdK6wfInbdfTSRh8lp0WAPo9chTVTK5CeQMkcu5yj5A32YP/UHCjqCO2R5iA5pwJL\nliRlyPayx7/zDa+rjlHGLNcD/vVzfqwuuMjf0aQ+4v0b5FeP+cJ7y93kYy5m8PW7M0v/llN85HEu\nGX5o+JVcMJwdrhd7pscNso0Yvtlx706C91wzLRq+P/swe8ukA+58rZjTs23fcOdegn7vUk1zii+/\np//A5dbdMz3PuLz7PfriLm/s39KfX7Mst9jNY75Y/cCjRrB1XxD9+mM+v3GYuR0cay6e3uGVa/Nw\n+Bbzao63zojlaxZuyg/vNFf3Y9zmRPTuCbfViO1IlmVAPbdxZIRRA0Pg4icdLgZ36XHuK2xPMDmK\nVev+Q6H+7+XPoq2edCxKVfPpnRM/7hwCEVFMLY6IwKzx098iVv+aThlMHKFsycwe+NZ+heVKqmJC\nNpqTckl1yOfNRF/1pH4B2Iily1l1HBcK9c7F72z8IaBvG0Y94jEgz2Apl9aeiFYrFA1+o5mSBltl\nuJsdeSmw2gDpnxktmE02pXRxgxp3WDBJCLXFMPWoeY8gRTcFJvRRk6SzwPgp5+mAPywRa5+yTLDj\nijCNqO0Dbi+osgaZ/0QhkCifIVRYuw4v6yiMR5oJzLRgCHscR2AKSUjEFFUc4yPzwjAPFGZw0bYm\nHFPGzoLJ5uQGWK1B2BVlEIMZSFof5hMdLk64J9jG7PwK1axJRAe1RzzZHEyKHCZCZbAWCZYSGH1E\nhBFgIdwBbxyRjvtzrQa4zQQWpJaFGCVT1yJCj+M5Ri1GZAHR5DNRIhYRLT1FaRNMI1L7yKVD1Fkg\nc05BT/hv3+JEn+LYX+C+sxl6ze3Fp8wdwzA6OLMd1iHm4eWO4+hws2/wnh7o6oL37x/BbM/7O/f4\n3ecHvv9Q8bQ33BnWvL+ZSGMXee+Kd2+/YfmhjX1Yk2YlF8E97F3LrWz5XMz5/TDyZt0j5g7Z9hbj\nuMx2D1k+nuA08C67IP7uBQ/VnNMQ0mUV8uP3rMsPOds1gxXgVIrL9GtM9JC6vyJ48Zyr+wHffvdb\n/Lni8XjgRTfyNJmzfnDm6/YrHhf3GMK7eIliaCUHuyFVFZ3nMQ0zlqXitLKYHQZGc0LEkim3cLKO\n3Ba/GKd/Fs+9zWjBPCNb/FOML7E6m2yhiWctw+JAdegxRjCVNmpoafTIfqrxfv2QqT6TbmKkNzLK\nI/XU0sZ7gvmAn/ncxAV2FRMfU87v3hA6gqY90GsPZ2YxrufoPsFyLDoZE8gIPewRjc3UaFwJ3tRy\nPs0JHAmVg2pXxCrg2Iy4omVUIWNrM9QVuZnI/RSdp1g3PkGbEImSvbunGVMWvaGbSSpvh71VXLpH\nxJQwWgrn8FOnqemUoWMbz59xmgLsIaFYGNzGIu0kwV4wWQ6u6bGHkKVXUKZnLOWwkAsKy2OSFqfW\nx24Unn8mGAdw9pgSlAbbkVjaYSZaLDeny2PqqkecPGpvIktt5LSDoePCWNS2xE32eHONiiVjXzHa\nhuC8ZDQDjZ44WgGCgHbIMFaC5WoGMlQv2JmEk68YnY7j0WCbHs4xsdS0cUGloB8ixJAhA0PshlyP\nE3JbIIXLQXqkluF/nb4gf6VIkphMCGJLITffUuiRTHfYX0quWwvndsZtOyd4WLF/6/H74wopbX6r\nDI9eCt4vrnj4wvCynFHYmqU4c24u2LYOzu+vOBuXo51yeXbQL37kEGZcPDoQ311yuwzZWBXlVwOy\nVgSDy9n+iuuvJS/SiKf5LfH9e3w5CvRv1hzLT1m5AaHl8UC+5VGrGVyHY/Nr6sJjyVfsVxGOPnOV\nHfFcm9fHPePFfV4eck5fDyx+gB/FG/7Jf2VhZMgiBc84WKcMt41Il4q9qZm1Zw5SUSsbMTkEc0ml\nYmT7y3H6Z+EsLEdhuTlWusHCYnBLJjVnlBlhEfIhDzj3HvboEsmYaZhwjx72jxZDukLnOVbVIeMA\ngc+yWSNOHugOU3lkQqOslrNJqJOB2NhIPeHUFVahGVXIORHUsc1Z24xyRiMqTtma4xBgAofEWEzS\nI5ISmSnUmKBGm3LKUGeFZbU4qmesWoKgoVIF2u44hy2WNUfsbRaxQesCq/dgCiiNZFtIRL+nwaK+\nmBMNBXIcUcLQljdI70hhCmRu4ZqI/TCwn5X49S0nZ04ZV6B9Il8w1RWlpRlVTNsm2IGDkA61ClCi\nZhojUvsWvSrx9x2BC12sEIEhmE9kRmGbCScJEKeaYPCRk0BIH8+cUUdF3ZTIXOGNKVnZU81tFn2G\nbjUil+SyQHs5oVMhBs2QVBh7yULbzJMWu7YI/Ql745HMzrS+wip8XOaIQGGpCRjoUp/UuOjEpXLP\nJIPDGCz4d3/zd4THa5o/Kp7ftVFVxeK4YPVesps6Wsth0A3dWvC4aei/3TC/nHFbGBJb8yfnEqVL\n7p1iTiojtp/zdlrww/QZM8/BX31JlEecrn3c4Br3kzOHmUbyLX8qNjyMDNH5zPcvHuB9Igm6E3Ox\nYeH8iuHJFzx69y3b7SPef3vg93cHovMLHv+q4LDTbPcNYhEg70x47x0+nAueYMNkWAcuhzoi+sDQ\n7C2mJwHmTw2OM6E/6QkfPuHu04g7955gkyD2HroDDNjrjvPtmZUFtT0gFwHhYsEqdOmmhmWnoPlH\nwqI+jYKgXxJ/+pZBWASVIhwMpaWQvo3zK0loamIXnHaPG7lMbkukX+EdDDJZkk8dRrYkly75tkdb\nPreNzdKZOIYd4+hjRE/aLBnnPZaWWNmcRAqsbE882SyHE/PZkaTv8LoZl71mqUe6U432DK3Vcw4G\n1KDo04JZEpKF14i0Jgkd5LBmLlz0oBHKJ9AebptRHTSLixDpGE7axYgQ2YZEsxARzQhti0COZNQU\nZPhBhW2VsJaoBubnnpnjUnslOrGYE9FbkvhWI/YRuSk5mhGpLGS9I80qkknTlSds1RJ6I2HqkvmK\nzg7JjobKtrDsHfak2akJfRyRk6a0UvpjjXB8gjTG0zHlrCXSEdN4QaottC2ouwrR+FjTiZO3Z93E\nZKpDiwRlzxB9hO24eHrCH3JqP0eXCc1gMzFiE+A1MI4ZziylFztMV9IZB09KunrAXwiaCeZtgpaG\nrha0z0r47ZqF6ngwVqS/usvenVHcf4G/VnTSw8s8gldbfvhwT+gciPQesV7xIKiJZcXX85Q/Pvmc\n052MTj7mw+kVH4x/xHr3DP/692yTntiVVNNIecxpFwuuq6e4zZE38h1peAe/q0mLOV+tZ4RWj7vY\n8lH3CUezYJP8yDKxOby9z7nqabREtxlZ/Bp5iPlezunlN3z53OGr5AVReZ+2PKLxOD/bYmYjFzuP\n2QVksUt/CjltJ6bhkvjTf8E4nuhsi+TSo5oZ7EliOUuMO6HHGEWL7PYMVsU0NfTyjL0ofzFO/yyc\nhbSg7XI+nV0QHRVdEHNKPRZ1gyN87DxH+hFKDoxJiNdPqJnD1V/OiNKRqYLIspiVc+pzS7DZMSQF\nIl7RdhHLrSR2Sibb4kYV1JXFODjsCxs/Gpnr4P/k7k16NUnS7LzHzM3n4ZvvvXFjzojMjKrMqm62\nAIIEF9JSWvFf8Adpo50g6C9ooZUgQQuKAFuqqq6oyikyY8iIO3yzz6OZaVEUQFBqiVARZKEP4JsX\nBnfbnIMX/g6HJu84+w4nkXByfIK55L4ZqAJBFA5YbVgaQxaGuK5m2IXkuqYxc8Iq4HgYUWJPLjTS\nCC5mHs1iS+tKzHrg2DcUnYMOHERjscGBRkg2lcB4cxhahmFk5UkCvUFaRbcViDhjd6VoxYiWFlMJ\nRKeIZjPKqwbPO5JZwXKa04YCI0KKyUEvHS79lGDmo+oJW7WMsU/guAxhzHzTYo6KYyHZtBewrpFi\nThcP+KmmHTV71YOXEwnDKaxYrs+0XgTLlHEVYKMKn4hkkth0oF2kRGxxy5Ywmigawewsyb0Q02QM\nsiVae+iug7FnH2RY01GdwZErvE6Dp+h8hSNG6qlmqiNOUUF/AE/U/Kv/7bfcbt9xZ8D94SFdOWL8\nNzzO1xy6W/ox4Kov+XZTEraveDwLGM016vgHflCSOrjGOe6YVwojfmZSBf74gvbqGQ+spms7vjhN\nXK0KsrsIsbxi9Unghy2X8zXt9IjXyY7n/QXypy2/+DAnfyrwf6p4P048eAn3c4X44prx+Y7Bzpj+\nKLmczWk2AZW34Wlzx4NWwur3+OXnvLk6kD3omO3PLC8zksszn/IckcecP7W48p7xyU8o+YZ//upv\nkO2ScVbTVZaua8ipsF7P2ZHM3ZDoEHFSmqmSZP0cMwoC5x+II5k1Ajv6PBIr+nlJZyWx2WNETF/t\n8C8vaLWPbjwGv8MKiHYe0R+uaL2Ovq0pIx/R9zhjSu+ELOuYi9OEDAcOcY1wIxZmh+o1KRovOhOK\ninGYODaQzjOSocezDem5YdiPmLmmr0Z0saEOBnpnToGDlA3BbMJOKZkc8FWMkoJ4MSMQEq/LGHIP\ng0TNWrxSIdGQKwIUYZrjlEtMXXEUO9jmKCS61KixQM1PnI2Pg8brCpzbkCDKGIoVc79iGDtU3ZPe\nORgNuUhp+4lYr7FNxqwaKAdJ17qUXU8VSXbGA6PxvJJUWeq9A1cZ6ynkGBSowWd0DEnvMtmBWEmi\nAawTMuWSTZpSb1MWbkc0DSzqBtsvIchp+5DamRiPDqdpRbsIuQ881trn7MREixw2HbkTct4emLKI\nrilA+5DFuKJErUZ8LyHqK4KixqoQcY5JlgLV+0ReS7c9cZDf8+R+xH3+Bfare6ou4+Gnp5SJwp4C\nLl79FufyAc+LF6SMdKef+fkdFE/mhO9ivvjJYIKHdI7m648Fi0PN98mZZD/wWyflWjXcHW/w3ixJ\nHQe3uOedF1KvFZ134oU9svhjg/i8wDw/cFoYboMdP6knSNvztlyh5AN+vnnNfnbFqQuZfV1w8+ln\n5Icryr2i+VkzfHnNi0uHerznoTMwu5+hxivevAu4fhvw5VXIsH5D4lX08gvmveX+jy8I/tmaYSpQ\nEwT9GTX0eJNmZhqCxGHXnPCXJaa7QNYSCUTJinH6T9zB+R8KRoIKRsrrX+Jbh0jXeN/fco4LArVk\nzlNMKYkvB9JjwjDUtFGOXecstx6WHm0sInNo0h6vdGiNxxTtMfmEihTlGFPNFZmf4s4ipPOnaoMO\nQ5yswztFVK1PXW0oA48mPrNpS3ydELstydmi6opxKPHPS1zVs5zlnKTEzIGZz7nziAKXKTiDgkQm\n2MlD9Q6JlxDSkwwamQ8E4cgQpCyWiiiZMJ5AuBd0U8o0DqAKAj9DuTP8y46THkh6g1NfUc01+74i\nDiWla5hilz7oMckd0ZjjryNwj3Reg2gbvEmR9jN8Z+IwaWppGFhDs6e9cuhrcK2kzgza5ES5oBYD\noyoZB43toD7saMVARcY4GY6DR23uKPslxh3ofMVqqljmkmDYsW5rVHQmWkjGcc1im7NEIxaXeJ2B\neYSZKrLdmcBxkUVAowTOuqdNJVruAIfIzwn8FCcL+V9+fM1p9pLsak30/hbn+4FMvqbyP+C8Exjf\novtfkU4j9bM54phg3BQ5VpydNY+enjitK6LHdzzdX/Lt1ReY4Zovbs84ySe+HJaMzx2CCx//Kwsv\nYuz+K/4qOqBXGt95idcbsleW3ozcfoBZLxm/d4nmkmb8wDP1DTc/tDD3cP7uR9LrnH7nsflyogkb\n5sMJfXXFJCxh7iFvNKcfAvrtM3r5gYdOw1205dAeKf2Y97OHPDUn4uZrzPOehWhZGY+68ciFA3KN\nEoLBCKwd2AgH02kiBGfhMtJwHGuG/B9KZiENUTqyTL/E6RcUbk05dlwWMUqB3CiccGDaDhiTU5mI\nrJizMAF73zLPLslMQq061DnkVJaI2EV0Kd2sxRYLglmDbpbkXYHdhaRDRNSkVHcTrpmzi8642iUV\nFTrwUU3COfGIteUwG0ErmASibDhIqExMby6Z2ZBTs8MtBvq2oapzvLKnsCVaK5Jzib8xeHcDvhMy\nZQWuDCj6EMc/UZs5kzOjP1g6Blq2OO2KeB9TDAXt7ozUlnk/0FvBaS1YyARfxdzbihkT7vkEek5X\nbqhUj24gHDzSSJGpGbJJ8UNJ1Zs/7Z3oWnrvxLlMaKuJyyuHom1ICkkfu2wvN9Stxi8NxkgaJRim\nFIRm6gomryWZJRgHCC1uJ5mLknJeMaYnZpXAcVyO04p8ODOVA9puOJeahRIgBrI2g0qj5y7N5NMu\nztTao99nyNzBZYXnudizZBqPmNpwevOOWH7gXbkkCa5x+qe4hzVm8Yjtlz5+CrvdPefTnvKPP1Gp\n3/D+ZcGLXx35qztoeUCVZzjff4avOr5IfZJkoPqiRnl/TeAIpI2YFSO3/cT5u0+8f/qaKRG8/O6e\npfMdx6Pgw80V4Z1Bu4/4/bN7nKDEniuC4gHFmxf82lqSDwbxuaXucnbODT/nCQ/CirejYfVesNM7\n/k41hJeGTKwYLu6wn0V4y5oH9WdsLkDeVfgdiOOO6a4jG0Pi+znHWcvSm/DEhnnacPYjlK8Zd5L9\nYOgrhbZHLuaCypkzb1wcvfuzefoX0WehEFTtkie/fovySxJiPiaCR64k7iY+e6oII00VWQZ3TTSc\naRj54/oFw4eP9GakmjesihEd3ZMtApTQnIcQx1MsmhNHKWEQrANFLhOmqWGKVojugK4DmFms3zMN\nHYnfIkeF7FM670AmFf2VJdz2EGYEsiM5aOqNh2oP+PUcF4sz01BBLWes5g7NoWQyMcVxwJEK7U0w\nrVnLI8FYkAofU+QQZCSZYHALAifmoAbQMUQB876mmHqIJyI3Qg1nhjZCxzVh41MNPokvyUuHhd6i\nFg6OtqAVZSkRcY0ne6rShd5nXPR4XYpRAyLpCKqUypQ4s4TgpPERdKKndxVdrEhFQzZZytUMcepw\np4TcbkmwdEmMU4ASkqLP0IMiDi1H1yesG3zRM2jL5Uqj65EL5VLfawY35KhqVpcR7VD8KYvo5qwb\nTaUrPG9An8BNBo6ui+4cVOpx++2/5sGp5nV4y++PlvSxh6FhfVPifZ4xdQsWcqJ59pgiFwR3CV/t\nfe4flkRPfMT2hjTd0S/WfH8YeeXv2bcl0/EVJ/c9jx+eUcUvuL/+iuz7PyK+fsVZb/HiOcaeGd/l\nhINl5Vzy0bWoLOTRXUapEzpZ8kTt+fFBxTzUVO6aL0WEXwSI/hE3U41+5cFi4LX9A6tvDJ9dPqJd\nb0lbwYd7g30kidqQyHb8gTUPFx5lf0TGGeFlgn//t2zFlmBa47Y1rrnjpJfE6xPHPmLt+xQzncA4\ngQAAIABJREFUiTSGrHMRvYvSBcMioXb8P5unfxGZBcbQDyNUn3E69jhFw+27LW7X4bgT6XRg1xqm\nw4JQGnwxEj64RA5nEkejjcQ5tajOxxMwjQnNdCKdDnj3I5OXoYcZqwxM76LSgkoucJqJWZyCDkjb\nGUiDUz5AYnGShLY/4MaKs5ihB8HuYs3SafFNwHZhGY1gJEUIB18CRcC4TIlsQHcUWDvhLwRB1BMb\nzdxqlt6I0ZrGBNS6ZYgEvWhBw+AYiCWxmDDLBoFDqyyZt6IuFuzbHE8L+slCozCpZe742PlEIg3t\n+oK2T8gHQdUO+FFFXATkZ4VaOlg54uY+TtCzcnqCZmIMNZPqmWqHaVaj855+19G7EeYw0s9i9lmG\nri2x7WmSEq9dEEyGuVuxNkfqSTArJBcG/MLHmB3juiWME9a+oup8KjqIYspEky0FsQJEzdg4RJs1\nV+eGInSJWJBInz6ErRezjlxW6cSyH/gfP7j8YXyJP0/5q2zBk7cT6f0Gff2Y1b5jNY0s4ohomGHT\nj+jHJ/QrzUNTc/j2zDg8wKuekOkjOl9y+9HBpyboLbO7JaW85HZ75Pq+pn/4Nc4nxebuATcft7if\ndZym52yjJfevEuzjLb+4bPgUTLiOxpV3vH3ygqs24/TuGS+/OfLB03x7uadQcPVsyxnDRsKquubx\n0yXj3cj+zWN+NjOSL3w2756Sd5f0T2+J7q85HhIid4neZrzROcPVmiCe00VH9ulAIxYs3ZyhVQRR\nwyHImaPp7j3awWUKGuZORydPqLr5s2n6FyEWWgqiCV74BbGbcLYRliXMR9A1TfoVYS6wM8k5FCjr\nU9k9ztonccCVMPdm3M18GrWmHbdM1YxcSKJ1hA0agrJEDweauOZivWImJnJHkgeKbjES1g3xfom9\nmCiHNRMuyplj7gXLrYtnJGEnaExG6eckviYy4HotnRg5r1qE1+PQ09qRhj1+EBCqGr8U+EuBk3WY\no4OKE5JwJBExhezxPYkpXUy1oGxHukkQbjVxWCPHhP7c4YuaVFrOqsdb+GhCZrXhGHi4U4wcT+jz\nHk9JUnnELAPGUKCChqUNcUvNSsZIYXGdmNIX4GeMyUQwZvhBhz6mHLIYIWesR02crKk6h+UR4uDE\nNA9QjiHQJZOZqNqMzk1Qk4detVSmRIUty5XGu43Z65yj5xOLI07nUh9Krtwztj5TTiX2rkXHirI8\nwEYR1Sdy90jfj2xcH7+PqI2D2LqcPY/wx/+By/0tw5DSHc/srn3U+JHAxOSHL+meJAxFwNFMPGyu\nefzJp5AON/MZqaNJvNd4qmM9asZozmBb8tkM63sEF0d2zopHFwvM9UjX9Oz936Ou75HxC4b+GdnX\nEZ4ruHY/4W4/52Dg2ebEFDQsX17yQHyg1JbZZcfu8YB63fKwuWKfdAzunM/enKllwvJJyrezE+dL\nj0ubcH4uycyMRt2zyO445R3RuebRl59w8wNJKHkaBrzPC1TocmEFuvSJUpcqjVBW4YoNUaFoTEng\n7xkzyVB7HK3EOQl88Z9++c1/EMhJ4ltN4Qii2CWYpxyan6h2MeVMkz7zSJhQg4DTntosWOHy9d2Z\nqs05VAWHwEW2Atk4+NOSwThICbve4Two3MzHcVP0FHL59T9mEA7u6sDUj7h1yOBU7BNBW0kyfUKd\nz0zTmSFbcNJHirZjqPaM3UQoBfaosN0OXQb4Sck8d5hiF9UkEDa4XoZOJ6pqIvSXaC/m2LY0yiI7\nh3LUaKfDqhjaglo0WJkTBwbTWVAeU2Po/RKlYqbGB7HC+gGmOZLEMZUb43o5KhdUKx/mHoU4YlyI\ntSZoQ3IFuV/ixQmTERyGhKPY4UiD34AcDYXTMfMUbeDANGJ8ELZHTC3L0ufoVzTGYKxBTgI70yjX\nZe44iKAnW+WYUtA5Ln3RsB8kxaYkFDGrAg7dCstAEyfse48wvCDWGcgUx+2ZTwvOosdg0cqhXhmK\nQTOoDqcuOF90jL3L/+EN+P4TwkNO+2TJMROEa5cgLSnbkbsf3xFc3bP2PabA8sYviMQNy99CUN9z\n3y744Apuzl/x6uHPMFtTuiHH+ZZm1bH6rqS9EHzc7tkdPa7SBeLuAfv575l2R8yH1yyuJOciRucF\nDSXTHwX5I03YJni3cwjP+O6RJx/XJE8ucZVk3tYMbsKtm3K5/IbqvSEdXpFldwj9G1yd4Fa3BLqi\nrUuCjeDY3/K+8Ph0mjM+CPjmxzf88sk/xTQH7vWCbOFTjCWyssTSRYmKMI4RnUHYjKSqcCPFcnDo\nZ5ZY/wPxOrWO4KRqfCsp65J42hJ88wGTGNrDBYu3imoeM0Y5UwLtKkfUgpP/CCcI8IMQk5+wnmSM\nNTbtuFiMLG3K3BFs3JrJbRgqUG3HA3OHbwe8PCYxA0n3pwU1TnEkCQdOo0s5KrQQJKpjIT08HbKQ\nIVli6AvN5GZMIqAdK1wjuXf/lOGIXtIyJ5m5eFWMmjYc3ZppuGfZxtio5BhZFlnMYUy5LC11c0Wy\nrrlSf6o0aN8FR2O7ENcO9O6ReF5hZIvfeTTBGk8d8QOBKmYc5w6J1ehxgCqmUQqrXDwxoiOJM3nk\n5zN5VON7e+IpwOtGjquAoIm5ihLOBwX+ERtkqKhmXCQMwqdftQRGQ+QiahfPTYmbhHJqOLuak4Aa\nQSAsvu4YwhWBChFViKXDxC6bxZl2kRDmNW7XM+mS3BcMvmWRp6iFizuNxEtF3Av83QIxesjJofJn\nDGKJtRrVpnhPcnLbE2Q/8eIYclKWtrjj0SrgCwX54QK+f8P9tzGfp2veDk/wCPn5i5fMyz1CX7Jz\nXmO+nZjduowfey67ClNr3F/7FDc/4e9e8osvBbV2CfOfSbcZH9uK9+WaOy14mkvkOsC3T4jcNS9e\nW97c/8wPnGhuFO1J0HBBeGzZngyz+Zx2bLkPAr59F2PckHjrU3kvia4DvPo1+ALhGp4svuLmRvPZ\ngw3zD5fMfqHZ5Q3/SDo8+afPCOqE5DgSmYBp7FC9oJEddeey80p6taL2TiAMQ1BzXCtiHIbszx8k\n+4sQCzSYSCN8DxVris7wL42D03aEcYf/5YIx3xG0Pk7goGxGn4TMr/e4RY/b91zNF1zoit7NSVVI\nua85WAc5SZoipG9G8n4itHP+5tk/YZz1aDUi25TmYiLpLcaZU00FqJQlNcpfM7kBTeqzmA10fkwl\nwReWeV/gCIt7aZn8BTgTy65F2xZRj+h+pFEjOsrxpoGi2iCckVmRMdUaUytmjcPJ77HJnmEStK7F\nPzlksibpPQyKodqguwRpDLQj0RiRVC3N2WE8ClrRkzg1tTPDiAixcpg5Efpcch4NwzZmttGMYkOi\nNWMcIEcYhyWXdY2aN0yDZvIGUsfFnySy6qDp6TkwdQFzNyWtXfxVjmTCKo+5GVFdw0WTIFsXmST0\nwYZEnBGFR9ZHZEw4TUd+53A5llSbjFmkGHPLpZ3QTsCubxF3I10pODge00wSrGEwLkunQRifB8cj\nvlsQtwbvw8CDzqP6bsH9PuUyf0zy7hcE63s+PhbcX/3Ifu3w6+AN/oXHy+9rvnv+E1/uvkUKA/Yn\nrs0Vw5OAOB35xbwkb0Js/ZS7vcvD+Usu5m8Y29/R/BjRXwjQI9PS8vIyp34vua9Ssp3k8PYD7705\n6kuLTFOevfqcp798jHwakq41p9bDY8M3s/fMvnX4rK75ov+S9sWR3pt4/NMP3PKIrrvgd25DEn6G\nDQwPk19zs3S5fTGyf/OGNnrPj7HLk/RLpo2i3/QMpx2zdMWgJ7Sd4SeKjV0xtCU2WlI7Ec0uwJ96\nunLA7P78ashfhFg4YsJ6G+xQcT4GzGNo9RHXOCRGoJoYMV9hnZLlOcHv7zl3E3ZrsaOHm03UdUNe\n+0x6RX03krkjq3mOW070fs+qiHGMS7P0ieSRNp+DnMOmpd1JWhEyX5YsKtg0NUV2wShzdLPF806U\ng09Q7Zn3BSURlR/TRT5jGcJYIAaNDcEJBlacKIQkFh1d7zF1AZezI5aMwbfEGLp+S9Hu6eWcuFLo\n5oLwpHGlYYwsR3XAFR06vaezOYM7R6xdHNuThC1+mlFsjqyiFtO2rASEtYM8BnQ7hckEER0uiqEI\nkCHYCUwRE9sUMWhyGeDdpUyeZBU67PoYLQraaI5TCZJshap7Ohp05VJsFdOuYa86CndO7EZoa/CU\noRYO665m2/SYeYXnQF6EVJll7mqOSmPP95xdSTH3uK8i0t6wiCLqqwHfSUnOBu1KRNMhrwaq0mdJ\nh7Egq5hHaY5YOeTemg5Y/eJMO5/4npw/3jzguZB4N3Ou44foy0fcHN4zvPjI8tNfcRJPOT5XJJtL\nvP5E/HbgD1lNGQvs9YAX1cyujty9e8/PF5+xz6+5//UW02xwzykvih5NxGp0SLIO/6uJJCyJxTdM\nHxXr8JpylHznv8G/6cibgs7dEmVvUa8fEX5xS5zsMeItz7cJV5sD2/4VgckI1Zm/vvuKbeTx0+l7\nWP+Ic3dgcQr4pf+P6FuDHhRf/LMlXQf9do6z8mgHcJbgCge7dTk5LbaPWO4b+nEi1gN+pZhUwhA5\nfzZP/yLEwjgOS13hyY5QJuwPEH57hwoCtsDzv/ZwbUtylohA0VhLVPXcvNpAoJmMoHE6nGBiPeU0\n7kgexRSnkDKokEPAadHgLUqsW7LNXpGYM6bc4t2NxH5L33s4O8NhNJi0Y5ha3G7E79c0zpwxCZH+\nDMc+ADGQJhZxsJjQ4lYaf7am2lsia2ntgqh0EWpBJAQiGxn3LjYqCKYzvkhxNwtWdsnS69BeBNPI\nrW7YBynBCMvRJYtLFuOGMFkQqAatBYUbcGo93OqebJsiexjjNf02R8VnwhUMrsEUE/no4GBonJ7V\ndI+MezxRsbUQzTq6AO5nB9Q0kbsRkR1YNz1JZdCyZzpqHE8x2Yn+wpAufdw4wzcjowN5MWJCyxSk\ndAfQtudKbJjqkZMWDIsANSruRMZy0sSjR2pjrpqOjXNiGB3q5kB/NoS2x5M5QhpOaUMweGSXHrk7\ncvDXyJnLd1PKD1nN8xevGV62NG8+YIqBL689JG9Rp69ZbCTffjTI+AbPfYR495Kb7EDWH2jzX1H9\n+AmjP+fgL7HHgkwo/F5w8/6C2actS/OYUnxH25Z8/sZhrA35y0u+j54wLCfGIKA4pLyTB3CXzBLB\nN49Lho8fOJxv+OybFeU00XkLvnxeIO4znn5xw+9sit3/Ajvz+UnfYPM1nluTOB9ZOxJ7Ktkdj8zS\nl7QfLJxCVu2INltm5leE8opfvPwvSNWJ1bqiqVOSsEQ5PePUoGYl032H8izbREKgcFYO+9FhPbjU\n7T+QEXWsphgs3XRNmuWE/ozvxh34PXGkuTFXWMehiUJ+FvfEkUe7DHl0WuDMBQqD1yiCUFNXHher\nEAeD8XxCnRFlDdEkqfuB8RzxN9OZQ9CSJgonhi5cEmYj+nLBXASczy5TG+At1tipZBBnZH/Epi1D\nOoL0ofTQAIPG3wj8sYUo4FgL0qzDDzTmfGYSBY4OGJI5g/bogzU7v8Stc8QDRX2AKjwyXRzJNhOL\n1lJ2ljGaaPMVKLC6Z9xmiL7ElRXaSyjSkHHt0+qJfndmkg5V5TEN94TSYHHRNiO4nLBqokrWdOcQ\nwp4Lf4+tOwJ7JIpCnMowtA1p6tM5Fpm4VMsQf6aorWaYzXGNRpwUrjrTdy5ZfyZQ0KqJ4Hhkig/o\naEZ9UTGLYvzFEb86UOgGj4aq3OArODqCRhpEHWEua/p4wdIzHHqBtoJI+yzvXYJ2x+mYE9QtsT3z\nc6kQ70rSds59a9DfG+7DR5jlmpMTkZBzn1rYD3gPJG9/vGA/3LFbNKjrHe76OV36O9KLpxxWkCUF\nop7z6WSZvVeEriZ8mBLM71iU10zPakrxhDs+8CqY+KW9YaHnPHwx8lD/wOR4XAVHQv2EX9/mXMlr\nXgD9K8MukwzXf+T7b37JB+FR/Zji/Njyd5933B0axH7NPW/ZPd5xv3Rop5qbJ+/56skNgyyptCK/\nzHgTGvTFikd6h4oH/vHKpXAltlbU5p7i1IMIiZuAZrAE7ozFzGUdB/i1oSxKUsdSJD0p/0DEQmuH\nSCSUa8HJOMSiQeYDQxHC0WEudvTG0mjB+qdrwq1LUFTo2x31ODHWE2KRUBQOAQ23RxhMi8gKOmPQ\n+yVDq4mzB6TRmfqf/OesYpfBGHo/wT8NOErjtWAEiNSQBAXqILF+yuzeY1Cag1iQlw3KaziqO2Jf\nkbZw0AusO2AjB+lETPRY23NcjjjNBdrRREmOkprB3RF2HkMo0dPEIhHEQQC1i6quOHklibqgSBUq\nrpHREdE0DJc7Ym+DU1eMOidsJoL+TJimLOWcLhyJA0VqXU5xiZQBqTfR4jKvF6TVlmAzI4g87r0Z\nO3lFXG/wTy3aaDZNi8kL8lhyPuxIGpfuYEmNQIw5Y9sglgXTMGed+JTEWKNwhxGrL3AKgdUOzRnq\n0dDlA1PisUDirsCft4hEg9kztRk7P0eNitB3oTVsshlHFF2uGJeasg8YY4+AgCmGbz79Tzy4iPC2\nSzrnKdH1jEef3VIGR9LjR67WLsebG/LjU5KPH9F24OrmKfNwg9l6iOk1z1WE+mR4wlu+Ew3pmHPV\nLajnJ6bLH/hNf4EWE+Hsngd9zHZ2y1fXa/7u07c4MuM304D5+Xv2y8d071PM+SvetTveJld807QE\nU078+w3jfYn45lcslzuSVzPsteRCPuHZmxrx6hnZ84mF0si3Mx7/9orT/lccihnO/RMOCII+RRYt\nUTvgTbf084b9pzvqICbZJnh9w6V0sdMlOg85RRVLRxOMJaM+UW0FjeeiUPg6Iq0ESg9/Nk//IsRC\nCY0YcuLe4rk+nU3QH1zmek+8KMhyRaJ6/KHk1n9PP68Jsonp4oQql4SrS6KxIZQD7VqRzUpMt2QR\n/BV+6lLJE3omEPZMe455cV6x367oepdA7kkzTb4NOVZ3TDIj9pb07ox6quiUYVjMuJAhy2JiPUWM\nvWEMYsbwBIuBqChoz4pA5vQbybFwyLXEKyRNaMlczWRaandG2CQYbfDbjOas6XWBIkKZGaItiJ2U\npt+jihlj1LIXS/pUkRrFZAT1ck04yxi8FKfxab0OKUayVmB9Te8syYxPoHyYNMGup1xM4AiqXUV3\ndAkdl0B2OM4dOozIfct+XHCYFkjhEycbpHdk8juqeU40LPHdAKzDyS3IS0nSSzpf0LQp+2jPehFQ\ntB0bMZEOAXHskeQCtKHXA6aFcyfRw4YgtASdi3Oa6FSJVQvaZsDtPWw00h0U1oTMKk3eC0w38cd/\n/RuObkzZFFy7NX3oc3pvmaRAyjNvPkbETULx168poo7suudmfIdwbrncbxCOS/TjSPn0B9T6gmd6\nwbNwjbrwON9rHpU9s48faQuf4DVszJrrW5fbn+eIpeZOh/z1p0v0ow1Od8evnS3lrOXaFhTVjvXn\nJTfZhvqqJVFz6idvqPuSB+3A8VaTX92RvMrR3+9Q5zOf7iVfjJLzr9/QXziE5xM7N+TxdMcod/zy\n4UT3wKeeP+Kut6TKI7Wa2p+4X3uUjgJ/QElYS4MuwfoRQ5kSbUZW9kSoLGp5htmIe5n92Tz9/xQL\nIcR/K4TYCiFe/1ux/0c/U/En/NdCiDdCiL8TQvzNv88ltAPKl/RDiTpZOr/kb6//gPQF+X5N8MhF\njxMiCfAQ5OUG0QvSdIHrSPpTxVEPRNKQHAWNE+LrI766RYwlLB0WY4q3HYlNz/UriR82RO6I1S5G\neiSZR6xjTFTQVCNhUBOtDEPb0vd7mtJl53Xcrc6IeEN0dpHdjHMbIhYOcWQoBo/lfU8ahpjRxZut\n0OKe4+QAEW6342wDQiYaRxK5NV4fMQ4SN6iwaUMfnpB6jeucKI4ZQQGpk3EwPr0Bzzkw2+/ppKJN\nBmqZIQaPYWVphgA/nyirjrIWqECjlg3z3uHsz9HLETeJmE4VfS2xo0tc5riN4GLR405H1rVGmw7d\nhszkhDcFKDsRjlDJFF1YTHpmWBYYLyAeGh5wQasrNoFmTC3nocWpEnrlohaSdIoZlUUZl3UzUrqa\nSQQcrzxMO6MJzrBSxElD2vZ0cx+56QlmAdkMslHy9n9+S9t/4nnoY9pHJNEd3TLjxbAF8wrxUJAv\nPrLuZnwtviA91qy+muF+eMDF44HdtODdU0kfP6Laf2JqNUa0/KAVj8evuatechkrCr3C/XLOD+N7\n8gcSHX/k4vuIjdXcrm64647cLjx+rB4Sz37g3H7BL6sv8d5eIw6G6vIn8uWKzl7w/PIZwbsbXj65\npb+w5HcPUF/1bM1DyrWkWUAtNEmz5+EvXxCdK87VC2YPnvJDdyD+8S3tpy35teVx4qC1IZM1XtcR\ndzPC1HAUI/ceHBMXVzok7pmTCNCpRcUZWkQcJVD/x1l+898B/+W/E/v7/Ez/K+Dzf/P8C+C/+fe6\nxGRpfZeYgUkIRjei//Epk/cATx6I7Z/s5JWU/Hh7g8vIofFRpytkX1KYDhO6tAuNs4TVrkSsLF/1\nz3DjEFkYprZCLwJsMqcaB0I3xosWTKeRRlnadks9M6TdnDhUeLnDYRoJR4WpPYJY4bkNl/cr0tyh\nik+MjWIxTYRVzXhwsVpS+tBHLm7q48odGxTRucE5G0TgsB5H2inFrUY6b8nBjgi3RU0zah0iTy7u\nsmf0QjZaMKkD4gSyb+m6I9auaFcRYyswvcfFvqXZHGl7yaQ09awjiBKiVY4zpdRjwJ3S+OcGo+dQ\ndnihRyYVO2GwmUREKWNe47gehRvSdJY+8XCkQ+/AJBsmEcFgmYs5iV7jGrgoJK03Z0x3NKOiriXn\nOiSMZrRzSJYKWwsGb2AMJuam5TCTDG5FLHrW1ciaitif4zeWSi45GXD9kGFwMHmOqFzy0fJ6969Z\nFr/m5yYkHQ3BD494yUPux0t+J0+8LJ8ysx67yeF10XH7zMe8KxlCwzFPmZcZ63wg+W7GW+8ztg/u\n+M6GPFE/8/E/O/Gkc/h4DIk/b/m2O/H5bcCT4QJJgOs8xHg7Mjfk4oPkF6uM6ctbAr7iNmqp5rdk\nSiBrRXB4jrsLCCT878VPvPt1yNsgwf625EZ2PM5LNubI07PAPs2ov3vBkhW3/hFn1eBe/8wkKi7X\nG9T0hMunKZ/97hlFYhhFgpitGezELm7Izx6zKMTamNAZGZSkCiOWxwZ3l3I+1JSqINr39Ml/hBF1\na+3/Cvy7rqp/n5/pPwf+e/sn/Ctg/n8ZDv2/fkNI9F6Qaxc38wmEQ6M//KkbTiVs7xMc21OPLi+e\nKeK0IpkGbs1bTqnP1dpBnGbUtSCvO8rljLq84N2DCnv2icWc/XFA2h7Hu+Pi2VecwxNajBzXGZNt\n8ELJLPTZzwoKaSgyCKuYYWVYrjyaRuBYzTkw2FlBek7xw5E2leSdwp+3hIVhNoQEQ07s9Rx3AZVd\ngCPRVjLsYnaxwFn0JKEL5QFGCVrjtVucYEJ5A922InU7GjviNBva8IxsVsQ4tA2UMsDP7pk5PtOi\np3ACloGLOhuUEdAYbKshdIhOPUllEa5mbc+IbMTrBSYuCTJJP1k8XZOn0Lke3kEwUxUyP1G0Fk9O\neE3K5GlUs6daasYmB+uAtyMSJ+RpAmfJlBoYNZG9Z2gdxN0Z3Xl45wXLMWPrSVLrEB8CAuXRiISx\nT+iEpRt6ZGDYqInl1JHUEeXC4ex2RIsVb/+lS+UJTpuJafqWW9vixYa7nxqeXFzyh+Vrqsbyqlzg\n2nekp465dmnXf+BY3yAevmW7+RziWzY/vuWVeoz3uWQsPuNJrmm/Bv/iglgdmO8e8e7Jl9xFv+Ui\nt5SP3yEGl+bNkvqzl3R//ED/3qLeaRIVsKvg/eX31F8o7maW6EnNst/zVzcP8es91/Y5zy6vefBk\nxc0qpF+7fHpUcP/xe9YPDLdP70h+3/EHuWDhJSzGn0l+qLiUHyjq72le7sjvNF4bUexqZqHLondx\nFy1VuyM4Hgl1R+uWWCkY59CHLsuLgVQHoATq9Of/cfj/+4a/z8/0IfDzv3Xu47+J/d8ghPgXQoi/\nFUL87eG4x91MxM4M00wEjstY3WDtnL2N8GY1oV7gjC7lRw+CgHJuWcwvWQYTekiInBMrM2dsLNPB\nMmPLg6XPyRqsV7N35mDmDNMlSkr83DJWPbaG7CggyOjvT5g2IigF4aTw0gj/2CFrS5jUKG/JcuYw\nOA2dGWm8inacMAJaNcdfdtQJFNGC+lgRzAVOUyGDFUWWML+ouXAGuqFjLBuMXbK6FPitpA8cesen\nsjHzuWGsLW2SYNYnXCcFaRms5FLVrHYN8XbB2PWM9Zyw93COFU5cM3QjRkn6UdCP4LpgTI2QgmM5\npy881CzHL32yGsSo6IYOdV4TaI2zGqjSK1S0wZ05TE3MKRlQVhBOlyyUwJ3Amxz20iFsB7YIku7A\nMAXMpphDCFHvUPgbXL+kVi3DWLLoLJUVICZ2U0XfFKjZLe5tTetLsB1aDJSOTyAGcGISPFwH5MuC\n6fSGR7wjv4nRTxx+84ff89nLhuyT4bGvGB9v+HHtgDKI+CE3w8DqQ4owDykPM9zXEuVHHLKJSYV0\nn97y6eVrDLd4tyOr4pYfHEn3eEFaFazEC37vplx/guKRxDyoMe4N0odnQ8o3fYl3GtlcPaUYFZt6\nYP37E3fTQLmK+e56x3XzBFUJEq8j//4Tj44OgpxX37o83j+lCG/5P7l7k15LrixL7zvHjvXdtXvv\nu+89b+ktyXAyIzNLVSgVVDXTRLMaaqKJZtJP0g/QSBMNNJUAQZAEZVVkBBlBOp10ev+a21rfn6MB\nE1IChRQqMwqqQK6hNcCZrAXbey/b69n3FofLhM/bN9yakfeLXyFXPjuZcdAXXH5c8Gf/6jOOKxhH\nQ35a0SU9ghEtwAkke7FkHlscoQhuPcYW2jzD2ieECzgugn8g1f9f/NFyY4wx/BKQ/Pf2ycgHAAAg\nAElEQVR97/+JL1yul9hmpugGyuWOfJsTOhq7Bjs94XuaCZdsanjXBJzGFk8abpu3VDeKpj9ilMV1\nbRH7HkZKSgXJckG22tJVinLzPadyxlYtU7jD1jOO9AhMzqhTmgm8+AJ7ALns8HqLajIoD/JAUZYJ\nDjWDaUlvfom5z0RKXDsIZ4WYe6zGwmpu2HRHEtclMgvKeEbKK/x9jWg9dk7IedMzn/WMquaYW5yi\nhjDwOasdzqShtRWnekLYN4jJQpuGzDsi5o5rS3GIfea4pJ0c8ME6aZokIvYjrF4yWj1CLZnrjk5P\nRIsl+eTjzCf8CdqTxTErKL0VloLEcUnPO+YhZsw7dAtDPeIMhqQbMSeFtCaadEtLS+XPnEqfsFpS\nbFZkY0az8jBYHKIWexTM8YnAGsgnl9EpUCaiC2xsPTB6Ame2fxnRnjbkmxbHFrS1pJkzutuOwS1I\nB4M1G2TZkR2OkD3l6hRz9esLvJcSnp5zfHufCTDf9lwq+JUuCcRDyps96mKi2/h0T7/DjlwcKs6W\nMVHwiO+tG1aN4eL2S3749IQfote8Kc9YNw563/NBzNjNJ+67Ls74gqRZUHYl/TRSWV9iBRfIrwaO\nccyqOfJieYcfWXHngeaLWXL+ztB/2vNWwtvumk/BkSfZRF6WHIJLtB1jX0Y8f3/JD2eCRSe4mh6z\nuLmL+6rit07J/IVN0rV8u2oQ4h7LvCeSCksPtL0iurWJwjXak8zaYmXbDP1Id37El0fUoqRydxwI\nkM3pj6X6P1gs/q4804/A/b/13L2/ufb/DWNzbA0rNLpcEIQLun7mw6lhWQks43K0rmmthnrVcDZo\n2IPNP2PenECdk7SK81hRCw+5sdCVjd2fc7oJmJcOZ9/Ayms5OS2x2BBYHntc/D6jTE+EtqR2cmaj\n0M3IrX+L0hW1vWGYclp3D7cJzuhw9GZMVlJ6PSWKpalwC8MkF3T2mn5MMaKiLQasPmEnPcKop+k6\nouKGUa6pphTfjQgtSTgnDGPBjQAzh7QIzsMIqwhxjwFNH5N3hthbsZYTrm3TIwjdjkpJnNSibDVN\nMVDHKWttY2rN7BcU8ZphV+FYA94ixJwrglSxMpomnzjomcKNuRYFQh4RKwvPO5DQM8kObXfM5BTG\nwhs1zuihzcjg7CjCntDktJsKVQiycMdS2oh8xTDHyN5iqQbsY8ZuzmkDl6SbcIOBxE7oiw6bI4kR\n+FhYkaAfT4RZi9UuORlJbdlUw8BudPAP7+k9m6c/9ahswNotscMc3I44SlHfadpSoJKJp47m8vxr\n9lzinS7o7Q35i7fshk+szn2eXI3szz2Cjy4vLnJofR6qHrVdc2EUD6v3vPU2tFbOm8V3/HjdIe5q\nkqMkvTPyNmyZ35zzZfyW6ipHCBvv+IlBnnMlRgJ34muecf8osN2Yw8cL5szhOnV5nmtONYjVB7b1\nTyydke2F4XGncZst2V2Hu3VPrhK6VvHi8IZ/+V/85+Ruw3QRs44UqIZBBMipp+4dgqCjMQmzhDGP\nsaclVQthfMYMrIP/eD6LvyvP9H8E/qu/mYr8cyD/W+XK3wmDxlQOlaWw6gl6QyI9zi5ecgKYBOti\nSRuusAeD8FPC9Jxfm7cE4wZfGcZFyT4ckEbhfCrxgxXjlyPLMMTiwB8OOw62xN4u0c2Rk93iiA7L\ndRHFGfatRVNEZOIaf/RRxmFwR7qmxAs2LI4rzGJm1kewJdPkEpcKK3EZI4FtNG08sehPSLdDCI/W\n6VFOxWW9oFIetnHpFhb1JJlMy+iP5LaHrmZyaeF4HSbtEEePLnDwjEZyIswKLA8aWTG3DeI4k7gp\nkxKcmQOmK7gIJa1aENmws2AWBZ4CYfZ0VsswuDSqhPFIfluzly6BtWfRL5inkWUdE0uFU4PqLE5+\nSmdi1Aw60wzjgXHymY41q9GGMGMTW7S9w2Ic6TGoyeGgRkKj8Ki5TQbGcIM0A9qbWbbAHCEPmpup\nJFRLJpFR7QLEOLA+GlIUZlrSmVtGJNPYMPkpalOxfrzn6+4Kf7LYELFZKKL1LQfnHfvyM/bywKsl\nzPuU1/4C98cRoQ88mCKON6+I3obcCe7wfviON3sLM2XU8RXf1gvuuILav6apfqCZW4L+Cd76mlVc\nk90ZUasc25wQ7SXv3J5n3k943it+by/Jny25sd4SHI9U3hvWnzbszj5j/yCmGyvKQ839zcSP7488\nedvxYetR/Crh482aO88zmjZndRPxuwdXvEpj8neS9GrA675Dx5cU9/6SfxV9zlAZpv2RXb7jrIkx\nSc9YeMSVYBIh2pNY+wFnYXNcT9h1Sr2bMXlLdfwHMv1v4d9ndPrfA/878LkQ4oMQ4r/m784z/Z+A\n18CPwH8H/Df/XqcQcC48JEf+xb+8+8v+ri5md3VNOPoMB4d9WBHle3T9EjE2UF9zJTZYXclp3mJN\nIeumZ9BHBifG+BXxdsMUdNiWT0nFsnGoz3omNaFdi9CUDFaDHd5gxUei5cTJrMhDi6x0yMoJT0WM\n5Ch1JFcWJ1cxOyVxGVH6R9QAxcGmC2acwma3MajBRkqfpQvCcii87S+/x2cWwVaRUnN+srGljTPm\n2LYk0hlKJIjcZSVP1OWRwkkoHIXYRyjvHNNHDF6Ms95TFBosn8ooambqrUsylohTzspxSYUBXELj\nsBjOMVONO6xox4xheYE6CeZsjaMbXNelsyZ2s0E6AaUv0X1Dr3KqeMm5cTkv1/TCQ5zHjP2AJRqq\nw56oDTmNiskdkV3Kpu4pUvAah43TUt3uGK0AVELhz+yChnK5IkhSVNSRuEc8f6KoLNAOahky1IJm\nYxG7Bca1CY8npAqJ1CN2sWY0M1Zrc338idtxjboUjPJ77DuP4L1L/WIiHs8pdMu9+T3WODOaDQ+f\n2rTzS853d8m+Klh9mmjbHud2II9hvv+QZrmB0wfKiw+YDw+4MhekbxVSOZhvNcnFlvPDJ17Lc4SK\n+MsuY/n2A/X2IeXlHbLTgFz9zHE7Marf8mHTkTz7gBVnPC8veW8iPnvyAxc7gVXf0L114cNj5qrh\n2c3AuZYUn9/QOwGL7RlcX/FO/55f/+t7BFkCSYSVONAVTLaHSUamsx6vG4i2N4QrcHeaWM4Mzolh\nKckynyn+/yG+0BjzX/4dt/6dPNO/6V/8t3/fQwipuY4LrKPD26s7zME7DqNHeViTRC3Kt2FyObk+\n1uvPqP5TTeOmyKcv6WdJFlhYdg1Nhm9cHFfSDSOfK+gqQeSNRMOEmU+srjd4ZoPqDUV7Q7qYmQuf\nw8rHDCXMA/5hwRh0VMEZcm7IOoXwOlK9wxwX6FRjkhJdrfD8gdaSWE4KokWeVoz6RIWFikeiWx9W\nIUW+JQkUe1KSdEbKEbeuGYclvZNTH0vmUJG40HZnOKHFfDgSE7KXPSjNRrQUQmCMgOFAuYqItYNy\nfcpUsiTFyW+4PY24ywWmHLFiiynaQR2i5oJ2nkmljXsmmIaWY9oR7xWj72GfCfKbDm8zEZqUo/ZQ\n+pq58+iiE3IKGPaKxvdwixERGPJpYu4TLNUxyhIrnGBuaeVA2494ZxvUac88bjBOzkIKmn5CVi5u\nJDiJid4HpKGvI2ShsZ0aMRpO9gK7njnuCnblFkd+RT5/Rh9pqsXIF9GKH/oR77unLJ63eK/fYzMT\nzgvgA/3zgeH9msB6gzM9pH+/QjsrXN5w/Y3LxVcOcXfBDz++5M7BYbJKzjOfag6JvRsO2Y+c/e4R\nt7GDdC/oz2d+okapiM+qE178jDevCtwHI9aPFhd/OVAdBe/3j/G8f8txe4/Hj2/58Drlw50/8Piu\n4jx1+Ou848vlLZKUMi54cnLYrUpqKWlrxfC95s1mSdgN3HvkwqmA4QJj1QTWwGSHDJ1mFre4uxgn\nMhzqHF85iHzB7GumAQZ/xN0dqS9s1CH8+9Ly38GfhIMTbXFOzMad2agcdxtj1RUffsjxpMDRM4Hr\nQ9zxU/0SezyDxqFwM4bAp1CSuTLcDj3Sa2nKhrBfMjgjGIfRMfxvP0wchcQNj9jFNZ0/EIYJBwMi\nClnvW5auwF3a2CsHVS9xBxhLl30f0HEGuzPswMHdK1QLmW9hxpp1bMjVRFuObIaWxtOkMibZzexj\nm1Nl43uKkzMjzzv8/Eh5bCksH20MbuizCJcIz6ZtDHYGfl4gHZtDcmQdS1bbkVOfYMzItDX0KiU9\nKca9QjYNcV5RNzMnR2NZGUM104uBTs4cxoxFVGMphWcihK45tB6zFphixRyHRH2FPXWEFw6agBaF\nnn3M6MKgCIqMuHbw3YlIaaQlqbkED1L/yKx76nhCSI906OhDj+y0xsUQzxFhs8MeE7bWhO9NdJYB\nbyYdbVYYlqPGxyCSHSYMsJoAd6tRZyP/57tX3NsmOK+u8No9ldvxxU8D388Jl7sN4SJH/7iHs4ZF\nfI/XH2MO4T2imwve6zUfhnvcybdQlezOaq53d7DFJcMfelR5IHQUZWaIg5j5+yPv7xpeHyL0e5sC\nQ3nvAcO7Kx7GKz5X97G2PWq/QY9bQvGJKb7PvWXLboR4iknbA7L+DP+R4vg7EPOCsN9QT4qr4i6P\nPY9PM6wON+xuKyYrwv3hKTfKZZ02bNyaXwc9/eGMj5/eIoNzxLpEXUecWh99EzBIw1AK5sRmF0Im\nl5R6pg9yDrJDmJ6NkdiXMxMR/fqPp+mfhFhIo+mthi6A+//co7VbEitj17zGsl2KqMM57XCHlMXU\nUvU1ejMy/f4LxnJisQvpwog4jvDbgFXKLzX+ny+JLEM5WzzX/4azLANjY4yFNdicPM1ZU9M7J2bH\nYx4G4v3EKCXFWcfsHTHkeEmL5YFzfmQ37iiiDt3NiP6EVJAfAoK9JEp9ijhAS5vtNFDFSza1YQ4k\n7jQQaouz247Gs0hFRDR0xCtDb2b6WiG0h3JSWmPRpIY0BWxJ6010yiGxRsZmJvJiYlpsvyPwW4SR\ntEbSVTucwWegQMcWthsRSQffy+mmM9q5pkw1brAilB1O1yHNiNtsadyZXmloDPpQM5kSnIHRgzGp\nODi3KMvgyJ5GLWi9kbgcCA41ctIYbSFyjT7G1FNAUp44iYG2OpFbgi4y1EWLIkOLAWlgqgYmsyBH\ncfR8buIGlQvag2YwBjyHbhvx+8P/hZWW1L8euPtC4iN4mRruY2G8V7iLEyfVcK0/YwoNf3FZ8Wis\ncZsTD7vvaR5YmF8l/Kg85OginixJXlgs76fshUu1WVOYF+RbxcfLB5hTwZg4zP2K01/syX+84YuV\noZ2XvDUHskcd2/jAm9srpN3i7bdcL7esP7b8TtxDLHI8dyZ5JRHhzMX0nou3hnddwRS/4e3LhIfG\noog1kfuUU9Ih771nNS/pGLl8rHnpLHhw1mCCFZm9x8FFn1eIoSdyd5gpxLE3KDGRjprenzBygT12\nKCekKgJOXYAxPqroWJ3mP5qnfxLbvYWQWPXINDg48YpI2FjuxE24YOcUKDGT4zI3A9L3yKTL7bhl\n/SWsYs1IQ3OUBItbrGVC1VboHv7prcEMA+M08m9+cqlFjpwTak8AAnusuHU8UB65mkn7BOMIem6J\ndmfkgYuzPCDNhBh/2T6U2jZ2ZTO4ksrLMdYSP+iog4o2N3j9xCxtfD8msHfk6yWB0HQyoDz5OHJm\nkjBoydwb5LSDekUX5ajGRnqGYTJoFUMv8MaJ1tSIaMQcZ5ZeRNW2jHgI0TLMkigSuJ5muLGx0wXh\nYYc85tSzoS8czjyHoWvohcRrXA7FEbFKyL2ZsO85JRGz9JiutzSpIA58jq7mXBg6HVHWPq7TMw1Q\n1zG9GrlQFxxXt7hdxuhYWGOPmpcUuqA3HpEOcVKfcNCQCOZDiOcHdGVFZ9loaSEdhW4rzCCJlEN9\nmjkuliyHlnGw6MKKjXH46f/4K4rOIvgm4oc7e4IpY3V3Jjl9x3TQdAuHu2cxxWwhkoIf5A5b3iXP\nDMq6z4tdw/u8434iES/PePPlFQ+uF7S7A7cP4fzdHXb63+I+fkYWafSVxWd3LT7kmjTfEDz9yEFq\nhPmBZvA4YvEr3fCHC8mDbcSbjzPVecJZnPNldEK8A+vLAZV/4Lv1C3Y/3eI/2/H5d3foBYznLYdr\niVP9Gc7l9zinL3E6lw9hzdPvJ75dJFyWIdf6FZdS4Vw8QfYa15G4iQc7ByKD0jW5CsnGmpNfI/wI\nfViR9QUnLZgtxTg1LENFM/4J+Cz+Q0AwIfoIZ2MR21+TDwfGuWHf/zWrwcKbQuYwQSWSMLM5KIls\nlzz6uaYUJzqlsDcz/mHFbEasEEJ74IN6gJhmzpXm7f4nZKWorT2drxjdmbEPcewIJ2+Z3BZr7uhs\nQTw6HHxItSEzEYO2OQmXol0w1zG9Hsllw9r2EY3D5BicYcJLBDpZs/Qlhh3H/Yw4DeiDYGp8zqSA\nzAYM/WJi5YZkh3OG6ITvZcSmgcbDH8HfFczzgDcLXLnGKRMCeYYWPdKZOZMKe5Qox0WWHdZ1T7hW\n1KeObpkyhT44MdmyowsdirOBoBdkxQn7ckZZNVk34JzHiH5iVdbEZ5pZ9bitj6gGhtmiGTU4HiOC\naTmwTE64lOyGLQLBodjD1hA7ApmU2B74c00buKi2ZJxrZDtwskZoBgI/QqkFjBNtNVIMimVk0cwC\nGRuyLkfWMcIrCCuffNLs/+ca//yS6MuI5+ePkHuLZIq5Nb9i3LwgVw2vPY09aKaPBy4OX5J+GEny\nlvDjW36Tr6jm+5TnDzksDmQm4FNwQ/2oZHq9Z3f2e566Gaq0CZuSaNNi/3xEpgOHSPNKNfT5hg9l\nx8Uu5qk+w14b7OYhu7LGefCUe+WJfXvJz6rm5f0lv3u951g85PPxGx482WEVdxA645Dk3FYt+tGA\ntH/Al2uq7Ft+FzhM1wN7/wFOq/l49zv06jFMd/nx5+/Y2w5YoK4dUC3DycIKGjhdUwxLFOAVNnvr\nyJXwsaRPVniYMmCrZsx/RJ/Ff1BooTguO8ysuBd+QXgmma0A99uQW9vCyz0ir2F5lPzVVv9SE7YH\n3gsfU6wwjcEcQuqzhkMdEPQhJusJ7AdoY6GrmcWNou8G0jTDRaFnSSYkUTvS+xELHTGrjKrtsPXI\nedtxnI4chMDeaSJTMqYFs9eT2ymWP3MaYrxIEBhJ3ywxORgxYXUuw7zEXgoSW2OPDe5Q0VsNQ3FL\nP1YEjWHoe6bljD9KvAO48ZqtHJnGmj4Kme0Ko2PCecJdFmynkUFZuLPNmDps5xlVgs4M+TLFnnrc\npMQeSmITkDk9jtzgG0VqGdQi4DrSdNuI6AhSTsymZQxmTOIzNRZZLij9nMBOKRuBZdWc2df4Q4uW\nNfsqwopstG2QNxYoiY4E1sljOmm01ZAsHTyd080xc7hmF/kod6aJbSZZ05Z7pDFYuiddFOR9g9An\nBsdjnFIsp8Iaz3B0TqQ9frN8xfpm4qr2Obx7TfjlK455x8X0DVfxG5LfrNCHS8RCsehnXl+9J7uz\nok4VicmIzxTPPtNcfNtz57OSey8bHmyfcnVM+Gp9B6YOOdg0Nx3tTcPw6T4/niukZ/Ps9orNPoMl\nBMuv2BY+ej5wfWXgJKgXS7iB46NLnnqfsL59xCMrJLmj6cIdxYcXeN8/Q4bvcGXBxdtH/Mp+wfm7\nc+TjicL4pK9f8LyJeBFGhOkJ/1nM4pDR36m5/fUb7vsPCE4B4yAwCUwzLP2R/iZjXjtM8y3xpJCm\n4iwWOO6AXEl25Mxpi2xCrPEfSYq61jPGmjmYHO8vrlBbD8uZ6K9e4U0jQzIj+oEhHnGvfmS0PUIh\neZA6uElH1ysC5wb7aDgb9tRKcOgvePy8Z/ID5thBD4Z5tUBezTh7m/XQY3mSVkic04jQNZW5Br9H\nWyuMECSWizwIorOJXqWYk2T2ey4iyTQv8XSDOsHgtMSuop4WmFYzC4UXGryjopg87MjF8jRV39CG\nDgvH4Gc9VdSR1wO2bxh0za4qiWObMMrICoXrgp0USCmxu4hgfaA/StzQUOgTrhqxNzAf1uB0HHqX\nzlK4MmMYcqYqxux26AHoY3a9h+fMOIsT05hQjxF1nTOZhCLf4qqU0UuYZ/DHhtho0jnl0LhM4wWj\n8lktBtJZEogQ7QzE6zXCjSlnsO0QZ7I56YjICYjNLXVbsaxH3GmJaLcYSxCTMaw6uoVNPWbo2UN7\nCZvRcNQtxQinRccpShlX8OkPAmUGnquSanyOPNyhTk+8N+csyxGVRSwXPen0nkYuee4fePOTxgtT\nok3HInrJ6xhePmh413zG7eWBn+RPyLri40PNi+kpb+ae2X2P45R0lzfoquIg7nDlJczKonz/nnvX\nn7h3WRFhSIKAh6OHlZeUj458/mHgY3yX9OKG6d0nwuMLgsHhdTbiXJacIRB3JO/DnGvrN/zQv0ZP\nD/l02PPzZk8eC4oy5+cbC/Fhz51SwifJ3VeXfPl1RC0rulPL5I4wpuztgUy0rHOHtVpTFy6z3ZOL\njLQJCfodwZnL8uQzV4reK/5onv5JiIURBlWeofOEv9yG1Nn4y2qyuieeE4Z6wpkcCk/RP/IppUMv\nbKpSYB0n1lGAY61hVtwuFwxuw7KF9/YaxyvodMQY/p6014wXEt8ukZTsuoI6FISJh1MYQuecpF7Q\nySOznKhCTeBoCjMT5RW+cMksi7w8cNEOzJ5Cmj1zkTAiSd2ZOGmZso7Zamllgq1LpOqZB4uFt8Eo\nTeUJTrc+g3RJVIWZljRiItEOVqE4iA6xrOluFhwKh26qOc0W7uiSpj7b48BS2FitpBwGLEejri0c\n38WdRoZpzzz4aDFSnLtYzYlRHUm7W8J5whpS5uQGzy4IapeoPyAXkpM3Mg3zL5EA6UizcDlagtAV\nRKLGmQYqBMUosS2bhWdh6warLzGZYeKIFP4vXyxjQB6sCMMWGU+0ccWwWFI1JRLN2k4IihVzVDMR\nElQWLRNeYkOiseiYhp7jJHjy1OZ9KXiZv+XJ+IGrdk9sZrrbPUOyRt0JuAk/8v7TU/rnl7ypXcqv\n3pD9IeK2cFH1c+LfvOXcFPQ//MhCPMa+CEieXWK/uuInkfPgsSR6seHH7T9het3z1LvH16ef6LuS\n0wfNw3srZh3xfttS+YY2ixn9CnX+hIe/f0s9CZ7IV9ykV9Qm5GaYyS/v4wQnvlER/vhr9ld7Ph9c\nGuVybvtUH9+z0iH17oQjbnlreVgPBH5jU4iCSE18SC3uPwqxpY12FxwqzZjtcYKZ/UYjVMUuhcwt\nEfYSf2szTRVHbbB0gBwjQl0yjX98e/JPQiwwEPY7VmnJm7OHiDlgKgW/mVJOYYH2BbYT4ekjn/32\ngEHSrmaaJz+gznqqWrOXEiusUNc1yRhg3B7/PONWarq54LsopQ5rOtNRKZ/cXuPGLtluoLY1h8yi\nG1taucfUIXYyktYeeTTh4CEXFv1syGsBUUbpFRSFQfoTwkhEd0PV5QxWipgnFkIgF4py7Nhrn8np\nGJJrhPZx5BovyAllTVVP+IeK9ezQTw2Vv4dpYldPDOuBzKopgpFlZegnF9HXWKODnhui2SPBo4gF\ndlqxPA4Ewxmu66FMQxc1eIyUWco4R9RJTN5ZDE6DXbrYns+06OlDl7Dx8AebwWtwjwHsM/xyZNkK\ncltyQmJJh2hu8d0J0xVs+5DaaAoR4pc1wRxhqx55qhmnAtOWNL2LLBxs0bBUksUIVt+wnytGVbHQ\nKVk50QQ9TdPRWx5J0KPHCX/U3DkULPKZ6b6NqWzef17z8G6MVyZcGMX+W83Pn97zvLPJnr3Evqm4\ncAf0TxO750eiJwuK8TVjnBH4a4anX3Gwd1yKPavJovEe05x6HONhTglfxwXP1g6It7xXDnd2ijub\nguLjPfqmYzXaJFPAcBzZXljII/z855/T3XmP+cMlXzR/jkkkjz+T+C8bAtvnwZsD77e/oX94l1df\nXCHWS26LmHICcSfAff6QbgtfXza4s8H/wmV6ZvPAFZybhq/+8j8jDRw81yHWHZOOGYoR11hUYYo4\nNVRjSjdAfz5RJQrXv6C3d4jlCE7Gyug/mqZ/EmIhLQtHhhy14p9eLGiKAOU5PDI/4o0Tcz2ST9eM\n4ozxi4KobzhvMvI3F1CAires55G2lXgCjk1J7p14dpwItQXScPvNS9wxIx4tgkjQTSfCrc/RbvE6\nRTyMaK8idJZM/UjVheDDnPd0O81OKCQBTu+QOh2RYyHtknlw8OwjYWqTrWaabo/qYsrJoKUkDCNM\nfqRszkGnDJZHKwbkLGhVQpoEsLQYEp9hTllWMbE1IMIUZEFpZqzujNtIE00NnAIiN+bopWylYixz\nnLxCDSv6lU1tH5l3HkrYJFaMzMGvJCYv0cJBS407prRBhO5botHHOxqmwKepS5xyiVi09LakaeF6\nPhAdBFPkUvUzlaWY5MSUOIS6Rhw9PAtqT5KLhr1JEWFHKUY2rsC1FTfuiNtLehom75zRskmH5BdH\nqgBHtDhDjVgJVnJk1BaqEMio5yacuXUiJmuP0wJ/vUEcUj72H4lfPMH54hPrhxmv9EBz/TlXW8HH\newHxEp5+v+LUfcC98rAfTMjXP2H1J4ak4TvP8HH7iuB84usXPW9OEa8//sS1NNysLF7Wj0nyM6YX\nNfU25dbRtH7AjYoori6ZP0H7vUN23hOON5zewHzXw3pbou6M5N+/ZPq1Rfj7kME35Is72LJl9RqK\nRrLaJFx+1nOWvyKYBWcvWn6Uj7hnzYhvIrqfB96y5ef6jOebP2NQW/quIJIJtl+zila0eY02go09\nM8Y93pDTmRq/GQnagln7zMVIMHUQ/iPJDRFGcjv7rOYF42cNF2okbApeXrt0hYtZQxtJVG94901D\ntLA5NSWWWVEOCc6YMlHRTWuU6BHDini/pl5eQ9fiMpEdM7TYU3k9VdciUFiLgbXvM1Y1jVnilz7t\nfESFE1MkGSyPMJV4gcRpQ+yoQw2KWzFA6XFmrWiNz8kFtobeipFjgAyOWNaEtehwLkUAACAASURB\nVNsRCJ8sPcNNd3RNw+IW1ChpLBevN2g/pT06VFZJ4h+p/RxTBKi6gm6JGT2kfYvdlBRxzHYx0oQn\n1gcHW/bg+VjBQNtbtD3o/QLbVMy2R1tvMbGisAukZZhPJQuVMLQQyY59qNAyxDIjw25ARArlCPTY\nMTgnMm/EViHK6VkC2egyHHtcEzD3PpMriaKcqN8jlUWyVITVntpyMEZSOZpWTfhtjLJt7Nqnk7fo\neEbNR7ywgqqmlhFzbZiPPvng0PYjYuXQ1wErI6nkGy7cCy7uN9xbfiK/qnisZt7KHwm+i8n2H3hS\nvkCN19xhj6ifIp0V9Z2C4uoesWuzzFOMEjxZZMTzObp9zqO7C25PP1PIZ9xd17gXZ5jmR8pvPR5F\n1+T5e2RpM36VMh1arObEIm6pyxP91wmc17z8sWO9G7DmkJfLT5TySLK/Inhhkfy1w3R/yyp9gHh7\ng3yzRD9+xBdmzX4FP2vJ4fQVzveSbZHDx4+Mh5DyVwcea4vPTin2/e/5/J/8M9ThgtDquFlY6KZn\nP4CXCBYTlDqmqzrmhWIFFHVDG7roomLKRvahi5n+sTQ4J40XdijniOV8xjAdqeUZxWcTqzhh3CcI\nk2DrijF7yDBKlqYnuXuFr1zKuqU0mlANFM6CxAimZOKr4HPsKEQEIe+XPzDuFFM/0zU+tuowlcKa\nJX3YYYI9ZjRkYsMoY6YZoumEW6wYrYKZIxwHTpsd57NBjDFDaaEZWJkAkflMxseKEo69RzvG+JOg\nsY8UcsZUHqM1MWc1s8kJupBElKibG7Q0WK2hDwNkFzCmJcGsmPwTiauQbIizNfIo2VTQ5SPVBEmQ\n0gWSkzBMwURSekybI/gjllMgcbCKGToX6Z6ROBP25CFkz76eyMoI6Q40iYVZSDzT0y33GJbYzYIy\nrBGxRamWzLKgGFpEEJIfHFynRCKocTlGHulRIYoFvV7g4GOFPtG4wiOlCU9oe2BWNQBFG1I0S06B\njY2h9HtUNmP5LqlzIDAr3F3K0Fs07V/zcB8wtkde7b7g2n/M8GcNavsC5+MzfLnh+31AJQY+nq24\n/WKJt/4d2buBZG9YlBXV0uanzMY2Ni8PEzefDGL/Enn02QwPEFdHitlQpQPBZ3d4Gm3ZV2vm+xPV\n/ATzXcuj6T3t5wv2D3rU2ZaLj5rlJsRVB8ZkoJlDVn+wOWwWvGp/Rfhx4Hs14n0c2VZv+dq5T5r9\nlkZPFIsb1vsrcO/hPHtHHRckx2e0aYIzzVzsZ36Whsnx+Tp7gTm/x9bd0UwZ4tRgjSGBA6JPaUsH\n1xgWCxuv7djjIc4XBHNBKjN8M2L8kt5p/2ie/kmIhSUFUzjB0WYTzYxrD6yJm//1Gw6lwXNvya4r\n2tLjdpIYt2e39LnMCmQiseORzg3o04KlKMllyTiO7DqDMyv6Y4eqJH4W8mjxNcvZQvSKg5oYaDjT\nEl8Y5CZhN3f4asfaHilsgy17vGqN159hC5/wKCnyEewjnTih3Jjbw5H+2MG8w9/uGUNDII90lyko\nWKkK6RriURKeAlyzwvaOjCpkG6yZbIM/Teipwe0Fbuuh1gGqTRmVIg1mmiJHKk2ucs7cc8bFnsaz\n6EZJdPBZNQUnZ2RuY0bPp5mXKLWkXEikd0LoPY5taBKBdiS+k6KEIN8GuK0NrWDQIdM+ISPHTSca\nHeLOCqc7UNs9jh8jpGaixbdGHJkSDQNqkBSWYGh6OjkS9SNBI9DDAbeTbBqfvrU5ioFABViBYJmd\nmIuanZ2yDCHOFe7pilOdoo0k1yPu0uKv/octaiWoX3nY5wF3rQ7/tyuqX79FNxOnX534s9gjvvie\nC/Mdye81vXPOp6cBx2XG5GuuNJzr15yePkXuB6ygxkRfM3kDrmeDDVfFkueqJJl2SHmPuDghtMvV\ntOXibsL2ro33vcWj/h4fXY13TNi8e8fnz2JUAF+sbhBfFmxCh7Rq8bINiy+OvPefEFkJ1w9OfKO+\nJv79R66mA8W24Vc/5OzfJPjRwEEdWXwY+PG5zW+1pLM1t7evWeiYdBQstCAMDIE9M9ghYdWjy5nJ\nmWkbi7qZyP0FZ+3IcmgYO41lz1AqzoYMK+/+aJ7+SYiFMZpoJ9lZA+urp1h4OE6L+9Qlswtkb1HZ\nEWFYs45uMEVMUBtMe4+6vWaUIbJr8buANohZyZ5B2Dx+fIGxXLTroHVGrS2cWDNYHfGcsdCS1orp\nG4fR2PRmIFsbjvOSSlt4o00/tTTRkcZcUfoabz0T2JImWCJ1TNvcEDhnVOcj87igsUei24G5SXGn\nLfVxppQWQy8IvIDZ3THYW2rHoi9dHDMzzQ5ubJMYD3Hh0+uGaTgg54EhGJFYOFozBSW/OM4mhtEi\nBZzmlx7CNp1Is4JMH3HLEBxD12l0L5nsBKNmcnuBO+9ZCo9g0uiwxg+2GDnSLyRqGhkmB60HpmFH\nWvTYGoyVEZQRITW0NcYT7HObyj2R6xUqUKyWA+oix7cmhq6jCw2THWKbA9VkmGuHM71mlB1TecIc\nXVLHJ5sK2kaytTW+J8iGPV14xFrZKHPk3dUbyh+ODM8rNh9fkX8s2cXvaX9fYC1/YnXcUJua0x8y\npvkBudrzrLL5fPqEt4LHl5esY5+PXOJ98ztS54SOEx6V31K/aejUO95wRXj3SFf7vK3vo3KHPnEZ\nbwWXa9h/CnloXzBbE/q7E0/bz/j+8g+8fHCB9bbm06uEt3di9r9/hHz3HYsHLRQN0ceUu+sR96wm\neFPgHo94zzvS4hIvWdC6Hvldh2b3kcsoRz3oePKHkmn7BP/pOfOfPec/+RdPqPIjVaexpIshQopb\nZnPCWJoohGF1wAtcFhwpZ59u9siFw2QNNKGHsa7ovcUfzdM/CbEQCErPx3Mz8FvG3sZxAvLfWMyj\nYD5bEcwDx87B6z9SiC2eO/GhXdBYIU43kYwzcwNmhlOS4Pcl2zclw75DTj6KPXZe0w41nuoY4oZS\nhUSdxbysmFsL0/SInU1Wa+TJIMQASYCc1yxZ4fkdw+GCOXCReod3JsBXuFgsBgNo0mXGvF4wpS16\nu+GcFfFW4mtJYUZqtYHRRusQN+6ZnQ5XG3ZTCFPALm/ponPMQWOLDpUbDv2ewktxZUaiLabCgrGj\nv9lh2oHRCsmciPykOQYrjD8gnRuChSaTLdZxIip85H6gPmQM5cBVDF0xo/qM2bGx25bU9VgtZk6W\nhxk98nTF2GjapGAIDDpMGDqPJO0QdsY4+8wL0PsO3Ur6xiONGtQ6RXc1B5mzHy1st8IPCmRX406w\nzNY0wUBeWxzHCT8/sbJcqkEyq3P0tMCRJdNB8r9cfYcVGtI3lxSbpzjRZ6wLgfXki/+buzfp+SzJ\n8rQeM7vz+B/fwecxIiMip6IlWDRCQkJCYgFi198BNizZsekNEmIHK1gjJDYsEP0VEJBDZAweER7u\nHu7+Tv/pzrNdY5FZUrdQUV2ZLapUP8lW9167RzKdI9kxO+fBPS7we5uP1SXC81jaA9HiIT/sV3zr\nCz5WNT9Ye+zXNunuimLzgmCeedE59E9ssmfPWL7/GY9Xz6j/0KMth/A4srvM2KcF94Yn9Drn8sEH\n6g8H5H2JDGJujxZqe8kmf88PL2LMxhCOSx77R/QXAdFi4OtBcTu/oS0M7o97XP2YL1YdZpfgHSZO\nZ084ticS/z2LFxLr7QWqeUrh25wlNfVwxfijzfz5v4clHJbuGVZ9YJgsHCOYbEM4WbT1kUA5iGOL\nZTxcNdDbA6lSuF1AXuRkTYjn//314Pw3Ki1nLGtkHgQjIb11Qh0zirVgThVJ31Cea5gkX+afs+xC\nDJLNcI0VhjhDQmNDTYOxLRa9gzYzK7Uik4K1rdGWwyAtlr2iC86ox5DJGVDJRDsLukojHImxBjof\nejSnMcEubKyo5bS0sEtNFhnKLsTJNmR9w8Za0lPRthtkl5EdOsadwJpShqiiT2tu1yN+EuB0AZIK\ntzQkgc14HPFqUFHDRve08x1nvsu2P4Gj0F5ILyzEybCVHU6/p9Y1g7vnTMSU5z5dPLKQNtUefClJ\n1B5nEswnB0ZDVwq8dKY/sxDuhDJ7hnOD21b0JHRxjo1E1pKd0cihQtETOC2bCqY0xx80qnTJb3es\nL1z04DP5E149MtBjRELVz+he0nQrxA5i5eMZge/P1Mpm9lP62EcHEdZdjbIE6+WEN67Jzx1O9kji\nrhgjkJYkrUJE6PDm/3pD++mai81rLm8aPkZ7rOVz9Bsf81Iwn9VML79nVwVodUG0cVg+EojXLwjN\nT1zeQui+pc62VP2PFKPmg6/x3r/k5e0N/uYjP12/5Wx9yfHdPaKnEfqQ8ShrcR7/SPr9Jb+jY3y+\nZvzwnqj/PU+dE6svNUkSM6uBdHMfZIO3sXj7hwt2UuN6LXazpDJHvnns8dOvWq72Lm+nlvN7O7of\nj/huyIO7nzF/8yuKZy7rCeIA7lYnPrGfsgjhP352hg5ncq7BtUimHuEs8CwH7VjMwRJr59A5M+KY\nohxwtY9NDNOMCgza7Rntvxwy9A+ikExqQWhJNC2t7qAXmDMXa3+kFilyBNFZyEDz9PvfILbQ1DZN\n7rAyBUYG+LWFSBx0P3JyR6bQQl9MiNyhDm+xjGT0Ch79+nNCu6Ksetb9htaD0PKwvJ4DAx0GR/T0\nUrAVgn06sDYGu2qZnJhtdkcjzmkcw2KOONY7hJZsjMt+CfqUskkyxJAyhy2Ncdng0uY9ozPgTwIl\nJGM7IG2HxmRofY6ZRmw7pCkUwgqwBoW372hil3EbE1oDdrtGKYlT7KnPBP4BZlvQpgXrbiQrQWlF\nK2o8GWF1HcMUIRQ0dy2uCrAcjS48oqRDqBHRpIxOjbOdkTqmKEficOTWETjOwDwaxhE2QlC5HsUk\nSBSUDLAM8KuRyOlBOhwajb2o0KODmGaSyaNqPJRd0Ewaa3Tx24o8tJlah1VYEgU2yZ1NfR5wLGYS\n7ujtJUUyklSaV1wTlAvedxHpUxfjBiyrd9gJvG3OOP3o8ln8K35zf+bU33LXlNgqZXt+5Dx+iVm0\n3L7b8Em6I/vwa+7Mb5jfzPxIjZF7Pl8+4fnGon/zLY41U374FfaLB8zffsvXfsXKtvk0es51MTLe\nC/nW3jLdCR55A/N1xMY4fOh+4HPP41UWs3nREIgzbtqALx4c+e5DS/rAwn3j4lwukL7DN8Mdj/0A\nZ5nw9tRif27Rvv4B7q25S0LOXt/jK+WiVyc+++yfcqSFwaHpO4Qnya2EYLfEjgpsrbCCASvyUfbA\n1AgCmaPlimKeWZdLWLuIuf/L/fTfgK//xdJScNyPlGpiZWLC0KbNB0IPBjnht4Zp7HHnjs4VnFoP\n1Vs8cAeyvU27GBmcBbYSmK5DZz0yS3C6hrV/hwNYWcIi8ugf/1OO+4HZrGi9Amdq0foa4bukKiKR\nNWMWIYeJsXewSxdRSkzfYuoBFUEVN2hvR99lRO4G2w04qIkRj9js2fsx6AmxT0mGgL5x6cwIbYwJ\nWk6rEe12TAvNEKxwq47RMeRhh1wfsLqZKpUMy4nJKnEryIee0snoxz31wqE1M45rEQUOwV3PUG2w\nxQIpBZnn09kZcvJxhc/oFCwtC7lUzFIgLMOxG2j3OZMncI2POXlQauK0x85nFncrVJeh5cx5sKSJ\ncs4WENo1WQPpQdHtRsZyZnRddN/jbDw4OijpUraGvPEwuoIhQhsXPdfoMELqFn9h2DtL7mpDn7SY\n3cTay6mUjed0TJXDPKc8F++4/mix8AL2zcCLr76nqhccdYiMr9k+fc1v0h94LhR27vK5nvE+xKjo\nkt/WEzel4HLxhqvrc9TF71hufo3/6DFPh4InwWN+vOo4/nTGXjvIbMne/g1L2WA/tHicBoRVT3Mq\nuTx+IPl+yeJ9zP2mYMoKGm3RRifc4D4fUoXlOASHO65PNk+LD8hGEHgn7Oo+Hy93JNERVR7Y3jS0\ntsLrrzjvAxpnxJUptjNx7+sEd1Vwqf8Ipa4XBbGpsc4COmXRJS0+Pc7SMJcTuunoR01859LZEsuX\nzE1EHlgYz+IkB8xpYnf6R5LgBIGvDI50OOqJ8qhxkona7lmONSczs/EjpoXhh1ATzQNmA1dpj2cE\nQeaTOhOnUaH1iBtY+MsGKTx2UUJ+CihEgdQB/26+Y+XNbBc1zWBRen9sFCvlH0HBrrwkFj2h0gx6\nQsQ5k2doUvCkx1QuSOqS0U5xxpHCG3GnEc8biUYfd6mhqsjGCZ0MTFNLOxjk+o8QJdota7Nh6GLk\nXYdfQ+1bqDnHOia0xwnl+axyQZmHnLcubtyzOES0vUGkCbEOUaImG0tmZrADhvNr/FVH0QYsxg7L\nD2CrqFYalVlMoWHkSDMZ+nYg9FM66WAXEoaMcbDRYc7cjuTLECcAV67Y7tccxR5nAmFGTrcLwjij\nshyS7cB87jCcNKgN7p3GSjyK+oRvj/RnkjgY0IHEYWSeZ8bDyORLhClJhhblGqZ6yTx31HLJYoip\nTi5LmZN5BX/45jHOwx1Ok5PG7xnTpywnHycPOD85RNFz/O0ZH/wD88OJrzuNeWq4+/p7fhlI6mnB\ne+Vx2r5Hzb9AJQXTu2s+Lu/xvtF8ujzj3vOeRy+fkT7uGLotP13bmOVjrqMl1794QeCE9Nkjjmfv\nuBVw+vQJ60+e0g571sGO+4eJ1l6jXoaMm0dcBNdY8QEim8vqC27sd2wHj6t+gdgV3FzYXG478q2H\nO2ZcfhwopoCPHw3fsWeZ7imWP/GzNz+RaIPKF4QZeHLJvLtgoiYbC8JFRJdukWZNG7ugc4asp4sl\ni6EliRvsAISZWQT/Pxyd/g34wv9KCPFRCPHbP43/6F969l/+CV/4SgjxH/7rGCGkxtMWi8onWbu4\nvk2fpcxHi8OUcmYXjAeJd0iw9lvUJKgPOVO9hWjipDLMOLK0HVI7wG8dTDdg4pw1Cs9JWRibTve8\ndgy3QYBuJNvQYWgm1GmJPjR0hyWnsSBfOqAFjmcx5S7C6pkbn3I906wqQn/FousZl2tWlqFchTBb\nBJOkaVPOKp9x7Mg7m3zyQR3+eP07HiidmtOU4ekeGRks0XJhJuYZFk5FqByaOGN/lpNYPaegw8rh\n5FTYjkVid2hXYncxQq8w0lCsKqY+pGkMi4uZ3PMZ8oGyLllkJSQwejGTTIilpIs0Az1+osmiEqoN\nQdgxyJnGmuDkM88zbWFzDBRBbVHUK4y2SH2oJxDJHZXQbOoJez1SWwONb5PbR6beIUpC4nKkGyAU\nHcqNWNEhtx6WHTB3McoJ8GZB6Rs6EzDIDqUmIjWyryICNbJ5PmO/C7CnnN1pwfeuwtgTrqW4S0rk\nIHj8h5QLvaPbNSzVI9qfRh58uuC75g3nVcFW3Cfy7qHklzQffJbByKcHRfJy4lTs+Oo64g/DW+Z3\nMy+8lEL0vKkzVuOMXd5yZ3qaJ9/AaY2//obm69/y7fXIeWThdBG37hWT9Z7pruTjfIs1etymn/Cu\nueON/A3P6oj27SX3j7/H/iRBvTH07+HmWvP9kyXxw5z1ZY9+/ozPl3uOqmXp1LySUGmXiRytbSxb\nEbq3wIRraW60YnO7o4hbGtXSGg9nEaFbxewVtDc9VmBTW4qqOPuzAsS/rD8XXwjw3xpjfv2n8b8B\nCCE+B/4Z8MWfvvnvhBDqb/uBmAyOZ5MNDZPMwNKMsmNeeKT2NdiKwYNAZJxHiiZsWK5s5u09vNLG\n9BbloGhPFbe2pIoKplxgGpfxzsVvalgKKjqW5/8EIxtmMdBOHbY3YoaCMtZUmxJ7kCi7IlCSzDux\nVQYlLDxrQJYV3RRSTAosgywOnJqWrexxPUllD7iU4BesvRjRSZL0hOzX7I8O9WywbcW2MXhSMIWC\nfmXTWIbRm8ltj9yfCWpJrCM6u8UtFMqTeNpm3Fu0xoHjSGsZfPtE1ykoN1ilpPY1B0Li2mJhLZjt\nlipwiHcB/pyRDC61BqUr4qFnyEHNiqORHMWMd5wJig2xgiGemGSF7R2QYkPgGmTv4nR7pj7F1AkB\nNjs1oCabBMnoj8yZxybqqTKD7dS0i4QcC6+ryJ0AnxI1WLjCoPIBx9VsXAg9zaKt6GKHcdEzbSbq\nVmOfjqzPe37/SUA3XfOiMHxYvuXm+cxUf8bx+wP++IrlfmIbeFiujXv2BnSJdD3k9BO7U0o8uFxF\nXxB++hVvPcV3i5DLQ8P20Qc2y5Ff7he8v5w58Q6/irh/cujDFQ+dEicfaQqJNA2Pkn8L/eAFYXgk\nGCL0xweMz0KevImZbgNedk/x3sY8qL7nYipYmy3FNPEsabnynnN7WhOd2+TrhAfC52HaoF+NxLeG\nxe8nPowvkfkvSYZ7XDxIoffpN2cIAbM/k8cpWm9whSAebHbpFml6FtlMKAxFvkcGgu5WgLuhqzz6\noccTh3/9qPA36M/FF/5N+k+A/8kY0xtj3vDHLt//9t9qhLCYF4aF70Dj4k4W6eQxzzvsfEPljig7\nY+dccLiemVSIXVqcc8McOaT+zGwseiVx+5lpiolSgaFGhzN93DEYD0suOJsk7DycSqCnCK/zGFxQ\nlUuSw7iwmGfNcZg5OzlMkUTtfRx7oFchyVwQaklZzRAuUEHM/uAzIhGexLE2aOWirAx5cUKcXCK3\nw2ZCOB2OdCGcEVWGS8qw7wh8wDL0dYOUAQfRMcmBvt3gzw6F3dNtFdKOcWqJ1jlJ32KHLitfk/YF\n4dJGdC466ymTkSLM6awz5DDTbHPmTjPZOyIzg9iCWhLOM91hYlrdsA3AEwHjsqdcS9yhRwUSy0o4\n2gNGjdy0Ppm9YF1Lolgym4Gtsch0zq2q2cgWMWiU2NLEmtKE6FuXTVVTWgvmaSa7GXHyAt1UKFkx\nNAFtb9PFNiIOqXTOOCv8ZiSaFdP6Gemtj7sLceYLjmc5wd3I/hhycajI9Bn1rzU7OdM6Mw9uPvDi\n9gGHJmHML7l6+Sn15kdm22d6lXPz9Uv+Klrx2fCRu2XPrrrHtJv50u3xswmzcTgLMl6n5zQnzS56\nwtAOeMWWT59e8GaaiKt3aONzjG7otkeWX3cETxvS5ze8Uye+eVEiN4/ozj4huddTdx7fdTHe4oat\n7iiimMXmLe7iI8cff2I6D5CPDJeP3+Klr3GGr3lDS2XbRHYNVsGAwEyCdOoxJqfQE1Vo8K2W0XFo\nzkZybFx7RastptBCuB2Bf8OsXJzt32+nrP/8T6T0//GvKer8mfjC3XFH3ubcMlEOMbPvUaYT6y5C\nWwrvKNDelk1wS3n2Je7oUIUzG+ljmYFcuEgp8PwZK1Ys4hNHZ6CVF8zBnqFdogaNkZLHLzripU2/\nSjF2Re5K7CBmDmu6WGJPhhUei3NFpjzGvct+OdHN5yytmcZeMNNg0dG5A0NV4Fslyp5os55aj7TC\n0M4+q90lRSJoZctibmkrm16cMHbMIV5gOg3Co90JxkqyWEQsJkOsY5ypZaEFO2ljHQPO5gGtNN3Q\nUqeKXMzkXc+hmMg9j7uiZWFm3K5jvXfw5hRXjfTYSHnOPPlMlUVu2bhyj5NbdLGD5cys8xW669jZ\nNaGbMZYVhUixmwE3m1hmIN0TZhoJFlCezahDzjRFjFaFNgpja+6EzexoTu3E3IcIWbLxjwwLD2ff\n4ToJdhJTGBiXCbnvMYclWhRIKyNzQ2yl0GYi8lze3UHxoefDZc7Lq4wnk8Gdr3nvr1jcdJzstxjZ\n0LWfk2w+p3sl+fETeL/VyLLmfKeJr25ovzeU4cRT1fF4+z2/+9EwvZwI/9DgL0YeHP/AA2FwRcr5\nmwqOa34pviMNM5avDM7jlKOn+ej4TN8A1S/Y3l0RpyPXY4v/wKH62JIWF7QejDcRN1ND8ZWLrBe8\nEA7R498xjc+53q35hSMRpwWFfU51NjOLhHd3Njp/iPQu8MqYy8RnDh4xljUpI62ZMOPAPM9Y1pJU\nn7G1OjxtUCImFTHG0bim5iwsSMaZOm/w2oR4OnEq//4SnP898Bz4NXAN/Dd/1wn+FXzhaoXVjKh6\nwgsapqZk2YMzK2r3wBBZ9O0Naky5lQrbbelkx/Xpiq62WQQjlsmYJ5++DzgeXcLdls6/xcPGtStM\natBCUup7BPNMMxsS1+ciyBmtnqTycWVFVwrM3FGdfOzUYbRbHCOR+g4zdojcoU0CRr1FY2O3CmyB\nyDxQHmbO6WrFwEjpFFgHiRw9srDGTlLkacGuKhkdh74ER40UcmQjHUwxUAjNIEr6zmXelthCYy9s\nSpUSpuCmPWnpYMktvuMS4xAxszATOqwZtpIpuOWYnxD7gsWioTUZWecTiQWrWNO3S0rdM8iQ5Syx\nVye6LmVp++S7M1ZxhJI7RtNRiQLld/j5kmib4RYK2U00vkNsTVR6zWZIWWcx63yB522w0hZpz0gd\nUk4+Yw9u6GIXGV3bMsoY59jjZorJjkmnkbGTWIcRlMfZ6NEqyccv/wWEIZUr+OlXAd/Hd+zrC37N\nJWOy4/yeh3l64uOPO+RPhkuvYuEK1G2KEQ67NmPVx/z8WcqlKRiie1wlS+5vPnD9g8X+TPChcXmz\nXrPzOnJS3n/2a3b391zdeCjPJdZvCIZv+FV8xnzzik82PeXj39E8WXF3+IzwfsRtWTI4P8ce37PW\nR/6q1vj5LU95z/z4wNsm5t6Pv6Le3zGtXpG92nBwC7xgz88PCe8/2shA887/lqap2D8JyceMz4LP\nEZxR7A1eVDDJE3Y+47cleW1ozYDMFJR3HHsLMbbsTcwkInZqxjlfUHaa4kyhkr+nEnVjzK0xRhtj\nZv4IE/rrrcafhy+0DNbmDH/j0OQ2LSnz6HOcBBuToCqbTfOY62rgcVHS0xDXW6KfR/ThBNPEsNVE\nYmTuwDMJ0imwkQylTd/GFDcZUg9s1gF3esa2e/Z5x5xPjMeObBsjWoWRLbNwCccJx9ySLAV932I3\nYLsB/nxLI3Js3yBNgz/bdHnMaTQIr6eyl9j2TGQZJAH1VhNEI2O4xlMnYA2eiQAAIABJREFU3Aks\nDE4D9tJlXkjClU1uBmq7IxoixiiEwSXrLOJxJGttgqPNWB5wO4GwFKv6iGx6bG0g6FF41DpisW/o\nhgscy6cLZmTnMs+GTSrpqxmdxwh6Gldz1mSodceh9xijiWzuSbY5d/0ddbclWVwwizWNJ2iCDqdY\ncugLRNXgDkuy0UZMioOuyOIOGJnsEWtIUYcC2SkSYTM2DXVU0IcO61EQuhX50mfwNJg79pYLZok9\nWrTHnDsE3Bb8L//iG1gV3J/WPH3voE5PeLk2fPlYMi9svsoD1qFNcBHSbEZ+kAvan1Li9Q+s3JDF\nz0d+HAW/9xqCqzXZPQG3Hd1GcO/+AtEuWScrHoma8WAxP/uJp+13dHuP5eIJ/XfX7NJn5PrX7I6v\nuL+5ZKe+54vqCeFNTOMYprLByiJkuGOX36f/LqK5lxOfB3x//pDm+iXx/W95fX7Neljx+CJg9/hr\n5uLE8OFT5LMTj9cfGJczdXnBo33N/uqatLb5d/6DC5plzuwkzB6oBixWDH2Is23wjg1NNGJEzKAz\nrGrEqANdsUdNS4K7E1YY43aaOfs744j/X/qzgsVfc07/pP8U+OuTkv8V+GdCCFcI8RR4Cfwff+t8\nBnzT0JQT51HLuZ+TL+9Aa0o/YxSGfq45Wxv61zPpznAca8q390n8GsteEjYpc2Sj3A5l5xS2zTAn\nNFikxrDdRkTZiPPoCYnuiQ4VQepzWDroMMKuZopgQxL1nIqa0gsZapeiNCwZKM7XjFaP4ya40mDp\nhqiMcNyOOBpw5wFdR/hyYDFG5GaASXCmIw7jkrSfCCefYjGzGGJ82WMzs2x7gkywSVz8UcEwo7qW\n0OuwdImRI7Y/YwbQvscusDB0NHFCriway9DkI7W0ccoC5S6JAkEoG5xxRV7VkFvkBqzYYlJHlKoJ\nfUMdhxSzi609vLzEb2OGvYeVbwjjO4axxVEZ02wYR80oFYmzQCxWuG5DXLfE3h1iFph5oJkGLDkz\nZCN+6BLIE5lXErsu9k4QqIrDUhGHsGUiaCyW2ZJ1b+MLg7oYuFAhaaiwHQ+d7lkW77jeW4wP9/hp\nww/ukfP2FfZak5YRV2WK6I5YyRXpJ4a7jctof85JTERfP+OpD5/VS/LwLdvXDU8jBzV9ykl+ZDEt\nSShQ1RNSz+Xx+zV/OK2J5UdKPRJtn1GrDtIMe1pxY6VQrfjxduLHy4/o9A2teYS8WOH+pFmnr5ks\nF9XlyDdPSK0jlXpH4L5gWsP44C1vbx5zf3Y4tF/w9v5ripsH/DiM9Nri/mrFD48/4UJ8RtscePRp\nRM+SeDogmpR+c8mw1Sx7CDKPykj6qMEeSpbSYCc2W20R46KiA+XFimZqmeo187T9c1z9X9Gfiy/8\nr4UQXwohfg/8+8B/AWCM+Qr4n4Gvgf8d+M+MMX8rsEBNNv2hIZwEx95jbwacXCFch3qIMZYhXYTU\nveSNfc60TrkIfVRqccoC7g4nhD3S1B2pW6DCkXujQLUFm7CiED1jPtNsWu4vXcZEk+s1YTcjjcKT\nHYHRmP1I1UX4eHRez8hAGPeYOCIYSsgihNcQXSuqwWWeMg5WQOk0JJaLEiUqhP4cxllh6KiN4UyV\n5JbFvnOJq4qdbdFLwTjd0nUp7TRwZ8BVa9ieSFubrrPZWDbanVlmDcclRIXAqlJqbyQYSyK3Z4wb\n5vmCvrcJTErhl1j5jJ36DLGNCSJWAQRTjmhOjKEmNFtMr9EnQShTwr5lWsEoWjzfYdr2RI2LUwxM\nDixmF2Wt6OwbalrUoeUgJfYARWMRrSNiawRLEexOhNsWakPjSow30vojTdByqhUbK6YyFncHhyLu\nKWk4iJy6gbwdKJIefVcx2RHv/s8PzNHP2STf8PGrhv7+kaSP2Bye0rQD94Iaf244y2omtWB895bw\n0HAVtBzznDz8CvdixLF/4KYO6a1r8rDhZjdQf2gYq5Kf9rf8+ExwVB5C3ufTOGcZPOXsJCmTa6y7\ngOHViZ/SGd2/whYZiT/y6M7hxR9+xnOno9Ujh3MX+77iTAlYLNEPWw6VYd5YBFcn7n8QbL0H/PxC\ncTq85P69CefHewinIK1tzg4di3d7ng8f0PUV1lry2Rf/BCc/YFkSJ+iRZUO2P6DPenIrZ549ptol\nUAtOmaCdl3RBz9FWDM4ZfpYTBi5ekJGu/vJ7Fn8uvvB/+P94/58D//zvYsRkTUzKZZwhihWiTejE\nETvuiDOJk7Y4syQaZtR6oG8NjpR4Zy4iyFkUZ9jMyHakC7dY5hxtnwiDFbnI4BwKIC4SHlc/QzQN\nJhrJ5w7ZBfRNTbBp2dz1jC7YjkebWSgT0ZQuZtSMzoBJThy0w3rZEYyGVhtoO6ZOYdIJ6oho1Oz2\nPWeLGe34CKempOXsEHOnCjq3Z2tyiilicM6Y7JHlHOG2E711ZD64THaIlHtw13SlQiUDZ6eBcgP+\nWDNMEZMccWdNXQmU06P6jGkZ4h1t6jNJU7X4tY1KYJAWc1hxEgnnOIz2kXmwcDYD0jjMSqA7B18F\nVOGMVfXsAlBCETgNQ+Mw+Tes6y371URSGRzVoWxYBwGGHWW1wDUj+cIlqnw821CZEaNH5DFGxjnO\n7CDzlm6SiLOJQI/UJmbbJ3T2CTuX7HwQaxvZ7Ml//4GFnukDi+DlS5LuHfnB5e29b9lcufyQzqyr\nmumTcya7Qs4vef5U8P30PesXM+n1c74cX+N+d8b5L3sOrwccnuJkOcrzmO7dZ2w+shbXbN83uJ7h\ndN+wuX7HK+Xx4uoB8tGXvA0/Ifr9d3hWiF1+xuR9Sb44J73M+KpZ8OQoefPyCvnuAVcPfmT5xsZ1\nlnS9hbryuFZw9tCmKn7gUGrGey7uty7PXrbc7u8Tbd8xVx7vUsk99x53916hX/2MXz59hjcpSuUj\nJg9/nBhnhZha3MkwpQFpppFiAKWxLMlcSpbGo5x3DOkK7ySZpaEq/tFwQxQi9JGypD8dSZlxdUrf\nCLq1h5xt7p8/YOhivPqWMLBAWSzefsXkRLS+5MSATJYomaHakaz2kdkBV6+xuxoVaaalwLw0OO1E\nXJ1I7BFLlTh+S3drs1c+s7ugwSfYdthLRRD1WJQYIwhPK/wixjgunmnwlMdm04NI6O0GLQ3NlJGc\nddS+pIk78i5g7AWj2xJ5AY4fkFsWk9/SVzOD39HrnMlrsIYYGYQMPVhNyO1dhTjTZN7MbtkzHRVe\n2zP6DpbvYxULVr1DrGuShSArK3zhUOmJhZZ0wUCdS+oGnN2SxSghmxE6RQwBdSnYFSc6y8IbfTzb\nYtSGpHdIR0Ns+4w7H7PMWJVnnAKLaFcxRD2i1bRCMmUllfCx45kuqAhOCzyn4OgrZBOi6xA2E0vb\nZ5pBKIMdzNjtgDzC2s0ZNyWEE6P0CMYUMSmkE9JuPF4nDUqPLMYvedu27Kua0Pkr2nnBIjbQNIyn\nluMwsHoScXU1sx3O+Hi15IOd8UI/Inq4pSz2PG1HHhxbrGTk9HyG6x2LBw6j7/Je/Yy7i5noo803\n9x7jL9Z8O0J9uGSZ95iLvyJfRZwu3pF++gjv6oq7aoHOwLs48XTekD0o8fQ9LGckHd/AeYOTaJTz\nka8M+PmK+/c+ASdi+WBLv1tRmVuKpcQpn3JmTZSHP/DC/QWRPWNKn9npSbMWT46wstmu1pDPDP0K\nX9nkviSTATIK6A8Zw2hxWhcEcouYcgp9g92viNQ/Em6ImAVVPzMnhmblIHsLW5RsYoe1mpFexcf+\nipM7ULkHDvucubkm6H4JnY9oclSumIeBdy0UviHetkz9GmEOVK7POm9xMhu3bckji3zhcZcnNKPB\nqSVVOuK7LV6R4bYt8TEgsHrqyaVgwPI1R5XhG0HbRmSJxTjUnPZb3LhFnRYor8dYK9CaMV/SHgR0\nOdHoQuOgJ81UNiQFzO3MYuyJ9w79RpBnESLIcasdjtMwLBUbCdHYs5xrlCuxEsE8uvgqI5sK5Nom\nnwIyd0nmeKwDB+FqLpqKRtsoCyLbYu05DKrhOOXceDWtbWhdwUJJ7MlHxQO519I1LSoXVFHHUY6I\nqsZVI+LGMHkl0mnJY0k+x9SdxA8F0iQMlSSvNEmR4Fgn9Gih2pYydbEsG7+r0PaMs7GoRo9xHFB2\nxzG1OWqBrhOc0uCEFs6ww6NAVhbZ7opgecdtdsmN9pmThPSxR/tNz2Wv2fZPKd1fcu0seVo8RH5/\nhzqbSX+o+Xx/hklqVJdw5uYMHx/xZhPy22OBP5T8Uklce+JYHMjHJd29N5g+403esDhlrFMFpkJd\npkynW9bnP/LiymVj3+PmlYNz9hlXYmIqfqC8FjS5x/HK42F6zVnwgG+fKj45HNFFxZR9wuq9w+v7\nO8zbI+d07EVJEiyx3AnvqLntG7JUUugl19cfmYIjvtNg6Q0mDWFfwnDHvpzRqWIT7hlOmrDtWVh3\nOK7EimNcNRLNCSNHum6Jb4dMW0E9/uUJzn8QVaezMSTuQC1DosLizss5710OjUXTFlh6y+WDlMPd\nT6S//YwoXmE3GV96H3C6AX/Zo+Ylc58hogXB3mKUS9qoIso2XPgz3dojP84UtPiVpgsEcQxF5pA7\nM85s0TcC1jCqBfF8R5uvEP2OTSIp6hmBReXf4AwefrWlT+/QUjOdMvRaMB8q6tWMU9osLMEgBYVy\nyMeW9aJlsnys+YLK23FWLikdiYh7zOxA1FGcFPLCwWSClYTTBqypwpIGYTS+nuncDl26WI7NNBm8\nqGKa14zFgJwTclHS6RSMQnp70BGnpsVZO9AqLCvCVHs2nqasHPRWkd/FpBsLd7un20e4tSKxLY5i\nwo8CxpOkUx7DaYc3OngXDsXsYLUGOz2xkB75QZFvbDq7hJs1KzmgrZZYK7Tt0/QNZh7QfsN6thmH\nlMEBd9SodYW+jtHWkU55JM2EtB1CUg79moePDR+yhPjO4sMm4zKemNtz3tYZXLY8Knq+7lY83pZs\nvw1hE3KdfkO693HLdxzGhCdPNZMcWHRPCJ/A//3Ndyx+HrK+OWe6K3gsn4HVsN/GxIsfuN5fcC/9\ngbZ8zP7xz/B2b+ge3lJyRbT/hPks58FwZPP4jG+ciPR6pK9zXn+95pP7mofOgvDFEal3SDlxrwrQ\nvOBVNKNuPcJ6h3Shbwyp+DnZqkIdJtwLyd0+50WTcLQdVtaRdgeDSmjHic2mpmsNorLQwQ4nTanG\nFerkYNKKaLWhGVsGHXAxjdRTT323Y5H+I6GoC8vgWoZQB1SjhdO57CJFLCvwNI2ZkWuFnQZUD3dk\nbU+pJaqxSDzNkRQjWw5n0HKFvrhjWJ5IfYMjM3obHByC5A4lNaHYEtSSiQF7KYmCNTM9JgyZ9gNJ\nXzNpn84vmVKFEEumdInlu5joDC9Oac46tNxwRo67DVkJGyFWWLWLcCz6SdJZHrHxcUab3N5gxB/b\n+PW1xXEtkesjTjbQHSY2GCJG7NLF6SJy2bCoLFrbwRaK7hjTMlPIDXWgcYzgqDKMkMxzjWpCejNj\nVIxKWtTqQNItmJ0d6VAR3HpczjFLaRjGGVNECDkhDi5bLSlkTT/M5OqPTIpeBbjBhDeULFROWEJg\n1gyRhRw0ghmlobAClD0yX1R4dU5gQlJlOC1nlLb/mFieB+KTz5IZ0UUos6AWB/xDQWMPFJOiD+CU\nGdIyZFRLcq8hd47cVxPyrYf2a66fQ9wbXOuKD+EVffEOq3FodiUyFny0Lzhe7PhwltLNj1Gbh3x8\nkeBOFbdugfv9PRwxcZSvCde/wP/2yGqXcXgB7+dv6NTAZf491tWScfeK8vhXdHd7ns0F6facqIx5\nIh7huQNd5XNlQ6cdXP2BfbrjYn7E8ycnfgi2fJQlP2mXVfOcS+MzPlwj3v6IKBKUe8ume8BdlyAv\nvqC7d40468iTmJ0sed7ZtPaBTZPQ3S3wYsnCH0nkRL4fCaeY1l8gHZsmGwgr8GSDaWayWTIVE4vI\n48bWWK4iNSm1W//FfvoPIljME4xlgHXqiaMWkZTIEbLeZTCKIK3R1SXV0FDe9jheTWvNPFpcMM0+\n57pE6Qm593lQpehK0RuJ7jp05NLUI6KYsKSD9meMfcSENm3R44qOcbzD+AuiCYJNhHF7Mnsm9GIS\nGaClwhQd/TCQ9AOdBJVZDMcKaWbGvuGwy9l4M0JNmMaDscfWMyQ1nt0yVRo/W2JPDmkysbiWjDeG\nPJyJo46xrqldi8rRyOCEg0duVQRDStEH+FGGI0aW3gmnD9C+xBE+o5VgTQ2ebRM4JaZ2WBU9Qbdm\nHk7QeSA8qnPNoDS7U0MQKwrR4YwLpLTJ5YCV+eTuChnEGCciqHsCAZbjMSOx4o5aDPi1Rz60rCKJ\ncHaMyjCdJrzmnC61aPsZd2k4G2zsfYEVDMxAufIouyWTP7LrMyi3hDiQDIxN/cd1ttfs4hHaA10l\nKI4XVM5rJvEOazrgvK14agX0W8nFfRsdP+Dk3bJ/+CuiD3d4Nzuudc/D/IpP54b23QeG3/Uc7IeE\nrx5TXr7hynzEGQ12M1E+FSAsNnfXDJt7WCvF6cUzyk7wxSc/Zzn9ls0jwavJYH91ZPJm3n0zYW0+\nYnkn4u6SV1XD5nXJvTCAXxz4/uMz5u9eEf92g391gT70vLMP2OYnPp65mLHF39/nbrHHffoDX2Sv\nkLrD7j2aZiB8PdO3kAQbMk9h+wbThFTzSOsoQstnYCB1GvSYECcJVW9wowZ3Guj0Ha22GIoDQT8y\nCUG+ahmGv9zV/0FsQwQzjTrhGYE7JpyXkuNaEs0CoUL66sTivGESPmpqMHVEeKa4efglIio4lRGD\nNxEkFu/yb4imJUZJsmpBupqYh4HbtiUIF0SniE4ZGuWxSntspSmURTIKpllTZBaujthscqrK4A0d\nQzCxmWPuRM3RlCAntn5FlDiM8gy7OrGyR5pAESsL4eTMo0bpBXdTQyAWiBZsVfw/3L3Jr2fZlt/1\n2fv0/fm190bcG31EZkR2r15RNk3JgApZtmlkTxAjpp4wAIkJc/4CmCFGheQRgj8AVCrJE9P51XuZ\n+TIy+u5G3Pu7v/707d4MMgcGA+XSE9ZTrcnZZ50j7dH3q7XXXmt9aUVEV4DpXSLahJEa0Wis2KTX\nU7qt5ui72F1PqmJaNthtRCgGxolke2kTTHqycmTpWyi1IZss8PaKgzHBmDQYhYuT96yJMG2DRnek\nmUXpbfGlh+9FiMoij0ZEWWJMYgZzBXVArDq2rmYx8xj7GVW2Y/SWuD5M/I6iEEQNjK7CNqZYI+zG\niOXQUNQpfVdy6FcYocEgHFx3xO8T7EChshalLMLQwKg2VJ2BaG3c3gInx2gNRBfQO1Nk9wO/lBve\ntTPckwkNe5rlFa93mrOPPh8jTRTX3Owec3j7CUtCd+ecdv+Ud+s5+VJgnO55PBupxh+pqimXesGd\nyQTbzim9jKj9mjePCkwZMct3vD5ajOuetbVGXJcMX9wjwcS+0qh5yTWn2F8dOBwMjqsdXn9AT+e8\neTJFfLI4bRK+tn5ELzXtIeJl/5Hb6S1q2+Hp1QrZjzwaL8nvuSTFgvalZHd3x+UOpof7dOfvqepz\nGjUwQ5LaR2oUhYhYSp+qcxDjJVUU0lUO07piGzko10W3EicRJGuBMnN2sSZeC4YxYZHlHKPJXw7E\nv8R+L8jCEGAKjRRz9u6WZhZQ9xpHjnii4+h6TBeS3hRIFTBgEm4P3JcGm1WIZWc4fkzWKNL8DtIo\nwPWYKYtmVPTzKTdOHWp2mMOIDmvMwqcKBVGRQA2FL1HJAY6aWvjoIkHGEpX3BCPsnAzRKwI1Q9eK\n0vHoshw1wMT3adMjWnfoUWK2HkdZMLg74sGicXOsKGKvHXS3pQ0lqnehFzimgWULduYUuMQ5uYFz\nzKicgXwMUaXAQLGTEm9nMpUhpnOFrmyqTmI1momv6dMReztgxAV9b7H1XIIux7ZGRnfEOIwMtkHg\n2hz7imHU+O0BM7HIdIGvPQyzwhkWNOWGnTsStQNWIHFVhex71HZAJQa952I7e9YHEy8YCYOExjLp\n2eK0inJqEhgRndFhHEMMMVLWJe0AKiwx6glq0ESOgy58lLelClPmQYnX9pStwT/+77/nBxEx8XZc\nuB4n1Qs65w+4kf+G6pt73BE9xa8+cXC+J57exOlu8OJjw5OTMz5MVlgfRuziHt86DXJ54IvZNYv9\nCS+DLZ+9OqHxTTbROx7+GPHcWdGetyxsg7G7i2wfknqf0K9KRBqRzn14fo/z3KI3cz74JbeSr9jI\nDu28xmkV6R0b91PLWxbsjj3fnP7A+dFis15x+/4EebpkqF3ejxVneuTZak984zZ5IPk8D+lvvidv\nLXR9gZzdJ/jjP6I/eDCMzIOGxu1xcMnlCXHR4UYKKUfsI7SiorIGxtrCDFpyqXG7FNMakCP0KsAz\n/5ponY7SoHIEebJj2FmYRDi6pNuM5EbJ3HHZ11OivWSYWyxFTW34vH/2OYZXQjxQ6y2yObDfwIoG\nd2NwmOyohYufV6iVRbE+xQgiLB0gZY+bmxhWhTq1Cd2Rvo+wIpu5DvDNHLMbIFyw6QLSOsRoAyyv\nImg6nHEN8YhDzU41GAcb1fRY3UDWCjppEQ4e7qGn7WLswsAcHWJzxG5thn1MP3egNGmlyVzkxOoG\nw1oh3Q6nt0l0xyReEDkDaWRidFCIHXVr4QcduhlxxBxRGQzdgDE3OGYnGIsAYywILYvcg3IfcDRD\nRO/QFSNGLVHxHiMJKQ4eSRPSZgJlzNHjHr+fMRxLdK9pZIwd2uyNhjpKmQ1gNRlyK4kjnyYT1J6m\nPmxJ6zl+pJjLKa3WWJbPWpcUXomYTJhMp0T6lHa08GZLNuFAHxfUSYJsDPbFwFXdMHQV6+5XuJ9Z\nWD+anFk7suEh3ocjK87g2mL85DP+oaC+eYP3zYSnxSVieMvqzZxbz77g9D7cuq84UQG/aO5j7xOe\nFxGfvZhTmwau+R2WPiHzFPp+xBfqLvn6Eclsx3Sq6IOW967gV3rFybGlFa+QjqDpfD679vhYXCCv\nfeTH+0QXvyBsXOpbLflxinN25N3rUzaByX32iFxyIQPy5Bl3lxnt24pkWXKYvuH8XUoT+6xKH65u\nYy2+4n6t+Lt/M6JrazzbRzk1eyIaYRBlB1pdcZQOpjWBThObDjgOzlhRjYLREwR9wS7waSZQ6IrW\nsH5nnP5ekIUB2LlEqRZnEnHr/F/FMSO6qUffWbQrzQ1H0HY9Q7ej9lwCN+drVTMxEoZ+icQjHiRh\n1GH2IdlkQFQBQ7clswd2ScYk2VGpDZuiw1QlhxlcG4puVaO6DlfYiD6h9HdsO0k1HMnLinHcs1V7\nLMuk2wb0g0HVgXVMiK2RuJGMiaYuFF0XgGgQfUBeSIQJ86aljnK8vgfbJxQt8VTi7SDuWkzfYLhy\n6LIji1mN2RhYTcV7JVGHLbg+WWVihgOe5+BYPcUmpHZaRmtLphSqKCk2HWG4Yas0UttcBxWBtpnd\nGLFDA7fsGVRF7wxMDgaF0kSRgyM1nqFxtWRvQa3XzPGwk5JUSdoKQumgs45VFXD0I/QJVFmH9gKq\ndcegHA79kVH7KAH+pmAstsyMBIyBWmdYbYvZlEzdA5gZonZpLRuv71HDjkSHJJaBjmx++xefCNaa\nj2nKkFWcfbomc3fMg4Zx8ZY6PyB/ayBGBzPNmNx5gJIzTu+veHr+inffjvQfQ+TMpFIdL8Q598/W\n/Pi5S5e+xOj/gOzbV3A4cuMvOl7vYvocrt9YPOeadgXFGPPNx4qr7IAVnNAdBAt9wXsnxzBuI+cj\nZ18rGnnFcPUKOZaMyVvOX4EvHc6ylne9ZqOPuO0VyXHCp9+4+Gc2WXrC+cec13dKXnsas78keGLQ\n9694Oq34o+m/CcJgTDuE9jB1j7vKMORIbXac7msOVkkXteimRq1Nqhhi18PNE+rWwcty/EphehVG\n9tclwSkE4RARlRKnEYSff6I7jnilZJ6bqFlDMvwrKMdGuynudo8qXLZhiChGltXIYFio6Yz1yiCc\n2CRCotOOuJswGQfkmLIxFtTSxJYe1agwOpu0AeHXdIHFQE/bjThugExaBveEzlOk9oSlCNBhjlis\ncRaKoThhTDbszYoiqNC5R4xADga1GWKxQdoDigVWVOH3IDqJXpvkR01hXNOpnn3aUV07aG0TNh5V\nbVOmAfRLArdiu4yRckvbumDZ1KpltV7gjAZ+O0XmIV10xPEczNSgUzMowA5qUhHRS4vtVcLoKPBa\nohPohU3uKEwFSrds+xV51LMZM4Q2aEaXtW9x7EYKK0cUa8xjgmnUBG6FrG3kZURkeNgBBFYOjoXq\nXA6doNcjlRfjh5APGyZHIAu5jDKq3OagNO3RQfQNp7sae1A/6ZzYNr52sP2SX6/ek2SKL7ce8o3P\nc+1ysox4NZEEL3vWtuJ9+IDE2TA1thyKmsd3XeofLznVMZ/HNpv2PbPrd0gvQVcbVH6X8+wp0Tin\n2Pya2dcJMi2JZj53T3/L3UcG96qKe6qgETcQN59hGHc53jLpkhn88j3XzjnhyVcszB/pjZfM3h54\n0Fo4/ueE3Yqv3QHxjWY7eU/n2qTf3IZVycaOaUcPS45k1wn2c586u8cXL6bcHkry2VeEz99wX9wi\nrmq4ERF5IA89xhgQbjTtYk7nzwnNlKNv4m4cHMekdX+SAG23KWossBIoRoU5C7k2avwqxQl/90lZ\nvx85CzXSORLHCwGNffIAO3nNuD9AFGD3ink4gLSRxYGSn1TJVo3PNtjjNZJJlXOsKyzjCiEEndJM\nBoGYSvgupTUPuMeetJNIKvTEw6Bk3yaklkkvR2Q/ImwXXVb4RoRfwGphIP2WTeZC3WI0HteqIZxL\nuusl6aSnbEArA3c+0m1zJv5AXhhMPY8+6ZFF9JPa2Kgo3RKnMQgrSYlBazoYTo7teDR9ThbMSMo1\n0vKJ1YClcj687QkeXZJf3sAXGter2QWSeTHSpiXT44xDvMU1Bvr3Lh76AAAgAElEQVSywXc9zD6l\nLw2GyRbfc9EHgZ/YbBqT2SDRIaxNl2Q/UMWSk2YCjWStaoKkICxbNo5LeKwgkgi9QsiQ7uBinuzY\niZh0IjC1gemmuO2RNgkRrkfRrBH1hCaIUDpHCJCTDq/7qV8l7CMau8MMHCrDpkZjKYVlXlFL2L22\nePr8ii7VhNuAxfmEuTnimDVV67EdVwzpPeLNt2TqBrfYkZUfaHhMO+25vCjwbtlYtPw2g2S6ZtRX\nvJ6foL73SMaEabxlPA68uzXjcxXSfeuwf/w91tJmWjyimDvcffeYp4OD6kfk+xVtdpNrtSM1n7HX\nituyJ+slxec7fDfkcLjPwrxms5rzSES87Wr48ciD+y6n2if79JLh7h1K8YrJO/VT5aszUny0GesD\n9mc3efd8B0uPP/67f4LqNoyjZF+HdFqT7GvcQFIVPcPco3Ilk2tNeRqSN0dmlsFaxMzbHWbQIQ8B\nUeAzmke65i9t0fpL7feCLPoRrEpx6Dw8v8epz1DrgXbp0+Vr9GxBPhUEqsNoO7JbmpuHkIdRh2cG\nNE7AaE9IVM7W2ZLvelynos1bmGh+E7zBx2MQYMdQ7DW9DbHw8a2MxrbRh55JGpMNW7LGwegD9KTA\nOxqMnUGaGOxVgCkUae8yHiz6kzVjMRKMgp05p9zOmMyuyTcgbcnWUSRaQ2cxYFKYFYavCGLFbnfC\nxCwYDRfbVYxtT+2ZTOuRwkrAsBjaiG8eLTjvJpjTPc8cA/PjXZqzls/HK6yPJ7RORtab2I7BZPeJ\n+g/OaH67Y3PzyLhPOZ2XaBGS7e5xu7/ibXJN7S+ww4K6GUlfzDHOeorNAXXP42R1kzrPMO45uAeJ\nUDXKP1K9X/K8/AuKcEe09YiihmPfYeopgdUwFg6D3xHRY9sxbbLHH04RToZuLbxDSefMifIt+1nA\naVlQuA5NZUCwJ+1m7LKWWIe8KN8g8xP89C3q1pruwqC70cL7jrt9zJs64Ik+cn3/c3ZKMnuTsezv\n8vHse05eP+FB9JZnVUI86/hGjHz89Y5QJtT7Dyztcw71My5mc5x+yvnhe94VJsMXa+Tb+zx4FCCP\nr5jUFpYfs7xxZJAn6Mev+fTsyDKds7ddHhodF1qxvGegPya8MWK+0RPyXnMC0GcE9ZKKFerqhB+C\nX2EFj1Fuwdf7J3TJBZM7cz7+sOZ41+XmboV1VXMn+QLhHMl0iaHnqKomcgo20kUHA6s8x2CC3zYU\ncmAVpNj1BpkKjrsY3ewpFhLdLSn1isD00FFKNFz9zjj9vTiGWBYcgoZA1dSWxb8RT+mSI/FBQH8C\nuyuiYUJjaJpAUv32AzUFMnxBjEU0ttSyQXsp/rsDw5DhhAbNCG0dwNUWL3eZdD7HxsBcKvxec9hp\nqmBEjw1GE1DtcqLawFEjSTugDjYEPTqWFPWKSXUgq0sqDwaOBHtBLecUns0EzWTRUugUf2IwhC5e\nVnLsRq4dTeg6OHFHsp5RqhTVtgivQRWKQ17RN5JwMNkXBW5uE+dHCDOawqZ4+J7q7Qzr8ibdyTtu\n60vstuOgLnh+94BMGvbLLS8WZ/gfSw4PTer0NrIYyfSUvbxJcPjAvpxQVRpHTjg7VDw5nCA/UzhR\nR+feYbg40lZrgoeX7PQV9lWJvxMc+5vsvs5p9h2miHFcSWtHRLi4akNbW/TaI7YDygJkDcgF9b5n\nNJeUhoeeaFS/w0ls5MalthO8xsLtdoidz7EV+MsUFjnffvc/EXUvafctXV0w/xzijwXD1iY52XFy\nLrkaKm6U19yxX2HqCa+n12SXBsf0LV1xh1+eHOjfr/nR9zm/e0Y6abnRznhZPyWZz1GvDrTxD9j7\nuwx2wa3djBNX8qp+yvOLFHTCrt7THQ/M99+TPD/noXFKN2gGPN7vFSe1wbs3GQvLQZxseDf/jvdJ\nzOEgeG1IxGJDZfX0y2+xphYeFQ8/pDwL3nHZGrx7taWVkttGyrRweGPMEQjeHAf8CvpmTyxq1jQI\nq6TdB8wmE0Jl0GqBLS0cMiYiwtcR07nEmfaYR4/ANPACF6PoUD1clb+7ivrvRWQxKE0gfHDA3x+x\nZopBe+gkI0tHImHhPTYJpEHtjD9FHAm8mqZk1MjYp2otBv/AuzYiXkxZVzkymSAOJY57i/3MwVQa\n1Qs6bTPuFYNsmFgh+9HG0hsY5vQC1LhFkGD2BccsxLPrn6oXMZiGgvywRYUOtTcwZhI7DsjdLYtB\nowaPKreRiUcTuqTHPVtvxs7PsIsJu8TCkgOm17HLbKxZiGFK8r5B+hFpK8lNiS1cpiJnel8w/3Cf\nv3hyxH/+nlDc51p1aJUyxN9z46nHMIzc3Z0jwpHj0ia6spkEJc2TnpoFY/+M+czk6mbHZ6uIFzuH\ny+aUWjjc6Tr0iWImLGJtYNw6QXyf8viJTXZD8SHpSMRzZh9jnLFHriy6qYuxLthPG4x6gQxLdC0Z\n1yXmENCeNoRNSeN6jHXJIEOGboKoWg62RzjZcjxITMvBkjap2VAi8Nc2x3RJ+Y9f0Z/WLPVD0vwF\nzz7dxfc+Yk5iPhhnmFcuevkSu55wtTtDJt8ytJLl7jHX3gY//YHy/Zcs0+e8j23ev7Ax78/Z+zu+\nfP8VcnXF4uHnVGx5Y73FVl/jn10ytm9Y5A/pg4qVWnFn1nFxeR/3s4g38z32C5fY/shnn2YM5zfp\n9weeTFqayZ67xwnDYUJ4+wXbOz2NfYvp64av7uX8sJtwfzfDuf+OLS3WaxffPmV/M+fBhw+IjQ1+\nQ71pMaOa8EGGqhqGcULuHBCmh59rmHYUQ41pmPTOgFI+pmpoxBFrN0PZ10waj6vIwWp6Ylq0GdFL\nwVQ5vzNOfy8iC4FJ4LQcmxzLkpz5EUMf0YkJ7u49XbNg4VsMVku5k2zXDtFGEe07xsLCyzbM6LD3\nE8pyjdFnnPYexmGkX3gcnv9TrHxH0F7jTQuGwSKZ21h2SJPZ4DUMeko3AyVzzInLmNT0JybSLIks\nA2EaiGCPfeyYeR5m36GaKY6/Z9IbTHWIEA6+6klcjd0esSlppwtOhh1iOyUeR0SvcdCUcsQLHbSh\nEEriBB7RVmOFYJYH2rBH9TOCYYL2K2bvbIalyZi3hNrDa/ZMxGesv0wJzm7ydvmMF7HJYWdzPX7A\nPpxxYipuXj4l7R+gY1gdJrSb+yz9j5i+ZHk2sNtMqJ6fc2w0h1s3Wf14wJu+YPv6KcZVSVOOeE/h\nRaPoVUhtK2QNuesgZYJIO6atydzo6KIYceLQ5SHFwcCsTWzTIDY7VLdn4muCUdHbPTNzIJm0aMdj\nFc1pSmhUTmOO/G9//oqkPWc2fYvt3OJ+VWDXI6vZhOHY89l5x7ROeZsoHo9H5OIJn4dnzG4/4/yz\nKW75BMMUdPZ91Msr7Idbsgubz7w5w6Oe7S8kR1XhX77DriSyesPxEPLUMekuXRaOw5O9T+1b3E7e\n8k5teHLVwG3Bne0AJwlmFLIl49204vI3HuG1yTbRiGcGN8p73Ow7jo9DNh9aTCPiWj6ljU6wN3vi\n+ITRO3L+dkvxMGTnay7KO0z1jrf6Hca2pRpnhCcFKlqwNBSjLfHznqEALSpmfcJyzLEdC6FOOKgM\ny/JRpz1wjTRq6olB5te0ukR7f01uQ4TW6H2LbUEX2ry4dwvPrmi3gi61GatLDo3i0Iz4ts38/C3t\ncoIyfdyFQzk54ThAIwYmqqIu5uz6AHfhYRcda2dk9Kb0QtMUEFoeedEzVRVN0yPXBknTMLlqkC7o\nfiA3LcxakJoBhbKANePO4biUHKqO2G0x2gZTOohjx1D5VFlMjc3GiQm7GbpSdLVk0BrTlpRRxTwq\nEdeCyJZ0RkuNJCwsHFpaa09tVrSmST20FB34W4c34ZHb1h4rv8kY+aTTF4yjhkHzqNA461eM9in6\nwwViUSGtGd3iissfXORiZLF5h94ozswt3H2FfO8yD0NWP2REv/hAPD5jmCnc13vab3asbz1hs3xA\n/6XA1NdY955w+06LN99geRKht9hjzrypGTOHoRLkk5CoNBBihzBGDGmxdR20NVIMFcIxMehRhUk7\nTKmSkPZgksoMc7NhSAcaZ0LQHnlp/hOK2YSP64F30uK7x9DfPKN5do2zcXhvO8QixB2WiEVD9+aC\nl96UYvyc4wZMe8dKXbNJnuEZM9ydxelgsSPn6kVL9TFEvHa5ODyk7e8Rty64FUblsfV/IDNKXnLO\np4t72NIgOXyC8MDtXPHSEshtwXZ4hz2bMt/9knvmHV44MQvHJu5usAtr8krQP7Pxpo95tGgoY0F7\nbXFZJJRdQ3nSsfUSjrVNbwTcnvbUt79BPhCs04eE8QFnn2LJAj1GpH5I5vZoaaBiTVko6jLFNwak\nu8YJPTIRItYJqV7SBjbdUWBhMw99Olf8zjj9/SALRo6WixUNtNmBRZQSe4ppnPPhoiWMl6TuGZEn\n8EcLe9Xg0CMuUrJNRj8aEFrIXjMZQ6zuQDzp2HQ7htqnHyuSscQtElwVciRDGR7N4KFOBlLhkC06\nlBWS9lNqnaJFRyZHOvOI3QxQjiAFkVQ4pwarcQpBhSg9CCraaiQIBL2IMawVedCjxAz8gmxmERqC\ntg7Y5wPdXFMdaurW4ORQo2cZolZ0oYHsQxxPMu5STE9Quxe4lwMvUoWlLULX5zDOeXPXYVu/5GlX\nsD6Hk+wTj4Wi/FQSmWvMY0NqSZznT1DZOc9P7nLRdeSblNWy5Ll8zxfBNdc7i43TER5f48wMnLcB\nF2/f8KC5JKtc7gwPeL/6RKw91ioA26YLQ6wwpe1HprWmigSaNbZb01aCpDPoDAfXOyJrSRx4xEVI\n7w+M9khUWwjZ4TkWm2KC44I7RiTJNa7tUo0O6b4m6e/iNPD1i5GN7zNLNtw9gYj3DOOAV/+at/GC\nLz4fMF99j5jAafOSrtiT3MpwLz/j0XSDpTo+nI1cvq4gfgdnJebD75h+ucE33jDpbxJWW75+m/P5\n6SPWQ0Jyf0U48SkXDzivT+iz+1yKgrP0AVur5eb7BZMq5sNmxdofuXPrQHK4Zv1ZTpilmHaFPH3D\nh2nHxdsRS3yBfdzB/ZHw4Ybg2qaTEbqwODZbPp0sqa6+p9l7THuJ6mxGZ0c5WBTtnrptsPsAt3HR\nlUC7HaPKOdQGwz7EDTVtnzOmAoeSYDQJgaocUMcjlpn+zjj9vchZIAxGu0WJGVZ8hat6ul2FHQlu\nOhdYQ0TbH6i2AY0t6T99STfLOT27QPmKQB8Ic0VuGpBUNBMHs9BwnOAHA9cZaNlQTGY4TYgOR0y9\no05dZo1JMR2Z7gYac+C4E0y8ntYrcPMQX1lsbEkyC9GqZrtzCEaXJRvWnUM3LTlqSTyatOX65zJu\nH1xJH1wx3Z0inY6NKLCJaJVJUAicZUJ9rUFkaNPGqnqm3gyOG4rIYWYMZBh8++1LjmOHqQ/k0T0m\n2xxnHkI5UrkZ7t6ltwxU+tMtz1zmFJZPNyrEaNIlPtbuijgQ7JwUWxiIXcWQDpB5TBKJyHo2KJK4\n47/6L/8Rf/rf/jd8UAa33rRo+4L4vs+HPGA+Cuq9xpi49KVi0AbxvENtGqL5DKVaBAGXaY7Y9pxa\nEUeno8ZG+hlqdDjVOVtXQ24gHZcozDCaOft4w+baRp2M3GDCW6+is2285xc0kxMmHzsc/5dclT+Q\nXCrKr7dMPvyS/HJExQ+4d+c99UdNdnYbN6pw+w1zd8Wrg0G0mPHFpeLpF0vaFzHVaHL/8CXV7nta\n4wvEk5e8vvC4rRuu5TVzL+byh5ZEtezvubxbbrH6nrS7hR18JKtTsqhnsBtmpze4wTVPs2ue2F+y\nvqh5ePstoTGj6qdM+pzuxgEnLDi8BUt5pBc+7fEj6u6A+TbGnNrEf/EtZ9YZ/3Rn8cf3ZqjIxxYN\n6W5ARzGV1ASFRb0YEbWgOY7EUtJZFtQ2h3JFkMwptzWNLjA7A98KCb2C3pCU4l/CdG8hxC0hxJ8L\nIX4QQvxWCPGf/uyfCiH+ZyHEi5+fk5/9QgjxX/8sYfitEOIP/7I9tFKYrcYaVrT9DW73/FQJeIz4\n7v+oGQ2T0D5nMd1iDCv6exmHVPCWBXMLnMrHalvmQ8vrySmGrNi3DYZzwMCgPfaYmYcv1uz8DC1b\nVGPibwO0glCVbGYWdlSglj11DG0RIWNJEQv81mRfAjoi8Qt8KnQYo3oDc99g7zWaFtH6eFaLbZsY\n5Z7EEHT+gSHsMFXD6B/xxx1+vYW95CSp0HqGaWkOakK+NVFTg6EIacOKpOkoLBt0Qed6zA8dTtxR\nNppK7jDqmCoViGFPoVzsQVOwZNA1TqvpUgfR1tgiYhwTnLKkP+TEXcxk8Jh4PXIzkMmWyHbpjgE3\n2nesGokSMU+XLlf9TRJXc+fqNRtMxDjSo7A6AzO0QJroqUnb9pTNwNwsWFwLTmKX+rom9iMS2aFz\nhWElNJFFbDsgE1biCl2HmN0GuU1ZTCxOB59iFRA177jxco/8wsUzCxzrHeksYxvNaW4+xs8ecz0r\nWM3fsbcUu7XNmxKqp3v8ysSzFYmdEt1L6UKH9cMMsX+GnQw8vr6mnJUMzR3S+/D2YJDKOS9sB/M6\n53hQPJnPuZH8wOj/msk7H6Ub4vdrsr5mwZqFuWJ6nWCb3/LJ8rgTPWFXZTyebvDUfeqLGWbwhiLU\nGG8esP+tzbFWGNzm1c2AboxYyc+RZyFidiA8+4pn4sAi3vPVv/3v0R5rDiKlUYrikCGwMbyMut3Q\nNCHGTJDNLdyyA69AOJJAG7iqYqldJpOMobGpuynOzkHs+///yQIYgP9ca/0F8K8B/8nPMoX/BfBn\nWutHwJ/9/A7w9/hpqvcj4B/yk8bI/6cJKYlCgWsEJI1GndzBt0OGoKVamEil0c6erZqRWC4mG5Iu\nJKpj1DCjNXpKt0dEsM07TOljiYC5GmiLgbZuuPZAZ4qJ0JhNQz23aHyJ8FrQNkLMGfMWdpJ+PyKt\ngaPb0nolY9yzlAb+0FPlCYMF17WFpU0sX9MohyEc0IuRVih6x6ZLHdzRxCxizCHANBdEuxZfzzl4\nBgYmvTBYpy1ZmdB5NZ3Zs8kUXlIg8ehNRbcykP2cyljSUjIUPsLNQMYgAD0yEhH2BX6o6PtLglHR\nzm3mVwaitnANj+Mgia2QOTbtSQHiSF92tAoiEWA3GZWZ8e35DIeW6PwlytDoWz3qWPNtb5PUPY1r\n05U72uUVYV4yMDKpBX5Q0+iRqpxQ657M7ujnIfp4oCxAjxbJriOzTbKuQQc1tjJoVc0hmODEPccR\n8rJn5VV04y+p5gm8vcHe9lknf8hF7/FkO1C9f8v45hXG5Se+2kAwXqJvFtx47HD70RHUFdffSp4n\nBvVLF/udoHzjcf4pJjg9cDFJ2I4hC/vIQj/j3mWIeX7JPJXMLYvl7ZTXm08cdj7Nt1P8OGO6fkD5\nuMY1BvYbxW6cg2+xOH5BF/TUHwzkDRe92FJvVpTOd1QvPa6ZUlvv+ShsWMyorzQP85aPf+BghW9p\nwgn5q45dlTGNJ+x3S/6DGxFWYOO2Emtaw6hpi5pujPEGBwabcK8Jao/CKmlEQKRCDvkKW8Hes9Dr\nOVIeSYyRyjjiy38JvSFa60ut9a9+XufAU35SGfv7wJ/+/NufAv/g5/XfB/47/ZP9L0D6f5MO+Of3\nGAfyKmEjNdKo8aKCq05zwMf4vgHbYexvo6kpTI9dfpNjqdDlBYfjFc2gcfWc69bnqxclMu8Y3R56\njUgbhtIhaAeM248YfMFoK6JNiwrXmJnDcDCY9xUVBpFto0KLwe6YbzzMjY+T59RhReH4NFFBPvTM\nbI3jWgxaMlEDg9FhjwZeGJLuDOLRRB98dmLkkFfUjByCKaO9YtAGpW4YGTGbEYFGmANmeMS0DNJd\njDV42H3MGK+pPBtvLKgDH2k16GuDPO9oVIsnOjo/RImRwvQJpguK4ARre6QNSoKxozW2RFJSNzba\navGuQvJ8TtVHSNmyMww2sYvvWDhHi0xcoq/vEmU2UVjxNnhAkirszmY6lsROwrhL2eqQKpNso5Fy\nCAncKUPcIv0FbmHRVpJKmPheh2kq+mmG7AV9YTM2CrtVGH1B0xnksqLVgsEWnMWX1Polp03HeNDY\n7xRJusHvBtra5+SxS/T1Y8re4tWm5mLfkInPucx+jRhu8ib2CY2E6TUUSxdx9z3D2Wvar1IWxQ3i\nyuHL/Ed+WwuOz0La5YHFh8ecbh2cwy3U0+9Zni1xHpggUtbJTYzzb0n1gh+PHV18wqMluOElr82c\n2fcZbXfBrtvzbAuHOznm+gFZopldCXIJXzoVynd5cFbyafYRqzXxvzvhTF1wx5kSH0cumbD0Yfrl\nV4Ttms4V2IPCndosB0lml7jKgEVFiQnWhpPGR/cthTIZLZNx4TA0IdfWHsOKqKwWx5wytr971+lf\nKWchhLgL/BL4X4ETrfXlz5+u4KfCNf7fJQwv/xkfQoh/yE+RB7dvneGYNfbWItcjYR6xSLZs9Yy9\n8Yxu/Bv84rMCowY/HsiHX2NM/h7nf/QlifGT+E/Xd4ig59Xsgi5KkIcryqWD1VaEw4rO8eDtke7Y\n0jUxTdDgNA69Z1EMivpY4MewMQaSamQwbbZ+QVAMWGlEvfcZ1DWJNFFTl34rcOY25WYgwyfOTDKv\nIrYatBo47gdk6CJFi6k6enNkUvrYhiBoNN0c7HaCEa5Rm4i8i+hme9LWYb/cEW4MWsck6SbIcIdQ\nGgpB30yprQ7Hsmm6kdpzCa0VLgHmfktrarrBYVQWVtjQeDOM3EE6JbPGpMdhf6pxdEe07WlCm8ir\n4Nrh6IXcyn3u3LqD+7JheLynrA3SzYqoVXSWwo3giMB1CtzAor0GpVrKrc1ickXTLfDIOXY2Wh3Q\nhkCbA3J0kaPPtDBRokcLh8GXFFKThgPDmOILydv+Je7BZXE3h2cj02XCGDU022scHmLLDc7KYzPC\nvRs9H+IvWfRvqIsr1F7yW3PO8qjRpzWW63C7fYbaSz6Ln9C+M2htkPLIs8AkEDbvQ5c7rkW+7hGj\nxevFivN3j7lSNmovOYs+0L65RTR+xu7BG26cfE72w1s+Xgc4Ny1CDdF44Hh/Tvh6YK59xram/3Jg\nPvjsu4Y76UhdK5zVO/rDPY7LE862n6i//ILvSpMHVchwf4+hB2rP4tHje9S+RzdsKHKfWpoYUY23\n0Thuitz2GKrGFDad1xOULp06MDgaNQZ4/ZHA0ai2pd54OPGOLp7+Fanhn7d/4dsQIUQI/A/Af6a1\n/r/QlNZaA3+liaD/rHzhbDEnDyxas6KNK249ucNhs8Df9ayMJ4ws+aTvYMQth41Ns10iNwPsM0Y7\nZTQrmtAikJr8xMWSPToMsGuDdphyFbtMVUV/Z4Zqpxizhla1DFZF2YHtdthWSK0iAmkgG0k5tFhI\njGVKLXrSyYBHiidD7MFBzTKGpoFEUE8N2mCH2jtk5RSZCCapgeENeGVIjMWpPbK3drSuSTjx8ITB\n6JjsMOiWApVWmLspTRrQtRY7IWiFTePtKdYpQ2fSYNHNcvSY0wY9xuyIK1qao+Q4Qj2zUcolXPYs\nTBNZxBjNiqlR/kQSi5Kx1aTjGtWbdIsB7SiO1wnNFJbVFS9Gn/oqxYlqsuwM+abE85cI82tUryk7\ni8XYoUuTLm8wtMswWkxSTS8Egz5ycEtMLyeIQpreQ4qQeGbSyA2bScmoS3IhGc0cK9C4fY6rco72\njv/9z57BScOH4iveLkwwP/GBCTevLN7XEaan+bVlMh0y+jFltvvI+qLnU3GD5jbYN3tu3nLYzgMq\nK+PjLsGUktf5c964T3GWGssbQNRIa4L2PtKVPYH/jq6rcXKH98kGL/mRB5lJYHYUIuBNZFBe3eTq\nO5uzuxGbcMYkXBAte34TLDkXPtWwZ+U5HHdT8k8VVz86lNeXfKocyonNqT7lw90SUV9gWZJN9R3R\n0CEfHSjiCY/0CxZvP6C7hK7WzIYTtFUzl4LxOGK6Dd3YEdolqWNDnWC6FoY8YooJCRHZrqSam9Se\nwSGuiF0DNcwQTftXgef/o/0LRRZCCIufiOIfaa3/x5/dKyHEDa315c/HjOuf/X9lCcNxkKSVxWA7\nmGNNKSROoLD9ElX9E6T9t/lmuCaqfHbigDIa4umAsReIdE++FkT2HlM6LH5lc1zvSMQ5jWjpLVg1\n3yIthyfHHdLZY5kGMoZy6zKzD3SOhTt2tE6EqXKMpEUe54xJR9/U9J1LfTgg/Z6gXSBNQTe4qOFI\n2pxg6R7hWwhHYDoth73HkHaIpsE3R3QPeWmz0BNk27GrCixShtMO4xBRGz2+6tCBQ98JkjbAGBVD\na2AmKZmVYzUefS/ps5C5dYC2p+st7KFGWwqEz3VVc+K75HULE4nYWwgnot5bBL4kKH0ODoSVwBE5\n9CGecMiTCrXJaU+X/OLBjj+POnamj3A05480m08Dr/VHXDtjVbnUdk/oRRxah8QqCYaRUds0RHhS\nUGmBzBJ6S+DH4OY52yRGmwp9rOjsCIs1/tqhSgKurBF/3dPFkoVY8PgP/2M+K5acezuuZjl/p3OQ\n/Ov8u/lNPt77I/7Wteb1dOAXw5rfeHf5d3YfuFCnpOKcXXLKjcucv53NsUTHd//WBmNlEN0dmERw\n/UbQOjf4j04i3gxHevePCD5UJNuE939nZPlxR289IlUFxV3Fp8mf8O9XnziQcv3Y4+EV/LA2+QeP\nDQyn4YdnDg//xhvu+1/zt/7DZ+TPesZHc5ZDiJG/YdfcJNqU/Mht7v3NjD/ZRzj+SD2zKf9P7t6k\n15stvfL67SZ29PHvz3mvM52N09lUUnahAgQIMSlgUhM+AWJeMKoRM4Yw4gPwCZjCgE/ADCiVLdKZ\n6bzOvNncfN9z/n30EbtjcD2wwBJlpbBSXlIoFBFbipg8K2I/e8Vav/mc8/INMIEffHPg4f8Uvz4Z\nzIPQSy5eUOmUy3FA3TTVpiC2A6PI8NsV3QrCrFm3kF4Ul6+hREMAACAASURBVOjJ8i2hDZjQMzUH\n0vnKrd5Qub8HWz0hhOCrUKEfxxj/h79x6X8B/kvgv//r/f/8N87/10KI/wn494Hn35iu/K2QSeDG\ng21hye4nxqKnCnfscMAhmbon79UBqgVCyTyfuKQbPt8/UZ92qLgyDTVlPpBvJWluyEeHtltiPTO8\nLbwnku+V3yEJgfWWMgaDqgu8GZlDwtSsmNjy9Du0vFKKOy7sSZPA6kZ2qcH3W2YjSbuImGfUxnBN\nz+Ruy3AvaZqWOCdk6skSJU3UvJsJOkHcOuL1Ti4926PlYZ/kwbHII0X6YBEnNmtLkUr8dGdNd4xF\nYCMdSlXEu8OzUJ/g2W9I/ZM+36IBfV8o6jugOfuObN5wTe5kqaS6F6z5hUob2hBInELYjKQquS4z\nWX7hxRR0WuCigx/vEVvN3I788a++4Fc6cNB/Qf76J3Rlgr7moGdGv/CyDyxdippTpmYmUQPzIND9\nkZC9EV3OahK8n8nvCy7LyVTAiUAXa5KtZ+ZCfQH1ITAuDf/sn/+A//g//2+5xYzDNUFIgd136Lli\niJEmfxLHA3a6ksgtQ91S2ciz9cxxR2ZG6lqBloS2YMru0O1pjjfeu0AsjuSrINieehxxZYZ0AVVV\nyDGAePJWHEl8T6qgVYJsnLB+i24E6dqjw4w2DVMfoB5ILyV219FOJS8h0rkJI3KcqcmUZ+pbbJrS\nhBWhSq5WQTlTecFctviu4KXYEN3IA0Hue+JB0FxnbKZo7gWd7tHXjEUlFNsRNXqUikwuYvKKNT1T\n6RMmzhT5iAoSLW4M+0g2KlR9+TuTw/+rTv8NxvxHwH8B/DMhxL/+6+2f8xVJ/GdCiJ8B/+lfHwP8\nr8DPgc/5KjT5X/x/3yKSpxotPDE45LmnrRWdeuft9gltLJ8dO95dil6f6PHPqdqR7+QKrwJrM7BU\nCdf2yI+ShDUqmmNgEHfMfcGfBU3U1N//Jq3ZIJTgRZXsszfojoRkwI8WHUsaNxPkES8FRWLp1xnc\nik9nnByRu0CMN2whWFJH0QlGaQhixFpJKxTKKmJM+YSmkBkvB8Fm9jgcfpV0q0AsgnipOS4XhhW2\nVmBjhZpWRFWQuYXt9CRpE2oc84tG5pa+HVn0HZlIAj35UCOosS75yvYPQdho9naDl6Bf3klrQWhz\nSqdYtwL9MjOEM5nQiFXhbgNZXeEePe+fnbn/6Ee8iF9z/qOv4yfJ8HKgkYqYSGI5k4kGoUrsew31\nxBh6QuexnLBZw+GwEvwLZpvAJElkDrVjXiGdU+RUkPc9tktxekcZK4ZR0wyet75i7gvK0dKdeloP\nk9gRs44iG7g+TvTZnWgq3naGsFT4SbJuP1DJkXUzc30arHOMccCOW3ztiecNxpwIvcV0d/Qsuew8\nFs+czVxazTW705Ub6qQjCQUsK+YqSEbDdjNTBsHyFIzpB87zwDTn9Pcjj2JFjxWv0iDUSJLV+Lhh\nqlo6r7BB0qiJaWdZUqh3D+QykMuctX3hgOAROvrEseqUPtT07cJ7tmGYAoMeOC4GnyjmIHl8DAgq\nrn7GVyWzT0h9ieoWViRJIpjLksJp1GNDGDtGq/7u7PD/wL9JfOH/xleLdH8b/pO/ZXwE/qu/01M4\nQRARMZY88zNBfYZ1KdtpYcOImBPkosmWCZE3lB9qsnLmy82GLmiESCi6SB49J/FGniTYV0s9Nwzi\nQfUFRPHkw6qRUuPoeNtLzKUhyQK7N8WyKXCTIplmtpnAk7KGG7LVhOaFITq0eOLeJnR94Bg17/NH\n/OGFbP1E/uHAsiaovmU5VmQLyMkiLazFRLoekPKGFHuIEy4mrKeItweyPnDzD1wMxLIinSyhMbiH\nog8j691Q1QHtDEuaEYceYVZQNV7OWB2Qd4ssN4i+ZztHBu1YkpzxZtnlNfIouV9GNqliMQK77ImN\nQKuKxFqc9FT5nublgVI/4FyOvAfYfP/7rPIv+fCTM/Z9JBEfCKeV/HanS2qkTag3BaPpMJeWYmfp\nngI2mvFeUakzPhcsD4nJUqZ6QKszdiyxCPTdE/InOQ1OG5ppZsgimTTUHaiXnmefYwuNuQea3ULE\n8/CW/bjQyYlbXRL1jT5TbO6Q5ZKHT6nTwGQm5qVnNK/YxbKpVqY8opzgdN9xrwTpVJFuP1IuKa2+\nM7kDeVwwckdXOexDsFsyejGiNiViuVP5hFVKAne2fUNHQO8S3CMjMx0TLVuxY1wmlhcQ64asddys\n4bWBwZ2IRY9MU2yn2bqB1grSqWNuNuT2BbfOaKNJ0pRxmalLRfu88ZLUTEZRjYL87nCu56EEoZ5w\n3lA+PMEYdIA5eNY6Ytzvbtj7eyH3jlHgnzmzcNgp5ahn5NNxbbbwVwonDev4bXJnEMqx/vQFd5aY\ny8qeO8JuKZuRXs+Yj4qoW9RffR32it1O8ONvF6wi8tMExNgi1opiHCkLh1gCEyV2ClRhxBwn3MNj\nkoRBbIgnT/NcmdNIeBHYoqbPL/Rx5mVIcaFn7SqWTwvmeUH5hPCULInFNz3J5sLcSPrjQLLJ6fOe\nJFEU+UjdLgi50lQLZaZQMZCMV64xwPTE7jNmXbNRmiTpeZQjcozEXCOC5kBCPrX4/Yg4bjDmyXos\n6baKXjkqnhQb6EfP2Z2pjODeCoY2x51mDmlP4yfOnWdaUnAfMT/6IduvKyYyXu4Dav4xX//8m7zT\n4w8JKyv1GOgdqKTFPlbW6Y0wFXTVhpUcW9bouUDGCS0kavxqSbQpH+juBXWWFD4i9MixcLz7Aywj\naXgwbTXbOTCOHuEs78uKmVt60dCaHe7W0fmCoBNkoTnOlr1OOfma1ygJ1Q5bGoql59mX5KrCpyf6\nzHJYHkxPsHePS2F+WTgsPToZ8I+cYBr8rEhlz9B1iOWODgmnfAYtyG8FRYzUIWdOU6x37ELDc99j\nkgXPGSkLYrbB71NuZ0ViNC/PFZEEHsVIbd+IakujW+IkOA4Boyzv0WOTnFSsvKpIsT3zWhpKPZIR\nGY8jgwgYDgybHjVFtDTcREoPxJhTCsk+N3zcNTgrucmZpBE0S4nQv7v5ze8FWWgpKZszQ1ITfaBb\nUvzGUemBtT+z7masmBDWUcyWrx1+Rdjv8XnHnGv2+oK7JygEP94Z4pDjq5Tk4YjyhPnV/45aAv9h\n/Q12J0nIJtZuy301OCGQJ82SV/Sq5nYzZI1E+pksBoLb0uuWbFrJ3zRbm7GZD4RRIlKBu9fkUSEl\nuI1Dbx2DhKxdqMeMdW2YLjtqem4CjI7cbMQ/c1pTkXVPxntBvxZsdIXiM4qomRrPPDzYyztYw+wq\n8h6s76myEic0FDfaRHNYFYO64yYHMUH2Ay+DIu1SeJ/YHQyBjGcJxkwUCsQn4GFpzQx5ycZOjLZC\nfvYbfvSbX3B4KnSY2bNl1oawUWxFSpo/cWEgUZYEwTGt6bMPkN3Z3u/MV82u0+QEcmG4WU22h9e4\n4d7lPLM3lpjgQ44TDW+rRAVLagpWFdE96NySbS2PWJI8dsRdQr0E6vrKLA8Y4UnpmcVMcIbuthI6\niW8yxpigu45VHqBZeNhIHmbSO/THjCyk7Nij0GifsSYBz4ZtufDULWW1YVq25LVm9YbN/GAoPOr8\nRmEi4BjKjmr0yHzlVkhUKwmmQLUZG/WV89mBkmPSsyYdvjkg2oWy31Hucy7zymgUbT3iF809LSjy\nLX4c0NuSeV5xbQpPyWXOedxbSluQTZ55eyW9wCgVpJptGhDa0+QDfaaIz46dfZCkEhEWbNvR+5Zl\nuv/Odfp7QRZBeNSUoS1kyQ7Xw3ZM0W7DvzodKXvBbu+JTWTabvB1yTTONPZAOQjm9oWb9gTf8/X6\nwaFOMX/6a1Zj6Icr2e6PSOSR/N/6iB8cq2/YHN/ZeEvlH8j1ggmWepmpNjnrqFi0BJtRdx53qCnL\nGl/lnCtPqhLcZqKXhqR+x+0lWmjKa076sOxQrGWCiiUFCZnvuIQNqu/QzhJaz/2UoPorqynJjgPF\nKknTAOLCnA4UscbbmX67R4sn6RLxxxeSyiBXh/UT2iWk5Za3R4FvM/Ik4mOPmCeeeSS+zGSvijh+\n+koEtCzMVYVcHNumpm8ikz2RJ2dmWTAGj/3Nwp/8sOfX6q/Y3r7NL39x4id/+EtKU5K9RWQ4MHUC\n9nuMLHgmdwQt4V2iaWjShDZ70Gd3TO4QPmdwmkt5R/sFvaZ0hWFIBEl35UVK6kOK7wN1eSDsnrin\no3xIDtuJJZ2QIrCGlvEWyLcridgSlhfMmHCmZrczzHKBbiSoSFvmxLXF2I56HanDSHJS5LOmrAR+\n44ndQqTDbk6YsHC1O6KF3kZ2zrGJgXUj0VIjRSRmG+J6ZVwSxKRZhWQnRj6UHtEsyCTi6gzhZ9Zb\nSegNXkl2SUB7RVdKFuG4CkUzB3b9RHXX9MUNe4lUN88hr3GXgWQEax3PRIAZ0UcYw8yZnh0HHi+C\nupSQOKy9U+03mLgnjp5sc2KddyTFzHZpKBJNrrf4fyg/kkUhGO2OUAWKbMQ7w72C7TyxXzz5UtBu\nFrTasLy1/Cs/8O8Fg+gVQXjS+s6HELHHDV98kWGVofji+8hppAopv/3ir2jjO9Uvay59hTms3Ls/\nQB4cQmR417MLM30+YacDtWnRScW9n1l2ge1lQccZt8s5hZl389UbvLgnlOkGN410W8tD1OxFh4gr\n+lkQipHpIXCniq2/MxhD0q2cZM0iLWPYMhVnbKzQ4sr7eOC4KZDdR3xSsG8k+hJZVEJfTZye8C4V\nbrjzoiRXt0W4GbF5UNuC6Le41UARUTJDXAIuKbjlK5V0TGZP6mCUKTxHkqmgAPJ4YC2uHNyO9Vsr\n3f+45WvffuXj7oFJof71C7/8Zs56zFhHQXUKPLkTVSQzkWJZCIWgMx2TTmC2VM8dJtNkWUd6sSRG\ncE8tUlTEakC1YLaSh51wSwkFyMsTVylsAU4YqnPHTub0McW3M9n+SLh7Rh7gDbYt2G3OrOLEEhbQ\nNdXdMr7CUVUID1cgWSbcdsUNnlkrml2k8QNzUiHihdUYTsPMm93yur9DSLmVOc3d0ucwKoFNU+Ik\nkcmDctY8hOcZU5rHlVhnJG6lt08GvyFViqmYqG4zN5WxlZD4yPf+5IeQZ3ytafnFXy784LDwoy//\ngH/xL/8D/pt/+d+RRPBas8qAamqyh0eMKYtJkG2KCE9EP2A2msdw53RqeLOG+nrHKsHrkrLMT6Zj\nhaFjIVCWG/LnG932+DvX6e/Fl0V0Atk8wb3zdAvGD/h+4LoO/Oz2c9akR1vN8LxgXzcc755pJ3F5\n5LqtaUPgLalY1pYfnB2dvfLZ4UJbTahdh/zFhWoqeP7TBqJjvacc54WNEKhVk04zi5GoWbHGJ/dV\n0U8zn5mAfAiIGWtVM3mBVBJzgXSwRGMJN40oJHE9sX8YlrFm7iae9kavB+LrTHM5k9wVOMe9MtxJ\nkGeJMCvlWWFlxtAYGuAsejbiSNdd6IcRe+qw60R6i0yLJpaKwmS8eYfsHW6JFHlFNtcwLEjdkSaB\nQrTIciHMT4TKicvM9vkgjJGkbKkSw+wVs36yqidTVnBzNy5rTfptTTF8ySs93yh+CV9/kN++5OYd\nezWir0e0rdD9Ec8Jm+XcFkiHirgOlGXJkGkWveKmjOuHCDQIE8m7AtPtKK1HqZo6kTTjiqm+6sHI\nPCPGkjqxVDuBOuTUd0l6LOERKILChS01lrEccTpnaa/YpEAkN3RjUJ1kUID0yPSB0AW8R9JTglwi\n6tLhVEI3C/JLw2wmrpVgqztWf6LdFOx1xKmScnVIm2DXnua0kJsDMWlI40LeSNYI5jrjY4bIN/gX\nyaNIMbPlWh0xNnJd34lpCS18N/6KAcX388hfBU/1A8X0izca34CEoTBYkWEvI1e/osuJZJ7g6Di+\npvQvI2KuiKnEekhLy1AUyF2B+7DQ5hK9SqY24F5TnjHgTx9Ipn8g5jdIWLyiuUWye4Hqak5N4EMh\nOegdSxIpipScBDEMZB+/xtxCMfVs5id1mVHXC040dNIy68ju+CdIk9FNGc/CMruebz4WTqWj2p/p\nkifLoyWZPKX5QNW1RL1CAzEzqCUwJ4ZCCWwyYLsre/cEP5IcJtYpcC4V/tSxuIxNeibZSKLU+FRT\n5lsyBbWtUR8O+KKmmE5YWZOHALsRWw/E3QHz8creRUJwlDoDO7PRAj97hqcj+VBSbjPW7MGHUZDp\nGvwOR0dVSMZxIuoL+WFGqxVlSm5JwaekoDq8kDMRiwJX7/EJJKLmWSucatmrQG8M8mooTyn33YR/\nfuLSPmE1fHn9Pj4KkqxEpE/GLhBfJpI+Z2oUwz3QO41WFV0WOQ0aHxUMgcVAsu3JYsoz5qT3gmoL\niXpwESNtq+E2EWLCeEl4jxEfFHV9pxxK7mPCfXwwbUeiG9D0XJgwSUevJdG1mKnCLiUf1h43KHzr\nqGOHymfCBOuzJF0MbhcYr7B91ST+wN0qijynE5pARp4WpGVgtD2ZdYxvA2PsORcVZSo4qBLZpshw\nZnEjVmzhLPD2Ay6JyOJJ/gTRpoihZS5qjlIxZY40M4xXSf6Pa9rNN0g/HvmyT5H1P6L48lek7Ym3\ncoKloEwMpbpTi4R0JxnzgkZEdu+C+ZyzX15Ylp7XKWFuQdFiTMrjk+DmS+peEdMAMcc9KkoteDxm\nmuV3n4b8XpCFInBUnqQQ5EkgqIn1EXi3Ox7nX+C6mudVsWpJXcLnf/wldbUQzPfplWFoBeI8kgEu\nXYg242fnv6R6TAyp4OIFsTny68++idMbzNQw7VPi6sjNk7i+04oPFCScnhK1zPSHlNh5VNRkhaJq\nXritCqsTZjw6ge3d0r9FvF55jA1r8PhhQaUwTxNxOnFJe+4+0s4P7rueclDEMpCheZERl1yZTcU0\nzoxmYBpHHo3jKvdwLNFxD+eU4ZoxTyVvY4QksNu0HMqIMwunouSmYVUHFq/p386YMCD1gu3PNEuK\nVgtLGNl3liVxSH1FmxOxFITUUdUja0g5qAPVh28QRYroUrqixdqvkf+sID4/Q9cNj3alCo5kDJRm\nICYdq1c00wJJySpGUhPIh5RGSNKnpLAzGkmwT4YpJ902HDYOt4+M7kZ+fJAfR46TJ14zLvuWEoVZ\nBdWwoXgmJLFBhwmZzST5zFHuuKsLMtUEUZBu9owbwW3aE0KJy29U5UT/MqNDjjzcub+1XBoI2cjc\nXnGZxSyG9D1nXhoWK7h3CcXmRCIUYrSoRyAkC1cHQUmGjaOeZ5JsoCl7onlliIZRzUi5kteS3Ztn\neViaYUtUkrIYyP985ovP4b7/MZ+5CrOuVN/+Q35dJeytoV1T/NnjtcYfEoRNceuKTD23Ddjdg8sc\naI41azbjWWg+GTbzgNAJvkvp0CjXw+Ip0it+vpPEwM3+A2lwIiLnRwnqA23oIV3Im1e245Pqi49s\nTca27gi5ZHzrUZ8nhPNEJv4vCBtspXiSs8xP9B98QouKV/cNtD5QPreUfqKWHd//g4Y+efI0MwcC\nayaYJ0kbFE1/5hOarl7Z1CsHL4kyMm4XmI8sRaTShnHccJCQpRmdT5HCMg8a4S1x8bhjwdwG3EEw\nLgH9qcCIJ5k1xPtIUCvWOt6vgmWBfPaIfCJNFXntCNaQZAsyd+y6hUL0cBDkxwtbsZI2Pd1TcG9r\nptmS+oal60jSBBtaCm1YdwXyLqjaHQ8i4xoxQSB9QKQzGY79aNiWN8SYUAw7pnTGecvrX/yWzy+B\nl/kDU/IFmZvh8x7/j3tk2fJM7pg5ZdlqtstKJjQmbBAuYLYTs5rJ1wOTXtC+IwwpUzojN0/WSrHW\nnp1yxPPI9LhhlCY/SPyckF0r2qkjqyL1KlHzSrEYxlyzbsBnHY0M6LagYsM8teQhsKkGniYhzB3G\ndcjtghEjt6IiKoX9lBHGjmY9cPoA+Jb9U7C3GtFJpmzG09HOgp0eoWkJ2YU1STkVCWulWR6aPAw4\np0jbCvtiSaqGsyqpE0EMC1JvkEVKnBLO+Uq7HfFeEEJCnDJStfLD71e4X2nCHwfK/cr6yRNnjQkr\n6c5COuHnSOpGNn6k7gqiqwm5p+43bIqBab2QhIJV1rQfUigc+daSlRcORuHGHHuSaOGZkxO1kRyS\n6ncu098LsnBe0xQdY/IRmexZXeD6bIlZxf/xzSOteDL4LTwGApLqO0/GbOXwRx8Im45D3yJzgU8U\nP18cB+UY/2nKLCc++l+TJS90Oqd95uyfmu1SMkRDPeegIS8O3F8jL9GguoBtM643yxAGtueG82ak\n60eGYkWM70wzdGgyc2HdfaAqevKlJCQLUkYOdcXL5NgLTfISqc4Zc5GjxYlZw7wmJK8jtq9ZxIl0\nrNGiIB8M+8pQtUfUZeJhPHeXEN7PhPCKqxz4hLJoyYoemTfY+4JNI8laofUO1pXS5GQmZQh3RJTY\nRaMuOzK9MEqP/5gwRg+PhMtgYV7Q11d2oeaLbxz5+jZD/sAzNS8klxaDwnVv+Ivk0O5gN5MvD85J\nj68mRmkpqkB3y5HBYYZIKhumssZ5TYYknyuEmrFTIFkamrQmmRPam8WKik1Xcstz5KkiCkMqa86q\nZH4psY+I6DfkiyBWCZUJsETKQ0SGLbd7RrHMxBT8skVlLVoFmkeGsCsJlkMRuTsLtuZExa3UeO3w\n9cCrSLgfDKW0PIuMY295zuordeuY4uaa9LUnblNSu4X4YOxS3BBQjzd6aSl1TZU5ov6E2zhipdjf\nN6T5QtCWsT7z2285Pv/XC394bLBngXwGVJmTKs+4N3Cu2MaGzeo4i0ArezpteOoS2Q+0zrMsM9GA\nbzSZesONE90YkNONTOT06ZWTDwTnMGlJvUQe1tKvfz9y7//foROHigteGlhm1nqPbgwTmvwmMGWK\nX1Z8+spe7Yj/5419XjFoQfkAu2Zs8ow0jbg/t4Q7/JEX6NXweqzxdmF1I9/5cOK9Hlj9yjwmBGEx\nSyC5T0ixJeYKqRJG48h3PU2+Za49u2g5pCUahZagvaHMWoRKeV1uiPOG9fSG6EakFYzecVWSi7yQ\nvWuWXQ6+wx3vSB84qgFpBeHwZEomUtMilEA6zTi9E/2VvdJsuy15mlMcargHNBV2nbBSICfo7UhW\nekQ8MNWafnIk00L0I2vu2Zkd0hxYk5kVjx8lczhiq5W5qbmFnCyWX6lno2XKB751a7mElZ/++YgS\nL7x8e8PqDfPuezRHx5I/UG7hLBWQIrxh0/bYKmMSBb3do8KFbLW0rmPJE0QWITrcsMGkCUFNDKlm\nrjWz3kMYuJRnDnIhORfEp2NKJl6rjvSiiMYh9MQ1lFzTmkE7utVy8Q34QAyasE+YOoPNr1QPw7CO\n2GImVw3lpsfZim3ImKTkPJ3JY40RDZSGyzBQjYq+jmQ2xU41a7tDxEBnA6G/oWxFNBZWR1FX7Ih0\ncqCQNZuoGS8PUmURLmNtLS8u4DdP7FxAb/HPHeN5TygtnxrDb+2NTku+HDIOXytILzXhtBJzyVgI\nVBepdYmsJdnUkukdG+EIKmF1inF40KQJezezTBuyStCLkUUHnLYc9cq6FLgs4OucdPMPJAoAr+gm\njXskuKJifk5kd4lVI+M0Y4VnmykaO/Bp37H5kw+E1mOGJ6OU2KIhLB0JJd/44cqyWXnaJ5PpePsz\nxxo122nDuGbkXYWrUrJS0G8FWkuup554M1yTQFYGSGoK0ZC6ldQHTBR0OlBGMGnFHBb0NWeYtji1\nQZcBekFXZjR6ZF7uvOiCXd0wNwq3vtMUkvLThirNUJkizoF1fOHV58xpw6Wa+RRHpNozrwdCcCil\nmb3g1hseykMPm6ogqBmT7fGTYKpX5PDEfvyEUFcMW9oxI07wzBeUuqHylOfuxrpAKgZG31N/8pxC\nQnxZ8FvPpCemOePzRVL97BPZP5rJ5a/51W+3zP/kC9aPPyY8BGmiyGbJKQVTGrSTxLCFt5H9diGP\nAb0/Ms5Xdn2CzWcyJL0KFLVDOsHVjBQO0kmhVc/SFmxEziAsIZ6x+5rUBxbrGeqIWR/4RWJPKwfb\nEvsN/lVTPh6YnaQRF5KHJW9G5HxCNYokL5jWkpseuGtogyQOI1ZKdqcXtsZglxUeLYktKH1EXQ0G\njU3glUid3KjUSFNK+ltPuCpE3nHpHW95gS1PjMdACJI6VsS7oHUe4RJaBqRbGcMFOLKVK+pxZuPe\n2f36hW/vv4cqfs1nL5Gf/nzEvpxZbhfuj5XeN5hM83yUnDTMmWdNNX09IZzlIAKlFXQhg0Jz2lx5\nrCf0uUHqim6uUXfJfbowCgiToh3/gSg4QZBvDxhfsp9HytUh8pbGSJbf3kiumlZbQunJY8EwroS9\nIFM5+JWeEZlb7OT4yU9f8bbH28/w/cQm/hkyRh5e8+/kM+U+YPuExTo2i6O3ivy6Z9O8U7iZGUk9\nz3SxZxCCmUi/TJj2gQ2W59xj44a2kZRxoF1aTGVx6QFcymNYKKoMt3bMi6bLYEj3kCpyM6OtQzQW\nn3o2ROZbxIae/UXyGhvK0tEJx1KsBDVzMBeKuKILiWdiGFbs7QU1B0xi0BdHXwrSD4ZEJliVcBoj\ng3HIu6d8SNY8oehfaExApSUfmg39XuA2D6T31L1kpx3GJXwoI9N3v8F33Xdw6ZMfvnzOH79Jcrtl\n2DbExHLWR66+ZF5XrplCLZp109NfHeLw5HGbcK8StW/J+4m3Z4mUNWnrGYYtqU/owkyyN1RVQZJ5\nbBJYVk2S7smk4HYuyOsdYVkRekdzVORzz6ghHFvMJSN70WAXps0LLgiWwZIcrtwktNNArgfMYKkH\nh9pdEXVkXkae8cE93ljLFe0KYiV4qxybaNDJk9wZ4mkmasWzktzmiBEbiiwgg2QrInr5RP7pSuFK\n5g7usWdJDDtlyPxMsUie9RaZKkp5w754jum3SL/+gef+J3wqBm7tP+bMXxLVBnk5UZUN6c5TTJCH\nlZBduT5atoPD3Ab8o6AIOUpn2ArK1nJxhk92SzN7dFY5XQAAIABJREFUGr0QoyLXM++biERRrSP5\nEjnGv5PdzN+K3wuycNGRji29uDEeAuNOMdotdy1JI9jDiFuutGJhuHu+/MnntCtkv/HUa8UmTuh4\noFgkc/crxpjxp6ct9rOUNvsuqpFs+cTPv/eB27ySyBUWYAyMxwyTKh56A72ECHEsYahZQ09qBVlX\nMJoDtlXs4pEsMxyfK0Ln+LLEtZ5d0lOkmoPYoMXMiGLIPB88FA9N93S4nUbFgU+jxK6SdpWY6onq\nS8bMMEqNveeIwxM1Z7RVQHQVLRO7eGMpKkJsEAxco0NUA0vc8JpaihH87BHVxO2DIA4bktTS7wXq\nfaQ/XAh+j+tG/G1CWEHUkuAyhIu0QwpcYZZMN8/ym5X6WnEf/5Rkt+Nb55oPuuU6G4wZET6SFJZj\n99WqQza9sjOOdJKs9YR5rwkhpTUaWUAqPecwsNkOmKXAMtLGmTH2GCtJhGCzAZOMBFb88cJ1sJSi\nI2luLEDlHdbZr2IltWV1JUrWzLpjbjxZHqmfB7LF0siMwqU412CkQdkSly2kDzB2pRQFmXb4oyKM\nmt0amZpP4CTTceTSzixDQZAj5I4sXeiICGAaNTqp8ZuMdIBVXdjtKjIjGZ8j6xZC1qCvjjUo4hAJ\nnzacZ8stNWyWktP7jBlGvpZ8l3/y+mOEX6lkiV4nsswzVCleVpQ6YKuGtYjE14jdNTz8QpJWzCHh\n6GaKaFFC44+W3d0Qk5WtNrzYiF5X/KHFreXvXKe/F2ShlWZdZthW0DuONhKcJ73OSBzbu6LildUX\nvJQz4TsajIbj11iTEV8cWLuOR5XQfFfwWii64oHxJT8zHpcNqKzi300EaqhY7I3N6ljkgc2a0JUz\nPqbkdckQGqwONF6z+hofA1My0IQHssm4qZXiHphFxSDuqP4rPURnPfk6cR493VtB6TXpzTInd0ov\naDaB7qEQhUPrirzYo3XPmpXoo2ORlrl4MKc9TDviRlC6kWtwZDvPeT7h1wcus2zrknAKrOueUsy4\nq8G0OXud0b5r9jdI9x2lSGlajz8YxJDz7i7MiYTKks8d7pKQrBm3ZiDkgnSV/OrlD7Frwf3DL/jy\nGxXny4/5Tftb+vQjD+dhGEiTBNfN6A4eYyQPHvIrn9aGqzdsJ0MpLM9hSyVSspugGzT5ywbvFFM9\nkdOQqYX6Iekzj/crWMFdAqGD65Z9pcmzgLxL/Bhh0KR9Qq0d3o48dIKfrxTk+PYrl7Jn8aBOJOlz\ny73wlKmlXQ70k2PpanRjKB8bbjLnOW4QvWW7DPg14IxA3gOjk4i6Ic9yqgk2QtOvHZvc0hWGeBxI\ntEMZiZWSxpfY64KyAl1DaiK9U/hjAKHxuaXC8rV/e+Eb7x/5+WcZP5kmPuQ/o/3p59zziu61p+9u\nrPHE4Czx/aumLbP4qqGZDxSfPOrsqNsc0UZindDOR+T6pFMfMeeMtrRIb1CXhrMJBF9S3h1z/fcQ\nBfD3gegdg4vUzx6bBfrJUmQLMoHIVyYf/XCjEStL51keA0mnST9G1sZSPgN2WlCrIFme8GYpEwHT\nEzH/huKsmVpLYhp2RKQ8MNucsbiTxonT40kZe2hXXp4jrnwSGchTz7QT1HuD6xYS2YNxnCsF5o4w\nFUsVuB9X5iXFNjnRt2x2A3GdSdYMcd0ik3cun7bEtCWyxzwmvBTkyjOPFrP01CNI6ciM51RNDI8F\nZzMOn3niE14ah9hsaMaMe7rAmLNPJ3qh6QgMu56rK2g+BHy4U0+SbrZcE091VUhh+VBnJLWilVsS\ntmQ7zVgEinuJMBK9bkg7T/pqSH/1PZq331KG7/DZ6Wt8+vr30Dqh2LzgnKbeVmSVgt1X6tl81cjs\nRjM4nrqmEwupc7hUsijPtloJ08xsVtI0QZqE+60i6JSiHVgXgbwPJJPleT9QVjD7HN/XiG2GWO8M\nxxLyDF1LpjySR8mcHMi9wuoHe+PYzBUfLxW33YOshyQbEXi2vqKoVqZZ8Kwi6bTSpBKZ10S5pasy\nmsuJW5GSLRBvN2ZvCVoRzJYJw5OE+lOKHkuWa0rpNY9m4JmvqEPkkrVkq6Kac1Q/Ia+CTdFRqgNK\nBvI/q8gTS+JHvvathrhRpNUPSC6fYeYKayPO9iT7nribUEnBkHnu043mkROyHFsleDdCZbBZwHBj\nyQylOzCXKXJ6IBbFc3PmEAzTXnHfnRjM717qvx9kgaB8eaXNK4wIaJ/w3NSoZmZhx7jP0FKyjpG4\nD8hPf0Sx3nj/3ic2jx2tcIz5HsTAX/5FwzMuLO8bwrRn+uWTm5ooicS6YShh6wTdYQVXcH9Yztkr\n3eS4C8d1HYlDhS0X9JzSTIbZA4ccaRuOLqEZOrqm4egExnTs7CvHaUaPHVHv6ewLqspID57RXxg2\ne4z2lF7CuCLriFiuDHMFscTpkv64sNOa9Gbol5qDXBmkwL5rhJLMDBzGjtZbcJImXOidIVaRTKS4\nMadJV4Y3hzIFt3ql3mfs9ZH8EPF+i9Ma0w/kOqUjMo+R0zkSPusZlwfxsHCc39jxJb/8wUfur99m\n+Oydn4st8+YT1SWg5g4zQ/J0KGUxy0qZeB4i0sw5IXc040jYVRTeY24jvsjA5RAD/qaYzit2Wkgr\ni58iiCPVFGm1ZTGwLyNL7IiXiWez0j48U1lTJx35YDl3+f/N3ZvDfJNleVrPvXFjX//L+37fl0tV\ndWUtXb3NNCCwMMABAwnhjT0CYYyFiYNGGo2DBHjgYSKEiTHCxUVConrLrqruyq4lM7/3/W+xb3fD\nyGpAre6ie9Jp9ZFCilDo3hNGnKN7I875PSR2RWwL3q44sxMrwTaO6GykSaCcEubCczc1qXfEuWUd\nUqJEcug0u2xptxDXrxg8T4OnrW5kKiH0K1laEJcLxlQI0+HPBZXIuB09SSqJy4HHduNkDJGJ6W8e\nM208sohNTugsgBrCNeXhJPtJ8OOnnTn9iO//4Znz607Vf4vy6f+kHQZM7zkIR5QXhP0Bfw9wPkSb\nnNxXTE3KUgZkqydKa0YxYYeFuY5JxxJVDUxWUfkY99QRjg0vJkS8BsTWQZB+7Tj9e9FIJhDcL5Y3\nScwjDamzGye3MN9jyqeOvlsJ6hJrMoRI2K+ehzxwbkqMndnkgTKQRH7nWLekRcoHx++gzpplkQRC\nQbEx3zWriiC/U24RrlzR6wE5tWQiJSxjblWBunR0bYWMHAt3TveCVwvpW4fbE4pKk3V3HhaqLmIt\nLxRHiQkh3m+k6zO3KqQyHn8E9bCoMkJsG1dfEa6Cgw/xScs1T5Fu5jCdubkVkwrOWrNXEYXMEc6R\nLBttmRPZB0/JhIhzLn3Bc+7YR8tUS/RqaH3MMZbcZ09TbbBFvFrL21tAKWfc4hmfJWq54k8N+3uJ\nUjfMXZC5I4yef/Jf/TP+83/+nzLdG8oUZgIOoeYyTPjDiruGWLkxHDTFQyCsxfiUar3j04ikapjm\nmUou2LxmGxxvE4cJLrj1iD0upNQEXU8QObwqSI1CJyUy8eTrwlAITo+IaxShupg81Sz7xD0uqY4r\niZFsRiK8RXmDKAzb5BHPR8w1QIU7j0PL+bVmjDUtgmcxkgcC2+90ZcD1f/8J//5/9juoNwUffd4Q\nfhjxf336Bb9bFwzvdm5flnzYpdh3K/fwS+bxLd9feoyxzD+4cr/8NocvBfP3fsrrZeNbHzzx8z9+\nphZ/inWCj8/f5o8jg3e/5Dv3gjw68pvLBffRhct3/g2a7krUt/yk/y2+9eGIFiN9DMUwYKQjLDNW\nd+dUHlFXTeEUl6rj1gjyR4roUvI0putvhCcwLxoTL7ijQLQHvHGUZHC8gQ4RU/K14/TvxcoC7ziF\nnluws08L25zDLimykuE1J9hSrJvYG43tRhrd0+Qxoh9ZE4jtjTy8c4tikuA7+N3zXrUsa0a9fEFU\nSca5Ig1WXBQghiNkAtsrRH0nPS0IZdCTI71coMhITyNC7xhdMseS5zeW9CKo3Xv8pshLKKuMVVms\nbVhauHcxsayY1IjvNau9sc8ZQ2Ppth3qZ05ioBQt99IiKksxzwTtG3yysMc59ay4RBN+Luk7j2su\n6Nzz9LrgIsHqJbcR6qOhGycePqOZd7KtInjcaXOozgHBI+RVr0TsmOKK8D3iGCJWcFGC3FpOOCaT\nYxOFCjq2ZuXNIFg5c45jNrET+45hzAlLz21uSIwnqgzisRGGGSaWiODBo05ICkswrJQB9PrMJHqK\n5xjdGtbXlCiUqD6gsC2LC5FDgc4mXu3EuDsCFTOlJdPrznTW1NpSVxuT7vBLQ7g5HluJ3F/xi8Ts\nO3EUML0qyiGE15H5sKL0Trg/sQYeoXLKSjDrE34U3Is3ePEMccjBn/nmWPKjTdH7P0Z98w1Cfsbr\nn5542mfe/97OdYC1faaWP+OXzw2ffyunIabeFMMnL/R//gm/m/024c9Wfid/D/+opi++x48yx5vg\n53z3+Ez0yYZ1M3/mAqIyZPzpe94fRz43GcH2KfLdyqnSNHvFEKfEpmTXI7ExWDcyPu0MYqeaPOVF\n0DuJiwQ6XDhEDtHC4/SW07ohvMQUHeGTRb25wxpTxBFNfvvaYfp18IX/XAjx+V/R5fzLMf/lr/CF\nPxJC/Af/fz5soGhLy9F3ZNYTnDOGMOEFR5QZohqCxfMm2anShcvHF/p+ZvvF9whkyNnGvBITPDT7\nn3+JimrqdCPd7jzmhLStcIcYsojQeJzUlLvhqc6JY4W+1Wg1QAyujnGjxF0LoiAgUSN9dGG47yzJ\niKdgSFLEtSQaPUkWsgeSOIlJkoQtEsRaUVY7cs15kpbaLtS5Y7pYxjBljlL8vrP7lCmX+OPKfV+o\nW4fJJdFS4wWU9crdQLF81XjmRMVmaqosIrxVyNST6ytCbhTplSI9cBSe1gx0fuO4rMgqoI8tmS1p\n9Q5DhJpgM45dbGxHQbIJRHUketR0QhC8jly3FcIdI2N83uMGhZEj67FGdTlOWIZ8oyoiCl8TzAbT\nx+hgYTIx+fAg3BoefuNmWlYqoqnFYbn5CoNhjB4su6VBIYVEbhecCAiDGLRBHh703c6+gQ0dQbuR\njg+8fQPVmTDI8KFHPHnSMmNJAzJ67lVGyoO4gsR50m5EaAPvEk5csQq0PnPtPuP9tJJ9c+KnP/6A\np3rhh493jN96ZXhqmV5/iu019Ydf0EW/QS5bPvrpn/MH/UYc9RT5C9L/kC/Vp3x2gB8yUX6q+ejN\nT3i7t7ztPmT4ieULkfNp3KM/ufKLz95hqoAPuhKVTXz/k2+zmZ3FBbgioZks5hTgCo2va8Zbgb5l\npJtnDDUrgkO2UfUT4ZQiCg+HELO9Z0trXmZJshYE71cem2ZUK/0aEgVvv16m4OvhCwH+O+/9P/7V\n8a8AfnXvnwC/DfyHwH8vhPi1aqEhlmY2PBaJ2CxjYFHTjSTyRCYg3aCh4P6isfaJ10cAzcLxN0Fb\n6JIS7oL0nLHlv+RiLe8OJ6TJceFOV8+sQnLbc6L8ygR04ZGJlm0+wFNMmEaE08QaeMrakJxasqMn\nWCPYDtiDZF8D9pMmCXtan9LGM91cI++CV22IEomcR4YqoFtKRGzQq8WJEmNjYKLaNHlckW8V2nua\nW03WxxRSEskHUT6w6zvrCn4NadZnjM2Z7w0jIbXYEP6FqV6IxgITCMb9yCON2dTOrQ2o2xIhE+5O\nYL5UWF2hTxonMuomoJ5jnuKUtgzJHh1zVjLPGqtfyKKSxcY8VT3rVlM8UjwBpyrmTXhitRuPKiA9\nCvQgua537vOG8A0BHV2XkOx35LHGLDvKSpr4hJWvhFpSVRX61hNkKwSCw7YzJDtpM7CZE160HCuN\ndx53K4iqEhFG5K5HNyERBUm6kTx6Nqm47Rtrl9HLndPisf5I1lr6RWPnlGBy9EGEXiVrv2PnglM4\n45Qi0BmBvWGnlnP5wLU/4xufCL57fWFovsE384jpWbDfv0vcGV4/E/zyo9/jN66/i9dfUu6esKxI\nxcbhNeMH1Jg3B/gLR/1aMh1Hso++oPgTi3wc+T19JNwLojbidv+I+fX72D/whPOZYHdMyZ31/GC8\nteByFrtQ0XIqHX1uqNUBDpZhcPTNjlxG1j1klQpcgheaMi3ZEUxvHe9iydEWuGlmesz/mini/7Wv\ngy/8m+w/Bv5n7/3mvf+Mr1S+/+1f58MJwVIJEhERZ5qmW7HbkSpwSDPTGrhvhrhJiaqND3/5wlEd\nufEFh2zC2wvPx6/Kjf/8oydiJwjDZ1bX4tcvKfxG1d55ZxzCFeT5QiWuTLZCDTOZ8yRbjc8XnqaG\ndYLFHVnGjbgaOVYzevDEFOw6h6nC1Teq/EiQXpHVhXfWET4mAnXgsEw0ucNRo4qcfYV5mcnPmt4P\nLAawG26LGWPDJX4hSUrWw5H1HnFuYqqnHhXdkTk8jhkqVyRiYDWOZTuiHhaRB+yHM4udaZaUZTCk\n55l7IygbwdnvqLPlKc7ow4JT54nakaWeEG3A8+QofM67aaNxBheBjzpEBu/vcIw61lJgdIC4Wfxq\nKKKB4uoxr2857YYmLknETqNWelcRq4gxipl1gM4M0pU4E3IgRZuG4T7w5jkgeziMDHm4GGccQ9tQ\nBRPIA629YTgxZIpxXnhz0CTnI8IsBHXPojvmMOJJrVSTJs9XfBKwhiHVbWBXlidT0BV39GnHpzFp\nLllcgKl7tskzr59SvvH48CPi+hOehoTj+DHX9Et0+Dtsf/ZT2s9XsugXpNPMN/0vidOWcRwo3m0E\nL99Dyt+kcR9w1G84vY1Z+o0w/xJRb9jjjynXhs+/+B76Ew+HCfPyIahf8s1vjggz8O0f/Azx9KB4\naljDE8oK5i6hKEJCldDsG6ap6fyED0PE48beFygh2NcMd1gptSHcBmSe4uIQqRbW7IH8smbWCa0Z\nSV2OUvvfOin8TfZ3+mbxV/CF8BUf5A+EEP/jX1LU+Zvxhb9uZrJtJhEVGwWDjAgPVy6PhfVQE+wD\nb3KDI2bqFeNvHbi8Qv9ZzUtwYPuNFGchdiv5nwqy7E6y/oI8K7l0If4mGZuYxfQUvUMKy9A+EesZ\nLwLCy0CXXtCLZK4fyDJF7xaZ5kz+BJ1AhYaEB6GaMeErB+l4fd/iXwUqyGkTRxBZwLIlCaNu2ZMN\nMUKMBa0J2gRfNSxpx1KvTOPAXgTk24n2thJdRqJ8wY4FZsqJiDGb4bjAUl7xoyKTCzJWrKeCMI2I\nthmZOxbV89xYVqeItwW/p6yHmoOJWIbpK0m4Y0939uxK4I8Lc7Wx5Ap2QysFm3hLfN2p3cS7VDD0\nNcQ3Dn6lTROm8E7HgaFeqP3GeDZMS8DuT3grSZUlkCNZbgi697h0xs4Wf14JohxxGsiaBItjSg4c\n3crTs8UfV6JA8hAlcXujFAV5B4ctRNYLl8XzsmjStUG6hGkGX0iuZsMnMbbXmN7g84C1jGjqjlGW\nnLqCIVjZ544ICBvDbg+gBR/+YGL2H7AePB8uI/ZdwY+On8N+4ovyx/wjBebbP2B5TUjOP0a9/S2+\nkX+PD+8ZPw8GfvGP/5ifPW4U040tN4zBHVe/xf3syK2QZE+/Qy8uuOeIt+LOJ+cLn+2a2/zMnx4k\nTnzBZ+33GcQbXO/R04MxMByfCnQmSFbFnijiXZNPO/42cXEH4nRjShKqvWB3De/NCb8YskHiQ8vg\nDWIuUG869ikltg2pmiEr/y6h/tfa3/pvyF/FFwoh/gfgX/AVtvBfAP8N8E//DvP9P6zTjz7+mHCP\naJVFFDHZbcMdzgQzFNudSNZcBoMaQnwtCN9/xpuD4C8aheok9WvLZZMEcsG9wuob9Hc/Is0T7nmJ\nrUvc3n6155cjbmxoyomlDwiOE7sPyEwCRUWsX5FiYPcZkbhhF88QxnhTo+MZfbWEpwOte1CXMUpZ\nwi3GrwGXRtMMMwQRLqrZHi0ydLRlxtOcMY0LPrUYtRGLJ54OFjk7tqLD+YxwjBAeXHpnGRzrFCOq\nAbOXRK0iVDl7MJBOjiSYEb4kswlmM/SHDPm6Ep9GdH2gvd85m2eM6xjPmsP0jMh3RntHdxXSzoxh\nShgFBG8GwiFDrR4Rn+mzjnGzuENEfT3ThwPWK0ySEcuVctrYkGzuwNvghk0Eds6Ics1iFeE1BCYi\nGyPlHX054BNH8cjZihFvNDIUDEFM1QacAou2hmWLwIToOSWMPWN0RVxj6mxDBA9WU2P7nOdjDty5\nLZ70YFmnGq8DcgRjPtOtb3DKsRNQa02nnunMhfKWYRKNMRnfTP9dfvnDP8AXjkHs2GCkcF+J9IZL\nhlI9MtdM9wOBFMhm5zH0vMuAMWGrBdMaobcWX1c0Y886v8GcNk524mYKisRg7wO+qRA3yQ/+o3+H\nj0dP+OVb/vw7Z6wb+fh1JBp/QpJFZH2MXTbmOuHgVvZBY4IHQxWR3xMkETKdmG8L7THCrxsnWzIk\nkO2WdojJ9pn96YniJcVWK4G37MajVv23Tgp/k/2tVhZ/Hb7Qe//ivbfee8dXMKG/3Gr8rfCF/1/W\n6fn5iS6QiEwSXzxBnvCD7Lc4TY47EcQbhVpZDgF+d/xwaXlMhvOnFhVIVPWWRoyUYU6mLOk6c1pC\n2vGV8S/ekywg0xOR1sxFyHoCsc9EcQbqiAhSpLbcxA29pWhT8GRGbjpHZc+IIeWMR8SGhZ15CxCP\ngs6DDVJe5K+EWEXIdK7JdsWqWk624XpIaV5WXKwoM4uYNqJbSeV3/HXEB5DoiqSFPTJceriMEfbc\nsPiFZN+YVU+cpqjVsEeeIJt5WLiphTD3pGFF5QOG0JHZAtXNNHiG/JVrlJIHMVs9ch96xPyO1Buc\n2Dk2ITJ5padCFiV7c6fNrhyniNhWPD9ueNlx1AWHcCTqVqpRczlL+sMZoQbsVqF1xj2o+HIu8SKn\ncyFN2GA2S10diAPJlmxcqwuPMGU3NVoJ0lWzJwl+T4ms4GkT2CeDMSs+lihbEsoCKwIecUIUL+yH\njfskaIcnyqLgImGJdxK5EYQT5vJMvLUU2UTMgjIFyX4jyHOM9AR+YZYPZF7yGq/YBZo9w6w5/aNG\nPjZWsyBSS3eRhF7gm5VOKIqqYJ4KIIANjsaSWk+zBTiXs59n3CpYeknoHyxLxlgmqDlgOwx8/PMX\nusUyPf+cb8mf8KH/OT/9IOTzDz8iW3eMB5nEJFvAfZLk8RtMUFOKhkCCqFrEDkoZVL8ijKD1hsMU\nIRAcNkdRP6G6jvXgiFfPZDw7Ecvafo008ZX9a+ML/5Jz+qvL/wT4o1+d/6/A/ySE+G+BD4DvAv/H\nr/VhPGuSEsgr1hXo3bC997gIjEgItw0dWOL7FRcfIPkOVvW45B3CzGTRwKRCzKvm8hsdw6cVL9sd\nER744J3k1bU07oA8KeS9JYhWlvSJ+T6j0gvbfESGCSr0MEYQr/g45nlIEIVjrzeuscaJiqi5ofae\n+RhzlgV266k8rIed6RKznzT3g0O5kEVYwtbSv61BWJJFkR8bQqtpVYSKQeyCPtyImgXbnUnijUlq\nQulxWck2Bzg/sBQWl84U3TOvVpIUK0Vn2KINswlmWVDn8Jgn3OFMoS3r3aLCiH3SBCYjFJZofo+M\nYdFHigHC5YBGEPoHUjkm9YYs21HzA1vnmJtCItFThYwf+DAh6XeC/EbQ5xgv8PGA9CsqTqlHWPIF\n31WUUcNDvJJmCWILaVRNsGo6GRE+doQQ7G8Ee+RAtzQ7xI8Al+Y8MOQrmGIiEg7Zp/hCkqxXnA3Z\nIs0xsWRLTSF3ZB0zIklPPbFKcJeJLiuYTMdZ1ehxYUoj4uSECA0vYuJtYBm14lUaQqto/IB5q8kn\nzewbsnQisle22xnlb8TUrKeI+92iJo86bOy5QNqBzAa4PWdWjqUBFVYkD4NwMG5wCDP0BxtDAnLu\nqYcPeRkWPlGO4/6M0wn7ybH0K+WmCeuIzoKQEend4I8S0Yc8vKKONOMKRVng6GCOQBq2fOemLUdf\ncleCTUnKVTA+hRzTr78N+Tr4wv9aCPGHQog/AP494L8A8N7/MfC/AH8C/G/AP/Pe/9r+WOcd/j4i\nlmeyE+ADxm8f0Zkg0hHRk0Wmniw27NtK9emIVYJv/0ZEkiwEKiNQIZVY0C+/pF6v8IPfJ14Njx9+\nSppFJPcbdu6xyrGIiE69J/czLnwGZ0j6BDmW9FazLzHb2CH9youaydTMwSXAhHrEeBFzcgt+X3k8\nQHpFIQNOZ8HTTXJ6eOouQckRZWOe7iuhtcyhx4iWrdthdqjrgFYLh8BT9QVpaCkbQ65T+guke05w\nGNAqIgwLNrtgG8cp29lTC280rgqY0gSvPXKG/FDglp1LpxBPz4RRR1IE7MlEaQ3TySOqI2mx0yUz\n69FTlSNd0hDIkFJY6A1b2XDddtJ4QZcbNA+CIEB2CQQZSjSMWrE1AVFyptlCzLhzP64IEzEpC+lI\n+nhGOM3uHKazvASCtOyQlWX3guQ2oXxL7iuEOOBTQZz31HplOWuECRAqxxcjsbAs6kBeS5pYYnWF\nNx1bZOjXntUbRh+zuok7CU2y46MaH6202RHfDiyj4DCNHHVJ9yiZVcDz0qH8yG5jwltA6FIW/WCe\nS4YqpNc3ZNXQuzuV7zgGsCrJ4xIgRcC6wUNaZDRzDGJOo6PwCZHSNGHBwfZcAsEa7Dz9UUOxnXhZ\nPuPkzlzfLWzpj7EkuJeJvJy52QKxZRyGkGKdWIMWvc2sRwiI2TPPyoE0GKAtMFGCEiHGzxw2g2bh\n6dqjw5YoAX11XIKv30j2dfCF/+rXjPmXwL/8uzxI9iyQLztjNMGWU3/8OcOnI5aQ/aYIzjFSFxya\njPy8UxnHq/ySVUqmk8O6nrjOuVeKYkr5XtszfGD50TRQhBNXI/BFgHIHhB3J9wNxHcLrDZE/YdKJ\nlAtJmjOrG0tVM+8BYtvpY6jdwLlNMDamXVqsPhBmM4fIE4YLug3YleB+WskfC4E6EZ1j7AvMmSUY\nDcQHlscdJUPSdeERxhw7gfPQHhV27klNgBf5YtIeAAAgAElEQVQFz+ceYR9sU0Gd9sih5lwHyN5w\ndQu1LHBXzXAWKN1yMCnTs2Z+KM5FiKh6HsOOWhPaoiMMcqajQowFnpYg9GT+hJxmzK4ojj1iCkgz\nhd0nkDEKD3mOeVhM7Uhziy0NwTyj3MYhi3msKYscEXVAs2fc77AdND4Bu+5E9kIcpxx8yBAbfOLR\njzOyGEhFyiU3pF3BzgWTh4g+pPUVSlxIpoq8jGmvd+qwphUjKhEMU4mzGi+/JK/eEpgrSiuM34mN\nQPsU+byztvCc7niVovqZNK8RucOT0e0T58YxzCW7yIliw/h2Zbp4ngpB0sdsqaDkSHy2eCXYopL5\nLpBKk7uQOOqZ7yWEAyFP7I+d0LzyXoTUry36bIhlAifD8+Dp3HeJ7Z8g3CcMY0Tz7YW3P9EM/+Y7\nQjkzH2DQFcHJ0A0xJ9+xhBH53mAiQzqP5HXEEBSkKsS1MB1WkjXlZYvw+5GsXhmNZt0FR1lziTay\nxDKJ9e8Sjn+t/b2o4FRSYSdNEW9UeUJMyu+G/xZDXHOeIUkEwxIzpTkdjuHLBVlHqPRDwjFGrgeq\nUOGmmA+/bJnvcDrHPEeKznwL/DsO54R5tiBn8mllEQubW5CpJdCvhC4h7U/Mu0O9pBysIDeeOCyJ\nfYxfDuzhgAheOJY7ajNsMmDwOXOfIq3gnqScnMBWBUIYzPwgeNLsuSViJpJ3XJ1QyI2hgIaZqVoI\n3Ia/jkRpiZUVybHHXkLWR0zgRzqZ06ZXhEswzUKYZdhxZPIl5TUi0TW3AEpfkDWONfD4oUS4kPE8\nEixw2gPca8heOFyac+8jBqVxxwwjdpJF0DOz0zOkUKFpBkHnVpSccDqFe4PSISugbiVKK6LkQSJP\nnEdB51eek4XNOjIbUAUClbxhG3eWdCeJRo43GPyEYGINruASpDUsx4JeK3JXEkQtNRGyiumGGSEL\nZKMxwU6ahqTK4nSLqDJi7wiXmrG2yHjHRZLQLcTbEXkomfaVWYZYFbO5kPX+QJmO0654DBvSOZZF\nUz4kR5dyiCXvh5Bwq3F7xzpc2W8d7npF2h1bSmRjiasHyp6RgSG2CVL2OKlxb97gORAdNa7L2S8Z\n90eETTP05z23b/6AIfoRLq6I9Y0/qc8017+gTQuaW4nsclSwkcUrQ5AjsozreWOzK0Y+0Y8T0V1R\nJwYTnkGlBHOArF8JcMxDTHQ/kDyl3JXDItHrjBr/gXSdau/R2mLSFT/tNMmN+vFLkuE903HDDTky\nWYj3lnM30H88034ZsP2RJm0U9XLBXHcsO/ZxoHSC8H5mCReW+edo+x7hZta1JBAZrihpXMYeZ0iX\nga6RcccuIMksm5IM647NHwTCMmtL564EgUTKjGURJEVL1s7kbgY70weC2MKCRDpHXFj0kmP1iBAd\nKvMIU6N8iC0skfYM9g3pvSJMK4hqYiFZp5n1RdPmAe6UsPmQZg6Q65GHEQyTRA0xyxxSnUfU2ZLK\nhTBL+XLtScgwRnE9zZTVK5mIKIOSq14J3wQEk4J9JEkN4WhQlytTGONSTV5LJlcQFBtXNzLFGXWw\nsB2hCgyIlfeLIHGWtbTI3BE9KiK/siWSRFk2kfPcFfgo5jWBVk74XaJtitcRrXZEVcLSFuz+HdK/\nx+U7pdthlrwqDdkKsWEfYT8oyjhi3FqE9Oh7RChnzoeUmAp/hxlPfjsSa4H2CYVKELJFLIpCRZjl\nQuavyEWS6QxTZ6yBwAYH+mbDpxP21LGMHUtRECYR5vnG0QeoucC8lSQiYTElbt6QLxmtDHmpB5Ii\nZ6DCFZZNwH29Ep0fTAOkdsCceioals0TNFeqfWNdn3DHiJYQEVsqnVLzilPiq3d4rYhRUHbI7YWm\nHVnmCDNf2cqQWY+8dgtd5jgjuB5a4v5IundkLiIUM6FciR4FTzYljkJi/Q8kWSgJUZGwtQGTiHBl\nCME3iDlTTBpfzQQ3hyo0myz5+ZeKp2PK45MfI/adLUq4RwGTfvCFeWJUI59/tyVYK05qQcmGRYU8\nJYrQziTtyqxHxOJRm0M9B6zasBQhSjj8cSbLAlLTkIqdcj9jtSKcPLNxlDrntluSTCKeEoYYlM2R\nkyITlsTF9ONE1jjy6IDrDyxhypZcya1D3irSBKL4ijgN3KKOMH+Q3m/ozCHUEbMHaD0xZ9DZmXS0\nxLHjIAuSfKaIFEuX0OqEPddUSYscUoLdYmOPNAWDO7HJhGRzmFRQTB3P7s4wlfQ7FNLgfEyIoLM7\nax/icBhnSUJLWVqWa0a5S+5RiGoEkVuRicJtKzc9I4RCqIFuyTDtmTneMamjX3eCNqciJz0kPAU9\nOk5wmcO6Fh+nLIGD5C3x4hl7xSGHNI+IrWQTJZl6+apQCYOkoEghzgakmZBRjTNXgnLCmAdjMhGu\nEGZX2qQgHVaW/o5YYpLqRLlXJPGAyAJsF4JSqE3RdAtB0RAMT8SmJu8iymnDPwRhXDG9GwjnkD4X\nkMJqV5bnFSVK/CPCd5o8nel3zdtkIkwF4V0SIpnSI8LGmPrBEreUY85SaE7zB3z48wuXveJbrwlT\n8SFzkhHmG+dypuxWgsBR7QdCI0DE2Dgg8SfSfaeOj1TPFtqWcZlQGkp5w7+JuTuHL2aU20mbiT1Z\n8CKmKMOvHad/L5KFkJ7CRbjiSBHFvA45Y/HMyyp5tUdupNhcMV8r9nDkO9uIHjRP+kMmN/MX128Q\nZjFWST58/gmrfcsyfY8laflcHlBtjDYx4+7huvO+EkxFQ55d6JqA68tGqBtWszF8ecQuB9rbhDEG\n6zXe9LxNA8Y0YA1iejUidYOYNpZXi7QeKRyo9wQWwvBGnihut4FZrOSRYb04xBVEOHI9TlgZsSZH\nwv5IHYeYsKTjhFtykiOkQUs1SdIu5FBY1POGuqys64pNIIpmMBOl8cTRM49Hic8Eg3zA1HMKO7Kb\nIjMdotJEs6XVcHM1qTBIndBrxV0eaJqZMsxQGOLwzn4tyScPS0qfhNyCE2pfGHpPU0UIVZEQUK1f\nUcbm4ETAznaasM7B5Di2G/mmiYYL/R4y3GrkNFKlFhkLzs5wVgarXxiOCWVteRQTZTcyyAiZbQir\ncJOltHfysWDXJS9y51HAw9+R64FLGyEOCUUcYoqK+LViia9I2VAfKm4MTKYHOpIUum3DuA1fj5Q2\nQJVPqE5jgittE4OxjGFEtga8WEs6pGS9IiRBcqP0innISF80YSgI6RgSQ65SFltwfm1YQokqY5pl\nxC0RaRdTpzWf599CtleC6gvuv2/4Rv0Ltje/4KPxSqICRl8yio3x3cqsAi4YVBIxNjXnpKVPrwRx\nTptZ4mUjzyAeKvIlZTANyT3lnG5Y52j9ETutqFdFYEfGoPracfr3okXdY1k6ycIdFR2pyxe+9duQ\n5Fcq54kkqCTCZQ6TJPzsKWbKJOvLTGQTSv0zhIejPDGpgkTtfLDcSfQbltGxqjtpeGDVC4EQiNiR\nbYblUVCFKSQdQwBNapDhik9B9hbZbuxBhS56ZqFZ94yn04JxHnvf6JuAtAsJXcFmFOYYwmtOGAnG\ntKd6LgBNH86c8hCzlLRXT2gdYdORhCGXPSe5KFIXAXfqpMRoh9wdVz+RnxsCfyS4bGynE8n9wRCc\nWAtNmsXoeeWhN1A10gu2W0p5WLmMOU9Rx+wSdl2QVRPplqGzmcf9iDjseO2QiYO7x6eScGuId4Mj\nYdgT2CELDNr3HHrLo07o+w2xasajJlpj3NKixoaqbLkMDUUdcH2ypC8acfbYOaOM79xFjukjqrHA\n7lc24chyy3N8QO8BUQyyf8MYjZzMionfMp4mGmNgz3iVmkMqiN432BC2w8YSKbI1wF07XOHobE6S\nCJrlDF5zfUwcOaD2geltRLjXxMcRt8esrOjKUok7gToSyI18slBJnA5wUhHWX/FgdDQRjQfiIiJY\nBB5LHFuCyDNYSO8B0R7zOF/x+UR9eWZzE2vdwLihy4n1PvGUvrDjuEnDhz+T/JmpKL5z5w+/URO/\nl8Rly0M9kflXhNE0SqKnFL9vTP4t8fOF5GVl8CE2OCKTDV1Bsq/MgK0cgYmx0sMsSQPP8nZkey04\nRv9AIEPWS+JMIU8bffxKfI1wVOwi556eEXIjsjCXO2J31D+/IbqVwjeYGprf/AaVhHtyIXrvyRvL\nd75d4LOF/fweiWI3F97mBhOnpEuKWzcGFq7JwsVuhCbCd451b9BzCerEfEzIpCBbYlYCzkvG+2vE\no8tQTY13Z6agYzoLbLNzvNZURc8cruRxg0Kz3hPko+YxaKROOUSCJqu4xA4xbGRVT3ic4e2AI+M+\nzUhnGI8pUZJi3J197bm/WZm84X1RYu9X0mWjvacYPRJVClUZgiqkTmCac57cRKsr8ikmXDYSEnat\nGMYS3J34vlDKgMTAmIf4yZIXkq5UpOcrWvWE8Q2lC8Jt4yIrgviBtIrwbc6boEAWPT7ISI4Tk4hI\nVYRsZ97YneZJoy8leZTxupyo1cpz5umPIamsCM4Zt0Ux3Re2u8Y6wUndsfHEToK/W5I2RczwOo6E\ntKw2Yck0XRUQDSPVrLH5gI5O+DAiGlvyYGaKHOa48JzmhOnKbSjwjwohN9zVkKiRoLdEs+eBRMQB\nk9FMwUrXzaTJjdALIt1jVM4kYoh76GP2Z0Pvb/hMsyfqq8I+nbMGV46yJOMJ5a+kzUL20MQ6IeQN\nRZ4QfPkl77q3jNPHmG8++GAYKb/4fX7w2c4gNF+KHBEtzMRYMTOOArc5GiKkfI9+H/Ioa6ogJsh3\nlA3I2xAtPeG+U3lI9oGTOCGGOzYxZHuEP4zc/D8QDU7pPCqGZgw507DWIfJwIp8GYi2oiJjXmefX\nit3AL8oIk46c5HuGNuMn14hJaaIp5RGP2HFkiI8kXUo4wP1YMo1n3i8JXjpUtuP3iaeTRFhJdIiZ\nkhVERrkZ9rAHu5Dtir58RZ0mSnUAL6mUwfsAJyYWBXX6xFHn1EvMUlyZ/cYhOaIuCfPFUYcDzRuB\nrN4yRFfM4tFqJ3txVGVIGKZISoKtxDU7x3njpiPyOcOmEXMvGeacsg8xXlA6i2kCIumIzyPuIPBr\nTOBWAntFbANn53jEFUm1Y6OJRySYxg4RhYTFSiwKsreOse9Ix5ZVprh4gflBngbcMRQ7JPuBILt8\nBd71DvkS4/Y7futYrh7vckofcncKs5yo5gseyXUScEmR1QhCAx3jmHLhSLPvrElALC3Rk8b7lfgM\nYs25OM2aQiADNtfjmgUZZuQKXOLYzJXM7ITdDZlIpmigyC21ApaA4I1j0hVe3HFLzJpp+khQ1xE2\n8uAdJgjojKCMj1g8aa/JHxdyccCbFJ7AmxB3CNiDgGDdKfYEIxMCNTGZJyIbsw0Fg5tZ5wwZrOyn\nN+xdzq57eAPbWLAevirf7/srU1Rz+87HmA8S4vtfMH6aM387YZU/wX2rIaljCn3F3GJSnaOmA+4w\n4CPPXFrm5EiRbkTLe4wKuMuJaIvow/tXokJJg6RikgVrayjKkN3BQ0u8iii3fyDcECsDRPegTzPM\nGBD7EPUmIlIFibTc+ok4FLjoSi0Dvp9qnm3CT1UP6YVPFkc+LQRRQV1kLLkh+uWdS7QQ/OznVNvE\niYGs3rCFR04haRGyRAHOSpp7xUFqtFyZS0kZSOLII7YBKWP2l4r+trBFdwIpeVY5zo3IS8s96ND2\nlaGUSEpcWNPNA9Zr9oOnjS3uGtEEnqqW3JuB6P/m7s19bUuuNL9fTHueznDvfZlMkplkMpNkF2uA\nAEHttiBAnmTIl9FA/wHtSK5MWbJktiFTgBwJAgRBQBdkSmpJzaoiWcVKsnJ+7557hn32PEWEjHwq\nNBpdVSwQaBC9gA1ErFiI2M769saKiO8Td4Ikorlb2tHTTT2quxC5mTpJiMaeTI+k55DCeSJ/ZZhG\n8s4yDSP+vLGKkHiKya5HFvvNCcplloxPAS5SpH4hEROztGgdkIQxAyPu2eKzhXkGHgNuIsCqmF4/\n4vKCbXRIIUgOAW3ecV8hu3oiJel1gZGP2DpnFj3rbcAWCwdtiMyEeNREheIxkHRhjh83BjdC73D5\nQKo9t0vNqFb6U8EwxkTHIze5MUUXZHZEXL7RychSR3ZXXNsXpkLhu0e0yNkQHEmIRihshVoNDC+Y\nxCGHnFwO5L1EtN9QMU6twQYvFKbBtyOHdSQYBQ0NY9ISZYK62nNRHUptpF6yrJZNtIh6pg09bu7p\nXEOzeGL5QlCOSK14nC2uOtFtlmAaWcIXgiFkO3mWWLHveuRDC1hKcSU7P/IX97/ko487to9CDrHg\n/FDSdJ+i2oAhqRBi4y40tdwQ2mBMQGY9h0gz2z1jntMXloMNuOcLWXAgSu5EW81yPVHWoMuRWmqy\nyaCTnESE6OS3v3X6O1GzMJtjifcw3jHlQjPCq2uPUp6Xq0XGgruTdBksE3z6+gEqxbq9IvQxn/BL\nnJFMg6RfYkppCIuFID3wl/sc/dWEVyuhk6heES0Lb5IDhoY8udOHDt8fGZWgMFfaWcJOIl8E2JhA\nWvpU4SLFenIMrybWLSOKv6Eu23SDuZ6wlCTRTBYKNt+wCyTNtLKFPefGYsxGEsecbxtJHhLkFjFo\n4s3jFkkXbxSzYQ3vCFGgxAljDvT+BVZDVHl215Rx19Hcc2SloD+zrY5BSYpOcF888zLgU0cXp1Tc\nwLe8NCMqe2SPRoQLL7cVbQ0Sx+N0pZ921GmDMiUZhuU5QD0YfBgTt4rrLDB+wsiFfhdQXUqwgrYf\nCIqIMPG4WTBpT7/M7HQOLsZHC7slZR41XfSML2GvQ+rgDbl75PrmRlpUJG7GDpbtMSDfFsbtkYAr\nxV6i7jv8/syL3bHtM7brgk8zdFvTnA1pUaL8ANMBt76hzx9IDw7fBuwKxzJYpkzj15X2mKL1RFAb\nRiFYxBE1KmZbER4V7WhZBUiZsRMDY2cZYkkcPoB5wUlJ4DQ9DTsvWeeM5JXFjAlKRbwsdxKfsg03\n+s3grhnqKaFdr/zyn/8v9E8Dxh9xU8805lSHDrXm2OUN0h+RcU1CT1oeGJ47LvuN9DoxhJJiGcmW\njaHfGI6G3EEbd5SnjeTxienlBGaivlbIeKbdctL1gl53XLJ/Rwh7V+Xp1IUtjqllAKEmKX/MTErx\nFCEzA33PfCvJk5B35557PeOHgagr+ejbM+vqiBPPKC1XO0NcYPqQH/S/Jgp6NBNtLRkDy1lsHH1H\n+Dwzaod5zpn0iFgc9+se1ecEzxXaVrhlRQSQzxG0kpSc8t6jBEQZXK49o9xhRM6SDnTKIboImSrE\nFhAvO/SqUCYkHhWrKvF5yCQMerHIoWMrYdUxcfvE5QgmemJrBnQiebEbu1QTHHboSw2mIRxXrNMU\nJw9JQFblJC20j5a9FRyyAL20REpy7TRys8h9QRW1nPKa+UWjkm8Ondkkx2cOaW+UvSL3hqSXeCcZ\nW8/S1TSrIz926GpmKwt2t5FN1dhDSBBm+GEiOStO68o85ZhVc087lp1F3VYCB3IeqZo9cZLhmp5q\neUKtF3bVjj68cQkd+UODXXbIek+WTbDsOQcbw7biLnuSdsOeJjI7kdYT1i/4h4E6gnut8fT0D4r9\nqGnbFXzHeF9wQ4HoBaGIiWVGugJVD4RcxchYntFpj2MmCid2c0zXT3S7jTg25E3MONQktz2qE7h1\nwpeKCU/pMgI70cgBNTYUOoJy5rAdGDLwRUNyA78ekGai6A3SNWQi5piBFJLVzEglsA3kQ4z0OePm\nGMQefMu412QvV3SS4luB3qXMc8TLtWNyCa+J6OsbuS3pK83j3hFsI1rA6hIaPZG//JsOYf/97HcC\nLLSQ6FXilpDAjUTLijUXgtHS3p5R20JlDsiypukXutAhI8/Td1JkfoPrI4w58brgrUWrkNWGzMPM\nV18I+mhDlIKd7IjaCBUIrmJh2T9Q3I6sTx4ROfzUERYzRq1g7kzHO2EQ4+aEJb6xyJFTdmUpV8qX\nAH+zVHlI2nlGPRGOO/LB8KwtLSn+OnPPWuZFERaSNbCwnqGTJOFMu4SE2Q7bGpZ8Y9tdObiVyTu2\nvWCeBQ/LwrCWJMOVq3qHKdkh2gDSCfl4IggypiGmSQQPHi6JxS0bgS8Rd4VFs4YzSduzTp54LRnl\niLrltLOlWDzDeGQxK3O0crpeOC0pw2EjyVsyMgpniMTGPGt6UzNEJWECUX9mC++UccF1LwjzjHS6\nkRcpDIqsKXFpyURPnBdMqocmwZWKuZrQacQtGnlcFMUlYhot6f3MYDz2prmIN+zWnCQRtA+eOB14\ntUvpkoSzWNF5SOYfkSyERYURIKTiORvJi5VZe9IgIiGkTi3jY87WPLNcNMNLhBxj9uHM41yxtznl\n3WJqzSQGsq1ksk8MS023X6lmySxblkQwdDmhb2mWnK69IHpJPAuGcaVPZ6SvuOR3rIzYhpk5vjH7\nE5PTnAkwJob4wkV7tvuKYWSSBWobWYqQbhGMVwXFMzLICfuBNt0zyo1BKrLGUkULiasIG0/54FBT\nzmU/s40Dz1uD0QKTN+h5RjSaK/1vnae/E2CBkCxhyT4UxIOltwnvpu+CGqnsA3njEKPD9k+U453P\nI4OTJdF0ZZIFv+oW4lhzcQ27eKBcNFtnkUWLXyVEKaKZ8f6RqFzZ0pWgCUm2FiEEDB55EjzIiSKa\n6cuZcVeSGMdqr0jfgy7QpkClFfdLzlApgtDSxTVN9kwRO+S+5RIsOC8p5wGfFMSzpn28sy0jIjGo\naIcyGtGE6N4xqhuh3tBbCG2BnwfibqRuZ+pk5aYGMisRMiShZ5QNbrcnvMNtiEi2iSR+Q7zG+GlP\nEjsaB8ZsjDlobdm6EjEnjOFIqW4ku4ogGNgCTSca0n5lF0EnU0qTI3EYdWe0hsxt3BPLPAfkWQat\nRCwL2rxiSGCbdwzDQlR3cO64JkfWW0smBTJvSHxEJyz3dWPxG6k4YSxkgcMvEvXGI4cdq1kJgiO2\n3GOTjTZ0RJnE3UL6cqHynpacjjsm6QiLkrhLcZeeh3tJPsw4JeAckM4KWafIoeA6LchwpNh29HXH\nGn8jfC1Vzi5aCAk4y5ZnecImG4EqiAoYs5qj7fB45rvDVjPmUTN6UEcQQ0WkbmSiogtSrLbITBO+\nLIhuIHArSg1IWTB3B55chJBwMBvzPeR8e0WxtMxbyd0nDMYSxynDbSQysI9BmYLDM0xGsPcX3Nog\nRMTVXDmNhkS2BMsL4urYgo39JMnWmKBVBFuAusAt9piD5WkLfus0/Z0AC2E3jrcbt+uMyj2ZuvMu\nmuEo8GKkKyJssBLnb8BXvP95y1S3/JUKSK49PxiuqACQAZdLCmKhDXuKyDLuRoJ+Rid7hqJn3Db0\nmwcqremDlEn2LIkl3xu2/ZGpWdlTIbsb9TVFBQHsM8bljsQgLj3m0LKqlWbeIU4ajeZ6C7FzypOR\nvFNJ7ialHhVqLtnfBKIPWJeQ8tqggitTPJA9LaxWIK1DrgGusEgcc7hROYmMX1E9eDrhuI8JvQo5\n3ODeW/SuJvQFUygwrWeVntsysXUZ1RrS+RQ9dlRJiFsW+gdFjmLWnnV4ZlOeNJ2I+5UmCThHO7JW\n4jcQVYhaDJly3O1GGN7wjcD2HU6EhMWdzg+UYUIQD6Rxh05WbBGSzS2DcrjIsNQrdr5yFI+4UBD4\nij6qoF0Z/Yr1G87A6+KKlwFXfUPfPWrYmLDIOSaMDWYxnE6O4n7BNp7lLimUB7XgjjFWjfjc048T\n2jimdaWNX+BYExnLLVmZ6ShygfICHe8p9x4b92w3jV8TpD2CjxjWE05VpGgao3E+5NXe0Ig9vAy4\nW8p6T9DBhNQ5xm94FeNUghkqEiXZ/MY8GpxxhCj2AEHGegy5mpzB3CnEwi3OwU24eqW4h3RcCPWE\nGxdu4UbkV+4JmFRSLwdyA8VxJA4jKjPzolPkIacNdkxGc802xi0isDO9SLjEIab1aLdS7/9WGtzf\nyH4nwMIJiT9adOxpVsM9Cmnf92STYdh7AitYDKz3mEHAz6aNYyj53qnhmpX8Sn+IX1b22UoeW7xc\niF2CbAN294pAw8t+ZjWCIbQUMbj9gp4bXKmpnj3bfQRZ07sHTN2jo4pDsnHXEZN85rhJJlEjUo/u\nDHIKmdKJ4JjDPSc7BKR+4NkK6rkhd57Qdt+wbVUHrBEE8copDVgcFL1nXQuwCUJ6lGuIxMR9SAiW\nhFamlPUV26ZEc8su6BHpiChzbObp6xI33OgGQa9LjroltQuJalGvZtIFEqmYt5DUT9jWMqwRWygQ\n8xNSFmQz3OM9hb2w9QHdrmVQDaKF1lvGQeB2Cnl5wBc5ywx5N2D9ExmSoQtQp57lJri7ilSF2CAm\nyR1D3aH2BW3umDLLdrGI/Q0pHMpYoqvHbwFFFhDXJVthcENFVGmyzBCamNEA4kqvA3ZasxFR2Iip\nVCzNwGAy9HLlMiVcpplMweQlES37XjLVKfm6ITaL7Q3TlmHXCrqV4fmOvVUM8cbR9Zi0xauQNdvR\n3MGpCnOd6BfPeLuwlyuUOQezYUvJZmOSIaGJJ0x/RQWW+rHnjRKk+5xDtkdcHGp2qFCyGotuBOn9\nzrHI2LIb+e1MJiayx4GgvKKNZlYlkek5tI5pDNjFPfOqKTfFogPqHqImZW47hHOs3YbWN/Q2sfMR\nqAZ1THDDDe1mChvQLynJ386Z/RvZ7wRYCA/dLcQYSM3CYZCESUjfRmzDiL8mFKkEWbCLNcVHES9J\nxF+Omr248853X7PJDiGOCGImUxC5keciQ4eGQYaozw17qwgnjV8c/eiR80QkLefMMtgc04aYpaNW\nK9bDRQv2w0gzHWkGqNqSqouwIkF48JNCbAYXt1hAWcjthh1DXiaJN5JbkLOqC4d+Y9ApZdOhxY5l\nCTAiYAsEC3saq2mHFekypkoiY4NLN2bvmHzCKdBUt4XprNmZnj09cZng5w0SqPsI5IqJDe25ZZAN\nS7QS0tC6gkfXMQWeufH4nWWaL0xbQG//pDcAACAASURBVDjPzDLiHTtRuT1RVuCdI9ke2AtDeI8Y\nxJ3ATGyBJT0ogumMGyWkgunwSBdb9muDaxbCZGQcI/Ipobsa/G3PPCseH0O4aWzbsOYPTIcdq7/j\npcaGjrzWZO3ANi1s15VlfCHSjqtKMN2AS2o6UbAoeFoTTHhk4oSVBY/pmXDRDEVGKiRmd2Dexahd\nz7P0aOGJ8pZkPCPmmjifqcSezQyMcsI5RXlOuV9G9LwQlQvb/Q023/FqL2mSDNE23LRhRJKIlqg3\n3KMrmxD4dMPfwY8j6bQxTB23ekYmGUspGcYBrxqW4o5QmnFb0HMFkUfIHUPrWO8gx4Q4vRGlIee8\nZcsk23ggNJ5GDOAlD0nKFl6ZbcQ+EWi/EoYpxidIK8mznHkybCUs1ZHTHpS9MHf/jlxRx3miLCS9\nhahGcc0s0eN3WI8D4eBx5YRfJFEx0WczTy8eP8x896PfB6m4RSljqLHNim8vTNNKHQj0uDAngrK+\n8/6/tzB3EfNiqIUjHDYsO4ZTRpgWBChOs0OrBZ8kLO6KANpAUnQd9gHEsWdLO9wcEM8rIpTc7w1h\ndGQYN8QGbl6JdESx9ES2Q1qHuRZsZkKtd9bsCU9HeJTMi8NtE30oqIL4G57PSpGvC0ntEG1BMiSs\nm6IwnjpfaZJnVmYGHdHcOhAb6xtLeShAJIyTxGnNjpi46Zl1jE5jejLoFesQYqYXsl2EkgFS9Mxd\nxy2S4KdveCWDkc7MuEkRyRn3FDLRYfKUq0/ot5xVe+blxK7vSI1gCUOyVXC/emwkkcFCkDm2uCdb\nZlzriMqFNStZLp7temaNY+LuSrjcOR8sCYIpHFE+wYwVMpQc7p5xSGjiHaq6s8kAq29swuGjmG4c\n2NqAXi6ItmNKWu6t59ZIyosjjFKm9Yh2OYEK2YyiDxP66EocTajrHrETeDWQlYJN93gmZBjRhTO3\nS0iwTbjcsGsXct2RNinXYEW7CNsNrO6Rah14HHJycUQmIbvYssMQhCvqaeK2eVz9gDsUiJcIsQUM\nhQH1gkhLbPRAYD3BnODbEqF3PF0CzvYN5XmkeAC5epwXOBNjXIGcG4YsZJkGvPFczA2/BFTznb3c\niOeehJQuMszbb0+r97sBFnhEN7HFG7dIEVwkez2ynQeKA0TrwjIM2KvAuZap+4ogq3hzbxgliDFF\ndwlT2tBLSS40LohxhMQTXIuA2+mR1q+UZcAxdbRZRZY6ShbcspBlPc6DyTwHPFntcTLFXjRBHBFf\nAqaxpOljdv6KDjRHsRHlGcqf8VPHteoxgSLIOoRJUMUDa2fxwYiKJdkaEgYtqxT055GbHynMRuDP\nGLGRFB2H5sKb3rH5O9pLukQiVUvgB6xVpK5gkY+kqSR+SjG2BKkQ55pRKqRukLmjziSTkWyXEDOd\nIdKIuOMhXbFbQuMS6mjFiz0meEQ6RR1vhMudaLIotUC+0TmHOBu8MhTXBt2szOsdEdc8LWCtYp4t\nUb9xSTOk3oi6kesSIK8LldLc0gAhX+iGPcc1Ygsb+ixABAtnW5IkikMXcNovhEuM1R5ZSSYRcn3Q\nFCmo1hEvFYOGuS3QU429Cx6LGfHOjIgEYhcRz69wW89BNDi3ZwkWku2KnUbGdMNkG9t4RduCKdhg\nLzk1BS9U4Ayx0SxixoUxgV2J4hlnSyZbcVF3OpfTBCeywSDnnidlUMHEKd6xRIKpGmibkOcp+Ya6\noCkZ3yyoW8FhuxC0DWE1EnBFnRf6OCA73YnMwvI4sjYbddRSrScac6IiwW6PzDJl6BOuq8CHBZM8\n4dyRwiQQCKx9IbkomtFSVx7fCYSwbEz4u2CXlb91lv5OgIXQHqUKgmwgHUN0YtmvC99yGtFqBrUw\nliFap6xX6OWOqG8oPv2c5b7xbmuYwpVWWEoVs5kaMwoCFfBsb7yzxPy+SRFRSzAKXGwpoomtC7iG\nmnCaOGlNXMGmcvy15hblVMwUBs6MoFpu95bDNlJHe05rB6pl9R3LYinKR2Qv0POerlsIgo3GteSJ\noxtC/AS1t4RTjxKK8BCy9xtSSKYtoxlmYl2xJHCUC/Zpx7YN2LAmkTG+9YRjTjP3BNczcuoYG0PC\nnTJd4GHDbZalrVC3gr1wjO0DJnrhnq+E3YLyHkxGnwkq3RK1gk11ZFZQujv5olFHxRbEOClwbmLZ\nJD5fEeNCHSiGQ0AUx2xrxRDsQK3MmeElmtktK8dZMyaG8qFjUIK6jXB6ws0V3g8MdiSPInZLRnCv\nUPLCLGL6deTxGrGpgTockdxx95mt9czjlai4wdiQJ46khG23x6gJMT+wdiWvIotTM5OaSDKFSwIm\n26PnlHW1DLnF1zvkHJIow1AK9DVAizcc5DPa15ipZu5W/DWgPd/ZXMRsI6jO9GLgOAWYqSaRT9QS\nEh64mpJqXQjHE9t0Azz7zRMdzyjlKYOJIhWkh5ZroOhSw6AM416zKxNmWXDZ7fB9S3b3LNqx3jwX\nKgJZ4vxEHY7YtWU9TFg5Ed1PBKFnUi3+zQvpsOO4SoTPMLIhazLuiaFzmnSN2B/3OPtvoWYhhIiE\nEP+nEOKnb+UL/6u3/g+EEP/HW5nC/14IEbz1h2/7n7wdf//vWsOhWCNN38Z0PiaVmtMVMv2K++S5\nBZr4mlKUGWtqMO6ZOdD0cocsFtqww7mAcgrRrse0BWQh2j4T5grhoIx/xNFk3PWFqwgRb1p0oDCu\nxoo9lZDMXjFfJUv+xM7O1K1nTRypLulyzzul+uaL03leiZntWuCHGB+UTOZOPsXc5JkwL+gSQzDm\nrFuByQeGysKw8dLsiaKKy7BhRsVw9vhRo1PFde3Q6QG0JH/TM78K2LaKu9eMLsTnC0mR4daQN/7A\nbpU0qeTWVyzPhmgLmIUiCGaGsWcnriTuG4HlWyhwtwIXRWRjxv0cMIUQmILn/QsnGWIuA0EzkI5X\nkslwsXs2ZdkPM90oSMaAPY4kjOjDhn6ZmWN4OkkefILVPddwIgxnpqvnmNaEdqQcVvpjx26F0Cyc\n1YCJzyyJBlugu5ZptWzRSD95MmlAC/Q68xTXqDTDuAylQoZLw2UICZYboVlZbE2jak61JHu2hOmG\nsRFNI1iPGUF5RlclEY7edsS2J4ws8WUhTBMyJxi6R3RQMi4J4SEm21seqoDQG+JesfaK4CK4qRjp\nJCECnKOvFnYBXK0ltQK9akSgOYcvmMsDW+8xrmVTjwTuQBjGZG4icR3rlDJfUo6DR7cNviyxRUIq\nYlAlyeC4ryPkB/Isw3fgO4WYJNIadkKxZJZGKkzxwov2tLrFuoy791hXIOVKJzZW7zHTvx0+ixn4\nR977PwD+EPiPhRD/AfBf84184YfADfjHb+P/MXB76/9v3sb9HeaZWcliwW594eZXwipE/zgl0pbS\n7Wmzhi/qT5DknDZIRcwH4Q4bOcbPO7ZWE+C4CoFSHSueFMW0OrbRIr9XYjvHdj1QtgIXBFxsi88l\ntpCMoydvBXtzpglXtMjw0pA0ms1sHG4hax0yu5zsaaJOjox6JnA9QzMjx4ntGFA6hZsvzHJiCkZ0\n0mHHnPB85DFJkOUM9Y1KKBwBhfEcgoFh8Bz9Sj+C7CQqDUidJupbVOGIFstujlg6iZcj7+iBenfm\nqA3KvcBTCkFIEMPAgNkMygVcB0s0JESzIswa/MsNYyyJk1TjQkzPwWqsGjkX0GeWpZAkbUeyzIgi\nhiUltDk6X7j5jtZuxLcNEFR6ZjkYWmNwo0IWCtUeQXu8g6Cc6KIdpo7p9MqtKQimgLn1xPICTmPI\nKfIFt2iMdJjNYecKue2ZRYbRDW07MGcauXMId6KtNb4ztOGeo1KoKUXoPYEPCYKaQx5RDDfU1bLO\nELQVXnqM8TS9JtqPOLt8U6A0gimeQUnmNxA+W5p5JGs8W7rg04Qw74jMzJzt2NyZzC+Ebc3JX8lF\nhiifII24zuCiklSNtMdvuD1G+wLDnb7VLDewwY5NvXCPeu7CExIyXSfuU4Td3THrmTna2O8CrFxw\nfsNojdITD3nA15FhmxzVeYfyB+ZLjjQhqchIAvnNdvnkkO2AaheUWzgF9783OPzr9pvIF3rvffe2\na94+HvhHwP/w1v/fAf/p2/Z/8rbP2/H/8K2cwN9ozoIVjjdqxeeSMFIQbnzxS0WahrxWNWZe+IPw\nR7j2ykFVeLcwuTO7Yc8p7BDFDTdEPFgQNqCqO6664GAyOGyk8ZdId0cdZnp5ZpUQiRTTOoQ7kwmB\nLzMGoUkZ6cIBnVzRyUhcz2zHDJtPSHuhbnpMOIAOEHYl0ylTKLidLF0VEbsjxVWQSU0XTByWG61t\nmXWDXwpcZGico0sMWyg5BTFBoanbGOsWJhniIs3ULujIUyyOe1phixpjN1It2KKC3RDwcpbsRILq\nPDp6Jq0loY7pl55ZWzKfY53HHr4hdBljTS+uBE89tzKkjid0nxNtOd7FxNeMYDBMWYRlQPmBKXOI\npGY1OWqQJKOiFZJ9LHm5KJo+YPErd5OzG/aITGF9wpg90PsY1a2sXYwNA0yxEtqYTVagI+KnhUl0\n6F7SWYti4b7GJO1I9nBGWuicxJaQtp5sLfE2wamU4KiR9TODkQjbMwcSISZWGzD0kqF0BEGOGzxD\nZNmHAy/NI8FSMcqVNs4Q65HZD2RDyJJ0BEeJiTRFGTJ7i9GCg5DEt5B2qSD0qBZcsGJ1xUEHdFrR\ntQ1qjlGBJ79FtN6RPnvu5oHQP6KXCfHKE4uVWgpKLTnYmc1JpFAYlRMOFuWPREVCqTeaIUCfYiJW\nBhQmTBHtM7tU0j5GNNmZpFwZ9iFhkBGqnlFeQS1E0coheEWeetalZh/+9hWH3+gi2Vth4/8b+BD4\nb4FfAbX3fnsb8q9KFP61fKH3fhNC3IEDcP6b5ldKorcaBs1dHtHzQFKOfPpX/ztLVlKqldH0/PHp\nf6UwAWKGTin08cgv/vJTTCUwFmYR8dNpwasL8r4hNsUvfvElO4BRM5QzqVgwOmUOM1J54XTWBA7W\neGO5Onweko0xwdbTTrByQO7PDHjywXCNB1SsSBpN7zq0rKiNp3Q5noD4NjPIDZ46hqbk4ErufmFR\nC7smwD1e8U3MMVpY1wth/Ir8/IaleiItJMt8w8uSlwV8oHmMHd3rhoMYmQILgeKsI7K+Zo4tjA1C\n7RlDSbNKkqoHP+GPAn9bGGMwwUrkSjb/wDBPhBLu3vKkPZfGcF/PlGOJI2B8FRK1d1y6YLaKRV/R\naqO/HSk6x32/0Q2GNBOca0Oyi3DbDdE74mjg2ewoaNi7gM/GC//wH/wYzh/wUbLx0yfB0ye/onj6\nLm+ylSf5GU3wLXTrEZcHdtlINzwzHVJefq1J3/ucY/VtJndFn99nCj+hee0I03cYQ8tx94D1PbtG\nUadfs371Lpn11Pozoh9+zOlftrz34ZXilPGL4MDxdueQfYrG8Cc7wU+yhe32hNoaXt+OxB94zsEB\nXv6KJZ/5UH3Ar8KZ/f/7KdGPBWUX8unwHcT1l/Tfz/D1+/joV/yEV8xfe5oPnnF5SPizjfNHC1ye\niB8Hnv6spi4TlmRm6L/HB+/dee1eEb8e+Wpb+cP3J365liSfvtDakOXhNTpJ+W5vaMOa/fyK2/4N\n288rbtm7/Mh9RZu+xxA7oumF3WNCra8Ef3Hks+FLHp4+pD5/QvLqY4qLp/6OZfrsz/6m9PuN7TeC\nm7fKY3/IN+pi/z7ww992YSHEPxFC/AshxL94OZ2Jl5DAehYpEGzo3mAPC/EGnB2pFThC/Bxz8gH5\n7JgZyA4d43lmaSEuZw7tC6bP6cwBEztEOXBWM8tjTzhbbuOCqBNCP9B7R1pGlNcBZzVztbHqgVls\n2LzEOMUlXmldQPASsVSOXe4o6yNSb2gd4fxANo9spsX6M/eyYdlZtiXj0Y+ofiGvMpIHaJ1jHjOM\nc7xsGrEKrvUNle6pZEfvWkwmmI49Oloom5DmvCFDQbcrWJeALdgQyUqfeoq7Ax1xO3qMOhFuMVYs\nzLNG1Y/0xSNlXDHe93hArm/wbFRhjL0abgNUQUaehQxyRCtIrw69hdhxQo6O4CZxjWHvLaNZCeSO\n+PCC7fZkgWfkSiZjokJxThTKTsQjNKHhySveL97jO68GpvuVp1866h8ovhYR0Ref8+evX/H4+kob\nZmT7T1jWT7lPGU3pUToh4QM+m17zehj5NJZ89fUrvvPBE+9958QrXjhPE8vXLeZ0pf9qYPzwK77+\nB5/hY8Wt+RNE+hWBq7m+v/Jt8wXNR1/wJv+Ay8MPqJqET/37/Jk1rOHHvPe0p48avvPzF9wcIF/D\nzx18vOYk1ROvTyH+9A67dxcOj3/AU3Pk3dNGGiU8f7kgvtfzlBrCX2qI92SbZD4UZD8b+MXxu1Af\neMfucUmI/HmFnZ4Z+l/wnnvmCwbmn28UP4QtajDt9/nx5xWfLo7q9g61PdOffsxVFKxa8uVO8Ot4\n5pb8mvDU8vPXG6dfO3794UD5k0d8bzCvjjTpL8m+J3nn9IaufPhtU/bvtxviva+BPwb+IVAJIf7/\nP5N/VaLwr+UL346XwOXfMNdfyxfuHw+MTjLuNKUecRFsYUrUW9R445p2YDZ0LRG2weO45IJVFqw+\nJ95XZIzM9CzigXXuSHWD8meqBSrdYldJ3eVEMqbeXbk0kvlFEoaSNUuIbg4dJOynJ9QwUV8tWV5S\nvFwI6pSVFj1YmHcs+gW/xNzDFVctROlKuGnS4oHl/oTQC/Ea8LzG9KvhPHWkIsFGO6y6sqiVODRc\nlMZFiskvXBGUgUWvHu1TypecOGjx20JSpSixIIYEQkna7MnWHaqAMkuY3cjY79g2Q6hT9n5mzF7g\ntkF74+FhwtoJJfYEaUK9tFDEOD1zbjemLsHme5Ldgk3OiCginBLGHMxe4uaBi5wZioDlPtHaEi8v\nTDbEbTn1ECDGkPRFEmqD6CMwI+fwC9RZcitSXpse8fAJzu5Jz56Tg3el5y/ue/bLzC+uBa+fdmz7\niA8+66mOd5avVt6VcPzq93g/+lOijy1vuoDbi2PQJUXTkj9Y/uRbJdv3PmSbJt792fepxHus/ieY\n6ockL4b+65CakIefP3C8l+ThV3T3Bx5/PrNPwZ+/5uXlRntSCLnn4/uebJ/zeGnp7J8yvlfw7lPB\nn5dXZtXy5Tu/oq402R99wa4deecnE28+MXy5htxsS5asPJrv8qNx456/w/fLjObVxvJckr3x3D/6\nBUtT4ModX6kS73O+/45C+oHjtxXplHA6vPCDrOXXtsU9fMQhfCE/vuYPDx3R4cZPio0f/exbnNKK\n+Xjk8O53sM2BcZY8lH/Ft7oz3z9/zFzX3MUjxfR3aJP/Bvab7IY8CCGqt+0Y+I+AX/ANaPxnb8P+\nc+B/fNv+n972eTv+z733/m99ic0RZ47YaOp8xtWOs+mw6ojKUiq34qMNrStII2QYsDtdKDNDtIZM\nAi5+z9RBPd05lgnLPSS2GrE5ZHugMxL3dMa1jliU2EBxiDPU6UI9ZszGsbd3VnVliHKe7MxtA3XI\nWdxClO8R28jZzURxxCZuvBIFlpymFgxtxRBZHl8JdlJCNJIKyRo4slTgnMCvN2IO+EHgJcThjtBq\n9OYIbwJ5BbtEqGVkMJahmNCPr5hPPZGMEJknVLBJi7lbWAXhJEj6jDBskWZhHDTSpjx0DwRVg9gc\n623DTiFDMpLGM7PxpHFLcJfocCY8asLY0l81Seypxzds1UjGxGz3pKqkUjFWXqiU5Kle2VWGLG55\nGHuK0eOTiCDfKIgY96DDCLH8gE1feH2teSfseX55RH7ZoY3g2z94YnYHoo9SPn0J+VE088Gf5dz3\nZ8S7e77eF9TvtmgXU3/rc16SGL58Jj6u3B9fMbsS+9DybL9Nun1J/7rjA77H5x//kvhdySsDu/hO\nH+eYsSHsNJ+9N3P9jmXyGR89KQIisiBli2eauSV/GQgOC6v5inxNOQY17fUPeXP9hM/qkd97SWhu\nObsl5eNxg/GRT+eYn/7ZnfmDhXTTSKcRDy2ffh3yp/NAol/zHEveKyY+iRT9q5Wv3BPr00h8nfnB\n91d29oRwE8viWK47/A8bysePEf5HbFPLzv0p482xvTNwMy3yq9+n4SvuRiPWG8c3/5KHc4AZXhOf\nK15nR352f0WX3GkfCq7ZlyzDT//+6PCv5+lvEPMO8MdvZQr/L+B/897/z8B/AfxTIcQnfFOT+Gdv\n4/8ZcHjr/6fAf/l3LSC0pL1PTE1I3FYk+xnlFV3oaeyA7WNexAPRbqK9Lwjf0O5CrmajbhvE9Ubp\nTqQ7S7ib6foGU81MxnJSBXU+Uswbla0oH0cmsxJuM4MYIHrCuRHrDJNb6USMn65MQhPPNUZr8tAy\nhpZx94hfIy4STCiohxsuGti2FOdv5FfF4kdOryfckpBqCfPEIGKa+cayk6QreJOgFsnCFZs0hHnE\nlnte9MY89QSDZ0hajNAUtwaVaxbVEPch003j14572DFNikE5sD3rrWQnN+RiqXeaJZgIY0eflpwf\nKlITkIiMrZ7RrWRwjiCQVHPMrd4IX1bS/cDZG6JdDPWe+2WgvD8zFi3dWONbjd8Uzy5ka2a4B5xy\nhQwm+quHNWJyJ9qbYvEbxy8E8xbzk/OR5+//Ed/7g2fU/D7q3ZYvzBveFRu7rzM+bATtsOP/+Tgj\n54npsvFHP1tZ3PcxVDydKtIvHiBTBD+1xJ8ZDpcvOP95CcHnvFo+4gP7NSb7km37kBs141d/wqje\nED8vKBFy+9Yz3613TA2czopRL3SPG/7PB34ZfhcdvIN+/9v8+faC3ia+jHe89Ctr9HN+75LwUTXw\nC/uaR60Qvw6Z7h1/ogLeXStk/BO6y4VbYnn3B08s/x937xWl6VWd6z5fzt8f66+qzuokCYWW1CIp\n2AKBwIAJJtmA2QZswMaw8TbBwsgEAw4YGwzeNmBAgA0iCYwwQQIBMiCBECh1S51TdXdV/fnLeZ0L\nXZxzxjljeIcx9jB+L+fVupnPWGvNtd73VB/KjE2DdTpJHymKUY0h0naBPDjBrtOLKCcd2HwuSiax\nNnM4lsqcPrBMP8vJDo0RJ1dZa+ZcKLYyZDetBqTDFzB9uEaOa9JZQrolIx7obK4aDqozlmyfXjik\nOQXW+ccxV89y5tgUY5bg6O3/FT78v/Q/El94P3Dp/0/9KP93cvr/s54Bz/+fWYQkNSjegDIraCVj\nxrlJX28hlyGj0kJfKvBmQ1LVB9PEKxP0SqNMK/KBjDRXCQqFtiQRmyV+3oZgSmk42OUY2VrEMHOy\nOqYZKmCEyJaDMnURnRHLEqSRhhz28NoNtWqRJzqGI6jWSqaOgTQP6AqXVJ1RFTZVVOMoFdW0R7lQ\noq7bzLwAJ/dA6VAEQ+IFh65QqUqYaDqLZYsyiWgqG5c5et2CToaqFniyYBLIlJaNl0cMDJd5rVC3\nMuyJjWynjFsz+pKgqSyUQEF0G+JaBSdG8RyGQmEpNSnDgKb0qbMCWTRYo4baE0QxlJaBm6WocYui\nnDNVVRakIatmh5aokCoVdyKzvijjlj2qeEatS0hmBVWPUkrpuRKpbWG5CZboIjU1ykJKNtdxMxdJ\nkmiyigeto5z2VTrTGd1jM0buufg7z3La6OCEgmrbCvM4YcO280gOn6WjjIjDbZjqKqtGxaNUm7JY\nYJY9yDlbNyCkFo2oMVYF8e4umj5h8UGdA80hFp09rB8JaCWCntZlvLOFLgqED2cTD3PfAqtLgqXJ\ncWx/J9EoZbY5pYk1NhcZuuuSHIrZfknF8YGHe+IQ9jkq42GXM4WKVNRs7ayjHkqIzq2YUXLxIZuk\nuY8tS7tZNH+NCy7s0M+3sfS0GRsu38VwWlHt3Ep28me4B3Lut0c0hx9msqOh/eN9PDA2sOoWSTdE\nNDYbzz3A+nSJHZ05lesS75+iLG0lOiIzVEZsG5iEzphZ2UZJFaQzDbuXBfv6u9icn+WkK7O0/Rza\nVUN2yuKgvZMLxAnyZCuzTT5M1/5n2vL/o/8QtnpNDTRjzLZNnLu0E4PSSFGcEj9tmEc2vkgZNSZO\nLiG3C8LUpdMNKAoXQ64INAMlyrEiD5kx636PgVUShDmdYsY4A68FQU/DCi1MrUFRC0bZAqo1QvUk\nzHhOIqu4w5RGM9AnEkk/xk5joE8gZdS6gR42zGho6R56CfY6FN0INVkgb3KaBRU3lanXUoIFC6so\n8FId2a9JjBLfm5NGJbYbkMcWaBEzSWBIPeo0J3d8qkBHao3RhyaJkDBXO/jtGXmcUykBmeljZBJy\nHWFmXdACFMVjVRliSS6lqNFygaumNE7JPHTp1wGVriCXgmkxhb6HPKmYVTZWZ4wxGSC1IHcanFGJ\nZGlkjY0zqRAdDSNXsUuTYVogGxamFOLXq4zsJdpxjmTJyAyplQ5yrCMtLpJScK65wEORyU5qhNvG\nnpgcWtuLtfUExtFzOHRpgRtmaIVLlR1i2uqyvOUsWXKW0I7pXXgO1eqcZX2Ve+sOnQtHdNRFtGQX\nYXfERVbIkd5xjANdlO0hY8VFHlWIwRr35X3MLSewzZTF2CcqHY6nx+ls7uJlq1RqnzqeEnc75IaJ\nfqJG2WLgbFjmTHaYRb9GHmtYExjt3M2fvOK17H7idezVF9GUnMbSUbSQJHexlQohHeWbx0+jHTzJ\n5qng5OnTWDueQHfrhOv3dpGkHSiJBLZBqkhIZYwn2/z8xCH85Aifu+lGbvxKG30Wo6s+P1fm9MqU\nzYvnoa6d4fgOeNSKSbbZYn2XyXoZsvFon3Rbj4VjEWfPSdliHMfYVJJOQdEa5C1nCNdP/ztd+O/r\nPwYsGoFbe0SNhGFkhLOCTm5RL6uktoIyCVF7Pp1kjcKQqBqwJCjrlDqwEL0KMWyoXQ09jhFUNGKN\ntdpHyiQaV8XNdKzQIFSneK5KOFaoSWgZUBgmTaKh9kqaWYem15CMciyrh8UqiSWQkjGlL7E065Eu\njDGHNTM1QqCgGh62qmM6q6wnz7DMSwAAIABJREFUC9hFzaRqoSzUFJVFTUlPahiLjKpQqZUWVS9C\nmlsUekBZNPQKSDshpdZCKwIk0yKMBeZigUgznLJNZXnIRZsqK2g8HcuSCKQYvQqoUxurCKk8A2cW\nM+/PqWWLrNYx84i6r1Kum8RaQbdVMcAhSyqqdoMrR8znHcZWgG9JpHWGZbZJhinlgok5TFFnGqUz\nJHR9vFoh0CPCooc7X8NR1ql7fYqkoG4c1HKEW7ewHxjiHA1Y6U7ZsViQn+rRhD7TM2u0L8z42UkP\nCw3tnoeorEsIqgc5d/DIxev+9YvRjRHZKZehAoMdMpq6jBdOmK9vZLObEUcRXa9FGYzYNe0RKh4n\nT065uKdybxri5yat9io75I1kU5UqnqJbCW62A1kUtE93OLltzPLBPchVyHSHx30Ti70H5hxwJuyW\nLmK+dB/bnvM0PvT297Njg0ZmeFRRSRGtcff4KD//0VfZf/eYOx44wNpojDKucOoCJ3EZn3OGHstY\nzhGsNYvT003Eu4ZsClTOP2cHFzzrGl76mOeiXryTK3ctM5EWefOOJ/PU37uLL735vXz7jvtx/Jrg\nAkEsQb+OUR5UqWQTe2yztdFQI58z5jp9e5kjiwbewyPS3RrL6YXM5RFH/IZI28TFrRF3rQT/W336\nHwIWkqoh/BhjrJD1CtwFh2ZcIyYNSjsgdwTJmodkLpKKIX3XZaJGlGUfuTNDGZq0zBppmjBsNWiB\nwlLqUDig2i5VXJJ1c+JMZuBorNUNaAGqZaPLEc2aRyBC/KKH11pDqnw0JSbzNLTAp84NxEKCXyqs\nOSlUAmvQQwxl7F6ISEL0oWDY9OkoMlmWog0ErVnCqq/i6RVBnNMKYGLptNUR+cx4JIhI1DSGx9w3\nseQMoxYogcnIqzCVAVU1xDY8UlPFoSJVaxRzhhYuUFsj/LEgVBpEGqPIOnVj0HRy5MaimgrSjkpY\nSqh5ibAVpGkJ9oBxvoZvGEQoGEOVxk4xyzZBWdNMcnLfwFoucdZrYhUUoZJXKVYwp1FadMYVJTW1\nJhPXPbpCQtVi6sYhyBeRpAl+R6Fc2MGm/kGOHVigGgTs8nzaRkj71DIDY0Ist5FyQSQdw17JMbd2\neViz2TSfcjoO2GxtwuyEDBWfzmgde203Rzbs44HVHh3/BFm9Ac0pKL05K8ePYfsaDyce7XxCi/M5\nGeXUUo7IFIwljYdql42TgHBiEGyGNKw5cdEY+YygPh3g2Zu5/8IVvvfRf+D8XVczPmtiWyFf//Dt\nXP/TW7j14a9y0Xwriu9Rnj6N/aTH8ss7ruSGP382Gzafx8XJJvxtMyZmD1eeEa0JHLNLqq4SlgrH\nTpVYp8ecefAI37v/O1z6T49GGpt0FmF4YiOLTouXvO5VvOuDX+M9/pB00kHr1fzJDa/ljtv2UY4b\nCucU2mJE8EDASa/Hrn7E+n0G3hJ45w44fbqiXjzGFqtLc1RB3XASzv7vP/eW/p1Bxf8R7bn8UnH3\nv30XAoEQKUm/SyvRiMwxZVCTaxJd0cUQIetlgbTgY0cKdpQSOTWW0yUuBUW0jlrraKjgSUh1QeR6\nOBOFSpNQ1QLbMmjW5owXW+jFGqg+7XnAtFqkoyWUuUWlhQjfJa+m6Kn2SIqZDkrpojQFUlVTdAui\nwoZyCqaMM1cIu+BOuxTVGEeqGXVa9CooJJ3KCsgaG2tU4vYi5s0C8iilGYSo5QDXnBEHbaoC1FaF\nUWrMKwkjXyfqNZjzAUKOEE5FhU43sAgNCd0KkYWLPEqYWya9OiXwC4yhhmMYzISC5Y6p0gWqtKE0\nEipNQnJ1jGlMLRX4tcbUtulGGbVlM8lC+r5HUEaoDYjCJVdUVLPENUPSQsGdejTNnHyxTdPkWNhM\nQ4l2npIOQswSzu4reelTXwDaFFGUHHWm+EZFT7UIfY282Iw1fICV5YrzTpzHSnoQs7MMjseKV7J8\nekYRLpJtNNnizViXFTYcHdEMtqGGJfdOSi7anHE8Kti+uEhSn2L1QA/TzEiiCkuNyXZn2NJWRJPT\nOZawZm1kszbn7GKAPs3oFQYnbI/O1r388OaP0NJzxjOZB++5kxte+1eckX8Gym6uss+he+3lXP/2\nZ6IZC3QynUiVKGYqnXbBjx/azw9/vIK/nnP4wJ2k4xVSe8gkEGxWN7JwxWa2pZvIzhd0A4PHPOM6\nNps7ONlL2DzSqN2IJtS5+76Hec0H3kd0/5c5WW/nwks2cZX3S9zw2Tdgygmj0yUve8pLuCeasLS8\nwvp9y1x87irNesrhBQvH3kZwb8oGU6e1NOV+yQHPoDl4P/GsuEcIcfn/ap/+h4DF3ssuFd/83u20\nk5JU8dDsnNSSaScZo9hG9mR00yBhiJ2oOEVF7XuU4wCrL1hb82l3JXKtoTWCSUdGmkO7Cpn7Bm1L\nZS01QI/RJ+BaKkWmU6sVeSMhuzpOPCYuLaqFHEYmWisF0UI3G5RhQWQ5NOkcq+VgzSVyb0KlmXgz\ni8aTabQRWtOlrAukxiUwclq1xLzRaGYJTiumljXMxiOvNaL5lGXJIKVEsi1KMyZO23hWTFpquLGG\n0UlIG4faCClmFVYtk7VsWpOUsilodI2gMpFtAzeaIWyHPCmpXB3bynGHOhOzQWtMtHJGprZpdWfM\npxJuJycZgus3DBMbr22hiwnSeo9wIGMOweyNGc0W6FTrJD0HW6oIxiaVNEfoPbrunCxrcIouQo6Q\nhGCCj2YleKXF7Oycxzx/M3W4hYUzJ1A3WDyYbcTX1wkXN+NyFGv/drIdpyjEdrYZEftqm/Pyozxk\nRTiFRLWyDcsL2NDJOJM5SMUUr3IJllSWH645sXMRtzhCntnEXosLxhPyRmYt3kJzvsDhASblLs47\nc5ih5sMoY+I5nLMWcFDbxRs/+Ebe8NJr0BKTz93yj3zgTZ9hsvkQnaDN9R/8R657ysXk4wX8eUnT\n0fnEJ9/Ju776MYL7ttLNUpTdGqerI/RPbWBpUbCwdD4b2lvYebnFibNjNuy4kP1Hf4q7cpqhlZPc\nvsaonRMNDfxOwdG2gXk4YvHyPkvqFbz1Xa9i98VtpGARw9L41G2f5bvfv5d/+/qt7BYKT/6dZ/KW\nN70O5h0m5RFe/OJfY3+m0kqP08x8TtewSVlDdBq8yORwvYuqOsbGyuHgqVO/+LC45JI94u5v30Vd\nRpSmoBIyee2j+ypWmiKrJXme43V8xqM5QpXptHziUYWLQ+HGGJlGVk1IJBVLNqlsicywWAgrpKSg\naWlMlByr8gmbCs+pMaYxE6+FImWYs5DaV7BCqHvAxCDpONSjdTq+hZo3zJUOeVTT7iXElUNhVXRi\nhVk9ZcG1IbBJqnV026AgRyssItWlpTfM8gLUGtlwyYYhppRjm4K47iK5BdQqFBGe1iINgQUw8zmy\n1lAjmGQKZlDi9gYkdYMQGT6PAC2TNKgyGjEjMPrIZoaYVXSzDNVoM3V0KkmgxQG5KFk0FLK4h2VV\npJaKHUdMHAtTVkjCdSqzRTeYE9sGVe1iq2MaSQVDpprL2FrKXF5ESDVGM0NEFY7iUAgHu5wz1kD3\nctRK4YKlbSyUS9TbHHDGnDq4jLRhHxsmXU4NGsSxhF1Si/nAYLSgsOPklHG1A3/bOnEhIx0d0b54\nA9O4RgnAXi040OmwLEdUXYvBoZyTGGy6JGH4kEqvSHn4gorHrKScHjWIXTmhXSOb24hXxnirMxav\nvpY/ftkbeOyvP5bmrOB3Xvp01g/+HGfjE/nbmz7EntYimSWxcugQn/j4O3j/p+5mw2ANbViz2bia\nX33/i3jpk3bTkncw902UqMbIPIQ7prZU0qFPZ0GlGqVoXgQMqJM5o6rC1z0sb042Upl5Kks0rIRH\n+OqHb+dEscK/vP/LrGws2RnqXPj0Z/Oe1/0XFpa2E5kqWrDGY17+Ojpnx+RNm1e+8TKe/9zXUtUy\nv3vlL7G6H4pWxYHBHCWI0bfvJdt/kiuEzMMbFVb2H/vFh8Weyy4V37n7HpykJqgzDEvBxWA+LfA6\nNVpWkWEipzH5QpdiCI4XIycKVa2QDgL8xiKQ5+j4VDMTzZmSSTXEPSTpEfcqJy6YygFNS2DMbNAT\nEsfDKmMiy6A7zNDaGrMpKIaNIs/I7TbudMKsZ9BGpgxVYkemF6aERRdXm4InI88V8k5FMpdpWzbS\nvKLQMxLXpkJgSxGFrGPIMZlw6a/lrMsOwpGQ0wx6Jq1cIjMkVObYY5mh00EzppgTFeGoyCroucE4\nHiOpoOs+shaSSzatSkaJYhJbUEsGtsiQM5+ZX9CRfWZSQZ4kmJ6EHpqEjoZbz6hosCaCaU/glw1m\n3UV4MsFkBo5DWkU4kUrdbdEKUyZFRWlLGJVEpxKUyEQ9CzfMKLJHvm/XCxplOMQ+KLjmeY+mthyi\nso3RmpM1AfaxKZJ2Admu/ZTRApmbs/DQMs3yAWJd4qwjWDjagcEmemMgW6daiCjlPmUzZjWQqNOt\naIsp9ckTbNYFp7dfxJbsXuYnthBtllmWjlGeVomVNmJXTFjY7FB3cNsPbqUqBW1X4ZIdl+J2+/z2\nq5/Bb73oJcy0kvu+sI9bv/cd/vH2O2hW4ZKX+Vz/G2/gkp2PpXYzWmaf8Bj82+mv8NCPv89nv/Ft\npod0nL6BfmA/ynaJYVKzJG/nRKbQDI+gb9nNjnzKqmZBJTjtZlgnJzxu7zKbH/sCfvsJ53DBZVcR\nm1vpNhNqeZE779rHP//jG7n3wTF5s86akfPp99/EZY/bS9+q+Ou/+hs++clPcHZlIy+74fG8+ZXv\npTZmPOfpe5jMPI7N19k4387QH9KTZNzjMfuq4S8+LPbu2SN+9MMfIecyileRlAW12ZBnCv2oINB9\nUAwMNSWxVNxpjK5aVGZBNDPQPZVaq3HlhnmcUDYWbpyRmxp52YBW06s9Mjei0NsY61PoGMRNjhZ2\nMPQx1BB3HVpFArJHHWTkvQpjqjFHQbgSA1UmSAUeBk1ZomQJQcfHVNcpsNCmOmFPRcll/HSdrPYp\naGjJKkpHZramodkSKRHEFdYgpxl20VoRyDJ2WTMKPRQvRgkMEm2OVpl4UgetCYmXLJLhGHXQpZsX\nzBJBW6uY2m3scUDTAjORGFYpSl/CXW8oRRdNHROqCrZrEq5LKJKKq8Y0qFhOi0Y0jJJHHMJGZkUn\n1Qh7CSouWpiQexrNRELrhjSVTZUWoGsI5jB30QaCvNFpSSHapE9kTigUjXhfzbOe9yTMWEckIStL\nh3HCjSwKk8mWjPG8IRnZmF7ARk3CzFvIG00O1vsQSRvz+CY8a8IZv8UFlk5jjng4OMOjeuezisag\nOU4qmaxWDbIWYEkbmNynsMVpMy5WMUyFoFinMreyQTnID06NkIKSv/yb9/HZj3yOpUrjGa9/Oa98\n86tRZgXv/ORn+KebPkwbaA4W/PkHP8qzfuVyLEUl660xizw++p5P8fUffJpDDx1id7YN6bwjNIe2\nIZ9/mGC0hcde3MHbtpOdRo+yo9NW4a7MpTmyztnhz3gwbLPzxH4enkzoZwM0X3Cg0rl80KVzWZ8b\nXvNatl9wHnp7CTEr+OK3b+aOH/yQ7//wB+QHD/F7730bL33xyxkIGWG4XHr+LtbUFq9/yYt4y/W/\nz+mjFZ++9a184MZbWRRthsMz5PMNuO0pJ08e/k8Ai0svFbd+/2fgxbjIVIVGGKnIYoJkF7hBH6OV\nEAuBVeRkWo8yasiNgAUkxvYjWRdqVZHNQtqWyrTykBsFa1BiBCmVcKi9lKIRVMLGL6ESDXFYgmwj\nXEG3KplaAfa0i3ADVL2L1ggmVYBaVbiuQMoswqhAkhuwoavYiDAkdjTKzKZbzxm5Pm0tJpU0NCmn\nGS4ijICo1pD1GbVi0G5UmtBH6maIsUI4aOjKDZMsZsGUWAtLkBZZUhsCtUIODLRyFWlpiWR9SIOP\nPagIMgOaCqGptJIRVWZSLOpYcYaoLeJSRbQzzAwcWWdqzLDTPqqZIosCLW046/bozyQasyQxVLw8\no2SGanbRhhqr5oi+2SHVM7RaoyklNClG1C2mWoxSFfRnHpEvURcNvqQwETVr5YyrL7mETU3Akd4F\ndNyGhRMJoe0T2g9hWEvMCwttKrPcPw2KTxBZDOPj9CYewhiw1VtlWhaEzlZmTsPWiUnWO84ZdRvW\ngZJ++yHsbIlDWUlnycOuO9TJHEdZRTltYV9V8Pq3fI4nXHoFt3zlDt748TfQajT++gUv4tr/9vtI\nlcRzfnMvP/2SysWXxnzsvZ/Df/RFUCd4hsEfvvQPuee2T1Nubjh8UubCDVu54rrf4O1vfxqpshvN\n0ijGGZ22TT5dI3E7tAuJqNSw1YyaGaLto8oxM8mlu2YRKzNy18EqJMKqBHk/t978aW799pz77voC\nQ3+Z3kTi6idczp+9++9RuxJ2mnHHzxre8/KriAdTwq2X8Qe/+TKe96wXkNUaz959GUc2T7jpde/m\nl57wNGLN5zFX/BL2sVMEPcF0NWJWzX/xYXHJJXvFrbd9D90rqeYqVadANBJKUOJ2BVXew8thWsV4\nwqZRZQRzEqHRdFXcICBzZLJJB91TkeMGg5q4VqnllF4jk0kxpiyQpYZhT0esCyy/g1pMqIRL3cwx\nWx7RJMEUPqYmkRsCkY4Rfh9tAvNBThsbqRIo0ggpUwmyCnotWolOqgyJtAF91pElnzRuiGIJfVFB\nNAlF2EaqJ3T0nBAZGgvHcyliCcMM0XKVvElQZZW61qlVCHQbM1zFkhcppXUsXGZOQCG1kUYSqgqq\nE1GlDb6nk8UeiTvGl03koYusD5GNBaZVimhiFGWAGUXoQkORQtYbGUc1sZDJpBpNhExrH2exIpvJ\n1LaDmU4o9Bo36aDRoEg1c0VguA3xvKHteUyKBtdR0aQp4zhnkR77xkd52qOeT7U4o9tIxG6fBbfm\n4cOCzcVBzpzfxzmQsiwyzmoqiWWiUNAT5xPOEhJOctGGBaJ1hxPZAaoBXCidRyJyVkYRbPXx0hUC\nI6HbtEnVBcKRYJAFGD34zNdu4tzl7Qi1ZOeTrsQZpdx63wpblYCxmnDlM56DPxvjbt3Jt/75y4S1\nzqHRGnf/7Qd408e/QJ8+l+/2+bW3vpRfueY6FLGIbTYoaspdh/ex/5af8Kmf3sfKsZ+yPI44I2sM\n1hLyhRmZfC6VHuKbc8YPbCGXdbQNKyxFMofmHsvnrtBznsIvP+9XeN1vbkWr96CZHUolxafini/c\nwavf+iGC9B56jkZy7i7++z/8BXsGl1DKBr/9qley77vforfk8fL/+iae+8wX4gqNPU9yyTWV11z+\nCl79/j9l5e4VnvyHz2JDXfDTn5z4TwCLyy8V3/zJXQzSmEg01IqHMFPMTCUJaxpZw3EF6lRB680R\nic3cd3GaCVmkoiYpttultkrqeYXm5Ezw0BAkjQHxOrrTxpBy9NxEyWoiV0JWNfS0YeLXuI1FNh7T\naUFRS+hZReP6JDMZczGCqoXWZMwzCb+Mafo6k3FKv6cjRAdpvEbldKhjHc1eRZUgC/sEYorptEnV\nGjk1kESAZKh0VQO5nLKayPT0HkGWI/yGvpFSZy2GCfS0kLrVQCSIqzbd1pj5ugWDBG2mYSgWidAx\nrZpQaHQSmPgVMMOrXIQpmAnBkqgYpx49MWGMjVxK5JVG15QokglSW0PLLCg0Cl/gigaRC+YFYGVU\neUKjDxDKHKXp0GpiZli05TGy5jGbg90pyLUcfQqVUSPPe0jzKY+/7mr80Zz92yrMcUasLrJZn1C4\nHt1ywoNTlc35VuyuztFVWGoKZMYogwHH1CMsaBfiezGnH0zYqHaZt8/Sc2YcDk024ZD3JDpHDUJv\nhj7dhnaOTNOKufNbt7B66AQf/Pjb+drtx/i7D/0+j977am7/0Y94/mueyfkLe7j6mXt591vejcgN\nPvrNm/jwa/8UKVqjbBQ+/q9/zSWPfQHarMRpGfzZ529k/+fv4scnvkTibqI8e4KN/YuxVY8lZQcX\nv3Yrv37Rb5EUCedv2EYq11T9CFKNvg1Z47MyOkVrOuO28cMcuvle7vnB17l7dJRIL9gjP4r1SmPT\n8grPf9XLef41b0P3a1yloYgsXv7fXsvdX/4ihvB48Wf+jFf+yjOQgglnzjzMVU98EecYG/j8Le9j\n57YLKeQWl533ZGSn5J9+cBM7nEV+9dqd/OCnK7/4sNi75zJxy7fvQrYmtEMZYVZQ28y0FLPWqDsd\n/BzCeIrqdMiKdUzRRhMmcTmikko65jKGMaWpVbK5QtBR6OcFotZQCpO5mCKsDsKtkMuEKvXotARJ\nmFGIFFezKMoKWylJUp9Ckul4c0gkqHyi8pFRYjyBShkg6WOMQkVTLaKypqOoyKVgLilUC2N6SYe4\nHFP4fTojiaHa0JSCfjdFyi3yWCDbIaJySAmwG4uw8tG1IZq5gB6npGqB006pZ4vMWjl+VWBOdSZ6\nRG3aYOmYYkycWOiqh55EpG1BM1exWyFF1qKOTKzeKiIxaSqNqokQlUEtKaidHGPWxTMS0EJipU2W\nV2iSgShjzE6DNjKYU9CiZE12MNQMpQbL8JjoFdLIZsFtSK0cc2Iw1ys8LSMudGon5LEL19JsrEjP\n1oQdl83elNYkJxwucGqDhsg0Bt0zDOQe+44bnNcOEb7O8PBhPKlituU8FjydLGyI1FNsmdQcXx6g\n5RLpOEPfdIbOwx5+R6NubeXJT/ptXv/up/DnH/0kH/3Ip9i5xeLHN/8blalx5Z5rWU1W+asbP8+T\nLt2NkiV85Muf4OY/+EvOLMK/fvwTtB91KYPKoDYkrr/xY3zpnZ9FMeYId4kNCzqvuvoFXPe638TS\ny0cmVUJHtsHPauJacPahfUTOmPtOgHZklXW3YJu3l/O3L7LU72I6GrmbUDgKC0WfaZTScubElsrt\nnz3Ou77xR2jHKw4fXWVDP+A3Hv88/ssNb0EyDXq+xz0//R4ves2fMJ88yGU7tnLLzfdSNzn33H4X\nv/uyV8Dl5/PW65/Oc696Id/4xoP8yWtewxW/fiXvePs7WWpv+MWHxZ69l4if/+QO8kRBzW1yKcQQ\nMJQcjNYIVRKo8z6WUTFXVZqwwu/OyIMBspVRKSl2ZDCvddRmSirL+KIi1SwUI0cVLmZgUzdTStlB\nW1CoZzUFFaUh6AuDWaXiGquUJVRCQi8h8xoMVYL5gKo9o84bLLOLGtZUTU5p29TVjKRy8JQGTU3R\nK5P1KqfnqCShjKboJFmOUUsYPQnUiEhqUcQSsp6iUmCWGkksY3ZVpJHGbLGkNdGJ/Bgl1LHliNLx\nsfOUXNOIY41GUejpc9TEZ96MUKQucg+suGLSFCi0kLUhrtahjucovka57jLvJ1hrgspt8EqX3B+j\nTQXzto81k5BbKkY+RzI96lIhNsZ0Go1VCeTUopU2zPsmep2gFDZqJlA7GWlekGolC5HK3KxoqYus\npBkv3r2D6cIyWqkQnigQ52pMxFmch3TU8zzi4Cw7nS5SsMoZdycbrdPsW1tki9FQC5msfwh13/ms\n1nO2XtZh9XRJvjpil9vj6LZ1HpVv5uDp+5AXW3zvc3fS3TLg2t2XYG7p8vU7voWf+Hzoj97D3+37\nAldd8xhufNtfMa7hnp9/kV9/2R/xqM4mbrjhfVzxtL34cs2vvP4Gjt9+H2vZKt7pIS9+z5t482+9\nBTcfIneApGF48hj/8N6/5MY7v89msyA7CIfbDsqGkp0r53KgfYDNaRc7NtA2zki0itPzPpuHOqE4\ni7a7gzZZIazPIynP8IKXXMX1L34z1QVbsCWDMqqwqg7v/+Kfcsvbv8h9y6fZeLjHuc/Yzlc+9iVI\nde46fD//8MW/4Jtfuotdks33fnIfTVvm9178Nv51/xdwIpM777wNd4PEFbuuZTaJOD39T3AMuezS\ny8UP774LkgbDzRiPYmzJJaplVFfHzhpMQ6bJ5qRSm0CNcbMKr9cwivsIWWBoU+qkQ60H6IWL3qpo\n4inYCoVosKJFYj9Amte0ZZ+RE6LEJoUl4RZzMq+DVSekeY0S6riLFkq+Th3o0FdQ85KxbNJvYioW\nmUcSfqtmXswhhU6nIMv7NLFCZU8wTBnqgibr4GoVo7rG0nXqIqSqTWQ9phGLdFNYK9fweoKIAb2w\nRoiGWTejl6QIYZEiY6Ypir9AEIzRpDaSHqP6FdVagWz3CIoQv2qYdSoGkc9MN2mnNTMqFG+OqfWR\n5zW5VBIXNX3NZlRN6UsmkZ1Tiz7CkGiCOWppUjslHQOCJkdkNZrQCY2Sjgpp5lNWGo5fYYo5qbqA\nLuWUgUbj5pS1wJuk7D/Z4RVP3oG20eZYoSPZB1lYtSnC3Uw2nKJcN1kqQjRrAWXHGc487FNuXWWr\nsYh7qMUDWxV85zj5fpOFDQlKvshKOmOnt8BIK0iOjthhdwg2NVx6yZP4xCc/zBte9gE+efd7ufm/\nf5YLrvhlxPphzjvvyXh7NnPg377CLNV50fNey+SBn5EIn5tuuZFzdi6TUvOO5/4B3/jxl1gdbGFg\nJNx8w1+x69rH4zcqom64P1B4/wc/yFe/+Bl6LQl7eISju1p4ocXu9Q3sef1uKul8LnL3sNGT0Doq\nW81F7lp9kGrV4YC2Hy+4j9u+bhEHX+BItsR2OWC+YRfTYsIOt887nvdGnvr7v0rOGL2Gz91xhm99\n6n188Zs/5VFxw54XL/Oev/8ablUQVhnv/v0/5Ptf28/Vz/D50/d8CbNq85k77uTv3voqNl19NV99\n74c5kD7Irz3pKRw4fPYXHxZ79uwVd333m2htl2yoEcoJUlOithvKokZvLKQ8RUZFOA2W2SMIJ7hq\nhzwEfZDAUMZuZ0xnHsZiTlwX9Mcu87pCbpmU0ghPeJRzDd2tmOcC4et0lSGjaIDsJEhzncosMIoE\nKe+Q+xWtwmbqDelMWyiNTLig0Gpq0qGC20sZpUCVInV9tErBkANEXFAZNmYSE2QOct+mmo7RFizs\n1ZxChtoVSGaLMo5QmzaU2acGAAAgAElEQVRlFeH3aqpZytxYxC4iLD+hWOugyaAYgtg3SYYTJM3H\nzUqCRTDriEzW6aUmhZJQBx6qEmAqNmUjg1dSaCFmIRiHMoY1QJYqWiJjPWnoWwVZraEnKuOWiawK\nlFKlm6TMNQOHhlgotOwh64aBetZEkVU8Z45itEhilUBLsZIADAdP0ZkpOTQes6MnufSZz+OC8RlE\nf4hibOXwesOWQcZ8PieKumxydEblnOGSoHu6TbwjoV03rIsIc2og6buhc4TifoP2rorFNUGStqm3\nTVlZP4et9io/O3gv44nguY9+JkMv5gc/v428SLj00btoZo/iw3/xZzzt+ddw/w9/zJOe/jx2Ps7l\nhb/zNn73Oc8njwKuuO5arHKEdVjn0//ySTZd/RhkrUGS4V0f+yRfftOnccQq9XKLYm3Ec/7oGfzJ\n69/Lmipwoxylsqi6Mt5MR/ElKhRqpaFaGxPTQSVFa5cUiUyv6TIxoaWkZHMZtZUSTzTe/sdv5juH\nbqeqOmj37mO0zeR9L/8dXvBbr6JpW8ynNYfmq7z66U+ktEF4j+XdL3o1V/3eL6NVFedueTaVMeVb\nf/9mLr7mxaT5Ko/+pWcxlx7m1HcOo8k6er/7iw+Ly/fuET/5/p2MDIlOWDLt2EjUNHVGN1YYOwFW\npuMbHSZhSMd2IS6YeRnyyECTcqLFR3YGziinsizSEmxDYe4p6KzjF0ukcYBW2BRKidoEhKqN5mco\nlYOdSUiOSVCtUsw7iHaJG0sUskXlDTHGJrYnkwmbQB/RGXdpFueEgYtkqvS0miLPyYqGurQxm4Cc\nBpcFAiVA9xpcUZIKm8rMaeGQRxGB3kPPA+SoRlF1Mt/GyxUatUDSI/IIHFWwXlm01YSsdh5xu4oF\nam6BVqLokJkSxUjGUVPyfo+8zOjJGkpRMTKnKGsdisEMY9an0CJIK1odh0iK6YQVw8rGFSZlT0KV\nauxYYmSO6cs9wlmC01WZyDUIj26ZMNMSnKSNlkHYkiikmIFcMp13qVsFXiBTSFOuuew8rNMqwVYP\nP1yGUJB2A04Ki4VmyqplYdhnSYqcXiQYbNzKmQNTBrHEeHsbY7xCVLQoNwWYq+eQbzoFKzrxtoLu\n6iL3PbiPW776ed7+5t/l3Ceey81/+xXu+uqPeMZbX8Grnvsy3vFnf06dyFx+2RX0tIA/fvcHeNoT\nLiWybV75wndy93e/xJbzHP72G99lq2pTdyUOHt3H65/6AvZngnxDh9+68qn89Tv/ANvrMlwb03Q8\n7PGI4eqEm26+iZ+cifnOV+9iS+cw7bMt8r4gX3RIo7O0td0cW5mhbW7YfFjG2J4QHSswrvV59q6X\n8tgnXMQvX3sNk6xEtWq6RZdpM+ON7/5T7vn4P7PiOpRRwiuu/nXefuNbSKoOh8/MecUTrkTxMwhl\nfnzbv5Jsv4CHvv513viW30OUKe/43Le47vIBb/6j9/Dlr3+Oj//j57j2qif/4sNi79494tu33oPZ\nlhDjjECY9LwQ0hZhGaN3GyIkrIlM3Urwiobc9imaHKewEZZKUq3iTntM/Bl2LFBdDeQSKXTR2hE1\nKnXYIvEjaiRISrS6T6XGtMyGeJSg2ha6XZPLOVnk4KcQ9RxMCdJJSN0xUPIKUbvYZkhVFbSiilXb\nZDnJmAqZZiDQ6UCoIadraLogbqu0Ap+slZPOFMoqZNHoEbsN9liilipmkqBxAhyjj1XNSEIPzUpR\nhEIQGdAPKcddJDvAlxukwCVXUxTbxNLmUNbkWYfKVaGY0ug6opKQVAV7npO4Np5REmU1SpGhSx3m\naoSu2zhphpK2GUo5fSEh2wmrtoWcCzwlIB238dyCWEtQEwW104ayQIliZpKJgYOqRyhKTRkJHD+j\nkQesnhzxmGc/jsGJlFjYrJtrdMVOnGIFI93AUV1isG0V+YhEJEuMlxZxVm2MzRlFNWOXtsRh6zDp\ngykbO8vkRsT6YoIYn88SfQ7/+Kt86v3Xc/13P8Jl9nXc/Pn38/o//gg/+Om3+acPfIzd521h/XjO\nU5/+eNr+Dr7+0FewpvDCFz6O+UMSYW/Ih972WbZccznLbXjCf30WP/v43SyfM+Jc8zn85dfewQ59\nC6rjsy4KRj85xss/8Rccu+tf2DYtObTkMDjtk26y6YcKj3/uFWx/9OO4OF6mfY2MOT0fx5lz5viM\n0+UDPHx6jLgz4G7tEKNbDyI5FbHlcTLIOPfsQSbdXfz2s67kD/7mXcxrgZHoRKsZ39h3I5/8669w\nfLbCRYtP4JbbPkpe5ShBw+N/5ykcPrCfcy+/jFs+/FkGWcM39+/jrS+5DueC3+Qzt/w9az9Jef0r\n9vDD/f8JpiGXX3aZ+P6tP8JwVHIJgmoIdNHymrLWMBqVlh9AatNYI8bWIlq+hiyDG7hIZEzthrbR\nBwKaSkFUGYahMitUJCXFnoBqaIwck14jMdUlWms1clemUXPqoEBoPZpiTCUvoOsjksTFbcXkSY2k\nd7HlilkuyG0Zf5Yi+zCXKwylRWuUsq7YWEVA1tJYzGPSVMfoC8pYRhcqw8qAtkZ3EhP3C5JYQtEq\n2oqC2nSItYJkGCMtSShDk7If0Z1pFHg4XkoyAacHeaYSygaaMcGQFaRCJtQSekOPuaWi1SF1YVL2\nY0TiUWPSMaY0skQ0ArOjEukuThLhxT6FLGiUmsgJqUQHXUnxpwnTrolIc4g8DL1EshLspMO0q+CN\nCjDmlGYH4ojG1zATmVRWqKOYXqvgbDbmiVc+g2zkEG+d493n0L7M5syRg4hzNtFp/i/u3jRqs7I6\n171W37/9+31fFVBFNRR9V4USFARBFAUUAY2KEkTFJjHERAW72EWDxga7ICEaRcWoRBSUoIJIL720\nRVEUFNV93duuvn/2Dzjj7LHP2Rln7Jxk7OxnjPVjPWOtZ/2a95j3Peead4iXtpDCmvnhlMKp6Var\nsdftoHq0i9VZQsqnzGcH4TdT1LBBvm6BfL6FpfucdMAmnl6+n99ddzeyWXLssX9JvPQr7nh8kUSP\nOeWoQymHMeec/6f81YXv5N7JlNe8YRNxYXDWy07jOx/6LqVVcsqZL2XnXQ8wWLeOGz55FQe8dBWG\n4SHUZW749C185qfvo2ioGEurmR/cweFnvZMP/NX72bi6j5dLlI7BUAIkgaLEeAMDyZ0QZE3URkpz\n2SI3YopSwS5bJM6UXJPJtAp1IOOPtnHJB77HveV1GJsz/FlQHtN47SUf5cPvPYvS11AVn12/vpMX\nf/6jFKnHoZbN5f96KSvtNvJkNy/d71wUO+IXv/gxyX7rcXKLP1p/EMZck/sfvpV0bNNa4fzHgoUk\nSSZwK2Dw3PyLq4UQH5ck6TvA8cD/ZXV0nhDiD88bCn0FeBUQP7//wL/1jY0bjxLX334bdZBjyCme\nJFHVOrVIEVoPYQWkYx29L2OoEdW4QJE0NKNAVroIfcqy6KL4MYrpUOYDyrxJy45IdA0xyqkND8uK\nUYOIcWsOj0WqTKLhe0zdEE20yKWaWoKG6lNIUGsqYtLA1mIGVooctGjoIzJ6JEpKJ01RUo0pFZLo\n0HTnias50jzCbOlYMohwSClaiDJCkzUkEuqsS9qNcQSkmomZqCxVIVKl0FQ0IllDjiVojfBSQaGr\n+KGDW6lMmzHeSKLSpli2h9BN4mlAU5ZILRNNFwyl8LnsSnOIfQW3NSYYqrTnTLKpR1Iv0MxnQIqp\nPBe0CTkpTqZDWBM7TZIM7FaGEDFWLpANQZ31mNYJRAK3aSD7MnmjQBEJaiYQikzulEihQeyaWNEe\nDjvqROLdTZJ9TFYOcuYdGWP+SayD11NtHxLORfT8DvO9hL2fklhs7sWB9pPsKdbRWlTxV+1kzpyw\nXWkzt73iyQ0j1m1bQ6OxwCjt85nfXEnbV7nkvNexkEXcfc8CWxKJs447lJcd/1Le+qVPsLHd4aPn\nnM1VN9zDCW84hSsu+xzDwOXmpzfz6ZNfzO4Nh/LLK3/K/t1Z0ENcUXD60WfyQDhPIsHG5mr+6bd/\nT99YRVlPsCIXTVcZLzzApbffgLJribt/9RtGW5vIs/Ps2T1BbyrU3gFkecSaasSuPTO4KxUoVJIg\n4OiNL+SUVx3AEaefwb4zHZxcI3FczDxmtGPM+X9yLreOt2GvXsGK5Qnv/fTfc+7rTqRajHh4+UHe\nd/IHKZzH2OugdXz3J/fTKiL+8kt/w43f/ynV0oBrN9/Lytk5PvHGv+UHz/6Q+761lZWHWf/hYCEB\njhAilCRJA24HLgTeBfxCCHH1//D8q4D3Pg8WRwNfEUIc/W+CxVFHiN/ffPtzVnt2iuGqpLWLSY2o\nAqqxQy4iVKlFVgdIPZdGWJA5JUpSkZg5ld6iEanUAdCriH2Zhl2QqBle4RFkCSBRktA2JQq1RTaQ\nsJsVlVySZxlK6WG4PlVgURU6ZisiVE2iqUDt1rREioTJZBKhm13KdICruNRRxHiFhh4rOEKnVDXq\nMsasBUM1wakUMDrU8RgcB00OoTLR6hpNWMxrKVKsY9gp+tTGdGVSNcOOKoJIQ++HKKKBPxGYyoTY\nqWlGMklLJs4qvKCLrvvkhUJqCgQ5ujCQo4poVmcu0Uj9EDFTUNKnqMeUqkl7qULxNCZ1hK10yDKJ\nhjelkDL0ZZNpVyYNBaKSmGm4DCYDWl4HMS5RumOqzMI3CrzEhCJE0br4QqHUMoSZsPsJwbvOewVb\nn6zp9nfTyvZmvr0DZbQWWyvxZ0zUJZ+2X6Csk9n+VBNbPE4ibaDZ2kU6tlnhyuwZhygHG8yNUspW\nl642xxP3+yTdjIPiZQqjw0OJzM2//AqHHnEirz3rj1h6dif3/GoXQbtix6Pb+eP3Hs8gT1m67SkK\nOeeJ5WXOPPI8orUDLvvby3jN8QczSltcc+P1XPqtjzF+ukTXmpx39Ll86mvvwtdrHK1mKXPIg0f4\nh4/dxL/c8gOiyVM4k4PoHhSQbt6Or2mIUsaamUPpRchqgTVfslsviUOFNeq+zPt7mCumbEtltLkj\n+JNzTuWPz/8LDt5XR1IlfHlMp7b5i09dyM9/8mv2rfvMz8MXf/B6XnHaOVA0+Mk13+Siy77OynGL\njbPH8aXvfwHLmvKCDS8k7DZZ2Si4+peP0HUFTusQNm06jDtu//F/Hg2RJMnmObB49/PX/xtYXA78\nTgjxw+fvtwAnCCHm/2fnHnn4RvHAr24gVHRko6CMauS+Sj0oqFsuXmQRyRmG5qOlkCgQmzpVVdLJ\nPaZ2gaxFFLWMGrQoFRnJmaAOZeSugvAzqtqhIWp8V6Nj5owyDbeySMIAowZtxiaJB2SZgmo2sWKJ\nWAlpSC2EnDPNVNR6CUc2yHWT2KiYSSLSvI8yk1EFEqptUqQxIpEILQnZC3CWHfS+hiSmLKU9PG2K\nMS2pPZdRHjCTu+SShkglUjvCdhwmy1PMFS2cSUWU5qTNEFetMX2XuFKJvYqur+J3Y4xRitTtEw0k\nXHeEpPeIxhmNVolSJtRBH1lNWfZKNE1HqVW0CKoqJ1JkZtWA0G9gdTOqWiatLXJzRDOrkXwL2UpZ\njtq4nSUUpUsUjqkKQU/to7TGLMUmbmGTiZhSBGBb1LKL69eMduccctYstSqzrykhb1/FQrmDuRXr\n2CFtZW5qMS0aeHN7iD1op/vz9BO72A+D8aExK586AL98DGP9Bp5VfbSxYNXCbqaOQzxXsdczK/jZ\n4v3MqvCjX1/LcS85i0NesQF92uaJW36H3pL49AfewY8vu5oX/fmFfOejH2QwbvLqN+7DYwtrOfol\ngqu+cCuirPntrT/lfX/5HnJ3FQeqEz554ec4/k2nkOUCw6z56/d/ilt/s5nNM4/R3pxhqusplJhX\nvv141vfW8oJ1Z3DgyXO09IRySWJZU+k4GVFso0kgNTPSXEFVYhYGPf71mpu5977r+NmNP2Af4yDc\n3bvZOlOxt9zi/LP/mDf9zZ9jRoCUIRkup596Bk/PD5itnuZvv/QjXnTyi9BGGQ/u2MI7Tjkd3P15\n6PYfgtOl9nWOPqxBvXold99xO7XR5iXtNTyQLv7Hg8X/aF8ohLjoeRpyDM8ZJ98EXCyEyCRJ+gVw\niRDi9uffvQm4SAhx3//s/I2HbxQ33XADLg5TU0WzCyylYBzKNEoJyVPwMx2RVLR7UFeCSM0glsgC\nBdtOiGOdfrdAlmSySmVaWszIEUEEllAp9ALdA61usBhIzLYigjymDvvIZklZZlTNnHYk8FMZ2ZbQ\ndINwMMVoeiSiRioV5ERD6BJSVtJoaBh5zbCcIguFVtdispiSNQycdEImunhSSaEoUGaEpota+1Su\nhzKIsFwQqU1RqaCMyNsFjaKLKcYMyy5y5aOZkKctTHOBsOjTNmP8gYqnwlQWVLbP7FAhm5MxJIfJ\nYkZ7VoKhxFQvcXKHzKio5RivqJhmNo2OjlyEDEOB6BdUeLQrnSwXVJWPIwqS0CQ2JNqlSqFr5A2N\nNhAPCwJ9yiwemYjIPY10otDWNUgz1KZMohboVcGjI51jNx5Ax5LQQwUqlUZfY3FxmZah4Oy7il1T\nBTt5lrC9H/LSFhI9wxEy/fEB5NKzPLt/E/b08CZPEHttDtZtolaFHnS4+p4fM9dUUYMOUZJzzgff\nz133/Ctbbn+Y+dESbzr35ehbl7jshh9x6IaT+MFln+dvv3gNa9fP8IXPXUL/2L0o5AavP/50dj+4\nmbl1DW564CaciUpalTz2VMwZbzmTql9S1wFrM4PVh5/Chy77IPv7Paa1yaxWEbenSGFJZnZoFhlT\nyyIsF1iSIubujXFf3EbJ9qLIA8wkR/Q7hOMKOjpaOY+braDa/Ci3b9nOez52EbPdPk/tSujOSlx/\nyzeZS9cSuimdCI654DievX2edbMmJ77iT/nYZ95HEbscc8GBtJ+OeMfFl/Cyk99Cq7nA2RtOZbem\ncvV1v8buW6zsmP+pmUULuIbnaMYQWAB04B+AbUKIT/1/BQtJki4ALgBYtfc+m+7ZugUTBTENSZWC\nVttmtBQw58osRDNoakqt1MxYJcHUJdMi6maGEjexAp3aytFkFUnE+K6gnqhYbYE3SSksBV9YOGVE\nYajkhk3BGNMvSd1Z9KWAXNMwOiEVHmoQULgmyrJAkWLcLsSygrLkkXZi3NQDdYCS94iUHKEF5L6E\naxqYqcKyaoI5wZ12qD0FR5sgtBYiHKJYFXWlEik1QlKQJYc09WkqFRPfQLEyGqEDMzlKaLFk6fRi\nhTgpcWbGyLKOv9xEuMuodYssjxBeQWvsIqQSxSup9QYVgnowpKKHow0oTY1pldOVZkiTEblsUFQ2\nogKUIZ7VwMhNKrHEpANWYaIkElEaUpkWrbRJ0JnSWrbIFR1NLhBODEbFcmAh1VMcqU+ZQVOpGPQk\n8iTh5JmXITdT5ucK1i7uZKe9iva0YGZ1wCOP9BEHFPR3TrFXaXi7R2zr2oSLEUcWczy4HlbmS7h5\nyZPpgbjLFr5UYO+X8u3vf50/6r4EyxpiWDKK0aESYx68L8Qrn+XNp/0pc8d5/MunrkLZx+TwM16P\nuHMr7/jKhbzpzHfSVgve/eUvc+tvbkR/Ygt3PvQ71BWHkiRTHtr2BOe9+V10nswwvd288e/exzlv\n+xhUMoZakEo6zmLMTzdfy3Uf+il3p0Omzz7DQbnO5qpFvVLCGz7K7Hqb+KkGtR3RDVym+4TYUhO/\n6uMPHmf96Qdx3hnv4m2nvZysbmMKhSCrKYwJ3/mbb/DTX3+VpWcNwnWrOeXgTVz+ha88NxLxccH6\nlxxLf+8pO1s+T958D3lp8d1vfZ/Lv/01Um3EA/+wE3lfiT8762T+8GTJA3d+gca6l/znVkMkSfpr\nIBZCfOG/2zsBeL8Q4rT/FRqy6YijxG2/+y2JV6AJmbKsUNQmyBKxyGjkGmE1RFHbWLEMGaiUhJ6M\nCMaY7T5GNaTQHdTAZCKnuF5Bldg4dUGZGfiaSsUSInGQ2hbEQ1oI0DUmVgMnjQi0hJnIJbZUNA2C\nYgxFn3YVgFVTTTroVsVIDLBtlXykUnsCxzIYz6c0dRlZTwl0QT6FuW6HKkgorII818jiHFk0YHaM\nUzz3bwuTZZa1Nq22jEgrpGhC1mpi+Cm6kiA8l6VKx00gbcgopUKxDFhTZqgJFQNNVajMAieVGE8r\nUjVBK1p0+wlx0cKpRlRGm0KBeDFB7WjotUKuJlSlSSuYkBs6qjAprQo1mjKQ+3RFTqEkmI2KybhL\nqg2YidsE5hhZaaJHI1IMLKlibGqouYZXpgi7TSAqBlXMBfu+gM0HRGRRH/Npn9WHDZCemmPLqp3s\nPemyQ6k4zMmQLIdgO3hGi8VGRIN5xlGXKRXO7g7+qu2sTppMSotP/vmFnP7219F0VKZyg3qS0WuE\nyLbFs2nEK/fZj0OOPYt//MGlyAG8/OxTeGibz0O/v4uWa3Hv7Xfw4fd/kp2zu/jQUW/h3IsvpN3M\n+eJHLuXKH/6Q0VwXZbidb3/hEk484XwwJDJdoooT3vfZr3H7bz6KunNfgrkhqq7TmKwjDR5AeIex\n/wnHc9jKA+jtW9CfCCYm6EsLPEpCPlzip/c8ydp0gawYMVjSSTfszaoRPD4q6Rw+5dov/4aD1u2H\nqlcE8Yjr77+HKy7+CUW4m0J7kLNP/xzvu/gcailDjg32P+0lzG7Zynv//l94w+kvw2/WvOnYl7Cw\nI+K6311Lc7bPm895H4/86+08Uzz2Hy5w9oFCCDF53r7w18DngPuFEPPPC6BfBlIhxMWSJJ0K/Bn/\nt8D5VSHE/8OM6L9fRxy+UTzw+5uoEoXclkHIGPmUceVglDUSMk5LZeJLNJoTqtQilnSqAhqNgky4\nxHmMpoQo2iyWH5E0S+qFjAwHo+/gTjPKLEH3GmTmAFlpItcB0wl0Gzq5VDEpG+jKAFXuI01q0iY0\nkogiVZFkh1pkJLWK3Ymwy4oiayHnEvQXWc57NJIScp/a1aiDHHvGQQxLqHJUTyfPDMrMop5NseoU\nTc4ReZNEglKSMaqcOKkoDAPbSIlDBUs1cPMMUcssVhGtVgdJyyiWTXRPoBYFE89EGSSY7QpjOaSy\nekjKgDibQXKHxFEHoU7o5ipJrWG1Csq8IpZ0kBRQVERaICc5iuxQKyOyooHdU8lTGYcQXy6pwxzF\n7tBVAoShkS4nKHKT0IvQJjKmYpD3a5LcQYpSmuoWDj/uDShPy0ytgma2yI70YA7t7eSR/hxmvhNX\njXF8gV/uTS6pZP52rLbFdFFiw4omS2JKuSTYS9bY6nTY/4j9uetnVxKmGY6mkKUpJSZenlK1PFas\nexl2Oua7132f+Xuf4Rv//HGiAdxy24PYc3DOQaexI7qXcWsNt1/zTdQ1R7BcKJx3zAuYV6HO5vje\nW9/Nse8+lWQSgu3ynrPO5Nptz7B+uEiybhXxYswBs3P8yV99itedeiRTPcUoDYZJxl6Vx0QtsBQV\nlBih6PjqlJlQRjFlCt0i8DPcokRSdO585Gdc9L1fsPT7a+nMe+yo9qNrLvPSU17LRy//CP28SVUH\nZF7Guce9it1SRlgW3PhPd6GvNHCzgDMuehsP/fgu1rz2KG767tUYA40LP/F57rzvG1z6+U9y3AvP\n5vwPfYkrL/vcfzhYHAZ8F1B4zu7wx8/Tjd8CfUAC/gC86/mKiQR8HTiF50qnb/239AqATZs2ihvu\nuBl9YmH2QkajEkOtqG0JLbDRdYOJNMWQW7RERW6HKFlFWrfJigSpKCmRmVFyBopHR5iM9QRVEUhj\nG0dbJu/OQDKm8gsqz6MpSqapQ96s6BRTsqQL+oTEqmgsd6jtGlmEjJwGWpii5xq0JliFiVS7DI0S\nyY9pOAWjaRPVkDGaIE0CqnZJw+8QqWOS1EFvRxRVTUdpES1l6EqNooOUlywrErJVYApIwi6yUdJP\nx1SNHkmo4VY1/pzA8SdEhkpDccjLgECRoZbRfIukAY04QLRS0kED3ZDRrQo9kxhaEnmtIU9SNBGh\naS56WaLLCVFrjgLwqowoNhFWhlHK1NUAPXaoZyLS8QokNcEwMtQyJ9Pa5EJBCkYktYzar5HDJoYy\nIqt75G6IOU6g3WRyf8RxbziEFZ01PP3MhNXrdzLZriHpDfRIolFNWFjZZzLKsN0CYWZUSoN12ySK\ng1IsEga798Yd7GSPmaOunOMfPvFjjnntJoQaUeMghku4hsu0CvnIez7PP//sm6w+xMOW9mfL5oc4\nqFjNcV9/Ex8+/QL8pzQ2nfMicsvlwhNfxkVf+giGLLHP4acxa+9iz66K++65hxlDQZEMSlfhxDee\nyrNb7mJWL9GVNpQR537y+7zhJS9ALS0sq2bsqfRrjYVSx42GuLVL3CupippMtjGXE6pWhBg3aMk1\n82VB05CpFZdIGtOwJf7567/jew9eziNPbCGf7zPnPsqKY17Bb/7hBxRpTqEZZEnEaw8/lF2SRGPd\nLBd/+krevGE1dS/m+KNfxNZ6lp9/++84cO2BGEqb9Uetp7+t5vbgUdRihOmu+a/flLXxqCPEbffc\njRQHBJEM3RJCBUoHVckxbJtiOqFRthl2BfZwhLHCYbCgoben2JKDKRdEhUsYTrClnEIz8eqSkeLR\nkiPUqKBs6khRSWXa1IZBHgQYSkWVtZCdAaHvIKsCq6UgoeGMSpZ7CrIfYEig5vpz4/4UlUKysPIJ\nDaciyhWssiJJZQJZY7bdZBxVyF6E6Tv4bo0c+DQkl1LKST2LvKqZyzVQl8hFl0iuaEYKtRMz9Gs6\nDYNsUmP2HYJpjK0m1HYLfSnCn5Ep/YieJBOZOlYSk5Qyqd5Bj1KUvksYgWMGJBMN+hl9YbEQlJi5\nhdX3KZZSRC0jdcAZWyyYBnNlTIRBbE5pawojIWgUHlVcYTgKETXN1GCgVjRshXxckFgJitfGG4bU\nVcSktmgYgsJRiMZ7OPXE4ylrl/kd82jaBla1p8jWGMVIeWios6+xhiIZE65cwXTzI7QPPAyxZQur\nuw3kPTaP7KWxegbwGwQAACAASURBVOcjPL1mlsnmB1mqBXODGYruMpLSZlAWuJnOX3/4Eq6651o6\nI4EaPYrctNmuyHzjrZ/jzL84j5/+7Eou/ezHaVYa37/7aaxkmcWFCa9+yXlsn32KT1z8Zd5+2mvw\nLJs0CXj3KS/ml0/XKKuX6OyWueknv6a9cRWe7zKWSpxmjPA1vnXN5Ty++TGuvvYOVi9azDdjMrvJ\nfjv3sMfr4a0s2L3NR8ZDWu+yNt/GIjrdFfvzd6//IAeddwK6FKEmM1BO0QqbJ7Y9w3vOO52djd0U\nT8zgNgfcct31tI48jHxQcvU/3sonLzuHaEli9atfyO9+eA1GUHHq649k6ckJUbKOO7ffS8cSHOR2\nmdmwD7fdfRe60f6vDxZHHnmEuOn2O7FNg1KU2Esjwo5FEktoToU1dQnlFFWvUSqbTIFKSjHUGr20\nmJIj1yXEMoaioxg1kaMzF1WIKmZZyZCMPv2kZDEfMdOzmMYqjUhn1Mzo+imJ9ZyfpynPMJimlLWC\n3dWQBgU0fWq5SzMbMzWbOEHMILORWiUNTaUYK5RVgiWD0knQlw0q2aT0lgn0Bq1xziDPUFbM0M5l\n5PGIqSVwNRtd0wnEMqXUx57UjDTBTDNjsiDRIUBYfSJ7GXMkUcodcFJ8IbAjBQMHnBLhSFSJRD2Z\nEsouqhdi5xp+4aI1Iqq8QCkqHL1HGs6TdRU80UKd5MSaQ8OMSCOBSUaiGwR5hNJR8EIXvzBo1z5a\nJ2dUCdqVjQhgbMh4poI8nVA0WkRBTaeOEG2ZoVrg+E0CeQtnvfTtbCnnOUBeRakklE8nGP02242d\neEbEvJxy8OaDWNp3G+0nJaTuaqJuzrCMMCuTOGiyapXONy74KkedsYmRlVOEPorVZjbJSQS8+sxX\nsnnX3cS2xsqqS6p0GC8uYK+U2cureN3Zn+HjF1/IKcefzNd+8i16mck3f/45/vHLX2dxd4tnBrdg\nCYsiczj1gH3x9+kQP2swtVO2//4OcGvi2CK2ZPpLU971tYt45Df38aixByeUkdwp0jMOUaixv+0Q\nrWljDDV2eluxVvYot01oRTO46zTCe3ezZ7+9cD2fOVGgBj6PWyVnvvwkzj37zzh41Qto2wohMkv+\nsxy9/jXs3Y9xzBQrXcsP77yJ3pzM/JLKtz/9WS6/9ysoT61g+/ydKIbGW045lvuf2kUSZDz09DLI\nAYesOJmZ/Xo8cP/N//XBYuOmTeL6O6+nRx85H5KlBqVRUkUyqpmTFy0a9ZSgKfCUiiz2ULTnehxU\nd4yZNlguCvp6gV9nyF6XpIKZoKQyJCRLZbIU0dVUEnJyVyBLgHCohzmKLVBLndzxcTCQJgmJKVN4\ngjp2sCKN3FbQipqok+KENUZkUJNSCpi6BaplYgcZTt7EtxMkTScNArrCYtCocCWXOFmgbfWZ6jmt\nocTATdBqCzmXsQuduEhwJJWkUSGLHF2SSYuYSm2TJzFdzWIsKuSmRlYrGH6OJEzaCgyrIW2vxC8k\n0qCJYcaktkNf8hFqhygdYuY99HpMWRtojmA4dfAaFURTAkXDKnNss8FSrWHpU7RJhei5KDUQ52RZ\nRikZ6HpNYsv0UpfQicglFc+XKA2DUJ5HC+eQ9ZBwIjhk0yto9DYzTvsc6CWUEUhLXfS8YtfKCEVq\nki8vk+7foDF9FtG0mBlKZOpadu6B/awBe9Scbbu3U2Ypdj4lUjuERUCPPh//+Pv58U9+RG7KlEMZ\nrTNH1nsG/2EbrbWaT3/mY5x/xgv54nev4u3v+BNassphJ6wmVaHbbnHzP92GNVNw2zU38N6PXESe\nbsBwtnL15Vczd+AhaLqMomv81Vv+jAe2/op0h4cp7aYID0Syljnj7NM45ZTXsO6kY5HMKZXZwQgS\nSiNBCRuY+oSaPmUpUbsjnKlA6IKdgwaf/Po7ePzHW9C6PuNxRO32sN2QIw8+kM9++UrAQbNTKqnk\n/FPeRPDoAjuMBT5/xTf5o0OOZs7r8XBwN68/6eV4ezrcO32awWhAx5I5+YCj2DYXcufNi6ywJPob\n9yd46P8AK4CNGzeKm++9AzENyYVMx3luxH8ZheSlSTZTIcc2DVmjiAPkjoeZjhibM6j5EFd2CKQU\nZVpRthsUiUYHgXAShpKMFmroZkkjFeSRSSqPUNs6duKy6CzgjZqorZxYAqsEubZJzQQ5zamVGkdp\nMy5rbK0mrSy0ZEhZCoQMVuYSySXdWuDLUCkOhlzgC522VTM1RvR8iTAzSeyQZjhDsKKgziravsW0\nXkbTBarXQU4TEtOjmUyY5k1aPNcrUckBql5hih5JMcSIPfCglkoiDebynFIvmEgaZlQhLIksEZiF\njZJHhL0+bgyqNmaUgeIIlBAasoyvNMlFxGwcEzgeeaKiukPSqEFPsqlaBeMyoV0U1HqLCRH6xEXp\nyJTRAqVp4ZSQaU2qcogsFNzEoSoy9CBh0ylrcf0ZHrY7rLGeQtm5nkavYrSiwC0E08lTtJvrefKJ\n3airVrNmoFPNLpMuRUx1mXGrYMtDDyMmbXqVjmov40sWttGkfHrIprecjvngIuO+SWlOWCutYpBH\nbE9NplvvoCYiIkerFbZtvZM/fvVbiWd0Tl13HJ+46irm0oLz//Jd/PTnd7KflPLbx36Opu9FnPdo\n6TFn/emb2frEnSiLPUpnF1GtculnLuXoV7yeZllhayljQye1azqpTalp1IMAtY6YNJsYek1Wm8gT\nFVlEuG5MkEuoLQ1jIiEpDWzH55+v/Be+ct0vGD7zKzpPO2xmlhed4vGjK2/AnpYklCwZ8xyy97Fs\nWLOetatfwNX/+Anidg+j2snRvZcj1kjc+oO7qTZYuLrChjVrWdN2uPr2x3DM3VjG/wGaxeFHbRK3\n3fArbMWj8gqmSoaZK5iqSz3xqfDQ2wXJ1CcqGvRVH9mEJdFC0XLqWKVOLea6AeEwRGs4aEVC5Haw\nAoHsAHLIYNpGpaKqJkiFhNksScwZpGFMq2sSx6AWKTY6opQZNQQtJYRJxkhp4Og+md6m8CVqE0gL\naGZ0lApRwXjSYaYzIa8L8olGigvNHDuysdSSJU1Bj3OEV+AMXSrTx4lhUTGZVSTGVUlZFQhDQq8V\nSj2n6ViwLDHSp5iyQm5J9EKVsWRQaDF9NJYdh2Y0QLGaMJDR1QTaLtPJkLrpoQYgjIzK19GdDNuS\nGaoGlRAYSxMaostio6IRK8RmSVfPWS6a1PYy/VFFKtlYtskkHVN7Mo7cYOr79HWFaOqRzGWoiaBU\nc5rTBlbHh2mTzeWUk47dRGZ66MpW9jYdJlkD/1GZttdm0FpkXyYMFz1YWZHZDbRCozV1Gc8+iz+N\neee5Z/Pxj3wbZU/N2A5RdajqhKZt8cLOgQxmcuI8Zl1zJW1thofj++nvMrllugWRFOhlC01VkIIJ\nOTNc/N7TuOyK75ClM+SNAaef8HLG8xF9s8+PHr2TItnNnNPhiu9/k+9d8gOezHQmo8e45Iuf47XH\nnEdj/4Bak5FCKGhhDiVufuAu3nfh55k3trGvuUykWCwrQ/YNFJTBBvYoBXYWYDZ24Vg6jWoDh55y\nAl+8+AKsfZoMExtZ15BVmbDyueLyf+IL7/0b9LbDeiuiKR/MjZt/QzDykeZmedkr9+GRsMH+acRn\nL/87jjj6NZg7YlafvImDJYm6vYbf/ex6yu48K9qv4WXr+/zTr66hM9f8d4GF/P9fyP+vL0VUOI7F\n0AyJJB1nUcYrmpRTSPM2sqYQkVObHZrCYNhqM6o19DrCSiPUKme2KxChSW2rpGnJYjaLnKekbs1U\nGpMg0/Ui5HIZ1VTQ+wZlqiMB7X5MOB4h1ZArAQuSxkCbQBEyyA1CdDS7xpIEItVpCBWjFrilghcI\nRksdqomMVvmEw5Ii8/AaJbYk6EUFsj7AzxX6dYZbCpyRiaImxHVK2jfo4RM1ZJSegWIDqoHnVpiO\nSlmZTKnpdBQKt8Sc2gwUDxQTW/Koagl9GVTHI01CFFUwbqUEk5rSMTHGUxJVwitkmm0NlAIxKGig\n4kzB1GYZtTRUK0TyptRxRDlymXUWWLEI4w5kxIz8IZKhYac1dRVgCZuBVFO0ShpBAWlNtzKROymL\nlcxUVtATndk0okgj0mA92/8wS6Yu01w5YdDfytoFl2f7JVN7DXK9mjllmdAf45oPwVaF1WqHz737\nw5iLgkknRNFkOrGJnjRZXLoPey+fWNrAikjh8VRism0eVe9RH+NQjrq06pXIIsFwfKK5FciNMX//\n999jqeGidSbc+J1fEYZTdkwCvnXNFWhlwEzDZH7XLr7zl1/joaGOVO/mgx94O3/8jrcxu3eMGXdp\np9CqIz7+gb/ghFcfyRvf/afo/tMc0fUIgg6rdmj0/cPQGgcjrVOoxIRqlUTWOhg5aDJfl/zm+qvY\n78gX8aVLP481HKHnAQ4Jhmzw8be9hQs/fRHN5t4oUcX2ZJH3vuttJEYTN1vim196EB7ZwXZRcf47\n/xYrL7FXNHjzm9/KY/2c+WArxkyIPl7JhnU626w9uK363x2n/1tkFhsPP1zc/eDvETmMixyBhZ2n\nFI6MqiskWYGqJJRRi9mGzAJD+lGPQJrghh0kNyFzUsqyQ1YN6WceWTlBr3v4boIjYlJNppqouHLO\noKViDW0iZ0K/alGWJZJaELsZ7anNYpnT6QjSsUvemWCmNpmVYfkate5hBssMDIWG1IVkidps4FQx\nSWEhyRKGYjKxcupKwakTAqXEy1Xy1CTtDpErlzKt8CQbJa3BMwiTMW6zQa1NyGuLPImp9QovNUjR\ncDyowhCz7iHiAJqC0HcxZR1dDpBcGUkLmZfaKLlPJTdYgUo1GUNLQhpoJF2DNK2odZ9GVaPLfSZE\nOCXkqokjl0RCgOIgR4tIqGRyi9pLMccOkVTgtGLMUULcaFEEKW3dIgsCVLfHVJ/i6ClTPLyJyTNS\nwNuPOZyRNwN/2MrSxjnM8W7qnQWz7RU0JlO2rBd48RryYhksHWOyjNdrkQ7nyPdXuPOqa+h1ZhDF\nGL800dKaSnLZ95A+ygqPdXUDraFwzx8SGge0sLc9yCPLKa7iM0DgVTaaNGKo9pkrfZ4JM0479SQO\n6BzIvY//lhWzDrdc+yhWS0NEGvuv7aFkffx+iwNnRlx7+2ZKKYWwoswF5fAJjnrVe2hV23hKrekU\nfWaEzdNhRa8zISgU1qsO+6w8nANO2YsBs+y66xfcugWK5pj1pYz17DJ7DmyxevOESl/DnSu2YE8N\nXnnCMVz2ncsAA23awGLMi488kSdaSxy8Yx0P51OWxveCWpDVDh/68oXcffWNKKOE+zZvo4oyPvSO\n87ni1sfZv1Fxyw034q+yOb1/AvOrcnY/vOW/Pg058vCN4rYb70MjJvcqMhJcxUCXZbKpRNasUFGx\nlw3ybkkVVRSlRCU7SGVOU0SEUokrgWh1qIuAQnlONFxQJszmTcapQDdsSifGnKSUmo1dTxg35iiU\nnJm8JgCqPKAtN1mSJ9R6j3a6hFbqZGaLJPWRFAc5DiirNp4mUXnLTOsus9OEUJOwPAkmAZMa0JoI\nqUQQYJUmeeXR7I8pojZGKRNJI6rSoSkXFG5KIBo0tArJN1DdCSgFE9mhOdHwmyHuosJgRsWgIqtc\nulPwO8t4aR8hYmTDJlQy7AULqVMilxpZlGJZKkILmEpNikihp05Zqi36dkwW6WiOhR8tYGcSyUwL\nrxyjTmxS8ufMkFUNSUhUHQeFkGTBxdbAbQSgVhT1HFkCQq0oaxk1HRBZJqPHM8541bHoawWNPTl7\nJmNmNuhoW1cR98DOCrb3dczpU+g9k/SxiCVNZ599Ddwk5LePLiIXGYqS4Y+bdFoFeZny1XddxCUP\nX88BiU5tFczXNsGSQ6Pj8+QtD5KkNe4+NoNCpzGWydUETUlRGwXH7P86hospcv0HpvW+bBluRuRD\n1Gqe/Q58AaZqsapj8pmPXMtL37CJYSrTzQVXXPl1PvLpz7PaLXiaFoeKMeNmk8OOPY0zNhzGiW8/\nHYocU2thyBKlkZItWch2iJ10iDsyYjhCrTTMOaiedHjPh07h6ttuo1APZC6OaXsTrN7eHPPyV/Gx\nT74fM1Gp7TFTcyUnH7eKJ3YFrM4cbrj+OrxD9sYONL77oyv4yKXfZn9/O7c86ZOIGCtWWPWyw9ln\nd8zdT86zK1/idQcfxH3T8X99GoIqkDtTKkNB0QRu4ZKPMqTYQ2qmWBQoMcS9Ab5UolYhaSHjaKBY\nNfKMg2nBUkMllTPGloeqyizECSDjKwmtno6hTGkgodAkLKEW4CQBrSii0qYUowC9LhkFJV4tmB0u\nMo1mWPIcJHzMxKNQB5SNAstOEGKBSBJI4ZhSSbFcg/FYZewatJQedR6jGya26yF3W1iKxMhvoyQx\nuTTAKWVqpixJBrXepxUJsrpgWsZUgcd0WaBOXErNQJQtFNlFL1OsgYWajqicmjxuIpdD5Conzqa0\nEg21vUwWJqhKhSWHJHHK2KixxACnzggROGaE8E0Uy6LWSsp6llQo1PiE8RwCHVMyGPRtXFsisVwa\nwkfPoaPXSK2YfCCIl5uk+YgqqfCMMYovYSh9jLBglVQw2GsB7Q+CzdaYntJF27mSh3oBjpHyqGqi\nLU1oBSqNnTX+getp72cx2LnMoHE4WaVRGjla3sZRczRDx7QTvnLfDaytWtSDMTsCFdPtoFkVm178\nKsw6pLOPRCXVNHOBbi5hmzVFq8F7XvB26mFKq7mA1TkMbx+JpW3PsOX6X/OiF72BhgdvO/fPufnO\np3jhWRso8pKffPdKOi9s8uEvfIFZbwYp6/DGtQdw25Pz/P6uJ/nqV77MmW95A3JSI3kmpDFTNSed\nNii6Y7yswdgbkJZD1E6bsluxGxVtheAfv/ETFubHTP/wrxx80oF0Vu9PsC3jd7+8nE0bD+A7j92G\nHOiIAdx223189S2Xoe+1kpPOPpnbb7mHUoI3XvBnvOfNF/MEh3D8occhGwmqrPKpL34KqaVy4Xs/\nQMee5dS/+sy/O0z/t8gsNm3cJH7/q/uY9hLqJYtec5GB2qc1mFK0mmj6GDFUqEodDVB7GSIvSdIW\ndTVG6zaZliFiZCF6Fm4ZEaUpRrODWI6RakHuRTRUiGQbe6Iw1WTkvEaRMjoNnSUFurUgHtvIbQVJ\nTGDiEYkI28yhbiCUiDg3oZdgLsjoNDCtmKBwcK2IJDeptJQy1tBnI6IFD8kcoSgGhdpAy4eUchc1\nymn2YiZKkyrx6Ucek6ZCO12mrtrIusa0qMi1McIQzNYNJmWFmfiUhotlwzC2qJICq2vQHC+x6DjM\nTGV8I6JWmzgyUBVQy4RFhKNXRHkLTw2ZNHU6VYI/kfF6LnmSINc6tRDomkwSShhNiXGd0NEqJKnL\nKK2Ry2UabhslDAjjGscBnx5WWEE3QFMKiqVZYmMR1WmxY/oQZ+57IuEBh7L3UsmSpRAPd7OX2Au/\n/RjLUYcjRcQ2PWVl2WTsRAxt6ClH8egdP0erUpYNGS0scTOPcDbn7ee8lKXbF5EVCWFP2R2sojN9\nimf267Drzl0kWooYQKsZUhUzhDoooxEPXnc9f/3Zi3nWllgaZxzk7U0UPsKSsxF1upnUPIgrvvJF\nXn/SC0lDmQLByae+hHy6lXYwy3IUYq3wuP7hX+LFe6HlFWlHojRCtMzg3mHB9y74EJu33sKjwbMo\nqw7BkB6lPVGxkv1gWDOeW+aFKw/ljy44iQve9E7iaY6SeVQdHySDRpbz8298l7/49FWsWjFid2Vx\n7Ny+XPaNz+Mc3CdOLOafuI8TX/kWwlYTVTzB0lM5Iqy45ON/zi+vv5FkZZ/bf3wT/629N4+2rarv\nfD9z9d1euz3N7RsvXLjSCLEBQWMwGNRKLJMY0dg9Y3hqapSJSamoFU0qiVqWTWJDniVVUUPUJGpE\ntDBgjxoEpRcuXLhcbnfO7vdefTvfH/eYR2VUKU+s3HsZ5zPGGnvO35xnnd93nLN+e805f2tNU9G5\n7CXP428fuIU7PvdPeLtaLFuPgQnOuqqAISILaNolg7xNMxiRtxwMbUbe95nXGkYjQG1p5DGUehfd\nS0k8FW0u0RTQOjMQEVWg4LgNRD/C1xQyWdF1LKKppDvUSFsGtMBdSJGNNiOlwMl1lFiS9iRS5KiG\nTdgLaLUjwtoGEZE7Es800PoNkk5JpE6p3YhEJkxEhJpDEutUzQJGKosywTMt2l6GWodIVaFRKrTb\nOtOhQpfBsUfwZUw+ySCpye0xUzunJUKIdNR6AUYVOTr4KmZVEWQOpOA4Fb6IKLQu9ixDNKGZtfDt\nCZk1JddKcj1FM0wCaxGnozArVVpRTpjU2A2XsICiNjFcl7yKyAMFOiZ5PEOJFYyxSVBNWRA5rUjF\nkCmlJdE6NWki8YOauRMjpMM0rQlaY3zXxQnG6COTld4ZiH13cv8kxu8f5pRdEYoxZXNb5yypkS1v\nZZNm8VCxTHqkzYaHetx8wweIYwdRNmhrJWrtYjQLXnbOZTzw+RUeiFsc6HcZ93sMTQPVs/ibd11B\nUK1SViG1HqKELhM1paPXVFaTl/+nl7GPOdFBhT35BkZHVzCHDm3zEFqh8M4P/SGX/sopxOYIa3nK\nJf/2bAZTnYPeZp582Uu4bnoL3/jedfiqR+1LRobOR//ocs5pbeK5S7/Ec/dczGePfoz9foIRn0qp\njJndpqIOTuHe1mH0Xh9juMgPolXe+aFPcMmpWzln8Uz+5C/fi5MVxKsuiePxi698Ofcf+hIvuegV\nlB2Xb+b7eMpzn8a73vm3CH/Chl1n8r1v3sVSNGZXZxfP2PhkhmnF5e/7I1a2dzH37eUXT30KSXfO\nez/3GZRuxW88/Tz8ifaor9MTIlggBJPawpsuUFDgRCm6qZEaGtPIZ97N6XkRhVxiOlGJKx0paqo6\nx4lqAlNQVSX+fJEux/ZHNZIppedRaHNsWyGuBUa9zLChYBQZemBS1U0MpcKOG4jCIPFLFvKKRq4S\n5gbmUIUc2h6kbo1eGhRGQqEGqJWCbDookU7bkHilYGbDkiqxSHBtQdmsKTWXWqj0bB29trAbM8Jp\nhdtqUNBCUUv6XoKrBcQa1LqOURcMbB2z1imTPiu9Gd0oQKhNxpZOlmZ4ZoYjFeaVTanNUVwDURfM\ne/LYi3aHHQxRYKo+DQROANOswmvWSL1NHSkk5YxGolKmDsMMqtgk7QmyQKF0JbJIWdVsOoOc2hBk\nbs10ZmFJj3Tgkmg9ardAui6ZNGkXHVBVgiTBULtUdpNTWwOWyjbNLSsc3iJJY4ewbtKfSG7LmuxN\nEszWBlJPI+nNGT6+Qxpvpa0LAuZMRx5lGTM3BF8+9DXCMzeyYLmkOx+kv2uRx7U1dl/0Wp58zsW0\nLIf20AZXULRjVM1gNIx57+++Dlp76KZtysrg8IJGsSskO8VGjAPqzQb/9pdOYzWUOAOPN738jxkc\nKKjlfjr9EW/7vVdhqC2spk4VtzDUKW986cv571d9hqxoccv2hKXl29kxWmRXtMqWRoC32mebu5Ha\nu5fN9SJHZj4i38uEB9mdHeDAAzbKwia+9vn38Gu//Uq2bhxhRiFuq02omlz6F7/HcniA5A4Hy9a4\n8nMfQsxsUhq0F2KsjU045HBHQ2Vw+ChV1uNLb3wHysYF9jXu58jN+xHTiN8893kQ5VjNyaO/TE+E\nYcgTfu7n5A++8S0S16COa3KnpChCzJGBI11UETHVdRQ3R4ttqFUUI6HMNGIjRWlK6qFA75iIsYoo\nQOvquGGf1NcJBjpau0EhCpZVDSli6mFCZnSIGzGNJCNzarzaQ4RzSnUJXR2ThTUz3cDPNbQWaGXC\nSuzSbKukoUpTG6NaFStjBast8MMF5k6JmZfYzpQqX2SiS7wywpIVqdCYhqB6KVIuoEpJpYQocYFm\nqRDZeDIkbxTYms5Y8/GnGqE6prCaNM0hSrRIleYkYkrealPXMxamJqnukFkzlExB9QuSVYWFrkdc\nW+jzVbLCJ+6YtJQpeqExm0tsKyfNXVicUeQ6dazhKxZOUpIaDkZjRKwuIIczGrpgXldUuovuVchp\nSKOoGC4u4a/UVMsBhfTQh0OihklXbTGZ3sPW5z6Rx+/tUPS2EBV3sqA2uWMIZ+Rd7tNSFrco6Dg0\n0hHj6YwNOzfwxZvvxBAFeRUzjQXNNObu0QFe+syXMUpLtraPohzcQXW24Oj3Fe4PvkUha6aRw6I7\nJXclYe3j1SW5qvLM87dgHIgJwz049X3Ura3YfsT9I5XUcLntE1ey4Wm7WRk7/MYp5/GAF7CtlFTP\nbnH9+64BX8fJGmSV5G3v+lP+5sN/TuEr2FsMuLmLvbAfZXA2Zz0t44JffRG/sG03rYufzcYoZ66G\nDBzB3jtuRn77Hv7j568k2VsxzDOWWovEjSHmQwVD18RSezz0159jds4SYjjA1XVe9+wXc9P8e0yS\nmMnSLm7/2N/R7i1QLeh88Qs38ydvewOjBwuODm4hng341Ze/keHd32EWjLivfz9Z1WT7k84gfugg\n8Tg8+VdDzj3nifLGL11P1aqZmBaN0sKY1wztEcuOQzbU0b0A1ehRDCcUSoUmPZRGTl5J4jqnK22S\n1CJZyGnGOcPCpJnDvJHQSTxmzZzGMEVp6qShRyJT3NpE8QOK1EPzU4rUwDUixqVGq2qg20PyvmBu\n1dSGild10MsVwrJL3lPRsgBn7hG4FR0lR01MMk0BKQntEDvQ0Lsq2qRm0PTQ4hS/iImLHM1QKUuT\nvKvTSWNGZQtNRLS8iKxsomoB+ahHqVTgz8imLZalwkw9Nk7uBLBqKvRIyNo6pjTJgxizUAlthazK\nUCoPy7bRjRXUvknZACWykY4KpKiJw0zWtHszZCWZjCuMnoVeGZRZitBdZKjimVAwQ0YdsCYoVodK\nWQFFoy5bOGrNbGjgG33iZgM11ZlUGkfnA37pzF9gcVeEtS9kdZuKGvn0Dhcc2BRRjnWkIukszRkl\ni5xhrfLfVdCNmAAAG5ZJREFUvnMHTXsbPjGTTEWzalp6zNLOi9k0zJFNj5XOhN37PYydR9h6+r/j\n439xOSIWiE5JpVgM3Izlfs6DKwXPet1TaNzeYOQWtJOacT1h2tvEcrtgKZC8/I0v5P961puYeDnt\nUmNuJLz1Ve9k8YwtvOlNz0fvL1HZIc961TNY/XrB4Thge9fgaEMQm/v51Nuu4ak7lmmdto1g3qBQ\nU7xUI+8KnFJlZsSocUodF2TKEhohUjosdAX/9YPX85Y/eC7m5mU2Gj1uzUO8tsWO05e54WOfxgwl\nU8NEiyW7n/okPDdBLxe58Qc3oEYBZgi/85F38/lrP0DOmax+41pE0eIDf/dZ3vHWd3LO80z++i3X\n8dU7v88b3vnrHLjhX+G1ev+nOefsc+XXrr+GwljEdUuqYExSWRiejlCPveFqME9xqgUspSZoRzT1\nnCARZEoLPyjJRYnSKCgmNr6SkesCXauIvZoUgVY3MKdDshbIwQJdJyYkxPdcVkegGTai0KiaI3Rd\nIKmQ0bEhStAt6OUqgzhHESqK52DNochn2B2BNleoHJs8SZB6A1NRMKyC0Uzit2JiaVMTIOcttG6A\nqCpEsoiu55SGiTlYYe728JwZ5Cq5qmFUNfq4ZtZzqMsQU2+TBQMMDSLRoeuoMIGZOsKQHUpHIVMG\nqKGJJSuk9NHQKK0+ugnxCCpTQrHEojZk1QdvrJP5FqRzXN3BtBKyzKJKbfRaoPslVTSjyDVm0kTT\nTTw7IhYV9cTHU+ckHmTSwMgiHMdjHKhoPYk+SxiHR7ng6U9E9jfiNfs0Gz0obThYcNCLWHhcQHWg\nQ6p3MMeCqd3njtvvxm1kGJXFJA9oCpDGEhde3CILd7O6f4XtSzH36CmPm+3gH++9gUq3WdJmzHOV\nWjhIdYrQFrjo/Kdw6EDOxmKM1XVAnTFpbUcMVogNweaFDtd9+ya8UjAoJI00JMDDb0Jyw03YF55O\nqlicvfCLuAshgzJHm6zStpb4yNvewzkveBp6GpGpPqKpEo9L/JaGzBOQLkJRoCoRVYDatEgzB1NW\nyEAw8SZ03Tb9VOHmqz/Mb/zuH6CpOqa3xM5GkwePOuzdfy2NLGKedjBbAacvbGOL7XOkrth/z2HS\nZklYZzzhgudAcCt/+uo38dJXv5Jx5PLMM3bjbdnKV2/4DGmtcOGpZ3LXgdHJP8GJWlPWXZRYMk8E\nmbFM07ExS4eYMUoc40sdfXFCJgTlVFIXDWyp4ZgJQZUhtAw5d6h9Sd0V1H6CpjWx0ibuqMKZDlBb\nNj11GaHmVI5G6nUYZhK3W6JIiShrFgKTLLcQ0yYSDU1xaSgVaSkwGiadtkExHCPMmKKpE5VtCtNi\nmtnYDriOxDAUCpHR7mqIsURMXWyaqMYMpTTwagNLWaUwp8xlwkQskVsSoygQWY1QPYqsoN+0qSuJ\nqCrUdIDZUimzJj0xZD4tqURIR9XRlDHuvI8tmgi7xspB5CqhOUfmgnhaY2oGSsug7RYUdok5MjGw\n0eqAXJqkVU7Yb2IGoChTUBJGRUiCSak2qLsp0lWIZg5e3MYyBYHuY8xcWrmGZldUdU5HBPiyQjNa\nLPRKtP5uylNVWpsXcA61mDf3c+DcNtWmjQzvLelvGVKI/SzuPsAv/vYFNJsa0pDMnJBGwydsLvOf\nLnsJRuHhPJDQ2NDGUxWato//3G00yoSuOiMUgsLLscwpLUNy/x3/SH7XveRehnjciACPIFhkaTXE\nKnPkrM/V/+MmrGROMAfHjpjqLo6dIAYC+YQ93HDHIZ7UfDLj7YdplQ22xk0ue8UrueuWb3L+qy7B\ndjX6rk+tazBMaC+ofPv2W7nqi5/lv7zu1bz4lU/jN8+7gH//7z/AOz99PTfdeIhV5SijpQRHuoyO\nzOjaMc/5+Rdw3/69HDg4Jhyu8sBIUm4I2bXrQkJVpWxKtDjh1nvGlDOXamfO8846BzmRGJXFrd/9\nNEpk8YH3vouaDp3E47PX3wPpKmc+++cpZJcPX/XJR32ZnhDBQlQSXRnjLGVIRaVQc0IUKpnjVJKB\nClGzpMgLZLOP286ZRDMUM0aPJQ0bHK1CaysQZFSKJJt6BMaAaVEhOiDbKkaQM5IprhLBMGChzilq\ngSc6ZOYE3apJpYEqcxpOTqOy0U1BnlTg6YjEIhpGuJaCUzWo8oyOCzgqNMckskNQSSgS4iRjtGog\nvRJLzzBDE7XRxcybJIkDLJENlvFriSP7+MqYQeWRmSZ1PiV3TJoVdMwZjueiKS5pv4nSq4gcC0ON\nMe2C2PQwGz0KpYUa62g5JLZO3VyFwMA0KlzbIG+6tCsTEaoEZQ8Ml8oPiKYmvTQl1SpUsyZs2cyE\nJGyCJWucRkJsBmgTn7Ie4XsKihsRKhmKETC3JLErMSqNIvEIWqDPbEojIcp1rB4ooxn6XSq37pnS\nv6uLHxzGLSVOdgq7+2ew2zLI0y184h1XIgmpRI86EqBkJPGEL+z/JpN7lri7eYTlZMztno+tNvjG\nX30U2oKgdhBZQSdvYyQu08ziVb/2MhJ3Gbo9ECYPDVTm1QGmrfvZO4z4wp99nLYZMMo04taIMtFo\nGSFxVJE3+pixwkU79hDmFbv29VA6h/nPf/Z/c9kfvwNZKRw+BHktUcOKe77+Lc4/99e58OwLeeFv\nvITLX/tRPnr117n2C0NWGvfxV7d9iv/+mjfxb/7Dz7PnlIvZc8qpvP39b2bBriAKCYwmdr6MMq6Y\n3rOXMzWX3T88gqKscurZ5/HR//gR1MzDWOjz/hs+R9nPObiis7j7fKo6xpws8qrXX8o+p+Y3L3oy\nq0XNzp6NXy+iDxq0oilPPvenvqH4Z06MYKGCYriIvklnFrM8n1ImOpQmZWHjN7uQgVIIfKUFukK7\n6JDmS+RBSFRG1EEPezikaWtoc59KSzGDDr4/RR9YyH6bSqtp13NCQzDvtolUhUYpyYjw6x6qNiZ2\nKrRaRaohiVswzyrqyEf0M9xaA9HAaVlU7hirMIhXQ/LZHGtsUiWrNOYlVVXTMJaQygi0DdT2lMyM\n0I+qKKqk1FOGckTVSilGJbVrYsbLyLqB1Gs8DeyZRLEKVrJFRG0zMwVuryDvx6g0cBLJallCVCGy\nmMI1scsBrl7QqBOs2EK1C5L5MnmqYcxTlNGcgQKVHePVEWpgoyophWrTzhzKKsApEsyqiykKilwn\nHfo4So6p18jCYmzEjMwQ07Wo8xqKikYxZe510dwctdIp1ZhyYjCullHyMRssjb0LPqc8UNDZZbC8\nz8SKRrhnmww27mM297jXP0KRF4S2jqVG9GqDTNexpEO8mjEiwFF8bncjWntnKA/4HI105plNow5w\nXY/VbMrAiyiUHKW3hOYcwQxuY7QvY/PSfWzZsYHVfAO//2svYtcvX0yWVfQaFd5IwyorYl3idXMs\ny0C0E47uPcysucqBesaH/+HTnPfil2CqQwrRptuVaEHOf37zK3jG770GsekA945S0G38nVN27IFd\n7THxHR4LHkjlKLsOrqJtiHFWMz5/xYd50e+8lEnSBJnjS6h1wayj8bHr/pKVzXN2CJ8tyZwrPvB+\nJmWGrG12ntKlN9rO/XsmbCk0zOI+kApvveSNbNB28cMHVvjuN77Aqsx5weUXEZT7+MevfJ6qNB/1\ndXpCBAtqcKqMpJmSehojw6JXBZhqhG67yNGUjuOS6i610PDqDtNakschib0IZY+ynZE1W+SVxTxb\noe02CVoTikIyxSbqaehBA8YKet2gOypxpUBraoxLmzAfgG3jzGcUiouIl/GHHnm7wJMh+oJDZI+o\nRMRkWjNLe8hGhaPq6B44tUauLhH4KaGdk+kD9IZFmUbUMw8jLciMnIGWUYQmvt2mOdQRhgG2SlTn\ndJw5Yl4zICVq+UQyxS5L5tOIViCZDXNaQsWOUqZtQc92kSKEyMWfzShqi1kMk4bHWEBLNSnEKjGg\nSIOgbrOkDnCTGpHrJK0QTVfJ64SJq1N3ewzihKIxIupnNJUGEkE1b+KaE5YdSSuuaMSLSGWOKFTa\ndoIa2nRX5xiqgocgTG3Mdso2V2fkOoxnm9h69B7szGPwwJzx7j7tDcsMZ/eQ/9BnNU7YsjdGzww6\ncUlMTtCJEVXJ9x+6ikppY+/pUjZW8Y4u0RYqm85exa9jPEyE1WFlVKBk4IUaV/7Jh3gwGDDasYg9\n7bJJ80g2Otx+2MPe7/H6j7+L3JckjgpjH90oiMsKdaCRlCp5Blmk8OvPOp0zN5bs3jxje+cc6kLB\nrLuUdsHb//5DPP6CM7jubx5EedCknxj4PRdLCjT9Iab7AzJ7A7MFm959RyjoMLS20wp9NjrL2Atn\nccPVR9i956m864o/IVRDWlZIa97Bdzey/+p7SPJVhkrK9Kyasy95PmqSoWgqN97zRZT7TPKN93D6\nU1+D2a2ZbnRZMhLageB1b/lj6jrmRc94K0G5hUsvv5w6sR71ZXpCBItDhw/x7v/6Hj742Q9z1Xc/\ny3VHb+SuKCW6KyGURxlZHnVUgpBUEYTxAMMSCEXStfosGAplFWJVOWmeYFsOch5A0iYTTVwzojke\ngpMz7GkUik66EDEaJcznNXYZYTVs5nlCoC6jAyN7Sq7ltDONEJNRWlFVXRpaiYKKnRYos5K4paBg\nEmsmvpJgah38oolI3bUnRnUqJSUSBaYS4lcl2DrUEDRT8lqnECnCrgmFhZakqLKD15/QSls0qylK\nJpgrFZajUho1kaNQRhZpZFKrGvNGn6DhMdVrHLeHW5YsNySjVMVou2hlRZpXpIsl/dojrSUTM0At\nPJSWjys1GiHEgxDaFV7i4jk2w0QQCYMmBlG5RDwWiJZJEJYIKsxGQVWrVC3JmIzJ1GCuCxw1x5QZ\n5iCmPORjGCHhQpM7ZYHdsTlc7SC8fT+9g3uo9RS9XuLcp+4hcCQZLbIyxcwsnKDizb93LWm/Revu\nO2g0z+Rx22ryzgJ/9oErEc4GhAxYVWI2tC1ccwFXNnnf5z7BHnuBbeEqYzZw55YWW4sZmvIgL77s\nGfiJij+pEIGgUCKEX9ESCioG7crALB1O3/xs0l5Gbm5lr72Tpz7+Yq458EWkEfDsp72UK996FfXU\npLRuZ+cpBum+MY2DE7ZGE5xbemzYcC7nXbCDX7nsxditXQTWCq3KJ6807sqgmJa0yhXc8QGu/czH\neOV5z2Tf3UMmTojfS5lu2MIn/uofMJyCU29tUQwP8Ir3vIOm6pA0NnDuOQ1idSu1d4jb9x/AVyyu\n+eSXuG/nEvP8bg5dfxPzruSiiy7BnzXRGg896uv0Ea+GrG00dDNweO2V/zuATwFdjm1A9FIpZS6E\nMIGPAz/Hsb1FXiilfPDHnltT5ILfQkQVk55KHUn8WUDgQReNMPOQVYxllGSOSqS2aAxGYDjkbR3G\nU9odl9nYpjICSFz0zoC80hHpJpzqEH5zM5ubLYzTSjabBtloO43l7TiPb7PbKhC2iwwU/AvaiBWN\nbusptHYdYcPyOWzNS1YVG8dL0AIIPBVROZgC6uGMynBxM0kiNOqFAn+aY7g60cyg0kPSdgN9mGIq\nklC16SghWl1TJC5GXTLXDBpdWB0lmGYLQ+0TZQpa06c1r5hmEcJVUP2abGpTNx28co4+aKJYhylb\nNvU8I7W76Am49YSJtLA1A2ErlPWMfNzCWp4QF20ctSBTMvSph51XlG5IRIVwurSmCsMyhEUFb+QR\ntWAh6jMrXLxWhtRc8klEUloUzRgrXsC1pmS5gZOl1B0TIRQiIdl/410851efyYaJh2kWHFjWCBsG\nrgzZdliwqnaZhznVUs43P/5BTjvtYga6xXI1YkUu4qtTzty2hyk9tsoRD0UlW5s29o42X/nuzWR5\nnyJcwM/HiCUQE5cwn3PR7tMwhcnR03cRT+9hq+tw/76CshREw31EYUatq8iyJClNlJ6JFiWotYZj\nmzzjl19CcmgvzuoDlMYWyp6NOlolqTIOVqdhtie0mhH6HWOcLRtZse8nPWTxxU9ezVnnX8BIi/Hn\nJrURoigeRZGRIuk6Lp+74Rr+/prv861/uoLT6818fzLB6PfJxU46Gx/k3Vd8lGed+gKc1hQZtnnH\nm1/DX3zjU+w6rDBc0Pj23qM08zFT1eYNb3gJX//ol2nYT+Drk3/CG0/Y8AtP59TJmAe3bWDf1d9k\nqAXsOes0Lj7tPK756j/+6yydCiFeDzwR8NeCxd8Cn5VSfkoI8ZfAbVLKK4QQrwXOklK+WghxKfB8\nKeULf9y5NaFKvetgKQ5WEJGaBWgW89DE7YyQocQIF6ExZqYq1AaoY51aT7FxKXQdT49JqgxN0WHc\nJvPn+KFkbkq6wmKUFfiLOnWmUsYRaq4iFyzsPCRFpZw55FWK4xjodoJSxAxVC9ssiNOabqFAWqH0\n2gwnJS2lZNzUMVcVGn7BQI1Y0mE07tF0NUIjRZAjMx0UjSLUURciGkctYiulU22nPiNg45EWC2eq\nBMslqrmId3+NOH0PfqukdThj04U72BEXjPIFTL1kwd7Klh0LjA0d64xN1Ai26j22OVPKsolezBiE\nLVpLBXN0hMwxBw2s3hC1ryBUk6EQ2FIjJqGBTShDFNVA00H1TIJkRqtuoLklWQnurGBmWRhSImqb\nYXPCkloxyUsIPNxOzLxcxItj1EIn6lT4iUaUrvCkZ5xBmSZYo/Ox5UEiGzyZMtZz9MRkU2ERK4vc\neNcXGTRslHmC2bXI8pxuJTh/y/nMWcGJJE6vw7w1YmhY7L3zKHkwQbcrvNik9j2iwzNe+4ev4Tt3\nfpvWgSbJ5pzZQwHVxia7Ux13qccnr/0SUhMokUKdRCiejl/VRJbEU+Cssy6gv6TiH4RkspfMlbh9\nk/mpW/AeqBhrCktlxKTssfPUGd7ZBm//7ffy8099JoGhoAwS4maGnHZYZMS8dpEd0GowTI1qIKl6\nU4q65HmXXMq+B8c0tbsZ26diVxbV8BBfe+h7NFYsHHsZRxzh9v19XnTps2g1XfbsfCrv/dRHUAsN\nJ0h52oXbyGObP/vgl3j6sx7Hl796O7//4lfTPO1+vvUPY+Z6xa88/YlMZJd993z3UQWLR5QwLoTY\nDDwX+FPg9Wuv+78IePFal48BbweuAJ63Vgb4e+CDQgghf0xUOuOsM7nu5luQsz4tCYrqkYqMvCkw\npxMUK+auSGIe2sutBytmgaDVWmG+L+SBlYLsiIphf587VAXz5pg7L3wAc3+HI1lIuxoxWalpGjF1\nYaOkKold0XYVsixkigLSxtFUFM0lIyadgN02MMOCDItKKVBiA4TJvJ5RooDj4AxqhJoiKwdv7hK2\n51RWzShLMKVFaZR0UpNBMafbKRisOsyW5zSnLpPuQ6QHE2ajoxy6U2Vya01LHmBUZDjf/w6hYtIr\nE9QvKwwCBb+ZEh1tY2sTAs2jVyWklYGh6MxFgNFtUJQq2iTG7VpUSsQsNRFqBEET151hzSBecDBq\nSMYmtaVhlzPGLZ9Wf0q94BMoUxpTj7lp4eRHMRoKZaqjhjW1q5EZ22nMB+zaDuMtFkZ6BmduyTii\nl3TGFrs1i+Y5Nvce3cUTdhSEosDqns304F7yx3UInYdYPtJGWwo5fHQbdycaofMgqdqix5x62WQ+\nDsFucOcPHmC1rOmRMHvSTlYmMc3OWbxg1yayyZhmq80YIFvFzWucZs4NX9hLYvdRqpxU20LRUVj4\n4Qp3bjqFu674L+SGhIGK2lFRsgKheOR1TSx1dO0IZakjx0fwunPUuo262qB6fMCphyMGTY3Hbc/g\nNpjZCq/9pd/ll9/9QtRhh5mc05wYTMsAN3KQrWP5Pd68ZKjqlAoYdY6GgjrxCV249q+/wh9f9X6u\n/8SHOHjPYZStPczNNc8/7xSuvSkmShIqVHY9fjd5ukTq3cuXb9uLfjgi6WlUpcGGjc/n29/5Gm97\nzW/xjVtv4hee9WQu/cNf48Pvv4o3v/33ect7/pyzXvrL/PDd17Dv/3d4+Bdx4BHudfr3wDuABvAH\nwCuAf5JS7lpr3wL8DynlGUKIO4FLpJSH1truB54ipRz+i3P+8/aFwBnAnY9Sy4lKDxj+xF4nH49V\nXfDY1bZbStn4aX/4J95ZCCH+DdCXUn5/bZvCnwlSyo9wbI9UhBA3P5rboxOZx6q2x6oueOxqE0L8\n2M2+fhKPZBhyAfArQojnABbgA38OtIQQmpSyBDYDh9f6Hwa2AIeEEBrQ5NhE5zrrrHMS8xOXTqWU\nl0spN0sptwOXAl+VUv4m8DXg19e6vRz4/Fr56rU6a+1f/XHzFeuss87JwaPJs3gjxyY793Fs+fTK\nNfuVQHfN/nrgTY/gXB95FH6c6DxWtT1WdcFjV9uj0nVCPHW6zjrrnPicEBmc66yzzonPcQ8WQohL\nhBB7hRD7hBCPZMhyQiGE+G9CiP7akvGPbB0hxHVCiPvWPttrdiGE+Is1rbcLIc49fp7/eIQQW4QQ\nXxNC/FAIcZcQ4nVr9pNamxDCEkJ8Twhx25quP1qz7xBC3Ljm/6eFEMaa3Vyr71tr3348/f9JCCFU\nIcQtQohr1uo/M13HNVispZB/CHg2sAd4kRBiz/H06afgr4BL/oXtTcBXpJSnAF/h/5u3eTZwytpx\nGceS2E5USuD3pZR7gPOA31n725zs2jLgIinl2cATgEuEEOcB7wLet5Y7NAF+a63/bwGTNfv71vqd\nyLwOuPth9Z+dLinlcTuA84EvP6x+OXD58fTpp9SxHbjzYfW9wIa18gZg71r5/wFe9L/qd6IfHFvt\nuvixpA1wgB8AT+FYEpa2Zv/n/0vgy8D5a2VtrZ843r7/b/Rs5lgAvwi4BhA/S13HexiyCTj4sPqh\nNdvJzpKU8uhaeQVYWiuflHrXblHPAW7kMaBt7Vb9VqAPXAfcD0zlsZwh+J99/2dda+0zjq3+nYi8\nH3gD8KONTbv8DHUd72DxmEceC90n7ZKTEMIDPgP8rpRy/vC2k1WblLKSUj6BY9/ETwZOO84uPWoe\nnmn9f+p3HO9g8aNszx/x8EzQk5lVIcQGgLXP/pr9pNIrhNA5FiiuklJ+ds38mNAGIKWcciy58HzW\nMpLXmv5XGcmc4BnJP8q0fpBjr464iIdlWq/1eVS6jnewuAk4ZW3G1uBYhujVx9mnnwUPz2L9l9mt\nL1tbOTgPmD3slv6EYu3J4iuBu6WU731Y00mtTQixIIRorZVtjs3D3M1JnpEs/zUyrU+ASZnnAPdy\nbNz4luPtz0/h/yeBo0DBsTHhb3Fs7PcV4D7geqCz1ldwbPXnfuAO4InH2/8fo+tCjg0xbgduXTue\nc7JrA84CblnTdSfwh2v2ncD3gH3A3wHmmt1aq+9ba995vDU8Ao3PAK75Wetaz+BcZ511HhHHexiy\nzjrrnCSsB4t11lnnEbEeLNZZZ51HxHqwWGeddR4R68FinXXWeUSsB4t11lnnEbEeLNZZZ51HxHqw\nWGeddR4R/y/97mwJkDqUgwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb6240263d0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQsAAAD8CAYAAABgtYFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3MmuLUmi5vW/mff96nd7+jZOZOa9WbduoZqAaoDEjAkI\neIEaIca8AC/BEwBixACJQUkIwagkMiMiI+P0ze73Xq0v7zszBllCNbnULYK4BOj8Zr5kWuYure+T\nu7lpCa01X3311Vf/JvL/7RP46quv/r/ha1l89dVXfy9fy+Krr776e/laFl999dXfy9ey+Oqrr/5e\nvpbFV1999ffyi5WFEOI/EEK8EUK8F0L8l7/UPF999dU/DPFL7LMQQhjAW+DfBy6Afwn8Z1rrP/8/\nPtlXX331D+KXurP4J8B7rfVHrXUL/DfAf/gLzfXVV1/9AzB/oe89Ac7/teML4N/5uwYHUag9L0Tr\nBlMIAtulN21cw6JoSqquRggTE4nvGvTaYxgG9FDT6gZDgeG6SEMjBwPZmlTtlsbShGaAY4HtTTEM\ngWlaCK3RhgJhIBjQCIxeABolQQoDRQcYGINCIZFSoZVksEB0A4ZlMfQKw1ToQaC0QGuNMIBBYhoD\nKIPeGJAKBiUwhQbTBDSD0pgDaEMzaAlCgxgQmMhhQAsDITVoiZId9AItTQw5AAowEL1g0Bph/Ku7\nQwGD1phCoxRIbaHNAd0bKNlhShOGHq1NkAMKiakE2gA9DGipMbSBNgZEb9JrBYZECJCDQMkBJIhe\nghBoMaAGhWmYDEIAA+Yg6IwBiYEeJKAwhUCpHiEkSAliQPOXS1ZKAhqpFZiCXptoGkxtU5UdRb+j\nrUqauqWoO/RgICQMaOy2Qbs2Ax1mDWiDzjKRvcI2QFmKhhZ3MFDCpG07pDawxUCvHYTdI1pN6wwg\nBJ6QdIDoNX2vcYVC2TbNoLHMnq4SGBgYhoEcehQS5bTIAURvIIRGaoPW0ghlIZTA0CWVaWJLE9m3\ndMIAc0ApjaFtetHh9S7KaWikQLQWjmrofAOn9wkmDsI28aVHGDpo6WAI9ZdfgFIIA3ptAgOgMZQB\nhkAo6KWArgcTDA1/+MN3K631/P9uqH+psvg3EkL8c+CfA4xGU/6T/+i/IMs/kDzKmMz+Xf5p17F7\neMK7/+Unzr78EbloMB/8Mw65z/2ZRXXzAx+NO376X79gPv0bXv2TB/ztzRqZ/J6Pry/5F7f/M6OZ\nxfGrOYezE/69w9/jfhvwzDum1QGZkyJvZthuThQmqFXLztpijqeYRUse5Ey2CWbQkWsDpAXNCtuY\n0emWfnCIpKAoM3QQ0KiSqd8zVJrCGpPUG/ahSVy5dJXAiQd2FQwjhbftMf0IM9tCMkb0iqzuSSzF\nPjSRwsa/Kdm6ILuBsRPTey3tRiPcirZPSLySpdVglBbCt4n3GUPvUh3UVG1EOChk1YElsRzBFsGi\n7rgtK6axiyxidKyoNztM10d7HW1polRAY5aEkaBsDDx/jd8e0Vpr3Dxhb9RUbYvtDIz6KZ0hMNSG\nonJxZhlDYWB5ITIVrNyMcC8ZHAMhXYzWpTN2mFaANgVOsaY1PYqoIVA2Mq1wtU0RO5zLLfkSzv+3\nf8F/+9+f8Tn9jqv8PU8zjxvesbVKmtVjfhtPuLrIscUXUtdAFmPqeUabDjx5FVBVO0a7h7Bw+FNx\nwcnyiIW75WOU4dia43c+67lFt5hSfb6ielZxVJyS3Y5RZUF2/wv3z204kGzvJliPNI/2A5luKe/2\nFE//mqfWCnVRcdfZjA5KhGljuxV9Z3L1zuLogcfBzTE/Anb5megbTfNmgvnshtM/H7O2c2LvCf7j\nN3ypfke9WXE/DHn46BFHv5/ye+sl/+w/fgyjf0oyHoPMcFoTz4Z9q+gDGCuDZQrCDJgZLVuZQTVH\nj+/wWkndTFnMzC8/J7O/1GPIJXDvXzs+/Vef/Z+01v+11vofa63/8STx6J/0rHVP8qcj7m8tzq2I\niyhk9tghfnSPy/4VDzYDJwtJX+VY4wmHyyNa/Q22veX5d4qmOWXPnu2zDYeLguzcJFnuCFYZV+GC\nF9YLtmbCvhkI6zE4G9reYrXOWR+sGfcualnhBIKFUiANusIkcj3CtsDuDsiDFK838fstuSdQTkyf\na8KixagddkqihpQqiqF2MdqCwmkohgriCtkVtCTkmSafTaDqSMWOdiTYDx4Khdfd0oQtnbBph4D9\nkJE1G6poh9fWNM6Wzd6jr0Z0YY9TDmTSpKDDWQ84KPwqw/ZbGt+mUxons6naAHMxQuSCu3jJnS7w\nLUHlOMjaoowF9WSHN6poNjA3DZqVyVZsqFcjtirFcgoOooTIGXFb19gD6DqmN0GuJxj1GIyOvbNn\n0SbkIqCxXWxHktobklgivJRgWNGM5uzdlriYI3YGeXjArRWh7iysOwurXXOVS7759nuOOWe26TC8\nD4zfPKA1pxzebvjjzRtu7wtWUwm9gf2g45nrYMxb1quCbnjAT4cfsbtLgquELqq4UyuMbI7belw/\nsbhe+BxfbOlnC45uAqyzEff0B45mEc89TWc/YSQPGMmQx5QYbYTHnuDgMbwvqTrBvpowvj9nX9ik\nlxbLjYFlzSie9FyvBZ/rax4n7zk+GOFtPebfXrO9Cem+Sch/F3MnKr78aPLw0xmvDg7IDzus5ppE\njOhelLyvTcJtjfJaBuniOyZ0UHcdgSGQdMwDgTnO2VguQ+QxmrTo2sWVBkGvfnaof6my+JfAMyHE\nIyGEDfynwP/wdw0W2sC7XpL4OX+2NNfdnqOnJq/e79j6E8zCZmbseH/wDntRMTlZsNMDd/07Tmd/\n5sAd6I59LsYpynfRV2e4K0n36IbEcTn0BYvVW3ZfBK5M8UuLxsogCgjcHG0MzLeS3BwYEgeVZvRM\nsW0T+oxsnbJpW6QrEHVLqwSOo3CKLa1b4FHSGJqqkVhug0WEpXO0U5NOY7AcQnPKeDWAnuOPYZhq\n6l3NOkwJrRkmgmoQhCsLMUzAazlsB+KZYvAljmUyLU02/pipFpijjEmXMdkorLDCljFy7uG6IULX\n0HtIwyDYbdnLHOUITKtl2jrUemDcBZi9AZGm8SqqUGHtGkxh4G9tgkhz1w1ob2BiwWgkGKwRWXnA\nbdGRrjKkWbIJNuwcTaskfa+prIxuW9L1PrQ73AVMdY2qekaypyLA7qdo5eCXPbEdk5LRezbOtsAb\nFUS1QbfL2byuGSce3ZuIL+sTkv3AT28E5e8Ex7XN+ijg3sEx6q2JsC1KPyLeGnwRIw5LRc8E6/qM\nSN9jUBYzz6DMJNbJQ+ZdSeifcni949ufllylM8yrjJ0+ITv+EXXwnO7wI+tySqsr1uE5o+Y16nzG\ne3/DuQzJZhtCcYcrpzT2WzYfoZ+NCMWKY1/w+vMHgiwimfrMvT1v+hH0t9TbKfH7iG9sE0fsSd4m\nRG1FOVmw/7bEPPsR1zhmdnCPhX6Cf/OYrjtFPfWIpYtpdDD07IYWb+YjNyPYefTCor2z0WnHKC/o\nKsVIR2wti9Jd/+xQ/yJlobXugf8c+J+An4D/Tmv94981vmcgGz/kyA6wXyQ04o7btcfb4pbjTcvV\nrYtzYWBfveTqfzcxdh8xkoSoHuPNI9bijk97wZw57qYhTZ4hg3sYH56z10/5Ik84OUjYCHD3IcE8\nxdYDyQApI4QTU3YH2IHA6W32kc12nVH3d+zsgN5rmI19OlGhrBHOZGAjx+hhhJeWOFMDa9ozxBpp\nHGCaO2SjGDUN4Y1mVNpshpSN4ZOUKbLvCYsUN26INwabVc5YdDhBy16VdI5AqTmDdBFZg5tV2CKi\ncUZo1VK1A5Vbkjsa0w3JWjDtO5ohI3cNgnpMbhakg6TsPWI1ZcSGSkDdrhiSEKPJmLc9aTUQryqC\nLmTidzhNSG11OPsGo6gZOpO71qWstoSyZjwUxB5IZWMNEf4uZtpLTAsyq6HREUbj4nYdjWOR5C23\nncQbwGwjjLIhqzI27Zi1WTDclbhtTRw2DBS4uaYar3jpn9DXV7z5eMN3XkdVX3NeuJwmFmlxzt6t\neD5WZGnLvcOPyP0Cuzxg/fCG8fUZ6tEj5rcThPGCI9titRqzTDviUc/5KudyNMa4NHlTPWTjhMS/\nEfSdZBI2NMYxny5WnPUQ7Gd04SeS1yF7OeJj3CD8hPtVhXq34OhU88E4YzTx8I/vONaXGI9dipsB\nrZ6RJgckoiA/ibDNAqpvOXlp8F495Gq04vUbD6+7YRzYLFwH9/OED/I3PAklZbviiozRdEJkRPSX\nYG9b3MaiaBNGCbSrgl0AZWCQZj2TkcQko3QPyL09udkjB00vfn7Uf7F9Flrr/1Fr/Vxr/URr/V/9\nX401lEbt7qg2NbP6hrZ9xLyyOOQpm87BezhQHy3x7ILpY8357IiTsOONt2CXBzy8tZhMP1A4F6yp\nCPfw3irQJzXp7WeGesKVaePEkk1YoNIxzXqCJfaIMiXWG0S0xE4TDH9JkjnMTIXwx4xNCw9Jl5s0\n+YAsHOpaoMod9ZBTjzSV8JHbCXXa0xgrmv0UoQWZIeh1Q+8oJoZJhMHGi9hnHWU5xUGRTiXTiUl/\n6xGxgSSmSsGSkq2vkVj00568UxjhntaTWEaPnflIWbN2KnrhI7OEcTbCbip2XY1thxi5xxDWiHJD\nLgV+0LCzXAy7IRVHbCyJFQJ+RKEVqSNxqhThj8EwiCxB4k2ZdR7aHuF0DSsvoBlyGtPCmZY0Q07n\nmKimJooU1tAhIgvPjDH6kHWuOBga7myTjQV9t6f1AwJHQWtRRjVJJLm51cRGRC98LKUoopR7Lx+j\n7StM7YDfcuC6uCMHnAltHiK1QWxWVLOQ+4cF+vGW/e1LvIWiuL5i/+KW8aOKN9kd1+l7pn9V4Ph3\nvKjWOLVPcXqOOLji8oFkV98wmUZswpydH3AibjkVe7Z3HzhNntMHC+qnioPLW9Twga48Ze+9pzJO\nOdpAcF1zE8TUn0IuLxZ8SU9wq3OOxEcc8wTz7Ign3gmZU7L/oeG5+4HRu2949rDAnp7wpyOwCp8/\nGzOG+RfevYF1Innswaa4Y/QoprEKtpFDbWi0r1DEWNYMbbfsvQJf1Owoiccmxi5j3se4XolXV0TN\n+Gdn+lexg7O3HMZGyIV4iFoeMDk8oxQ2weE7rOYdJjvKyweExmfszUeC8Jz3dcvT8prSz7H9mODs\ngHtuiz35yPj0hnvuOd+qj0wf+LxKbplVBYf9HdFlz3rICCwYLAsdzbEbA1WalJbCWgoMZdPEI5q0\nZttnyKoj9QuSyGQqCwx3R9CNsGSE20bU4o7BEIRBh5uNsfyU3obECRnGPYMhKIuSPknR9Z7E9bHE\nlqIwmOQ9mdFAsKPvZgT7FarZw6bBb27J5Y6gDIjljipNkE2A2Qi0U4JngOHgbysyUdBQMnTgzhT4\nf1mPsEsb2/BwrZ6q9TiocvKti5PcEDkVdAndkKErSVJPKAOJ3O4o4pIGl8wo2TcFvlihh5iFeY1S\nNvPxDlE5BFMXu1yiA0FdmoSuYlAGqbehigTWDIYJxEOD6kxyLbHFmp3YMa4bDgaP5X4gOogp7JKg\n0tz5B3xkRFec82RweXxlEtUp+r7kbH3HtPbIrmK2Hw45K8H+WPDTXU395Q6z6UhvnxInLgerErm2\neBg84cV0Tn+1p/8y5oOYsTHWxGrM6Ghg8m6g+GywHy450SsetJ+pZgZe+wwdONxYLut7F/Tdgrvf\nT5m2v+P2uMW2DPrrtwxuw0dpE3VfuBYdxnHD5BuB4gHdsmb59gxf7TnbwejeR9LFZy7TGCfa8nEd\ncBX/wPM/W5DDb+6949newj3OOXb+mosownt2xPH5hhNnRJ0V1MLDUDV9ZhIGgkTuONy2DGbEtAmo\nUkk9dqh1BZlFH5oY7vCzc/qrKAsN5OojcfiFPvzCrf2YbmVy7dqsLEmkeg6NlNFkRmjC0I5Y0FDf\nszFLi9dzQfHNLavKowmeM1QOF3nC5+wFJ8tHmKOG8tjhZtqQuRYHk4BtrJBFwKhdkjoWfuRShxUW\nDkUvqeuKyhPEQmJbJmGrkNpEiRx7E1MlO7RZEXUO89WUWOWkakxt7OgGwV57LHcNkh5PlCgb2mGM\nH2hyUaKnIbbXU/uCUROyDWy6NqV2xviOizWkNAloJmRSszZ8WmvJiC3b6ABhGNS7EDe16L0Yo09w\n+o6hCvGbht0uILc2eJFFLx36bMJgpSxth0VYUmnI1JSsaAiZ0dgrBmeNzCWFkdATEPgKIzWxrI7d\nMCK3WvJKok3BJnXZa4mxNdjIEUiDobOx7Iw20MQ7yVDsIDfJy7+sn3ga4tiARkIrQCYIqRE6RDc3\nOEnMYO3QTkYjW76joLdzttVn4ntPuSkL3OiAO/2ap/davG/eEk7BPjrgmcwJHz8mOjwjDFxCecqt\n5/E9OVV9x2s1YRM/oF2UuInJbJ/ydr1D301RsxmdecqRqWjPj5iaJtfiBfZ5yklQ8OJ1RaEm3Fv3\nvCxrlPwThe+gvICzo4cUZ3PC7hR1OSdpHJzsCutaMTu2uSd/z+Dd5+Npw2RRMJz3ZMkhqyOP0vZA\nWEz3r3irfa5nl3y+nFGaCX3Yc3dxSaAPODbPKfwpztGS0GyJGonb1Ljtnq7JKJdjdlMQUQqmhUoK\nRsWWYrBomoywmCD8X+8C578VqTVekCCYs9kY3P+UIoI7inbCcTLBqg/I+kvUdcpraaF3IaMLmy9n\nipPe49QYcbgKmQ+SnQgwZcShM+Xp8IViuOQui6jf3cN3jrCjMZXMOFqZqLzDi6d4vWCVK8KNRWlA\n63XI3sLNe9rARcgplQ2FuWZrHFKqFLN30Y6A0YYmydiPfQ7tmtCf0rchwhhIDI/OsdlmEs+O0XTU\nhs+otxB1Q5t1mNWE1F1jDlBoh6ReMwQ+ayfGuEloy5S2c7C2JVK4VG1ELDKCfoEbgCNM4rDDMLZU\n85gqrskbF3fQ6GxBbfvsS40X7Aj7AOEn3JY2YzlmrBvGRsDOV4ycgV6ahK3JNEqJtGQYNkSixHFq\nrLLDdD3swMfAxbF9oqFip2ratkDrFmdqsSs9uiZHjiJcpycMOwRQBT2VbKiFixPFzFwPcyy4HUJG\nRkuvNGKXI4aGw/OYg7P3jDT8tJywlQ3v1Z7xJ5dwXXJIQJl3WN0Bi6ImkkvMxCD+9Jnu2uI8+IGr\ns5LkXHDc5Yzed7yyvmBeh2TzktMyYR4KvPAh42rK0UwQ+e94zVOscE9ZK/zkDfV8xsf8r9h8c8Gr\nQnHe9pTilI0153DzASuboS4+4x9suItycBvak4C2dshPC3qWXN9cYyx+wgw0UXdJm/8ek5KD2QUj\ndc6Q9tiORBz/yCSRjDZTwvmEV3d7/L894Cg02EQnZIfXXK9HdKWNdDpkpOn9hMxP6GSNMVjUa01u\n3mEVFkpLwrBnCBaoaIm1zX9+Tn9+1H++jo7IlIyWDs85oT9ZMakzFmdTrtwt7UHJgM2w6XhgnHJv\nE/C9ccOr+yGrUU9/EyDClJ/WDfebT7y7+gGzFRTmfZJ4xOGNA/e3hHpJI+9wlx6t3KE9l7qHJuiZ\nxh72wqHxwBoyjKHATGp6KnRQY2mbtggZ7A3tMEE0NlXbUq5t8szFyRyWqUAU4NgZfuHQeCZeFuBP\nS4p9hz049EvNtmkQbUPvC3Jzj5Va2FuXmeeiYx97t2GwHdTY5cCF2EpR0kSJGNPvaEqDdFihswEa\nTbtSZPOE4bbFcjXaglCDuVghVj0j2yArEmTVIlnhGSn0NqumJRM5k7ai2h4gV5BOXPa7kGLbk+aH\nmKFL1kxwx4Ky2dGWOZFsCDuNX9mYhs0oCphISShSLKcmEiZdOYBziChcqryn7sAUJbHwkJuajWGT\nKUliZZiTjjqPsHqTobvHzoL6/iOGN1vu3V3jh8+Q729pQ5NCFBTlCXLs827Q2HXJ+8DhQz/m6vg+\nbXOIp59y0Ke8VxbWzuXzizWi6onaEv3dKZ/iNdujCKP/ng9NRv4ngR4/Rlgb1JVBVU7IVc/bKOVp\n9Jr8B8FHZtin14jmA+Z+Q5A95mhh4VszNpwgxjCvl2yaO8LtA6ZFRJF5bB47DMUh1oWBZb9AhD/h\npIds/6RoT77BfOXwfmPwqnuG2Xesonesy4ovjx3G7QQ1qykvU6LzEb5hUwYR0qi40Q6D3iLSOxYT\nh6E3Gbkeoz7BMQZyO2K3sXDJqHBIA+dn5/RXURZOZzNbH3BRlfzkGMTdAf3Lnnz0iUle07Q5XSK5\nix3UwSc+zH7C7h5SrAYW1TW3xy039QHjQ49wO2Isv8XZBFSNzY1w2T0MWawsRBEybwNS36aTNnnb\nINcZtXTJOoneLRHaZug09cincA7Q24RcOHhrTa88YmyM8UCrdthdzDBpiH2fMrhl8GqKoqCNwelK\n+qxENiZ5OUXj0tgtk0Aymng0vo/jCKKsYS8MynmJ8nIyr0b5CdP9msToWMaSXLmIwCFwUkxjjxEL\nnH2H1bXspyVu1DC+zYlCByUVSS7ZhTVWb2LSkvUKpQqEAa0O8CqJaWwxTINg5NCInsDdYHg9va6Q\nqkYnHpHbUtg5UdAxCEWgArw8ZtP5iFHG1hMEdo2wLHb1GLoeexhjuQ3FqKLv9tR9Rzj20FlNEptk\n65ztyCHapURFitP0rDcBZlgAkmWiiVcfUJse6z5UDxIs+wtGMsEqavoHE84nHf3FW2b6gkF4PHyt\nae2IMR0v7kckyRnvH6x49PASZdZEucuSl2T9F56zZ+b6VM2MnU5wn1jY8g2WueOv9zdceXBV9Rxf\nnfL4B81bVzIN7+H2cKxDrj97BKs5+nCHlO9YJCPkcIPf3bF++g3GIkc0t3xcV9wLbWzhQjUh7h1u\nVjZOOse6NXhghjg3mkZ94snkO84Cn+XbCmkVrJIdzf4pjr9iZlhMnUdoZ0yY+EzCLXVqEXQ5e2fM\ntPVgnxMKFxuHbVaRejZxUYCp0HsLq+7w7epn5/RXURZa1KyOSwwET7of6NJblhdT1vuIPP5rtmch\nverwjp6i3j7lQIXIxx52XqEsi0dvv7Bob4liwfnhjnUreb+okSchTVjTDjl1VNPHBStXYvkNWVAh\nkwHlOrhZhmM0bGSAY9qEi5BelcxXJQEwpC0bv0P0K3RWwq7Gnvu0wQZZSAyro8VmXPZMjQ5zMCmi\nDulBL2Gk7hiiNWO9Z+s4iHWBkD3+5oCt7+L3klkasLlTdFVCVnW0xhhSE7EdM6pi7C7Eqg3atWTf\nS+ooQiSSUVqy7yxaT6FVi9kE1DaowkFWPtmkJHIH+jHUpsdCdOyNCXeDhbYGsjbHES5VY1Jqj8Ty\nsGRAmG2pDRsBdLucTiv2oaIyLNzdll0a0/ZQOQmUG6xqSdtICl2zv1kQ3El6u6aeliAKgkiTr8ag\nFEe1RFkJ2B7FEDKEDnIXkdoK06rZOY+w0zvc1SlffvzIp8sZRS+59D6y+bTg2ZcOd27jOL/Figfe\nLmye3+Q4b3veXv5EHz3nUP8NV+IlZw/GVEPEsbfh9K8iNuM9tb7kgVOBHcH3AXvP4/Bi4KMT4Rwf\n8zQbke+3rE56vjmzaZPP+Okb3quMh8cpJ7M1qTL4UtdY15qHo0PK2SHT795ivXvA7sUeHSrMdcVR\ndgON4IYKvz9n+TzHe3VN9uyA7eoa4+3A2cUCcXvFyychx/O/5WlWMLPXTDcV5ReN+3RP12zJixyx\nFoiZS+ElzNKOrVmzM2L6Xc+NBOF4yH1LMYLIsKjnOcXQsRfBz87pr6IsBny6YMfT40uKxw84tw9I\nF1c8fmkwv7igcSrq7il6v6aYNNw6xxx9/5qzb3Py7pSd/Zxz7xivn5G+k4TTD/zu4gP5xTueOSaH\nI5/sNoNWs6gzdNmwGCKSomfQKYnsUVuFFwoqWZMrxVj03EiLzAARFySN+5dXjLaHK33MVc2hOyCb\nnrtuQ7yNKYKedGYzzlqEYQA1lr3H7CVD5nGziVnUG+6CmHDjYFstcmgwxj40JouRR5dl9JZChZp2\ntGYmwBi12HRI2dAg8bCYO1A2Fis1YEUt0pVgdjj5HhlIkqRgR4O1t0gHGxoLWRqUe0iiFcbaISoC\nBIKy63DHUNUFzbrEjCS7kUkne/Rg4fsuZeZw0KbI0EKPA4ZIot0ST+7JVEI8NnFCGOsSc1SQhg7o\ngSGfUagBkTmMF0v8RcONoQi0QPVgOhK7VwwjhzjOcDFY8QU9DXhT7dgGL0m7K+4bCfdejHkcKozn\nBjdtwE7CNpVMdreUbo3/20ueeM/gTxsu0x3ejcts43GyKhiObyibmLt2YHo5pfswcCJTHoQ3cBRx\nMfLJ5xYHb3ds5Vti/5R9GfPptx2r+JS5HzAxQ3ASVkf3mb6PiKoDzKcuV/k1I72gXRhMHu4o37o8\nM1N+enDFfjSi9e9I8oqzoObh55aL0kSaDrcnYzp5n+obEMkRyy9Tvjg9KhKseMCgITi8obu+x5Pf\nuBhbSTkb0Q4dwb7m1tgS2lPC2qSyKqxeUgUmMpIkbUzpNaghYGQdEqXNz87pr6Ms7JrsDwesbx8Q\nvBdI0+ThtUE82PxZr7hnjLk/+sDZvMMZa6Llnuapxew6I911lCcrqu0dK9fi+WnN0fWM94fwzfQ5\nbX1LTs69xzOM5piuHRA6YshLKnOgMA5gkFRGjmUIMGtMZWGbDrOwxHUV9tJjJ1tc5UHqYcgtha9Y\nKYkc23iGixHXyD6gLwPyJiDIehJrzq7xWE1nWFi4M4elpxh5t5QHe3TYElgeg7FEyBvSApI5eENA\n1kCLy9LtuC1amtChqjpmoUSmIIYQ5WZEoxl2a9CpALGPEFbCbrPHHmyEZTKIHieoUe6AGO3AcugE\nSNNi44BT9liEtLpHGH/ZLWqqgV70TO0NpUiorAjHd7mTHl4rsNuG0TbFVDNSo8KNBnAMVksX7QZ4\nTkno18i9ix/smPY2yra42xhYvUDWFlW3RTsFbZgR+ilJv+S2McguM/Zexhu7Y2oYHIXvGZ0U2P2O\n7qLikzdgfow5DmxOs9dU9045OoDbxOVjKdhuPxJOJ4jKxRTfM2sdLicut2sf4+aM5DTgLvC5Cz+z\nvplz47f0IxVUAAAgAElEQVQU9Zp6+Ql915K9jElOQiaHivtOxv7Ph5x+Stnsc4xlTnY+Zf/HhtUB\n+IuEH7tL5vmM9LVgqY7pzyaYLw4YRjXz6yl3pou/u+H0gcUT5z7XixmO2eD+ueOhnbJ4VhC/H7NJ\nPzN2t1hvXnMe3+c30Xtyx2GW3cNJ3/H62kOMYOgV48pCyAZ3JHH8DRl7QjlC9oqjYkOhDDb9Dkck\n2Dpnm/UYwv/ZOf1VlIWhFQ9ebbDsJV8il4fWDX1wQpV/Zjxe8P70DX7u8k030J1VhJ3AvXVxwuc8\n8wcOsh571DBSNcUHm3y2Yr5s+YkP7HchK3NOsIPb8JyhNrGUwd732AcxliwZ3IHQdSnKjGQwidea\n5U7QlxFD32AIh0g52JQkk4bSDhnLBaEMKYoO13XQjcJqLZRzQ5hsqWPBXt4QhhVGO+BoiZeZhJVg\ns3EZlTHDtqEualAWd1MTZzAxGwPfApFUNFlAIhR+UOBvG4pkRto2iKCgy7ZQxNjpjrp0cfOUPALZ\nb4lDl8rwGAuBrUaYVoaxDxGrCEv2GDuHcbxl0QwEaKx+h9pbTAnwDFj1GXoI6FZz1H6Ft9pS53uC\nvU9mV+x6gyKImPQFg7Lw8hxj1TE2DBoJjVjgrFukE6CExRBWWDrAUS7IBeNa0CxGLPUEtbIxNiMy\nYeMYLt6k5cVE8Dw3uPWu2GcdRnWf0v+EfefR95/5Uf5E0VySymfMNnfg/SPmyxUHX37DZPKM5XXB\n4mSH8eKvuRhlPLsJ6asjVicL/Cpks9sz32uM4gxvFvCwe0r9coz2CzxTkBchN2c17tUxT+85fDzs\nmL18gvngd+xPXcpXKavKQ10IZtEBn/WSkXdFY5yzPPU4am/ofvIYVzUnP57TfaN4rw85237A9Drq\nmyPWBojLJcVwwyTe8PLxCd8/94mFhZ+t2d0+5ejZiMFbc/wqgKFn6wlmRs+2bKhKn1E1ZZWaWFOF\n7W0RcUYeD0hnTBdFdEWOFDPMULAJ/n/y6nTo4do36Z/2xJcl2jzmOvXZOGMOHZPJd0e8vj/BKwsM\n7xCdNbzuInp5w81+Q30bQHhK1Vxz9ijG+zTnTGlmTczWm3N/3TLEPs5whLJNKk9gV5pp0WEbmnVz\nwH4IMfMEZUAeCzBNMrED5TG4WwzdMzg1lBm9rUj7ilSluN0BNg0yLPCtPbqcUvYG+RqGWjBYFiNL\n4GKyS/YMfsfE7LlzbJaxgxwtsJkSK4PCEKRZR2ErYpEziipsv8PSY/LIRJc9KAMzCJFhgzNyMZOA\nItQgprTOHYWwKVSG03qofMALOmTmMjEH8oVFmkfIhUejJcvAo7RtunaMJSJ2cUOjNZEb4ymLdlIS\nMmUZRCRWRO0qkiLn0KrRpaA2KpJBso/GMOnAhGFQFOuK3XSBsDawjVBLG617uqnFtl3RsSLc54Tp\nCt/W6EQwDgRePuC5U67fHLFrduz/oHFvLabmQG4GXH67Z9J5TEYT4vMAr/qJdOHzp88XuCc+I33B\nxficcLrH3E7Ynp/z8KrnTaSQ2xR/6VApOPQVUj7EeDBns3FZ31o8bUqS4ZDL85q977N6KSnvf8et\n+Sd0Ivnx9Se2K43yStrqPsb4E7f9GVvxCeGblPsts/FzXn7+wkUHrRRcmgZ5LDE/fkuxy5Gr+9gf\ndpilyVyY7IcxRhkwdANvNjYSG2vQzKIDHv7mis/vBuwwwgwHFvevCIVPdgdTMwPLo3QVgTBoW8nS\niYgtRbcM8CrFeJtiaI9IKRqRY6pf8Xbvfxu2ZVHfaqpuTjotuV1ZHFff02z3/PlLy+E/uiHpb/nY\nvaQ6fI//VynCK/hcNMT2SwIj46Q08EcnvNzv+fzqlunoW+rDO373+ArR92wqg4VZUskIUwzUYY5U\nJWXq4SYDQm5xZEpW2wi9RRkZcTNmFOxwAw89AScd06qQQRVEWjNvIyrvBl1Lmq3DDXMSvcUOJwSO\ngdVp+nrgrs0g7piUFUKGdHFEtNphlT1JNcAuY1f2uENDECYkrUIxZ7+v0esWYShCRxD2mmRsYq8E\nyz6kqTr2u5pxWbDvIdkF2AFI75DeyNloj5UYKErFpgNruWKUlDR1T9+GaMAuRxjRNfm4R+9NLJlS\nGDVxltNIh95tCSuFYQF9ztbw2JcjpE5pSpuqCal1zbo3WWuHpo2wbMF0VyDUnNIUdLbC7DvEsqOp\ne2zHow97BkMhpcndJme7d7G8GFdd0Dz+TK6u8Rdz3mmbWt1y9P1jsvY5bTpmv5wRuA7vrw85fr1C\ndhXVRc7r36ac4mDtllyOcg6Oj/lpPPAysDg6djk8XROcTUnuhSyrhsl+zDSqmTzccWcMlOUA4gKG\nNY/SltHmHk/1E46rOU8PJhxc/pGjds3L+Af+Kq34VoV/+a+MPCf+bYTdtqTJCeFcMqu37J+X7MIJ\nBwdrXsUNOvnIOkgIFgUOIIeGR+Ec7/49HnspsyzAeTllWcd8vn7C5OGEXveY779hu3/OsJEY846d\ns8DqDMpVQeXXzNIKG0g3YJsRVaWofPCjnDu7YaQlwZD+7Jz+KspCtxbfbE/oVzMeyy15es7ZqzkH\nwzHWuOHybswQ3scxK8T3p+TCxstK7u0tzsMLsicPsXOFOHf4bFcsflpw3NaYs2/53n9GPDnBeqS4\n0hIlc2wBphwjhIFrrfDTnIkzxvUH7GoDpYNsJlhmTWZD1bpktUF90FBPCrxygvY0K2Ui+4hyUGi3\nwY17WqVptaYPx/RRROgE2PZAV6a0zghqC3NrIWRAZ7X0VQmDx8yCauogqopetMh2j2NbDKGP7kyk\nWuKGiu02prZyDu0MvxuIPMU2UYwON6R2haEEbQ66l7hzhS9r9EGMadhU9oS9aKlbKLRJYPSUQYeu\nA6adSeg2WIaPvu0ohYF7VzCiRroDm92WLnbpehszkISRBbaHWw2IvmHSjhHBQFRprCGlw0ZmLeNe\n4+op6aQisToMJ6SpO6rCwJ54tNpmPpiYjknvrklXNqeX9ymuHdr9jnv5Oa8/l2zdjxzqPxCd2nzz\n5JKMhGeD4I/1YwJ8EhHy/A8TPuiUyxevOAq+wIeMg41La/rIpcnn1QM++S1fftBM7wmu+nOkNUMk\nA+qDyePDY56nz5m5Ie9WHeftjvPPX9jqjreTnNWrJ5w3EV/++IKzneK7JGSWexwVHeb5A27WLdvF\nOcbeQL56ynQT8uj2krXcYVYO96ZQnNjo7Re++H+kPpryoxHz4eMfGC7W5OGGyOpod+8xdx2Hkykr\n92/YPDN5uBeMRMewdJBGTpvcIYWLbwiW8ylOkaFMQT+5w5osMVqbfRfg6hrTdMk9+2fn9FdRFoiS\ns+c9nS5wmjGOpRgPDWsnZzo8Yb+PePTWYi9v6R6m3NyMefYk4bOdcXo54sD8AfPROderjOmmYDgW\npIcadekiOwexeUPfzei3e0xLURc76t2e2zqmmUyoxMB205H1C4QR0/cBC7dhlVR4bUibZyRFDncd\nZhnjWVt042LJPU7o0GUlXm5j3bXgxjSqpsm3dCpgZQwEaw/TTWgti66sKFuNsgdCW0PSIsSejdJE\nmcCyanTtUNtjqsZHtDlNndLisq96pF+zFw3XnUHgVdzZMUlpkK7GSHeGNjVTV9PqjuA2pRMeJhZV\nURN5ArU2sKlI3DWFIdCuix6btKzY5DbZpmASSJypIBBwm4Zshh7L8UCXLGKb0t+xtTSOUyLHYAuL\nwqix65p9BP8Hd2+ya0m2rWl9c1pdr3rt2re7h0d4RJwT59wrmggJkSDRgjfIHh1egEfgNfIJEA0k\nBMoeLXTROXGi9CJ8u+96r9KW1fXMRkQiGpBXIkCZOkMyzTHMbI6O6f8159C08RtmQBoo5Ghga1RY\n5p5xO2IzEVhK4YaKcVVTFlB4A2pSYooSazdl5+vEXcIizonvB3S3oC0U8rM5Tf4NvX7Fd/kIb9zz\nNA85n1mY3Qjle9z/YYZdO3zRXBHcPyfs7llNf+FBxdSiRm1/4ChY8eyk5CArLtxLbh/eYHxf8OyV\nIpa33H+9Z1uFfHPScjHJqZdfMdlsOP0UMNd7vPmOyaimWn7Gi70iORxzY+lI54HpaMuLDyHFlUux\nWjN/qtidemjaV3xvDBySb7Cljuud4IRH9O4jo5/3KNPAG1yGB4+nj6dMX53z2esR/SrldbfFcR5o\njnMeZwJnquM2Cr0bY847sp1HMOwx8zljH5q1osl1ut6jMXrMSrJuFJPk74QshKHzufqFZzJA9jWy\nC3iyXFSWsNx+5E9azPC843Ryiuk+4duS6sMRUyFoxh4Pnxwe3y0Qfy5Y+8/wkg/EWxMn/R5ZljxN\nl0zefyIwZgwqpIpMjmTA2OkI+gRpN0SzgkarAUkX1RxKRVBrqLpCG0x6zUWzfERn0Q0RQ6bhdSbu\nOqEJdRoDqmmF1gtkMzANNKy6xmsq2l5npWyCZCAQDp67wytS/MEn6z3aLsI2FaafcfDn9FaBnZd0\nYUwagNF7JLGLNdT0SYdumATdnKwQjJsdh8pGhgPEW3o9YHso8IKWZhnh1hl2NRAKjcOhxIws6lrQ\nxx3Lg8QpHtitNZo4wPIEJgaZa7NLa3Ldwx5SFn7DyOpwckUbd/RlQLgpqWRIVbUEEjxq9NZDDlvS\n1kIWCikqHLukMQx6s0GrBQwmnRhQIqQLHQQGejqiTUIaSzJyOnr7LUNZ4kweufW/YB6G3L6r6OqP\nHH4omX64A61hf1QRijXdi4z0qSYbfsBj4NDrvDU83mo288NrtqbDcPlA5LymPVxAO6PIzpDeDjv8\ngt3plNu7U5rygP0Y8tnhDVempDJeY1nwcRRwt9wRHwyc76Y87B8Q0SPDucZhK3n+/JirfsFaf8WH\npuILv6c6XnJ7YRHuX/IgH7mwImxjjR5LqrMpT43EsF4yfP3A15lOrVa4pcXpsxKntPl5d8OR7mKP\nXPwW+uuA8bCn1Bp6s0RlCXUyMLJqYuWSyoS+dbEjE7vR8eQBDhalslg2PbtW+904/Q+CLIYa+p/O\neTIqDpFAikfO1iFWd8l304G/VTO+++493o83BEaElJ/Yjj/Q7TyepjeYymb92uMkOWL+6FDLCZe7\nnvqzb5jkNpf7B9Zfdkycmmm+xU8CarOnMHOSrSSJDaquQ3YGvZkxHgzKtkUTFUkRUA7WrwU854nW\nb+ibDuXu0ZqA/cRHswekG+DlEl1C12usZYnnHLCNHIwdzgDbXGfjWuzpyEdz6sbGkTq+V+HWHgdg\ncsgo/B7MjqOqx88GpLIIZUmDTWu2jBubod4S+QG7wWc0GDhtgS8VcldgOjl5I+jXBobyUPqK2pLI\n0MNxKmyjo1oqnqw9B+FgiAPV2MLPHJq5Td3WREIgJjmOF5CpiDQNaAtBO83xu4HtsMCvGlRf05QF\nTwcNZSYMrgdeTGs1dH1PuzPZ9wZVbjEuQ3ANDDWid1qiRuH2FWs7BX2F4Wqs3494qEa8jwRbc0Ff\nrpgbN0yyLd4hpNSnzKyesjnhvKgY1gvMTnAfeIirP6OlJ9zcnhI5B77uLhEX94z0W9ybr3BOfsIY\nfsbZX+PJv7E67Dm623DT24jJgcsrA182/CU54+TnmPf7HPX0iZdomO8W5E9r3D7h1DzjlV1QrT8y\nG1W8+/HAmfuEebXl+VmBfGERxjd0tsXo5C3HekXyIFlZAc+2JbIS6H3Ctlpz2L9iCAziizNOnS0f\nrxzQar5sRojTHcbLHXfrGeb8Gn1r0aUaZWowdVwipaHCEg0HqVvUpY2VmAzeiJ0cEZoZwlUUvUTI\nv5MCpyF7ricu2vDIw1OMER2xvrYYnzxhjc6Zzg78cX7JY/A5m+9C7soJw9MZjq0z3x9xNllgbzt+\nurnnEDTcpvd8OyuYf1zjLW/Yi9eE+QX3hcYhMDiIjk4v0EwYT0z8cUdgRLh1idkp4iLDNED2M1pz\nw2guaFc+9t7DLDqKcYDZ6NTdhoAecpuibmg1jfRwIHRcgp3LSluSx0uaLsJpFJOjnpldsNQ9GqPk\nYMYwpPRmyb5sGR1CHqwKETs4SUlrR8TKRYQ7dk2IqfuYGqzCBvDYFRvMwkRDR1Q+pWvR+zZSeeSY\n9KqgzAzM9RFmV6MXa/onm9rw8ErQqw6Ru4SGxrB7YB/l2FufqGzZeh7pTpK4Am1QGFpCONgMosIQ\nBfYoJxulaHaEMhXzWUfuQZCkdF2PboKWRoxnFUaeIdqSquso6zWNfiBVgsNB56ClCNMjVA5Dqijn\nFtNri8Tz6bor1h8zbqMT6pHG2jggvlpit39ARD+hX3e8nf3EMMyZL+5wpzGFbvDlNz22CrjyWuyr\nCZeVxWPxFvd2yuzIpY1qsodnjNRnMLVYxj+yXyX85euWzXaNLx64PtV5bW2YPnfw5UdEcANnJrk8\nR38Ju53PxHMx3ZTLLyO4Mzg5ydmEGp9qi3fxlxg/2WT3X5Bfm3TO93B3w+5MMdsUfFmXiHcds+st\napbRDQZ4EY7TsL+fkFk+2bWP8dMXzOqavXNM3xZEgWDiDexNAa2BGDz8Xc4QFmge7MMWVQ8cyx7V\neQRCIq0ML/g7WVm0QjIUKZFrU5s24fGe0z9/QGQNRtJyvKkotScm4wP55ZYXdYxrXyH1Z/SHmN7a\ncNJMmZo9B72iy02CsKJ93dB99DnUjxAoFprA1nqstkJvJG3doecWdnLE0A1UqibVBqRhEw4Gmkxx\npWS7FThBSrFQqNxFaQMHt0daLiJtiTqF1+X4hUL4EX1d0Os+822NkhXCMhi6hF2boZ4adiJDHzq8\n1kO5Fn08Zix02qHHagN0bwdCUKQ6QsKgGZhqT9WV9MEUrzPo7AN9LYlmA4ldIL0NWjbgmAc830LP\na5xpQ25YJLJCN2FowEQh0g7LOKL1Fph2SqUFzMY2Oi7SqOg0xbgXRF5Ht19TyQNZ4JP6PuUauqoh\nSCy8VY887KjKCbvaQ19JSkvDlhNk61Jo0K2gGwJyzaLTauxqgd67jDSLQU8xhEtvCvoANkNLNLri\nQb1nNuw47wPE8y37JmWh2TjBSz6L77m9uOfj9wuapYf05gT9T3RvFZ3VYA4/kHwXE90PnFcl3YXg\n48PA6I8BPxXwoRuTxK85faZx2P3MKkjYiAV63BH+6JO+fs6F85JjXWOdL8neCArnK4ZzjepdSBl9\n5OHR5RALflzF2MGcKHvg9nzBzbahKHQWDwODU/L8y5q6yXnm5XiGgda5WHLgur7lwZtgh6AfPfGU\nuzwvBftryUXQY3/1nmf/kJJ88yXJ5VvGrztoTTRhkvYliAGLgnhusEkKWNZ0vSK1S0bmQCTXxK4k\nD2LyCvC1X7vO/077D4IsOtGznO55OEjCY4eqn7H7/iWHSPIilPwcBdwMEXfiIx1j5FkL3WfI6DsC\nT6PKBcZaoS4nvLD2jBcG9tYmqS8Z/fmY6cWCYl+gOxqDJRgHBrEumFZjKj8jFlvKpkVEBqqO6I2S\nWubQ2zhRhycLms5keHLpnRy73iMsh6KS1MIlcTRSe8ouMOn8gULlCE2xd0rcNkepmkw3sJFUxhjv\noBOIX4ucVV/RzDSUAzUNmp/giWOS0MEgxrYGDlWLLjyqIUPPd4jUIGg8CCL2iYXhtMjaxPXG0Phs\nlGRk2pRtgCkfEdOSpKkYdJedmzCd+2xZMabEVQqj3HJIxvQYHISid0bI2EaWE5g5+PsJg9kQeQ+M\nhUYynhAPOg2QzyOUkeOnKaNAJ2hHKKOAqqdp9uiuxNMOzO2U0NURE4Gwcpq+xhM2WiywmhrRpyzV\nBvG9gdZ/zf59QPL0xGn3GV88adxZB4LDE72fMHOOsPQdRrnj5UOBN5yibI3R44i+WaKsI+6W18jP\nHnDbO3L9BPE4Y66f8fkmpDP/hpncsXdfceK7yKlPH54xMU7pVc3bec21XRI9/4R2XpIUa866FsPs\nKJMFl25M3B5hWX+iz75lyGf8+e4jp/Oezku4da74ZnVHtQl50q5p91NYCmz9hOT9wLI74WIniCKN\n2v4D7irn20xjY+V8GG4xNy+pc58xAn//BeJthDXUEIxphQk1DDJCtDUaLodhCobPuFfIvEXHga3B\nrPXRLIlcN7S1+N04/V1kIYT4KIT4TgjxVyHEP/12byKE+F+FEO9+G//5fl6Dg6kizj+bEX+YUHQl\npwuY1YIf8kf67JFzbcf521ec/tKyj5fU4i039pS3/hEfkyVelND/5PAUSJp1Th4ayNE7rO+2qEnB\n+M4mZ4ubjiiFQroO8ZCRxR6WrtFbCqF1TISg6wBzgRxaimSG8jUSqePO17h1Q5MFeLuMyK3JnQoj\nHhgnkujQYqQdYdVTaRXjoWUtHHSlobmSXjMowhJzOUXENZ3uoSkLvczZ9xlZaNErl23ZU/UDSp9h\nlQVTwyIwFZPIRh98nHBLrvVMDRNtBNKw6bopqV6xaw/MNxld5sDQYOGhqQ5XC3BMAZ5OU2wRSnGI\nD2CPIJjRmwOBvWewBrR4QzIv0bo1812I5h2Yt4IhnlCMQtBzRt4GzdYQ65R506I0wcqN2Ts7+ryi\naQVm77AxNazBYCNNtA6a+pFDOkbYJh4V7dhAGzJ6Qq6NMafdBdX8O47bDX17TqieqNw5nfmCQR7x\naDn8uP8RL5LcHR1Tn+/4+HBNcWkxqe54MB3W9gdSo+KHuwXp6BlfK4uf2rdoRw37y09o3hk/h8cc\nzz5gDj0vkgLfG2N8YTCtaqLthi9/fMnu4DD6MJBFAR+evuT1bEMetbzX97x+Beeja8xJSLdtEVNF\nsn9O+/ZrCs+hPw55fLhn+uVXHGYjws1A3jfklwHeZcbdbMdB0zhJ90zkF/zJzzGCNRP3jLMjRe1K\nXtaKj5cVeC2mBaLoCVQFVo+n9owOPXOhmCRrLBT5UBPrko3sMWYl60oiRINmzXGb/e+BOvD/zcri\nP1VK/Vkp9R/9Fv93wL9WSr0C/vVv8b/bhpo0X+AWKcejW0wiCgElilfVGRftS8rmnC7waU8jpBGh\nEXJR6nwp7hktNfLjjlH/AXtd0l5qaK2JfAO5mnPYBFRf3+BoHWslqNYwUjXuOCAcVzSWRiAlVqpR\nGBnLoUPZB1Ldwyg0zPyA7ucMjcVeD1G2hjZSxMoh0gS9bFgDjdnR2qCPJ4zMko2aEHQ6eRPTk+Fp\nA9NdT99A3QeYZYVNzaA0RsMS30gwREnUlXhNRF/EaJrOtjZRVUbT9VidIKfDr2C3SRknA+nWIDUq\nhiqm10L2YYj0DnhKox23qBKczoCoRUs8UsPDlWOs2Qz0BK02UMGKbGsR1hmtHJilKYXZk9oDSebT\nZAnZKEfFOVbr09gCW4ywfMUwmtGOBOHjlNE+xG1DfPPAyGoIWp1sbDJtC3Ztw5DbuKqEwkRUJX2i\n47VjtEIwc3Walx3Ze5cr3+OjecvfPpXcz99xus5prY/Iv7gsZjpSFxSrHeJaR01n6NVzHoTD8jBw\nXA0QPCfqeh4/uYjqHq0/wnNtujhnfqg5HzU0dzPutzG3iwmTUc311VsmyY7Z+Jj05Sea7Bjj7Jiq\ntTk7eWS4l3x1tmP+cYrbXCMPBh/iOVcXFWkzZntkUB+nDHbJp51BrlnM3j2yuCsR21eMJivOLMn6\ng8tsc4JT9BzcDnHyljd1y+kItG5FIw2cQ8ubvML8mLAzlwyrCrlQ0NqguZRSspWSfhhIW5+6zmgy\ngUdA5Izp14KFFDhdRSVT1ND+bqD//7EN+a+Af/Wb/6+A//qfm2BaOk/lwP16x/TyC+TPJu9v/0af\nLIm7O7Zfr+nqlJvmJxq5oa6fqGdrbrWUq2nMcbAmdgWr05pkLWl2DdXM48JdMDI8xvOBR3lJcxgT\n5Dt8t8Xcl8hVQt0azFKNdisw0Gi1kF5O0ToT3y0opzsce8FITMgwWWoQSljHGnqokbQm1thAP1oh\n3TGjLKTYSiphEDQKw9KYjSZYlU6fFuxUQ1wVxKGO6TTEWUSd6yBSymaMAwggNxWe5rJlINIz8sUE\nE4tdDXVtscVARpK9XRM0DTPzgGFLRlaMbjyhFWOGrkVUFqU5J45q8scG3WzoZY6sCwQtWd6iRWs0\n5eB3FekwoXdmUGn0YonJHlO25K2HxoBNQLRNcOoZKwXKsolFjqN0GDckXskBDauW1NaIwa4Ru5ah\n7nDdEqfvMEctlTeQHgmcYI8yKtZBgZVJ/po/cCkEp9clL9sVnnFM/anEfZ4jlx5jORDfe5grwTMj\nhybE746oNzdMLUl9/oQX1PxDv+NZZjBPB25cxWJ0yy/plqduye2y5GPscTy54bQc+Mx8QxP/yIVx\nRtbWdKOWj47Oor5nt/xIqKXcfmeR/nHgPh+hXt+zXhnoI4PpuGS5K0hjB4OMV6XDbH+Kc3lPKGY4\nly33Qc2bz3/BMM/QD2t2wM8EGOacWy3mWhiM6gPF40u8k5e4+2tmms3p6Z7ee0HVvKciI+4V0jDI\nSw05BEwsE2WMCeaS0d5k3mg4hg1iQzeWpHrDUDgoq+egjn43sH8vWSjgfxFC/B+/KYwBLJVSD7/5\nj8Dyn0vS1AMvLnsWyw79w/fY0x8ZnX9F43/PtIiJegPMUyL1gsNOsRiD0zucfTrh5cFhc6Uz6weW\n5TO0oKQ9Nfj8+g1SHuHNYo6KB57vNQYHkiOPPNApDMFmGVKbGRtHUASCjW0QFA07ryFPTPqmQpSS\nst2Q7lqiKkf5NX0vCMYdVpcxanWaYcBkjDAEbZdQzwrcvSIbCQwHdGniuBY0JpOZhVvU+HmGUC6h\nVyC1Eq2smcqWQ92TjXystCeftcx7D0MaqLIlTys8e4djGzijDMM1sdMGbZQQJxDqI9RKw02WbGc7\nbEoalWInB6zMxlEeTuUyzTX2WkdTVSixoC4s2qShdiZM/R1e1bA1Owy/p+o7zNCBaYvXdjih4glJ\n5TYsyoFaSaLUI1cOVtnQFRNMr0AYHYWZYDcGnufTepKun2MKgziXtAeBW8xx1cC6qYhai41R0xY9\nxYoQ+v8AACAASURBVHzCty9NbtOazegdr/IZ8lNBcasI5nOayubmG41KT0kXOcFmjVQWxtGMbqPx\nfTVn862iep3hnt5y1gWU118xjld8lg0cNiOcu0fy8owPS4Pb+nPa/BTHr/h0HHH11PPlQWLPxnhK\nYe0LvlBLgv2UC++ew1rHWCqsTQc/PmEJgXWREzlQzjSEpfCvRlhfx2Tagsn8mq9uakarAx/2Aq9t\ncU469DTmxZPG1p8Q6V+x+HzN/WFLVn2Fqk9w/D8QqY7o6HN0N8JViqw/kJk2+mBSVQ2F80DflRz8\nEmG47IqUeKtockGbpxi9R7Ezcfn3vw35j5VS/wj8l8B/K4T4T/6vD9WvEu3/tzLtQoj/RgjxT0KI\nf6qKhID3rH6B7+0/8sNSUvQfOPhf86Z/xeqmYiOf8NUOU9mYxYyx03JLxp37HEyP7Zvg1w9w5LIc\n5uTa5/RpywevpA7+wEdRoVsGYxr6tEK6PW7R0xVjptLCaR0ioYj7hllnY/mwOYxpbYPUG1MpQTq4\nyLVP3tbUhylDUrNrW3Q9Qu6hzjd4Yx2jiGg9hbXeUFUarV6wN2Jq1TCQ0fkRuuxJspIqbhimgtYc\ncch6JvUSlCL0U7pEI+ty1mZOUIKuSXJ9hJtLGm1G89hgDRVmP2LwA6p9SiY0LHq8Gva6Q9BIGk2R\namuGiU2mp+x9yVJ0eJ1gEBX7YiAyB1q7o4l9xNjA6FzsIkFZM5q8xD6EpP2IOhvwpy7VPiNTW0Y5\n7IwKaZokfo1tAqKljyLMfGBXlHQFDAfIqwOJH2DoEnOaMiRA7LKQDknhsNefkPcjPvA3gutfuOmP\neV007F4I3p1L+jpidbyCasGff5kz9V6R9j5lUGMMRxhPkrr0mHlb1EnK/kbx1C75jismxoqz56/Z\nX6yIPk8JvD3NomF2q5N0sDn1+eDs+dO9j9GFvFUX3C583j59xUhfwOUDd48HhrzHK84xngSP0YCQ\nr2lG52w/7Ugfd0S3V4ydnHdBzfRxwfVjwftiRv085NOl4mWdMP2q56i7YZlMyS0Hq5XEZz8QFzlN\nsSA62bG76LmrA6wpDPaAI3Wy3MCpWrTDhlLsccY1bjlF25r4csQwGhCOgzMymagdo86g759g4iHG\nwe+E+u8kC6XU3W/jCvgf+FU9/UkIcQzw27j6f5j7f8oXBn5I40yx/jxjcVxwVi4p0gHxPiH4omWK\nzSSMkEaJWdi8ca/5eT1l0vnoqx8RR080n2/4+MuG4uOBff+AePYRIXWa9DmW9Y6ojJCHnnRo0YOW\ng5CEbYdbNgijQZgZhWswwkEMHb0r8UXHCA2tz3HGEl06rPUdLjp6IDEnLvNJRs4a1YMuHNLcpW02\nNCqimVmY1Iiyw8omBN0IVS7xrBKt01DNAJOQESZmkxBKQavVRFpFX4X4toFoQux4xl47YI0mSL9l\np1uEYsDVK1ZaCDQMpkJEOjPRkeothewZ9A4MgVA2nhyjJQJRm4gStqbH0AmmrcSTYGYOQRmjj3K6\nfY8rB/aGwaisqDSJb3UMRYdsOwa9xO00Cm/MximxjAHn8YmaEHNosXYhyb6hUBPGc51DJ/H6iFlj\nYmuSYbAJqoYuiOnlr02Mp2HCZ5pBZaTEyRHm0TG9qXPrXaDVU85/HIiOVszfNrx+/YEPzxOelIVt\nLlgcK5qTkqeyZni9g5tTqvtTdsstw9Mjf9IVw9mE3Xd/Y3VQzLsjNuqU9eOYTTjia1Vhxh8RbwM2\n2oHFVHHmf8fyk4QG9ocdhj3BGY2R7XNG+j2D6bC6ycn0R65Sn6PLU3Q58BCOqIwp57lDNm046Q2O\nng5U10tGrYPtfIYWa1TDkr+Ob2j2Lfw8xck9JutvWC4C2vWA1wZ4dYu1Nsg3BqlVI3od6hGzZYCV\njMk3LvtaR3o6RQFVZeJIaDKHOhqhWzV5MGPS7empfg/Ugd9BFkIITwgR/Fsf+C+A7/lVpvBf/vba\nvwT+x38uVy8U6sOW5WrF7PsD+keN12cNy3mAY3YI+8CkielmJgKdWa1RxDXaPGHqHlNXc8zvCub2\nMctKcPLhFO2dzYP3M+P+e+J3IbNUsvNqnE2IKWa4lUauwJrmrDQDleu4qsaaSFaHAbPvkbOcvN+j\nsoHgoNCHgrkuSD1Jrce0lUu91zGrgDbowP1V/0Ojp5E187xlM0rRHA/X6ajGLYncsC8VSeCipkAc\nE6sEHIWwDrSa4LDS2Wt7NCQuHeNogMYnPyimQqIbO5JdT69rGGZLXBlMNx3FzqCObArbQAwGE8Cs\ndAJNp7IbekNhyRKncuiyHE3zUK5CH2xiEVKFikwXxJOYVguwswahSoKu4DBk4EjyaYmdKg7jljAQ\nyF6jKXWGiY8mTVRbYo/2dFGNLjfUcYtLiiSntxvKRKF1HXXv0rg9ndXiFBpVJtHrijNdQ7vX+ZTs\nsD/dsF8ndB//ytMfF6zqU8rPWlZdz/Bjz4mh0S4L7t4ecVrcchy2vHh8TfGVpLYcpo9/pHrtsTkP\niXawGr/ipR7yTr/m0lrwov6AFW64jj36bU/0omHx7BLR1OgfQ7ZnT4TVL5jnBqvbWw5H9/xFu8EN\nLkhnPo67oF1M+EN5xfDewB295HwTof38kURlPOw+kHgfCGZTRnbMJISn40cO5gMHkfOnZw3jl2PU\n+RvsZsYuekPTPOJoFbPDlGd2Tz+SSLdgpjd0IeAacGgQdk2nHxCjFXWbYYaSLKspyj2hd8CMO1Zq\nRJUdMISLvvn3W+BcAv+bEOJb4H8H/iel1P8M/PfAfy6EeAf8i9/if6fpvUbQn1L2X1PNY1rrge0w\n4+fbR8Rqxn48IhY9n2SE+TLBSkZoZ6C2MYX1iLvY0H/5nPczne3CZftlx6otmFQWzZlHctFwd/kJ\nXTPZmQJZAoaOblkkqY2jpWTjmP6pItMrLKekqwtkC8LwaJVN65TsxpK9aaNRMe5c7D6mcTpkKxkx\nINMRfdZT2CFdqcgiF2slyZsD21KidzXz3qGrBoQ0GW8MmDrQWjS1RVNMsVPBeKEYa4JYW5GaLrum\nYWQnDKqhH3qCdM7I7vE6j6ax8ScFe9eiDXW6pCdIVwhLo08tkihgp2uMG3BDyLoJLAaW3YhK1RRC\nJ9FSJv2WZuVjryzcek5l7Sm0jmKsY1ojqCNMcrraou1LhtZE2zYY5kCobSkKgZenHCxBm0/xujkd\nE8yxhuYqignsIhfbKTGbnMzJafcS03Ko5T3dxOc2O6NJP1Iub4iuHOwLxddjQbH8gt13Gs9P9vTF\nEUF7gXMW8pN+xfwavH/cc8gnxLGN611Tval4Jg2KeUJwG+Eh+GtrMF1cc73VsCqJ5uzZPhMsPuQs\nJwbm5SvMYcbN6q+sHhPU8zn7VY0eRGxFTewu6etT/pw55OsS65cNTjjGLipuT0o2pwXNwyeErKkn\nFtH0lGZzRvrpgm3XsRnOeXizwekUa/mcsjVYi4hhuOHi9pwr10UY5+gTB+kvGRsGt3VP58VMLYek\nkCyaEosdT4MDv53i1WIdaU6x1Q4CSYtBuvWolElodAzOiOIgKQL/d0D9V/t/TRZKqQ9KqT/9dn39\nbyUKlVJbpdR/ppR6pZT6F0qp3T+bS5esvnqizK/Y+C0TERLeD5x9odiIhPP7jFZUyGtYJQXJtOL8\n8UDcnmLe+Jg3X2E0FedFRjFXqI9P+NZLxmi414ovVIdRCLTCRdh7OqMEdErRMw1disFE6jPspUf9\nEKH5Nfqho8gCwsrFMwR272NRo5ctSlg0hUlaRfSlRum2rIaC2t0xsgR6bzIJTZy1i/RNXN1CMwvK\nwmRvdJhKI6prEqNG9C1Wb2HrklZs2Q4KkSo6ZdNpM3ojRcqOpAmIbBCENH7P3jLozBYx9OxWDqLL\n0dIavJ7E1H+VW3QVQ14zUQ1ZbtEpg0gbMJqKbd/hBi1VkmKIObEeEIQ6UllIvaTJTLxhQflgkQ0F\nCqgLiSEzZOQxSIfOV3TtmMRYMogcPfi185YdVEgVE1UFxX5MLUqkYbLcKWqrQDo2s31AOA4AhWgd\nzC0MZoP/LOL8zYEP9RXlm5L2l4g0rFh82bLdhdweevr2gaNdy/BmjKjW+P2MxZlk9adHeIrphphG\nFCxHMfYoZndj4M46/JsTmnOPF5pFpmf4O8Hu0uKwfuTCW3Nd90y3M168ONBUd5h6xFHiEsRjXgbv\nMe4/0WoliXmHNg/RVg+Y5zuiDw6v5AHdkKyLmtp5RZC8YRxco0fXeHTM2m8JXkOatoycFV9vdxjZ\njv7QI6Ym7l5De/J4+XGO7CTpVxkz8Yj/oBOKHmW75OmAqBWLSLDLPPRRz3iAvG1I1MDItoj6AA8T\nn4LU7Ykc0MMMvf476cEJgrufxkRHNr494kGN+UWlyPUxrx5MynrGIb/kzG248CJGqmBzWmKcXeGc\nO1jO95jtJ1w/oOp0/LMvGc7g6h9O8dxjvg8/xzB8WnuD6McYiY6QgtbQ2cVrJntFAKRdhzstUBuX\najYg2oLMU3R6x5NVEpQG1ajCrDqcIaaPFJFfsuh7xsOUQc1oqg7ppIhdgSKhzDvWexNHs2CiMcSC\nke1z8CSOqyMGnbYuKZyKDjAQNKTUCIJ8T6+biLQkGjSMOKcYnnCkZChMkgFcy8FRPUrvCJ2KQrgE\njJl4CmWXWAMYVYc/6mhFSxbsMXKbYJRTJor5WKPWtoynA6VZY4oWv8wZi4p0iAkmJqH08b0GpQJq\nb0ST+4T9gC4bfE1Dq9dINaGvfCoL2s5FDBa5HSHNjEHzYKWR2Tmq64gteOxsrFbSliGdaiiLmvmn\nkuu/CN6djNGahmzUky/WvPjxDkut4OkWx4h4pOFNtkacPTB0Nlcf1lg/lEzWCY/Pdf5ovSK+eM8V\nR9j7AP0koMxuEM4NYyfgvX6BNDw2KmI/LLg/6Yh/cogCHTn22fziYKpj+syBSUVvSN65z3lxfEnj\nK0ojJNlN8P2A49szJkbOrdgxOhVkuiK/uycePeN0GLE8d3Bbi/RizEM5w9y8Isgqbi9KCl5xmwS4\n0SP2+BPBZ1sMe8vLQNEkFWP/CM4nfOwK2sZGdzsOusuqz5CVRA4asd4zcRSa7kG5Rdk9yfFAbo6Y\nbUySXUPq6FTW38sv6nqDR09wfYY5hAxlxsy+xJu/4c0/1syOK86MFdrljsdBYFUvuXh6jhXP0EP4\nVJ3QtHC7zRHfWnRJyuz6itPHmKjIcXdXlB40K4tjPacxGoY2BSWY6mP2EwO9h86o6eMDpuyYahaa\nLnE6habZsNPILYVXTBAd1HZLL1J6OyDvInpR0+qQ1AtEAlnXkHoVy9EIPSzQ9y6NEIynPls7QRQx\nWdkQFj2WHdDnPuORTejG7IcpyrYgtfB6gTU5YtByHnyP+mDR6C2yrwnsDFc8ULoudiDJggG/UVgq\nZ0gtmnyMoVwe5xp1G+P2Gm4mWI8G0q3AUT0rOSDrEb3U6NuOSjXkrUc3kZhDTdL0PDUlQ6vQPJNF\n3mPnOX1loDUtQ73FKcYEzQapBM6gU9QCQ4HTpDiuwzipEdFAwQg79TF3Al/FVLEksRXOMmByYrE6\nsng6bnDf1UQnM2ZlwO1uydNLl0p+RvPSQhV7jNUM8zLn1c0LCpkw9Aa9PWd6FzJ9eMYP5+8RVoix\nf0c9SZhnOy7yL5DTBd4Hg9GuQzccxmOLo/6Jo0cd+9jmJF/TbrcMomDdb3mW3VEHCU56x5fDA03u\n0+xbZqM9p5dv2LkhZW3T6Dbl9cBw77P0XU6DjuVuT5ZEtM0J++UTzsYmkZ9QsiYpB7brf+TQx3Sv\nz/nplzlaL3nsHhGXNe7rY+aFTWkeqOoHTs2ASZOiDMW4k4z3gvkUmhZCd0FMj9kUFJVDF1f4vUmv\nFB0laB1yVzEd/k60TrVhoJwHbJ43HN5C+GzAzB55+PQNZ1eCIRwx6D3Zm55jbYvWfMv7ZUR7UfAh\nAb+zaQ8ufrjBQuFtRsR/OCIdK6ronPMHl+P3FqZhg60YHBNbMzCFTt8bWE+SLm7QNi1ZZJLIjq60\nqRUksYEnBqZaStcMCEsntDua1KVPWuK9oBhqnLxHkwLDbai8GmcUMi6hyUvCziNxN2hDR7up0QnB\nM0F0rK0Bhx25zNmUip3usbQ6RvuOwrEprBYee2LhEvogI5+kAXOS0toh6HOW/oY+E7iJA1rHxlSU\nStE7BQfrQJDnJMJE0xoS06KPfbrJgr3y0bcGui9puoxI88jEBKyB7GlAN2GWt8y8ChUVjMSK3q6I\nTRPfHKirgFSL6AKNzRxM/YAtTSpZ0WUx/bSmaTRi36MuwTf2VIscQysRk4ZMKwjXikSl8HDN7OkT\n0v1EcfGB7vpbbk9XiLal1QomHw+0P3cM+YHos0fm6wX66U8wUQxHcPviJ668E344bwmEjvruEun2\nnHozvg2fs3mWk94r5PkNlrbCSRWbD2usyiZZjLjfFZRriJ8FlOcWLx8aysuWN2nGk3PJ04dz7ucC\n0xYYveRDewzte67KDb/MPewgZDvb0nsFV4c5xbLlvWVQr+5YFZfsZ3f8sZwxP3cZ1z2eu+bSy/nm\nzRb9j2AtZ2i7CMuoeVO11KOSKDrFrTT6OkGOJJKedJwjF4pDFRNUUEjQ9J6+nWL5Lb3Z0yRbaCt6\nGSCUj+VbVH8vwshDJ7HvHG5uG2pxS3+zw7hIEWrFkDxyv7Epzk1C9zV3jsFTNMPJO6zUoNqtcZdP\nXOoLnn7x+Oxrh09tzbmacuqOKT2F9scQc3pg0FNINbq0pG0chs2BxC/wF1vkyMZkDIOPCm12VYyj\nW7gTgZJ70KBtFH265mA5mJ5E6xTGOCOyNVaiJmp7tFwjMhzoDFatSVPptHWOLW10lVHaGU5cIWOf\nqLRRqUsmFVNTxy1cgqpEWTGZV0Ct01UNhblhZNcY64whafD1A03X4SUuWa7zWELZO2RlRGn0TLOQ\nIToQpuWvimGaZOJEDOmeIxcsc4OzVRihyTis6YuBbtORlxmjxSOqEYx0DV/36SgQpoPqO/bWmMN6\nismBQ6+jGyWGVGhGj3VwSZMF6a5jQkqPgSht8qRHlxVV61ENEcZeJx75dLWJ0Acqu6PJplTTC+ro\nhOkhQbQvSYqAV39Zcv75wNlHn7d5iW0nHGnHbH4YsKxjqqc5u/0Zrt+TPF0yP2px4p56t2Rx3KHM\nS67e1nyjbnie97hHFoN2hr5tMNI9i2BG7l9yUjzQ91t+CSu2XsZCO+NNN2JvKP5QDpjFhsnlW3x1\nxdXDc6p4intjEC0ueDGxUfEZ8nwgXD1HpQXjLx6pjIbg7JbM8vnCfGLXveKHuiN3B8Ljjqbt+bl2\n+OXVI0a1R703cC+O2WcuR9c5UT8n/Ohi2g7GyiOuXIrSx2pN5DrEcB3K1qRTMW5hMPQ1be7hRj26\nkIRhShZUjMcK2Xkklf67cfofBFl0muDiC8VXy4jw+Sse7Dn35TFHR1PWi1f0gYm71VDlE68eIvRs\nh1bXhIeK0PgTu8rmL37PZJKzefNvuHuPXU2WPMnv5x5axyePTJ15M6+qW93kQ5ArvgUfiBvuCIKP\nwhUBgt1dVVekzpOZR3064gstnYtqAo0hm9OYO5gptAGx+SMQ8I0ZPBzmZg0nkaLUPnC3zlHpV9q0\nojBaJj10YmAy1SmDhtZxGVTFXk1I057Ez7HLFmuvo5kRZVCgVVv2TYQYdYw+pAgGGg5UrU4U6hiJ\nichLJqZJuZNUrsSsKgYnZeF7GJMO0Zp0VUm0jRFRjInDaCh6g7+2tGsBZedST00aZuTthKKI6cN7\nlgaM3Zw8bymNmJmjI/c29hCwc2tcoZC1i+HYeF6GlUhKL2VynFBYLukuRtoDY7sm1UPu6WgsRadl\nOMeMetcgVUMYzmmlz3Gv06iOxo5ZawNyrtHUFtVGoQ4jzaxj8CRmuEbrpvhZhtP1RF1OOUIcFpSG\ni2v3uFlOOBTojsYJI2HS0TgdZpFimC6DUSKEgTY2yNLgzfV7duoUXb9no+ns/lAidh+4iSd8u/BY\nPHpAFX/k+1d/oIl+5uYSZHON8XrGBQNaA7PPG15OvtIXikvxiTj8xFVVoPJP7N54VPqAHASDkZBW\na6Y3Cf245PGF5IwSv/ZIvq4ZT1teGYLPZ0946BcMX3S29xMeLnwWjyx24Tv68TO72R2PxmvOjYij\nW7Lpn7G/hrzrUFiQTfgYP+HVccAzjmjWNV9vv+fHjcTfzvDHH7C0kKVncd/cUJx5CPPvaZc6rbqh\n9016uaVlTRDBLuvYiQKx0zAnGrEMkEWJNnR0QUVbCPrQQh5cjH5EpTtk1qGXye/m6d+EWAydBjeC\ndHLgxPyCa0U8ZMdvbIjTHNNv2G5dtj+12OEUf31CZkFw/gJn/iuPWPHAtejiU8qXPZvsI5Mrj4ve\no7F1vPsLdpZDEi+Q2siYgzOArlJU54MuiK0cr4BhZlNOLcI2gd6gMiUUR1JjJFAVdj3Fai3iAbIB\nSgz6f46O090GXTUUnYO7czm0CVLr6U2B459QhhlDOoKbE/t7WttD6QlNPVIOB8IyxR57MAoW8Z6T\nesneANNJ6Rf2XysYhYCxYlA2Q9uQ+xmGsnGzBmkG6EuNWh/YdS2DqXC8lFQIhmSB6Q2ovcIeZ/S+\nSx12FJ6Fr45s2x1mMdB5Pp2S9L5g1kccep2hSahdgRXqyERDZ8RoJdXsQGE4jLVgOwmR056i7Wna\nkbzx6CyP3tUQSpJpB5TbsrQVFjZj3bFMLZR5z9jnmKsO1bzg8P49fjdhInf0nUU1fc6wSnmz6Plq\nFNiLJ3zWP3P/ZeCREdB+9yPm5Vt4uMbcZXjiFffjhIO1ZXj/dygzxtv3HNSUyM3R5DU3g8voPKY8\niTlEPcPihnVfkzlPeV4HFN0CfXnBn98NWEJxf/+cuvyOZ9MEeTjwj3nLxdZlc90Q6JfIk4q3PztM\nDxmN1vBDPSfeP0S9HzCFzberK958tZnaj7j6vx7gjB+5erBjetky0QfiN5/RnpSYVyOPcg/z/D3t\n8kj67Ce41yg8G7I5VWdgOjqh4SBnKcauIWkPjJ7NYHeoxKCSNk2taIeWUTUow0MtLZR0fjdP/ybE\nQpeS8qmFuZ3zp1KjsP+Rm9szXuhTwpcjSm15/HBE/y2D6J7ucsZ8v0J9LVluFxRfnuJ8GejrGy42\nHno4Zz14pA9s7PaS6/kvnN0G+E3OiEHaGvRJRCxDZmWF1bXgTBjVyDRRCG3HbrBYHgqao8vybMrU\n9UgDjaGqCFOL1KgI84hJY5MddeoS6Ac8vUM1UGJiDQ4H4VLYYPaCzJZ0VovsDGocIk2idRZSNVjG\ngOH5SDFQly4H2XMvBY50KDWHTgTMOhsjy2lCD9vc4OcugTnQzxqkW6O6AdYCwcBgODiVg+57qL1L\nJ3cMQ0k07Qn6gnAc8MoOUzbYvoPZ9BB6eKXNNOyYFJKyy1CapLbm+HJJW67RrR2hGbHrQmQjGRSs\nw4agrjBEgjAsIhN0w6DSegqpOG59xr5HaHDsY2wd7Lajmg0YGrj+knezkQdqz/nJBffbhIkxcPOb\nxfbTlvMXNReHDZQN9AaWmPD4yWM+fJX4YoOl1QyvX6BaE5O/4JUGBg8ow3c4oqbzz5mbR+6cHLl+\ngheveFcOTIwdyp7g37bMPzxjemug1l+Ivym4/G2HJR4S7a6YvPjCzbe/0H5Y4i6uce487pxzgsmU\nttzh2gZxn2FIh/5MkU33fD2RzM1zTvu3NIcp3/i/kphf+WbZEcuAQzMS3H1E/6zT/fiM/Z3Ef/I9\n7+4tqsUDrPZ7lvpr1GnPpIeF3zNk4FoapVIYo2BctNBqdG6LcD2GaYJ0R+JqpJ5GdIPCGBXtsQPn\nv6KD8z8nekYs4wpzU/LoumD5xWZep1RbwbtNzOn+If3hhgfaY3i/5P5dTqs5XJkmedRxuBS8e1lw\nPo/p797z1ImZ9xFBNWP84ROXxoJhuqVydIrMw1EttlbRVyb72MSucvK0IZgYpI6Glji4YQz6jMgU\nDOj0iQAjxYp6DqaGb1f0omeMC/ypQWhVqEFHuJJ2BoaoEHrDZF+xKAtqvSQ+Kha6QeHm1GVJh0Bf\nBDidjzUYbFrJfkgRVUmwCwhVR4mGX4xEuz37VqOJQ9rcxdAndMuO3UFHSx0KbaQeS7rAQm0NrHjH\n6B7Qs4Hl1CSeRXSajrWe05qCsWgYowldrjMaIZqaEGQ1mlbT7meU5YFBlrh9iX1MaJuaIJox66do\nO8Wpb6L0CRNnJDy4NEaMnypE3ZNoAy42gR0QGGDFoPlzajQMYbKuoJ0qjlJDPy6ozRrbEPC04mas\nyIL3SP0R42mGt7vDdVKmK/juKNiod8zrHYddxKuTT5w1NgY/EF5+IXM2rNQrbkaXjddwnz7k85jT\nLXyOS5tyeMDJ+orVKuLp6HLYDmz5M5+LJ1jTO8rvFeWlx/mvR9wXEc6jOw63Dsa2RPIj+1cVInqK\nOZpo4pptfMIq33J7+xDnxZp0YXD5PqNpMlwv5jg1qL9p+Bq2dNmSM/sbqkXFulA8Ks5pkil/eTGQ\nbDWKJuVFemARljzb7wjGhncyxilNDrHDOtNxrJxOy+kDnUJ2aNWIZnV0+56mHND7CbPRZW+PmPlA\nRMDWKrC8BF//d1KMbA6Kz+qSbWij1I84r2xu9QWfzipe5CWHpKBpfyIbbvnHyYrlPGAXbTC7n5kM\nI566Qhk78t0dVycu7zRB6hgc5MCTt09Z+QGmNkUvTYxYo+w7CstgGFvcfc6xB9kJpBZRpwdCUWF2\na9qpoFM9zfHIzrFxlI+WuIhhQEs1Ot1AlwI1tJj9FENvEceCcWeRRzalE6CPHr03wTwUDGZMW6WQ\netSVxs7MSNORYSgx4g493WBEAe6sQxMS0zriZw1eDMUElDNgyZ5hUdPfF1SHlBPpMlgDsjIYxhxX\naohTBVWMVmikOpRJw1hbOHXINqyw9zqZrmMdakJrTtN1lO5IqwS9UKi5oDcVfhsy1Cc4CxtleOUg\nKQAAIABJREFUaOh1Qit2FBYwbNGKjt60KHyJ1Ld0kxjbNglai7W9Ii1zmnTE7Cq6WqO1W/Qhx5uE\njBuJO7RkaLSFjrHeUL03GP7i4R2+5WPzM68Sh3T+gg/Xl/w6GFzlisnmHLSKhXNHcfiJDzuftx80\nyrGg6EzcxTXiuCNcfcRaVMRzSG7u+SINZqc7fhYmPwZLPptXuMMJF5/+iBN95uDZ8PoN97u/XgI7\nfL5FWg84exihJw+ov96T/jxC/R59qhF2FpfDyHwZs578hu9+R/8243p+Rzh7yeG3zzA5EIkLXpzu\n6OwT3r2+o/iiCM9r1rMOUynU25z4VPIkeI52CY/qC748e0o9mfI0X9JkLdaYEpoJe0viVj6qKBiy\nmFWvUdSCbhpieh2DnrJuFZGpaHtF09rIVFD0E8bk34nPArNn9qeS82nO/aRmeBuy6D7yqv7E5/Iz\nfZBQPb3DedLz00QS3P0TP7g/oqIn9Ospc/MFYd5zfWMRMWIHiuN5TeVatKbgwXjDquxxywyn32Cb\nNvZQ4Z5Y1Lpk7GKUnbOtcmbKQ6kBMxCY4kgZ6FSDjnvMqMYWa5lja5KVZaL3R4ZS0boOBz0n6XK6\nVuAsE+xDi6NLKn1EjC3oDq4+YqgTSk0jNCImOxvbl2TDiC4ctDjEygRO5dP2CbK10N2alaZhZjFG\nfqTJUrRMoAcdU++ELqwxqobGV9DPaPdHFkPLRHUI28drwbYrWmvEHPfEusnaE4jWZadi8rFHJSVW\nU1MZJZXp4K23OJ3HYWLQmSmyLhmDAYYlo39CXlfUg8TQWo55w7ys0JoTnKRmk1eMhssii3BaA8wR\n28hoYoV17Kl2NsGhRGkjUvhEYY49KMazGWv1jqm/Qa2+oOcG6sF7RH/FM6558CRl8I6ocsfX9xq7\ncsZ4KngUFZyb1+ShxHtxRpk8xFUbNnHIeA+7UvI4mHKxyele7/jmG5+qrAlsAV5M87il8ELW9x3i\n8hTzWLPoHlHMYsqvR/JZg5Z/4O+7joU74V31mMvDjuFhw/rwC30Rcl55JMUnElegohMO1Rpres7j\ntc0+CbnqzkiCD5xGEdJOqG5fgDBYPTMxGw3zTyXpds+v4ymbH1Z8s7qh1N7QBvcI3aHSJYUuWSYO\ne6FA1tS9RaiBbijsKqcqfYLjAj8pwLCo3Qbbqxm0EOeYoab/Xg44hcFZULGTVzzqGswxoPG/Yb+V\nBJ6B7ZYY7Q47n7P5umMYNd6uf8Zgy9XyM7ZMqe0z5JMBbTtjefMW7+AhB/CUxv0nG63PqGY+gzGi\n4prKdlnvE5zWI57qFJrA7SAhBf2EurMpcoFsYNoW9DMPK/dYpza6UzP1oMej1XrGlUQTPn7o4lge\n4jDFjCS6ONCGLbqpk4ucbQGtc4cUAttOKKMjLXuipUDVMcNYIRYNfaWolzat7ZDWBlExImSFa+kc\ne5NpqVM1IeZuS4WGFbqMUiECjXrS0+xOqLuOXuvAa6joESpnUD6VLli4DnPtgK0fGJ2OUvOp/IDJ\nxMITO5TlMsx1hNYzbzQK18UfNY4MDEaPtnAxTI1BgllYbN2eoT1QhjUeS0y24A4YCxdbg3Y3Q2sV\nmgXu8ghthj+6uEiQBiIq6Pb3BFHDm+bIb/mMaHAZ85wmgjv3KaZ7wqJ5wkQ2HHuD8eTAlM8EIufr\nqwH5jyFf2prY29K8tAknEzqVM3deUF3bzIuR+HGM+b5DO9+xun1Ae9rQX3+C7oDuXKKtdhy9JXfl\nF5rbCd3RI74Lqf9wztp5QN1e0ywKPk8qcj9mWUmadz677AmlP2VSrfhmdUdzdeC5+QGKLU34DutG\nJy0Vq3vF3mxoH/yFyroi/XjkO0vj0/Mj0U8xL9N3RJsZghBv65HVEVa8xylcxkyiBzVuayCEydRd\nY2g+ovOxzYF5Y5KOW5yox6oN7EZyUCUnYUsjbKzt8nfz9G9CLPRacPBT8o9PcC8ssr/L8fKORWAz\nfXDKodVwvgT8ZRxwmifsn8+4NC/YTSzCtcbq+iHPyzX6bUd59gFzN8F7lPLjxxTRXLF/9ZTl6RnD\nRmNv2NT9FDPLGbWWRvS0+xatdzH8gmjuI9VIU440YYBo9lSaoJUVtqVh+hWD1VMYFcqp0XwH8yRD\nDClWFZIHGYOfkhgNWWXgyIJ23+I0IcPY0GYWunugRiCkx0RT9KPDWGQoMyQvGvr+iKEUoskIKhut\nKZG9iVn7nAQtSiToMgMZ4+gNpaE43fg4eYI1Ko5KMFgSXVq0UhCaAVUr6aqSbrdhX+XslaB1HPSy\nxfNGYqekzzPMuqWVFn0psDqNlAEbCzPpCcyObLWjrwf00aOpXMZZiaVsLBGDMGiDNWnlkhQF23ag\n0DTqoGLQW1K5oFU+aAF5mJMcbap9Q3ufcmHM2dgvGS4NXj6t+Mti4PjeQbsOmYRb7vMdXnDNXfQt\nP541RM2c6uecN/6eyTBgyCN/LO74XLsY3YB7veJ5P0ftO1azjOPkB1bs+TU+Ms4EL/QPXFY1eb+k\ncm1eVSaHs6eMYc6DP1xg6Qli4fHz7Mj+/oZZKjh7MMGWIUd5wuIfSlZnMQQtdf1PGL8qHlxISs1n\n+OMlt7bO68BmTo/jOXzTtvhTHds+4RBaLK9/4Pmk5dDeYNw/oj9codRT3GnF5sWE5w8fcpY5rJRE\nmA2uY9Kqhmw84tYRY2pyFCtMX6c6RuymGZqh0zsz1lIiehu/H7jPArwIRJD9bp7+TYhFbXUEJz/g\nPd7zp1vF+k8NW7umCB/wbp+BcUL7wuOFF3H92GJ2OCNdWjx/nXPmPkT/5h/5uvqW6omi1jykbLlr\np7QPRzazGO32PduvHVgbjKNPUA30OMh4QC0LMmEhKonsLRJh0dQangoYDj1zxyXTJtDotGNNs/Fp\nSgdGC99V9Gsdu5gQ4FJMtvTKw9XmmKWAYsBIRxJbonDR7JbO0gmdkKz0kceB8V7Q6wfwdbp+y1Ro\n9Myoeh3T8+jlkUMs0dqetGupZEC+8CilxvpEILYeRpOj4hTdh9ZcENIipYOeZETSoTjmdIWGb4A5\n9cHJcByd1lDoVohh96i+onF1shIGv2BoB1Sd0tkm6XggiVyOumQeaMxkyjA06G6NVykapyJRBd6q\nR+U2k2jEnygsfUNcavRtg93DPN1g9zXt1KVQCj/cUAU6xekT7jxJ+67HfJez/nzDy3+4R7NbtBdb\ntI+PSLYW5bFn2giG3TPeZZ8Ry6c8f+1BGUL8PQftIZalIZOHZPKCd39YkeQJzxYBeb7iMvWZLw0+\nFed8XbSQTnjy04xX+oJErniRGFizGc3PDaf2DRN+xqCG7ZKP3x25E19x6p7v29dozyT9+wus6T3W\n5Tcs9Yxu1aLOHlHsdSpXY+7bGF8vuCk+Uz03eJb9ymN1TXytEZy/5l04EIqXTKK3GKc/cP+44tqK\neOVskds9g9LwKh1lBJjWiOp9RGNTRyOaspk60JYDMjSIxgC7sMjKhIVxwAlyct8m6ju6THCord/N\n078JsTClwWuhUU5P+an/wvDdgieXX8j3CRdzC9uu0F4bvK995nefeX9RYxcKxo4PzzT0Dz8hliXP\nPzzF+CyodY2TLCdZV5gVxG1EuRBEkxBXDHRFxig1/MogSmOWXoqrFaRqgDwh11a0vsTWc45NSGgo\nLArGwUTNWpz+SKxC1MZEc3cU0uSgFWirOdbaJxMbyqoi9hW5JXAxkMuMSSMBj3FXcTJKxtBnPHGh\nijgkHXNp0LoT8DOCIWC3MXADwayzaa2B1tKQY8lYO5jKxhsPKH1AGQbSmCPHjr7rEJ7CaGuMoSUr\nKvLOwvAH1p6FcWwZShPhVCwKHZst20ojlT5GLhjsJV6igaljGRGB0+KmPkaZYI4HUt2ibxZkckA0\nA1nrQ9LhGCV718K0YVzZHAobr5hCUOH5Cs/OyCY6hypk3GWIQbHrJ9jWSHxbsDfA6m8QScQ6EPyi\nXmI/GMmuArZnb7m4tBj9H/gYfoBvrzmNJ+jVNd2Jx8Ir2PYNnw8aaXzLbO6x8H7F63viy4rP6Yqj\nyPm6k0RiYDzaGPFL1OmWD7/9wrsPn7gZLa5GRftxxc38K6lrU3FJwCnOA4F9lUFhMekjZGRydTPj\nqfGOdPWQ71cf+fV84I35A8v7kj8uvvDoxuZ4e8fH8BZ3CPAOBuPyjD+pM0hC6q8v+XYX8PW7Hfmp\nR3Z14Lvdnm9OnjLcP+Td6YT8bAC9Z9AaurRDNRqnpyYzOZLODFZpgO6VlMeKStUEpkCUGsXaonIc\ntPWAEZVI5WJI43fz9G9CLNpa8XKX0vyTz8+LmOB4x89vW9LthtmvW86EYDutMJc1tXWO/bkhv074\n/N2EJ/uMRJScXsEhzDkGGc4L8ERCakbcmwnmtxEBI3XfkgwGlREwUx0mITJsabUQY3SZJRGxrQh9\nnzHbUwcuulPjDAb26FDZGno7MnoRuy10c4Wp6/jVHquuQWvpTht6HELlQ20jjiFdn5BnAe3EwXYG\nSt0hNWvUvkYdobMdZrpBolmwXWNmDbrX4ZqwPYRQOBiq5tTc0WaCsIKiGqjagGOjowmbpFD0zZIh\nq+mETtL0VNJnGKbIRY022sjRxe0neFrIWNjUTkWlZoRZh5QFaeCwYE8/KHS1Rpgpw71Pr9WEDBgH\ng0j6aGWG0VsMjoWMSxbNnKhXTMMa4Zsk5ExqjaKWNN0UvTbJCwu1i4m8FsO2iJ2BiTsgcphMPGZv\n/0+EGbCSHbN+xdm3A8WHVzw8yVh8vGC/m1DWv/Jq+5KP6Nx90Pjg9tyaLZ/KGZGrcS6/8sedgyZ7\nEk1x+XrJvDvn0WLCZTDjm2dLdJnyQH5gMVyTvtnx6PGM5/o3GIs9z/fv0YLveHb+mPw+oj8NqH9z\nualWnD7uGNMBYfyZrBv49skHzOEx35m/MT6eo3285LFdkyYbhqPPp35N9PwpF/ZAOtSsZcGmSHie\nJlzYCfJlQSl7FqXOcpDkLxPIX7E23xIHDs7nFk8JVF4zpgpX75G+Rpp2VG1BMByYiZygCplQ0A2C\nnaYRq47SL6lymJ0a0I+M2j1e9F8/g/M/CxzVsPKOXJ7nvOh73IOP/djjgeXxi6/x+v0pT7IGKQp2\npx+YPjJYPlly9v4B+82E+dMGXd0xqRRNKlCvXe6HF8hvY+T8GV55jyUktrSIvRbDSVi1FTKHQjQ4\nWkU7GUE1DFqANTYI1eNWNfbWJJMNpquh7Byncci2BX3YoamMVLmkuoPjWVhahS0KprlHpmyULXEX\nRwzDxHI3OMWeYluBZeHrPpF7ZO9pOKJgGBr6rKUWGonjsOtaSk1gmbCdtJhNQNGaFGpkNBq0uYV+\nzHEXB+z+iFvfk3iKSG+wipxIeGhBh21umVchmq1j1A1NAM6Q4BcNXuHQ9wek1zDuZlhdx942GGMD\nuzZo2xmuv8FwW3ZlTDXXOMiEhg69G+jSlsm25G6iUFGESGIcephNqGcGysnx/JG9r9GaNmGQYR4H\nJB1ZYVB2R4Yxo7uH9eOfGA85i0wwWhHx8S3luEPenvBlOlLYHdHEZ4g2+P0Z2uOC4R6CquPkoDFJ\nak4Kh9WzEF5/QAU+n+Y9g9Yhr3W063s+8povVwb1eKT/Kkg9j7HO+ZRc80A/5c+vXF6Yv/D+tmJ6\nWjHfXzObfOQn+4Sr9oQ5j6i3Du+ZsD1O+fB0w9XknLxyeHy6oms9/LDkN3fCRfs9bvOarXfJ42iJ\neT+SJyPVaPLVjNi//oKxGCi1jMP9I57eT0n/ruRF+t8yRHvEk1M2nUC6MV7dsJMLslzgiwJtlOjC\nx6hPkINkiE2ctiaoBw6awBQn4HfU1UibtbTDnN1g/26e/k2IRSctHhQOu+MXPqkzmqqjWj/jejEg\nn06wz77ihg3mPuT8TxZV9pa36UfEg4bN1GDyecWXPz7AWKz4SfO5UzGPh498137mMvzK9XXEQSk2\nyYDUE3rNJjrrqOcdTWWS54pRH8kXLeNR52B7+MLBti1Kp6W2ddb7A9PSxjWOeGcBmiUwjjFm5aCo\nycUUTdM57nQOsuN0MaIKh0qL6fsCc5zS1C4L2YIzkOkwZAqh6Vidh/JDtCAidhaMlcmsG4m9hDFu\niIqEo5lT6QbaPKAjY3JMkZOBoYkpjx7l6OBWDckUdN8hsyWqbLF6C1V2NGWJFDamJejHEDSDQ77H\nix3SYIrRD1hWxZjpCG2kij3c5p7RtRiqOQYD42igH1qKUCC9gnjecOfanFKhVg5rcop1i5AZVb4n\n9Fq6oWW2l5yYklILqdyCdQ2uM0GOOkO/5OhccblZo/kt3kvFTuS8qW1GBMlyz+BpTPIN/vgAe7dm\n9/4T3+ymXDxZMrN1bD/DmkhaTSdQO/j2W87LkpkJw8rCubjGORl4nj5A9SbeiYFVL3i8POK0T+hO\nluiRjv+lob5ReHqMO3NpBp2JYfLmc4twK+7GWxpN49upYL50eV4J+t0R7WqHcf2IYXHLXw7PmVz1\nhFZF8/4R3etr2rlNenHK3HmMbVhkIqSIzvAwuNhbRGcfkLMzrI8j68Uv7HTJorrF5wbN0dBtg9jP\ncfQ9Q6lAtmSdgVrkjDJh7G0qGVAYiqhxoeqJRYszKo6zEzq3Zb7/d/IbghS8ubnl2emAbZscHt9y\noa2I2jNm5R1tJtgU3+Ks7tg+79A/zJDWwLX/Fmupo4UXqH848PrTD1xHBfHYsK4X3L1esF+95MLu\nOC9cNENHSyIWFhR7G/Y1vW1gRQHjuqXfxJiiYVLCoffpNzm6MRCmHVFvYdgHDv4Cq9/gJNANNp6R\nY/YtUr/j4GrEw8ho7GiyilKMMAz0IqCxt+iWJDElQz7Qyw4j+Kt9+77tGDOFV2woyxWBcSTTWrRO\nY6wkYjxBsydovsdkVWLYHuk0ojdC8jzBiVoM3cPzNdxco3IzWutArfmMjo90DcygJHA0qk1CqlVk\ndk03UzAahMccZ7FHq3Umjs1eQq0qkthntxmoqgODbeAJi1gzMeQMHR8x2MyHktUBVk7P1NfwfJ1Z\nIYgsgyJX5InGdp4yqp5apcg+JjJK8hwCa2SQismJZLS3HITD+0OG1ihc6dCeZXSNhRvsuQD+1Peo\n6QQ9eMEv8RFxv0ZLzqlNyehtKdoee60Qn18jbiXjuMJI36D3OR+mki67RTyw0LPnDFXO7sNTvnZ/\nJp5qdOtf0S4eI+sfsa01RZNzr+ccT4+cWQneV51lMKeVBesvKfYXndTtUN2S/I9zlLUhixUnVKy1\nO+6VRftiT9rC7eYDYl/wNbrDGzouVcdz7Yaf7wp2Q8ip/YSrbCB+otG2f4+4ukS1LZWnMA6Cld2Q\n5h3KVJi6omp6GhNU4lN7A8VwIHYVWpciDJNe18m7DioD2VRMCxuhp7+fpr+f6b8fclAsnW9JTAvr\nZothPKR+btNH0LUXXDzcId03NE8cph+e8+FljHdlMf1NYr2uGU4tuqXB8/YjtT5njH0eSMXU17E2\n72kfndO2GULTWdsWhz5nHDTybsZ0pzgMKzrPwzQ1ElVwUBWuIymsCaneocuEJB5pszNIKlACYQja\nSc04OkjDYew1tDRDn/ecKZO0F3T+wLjpEb5BlfhsbR0RSnTtiDbCxq4RRoUmgemWLLAZlItPAJnH\nqGk4eYOlBoz+iFdsyBc22jASFSZy0NAXOtVQIIaB9NAQuCGucJimIfYwIGvF0THRe4P6cOS4mBDa\nLU0TMUnmCFFTOw3ddoqyLI6N4jS1cGod0ZtoukEUwcQbGWgYA4eJoagHk/tRp/EDdFvHNXa0Wc+q\nrckMDyMLMAwNzbaZjzZUCZQjsq/JfINwUqFuBmw9405MaT884bD6wmV+h6pOmI8bWmfCRFxwcezZ\nBBqiELy+Szmv3mKsR1L1hL5v6PY2Kzmntit+6y3G2Gc/U0x3D+jlD3x8/Q1e0ZFqA+a7KR8PBdV3\nBwa7ZN484+SdRtg94oF1x6flP+Hcmmit5FndcpNccqMb7MOQ/fYe/eiw7GJoP4Bt0n/zlpNa8Ytl\ncfnJ4OzZkR+zb1nkX5h1JTjf8+P0KeNDWEx8Kjru4wOrespZ/Ef8pwbptcNZfsS2JvzB+ILSJKP3\niOUuonC3GLrP2AV0UicbHAJnCUXG0PX0rcmsdjgWPS0Ooq8x+yNucco29KB22Y0dpftfwMEphPhf\nhBBrIcTP/2L2/9lnKv6K/0kI8V4I8WchxN//WxbR6CPGN4K9bGhMQZh8Zt7eYfWfuThs2L31SYpL\n4i8lnXqDJT9y+PHIdH7BfNrz8erIcrCp7YrlpwXX6gO/RHfszJbkUUC2usOxLOyhZtY0NGLOzHWR\nyw3NLMNpQhwtxW5zAi1EKyF3jnRKcmKZbHwTQ3pYAShRUG5nyKpC9hU7R0PWEkeMjIFNAiAnLAUs\nzSOdPyB7HdOtCJoj+s4CzYD9yNg4WOkJGAIzB+fg4EqPznKRQcputKgmFseoRhkdfeehJxZtriM1\nhdGn+K1krD00s8C3Te6PI6teY3RTBmOkdEr87kB1kKhAZ5mUdJs5mjUg3ANG36KOOsEwcGgNVNBx\nYMTSfOgFnu7Qlw3st+j7nm0lkGg0uYafpciuZhInNKODanV8d05nHSimB/RkjnVcU2wjCkKG2KUU\nNU5tU291ZNAirJj6s8/+wXsyIWjKhuuVpB8SsjuLsr+jNaYsbwXPT3WkE5OrU5Q5UE93vPFalg8j\n0tJCPYh40rnUX+A0/ZbP/Q3vZ39BmTdYdwa3XYfxKEOOEUH2mPZBSXVpkJ121Jc3pL+0nJkL2vmW\nr2NBtnjMWX7km6Hj++yWbmKyezKytU750zjHfA3DrxO4MVg80dlFJl3vU7+UpJ5Pfaw49Wre3n9G\nvEnR65jj3MBpbNxMJ4lWFJ2Ov2xxJh61lrONX9J/6/JQOoxuRKBNsROdSbSjG2s8zafaFxieSa62\nCCS7cWTQBAYtx0DgDAV5lxL3W0T/V+drLn7/vuDf8oX/Ffjv/oPZv9Zn+t8DL/75+R+B//nfsghd\n9BR/qnlofsfjRyX+7cDxlzmoM65OnzN76uEuB24cSfCqpi+e8X1hYiQeQ5pTdxmf6oSVOZI9fc+l\ntoDhOY/mGUYqaMeaVZTD2GI2KUbXkI8Fk9bF6yzcbKAeB3anDpmdENsjofLAL9nfHwn1mKESVM0a\nq9EZlwJz0qO3ME8TaheKOiAadeIsJBkGCB02dUSoPMaqRdUzbGlTOg3OGNJOBgIbsnhAaTs2uonF\nnko2KFFi5DPcdI8nbczUpkZH2g6D1WHYoKwDjiGxJQR1CbVJZqWcaCOLpKRpNXIJjjLpuwHdG5DZ\nQGvluNqGaCho8inrxiCaNxz0jEWhM6tdOksimh2mW9PLntR22FsL1MwhcA7sjiM6LfUwx7FcqEM8\nXWHGPY3WER6gTSf03opEhn9tj7calprOEE3QXYmr7zmOEpn0VM1rrq4z8tLiTWBiRr/yPvUQ65Ru\nSGCbcH0O+SdFuRywnt/wanFKcDvlaXWD/PmOfntkZ05ZPRvRh4g72VGIiheXE5JliRFPeenpnMqY\nR/2BetMwr8/or3USEXCooHgVs0p11vpTXjqXTKsW5zTn7tVjEqNiOL8g/OUJUf1PhHjsFkd036V9\nCHfbO7LYZ3Odcb1Lyec663DBvv/KdFywlAvaomDVZDy+veHgnDNTJvbXK9rmPTfzI+dByCM8/hvX\nITM/0O2/sFMF5jhw7GzMegoyQTNczIOHciWtBYNrYYwNnj8S6JJRd4lsn0JGRLOOWe3hVf8Frqgr\npf534D9M6P7X+kz/B+B/U3/F/wHE/0/h0P8fjH4guewJ3r7lza8zrIcBkWfD53sa3lPfbqj8DWZw\njvzoYK8Tjobg80OB/t3I8xOHc69BX1qUNw8YZvfEMoG7mDFOENqSaBehtJ4iOMXubAZNo1AmaR4g\npiVwgqTAaQPGaCBtEjStxQmWaKrC7XQKGeOc6Ggk7I4+iQ1JILCsAlfT6JKK46ih54K7tsHqjgil\noamOWB5JmhrbhmOREx1r8kZCKphXMZqCsVeUeo6hTPS2pI0n0CUY7p4wbxg0QdRW4KZ0qcOwHqn3\nNrvQ4BD52JikvcUWRWVHaPXI9tBysJd/zQc1PI6ZSWJBFijcaUfs9myyEd+U5NGBtK0IOLBpBvy9\nhXBbLBVg1w1DmtIPS5y4p3NKBFtULZBNgW4Iyg4wGorepO06RlehnwyM9oG+DtF2O4L6gKllFJGL\nUiZiAhdnFo99h5P0PYt6g56/QtN1OmFSiR+4z2L2tzHLuuNFfUHSW8j4Z9r5mk/Hls/f7PhDXNC/\nu8I6tnwJMw7pR57Mf6L/hznT/ZxNmPFl/JZf5cj7ds+h2zDGA93pNV6+4ezWwTymXJz3nHufuEoO\nvNuENDdPOX2bYIUmj25fk3i33D2eMhvv0DudSz1A3VtcjgPB+gOdrhNEn7hoJshiwzKpmQYdH4JT\n9MzgyW7K18c/8fRsxZ3R4cdPGeYOTwe47R5wz47XVwrXXjJ6p8ybCDkrMNsIx85Zx4pkvqf3e0Rn\n0ncestNwRE8rY5KupQkGOgFKOyILwd5UYPxHQ/b/o/hP3Zv8a32mF8DXf/He9T/P/l/4l/WF+6xH\ndyp+GyMmcx9tH/I5zgibjjA7I3VtrJ8riu2AdfYc76LC3Z3Cuys+i5a3lo3ZTJlvn+Je7MiO5xTC\npX0V8LK5YFkPKL9GtC622JIDWnoklDWYO4pqhicGnEEyOhVdF6J1PvoqQhZbzDQDsWfSFkjl0KUz\nFlPFYEhEM6KJiH2dkEx6IqvCZmCqSxqzp3Z62landzQ8z8fNNEzdR0QhoZETBR1NJfC6mHxY4Lc6\nottznBnM9BFpOtRlTCnn6LWiC0waoaFFKYMwcBRIY8LC3mJXGv64JbAVJweBV3uEUwuZKnxLsOj3\nzCKNoZBociSRJprw8bQzMBV25tHPC7Qswg6WFLHFsRsYiiPNtEM4M5y2ozlo+I2DPwlVDv8/AAAg\nAElEQVRY2TnKWcDWphocvI0gki2Ls7+eeZj3NTawNAtGxyS1Z+wzA3sXYOg2Yz9yu7rgXXWK6JaI\ntzmuecXp/YaLl++5lF84HyPiRUL6dyNtsOflek63m+I4Z5wTUcnv+LoQnD2umN7WPHkU4kWSKtrj\nLT+Rug3zXJFrI9+io17NOf/uIXdXEtop6TLhWj7F2NcEtzGH6ozQMHg1XNM/NLhvH5LuL1lPLtDi\nnsefL7AuZyTTBfpR8tvlNZPY4KCfc5gdKcrnvPm/uXtvZU2WLEvvcw/O46eH5knOLqtuGwjQ8RRQ\noEADHgkPAB0CVIgQYD1V1ZfkTXIzz8nMw34enHoEhGrDjBnQQ/oWpstmiR4ebq6sZeG+d6zlSB74\nS6xHGm1lE4YHto/uKZ/3TOye93uFyGI+3L9j+/NrjMkrpPEJpXloT0JuvkS0oiGfbigSi4oEXY4s\nmhA/GYgswRibuJlgrgSdjHFliXA07C5EWQXiEKCHEreTaOPiX0j1f4fffZD5D+WZ/kfe+3/iC33f\n4/huwflpjDG74ZezO3phcf/iKbV7yWsbZk+f8F1yxe1qgzRrxuIW4U04/vEY69Oaz43EVg3jRud4\nZjCVMTPL59rbETz0/1KzNw3qwsGkonYWrHITu9MpRYkpd/RFibkyaPcSxyhxZxrZwmP0IkzXZxf4\nlDKlDQ4c1jZj72CEMWqToGkG7mixHwvSsaFocszymGGvY8xN0m2GomcULqk30PV70kTQpwPD0CED\nmPs7KtNhLQdCY6TdgpFrGEOJa0t6MXDIHZx8Rl+dkC4kBDsmY8mmVhw6i0wq8sohdwtMs8JuJHoD\nJBJBhBQurjZD6zRk2tKuUgx9D7agbRqG+5HaTDCdAT3NsewW09DR+4pSrSmUZAjX5HZCvS+INQNl\nCg4Tgaw7lG7SeZIdDanq6WONgz+wLWrQJ8j7EduwKP0Ssx7JVneMh1vOxjfcWBuKyRnjF5sPr202\nV0ds9YZ3YsDtYu7fXdE5EcXcZ3V9yuR6S//iiLr8wuLdBDE+472uk3/4QvlEsul9bovvGAJovWcc\nO2+RTsffFQPZfsPJ4o6LfcK37hNOHx0YZyb76a+cXV8TXp3x5ixnfXnPfJ6zmL3DVBOsach9q/PV\n1lA/m1x+oxGPil/tCYb7iYvVBQul8+LqhhuRcGc+4cNQce7k6LsjJpuY97d3PKkj7PuUJ5rOQn/P\nkXHFfG1j1PeE2ch0dkXclnj5iOkoXLclR5HliraTtBUMXY0pGrLehKGgVS56MtB0e9qDgWGV3G8E\ngZFjVOXvpfq/WCz+uTzTa+DBvzfv/J/G/oNQ5siY77FUwDKvMYZXPLrL8T9qPL4+4aqLuJL3/Co8\n9rMZ4U3M+lxx/CjjVrtisjjiSfMbV5sWr55gDyU112xZwyDZv/mEO5ygG3uEbmJ1PlNXxws0DrGO\ngUOpD1iliQwl+nKgGT1EUbEQkCmDvuqJNjraIJjuetzJimNy2u0Wywqw9AkqjYilSSAHzBwarUPX\nJeKgMYumSKHTjjXzZKBppgRtjDOvaeXAoW9Y1w6REEzigH6dk1ga1WjSSEVpVIxWgz4IVsFAomVM\nkPSlyfbQIg/H9I3GqMCW/V8MUgyHslKYtqSyKwo/Je9AV2taQ+DpJVngkuo22magn4ZwFKHJAbtr\nEH5DfA+lnVMlMwbHo5M6lgbUBmI6Yewd1HiHP+p4scDpTDS9w6k1TCuisQXuMMPzQ7asMJwDZbvH\nVx4lDep4gXOa8SY5w5mllIfPxJXiwY9nTB8nPLQH4ukvSGXyRHvOrHvHoF8hv9/D6ZoyTfGqCzZP\ntlT7a46nR9TWM8xG4dUpiycf+b6ICA1ojmzaNx/h8z1eM+Nr5tG1inV24LY12d6c8LWfYL96jnyQ\nY3z9gbPjLflxy5fqMfYKnqmAjD1Ho8/iaMXyc4++Hnigck4OM2zrI5/Kt7w1OqT9kuXbL5y3c96P\nU1p9Tdr/ytE+xO4/8Oj4wIdTgWGYyPYlmu2wcCSlqLHNOePcZ6ssDgcHZzCoKos67DFdn64bWPSS\nwncYtTWN1UJX4zQdjmbzl9pVgEZEMuokvvsvpPq/w79ULP65PNP/Dfgf/qkq8t8Cyb93XPlnYY8j\nV5FiV+15u4uxP1/zxjvCci+pFp+Zmhucg0X8g8tJsWWzHLB6k69FyuNnS7Iw5TIeSV/cw/KeP310\nOCth8+EeV4/oHmj0VKyVj7JrhqBir29oigNWAn0lMRIPcWTRuwqqjKoV7Mecat8h64TRchnmOfXW\nhNCnTAfu0obYiNC9FJcdE2/FuulRRk+r+QyTjKTrsNwNqajIekHvZ7Siox00En9PUplEHuhZi09F\nZmnsGCn8JTNjpKgKrG5Ayyv03EXqCVo6goJ0VCRhzLz3EHGPRYJlLWgmI2OmMVQlVdwj/Q51gCKd\n09g79oZNKwPycWDmWajUYS1M5KEi2uZY7YxG5phKsQ5nyMHDMkZGbHyZ0e0E/RCDyDE0KJIZ0qqw\nR4vWXyP3C/paQ9vo+K3ASBNUnoH0UMpF9oJclmTRlEW54qA/5LlT8PmXnHJ+zK/DNb9p76k2DyjK\nh8xWUwpbQxx9ZfVWkPY58lNDdXvOojqhXtcs9YDpwcYfTA5Wz+OVRacCijzn7sZGl585+TileXrC\nT+FL7qfvME9qrh5PGD8qVrbD8qnE2yiuWkFa2px1K3YyIvlVMfYVh5M/8dPhDjwd99okTSP8wCCc\nQP95z35WsHki8LrvePbIx/j4M58fHXE9+0cWv0heJg5W+pj1xOBX/xmX4jl99pid9YL9/oZB8zmc\nu1x4BV+ERKYZmjEQuzV9L9Edg+PCwutsaqfm4EY4SYOIQ4J0JHVscs9Fs3tmlqTpdiAaorpFq/8L\n3FkIIf5X4P8EXgohvgoh/kf++TzT/x34CHwA/hfgf/pP2UQ/tJybS/xTg5OntxzMgkX7ibJ9yAde\nEXQGE0fQZj6aFzM7bEm+LCCzKT50HH0cWEYRF9aEq68bjocc7Tuwm+f4d1vM+gFmOaA7LY5mIQeB\nOTj0vYHRWbizlnZasaeiPlj0KmQWa4z9nCoa6cYZnqkoa0VkWSTFgJyGOO4Mwpa1HnMYHRrfYZQa\n+zJGW+aYmWI+achNC6vtCc2GcZziTAsm+gGzc7CMhqEC07UYhxgz7TB2Er/fIDtFPyj6MMaY+RT2\nnsHxGeWA5/ooMdKXsHIVltCp5i6et0KqiEDr0L0Bue4Zuh5daNjLNTOpIwwL2f4lB4U8wbRumWsa\nmufQeCN7f8NYxrSNj2HsEJlOH45MtzlZ7uPHksjOENJAJg2e39HfOdQplLpFf7TCNxwqbQOZoPJb\nVDthorUEgUPsObitiy5Lquljzm5/Ic/XTFvB/nqLcyZ5cTHjtOhxdp8xZ3v288/c3OSI5xIr9+kf\nCBJbZ2juuIg7un3H6NxTX+15uu5ITnLGoeXOtdC8lk2b8yW0uXwzY95eczQ+YNkX+AeD6g/HhB9W\nXG0kudFyfFugz3bsBsF0DKgWGlEeEtxbvHIeI+Y7bk/u+KZPuY0LEt2nfHBM+jbCvVc88X6iSSJG\n9xuG4MA8/wbfMXn3fM9Hb4dznuMOJZPsI99mWx67b4gnP2Aa50z7M+w+5qIcEEJjyFvsQtJoA7Fd\n05NQORuEsBmKLcpo6aoaXbaMaU4rG9ZDS9MlLO0pnmWDZxNWv7/P4j8aJjCO43//zzz67/4/5o7A\n//yfuwkhdaz4K1+zli/mt1x0IwdO6J4Kfri64X05pXVdlqs168anCwTFq5Kz/+MB6+cC9TLh0EGW\nDEwvvuc661n3Id/EO3L5gGXQYeYRkdiwqRsCa0SuJwSzjqzuCLYuSaSQg4/t1mRNQJ/DRM/JGp3O\nSalLE8ew2BkNY9FSbQZOZgNpNrIsBXezmDp3OBold05P02ks9Yb7RDBGPZUZ4pYjkZOg6hmiOdAb\nOkbl0EwV4abhblmh10tGcY/URlYHHW3qkfUj1uqANp/ji4QqlUjLwjwYuFYG9YAmE/Q9qGUEKmHw\nJMO9gTG3yYaCJVP2xYHKbLFHE6U5BK5OX+/pPQFdQ6fr6GKKV9aglSTxwCw95iDANWs6PBZRg9rM\n2VprFrlAWwZkq3u6acOk0DC6gbYIsNoezx7JfZvFIaALarr7iDY+IKQkHAWrm55kUISFYLySrJ5a\nyDd3uE6M9TblN9XSah7D5JhZMRK3V9i/PePW/ZGHvsU2kvyWGwTlDrNp2Tx8jV21+Js9R+mSjbpC\nfHpE+/iSRGmc9yBfVORrSZrtUftvCNYVantP+SxFmSnOe8Uns6PbnvDg4c+U0uKlZZIvt7iXPfui\nozYfEX5pOZyVnCoFHfy2jei+T+l+1vjVXeAsrghWZ0Q/aWB/xO5ecnYTU0UR609v6Y9c/M5gS8g+\ncJksDny32FKZC3y/R1U+WlQTdiPJxGfcFayLHg0fWwwEzYHUC6hLnWh6oGmPULbCrSvqfMQcXJpO\nUNGiVzpilv/n0vL/hb+JDs6+HllfF2gbg/nuFsfNWfQ9dXPJP05m/DauWZtv6J/mxNNblBvwUtTs\nX79jsnW4T7/hNS5DPcDlHSq75MnaopFHiMc5bQO1lmI0IValMHsd/7ii12PmekXNimiwsYYBI7Xw\njAZDy5EiRGoBXtsiSMnTDqcBaYQsNYeunxHaBhxP0DuF07es1AFHpMwLyV0RIHSbubSxNY1KG1lp\nGvm+QZMeR25HOS0pk5HMapgfYoQ5oKRGX8AgNCQmwWiCE6HWWzYqoHR7nHpAixvUMJAZGnulY0xN\n+tREa3yaXMPRTNy8ReYa1bRn5nmkuyVjnUJqYI01Zmti1x5ry8cUBXW3ogwr8r5ikfXsqg2h1mHX\nA/UkIxfQLhS6K9jNddZ3KZ02Mjs44Cp0YrxGoPyWItKxDgZ9WKE7NUXcEmEw7k0OQYktBibqQN6f\nc/t8RP+5guYF7bXPHx8tuVhmDK3L5LNJeqWzlt/y69hzMvmOf6vbuOLAi0LHOO5ozp5hyQa519ku\nJny+93hy/5ppUHJ8r+PcNtyvb1nrNZNwx9ZZMnOvuXxpM30+g+wM56bDz2boaokx+Qf6G4PkbU9+\neeAue4hun9JcH3jw9SeW0w+sE1ipDU074cV4x0ndEX0z5XvTpWPJ2ukRx6fMzjWqk5avLFmOB/zy\nORd351hlwP7VNUH9kOnok14/5OFWIunpNcUuGensE3pxTzdzsY4EM00jqBTSdzF2AjWRjGVI2iZo\ne4nfhEwChzLqybSecJAQZDRov5unfxNiodngiJdIcc3d5BhV7yjrDU/3j3lx/4UoOGVhGYjtwE1x\nxot9xM8/Ttl9+o76ZcJ8VfIP1z6PjVOS0ymPJi2c3yFCk7aJKfItZi0YK4tuGtKnCtXp+OWIHHws\nOaMeQrzRo9QMhJGD61M0B8S4Z5AzpO4xThtqzWGYJeQTHaPbkOKQKIEhM3YWTDyNTpcc3BotKrC7\nirSrsPYH+tEkpifWBvrRoJOKHhfpFVh1T28VWFLjWJsyMaccDQKzqZHyQFybTM0jjoctE1wys6JJ\nRnSvRtiSPrDphUbhDVgU6F5DIySlTPAHF1M2rNoDmp5ja8d0oUmpKzo3RqPA9gecQkOzjpjXE6ZO\nTN5ozI0IFSh61cO2x2gH6vsBW0yYrgWLBQTRnO30wL7WyIeO9bJFU5LldoKKMna5yTgIdNmztQu6\noSBKaqYywHF9vj67Zki+kD065ajfsjC+8Phy5Kc45tuXW2bHGdqTT3gPDgTfr8kyg2+v4J4CFl9Y\nfDEJ66+Itza195WTbYDh9GhP3zBu7rg/foJnaPgX59R3OsX9N7z2VnxVW/7ubmSTajzau1SuItYM\nrOhnjM8nGA9y5PMK9fApE3FP9ahn+kSnx+fX1uZitMgzC6/8zI3mMVMa+x/nXB3veDHYqFOJrVK2\nmxlfvDfMhzt2wkO3DXbnElUJvvls8cDQcC1F/GLBTXLOZZpg2y4zc4Kt3zPNfJxyjXZfszcMcmME\n1VCLjniXU8sRmxCshF14R7VzGNKIYNzRWimNbaJV89/N078JsZCdRqPeUFQOR5c1zqkiWs65W3zh\n68kRi2qDnlgIzQMfmvOR437Hs+gK1cSYZwJDNZjVyPnwhW7oufnNRXdNTjZfGcwjRlWwFhlS8zCt\nmF532DUlG7MitVsa70AdlIxWgZ279EJRT2Ks0SFsVmCMKGboVY61EjT5nkot0IySaNhSlxMWWYY+\ndmimhabrRMrHn+fE5oSNoaHEjqJ36IRDoWtU+YixaYj1ASlOMNqevmhJ8z29mdLO9xjNgbaqSeYa\npdNxaARN7+J0MwJdYzBsYtMjUDp1ouiamsZtcbYhpSzRNYdBJVRFhVQ+Y6BxMLY4Q4YzTMiCLbkB\neqeRLkOabiTtNwx9Qq9BNxlp9gOGK2nsGaXhYS9LZNOSUqHWDvZGx25M5o3JYGoMSlGGkp0lmKQa\nrnWgLhuissfLPewYhqhkqBoC/4bi/6pY3dg0YsXH+Zw/ZjO86AP/5reWS+uY9/WWY/0ViZMx+SrI\n7D8jnq04Wmi44YKPTz323oHQSjFnC5KLirCYg+Xjnr+g/cUgn5oc2vd8s+1YPfmC/DASRef8ZPxM\nMLvms9rxh/p7TKvAvX/Jw0DSaq+42JuI4pZpGVGlMTefbcqnp0xZQiN5elD8qAuO9ANfghx9ekP1\n5pS77i3WXU2T95S+yYXzlDLtmTh73Ge3LO8+U7yaofTHpJYO/Yono2T+hw3Fqc+OnHEc2ckFaSPR\npI2wwNTXtE5J3kLgu+i2APmXyhuyR9YzXH9HOBMIw8XWdPpUY3D/9Zqy/rrQBuZn55y6U4b0E6v0\nmMs+4eRGIS5HrqoCbRLiHpZE0XtE9RHzBegnZ3B4yzUtD2YWurNjvAnYDBeU9TmNkWH03zGmA9U5\nLEqLYFuDZjLKDYFnIgqbaVexLGKqssLLQsoYhjuFKLfoVsU+WpB1EmOXYkQazBzQA/KopxQa5cZh\n7ATaImQlp7Syxj7YaGnNervg0O4IlEUgXQwB5bgl0He0k4DR8BD5hG6+pastfGGAK9GLmLLXGBYS\nb3qEn6ToeocxGFTqDhWMoFrSfsI2L7G0ATkb0PseH4+t2zMJa7SkZIhrAjlBawxkKpn3MW6jodIe\nIZYctxrtkGKWCUa9R3QWujJxQgk7DcNuaQ4llsgJ7ZY0M+jaFuG5qEhSy5Zm7FhhYrU7JlrMMFaM\nTomkJBQaQXOMsBuG3qVIFU0Zos48Pq4SHr6oWJ7teHhtUWgJx3XP9ibij09d+s0X5gsT5809k2FJ\nm3bMXMEX5dG+zxirG6a/GJxmc9rY4Whrc55/YPPoHT/eumzUjtnZn1nmPove5sfvDxz3LruuhKs1\n9vKY5OeUkycN+8OOnx9MWTe/8Xkr6L80lIfneM0TzMcd15stz0VPL0e8C5+vjzd8bk8Qdwbt0BH8\nfIo8CXk678mvF5jpCs2WHMcd/e496vUD/tRfgDznMhPURov61sG0K57kf087U9S7niBzsZyarkqJ\nszXa1CBPLHAmmGqgH2z6EaTIyWtQooCsIvQjNLNiO8KGFmnX7GxJ67Q0+uR30/RvQiyU6BC+yZWn\nWBtPieeKV8GcX+YubpVy0ghWu5afH7zD3C3xVzF3asHqXhEyxYwM0iDkze0lV/Yd+pFCe/WG03cZ\nh8UHjmY2NQZlNHCQA4O7I00t9qMBcUfpe9wbDY6mSOc5pD6h1zO3A4x7A3PcMUESmCb5WNJToLKC\nSb6HPELaIf40o97nxF2Cmw10hkM/GUEN2LUkNzpKy8bOCvyFjlkNWJ1OVLcMbkFR+iRWyNYsEd2U\nPqiwNJ20sJD1htbXqSoHzwmJ7DlZV1EbPtq2gTpnXxt4iYHXSMq+YNHXVM1IMhHYpcbobtEZ8caE\nKtAQmo4ISuwxQzUharBxLI9eCnQtREqDRJfsnD1NPXLwFwy2j95LZFzi2RqmbBjGDiUsjPwIGUss\nU6dOE/S2JWgCumakzXv2SrFJQlIxotseytK5ux15Mp3z6/Uc49Nzfl184LTsuP3e5VpEHKUHLqav\naFKNj8sZ1aXg9vERHz884JFmcLfw+XTzB/LJJ66ne7hz2fk5X29G1LXitJYUMiXvQ67uXYLtCS8/\nP6K4WbIWNuqk5JFxh3HyHVc/7tjJkKPkDvf7nsXf3WK3guL1bwj/E59XXwknE24erTjXMm5+uaGs\nA+plT/TNEZ9dyXo50F3vuMq3vAyPOPn2CK+7oZN3XGovOXt/IB4umd6VnD15wvTWxFunFNOc29NL\nltdr9PgxJ1lBg0V9oqNci6bbMYsL9C5B1wWBEtiuTWFKLM2j01x6q8Ec9kSdJPbnmDubcbARWYap\nOcTr4nfz9G9CLGQvyDobb6/z0PjIx49zbrqRk9/mrFhy8/QJ31o508JhUtwwFjYvxHsWQ4ncztAu\nK9yPb/h2MWB8o7O4vWNMfKyzKbr5Gsvv0QqfsmrQ9JJ8Z3EkHeZNT5zqRAdFWGb0ErpGZxzBFDZ1\nk9Ni4eoRyhs4OBWuNAkZcUOHdb4k1Go0OZLnNrXvkLo6nqNTdStofcKlYhwcwk7Hbrf0ukZaxigR\nUmcd9VjSNgNYFnG7xUhdqqJAbm1E0eB4NZmIMQtJPe7IB0kqOvxeErYuTlQy2ks0L+UQ9hjOgFIT\neloG22BpuxycCYcmQG/3VIuBft+zlQcOg0XXCfYc0M0ClQjktEeXFQfbYL7WsKqBPvLRux3Ofk09\nKILEYq8r7Mwm0Stk1FAeFajDiiaL6ZqYMdFoioLEntAOU4SXM9dSlgFgOYih5+ziAzk654HLVf0L\nT3YnuNstw791MJ0NKYJ3xc/IJmHUS5yLa17d1Twi4PPlMZZp8tjLebx8zYInPHz1DqfeEGkhvVnj\nz2YcHZ5zajV8txyozww287cc65Jmccr46Rv2NxFLreK74BvaxZaVrnj8YY67WdIHOuXVKzLP5dA9\npQlcDu1zZBLy8jjGK7/i9ffUP7/nWfKQxlwxuK+YOQl/dG/JtzsmpzrDjz4Pqi1fzBmJY7HfQ5W0\nrK1rCjPksZcjsoGN94qLdoE6PcEB+l2DNQqGPqIyDKwMDmOErlrqu5TxMKCFA0YCM2UwDjqp1jBk\nOpqs0feSmTJwU5sN7e/n6e9e4a+AHoGX/cJ4UWJ2r7h4+pW92LM34In4itlcow4mzd7h0+EFVZ+j\nXYc09Q66z9RaiHUxJy0ewf0JrXGCmZn8tNowya/INhLLrRk6F6OTaF5O5RooUSKkQoXQqhl0Gp4z\nUrkVW3+g1B0Gd2TcJeg5uI2Ob2gM/Zy+bjmJR9LeRQ8Slo3EGP/iEN7904WT1Y1YucVgWNSNAqZk\n4Yiwc3Zujj9tMY6mNAwY3Q45CYjIWVqKerZDeAN9OSdQgkwmGMrDLXNm1YCV2+y0lkTvGK0Vdu8h\nNYUIIpQ+ssNEbFy481FWgz60aO5I1xlMzBRRhUi7BEwcLUaKI0ZNJ1zPaaclssxYqZwuXuK2B0wz\nJJnO2esJieyYaC3EewIRookWa2UROz52vEPaJWps6NyeSdugOyU4A7s4YpXXhGWBIxz2tzFv7Jg+\nSTleurzfm9Cd8t0fSroLg/PNjAe3LRsx8NS6JNYzPusmX097vOgDJ1/33J1KVtpXmpsbxk8PyMyA\nlBjbeY5lfMA/+sjNl2d8ER7X3kCsN3TDniA2cTwLZzkjuem5c255Xfk8ubf48bHBer5nflpTnP7E\nly8bjOqS8G3P8f1HrsaRq9uM04XH5LSDyOHr4sC3SU7b/5EbBp597JnObf74+YjKOOezVlOoL1xc\nTdmf3LG7uGS2GvG6W+T2NY76O2Rd4U100mtJu9LwlcG6CzG8HFsKdp4gyhNKqVCmQPd89ppAtRoi\nCuiY4AoQVULvWKxnFakyQGyY+up38/RvQizkKBCbc9J/nFH7vxKIKZ6ZM44f6H94he33/FRLRH6E\nNklJZjZ/Po7RTivM81OO4xDjq+COHUXZkbuSc9fFDAcuDYPtuEflI56bY/kDYRNTyhVGrehtHdkF\nhMMBw41oWpClhdsMxNKiMXWEYYI2ImKPDRpml+AEHq2ZMw63FJVALFrc4oBTttTDSDWxSeKBRFQU\n/h4Z6dQKvHSKU0NvKuq7gnq9YTQ1KlOx7xV7qbh3A8hdahFjGzW9lLgEmFrB1h7pvQbh9wTtgbCe\nMh0WyKGlT13W2zV2IwjahoicRAzoSYUzmhSmhq508mHGYqgwcxfYo5SByhXF2JELKJWGH7sY5hyn\nVHSGT9OlRFWF10vMUYLySbs5nd6CEWB6ij01VTciGo12GmIJg3baUAiBlfR4ZYvfauRewd2wItNu\neZJ8YpP8yG/XB6KTFavTL2RvExxdo+oDQuM1p7lHSsSb9z5NUHA8+YLRmqy7OSdvJXqjc5w1KExO\nZIJqJPbxlj+1ExrLR736xKPsDd+179ikcPAl5d0ndu0tvrgkObsly+c0o8WXRxEnY0z0i8FNn3Ks\nO7z0vuXp0Ug7q5hODOYzxYW2YEjOKeuBk+IZs1uJOI042/w9p4cFnwNF9cnnD+aaYpmxcEPcRwP+\nAUxrgvkpxpsvuVx3uGefWSy3zJ8GdB/fET+8wjpSVLpJJNY4W4GsLDTPREQTQnOClDO8umBetMy9\nkqw1UQravCXTDVq5Qx6gkA1i9Nn8FZj+NyEWmIp92KG+ecf9JKLajJjWkt58zHZcIVKNp4stuBld\neYTmmChjzyp7xGYXUdg9Pz42yEsdcR4yswTpqcEQCU6OfB5NI1x/gtXF5K1B4xeIe4O1cCjlwK4t\nYWKiHVJUXTJvMvo2oSahqiT70SPpOsb7PeNGcjBD+m2CPg4svAllBuvCo2FCpwuinY1f32OvOwyV\nYjc6HgmYe3JvT56beIXLZLJkZIKTaixSH7suGQyDIO9wXR+nFvRGw9gV5FQEvrM1Xi8AACAASURB\nVEbc9GiFYt921K5FOwjaFuq9JHAypvqSzMvJRhslQ6oZRGFH7UqUmjM0McpR3E8cMtMA6dHbK6R3\noNE1omnDsJZscx1lF1jsEIPESAS5Z1BnMxwadjuIuxHRFnTjPa5Wc+RPKfQYb5DMGx1D03H2PrEu\nqJXOXld4KqPpLBZ7i+PkNdb7iN0Y021nbP48Y9IvCZYddbKkO9nxW7zFWxq4nPDqkeKkvqc2Ym4m\nE+TFmsS6RP+i8aZ4xl2gkWwtLuIt89UFs2VK/2uC8bNG0r3iw+2Eh80Tjt0NKp7zbHLE/acJh8pB\nvBjpNMXkI4T796y+fcrpe4PjocLxL7m8+YbpYc3t0Z7iz5/YiFvc2w94HayCa7LHN3z8NCdZ/pH1\ntw5tXSDqG1aPZ5xe7wizPebNBvHaJv6i0y6OuT8qOTqfsf3gYT3IqM0Kx31Bl2mkfYs7tpT9SGaa\n5HVLn+XIaseoLEynR1QOoyVoTI8wVXRDhT13mVo6R4aJazgsDEiijon9X0kwskJjuTF5VrqY+z1b\nJOc/f+JMbHg0FDzc+VTeH1DHgsf8xjSu+cEwqZdf4Nv3CE2hvxvw2p5T/Yr70iF9W3I+f0W/h74z\n6PcH6nANbkCNTjtGzOYmbqox7wWbrqP1J9jNAhV7WKMLnUk8NLTmDkJBj4npWTj7lMZckm4MRJYx\n8WwcM6f0d7hmz703YpUBhS1R3RTXCMg0Hb8ER4BwWjoEd8MWYy6oOoFGjhrn6KOOxCRNGgq9xzhM\nEG1J7HSUB5PGHijNCYFp4bUOUVNAVNIEHeZgY8QdMo0INcVq0iE3Erop2jqhMwrmZk6t1uhZjW2O\nmKPPxNFpdrBQA1U5ENsdwWhwlBaUnY1SNf2Rg9jquJN7pJSoyGXTlDhWiLPzaMyBMtkRbnN6p6Dx\nJEVWkWiS1lGYY4fbhQzSY6l7qDHmJljxy3eSySAYgx2L4B9o9M80o+B5lDNZz6jCe3o7x7nZ8um3\nKbtecfpxxqsPLnP3OTdUbLo5i1ctzuLAhZ+yDeEwfUfybo72/QT5KkZaLvJ0z1bprESNWW7pp9c0\n+Qo5V8zKnv2Jw8LaUowX2NuR8Qedm73HnyyDLPzMxnvM/mtIEbfMp4rrqUb74SGRSGlSH6EylpvH\nXOQ7jLMn3D1+xvQ6oY0L7oeGxcIgu/xM9VTH++0tZedQ1CWvXx+htlPKKw/tWUHlaYSMYJlo+gIz\nKtGUYvRgZc3Z9A29maLGDYVlooqRRpNQFZTpQG4VbFXLWGhshhjVtrTD8Lt5+jchFrI3WMUrnLuB\ns2qGPtZ8so8xmpi8KfnH2RRN3PHM/cJGtrz9WZFmCfyjAbsXSGpeqobu/BT1a8vTxuT0G41D9wG1\n2aGtevJ4RGsGnF2BoY8cLyoaWSD8giIcMPIZfrJmjNZk+R7lK0QpqV2DUIfovkFfmFRpyn7iMoR/\n+TO1YUTDImh9vBKqusL2KtZhT+eGWPGO7rCiPthoho8ULqI2CWvJopOQ7DEWAfcteO5AmOnYfUGP\nQzPusELFEDmI4Qg0he5ojGJL3/fIKKPSa8zeIzI7BuVR9ynzARpalkonCDKQDcPEwV935JnHsrYI\n256u1KiKO9ayJ4p6tt6BUGYYekDhgfJC/IkkDlysasCf5sg6ouldlknLVIsY7jWq0SAbIqrIJo8U\npVFj7RWmp9ObJvWqRoYB1C3j1KTQRoyl4rE7ID4kNPRMwynvDhPKD6fIO/goB+7CHY+7JZe/zrh8\nOnA0zjlSr/mUJrx/qnH4raYWzzBebDG2Ow6rT9TmMywlCVYlUaMRvZszvXT5dPQjJ79JjKefWe1O\ncKRg+8XBOf47XmsFYbNHf/OGZvqSbfCOdVuRfPXRv4Q8+Jjyw97mPPuI3D/E9J5TBYpl8JzNec0k\nbygzhWV2ZIFi/z6k27l42Za3+5rh7IS5t8AqJ8RexPVdx/kPrxh2FSfWKVzqrIqG2X+jUem3xGJJ\npvvIyqWuN8hdjGv32PkJtsowxYi9DUE7oksrhFUjJwXRPMTuPKIigr0klwcWlYZZzxj3/2Vs9f5/\nx6DBsX3EtaoQL+fciwbv4Z7LF3d8KV/yKNKoU4OPaYhz/JxXIqFeP8GVGk3aM/u4Ij+eYE0+c3/x\nHPNsw7SRRGWAuohJ7Bp3qzN0PmKeI4Rgnyi0O42DiGm7Gs3dU2kRei2ZaDHkHYOTU8sNo9QRwqXa\nF+hx8xcX5XWBaZRobYQ2toxFTydsuj6m6xTL0iAUAyL36EyLWWig+gx7VTMlYSda0lJSxQb9OkWf\nWoxpQS92rKc2EYpJGnKoSqq8Is824LtUI2hNgBoMdp1JZk2gLlEbRZkeGOlQfooWHFHK/i8WgvuG\nOoFGCzDYUlgTal1hWFt8N0QaFlZuI8Yp69yjdypkXtJpPSp3ub9PKYeWZDTIOhPba0ndnmGyRtN7\nqkhjJgSxKIgch1lvk9oCX9b4ssKY6thJj2Mqai2nHDWu93estvdYxx115ZEk1yy0LUrcUtYK6+2B\nh94Ng2Xx/bc75uNA9HBPbyr05y7GKmcbGEzkbziblqj1eBhOyVcWmtrR+BdMZj1VeceVLPkhecD7\nH87QqidM2pI8hPKoxTy6Q6sd/hzVHNeKqu45vpqiTzfcpQa+d8B9+ph3/ch60hB+c8PTxXvWnUN7\nuEdFJp1/zJMHIyfzDR+dCetHOcf9mu7O4eELDeeNxS5UyKspd+YdLxagrw0emDlN1CGeKOyHT9jn\nCf493HcKZzMw6isWroZj9ty3Pc7Y4Jc+oaoxfYPG2RBXOmPWknc+dVZQew29vEcfbNxxgtQVsbWj\n4F/Pz+KvCtE1vGkgtHV26sCjbo3+q2LSHujFO/yvH+lKjf5zwsLs2dpLWq3BXS55oV3zrta5PZiI\nbcTF+xvSceCnT1uinY7aBjh+ihgzROwgs2PS+xLbdxjDFFs1yGjK6Lhklk5m9XS2gdYZlMOILm3c\nQpLQMu8j6C1iGTI1Ilo3pThK6N2KzZGJaFpmgclESoTtkLclhq+IOofR2rO3RgpNkls2s7mPZjVo\nnY1rOBg7D+XU9JbBLJH07oaDreHmHv4Q4fdz9LWiq6FuepTeE+YNo5uzFRa6WBIEA4eDS9WMWOXA\noHKSIKLzHKYITEsyDjGFWCEGga5FGIPJZKcxyAa3FSwWHlYi8WROX7V0bYG0ZviqR+t1wnZA33tE\nImUje5qhQB3WaFqG3CjGQqN3JcIy6QvB3kkYSwszgENXIpWLVWqcFZJmqbF6d0OwTLnxa742jzHO\nevTYpT03+LK6oF9V/Ja0NLZNdqu49HS6r2AFBRedSfjQZJ3P2FuK3W3DZPiZdPOI2C7p7r+iFhVy\ntuZPpzu+/dHHHXeczmwi6xXT2mXIPd68aXiqLO4HaK2fubJnnJdz+ueSrw8e8P7umsnZjGPZsFAG\nb6oQ787j/jDy+GNOe3KP/2HCsIoImp95/OWY8ahnLWZU5gm1+Y55lvCnxS1SdfS9xRsq1t7fozkD\n2n1MkEnOZgJt4jPJWpQrqUMHOcZUZMx8l8HVaYeWnd6g2ZJCRXRhimYEGLIgbTp05VJZNu44YugG\ng93SCwu//dfzs/jrojd4bdZceydMqoDP85jGbDh903PutWwePuNwvkN8+x3v9xXSGpBiYFxvqLZ7\nTn0f2/2CnhSYJyXrmxlHy4fAEndeIpNjuiikXO3otJap7zEaPUU5wRxtqh700kRzBmK1JDUl1dTB\n0W3UVoJUBHrEblFg0ZE2CWKAuDvBHGNaoVjKFEscUcgCoVmIKkViMhgGou/Icx+ZuwT6gLJM0ian\njX3qvaT3M0JR0psTROex0hJELvDQ0UedMTqwmm7Y+wJ7EARzEF7L3tcwNgGTYcvebelcgT4z8CvB\nvu2wmNAlCs9yGHSNJtjTRS1h5+Ay/uXT/VCyGXsya4qRK/bJlkKzMVsPW0zpXQ9RZ4xtiJEnmLFi\n45Z0rYPIfYR0mc5O6LaSYnBRaYtYK4zugNQbZmVEH9RsLJOZYaBtCmyx496PsL/+39y9SY9lS5qu\n9djq+7X77e7h4dGdaE6XmUUhGDNCYoKY3f8AE4bMmNzJlRAzGMEYMWSA+A1IVGWek6eJiBONh3t4\ns7u1V9/ZWsbgZAmuUFG3MkVRqk+y0Vpmssn7Smb26X1cztuRT0nAl3LDi+cm1wcTOTvywFtQNpeE\ndzva9nfc3rp0j5Z8FY04j3VCOfLLcs9Qn/K1VtLvepYZXMandNMO7Sakfj7i1hOeVI+YN4+RD66o\nbQO5CVn++JbNPMGQB860l/hvNZavBFoTEKuPeD4sshTBFWa4pDh85JfFjPGwoVPQyzsuXu1593jB\nx08+uypDO5UY3QXFCzjpbR5+e8fxDxH94jlX9iOcBdS3T9nLLau1zWp3yeNLm1/OImZVQvN+RZ4/\npapiJsLBTSF1RkYC9EznaEmOE/tX1GWSY1UDqjSwrJ5A1QTxDCEHZG/SLSqkLalaj6MK0f1/IU+n\ng6ehNTFLv+G261m8yxleWPwfdkQqI8IPP+O8mfF0c89kfsXNwzX2mcZhtuLw5TOiZkQNCxzPRc4f\n8kLtUKs9Dp9Irc8QS0RjMNN83E7Qy5a2NZkFGtWwg7JCRYpJXWPaDdNthZZVCEOiWyZ9GyLdjFnR\nMzQ+tppSBvckqsISDaOC/bahGY8Y256qHNmHAs8xyPHY6SaNUsyCBmGMWF2N3zZ4dw5TX6LlEZUN\nXZUwro7MvB7TiBF6QRLWJNJkoU9Apuh9QLbTsdsSd5jhDwplG0w1BytZYCcNhduDXmAYKdbY4bFF\n2gMCF9NuaB2HgzLQFxbhiYFnzDDJMLQCR/QU7UgyHxj9DfZYYNoaAx1mrKgbhT+ClCNWpFOpDLX5\n9YK1nxuIeUU1N6nSkENtoYYcJV1E3kPsM5g+tghwph7vQkG5mLK+/p67q1e82Wyw6yXKiBl/+kC3\nWFKtFowPv+dlvEGvP/D2+IHwl+9wrBmPB5tJKbg69YmmA9/NSs6jA2Uw4fdK4PpzfphqfFr/zET+\nRH7pYWYLvMkV7bOK07/JMO+fMDobBveUTTJFNAOefIqVvsW7/sTk3mZya7BYDizVyEE/5a/0juxC\nY7w1ePbmnoeGZPvyGdJYMTl5T/4eDmKLe+nwSPuB5Crn9GCgkgnO7Jrz6wuyX3ZsH67YeAaPs3sO\nf6VT2AfU8if0SNIdE1QEIiuoi5Jk1JjUOidtwf5eIQJJr1pqTaOyO1JtgZUMVEaBJwva/Yjptgxx\njz2UDGHzF+v0n4VZ2HXHzeoXpsOSRvdx1AVuY/LXLyK8/QPG/Amrixt2roPsBfbr71lsPvE4E/Qb\nF7GYcXboqPYubdUzni852g3vHz+l5BHHscY1OwarIFUFTewzSXVUUqIsgZIG5VZitDZjW5BYDb02\n4Bg2oWqxZho5HkOk0+uKajTQhgDDGNDue9zcwIvnKMdAORP6wMUtDVokskqIORCpgsT2SZSgaCV5\nO6VapwyNQW5KuqHE7Gzs7ZyiDdkbGl3joBsSUekYu5TV4FOEKePMoDEinLClnhmknU4vQE6gnrkY\nrk9gDAhiWrcFaWBnA6M0QZuiVykmGseupcZEWg2GrdPYMbQOM9PAzgdEO8O1FUgXHR+LgKas6ERI\nHUn6VGF7NpZb0pYOKOjECcPQM8Qjjjah8Se4ux7DlmybgmqqUSuXYdQ5u75h18V0Zs0mfIP5/opy\n8oHEuaFZGny53ZKvz7jI4efEZHad86X2gLGf0N1qdFXG3fEe2/jEUYUE+1Py7AVfvt+iZT3OdxLt\nKkJPv0b/+Ajt6Qm4b3mzfojxbo2w/goZ3cPa5X6i2J5FjM91qpOf2R9crk9WpGfn2Coglh0dp3hR\nR1rBk3TN0Ym4/2bBdBmychs+ZxuauxkqSrgdI9Rqw09qxZNgzt56y7PjHD9RDI8Kps8huN2zWFpo\nRsyL45rfnhhk8im2PmKcjRRtTS0kxlxjGqRk/ch98GsYcShs1obEtj38ysI93LEzWjpczD4imrik\nhUYwmJhDg1//C3k6VboguY34IDKiw8+o+I5cfkFyULjdG/bn7ynNJwQHl0O1Rqt13kdr3jrXNMGR\ndr5n++IWd5biZi0fdlue/Rxi1x1m1rPwepTpkkufeTAhLDQEijTyMdKQwG84mWgcpyl708DwA3Q/\nYhQNhz7mqHqCxqZQBvq0wBsVganTazV9OOEoW4pmxLd8Sh300qCqK+pmT9wq9LlNo2ZYjUPM5Ndj\nhCUZG0jsHqM1mWhLRKBDmDLJUhxh4DspduvjjwP90qIaJWFrYJcWhmoptileXuA0No2j2NcD3j6H\nxsBWM7IM5kqhlEAZAgpAVchJiOYJbHOF7LpfWSjjQMZIHsRoo8K0AxJb0HQakTdixCOpslAqRvU1\nVALDgs5oyK2RyDXRdialVtL1EQvTwpt2RJmJtozwjpJlrjHsNFR4oLbfUEqPov2Zu6NH+k7SP3iM\nsToB7ZT0LmD7ymD1w09UH5+iiYrfT2YcPjUMT23K5+/xgyccX4HLinrecfLEYFN9pv3yQGAcef1l\nhYh0YvcNV0/v6PMP9HdnXJQ7Pp9vuVu0uKIhvjywkte8uBJM38TI4He01sD09oi6/o77Sc+bjWJx\nl3P5U4Z384rLSNHUAdp3NZfqBOP1G2qxYAxnPLjo+VJA1X+BuzR5Z2WcHJ5y5SiOTy54a3/ikBwJ\nH6wIuwP6k4H9yYTEeoHsevohJ5VTQtvA0n2EmrLTDDSvwetG2rTD0FuKqU/daexNGzPSWFoGq7pj\n7/RoNMxbjb450lsLdkr8xTr9Z2EWuhK86jeYdwa9NcOYz3h0GBn9Jcn5QFkY1MJja13ztfIRAczT\nKV/HD4gOtySFg5AtTjvFGU+YWR678RT30x2R4yHynLIymOsatBtqNZIGOXgHItNkcBR92xNtl0xl\ni6f3uKWNymYYyx7fSND0hjZ1GeWI6Y9gZ4S5gWUlzKdzFn3Krjji6jtqX8Ne9oguZi+mZKKlcyz8\nrmAoOkYZEMsW5fWsjZohasDMcPOBxInILBfd6jEyHd+sUGqOXjTYjkZajPRxS2HYxLqBPRpUvkWQ\nVHidDr5NW+/R/BRL23OoNFLdpAhbZvKIVB32mNFpOv04oioPU+tIj4JIJYi2RwtyRnPE6TTyvKa3\nK+gqxL7EOdlBVGP1cwyjo2tgcCaopkWeSCath2+kGG2GOBSkHLH2I4VrUcwcptMtbjrhVAo2TYEb\nn+FE9+j2yCT4TC8P1JnB00WE/3lGf2oxf2lymjzjYpJRfrlCfSzorr5grBJ0ThCfP6PuRlR7xzyZ\nYZchq2nDMx4g/ZL7Kwfj8owgNbl2R+6uPU4/WjwJW7JTm59ePWZ/k1NENWXT0NY/UT+eoj9+huxH\nHmoVD+e/YePpPJ8+5s75ifVeZ9HUOOaR7JcdR+mzigS3e5vL3QPGTrG/6jlPLNbRHWYv6NMd3uVb\n3OMKPegRxWc+PnlE43ecf2rxDi1LalQT0WsSY2/TaRlWtcWqHOamInR3GK4PmQTdQKqUQPXgRBxb\ng8GumRYhIy5708L2bEa9Ya7bf7FO/1x84X8thPgshPj9n8Z/8n/79l/9CV/4WgjxH/+7bKIxNeTF\nC558ZRLWF1TDHa0+4F4lLMo5i/MnWJ92nPct11FB/vQbzOoTu7plGb9kfZNiJg/IVnt+6T7ireY8\n1lzMacZB7KlC8KKacmiQuk/jDbRagJ+u2YQl0cZGt0ZGNljZhDJ1gI7W1VjqGtV+Rl6BExyZl6fo\n5gGVTACH/TADkZL0Lkt9pCodovKeTq2YtTZe0ONsLUwK8sGlEjmyHugmDU7qccgdfNOjN+Ggt4h2\nxAwdNM0kEZLClgTxjoGYzIA4njCkOkbTcAxHMqNgLlvyyMf2B3wzZuLrbHEZwhDdMYlqG6sYKJaS\nPgnxKp3FoUaYGn0vMBwdcyHQfQ1cjfHok2Yw2hqBFzKUPoOuiEKF3AfYhouhl1SmwNBMJowcHQOn\nsumznqDWqEfBEIYQuWh6huYKglxSFBb35OyuTNrFnOaHH9lcvsTzlxwyjZPbGetgw+cbyWhM+SUu\nOfycMoQ1ibUk6r7DCS0ezEvsTwWPf0i4mTwl81y09hnjo1tcq0NFEeJnk7NDwYPTjrKv0WYPmc6O\nTMLP3HzxhKtbB6c5IO5atJc24dWOxn7Aq3ZC9WnPPP/IRfyE49LHjX+Ptov4NDhUj55jzT+jXdSo\nac6X3y4ZvyzItWu+aq9wPlcoFrwwtmjxEVtzMScFc73l7iQiX2q8+BTT7J4TqYxe/AY5lFTPTQYV\n4yw0VlpO53us5IxKrREipxlssmSBq5koc8lQp6ykIO8yRAlCl3SWjmG11IaBKwSoCk0b2Gv/aFrH\n/6P+XHwhwH+rlPrdn8b/CiCE+Ar4V8DXf5rz3wkh/sE8Lw3I5Y77n64IX2xYdOd04weO7kC3P6OS\nt+Qrja5WVFbG5GPPlQoo9is+LjKKaYPVufBmxB0Dkj8e2X5xT6mFxPqUrPDRb1qwPQZLMms09P5A\n7kss4TFaNXs1kDsW9zRo1kBqZ1i9YnNXQFAxhA2TzOZuTNgfPXpSumlJlGuoo0MbVtStRHhQVwqz\nK+hJEQKypU9gD0zsBj/2kMFIbpwQWiPO0qEpc7K2w1E2Yd4xdBb5bsQNTRxhcdcLzGYk1m2kLdHC\nkfAo0YYFRuQjrYZpXpPnI9U2oeg1LFVSDQ7GOFAMCSqY4Q86kdJowohjYDBkB6L5nqSBxeCi9RHL\nrGScHvD7IxxqXNem1Sv0Y8vgOjiWj69apN7ipz1u6bLbmYRtQmsOCPNIF0eMgUthGvSdRjcdiAuN\nth8RpmShdbSnAU+rFs47Fov3+JcD7YeYK/eaq98rcueSbXDL2ds5+75HGfdoXUL32iE/Brw3Lvnw\nW0V/0vDK1THlR+67LSfDKT9mz/l4XNIEVwyioq1D5qtLjuqS6S8+H9anPAkEXX6NIdb0Bwu7fM7n\ntcUQ9/xUb/l2WLIrvkCeOuRjj5DPiclY1Z8Z38EwnFClF8zzEPQ/YHw342w3xf5th/d1w+Vhz9un\nJkd3ZPvG4e3iSPW44mu/RBcxH758zOrLe9KDy3+4vUHMFky2e3RvxzAMpLceuczpph2+t0N4cxAG\nnWjZIumqGoRgtKd4xpoyr9CkSedEZKaB1Q50esFwnDMmFcHxn8As/h584d9X/ynwPymlWqXUB35N\n+f4P/qFJAkXc2YTPfPJ3CutQok595MIndO7wugwtm5EMz7A1n/XZhgtxTff4R+JjwfbuMRNRMzkJ\nOKt8rN8pdp8mnE4czKYjDJcQS9B0+hK2XYnfTBjFQCMP0A/YQ0XgQRy6kB8gsWj6gXHqMqlDbKOj\nGAJmGkzCjtSBbphSOg1qLjlpp3QzjbnU8YITXNugjlw0vcHfV6RFjRAOVm9ibkBvtiT1iOy3SCHB\nmGOpkd6vqNsCzZS4msVQuAhvQjocOR4PGIcU25CU7pKguIV9Tp31ZJpCs0CsIhos1G6CO5R40cio\nNITRsa8UrZEgGkXshui6xSCmxGZFJ1I6K6eLLJp+xeCeoBYtZa7o3F/TnvrMwaJEtlNk3NMNAZ4t\nGLwDrmsQZwW+rdPKgXHYMRl3LMYDRhPRC49e70G6aFZNdOXSBxGG9RW33QOu5rdEz0rcUvDytwFf\nhjHPb87YrVYsX/akbkdjrSi+FaxOOh60Cv3qQFnOKZXDQzOmny/IDI/R/MiF+JFKzFlcdISBy8Z5\nQZcckA9vcf+gs0u+Zzx7yut0z+9eXOEZb8j2I2b7PX66ZicG3ItbbpIfeLm9Y3evk389w55brNcm\nN4OBt3yLeQKHv3nG6dOMN7rkp2yCeOsxXU15/vOC8qolenJClw2oQpHvQ9zyPc7nCrdsWL2y6SOL\n9UmDHguqds2gZYQnGTNz5FjYeDLA7jOqNEV3c1Z4VNMGow6o2TKGA5VnYasWWemEdoJV9iipUS4b\nhoWJM2//HSX899dfcmfxX/yJlP4//h1FnT8TX5iXBT9flbyrBpqZTULD8dJncH7h50drdrcx7vZn\nJouAEMW1fcrnXvEsa9nmGY/ChJ8fwf0sR7/4zMlNxvKrhJ2/wLcLvEKgKgurONJELhNrhggLQpXj\nVCbFbIE5QK9PkKaBv9IxFhKpckTZcogqjGxCMM/R64BCeRjZHL0d0NuMjSzpo5IhGWhHm6aVdKJi\nMpqIuxh7rrPQDI69hLammjb4BrjmnNEQmJaGn0jENKIypwTur8JX6YgjFPO+QE0ipmJEQ+DIASkU\npbWgtufMZyGh2WHaFWa7RSgLS1OQCqptSDhdYGeCpadTeDq2rJHpgOsNqBpAp1cTsmKk6g2Usycq\nO1TiUZqCE2kRMWHwU8Yehn6HXi7ww4GkNYj9JX29oB9NxrJDGgeafs59dULjLOmqBKPb4gcB9ahT\niyV6ZFO2l6gfLtE/vcZtV0xyj8fNlOL7kD/GGR+tknaSMr73ebhVyCyib3X27hLZW4ynv2GfDRw+\ntPS7NWO6I7z/zNgv0Qm4qHV+PJ5x+yng4e4t4qXBL/kXaIs93vYFK+8ON9D5/ZsZ2t2K6VIwrZ4Q\nix39ao5ze87Ticl3MmUqP3L3+o/cba+YijvOggrjqmVEg+kt1/YTvkg73A8ppw9uqB3Bu+c/oz0I\nuUl+xDu+4lzYfFomPHg3QewPfBz+PdzjGbLp2X9eUl/7rNIN9aAY0hnNoLOm515m7CvFZLChWIO5\nIxwt5KzA6R1U0rM2XYzBYxZIyiEknfhEUjEOJVFjIo7OXyD1X+vPNYv/HngG/A64Bf6bf+wC/xa+\n0HD48tHItz5kMiYaHhE0nymqEy7GewLg4bcR4uRvuLm1GP72BywZ8C76Db9dhCTVkSpNeHTw0dqK\nD3FI+31AY9yyzW2OrkLpOqMTEWUaeSuwBklqQNMqPFL6wERkJb2tU6kFJtn3kwAAIABJREFU9i5m\nGgZEUsekwp4mZLueUu9AO2JMJKGCyo7RtqfIvaSPHHr/gC4F/SGgNQdksCPJfHosQrMkmVsIzaTr\nFG6R4rcGYSXBd8izGk0f8THpXEkZuRz7EWFYaAg2g0vlBiSDQeBI/CZDiJxi7yIKkzqf0vc6pjNS\nKJ1GlIQiR8iSxC8Q2siybNnaEb3SUHsLV6+oZIfbaIShh2WAI6A0LYLBQYx30GpUYos5KvZmRy4V\nTWDQiIZwZZCNCUl0YLQlO9+gVRahmWGJO0SfkxkaJdAYkpluYBSCdv8Rs86Q5wnJxSM8M6Gc7fix\nuAWjYRb1dA8/4TUTdqsjN+sIx/yM9UvPIq8Y/FPmhmIy6WhPXEb3PeeFzo0R8rKz2GWP+O6s52yT\ncFxckzx5itqfEsU7nInClRnTo8Hq44In7oEfHke4iwzt4ZTsscDsb3hnFLz/xeHrSUwtz3EuLCZP\nAj7c77h9N+Hy9Gv6bU+1mCBvHN5PH+CqJT0xi+aa0+4FXZLzqhoo+EBlJjztoJ0+wPI7pl7CRZfC\ny1ckD++xH2g0ixPs1MJsR6pQUtoS34cTbaQ3a2aThJ1mIM0cmUbUGLgUVNqO9FSi1SW2UKhDR9W3\niKOGFjggjn+m1P+v+rPMQil1r5QalFIjv8KE/u6o8WfhC3EGtp/XFCLCqH/i+7mJG68JyxX3yZq1\nm/PmXUQ8WvjTlqWQHL58ihsc+XR9xjaYcvHxIVdXLlfuGtE5dLpALx8z6SVCExiezujWNHEFfcdQ\neSyFBHeOdhQYbcTge0wrCOsa5lvyUVHNbfphyUa3aeYWum3ilhGlbjBQAyZLoyb1IzwR0w1THCcj\nGGucqmLQQ0CnNXSGPqZLHGwZo4wpqRswdga6MaPUczyp0DcpG9NmMhS0tU4bDuybASMfcKYOqknx\nao9clzR6gN/7WJpADzxiG5raxqHH93SMiY/hLcComHY6cjQZ9QWiaWnnDfmkZasXlMLnYEiKqkZL\n9yTNSO4XZPaGRWfRjS1trtM0E+xSIGTMcsgxJdTdPaZmsRglVtUTNBonbY+lTGSsMGofMTUJdAfR\naRyaAadN+eA7tHceyR8L+s0H3pUJNXMm4its18HKbKKfpqjPLdIyGT5U6PslhfaQ770J6YeP+H9Q\niPbIwnvP+ouXbII1nd6xDSsC+x3Pd9fsHkx40YfM81tOpoKT24EkG9mNR26LHUX4EbM58NtC0TQn\naDG041NqZ2R+yJHC5a7yMb+9ot1EtJcT4uEM50HGw+0PlM8ucMcMnAazLmhnW15/2JGfPueg7ZjH\nNabzhHX7mMz6Fs/5aw6PMiZCx6sj7i56MnvPIn7EMVyjH/fopsfRK7GOBqPe0+QTNrqDqqEaW0zN\nR6kF4djjOS0HOcHVbShLusKmzBVx0CBP5xiOh2h3qNn/T0lZf8c5/VP9Z8DfvZT8L8C/EkLYQogn\nwHPgf/+H1pO4zIIO/f5IsDrhm+CG0b7mUHU8snTUqcdL32efn9C4FZeTl0TFlihvmb2yeZqkzL7+\nSL8SFFdTvth1zJ2W9TTDiSIMOvpRMdAjtzruXFASkFeCcKgRcsAtaxwhGKuRg6zQ9g6kKd6xItTh\nJDfQj4IhNMAE87hDOhpRv2XvF+idRGvBrXbIaqRbQFs1zPQerdvQahZJKxi9EqwWUSUQbMn0kbEE\n3BBN1ERhzNLoadIp9rBFLxuE66NUidM1+KbD6NcwpvheSmcMHJYJxzJl7BLmjkUpA8ZyC5lDXUGR\n+xzHkUZ6yL5n6Y/IDVgHsKs1tlEy0xSL3iPzQ+LWwGlclAedZdAyMDgGUtzj2yGx5tDiQR1iNVO8\nrqba2gwnOqYxJe0DlN4RdxGVN6DvLVQf4LYJptVyOY34Oh4QqmHX9kz8iAehjV97BOs/YDQD5vsJ\nBvD8+WceX/k8fRSx6j7wXPrEm9cYzVe001viizU0Uz7cjGjOH3lCx1nds5wIvDOT4G5Pmi65Kh6h\n3xW8mbScVhJTf8rdxYzyfMnNg2+4da6omgVvb/9AIC12pc+DZwGLbI67Tyj/ZoUdzJhaDtuZxfIQ\n8UP+nKg1GdwXOLMGT3d4KCY8OfWZH45wCPDm3/LJDJnHN4R3kjfNa764f89N5xG6G+KNy3xb4nz/\nicmmwwgDumhPYHsM04ZmG8M0wQh1Gt34NdZR636N1pvWlIXJymhg7zMt5hQzC2Mq6bUQWx5x0VG9\ny/6fghvy9+AL/40Q4nshxHfAfwT8lwBKqR+A/xn4EfjfgP9cKfUPN6X3I2+UT7YJcPt75MYh88/5\n7fGSqtMYXj/AXI9EnyLanyKmy4HIvSeoRtzXHc0y530K0apmbd7w4fGB2bonGCrG0WZM7ugtiewh\nnoKV1ITegXpcUjUVaayxnZQc9mAMCYPUGI0Qfy4xIzBqSOwC3dAI5RbDVzizkIgepfnEtg6RjlcL\ndMNnCAXlfsCbwb0mkK6DP+iMToHIGwJdx3cGJkmIVXZU1oHJ7oi9niEFFNuEaFERBBGhbTGt7vFd\nRWLpKNtB7EoctUAyp7MGrCTGEjGplOztkWkkqI2IIOogbAh70L01YV+gRxl9WxLOIQ4M9CFlkkSU\n9UDlmVjViIVA2iVhM3I0elrhoEuPoHdQVkcuWzpNp9YaUrenSXyEMNF3FlV4IOoF1W6O0nL09Ejg\nNhRBTdHoTMKYhTlwfYz5/nTP8tlA5fyIXcHtdUFfWxhGy8Gd4p8AfwyZEYE+4J4FfHK2JDEQj9TH\nhPFSkN7vaYoN8+4bSr+mvymQyQXi08BhUhN+VfCye8NrUWDFD8gfvuL4+BNfHSSLo8eJccvZ3ZxY\ndTw82JRjjRg6NvlA8vU76gcOcWzSbHvyIaeyKrbNe76Zf+S2P6Dall4reGgm7Och99cr9rM7VoNO\nVV0yHwVv2xmFGLi4GrlZr1gvPBrNJZw+oJquiA0dIXS6/sg8naFpBka1wF31TLcOZtnTrQYGPWAQ\nEg0df7DQ1w6V3pC70M5yxrTDPXiUWY6rzUg9k2Ot8A5/eZ7Fn4sv/B/+X/7/18C//sdswlYSvYH6\n2QTz7WM2J5c8/EXj7b9/Sl/fsHkyot7/wMPJKb997vPdvqB9O7JaLhnGLbJ4SFLf4a58Vq9OaM2Y\nn7sLNHPBedlztphyt6tZaDayd2iUgWY1GAfFaPcYzZyh69D1I4Pl4LgtORrx8CuEl8AlLBW6JdiV\nHnZgYxUd/eijhpEuMxBGxTjvGUoP0xa0oaRUAqMBMSrkKLB0h/moU9cd9hDTzy3kvieKHaQ8ossY\nmeu4rkV5P6GyUpbeSKNcjiHMOpvy0KDFNq7QMGrJXB9QRsUuKljKKUnWc7RrVm7KblwTDwcO7kiU\nCIpghhwTBhcm2sDBNRFBQNknjEWEZexp9QCBwMpMkplJlIIcc6yxBd1iDGxG/YjoEyauTar51J7G\nSkE6HDFGyWFeYWHT6hbmWqeqdCadT7lsqIqesA0I8nc82plcqw73l5ZdMaE5+Y7dD1/RnEua8IC8\nVjTfzmnlR8orGyeeMBMaXWTD6j2TJuSm8QnLOYb6ietqzdNJxac1VA/OWYqH/KYOSKs7nEbQu69Y\nfbhmPK84+/icn+rXfD1taU9KPhkPeTwqfm/EeLXggW9zc5Sczxy8Y8/70z0PtzZxkHHvfEGvrfhh\n/rd83c+oTRPxk80fTjd8ealjWgWflcHt3MS5WaLMn+HCIB0f8ag0qV8r7L82ofNpx49MhxXDwxVC\n2QgjpjUHjK6nziRja2DMQux0Sz3a1FuJrcdknsRyappyxDVhLHpGq0PJGegCFevUuwLhFZiRRn38\nF9LB2WISpz/jam/JtYKL1zrXUxN7UxBtQckRUxjEbsRrOaH/tEI7fcW9s6H3K46MuF+GaNcHLivJ\n/tOO8+SGs9TgJD+S6R3ztUnpuZR9Tr3a4HQ1tiEZxZpfW5hGZuNIFbcEOviHLbkw0Yc10U6n0XXS\nriCydQa9oG8bMt/E8gtKo2ba2aSiJdUqxCiJhYaruUR9h4xbdFkRiYRuGeBYLb1p0h8ydL1FHkpS\nDXZC4ccdYx0h7BI/GjlYOp60EUmNRUHPSNONpNmeQ1QxuC61JvANn77V8EaFd2zoxQlBvQfTQPQL\nurlG0JXIcoJVu0hhEKUOoTzQay2Gp1PsF8yCkUEOaJi/4vEMGCYmMtLpvRyxKfGlJCo89F5jGCTr\nsqcONWQ0oRxO8PoJ1mZPdSsYEhfsnm2wQ6kJAzX16hP2acub9pTPecMH8YSl9Y7HneCZ/wNtvWV4\n09J1OvrnS66aAnc9IzF2dEbH7rDhsA3ZWh0X1mfK6WcyXmJc/EB+vaB1Ry4+V7S/VFz9KLDCJf2r\nRyzXG5L5BSf2Cz5bPzK3O+qqx3ZcwmjLyI6TM0mw82iNLU8nU/SDZEw16myClCv2n095eg2xfsuX\n3/u8Gx3uPnzPezQedGA9V9w8kPQ/DMx2sDZvOdef8pVdox8SfroZKHyLRs84P2+ZTH7Hxfk37KZz\njs4NxnFEaDVKM7EDg4nfovSO2opYCQs/Lji6CbIzyesQBoFpDgipoacaVjAg7Q7z4FKvCrTSR8t0\nbCf8i3X6z8IszKGlOQs4hgaWB9+frlk2kk4ZLPY239zdEKy+5H2bomsexsWO85VJks+Ru46OmvCH\nI34946JPcJwVx7XB/GOGWqzRR49qVxM4GYaYMr9fonkjUhtYTsARLrZugzGnKnSSNqYJIybVlMFo\n6EKBY5vMBoWTSpz9SDtzMHpJYa1YBrCzB7TawRaKTknStkLTLHR6jF7RayVJY2Mke7a5hSxTct2h\n1X2qmYaVg9HU3MsRMdXxNBehabiaREkb6blURswksHBCE1sFRLmLtAwcp6eWBoOm0U0Cjo5P67dY\nkwFDjoTBnnAzsG8Ek0jDFiXOzqZXFYfKxelPkOWBICw55pLRisEr8HyHxneZKAdNtNTFmmoBTWlT\n6ZAKmKYW3Qk0Y8tCG1nVJQyKNrBwZjF1kOC3Bj4ulSGZxoLdW5/f/w1UVwPtx1O6sKbkyCbqCGOH\ni7XkYj0lPWlJHzznpXrEYdxRcsHMdPjCf8TT9YTtsOb+84rxduSx2jLNJsi25cn2N0jVcPrU4lwX\n/Jyl/LJPaPWUF/ENh/RnVosA96lgKzqyXHITaNzc9jjVAWd2xL4f+VD/wK1y6VZH3MBD127Qxluk\n+JH5wyMfTy/whobi2Te8tBIWE59qNHE/BTxbmHirj3wcQt6u3vLHccbjxufRX52hhxPWn56yVaeE\nNxXG51uqfMBE0WsmdWnR6A2672MXAlmOYCmK/cheTVn0LgvvgJm7zGVE2Rt4Roc9h648gNCQjo1d\nu7RhgJAepf9P08H5/3l1hs6yKnn43Qse1BnTtYbjTaBPyL7Z8b18yTQzcF2fYKxxPyvU6wYhPqKH\nv8F8IHDHB9STns3wmC+zO9rggh8Dhere4+1rcE+QlcToN9RrwV6bItHIRknvSHLbZ7BzVOEy2iVz\nS2eMc6CGYYd9nLCZKFLfINNG3ENB40HUDygU1mjRliN9FNCJgDHQKYTOVsX0ZYxSGhPDoY91loOD\nnE1YTEYsNJokQpor5rXJZOzZyz1j3EDd0xcWrb5nLXy8jSIpDGQ1EKmOxOwpDiPV1sTJFXU4IJye\nhYSwypEbi8wEwRwZBwQKBk0yCptdCPYIfiRQ+YBwQlzHIohdTDWCZmC1OZHcU4qCrvSZeQVqcJmE\nGkNjYnkeutAosxJXHxhTQablZNZAWfbE5RFLrhFdTVdbrKqKok4RJx3PXzYoQyJniqVVcbjUEJtv\n+OPEwDyc4zkNU7+ievsj9b3FxbuAV/aPJINOdStBM/mCHGfmMVv73MiKMdc5i2YYVULs3fGmdXnn\nDbz85YTJ1qSrJLv7kjT3GMtzAutb7NAl2D1gfJ1w9qjkPtYQyQ6zWfNksLEx8M8iLvIrxDQm+nrO\nrfUClTWo1Xu6jz0vPrzj5pnB3XHJp88d4knEsKqothm/cUsudiecVhHvyg8U4iNPnI/o1j3lmeTy\nYcyld4FVl8z0X9m101gRtTF9t+FWOJSmpE89KrdCiYKq6yn0OdEKmO4xdJ9EmGhZhOPM6f2e0FdM\nUoktFLpZ4Gf1X6zTfxZm4SqLy0zn5uV76tjkXN/gynu+cEbSHwe85Q/oaUI9OaO6rFAPL3j96APy\nMOd6v8GXa6rZNSrckoyv2cZTgiblyeOOe3VOu7AZhyN5Mwd7ineXYu+3hKZFvy041h6RyNFLG7Uw\nsGVN2hhoYiQ0pwRlTx6VOJWPtHtW8ZRmXHGyaxBtSoaG5/QoS2H2AxOpsA6SRtsgwgZNK2k1sGqN\nYxez8QdEA13rYIoSV/YIf0ftjmhdjdVYJAedNp8QWzmN49NXOb1RYLmKqVGwNTp6rSFujlSGjvIN\nJoOCrYEWpbSmA0uDINMZh4xR3TJMDfJCYtYhfp+TxyF12WPpFUiDbge6IcnrntG2SMKGyp7goGPp\nBW3pEesH+rzCDgusvKab5Lg9aInFIc7xwxljb2IIF6yRWO9JPYFmHSmHDmkssLcVhzcVy+qPVJcb\n7HSF4y04rXVCY8cfnB/RBsF4qREuFU0QMv7uBu3+gmldU/s79Nc/cqfVTLQ7NmFLbVlMJhZ95HIZ\nwg/6c769VFT5z1T+NcdwSth4jAmcnzoIPlMcG3YiJ1lsOBMO10GI3ESIbyAK5uzrC2ZiSvs+o9l2\nFLcbys2UuT7w9viEi789p1vOqeQF8+MDOvOeYd7hfizwc0HJBe/9h2TtLV1/xfziEfsPAebmOZyt\nsYwZ3VIjcgacE4Gb2FiVgawbthT4xxlx1BMXHt5iw0Q6qMbAjDocuaNoWprMR2mCOMg59DVNecCT\nPTspOWg6jitIJwPDOP+LdfrPwix6o+LRLCB6c8Lb44LbdE0V+ry7dzg5eUCzXdCbJs7+E2nfYx56\nzE9f8SQwkH814+HmmuT0Eb3sMawLes2m1jKSdoVudYyNh6tbyEHS6JJsZWBbU0oSgjn4CuTO+PWC\nLk2pdYVrtzStS9YnKDvCw6GzLCajhtSOLLQjx0iwGVv8YU5ROgRTi745UlgVBiZetUJUA04zYpo2\nmW2gFTlWqjPSY2sNlfIJFwV+4dIJk9weEJ7JbHbAn+7YKgujchntirSNMKOMMQswawdba9GnOsYM\n2k4nKzTyqUZaWZSpiTjkbA2XtJmg7Sc0jcHcBcKKxrAwdhpeDZlxJCxrKtNgzC3G+ZFRdXipC/1A\nlnnU/ZoxqjGkz34eoBlLkr5DmSOmGjH1HvOuBU1hqQRroTE4c26zHqnPsNIJjhMyvb3H1A3G1cCw\nvsCKJlwn32GZG7an15RXj5l1T3ijWyzXA5FySbY9dS/YLbZUtkV8foJlPOXRYcabfORJoTCPPu8D\nm2v5llWreGlWDE8Snn79WwQnPFxrRHbI4qHD9jjnc6AxjT7zSrxgezwyDadEv+TMzxQ9Gj+rH5mb\nGUM80Lo2+/BrJqcXXBY/sutbWstj9wWMvkNxbrFNew66weKXp5Tnj+jvVpzZV4jjJ/zpU7zPLevp\nhi/1J7z9Qqe977CuNR7Jjpl+ibvtuY4jsFo0fYXpeKTsGfcmbrtHT+xfLz59m7Gx6QqPtjTIhCTq\nbIoixln7zEJBpsdMK4uZoeEkJVZzgvUvJfxGG002J3N28TVPzyXZ8Yb2zqR4VGBOBx6aLmIVcBa1\nPF5NOckdpi/uuQtM5h8+8fY85KttwWNf59TdMJzPudDPSTc1YeEhDEFvBDDtmHkKIRXHLifue7LG\nQrQphggZjZjppANpYFaS0BrxfJOuLOjyHD3rELZJToSaKHRdw7U1cqNnrv2f3L3Hr65Zet3322+O\nXw4np3vuubFyk93qBFo0bNADC/JAnmqksQEPrD/BU005swDD0EAGrJkhUJJps02R3dXsulW3bjo5\nfjm8OW4Pqg3YgALpMuSG13BjY+/RWtjPsx+sNcWtUrqlg0x1tLqkMlfIUiVyKzppSs2MhmzQ9FNK\nxYC5i9Rs8tRHkQqLVUhRb7K8MHiTbfKgGuinFZp3S/awTVePkK+bnNc2440lSV4wF2ss9ZT2fUBj\nIRicw9RwmHUu0GQD4etkiwc+eCpN+wPXSQSpRT66Ybwx564uyWoIygrGMypHQ5/oNJIQVVEQCx1H\nRnhOTWqUzNcJraRmltd4tUo4NRBSpVIrdL2FOjJp5DXJOGIxj+g3SrpxjmEtyOYZF/0D7tQZK22E\nG11QlWMWxR6n+T5dw6LyEvx1xra+4Oq2x6VlUTdTxrVDp1ZZHyxIbl6Ddo+cm1g7OVfNLXqftthX\nm4ThPlXbYGwrXM5WJPoFpXNJlhvUM4VbWeLenrFzKZHfHIA/4+n6BZfWO2pcKhSuF232N8GzJtxG\nAev2DoPWLali4nktNq2KrbhiaJvY5gc2zJSDrSmH9RbFi0t07wEjgdnkCb4h0S5G3FnPUX5zxOX6\nhvbZFMNqs/X4lslKYRW/ZFlpWK5NpOsUiwKLkrKtUYiQpNNCWjUyd2kHS3QzRegJjjbGa1hEcozS\nLVgtA+rSIQnvMfwInIzUjUmo0JfG9+bpv/fr9D8IBDiTCcfC4u3NPSebe1wtW+ybLg/nGvP2DcbD\nW/x0k0CVnGqnDMsC/WbJ1PH5YtFEOFd8WG4hTZXDxTtm+5v87fZLDPuOdKVQCJcNv8EyqMn9FMPr\nMlnN2RABS61P1JigLF2WsoERmaRGQVJodMs1D6qHbjuo65RxJBlYgnKhkLc10Ns06pjKNogjn0ir\nGJYZSlunrGrqts4Al1lRoPgaVRmxCG3UhkLi3dOdDqH1nutRh0nyHtX3cJxN7H+ZUR2m3OPhfZkw\nav0L1OgJY3XGRzddXn8zp+uMSQcFw6TLvEhIJhc0d27p/S+fkm8UfBW8IZ+XzG4djuQFv2p5DDa+\n5e16hwWC7p/+irilYSuSm61Dls17jh8kflqQurskao6vZsQtEyfN8aeSslejSg0/XxE6LeRMQSpr\nCpnhGkOm9ggpDRzHxpRQZhqlp2LkAaIWbJprztsei189ZZyPEcW3bMwf0DsXvJkN6VVX5D2dXr5i\n3n9K9+IedWdEnNmE9w52XiPZoX4uWVwlVFrO4bvXZJpGurfDyyTiXaaTtto0W5JayUnVAb2rV5ib\nDo2o5quXT/j4/RnX9QOr2ZK9ukM23yXwdcx3EYc7Nu8fnvHCekfzrkckvsbvfoH9dkFraKKWIyab\nA6qLgNTY46q3onfWwz2uWMgO1Vyl6hrkkzuyeI/jTy26X/+aS19lyzwizRYstRHx2TF2Y5ulc8XQ\n+D2M0RVLMcC0EuTMx2rrFJpNtRAoHYOkNsjDLg0zRrUM6lWbtRT0hMo61fEMqDFxdAGlTVSaFOqc\nfqoi3NH3punvhFjIUvLQ3ORZEWPt3xKfXdJ/OmGSf47Wek1LmZMtDok1BbmTs33dglGLo8EC9WiA\nqsJ8XmOOx2hiH79rcbSGd/2Cp1oPZnO0KmISN+h5JaNa4hkPOOgEjR5+khIsbLzaRoslmRsjlRq0\nEtZgqgalvkb6Lh2rYjWboXQ7uKqOECv0MGUa9nCdgHbRorAD4tImz2pUWbLyEqTcxI8j0lLB6GTI\nWDLVh+ytc/7ETUkvz4mrb6l+MaTT+t/4euFTl2Nq+SnidMFHOwVf6W94cubyT3ZUlGxEMbd52Tni\nL5JfohX/kuPkOfd3K1Z3f8Hq0R2deJ+8tca9LaiaU+5fD9hJxmTKFaemSbF1T/c3u2xtXRK9TRBb\nNkdGxNXBPnurU9z9R1TpmHwOsq2hqA5pEZEmKaapYmoLXNkls7tY5ZK4hCo3cHoNnEqQL3P0SoAx\nI9O6GHmFWakkpyEbs7/iy8ktq2aP0517vPc76LMFLXODhZfy1qx49PqSSlVYOkMG1x94pe6gmQ2e\nH3/gbLXP5pHN8lQhKQ1utAVbQmfVNPFs2F8l3DVHuHdd1r7EGHyELG/RipAn4ztyecjG4VsqQ4d9\nm7w8x8w0FpsujeKSj7YM3t6cwLMQZ/Exq+wV49Zz9howHhtsru/5SvN4JjLeeVA2Ml5fT9isdVzP\nI1o4qI+3aPvnrMNj7h6Z7BsKZ06D7TOFfSXFsn0Omxkbnc84NE+J3AGb+prlsofZqNGXEHslhsyo\nRYlbSLyBICo1bK3CkGPSrI1W6HTqgIXeI8lHeKJPrSooYU0bhftmTjtsfW+e/k6IRVnXHI9DXvVu\nCecv6B084JaPqeRrFvUTDtfbjJXf4OzvcX/tUJ5cYn5rcbsJ3Tced5s2euww2zEZXl5hH3/CtTrj\nizBCN3TmvktDVrTUJUpZsxEYZNImNHOcdUqkVjSHKnI+YZQL2q5GQo7IXMKejT7KUISCm4ZMdQWz\n0yFeRXiWg1QLFrZGs0gQuU9dZhRFh1qApktULaKZtCjlAr3IkDg4icKqOWUz2+TDWjIvar69/xOa\nvxjzdSNGPfsLBo9KvvmlzmerLzndKPlyafIkVfll0iIYpczmbZAWp/WfMO5usSVtfl39DxR3WygX\nKnvjGUvtX1E09tDHkqSzRszf8+tKQfprrNMPBCebnE/u2JiqzEaX/MHJHv/74zndcsHhD58wCaZs\nml2sVsBkItD0NbYuEbVHmUe04h5Jc0QddAj7DWCJHXukSUiMi2xq6AtBJ25gGDUzI0K9CRhah7xt\nnNHsLYjeSHp3Te7ta+ptSaKHTJQOz263uD08Ixgl2LM+s6HGZ3crrtsLOHWJtEuSaQe9bTI6qvCu\nloiLASK+RBdDtHaHrpYycyWVrEnuA7zpLq/33/LYqJhZY3wlRX6r034ypn7XR9kYsZPnBJbJq/MD\n2v47+oHGW9eikT1DiiWJqEiXQ1aPmrhTMIolO7cBhW3zaV8lnFpohFwf2eTxHYN3m8yHKY36EYER\nsFO/ZW19StZ1GPZ1ms8rYvMBWfepw5q01aeQMVpSI8yapinJLQVzUYp+AAAgAElEQVRR+Ch6wSI0\ncMsVojYIhUMtF2SlRdFuo6RzLOkikoB17SB7K6qJgaPpFEy+N09/J3oWQprc7I8ZagaPjVPOjA1S\nL2Yz2eUzZcrX+S1NBB+UgEePfMzlIXE65nhd4/t3PNUyyuqeppzS3nUxsgfcgxMaxpRcU9moDJyg\nRJYtKA1qGaF3mzT1BgkOSiOlftAoXPArn3TlUC+auMuUbNYkMw2KVU7SUOkGBc1SoZe7FGlCjIVR\n9siBTFTEqoHVitDbObpfkxk2pCphp0mdtwnbsKgyWnODJImYdN+wkU7Z/RqWs03WZ3+GN1f4zTuI\nzhT+0nNRUkHvT2F80+bdNxXRX5kk869Yh7e8jmbkv5Aw+5rzVyn+2zfcqH/B8pdrfvG+5lfn/5p5\nGBB8ecZonXOdviF4+AVvzA7qLEBrJpyFGVkv46vYZSoCqiOf27pAzz3uhSRVWmDZdPweedGnrHXs\nxGDsLHAYkugKaV3ATCcOAoyswF0vaS8i/K6kUmMUPcKSOtnmBmVcsfA1tNrHXGusREzLkzx+vyC8\nzng8GXEn7siSHbYHNmrjgft5i/ngmJ7Q+ZAc0Le2ubcjGuYNh4nPem4RySVL7yn3PYc4fE1etJCz\njL3RlKvpFaPNmKG5weK6Tb+ssdxnPLIe8dW7NtdWj/tZE914xjR8hGecsXffZNHpo1Vz9Nk1h8WI\nuTImNkfIdMyj6T1VDDcUZI7B63CLeVKQei5KMMFJdnAfZfTNnNp7w06WUDhNHj2v8Lc8ToMVerak\nLhsErkZDbeLMMkyhYRshYeKSryLywiFYCxRLx9EMsnaFsCuEp9COW8R1jqosqCoDveVA5SPVBUpU\nIuyYOl+Sud/fsPd34mWBJjBHJzjha9Y3NXvFKa2ffcTbVsR2pfFRtSQaGYjMQhOv8NUadfcY8yJn\n8rHk8WjF0apmvrFLenNBWB3QqGZkZ1/QPLGoyiWldMmSFfg5Ue7TSmfUmYntZhRZg3SjwJ4PUMwl\nedOEwmUexPQbK1ZxhVU1cGONtb7A1QRJlVOVTdrqiEq1SVxBNl8iWxaRIpELA0tdkqsKk9qgJVMq\nK8OK2mTtOcwcKCccrgq+/dLg1/6cey3AWk35NlFJxg2mToLz5Ywbs4/0Ytp/tqLcCRhVTa5zsOe3\nbK0MTu1/xt3IxSibXN+2uKxKit0z9Cuf6rrkz4L/lS1pQuOWVH9GoT4g7v8nftUc0D7scD/r4XsK\n6g8m/HT0EjdOObA7ZFqCpVcUVYlnS9JgjZKr6B0VrfboKAUzdYVmC9qpx6i5wIpzRNrGNNdEjSZu\nVBE6Cs3Qw+gK9FHFJLumUzY5n2lcxjo7YsWbzCU6HrI6k8wfjTlZD/mwuuG2u0UjHtFp5lzkMw5u\noP9YkFxkKKKB2WrydRnzZPOAq5nFjrihc7Wk7D7mdn1JowrRjp/wbFIwuVG4fu5iuV+D3aB1dklh\nH7PhjJGKjYrNN9orHG/AUf6IeSfB/ValMqbcR4+wj2P2P1RMDu7RjDbTw4TRNEdTdvHCCxbdY1Jd\nJZtY7OcNarfmLDFRVhF7ZYfi4waJuUkoHRTRYbBXUWaH+GaNt9BZthKq9Ltv8EaogZqwyloIK0J1\nHNZijpp3QGuTRDq5FaCpLmbRQY4FjW6AoUREfoIuLXKamKbEKWasi//v/Cz+X4WqFIRTBRE948rL\nOVWaLBfnbCS3jLU58sYg3e3gPZSodp/Na4duGrAoY3irEQuf+8cn+F+NuB0IpA3+eo3Yd4gXEZUL\nRRUQWT7mysb1HRS1JG7YOFjoi5IiVEllgGHVKLlCHk/ZoMtCSyhUF6EtmIULtBym6ymZ4aFRs0h7\nFPMCoeeULZ92bpFrNbZTs647SJHTV0zUcczC7qNYIdW0ydIHM23xRok4syc4yoLR3VturjYJJ1fk\nekLYPqWzHGP3vmIzmmNvf2B9XjB7n/A4UXDy16ycEkuq7OYV2TRBGueUOyYLOedtd4E28On3V7zb\n7PL6ocUk+nPWZzmTOkSsloxfrYijK4aypFycMW28oR61ya6nLN05aSGYp4IAQdrQKFQFTW2QaBUr\noWHVPo2RTRZnNChouTamlaDjYoiC0JoAOot8zbq8Za1/IO2UrF6/IvAsxOOUs6FLfKqzPz/nUE3Z\nqHTOgnPqrV16lxd0rkG72uOzTgPz6SH5+28oM4OmXePf5WyKjAvnDstZYfR1rtoain6NOtYY7Oxy\n9yohnm7hbtVsBiq7uoVRt8kSnw/ZLaXapz0v8Lc07Hc7tO/HxFqNW32gaFjspjH7WzXJw4oFGv15\nl9H5e7qzFWLQZGP1gXOzg302RoY+cVwz6l3yrqvhB7c0FI1ow0eLS45fa2wsZry7uAR7hzp0GHg1\nSa8iD1TsTkkLwbyl4zkGXkvi1hlWoWCsPHS7pE4MQjkmzxJyK0V2lkRmiB1bjIuUKHWxlAZ1uUYq\nE8yVg1f+/2SCs8xVaN4QnUw5iF6wtXtPPtlhpO7AaUVa7aI7VyxbDlI2+LCt8rXpMZYpO08tbgch\nw8UV02c5J7dtullGUeSI2zHLSiEtXFxNYFghI2mgziVj06EMAuIyZi0rHE9H0RxQLTIzpV9aLLsz\nvLjPwE2papNeQ5LbLqpsYDCnqgpEssbwwQksWpVGqc1pr2sS3aKrBviVTWJmBK6HV8/JhI3uRlih\nIN822alewnaTofqC1uYjxNacdv9nmMcjDqMfsP7BBmk2YGg84mHwKYPPO5if2uS9hO7nA6S+5PHR\nE0bCoe9sk7z8mB8HbbZ3fsDPrRdsDZcU/Wd0shlfdI7YfPYTzCZMshOa3RhdVuxGDZT6PdFFiCG3\nGMaSesvBTzfISJCBipJKsnWC7yTks4CiLlGmMfG6Zl1nLBsGqm4xzh3WmJSVQ7HU8Rc9CgyMrkI/\nczEnHdKZz8b+HtUkxzp7TU9kHB//FZPgBUEVU5426W494Rlrpv4Go30f/wCurgKW76/xpIfqeux0\nMj4cbCK1JtpVgCYqposR0t8EuaZ1ssndskWnb7MWElc5YzqLybQT9KVForVpYbNRjrl7YZPeVxw1\nHEg2eD+NuR48Z219xdePhiT5mMOixbrUUVKLvfwFYjOnc/seK/+YTTFg93ELZ+FgP3fY7uzwYqFS\ndlRWBx6NTpPxw4CpmjO3HD5+MWB/3CN+YWHQJVV0Njsr7EmOElSYK5/YySlVjdhywF7RLkz8NMYy\nK3RniN00iYsVxczEQkNUa3pzE81NMNaCbuoQZh6ZFmA3Vt+bp78bZYhasrOMuUs73DUTjh96rHZV\nOucZ3Q2db+YSZ9VBzRvcijv241006y+56Rrk3yzpfB5QbXcYzGB1dMdK8/EYcv60xwANI1gwMR1k\nkmA1XNJlAoGkUSioVYWnVRTrJWGmYCoeIggJdY/GvUPJmEJp4ToawTJHdgIsrUudBFRihWgNKKIF\niSUw1hZad4N5taBWVpTNCndmoXYEcrwmtWzUukCXJoa0iWYRhrvELZbkxXOe/TSlXn+GfPiG5O4n\nyD8scK5/THs3532rw98zLpm8OqSyfKb6NUeNbe5+FKMOCj6pn/JuGnJSlZQ/TVkmkrGrYHWf8Olu\nn87TitOvEwzX5OEP5gwfNOJCo+PO0Wwb5b5Jd/+E+7MJo89n+KM9vIMl1dxgoCnU0ZLY7ROkNbgh\nlvBpbljE2RRTdgjyDFQFshWmI5myYohJkJfIpQTZIWrB8PE5v/6fdeJshWN+w8Js8eGbmMPhEQM+\ncNpwqOcT9idX6FJwGB4wzidU4TV2+YyqmCLUBCftcuHv4Lx+IGlbdDMI5RV1x6CnP1DPbWphky/u\nKBSdRq3wXmvQ90IajUvGnkK+UsHNUYtn6FfnpEcmi29XyOY2Yr1kyy65OH2G+vGMi9TFit+h9g6Z\nXaTMdnwab3w8JUF7dkMZ9JgtDUIF3FfvuTQG9F5MWCx67E/XBKNL+u1PWH4W0V+H3FQ/ZquX8R/V\nGrdCYzeDIOph9mNC5qixoL1uU3sZciKw2wahWaI3K/JUpRlNKLQuuT7DKQq0wmXUtumJgn5mEykz\ncr2BUVpUuo0s/ro2uv92/E6IhYHGnbWHrd1w0rgjlLuo/oRhYiNmHdytNcp5zmA3piuH3K1yquAj\nnm5E+OED5yOPRk8luLrEf67jJw1WnYThmxLzOKOsBGZl4fk5y4VAbdmYdUiiOpTpCroqYt5hQEbl\n6hAoWMYSoRus19DP1hSiidVbUecNCmOKr7eJypokTtCUDnoxg65CWYFfNwmVJWXVoRIVMspwtSZx\nltA0MpYNmyoGP4f4wOHnv/wjxsdfsZU+5fIw5Jn/c745jHFcDflkxvGD5PnukDPnIz479nmYvOEn\nj3+OdXfHt+Mem5/3GAQFTWERiwX+xQYt54zfdzPWrT7GfYq5djk4vudSuaP1y8/5ZjLCdB3u7i7J\n2jEds0JsXfIHVYfyWxX1xzM0rcmiO0MWLn5u4RlLLN8mHLkYoiZvlci6wbi7wI8dolTQs7skpkB7\nmFF1C3AFHbtPrQUYAXx1W9E+uWD5z0Km71QeOvd0vXtmX7foeLtsp29x7D2uLINd5xJruqK/nXBR\nP+bjecxpv8VgsMc0NCi+CdjYFSTXMfXTAVzVRGuF/VDy7Y7kkbgnx2c0WNG8XCB9BaNT8nYMe82C\n1TjDGe7A/QprZwc7m9Df2WYdTglsjekbKF+WfPJNROkZnLKFJQJGVotj+RXTx3v4VZO/er3No/Y7\nyoMe6zBh2NnkxjWI0phnlWS5Macf9bjqfYk6ekr/aICI3nCQ/ITMyCinBZpWE6saUnpkyxRFaLiu\noJ462O0FQdLCVyqoe7StJaGtU+Zr7NKh0GJEHeDhIbKUpVejGF2quKDVlChVwqIovzdPfyfEIhNg\natAOBEv/GW4FoV4itQ2+Hrwhuw9I6orj8ZDRyweM1j7661csVzlmvc3JsEG4XqB4LVbzjKXR4ZP5\nMbudtyjjE2LPpl+X1LmKN5CoSUxSx0hToKUSUoe0UbOgxF3ouC0TEXiM7RTd7zNRZ3RlxTwArwJR\nKuhGjaaZtPUSJYJKaVCFayIrY1A0yGcOuRejtSNMFMaaQ0/VmU5U0MDIEmLfZjdacP54ynDfZ/lm\ni61oTrxVcZQ49Godr5eS7egM7l6xEW1ykd/yn37xkrAc8fDZEZsXu/TCBW4h2HbXOJsn6Ht3DO6e\nsNKmzPQ94s2U1qDL3Bvw7ENFf+iy2L/lqzenWPubKOcjSsPGKlq8bw54qSoYfsTkxkHdb6OJmFxX\nWIYCP3Zom3OqvI2QGakIaD3UBO0IEfqITkkymdNrqVSBjtQKKiUk02vyuYrMNxmfXRCualbDPXZv\n7hmlm3yov6XVq5nLJpqSEFo5Mm8y0kt864Td9Ct+vdvihbWDNDJWYcxjJWW5rBl0BeeKRGPG1tER\nr8nxlwlGx6dWcvRsyWxgshsdc2+es794hO7CnJLYCDB3E8JJRNs2OPUn7N532e+H+OsIP26RSJsr\nHdqqh2w+8OxqhGwNkIbNxe0d2w3It9pcrSL28wxzMcS8O8OqW6SPNdzfFLwZzhDpPj9a90j3E7rR\nM65Z4D885vHzAiWMSYWJm/k0ap1QUaCcougtFqpKgxDykiJTiCwdz0golg4IF6lnFI0O0WxK4FkY\nmYXeKPCNmipLmeHieN/fz+J3QiwsvSKTGatuibxfIHYli2zIV/Wv+fh0n0lScnVUkyhnNF2DvF5j\n6QOUSKI8LgjmK769F/ScCTr7NJ6suArmnLzcpfKXKLMhdUOwCAz0oiBVYwZZgzJJUbomokrJlza+\nGROpJYowESh4cUChBbjJgGlXIHWVcmYSDGvU8Zy+55IubehmpJpKPVFoWj4rLQBXw0tylNgjqiMM\nN2BcQ2vYQAqFlZbjZEuWQY+dDbjVHF5qC66zNkc714xmHfaESqT1aPk5Mi9IPmxx9Pw52dmM7fQL\n9pVTsoOKsfcRrZ0OJ6+mFPYGXeuCK7NJN5my9ZFJGbWZXM8wGxWN5h+xcv45T66fsi40zi5HqM01\nzceHrIoML/vAm2c/oJ5k7PUNtIVkpRn0MbBbAnUaI5WSeABptcIqbAy9RBUSXShUgaRpNhiZAYPQ\nIRYKea3QLBTkLhwvC6R1SFb/OU/iKaPqkKo3Q1s6VOMG0V5Jko3ZWG2TJymrwS7B1zEb4il+uuLC\nOGfnweFJ3mHqj2mzydt5zY7aID700e9STnYdPoQ1Z60reic18/MXPBnckedv0NIukfmeyekGT3cV\n4ps2wbbH0pLs+RLn9QL98ZDizGWeN8iW7yjkDkmSsyskN+9jAnfAXh5Sq10IXuC2C8JVm63kjsut\nR2Rnp+gHJUU95m5scewrSC+nX3QwX5RMpcHRZsnBRy5b9jlcbrPeyxiiszBWVFETpa6pfJ14pdGN\nV+Sqj/B9RBlRZBVlLVB6LtY6Rzo6ebqmb9tIW0EEBUqZkIiaWOkhvYI0/f5OWb8TDU5ZCjZNlc1G\njr6zZjS+Z6s+ZZuaC9vnRhUUdhs/2WQWNHDOE27MBdV6hmqEKHKDI/OB7v7H2DOP2YeQx3ZGsFJJ\nMlBaSxZxSMdbI5qgiR7rKkRTXNJFSam26HZyNLOJaoKRrgm9OSo+jqajlxlWuKJTGjAYYZYZzcGQ\ndSlJm2tCkdKUCZYVUhgpDbWFMhJkVo+VqyMbHnVpYIYqSa6hzBc0hIeaNTDsgHBRcVQtSIXFI6ON\nk33Elm0i2h7rYURajZm7+xSdhG7SoD3cQrywaD9tMOwe8+g45bF1T39HRW6F6Hs2nadN+p9vMJBt\n9CLn8EWHj8MBYRWQqRr3g7e4P/gWLUtwrQbZ2QWf2h3W+ibN+ZRmd4MElbBWaBoBsb+iIStEWTHP\nBdo8QQRtlEylrgxE4qKXS4JKIusAd9wENWBDtVCyjCCMSG/gQp+Des83e7swTdB37tAexqhKhXm0\nQVs2yWc6ptrDa8UMBxGVV3IvQ9qrgM5VF6+1T7jbpHOiEPjQawT00w/Yd3POTxzGqYWOxdHZFs5a\nZ0M7JelbjMUBe0Ile9Lj46FH1V3SbViY/RmmgLdyxvpog9qyEHmMMlCQlo77ewr2nmDaVHhaC4qu\nhXtfM4jucVs1jn+Nqxqs9Sbb7RjFUNGqFvW6w+8dHOHs/IBG+jHFUGM6CmgbOWkzYHmv05v+Pj1F\nI9M9wpWOFBUaU1QlJC8iXEMlrRVq2yFZQRbYGEaGqHVW0YhlrTJLKhapSVGYpIsKWjXjeQNMQSNa\n409TXDX43jz9974shBC7wD8GhoAE/lhK+Y+EEB3gnwAHwAXw96SUCyGEAP4R8J8BMfD3pZRf/rvu\nyIqKeXvMZDwgG71hw28Qzwu8wRYH5jsmwsFdazRWt4waxyRmwLCdUeS7ZBOXVe83TJVttPeneAct\n2s+PaWQdogOHbRmSB0OKVsV6pmI5NSUCzR6Q2Dlm2iZT1oSBga9VVMIgq3OcWU4+VEgjC9MA3xQs\npKAdqYRak3wt2agzFkVF5jaZKimVqWEuHWI7Je4kDB8yxt0aIoesVbIZC2RcUCk1SrZg1czRdQs1\n0rhLUoyOSSym5CrUURfHzunEJWHdRk2a1G0ToQpqJ0OOWmTGPs1ORTLOWWoKbluhkwuK0kQUAS3Z\nZF1KfFvSiea81326C8lx9yVfOTf483cMD65wz3sUPY3T5AMn+XO2xlOGX1whr7eg77POAMtCeQjJ\n3JpWJCm8AktXkMuK2aDATDWKRMcwdcBFaAVTr0s9DXDVFiZjpOWSbvq8Hd1TygDnmcFy0sexCnjx\nOcQWw5WDdbCHbefMnJ+SvLnm59sx54MXWOsas7rAH8xRThXMsseWN+DuUcK6fk57ckYVHeBpAYnb\npP1MITcfYS6vuPEljXyLoJ1ygIlXjbgLD5CDGen9Fp9sdMjWOtHRHgMlQfkhfCXnPDs6plyCtPZw\ntlIYRnweRFz+ZIhxtk/vyRuawYBRMOLo4CnNxT3ZT4Zopy1QVW7Xa1rtS/aMT9DDAvnREXu64Ed2\nk/qwi/bxG6RoU01N0FSENNGEQO9prBc6vrFCek1kPWVdg+60yUeSul2jKBp1vYTKxxFz8laHaO5T\niwpbD0lHPexmRkSN0Bv/z1Xit/jrlCEl8F9LKb8UQvjAr4QQ/xz4+8CfSCn/WyHEPwT+IfDfAH/E\nd67ej4Ef8l3GyA//nTcYCr5e8+CYdB91oIyZNkC+U1i6TyE8R6QGNAUeM3xDMFFSLuU3/Eh7Rvlh\nQKNjku90UCKLm/uaYmfObrlLUhsUVY05F+j9iDhNIKnJtQZaGTEua6yiiS0rZO5gyiVSq0gbfbqB\nxBYrlk0LZaXjqDNi3WLDgEjJWYQOqhC4rMko2ZQ2kaVC5WKKimjoYFCR6jUb84xIaxNaAe3VgLmm\nYqbfzWdoqYVeZrTsNbndRg0DZBVirmGRduj3HsjCCWvpkVhTnNplZaY0mik5kpboM0ZBMyCrJb6W\nYmolk0xFkTNcu8Eizoj3LDb9x0z+xT/l6azga15SNf6S0bMF9dURrf4Rz60FmvIDHi5zlI0CTRe4\nqYYSxsR+j5adMZUZ7TBB8TNKtY1dpKCkKKYgNDOMPEGImjqVeN0WYr2i0PrUy5LPFmOu1c/4qP8r\nfvmkTU+00do+jXFNpzlnOTyikVxwHj/j6dY5g/JTrCcrXtwZmHtD5rbk0ewJtzsf8JQQVT+hf3jE\nzcOSZ8YLcCJCx0XIbZLSYqK9Rz3+hP9kmvPNj2O2dQfrxsX4L45xogmDW41oWHETFzzOJdmOQ3iZ\nMXj0c/7z7IqicFg3ttA3cvZvLwgGJ/hPBZuXXW6flWjhJ+xsZsgXJ/ijmOpv+Xg3A7SfVji3b3Ab\nuwzHv8f48Iq83WabE+r+jODRPn/gCjKaVIsNer5OVaYYSxtDLiBa01E1cDR0saKgR12sqJUlA6dH\naM3QxwpQIaWKtIbYYU2prHBWTQLfxNUyqiRGsZq4/4EMe+/5LkgIKWUghPiW71LG/g7wB7/d9t8B\n/4rvxOLvAP9YSimBPxdCtIQQm789598IQ0CWeRz05lx9LVmEFS8Vh4tPKnZHr6g3D8jXt6x6NSeL\nDd5bt3TMI0bet4RaQb8xZ+Tr6K8K+DxAUTVm6c8IxYzn+g6VV7GsFMxKoZ0aPPgV1ionNzr0qoR6\nZlG4I9JGRSPyCZ0G3mjCuOXTpU3NmtKrMBMJSc4ii9BSQeaZ9M2E2VyjJXrMWwv0OEF0VOy6wzKr\nsHOBjU3mKojFEsVpkeg5ZBGqLclDDd8oQWsQaBVaruPWNkWVEXoaXhaT4ePYFYYUhNIgljkdI2Gu\n6GiFTmGtsXIfO6uo9Ii11kKpc7pFRShaRFGNvh5A6x3huM/Voc+bXzd4aN7i/KlgeqJivWzg2Eui\nls37px/43NuhQ0YRjRCWTR572ExZqQbS11kHPlY4p9QX6KpPHEagarTqgiI30LOYqq0hkpC6NKFS\nme5K3LnN5mbN3FI4UX/GorBo+Ve07gfo+7+hfOVx/eKQH9+6RAcqmy0D7+UXDJVrxsomTvdv4fZf\ncXLyh7gdm2sno/8q4uw4RPUqDsITjONrxu/7LJQVR/1NFOZsPmmy00yo1Sbiw5zsaJftS8nykcV2\n+4LtZJN2OWWuHvLIiLh9HuDFz5k3VDpKzMGrNe6TDVbdXdRuwe//eMK32hbNr1dkH7Vofu3w9BPB\nxahg84cjpg1B2n/Gi+GCeUvyaL6PHDU4eamjNj2MxefEJznq5Q7bvsZU/y45LKsEWkdhsXbxWhnR\nGhq2S5bmDNSaIrcoywSx9imMnLbXIFZrNJlSkODGXRZRSXMdMXdLGjqUZY1hfH+nrL9Rg1MIcQB8\nBvxrYPh/EYAHvitT4N8eYfh/EwshxD8A/gFAy2sQaGuWdZ+h8PHiiHc/CTkMmtiOS3JfM59YbIU6\n5YGG0TOR1wlHdyc0t2ImCTBesWgs2T+FR3+ksbIj/vbVE+62QvpLgedqZGpF7fg0FwrFcIJKwixw\n2LAWVO6AYpoy7wrseUzWHNKPA0pRYWASZgGiAsvtYISS2pSQz4gjh74O03aEv/RZNipYJjQRbIic\n2HUoyRF1QtmqcZKIwJD0qxpVqRgHDYJBQTUd004Es14TO4qIuwbW1Eaaa5Igw0xcEGtUc4CmSPI0\nxxFdHHXCPBRIZUFmK2hSRS4XGC0P6aS4oYGmpIiNnL33JpW6Jv1wwKB5yq9/cU7wWKBrTQ7zERuX\nDWZf6Bx+08M78JHNLVaVYJBMSIYWxbSkoWhURYmug5LmUA1JhUI7FwjNZBpJnKaCkqrUSQKWSlA5\ndDsJrZHJWvF4etDkL9eCJ+qa9x+lHN/5TI8WXG/8kBeeQ5HPebbjcKembH1s8lX6gsXPPuLI/YpQ\ngDH5BM/t8XD1hp1Awf7kC56vStLnMwZZmzResfN8j15+xcHuAcWbivluSdIIOVq3OT8KMBWV7R/d\noX/dRet8ROdqzZ6xg1Jm3D4S7HVsDow9yq2CmzTF32nQ3rkimzmMo5TN6iVFL0R97qMpJt2THKte\nEu9u4Kp7OFtNVuU79N09Xp6uWT9TCF7azJYNOuUeR4c1+m4PZzYiNdp0VI3cjrE0hYmq48mYQgzQ\nXYUyXiJMqBOfpbFE01S0yqKZK8ziJc3YQvEq0lTFEgldtaSSBYrSJy9yhppk4X//ce+/tlgIITzg\nnwL/lZRy/V1r4jtIKaUQ4m80Tyql/GPgjwH2djZlpT7CDBacGWfUFDzPPsYzFL5UxnhpC+OpzqQ0\nWLRuWeYRsQY7mcXbB49n85zSbHO3uKfYfcHtQ5+DHzVJejdU1hDZKjFzHaIKITNW/QAxF3iGgxys\nKVUTZRKBUtAsQDE9qmDGtG7jDgvMKKBs+qSFxC/mKIqF6oAwNOxVyrjoocdLojZsxB5Le0kezQla\nCnJV0c91xj0dLcipahffWpDYJkLLkYWGEuu0lZBFs01LCdUsCHQAACAASURBVIhrF5Hk0J5Sxl2M\nzIJeRBE1qGSAm1VEDR9FjYkLh8KPIO5iZgqZvsJpZASUZJWOZ2WEWZucFHtDI5Ejds4npHMN59GQ\n8TzENG7Qw8+YP4n5IvIxn6QEey6KLvGyJVkHiqiiX/cZLQWaFiMF+MIkVxZoqY/aLYkyAxYVebPA\nsgMcq0kSZ/SUCat1g6YWUzR9uND47JMtsv0ZvUhif7GP+o3B8+dtGqcxX2x0KSZb7Dk/4uZhzu+/\n8HkySThbD9nQVMRzi/O3Fxz8/L/En/+Gbusz3ozv6T07Ynk7w6j/LpudK4rOJ9RFRvzZIT7wH68s\nFq13HCz22dcjvl39iM/+Vkyzp/LhoyvSxqd8vPiGTlsjOXfobiwJN7sc3dQ8+btNLs9/D9kr+Wk9\nQtmE/qpi42DI5esF8fMGn5x9YC8HqbiY7S7TPZOo3uL5T6Y83PSZugUvXhQkVkln7iC0Q1bNEW6m\nkSHwLJ8kBWWV4LZ1RolCU8lRDAe/XCKHBcaspt1wWFgay3iBJrtorZJCl+RBg0UnQc1Mmo0cJQ0o\nq5QSDbP0/ib0/DfiryUWQgid74Tiv5dS/o+/XR79n+XFbxPKxr9d/xtHGJaVjnUTc5CbhGmCplZc\nx2uOlyOMx0N61TuS6hG17bOr3WJe98mqG+ZbAkca6M/gl+9zePqC4FrB1h441E0uJxFHtk2dzimT\njNA3kJoG05pGW0XKDCEzysgkc2pabs587OL31yR5F68h0GROkSm4jkUeKEwNl15jjCzbeOuSRAjs\nxhSEipNGZBboRYM0t/HjCWnaYdaZolYGVctG5msC0aI1k2BX9PQJieoSoEC5RtNKSl/D0EqCuINv\nSLIyIVnaRKZJt9KQ3hxbAS3tMq4qrMqlcAVpWFCVCsguqi8oy4JQKjhijhFbFDeCu+1tGtYZD7+5\nJq/6bK6vybs26TJGuW+RfrLJwl1yeNmmdVyyGjTRSXELi8oJUOoWqgPZesRKtRnIhFCoTCtBu85J\n/JhuoiKzNtIzMGybIiqRLCntNl1W3Pcd3FmM2/2YrpVx6bbY/9khvTdXqD/Yw75zWTx/YL3u8fPH\nPR6StyRPN9hBkKkVe2GJ+PEXhHfQfPGHyDri949MZjc99JNdSlNnUyso5QGlJll8UBjWGtbR/8Hd\nm/T6tqT5WU9ErL79t3uf9p5z8rZ5KyvTdhmBsCwPYMqUGViM+QZ8AkZ8A74AM5BsCSFKsmQbU7gq\n+8ybtzl9s/f+96tvomFwa+BBAS5dC6XqHS1FLGmtNfg9injf+K23YiufUF5pssun/JQj4b1nvBlf\n8iOesMwFx+0/5ukrzfGJ4fPY0ace0UqjIx+3lcSdIE7ucWje8Zm2HPqG66cxk59zfvAZ3oOKj776\nnA/3XvJnxZ/w6uIh9j9m9eV7Pm4SLsmJe4cM+dSnqt4RlSuObURUHanmjC7okIucYxtw3d0hcp8+\nzLhMjkysyWTPpYpwSc2qjLk51YyTxBGQbkcSB2LW1HdrUifwtzegc+rL/w+l07+ubvyPwO+dc//D\nvzP1vwD/9K+v/ynwP/874/+1+D7+E+Dy/5avgO+NZH78FW88aKOA+w/vsTUZ0s/59PWSs43oXr5E\nvvg1z7+NqJo73u0XePkFb6foX1xzf9vy4FXPcv2WR0VI7td8Wn4Kd2/Rw4IqipgnhTxb9KpFjopj\nX+EdM6ZEUSqDtyuJhKLrgcDCpaY9eNQhHExDpDSJrnHDikEIrFsyCoWLroCUPhC0JiGRgkV4i5kk\n41VDEZYY37KYfMp6iXAT1bWHC2f2ck3vBaRxzNIvOKsNZXcmOrXYQBKqikHkNMWImkCFIUwBxlPc\n+A6mgb6tSHY7HBeiccafLd7cIuMARY1xirtlyvv7Ddc3Fb8cfsTu6hpxeo5UKQ/e3ON35Vs+DSze\nmxn19lOE+z29H6CQxCom8MGljmWhmdsBL4ZwNuyEojcGVyc044DIItzscywFrtNcBsd4dUGHGUGn\nONuZzG/JxUR50fR+xPVx4BFn+m1MMxqaqyNx6PNwBSfR8nB8QD4mpPuSJ2aNJmIhWz6677iuJsrK\nZ2dXJGVCmFuehSMcIk7GIzgYNuWFOatw9Yg1S8Ix5i4JUJsVd2HPs+QhV+IK2oTSOuLthfsYOhng\n6R0iiqlEg9dK5nFgGirMeE3weMHiYUr5MKIsFzyTD3moP+f1FwY/fsownnliWu62I7l/n6rriPfP\n0JuCrteo4CHjTpMt7gj7iXA14puC1RiiwwvNNWAt0zQR+9BUhmMQIleCZZyhVQerEbH2CFOPQWhm\nYbgoCPyKPtix70H3M1kx/+3I8DfEv8/K4h8B/xXwayHEL/567L8D/nvgf/rrdoavgP/yr+f+Od+X\nTb/l+9Lpf/P/+YTZEq5Cjo3g4+ATfjs4wrBm7AuuueFWhHjPlui44p6ayd8+QTy8JRk7rn428uFF\nRfFS8zxbcbXZYsKQ6bnl8njCbR4Q2wtOCwLnMyYTsSyYEoepIdz2NFPHNCvOccAmPNKOAS0XhmxF\nVu2YnE9CjO564mLmKAb80DCOIeUU0rkLqVPcNY6rTNPdKWxckArFJCfOR491vECOJ2o1E7cwTDtc\ntCA+n4jzgH7WnG2AV48M/oJOdKS+YydTikiix5AmabDRgn0VEAnJPW/mEA5cRQuq04l8AnGVoduI\nPKzRk6bvQ2ykWZ9b3Ok+N4cZv3zHZ3GDsT6/fp3yrfcNi3TDm0vBP/QGPu49uus1SzFgbnsqBcor\nyHwJQ8t2FcGU0l9b/KohKTUYxehiqsuMHh16btBRThD0mFniDzMi9XHyinkG56ecgwuJCajSO7wh\nIvSWpLpirgye8Bj9nsANVGWINga3PjEcDOLKQ/UhITlWfaAPrrhuHP5VR39UzLlmiDLyoGeafSRL\nNrJGRo7Yd5gPV9h7EhMF5PKMHLYcsgZfC9RJ4jJD72nC6YBNrzjUDV6gkAmUZU+nBPf8M4P0KExA\nVxV4fg/bHTdeT/2bGPwVv7sKKb6RZH/vOy4/98iW94nvTwTthPWW7OeJMpmpuyXLYMSbO2QRIxFc\nIRimFTfKEYk9iQsofZ99ZNGNw7qZSZXgWpgVMhqJ25AjB0IHJl6R1RPOCo7OY9P4fzsy/A3x71MN\n+ZfA/9NZ0f/sb7jfAf/t3+YlhO8R//IR9372nN92D1jVB/zngoV/n2O0RGxP5J7hY/WMnZhQn0iG\nX9bcfb5hVg+x5g3NJz2r04H0RYj5qMH++EB6/TFNPWGjiLI12HxGdRNRG9HlE8Ku4WYm2TQ4m+IV\nEld55CnQWvwJdLxkM06IZOYU59DcYdch7pihZEubaqwduaFAigS6E1UBKgholcXXMS6rmE4R4+KK\nqbshCRRqEAxTzSJT1DbEhh7bi6FNEzI54XspsnPMSUATOPKjI401x/qGLHOkQUhzkSgvpbc9vdLM\n9pqiERyFgbaADJK8xYX3mfV7TuENyn7Mw99cuKg1X5uK8jPHehCMmcdaB/xSHXj62R1PqonLOSXI\nAlTUE+5htj2ezDnbmGG+474pIOo51j1FpLBtRj6PyPUCJxXpWXIMQeoEt5ywzciiHhGrGNvGxDJj\nrk7ILKERCr+E896QL5Zc+pp5Ibg2W9zxxEXAsFAo69OeOxAho90xuiv85ZlqLpHjkSBZYN1M5Ayh\nDdGLjqaKiTYFvr3jTEAuBhaNA2WYmiW9f0BVHr4d6ACkT3SdQutjxwNXaUynCgbbYxuPOJEMdUa7\nPWE7D2d6ukFxHJ/gnX7Bh3cTX0X/lvL5Q5r2xFfdmv80uM+H7cDTDxnmAVi/4kqHzNbDTg0yTzFq\nxp6PgOOgrpH+zFUkOVwS7MpnuJzxmplsuUFfvv/GJg1Ih4povGIWJzZzhlzFXMaGWizw147r1tAl\nf0cs6s4Jzlu4/cOS8O2E3secPw6Js+cIT7BVjk0jObs3mFhjhpmn6xPFiyOHP1iaeckqesDp3RXm\n2YXQKeTrEX03YLMTtu1B5oT1Es+D1o8pRh8XzowbD1knNK7Hu5u4pDNmSpDdhsHOjNJxLBXTrmZp\nz0jpsWYk4Ug1e9hoBOvwZkkctyDW5FFBdoxJ9h5Jp1AnTVJKyn6miK6xaYxLQ+ww03oBoaugVSj/\nQhTCXpwJw5HTKMk4gjchspA08lmka4S6otFLXN4QiwDVG1KXkYW31K1j0SsCKmSv0X5J3N9hJo+h\ngFx+xyAHXPgd9uk9RnHA3K0IXh+pHsf8pAt5vxfIp5+Q5g3ZmOJO0NyT9IWHnBvEcaLMA1zm0VUg\nhMRaR7yOCVXEvqvxpok5leQmJyJE65gpSTltAupLjPSO1E3DJDxcP9KKFPvBY1UGeLqlLFcIFzFx\nZggmlDEsBo3wDCayTDIgimL8osbeOXJfkjVXBJHAB2SYYGVDrVJsODHIlnbeUHQOlafse8scT0wT\nzElMaUK6yBBftfjnkrgbSVRPFJWIUJINLUJXSM/nUEu67UxYK6JLSp6sKUiZk69p311T5+94+1eG\n7/Sf8/ubX3D89QvehL9haga+3X7L2zch4HE6KXrPwy1y+mZgkgtif8m+9MnykTFsEJWknBLcraLt\nliRlwtA1OCuomQkaiek9qm6kcYpKzChzIdQpnt8S7itO3Yi4/PBtyB8FLCZjKEqf7t6G4vwdiReS\n5+/5OrO0ix15OPCm+ED13RWLPufE13wtnxKmHpvgBV9cOV4Nr7lO9rzc7yh3P+ObzuN2uWd5NqRh\ngfUPHFXP3CeEbuRcNQSdhrYniGa08kjEifS8YhdqRHLHnFyYtSY4Ok55we0iw7MWbRSj77Abj1Rb\nen/NIvZoKblL9gxaMOU9/SrjImai7YpmMvRFixMj/dkShy16ERCdei75hpwZJ3LkfodqMw6TIJQX\nhM4oxUSnagbjYeeeQDe4+o60i2niBlX4RAtFkAQIz6LCkdLPyH2LV010/pLYByFSvsl7Vl9+BPNn\nRL+M0O2GN/6WcBFiOsXzIKS4Lbl99x7Xa5rlRLgoCJmxTmJXPunCIAZH9QGsHzEVAYck4GQ6BmPw\nSIiHkVZqfHPGDDvud4I66Mi1j7eyzNkSjMHzlpBEpNWO7lpy2+acbYDijKr3BLXA5D5S5nipZFhH\nGFGwFTPnQEGliK9SulAw5jNurOnHlHNjkY0hrEa8YWRue7oATn3MpE/IsmKeQkYMuWu5DWq0SdD7\niGLd0znNVE/oRmF0zcmGyFmy7xVeOZKOBhVr/OhMF+3QK418lfCL5Pe0/+z3jPv/lV/8M82/vez4\nuvo3vPzNDS8uBx7/yiN82mFeOYZtx3xOScVAFKfMvcRGGtU45GkkuJS09ojbSvxCk2x6nGhI3cg5\nTFEuJ8w8pD+TbH10KCnLnON5JmwGGCaiKEfmC3ziH6zTPwpYOCye95yF/UC+eoLevqO5e4C+WTNy\n4v2rDtE8YfvTD5Se5cFJUd5prH5M1D9h2jvcYYknRu5tnrKLe358/wmLN1d0i4fUPVjfJ4kjwuuJ\nbrhg1iWL0sP2GuVnXM8eY7qmNTXruqEVBZEQhLnGJZKwdSy4MJQpF78kjAOy6owcl6wPJ8bqRNlq\nsmFDdhF4fUS0b/CmltH45KHD3IY0WJIesALRCQ5Fim+OyKLDJBqWAdooFq1P4kVM1Ph1iJIetXKE\nOsK2ECQ5hxK8LmPnhUzaMJ48pGmRTjGJiPgQg3DM6ogIl0Tdp/jVl9C+oIn3jPcU7/cV11XNq/wR\nzdTx+EHF9ReaR/nA4DtUA0Ya0moiG5b4rWE6ddQyJM08glDjHT02txHhOWQKI/wioJcQni6c/Ygh\n2HC7GticDVNQk44O2wyU0mcuK1Rr6FWC2FdkkaFUKRjHJttyUCV6v6DxB/qdYh4qkilmn8QkB0U2\nBUzNhLmcac6auC8orUAvUxjWVN5EnkaUKqGwEp1UWJMR2CUzmsV2ZqoKVjpnHdSMG59TBwMJvkvp\nx4mpvocH6HxDspzQe4eMOnqXYMKceJBEWnEbCO5+ZXmrv+FXzY5Xp+fof/4vmP5gudkNjJcXXBbv\naC87/EWEOuZ4+o7soKg5I9WepjIsp4LAZKhZMaca2XSYuUe4CUYfMUcsvIY+HGhPJ/wygZs7VmLG\n6wdckGOvBUWo8CIPLS8cxx/uDfmjgIUIBLX5iCdvlsQPSt7dXaHI+GRreNrMxOVHWHvi/N2KD1lL\nJAzhJyNj3VJ7X3HmPdX4gUskiavXTJeR0N+zSN+S7Q/4tsWojCGomLolebwmVjM9kK5jOJwxRtLP\nEK48lA7w1Jn4Ygimljh22KsZ/9bStgGBHOnEQKJXDKpCrT36cEVc5HTJSH3VkWpLUipYOyQV9mwx\n1wHJReMEVN2GTShRVUCkYtrJ4zgbjmNIEEQcUsM8+phe4dIJO3cUUjJPHpdA4PIOcWpIdEcyKy62\nQy989MqiowFvqOnSlpAUq5aczR61/y3Pypf0vU/YaKRwPPvoM+qP3yLzl4jwBlfXmDZCP/gEP3zM\n4Hyskhw8zZxWzBH0y5h173MIJmwfkawlWp3xYouUA+28Y+4lXnqfoFbk8UShR8akpT+EtJOizjQt\nM24SmCAit5o5zEjaikrvuR00t6eRRdTgcsV1YJkEiAuMsWbRaEbbcbkeSXSBn/kUaYfyFOcc7qmW\nozmTxUsuYYPxE1RlWJ01NjyhG4sbJV0vcTahSUdm55Pt9ozCsrI9k7TY1GNeVvR9g7s7IhtNEIxI\nEbOWM5UTyNTwbWHJ6x7/8g2/+nDi1fsC//A7qsXE7+sbzu9fs93XPO8Nj/UjTNMg1USX5cz+TDCt\nkF7EPV+jU6jTAbIL2vn0JqRWUNcDUyaptM/QKIyLEDJCDh7neyWdKLltJEHaItuUYyFoPUV89Fhd\n/x3ZhthJYY+v+NWj1+C94SfNS7brbzCLiN0Ztt3Ex1eguiPVt2ferJ/w+vmWq09XjJ88xq0KvO2P\nSPucdmFZeTG/eesh2yvqaIFOBW19gONEn3a4SBCdHfrkmI8tZhMzlgK7uFAbH8vEnCR0xRZjJZMY\nSHVPtUnwVj1LDO4YcjEa42uqMWbdCOahQe8zsmGiW0/YENTpPkZPHJgoaGnzAK8YWdsGxgWbsido\nY5zOiZOIZSiZXEVqamzSIMKA/XkkbCKsTmjsCd8b0GxQa5+6GEj1jvse9Bj0KcdzlnaOaJuCaFGR\n2SNKGdY/fsR393O88THn45n1+Q3P9S8xU8jDS4m38PDkzzhm77Ff+4S373CBRpiQBIfWgkukSZjp\nfY+trpmTEWk6PLOgrnu8IeQeBVmo0OKGaXa0rWJsFtjOo4gkRCfyrmEoU9ZBAGOPVpayt8gpx6iA\nMozxnUQNI0F4YtaKdNNRFAVuOHLJNJ6fs24EZ7EjFIpKh3TuwFpMiDuPbJtj3B4nPAJTUa00ewnN\nHGGWmqAVqKilEZbJWzBqDYFiqTtCFdPYjNLMBGPPZpOT3lvRiwXKW+COICuPsPEZnMN97VG5b5HF\nmdjTrL9+jpwHvn294eFdQ7ML6fxHfKk+Qe6+xi98Mu1RDDU1AVMAQT/RDT5StCSdj+s9PJPSpzN5\nvcB5ktwkZJ7G5YJV15KKDBdG2PlCLEdyL0TVJYg7Vs2CufuAtxi4VMsfrNM/CljIQKDVgqvdn+CG\nlt1HH2NfPGLqXmBJOD99wc9/q1mmI9uPAqLCZ5X/mqh7ydUrwaPFkvx4w27pU8unrCLJT5zmZFvi\n0KGsZh1vmUsobjN6XX1/Um47M5Yxek7pnSI5xvh9RbdYoXqHrBp6B2M3YqoN3mgY5whuOrRa4l8J\nGruGqqbhFi4ZUTJxdinjOaExIflUU4xrFsUa7xSTzgNhYDlmHkIZmi5nwDCWgvAU46oLfjQxFSVD\nbmnCjjiKqaKRUFjMRhK6JXWnyXeKabbo2OHOBiMciRypdI9NBYug527S+HPOvWrDC9USfaiIVr8j\nj9fcrUuydyvSs8/OCDa6oL99QXL3EUk5UqGxesQMM5m3ptCS7XCPtlmidMcU5HSjxbtTXLIWsR4I\nNhdEUzO7Na5eUFwb5m6CbI+JCkQ4kQQTMwvUeeIwt/hRxJSmRKLj4lkSkTJKn2TpcZutiM8Z8zQQ\n1golIrYClseEwLT0LkTEOfNRsi5TTAfT2TEtO7yjIux8Rq2YOsvc1IQby1p75HtJI0Lscc0ay72j\nROg1JluivA0In/XqiCgtkbfmrHa0g4XQEWsfZQJqAsymph1Lok+PdO2PiJKYWoN7anjxrsU9/I6v\np3fIj19xyN7x3IW4jz9B+DljvsckJaupw/otWkGEYW4S3KJGeALVdizOM8d0QAUhN13IwVgCNzKx\noo7OVB34fQDnBmlmYtkze5Yg3ZOPS7oho5TND9fpfwCt/+AImbm/aCncK+b3Pla9IF473k6fs/z7\naxoMydzz+tlDig8p797csrl8wXsiSj3x/g875rAlUt+xeR3yfBux/9P7HH+0oQ1aqs7RzBPp6NOW\nFcZOjFkE84BqY1xgiAOD9iRhmiC8CdWV9KHEujXelIFuobUszkd656FWE9PtgD915Ns1Y+GhojPa\nGBY2YIx7lmdDlY9ob+AwC+apRoucyyVD9R5GOkQ+E3oWfwjo8gvNAkIbMdUdSTVzpdbMiQEt2A07\nVuPMIAbWHuxMBB6cLtAUEfdOIWlkMfOG5TjQhT1X7QKtBTdxgP9dRfa0wX/9kEt5whd7Fv2Zt6Zl\nvVrw7bsDWbrhjoDvrt9CJpBZQ2wCBjPhEsE+qHGypitSpoMldCl3wcymWbA+bRFtQuv5BPZEnffs\nhY8LDbmSqFNDpQ16SOimDhGVhFqS5gOLbuZ2mRGsLb7rUUPMPLRsD2e65QFnZ3bBihMDjVgyMDEm\nAZM5s/EgFSPDqcJLBM606GNMn9dYpYnrGT9fIoeU1S5jJmNcV4TLPUZ0TIsjY+noioZosDhVM/l3\n2Mqjsz13w8jiLNkEF6Q+ouWJJgChHL0qEQSEzzO23Zlst+ZTncBrSffkC8I//ClX5hl3549Q3z3i\n2YN39F8P2NOJ2ffRF0mbZviix50V50hgry7IpqQveuJlThhNbPuOlUpYSMcqiJgiTZI2rCON9i7Y\nMMdgsFvBwXjg5+zslq7sKdVE0/5wI9kfBSzGSXEM4UUeEnUN5u0TxrJADSGvXu15+PIzvlhdYTnw\n7nHAk9OaavWKTvt882mKWqzoT0/o+RG3ao9/UzG3F1byQucW3NvkBEYSFyHRHGNMjJtAVZY2sFTq\niNmf0JOkPygCQDoHRUsuLMb4JNbSJzDIhGa1xj+dyDY5hSiwumY551QTLEWLmBzYgJ1pWQ4bNIKr\noMHIED8/MiuLP9Z4ccXoOvqzpohqXGsJxYZIRrhxQVAsMd1AdpiwasW9zKcaCpZ+hOt2JAvFGpCp\nj/QEdXzh1FiycUeVjDgp+ZArRN+wGG4YHz9CffMFH/6kIpTP+LQSnH8S8yh4yIf333E/fMS8LniY\nnfl0VORmTbnbUM+GYHSMbY3XORLfsWwb5msfOU3EJqaLZ87exBwmDLnDqZSo1qxnQ574tLNjCA1O\n+Rwbj6VVxN4NiR7ZVZpd3LPtRvx9x1B3xPMNrYaLm5gGh8vXXJmWZLjgNUdcPOPPEsKUS3vmGHlM\nQUznLOf1fWpnmV2ASkrKPKV2FdFyYs8AxS3GbSj7DdYfqduCC0fioaOJBQwTdQPRIsM4gT8FOL1k\nOOcUg0b0SxLVomzFar4wzzs2uaL7U8HLjywvp5bXxSM+8Q6IokXwlvTxwMHMmBcN5y8NVRGzOV8h\n8wHdSMx+RRPNFKkh6jOEqVgfJQdh0R2wWtE1R4JUc9aGwvmchxy3z4iEwgpwvmK2J+gn6t1Efh6I\nraLOWyh/eJOhPwpYOE9jv6l4ON9g7ResrwaS7jVRduEnfssfgq95ay0P+48YGKjVaxIdsFFrHv/8\nD8xO8OCLDzycFffSDhP0jPOaZOy5blvGHbA8smsvBNERpyGXgkYsMMHM8lCi5YJ0rVmlFbaTzOWR\n7eARtzVlcOA20FypAeunhKahHz12dFRyR3cWtINjXimOXkCtL4i4RghJazXlYBD9iPVjQrti7XX0\nsmDcGfKTpggD2nlCjo6GCdF6LNcVl67j0seIck0wz1wOAZEXYXrJrH3GucIZj5VdkISSvrVkZQ/e\nPRYyQ/U5mZBE6yVzMPPx0PNBKELusz2fuTkvKdyC9irk8/WX3OMdXn3HjbWM0xVdeqDxQ4q1pR8i\nXLtA2ojB+FTOUh46Ck8T+Ro1DKj0QtSPzJcFcjGSrzZwbugbD8MCScraaTZBxSkR6FZi/TWqX5HP\nEdM8c1gUeOWCNpOEU4rcFEwmJa0uHEOBm67wwwVJFEH+vUszGjxU1GHSC+WUYo8Dy3BGxhntNDEZ\nD90o7D4myBJm7TF1NU72xNGSKGkgCIjnBbraM7grTLHg3AREk48aDbvkzMU/YfSSNutBF1SUiCbD\nC1a8Xu/puhnMB1J+yoMqgOEG697Q/TTjs3GJ9/grvnv0GYdf3OINYIueSXT4SLxcsCxzJpMg2hiR\nGPpgyar12Svo6jODkBzqDisGJpcQLw2NiJFnD7+uafMM1a9Y3UuxaURlJyCh32cswvEH6/SPAhYB\ngoVf4PJr3qYvOBc+7Ydrsq3lF+EnBE9WrPp3pLfPefZe8+iLGNE8Zhg+8M3PnlBdEl79auJ99J7D\nKqR/OhDszoztQ7QzDNLibq5IwyXqHBMWPs47YWnYVhF+bvBTEP3MbpaIqKMcMm5VwTmf6YaUotxw\nbGLi6Y6kyvHLgmRfE1tBbBxDPGHrHDN0JGGCN8BqGRFsL3RY9iahGisug+I4R6yDDhLFKfe/z7TP\ngkFJgkuAXtcIURBXI3m2o68HgiBg4SKUHtjPA2lZ4hWW0xTThuAqw3qzQV1S+sVI04VMS0sUNPTz\nTF6veEeI1K/g65nfXcG4rdjJnCy84auj49sg4jdPjlQIbAAAIABJREFUb5mWkld5SuUlxMmB5rYj\n8I8kZUMWOPzYw/NAhJobDE0GVQjaX2DEROzfMh9T7qoDnYkJtEfmVaiVx50TtF5BHM2M/hXK7UhV\nBZ1k2CRsvZFhDPExLDUUCO4NilY4wmbCu75BpheOdY/SAaF3YQhjhjMkNqcLO7a2p/YNdgLPb2lM\nxcqOFP6MMpZ0SIl6j2O2RwwX+npi9SGmmU8sF9dQQoIiiWtsv0CJkSUrFjjkqiOwPsJYVoUPgWG2\nd5iDQn2nMc2X3H+muSxfku8Vc/8jNs0Vr19e8F96bG7e4a4fk7WGYy8JEKCOuLZBDSFN3SHiPSOC\nINTMVuOcIigL0sRgbc7CSM76RNsoRHghXIGKLIuqoWsc1eBRSB9ig97XhAYq+8N/2PtHAQuEx/Gx\nJZ4iFqtPKJ6/5Fy8492pYtPvuTYZN9Masf4cL17z6yHkm2evIVzx0beK7FnFzz7+EcFCcKUFP6me\nwqcd6RF05Mhsi0tb6kZysiWRE3RaQ66YhWFwEUooxsmi0gWznPDGmSDqSHVAshJEDkzUc4kKdDFS\nVGdsrmimGJPlOCYSCVF2j2iMMOaa5qzx7mLcMmHhC9LVyGZqudYRRhtOWiKblD7yEMEKt/JZ+A39\nUdFXLcHVmkaAdD0mqxkXHS7tCKKYoZ9YHmNCryXqavosYq7OKOHIjKb2bzG14lhPdM1El0qSuzsW\n5ces0p4v489xSU6+XvPpbcTisx5SwSfh59C8w3LHvWnBMXREytAmMxcdUssLbpiJTYGJAxaLiFkH\nRIQsRcOQwxQqJgXB2pKJgDDTeJVD6jP+FDGMFWkNadqxRzEXS1q+P259mgXSQjR57BUc7cDZ+USU\njIFiMILWW7CeNYntmQjJg4Q0KWlOmmC0TLbECIlvKqYpZVltcHVJG1XIbERGhvC+4yCf4KWauwGM\nesl+2XM4f8fcfkv6TiI8w+HwNdnW561TJDcJwauKtKiYpOD9BIf9ke7mzDk4o/0BV3zH195Lpq3j\n11dXfPTZiGtGHiUXHi5nouOJ9Ob3NP6FPNQUF4+IBb4aaY2m1DFtrTg1IW23Y0wM98uJCQ9xitgG\nNSZ0+MGGpRmh0DSmQsZLRBCTSAW9xcQjtvM4yZlMTsj270gXdYwg/H3Dm48dp293PM1nyt1jhuIF\nd+uP8D8k1Kt39PVDullT2J7s/IS9fc7yi58QGs0vu4j89iWz78GPP3Dt/gz7ycDczIhCodqRTRYy\n+ZrhHDCPWzZpQx3umURIdjREhSRVPU472kXI0EqCRCGrGWGPbBKf3TkmzE8cvACXBGxUTTPOpGnC\noI7EZoF0htVkqQvJ5WLIGon1JIm+ZiduiZMlQ5ihPAjPJyYyguaIyJeM+kCC45TFHPqBIl3DXMFU\nEAwT1dJi/AkGQTvHSD1RbRK2RnFMO8bBId2Ad4pw4gILgZ4sTRqQX33Gyn/N2198jrUX/smX/4j2\n1Z7hzz7iwXDhsXyAf7Pm45+tMIcAkzasbUmVeixo6EVO0cSYaKKrBpSYCJMFUVyR+QXDLEm1JR1i\nLrLC36/QKAbTMuYeci5YmI5BrJBSYS4n/NRH9Tvs9ZrwMpDLnibwsJ7E+A1yCJicwd86ooNkCH3i\n2wglJkZVcDpfCPUOt1xT1hG+H9IsaqJDwXulWJ8PvB0Mkp/T3z1lbDWL8A9YdZ9zV/Hn+gP2+oK/\nW7M3Ldn9iXH8gv30r3k/DZSvQpLszPRNza/4GfuPD9z7tyOv+2v+QWAZ05e0SU/7l/fpfUn2F+8p\nf3umDTtW85Kvvk649w9avlqc8b0t6/inrPMPJEphkAyLHH+SdOKKYrhw9HukcOQ6RCJQruF2WOGp\nHb3w2VY+pzTgujvRiwB7V5A6ibfYMYklWeKojKXrfcpNjCXAAubyw6shfxywQHIQf0bu/4bLM82r\ndx+z/vE3iPEBrlnjm9+SBM94n73kgdGki/t8u3tB+P4BvnhFti/5e9mFociQ3SNmc83N7zL6jxKu\nE4+mHAk2gtkcKd2Wzu+RouYyrgizkMwYlNMMWjJdMkQewyzxmLBG0M5HAiEQjUXEFy5eQMnM+aC4\nW0ikdciLYNYeUVlxayLK/EQ2bKk9wVEZFjrkMDQgEnTusdR7rLMYEzBlPsNscPKMSBLOs2Azj9TD\nRJtmLGNLPEKVtLgWpJioEg9hRugLxH6gc5oyKpmLPfVF4i1yItPBvEIVPX0/cDjVeH3K/e3P8Yo1\npw8zVjqax4pPbMff+2RF9EVPVz3mTz/KqLXDnlqMF2D8gHSEOhjwRhhyhY5m8rOGyXLe7snrnEpY\n+jDCjxo817K/i/HalrQVxOGAmHNmdUGPMWPkEcea1gsJb454FBzlTJL1dKOPFIZsiFHRhZs7n20R\nM4kctbjQVznn8Y60LMkJuIw1UaqpVEKqAl5un9PsMuT0grvGp3qfsFn9iip5zIvdxNX6X2KGgmFt\nyd5U/O5eQvTrmK/dHbX/f/CsjnBByTeXmXlXcvAH9vyC/NUWP9hTkfBvhpaxf0cdPqV73fJQ/wW/\nih7ixL/C/uU1y89/R/qjn3JSLbn/n1M4wcfTmVc/eowzKbY9ETrF0ffYJCO3+ZJYG9SQM6gD+XjN\nODdc6YpeCbRMsWvD/VvFLipQmY8eGmJ8pjAgqi7Y3pJkKZ2LYX+kW2g2XkBoVz9YpX8UsBAO4o/e\nMj9fspIL1OavSC9/RlHVxFnD7ZCjwt8yHZ5x+rRj/1vFXI18kR9I9p/zcvgOER9ZRH+CezwwmJ57\nj9+wuF5y6Ec2asScM8Ihpb8yZJ2DTKGEoao1ZBlTMLOaZ+5Sg1OaWAzINMTUJ7ZlytikNEIje4kr\nDd6xg2XD1UEhthHnoaMQE5NZE0qJ38BYCILeweDTqZrcU0TE7FRLexCE22v8oEHII4m3JmoHpm6C\nzGevBNHaobqOWQm6viUqPKbWksWO/pJQ3d/jBRFLL6YaBEO3Y7QpUTSTVRW6kESXERKP1qt58ngD\nzyuaz5/w8KsDm398n8VdyMtLy5dywar8nJX/E/LthRfBhQfRA1oV4yof684Y35FPKZoREzuEBb08\ns7izHO5KKi7kS4kXRiS3a+pNRSoUA1cE8pYmrREjRHPBEBl8N+DPAq9ZEsWSihEjc5AemTzQRg4z\nnpBjiBfNnOKMpT4ziwizbEgbQzf5FOOJMPI41UtsYulNjXh1TfLyD/zrt5aV/Tlv3IX/bb8mff4e\nl3zN8tEnRLuvkL1gfPCE3c1XPJme8+v/PeCT64oXSYb8ywt3LubN/wXFw2e89n5D2wR8lMLrV/f5\ncV9Su9/xZjshi1/wf9Z33PyVwxWfkNi/5K8Oli9rwcNQYHz49LKl/vQFXCSyKRmeLAkuA74Y6F2M\n3LcEMmKIPfz4GmXOiCBmMC20JQQWc6o5bUvWpmJ/UZQOzuWEV2XMsYeYNJ0ekd2AStYEw5F2IWm9\nvyPtC7U3cTttKb/suP/LG3a3f5++GDCh5DS84+qzifj3UH18RXbWiIXgxdMv0b9s+WVU8Seferyy\ninevf88/PP0T0jRgH99n22mcSegvCZGUkI/fryCyHm/wmbuAwDPE8y3zwnGcE8K5QhIQ2png6DGZ\nBXXUIZY78vMCL93T9R6tcpTOY1hKuHGIbYkzHdllwPkht6XCyYFrI9GyYapHpniD0KD2A2RrBjcy\nBD2qE8yRwjWSPpZk9HTye6NQoHr8znCOI4SusSy4yD1R3LFoI+be0PuOQsIhvuLeDgihuR5xxx5b\nGuxBkSwVenpN98VT6g8/4z/avuLOOzL8/R/zX1wk47QgkwdOxQPiiyZKFGqoQDs2ImZgiWHAzD3n\nsiG9rBjVNcgdk6/QheJemzP3MXq2dFlN24O3uuPqVHIqJVIHBGYktAbvIqilY14v8cYd6v4Wbs8U\nWUh4idB5gHAFcqwYE0PegXfsmCbLEFcYvcafBULX1GsfeRMwB0dW6cybpmfOer4VA/mHf8XPv7uj\nOt7y+nHNhGX1zZp/sZ9wb74idTnq7VfcVxkv7xTHRw13v9ygT39BU0RMs2X7IaGPv2P7yYV34wPe\n6Ibddy2/+/GvePz7gNtiZP+wRf+yZpvXvPrzmSGrCXXJPv45j8xPOB0cX3/+Hd72E1aLI0P+CHuo\nIMwIWo8OQVhKBtlT7C6cr8Esl+jbmcxLqESNLjN6F7Gi5+6yolQWvbggug1FeqTRHqOWZDLBeB3S\nWHpPkJ8S0v8ACc4/Clh4RvGT9XP8337J5YsE8eED805wHVa8+ygiv8C7ZMF97xdU/SNEWLH+nePD\n5wfS03+MPaf0Y8lVPaOfveRm6fPTKqRPQ+4vMo5AnzRcHRy278lNisPAuuPoBIKCoZko8wQbeNRz\nTTIp6qgjJCC7+Ayxz7BUpHNJIAY6owjmjJNsWW6hqVqKXII3MSwzvDvDJosgdCDBI8fTFh3XxIMi\nlIamrlHZGmt7jD8zixFPekRhitk5Km9AhhOx8Ij6isEr4AqKIUcnMe3dnmQRoU+OKupYjxKR9JAV\nuDsDzn3vG1k6XGXZlxHeZeAj7dj/6Uf4TrM9P2EXvODJ/83dm/zqkqR5Wo+Zz7N/4zn33rgxzzlU\nVlZmUk01Qr1AhRDdiF2zYcGGBUis2SGh3oFYIsE/gFiyABZILGlKLSqzcoiMjPlGxL3nnG/yz+fB\nBha3WpREV1FFtFCKV3K5y+Vm5nL57zU3e83fZ73my2bF+9G3OMWKYXGZVMSqkFROTXRoIBJ4YUEg\nPJYUyuqCiAvkqmVz0DSJwygeWE8Sle5gviLcBOPFFMuA6STXfEGqNaNYsFEM2iBvA5yhwbsBTpIq\nbwnHkiDuadwCd5ixWYcYfFyvJwp8AivQaY+wId6Uox9B0ih6QrLmG6S5Ij5q+e2jR3zyyxe0Aj79\n4re0WF6fXIIv3ueL7jPe9C3OJ5pfx2tOX0a8s+y5e/4xl11J/7tvSJ9UnManlN9MLFeX+/hM+KLn\n2Vu/oPjlU5rLSPPVx8z3McuxJ3kxkk7fkomGr/3XMN2W6Y2It8eJ2XkT5xgyyoxuo8mlwU4jnuuy\nDD2+cGmMz3UbspkCjqPF7gOu9USa9ugTGFchUohWZ5bjFqNAhCPTQ8yYz4Qs6MiSV4Ymcth7Oafr\nTLKtv7NOfy+iIdaTfKx3fKR+i6kf0OOWzb6i8l1eff4Oz8+vo1/bcv7sQ159HKIDwyuFIouf8or/\nK/rwOdt9QPx0xt8b3vAsVryG9mfuOSHHE2WXcHVD9CrlXHro/cS56lGeIT5OJMCgz7TdzF5aOhK0\nKvHihbvkihIhrjqAXFDVSJSVdOZE4Qb01454UoxC8yIqcI8TxXpNN5wxvUbYhiWA3F9omonrasXg\nuQz9lrg7sndT3MuZwE3wTMjRzmRrydbTuH6IF6aEQYTIPLbqgHBdltMVYz20cNGxQ6AG5nhkFAl3\nQ4CWIXMKVxamUXLJcrzLLSJWmH2FqTSPhpcZnoJ8y/PpRJ51LMmG+ThTVwIvdzkKB90G+H7AMjmM\naiEmI/Fm2p1Dpc4MU8akepTXs5kEJnVBXXGDgKBOGdKFKUiot7AEW8z6nnDXkgYSRkW3xBgB0+Kj\nvJSRkFpNrKaOXCyUac1yLclmCUoTOCOtN9JebhBTQjN0jHcTyRgwWMFGvY77ic+LvuXmxafo+Z7P\nP3vGa+Yd5O9G9OdvUOsLT+6fMpm3+d1pSy4Ebz/u+eX8EbM70nzV8+ryLaJ/A7UYzvOJ2jnjftEw\nxjO7rwXRt8/I8FllB+LT5zx5w+fFO3dU2WMO2Y9JHJdH5YnfvvgaE33NkwyS3Zbg8QrPO2FXe65h\nySJTAhszdJKtlZTWcKovKD1jaoWbaJwlYgo1QV5gJx9zAik0goLg5DIFGlcHqO3C4mZMXkHojbTu\nhBASJb77nMXvhbNQs2L+VUX8asJlsvTDgX6xVMP3mDfwxrbh8UfPcL7/KX9xjYjPAZ84PfYc8bzK\n+Parmq/miiqPuIu3PHueoVyNCGKKUYGzQ0c1SdTS14pgcmjOLqV02PQx3U2GMTHuVZNEFnPaMEQL\n8TCjBslNA9I39Dqjpcf1btFuzyI3NOKETBzCncSZRvA1emNpzjNuHjBHPpPaUlwEg/XJIo+0usep\nHthmIwOWF9wzBjlDalmES3qSYH1qWeL2CjueCWyEuzxgkExXgS00qe+yLAGlP6CCmDkose4MsUZG\nCpTDaD3WywOx8ki9iqhV6DrCGE1vJMsUoJOcLMkJLajOp49nAt/HXHq8hyPSS5higQgSIm9m8Crc\nkyUYAhxHYoeOeLdmOrl0jo+jApQoCBaP1rlHMoDV5JcY//CAIkc5M9WlYe5rdtJhYaA4x0zyijt4\nbK1PFXgoNXJBEiY98+6B0M1ZKkFCTOnck8YLa6tJ3YGTabmVZ353q/mUguyNPZ/pDWO+4u0/fpfB\nMzwKXyd7TdG0JfrHa3bzwGu7d/DnlOe7mZ+IV3jlzdd46oaYH+2Q7Nm81nLzrzusppb5ZwL7wY7x\ndUm+cam9Hfu3nvJeJDlfXhDdv876nZjb8YCOzjx3U27fKzlvE57/tuP2c4+nz76idWK665Wkt1Ru\nS7CXxKXmMmqUzig9jWcDiBvG3nDvG5CC+3ZkaATx1kH4C+gBkVxAtBRLgFP5CNOgOXBaWro+xBGa\n8OR/Z53+bRL2PhVC/K9CiN8IIX4thPhP/vL8fyaE+FYI8fO/3P6tv1LmPxVCfCqE+FgI8af/T20Y\nRxD/4AnTFBIMkvH1HUWwxn/9Gcxn5NcrwncinkqPW/0td2qi2L5FbS689eGV118vecWMvPjynpvn\nPeMPD/zu7BInll6uSbMjnlXIRlDGC11kUGsBomBZDFNbMfsNvbzFbXKOmwZPZfSewR0i+u0Kt7Hk\nVYu4OFR9z6gaRu9CVrnUnUU1HouKcA6SXkcU+xltOuQIK32l23WM+swwOmhnRRskiL5jmSKkv2ZJ\ne7IgppgkQ+FzdC/opMJXJbO35a69IhqHwSlRa1Ba42cO6IUmDBhbS9S4VEKTP5yQjmaV9MgbBzfY\nMqqB2pF0q5w5DAjlgO8XCP9KOVVEaqYvR+L0QJjHROkRsQmZ3BTPNnTDQHd1kW1MeEqwqUUFC3YM\n6fMSLorCj7CmZBAW22t6R+CbkKlW9Lqjc0fcsERdXPprQklE5CQcXE03pFS5Imt9VtHCJdGMU0zo\nBBTnmCHyWc4h3WLodivGYOFO3GCOFacCZi+k2Anu65G3PQPfWwhWNek7hifW8ORw4t3lEbsf/RjS\nJ/zhTciPDhGVeMTyuKbF8OH8U9onr7HfONz+aMMb2+/x3vdj3mx+xPvHnyFv3uOVXOHZmSfhTyjK\nV3j64T2Zs6D/3h/w6v6nZK/WnF68wL72nOvRUJeG47eP8E63vBlp5uIrzk6ADAxmXHDjBifqua8m\nhiYgTxXeaBDzHld2UFnypEecMiKlyfuBuRy4dDlDbhhjnyiOcBOXyhmZNhFBm9CWG4o4JlUduY3o\nne8+DPku+EKA/8pa+1/81YuFEB8C/xj4HvAY+F+EEO9aa/Vf24KWLJ1BTc8pN4ri7spgfPbrJ7Rj\nzfWHFeb5Ge3+Ca/UI5md2SwDTmVpTj/Cvjrifvkx339jpDUXfjL/Ectjifj6RBxtOFwNmZcwZj6+\nvWDnmvWyMMYzbu0ith7mzifxDMY/kC8Oigvz8hJMpA8Vzs7lOsYUw8S0mrDKYVWlqEJiJ8WwGOJ8\nZrMsmLNFFCGOzGjChUzMzOQwOWTrCefYMaWGQwZxnRCcHdQjyVL1eMqi9YgVAVslMcuF2cbcRj52\nFtihZZhX+KGmEzWpLOmuCicy9HrE15ZYbCG4MNYu6BFMhNUR27Wh0Q8Y36WUBZ1YqMM1aSjpjyfC\nyjLKmGWyxI5EV5r9umWxMEYRnqm5phlO1yLChJSJeu1hmwNHVRJIy6yOrM4RRvSMmcAdHcxK4Vgf\nZX1W8wWJw1WXtFkPnWF/WliUxIk8egGhs5C7IXZ0mPSVYeOymRWWiGU/0T9M5IXi1noctwmpo5Ay\no78bkTbneWR599lr/HwKeVcoin/1Qw7xpxR//sDr655F/AH37cQHc8jNbctmSqg+WNg8yRjHzzk7\nT4g/ydg8vdCmlutNzHu3ClmXZPc1r7xzi//QYf/0j/i1/pLHKuX8G8P8x8/4on4dG3zD8kuD+1ZP\n9LzC/fAxbfIFZ/MHqNffJvfuiYacJTjhLy/fO8+OtCbg0kXs5ciDDMhzyWw2uEOPs1HYysVbSbbV\nxFUuZOOILLc8HDVF6iCHEDl3BDuNPlhErMGPOVCxj/4/CJ3+DfjCv87+HeC/s9ZOwBdCiE+BnwH/\n219XwJczT/S3vHj1ByyfL1yr/x0jfkb8TY2+Kbj5TcBH7z+Qe79AyAh1I1DDwLxTPAS/Y3+3xaye\n8Lv7ip/8wKFPel6Ja+7WIekUcGtd1Dix+AnLUBL6ius8IUaHSfgEl5YkUBzSEKqAzAHHGpy1JLku\nzPH25bPQC6QRRgsCBf6jmeNdRxxHBA5M/ZY+vKMQAbo1oCaW1KftdsShQQcj0ahYfIebeIM9PWBu\nXK72DjVsCJWh3XfsreR8v+KSGuR6oAwsxwpWdmBpFWVeMYQx4xVi54xjdxSxpu19eldwtSe81tKK\nPdl6hmlADIZOpKRNypQbxuCKuBY8MpZprhjSALfX6MRgGkUbhpTRlcomaDVj/Zi57F+G5DKJuLyc\n8E0XlyicEMEF6Ub4/ZbjfGQdJahKIQtBMJYQncDzEbPPkoHTtjijpctmKj8lnmesbuk2LpwU+ubC\nSue0yiMQNa2ToqcryUNJuXJYugl0zNZcOJ8kyulJ4pipqwichetP7/nZnw24H/59fvFlx7jfc/c9\nxaO2xg1D3N+cyT/cc/r0Sxwv5cs3K177PCT80c+I545nrz0QPLpBtg2++x7V6lPeX/6I+v2OV/IN\nJ2eg0SM/SX+IPj8jetqw/t0jCl3zzfZ/4n++2eGKF7z+qCD+wuXpWxFN/RXPxB8TNQE/ThThesd9\nt4DZss+PyComXx+5WoW4pixjQjjWLIFLLCf0KkQ1HYsXE/qSVsSopSK7Kbjeu4TOlSZKGYaKMpQc\nA0M0dNyUC8v03RP2fhd84Z8A/7EQ4t8H/hkvvz4uvHQk//SvFPvn+MK/1qwMuB883q8feHB8Hi1r\nvvlXfs3q2Vsc7j5n94rmtU897uLv84X7BTdeASLF/KbnlfcDPosWnlwTwshHHEu6T0NuxWtcPEm9\nE4jI0DmajeqZvJi+6XFWDkVsaJHI84px03NjXAwxzeZE1Ib0reZhPbK6hLhhjzMqui7FKRVTciZo\nU9JMI8aKcbklDhSVTrEarlFMKQ+sekvrT0jrMzslF3EgjxSHWmECg3Pq8cweHR7wJOiHkHaz4BQX\nPGVJbIaqL8jCY5gzJBVCKKYx49btuYsTaEbS2cUEI6EW9DcJ+1pB39PnEwSK4ppS2ZHZWzCXiEQO\n+CFchWa4huzSmUVb9OKTOA5uG3D2epJA0wSwNleOZxfHkeSty2Vn0A+wiQZcO3BRtwTxQGJmkk2G\ndCTOISKs7rFOSGQ0qrhQJwprDKFT0qozO/kI1R0Q8Zq2XwgPI1ZalmnHyVtw9EQgNgzSRcuFSyAo\n9ExIRB1VzLVhu/HRIqCeBMp6iDHmldNA+P33+XT8iB/8A01efcjnl894+sGKk4lZHn1IVT3n+z/+\n+9zpirQRvPvjgipqqL58l59uFMuth/3invXfc/lyncE88eM64rPpCX8S+ohXTxx/vuHy0x+Q/MU/\n47MfwurbL7j75ilPLp+jGwHhlxyfJizfVix/OpGZX1HKt/n62rCLJHsbvpyXWW6ZyzOxtjg6ZADC\nwVDLGa/PCYIj1snxA0U7asLhypB6hA701wlNg0dKPBrStc/RjfD6hUIGtIPHPHZ/F6n/C+274Av/\na+A/B+xf7v9L4D/4O9T3f7FO8xXSOAzDgpoHptWeDz5beCgObPKnaDfg/EXF60/uiOqZn3/RMnYO\nb4WPGNuBMErhtoODJipnhDjR5f8H3s0fwoOLCH3W1Ui99hFLi5cXLPoBG60xFxeZHzCngrPbsew7\nykvJEPbIJSA9Kpx05HRxKESPF0E/XXCdFLwEMQc0gcvenahcja8HjuwQw4SKPC6z5tHGQy8XsnjN\ncgi5JgU7jhh1y1FeEXZETlB5W4pNj1e7uFFG7Thc65GpdClOGV2piM4xC5Y0Helmg9dYSGLGdoBb\nxYTEaWuOwY6NFESTxlxHlgJWZw/txhCe6AkZ1Igf97C5oZ0cxqQnqwTTpKl3Fs/4jOecwKk4uQ6b\ntWSuOty9Ja8kelOjTyk2kugFQuHDciQbtmgzU2YW4664OhPhNcEOGr9JcX2XS9yzsgnnesBfbzAn\nwSwHLAtZviNwGhw5oZcSM1tMpNhGkl4AV4frqiaqHTpHYE4jYheQDg1RMWNqcF99xH27sIk+oHn+\nDN83PL35HidRc9sJTrOA1euka5+39Y7lvqe1mpvoCbc/eY635GjfIG+e8HyYeMuXHO9T0tWZ18II\nXza4D2+w/elI+SKA9z9A/OLP+Crvua59guxVHm4u1L+YWY93rP7tJ+y+esTjrMATgvKtHD0NtKml\n7zzC3YGkCemtIAxcirDlkvm47YbZuWKXDcpbUG6PM0NvfFLHxUpDFCiUKnCLE6ESVGOA484s48IS\ntnhLyeh9d27I3yoa8i/CF1pr76212lprgP+Wl0MN+FviC621/4219ifW2p9EmYssG9L9mnubcag+\nQbkhxd6nHCOmn3/C+vt3fC0ifrlKcFcV7u0dp/1CEHrEecOp77FHn3rVs4s93Cpkki1x3BI0LaL0\nsEeBFhFRICj7gg6HIl/wogBNS57nuHPE4PQMJiDgQpNrvFGRbBZEFnIUNVkA/ghOB0vk4ToN1egw\nJQabboiTCi8f8IaZ1LGYYcFpEio10GaSVLWKfzquAAAgAElEQVS8wKdLOmInJlxpVoGPcCzTOKFX\nLkordL8gVh656zMFJ9Zux+BpWt+F3idwA0TkUKSGNhbM9wP+nFF0kkBYerHQDT2Igl4OmN2F3mkJ\ndYHbRljrEA05+34kGHy82sMUISJWbJmJrCFKFb2Y8cuU6rhQzyvahy2T6QivIWEuCOIcxxyhPaLi\nW6rBxawa0BVBXbMafKqkI7aSIRL4WUdYa9pIQaGxVctoLIlVeLcOAQfq88yoNii/otYOcSU4xS6x\ndWk8hZlDXD2wznoWWTA3HWdHssybl6FOfSEJKrKw4kkcvEyCpO+JVEKTLwSZx2btYweF8QVxInh8\nk3KRVxxerg2plcuAYt20uENL7HZcNg6rJeQYp4xOhVtpnHCm7Vseyqc8+jRk+7ykTL8l+vwTHr/y\nCHGz4y+CnjmuMVowvxOwTCcmtcb3cm4yF30J6KeZLLTYriGYbyjFlU3SsDgW4SpcfUL2a/JVgMnX\nTEw0CHSzcHUdjtWaQWwovQRoiHcFyxgjjCUOr9/BTby0/9f4wr/km/5z+3eBX/3l8f8A/GMhRCCE\neAN4B/izv6kNawO0fo/PLyfeiwU6fY+p/pxovuHBrzDfe8T4dU5vFW8aw+MoYTo6FOFHmAic/p4n\nDynrt1/QXwWHeI32E0a7YmLmWix0oifLLdn1gGjOCEeSVnAwC+c5YQgLRLew6nqiWJLbijZzwMmw\nS0DaWAJ3xgSSK5Jz2qHcI8rO5FFIkC+spgQhBXpwKD3NIlPSRPOQaq6Rxzh5KN3SRC07t2eqepJY\nMPWW2UTsmw6lHXwzIqaZcmXAadDHmUL7LFOIKHLCOaRbAhqpyCaw5w4beEQ3lqI7cin3THYBsdAm\na/TGJe0zOpXj+TEPY4PcDmzNQDe4dNOEERVuOuGdakxfcqodLiZAtUc2W4/i2IDn4EiBV1xZSpCJ\ni7gaxlajdppL4aDkQrS7Y5gSzjpl1grRKzb+hqaLiVTAQQr0TlCaFE9qcpHjrx7odYR5CGjrAhkW\nmA7i0CfcLPjulYCZJh8ohItrPZCWYE4QyuLqifUYkLhXxnjmxvj4KkBUGVXskOs1olkRjgJ39Ci3\nlnRoiUXPVLn4iaVxfdYmol4S5mXGHQLaaqZTAVY/YmKicEOa6EBZx/hpwpgC3oi/fMBQ+zxPbyne\nLtFtBE+/z/NqIH2kKeo1Vbtl9tZ8/SKm39yw3NzRmJp7p2PleERJSju72GxHPd2juhR9GlgImT0N\nbkI6zXDpEHONrT2Sc47rp4ilJtxN1NOFvhlw2j15teCGkst2Zjlmf0fX8H+374Iv/PeEED/i5TDk\nS+A/fCl8+2shxH8P/IaXkZT/6G+MhPBycYlsO6LQ8PHpOYFVfL3PePrFHe07MfO3A/vZx1OGKX0D\n/5Nf8Xr/BvVnCY+DE3fvOeijIG3eYLVNcZqKb26fsp8XhIlZiZ66W+ENlunRDe2xY2Udjgm4S48/\nRAyO5aIbcHLWV4m7mUhOC7F35riWFEOBERXeJMlizbEROCJhuVxoTYpNa1b+gDUponRZpoRr0XBz\nKtgOC71euE0Vg+vT1gHS71AbD63OmG5PWJ7QKmEne+rZx9nOBNcZlpJofWXRKcqtcQ8Lw84QnHLU\npLjYCBuPrBuHRlnm0mN9f8/gp+hUsb20dDJiiUMyB4JxInYUXhfQRDF+fKZFENQuKxYGV+HsEuIl\npG0fiPcul9ESlD4br8dOmvm6kO1dGlL0TYdVDt55wya9YieXpgnAGrJYcA3BtyFZM7AuA9SlQlxL\nwqlnChsGsUL7Gre/IZELOr4ytjErOWNwWdSEGDU2cpBCYeoFGYKftFwDwTKFhN4Vx0tZVIPSa0wo\nqEaXZL7iFSPOOabPYL30nJVkk+QsbcPkJVh/Ai5cOignhyEYiV2XUU0s7kgQW2RsMc49kXGQS82s\nVjhzR5tJEqkZa8FDCusPYf7qC9T0JVMk0V8abt9qSZaUm2rHGzcTB/Ec0TpYVbL0Ed7UE6Q5Q+Ey\nDQJnSlE8kAQS29c4t3tyroiHicjcMJUDV7aspobDyme9PDCGCbp1UZ1GsmeUhjJ54Hh2SW2J0Ybg\n5run1fsu+ML/8W8o80+Af/K3vQmpHLzbI/rXt3gfSLLuwC2W6eCwlieCcc/4ZEGsNP63H/PZDzJe\n+6f3rFzD/A4Uv9U46Zc82z4hbR9Y/eTH6McTnruQBD0PU06IZDIj86iQQqI8g1yurJXLi6TFGwZs\nCOtR8BCciGz2Eqd39Uj9BDEckH5M6i6MOsMWEagT62nHWSpSFbNIH69RjL0g3D6QdSXzWmGswK8k\nd8bjxmgWEXE/KMoppSsclk3D2CSEi8vJW4H/gHNd0acT2WXgLDWqqgjyAjYQXmdiUTOsXEQ9MXUW\ns3ogXG6ZTIe+jYn0jLuUjOWMM43kzULtdXhihSOgsYJQSuTVYfRchHZoT2u8tMHrato5QIY5Q6Up\nMMyOi3I8/LBFaENzH1DkGi0l8yVAAJdlyyw6KAJcvyNSCUWXUDmKZTb48cx4ExGfF5ZkIklKnPGA\natfI7YH6cst23GJujjhqg6ovVDl4c8isWsbGYRUaxmpB+xPC5uRODzKmNZIgKlHemXy0zNZlYI17\nasnDASE6KgnbcMW5n/DljNEZZq4p3Yh6tmjvShyNHByDckq4XDFzjNUDS1GQxA3dOGA8lzh2EYPm\n4eKwSRUfAB8daurybWi/5NvuG4ZEcP0oZP+jJ9SBYfikZv92ynbX4TglpzzCMS7+yXAZriRZyZAv\nbKobTrlBqAd0fyL0t5RFy1Bf6USOKzQPSAozoiS0pxGzsoR9Qek8cC8c6kqy3SfYB5eVN7Mc57+t\nHP96nX7nGv5lmAWtDHnynO2vV1ytx+fhwsFvaL+64YtHn9N/8S3bn/cs7g3Os4L7p5aP9ZYmfB/5\nyg9IW4t/nvDCLe31QN4KChVyORYE15ZgOaHzAOksTLHhnA2E8Ybzotk2KbkoCbDMWpL7LsuDT9CU\nrF1NS0u79RmVQfkaT0tWxyvOyeIFDcVGkuQWTyimqWcuHYzMMX6FnEf8SiMdw6aNOYqYNJMIa/Gy\nhWI+EoqeLppQUrEJ7nBEiZdZOrfF8SbWhxA3kWS+xBsv9JlPk1pCM6D8jiJwGMcQ1TxQHuTLHmpe\nGAJNKGAINEMMfmuZ/YX7PCSbJur6wiWCbCywNx5ifaBSCd3kUQCT1xIKMMuEDQeqMedBGdqyxMaC\nbnBwtCRYT8jgBN4Za0bEJNhcLAwzFSFb32EdGLo+orirwbgEFux4QjYr/F1N3ktM0nGJrjRdwtWr\nQcTcHDaIPmDy9gRBhBEerr8g3D1jG1EnJc7QU2YD3agoqy2TzHB0RFRqrlmIclyUyPDzFMXEOm9I\nnZRUdiyLh8wSilRxdgbaJkTeg+jviZwRU5wIixnl3zM5PqF2wb0iOoOeFTZdcNbAw4Uu8nm78qim\nkTz4Ia8OkiS50AnDzSsNqnxCvynwP49wHMvt/YJsW0avJYocJkeQuIJrUFEuV7Zr8EKNGAzG9DhF\nzLa6Z9EL6yBBCENAQWwjVsJhiEeszNj0ObkseRACsRm59BOz+91/A/u9cBbSEYTPa1RWEDxpePWj\nlrEOuXnnHbzsW1ZfSJLXNOL9R5R5z416xumSslId7fMB++y34DziLXHDtYMbPqDLGibVs4s0cpUj\nCzDdibAOkd6Cay2B2xA7IZVuaVD0qsCsasZe4kYnpO6o3ZhgTrFqIVOS1o2ZJpdha7nfa+ysaPTE\nXI2MXU+kQ+b+grxG9FfL8aqovJjJn9HbDvBQ04XdNqepIl6QMywlnhxY8o7RlUwCqiYgul9Rqw3V\n2iCmDZe5w3pbwj4gbz0O/S253aDnHCeO8dY+h42kGK9Yz9Kfa6rJJ9MKNbq0K5flqhDtzAmJcRPW\nnk9XQnFnCE6WTI6YWXBYxQTsuCQBNs6YW5d4e2I7Lyh7YRuHDFxZtHqZHzKP8CfNfr3GTa80q4zK\njYlQKGG5Zhq5GJyNxKgGJ4xR7gbiC9lDzqwsqRF4ic/OaWEKEJ7hEFyY1gYtZuxkOLseXhEwqiNe\n0eI2iiHSyAeHbSg5a0MytmSzx2Jh5WuwLvPJZ5oWfMdhvOQ0g6X1OkIn5fJwonUVfirorEcWZNzM\nMTaPKI+3yEbgXjY4hwEx+xRGM84nFjXiSs23TYu8ldS/bRH9r8iebEliy7frhMe7Dzl9duaXc4r3\n9Et8e+LL8Mr4teQsZorIQ+Yb8roAagYzo3ODlgLVbfHnPagB6a9wmo7OFLjzyDkAq/d0dYPreziT\nh0fIpZWIvWDhjHPuWbAUkcYvzXfX6Xeu4V+CTZ7iekkR0QPGZHzsvoqbBdhvP2Ls38BZfD758jFT\ndcdH6YFk9wN+1K9ZXk/Yn5+Rv/cGl7ccDrXhbWmYj7+h/N17tDalSi7EzZHpvCbZ7OgSH4cQDiGO\njiFK2N0MZGWL1BWLmVglhnkSGDuxWEPuNUzK55JZ9pcrwWxYDjmb8yNO2xBXBcykDEnIpVjI3IBm\nMhjWiEcefgiRTlAyYT1d0XPIw3AgSy07bdjgE7ku1nUJr5JEngmNpQwnJn9gvcxs7T2eUoxnh8x7\nweCPiMVQuw7z+oLsXPxjgbxoLsXLnitZlaj+nvq6I7QDhoRsC1EWE2zXlJFP54dMvmFJJdPtltmR\nRJELdcXElXmpqJILiddje40SsHc81Gi4MQMqc1DxDiFD5tnlah8oTx4DinwemLKB1j2xEg4m0Jxq\nCKXCWTTNKBFxSGU1jS3wI8EyWKwnmeqaOgspE8lNe8Uanz7scHpBfxrYuA5FPWIDhzEoGTcLDiNu\nqDmlGVXpoOaecyXRNmPcQWp87nqP0Bf41iNNInzPpfQ3hGKPbnNK02HClmsWMx0z3PRA51t81UCS\n4coA4Rp6EeKmBQkFRbPh6Fuit1/jGnxIcu6Y7QOPixnGie+/GfGkWCFFyN1HOaF8QiyO+PuF+iLp\nlpluI1jPOdq4pKNhyWAKTihjUNnCfLVYB+qoRcclzjBDoyDYYNIGx4/wpwv+dkH1FuNKHLfELD2O\njBi+O5Ds98NZeIvHsLa0X7tUZmT/6tdErsvn04KoFV6+48nrG47rlh+e/oD7ryytNuRf+Yyzw/OP\nPyF7lmGL36K6gMvjLVPgsfUrfBVxWt3gS0XTzjCdsTUkjksnrgzMLL2l7nLMZkc07hlmB6stbZSR\nBDMvZMJqdglOMTjQOiPGDjTBgu4H4k4Rr0aUgVg4hH6G4/XkgSA4x/heR2Mm5tOJKw7XeeYm3HOV\nM2boIahYhEs497RKIuYNo+2oo4I0HOm1z0OxIaktfjxg5RovT/DkmU1d4Y8rwuBEY2rc0CU/pJjz\nivFwZOsZnLjFJA7cu9R6BHuF85lGdPiXgeQgaXDwxjO5lVxShU9MXrkExuJMJWc/ozUOlVojjM/Y\n1kixJ7z0bNyRbBHYOCF+yDGZYmMGnEmwqmMC4XE+SNbDhXy9RrlrDqEkzGucc4a/G7BTj2sNZW9Q\nrsLRMZvTyImUQ+qh4grhxIj+Qu+7mCFGOpIyWAidkeYqOScabXsenWoyVRHjszY+MqoJLy1V2LJy\nFEr0LLuZtodrMfMQanzbkemeLt5ReR3yPLASgjkIkFZj9Ywer9yvJq6TwfqKStSI/g6dXTnVEcnn\n35K9l/K53pM+zUjF25xvG+KgxtVH8gfF001Dv3+G2O4YHlKieOLm2sJ14Swsueui3Q3LdcJWIa6q\nKUVK68ywCHIL3uXCekwY1wPhPOEeE7AzXn2L7TwqwNMhMu3x6oyLr9i5313qvxfOYnEXfB1ws3qN\nR7PE/fodtl8eeC/e8PrNN5xfe8E3akKZP+AX9Vc4ukW+ISH2+EbA4w+2RE8/5i59h49zn93dwqvj\nr7keNPaU4I8Dxh1YFp95CknXGpOdUW1C2Pc0i0M5CXaNpBItcpQE/p6l1VjPJe9BuC2LaxkjiRQ9\nbtbhjxNJ4NClLf1dSXnxEVJiKkugfML8SpwOTCdLGS4UkccqEiShZTQDaXPF+Ap1LNF1yrmTeKlB\nzxAiMPMDtb96ORGJQd6keJGglT3D5BJNPocgJBkmxMmgi5LMSBouVH7Nutix2AA5ddhWk5Yj8+jg\nSg+VClbHlDbU9OGRrbyy1FD5E143EQU+pqhZ1Jr0OiDxEalkVbwkp3duSSVmTODQew7n6Yg20CUB\njr/HHF0uGGTcEXUFqaOY0xx9bOlTgz8PeHpE7xpi4SKEwVYjtZyJkCixIFYzW9Ngx5D9UQAeaRBj\nSodKTbRzQHevSI4RrutjRoGwKQ8yojULQlQMy0B/8LFRCK2kiSMmN0DZEKsdvMvEepy5nBsmLfG7\njtXBwa4z3HyBw8BuKMnEmjC07BofIwP0tCZyR85hjE0D9v0Ds/sKb2vN4x/vucnfY7vf8DPvTeY/\nfJ90/wH1+7c8e3vDo5OkO1p2e0mV+CybNc5mQDQ9bjvQ6gNBJMhSny4oEaZBOCnNymBml7CI6MyF\nrBk5LQE69VCT4bw64KUT0h0ZI4OUIG9ndifLofrui7J+L5LfBNag3rjl2/kT4od3KV/9CjN8gA5+\nixu+y6tjR30wDJdfkdy8zenpJ8x/vmL7tgH1Jp82d+zZcPv1M7J/4xHPX//XGN6deM+uObcHdq3L\nyQYUEupUMR5CcrUwuS29LLDFheUuYBI9NgjxdYWjIuS+53QpCR2Dn+5Q80IsczwZUM0tiech3YXo\nanD2M+3cYyhxbmf8c0B7Solzh7gcwd1yiu4QFwjcifkiiX3DGMSwuiMixKn2SN0Suj5kHn4z0Cwj\nXacxYcusFoxevySXLxWmvGF1HulvfIxuiAG1GNwsZQwHxutCvxj8tcSxMS0G3xe040DmLtz7IZsm\nYkqvHCeJERtcqTC+SydAy4Sd21GlBWJUJI0HiWDwBbdqodtrqjtD2gQEXoAsBrJZcpE9pkzZNppT\n75F6Zyq9w1kurLyQRc/IcSaoU1zfo14plIhoch8OFmMVe99y30nCoGGDR+3P+KPAMx6u8oljTWUh\nnitMIrHRwlptGZEEFpSfIjwXZ6dZdTPaFVhy1HJiagMQUG4Up2Zi1Ia0gDlOSS4jd3HATXPhofRZ\nbfaIqmEONJcgZu84rF1BMMKD61BMoEWD88ZTouuF+eYF/yh9kz/XHb1skes3uL1zKbY3/GD3CHzN\n4d13eHKCwc5kfYKXOOhqICKkKhwCFdPXLWEekV8OPMQBoelIziFVtuCYhmm9RqkLfjJSi550MuTu\nnk6fyEcHExjcJQQdcn10JGHznXX6e+EsZmH4wemAt+x45vXY64r4ld8RSkmlnvOV15K/ujB0IbL/\niPdTya91zqt2wjQfsy0lQWZJh8fY6weEGt7tFMIuRPkasVjcCQKr8USA6zXYqMS3V3pREVU+0bpD\nNQMyiLgfE9ZrjdMrrHehnxOS1uD6F+qpwPeveH7O4PSk9xmIkf7YkeY+x+sJ4wjqyHAjQ8T5ivAV\npvTx5wQ3mRn6Wza7C7JaYVF4g0AMsKQXmtbDhC+w97fEFua0JwxTglGzeBvG68T6Zksvzriyw/Ul\n9qEi8yWtnvHiBrs4bEafrjgjnTVpoxkdRTJJOivYpiusFGxXktncE1xSJtfF9yVmXnDcjmQqsKPD\nOLfoOaCULotsUc4EfUoVW3wkwW1OQg/nlEqcOfUg/YT1BZRYyCW4rSTZvUBJB3EumJoaaTaMm5HM\nuGQvziw3MaNoCDYuD2bDrW+xUUUwb+jEgSXdsLkONHJkkob5BGVZ4BdrTneKjbpSDSfCFPSUofsW\nX62pfRdVtNw2GbM9Q/wIP2ixl4nJSrIR/FVGdU1ww4FmNbMbfJoFbtRCN3bIxGG0hrD2qFcz9h4G\n35C0IU4Y09aW26Rm/f0V+V885eflPR/8m/+Q1t7xaDzz/A/XvBftKG73dF8JdKC4khKNEtU6zHNL\nkTnMtU8pJNQ9brHm6l5QXoloG6agYApmys7jUsxsxRV9NpgVCEIaL2QlG8qjYtwVdKcBmwWsRk3h\nWh6W/59k9xaLx4uLQccBO9XzUXQktnv0IaFcHSi9/5O7N4m17drStL4556qrvXZ19jm38C18fW2/\n51dERpBESAjRQTRopYSUSQPRQ0ADBF0a0IAGHXoIFBINSKUIpVIIECAljUgJMgkpIyPec7h4tq/t\na9/qnLPrVZdzTRp2oiQlIoIwmXpidNbe2muv0fo/zTnGmuO3eXkz8ZvZQ6ynR9Qu4P7yJdfNY+bN\nmn32KfXFhlXp8NP9xwTqCY25R+gLpkJiBCydkTEbETNDLQLKcWTZzumsE8MqoelLJuXhobG9ibKf\nSFrBxtZsLUFeC9ImpBMe9kJRH0qIbIaNhTpaqDiiMRaYFqMmfO1yWx+YrWOa2kfrkmSEUodMfclO\nSCwchlLiO3OGQDAWAmEmNvaK7eyMNSrsQ48dTRRNBkWBOxPIbYSTSDoxYgc21hRwaBRMB7SYIbWh\nMAHB0WOczpyWCn2eGNSMy6TikB+ZrIlkXCFih4OjSSyHXhkUHdFRsV2eucwX1M6aMBgYrRHZXHJW\nB5zEIugMVSeYspFz0OHEhnkBJxy8nWRaNOTFSBqFDHXJVCUwlhB3WMZnNWimJuCcKPzNgnCncAOF\ntBqStqEyJW4RYNUZkwOqbThSMuHhbQV2EqGmhqLq0Jch/Vah14bgtGRMcoZ+Rp3WrIyg2gcMuiOd\nFtT7G9RqQeiU7KYE4yvWXYnrttRHi6VIOdo7lBNxKCSBihi7jHCh6LUFuw6z+u6V9HpK8HWJmARG\nCCK7wX/vAX/Z1zilz8H/gGvO/Msq4ThI6tc+iwtJ7SlseaYwHRLBLJtTWIp44XIseryFSz70iK2H\nkgOeAi8qkQIaB+aljfQ7RmZ00wlqxVJOTJ6F8VZkgyEioVAt507g9j5Lf/zBOv21qFkoJQne1gyn\njO4YEUU1Bot3sfGLGYvzmpnX8uxJy+QoPo58vpyd6eWJ5cVnmAsbO3hB21tMlzaqOZI2BjnUjK6m\n627pS0NhWbTGYhla+I6NSEoikxIfOkTZMvMsXGmR1XPmuLT2inO3Yu07WEFLuRAIcYLzicAB6fnU\nY4foz4CFdEtWFz6uiUnKHEcbWtGyGG5xq5ARQVI6BHGFGBtCecPGLWj8AbwKqU+sAkl1qwkqTVV0\nNCplaBQzHSAjSWqvyMMBV8YER5fSz2HqmLsVwlUYq8WEPkt/j59IZpOLjWS0PFb+RNHVzFOPWK0h\nKjlbIxsxI9CSqR2Jz4LT2sZtLjgMNp4WNO2Ee6gophz77GIPO4Q4EQySNCiIQo8pn7gdUwIj8cOe\nwY7ocVFKcIo8bNtnCGEYOkx1oo1cRN1hFyM6O9PTI2tB6VnUrkMnfea2Qkaa0ViIeCAYJdakABtf\n15gpZOginJs9dWhhxpGtzqlqm647ohqL6uThjDVjYHNycoJgzngzUrRzMA7KdRB6wh+/G5CcJwcY\nDOEsxPNHVFygPckkA0x8xLYFw0lQC0XZdGxtg6gdeuHjtAp5OCF2Pi+VRVyPJLv7dDphkYWoec4o\nd4SdwM59vMzGnS5wfJu+szixx1cCpxgY6wb8HJN2NFFMn48UciAfBzpstBXSWtCzQooZVRRSUzKo\niQUlZXwG5bKKNNHSo2/+fzKwV0vJ7LWgTiPseM+F41ANDR+PCYnIGaMzzZsFi8uMT7/pudMbptzi\nahbgvVWwOgyUsznnH9UU4U95mQa41z6bqSNNFFZg0deSaJRE0x6RWfjC4rCe4WQTTqKo1YzSNcyL\ngkVQwSgImzXNxQTHkUD2qE5zEyqkF6CmhKk9sPJ8bldzVmeoVyG2OeBFHogljB1x73ATV1yhmYaI\nIdIMw5qVs+fURhS2QRWGqRdEeg36zGhJYhVSLHqujoLTVUZy47GeYDfusL5/eX4SErtWtBNUUYST\ngyBHu0f6I6i+4XgZ4YwlgedxqGDtr2l0h6k6ptBBipTaumYaPQIBjZqjGLD6HYG1oApH1DDQe0v8\nUcNswjo29F5I7E6U44rgqNFzD9+c6E2Krk4M+4IknDCFIESipWY9JJzHnGmKyLuR+aLDr2xaFEkk\nKI1mLHpEa7FQA0fLxu3nTEairIp64+EdAuxZiZQOp7EnnRfUO0WT9/hXKbZT4RmXauFRK4lddIhV\niOk0Tg+WLImsCSkNYb6mSQ1DcEHdnLDTGM4Ww5QwDnsC4WLykGlmczR7lkfFYeng9CVx76MIwBpA\nlrhNQtZLqk3IYE3MO42JFTNK6kFSS8XStaBcUQwDdmgYVM8sKGjOgpQaefDYzw2eHWENE46r6U6a\nWAyYxKOpLdxR4fgHVB0Rjh6m39MpH1NpFt0CsYZ8Sgjp6OucthlpHYEz83+wTn89VhZoPrfvcjYW\nrhj57KOQwOl5uvyKXpe89apHXq1Zv9bcffQ+3iJj5dxjcJ4hrXcp7vjIZ3OuzBva03MefRWyePyC\n83rkqHN05VEvbE5+xUEn1OmSwfRwusEPz+R2z0ob9MFi50QcnIR2iNjLlmCSnExPmySU4wqkwC47\nrKZHWRbZmKOQ5PFIYxrkyUfuEkyfEYuKsYVl25FhKO2cVvYkukOoEFfZiCRHziwsT9J5PU3k0AuP\n2vFxdUIXDehMU104MMzxPRdXLBikRbmwsaTBrUOmrEHPS6pziN32DGKOtTSkeU9ChbJznIWknSTl\n0aH3GmRjMetbat8Ga0C7MYHJmU8jsT0nm3c0boUJHQbZQqsZxBkRKSbfJ9MDo72nTvbINsOaBsa+\nx09ilLSwS5/c1YSxQ9SdOcqSfmVzsQqR04GpNsipwDOGrvWJ+xJHzBitI72JGHBp9AF73RD2HqMZ\n6eMSB8XhZOH1LacuZrRmbBYz2tsKt11Q+1AOgtnBpVtIYGCKBiwrpLAm8uWCcVAIXZLLnnbSKHdk\nOBQ4JkWmDbZykLJBDAPycCDtJ7J4YtXYLj8AACAASURBVOoLrL5nK3xKp8S67dHzOYNWNLYicQuW\nfcCYb8gPit6TjHaIG/foLmGnbvDnLU3j4RQB421AHZdouWL0etKsos0Url/TdmfGYaCyOtyyRIzg\niw47n3NUGa1boSJB3E8s0hzMke7U4dQK1SgCM1L7AgaLQv9TOHX6TyN6OdA3GZe4fL1/i3s/y9mX\nD5FjwKMi5LPK4aLX+KuB/b7GayZEMyevnvJ6eo797BLPjtDNezirO1y/YxOGb7FhwMMjTxpmWUao\nIhbVRFi22BcrHHXByQqwTUAnW2aiR2ITDiNqJnHmJ4bdmWnmExwnQpPhFzZ+EBDaI9boEJ4FOj/i\nOi5zBm6ShNOVoXEazvMA3zszdJKhtujrESMgCyaOW0ktO8zBJZoEIp/oI43VGPyZTdAbOjmS4SCT\nBZYW9PMDztGH0DBNI+HYUAnFkAqUMAQ3himsmGSEq3t2bcGQlJhsiXvqsPYau2sIFhkYB72UWLbF\nuLcxo4c6TegpJrMc8qbFalrCQ8R0cpg8F5nYTN0cScLEDjV2cHLpRULdwChSBllxygekbXFMO6gd\njsDtCkSQ4vcxogDZXmINCjMfaMIEO8npwohaNVixhzYN87DDtRWy1ZRjyxKHpKk5jgJXDVRxixCa\nWHdk5w7WPtVMU7g9ofaYrD3LbuLMHKee43kFsTVD7UqkdMFEJNrGGSWliXFmEt8I5uUEVkKjY0Qo\n6OWKfhKIVhPVHn08x3ENTt+QLwI8ZTgENXP7gFNq2sJF2xNKNszOFkFe4TYOY2RIm4giE0zBQGzV\ntH6HEJfI5UhVzWiMYj3f0d8CjUSoGXMzMZk5aVNRex7n4My8j3DGgnAM6f2O8kZwvlxSjy6BLLFc\nhRdF+HWIr86sdPSDdfprAQsxOOghRTgZs1Zif7pmWUxsby+Y3k6x3h1x4okPr0eW9JT3V4w/uiHe\nDPiHht7pyR5+Sz11rL/aszBb3gyKwiQ4vsCtJAcVEFoj3aJhF9tQHAnHho1XsDjn5GNHFueI0SYc\nfWwUVnNF7oRIWbEPMjrbwg4mvFZiNRmWHOnnPhsLVNUxbX1WR8OkC4Z+QdqeOdSCzoQsUiBe4gaC\n8Vgym+eIRU8UR0i3wV1I4ixH2tD3LaLPWDQ5UaCYNxP6dKIpIqy+wJyOeEqgxIRb9PhDyRT2VDMX\np53h6ZjBcXCFxGeGcCemlcRJe2qlsNoFoq8IOHIsFZHdI8OELDZYVstM5zgu9LnEHXr8ZKKta4x/\nQHcVoj6SOi6erZAOoEtcx8JWCl8u6dOGWhqizmWIOvwBkltB75wJhabzeuapZueHiCwGu6NqbHrT\nE1suY1UyzhVFniH7Jbav0UOEyHsO9oxAVAgrxzvOGUubbAxQEmZ1y9CPWGeHqhbkls9xiLCmGnua\naKyY0TVwITgKEOkW32nIxQ5T1CSuJHdzcAOmQqNrw6RrhqCkbnxis0S6OfNDQygh1RFO1aH2E6Zz\nyO0FfbCB2ZlY7AnCBdJvGIOQ82BwDzt6t2ZyJaFTc+vZTFNLmLWcpo5kpZmskEassFKPcTkjuGjZ\nziIOzgl96SLzDlm5CEvjaMnByemMpPXnLLc73AvFrgqRTcZ+nxHMStzRpvv/oODw6wELS/Kz5Wds\nNh7NnZz9wx558TGzyME7Ozz62ibPaj5gxVHvGF5n3NaS6puRm37Cf/qS4Ysl99qcj4zN6XSHrnrF\n3BoYxoGoSwjLnmEs0OWcJJfsIw8zy2lzTRNHzIMFUSZJooGuH2jOhirpmA8CrRMWzSW9E1HWiq1n\nIE3pEZQKhnFB5ta4m5JS1syykdbWVKPLEI/YSHamYJIdbCEJVogsxi1cxr5hvE0RhChzSdNXyGxA\nKAurXzAcDKcJ2nRFYkZqNyUyFpkxKONSqoQ6GFieQ6RVEYqM05BT+j1DE3Landj7J8hmKKUJRY+u\nGxwlOexWJNLgiBEpDiS9ZPI9mmLEchSBm3AMO5y+JJE2TREgHMN5NWNb2qBqlPFIT2tCL8K5LQid\nDPdgYSxFNHSMfUiHQSxCNlvJQdmcqoHqoLHUwDT1DMVA3Nu0vUbaNvF0gTUK3MUFweaI3rbM1IjV\n+tiewG0jIjdA+BAnmtDVdKmLkhGTdJjmipknUNbIcpoYy4nBPxD2PkWjcLcTi7TjaBZUeUJSLZmH\nmnI7EccJDBPCrxGJz1FFzNwJdxZSNhmOHVNaArft0EridSM6Mdi2JEDS93uiesYw9ym9M3gRqge9\ngjy9JBQBftTBWbJqFO6g0ZOGvCdXHm1doLYjXm3hFx1eZ1hMhmW/oj5UxF6BPdNk3cC0WjPlIU4t\noLM5YiNvt9gJjHHIFEvOTk8Rxkz+D2+d/lrAQuqWL9YOL9qCx0mK3428dn3y9gu+aXLejA9AS/at\nZHN+iDzETJnCfrDHHS+Yv4j40ZXHeKfAXwts/yus2ELXM8QwIhSIK4nsZmhH4S4b5oVPPq5RMsSa\nehRHgmhObzTdTDJOe9JdzXB5IqkbmrQn6TTCjjCNw2FQiEIwnRryaMJpZ5higx9orCQhnQ2M5ZxI\nekzrM26fEI4Wk2zwohN7LNrRIgwdxgjarsRd7/CqBcHFxG2gkG6DlyjCokJOJwZHMBmLLpK4todR\nNsp2sfOA7VTRZRIbG9NMWIDrWnirGXYXYNkdzRm6xqCEg+WvCLwjQ9pibEUhFpg0wzgZXR9jrAY7\nsbDcBbJQtHlLNNWooUMcbFxbUB6X5IsOeXmiPB0RcUq3d0nTiGUZcAoFqTG0wsEVGZ3oWApNsLTI\nFzaWlFTKsKg9xBLCOsK+nWAB4xhSn44MpY3lX3LrGU7BhFMpurrk7Fvo2mEca84GxuHA1E1op8Hd\nCmQ8UWvJZG9JpY1jJHv1isjtyC98BpWiOeLqEdKCVq7w9JxjbngjPEQJQXlm7nVMuYPel1hKcNse\nCQaX8WSjU5edHTNNBYIK2Z3piRHtDjnamKbHCImUHYuuwstahHbpr2eUF2dGbyKarakSF+n4BMVA\nGEhqq6EPDNNoqEtDrmvaaCB0J7BB5BGJSRlvD8Rxi0wnPC8naVeMdkrUDpyyPWbvYzUrhGngTfDD\ndfrDpf7Dw3ZstLnk8dxBv54Y/HfYFANp+2Oc92B4YjHbW2ySM0FyZHvHsExS1vHE3QeKRPm8Lo/M\n6vfph4fohYLJxTQ5VqCp1ic0mn0IMt9jdpqizRmsAttq0Ai21YzK9FTCYmhKVGhRqJRzu+DoWgzH\nCuMLhHdi0wtCu8cXPcthw1AOmOZANZRkY4I4TPi1YRZf00uDaWJaecDORmzb4zBIwpWDH1bozqHr\ndxjVw9mmWZ85ZODbNmXrMbkFZWDTDxFWZTNEJxp/Rj+VNL2Lcgx5BP46ITQOMv3Ohdw1JXXVM22P\n2K3m2IVYfYETaZrE0FFguT5TbfDUnJm4oepnjLmFb3L2g0ZxQpYCuXAgACuOMViIMcO1HKJQs8Sm\nmHy6aEnZNDgj6LOFkK/wbmY4qmc9KipCDuEd6AZGnWOZEfug8Wchz0VB8aL87lh9cmQodsRRw2Ke\ncDvWnKaWXtwg3AIvNuhNTVZqLKsnGhwu3Ia4mFMlDRsb3MWJur1Ga8H1OcWw53COmBlJ30nafsuQ\n7RGyZUgUnTUjVRnDumUqCuK6Yuwqrt2aNxW8akZsy8JZxKQqYRxb5OSgvp2Ikhypl1i3HZMzom5z\n6mVHsD+T9DFl3lKXJ2jm4NZ8PVdUaUV/vWAnY14cNLFo6NUZHdRYQ08iYrK2oQxOhFVP/dpHlq/I\n/YHBdNzGW74tDXIRUN+G+O4S5drI+xrpF+R+jY5hmMHpeIsUYI0/fJ7Fr0XrdBol6/YOeXXL8l6M\n87xExxHOjyPe+crimXUk+mfXTHaE1XgsU5urrxWvxt/mTpZhLW3W6z1ze4ZZHXjr8w9YXaZkb1lM\npsdUDYtxwJIKs15Ql1tEc8lVXnCmJ3RLonGOyj1mY83oJ1S0bNwTk0m5tS3MFFBnPekYcloqFAHh\nKNhuGjgPWDKmshVJIzluKsRuxEyXrKOBfDzid5e0yx3OrY0OO5qjIZRzzrNbrFsPIQ2DTmn0DcGg\nmcoZ0WXBobCZNw3EEeNqwm8mwnaiaH1c74aqUGwSh5ujxTxymM4O/aIj6tcYb8s0WejRIKMTzuBA\nawjchlIFtG2F7diMRUvn2MS9pFUKo1dsgFu1ww226FoR4pMdDEm0oBAjzaHGcUJeixtSs6B58Rrm\nNVUw51x8Tl8q7vsR/VnQn58RJSM72bIeniA7C//JM75Y9Py4crm8vkf+voUoQd6e2J9eU72lqPfv\nUSxveDSGeNIw7npeXLbcNQn+yxY2Dr1fUP7ywPYdzeVHH/D3/ZJ7SQrr12QvG5zVkqmZMfh7vn6+\nZuF8xvKt+7yoei6OLjszklslj5OY8sWnrB56vNwvieI9b8oZ8bwienHiSyN4+xxxaLZYSch5H/I4\nfsU+G9G3W96eHvEsO/CwtfnSyXnU9HydXKPNPa6SiVf2J7SZi3JdrjKfvLgm3guq9xdkb87MD5cM\n9z7ly9xiJrbEl+9TfrljGp4zPQx58crj4RvBp+9YyH7CEQ1fsOXdsOeLT22GeYisX3JnCpn8gNKK\nudg1FK6PW3zFN/ryB+tUGPPD/QR+aDx957H5d/6z3yU49qjao74aebf8hCaVHPsV9qzC//DM/tFv\n8HD3gmZ+xVfnhse1ReG+IOs8wp/fIWmPDO7PeCd9mw8eO4j8THc3xd3uGeMlPR3aqmFY4JUNU9Di\n93O0lZO5KfawIwptzBjT7g2WOmJPLpkMsDxBGMLNsUABfrqkq87Q2URTQO1v0RMEek6b1sztHrFP\n2Okea2PjHn2M29GWAmVOEDnEU8IhqbDakVT49LqhzwOGhYVUFf1phj+U2BuHOj+SpDHyVlJZoGSJ\nbda4MmewPUo/xy9nOFbOcVqSTDWF0jiWInBsTvWE2wo6d0BaGlMnxKajHDSaAWuZME01lmUT5ANn\nZWN7HaNdo48zZtpBrwW52XM5OAhVM1kd+Z9k3CQa+dWC07Ejc09EYuDbBy8Izz73Xi15+bgk8O9w\n2g74eiQILQq/5clWUMUh4fE5H28kQfcOwavPGSeHvR/yI/eGl0vJxnubEzXObiKeEvyqRLua14xY\n4ZzxWOLHO2aHNeoiZli+5HM1kRRz1rnHmPkMs1+xOi74+l2f6vmJDy4TbvOW+mHH/PV37cjokeHz\nr/f470/k+W+wfJ3Tbt7w1t6irq+wE8l1+TXi7hNE+hXzW4N3vMvNTyIik3PdlfzsTUypjlh3B371\n2uVRdoWzfsM3PGbcfUH8KGZ1XVA/fEhUf86brzXi8h3SJiTP35DGBUX6iOjbkTdPW0T9ksX+Ic37\nAfdfnbkeNKtJkk8NafoA0+RMDNyeX9O+tSB1Apa3JS8eFsy+TFne7eCkeX4x8Fd+61/9I2PMb/1F\ndfpnwkII4QH/G+Dy3Urkbxlj/sPvh/H+HrAE/gj414wxvRDCBf4b4DeBA/BXjTHf/Gk53nn6gfnr\nf/tvcPtZzdXszDevl/w8ssm1IJ/tcNu79Pc+x/r2LSy9w7EdnIdQlyHlPOHenwwc/IhL+yPs30zx\n4g9Ivk0Z1tDnNWahMdbEtO8JFwrbWnHM96RVxPnSYdMN3JiGtQ4Y9IFmvGBaNEydjeO0+Cc4GYcL\n+8w2uiTVmmLULF3FKAzjucRjwIRztrpl7ZQ0ymU42cxEjbQlBGsy0eNNGmcauD0mrIMSKqi9EGk1\nqNomcw/I3kGqERVf0LdbLGeFqSWz9IbjOSagQowe9jrAPhw4S5tIjdTWRGIWFH1H4yg2fcshgnEw\n+K5DPbpcYBBWyXnsiac1YtRMU8E0ejRuhy4lnjsyiQilJwpGHMtlUC6LsWKUAiV8VNxxqlte/LKm\ntb/g/MmH3OxX9K977IefMby4h1FnXm1qVNRj5TOSw5zqrZD7wUf88tUTXPmS6OYBdx/6MPuK/nOL\n+oEmNhfk4YnupccizRgGwzF7gHrcEe2+5Vv/AVe7HTeeIB09/MWB6eYhq7u3bPO3OM0/Zf3MhnFg\n+85v8OSzLZ+8LQi+WhA6EvmgYfbNxLO3n/P4kHLs5txRrziPV4SqZ7Bbqn7ONrslmj/k7buv+NyC\n5HjJeP2C7OIJJnuB+47g3hsL1ZV8uxkYv37K2z8xbH9loy8nnPMt+4cJ6Vc+a3eLtd3Qrzpep6+R\n+Zw0umVxPVC+9y6irjncwuMkoA96rr99Rd6lXH2wJVJPGaeaMS/AdXj1RcnVo55yCknclu2tZnM5\n4h1+xJfNwLtPG15+bLFYXSPLdzjHR1Th8h/8J//eP3FYCCA0xpTfWwL8XeDfBf594L8zxvyeEOK/\nBD40xvwXQoh/G/ipMebfFEL8NeCvGGP+6p+W44Of/8z8t//9f8Xi/BgvcHmzekPaHHhzMePtTyBY\n3ueFeMO9bciXauLdxYmXN3P46S3TJ3d564nNdVmiLizunHy079AGI0les59dEGea1h6JdYtqDbk9\nw3ULzm3KKs04Fw62N6FGRdEJllZJJ1ZM4x5nFtMXA2NtMfeBFupZxVhNzPSSramRsWKhHM6mRNs+\ncZvjTS5bWxFOPqWGhTti5z11KpGDh9Ej05hTRwZfLojzjLbVlJcp0S6nix08AXKI6IsdQTpnOzQ4\nUU0iEsashZnCPnTsR5+5N6GsgUo7uEpSj5JJ1MSWg7EkVdsxtXNMtEPJDba3I8oSDpxJlUUrPSqt\nWbgRh1wzT3pOtofUNet+oqsCqllOqA1VF1D4A81XDbX1Id/8vSMfvvw/qL695cXLiPPwLeaRx5RV\n3Ln3BOv4jG34mItXHdaDOfsvJi7e27H/rKZ4d+D+RxusOxGvbz7jbTXRBk84xAV5sGIjR3bHL5Hz\nR9w7bfHlik+PKWH8S85S8bM8QN9bwxY+yW94cllibgOeL9Y8yF6Q/NTwSb7m8mbLculwEDaHNyu8\nVDPvHHaLE3euPa7lFU38C+4XD7FCm6Au+ZMHO1QZcDEVWMkl7puU46Oay27N622BVb3gXvsAsTnz\nq+kO6wUUN3vu9gPf+iWz+UPkC4E1fcI+WPH2WyXtFzOcd0N+echQOuO92wfUvzFy/DBi/UhTv865\n6DTP7QAZv6G/uEvxxQ7vvYnNm4b4NPDszgX4He/rRxivIO9arreaqylkd3Vg/ipAr1ZE7Z/g+Zc8\nc3pmfczf+pt/458sLP4xcATfw+LfAv5n4NIYMwohfgf4j4wx/5IQ4m9///kPhBAWcAOszZ+S6Kc/\n/4n5w//9l1TuwHmU+NdvCO4+wHk5oq4M+rXmzd2RB57LdNNxGxcEtQ3xjCHrSDxJPynU/IS/c8H3\nuZUeC7Oj6gKctMIcFXrtIgqPOFGcmorElPRFSm96LBlgJxlWFtB7HoUqcboJSykGayD0Lcyhxr0I\n6XYu3rKg0xa6rhFBwGB56PzMOC5ZuztuLfBqCy1mpIuM036J0lvCJEKNJWMcUlcGt1M484LxZFP1\ngjiWjG2MF9VUpwjLOWGpkSmwmdoRB48ybAlMTAbI1mbwjkgkaTmiO4sp+m7+xdhB2FvUro3xBpzC\nZ5p6uk1DlKeI8UBuDFrEuF6NXwTUa4/g2LCVIbEw2Cm4zY7GWTBlJXYqyLKIhV1wFgc++V/+kF/9\nUckvPv6KX7z5XxHiimiE01AyLl8QBZe8+eaWy3sjpvuAzv+MO+17vHijeOJmFPZLutRDeE8Rx9fE\nVxH1KcWIj8nwqHLBvbzA/eA96i8/o72/4XyG5ubA4x8rXjbvcw/D6QXcSQy3zadcmff4YjowvXdN\nPP6Iq+tr3IPLL1yBvLslimwCvWD4zOXeRcbRqkh3D/hkuOXpRvHKWeLYA+eXivmDMw93mmddzuat\nBzTqNfp6QrYXbKTHzaVFNL6g1neIogzny4LBuuI0nMj/ksf9z9aUDw3pIDn1X1O/mRBDzePkHt3l\nmtvuJYtXdzinn3DpWHxev0fg9EQ7mxv3hncuD9xWc2rvivuHLbezGavdN1x7Fk8fJnw4XeJcj6wu\nGrj9mtd3Fd5tyNPM4+TMmN3ZM+RHXp6e8tmXv/+DYPHnKnAKIRTfbTWeAP858BVwNsb8w6Ns/6hF\n4V3gJcD3IMn4bquy/39MICWH6ciqmjGktyxnC27qnDuXmmMviB/XzPqEN+eS+VxhnzymTQRZQTx3\nccYGMy05Ng5tAK4ekH6Ld0zQxsHqQ1hq+n1BHYLdFiSBj72N0DJDOxp0i2XNyC4GEpnh3UAsPBrV\n4mmHqXIZHAsxWDiypd3N8MKGnb8iqjp0IphHAfmYo89LVsJiXBjqccfxBtLUcMzn+COYcoPd3xIs\nNxS2xi5sHG/A1Rk3rsNFPdKfC4Ro6Bc2diYZbQfRTPSmZVZZlL5FNB3QjU1XucSiZohcxmDCamZ4\n7pZebSDtwLbQu55eaSa3xGxD5KqgQaHaJX7foKWL2Bi8StExsg4aTplN12hqb014LBF2yk5rrmrN\nYCa6813aixOCP+Kreznuxy62GTnIlzjdiT6e038C+Xvw4A8bfnX1KU9rwzPrF8ziC/7eiw5n3nI1\nK1DfLHh+suCmxy3+Ps7mMZuD4MXDV1hJSvBRTj1dMTxvuSJiUjlye58u+CN6veBFWZK0HWKR8tmL\nr7nzbs3uq4Yhek6dbfjF3Y5HzZnbL2v8hzHnz19xTnK2zwTvOTZ/vFyj0oFflXs2LmSDjcwL5jLj\n0+rHWPbAl68sZhf3iYo37O4rjkebt3ML63Sf8rGLbCPeBBX+KiMtL8jygVxuWb1ekaVbpudHCvc9\nlncVL7eK8dM/xmkVOul4fdjQvHXN8es/5uB2uN1dFvcnPv7iAdPTzxEfF3z0k4CLr19wO3TYgeFl\n1pPs/y7XJ8Ume8re7eiePyUPGrI0IH32EU4dkt9zUfrwF+HD/12mf56bvnce+znfuYv9ZeC9H5pY\nCPFvCCH+gRDiH5z3R+ahg5lKFtuIw0IRJwW37kRiJTgNBGWA7wgmIuaWxkwlKhlwcpextGmFwXNi\nrCalm0+oeiRfd0zOLSd3z1htsawe15QEhY1dHjjNzlQzj9CMGF/QMmANDmOlGBKXs9KU0kV7giCU\nDJZCDGfk0kMKTWlAlz3KsxmOPbkFyksR7p7swlD0JVOfMg9sMq/C5czoKER8pB1nTOMB8olzLck8\nG5NeEinBMZLoC4FkiVdE7MYEt3fRVo+O5mx7QWk1MAj8xCdKJuqFwTKGaLCxg4prI+iaGzQW3r7H\n3YxERuN6Aaxs6ipkmBRdVjMlLTSaKa/Iqy1dIOmGkfnaEFkt4XZP54y47YRvDHgnhiCmnH3ErfMt\n19YbHr34nDytKGLN6Hmoy4RwP9A6X/Lurc2X0sP2l7y0erJ4xCqA8SWxteZ5/y4yv6a9+ox3gpY7\nq5ylONENv+Tuy4JDfuSrvmOvDbPqa7Ldrzje9LTnEvtXJ774SPPWoPk8h203sTExBWsKe6Rix0cX\nA5cvPid7ecNVNDLqN6z8HqOucJ/Y9OsrNudPuHydwc3IfLCJ7p/oPygI2ndwfmJ4/H7He5c9j3tD\nd+/H/Nwt+WeUw+tlz01cMj9K9t5XPDQWJnyb/irk8U1FlJTUb7mwW3DmLk+mM+6bETs6sWtT3qQ+\np0XEnWjHm2dz7HdqVrVNf9cgw1t02rH+8B53o5GqVDibidRUJO6CcfsNceLzYN3ycawZB8HV9kMu\njML+7EPSt694ljlktxl+UvxQyf6/a50aY85CiL8D/A6QCiGs71cX/6hF4T+0L3z1/TZkxneFzn/8\nWb8L/C7Az37z58YqFOcwJlWQ0EPm01gWY3JE6QQdazwNY1bQRRFBc8LuV1jenoENUwLxdKR1FKvW\n5yQc/MMZrRZYo0b6OWcbLgrFITrj9Cvm4UB3MPRhyNQNzB2LlhacGnP2sZMEa8zopMu53TO1a6ww\nIt8dmJYKb0xZ6gNGWCx0AseMU+DhTikcDOkyQhmNLDWWmZGYia2joYxZph2it5gvLabbgWmE3bBj\n1l9QiVsGvaGRE7ICYUb2k82midGM+Lqn05rTtMY6VSwvOtyDQeiAIsxo9QXSbgnSBefphPA8vGJk\nazxWZ0W93DMwJ9nN2QUZ9sHhtKihs0kWkka1uN2cvG0YlA1hQNiNZBvNoEuyyKG+sQn3Dq23YdNZ\nfHt+gHcpedU+I96uua4NtnfDYvGQ7PVzNu8+4Nv9c5KpZmDNYbWjXr9NJSJ+8kVBo3s+OF3xfHXC\ndQThVxHf3L+Hq65JwiV3vjgj24Hj1Tsk+XOKuynb1Cc9LXgSf4k5vo1YzYiza752HZ5UXxBVP+Kl\nesZb5Qn7nSVf9zP654ryvMNRMfP7ActtztfrifX8MXdu9lz9dMOgFNbhin/hvuDZoWKx+w261SOu\n3v0WeXiX5t4neL+8y/mJx28PHSx/h+uf7Lj32fvoe3e4t/6Cpe9wTN/nNuqwdUlQjAzhu2zNNYu7\nFoUY+MkcRt3yq2d73hWKuVjSn4+ElkejwLIlD/Idn77nMNwYfEvyqnJRD0acY8Hy5VOq4JYvvp3z\nJDrxvHVxgg7z5mNc/ylizGExoRaKvMr/4pT4Pv5MWAgh1sDwPSh84F8E/lPg7wD/Ct91RP514H/4\n/i//4/ff/+D733//T6tXANgYjuFEKrbIWuE4AWcxIB2Bs1/Suyf8vqNxNcwXmFFRtGBLTdpF1LOS\ndN/RTRJ/Kbk9VURjzH55hV/f4JuQqYiRM4lGY0oXLzFkZQ/BjFDf0vgp6ixRsabpLdZ2w06PWLmF\nkzgEzYSd5pykhR9sqPKcSUzINGXqGjyZUw8LbPdIXc9YjDv2uxmpY9NhsG47ROSw2X1nKDwqD7c0\njNtbuFzQ3rZsljP08RbsC2ZmYJxGtF+gfEUwOjRTwOAfGRyB186J9Q7f9Tl1S8LFgXObY4sYu9/h\n1x6FrxlyF9+t0OmGlXfgWNs4xMHLzwAAIABJREFUbUxQnjHK5iK00JFmkgGDVdLnlyQ+nMaROQLp\nCrTJONkJUwFBmKBPA3eXBX8gI57+/sAflAFGNWz6jGvZcPHS4UALb/tsP+m4aws+bF4yy5+wevoN\n6xvJ85s59wbBq4tfcHqiOB3nLNqK8VXD2/gcho9YyTnrEfRHUD2E5XZgP8LW2iBnLkFhs1vvSeMN\nzalifjWwLJf0335O//oR51XOUWyYdxmRMqQnn7XM8L2B0Dxk961N8uPfZDX6rJcG7+mKy8Hj4zdX\nzKNXhHff5meyoBEp/VVAv0ihe8Oj4rd5+59/g7r+Kf17JfmrCun8FveeDHxxfyC0Oq6GDXdFy492\nL+i2IbufP+VHr7/mZbzAUz6z7YHq8YnPPpP8c4s5mdBI7xrl3OV2dcvijaYMU1QXcamesb0Neef8\njK+nEOXPWF3FbOVnZMcL/tLVjE9Pgtmy4MHrt/jI/5xHtkUve5Lbgf71EuLdX5QR/1f8eVYWV8B/\n/X3dQgJ/0xjzPwkhPgV+TwjxHwO/4Ds/VL6//nUhxJfAEfhrf1YCPdmExiOTmoUyHGVN0M0YrA4d\nCWoMoRWgOgsnNwxjjm+WDNaEWAzIasBaeLRlgjofSZMV49gghyN2bxO6Hjpq6Cawwoo0VvTViPJb\nor6hDFb4B0MmW9IqwYsLjBUSWCP+XNMVR/qFQ2d8oknRHCYsM7Fwa9rOovMstFKsJ81ZKCw3Yz+6\nLHSGHmKGZUji52S2hRkngt2KdtMgxMjgBkS7M9YqpFAV0ZTgjw1d0GFSj2Rc0IiRqixIpgRPxwR1\nxlFrghns9Yy0OyJljC976rLAmXyU2+EZQRjYFCrBNA31/8nde+zYkqxZep+5uVZbi9ARJ+LoVPfe\nKlZXdxMkQfBh+QCccMIBwSaag6rKvCmOFqEjtvLt27UyDnLAYQNMNJDo/w1ssBaW/WKt1sArNHKt\n+N3x2WoodYc8tkDU5PaYqQmrXYnXy1kVDa7Q2EkNV0iMbkvKgNpLCYjQ0zWFE5FbFslZQrc2CK8F\ni70U6y7gY6HT7Svc7AT/Cxy8viX5Okdqt8ySji+HkkF7QlgJYkujNK9Q5hl/31xS60Ps9T7SyrD6\nNdvQIrAkvfu3zNUFt4nONjYYFmd09wWZPWTW3HJTuMRnL1HOO8aWSXKp0fYc0k8BUjeIzgTD6ZRJ\nO2Q0Cygzn+PcYsglo8kLwi7mtbQ4mT7lhhav9w8cv37LZZsQX+/z7CDE7HtoVc3PezCXCbZ3wml3\ni/k8Zi8yGd89o5hpZPmaufyO+4s7vtt6/NvJ/8g/lj+zrQ64PLnAvvmRf3/eY5fcMb6fIvYUaqtx\n25lUeouRXFGetLhlyN7fJlzXNfpdy7yf014VTI9Njj9vKPYeCXoz/FXGry64BmzHbxm0LoupQRJe\nYhT7sPxjhPGnWMr6299+UP/Pf/rfKbqQXQl+nmDofTq7oXUK2AlKQ8euNHZ1hhO4lG1OJyw0w6a/\nS9mFOU5rYiUVUTfCYEMgJFlXooSCgU6ijQjqB0gEliEQmiKyAhxNUWUJJWOGZkNuF3i5Qe0o9LsM\nhjbdziYKFQOzIt0FdGaGvgF7UBOVioEV0G4zZFdT+jXKnNEmLZ2xod94pP0tehVA5lH0HumvHe6M\nCrur6boxrdDRB0uGpUC10MV94mGMKgRNbYPeMqgEWxXjKw9tZtA2FqpusKuYla6j1x5CbyjSGluv\nCbQG6h7CTqhVTWHMMeqEzi6QuqSr29/VUe2R2Sa6XGFsJbk1ojEigl1FOjTpPzZ0niTOQ8z+Gl0N\n0G9guy743778Zx7/0wf+j+3/Svt/PfClczi6WfK+W9IdaZwVM34bCL5xHojUATeq5viNpH3SIKoB\nzU2HsBXdWcvincWcDHfqUNsbVu9XxOennMgN2p3Np8jGOqtgY7MXetjblM5+RyRGPIQl3nKIIW44\nPu6z/SVF+h2T7DsubQ1jHmHbPXxl4YdTXFfjaL8iVT1ODlzUdc3i2z323waUhznD8e53D9emRkZ/\npbAvKYXHKjW4OG25b3zanz+z/7Lj4/ua05HD28ERrxYt2+Ajd+IU07jmqH2J1Co6ecnffzziSLbc\n8YFRc8r9IEaoNcUi4HCTcD8r+Wg0PFm84b6GJpmiLx94t+jYO455bLdcrqZo1RV82TD1vyd/esN+\nLLhcrxgPWz5qFhN/RvcvtziDmvWBZN+col/e859v8//605D/2qWUoMkEdqij2wqp6ey8ht5SsXBC\n3LCg3ikGGohBTR5t8IcGiBSR5mR2h9367HSLji3D4ZZdM0S1K7R6SqNFWIaNQ0SRjnGNDUoptDak\nKyVabSDMmqGxpdaGyK1BVghkrLGWFb1GIb2ONq2QmxxbsxHODqkHRFmBZtqUUYtDQ6YLdCnINwWW\nntPoGg05dT2mSApceY98NHmcKgJcuqbGqlpqqWMWJksjI0gNDHuDpjq6pse0V9GlGaXuYvcmlHKD\nUxaYogbdZZv3EfWSpm8R6BpemrAMHXrCJco6TEun3Q0ReoRl+aSVRa2ntNKlK2r0ymCi1TSFRiYn\nTKody9ala/rMkiW5P6RjiarX2J0LywTNkjzuPzC6d3jf3CLjE37Lbhli8PkY/GbK3dcRvz1tCB5W\nvPVN7ExnMP+CJ0d8eG8QWg/4xR7Xva88i2D0JCT5u01avSHu7SOfC56/V6gzk0+1yxOnwS5N6tGK\nlbjF3A/5tHPxHqYYiSA5uOQvPYs3P1U8+Yd/4jDXeesumZUmTMf8c/M9nn/NYzAiU8f05I6nh/eI\n4BvSJua7ry3XpoG2uOHG+5Zv2iWyt6DKCmThku1JGmGT/xhzfKjxs9zj/u6eoeniDjqcyxJx4NJb\nWZjje9TViG3ZYE1XKAmzvVu6+imvJ5KFcc1wIZHNKTxPWH52kPsf+Z/US+Kxolndk7x1qJ0nPP+n\nBvUuJ0sS/l34lY+lRjYZ4tQGj9cDPrhvKbUXzL+mvJh3/KTVXJzMufuyJjcDRLxjN7WBPxaO/Kc4\nJKMDvZY8Lku0ouLRtHE3GypTYFQpSR7j6jtqqaFJiWdLik1ArUbIzKG2gHaL064QRo+1EljWltgI\nSeslemiRoRAteEZJbbisnR6FXdCYCXrYYBYWumWTLbdkVkzd66ipGbc1wjYpsgTXrdnpMywvwqgm\ndP0dw8rBzQM0S0doLkmvQVqSbpyxdUqsukNTin6zBV8nduZkc4dg0ZCKFhnlNGaNToxluxirPirQ\nqV2JaQoaOyNb2ZR1j8LKQVtQxjrpzoA1iLVEuTsa3cJFkG3XZN4UfWWw7naoXklnaWDn1MokriHr\nchphoJKUkaVRaRuSKkWzQoIGIlXS12zUKIGshSJDWYp5MMFQLsZMYZgho4eSw16EEDuiBAa9Y9L+\nmuH9Ac4uRDuqeBZ3mGvJSWZSLA3a4im/jgTaeApGiv7skvlaUN/3ebws+fzEIEknDKqa/NeWpvOx\ntwl1/cDmKOI+VSTZFE0qWsPF8wMmgcuLkyXfLU54l5v8bXjOrNkhuwxn75zwbMR8PsfVthQnr9kf\naDwPNnQXMxi8pMo79gd7vBNbBk9SxEnA0/Q3MqvkYalxfXTN9qnPpDdkVio+y4zazbHHNcm+h3uh\noNZ4WvXAyJDdGM/eY2eEuKOYRa8l6b3i6OAJi/ANsreH3f5AGR9xaDm4Tsnp8Q1nsyM08xJDdzGT\nZ1x8U+P+bUg5CYhFzd4POR92BYXh48qE+2LFy6FDJV8jJzvWLwzedyvmiynytqL37RH+UHGQn9C7\n/eO3IX8KsuiQ0Cg0D6JNjmkI6s6nrCsKfYdX93HSGUURESeQ+gPMbotfr1nZGnYmaYoJhfIoKai3\nFtGqoetqmnBEriz0CtJFQ1uVqEYhqghRK0QaEDUanbDJljmtVASyo+rWOMOGzV7ANskwhg5a62MO\nH9jtfCgrokbSGSbbvsLp59R+ir/sEauGUS0ZO4LOdJFyyGZXg7CYVzHqPmPr1JgLl8ya4WcdXWfz\nWG6ALbluoHYDnMrGcDVqd0XWljTlENlNwWlp/YrYr8m9lsoombYF6TqirCBMa3SZ0av7eKlGu8to\nHQtZdxS+YG50DLsae+DBtmMUgrL6dLrGol8gQpcFC2RR0IVDzMrF0gJUkpLKDS0DsiIlkPvcrWrY\nEwymFW6uMa6G3GgVV5s7BumWe/mZh5HO7XrI871beq3Dt0XHON/STwOqbop11vKrlbOYx7QNlF7I\n9qrlfGbz9fkVb32fvV7IfNWQHcLA6Bjd1Xx9VGSfhnRux854wtXemn+yJ4xf+Giug3XhMHbm7Juv\nefbEZrP/LWNrzHR0iGlZ+KVDf21xN7rkXizwrBHtbUphjoiHQ25vK+LunPixRYhrrj5rjAybb82G\nXz4tEfaMb7523L8PaVXLQ/8Luw/3vJsWZDcx2V5GfzriuTMlWG/46e4tcuXypQnxsnc05xVV+5H4\na4u1ek4qj2jDAakmCEYajf49B5HG/qLj4H85Qk33+OEfzziyznny4gT3n05IBgWTzRrz7S3VlUP5\neEE+zPlS79F9fcdZJWn+2pF4V38Yp3+Kbwh6QzRp8XYKV4dFnVOPfeoHjZmSRG5Bbmt48QTP7LCW\nsDYEVTzADmOqMsRrEvStgRV6FEZDXgqaOqXXWghSogimwz5JIim0BT3TpOoUPU0jVTmZGTDWAmwv\nIVI+QkoyOpqyIyhMcr+hFi2+0DBURWspNDtk0WyZNz61LNg0I8L5GrsekbYJejQi8jOy7Zp6ohg0\nG8pUIkODSemCviNVIYXUqSVMGkFpWuyKgnoA2VpDZAm+PWBhGYy6GOISwwuhMHBKSdx/RGscOtdm\nEMPS7njQU/RWURkFamdiKEWiP6I1Nr0Hh9IJyY0Ep0rRdId2NaZDsgkbxnlJV1uYlU2uZ7SBhj1P\nUeS0Uwen7JPVGv0KfmHHXhyzzkL2bpYo95LKdnC/bJBPA8ZXcHv0hOfJkk97Hu/e+aBFfNQcTvcH\nlJdfiR8NVFHz+uiQ+q3OR/0rTwzJUkx4062Zlx7rSqdaN/zatzj/ck1dwFVvzneej9aXXLoWYd8k\nXJwzbua0nUD+dxbhhyHOPEXPa/aqgM0PKXGjYWstm5mNs7shcwLGX19TzRWzC53lpo8oHphNEppi\nSjoW7IdP2MsE70TKl75k+PCMw/EbwustysiZTCQ/qWN67SPR2TFhVdBrYlrR0qwLHlzJJrzhb5FG\nYvRI9LfU0295kZWY7pQnxwHZj3foX74ShGek41PKSmHOtohmxqF+wjDc8cmv8TeK+GjO8XSPfPse\n6/0I/YXO/32zYVQYOM2au089+CZiJzzSJqHMejjJCPhjBjh/CmUh0JGLkKJOWHdgR4Jy0WL1FrRZ\nhdVU0K3Y9RvyqGWhYqzSpw5K7NynaddsLQ3D0KjkFiVbxCDBsgxSlaEKsKYmpZbRuR3Cdtm6OnXe\nIzYaNJEwsiNUWlHea2hKMNm2aEowUiWxn9EtKnyzw9xYZOOGOq5xI9AbH6Vp6ImOHTxStUP0TrBr\nfConod+BGunYDyFl7lL1fPqdSedIYrNHZm8pRAe7DUpqpH6F7VaM1jUtgr7usTa2mBWUnkddT6gN\nGBQpW/lIYHl0rU5nd3TTlLm/xbZqNOGQigF2X1G0Gj0rQA1a6rGi9hYYmiJvxiSyI52uKOwVpC1k\nAevehjTI8E2BXq5hW7KL5piqYrdWBE7H/b7FUezQzgJ+GMV0JyVXUc57/5K4N8NzQpZnA4zslqW3\nB22K266o6h7HFz4L+zdWdp+91qA+mvAmumdxGqO/7LjOC9wLkNKFLxlPuxvUa4lkgXFoUr3smD/p\nsdJTWpXx74cW3/eWnH7zlO3eMaP5kP9QSEZDnW97R/yHoUHufc+JKjm/mXL1KKnflDwpnhLJDE8+\nMg5iNO0DdfuJsxSayyHNM5di+Bvpekf0LuVgWDHRGsRkwebhgtawaK0D1pbDWR9EdMQguuUx+0ob\navS6EZlKWMoITb4gWe4h9Ue06yOqd++pri4pHxbcprd8EnPqJy8wsxS5KflmlRI2kuMgILvQuRxt\neL56ya13wl+PIu6CltD9DqVf0KyecNH2UMpBZ8zpuENfu2T6gMP7kIt3Bbvnf3yQ8acgC2jQRU4o\nBthaTds30ewcv9DZKIGbjjBaC03oDESGb9hosy0DwyERGar1mKiUVa+j1noUlUkvgiJxadqARhZU\nuYnVtXSpoItC3EdJ10VgxJTdHulWguuj5i3momPT3yLKBJqa0Agxhj61qmj9hkZ3ST2fqieo6x21\nJlmmHd5DQCkatu0KLYzx8oKuC2GdYzgFWZ5i7La0woQURLqkpzf0G5/OMWiocFtBtfGhdaGnyB0N\nldlIv8M0W7SgRF/YVCJEuX1U5uLjUaYFsgh4SCzstI/yDNrNksXCpxvpmHlH2JkUbYHqLNKmpshS\nnEojXPvogcNYa1hYDW6mcJQi1U2SYIThCfrOArFtadwdebrCVxG/GoLlZsC/FSH5+gbn3OD8Ycxh\nG/G5vsWIrzjEorz9jFvYLOanVK9jLndL9CvJbjbBuIDi0sXu7eEtRxxcvsASgs/JNU6+x8Ow4Se9\nxV7b9MpTPn4q6eIZ1qWiN3/K5OSCnfGcev/f8a1u8+QvBf63fZScMHdb+krjsxoxLT+gP9h0w5J9\nKbl4IckPIfqo0ExF82FNl5S8zCquZMSlF9KuHnGSfar5krvvHW5u1zirLdtox+mThqvTNT/qS3YP\nkubnO3avK8pG8Lo74Ce9QzxeczPIeZEWFOVvbMc5j/sHNKsh2pFFGcx5982cebzH88l73Dcr4t2Q\nA++Gy29rtu0V+e6RcyPnh88ThBfz7OVLDp4e8SzpszcrOf+fJ7z8H3L07/6RI6umPLjGe2ozMG/4\nJr1jtb3lk8j5YXXwX4bhf6H+FGShOkHZN6i0HMcMaVKdsNBJjQ7RwNJf4fo2vkrA7oMV0ax9mqrA\ndKA3zll4FhoCfblGbzLWfYnwFH3VIB0dLdNIEkXVNIz8Dk9T9PtjwrWJU8d4TUvULjGUpKCiZoyt\nVSz1jrIqMKSiWHhs6OM+lnQ4eAuJVD5llxKEFo0ymG5yxlmIJWyEZiN2EY2pYVcOfc2jVkN2zoLF\naEPgeGw7h6zMcYo+v+dTCUbSpZvuGGw6Mj0h8AP8RFHEDiUSQ3+kmClCUZDaMaYssDwdRIPR6Bhe\niZ5WGLqBOdkyKE2WtUMlTIzcpcwb+pWBN9DJ24JSOlipxdZ1GGoNeTkAz8ZLdJy4IldjCl0QVdBr\nTKRwMfKGs9fvWI0/8PoWouAcdxcgkxlbz8J5GGKVR/xbpEFySNzTONop+suCg+Was8MByt+SP16y\n/3KJp+sY+0tiuSZ/+oJXq0OUfsV5pqM2z5nmO4zXE44mY9TeAMs/IBwsuXhp4vQbvtVmnB7N6fde\ns3e/x+yFwfrVkE/pBHnkIiZHvJ8LruYlYzMmqfq8UwWBPEafD/isVdjDgMvkFTLS6d0sKYMjjlc9\nxo8XuEXL9mhKoSt6xwafFw9Mr12+bTzOm0fik0MmmwXTOkEbDAkvS667jrra8GZUECxdZv6CjWEz\nn9zT3R8jN9d8fwnOROda/gX7wsY8fw/rCbtO8GrxjOQ8wVzcsR2u0J70mecrxN0BE6fHqbtP01+w\nSE65sFzM//iUv9lj9tHR00OSh7+we/6M6cmGt5M/7pT1pyALrdMIcofGbYiMFlklbCYVdu3R+h5m\n5hALSSl91m6DtjMIa5dWxlhSkLQjfNUx3LbYk5BSdPSWOt02pZhIdolgMGyh6mGPE9ZiDUFC1ywx\nTJ2iLugcgV74kJQMxj52sSZqO3qVAYlHpXR0zaBvpPh6iC8rxHDHpA+aobGxHDQ7Yt2vUL7C2Tps\nezmm62C5LvEopzFsKjb0H0YEscvaBTd10ewdpq1h1C7xriMJW1QqiKY6em4QPxZ0XoNprdCsGlHN\n8e4zSAV251GWgiqraLYGA5nTZB2Ob+L2elSlRy4lbqv/3tT1F1hWn6azSSoNaZrkRULqCgyRIHOb\nnikwI0ljVGRag5auMDY6hTNmNyxQVFR+gbnsceLYfDpcM/v4GRFN+HwkybQeUy3hc1Kzp43IjYKT\nncnlScN0mHI/3+d6E3J+FXDHHFF7lB8/kKlDFlqLlVyzPM3YXzksZj4vJi5ftg6D1WfiRnCS7nHy\n1x7PpxbO/THfq1OkX7MYDbG0Au3FIxsxYhZZTAa/cXrTY3cZ0Hm/BzXJ8T6uMeBwk6FlD6Ql6IXN\nQzJETn8jqU0eD2EeKr6079D0j5iUnDUB7+s5wTYkOUroHWq81Ww+q4BtrbDUlDKc8On2EtnssLoM\napvh+oyiP2b9+Jqnb2/JVo8E4x+5mo1o9lb8+DHlSP+M9XXAtTVFHeWcbza8rwsK/RTsZwjtFZaZ\nsgg3BIbOxjxhFrkcl0e8HDu0+/tMrwbE1l+471LMYYz3+gvN9Y5lVDGVb/8wTv8UDU5Byzro8IWG\njHJ8fcrusWSjOiBC1CP0RYrqt6gCKquldddouqLLAqxmi5ADIm+BG+UMjBbZSULbRM+3BGFHrCSe\nbMmWPuOwJjOHFNsM3TYJVUMcdlhNQmv3SeMYWdVYxhjNSQmslO2mAtOj3VaoDgQ+aVIgiDHUENuN\n2VY99Eyj8BV5UeDu5sh0STey0YqaxKgRjaSUMWlrYq4sjPGGKDUZih1VVdAjpNkZ5FVFuLPZFT16\n45ak2xLkIbqZUM0lzQaktLCzDaU2o/QFurekaCSqkhRLSetsmEiTOCkIRU7ZBqSUuPmCrmcjpE7p\nWqgmQi8UZZVjK428tCg1HTmokI1OUvv45pqeWVDEI1LVUtUbutWM5NeWaaLzIJ9SHvyfqDrkhbZh\nOw1wpneYlwmTsclukeDHIelwn+8mCZndoloHp40RjxruZMSdKjhITbZ07EVrCL/B37xnmUVMnreU\npcs/n++zPnXIgoJo9R17T7ek/pSkX+Dp2e8mu6nG1aPLYrZhbg+5X60QRxOcnxw24y1S36Lpfa7u\nO54exmS5iXGcYV11+EpRug3RWmGZLZ6pCJqQ9dclbX5LP2z5RbgE722ieYVnxPjqnJ34wHY54NSc\nsbZKovSI44uI8F7Q3Jo0f3lLXr/CfWypzgwWuz0m8o4rZWLnNxRXLtv5NWLpIbQYFWacZQ3y/QKk\nRadNKWKXhZ8gzDvG7KOcBZVtMWmnHE1yFsma2bXN0+IJv+1d0n7IePFM0l4p3n2RwPs/hNM/hbIQ\nmkBTO7SliRi5LPUK098BDUPXJx9ucPQaTe0Y1zYyd7DqEWIxZ2uXlJWJ9GrcWOH0bPTKYaWFtF6P\nwnHIyjH9haBhRdezWCUV7rIFv8GuCrZlR7FyEVXDNtrRei7OQKPrDEStkJ2GYvq7SW/bI+0K1C7D\nq3JaH/KqoSpalCrpNRuqssV1SzA2dL6BTDT6hUuvrNEdiyawMQxJGSqSugemQ2wrQkdHH8cY1ppQ\nt8Cv0WRGtU3pZJ/IilBdj6q22PgmppuR4qLUAmMTs2v66OsJRdeii4aJabKtdGpnhBjYKKNAFYrc\nG2LmJn7ho+9idBlidBC6GtmgxbHBcDWMosXLTcaiYteZVFqB7NfUToVu7WHMFuw7GjcDFy28p/eo\ncfrrZ370Dby7lNOvNbe7gFycERslyIYbOyN5o/gsTS7rj4gULC3E6QYYHwVKFAy2BdHNMcbsRxZn\nM+zXHcaJTvB6yMoc8r0ImWaH/MPZKatgRmmZjHcWwdt7ZkZNKnxm7o5ZP+ZWm7P33CcRj2QTHW1i\ncZX1qKIvHNaS29ERbmoyTeYUT2yy02+ozl7iZwd8TR5Y9c7pjvpUM53x6JC++5rB8R7HoxloNxTV\nIWH8E76R0T7NuGq3HDdvOfN+4fbnG/Kg4lP4jtPIIRh+JdIDLj9WnOc2pq/Tvx3Qzk2s85bpPXy7\nvGTRwO1jn7ftA7+cn7OVRwSOgOEYuIB9m2l3zW3rMF7DprCQKuXJXwzO/uOU1V7I+dOnTI/7HK4K\n1LdPuTDCP4zTP4WyqOkYbUPWgyViN8ELExQWuiVJSw10RalpmFHARj1iulNqrSIOTKZ1x6LLESsX\nKzRZFgadmSDDhq7SKZqIvjBJdIsqHNPTd2RFn8zNMVc6BimBpdAdRayP6a8a9LhiqzpMt6RMCjAm\nDOyKR7v6XWksQoSbkJVj/Dim0izqXIAnePQULhuySMfXeyyrHDvoqKuKJi/pGTaxENSqYCRz6lRi\nq5K0EcQ6hM0QYbZsRYKIGnp+iDJS5DJnrQnKJicYwmCl8TBqGVh9zMLmXhqw2SD1CN3oo3ca9yuL\nubOhoSJKM9xQR0ND1B2FZqEbO5J0QLdTDEVLZwgaYVObFcY6odEmBHrNUs8YmwEpHe2jYn8cU35t\nKLIxn3yNo9sp7zZj3p1uKB90frjbktsb2Nc4+jVkWWQ8cU2EFyB8m5VTMn9/w/K0pbBGrN9/IfzO\n5mDTcmOcMtIX2MENHy+/xfVTTl8dEFjPMVKNdrZBTl4Qtvd0es7TzObm3mM38Xl+YND4j6xTiWMO\niW41LjYFOz+hrH2eVI+4q4oPIxvfDPlwukb+6nJ77DFdQf/xLdF+j3y148VoQl2cYO39wvuox3St\nkKcd7hfJsrpCPT5jhUv3vcWtMsnfvua1fU/z8ivX23OyUqLHb9C1mB9MizgbUd9eE1QblPkXfs0y\nXj3s81MX8Y11RnEZcesY1AcaQnTUixG9s4zt15pSfkLaL1D1FvIlY+0pa3dLJ3cM5juie429/gVG\nm1C9fc/kySGO9Z7t1wnpf9/j7K7g08T5/+7C/3/Wn0JZyFZHqzXGuyFeWZJuTIzWQy4rqqrFzAe/\nL1ihI1G0eUujWvx2w8rqGI0D6nEEpseg1QnUGKcc4W5WeNJGWSFZ42PlEEUlab5GJSmembAeK3a2\nRx4JnJ2iGHesVYMauqSp//IQAAAgAElEQVRGhRJTUjOCvKPfhliNRiwMjMYlEFBVv/twWLrDyCwY\n7lxkHTJG0lIxszzqyKQKBOZ4SJYp6nXHqAlJzRLHFSTDkNbyaByXrq0pZI7NAKfTeJAS1ehsRtCN\n+7iuzroWlMLCFRpp+UCtlri0jLwWzTbBkOh5hidLyrJlLQNaJjSpwzhTmFuTumqJhWBc5wino+4K\nktbFW2kYq5hi0GEEkBs7nAziIsErbUorIcbH0nq8aTuKpCL//JFgb8n5LsIf3BF5Z+jZ98Qrn/Ro\njeUPuF4MseyWa+tn2uQTN3+Jed7vUbqCl16AeLvj+kgy718iLuZMBwf89fuGvTOXxD7k4HiA+Y/7\n7L06Q595hJNz7ooeZWmjXkj2CcnXPeKPhxx/iBgWf8eb37IaX5PlI5qhRxJs2T6H+fiUTIP9m5AX\nJxXGtY02NliuztHyDS+rhqKc8HCk0V2N6G1PGOka952LqW05/PgtxXnG4UGJdRnhLU+wTn/h/XCE\nvjvGlB95NXTRJ0fsf2x5m/h0yYatcHCkTir/jVfeF37e+8rh6Ra17PhsrTjybLzEZHA35ps8RhfP\nmXgxycjmq5/y6fYjF+2EN4slj13FE7UPsYOx1zL8WXK70vj6w5TRJMWxv8X9/oBvvCmP4zlHF/+t\nxBdqUAUdldmyMwSuF7PrKmodqDtc0RJoOr5owRtgjxWqKKldyWSxI2o3iLqHSjcsQ4FlPWBsHlga\nI9KVh1XVGCrCKwQ9x0KXHXXjUMsx/eUQLxMUexKjFZixhaIi2JX4iSIINGoRonwDsWmg0XFlwlpP\nyDtIAsjDktq+p2h0pGugGwbbQLDTYto0w7Z0ssil6SJc12LsV5SBicw9ss6my3WaqqBxbCItpUlD\nYq+kI4S8JeoUg4WG/WiwIkYjo5A5ba3olRql49LokjbpSKwe9SojntRYY51OGpjVAo8VIjOo6o7S\niTC7iK6wyXo2g5VJ41kY25Sqy+hqSfdo4eUxKrcoDRvH0lCljuoEQZfy6eiRV3zm5eA7vP1nhNUJ\nZlqQegPK4O/8chJRZwOqaMrs8ldc75EP6MgrFyFe4UQ+P26X1Kv30BfMD2wOVw5cxkyKO5rllroX\nEJw848LuGIxc/kk5zJo+nrPD7SVM+iWLwxl2/JbOMVkaPuv9gH+dnPH34BT9VtH3XtOff8F6bFDt\nEdVGUf+2Zun1WRi3tOsa79lbjLzl8ERHixyS+jWr/RXGLsfeG1F0C5ZZRVoGiN0a4+UHxOeUhWsw\nrRSuIanjPgfaJb+8/4Lvdtx9/RnDECjzgt7rW2p/yNOg4K32hO7Zd2RnJge3HiHfs3U/I6en3I83\naNUKY16g5TmzNuZWPqLcgurDEs01cdIegbXCqgb8uid5nx5y/nHGYv+a04XPX+9yau2co/sZ/9zo\nlMkh3x3uOKv/G1n3Fqr5fQKSFzT1jl3SR5LT7/UZTQR5p2i8AZUfU2kdjb6h8wP0siW3dYzSxqlr\nhGlg1BVKm1KNe4g++Epwj4sxCLlnQ5m4eMJEtzUqLSad6NROhRnV5M6OxllhhiPafg+nb5HoLY5K\nid2E2GsRtoUzyOjTw+jDQNewsw4zG+FgsdJTui5HVBY95bKkovEiqA3yuEdaFCwcF7FKaLsaKkGt\nFVhuD7EsCXQTzVoyWpRsHYllCsIc0rGOCgpEOCPsFP7AhlijDR3ctqHUOjpHx2dJMKkJM5MqXSEb\nl8Iasgsd3LFESoO6DIhDF8teUakdxWhFvbIQuqBtFY49ZNZvSJw++sDFoUCIijrfYfdb8thg/66P\naHXivKWw3xLXb9gUx+yVCfPHV/j1isl+wVqPqPyWQXtM8u4dpuGi7z0yjeY8jV7yctcQPfb41RCk\nsw2Tc5Ot6qO7Oav7BYftI9H8kN3NA5+bknbaY3YHi/SAuic5vfo7TjVnGfoU5o841ymT7hF7aRBq\nLk18T61JzvX3XMePjGPF8Kgmu/uVNvL42k4IHl6yjdYYuiRvD7GSiP13A5wrDW3loM0k894pB7sN\nqwuN+k2PRtmodyUPwZD15jNdl7HNImZTk3X+DXF6SLcp+Ty75FGFLFJIZxccPf3M88/v+BhbWI1B\nvLokUz7m9hFnqWP1HYr7JeL5Dq2KEfSQD6eMj8boSY908K+0DMmmS55VKw6O31L88DOL+oIP7MA4\nYLzNEM5X3p0dcrCX0n+cEJ/+caesPwVZtMog10p0p8+gZ4EeU5fQ6jGrpYO0K6p6RyMm9ESMnvTR\nohRfgzSHWkFdWDy2vz9opa+RxPSLFN1pmZkragS+5oG5IPVMGt1F13o0bUvnhQRFD80SmJrC6mLK\ntcVCbdCFRMtKtI1kIixMDTRtTqxXZNGGLmooei6ejNCqjiENVtLQdBF1VyJVH9nZ6PqanrGlrRt6\nqqTVPFptyM5p6RkSZQqUYZIqD4MOOXTQdgLFlsZpqKixbANZ7eiKAVkW0/d9tJ0PyqQvF+BXPEQ9\n2kXHuhQ4mqQamIhMYTYm8WrB1oHW6xB5QbOVKNsj2xmImYbeN+lCSRvmPKgpmt4hHwoq00FTNkI4\nBFWHW+bo/R2/aFPqoiVvhyynRyxGSzbxlLeDJfXllLefhnw3MHm3CdFVhfnqgrjbIT/qyMFHVskb\n1uUp6TON1+tDFqZJUntYX2KWewPOpwMMS6LpJZP+Mf1Rn7yu+Nj2mU5/JFrWVEGfbFxyUt/RTU6Z\nnHW03j2yuWMVFjxOEraXF3x5ouMYLneWS55s8Y4kzcURZ/2OVNPZd01SU8Mf/0Z7HGJ8V+GfmRT+\nip3yuD0U3CkDrTti+2THqneHfthD5j8iLnKe6jb+wx55a2DmMeO5wenBAyLzefVrQnCcc/dGcS8d\nCnnCPO9xq8csYsEkCNg3xxwYG6ZpxqEzpJL7JOmOb6wTxN49dx+vcU73Wa9NOJZ8O7qlu+0Tfu1x\n/+MrLsY5TwYp63HItAeWliFUjjkbMz14xbPRP/9hnP4pyELpCuXodCrCzEp8R2G4JXIt6IUtjllT\nGTZkDVoCtRmRDySdquk7Lp00aRuLAUPMuMVZhFBo6J0iDTMeVIC/TWmcGkvXcRyHftGSpgVepWFs\nYwzR0TQ9VObQxSGClllss8221OMBNJBiY60ztg8Kr+ioQh1l5wRlACONpJaUlcnK96gyHycQOHsr\nRNNhaRbr2mYYDDGkjhQpfqbQdJNtWRGgISXYBpSuJGk0BtYSURiUmo8tA6LHCG+dYYwMAnvIgwnr\ncM3a1oi2Ok00RAobObWYtDVZPcLstoRhC7kk60Oz8zETSR8Hze4TpltGTkOw2lI+ttBKiqpCqB27\nRYVmZXSioG1NMq+kykbEwiVtp3iTnLuqYiQaaiKMJmde3RB8aekdJvSep7T+khff9UnaL8j3BRPH\npV8FfG0Eycvn9FyDMLPI8huebj2u8hPKWcL87yHvfispP805rA02lovZwIsbhdPfoP/aZzbb52sa\nkmaSTJ8z+7IlzZdsh6c8qQuMK4dxdcHu21uKRqEbe/ibA8R2SNlITjNJMwqJrWse6wmfPn9E5SbW\n5RWruwi9/cSn3GL/UbL8l3sO+hsyQ7IwayYdROsd5p5BsP6O5bAmsEx644J7z8NPI1a/TpnLlvRE\nsJYTRk861Ptb7o4cHq2E2RONi4sQMkU53fFlWZPKc+qJwYfYp6cd0929hdLjxd86Dr23jC5O6C1z\n3t+63PgV/3o+JvzmCvHwyK1mYf/2njKuKKTJsbBg2/FomDwMoj+M0z8FWSBa/MpEyJzKG+Ekkkbr\nETWKdNfQ7EzqfEfdN0gmIEzJLM3JCpNSuqgkZjeNaJWGZ1WoMEMWLmghxn2NnRps+oK6LpCGhVes\n2DUaQ6GIZUmhVeyClEZPkJ2O6Xd0ZkHdGkxzGz3PEL5CuhXJSFGLFamuCCpIOwdNVaitoBzBLtEw\nNhZzOorHAVU0wOhMClsyUjpJU7NcBZTDiqKJEHVLWxXcJ/eYWo4T5XSNhagyNroGRkCYSlSboTGh\nCAbIbsVjmmGZkv6mh7eS7FkjxKDBGSl264ZOeniOQM8a4mVKYETM4xm+vqLSUpLcw99prCqbrROS\nCsA2qUNBX7potcNMtMTGkIFqWS9LNFHRuRHWUMP0GjqhcfzkEr2tmW5NBuU59/4BkRkxi4b0djE/\n18fIrx6L9ITzE4H1mPPOfs+rZZ9X249cux/YBTXuscO29pn6/0I9ekZuOzT6lvb5FjFp2VutsbyK\neNBwPPA4HI9o0s+YI8F45BJtU259yTjtePIvGb84r7gdaFxd/4L4qcdoc4jUb/n6rEW9cug1Ax6C\nN3Q/fSDd/R7gdD7qEJ7PauLi7aXc2HCaf6RXJbh9n89awrSL+TapuUwm2OmUYVMg4h9Zxx0/FwPu\n3zao+orfrJJ7ecDGfkDTv+G7YkXkrXFeTFFZi7vq096dc/3Q5763pn81RE6f4ZoO1q83+COXW7Pi\nJnjJ4bVJ8rNOEelcfW7otTX78gkn2W9890YnSFd8FDbHUY4zPuKz1pAcdawqn8OzEfP6mvFu+odh\n+qcgC9UJVGYxKkKM3ZJV2KNqDRxPZxRsaJRgqEOwuYeFjkdD6nUIYdN2BdMx6A8KZS1R9RC/sEl6\nNjJWpOMQpRIGek2/saiExX0yITRWVL6OKhMm2pC68hiKmqRW1OYKv9VZaRrJOMbVPQpc4o2J3uR0\nsk+bB0SNjSNqGrFFmkOoBLO+TSU7cqsj+H+5e5Nf25bs3OsXs67XXOVeuzi7OvU599y8WTynbVng\n55ZBIPgLkOggJNoI0aRBG4kOEh0Qf8Jr0ABE51nPaWd5q1PtU+561WvW9Zw07rFIpPRLpy9IKT4p\npKkRMWNEZ3yKiBERn9HhVhmKlNGGEpJUI9Uypp2irQcoRoWWyiBcfNXF6DTiAfhJQlk1NMUAqYBU\nT6hSA93MkOWA7VrF1hLqJqbZaWAYkbHBWssY24qRJ7OlJo8ChO8wtDrK7ZBNGdFYQxQN2l5GoVY4\nqoQVqvT6LlaV0C1KOilAFi1rpyZTZGa5hTUSyNEYO9QpwpJtsSKxI96m9+lKEy8YEq0qmolBIT3g\nuh8zv1XZaWJeHMjsTFa8vbZJ98cMXZliOKWLFO6s94nrOVdixdJ0keyfMJBfsTRtDp64JMsBYn+M\nfXTC3eMn3H86YZVJXCRj9M2QexMdzm+p7Eus8ZBzX+bKnzAuv8aRVUb3nnD8ucTY7GPUIXtXChdK\nS5ZEDJKHyOoIWam5tvpEzgG9jykDx0L8ZkDUlET6MwrzEudoSds2vBMSt6KlN2kx93Wq2KSSn+Gv\noXlwxel9mQN3nx/GcDdL8GuDD+ffkhDSXCdMNwHS1YIofs9yZNNaDbWv8CKKWRQrnocbltylfCFQ\nnYh+16Epa6paIRvaVA994mYP9+Zrbnr3uX5a81rfIbd7LPr7XNgOVr7D6F3Dg4VHNZOYDB4y0f9x\nJY5/Kn4vWQghDCHE3wshvhRCfCuE+G8+2f9nIcR7IcRvPpUvPtmFEOK/F0K8EUJ8JYT40e/zIbcg\nqS3CadmaQ9QwoA1KwrZisbGwNUGqaNTSlKbTqW5dqnhCLBs0WcOmkLFGJVYBK39GVuWYYcacBeYm\nRs8hXXvkekW8FvRYsjJkEqGg9vpkNJRtSL3UMPUWKZHZsmVYBtjrjiSTcBSF4aBCW9uYgxJPifC6\nLZbikgvBQk1QgxVVmzJuK+Qsp9Y60oFOKwlGw5hlP0FWF3hZSWcssQsXlC1yFlPEJWuzpCkgTD0c\nU6dX13RKQScXFA3YwqQOXLqBSV32sAqBmId0cU2e2qyrkoUVkeQNE1unUz3yLCVuNcJ+RWe6mOkS\nvWgwSoHm5ZRNRlHP2FYltWUwVFMWjUGZywwbGS3bYjQK1SImYknSNUh9H7tTMNUh9khBMCQ9bUim\nW6pQRX38nImc0586VAuDcazQM3a5u6dwrXxgh1PUqoLdgqBc4HzcJ76eMC2/4fqNjPPuGT9hhndn\nxNHDXf66P8A/MDkZusTehCP1gAOvxd2VSFbv8JWI+8khu+c1B9aY/XqB6jzhZOOweBEQXFms69dM\n7roo4ppsPePhrQPvv+ajXcAQei9uWVYpVf+IN9cu7eOY+9cnSM4rLFlDeqvwoDXYmbX4qcJulRBe\nFUT6Y1LnG/Z8ncdLmdXKIp3XfCnd4dbXOV9IGIVAX++SHY55PTgmP3CRxhbZmzck7QcOvi04tVVa\nzWdPLZE8g+LeO64/7BH3WuJBg/n5lJvzJZ9Xz/m4jtg+9imXJuH5Wx6FM46X78iFYP+8JXQdosql\n7rZ81GpCveJiZ+//e7IACuCvuq77AfAF8NdCiD/9VPdfdl33xafym0+2fw+4/6n8Z8D/8PscdEKi\nqjVWdcegyLGGBeO2w3M7nIFDXEgYGwWtWVF5Juooo/EXGGaHIWdolSBLbRLJQ0pMlK4mMCx0zyOR\neygDC2u4piwN1GGFavUZ5g7DBjrWKJHORBnQ7WhknUct+di6SjOYUONQ9zaINmV1u0UMG9xlSzCw\nyLwxQbakpzX0sxjTblE7mcaSkIYThJKRygFZ2dBuVdRuQKX0WBsVuSG4NTs0TaVxWyzTRSo1GgfU\nXoyStQh/TSNDtbHQ9I7Oyag8HbnKUQuFPO+QxQAttfC7LVqnom0FliWz6BocPaesDHy9Q1NDkNfE\nbQ9b12kMjaDIUUsFte3jBy2x1FKVFl6loPZK8kxQlTWKv0XedemJEeYkI0synG3DURZQVV/zztOo\nzl8zCRUOkhvkbx5DY6Ber+mlfW6cmnnekcpLdjenSNELlu1LvpEsglLGPFzi2wrDfsfhFHrOmG7Y\n44fDRxyenOD5Cob5I95c+dj6FFVPKE/esaoL3q4SrpwHvFYu0advyOcrbvdNbOkNGS33TzLm0YqF\nLLgKTrhtNe72E762VfTDAVVcMz3rcO7eY/DOYSu95/HJOdfpltemRXF7n6UsY9XHfNBCFuIjH4wD\nllrE5PNLMH/BtGr58tLmxSbGNY84NBIkWaHs1rTGEb0pXCpveJhdcPL+A5pfMTE8Du8UjHsnvCwn\nmEc5w/SCj1JOHrxiut3Bt58zeVugfLgPocTIP2F285jP7hlsrmz2elc86e5Qlz6qeMBObVA9nnHg\nrWiPHUJRoWcFinzLva++/yLi957g/PSM/z+8mqF+Kv+2y/H/EfC/fPrvZ0IIXwix23XdzT/qQ4bO\nqukXgtDrKLcjZHmFNRO0lGTWCNPNaeoBIg6oLQ+lqejUGfHAQ1nYDLQ561zHdjLaVsPWQjqpQEEn\nWHuYMvh2CtGYqAwoxjm9uY6fWbTTmOUavE2KVqnEso9RCOymRRnBqlSx9BZzMECKVmz7MNqmrEqD\nnqYRrzts02bTJdSdjaxskEWNvWnRlSFOrdB6S5zbkNCRIR9iBVvknk5Fh6YVNCLA7gaUq4BGg7kB\nY2OAWq+oewI3NdhkGqaU0LQVoVMwEDW1mtGuS8LxkEnQMrNdsk2NKuus9S3yd+/k0eYedlUh2QmV\nZqJVLYVqUAsVTaTcDlXMECTJYavM0KodlG7JEJU67oMaYwwLVnMfd6iwXB8gVR7N+jVP1l/yq1yj\nm7wl7kqEphG8zrixDfxRhxoo1OucC6nD3y7ZHAxIlTHHxRXt/T5t16O8CojH97m7U9GfjAkzizsP\nfsKx5iGJXcb3dLLZFuXG5ZwRrxdvqN4GPEDmcnjBoNhFvFeoXBtTvKeNBlh3dV5lN8j+gB255TJ/\nzw+PdeLnJsMHG5RXO4xdD2cyQw9eohw1TOYyysUWcSogKYiac+TjDbfzFO1tw53mM+aDb4nMezQf\nVwRpxfJhy+i2IpikJFcr3h653DsoKNqI1bpBU+9hOyHZG4sPrczw9Vs2FUg7x9SyjD2MKd/WDL0T\n9KVCb3DFTS0x2ZsgmrfExRHqNsfdXIMqcRk8Yu8kp/xapz5QWZQnrIzX2KsTdtIDAjdhJzApHwmE\ncsHlu0PMw/M/gBZ+N/5JdCOEkIUQvwHmwP/edd3ffar6bz8tNf67T+rp8FvyhZ/w29KGv7v/uqW2\nKjJZxq1iLHlFpU3IJiqZ1WesFCSShWhv2REZpVIjShm1smjnJoJbKk/BKwuUyiEVDnokY0kqRtWh\nyylOX6MpDFZySatY9NcmspWztQWr24xhVdBaKkqrIooSzysRfkO5KhkVMtmqQOQr5hZUW4eoshCO\nB6aFi8paL+i1DZKyxs/7iK3JZjxGddbEvRBRWMgGkMjYZkq80yNVV9htg9I5ZFmDqc8YtDqYCqYh\nWGc57VZmqIwIqoam3yGpFp7us9OVFKqBgYMixgykDZuyQEQVrZJglTVeVKKXQyKjR9ttSMYuWdSD\nUkWpJeRVRj0yqFqJaaajtSqN1uI0NpUVkKoSndSnajL0MqMRGv5AZy51KHVDKgR71QHf+Hf4/E7K\nxpIZrXUe7YQIa81dZYzqNDxJN8z675EIGVYym/dTzNUZs8092k0Ar1OKH7S04wHZxmLq1fzFn/9L\n7jUdY+eHyJ8/xpyVNJM5dv4c+eZr4o89tN1zYm/N8pVP6Quu753xYfCc2jxkrfic3+ioxmfs1DmW\nq3NXjXiXeWR3jygkh+Dhe3LnI+cFRJ0geV/T5Xe56Qt2b30e1zG53WN/9QX3PnfxrM+x2zccR30m\nRg+tq1HuVgw3Ku1nNWQO/r6N3F/SXV1wcd1jZDm8D2vaVGJ5GHBknjNO7qEe7XBXe0+TnVO7NZeD\njtX1BvWooZ7WRNtrlC9z3lT7rMclN4VJvGuhPunjViuSsyNixjTukm37Eq3cYUe+Jay/YeCodDzn\n+vqK6GVDfZqhVXf+MGb4HfhnyRcKIT4D/mu+kzH8F8AA+K/+EMe/LV+4Wq1INyGlXVGUE/JkiK21\nFJmB59UUFfSyOUXSYyFbkMZ4PQ0tc7G1lEIeoqxtSmJKzaFXBSRVwSoEIRuknkqEi5QrGHVK0eUU\nukWsSnSdia46FLpL3qhsjBqzF9CWElLRwcCgdhW8Xo3jWagbh75V03MtOmuOTERq2/TWFZt8gF8J\nRBnT7xWM4xRN7VCjHpFbEVodTd+kiCT6UU5vq5FXBYbcgSbIMVmpLepKQ4gav7LBcVhLJYNBQS9Q\nKNQ1bbUiqTvKTc5CxMhqRjTX6YYVTp2RFB1rb0k+cdCqjEqNMEoTe17STmLSokIRAU5/gL8JsD2T\n265E7hQMI6AwO7wOPBOS0RItFbRqj25dIi1ifCHj2BlVtqRrVtTiVyzeO7ivRpx9pvF12TBybJqD\nOcVlR7jIOW1U6iDh1WFHor4n7ikI/RcsdgXN4Za7VzVPZ2t+9FcP+fzPf4r8zGLx4x4HX1TsXs7Q\nrI7sZxHPlwUf4zPm8zN+/fKar8oM87ji4hcvSTdT7q5ketWSlb/l4PA9RXLBZVJxmUYE5inTdkWH\nQvxiwCSwWK52yeua20GMfn/K1701i3qfcqrz/B48lFOyhcK72yl6/Jqrnk4mOqQ4RA2O2Xs3ZVJJ\nBI2HGFrEixT9g86b3ZQntoyUVvhyTE2fUQh1ZhOP3tOlFVcXh3jzOa3YJZxVpPdSEvc1uaxwr7fP\n1a7BZLdkmHY8Sip0p0+9mNBv1/R2rsmf1ZhaDy0omOz0SKYmo6cSLC9ITp7QjCeoB8dQvGMQfL8b\np/AHZkO6rtvynRLZX3ddd9N9hwL4n/hOAxX+b/nCf8BvSxv+dl//Y9d1P+m67ifDwYCRrtHkHW27\nQXZVtFAgMo3iNkNqNFTRYSgheilhuTYNMXUb4RgOwo7Jhylda6M2S5Zuj0YaoXgecZmjNDFdPmcz\niah7JoYlUccrRKnS0xYopo1cVxiKhKzr2MUOqSyIggRiE7mLKTYQJwWdWlDrGqE8ZxANKTsJWNNN\nZWQRo8oKWykjCnWyrCSqx5RuhEWOk1colFQ7kFGRjzskJ6UOJfrGCBE3DMyGaAhVAkoWYQQN9qIg\nXxdUBIi6Rrg+GA2aLuFXMomXYOglXt6nMQdoioUnT0kyg3Um0eYNia2jdQJnUaD5EonikecFkWlT\ntRVaJQiajrzqYYQqcVeQag5ebSD7EYHcspYlGqlCy2qudky8iYGfZRwFJtkji54Xc+/ykHsfG9b9\nEevnW/ZFQjwcUC+nTJRnDOshzYMHaO0jklCiig8xnTEHd0/Jjv4SY39I0esz1e/zaH2XZdan3n/H\n4nbOjXLGVXzBIoKzi3esvozgFzH6r97h76UojUG4+zmRsDE+jticD0AvmXKP3vsTgg86L+cW0se3\nHJkSr7uWe4nMyHPYTY5Y0WNYjHm2I6jtECm6RLYTxHHAE++KeXbKfD6ioiB9kRPpKz42KYnIefQm\n4eDbEM1r0MdbRCJzu5yhlT3Ww4JIfcXteEWnlvjlKVJcobghY3eApb1HaywsNuTfunjSLvnut+yt\nx0gfJ3jzIb/WHJI4QYo+cH5yhxupj3q9piky6Ea0yQorGXF+dsIHr4dx9p6H5ynGhwxbOiKzv7c8\n8T8pGzIWQvifvv9BvvClEGL3k00A/zHwzadf/hXwn3zKivwpEPzb9iu+G4XCrCrpmRa56MBa0Vkp\npt9SKSqFtUBmhCm75LZKG+XkG53QrqmZoScdyaYj9nO6RMavJWojQO4q+j2ZLhjibcHEo4lT/KDD\nUxQaXadKJrjNErVvUkYyttkwY04d9VDHHXWeUUUukj8hbvtYnQ+RwE4mNHlJ1PZoTZPtvKayBI2S\nMXA1hCbQ5Bo5nmNpJWo4oshsPLlFijLqQqLZqjRbga5mxOGCxIG69bAkG1suiUcq+lCi6ZuoRoOe\nG1Sdy4YNRm5T2hZbrcPcDDAUk9yosc2ITlcpkzVDY0mthjjmmGEOhfhuTV9stuSZoGhymjYmSkxs\nWeBbW2Q7IpLBbQZkKKy2BlEwZKikKEqMphp0C41mHvAhvyJpT7mdTIi/kVk6UEgz0tEd9HnJUPHo\n1gnlZMuGFSozcrj/gugAACAASURBVKXk0eY1an3BD+7e4YeLBbulQnl4wsETeGQf85eP9jmY+OwY\nNv7lNa/+D5m/v/glZ68XPH/zS37+5pap/o67bUr3VEZ/1DJZW/TFmOngNfs7LveMF2itSdvdoXUi\nJO8d4iBkfF/H8WwK6wOKcpet0pG+uALPoduYGDsly6IP1QFj5SFBoHLWXHL5rU7tpvg/nmFKD5nd\nsxk9snn4ucLCe8xsmPLG2GG1M+e26aNcZcSDKefGllOGBJoP3QPWdUU3XuGbFtu9A+L1AF2ekvcG\nVJbPROnx+uWK/PUx7x5f01Tf8s3ue+xH71kUe5wdF4gPFVa7QFp5zJNbyvtT1L015Z0Wf/ISZemz\navt8OTTwH1bsKTNkt/jns8QnfB/5wv/zkw6qAH4D/Oef2v+vwL8PvAFS4D/9fQ46ucWoxwSbBc7I\nJM9K1krNuKhIGo9OalkBWmFjWUtSyyNZb7Eai6YwEDKYUoLoDLZWhRVuMVyHoopxVBPLCbmpXZyt\njlTItE5CKbdUlYks1cSpj1MrqJ5CME9xjQ5bX7FIHCZ+Rlv5NG2M46UkpYKaQatLpHWNqFNiYTMa\nZjSrFqHqhHGNTkZtGxhJQ5HVRPKKwaRjuzKQPYPUijBViagxiGKXsV8hzwsqNadVBJKQkJY6ubwi\nHXXIjUuqVJixjBqP2RLTq6EWBk1XsUJmXIdEhUBpFTrfIJnJeD2VYpui9xPCSuCWEpUrcAsZo/QI\nKgPqHKyGuLWxkxphGZT1DHluYE8suqXKRnh0Uk1SgbZfsfdhRBsU5Hffsf+vSi6na5pExlBc3uS3\naJnGydMZdfGUVJtjiymK23J/o3CjpGwrjRN5Q7y7Q95vOBrn7K72iP/SZ3sbMXoms20PeDeouHpV\nMioUfnbzlvFXMkZxQzlyuTp8Qr/qEM0RQkvZ212wqE7J3nRsdx/yTJ3RaTuU5TWjUqLzFZyw4ULb\nY7B6jbTJWJ28pVX34OYc2dZZXHS4DEgPKx5eX/PW3uP4tYq3V+LIH7i+GPJx9YEvHuxwnV2xL3dY\noY05EBh+j5WiIL8dojsuXBS0tsT1VUAxACO94ujhKcvVBbpU8OhqwOxYJ1i/5lEteL7x2OMc1XnI\nYPeKyfUOzchnJtkosxm9JkEUOvKOw0q7orlvMLz+jOH6ErX10E6v+XghYd1/RREO+VE/5N17g3Aq\nYZfv/hn08P/EPyUb8hXww99h/6t/pH0H/Bd/0CBage5vaIRPW1Zo5Rjb6dgGOfowpkl1KmWD59ts\nViN8ucTWhyjymkhXkUoZpW2xZIe0XSFpCk4j0dNlWBbErUzf1kEENI7JSipxOo+x2hBqFX006rIi\nXwVoUxur6pjFOpIeUhYylQiohYJTjrCFzNyZIbUKTS9mKqusspBVOML2t2TCROsXFGVDlXWYI49u\nKzCaFaVlomkSUdDhSWMkAhxFI2xWVEuDVEup+iq7CaxiCX+wIVI8tPmGVpVQ+yZmkZBYLaQFG9lF\nriVUETPSbJaqjlKUdE6FsS5Bc1CjDrWLERsPX03ZUKG1HqUyQ7F9VDr0eUSuKYhSZ2taqLM1pt1D\nJmabx+jegEGxoW1HxI1gmS3RpztsdresX7wnnw6p/nZKup7x7lZHmjacjBTef7NHvpcwfiWRm2eU\n/ikvjEtqYTCu9ji359yzxkx3ZHaHLk/NMT9sf0z7uYpz0RGrEubfveb9xxD55d8iXvX4eXaBO06w\n3Cd4qsZO7y7OUOXpsz+hyxQcxSapPzJ2oSxbus0ZN/0d9JcQ9d/RX6hsw2uCHZdD44b92xGRvqFN\nd9luIu7uNNg3OR8vR1RWg1m1NOoV2v5dcr7gx/J71vqEm/6Sw3cPSQ7OaIYr/EKm3W9Ybl0O3DVO\nf4dk2FLehijH+9izhPDQpA0qNqsNw2bIb8pzeqLHXdvlxSjgi7c166dTxIsXLPcFI2nETQCP7ie8\nrT28skAPNRK/ICmf0buQqMpv2J7eITZ0DtSXFN7nHClfcm7dMlvdZ2olVOsJ+lT9Q0Lyd8fp9+7h\n/wU01HSyjFltSZU+Up2TCwPX0GiVBNPIqNQeUZFgGxJxrSAkgWUoKKJFyV00RaORatA0lLajUGsk\nWiJNQ2gtKrDN+/RJCYVC6Jj0RUYfk7W0wbArCk3CKwu2omSAhmLozJcZI1cmTEpMw6GUF5jhGL2K\nqW2Z2zZhqPpkUwk10sjkGEe3SDIFq42Jb2WEWmB4JmQelrYm1H3qck2aDHCGEaPIIrFi1ExBLwDV\npK9obLYxAzNj2TqossDsYuK6oskL1NrGcSNoCpbZEDPdIlwf1zGp65ZctPSalthv6XLIHQszBb90\nqPWGMhixyWK0pkNWG4xtR2hWOAsDtd/QpQm53OJIfUgLolLFGlc0Royk6sRvSh52R8ySM7zsFRoK\ne0mf9ItL/HdDvk7nDCYjjp23qAcyl+sfsMrPsepjJqMZ2lmNu+NjTlTS4T0k419QPnCYPKmQYsGH\niUrw6u+5NjLaD1dcDGquonckD/oMgg55kNLPDvjpn6jsG4eoss2hMwX3A99YOrdnNsHNNYY/4dHC\n5Gawwawe8koxOP1iwfJ8RRl1SPdj3MVTop0bjjIdSzS8PJhxus44P/CRXqxwvI5FpLObvGeZGDTy\na65+/pSqDugSlcru8612Tv/DiDv6nLSbEkQ3pNsI5bMD5PKMrXTKaJFTig3j8X1Ks+RoWyOtaz5e\nT2mVATcnIdaHlGJ6SvdeIRYLsumQ5IXgyU5MKhqs2wonMTg8/IZ5+5DyWGbnYsO10XI+fcSO1lFX\np0jyFamp4hbXjHOZ29Xp947TP4rj3lKrUK4Nusym6UAtM+R1QWvUFLWHUsj0SnA1SPWYgQx2JgiD\nHnVTUxsBlatRSDV6Z5BVMlYDtdIy9G20oCDRF1huxNZq0Gofo2zYRhp12+CbPXLZQ6pbEgHu+rvH\ngMOViqdUSKaEXrRUUUNRq9R6SGAVtK2BUg0JpQQlXhDIFqOiT7cQ+H6JWsOwl9P5DU7oUYg5Xa7C\nRsKuO1y3QS981nZBodvUrkRGRR0LVqqgMR1KpUUWNVkVEDQKuaHRNR5GWxJtHTLGDHst5H3acE4Q\nVlhdhC8NaN0OEcV0eR9TlLhyTKOHJAUMRIni1Yi+ILMMKoZIsU0k2dSxz7J0kAxBtZaIigj6PqQg\nty69LuLursyZ85JK36OSavwm40U5YPPOoSfd8GCww+D6guL1EzrFJRl8JE9qjI8vSAuL8tE1+/sT\nDvWOZ67CD6c5f/HjCReqRWlDf3vGdRxy+bd/w2b4C9Jvf4V0OODO7Tuc3T7P1Gf8Bw//jHH2l9z9\n03+HyfAO3s4uQW9Co+8zWV3h9T0mzi1n5TV97xrHrDjaztkIn4PGYBxOmQeCVVtjazFFonHZTzhS\n9rHv7eCJCOthQrwHN2++5l9bgmKw4OvrI6RRyfpOwqZe0t52tAufrPyaWSEoRwXSzTn7mYP28xds\n5gFjZctV1fBRPaTSFHpqD2mgoFUN0cOSds+ml8e0acCdecnQhyOr4eGHFkUvEcOMy35K6diox895\nNxvSc5fsLToUY4mqHKMnZ+TpFYVmYzSPkeuA9ewOl7sjnm6t7x2nfxwzC1HjmAV5XaI3CbqqItcV\nyVrHnORkro2GyrYzmWwqcmdJpsmYkoo+t6icmHJdENUtumfhdiXIHemtjtmb0ag2xlon7m/wqz74\nHSIvoJcSVA5CGHSFimIN0KuA3MtAEui9DKmxyOY1kjSgklY4CCKpj1o3SEaJ1CmITYMYmbibjoW6\nwiw8zNxGkmWkWEHr5xRNTq8ZsLZCVKkkrzoUp2NebPEXLbquUHgKcggrLaJXO6RpRWObOP2MeCMQ\nywzNsTGlkFYXaFpDIq3IW4N2IKHnGrW7pZx7SJOCTdMwtl2WqY5R50RCB11mGGXEvT7DImemxOiK\nTWVE5J3KsJqzkcaMWROagP3dBrGrRSRaQX5r0DUCz6+5P7OgSjn/GHG9O6C//jVdndH5Mll7w8Cx\n6fbnpG1Od3uCKy7Z9UwSU2WXRwy7nFT9CXd+dMTk6Ygrbxd3Jti8zJinEa++fMWHNxqduGR5PiDt\nSaD26Y+f4B86OActB09DdpMaBgd8dRuhTyXS5Ude7Vzj/HzG830TRZ/y5bcFP+2ZbA88lPMrNvsJ\nac9huP0BTfSSN/sKrjzgJDV46dZkly8x6NhsBOvhiNPTBekmQV4c8SP3jFdKj2PniDRW2GsyZtYh\nt3ZFNbFwzlfkjzTUKx8RetytfsPXyhkTfY/GO2N11ieyLFpZxhnvoLst4/UMzVKop1OW20uM5R0y\nU6f8XGa4LlhvXXrahlru0eUlpeqh5xeUY4gbjWn6Ff5Nn6+6KXX8nr2y5sx0+axsKOKExbj63nH6\nR0EWcgehLuNaDtW8IrUcnEZG6adUkYPkdsTtDLVyieSSOOvjeyGa1lHYKani0hkN/bAliJZkTkMW\njzEcwQKBo5VkjUqXDinKEE0dorcF6sqjaEKE2yBoEFuTvOqhyQWlb6MvE4qehjlJSecN3cimjHX8\nuGBmR0jxGN0Q6JJB3rkYbUwvHpFLGaoeUjcdS0PgVdCoOpkboheCJi/QTZVtndIPGnJ1gKZVpGWE\n7g6RNxWNGtKzhhRWjSj6SPKS2lQxrJy8kzHKmqaQ0TyVslIZNgGSOSSvSppBgrzwEIOCmyZBawMS\nIXBil64xUSdrmnbBrTlEI8MNFKo8x92R2dQ2/W0I+ggRSyhNimk1VEkOnY6ruuSdRWxn5FLJ68sN\nyanL9OUV0m7F7bWPcj5D8UZcHmVsrhV2ChuruCEZ9rmydrmjZjSezuXE4NFnBlP3M+5WBcO5xStP\n5sX6NS/TFe+44EN1we0rn11T5tGRybz8jNFnO3z2TKWsTtl/6rM8a9gpz6mPAy5+LqG9vUD7Tc4v\n85jD2CAsX3LHkbhJ5/R3I26vDqEZ4hoLqqnAzvc5ykvaQcM3a5XmPCe9J0i1PsvrKeb6in44pfx8\nQVf3SZ4esxeFLOYLjseg3NtlHF+hBg+YDC7J5M/QzmW6R1/x+sUxSvyEOw2UKjRxy6SfYocZF9ou\nh5MliRizPNnHk0ouw+dwe4/+gcRoYHLzRuVmcMbOhcl2xyfdFqDZHEQa32oy5azAGzylcGLMbcbQ\n6tj3R7x4s+VHqcHXxxvuOWM+iNX3jtM/imWIQKLXOGy3EvXEphZrMiNEyjMcvSBcr0hbhU6OMRWF\nqRwgaTrlTGJb2Hi1CduGXPcYKRa2cBj1M9q0Zic2MW0Fv0uQnZxO7dNtZuAYhMMS02vQEx1JbpFU\njXq8AUfH3pSUfk4VdKyEjmmskLcStbIgFwrTzMGxGqoyZeUXFHlBJko245ROasgXCollMmlT9M5G\nUwT1JqMODXLXRakatMyl9UY4LnRJQGuM6IKMoaqT1n2koiUuFFQrxFds7ERHKTqc0qLLbBISnNTE\nQidqxqSbgDiRMMWQwIiQCw2zAeE7SEgYQ4lkvOS2kElbl94io8kl5lpFZCvEswJ5KdO0NqWS45kS\nrmqyjhLyeISa1cTKmr5V0XY5heFxXC/o1yeE/oLuRqUfXTMfP0YyNQ60hOmhx0jpoe1N8V0DL465\nEWMmoz6PnBGP5VPCOx9x0vuUscv81zPMQ5XySmFaBQQ3t0hWju08p1IU7jxN+OnVLWR9TGvA6qPH\nqJlwcbLDne0E2XzHm48NXyVXxNklf/t+Q1TMOSsSUvctXy839E9C7vWvGK9OGVzeYJ72+BhLfDhf\ngvkcf3fOanVEXfXZ0zsed6DurymrHZT75+Tf9Bhtf4B38pBbT0ZRfD7e3MfarWmDmo2vYexrdOoD\nRs9qNs/W+IcN6qlB008oo47Zrk05MbgNffavb5jGLZfrDVN9ws5xTGOGhG9lCrlkUg+YGjZycYXx\nxQdiPWXRvaRlwkNNprmGmGuSVsb3XvK+2FBMdG7iS6SrmOLbhO/yDt8PfxQzi1bumAcLep1Ktpbp\nNbA2XFJTMCgzrIGGu9JodYPK6YiyHKWAsovpGom2yBnoOoFSEysJZdih5AqN1NHoCl1okZUtFQK5\nk1CNlmjbIVsNXa4giw11ptJUFX6lUBsKdZeQBC7jgUawjrHaAbFQcMoJQl9Rqw7lVkJVa0xpiBIu\nSNUJ/TQjEynRYIKahLTozClQnZBqPmJoKljSjHKgIichieFS3yp0PVCbDoeOUC8wq5KVrSBpIbdb\nHanOkAwXp3EJoyWe76E3HtQxetKhmhmh3DFuE5pARh9KSIVOI4GhxKxyDTnQ6NyGKTq5ElBpQ8ZR\nw8wK6Is+7Y5GG0KVBeh6QzJPyAwH3XQRRYpMD8VVmBUdkpBwtxcg3edr++/RuppEUvDuT1i+Nsgn\nr5CuHqJlCdvempmf83BxgnI84yQZMO2PGYnHNKbEn2Wfc/XsGmPuMC0zvv3wJfXVius4pfFq/AuN\nK/en/If3jgimFtYPfkL/dJ8eh+weNtTXJa/jS0Y/+zf8+sNLflkuWdvvWQUOX6xj8vSa8M9+yN2o\nQb5jsUufhbA4Ht/yNoxYfXlBY+T4xzpSto+UdDzdK+mGawz/mJtKwm81hhuZcLlLJ9+wuTS45Bec\nXPp8eBIwPfmKbzc+O9VdEvsNfqFzYU5oS4Nn+mfMBwFoDvff3UH6TOPmeY2kLMl610i9R9xaOadn\nK1pxQjjN2NE+8ja2uTt4zVVwwDfOgLum4Oxjx7NQ49vxFtVdM1MOsIbX+OFDePCa9+zy8LnCzrGJ\n2muoTJu3RYB6/f8TrdMWwDVpvAZVzkh9i8bKGdYVpSGTZRmhkyCpKZt4TS8JMfUCx9boqzL50GZm\nVOhRhpQouAMJqZRoTJtag6StUHsNo6WG3N6yrKZ4eku1cYhKQWE5SH1BIXJEaxJkc2JRsCNHtEKi\nsDuwC8bainXWUJl9krxBlxPsRiEtM1rXQZK2lE6Bq/tock5nWKzLDqMLaTERck5ldiQ4rGc1dqxT\n12vaaYPVTPDiJYWhIjVQSjq6aqI1E4Yd+IZPkxR0cQeyT1JqSNWCtkzJByZN3MfA49ZuqbScaC3Q\ngyVxpyGyEW5kUbRbjI1MWMsYqymxvaQcyuiqhCCm3MzYEoJZsw5rVCdCqhO8IiJtHbJKwLZiaoaM\nNxWaW1JPEpw3b5nPNFQ54ebVilX9nOHHKd2wRrUlvChG+7iLEeWsFw9YnQb4iY+xKxg8nNAvpli3\nJmqVsPn4Lb/4O4Uz+wPdzMNtHhLuqPzFT3UaXeFhanNaHOEuK6aHAVF2wW/mEdPLgP9N8lme9Ul+\n/prmb4ZYyRtC+YZCuYNy9pKyfIyq66y9a+RRTh4toaroHsLeqU0wNziazynv7BClBbehRpy11LNd\nunDB69sZZXSL7cWc939FEm140TbMrv41b5d3sJ6vef1hRvN3Kb96f8b4XcDh2RXnywRfecO9IKc6\nztkUF5xoMY29Zrk2+Fh8S//NGaH7mPzRNUfXC96vJTKj4mx+TKAu2JtnvPqYUlsB4cOAuzdPadc1\n1pWHSFVaNgRnPe5GNeHTkKttjWSYeI3HE73mjjn+3nH6R0EWcg1uUJGrNoWsIbegpDqLKEUJBU6z\nQyZqbrsSvQeBGBAVBYpmoWkFJRXjpMUYtjiujlFK1LaHq8Romw7dSNhSk3YBWTXB0Tas0wrbCNF7\noLUNoq7JRzqVIyMZGsO+TldbJOEWS1JoNYlENTClkDAqcCydBIutV6KrMl0XY1U1VSJBJMiSDr2R\n6AyTsppg1C07ukMstZi6hBhotDsCO+lTLCFTE9LWIXV1SrtGrytk9btj4nXZUYmA8TglGcp4eoqT\n1nSyiqyBs5hh7BQkrc64tdjIGeNKI+k5jOs5WyXC1DckjcC2ZOQoYTHMcORdNKnBrmxWqkfuqHhe\nim4OwOzIOwvLVli5fYwWclNBq0Kq8x5SUiM6i/d5TTmZcH8w5iyqCeQJe/saL7iG2S1bbc3S28dW\nYj7oDafC48HwlOp+zs5kwv31PcLRBZvE58t4waumRU1+xjZ1+HX+CxbGlwxPLYaTlGeDXR78uY94\nukQdDLjt5ujxNe+2v+bdmwvenP+SbflLnEqgT9f06z7l1ORD9BH55BEn/+6cPyufoU36yNYApe7T\nnOyw3wZohsleo6MfHaGPS6zmLvZ5zG2xoHl3y9+8AEuzeROs2LLFWq25L8tYWwmJOyhBzKi3y0n9\nlputipge8fW7GRfeJWgrfvVvDH61OmPmp7QzFeNJwhfSPkftZ5xoD/kYZLjFC65en5C3Qx7vWjy4\nMyL/wTW6VoN5xdSMeOD0sTKJ2/2vsZQDzJNrYttmzwsJPlsQbBfILwuy2uR5WuDHHTcGqPPvH+p/\nFGTRALmnoIQ6XlcStR1GIuEPdDQ1Icoy+uUIPW4ZpH1cUaOWE+RuzbbSGGw1KqmGpKXKIrZtgWMF\nGIXFXNtSJWBpKcbIxZ8ElHqB1tkokkubOaRdSxlYmHJHUUlosglqRWE39DQHc+MQxzVOJGibip1+\nhaxVFJ6C0RkYTYymyyztCaQWSr/FzVTSskZWGpBl0sZnZnXItUDemIxjAwqdzuqQpRq9Ucm0FK8q\nkZYm8dSk3ubUqokhC8hk1mkPv52xaWpKR0MxPCR81o7Fci2xI7akIUzFmECSMLdQymOqwKaTJiCb\nbNyKuudgrlvqWcViW5JoKXLQUHctbeiS5xukQMXsapQC2hpke43n5ESOhja9Jj1oaYuMsa6xd16Q\nFB+o+i1PtAx3O2a45xL0a/ykjzxcoOotlaJz9cwlyqccn4B4OkUYoOsO61yind9wflHxyl9Q/d17\nhjctSvg5w6FFYv+Y/sF9dq2H2PqP6AqTsHJ4HVTYv95ye/0z+s9/xfybkHdVTbzUeSuPEXLBdPQn\nfHH3lL3dXTaTQ34s38VN/q/23izGsiS97/vF2c89d99z37P26m040zMcScMRRiApQXoRYAuGbQEE\n9KIHGbJhizBgwE+GXyzbgGGYMA1LgGEbpgyboCFRJIecYXPInp7uqu5ac19v5t33e/bFD5UjtQhq\npjXVYlU38gcc3Igv4p4Tf2TGlycivoxwUYu3SJk5srFB5aJOJWeyY7fJ7gScHZ3TTS+QnMzwpF2W\nF21S1RTfXF1hkt3CLP8FFoy/zO1Fk1vrOuXCNtVKQPGNNPcWIuaSLG9902B0qnF4vsNo2SClnpNq\nh1QWazzpFzkvSoT3TnD1kI3tDN4oRTz9kIfLaZwGOKdPufckTbFVQwt9ziYxdtBHSslkxxIj/ZjG\n0xprkgEXi4jLhKa3jXVzC5FzkdM2+9EeulxjP3P+0v30tZizkGWZ2NUQesTAyqK3R6Qkl+5Ew3MF\nmiyw0x5aENKyHUqJw8w3sf0iShyTmBNiUaY16VEqp8GGoBUztHxUISEhsLplYl3gySlykkmghghD\nxVBj7NYIOa2RODamyKKZMdMmONUYx5cRJZ+krzDMCoRSYRArRK5NFE2YpXxmkobeDpGrE0J3hj+z\nMK0AL9LQ4wRD7iP7BUIZJkmHvlRGyYJuD/F9lVxGJx5NkMsK03hGGokkcXD1OoHTJ1HSxHmBHnsM\nA4EeZHB8B8VJmJhT0lIJWYppRSpKZkpLj8kqMZ6SoExGFHIWMSZFIyLsgJ8e4hQUco5GGMl4U5OS\nMqQjl0kiCS2aIUtphoZNZaaTnrVA1xgGPpIf4nRNJnUZN6WR9vdpyBNYXKEcZ/A7DxjrC8RHRcLt\nNP6oTyFnsCdrfGNeotCTefM2mMU5fs4MOLUa1PspHOOY46cBnvMEMZpxsp5h+3GBIKeytVBic3md\n9JJHTWyTFNrMKilShzaHD4bsyYfsDeFJIBjyGCNRkeZv8+bEpjex+KW/YuOJOkHqDZaLI3L5Zb76\nwOXoXZe1iwrBasTFHtjTU8oTmw+mj9hW+jzpG9yf1qmvfJ1+ZUrQrVJZyPHL68ecSArqChR7W3T9\nMYvlIengm+TKMU3lhHg6pDp9m+nGkPP4EStHaaLaAr44p/GHx7RvbbPWhVoqQ2NtntLZAs/vf4D/\ndJOV56e0y+sM73WRzoaopRS2kkNpmgSXMkOrQlRJeNOC5qDF6MLgyIvZKt6mcWNK8iRhTdG53Cji\nJiNmPRt55fZL99PX4s0ijgUiUkklCtXAwSTLJB+gSAkibWMKjWTkE8VZUpqLULIUGJFWBFF5yAgL\nP5yCopAMU5iORjrvktFiSJcxtRI2MpPQwbFD+gxw/CG+FtFzpiRZgZmKiOSEkerSd1VSioEZCEJ3\ngtJ30XIqWmCQtGcUBzaq7iCFIaGSIjMz8CtZrI5HRakzEzZBqJAJx7hMkGONOJkR+VCeZCmKLpmJ\nTZCksRIPR5Lw4giznycKIjqWhB+lMY0ORcvClMcoQsYXU3ITFUcSqBmDlGEipzU0OaarOmixRjgF\n+gnaNGY6kYksHduz8MYwmXpMrAqRMEmGEUEgoxshJiaerJBNPLwoRNWraFmF7DhPF5tZFBOkMliD\nEEXIqIsJeadDWmyQGa5xx6wx0DyUzieo0jqFkcOSdkDQGdNaKxAVK2SnPgdxQDPvE2YrzLWW8Cvz\n1G4u46QUtJZCVTyn62YYPssRPI6IlwYQC/LBjETkSXnrHKpT0qc1ktMsxvCAHdlmbxpj9kZ4zZje\nSCdoRkSuhLMqUb1hEKff5a2vFaisGtysZSiejOhXF4nPNsjqGS6CIYuLn0A0h9eqYc7S9NQb3ItT\ntO8ukyqUKXfzpJY8UkGIGxepKXV6F2tM9Bmp1RVC4y6ZUMPNGkSZOe5VFWa1CGtOoZ7dxJ9zmEo+\nvf2bBLJGLPk0ijZ9pwNmG8sIWNLrvB2O8MIMjeYJi24PLVfj8mCR4dTBkC6wTYncwh75pMbRY42h\nf4k1UdjMDznXd5GiMd0QWpkRK08nqNKI7KxOefrym9+8Fm8WkhySsyT8pM9AzpDNRXiqguxJhG4B\nQ0yxPBcn9hbtiAAAH3xJREFUVpmJhCTWccszYg/0qU6cMkkkQXU0ZiRdYgQqfbeCpvbJCw8preJL\nLgVTJ/YlZqYJU0Ew6VK2qngdmb47RSvqCF8QDkOiqk/UBKuaRulCovWJ5RKabTPNyOR7JXwmuCMV\nJ1EpuD79YhotbiKbGYSbYIeCrF8iifpoiYRPGl+YCC0gDBIU3UZMIZklyFWDwPNJSwLZlZC1GMnP\nEYYCBxM6CemUgVowMMKYwOgjJjqapxBPfCrZDEMjIOeUmdrQVfrk7BxjbHKKxyQVghGTjkKMjoJc\nKmJoAXGYxja6uLMcckYQqiEirTIYQkWzsXUHyzIx8QmMNJlIEHYTTqcJjnRC23tOtGlQfuAyKQuE\n0eCTI5nqZg19NyRt2ihTl/lajUVdUF9TiWqrFAoZ8r6FHTVo5lyMyxbfnYyZPH2PVD5kNT9EsX+O\nX/jOPKXpCjfv6WxNVulu7uEPz2A85uMdQeCfEQ126LozjIGKujLHKDjnLdWifuMm26IOcxZu7Q4y\nKcqjNZqlY4qqjlXd4fCwwdqlxu97Mp54xILiIKdraLkAoXyLZWHTkmUWqyUUR8VP9TiettkKRojK\njMajdTILZ4zpcTmesfpIZuNmFbljsZA3oBfQD8sc/XzArX6Bp+MpDbNAeKSRJBpjKyTX73G8kaHS\nKzJd6NJLSahMcL0Qq5dw/85DHo5LbFZTdHpT9s90qp5P7bbBs+OY/kpMSc6wdZJld36EuSVod6cg\nplj9WyjlXQop96X76WvhLESo0BkEmAWTXNxlkFhYoxJ6KmSgRAhtRK+7TDHVI8ylybh97GaBnBrj\n6TLeyKOkJkRBlaTgoSsCr+Wi6xGSWcTpjYgljWGk48wS6gCaR2QbzJwZshJQikz8cUziKsRmAOMY\n2zRJ9ackJZVkrDOKu1hGEXXQx5FtVN0gM7OhJhF4FpmoixNXMESCklaQMfGTMSkrSzAc4xpNNMpI\nSpqM06Hry8yCNPlQQqRgrPRIyTXkchupX2bmD4jyJqodUKzIXA4VDKESMER0dZJkSmyomJmY2NYw\nghFyZJCoMYleZoiDpYI90SjoYyZRBjsWGIqHPNbol1zycYwVGsTmlFw7YFjT8CKbatpkKqeJQwnH\n1UmyM6TsFG+cJiwmrEkm7WgBp+Yi/z+/SccrkD5LM55kWNmKmfZCUuljUl5Iu/Y2mW5EZy7D/NwN\nvlmsoBZD9royxlKO/gO4SM1wp4c05z3cDzQyhTTn947YzKyRKRhsHa0RL02pTYtM8z6POxGS/Rz5\ne/vsOWfYR4JW6gnGM53yUoqNBQPSa+ipPrfNHNl+ieLtMXr9BM03SJ/MEwxG2KLPnqNTHjbxzgN6\nN+9C7pQbc7eYqFkK9pi453GYUtnsNfmD8wihnPNEX6X0/Uvc7TMyDy+Rh1XUjQnvaZB+1kXtKohS\nDiUz4J1ixEq8joFHbmPMnH/KSDSJkGgMMsTNefRkRBfB6qIg8bv4RyamPeBkLU2wv4C+NCJ6YjDz\nFNargla2xfR4g7R4i7H2hE50i4KpoPQ1JkaP7aKPE99mmH6M2kqw9J+4Wd1n4rVwFq4cIgptLtsW\neWyEPyDZ3uZi0qVszpOcRKQyl+iWiTbw8fQ01fwFnUFAoFZJ6UPCjotZ03HJc+Y1sLwMXqTgHI5I\nVj28S5OC2WUWzmFrYA4V5MyY2EgQbpFZZgpMIdQYxSqOmaKm9XF8i6noUhgbpHWYlaeUUgbjmUQU\nuihlDUcKcX2fXJKgyRBJHlpgIzJZzDhHgouSylFyR/TyQ/JtD1cyKekSbiQYJQlVBeR2jVk2RpoU\nkAsyph8zVUziJKYZq6TzAeHMxnTS+LGGUtCJEohGQ6LYI6qn0d0pcmRhuT3kREZWdMZlhbGkojou\nshFgxx5OJGFECn1fRrUM5NmInpQgLgtMLefFYU+WSlqTaVohVi/Gy5XwLAcxTbCdNJmmhC2gXbPo\nPjpHKmYIJw1StkukLxJlysg7JaQVicUFGSeVRbmMONlSWJm7xUbrDO/ZGL+5y8c/3CWKJJyPi6Tz\nE07dLN8YLJOVlll6+x49RaDn23RnEqVmCV9/jwdOg0s5xH9qkAoFudYCKxsWyWaW7h34mwUXUn+J\njXdXqeUMPN+lOczgdDso6YQL74QnjzQumy3OT2NCsci2F6LZcwzsErrf4UKrkTMf0GtOCXcnDPwB\nuUKafuOQ89Eudl9D8qYkqy2Kf1hhqtskuQzZeMyC/M8oHC/z3ptV1pPHeFId9SZYj36OzN2nHMwc\ntP4up3LMenuIvHyHT9pV3rJWONaPeC7FFGYPmRRv44wEqTfLRI0POAxuEUoalXqLlD0mmsT0VYGh\nnNGSLQoTldawRmXuGX6ujpdKkOPiS/fT18JZ+LOIyQ9j3HqDJ5pPTpPY++77yKFOtzqCQgWef4y3\nYhCPyty1NR6kR9xdztJ5FHDCGMmIyVV8SqMRwZGLmcvQEREZrUvKn1Lo3OexvU+5HHLQWODu0oxP\nnqe5q0Y0OWemTdFJM9+cIN0okD7bp+NblAsSxqjMaahQjY8p+iscnfbRN/ssBiC6C8yCAYV6SOIu\nEyldAs1i6hpUiTjyY1b6EkeFHnK2SCmwmRQNAnKk5BDTD0mpPcauoGDoBJLKRaJTk11UrYg2mxJM\nVOrZGB8Jc+jgzA+w+xU0ESGHEVGpRDJrIpw87tQimx+QTFLIBaAtg5lgxCZecYIXyIjZPOa8izWZ\nIekWhq8QiSJxJkT4HVJGhRCbwHYxXIlcQWaaiVFDmzhIqM4shtkOSWrA5GxGszvidm2B3/3Rd3Fu\nLXFnfM55sw1Myaz32Orf5Hh5jlvbNRaKq6Qy80zbOqMbMyb2KueffMSIPNHzMVF2QGZaJG2EzElV\nbuXTtMc5UtUuem4euiEfdmJkqYL5QMDkHKNooJwFxHKBg6rFX69kSFJ1Suvb+Btp8oU6ymzMwJOp\nxyGH6oxQatPbzzAd/Q6dEHx7xso7MZXLKueVNooL6/oZ5/4HHEfnHOx6ZM8kRrcj/PeH1KsrKAuL\n3Dwfc5krMDqLKLt5uqmE5dNjDpYcLrtVNoc/QBwvYY4tboR5ooqN0AWBL7Ocz1NdeYdZa8bZmk3l\nfAd1TSeZ28SQZVaGKTpSiYEXUKvkiPY9mM5TMLpcNpvkJMhsFtnpp1hZec5hL+KtrSVm0SPYq+Ib\nIXOHCXmjQ6P68nEWr4WzsCczHu39Yy7fq2Pd6eE2S6w4ARerKQaXKW5IZ7SlDTZxeezbTBUP6+kF\nP2gmyNbbBBzS6JiITh2r1iV71GQpBxePHfwlla0Px7S8h0wWGrjHHQqjH/G7exvMZm3aKwliYDAL\nsuT7B5xYZeyLx1R3bmJoD/DadS4rE4p+jh+aVVJ/3CYTxcilkMYgzWF7D22hzq2LAR5Thr0BRvGY\n8uAWH1WmzGVa7HQ3cOstSjsmbtFASR3iHrsMb/QZnWdoZVNsLTXpjUMu2gr39S7e2Qa7KYd0y6GS\nm+Nxd4JZzeAWA3IUWGzqOLMnqNnbnBoH5AKJUUYjVHukegl5N4859RHjHk5dphC4uDt1emaX4uKI\n6cBDF4t4QsJpOJhlnWgoSJQqjWHIgjLlLF9CmBdUnAWyUkJPGWKNMzjyBfl4nhN3D7m0h77YI/je\ngOWlLDt+i84wy5pzym4mS71ZwM2ZzE8cipMu8dstltcNSuqAWcPgYjRkaHlMtCFRx6FeVdDTOl8p\nVDDf6DOTLf7qjZi8ZuEZEcWSTm+vw+WTRzR0hx27hnz2B4iaihNVWG5GdDMVvvr224j8GkW7yDhR\nSHSbdCrDBIvusMN518N7uk//Ych49jHPBi7y+/dxS7+PWixwap4z+HieYdsjyRsk+pRyfhMx1ai8\nYTIreyz1NnDfgDsrAV7rEvNiRlJdY6K1qTQcrD2FoVxh9KFMMj8m8UZkSimyicmkUuXeZMqpccLx\nLZtpY5FZ5yH63E2eX7RZU1bILcfYuw8oWhWS/QGXK0sYqscsTJDrq6gTg2E+xkdhelTEX4cHH8PK\npoSw2hyOVd6uqzwfb5Jt7bx0P30tnIWiBBw1y4RigDRpcnFc4fSeTvqDkIIIsGsDegsnnDZ9tocr\nPMo9oxDJ5Htb7Oz/HpU4jbQUoR9rZD+5RJqzuZB3OG+UKHf3eaBsMC2eYY8CtPQlB5hMUs+4P5UI\ne2ka7T6VZMyZXKQQuAR/GJNkv0ezqFHsTzCOyoyXJ0iiR9qf8cgTSO9lqW0ek+tKdBo9dtdijOIP\nOJYEd3YK/NHWH+FFiwSdHNnwEeWLRXz7IfZMR+4J/FqPwfc99PspvKjJg0c2RYYMpCIH2YSTTp+s\nGZPM5bjo/BAVHWYeJUmiJdfplQKsZha732JxuUrGTTg7OOZmYZ1IVnmenrJqF1AyKaTTZ1CFjq8S\nJArNrsxcJqGRjFg+KHMW7aNmVCx7iePkGKNgICXLzM1c5EYdOT5mvGVSQqER2EimxHgYIvYVpJNF\nrMYpZ6NL2skqK0d7WNKYk1WLW/EGdneH9cICs5ognVnhK45FbLTxY4NRc4HlcRsOJjw66CLxISeX\n84zTY3qlGevK3+BO3uDJnkb9a2lW24Jd+ZBUAIejLOr4MaZ8yYFRJGhFrJdN6ptb3LyvIIclNocq\n3vKE7EzC1IpEg4jdiyPEYR5n+ITH+oyGv8dJpkW5leY8+x6hssrkaQu8mKwKo/kBo8kFavc+wc0X\nR17mZgbaLOLdKkTLMUf5DYLwDgviY9bVPg/H83jaHOPbFwzsCcXzPN1ujsriMc2DAvdyI9a5j5wf\nI9nbSBeH5OMz2oUcxZ0Gg3e/htJNWKrL+FEF9Sjg1LiJdd6kaKUxy4LlfY+DhSFbD8bUCyk6MxV9\nL2FjI4UmbXEcnrIer9EqD9geHhLnb718P335rv7yuLbDk0ddVqUu4+M+R9lTbj0LGccJqn7Aj+xl\nOLykstfmny8ccuehzidbGtGDD5lG86jSmEnQITX7hO+HNTZOOvTP71MpX2BrQ6aWSzwdc7Gfx5pv\n8NTQqQ08/tn+GlL1EVrWxv7/CrTXTJ5KU7LZVYbNGf3nAZX+CQdvLLF4Mcb8KKThNemVM4izFOKR\nzMGNEkbjj7gc58lnTHYPBgzeytH+gwRcgbIS0xvK9KePsIZtjKmFkivR641oCRn5jz9g+XRAQcrz\ng5rPuvyE1vtz6NuPOH/fRDOz9L1zoiXI9KucrObxD49Y8DzCGwI/TnFydsD+s5sYiwJ/ekx8/AxW\n0zx8vgnakKhepP3QpS/aZCWfTKXLB4OIsHSf55Udbg6bPNl1UNMm3dNz7o8N3lu4wMw5FMZ5tFmB\nM2lA8UJDi/Y4juaoWw/50LVJ+buMuk0iT6VctTEulniafkT6xCLywUmp9CpD1v13KOVtxjdz3Duq\n0PiKgTkcIw+aPFipYvzJDmdrRdTmCN/JUxb3qAQt0pW3Ka+GLA98up0WTtHGq444nwxIphvgDhBO\nEX+1haL6kMtjjLfY+gUJeVvCTyVMYx1f6uIV6ixc+PyTyymxNuX8ss94ppN1yhwO+tQ+HnA5H5EK\nA1LmHSapPrrUZ63+BjltFW+zx/z8AuXxXe4labTcGfnMPdYWWqTnC0x6N4jMNtoooD9+RDK4gzse\n0/be5+Iw4IOpzdx8i+/O5vmLY1gtbDDYSHGjtsbjPz5gLe1yqLssNc9BmnF8cIflFR8xmdC1Q25q\nGu5ExskNcJURm8ktWlETf01m8cLlNC6jzGwaXohUSBG1L5lK8wzmXKLW7kv309fCWSiqibjnMEiF\nrDtZ7sza7Mghq67LWNwnd3mEc+s23fUMd0c7nMsr1FvHnEUJuSDDse6w8KjKxdKI5alLN5ojl3Jx\n/ZhD5wRfylAcSoSLPh8dV6lOhpyWDcqdpzQrSxSGNnteF3FhICYRzYWn9HpV8oUDmnaKyYctftBd\nAP0cqTglrxmE+QdM5CWs3x3wqBIQdCfgPCBUN0l/r4FWPIWwzG8fddjuZNkdCOrdPFJ3TOmOyRN7\nhp8usXImcVJ0OTYvOPhBQmNZZdHtc/RH8ywsH+A/NilVcnRPHHbrfZhYLLQnTFZmTD+6Q5B/D71r\n0Kgr3PqTBC+YIMkOR4HJ9tilGTxnsl/kwwWXOS/ArdyBg30G+Xne+eQjDvUGz0oWd7sGh/YjpMwh\nR8WI8j8vkY0LPFmZIVu7pBtjTrtFFgdN2jRQrBSKovHdRpueYhCHzxg9AqWoozQWyccRjXcOWZ0l\nOA2B8i2XwF2nIJucaBHZ1gy3GfJDtQ2fPME1elw+tclvLnHTnaMCWFvr2NUia+N5+vUhnZRC2PFp\n7Z8TOB4j+Rm9ozzhmkQ5PSXxttgSKZS/lMNTEiy7SqbtgS7wc1WiwGffH9KMv497fkynecRkPGHv\n6BykmLRykx1nwD3ZQrNjmn3BnfkVMrcttmZpjNxt5rd11p0baJkL/JVtlF2VBW2bQVGwtNVlb7jG\nm60Ddm7+RTY/dPj+2iFr03Vs1SJz+AmdRp+pWuZy3kEYF9xzyuxXs2RSNSb9DHOiTby/z2C+zjsV\nm7i6haP5GF4DL93G6OdhUmOSTDn0T8nV66Sn56Tmt4k/aeDVepSKc2TjSy7cDPnDS0a2jsKf4wTn\n1Ya9PwIaSZL8NSHEGvB/ACXgQ+DfT5LEvzps6B8D7wA94N9JkuT4J91bNeFNp4BirFHSApK5Eb+k\naozG84imTb+8ihvtMbXTNDNv8ZYx5dEsz817GVypQ+fsLXzrhDelb9IW+9xYdjg163hPFe5G7zBR\nDDqXJ9yQC5h6lcdGhWVPIncrhy4d4e5lyJYkEhbYuNmkfelRrikMrRQXrXXmtT1S6hHDrSXmnyvk\nKjHnoUSuofDwVov7QYo9OwuDTdJhH2exgKTJOMqY6Ai6+Qj9kyq7aw0MzWXo6FRU8Hfm6S7apM9A\nDSCbaVANBO1QME21iY6W6XQ8Bu0zxrUy/ieClPB5virIfpRBH39E7k2JZjNh9LzH+/Ij5jfu0Dh0\nuRUp/En6GavnLpPlGX7rhPFohcvxHxL25vDmdvmDQYnaXJPk6ZiPOgvEcym8nRZCW2YknTIXP2XW\nyjPJzjGdzthKB7xf0DDOfXYzDVJmhH2iMsr9kIaj4sRllOGYURHU+ROCcY1uYZHl/AJGYrJR26A3\nu8nd7SK7R03y+oSths+ZZRGFXVyljekUaBUk3CDhbcPB7jfpb86RBHVqvQQ78SA/JrHbuJJGEjQo\nzCz8QpXleshobch3TmU2N6t4SQ8zV8XDpj/UcA6fEU0El80m0xMF266haxPC2iqKckR35rGpDJBN\njf1szFtbcxQXq8xtbDJX1tjoFXC8LYLtHOnZmCBR6C8X8bURRVeh31eYL0m002/zncPHBO8W+E5U\n4fToLXatCxr5DP3zNveSY9oPdhDb36avdVgcLlCornGjfMLzp2NMY4Ph4oCu51AYhuzHfer5Fr1e\niSDX50a8SqiEhNKEUq9OMljgsbyPlKkhvB5COqNjZkjSfUajeVQVzM9hd+9/kwjOvwc8+1T+vwb+\nYZIkm8AA+JUr+68Agyv7P7yq9xPxkwhjS6AlgnG5SjLWOJbSJKUpvYJOfPM5txWZG0qF5UTmNClw\n47ZMyonxO3fYkBQq1irT0jELS4tcjLe5fRyQ+fopQW2CvTph86sZChSxi3nuf0VDv13Ek9IsJOuY\nX8uRyuWxch2sJKCQXSTp9sk5db5Rm5Ka2yD8+h3u2Db9uZjD0SVG710a6TQLxRpiMEexLNiyRqze\njSnnS0iTVcLcbSyjhLOis3gjTy3U0TNZinmN1oWCVRmy0nSIohyNdZtapoRmzjOfs1jOriPVLFbu\nZ8neiSkWLlm8dcRaxqA2aVCcDbDMeQ6ejJlkDBazz4jENu3mJfrtInszl8k04sxN0ReHqC2Vjtkn\nPq8g5kHtdnAyuwwGgv1UmYZ2zpmckDGWsZJT5IrNnh0TZQwYjJmKDt1xg5nrcJI9oNiSkS/SFFd9\nMjsFihFUVnf4ePOUN/I2/lGaO+4FpqSjtlJUCg6xtIOaOuboZEKw7HHc69EvCaL+Ps7EYRbXOMyY\n5JWIn7tTQ+2vUJELSIZAD09oDTv0jWM6H0i00wfYOyrmssN8EFA1YJhf40bvWxhfyZJ3FuhVliDn\nEZVURukeTxY9DsfnWHaJy0wfb7/F/kjl9qHLwnEJNdfjrHsLU57j2/PLrM6tU9HWWJluoQRfRfv5\n2yzd7lJKpvh6hrSdJa1E5D0F39TIpSzUULBCj8niPSRljoz4Brm/UuAXbs3xdvYbVOW/wFFP5rkj\nE3s7pM97OGsHWIs1xnqZcHUOf+EYw0mzf2ajdetU+jAe3+SipZGav8FkcQ/p9iJGcA9z/ilN9Yxq\n2WK53+Q0s04zVUGzM8xpOkrVpLjYIGtOf1o3/Kl81uMLF4G/CvzPV3kBfBv4jasq/4gXZ4fAi7NO\n/9FV+jeAv3xV/1+LHCd0P3BpZ3tc2Bf4rkr37AG9nRbD2QOaQ4XvhR5+aYrdjogqguiJRdJ2ydU9\nbLnLmTUm2vf4KNjBTV0wnUvhHpc5EjazPYnWYZowP8Aq7TL6kUuofUjfbPNYOyH70EbJgZ6vkBhz\n1KJz4uyEVrvMQz+g3zJZHLUJ1ICFqMSic4N184z1aYflkwqW2kfuhQysRdrjDQLRxJzPU5McVvNF\nlh5tcBLFhLbCrcU8ZVsjs/wGucWYdKiSz2a4a22SU1bZ7RZ4PipRmp2QUWwOFAM98khrq0juHJY4\nIxzf5biQ5Sw9YDO9SdS3mGyXKd4pksuVWVSmmCsCs53Hr3sozgIL8RzxIIcWF0jiIeqkRr1zj+Uw\nZPtCsKx8ha2JRqzNmJoGg8YmhbWIacFhJM54WwREeopCfMqKq+DNe+yXB7T6J2irY6bVFWbhFqWz\nTZrhCEvkmbUyVC8DqsYBvi1Yrt1grZXi3naJu+dp2rkBzw/bJLky/ctVtLSBfqRQM+YYZSTcr6ao\nbteQUJG9FPZ8i/SziA/nZczTEReyQJEqHM9LVFhFD1Ik8wnkCuxLPaykQ/cyR+Y4SwHBxvM2U/sh\nPblB7XGDcaqBHRwh37Np589x8hnml3vYvRr6eMyGt8nKN7/G/LcU1jchq8jMRnOMVAk/soixMITN\nQI/xOh5j8ihhkZgccjIiLvVRki7y6hbJ2jfY0kd8bWFEbquMXogZT2ye5ltM+yUUpY/vrZEbZXHb\nEuqRSn1b0FYfULuRZbScRV6xkPtNiANS/SHrukK7Pc+Kf4ucHtOt1gmjAbWBiz0V2EkNsx/SPrpD\n0B7+m3mGP8sPfJYddIQQvwH8V0AG+E+Avw38ydXbA0KIJeCfJklyVwjxmBcnlp1flR0AX0uSpPun\n7vl3eHHKOsBd/uUhRV82ykD3p9b64vFl1QVfXm03kiTJ/Kxf/qlzFkKIvwa0kyT5UAjxrZ/1QX+a\nJEl+Dfi1q2f8KEmSr3xe936d+LJq+7Lqgi+vNiHEj17m+59lgvPngb8uhPhlwACywH8H5IUQSpIk\nIf/qeaY/Puv0XAihADleTHRec801X2B+6pxFkiS/miTJYpIkq8C/C3w3SZJ/jxcHJP/Nq2r/IfD/\nXqV/8yrPVfl3k89jt9BrrrnmlfIy+1n8Z8DfF0Ls82L59Nev7L8OlK7sfx/4B5/hXr/2Eu143fmy\navuy6oIvr7aX0vWZJjivueaaa16LnbKuueaa159X7iyEEL8ohNgRQuwLIT7LkOW1Qgjxvwgh2ldL\nxj+2FYUQvyOE2Lv6LFzZhRDiv7/S+okQ4u1X1/KfjBBiSQjx+0KIp0KIJ0KIv3dl/0JrE0IYQogf\nCiE+vtL1X17Z14QQ71+1//8UQmhXdv0qv39Vvvoq2//TEELIQogHQojfusp/brpeqbO4CiH/H4Bf\nAm4Df0sI8fI7i/758r8Cv/inbP8A+L0kSbaA3+Nfztv8ErB1df0d4H/8c2rjz0II/MdJktwG3gX+\n7tXP5ouuzQO+nSTJG8CbwC8KId7lc4xIfsX8W4u0JkmSV3YBXwd++1P5XwV+9VW26WfUsQo8/lR+\nB5i7Ss8BO1fp/wn4W39Wvdf94sVq13e+TNqAFPAR8DVeBGEpV/Z/8XsJ/Dbw9au0clVPvOq2/2v0\nLPLCgX8b+C1AfJ66XvUwZAE4+1T+/Mr2RaeWJMnlVboJ1K7SX0i9V6+obwHv8yXQdvWq/hBoA78D\nHADD5EXMEPyrbf8Xuq7KR7xY/Xsd+W+B/5SrQ/540c7PTderdhZfepIXrvsLu+QkhEgD/wT4j5Ik\nGX+67IuqLUmSKEmSN3nxl/irwM1X3KSX5tOR1v+2nvGqncWPoz1/zKcjQb/ItIQQcwBXn+0r+xdK\nrxBC5YWj+N+SJPm/r8xfCm0ASZIMeRFc+HWuIpKviv6siGRe84jkH0daH/Ni64hv86lI66s6L6Xr\nVTuLD4CtqxlbjRcRor/5itv0efDpKNY/Hd36H1ytHLwLjD71Sv9acfWfwr8OPEuS5L/5VNEXWpsQ\noiKEyF+lTV7MwzzjCx6RnPx5RFq/BpMyvwzs8mLc+J+/6vb8DO3/34FLIODFmPBXeDH2+z1gD/hd\noHhVV/Bi9ecAeAR85VW3/yfo+iYvhhifAA+vrl/+omsD7gMPrnQ9Bv6LK/s68ENgH/i/AP3Kblzl\n96/K11+1hs+g8VvAb33euq4jOK+55prPxKsehlxzzTVfEK6dxTXXXPOZuHYW11xzzWfi2llcc801\nn4lrZ3HNNdd8Jq6dxTXXXPOZuHYW11xzzWfi2llcc801n4n/Hzq+qqQ3zFFCAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb61f6cdd10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sharp_test_noise = noise(sharp_test_noise, 0.2)\n",
"soft_test_noise = noise(soft_test_noise, 0.2)\n",
"plt.imshow(sharp_test_noise)\n",
"plt.show()\n",
"plt.imshow(soft_test_noise)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"## Check gradients of test images"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# compute a gradients measure that should prefer an edgy result, thus a sharper one\n",
"def gradient_sharpness_metric(data):\n",
" # limit gradients to one colour channel (greyscale, remember)\n",
" gy, gx = np.gradient(data[:,:,0], 2)\n",
" # get norm of the gradients, thus looking at both directions simultaneously\n",
" gnorm = np.sqrt(gx**2 + gy**2)\n",
" # and produce a single number\n",
" metric = np.mean(gnorm)\n",
" \n",
" return metric"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"source": [
"#### Inspect clean images first:"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" metric (sharp) : 0.023001\n",
" metric (soft) : 0.00670288\n"
]
}
],
"source": [
"print ' metric (sharp) :', gradient_sharpness_metric(sharp_test)\n",
"print ' metric (soft) :', gradient_sharpness_metric(soft_test)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"source": [
"#### Now inspect 'realistic' images:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" metric (sharp) : 0.0353338227318\n",
" metric (soft) : 0.0212094832647\n"
]
}
],
"source": [
"print ' metric (sharp) :', gradient_sharpness_metric(sharp_test_noise)\n",
"print ' metric (soft) :', gradient_sharpness_metric(soft_test_noise)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### Check robustness of metric, looking at the ratio of things\n",
"A higher ratio should hint towards a clearer identification (or so the idea)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" ratio/cleanliness of results: 1.66594453485\n"
]
}
],
"source": [
"print ' ratio/cleanliness of results:', \\\n",
"gradient_sharpness_metric(sharp_test_noise)/gradient_sharpness_metric(soft_test_noise)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
google/starthinker | colabs/google_api_to_bigquery.ipynb | 1 | 9224 | {
"license": "Licensed under the Apache License, Version 2.0",
"copyright": "Copyright 2020 Google LLC",
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "Google API To BigQuery",
"provenance": [],
"collapsed_sections": [],
"toc_visible": true
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-001"
},
"source": [
"#Google API To BigQuery\n",
"Execute any Google API function and store results to BigQuery.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-002"
},
"source": [
"#License\n",
"\n",
"Copyright 2020 Google LLC,\n",
"\n",
"Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"you may not use this file except in compliance with the License.\n",
"You may obtain a copy of the License at\n",
"\n",
" https://www.apache.org/licenses/LICENSE-2.0\n",
"\n",
"Unless required by applicable law or agreed to in writing, software\n",
"distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"See the License for the specific language governing permissions and\n",
"limitations under the License.\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-003"
},
"source": [
"#Disclaimer\n",
"This is not an officially supported Google product. It is a reference implementation. There is absolutely NO WARRANTY provided for using this code. The code is Apache Licensed and CAN BE fully modified, white labeled, and disassembled by your team.\n",
"\n",
"This code generated (see starthinker/scripts for possible source):\n",
" - **Command**: \"python starthinker_ui/manage.py colab\"\n",
" - **Command**: \"python starthinker/tools/colab.py [JSON RECIPE]\"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-004"
},
"source": [
"#1. Install Dependencies\n",
"First install the libraries needed to execute recipes, this only needs to be done once, then click play.\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ed11ce30-005"
},
"source": [
"!pip install git+https://github.com/google/starthinker\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-006"
},
"source": [
"#2. Set Configuration\n",
"\n",
"This code is required to initialize the project. Fill in required fields and press play.\n",
"\n",
"1. If the recipe uses a Google Cloud Project:\n",
" - Set the configuration **project** value to the project identifier from [these instructions](https://github.com/google/starthinker/blob/master/tutorials/cloud_project.md).\n",
"\n",
"1. If the recipe has **auth** set to **user**:\n",
" - If you have user credentials:\n",
" - Set the configuration **user** value to your user credentials JSON.\n",
" - If you DO NOT have user credentials:\n",
" - Set the configuration **client** value to [downloaded client credentials](https://github.com/google/starthinker/blob/master/tutorials/cloud_client_installed.md).\n",
"\n",
"1. If the recipe has **auth** set to **service**:\n",
" - Set the configuration **service** value to [downloaded service credentials](https://github.com/google/starthinker/blob/master/tutorials/cloud_service.md).\n",
"\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ed11ce30-007"
},
"source": [
"from starthinker.util.configuration import Configuration\n",
"\n",
"\n",
"CONFIG = Configuration(\n",
" project=\"\",\n",
" client={},\n",
" service={},\n",
" user=\"/content/user.json\",\n",
" verbose=True\n",
")\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-008"
},
"source": [
"#3. Enter Google API To BigQuery Recipe Parameters\n",
" 1. Enter an api name and version.\n",
" 1. Specify the function using dot notation.\n",
" 1. Specify the arguments using json.\n",
" 1. Iterate is optional, use if API returns a list of items that are not unpacking correctly.\n",
" 1. The [API Key](https://cloud.google.com/docs/authentication/api-keys) may be required for some calls.\n",
" 1. The [Developer Token](https://developers.google.com/google-ads/api/docs/first-call/dev-token) may be required for some calls.\n",
" 1. Give BigQuery dataset and table where response will be written.\n",
" 1. All API calls are based on [discovery document](https://developers.google.com/discovery/v1/reference), for example the [Campaign Manager API](https://developers.google.com/display-video/api/reference/rest/v1/advertisers/list).\n",
"Modify the values below for your use case, can be done multiple times, then click play.\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ed11ce30-009"
},
"source": [
"FIELDS = {\n",
" 'auth_read':'user', # Credentials used for reading data.\n",
" 'api':'displayvideo', # See developer guide.\n",
" 'version':'v1', # Must be supported version.\n",
" 'function':'advertisers.list', # Full function dot notation path.\n",
" 'kwargs':{'partnerId': 234340}, # Dictionray object of name value pairs.\n",
" 'kwargs_remote':{}, # Fetch arguments from remote source.\n",
" 'api_key':'', # Associated with a Google Cloud Project.\n",
" 'developer_token':'', # Associated with your organization.\n",
" 'login_customer_id':'', # Associated with your Adwords account.\n",
" 'dataset':'', # Existing dataset in BigQuery.\n",
" 'table':'', # Table to write API call results to.\n",
"}\n",
"\n",
"print(\"Parameters Set To: %s\" % FIELDS)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ed11ce30-010"
},
"source": [
"#4. Execute Google API To BigQuery\n",
"This does NOT need to be modified unless you are changing the recipe, click play.\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "ed11ce30-011"
},
"source": [
"from starthinker.util.configuration import execute\n",
"from starthinker.util.recipe import json_set_fields\n",
"\n",
"TASKS = [\n",
" {\n",
" 'google_api':{\n",
" 'auth':{'field':{'name':'auth_read','kind':'authentication','order':1,'default':'user','description':'Credentials used for reading data.'}},\n",
" 'api':{'field':{'name':'api','kind':'string','order':1,'default':'displayvideo','description':'See developer guide.'}},\n",
" 'version':{'field':{'name':'version','kind':'string','order':2,'default':'v1','description':'Must be supported version.'}},\n",
" 'function':{'field':{'name':'function','kind':'string','order':3,'default':'advertisers.list','description':'Full function dot notation path.'}},\n",
" 'kwargs':{'field':{'name':'kwargs','kind':'json','order':4,'default':{'partnerId':234340},'description':'Dictionray object of name value pairs.'}},\n",
" 'kwargs_remote':{'field':{'name':'kwargs_remote','kind':'json','order':5,'default':{},'description':'Fetch arguments from remote source.'}},\n",
" 'key':{'field':{'name':'api_key','kind':'string','order':6,'default':'','description':'Associated with a Google Cloud Project.'}},\n",
" 'headers':{\n",
" 'developer-token':{'field':{'name':'developer_token','kind':'string','order':7,'default':'','description':'Associated with your organization.'}},\n",
" 'login-customer-id':{'field':{'name':'login_customer_id','kind':'string','order':8,'default':'','description':'Associated with your Adwords account.'}}\n",
" },\n",
" 'results':{\n",
" 'bigquery':{\n",
" 'dataset':{'field':{'name':'dataset','kind':'string','order':9,'default':'','description':'Existing dataset in BigQuery.'}},\n",
" 'table':{'field':{'name':'table','kind':'string','order':10,'default':'','description':'Table to write API call results to.'}}\n",
" }\n",
" }\n",
" }\n",
" }\n",
"]\n",
"\n",
"json_set_fields(TASKS, FIELDS)\n",
"\n",
"execute(CONFIG, TASKS, force=True)\n"
]
}
]
}
| apache-2.0 |
boya-zhou/kaggle_bimbo_reformat | notebooks/5_random_forest.ipynb | 1 | 22221 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Random_forest_regressor\n",
"# extra_tree_regressor\n",
"# sklearn.svm.SVR"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"from sklearn.cross_validation import cross_val_score\n",
"from sklearn.cross_validation import KFold\n",
"from sklearn.ensemble.forest import RandomForestRegressor\n",
"from sklearn import grid_search\n",
"from sklearn.ensemble import ExtraTreesRegressor\n",
"import gc"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1_predata.ipynb preprocessed_products.csv\r\n",
"3_xgb.ipynb ruta_for_cliente_producto.csv\r\n",
"3_xgb_prediction.ipynb \u001b[0m\u001b[01;34mstack_sub\u001b[0m/\r\n",
"44fea_bst.model submission_10_new.csv\r\n",
"4_keras_nn.ipynb submission_11_new.csv\r\n",
"5_random_forest.ipynb submission_44fea.csv\r\n",
"6_stack_model.ipynb submission_nn.csv\r\n",
"agencia_for_cliente_producto.csv submission_nn_xgb\r\n",
"canal_for_cliente_producto.csv train_pivot_56789_to_10_44fea.pickle\r\n",
"model_nn_10_after_l2reg.h5 train_pivot_56789_to_10_new.pickle\r\n",
"model_nn_10.h5 train_pivot_6789_to_11_new.pickle\r\n",
"model_nn_10_whole.h5 train_pivot_xgb_time1_44fea.csv\r\n",
"\u001b[01;34mold_submission\u001b[0m/ train_pivot_xgb_time1.csv\r\n",
"\u001b[01;34morigin\u001b[0m/ train_pivot_xgb_time2_38fea.csv\r\n",
"pivot_test.pickle train_pivot_xgb_time2.csv\r\n",
"pivot_train_with_nan.pickle\r\n"
]
}
],
"source": [
"%ls"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"dtypes = {'agen_for_log_de':'float32',\n",
" 'ruta_for_log_de':'float32',\n",
" 'cliente_for_log_de':'float32',\n",
" 'producto_for_log_de':'float32',\n",
" 'agen_ruta_for_log_de':'float32',\n",
" 'agen_cliente_for_log_de':'float32',\n",
" 'agen_producto_for_log_de':'float32',\n",
" 'ruta_cliente_for_log_de':'float32',\n",
" 'ruta_producto_for_log_de':\"float32\",\n",
" 'cliente_producto_for_log_de':'float32',\n",
" 'cliente_for_log_sum':'float32',\n",
" 'corr':'float32',\n",
" 't_min_1':'float32',\n",
" 't_min_2':'float32',\n",
" 't_min_3':'float32',\n",
" 't_min_4':'float32',\n",
" 't_min_5':'float32',\n",
" 't1_min_t2':'float32',\n",
" 't1_min_t3':'float32',\n",
" 't1_min_t4':'float32',\n",
" 't1_min_t5':'float32',\n",
" 't2_min_t3':'float32',\n",
" 't2_min_t4':'float32',\n",
" 't2_min_t5':'float32',\n",
" 't3_min_t4':'float32',\n",
" 't3_min_t5':'float32',\n",
" 't4_min_t5':'float32',\n",
" 'LR_prod':'float32',\n",
" 'LR_prod_corr':'float32',\n",
" 'target':'float32',\n",
" 't_m_5_cum':'float32',\n",
" 't_m_4_cum' :'float32',\n",
" 't_m_3_cum':'float32',\n",
" 't_m_2_cum':'float32',\n",
" 't_m_1_cum':'float32',\n",
" 'NombreCliente':'int32',\n",
" 'weight':'float32',\n",
" 'weight_per_piece':'float32',\n",
" 'pieces':'float32'}"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"predictors_10 = ['agen_for_log_de', 'ruta_for_log_de', 'cliente_for_log_de',\n",
" 'producto_for_log_de', 'agen_ruta_for_log_de',\n",
" 'agen_cliente_for_log_de', 'agen_producto_for_log_de',\n",
" 'ruta_cliente_for_log_de', 'ruta_producto_for_log_de',\n",
" 'cliente_producto_for_log_de', 'cliente_for_log_sum', 'corr',\n",
" 't_min_1', 't_min_2', 't_min_3', 't_min_4', 't_min_5', 't1_min_t2',\n",
" 't1_min_t3', 't1_min_t4', 't1_min_t5', 't2_min_t3', 't2_min_t4',\n",
" 't2_min_t5', 't3_min_t4', 't3_min_t5', 't4_min_t5', 'LR_prod',\n",
" 'LR_prod_corr', 't_m_5_cum', 't_m_4_cum', 't_m_3_cum',\n",
" 't_m_2_cum', 't_m_1_cum', 'NombreCliente', 'weight',\n",
" 'weight_per_piece', 'pieces']"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"predictors_10_target = ['agen_for_log_de', 'ruta_for_log_de', 'cliente_for_log_de',\n",
" 'producto_for_log_de', 'agen_ruta_for_log_de',\n",
" 'agen_cliente_for_log_de', 'agen_producto_for_log_de',\n",
" 'ruta_cliente_for_log_de', 'ruta_producto_for_log_de',\n",
" 'cliente_producto_for_log_de', 'cliente_for_log_sum', 'corr',\n",
" 't_min_1', 't_min_2', 't_min_3', 't_min_4', 't_min_5', 't1_min_t2',\n",
" 't1_min_t3', 't1_min_t4', 't1_min_t5', 't2_min_t3', 't2_min_t4',\n",
" 't2_min_t5', 't3_min_t4', 't3_min_t5', 't4_min_t5', 'LR_prod',\n",
" 'LR_prod_corr', 't_m_5_cum', 't_m_4_cum', 't_m_3_cum',\n",
" 't_m_2_cum', 't_m_1_cum', 'NombreCliente', 'weight',\n",
" 'weight_per_piece', 'pieces','target']"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"f = lambda x : (x-x.mean())/x.std(ddof=0)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"train_pivot_xgb_time1 = pd.read_csv('train_pivot_xgb_time1.csv',dtype=dtypes,usecols = predictors_10_target)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array(['agen_for_log_de', 'ruta_for_log_de', 'cliente_for_log_de',\n",
" 'producto_for_log_de', 'agen_ruta_for_log_de',\n",
" 'agen_cliente_for_log_de', 'agen_producto_for_log_de',\n",
" 'ruta_cliente_for_log_de', 'ruta_producto_for_log_de',\n",
" 'cliente_producto_for_log_de', 'cliente_for_log_sum', 'corr',\n",
" 't_min_1', 't_min_2', 't_min_3', 't_min_4', 't_min_5', 't1_min_t2',\n",
" 't1_min_t3', 't1_min_t4', 't1_min_t5', 't2_min_t3', 't2_min_t4',\n",
" 't2_min_t5', 't3_min_t4', 't3_min_t5', 't4_min_t5', 'LR_prod',\n",
" 'LR_prod_corr', 'target', 't_m_5_cum', 't_m_4_cum', 't_m_3_cum',\n",
" 't_m_2_cum', 't_m_1_cum', 'NombreCliente', 'weight',\n",
" 'weight_per_piece', 'pieces'], dtype=object)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_pivot_xgb_time1.columns.values"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"train_pivot_56789_to_10 = pd.read_pickle('train_pivot_56789_to_10_new.pickle')"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array(['Cliente_ID', 'Producto_ID', 'id', 'Semana', 'Agencia_ID',\n",
" 'Canal_ID', 'Ruta_SAK', 'agen_for_log_de', 'ruta_for_log_de',\n",
" 'cliente_for_log_de', 'producto_for_log_de', 'agen_ruta_for_log_de',\n",
" 'agen_cliente_for_log_de', 'agen_producto_for_log_de',\n",
" 'ruta_cliente_for_log_de', 'ruta_producto_for_log_de',\n",
" 'cliente_producto_for_log_de', 'cliente_for_log_sum', 'corr',\n",
" 't_min_1', 't_min_2', 't_min_3', 't_min_4', 't_min_5', 't1_min_t2',\n",
" 't1_min_t3', 't1_min_t4', 't1_min_t5', 't2_min_t3', 't2_min_t4',\n",
" 't2_min_t5', 't3_min_t4', 't3_min_t5', 't4_min_t5', 'LR_prod',\n",
" 'LR_prod_corr', 't_m_5_cum', 't_m_4_cum', 't_m_3_cum', 't_m_2_cum',\n",
" 't_m_1_cum', 'NombreCliente', 'weight', 'weight_per_piece', 'pieces'], dtype=object)"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_pivot_56789_to_10.columns.values"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def normalize_dataset_10(train_dataset,test_dataset):\n",
" train_dataset_normalize = train_dataset[predictors_10]\n",
" train_dataset_normalize['label'] = 0 \n",
" \n",
" test_dataset_normalize = test_dataset[predictors_10]\n",
" test_dataset_normalize['label'] = 1\n",
" \n",
" whole_dataset = pd.concat([train_dataset_normalize,test_dataset_normalize],copy = False)\n",
" whole_dataset_normalize = whole_dataset.apply(f,axis = 0)\n",
" \n",
" train_dataset_normalize = whole_dataset_normalize.loc[whole_dataset.label == 0]\n",
" test_dataset_normalize = whole_dataset_normalize.loc[whole_dataset.label==1]\n",
" \n",
" train_dataset_normalize.drop(['label'],axis = 1,inplace = True)\n",
" test_dataset_normalize.drop(['label'],axis =1,inplace = True)\n",
" \n",
" train_dataset_normalize['target'] = train_dataset['target'] \n",
" \n",
"# target = train_dataset['target']\n",
" return train_dataset_normalize,test_dataset_normalize"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/ipykernel/__main__.py:6: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
"/usr/local/lib/python2.7/dist-packages/ipykernel/__main__.py:14: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
"/usr/local/lib/python2.7/dist-packages/ipykernel/__main__.py:15: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
"/usr/local/lib/python2.7/dist-packages/ipykernel/__main__.py:17: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n"
]
}
],
"source": [
"train_dataset_10_normalize, test_dataset_10_normalize = normalize_dataset_10(train_pivot_xgb_time1,\n",
" train_pivot_56789_to_10)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"train_dataset_10_normalize.to_csv('train_dataset_10_normalize.csv')\n",
"test_dataset_10_normalize.to_csv('test_dataset_10_normalize.csv')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"train_dataset_10_normalize = pd.read_csv('train_dataset_10_normalize.csv', index_col=0)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(20768652, 39)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_dataset_10_normalize.shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### prepare for stack model training data, 10% sample, 40 bagging\n",
"----------------"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# from sklearn.externals import joblib\n",
"\n",
"# for i in range(20):\n",
"# train_dataset_10_normalize.fillna(-99,inplace = True)\n",
"# train_dataset_10_normalize.reset_index(drop = True, inplace = True)\n",
"\n",
"# train_dataset_10_normalize_sample = train_dataset_10_normalize[predictors_10_target].sample(2000000)\n",
"\n",
"# train_label_10 = train_dataset_10_normalize_sample['target']\n",
"# train_feature_10 = train_dataset_10_normalize_sample.drop(['target'],axis = 1)\n",
"\n",
"# gc.collect()\n",
"\n",
"# clf = RandomForestRegressor(n_estimators=1400,\n",
"# n_jobs = 11,\n",
"# max_depth = 22,\n",
"# max_features = 'log2',\n",
"# bootstrap = True)\n",
"\n",
"# clf.fit(train_feature_10,train_label_10)\n",
"# print 'model already fitted'\n",
" \n",
"# # save the model to disk\n",
"# filename = 'RF'+str(i)+'.model'\n",
"# joblib.dump(clf, filename)\n",
" \n",
"# print 'finished'"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"# submission_10 = pd.DataFrame()\n",
"# i = 0\n",
"# clf = joblib.load('filename.pkl') \n",
"# submission_10['predict_' + str(i)] = clf.predict(train_dataset_10_normalize[predictors_10])"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'train_dataset_10_normalize' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-1-b901674e841c>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0mi\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;36m0\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0mtrain_dataset_10_normalize\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfillna\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m-\u001b[0m\u001b[0;36m99\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0minplace\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 3\u001b[0m \u001b[0mtrain_dataset_10_normalize\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mreset_index\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdrop\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mTrue\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0minplace\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0mgc\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcollect\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mNameError\u001b[0m: name 'train_dataset_10_normalize' is not defined"
]
}
],
"source": [
"i = 0\n",
"train_dataset_10_normalize.fillna(-99,inplace = True)\n",
"train_dataset_10_normalize.reset_index(drop = True, inplace = True)\n",
"\n",
"gc.collect()\n",
"submission_10 = pd.DataFrame()\n",
"\n",
"for i in range(20):\n",
" train_dataset_10_normalize_sample = train_dataset_10_normalize[predictors_10_target].sample(20000)\n",
"\n",
" train_label_10 = train_dataset_10_normalize_sample['target']\n",
" train_feature_10 = train_dataset_10_normalize_sample.drop(['target'],axis = 1)\n",
"\n",
" gc.collect()\n",
"\n",
" clf = RandomForestRegressor(n_estimators=40,\n",
" n_jobs = 1,\n",
" max_depth = 6,\n",
" max_features = 'log2',\n",
" bootstrap = False,\n",
" verbose = 1)\n",
"\n",
" clf.fit(train_feature_10,train_label_10)\n",
"\n",
" submission_10['predict_' + str(i)] = clf.predict(train_dataset_10_normalize[predictors_10])\n",
" print submission_10.head()\n",
" submission_10['predict_' + str(i)].loc[train_dataset_10_normalize_sample.index.values] = np.nan\n",
" print clf.score(train_dataset_10_normalize[predictors_10],train_dataset_10_normalize['target'])\n",
" print str(i) + '__predicting finished!'\n",
" gc.collect()\n",
"\n",
"print 'finished'"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"# # gird search \n",
"# # create model\n",
"# # svr_rbf = SVR(kernel='rbf', C=1e3, epsilon = 0.1,gamma=0.1)\n",
"# random_forest_regressor = RandomForestRegressor(n_jobs = 5,\n",
"# verbose = True,\n",
"# # max_depth = 5,\n",
"# bootstrap = True)\n",
"\n",
"# # grid search epochs, batch size and optimizer# use a full grid over all parameters\n",
"# param_grid = {\"n_estimators\":[1400,1600],\n",
"# \"max_depth\": [12,20,25],\n",
"# # \"max_depth\": [5,None],\n",
"# \"max_features\": ['log2','sqrt']}\n",
"# # \"min_samples_leaf\": [5, 10]}\n",
"# # \"min_samples_split\": [10,15,100], \n",
"\n",
"# # more complex para:\n",
"# # gamma = numpy.array([50, 100, 150])\n",
"# # degree = numpy.array([5, 10, 20])\n",
"# # param_grid = dict(kernel=kernel, C = C, batch_size=batches, init=init)\n",
"\n",
"\n",
"# grid = grid_search.GridSearchCV(random_forest_regressor, param_grid=param_grid)\n",
"# grid_result = grid.fit(train_nn_time1, label_nn_time1)\n",
"\n",
"# # summarize results\n",
"# print(\"Best: %f using %s\" % (grid_result.best_score_, grid_result.best_params_))\n",
"# for params, mean_score, scores in grid_result.grid_scores_:\n",
"# print(\"%f (%f) with: %r\" % (scores.mean(), scores.std(), params))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[CV] no parameters to be set .........................................\n"
]
}
],
"source": [
"# # evaluate model with standardized dataset\n",
"# # numpy.random.seed(seed)\n",
"seed = 42\n",
"\n",
"# # parameter for svr:\n",
"# # C = penalty before 'square loss', the larger the C, the more bias and less variance\n",
"\n",
"\n",
"train_dataset_10_normalize.fillna(-99,inplace = True)\n",
"train_dataset_10_normalize.reset_index(drop = True, inplace = True)\n",
"\n",
"# train_dataset_10_normalize_sample = train_dataset_10_normalize[predictors_10_target]\n",
"\n",
"train_label_10 = train_dataset_10_normalize['target']\n",
"train_feature_10 = train_dataset_10_normalize.drop(['target'],axis = 1)\n",
"# # gamma means parameter before(in) gussian kernel, the larger the gamma, the larger the bias and less variance\n",
"clf = RandomForestRegressor(n_estimators=1400,\n",
" n_jobs = 11,\n",
" max_depth = 22,\n",
" max_features = 'log2',\n",
" bootstrap = True)\n",
"\n",
"\n",
"\n",
"kfold = KFold(n=len(train_label_10), n_folds=5, random_state=seed)\n",
"results = cross_val_score(clf,train_feature_10, train_label_10,scoring='mean_squared_error' ,cv=kfold,verbose = 3)\n",
"print results\n",
"print(\"Standardized: %.2f (%.2f) MSE\" % (results.mean(), results.std()))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
keiikegami/envelopetheorem | ほうらくせん.ipynb | 1 | 181033 | {
"cells": [
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# -*- coding: utf-8 -*-"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAY0AAAEZCAYAAABrUHmEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzsvXmYXUd55/8pSdZiydosa7WklmRZli1Z3mXjOBgIEAIE\n",
"mBD2TFgSICEDk2RCDAmBQBZDtvllm8lAMoQt20wgG3GAsE0SsDHeN1n7vne31N1Sq7f6/fGtl6pb\n",
"t869t9UtS9D3fZ56zrnnnqVOnXPeb73fqvd9nfeetrSlLW1pS1takUnnuwJtaUtb2tKW7x5pg0Zb\n",
"2tKWtrSlZWmDRlva0pa2tKVlaYNGW9rSlra0pWVpg0Zb2tKWtrSlZWmDRlva0pa2tKVlaYNGW9rS\n",
"lnMuzrk7nXN7z3c92jJ2aYNGW74rxDnX4Zwbcc6Nyzt7LpSYc+4DzrlPjuc5z1YupLq05XtL2qDR\n",
"lu82ceftwuMEWA3OP+Vcnr8tbRkPaYNGW85anHPLnXN/65w74pw75pz7g7B9knPul51zu5xzh51z\n",
"f+6cmx3+M4vhPzvndjvnjjrn3puc8xbn3P3OuRPOuUPOud8Of309LLudcz3Ouc3OuTXOuS+Hax91\n",
"zn3KOTcnOdcu59zPO+ceds51O+f+0jk3zTk3E/hnYGk410nn3OLC/X3cOfc/nHOfd871Anc655Y6\n",
"5/5vuOcdzrn/Evb9QeA9wKvDOR9M6vC85JzfsQCStnizc2438K/OuR93zv2bc+63nHOd4Ro/mBz/\n",
"Rufc9lDnHc651xXqXVWXpc65v3fOHXfObXXO/USDZ/tDzrnHw3X2Oed+PvnvZc65h8Iz2uace2HY\n",
"/ibn3BPhmO3Oubc2OH+xHdvyXSDe+3Zpl1EXYDLwMPA7wAxgGvCs8N+bga1ABzAT+L/AJ8J/HcAI\n",
"8CfhmGuBfmBd+P8bwOvD+sXA5rC+Mhw3KanDGuB5wEXAAuBrwO8l/+8EvgksBuYBTwBvC/89G9jb\n",
"5B4/DnQDt4XfM4BvA78MTAFWAduBF4T/32/3mdXhucnv9wOfzNri4+Hc04E3AgPAW5BV9XZgf9h/\n",
"JnACWBt+LwKurqh7qS5fB/4QmApsAo4Az6k4/iBwe1ifA1wf1m8JbfK88Htp8ux+CFgV1r8f6EuO\n",
"u9PaG3VWK9uxXS7s0rY02nK2cguwBPgF7/1p7/0Z7/1/hP9eD/yO936X974P9Xpfk9E7vxqOeQSB\n",
"z6awfQBY65xb4L0/5b2/N2yvo6W899u99//qvR/03h8Dfg+BQSq/770/5L3vAv4BuK7qfAXxwOe8\n",
"998Iv68FFnjvf817P+S93wl8DHhNcs5m5y39/4HQhv3h927v/Z967z3wCWCJc25h+G8E2Oicm+G9\n",
"P+y9f6LBdb5zLefccuBZwC967we89w+Huv/niuMHgGucc7O99ye89w+G7W8B/tR7/68A3vsD3vst\n",
"Yf3zoU3w3n8d+AJwR+HcN9O4HdtyAUsbNNpytrIcKbeRwn9LgN3J7z2oR7ko2XYoWT8FzArrbwGu\n",
"BJ50zt3nnHtxVQWcc4sC5bTPOXcC+CRwabZbep3TyXValX3J+kpEaXVZQYC4sHxoy5IPyH+nzt77\n",
"U2F1VgDgVyPr44Bz7h+dc+tavMZSoDOcw2QPsKxi/x9BlsMu59xXnXO3hu2XI6ugTpxzL3LOfTPQ\n",
"X13h+Px5wLlrx7Y8A9IGjbacrewFVjjnJhf+O4CoF5MVwBBwuNlJvffbvPev895fBnwY+D/OuRmo\n",
"15/LbwDDwAbv/Rzgx2j9nW41vHO63x5gp/d+XlJme+9fEv4vAWgfopVM6sZORlEXvPdf8N6/IJzn\n",
"KeCjFbvmdTkAzHfOpaC5glpQTK9zv/f+5cBlwOeAvw5/7QWuyPd3zk1DNORHgIXe+3nA5ylbVntp\n",
"3I5tuYClDRptOVu5F/HedzvnLnbOTXfOPSv89xfAz4aB3llIuf9lhVVSI865NzjnLgs/TyCFOgIc\n",
"Dcs1ye6zkFI+6ZxbBvzCKOp/GLjUhQH6qupkv+8Depxz73bOzXDOTXbObXDO3ZScs8M5lx73EKLm\n",
"poT9foRRgERNZZxbGAahZwKD6N6HK3avqYv3fi/wH8BvhskA16Kxp08VrnORc+71zrk53vthoCe5\n",
"zp8Cb3LOPddpwsOyYO1MDeUYMOKcexHwgoq6NWvHtlzA0gaNtpyVBAB4Kep17kG9x1eFv/8MUUVf\n",
"B3Yg+imdHdNIab4QeMw514PGKF4Txj5OAb8O/HuYVXQL8KvADQhc/gH1dBud29v/3vunELjtCOer\n",
"sgC+c75wzy9B4yI7EJD9L8CA52/C8rhz7v6w/j4EdF3AB4BPF65Rec1sn0nAzwL7geNovOCnKu61\n",
"VJfXIgvwAPC3wK94779ccfwbgJ2B9nsrGqfCe/8t4E3o2XQDXwVWeO97gHcii6QzXOvvSvcRgKhR\n",
"O7blAhansba2tKUtbWlLW5pL29JoS1va0pa2tCxt0GhLW9rSlra0LG3QaEtb2tKWtrQsbdBoS1va\n",
"0pa2tCzfMwHSnHPtEf22tKUtbTkL8d63HAj0ewY0JP5nkfXkwrKV9XzbZBTLKC1TCtualSkottJ0\n",
"FFdojFbdB0JpSU6jOfy92bIPOImmqNryRMXvHjRF8hIUe8jKXDRXfxrwx+j+5iPP3/nJ+tSzuLcR\n",
"NJX0CJqGeSRbT7edCte4DHkSfxCFIvlaOMdS5Jm+ONS1FelD01EPommte0PZF5YnUTys5Sh21lLg\n",
"38KxK5B3dcHZ8Tv3Z9fYGcquZP0gau9FKKTGQuB+9C6tovF01D5gW1K2omnQg8B6FG/KIf+IFahd\n",
"SuJDnZ5KysFw7G8Da4ne/Usr7q8LeCyUx9H026uAXwnn34k8wktOofuBB5Fvy75wjV8K+x6h7DF+\n",
"JhxzP4pCcDWaEuxRTLMZhXt8CvhWuNcXALeitppCvW/OHnhrD/yve4CXo+nTg+i55PX4Jmr755PE\n",
"Ssv2O4iewzKgyi9lL4qTdiv65nLpQW27gXKEgz3hPpYX/jse6jQvbhpd4OjvmSm3sjQu6HsZQcr8\n",
"NHqZreS/K7a9/Db43Gcpg0G6BH0os0KZma3PphYEqsoljC0M+WmkMDrRi5qvJ9vWvgq2/jp6mRcg\n",
"5dCs5MqgkZxEH6sBQr5+GDmvzUWKalm2vBx9gK2EIDmMPvo9fMd/5c5b4au/hxTLHAQCq4DVyXrJ\n",
"TySVHuTTsDWUbUjpDYZ6r83KcqqfXz+wBXgSKdAtqKMwLdRpfVLmV5zjFFJcj8HLlsHf/Wm43lJg\n",
"YyhXI5DNZSRc+yEUd+w4UsJXANcj/41S+JFTwCMIJLaHe1+IlO9NFcfsRgDxBHon54Tz31K4twHg\n",
"ARRMsRs972vhfd8HH8pB4gQCiR3hfjqA29GzSGUfAoku9E3dQL1HfTdylu0M97CZWrAYDve8D7Xn\n",
"TVndz6C2PIme+1XZ+Z9GbWzvscmI/nNXTWBLg/+P6EE8UrHe7P8R9DJaGcp+Nyvp/qb0h9BHYZFM\n",
"p49y/WKYMw+4jTIQ2PrFjG++iR7qLZDLgBvRR//nlIFgINQrtUAuTdY31G571XLgp0dZt36i1TEF\n",
"KYK9wO9SCwj9qFeVg8Gzk9+LaM0S7EVAYODy/5DVtQd5Qk9Gyn9FUq6HzZuAV9D4extECu4ypDD+\n",
"HjkC7kdKYz4REG5Ewf1WNqj3cDh2BXqnP4AU4kCo/1UIFF4OrKMahHsQmExFDoF/Feq6AD3HjbBh\n",
"M9Xe3ydRR6UbWQ29SHluQM/sFZSB5XSo00ng1xBgLEKg8sOUY2aZBbADWYIzEHDdAryysL9H38sX\n",
"kNJeihT2T1PzHU1O9/8/qGNwJQoA+cLCeUeAfwx1vhH4T4V9QGC2H7VD6TynkCW7nAiMqfQi0F0X\n",
"6p3f21YEqldm/w2hb2Ul9QDTVL7XLI1f5NzQU2dbpjEu1BTI8fbOVnY8Ta3lkVsjOQiUSg9qi5ya\n",
"moM8u28B/hUpuRIo5L2yVu7NQoUcaaEMIJBcjBTJL6Ge7TcRaC1KSit18eG8B9BHnC8PEa2E9Ugh\n",
"TQltcClSzFU9cpJnd4BIR+0gUlR96D15QbiXAUS3dFBDA9XJCHoGW5OyPZxvOnA3isy7G4FIB9Xv\n",
"4iHUEbCyN7TLTyDP/5NI8a+ouL+TwKNEaqoT0WB3o7Y6EH6XOjV7iLTUQWR5/UKoq4FOLj2oje5H\n",
"SvxFKEz+EPF7TqUv7Psg+hbejoCvH7VVKgPI2ngIuAS+8jp4ziTKdNMOBDjzgB+kLL3o3RxEz7hE\n",
"zXWG611DbWBPk1PIWlpPbSwzk31I31xW+O8Aej/z+wyhaNzc0Vga32ugcb6rUSXD1FJOjSiqqvVe\n",
"6kEgBwSPem2zspJaIyUqai711NRY5BT1FkhujaTLPvQxXope+gWhXEZU/ouT9VGMl3CSajA4EK5v\n",
"EXhTSyQtS2lulZ8hUlJWdoelXeNyRP8YLWXLRmMuQ+E8O0J5GoFDdzhuFepJrg3LNVS3zwgCqhQc\n",
"jiBFvhIppKvDsoouGwzHGUDsJo7FXIvAewNly2UoOdZoqWmh3teHUnr3OpGV9AACFVBb3oJ68rml\n",
"MhyucS9Spsbv3xLqlivtoygu19Zw7DJk1a/J9hsmUmq9CChuQT39VPrC+fajZ3E1Gm9LFfNpZGkc\n",
"I9JWKb3mwz3sQ99t3jb94f8+9A6sTP4bIdJxV1JLdfWgjso81IaAG9VA+PcaaPwWrVNQ6XojeqoV\n",
"GqqqlKipfFnalv9XNUaRA8N4SskiOY0C7g0iuuMo9cBwGn3EZn2Y8l9ALRik63kPqJn0op7xYaSM\n",
"NyPl/Oth26FQlxH0caTKPweEnIOukiPhGleinu/HUbyrveg5z0Qf7krUG0+XpcHMVI6GOm9E78sv\n",
"IIVwCrXlSgQwBgxrafy8D4T/5wBfQhMWetF7dAW14DCv4hyniFTWw8Bvouc+G/WGDSCqBtU70TvQ\n",
"j6yn46E+1yA65lrKz92iAh8jRjHuQEr1espWxzACgq8C96D37kaUtyMHIbMWBhG12IMomtuptxZt\n",
"332ImluMwKQ0wAwaG7oXtesNVA/234faIaeNCPX6BgLhUtj7PjSWtL5wb8PI0lxJfUekDz3T3BIZ\n",
"AjdlIoPG+2idlqr6rxk9NbXJ/2mZzjPrC2PUVMkiyempbmoBIf1tymE+UipW7kB0xX7gK8n2dL/R\n",
"WAEmZ5DiPFYoBgKHQxlEymdxKO9Gyuv+cA+2/VJaG98ZIFoeVtLfx9AzXAw8F+V9OI2UwwqkQJpR\n",
"YKdRj3w7kZraQZyZtARl2rsO9QIHkKJs1JbHUc/4aaL1cQyB6A8B7wrn2Yl6olXnOoF6pU8gK2An\n",
"Uj63Ab8Y1g9QrSj7EMBZ6ULvw4fR+38MdQ5KspNISx1Bz/EdVM98ItTlATQg3oWCKa5F71DJYtuL\n",
"ntXT6Bm+ET3PIeqtxwPIQtiLAiqupUxJdSPFfhSNCc0mjo+YDKF3cj+ipEoWVA8CELM6S/83miW1\n",
"E7V13inxxNlnOXCdQKCc3PvEtjTOdzVKUkVNNdpW+q+HehBIwWAQfWRmicweQxnLBIkz6GPuoh4A\n",
"cmA4GvafQbQ+0qXRUwYEC0dRN0/swedAYMXGEpYhU31ZYb3BWMV35BgCBaOjbLkfKe7ZRMWwGtEe\n",
"q2medOgwAhoDme3hvKD2uDIrjSya/UhxGi2V0kpXh3IN1eAwmBz/aKjLcLiHa0OpoqXOIOX3MKK0\n",
"TiJAWYcsgusqjtuLAOJh9D5NQ4r8Jso0Uy+ifB5Aiv3icE+bqR8n8KFO96Lnd3G4h83UW0D70ZjE\n",
"ofDfemTFpJ0FjwBwC9E6uoVasLZZULvDea6lvr0fC/c9C1krqUVpVsYAet7p+3MGPZvJoX7pd7IP\n",
"tfkaaoH1KHAK3MqJDBq/zjNDTw20sM9gOKdZHNOJfhvTG2ybgV7gmU1Kvk/JFD5bOYN6JJ1EAOhC\n",
"A42L0UDwN7L/bNbUxUSrI1X+OSDYcrSWSRfR8rgI0Qq7EV12KJQT6KO5DPXiq0ChFVpskAg4t6Je\n",
"53vRQOmRsM8iIjWVlmU0tjTPoN7iTKQ87kWUjM3EWkYEmDVIYTYaGD+BLJDVYf0dSDFcFOqzDimU\n",
"axqcZyAcswy19X9Fymo2onGMmqoCF7MsBlEO8CPI6tuIeP2rKT9zo6X2Ip8QG+swgMg7C6kF8EkE\n",
"aCuQ0t9AfbubZbEX5RCZjxT/dYV9Qd/u34U2uC7UvbTfKeCfwj1vpjwTrBelCVgR6la61v3IGinN\n",
"ZupDIL2eeqt2AIFCyVLpQm2at3cfNTMtLxBLwzn3Z8CLgSPe+43Zfz8P/BbKE9wZtr0HJYUZBt7p\n",
"vf9C2H4j4o+nA5/33r+r4noe/Icoz4xqNGsq/c+c+FJnvqr1qv9M+Z8NTTMWsaQ8Vsxhb7RlBNU/\n",
"paXmo17N3ai9/gb1hOZTS0+djYXSR60Vki8NCI6Fus0nWh4/i5SRzVE3Z75WB/JPIjDYR7Q+0nWb\n",
"9rkc5dL+T0Q/jJWUZ6qk4hHgmBWyPZRdxBS3N6HxAod6kZfTeJxlgFpa6mniTKelwO8ji8Om75aU\n",
"GMh6fZJITW0L516GlPb0cK8LKdN8p5HF8QiRlpqN3pFZqKdfdR/bkTXwUDjuNpR1cQR9/7liNIe8\n",
"+1FPfjLwc+E+S7TUUDj3t9B79BLUay9RTUOoA/AwaqvXUH6Ph8L5nkLPbGNhH9AzfAoByOWF/0+H\n",
"611GecyiFz2Xq6kft7JptJdT/1yto5dbrx6957kVOsR36PgLBzTuQA3wiRQ0QoL7jxJMU+99p3Pu\n",
"auAzCPmXocG7td5775y7D/gZ7/19zrnPA7/vvb+ncL0LkZ46E0o6Uyr/XdrWVyinKrb3oRdgOtHq\n",
"SOmpOdRST3Ma/DebsY3BnCJaHSk9VQKEo6HelxCtkVJZhMDgMlr3QTlDBBujp1JAOIRA1maQWFmW\n",
"rTcD/kGksHcXSjdSPssQVZFSU43GGCD2LNOyM9zXJcQB8XWhVA1Gg9p7S1K2h/PMJVJS14S6ldp3\n",
"CAHT46HsCNsWIItjE9W01CniTKkniD3caxAtdS1lgNiCFKvNAJodrnMTZQtnP7J8tyDgW4iooesK\n",
"5+8kem4PIaB9FrWzjwjX/Ua492H0TtxBPV25FVFOfeg5PIvawfqR8P8eBG7XUg8mW9A7Y7Ok0rY8\n",
"gUBkEmq3FEhOoucxm1pLYwQ95xnZtYbQN7CYGiv7AgENAOdcB/APGWj8DfAhZPoZaLwHGPHefzjs\n",
"cw+iG3YDX/berw/bXwPc6b1/e+FaHvz7qXfia+Tgly9tRlQ+M2poFOsGAo5IPZVoqapi4xKjKeM5\n",
"2H6KOFhuXtxdaNbNrcjM/hi1tFQX+rDMoc8sjyogsJlTo7FM0jGKQ0jp3ok+xruS7adDPRajjzil\n",
"p6wsobU260If2SnUc+xBjl87UIfIQop0IKWTLpt5jx8OdbdZNu9Fg7DDqO3WoDa3ZQfV7XUGKYkr\n",
"ULv8HnJYm4SU4lUIXK5CyqV07+bwtQp9C3choLoE0SIbkNIq+GkAMczHMMqoeCD83oSU99qK69oM\n",
"sS3AHyEFuBEBRD7l1e51GgKHPwzHX42slRw8R9B36BCFtIXolJcrf5uBdRA5Vq6kHgBS+Rp6PzYX\n",
"rmvn+3q4zrXUA7JHVtpU1L659KJ3b13hWJvQkl/XEycipDKC2qvkp3HRBQ0azrmXIaX/s865nUTQ\n",
"+APgm977T4f9Pgb8MzLj7/bePz9svwN4t/f+pYVrefAfpnUnvtJ6q1RUo9/ng5oaIFodNjCexpSy\n",
"0ui35YE2KyWlpuYjp77VyEO1h1pwmMfZjamcJFodaUmtEZs+OwkBjoHBzyBF9ni4X6OsWm37w+ij\n",
"tLI/WbexigUIZO4K17LQFStpHsakF72/u1DnZ2c4/jB655YhALqTOFV5GY2tqX1Ei+HpcL5+9Lze\n",
"gWZ39SAAqJpKO4x6x2Y5bAnXnoVmPC1BVtKciroMEAe1Hwl1n4nGYuaG+y4B5jCyHB4Ky5MoRtPL\n",
"w3/2LabSj3rp30bPZ2m4z0lEJZ+KWRGPo+/xraFuJVrqUNh3P5pttor6GVCgDsID4TwvLJwH9L7c\n",
"jzoQJdrqTDjHHARwufSiZ3I19VSb+f+spjwT6iLqqaq+cJ68k1FB5Y1uyu0zFkbEOXcx6k09P908\n",
"vlf5wC/G9Ttp0YP6XEmJhmpEUTWjp3orttsYRGp5XEIt/WTLtTSmqFp5Ht9Xsb2XaJmk9FQJDMyH\n",
"Yg7R+liYrK9Kftv02Sq5Jvt9AimEg8kyBYWj6ONbhD5ysz5uTX5XjVWkPd8uBAa7suV+orWwClkI\n",
"HYiOWVNxbru/4XCe7WiMwaipbqQcOoiU1PMpKxIbzzlJjCu1BSkl86GxAe0fRe9Ergfmhro8TQw8\n",
"uCO5r43Ieng19eA5K1z7YQQQTxP9PTYi+uV1Wb0nIzB+BI0b7CTO7LoJTZPNgWgS0YHvQLiHK5B1\n",
"8EPUi4FPd2ij69BYR3rvNq70APq2FlAOQXIMTZXtRO/wTYVrWptdhDoct2X/P4HeldmhLtcn/x1F\n",
"z30mek5rk//2huuuoLZj0IPe9+XUUlhHiY6zATC+PAhfHoEpJWBpKs+YpeGc24jGKk6Fvy9HjbYZ\n",
"RaXEe393OO4eNG99N/CVhJ56LfDsBvTUezi7eFM5PdWMomr0u59aaip31mtW8llRs5r8Hk/gTf04\n",
"bCZOF/qoX4M+lp+jFhi6UNuZX0daUkoqBYVLGR2lNoJ66AYEFyGluQcNhh9CvT1z5luSFQOG5TQG\n",
"IBOL27SP6JD2EIrUeiD8v4AICGlZSuNn0o+UiUO0xBY0Q6kHPf/VSPlZWUO1I59HIDMZKZGHkSPd\n",
"CGrvq5JyBWUFYee4HLXrHyJaxWbymId3aVAX1PaLw3l+I5xrKdHDOx8rALXfAPouvo1mPy0gOuSV\n",
"/DpsUsJh4H+G+t0U9s+By3rUvYhKvRh1CjZS+2zMshgBPhuOexZ6jqmYpbIbAcp1qENQkgfD/tdT\n",
"fsefCPUtHX8CfU/59SFOOc6tigHUnlVtkErJ4hoBN+mCpaey/1J6ygbCbyEOhF8RBsLvBd6JkP2f\n",
"aDwQ/t8Zn9lTVRRU1bZ0e6thuMdLzlBvkfRSSz2daLI8Gc5lYUaMnjLl/4PINLcwFikwzOPsgKuL\n",
"GO48Lfk262UvJILA25Ai24KU8GgGygeppaL2UktTmWm/DCm8u5HSfjTcbzNQGAnn3JWV3ajDNBuB\n",
"xd3oQ99F3cBknXQSQ56b9WBhRG5BQDEJtVejGV27ibSUUUTTkAf69aF+VQ6p/eGYx4ghQGag8ckF\n",
"RKWey2lkQTwU6n0GeBUKGFmimECdk2+F65xAlMELKdNHhPN+EwH6dSgOVUkGkGXyBHqfXl5xvm40\n",
"vtSN4m6VZuN1hzrORECTyyACkIspT7PtRs/jGurBvEGcLw6hZ5y3W0+hngPo20nvsdDmF8iYhnPu\n",
"L9CLcSlSBL/ivf/fyf87gJuSKbfvRVNuh4B3ee//JWy3Kbcz0JTbd1Zc70KaPdWIemqlVFFS+e8R\n",
"agfOzQpJAw3ObmF9rLGm0kHz1AopgUEneonnEa2Phdl6uq1ZCA4TGyg/WCgGCNabTy2P5cn65TQf\n",
"q6gChV3EiLDLidTUqmS9kef4EWpzYmxDCmISaoe1xMHsdVRbHxb2/CkiwPSisZ41SIFtoMyfQxzz\n",
"sNhSu8K2S8Nx5shXaqdOooe3eZYvRIr8BspWRx+yNizw4JRQz1tCHXMAO4mU9WPhvuYiwLuxcD+d\n",
"aAbU7vB7OVLwubXZjUBnH3o/NlAfK6oPdVwPoba/nvqZXDtQe9tMp9Q6M2dC81vJnROtI3MZ9TOh\n",
"tob1fDKBxdValmwbRN9BGhxyBLVbOgU6Cex4gYDGMy0BNH6O8Zk9NZo4U/l/UE1J5dtK+6T01KyK\n",
"5bmgpsw6SYvFlXpzuN4voF6aAUN3qMMcahMwpfRUDgKteFinMkgcmzhIjAa7Cw3OHwz1mEy0RiwB\n",
"k60bIFQp2lROEK2P65AV8Angf4d7nk6cMbUqW1b5RJgcQFy1Bdn7MLKebZbTWkQj2bIq/AbEqLzX\n",
"oTZ6G2qnNOz5ejRbqGpywJ6w/2wUyvtT6B0zWupaqqfzHkRt44DfQYptOQKHGyhHaj2NntNUxCb8\n",
"C1J4N4djciAaIjrI/juKKrwaKf6SM5s58D2IJmxcjWip/Llbb3sHouKuRs8kVeJG5fShkDlrKM9y\n",
"Itx7V7iHEgW4jRiVORdzii39VxWCpTTZwHRYboHk1lnBWpvYoPHHjN/sqVYoqfz/Zzo/Sckqyemp\n",
"FARKvy0Meh4B1+ipK9BMpX40zTAFhVaD/aXiiQPizTL0nUK9xxQI3oZ62lvRx7+E1q2RXmI2vjQj\n",
"316kcC1vhUVEfRcxMutKGmfPAymOXdRn5kuj3L4W5YM4FUojYDhFpKW2IWpwH3pXlyFqqNlsJ8Ix\n",
"lnDpcWLSo9ehweDE0atYh8eQ5fF4uMcZaMxxEVJ4JVA6gZT3A6h9R9DMpyspx30i3ON9oZ4GhB2U\n",
"ufg+ZB08gsDojegdKVFYTyPr5CQa1C5ReMNhn22UI9yC2uJb4Rp3UN9ew4hSu4jyLKrD6N0uWVBH\n",
"Q73z9+EMur/8W+tHbZi2ow91yLc1AYSJDRrnuxpQnhnVYna+72zLQSCnpixD33TK1kgpD0ZVaeZP\n",
"0Eg8UlhpZj6LeGv0VAoCNqhuIUTGKzvfALV01AHq6SmbwbM8KSuSdes1N5JeasHAlgdCW9jMr7Ss\n",
"pjGoGTAYOGxFFsBQqK9FtV2LLICqeFXD4RwWW+op4pTMVcTIthsoW1xGg1jgwd1EesloqWsoj70c\n",
"IYYuPxC2pVZHafLBMTS+8DBS5jPDdWxcM5ed1FJNHciKyAeUR8I5H0QdIgtfnofnGCCCxEg4323Z\n",
"/Q0j2swc8zZQb+HsQW0NauOUsjJfjG4E7nlU223om1hJ7XM9He7XJo6Y9KP3OXc8tfDqKT13gtoZ\n",
"kSNhWRivmtig8TOM3+yp0dJTw8RZU2eboS+lp/Iw6Dk9NZ7UVMkC6ULK/w5EgXwKTVYwYDhBzDVs\n",
"tFSakCl28v8+AAAgAElEQVSlp6yM1jI5Ta3yvwQNiD6NrJ+DSOnOIFojS7N1S9fazAocCeczq8Om\n",
"Y74TKRfzoi6BQolaSKUPUSGDSIkeQmFJ+qlP1XplqG/V8z2FePO16H34X8gZbWY41sBhHdWgeyjc\n",
"71JkRfxaOH49ccyi6p5SWup3keJbjeidGygDZDcx2sBnkJK1cYurCvfaRwS2TyOleG3YPwc8myU0\n",
"hLIKgpR/rtzNuhlEIe3nhv1KbeRRVsaZ4Z5K9I5FGaiipHYSadtcjhHHIlMZJsb5SsV0U27RBee8\n",
"un1H6ew7sUHjY5wbeqqVMs4+J03lNNXJmHqoH5/IgeFE2N8RB8XTZEzzkPJ/Z/j9TXSfBgjNqJqS\n",
"DNNadr5j6IOYRS0AvA0p6u3oeS2h9VwcR6mlpiyP917UFlPD+VagGFM/gJRdN81BxxIl7czKPqKj\n",
"3ZXAB1G7HUHWVtXHPRSON8vj6XD+IdT+b0RTjs8gy62qbgeJIc+fIIZ5fw5qyxKdYdJLjC1lM61m\n",
"IlrqMsoKC0TBfBtZHYeQQn9PuN+SQhsgxonah9rqnVQ/1+3EmVJrqE6l2oNmQO1CIHpHxX5PIuBc\n",
"QtkHaRBZGz1oFleuuEfC8VMpBxvci+6xRHftpZxPpgt1kPLnYt7zqZSovhYoqVQmNmiczyp49IK1\n",
"koWv0X9pTozSWIXNmsoz9KVWySXUZ+Mr/W5lYLhKRojWSGdh2UktEBhVYvGkzPpI1+13aUphlfQQ\n",
"6agDSbHfx8J+5sy3gkhL2bKV2WNpqta0WHKjDuqz8pVoFhOPgMByYWxFCtEUwxpqw54vp1oR7KIW\n",
"HDpR+3UQw55fTRnofbj2I6HsCdsWE2NLXUUZWA4ggHgQPePJod43IOu0RH1uQeMW5vS3EFkpNxX2\n",
"7yemaD0Z6n89GjjPZ0odRWCyJ9R1HaKvcoX8OALD/nCPm6n3nn8s1G8ycbZaKnuRtTQp/J8+55Fw\n",
"/h70HqT/DaNn5NEzTe/BvpEOasH4IDGAqEk/0jV5Jr+pRFD2obRgdUxs0Hgr54aealYgJm8aTWa+\n",
"0j4pPVUChPGkpjxxTnhuhXQhRfuj6CP4RSIgnAz3m9JSabHtKRiM1jLpRh+SKf/5iJp6FM2aOkTk\n",
"/S0j39JCaeS3YNJHTNHqkV/KcaJDowUezEFhFY0tnWGiBXIzaoPfBT5HbapWK2uonpY7hEBlMpqc\n",
"8Dh6JtPCcSk4VI1TGa24ClkE7yb2kA0gSmMmHrWN+Q38d6Q4r0AAsYkyzWOzf0ZQXKluIs1UmpVl\n",
"wHASBTW9FFFIpWiwNgC/Fc2quiacNwcT63XbeMtt1I+x2D5PoPf+FupzZTjUfnvCPZSUsY1DlNq/\n",
"KmLwaSLDUbq/VEqW2iitipJMbND4BKPL3Jeu5/RUqxn6xjOPRati1khqgaSWSEpPlQChO+w7mbIl\n",
"Mhcp6ZehD2R7OM5A4WwGzweptTwOV6ybH8dcBFopNXU5+jCnoV5iK9yteXcbFbUnWd+PPs45RAvk\n",
"7ai3dwgpwmYzs44RkyTtTJYW0XUl8ArkJHaGSLtVyT5qw55bfKmZqOf838J991MNWEeIIc8fJ4aS\n",
"2ISAYjLVM5hOIovj4XDsKfQuvA/1dqsc8nYSw51biO7/1qCO3cjisIHwm9D7VpLTYd9HURu+lnI+\n",
"EBt4fjjc249Q9kXZF+o6BU3fLuXqeAi12x2UKaFH0LtRop22o2ecTzseQM8mjzFW8qMA3ff0bN9x\n",
"oKNymdigcb4un1ooZ5uZL12WgMDWPfXUVF5Sx725FcuxUFPD1OYFL5WUnjLnskVEOqpqfTR+HEeJ\n",
"dNR+aumpA9Q6860olMtpDvqnEciUUrV61GM2C8QSJq2ieapWo6UMHDqJyZIs7PmVlONLmRwienc/\n",
"gdp6EqKyrgmlES21HSnYh4k5ORYhcLmWalpqK6KlHkEAMR0Not+IZhiVes0PonGLg+F+ViMQLI0D\n",
"HER+GTvD7xUo2VYeysRmQD2JwGQx8uHIrZiDCHS6ibOp8oH+PQiUhtAkgzywoAWLtFhS6Xs6hCit\n",
"M+iZpVRSH5osMJda58YR9B7NzOprqY+XUks15dFrE+e878hZgsfEBo03cnaZ+5rRU1WZ+iz0cmp5\n",
"pNRTM1qqtE9OT13CuaGmRihbI7beh+iPEdRjO4CUXU+4zwXU01L5NgOE0QDUCHGw/HC47mLUI7wf\n",
"DZIeQ+2wkFpqalm23sqU3UNE62MlopG+Gu59ECncDuqBoeS8lsoRpJRBlMhh4PXh/hZTCwxXUj2u\n",
"4tGYxRHEvw8ga8jCTFyTlCqryPxi1iPL4d3h3lJaquQvMoLotY7w+7fDfZgzXCkEhnnmL0SA+3vo\n",
"vb4lHJM/kwFi0M1HgC+G85bCktt4zzDwt8iKeFah7jZI34mc9zZRnpo7CQHK0+i5pxaFKeAeBBil\n",
"WV4gYFtKOc5TN+VOUDo7LL1eaQxiHOinZjKxQeMvqaaemv1O6alm1JT9fz6kZInkpYeo/EuAkFJT\n",
"c5OS/t6EnNBOoB6RAcHZWCgDSNkYDVW13kNM02rWxzLgJ5Gi3ROu30rQQdDHuZ+YszstFu12CQKL\n",
"NQiQptJ8dpPdU2p57EAgYTOUzMP73QgQuqgOVw5ScGnY863oOdmYxbtRezSipTqJsaUeRwpxClJ4\n",
"d4XjqqZkdhOpnafCdRagyNRzKCuvkbDvA6i3fwoB008W9jXZhvwzdobj30h1jo5dyDfjIFL6VbGi\n",
"DoRzHkedi9L5usM+fWhsrPQeP0Ec9yhN7X0UgWF+fptMsIR68E/D5qTSi55HCroj1GcutI5pE6/u\n",
"scjEBo1n+rIj1FsfKc1Uop5a+b8KDFJqKrVA0pKGRS+BwVipqSHKdNSxwrYj6COdQQSBvCxO1lut\n",
"1zBSJDZX/kC2PBz2mYMojZXoQ1+ZrDejwTwxVavRUwYOlqp1FVLoaWk1VasBhDkGLiHO1FmHAKeK\n",
"4uqmFhz2he2LqbU8qqyHrcR8GOZhvhR1FDaFa5cA4glESxlAWEa9G6nOUX0fGh+wgHqbKM9YGg77\n",
"PYgUrYUvv4n6DtpWZHV2EUOL50EBT6MptwfRe1WKTLsfAcEAsqauzf7fF641HXl4p2NRp4h5O66i\n",
"1oKyzlAeRaAHfScrqKUcD6P3ppFznrEh52AMdWKDxuuop55G89voqSo6qmrGVGqZzKCedhrN79J4\n",
"xSWMPzWVWiKl9R9HH9L7UIyg4wgAUmqq2XIRrXt1g9r9ENH6OIz4+RcgBfBfiJFZLSOflcuT9UU0\n",
"bytLbrM7lJeFen8QZZW0sB8rQzsYKKyicSTjPiLAPBspx99BMaZmET27DRwa0Vz7kdKy6aj/A8Vs\n",
"WkQtOFTNEOtGPfrrkVJ+b9i2nggQJfA0P5G16Nv4rXCcAcQVhWP6iYPm+1FI8uVo3GI99c+jM+zr\n",
"gb9ESv6WcD/5IPEgavNd6D24iXrvaqOkRhC9aOlo8/uaQvRB2USZkjILNb+G7XOQ8kD8QLhGPnA+\n",
"HI7LqbzSoPZZOOedrXgu4zBHWTKhQeNvGTs9lVNTpd/nY8YU1FohPdRTUjk9lYNBN/ogJlNLS+Vl\n",
"IfAT4ZqPIMW3gOYB+arqfLiF0o8AJrU8FqPsa5eij7jVsCc+nNMsEQMGo6bMUjDL4/uIMZjO0Nzi\n",
"sfGKtFjoj3kIXF6MHPAG0btW5YBnUWmtPIV6o5ND3d6ElGnVbCfQ87aZUo8j68Uh0HtPqFOVMuok\n",
"DoZvI/pO3EV1W59BVsG3UbuOoHDkz63YfwBRWN9GnY+liJYq3c8AcabUIJr2XJoGbLGndiNwKznv\n",
"9aOB8sMIwEvg+hQxr09+v6dQu3ZQb7X1EzPq5fdxMFwrp57svUullPfiHI9jeGZxknt4IbdzLw4m\n",
"NGg8k5dMB81Ty6REQTWip0q/S4Bg1FRKS11CPVVVoqfSMhZqahApNKOimi1tqqgBQb5M11tN03qa\n",
"CAb7knUrJ9DHupgYAt3AoQNRA82u1UNtNr7dCBhMGS8l5u62REmNnO8IdbNQ5VvC+Wy6r1kdZoFU\n",
"+bT0EsHhCaS0RpBSvYYY9rxkPRjvbgBxkDjT6npE3+Shvgl1fATRQRan6TKiQ17pWnvQWMRW9J2Y\n",
"E90m6oHrIFL+NlNqOQLxfAbUSTSjai/qvK1DYJoH5/s2atspxJAqqRxFFNggeidyWmsfMSrttdS+\n",
"K53h3Bb6JZVdqG1WUfseHEDfbUpb9qN2nZ1tS53z4BxYHRfRz6d5HT/KZ0GAepeDf53IoPFKxk5P\n",
"5dRU/tsigqYWSBU91UrJKaqUnkrBYLx6HsOULZC0fD8Ko/HXiJowamoa6nGVyqWFbaNJSGXpKg8n\n",
"y2tQ6IYvAD+PPqxLiFRUurT1Vry7jxMBoRfFgTqDrAOb2thBBBqbNdWISjJHvm3ISnheuI/XU5uq\n",
"1YChg2qF0IUAZlG49n+g57CAWnCoig/VjZTbJqQ8fzvU62oEDtdRBiabXrwOvecfDssbEECUHPKO\n",
"oo7BxWig+YuI/7+NegthGCn/eahj8dfhWqVevs0wGkJh2xehGU557x3UjlWOeeZXMoisl6soU1Kn\n",
"0PMqjc0MEf2UcimF9oCyc17JgngGZkfBJAb5HX6e/8ofgDotvwT8LUp05ycyaPwj9ZRTiYYqbSvR\n",
"UyVq6pmOMWVi1FROQ5W29aAPKAeDPnSP86i1PvLfP4o+kO3onhcwurEJkz7qgSBfWppWc+ZbnJSf\n",
"QMrkYKhPK9bIaWpzghs9tSucB6TMOhAovApZC+aM1+j5nkFjFZa/25aWfMk8vN+BFF6jmU42T9+s\n",
"j6dC/Vy49+ciJ7ZGSqWPmE3vMdSmIEvo58N5qnqrR4gJk3aH66xC4eCrwP4Esji+jZT+VPSMOir2\n",
"P4YsjieR0v4BBBAl2YFoKQsd/rzCPiPh2lvQe/FiygH7Hgz3dDNl6+kJ1Fa3UA9WvWiiwpWF/46h\n",
"9ys/pzEEudXVg96DtP1LMbvOIXAM824+wod5L+hb+ADwcbwfsj0mOmg8E5fyROsjtUJsvRHt1Op/\n",
"ORhYrKmUjmq0PpsyKJzNmITJAPqgjX5qVDpRD+8SakEgpaesXEbrJngX9YBgWfkOhjqaJZJm5+sI\n",
"pVk02uFwrl1ZScdBUlrKqKlGgNpNBAWbTtsTjrmC2jzeVbk1zoTjDRx2EfOUbyDm8S5N6TVa6qFQ\n",
"LEbUamIe7xLXfwqNQ3wLtfMkRO3dgiyVUsTVhxGoHCHGf7qd+nYfQsr/IQR8c4gUWU7P3B/ufQg9\n",
"y9uoV+ZPhjKMgO+G7Dzd4XoWODAf4DYKci5qx/RYi3q8klrL6QzqMCymFixOofc0jTlVcs4bDsvJ\n",
"2X7jBB4jvIFP8gneiNO1fxP4Q7w/ne850UHjh2lMQzXbVkVL2TrEzGO5NWLL0dJTecnBYRbjx2sa\n",
"NdVN2RLpQr3Ud6AP9ccQCFj4ccuDkVJQ+W+jqkYzWeAY+jDT8qxQ/gr1jkxJXk49KFwe6t3smsMI\n",
"AHYhJbEc9Wi/Ge55GlKMHdRn5Wtk5RxDVscONKA+G83C+jpSNOuJwJAHqkulF7X7QLj3TuCnkbVi\n",
"tNRG6j2jTboQMF0frvE/0XjE1WHbJsqD292oza9CnZYPo+d9EzFmVi47kSKdhGimI8Tw6Pn9dYXr\n",
"XoQsj51I+edTYK33OwWN2+xGoJM7LRr1cxRZDbljnllXI+E8V1AL7Pb/adTGpcCSpaCAJlXOeXCe\n",
"6Kf0cs/li3yeFzONodMoTthH8L676oiJDhpfZPzoqXz5TGflS6WfSDv1trBeoqd60X2Y1VFazkOz\n",
"UNYh6mgQKepWw4+ncpJIQ+XFtneidl+AemxLwnIpmvJriuFSWgPOo0TLIy27UHsYKKxCPe23hG2N\n",
"aCSTQ9Tn8DY6aQkaGH0pUmBV8ZlMbFD8ybDcg5TLAqTYfyrUq0rh9CNl+Bji6Q+F/ZYhkFnR4Nj9\n",
"iL55kJiDfCNqi6o67yfOaLJsgz9F9aSKLcTw5bPQDLASWJ0M+21H7+arKSvpnaG+pxAol3xhnkTP\n",
"xLzsc7HQ8DdTbxl2oXtcRz11tJ9ovefHzMr2H0KAlHYwngHnPJ3yah7j37mdufQMo4CPH8L7A82O\n",
"nOigca4vk/txNKOnzqacohYIhonWR05DVZXZ1IPCWKgpi4dj9FO6fizb3hWOmUstDbWksN7IQzoV\n",
"m0JrILCXWlCwgHyLqc3MN5rw5yeozcZn6+bhfTm1ObzX0jiC7mliNj4DCPNC7yDm8F5Pec4/1GbT\n",
"e4w4G2k+MZveRspK1GipBxFtdAwpuLXIGriecpscQ7TUg6G+05EFcgtlZXwMDYA/TkxLahZKbp0d\n",
"QDOgDiR1KdFN+8I5bfB5M+VYUQ+jd3M5snLSjl0vorYGiaFfUtlKjPHUUfhvED3r9B6OIqDroBZg\n",
"D6F3ObWwTqL2PcfOeZ4l7OffuZ1V7AFZ5u/D+62tnmGig8YLGR96KgcDM5urrJCpSWlEO7WyPQeI\n",
"8XrJhonWR9XyNArd7dFArHH5M6mlotJlvq1VIAC1a2qNHAzLFyEl8CcodpEL5zc6Kk/VWjUWkMop\n",
"asHg5eF8vwF8NpxjNfVZ+Rp5ePcTgeFSNOvsSZRVcC5SOuuI4FB1rjOod74n3PtkFPvqAFLYGxFA\n",
"dFQcfxz1pG9Az+qTiAbaQOPQ5QeQcrsKKejfQcr5RjS+kNNM/eGY1ejb+Fi471sph9Y4hp7baRQr\n",
"ajVlD28LiX6aGOY8p65Oh3swn48N1IKN9d4NLJdTpqT6wjnmFY41GjZXoJaVM7d2SxblM0RHeS6h\n",
"m3/mRdzOvaAZhu/F+2+P9kwXDGg45/4MzW444r3fGLb9FjIvB5BJ+ibv/Ynw33uAN6MH8U7v/RfC\n",
"9huBj6Mez+e99++quJ4H/zXGRk9VjVOcL2c+iNRUTj+Viu1j6VoNDFJqKi8pNXUV4tJPIerobKgp\n",
"j5TYUSIgGBik4NCN2tfoKCsr0IymSURl0kyGiBZImpFvb7jWIOLFDRQ2o/hDrcyDP01tFr2taOzC\n",
"fCyuQErux1FPt5HSOEEctH2SmAJ2NgKVNyErrOocA8QkQkZLma/FmyiH6TbZRQxdfhy1/e0oGGVV\n",
"fZ9CPf7tqK02Aa+s2L+HaHH0I8vkOYX9PNFXpA8Bbe4rAXo/voGA51kV92Yxukr+FqA2Ph7qkls9\n",
"e8P112X3M4iAMY+APIi+i3x8xcAslfy9GlcgmcYp/opX8TL+CYKvBd5/+WzPdyGBxh1IWX0iAY3n\n",
"I0eSEefc3QDe+7ucc1ej3ME3I172S8BarznE9wE/472/zzn3eeD3vff3FK53rumpnJKqWhrFVKKd\n",
"Wt1mIGAhCZrRUSktldJTVsZCTfUjADBKKl3m2wycFlCdlW9JKK1aJPYRW1ypPGWrhT9PLRAry6kN\n",
"MV0SGxzfmZW9qP0NGIySupJ6eiI/3w7qU7WOIIC0REnrw3lKH+sIUtRPInB4Glkj84i01LWUo9oO\n",
"I2X/KAKILiLFdCNS/KWB+O1ohpHl0LCYTrdSpuEeQ+McFhRxddg3n446RASTNHx5Pvh8Cvg3YqY6\n",
"yxiYSmc4V384Ps/P3R/uwailfMLAUwiMVlHrczOELL3ZWf1H0LuRpzc+ReyIpNfOO5jNxrYyaYwt\n",
"kxngj/lp3sqfQuZr0fo16uWCAY1QmQ7gHww0sv9eAfyI9/4NwcoY8d5/OPx3D5oxsxv4svd+fdj+\n",
"GuBO7/3bC+fz4J/D+NJTA+jBT6Kakkq3TaNMO108im0pSJwraiot6bZ3o4/tHcDnw/3PoD5DXw4E\n",
"tt5KiA+TQWJWvjRV6+tQz/2DwKfC9S3UueXFSMGhmf+IxQrag5R5Z7i/YRTFtwf1VFdnZRnVX7AP\n",
"59salq9Hz/5dCHDWEAdk11Gd9nUIAcJTyIlxPvAJ5CC3lggQayrqcgyBw3UIUD6H4i5tIObEKAGE\n",
"OSCuCm3zJ6GeN1Hv6WzX8Qg89qLYXNeH/fPz96DvYVqo2zbk4Z0DT8r534u+n+uz+7QQGz6cayW1\n",
"ijrt0e9BgJRaFKaFLapz6V3ppfzePsP+FI1kmPfxIT7Ir0KFr8VY5LsJNP4B+Avv/Wecc38AfNN7\n",
"/+nw38eAf0Ym9d3e++eH7XcA7/bev7RwPg/+G5Rpp0aUlP1nwQdzYDhfznygj6YRHXWywXYDgjwM\n",
"ui0vpRYMFgE/FK57NPw3WtCyEOhVGfosfetJ9AEvIdJSy5Cyfklyrlac+U5Qn5HP1i0vuQ12rkYz\n",
"nFbTvBdovcwdRMvhadSmU4mOfC9HSr2RQrH4UpYs6WlkVV6CetOvoEyvmAwhq8Mi0x5G7+1KBFgl\n",
"RW+yjZgw6STqlLwY0UIlSeNKHUTt9yMIyEvyFLI4DiML4ccoj90cQp7tRxDov4h6C3AQ0S17UNve\n",
"UDjPdtR+Kwp18sgC6g/H5s93K9F3KJUT6H3InfO6kYWR1nMAtUn6rM8RHTXCj/Hn/DlvbuprMRYZ\n",
"LWicl2mkzrlfAga8958Z3zN/4La4fmcoY5YR9KKU6KjSek47nc26UVPTqM7OdwkRBBZRCwjp8mw8\n",
"ua1X2EN9Nj4LeZ6DwmmkNCymVJqRb02yvoTWLJKp6KNNqan9REA4SJxJZFbHSjRl2H43us7kcD87\n",
"qc2JsRM9g6lEoLkCTQcteQmbOARYFvb86XCuAfQsjJYyJV8CLB/qYLGlDFxmo8HwTQj0SrSUhcl4\n",
"OBzbiwDiGmQRvLJwzREEEPdTS6HdiMYX8/Gs00jxPxLW54V9X0e9Ltkb9j2K2uw6BI65sv0G6hxO\n",
"Cu1yK6Kv0mv+O3oXliIKOx3f6ENAA6L80g7qCAKREQTOKbieRO/Tcmrb0zpeS4ngN4KUdhqVwBiK\n",
"ydRm2Mun156FeO7kX/kXXsTUFn0tRiPOuTsZg3J8xi0N59wbUZKW53nv+8O2uwC893eH3/cA70cv\n",
"8lcSeuq1wLMb0FO3U089VVFSpf9yUIBaC6QUXsRmTLWamS//rwoUzlWsKUvIlOe+eAnqNf8J8Kuh\n",
"XWZTzspXStc6mgHzNOhgmp71vyBF/S4Ujn0+9eHPVyJAaDZWAVKcu4kh0FeiHu63wrUWUpuNr5XQ\n",
"5+ZAtwVROrcC/w/1AjuIwQfXEZ3fcknB4Uqk0L4B/FE4zhz5rqg4/ggCiOtRG/0zoqWuRcr5KsoA\n",
"8TjxeT0O/D2NAw/uRO0+NZz/IFLoKwvnPoSeySAKA9+BQC59j43unRHOtTtcP48VZdb/NqTQU2or\n",
"7cXvRSB3UeH/HsrfkX3npUx7Vc/qGWIbPOt4kv/gdubTPSpfi7HIBU1POed+EE3re7b3/liynw2E\n",
"30IcCL8iDITfizKq3YdexkYD4d/m7EKjW8a+tJxPZz5oLUNfCgI5MNgU2qnUJ2GaR32a1ueg6Zon\n",
"OTsv9FPUZ+Mr/e5HYJSmZ12GFN330/pH6hHQ7EmKAcQBpHzmESPcXoFmZbVCeR0l5sSwpTngLUaK\n",
"/QYEtI3qavGlLDLtk6h9pyOweC6Ne3zDCJxsttEh4ljEa6meLTUSjrufWv+J16DeeEmOIDB9DPXe\n",
"56G4UiVfDnPKM+/1m1Ho8VwG0HiFjaG8nPrZcCPh3nYhcLid+jY9EO5ncaH+HrWvoz5vxwBq/xXU\n",
"TwY5iN77i7L9R6jtAJWm27Yy624U4lnGXv6NO+g4S1+LscgFAxrOub9AL9ICpCzej2L7T0W0AMA3\n",
"vPc/HfZ/LzKJh4B3ee//JWy3Kbcz0JTbd1Zc71zMnmolZ/gAo8vWly/zMOh5hr5SxNuUnkrpqPz3\n",
"2Xhym6TWyDHqM/KloHAm1GdRRbGYUwtpLfKt9VzNEklDoe8O9ZmCwGZloSyhsTIfQkoqBYXtCCzM\n",
"w9tiTK1BtEaVAx6hPmk2vm3E6KdriZbDVZSfiUe9+seQkrfZUrPCcY0i0/YTAw/acbOR1XEz5fGO\n",
"U0iZPxDqPi3st5lygqVdiCKyGFRXIOWeD24PohlQ24kBEJ9FvcK2WWEjYZ+bqJ/e+h8InJYgiyr9\n",
"vy/c82RE+aX0kk1LvqRwL3vDNVNLyaN3LQeQ3FLxCEDyUOxjsEI88zjOl/gBbuBhGIOvxVjkggGN\n",
"Z1oCaNzM6EOje+rBwWYllKionKaaRpmKKv3O/zN6KgeE8TKHh6gNJZJaIikYrELT9x5Ag6SOOFhe\n",
"ysqXAsJCWs+FQbh2DgaHgA+hj/+VqAebZ+ZbRhy3aJaqdYTa5Eu7UYdkMeq8fA3RJwYKVkqhr00G\n",
"EBhsQW34prDtLehdsJDnV4VzVVmqexE4XIw6VQeAX0b0mIU8r5otdQiNJ9wY6noPorWuQ4q1o3CM\n",
"5bZeh96zryKluhnRR/kMoX4Ezleg9+evEC24mXrAOxrOOR09s72UPbwtP7olWNpErQWTZrZLI/2a\n",
"pD37w+idK7VP7tdjSr00E8que16c82bQx2d5BS/kizAOvhZjkYkOGo8ydnoqT4RyPiSnpkpJmYye\n",
"ynNjpNTUNMqJmIyeMiC4ESnp/nDMaD8aizNlJU/ZehgB1Ei4to1PGBhsQoqvVbPfsqbtzsqeUJep\n",
"1CZfuhVRn80Uwmlqs/FtIw5mzySOP7ySxp7iPtTHIts+TgzjsQZZAC9rcK/mN/AYsiAOo3d0FaKY\n",
"cm9pk35E9TwY6j+EFOybKecCMWrnPtR2DlkoL6PcTk+GfTsRwL+acvypbaEOvcgiKYUfsci/MxBN\n",
"l4PsgfD/MgR4qZwJ9Z5P/fiKdYg6qG3fkie4bc/vIQeTcQOSyQzwJ7yNt/BxGEdfi7HIRAeN8Txl\n",
"TkNVxZoyeiqno6roqfx3HgbdU2+BVGXrqwKEuYwuAVIqHvUMzQpJl7ae0lPD1ObCsGWepe8yWvvw\n",
"bJA8z8pncaYsrEkHMUlSumyWmdCyr1kujO1IwZuzllkfFvp8FdVWwymk2NKMfL2o572aGD4kD3mR\n",
"itFSjyF6ySKrXkMc2C7RUhZb6QFi1rhFyOK4gTKddhjRTOa1PS/sfwv1YxcjaNzioXCtSxHYbaT+\n",
"Oe/lcIMAACAASURBVD6GwKo/1GEz9dSVOeb1oXfiZmrf0ZFwP8cR0F1HreI+iaysmag9L8r+24EA\n",
"Jr3uEHq2S6ilyHrDfynwn0HP+Zw45zmGeQ+/wa/zK3AOfC3GIhMdNDYxdnoqd+ZrRFEZPdWIfmpW\n",
"cmAYL9N4kHL4c7NGDARGgP+NFOBVxGmspex8VgwMFtL6R+XD9YyWMlA4gTLLTUID4f3Uhj5fRm0Y\n",
"9GbjNCepTdU6giZS9KIetHHdaVlBYwtnHxEYXhbq8mcoTpKFPF+PetRVVJ3NeOpGfg9nUB7uS4mx\n",
"paosiINIKd8c9v8CUrA3hFLKod2DeuMWyO//ondic8V19qD38TL0XL6KqKbV2X4D6DkuRc/q60jB\n",
"53UwSopw38uopRV9qI9NrT5DrTWUWp3HqaUOTTt7Ym75XEo51c+Dc57ntXyGT/EGJp1DX4uxyEQH\n",
"jS2cXeyplJ46n858UB9rqlG2vhIgdBFDfaeWRx4G3eipq4j89dnMGOukNujg4Wx5CCnySUixLKUW\n",
"FG5GiqnVD7qTCAjp8kC4hwXEpEsdKMZUo7EKiI58adjz7UTnwA4ECs9BVFoj2U8Mef4kAguHgOk6\n",
"lBWxygocIA4SP4aU82Rk+byaeirGpAs541m4cxeOeRNlkDXfhofCPc5CM8tKWe56kXXyNGrfZ1N2\n",
"ujuELJPj6H0qzabajaycyagtc4A9SHTcy4HtJHouq6inmCz0SL79GAKqtENQomDPAR3leS5f4p94\n",
"CdMZGHdfi/GUiQ4a43Gq3F+j2XpKT1WVZln60jDoZn1UhUJPf5cAYazUVCuZ+WyMwqOPMs/Ol5dW\n",
"gg4Srm00VEpJ7UPK10JZdFCbIKkDgVGzGVM7qc+JcZKYqjUNfZ4n7kllGHkXGzg8hRR3CjAWX6oq\n",
"xtZuBA6PhHoMUhtbaiNlqq2LOPPJpuCuRDOQrq845kmk0HejNlqOxnnyKaqgdv434kypNcjiyB0K\n",
"TwBfRu/BJQhI8rGLM8gS6SLm+M7zcxsltTjcd6rgjyPrbkHh3PvRs1tDLfh0om8yH0jvptbSGUHP\n",
"8aJs2xjHMz3X8QBf5U7m0PuM+VqMRSY6aKxn9LGnUnoKojNfVRj0fFtKT7Va0rhTKTU1XrGmBqin\n",
"pvLfBgAfQx/lnah3bdRUmpEvX7cxilY/sAGi1ZGOUThkrvcgT+451GbjS2mp0kBuKiNo9s4uYk6M\n",
"O0P5e9TTW00MPGjUVKNgjscQOGxDCv0l4dzvDudYn5Sq85xA4LAbWQtTwj0PIyW5iWoL4gCipW4N\n",
"1/8iskBuREq6NE6yl5hFbxD4c9Rz30w5A94WBHCTga+gHnspfPl+9AymhDpMpt5n4hTxG9kbtuXW\n",
"i8WT6g3XzxX5JPRNnqB2zMH+qwpTPs6+E6MVTwc7+Tp3sJwD8Az7WoxFJjpo7OTsYk9N4fw784Es\n",
"kjwEeqPfORh0oY/STPU89Hm6vgB90Ndydua4jVHkYc/zcoYYZ8qm0RoY3EpzMDCxabQ7iaCwKxSz\n",
"FozWWIVm3Hx/C/d1jJgTwwDiCHovlqAe7jUofEcjUD+MevRPhOXBsH0pauNXUW1xnUGK+BEEMCdQ\n",
"h2QtcuJbUnHcXmrjSk1HbWrTpkv7fwNRQMPh/K+izP0/HM59Ilz/ldQDySlihr55iArMz3UU0WDD\n",
"iLLKrTeL73Ul9YP3R4lpaNNrD6F3YVl2vdNEH6d0X0ftsxtHgPHM5zhf5jls4jE4T74WY5GJDhpj\n",
"PU2ema9RCPScniqFOc9Lvo/FmbLZHDk11SwMegkQRuMzkcow9Vn48nVbWprWy6jNxJcubb00P750\n",
"7QPUZuVLs/PZjKTlRFrKSgfNZ0wdIQYdNIAwusBStV6ZLBuFbd9NzIfxBDFr4HIELhZjqsqXZD8a\n",
"e3iEOC12ATG21DWUn+Fh4mymTgSS65FVcA3lnvc3keI/jtpvPWWgHkGUlAX7uyzslzsG2n47kbJe\n",
"T31k2hHkmHcYtePN1M7M8uH+u1DHIZ9Oexi18QpqKSaPnl0ecNAiA1xGbbuVwojk43ZjGruYQS9/\n",
"zY/yEu6B8+xrMRaZ6KCxhrOLPVXKzNcoS1+6T1U49FZ+z2T8w6AbNZWHPc/XjyKa5XY0u+hzlLPy\n",
"5dn5LqP5wHIqJ4nWyEEiNbUQRQjYiQLZLSPSUmm61stpHnTRUrVaOYziZ01HzncniGMVBg55pNNU\n",
"eokJfg6gUOpTUTa9QSIwXE21v8YJNOi7PdzfLOBPQxuYX0pp4JlwzBNosHgWotcOIIAoOeQNIwvF\n",
"8mYcQ6Htr0NjJDmgHEeD4SvQ8/laOHdu0fQhELk07PcUAon0+oNE73WLrpzTbTYxo584pdjEFLlH\n",
"Hal8zKORc17JYjjnM6QmM8Af8Q7exsfgAvG1GItMdNA4wNln7jvfcobWsvOlJQeDnJpqVBYiRXE2\n",
"H9gItVn5UlCw5VGiM5+FQF9CBIXbaJ632+QEMYRICg77kcJcQEzPaqErqigdkzOo52rg8HS4xjBS\n",
"kpYP4wU0zgXeRYxK+zi1Hs3XoCm6VRTcaWKyJItMOxP14F9F2VrxSHnfH44ZCPV7CeXw6kPESLbH\n",
"EAC/CAFeLseQlbAfKemXUA+uI8hS2IaU/Qspe4A/HOr2fdSP9+xAILiR+nGWfeG4fKqvhR7K26SU\n",
"3TEHmXGhoxzDvJdf49f4AFxgvhZjkYkOGmM5RU45tRIG3dZLtFMrv42eGkTK3jLv5Zn4WsnONxZq\n",
"aoj6THxHK7adRB/kIiINlYKCldE48+2hPiPfXgRMhHtbQaSmDBwaJUqyc1tsqR0IGHagHu8lCBSs\n",
"rKNxfKluRCkZQOwL25chcLBSZYUdQYr74VAH89behHrv6ygrNhuHeIQIKhuQQ14pYGEXCvhpU2QX\n",
"hn03UT/ecAT5mhxFin0D6kjk+20PdR8iDqrn79oD6DnOQYP0KRj4UP/uUOc8o95OojWYApCFNFmR\n",
"Xe9kWKZgMUAcnzQZp7GLEd7CR/kobz+neS3Ol0x00Lic0c2eMlPWUUs5VdFUpXVz6GslO1++NHpq\n",
"vAbhz1Cfma+q/DCibj4K/Bq1VNRC6ukp29aqdeCJSZfSsg8pprcgB7K7iJn40ox8rc6Y2kPMibET\n",
"0TNvQErqLmLY8yuQYl5NdXtbfKmnQ3kxAoJ/DMUCD15D2aEOIi31ZDh+MaKXHiHGiCpl8hsOx2wJ\n",
"x00H/hYB343U57Im/PdtZJlcisYktlM9brEl3P+0UJ9hBCZ5BNe9iGLy4fxrqQcBm900gJ5zDgQ2\n",
"S+pMOGdKMRolVRqkTtvjvMSFSi/3g/wjf8crmMrwBe1rMRaZ6KBxjNZnT51vJ75UBqnPwneyYj39\n",
"nYKAecbOJ1oejdarckU3kyFqaam8HAj1mYIUl1kgtlyO6KNWB8j3Ey2R3URw6KY2UdJqBBC303x8\n",
"aA+1yZJ2ECP1riXmyagKIw7q9T+elP1h+xIELC+gesyiD1kcDxFDesxFz+RHKA/sDyJFbwmTQODz\n",
"Wso01nHiTKnBsG/JsdCy5W1Bz9bSuOayDYHSIBprWZD93xXqN4SeQe5U+DR6Zvl7N4SAbjH1wHQI\n",
"vUN5DKkZ2bacjhojuHg28QBf+y7ytRiLTHTQGO1hnjgQ3oyCqlo3eqqUiS9f5ttOEQcJjXJK6adG\n",
"S8uLYSBwttTUIOop5pTU0cL2/nCdFASWUg8MpcxyJTlGbYrWdNmLlIvlBbf4UmY5NMv+t5NaaspC\n",
"n1uq1jRZ0iqqgcamw1rY8p0IzBYSo9JuoF6JmnSiIH8PhXrYsTYYfiVlCuVRYi6KIWTl3YAUeml2\n",
"15MoGZTd4zoEznm9PJoB9WSoy0qk5PNn1o38NnqR4r6V+rGDJ8I9GSWVgp1RUn2hLnkYkKdCPXOK\n",
"7UhYppbcCDFzXrotd85rASwa7eJZzm6+xrNZdR7yWpwvmeigsZDms6e+cwi1fho59dTq75SeuniU\n",
"6zM5e2WfyxmkoMzy6MyW6fo1wEeQMns1kX5a2GB9NCHQB4hWx4Fk/SDqGb8AORV+hpiJLy+tzJhK\n",
"QWEXCjG+FNFtO6kNe55TLKn4cLwFHVyM2uUA8D6k9DYicKiyHk4Sw3/cGY65Fyley4dRmrE1TJxl\n",
"9VL0Lv4lej9upjygfxgN3t+GwO4eBCQ3UG/BHUaKezXqrHwD0V15W+wl5jvZi551TnFZPCmbCJHX\n",
"zSipfvR9pRaF0U1VVsF5dM7zzOcYX+J5XM+j8F3oazEWmeigYTGOqsqFKENI4RjlNJqlAUFKTVmZ\n",
"1+D3FbQe2iOVPtSTTUEgXR5AimkG0QJZlqwvRwqrFemmPiOfLW3GVAoKVWMFqZwghuQ2auoEUm5r\n",
"0HjIBsrZ40wsLLcBxO5Qn0XIie/51M/8MelBFsdDyIKw/OE3oTGmEmV3AlFS5tswDQHYD1Pm/I3C\n",
"6kTA8wLKiZh2IlrqBAKzF1E/1nMoXLcPDaavyP7vQu0AskTSToUnUl5XU/v9WcDMVdn2XtTuqcVi\n",
"M5PSuo0y+my1XEwPn+XlvIAvw3exr8VYZKKDRiu7VvlpDGQlp6CqtqX0VE49leiodH0AKYGUmsop\n",
"qqptRk/N5+xjTQ0Ss+8ZFVVaP4Y+1EuIQQfzYuDQSl08kYoyILByMPy/gPqMfKsQ8DR6wXuIPXcr\n",
"+8I5FxKj0lrSpCqLZgQpYIsttRUBxlzigPgGqqf2HkfTVx8ihtRYRhwMzxUwoY7fRBagTR/vQLOV\n",
"NlKvKIdR/CdzyluQ7Ju30QE08cAGsDdTD252vmPo3bqJenprF6K25ob7SMcuRsL9jqDxoFT52ySD\n",
"pdT6tgwjcFpCLYC04px31nIR/XyUn+DH+TR8D/hajEUmOmjMpQwKJo3CiFRRUKWS7jOdevopL1X/\n",
"tTIY3IoYNZVSUlXrU9BMoB7U659PLQW1KPttNFWrltpJYma+vHwIKev3IkWXg8JKWp8xlYLCZcB/\n",
"QwD4c8SsfFYa+WwcJALDcTTjajKiuizd6gaqw5b3IZB6jJhv4lHgX5BSvY7yNNzTaDC8E/ghpBA/\n",
"g8DkJurHbEbCNYYQDXUK0Sg3Uk+ZDYY6XY3e0ccRmOfpT08gpT0/3Id5aaeShjg/TP3zGQjXsGUq\n",
"Rj1VKfvSAMM5nSE1iWE+wC/zPu6G7yFfi7HIRAeNM1y4M6RKMkykplLaqdG29HcnMRf1/KxcWtg2\n",
"HymYZulSS9JJtDxKgGAJmSwzn1ketm6+Fc1kmForJC1GJa2kFhTyHNO5DKBxjzQq7WFi+A/Lh/H9\n",
"VAceHAzH26D4HqL1sgHFVSrl1wa13YOh2HGL0JjEcygD8m5kcTwZrn0p8AOUHfi6Ufjy7QhcVqNp\n",
"u3mb9CJLZh/RyS+nKTuRz0UPotvygWpzZpyKACu9Rj+i/OZTDz77UAcrtVxK0WehHoDGYbxjhDfz\n",
"MT7K2y7YvBbnSyY6aJT+ahRCpBE91QotZaWPaoqqqhg1lVNQpTKnYtt8miclqpIhpOwtC9+RQjmM\n",
"PrBJSGmZJZIDwjLqp0Y2uu5WyqDQQ22MqQ5qs/I18hHxSJltpTZVq1FKVxLB4Soax5fahqyFR5ES\n",
"tCmxVxPDlldZRF1oFtODyIqZhKwHi0xbsjqGEC30QDh+JqLAbqU8TnMcWTL7kLV6JfK8zge3h5A1\n",
"sg+9a+uQNZSDyf3UzoLKPeAtN/k8ZDnlYUQso17uS2LRlPPZaSfD75S+GgzHjvPYhef5/Av/yEuZ\n",
"ytD3rK/FWGSig8YMaimpRpFtq+ipUpnW4D+jp0ZbxsuhbwApkc5Cybd3I2/hucDzELgtIlJSpfVG\n",
"ubBzOUJtilajqY4Bn0RK/w3EqZ4d2bJRmHKIiXjSREl3oYHeP0bcdJoPo4PqdrZYSuZQ99aw/98g\n",
"8NkYyhWUwbAXWRyPIiDZjADr7xFAXE95ttZxBA5TkJXRi7LqXRtKriRtIHwT6qVvR216M/Udht3o\n",
"/V+FOibbqI89NYQ6A8uIfjClAW4D1WPUWwc+1NNmS6X/Neo4PIPOeZ4b+RZf4vnM5eT3vK/FWOSC\n",
"AQ3n3J8hE/mI935j2DYfzX1eiQbUXuUD4jvn3gO8Gb3I7/TefyFsvxH4OPpAPu+9f1fF9Tz4Z9hj\n",
"dEwyhCyUlHo6QT091aiYo5NRUc2WixldsEHQ8zhKtEYOEykpAwbLMLeQmKJ1WbJ+Ja1RYt2Us/Id\n",
"RAppAbWJkq6leYypvURK6imiYl1ITJS0mWoP72FkbZjlsStsX4RA5XaqaanD1GbUm4IU+rMpZwC0\n",
"wXcbCJ+CqKaXUXb4ewLN+OlG1ueLqJ/WO0S0JEaQRdKR7dNDDIO+gXpK6kS4luUuT7+xTtTGa6kF\n",
"/TPhni+nFggtU2C6LaejxvAde9awla/xbJZxCCaIr8VY5EICjTtQL+oTCWh8BDjmvf+Ic+4XgXne\n",
"+7ucc1ejQcCbkZL5ErDWe++dc/cBP+O9v88593ng97339xSul9JTzSipnJ5qRj+Vyhmq6an8d16G\n",
"0Ecyi1r6KaWh8m35f3No7stQJZaP4DC1YHAk29aLqIjU8jB6KgWFVoGoByngXdQCgwUKtKx8q7Jl\n",
"M2DoQr13C3u+PVzronCONFlSo2m5h4jjCE+h53hJOM4sgarouJ1EWupQuPYVRKujpPR7EH1kXuEL\n",
"0PjMzZSf7b0IAE4TZ0qVvNafDPfhUfvdSr1VsgMNxF+MKKecbjsU6jWfegvoVPjPKMpU9oRzptbJ\n",
"MAK23MHPcoSn284aLBZymC/xPDbyBEwwX4uxyAUDGqEyHcA/JKDxFPBs7/1h59xi4Kve+6uClTHi\n",
"vf9w2O8eNKthN/Bl7/36sP01wJ3e+7cXruXBT6V1SmoS+hByeiqnokrUVLotpadmUktBVf0eL5+R\n",
"QUR3GA3VaHkcZXG7HvhJpFgMBBZTCwpWmuWpSOthlse+bHkRoqZOAa8nJn/qIILCMhq3yRAxxpQl\n",
"S5qLHO860XTJDmLo8zVUA+oZREdZTozNqIe+BfgLYsjzqyhTWz3IGngEKew7Q93+jjidtuStvhv1\n",
"5jvQuMERBDI3UJ4gsC2c9znonf73sF8eVPE0AjhT7Fsph5PfjWgoR0xglEpKSfVQO340QozRllsF\n",
"Nu5w3pzzZtLD53g5PzCBfS3GIhc6aHR57+eFdQd0eu/nOef+APim9/7T4b+PAf+MeqJ3e++fH7bf\n",
"Abzbe//SwrXGGuX2mRTz7eijlpI6QT1NVfW/hUG/tEGZn6wvYPTUVD/R8rBQ6EZPGSh0hXqkqVnT\n",
"vBhrae5J7sP5LOT5rrDcTcyxsILanBh5oL1cjhAB5smw7EcWmgHD9VQ74vlwjAHE7rBtSbj2bVTP\n",
"BtuDAOIh9Kymh+s9j7KlcwpZBg8ihT0nnP+Wwr5dyKt7T/h9LQoXkouFah9AlNJ12f/9xIH39dS3\n",
"wxH0DBZRT2cdQs+lg1rL4BjR78hkICzTd2Bc/C0u4gx/zNv5CT4OE9zXYiwyWtA4bylOA/U0zg/3\n",
"/Tau4eHOIXjuEK1RVCV66swotvVRS0k1oqtGiNbJLCLVlNJQNjNqVcV/cxhbGHQLO14qBgz9oX5p\n",
"Fr4lSLncnmxvNc6UBRu0sOe7kFLqQtbICmI2vtuA16Gxr0b36RFds4UIEEdQz3cZMbbUW6ge0IaY\n",
"iOiJcK4+ZGVdhQDiHVTPljqG6NRHiFOCr0IUk4UFyWUPCv1hedJXhnv+2cK+vShB1tHk3HdSP2mg\n",
"B3W0TqPnciv1OTO6kMUylTLYHEL3vxw954XZsftQO6YU3QDqRKyglpIy57z0+VkIkSZ6pzFL5Rji\n",
"l/kQH+SD0Pa1GLU45+5E79DZHX8e6Kk7vfeHnHNLgK8EeuouAO/93WG/e4D3I0XzlYSeei2it6ro\n",
"qVm0Tk3l9FRKOY1mfTqRdmq2vJjxG6hPqam0dFZs/1WU5/m3kcLKQ59fRm0+jFan8g4Q07PuzdY3\n",
"o97fIygeVBr+fBVSTM3CmRwmWiDb0ZjIe1Dv+FNIyVnCpCupnu01QsyI90S47jsQYPwxorSuCeeo\n",
"oqUsMu21yKdjP/DF8HsDZee2J1GP/nmoXZ9CyrnkwHcG0SuLkXK2iQHXUg94W4nWZCdxTCiVPeGa\n",
"F4V95mbn6Uag74j+PmldbGZU1dTXZ3jiyQhv5U/4H/x029diHOVCp6c+Ahz33n84AMXcbCD8FuJA\n",
"+BXBGrkXpSO9D/gnWhsIv5DlDNH6MHoqpZ1ONNhmvz3irEthz+dRTtc6mqmzhLqVQp+nYdHPIEVj\n",
"lNSKbH1lC9fppTYfhq1bmPulxMi2NmOqEc12kpgPYwsaGzD/jysRMFjwwZL4UAfLqJfSUtcjiyB3\n",
"XDOxZEWPomc8B9FCz6c8ndgc+Cxy7nLkHZ7PNBtCwPM4siQsU18+brE/7GcBCnN6awgB+DEEtPnz\n",
"sbGoddS+L9Ym87PtQ0h5LyCChydSpyZj9LfwvIzP8je8iou+h/NanC+5YEDDOfcXaGrhAtRb/BU0\n",
"WPjXSKHsonbK7f/f3pnH2VXW9//9TBay7zvZNyAJWyDIIhKEqrRUq6JVwbXuVVArCloL1lYFba1L\n",
"a1UUtQouiP6kVkBUtLVFWQKEJZCETJLJMkkmk2Qyk8z6/P74PI/n3Oeec++dLZOZ+3xer+d1zj33\n",
"3nOfc+fO8znf7fP9CEq57QCusdbe4477lNvRKOX26pzPs2C9+6e7I+2eau3m/lGyXVNZ2060eKQ7\n",
"8oWS5+F+SAqT6Pk/YBe6082SQfdChLvddU2gWPI8vZ1FZS4yS1IJ7WXPfcV3q7umxSTE4Eep4jvQ\n",
"b+oBEuFB30lvOoWy58vJt5ra0A3KkyTZUmPce0op04K+q7uRJdGMrIaVyLo6Kec9/4dkyZuQ9Xmq\n",
"e30WCa5zr+9EJHUBxWnBFrnVtqPv65yM1zQjl9QI93mhllQ9+l9cTLGlUof+HxcGx/cjK6Sfi/Ms\n",
"5/I77uXFjKcl1lr0E44b0jjWcKQxmdLuqDCzahjlJdCzngu78GV15guP9aUM+mGKO/GFEujpXhhv\n",
"BD6Misi+RmEnPr/17VtnUbkm1gHkz/ZkkN6+Dymxfh8tzGnZc68zVWpBaaFQ+vw5RFbXI3fbTYho\n",
"PDmUSsvdQaIP5V11w4GvIhI+FRFF1nwOkSjTno3iAHVoIfb9MMJ/uDa06D+Len2fgAhuItkpsrvc\n",
"/C5C3/3T7lrDeNEe9Pc9CS3IOynWndpNko7t28Om53cwdd5QptxnRoVup2OcGWVZykZ+zVrmsgti\n",
"rUW/otpJY6CnUQ5eBj3swBdu87rzNaJ/4LQFkpY991vvnvKEUGmw2qORfPnzXYiIutAdcrpFa5oU\n",
"KsnUqqOQFHygvAMt5kuCcTKlJcu9S8oPH2RfjNxRpyIXU9YCaEnkQ55w8+hCi/eZ6E4/Kxje7l7v\n",
"60R8X+7noUK68LPaSDKrGtFNxdlky7F799V+ZMm8kGJyPITqN/a5514QfGar+yzfNS+0nDYicllF\n",
"IYE0I5JaEJyvkeIWxd2tDM+BZSp7uZcXs5pHIdZaHBNUO2kcpHQRX9bxUhpTWd362ikteZ73nL+r\n",
"CyXOQwn08HE6btEb1xRocfOFe6EMuq/69qqnoeR5eoRujDy0oAUtLX2+laQd7DyKiaGc9Hkn8FuS\n",
"nhjPoe92Iom+lJc9z6szsag50iMk2VLjSJotlSri24ZUgj1BTEMWx9kU11DgXvNjRGjWveZ5KLMp\n",
"vM4j7rU+aH22u5YQm5AlM8rNNYxNtCJZ9hp3PWGMZDv6e4ffURdyVU2l8EbDC2umXYZesy1NND0m\n",
"i7E0cQev5CXcB7HW4pii2knDi+Z1J3sqzy1VShI9S+o8T/7cH+8rGXRvfZSTQveEcCnwJXTH+nHy\n",
"ZdB9QV8l//S+B4KXE9lKITHcgfzwNyF3UNoltYDSlk+W9Hkt8M+IwG511+fFBxeRTzJ7ELk84bYf\n",
"ddf4M0QU5dxS6xCxXIDiBdvRXftZZBPEIfQ9NyPpj05EmqdQHKNpc+eeigL8PvEglCRpQcTmi/f2\n",
"UBy3OIB+X2Mpvuv38/JZauHC7msmBqQ4byRHuIW38npug1hrMSCodtIY6GmUgr9bS0ubl5I9T7un\n",
"vNhgJ/rnz5I8T49pJGRQShk2C3nS534cprBPeBinWEh5gjxC0rc7PZrQgreQQunzU8gPZvtUWq8t\n",
"9TQiquGIuLwy7Vlkx5S6SLSlHkcLN+69ZyHCyNLN8npNjyALbRi6/osREYXYiQLbteiHOhd4McVk\n",
"0oyshFr0Pa5280/jCCKnvehvfSHFEuWPu3OdSXHG00b0PYcFfTtJEjDS54LC7z+MheQgPyO3hg4+\n",
"yfV8mM9CrLUYUFQ7aXhfe3dGOY2pLJdVlvx5lhy6P5Z2TeVJnedJoqfjFb25E3wS3SlnSaD7AGsN\n",
"Ipos6XN/rJwSrcdOtLClpc93okVrInJFpYlhSQXn3oIC0E+jhf6we88yCvWlShHlg0i+YwP623ht\n",
"qdPR4pyXteUVbHeQ9OE4Gy3KWfPejwK4DcgCWIUK7rLm9qibVw36HrK0ohpRQsGw1HWm0YFIqcZd\n",
"S1gDsgURwEkU/o6OuDmGacQ+wyvLKimDUuUbXbybf+VLXI2JtRbHBaqdNObTO/dUJeMEkoruUFsq\n",
"b/RJP2OSxkuVjHqUAnonWrCvIV/+fCblU1w9mimUPq8jIYUa4C5kEX0YkZ23PhYi4in149xHoez5\n",
"JlRZfTUivG+QLJjLyW8t20CiLfU08FZkcTyILJzTKF4803PwRXyXufdtdfM5i2zX2hZUn7HKzW0/\n",
"+l5CWXKQBfEsskhGUFiAl8YG9H2NR3/3sRT+jppJkiKy7vwPI+KoNBOqnwv1LH/GT7mTK2Jfi+MM\n",
"1U4aAz2NPHRSrDNVqRy6d091IeujEhn0aXRPcBB3/t0U98Lw+7tIrIS0wu18kn4YWX7+8DM8yaSJ\n",
"wefdz0ZWg5c/X07poHsdCTE8hYjSkLilViD3TpaAYCfyoT9GUvA23F3HGSjzKet9OxH5rCcJrB8k\n",
"QwAAIABJREFUoK9CJBBWt3eguMjD6G/pNaVCd5NFJPUUSV3EhRQu7p3uXDuRu+kCspVnO901jwye\n",
"q0XWUdrSOYJ+fzMpLM7zel/pz+7hjY9lDX/gbl7MFA7GWovjENVOGnV03z2VpSdVzl1VritfenRS\n",
"KIOeJ4GeJ4fu3VM9+af1d48b0AKdJX9ej+5KT0CLdih77rezujGHh1HwuTY1minUmEqTQ16mkscR\n",
"VEj3LCKIvSS9KVYgi2oFpa2lp1EK59MkbqlVyL10GvmusXXus/chC/MkFBTPymoCxTh+jX4r01Gm\n",
"1KkZrzuEMqWOou/9AorTlNtRR782kkLFNHyvDF+4lyaKLuRSm0Bxmu5edP1hnAIKLZZekcVJbOA+\n",
"LmWu7glircVximonDS9K1xP3VF53viypdJ8RlXZP5e33VUZKE6Vlz9PH9qEF6P8QIfwVifURyqDP\n",
"ovK+HHsolj734oMvBj6C7t5vobgnRqnPaEWktjE1GpESwBhUhDccuX5WkJ99dYBE3fUplMG0Flkz\n",
"DyILIs8t5TOj1gNvQGT5NFrcz6Q4iO4L+DYAr0Q3BZvc3ELrqBXFdxaiu/3DaJEOSW47+n3NcOc3\n",
"FC7ih912HMUuKUvSQjh0QfVB29RKYZnDDn7BpazgGYi1Fsc9qp00BnoaWWgnkRJJa0iVk0L329A1\n",
"VcmYRuUBa9CdfD2FcYr0dj9ahGZSKIE+lyRmUS5Laz+J1bGFxD11xL3XS577UUq3aj8JMTxFIiEy\n",
"B1kdq1AwOGtOne49niAOkPTPPhNZEVmZQRvQwr+RpOjvXOQKCv/h9iLC3ooW64Uo9Tkknu3IMjmE\n",
"/maXUGwtPIZcUlOQ1ZImg8NuXqMprvvY7Z5fHLxnLyKrdED7CIWk3qP4xgQa+Skv4yL+G2KtxaBB\n",
"tZPGc/TOPVWpHHq5Ln3+mEWLwFgKZdBDmfO8Y9491ZO7RH+3uQktsKH0uXdPtaHF1bumQlKYS+VB\n",
"8nbkynmOhBx2u+emowXMq9v6ZknlUjf/G7m7nkUE5gvkVpEQRKm4xzaU9fQUWhwnIHfUmWQr03r8\n",
"FrifJIvoNEQSWXGbdqSpVkfSOyMrU8q6c24h0YoK+2tYlHJ7AH1Hy4LnvXjhGIpbr7YioloYXJdX\n",
"IkinDmcV5/WILE7gKLfwFq7idoi1FoMO1U4aK6hMCj10T3VHCt27p7Lkz8NjfZWN0kS23HneGI6I\n",
"Yjjq0jcWuaHCMYPKCMnLn6eHl0HfCfwTChzfie58fV+MxeT33vaoI1Gl3YhI7r3ozvxhN5ZTWl+q\n",
"yV2v15c6H3gVSa+L08l3S21EbqZNwLtRkHk9WvzDBRvkNnsAkfKfue0msvt1bEYJBF4iZC/FBLcP\n",
"WQQL3bl8K+D0tRl00xGmvHa4546R66kQNbTzMT7BDXwCE2stBi2qnTQGehohfIOmFrQwlJI7z3vc\n",
"iSyOdPe9ctvuCCM2klgfaTLww7su5uWMuZRetNpIGjBtSY09JNlKaUXaZeTXAhxBFsMTiCBq0R99\n",
"Jonc+Wlku6U63HsfQdlSvqXpqSitN7xrh0S3yRfw+b7faynWofKZUr6obgoSIAwFBQ8gN9c+9Hd9\n",
"QcZ8n0BkPA1ZRGF3vFpE+unaik5kVU2nMOvrCCKjdCadFyb0yLEw8gyPLv6aL/EF3kcNNtZaDHJU\n",
"O2lsoLw7qpNs91SWmyrPdZUlgx5KofueF94C8e6pSWS7ofKO9+Qu0t+R1qI79d0kxOD3G9Cd8RSS\n",
"xkthq9a5VN6MaTcKenpS8K1axyKrIy19voTsKus0tqOaj2fQYtiJCNELD66idIrvbuQy2oQylCa4\n",
"95yBCCLLLdaFJFAec/uzUQHfarK/h+0oA6rTzeV8ikkCdBf+S2R9nkGxVAiIKOoQaS4JnmtHZORj\n",
"SmkcQr+5LCHD8RSu+r1ss2p5JT/kdl4X+1oMIVQ7aZxBaXdUeGwYhW4nv806ln4uTQahW8rv9xUO\n",
"o7vLhgq2nggeQ4TzQXcO36p1Vmq/3KLtcYCkB0Y42oF70PV+Fl27J4aFlI5XHKZQkda3Gf0MIujv\n",
"IivkZLL7akNSm+CVaU8G3o7I6n4UW8gKqFvkRnsIWTzvRX/fx8gXZNzoXn8hWrgb3XnC7/EAskzW\n",
"kBTmhYv3IURqPoU2vPNvQt/dKIozoY6STWD9qB1luZDf8DMuZzzNsdZiiKHaSWOgp5GGb87kh3dP\n",
"heNAzvFD6IImIDdFJWMKlS8cncjySHfjS7dq3YUWomkk+lKhDHq5Vq27SCTPfW+MOnddU0kUaf3I\n",
"KqYDLaq+RmM9sh7aSXphnI7cOFnz8TpMjyFianWvW4kC0Vl3/fuQ0OAT7v0TSeTRwzv1HSjGUY9u\n",
"Jk5F1kk4/z+472OsO0+YNvyMO9dsiiVCtpGINKYJw8vopy2uLvR7S7u8SqTclop9W07hKe7jEuZQ\n",
"D7HWYkii2knjccq7o8LjrRS7o8pts1xS6ceWYktkHIkLalKJfb+dQM8C6V7ldDtK+0yTgt960UFv\n",
"dXjxwTQpzK7g8/2K85D7LE8MvlXrXBJdKa81Va5qvB21/l2P3GtdKNPIF/GtJNsF5LEPyY1sRn/j\n",
"mcgltJpit4/HUaSeW4e+l+Uo+2lRzjX/F0nhnO/wF5J1K8ok84V5YRU47hxbkUsqtIha3PNLKCbT\n",
"Xeg7SROIDz6nSa3HUuUz2cm9vJjTeBJircWQRrWThs9j7657KnRJldo/gUJXVJabqq/gXVOVjINo\n",
"AX8ALcx/jxae2RQSw+wK59iFgrG+E58f293xtcDNKCPoaySxiqWUTtHtQGSwITV2A19HC/w9aLFf\n",
"SX6tRqt7n8+Wmo1cTG2oGvsURHxZ73sMuY/GA1e6z/KurVDLqpmkCdLL0W9mO8Wk1Y6IczZyy7W5\n",
"42mX01H0/S1Df6fw7r+JRKcsvP0P3Vf9hgk0cgdX8Cf8CmKtRVWg2kljoKfhcYRCt5TfeldUept1\n",
"rMmdZyKJ62l6ajs941h3uvO1oLvVcHhSaECLlNeWWhBs51D6Dta3avUFfJvRHbWvCfG6Uj5jKk9G\n",
"pA25bXw67XMUBsRPIz9bqoWkH4av35lJUsCX1VlwA3JLeSXbRSiVOIyptLrXbUI/ukUoCyp0Xa13\n",
"nz0SFeaFdRJPou96IYUE6eXeh1EoX27R32kahSTSTHEzpW5ZGKNo4Wu8NdZaVCGqnTQepOfuqbQL\n",
"qtx+6JLyxNDiphO6pcaihW1ShaO7PTBw1+KzlXaiQHBICrtJFu50Jz5f2OeJYRKl4e+EO1Df8WfR\n",
"IrfFzcF30UuPRZRfyH6DtJbS3fRWkpDDwhLvPUDilvKZT6tRfCGPlPYgqZLD6JpXI0LJssQa3LV2\n",
"kZBJKAhpkXT7LvQ9nkVxLMErAq+kmLgOotiIt0Y82tD3kdXIqYLU2XwMo52buJa/4fMQay2qEoOC\n",
"NIwx1wNXoX/A9cCb0T/g99E/Wy3wautS+dzr34IW+quttfdmnNOC9cqgWUV8WY+HU+x6ynNJZbmn\n",
"xgXbvnJNWZKA+D7kAgq36f3DKNvmbnT3/jm0yHmXVJocKkm5PErSjS+93eo+6/MomPsrdCfti/nm\n",
"lzh/F4ksuB/bgHcCf4ru2p9ArqWlZAdu29Dd+ePodzMH+AAir/9Bi21WptUBkoZJ56IMqMOIXLMa\n",
"Jm1EbqlzkcvNC0+GZP4M+hud4x6HXfO8K24JWszDRb0RkVX4D9uJfp/h8T6UL+/k/XyOz3ItNbGv\n",
"RVXjuCcNY8xCtNicYq1tNcZ8HwUWVwL7rLU3G2M+DEy21l5njFmBAqNr0IJwH7DcWtsVnPd4cU/5\n",
"Qr7QNeXdU+XGYbRgTkJ3lt79NIPENTU9ONYdstpPdke+Xcg11YII0NdqpKu7F1Febn0nIpJnSMhh\n",
"PyLhhSh2sAKRw8Kcc1h3Dp8t9QyJwJ/PlspTpj1EUkm+Cy2+C9HvZzXFpHYU+e4fJbE4zkIWSmgZ\n",
"bULEcxi5urIK8552cx/uzpG2JnyBYYv7DtLZXp6o51L4HR9y80gHw0Ny6gaZdHEFP+Q2roy1FhHA\n",
"4CCNKSjT5lzku/8x8AXgi8BF1tp6Y8ws4H5r7cnOyuiy1t7k3n83cKO19oHgvBbs78h3S+U9bq1g\n",
"tAWPs4ihGf1zj0H/4H54S2QCiftpcoltT6yVVuQWmoRcUPeR9MPwhLDbXfMMCov30hpTJ1LeEvEu\n",
"kefQ385Xeh9EC9kCEvFBL32eRzR+sduMbgyeIalAX0YiPOjv1LNwEPhXd53GXc8atPDnpQQ/gm5U\n",
"QNd9PtkWh0WB+ecQOZ9HcXEdyDJ5AllaZ1JMNnXob7CS4r+v7wESyq0cpDiDrhfFeZYLuZ+f8eex\n",
"1iKiAMc9aQAYY96O9IqOAPdYa19vjGm01k52zxtgv7V2sjHmi8AD1trvuuduAX5urf1RcE4L9hKK\n",
"s6NK7Q8n3wWVN3zXvjQhjKPvXFOdyOJodFvvgtpD4pZKj1YS197pwLcQYXgJ9PS2kgVnL4VyIrUk\n",
"9RWTkfjfcLToTEIL+jJK12zsJ9GW8oV8JwOfcPO/151nec4c25Fb6jFkecwF3oe+K69NlRWHqUNW\n",
"xNMkcue+2VL4+hZ0M9OCNKVq0Pcfvq7Bzf8cd55QorzDfe4CsonuENnfVVYtRR+4oywrWc99XMos\n",
"9kKstYgI0OekYYx5lbX2h+WOdWOCS5A8xIXobuqHKMD4RU8a7nX7rbVTckjjv6y1dwbnPR7cU+nA\n",
"eHo0I6vKE0He1jdD8hpSebLnM0iqu/NanmZhHwkZhNt69AX6tFHvlvL7cyi9gB0iIQY//F30LJJs\n",
"qRXkk4N3S/meGJsQqUxG7qgzkHsq65r3kmRLNSByPwVlLWXVZ+xEGVDPIYJYjLSiQpLwhX77kCvq\n",
"PIolOzYia2kkxS1hfXowyHJKE0M9Ipl0HKYL/VbS5+hBcZ5lLtu4m5ewUh8fay0iMtFd0qjkzvMj\n",
"aGEvd6xSnA38r7W2AcAYcyf6R9xtjJllrd1tjJmN7qxBd83pvPi57lgG3lsL1gIWXrgPXrGPYtdU\n",
"uN+K/MmVuKn8yIpXdJE0XhpPttz5BJR2uSjj2FR6ljXldbCmIRfITyjWmTqAFsYZFLqjzgWucMdK\n",
"yYvjrs+68/wnuoPfggin032+J4ZLkWLstJxzeXZvQa6lp0jqFJajxfUKSrulGpBL06cHL0a/rQ+Q\n",
"XdNgkRbVsyRZWZeS/Z3vQO6rcYio/izjNXtRTcw8ZOGFirjb0c3ASve8Rxf6O3kL0CNdnDcx9Vpv\n",
"Geeg+OuZTAN3cTkX8ADEWouIAMaYtajOqmfvz7M0jDGXoayWvwS+R/LrHA+ssNaek/nGch9ozOlI\n",
"V2gNWqy/iTJVFgAN1tqbjDHXAZOCQLjvPXAfsNQGE3eWxmWUl0P3x0aQL4OeJYuepzHVlzLonRR2\n",
"48sbnhBa0d/jOyjIextaxNPy57MpTwj+s30x3xaSfhhb0IJ+FXA1ynj6JUlwfB75196MFmkfFN+I\n",
"Fu+voO/tt8iKOJlsnSofOH4UZUwtRmTkj59EttXxNLIOWlHXwuHu2rKq3DejwrwXuOeztJ1a3Oef\n",
"6uYdxhbaSNJss66hI+Ocfa4VNZoWvskbeDU/glhrEVEh+sw95Rb3M1Fl8cdI/tkOAb+21jb2YpIf\n",
"At6I/nEeAd6KFr8foGBiLYUptx9BKbcdwDXW2nsyzjnQ7ikfIPcuqjw9qazjje65EcjqSOtJTc3Y\n",
"9zGKSquEO0g68WXJnzejRe1EtPClmyUtpnS8phO5eNLksJWkCO8kRApe/jzvXM+hYPITaCH32VKn\n",
"IUJcRTax+Iwm3/vb11ucS3HBYxuKgXj5ct8IaWXwuiMkRX5eTyq0JLa4OY9CFk6avJrQb3gShVZy\n",
"J/q+Z1MsUJi2eAKfU+nQxgjauIkP8n6+CLHWIqKb6I+YxghrbbvbnwLMtdY+3rtp9j0cadxDZXLo\n",
"XWRLnpeSRw+lz9Nb0OLhLRDvnsqTPA+PTaG8+F8WDqEFbiaJFPjuYBwmIQQvfT6fwp4Y5eTPfcVx\n",
"E/Blks58Pj13CYXEkCXhkYZFAfvfuWsY5d53KiKJUq1e61GdiBflW4UW7SzhQZBr7puIhOYiV+jC\n",
"jNd1IpdUE4qFnEHxSt2CuurNcp8bYiuyQLIqyL1QYhpZfb4r/+elg2v5LJ/mekystYjoIfqDNO4H\n",
"Xor+GR5GvtzfWWvf34t59jkcabyMyt1TWR358iTR04TQX1pTnRTLnedJoO8hUXn9Olo0f0Sikupl\n",
"0GdTvq4CCuXPt5Eo0+5Ai9gdKBD+C2S1eEskz9JpRxbAMygI/Axa1D6NyOVJRMQryHYvtZJInq9H\n",
"C/SbKC6WC9/zKPLhrwBe6F7ve5Cn0YTiEeMQiVj0/Ycup8eRhTGR4mD0UWQlhs2YQOQyOmOOfeSS\n",
"6uJ13Ma3eBPDY61FRC/RH6TxqLX2DGPMW4F51tobjDHrrbWn9nayfYkBdk+lZdB9DUeoKVVqvwkt\n",
"WGk9qbx9X9RXab7+EQp7YGxL7fuMqakk6rbphkl5fSw86hE5eOHBTe7zxiHL4RTKy57XklR4byEJ\n",
"qp9K0jApDAT7pkQPueuwiNTOQa6p8PXbSOTLR7q5nU+xBMc6N4dh7nNDl1Qdcp2NQllS6b/BTkTm\n",
"JyHC8NjvXpe2MsLivAphuZj7uIuXMZYjsdYiok/QH6SxHngRcif8rbX2D8aYx621WVLPAwZHGnfR\n",
"PfdUlvR53n4ofx526PN1G2mdqbT0eSlZ9J5kTTWiBXoOCsJ+l0KdKW+NTEAuKC82mB55mkweHei7\n",
"Gol0oe5Ci2YjiRsmTQ6lWrX6u+xfIqvoAFo4l6PsojMoLZteC/y7u6bpaNFeQ75O1iPus8YjIsmq\n",
"BofEmlnkzpdVMf4Q+q5CF5hFJDONYtdTVj1GieK80n0tVrGen3MZc9kJsdYiog/RL3UaKBD+O2vt\n",
"u1ydxc3W2lf2bqp9C0car6K83lTaPVVOa8ofC91Tfa011UmhzPneEo/3kzRH+ne00P0nciV5fak5\n",
"yG1SrlWsD8x62XOvM7UZWT+XAv/g9u9F1sdS8knOunM87cYGN+c3Ai9DRFaLrIjRGe9vprBh0guB\n",
"P0cL9z6yq7F3oaD1FiR1PgNZeqFl04UsiZ3Ai9HfNrzj73KfvQDFmcKV/DBJz/YQWdZDL4vzLPOp\n",
"5WdcziqeglhrEdEPGBQV4f2BAXRPeRn0tJzIYZKCvbQEetbjFrSApWXPS43udOfbhxbJbRmjCZGh\n",
"V7b1w7unShHiQZQ+u8ltN7hrGene6xsmrSCfYLahBfoxt+8LC33W3uKM9zShu/51iDxHu884l+KC\n",
"Oy9f/iy6w5+HRBZDy2Qzip90IKspzKTaiL7DGRR21LOIAEdQSGad6PuZEhzrVnHeNPbw/3gp5/N7\n",
"iLUWEf2I/rA05iFtqOe7Q79Faa91PZ5lP8CRhpeurkR/Ks8dlXcsJIZmkg59oaSId095TalQcyr9\n",
"OOuOuxz2IbKahxa0W9Edt9eZ2o8WqRkkabR+LEREUc5K8u6VVtT/+2kSfacZyBW1DC2kp5AfcPcu\n",
"mSeBr5KIFy5HLqkzKdZdgmQ1fQy43e0vQBXep5G9CHegmqJGRH4XkN0QqhGJZs5ESQRh9lg7cm/N\n",
"pjgTrANlpYVWT4ebc4+zoQDGcJhv8Qau4McQay0ijgH6gzTuQ/7y77hDVwJXWmv/pMez7Ac40riS\n",
"yjSnstxT5fSmsqTQ+wIdaCHN0pUKpdAPurlPRwvw6ShNdC9ySZ3otuX6YeDOtRXdLW9NjV3u+a+i\n",
"u/iHkHtoGdmZQh71qODOj3rgEuBd7v2+GC/rezuIrId1bg6vRoHqJrSATwle30kSCJ8KvMIdz3JL\n",
"1aKsqvPc/LPu+je457II5hAi9rBGpBfigcUYThuf4jr+hs9hYq1FxDFEf5DGY9ba08sdG2gMkHuq\n",
"lAx6I4mLyo/GYN/7wUP58xnBvt9WWsvRRqJwu4MkXlHrjnW6cy4k0Zby+6GbJ41W5JJKa0ztRkQ8\n",
"D6XG+pFHXDsQOTyK4im+l/hZKFidVb2+G4kJbnDXNhNlSp1OMQFsQQoDDYgEsnp9b0NFhJ0k3QPT\n",
"2IiIfHEwnyOIVOdRSCKhIm3FxXmGTv6Gf+ImrqMGG2stIo45+oM0foXcH7ehX/5rgDdbay/pzUT7\n",
"Go40bidfYyrcz3JJpUeoR5UWHwxdU+GYSKHceTj88e72fe5Alkc7Wri2om51aRn0o8j1dKIbcykk\n",
"hnLCgx3uuxmD0lS/jRbiNnddy0gW2pPIlyjxEup1wE0kMY/lJAQRWhCQrLC/dOMEZPGcT34K8GYk\n",
"YT7FnTtMlQV9Z79EVsMait1zbcgaWkwxOTej300fFud18Qa+zS28Nfa1iBhQ9AdpLAC+hO7YQBWx\n",
"77XWbuvxLPsBjjTeQuXuqTw3VNbjtHvKu6b6QmuqFVkc+5E7Jy2BvifYP+rmMgO4BS3YvoLZk8Mc\n",
"yhNRF6ptqE2NLejuuxX5+D+PFsTfkKjd5gXfD6N4hZcA2YliHDe6z9qAguNZdQn7SDrqNQDvRXGL\n",
"A+g7Dl1Cjej3txm5pOZS3PLUz+khRKxLyF7MNyGLJStQv59sQisR0K4Ulhfxc37EqxhHS6y1iBhw\n",
"9AdpfAt4n9eaclIin7XWvqVXM+1jDIB7yrumsoaXQU9Ln4ePO9Bdr9eamoEWsfQ2vV9pMdgBEp2p\n",
"HW7UImLwd/s+SyqtMTWfbG0nSFq1+l4Yz7rz4+Z2GkqjPZV8ZdutqB7iUeTiGYYW9DUoGB4mBFhE\n",
"OF4DqgZZEC+gOHDeiNxXu9D3tAoF2dOoJ8mSOpnCAHcnSZZVKJ64B31naXebJ/Bu3DhYTmcdd3MZ\n",
"syTgHGstIo4L9FtFeLljAw1HGt+ke+6pLEn0vGNNJKQAieUxnsKsqbR7akqwTe939461GS1gw9CC\n",
"twlZHJ4Y0tXdaflzX+W9iPIxkQb3/jbkW3/MXfdoEn0pP/KC4l4l9iCyNhrd+09CMYjVZNc5QKJJ\n",
"tRmRz9nI3ZSljdWJZOAPIbJaTbE1ZBHpdLnzhMR7FJHhUoqD2gcz5tkDS8OygOf4GZfHvhYRxyX6\n",
"JRAOXGyt3e8eTwF+c5zKiLyLYjdU3jbPDZV1bBQJKfSVa6qZxPrYhxZ975KqT233okVvPFqov4Zi\n",
"E/+FFndPEKUymzyaSNqzprcH0aL5FbS4+yDxcvJTgo8gq+NplMm0zc3hJnSnXuvmlZVhtIOk3qID\n",
"uA59v1md8nCf8yAi3D91x0Idpw7k6hqBCCQLm5ArL7ymTvRdhsd7pRU1g938hJdxHn+AWGsRcZyi\n",
"P0jjDShX/AdosXwV8I/W2m/3ZqJ9jWPsnvKuqbT1kd4/hPzinhTS+41okRqPFsEpJG6odHtWP2ZQ\n",
"2cLVheIJWfLn21CMYipyRS1JjcXk60KBMpc2pMY291lTkcVxGrIgsiRJLHL7PIaI6BAi4mXIilhF\n",
"Mak0IevgSURM3uI4jWyS2Ix+l8uQNZH+8e9357Hus9JxilZEmBMplC9pdXNIu9kCC6N0vHs8B/kO\n",
"V/JSfgax1iLiOEe/VIQbY1YiSQcL/Mpa+1TPp9g/cKTxVQpdUKW2oTsq3IbHPCn4rKnxwRiX2vdy\n",
"51ljEt2/e/WB8jEoHvEkUrf1xHAQLcZzKJQ9T+tMlXKrHER36GOA+5GU+G4SV9gpKIPpFPIzmLxb\n",
"6ghwA4ovTECLvV/0w5iJX32PIsn1o4jEzqewD0Uaz6Jg+CKUnJEV63nGXdOZGZ952D0XXke7m0ua\n",
"xLrZ16KVz/Ne3sXXINZaRAwSVLuMyDUUu6GyXFNp95R3P5XaH01CDH3Rbc1bIn7sI2nRmh770So1\n",
"FdVPfMPt/4xkQZ9HecFDi8jlOXRnvtnt73TPXQZcjxb8R5CLKi+gfRRZHE+jFNUdiBw+jb6v7W6u\n",
"oQVh0WL+EKqDWAi82T3XQnEK7EGS4PbLEdlmFdStR66l1WRLkW9HbrKQNHsQzM5GDR184I+1FrGv\n",
"RcTgQrWTxrH4qCPI6vCWR1PGOISCyvuDcRAtUhPQ4j+VxD0VtmidRXbaZxaayZY+34YWsZGIYJYG\n",
"o5TKbRMiBU8OzyGry3fTO92NPAmQjYiA1rv5TXCvP4dsK2ILqgvZiRZzL18eVpBvRq6uNkQ8Z1FI\n",
"5I2InIahAHk6iO4FHxdRaIE0IlLqZnFeJ2/kW3yVdzCSjlhrETEoUe2k8SWyXVF57qmjFLqgwv3Q\n",
"PdWJ7ojHo0VwfLDvtxMpJAW/X4m8RxqdJP3Ap6PF9v+QpMs2ZD14+XMvPBhu8zKVcNe2x533MPK9\n",
"16I7+unIJeXHIrJXziPIEmsDPuHO5zvqrXHvzWtGtAVJ1ExElsIasutMjiJZ9vFIDiTrmragv9Eq\n",
"iq1Bn8EVZmFl1XhUAMvl3MX3eE3saxEx6FHtpHEt+a6pLPfUqAqHd0/1srALizKEvBXSQNKRbxeF\n",
"bVoPoQVtFiKAr7m5/BSRxALkdsmrrfBoQXfnm1JjMyKMie68s5E1MY78Vq0dyHrw2VJb3es/jayB\n",
"PWRbHe0oEP4gsiJehmIcYTU16Pt53A3fhCmvMM/HLEKC8FpeeXMp932VgOV5/B//yeVMoxFirUXE\n",
"EEC1k0Z/f4zPrDkUbMNj3j2VJoeDaIFLWx7T3HYmSZtWP0plNKWxh8JeGH67A93RTyZRpPUjdM+k\n",
"0YbcO154cJM7Nh4Fwv1inuXaakOuo3Xufd5iWYPcUqGr6SjKgHrK7c9CyrRhM6Z6VBTYggLYZ1NI\n",
"FvXIQhpHsWWzjaQXe/pzuxHPsCxhEz/nMpaxGWKtRcQQQrWTxj9T7I7K2w/dUOWGz+P3bqi8MR4t\n",
"1GlSmEppN1EWjpJ04VuMFtSfAXeieIUPYs8mERtMjxMpvSjucPM7AUmP/wi5miYhcvDCg1n9uCFx\n",
"S3UAn0TkNR0RyllkN0zyVsM9iFzmI3dT1mtBWVIHEelkBeZ3uM9fkPE5Byl2B3azOM9JKrgzAAAg\n",
"AElEQVQyk938kFdxIb+DWGsRMQQxKEjDGDMJVTOvRP/gb0auj++jBaAWeLV1AUVjzPXAW9A//dXW\n",
"2nszzmnBfpRsV1TWY58VlXZB5e1nSWN3F10kmVJpt1QDWnDTrVqb0F3zXFQL8Xl3jntIemTMpDQp\n",
"dKGYRy2JIq1Xbx0JvAPpNx1C7rDFZBfidSLLw+tL+Wypf0DxnbyCvGa0yK5DbqF3uvdlZUA1IIIY\n",
"hboFZl1XnZvrKRnPN6G/aZiB1WP58gk08l2u5HJ+DrHWImIIY7CQxrdQVfk3jDHDkdvio8A+a+3N\n",
"xpgPA5OttdcZY1Yghd01aLG8D1hure0Kztnf7ql2EtdTqdGE7nI9IfiMHUgkztPaUuHjWVTWM7wL\n",
"LeBbKBQfrEUL9gnoTn4JiSLtcvKlRCzKkHoCEcQzyBqbgBbq09zIUrU9jDKlHqGwvuN8ZK1kxSQe\n",
"RN/LWGSdhLI0jYhwmpG7KoxfbEff7XxkyXkccfNJz7PTvdckl5r9PzKKFr7Ie3grt0KstYioAhz3\n",
"pGGMmQiss9YuDo5vAC6y1tYbY2YB91trT3ZWRpe19ib3uruBG621DwTvt2A/TeKGCt1S4eO06+lI\n",
"icdH0AozkmytKa8zFWpLpfcn0r36jqMkooOnuXN8E7mn6tCieALKegqFBxdSuhvgAZL4wSZE1i0k\n",
"+lCeHJblzDmdLfVJRJBzEamfRXHcwmdKtQD/gb7HNYhMsrAFWURnk51yXOc+I2yY1EZiRXpUXJw3\n",
"jHY+xif4Oz6BibUWEVWE7pJGn3Ue6wYWAXuNMbeivP2HgfcBM6219e419SRaSnNQ/r5HHflVya1o\n",
"gRqOFqeswr4RZGtMhfs+tXYcfaM1dZBCXamsUY8Wv3GIEM4HLnLXNR+5hOZSvmtgA4X6Us+iO3OL\n",
"Atmfda+rQem7Wa63ThSgXo+ymepRXOHj7vlWdBceohZZEc8h9+Pl7vgY5BLzaCVplvRiEqLz4oqQ\n",
"yJ8sSb3Pxz8OIDL2f5uRFJuapuRDALp4M7fyFd7JiFhrERFRFgNBGsNRTv57rLUPGmP+BQnW/RHW\n",
"WivLIRd5z93QR3MM4V0eWVpTh8jWl/KPD6HVagqFmlIzSTrWeb2pGWTXDZyAZFw8DiMSCIUH691n\n",
"zSLRljobuIpsovXW3jZU5b0epdQeQYS5ErmNLqPYrTUeiSk+iFJqDyMyOw24GGmUpdGEaky2o9/A\n",
"MiQDkiasZneuZkSSJwXn2IpIdTGFcZQG9P3mFOdlwfJSfsJtXBlrLSIiuoGBII06oM5a+6B7fAeS\n",
"sNhtjJllrd1tjJmN7rxBbpp0BfFcdywDr/4NWKvxwk3w7s0UF/a1U15nqpWk8ruTQq2ptMZUWmdq\n",
"LlowQ62pSlu0ehwiyY5aixbVv0N35bvRgjgZJQykiWEJ+V30cNe0HVWCdwLvR4vwKPfeVcBLkNWX\n",
"lWHU5K63BSnZtpIs/JeRX8D3OLIUT3bXk0WKh1BK7anIugqxCxFqmCXli/OmBsdLEIblfH7HnbyC\n",
"meyFWGsRUWUwxqxF/4s9e/8ABcJ/C7zVWvusMeZGkqyXBmvtTcaY64BJQSD8HJJA+FIbTNzFND5F\n",
"+cI+754qpznl+2X0VmvKIoujgaS6O60v5R83uNdOQST5CuBKZLFscsdmUfoO2iu3bk6NrYgIJwI3\n",
"o5jHXkRmWWJ/XSgI/hha8BvQYv1h9P15YcI02lEQfB0ildcjAgulxX3x3jbgQrKzrrYiV1VYnNeJ\n",
"sqEqbUYVwLKS9fyEl7OU5yDWWkREAIMgEA5gjDkdpdyORAvbm9GC9APklqilMOX2IyjltgO4xlp7\n",
"T8Y5+yt76ij5GlNeMTXUmPKj2V3XFLSIzsoYXmcqTyAwDZ8x5XWlPEHUIsIYT6Irtcxt81Jpcefx\n",
"RXwb3Xy9W2o1ijllNUDaiqyHjW5Oc5DFsZJiUltP0jFvPvA8Chd+XxDYgiye2annOtxn+YQCjxY3\n",
"L0dIpb1Rc9nGT3gZZ/EoxFqLiIgCDArS6A840vhbymtOtZGvL5Xeb0F30KHWVLidRFLAF2pNhXUD\n",
"pdCFXHK70d39JW6u70SB7Ca0UPpufAsprPAu5WqsRTGT0Ujr6U60cHu31CoUP8g6xyF3rfuAzyFL\n",
"7XTkRgobP/niuTbgx+j6n09xphPI/fckSucNA/ud7nPD93Wrr8UkGrid1/ISfgGx1iIiIhPVThr/\n",
"TPfdU6PJ1psaS+9jPu0kUiJZ+lJ+NLl5zUIuuLejXth17rkFlCegOuTG2kiiL+Vbtb4TxSt8+mhW\n",
"Sq5vmPQIciE1oVjJm1LPhz+svSi4XYuI54VkYyuyZs4iWxOqloTU0uiRoGCstYiIqBzVThp9fdpQ\n",
"aypLd+ogSYV3WmvK6xtNc2MGxfpSc9y2XAot7vO2BmMTWrhHImJZTlLIt5R8//8O5BJ6AhGFL+Lz\n",
"DZOyOuq1IzJ5xH3mKOSOuoBinaxdKLDd7K57DYWE0Oo+uwNpRaWLGRsRuaX1pyoqzhtOG3/Hx/ko\n",
"n6IGG2stIiIqQLWTxrVU5p4KdaXC4r6jaJEcTaGu1ESKtabSOlPTUvvdCdgeIZEQqUF6TLuQhbCT\n",
"pL3qIhJtqcWIILJcPx67kHU1Ay32vn/3EpKeGFnaUl1uTmOR5fJtZAmcjSqzw2vzAe9HUZzlPApj\n",
"Ex7tiOiWUlwb0uqOlUg8yCYLQwfX8Hk+y7UMw8Zai4iIbqDaSeNLlNabGobuyivRm+qta+oockml\n",
"x04KNaZ2kfTDmINcU9cjq2Gzm8scSmdMNSFr4Vnkt38WFb6NRPUS16BFvYVs5dwOVJvxGIoxHEUF\n",
"eZdQnP3k4ZVsu4BXk+3u2u3OdwbFKbE+fhPqZ2V8Xqm4RRev4XZu5S2Moi3WWkRE9ADVThp9ecoO\n",
"5HoqpzXldab8aCCp6p6GsqamoQXyRBJy8K6pcuTkW5bWUqgzVUciPX5yMPLcXfUkqbSb3funIKtj\n",
"tXtv+ONpAH6PCMlnSp2HrJ00DiMi2Yusn7MpdDsdRlbLWBS8TxfieYXcFGGUIgvLC/gNd/IKpsa+\n",
"FhERvUK1k8Y1FGpNZelPeffUEbJ1po66140icUlNDPbTjyeTEIPfdkcRtwFZIDuQhXEK8GvUBe8g\n",
"cgUtQO6o9JhHvitnr3vvUhQjeD9ahRch99KZZDdbanfbEcD/APejBf4CiuXLfSbTAffaUykuvgN9\n",
"3/Vkt3jtZqDbcgpP8VP+nKVsgVhrERHRa1Q7aXyVYndUlntqdDBGBY97qzV1GFkde1PbvYgYdiCS\n",
"2Os+ZzpakJcAH3Pzewbd0ZdSu+1C8YMNyL20wZ1zOIp1fBwRzmGy3VJHkMWxDtV8DEdZW3PJvs33\n",
"8uW7kFZUFkHsR+6xFRRXwre4c4aurIokPxZQy528nNU8BrHWIiKiz1DtpNFXp+tAmT8Hg3EoY/8A\n",
"CSnsQ3fgE1Dw2Uuhe8nzE9GiPJfSkh8eh5Ab6bnU2IoW/DGIHNJ9vPOC4g2IHNYh11anm9NZqCgv\n",
"rLewKEX2YUQEvuf32RRKjHS41+xFFtZqCi2HAyQyMGkSaUZEPSz5uGzZqBns5rtcyaX8CmKtRURE\n",
"n6PaSeNdFLunwtGGFt20eyo9QHfo45D7aVKwDY/5am9PEpV2hutEFkedGxejhffzwPfc89ORBbI0\n",
"NUq1aj3gzrUKLeh/644tIHFLhQQBia5UF8qUakJksjq4Hr+idyGrYzaFCrQevkgy7FYYBLrzjYxx\n",
"HOLLvIuruA1irUVERL+h2knjW+S7pYaTuKfGUOiO8o+zJDO6Cy+BvjfY1pMQxEH3eSeiu/ALkF5T\n",
"u3t+AaU1r3ai1FUvAbLdHZ+LYiGT0KKdlfZ7EFkcjyHLaDrwLrKJyFsSG5ElszrjNQeQ9bMi4xzN\n",
"FAXlS3ujhtPKx7mB67kp9rWIiDgGqHbS6ItTeevD60odCLbhsUZECl5wcDJJN76Zqf05iCDmUb4z\n",
"XxeKM/jK7k1uNCLyW4oW6ZVuzMo5zy4St5Sv2ZiHiu3WUFxlfhhpSm1xjxcgQksv/F1IT8oTzqkU\n",
"ssAO9z2kA+edYA2YXK2oGjp4L1/kM3wo9rWIiDiGqHbS8H3Es0YHiXuqhUKXVAsiCx+o9XpTkxAJ\n",
"TApG+piv9g5SRkuiGVkH2xHxXIEW4yvRgn0ChdpSfuTJrLegeMcKN4dPufMsQ3GLsyh2FUHiljqA\n",
"XGKeJPI+5yn3+qxMKN/RrwSyrIwuruQ7fJV3Mib2tYiIOOaodtK4nWyXVPrxCSTEkB49lNwuQAOJ\n",
"K6o+2N+NSOIIWsAXIGK4ClVmN7o5luq/cQC5ijagwrlaRDYzUYB4FvlprLuBh9z7jgCXIjHBLNQi\n",
"a2JyzmsaEeGEabvtJEWVDnnuKMsl3McPeDVTOACx1iIiYkBQ7aTR29N4C6QFuWoa0UJ9oMT+fhS3\n",
"6ESLrNeU8iN8XI6cfBFceuwm6ch3Mgp0n0b2HT+IpB5CbqlGkv7fz0MZVyGeQCTRgqym51EoLGjd\n",
"84fcZ6bTbTvd/GZTIFUOeWRxOo9yB1fEvhYREccBqp00rqLQFRXud5LELFooJIlOkk58WVpTvpBv\n",
"WsaYTOW1HT5wXIvkNZ6PFuR3oNV2GiKGk9w4mfz03KOoLuJkZF18xZ1rOVr4z6TY6mhDFlcNyoDa\n",
"gVxSc8jGDhTTyGqY1I3iPMtyNnA7r2N17GsREXHcoNpJ4w5KZ0+FhXxpzaneduhLy5/vTA3/OF3M\n",
"twilqr4fucYaKS082IJqFPzYhEhuGvBB5CbK04nagFrF+sX/LWQX++1Flsl4lG4b/oh2u/eF7y1b\n",
"nDeLHXyXq3gh90OstYiIOK5Q7aTRm1N0kEiepzWn0vu+kC+tNXUQEdIU5NLxBXwnBvvlivl8l7rn\n",
"SMihlkLrw2dMZdVGgDKtHkUV4s2IiM5CVke42DeiTKn97nVrgjlaRDhtyHJJB7mbENllFOclGEsT\n",
"X+VtvI7vQ6y1iIg4LlHtpPGXlM6eCvWm/NYiN8vEMmMqWljTo1TgOg3v+/dtWl+I4gCfA36ErIBF\n",
"KOPJV3hnSXWAFvJn0WI+EhXkPYUI5WyyhQd9plQLcDdyfa3MOX+9u96wbiXonJeNEzjCJ7me9/GF\n",
"2NciIuI4R7WTxl3ku6dGUKw55Udv0EGiL7WHpMp7R2ocQQHwE5HY4FrgZSSCinkV3u3I4vBFfFvc\n",
"671b6sQS73uIpBHSJSi+EaIZuaTGoQyuLL2pKYXH871Rw2jjOm7iRj7OcDpjrUVExCBAtZNGT9/u\n",
"pUXSelKh7tRBkkwpTxDNiAx8Ed8skgI+P+ZSvtJ8J4VFfL6b3iRkcZzqRpYybSfKfnoIkRXuM5+P\n",
"rIk02lEA2scnViMC8uhwnz+eQkIqWZxn6OKNfJMv867Y1yIiYpCh2knD372Xck+lx1H39lHIR+/1\n",
"pPIK+aZSWOVdrm+3x0G0oG93n/kXyE30SrSQzydp1Xqy22b12WhFrq1l7vnvIHeXj1uEGU6tyH1l\n",
"EFmMINuigPLB+AxYXsTd3MaVsa9FRMQgxaAhDWPMMNzdsbX2z40xU9CiswAFgF9tnVvDGHM9yvrp\n",
"BK621t6bcT4L9l7yM6e8e2pMattbralWigv5PDlsJ6mvmOquawHwVpTemqcNBbqV30RSP7HVHZ+B\n",
"3FJhJzyPXahh0k5Ean9BcQyiFQXKp1Jc59FKUhCZmkr4e7JcwP/wXa5kgWSvYq1FRMQgxWAijQ+g\n",
"O+Tx1tqXGmNuBvZZa282xnwYmGytvc4YswK4DWX3nAjcByy31nYF5+upe8rXaRwhcU3ljf0kBHEU\n",
"Ba9noYC23y5IjTxNKI9DJK1an0VE4WXPV6BWqaeTXUNxBIkJPkIS5D4NOIdiC2gdIrOJyCWVzqRq\n",
"IWmS5Kyb/OK8laznh7yKU3gGYq1FRMSgx6AgDWPMXOCbwD8CH3CWxgbgImttvTFmFnC/tfZkZ2V0\n",
"WWtvcu+9G7jRWvtAcE4L9jLyNac6SAr6vNZUDYnV4QvYpiA3TTimIP//LDcqkR3pRIHwrW6chTrz\n",
"3QF8maTC+2R33GdDhTiMrK9VaEW/BQXEz6NYMBDk8hpB0pf8tIxzWvedVNRlcDZ1/JBXcQEPQKy1\n",
"iIgYMuguaZTrT91f+BxwLYXpqjOttfVuv56k78McVE/gUUd+1tCHKdScSmtPeUl0P3rrmmpC7qdw\n",
"bHOjyX3GfJRKuxoRA0ig8Iqc89ahrKfH3H4Nqst4t3veAG9Lvd5nSj2DCOAvSFRpfcV6Kwq0zyex\n",
"MoxebzvB5KbRTqKRr/FWXsmdmFhrERFR9TjmpGGMuRzYY61dZ4xZm/Uaa62V5ZCLnOduTJ1vrRsl\n",
"0YIyoLz14XWl/NgfPG5AxNCJXD2hxtS5wGuREGFW1bVHB9KU8m1aN5J0szsJWSTvoDCzyaMBkehm\n",
"Egny85HVkcaziHSmIgtlReq5/WDHgxkhwiiOW4yliZv5EO/i32Nfi4iIIQS37q7t8fuPtXfBGPNJ\n",
"1HCoAy2SE4A7UcxirbV2tzFmNvBr5566DsBa+2n3/ruBG6y1vw/Oa8FeQrbuVAdJC1cfvxiG7sjT\n",
"YzJaZKe4MTXYzkDkUAnZHkJ1FVuQe+kqlNr7RmQdeOHBlW4/y03U4MZy5E77JoqVnE+x1Ll3STUj\n",
"iyBLmLBscd5IjnI9n+bv+Dg1+p5irUVExBDGoIhp/PHDjbkI+KCLadwMNFhrb3JEMSkIhJ9DEghf\n",
"aoOJO9L4XwpdU+n9kSTk0FvX1H4KdaXS+3WIoKajZklLgNchwim1aG9B2VJPIvfcMGQ9vDLn9bUo\n",
"wH0UeBHFGVXNyEI4kQIzIluiytDJ2/gaX+S9jKQj1lpERFQJBktMIw2/+H8a+IEx5q9wKbcA1tqn\n",
"jDE/QBXRHcC7Q8JI4fxufKZ3TTUjS8AvsvvR3f3+nP0uRAheV2ouihWc77bzySeGYcgKeMKNp1HG\n",
"1ngU0F4DvJeiFqngXv8wipVMQq6wlwevqUPENcfNy53HdtbQVdPFMCPCSLujungFd3ILb2Ny7GsR\n",
"ERFRBkOtuO/5FLqj0vvtiBiOoJVzLIlq6zi0cPsMqakUy59PRdZCOe0li2o0fHX3pUg65DvIDbeU\n",
"pML7FLKzsLaiYP10RDK/RFbHsuB1HYj42xHxBcV5pQRoLZfyC27lLcxlB8Rai4iIqsSgck/1JRxp\n",
"PEzilgrHSEQOvdWa2oMW8rrU8I8Puc9ZhGIKF1I+4LQNZUqtQ1bHONT2NSsmcRhZGweBF1BcAX4A\n",
"kWEqPhISh+UM1vF9/pLlbIJYaxERUdWodtKo9OWHSVxSh1PD98TYh1xRaQn0ZmShTCVxQy0IRinF\n",
"2/2outu7pZoRQZyM4jVnUBwMb0aNknYiMjgDWSppeEHExZTpnLeYTXyHqziP30OstYiIiCCSxjkk\n",
"7qhwtKFF2JAU9I0nu5BvMnINzUqNMFspCy0offZZ9xmXI3HD96A4wxlIbXYFxfEki9JoFyEX2H8j\n",
"EjiXQpeYD6a3u8cjkrdn/92ns5sv89e8kjsh1lpERESkUO2k8TjFhX3D6ZuCvnZUo1GPYha+ynub\n",
"O26RFXIKile8hvxqa4uIZZ3bdqLajqsy3tOJ3FfNKFCeugZrDbbLUpMZZ5nIAW7iQ7ydr8Vai4iI\n",
"iExUO2lU8tIjJPUaPmMqq5ivAaXR7iLRg5qDsqYWInfQYmQZ5PXXxp3raZKeGEdRLOIMRAKLMt7z\n",
"ECKkEYiAgtfYnYau6ZZhmVbGKI7wD3yUa/hC7GsRERFREtVOGmdSmDWV1pzyWVNjUCxhLHJPTaWw\n",
"iM+PmSTV3uUsFN+qdQsKiF+JFvyPIZI4jcQtFRZJeB2sKSiQ/iTqvpe2ODwr+GypTNTQwfv5HB/n\n",
"RsbSEmstIiIiyqLaSeMZiov6RpDIofcUTSgW4Iv4ahFB1CJdp3GoiO8k4C9Ram4WOlAw/CEU6zgB\n",
"1VosDl7XhQLVw1Ca7R//oIYubMA7hk7exDf5Jz4Yay0iIiK6hWonjXIvCwv6DpNIdexP7TegRX0X\n",
"slamUNiNbylazBeTrUoLshoeAx5HjZMMsl7OpSg2Ae6znkBEciqpmosaOroM1HRmxM5fws/5Nm9g\n",
"Og0Qay0iIiK6iWonjVPILu7zgV9f0DfebSeiwr3pqa3f966pclXzO1HG1HPAS5Fr64fIoliNxAfD\n",
"ZkcgkphNEhRfUsFnOVhW8zC38TpOYiPEWouIiIgeotpJo5bioj7vnqr4Swmwh8JufHWIILx7aTHK\n",
"mLqc7KA2yMJ5BMUrOpClcU7wmk6d384Gk6oSLwxyr+QJbuVNrOFhiLUWERERvUS1k0apl7SQuKSa\n",
"Utu9buxL7e9FWU8GWRsLU2MRKsibkvM5zejOf507zyj3nhegAsA0mlBm1USwy8G4P1xxcd5ctvN1\n",
"3sKLuA9irUVEREQfodpJYzHZhX0WuaMmINfUBDcmoThD1phOaevkEFrwn0aEsBj4H1SUdx6yJkLh\n",
"wSZ3rAYRyrTkM7KL86ayh3/hfbyO71GDjbUWERERfYpqJ41dJC6pEan9Yi3w8nDuIraiLCk/dpNY\n",
"IKcDL6FYSNDjOeSWOoQyqy4omDNdnSNor2njhKI/2HgO8lk+yF/xDYbRFWstIiIi+gXVThp5Tx9F\n",
"C3eT2/pxEMUs6oPhi/kWoUwpP5aR32r2MHJLPer2Z6BMqdPDuYymZU8nNXPbGJXSitLfbAStfIjP\n",
"cCM3MpzOWGsRERHRr6h20piL5D68FHonWo3HokypScF2KspgmpPazqF0TUcHatG6HlkO85Hy7DrU\n",
"U+MUCv1M7cjiMdDVBjWZKbrDaefN3MoXeQ8nSFYq1lpERET0O6qdNPaTuKZGUL73RR6akabURpK+\n",
"GFvdc7OR9fDnKDAeog1ZG7uQS+rk9JM1dNKVmpahiyv4IV/hHUzmIMRai4iIiGOIaieNrKfakSvq\n",
"AHJHpbeNFLZq3Usif74ULfh+LCI7NtIA/BbFOkYhS+Oc9GtH00I7w+kI6gAv4T7+jXezPNZaRERE\n",
"DBCqnTSmI5LwYwTKlkoP34HPj5koTrEAuabyvrwuZHE8gRorTUFuqUbg+RSqz3aByQ2+r+VXfIYP\n",
"cXastYiIiBhgVDtpNJFkTPWk/3kXsji2osynDW5rkazHmUjyPKvZ0gZD14FhdJ7ZwYjM4rxTeZx/\n",
"5x2czwMQay0iIiKOA1Q7aYSHW1HGVHo0oIyp9NiFXFijSTKmViJ12gLBwBQeR1bCcLArwJyUPFVY\n",
"czGfWv6Nd/Nn/BxiX4uIiIjjCNVOGpNINKd81lSYMTWTwkwpX/Gd15nPZ0vtAS52xx5EcY6UxVFc\n",
"nDeZ/XyJv+Z1fA+UxhtrLSIiIo4rHPekYYyZB3wbxRMs8FVr7ReMMVNQmukCVET3ausWV2PM9cBb\n",
"EBlcba29N+O8Fmwbck31RGeqiSRTymdLdSGSudiNgvNOZV9bO8NHHmJSwYlG08wNfJwP8DlG0BFr\n",
"LSIiIo5bDAbSmAXMstY+aowZh4LJfwG8Gdhnrb3ZGPNhYLK19jpjzArgNiTLcSJwH7DcWtsVnDft\n",
"nrIkPcHTGVMHUYbUztTYi4hmFnJJrXLbkygmn7axHH5iLtsXbWP+5CN/VAmRlTGcNq7mC3yMf2CS\n",
"0mdjrUVERMRxjeOeNIomYMxPgC+5cZG1tt4Ry/3W2pOdldFlrb3Jvf5u4EZr7QPBeSzYMe7hcKRA\n",
"O4GkK5/vzOczpfzIy5jqQHGLhXpvZ9NI2ke3MaoowD6Mdt7GLXyETzKPOoi1FhEREYME3SWNnmQY\n",
"9RmMMQtRRtLvgZnW2nr3VD1yC4EW9TRB1JEv5dHSg2l0IXfYk27sRo2VlgOv44/V4cPGtzGMGjro\n",
"cl9bDZ1cyXf4e25goWr/Yq1FRETEkMaAkYZzTf0IuMZa22RMQnTWWivLIRc5z90IdHWC7YSLWuFS\n",
"340v3ZVvN4pX1LnzTERZUueguMn0gnnSxTy2s5PZdDCSLoZj6OLl3Mm/8h5mUQ+x1iIiImKQwBiz\n",
"FtWa9QgDQhrGmBGIMP7DWvsTd7jeGDPLWrvbGDMbZSuB6hnSne/mumMZuHEMKrIbhSyEKRRLnq8B\n",
"rkJS5hnXb/ePpHVUG6PGGDqwDGdbqg3GefyO73IVi6j1c7uRWGsRERExSGCtvR+43z82xtzQnfcP\n",
"RCDcAN8CGqy1708dv9kdu8kYcx0wKQiEn0MSCF9qg4lX2CM8xDbUanWDofPQyWy4cDNLnt/GqCL/\n",
"3lKe5Zu8mQv4X4i1FhEREUMEx30g3BjzfKTV9DjJKn898AfgB0g1tpbClNuPINdRB3Jn3ZNxXgv2\n",
"KJJBb3WjkULJ892oR8Zh5JY6A+wLDHaNpSYlbpjUXMxmBzfw9/wVX2c4nbHWIiIiYkjhuCeN/kKq\n",
"uO8EVNQ3HXXGm4mqvBcDS1A67fiC99IJgE2pz05lH9fzKd7NvzGao7HWIiIiYkii2kmjotcOp33v\n",
"GTxqT6RuxsOspo75eMtiMZv5AP/MG/kW42iGWGsRERExhFHtpHEYuaVaUNGeH7XA1uU8M+k8/ve1\n",
"dcxb/d9cSBuJruBSnuUzXMtLuYsakU+stYiIiBjyqHbSOBG1aZ1KUry3ZDjt5wCndTCiKG4xjib+\n",
"lXfzBr7jn4i1FhEREVWDaieNkq+ZQT1NjMPLf7yG2/k81zCDvRBrLSIiIqoQg6oivB+wC2gxdB08\n",
"iWeGreX+ZeM4PGYr87mPS9njiszPYB2f5YNcwq8g1lpEREREVIwhZWmMpWn5tXzm9WNpfudTrJh+\n",
"H5eynfl/fM0a/sC1fIZX8iNqsLHWIiIiouoR3VMBZlDPFdzB6/kPnsfvMbGvRURERMQfUdXuqYVs\n",
"YS51LGEzq3mEC/gdZ7LOZ0PFWouIiIiIXmJIWRolriTWWkRERERkoKotjQzEWouIiIiIPsRQJY1Y\n",
"axERERHRD6gZ6An0MZ4BrgCeFwkjIiIiou8x1GIaI2KtRURERETl6G5MY2hZGk9ZsrAAAAZxSURB\n",
"VJEwIiIiIvoVQ4s0IiIiIiL6FZE0IiIiIiIqRiSNiIiIiIiKEUkjIiIiIqJiRNKIiIiIiKgYkTQi\n",
"IiIiIirGoCENY8xLjDEbjDEbjTEfHuj5RERERFQjBgVpGGOGAV8CXgKsAF5rjDllYGd1bGGMWTvQ\n",
"c+gvDOVrg3h9gx1D/fq6i0FBGsA5wCZrba21th34HvCyAZ7TscbagZ5AP2LtQE+gn7F2oCfQz1g7\n",
"0BPoZ6wd6AkcTxgspHEisD31uM4di4iIiIg4hhgspDE0BLIiIiIiBjkGhWChMeZc4EZr7Uvc4+uB\n",
"LmvtTanXHP8XEhEREXEcYsj1CDfGDEey55cAO4E/AK+11j49oBOLiIiIqDIMiiZM1toOY8x7gHuA\n",
"YcDXI2FEREREHHsMCksjIiIiIuL4wGAJhOdiqBX9GWO+YYypN8asTx2bYoz5hTHmWWPMvcaYSQM5\n",
"x97AGDPPGPNrY8yTxpgnjDFXu+ND4hqNMaOMMb83xjxqjHnKGPMpd3xIXB+obsoYs84Yc5d7PJSu\n",
"rdYY87i7vj+4Y0Pp+iYZY+4wxjztfp/P6+71DWrSGKJFf7ei60njOuAX1trlwC/d48GKduD91tqV\n",
"wLnAX7u/2ZC4RmvtUeBia+0ZwGnAxcaY5zNErs/hGuApkqzGoXRtFlhrrT3TWnuOOzaUru/zwH9Z\n",
"a09Bv88NdPf6rLWDdgDnAXenHl8HXDfQ8+qD61oIrE893gDMdPuzgA0DPcc+vNafAJcOxWsExgAP\n",
"AiuHyvUBc4H7gIuBu9yxIXFtbv5bgKnBsSFxfcBE4LmM4926vkFtaVA9RX8zrbX1br8emDmQk+kr\n",
"GGMWAmcCv2cIXaMxpsYY8yi6jl9ba59k6Fzf54Brga7UsaFybSBL4z5jzEPGmLe5Y0Pl+hYBe40x\n",
"txpjHjHGfM0YM5ZuXt9gJ42qi+Jb3Q4M+us2xowDfgRcY61tSj832K/RWttl5Z6aC7zAGHNx8Pyg\n",
"vD5jzOXAHmvtOiAzr3+wXlsKF1hrzwQuQ67TC9NPDvLrGw6sBv7NWrsaaCZwRVVyfYOdNHYA81KP\n",
"5yFrY6ih3hgzC8AYMxvYM8Dz6RWMMSMQYfyHtfYn7vCQukYAa+1B4GfAWQyN6zsfeKkxZgtwO/BC\n",
"Y8x/MDSuDQBr7S633Qv8GOneDZXrqwPqrLUPusd3IBLZ3Z3rG+yk8RCwzBiz0BgzEvhL4KcDPKf+\n",
"wE+BN7r9N6I4wKCEMcYAXweestb+S+qpIXGNxphpPvvEGDMa+BNgHUPg+qy1H7HWzrPWLgJeA/zK\n",
"Wvt6hsC1ARhjxhhjxrv9scCLgPUMkeuz1u4GthtjlrtDlwJPAnfRjesb9HUaxpjLgH8hKfr71ABP\n",
"qVcwxtwOXARMQ/7FvwP+H/ADYD5QC7zaWntgoObYG7hMot8Cj5OYwdejKv9Bf43GmFOBb6Ebshpk\n",
"TX3GGDOFIXB9HsaYi4C/sda+dKhcmzFmEbIuQK6c71prPzVUrg/AGHM6cAswEtgMvBmtnRVf36An\n",
"jYiIiIiIY4fB7p6KiIiIiDiGiKQREREREVExImlERERERFSMSBoRERERERUjkkZERERERMWIpBER\n",
"ERERUTEiaURE9BGMMbONMT8s85qFadn74Ln7jTFn9c/sIiL6BoOic19ExGCAk6B4VW9OweDVNYqo\n",
"EkRLIyKiBzDGfNwYc03q8T8aY672VoRrVPQZY8wfjDGPGWPennGO0caY77lmOHcCo8kRAoyIOF4Q\n",
"SSMiomf4BvAGkBQ60j37n9TzfwUcsGrkcw7wNicFn8a7gMPW2hXADUjYMFoaEcc1onsqIqIHsNZu\n",
"NcY0GGPOQI1rHgEaUi95EXCqMeYK93gCsBTYlHrNhaiTGtba9caYx/t/5hERvUMkjYiInuMWJPg2\n",
"E1keoWvpPdbaX6QPZFgb0R0VMagQ3VMRET3Hj1E/97OBe4Ln7gHebYwZDmCMWW6MGRO85rfA69zz\n",
"q1DP5oiI4xrR0oiI6CGste3GmF8BjdZaq1Yhf4xJ3IJ6vT/ieojsAf7Cv9Vtvwzcaox5Cnga9YeJ\n",
"iDiuEaXRIyJ6CBcAfxi4wlq7eaDnExFxLBDdUxERPYAxZgWwEbgvEkZENSFaGhERERERFSNaGhER\n",
"ERERFSOSRkRERERExYikERERERFRMSJpRERERERUjEgaEREREREVI5JGRERERETF+P+zsSjNWali\n",
"PgAAAABJRU5ErkJggg==\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x106c8a1d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#コブダグラス Y=(LK)**(1/2) (w=5 r=20 固定費用100 ) Y=20x+100 規模に関して収穫一定\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"fig, ax = plt.subplots()\n",
"x = np.linspace(0, 60, 200)\n",
"plt.ylim(0,1500)\n",
"plt.title(\"constant returns to scale\")\n",
"plt.xlabel(\"yield\")\n",
"plt.ylabel(\"cost\")\n",
"y=20*x+100\n",
"ax.plot(x,y,'r-',linewidth=5)\n",
"for i in range(1,100):\n",
" y = 100+(5*(x**2/i))+i*20\n",
" ax.plot(x, y, 'b-', linewidth=2)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAY0AAAEZCAYAAABrUHmEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzsnXe4XVWZ/z8rpBJKEhJaCAQIhCQkkEKogdCbNAuIgr2g\n",
"MjAyOoLOKI4zKjgoiowz6k8d7OIgikKkhN4SWnoP6fWm3dzcm1vX74/vWuy199mn3XtuSe5+n2c/\n",
"u6+9zj7nvN/1ft+yjLWWTDLJJJNMMilFenR2BzLJJJNMMtlzJAONTDLJJJNMSpYMNDLJJJNMMilZ\n",
"MtDIJJNMMsmkZMlAI5NMMskkk5IlA41MMskkk0xKlgw0MilJjDFzjTFnd3Y/ShFjzAeNMX/v7H5k\n",
"UliMMXcaY37Z2f3IpDzJQCOTksRae6K19rnO7kcpYq39tbX24s7uB4Ax5hljzMc7ux/QtfriJEsS\n",
"2wMlA41MOk2MMft0dh/aIsaYniVc1ibFWOF31NWUtOnsDmRSvmSgkUlJYoxZYYw5z23faYz5gzHm\n",
"f40x1Y66mhhcO8wY85AxZpMxpsoYc587/hFjzIvGmO8aY6qArxljehtj/tMYs9IYs8EY8yNjTF93\n",
"/QBjzF9dO1uNMY8YY4YGz/mIMWaZ68NyY8wHguPPB9e1GGM+bYxZbIzZZoz5YXCuhzHmHmPMZtfG\n",
"ze761P+Gew//bIyZDex0959mjHnJtf2WMeYcd+1/AFOAHxpjdhpjfmCMGZ5sP7QAUt7RncaYnxtj\n",
"7nfvotoY84ox5pjg/u8ZYzYaY3YYY2YbY8ak9DunL+74GcaYmcaY7caYGcaY0wv8Br5kjFnj+rAw\n",
"+D3sY4z5sjFmqTv3mv+ejDHfN8ascn17zRhzVoH2U99jJl1MrLXZki1FF+Bt4Dy3fSdQB1yCRovf\n",
"BF525/YBZgH3AP2APsAZ7txHgEbgc2jA0hf4HvAwMADYD/gL8E13/SDgGnfdfsAfgD+5c/2BHcBx\n",
"bv8QYHTwnOeDvre4dg8AhgGbgIvduZuAecDhrg9PAs1AjzzvYQXwBjDUfbahQBVwiTt/gds/yO0/\n",
"DXwsuH+460+P4Ng71+R5R79wbU5y7/dXwG/d9RcDrwEHuP2RwKF5+p7syyBgG/BB96z3A1uBQSn3\n",
"jgRW+baBI4Fj3PYXgdnBdzHWt+HaHujavw1YD/QOfke/dNv53uPgzv7tZ0t8ySyNTForz1trp1n9\n",
"w38FnOSOTwYOA75ora2z1tZba18K7ltnrb3fWtsC1AOfBG6z1m631tYA30LKC2vtVmvtn6y1u925\n",
"bwLh6LMFGGuM6Wet3WitnV+gv9+21lZba1cj5en7ey1wr7V2nbV2u3t+IdrEAj+w1q611tYDNwCP\n",
"WmunuT4/iZT45cE95dIw77wja+1u98yHrLWvWWubgV8DJ7trG4H9gVHGmB7W2kXW2g0F2g77cjmw\n",
"yMoH1GKt/R2wELgi5b5mBJJjjDG9rLWrrLXL3bmPA1+x1i4BsNbOsdZuddu/ttZuc+1/17UxMqX9\n",
"fO/xsoJvKpMOlww0MmmtbAy2a4G+jnIZBqx0oJAmq4PtIcC+wOuOktgGPAYMBjDG7GuM+R9HCe0A\n",
"ngUONMYYa+0u4DpkKaxz1E2aMvISKtJaZLmAAC7s05oCbaR9hqOA9/n+u89wJnBocE25voTVKcfC\n",
"912H67+1djrwQ+B+YKN7X/sXaDvsy+HIeghlJRr1x2+ydinwj8g62GiM+a0x5jB3ehiwLO1hxpgv\n",
"GGPmO/prG3Ag7vtNSCnvMZMuIBloZFJpWQ0cafI7cEOlVYUU4Ghr7UC3DLDWHuDO/xNwPDDZWnsg\n",
"sjKMW7DWPm6tvQgploXAT1rR3/VI6XkZlu/CPJ9hFaJYBgbL/tbau1OuBdjl1vsGx5KKsSyQsdbe\n",
"Z62dBIxG7+uLJfQbYC1S1qEcRR7gtNb+1lo7xV1jgbvcqdXAiOT1xpgpri/vc9/rQEQppllexd5j\n",
"Jl1EMtDIpNIyAynibztLoa8x5oy0C5018hPgXmPMEABjzFBjzEXukv0QqOwwxgwCvubvNcYcbIy5\n",
"yhjTH1E0uxCFUoq8AzzIT3KrMeZwY8wA4EuUp7R/BVxhjLnIOYT7GmOmBg77jcCxwWfejJT1je76\n",
"j4XnC/Q3/YQxk4wxpxpjeiELajf530OsL8CjwPHGmOuNMT2NMdcBJwB/TXnO8caY84wxfRCtGD7n\n",
"p8A3jDEjjGSc+772A5qAKqOAh68iv1KaFHuPmXQRyUAjk9aIJVexWgDHuV+BRp6r0Cj02gL3fQlY\n",
"CrziKKgn0GgZ4F7kTK8CXkLUlb+/B/B5pIC3oMigz+R5Tlpf/bGfAI8jR+7rwN+A5gL0Wrwha9cA\n",
"VwFfRg72VchC8or++8B7jaK/7nXHPolG4FXIOngxT9+KHQMp4R8jB/YK1+Z38nQ31hfnd3iX628V\n",
"8AXgXd4fkZA+yN+zGQ0KBgN3uHPfReD7OLIkfoIc+H8HpgGLXd/qiNNh73yuAu8x01FdTIz8mJlk\n",
"kgmAMeZS4EfW2uGd3ZdMMumKkqF4Jt1aHA1ymaNnhiIK7KHO7lcmmXRVySyNTLq1GGP6oaisExB9\n",
"8lfgVhfim0kmmSQkA41MMskkk0xKloyeyiSTTDLJpGQppeDaHiHGmMxkyiSTTDJphVhrS65asNeA\n",
"hsTeShTqmFynHdtTr+mBahD1dOvE8onx8NN56efeWdLu7Z1Y+iS2O9Iy3QVUoxDO6jzbVSjcNlzv\n",
"QOGeB2m56PPw+NVAA/AASqQ7FGWCH0Jp/4EtKATUhxAvA5a4dQNKdnsI1a56AiUIHofeaVIsquP1\n",
"FvAmqmO1BvgQCjFdj/JOjky5dwEKPX4ZhSn/1n2OTcDBiWtXoZDXp1B470T4l93w732Dazajul/L\n",
"gG+jvIuwz2uB36D6UYcn2p/v+nAlrpZWcLwnUdg06LtcicKLvWxAta96u/0W9L0OCK5pBHq57ToU\n",
"fg16h2lKLt/xFLnTLaWIpZr92J/aX2PtDSXetMdIuQPuvQw0+H5nd6BryBEA49qhYYsSuxrcEm77\n",
"/doylzpyQaERFSQ8wC0HJrYdIHBcsO2XRAmNd/IKewOfSPlM25AC20AEDOGyE+UkHIUU+VEoM/0T\n",
"KFGub6K9C4N3tQwVQ5zv1gtQUtxxwATgNOCzSPF78ds1wKsIJF4FtqNCgGeg/IgwSe9gBJjTEUis\n",
"cNdehgogOsXbsy8CvYdcm8NQQchPunb2Qfkef0RgNhb4NFFCXi3we2ARcBECDBBgPIoKVV5BBBjb\n",
"XVtHuutB7/MvwLlEgDEDfd++Ou9S9D0e4vZnEdUKq0bg0Qv95nq65+8m+i48+IVg1kqx/AdfYn9q\n",
"NwC3tK2tvUP2Gke40NLe53ZtnnWhc3vSNS3oj9Hk1onlwivhiT+mn4styfvTwMBvt6A/YtL6SK73\n",
"TVn65znuz+1HHBj86LI10owU3xYt/zQC7jkEjez/B43kPUjUIaA5FI2kjyQCBr/eL/mAhGxyzxqF\n",
"QOIryAqpRQmOY4JlFNFoOZSdSLn1B76BIrgGAKcjkDiN3ExqrySXoIq4hyJFfB7x0iBecW6Bc5+G\n",
"p+cjoBibeGf7oGq6a1BNr+MSz1uAEh9vILfsyX8jgAqto80ILMMCk3XoHZ0YHFuKANBbCEmraRuq\n",
"kht+lqSEFkaJQHEnpVgag9jEFmHXlVj7SPF29zxRKbfS6am9DTS+SNemlSp1TQ/yUlPsA384FK7d\n",
"WviaVJoqHy3VO9Gn9pZ6IusjSUtVEwOFd5YqpGB6ItrjIGAwPPxVuHoCyrreiEbyhyHFl7QS0qQG\n",
"USurgrWnp7a5tm5Ho+4FSDGORACQJuuQ1fGGWxajEf+fkfJbihR28n2vRFbHS+7+L6Gy6FXkFgCs\n",
"QpnYT6Dy9dcDO+GZ/WGqv6YagdPzwA/IBeoNKMv7XOIAA6rzNQ94D3GFvRgp7ROCa6sRzTUqOLaW\n",
"ODXYiAYm/YP9nkG7tUS1upqC+0KAKIOaAniG4F3kEUstfelHw/9i7UdKb3vPku4OGp3djb1Zmihs\n",
"iSTpqV2k01HJ4yE9VU3EXXsq6kDiFFVITzlgeGfbj0hLlRoiy2M9cWBYhUbLB6CRe7gc55YBuU2+\n",
"IxuQYg2XbQggxgETEUWVHNGDlOZbCOheQqP/Y5HlcRa51GMN8ByipxYARyOwOI94YcSNCJyeQ0r7\n",
"KlR+xSuMnUTU1UgENn7UXw88CMxBVNP5QbuPu/5eEvRtm7v+eCLtvB35WS5A3xfAK64vR7v9eYhf\n",
"PdDtzyfyhYRWyE4iKjIEFS9lgkhSLPfxWW7mv9cCJ6Ky+XuldHfQuMftdlVaqVLXlEM5FTsenssH\n",
"BAaN7tLoqHz0VP8822nn9icChD60XixSVqH1cQGyKO5ECnW9W6rdM73lcThxYDiS9BLeodQgi2OM\n",
"+/y3IYVb5do7MVjGkA4yDa6vhyHle6fr7yRETZ1BrpO7Hr2nJqT4+yIa6CLio3z/TgzywQwB3g2c\n",
"Epz31NQ0BFDXE7cKQAD4gDvnqwD7dh9AABIWFtyC3nU4S18tsjBCkHybCCxAoHZIsO+/I9B78j6Q\n",
"0GGfdN5XRA5jNevEtl2Km+Njb5XuDhpfoTjlUw491NH3lHptIXqqECVV7J40X0Vb/AutkSYiOirf\n",
"eitRxJQHh61IkQ1Eyt47r+9DI/f/IwKIw8hxmKdKA3Icr0wsy9Do/wA0Ur8P+RjeREoxH9hsRSN1\n",
"T0/NQe/952hkvwyBVfKdV6GIqZfcM6Yg38lOBLohh1+NaKm/oxH7V4k7iUEK/DEEUt8gF5Q2I2pq\n",
"PEEkgZO3kQV0A/HR/EK3DkFrBwKccJ6TFQh4vKKvJfKV+f3Qagj7HgJHBZzc+aSFBnrRi5afYO2n\n",
"2ucZXUe6O2h0djf2VvGcc30J6yQFlW/b74f01C6kFEIqKklReXpqMLn0VDlKpJ7I6vCLp6dWIt9D\n",
"L3KpqeEIGAqV7K4B5iJwmOuW1WikPx7RUhOQ9ZEcJVt3vQ+tXYKsljPQpEQTiEc9NiKKZzoCosHI\n",
"13ExEcUDer+PoOls90MWyrnB83ej8Ntn0ej/Q0QO70bgTyiK6Uzis+l5aupyouinre76kUTWxhYU\n",
"2XUJkfXgy7d46+J1ZJX1QRbEavS+QVaKf+fbiaw27+OokMVh+QPv5n08vBw4iW5QTqa7g8a33G4x\n",
"yqcceqij7ynlmvakp0IAaESKuBeFKalw21NP+dbJY56eOpD0yKJyJJm7MQhFHs1Ezl4PDlvQ6PVw\n",
"ImoqpKeGu/1Cf6QGZBn0Rv6GR9B85+uRtRNGTZ1IPKzWSwsaeR+DRvfXuXbHIeV8JpHSDO/Zjd7f\n",
"vyBr5SxEEY1P9NnTWP/h2r8GWSk9grZ6IOvlQeB9ro1QdgI/Ip2aehD5WY4Irt+GHOKnBsdqEJCE\n",
"0VWryI22GhLshxZGmKMR5m5U3No4kVnM4eQWYArxaYr3WukyoGGM+RkafWyy1o5NnPsnVPN/sK/d\n",
"b4y5A/gYUl63WGsfd8cnolDAvmgO4VvzPM+C/Trl00ftQUm1d5v56Km2HgvpqT60A1dcRHyC1w7i\n",
"lFRyP5nQV4WUiZ9K1C+fQgr1NaS0PEh4J2yxvqxFVscK4vTUCvS+jkVzfhyDRtuDiSvQUOqQU3cW\n",
"sghmIaV+K0qe24QsgKRDdyeyJHy+xr4o98EisA+prHo0//lj6F39nFyHcAOyDv4K3IwALbzG51YM\n",
"Q9ZKeG4Z8ALw4UQfF6H/bZi8twW989CHkQyv3YasDv87C30Y0AG+i7g000xPesC3sPbL7fusriNd\n",
"CTSmoBHGAyFoGGOGoUlaRgITrbVbjTGjUebpKcgEfRI4zlprjTEzgJuttTOMMY8CP7ApjqmMnmo3\n",
"KURFFaOniq39Uk2Uq3BgCYunpcKlHN9LM+La1yHLwK89KKxy1wwlytc4Cim849x2vhFuPXICh1FT\n",
"y5BFdSIRNXUy6ZbVCgQQLyIrwudrnIX+H6FvwiJK5ylEZfVDzvDLifspahFQPIoU7+XuOu8faEAg\n",
"8jQCveuJrIBmFFH1BnK2XxK0+7jr48VEuRdb3PXjkTMf9G5fQIl/fV2/nwImE4HEq+7z9SCagXCQ\n",
"O7c12PYWSGhl+O02RExZXuA0zmTGW8CpWNvQunb2POkyoOE6Mxx4JAEaDyLn25+JQOMOoMVae5e7\n",
"ZhqKIlkJTLfWjnLH3w9MtdbelPIsb2lA+fRRe1BS7dlmqfRTucdCAGgkco4nKahC20nqqZTt/SnN\n",
"MV1IdhFZHd4KeS9RVNMiBA4bkYI5hMgpPox4Qt8wCoNQC/ptrke+hq3AjUjh90Yj7jBy6ujUVuRU\n",
"PhQp+08h62MkoqXOIvIRhOKT3X6Hpkg9FUWITSY+Et+F3u0DSCFfhUJwvT/EK9i1iLp7H5GS99KE\n",
"KLf3EdFk/r4/u2eGtNsOBJATgmPVCATChMA1xC2yEBSsWzwg5IuaqqhcwGM8wWX1wESsndcez+iq\n",
"Ui5odGgZEWPMVcAaa+1sY2J9PByZ4F7WoFFeI/FJ7kNnWJqESWhdhUpqjzbT6KlK7Ie+io6mpiA3\n",
"UirfEtJSVUgp9SfuHB+BPsdupFRvRAruYErjwTcRT+pbiZT8MqRMj0LO4jOQYvs+Aoe099ZIlBD3\n",
"FrIOtiAL4n7X3neIO65x7c5Eo/SXkOX+O3fuKuD9wbVN7rq/Iuf5/7rjN7h+gpTuk+6aK5Af5DDg\n",
"Lne+GlFTB6LEvX1Q3SoQID4FfDx4PsjSMAgcD0SAsQmB1tFEWf6LiKKojiCeczGIyLltiA+segfb\n",
"4bttg1URl32o5wn59u/oboDRGukw0DDG7Ivm/70wPFzZp9x5R7Q9leIZn5kUEEsuBZW2nzzn6add\n",
"ebaTx2qRMoTIIZ5M5vPbR6AaRMnoqUKZ3X2JR/uAgCaMmlpD3GexC42Mw6ip8xE9NYLcXBI/im5B\n",
"TuAwcmoR+p+dgDKrL0DZ3GEiYk/3GTcQgcRr7vipyHn9OeIlTfq5ZzyJkvX2cX38HJHDGgQU0xBQ\n",
"NCN66dtE78yi8iCPIyV+IxE11YIiqt5CAQUfJ5K/I8C4kqjW1CZkgZxFlOvxNqK2rnb7TSjSa2rQ\n",
"vzeJrJwt7nP6PJQm19dmBPaGuPXRRrEsEpY9TTepXWeMmUoblGOH0VPGmLHoB17rTh+BLIdTgY8C\n",
"WGu/7e6bhqbdXAk8HdBT1wPnFKCnvuJ2uxKV1BH0VJJyau2+B4Bknam0siLJCKp+FE7qS9v2NaeK\n",
"1XcqJvXkOsePQvTJkyiPwgNEE4rS8U7xw5CSHE4EEElndFLWo9H8aARa/4qUZRMaTY9FI++xSKGm\n",
"WR+bXL+HoUCP+10/TkcgMZHcQZ1PfnsLDcBORkBxFnEg89nSzyIK610ILJJgV4eo4isRKHjxo/j7\n",
"kEVxZOL4o65/YSLeTvR/DetK7XD3hEmNG4hTVWFmd1giJJ9UzMIAy2f4If/FLdXAWKxdVZl29yzp\n",
"8j6N4Nzb5DrCJxM5wkc4R/irqLrkDDQiKuQIv4f2oYi6yrVFak6VtKTd34t4SfTOkJ0UTurbgSiM\n",
"ZDl0X/XUO8S99fEZpLTfQPSQB4hSHOY7yI2aWoFGzdvRb3Q0UvT7IOrpGNLfnUVRQ2FS3yoEWr9w\n",
"/Q05fS8tCBxeQPWhNgJ3I+UehqB6mYn+H3PcdceSW5vpBWQ5nI78PeH5XSgBEkRnhcp5OfpPJhPd\n",
"ZqPfUxg1tdbdG/osFhMvlb6eXF+Ip+bCUNs0Z3fFZH+2Ua3X/iGs/WUl296TpMuAhjHmtyja4iA0\n",
"qvqqtfbnwfnlwKQg5PbLKOS2Cc3R/Hd33Ifc9kMht6nlibPoqYpKMpkvLXoquV2ovlS+/V1IYUAu\n",
"NZWW2BcUInxnKddK2U5kdfioqTDreyuijny+RriMILfabChriZL55qAQ2wakMMe6ZRLpYblbESU1\n",
"A/n36pB/4CzkGE9mmXtF/oy79mxkUYQhrk0IcB5BoHyBu8YXBrSIZnrctX89kdO+BVlPryPL5+Kg\n",
"3ccQ7XYNUUXdta6t84Nj89A79fRgnft8ZyNA2u3Oe19HmLtR4/ppiIOkt0baaHFYdtKf/aj7I3At\n",
"e0vCWiuky4BGR0tQ5RY6L+muva+1FE7SK2VJu9+DhA8zLFZfKi25rx/5E/jyHdsPKeG2jCCbiDvG\n",
"t6AIo4+58x9Eymg9AqqBRMl8PrHP01PDKV70cAdSmD0QADyNJk/ahZSlB4dxaASe5m/Z6fo0Bo3W\n",
"P4b8CT5q6tSU+3zyWw1wLfIZXIgUcEin1aD3ugwl9V2OlHbSMmlBJUYudc/14pXxjxFQHBVc3wMB\n",
"zMnkli/fRLxcSFreSZjJDVHyIcQtjBAQ8m23QSw/4lPcxE83oGKEW9re5p4r3R007qNr0EidTU+V\n",
"e42npzq6zpSXcJa+Qol924hHTW1DfU7mbIxDkxtVozBWDxKlZJzvRlTUCiJayi+bkLUzEk2ENAZZ\n",
"KYPIXwp9FbI6/LIUWU1fRzRROF9EKAsQnfSCa+MjKKkuWUcKZNk8iiyVmxGQJMNTX0HU1LFo0qWQ\n",
"7qlF1FQDcWc3iJJ7EhU8DH+Lb7nPHFo2K4mi2LwsSVyTjIAMgSPNooCK+jFgBAtZIj/9ZVj7WKXa\n",
"3VOlu4NGZ3djb5BSa0yl0VNpdaYKrXchK8c7xIstg4iDQ7ml0HchSsovYc2pFW67H6Johrvl6GCd\n",
"LOwXShXybcxF1sMcNLL21sd45Dw+NuXeWhRB5Euhb0fANwVZHskSJOtRUcKnEDCehminMK/DuvYe\n",
"du2dh8Js9w/OT0dgMxD4APLL+HMPuz5Ndfd6+SsCymuIHNpvu2ddQgQYM5HVc67b347oOl8AcQsC\n",
"Nv9OVxDlgmwhytr3IFkhi+OdrO8fkKe6RHeT7g4a/kfQ2TRSe11biJ5qS82pRqI6U/kS94od8/RU\n",
"KQl94Yx9bQn7tkTU1GYiC+QkFFTxBzSr3Do0ot8fjXIPTyzef5GcBzsp9WjkvBLRPnWIw9+E/BQ+\n",
"YspHT6X5P3YjYJmE3vn5RKXQpyCqKHlflTvmp6ztg/wT5xKnezw1VYtCby8kDhQQWSB3IUvn7JRz\n",
"Pyc+A6A//hQCv9Bpv8l9prCO1DoUWeUtnRb07tKsCIhbG+1YW8ryIqdxBjPmAJOxdnfl2t5zpbuD\n",
"xo/pGjRSZ9BTbSmJ3ovOSeYDKZxCiXzhso0IHLagdzMIcf2Dg/VNSIm9hRTt4RSeMMlLM5HVsQKN\n",
"oP32BgR0I1DOwQddn5rIX8uqioiWmo3Aog/KhfgE6VFQuOc975aFaHT+bdIzopeg0f8rKCLqfSnX\n",
"vYHopwEoWS8cqdehirQ70XzgoXhq6pOJ468g6+eo4NhCBJw+MKHZ3T8iuCacL6MB/e58P/LNyOel\n",
"zRTV1fyRP/G+emAS1s5tS1t7k3R30OjsbuzpUih5r9CxJD21i8IJfn7bT/EZUlADyKWl/LEQIMot\n",
"hd5AnJpah/h1T0+tdu0dQTxi6ihEKQ0jv+wiSubzILEBgZV3ivtS6Mk+NyBwm4konnXIB+CpqWMS\n",
"11ehEf9TSAlPQNbEhMR1M1D000bX1lXEgdNTUwegENvh7rhP6JuPLJnQSf5n9/x3E1GD813/Q4vm\n",
"Gfesk93+egT4PjR3BQIdXwK9OmjPlz/xf2ZDBcqH9KOGWnXvZqy9vy1t7W3S3UHDJ/11No3UXte2\n",
"Fz3lk/lCuilJPxWqN9WHeIRUuBQ61taKBD5vI6SmPDVTh5TbOkSh9CGKlvLrECCOoDAINaEw10WI\n",
"ojkCzQ3+JwRoY4lHTg1JaaMZActQBHy3IIV7KgKIs8i1WnYiYDkI+BZSuBcgWiukiWoRzWWQM/w0\n",
"lLQXlibxmdQ/Qgr8nMTn64nypc4iXrDQU1OnEg9xXofea9jnZF2peuLlfZKO/HbNxZBYNnMQg9n2\n",
"V+DK7hxemybdHTR+QdegkTqSnqrEfmeJn6VvO/EEvh159j09tdndO4C4Y/wgVCn1OnftGgQQxaZt\n",
"BQHyOnKjplYiS8Qgi+MEpLx7kjs9aSjVRLSUz9loQr6L75F/BL0e0VIvIOvlMFRHKm2kvQLlRjyL\n",
"KKybyVW8sxA1ZVDEVii7iayHzyXOLUXWSDKhbzoK9w2d828gsPS+CJ9/431ETQjEvSUSZoHno50q\n",
"BCCWu7mNL3LvRmAc1m5qe5t7l3R30Ojsbuyp4h2V5dSYSp7LR0Pl229CfH5aMl8ysW8g8aS+gygP\n",
"7JqRgg+jpjw9tQIBQwNxyyOMoDqK/OHIu5FfYR4RQKxAgDYWOeUnIusjmTHe4u57FQHFCve8KchB\n",
"fXzi+mqktB9HdNrJKGpqMrnhsA+5z3g68sGE1sAzyA9yECpo6Kk36+5bgiyZU4Lj3u/xHiJrY4br\n",
"89XBZ3sc0WtHu/356DvzUVILiOpS+Zkae6HfQw+3hLWl2uTLOJpFLNcMtJfgEoYziUt3Bw2f0NXZ\n",
"NFJ7XZukpypRc8rTUuUk9IXbhWpO5Uvw60/by5XsJJ6z4ZepiD76IfAzolLoh5IbNTWMCBSSdZmS\n",
"sgqVw+iNFPoTwD+4zzSGeNRUmv/DEk1WNAb4LaKJxiI66GxyKzjXus90JIoEewxFNV1AfKRf79rv\n",
"i6YUOJpcH4Z3uj/g2juHSBl7Jf0g8RBfT1k9jyyk0Gm/BoFOeGwd8Qi05KRKyfm/21neCa+9F2s/\n",
"33HP3bOku4PGbyid7qkEZdTRbZWS3FfO+Xbgj0uWRnKjowqVRN9MFF67Gykj7xQPI6c+hZTZAmSp\n",
"HEppn7OK3Iipt4kmZDoSjfxvRsl9W5BPIe3PthuNsL1T/A00qh6DqK1DSC/Ot5Wo1tQbaET/M9Kj\n",
"s9Yja+FZ5Cz/N3JH5XOR5VCPssNDqQf+4tpJluaZh/JFklFTTyCrKfSlvICoMf+ONyMg8dbITjRI\n",
"8OfDrPAw1LbNzu64WGYygUm8NRtNqpSF1+aR7g4and2NPVGK1ZUqdq6e/OXP8yX61aNRcSkJfQci\n",
"eioEh2JWQVI2kRs5FdJTO127w4ksj+FoxJ5WCt1LCyrXkcz47keUs3EyUrTJjHFvecxEs+4tRGBy\n",
"JqKnxhGGtJu9AAAgAElEQVQHgF2IVnrS9fkERE2dTq4P4yFkCUxGdFLo03kGRU0NQWHD3jJocfct\n",
"R0l649zxZuD3COSuC97FUygv5Eoi/8yTrj/eunjNvYM+wbvy2eHhfBo+vwSiPI02+TQ+wk/5OZ/c\n",
"jSZVmt/adrqDdHfQuMHtlkP3pK0r0UZ7tJUveqo1kVOgP2WhelKlUFVhzalSEvr60/ZyJZ628YuP\n",
"nuqFyoesRcrSl0IfTDxqaijxgoTFKJMNiJpaiXIsdqNIohZkfYwjipo6lnTrYyVS5GciC+DjRFnf\n",
"U8id3a/R3TMCAcu9KAT2IuKJdI0IUAYguqsvoqZCa8CHsf4OKepzgz56aurPyGLwUV/eEnoF+TZC\n",
"K2A1eo/hsSri4JSsMxX6KfLlZLQ5FwNgAFvYpq58Dmv/q63t7e3S3UHjj3Q9Sqm96ak0OqrYNW3+\n",
"Y7ZRfGx+WrRU2rKdCBiqieobhbTUYOQXOBdRR36K0VIAqhpRUcmoqRXu3OGIkroUlc+oI//shn6W\n",
"Pu8Un+P6cwzwBZRPEWY9e9mJKKHnkYO5L8raHkWubEJl0KejUf0Pyf1OFyDndTWixMLz9ciq2Ewu\n",
"NTUblQ/5cHCsGVkn5xMBbAuykMI8jmUIhP17Ca0J/1xvqVTM2R2XFmroT392/xm4JguvLS7dHTQ6\n",
"uxt7knhLpJwEvrRzu0mPlMo3a5/PBE4m7g0ocCykp8othb6NeBl0v16BgMH7JoYHy9HBOl8pdOvu\n",
"X0A8rNYgRT8O0VKTyJ3GFXfvTAQSs91n9VVuJxIHlXp33ZOIPjoalTE5kzhwzUJAsQpRU9cStzie\n",
"QbP4HYQsJl87ylNQq1GSnk/Ca0STOB2IIqS8RfA3FDLrS5DUodkDz0cDlBZUUt1HX3lK0ifwhfOH\n",
"eCAJgaOVIGL5He/lOh5aBYzHTbuQSWHp7qBxrdvtSpRSJdtKo6eK7YfHfDsG/bl7Ul6tqbTtsOZU\n",
"sWS+SiT0NZFLS/nlRqTsb0VzSNQh5ZSMmgpDa4sVPdyOfA+LUMTRUSinYTrxeTL8LH1pn289UuiX\n",
"IEXsKaYzEEiMSVzfgqyV0Wi0fgtS0JcRZW77d7EVjeb/gHwDVxF3nPsJjv7i3sVZwTmvsB91xz1A\n",
"eqf0q4iGg0iRryRePgRyK/UWipIKHd4VtDBgCtN5jvObgbOx9qVKtbu3S3cHjb9QOTqoq60hl54q\n",
"N5GvK0gTUfJXWgLf9jzHNiOqJVkKPaw7dRP6nG+jUXQppdDrSK819bZ79mAEBqNQ3aYe5K8ZZYlm\n",
"6ZuDaJ61SMneiBR6WpRQPVGuxqvoO78NgVRSsW5GobdPur78hFyqaxEqBbIR+E7iebXu3FYUCRbK\n",
"y8gSe0+ib48hp7sHxFpkYU1MPDOcTyNZZ6pYiHWbAKQPdewWTn0Za7/V2na6o3R30OjsbnR1scSt\n",
"jyQ9VYyOStuuIz2BLy2xbzdStmmz8uVbfFLfEOLVWkuRGtKjpnzm90bXn+HEo6aGoyif5BSsoWwg\n",
"XmtqPrIivPVxEqJn0sqpr0HU1AwUWtsHjeinuHUYrdWEfB1PIsU8DFkcU4iDxWxETa1xz303ccf0\n",
"k245GJVB99RUE/BLZKldS2RF1KFcksOQLwei2fxGElFYW5BVdGZw30oU3QWylA5CwNVIZOWGzvBS\n",
"5gYvIJYNHMwhVD2BkvhaWt9W95PuDhpXu91K0kFdbZ0vua8QTeXv70FkdSST9Iol8SW3+1I4kS8t\n",
"sa+tCX3NpEdNVSFFfwMarX+CKLEsWW8qnKUvrT5UKDUoamoxUrbnoQS4ryGKK4yaGk16aO42BBAT\n",
"kfL8OAJQX2tqHPHQUotAaCxS0h9GdaQuI168sAWB3mEoX2MjuZnfPoLpCbc+JTjnqaknEE3mQ4K9\n",
"JTQLAZ9/Vg/k8wgTF/3vq3fi2D4p2/mkjRTVO7PwbQROwtqNrW+re0p3B41pdG6kU3u2UcpsfPmW\n",
"riIWRQmVWgp9B1FC3xb0WZKz9Hkr5DKipLs+lOYw92GtK8iNnNqALJuRbvkkAp0wAigpK9CI3zvG\n",
"V7m+nQf8I+kKshHlM7yAqKkmBBTXpFy/BVFFTyOFfD+5+R8LUa2pzYiaCq2RaneuidzEvWfd+SuC\n",
"Y9uR7+bdwbGN7nhIRS0jmlzKf8fePxLWmQppqook801iBjM51QIXYe2TbW2vO0p3B43O7kZXlZCW\n",
"8ku+hL1iCX3hdimz8/l1AwI+T0cVKoEe7nt6aiDljUjrSI+aWo2U+1qkUIcnFh85VWhCJj9LX1iQ\n",
"sMbdOxaF1Z5CblkQf68vg/6a+0yTiUqhJyvAvopopVlolH858nWEYDAPgcFaZJVcQzxH4nGk/Ici\n",
"a8w7rRtQMcQ6NA+HLx+yA/gjsoJOCa79q2vfv5slCIB8WPBG9B17ayd0mnuHPKRPWVu2xdGTehro\n",
"i4FvYu1Xyrk3k0i6O2hc5nY7M9KpvdoolKiXbwlpqaSlUixxr1hSX0hPlZLQ19aoKYuct2n1prai\n",
"mkv9UJTREvfskJZKJvUNpbCSakBO7UWu/Y8j6+NspLzDqKkxpM8RvhMBw2B33feRRXEW8gGMJ3e0\n",
"PRv5U/oh62Q4iro6IbimBfkujkShrksQUIQ+GB/R9LRbnxyc8yP+p11fPAB5xb2UaPIkbxEkK/om\n",
"gwGSfol8c3xXKGLKsoJhHMXaF4GpWNvU9ja7p3QZ0DDG/AyNijZZa8e6Y99BURgNyKT9qLV2hzt3\n",
"B/Ax9CO9xVr7uDs+EfgFUlKP2jzz+jrQmE7XpJYq0Ua5Nac6s65UmrQgiyOsL1WoDLpfPDVlkfJL\n",
"qzd1NKJQmpCiLmXu8BYiqyNc3kYWSX9EuRyPSmWcSuEooPVETvFZSPEOQL6ML5MebdWMKtK+gDKv\n",
"d7pnJcuRg97NNFS+owVRT0lH/QJkIWxDiYG9Evf/0R37cHC8BeVd9Cc+F/hqZMFcEhxbiixF79yv\n",
"QxaW9w0l60yFwNJGZ3colu/wT3yB720DTsbaVZVpt3tKVwKNKegH9UAAGhcCT1lrW4wx3waw1t5u\n",
"jBmNJn/xJv2TwHHWWmuMmQHcbK2dYYx5FPiBtXZayvMyeipXktFS+eipYgl9+dblJvT1R0onmbyX\n",
"L7HPz5fho29KlUYiSipc1iPKZLV7Nz5fI4yaOpZ4mY6k1CBlGk7jWoWsj5NQMt8kcnMZQEr1VQQS\n",
"M1wfJhFZHqEfxhJRU3NRtNO7yKWmFqMcjTWIOrqaODX1N0SFHYMoKE8R1aLBWO/E8fXIb3IWUWn2\n",
"HciiuZCIVpqJwNpHaC1EFtI+5IJ3mLfhLY1W15YazWzmyUd/Fdb+pTVtZBJJlwEN15nhwCMeNBLn\n",
"rgHeY629wVkZLdbau9y5aYhuWAlMt9aOcsffD0y19p0Z+sL2LNgL3G5Xo5Y6gp4Kz4P+mIWskVIT\n",
"+vId60vhhL7wXCVGmNVE0VLJ9dnIqv0J+t30IiqFfphbwjLowygMQuEsfYsRNTUAWQHbiUqg+3Xa\n",
"/OO1KJy2EZU2eQKV+/AFCSeRm1+xEFkPByNLoS9KBAxLibS4vo1w7c8i14fhM66fdW2F94flzs8i\n",
"buE2oRBZ77PwCj5Z4jy5n+ajaBcJ/Bjfx9p/7Ihn7u1SLmh05qxtH0Nx4KAf6SvBuTXI4mh0217W\n",
"ku5c9PJ1uia1VIk28tFTXa2uVJr4hL6Qnkom8eWbva8KWSoHkh45NYooa/k6cqOC8knaLH0r0O9t\n",
"HzSKPh45tQcgBZpvVLsFWR1zkQ9jIVKqE4lqO13oFi8WKfznkSVQjZT4He78l4JrdyJq6gn0n/Bl\n",
"zicQzQ0+F+VpbAe+7Y6d49abkDUyGHi/OzaFqAbV8a6vPdF/cR76ria7aw9AltFJaNBwAPLvHISA\n",
"ry8CcE9ThbW1Kjidq2U5R2Nkgf1z69vJpC3SKaBhjPkK0GCt/U1lW74zKJ421S3dUkqxRkpN3iu0\n",
"XSiRzy8+RHU/0pP3PB01FOU6+OODKH+WvgOQYtqAaJYwasqXQV/h+n8YcVpqAqJXhpOu2Azi6OcR\n",
"T+rbhBzEY5Fj+8vkzriHexevoUS9V1wfJiAr6cPkJi6+iqKe5iJFfjkKsQ2tk4UIDDYiwLmNuEP+\n",
"YffM0Sh3xVsD1YiaOghlf/vjC9z1lxFFQK1Cvoxz3Tuw7jOcir4X6/rhrZntRFRX6ANKK9JYhlh+\n",
"yGcYxvqtwLVY29D6trq3GGOm0gbl2OH0lDHmI2g0eL51E6MYY24HsNZ+2+1PQwlUK4GnA3rqeuCc\n",
"AvTUFLfb1ail9qKnwmM+CzbNKkkrPdKW6KliM/SF60oMTPLN0leFlNHdSBGOdp+/0Cx9R1KYSmlB\n",
"wLIYRSWNRwr5u0hBe1rKJ/alzT/egBzcaxF1tBz4PPLZTUG+h2SuxzK3PhZNvLQduJh4XaoWpMCP\n",
"Rwp+BvJhhAUR/Yj/Bfe5w4RAHwk1k3iiHwjwm4mDV5jB7akqX2bdS74oqYrKZF7mVc6wwGWk+DQz\n",
"ab10aZ+GMeYS4B6k+KuC67wjfDKRI3yEc4S/ikz8GcipV8gRPpOuSS1Voo1iQNBVxUdN1VC8/Hm4\n",
"78Nr65EFkawz5ekpX67D54GUQn9sIT2hbylSfMNR8trxyAooNN/GDiKH+GxkGfRGVsTHSS9tjrvu\n",
"OURP7UD00NfI/S6rETXlE9e+Ri5F+xayKuqAfyc+ol+NwG4kcqR72YmoqTOJwmtx/TksOJZWAn1p\n",
"4p4wByMElTZaF5K+1FKnJr+BtV9ta3uZxKXLgIYx5reIUx2MzOevIb62N1IIAC9baz/rrv8y8nM0\n",
"AbdaNwl8EHLbD4XcJuv/++dl0VPlzRPeluipWvLPyheuvdLoj+ipQuXPk8c8PZUv+zpNLKKL0iKn\n",
"wln6BhNP5BuORuTHkj+kthE5xsOEvjVEwDUOWSUnkgtcdYhumunWNe4en9CXdKTPRP6L2URRU1OJ\n",
"A8oiBAab0f/sXUTvyqLw2jmuT1cE925EkzEdh2pKeWXxkntPVwTtzECDEl+YcBeywMa7/Rr32bwv\n",
"I8zlCMHDWyCtsEQsmzmIwWx7CrgYa5uL3pJJWdJlQKOjxYFGWMa5Neu23NuR9FSyrpSlcAXcNCul\n",
"lNLn+c6lJe+lHatECZNwlr7NKds3ocS1T6OM5UOIEvnCpD5PTxUrergGKcZF7rN8GCnUW4jmyfAg\n",
"cWjK/c1EVseHENhciywPT00lczbeRkr2ROTMXomipkYH17S4Po1CtNnLiPryn8cD5iGuv0cTZXg3\n",
"o9+HDdqAiFra5toJQSmcgtUr+0KlPyo+Ax9YHuAD3Mjv1qH5MTa1vc1MktLdQWMWbaeH2nvd2nvz\n",
"gUBXljBqytNT+aKkkvTUFiLFNYQ4NRXu+5LdpSaP7SS3BLrfrkU+D19v6hqUy5FPaogAYhZyCINA\n",
"7L3EKZ1QFiAa6HlkdY9FocJJX0sNcWrqX1L68zoCmhZETYVWzmJUlfZUogmTQIECD6P8DO/wbnbP\n",
"OouIaqpBjnAPXi3IGjkiOL9v8Mw0UGk1gFzGX/gbVzWjjO8XWtNGJsWlu4NGZ3ejM8RSvOpt2nZb\n",
"oqdCaipfUl8Tskq81eHpqbTEvrTtwRSfuzspWxENFVJSfnsNskwGoFG4X4YH22mlQHDvawkqfz4L\n",
"gcQK10/vFD/FbSeVZhMRLfUiAq2TkBIPFbSXmShqajayGq5AkUshIM5BYLDNnbuYeIjrrxAY+ulv\n",
"vSxDEy5NRJVtvTxCbkb4dASc3n+yCoGDB4yVyHrrQfSb6kP0JyxmmRSUA9nCdsUYfBFr/7M1bWRS\n",
"mnR30PBca1vpofZat+Ve/8cMZ+EzROXO0yyRQnRVObRUcr9QMp9fKlHGpBHRUOFSFWyPRPWZnkQ0\n",
"0mAiOiq5HEnh+TFwbfpZ+tYCX0Wc/dlE82SMc0uaBdKCHNwzUSjrADTL32AEEGEJci8rkFU1ESnq\n",
"uah0Rxi224wAaywCg5kITDzN1eLa8FFTo4PP6hPv6hF95Uub+1Do9UQ0VkhXhaVYCtWVagdpppb+\n",
"9KP+YeDd2Tzf7SvdHTQ8PdDZFFR7rLviLHyFpJF4vkYNoqDCZL582ztQ1FAfpAgPJk5L+f3JCCRK\n",
"VWK7iSip5FKHfBQ+amoqkcM3X1tziZzis5ByH4f8EVfkuW8xipp6DllGo4B/JXcu8h0IDKe7/duJ\n",
"z2UB8l08ioDoduI00BuoHMiVCGzC5z8LfITIOqlBNa2uIAL7lQiUfJ2prWiw0DfY98BUwRpTlpc4\n",
"ldOZuRyYiLXbW99WJqVIdweNzu5GR0oLpVNRaceSlFMaDZXvmiQ9lUzw81RFaHnsT0Q/pS0HJvaT\n",
"SrSYVBPRUWtTlq1I4YWUlF+PIL+D3CJQCcNql7nrT0RU08luSUZeNSNaaoZbvP/iHGS9JD/ja8iv\n",
"MBsBxJXIeR5abXPRRFC1yCI5jwgsmoGfoyimi1GpEi8zXfsXEc190YLCbkcR5YM0As+453qAeNN9\n",
"1l7ufaxE7w7iVkmhuUZKEMtt3M093F4PnIG1b7S+rUxKle4OGmPofAqqvdZe2fskviQFVYieSlvn\n",
"o6GSS9r5jqCmmomoqE3k0lRbgQdc/7zC8xFTYeTUEcQL6+WTrUTU1GJEKw1Fc3vXEUVNnUSkMJPi\n",
"E+5OR9bKXe7e0xA1lQSJ5YgeOhMp9FcQEIQ5EE0IKE5G4PcK8fDaBmSVDEGWx8lEviAfSLAD/Y58\n",
"aK+3DDYRWRLeQgiLC0IuEISO7TaWBYnL8cxnkb7Kj2LtLyrVbiaFpbuDxnK/uxeuvcLfE8RP0BQu\n",
"O9GodHsJSy0a1YbRUsnIqWNQGGup0TkN5EZM+fVWpDxPQPTUSWhEnk/qUTkR7xSf446diEboH8hz\n",
"3zI0in8WAeI44IvEp2gFKfm/I2qqD6pDFU4KZV0b05Cz/POJ+59B4HIDcd/Lyygx78bg2GoEkucH\n",
"x15H4ON/b6uIKv+2IIDxVlUaHVV2xFQv6qlXIcL/wtrPlXNvJm2T7g4and2NjhBLYdqp1HUh+qnY\n",
"ko+a8lFT4QRNYc2pfBFT4XoQuRFFxWQXEQ2VjJxai0bzfYhHSvnlGArPv7ECWRA+rHaJ+3xjkWL1\n",
"ORvJ3AuLlLSnp3YiGugcBCzJz/gGqngwHyn6K5EFEo7kZ6KiiRbVhwojoOqBH7v1u4mXD3ncvYcr\n",
"iQBqF/KHnENkbVQhUDnN7TehMOIT3f5OogKF1j3LU1geKFphfVjWczCHUvUScG5WV6pjpbuDxnF0\n",
"Po3UHmsT7KfNwpdWATffNb0ontSXb7sfuZFTyQS/StAVLeSWQE9GT30IZTT/K+L40yKmfM2pQlO3\n",
"gmichYiaWogU6QXAvWhEP4YIIEaQPopehgDiGKR0f4bopzNR5FTSZ7ICWTrnopH+dERNDQ+uaURW\n",
"zATkR5iPLCBvAdQixT0QWRaTiEb93tcQVqOFqIhgWN48VAL+txau21Esv+E6rufBDcjxva59n5dJ\n",
"Uro7aKxmz0vaK7beUygpLyE15S2SfGXQ09bVCHiGFFlOp3SnazOiYZaTGzXlczdGIXrqBFRRtlA5\n",
"kfmo3pOnp2rd/acBHyU9emgpAiCf0Dca0UqHJK7bgqipFxFI/zORJQAa/f/dtTOGONXUjKyVeSiD\n",
"3Yf3tqBIqr7EaajXEJiNDD7bQqJoq2bXV18mJKwxFVawbXU+xrX8mt9zQxOyMLIEvk6Q7g4and2N\n",
"9pRitaRKPdZI65P6dlO4DHoL8cmZQnqqlIgpf6yc0W09uZFSYQTVBnfdUcgKCJejyfUnhLISUVML\n",
"iDK+exJRU+PddtpUrjPQ6P9VpHhPRFbFFHKtjjdRst5C16+rieay8PICopN6I/ppXHCuGlk2fVAm\n",
"ulfyFs1Z09O16ZX8SmTBhEmBs9D7P8rtb3TnfFjtOiKLLXSWt7oo4VBWsUaPuxlr729NG5m0Xbo7\n",
"aPgffGdRSZVu03+RhRL4ClFRadshPVUsSip5rB+FZ+irFJWxlfSIKR9JdSjwPTTK96U+huZZH0bh\n",
"UfBuRA8tdMsQ4DPIKvgesiA8SJxAOv22AoHEAYhiehQBxhnIIkr6L5Yiq+ciZO086e4L8zD83B2T\n",
"iBz2U4ne8TaiRMvXiYoKQpRDsTpo0/+efMG/fYJjhSKkoMJRUnp4A7vpR09aHgA+kiXwdZ50d9DY\n",
"RMfSSpW+d0+XtImZPD2VXHbkOdYDjf7DJL5w7aOc0ooFpolFFsdyInrKb29Co/4TEDiMQrPr5XPE\n",
"NyOr4023zEagMwKBw42klz55G3gaAZHP1fhH4rQTrj/TUOjsQERNhU76BlTyYybyu1wanKsD/g8B\n",
"661ESn4XUf0pn5/RjJzjZxNRWBsQkHgrpQoBj28nnNK11XSUxPI2RzKcNW8CZ2JtXevbyqSt0t1B\n",
"o7O70R5SCi1VznZITxWKoEo7FtJTyQXi1NR+xOmpgaRTVOHxAygPQJuJaKg1wdpve6fqEUhhHktU\n",
"Av0YCudurEegsAD5MOa54yciWmoCoojSJnR6DfkkfBn0UchKmEJUOTa89mFkSYxAEU4TEtdMQ2G0\n",
"ByH66ejg3AbglwhE30MEWg3u+NHEa0q9gIDAR15Z5B85lcjaWIiAFPS7aUi0m8/fU4JYfskHuYHf\n",
"bgEmYe2K1reVSSWku4OGH312JK1U6jWp3SY9UiXpCC+nplSxa9Nm6Ct1Cemp/Wgfaqoajbg9PZW2\n",
"/jUapZ+PgOyIPMvhFKem3kZRUwuQgv8P94xPIWf1aGQZjCHdwb0cWR2NaP7t19HI/nTSo6aWIHrq\n",
"UgRuT7nt0OqoQUA12V27nXh29zp3fU/X73CiJ++sDmtKefopbYKkJDXVrnWl3svveJDrW4BLsPaJ\n",
"9npOJqVLdweN7XSN6KnuKEkrpCbYzpfUFx6vRu/vQCIaKm0ZSvoc3PlkE1LsyxLrDQj4jkWj6tGI\n",
"8skXnmvRCPwNt8xyn+0EBBDXkU5rLUXU1PMoz2Ec8pkk6bXVyBcyC0VU3UYccKpRyY9FwFVEuRQg\n",
"KulBZK1dHxxfi0ApnHdjO7JuLgium+s+v6eiwkzx0Ondpqldh/E2q5Q+8s9Y+51y7s2k/aS7g0Zn\n",
"d6OQtNaSKbemVLFr0+ipYounquqIg4FfLLJCQkoqWXNqYMo63C631hREJc/TlnXIgXsoAoYRRBTV\n",
"CCLuPk22IMU63y1L0Psbjaip8Uj5p/kvZiHfxatI0Y9B9NBZKdfPRDPsrXFtv4eIFvLykOvLEYia\n",
"Ci2S+WjiqRORI90r/SqUBDgFzdAH+o4eRVaTz+6uRpbWSW6/HgG5B7QtRNFloU+jbMd4L+qpox/7\n",
"YH8FfChzfHcd6e6g4cMD2zM6qmA3yE8ztXZdrJ5UqbWm0mbsay09FYJDJampHUhpbSSiqJLLx9Bo\n",
"+i6kUI9AEULDEtulUFPe8vD1pu5zn/MGd/8YBBCjSadsViE6agvwCaSA/xcl9J1GLjU13z3rGvcZ\n",
"p6Ow17Bk+1bXzkREPfUkUvy4c0cjIK8isowa3boXsiZ8nSlPSe0M+pNU+mlWQwUT+1rYwCEcQtUM\n",
"4Bys3V2ZdjOphHR30PBRGJWknDIpLkkLpCax9jRUvrWPmjoQjWw9FXVIynokpXPumxDts8wtS916\n",
"HRo1H4cAYRTyH4xIbwaLlP2bRNRUnbv+VOIz4IUSUlO7iKalTUZNLUfJd/NQnsTniTubNyL6aR3w\n",
"SeKO8CXIUX4KccrqdfdZrw2OLULv2YNQnWt7uNuvQaCZzB737yA5KCpBLI9yCZfy+Hrk+M4yvruY\n",
"dHfQ6IhHdXTuRzE6qtS1XxrQKLtciipJT9UgvtsiayO0PvYL9vcnoqKS1JRfWkNNbUa0zupg7bfX\n",
"uM/po6Z8xJRfCoXr1iBqaT4a6c9F73AMimqagOictKipOSjnYgZ6V2NRQt8ZKde/jKipjUjhv5t4\n",
"noZFM/AtQMB2NfHIq6dQVvp5xOf9mIeivi4neq87UdTUeURO7wXoPfiQ3rXIajHIEmkMrvWWSdmA\n",
"8Xn+k+/yz/XA2Vg7o/R7M+ko6e6gsR+tq+lUaN2eDvRK0FOlrAvRU33JpaHyHUvzW1RCLBE15ekp\n",
"T1GF66OAn6CR/ieJR0oNC7aHUjgstBHRPEuJQmq/gCyOryLAGY18BWNJz3hejqyODcDNCMR+hJzi\n",
"Z5Lrv5jjnuepqReRMzoEzHXus55MNN1rWGZkMQoC2Ia+y9C5PcB9LkNkifkIqWTWdjJCquLJewDj\n",
"eZ03FPR1I9b+qtLtZ1IZ6TKgYYz5GRrtbLLWjnXHBgG/R3/+FcC11s3MZYy5A/HVzcAt1trH3fGJ\n",
"wC+Q0nrUWntrnudZsD7bNaObOk689eGXXSn724Jle8o+iJoKE/jSlmPJzXPIJ1vRb2xZsCxHI2o/\n",
"GdNIZEH4jO98shgBxOtodB9GTV1NulN9IaKmXiCaU+OT5FbUXYic2W8j0PoscQW+GOVxNAL/QBxk\n",
"XkBO8muJfBvNiK46GFkwEOViTCayeFaikFwPrlVEeSttnonvALaxnUEYuBtrv1Tu/Zl0nHQl0JiC\n",
"lMYDAWjcDVRZa+82xnwJGGitvd0YMxr4DfqRD0Um/nHWWmuMmQHcbK2dYYx5FPiBtXZayvNaS0+V\n",
"Y5m0JxVVDj3V2nVYEj2ZtFfKsTpEdXhg8NRUSEuFVkgygS9tXW6tKVDUzzIiKiqkpdYiBTsY0VI+\n",
"amqEWw5Lac9LA5qG1Sfz+aipkRSnpuYjZT3TtTMOUVOnkWv1TAf+hOi9M1EIbegTaQL+G1keZyFn\n",
"eejU/x0C3KuIhwhPc9ddQPROF6Lvy5cZaUFWzMnBfhWRnyV0mLeqrpShiVr2pS+NjwJXYt8ZzGXS\n",
"BaXLgIbrzHDgkQA0FgLnWGs3GmMOBZ6x1p7grIwWa+1d7rppwJ1oNDTdWjvKHX8/MNVae1PKsyzY\n",
"PhSnmyhz3ZXoqWLUUynnPT0VUlB9SzwW+i76B/1sq1QjiyNfxJRP7HuaqL5TH6JIqTB66ggKK7qQ\n",
"mpfVJq0AACAASURBVFqClP0VaDa8XyCwGIPAwU9xmpS3keWxGLgDKeV7ke/iDHLrOL2FrJ5rEKjN\n",
"QoASFjpc4vo2GjncjyWyKpoQSI5EQHIokTWyEVFYaco+tBL8MU9FtQslBZZFHMfxLFsInIa1Oyr/\n",
"jEwqKeWCRrtlfuaRQ6y1G922/7GDRkuvBNetQRZHo9v2stYdzyf1FepnJqXJbnIpqTBqyvspQkoq\n",
"GTVlkHIcSG6k1PhgfyiREs2xNBOyBVkfHhx85NQapDiPRVTQaJT57ct2fCTRjk/o81FTbyHrYAyi\n",
"pj7urusPfCW4bw4CuJeQcp4StO3n+sC19xcEimehjHKIHNszURn0/oiaAv1XGhFltQ5FY4EAY6u7\n",
"/hL0Pnu6Y8uJZ5T7sF2Q9dibyJJppdMbQHNjHM+y7cjCyABjL5SOBo13xFFPFTZz7gy2z2nRYK5D\n",
"KKSOoKfSKKdixwrRU7tTttOOhdth9BTEqam0taegjiM3YspHTZVrrTSgEf5q4hFTfns3ApowWsoX\n",
"6ys04GhB9Z18Qt8ipJxPQKDyXuDfSC+Dvgj5JV5z90xAtaY+S+5/7G8oya7ZXXMbcT/NLuB+9zkv\n",
"Av4lONeMaKuByGoJ/Q5/cM8NM8KnIxrKA8YmBA4eMMLkPT/3fKsB49Pcz/U82Axch7VLyrs/k44S\n",
"Y8xU9NtrlXQ0aGw0xhxqrd1gjDkM/YhBFkQYbngEET99ROL42vzN3+n/RB1VOqQ9174ceqk1pYqd\n",
"70luVFR/lFiWL2IqX82pNMXZWqkmskI8FZUWPXU7yoe4F0Ue+YipkagGlaenCk3M1ETkHPfgcAqy\n",
"Nh4HnkC+iJvIn9C3EoXkzgG+jpTtXxAtdQtxOqsFWQurULb3KmQR/IC4j+JN5IMZhgDxtuDZO5FV\n",
"Nsy9i3D+bF8CfTfRvOQ+ma+eeKFCSzw/xBL3o4RUVdm048m8zn/LGPoHXBBLJl1TrLXPoAESAMaY\n",
"r5Vzf0f7NO4Gtlhr7zLG3A4MSDjCJxM5wkc4a+RV9GecgUZplXaEZ9I6SUviy0dPpS3bkVI9ECnM\n",
"tGipQ4LtYlO2etmOlLOnpfyymii72lNToxAVlMbth9TUm4hK8qG4pyPndHLWvRZEYz2DwKIXop0+\n",
"TBxom1Hk01PoPV1OXMH70uUzkKVzXXBuC6KmhqCKuF5mI9rpquDYXPR/8hFbG5H154E1nIkvLBNS\n",
"lqUxkCq2KoDsXqz9fKn3ZdI1pMs4wo0xv0UF4AajH+tXUfXPP6DaNyuIh9x+GYXcNgG3Wmv/7o77\n",
"kNt+KOT2ljzPs2Ab6Pjku/Zat1B+Yl+hY02UFiGVL7oqzPg2pJdA92uf0Feo1lRroqZAI/wwWirc\n",
"3kVUa+qYxPqIIs97DinZeW5pIQIVX2sqzcJajH7XM137kxEAnJzyvD8ga6YvAorziVsmG4H/555z\n",
"DVGmNijC6TdECYNe1iPL62IiR3i1+yxnBNctIprW1bprPGCEIbZlAcY+NFDLvvSm+a/A1Vmk1J4n\n",
"XQY0OlocaPg/QVegl9q6Ts7W19Z1L9Kjo0rZD+mptCJ9rRVPvVSRGy0V1p86FfH8LwPfIF5nKlwX\n",
"SjZsRhaIL4M+H43C70RWxC+JAOIE0utWve36MAeVUG9BPoZTkN8gvKcBOcKrkUXwNqKTwhn2WhBY\n",
"TUJg6yO3vKxB9NO+RFQUyBnfG3234YRIyZwKv99OEVMtrGEoQ9nwFjAFa2sq13YmHSXdHTQ6uxvd\n",
"RWopTE3tJDdSKrltiaKmhpBeZ8pvhyGmhWQnuWXQ06gpT0+NI91v0UKcmpqDLK7RaPR+CbkTODUj\n",
"Oulpd09/lC9xHXFrYre75ml3/APEgaIG5XAsR6HA4YRM8xDIXER8Fr4nkEXlS8bvRpaGd4BbBEDe\n",
"b1hDFDIdgk4ZoGJ5iqmcx3PrgclYu6boLZl0SenuoOETztgL1i1ULqnP01NJOqrUfU9P7UaKJllr\n",
"Krn2YJBWZ6ot1NRKosipZN2pXQhgjklZhlFYGc4kyvae7/oW1prKV0pkPqofNReN/E9H1NSoxHUW\n",
"lT95FQHgVYjGCmUBKko4DNWhCufmeBNZOJe4z+PlZRStdXZwbC6RHwgEpE1Efo1twXZomZQFGHfz\n",
"Bb7Id2tRTanXS7svk64o3R00/B+lK9BLbV2nRU+VGkWVXLe2FLqPsPKAUCgyqVzxUVPbiWbkS0ZN\n",
"bUSg9yYCrOuQ0k2bpS9ZhjwUiwBnQbAY4MfuGfegRL4JSOGnUVOLUUjtW8C33LGfIKA4KXFtLXJ0\n",
"GzTn+AL0fY4MrqlDjvDL3HWriea5gIiqakYK3YOWL/cRVqD1s++FVkMrwmZLk+v4Db/jgxZ4N9Y+\n",
"3B7PyKTjpLuDRmd3Y28XS/GIqZCeSqs55aOmDkAcfTJKKrkcSmmh4TuJaKlwWY0U6TFE07cWo6bm\n",
"E83QN8d97pMQNXUBufWj6pH/4ml37yHIMX0FccW9A+VovIYU/8eIR2CtJiov8ikiH4ZF0VRr0Vwf\n",
"Hiw2IevlEiJQWUYUkQZylA8JPmtalFTJADOON5klxuwLWHtPKfdk0rWlu4PGFjqfVuqM6Klix1pT\n",
"Bt0vPmKqFinftNn5wmOF6kwNQAqtNc7YTWiUvyZlqUE5Bz6ZLyyFXixq6i1UzG8+8mP0QKDiqal8\n",
"c4PPRdFQi9znPgtFNQ1PXNeELJllyKdyDbnzdjyFQGciuXWmHkLf4ZXES5X/GQUIhIUK3yAqUgiK\n",
"UBwe3NOS8llKBoxBbKaKgzGy0G7KZt/bO6S7g4ZPBGxP2qgjqKlKR08VKnle7JwHg0pSUzXEy6Cn\n",
"RUz5/WmIMvoiGqmHs/OVGjW1kqjO1HzX9p8RKH6DaIa+keQqUIuoqZdQzah73DW/QtTUcYnrdyCL\n",
"YzACktkI0MJs9M3Ih3IJUeFHT681ub6OQhSeL51iETU1hDg15S0Hr/yTEVQVoal6sZsa9qM3zU8A\n",
"l2NtY9GbMtkjpLuDRmd3Y28WS5yGykdNFZuhL4yaOojcaKlkFFUp1FQNCmldRv6EPp/MNxqBRJpj\n",
"uwn5Et5AfpS57rrxCCDOJXfCqJ3IUnkahfQeDVyKcpRCWYuop2UoyumjxKvlzkRJgYPcOW+NbUNJ\n",
"rUOQFeJlhvtsPrqqwfXX7zejd+6zvsOChqHvowRpZhMHM4Sts5Dju7r0ezPp6tLdQWM9HUMfdcQz\n",
"Khk9VU5CX/L8LnesB7mz8yVn6vP0VNriqanWjHprUaRQWr2pnURRU0l6qhg1NR/VZ5qDqKneRFFT\n",
"4xHIpIHWW6g8+TJkUZyDavkkZwTcBXwbKe/x5JZAB/gfZFFcRjz0tgHljowjTjmtRZbI1ODYKvRd\n",
"+LZriMrG+H54a6zMXA3LG5zEeOasAk7Ppmvd+6S7g4YPR2wvmqkj7ylET5U6S19IT+VL7Cu23Z/0\n",
"+SNaK2HU1FaiKKnksgn4V+ATwK+BZ0mfqa9Q1FQLUqg+mW+B2/8bejffQqP+8aTPD96CAOUlBCr3\n",
"IhB+CM2DkSyAuIFovu4x5JY4B1FdVcipvh5ZVF6Jb0YhtIcTV/Q7ECAnkwd7045RUmD5Ldfyfv64\n",
"HTgTa+e3z3My6Uzp7qDR2d3YW8VHTaXNzJc8lm92Pp/Qtz9R1FS+OlN+KTRlq5ca4sl8fr3a3X88\n",
"UUKfp6fSqKkGBBCemlqE8lEmIGrqHHLLiFQhSulZ9zlHI2tiTOK62cAjSPn7SZe8NCIQW+yeMyU4\n",
"N8vdeylRNJSf7/tcIjBfht6fr5a7nmiyqdD/UVYuxr/xFf6VbzUAF2Dt86Xdl8meJt0dNFbS/jRT\n",
"R91TjJ4q51wpZc8Lbe9D/ogpv30g+etMtYWasshfsJLcqKlaRMmkJfQdQWEFuQR4DAHEYqSAT0JW\n",
"x0QEMGn9fRlRU2vRtMXnuOXAxHXrgO+h72Aq0cRRXupQaZSD0JSxYRjvcmTdXJ44/iLymfiIqRZk\n",
"PYUgtZlo+lmfv+GvLZmW+gAP8Gs+bFGZ8wdLvS+TPU+6O2iE0S976roSSX1+28/S15rFz5VR9nSf\n",
"BSQsL5IWMRVunwv8HDl3f0BuMt+RFJ4vvAU5xz0ttQCNyP+GrJ3vuXYmEJXkCKURWR0vI0rruwhI\n",
"H0fWQDJXYzECoRsQEMxGyjxMtnsBKfxj3WcMS5XPQZbKPsQV/DqiiZf8dxEWGIRWzuOdT87gOV6U\n",
"H//zWHtvpdrNpGtKdweNzu7G3ihN5I+aKjRLX7LelE/oS5ZBH0J6Ul8pIb5+rvBkQt9a4lFTY9z6\n",
"BNKVaz0RNfUGym/YD1kcpyNKKQmeK4lm52tAfoz3EHeG+xLo091zr0YlSbz40N8G4IPIIgMBxDR3\n",
"/9XB9bPdepxb1yKLy9ec2oXeWytKg0iOZinLFUX8Pay9rZx7M9kzpbuDhp8trLMT89oamdXWZD6/\n",
"bqC8RL6Qkqoj4sPT6kslt5P0VLgeQPkJfV7hzUTWhqek1hKVQR9EfIY+vxSbe2MpmpNiHgKZfZEi\n",
"noCU/zF57nsCJfTtRPTVecBp5ALKW8BPXf+uIB79BAK6PyIq7ELiNNg09M7D+TVqEGCEpc7Xovfr\n",
"qw6Hc2OEzvGSHeUHsI1tDKKHPuP1WNtS9KZM9njp7qDhR2AdSSl1JD2Vb53vnKenCpU9z3duXyo7\n",
"s+Mu4nWm0hZ/bgjKQ6gFvoCcumEy3zAKl2hvRNbCIgQM8xF99DByGP+EaA7yYSn31yKwehkp428h\n",
"oHgZJeyFz/YTLz2HJgvrSXzuCv/ZH0c+it7EFXyDu34scdrJF4cMLa5iEVOtjqTqxW52MIB+1D8H\n",
"XIy1u1vTTiZ7nnR30Ojsbuxt0oyUZTJCKrntAaFQGXQ/MZOno9JKoJeb0JdM5vNRU/0QFRXWmjqe\n",
"9IS2WhSl5KOmVrt+noZG9pPItZLmIcppBgKQc1GZjxBMdiL/ySwETDcQD7315UuGEaeg1iGH9+lE\n",
"Ux3vRCB2NtG7WYysKv+Zaoh8PKH/o6gYmtjMEA5i+xzgHKzdVuq9mez50t1BYx6dRylVsq1SEvZK\n",
"ucbTU+WWRK9HisdTU6UsaWXQPTVV7ujXK71FREl9PplvtevvYHLrTB1DcWpqBSpB/qZrcyCyOCYg\n",
"H0Yy98LLHxF1VO+uPY/c6rYAf0U01lHAe4lXrgWF3i4H3kXcAb8L+TfOI+4Xme365BP3mlHAgP+c\n",
"Tej9tmJODF2+mOM4juVvo1yM9aXfm8neIN0dNPykM101Ya+Ua0upOVXqud6kU1GlHCujzERRyVcG\n",
"PW3djJzSA4Gvuc/haSlPTRWqNdWIlPL8YFkO/B9StL9GQDaR3Axu39dXkIO7D3AHysdYinwT4XvZ\n",
"jayF5cCnEb20i/gETWuQ4r/Mne9L9F2vQdbJIOLWwQbXtxAAwnwLqMgsfJZXmMypvLYRAcaytrWX\n",
"yZ4o3R00Orsbe5OE1FSxJaSnkkl9lngZ9GJJfaXQKjuIU1I+oW8TUvQjUcSUX44hXcFWI1rqdbds\n",
"RcByOqKmkkl6zagU+XSU53EQqgd1YaL9ZagE+mYETlcSAUUD8HeUgHcJcUvkGUSXXRpcPwtRet6y\n",
"2IaAy1NdoX+kDFrK8giX8y4e24EoqVml3ZfJ3ibdHTTepGsn7JV6Takz8RU710B6wl6xhL4e5EZN\n",
"5dtOztLX1oQ+X7V1LaKDkgl9u5ESPRaV/gjXQ1Lag8hBvAxZGvOIHO6emppEbl0oLz9CfoZ+yBF+\n",
"Aek01j3ISpiMFH+YR9KM8k2Goozw0MH9JgKwc4JjtchvcXJwzOdshNd4P0oZRQgt93MTn+XHu4EL\n",
"sfaF0u7LZG+UPQI0jDF3IMegr+3zUaSEfo+44BXAtdba7cH1H0N/jFustY+ntGnB+pDE1tJDXeGa\n",
"NHoqSTuVup2Mniq15lQbaY+YVBOvM1UocqoFhXueBvw/d32yDHqh/I3dCBgWI2DwIbV/Qsr29wgo\n",
"JhDlRISyEYHDSyik9uPot7iLXKtjE/AksqAucfuDiDvxX0O/61HEq8xaBBQTiCt7XxgypKHCSZOg\n",
"LHBIE8u/8HW+wdebgauw9m+tbyuTvUG6PGgYY4Yj836UtbbeGPN7ZMqPAaqstXcbY74EDLTW3m6M\n",
"GQ38BvHJQ9Ef9XibiCHP6KmKSj3FI6b8OvRXhOsdSAGWWgZ9CKUpw+0ICJa6ZZlbb0ZKOUzmG4MG\n",
"IWni57Twc4PXoBIdZ7kl6cCuRTWmnga2IOvmYqJS5CDQe85d1w9ZFGHo7Wr0298PTcbkwXk98qNM\n",
"IfKHbEGZ6OPdftIBHkZLlQgklk/yP/yYzwDciLW/Kn5PJnu77AmgMQhFxJyGRl9/Qmb7fcA51tqN\n",
"xphDgWestSc4K6PFWnuXu38acKe19pVEuxbsq1SGHurMa5L0VGu3w5LopdJS9a4f/Sg9ason9SWX\n",
"5LwTpYgfje9EFsfqxNKEcjZ8tNSIYHtQSnsQKdQlqNT4bARqRyJKahJSzGl5H41okqZlCNzOR+G1\n",
"SUd8jbtuX+Ai5BMJZRmKqjofzUXupQmF5Z5ObkmRkUQWxy7kq/D7YT5HyQ7xd/Mg/8e1ALdi7Q9K\n",
"uSeTvV+6PGgAGGM+hfjfOuDv1tobjTHbrLUD3XkDbLXWDjTG3Ae8Yq39tTv3U+Axa+3/Jdq0YM/1\n",
"uynrrkA9lUtPlUNRpe2H0VN9yaWpkudKqSpbqlii0iLbSC+DHkZNtQDfBD6MQlZfJz5L31AKU1O1\n",
"SDnPJ6Km/MRHh7n1YAQQaTWrVhBRU5ehRLzF7tpkGO88omS9491nCOf6rkPO7svQOw0d1JsQWBxO\n",
"XOFXuf61Kpu7mJzLk0znQoBvYO1XK9FmJnuHlAsaRZOojDHvs4kql2nHyujgscA/AsORUnnQGHND\n",
"eI211goE8kq+c0+3pk+ZxKSewlFTydLonp4Kl5CaSkZNHYJKdoRRU0lq6kK3JGUL8agpT0/tcM86\n",
"Ho3kzwJuIq7srwm2VyN/w2toVN+M6KwpyGLwVouv6bQFAdmLCAAmoVpR3jo4BNFmf3P9ORblaHgQ\n",
"3gfRUkuRszukrKYjwPb+OIsiusYG968iossa0f/WkNfKiGPNBGZ4wPghCmPOJJNWSymZt19GyVDF\n",
"jpUqk4CXrLVbAIwxDyHzfIMx5lBr7QZjzGFoRAYaLYalHo5wx1LklpXR9vnb4Cof8gldg3oq5RpP\n",
"TyUpp3zH8l0TlkRP0lO7U87Vo9FwsWgpv30A8hcko6YGUnhipHziQ0ebgV8QlUJfjaKGmlDuwgi3\n",
"jEQj/REFnudH+AtQLaiF7vOOQBFO1yGQSKN3tgNfQaB4PKKdrk25di7wAArrvRqBSSgPoSi2K4nX\n",
"k1rinhEe2+aunej2LQLwEDB6Befy0FIRYBzPAl7nVFBgwa3sLeGSmbRajDFTic/8WN79+X5DxphL\n",
"kXl9HZo/wP8S9wdGW2snt+qBxpyEwh5PQX/gX6ByDEcBW6y1dxljbgcGJBzhk4kc4SNsouOOnvJz\n",
"KFe6HlR7J/75dVhHqi3Jfb0or85UHypbAt0SLydSqAz6FnfPp9FgZBaidoYhZempqUKO3u1ICS9F\n",
"Snyua/sRRPlMQ9bAaHIprmZ3/QzkjL4NOdDnueeHgNSIqtbOdNf1JB4VhevDauT7COezAPlTxhE3\n",
"BWoQCIf0QDKRr1UylNWs4kh66P/zIaxtbmubmex9UjGfhlPu44F/Q9Nu+kb/f3vnHWdXVe7978pM\n",
"ei9k0gmEBJIYqnSQAIKIV2yo2FAQ9FURBL1SrldRL/elWK/e1w6CDYOKolchcAURpElLgBRSJqRO\n",
"kskk0+t53j+etbLX2WefNu3M5Kzv57M/u5y996wzyexnP7+nrHrgYelBfxpjzOdR7do1e7sM/cNb\n",
"hv6hVpOecnsDmnLbCVwlIg8k3DNkT/Ucv915khQV349nTNXZcyqIPI9JpGdLxTOnJlOYbl+D/r9w\n",
"xsFJU832PvPRflNL0AdztpqLdehD/2m0Tckw9AXmDcCJZD6sV6Pxi5fR/6Nno16Hb8ReRuWrTlR+\n",
"8rva7rTXj0I9EecdbEBjJmcSGZZX0d/ZFO/aKfaaFNFLSd5Yx0HUsINpDFFP572IdOY6P1C+9Hog\n",
"3BgzVEQ67PYkYJaIrMh5UQmwRuMhercPVE/XxV5TSOFeocV9SRlT2fadNu5LUPkWl0obX3K1+EhC\n",
"iGabM2iG0xr0bf01tFgOoqyp+ahcNN/uZ5u/3L2t/xOVZl5FvanF6EM9Vwv0V9BJlypQOfVcklN3\n",
"70If/KejBX++IWlAPeo3oB6OoxNNyz2VyFgIOmGUP556ogy0olqGTKCWXVRRSdefgXcg0l7otYHy\n",
"oy+MxiOoHluJZrTsAh4Xkat7MM5exxqNt7rdItb9LUXlk6e6U8QX385W1Jdt3SsZOpYu0j2PPURy\n",
"VHzZY8f7NuBbqKG4G31Az7HraXnGV4MahLV2eQl94N6Pvt3/Ga2/OJzMB28L0ex8L6Op32Pt9sLY\n",
"+btRb6ICjW00o2mvbmydqKx2Cmo84xlTFaR7P4J6a760FZezimYcdexiKsPo/CvwL4i09OR+gQOf\n",
"vjAaL4jI0caYy4DZIvIlY8xKEVmS88J+JshTPaKTqKCv0MVN3eovzajhmmQXv6hvml387aSq7Dgp\n",
"NPHhNfRtfC1qJDai3sRM1CAcjspTR5I5XzeoMVuBSlPPoEH2Kegb/+lkVnx3oNlS/4sapkPRlyff\n",
"a2hDpafV9vu8k8jTErSX1FY0E8yl5Laiab2HE7Ui2YMaWudpNKIGyZ8qNuGPOv3waBqoZTLD6Xgc\n",
"OA+RxoTfQyCQRl8YjZWoe34n8AURedoYs0Jk/4RHAwJrNP5M/8hIfXVtbxT1+fJUrqypNvShC1E9\n",
"hy8/jc2ydttOnprkrf15qwuhk0i3H4bq78+imVOv2c+Gohlzc9GspwXoA/dQsmf/OWnqEVRC2mLH\n",
"fBSRNDUldo17Av8JnaxpIpphspRMya0VrSmZjBqK+EROj6IBfjfpkmMVaiine8e2kt7Hqol0w1PQ\n",
"H/NwmtnDZEbR+k/gjYjsK+S6QKAvjMa70UD44yLyCVtncauIvKtnQ+1drNFwYxroBXzZzimmcC/X\n",
"MV+eihf1+fu9mTEF+nbuJKk9pBf17fCWGlRCGoZ2BvgZ6rn8EDUOB9slWwNCx2to/GMNkQcyBLjP\n",
"rpejnkHS7Hy1aDD8UTvur9n1joTzV6Iex/mo0fJbeIAauTXoy5Xf0kNQL2Qh6QZgD+kV7J30YJbE\n",
"4TSzkyrG0bgCOBORPd29V6D8GBQV4X1BkKe6hZDukTjZqTHHtr/2DYSbK8JJU5O99TT07dpfF1LL\n",
"0YEahk1o5tQG9OG8CZWtDibyPJagElNSYLwJDYg/g3oyDWgQ/XS7VMXO34XGL560v6PT0EmTfI+j\n",
"Go2bNNvP/RT0jWgL9dmo/OV4zt7P1WF02HMXePuGrAYk0/EYTgs7mco4Gl8CzkZkZ+KlgUAW+sLT\n",
"mI0GCE+zhx5F0163dHuUfYA1Gr+n9MV5PTmnpwV9/n4LmRKVv6TQN2Lnebh+U2NJl6Sy7btqb7dk\n",
"y2LKRjvaqG+Svd9ytKJ/k11qUW9oDhrIdsZhgT2W7T+5Cyb/AQ2q70MN1+tRWeoYsstoX0NTcg9F\n",
"mxEmzcz3LPAXND33TNIf8C1oJ92zSfdWmlCD58cB60lv3VJ0bYYajIMYR9NLwFmI7Crm+kAA+sZo\n",
"PISmDrqOmB8APiAiSW0eSoY1Gu9zu966u/JRsZ/1xr2S5KZsMlSuc1yMItfSmxlToA+9WiLPY4+3\n",
"72Sp7XbdYMcwH40hpNCK7elE0lSuIHkXUZ3DGqLsqZloDMMFsY8hOSi+ES3S+wfqCXzQjnUU6Qal\n",
"Be1Yuxb4tD0mRFlVXWjc5LiE8Vbb8fgSYLwQMO46FBXD2MVBjKV5JephBIMR6BZ9YTReFJGj8h0r\n",
"NUGeKho/WN5CujzlL9mO1RMZhzYiacoFxSejRXcuU2q6t53UUTZOK5HXUU2UUrsFNYrzUK9jMfoG\n",
"P5/kWoYdRBlTK1HjehRRMV/cQ3oRlaZes2M9F/VSHB1ExX5z0J5WLk22Fe0llUI9FWcwXJfek4mM\n",
"wqt2zKDGBwqcJ2M4LdRQxXgagsEI9Ji+MBp/Be5AWxEY4CLgEhE5uycD7W2s0VhG8RJRb37W03vl\n",
"k5yK+dyXp/zFtT+vJPI6/KK+fFlTY9G3al+aKjag3oJ6Ha4g8GG02Z8zEvWoYZlLVMznlnj8weE/\n",
"eH+APtjbUK/FZUzFay8c+9AWJpVoncW5dlxxvmfv/1bSM6BAPZJK0mMYoGm+r/N+bgf67+M8mqKC\n",
"4MNpZhszmcTeFajB2F3otYFAEn1hNA5Gu2OeZA/9A/i0iLzW7VH2AdZofNjtdmPd30V+/rVDKL7t\n",
"edK5rudUtmyp3m5/7mgmPVvKbcezprajBmM0Gqf4ox37z9BMKSdN5aoqbyW9mG816omchXZwrUOl\n",
"qyPJNGadaDD67+jD/AY0TrKdTCOwHi3WW4IGy+OFd5tQr+dU0iu2XeLANO/cDqKW991mFI3sYBpj\n",
"aXoRTasNBiPQY/rCaNwJfMb1mrKtRL4mIpf2aKS9TJCniiLeTqSJ5OyobBlUvnHoQr0CX5qaQiRF\n",
"xQv6Cql4biCq1fANRC3q8RyGeg2uz1R8vguI0l39Yr5xqER0hr3epxWNTzyKxmeORef59j2O9UQ9\n",
"ps4ivdDveTvmk4gMRgMqYx1HZMA2EQXy3eyTeVuEjGEfO6liJG0voh5Gbb5rAoFC6LOK8HzHSo01\n",
"Gj9n4BTqFbNOUXi2VL5MqnimlL/v3nhdoHwk+lbvS1C5Fr8JoZOWin17bkS9jgmocXkYnSDJGYlm\n",
"NHjtCvl8eSopqA3RTHYp4AuoF1GJGpQT0NhFvObD1VM8gXZankMUv4j/AVUDv0XjIMfHPquz93gj\n",
"6V7cJtKNpNjv5ryogvtJjaOOGqoYQccLqIcRDEag1+iTQDhwptiCIetp/G2AthG53O3mWA/EYxBW\n",
"7wAAIABJREFU4r74bH3d6TkVn6Uvad0jeSQLjWRKU7WkF/K57XaieTh+b8e8DA2az7FLLk+knvRs\n",
"qZVoT6jL0QyoLUTzZcSpRWsn/mHH/HX09+Hm8XC0ofGJlcCVZEpcTfbzc2KfCZlNB6GHbc4nspvt\n",
"zGA4Hc8B5waDEeht+sJoXIxORrMMfcC9G7hJRO7qyUB7myBPFYQr5vO9j1yz9MXlKZcx5XpNCZn1\n",
"GpPQt3o/W8othQTMa0nvM7UWrZ1oRT0T12dqEepJJKXmtqFy0VNoUV8D+jBfinoL8Ws2ooV6G1Ap\n",
"7U2k11S0oo0PX7M/9xwiw78TrSyfRyR5dQEvkF5suI1IRkvwMjKzbavYymvMZRidjwNvCa1BAn1B\n",
"n1SEG2MWoxquAH8VkVe6P8S+wRqN2xm4hXuFylOFSlHx7aT25/5aUI/E9zxGkVzQl+2YnzU1keJr\n",
"PfYRSVNVqDR1NyrlbLO/h6moJ+Lmxzgc9RyyeSDOU2hAaylq7dhej8pSx5D5pu+e0F+3P/t4tEVI\n",
"0hwcv0CN3ZvJrGJ/0N7f72Plprr1z3XyGRRoMA5hHeuYzxCddOztiDQljC0Q6DHl3kbkCrebYz1Q\n",
"5ali+0vFj/mz8cWzp3rUbjsH+8gs6NuDSkaukG8H+jYu6MN8NvAr9CH6B/RBfTBaCJdL499G1Gdq\n",
"Dep9tAC3oIHm9agxSnrwr0ZbgjyNVmu/i/TGgI4NqEdxLJp66/eRAs28mkI0/apjI5oN5lNAm/Pk\n",
"Wr7FrGAlR2G0h9Z7EWnNfZ9AoPuUu9Eo9TAGMu0ktxNJypbKlkHljMQ+9GnnHtL+Mgn1FqZ7y1Ty\n",
"B30F7fhajb79r0eNw0b07Xw26e3PF5Isd+1EZamn0NjHMLSY7wzUuPjjaEUrw59CDdAxqEfhFx8+\n",
"i0pc49D6DNeosAWNj4wlve/UCtQzcvdwE0xBmpeRbDBO5HGe4DSMemAXYydACwT6inI3Gt9j4ElP\n",
"hZzTRWH9pHIdi8tRfsaUIbNuYwT6YBtbxOLmx8iWxZSLXaj3MQXV9v+GttvfhHojFfb4PKK4xeGo\n",
"F5L0H1rQuMok9EH9ZftdD0HTak8mc7Y95znsAL6KGqI3ocYizno0Bfc80luXg3ouo0j3ONpRQ+L/\n",
"bvyJmJKthMdbuI8/8TbQmQY/Hub0DvQH5W40rnG73rq78lFvflaoPFVsv6m4PJXUY6rbLbdz4B7Y\n",
"tQnLHiIDsR2VqiAq3rvLjut+1ADNJXcLdNdnypemNqDy1q/QN/919j7x79qAehFPovLWV1CjFZem\n",
"WtDW51uAj5P5cN9kv9PrY8e3oQF+33vpRraUcAm3czuXgTYHvRqRVJ6LAoFeodyNRqmHMRBxGVNJ\n",
"SwuZfaUa0CyppOP77HoI6T2m3HoykSTl+k0lxRjixFugO+OwAzUwrpjvCDR7KR4/cN9zDWognkSN\n",
"1UxUljojYRzrUcO1HfU4zie9M22N/VzQ+g2X+SRosWAnGvdwrEINlwt4+6m8OWoyhM9xK7dxHcBN\n",
"wL9zoPxRBgYF5W40vk3f9ITqjc/yyVOF9JrK1X8qKV7h5Jh4YNy1QY+3O8/WEn0ckXHI1eIjiRT6\n",
"AN6OPsSr0D5Tv0CNxD5U6jkYNQaHocZhIdk9kDb7nUfb+/zajvNoNGPq9QnjdD2e7kFjFCehxiB+\n",
"Xhfa0flwotY5DudNLfCOpVDPZWzsWN4MKRC+ztVcw7cBrkPkluSvGwj0HYPCaBhjJqCtsBejf02X\n",
"oEHLX6MPj2rgPSKy155/PXAp+gd9pYgsT7ingFzndnOs+zMzKt+58aK+Qrbj+0PJPjtfX9BJJEMl\n",
"rf0W6PvsmKrQFNrv27EvR9/c55I+A16cJjR+sBp9k1+DBuSPAm5GPZRdJLcR2YgGuZ+x53+U5OaA\n",
"L6Cpv+8iMyuqGQ2En0b6E383mgTg36vI2feEu3k37+W3KeByRG4v/NpAoPcYLEbjTrSq/HZjTCX6\n",
"tvdvwG4RudUYcy0wUUSuM8YsQjvsHo++qT4ELJCY5hvkqUT89ufxIHlSplS2luiuqK8ZNUZ+ttQU\n",
"b9sV9c2w60Jm52tAH/Ab0ZeFjaiB2IvKO66Q7yg0ayrJyOxD02mfQg1LJfpCchYa5Pb/IBrR/lLP\n",
"o7GHM0jPfmpD/4/tRj2Wxd5nL9nrT/TuuR41fhXe9bFU23Qvw9DFo5zOaTzRiqbU3pfwnQKBfmHA\n",
"Gw1jzHjgeRE5NHZ8NXCGiNQYY6YBj4jIEdbLSIl13Y0x9wM3isiTsesF5DYGXmZUrnOFwgr3cm13\n",
"kGkY2u3PiE/GNJJ0eWocmbPxJe2PR41Csd5LK+p1bEMlnYNQb/IeVJpqRWMjc9GKbZdSu4DsMlgN\n",
"msIL8Fl7nxmolHQKmfEO5wHsQwPhhwJvsT/T4Z7qT6IG8izSvYZ21Jgd7h1L2fEXMjfIfiroYCWv\n",
"YyFr9wFvReTvxVwfCPQ2xRqNvsisycchwC5jzB3o2+OzwGeAKhGpsefUEM2bMAP9Y3ZsITMF0tFg\n",
"18VmOg3p5nU9/Syp51QxGVQVJM/SV+z8FoXShkpQu0nPmNrtrZ2RcC3Qp6Nv699ADV0VWpA3J884\n",
"d6Jew2pv6QKuQWMRe4D/JNOQNRFlTO1E259PtWP5euz+99vxnYMaDhfD6LL3ONaOcRhqMPaixrYS\n",
"/bcbRQGptI4RNLGBQ5nOzu3AmxBZWch1gcBAohRGoxL9Y7xCRJ4xxnwLuM4/QUREPYesZPvsK700\n",
"xgOBbJMw+fKUnyWVa7ueaOIgv4jPl6kWEklT2VqgV6D9nxw1RLJUNVExXxf6YrDQLpehD20/uDzJ\n",
"rtejXWafQtOAq9D+Up8ivWaiApWkHrPf/Ujgvd44jb3PBvuzTvSufRU1GH6H201ENSQS3SPZhkyh\n",
"hmoOYTQtr6KNB6szTgoEBgGlMBpbgC0i8ozd/w1wPbDDGDNNRHYYY6ajb4KgVcJ+KuQseyyB9/6d\n",
"/X/AZ1fDxzYxcLKnkj7z5aliZuXzP+sg3UD4GVNOjkra9uWnceiDfn7s2FgiA1Fsh9x61OPYjmY1\n",
"TURn1PuDPTYENTCHoJLRYuBCu52UntqFBtenoYbic+ib/lGoLHUhmV6HK667BzVI5xDN9e2zFW0R\n",
"8ka0KNCRQo3Y/NixFFHhoGclkg3GEl7kBY5miGZtvQWRnRknBQL9hDFmKekvb8VdX6JA+KPAZSKy\n",
"1hhzI5EuXCsitxhjrgMmxALhJxAFwg+T2MBtTOM/3K637kkBXl8fSyrqK3YZRrpBKGiOhm7QSHIx\n",
"n1tc1tRO9AE/iSjWcC0aF3gWjSXEZ8nzSaFGYRXwil3XogbsB6gx81tz+KxGW3usQh/+7ySzf1Qr\n",
"Wsi3G7iYzKf8c2hcxY9V1KOylPvdZpGk4oeFC/g9f+CdAH8CLgqNBwMDjQEfCAcwxhyFptwOQx8Q\n",
"l6B/2MtQrbua9JTbG9CU207gKhF5IOGeIXtKic8P3hJbJxX1ZZOmGlDJJ4VKPVO8ZbK37WdNVZHf\n",
"cHWi/8Yb0Df5DXbZif6fOAzNmFqEeilJBYIudvEEWhFeifaWOpt0zwDUk3gY9Xxmo/2l/PboL6GG\n",
"5mDSM6lcU0TXJl1Qg+UC8XGD5CFczTf5Bp8FnVv8SkQ6k88NBErHoDAafYE1Gl+iZ8V2/X3MyVMd\n",
"FF/UlyRPQfqsfCNj227f9ZwaV8AykeK8F0Ef/ttQ7+NsO6YvonNzu9qNuagU5bKmFpK9erzWXjMG\n",
"fdlYjsqUp9glXqfRar/nZuBHaHzijWTGWdrsvc4kPZVXUK/Jv28OAxFH+BGXcRm3g3pZt4Uq78BA\n",
"pdyNxq1ul/zyUHckpd6+Z1yeGkqm/BQ/Ft/3C/r6ir2onJO0OHlqu11XoG/iM4ALgPeh3spm1EDk\n",
"KuarR9/4nTS1HjWK5wGftNspMh/+dags9Sz6wL+BzMwsQb2SV9BZ/uK/rxfRVN+R3rH4rH55p2gd\n",
"Qid/4w2cxhPtwIcRuTvX+YFAqSl3o1HqYZSaNtLlqJYc+/UFLG2ogXPdbackrKvQWNMMkmfRi1NP\n",
"JEf58lSLveci1Os4yq6THtIudvGs/S4Ho57EiaR7A41op9o16MP/HNI7325ApanZpHe6XYd6R65C\n",
"3LUnt4bIxS7SYxijaWQNC5jJ9r3A2xB5NM/vIhAoOeVuNK6neHko1+fduaaYewrJ0lT8WK5zOkhv\n",
"f+5LUklrV9TnZ0klbU8it1eQRAcqS21F4yFvQg3P5ei0rR32vk6Wmo8ahvkkZ/J1odl2B9v7fcp+\n",
"RzdJ0hLSjUqX3TfAd+zPOh81ej4p4K+okfGr1gX1qvzzC2oPMovXWMsCRtJWDZyPyKp81wQCA4Fy\n",
"NxrfcrveeqBkSsWPFdv6PEm2csagrzKmukiXoZLWu1Aj4VqMzLDLpWjPpm2osZidY5yCBsb9jKk9\n",
"aOzlNnu/BjLbknSg2U5PojUfl6HGKJ7GtBptM3IBmd7QKnQOD7+deSNFGMyzWc6DvAmjNSDvRGRX\n",
"odcGAqWm3I1GqYdRKrrIzJJKyppyM/X5RXv1Wfa7UOPk95byZamDiAzEDPLPISGo1+BnS21AjcpQ\n",
"9GG/CPUejiF5oqc9qCz1BGqsJqCFfEtJf8h32PNetuNaimZkOV6znx2Cptc61trv4s/ONzIaflyS\n",
"Eq7lZm7mBtB5Qj6GSFue30MgMKAod6PxWQZGVlQhx7qbLeUvrajUMpT8stRoMvtLxQv5xhJN4Vps\n",
"K5K9qAHYhj6o32C3L0U9kqFoxtOh6Jv9QtRIZMuYqkGlqAno1KfL7XWnommx8Z5PbvKj++3PfQtR\n",
"Kxqfp4HXxa53xZJFzKWe4ne8g3dwH2hx6i0hQyowGCl3o/E9t+utB4IUlXQsm+RU6L6Tp/qKJpJ7\n",
"S7n1bvThvAs1XBOJvI7r7XozkSHKRgORJPUK2p6jC+0v9THS4xQ+a4HHUVlrKZo2G2cT6pWclzCG\n",
"tWgsxb9vQfGL4TSzgiNZwPpm4IOI3JvvmkBgoFLuRqPUwygF7eSWpdy6meQivvi6ETUCroVIkjQ1\n",
"jShjKtdUrY4m0jOlNqIZSm1EGVOvQ2WpQxOud9Xkj9trh6Fty88hKrQD/Q/wDLASffifHrtftf35\n",
"rk8W9ru+htaN4B0bklT4PZf1rORIxtC8Fe1S+3wB3z8QGLCUu9G4gtLLTsXKU8VkSvn7oE80v5gv\n",
"Wxv0+Ox88Rbo7thkCkub9UmhRXxOmnKtzf8H7ULbYe/tMqbclK3zSC6Wa0M9lMNQyevzqBdzMhpY\n",
"nxI738Ud1qLzZJxP8qRMK1DD1M35vIULWcY9XAQaeH8XItsKuzYQGLiUu9H4idul/wv1iv08nzSV\n",
"S54aTvENBAtF0GK5eAv0eCHfNtQzGYp6HjNQg3Ad+mDebI9lG2e8x9Qa1COZgs7KN46o4aDPDjRL\n",
"6VVUXrow4d6b0eaAbyQ946oDrVafGTuWJ34jfJuruJLvAPwE+FQIeAcOFMrdaJR6GP1JivRivaT+\n",
"UvGMqWz9ptzSgj7kXTFffKkiPWMq3wREgqbjOklqI2ocdqNe0HzU6zgGzZpKeutfhRoJV/ewEK3/\n",
"iE/N+hxaqOfar/uG4VX7M48mqvhuQo23/Q6SApOREjyUNh7jVE7g2U7gSuD7IeAdOJAod6PxMUpX\n",
"qFfs58VIUfG26JA+N3jS4mbni8tQSYszEkVkDwH64N1K1GfqAvQhfC3aILASrc84FJWsXBPCbNPA\n",
"rrPnD0eL8zahhXynk94eHyJZagfatTYe3wD9XW8kM05SgHcBs6nmJZYwjsadwIVhlr3AgUi5G42f\n",
"uV1vPRAypfxjPWmHPoy+m5UPNJ4Qn5XPX1whXw1qwMajHsdMNJZwPurZtKPyUjZ2oZKUW/ag3+1y\n",
"tNI7qTngXjQQ/jJqHD6ScF/nyZxN+u/JyWh+tllmlNv76EKWsYyLMCpzvRORzTm+TyAwaCl3o1Hq\n",
"YfQXSUV72WbnayRZnvKXvagRGEVhhXxTyfrA3U8D6UV869HsJVAjswjtL3UcyYV8W9GuuCvs2A5F\n",
"vYl5sfNWoNlSY4EzYvdagRqKBd6xvewP9mfaDUOKH3A5l2uH2juBTyDSkue7BgKDlnI3Gh+h9FlR\n",
"+Y7lmpEv38x97imXVMCXdMz1mUpqg+4fm0hxgXUhPWNqKFoLUQe8HTVYk9AH/GHorHyLyD63e429\n",
"5zQ0ZfaX6HSsbyDTSLi25/tQWepMMntLdaBGa5J3LIdnoYyhnqc4kUWsbkdn+PtRiF8EDnTK3Wj8\n",
"2u3S99lT3c2ucvJUMYV8bin4H7YbNJCcLeUX8m1DPZdh6AN+FmoIPoV6H3vQt/hsPaZaibKlXrb3\n",
"A5WTPpTlmkY0EP6y/VkXJZyzyp53fOx4HekGJavhOJm/8zBnM5yOajR+8WyW8QQCBxTlbjRKPYy+\n",
"Jl+PqfixRvL3mGpGH/LjURnqICJJyq1d+/NZ5M+YSqEpr+u9ZZ0dzwSi/lLHkVxPUYvKUi/a7zsP\n",
"9Sb8bClBZ+3bbMd2MlEMo40oHdcF9jtAhpLRO0qHewvX8nm+Bjol68WI1OX5joHAAUO5G433M/Cz\n",
"p3zZqdDCPscw9KE9Ms/iznES1Pgca3/SoUJoQhsPuuUMtJr6LnSWvKF2fx5qIBajElWS91GPSlPz\n",
"0eD4Lfbcs0iPQ0AkS9UBz6MZVfGkgHpyB+DTGEUTT3E8r2NVCvgC2j8qVej1gcCBQLkbjXspTE4q\n",
"5fYQIukpvk461ldFfI4U+iDeRdTqPL69iyjuMJ5Ilno98F57jzayG6AU6m28bJcN9l4LgWtI7vfU\n",
"CPwNzYY6As3Mit/zOXSuDb+VSRv6u7NGKlmROo5neIzTGUHbTuAiRB7OMvZA4ICm3I1GqYfRVziP\n",
"o530GfjyLU6O2pdl3YV6Jb4U5UtUbtrWWRTWY2o36bLUGjuG0aiBONIuhyRcuwuVnFahD/65qMfh\n",
"S1idaAPCvUStSBzbUTnKBr/FWou4JJXiP7mB67kF4CHgQ4jsKOC7BQIHJOVuNC4kt1w0ELadPNVR\n",
"wBrI6C8VX5KOjyZdhkqSpsZRnBfThQaunSzVic7/3Q68GzVEM1GpaQFRMV9SDKQdTb9dgBqI29DY\n",
"xJmkz3vhzh1mf3Y96fNfOLx5LyCbdzGRWh7jNBaxugv4N+C2IEcFyp1BYzSMMRVo4dQWEXmrMWYS\n",
"8GtUbqgG3iMie+2516PzMnQBV4rI8oT7Ccj/uF1Knz0V/7yQrCl/u69lKdAgeJIc5W9vI3ooz0Ir\n",
"s+eg2U5T7T1yBcc3o/USK9AAtUENwzUkV6DXo40Ht6Bxi8Wxz+vQGo7FpFsGryAwbjSEt/Anfs87\n",
"qKSrGngfIk/mGHMgUDYMJqNxDZpBM1ZELjDG3ArsFpFbjTHXAhNF5DpjzCI0b/949E32IWCBxN4Q\n",
"D1B5qovI88glQ7XG9puIJKgkWaodNWJj0Qd/lV3HlyrUUORrL9KCGoRX0W6za9GYxHDUQBxll6S2\n",
"5zWo5LQejVMsRGUp3xDVoy8YI9D/By4A3oFKVVY6y/QwKujgbi7iQn4HcA86u97ePN8nECgbBoXR\n",
"MMbMAn4K3ARcYz2N1cAZIlJjjJkGPCIiR1gvIyUit9hr7wdulNibojUaF9C/2VPFfC6kZ0dl207Z\n",
"c33PZBiZmVHxtb89Bk1vHe+t/e1iW5HUoR7Da3Z5G2rAfwj8xt7XyVKHo7JUUhaTL0t1Av+FxizO\n",
"JHOWPec5rCO5OWLe/lGLeJnHOZUJ7GsFriIU6wUCGRRrNPLOUtZHfBP4V9IfLFUiUmO3a4geIjPQ\n",
"+QscW8heWfxpBk6WVHw7W9ZU/FhfFvA5WlGvow5tFZ5tabLjPgiVpOagktFM9KH+MbskUYPWWqxA\n",
"vQgnS33Kfl6JSlSOHei/cyvwVjQuA1GMY539+a4T7lANdpuE31eKr/BFvsBNrnfUhxBZned3EggE\n",
"CqDfjYYx5l+AnSLyvDFmadI5IiLqOWQly2c3nhNtL7XLoMP3SPx1MyoDFbJuQmWbfd56HyoZQZQx\n",
"FZelFqJ1F1NRw5BrQqYKO7b1RJLUq6iUNAyNTS0B3kFmKxBQ4/806sGMQNN33x47x7VRX0RagFwa\n",
"wIxVg5EuSVWxnb9yFotYnUI92a8i0kEgEADAPneXdvf6UngapwAXGGPORx8W44wxPwNqjDHTRGSH\n",
"MWY6+qYLGvT022LPsscSuPE8Bk6WVHzbGYNs2VKu5XkF6V6Iy45KkqHi26PRh302WSpfNXecFiJJ\n",
"ajM6Reqb0Qf+J9GYxaGoNHUq8H+IPISk+xyOZkv9yG67/wMON0d3B2osDreLw6XReq3Vzf6PPsl/\n",
"8x0+zRA1ZB9C5Ikiv28gcMAjIo8Aj7h9Y8yXirm+pCm3xpgzgM/ZmMatQK2I3GKMuQ6YEAuEn0AU\n",
"CD9MYgO3MY1H3S4DK3sqV6aUW/cHKSLvYxdqmGvIlKX2orLUaFQSmo0+vN+HGrXknFZlO1Hn2c2o\n",
"17EYuJjkqvAVqJdyGDpJkk+tHYNnWDJ/9ARqeYDzOIF/gsZZPotII4FAIC+DJabh4x7+NwPLjDEf\n",
"xabcAojIK8aYZWiTu07gk3GD4fGGPh5rX5Ii0/tIyppqzrHfTCRF+fKUK+SrRGUpP2OqCjUKx9nt\n",
"6WROZpQ01o1EGVPr7M8ainoeR6GNBWclXPsSaij22Z91Flrw52gCVqPFfZP1kDCElKSoMPFU2ov5\n",
"KT/mYwylswa4HJE/5hl7IBDoAQdacd+ZDMzsqaRMKbf2M6V8WcqXp0blWEbHtp0c5S/jyd55Noku\n",
"VIJyGVNdaF1GJ/AJ1BDNQ7OgXofGLpJaiLgU39n2mj8CJ5LZV8q5D/GutGRzasazhwc5h+N5DuDn\n",
"wFWI7CniOwYCAQZJym1fYI3Gk5Q+SyppO24M3H5/FPA5GtGH+G7SJakab70HNS4jUC9hDhrQvojs\n",
"U7Q6NhNlS+1Fjdi5aAwrTgPaN0qA00j3eJtRSSuLF5ziU3yXb3ENlXRtAz6OyJ/yjC0QCGSh3I1G\n",
"qYfRHeLeRzxY3lzk4stSe+09DOptVHnL1Ni+k6Zy/efpQpsNumypDWiK7DDU8zgWLb6LB8Pb0b5S\n",
"G1BjcjwqPzlcQ8Pp7DdOmR7GDLbwIOewiNUAdwDXhEK9QKBnlLvROJXSZ0klbScZBdCnYrxmwy3D\n",
"ibKjshX0jSK5kM/PnCp2Rr5twCZUlqoDLkE9j5uBF9CYxRI0DnFElvtXo7GT0WgsaifqcQzzzkmh\n",
"Xk0beSrODV1cz83cxBdAZbPLEbm/iO8VCASyUO5G4zkypaFcslF/nZtUxNdftKAeRx3pUlSNt1+L\n",
"PsCHocWUs1Hj8C4yp1L1SaGB8BdRz6PDnv8RMms8BO1guxetyfAMSKoDzNAkJ2cJL/Bn3sIstgnw\n",
"XeALiNQX+N0DgUAeyt1olHoYxeD6SiV5Ia4NehOZhXvxYj4Xq4gX8zWhBmoiKkW5rKmp3v501EBU\n",
"kVuW6kBrH1y21CZ7bDwaCD8GLQyM36MaNSid9vNF3mdiSO0UqEqK0Y+kidv5KBfxa1AP5+OIPJ1j\n",
"jIFAoBuUu9E4nuyFdRT4WV+c6wxBF5FYn5QtVUnUZyqfLDWKSILyFydN+UVz+UihstRmu+xF6ypG\n",
"AN9A02Tno7LU0SSn0rajXsss+12fQlNv/QC6/e7SBSaLbCZ8gJ/xfT7JGJqagX8H/guRziK+TyAQ\n",
"KJByNxovUZxsVOhn3b1HBemyVDFprz2li6jF+U5v7W/vRb0AP1vqELSdx/gc925GPYgX7b1GoW0J\n",
"jks4t9qefwTe9zekkNivYz5r+C3vYgkvg87XfQUimwr+xoFAoGjK3WiUehiFEJej4tvtJPeTSjq2\n",
"L2FpJnvbc7c9DZWl8hXxNaH9n9ag2U319t6z0Eypo8nMlGpE02lbUUMxx31gSIkhZVKxkM4Imvhv\n",
"Ps2l3AEagL8auDd0pA0E+p5yNxpHUbzE1J3zCr2Hi1ukSA+KJ3W4jRfy5ZKl3Ax8cUlqPNnn6U6i\n",
"E81Gcv2lUsAHUcPwDVSyOgKNWxyV5d470fiIQeMe00gzJMnFeUqK9/NL7uAShtHZBtwC3IJIcxHf\n",
"IRAI9IByNxpr6d2ivO5e79qg93emFKgh8FueJ/WWarRjHYV6HHPRKu3z84x3I/AsGvcYgspRpyWc\n",
"9xrIBDBe6/t043Esz3IPF3Io1QD3ov2iNhb3VQOBQE8pd6NR6mFkI95XKqnTbQeZ/aSS5KkWVCby\n",
"W567Ij5XzT0FlaKmJSxzyN3yHLSL8Cq0B9R2ouLAJWhh3uTY+W1og8IKkIVgbBDe/XtE/x9nsJWf\n",
"cCnnsRx7/ysReTDPeAKBQB9R7kZjIb1foNfda3xZKl6452bji++79uajYuv49ng0lXYiMAk1AsXM\n",
"xteKps1uIppJbyna3uNW1OgsRmWpaQnX77VjMGggfAq5U3YZQTNf5xo+zo+oIFUHfBX4b0Taixh3\n",
"IBDoZcrdaFRTfFFeXxT8uayp/qQVlaXq0GK9HbGlhmi+igloltQhwMloDUU29qGz37ksplPQOMd+\n",
"DKmuEbTSwsiKuO2opJ2r+SZf5KuMoakd+A5wEyJ1PfiugUCglyh3o1HqYcRxslQ7ycV78WNu1j23\n",
"bko45vpLuaUTfVKPQWWjaWjRXnyZSe7ajXZUYnoFNRApe7+F6FwmY2LnN4ykeXcKM7uNkQlxkBTv\n",
"5F5u5xLG0wBwN3BDiFsEAgOLcjca8+heUV5vFvyBehqugC9JmorLUyOIpCd/GRXbH4fKUb4sVUzt\n",
"Ry0azN6IehDvtz/jUdSbONIuSam4Lah8JpDqhCFZPKkU5/Igd3Ix03TyxceAzyHyVBHjDAQC/US5\n",
"G41t9L08lW+/Pwv4QOMQe1BZag8qRW33ljrUeLmpYOeh8YpTyJ4p1YB6HTvQ2MWpxLwUQxcS61V4\n",
"Ev/gp3yEw3kVtEX6vwN/DPUWgcDApdyNRqmH4cglQSVJVK1kylFJizMQDfbnVKLex2S/BOo8AAAO\n",
"EElEQVRUgpqBGoaZ3nauhoOghXsvogZC0JqLRWhdhvcfSZhIHXuZkFHJfSqP8W2u4jidEGkt8EXg\n",
"HkRSeX9TgUCgpJS70ZhN/8hT8Yo1f991i3XyU671cCLpaQzpUpS/PxaVoybbdTy+kIsOVI5aj3oe\n",
"b0UNwzbgf9CeUseRMcmSpMBY6+C6mKdzNg/yJb7C6TwGmoX1ZeDnoU9UIDB4KHejUUtuGak3jg0E\n",
"ulCPo9Zb70ANwVY0DXYIanCmom3OF6OZUsMS7gdaGV5dQedoYEkXlZ505dtE4Rwe5Db+laNY4a77\n",
"v8CPQ/psIDD4KHej0d8/NskLcZJTIes20uWnxiz7jahxaEef3sPQ2ggnQfnrGeRvde4K95pRwzIH\n",
"ZAkYL7idXphXQSfv4F6+yWeYxTZQz+Vm4K5gLAKBwUu5G42ppEtISbJSocdAn5jxX1A2L8RlSmWT\n",
"puLb8UypuDw1nnRJaiKFB9k7UbloHWpwzkezpHagzQQXo3N/e8QVN2UYbbyfX/AdPs0YmkFTcm8C\n",
"lgUZKhAY/Ax4o2GMmQ3chcomAvxQRP7LGDMJ+DX6MKsG3iN2/mdjzPXApagsc6WILE+4r4A0kF9i\n",
"yidHDWTqSZelnBy1Dc2SGkokSc0DTkRjFhkMpb19OtupY8KwBsYR/+pjqOcavsG13MooWkCNzX8A\n",
"fwgB7kDgwGEwGI1pwDQRecEYMwZtgPd2dC7q3SJyqzHmWmCiiFxnjFkE/BLteTQTeAhYILEHVx/J\n",
"U9m8kqTjrq25k56S5Ch/u5nsclQTaiBq0cwqQQ3CZKLsKH+ZRWY/KJ9W4IWJ7GEqNYfUMXHqTqal\n",
"ZUY5ozGPV/k8t/EhfsZIWgH+iHa8/VtInQ0EDjwGvNHIGIAxv0fnfv4ucIaI1FjD8oiIHGG9jJSI\n",
"3GLPvx+4UUSejN1HtLNqUVJU1mFRuMdSQSQ55VqGotlSI1Epyi1jY/suhdYt2QLXcVpQOWozOs/F\n",
"DCA1hM4NlXTObGdE1pbphi7O5y9cwXc5l+UMQVqBnwLfQmRNgT8/EAgMQoo1Gv3dtjsNY8xcdH7p\n",
"p4AqEamxH9WgwVzQh59vILagb9dJ1DB4MqAKpRX1OGrRtuZb0d/BDlSuG4FWhk9H25S/GS/9N0Xl\n",
"Ye1UMpxW2hmWVmNRxQ6u4Dtcwk+ZqcHtGtR4fx+R3f3y7QKBwKCiZEbDSlO/Ba4SkQZjoue5iIh6\n",
"DlnJ8tmNw6PtpXbJSyGeSa7jKTQLKi4/JS2uv1QDKkVlW9rsz6tAaypmoxLUbLQj7dmoMU0MjFfS\n",
"wRw20cZwtjEDoYI2W9BdSTtv5n6+wFc5nn866/I34HvobHkhEyoQOIAxxiylwIdjEiUxGsaYoajB\n",
"+JmI/N4erjHGTBORHcaY6ehbNeib9Wzv8ln2WAI3jiI5AwrSDU2hwfFcn7uJlvLJUq6Ab0xsGY96\n",
"TGPQzKgpRJJUIVlSArJxBK10MHROF5UVhi6G0U4bI9nAYWknz2ALV/FtruabDKULNGZyF+pVvFzA\n",
"zwsEAgcAIvII8IjbN8Z8qZjrSxEIN8CdQK2IXO0dv9Ueu8UYcx0wIRYIP4EoEH6YxAZuYxrJeaOD\n",
"j3pgNypJOTlql36UGjWNHfMr6ThpBzNmdObowF5BBxdwH5/j65zCE+7wc8D3gV8h0th3XyEQCAwG\n",
"Bnwg3BhzGtpVdQXR2//1wNPAMnRmuWrSU25vQFNuO1E564GE+2bLnipEYurO5ymS5ackWSqXFNVI\n",
"1N58KBoon2J/D4foIoeAyTLbnjCELlKe03gkL/JRfsIH+AWT2QMaq/g5cCciK5PvEwgEypEBbzT6\n",
"Cms0/E6suaSmni4uE2o4kQSVtO+yocahclR8exIa8M+bITVc01/3xybiLOYl3sMy3s09LGQ1qAG7\n",
"D82CegCRjnw/IxAIlB/lbjRKPYzu0mhI1UykruVgNg2dxo6DxtA4cR/jzGqOYAuz0jwJgJE0cyYP\n",
"82b+wpv5C/PYAPoL+BtaJHkPIrX9/1UCgcBgotyNRhe55aXeWjrQDCeXNZVtuxGd7KjeLvvstZXD\n",
"aRlxDM8fPo0dS4Ygi/cxfkY1cyuqmUtXQn7CELo4gtW8j19xDg9yDM8zjP3Ow+OoofgNItt7/MsM\n",
"BAJlQ7kbjTH0jRzl2p0PT1i7bVeo5yQotz0emDqEriqgKkVFHikqiuUbUhzN83ycH3Apt7usJ9B4\n",
"yj+Ae1GPYnPxv7FAIBAIRqPUw8jLaBoZRz1D6aCDoexjHM1p02OkOINHeQ/LeBe/pWp/5jGNwANo\n",
"nOLPofguEAj0BuVuNFroGznKL+Dbvzak2sZRP3QytSOmsnPETLaOmc3myROom9xJpWlnGA2MpZbJ\n",
"bGEW65lHDdMzxl7FDs5lOeeynHN40DcU64DlqKF4BJG2jIsDgUCgB5S70ZhMuqQUl5iK2R8KjBhD\n",
"w+jjeHbmbDbPmcDemaNonjmE1MFdVMxsY/jkfYyvqGMidUzcbxzqGZ91nCNpZiGrOJ5nOJknOJkn\n",
"mM+rrrikFq1D0UWkupd/TYFAIJBGuRuNUg8DUMMwm837lyNYzWJeZhGvMJdqhkTjrEVjE4+hhuKF\n",
"0HY8EAj0J4OqYWFvM4qmdoNgEIaQwts2FXSZIaSM3R7ifx4/3yBU0slIWhhBa8YyjnrrW9QxiT1p\n",
"2zPZyiT2ZCtLX4caiMftek1oNx4IBAYTB5SnMcC+yQa0Zcdz6JwhzyOyq7RDCgQCgXTK2tMoEXvQ\n",
"KVBX2eVF1EDUlXRUgUAg0AcEo1EYtWg/LLesJzIUu4LEFAgEyoVyNhpdaIX2TrShX01seztqIDYh\n",
"0lCiMQYCgcCA4kAzGpejbTo67dptN6BtPNy6HmgNHkIgEAgUx4EVCC8imBMIBAKB4p+dhcwQFwgE\n",
"AoEAEIxGIBAIBIogGI1AIBAIFEwwGoFAIBAomGA0AoFAIFAwwWgEAoFAoGAGjdEwxpxnjFltjHnV\n",
"GHNtqccTCAQC5cigMBrGmArgu8B5wCLgfcaYhaUd1cDFGLO01GMYKITfRUT4XUSE30X3GRRGAzgB\n",
"WCci1SLSAdwNvK3EYxrILC31AAYQS0s9gAHE0lIPYACxtNQDGKwMFqMxE9js7W+xxwKBQCDQjwwW\n",
"o3Fg9DoJBAKBQc6g6D1ljDkJuFFEzrP71wMpEbnFO2fgf5FAIBAYgBxwc4QbYyqBNcDZwDbgaeB9\n",
"IrKqpAMLBAKBMmNQtEYXkU5jzBXAA0AF8JNgMAKBQKD/GRSeRiAQCAQGBoMlEJ6VUPSnGGNmG2Me\n",
"Nsa8bIx5yRhzZanHVGqMMRXGmOeNMX8s9VhKiTFmgjHmN8aYVcaYV2yMsCwxxlxv/0ZWGmN+aYwZ\n",
"Xuox9RfGmNuNMTXGmJXesUnGmAeNMWuNMcuNMRPy3WdQG41Q9JdGB3C1iCwGTgI+Vca/C8dV6Fzu\n",
"5e5Ofxv4s4gsBI5E57YvO4wxc9HZPY8VkSWo1H1RKcfUz9yBPit9rgMeFJEFwP/a/ZwMaqNBKPrb\n",
"j4jsEJEX7HYj+mCYUdpRlQ5jzCzgfODHQNnO6GiMGQ+cLiK3g8YHRWRfiYdVKurRl6tRNrlmFLC1\n",
"tEPqP0Tk70Bd7PAFwJ12+07g7fnuM9iNRij6S8C+UR0DPFXakZSUbwL/CqRKPZAScwiwyxhzhzHm\n",
"OWPMj4wxo0o9qFIgInuArwOvoVmYe0XkodKOquRUiUiN3a4BqvJdMNiNRrnLDhkYY8YAvwGush5H\n",
"2WGM+Rdgp4g8Txl7GZZK4Fjg/4nIsUATBUgQByLGmHnAZ4C5qBc+xhjzgZIOagAhmhWV95k62I3G\n",
"VmC2tz8b9TbKEmPMUOC3wM9F5PelHk8JOQW4wBizEfgVcJYx5q4Sj6lUbAG2iMgzdv83qBEpR14P\n",
"/ENEakWkE/gd+n+lnKkxxkwDMMZMB3bmu2CwG41/AvONMXONMcOA9wL3lXhMJcEYY4CfAK+IyLdK\n",
"PZ5SIiI3iMhsETkEDXT+VUQuLvW4SoGI7AA2G2MW2ENvBF4u4ZBKyWrgJGPMSPv38kY0UaKcuQ/4\n",
"sN3+MJD3ZXNQFPdlIxT9pXEq8EFghTHmeXvsehG5v4RjGiiUu4z5aeAX9sVqPXBJicdTEkTkRetx\n",
"/hONdT0H/LC0o+o/jDG/As4AphhjNgNfBG4GlhljPgpUA+/Je59Q3BcIBAKBQhns8lQgEAgE+pFg\n",
"NAKBQCBQMMFoBAKBQKBggtEIBAKBQMEEoxEIBAKBgglGIxAIBAIFE4xGINBLGGOmG2PuyXPOXL81\n",
"deyzR4wxx/XN6AKB3mFQF/cFAgMJEdkOvLsntyAUIgYGOMHTCAS6gTHmy8aYq7z9m4wxVzovwk4A\n",
"dZsx5mljzIvGmI8l3GOkMeZuOzHS74CRhAaLgQFOMBqBQPe4HbgYwBgzBO179pj3+UfR1tsnoPO+\n",
"XG5b1vt8AmgUkUXAl4DjCJ5GYIAT5KlAoBuIyCZjTK0x5mhgGtrHqNY75VxgiTHmQrs/DjgMWOed\n",
"czo6qx4istIYs6LvRx4I9IxgNAKB7vNjtPlfFep5xKWlK0TkQf9AgrcR5KjAoCLIU4FA97kXnXP5\n",
"9WinZZ8HgE/aaUUxxixImDHvUeD99vPXofN3BwIDmuBpBALdREQ6jDF/BepERHSKhv0xiR+jM8Q9\n",
"Z+du2Ek0/7I753vAHcaYV9A53f/ZX2MPBLpLaI0eCHQTGwB/FrhQRNaXejyBQH8Q5KlAoBsYYxYB\n",
"rwIPBYMRKCeCpxEIBAKBggmeRiAQCAQKJhiNQCAQCBRMMBqBQCAQKJhgNAKBQCBQMMFoBAKBQKBg\n",
"gtEIBAKBQMH8f0gI4SnTzMBkAAAAAElFTkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x106c8a390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#コブダグラス Y=(LK)**(1/4)( w=5 r=20 固定費用100 )Y=20x**2+100 規模に関して収穫逓減\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"fig, ax = plt.subplots()\n",
"x = np.linspace(0, 10, 200)\n",
"plt.ylim(0,1500)\n",
"plt.title(\"increasing returns to scale\")\n",
"plt.xlabel(\"yield\")\n",
"plt.ylabel(\"cost\")\n",
"y=100+20*x**2\n",
"ax.plot(x, y, 'r-', linewidth=5)\n",
"for i in range(1,100):\n",
" y = 100+(5*(x**4/i))+i*20\n",
" ax.plot(x, y, 'b-', linewidth=2)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAZMAAAEZCAYAAABSN8jfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzsvXm4JVV19//ZPc99b88NtAwyCSIgiAoSUHGOmhg1JmYw\n",
"xhgTfcHEGKf8lAwah2gMml/eRKMJDmhM1ERFBUUcUEQcwAkBmaeeh9vdd777/WPtRa2zT81V59zb\n",
"5uzn2c+pU1WnaledqvVd67uG7bz3DNqgDdqgDdqgNWnzZnsAgzZogzZog3botwGYDNqgDdqgDVrj\n",
"NgCTQRu0QRu0QWvcBmAyaIM2aIM2aI3bAEwGbdAGbdAGrXEbgMmgDdqgDdqgNW4DMBm0Ss0592/O\n",
"ub+e7XGUac65Fzrnvjjb4xi0/Oacu9g596HZHsegNWsDMBm0qs2HPueb9/4j3vunzPY4AJxzVzvn\n",
"fn+2xwFzayyhHRLP06DltwGYDFqd5lo9mHPz2zxev5tzbkGJ3RoJzJbv0VwT3q0+T4M2O20AJoOW\n",
"25xzpzvnvuec2+ec+xiwJNr+y865HzjndjvnrnHOnWK2bXHOfdI5t805t8M5956w/kVh33c553YA\n",
"b3LOLXLO/Z1z7k7n3APOuX9yzi0J+w855z4bjrPLOfcZ59zh5jwvcs79PIzxNufcb5r1Xzf7zTjn\n",
"/tA5d3MY73vNtnnOuXc657aHY7wi7J/6jjjn7nDO/blz7kZgJPz+Mc65b4Zj/8A5d17Y983AucB7\n",
"nXMjzrlLnHNHxce3FkPKPbrYOfdB59w/hnuxzzl3rXPuGPP7v3fObXXO7XXO3eicOzll3F1jCevP\n",
"ds59xzm3xzl3nXPusTnPxGucc/eEMdzknHtCWD/fOfd659ytYdv1+j855/7BOXdXGNv1zrnH5Rw/\n",
"9T4O2hxv3vtBH/TUDiwC7gQuAuYDvwZMAH8Vtp8ObAUehWiXvwPcDiwM+98AvBNYCiwGzg6/exEw\n",
"CbwcUWiWAH8PfBoYAlYA/wO8Jey/BvjVsN8K4D+AT4Vty4G9wHHh+0bgJHOer5vrmQnHXQVsAbYB\n",
"TwnbXgb8GDgsjOFLwDQwL+Pe3AF8Dzg8XNvhwA7gqWH7BeH72vD9K8CLze+PCuOZZ9Y9uE/GPfq3\n",
"cMwzw/39MHBZ2P8pwPXAqvD9BGBTxtjjsawBdgMvDOd6AbALWJPy2xOAu/TYwEOAY8Lyq4EbzX9x\n",
"ih4jHHs4HP9PgfuBRWHbxcCHwnLWfVw32+/DoOf3gWUyaHntMcAC7/0/eO+nvff/BXzHbH8p8M/e\n",
"++94aZcC48BjgbOAzcCrvfej3vtx7/03zW/v897/o/d+JvzmD4A/9d7v8d7vB/4WEWp473d57z/l\n",
"vR8L294CWG11BjjFObfUe7/Ve/+TnGt6q/d+n/f+bkSonhrWPx94t/f+Pu/9nnD+PPrFA5d47+/1\n",
"3o8DvwVc7r3/QhjzlxDh/gzzm6p0zoP3yHs/Fs75Se/99d77aeAjwGlh30lgJfAw59w87/3PvPcP\n",
"5BzbjuUZwM+8+JhmvPcfA24Cnpnyu2kEPE92zi303t/lvb8tbPt94A3e+1sAvPc/9N7vCssf8d7v\n",
"Dsd/VzjGCSnHz7qPT8+9U4M2620AJoOW1w4D7o3W3WmWjwReFeiI3c653cARCIhsAe4MYJHW7jbL\n",
"64FlwHfNcT4PrANwzi1zzv1zoJb2Al8FVjvnnPf+APDriGVxX6CA0oSUNitgDyKWDmHMdkz35Bwj\n",
"7RqOBJ4X3YtzgE1mn6q+irtT1m01y6OE8XvvrwLeC/wjsDXcr5U5x7ZjOQyxNmy7E7ESOn/k/a3A\n",
"KxFrYqtz7jLn3OaweQvw87STOef+zDn3k0Cj7QZWE/7fqJW5j4M2B9sATAYtr91Pt0A50izfBbzZ\n",
"ez9s+grv/ccRQfgQl+04tsJsByIYTzLHGfLerwrbXwUcD5zlvV+NWCUudLz3V3jvn4wInJuA99W8\n",
"1i3m+5asHTOu4S6EqrH3YqX3/u0p+wIcCJ/LzLpYYFYCH+/9e7z3ZwInIffr1SXGDaIwHBmtO5IM\n",
"QPXeX+a9Pzfs44G3hU13A8fG+zvnzg1jeV74X4cRajLNUiu6j4M2R9sATAYtr30TmHLOXeicW+ic\n",
"ew7iH9H2PuBlzrmznLTlzrlnOOdWAN9GBPRbg2WxxDl3dtpJgvXyPuDdzrn1AM65w51zTw67rEDA\n",
"Zq9zbg3wJv2tc26Dc+7ZzrnlCNVzAKFiyrQHAQnxw1zknDvMOTcEvIZqwvzDwDOdc08Ojuglzrnz\n",
"XRIosBV4qLnm7YgQ/+2w/4vt9pzxpm9w7kzn3KOdcwsRi2uM7PvQMRbgcuB459xvOOcWOOd+HTgR\n",
"+GzKeY53zj3BObcYoSfted4P/LVz7tjwPDwi/F8rgClgh5NAizcifqu0VnQfB22OtgGYDFpm895P\n",
"As9BnME7Eb/Cf5nt30V8He9FHLa3IE54BYhnIprqXYjW+nz9Kd2C+jXArcC1gcq6EtGuAd6NOPF3\n",
"IAD3efP7ecCfIIJ5JxKp9EcZ54nPabe/D7gCcSB/F/gcMJ1D03UeyPt7gGcDr0cc+3chFpUCwD8A\n",
"z3USjfbusO4PEI19B2JNXJMxtqJ1IML5X5D/4Y5wzHdkDLdjLMGv8cthvDuAPwN+Wf0dUVuM+JO2\n",
"I8rCOuB1Ydu7EFC+ArE83ocEDnwR+AJwcxjbKJ202oPXlXMfB7Jqjjfn/VwLOR+0QZv95px7GvBP\n",
"3vujZnssgzZoh0IboP2gDRoQ6JSnB5rncIRK++Rsj2vQBu1QaQPLZNAGDXDOLUWixE5EaJjPAheF\n",
"UORBG7RBK2gDMBm0QRu0QRu0xm1Acw3aoA3aoA1a41amQN0h0ZxzAxNr0AZt0AatRvPeNy62+QsD\n",
"JtL8XyChiEuQUNIlNb7PZptE+Pox02t8f9qT4POfKLn/FBK+uojOe7KU7vu0FAkbfRgS/nldwb55\n",
"x1rc2l3LbReH3tFmSO6DvR9Fy3X2HQ/n05yWxaTfE/18KBIuvBQpI3JVwf5ZnynPcuq96EWzz3HR\n",
"Z5l90j7H6QyTjp/hpdHyo5Gw9aXAPviDu+B9X03ZL+1+2uXZqnAd39Os5Rrbk2KoTdovjM9ELJNW\n",
"rmWCRoK80nddN0HyMlQVyinLLz0T/uXnJY81m1TnOD0X6ke/BG5/RziXtoUU39u2PvsEmqltgo57\n",
"9uoV8I67Sb+XTT5t/ss8EqFeRUgXbY/XLWp2ay6mJrCqItIjwf4gSHqSHKV5yHMU34eWvrslA8uk\n",
"u72FZsJ9hmzrpYxQHyrYnrW8sN3bcBhIElyZNkV5QX0mkoT4AyRxsA4ATITzaiXcOgJ6Tfn9X7ga\n",
"+ENav8eVWhkNfBo4H6lZdR9wGZLNX0WoT4XzqWCI7sU1v4+EO+cJ7FVI5eUqgn+2WpFgngc8EqlW\n",
"PAN8HUl6HYMfPA6pIJ33+0kSkFTLcgHVhfeGCvvP5nPaqP2igckUUjl1PdW1+iXM3iQ9nkbad7zO\n",
"HYOUR8871iRyvQspJ8Q3As8LY70G0QxXl/hd/NnnZ+4C+6VNbTzvcxy5tx6hRVSrzNK0VyLFE1cj\n",
"meWfCuvXpOybJ+QLrMy3APxm8T2r3CILqCcau5ZsUY19PvnC+RykAOgiYA9Cy44gJfOXwu+sQqZU\n",
"yBPus0Vpxfegze/TdFo9IHRq4zaguTpbGsXVIuWSum4aEQJN6ZSiz3jdbL0onmzhUeaz6m+0xfe4\n",
"ipAu2h6vmy3tcpp2BHfRdvuiWQqmrKZe5/tsKHpZlFZb3yfDeVS4K0jG9yCrl9kvfjZT7qNrxQH/\n",
"iwYmF1NfqHu6HXj9+Jwtn0Xai5JHnzwPERr/BtxW8nf2Ux39C6gvpKtuny1/hVqaZQTz6UgNsjHg\n",
"Q0gNs7KC3TqhrZXZK8E+m/d0imLhvBCZR2c1AqxfAq7N2d9+t5QWyHtpKa2qgrvMPrPx7qsj33T3\n",
"sIHPpLstQfjROkJ9tigufUn6oaWPkTj79UUpI6QvQITIPciMfJtL/GYuaJaQVLbttcauWiYUUzDa\n",
"n4kAyRTwGUSYHZez/1zh1+N72rbmHkdqxU79tPtxLvAryD3ZjUTBjQInp/wu7TizIQutJZnW43tU\n",
"ZZ80f49GE8bX/8E2LuYXzTJpcogq4YxtfGp0URzBVVUTr/qb2VIgYtDspWCfptsJ3QtNfa7w620L\n",
"8/jeamizJwmcaEs7T+uzAZJxuHgTIZ+2fYZO4T4Puc5lFN+vOr2C1TOguTpaAJPXU0+4z5Aeetc2\n",
"BWPXNQxtrN3SfBZ5gnkzMr/4bmSe9qyXJuv3ygdb0Oy1cJ9tfr1IWG8AnhjG+VkejDAq9XsVSvMo\n",
"FuxtCPjZorXKCOglwNlIBNokMi/LdSn7xceYoDP8Ni1Kq82+pOV7U6bFtGDcJ5DJzY4Ht2BO01zO\n",
"uQ8gc0tv896fEm17FTLXwjqdM8E59zrgxYhWeaH3/oqw/gyEp1+CzA19Uc5pN1Bd8M8mxaV5Fv3Q\n",
"2PUFSqO38r4/MYz1+0jMcVnBPpuCaJLe0jD6XUNxoTsqLqufiEQZOUTwbQNOydg37R7PxrNqn9Mq\n",
"GnrZfazWDglNmNfPB54U9t0JfA353x9T4rezYfmk3cODKeuq9knk/tkWB0XYvgKJdLsAWN7mBfbM\n",
"MglTde4HLrVg4pzbgkyacwJwhvd+l3PuJOCjyCx+hyOOs+O89945dx3wCu/9dc65y4FLvPdfSDlf\n",
"E5orFj69FuzqjO4XBTNbLxB0Jyb2Srirz8JmQrehmeftM0ccqJUFeN52S2tBeeunbI9pndkIQomt\n",
"yDa7tXogobTK3Is661swCNqhuXpmmXjvv+6cOypl07uAPwf+26x7NnBZmNnvDufcrcCjnXN3Aiu9\n",
"99eF/S5FnGxdYBLan1Fd2CvFVVdYp+UCFH2fbX69rLC+AHEIfxVxEJf9vfqDYsAsK7yXIzP4VRHw\n",
"s+ELSvMDZfX5wLMQzfCnwL/TrZmmHUeFU54DtaivIl9I2T4b1mQZgBxF7t25SF7OOJKPc33Bb9Iy\n",
"yuOotyIhromcZfbtt9KW5sSPn6tFiPW7OfxmLyJDvxO2/2MbA+nrC+icezZwj/f+Ruc6gPAwJIRP\n",
"2z2IhTIZlrXdG9ZntWOoDgZzgV9vQzPPc6Aqx15WMC9F/pPjkIf1LuARKftk9dl0oFbR0OvsY+dV\n",
"T4swSutrkSl6VyBT3X4XOKPkb2cDJMvckzpd56bPy1NJE9jLgCcAjw/77wC+FbY9Odo37v32TaY9\n",
"h2l0VhbFlbU+vm+QOPHj69flDcBTkXcXRDG5CZGjG4Dnhv1aaX17UJ1zy5B5nZ9kV7d7lov/OFk+\n",
"P/TCZrWiNgV6ngO1LL8e76Mae94+bWua84HfrvG7toR33j72BctyoBZp42sKtse96TO7GfitCvu3\n",
"RcnkCSnl3POS5vKol/ge5u3bhnBfh4RVl2k24KSOEM8Dgim6s8mtgpEm4OPljSX3b0NBWwQ8Aq5+\n",
"BFzdwuE6Wz+1nocCRwE3BKvkCOC7zrlHI0i5xex7BGKR3BuW7fp7s09x8f+hmvCfplsrKivgVyBl\n",
"W8qAgF03lxyoWffGI5r0QiRQ4vaUfdK6+i3UCqoa9ri24v5zmZLR+3UB8uzvBf4BeKDE7ywtU4WS\n",
"0XWxwpEn3GfjHpYV4kOINbI8rPsYSZmgtGNY5UJDme39yxLW9vsQnYEmeQK+3++yvVdpy2Nh7KeF\n",
"MQL8GKGo70r2P/8gnG8Uib+8po3B9Q1MvPc/RFAYAOfc7SQO+P8BPuqcexdCYx0HXBcc8PsC4FyH\n",
"aMiX5JzmVIpBwH6fDQeq1jGqooHX3T5DPQfqE5GX8G7kPzuq5O/mGiXTRrSM3kdtVbT2X0WAZBwp\n",
"MvhwJMgkDwhmI4xU72GbWrt21d61zadYY1+GgPDZiMDehlCDm5FKDFm/7TelZRWLIkFfdj/Nk4LO\n",
"Ssz2vqV9Phy5Z2vDb3YBPwvHe3zG71p91noZzXUZcB5ycduAN3rvP2i23wacaUKDX4+EBk8hc29/\n",
"MazX0OClSGjwhRnnqxPNlRaL3QueXb/XdaBW7cuYHSvIUjJtCfK0ri9bG1EyRfvOxn1US7KJEM9a\n",
"r7SWLZi4hHKUTJ3lfitsVQR3FRBQhUL9jxo1mCfg63z2W5kYa6sE/S9a0uIfUl7AT1LegVpFiGdt\n",
"m40kRWsFle3HIXz0fcDflPyN5lvUoWTqrO+3cNf7WFaIH4/4Bj3wryRRM1n7a8SWCqleCvd+01rT\n",
"JNdcJLjXI472ZYS0AuCGjP2tr8cmcbYp2GdRwHfds/gTJELrBPObK4ArkerIdv9xuqsuq7WzFNwX\n",
"B2BiWgCTD1Fe8M9GeG6vNPVYuGl5+aqO1KXASxFr8hoEUMoAQb+1z0l6Q8nY9ZZiUGuyjMB+BBIC\n",
"7BAQub/Eb/v9LKbRWk2omTQBD+klQ9IE9nKEojkz/G4r8EPyqZ25KOCrfloK0FYNTrtXurwaCY8+\n",
"E6GVPXAn4mNelPG7AkV2UE6lo9WguYqKrNUR4lnbJsjO6m1ba58NoJyiN5SMXa+TalmqsImWXrSt\n",
"n22G8tp71WXl4FVYxLRWkaA/1DX4qp8TdFs8afes6nLaun5Z2J7O64yu2V0wABPTApi8iHKCf4J0\n",
"SqapEM9a12/HtKUWqgjxX0dmUvw0klRadAx96awfqFf0TL/vYZrfIm95OfBCROh8A/HzZWn4cThu\n",
"nCvwv0XAb0byRJYgE1i9H/gR6fdZJ3WCYkqriaDvZ47UBKnCvWvdWmQOe3Wu3wl8ArHe7P4WCLVp\n",
"Kf206w/dvWEAJqYFMPk45YR7v5PqrObZC61dl20l4qra+EOQ/Icp4HMkeRt52ns/fRfq3G+Djsn6\n",
"vc0ZKBLmdnkj8AIEUO5FeP5DVcDnWUjx5zidLaZosgT2CoTW0jJLW5HIowUp+/b7WbPPWZZwL7Ns\n",
"12n9LPt8WWsnQ8izBYnE0vSIUSRMf3/Kvg3k2oDm6mgVaa6yWapV16etm6bzJeml9t5vkExzTLe5\n",
"HCclltXGf9E0+KrCPytaq20tvp/W4jjNBHra8gSdTa3EWEinCe4y63R9v+6TKq3x9Rasc385p2tz\n",
"zVL7TYqF+xiJBlVVYA+TJDSV/W0/tXfN9q0quOcjdc3mIXXT7krZJxbw6ruoKuBXV/jNXBTwdnkC\n",
"sUgegjja/xqpYJv2W52sSCO2qlI0wxnr07T4fjUrvMoI9KOQ6QwWISVR/gn4Scrv7ERjGnlkAbFI\n",
"oG8ouV+/fIszwAGyBbp9nk4CHomA2gySqv5fwPZov7RikjEQZvXlSOScfm+l/aJZJp+iWMD3OzQy\n",
"jjxqk5rRZeXgY2qq7Od5yPSx9wA3Fuw7FwR8FU0979NaPjZnpYwWvxwJoT4yHO/bdCop8e/6GRSR\n",
"BYpNaRsNAbcFE8to6CuRRFgNY30Amfp5ccZv+xUdOE0i5Ctq86nrNNjBPlM2HyVPuD8SmXJY368d\n",
"SDTl/JT9W36WBjRXR6tIc/WSmrFA4UnCc6sK+DQwnIsCvi3Bbj81tDnWSNukaPp93zQooqlAT9se\n",
"h+PGAj2Pgqmyrl9WtipgbQn5g3QKeRCBXCTky9xD2/ulqMYg2KRPgLtqACamBTB5LsUC3lFfsM91\n",
"AV9HcD8SKftxC/AXOfuNhfPUoWjKCndd7mfein1Oygr0s5Hkukngb+lMrLPPWxyxVVZAVRXy/Wo2\n",
"+qiMQD8OqVq7ELFGLkEc7XbfeNZDzespK+TLAkG/gLCsEF+GPEdHhd/tBD6O0Fq6j53HHTqnIVhO\n",
"+rVWXb9gYJlELYDJ5fxiCPiyn0o9VKVodHk54mdagRTQ25fzu37Sg5q3UlVDLwMEajFmcfFFgvt0\n",
"RAiAgMiBjH376btQ53SekK+qzaclIKbdq7R7tBoB26PDbx9AKNS03/fLbxvfo6Y9K6O8SKCvQ56f\n",
"h4bfTyH+tv10P3f9UKpmwM0bgIlpFWiuXgn4WIvvNUWjy/108Lcl0NO26yRGdqbEuhp73r79VCiU\n",
"Dqwr0LPWWcomjtZqq/ebsskCwKrdWoTQrTRU1dyztvWjTZJNZ+XRXPG2UZJnJs7VWQTu8gGYmBbA\n",
"5FnkC31P7ymapfS3Dpd18FcV7i9HtMcPILPWpe2ruQTzqCbQqwr+flo+dQT6BqQs/wLgP4EPp+xn\n",
"Z0Ws4ruo2ucaZaP9FITWmo9UnH4ncKvZPk4n9Rc7p6sK9LT1/VIWxikn6EeRRODHIQwAyOyQlyJB\n",
"CKoc2CoFGtKtdJ+9xjrLBfdkQHN1tAAmXyJf+PezfEEb2nre8jjdpUWqCPQjgachYPRNskMv+wWM\n",
"8T1rQ5PX9UptQQKKVfphyL1aiETY3JOx32xSNk01ewuE0B1FlCfoh5GIQE2uewCpFB7v169naZTq\n",
"Gn3W+jgM15ZXKRLmxyFTDqwKvz2A3BcX7d8PuaTPh73OsOyeMgAT00rSXOpAbJuHt+u0DleRJt50\n",
"Xb8SFLWuT1OBnrVOueeie9ak90tbtfkEbXZbEDCL1mrqkO0HEHqq0TNF6+OyNKrRZ13n8px1Wcv9\n",
"COm2ykGKsC+9HNcVUwtZUwbi6w+f7pUDMDEtgMlTyBb+U6QXa8sT3HWEfD+zXbO45qJ1y4C/RAT5\n",
"i5ESIPF+Sm/Zuj696HOJsonvmwf+GNgE/BR4AzJjot3HZptnhZo2FfT9cMTmhZtmrT8TSUKcB/wc\n",
"eDtS7sPeG202oq0pbaPL/bB09L6UEeYOeCwy06EL6/4r9H3hWGngZ/05GQI/97Mh8A1oro4WwORr\n",
"ZAv5fiWN5TkU21inDsay2a5p/RyEx70fyXZP26dflk8cbtpWj6mtqgJ9FVKEcE043s2kh2T2o9Vx\n",
"xBZZAGoRqlBbSHlhPoyUQd8YjrEVKdRo9+mHNRhbOlWW43Vq5cyQaPTQ7bhP+1yFRPmdgMgZD+wO\n",
"x7V0WK+bfU4qfLp3DcDEtBI0V5qjug0hb9dPUS0RqmrvZ8hpVcqmCmdvc1bajJm32/pFbaVFbNUV\n",
"9LrelhOJ8y7qavLxPZsNnr4JhaPRftqUvimjsZf57EcAyBjVhH3aOs2ytxYOdPtxltN9D9K+LwN3\n",
"wgBMTAtgcj7pAk5LzvdKyGvvV7JdE2frE4BfQ/JKXp2yXYvfpVESVQV61vp+OWKrCnnd9hwk+mY/\n",
"UrPsJvMbK9RiiiJPgB/qPP1BxKJ9MiLAfookbN4ZtqmAiyd5qivc49/0mj5W32BZ4X4YUvlYrbNb\n",
"gH9B3istO2OtHHs/MoR6KQDogZI0oLk6WgCTa0kXYv0SXk0omzIAYRMU6wj0FUg9qcWIgJxM2X+2\n",
"HbFN4urjhMSs+5G3rHTFDOIHINpnrvH0ZYHAZplr2GlZob4WSbTT+TS2kyRr6j69tnTie1Kkwed9\n",
"TpEIeki3crKE+makasS68NtJhOLTyhrL2r/0rpZ2/Vn3I+27UuXB3zeYtrejFdBccXXTXnRPdxmI\n",
"tugbXT9XHbFlI3TUNLdO/bacsXOVp69C4egLHecXNKVw+nFf1NJpIuT1NyrsIVEMFlGJusnd1mvg\n",
"UzqrqpC339MmuppP8u5kXWuZHlF6A8ukowUwOZt0jT+t8mabgr5fOSx5lk8ZQf+XyIQ7b0eSFO1+\n",
"WlyxacRN1vZ+vMRQn6c/AXhZGOO7kQgc3UcpHKUrmgr3+LMfwQ5VhfoYQoleEH7/feDNSI5NWk5K\n",
"HJFUhbqJl3utNNmEwzJC/VFIwMEi5Fn4HPBBxMmeNod7WQGft18vqU5ViEJ3x8xpMHHOfQB4BrDN\n",
"e39KWPcO4JeRP+jnwO957/eGba9DwlSngQu991eE9WcgU6AuAS733l+UcT4P/vt0C/t+OayzHLFl\n",
"tfa89ZqgqNpZHWF+FFLiehKJTIqpsrnI01ehcKCT2qoizI8AHhN+v41uCqfXwk2DHZo6Z/XT+nXS\n",
"BFyRUF+HTBO7OhxjJ/LO6vZeU6EalVRFk0/bpvchLeGwSOCvQBSME0moTX0XtRJ4L5u9B0U9vm6l\n",
"sjQ/KS6hopF7oc/xaC7n3LmIA/NSAyZPAr7svZ9xzr0VwHv/WufcScBHEQ3gcOBLwHHee++cuw54\n",
"hff+Oufc5cAl3vsvpJwvj+ZqKszzto2Gc6T5MdpaPhR5el3WyC2NSioj3KsAQT+UBbUImwp5q/Vb\n",
"YW/Dcptq9f2wdOyzUkfI2+/qrI6Lb9bV6Pt5H+yzXqcfJMlT0uuP78GKjGvLWq/bKlCb7dBcPdMw\n",
"vPdfd84dFa270nz9NhJVBPBs4DLv/SRwh3PuVuDRzrk7gZXe++vCfpcCvwJ0gUloZ9At/KEzqqSM\n",
"AF9XYf9DgadfB7wNEWLPRvICdB/VXvJ4+rR1wxnr489+AGEWtVUk3JcAr0VySb4RlkfotnYUBMsI\n",
"9TUl9u11GGqapVMk5MeApyNzjgNci8wcuZXuMFR7P/L6xpR18T3pJfWZBnp5ALgSScLUSby2Au8D\n",
"vky3wLd0cJ6QX5+zrZeKkI1OO4Ao9ln3IZXtqdpmc9reFwOXheXDkIdX2z2IhTIZlrXdG9ZntQ/R\n",
"KeznOk9fZtmT8PRlNfY1CHWj388M4zyATJXaT3rLAmFVDT7vN1nUVpHAXxe+DyERSsvCMR8C/Df9\n",
"oUbjF72KJp+2r/owIJXGyLwvq5DopPWIIqaFCPcAxwOfpPfAp/6LOlq9XValyEZoxU77NG1+JVLs\n",
"9GTkXkASsLMKmePnL3pw3dryrjELAHS9ve7YsllAcr32uu26k0hK4TduswImzrk3ABPe+4+2e+SL\n",
"T0qWzw+9Jzy9Lo/RGRJYRdiX3bfNtpYkvFPbFOkvZ10hr59qvmvIZZGQ1+/rS+zb9n1ZhoCJbWkU\n",
"RlUhb5dtZI69J0U9flbSetsKwZBZjpy1qdddttsMc1tZuYjKWYMEjmQBQ9vPwzwSYCXleouEfNy1\n",
"WnLWnO2xkLfXuCFne83rvjr0dlvfwcQ59yLEnH6iWX0v8rBoOwKxSO4lqUSq6+/NPvrFp9Ap1KYo\n",
"5unjdWtJHtwiYd+vrNkmwv3XQv8K8CdmvXLVlt4qEuL24c7bfxm9d1rb8MsqQn4Mido6E3G2/z5S\n",
"T8qG5xYsGazUAAAgAElEQVQ5rG1fh1RgzgOEueisnUAo418Kx/gK8FdIDSlr5aQBX5rwX48EeeRx\n",
"+b1so+RTOXbbKGKJPI2kou/XEErLMiF6/cvI1/JXI4xJ1vZeytmDJNdmrzFeXozkUJ0B5y8Kivbd\n",
"wP/AX768jYH0NDQ4+Ew+YxzwT0XmODjPe7/D7KcO+LNIHPDHBgf8t4ELgeuQkLw8B/zP6RT4/cqa\n",
"bdM5a192nSK3rFYfL69CQhrnIy+JTczqNb1l8w6KNPey37WelGq0ZTT7+D6dihRunEGS71TZ6LWz\n",
"VsuiN+l6T3Sio3ga1yxBH6/fgNyHpeE4+0nowl7Swmn3oKqWP0F3XTFLA6cJc7t8JELhKcBPkRSB\n",
"7VWbolvgpwn+LDDQvJs4Qk8tGwt0MehtQaisNWY808j/7fRwcz2a6zJkjoN1iCPrTcDrEB5zV9jt\n",
"W977Pw77vx7xo0wBF3nvvxjWa2jwUiQ0+MKM86VFc9kEvKbCPf4co1rIZVkA0D5b4ZdNqJ20mltN\n",
"+lx21hb1KXNsK+zKaPlF23p5H9Tiqyrk7TYL/NpiDT9L2Bdtnwtafto6ZUJsCfj5JNUG8gR+3rpe\n",
"AnwAd7duToNJv1sAkxNIHuZR0kMuqwr1rO+9jlKKhVtVIT8GvBdxKr4K+ExYr8mJRcK+bPil7XPZ\n",
"WXs28FLkZf8z4PMkAt+G5zYR8rq+1zRfnGFdRsufAl5AMn/95cBbw3ZIp/fqCPsV9JbWK6vl6/J8\n",
"4ElIaXgX1n0YSdpV6z+m86oKfP1dr5pSePZ60+7BFDLb5WNJ/F57kWf980hghc01CeDuLhmAiWkB\n",
"TO4meZl7HbJrq+qWFfJl9lVnbRyJUlWjfwgS4jgJ7DDb+phZW9tRa7uldJTaqhp7vwVJPgN5ubQk\n",
"fS8FvgW+plp+PAdG7LQtEvwbkcidxSQzWi6if1p+WcGfZt3ETmubf5En3FcjMx0eTqLZT9F/yyZL\n",
"8MfLk+Q76VfQfc3a1yNU1kaSa7WRbQVtjtNc/W4pNFccftkmfz9BumOyjjYf97norC3qWjI9K0qp\n",
"iZbfL4FfVcjH3YbnapZ1U0pnrmn5aetG6QR86BaAVTR8a931qqVdU1kQsEUSIdH0LY0X91j4p23r\n",
"xXOu/rD4mvZ3rncvH4CJaQFMjiJ5UKCeRl9mv7nurD0S+HskMueXEMtEBX5Mb1XV8tPW99LamYiu\n",
"rYqWvwb4mzDmTyD5AjY01Trx6wp7XTfXtHwP/A4S1ALwn8gzoaCnyZhNBH6vwS7tWvPonqOQpFyN\n",
"AP0pklf1o/BdCyWmXVdZ4d8renss49riPopYIeeQhLNPIrG+n0EitBTg7P+b091jBmBiWgCTrSQv\n",
"92w5a5tQOxMkUTVVhbzd9nDEzN8fxrqC3gr8SZpROVlaflZZiTLCfhjhjxeQxPn3W8uvo/HrjH96\n",
"/UrJVRH4G5GIpYXhOJP01sdXl9rRZa2QG2eYx0I9S8hvQGYOXRHGU4Hiqdym6RbwecLfbtPnMM61\n",
"UV/VCiSJMu0ah5Dkys20rrgMaK6OlkJztZFZmyXosjKMmwBAr7XbNHqrKgDY9QdJXlobrVJXs59t\n",
"Lb9I8Mfr4vpaccROVQ1fl3vl61N/Vh1qJ/ZjaLOO6yoafry+V/+3/td1BL8qNHGRxDRtPwsA4t6L\n",
"65xGSgBlXVPatgMkPpoZcB8fgIlpAUwOQ27UONkURh0h3y+KS7PRm2j5L0GSFD+J1NzRmRNt8bw2\n",
"BP9c1fIngTciSWm3IhFM+8Jx0/IR6tI8vYpcU567qsB3wB8gEzeBRCy9FxE2ju7yGlWonV7/52rZ\n",
"Fgl4K+jPA56K/A/TSCmcS8P2IpArI/x74cOYyLnOWPhvQKisU0isrB8gVNYNJNF3WkHAXtfKlHV2\n",
"eXnnsAaWSUcLYLKH/gn8plq+3XYwHFsjuOoK+1UkD98I8qDNRS0/bbtSALawYh2B/7DwOYP8V72i\n",
"dzSarwyNk7dOaS3orKlURbvfBByDCBfVpnvl0C2r2adtO0D3/OULSIIV8roKwiORWn69Trq1Powy\n",
"wl977KC3ocd6nWkCfmXoW5AItF6H2R9Ixu6OHYCJaRHNZX0aTYR8GsW1iHY0+7mi5Veld3Ruldi3\n",
"U1fD1+VeCv0m1I4uK8XjkAdtId0Cr4x2H/deO3TrCv8xOkNzLdCVpXXi/XoVoTVKPtWTJfzjREMr\n",
"+JdSrOGnrevF/2mBbYTu60hbtv4ZVS7iKZvDmN1rBmBiWgCTtcgDYn0abQh7/eylNqS+mrqCfwKp\n",
"wrwOeCFSkkYn1Goq8O26Xll9KvTravrPBX4beYl+F/ge2Y7cOsI/ogZavW4rDLIEfLx+IfDHwCMQ\n",
"YfEBpLbUDN30Rx0A6JXvxl5HGQAYQmjbU8LvHwDeD3yVdDqrCgD0AtzUh5Em4ON1S5BJ2R5LYonc\n",
"DXwWmRJhms4wa7VeipZXUMkyHdBcHS2AyShzW8tP264Z6Ra86gj8w5BID6UReiX0NZqlilaftd06\n",
"8VXTr6PdH4FEMOn4egX6sUO3jtZvS85YsC+j2WvfhNAhvczBsTkKVYS/7mcr5cZl0csI/WEk1FcL\n",
"MfbjGssAgLVobOl3O4tjmnC36zYj72uvFBSQ+29BLWfZvWUAJqZFNFdTLT9t+ySdXH5TDV+Xe+XT\n",
"iEMY61A7druWHomFXx3hr9t6BfxTdAu+OoJfy21AflJaFQugFyAfWzdVhX8cpRWDXFnHrl3Xi+vU\n",
"siJlhX4MbDGdZemeshr/SnpjtekzGAv9LCDQZNH4f7MFIFeW6CvADQ/AxLQAJiuRm9s0+zZNGPZK\n",
"21Vrp47A18+HA5cgJdUfGY6ZxunXFf7L6b9Dt4zwPxp4ByL4LkGil2z4Zl1uv5f/eRrQlQGApcAr\n",
"kQCDaeD/ItFLVvCX5fX7IRwnyRfw8boDyARdzyOpK/V14F+RQrEaiVck6NOW2wY2TymNnxHkv3ok\n",
"En2mlXv3AlcAV4br1nc1bfxZvUXfzIDm6mgBTHpJcVihX0fgp1lBM6RXFK0q/I9BBEIvr3+cdCFX\n",
"VevXiB7Voqpq9trXIhnAvUxOzbvmstq/LbPiSGiQKkJ/I0KN9Oparb+qCgCM0BmhpePLonuyljeF\n",
"3isrXQE8S+hnrVPnvF6bzTUpEvZrESprdY+uyfpmbN+fsX6c7lL2gZpz/zIAE9MMzWVj1ptSO7pO\n",
"Ka6yWnwZzb/XDt26UTxxBJMtslhVs0/br1fXbSur1hX+o+Z642uuo/WvoDcC8iDFQj8LAOJZH9Wy\n",
"qaPx9+r/rMD3dyzbYolW+NvIrDLUTy+uS/0zaYI+ras/VSPq9JoW0AnWq6Jxx9+15yiZA8ukowUw\n",
"WUq6Q7MJr98rgQCdDt26dM9rkXpE7wfekHH9dQGgV6Gcet11wjkdQmkdDVxPMgeOCv4qvH683IvY\n",
"/gnShXqR0F+JlMo/HhEq7wX+g8R3U0bQpy3PBb5/IfAs4AkkZeE/ikQxeYr5/jRQWEH7VOyBjPHH\n",
"/SDyPz0RCRoA+c++gZR+f4BO6jVL8NvvbYOZAvS+7vG75w/AxLSMybHaajHP3VTrH6MzT6Mut7+a\n",
"zumOe9HKavVF+2n0SywMqwj9lQi11cvw5DRhWBYARkgCFXRyJAtyZbX/jUiIdy9aFb4/vk613CxN\n",
"UsXZuxqhfnoVoTVGtsDPAgWduTEum2L9GFlCfwihH4fojU8xHmsMBPa7pbG06eRcNj9oVfS5Gtyj\n",
"BmBimgGTOsI9b9sE9evxZO3Ti8Qmy3s3Ff5jJD6N2OlZR+tfQW98Oao5lhH6aQCgfD8kAqQqzRPv\n",
"27ZQqcP367KdE8SGIlfR+G1v+7nV8iJlqR+lf9ISDdX/VkT5xOva/L9mEAGfJ/TtOgWAOMR4AQnD\n",
"EAv/VSnrGl7HgObqaAFM4lyNNgCg38XZygLAFBINsgp4GnBjNPYmADBXsnjtuouA5yCRML8J3Em9\n",
"sE67PJf4/rXAa5BginHg3Ui9KevILtv1+toOvc5y+ubRQMciSbRHhmPchERo/YzEl1FE+djvbVOv\n",
"sTWTBwSbEGrudJJggxsRKuunyH+VJ/TjzzYVLK0CYMEs/nTIJGlnIrW/QhuASUfrIc1VVJytqvY/\n",
"TaelU1box/uuD5+9aFWyePO2j4fjpTlBq2j8G+md/6Yq3x8vq2ZpC+9V1fg30Juon6pOX3t9k3Rr\n",
"zIsp5/BdhYDjenpDSe6nWPu337Vellqh+l9p9nye0F+FgMgw7VvX4+QLf/s5TmdeiV6D5pWoFRP3\n",
"ITP+jP9iACYdLYBJmeJsVYS/jeKqo/Wn7dt2eGfdLN607fqgWiqkjsavy7MZ358FEBqqG9N4VTR+\n",
"+72XTt88jT+N/rGUlgrLMtp+/L3t65pBLMo8yif+bmdw1AKgC+ikIotAQJfbfA6nkbnUi0BgH0Iz\n",
"2ogspRr1OmIgy+oraU9uqLzYmYzXnTMAE9MCmAxRj9bJ2j6Xsnjt8jlIdM/tSDJUVu2eQ5nvH0HM\n",
"8b8L43oj8Gk6hV8ZrT/et23asozTNw0UNiEzPx6BPBPvAL5Mp4Ap0v7t917QP1W0/wmEbv0VRAGb\n",
"Aj6HRKBNRWMuQwW1GVk3Rbbwj9ctAc4HzjVjuBf4AvAdRCakCfs0EGgzcu6gGW/cdfyLkFptZyKW\n",
"iLbbwth/jLxL0TjdU+c0mDjnPgA8A9jmvT8lrFsDfBzhT+8Anu+93xO2vQ4J85wGLvTeXxHWnwH8\n",
"G/LHXO69vyjjfL2guapm8eYtj4Zj5mXxltX+N9Cb6BG17Jpo/0op6IRRdbX+YXpD/WiobhWt33Zb\n",
"vkJnyKsi9Fch9E/bwt9SWmW1f7VolAKyzuw0rTkLEDaE5TbbNPlCP/5UytHmmSgNtJR0YW+vYT2S\n",
"od62FRNfQ1rfj7x7WdFY+h7Zca+mk8ZaRW0abo7TXM65c5GbdKkBk7cDO7z3b3fOvQYY9t6/1jl3\n",
"EhJn/iiklv+XgOO89945dx3wCu/9dc65y4FLvPdfSDmfB69/TFMAUE3Lzj9QV+PX5X7G91fR/veH\n",
"Y2mSXh2N3/a2r9OTUCRltX7bbZKevcaylE/c26QpZxDKpKz2r99trTTojEQrcvrGANG2k36EhAbK\n",
"E/4qSNUXoIJIBWiaMzsPDNoEZ6WydqWMN7YIdPz2GVOKcQmJ0I9BIO5tPVdTyPuyI4xxb8q4R+mg\n",
"39y75jSYADjnjgI+Y8DkJuA87/1W59wm4Grv/YnBKpnx3r8t7PcF4GIkYucq7/3DwvoXAOd771+W\n",
"ci4PfhPNNH67PBf5/hHgXcDTSWpRVdX44z7bmb4xKCwHPohoW1ciSZnWr1FW+9fltoWljZrJE/rx\n",
"uocgVN1mBAzeClxLdeHf9n+mz2WR0Lfr1iFl/k8Lx9iK1An7DumCPq+35dT2pAv8NDCYBs5Gkgy1\n",
"XtYIcBXwNQQY+g0CB6IxpoHACuSen0FiCXrgFmTKhZtJQHh1yqcuR6zGHLdMIBVMdnvvh8OyA3Z5\n",
"74edc+8BrvXefyRsez8SbncH8Fbv/ZPC+nOBP/fePzPlXG3TXE35frs8SWfiUJ2+AnkYVrR5kaHF\n",
"Tt8ibT9tX6V/1OlbVeivDNenRf7aaiosq2r/uqwWQOywL+v8XYlENrWdXR+PtQwlZJMOldLSYIs8\n",
"rV/7ULiWNv1O6nPKo4HsNVhLJs7LSBP4dt2aMP42Q9/LgMA+ksnGdOw2OVL/gzQAGEZoxDaDdw6a\n",
"ce4Fd1YbYNLLKV1zW6CwWkayNxyEqQnp522DZ91LPe1/jGK+X4FhU8F+K2k/pHAaMcHLCvq09TpV\n",
"8Dy6QS5N6G/I2aftKDWP0AwxvVXWGrAAEINbmtDfnLFP27TWJEI/FAl9+2l9ASo844imuB+Tcp2r\n",
"aNfangjXojRdkU/AZprb61hGOgisM9ehgrXN/2Maeb62kw0Ce0kismyBROvLUCXPAsBGpLyKva62\n",
"xj2ORGJtD+MzoPBgBNkUnf4X9YMtlDH/+8Pgaw+FhUtg4QZaav0Gk63OuU3e+wecc5uRkukg0RK2\n",
"LMgRwD1h/RHR+nuzD//mEykW7JuRPzqPBupFpm9drV/7fIQWWQY8E7iffO1/E3Bcyj76vW3fhhYf\n",
"LEP5xN8PItFMTwjX9WIE0LM0/dXIs5BlHbQZnKBRNEVCPwaIExFaax3yor8V+FHK9WjfhDyXadfb\n",
"VpskXWhmgcEB4JeQpEONDvom8LGwLQ0EDgvX3isQKLIErFA9FXgynfWyrgWuDtcc0z/DSHCQXdeW\n",
"Ram5MVb4x0CwHkmIPI3EBzSNJHj+ALiLTvDSckp2vCVk+u+Gru29DS4raf2mud4O7PTev80591pg\n",
"KHLAn0XigD82WC/fBi4ErkNCDfMc8G0NPS/Ttwoo7Ee0A+tMLEv5xOtW066QjLnyqtr/CAKShHEV\n",
"JX/lUUGradcCiP0aZamg/YjA0WaT2oooINvbTnBTQVTWJ6D/jWqmcVRTER20CqGD2nRqlwWBfXRP\n",
"/KSatZYYiS0B+zlMu7SiBeAsIFA2Iy2aTGksC1y2DyMKR1u+vTEzvrQ+hjwbmmwLuL+Z0z4T59xl\n",
"SA7EOsRB90akPMR/IM7IO+gMDX49SQXYi7z3Xwzrz0BCg5ciocEXZpzPg7+P6hp/DAqjpCdGVQEC\n",
"/d4L/8Y+OqNMqgDBPsRM1ge9qtCPP9u2bHeHXob/t58ajgydhSSzhH0WGLRNa40iFWOLaCB7PUqp\n",
"QHeUVhkQaNsSUMpxG8UgMIK8vzZLewGdVGMWENjltug4TZZ8gCTCLA0IbESW+jMUvJSGy+tt0lgH\n",
"EAprG91AoGXp0+5xGmgNRZ8Z4zwEHPD9bAFMjqOe0Le9F/RPE+1/BCnX/W6krtGvky7Yy1oFbVJ4\n",
"k2QLxTJWwXOANyEv8auBG1KuqQwQtPmfxRp0Hg1kfQKPRKYAGEbA/m1IsliWwE8Dhdmgg7QvA34D\n",
"iXDSsvCfRMqoq3VWBARtKU8TpNNAaUBwNPAkhBrSe/dj4KsIJV4EAm3d8wPkWwQjCDV7OpJYqO/h\n",
"FPAThALdFo0vBoM2QHZ/GI/6JPeCe9oATExrkebSMuR1hL79Poo8pFn0TxVKqF/ZwGWoIM3bmEdC\n",
"31WhgOz2tmg7TQ4rSwPZ9Upr2cqzeVp/lmXQVqsKAuqgj6ObiiyBWINt479Q6rQMECilGNNCSi0W\n",
"WQNraU+JUAGb1fch9FDsiFerS2uWWcGvy2vJrYtVqU2QgED8GY9RAzYcidWyNBrbELAB3KYBmJgW\n",
"wOR2qlE+aXTXAuoLfbvci+S9u0kX8GWAQSOc1BSuQv/Y3nbexn7E6V4FDJROUUpCX+aqINA2rTUC\n",
"3Ed2ZFD83dYJU7pCfQJlKaE2/RrjyH8RJ7zFQKBJk/EMgFaoFlkEbeXKKIDdh0Q5pYGBjjctmkzH\n",
"HFsBMT3UBthqifr76aSx9iDvQTy1rvW7aHSpgoAFhCEa3c8BzdXRApicTHWhbz/bfDHVwqkr/BXc\n",
"1Pf0buATVKeAtLflELZzNpSlgew1HQV8KIzpk8A/0yngZ5MOKgsCB5D6aK8LY9kOvJOEVikDBG39\n",
"J/b/KGMRaJTT7yK+S5Bkt0+E6ygCgtW0o1BokmGeRaD00BAS6fc4EnroPiTB8BZEkOaBQRvU7gE6\n",
"qKGu5VHk2X4kUuZd/YnjCI11U7heCwAWEJoqn+of2mO6fh9HogWPQaYEsP/fCLiVAzAxrSWayya4\n",
"VRH68b4TJBZOXQqoTe0NksJ9VWigmEqBdMvmUAEBtdDUorGUSllKqE3rbJRsoZ+2TqOcoLMsfBkA\n",
"UMHVhmBVwVWmx+VS9L5rqZEs/8BqJMmwjXutPpg8MFCKKK69tpDOrPKhqK+hHZpwik4gsICgtbvs\n",
"+GKrRQF1CKHV1iChxsspfOcGlklHC2ByE/X8AAog88gX9kVAoPu0XYplPxJjXhUMRkgK+MUhrnn8\n",
"f/y9bTpoAonms6W8i0DgoPm90kF59E/aurZzUHYh+VBlgGCMzvpNltIq29sKnvBI1NzddArVuGsC\n",
"XMy/K4ClWQF23Wrau9/7EctvK91goKAVj1Uz462gTQOEtsapycT3IDSWAoJGjGniJnSDwQo6wcCO\n",
"rw2f6WQY270IzabW1Di4lw/AxLQAJqdT3x/QZhivnfSmjPaf5hNYh9Q6mg88D3mZZhME6loCI8gL\n",
"8z4kkuU2pN7WPKoBQVtBCHodVSyCCYRmeTWiKd+P1EbbSTkQWEU7CobmPJTpI4gwfRbwbJKy8F9G\n",
"kvYWUgwGbdzzg3Q7i+PlfYjQPxu5z8PhtyPAt5BIJx1vGiCsamGcSmPZsdrvU8BDkWf4BBLwGUVm\n",
"Wfw58t6ngUFThmECAX87pt3I/VmE0GvHIgmj+r575Dm9J+y7JIxLx2aSYQeWSUdrieaqIvDTto+Q\n",
"JCmWpX5mEwSKQGE8XE8VSyDe1ta1aDXUqkCg2qqN1qpiDaymHd+GDXctSw/FDm6NxsnzD+hyG8qR\n",
"glcRGMTl3/Veq9M4yxpQwduGr3If6f4C7VGl3A7LQGmsNMtgLc3vpVYhjsFgD/J+TtBJYWmS6aJo\n",
"bAoG68P3Jnlemj+0G9wxAzAxLYDJDdQDg5FwGH3w5wIIaLsTMe2rgIBm3mvdrSKtP2tdmzkpHrFK\n",
"bC2kPCBQ/wbIPY059rIWQZu01laEbiwCgoN00xk23LUIDNoCMBBBdReipWYBg47X1v9Sf1IRPdSG\n",
"81jbKELDWPpNha8KXQ17tYUSl6SMLbYO2lIItiPvpNJYSmHGBShjf4aOZ5hOC6HpuNTP+0AY1y7k\n",
"/4wBSv/TxYhSsiIZhzt5ACamBTB5LLMPAk0sAbUGXgL8NXAj8CqqA0FblJ2lVapYBPuQF/6PgT9C\n",
"Huw3IBE4VYCgjf8kqpBaih6aQmYNvBARVPcA/xS2lQGDNoSrjjvLIrDrxpEaTb+LJMSBCL3PIgBe\n",
"BAhNKbgpRNOOrQE7Vn0mTgMuQGpg6W+/jySsTpENBk0pN0tjWctAx+YR+uo0hM7SZ28/Eol1d/ge\n",
"g0JTiu0gSeUHO6YxpLjq0WE8liobQxSEncg7agGqBqU2oLk6Wgs0V1MQ2I88gFUsgbRtbZUoicdZ\n",
"FghGSLSrOtbAatorTliUVZxFD2mzTu4i/4AutzF2jcwpAwYjJBp3nHSYZw3Y702trzGy6SE7dlvT\n",
"yVoGy+gW/vH3XvkNYstFNXFPUmZEqaLYKhimnTpee0kHhIN0547YRMeldALTGoTCahLBNh2NZRdy\n",
"b7Qm1ySd1OkicL81ABPTAphcR3UQ2Iv80ZaGqAMEbYXxTiIvwCRimVQBAp01Ued5rgMEbdcTuw8x\n",
"v8sAwQE6aQIVqFXAoM3Jlu4JY88DAxs2DUlBxTL00BDtOI+17QRuDZ9pgKBzaihwKS9vaZgsMGjL\n",
"UpxAKLfbonHuRWguWzrdZm9rwl4aIAzRToDDmBnbDkQYW0Cw4c1xSK6CgY5tNc3vl5b5vwt5FmNw\n",
"iseiNenWmF5iHAPLpKMFMDmfer6BNgSQTcKqYxEcQP70zyIRI5cAX6EaELThyIxLYpTtSmOcjkRu\n",
"LUIqQX+B8mDQBj2kuRtlLQP1F/wqQsktRADkX0mic/IAoQ0lInYeZ1kIWtDyfOAF4fwgNNFXwrYs\n",
"MGiDn4/HFFsKexEl6BikxtcjSATZLQiVtYd0QGgqfEfNmKyFsBsB/PlIafzTSJI19ZpuQfxhC6Ox\n",
"DdPM6ostll0kVTa2IBTWEdE5tMjjQeR9UFBoYq3sCefehTxrE8h9Xw9sBrdsACamNaS5bNnmOkAw\n",
"SpKkGINW2d5GcpZmQ8fjLdO1nPz8aFx5VoBd14aGrVEvVcBgjE5rxtJaefSQrmsj8ziPHrLfNe/H\n",
"TrKkMwSmAUD8vZd+A/2uuSVxZJE6uS0AxIDQFFj30QkCMSDY6r6xk3t1NKY15rMJiO4nAQI7ppCj\n",
"0WGxWFpNrT0Fg3U0oyQ1T8SCwkES+spaKotILJVV4fwbyVQoBpZJRwtg8g2qA8E45cpM5/U24vFn\n",
"kBdlIaIl/YzyQHCQhI+tQgnZ5TZ8NSrU9wE/JB8Y9DOusVWWHtLelo9pBrg99CxA2EfCOUMS/pol\n",
"/OPvbVKhdyK5DRYQdpMArC32p8l7K+kGgPh7GxF808gzrBq/jk214jRA1bDnmC7S722MSxMfbyGZ\n",
"8VIBQcdk5yBZhtwXSxsN09yvpizGvQilpnLITj9gQ4PtONbSzv04gNyD+8A9dgAmpgUweTLVgaCN\n",
"h1RzIKpaA5YeeihSNnsKieaaoTwYtGHVqHVW1jLQsU+HcfwbQm/8BKkjpj6oPEBooqnZcRfRQ3ad\n",
"Flf8deD3kZf2NuDDdNJEaWDQ1G+Ql29gv2tY9BDwfITWcojScDWSJBfnHtixNrmn43RbBXZZrdg1\n",
"YVyPJXmHtiFU1lY6Hd4qhJs8p3ZcsZVwEAGAk5G6Y5vM73YjCsJORChbYKjrZ5kxY1BLQUF8GEki\n",
"PJpOa32CJMQfM4a6iqhO36vFLUeRd24dcv0xU6ATxs2QAHdoA8ukozWguapkFWfRQ4so1vyztrfh\n",
"2NT5rIusgHidOrznkVhnZawBXdd25nEZQIgnwoprEuWBQYaZX6nFY0sDA723Nu9A61HFVkEaIDTV\n",
"fJWaiQHBjtXmbFhnvLVe0qyEJgEaU3QCgQUGtVpUO7cl6TUay1oHujzUYDyjpIPCKJ2RazYQIB7L\n",
"WkSA11VKJ0hAQX0qlkLTnBqNAFtGkiOykfo0npbU2QXu2AGYmBbA5CqqAcEB8usMlQGDNqJIRpAH\n",
"xCHO1LwEM7us9aoUzIqEf7yuDdplCnnQJ4Hv0pnMlQYImlAJyWyPeQAQf29KKapw0Lm1byMbHLQC\n",
"AHQWVcyjiXS5rUS+3Yglch/dgBAnyimdlUcXDdOOEuARmuRmJAdDBbLNNIfOel7L6aaM2nAwa9uD\n",
"0H83h7HY4ogWFGxYrgWFNsYxgbwDdyD/mZ1jxP5HS0n8KmtDX919uEptFAGlB8IYVGGIwUgVhrXy\n",
"fSJcFEMAACAASURBVGCZdLQAJs+kGhi0Ef00Tnlncbw8gTxgrwJeiQjjd1EeEJoKVnUeF1kDtmtS\n",
"H8gsic9BAOKtyMNcBAa9zjewy+rjcMBvA7+FvFi3ICXX55EPCE2smEnSI4vi7xquexrwQiS6ByQc\n",
"9KuIwpBmJQxR36L1yH+bZSVYi/uxwC+RWAAHkVpZd9NJG+m46t6z2MGs41FLYQnwcITGWmt+twPx\n",
"PYwgQlJBoe67PUliJWhXC/5whMI6gs7r3BvGO4kohWupZ6motbCTJOhgcTjeBuT+2v98giQdYCn1\n",
"gHAC3KIBmJhWk+aycwDUAQPLP5a1Buz3ps7jSar5C7QrGGgoZBXLoF9+A11WukgT+jRBLo8m0uWm\n",
"GrhScEWAEJeG16iyPLpIKZomgKXRT7EfQb/rpFBxTsLSaExrot6EytpPOijsIdHSteaYrY1lgcBa\n",
"CnWVjyk6QWEnSeSlUliQWCvq6F5NYimso/4zNEZCX+0hoa90DncbjablTVYj1NVa6jEe4wi46nuj\n",
"ZVX0/bHz2q9Crm8I3PwBmJgWwOTzlAcDLTlfRfjHVk4bzuPxcKyDyGQ/ZQBhDHk4FlMdDJoKMJCX\n",
"QrWgHyGJcnngoOG7ShWV8RvochPaQR9uh7zAP0ScsWmAoKAFidBVOiCLLtLeBtU5jVAjPyZJmNPx\n",
"xZnnSlkMkU0bNXEw27YXoY1uNuPRyKM4Ikt9QjEgNAUowrl2IhFsN9M9M6HeFyss10a9abDNHsQK\n",
"uoMkEtEKauvT0HDgphn2EwgYbkXoKw0gsfdck3vXUgv8DmGayzn3OoRymEFe8N9DNJCPIzV77gCe\n",
"773fY/Z/MfLHXei9vyLlmB78cykPCG3wxjp3dBlrwK7T0ivLgM8jkVz/PxIJUwYQ+pFvEI9fBe2T\n",
"gLchL++lCJjkAcIQzYSa1n0qYyHsD+NcALwIiYQC8Y38D/LyZYFDk3s6SrdVEH/XTPmFwDOBZ4Tx\n",
"TCP05o9IfApWIA81HFfsYNbvCgozCHX0eBKKbRoR2Hci99KCQt3gAJ3rQ60Emy8xFo57MnAKnb4D\n",
"TeLTBNImvgVrLWgU1MFw7ocgFJY9to55FPmv6obkjiIKwk6Sd38ISRpcR6dSOk3iC11GdcVPgxws\n",
"/bWSdDCflOO7eYckmDjnjgKuAh7mvR93zn0cuBx5kHZ479/unHsNMOy9f61z7iQkk/pRCGf5JeB4\n",
"7/1MdNw6NFdsvZQFBA3v0wltqloH/fQbWEELSSXhLD9BGiCspnl2ch4I2GUNN9axKiWTRxfpchMf\n",
"mN7TLD+CdjvJlbVgsigjXddGBnMMCupTsMlz1smcRR2tob4ypWGxMShY57tSSJpAt4TEl9CGtWB9\n",
"C9othRXnjOj5h0ishfXUo5kPIsCgeSpqIamT3UagrUD+g/WIz6POtep7MYIogfpfQydtpUBbo2ht\n",
"O5ZJWwlfVZo6RZc556aRG3EfMp/2eWGff0fi6V+LTOxzmfd+ErjDOXcrcBZwbcqxP0V5QPB0xuqn\n",
"Cf8tGdvb8hssQ4TMrcAPyAYH/T5OUoAxixY6DJmDOt7WFMD2h/HOQ/6vb5MNCEoBqJ9DwSsGgiMQ\n",
"TdQCQxM6ZDqczyFC5XtItFYMDJrHYYVvnIMwjLycx9FpJdSlCPVcIILhRoSyifMUbIl1zWTWseg4\n",
"jjXLTSOAQITwrWFMO+ikkCy1ppndFgweRnMLCuSatyIW0W0kwBQn8ammrT6No4AzaSbLJsO570Se\n",
"betnsHWvVpPQV1uoLwPU2t4ezjsW1ttZFzX8WN/hqs0j93AfSeCMUuNKAzZlDTpa38HEe7/LOfdO\n",
"JFplFPii9/5K59xG7/3WsNtWxBEFIhwtcNyDWChp7T8pBwZNhIK2GKiKqCIVsprl/ijgP5AH6RIS\n",
"CmY4XF+axdCE81UAK7IQ7Lg1Eupw4IPIQ/79MO4h5GF/CEKTWLBoIuA0wqyMlaCO70XASxH6CCRx\n",
"8koSgFCB10sHs/2uIZlbgN9AopBcuK5vh/3WIKCvFkPde2a19Nhi2EMilI9GkgxPIhGCWshyKozh\n",
"CbRrLSito8l8J4duFZttYaweuRfnkCiVVdp+EotBaZ5pRI5sCd3Ku4MklNNqRLE5gvJNQ6PVKpqi\n",
"E+QWRvuqn3NJGMf60E8qcR7LLKiPJLZ0PYllBAmNvozOJM64jdFSGHshzeWce573/hNF60qf0LmH\n",
"Ap8BzkWE6yeA/wLe470fNvvt8t6vcc69B7jWe/+RsP79wOXe+09Gx61Kc1X1G+h3ddyrL6ZsZJEK\n",
"2V5kJ+d9nyChY8rSRTr2JmONx5MXhmqdqNaJG9NGbTmYZ+gGgRgYLChAZ56JpYxiGqmuhq4z36WB\n",
"wi7kudOcCRsJpH6WmD5qYi3EvgXtlmZRiyWm1FSY6nIdpW2EBBjSorBsZNJSEi1+HUIn1VEWDiCW\n",
"gt7ruKR97NxfgwBVVUE8TeKvsRFeej9j2qoqo6B0rZad1/tlZ0tdQcf/0j+a6/WIwC9aV7adCXzT\n",
"e78TwDn3SSSW/QHn3Cbv/QPOuc2IxgISPbHF/P6IsC6l/cGPYGJM+jk/hld8j3RwGKPYb3BEyrZh\n",
"mkel7Edejs3In3xluJ48QFCtRsNi04DgoXQDwxDNrE+dY3ox8nBeRaJJ7o76fjppI7VcYhA4OlrX\n",
"hB6ZCOdyyD26loTWSgMFFULqh4mB4Dg6QaHpC+YRzf96JBJHw0Qt723DdWNQOJVmvgXbppBItu8j\n",
"z5sNG4XO6CDrW9iMWFZraaZcTIfz/hSxiOJ7YBP51oV+JPBImrEIe8N5dYZM1ThtQcbVJGVIjqp5\n",
"Hk0z2IGA0gE653vREvoKeBsqHt+TzLk0QhIUoGCqbMsiElYno10dOsCMKnGNW6Zl4px7GvB0pIbR\n",
"x0herJXASd77s2qd0LlTgY8gNM8YUtPpOuTB2em9f5tz7rXAUOSAP4vEAX+sjwYeLJMXU85CaBK5\n",
"Y+ZOrmQhHCQxqV+LRLN9J1zbMN3gYL83ESQHKaaL7PfJ8LvFwDsRoN8N/AsCTFnWQi8czDEo6Lzo\n",
"i4GXI5FlIOG0Xydx8lqAGKY+KOi4YitBlzWPwyGW9q+ROLZvDeNaTCdItG0tqONb62Wdg7wrarXt\n",
"QaIjD9JptdQRICosd5pP1YA3IBTWCSTaulJBIyTUTp3nZC8ioHeQaPTLEAp8S7gebTMkVRaWU916\n",
"HQvnUqVTLeX1dMsNtfqrKmx6DUp7raD7Hbc+trJNfW5avbjk73scGhyE/unAXwH/nxnYPuAr3vvd\n",
"tU/q3J8jU4zOIE7SlyAg9R8IB38HnaHBr0dCg6eAi7z3X0w5ZhWaK85OznIkx991LgILTkV0kX5v\n",
"wkuOUQ4I9LvOljiPcpFGbTiYbQZzEYWk5e4dSSmYNMooBoW6GtRe8kFBrQWbN6FCJC0Cqe1IJAsM\n",
"NrHPJtRpkpnSSLq8hnpguYdOYFChbyeo0v9HS6Gsi3odoB4nAYYddEdhQZJHs5zkujWMturzGdNX\n",
"1rGv91eTBocQ66Qq+6BlTCw9pv4LOxNl1RB0tXYO0JkYu4hkuvEqx5sioSo9D1qibmlfQoOdcwtD\n",
"JBXOuTXAEd77G5ueuO0WwORSigFhH0mETFkg0N4kIkqFLYgZuhsJic4DB52CNq+mUdr3pg5mrQQ8\n",
"gyRS3kI2KNhCkVlAYD+HqQ9YWlbDIS/F1xFay4KDTnYFidmfBgptWAuWIhhDIvJuICmHoZw1dFIe\n",
"yu/HwNDEigL5L+5GFLQ7kHsR14XSTG8Nj7Xg0MQC1rL4NyGUXgxISimtIXE+r6VZRNRWhDK7j8RC\n",
"VHDQAqBpuRxV2ggJ4OokW2pNKNDVYTpmkGd4hOSZVaWhjm/VI/JCQVl9JCXub5+SFp1zVwPPCoP7\n",
"LoLy13jv/6TpydtsAUz+iGJwaFKRNW1+5aLvytMuQV6eTyI89PsRHjfPWmjTwZxnLShozQd+E7go\n",
"jPmjiI8ky2KoCwojZFsJuryHRCCtAF6B1IgCSXS9ns7SF72yFhQYNMFvCKGzzkZe1PEwnm10gsQw\n",
"1ZuOI7YYlE6aDNd3FkI/agTYGAIiIyQCtM5zrlq8Pa/6VjYikUfHkTyXmnMyTiK8q7Zd5pwj4Vxr\n",
"EUr7cDrfgYnQF1P93bBVeReSBFLECqINLy/bNDIMEouqaaSsvpMLaebTKEGX9Q9MfuC9P8059xJg\n",
"i/f+Tc65H3rvT2l68jZbBZpLfR5V/AgaHaFZsGWsgzYczJrsl0cZpYGCHWcedaTLdR98DZPNAwXl\n",
"9K12rJEqaVZCr3wLtk5SmkM+jkSyFkPdOP9dpAPDXrqT6zT+X89trYY6UVHTJM5gPfduOikla61o\n",
"/sh606sC0ky4PuvfiOtD2fMp8G2oca79JL6NERIrUCeJs7W2NlI99FpD/zW0Wa1da11WzdNQS8RG\n",
"WWn5leWUB41pEn+dWt+LK/ze5jLN6yeY/BB4MpJI+Bfe++ucczd67x/R9ORttgAm76MYHKBT8Jfx\n",
"JQzT3MG8G3lpliM0hCb9pQGFRm9pjZ+yoFDXkjkQ+vpw3h8D36AbHNRaUCGcZhm06VvQGmAOeQm/\n",
"TDLRkQKD+hc083gV3WBgl6sKFR0LJBrefcA1YSzq51BBZkN204ChrhPatu1IVNZP6KyTZSPDVtMJ\n",
"DOtpViFgDKHOfoYAhfVvWHDYQHMKawSZhkGtLUuVqQ+wbggwJGVm1FJZQGeIcZ3jqoA/iPwn88NY\n",
"V1H9PkyR0JPqP6rStJBmSXDpH5g8D3HAX+O9/6OQJ/J27/2vNT15my2AySuZHQdzHihomfNzkeTE\n",
"g0htq7xSF3W564MUWwm6PBp+Mx94BPD3iED4DvAt2rUW1EGp507rmm8C8gJeCDw6fL8RATgNrVRg\n",
"0MipKk215zSLYQcJneSR+/JcJGoIRIj/DPlPFRjq0FkT4VjWathOknnukXDcc8y5ZxABu4+kREdV\n",
"IWPPq05ptRwOA05EZsvUd0QnXdNZP6soKxrJtY0keGU+YiUcjvx/dt9xRHBWsZInSCwgSAAtfi6q\n",
"RkZNkoS6a95HE6pJk39no+JIiXYIF3rsRatAc9kM5rIU0ijJvAJlnMza64YgW+FbBAoqhFUTKmMp\n",
"9Mq3YOskWc11JelWgl2uw/FrAlgcrqoCWukkW1XWWgyx1VDHCa10VgwMO0gEdRyZlWY1xFnTZdoo\n",
"neAQl0KBzsgoDXHVPIeqASX7EHDYThJlFJceUQ1/mMRKqaLAqd9GKSYb5aWC3T5PZYWg+js1ekwV\n",
"Bpvjs6rCWKfMsfT9Wx562WdoJvxeqblFlAet2Fou2DVvt/5ZJlsQjfpxYdXXkPDce5qevM0WwOS9\n",
"5AOFVictAoJ4uS4oKH+/H4m/nwEuQyJQ0sBhlKSWVRoAtG0t7Ca5vh3ApxFhYYFhhMQpqVFwRcBQ\n",
"lyYYNb/dDXwRoZK0RIaGRyowLKMTCGI6qQ5A6cyRunwDQmltJxEcMZ2l57O9jp/Dtv3h3DeQ8OMq\n",
"dNS/onSP9jpWkrYDyL2+mSRoRH05GqK7gWSq2DptGrmP9yMRXzN0Z5VvoP5cHtbPsZDOQqxV2yTJ\n",
"9Lk6b9FKqlk4niSIpKkjvYetf2DyJSTJ8MNh1QuBF3rvn5T9q/63ACavIR8U6uZ6jNNJ0xRZDHuQ\n",
"B0m14NchJce/g/D+s2EtKKhp/Ps6ZFbH4xEA+TSdtYX0s0449BTd9FFMKY2E/XROmT9BMr5BBOht\n",
"dINUG05oXVYacgZ5Lp4CXIC89DPh/NtJtPk6+RyabKfavE2Gm0ISdc9G/gM9tlp2S6mu1c+Y8ym9\n",
"pPO0HI7QWA8x55pCrCcF5qrn0esZRZ6dTQhdZp9jDTKoQvHsIwk913DZVdQXxpo9rnXcNLy8TtNn\n",
"do4CQ5Xmmc8U0yzqG5jc4L0/tWjdbLeSNNcE5UFBP8dJomyKrIS2fAs2iS0LGHQqUc2jyLIS7Gcd\n",
"B+wkxcCwi4QX1pyTmD5qwwltM6FjcFBnvFJaajXEFoPSPHUc8RqpFPsdlDaBxIJTq8laDnWuezcJ\n",
"GG2jm6axkWBDiOWwMZyvikWtc5dvo5tiUge4nXRqE9Usv4N00mO2ZLvW9tLQ6rIAqnWolNrT42mS\n",
"YFlLQsHmIMmcM1rRuwxoeJJE3AUVxt+H5lnAFKvYw5HcyancyPl8hXP5BkdxJ/PwOOgbmFyFVIz9\n",
"KPLHvAD4Pe/9E5uevM0WwOTvyAaHvSR+jyq9qbWwBCn5cB8y+VcaMOhkONYyKAKGmvM9syOMaU34\n",
"/ikkKdGChGrs+mKmgYFdruuEHiNxlm4HPotEDGlmtJ23QcuSpAHDeqpTazMkwhjkGbkamaRKk/10\n",
"u9ZAsv4G7VVByRLYE0hE1ndJKkrb8NlV4ZwKDlUtFdv2ITTWrSSlfeIpXDdRn8I6QDIboIbRx9Pg\n",
"Vm1TiAW7FwFQO3dMVSpskiTEVxP6qjSbCDvHmmcBk6xiH0dzG2dyPY/lWs7jqxzJXTGa7kCegVuR\n",
"9/5WBx/pF5gcCbwXeExY9U3g/3jv72p68jZbAJM3MrvWwk7kgZ2PPPCbEHpwKHzuIx0g6tBvOt9z\n",
"WkSSXVZn+DxEU/8jJOluCvjvsC0GiaovapoTOqaX7Fzu6xFa68Tw+xsRHt36HqqC5RTdVoP2ERJN\n",
"eAty/ceH36mvAERgV82W1vNuM12tlQkEaB+DRIbpfT1IotxUFd67EaFto6T0uo4nif7SsSlVVCWH\n",
"YRudz45aIjHVV6VIoEbRHUDeD80gryucLTDU9Wm2VuSw900oqZXs42hu5yyu4zFcx3lczVHcGQPG\n",
"dgJQYEADuJVQoso255zvF5j8O/BKrcUVSqr8nff+xU1P3mYrQXNV8S1YYFhBsZVgl+s82GOUAwbl\n",
"kRUYsiyFpk7oA2T7GnTZzuuu2f3WUoh7VQtPazil9d10RkktQv6n2GrQXvXcO0mAQYFibxiTjVLT\n",
"fA51TGuvovVaP8dW5D/W+km2HIlNwNNeBfR3hONbWkiVjEUkYbXrwrHL+jj02d1DYtHZyC5NTCz7\n",
"XhwgsUR0fHqfy97XCRLlRcdR9hmweVQFrU4txvzjzWOalYxwBHdzOjdwHl/hl/g6x/Jz5nXKtz1I\n",
"sMTNCFjo5614v7f72Nmtn2DyA+/9aUXrZrsFMHkL2cAwRXZNpKx1Ted7PhZ5Ab6MJAHGfgctwaCh\n",
"jkXAsJbqmpQ6occR5ysInfN1Oq0I5fznkwiArL6O6jHzykcrrXU/4vS/A7kXKjzV36HRQ2nUUlWA\n",
"tKXqPZKzciVy3Rpto3SW+lms0K7qf7BSZgaZUfH74ZptZJwCxKbQN1I/oXE3YmHdQXK9GoG0Binh\n",
"U4fC0pIpGuWnIbAa3lw1QENrUimgqc+v6nVPkgBX1d+2jQKVmmOaZRxgMw9wEj/h8XyFC/gSx3ML\n",
"ix58DQGRJTFYKIDspKW8jn6CyQ3A4733u8L3NcBX52g5lTeTDQx1wg11vuc0KyFetxt5SNWSeSKS\n",
"7DmClNm3Y2rqhC6yGnaTRJ0sQRIm/wIBgO8gBfniMNaqIDVCt8Vgo5a0hAqIIPtTZC4Tj/gldlE/\n",
"W9o6iy3FpP4evfZzgKeRgI9SUAqWVfMftpquOR0TiEA8HTiDRHueRO6R8vxl20HE7/AASTQWCI11\n",
"bBi3NptLUqZNh7GrIrOYxBKxYFlF2I4hWrJGxa2k3rs2RZKvUef3swoQ3W2GxYyxnh0cy62czTU8\n",
"g8/xCH7Eigf/UkCek9voBotbgPvwfqbr0C23foLJ7wBvQMrDO+B5wJu995c2PXmbrQTNpdRNGWDY\n",
"gQiJFeRbCm04oeNM6DRwUJ5zPkmoal6vo4HuIR0UtFvfi87amGY1KEDUzZa2Paa0lJJZRafVoMtN\n",
"/A/6ORKdz+aSbCSxIqqcawIBBz3HPjorCus5Vobr2Rw+y4LdQcTq0aQ8DaDQOb9XkCQRln1O1Sen\n",
"0WPWolpJtfIs+0iAl3CMIcopU56kqq7O6lg2wqrH4CKRUqvZy9HcxhlczxP5MufxNdazw57cIwpc\n",
"DBY3A3fi/VTKwfvW+gYm4WQnI/NDe+Aq7/1Pmp647WYc8GnAMEI1YGjihFZn8yMRYfEeJEnRgsRI\n",
"+E1W6Grc60QMaTTbkYgAvh3JF1IhvYvOst1rSQeFJtnS3oz9TuA/w6cmQio3vYwEFJr6H6ZI6MkD\n",
"CKV3PZ2Z8EpnbSChlzYh11slA9m+gPcjVNbtdIbsaoTe5nCOuomFO5B7dzdJFeoVJIEedaKl1N+h\n",
"IfCaJV/n+T9IErKsPo4qzWakzyELAxwzLGWUzdzHaXyPc/gW53M1p3Jj7MfQcjs/IwGNm4Hb8H6s\n",
"/yMv1/oKJodCC2DyTvrnhLbfRxHhoU7o1yEUy/eQSKU4lLWqYLbJd1ld/SLqsD0S+FtE0NyPTGlr\n",
"8x6qCrVxEs06ppfUIa/a8EOQMvZHhHU3IcKmSf6DpZg0F0IBYhiZFfTM8JvJsB/Uc1SrFbEVoRVV\n",
"EJwQzqFTrnpE49aqrWWazsNxP4mzXe/ZMXRGHVYph64UlgKD+uHqzpGyj6Re1jLqFRtUunEOhtPG\n",
"TaKlhtjDcdzM2XyLx/ENzudqhunwZ08hPrCbENC46cHl4Ao41NoATKJWQHOpMC7yNejyBIkpn9Vt\n",
"1FLV0N5J8oFBuyYmLqHTSkijl5pmS8f00k4Sp7xW442thrr5D7H/wUYy2SitxSQRTNZJvYlq/qa9\n",
"JH6IreH6NPIIkgmPlD7bTEI1lbVUDpCUCbERU3p8rVm1DgnfLXvsGRIfTVwLajFJGZJNlAsYmSTJ\n",
"srfTvGpibhmLwpNEXGlJlJWUew8q+kbaZqtmWMIYm7ifh/NjHs9XeAJX8XB+zIIHA/UA+Q9/SgIY\n",
"+nkbYbLAX5Q2AJOomXIqMTjsDLuUAQW1aKpGcem80dsRzfIYhBP9IJ3goGVWlpAdxmrBom62tPpN\n",
"9gPvQzQp1eY1ckmT8GJgaOJ/cCSa9S1Ikua9dE5jqnOtWGDQ5SpVgCfC8RTEbgOuIJnlT8+l9OZm\n",
"0+tkv4MI4BsRoaI5DjY8+LBwLVU1cY88H3ci/5MWpBxG7su6GsfbS+LAt/PQV2maWKqlgapE8E1T\n",
"+j60795wTLOSfWzhHs7kep7O53gc17CZB+yZtGxOYl0knzvaipaa620AJlELYPKPpIex1p03Oqtb\n",
"7X2ahH/fAvxfRMB8GnlLmmRLj9JJLcX00jaS7PmFiMD4E4RiG0fCf5fRLP/BWg7aLa01HwHPV4Rz\n",
"TCNAMkMzR7VaEnqN6rw9GalzplFN+0MfphrV9ABiSSjdpEmGhyNRWUeb/ceoVh59B1LxQOfLmI88\n",
"G0fR+R+UlaKaSKiArSVNqlrEMySl1RfX+H2dWQh72ISaWsMujuF2Hss1/Ar/zen8gFUPuiUBAdZu\n",
"Wgp+jvfj3cf939UGYBK1ApprH/mgYLuW+CiyGtrKlo675nzMQ6iDLMuhTf+DLittoZaLOqhjiqmK\n",
"o1oFYQwSyu3b+kyrSayHTSRUU9kHfT8JQOg5NL8FkuS/NYgVcVg4R9l7uCsc29bIUgGrYbFrSWis\n",
"MuMeIbEaD9BNYalSVNQ0H0R9HSDXuxoB2iKFapokkk2jy8pY6BpIUfA8NLE+PIuYYD3bOZGfch5X\n",
"8xSu4DRuiPMytiLlaX4aPnV56/8WK6NOG4BJ1MzkWGmlNOwMcHn0UtNs6TORl/DjwFfN+l0kcfhZ\n",
"wNDU/wBiIXgkjPvrYb1qolraPqaX9HtVR/VORFNXa+vHSP22OEpMz2kBYjPVKK0xEi16Apm861th\n",
"2WbAqz9Ce1ma0Eq6cURr/VE4r0Z+aeLf4dRL1NuGRPXtoZMa25Dzu7Q2QVIs0YVxVQkw0Vn8NMx3\n",
"DjXPIsbZxAOczvc4h2/yJK7kVG6MYehuOsFCPg9RB/hst0MaTJxzQ8D7EcrCA79HwrEfiWTxPt+H\n",
"OjLOudcBL0a0oAu991ekHNOHaXubZkvvJ9tqsFbFPpJS7huBpyJ1r/Yi3L31R9TNf0ijmGLfx1A4\n",
"90sR4fJ9RCC24ai2VJP1e5wAvCxc1zTyfy2kvBMYRKCpBaHWhEakTSHg8XikRPsCEj9AlSJ9+xG6\n",
"6b5wDeoUXwWcFq7Dzl0yn3Lq80EEGLSU/gIkcm0L1f1cSidqra5VCNBUsXgnSSKvFlPeBGhxgqUq\n",
"TUBjM/dxBt/lXL7Bk7iSk/hpnJtxG92gcRPej6QdddDqtUMdTP4dyaL/gHNOnY1vAHZ479/unHsN\n",
"MOy9f61z7iRE430UohV+CTjeR5mhOTSXUjtF9NJ2EkGTRSk1rb+UBQ6alayRNVpYL6aX6jiqbUZ1\n",
"DBJ7SGpNaTa0tR7UmlhPeUmyj06AeIBuH4tSWodFvex1jSKO/fvMdaRRThsRIX845ZQKj/wf1t+h\n",
"vhq1fpQi21jieBqJpSHAtvyHRqmVsXJ2kxSrdCTO+SLg1nnJ9ZwFPh8fEKNd0NjIA5zKjVzAlTyF\n",
"KzieW2x+xhSiSMagcTPej6Yfd9DabIcsmDjnVgPf994fE62/CTjPe7/VObcJuNp7f2KwSma8928L\n",
"+30BuNh7f230ew/+ZXQDxELKgUMT/8M4okGPARcjZriGc2oSnZ4vCyTqOKr3Idr1QqSM+QfDehvy\n",
"OUw6QGymvNWmGerKwYPk0HwMEXKapLeUTqppc/gsm9OiBLjSbVsR5eFOOums9QhAHB7OUYYWjOtl\n",
"3Y4Irb0k4LMOAZ8yQGGb9QuNkoQAb6SaZD5AEg4+RPnncYYkuqzPVoYcbwETbGA7J/ETnswXeTqf\n",
"5wRutuG2Mwho/Cj0H4d+yy9aqO2h1toCk9mY4P5oYLtz7oPIzHrfBV4JbPTeK/e/leSFPgxJuNN2\n",
"DyJE0trj6E3+Q/x9AhGcCgSvCb+/BakU0KajWpe3k2jeK4CTkOTIhSQFBF8TzlvW9zFBpwWhy3FV\n",
"4JOBlyBAMoVo7kcCby95nsnwm/tJaCetwusRAf7UcEzdfwK5jy8scfwdJJbKXpLZAx8GPBz5ruDN\n",
"nwAAIABJREFUrxxJBvw84KGhp7WZcCwtI7MAeebiWQS1zScB6vg4ei81jyUvgmo5nZaK5twsIl/6\n",
"V5z5r77c0Oip47iZJ/BlfoX/5v+1d+ZRflVVvv/sSiozZABMQgaSEBIJEcLQAWRIQEAEGVTEEedH\n",
"q02DQyuDdqur1af0U9Cl0k9FG3mtMoqkQRLmoJGEKSEjmchIUpmHSlJDqvb7Y5+Te+vWb6opNe3P\n",
"WndV/X6/e8/v3pvK+d6999l7T2YxvQ8ZcIC5PdOisQhzT3XYLHCn5bSHmPTESo3coKovicidwC3p\n",
"HVRVzdLIS77PPp7jvWLxh/RKpujiSlsOx4bzHZp6L99k/Y6wpUlnVOdyN+0mcUPEukzRejgt9bpQ\n",
"rkF2IttNY4GI3xlFIlbmTVsQZ4efhdxaPUmqD9fRUCDiBBxrKUUf/mASS+J04AoKC1552GrCmBvD\n",
"98REOSXJxRgUznkUSdvffJSRCEUcbz+JFRfdR8MxgRtZZLxY7DLtgopl14diIlMowF5J0r64HBPr\n",
"dMwll3AdTO1f4EGpCeGQHAj1HMEejmdVKFL4OOfyV45oWKRwE4lYxG2JxzS6J+0hJhuADar6Unj9\n",
"IPaEvVlEhqnqZhEZjk30YBPJqNTxI8N7Objkz7C3Enbvg6OfhNmzsPhD1r0UJ7XWyKg+FjgBs7B+\n",
"QTJpV2P/4dMJc8PCtUxNvS419hL9+ZuxyXwwNpH9B/YkGP3LvUiWp8ZtYvi+oZSedb2FJGsbrCna\n",
"QzSMIcS4xwhsJdl5lJ4YV0USLK7H+r7/jaSjXlydNRKrlntOieOmqcByCuK1xEl+NMWFIk1c0h0T\n",
"YIeEcY6gNFdhHYloDSARgQEU/vfP1bypxHyX0mPwvaliJBuYylwu4Dku43FGsCm9004aCoZZHKrb\n",
"cwzodHBEZDowvdXHbacA/Gzgc6q6XES+TVJ9dLuq/lBEbgEGZQLwU0kC8OM1c+IhZvIAbROojr+n\n",
"J5PhmJvkB9jk9xz2ZBtFolShriaxHrLWRAVJi9U+2MT9FaxD4QFsCesxlJ51nQ4wpy2KKH7xif8U\n",
"4JPheg5i1lWpSYHRDbaRxKKoxJ7ce2Aifj7Jv3l1ieNGi2I9SbHMOiwRcDJNrzW2g6T2VlyJ1pSm\n",
"ULHZ2kFMqPpTuqsp1qwqYf/Wi2+UBRfVO3idaczmPTzBGbycDobXYgHw1zPbZs/T6Lp02gA8gIic\n",
"gi0N7oWV+vg0NtHcjz01rqHh0uDbsKXBB4GbVHVmjjFzreaqIb97Kf17JSY82QB19vemlKPYRWNx\n",
"SL+OInEEjVc1DU/9LDX+EbOu01t05cTSFv1ILLO4jaS0pDjCWBtpKBQxKTCu0hpM4iIaRemrnqJQ\n",
"RNdfjBfEEurHhPFGUfye1GIWcHRBVZN07BtEIhzFzil2EIwFNPtSWgvoGizWUo/d8/4UVoT6IBqt\n",
"1EJW6cN+RrOes/k7l/MY7+JphhzqZADYfV5AQ9FYhmpNjgGdLkynFpO2IIjJR2hY8bUnjQUh1+tS\n",
"+zLEpZ7xO6ZhE8zPgGexyXUfSQXhKAq5xKIpWddvhXMcR1LW/u8kk1xMhkwLRPy9FPddvK4BJG6b\n",
"Z4HHwvfFGlRxqW1ThaKW5Hr3Yl0n36Bhr5BRJO67prCX2EgoyW4fQekCCXaNMWekH03rx1KDiXUf\n",
"2qHMiFDHYHYxkWVcyhNcxZ+ZxFLKDyX9U4PFNaJgLAAWorolz5BON8PFJEMQk/8hEYumuCyqaGg9\n",
"5Ape78EsqWGYIFwJXIs9uS6k6VnXu8ltSbxFUhCyHAvgvg+4Khy3Epv0S112WklDa2IjDZcPl2Ou\n",
"p49iE+JBbFItZVJPWxQbSBYyHMTiKRdgK6rivlDctVMNrAvj7gzneUwY59gSzikSV5DtJIldNaX8\n",
"zd5wzn0pPRGzBJ9Uc91WSjk1DKOC03iZ9/MwF/M0wxoWLtxIIhhRPJb70lunEC4mGfK4uXaSWxzS\n",
"r3djT8e5LIi0y6nUQPleGq9wittmktjB0TR0N6W3Ur5Lsck7KxSbaNjR7ijsqb8lrqcNYexYuymW\n",
"bB9MYlGMprQYVQUmFlGgY0mUPiQrs46jeFHMqnBO20mC29kujIU4kDoWzCI5msJLd2OhRAn7F1lN\n",
"1fxaVP3YxxjWcD6zuYIZTOd5+h1aY3GoR8xrqW2BB8Sd5uBikiGIyftJxGI3jQv65RKL5mRd12Or\n",
"IfZg1XLXY9ZEGTYh5hOJUgPl8bsqgZPDuI8Dv8Mm3zJsMhtO84WiAnNpDcBmvifDBjahDiSJUYzG\n",
"7lWxp/pcZeHnYK6//piwjcbEophgpmfjGiyOtgkTyLdh19uU0i27MYup1IUESrK8uQ2p50j2MInF\n",
"TAvCcRYv0iN5MKrCLIy0cCz07HCntXAxyRDE5EkSkWhKr+tcVkR0O23CJqMjSUTha1jy5UqSsuWl\n",
"lpffiglFfNqPWwXJKp/BmOvpn7CJbysmAM2xKNaTBMrBXD5nAh/AJuNY+K+Ye07DOOvCtp2kyvAJ\n",
"WPwoBqZzLWnNspekf0cldp0TMLEpNdE09quJMapBlGYOxFybEvuJt9aKqnoGs4MpLOBCnuUq/sxk\n",
"FqVH3klD0ZiPdfBr1x7hTtfGxSRDDjdX9Jlnl8Gmtx3YE3M+SyJmPZfydFpNY5dTWijqSGIu0Ypo\n",
"qesp/owrtsoxayOOGd1Pwyg+G1Zik/u6MO5OGrqghpD05Ih95QuxM4wX3VnRvTeAxEI5tsh57SPJ\n",
"aq9KHR+LaBY6dhdJ3CMG5guJVFzx1dTe53moZwg7OJnXeS8zuJIZjGdV+oTXkwhGFI91vgTXOdy4\n",
"mGQIYvIeEqEoI0moy25xtVOp1st2EmEYjz2JPwP8CBOK2IkuCkRLhGITlmR4JOYm+g5mVcSJdCSJ\n",
"SMStWJOj6NY6MpxnPTATmB3G7Y8JzhhMKEZTXECzZeFfw/z4MU4zOozXlPpSMY7Vi+JZ/2lqMCup\n",
"F6UtgGjl4lT1DGEnk1nE+3mIy3mM41md/oINwMthewV4BdWtrff9jtN8XEwyBDH5G4VrKGWJ1ksh\n",
"iwKSLoqxHlYZtoIrFm8sRj6LYgP29B1jIGOBm7CJ9ABmLZSyxHUXiftpXTj3fSRB6XOB92ICEXuN\n",
"FHMlVWBximilxIz+qVgcp1RX1FbsOndg1tNxlC4y1ZgbTDA3YinZ5tElVKxCLs3Tk3oGsocTWcLV\n",
"PML7+BPjWZVO/HuLRDTsZ1JzznE6HC4mGXK4uXaRWyBirGILNqGNoHUsiqxQxExtxZ6Wc1kUoygu\n",
"egfDeGmxeIukm14sOBkn6TEUdx/F+McazBUVixFCskrrOEzcRhYZaz9WgbcCc2fFulExCXQMhS2n\n",
"SswiiS6pPiQlcPJ9bx1J9nl/zGLLs29Lyqor/alkIm9wCTO5hoc4lflp4aggsTiicGzKN5rjdERc\n",
"TDIEMbkAE4qtJJnYrSUUm4HLMAH6BlY+pQab/EbQWCRGU1rG/HZMIIZgE/gBzLW1Fnu6PiK8nxaL\n",
"YSWc9xZsQu+HTbp/wZ6We2GB6jGYWIyl+HLYGI8BE8hXMBEYQrI6q9RVTzuxf59eNM2CrKeoNdPy\n",
"1rDHs5Jz+StX8wiXMIueh9Jj2AHMo6F4vOUxDqez42KSIYjJy7SORRHbq/YiEYr3A5dgT987MFEq\n",
"NoHWhPHWZba4OisG5D+K9UOJ3QSLleuoC+OsJXFFxSf7Xljtq4sxV1QspVKIbZh1sY4kWH40Vlyx\n",
"1N4eMRlyL+aaK2X5LyQWxgCKxzvqMbVo+R8+dQxlM2fzIpfzGB/gIQaxJ34cY0BzwzYPWOXC4XRF\n",
"XEwyZNxcxYRiExanyFoUacui2IQO9vSfFYp1mNgIZhmkrYr4s1gjrFpMKKJYrMHELTbayloWoyi8\n",
"xLUKE4vVJCVf4tLY6NIaT+H4TGzPG1dn1ZEE20dSvNT6Fszq6kHSZTDfOVeHffuR13JpihViSYCT\n",
"WMIVzOAaHuRElqWPXkFD4ViAanXusRyna+FikiGIydmYWBwgv1CMDp8Vyy+oIhGHMqzp1RasZ8ou\n",
"kkqzY2jogio1e3ttOM9TsFnxHqwicuyOGIViXBi3UP2wmA0f+2HUYm6txSSVjMdjVY4LJWmm+6DX\n",
"Y3k0qzCrYVS4tlLzOGIZk1JWZJViPZVMGXUMZxPTeJ5P8F+cw98ZkPTh2E4iHHOBl1Dd0Vrf7Tid\n",
"DReTDEFMFmNiUcqqn3QCXnpbjwWVY6xiDPBV7El6E0nWeCH2k1gU0bqIIleGWSbnY+6tMpIM8ULs\n",
"ILEu1pDklvTGsvHPD2MVe2Tfg4nExjBGPVb36mSKr7CqC9cRW/iOpPjy6lrsuvtQMD7S3GZOSj/2\n",
"M5FlfIAH+SAPcgIr4yj1WB7HHKww5lxgtburHCfBxSRDxs21j9xCEcXiIEkNqDE0tC6Oo7jvfi+N\n",
"xWINNlEL5vqJVkX8OYriSXNvkghGFLW4bHgkZlmMp3jAeysmGOtIyoikXVoTKCy4m0hqccVih7Gp\n",
"VL6kvv3he+MKqwItk7XGzj9XyfXCWijUczRbeSd/44M8yJU8mu7+twsTjTlhm4dqZf7LdBzHxSRD\n",
"EJNTsSfnPuQWifiz1OztNVjjpfFYR8gfk4hFWiiiS6qQdaEktb0mYwLxGvBzknIgsS/5eMwVV+gf\n",
"OK7W6oMFjP8Szjm6yCZQOI4RS8uDCcFyzD1VSrtaMCtlLyY0bbbKqge1jGMV03mej/J7pjE7PdIb\n",
"JMIxB+vHUZ97JMdxcuFikiGIyWpKy97eRkOLIu2KOoj5+ccBp2L1sRTztRfz/+/CrIo3Uz+3k2TI\n",
"vx34PBbbqKVw6Y66cPyqsO0g6QtyIVZfq9gfQBUWXI5WRu9wTaMKHRS+ZyPmnjoGE7pC31WN3fN8\n",
"lkgJp2r05gAnsYRLeYJPcA8TWZH+jrlYa985wIuobitpUMdx8uJikiHj5orZ22tp7Irah7lssm6o\n",
"sRQXoli9NgpF3CqxiXQYiWVRSsC7ikQsVmJuolqSPu7jMQvjePJbU1F0VmIiWR32Tbu08lkOezF3\n",
"2u7wOpZryRcHqcJErScW98lxr5oW++jLPk5hPtfyAB/iPo5lc/rc/ga8gJV9eclXWDlO6+NikiGI\n",
"yduxCXkYucViHMWD529hYrERyy0px1oGLw/HRrGIP8dROOkvBrxjU62dWN/4fZgb6gRswi8Wx9iG\n",
"CVMvbFJ/Mrw3DLN4xpB/Bk9X8d2CLe89BlvlVQjFBLSAG6tpLqx+VHIar/IZ7uYynmAohxr+bScR\n",
"jtnY8lyvlus4bYyLSYYgJpspnh2+BxOLrDtqIzbhjsaE4lrgLMzVU05pAe9oYawlqWU1HOtxP5Hi\n",
"M+8uLA6wHLOuopVyIeaeKkRd+P5Y7+ttWGymUBynChOXWMIk3wKBYPVJE//gLL8jiscVPMbRHOrf\n",
"9BbwPCYcLwBLPd7hOIcfF5MMKTdXTPjLisVq7El+CA0ti1ID3hswoYiisRqbtOMS2QmprVA+Roxj\n",
"LA/jRBfTEZiQnYgJT768kn1Ydd5YzLEHlsQ4GrNycglCzJjfFc4rlprJtW8NsB90AEgeN1a+S1P6\n",
"sp9TeY1ruZ/ruJch7IofbgSexsrQPA+86Ut0Haf9cTHJEMTkOMwiGEtuwSiW4R0D3j2Bd2HxkU9i\n",
"gjGGhoJRShyjCrMOFPgVZnUMxdxSJ2IusnzWwE7MrVaOWUfPh/HGheNzfXd6pj+IWTe9ilw3lNbM\n",
"KiflVHMSi7iSGVzPLxnBoTqH24BnsVL9zwArXDwcp+PR6cVERHpgxfI2qOoVIjIEuA97ql8DXKuq\n",
"u8K+t2JxizrgRlWdlWM8Bd1D0wLe8WcF5uo5HhOKL2ErrtI9O3LxFmZhxG0bSbn0dwPvKXIb6jHR\n",
"WYpZPvux+MQFWLn7QqzFnvajwIwmvyAcCNsAWlyepI7jWc17+AvX80veweL4wR5M8KJ4LHK3leN0\n",
"fLqCmHwFa017hKpeKSK3A9tU9XYRuRkYrKq3iMgk4PfAP2CuqKeACZqZqFJurhjwzgrGesx1lA54\n",
"x61QPkY6jrEcc2/tx0RmLImV8XbyB9CrwhhLMXdTbOR0TDj2JPLXAtsUzn8nJj4DSepy5WJ72MrC\n",
"dTUSV6FeBaWeHpk/oNyCMpgdXMSTfI5fcwHPUW4tQ6qw1VZPh+1VD5g7TuejU4uJiIwE/gv4HvCV\n",
"YJksA6apaoWIDAOeU9W3B6ukXlV/GI59Avi2qr6YGVNBh2IB56xYNCWOcRo2Ud8N/AELoEexOBFz\n",
"l+XLD9mBWQwnYWIxB/ifMMZJmMsrn3BVYgLVE4uFzAtj5BOa9Mx/AIt1FKgJVvqqq57UcAoL+Dx3\n",
"cRUzOIZD6RyLsQ6NM4EXUD1Q0oCO43RYWktMSu1B0drcAXyNhk/NQzXpSFdBUvr8WCAtHBswCyUX\n",
"6ykex0i7pVZgAjAQC3qfiwmJAp8NWy7WYkHwpZjlE91hk0liLGBl5d+ZObYSWIRZG3vDvtMwkYr0\n",
"x1xdkW3h2gRzaR1JQ2XoG7Yae6m9mpZxXs9QKngfD/OP/JJTeD0evQNbgjwLmIXqhiYM6jhON+Kw\n",
"i4mIvBfYoqqvicj0XPuoqpqlkZc8n327F1TvhcrtcOZC+PjzmGisDMeMJ7Eyrgs/cyXoCbYqbDkm\n",
"GMtIyo1EV9lk4Apscs81c1eFYxdj4ngQc4ONwyoFn5XnumIRxhqSFV4jaJx9X4st6+2JucvKOCRi\n",
"QmNLpOEpllPNqbzGp7iH67g3VtWtw4Q7Wh+voFqX4zwdx+mkhHl3equPe7jdXCLyfWwiP4g9zR8J\n",
"PIzFRKar6mYRGQ48G9xctwCo6g/C8U8A31LVuZlxFfQYbOI9kYauqUJZ4HuwSX8NcA02634Kcx1N\n",
"InFPTSC3+B7EhOZt2IRfgbnwjsJEYzK5C0fGuEkPzK21NIwxOs95RqoLXEsBlKPYxoU8w438lHOZ\n",
"Ez/YCjwOPAY8SVj04DhO96BTx0wOfbnINOBfQszkdmC7qv4wCMigTAB+KkkAfrxmTjyISaHAwEYS\n",
"19RSLCC+hyS57zpMOPItk1XMpbUobJvDdw3F3GGFssnXYhbKNkyQziN/fawDWJC+H+bia7R0WKhX\n",
"RaS4K6ue41nNNTzAjfw0XapkPhbLeQwrU+LWh+N0Uzp7zCRNFIUfAPeLyGcJS4MBVHWJiNwPLMGs\n",
"gC9mhSRFbOiUFo1l2EqoMSRWxifC77lKq5Rhk/kiTADewCb4IzBL5RTgBnIHxWuBheFcYw2roViv\n",
"kMvy7P8GlrgYKx0fhcVvDiHU7yujvlcdPcsBlLLwD99YO8uo41Re4fP8Xz7E/RxBJeH8n8IE5HGP\n",
"fTiO09p0taTF4Zg7anLYonjka5NbgYlGD8yHuBS4FYuJTMGE40RyJxZuxQLo4zCRuw+b2U8nIwaB\n",
"dBfDfZhlU6Avidbn7vfRmJ7UcD7P81V+zLt4ht4Wh98BPIq5EJ/ylVeO4+SiS7i5WpNM1eAsu0jc\n",
"U4swy+EAZglMAW4kf0OseiwmMj8cV4mttnovVgY+FzWYhbIBO6mzSVanZcfeEsbLkaOS32vXmyou\n",
"ZhZf5cecxwv0oJ7wfY9gAvKC5304jlMMF5MMQUz2Ya6pRamfb2JxkWhpTCF/UHwv8DqJcBzAlg2f\n",
"ApyBubmy1kJdOOYNzOIYgFk2J9PY6tgfzkew2lgNEgrLqKMeyfEVRm/2cxHP8HVu5zxeiDLzBvAn\n",
"TEBe9pIljuM0BReTDEFMxmKTeFo4xuU5ZC2wAEtSHAn8MvX6DExwsu6tmKsyNnz2ImZZnEljyyPd\n",
"2ONAOLZY+ftGlFPF+fyVm/kBF/N0fHsZ8EfgAVSXNHVMx3GciItJhgJurhrMQlmAWRyLsYl9AnA5\n",
"cGWeIesx6+RlTEAUi8FcQ+4YynYs5lKNCVKO/BXdL2gfpaxgLKSMOqYyj6/wIz7Aw5TZdb2JCcgf\n",
"gYVugTiO0xq4mGQIYrIVE4y0cPTELJTTMYvjZHJnyUfheB1zRw0J++eLd7yOLRU+iPVQOZXGlsce\n",
"YIdQP1wpS+WG5IqFKBN5g5u4k09wL/3ZD7ac+T5MQNyF5ThOq+NikiGIycmYAJyBiccUcif4vYG5\n",
"iq7ErJSvY+6wszH3WDbWsQMToAHYCrBlWJJlvp4jxfq7H2IQO7iBn3E9v2IUG8AC/A8C9wCzvfKu\n",
"4zhtiYtJhgJurhXAKyRWRxkmGP9I7nhKPbYSax6WZDgQ+Bi5iyiuxtxbjSoGWzC9jFyrscqo5VJm\n",
"8q/8O2cyD7ETfwYTkIdR3Vf0gh3HcVoBF5MMQUxWY6IRxWMbFkg/m/xWxy7gr2H/vVidq3OwoHrW\n",
"HbYCE5BemIA0yHrvzYGDB+nZsy6nUaKMYh1f5g6+yF0xF2QFJiD3orquWRfuOI7TAlxMMgQxOZ9E\n",
"OHLFOqLVUY2VZ1mEJfZNx9xWaRVQLHN+CBbEX4ElMJY13EUo1KiwB7VczFP8H77KSSwFKwB5H7Z6\n",
"7O8eB3Ecpz1xMcmQx821Hfh72BZgFsU5WJJi1nyox4L2r2DicRGNM9lrgA2gx4KkOjA2DqgPYRs3\n",
"8lNu5nb6UA0WZ/lPzArZ0ayLdBzHaWVcTDIEMVlAIh6LsMKQ08J2Go3Nh3lYt8Cd2IqsCzDrI80W\n",
"zLV1NA16jqTTSBKm8Crf5zYuZSZigfiHMBGZ7VaI4zgdDReTDEFM3kciHlNoONMfBF7CBOEYbMXU\n",
"QOB8Gq74OkCSHb817Fv4u6njGh7g3/guk60n+nbgLuAXqG5qyXU5juO0JS4mGXK4uWqBucDzwKvY\n",
"st6PAZfkOPwVzA01EhOiQ/TgYI2gvQ7mCKqXU80X+E++wfd4G1sJY9wB/D9U97f4ohzHcdoYF5MM\n",
"QUyex8TjBSx/ZDrwbiy4nnZx7cUC75sxV9glNKgsrFX92bfzAH2G1x9a/JXERfqwny/xE77Fd2I8\n",
"5Gngx8ATnhfiOE5nwsUkQxCT6zHxeBcN+43UYMH1qeH3J8I+/VP71AE9oL4WynImHPZhP1/mDr7L\n",
"N6MyzQC+i+q8Vr4cx3Gcw4KLSYYcbq4VWB/zuVidrFuwzoVpFmAB9mmkckqEejRlyPSimn/mp3yP\n",
"b8b8kIcwEZnfBpfiOI5z2HAxyRDE5BFMQJZgrq33Ae+kYSB+HrbS6zjMDdYDTEDKqaUmFYsvo47P\n",
"8Su+zzc4ih1gvUK+ieritr8ix3GctsfFJEMQk29jAnJK6qNqYD22imsN5v4KLjBVEMmVdHg5M7iT\n",
"LzOeVWDLh7+O6pw2vQjHcZzDjItJhoybay/wGDAbGAXcTMPM9RW9qRpRTd9GhRrHsJp7uY5zmQNW\n",
"Uv4WYIbniDiO0xVxMckQxOTXwF8wy+NjWBJivEm1wJM9qB1fR/kEeytZoVVODd/jNv6FHyFWOv7f\n",
"gJ9761vHcboyrSUm2aKHnZ1y4Hckq7SqsWTF/pi1cllShDERkjOYx0zezRB2EY6/GdXNh/G8Hcdx\n",
"OjUFO/61BSIySkSeFZHFIrJIRG4M7w8RkSdFZLmIzBKRQaljbhWRFSKyTERyJR1GPokJxxzgX7F8\n",
"kygsQ45kN+kyKD2p4ed8gZc4kyHsWgtchOonXUgcx3GaxmF3c4nIMGCYqs4XkQFY9vnVwKeBbap6\n",
"u4jcDAxW1VtEZBLwe2x11gjgKWCCZpIDg5vr37Es9A8BVxBMj4HsPFBPj757OfLQ/hNZyp+5moks\n",
"B/gFcAuqe9v04h3HcToYreXmOuyWiapu1pCfoaqVWJB7BNb18J6w2z2YwABcBfxBVWtVdQ2wEks+\n",
"zMXlwH+HsWoBhDrdzeAGQvIFfs58TmUiy7cC70b1n1xIHMdxms9hF5M0IjIG650+FxiqqhXhowqS\n",
"XiTHgvWzDWzAxCcXp2HFGe+Cur0ASg+Jrq0e1HIf1/ILbqAP1bOBKajOar0rchzH6Z60WwA+uLge\n",
"Am5S1b0iiZWlqmpuq7zk+ezqWXDUUBj5BVvIFWs2CgPYw1zOZBLLAG4HvuErtRzH6W6IyHQsYbtV\n",
"aRcxEZFyTEjuVdVHwtsVIjJMVTeLyHCszAnARixXJDIyvJeDR84D+mbLoRzFNhYziaFsrQduQPWu\n",
"Vr0gx3GcToKqPgc8F1+LyLdaY9z2WM0lwN3AElW9M/XRo9hqLMLPR1Lvf1hEeonIWOAErCRKLvpO\n",
"ZOnWtNlyNFuYzxSGsrUK+IALieM4TuvTHqu5zsUy018ncVfdignE/cBorOzJtaq6KxxzG/AZLGfk\n",
"JlWdmWNcncqLL77EP5wVrZKB7GQO5zCJpfuBS1F9oU0vznEcp5PhGfAZknIqloxYTjXPciHnMKcG\n",
"uBzVp9r5FB3HcTocnXZpcFvShwNYaonyAB/kHKuvdb0LieM4TtvSpcSkij4AfIrfchUzwGpr3VPw\n",
"IMdxHKfFdDk31wD2sJ2j6UXtKuAdqB5o73NzHMfpqLibKw+38r/pZcnv/+xC4jiOc3joUpZJXyrZ\n",
"wCiGsHMuqme19zk5juN0dNwyycHnuJsh7AR4ur3PxXEcpzvRpSyTVYxlHG8CXOwruBzHcYrjeSYZ\n",
"RCReSS0wCNX97XpCjuM4nQB3c+VnrguJ4zjO4aUrismz7X0CjuM43Y2uKCbPtfcJOI7jdDe6Wsyk\n",
"BouXeH6J4zhOCXjMJDczXEgcx3EOP13LMmkFdXUcx+lOuGXiOI7jdBhcTBzHcZwW42LiOI7jtBgX\n",
"E8dxHKfFuJg4juM4LcbFxHEcx2kxnUZMRORSEVkmIitE5Ob2Ph/HcRwnoVOIiYj0AH4GXApMAj4i\n",
"Iie271l1XERkenufQ0fB70WC34sEvxetT6cQE2AqsFJV16hqLfBH4Kp2PqeOzPT2PoEOxPT2PoEO\n",
"xPT2PoEOxPT2PoGuRmcRkxHA+tTrDeE9x3EcpwPQWcSka9R8cRzH6aJ0itpcInIW8G1VvTS8vhWo\n",
"V9Ufpvbp+BfiOI7TAek2bXtFpCfwBvAu4C1gHvARVV3arifmOI7jANCzvU+gFFT1oIiFMdzmAAAF\n",
"R0lEQVTcAMwEegB3u5A4juN0HDqFZeI4juN0bDpLAD4v3S2ZUURGicizIrJYRBaJyI3h/SEi8qSI\n",
"LBeRWSIyKHXMreH+LBORS9rv7NsGEekhIq+JyIzwulveCxEZJCIPishSEVkiImd243txa/g/slBE\n",
"fi8ivbvLvRCR34hIhYgsTL3X5GsXkdPD/VshIj8p+sWq2mk3zOW1EhgDlAPzgRPb+7za+JqHAVPC\n",
"7wOwWNKJwO3A18P7NwM/CL9PCvelPNynlUBZe19HK9+TrwD/DTwaXnfLewHcA3wm/N4TGNgd70W4\n",
"ntVA7/D6PuCT3eVeAOcBpwILU+815dqjx2oeMDX8/jhwaaHv7eyWSbdLZlTVzao6P/xeCSzFcm6u\n",
"xCYTws+rw+9XAX9Q1VpVXYP9sUw9rCfdhojISOAy4NdAXJHS7e6FiAwEzlPV34DFGVV1N93wXgB7\n",
"gFqgX1i80w9buNMt7oWqvgDszLzdlGs/U0SGA0eo6ryw3+9Sx+Sks4tJt05mFJEx2BPIXGCoqlaE\n",
"jyqAoeH3Y7H7Eulq9+gO4GtAfeq97ngvxgJbReS3IvKqiPxKRPrTDe+Fqu4AfgSsw0Rkl6o+STe8\n",
"Fymaeu3Z9zdS5J50djHptqsHRGQA8BBwk6ruTX+mZpcWujdd4r6JyHuBLar6GolV0oDuci8wt9Zp\n",
"wC9U9TRgH3BLeofuci9E5HjgS5jb5lhggIh8PL1Pd7kXuSjh2ptFZxeTjcCo1OtRNFTTLomIlGNC\n",
"cq+qPhLerhCRYeHz4cCW8H72Ho0M73UF3glcKSJvAn8ALhSRe+me92IDsEFVXwqvH8TEZXM3vBdn\n",
"AHNUdbuqHgQeBs6me96LSFP+T2wI74/MvF/wnnR2MXkZOEFExohIL+BDwKPtfE5tiogIcDewRFXv\n",
"TH30KBZkJPx8JPX+h0Wkl4iMBU7AAmudHlW9TVVHqepY4MPAM6p6Hd3zXmwG1ovIhPDWRcBiYAbd\n",
"7F4Ay4CzRKRv+P9yEbCE7nkvIk36PxH+nvaEFYECXJc6JjftvfKgFVYuvAdb0bQSuLW9z+cwXO+5\n",
"WHxgPvBa2C4FhgBPAcuBWcCg1DG3hfuzDHh3e19DG92XaSSrubrlvQBOAV4CFmBP4wO78b34Oiam\n",
"C7GAc3l3uReYlf4WUIPFlD/dnGsHTg/3byXw02Lf60mLjuM4Tovp7G4ux3EcpwPgYuI4juO0GBcT\n",
"x3Ecp8W4mDiO4zgtxsXEcRzHaTEuJo7jOE6LcTFxnFZCRIaLyANF9hmTLg2e+ew5ETm9bc7OcdqW\n",
"TtFp0XE6A6q6CfhgS4agC9eEcro2bpk4TjMQke+IyE2p198TkRuj1REadv2HiMwTkQUicn2OMfqK\n",
"yB9DI6uHgb7kKVjpOB0dFxPHaR6/AT4BICJlWF24v6Y+/yxW+nwq1hvjf4WWAWm+AFSq6iTgW1j5\n",
"CrdMnE6Ju7kcpxmo6loR2S4iU7Dul68C21O7XAK8Q0SuCa+PBMZjdY4i5wE/CeMtFJHX2/7MHadt\n",
"cDFxnObza6yI3lDMUsm6qG5Qa8p0iBzWibu1nC6Bu7kcp/n8CavYfAYwM/PZTOCLoW0sIjJBRPpl\n",
"9pkNfDR8Phk4uW1P13HaDrdMHKeZqGqtiDwD7FRVtbYPh2Iev8Y6/b0a+kFsIemhHfe5C/itiCwB\n",
"lmL9eRynU+Il6B2nmYTA+yvANaq6qr3Px3HaE3dzOU4zEJFJwArgKRcSx3HLxHEcx2kF3DJxHMdx\n",
"WoyLieM4jtNiXEwcx3GcFuNi4jiO47QYFxPHcRynxbiYOI7jOC3m/wN5yNe3d+wSCQAAAABJRU5E\n",
"rkJggg==\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x10624a310>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#コブダグラス Y=LK (w=5 r=20 固定100) Y=20x**(1/2)+100 規模に関して収穫逓増\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"fig, ax = plt.subplots()\n",
"x = np.linspace(0, 1000, 200)\n",
"plt.ylim(0,1500)\n",
"plt.title(\"decreasing returns to scale\")\n",
"plt.xlabel(\"yield\")\n",
"plt.ylabel(\"cost\")\n",
"y=100+20*(x**(0.5))\n",
"ax.plot(x, y, 'r-', linewidth=5)\n",
"for i in range(1,100):\n",
" y = 100+(5*(x/i))+i*20\n",
" ax.plot(x, y, 'b-', linewidth=2)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
tpin3694/tpin3694.github.io | machine-learning/f1_score.ipynb | 2 | 3004 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Title: F1 Score \n",
"Slug: f1_score \n",
"Summary: How to evaluate a Python machine learning using F1 score. \n",
"Date: 2017-09-15 12:00 \n",
"Category: Machine Learning \n",
"Tags: Model Evaluation\n",
"Authors: Chris Albon"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a alt=\"F1 Score\" href=\"https://machinelearningflashcards.com\">\n",
" <img src=\"f1_score/F1_Score_print.png\" class=\"flashcard center-block\">\n",
"</a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Preliminaries"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load libraries\n",
"from sklearn.model_selection import cross_val_score\n",
"from sklearn.linear_model import LogisticRegression\n",
"from sklearn.datasets import make_classification"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generate Features And Target Data"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Generate features matrix and target vector\n",
"X, y = make_classification(n_samples = 10000,\n",
" n_features = 3,\n",
" n_informative = 3,\n",
" n_redundant = 0,\n",
" n_classes = 2,\n",
" random_state = 1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Create Logistic Regression"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Create logistic regression\n",
"logit = LogisticRegression()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Cross-Validate Model Using F1"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([ 0.95166617, 0.95765275, 0.95558223])"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Cross-validate model using precision\n",
"cross_val_score(logit, X, y, scoring=\"f1\")"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
SylvainCorlay/ipywidgets | docs/source/examples/Index.ipynb | 1 | 2451 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Back to the main [Index](../Index.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Interactive Widgets"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"IPython includes an architecture for interactive widgets that tie together Python code running in the kernel and JavaScript/HTML/CSS running in the browser. These widgets enable users to explore their code and data interactively."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tutorials"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- [Using Interact](Using%20Interact.ipynb)\n",
"- [Widget Basics](Widget%20Basics.ipynb) \n",
"- [Widget Events](Widget%20Events.ipynb) \n",
"- [Widget List](Widget%20List.ipynb) \n",
"- [Widget Styling](Widget%20Styling.ipynb)\n",
"- [Layout Templates](Layout%20Templates.ipynb)\n",
"- [Widget Asynchronous](Widget%20Asynchronous.ipynb): how to pause and listen in the kernel for widget changes in the frontend."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Examples of custom widgets"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- [Variable Inspector](Variable%20Inspector.ipynb) \n",
"- [Export As (nbconvert)](Export As (nbconvert%29.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Examples using `interact`/`interactive`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* [Beat Frequencies](Beat%20Frequencies.ipynb)\n",
"* [Exploring Graphs](Exploring%20Graphs.ipynb)\n",
"* [Factoring](Factoring.ipynb)\n",
"* [Image Browser](Image%20Browser.ipynb)\n",
"* [Image Processing](Image%20Processing.ipynb)\n",
"* [Lorenz Differential Equations](Lorenz%20Differential%20Equations.ipynb)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
SylvainCorlay/bqplot | examples/Index.ipynb | 1 | 7017 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# bqplot"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`bqplot` is a [Grammar of Graphics](https://www.cs.uic.edu/~wilkinson/TheGrammarOfGraphics/GOG.html) based interactive plotting framework for the Jupyter notebook. The library offers a simple bridge between `Python` and `d3.js` allowing users to quickly and easily build complex GUI's with layered interactions."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Basic Plotting"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To begin start by investigating the introductory notebooks:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. [Introduction](Introduction.ipynb) - If you're new to `bqplot`, get started with our Introduction notebook\n",
"2. [Basic Plotting](Basic%20Plotting/Basic%20Plotting.ipynb) - which demonstrates some basic `bqplot` plotting commands and how to use them\n",
"3. [Pyplot](Basic%20Plotting/Pyplot.ipynb) - which introduces the simpler `pyplot` API\n",
"4. [Tutorials](Tutorials.ipynb) - which provides tutorials for using pyplot, object model, linking with ipywidgets and selectors"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Marks"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Move to exploring the different `Marks` that you can use to represent your data. You have two options for rendering marks:\n",
"* Object Model, which is a verbose API but gives you full flexibility and customizability\n",
"* Pyplot, which is a simpler API (similar to matplotlib's pyplot) and sets meaningul defaults for the user\n",
"\n",
"\n",
"1. Bars: Bar mark ([Object Model](Marks/Object%20Model/Bars.ipynb), [Pyplot](Marks/Pyplot/Bars.ipynb))\n",
"* Bins: Backend histogram mark ([Object Model](Marks/Object%20Model/Bins.ipynb), [Pyplot](Marks/Pyplot/Bins.ipynb))\n",
"* Boxplot: Boxplot mark ([Object Model](Marks/Object%20Model/Boxplot.ipynb), [Pyplot](Marks/Pyplot/Boxplot.ipynb))\n",
"* Candles: OHLC mark ([Object Model](Marks/Object%20Model/Candles.ipynb), [Pyplot](Marks/Pyplot/Candles.ipynb))\n",
"* FlexLine: Flexible lines mark ([Object Model](Marks/Object%20Model/FlexLine.ipynb), Pyplot)\n",
"* Graph: Network mark ([Object Model](Marks/Object%20Model/Graph.ipynb), Pyplot)\n",
"* GridHeatMap: Grid heatmap mark ([Object Model](Marks/Object%20Model/GridHeatMap.ipynb), [Pyplot](Marks/Pyplot/GridHeatMap.ipynb))\n",
"* HeatMap: Heatmap mark ([Object Model](Marks/Object%20Model/HeatMap.ipynb), [Pyplot](Marks/Pyplot/HeatMap.ipynb))\n",
"* Hist: Histogram mark ([Object Model](Marks/Object%20Model/Hist.ipynb), [Pyplot](Marks/Pyplot/Hist.ipynb))\n",
"* Image: Image mark ([Object Model](Marks/Object%20Model/Image.ipynb), [Pyplot](Marks/Pyplot/Image.ipynb))\n",
"* Label: Label mark ([Object Model](Marks/Object%20Model/Label.ipynb), [Pyplot](Marks/Pyplot/Label.ipynb))\n",
"* Lines: Lines mark ([Object Model](Marks/Object%20Model/Lines.ipynb), [Pyplot](Marks/Pyplot/Lines.ipynb))\n",
"* Map: Geographical map mark ([Object Model](Marks/Object%20Model/Map.ipynb), [Pyplot](Marks/Pyplot/Map.ipynb))\n",
"* Market Map: Tile map mark ([Object Model](Marks/Object%20Model/Market%20Map.ipynb), Pyplot)\n",
"* Pie: Pie mark ([Object Model](Marks/Object%20Model/Pie.ipynb), [Pyplot](Marks/Pyplot/Pie.ipynb))\n",
"* Scatter: Scatter mark ([Object Model](Marks/Object%20Model/Scatter.ipynb), [Pyplot](Marks/Pyplot/Scatter.ipynb))\n",
"* Mega Scatter: webgl-based Scatter mark ([Scatter Mega](Marks/Object%20Model/ScatterMega.ipynb))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Interactions"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Learn how to use `bqplot` interactions to convert your plots into interactive applications:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"13. [Mark Interactions](Interactions/Mark%20Interactions.ipynb) - which describes the mark specific interactions and how to use them\n",
"14. [Interaction Layer](Interactions/Interaction%20Layer.ipynb) - which describes the use of the interaction layers, including selectors and how they can be used for facilitating better interaction"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Advanced Plotting"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once you've mastered the basics of `bqplot`, you can use these notebooks to learn about some of it's more advanced features."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"15. [Plotting Dates](Advanced%20Plotting/Plotting%20Dates.ipynb)\n",
"16. [Advanced Plotting](Advanced%20Plotting/Advanced%20Plotting.ipynb)\n",
"17. [Animations](Advanced%20Plotting/Animations.ipynb)\n",
"18. [Axis Properties](Advanced%20Plotting/Axis%20Properties.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Applications"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, we have a collection of notebooks that demonstrate how to use `bqplot` and `ipywidgets` to create advanced interactive applications."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"19. [Wealth of Nations](Applications/Wealth%20of%20Nations.ipynb) - a recreation of [Hans Rosling's famous TED Talk](http://www.ted.com/talks/hans_rosling_shows_the_best_stats_you_ve_ever_seen)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Help"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For more help, \n",
"- Reach out to us via the `ipywidgets` gitter chat \n",
"[](https://gitter.im/ipython/ipywidgets?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)\n",
"\n",
"\n",
"\n",
"- Or take a look at a talk given on Interactive visualizations in Jupyter at PyData"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from IPython.display import YouTubeVideo\n",
"YouTubeVideo('eVET9IYgbao')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| apache-2.0 |
QuantStack/quantstack-talks | 2020-01-09-PyData-Heidelberg/examples/gradient_descent.ipynb | 1 | 5397 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Notebook served by Voilà"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Notebook copied from https://github.com/ChakriCherukuri/mlviz"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h2>Gradient Descent</h2>\n",
"* Given a the multi-variable function $\\large {F(x)}$ differentiable in a neighborhood of a point $\\large a$\n",
"* $\\large F(x)$ decreases fastest if one goes from $\\large a$ in the direction of the negative gradient of $\\large F$ at $\\large a$, $\\large -\\nabla{F(a)}$\n",
"\n",
"<h3>Gradient Descent Algorithm:</h3>\n",
"* Choose a starting point, $\\large x_0$\n",
"* Choose the sequence $\\large x_0, x_1, x_2, ...$ such that\n",
"$ \\large x_{n+1} = x_n - \\eta \\nabla(F(x_n) $\n",
"\n",
"So convergence of the gradient descent depends on the starting point $\\large x_0$ and the learning rate $\\large \\eta$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from time import sleep\n",
"\n",
"import numpy as np\n",
"\n",
"from ipywidgets import *\n",
"import bqplot.pyplot as plt\n",
"from bqplot import Toolbar"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"f = lambda x: np.exp(-x) * np.sin(5 * x)\n",
"df = lambda x: -np.exp(-x) * np.sin(5 * x) + 5 * np.cos(5 *x) * np.exp(-x)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"x = np.linspace(0.5, 2.5, 500)\n",
"y = f(x)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def update_sol_path(x, y):\n",
" with sol_path.hold_sync():\n",
" sol_path.x = x\n",
" sol_path.y = y\n",
" \n",
" with sol_points.hold_sync():\n",
" sol_points.x = x\n",
" sol_points.y = y"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def gradient_descent(x0, f, df, eta=.1, tol=1e-6, num_iters=10):\n",
" x = [x0]\n",
" i = 0\n",
" \n",
" while i < num_iters:\n",
" x_prev = x[-1]\n",
" grad = df(x_prev)\n",
" x_curr = x_prev - eta * grad\n",
" x.append(x_curr)\n",
" sol_lbl.value = sol_lbl_tmpl.format(x_curr)\n",
" sleep(.5)\n",
" \n",
" update_sol_path(x, [f(i) for i in x])\n",
" \n",
" if np.abs(x_curr - x_prev) < tol:\n",
" break\n",
" i += 1"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"txt_layout = Layout(width='150px')\n",
"x0_box = FloatText(description='x0', layout=txt_layout, value=2.4)\n",
"eta_box = FloatText(description='Learning Rate', \n",
" style={'description_width':'initial'}, \n",
" layout=txt_layout, value=.1)\n",
"\n",
"go_btn = Button(description='GO', button_style='success', layout=Layout(width='50px'))\n",
"reset_btn = Button(description='Reset', button_style='success', layout=Layout(width='100px'))\n",
"\n",
"sol_lbl_tmpl = 'x = {:.4f}'\n",
"sol_lbl = Label()\n",
"# sol_lbl.layout.width = '300px'\n",
"\n",
"# plot of curve and solution\n",
"fig_layout = Layout(width='720px', height='500px')\n",
"fig = plt.figure(layout=fig_layout, title='Gradient Descent', display_toolbar=True)\n",
"fig.pyplot = Toolbar(figure=fig)\n",
"\n",
"curve = plt.plot(x, y, colors=['dodgerblue'], stroke_width=2)\n",
"sol_path = plt.plot([], [], colors=['#ccc'], opacities=[.7])\n",
"sol_points = plt.plot([], [], 'mo', default_size=20)\n",
"\n",
"def optimize():\n",
" f.marks = [curve]\n",
" gradient_descent(x0_box.value, f, df, eta=eta_box.value)\n",
"\n",
"def reset():\n",
" curve.scales['x'].min = .4\n",
" curve.scales['x'].max = 2.5\n",
" \n",
" curve.scales['y'].min = -.5\n",
" curve.scales['y'].max = .4\n",
" sol_path.x = sol_path.y = []\n",
" sol_points.x = sol_points.y = []\n",
" sol_lbl.value = ''\n",
" \n",
"go_btn.on_click(lambda btn: optimize())\n",
"reset_btn.on_click(lambda btn: reset())\n",
"\n",
"final_fig = VBox([fig, fig.pyplot], \n",
" layout=Layout(overflow_x='hidden'))\n",
"HBox([final_fig, VBox([x0_box, eta_box, go_btn, reset_btn, sol_lbl])])"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
},
"widgets": {
"application/vnd.jupyter.widget-state+json": {
"state": {},
"version_major": 2,
"version_minor": 0
}
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| bsd-3-clause |
savioabuga/arrows | arrows.ipynb | 2 | 763487 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# arrows: Yet Another Twitter/Python Data Analysis\n",
"## Geospatially, Temporally, and Linguistically Analyzing Tweets about Top U.S. Presidential Candidates with Pandas, TextBlob, Seaborn, and Cartopy\n",
"\n",
"Hi, I'm Raj. For my internship this summer, I've been using data science and geospatial Python libraries like xray, numpy, rasterio, and cartopy. A week ago, I had a discussion about the relevance of Bernie Sanders among millenials - and so, I set out to get a rough idea by looking at recent tweets.\n",
"\n",
"I don't explain any of the code in this document, but you can skip the code and just look at the results if you like. If you're interested in going further with this data, I've posted source code and the dataset at https://github.com/raj-kesavan/arrows.\n",
"\n",
"If you have any comments or suggestions (oneither code or analysis), please let me know at [email protected]. Enjoy!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, I used Tweepy to pull down 20,000 tweets for each of Hillary Clinton, Bernie Sanders, Rand Paul, and Jeb Bush [`retrieve_tweets.py`].\n",
"\n",
"I've also already done some calculations, specifically of polarity, subjectivity, influence, influenced polarity, and longitude and latitude (all explained later) [`preprocess.py`]."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from arrows.preprocess import load_df"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Just adding some imports and setting graph display options."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from textblob import TextBlob\n",
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib\n",
"import seaborn as sns\n",
"import cartopy\n",
"pd.set_option('display.max_colwidth', 200)\n",
"pd.options.display.mpl_style = 'default'\n",
"matplotlib.style.use('ggplot')\n",
"sns.set_context('talk')\n",
"sns.set_style('whitegrid')\n",
"plt.rcParams['figure.figsize'] = [12.0, 8.0]\n",
"% matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's look at our data! \n",
"\n",
"`load_df` loads it in as a `pandas.DataFrame`, excellent for statistical analysis and graphing."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df = load_df('arrows/data/results.csv')"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'pandas.core.frame.DataFrame'>\n",
"Int64Index: 80000 entries, 0 to 80025\n",
"Data columns (total 21 columns):\n",
"candidate 80000 non-null object\n",
"coordinates 87 non-null object\n",
"created_at 80000 non-null datetime64[ns]\n",
"favorite_count 80000 non-null object\n",
"geo 87 non-null object\n",
"id 80000 non-null float64\n",
"lang 80000 non-null object\n",
"place 743 non-null object\n",
"retweet_count 80000 non-null float64\n",
"text 80000 non-null object\n",
"user_followers_count 79994 non-null float64\n",
"user_location 53628 non-null object\n",
"user_name 79973 non-null object\n",
"user_screen_name 79974 non-null object\n",
"user_time_zone 50386 non-null object\n",
"polarity 80000 non-null float64\n",
"subjectivity 80000 non-null float64\n",
"influence 79994 non-null float64\n",
"influenced_polarity 79994 non-null float64\n",
"latitude 743 non-null float64\n",
"longitude 743 non-null float64\n",
"dtypes: datetime64[ns](1), float64(9), object(11)\n",
"memory usage: 13.4+ MB\n"
]
}
],
"source": [
"df.info()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We'll be looking primarily at `candidate`, `created_at`, `lang`, `place`, `user_followers_count`, `user_time_zone`, `polarity`, and `influenced_polarity`, and `text`."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>candidate</th>\n",
" <th>created_at</th>\n",
" <th>lang</th>\n",
" <th>place</th>\n",
" <th>user_followers_count</th>\n",
" <th>user_time_zone</th>\n",
" <th>polarity</th>\n",
" <th>influenced_polarity</th>\n",
" <th>text</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>Bernie Sanders</td>\n",
" <td>2015-07-06 01:52:42</td>\n",
" <td>en</td>\n",
" <td>NaN</td>\n",
" <td>1642</td>\n",
" <td>Eastern Time (US & Canada)</td>\n",
" <td>0.285714</td>\n",
" <td>16.378184</td>\n",
" <td>RT @DrTomMartinPhD: BERNIE SANDERS QUOTE ON #BILLMAHER, \"Hillary Clinton &amp; I Have The Right Message. We're Both Speaking The Truth.\" http:/…</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" candidate created_at lang place user_followers_count \\\n",
"0 Bernie Sanders 2015-07-06 01:52:42 en NaN 1642 \n",
"\n",
" user_time_zone polarity influenced_polarity \\\n",
"0 Eastern Time (US & Canada) 0.285714 16.378184 \n",
"\n",
" text \n",
"0 RT @DrTomMartinPhD: BERNIE SANDERS QUOTE ON #BILLMAHER, \"Hillary Clinton & I Have The Right Message. We're Both Speaking The Truth.\" http:/… "
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df[['candidate', 'created_at', 'lang', 'place', 'user_followers_count', \n",
" 'user_time_zone', 'polarity', 'influenced_polarity', 'text']].head(1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First I'll look at sentiment, calculated with TextBlob using the `text` column. Sentiment is composed of two values, polarity - a measure of the positivity or negativity of a text - and subjectivity. Polarity is between -1.0 and 1.0; subjectivity between 0.0 and 1.0."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Sentiment(polarity=-0.19444444444444448, subjectivity=0.2888888888888889)"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"TextBlob(\"Tear down this wall!\").sentiment"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Unfortunately, it doesn't work too well on anything other than English."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Sentiment(polarity=0.0, subjectivity=0.0)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"TextBlob(\"Radix malorum est cupiditas.\").sentiment"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"TextBlob has a cool `translate()` function that uses Google Translate to take care of that for us, but we won't be using it here - just because tweets include a lot of slang and abbreviations that can't be translated very well."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The root of evil.\n",
"Sentiment(polarity=-1.0, subjectivity=1.0)\n"
]
}
],
"source": [
"sentence = TextBlob(\"Radix malorum est cupiditas.\").translate()\n",
"print(sentence)\n",
"print(sentence.sentiment)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"All right - let's figure out the most (positively) polarized English tweets."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>candidate</th>\n",
" <th>polarity</th>\n",
" <th>subjectivity</th>\n",
" <th>text</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2287</th>\n",
" <td>Bernie Sanders</td>\n",
" <td>1</td>\n",
" <td>1.0</td>\n",
" <td>Republicans Welcomed Bernie Sanders to Wisconsin By Calling Him an Extremist. His Response? Perfect. http://t.co/ksaN85UuS8</td>\n",
" </tr>\n",
" <tr>\n",
" <th>810</th>\n",
" <td>Bernie Sanders</td>\n",
" <td>1</td>\n",
" <td>0.3</td>\n",
" <td>BEST OF SUNDAY TALK CNN SOTU #Sanders draws 2016 record crowd in Iowa-http://t.co/XnSbMweMbW http://t.co/wWqpmsVdEI</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31467</th>\n",
" <td>Hillary Clinton</td>\n",
" <td>1</td>\n",
" <td>0.3</td>\n",
" <td>@whitehouse but there is one thing i want to be known by all the world: my best wish goes to Lady Hillary Clinton. it's said and done</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" candidate polarity subjectivity \\\n",
"2287 Bernie Sanders 1 1.0 \n",
"810 Bernie Sanders 1 0.3 \n",
"31467 Hillary Clinton 1 0.3 \n",
"\n",
" text \n",
"2287 Republicans Welcomed Bernie Sanders to Wisconsin By Calling Him an Extremist. His Response? Perfect. http://t.co/ksaN85UuS8 \n",
"810 BEST OF SUNDAY TALK CNN SOTU #Sanders draws 2016 record crowd in Iowa-http://t.co/XnSbMweMbW http://t.co/wWqpmsVdEI \n",
"31467 @whitehouse but there is one thing i want to be known by all the world: my best wish goes to Lady Hillary Clinton. it's said and done "
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"english_df = df[df.lang == 'en']\n",
"english_df.sort('polarity', ascending = False).head(3)[['candidate', 'polarity', 'subjectivity', 'text']]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Extrema don't mean much. We might get more interesting data with mean polarities for each candidate. Let's also look at influenced polarity, which takes into account the number of retweets and followers."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>polarity</th>\n",
" <th>influence</th>\n",
" <th>influenced_polarity</th>\n",
" </tr>\n",
" <tr>\n",
" <th>candidate</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Bernie Sanders</th>\n",
" <td>0.096348</td>\n",
" <td>162.142172</td>\n",
" <td>14.758500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Hillary Clinton</th>\n",
" <td>0.037577</td>\n",
" <td>176.315714</td>\n",
" <td>7.561452</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Jeb Bush</th>\n",
" <td>0.026713</td>\n",
" <td>318.453703</td>\n",
" <td>16.174172</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Rand Paul</th>\n",
" <td>0.086817</td>\n",
" <td>144.550312</td>\n",
" <td>10.042045</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" polarity influence influenced_polarity\n",
"candidate \n",
"Bernie Sanders 0.096348 162.142172 14.758500\n",
"Hillary Clinton 0.037577 176.315714 7.561452\n",
"Jeb Bush 0.026713 318.453703 16.174172\n",
"Rand Paul 0.086817 144.550312 10.042045"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"candidate_groupby = english_df.groupby('candidate')\n",
"candidate_groupby[['polarity', 'influence', 'influenced_polarity']].mean()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So tweets about Jeb Bush, on average, aren't as positive as the other candidates, but the people tweeting about Bush get more retweets and followers. \n",
"\n",
"I used the formula `influence = sqrt(followers + 1) * sqrt(retweets + 1)`. You can experiment with different functions if you like [`preprocess.py:influence`].\n",
"\n",
"We can look at the most influential tweets about Jeb Bush to see what's up."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>influence</th>\n",
" <th>polarity</th>\n",
" <th>influenced_polarity</th>\n",
" <th>user_name</th>\n",
" <th>text</th>\n",
" <th>created_at</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>52023</th>\n",
" <td>89594.614397</td>\n",
" <td>0.500000</td>\n",
" <td>44797.307199</td>\n",
" <td>CNN Breaking News</td>\n",
" <td>Jeb Bush on Donald Trump: \"His views are way out of the mainstream of what most Republicans think.\" http://t.co/5K3Gi7AcQG</td>\n",
" <td>2015-07-05 02:14:26</td>\n",
" </tr>\n",
" <tr>\n",
" <th>55849</th>\n",
" <td>68470.590942</td>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" <td>The New York Times</td>\n",
" <td>Jeb Bush, whose wife is Mexican, says he takes Donald Trump’s remarks personally http://t.co/9CZFg4Nbcb</td>\n",
" <td>2015-07-04 20:10:06</td>\n",
" </tr>\n",
" <tr>\n",
" <th>47246</th>\n",
" <td>53754.716258</td>\n",
" <td>-0.066667</td>\n",
" <td>-3583.647751</td>\n",
" <td>Donald J. Trump</td>\n",
" <td>Flashback – Jeb Bush says illegal immigrants breaking our laws is an “act of love” http://t.co/p8yFzVuw8w He will never secure the border.</td>\n",
" <td>2015-07-05 15:23:20</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50459</th>\n",
" <td>53641.142046</td>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" <td>CNN</td>\n",
" <td>Jeb Bush: Trump comments meant 'to draw attention.'\\nhttp://t.co/chKrOnsntE http://t.co/bZnmLgyN7l</td>\n",
" <td>2015-07-05 03:55:25</td>\n",
" </tr>\n",
" <tr>\n",
" <th>47616</th>\n",
" <td>51601.878338</td>\n",
" <td>0.200000</td>\n",
" <td>10320.375668</td>\n",
" <td>Donald J. Trump</td>\n",
" <td>Jeb Bush will never secure our border or negotiate great trade deals for American workers. Jeb doesn't see &amp; can't solve the problems.</td>\n",
" <td>2015-07-05 15:02:22</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" influence polarity influenced_polarity user_name \\\n",
"52023 89594.614397 0.500000 44797.307199 CNN Breaking News \n",
"55849 68470.590942 0.000000 0.000000 The New York Times \n",
"47246 53754.716258 -0.066667 -3583.647751 Donald J. Trump \n",
"50459 53641.142046 0.000000 0.000000 CNN \n",
"47616 51601.878338 0.200000 10320.375668 Donald J. Trump \n",
"\n",
" text \\\n",
"52023 Jeb Bush on Donald Trump: \"His views are way out of the mainstream of what most Republicans think.\" http://t.co/5K3Gi7AcQG \n",
"55849 Jeb Bush, whose wife is Mexican, says he takes Donald Trump’s remarks personally http://t.co/9CZFg4Nbcb \n",
"47246 Flashback – Jeb Bush says illegal immigrants breaking our laws is an “act of love” http://t.co/p8yFzVuw8w He will never secure the border. \n",
"50459 Jeb Bush: Trump comments meant 'to draw attention.'\\nhttp://t.co/chKrOnsntE http://t.co/bZnmLgyN7l \n",
"47616 Jeb Bush will never secure our border or negotiate great trade deals for American workers. Jeb doesn't see & can't solve the problems. \n",
"\n",
" created_at \n",
"52023 2015-07-05 02:14:26 \n",
"55849 2015-07-04 20:10:06 \n",
"47246 2015-07-05 15:23:20 \n",
"50459 2015-07-05 03:55:25 \n",
"47616 2015-07-05 15:02:22 "
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"jeb = candidate_groupby.get_group('Jeb Bush')\n",
"jeb_influence = jeb.sort('influence', ascending = False)\n",
"jeb_influence[['influence', 'polarity', 'influenced_polarity', 'user_name', 'text', 'created_at']].head(5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Side note: you can see that sentiment analysis isn't perfect - the last tweet is certainly negative toward Jeb Bush, but it was actually assigned a positive polarity. Over a large number of tweets, though, sentiment analysis is more meaningful.\n",
"\n",
"As to the high influence of tweets about Bush: it looks like Donald Trump (someone with a lot of followers) has been tweeting a lot about Bush over the other candidates - one possible reason for Jeb's greater `influenced_polarity`."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"candidate\n",
"Jeb Bush 4\n",
"dtype: int64"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df[df.user_name == 'Donald J. Trump'].groupby('candidate').size()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Looks like our favorite toupéed candidate hasn't even been tweeting about anyone else!\n",
"\n",
"What else can we do? We know the language each tweet was (tweeted?) in."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"candidate lang\n",
"Bernie Sanders ar 1\n",
" da 2\n",
" de 55\n",
" el 33\n",
" en 19208\n",
" es 55\n",
" et 1\n",
" fr 447\n",
" in 6\n",
" it 1\n",
" ko 1\n",
" nl 47\n",
" no 1\n",
" pl 7\n",
" pt 8\n",
" sk 2\n",
" sl 1\n",
" sv 7\n",
" tl 2\n",
" tr 5\n",
" und 107\n",
" vi 3\n",
"Hillary Clinton ar 5\n",
" de 168\n",
" en 18100\n",
" es 841\n",
" et 2\n",
" fa 4\n",
" fr 202\n",
" hi 31\n",
" ... \n",
"Jeb Bush sl 1\n",
" tl 1\n",
" tr 1\n",
" und 67\n",
" vi 7\n",
" zh 2\n",
"Rand Paul da 3\n",
" de 14\n",
" en 19607\n",
" es 165\n",
" et 12\n",
" fi 1\n",
" fr 42\n",
" hi 2\n",
" ht 6\n",
" in 7\n",
" it 5\n",
" ja 6\n",
" ko 1\n",
" lv 2\n",
" nl 2\n",
" pl 3\n",
" pt 15\n",
" ru 9\n",
" sk 2\n",
" sv 2\n",
" th 2\n",
" tl 1\n",
" tr 4\n",
" und 87\n",
"dtype: int64"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"language_groupby = df.groupby(['candidate', 'lang'])\n",
"language_groupby.size()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's a lot of languages! Let's try plotting to get a better idea, but first, I'll remove smaller language/candidate groups.\n",
"\n",
"By the way, each `lang` value is an IANA language tag - you can look them up at https://www.iana.org/assignments/language-subtag-registry/language-subtag-registry."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"largest_languages = language_groupby.filter(lambda group: len(group) > 10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I'll also remove English, since it would just dwarf all the other languages."
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArYAAAIlCAYAAAAg8bsBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcZGV18PFf9TBsMswQFpFVFj0qKkg0mCiIAi4YFVAi\nokHQAAYk+EYEFRVEUQSTGHFBkU2DGwGCCyCgoIiggiiY4BGVEQRE9hlGYGCm3z+e205RdPd09VR3\n3Vv9+87nfrrqPvfWPVXdPX3q1LnPbQ0PDyNJkiQ13VC/A5AkSZJ6wcRWkiRJA8HEVpIkSQPBxFaS\nJEkDwcRWkiRJA8HEVpIkSQPBxFbqUkQcFRG79TsOjS0i3hkRH5/kvi+MiM9ERKvXcTVNRBwSEW/p\ndxy9EhGHRsS+U72PpP4xsZW6dxSwbb+DaBcR20bEpRFxb0QsiIjj+h1Tn70K2G7kTkQcERF3RsRm\nE9h3Z+BtQKMT24h4fkS8YAUf5p3Ajj0Ipy7eBewAEBFrRMRtEfHJie4zERGxU0Q8ZwVilLQCVup3\nANJERcTpwCuAHTIzO8Y+DLw3M2fcm7WIWAU4D7gZ+Efgz8Cf+hrUKKrv3z6jDD2cmatNwSHbrz5z\nInBeZt7U64NExHxgk3E22Tczv9jr407AV4EfAFeswGNMyRV8IuINwIHANsAqwG3A5cC7M/OPU3HM\nyl+eT2Y+EBHbA3dOdJ8Juhj4MHBtl/tJ6gETWzXNusCFEfH8zLyjY2ymXkYvgA2BAzPz/H4Hsxx/\nAvboWLd0qg+amX8GftXlbhOt2L6WkpwBvBXYD3gRsKRad2OXx+2VYWpWda7aO06jvME5D3gLcDfw\nZGAnYOEUh/CY1yMzf9vtPpM5jqTpY2KrprmrWs6JiBdn5uK2sb/8MYmIo4EPACtl5tJq3b7AqcCW\nmfm7iNgBOB7YGFgbWET5o/tHSnKyBeWP7mcy89iOOHaNiN2rbW4FTszMv3ykGRFDwBGUqtS6QALH\nZOb/VONzq1i2AdYHHgH+NTNP7XzCEbE18FFge+BR4DvA4Zl5c7XJX1VfvxURI7s9rkoYEa8D3gM8\nqdpnUfVYh2bmnW3bvQj4EPBc4AHgfyiVtHuq8R2Aj7W9bosp1bZDJ5AoLM7MH401WFXedwfWA+YC\ndwBfBD6QmUvatnsL8A7gqZQE8mbga5l59BiPuy+P/d4/A/gPSrvCSpTvz0sy8/623a6O8oI+BFwE\nHNL+Oo3IzGvajvPS6uYVmbk0Ip4H3BERr8/Ms6ptdgS+B2ybmT+v1h0IfAZ4YmbeFRGbAB8HXsqy\n1/cdmXlL27G2Bz4C/HX1Op0DvC8zH6w2aQFvjIg3Vve/lZmvHuO575SZ943y0rWA50bE1cDTgHuA\n04Gjq+f3a+CGzHxNW1xvAz4NrJeZd3c83n6UpPbIzPxo2/rvA2e0PcZx1XZrUyqqn8zM49vGz6d8\n79cBVgN+AxybmV9u22bd6nnuWq26GlijPZiq2n55Zv5jF/v8C6U9YV1gQfV6HJmZj7RtdmREHFnd\n/lRm/ku17/6U9o5NgJuAT2TmyUjqmRn3sa0a7yHg1ZQKz2eXs+3yKribA38DfJDSV3kC8P+AgymJ\n2yspHyt+qEpG2j0B+ASl+ngx8ImIeGvb+Mcpf/z+DdgN+BlwdpXoAKxFSeAupfSDvpHyx/0xImJD\nysfJcyhtBv8MbA1cFhGdH9+/A3hhtVwwyvN9JvAc4ABgF+D9wN/T9jpWvYGXUBKYPYF3V6/Dt9pO\nptqckhQdTXndDqH0HH91lGN2akXErIhYaWTpGH8h5f+l1wMvA86kJOP/3BbjwcAXgB9RXtvdKMnP\niyZw/BFfo6pyA68DTu9IamFZgvO+6uvyft5Gcw3lzVF7j+aLq6/bt63bAfhZldSuSfmePwnYl9Lv\n+zTgmyPfg+rn6BJKUro75ef1rZSf4XbfYdnPxOHVutGe+2hJ7Yg1KcnbHpQ3Ge+h/M4AfBPYMSJm\ndzy/n46S1FId86Yq3vFcCPwTpfXoVOC4jhM2X075qP9VlO//b4EvRcQz27Y5h/LG4EjgDZSfl1U7\njjPMY/+fmMg+PwIOqmI4DjiU8n9GuzNY9rr/O/wlIf5kNfYa4BvA56o3nJJ6xIqtmqaVmbdHxB7A\n9yPiR5l5yljbTvAxL8nM3wE/jIjXAEtGqp0RcRWwN+WP2GVt+5zVdtwLI2IDykllp1RVn7dTEr4v\nVHFcRkm83gL8tO1xfpSZ3xsntqMoFbtXZOYDVUw/piQ076BUckf8crxqaJvzqyr25RHxVODtEbFS\nZj5KSThuBHbPzOHqeDdSku69gK+0Pc73qtftioj4K+DfI2JzSuKyStt2j1aPDSWhaq9sERFvy8zP\nt626s+01uTQiXk5JdD8VEatS+hfPzMy3tT3GG4FNJ/DcR6wPXJyZX6vuXzjKNv9VvU6XjfI6TUhV\n1byQ8jH7iF0oye5OwIlVsroz8Llq/C2UivW2lIoglDca3wOeB/yEknhdQ0kUR37On0j5lODt1f1h\nymvZ+TMxkec+Ypjyff5Udf+iiFgD+NeI+BglEfx/Vfwjb6ZexNhvAp4JfHPkU5SxZOZlbXe/FxGv\nopzE9j9t62/IzMvhL78TfwL+Afhl9Ub0BZSf4/Oq7b/T8eYTHvspz4T2ycyr2+5eVlXOd6S80R1x\nS/vrHhGzKL/Ln6B8StSivKndjvKG5L/HeCkkdcmKrRopM39M+UjvxIh4Vg8fej4l+Ro5ziJK68O6\ny9nvUmCjiHgipb1gJcof90coienDlLaFiZyV3+7vgKtGktoqppuAXwN/2+VjjSYp/w+s33a8744k\ntdXxLqe0LYx3vJGT+TagJDZ/blvak9Y/UVoc2pdzJhDjBtXtrSgtCt9Yzj7LcwSwe0RcERH7jlL9\nHi2G9tepG/8DPC0iNo6ItSjP+b3Ai6uK9baUn69zq+2fR6kS3kX52VlMSWqHKdXykW2ez7Kfr8WU\nxGmViBiJcaw3dt0+906XUj7+3yozrwB+R3nTQ/W7uB6jf2IworMC+jhRptj6VUQ8HBH3AltSKsej\nqtpk7mLZz8nI/wmXLu9YbSa0T0TsHRHXRsSDEbGQktSOGVtlc8qnNEfw2O/ZjnT/f4KkcVixVWNl\n5qcj4iXAf1F6INuN9N6uRknKJuphHv978TAwe5Rt243sM0xpl4BSsb2yY7tenRzTojcnqIz0Y67c\ntm60Fo7lHa/9cX5CSd5G3NV2+5HM/NkkYhyJb+T7MOGq6Wgy89SIuIBSHf0ocEzVsz1Wj/Bor9NE\nXUhJ8HenvBb/R/k4+t8oH9vvANyUmSNn0T9EqdC+9PEPxcisDg9SfubfO8o2Iy0Ao1ZFJ/HcO7X/\nrAOcDLy/ahHZDbgjM38yxr4JPDsiWu1vntpFxD9R2kBOoLyBGQJOmkBc7T8nI8lzN9+v5e4TETtT\n/r85nfKJyWKgs/9+NCP/J3wUOLtj7OEuYpS0HCa2aprOP4b/BFwH7N8xNnKSzVaURGtFjjERrwTm\nZ+afImIpJanYMjM/PYnHancV8JqIWKOtFWEz4CmU/tNeuwrYuT3xqD5qXZ3HJ+mjquIcK3ld0Zkr\nfkVJandiWYVzrOPMGu+BMvN24NiI+Czl5+VAlvWh9kxmLoqI/6FUNW+nTDu2uGpR2JNS4W7/Xv6S\ncpLV0pGTy0bxv5Q3Dze0nSzW6X7KyVWjxdT53N9G6QnvNNqbmVdS3ixeX90/iZJg70NJbL8+RjxQ\nksKPA/8C/OcY2zwHWJiZR4ysiIhup6/7cfX1VZQTQsfS/vM41j7tr8HI/LT/OtKXHBE389g2mNFe\n9z9U65+RmUciacqY2KppOqfrubc6Q/47PPaP1Dcof0g+W51pfxfL/ih1dYxR7gNsFRE7UU4iexMl\nOXlTFdNdEXESpSdzmHKSzyPV8f8zM7up0BxN6Rs8PyL+nVJV+gBlJoZPjLPfZB1BSW7PiYhTKR+R\nfwj4SfsZ5ytglSgXDeh8TX+VmSOV3TErw5l5X0T8G3BYRNxP6f3dnFL5bK843gK8OiJ2zsxLOh8n\nIt4H/Jwy68OzKD3By5vPdEWcRjnJ8BHKyWhQktmvUxLwM9q2PZ3St3peRHyU0nYyF1it7XtwHOW5\nXxwRJ1JmRdiEUvm9vNrmx8C+1e/H74ENMvNLYzz3sRLHYWCzqlI5m3Li5ptpm30hM++PiM9TktsN\nKG8QxvJJyglh/1GdqHgO5ff0iZTfoQ9TetD/ufq9/S5l1ot1WFatHstffm4y8wcR8d/AJ6v2oJ9S\nfndWn8Q+7a0aI/3xx0fE1ynV1o14fIK8Z0RcBtwHrJGZ50TEsdV+p1KmOltI6Tn+78y8bTnPTdIE\n2WOrJuk8gxmAzLyYcpJW+7r7KVW9h4EvU5LL11ZfF7Rt2vl4ox2j8/63KUnqeZSZADagTBXVfmLV\nIZQ/9LtS/nh/hZIUzBvvCXbKzD9Q/uA/SKl2nUSp1u1Yzc06VoyjGfX147GT1l9DmY1gXUrS9THK\nR+m7jrVPFzEMV497OeWs/5Hl+yz72H2s17993fspJ+DsSXltD6R81N9+UtqxwA2Uj7QfE191AtqL\nKa/nd4DDKAnXf7RtN5nnN+a+mfldysfwv8zMG6rV36YkdRe3twFk5r2Uk5guB44Bzqe8iXlO2zZX\nVs/hIUorwLcpsxVs1HbY91fP70TKyUlvmMBz73QRJek8m1Ih3w74h46puqj2Xwe4tuPkqs7X4VHK\niZiHAs+gJPcXVftvSEkCT6e8mXpTFeP5lPaAG0Z5yHadr/velI/+D6T8DH+VUjn9yWT3qU5qO4Ty\nO/ntKr7NKG8URhxM+R39YvX8Xl7t+3HKJ0wjM4icTZnpZK3lPC9JXWgND8/UOe0lDYqI+CFwXWYe\n1O9YZqIoV7/7HeXqf2csb3tJmiq2IkhqlIh4PaUF5BZKJe+VlBkCjhhvP/Ve1X/9CGW+49spVUpJ\n6hsTW0lN83TKiUpPovRfXg/sVU09pWkSERtRLtAwTOkffuVYMx1I0nSxFUGSJEkDwZPHJEmSNBBm\nVCvCg3feanlaj7H43nv6HYJqaLX1N1j+Rppxhpcu6XcIqqFV5q3Xi4vlrLBnb/qinuU41/3++7V4\nTpNhxVaSJEkDYUZVbCVJkgZRq9XYImtPmdhKkiQ1XKvlh/BgK4IkSZIGhImtJEmSBoKtCJIkSQ03\nhD220IDEtrq6zc3AkzPz5n7HI0mSpHqqfWIrSZKk8TkrQmFiK0mS1HBDzooA1DCxjYj1gc8DOwB3\nACd0jO8P/AuwMfA74IjMvHi645QkSVK91DG9PxN4hJK47gDsCwwDrSqpPRzYOzPnAUcC50TEFn2K\nVZIkqe9arVbPliarVWIbERsCLwYOy8yFmXkHcDT85VS/Q4FjMvN6gMy8ALgU2KsP4UqSJKlG6taK\nsFH19fdt6+a33d4M+HREfLJt3SzglimOS5IkSTVXt8T21urrkyn9syO3R8wHPpCZZ09fSJIkSfXW\nch5boGaJbWb+ISIuA46PiP2A1YEPtG3yH8AHI+I3wHXAqsBfA3dmZk53vJIkSXXgrAhFHV+FvYFV\nKO0F3wfOoJw8NpyZXwCOB04D7qG0LBxJzRJ0SZIkTb/W8PBwv2OYNg/eeevMebKakMX33tPvEFRD\nq62/Qb9DUA0NL13S7xBUQ6vMW68WPQB/99RX9izH+dGvv12L5zQZVjolSZIabqjh03T1Sh1bESRJ\nkqSumdhKkiRpINiKIEmS1HAta5WAFVtJkiQNCCu2kiRJDdfy5DHAxFaSJKnxnBWhsBVBkiRJA2FG\nVWxbQ7P6HYJqxon4JU2Uf0NUZy2s2IIVW0mSJA0IE1tJkiQNhBnViiBJkjSIhlrWKsGKrSRJkgaE\nFVtJkqSGcx7bwsRWkiSp4ZzHtmh8K0JEnB4RJ/c7DkmSJPXXIFRsh6tFkiRpRnIe26LxFduK301J\nkqQZrhEV24hYHTgG2AOYC/wEeHtm/ravgUmSJKk2GpHYAicDc4DtgHuB9wHfiohnYbVWkiTNcM5j\nW9Q+sY2IdYA3AJtm5p3VumOAd1ASXftrJUnSjOZ0X0XtE1tgs+rrdRHRvn4lYOPpD0eSJEl11ITE\n9vfV1y0z8+7OwYh42TTHI0mSVCvOY1vUviEjM/8EfBn4bERsABAR8yJi94h4AvbYSpKkGa7Vw39N\nVvvEtrI/kMBlEbEAuA54LcvmsLXPVpIkaYZrQisCmfkg8P5q6bTfNIcjSZKkGmpEYitJkqSxOStC\n0ZRWBEmSJGlcVmwlSZIazlkRChNbSZKkhmv6bAa9YiuCJEmSBoIVW0mSpIYbalmrBCu2kiRJGhAm\ntpIkSRoIM6oVYXjpkn6HoJq54vjz+h2CaujQL3253yGohn54yaf7HYJqaOU11+53CIDz2I6YUYmt\nJEnSIHK6r8LEVpIkSV2JiL2Ag4FnA6tn5uy2sX2BU4FFbbt8IzPf2LbNc4HPAFsBtwNHZeaZbePr\nAScBOwMPVY/3nswcHi8uE1tJkqSG68M8tvcAnwJWBz4/yvhvMvOpo+0YEXOBC4DjgRcALwLOjYjf\nZuZV1WZnAvcDGwLrABdWxzx+vKBMbCVJktSVzLwIICJ2HGOT8TLtPYAHMvOE6v4lEXEucABwVURs\nBuwEbJGZC4GFEfEx4H2Y2EqSJA22mvXYDgMbR8TtwCPAFZQ2gvnV+NbAtR37XAu8qW38/sy8qWP8\nyRGxRmY+MNaBne5LkiRJvfQD4JmZ+STgeZQe2YsjYrVqfA1gQcc+9wFrVrfnUNoQOsdp22ZUJraS\nJEnqmcy8KTN/U92+A9gfeBLw/GqThcDcjt3msSzZHWt8ZGxMJraSJEkN12q1erZMZZjV118A23SM\nbQv8vG18btVr2z5+U9VzOyZ7bCVJkhpuuntsI2IIWLlaiIhVgFZmPhQRr6Qkp7cCawHHAXcCIzMe\nnAscHxGHAScC2wO7Uab2IjNviohLqm3eAqwLHA58bnlx1TKxjYjVgWMoZ83NBX4CvD0zf1vNm/YB\nYCPgz8CFmblvv2KVJEmagfahzC0L5WSxB4HhiNicMn3X5yk53ALgh8AumflngMy8PyJ2BT5Nyfdu\nAw7MzB+3Pf4bKfPY3go8DJySmePOiAA1TWyBkymNw9sB91Kmd/hWRGwHfIny4lxWNSFv278wJUmS\n+m+657HNzNOB08cYPrxaxtv/akqeN9b4ncBru42rdoltRKwDvAHYtHpSRMQxwDso0z8sBp4eEddl\n5j2UKSQkSZJmrJpN99U3dTx5bKRR+LqIuDci7gXupiThGwC7Ai8HfhMRV0fEG/oUpyRJkmqkdhVb\n4PfV1y0z8+4xtvl+RLSA1wBnR8RVHZP4SpIkaYapXWKbmX+KiC8Dn42Id2TmbRExD3gxcA1lot9L\nqsbj+ykNy0v6GLIkSVJfTfE0XY1Rx1YEKBP5JnBZRCwArqM0ED8KHATcVK3/FPDmzLy5b5FKkiSp\nFmpXsQXIzAeB91dLp52mORxJkqRa8+SxopaJrSRJkiZuuqf7qqu6tiJIkiRJXbFiK0mS1HC2IhRW\nbCVJkjQQTGwlSZI0EGxFkCRJajjnsS1MbCVJkhrOHtvCVgRJkiQNhBlVsZ21yqr9DkE184LDX9fv\nEFRDV/tzodEMD/c7AmlMtiIUMyqxlSRJGkReoKGwFUGSJEkDwcRWkiRJA8FWBEmSpIYbshMBsGIr\nSZKkAWHFVpIkqeGcFaGwYitJkqSB0MiKbUScDjySmfv3OxZJkqR+88pjRSMTW0mSJC1jK0JR28Q2\nIlYHjgH2AOYCPwHeDrwW2LvaZi9gGJibmV4SRpIkaQarbWILnAzMAbYD7gXeB3wLeBbwdEorwgH9\nC0+SJEl1UsvENiLWAd4AbJqZd1brjgHeQUl0Aa8dJ0mSBDBkWgTUNLEFNqu+XhcR7etXAjae/nAk\nSZJUd3VNbH9ffd0yM+/uHIyIXaY5HkmSpNry5LGilvPYZuafgC8Dn42IDQAiYl5E7B4RTwD+CGwe\nEX4XJUnSjDfUavVsabJaJraV/YEELouIBcB1lBkRhoEvAE8A7o6Ie0xwJUmSVNdWBDLzQeD91dLp\nJuD50xuRJElSPTW80Nozda7YSpIkSRNmYitJkqSBUNtWBEmSJE1M00/66hUTW0mSpIZreYEGwFYE\nSZIkDQgrtpIkSQ3nBRoKE1tJkqSGs8e2sBVBkiRJA2FGVWxvv/TKfoegmllzyw36HYJqaNV11+13\nCKqh1tCsfocgjcmCbWHFVpIkSQPBxFaSJEkDYUa1IkiSJA0iTx4rTGwlSZIazgs0FLYiSJIkaSBY\nsZUkSWo4WxGKRiS2EfFXwFeA7YAbM/N5fQ5JkiSpNsxri0YktsDbgNWBv8rMpf0ORpIkSfXTlB7b\nzYFfjZbURsTKfYhHkiRJNVP7im1EfBN4WXV7L+Aa4AXAfsAxwNrA3L4FKEmSpFqofcU2M18FnAmc\nnplzgKOAWcArgK2BJ/YxPEmSpL5rtVo9W5qs9hXbSqtaaPt6RGYu7FM8kiRJteGsCEXtK7aV4Y77\nSzPzD32JRJIkSbXUlIotPDa57Ux0JUmSZiwLtkVTEtv2VgRJkiS1sRWhaEpiO4wVW0mSpFqoZqo6\nGHg2sHpmzm4b2wc4EHg6sAT4KXB4Zv6ybZvnAp8BtgJuB47KzDPbxtcDTgJ2Bh4CTgXek5nj5oCN\n6LHNzP0y84Dq9mWZ6dy1kiRJ/XMP8CngHaOMrQF8ANiwWn4GXBQRqwFExFzgAuAsYB7lQlwnRcTz\n2x7jTGBptf92wO7Au5YXVFMqtpIkSRpDa5o7NjPzIoCI2HGUsc+034+IDwPvBQL4ObAH8EBmnlBt\ncklEnAscAFwVEZsBOwFbVDNgLYyIjwHvA44fL65GVGwlSZLUWDsBi4Abq/tbA9d2bHNttX5k/P7M\nvKlj/MkRscZ4B7JiK0mS1HB1vbBCRDyV0h/7zsxcVK1eA1jQsel9wJrV7TnA/aOMU23zwFjHM7GV\nJElquKEa5rUR8QzgIuCEzPx829BC4Mkdm89jWbK7EJg7yvjI2JhsRZAkSVJPRcS2wKXARzLz4x3D\nvwC26Vi3LaX/dmR8btVr2z5+0/KuOmvFVpIkqeGmuxUhIoaAlauFiFgFaGXmQxHxAuBbwGGZecoo\nu58LHB8RhwEnAtsDu1Gm9iIzb4qIS6pt3gKsCxwOfG55cVmxlSRJUrf2Af4MXEjJJx8EFkXEpsCH\nKH2yn4iIhW3LCwAy835gV2BP4F7KfLUHZuaP2x7/jdXj3gr8GDg3M8edEQGs2EqSJKlLmXk6cPoY\nwy+ZwP5XU+anHWv8TuC13cY1oxLbJ734b/sdgmpm6SOP9DsE1dDQ7NnL30iSaqSusyJMtxmV2EqS\nJA2iOs6K0A/22EqSJGkgWLGVJElqOFsRChNbSZKkhjOvLWxFkCRJ0kAwsZUkSdJAqH1iGxHzI+KN\nY4y9NyK+Md0xSZIk1clQq9Wzpcma0GM7XC2Pk5kfmeZYJEmSVFNNSGwlSZI0jhbNrrT2SlMS200j\n4hLKpdfmAwdk5pURcTTwgszcpZ/BSZIk9VPDOwh6pvY9tkAL2A84BJgLXAyc0deIJEmSVDtNSGyH\ngc9l5g2ZuRQ4BdgyItbsc1ySJEm14MljRRMSW4Db224vqr7O6UcgkiRJqqemJLaSJEnSuJpy8pgk\nSZLG0Gp4C0GvNLViO9yxSJIkaYarfcU2MzfruD8fmFXd/eC0ByRJklQzFmyL2ie2kiRJGp+tCEVX\niW1EbA7sBWwCfCQzb67WPyEzF427syRJkjSFJtxjGxGvBH4FvBnYH1inWn84cMGURCdJkqTlGmr1\nbmmybk4e+whwErAVPOaCxL+s1kmSJEl9001i+xTgm6OsXxlYrTfhSJIkSZPTTWL7a2An2qbXiogh\nYF/gut6GJUmSpIlqtVo9W5qsm5PHjgC+ATyzuv9u4FnAFsCuPY5LkiRJE9TwfLRnJlyxzczvAH8H\nLKCcRLYl8FNg28y8ZGrCkyRJkiamq+m+MvMaYO8pikWadovvvbvfIaiGVl1v/X6HIEldGbJkC4yT\n2EbEM4CJ/u9+W2b+qjchSZIkqRtN743tlfEqtm+i9NFOxA+BHVY8HEmSJGlyxuux/QiwedtyEfBF\nYLOO9W8Dnjq1YUqSJEnjG7Nim5kPAA+M3I+I5wBvzczft28XETcCa01ZhJIkSRqXnQhFN/PYrgqs\nO8r6rYE7ehOOJEmSNDndzIpwFnBsRPwJuByYDbwcOAr4tymITZIkSRPgyWNFN4ntocA6PPayusPA\nqcBxvQyqXUScD3wvMz8+VceQJElqMvPaYsKJbWYuAnaLiKcAzwBWAX6Wmb+ZquCq43pVM0mSJC1X\nVxdoAMjMGyPinuq2s9tLkiT1mRdoKLpKbCNib+BDlCm/iIj5wFGZ+aWeR7bsmJcBFwNnAr8D9gHe\nA2wMXAm8OTP/OFXHlyRJUjNMeFaEiDgQOAO4APiHajkfOCUiDpqa8IDSxzuyUB13e2BD4AnAMVN4\nbEmSJDVENxXbdwEfysz2RPK/I+IO4J3AZ3oa2eON1Ng/mJn3AETEl4F/muLjSpIk1ZqdCEU389hu\nCPxklPXXVGPT5fa2238G5kzjsSVJkmqn1Wr1bGmybhLb64A3jbL+DcD1vQlHkiRJmpxuWhEOB74T\nEc8CLqO0BrwICOAVvQ/tL5r91kGSJGmKNbzQ2jMTrthm5veBZwI/B3YBdqJUcZ+dmZdOTXjAspPG\n2k8gY5x1kiRJM4qtCMWEK7YRsWp1MYY3d6yfGxFbZOZvex4dkJkvbrs7q2PsDMpMDZIkSZrhuumx\n/VFE7DfK+t2Bb/UoHkmSJGlSuklsnwbcPMr6W4AtehOOJEmSNDndJLYLgaeMsv5pwD29CUeSJEnd\narV6tzRZN7MifAH4UETcCVwKLAFeAnwQOG0KYpMkSdIEDDU9I+2RbhLbo4H1ga/x2Erv14AjexiT\nJEmS1LUJJ7aZ+Qjw1oj4MPBcYDHwf5l541QFJ0mSpOWzYFt0U7EFIDNvAm6aglgkSZI0CU2ff7ZX\nujl5TJJD/2QoAAAgAElEQVQkSaqtriu20iCZPXdev0OQJEk9YmIrSZLUcHYiFN1cUrcF/CPwJmAT\n4LWZ+b8RsQWwVmZePUUxSpIkScvVTY/tEcDngN8DTwVWqda/FDilx3FJkiRpglqtVs+WJuumFeEA\n4HDgs8Bb29b/Bi+pK0mS1Df9yEcjYm3g3ylFztWAbwMHZ+Z91fg+wFGU6yBcDxyUmT9r2/+5wGeA\nrYDbgaMy88wViambiu0TKUlsp/WAR1ckCEmSJDXOF4HVgS2BzYC1gS8BRMQLKUnrgcA84Gzg/IiY\nU43PBS4AzqrG3wacFBHPX5GAuqnY/qA66PdHVkTEJsC7gctWJAhJkiRN3nS3EETEE4CXA9tk5iJg\nUUR8BLgsIjYG9gfOzsxLql1OiIiDgd0pCfEewAOZeUI1fklEnEvpELhqsnF1U7E9BNiG0mML8N+U\nCu4awDsnG8BERcT5EXHYVB9HkiRJy9WqlvZcclb1dRvg2cA1Hfv8vFoPsDVwbcf4tdX6Sevmkrq/\niYitgL0pAT9M6Zc4MzMfXpEgJnj8XUduR8RS4IWZ+aOpPq4kSZIeKzMfiIjLgKMjYl9gZeC91fCa\nwBzg/o7d7qvGqMYXjDM+KV3NY5uZDwCfX5ED9lCzT9uTJEnqkT5NZvAmysljNwAPVrd3Au4CFlJ6\nZ9utBdxY3V4IbNoxPo/HJ7td6WYe2z2AZ44xvAS4A7ggM29dkYDGOf5lwMXAntWqi6rK7Vcy84Cp\nOKYkSVIT9GOarsy8Ddhr5H5EvJKS4F4F/ALYtm2sBTyH0soKpS3hNR0PuW21ftK6qdi+n5JZL+pY\nvy6wmDKv7SMRsUtmXrkiQY1hGBjOzG2qhHYXWxEkSZL6IyKeSqnO3gf8NfAfwHGZeX9EnAxcGBFn\nAFcAhwKzgXOr3c8Fjq/OnzoR2B7YDdh5RWLq5uSxTYB9MnPj9gU4mpJdr0WZHeFDKxKQJEmSutNq\n9W7pwg7ALyltBWcCJ2bmhwAy8wrgIOBk4F7KLAi7Vm2tZOb9wK6UT+LvBU4CDszMH6/I69BNxXZ1\nRp+v9lrgyMz8c0R8DjhtRQKSJElSd4b604rwBeAL44x/iWpe2zHGrwa262VM3VRsrwX2G2X9bsAf\nqtuLgVVXNKgJGJ6GY0iSJKlBuqnYHgxcGRH/C3yPcsLYCyg9FftX2wRwU08jXKb9rcgfgacC9thK\nkqQZr0+zItTOhCu2mXkt8CzgSuD5wMuAW4EdMvOUarPvAv/S6yAr7VXaI4FjIuKeiPjsFB1PkiRJ\nDdIaHp45n+ovXnD3zHmympAlDz/U7xBUQ7NWmY6OKkmDYOU1165FrfTiIz7bsxxnl4/9cy2e02R0\ndYGGiNgIeC6PvyrErZn53Z5FJUmSpAnrxzy2ddTNBRr2As6gTOmwBuXKEIsosyX8idKmIEmSpGlm\nXlt0MyvCRylzjK0LPADsmZmbAa/n8ZdEkyRJkqZVN4ntBsB5mTkMzGHZnLZDTM8UX5IkSRpFa6jV\ns6XJukls72RZb+2vgH0iYi7wOmB+j+OSJEmSutLNyWMfBG6pbh8LfJkyf+0wcECP45IkSdIE2WNb\nTDixzcyT225/PSJuAJ4OXJ+ZN0xFcJIkSdJEdTXdV7vMvB64voexSJIkSZPWzXRft4wxNAxckplv\n6U1I0vQZmj273yGohoaXPLr8jTTjtGZNuhYkTTnnsS26+S09ZYz1TwN26EEskiRJmgTz2qKbHtuj\nR1sfEdsD5/cqIEmSJGkyevG5ykaA7xMkSZL6xFaEopse25d0rFoVCOAw4Du9DEqSJEkTZ15bdFOx\nvWSUdUuAb+A8tpIkSeqzbhLbzTvuPwLckZmePixJkqS+6+bksflTGMe4IuJ84HuZ+fF+xSBJklRb\n9iIA3fXYfpAyrdcwjz1ZbJjSknAHcHZmntvTCIHM3LXXjylJkqTBMtTFtnsBs4HbgFvbli2ATYEn\nA2dHxJt7HKMkSZLG0Wq1erY0WTc9tk8C3p6ZF7evjIj9gHdm5gsj4njgHcAZPYyRiLgMuDgzj42I\n04CdgHnALcCHM/MrvTyeJElSkzQ8H+2Zbiq2AHNGWXcHpWILZeaEp6xQRKMbrhaAy4GtgbnAMcDp\nEfH0KTimJEmSGqSbiu35wPsj4ieZ+QeAiFgHOBy4vtpmFcpsCVMmM09tu/u1iDgM2BG4YSqPK0mS\nVFetIUu20F1iewilWvq7iEhgKaU6uwh4dbXNNsD/9TTCNhHRAj4I/AOwPqWK+wRgnak6piRJkpph\nwq0ImXkn8CzgLcCFwJXAe4EtM/PKarOPArv3OshKC9gbeCuwR2bOy8y1gF/gJX0lSZJmvG4qtmTm\nI8B/Vcto448Cf+pBXGOZAzwK3BURKwH7UPptvzmFx5QkSao1Tx4rukpsI2JDYFdKG8Ds9rHM/EAP\n4xrNMGW2hZcAvwH+DHwJ+MEUH1eSJKnWmj5NV690c4GG11MSyRZwF/BQNdSiJJ1TmdjOAhZn5oOU\n/lpJkiTpMbqp2H4IOAc4IDMXTFE8jxMRc4AtKVVaSZIkdbBgW3ST2G4KHDTNSe1zgEuBC4BvTNdx\nJUmSmsRWhKKbxHbaEtoRmXkt5QpjkiRJ0ri6SWxvpVwQ4c+jjA1n5iY9ikmSJEnqWjeJ7bHAVmOM\nDY+xXpIkSVPMToRiwoltZp4FnDWFsUiSJEmTNpl5bJ8HrNkxdGtmfrdnUUmSJGnCPHms6GYe270o\nF0hYCKxBOZlsEbA65Wpjz5qKACVJkqSJ6KZi+1HgJOAdwJ3Anpn5/YjYkYZMxbV08cP9DkFSAwyt\nvEq/Q5Ck7gz1O4B66OZl2AA4LzOHgTnAo22PsWqvA5MkSdLEtFqtni1N1k1ieyfLemt/BewTEXOB\n1wHzexyXJEmS1JVuWhE+CNxS3T4W+DKwP2WqrwN6HJckSZLUlW6m+zq57fbXI+IG4OnAdZn5q6kI\nTpIkScvX8A6Cnpl0q3FmXp+ZXwcWR8RRPYxJkiRJ6tqYFduI2BfYfDn7t4CdgbUprQqSJEmaZk0/\n6atXxmtFeAbwD4x/udxh4DbgwF4GNVERcTTwgszcpR/HlyRJqgPz2mLMxDYzDwcOn8ZYJEmSpEnr\n6pK6kiRJqiFLtkADEtuImA98DtgJ2I4yZ+4BmXll/6KSJElS3TTlAmz7AYcAc4GLgTP6G44kSZLq\npgmJ7TDwucy8ITOXAqcAW0bEmsvZT5IkaUZoDbV6tjRZ7VsRKre33V5UfZ3Tj0AkSZLqxhbbogkV\nW0mSJGm5mlKxlSRJ0hi8QEPR1MR2uGORJEmascxri9ontpm5Wcf9+cCs6q6X8ZUkSRJgj60kSZIG\nRO0rtpIkSVqOPvUiRMTOwIeBrYCHgK9n5sHV2D7AUcD6wPXAQZn5s7Z9nwt8ptr3duCozDxzReKx\nYitJkqSuRcSOwFnA8cBfARsCX6jGXkhJWg8E5gFnA+dHxJxqfC5wQbX/POBtwEkR8fwVicmKrSRJ\nUsP16cIKHwU+m5nntK27tvq6P3B2Zl5S3T8hIg4Gdge+COwBPJCZJ1Tjl0TEucABwFWTDcjEVpIk\nqeGmuxMhIp4APA/4YURcA2wC/BI4LDOvAZ4NnNax28+r9QBbsywJHnEt8KYVictWBEmSJHVrLUoe\nuRfwZmAD4CJKu8FcyhVi7+/Y5z5gzer2HGDBOOOTYsVWkiSp6ab/5LGF1dfTMvOX1e2PRsS7gL+r\nxud17LMWcGPb/pt2jM/j8cluV6zYSpIkqSuZeT8wv31dRLRYdvGsXwDbdow9p1oPpS1hm46H3bZa\nP2kzqmI7tPIq/Q5BUgMML13S7xBUQ62hWcvfSJpZPgMcGhFfoVRi/5Uy5dcVlIrshRFxRnX/UGA2\ncG6177nA8RFxGHAisD2wG7DzigRkxVaSJKnhWq3eLROVmR8HTgW+B9wJvAx4RWYuzMwrgIOAk4F7\nKbMg7JqZD1T73g/sCuxZjZ8EHJiZP16h12F4eHhF9m+UxQvunjlPVtKkWbHVaKzYajQrr7l2f66M\n0OGGU77Wsxzn6W99fS2e02TMqFYESZKkQdSneWxrx8RWkiSp4Vp9uqRu3dhjK0mSpIFgxVaSJKnp\nLNgCVmwlSZI0IExsJUmSNBBsRZAkSWo4Tx4rapXYRsR84HPATsB2lEu1HZCZV0bESsB7gTdTrjX8\nM+DQzPzfvgQrSZJUEya2RR1bEfYDDgHmAhcDZ1Tr3wX8I/AKYH3gcuDiiJjTjyAlSZJUL3VLbIeB\nz2XmDZm5FDgF2DIi1qQkvMdl5q8zczFwDLAEeGX/wpUkSaqBoR4uDVbH8G9vu72o+joH2Ai4aWQg\nM4cprQobTVtkkiRJNdRqtXq2NFkdE9ux3AJsNnInIoaAJ1frJUmSNMPV6uSx5TgdODwifgD8HjgC\nmAV8u59BSZIkqR6akNgOV8sJwCrARZQTy64FXpqZD/QxNkmSpL5regtBr7SGh4f7HcO0Wbzg7pnz\nZCVN2vDSJf0OQTXUGprV7xBUQyuvuXYtMsrffuXcnuU4W7xh91o8p8loQsVWkiRJ42lsKtpbJraS\nJEkN1xoys4VmzYogSZIkjcmKrSRJUtN58hhgxVaSJEkDwsRWkiRJA8FWBEmSpIazE6EwsZUkSWo4\nL9BQ2IogSZKkgWDFVjPa4vvu7XcIqqHfffPH/Q5BNRRv3KXfIUhjcx5bwMRWkiSp8WxFKGxFkCRJ\n0kAwsZUkSdJAsBVBkiSp6exEAKzYSpIkaUBYsZUkSWo4Tx4rGlexjYijI+LifschSZKkerFiK0mS\n1HAt57EFaprYRsR84BTgpcA2wK+Afwa2AN4DDEXEQmAYeHZmzu9LoJIkSXVgKwJQ08S2ciDwKuB6\n4J3A+ZTE9iPACzLzpX2MTZIkSTVT18R2GDglM6+t7n8sIg4C/r6679sSSZKkiiePFXU+eWx+x/2b\ngY36EIckSZIaoM6J7WYjNyKiBWwC3AIs7VtEkiRJqq26JrYtYL+IeE5EzAbeBawGfBv4I7BJtV6S\nJEmtHi4NVtfEdhj4PPBJ4B5gT+CVmbkQOItSuf1jRNwTEZv2L0xJkqT+aw21erY0WV1PHgP4bWZu\n37kyM+8Ddu5DPJIkSaqxOie2kiRJmghnRQBMbCVJkhrP6b6KWia2mbnZ8reSJEmSlqnryWOSJElS\nV2pZsZUkSVIXGj6bQa9YsZUkSdJAsGIrSZLUcJ48VpjYSpIkNZ15LWArgiRJkgaEFVvNaCs9YY1+\nh6Aaeto/vrzfIUhSV2xFKKzYSpIkaSCY2EqSJGkg2IogSZLUdM5jC5jYSpIkNZ49toWtCJIkSRoI\nVmwlSZKarg8V24g4FngDsDbwCHA18O7M/Hk1vg9wFLA+cD1wUGb+rG3/5wKfAbYCbgeOyswzVySm\n2ldsI+KyiDiy33FIkiTVVavV6tnShS8CW2fmXGAj4H+BcwAi4oWUpPVAYB5wNnB+RMypxucCFwBn\nVeNvA06KiOevyOvQhIrt8HiDETE7Mx+ZrmAkSZIEmZltd2dRcrZbq/v7A2dn5iXV/RMi4mBgd0pC\nvAfwQGaeUI1fEhHnAgcAV002plonthHxKWB74G8j4t2UF+tKYGVgMfBq4KvAwX0LUpIkaYaKiL0p\nldk1KRXbXaqhZwOndWz+82o9wNbAtR3j1wJvWpF4at2KkJlvBy4HjsnMOZn5NMrVkF8HnA+sAxzW\nxxAlSZJmrMz8cmbOA55ESWzPrYbmAPd3bH4fJQEeGV8wzvik1Lpi26az4ePyzDyruv3gdAcjSZJU\nK32exzYz74iIQ4A7ImIrYCGld7bdWsCN1e2FwKYd4/N4fLLblVpXbNsMd9ye36c4JEmSaqdPJ491\nml19XQj8Ath2ZCAiWsBzqvVQ2hK26dh/22r9pDWhYrt0lHXjnlAmSZKkqVMlqgcDX8vMOyNiI+BE\n4IeZeXNEnAxcGBFnAFcAh1IS35FWhXOB4yPisGq/7YHdgJ1XJK4mVGz/CDyl7b6X1pAkSWrXavVu\nmbhXAL+MiAeAHwK3UWY7IDOvAA4CTgburdbvmpkPVOP3A7sCe1bjJwEHZuaPV+hlGB6ud/Gzmrz3\nNMr8aLcCPwUeycwDun2sxQvurveT1bRb+ogzxenxhmbPXv5GkgSsvObatSi43fXTH/Usx1nneX9X\ni+c0GbVvRcjMq4Fn9TsOSZIk1VsTWhEkSZKk5ap9xVaSJEnLsWKzGQwMK7aSJEkaCFZsJUmSGm4F\n558dGCa2kiRJTWdiC9iKIEmSpAFhxVaSJKnhWkNWbMGKrSRJkgaEia0kSZIGwoxqRXhkwX39DkE1\n8+gDi/odgmpo9lrz+h2C6mjJkn5HoBpaec21+x1C4cljwAxLbCVJkgaSiS1gK4IkSZIGhBVbSZKk\nhvMCDYWJrSRJUtM53RdgK4IkSZIGRKMT24j4QkSc1u84JEmS1H9Nb0UYrhZJkqQZq9VqdK2yZwbh\nVbCpRJIkSdNbsY2I+cCRmXlmdf/JwO+AjYFjgVnAg8CewCLgmMz8fNv+bwGOBNYBzqMktY9O2xOQ\nJEmqI2dFAKa/Yru81oHXAt/IzLWAQ4BPRcTGABGxPfAp4ABgLeBi4PXLeTxJkqSB12q1erY0Wd1a\nEb6bmd8CyMxzgfuAbaqxfYCzMvO7mbk0M78E/KRPcUqSJKlm6nby2B877i8C5lS3NwR+2jF+E/bY\nSpKkmc55bIHpr9guBNZou79BF/veCmzWsW4zbEWQJEkS01+xvQZ4Q0ScCawOvL+Lfb8EXBgRpwM/\nAPYC/gb4da+DlCRJUvNMd8X2fcAS4Hbge8BXWFZxHffEssz8AeWEsi8AdwMvA746lcFKkiQ1gSeP\nFa3h4ZnzSf6iP/x25jxZTcijDyzqdwiqodlrzet3CKqjJUv6HYFqaPUNNqtFJrjgxl/2LMdZ8ynP\nrMVzmoy6nTwmSZKkbjW80torJraSJElN5yV1gfrNYytJkiRNihVbSZKkhms5jy1gxVaSJEkDwsRW\nkiRJA8FWBEmSpKZzVgTAxFaSJKnxmn5hhV6xFUGSJEkDYUZVbGev6dWE9FgrrTGn3yGohlpDs/od\ngiR1x3lsgRmW2EqSJA0ip/sqTO8lSZI0EExsJUmSNBBsRZAkSWo6Z0UArNhKkiRpQDQ+sY2IhRGx\nXb/jkCRJ6pdWq9Wzpcka34qQmc7XJEmSZjan+wIGoGIrSZIkQQMqthFxMPBPmfmctnWbATcCWwA3\nAS/MzB/1KURJkqT+ch5boBkV2zOBp0XE1m3r9gUuzczf9yckSZIk1U3tE9vMvA84D9gPICJawJuB\nU/sZlyRJkuql9olt5TRg74hYCXgJMBc4p78hSZIk1YOzIhS177GtXAI8DLwK2AP4SmY+3N+QJEmS\nasJZEYCGVGwzcwnwReBQYHdsQ5AkSVKHRiS2ldOAHYDfZebV/Q5GkiSpLmxFKFrDw8P9jmHaLF5w\n98x5spqQ4aVL+h2Caqg1NKvfIUhqiJXXXLsWmeBDd93Wsxxn1XU2qMVzmoym9NhKkiRpLPbYAs1q\nRZAkSZLGZGIrSZKkgWArgiRJUsO1+nBJ3YiYBRxHuXDWqsBFwIGZefe0B1OxYitJktR0rVbvlol7\nN/Bq4G+Ajap1X+r1U+uGia0kSZIm4wDguMycn5kLgMOBl0fExv0KyMRWkiSp4VqtoZ4tExER84CN\ngWtG1mXm74AFwNZT8iQnwB5bSZKkppv+CyvMqb7e37H+PmDNaY7lL2ZUYluXSZQlSZJ6qQ85zsLq\n69yO9fMoVdu+sBVBkiRJXcnM+4Cbgb8eWRcRW1Cqtdf1K64ZdUldSZIk9UZEvBfYB3g5cC9wKrBa\nZu7ar5hmVCuCJEmSeuY4YC3gp8AqlHls39TPgKzYSpIkaSDYYytJkqSBYGIrSZKkgWBiK0mSpIFg\nYitJkqSBYGIrSZKkgeB0XzNARLwQ+ENmzo+I9YATgEeBIzLzrv5Gp36KiE0o1/Se074+M7/cn4gk\n1UVEbDCR7TLztqmORZooE9uZ4SRgt+r28cAGwMPAp4HX9yso9VdEHAB8inJd70Udwya2M1hErAo8\nhce/4flRfyJSn/xhAtsMA7OmOhBpokxsZ4aNMvM3ETEE/D2wFSWRuam/YanPPgC8PjPP7Xcgqo+I\neDVwBo+//jvYvjbTbN7vAKRumdjODI9GxOrA04DbM/OOiJgFrNbnuNRfTzCp1Sj+HfggcHJmdlby\nNYNk5vx+xyB1y8R2ZrgU+DqwNnBete6pwO19i0h1cFZE/H1mfqvfgahW1svMT/Q7CNVLRBxJaTt4\nnMz8yDSHI43JxHZm2B84nNJXe0K1bgtKf6VmrlWBr0fEdylvclrV+uHMPKB/YanPLoqI52fmVf0O\nRLWyC49NbDcEngz8EDCxVW2Y2A64iJgNHAsclpkPjqy3SidgKaWSD7Ay5Y9WizGqMhpcHdW4+cA3\nI+KrLPtUp0V5w2MCM0Nl5o6d6yLi7cB60x+NNLbW8LB/wwZdRNwNrJOZfrMlPU5EXMZj39B0vsEZ\nSWxfPJ1xqd4iYiXgtsw0uVVtWLGdGb4BvO7/t3fnUXZVdRbHv4UEkAARZR46oOAWGUQEFWg1gHFA\nHFq76VZERBBtoG0bFQRERCZFEAJZtraIBBVBwZluGtSgDBKmBsHGraCJjEvRBIMMAVL9x7lFXp5V\nlZBO6rx6d3/WqvXuO/fWWxtSK/nVub97DvDN2kGit0haA3gDsClwF3CJ7YfqpoqxNtxsXMRS2K52\ngIhuKWzbYRXgq5LeR7nNODQTk17KFpO0NXA58CTl52Iz4HRJr7F9W8VoUZGkScDjth9uVk/ZF3jS\n9lcqR4uKJF3eNTQR2IGyikZEz8iahO3wOPB1ymLbKzdfE5qvaK9pwBeAv7H9CmAy8O/NeLTXfwLb\nNMfHUh4MOlHSyfUiRQ+4uuvrYuC1to+qmiqiS3psI1pK0p+ADWwv6BhbBbjf9rPrJYuamp789Ww/\nKek3wJuAB4FrbG9aN11ExOjSitASze3FvYCNbZ8iaUNgIHt8t9pcSvvBrzrGJlOKmGivZwALJU0G\nJgy1pUhau26sqK1pTdkSWJdFywNi+6fVQkV0SWHbApJeAlxKWbpnc+AUStP/QcDbKkaLumYAl0j6\nFGV75c0p6x3PqJoqarsNOJryS85lAJI2Av5cM1TUJWkH4FvA33SdeoLyHEdET0iPbTtMA46wvR3l\nLyEoPVI714sUPeAk4BzgCOAHlKL2XOCEipmivn8B9gS2AI5vxqbSFLnRWmcA3wEmUe7qrAV8Hti/\nZqiIbumxbQFJc4Fn2x6UNNf22s34g7YnVY4XERE9TtI8YH3bjw3929EsF3iz7S1q54sYklaEdvg9\n5bbi7KEBSVtQVkmIlpJ0u+2thhm/1fa2NTJFfZJ2Gemc7WvGMkv0lAUs6qudJ2l9YB6wQb1IEX8t\nhW07zAC+LulwYKDpuT0NOLturKhsk6c5Hu1w1Qjjg5QHy6KdbgJeTWlb+gnwFeBh4Oc1Q0V0S2Hb\nDqdQFtO+BFgDuILSd3tmxUxRiaSjm8MJkrrXoNySzOS3mu3Fnr1oHhw7kVLQRHsdwKLncg4DTgbW\nBN5dK1DEcNJj2yKSBoB1gAds5w++pSRdQZl9ewVwZcephcD9wOm2b6gQLXqUpDWBm2xvWTtLjD1J\n+wPbA9fb/mrtPBGjSWEb0VKSpts+tHaO6H2S1gHuzMOm7SPpGOBI4BeUHemOsX1q3VQRI0srQp+S\ntLBraJCOBbWHxmynZ66lUtTGcJpWlc4ZjzWAtwA/rJMoKtsPeIPtmZL2oLSxpbCNnpXCtn+9suN4\nR+D9lL+MZlN2mzoM+MKYp4qeIWkD4JOUn481O04N2n5+nVTRA6ayeGE7H7gQOL1OnKhsfdszm+OZ\nwIY1w0QsSQrbPmX7qSebJU0H9rJ9R8fYTOAiym/f0U4zKA8Vnk15unlI+pNazPaU2hmiN9leKCkb\nO0VPS2HbDs8F7uoauwd4XoUs0Tt2Bja2Pb92kOhNkiZQ+irvtJ0tddvpmZIuY1Er28Su94O2X1Mn\nWsRfS2HbDjcBp0r6iO1HJT0T+HQzHu11FzChdojoDZJWA46hFLJXAl+mbL39fOAhSXt23gmK1uje\nYvvqrve5wxM9JasitICkLSlrUE6m7EK2HjAHeJNt18wW9Uh6J7A3cBxwX+c52/dWCRXVSPo8ZRb/\nMuB1wJ+B6ymtKgcA29verV7CiIglS2HbEpJWBl5G2VXqHuBa20/UTRU1DbNyxpCsltFCku4FdrR9\nr6TJwG+BtWw/JGl14G7bz66bMiJidGlFaImmiO2+hRTt9tzaAaKnrDk0U297jqT5th9q3j/c9NtG\nRPS0FLYtIGkN4AMMv6xTmv5byvbs2hmip400ox8R0bNS2LbDl4AXA98hyzq1mqQPD+0aNMxC/FCe\ndB60fdKYh4valvT0+2p1YkVELL0Utu3wWuD5tn9fO0hUtzuLdg3qXogfmsIWSGHbPkt6+j0rIkRE\nz8vDYy0g6Q5gO9sPL/HiiIgIsjV7jE/ZQaQdjgKmSXpO7SARETFuvLLj6zDg18BBwGua11824xE9\nIzO2LSDpCRb9EvNkx6lB26tUiBSVSLp8KS7LQ4URsRhJNwN/37U1+/OAi2y/uF6yiMWlx7YdXl07\nQPSMpVnyLb/tRkS3bM0e40JmbCMiImJUkq4AbgW6t2bfzvaUmtkiOmXGtiUkbQVMAdaho/nf9idr\nZYo6JG0BvN72WcOc+wDwA9u/Gftk0SskrQS8lLJT4d3ALNuZBWm391K2Zn+vpMW2Zq+aKqJLCtsW\nkPR24Fzg58CLgFua159WjBX1HAncOMK5BcBHKQ+GRAs1fZPfo9xi/gOwLnCnpDd39ldGu9j+taSt\nydbs0eNS2LbDx4B32b5Q0lzbO0l6D7BV7WBRxRTgwyOcuwA4fOyiRA/6IvBjYEfbj0haHfhUM75b\n1eJ/o1EAAAzmSURBVGRRVbZmj/EghW07bAp8ozkeakM4j3KL8SNVEkVN69meO8K5BykzdNFeOwJ7\n2n4UwPbDkg4HssFLi2Vr9hgvUti2wzzgWcBc4H5JLwQeAFavmipqmS9pM9uzhzk3GXhojPNEb7kT\n2Ajo7LPufh/tk63ZY1xIYdsOPwL+DjiHMnN7OfAEcGnNUFHNj4FjgAOGOXc05eclWkTSLh1vzwW+\nJ+k0YDawOfBB4OyxTxY9JFuzx7iQwrYFbO/f8fYTgIG1KP+ARfscB9wgaTJwPuUhkE2At1NuM+5U\nMVvUcdUwY1/qen8GcOYYZIne9AC5mxPjQNaxjWghSdsCpwOvAp5B2ZHuCuAw27dWjBYRPUjS3sBU\n4KO2/1g7T8RIUtj2MUlTgEdsz2rebwJ8DdiestTXfrb/VC9h1NY88b42MNf2w0u6PtpD0gCwge37\nameJ+rI1e4wXaUXobycAx3e8PwuYRLP8V3P+4Aq5okc0xWwK2nhK8/T7NGAfYCGwuqS3AC+yfVzV\ncFFTtmaPcSGFbX97AU3vnKSJwOuBXWzfJOlSykNkERGdTgM2AHYFftiMXQ+cTOnPjhayfUXtDBFL\nI4Vtf1vF9l+a4x2Ah23fBE/tIvOcetEioke9EXih7XmShsbupSz5FS2WrdljPEhh29/ulyTbpsy+\n/GzohKRJwGPVkkVErxoAHukaWwOYXyFL9IhszR7jxUpLviTGsa8A35b0acoOY+d3nNuZsuxXtJSk\nfSStWjtH9JyrgSO7xg4FZlbIEr1jaGv2nYC/NK/vB/6nbqyIxaWw7W8nUorbrYCTbX+t49wLKRs2\nRHudANwnaZqkbWqHiZ5xGPBOSXcAEyXdBuzPXxe70S4jbc2+b504EcPLcl8RLdUs5zSVsgPZmykz\nL18ELsjSX+0maTVgL2AzYA7wA9vd7QnRIpJ+R1kZY66kXwJvpWzacIftteqmi1gkhW1E0DxIuC/l\n1uKGwNeBM23/b9VgMWYkHQ10/oMw0HE82Hw9AFybTTzaR9KXgSttnyPpk5RfiJ8AZtneu266iEXy\n8FhEQFkabjvK1ro3AKsB10k6yfZJVZPFWJnK4oXtcCYB0yUdafuzY5ApekTX1uzHkq3Zo0dlxjai\npSStC+wHvAdYD5gB/EezigYqaz1dn9uM0UnS9sD3bW9aO0vUJekZwL62z62dJWJIZmwj2useyhJw\nJwIX236086RtS7qsSrLoWbZvlnR17RwxdiS9ANgauNH27GZsH8rM7XPIrG30kMzYtoSkZwFvADa2\nfYqkDYGVbN9TOVpU0My07ATcZHtB7TwR0ZuaAnYGZRWlxygPFX4c2Bb4LDDNdtY4jp6RGdsWkPQS\n4FLgPmBz4BRKP+VBwNsqRot6BoEfURbej4gYyeHAh4CzgX8Gvg/8F/A823NrBosYTtaxbYdpwBG2\nt6M8xQplEfad60WKmmwvBG6nLOcUETGSzYDpzfbsZwKrAAekqI1elRnbdtga+HLngO2HJE2slCd6\nw3mUnelOBWYDC4dO2L6mVqiI6Ckr2X4SwPYCSfNtz6sdKmIkKWzb4ffAZErxAoCkLYC7awWKnnBG\n83reMOdyNyciACZIOqo5HgBW7Xo/mCUBo5eksG2HGcDXJR0ODDQ9t6dReqaipWyneI2IJbmWssbx\nkOu63gOksI2ekcK2HU4BJgKXUB4WuoLSd3tmxUwREdHjbE+pnSHi6chyXy0iaQBYB3jAdv7gW07S\nSsCBwB6Un4uVaHaesr17xWgRERHLJDO2LdIUs3+onSN6xgmUXce+CrwR+BywL3B+zVARERHLKoVt\nn5J0s+3tm+Nfj3DZoO3nj2Gs6C37AK9rdpI60PaHJV0EHFE7WERExLJIYdu/PtNxfOII16Qdod3W\ntn1zc/yEpJWBWcBuFTNFREQssxS2fcr21zqOz60YJXrXPZIm254D/BZ4PfAAkC12IyJiXEph2xKS\nVgO2BNbsHM9C/K32eeAlwBzKnu/foaxLeWzNUBEREcsqqyK0gKQ3UdayndR9LmuZxhBJmwJr2L69\ndpaIiIhlkcK2BSTdAUwHvtjs9x0RERHRd9KK0A7r2T5jyZdFv5N0+VJcNmj7NSs8TERExHKWwrYd\nLpP0ctvX1g4S1V29FNfkNk5ERIxLaUVoAUmnAvsBFwD3NcMDlJm57PEdERERfSEztu2wI/ALYJvm\nq1MK24iIiOgLmbHtc5ImAG8Fvmv70dp5oi5Jjy/FZYO2V1nhYSIiIpazzNj2OduPSzrb9oW1s0RP\nmFo7QERExIqSGdsWkDQT+KDtW2pniYiIiFhRMmPbDj8Gvifpi8BsYOHQCdvn1woVY0/Sy2zPao53\nGem67EgXERHjUQrbdjiAsoTTAcOcS2HbLj9k0bbKV41yXXaki4iIcSetCBERERHRFzIr0yKSNpL0\n8to5IiIiIlaEtCK0gKT1KC0HuwOPABMl/RPwStsHVw0XY07S0Yy8u1g27oiIiHErhW07nEV5aGxd\n4I5m7EfACbUCRVVTWVTYDgC78tf9tilsIyJi3EmPbQtI+j0w2fYjkubaXrsZ/7PttSrHi8o6fyYi\nIiLGs/TYtsOjdM3OS3o28Mc6cSIiIiKWvxS27XA5cJqkzm1SjwMuqZQnIiIiYrlLj207HA58B5gL\nrCrpQeAW4M1VU0VEREQsR+mxbQlJA8BLgM2BOcD1tvOH30JdqyIMAEez6EHCrIoQERHjVgrbiJaR\ndAWLL/c10PUe27uNZaaIiIjlIYVtn5P0amAb4GfA9cA5wFuBm4F32L67YryIiIiI5SYPj/UxSf9K\n6a19B+UBsumUVoSjKDN0p9ZLFxEREbF8pbDtb4cCe9h+KbAn8H7KLO104B+BKRWzRURERCxXKWz7\n2wa2ZzXHVwOP2L4HwPb9wMRqySIiIiKWsxS2LdGsgLCgdo6IiIiIFSXr2Pa3CZKOao4HKGvYdr6f\nUCdWRERExPKXwra/XQtM7Xh/Xdf7n41tnIiIiIgVJ8t9RURERERfSI9tRERERPSFFLYRERER0RdS\n2EZEREREX0hhGxERERF9IYVtRLSepH0l7f80rt9V0vErMlNERDx9KWwjIuAAYHcASVtKekDS20e5\nfirw7qX5YElbSNrj/x8xIiKWJIVtRAQMNl/Y/jXwCuDi5fTZHwM+sZw+KyIiRpENGiIiyk58T7F9\ne60gERGx7FLYRkRPk/RB4DBgXeC3wOuBzwMvBVYHrgIOsv3b5vovAVOa61cGfgq8z/acjs98J3B8\nc82twEbA75pzWwC/AqbY/mkztgPwBWBrYA7wUFfG9wLHNp93L3Ck7Qs6LtlV0sLmeLrtD0haucnw\nHsr21lcAh9i+b9n/b0VEtFtaESKiZ0k6BjgROAvYCzgduAf4EvB24B+A5wCf6/i2PYAbgT2B/YCt\nKIXw0Ge+BTgP+BbwNuAiYM1RMmwEXAncD+wNfIpSUHdu23gTcCil6P4eMEPSxh3nfw78bfP12Wbs\nFGBf4CPAu4DNga8u6f9JRESMLDO2EdGTJE0EjgA+bvu0ZvhHzetFHdc9g1KoDhkEfmn7qub8usBZ\nkla1/RjwYeBi2x9qrv9vSXuNEuVgYB7wFttPNp+5GXDg0AW2b6QU00iaCewD7EQpwgHm276mI/Oa\nzee+E/g2pRXiQeAnkjbMrG1ExLJJYRsRveqFlJnRmZ2DklYFTqPMtq4D/BFYY5TP+Q2lcFwPuKv5\n3G90XTPQ/U0dtgZmDRW1w10vaW/gaOAFwPwmz1qjfOZWwCrD5BgEJgMpbCMilkEK24joVQua1ye7\nxj9JuYX/b8BtwKuAT4/yOY82rxOa11U7jocMMrJVgYUjnZS0LXA+pT3iYMrfq99cwmc/1ry+m/Lf\n0OlXo2SJiIhRpLCNiF51J6UA3B24pWN8W+DHts8BkLT60/zcG4DXUWZ9h4w2Y3s9cIikNW3PH+b8\nVpTnFQ63/WCT6S8d5x8EntX1PXdQ/ts2sX0eERGxXKSwjYieZPshSWcAJzTtBzdSVh2YB+wpaT9K\nm8GOXd86WpEKpWXgJ5JmABdSZoTXp1kVYRinA+8HLpN0KjCX0p4wNBN7a3N8sqSLKLO7ncX2DcAH\nJB1CWdVhgu3vSpoGHC1pJWAWsDbwhO1vLSF/RESMIIVtRPSyoyiF7CHABsDdlAeuHqfMuE6i9Nhe\n0/E9w936f2rM9lWSdgM+Q9mE4bHmc68b4fp5kl5KKXC/TJmdvR+4vDl/u6SDKA+6HUhpfZjDogfH\nLqRs+PCpJveFwHcpBfaC5nuOaT7zbMpqDRERsQwGBgdHay2LiIiIiBgfso5tRERERPSFFLYRERER\n0RdS2EZEREREX0hhGxERERF9IYVtRERERPSFFLYRERER0RdS2EZEREREX0hhGxERERF9IYVtRERE\nRPSF/wPm1UxDGsu8/QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b61c5f8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"non_english = largest_languages[largest_languages.lang != 'en']\n",
"non_english_groupby = non_english.groupby(['lang', 'candidate'], as_index = False)\n",
"\n",
"sizes = non_english_groupby.text.agg(np.size)\n",
"sizes = sizes.rename(columns={'text': 'count'})\n",
"sizes_pivot = sizes.pivot_table(index='lang', columns='candidate', values='count', fill_value=0)\n",
"\n",
"plot = sns.heatmap(sizes_pivot)\n",
"plot.set_title('Number of non-English Tweets by Candidate', family='Ubuntu')\n",
"plot.set_ylabel('language code', family='Ubuntu')\n",
"plot.set_xlabel('candidate', family='Ubuntu')\n",
"plot.figure.set_size_inches(12, 7)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Looks like Spanish and Portuguese speakers mostly tweet about Jeb Bush, while Francophones lean more liberal, and Clinton tweeters span the largest range of languages.\n",
"\n",
"We also have the time-of-tweet information - I'll plot influenced polarity over time for each candidate. I'm also going to resample the `influenced_polarity` values to 1 hour intervals to get a smoother graph."
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAuIAAAHtCAYAAABcXRt3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4lFX6//H3pIcOkSZFRfQgARUQsX6VRVZFRSzoWrC7\niCji2hB1d3+69rqgwOqKKLZVFMSCurZVpIpYiHoAEZEiRQiQnszM749nZjIzaTOYTEk+r+vKlZmn\nnpl5ktzPnfuc4/J6vYiIiIiISGylxLsBIiIiIiJNkQJxEREREZE4UCAuIiIiIhIHCsRFREREROJA\ngbiIiIiISBwoEBcRERERiQMF4iJSK2PMIGPM68aYvePdlvpgjGlljLnbGHN0A5+npzHmP8aY/g15\nHmlYxphrjTGXxbsd9cUYc50x5pKG3kdEIqNAXEQCjDHnGmO+McYUGmO2GWNOBw4CRgBZcW5efekA\n3Ars38Dn6QqMBNr83gMZY1YYY94Iej7EGNPv9x43mRhjnjDGrDfGNIvxqW8Ajo/xORvSTcD/ARhj\nWhhjNhpjJkW6TySa4vUpsqfS4t0AEal/xpgZwBBrbbco9ukLvAjMAP6C8/thOXByAzQxYRljhgNP\nAzmAF9gNWOA14J/W2tI4NOtkoCTo+X+Bf+B8PknNGHM88FFt21hrU4DbgEestUWxaFeQBpn1zhhz\nHjAaOBTIBDYCnwETrLW/NsQ5fQKvx1pbYIw5Ftga6T4RajTXp0hDUyAu0nhF+8dzMOACrg0Odowx\n9dqoJNAOJwi/EFjnez4UuMf3fWisG2St/aWaxa5Yt6OBfAkc43vsAl4FvgbuCt7IWpsP5Me2afXP\nGOMCngEuAt4ALgN+A/YFhuDc+DWkkOvGWvtjtPvsyXlEpHoKxEUar8AfQmPM2TjlGJ1xAstC4D3g\nOmutPxvWzve9ICj43i/8oMaYfYE1wJXW2qeDlnuAu621d/ieZ+EEUxcALYBvgVustfN963sBT+IE\nIO187V0K3GCtXRZ03H2AB3AC4CxgNXCKtfaXus7h278/8DAwCNgBfBPJmwcsstau8T2ea4zZCUw0\nxvSy1v5gjDkEuBc4FqjAeT9vttauq+mAxphxOP/mbw/swvnvw23W2nLf+odxst+dcbKkz1tr/2yM\n+QRItdYeG3S424wxt/kePwFs8r0X7a21233Ha+F7zTdbax+tpj37AvcDf8T5e/ApTkb2W2PM4cAi\n4Cxr7eygfeYAnay1R/ieX4lTvtEd+Al4zFr7VND2LwADgU445ZAPWGvv9K+31u4CFgRtXwpstdYG\nlvmW/x34K5BmrfUYY64B/gx0xCn/+dX3WnrhlFJ1BH70vfa3go7THXjI95rLcLLQ42u42QHnujzM\nGPOF79jbcT63v/vasRL43lp7etA5rsL5TDpYa38LO96lOEH4bdbae4OW/w94NugY9/m2y8HJWE+y\n1j4QtP4d4EBgLyAb5+fibmvti0HbtAceBYb5Fn2B83NC0DZrgc+staOi2KfW69gn+Pp83Fo7zrdv\nrdeLSFOjGnGRpqEP0A8ncBkK3AGcCkytZtvjcDKUx+AEdzWpLuMevOxF4FyckoKRwDbgPWNMV9/6\nTr5zPAmcCFziW/aGMSYDwBjTHCdAOQS4DjgFeBzYEMk5jDF7AR8CrXECoKuBLbW8ptoU+75nG2O6\n4AStLYFRwBhfGz8xxmTXcowFvjacBNzne01jg9afhZP1PQ8YjpM59Qt/v5+l8nN6GHgTJ2gMztgf\nC6QC88IbEvTe9gGuwgn62gKfGmM6WWuX4PxH4MSgfTJw/nPyH9/zccAkX1tOB+YC//Ld+PmdB3wP\nnOl7fXNqeG+idRjQxdfuk32v5XEgF7jWd77dwIu+GxKMMa1wPrfOONfbVTjB9Zu+THVNWuEEm2cC\nz+Hc1P4/37o3geONMelB2w8GllYThINTjvITzk1Dbd4FrvC9tunAfcaYEUHrT8Ip/TgN58bjR2Cm\nMaZP0Dav49xw3IbzOSygal8PL6HXViT71HUdQ+j1+QhEfL2INCnKiIs0Le9Yaz3AZ8aYA4FrjDFp\n1tqKoG0+920D7FlpijHmUJzgYBjwgW/xfGAzTvY6OAhZYK393LdfOU4gcAxO3fB1OEHTgdban33b\nfxzFOa7ByRaeZK3d4ttvBU7wXJc0Y0wmTnA6GBiPk3X8BucGpgw42Vpb4DvuYpxa8vE4mfIqrLVf\nBD39xFefezzwmG+ZF1htrX03gvb9Uk3WeBVOsPgf36LjgZ+ttT9Us/91ODc+B/iz+MaYD3GCxP+H\nEzDOAs7HCVgBTsC5+ZhljEkF/uZr+wM4NwEf4/zn4XLfvn5fW2s/oP4VWmvf87V9CfAnYKG19g3f\nsnKcgPYY3/fLcDrr9sfJ5IKT4f4IOBxYXM05vMBH1trHfc/f9wX2fzHG3I9zvV6P8974b3iOo/qb\nXHBufN4M/hmrjrX2k6CnHxljTsP5PINvZL631n7me62LcW4yzwFW+GrvjwbO8L8fODepl4edKvg/\nZxHtE8F1DGHXZ5TXi0iToYy4SNNlcX4HdGqAYw/0fX8HJ2Atw8lOZlNNuUtYmwD8QyUeDawMCsKj\nPUdf4Dt/EO4Tae3qDzhZ8I04menPgaHWWjdwFE7pSkGg4db+BKwEjqzpgMaY840xy40xxcaY3TjB\nS6sI2xOJ54FTgkYWCQ4Owx2F894GSml8ZSILfevA6aDayRjjHzHjbGCxr4yjB85Nyi1AOZWfwfHU\n/hnXp8Bn6fsstlF57QD4r5v2vu8DcbK726hs70c4wXY0bf4Y5zrL9d1ErsG5CfB3eu5Aze87RDAC\nkW/IwB+MMaXGmB1AT2q5VnzlSMGvv29QWyMV0T57eB0nwvUiknCUERdpuvylFhlR7lfm+15bCYZ/\nhI+zgbVh67ZF0SYXNXc6jeQcWTi11ntihO+424HNYfWvNXFRQ6BvjDkBJ1CegZM1LwPu3sO21eQZ\nnLKjc40xH+CUI91RS1vrWr4IJ8i80BizCCfbfrtvnf/9vxcnYA8Wj5Fl/OdNC3sO4C8bKcH5PP9Y\nzb5roziP/xz+a/Mp4A5jzFic62azr7SnOhY42BjjstZWe20bY67AqdN+EKd8IwWYFkG7iqn82fEH\n+9H8fNe5z++4jhPxehGJOwXiIlIXf7Dg/w/aZpyMVm4t++T5vnez1r7+O869DBhijOleTSfIFRGc\nYxEw1BhzgLV2VZTnXhHUWbO6455ujGkRVJqyH3AA8IJvm/D3zT+u8l98I4BgjFkH7BNluwB24nTS\nC2GtXW+MeQmnZr0FTtD5Xg3HWAicEPzeGmNaA0fgC5SstV5jzDSc4Hspzt+M53z7r/e1o7e19rbw\ng8dItCMDrcDpK+Cx1n4V4T7V3bCcgtPh+Vvf82nARJx69RHAK7Uc73mczqLjgH/WsE0/YLe19hb/\nAmNMtH0b/GU2pxHa1yBc8HtY0z7B70Ek13F112ciXC8iCUeBuIjUxT+axKXGmAestTt9wd7FvhEj\nlhOWHbfWfukb1eEeY0wbnMA1BeeP8MNRnPsJnA6mHxhj7sXpPNgZ+NRauzyCczyC0ynvPWPMXTj1\nzwdF+wZU4+84tbjvGGMewckk/hWnE6m/Tna97/t5xphvcQJZgAeMMa/gZAG7EhoI1VY2E7xuMTDS\nN5pKPtAi6GbkQZw69k7Ay75Smuo8hvPevuN7b8qAG3Hew78Fbfe07/U+ijOKyy4IBOl3+17PdJyh\n+Hbj1EDPstZurOW11CaaYe/Ct61r3xk49dxv+K6nlTgdebODRxsJ4wX282WC03E60V4M3G6tLQbw\n/Uw8iROM741TX1+TSTgdMB81zqQ3r+MEqB1xasv/gXOtjDHG/AOns7EbJ7D9qY7XF1yq86kxZhYw\nyRjT0XfMLCB8QqRI9gn++Y7kOq72+myg60UkqcWtRtwY8ydjzGfGmJ2+DjXh6y8yxvxonBn+Fpmw\naaKNMYcZY5b41q82xlwQu9aLJLzwkRDCnwcvr3Uba+1HOCOb/BnnjyY4IyQ8h1P28CHO6CXLqMwQ\ngjNCxiScoGUuTobtZF+nrerOX4VvYpN+vmM/jFN3+zecP/x1nsNaW4jTGewjnM6bH+AEOgtxRpmo\nSV3tWo8TNBXjZDin4fwX4Hj/GOy+8Zn/H07QNcTX+e5a335v42Sq9wOCM7M1nTf8sxnrO99zOBn4\nk4LatgKnbr4rzudW02so8LXlB+BfwEycwOg4a+2moO124ASwWYR2xsNa+xDOyB79gZdxMumjcGqB\n91Sk70F112tdn9sOnH4HnwF34rxPj1GZ5a3O+zhB8mvAbJzr6ZywoQfBuVHZC1ge1pkxvA0VOJ/X\ndUBvnM/vfd/+XXCC1hk4Q1FeiHOdvINTLvJ9ba+Pqq//fJxSkNE4nVVfxrlBXLKn+0R4HVd7fTbQ\n9SKS1Fxeb4NMGlYnY8wfcX74mgFPWmvTg9b5e7iPwBmSajzOuKMHWGt3+/59uhqn5/VjOL8QZuN0\npFoU0xciIpJgfFn6ftbawfFuS1PhG2FnDTDRWvtsXduLiEAcS1Oste9DYLikcFcCrwUNd/WgrxPM\nGTh32GcCBdbaB33rPzDGzMbJ2CkQF5EmxzdaRwrOKBSjfd+lgfmG7isHJuCMu/9c7XuIiFRK1OEL\nD8b5V3Swr3zLwZk4Y3nY+uW+5SIiTdHfcWpzLwbOttYurX1z+b2MM3HUmzglU2U4M77G59/MIpKU\nErWzZkuczivB8qkcp7QllZMxVLdeRKRJsdaeFe82NDW+vgJt4t0OEUleiRqI78bpyR6sLbAqaH34\nkF9tqBqcV2vZsmXKWIiIiIhITAwYMKDaUZ0SNRD/Ghjgf2KMceH0avdPgfsVcHrYPv0J7bVdq549\ne5KZWfs8H6WlpaxevTqibUVEREREgvljyZrELRA3xqTgDMeU4XueCbistSU4s5S9a4x5Fmda6etw\nxm+d7dt9Ns5YpDcCk4FjcUZYOSHS82dmZpKVVecsw1FvKyIiIiISiXh21rwIKMIZpjAFZzzeQt8s\nb58DV+ME5DtwRkkZ5p/Bzlq7ExgGjPStnwaMttYurnIWEREREZEEFM/hC2fgTBJR0/qZOBNM1LT+\nC5yJFUREREREkk6iDl8oIiIiItKoKRAXEREREYkDBeIiIiIiInGgQFxERESatJ9W7+LjdzdQUuKO\nd1OkiVEgLiIiIk3aks+3sPL7nfy0KqJ5AUXqjQJxERERadIqyj0AlPu+i8SKAnERERFp0jxu/3dv\nfBsiTY4CcREREWnSPB5vyHeRWFEgLnWaPHky06dPB2DSpEksXLiwyjaLFy/mqquuqvU4P/zwA//7\n3/8apI0iIiJ7yh+Au5URlxiL28yakjxcLlfg8bhx4/b4ON999x15eXkcd9xx9dEsERGRehHIiCsQ\nlxhTIN4IzZkzh+nTp+NyuTDGcPLJJzN16lTKy8tp06YNDz30EDk5OUyePJmNGzeyfv16Nm3axMUX\nX8yoUaMAmDp1KnPmzCEnJ4fOnTvTp08fACZMmMDgwYM58cQT+fTTT7n33nvJzs6mf//+gfN/8803\n3HPPPZSWlpKZmcm9995Lly5dmDRpEqWlpSxbtozRo0dz3HHHcdddd7F69WoqKiq45pprGDJkSFze\nMxERaboCGXGVpkiMKRBvZFatWsXUqVP5z3/+Q5s2bdi5cycul4tXXnkFgFdffZV///vf3HLLLQCs\nXbuW5557joKCAk466STOP/98vv/+e9555x3mzp1LeXk5Z555ZiAQd7lcuFwuSktL+etf/8pzzz1H\n9+7dGT9+fKANPXr04IUXXiA1NZUFCxbw6KOPMmnSJK677jry8vK4/fbbAXjkkUc48sgjuffee9m1\naxcjR47kqKOOIjs7O8bvmoiINFVerxePb7AUZcQl1hSINzKLFi3i5JNPpk2bNgC0bt0aay3jx49n\n69atlJeX061bN8AJqo8//njS09Np27YtOTk5bNu2jS+++II//vGPZGZmkpmZyR/+8IeQc3i9Xtas\nWUPXrl3p3r07AMOHDw8E+7t37+aWW25h3bp1ALjd7sB+Xm/lL7n58+fz8ccfB+rPy8vL2bRpEz16\n9GjAd0hERKRS0J8l1YhLzCkQb2RcLldIsAvwj3/8g8suu4zBgwezZMkSJk+eHFiXnp4eeJyamkpF\nRUWVY4Qfz3+eYMHb/POf/+TII4/kiSeeYMOGDYFyl+pMnjyZfffdN+LXJyIiUp+CR0rRqCkSaxo1\npZE54ogjePfdd8nPzwcgPz+fgoICOnToAMDs2bMD29YUYA8cOJAPPviA0tJSCgoK+OSTT6ps06NH\nDzZs2MAvv/wCwNtvvx1YH3y+119/PbC8RYsWFBYWBp4fe+yxzJw5M/D8u+++29OXLSIiskdCAnFl\nxCXGlBFvZHr27MmYMWMYNWoUKSkp9O7dm2uuuYbrrruOVq1accQRR7Bhwwagst47XO/evRk2bBjD\nhw8nJyeHvn37VtkmIyODO++8kz//+c9kZ2czYMAAioqKALjiiiu45ZZbmDp1Kscdd1zgHIMGDeLJ\nJ59kxIgRjB49mquvvpq7776b0047Da/XS9euXZk2bVoDvjsiIiKhPEGTaao0RWLNVV1WtLFbtmyZ\nNzc3l6ysrFq3KykpIS8vj0i2FRERkeRTVFjBzCdXArBPjxacdHr3OLdIGhN/LDlgwICqmU9UmiIi\nIiJNWHBCUhlxiTUF4iIiItJkBdeFq7OmxJoCcREREWmy1FlT4kmBuIiIiDRZwZ01lRGXWFMgLiIi\nIk1WcPDtm39OJGYUiIuIiEiTpdIUiScF4iIiItJkhWTEVZoiMaZAXKIyd+5cTj/99Hg3IypffPEF\nvXr1inczREQkAYWMmqKMuMSYZtZMUqNGjeKrr74iLc35CNu3b88FF1zAxRdf3KDnHT58OMOHD9/j\n/T0eD1OnTmXu3Lls3bqV9PR0evTowfjx4xk0aFA9tlRERKRuwUlwBeISawrEk9jYsWO56qqrAPj6\n66+55JJLOOCAAzjqqKP26Hjl5eWkp6fXZxOreOqpp3j77beZOnUqPXr0oKioiGXLliX0zKWxeF9E\nRCQ+VJoi8aRAvC4VFbh/3UBFZmaDnyp1r4649jDgO+SQQ9h///1ZuXJlIBDfsWMHDz74IAsWLKC0\ntJRBgwZxxx13kJOTA8Af/vAHzjrrLBYtWsSKFSu4++67eemll+jTpw8bNmxg/vz55OTkMGHCBIYM\nGQLA66+/zrRp03j//fcBqKio4N///jezZ89m+/bt9OzZk9tuu40+ffpU287ly5czePBgevToAUCz\nZs049thjQ7a59dZbWbhwIbt27aJz586MGTOGU089FYDFixdz6aWX8tBDD/Hoo4+yY8cOjjnmGO6+\n+26aN28OwNq1a7njjjvIy8ujW7dunHHGGSHHr6vNEyZMoLy8nIyMDD766COGDRvG9ddfz+23387i\nxYtxu9106tSJv//97xx22GF79HmJiEhiUGmKxJMC8Vp4y8vJmfRXtuf/FpPzpXbcm87/ei3iYNw/\nLa/X62XZsmWsWbOGfv36BZaNHTuW/fffn7feeou0tDTuuusubrjhBmbMmBE4xqxZs5g6dSq9evWi\ntLSUl156idmzZzNt2jQmTZrEjBkzmDBhAvPnzyezmpuRyZMns2jRIp5++mm6dOnCa6+9xhVXXMH7\n779Pq1atqmw/cOBAnnzySVq3bk3//v3p3bs3zZo1C9lmwIABTJgwgVatWjFv3jxuvvlmDjroIPbf\nf3/AKW9ZsGABc+fOpaioiPPPP5+ZM2dy1VVXUVFRwejRoznmmGN4+umn2bRpE6NHj8blctXZ5v/+\n97+0bNkSgPfee48HH3yQe+65h9LSUqZMmUJpaSmffPIJ2dnZ/Pzzz6Smpkb0OYmISOJSRlziSZ01\nk9i0adMYOHAg/fr148ILL2T48OH07dsXgBUrVvDdd99xxx130KJFC7KysrjxxhtZtGgRmzdvDhxj\n5MiRgY6M/kD7lFNO4dBDDwXgnHPOYffu3axdu7bK+b1eLzNnzuSmm26ia9euuFwuzj77bNq3b88n\nn3xSbZsvv/xybrvtNr744guuvvpqBg0axNixY/n1118D25x99tm0bt0al8vFsGHDMMawePHikOPc\ncMMNZGdnk5OTw5AhQ1ixYgXglOhs3LiRm2++mYyMDPbZZx8uv/zykJuWmtr88ccfB45/2GGHcfLJ\nJ+NyucjKyiIjI4P8/HzWrFmDx+Nhn332oWvXrtF8XCIikoC8wRP6uL2BvxcisaCMeC1c6en8Nu5O\nenXcq9pscH2LtjRlzJgxgRrxzZs3c8MNNzBx4kTuu+8+1q9fT1lZGUcffXTIPllZWWzatImOHTsC\n0KVLlyrHbd++feCxP1tdWFhYZbsdO3ZQVFTEVVddFZJxrqioCAn2wwV3+MzLy2PixInceOONPP/8\n83g8HiZPnsy8efPYtm0bLpeL4uJiduzYEdg/NTWVtm3bBp5nZ2cH2rd582ZycnJCPq/g1xhpm8Pf\nl8svv5zy8nImTJjAli1bGDx4MDfddFOgzEdERJJT+GyaHg/oH54SKwrE65KWRmqnLqQlcGdCgI4d\nO3LSSSfxyCOPcN9999GlSxeys7NZunRprfulpOz5P0Xatm1LdnY2M2bMqLEmvC65ubmcffbZPPbY\nYwC89dZbzJo1i2eeeYaePXsCcNZZZ0WcoejQoQO//fYbJSUlgQ6gGzZsiKrNLpcrJEgHJ9i//vrr\nuf7669m2bRs33XQTDzzwAPfff3/Ur1lERBJH1UDcS2qqq4atReqXSlOSWHBwunXrVt59910OOugg\nAPr27UuvXr246667yM/PB2D79u28/fbbUR23Ni6Xi4suuoj777+fn3/+GXAy55999hlbtmypdp9n\nnnmGTz/9lN27dwNOx8o5c+YwcOBAAAoKCkhLS6Nt27ZUVFQwa9YsrLURtQfg0EMPZe+99+ahhx6i\ntLSUdevW8cwzz0TV5upe/8cff8yPP/6I2+0mOzubjIwM1YiLiDQCVQJxddiUGFIgnsSmTJlCv379\n6NevHyNGjKB9+/Y8/PDDgBNwTpkyBa/Xy5lnnkn//v0599xz68yQ+/etbV3w+nHjxjFkyBCuvvpq\nBgwYwIknnsgrr7xSYzDfokULpkyZwgknnEC/fv247LLL6Nu3L/fddx8AZ555JgcffDBDhw7luOOO\n48cff6wyMkl4+4LblJaWxtSpU7HWcuSRRzJu3DjOPffcqNpcXUZ83bp1jBkzhsMOO4whQ4aQnZ3N\njTfeWNdbKSIiCS488HYrEJcYcjXFTgnLli3z5ubm1jl2dUlJCXl5eUSyrYiIiCSfFV9t5/OPKwcM\nuOCKA2jRUnNHSP3wx5IDBgyoNsupjLiIiIg0WSpNkXhSIC4iIiJNVpXSFI0lLjGkQFxERESaLGXE\nJZ4UiIuIiEiT5fGEPVcgLjGkQFxERESarPCMuEpTJJYUiIuIiEiTpdIUiScF4iIiItJkKSMu8aRA\nXERERJosr2rEJY4UiIuIiEiTVSUjrkBcYkiBeCPXr18/vv76awAWL15Mbm5uYN3kyZO59NJL49W0\nGoW368orr+Tpp5+OY4tERKSxqlIjrtIUiaG0eDdA9syoUaM46qijGDNmTK3Lly9fHo/m1Wrt2rU8\n/vjjLFq0iMLCQnJycjj88MMZPXo0++yzT5Xtn3rqqaiOX9N7IyIiEi68FEWlKRJLCRuIG2NygMeA\noUAGsBy43lr7jW/9RcDfgE7At8DV1tov67sdFR4vG3aWkFnsqXvj36ljqyzSUyP/J4XL5YpqeX3y\neDx4vV5SU1Oj2s9ay/nnn8+JJ57Iyy+/TNeuXdm5cydvvfUWn376KaNGjWqgFouIiFTl8ao0ReIn\nYQNxYBKwF2CAIuAfwFtAd2PMMcAUYATwP2A88I4x5gBr7e76akC528PfFu3mt0/qPb6v1t6ts5h1\n+RFRBeN16dWrFy+++CL9+/evc9tnn32Wl19+mc2bN9O6dWtOO+00xo8fT0pKSuBYEydOZM6cOaxZ\ns4YZM2Zw4YUX8umnn9KuXTsAvF4vQ4YMYfz48QwfPrzKOe6991769u3LPffcE1jWunVrLrjgghrb\nFZzhXr9+PSeccAL3338/Tz75JJs2baJfv37cd999tG/fnjvvvJNly5bx1Vdf8eSTT9KpUyfmzZtH\nRUUF06ZNY86cOezatYvevXtz2223ccABBwAwYcIEPB4PmZmZvPvuu2RnZzN27FjOPffcqN5vERFJ\nLh532HOVpkgMJXKN+MHALGvtTmttOTAd6OrLlF8JvGat/cBaW26tfRAoAc6IY3tjzuut318WnTt3\n5t///jdffvklU6ZM4bXXXuPVV18N2ea1117jn//8J8uXL6d3794ceuihzJ49O7D+888/p6CggJNO\nOqnK8YuLi1m6dCmnnnpq1G0Lz/LPmzePF154gU8//ZSioiImTZoEwF//+lcGDBjA2LFjWb58OfPm\nzQPg6aefZu7cuTz11FPMnz+fww47jEsvvZTCwsLAMd977z3+8Ic/sHTpUu644w7uuusuNm7cGHVb\nRUQkeaizpsRTImfE5wDnGmNmAwXAn4HPrLW/GWMOwQnMg30FHFKfDUhPTeH/HdGSvbr3JDMjoz4P\nXa1oS1OmTZvG9Omhb0NRURFHH330Hp3/j3/8Y+DxQQcdxPDhw1m4cGFIVviyyy6jW7duAGRkZHDO\nOecwbdo0Lr/8cgBmzZrF8OHDyajm/dq1axdut5uOHTvuUfuCXXPNNbRp0waAU089lVmzZtW6/euv\nv86VV17JfvvtB8DYsWN59dVX+d///sewYcMAOPLIIxk8eDAAQ4cOpWXLlvzwww/svffev7u9IiKS\nmDShj8RTIgfi9wFzgS2AG1gHnOxb1wLYGbZ9PtAq0oOXlpZGtE1aiou9slxkZjb8Pw/c5WW4yyPb\n1uPxcOWVV3LFFVeELL/88supqKigpKQksKysrIySkhLKysoAAusqKirweDyB5/PmzWPmzJls2LAB\nt9tNeXmGYAWlAAAgAElEQVQ5Bx98cMix2rdvH/L8uOOO4+6772bhwoXst99+fPjhh7z44osh2/hl\nZGSQmprKL7/8Uu16v/B2eTyewGvyf26tWrUKrE9LS6OgoKDa7f1+/fVXOnToELKsc+fOgba43W7a\ntWsXsj4rK4v8/Pxa2yoiIsmtoiK0NqW0rFy/96Xe1BVvJnIg/l+cDpqn45SdXAzMN8b0AXYDrcO2\nbwusivTgq1evjrgh0WwbK0VFRWzevJm8vLw6l//000+kp6ezdu1avF5vYN2WLVsoKCggLy+P3377\njVtvvZW//OUvHHrooaSmpvLCCy/w008/hRzr559/JjMzM+ScRx11FM888wzdu3ene/fulJWVVWmX\nX69evZg1axbGmBpfW3C7wl/T1q1bAVi5cmXg8YYNGygtLQ1sX1xcXOU9aNu2LUuXLqVFixaAE6z/\n/PPPlJeXk5eXR35+PqmpqSH7lJeXs379+hpfi4iIJL/duzOAyoEHNv+6hbw8lSVKbCRkIG6M2Qs4\nArjEWlvgW/y0MeZ+4Ejga2BA0PYuoB9Qe31CkJ49e1YJKMOVlpayevXqiLaNtWbNmtGhQ4eQccFr\nWr7ffvuRm5tLUVERLpcrsO7TTz9l48aN5ObmsmbNGgAOOeQQ+vbty7fffsvChQvZf//9qz1WsNGj\nR/OnP/2Jn3/+mUsuuaTK+mB///vfufTSS5k1axZXXHEFe++9N7t37+bdd9+lvLycCy64IKRd4a9p\nw4YNABx44IF06NABcG6UMjMzA9vvs88+lJSUhLRj5MiRvPHGG5x22mnsvffeTJ8+ndTUVM4//3ya\nNWtGmzZtSEtLC9knPT2drl271vp6REQkua1btZHd+ZUZ8Jyc9uTmtotji6Qx8ceSNUnIQNxau80Y\n8wtwjTFmAlAGXIRTkvI1sA141xjzLPA5cB2QDsyu4ZBVZGZmkpWVVe/bxkpKSgrp6elV2lXd8oyM\nDLKyssjIyMDlcgXWpaenk5qaSlZWFr179+baa69l/PjxlJeXM2jQIE477TR++OGHao8VrFevXvTt\n25fvvvuOESNG1Ppe9e3bl1mzZvH4449z8cUXU1hYSLt27TjqqKP485//TFZWVki7wl9TZmYmLpcr\n5DPJyMggJSUl8Pyyyy5j4sSJHHvssXTq1Ik333yT0aNH4/F4GDNmDAUFBRx00EFMnz49MNpLWloa\naWlpIW13uVzVvsciItKYhA4GkOJK0e99iRlXfY+8UV98HTIfwMl8p+GUndxprX3Tt34U8HegM/AN\nMMZaG9HsNcuWLfPm5ubW+YNWUlJCXl4ekWzb1E2YMIGMjAzuvPPOeDdFREQkYq+/uIatmysz4rmH\ntuWYwZ3j2CJpTPyx5IABA6qd5CUhM+IA1tqvgRNrWT8TmBm7FklN1qxZw3vvvVdlqEMREZFEp1FT\nJJ4SNhCX5DBu3Djmz5/P6NGj6dmzZ7ybIyIiEpXwCX00jrjEkgJx+V38E+mIiIgkoyoZcc2sKTGU\nyDNrioiIiDQolaZIPCkQFxERkSbLH4in+CIilaZILCkQFxERkSbLH4inpaeEPBeJBQXiIiIi0mR5\nPM73dF8groy4xJICcREREWmyvP6MeJovI65AXGJIgXgT0atXL7788st4NyNg1KhRTJ06Nd7NEBGR\nJk6lKRJPCsSTWEMGs5MnT6Z3797069ePfv36ccwxx/DXv/6V0tLSejuHy1XtJFMiIiIx4w+809Od\nv0lud21bi9QvBeJJriGD2SOOOILly5ezfPlyXnvtNb766iumTJnSYOcTERGJJa/XG6gRD2TEVZoi\nMaRAvA4eD+zaWc7O/LIG//o9HUQ2btzIuHHjOOaYYwLZ68LCwpBtvv32W0aMGEH//v256KKLWLdu\nXa3H9Hor29OxY0eOPvpoVq5cGVhWXUY+uATmu+++47zzzuOwww5j0KBB/OlPf2L37t2BbXfu3Mm4\ncePo378/Q4cO5cMPP9zj1y8iIhItfxAOlTXibpWmSAxpZs1auN1eVizN5Mv5v8TkfC1bpXPuJT1J\nTY0uy11aWsrFF1/M8OHDeeihhygpKeHGG2/k7rvv5p577gls9+qrrzJ16lQ6dOjAAw88wJgxY3jz\nzTdJSan7fmzDhg3Mnz+fESNGhCyvLSN/55138n//93+8+OKLeDwe8vLySEurvORmz57NtGnTmDRp\nEjNmzGDChAnMnz+fzMzMqF6/iIjInghOOCkjLvGgjHiS83q9fPzxxwBce+21ZGRk0KpVK8aNG8eb\nb74Z8kvm0ksvpVu3bmRmZnLTTTexbt06vvnmmxqPvXTpUgYOHMiAAQMYMmQIzZs358wzz4y4benp\n6WzcuJGNGzeSmprKwQcfTHZ2dmD9KaecwqGHHgrAOeecw+7du1m7dm2U74CIiMieCQ66/TXi6qwp\nsaSMeC1SU130GVjKPt0PjEmWtkXL9Kiz4eBkqzdt2sTAgQNDlqekpLB161Y6dOgAQJcuXQLrsrKy\naNeuHb/++muNxz388MOZPn06AIWFhTz22GOcd955vPnmm6Snp9fZrnvvvZcpU6Zw/vnnk5aWxvDh\nw7nmmmtITU0FoH379oFtmzVrFjiPiIhILAQH3cqISzwoEK9DSgq0ap1OVlZGvJtSo7333pt9992X\nt956q9bt1q9fH3hcXFzM9u3b6dSpU43bB2fTmzdvzsiRI5k5cyarVq2id+/eNG/enKKiosA2mzdv\nDtm/a9eugdKYlStXctlll9GtW7eosuoiIiINJbhGPDChjzLiEkMqTUlyLpeLwYMHU15ezr/+9S8K\nCgrwer1s3ryZDz74IGTbZ599ll9++YXS0lIefvhhunfvziGHHBLReYqLi5k1axbNmjWje/fuAPTp\n04cPPviA7du3U1BQwGOPPRayz+zZswPBecuWLUlLSwupRw8O9EVERGItJCOuCX0kDpQRT3Iul4us\nrCyeffZZHn74YYYNG0ZhYSEdOnTglFNO4YQTTghsO3LkSK655hp++eUXcnNzmTJlSo2dLV0uF0uW\nLKFfv36AU+9tjOHJJ5+kRYsWAFxyySVYaxk6dCg5OTnccMMNzJkzJ3CMxYsX8/DDD1NYWEirVq0Y\nPnx4SGdPjSMuIiLxFFqa4h9H3IvX69XfKIkJV1PMSi5btsybm5tLVlZWrduVlJSQl5dHJNvGwxln\nnMF5553HOeecE++miIiIJJ38HaX8Z8aPABw3tDP/++8mAK687iBSUhSIy+/njyUHDBhQ7QWl0pQk\n9f3337Nq1aqIS0tEREQkVHAZir80Bfhd83qIREOlKUno+uuv58svv+SGG27AGBPv5oiIiCSl4KIA\n/6gp4AvQ6x4cTOR3UyCehB599NF4N0FERCTphWbEKysHNJa4xIpKU0RERKRJclczjjioNEViR4G4\niIiINEnBme/08NIUkRhQIC4iIiJNkjdoQp+QjLhKUyRGFIiLiIhIkxQ6oU9Qjbgy4hIjCsRFRESk\nSfIH4ikpkJqqQFxiT4G4iIiINEmVgbiLlKBAXKUpEisKxCViX3zxBb169YrLudevX0+vXr3YvHlz\nXM4vIiKNj8dXI+5KcZGaooy4xJ7GEU9So0aN4quvviItLY2UlBS6dOnCFVdcwfDhw+PWpsmTJzN1\n6lQyMzMB2GuvvRgxYgRjx46NW5tERERqooy4xJsC8Tp4PB62b98eCC4bUuvWrUlLi/wjGTt2LFdd\ndRVut5vnn3+eCRMmkJuby/7779+ArazdEUccwfTp0wFYtGgRo0ePplOnTpx11llxa5OIiEh1/Jnv\nlBRwuVykpDhZcmXEJVYUiNeioqKCefPmUVRUFJPztW3blhtuuCGqYBwgNTWVkSNHcu+997J69epA\nIH7rrbeycOFCdu3aRefOnRkzZgynnnoqAIsXL+bSSy/loYce4tFHH2XHjh0cc8wx3H333TRv3hyA\ntWvXcscdd5CXl0e3bt0444wz6myLN2i+4COOOIKePXvy/fffs3nzZiZOnMh3331HeXk5xhgmTpxI\nbm4u4GTTv/zyS5555pnA/qNGjeKoo45izJgxUb0fIiIikQjOiPu/ezxezawpMaMa8STmD3rLysp4\n6aWXyMjICAS2AAMGDOCNN95g2bJljB07lgkTJvDjjz8G1ns8HhYsWMDcuXN57733+P7775k5cybg\n3ISMHj2aAw88kEWLFjFp0iRefvllXC4XkfB4PCxcuJBVq1bRt29fPB4PF154IZ988gkLFiygd+/e\nXHvttbjd7lqPE+n5REREouUND8R95SmaWVNiRRnxWqSlpXHyySfTpUuXhCxNmTZtGtOnT6ewsJD0\n9HT+9a9/0bVr18D6s88+O/B42LBhPP300yxevDikdOWGG24gOzub7OxshgwZwooVKwD4+uuv2bhx\nIzfffDMZGRnss88+XH755dxxxx21tmnp0qUMHDiQlJQU2rdvz3XXXcfpp58OQOfOnQPbXXfddcyc\nOZO1a9fGtZRGRESaLn9nTX8g7h/CUKUpEisKxOuQkpJCu3btyMrKindTqhgzZgxXXXUVu3bt4rbb\nbuOJJ57gyCOPBJxs+aRJk5g3bx7btm3D5XJRXFzMjh07AvunpqbStm3bwPPs7GwKCwsB2Lx5Mzk5\nOSE3IF26dKmzTYcffnigRjzY9u3bue+++1i6dCm7du0iJcX5Z0xwe0RERGKputKU4OUiDU2lKY1A\nq1at+Mc//sHKlSuZO3cuAG+++SazZs3i8ccf54svvmDp0qUYY0JquGvToUMHfvvtN0pKSgLLNmzY\nUOd+NR3/kUceYdu2bbz66qssW7aMTz75JGT75s2bU1xcHLLPli1bImqriIjInggE4qnOc38grtIU\niRUF4kksOOht3bo1l1xyCU888QRut5uCggLS0tJo27YtFRUVzJo1C2ttxMc+9NBD2XvvvXnooYco\nLS1l3bp1IR0po1VYWEhWVhatWrWisLCQBx98MGR9nz59yMvLIy8vj4qKCp5//vmIAn9p2pYvX87c\nuXP1nxUR2SP+QNzfH0mlKRJrCsSTWHhHxosuuoj8/HzeeOMNzjzzTA4++GCGDh3Kcccdx48//shh\nhx1W6/4ulyuwLC0tjalTp2Kt5cgjj2TcuHGce+65tXaeDN4/3Lhx49i+fTuDBg1ixIgR9O/fP6Qe\n/vDDD+fSSy/liiuu4Nhjj+W3336jf//+tbZXZM6cOSxYsICHH36YDz74gPLy8ng3SUSSSGVGPKyz\npkpTJEZckZYqNCbLli3z5ubm1ln3XVJSQl5eHpFsKyKx5fF4mDhxYsiydu3aceqpp3LQQQfpxk1E\n6rTk8y0sX7KNTl2acfo5+/LaC2vYtqWEgUe1p/+g9vFunjQC/lhywIAB1f5RUkZcRJJS8NCXBx54\nICkpKWzfvp3nnnuOGTNmBDoei4jUJHhCH6gsTVGNuMSKAnERSUrBZShDhw5l3Lhx9OjRAwBrLUuW\nLIlX00QkSVQZNSVVo6ZIbCkQF5GkVFFREXiclpZGp06duPLKK9lvv/0A2L17d7yaJiJJwuMNDcRT\nU9RZU2JLgbiIJKXwQBycDr2tWrUCqDIcpohIOI+vwq3KzJrKiEuMKBAXkaRUXSAOzsRUoEBcROpW\nY2mKMuISIwrERSQp1RWIB09GJSJSncpA3Hmeqgl9JMYUiItIUgoOxNPT0wOPlREXkUh51VlT4kyB\nuIgkpeBRU1SaIiJ7InxCH82sKbGWVvcm8WOMOQH4B5ALlACvWGvH+tZdBPwN6AR8C1xtrf0yXm0V\nkdgKzoinpqYGHisQF5FIeTzO90BG3D9qiideLZKmJmEz4saY44FXgQeAdkAX4N++dccAU4DRQBvg\nNeAdY0zLuDRWRGLOH4inpaWFzKLpD8TLy8tDgnURkXD+jLjLFw2laEIfibFEzojfC0y11r4etGy5\n7/uVwGvW2g98zx80xowFzgCei2EbRSROggPxYFlZWYHHxcXFtGyp+3MRqV74qCkaR1xiLSEz4saY\n5sBAIN0Ys8wYs9UY87ExZoBvk4OBZWG7fQUcEst2ikj81BSI+zPioPIUEaldTcMXahxxiZVEzYi3\nxblJ+BNwMmCBG3HKTw4EWgI7w/bJB1pFeoLS0tKIt4lkWxGJLX+QnZqaGjJUYUpKZX4hPz8/MMGP\niEi4inKnGNzjcVNSUoLHN8NPRblbQ6BKvagrhkzUQNw/N/Uz1toVvsf3GmNuAo7yrW8Ttk9bYFWk\nJ1i9enXEjYlmWxGJjfXr1wPg8XjIy8sLLPd6KzNZK1eu1FT3IlKjwsJMIIVt27aSl7eJbdvSgHSK\niopDfq+INJSEDMSttTuNMWuDlxljXIDX9/U10D9sXT9gVqTn6NmzJ5mZmbVuU1payurVqyPaVkRi\na8eOHQA0a9aM3NzckHVvv/02xcXFtG/fvso6ERG/n75fT+HuMjp16kBublsoz2fD2u1kpGeSm9sz\n3s2TRsAfS9YkIQNxnynAdcaYl3Ay3X/BGcLwc5yM+LvGmGd9z68D0oHZkR48MzMzpFNXfW0rIrGV\nkZFR5eezWbNmFBcXU1FRkVQ/u2vWrKGoqIg+ffrEuykiTYLX69SEZ2Skk5WVRWZmRmB5Mv3ukOSV\nkJ01Aay1DwHTgY+ArcCJwMnW2t3W2s+Bq4GngB3AmcAwa21BvNorIrFVU2dNSM6xxMvLy3nmmWd4\n/vnn2bZtW7ybI9IkhE/oo86aEmuJnBHHWvs3nEl7qls3E5gZ2xaJSKJobIF4SUlJYLbQnTt3stde\ne8W5RSKNX2BCH1fYFPcavlBiJGEz4iIitYkkEE+mUQ/8QXj4YxFpON7A8IXOc40jLrGmQFxEkpI/\nWE1PT6+yLhkz4sGzgJaVlcWxJSJNh0pTJN4UiItIUmpspSkKxEVir8rMmipNkRhTIC4iSUmBuIj8\nXv6A2+WfWdMXFbnd3pA5CUQaigJxEUlKjS0QD64LVyAuEhv+CpTwKe4BFIdLLCgQF5GkVFsg7h//\nN5kCcWXERWLPnxEP76wJTlZcpKEpEBeRpBRJRrysrAy32x3Tdu0pBeIisRdeIx6cEfeow6bEgAJx\nEUlK/sC1tlFTIHmy4sGBuIYvFGl4Xq83UH7iD8BTgwNxZcQlBhSIi0hS8gertWXEIXkCcdWIi8SW\nfzIfCJrQJ0UZcYktBeIikpQiKU2B5AnEVZoiElvBgXagRjxVNeISWwrERSQp1dVZ0+XLcCkQF5Hq\nhATiqdVkxBWISwwoEBeRpFRbIJ6SkkJmZiagQFxEqheaEa/aWVOza0osKBAXkaRUWyAO0KxZMyB5\nAnHViIvEVnDGu9pRU5QRlxhQIC4iSam2UVMg+Sb10agpIrEVPGFPYIp7jSMuMaZAXESSjtvtxuMb\n8qCmjHgyB+LKiIs0vNCMuO+7xhGXGFMgLiJJJzhoVSAuUmnr5mI++2gTBbv1X5W6VFsjrs6aEmMK\nxEUk6TTGQFw14lIfli3ayndf7yDv6+3xbkrCCw7EXUGBuG/AJZWmSEwoEBeRpBNJIJ6VlQUkTyAe\n/Jo8Hk/Ic5FIlZa4fd89dWwpIRP6BGXC/WOJqzRFYiHiQNwYc5gxxlX3liIiDasxZsTDA29lxWVP\nVFR4fd8ViNelunHEgx8rIy6xUP1fsOotAfKNMf8DPgT+a621DdMsEZGaBQetjXHUFNDIKbJn/AF4\nRbkC8bpUN7Om89iXEVcgLjEQTSDeEzja93U1MMkYsxJ4BXjOWru6AdonIlJFcJDaWDLi4YG3MuKy\nJ9zKiEesus6aoNIUia2IA3Fr7RpgDTATwBizLzAMmADcboz5BPibtfaz+m+miEilaEpTSktLcbvd\npKamxqRte0qlKVIfKjPiCiLrUlMg7n+s0hSJhT3qrOkLws8FrgVygKeBecBcY8wF9dY6EZFqRBOI\nA5SUlDR4m34vBeJSH5QRj1xwZ01XUA+4QEZcgbjEQMQZcWPMH4HBwClAH+AnYCrwtLV2h2+bn4G7\ngRfqv6kiIg5/0OpyuWrMdAcH4sXFxTRv3jwmbdtTCsSlPvgD8HLViNfJH2inpDi/S/xSVJoiMRRN\njfi7wI/A28AYYIG1Nvwq/QHoVk9tExGplj9orSkbDlUD8USnGnH5vTwebyDL6x89RWrmD7SDy1KC\nn7sViEsMRBOI97DWrg1faIzJANpbazcAm4CL66ltIiLV8gfiNY2YAskXiCsjLr+XOyj41qgpdfPW\nEIirNEViKZoa8W+MMYOqWX45TpYca+1Wa+1/6qVlIiI18GePa8uIp6SkkJmZCSRHIB6eEdfwhRKt\n4LpwBeJ18//3oEpGXOOISwxFE4i3AKorxlwNmPppjohI3SIpTYHkGsJQGXH5vYLLUSoqvHi9CiRr\nU1dpimrEJRZq/StmjGkJtAf8V2kXY0yPoE3a4owpvrVhmiciUlU0gXh+fn7CB+Iejwe32x2yTIG4\nRMsdNlKK2+0lLU0TYtfEH2i7wlKSlaUpsW6RNEV11YgPBuYEPa+u7GQXcFm9tUhEpA6NLSMeHISn\npKTg8XgUiEvUwjtolpd7SEvbo1GKm4Q6O2uqNEVioK5A/EPgDzWs8wI7gVXW2sJ6bZWISC0aWyAe\nXA+enZ1NYWGhAnGJWvjY4RXlXsiuYWOpDMRTq68RV2mKxEKtf8V8AfYnsWmKiEhkGlsgHlwf3qxZ\nMwXiskfcYRlxTepTu5o6a6YqIy4xVFeN+OPA7dbafGPM33Cy4NWy1t5Z340TEamOP4Nc2/CFkLyB\nOGjUFIle1Yy4AvHaBE/oEyxFwxdKDNVVmjIEeADIB66k+kDc5VuuQFxEYqKxZ8RBnTUlelUy4grE\na+UfVabGccRVmiIxUFdpykFBj7s2fHNEROrW2ALx4Oy3AvHEUFbqJj0jJWTq80RXJSOu2TVr5Xar\ns6bEX8TdqY0x7xtjTmjIxoiIRKKxBeLBGfHmzZsDKk2Jp00binh2muXTDzbFuylRCQ+8VSNeuxpH\nTVFpisRQNOMa/R+gn2oRibtoA/GSkhI8nsT99aXSlMSyaX0hHg9s/CW5BgQLH0e8XKUptfL/Sqhp\nHHG3SlMkBuqqEQ+2A2hvjKk2eLfW6ideRGIi2kAcnGDcH+QmmuBA3N9mBeLxU1zkjOuebIFslYx4\nuQLJ2njrmllTGXGJgWgy4j8ALwEV1Xzpf6giEjPRjpoCiV2e4n89aWlpZGRkAArE46mkxLkxSrZA\ntmqNeHLdSMRaTaUp6qwpsRRNRvxmILehGiIiEqk9yYgnciAe/HoUiMdfSVBG3Ov1Jk2HTY2aEp06\nJ/RRRlxiIOJA3Fq7FFjagG0REYlIYw3E09PTA4F4RUUFHo+HlPBBjqXBlZS4A48rKrykpydHIF7h\n1qgp0QhM6OOqYUKfBMuIu91uFixYQJcuXejRo0e8myP1JJqMOMaYQcCRQKuwVWustc/XW6tERGoR\naSCemppKRkYGZWVlSReIg1OykpmZWa/n8nq9vPLKK5SVlXHBBRco0K9GcVFlzX5FuYf09OR4j5QR\nj05lRjx0eaJmxFevXs3bb79N69atufXWW+PdHKknEQfixpjxwCPAV8ABwM/AViAHSAcUiItITEQa\niIOTFU/0QDy4Rjy47r2srKzeA/Ft27axfPlyADZs2EC3bt3q9fjJzuv1UlJcmREvL/OQnZh9fKsI\nrwlPts6msVbX8IWJNo74rl27At+TqWRKahfNbf7NwB3W2v44wxiOttYOBq4B9JtcRGIm2kAckqM0\nJbhGHBqmTnz79u2Bx7/99lu9Hz/ZVZR7QwKwZApmq44jnliBZKLx1Dihj299gpWmlJaWAs7NouYZ\naDyiCcTbAQt8j9N9XwAZRFniIiLye0Q6agooEA+3Y8eOwGMF4lWVFFeEPE+mQDx8HHGNmlK7GkdN\nSdDhC4N/H/iDcgn102+FPPzRStbnJ+7v+3DRBOKbcMpQAL4GxhljDgFGAyvru2EiIjVRRnzPBQfi\nwdlxcRQHlaVActVZVx1HPHnaHg+BzppJUpoS/PugpKQkji1JXE8vXMvLy9bz0he/xLspEYsmk30N\nlQH3bcCbwAigGPhTPbcrwDeB0HzgCKCrtXajb/lFwN+ATsC3wNXW2i8bqh0ikhi8Xm+jC8SDM/yx\nLE1RIF5Vo8qIJ1Hb46FyQp/Q5Yk6jnhwFlwZ8ept2e28L9uLkmf414gz4tbat621q3yPPwL2wQmO\n97bWvtlA7QO4HigEAj8RxphjgCk42fg2wGvAO8aYlg3YDhFJAG53ZcaysQTiwTcWKSkpgdel0pTY\nKwnLiCdTIO7PiGdkpoQ8l+rV2FnT99zrTaxgXKUpddtZ4iQ1isrcdWyZOPZ4TCZr7TZr7RKguzHm\n6XpsU4Ax5kBgDHAjEPyTciXwmrX2A2ttubX2QaAEOKMh2iEiiSN4OvjGGIgDgax4Q3TICs6C79q1\nS52+wlQpTSlLvkA8K8sZj08Z8dr5g2xXDaUpwdskAgXidcsv8gfiFXVsGRtut5vPPvus1m1q/Ctm\njLkZ6FPHOVKAQTgZ63rlK0mZDtwA7AxbfTDwTNiyr4BD6rsdIpJYmkIg7u+EWt8Z8dLSUoqKikKW\nbd++nY4dO9breZJZYyhNycpOZdfOcnXWrENdU9yDUycewa+ZmFBpSu28Xm8gI16YIBnxVatW8eGH\nHzJy5Mgat6nt8vIC3QkqCfFxhW2zGLh/TxtZi+uAjdbaN4wx+4ata0nV4DyfqhMN1SiSi9i/jS54\nkcRRUFAQeOzxeOrstOQPbouLixO2g5P/d4zL5aKkpCQQiBcWFtZrmzdv3lxl2a+//krr1q3r7RzJ\nrnB36M1PcXF5wl434fwZ8PQM5890eXndPx9Nmf9GxeOpCHmfKioq/0tUXFSC15taZd94CG5jQUGB\nPtswBaUVgdlQC0sT4+c2kn44NQbivnKPB+uzQZEyxvQE/gIcFrbKfxOwGwj/y9EWWBXpOVavXh1x\ne+YHfuAAACAASURBVKLZVkQa1u7duwOPf/rpJ7Zs2VLr9v71xcXFrFixIiEnwcjPzwdg586d5OXl\nBergN2zYQF5eXr2dZ+PGjYAT8GdnZ1NUVMR3330X8l+Gpm7r1gygMvD69dct5OVtjF+DolBengW4\nKCnZDaRRXuau1+unsSkuzgRS2Lo19DMuLnQBWQB8//0PZNTvnFp7zD+hD8C6deto1ixJZpqKka1F\nlVnw3cVlCXHt//zzz3VuE/U/XIwx3YGBvqfLrLVroz1GBI4B2gMrjDFQWcv+jTHmdpzhEwcEtckF\n9ANmRXqCnj171jljXWlpKatXr45oWxGJjV9//TXw+KCDDqJly9r7aLdq1Yr58+cDzs99VlZWg7Zv\nTyxZsgSAjh07kpuby5IlS9ixYwdt2rQhNze33s7jv4lp06YNbdu2Zc2aNWRmZtbrOZLdzys3AJX/\nBW3dqh25ue3j16AIeb1evvj0JwA6dGrHb1t24fG46N27d0LefCaCVd/8QjHldOrckdzcNoHlO/PL\nyFu2HoCePQ+kZau65yuIhQ8//DDwuL5/NzQGeb/uhkXfAlDqcSXE+1NXogiim+I+E5gMXEZlYOw1\nxszAGTqwPus3/gO8H/S8G7AQGApY4BvgXWPMs8DnOGUs6cDsSE+QmZkZ8R/kaLYVkYaVmlqZrWze\nvHmdP5vBZRcejychf5Y9vgGNs7KyyMrKCtz413d7/YF4Tk4OOTk5rFmzhp07dybkexIvZaWh1Zhe\nb0pSvD/B9eAtWlQmjtLSMklP3+NxGRo1r++jzszMCPmMy7Mr36/0tAyyshIjERfcsdrtdifFdRlL\nxe7KssUyt4e0jAzSwsemjLHgUb5qEk1G/D6cccP/BHziW3Y88DhOCcu4qFpXC2ttMc745AAYYzJw\n6tF/tdYWAp8bY64GngI64wTmw6y1BdUdT0Qaj+A/RtF01oTE7bAZPlOof9SU+u6s6R+6sG3btrRr\n1w7QWOLhSop8HWfTXVSUe5Oms6Y7aKhC/6gp4NSNKxCvnn9AlJom9AECNceJQJ01a7ezOHQEqKIy\nN62y4nvtR1KnHk0gfj4wwVobXP4xyzd29wPUYyAezlf+khq2bCYws6HOKSKJaU/HEYfEDcRjNXyh\nP+hu164dOTk5gWUej4eUOGeOEoHH46W01Am8W7bKYMdvpUkzBGBwRjwzu/LnIlnaHw/+KezDL/2Q\n4QsTZHZNj8cT8vsgEToiJpr8agPx+JYVRXLDFM1v3uZAdbM/7ACyq1kuIlLv/H+MUlNTIwoe09LS\nApnmZAvE6zMj7vV6q82Iu93ukE5gTVnwZD7+uuDyJBlHvKKmjLgm9alRjcMXpiTeOOIVFRV4vZVt\naYjJvpJdeCBemABjiUdywxRNIP5f4HZjTGf/At/jicBHUbdORGQPRDO9vV+ijyXuv7loyEC8qKgo\nkJ1p27ZtICMOmmHTL3gM8UAgniQZ5eDp7bOyQ0tTpHo1zqwZNo54IgjPrCojXlV1pSnxVt8Z8fFA\nC+AnY8zXxphvgJ9whhFssLIUEZFgjTEQ978mf+a+ISb0CZ7avl27dmRmZtKiRQtAgbhfdRnxZAlk\nQzLiQYF4uSb1qZHX99bUNMU9JE5pSvjvAtWIV1VdaUq81WtG3Fr7M86MlmNwRiqZD4wF+jTQEIYi\nIlU05kC8ITPi/kA8PT09EICrw2YofyCelu4iy1dnnSwZ8eAa8YxMZcQjEciIp1YNxP0jPiZKaUp4\n4K1AvKpkLU2Jahxxa205ztTy4dPLi4jERHgZRyQSORD3eDyBDqgN2VnTH2y3bds2MK50Tk4O69at\nUyDuU+wrTcnKTguMNJIsgXjwqClpaa7AqC+qEa9ZZWlK1XUpKS7cbm/ClKYkakZ87Y+72bmjlIMH\n5MR9vPpEzIhH8jlFFYj7Zrz8G86EPiXAd8Bj1tole9JAEZFohQetkUjkQDx4VstYZMTbtm0bWObP\niKs0xeHPiGdnp5KW4URnFeVevF5v3IOMuvgz4qmpLlwuF2lpKVSUu5URr4HX6w2MI+5KqfrZpqY6\ngXgil6bE+7r0eLx8+M56Kiq85HTIomv3FnFrCyRejbjH46nfGnFjTD/gW+BQ4D3gQ2A/YIEx5tQ9\nbKeISFTCx9yOxP9n783j5Ljqa/FTVb1Pz/RsmtFq7SottsG7Idg4YckG2YCQvCQkDkng8V4gOC+Q\nBENC8rLCS9iS/AgBDCFAwGtswMYLxo4tGduyZEmWSutImn3t6em11t8ft+6tW9XVe7emR9Pn85nP\nzPRa661zT53v+a4UIt7KHHFeEafoEHE3KBGPRCVX9vZKUJWpIi4FCDGjy98h4v4wuc3i9YgDjl2l\nXXLEvYTOsqymx5vWinzOYOfG3MzyKvSWZRUR8eW2plQ7fteiiH8KwHcBvF1RFHZkyrL8eQD/D8BD\ntSxgBx100EE9qMcj3tXVBYAkh7QbyinimqY1TfWiijgl3wBYcko+n0c2m0UsFmv4e1Yy3NYUZ5tr\navs3xaGKeCAgun6vhEnEcoD3fvsScfuxdlXEAXLe0rFiOZDjUoYW5paXiKcLOgz7FkdIEqEaJjLL\nrIhXax+qZWS5EcAXeRJu434AG2v4nA466KCDulEPEacEM5PJtGSZGoFfp1CqjDdL9fJmiFN0Igzd\nKKmIrwBVmXqZA7YiHrAnEnonNcUXPMH284hLUnsScb53QjN84ppm4uypFAr52klrLts+RJxXw9f2\nRAAA2WVWxKuNmKyFiBfsHy92g7SY76CDDjpoOS5nRdxrTQGaY09ZWlpi38MT8Xg8zr6rU7Dp5IhH\nowEEOCK+Ego2dWZNsRXxFVZseqlRURFvU2sKTTziH2sER16aw6MPjeK+b5xDJl3bpD+fdcj7wnzB\n1XDoUoMv1FyfoER8eRXxaol4LdaUMQD/JMvyNAABgGX/vhJAWpblp+jjiqLcWtvidtBBBx1Uh3pS\nU6girqoqNE2ryV/eapSzpgDNIeLeDHEKQRDQ39+PycnJDhFHaUV8JZBZg1lTbEU84BSbdlCMSkRc\najNrCiXdPT09rBNuM4h4KknG08WkiofuPo+3vmMLYl3Vja28Iq6pJjJpHfHu5RlbKREXBWC4JwwA\nK8aaUgsR/ycQe4oXZzz/t8dR20EHHVyWaEQRB4gqnkgkmr5c9aISEW+GNYWS7HA4zApXKSgRX+3W\nFMuykOOIeGCFWVOKFPFAx5pSDiutWJNOyGOxGCRJgmEYTemuqRYcsppcUPHg3SP4uXdsQTRWeXzN\n5dxEd2GusOxEPBENoitElr1drCmVfPxVX8kURflnAP/c0FJ10EEHHTSIeuIL+SLETCbTVkScJ9qt\nsqbwhZrewk/qE1/tRFzTTKZ+RqMBiKKAQECArlsrQhHXvYp4JzWlLFyKuFSaiLebIh4KhRCJRJDJ\nZJoyNtBje3AogvnZPJLzKh68+zze+vbNFck4r4gDxJ6yacvyRBhSj3hvNIiuEGlo1S7WlHA4XPZ1\n7V0G3kEHHXTgQT3xhTwRbzefOFXEBUFghVjNJuJ+0YUUlIivdmsK73elLeKb6bMeH83gO/ecx8xU\nayI0aXwhtaSw+MJOaoovXETcJ5SIWlParaFPKBRixK4pirhKju3N2+J4w89shCAQZfuhe867UlH8\nkPdRxJcLSY6Ix2xFvF2sKZFIpOzrOkS8gw46WFGox5oSCATYxatdiXggEGBqtSRJjJQ3UxH3I+LU\nM55KpZY9l3g5kedSIyIxml5jk1m1cSJ+9KV5jF7I4JWXFyq/uA6whj7MI25bU9pUEbc0FZZaH3E7\nffo0PvvZz+LkyZP1f3+1inibWVPC4TAby5qSmmIf28GQhG07e/CGn94AQQDmZwt48pHxsu+liji9\nydYORDwRCSLGFPH2sKZ0FPEOOujgskI9RBxo3whDuj68wi8IAvu/2dYUL+hjfMThagRPKsJht6rc\nDEWcEn2vitgs6B5FvJ1TU8xMGuO/+bOYeO8vw5ifrfn9+/fvx9jYGA4cOFD/MlQq1mTWlLq/oqng\nrSnNJeKG/bnkeNkuJ3DzLcMAgInR8qIFPWcGh4jiuzC3fMkpjIjH2seaQvdPh4h30EEHlxXqJeLt\nGmFYKgWmWd01DcNAMpkE4K+I9/X1MfV9NfvE+cQUemfCIbONkwtaFFdPXnM1MLgW90CbN/SRArDU\nAoypMcx94k5YRm3bZHaWkHd6XNeDisWaK8Ca0gwirjJF3KGDa9aSgm5NM6GWIbO0WHP9xi72WdnM\n8qjQjkc8xKwpWdVY1kjFahXxklcyWZb/EsBvcQ/RtfEesRaARxVFeXetC9lBBx10UCvqiS8E2l8R\nbxURT6VSMG3W4aeIS5KE3t5ezM/Pr2qfOM0Qj0Sc/dBMRbxQIJ/RKiLuKOLt39BHjETQ97//FPOf\nuBOFl19A6hv/hsSvv6eq95qmySaMi4uLdS8DX4Qp+EiSK8Ga0qhH3LIsZk0JcUS8i4svzKZ1hPql\novfqusneu25jDIdfJPtkYa6ArvilT07xs6YYloWCbiISLF7+S4FqFfFyV7KHAfAjxs8CiAH4Ftxk\nfB+A19ezkB100EEHtaKe1BTAIeLtpohXIuKN+rZ5cu2niAOEoM/Pz69qRZxFF8acizYjs00g4lQR\nz7daEfe2uG9DawoAdN32UygcPYjM9+5F6pv/hvC+VyNyzU0V35dKpdg5Q5ND6mnzvlJzxMPhMCv+\na1QR13ULVDDmc/NjcWcsymR09PYXE8kcV9zckwihuyeIpZSG+bkCNm6+9MkpizkyUemNOfGFAFHF\nl4uIN6yIK4ryDIBn6P+yLL8TwN8qivIV/nWyLP8EgP9qYFk76KCDDqpGPakpQPsTce/6NEsRp77v\nrq6ukheEgYEBnD59epUr4jYRjzgXbXq7vlFF3LIsqJwibllWUYxko/Aq4sEVEF/Y+7t3QD1xFNq5\nk5j75Eex9rNfh9Q/WPY9MzMzrv8XFxexZs2amr97pXXW5K0pdGxolIhrXBFyKMxNQAMiQmERasFE\nNu1vNclz0YWRmIS+gTCWUtqyFGxaloVF+44WSU1x1iWr6ujvqn2i1gy0wiO+GYCfXNIHoH3P9A46\n6OCyQqMe8XazprTaI14uupCCWlZWsyLO2tvHmm9N4QmPYVgt8W07OeLuYs229IjbEMMRDPzJ30KI\nxmAm5zH3938KyyjvMfYeo/X6xCsS8TZSxC3LcllTmqWIa5z/m1fEAaCriwgDmYz/HTkabSgIZPLa\nZ6vmy0HE0wUdhi3t90aDiHEK+HJGGLYiNeUYgPfIsszWUJblbgD/B8BjtS9iBx100EHtuNyKNUut\nT7NSU8olplDQLPGFhQXmJ19t4Is1KQJNii+k/nD2fwvsKQbrrOmOLzQMq218zn4IbrgC/e+/EwBQ\nOHIQqa9/oezrvYp4/USc/BZLsCCpjTziuq6z87KZxZoqd1wHw+4NQe0ppRRxak2hxc19AzYRn7/0\nySnUHw64O2sCQFZbfiLezBzx9wD4CQAXZFm+V5blhwCcA7ANwAfrW8wOOuigg9pwucYXtkoRL5ch\nTkFJuq7rSKVSDX3fSkXOh4g3SxHn24gDrSHiRYp4QCx6rl0Ru/XN6PqZtwMAUv/5JWijIyVfSxNT\nKOot2KQE208NBwDRPgyqSU0x83nMf+6vkf7u3XUtSyXwY0AzibjLmlKkiNtNcUqkoNDowmiUvI4S\ncbVw6ZNTeCLeGw0iEhRZk6blzBJvujVFUZSDAHYC+DJIsaYI4J8AyIqinK93QTvooIMOqoVpmg0X\na6qqyshvO6DVRLwaawpVxIHVZ0/RdR3nzp1DNksumpRYACuLiBcp4hyx0psQv9hq9P3uByFEooBl\nQTujlHxds60pfs18gNqsKekHvo7M9+7Fwuc/CasFYwtPuJuZmkIVcVESWJEvhaOIl7em0OLm3n7H\nh32p7Sk0ulASBMTDpDFa1LanLJc1xTTNpqSmFEFRlHEAd9a9ZB100EEHDcDg8obrJeIAsaf09PQ0\nbbkaQani02akpui6jqWlJQDlrSnhcBixWAzZbLahbOaViCeeeAJPPPEEErEr0d99rb81pUEi7rWm\nNCs5ZWZmBpOTk9i3b5+PR9whmO2uiAOAEApDWrMW+sVz0GenfF9jGAabWNKkn4aJeAlFXKqyWNPM\n57H0wDfIP7oOY34WgaG1dS1TKXgVcWp1UFW1ocJf1dPMhwf1iJdSt/O2NYXWVIRCEuLdQaSXNCzM\nX9rkFBZdGA1AtLdFVyiAjGosW1Mffp+Fw+Gydy9qaugjy/Itsiz/qyzLD8uyvNN+rFeW5SvqXdgO\nOuigg2rBk9JaU1OoRxxoL594KxXxhYUF5tcsp4gDQDxOLpzttG0uBSYnJwEAqk4sPJFWKOJqaxTx\nr371q/iP//gPnDx5inmeWY44b01p4+QUHoE1pKOjMeNPxPkahh07dgBoxJpCfoslSCzLEa+giGce\n+y+Yi05HWqPEJKIReEkdVVj5Is56wNrbB4upIFXEM2nd1/NNFXH+DhLziV9iRdwh4s41Ybnb3PN3\nK5pmTZFl+bcBPAlgK4A3A+i2n7odQGuMUasA2WwWBw4cYKpVBx10UBq8paQRRbydfOKtJuIUlYh4\nu3roWw068TBMu7Aq2vz4QrUFxZq6rjO/9NycEztJLQY8uWrn5BQe0qBNxEuQWbq+giBg69atAIg1\npZ7iQEqwxRIR09XkiFu6jqV7/t31mDE3XfOyVAKvpgaDQRexa8Qnzpr5hH2IuO0RNwyr6PgFnGLN\nKJe73zdAxqzlsqb0+hDx5bKmeO1E5VCLIv4hAH8O4Kc9j78CQK7hczrg8MMf/hD3338/HnnkkeVe\nlA46aHs0QsSDwSAjt+2k+rYyNYWqhd3d3RW3V7vmrLca5Yi4Y02xGkqCaIVHfGlpiS1TNptjjwc8\nqSnAylHEJVsR10so4pSI9/X1sboGTdPqOmbptitdrFnZmpJ96hEY0xMAAKGru+yyNwI6BgQCAUiS\n1DQirpZRxLv4pj4+PnFWrBnjFXFimVmYu7TJKY4i7vjU+Tb3y4GWKOIArgDwnM/j3QCWp23RZYDp\naTJ7Xm0FUh10UA8aIeJAe6q+lTzizSDiiUSi4mvbNWe91aAkzjTzCAQEl6WjWapyKzzivCUjl3Mu\n+nT5RUkAdV00quhfKkgDQwAqK+KDg4Po7e1lj9fjE2eKeCmPeAVF3DJNpL5N+htGX3MbQjv3lF32\nRsBniPO/gWYp4sUULsYRbK9P3LIsljLkIuL9tNGQ6eq8WSsKeYN1iq0GvEecomuZrSl0vwiCULHz\nay1E/CCAXwbAjko7R/wD8CfoHVQBaklZbRe/DjqoB7xHvB4i3o5ks5XWFErWqilMXY2KuGVZbH0t\nGAhF3Bf/IFfwqDWQJd4KRZwn4rz6RlNTBEFYEU19eATWkCJHMzkPSys+7nkiHo/HIUmEbNVFxG2l\nW6ikiJcg4vkfPQ39wlkAQPfbf4uz1bTOmkLHBJ6IN5KcQmsX/BRxKSCyu0MZT5a4qppsgsLfQaJN\nfYD67SmZtIav/dtJ3P21s1VnuLP29i5FfHmtKXS/hEIhiKXC6m3UQsQ/COAdAF6y//8sSI741SC2\nlQ7qAM3sbSdi0EEH7QpeEa+1WBNoT7JZyZqiaVrdt3nrUcTbadu0GoVCwdXASAq4b8G7FPEGVOUi\nj3ihyUTcRxEnfxMyuWKsKTaZBfwJLU/ERVFkE8x6Cjadhj4VijV9yKBlWUh9+y4AQPjq6xHefSUC\ng7aa3wKPON/eHiBjBR0vmqGIB31SUwDHJ+5VxPn29rwiHgpLiHeT/+sl4hNjWeiaheSCitnp6iYZ\nSa69PVv2NrGmVGrmA9SWI/48gCsBPATgYQBTAP4ZwE5FUV6sZ0FXO0zTRDqdBkAufqu1o10HHVSL\nZllTypHNfD7fUGRgraikiPPZ6bWiFiLejpOUVsMrgIgBtwrLZ3E3Yu9ouSLOkTGJ84ZTUr4S4gsB\nxyMOoCjCUNM0pnwPDg4CALOnNKKIl+ysWcaaUjjyItQTRwAAPb/8W+T1lIi3UBHnlfBmNPVh1pQS\nRJz6xL1t7nnbCV+sCQC9/U6HzXqQnHfOwfGL1QmUjiLuEPF2saZU8ocDNeSIy7IcVRTlIoA/9Tye\nkGV5u6IoZ2pczlWPTCbDyDfxXOVcEWsddNCBGzwRp7ela0El1TeTyeATn/gEYrEY7rjjjrrIfq2o\n5BEHiCJWz7LUQ8QzmUxD2cQrCd7jQBDc5CHYJCJOFfCueACZtN50Iq4WCqBHj5/HfaUo4mI0BqGr\nG1ZmqSjCkK+jai4Rr92asmR7w4M79iD86psAANKAbU2Zn4Vl6BCk5o0dXmsKQAheJpNBoVCApeuw\ndB1iFeorD1asGfIfS2M0S9xjTaHRhZIkFNla+gfCGD2fwXydiniSI/BjFzN49Q2DZV9vWhYW7eXx\njy+8jBRxAM/Isny7z+O/CKKSd1AjvJGFHXtKBx2UB68e10MUKxVrjo6OIp/PY35+HmfPnq1/QWtA\nJUUcqM8nXigU2MWgFmsK3xHucoeXiJtw3woPNMuaYhOe7gTZp80u1iwUyHILglvhpU19VopHHOCy\nxD2KOLWlSJLECDg9ruuzplTX0MdrTVHPnED+4H4ARA2n4xBT800DxkJzwxe81hTAUVrz6TQm3v3z\nmHzv22HMz9b0udUr4h4izkUXesdhPku8HktdcsEZeybHsiU9+hTpgg7D/h4/a8pye8SbTcR3A7jg\n8/hFANtr+JwObFB/OAW1qXTQQQf+KEVaq0UlRZzP3X7llVfq+o5aQRXxZhNxfnypRREHVo8oUETE\nLfcERBQF5rNuhjWlJ0GIgq5ZNaVC+MFFxFWy3FJAcBEjqo6vlNQUwLF4eGMAKREfGBhgxW8tVcTt\nxy3LTcazTz8GAAis24jozbcVLTfQfHuKNzWF/zs3Ow1jdgrGzCSSX/iHGj/XLtas5BH3KuK2R5xv\nfkVBrSmFvFFzcoppWi5riq5bmJ7MlXmHkyEOrFxrSi1EfAnATp/HdwOY93m8gwroKOIddFAbSpHW\nalFJEaftswHg+PHjlyQLt1WKOE/UqklNadfOo62E9zjQ9eKLPlXFG0lNofGF3T2hosfqgWEYruuH\nahNx3pYCcDnoK8QjDpRu6sMXalJQIp5KpWquo2DFmiUcbtSaQl7rjAPaGQUAEL76BgicPU6M90Cw\nSVezIwzLecRzS86EO/vU95E/eKDqz6UTtFJEvCtO29y7C8ZZV81Y8ThMFXGgdp94ekljCji9I1HJ\nJ57kiHiijYo1W0XE/w3AX8qy/DZZlvttb/gvAvg4gH+v8N4OfOBVxDtEvIMOyqNRRZwS8UKh4Hvh\n5hXxxcVFTExM1PU91cIwDFYnUskjXisoEe/q6qoqYSYSiTA1dbUQce96aj5EvFGfta47UW9UEQeA\nfK5+pY5v5gMAmkYbvrjVXVasqbWXNcUwLPzXt0fw2HdGiya7UgVrih8Rtyyr5u7U1SrigLtgUz17\nEgAQ3LbL9XpBEByfeIsUcX5MoJaHQtbNGxb++W9hFiqnjViWVdGaQhVx0wTyOWe8zPt01aQIhyVm\naak1OYX6wwUB2LaLiAfVEnFJEBAPO9cF5hHXDJiXsLkQRausKX8O4L8A/CeAWQALAO4B8CiAj9S4\njB2go4h30EGtoES8nuhCwG2/8CObPBEHiCreSvCTAe/kgv+/nhSXWgo1AUAUxbZseNRKeI+BQqH4\nmKBEvF57Bx9d2JPgFPEGfOJeT7Rh6LAsg7W3p3A84u2liM9O5zAxmsWZk6miaLzAIMkSr4WIA7Xb\nUyi5LpUjLnGKOO2uaczPwkwS/3doe3FD8VYlp5T1iOfI5FFM9AGiBH1iFEvfuqviZ+q6BcpPSxVr\n8t01+f3EFHEfawoA9A+SZZubqS3jnNpSunuCuGJrHAAwOZEre/wucs18RM6W1RVyli2nXXpVvFXx\nhZqiKO8Gsae8E6RIU1YU5VcVRam/48QqRkcR76CD2tAsjzjgf75RIh6NRgG0noiXa1AkimJDbe5r\nJeLA6osw9K5nPl+83oGGibhDArriAVZM2Yg1xa840bS0Mop4exFxfnKSy7qJOFXEzdQiTJvM5PN5\nVkPFE/FIJMIIac1EvMrUFMAh7epZYkuBICC4ZUfRe5i/fe7SWVNYosrOvej++V8FAKTuvgvaxZGy\nn8kfl6UUcd56wre5z5VRxAFgYA0hn7UScWpl6e0PY/1Gu3jcsDA57j8ejZxZwuTBFN4o9uJ1Zg8e\nfegiHv3OKJ78/jgE7hhbDntKq6wpAABFUc4pivJtRVEeUBTlVO2L1wFFRxHvoIPa0CxrCuCnhhbY\nOXjjjTcCICkq3glzM1GpQVEj3TUbIeKrZSyix4AokO2czRWvt6OI13d7m2/eEwpLCEcIeWkkOYXu\nWz7C0zQ1H0W8Pa0pPAn0FvS5mvrYhJaq4YCbiAP1F2xaFRr6SD7WFM22pQQ2XAExGit+D/W3zzSX\niJdTxAuqbc3oG0DPr/0emcjoOhb+6W/K1rjwE8tSHnFRFFire5cini3tEQccIj4/W6i6OybgWFN6\n+8OIdQVYp87xi8VEvJA38MTDYzDmDGwRIxjSgzh7aglnT6agHEvi1PPO3c3MMhRstkQRl2VZkGX5\nnbIsf12W5cdlWX7K/nlaluWn6l/c1Qt6gacn12q5+HXQQb1olIiHQiFGeL3nG29Lue6669h5eeLE\nibq+qxpUalBEl+FSWFOA1auIBwMJ9r+3sRolKfWqyrz6GwyJjIg3w5rCk1LTUn0U8fa0pqhc4WvO\n45WXBrj0kRk3EQ+FQuju7na9vl4iXqmhj+hjTVHtQk2vP5wi4GlzPzc3h+npyjaV3HNPYeoPb2ef\n70W51BTVtreJfQMQozH0veePAJCmQ9kffLfkd2rccVlKEQeAGI0wtJNTTNNifvFIBSJuGBYWIPJS\naQAAIABJREFUF6oXEZL2a/v6ybi3fhMZj/x84kcPzUNTTVgCcNzMYrHbxO4re7FlBzk+ZsfzGMDy\nFWy2ShH/vwC+AWAHgBkAZ+2fM/ZPBzXANE2miK9dSzxxHSLeQbNxKVI/LiUaTU0BSpNNSsRFUcTA\nwAB27iQhUa20p7RSEacT/WoSUyhWW5t7LxG3LKto3anPut7UFKr+hkIiRFFApAlEnO7b4WFHPSbW\nFPclvVF/e6vAK+J5jyIuRiIQe8j+8BLxwcHBotzqerPEq80RB4oV8dC2Yn84wHnE52eQz2bxmc98\nBp/5zGcqThIWv/4FqCeOIPXNf/N9vlRDHwBQ7fWQ+gYAANHX3IbITbcCAJJf+EeYS/539FSXIl66\nOZq3zT1/3Eaj/u9L9IbYJLBae0oupzOCTyMQ128i49HMVI5FLQLkXDzyEkm4Wuw28YyZgrYpgNe/\naT3e/JaNSPSR7XSVaI9nl5iI870Yml2s+W4Af6Yoyo2KovyKoii/xf34NfrpoAx45WXdunUAOkS8\ng+bBNE188YtfxKc+9am6SFy7olFFHChNxGl0YSKRgCRJ2LNnDwDg1KlTLduG5TziQP1EXNM0Np50\nrCmlQdczJPUWPUbByGydqjL1gofChLQ0UxEfGBhg9hTL0lzkEeDjC9trQu5SxLPFtgFq8dDniom4\nF40r4pVTUwzDgpnNQB8nrVSCFYg4DAOzF0ZQKBSg63rZybylFqCNEJdv/tCPYOnu7aHrOivq9ktN\nUWE3FOpztk3fe/8IQigMM5VE7kf+hgU6sZQkoei44cGa+tgecX5/lbKmiKJQc8Emnx/OiPhGMh6Z\nJmnuQ/HKy/Mo5A2IkoALYUJ4aXShIAh41XVkUrJNiCAO6ZJbU/jxutlEvBfAD2tfpA78wPtOeUX8\nclMwO1geJJNJnDp1ClNTU7hwwa8P18pEo6kpgKP6lrKm9PX1AQB2794NQRCg6zpOnz5d9/eVQyVr\nSr3FmrU286FYTYq4pmlsIkQVcaC4sRojs/Uq4rYaFwqTz2mGR5ySzkQiwZRR0yxWxJk1pe0Ucd6a\nUrwdvF7r1hBx8ruqYk3TYmQZAEIlrCm8v31hbJT9ffLkyZLLoZ49BdjjgJXNoHDiZffz3Lnva00R\nJVhwFHEACAytQ2jXPvL8aX9rHb0rUcofTsHa3NuKOO/pL6WIA449ZbZqIk4IdTQmsbtGkWiAfc6Y\n7RPXdROHXyTJNbv39WLG9sjzzXx27kkgGpMgCgKuEmOXXBGn/nCg+daUOQA7ZVne5vdT+6KublBb\niiAI7PaiYRirprV0B60F73f2RvKtZLRSEfcS8Xg8jk2bNgFonU+8Wo94rUScv03fUcT9we//gBiD\nJJFt7SXizYovbJYiztsaE4kEU9xMS4Xk9Yi3aUMfd7FmsVoZWONEGFqWVZaI0+M7l8vVdP1kingJ\nLumKLzQslh8u9g+6SC8PsacXCBBCmJyaZI+fOXPGda7zUE8dc/2ff3G/+3nu3PezpkAQoIkSRM8y\nBXfstj/fv0MwPZ7L+cMBRxFnRNz29IfCYlFxMA9WsDlT3T5hhZp9buK6weMTP3E0iVzWgCAAr75+\ngMUX8kQ8EBBx1TVke8hCDOl07TU2jYA/DputiJ8D8AUAp31+OukpNYIqVvF43FV8shougB20HnyH\nyA4Rd6OU6usl4gCYPeX48eNFRXzNAF0fURRdCRgUjRLxaDTqunhXAj9JudzvzvH7XxTDCIdJZGWz\niXiB84gDaNgjnk6n2bHoUsR9POJtG1/I3V3wa2zEK+KZTIYpjOUUcaA2nzgj4kJla4ppWKyjZil/\nOGA39bHtKYvzc+xxVVUxMjLi+x71pIeIv/CM+/kKijgAaKJUNDkI7dxLnjt7EpZP8zI6QSznDwfc\nHnHTtJzElBIZ4hSUiGezelFWvB8WbGsKtaVQUJ/47HQe2YyOwy+QSdnOPQl09QSxaB8/PBEHgL1X\n90GHhYAgYPH0Iqbv/F/IPv1YxeVoBnhFvBoiXsvV7HcArK19kWqHLMt/B+BnAWwCkAbwHQAfVhRl\ngXvNuwD8mb1MRwC8T1GUg5di+ZoBqmh0d3cXZRsPDPjPtjvooFp0iHhplFJ9SxHxRx55BEtLSxgb\nG2MKebNQqfi03tSUehJTAGeSYhgGVFWt6rbqSoWXiEcjXchmF4uOi0CDnTUp4Qk3SRH33u1girjp\nkyNuF5qaJlF1y3mBLyX4wjtvfCHgZInrs1OYm3MIbTlFHCD2lKGhoaLX+IEWYIoltokoChAEwLII\naS/VUdOLwJphGJNjRbGnJ0+exI4dxdnj6kmiWIf3XYPCsZegnT0JY34WUj9ZV15d9VXEAWiRLgie\nOMWQrYhbhTz00REEN293PV+pvT0FJeKWRbprVsoQp6AecYD4xGNd8bKvd6IL3cLBug0xth+eemwc\n6SVyDbjmhkGkCzoMWzBIeIh4OCJhJqpjXS4IfcpE9vBLgGUhdssbyy5HM0CJuCAICAaDFYWUWhr6\nnFAU5clSPw0tdTF0AL8GoB/AqwBsBHAXfVKW5dcB+GcA7wHxrt8D4LuyLHcXfVKbgk80iEQiEO0M\nJa8a00EH9eBytaa0KjUln88jZ3eo6+/vZ48PDw8zYt6K9JRKE4tGFfFaiTifs365352j+18QAhAF\nCbEYmYQ035piK+IRt0e8USIeCAQQi8U4a4pPjjj3fzvZU9wecT9FnJBpK5PG9NgYAHJs8scnRSAQ\nYHeVa/GJVyrW5J8zVAPaCKkT8euo6Vp2u819yh5PaMqLohRHE5qZNPTREQBA9y/9OoSQ3S2Ts6dU\ntKYA0PsGitJkAuuvgBAlx7R6unjsYrULFa0pDsHNpDWmiEcqKOKhkISeXrK8lQo2dd3EUoqM7X0e\nRTwUlrBmmNytOn+WnJvbdvWgtz/M2tsDxYo4AKQSFkzLgoAARtffgsC6jWWXo1ngU27EUvmYHGrN\nEX+XLMvfl2X5hCzL++zHt8uyfH29C+wHRVE+oijKYUVRDEVRZgF8BsBt3Et+F8A9iqI8Znf8/ASA\nPEi3zxUBXhFfja2lO2gteEW81iKmdkYzrSn8ucZvL14RFwTBZU9pNtqNiPN35y73gk26fpJILvzx\neAkiHmoSEbctANSaoqomDKN2+w+/bwVB8FhT3GSMTiKA9rKn8B5xXbOKtm2AK3qcGSXF5n5qOEU9\nBZvUeVWOiNM7COrMFKDbhb1lrCmAM4lYspM6qAo+NTVVtHw8QQ7tezXCV18HAMgdfJY9TkmdJEmu\nccJFxLsdew6FIIps0uBXsElTUyop4pGoBMrxsxknYrCSIg4Ag2uqS07hs8a9ijjg5IlTXHsjORYW\nKxDxUEzCGYt897krfgqBreXvZjQLtTTzAWrziH8YwOcBnAewCwA9Ct4M4Is1fE49eAOAQ9z/VwN4\n0fOaQyDq+YqAN+O3VJJDBx3UA55YLi4usvirlY5mpKbQSW8+n2fbhd41kCSpKHebEvGJiYmmT2oq\nrU+jqSm1ZIgDxFNOlbXLfSzydtWkqmppa4pVl2/esaa4FXHyXO3npXeSRS/2lqUWe8R5It5GEYaq\nJ4HG6xNnMYAAZu2GOOWIeD1Z4tSaIpRhQdS2ok5OkNdGuxBYu6Hs59JlT1vkvVdffTWbUHvTU1SF\n+MMD6zdB6k4gct1rAQCFg8/BMsg28euqCZDJOz2S9Lj/ec4KNn0V8eqKNUVRYPaUTFqv2FWTh9Pq\nvnzBJm1tHwgIiHcXj4UbNjkCweZtcfa5VBGXBAHxcPHyxEIBvGyS8zkbG8ZErPwkqlmoJUMcqM0j\n/nsAPgTgX0AyxSlOA9ju+44mQJblt4FYUG7lHu4G4D3jkgCqvupUU11NX9OKJBN6oYxEIsjn84hG\no+xx3ujfQWPIZDL45je/iZ07d+LWW2+t/IbLAKqqulQ9y7IwPT3tUnpXKqg1xbKsus8TXlVaWFhA\nPB5n3e96enqKSC/N+QdIy/tqB9dqQO0woij6rg+9rVkoFGpaXzqxiMViNW+nSCSCXC6HxcXFy3os\nomOwaCviXXEyBi8tLbnW27IckphO51wqczXI58n7BdEknys4n5dazEIQqy+mBZxJdjweRz6fZ0W+\npqnBtHTXshuG813ZTB7hyPKr4pZlFU1AFpNZBEPuZRN6+2El5zHN5fuXOh7jceI/np+fr/qY1Q3y\nfaZhlHwPJemFCULEpS3bUagwKTZ7+qAJIgp2HEs8HsfWrVuhKAqOHz+Oq6++mr02Z0cVStt3I5/P\nQ7iSKOJmOoX00UMIyleyiWEwGCxazhAs5CBAjRSf56qqYml4EwSQjqC5TAYCVxBeYMdl5bE0EpOQ\nSetILeaQzdr2wGDl93UnyAZMLhSQTmeLJooUs9NkHXt6g758q7dfRCQqoVAwcOU1Pex7Z1JkMt0T\nCfi+LywBC9CxWJhDIjyAE1NRbK5jTJuZmcHU1BT27t1bldWEXn/pPqvEIWsh4sMgpNuLIRBPd9Mh\ny/I7APx/AN6qKAqviC8B8N5z7UMN6S215AI3O0PYsix2EUgmkzh27BhTxsbGxnDs2LFyb++gBpw+\nfRoXL17E+Pg4+vv7i3x0lyP8VKFDhw5VXcTUzqAq5szMTN3nCa94HjlyBD09PThzhjQHDgaDvp8r\nSRIMw8CZM2eaOjEfHx8HQJRxv++lsW2ZTKbq9TVNk63jwsJCzduJEruzZ8/6JrlcLqDbXhIIEc9k\nyJicSqVc2yybFgCQydexo8cRrI03I5+PABAwNT0GzbpoR0YT0n/ixBnEe2ojx5OTJBZPVVUcO3aM\nne+mpWFychyadZG9lv+ukydPI96z/Kq4aQCmGXU9ppw4h6kZ93boi3UDi0nMZQlx0jSt5LFMJ7S1\njAuFfBiAiKnpCVjHRn1fY+jkNZkJ4lNP9QxgvMLnBxaXIAYd28jU1BS7433q1CkcOXKEkbmB40cg\nAZjt6sVF+3P7+9cgMD+DsUceREYXWB8Iy7KK1i1gaIAUwrxmFD332GOPYTGZxM919WFDZgHKU0/A\nGFrPnk8tknVLJmdx7NgkysEwQgAkjI3OIpuWAAiYnZ3AsRLbjUItAEAUlgUcfOEEurr9j78L54MA\nAoCQLbn/BnaYyKoCpmbOYGqGPHbygq08i8XrDwCZJDl2ZvUUEuEBLCzk67puPPLII0ilUti9ezeu\nuuqqiq+nY0u5Y5ZHLUT8KQDvBdfUR5blKwD8MYAna/icqiDL8u0APgngLYqi7Pc8fRjAddxrBQDX\nALi72s/fsWNHxUSAQqGA06dPV/XaWsA37tm7dy82bNiAkZERjI6OIhQKYd++fU37rtUOOokyDANb\nt251eWAvV9CiIOofzefz6O3tvSyOq4cffhgAsGnTprrXR1VVfPe73wUArF+/Hps3b8bLLxNlauPG\njb6f+73vfQ/pdBpr1qxp6nacmiINS+LxuO/nGoaBF18kLrxqv5cvzr3qqqtqnoDt378f6XQaPT09\nK+aYSSaTCAaDNZ3fhw4RbUcUwwgEBOzZI+NHPzoAXdexa9cuZgtKJTW8cpCQ223bdqEnUb0tyjQt\nvPDUOQDA9u2bsX5TDJZl4fD+c7AsYMP6zdi4ubgAsRweffRRe1m2Yd++fchkMjh69ChMS8PmLZuw\neZuzDUzDwqFnyfdfsWkr1m2M+n7mpUQuq+PgM+4mY8NDG7FjtztrYXHTZowkF0Gp280338yUby8E\nQcDhw4eRy+Wwd+/eqgSX4wcvoAAdGzasx669/jfTTx6+CLWgQbQVzqHrbsLmCueEuX4tDn/NuWt2\n7bXXIpPJ4ODBg9B1HT09Pdi8eTOMhVnMp8i5uumWn0BwN/ncpRtvQf7he5EYPYMt+/axybjf+fgD\nQ8eSFEJkYMj1XDabZePAf2+Q8Y6TB7BF0BHhXnPqyEUAGtZvGMa+fcUecx5Lc7NIzqUQlLphGGTS\ns2PXZqzbUP54siwLyqHzKBRM9PZsLLmdzxwbBaDiii1rsG9f8Z1b1TDx4S+9gMW8jl8OrsP/fO1m\nBCQRTy+eBzCGoYT/+HkoPwqcvwAqvZiGVPOYZpom7r6bUMsTJ07gpptuwtatW8u+h/KOgYEB7Nu3\nj3HJUqiFiP8+gMdBPOIAIb0bAYwB+MMaPqciZFl+P4CPAXizoiheLzhA8swflmX5KwCeAfABAEEA\n91X7HeFwuOpbzLW8thrwF8rBwUFEIhHm5czlck39rtUOajkAyLZdDdGQ9LZYX18fYrEYRkdHkU6n\nL4vjinq6o9Fo3esTDocRCASg6zo0TUMkEmGqIj0fvYhEIiy/uRXbsdQYQ4klXc5qwCv2Q0NDNS8v\n9UqrqroijpmlpSV87nOfQzQaxYc+9KGq6wdYEZwYRjQWQH+/QxIMw2DbwYg7dwUkMVjTNuG7Z8a7\nnWM2HJGQzxkwDbGmz+Ob+QwMDCASibBjxDRVRKOhos8TRRJfKIqBttif+ZxzfAaCAnTNgq4JRcuW\nG1qH6dgIAFKMWc4jvmbNGgBkvxmGUZKw86B2/1C4eJtR0BQaUyN3rLt2X4lQhW1oDa9DJkwmV5Fg\nED09Pejp6cGaNWswMzODkZERyLKM3HlyFw6ihK7dV0GkXv+bbkX+4XuhnzmBYD7LMuMjkYhrOS3T\nRFBTgVAMRtj9HL1rAgCz4ThO9q7D9efPuF6ja2QDdHVV5jc9CSJELsw5tpxEoroxeGAogvGLWaSS\nhu/rTdNCKknsLoNDXb6vmZzPYNG20nzr0AROzebwNz93JdJ2kW9fiXXoiZHHMvbETNMsBAOhso2I\nvEilUq7akPvuuw8f+MAHyk76qcOBTzUqh1riC08D2AfgIyB2kQcA/E8AuxVFOVPt51SJT4H4wJ+U\nZXnJ/mGhnIqiPAPgfSCEfAHALwH4GUVRVkT2H99Vkw4Y9PflXiB1KWEYBlMcgcsrPaQcqIe0r6+v\n7vbP7YpmxBcKglDUuIZOjvnoQh70jliz60WqzRHXdb3qhkJ0UlGvgFCq82i7YmJiArquY2lpCTMz\nM1W/jxVrihFEuwKuCytfY8GnStSanMJ7oWmLe8Ap2Jydm8dXvvKVqm+XZzIZNhmlBYqhkBNf6OfB\npY/Vm/rSbPDRhQk73s43wnDNMKajZHK0cWP52Dm+qU+1Y53T0Kf0a2hqiikGAElC8IrKTcQFUUQ2\nQcaR7qAzidu1iyR20DuWtJFPcMt2RsIBkOQUuztn/uABVxSea/lTSYQMMn5onvGDF6AA4MDa7ch4\nCjZZakoVNQ+0WJOfWFZTrAkAg6xg09+bnU5pLD2ozycxBQDGF93vfWk0id/46o9wdJzQQr/EFACI\n2q7pFFeRm8vVViDN58FLkoRUKoV77rmnbOF2rakpNV3NbKL7r7W8px4oilLxyFAU5d8B/Hurl6UV\noDu2q6uLeTDbPTXFMAyYptlQWsWlxuzsrKut8OVCRiuBb0xDi4AvlyzxZqSmAOR8S6VSyGazrtbY\npQpaKRGvNb2kEqqNL6TfXc3AXm90IUW7j0Ve8DURMzMzWL9+fZlXO2DxhUIY0aiEWCwGQRBgWZZr\n3Xly2wgRpw19AIeIKycPQTl1HPPz81XdMufXlZLPYIAeIyYsFJOMQECEqpqXJDVlaWkJBw4cwDXX\nXFNSwea3SU8ihLmZAvI+TX0Cg8OYqpKI02upYRhIJpMVXw/wLe4r54hbQgDBK7ZBqLJAINtFljsu\nONtclmU888wzGB8fx9LSEms9H9rp3u9iJIrwVdei8NJzyL+4H4UrrgSAInussTCHkEm2W8GjqVIB\nKivG0GXlkAlG8PzsFDYYBgRJIgWzlIiHK9eBxOLu8VYQ3Ok/5cCSU2YLsCyryDaUXCiwz6S5415M\n2ER8KB7GB27bgb985Dhm0ipm0nY3zhJEPLxAJuaLXK1LPmf4JrOUglPULeKtb30r7r//frzyyit4\n7rnncPPNN/u+p2VEXJblvwRQ6kw+qijKt6r9rNUOPkOcgl78VFWFpmltRXgNw8CnP/1pZLNZ3HHH\nHb5NFdoRtGCC4nIho5VAFfGBgQE2eF8O624YBlMhGlHEAXd3zVIZ4jxapYhXIuL8OHCpiPhKU8S9\nRLwamKbJJdYQa4ooiujq6kI6nXYp4qIoIBAQoOtWzVncvPrLx8TRLPHFRdI1cnZ2FqZpVkxkoOsq\nSRLbT4GAQ14Ms3iiSLtrXooc8R/84Ad49tlnMT4+jt/8zd/0fQ0lgIGAwJrF+CnihZ5epGyLx4YK\nlkJRFNHb24u5ubnaFfFyDX04RTy4pfrou0woCmhAXHf2x9atWxEMBqFpGk6ePIm1dkfNkFw8AYte\n9xpCxA/uhzq8k7zOq4gvzCFop+JocK8DPQ/mg/3YtrYLk+cVvNi3Aa8/dRz9u69kthQACFWhiHd1\nucenUEQqu914UCKuqSZSixq7C0JBW9t39wRLpqqML5JzdX0igjfvGca2wS58+IEjuLBAHvd21WTL\nOTMKIIG0yBPx2rJFeL5200034dSpUzh27BgeeughbNmyBWvXFjecp9eJamsLa8lh+o0SP+8FKdjs\noEr4Zfx629y3E2ZnZzE9PY10Oo2RkZHlXpyqMWFHTlGsBkXcsixfa8rlkCXO391olIjT840vagoE\nAiW9pctFxL2KeDWgZK3WDHGKldZcjL91XC0Rz+VybFIniWF2650eF96mPjSPW1NrI7MFW/2VJMHl\nS6Xq+FKaHHuGYVQ1WeYnWZS0BwLOxd4w/Ig4zUFvPRG/eJEUtY6Olk7T4Bsc0aYwfm3uJ51eLRgO\nVVZfe+xzdPrZJ6taVur0KtvQx37OFAIIVWhtzyMtEmLYVXAms8FgENu2EWvLicOHYKbJcRvaubfo\n/ZHrfox8byqJfJIcF14ibizMOoq4Z2yginhGiqNn32sQMnToUgCPPfYYAKerJgAEw1VYU+Lu8UkT\nqr+70tsfZhMaP3uK09q+NGml1pT1CXKHd8eaOL7yGzfgTbuHMNQdxo9t85+oBSdIUbAJx2JWrzWl\nu7sbgiDgbW97GxKJBHRdxze+8Q1mL+TRsoY+iqJsURRlq/cHwK8CuKLaz+nAvWMp2pmI836zWjyY\ny43VSMSz2SwjbP39/czzzBd5rVQ0k4jzZJMSoN7e3pKKZKs94qXugDVCxJuhiNfTwOZSox4izqv9\nohBGNOom4t4xuN4291QRD3nITjgiwbJMZHPOmFTNsvtNsgKSc+zoejEpoCpjq1vcm6bJigSXlpZc\n+4UHayQTFlmbdD+VcnzR9v/mMwim5oue96JrkaSLzJ09g/T3H6i8vAZVxEu/RrAz5C1RQrBCa3se\nS7baHltyX3OoT/z0uXMwAQjhMIKbi33ngU1bIK0hSms+Sdbd35pClo8flwqFAjtOMlIX0mYANwvk\n+ZdGJzE1NeWaUFajiEciEnjRfU5Vqx4bJElgbevrJ+JE+V6XcIhtPBzAX7/1SnznvT+GrQP+hZOh\nMSepJBQh65nP1qeI03MuFovhne98JwRBwNTUFJ555pmi97Sys2YpSCCFlR1UCe+OBeCye7QbEecL\nHvm/2xmWZTFryqZNmwCsDiLO2yz6+/tdRUz8cysRrSDivCJeqlATaA9F3E958UOzPOI0Vabd4bWm\nVFPU6iLiYpgps/SOSFGb+zpVZar+hj0+3HBEgm6kYVnO59VCxPl9K3INgXS9+Ph0rCmtnVTNzs66\njhevNZCCKeJh0aWIe4ndqP3+oVwKxmz5645lWYhOk9enQxEk/+XvoZ5RSr6e2lKA8oq4kCfX4sWe\nrbDW7yi7DBSGYSBjp6xEk7Ou9ZJlQuZzmo7jfRsQ2L4bglR87guCgMh1rwEAFLJkGYoV8TkE7buc\nfGMdXjjLBLqwkFNxw7bN6FZzsECiWPnOptV4xAVBgMG9bF7VcHTCf6Llh4Eyre6TtjWlVKEmwCvi\n1RefW4aOwAWHiAdsRZwvOK0Gfg6Gbdu24VWvIo3cvS4B0zSZaNIKa0oRZFnuB0lOOdvI56w2+O1Y\nSZJYYV27EXH+ArFSFPGlpSW2HffuJbf+MplM04vtWolkMolHH320prbNlGzTTOVIJMJI50r3ifMX\n+WYScd7KUwr0IrjcHvFKMAyDTfQbJeJA+41FfuCVV03TSiqxPBwiLkAUgoja1pRSRDxQpyJeYIq4\nm+xEIhI0w72c9RJxQIRgX8o13ceaQlNTWqyIe4n32NiY7+vUggnLMnFh4hkcPPQULMuCYVhFth9q\nbxnKpWDMlCfi+vgFJOaJGj8b6YamaZj7mw/DTPvfBbSqJOIJjeyThd5duOfeKYyerxzMlk6nWTFd\nPJ+BmXLG74GBAVZM/OTGPXioe0PJ4zW0i3jHVZvUe0mdWUIRZ0RcCkIVwkjmNMR27cVrJgkpPXHi\nBM6dcyhbtZ1is1whcA4mHnjZf6Llh1Kt7nNZnRHjUop4VtVZK3tqTakG+tgFRHJk/8f1JRw//W0s\nZo/72qDKwc/BADgCn/fOOz9ON10Rl2X5oizLF+zfF2VZngEwA+AnQTLGO6gClmX5FmsCpf2Jyw1e\nBZ+enl4Rt6vpySEIAnbv3s0eX0mq+KOPPorHH38cd911V9X+bl7dpdXpl0uEIa+INyM1BXAr4uWI\n+HIp4pIksWSlaoh4Op1m5yd/N6QW8Hfn2r1gU9f1oslCNYSWRRcKYQiCwKLYKltTahv7ePWXRzgi\nQdPdE+xqlpuSAp6IG7oFQQjZy+eniF8aj7iXiJdUxFUTeXUSE9PH8PwL/42CTiwlvHd3cXGRXSeH\ns4vQKyji+ReexaY0mVAbooixnkHoE6OY/9THfa9X/E2TckRcnvshdp/8OkRLRyat4zv3XsDTT0yU\nnZDxwklcK7jUfEEQ8K5f+zVckSHLejqr4h/+4R/w/PPPFy1ncAtR4DU7es9XES9DxMM9fYAgIJnV\nENqxBzsWpzBgE9NTp08AsGsXyqTGUFiWhaThjL95y8T3T0wjo1Zn86ARhuklzaVIU1tKUUglAAAg\nAElEQVQKUJqI89GFXQ9+BZZe3XeqZxREDPL5awsTKBQWsZg5VnOxpp9wCgDr1q0DQPY3P17wdyda\noYh/EcCX7N9fBMn6/h0AmxVFeayGz1nVyGazjFR5d2w7xoaZpsk6ewHkhK9GcVpu0IvA4OAga/YA\nrCwySidAExMTvj40P1B1l7dZUILZqCJuWRZefPFF1nL5UqPV1pTlIOKVPOKAcwGuhojzJKDeYk16\nZw5or7HID/xYRP393gxlP9D1kkSyXykRL2lNCdVpTVH9FfFwRKxZEbcsy1cR13UTol0c6HeMMFtN\ni+MLqfhBz83SiriBvObso3SOqLM5zrtL1XARwGA+XVERz7/wDGK6imF7M0/d9EbymfufxNK9Xyt6\nPW9NEcqwIPX4YWy78DB+avgVDA4RMvnK4QXc/bWzmJ32z8Wmx6RkGggbGow59/EYS87iLWcP4g0X\njyFidz6+55578KUvfYkl+QBAcPN2QBCg2YkffkQ8ZHMJVVWZJYse//EEKWBcyKoIbLgCYiSKtVly\n/CRt3zmdIFYitwtZDSmOiKuihZxm4JHj1VlVqSIOEHvKzFQO//2DCXz/QbKfozGJJQl5QYm4aBmI\nfu/ryP53dXRTO3sSEiyETR0xg5zvhplFKlW90GkYBhsrShFxwK2K80S8FcWaf+75+StFUb4MYF6W\n5fbJ2mtz8AVzpRTxdlKh5ufnXQQIqO5Ct9ygJ8a6desQCATYtl4p9gzLslwX5kcffbQqj7cfqWwW\nET9z5gy+/e1v46tf/WpDn1MvWpGaAjhkuJxHnA6ol1oRB1BTBCUlasFg0EWoa4EkSWx922ks8gNP\nxGl2dE2KuBiCKAJhm5DwRJxXKKnPut7UlLCvIk6Wff36Dew7eSLmRSaTYceLVxEXBbsBTL6YHAYC\nrY8v5GtyaB56Mpn0ncgRRdwhcJn8CCzLQJ5TxCkRXxOLIGCZMGZLX3PMfB75IwcBADuuIHaBc5qJ\n2Ot/EgCweNfnUDj6kvs9VVhT9NlpGFNkMjF0zW78wq9sxfWvWQNRBFJJFY9/d9RXbafnYJepQwCK\nJhHqyWMQAOw1svjgHXdgz549AIBTp07hqaeecpYrEoW4dgN0m4iXs6ZYlsXGMXr899k57smcBkEi\nxaa9atZeRhKbGQyKSH75sxh92y1I3VO6Lcv5hSwyXD3DjnXkPLm/SntKOCKx7O7vP3gR9379HI4d\nWmDq+J6rSosgEylyTgzmFyFZJrKPf6eq71TPkhqBmGiiy3COw/nkZKm3FIEfB7xEPBqNsruOPBHn\nrxENE3FZlsUqfiQAvw2g+jVb5eAvHF4iXkqNWU5Q0i2KIjsQV0LBJk/EAYeMrhRFPJ1OOy24JQma\npuGBBx6oaAvyU8SbZU2hF9p0Or0sXvtWKOI8qlHE1RrSAqpBNUScJi08++yzFbc7r5h6G2fUgna8\nO+cHur6hUKiIiD/9+ATu/+Y5X/LMmvmIEURjAbat6BhsGIbrgsqsKTX6rPmoPh6RaACaQZZ9B5fG\nUW4Swd/tKFLEyxLx1qempFIpdqxcf/317HE/e0o+p6KgOXdZTauAbGHcVxHfMEhUXWN2quR5V3j5\nBUBTAUHA3tfeAoAUjlq//j4ENm0FTANzn7gTFldj4iLiJawZ6iuHyB/BEEI790KSBFx38xr8zC9u\nBgAkF1SMXSg+P5in2Cb4XluN08hnDxKJBN71rnfhmmuuAeBzF2GzUyDKK+KWWoCZTiHEqdSFQoF4\n4+cIyR4aGgIAZFQDqm4itGMPEnacYjqzCMsyIcxPYOnurwC6hsz37/fdDgAwMpdxecR/TCYk//jk\nEpSp6tK4aMEmTRLqSQRxw2vX4H+8ewdueO1QyfeNJ+1mPnlybcsfeg7GXOW7R9rZkwCArqCAiOlM\ncJeWqhcSeb7md4eR+v39FHFBEKq2UJZTxO8FoFf40QB8HsB3q/q2Dny7alK0Y34vJeIDAwOM1LZ7\nwaaqqsxOQ0+UleaTpoMpALzlLW8BQFojHzlypOR7TNNk6+dnTUkmk1W3SfcDfydkOZRSSloFQSg6\nd2oFr4gDTnFrKVAiTjrSNW8SUo015bbbboMoikin0zhw4EDZz2s0MYVipTT14T3TlHjMzMxAVQ28\n8vICpiZyGL1QLGzwHnG+VXfJNvfU3lGjIs7iCyPuS61pqTBMcsEeHt7ElLNqiLgoiq68e123mDXF\n747NpUhNoYRbEARs2bIFA3YDHj8ivrg0wzqA0u6b6fxZ1tTHsiyWR04nV5ZacBU98si/SGx7oZ17\nsGXvPrYtT52/gIE//hsAhMjnDz3H3lONIl44Roh4aNdeV0fNDVd0YWgtudt07HDxXSq6n7rD5D28\nNcVYXED+pefszyV3DgRBYOvpvdtsbdjC/uYVccO2lgRNhxzn83nMzc2xCcum9U6jmYWcitCO3ei1\nibhlWdCNNKSUMyHSR8/DWHCuOzxG5rPIwjn2r9nahw12gskDR6pTxV91/SDWDEew+8pe/Pwvb8Gv\n3L4D1960Bt095buV0ujCYZuIwzSRefLhsu8x5mZgpsi1sCegQ+R6UWZys679Xw7MZsQ10OJBORF/\nnNNzMBQKVWzQRVHuVX8DonaX+7kdwJsB+LfQ6qAIftGFFO2oQtGBYWhoiHmt210Rn5ycZIMRPVEo\nEV8p1hR6Qe7q6sLNN9+MnTtJd7UHH3yw5O3rVCrF6g/8iDifqFEP+FqB5ThGKWltVA0HyCDJk/m+\nvr6yCjKvRjXTnlKNIt7f389UxqeeeqrsRKBZRLwdbXJ+4HO16fiUSqUwP+ccn6lk8fZyFHEnuhCA\ni+DyRLze1JRSingq5RCerlifaxJRCnzRGH+BN3STFWv6KuLB1ivilIisWbMGwWCQCSC+RDxFHovF\nunHrrbcCAHKFi0gtkn02NzfH1mPTDqeJjjFbfOPdsizknn8WAGmCI0kSGysVRUFoyw6Edl8FAMg+\n/Sh7XzXFmpSIh/ddU/TcvleRMfX82SUspdwRn+yY7IrZy02uodrFEUzd8Vswpol6GrnhFvYeuv+T\nyaRrfLHWbWJ/ByVun8+T44daUwAyLtFrczAYxMbhQfYcLdjs0XIQbIuJZqQQMPJIvPsPAHv88Vp4\nKC7MZ7Fg6bAEIBKV0N0dxM9fTfbx916ZQl6rHCawbkMMv/Q/tuH1b1qPtRtiVd+xG5sj16w1+QUE\n7aZK2ccfKntnkqrhEEXERbe1tqDNoVBlhCEfrOG3vLw4ScfyWjPEgTJEXFGU5wBsAfAjRVHuAmlv\n/x1FUe7ifr6iKMpjiqK0vmXXZYJSUTiAcxFoVyI+PDwMoP0VcXqbqKuri23nlWZNoaR3cHAQgiDg\nF37hFxAMBrG0tISHH/ZXA3gV3c8jDjQ2EeH3+3Iq4o0mpgBEheIVjnK2FMCtRl1qIg4AP/7jPw5J\nkiqq4s1WxNtpLPIDT075ouyxUYe0pRaLs9Adj7hbEQ+Hw2xf+Cni9Tb08eaI0/NbFIIQhQhThqtR\nxL37Vq/oEW99agol3JSA099+BZuZHCGL69ZuwlVXXQVRkGDBxPmLxNNLbSnBYBDrduwE7AmzX8Gm\nPnae+bgj15NulNTKdebMGei6jtgtbwJACjctlZy7tJkP4N/Qx8ykoY2cAgCE976q6Pltu3oQiUqw\nLOD4EfeY6k22MWankD/8Aqb+8HYYk2NAMISBD/0VwruvZO+hRBxwHwPm8Hr2tzTP2XkWyN9BjhwW\nCgV2vR4cHERfzBmzkjkNgQ2bEQhH0K2SY0TTU+jauw89v/TrrLtn4eiLxRsDRBHPwUTXdTG84ze2\nIxAQ8dYr10ESBKQLOh5XWlc3Ros1h400en/nDrLs589AO1s6J54+F9iwGVHqD7e3lWFmMTdbXSRw\nqcQUCkrEDcNg276pRNzGHQCG7b+/DGBn1Z/cgS+qUcRzuVxbtCO3LMtFxJnnLJNpKx+7F/xFgc5i\n6aDIq8btDJ6IA8Qa9IY3vAEA8NxzzxU1EQAckt3V1eUijtFolA0K9RLxTCbjImXLQdCqJa3Vgrch\nlCvUBFpDxA3DYFahSuvU19fHVPEf/vCHJVXx1WxN6e7uZvtpctIhBmUVcY81RRAE3zuT9UQAWpbF\nijW98YWUbAUDCagFsypFvDQRdzzi/tYUuuyts6ZQ8YMS8A0bSAHq7Oysa5k0zUCuQAj1xo2bEY1G\nsXaYdJYcGyeRetSWsn79egRCIUj9ZIKljTjNWSjyLxA1XOxJILSTFD1SIq5pGs6dO4fo694ICAKs\nbAa5F/cDAEyrvDWlcPwwYFmAICC8p5iIBwIidu8jd1lPHF2AYd9tcCXbDJCxW58Yw8xH/xeszBLE\nnl4M/fW/sEJSip6eHnbs8vYUo8eJIBUmnLQqI2kr4n39bOzgifjw8DACkojuMHluIatCkCSE9lzN\nCjY1I4XIMDnuwlddRz7DLnrloeoms4ds2xBHzM7cH4yH8brtxIJUTdGmOnIac5+4E4XjL1d8LUUq\nryFjkv2zcf0ahK++DtIwObYyZYo2VVsRD23bhaBKOJfY66ScXLg4Wt33lxFOATIu0/1GzwF6vFcb\nXQhUJuI5AGsqvKaDGlBux/LEoB0ugIuLi+yCz1tTgPZOTvEWagKO4rlSWr17iTgA3HLLLVi7lvj+\nHnrooaL3+BVqUjSanMLbUoDlVcSbRcSXWxGvNRedquKZTAb79+8vet40zYoKTrVoR5ucH3hriiAI\nbIya5QhtatFNxC3LKqmIA/5F8+UU8VK3yHXdAn3KG1/IiLjUg0LeYOf53NxcSaGgFBE3OI+4nyIe\npKkpLbKm5PN5NvbQMZcScsBdyDY+PgnTIvtjyxVbAADbthCvdCo9gfn5eaaIU990+GpCElPf+jK0\nMXd0au4F4g+PXPsaCLZynkgk2Dh58uRJBAaHmL0k99T3AXgVcR8ibttSglt2QIz7k7A9V5MxI5c1\ncO40uabkcjl2XvcO2x5t0wAMA4GNmzH8D3f5KuyCILDJGH9tVXVyLAiWCeuC04SHermlvgE2NuXz\nefZeeh70xchxsWA3xOn//Y9g7W6ifmtGisVyhq+8ljx2/gyMRfdd44vJLKilenOf2yf9C7Y95dDY\nYsWizdR/fB7ZJx/GzEd/v2zXUx7jSceGuWnXdjJRfsPPAACyP3ykZOyido4Q8eC2XRDyZLn0WD9C\nAXLujJeI1ixa5grjqSiK7Jinx3krFPGHAXxSluW/tf//XVmW/8Lvp+pvXOWoRhEH2uMCSE9qeoGL\nxWJsAtGuRNw0TUxOktvSfkQcaH97immazGbCE3FJkljh5ujoaNFt33IdIhstVvUqdZebIl6JiAcC\nAebLbQURr2adent7ccMNNwAgXnHvcmQyGaawXw6K+Pj4OL785S/jzJkzvs9bllV0oaQEZCHpTByX\nUhoMjnhpmsa2vejxiAMliHjIn4irqorPf/7z+Md//MciEkz94UBxfCGd2AYDCeTzBiNhhmGUnCyX\nt6aU7vzK+9tb0YyN94FTAh6Px9ly8uPUubMjAABRCGHderLOW7fugCgQMnnw4EH2eZSI9777DyD2\nDcAq5DH/yTsZ+TLzOabgUlsKBW0lryiE8EWpPeW5p2DmcxWLNdVXDgMAwntfXfTcuXPncOedd+KZ\nZx/HFVvJsXLsMBl7+ZSNvs1b2d/hq67D8Ce/jMC6jUWfR0GPXRcRt4WwoGlAP++cB5SIi70DjPDl\ncjl2XFEbaW+UHBfJLPmcwPB6rLv+NQCINSVEifieqwE7JrFA02JsnJ8jY0BQErDO09nyNVsHsLGX\nPPZXj5yAXiIMwDJNtq+sXAYzf/Z+6JOVyfDo+TF7/TWsfzXZF10/8bMAADM5j/zBYpuemU1DHyd3\nVYJbd8Gys9MLwS7EouR6OjVVXYFpNcKGt2CzFUT8/QDuAemeeQHAbQB+w/PzLvt3BxXAXzgqKeLt\nQMRp4UdfXx8rVvObtbcT5ubm2ODFqzKRSKSmPOblRCqVYkSBpg9QbN++nT32/PPPu57ju2p60agi\n7iXiq00RFwSh6Vni9XQKve2220qq4qXi7epBOxRrPv7441AUBT/4wQ98n89kMkw9putLx6elJec4\ntyzS0Y+CXydJDCPmUcTLW1MsF5l98MEHMTIygqmpKZw4ccL1OXxBGK+I803SqCLe39/PJnp+9pRS\nzXwAUqxZjUfcstxFis0CVQITiYTrGubnEz9/fgQAEA4OIRwhyxzvDqMrsgUA8PTTT7OibErEpUQf\n+v/gzwAA6slXkPrGFwDYsYW6BggCIte+xrVM1J4yPT2NZDKJ2OveAIgirEIe+ef/u2yxpqWpKChH\nAQAhH/X6wIED0HUdBw4cwJ6ryL6YHM9hbibP9pEgCOjdtBl9//tPkHjX+7DmLz8Hsbv8XSpKnvlr\nKx1rgqYBjSPiJlPEB9m1eWJigp0P9DxginjWOf6puGOYWQh2IaMY60JoB+lAXTji9omfXyDnyxV9\nMUiebSWJAv7kzWTSc3xqCV9//qLvumkXzmJck/DNLW/CVNcQzIU5zHzs94vUdy8unDoHAFhTWERk\nF7EeBdZtZPsl80SxPUU751iYckPrYRlk3bNSHN1xsl1m56tL3C4nnFJQIk5DIppuTVEUZVFRlA8q\ninKNoihbFEXZ6vOzRVGUreU+53LCxMRE2aYL5cB7v/12bDAYZCdVOxBxekHgC0nanYjz3d14NRlY\nOQWb/IXYuw6CIDBV9NChQy6vcCutKe1AxJuZmgLURsQBJzmlWURc43KNq10nryq+sLCAXC4HTdPY\ncS1JUtkoxmpAt42maVXFNaqqivvvvx+HDx9u6HspdF3H6dPkglpqrOHVR0pOqaqYzSdhcQ1IeHsK\nP7Z64wuB8tYUwPFaHzlyxDUZPnvWsQ4ATldNwO0RX1hYYNeBYCCBQt5AIBBg560fEc9kMux48VXE\nOWuKV/Wm8YVk2ZvPxKkSyN+BBOCbnDI6SqwlkdAQU2MjUQnxKPGJ03MrEom4RIjo9a9F/K3vBEAs\nKoVjh5g/PLRrH6SE46UGgM2bN7PzVVEUSL39CF9NaiyyT30fllm6WFM9dZzkkgMIX+lOTDFNE6dO\nnXKWVVpAT4Js+2OH5xkRj8fjkCQJ8Z9+G3re+dsQqpho02OXb6LHFHHDgD45BjNPuAdvTaECAfXW\ni6LItl2vx5oCuK8p+YJzDlF7SuGo2yc+Yivim/uL4/sA4MbN/fj5q8m+//wz5zAyX8xdzr7wEj5y\nzfvwrS1vwl/c+kfIhOPQxy5g9i8+CNNn8kgxNkEmrGuDBgSJixl9A7kznDvwQ5hptyWGNvKRBtZg\nvuCsd0qIoa+XTHZyuXRFi6qu6yW7avKgx302m8Xi4mJLPOIdcBgZGcGnP/1pfOlLX6rr/ZXC4YH2\n8mZSRXwlEvHh4eGirOlLnSVOm/A8+eSTNb2P2lISiURRW2MAuPbaayGKIvL5PMsV1zSNDSx+pLLR\nLHFKDqhqdzko4vRcC4fDvhmxXjS7zX29DYqoVzybzeLv/u7v8PGPfxwf/ehH8bWvkVbejTbzAWqv\nV9m/fz8OHDiAu+++u6gTbz04f/48286pVMpX/KDjKZ+rTcmMZZnQuW56fMGmWxEP1UzENY3k9d9z\nzz3kM+xxpoiI29YUQXC/3yHaAoJSN+suSJfdj4hTi4UkSa7xGCDebxpfaJpm0fYP8JOIFvjEvYkp\nFLRgc3p6mk0Ul9KEqMYiw5BspT4aCyAcGERAcu4Sb9y4sSiDOXH77yOweRtgmhj79N/j6DkBucgA\nIte/tmiZAoEAduwgzXBOniR+4ditbwZACjz1nHMMeBv6UGuGNLQOgcFh13Pj4+Ou4+f06dPYa3vF\nTx1fxPw8ubbUc0eK7lfemshbU2BZTBVn1hTOI06Pm8HBQXZMUmvKYs45/hOJBASb+mWyzrUwfJXt\nEz970kVuqSK+pQQRB4A/uG0n1sRDUA0Tf/XwCVcx7GQqjz88G8NCmHCeiZyFf/3pO2EBUE8cwdzf\n/Qkso3jMsCwL4ykyBqzvcwsLsde9EQiGAE1lsZSWriPz2ENYupeMg8Gtu9g2yYthZHRgcGAYANnf\nfok+PHiiXo6Ir127lo23ExMTLbGmMMiyHJZl+cOyLD8ry/JZWZYvcj8XKn/Cyse5c+Q2ydjYWF1k\nht+xfF4tD3oBXO5UEm9iCgX9O5VK+d4GvZTw8zuWUmeAS5slblkW7rvvPuzfvx8PP/xwUbFjOdDB\nw2tLoejp6cHu3eQ2IlXk+HUqp4jrul7zsWUYBrsw0IvrcnrEmxFfCADbtm1DKBTClVdeWRVxbRci\nnkgkcMstt5R8nt7SbwT8xKTSvrYsCwcPEhVN0zRXcV69oMSTwm/iz6uPlLQNDAywvzVjkZEsXhGn\nREoQghAECZGoe8LuJ4YEg3xMnI7//M//RD6fRzQaxdvf/nYAxPfNiy0F2swnJLqOL3p+x7t6IAgS\ns7CUI+JHjxKrxM6dO4su8HyLe6DYnkKtKUDzFXFd19m+KUXEad0OTXoSIKG7yyn8p51N45Ht7DG/\nY1gMRzDwf/4vEAjiRPdr8cr6t+CZGz+O9PZiIg44PvHTp09D13VEX/vjgCTBUgvIv3KUvc577rP8\ncB9/OCX1FKdOnYK8rxeSJEDXLZw/R/ZdKNSFiyNpnDmZwtxM5evk9GQOR17MQ7JVXyqCseYw9i7U\nRk7DsizOmuIQcXo95K/XfdFia4ogCAgECLFMZ5zrRnjvq8ms0bLYZMSyLIzYmfylFHEAiIcD+OM3\nkWvSobFF3P0SIbmz6QLe962XMC1EETJUvDVBJtRPJ0U88baPAADyP3oayX/9f0WfqU+MYkoi5+LG\nTWtdz4nxbkRvfj0AIPPYg0g/cj8m3vM2zP/jn7Oc9tjr3siOzYzUhaxqIB6PIiiRda+FiJdKTQHI\n9Yieu+Pj4667OtWiFkX8MwA+DmAUwLcAfNHzc9mDkinTNOsiynxXzVIX3nLezIWFhUuW+JFOp5kK\n5UfEgeVVxR9//HF87GMfw3333ee6YPolplBUsqbout60ycX+/fsZOQFQ5B8tB3qc8Sk1Xtx4440A\nyF2a6elpZksRBIFNOHg0kiU+Pz/PJp6bN5P2zpeDIr5+/Xp87GMfwzve8Y6qXt9KIl7r5OInf/In\n8aEPfQjvf//78b73vQ+/93u/h9tvvx233347I4aNgCfilfb1+Pi4q8nX+fPnG/5+7/ni10TMm9cM\nkGMjYdsUNH0RQ8P/P3tvHh9HdWeLn6rqfVOrtS+W5UVurwSb1XgF7ISwY8zihAHCkp18hsmEyUzy\n5g3vzcvMJ5PMbxImQyBvloRAEpIfiYEAYbEHsxgMZrEtY1mybEu2tbXUaqlbvVbV++P2vV1VXdWL\n1JItu8/nwwdZ6qW6uurec8893/Mlk+HYaLZHXOCtsNmFLI8wFUkmJiaYhUSpKr/11i4mymzZsgXL\nly9n16RSFWfNfAwSU7xeYhHIR8Tj8TizQyxfvhxaKOML6eOVUNlqUqUt1hwcHGTnSEvEPR4Pm89O\nnTrFzpnVXA2rLbPTZzbzMJk4uOwZh+ucOXOgB8v8Rai462sYrSBqd8LiwUvvCeg5mj0vUp94PB5H\nT08PBHcFbCsvBQBE24mFSquGy5KUKdRcbkzEqULa29sLcCks8JN/9/eRcXioD3jh9z149Y8n8Myv\njiISzs6yV+LdNwdw+OAYHHZy7dK5lSriljSpSx4/AjkSZnnogq86ywKhIuI61pRkUmJkdExRS8G7\n3KxhDrWnDEcSiCTI9zvXl9vutn5hNT6zhOwg/OuuIzg0MI4HfvsReoNRmKQU/urAL/BXm9qwyU+O\n77GgFyeuvQ8AEH7+t4imrUYUsY/fx6CNiEpz5mUvzGjRZuLQfgR//Pckox2Afc0VqPvxk3Buvo7d\nSxNpIm6zC7CaicCVj4jT8cVkMsFut+d8rNInTjnEdFlTtgL4VkdHx60dHR3f7ujo+DvFfw8X8Tqz\nFkpVU6l8FApllyYjGFlTAoEA/vmf/xmPPPJISVtsG0FJspU3tsvlYhfl6SLiAwMDeO2115BMJvHu\nu+/iBz/4AXbv3o3x8XH2vWgnBUBtTdGq6bIs42c/+xm+973vsdSVyaK7u5vFC1J1Tqvw5YJeYooW\nbW1tbDJ4//33GRGvqKjQbf9ut9uZzaVYIq60pVCl6mxITSn2tUpNxJUecb3vLBc4joPP50NjYyNa\nWlowf/58+P1++P1+XTtTsRAEgX3efERcueAEpk7Eg8EgG1v0spUplNGFSlRUkIk2KY6hoZmMp3oe\ncT1/OJAh4sqYQ5qaEksM4a23SfHoxRdfjBUrVsBsNqOlpQWAloinFXEDIu7zkeOMx0TIssyIeCQS\nUZ3zjo4OpFIp8DyPJUuWZB2vKGY84oCeIp4hm8U2JMoHugNptVqzLHEcx6kKNqkiblX4wylsDhPM\nghuXXLgZa9as0f2cFI7rtiHsImo7DxGppIyXtveio10tsFRWZjqW0vHXsZ6kp8S7ycJG6w9P9nRD\nCpM5RKuIx2Ix9PSQzf9NmzaB4zhIkoTu7m6ct6oKvMAhJZFryyRkFrKSKGOgz7iuTJZlDA/F088j\n1zK9Rpjf2EGuyeSxLlUbeqVHnEI5X3sdZCwYiyYhpn3xyYQEc9oGNBYaUT2X+cTTCSfHRzLXYS5F\nnOKbV7TBazcjmhRx9xPvoysQAQ8Zf3HwSVyQGoCldSG+85nFaPbakZJk/AO/Agk/8eEHH/k/kCIZ\ngXPwwD7EBXL8TZXZDgLbqkvBe9O7xhwH+/rNqPvJr1H9N9+HZQHZDVEScVGWYbLysKSJOI3JNIIy\nMSXfjqkyOWVarSkAHAD0+5+eI1AScWVCQaEoJApHz58IAHv37kUymcTY2FiWF3E6QCc+j8ejuqCM\n8k5nEi+88AIkSYLT6YTFYkE0GsX27dvx4x//mD0mlzUlkUhkkYv+/n4cP34cibDo1f4AACAASURB\nVESiaE+3EqOjo3jqqacgSRJqampw/fXXAyATdCEEThRFRqqNrCkAIUq0wcvevXvZtWnUmIbjuEkX\nqyqtMnQRmUwmVURyJjAdRLwYTJcizvN80UR8JlBIcoooiqxAk45rx48fn1JMHiVNVqsVn/oUSUfQ\nG2uMxlOXI23Dksbgqybf2VgowY7JqL09e77CNkhJu8nEQ5ISGBp7g5FmGiUKEJsToK+IG0UXVldT\nPzsp7FTugClVcWpLmT9/vm4RrlYR1xJxYRqtKXrN05Sg9pQjR46wXQ2buTarwZE9bQ9qaT4P1113\nXZY/XInQaBIyRx5/9XUNqPRZIcvAf798Ch/sGVJde1QVp0q2/dKNgMnM8t21uyGJtCWDd3lgmqPO\noDhy5AgkSQLHcVi+fDn7bF1dXaiqseHz97ZBMJGx4fLNC/DFP1+Cqhoyd+ayp0xEUpmEHZGMr/Rc\nUdHN5iG7PoSIZ3gI763KWnjrWVNkAKG0Kp5ISDCnrSlBBakHMkQ80XUI0kQEx9JEvNppgcuaf9yt\ndFjwrSvJORdlGRyAb4oHcGmgHdblK8HxPFxWE/7x+uUwCxz6xuL4yYX3QjZbIAYGMPp//z9yvLLM\nElMAoLEim9RyJhOq/8cP4Nl2P+r/7WlU/9U/wNK6kP09Ho8znhZJW1w4MwericyrY2NjOR0G+Zr5\nKEEXnMrUtulSxAMANvj9/iv0/ividWYlotGoSgWcLkVcr7W0JEn48MPMGqgYdXWy0POHU0wnET9y\n5EiWD0+Jw4cPs89//fXX4y//8i+xciVZUdPz6/P5dFejubLElVvh+/btm1RBZzKZxC9/+UuEw2FY\nrVbceeedWLFiBTiOgyiKhnnISihtILmsKQBw4YUXguM4RCIRpkrm6hA52eQUSgpqampOa9OpUqem\nFIvpIuKn6/PkQyGF452dnUw0uPpq0mhjbGxsSnUY9P5euHAhW1DrWVOM4vzsNnKdJ1MheCoISUkl\nZUQnCNlRNvPRRhcC6kJV+tk4DhgO70ZKDIPnedx+++0qAkSJuNInHtdRxGOxGBun6uoyY2s8JsLp\ndLLxn95zyWSSjU16thSA2E04TmD+Yu31KQgcU35LbU3RdtTUQklQCDjYzDVZuwR0ZyI6kb/QNzBI\nSK3FwqNxQRWuv60V9Y1kl/a9t4bw4Z4MUaU+8b6+PoTDYfBOF+wXrWFEXkvE42nLimXpp8BpFgN0\nXpozZw4cDgfa2kijcWobMltkxNKpJr4qLziOQ1V6ITgSMB4zhhV/MwvkWg4EApAkKeM3riTjuhQK\nInmUvB/ncIK32bKEMuW8UenIXKPBdMEmUcQJEZ+ITqjGcdr4CJKI+Cf7mCLeWpVfDafYvLgWn1lS\nx6IN1+wnEYO0eycA+Ovc+IvLyfl74+QEXrvumwCAyMvbEX3/baRO9aA/Qb4jm8DBa9e37lkXr0DF\nHV+CuSU7uE+5mKVEXBYAi7kShRRsFtMcTU/4my5FvBPA/wbwqs5/rxTxOrMS2mK7YhVxZfFjri9W\nb/Lr6elREcOOjo5pacygxOkg4iMjI/j3f/93/Md//AfefvvtrL+Loog//pHc1C0tLTjvvPPg8Xhw\n22234ctf/jIb9Gm1vBY0UgrITcQlSdLtXJgLsizjD3/4A9vuuu222xhxpX7HQnzidMJSKthG8Pl8\n7LNSFSzXc0pBxIsp4is1TjdxnS4iXqri01KjkKY+dAE4d+5clVeabuHrQRRFw1qMZDLJYgsXL17M\nxppQKJT1HD2POJDZ3k+JMZgsGWJHk1OM2tuz55tMbBKlRPydd95BOEosNxddcDlTQynmzJmT5RNP\n6LS3V5KDxkY1EQeyfeKdnZ1IJBLgOA5Lly7NOlYArL262UxIl26WOM1BL2FqiiRJOYvjAWSdJ7er\nGjxvybampBXxaFS/q6gSwwHy+Xw1tnS+v4Brbp6LufPJTsbBfZnxraWlhanr9Jp0rNsMiSffFSdm\ndvUGBwfx0ZGjkABYl6ltKbIsM8JNVXY69g4NDSEUCunm+PvSivhIwFgRH1Go5eZ058dUKoVgMJhR\nxKsy5Dr24bsAiC0FUCuvlZWVqvFESWBHJ6giLjIiDqi5jVDhhXkuKZqNH/iARRHOrcztD1eC4zj8\n72uWYucD63FtZQLSKNnhpWo7xc3nN2HzYnIP/DJSA27RCgDEohJ953UM2sl81ei1TyoFit5DFosV\niXTDKFEAeM7MFjy57CmFZIhTuN3urACO6SLitwCYb/DfghzPOyugJeLFKuIdHR1M1TEiioB6O5gq\no1QNpzfcyMhIUSkck0EhRDwYDJbUnnDgwAH2mZ999lnVLgBAEkLoObz22mtVN2drayu+/vWv44EH\nHsANN9yg+/o8z7MBUklGI5EIG6SpB/rdd98tinC9++672LuXNEK48sorVZOmsstbvgVUxj/qK4hw\n0kxpiulWxIsp4is1TjdxnS6P+JmqiOvtzikRi8Vw8OBBACRS02QysUUn9QNrIcsyHn/8cXzve9/T\nJevHjh1j58Xv9xsWhyeTSVZMrp0oOTkzIY6PjzAiTH3iudrbUygtgidPnmQ1Hw5rC9oWrMp6vJ5P\nPJHILtak95LVakWlL7OAoESc1oXQx1FbSktLiyEhoCq3xZJpda4FTU4ppTUlGAyye8FIEdfuTrqd\nJP3CSBGPFaCIU5tHVU2GgJpMPJafT8a+SDjFvPBWq5UtEmjtgu2S9YCDnEs5NILR//gx5GQST/zX\nf+EVbzPeq52f5Q8fHh5mlkFKxOfOncvGos7OTt144ipmjUqy6yHr86gUcQ+oWjs4OJhRxF0uCHXk\nHNOGO0JlNfuMFNr52mYWYEsvwkbT1pRkQgLP25idKbNbQUBjDOMHPmCK+NwqB8SRAIZ/8D8w8Bd3\nY/BvvorA3/8lhn/4txj5yT9i/NlfQ1YkyXEcB7tFQPwAOVbe5YF5XpvqfTiOwzc2LAQHYCyewie3\nfBNIW1RCP/8JK9Rs9OYulDQCi3OsqSZbWgBS6cvOaiavXSpFHMhejE6LNaWjo2O4o6PjmNF/Bb/j\nLMVUiLgsy3j11VcBEMJItzH1QCcASZIQi8WQSqVYVvSGDRvY5Did9pSJiQm2GsxFxGVZ1o3amizo\npEMJ9m9/+1t88sknAMjk8sorZOPl/PPPZ5OeEjzPo6mpKaffVi9L/PDhw5BlGSaTCdu2bYMgCIjF\nYnj//fcLOu7e3l4899xzAIiKd+WVV6r+TqMGQ6GQ7ha7Ehn/qHGhphJLly5VbaUXSsQL3VFRFo7V\n1NTAZDKxLfnTRcRPtyJeqmLp0/158iGfIr5//36kUikIgoAVK4iaRVN1jAo2T5w4wWoxnnnmGZa4\nQUF3jRoaGuDxeOByudhxKIm4Un3UTpTJuJm1TB8aGmL2lJBWETfwiAMZQWR4eBhPPfUURFGExexC\ntecyiAb2Dq1PnFpTrDqKeG1tLUwmPlMEGlN3RBwaGoIoimyhY2RLATKKuNVivFBUdgYtFagarsw2\nT6UkHDsyjjjLUOdUBMVhTxNxi75HnNqHjKAsbKyuUSuOFd6MDUNZnEvnCnpN8jY7nDd8jvwsixj/\n/3+Bzm/eg6E00f6oZi4matULC6qG22w2pvKbTCbMm0csEV1dXeyaVHZx9lVnjtHInkLVcrtDAMcJ\nsJiIdXVwcDCTmmKxMKVaTttfeB1FXG++rkxniQcnMtYUjuNgMZOFoHYOty4nFpLxrg70hcixNY70\noP+Bz2Fi54tIdBxA/OM9iO7+b0zseAGRF36H0cd+gMhLz2S9dyy9aLAsOz/L6gMA9R4bLmgh89JL\nAxIq7vgS+YMoYjBtMWv0TI2I19XWgjqQ4rIIjgMr2CwlEdcuRkumiPv9/n/1+/3e9M//0+/3/63R\nfwW/4yzFVKwphw4dYlsgmzdvzrnNom1zf/jwYTZxrFy5kq3Gp5OIK29MvRtb2WimVPaUUCjEFLKt\nW7eitrYWkiThySefRHd3N3bs2IFIJAKTyYSrrrpq0u+jV7BIyf78+fNRVVWF888nashbb72VNy8+\nEongySefhCiSNtW33nprVqFRY2MjqwvIZ0+h6kSuQk0lTCYT88gDuYk4XYQUkyWu1+XzdDWdOt3E\n9Vz1iBsRcWpLWbJkCSPLlPT09/frnidl583+/n689dZbqr/TcY0uXpXF4cpFrJ4NgCISTrJitKGh\nIXjSBG0sRBTBfKkpQEYQeeeddzA8PAxBENDWuhkCbzFMHtH6xPXiC5VNVwDAZiN/0yriw8PD6Ozs\nZOr2smXLdN9TkmTWrj2XIk5z0EtpTaH+cLKoIOdx395h/OnZXryzK/NdKe0pNjOxWBh6xKO5FfFI\nOFPYWFWtJjpOt5nFEYaCGSLe2toKgCwC6T3HpdM2hPT3fHw4Mx+keAEvv7ZD9drUH97W1qYSeqhP\nXEnElcTN4TSxxZ4eERdFGaMj5Pf+pWR8NqVtE1lEvFW9k06tKUrCpzdfa7tr0o6vNmvGj64EteX0\nmb2gyzbXTx+GNDoCzu6E++Y74b7pDjivugmODZ8hTZYAhH7xKMSxzHmUZZmlr9gU/nAtrl1GFmdv\ndQ8j9ZlbYFlErvUBqojrFGoWAuWuvsNCrq+JpEQiDPMUbCp33Aop1gTUijjHcUWlV+VTxK8EQK+q\n+w3++2L6/2c1tEploYq4Ug2fN28eFizI7eLREnFqz2htbUVlZSWzORw9enTaYgzpBexwOHQbD/E8\nz7yMpSLiVA2nSQn33nsvKisrkUql8POf/5xN2OvXr9fNyS4UWkVcFEU2yNJzS5uljIyMMEVKD5Ik\n4emnn8bo6ChMJhM+//nP63Zo5DiOvXY+Iq60gRSK1atXw+FwoLm52bBRFJC7WDXf8TidTnZtFuId\nng6cbuI6XdaUM90jrrfgGhkZYbnQq1ZlrBpUEZdlOct6IkkS9u3bByBDHl555RVmlQoEAmycpfcL\nQLrkAuqxho6/NptNNeGJKQnRCZF5QAcHB1kL8rFQAqIosu/PqFgTUEcYAqQQtbKCEAYjIq71ievF\nF2rvb6uGiCu7K+7atQsAIbJGC2wlsabnVFcRT1tTShlfqNdRc2SYvLcyJYQuUBobGyGL5Bj14gsB\nIBYVIUnGqj19XY4DKqvVW/88z2W+a0UnVXpNplIpdsz0PcyVPtR871GcqiIkyiSR7+HDDz9kLeNT\nqRQrtKfEm4L+OxwOs3lEuzCkqviwjk88FIyzhdSipV7wAqe6dpXt0i0GRLxQRVzpEQcAh12fiAu+\napia5+KUI71oEpOojgVhnr8IdT96At57vgHvfX8O3wPfQdVD/wc1/+tfwdnskMZDCD3xKHud1Mnj\nrPGQNQcRv3xRDexmAaIk4+XDw/A9+HeA14chOyXixSvioiiq+nE4LOQ+I1niJljMPnA5CjYL7aqp\nhJKIW63WonztOYl4R0fHko6Ojp70z80dHR1zdP5r7ujo0E/fP0sgyzL7UumgEo/HC5qQP/nkE/ZF\nb968Oe/jrVYrW3EPDw8ztZaqnm1tbeA4TjU4lBp6re21KHXBJiXiS5YsSTflqMC9994Ll8uFeDwO\nURThdruxYcOGKb2PlogfP36cKUhUhauvr2cD7BtvvGH4Wjt37mQK3g033JBVmKQEJRY9PT2GBDaZ\nTDJVpVBrCkDU829/+9v46le/mne3RelpLAR6C4PTpYifbk81nfBSqVSWpWIyON0Li3zIpYhTgcDp\ndLJdOvpveq1o7Sk9PT2MQN95551wOp1IJpN49tlnIcsyu5dsNpuqoYueIm60bRyJkHNqMWW23all\nYWw0oWlvb2UE0OizA0SNvuyyy5iNxMjeofWJM0U8/Txl63IjIu7z+diOGrW45LalZI7FaiWEL6dH\nvESKuCzLjKgqxz2aehIez9QOLVmyBPfddx/uvvtuXd88kLGmAJlzoQdKxL2VVlXHUAr6XYcURNzr\n9TJyTK9JSsR5gYP1vAvRV98KALgwFkSNjwgWzz//PGRZZlYqAKprHSCLRKqY0u9Le02y5BSdCEPq\nDzeZOHh9FlTX2ljB5uDgIBvzLBYLTHPVIh71iFdXV6O6uhq1tbX6jeyYIp6xpgCA00k+ZyAQyLIq\nWpevwgkHue8aokPwXLMVdT/8T5ibsi2hpupaeG6/FwAQefEZJLqI2ETVcM7pyvKHK+GwmHDFInI/\nvNDeD3PLPFge+R1S6WSbySjiwWCQjdE1NTVwMiKegt0ugOdMcLkI0dcr2NTz++dDdXU1G8uL8YcD\nxRVrnrOIRCKMdCsV7Xz2FKUaPn/+/JzecAqO49gksGfPniwPpsvlYgPfdNlTlD5GIxgR8aGhIbz1\n1lt477330N7ejqNHj2JwcDAnaRsfH2fFXcpJp7q6Gvfccw9Teq666qqiL3AtqCocDodV0WC1tbUq\nO8jatWsBkIFbr6iss7OTfbcXXHBBVtGkFm1tbeB5HpIksVQILZRFM4VaUygsFkvO7F2AXFv0+n35\n5Zfx/PPP5yWU2q10oKyIA6VRxU/358kH+j0nEglVUbYsy4yIf+pTn8o6fiOfOLWl1NXVYf78+Szu\n8JNPPsHBgweZorho0SLV9j8da0ZHR9l5N4oujKQJICUzIyMjcLrIa8WiIkKhjCWLz+ERp4TG5/Nh\n69atpC142t5BiYwelD5xWkRpTZPOYDDIvnMtEacecUEQsu79XERcrYjnKNak1pQSecSHh4fZmE6/\nbyDj8Y5OiOzYOI7DwoUL4XK52ftn5YgrFkS5Igz1CjWV0CPiymOk16ScPm08T76X0TTxWvWXf4tr\nb7iRPXb//v1MtKitrc3ajaWfTXUMBor4SCCeRXipP9xXTRTU2no7W0TG45nHW61WmJtbAcW9Rj3i\nJpMJDz74IP78z/9cd3etQtPmnlpT3K7K9L8TWfYM+8XrmCI+v6UelV/9K3AW47nXfePnYGpqAWQZ\nwUe/D1mSWFGpddlKcHn6JFydtqd8MjCOI4Ew+icy1/VkiLiyCV1VVRWzpkTiRBEHALeLfD49RZwS\ncbPZXDDnEASB7d4V4w8HgDNzBjjDoCRISjI9NjaWk6wePHiQbYUVooZTOJ1OjI2NsUHD7/erLA9+\nvx8nTpxgRYaTifbJhWIU8UAgAFEU0dPTg127djEFXw+rV6/WTTRpb2+HLMswm81ZikNjYyO+8Y1v\nIBAIZP1tMlAOpKOjo4yIUzWcYtGiRaitrcXg4CDefPNNfO5zn2OK1qlTp5iK19DQgBtvvDHv+9ps\nNrS2tqK7uxuHDh3Ceeedl/UYOniYTKYp2W9y4dZbb8VTTz2Frq4uvPnmmxgcHMS2bdsMW/jqLcpO\nNxE/3akpACE7ejakYnCmE3FtZjwlGL29vWyHUFmfQDF37ly8//776OnpgSRJ4HkeoiiyonN67a9a\ntQp79+5Fd3c3nn32WUbslLYUIGNNAcjCf86cOcaKeJicU7uN3D+SJCEpZtStwGDmZ7vNrquqAkQF\nv/fee9HU1MTuDdoqXmvviEZTEFMyXG6zyidur56ASXAw0knPGcdxjGxrPeIAWfSyQrO6upw2NWUu\nuN2ew5rCijVLo4jTuclisaC+vp79Xkmiw+NJeCsz94xyAWMUXwjkjjCkhZpVNfpEhxHxoJqIt7S0\nYN++fazZFFXEOY5jO8sWi4UV+y9atAiHDx/Giy++yKxPWlsKxcKFC1UJX1mKePpYEwkJ4bEk3BUZ\nKxX1jVOyXtdgZ9YUJSwWCziTCebmViSPESGHWlOA3J15qSIeUqSmkOPMWBUDgYDquG0Xr8PARzIw\nJmK+vwAB0WyB90vfQuBvH0Di0D5M7HgB8QNEEc9lS6G4sKUSdW4rBsbjeKG9HwuqiTXMbTXBbSt+\nvNemjznM5PxEEinYHORcO2xEXDpx4kQWjyqmq6YSDQ0NOHnyZNFEvKyIFwBKxJ1OJ9xuN5uAcyni\nkiQxxXThwoWsuroQaLunaSc7OlFNR4xhPB5ntg3lBKiF0sv44x//GI899hgj4fQ8aQeH3bt3M1+p\nEtSWsnjxYt0CB5/PVxISDqjViu7ubqboa4k4x3FMFT9w4AAeffRR/N3f/R1++MMf4le/+hUikQhs\nNhvuuOOOgokhfY+Ojg7dIlB6nSm3p0sNh8OBL3zhC7jssssAkCKkn/zkJ7rpN8ounzOpiIuiiD17\n9mTtRJxu4qok4qWoz5gtHnEgY0MKBAL49a9/DYCoujTuUwmqPsbjcbaoP3r0KCsQpt0yOY7DTTfd\nBEEQEAqF2PerJeJut5tNbPR+NcoQD4fJOfV6vew5r+96hTW0GRmmRJyHw2E8WfI8j7a2NtU5MOuQ\n2dFgHE//1xH85r+6MDoSV/nEYwny2akNg95jyqxnrTUFUC96jYo0KUSlIp5eMMyENUUZ90rHeUmS\nEVOQ6PCYOtqWWnWAbGuKMkHGSBFPJiSmdBsRcU9lOtEpklItmGjB5vj4OILBICQxY02hlpLW1lb2\nWa655hrwPI9gMMiuYaM5KJ8iXumz0PQ8VVQhoFbEAaC23g6eN0Pg1Yt8OvYoCzaVRDwX9FJTAMCp\nqAHT4xG9pFYRrQW0tgcA+wWrYV+9kbzXY/8EcZhc77YV2XGfWvAch88uJQu6Fw/248QomVsaplio\nSRexTqVHPH3PWdOFw+Pj46zwmKKYDHElLrzwQlRUVOgKFLlQJuIFgBIkSkbol5OrYPPgwYPsy920\naVNR76ck4larNYskNjc3swmikCYxhWJsbIw1zAFyK+I+n48NWnSgamhowG233Ya/+Zu/wXe+8x38\n/d//PR5++GE89NBDbKv3D3/4g8oOEYlECvJClgpms5l5+mjTHpvNptpepVi5ciWcTickSVL5BE0m\nE1paWnDnnXcWZSGh32MkEtHdDtOzgUwHBEHA9ddfjy1btkAQBAQCAfzkJz/JshIMDw/rdvmcbo/4\nSy+9hGeeeQY//elP0d7eDoDYIc4kIn4uWVMAsug6efIkHn30UYyMjMBkMuG6667TVYuqq6vZc+k1\nRW0pTU1Nquu7pqYGGzduZP/WKzjmOC6rYFMvoQIAIuPknLrdVtaCvqOjAzGJ2F6CQbIYEHgrHM7i\nzrtJo4jHYyJe2t6LWExEKiXj473DKp94LNkPgMQXDg8Psx0B5b1Ej2FcQVqVf883JioVcYc9V3wh\nl/X4qYB+r8pxM6ZRspU+cSBjiQCyFXEg4xPXvg6FstjRWBHP3KPKgs2Ghga2+Dl+/LhCEQdTxJW2\n07q6Olx88cXs38qowqz3rKhQzZXaa1Iw8fD6aIfNzGeIx0SE09crTYBxe8ywOwRmT6GgApV5bpqI\n8zz4itwN3yhoaspoNAlZlplP32zm2b2oJeJD4QQmkuRxcxVEvLe3F/39/cbvdd+D4CxWyBNkbuAc\nTpjnFyaiXZO2pwyFE/hjO3mPyRRqAtm1TZnUFJHZoARUskUTFQMpio0upGhtbcVf//Vf49JLLy3q\neWUiXgCoKkhJF/3yciniO3aQ+KO2tja2Gi8USiK+YsWKLMWM53m2Os/VDr5QRCIRvPDCC/inf/on\n7NmzBwApWMx1EdLtO4AoBffddx++8Y1vYOXKlYygcxwHq9UKn8/H7BsDAwOqyLKDBw9CkiSYTKas\nBcd0gdo+6ICi9aRSmM1m3HLLLVi6dCnWrl2L2267DQ8++CAefvhhfPWrXy3I869ETU0N86jrLaCU\nVd4zgYsvvhj33XcfnE4nYrEYfvOb36iUXjqYCYKgSm2YTkW8s7OTFchKkoSnnnoKhw4dUi3eThdx\nVe7WnAtE3GQyscXHgQMH8Pjjj7OdoHvuucdQIeR5XpXdnEql2ESnZ8nauHEjIwRGCrCyYFOSJEPF\nKpJWxJ1uMy644AKmvp8a3IN4chhjY+H0MRpHFxpBaU0RRRmv/PGEygLR+UkIE5EUGxdiiQGkxAm8\n8OJz+OEPf8jIq7IHQkVawVU2ofH7/XC73fD7/YYdKymUCrfdYayIWyzZyvtkEYvFmPii8odrogfH\nNYp4PIciDuRvc0/94XaHYLiIcrlNEGiEoYKIC4LACoAJESe/TyTHGenSjuebNm1iuyqtra054+iU\nthWtIg5kCjaptQZQk3KqiFOfuNmktibS+9C28hIAgGXh4ry+awqqiKckGeF4iiniFivPOM2Oj4/g\n3if34r6n9uL+p/biL57JxIxSIt7b24t/+7d/wyOPPGLYkdJU3wT31jszx730fHBCYfdZa5UTyxrI\n/XyK5pdPUhHPJuIKawpd8MUkttCl45Mky/j29v3Y00mEskKjC6eKMhEvANpK93yKeDQaZd5wGoVX\nDJREnGZaa0G3b7u7uye9TS6KIl577TV8//vfx65du5BMJmGz2fCZz3wGX/nKV/J6o+644w5897vf\nxT333IOFCxfmfPzcuXNx4YUXAgBeffVVtoihN8CiRYumXIhZKLT+6yVLlhg+dvHixbjzzjtx7bXX\nYuXKlairq8vpx8sFjuNU9hQtis0QLwXmzZuH++67D4IgYGRkBH/605/Y35Q+O+VnptdnPB5nZLIU\niEQiePrppwEQBau6uhqiKOKXv/ylKkbydBFXnufZZHwuEHEgs+h65513EI/H4Xa78aUvfSnvIlRZ\nHNfV1cUyefWIuNlsxv33348tW7YYjpdKRTwcDrOdGr0McQBwukzM+uLz+SDLEgZDuzAWIrY7gbPC\nXqQinklNkbD79X6c7CGq3+oNdbBYeIiijPaPR9i5SYpjOBH4PfbseReSJMHtduOGG25Q7QDoNaFx\nu934zne+g7vvvjvvGExTUzgOcKSJuLLIj8LtyUQ4ThU9PT3s9ZWLimhEPRZkKeJxWrxJUkK0sOVp\n6pPPH05em8s0cAoaF2xSRTw0TgiX1WrNasjicrlw0003obq6Om9aFx3XHQ5HlrUUUBZsZsg3tak4\nnCZWQAgAtRqfOMdxbIywtC1Bw//9A2q+99Ocx6ME9YgDJEucEnGzORNDalRIoQAAIABJREFUHA+P\nYt+pED4+GcJHJ0PoGCQL1pZKO1OTX3nlFciyDFEU8dRTT+ku+ADAvfUu1gXUdsHqgo8TyKjiFJMh\n4somdHQBr4wvtKfPdTIhYekSsvAfHBzE4OAgugMRvHZ4CIkoubeLVcQnizN3BjhDIMtylk82HxFX\nJokYtf7NBUrEvF6v4YS3aNEicBwHURTR1dWlaqleKHbu3Ml87BaLBWvXrsW6desMC/e0EAQhZ261\nFp/97Gdx8OBBTExM4Pnnn8eWLVtYgghNhZkJKPO0OY4rmf+8EPj9fuzevRsnTpzA0NAQGwij0Sjz\n0E63NUWLhoYGbNy4Ea+99hrefvttrFixAq2trYaZ5lrLQikGK1mW8cwzz2B8fBxmsxnbtm2D1WrF\n448/juHhYeZLBk4vcbVarUgkEiUl4meqRxwgiy6a811VVYV77703Z9MoCkp6RkZG2A7Y3LlzVfee\nEhUVFSorgBZ0Qg0Gg6pt9GwiTs6p00XOqc1mw+23345HH/0pUuI4+obIgo7nrWxCLhTUZz0WSqL9\nY3JOVqzy4bxVVYiEk9i3dwQH9wVxy/mt4HkBkiRChgiHw4ENGzZg9erVWaqqK92ERhJlhIIJVZOa\nQorEqNXEZOKZkCFJEpLJpOq9aFOj6ISIREJkCvlkQP3htbW1qrFAW2SZbU3JRBfqfTbW5t6gqU8m\nMSU3OauotCA4Es9adNBrsr+/H/FF5LVCY4SIz5s3T1dg+dSnPsV2VXJh4cKFuP3221FVVaX72WjK\nS2g0gWRSgtnMs0JNbQJMXb1DZU0xm82qmiFTQ3ZdRi547QoiPpFkFiGzVWBzjV2cwIVzPDiv2QfI\nMmQAHIArFpH77vjx46rd95GRETzzzDPYtm1b1uflrTbU/uPjiH28B84rri7qWDcvrsM/7+hEKr1Q\nmow1RVnvROcut41cW6PRJGyKpKTa2ia43W6Mj49j//79iNcTYm6VyHczU0S8rIjnQTQaZRNmodYU\neiEYrY7zYfny5bjxxhtx9913GxbtOZ1OVig1GXtKJBJhFoDly5fjoYcewqc//emCSfhk4HQ6WVfM\n/fv347nnnoMoihAEYcZsKYB68m5paZnUdzRZLFiwgG13PvbYY2yLT0kuZsqaosTll1+Ouro6yLKM\n3/3ud0gmk4ZEXJumUQrQuEsAuPbaa1FbW4uKigrcf//98Hq9quLW00lcS9nU53TnohcCOlE3NTXh\nK1/5SkEkHCBebzp20fg3PTW8UFBFXJZl5ukVBEFFBCVJxkRalXW5M+e0paUFl1xEFU0ywQu8FQ6D\n6EIjmDW+5jmtLly6jhzXipVV4Hnibz7WGUHbwpXgOSvqq1fioYcewoYNG3StDUZNaAoFLdYUTJwq\nqUGrViqV9/GQmiAXCz2LDZBtKcku1kxbInT84UBua4okyUxNzkfEPd50SohOcgpArqHgaD/5f5qI\nF2sz1ILjOJx//vmq/HslqCIuy8BouukRK9SsUn+emrpMljhQfCa1Fi6rCaZ0j/fRaCJjTTHz8PkI\np+Eh46oFHnxl7Xx8Zd0CfHXdAnxl3QL464g1gwp29fX1uOaaawAA+/btY1ZWLUy19XBtvr5gWwqF\n127GugUZIWoyijgVQl0uFxsf5lWROev48AR4c2bhEI9JzA534MABdA6FwcspmGRaa1K2ppwRUOZr\n0kmJErlwOKybw6ys2J1MtKDJZMKll16qioXSg7LdfbEWgV27diEej8NiseDGG28sStmeCi688EI2\nINIW2QsXLpzWBYAWSlVuJhcAACGRd9xxB6xWK8LhMB5//HEcOnSI2VIsFsuMfRdKmEwm3HLLLeA4\nDoFAAK+++mpBingxBZuxWAwHDx7E4OCgilgPDQ3hueeeA0BsQkpl1Ov14v7771ctniZrDSoFSknE\nZ4M15dprr8W2bdvwpS99qajrkkbBUXAcN6VdL4/Hw849JfZut1slVExEUqCODKqIU6zfsB42S8Zv\nzU/CmkKLNQHA67PgyqubwKcJjsttxvxFRD3b9+EIlvnXY27tbWhtvjhvlJlR9nUh0FPEgezr0+nS\n904XC0mSmCKuLXDPIuLhlMoik/Em69+/zJqiU6w5Nppgn7U6nyLuzajPSjgcjszOymgfkuIYEgki\nJOTreD1VOF0mWNMxlsOBGNlpp9GFGkXcYhVQU1MBniO/L6ZVuh44jmOqeDCSYLUIZiuPqJAZyys5\nfavJ0aNH2T23adMmrF27ltk5n3vuuZzFm5PB1UvrMG/iCJZHDmDvzpewfft2PP/883jppZdYZ95c\n0Ju3/LWEUIuyjJORzOeMRUXmE+/r60NXbx+sUua6KVtTzhBQIl5RUcFuCPrlyLKMcDictT06mTbl\nk4Hf78drr72GYDCI7373u3A4HPB4PHC73airq8Pll1+uq/aOj4/j7bffBgCsWbNmRokfz/O48cYb\n8cgjj7BBeibSUpRQerBnmogDZOHx5S9/Gf/5n/+JsbEx/OIXv2AWpsku3kqB5uZmrF+/Hq+//jp2\n7drFvh/tdWw2m2E2m5FMJotSxH/961+zIlXaPXHOnDno6OhAMpmE2+3GzTffnPX5q6qqcP/99+Pn\nP/85rFarob1hJnCuecRdLldBW/N6aGlpYd0X582bN6VJjeM41NbWore3l+0iGfnDAVKsqURFhRU1\nnjU4Ofw8JDkGs+Au2priq7KC5wlRuuqGFtaoh+K8VVXoOjSGUDCBIx1kt9SIdKqOzSD7uhDQYk1T\nHkWc4zi4K8wYHUlMSnmnULZdzybihEB7KswYCyUhiWSHgi6KWKdRa25FPKajiFNbiiBwrMDVCPR8\nTkRIYaJyJ2Pu3LkYHBzEaKgPnEjGGZvNlrcodqrgOA6+Ghv6TkxgOBDH+FiSEWKlHYmitsEOS6cX\nseTAlIk4AFQ6LAhEEgiGM9+92czj8OgEorwNdikGLqZvtX3llVcAEAvj0qVLwXEcbrnlFvzoRz9C\nKBTCk08+iQceeKAkxwkAfP8hzI+SXa8P9p7K+nt1dXVOy68e/6pzW+G1mzEaTeLwUBgWK49EXEI0\nKmJ+2zw4HA5MTExg9MQRWOUMH8o1ZkWjKZzqnUDrAjdb5E4WZUU8D6hvV0nelF+Onj2FKuK54v9K\ngebmZtUAMjExgf7+fnR2duLNN9/EE088oauU79y5kxVmrl+/flqPUQ+NjY0sx5rn+Un526eC2tpa\nXHnllfjsZz877QOwERoaGvC1r30NdXV1kCSJkYuZLNTUw6ZNm1BdXa1SsvQWlMUmp/T19amSYmKx\nGDo7O7Fjxw4W5XjLLbcYLgqrq6vx4IMP4mtf+9q0ZawXgulQxM9kj/hUoCRqkyXzSlB7Ct1NMYou\nNJk4pj5SCCYeXq8Hjb6rUOW+BE77/KIVcZfbjM/d24bbv7BQZfWgqKmzo3EOuS/G0vYP7XHoYSqK\nOC3WFDSKuF4hHStinAIRp7YUu92eVctCFfGauszuptInTr3JhtaUtCIej5NUGiUCQ5m8bboLYQQl\nUTfyiYfG+xFNkHjhefPmzciYUqUo2KRqOM8DXp2FBUlOIQtN5ffaezyM5353DB/uKa5/CFXEQ4rF\nqsXCo2sojIm0Kj6k6ZINkGhHGi+8efNmdp4cDge2bdsGnucxNDSE7du3F3U8RhgdHWXEv6mpCcuW\nLcPixYuxcOFCJljQIAwj6BFxjuPgryVzy+GBMFuExyZI53JqT3GFTzF/uNVqzWkLentnP1794wkc\n+HDY8DGF4syVYs4QUEVclf3qcMBkMiGVSmUR8WQyyYo7p5uI8zyPr3/96xgaGsL4OIlhGh8fRyAQ\nwPvvv49jx47h97//PWvRDJAL/d133wUArF+/fkYtIUp8+tOfhiiKaGpqmlGPNkBuymI6nU4XKioq\n8OUvfxlPPPEEG+xmulBTC7PZjK1bt+Kxxx6DLMtwOp26HSSdTidCoVDB1hRaj1BVVYU/+7M/Q29v\nL3p7e9HT04OhoSFs3Lgxb9Hs6STgFOeaR3wqWLBgARwOB3ieL8mul3Y81RLxMEtMMevuKnkqLAiP\ne2A2kecZtbfPBa3lRYvzVlXhVG9mcVqIIq5qQqNRcPNBqYgLgsB2qvSuT0r4p5KcovSHa+9HSsS9\nPgtMJg6plIzwWBJ1aa0jo4jrnxNlnGQsmlKd60xhY37PMLXhiLQAVvEcSsRFMYkJkezWTLcthYJG\nFI4MxZnCX1FphaDT3bW2wQ6XfQGiiT4sXXI+xkIJ7H59AMeOED4ycCqK8y/SLwzVA01OGY+kQGd8\ns0VAVyCCsOBGVXKE+b2vueYaWK1WyLLMvOFNTU1Z6WKtra3YvHkz/vSnP2Hv3r2ora3Nmy6TC7Is\nY/v27Ugmk3A6nbjnnntU3ODRRx/F8ePHdZvPUeTiX/46N949HsShwXEstlchNJqxQS1fvhzvvfce\nKsQxjKX0exRoj/XEcTL3KS1rk8XZOQOUEHqKOMdx8Hg8GBkZyUpOGR4eNtzSnw4IgoD6+vosP7nb\n7cbOnTuxd+9e1NfXs1iwHTt2QBRFOJ1OrFmzZtqPzwhWq7Wg1vBnO+x2O+655x48++yzOHz48JQK\n2kqF1tZWXHbZZXjrrbd0Gx0BxSnioVCINXRZu3Ytu14vuugiAMhqL3wmg27/nyvWlKnA6XTiwQcf\nZD9PFdpOv4bRhW798+nxWnDqBLleTSaO5YKXEi3zXPD6LBgdIWTXyIahhLIJTWg0gerawgvUUkwR\nz9gsksmkviJOifjo5Is1jfzhQMaaYneY4PIQG4yuIm5wTlRt7ifURJwlpujYOLTgOA4erwXB4XiW\n+k+bTZFxi5y7qRZqFgq6IIjFRJw4nuYV1fqKa6XPCrejDjbzTRgPOPH0z4+odglEkXQxLTQL35vO\nEg9Hk6gFOa9UER+wt2KxPYZocAB79uxBZ2cntm7dClmWWSfszZs3647RGzZsQE9PDz755BO8+OKL\nsFgsWL26uMhCivb2dtad++qrr84aM2pqanD8+HFVKp0WufgXLTztGgrDOp+QdNo8asGCBeDNFkjJ\nBBoTRHHPVagZGk0gls7kr28srPNoLpx+iekMhiiKTPHTKpVGEYb0IjGZTKfVy7p582a23fLCCy/g\n0KFDTCkHSBONmcrtLiM3TCYTtmzZgm9/+9t5C3RnCtdccw3uvvtubNmyRffvxXTXfPvttyGKJMbt\nggsuyPr7bCHhwPQo4merNQUgk1mpkge0ClcWER9XRxdqQa0ZAGBzmKbluuM4Duetyog2Wh+5Hoya\n0BQCkSnifPr9yPWZi4iHx5PsecUgHA6zdCctEZdlmSnidocJrrRHf1xJxKkibhCdaLNnzsPOP51i\n5yIaTbFYSm3UnxGM7D4cx6mO3Wy2zdiYW1mVOfb+UyRX32ewsOB5DjX15G8neiIQRRl2h4DV6zOL\nUW0qTS7Q7poTimjIJCScHI0iyVuxeesd+MxnPgNBEBAMBvGzn/2MRcbOmTOH9S3JPk4en/vc59hi\nZvv27di7d2/Bx0URj8fx7LPPAiALo1WrVmU9ht7/uRRxJf/S9gtZnCbi8ZSEFEfIOo3KNJlMkCtJ\nCp0gkd/lUsQH0t+f2cyrvtfJokzEcyAYDBqurowiDJVtyk/nVjrP87jtttvQ0NAAWZbxq1/9Cr//\n/e8hSRI8Hk/RLVjLOLfA8zwWL15s6NkuVBGPx+PMCnXppZeWrKDndKFUxZqyLJ/1inipoSyYB3J0\n1XQZKOIVGYJebHRhMWhbUsFsLy5P/kUWVXABIDRa3HWVSU3JKOKA/vWpah5UBImjoGo4x3EsOpeC\ndhsF1ERcSRbzxRcKAofVG+rAccSK8sxT3eg5Os7UcADwFWBNAXL77pVEvLqqecbmabOZz6ot8Bko\n4gDQ2EzEDo4jefW33b0QK1b52GJlfDz3d/jBniG88PvjiISTqEx7xOPxjJXp2MgEqMa+qM6Dyy+/\nHF//+tdZ3RR1Axip4ZnPZcZdd93Foht/97vfYf/+/TmPTYuXX34ZY2NjEAQBN910k+77UQ42PDxs\nmBKXi381e+1wpheB4+m0O2VCT59JzfFyEfH+U+mGQQ32vDULhaBMxHOAeo04jstSt/Mp4tPtDy8E\nFosFd911F1wuF+LxOMvfveKKK85qFa6M6UehRPy9995DLBaDIAiT3rI8k1AqRVySJLbILxPxwsDz\nvGpczfaI0wxxA0VcQYKKbW9fDEwmHtfePBdrLq/H/LbCkmIKSU75+P0A9rw1yLpCAsoccTKV5yLi\nLrcZlN9MJjmF+sMbGhqydlOV3TAdDoF18gyPZwiTsqGPEZZ9yoerb2qBzSYgEZfw4h968e4bZE51\ne8wF7TAAChuOzvlUEvHa6uKa40wVWuJtpIgDpN5g3ZUNuOXPFuCyDfWwphshsUVODiIuSTL27h5C\n77EIXn+ljxVrxtPfgdnCoytAdjO9djOqnOR80RCBK664ghUxtrW15f1cVqsVX/jCF5jw9+tf/1q3\ne7QeTp48yVLcNm7caGjppb+XZZnF/WpBibge/+I5DovSBZuBdDdyqojHkiI64i6kkLm+cu3kDfQR\nRbyuoTQ1drOaiPv9fsHv9/+T3+8f9Pv9Y36//3d+v7+g2AlKsnOBftlerzdrsqSKuBERPx1NWfTg\n9Xpx5513suP3er2s1XwZZUwWhRBxURTx5ptvAgBWrlw5Y80RphOlIuJKRae8KC4cRkRclmVMKIo1\n9aC0pkwnEQcIwVp+vq9gtYwVUhoQ5NFgHO+8MYgP9wTw3lsZj6xWEc9lTREELtPqPv0+gUCg4GuZ\nEnF9f3jmerapFPHM58nnEadonuvCls/PY175wGBhjXyUoMkpExMptgBgr9/cDIvZCQ4mNDbMTKEm\nhfIzWKy8qvGUFmYLj6XnVWZZH2gNRCQHEY+MJ0FbNfQeCyM1mP5+0qfCYhHQNUQU74U1TpUCbTKZ\n8OlPfxoPP/wwPv/5zxds4XI4HLj33ntRU1MDURTxxBNP5M0YlyQJzzzzDGRZRnV1NTZu3Gj4WJ/P\nx3pIGPnE80VHL0rniZ9KZ4lTj3j3cAQpCAhYMs8zUsTjMRHBdFOmuhL4w4FZTsQBfBvA9QAuBkCX\ntk8U8sRdu3blfQwl4nqRcvRLCoVCTNmSJIl56M4ERZyipaUF27ZtQ1NTE26++eayAlfGlFGIR/zA\ngQMYHR0FAFYsPNuRj4hLkoT+/n7dRl9KUH84UFbEiwEt2HQ4HKoFTHRCZMTDyJpitQmw2shEPt1E\nvFhQ4mjkEe8/mVnwfvT+MI52EQEoZaCI6xFxIKMUB4MxPP/88/jBD36AH/3oR3lrPURRZBGruYg4\nL3CwWHhmyYnHJSQSImRZzmtNUcLtseCG21rhX5bx+RZTxKqy4WiKU81mMxbPvwlNVdfB457ZOi4l\nEfdV2yZVp1CIIq61Hp3YNwYXeFhA3s+cLtQEgAXV+vZDk8lUtG3H5XLhvvvug8fjQSqVwkcffZTz\n8fv372fxtTfeeGNOUYLneVarp0fEJUnKK4RSn/jxMaJox6IiJEnG4UFyLsKuTJyxEREf6I+yn+vq\ny4o4AHwRwD92dHQc6+joGAPwEICr/H6/fp9ZBfbv36/qmqmHXEScKuLKCvXR0VE2wZ4pijjFsmXL\n8MADDxS0zVRGGflAiXgsFtMlnbIss8jCxYsXZyVezFZQIp5IJFRZ6xQ7d+7Ev/zLv+C1117L+TpK\nRbxMxAvHihUrUFNTk2VzUqqDRtYUILOVXIy6OhOgxDE6IbKiRiVocR/Ff6eLGUUDRdxooeipsECU\nEti95w9st2pkZAS/+c1vVN1utTh16hS7ZrWt7elxA8SWwnEc3IrvIDyWZF01gcIiHcln4rFhcwM2\nfroRbYsrsGRF4aTZ6TKxc6K3uDEJdphNbsx0GZfSmpLLH54LhRDx8VAmtcdmEyAmZazjK2DmFEQ8\nbU1pqyltQ7+KigrGM3IlnADqFJ6FCxfmfe1cBZtjY2N5+RftsDmqEELiMRGdaSJeM2ceKisr4XQ6\nDXuMDKT94ZVVVrawnypmLRH3+/1eAHMAsBLdjo6ObgBjAPJ2jxBFEbt37875mEIUcSBTsEkvDo7j\nzjgiXkYZpYQyW1zPnnL06FGmoJ0tajiQITqyLCORyJ7g6cSSrxVzmYhPDj6fD9/85jez+gDQDHFe\n4FQxeFpc+dkm3Hh7K+a3nVk2KWUTGj3iSBXxJSu8sNkFJBISXn6uF/F0hJqpQEWcE8LoG3kBwZA6\nQ/vw4cPYsWOH4fFRW4rb7dZNA6OKuC3dKMXhyvjRw+NJZksBClPE2fFyHPzLvLjis01wFNGAieM4\nRQOj7EUJ9dmXotCuGLg9Zvb5C4liNHoNAAiP6RcsAsB4WhH3Vlqw5gqSCtPEW9HGpRVcAQhFyWMW\nlpiIAxnCnI+I078X2liP8io9Iq78nRH/mlflgEXgEUPmeoxFRXQOEVG2ra4S3/zmN/HQQw+pOtUq\nUWp/ODC7c8TpSKptbTkKoKAKmd27dxsmOSQSCeb/drvdWQObcgslEAjA6/Wyjk9erxeiKObdni6j\njNkK6tUDSLqQdkvx9ddfB0AG2MbGRkNiMJsxNjaW5XunVpxAIICBgYGsiD0KpRVAFMWz8vzMJEaD\nZHJ0OIS8nueKSr4k8ZOlBC/IrAlOYDACd0WGIEYnREbO57Ta0dxqwyvP9bMmNwAgyyIrigaAaDSa\ndU11dXXh5dd+i6QYB8DhmmuuwUUXXYjt27fjww8/xKuvvor6+npdZZLmSTc3N+ueu/HxdDdCG8fe\n1+4QMBERERyJwmzJ7B7JSM3I9e7yCBgZBkYC2edCFAkRE6WZORYlLl5bhVO9UTS3Wif13hYrOZcT\nEylEIlHd9uqjQfK6DpeA5rlWzF3gxPEjETg4cn1EkoTEcwAaXULJzwFdrA0PDyMcDhuKDdRD7vP5\nCjoG+rqDg4OYmJhQWWco/6qoqIAkSYavN7/Kjq7BjHgUGo0wa0prpZWJJHrPlyQZA33kuVU15oLP\nW77xZjYTceor0c50XhBVPCc4jkM0GsVLL72k21lLGUs4Pj6O9vb2rMdYrVbE43EcOnQI8Xgchw8f\nZr/Xe3wZZZwtUCq6Bw8eVKkRoiiis7MTAJm4Dx48OOPHN12gkV4AaUChJeLBYJD9/Oabb6K1tVX3\ndZTF4keOHJn1sY6nGyeOmwCYAS4+a8des9WKVIpHV+dJTCQy91cwwAOwApAxNNINQQAaW004dSyz\n+B0a6kd7+0l2XYXDYdV56OvrY1YUnrOi1rsBAudAe3s75s2bh6NHj2J0dBRPP/00Nm/ezHa8UqkU\nurq6cOjQIXKMZrPu+R3sNwMwIRYfR3t7Om1MsAAQcOxoH4IhKf0ZgCNHOiDMAPNIJMk1MdAXQnu7\nWkFNxK0AePT390HkTkz/wWjgawA6O43zsHMhNsEBIGrtRx9+Aps92yI32E/OfSw+ivb2ALw1wOEj\nVljTJojBMUKfqu08ug8fmtRx5AIdJ2VZxp49e3QFiWQyyezBkUikoPuW8rJkMom9e/eqdmYp/7LZ\nbDlfq8aUxCHIECFDAIcP2o8hki7o5UL9WdeKEhNhDqkkOfeh8V60t2ef+8lg1hLxjo6OUb/f3wPg\nAgD7AMDv9y8AUcNz7wsDWLp0Kdrb23H8+HFce+21WUUJlDzwPI8VK1botoJ/44030N/fD7fbjWXL\nlrG85Hnz5rFmOmWUcTZClmU899xzSKVSqKurU7U/PnnyJPObrlmzJquxwmxGJBLBiy++CIB4ZRsb\nG9nfEomEyq4Si8UMx4Fjx46xn5ctW1Ym4lPESN8ggDBqaj1Ytmx21iMMnRjA8e4I7NZKLFuWKfZ/\n/+1hACFU1dhw3nlENFq6VMaOFwdw4jhR55rnNKJtiQeSJGHv3r2QJIlde7Iss3CC6uoa2LAWZsGN\n+rp6NM4hRKa5uRmPP/44YrEYPvroI9xxxx344IMP8NZbbzHrmc1mwxVXXKF7P/d2ngIQQ0NDFZYt\nI1bOwKkBRMYicNgq0dzkQsfHRP1ccd7SGWniZebG0H8igFTSgmXL1LVR7e8fByCiqbkJbYvPLJtS\nPqSSEg68fwwA0NgwDw1N2dykfS/5fK3zGuBfRgwCv/vkE7SF0jUuJrKIW9roxbJli0t+jJIk4ZVX\nXkEqlYLH49EdB3t7e9nPF110kWHPCiUSiQReffVVAEQdV+7e0GaFra2tOfnXJXI/3jjVjRgkOCFA\nsngBjELgOVx50XJYBGPr1KEDYwACsNp4rLpwScHXcTweR1dXl+HfZy0RT+NxAH/l9/t3AggC+D6A\nlzo6OnryPXHNmjVob2/H8PAwjh07hqVLl6r+Tv2tLpcLdrtd1y/k9XrR39+PiYkJ2Gw25ilvaGgw\n9BeVUcbZAofDwQpklNc7VcedTifq6upmVefMfFBacmRZVn1upVoOELJttVp1P39fXx8Aco7cbvdZ\ndY5OB6JRsvDzVNhm7dhbWWXD8e4IwuOi+n4aJIu7hman6vdXXj0Hv//VUYyNJlDX4IbNZmO1S/F4\nnF17nZ2dGBgYAABs3Xoz3nwlgUg4hdhExlPe2NiIW2+9Fb/4xS9w8uRJ/PCHP2S7XoIg4OKLL8bG\njRsNrVa0UYzbkzn/Xq8NQAQTERGQyX1jsfK6otZ0oLpGBBBALCqC58yqIlE5bRG2Ws2z73qxATab\ngFhMRCLGZR1/KiUhGiEKr6/awf7O+UxoD0awVHDiaIpYJRbVeabt89fU1KCvrw+jo6O670FtfA6H\nA1VVVQWNgTabDV6vF6OjowiFQqrXLZR/LW/yAejGhCzByQkYSXvt5/kc8DhzxxGODJH3qG90lPQ6\nnrXFmmn8I4DnALwHoBeADOCOQp7Y2NjI2rLSdAeArOReeOEFFjCvbW2vhLK7ZiQSYb7PMym6sIwy\npgs0OUVbrEkXsc3NzWcdwVRGeml9f9ouu+Pj44bFSrSYc/ny5WeXTXyyAAAgAElEQVTdOTodoKkp\nzhy5zGc69LpBplISAgPE/16vySy22QRsvWM+br97AWrTMWp6xcR0fmtpacHcuXMzXTxD6qLQpUuX\nshznVCoFQRBwySWX4Fvf+hZuuOEGQxIOANFIulhT0bHUpWjqwzLEDdrbTwdyFcCermLNUiFzbrOT\nU5S/8yg6u1bazdgtjeNQcxIfjRP37kKD6MJSgCZlGY2BdHFYrFijVwgai8VYTV++oIwF1U4IHIdY\nejUWHCfXRltt/nNB/eF1DaXJD6eYvaMWgI6ODgnAt9L/FY1169ahu7ubJTzU19fjt7/9LT7++GMA\nwMKFC7FixQrD5yu7axZSsVtGGWcTqD9Pm0FMc2Gbmppm/JimGxzHwWq1IhqNZqWmUCJut9vB8zwi\nkQg6OzuzohsDgQBTxHONL2UUBlmWEUl31TRq5jMbQIl4LCoiHhNhtQkY6o+yfPT6xmwFzmzmUVGZ\nicFTKoHxeBwjIyPMO7tu3TqWJtJ3YiIrXxsAS6NJJpNYs2YNfD5f3uMWRZkp4g5FPjuN2YuEkyzd\nJV8zn1LC4TSxAtix0QRq6jLnb9YTcbcZgcGYLhEfD+lHeVY6yM/7+0JIiuTzLyyAfE4WlAdRwq3F\nZLuQ19TU4PDhwyrOpfw53+vZzAJaqxyIjZBrdiK9iGyryW1RmoikMJY+t3U69+JUMKuJ+FTh9/tR\nU1ODoaEh7NixA7FYDN3d3QCACy64AFdffTUrUtGDsrsmvaicTidTCsso42yGniKeTCbZwNvcPLPt\no2cKlIgbKeJerxc1NTXYt28fjhw5grVr16oet3//fgDE9jZv3ryZOeizGLGYCDFNLHJliJ/pUBLq\n0GgCtfV2lh/u9pgLWmQoW8/HYjGmhvt8PuabzdXFUxAEXHXVVUUdN20TDqgbJVHVVpaB4Ai5V4qJ\nLpwqOI6Dx2vBSCB+9iniObLEaYa402VijZ4AwOtIf+8x8n1ZTTyaKqbPJkQFiEAgAFEUVbY+IEPQ\niyXieoo4/dlmsxXkNV9c50ZghAhIcpJcC4vyLEqoGs5xUC3qSoHZbk2ZEnieZ5PkwYMHGQm/8sor\nsXXr1qwLRwuqiIfDYaZwlW0pZZwr0FPE+/r6WKHm2UzEgex4K0rEKyoqWBFRd3d3Voyp0paSb4wp\nIz9om2rAuKvmbIDdIcBsJlMyJY796eYhWluKEZSK+MDAAOtsuG7dOmap8lSk29yH9JtSFQtVe3tF\nhrtyUTQSIPdKoc18SgU9u48sy2yXYaYb+pQKrrQFS4+I066abo964VZpV/97QbUTwjQuRCgXEkVR\nlRIFkLGTjpfFNnujSns4HGYikLK1fSE2l0W1bmZNsXHkIsjX2GggvSiurrWx+7RUmKWXYemwatUq\nRih4nseWLVuwefPmgr5MpWfuyJEjAMq2lDLOHdD7RqmIU3+42+02bBE822HUvVBJxGkkajweZ+cE\nIBNG2ZZSWlR4LViwyIPzLvDNamsKx3GZVvdBQpIHGBEvTIFTKuI7d+6EJElwOBy44IIL2O+pRzyV\nktm2/FRAu2oCakXcahWYAh4cyXR6nEnoqf/KtcfZoIhrF1PUmuKuUCcxVTrU/56ORj5KVFVVscWf\n1ieu/HexRFwpdlICriTihWBxnYs19bGBR7XTAp8zd3LVdPnDgTIRh9lsxvXXX485c+bgrrvuwsUX\nX1zwc5VEY7J+pzLKmK3IRcTPVjUcMCbitFjI4/GgqqqK+WtppjqQUcPLtpTSgec5bLqmGavX15/u\nQ5kyPAoFd3QkwbzXdU2FTf48z7MoTNrgRNu0jr4HfZ+pgnXVtAlZxJbaU6S0dWgmizWBTMFmYCiG\nXa/24b23B3Hgo4w6y+s0w5kNoOc1lcz48ynGx8h3qlXEvRpFfLqJuCAILOzCiIg7HI6CrCRKOJ1O\nlliiJeKF8q9FtW5EFUR8UZ5zIaYkDA2QXZ1S+8OBMhEHAJx//vn42te+Br/fX9TzbDZbVkfBsiJe\nxrkCPY84JeJnY6EmRSGKOABmT6G7ZUDGH75ixYqs3gVllJFRcOPMlmKx8vBVWXM9TQWlPcVkMmH1\n6tWqv1utArOQjIWyrQ3FghJxpRpOofXsz6RHHAB86TbyqaSMT/YH8cG7Aex+PVM8ONsVcQAIj6m/\nQ9re3qNRxL0ODRGvnv5aNqNW90p/eLGpURzHqV5XFEUWXVgo/3JZTbC6yT0gcBza7LkXuoGhGKtD\nKdQmVgzKM8EUwHFcVqRTWREv41wBVcSj0SgkSUI8HmfKxLmgiCtTU1KpFMsR1xLxnp4exONxDA4O\nspbOZVtKGXpgnuZgAv0nM1vhxZAVpT1l1apVWd1fgYwqrlewWSyoNcXuyFa7XRpVdqY94jV1Nqzf\n1IDFy71oXeBGXYMdngozTGYO1bU2VNfOsgzxNOwOE/O3K33iyYTEaiayPeIza00BjIn4VB0ElHAP\nDQ1hZGSE1eEUI4TObXAhKJNzV5XKXVtC/eFOl2laCsJnb2XLGQKPx4NAIACA2FxyZa2WUcbZBKqI\ny7KMaDSKwcFB5lc8F4i4UhGnthQgQ8RpnwJRFHHs2DHWSc7tdqO1tXWGjraM2QRqpYjHJfQcIwu7\nQv3hFEpFXJvYQ+GpsGCwL1oiIk4zxLPphFuriM+wR5zjOCxZUYklKypn9H2nGzzPwekyY3wsqSLi\nY2OZ79NdoTn3Jh5Oi4BIQkSV05LlGZ8OKLPEJUliu4DKDPHJgBL4oaEhJv7wPI+qqqqCX8Nf58J7\nnUOo5MyQgmLOx9LdqbppUMOBsiI+ZSiJd01NTXm7uYxzBlQRB0hyCrWleL3eon1/swmFEnGXy4WG\nhgYAQFdXV9mWUkZeVCj821TZLHYrnN57S5YsMVQcK7yEpJXEI56OL3QUZE0ppwSVCqxgU2FNoYWa\nPK+fqU994jNhSwEyCnUymWTWvXg8zrpqTlURHx4eZsXvVVVVRaVQnd/kxQmZjOHh0aRuAg1Aoi77\n2O7U9MQ9lmeDKUJZsFm2pZRxLkGZlz8xMXFWN/JRQo+I00nGarWqrAFtbW0AgA8++ICpQOedd95M\nHWoZsww2u6BSjXkeqKkvbvLftGkTVq9ejZtuusnwMcyaUoIIw+KsKWXKUSowIh5WEPG0Iu5ym3X9\n79UuMja11eZuXlMqKOMEqR1lKokpFJRrybLMer0UW593frMX37hmEXgTOb7e9A6UFid6ImxRPHfe\n9AhM5btiilAS8XKhZhnnEiwWC1MglIr42WxLAXITca01jfrEada6x+NBS0vLTBxmGbMQHMepVPHJ\nZBY3NTXhhhtuyBkfSgv5EnGJdb2cLM7kYs2zGazNvY4irl0AUdx/2Txs8tfi1pUzI5aYzWaWHkUJ\nOBUkbDabbv1CIaisrGRzD7X8TUYIvXJJLea0EEHJiIh3fkLG9tp6u6rpVilRviumCOXEW1bEyziX\nwHEcs6eMjIywWomznYjTKLhCiHhra6tqu7RsSykjH5REfLo8qRUlijCUZTknEXc4TaqmOTNdrHk2\nQ6+7plFiCsUlrT78w/XL0TCNHTW1oLyIEnBKyOvq6opOTKHgeZ5FI1JMVgid00pU7pM9EZaMQpFM\nSDjWRWyHbUumr/6vPCNMEVqPeBllnEugRFyZlX0uW1O0RNxisagU8LItpYx8UOZ8T0dUGkAsMOa0\nOj2VCMNEXGJdKpVdNSloUSFF2ZpSOtDumhORFCOQYyH9DPHTCW1yylQLNbWvSzFVIp5ISKxpD8XR\nrjGkUjJ4Hljgn74GdeW7YopobGzE/PnzcxbGlFHG2QrqE+/u7gYA+Hw+VRHn2QhKxFOpFIvNMiLi\nALBo0SL2tzlz5szQUZYxW0GTU4DpI+JKC8xUklOU7e31ijUBtT2lXKxZOtDzKsvARIR02KQ2FW1X\nzdMJJRGXZblkzQ+1xHuyRNxTYYE3fc9p7SnUljKn1QW7ffpCBsvxhVOEIAj44he/eLoPo4wyTgso\n6U6lyIR8tttSAHU8XDweh8PhyEnE165di1QqBb/fX7allJEXc1pdqKi0oK7eDodz+qZoT4UFgcHY\nlIj4hIKI61lTgLRfmdRxMxW+jKlD29THbBGQSJDtiTNREY/FYhgeHkYwGFT9fqqvC5BIWNptczKY\n0+rCaHAEvcciuCSd+BkJJ3Gyl9T2tC3xTulY86FMxMsoo4xJQ5mcApwbRFyZihKPx2G1WjE+Pg4A\nugVyZrMZmzdvnrHjK2N2w2434fa7F077+3hKEGEYSyemmEycIcmmhNFs5mdtJ8szERYrSdhJxCWE\nx1MwmRUZ4mcgEQeA9vZ29vNUrSlKBXyqtuA581zY/+EIhodiiISTcLrM6OoYgyyTAuO586c3jre8\nPC2jjDImDa0N5Wz3hwPZRDwcDrMIuHJDrzJmC6g1ZbA/it27+pFMq6nFYCJHoab2faZT3T9XoSzY\npIkpgsCdUefaarWycZH2UrBarTlTfQpBKYl4Q5MDJhpjeJyo4J2fkKzz+Ys8MJmmlyqXiXgZZZQx\naZSJeJzZUoAyES9j9mBemwcVlRbIMrBv7wh+8/MudHeOFZUrnklMMfZ+L/B7sPLiaqzb1DDlYy5D\nDSURp1013RXmSaeRTBeoKk4jbqeSmEJhsVhYJ836+vopvZbJxKNxTjrG8GgYw4EYhodIMf50pqVQ\nlIl4GWWUMWkoiXhNTY3KP322gsYXAmoibjabp+RTLKOMmYTVKuDmz8/HqkuqwfNAJJzCK8+fwEvb\newv2jdNGJ7kUcZOJx8VratE0Z2a6OZ5LUCnitFDTc+YUalJo/eClCra4+eabsWHDBqxatWrKr0XT\nU070hHG4najhLrcZDU3THz5w5uxflFFGGbMOSo/4uaCGAyTD1mw2I5lMqoh4RUXFGadElVFGLpjN\nPC66rBZtiyvwxo7/1969B9ld1nccf5/dTTaX3WQTIGAwEQPx66Uaaqy9iMpFO7Qi1nqbiiKtA44y\n4x2tWqn1CkKpU6diwQvWQbGt1aFiHdSxooI3rlLkK5mAQUGJIRdy29y2f/zO2ZwcNmd3k7Pnd/bs\n+zXDJOc5z26+y2/O7mef8/09z4M8cP921t27lQ3r7+MV55ww7mFCE2lN0dSpD+K1NzIGF3ZOf3hN\nY/A+3P7wmhUrVrBixYqWfK7RbQyH93Hn7cUNpSc8cUFbvqe7Ii7pkNWviM+EGzVr6vcSrwXxw+15\nlMoytLifM17yOE45fSlQrI5vWL9z3I/baRAv1ejpmo/sHj3evpNu1KxpDN6tCuKttHBo9uge/vuq\n+7I/YYp3S6kxiEs6ZPUr4jM9iNsfrumsUqmw8okL6a8eurNp4/jtKduru6bMHeMwH029gYHiF6Bd\nw/tG24kWdGBrSuPNlJ165sry4/bvjnLkkjksOmJqjrRvZBCXdMgWL17M05/+dFatWnXACZLdrtYL\nbxBXN6lUKixcXISPzQ8PjzPbFfGyDdStftdOOO3E1pT58+czMFCE3PpdVDrNsuP2Lyy14ybNGl89\nkg5ZpVLh5S9/edlltF3ths3h4WG2bNkCGMTVHYYWzeahB3ewaZwbNvfs2Td6gIxBvBzz5s+iUoH6\njW466VTNekuWLGHr1q0sWbKkY++lWbpsPkOLZrN79z5WPtEgLkkdq741xSCubjK0qLYi3jyI76i2\npUDz7Qs1dWp7hm/bWrwzMWt2z2hrUad5/OMfz9q1a1t2c+VU6Ovr4aWvPp6RkZEp3zv8gH+3bf+S\nJHWJWhDfsGEDe/cWgcSbNdUNFi4qVlQ3b97Fvn0jBz0Nc+cEjrfX1BsYnDUaxAcXdN4e4jWnnnoq\nEcHSpUvLLqWp3t4K0N7/h535q5MkdbBaEH/ooYdGx1wRVzcYWrR/54ja3tRjqW1dWKlA/xxXxMtS\n3ye+oEPbUgB6e3tZvnw5fX3+0tbIIC5Jk1QL4rUbNXt7ew/YQUaarmpH0gNs3njwGzZ3VA/zmTO3\n96Cr5pp6tb3EoTO3LtT4DOKSNEn1x9xD0ZbS0+O3U01/vX09o4Gu2RaGO7a5Y0onOCCId+COKRqf\nPzkkaZIag7htKeomQ4urfeLNgviOahCfaxAv04Er4p3bmqKDM4hL0iQZxNXNFlZ3TtnUrDWldpjP\nfPvDy+SK+PTnr7KSNEkGcXWz2g2bm5psYbhjuyvinWDxkf08bsUAPT0VFrfpJEi1lq8gSZqksXrE\npW5R20t8+7Y97Nq1l9mzD1z1HhkZ4eHf7QQ6e6eOmaCnp8LpL5o5pxp3I1tTJGmSXBFXN6v1iMPY\nfeJbNu0abU055ti5batL6kYGcUmaJIO4utm8+X30zSq2JBxr55QHf70dKE5yXHzknLbWJnUbg7gk\nTZJBXN2sUqnsP+p+jBs2f/PADgCOfsxc9xCXDpNBXJImqT6IVyoVBgYGSqxGar3aUfdjrYj/proi\nfszSeW2tSepGBnFJmqT6ID44OEhvr1u4qbvUdk5p7BHfvm0PmzcVY8ccaxCXDpdBXJImqa+vb/Qk\nTdtS1I2G6vYSHxkZGR3/zQPFanhPDyw5xhs1pcNlEJekSapUKsyeXawYGsTVjWqtKXt2j7Bt657R\n8VoQP3LJXGbNMkJIh8tXkSQdgjlzit0iDOLqRrUVcTiwPWW0P9xtC6WWMIhL0iEYHBwE4Igjjii5\nEqn1Zs3uYf5AceZf7aj73bv38buHioN8vFFTag1P1pSkQ3DmmWdy9913s3r16rJLkabEwkWz2bZ1\nz+jOKb99cDu1dnGDuNQaBnFJOgTLli1j2bJlZZchTZmhRf08cP/20b3Ef/PrHdXx2cydZ3yQWsHW\nFEmS9Cije4k/XKyI127UdNtCqXUM4pIk6VFqe4k/smU3u3ft47cPepCP1GoGcUmS9Cj1O6fcu2YL\ne3YXDeKuiEut03FNXhExG/g4cApwDLAR+BLw3swcrpt3AfAmYAi4CTgvM+9tf8WSJHWfgQWz6O2t\nsHfvCHffuQmAefP6WLBwVsmVSd2jE1fE+4D1wBnAQuDZwKnAR2sTIuIs4O3VOUcBdwHXRkQnfj2S\nJE07PT0VFgwV7SkP1u0fXqlUyixL6iodtyKemduBv6sbWhcRVwJvqBs7D/hkZt4GEBHvBh4CTgJu\naFetkiR1s4WLZrNxw+ib0faHSy02XVaQnwfcVvf4acDNtQeZuQ24B1jV5rokSepatRs2a+wPl1qr\nrSviEXEVcHaTKR/MzAsbPubNFO0pz6gbHgQ2N3zspur4hAwPD094zkTmSpLUbeYP7F+v6+urMH8Q\ndu7cWWJF0vQyXoZsd2vK+cBbmzy/o/5BRLwFeAdwamb+qu6pRyj6x+sNAVsmWsiaNWsmOnVScyVJ\n6hZbt/QAxe4pcwf28POf31VuQVKXaWsQr7aQbJvI3Ih4L3Au8JzMvKfh6duB1cC11bkDwMrq+ISc\ncMIJ9Pf3N50zPDzMmjVrJjRXkqRuM7xzL3ff9ksAjl95JE95yqKSK5Kml1qWPJiOu1kTICIuAV4G\nnJyZa8eYcgVwWUR8BfgF8GFgLfD9if4b/f39zJkzp+VzJUnqFnPmwOIj+nl4wzArVg75s1BqsY4L\n4hHxOOBtwDBwe0TUnrovM58KkJlfiIhjgesoWlJuBM7MzJESSpYkqWud+Yrj2LF9zwEH/EhqjY4L\n4pn5Syawm0tmXgJcMvUVSZI0c/X399Lf31t2GVJXmi7bF0qSJEldxSAuSZIklcAgLkmSJJXAIC5J\nkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmS\nJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIk\nlcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSV\nwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXA\nIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAgLkmSJJXAIC5JkiSVwCAuSZIklcAg\nLkmSJJXAIC5JkiSVoK/sApqJiPnAHcDyzJzV8NwFwJuAIeAm4LzMvLf9VUqSJEmT1+kr4hcBa4GR\n+sGIOAt4O3AGcBRwF3BtRHT61yNJkiQBHRzEI+I5wEnAxUCl4enzgE9m5m2ZuQN4N7CiOl+SJEnq\neB0ZxCNiHnAF8FpgzxhTngbcXHuQmduAe4BVbSlQkiRJOkxt7RGPiKuAs5tM+WBmXgh8BLg2M2+J\niJPHmDcIbG4Y21Qdn5Dh4eEJz5nIXEmSJKneeBmy3Tdrng+8tcnzOyLiJOB04MQm8x4BFjaMDQFb\nJlrImjVrJjp1UnMlSZKkiWhrEK+2kGxrNiciTgOWAesiAmAW0BsR64FzMvM64HZgNXBt9WMGgJXV\n8XGtXr26sedckiRJaqtO3L7wMuDKusd/AnyRov/74erYFcBlEfEV4BfAhyl2V/l+G+uUJEmSDlll\nZGRk/FklqvaIX5+ZsxvGLwDeTNGSciPuIy5JkqRppOODuCRJktSNOnL7QkmSJKnbGcQlSZKkEhjE\nJUmSpBJ04q4p0pSLiF7gIuA1wBzgeuB1mbkhIs4GXgc8CdgL/AR4R2beWVa9OjzjXO+XARcCx1Is\nTqwBLs7M/yirXh2+Zte8Yd7FwAXAqzPz6rYXqpYZ53V+DvAZDtxC+drMPKvthaolxnuNR8TxwKXA\nKdUP+Tnw7Mwc68T20rgirpnqb4EzgWcCj62Ofb765wD7g9mxwC3A9RExt91FqmWaXe+bgOdl5uLM\nHAIuBq6JiOXtL1Mt1OyaAxARz6Q4QO4BwJ0Lpr/xrvmazBys+88QPr0d9HpHxFHA94BbKc6mWURx\nqOTe9pfZnCvimqnOA96XmfcBRMQ7gDURsSwzP1E/MSI+CLwbCOC2dheqlmh2ve+vTaqusOwDNgNb\nyyhULdP0mkdEP/Ap4FzgmvLKVAsd7JrXfqn2ML/u0ux6vx64LzPfXzf/lvaXOD6DOOO+nbWq+tyJ\nwNEUb2v8oLRiddgiYojiN+Sba2OZuTYitlAcHHV/w4ecRvF25j1tK1ItM5HrXf3GfTswCGwC/iIz\nHx7r86nzTfA1/j7g25n5o+opzprGJnDNR4BlEfEgsBv4AfCuWojT9DKB630yxff2rwF/DPyKouXw\nCyWU25StKYVmb2cNA/8JnFF97NuX099g9c/NDeObgAX1AxHxBIq+wrdl5jY0HY17vTNzXWYuqs69\nGPhqRCxtX4lqsabXPCKeAbwUeE9bq9JUanbNB4EbgN/LzMcAfwDsBL4ZEfPaV6JaaLzv60cBf0nx\n8/so4G3ApyPiWW2rcIJcES80ewvzbuDu6nh5FaqVHqn+ubBhfAjYUnsQEU+meHfkksy8ok21qfUm\ndL0BMnMHcEn1xq4XA/8y5dVpKjS75o8AnwXOz8ztdc/ZtjC9NX2d15+8nZm/jYhzKULbHwLfaU+J\naqHxvq9vAW7MzP+qjn8rIr5BsejaUV0NM35F/GBvb1BcxFVl1aWpk5mbgHXA6tpY9e7qBcAd1cdP\np/jm/OHMvLSMOtUaE7neY+ijIaRr+pjANX8ycHVErI+I9RQ/Ay6PiM+P9fnU+Q7xdQ7+AjYtjXO9\nb2fs+7kqFPcAdRRXxCfRpqCucgXwzoj4DrAR+CjwjcxcV33r6mvA2zPz02UWqZZpdr3PplghuReY\nD7yF4g7768sqVi0x5jWn6A9fzv42wwrFzjkXAx3XP6pJafY6fwFFQPs1xev7ImA98MOyitVha3a9\n/xX4XkS8CPhv4LnA84GPlFbtQRjEJ/G2tbrKRRTfjH8C9FOErldVn/sAxS9oH4uIj9V9zOneqDtt\nNbveK4H3A0dSfD/4McV2hr8toU61zpjXPDP3UYSxURGxF9iYmRvbXqVaqdnr/LkUwW0hxc/27wPP\nb2hP0vRy0OtdvQn7lRS/YF8NrAXOzswflVTrQVVGRrz3MCLuA/4hMz9bfXw8xQ4Zx2Xmurp5+4CT\nMvPGMuqUJElS9zCIAxHxbuBsioMdNlLcZTs3M/+8+vwcircvt1FsZXcTsKu6siJJkiRN2oy/WbPq\nIooeop9Q9A+OUH17IyKOA7ZThPAR4NvVx68a6xNJkiRJE+GKuCRJklQCV8QlSZKkEhjEJUmSpBIY\nxCVJkqQSGMQlSZKkEhjED0FE/G9EvKfsOiRJkjR9GcSrJhmuR9h/PLIkSZI0aQbx/QzXkiRJahuD\neIOIOC4i9kXE0rqxcyLinjLrkiRJUncxiEuSJEklMIhLkiRJJTCIS5IkSSUwiD/aluqf8+vGlo41\nUZIkSTpUBvEGmfkw8EvgtRHRExFPBc4dY2qlvZVJkiSpmxjED1TbvvA1wBnAZuBS4FM8emtDtzqU\nJEnSIauMjJgnASLiFuDyzLyy7FokSZLU/VwRByLiROApwA/LrkWSJEkzQ1/ZBZQtIq4BngW8KzN/\nVnY9kiRJmhlsTZEkSZJKYGuKJEmSVAKDuCRJklSCru8Rj4iLgRcAy4CtwHXAOzNzY92cs4G/B44B\nfga8ITNvqT43B/g8sAo4HrgwMz/U8G/cBxwN7Kkb/qPM/L+p+aokSZI03c2EFfE9wFnAYoow/Vjg\nqtqTEXES8AngdcAQ8GXg6xExWJ0yAvwAOA/4MWPvHz4CvDYzB+v+M4RLkiTpoLp+RTwz31P38HcR\n8c/Al+rGzgW+nJnfqj6+JCLOB14M/FtmDgMfA4iInU3+KU/alCRJ0oTNhBXxRqcBt9U9fhpwc8Oc\n2yhWzyfjsojYEBG3RsR5h1OgJEmSul/Xr4jXi4iXULSgPKdueJDiKPt6m4AFk/jUrwF+CgwDpwDX\nRASZecVhlCtJkqQuNmOCeES8DPgk8MLMrF8RfwRY2DB9EX1bKXEAAAL0SURBVHDPRD93Zt5Q9/Bb\nEfGPwKsAg7gkSZLGNCNaUyLirylC+BmZ+d2Gp28HVtfNrQC/Xx2XJEmSpkTXr4hHxBuBC4E/zczG\nXnCAK4FvRMTnKHZHeRMwC/hK3efop7gZsxeYVd3ScG9m7o6I5RTbGt4E7AZOAt4MvH/qvipJkiRN\nd11/xH1E7KMIyLvqhkcyc0HdnFcD7wMeA9wBvD4zb617/j5gOcU2hbXdUa7KzL+JiCcBVwMnVJ9f\nB1yemZ+Yoi9JkiRJXaDrg7gkSZLUiWZEj7gkSZLUaQzikiRJUgkM4pIkSVIJDOKSJElSCQzikiRJ\nUgkM4pIkSVIJDOKSJElSCQzikjTDRMRpEbGyYWxlRPwuIv6qrLokaaYxiEvSzPNN4Nn1A5l5T3Xs\ny6VUJEkzUF/ZBUiSSlFpHMjMn5dRiCTNVB5xL0kzTETsaxh6BrAF+AVwcmbeEBHPAS4FlgMLgXuA\nfwLOAE6leEf1c8BbMnNv9fMuAT4O/BmwGfh34F2ZuWvKvyhJmoZcEZekmeki4GvVvyfwmIbnV1AE\n9BcB24E3Ap8GLgdeCTwJ+ChwG/CZiOgBvg7sBM4CjqAI8puB90/lFyJJ05VBXJJmpjWZeWPtQUQc\nbN51mbkvIh4AXgh8NTO/CfxPRLyCYnX8M8DzgBOBZcD66sc+Fjgbg7gkjckgLkmaiHXVP49qGFtc\n/fuJFO0qv274uOEprkuSpi2DuCRpImqBuq9hbGHd33dS7LzizUeSNAEGcUmaeTYDi1r8Oe8E5gD9\n9S0vkqSDM4hL0sxzM3BuRNwFDAG3AnsO8XNVADLz2xHxI+CLEfEB4D6KHVfuyMyfHn7JktR9PNBH\nkmaeNwJbga8CHwKOq443tpSM12Iy0jDnTOC7FDuyXAtcABx9mLVKUtdyH3FJkiSpBK6IS5IkSSUw\niEuSJEklMIhLkiRJJTCIS5IkSSUwiEuSJEklMIhLkiRJJTCIS5IkSSUwiEuSJEklMIhLkiRJJfh/\nAhMwvpEFiosAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b49ed68>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"mean_polarities = df.groupby(['candidate', 'created_at']).influenced_polarity.mean()\n",
"plot = mean_polarities.unstack('candidate').resample('60min').plot()\n",
"plot.set_title('Influenced Polarity over Time by Candidate', family='Ubuntu')\n",
"plot.set_ylabel('influenced polarity', family='Ubuntu')\n",
"plot.set_xlabel('time', family='Ubuntu')\n",
"plot.figure.set_size_inches(12, 7)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since I only took the last 20,000 tweets for each candidate, I didn't receive as large a timespan from Clinton (a candidate with many, many tweeters) compared to Rand Paul. \n",
"\n",
"But we can still analyze the data in terms of hour-of-day. I'd like to know when tweeters in each language tweet each day, and I'm going to use percentages instead of raw number of tweets so I can compare across different languages easily.\n",
"\n",
"By the way, the times in the dataframe are in UTC."
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"{'de', 'en', 'es', 'fr', 'in', 'it', 'nl', 'pt'}"
]
},
"execution_count": 84,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"language_sizes = df.groupby('lang').size()\n",
"threshold = language_sizes.quantile(.75)\n",
"\n",
"top_languages_df = language_sizes[language_sizes > threshold]\n",
"top_languages = set(top_languages_df.index) - {'und'}\n",
"top_languages"
]
},
{
"cell_type": "code",
"execution_count": 85,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtsAAAHPCAYAAACC3xa4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcXGWV//FPVVelqzudhWwkZGExclRARTA4IIKIgogo\nojIzyKIoqICDgoCOLKOAoOMMBlFADJvwU0EcRBQCgmwqIiBIhEcDBrIvhKT37tp+fzz3dlc6vVR1\n19r1fb9e/erqW7fqnqq+XX3qqfOcJ5LNZhERERERkeKLVjoAEREREZHxSsm2iIiIiEiJKNkWERER\nESkRJdsiIiIiIiWiZFtEREREpESUbIuIiIiIlIiSbRGROmZm15vZSaO87Qlmdk6RQ5IhmNkHzOzi\nSschIoVRsi1SAWb2ZjN7b6XjGI/M7Dgze9XM3lnpWGrEicBu4Q9m9iszezbP234K+GBJopLBfAz/\n+5KAmR1qZo+bWauZbTGz0yodk8hAsUoHIFJKZvY74F3D7HKRc+7rZQon12KgAbhvuJ3M7AbghEGu\nWu2cm1+CuMaD24CngecrHchomdkKYMEgV93jnDuixIf/FDChgP0LWhnNzDLAJc658wuKSkJFW4nO\nzA4GHgAOdc49MOC6i4ALgJhzLlOsYxaTme0I/AJ4EB9rBnhxkP0+D1wKTAbSwGvAX4E7gOuccz3l\nilnqk5JtGe9Ox7/AAhwBfBU4FlgdbFtZiaAKtAH4yIBt+ucwBOdcL/C3SscxRlngXuAbA7a/VuoD\nO+c2FHiTyCgOo6WLR280z/doVfvvaT9gInCec264v/lZ+P8D78Yn29PxgzDfBE4zs/c551aVOlip\nX0q2ZVxzzj0XXjaz3YOLTzrnXjKzWcA6MzvXOfftYJ9dgJeAjzjn/i/YdhjwG2Bf59xTZrYD8G3g\nQ/jR6T8DXxpwrL2AbwEHAluApcDZzrnNOeEdEIzyATznnHvzEA+j1zn3+8GuMLMvA58A5gItwEPO\nucOC6z6MH+15I/5NxQ3A5c65dHB9BDgbOBnYFUgBrwA/dc5dFOyzAnjEOXd8zjF/BzQ45w7M2fYZ\n4Cz8aOw/gSuccz/Muf7XwO7ADKAJWI4f3bw1Z58mfHL5r8F+a4EzgDcH22eGz5+ZteATz3Occ/87\n4Dk5mJzROjN7F3A5MB//T7YXeAT4D+fcdqNgwX1cDByN/yc9BVgP3ARcED5/wX6nAGfiyzBWA9cF\nz3EmuP504DPAbGAq/ly4AzjLOdc52LFzbBzq9x7cdz7PaQK4EPh3YA7QGex3qXPujiHu9wbgPeEn\nJ2b2QeDrgAFdwL3OuX/PuckeZvYP/PO7CbgZ+Fru81QIM7sM/2nOdGAjsNg5961iPu6cv/PPOOd+\nlHO7bUbd84hlxOc32OcbwHH4v9G/Auc65x4Nrp8EfBc/GDAVeDmI6+EhnqJJZnYv8Pbg57vxrz8b\nzexa4KPOuWk5Mb4B/+bzGOfcL4Z63oewTWJvZm/BJ6gH4l8v7sX/Db4SXH8SsARY6Jx7Kdh2MNv+\nPe4GfA94E7Aj0AH8u3Nu6cCDm9lB+OduX6Ad+D98Yh2+joaP8zkzC2928DDP3SM5o/R3mtmPgMeA\nHwMHB8f8KP71fUegG//3+iXnXKuZ/R143jn3oZwYPwtcBcxyzr06xHGlzqlmW+pWMIL3NNuWmbw7\n+H5gzrZ34ROfp8ysAZ84vwOfCB4PNAP3mdlEADPbGXgYP/p8LPAV4H34ZC3Xs8A7g6/jGVrEzBrM\nLBZ+5Vz3AXzCcRL+n/XlQQwfAm7Hl6kcBfwQnxR8Mee2lwOX4D+G/QDwYfw/14Ny9sky+OhW3zYz\n+wK+LOZG/BuQXwLXBP+0Qofjn+sPBsd5EbjZzPbM2ecm4NPA/9L/KcQy4K4grtwa9wPxb3R+M0hs\nA+2GHwG7CDgU/3t7G/CTYW7zTvzr47HAYcAt+N/j53Ie9+nA94FfBY/7evxzfGnO/ewLzMP/ft8L\n/A/+zU0+pUvRYX7vkN9zejPwBeAHweM4HtgZ2JPhZYPHOBv4OT4B/BjwSeDOAfu+BnwZ/zv7MXAu\nOc/TKNyDPw/ej0/cLgveOIaK+biHPbfziCWf49yKP4/+E/8cbgLuNbN5wfWXBtsvwv8dfgv/fA8l\nATwO/Ftwn4fjf0fg/1ammtl+Ofu/G0gC9w9zn9ucZ8G5tk1+YGZz8a9rk4LH+TngLcDvgjfK+VoQ\nxHwr/nk9GXhm4E5mtncQ82b883Me/vn5VTBQkOtY+l9L/5JvIMFo+PeAdwVvSgCew79OHoE/l4+h\n/+/1LuBgM4vn3M27gSeUaMtwNLIt9e7XwBfMLBqMeLwXeBV4T84+78WP4ID/B78PsAfwj2DbMvwo\n2ZHAT/Ev1K34EdpUsE8UuN7MZuV8TN863Mhljrn4f5Z9zOyjOSOT65xzvxpwm/8CfoZPWCP4msY3\n4v+x/Xcwsvcl4OJwFDu4300U8NFx8ObjQuAKfJIQHmu/4Fi35+z+vHPukeB2j+PLYz6OH5XaH/9P\n7Tjn3P8b5Dj/wJfS/DTYdDDwsnPuhXxjBR4IRtseM7NpwP+Y2W7hCNwgNubUsT5oZofj/6l/L0gu\nLgF+5JwLu3HcGyQB55vZ93I+lu7IGbV72Mz+Jbifs4OkJvd1uDc4DyP40dLcEWTM7A3Oub/nbBrs\nOT0W/5y+A/+cDhy9bc/juQqTmRlBfL92zt09xL6rw0+BgAdyn6c8jrMd59zvcn58IBhZPxg/qhkq\n1ePOO5Z8jmNmb8W/ITiC/mT3UfwnJcfh3/DOxo+aLwlKoEaywTl3Qc4x1gJ3mNkh+DfXbfi/lceD\nXQ4Gfu+caxvmPu8dYnvua8GF+E+F3u+caw+O/Tjg8J/ufDOP2HPdP+D5Hehy/Gvs0c658M3fP4CH\n8K+tua8TTw7zdzySPwTf3wS8ELymhK8rvzOzPQhGvfGj3F/Ev2kP3+gfhH+zJTIkjWxLvfs//EjN\nAWYWxb+IfhV4s5nNDkpN3oYf/YX+j26X4f/x9OIT7Sy+FCPcZz7+I+Vwn+uDffq6PhRgA36ENPfr\ngaF2DkZd3oz/h5TMieEk/KhbGGMUPyo7FrsBO+BHgHKPdTD9z8d2go+BNwE7BZsOCL5v91Fy4MfA\nB8ysOfg595/daLjg+07D7rX9bcL998CfNwPjvQefnC7K2TZwFM7hEyyAr+HPk/DrEzn7/Zrtf+9D\njnjmPKdzgk3hc/rLYR7TsILSqOuAq8zsp0FJ1Yg3o7DndRtm9h9m9oKZ9ZjZa8BC+uddDBZj0R93\nnrHkc5zw9eLX9P9ttOE/jQr/Pi7Dj1Y/b2bnBZ8mDGfg+fRgeCznXDf+De7Hg/ij+JHXkf5WPs/2\n59oPBxxrf+CPYaIN4Jz7J/B34F9GuP/R2B/4bZhoB8d7BF92UorjAWBm7zOz35tZm5l14d8UTQ6O\n/xj+9f5fg333wpeajeW1SOqARralrjnnnjSzl/H1uWl8acKP8LXMH8TPbu/GJ1EEl7P4MobuAXe3\nJmef5/DJ7UDhqGQhE4+SzrmnCtg/g098b2Ho0cUw9pFG0nrxicFQwvv5Jv0fZYdGmsTZRX/Xi/Cf\n+lBdD64HzgeONbP7gb2Dn0erK/heSNeNweId6vc43CS2LvzH9lHgGrZN1v6Zc3lzgb/3gTGGH3Wn\nhtg3L865U8zsKuAU/IjuH4HDhhmFzY2hIGYWlhF9G/+8RIGr87hpoY87jH3IczuPWPI5Tvj38VFg\nxYDrNkHfa9BC/Mj8F/CfjHyigPrq8P94eC5eC3zSzN4dxDaDkd9U/33guRaMmOcjQv/5PuLzWqDB\n/r5yj1cMYeK+zMzeiH+u7sH/T2gH/gNfNhj6If53dBr+U4v1zrk/FTEeGYeUbIv4pPREgpFe51zG\nzO7E1wlmgTucc2Fy9hz+hX6mc25g7So5+3waWOucG+of1lb8JK98FNQRwDmXNrMX8PWUT+eODA2I\nMYsf9Rqup/JK/MerQ1mFfyxvcs79ZyFxDhD+oz+MQWqpnXOrzOz/4etEW/B1nEN99F0Oy/D/iA/D\nf7QcOhz/pu2JnG1D/v6C82Owc6QYXSD+Gnx/D9uW8wxm4Kec2xzfOfcMvmvDXfhR2kOD70MZbfx7\nA23OuXPDDWZWaHeUfB73evwb0j3GEEs+x1kWfJ8/1IRUgGCy7PXmJ6c+iv90Ld9k+wPB98eD+3rc\nzB7B/62sBP46QqeOfP0R+JCZteSUkewKvB7/Ggr93Z32oP+xj+V4h5pZJKeM5ED8HJk/DHvLPAV1\n2qfjJ5Y7M/sYPi+6wDn3l2Cfw9k22b4a//s5AZ9s/6wYscj4pmRbxHfp+CrwWfxoBvh/Hl/CJw3v\ny9n3LvwEnB+Z2evwiWoTsJNz7ppgn+/ik/f7zOzb+A4fs/C1u+EI0x+Bo8zsLHyiuXvO7QcaaRRn\nsOsvxtc332lmN+KT04XAH5xzzznn/mlmtwKXBHXDz+FLT/bATz4L/RhYYmaL8aN76eCxhKNyWTO7\nBPiWmS3BT55rw08Qu905t4ah9cXtnLs/SBCuMbMFQQwt+PrUx4Ldvo1/vmcDPxltt4sCDPm8O+c6\nzex84DtmtgX/Uf4++PPoirA7w0j3M8KxZ9ngC/M87pxLDrJ94LF+jU9KfmBmM/Cj5ovoL2EJrQIO\nM7NbnHNhb/IIQPC7OBZ/zmfwyUUWX2M82DGH25ZrVzM7dMC2F/FvUj5nvhvMb/HnWxj7cAp63MEb\n0v8HnGi+w8TTbD8aO1Is+RznKfPdUy41s6n4v/so/s3pdwDM7FP4N27r8R0wdmaQCYM5ms3sCPwn\nR2/Hn3NLnXMP5ezzLXyJ3Eb8pNxiuAhfnvJrM/sffOnLBfguPFcE+/weX2bxzWA+xypGX/JxLv75\nuiN4bZmJ70zyp9zOMwV6l5ml8V1MDsR3ClpFf/nWU/jf84Vmdg3+9/L63Dtwzm013/Xlq/hyqVNH\nGYvUkbLXbJufXf9tM9tgfsWn281s+jD7zzKzG81sk5ltNbOnzWzOUPuLjGC7ETfn3HL8xKItBKOl\nwUjec8A/nHMP5uybwo9k/QyfjN+NH+l4V84+L+HrOV/Efwz9a/xkutwX7bB7x4X4BPWknHrkgfEO\nN0o46PXOudvwHTJm4rt83IkfwZmZs9un8N00zsEvBPMhfKKcez83BI/zQ/i6xLuC4z2cs89/40fy\nww4fP8d3K9hhmLjD2HO9D1/2cgb+ObsKP7oYHue5YPs8/Eflhdz3SF0nBrtusPvIrR/9Lv5j/w/h\nn9+T8b/nc4a6zTDbBjv+e/HPc+7XQ2z7OxzsdmF8Wfybx6X4kpuf4j/J6GHbCbdn4Nsb/scg8c3A\nd724E/+7fyfwOefcE4PsW8jj+/cgrtyv44Pz7Rv45Ode/O97AiMvUDSax30a/m/jfHwyfSvwJMGI\n9UixFHCcY/B/7yfi37BeD7w/KCMC/wnUYvwEyu/hE8yhErjH8cnhTUE8p+BLuI7M3SmYzPoC/m/w\nhiHuKzTU72rg+b4KPxmwC/8m/Gr86PXBwcg8wRvg9+EnNv4QP7fkC/jzdu2A+x6Wc+5J/CdHM/Gv\nt5fjyzsGLuqUz6co6/GfwD2Af2N8HfBWfIeTtzrnVgfHfBFfo70b/hOr+/Gv5Y8PuL//xf9tPO2c\n+3Mex5c6F8lmy9uz3sz+E//xy2H40bYlQLMbZFU08/1Jn8C/W/6Kc25zUFO1aoSZ1SIyCsHoctI5\nd0ilYxlMMKK2t3Pu3SPuLNsx357yVeAE51zdfPxdrsddTc+vmd0BbHXOfbKScYxHZtaIH8H/qnPu\nxkrHI9WvEmUkp+CXyF4BYGbnAMvNbL5zbuBqfifiZwF/PvzIOOdjThEpvmJPPhqzYMZ/FN/h5FT6\n23DJCMzsbPxI6Ab8R+efxQ9yDNX1ZVwo1+OutufXzPbBl/t8BP938tZKxDFeBTXjSfyI+Fq2XztB\nZFBlTbaDmrX5+I/qAP+Ru5m14j9KG5hsvxu/GtdNQcupjcA1zrkrEJFSyKcEoNwuwk8C+xt+dbwn\nht9dchyEb+M2HV9/+hi+T/KWikZVeuV63NX2/F6L76f/FHD4gLkDMgbmFyEKy+juAz4wxORzke2U\ntYzEzObj+8Tu6px7OWf7CvzHMbcO2P9+4BB8LeEP8An5Pfhllkc7QUJEREREpCzKXUYS1llPGbB9\nKn7FvcH2X+WcuzL4+Ukz+zF+QtKIyfaTTz6pd50iIiIiUhb77LPPdqWYZU22nXNbzOwVfIusZwGC\n9mmTGbzX79PBvrkiDL3wxXYWLlxIY2Pj6AKWutfT08Py5ct1Hsmo6RySYtB5JGOlc6j0li0bvL18\nJSZIXguca2YPAq/h+4HeM0Rt2Q3Bvp/Hr7S2J75l1Gn5HqyxsZFEIjHmoKW+6TySsdI5JMWg80jG\nSudQ+ZW9zzZwGX6SwRP4CZFZgobyZnacmfW19AsS8CPwPXy34nsBXxj0EBYRERERqWplH9l2zmWA\nLwdfA6+7hf5lX8NtD+EXyxARERERqSmVGNkWEREREakLSrZFREREREpEybaIiIiISIko2RYRERER\nKREl2yIiIiIiJaJkW0RERESkRJRsi4iIiIiUiJJtEREREZESUbItIiIiIuPSZz7zGX70ox9VNIay\nryApIiIiIlIOP/zhDysdgpJtERERERm7bDJJetP6shyrYcaOROLxshxrrJRsi4iIiMiYZJNJ1p56\nDOn1a8pyvIYdd2LONT8fMeE+/vjj2X///fngBz/IoYceyuWXX861117L2rVr2XvvvbnsssuYOXNm\nSWNVzXaN29K5BrfuATLZdKVDEREREak6kUiESCQCwG9+8xtuueUWHn74YTo7O1m8eHHJj6+R7Rp3\n97NfZ0PbPzgyEuP1O76r0uGIiIhIHYrE48y55udVW0aSzWYBOP3005k6dSoARx55JLfffntJ4sul\nZLvGvda5EoBN7SuUbIuIiEjFROJxYnPmVTqMYeWWjDQ1NdHR0VHyY6qMpIal0j0k090AtHdvqHA0\nIiIiIjKQku0a1pXc2ne5rWdjBSMRERERkcEo2a5hnb1b+i63aWRbREREZFC5kySH21YKqtmuYd3J\n1r7Lbd0byWazZTlpRERERGrBzTff3Hf5+eef3+a6o48+mqOPPrrkMWhku4bljmwn0130pEpf5C8i\nIiIi+VOyXcO6erdu87MmSYqIiIhUFyXbNSx3giT4UhIRERERqR5KtmtYV04ZCUBbj0a2RURERKqJ\nku0aNnBku717U4UiEREREZHBKNmuYQNrttX+T0RERKS6KNmuYeHIdjTiOzhqYRsRERGR6qJku4aF\nrf9mtOwCaGRbREREpNoo2a5RmWya7mQbALMmvR7oX9hGRERERKqDku0a5RNtn1jPnLwQgHSmd5tV\nJUVERESkspRs16jctn/hyDaolERERESkmsQqHYCMTlfOCPaMll2JRhrIZNO0dW9k1uTXD3NLERER\nkeJLpjOsb+0uy7F2nJwg3pDfmHFXVxeLFy9m6dKltLe3s9dee3HBBRewYMECjj/+ePbcc09Wr17N\no48+yvTp0znvvPN4z3veU7RYlWzXqHBkOxZtZEKsmZbGGbR2r9fCNiIiIlJ2yXSGj/7oj6zZWp5k\ne6cpCW4/+R15Jdxf+9rX6Ojo4LbbbmPy5Mn84Ac/4NRTT+Wuu+4C4Be/+AVXX301ixcv5oYbbuC8\n887j0UcfpbGxsSixqoykRnUGPbabJkwBoCUxE9CS7SIiIiKhzZs3c/fdd3PhhRcybdo0YrEYp512\nGhs3buSZZ54B4AMf+ABvfetbAfj4xz9OW1sbK1asKFoMGtmuUd1Bj+2muE+2JyVmAdCuZFtERETK\nLN4Q5faT31F1ZSSrVq0C4KijjtpmezqdZt26dQDMnDmzb3tzczMAHR0dxQpVyXatCntsN02YCsAk\njWyLiIhIBcUboszbobnSYWxj7ty5ACxdupQddthhu+t/8pOflDwGlZHUqK6+ke3JALQ0Bsm2VpEU\nERERAWD69OkceeSRXHTRRaxfvx6A1tZW7r//fjo7OwFKvkaJku0a1dVXs73tyHZ790ay2UzF4hIR\nERGpJhdffDG77rorJ5xwAm9729s46qijuOeee4hEIgB930tFZSQ1KhzZbp6wbc12Jpuis3cLExun\nVSw2ERERkWqRSCQ488wzOfPMM7e77uabb95u2wsvvFDU42tku0aFrf8SfRMk+4v7tbCNiIiISHVQ\nsl2Dstlszsi2LyNpik+lIRoHNElSREREpFoo2a5ByXQX6UwS6G/9F4lEciZJamRbREREpBoo2a5B\nYds/6F/UBradJCkiIiIiladkuwZ1J1v7Locj29A/SVJlJCIiIiLVQcl2DQpHtiNEScQn9W3XwjYi\nIiIi1UXJdg3qSoadSCYTifT/ClsagyXbtbCNiIiISFVQsl2Dunp9GUluvTbApMQMANp7NpHJpsse\nl4iIiIhsS8l2DQpHtsO2f6GwZjubzdDRs7nscYmIiIjItpRs16BwqfZEfPI227WwjYiIiEh1UbJd\ng8Jke+DIdmNsErFoAtAkSREREZFqEKt0AFK4sIwkt+0f+IVtJiVm8lrnSto1si0iIiJllE5naW9L\nluVYLZPiNDREynKssVKyXYM6g5HtgRMkgb5ku00dSURERKRM0uksP71hOW2t5Um2J02Oc+xJC/NK\nuLu6uli8eDFLly6lvb2dvfbaiwsuuIAFCxZw9913c9VVV7Fu3Tqampo48MADueyyy4oaq5LtGtSd\nDJLt+NTtrtPCNiIiIiL9vva1r9HR0cFtt93G5MmT+cEPfsCpp57KbbfdxjnnnMOSJUvYb7/96O7u\nZtmyZUU/vpLtGpPOJOlJdQCDj2y39C1sozISERERKY+GhgjHnrSw6spINm/ezN13382DDz7ItGnT\nADjttNO48cYbeeGFF4jH47z44ouYGVOnTmWfffYpeqxKtmtMODkShigjafTJdnv3prLFJCIiItLQ\nEGHK1AmVDmMbq1atAuCoo47aZns6nWbDhg1ce+21XH/99VxxxRXMmzePT33qUxx55JFFjUHJdo3p\nSvYn283xwWq2fRlJR+9m0pkkDdF42WITERERqSZz584FYOnSpeywww6D7rNo0SKy2Sy//e1vOeOM\nM3jLW97C/PnzixaDWv/VmNyR7cQwZSSQpb3n1TJFJSIiIlJ9pk+fzpFHHslFF13E+vXrAWhtbeW+\n++5jzZo13HvvvbS1tRGJRGhpaSESidDQ0FDUGMo+sm1mDcBlwIlAAlgKnOqc2y4zNLODgQeAjpzN\nzzjn3lmGUKtS2PZvQkMzsej2H9UMXNhmStPsssUmIiIiUm0uvvhirr76ak444QQ2btzI5MmT2Xff\nfXnzm9/Mrbfeyvnnn08qlWLOnDlcdtll7LTTTkU9fiXKSM4DjgIWAZuBJcDNwBFD7J92zk0qU2xV\nr6u3FRi8XhugMTaRCbGJ9KY6aFdHEhEREalziUSCM888kzPPPHO762688caSH78SZSSnAJc551Y4\n51qBc4DDzax4xTHjWGe4oM2E7dv+hcJJkupIIiIiIlJZZR3ZNrOpwHzgyXCbc+4lM2sF3gKsHORm\nDWb2ChAPbvdV59yz+R6zp6dnbEFXmfYuX23T2NBCd3f3oPs0T5jOqx0r2NKxbsh9JD/h+TPeziMp\nH51DUgw6j2SsdA5VTrnLSMJykK0Dtm8BJg+y//P4JHxZcNtzgQfMbC/n3Np8Drh8+fJRhlqd1rf7\nFjbd7dkhG68nO31h/9pNL7Gsp/jN2evReDuPpPx0Dkkx6DySsdI5VH7lTrbbgu8DC46nAq0Dd3bO\nrQfWBz9uBb5qZscA78fXeo9o4cKFNDY2ji7aKrT82Sz0wpxZO7PHrnsMuk/XK8+y7uU/EZnQwx57\nDL6P5Kenp4fly5ePu/NIykfnkBSDziMZK51DpTfUIGhZk23n3JagJGQf4FkAM3sdflQ739KQbCHH\nbGxsJJFIFBRnNetJ+fcrLU3ThnxcO7TMAaCjd9O4euyVNN7OIyk/nUNSDDqPZKx0DpVfJbqRXAuc\na2YPAq8B3wLucc69MnBHM3s3vo77JaAZOBuYBdxbvnCrS7ioTXN8uAmSs/r2TaV7iDXoHayIiIhI\nJVSiG8llwF3AE/hEOgt8AsDMjjOztpx93wLcjy8xeRHfLvC9zrnVZY24SmSzmb5ke6jWf5C7sA20\n92jZdhEREZFKKfvItnMuA3w5+Bp43S3ALTk/XwFcUb7oqltPqp1sNgNA0yBLtYcGLmwztXluyWMT\nERERke1pufYakrtU+3B9tuMNCRJx3/ilTQvbiIiIiGznyiuv5JOf/GTJj6Nku4Z0JnOT7aFHtqG/\nblvJtoiIiEjlKNmuIV29fvXIaCTGhIbmYfcN67a1iqSIiIhI5VSiG4mMUlhG0jRhCpFIZNh9JyX8\nyHZ7j0a2RUREpPRSqRRbtw5ct7A0pkyZQiw2chp7yCGHcOyxx/KHP/yBZ555hnnz5vH1r3+dvffe\nuwxRekq2a0g+bf9CkzSyLSIiImWSSqX4zne+w2uvvVaW4+2www6cddZZeSXcd9xxB9///vfZdddd\nufzyyznvvPO4997ydZFWGUkNCctIEiPUa0Nusq2RbREREalfxx57LK973euIRqN89KMf5eWXX6a9\nvb1sx9fIdg3pSvoV7ZuHafsXCidI9qTa6U11MSHWVNLYREREpH7FYjHOOuusqisjAZg5s78lclOT\nz4c6OjpKEtdglGzXkHBke7i2f6GWAb22p7fsXLK4RERERGKxGNOnT690GFVHZSQ1pDOcIBmfPOK+\nLYkZfZc1SVJERESkMpRs15DuvqXaRx7ZjkUn0Bzsp7ptERERES/s6BaJREbs7lYMKiOpIZ05rf/y\n0dI4i87eLUq2RUREpC498MAD2/w8b948nn/+eQBOP/30ssSgke0akUx3k8p0A9CUxwRJ6O9I0q72\nfyIiIiIVoWS7RoQL2kB+ZSTQv7BNm2q2RURERCpCyXaNCBe0AWjOs4xEC9uIiIiIVJaS7RoRtv0D\nSMRG7kY/UFScAAAgAElEQVQC2y5sk81mSxKXiIiIiAxNyXaNCEe2E/FJRKMNed2mJSgjSaa76EmV\nr3m7iIiIiHhKtmtEV1+P7fzqtQEmNfYvbKNJkiIiIiLlp2S7RnT2rR6ZX702wMTG6USCX7Ha/4mI\niIiUn5LtGhGWkeTb9g+gIRqjuXEHQB1JRERERCpByXaN6CsjybPtXyhs/9eukW0RERGRslOyXSP6\nR7bz60QSCuu21f5PRERE6tGWLVs4+eST2XfffTnmmGPKfnwt114jwtZ/zQWPbAfJtspIREREpA79\n5Cc/oauriz/96U9Eo+UfZ1ayXSP6RrYLmCAJOatIamRbRERESiibSUHPq+U5WON0ItH80tiVK1ey\n2267DZpo9/b2MmHChGJHtw0l2zUgk0nTnWwDCpsgCdAyYGGbSCRS9PhERESkvmUzKdJPnAs9m8pz\nwMYZNLz98hET7s9+9rM8+uijANx9993sueeePPXUU1x66aUsXryYLVu28OSTT5Y0VNVs14DcpdpH\nO0EynemlO9la1LhEREREqtnVV1/NBz/4QY4++miefvppzjjjDNLpNA8//DB33nknv//970seg0a2\na0BXTpJc6Mh27sI2bd0bCi5DERERERlJJBqj4e2XV2UZSTabJZvN9l0G+PKXv0xLS0vJwsulZLsG\nhJMjofCa7ebGHYhGGshk07R1b2TW5NcXOzwRERERn/w27VjpMLYzsIQ2Go0ye/bssh1fZSQ1ICwj\niUUTxBsSBd02GmmgpXEGAG09miQpIiIi9Sc34S73/DUl2zUgXNCmeZQlIOEkyfbuMk1aEBEREakS\nuWUklaBkuwaEZSSJAuu1Q1rYRkREROpVJBKp6Mi2arZrQFhGMtaR7TYt2S4iIiJ15pvf/Gbf5f32\n24/nnnuurMfXyHYNCMtICm37F+pb2EarSIqIiIiUlZLtGtAZrh4Znzyq20/qq9neSDabKVpcIiIi\nIjI8Jds1IKzZHuvIdiabojOnjaCIiIiIlJaS7RrQ1TeyPcoJkoltF7YRERERkfJQsl3lstlsTuu/\n0Y1sN8Wn0hCNA5okKSIiIlJOSrarXG+qg0w2BUBilN1IIpEILWH7Py1sIyIiIlI2SrarXFeyte9y\n8yjLSGDbSZIiIiIiUh5KtqtcV86ExtFOkAT12hYRERGpBCXbVa4z6ZPtSCRKY2ziqO+nfxVJJdsi\nIiIi5aJku8p19/oykqb4FCKR0f+6wvZ/7VrYRkRERIQrr7yST37ykyU/jpLtKheObI+lhARyarZ7\nNpHJpsccl4iIiIiMLFbpAGR4fUu1j3L1yFA4sp3NZujo2bxN720RERGRsUpnkmUrV52UmNnX1ng4\nhxxyCMcccwyPPfYYzz//PLvtthsXXXQRK1eu5JprriGbzbL33nsTiUT45S9/ybx584oeq5LtKte3\noE2RRrbBL2yjZFtERESKJZ1JcsNjJ9Hava4sx5ucmM1JB9yQV8L905/+lKuvvprdd9+dJUuWcMop\np3Dffffx2c9+lqeeeoolS5aUNFaVkVS5sBvJWNr+ATTGJhGLJgBNkhQREZH68dGPfpQ3velNxGIx\nTjnlFBKJBL/73e8Av3hgqWlku8qFZSSjXdAmFIlEmJSYyWudK2nXku0iIiJSRA3ROCcdcEPVlZEA\nzJ07d5uf58yZw7p15RmBByXbVS8sI2mOj62MBOhLttvUkURERESKrCEaZ2rzTpUOYzurVq3qu5zN\nZlm7di1z5sxhxYoVZTm+ykiqXN8EyTGObIMWthEREZH6c8cdd/C3v/2NZDLJddddR3d3NwcddBAz\nZ85kzZo1JJPJkh5fyXYVS2V66U13Ar7P9liFC9toyXYRERGpFx//+Me5+OKLWbRoEffccw/XXHMN\nLS0tHH744cyZM4d3vvOdLFq0iNWrV5fk+CojqWLdwag2FGdkO2z/p5FtERERqRcLFizgtNNO2277\n5MmTueGGG0p+fI1sV7HOZG6yXZyabYCO3s2kM6X9yERERERElGxXtbDtH4x9URuAlmBkG7K097w6\n5vsTERERkeGpjKSKdfW2AtAYm5h3e5vhDFzYZkrT7DHfp4iIiEi1euCBByodgka2q1lX0o9sNxWh\n7R/4pH1CbCKgSZIiIiIi5aBku4r1t/0bewlJKOxI0qaFbURERERKLu9k28xmjrxXXvfTYGbfNrMN\nZtZqZreb2fQ8bvc5M8uY2X8WI45aEC5oU6yRbegvJdHCNiIiIiKlV0jN9noz+yvwAPBb4CHnXNso\njnkecBSwCNgMLAFuBo4Y6gZmtjPwJeBZoPSL2FeJzmCCZDHa/oVa1P5PREREpGwKKSM5FLgdeCPw\nY2CTmf3GzD5lZpMKuJ9TgMuccyucc63AOcDhZjZ/mNv8CPgq8FoBx6l5xVw9MjSpcQYA7SojERER\nESm5vJNt59wDzrlvOOcOB2YAh+FHmr8OrDOzJWa2cLj7MLOpwHzgyZz7fQloBd4yxG1OBdqcc7fl\nG+t4UZoyknBke1PR7lNEREREBjfa1n9xYEd8gjwbeBDoAp40s48555YOcbtwBHzrgO1bgO1mAZrZ\nAuA/gf1GGSc9PT2jvWnFhWUksUgz3d3dRbnPxqgfJe9KbqG9s5VYdEJR7ne8Cs+fWj6PpLJ0Dkkx\n6DySsarXc+i0005j0aJFnHjiiRWLIe9k28x2B94NfAB4D5AGbgLOdM69EOzzDPDfwJuHuJuwxntg\nXcRU/Oj2QNcBFzvn1gY/R4KvvC1fvryQ3atGNpuhO+mfkg1rtpDetKwo99uZ7l8o5y/P/YGmhhlF\nud/xrlbPI6keOoekGHQeyVjV2zn0+c9/HoBly5Zx3HHHceGFF7L77ruXNYZCRrZfADqB+/F1178c\nZILk74HFQ92Bc26Lmb0C7IMvQcHMXocf1X52kJscCrzNzC4Jfp4C7Gtm73POHZRP0AsXLqSxsTGf\nXatKd7KVR/7o54Lawr3YcZIV5X6T6dfx59/7y3MWTGXu1D2Kcr/jVU9PD8uXL6/Z80gqT+eQFIPO\nIxmrspxDmQyR7vKMnGcTjRAtvIP1Lrvswh57lCb3WbZs8IHRQpLtQ4DfO+d6h9lnK3D+CPdzLXCu\nmT2In/D4LeAe59wrg+w7L+dyBLgNeBj4Tr5BNzY2kkgk8t29anSm+ycwTm2ZVbTHkCBBIj6J7mQb\nPZmtNfncVEKtnkdSPXQOSTHoPJKxKtk5lMnAQ49CV1fx73swTU1w0DtHTLiPP/549t9/f+655x4A\nPve5zxGJRDjyyCP5xje+UY5IC0q2TwBagF/lbjSz44FPO+cOcs6tBL49wv1cBuwAPAE0AkuBTwT3\ndRxwtXNuEoBzbs2AY/UArc65cd+3LqzXBmiKF68bCcCkxll0J9vU/k9ERETGvUgkwp133skb3vAG\nlixZwtve9rayHr+QZPsY4CeDbF8LvD3fO3HOZYAvB18Dr7sFuGWY27473+PUurBeuyEaJ97QVNT7\nbknMZGP7i1pFUkRERIojGvUjzV3FaegwoqbEqMpIKqGQZDvCIB1DgJlAqjjhSKhvQZv4VCKRguaE\njihs/9euVSRFRESkWKJRmNhc6SiqTiFvCX4D/KeZzQk3BJfPBe4rdmD1rhQL2oQmJXwHEo1si4iI\nSL0o9uBlvgpJtk8HmoB/mtmzZvYX4CX8aPfppQiunvUvaFP8ZLulUUu2i4iISH2ZMWMGK1asKPtx\nC1lBciOwF3Aq8Ah+IZvTgTfm9MGWIukKykiaJxRv9cjQpMRMAHpS7fSmyjRrWERERKSCvvjFL7J4\n8WIWLVrEhRdeWLbjFrSCpHMuCdwYfEkJhSPbifhgZfJjE9Zsg6/bnhZbUPRjiIiIiFTazTff3Hf5\nIx/5CB/5yEfKHkNBybaZzQWOwC/RHs+9zjl3QRHjqnthzXYpRrZbEv2rRrZ1b2DaRCXbIiIiIqVQ\nyHLtxwI347uSbALC3i4RIAso2S6ivprtEkyQjEUn0DxhKp29W1S3LSIiIlJChYxsfwO4AzjFOdda\nongEyGazOa3/ip9sg58kqWRbREREpLQK6UayM3CdEu3SS2W6SWd6AWgqQRkJ9E+SbFf7PxEREZGS\nKSTZVpJdJp1BvTaUbmQ7nCTZpoVtREREREqmkDKS1cBPzaxzkOuyzjnNsiuSsO0flKZmG/pHtrWw\njYiIiEjpFJJsXwLsMcR12SLEIoFwciRESMQnleQYLY1hsr2RbDZbsVWVRERERMazvJNt59xtwG0l\njEUCfUu1xycTjTSU5BjhyHYy3UVPqoNEvKUkxxERERGpZ4XUbGNmu5nZV83sajNbkLO9ufih1a+w\njKRUJSSw/cI2IiIiIvVg3bp1vOENb2DNmjVlOV7eybaZfQB4ATgROAWYEWw/B7inJNHVqa6kn4ta\nqsmRABMbp+NbpKtuW0RERKRUChnZvhS4mu3rtp8bZJuMQf/Idmna/gE0RGNMbJwGoF7bIiIiIiVS\nyATJ1wNnD7J9AtBUnHAEoDPZX7NdSpMSs+joeZV2JdsiIiIyRtlkkvSm9WU5VsOMHYnE43ntu3Hj\nRs4//3z+/Oc/M336dD796U9vc/3PfvYzbr75ZtauXcv8+fM5++yzOeCAA4oWayHJ9t+B9wAPhBvM\nLAqcBDxbtIikf4JkCUe2ASY1zmQdz6uMRERERMYkm0yy9tRjSK8vTx10w447Meean+eVcJ999tlM\nnjyZ3/3ud3R3d3PGGWcQiUTIZrP87Gc/47rrruPKK6/EzHjooYc4/fTTufPOO1mwoDhdrQspIzkX\n+CJwZ/DzecAy4Ajga0WJRgDoSpZ+giTk9NrWBEkREREZh9avX8/jjz/OOeecQ0tLCzNmzOCMM84g\nm/Vdq2+66SY+//nPY2YAHHTQQey3337cfffdRYuhkNZ/95rZ/sBZ+ImSC4EngI85554rWkSS0/qv\n1Ml2sIqkRrZFRERkDCLxOHOu+XnVlZGsW7cOgLlz5/Zty728atUqvv71r3PJJZf0bUun08yZM6do\nsRZSRoJz7kng34t2dNlOOpOiJ9UOQHOJy0haElrYRkRERIojEo8TmzOv0mFsY8cddwRg9erVzJ8/\nv+9yaO7cuXzhC1/gsMMOK1kMeSfbZnbIMFevdc49X4R46l530PYPyjCyHawimc700p1sLXnZioiI\niEg5zZ49m0WLFvHtb3+bSy+9lO7ubq666qq+60866SSuvPJKdt55Z8yMnp4ennvuOaZNm8Zuu+1W\nlBgKGdm+f5jrHgMOHGMsQn/bPyhfzTb4UhIl2yIiIjLefOc73+H888/n4IMPZsaMGZx88sk89dRT\nRCIRPvaxjxGPx/nKV77CqlWriMVi7LHHHpx77rlFO34hyfZQ6f3B+B7cUgRdQds/gKZ4actImhun\nEY00kMmmaevZyCxeX9LjiYiIiJTbzJkzufrqq7fZ9rGPfazv8oc//GE+/OEPl+z4hUyQXDHYdjNb\nAUwvTjjSGUyOjDc0EWuYUNJjRSMNTGycTlv3BvXaFhERESmBQlr/DeW9wKtFuB8hp+1fieu1Q/0d\nSZRsi4iIiBRbIRMkbwayOZuagN2BvfDtAKUIunr9BMly1U+HkyTV/k9ERESk+Aqp2Z6PT7bD/nBJ\n4Gnga865u4odWL0KR7ZL3fYvlNv+T0RERESKq5Ca7YNLGIcEwgVtEvHJZTleXxmJVpEUERERKbpC\nykhmAHllgM65l0YdUZ0Lu5GUa2Q7bP/X3r2RbDZDJFKMMn4RERERgcLKSG4FDs1jvyzQMLpwJOyz\nXe4Jkplsis7eLUxsnFaW44qIiIjUg0KS7TcB5+MXsMl1NpAAvkF/PbeMUtj6r1wTJFsaZ/Rdbuve\noGRbREREpIgKSbZnAA875x7J3Whm04DvOuceKmpkdSibzdIdlJGUekGbUPOEqTRE4qSzSdq6NzJ7\nyhvKclwRERGRelBIge4WwAbZHgM0HFoEPakOMtk0UL6R7UgkSkvCj263a5KkiIiISFEVkmzfClxk\nZvuHG8xsT+C/gHuKHVg9Cuu1oXw126CFbURERERKpZAykvPxC9g8amYdQAqYAvwFOLUEsdWdsBMJ\nQFOZupFAbq9tLWwjIiIiUkyF9NnuAN5rZu8G9gV6geecc78tVXD1JuyxHY000BibWLbj9q8iqZFt\nERERkWIqZGQbAOfcg8CDJYil7oWrRybiU4hEytfYJSwjUc22iIiISHEVsqjNBOA84BP4pdsPcM49\nZWb7Ajs65+4uUYx1IxzZbi7T5MhQ38I2PZvIZNNEI2qTLiIiIlIMhUyQ/CbwBeAmoDFn+5uB/y5m\nUPUqrNkuZ7029I9sZ7MZOno2l/XYIiIiIuNZIcn2x/EL2Fw2YPsrwM5Fi6iOdZZ59cjQwIVtRERE\nRKQ4Ckm2pwCvDrJ9F6CzKNHUue5kK1C+HtuhRHwysaj/sEKTJEVERESKp5Bk+zfAucDM4OdI0HP7\nfODXxQ6sHvWPbJe3jCQSifTXbWtkW0RERKRoCkm2zwASwMrg50eAR4E1wFlFjqsuVWqCJEBLuLBN\nz6ayH1tERERkvCqkz/YGM1sEHAq8FegB/uqce6BUwdWbcIJkosw129DfkUQ12yIiIiLFU0jrv4uA\n/3POLQWWliyiOpVK95JMdwGVGdkOF7ZpV822iIiISNEUUkbyZWDHUgVS78IFbaD8rf+gv/2fJkiK\niIiIFE8hyXYPoNVOSiSs14byt/6D/jKSjt7NpDPJsh9fREREZDwqZLn2FcB3zew8IFxLPBtczjrn\n3lXk2OpKWK8NvhVfuYUTJCFLe8+rTGmaXfYYRERqQTabJRKJjLyjiAiFjWxfATwGvAS8GHzlXpYx\nCNv+NcYm0RAt5D1QcYQj26BJkiIiQ+l+5s+s+df30PrzmysdiojUiGGzOjM7HHjKObcBeAj4iXOu\ntyyR1Zn+pdrLP6oN0BibyISGZnrTnZokKSIyhM5HlpJpb6Xjt3cx+ZjjKx2OiNSAkUa2bwb2Di7/\nE9i3tOHUr7Bmu9wL2uRqUfs/EZFhpdb4pSZSq1eSTacqHI2I1IKRku0JZYlC6ArKSCrR9i/U15Gk\nRyPbIiKDSa1+JbiQJLV+bWWDEZGaMFJx8JPAeWYWJuX7mllisB21uM3YdCVbgcp0Ign1L9muZFtE\nZKBMdxfpTev7fk6tWkF8p/kVjEhEasFIyfZpwK3A3cHPVwyxXxa1BRyTcGS7Ej22Q+HCNuq1LSKy\nvbCEJJRcuYKmRQdWKBoRqRXDJtvOueeBvc1sCrBDMQ5oZg3AZcCJQAK/GuWpzrlXB9n3QHyCv0sQ\n60rg+8657xcjlmrSP0GyCspIlGyLiGwnteaVbX9etaIygYhITcmrx5xzbiuwdcQd83MecBSwCNgM\nLMFPxDxikH1fAD7snFsJfcn3fWb2V+fcI0WKpyr0T5CsXLIdTpDsSm4hle4l1qCSfRGRUF+9diCp\nZFtE8lBIn+1iOQW4zDm3wjnXCpwDHG5m2xW+Oec25iTaUXy5Sg8wroZeM9l0f812FYxsA7RrkqSI\nyDaSYbId9f86NbItIvkoa7JtZlOB+fiJlwA4514CWoG3DHO7LUA3cC/waefcCyUOtay6k2349xGV\nbf2nhW1ERIYWlpE0vumtAGRat5LeuqWSIYlIDSj3UoWTgu8DS1K2AEOu5uKcm2pmceBY4Hoz+4dz\n7i/5HLCnp2dUgZbT1s7+xDaaTdDd3V2xWBpjk+hJtbG5bQ0zm99YsTiqRXj+1MJ5JNVJ59D4EY5s\nx972DnqeewqAzpcc8TcOOVZUNDqPZKx0DlXOkMl2UB/9+jzvZ7lz7uE89msLvg+slZiKH90eknMu\nCfzYzP4NOA7IK9levnx5PrtV1JbkS32XVyxfQ0NkU8ViiWVb6KGNl1YuI7VpdsXiqDa1cB5JddM5\nVNsinR3MbPWj2KviE5kycRLRjjZeeeKPdGfKN26l80jGSudQ+Q33CnEocH6e9/MEsN9IOznntpjZ\nK8A+wLMAZvY6/Kj2s3keK84IiXmuhQsX0tjYmO/uFfHipi08+zzEoo28ec+9R75BCb28bB4dm9fS\nPCXKHq/fo6KxVIOenh6WL19eE+eRVCedQ+ND8u/LCAtGFh7wLlp/v5Tk88+wYzZJyx6lf63UeSRj\npXOo9JYtWzbo9iGTbefchcCF4c9mdhfwd+fcWbn7mdlRwHUFxHItcK6ZPQi8BnwLuMc598rAHc3s\nI8Df8V1JYsDxwAHAF/M9WGNjI4nEoOvwVI00nYCfHFnpWKc0z4bN0JXaXPFYqkktnEdS3XQO1bZw\nMZvIxBaaZs2me8FuJJ9/huzaVWX9veo8krHSOVR+hUyQ3B+4b5DtHWxfFjKcy4C78KPhK/EzAz8B\nYGbHmVlbzr5zgDvwSfkr+Jrt9zvnBn/rUKOqoe1fKJwkqV7bIiL9wrZ/8bkLiEQixOfv7LerI4mI\njKCQQrMsvob7ngHbD8AnwnlxzmWALwdfA6+7Bbgl5+ergKsKiLEmdVbB6pGhlkYtbCMiMlByzcsA\nxHZa4L/P2wWA1Po1ZJO9ROJal0BEBldIsn0dcImZZYBH8LXThwNfAc4sQWx1ozvssR0fsiFL2YQj\n2z2pNpLpLuINTRWOSESk8sKR7dhcn2zHg2SbTIbUmpXEd35dhSITkWpXSLL9Nfzy6v8NhJX1XcDF\nzrlrih1YPammke3chW3aujcybeKCCkYjIlJ52WyW1JqVQP/IdsOsORCLQypJctUKJdsiMqS8a7ad\ncynn3JnADGBv4B3Ajs65S0oVXL3oSvqa7eYKrh4ZaknM6LushW1ERCDz2qtku/xE9vhcX6sdaWgg\nHoxyp1auqFRoIlIDRrOC5GSgCfibc669yPHUpXCCZKIKJkjGohNoDkbYVbctIgLJ1S/3XY7Nnd9/\nOSglSWqSpIgMI+9k28zmmNlvgdXAY8DuwfaPmFm+/bhlgGw2S1fSl5E0V0EZCUBLozqSiIiEwnrt\n6NTpRJtb+rbH5+8CQHLVy4PdTEQEKGxk+ypgGnAQEMnZHgM+Xcyg6kky3UU6kwSqo/Uf9E+SbFcZ\niYgIqTX9bf9y9XUkWbWCbDZb7rBEpEYUkmwfjF9R8g8Dtr8GaF3vUQrrtcEvalMNwkmSbT0a2RYR\n6etEstP8bbaHHUmyXZ2kX9XrpYgMrpBkO4kf2R749n0/YG3RIqozYb02VM/IdkvfwjYa2RYRSQ5o\n+xeKzdu577IWtxGRoRSSbC8BLgWODn7e08y+iu+zfVOxA6sXYdu/CFES8UkVjsabFCxs0969qcKR\niIhUVjadJrV2FQCxuTtvc120qZmGGTsCmiQpIkMrpM/2+fj+2j8Ofr4B6AG+C/xXccOqH2EZSSI+\nmUhkNM1hii+s2e5Nd9KTbKcx3jLCLURExqf0xnWQ8vNqBtZsgx/dTm9ar/Z/IjKkvJNt51wK+JKZ\nXQi8EZ9oL3fOdZQquHoQlpFUS702DFjYpmejkm0RqVthCQmRCLE587a7Pj5vF3r+8ieNbIvIkPJO\nts3sQeA259z3gT/lbN8TWOycO6QE8Y171db2D2Bi43R8w5ksbd0bmNGya6VDEhGpiFTQY7th5mwi\nExq3uz4WtP9Lqf2fiAyhkLqFg4DvmdnNZtacs30qvlOJjEL/gjaTKxxJv4ZojImN0wD12haR+pYa\nYnJkKOxIkt60nkynPugVke0VWiR8BvAvwNNmtqgE8dSdMNmuppFt6C8laVeyLSJ1LLVmJTB4vTb0\n99qG/sRcRCRXocn208De+DKSx8zscqB5+JvIcMIykmpp+xdqaZwBqP2fiNS3vrZ/Ow2ebDdMn0mk\nyf8bVN22iAym4PYXzrk259zxwL8BnwR+zva9tyVPnVU4QRK0sI2ISDbZS3qjX0ZiqDKSSCSyzUqS\nIiIDFZJs3wT0DXM6524H3gDcCGhmyCh1B63/muLVVkaihW1EpL6l1q6GTAaA+IAe27niweI2SbX/\nE5FBFNL676RBtm0GTi9mQPUknUnSk/ITaqp2ZLt7I9lslkgkUuGIRETKK+xEQixGw6zZQ+4X18i2\niAxj2GTbzM4Bvuec6zSzE4bb1zmnVSQLtM1S7dWWbDf6ke10ppfuZGvVxSciUmrJNUG99uy5RBqG\n/ncZtv9Lrn6FbDpNpKGhHOGJSI0YaWT7i8AdwHL8ipHDUbJdoHD1SIDmKpsgGZaRgK/bVrItIvUm\nNcLkyFA4sk0qSXrD2kEXvxGR+jVSzfbuzrnlweUJI3xJgXJHthNVlsw2N04jGvGjM6rbFpF6lApG\ntoer1waI7TQfov7fqeq2RWSgYUe2nXNtOZdTg+1jZrOB9wPXFze08S9s+zehoZlYtLrer0QjDUxs\nnE5b9wb12haRupQcYUGbUCQ+gdjsuaTWrCS5agVNi95ZjvBEpEYMmWyb2fuBOSPcPgJ8EHgbSrYL\n1tXbClRfvXZoUmIWbd0btIqkiNSdTGcHmc2bgJHLSMAvbpNas1LLtovIdoYb2f5X4Pg87mMNcFZx\nwqkvneGCNlW2emQonCSpMhIRqTfhypEw8sg2+Lrt7j89oo4kIrKdIZNt59yJwIlljKXuhDXbTfHJ\nFY5kcC19vbY1si0i9SWs1440JmiYPnOEvSEW9tpWsi0iAxS8gqQUT9iNpGpHtsNkW6tIikidyV2m\nPZ91BsKOJJmtr5Fu3VLK0ESkxuS9qI2ZzQC+AewPTMLXa4f+5Jw7tsixjXtdvUEZSZW1/QuFC9u0\nd28km80Qiei9mYjUh3BBm3xKSIC+JdsBUqtepuFN1TmIIiLlV0j29APgMGAJMBH4BfBfwM+BA4of\n2vjXV0ZSpRMkW4Ka7Uw2RWevRmpEpH6EPbbjeSbbDVOmEp3sX8tVSiIiuQpJto8AznPOfRfYAfiJ\nc+4G4P+AWSWIbdwLy0ia49U5ArLNwjaq2xaROpHNZvNu+5crpmXbRWQQhSTbSWBzcHkrsEtweSeg\no1YZcAUAACAASURBVIgx1YVsNpNTs12dI9vNE6bSEIkD0K66bRGpE5nWrWQ7/DIT+bT9C4V121rY\nRkRy5V2zDbyIT6wB7gH+x8z+BTgGeKjYgY13Pal2stkMUL0125FIlJbEDLZ2rVX7PxGpG2G9Nox2\nZFu9tkWkXyEj2+9wzt0UXP4C8Bi+hvtR4LPFDmy8y12qvVq7kUD/JEmVkYhIvQjrtaOTptAwOf/X\n5/j8Xfzt160mm+wtRWgiUoPyHtl2ziVzLr8GqPvIGHQmc5Pt6hzZhtxe2xrZFpH6kFxTeL025HQk\nyaRJrV1FfMFuRY5MRGpRIWUkmNnrgIOB6QNv65y7tHhhjX9h279oJMaEhuYKRzO0/lUkNbItIvUh\n1ddje35Bt4vtOAdicUglSa5coWRbRIDC+myfDPwQSAOvAT3BVREgCyjZLkBu2798FkyolLAjiSZI\niki9SI1yZDvSECM2dz6pl19SRxIR6VPIyPbX8T22z3TOtZconrpR7W3/Qi19yfYmMtk00UhDhSMS\nESmdbCbTl2zH5+5c8O3j83Yh9fJL6rUtIn0KmSA5FfiZEu3iCMtIElVcrw39EySz2QwdPZtH2FtE\npLalN28k2+M/uC2k7V8orl7bIjJAISPbfwH2NLOHGLxm+5ViBjbedSVbAWiu0rZ/obBmG/wkydyF\nbkRExpuwXhsKr9mG/kmSyZUvk81mq7pMUETKo5Bk+zr8ku3fYvsR8Syg+oIChCPb1dz2DyARn0ws\n2kgq00N7z6ZKhyMiUlJhj+2G6TOJNhU+eT1s/5ft6iCzeRMN0zVAIVLvCkm2/w14GbgCeIX+CZIy\nCp3hBMn45ApHMrxIJMKkxExe61yl9n8iMu71LdM+ihISgFhOnXdy1Qol2yJSULL9L8C/Oed+Vapg\n6kl331Lt1T2yDdCSmBUk2+pIIiLjW2rNSqDwTiShaPNEGqbPIv3qBpIrV5B4y9uLGZ6I1KBCJkj2\nAp2lCqTedOa0/qt2k7SwjYjUibCMZLQj25C7bPuKIkQkIrWukJHtdcD3zWwDvrd2rqxz7l3FC2t8\nS6a7SWW6AWiq8gmS0D9Jsl0j2yIyjmXTKVLrVgMQH+XINkB8/s70PPMntf8TEaCwZPsHwL5DXJct\nQix1I1zQBmqljESrSIrI+JdavxbSaWDb2utC9Y9sv1yMsESkxhWSbN/qnPteySKpI+GCNgDNNVRG\n0tG7mXQmSUM0XuGIRESKLywhIRolNnvuqO8n7LWd3riOTHcX0URTEaITkVpVSM32s2Z2bMkiqSNh\n2z+IkIhVdzcS6F/YBrK097xa0VhEREol7LHdMGsOkfjoBxViQfs/f58a3Rapd4Uk2zMAzZArgnBk\nOxFvIRqt/vbkAxe2EREZj8K2f6NZpj1Xw/RZRILR7OTKFWMNS0RqXCFlJOuBQ81s0OWwnHMPFCek\n8a+rr8d29ddrAzTGW5jQ0ExvulOTJEVk3EqtCXpsj2FyJPj1CWJzdyb54guq2xaRgpLtJ4GvBF8D\naQXJAnT2rR5Z/fXaoZbETDZ3vExbj5JtERmfUn0L2hS+TPtA8fm7kHzxBXUkEZGCku1PAl8qVSD1\npCvZCtRG27/QpMQsNne8rJFtERmXMj3dpDeuA8ZeRgLqtS0i/fJOtp1zW4GtI+4oI+rqG9mujTIS\n0MI2IjK+pdau6rs81jIS6O9Iklr9Ctl0mkiDPvwVqVeFjGxjZu8E/gvYL9j0BHCBc+6RYgc2noUT\nJGuh7V8onCSpXtsiMh6FJSTEJ9AwY8cx31/YkSTb20N647oxtRIUkdqWdzcSMzsaeAjoAi4Kvv4/\ne+cdHkd5ru97Zqt6L5YlW5ZsrwvGxsYGB0LABkyHJARCgECSE/LjAAnpHRJCgJNwEkJOAoQACQRI\n6B1TbYMLxr17bVmWVa1etpeZ+f0xu6tiSV5Ju6vi774uLizt7HyvpNHq3Wee73ldwGqbzXZlPIqb\nqHRvkBxHzXYo/k802wKBYCIS8WtPKo6JCm0qKgFJzxMQvm2B4MRmKMr2XcCf7Xb77T0+d7/NZvsj\neuP9QiwLm8h4AuNxg2QuoNceVPwYDeZRrkggEAhiR7BeTw0ZyZj2nkhmC4aCIpSjdQRrquDUM2Jy\nXoFAMP4YSs72DGBlP59/N/SYIApUVcEbcADjJ/oPeg62AadIJBEIBBOMQCSJJDbNNnT7toWyLRCc\n2AxF2a4ALuDYhvv80GNRYbPZDMB9wA2AFb1Z/5bdbj9mNKHNZrsI+AEwDz1acDfwM7vdvnYIdY8p\nvMGuyL/Hk7Id3iAJ+ibJzGThPxQIBBOHYH0NEJvNkWGMJaWweZ3I2hYITnCG0mzfCTxns9nKgFWh\nz50DXAx8eQjn+QlwGbAEaAMeB54CLurn2EzgT6H1nMBNwNs2m2223W6v7ef4MY/b3x3oMp482yZD\nEhZjGr6gQ/i2BQLBhEJ1OlA72oDYNttC2RYIBDC06L8XbTbbOcBvgLtDn94KLLfb7auHsOZNwK/s\ndnsVgM1m+xFQYbPZSux2e02fNZ/p89yHbTbbncCpwLhstsOxfzC+lG3Q1W2fUzTbAoFgYhEITY4E\nMMXBRqJ2tKE4OjGkja/XfIFAEBuGFP1nt9s/Aj433MVsNlsmUII+jTJ8zkqbzdYFzAdqBnpu6Pnz\ngFxg13BrGG3CsX9G2YrJYB3laoZGmjWPFmel8GwLBIIJRTiJREpKQc7Kidl5w/F/AMHaIxhmnxyz\ncwsEgvHDkJptAJvNZgHyAVPPz9vt9soonp4W+n/f4TgdQPpx1s0HXgR+b7fbD0VXLfh8vmgPTQhd\nrhYAkkzpeL3eUa5maCQZ9T9Cne6j46724RK+fsbadSQYP4hraOzjrdb/fBmKimP6c9LMVqTUdDRn\nF57DB9GmzRz2ucR1JBgp4hoaPaJutm0221TgYfQNkVKfhzX0DYzHwxH6f997aZlAFwNgs9mKgPeA\nlXa7/WdRFRyioiLqvZsJodpzEAAtaGbPnj2jXM3QcHtUAFo6a8dd7SNlrF1HgvGHuIbGLun7dmMF\nnMnp1Mf4tS0zKw+zs4ujO7bgKigd8fnEdSQYKeIaSjxDUbYfAWYDtwGVwJClTbvd3mGz2aqBRcBO\nAJvNVo6uau/s7zk2m60UeB94yW63/2ioa06fPh2LxTLUp8WN9kMfgwey0guYO3fuaJczJIyNjVQd\nWElQcoy72oeLz+ejoqJizF1HgvGDuIbGPu3/7CIIZM86iZIYv7Y5ZszCW3OILJ+b0hGcW1xHgpEi\nrqH4M5AQOZRm+yzgBrvd/vwIa/kb8GObzbYKaAd+h65YV/c90GazzUJvtB+32+13DGcxi8WC1Tp2\nvNF+xQlAqjV7TNUVDdlpRQD4gk4MJg2TIWmUK0ocY+06Eow/xDU0NtE0DaVe329vnVoW85+Rv7Qc\nL6DWV8fk3OI6EowUcQ0lnqEMtQkCDTFY8z7gdWAT+oZIDbgOwGazXWuz2Rw9jv0RMAn4rs1mc/T4\n75oY1DEquAPjb1R7mN5Z22KTpEAgGP+oHW1oHhcAxqKSmJ8/nEgSbKhDCwRifn7B+ERTVXE9nEAM\nRdluBr5ts9nO7+/BaJVnu92uAj8M/df3saeBp3t8/HXg60OocczjDeVsj7fYP4BUS+/BNtkpsYvI\nEggEgtEgnEQCsY39C2MMNduoCsGGWkxTpsV8DcH4QvW4af7lrQSqDlHw4L8wxeFNnmBsMZRmezWw\nHFjc5/MSujo9LJvHiYY7oOdsj0dl22gwk2TKxBPoEMq2QCCYEATq9OmOckYWctqgoVjDwlhYBEYj\nBIME6o6IZvsER1MUWn//C/z79G1q7tUryfjKN0e5KkG8GcpQm2/Es5ATAU3T8ISU7WRz5ihXMzzS\nrHmi2RYIBBOGeIxp74lkMGIsmkKwupJgTRUsjcsygnFC5z/+D+/GjyIfe7dsEM32CcBQPNuCEeJX\n3KhaEADrOLSRQLdv2+ltGuVKBAKBYOSEbSTGOFhIwpiKpwJibPuJjvOdV3C89BQApnIbAP4Du1Ec\nfUePCCYaotlOIGFVGyB5HNpIANKs+QA4fC2jXIlAIBCMnEC9biMxxUnZhm7fdlA02ycs3h2baf/L\nvQBYFiwh/7cPgcEAqopv+6ejXJ0g3ohmO4F4/B2RfyeNUxtJakjZdghlWyAQjHM0VSUYiv2Ll40E\nwBQa2x6orULTtLitIxibBOqqab3nR6AoGIunkvvT/0FOS8cyZwEA3i3rR7lCQbwRzXYC8YRi/yRJ\nxmJMGeVqhkeaRVe2ncKzLRAIxjlKSyME/AAYJ0+N2zrhc2suJ2p7a9zWEYw9FEcnLb++HdXZhZyW\nQe6dDyCnpgFgXaQb+D1bNog3YRMc0WwnkLCNJMmUgSSNz2992LPtV9z4As5RrkYgEAiGTzCURAJg\nLCyO2zrhrG0Qvu3jofl9aH7faJcRE7RgkNZ7fqzvCzAayfn573rF/FkXfQYAta2FQJUYoT6RGZ8d\n3zglEvs3Ti0k0G0jAXD4hLotEAjGL4HQ5khDXgFyHCfqySmpyNm5gPBtD4bS1kL91y6l4b+uwH/I\nPtrljAhN02j/6334dm4GIOvWn2Gdt6jXMaZpM5CzcgBhJZnoiGY7gXQr27HPck0UqZZc9Gh14dsW\nCATjm+4kkvhZSMKE1e1A7ZHBDzyB6Xr+H6gdbSitzTT95Ca8u7aMdknDxvnK07jeeQWAtC9+ldTz\nLjvmGEmSsC7UrSTeLRsSWp8gsYhmO4GEPdvjWdk2yEZSzNmAGNkuEAjGN8H6ULMdx82RYSKJJDVV\ncV9rPKK0teBa+bL+gWxAc7to/uVtuNevGt3ChoFn40d0PPYnAJKWnk3GjbcOeGxSyLft27sd1eNO\nSH2CxCOa7QQSTiMZr7F/YdKS9E2SHe66Ua5EIBAIhk9Y2U7EuOyeiSSCY+l64Z9ofh9yajoFD/wT\nQ+FkCPhpvffHOEMK8XjAX3mA1t/9HDQNU7mN7B/8BkkeuNWynHIaSBIEgxHLiWDiIZrtBOIJdAHj\nd6BNmEkZswGobd8xypUIBALB8NACAYKN9UB8k0jChG0kSlMDqtcb9/XGE0pbC663XwIg9fNfwVw+\ni4LfP4Zp2kxQVdofvJuu/zw+5hM7lLYWWu76LprXg5ydS+4df0C2Jg36HEN6JuaZcwFhJZnIiGY7\ngXQr2+PXRgJQkn0KAI1dB/AGHKNcjUAgEAyd4NE6UFUgsTYS6J2CIuitaqdd+mUADNm55P/P37Cc\ntBCAzif/Ssejf0AL/czGGqrPS8tvvo/S3IhksZB3xx8w5hZE9dxIBODm9XF9Q/Huu+/yxhtv0NjY\nGLc1BP0jmu0EEtkgOc6V7eKs+aHoQk2o2wKBYFwS9mtjMGAsKIr7eobcfCSLnngiEkm66aVqX/EV\n5JTUyGNySip5v/kzSUvPBsD56rO0/e8daIHAaJQ6IJqm0fbAr/Ef2ANA9vd+jXnGnKifH44AVBrr\nCNbXxKXG6upq1q9fj8fjYfNmYVdJNKLZThBB1Y9f0Tc/JI1zz7bFmEJhug2A6rato1yNQCAQDJ1w\n7J+xYDKS0Rj39SRZxlis21WEb7ubrhefRPP7kFLSSLvsy8c8Lpkt5Pz0PlJWXAGAe/VKWu76HqrX\nk+hSB6Trmb/h+eg9ADK++t8kn3nukJ5vnjEHOVVPKYtHBKCmabz11luRjw8dOhTzNQSDI5rtBOEN\nqdow/pVtgJJs/dZedatotgUCwfgjbOVIhIUkTHf8X1XC1hzL6Kr2iwCk9VG1eyIZjGTd9nPSrvoa\nAN6tG2j+2c0oXR0Jq3UgXKtX0vXMowAkL7soUuNQkAwGLAtPA+Lj296zZw9VVVWRj9va2mhra4v5\nOoKBEc12gnAHejbb49uzDTAl1Gy3u2vE6HaBQDDuiGRsJ7DZ7o7/E55tgK6XnkLzDaxq90SSJDJv\nuIXMm74PgN++m6Yf/hfBpqOJKLVffPt20vbAXQCY58wn+9u/QJKkYZ0raaFuJfHt2hzTCZqKorBy\n5UoApk2bhjF0F+fAgQMxW0NwfESznSA8PZXtcTzUJsykzDkYZQsA1W3bRrkagUAgGBphb6ypKIHK\ndij+L1h3ZMxu9EsUSnsrrrdeACDtimuQU9Oiel7a5deQ/cO7wWAgWFtF0w+/QaC6Mp6l9kuwqYGW\nu38AAT+Ggsnk/uJ+JJN52OcLb5LUfD58e2L3N3Xjxo20tLQgSRIrVqygoEDftDmRm23NXY9ifwzN\nVTvapUQQzXaCCDfbFmMKBtk0ytWMHKNspijzJED4tgUCwfhC9bhRWvUJuKOhbGt+H0rz6CmyYwHH\ni2FVO5W0y64Z0nNTzr6A3Dv+iGSxorQ00vSjb+LbvytOlR6L6nbS8qvbUTvakJJTyPvVHzFkZI3o\nnIbsXD3qEPDEyEri9Xp5//33AVi4cCGFhYWRZvvQoUMoihKTdcYSmqbg2f4gWuNHuHb8bbTLiSCa\n7QThCejesqRxHvvXkymhCMCatm1jPv9UIBAIwvRMfEhos11Uog8wAQIn8CRJpaMN51vPA7pSHa2q\n3ZOkUz9D3j0PI6dloDo6af7ZzXg2r4t1qcegKQqt//NzAkcOgSyT85P7ME0pi8m5w+p2rHzbq1at\nwu12YzKZOP/88wEoLCwEwOfzUV1dHZN1xhJa/QeYgw0AWINH8LVUjHJFOqLZThDdsX/j30ISJrxJ\n0ulrod09dm7XCAQCwWCEY/8kiwVDTn7C1pUtVgz5eszgiRz/10vVvvwrwz6PZdZJ5P/u7xhyC9B8\nXlru+h6uVW/HsNJj6XjsAbyhpj7zWz+IjFuPBdaF+rmC1ZUj9qK3t7ezbp1e55lnnklGhh7MkJKS\nQk5ODgAHDx4c0RpjDc3fhXL4pV6fa98b3+shWkSznSA8oQ2SE0nZzk+fjsWo7x6vEVYSgUAwTohs\njpxUMugo7XhgKjmx4/+Ujjacb4ZU7cuGp2r3xDRlGvn3P6ZbdBSFtvt/ieOVZ2JQ6bE4334R56vP\nApB6yVWkXXJVTM9vmTMfKTRx0rt1ZOr2u+++SzAYJDU1lbPPPrvXY+Xl5cDE822rVc8jqR78ipnt\nDacDkKVuw9Ux+skrotlOEO7Q9MiJEPsXRpYMlGQvAMQmSYFAMH4I1Cc+iSRMJJGk9sRMJHG89BSa\nz4uUnELa5UPzag+EMa+Q/N//HbNN30fU8egf6PjnX2Jqb/Ru20j7X38H6Ap05k3fi9m5w0gmE5b5\ni/X1RtBs19bWsm2b/jf53HPPxWKx9Ho83GzX1dXhcrmGvc5YQnNUoh39GIBt9WfQlXIuAcWEQVZo\n2PrOKFcnmu2E4Q10AROr2YbuCMCatm2o2sTbbCEQCCYe3bF/UxO+9omcta10tuN8o4eqnRY7W6Uh\nPZO8ex6KWDEczz1B+4N3oynBEZ87UFNFy70/BlXBOKWMnJ/ci2SIzyCkpNA0Se+2jWjBodfec4BN\nXl4eixcvPuaY0tJSDAYDmqZRUTE2PM0jQdNUlIqnAI0OTzZ7mxcx/aRJOCz6156jrKejbXSHIIlm\nO0FElO0JZCOBbt+2L+ikqWv8/9IKBIKJT9izncjYvzDGUPyf2t6K6nQkfP3RRPdq66p26hWxUbV7\nIluTyL3jDySffQEArndfpfWeH6P6vMM+p9LVQcuvb0dzOZHTM8m74w8DDt+JBdaFuv1Bc7vw23cP\n+fn79++nslKPQrzwwgsxGAzHHGOxWJg6VX+jORGsJFrjWnDoX/OGmnMxmk1MLkkh+6SLAEizdFH5\n6drRLFE024mie4PkxFK2s5KLSbXkAsK3LRAIxj5KVwdql/56bJxckvD1w8o2QOAEspIone09vNpf\nxpAWn7+FkslE9vfvIjVkUfF8soaWO749rDc2WiBA629/RLChFowmcn9xP8ZJxbEuuRfGScURe9NQ\nR7crihJRtcvKypg9e/aAx86cqccMHjx4cFyniWlBN+ph/bpq8Mym3jGN0vI0DAYJY3oJbuN0ALID\na2luHD11WzTbCUDT1G4biWliNduSJFESigAUvm2BQDDW6R37NwwbiapCUzP4hjflT87IQk7V7RMn\nUiKJ46V/oXk9SEkppF4x/ASSaJBkmcxvfo+MG24BwLd7K00/uQmlrSXqc2iaRvtf7sG3WxeRsr/z\nCyxzF8Sl3r5YQ1aSoeZtb9q0ieZmfaLzRRddNOg0y3Cz3dXVRWNj4zArHX3UIy9DoAtNMvFRxecA\nKJvRbU9Kmb4CgOKMKnZv2DsqNYJothOCN+BAQ58WljwBRrX3Jezbru/YTVD1j3I1AoFAMDDBOl1N\nllLSkNOH+HqsKLBlG2zeCh+thbp6GKIqKElSZJPkieLbVjo7cL7xHABpl10dN1W7J5IkkX7V18j6\n9i9AlgkcPkjjD75BoMebrcFwvPQUrvdeByDtqq+RsuzieJbbi3DedqBiH0qUSRo+ny8ywGbBggUU\nFw+uwBcWFpKaqtthxquVRHPVotXpX3OLaRlOfwZmi0zxlJTIMXLeIoKy/nueFVhHbbVzVGoVzXYC\nCMf+wcSzkUD3cJug6qOhY/TeOQoEAsHxiIxpnzxlUOXvGBQFtm6H5pA6GgjCjl168+0dmsptLNYV\n9RNF2Xa8nDhVuy+pK64g52e/A5MZpbGOph9+A/+h/YM+x71hNZ1P/BmApDOWkXH9zYkoNYLlpEUQ\nGv3u3fpJVM9Zs2YNTqcTo9HIihUrjnu8LMvMmDEDGJ9525qmoR56GlDBksvmI6cCMLUsDYOxu7WV\nJAOmkmUAzMzdxZZ1taNimxHNdgII+7Vh4tlIAFKteWQl697HGmElEQgEY5hAOIlkKJsj+zbaZdMg\nT9+rQlMzfDw0ldsUarZPhCmSPVXt1EuvwjDUuwkxIHnp2eT95s9IySmoHW00/fhbeHds7vdY/6H9\ntP3+F6BpmKbPJvt7dyU8i122WrHO0+8YRzNNsrOzk48/1mPvzjjjDLKyohsdH7aSHD58GL9/fN2V\n1lo2o4XEvcDkq6iv15NbelpIwsiTzkbDgNngJzO4hcMVid+YLJrtBBBWtg2yCZMhaZSriQ9TcvQX\nhuq2LaNciUAgEAxM2EYSdcZ230Z75nSYNRNOXQjzTgKjsVvl3ro9Ki93eJNksKFmWPFu4wnHK0+j\nedxIScmkff7aUavDOm8R+ff9DTkzB83jovmO23Cv+7DXMUprMy2//h6az4shJ19PHrFaR6feUISh\nd+sGNFUd9Nh3332XQCBAcnLyMQNsBiOsbAeDQQ4fPjzsWhONpvhQK/XhQlLmXA416ZsgTWaZ4qkp\nxxwvmTOQ85YAMDt/K5vWN6KqiVW3RbOdAHrG/g3ptuU4IuzbPtplxxecGCH5AoFgYqFpWi8byXHp\nr9Gerg8EQZKgZDJ89oxulbuxKSovdzj+D0UheLR2mF/N2Efp6sD5+n8ASL306lFRtXtiLrdRcP9j\neqJIMEDrfT/B+bY+3lv1emn+zfdRWpuQLFZy7/wDhpy8Uas1vElS7eogMIjtpb6+nq1b9U2cy5cv\nJykpekEvNTWVoqIiYHz5ttWaN8HXCpIBefp1VIaU6qllqRiN/be18uRzAchOasHqP8SBvR0JqxdE\ns50QvIGJGfvXk+Ks+UjIaJpKbfuO0S5HIBAIjkFta0Hz6vFfx00iUdSBG+2eJFlDKvfcqFVuY2Ex\nhPKPgxPYSuJ4uYeqfcXoqdo9MU4qJv93f8dUNhNUlfb/u4fOZ/9O2x/uJHBwL0gS2T+8G3P5rNGt\ns6QUQ14BAJ5BIgDffvttNE0jJyeH0047bcjr9IwAHA9onia0Gj3eUJp8Hh4tn4Y6N9C/hSRCWjmk\n6r/zs/O2snlDM8Hg4HcMYolothOAO5yxPQH92mGspjTy0/VbUsK3LRAIxiKBuu5ca2PRIBnbigpb\nt3U32jMGaLTDSBKUFMNnPwO5OfrnGpvgo3X9qtyS0Yhxkr7+RE0k0VXtkFf7kqswZIydJC5Ddi75\n9/0Ny7xFAHT962E86z4AIOPGW0leevYoVqcjSRLWhaFpkgP4tg8cOBBpki+88EKMxqFPtQxbSZqa\nmujoSKzaOxzUymdBC4A5A3nKFRyu0GOVjSaJktKBhw1JkoRcpKvbpVkH0Hzt7NnRnpCaQTTbCcET\nspFMxNi/noi8bYFAMJYJj2mXs3KQk4/1dgL9N9ozBmm0e5KUBIsX9VC5AwOq3KaQlWSiDrZxvvIM\nmseFZE0i7fPXjXY5xyCnpJJ314MkLT0n8rmU8y4l7YtfHcWqehOOAPTv333MUB5VVXnzzTcBmDp1\nKnPnzh3WGlOnTsVs1pNPxrq6rbbtQmvVLTPytKuQjElUHtSb7anT0ga0kISR8k4DYwqypDErdzvb\nPm3B51PiXjeIZjsheEIDbaymQW5xTADCEYCtzsO4fNFlgwoEAkGiCDfbpoEsJCNptMMMpnLXN0RU\n7nDW9kSM/1McnTheC3m1x5iq3RPJbCHnp/eRceOtpF31NbJu+dmY2ldlXbAEZAOoCt4dn/Z6bMuW\nLZFhNBdffPGw6zYajZSVlQFj27etqUHUQ//SP0ifjpT/GTzuIA21IQvJzOP3V5LBglR4FgCz8nYQ\n8PnZuaU1bjX3RDTbCeBEUbaLMk/CIJkAqGnbPsrVCAQCQW8C9eHYv34sJH092jPKh95o96Q/lXv7\nzojKHU4kCdRUjetx2f3RS9X+wthTtXsiGQykf+lGMm+4BclkGu1yeiGnpGKZfTLQ20ri9/t59913\nATj55JOZMmUIMZb9EPZtV1RUoB4n+WS00OreAc9RQMJQfj2SJHO4woGmgdE4uIWkJ/KkZYBEkslF\naaadnVtacbvinwgkmu0E4DkBNkgCmAxWijL1W1k1bVtHuRqBQCDoTVjZPib2L9Jo66Ou9UZ7+sgX\nHETlNmfmA6C5HKhRTgkcD+iq9r8BSL34Sxgyost8FvRP2Eri3bIh8qbso48+wuFwYDAYohpg135d\nbwAAIABJREFUczzCzbbH46G2duyl42i+dtTq1wCQCj+HlFYKELGQTJmWhskUXTsrJeUjZetvYOYW\nbCUY1Ni6sTn2RfdBNNsJwHMCbJAMU5IdztveOuHUGoFAMH7RlGAkZq9XEkm8Gu2e9FK5DRAIYGpq\nJ+eCryAnpYzJTZKBQIC3336bjz/+GEWJ3tfqfOVZNLcLyWIl7YvXx7HCE4NwBKDS0kiwupKuri4+\n+ugjAJYuXUpOTs6I18jJySE7OxsYm1YS9fB/QPHqfutpVwLg8QSpr9FjhstmpA3pfFJoo2R+Sh05\nSY3s29VOV0d8h/qIZjvOBBQPQVXfGJM0wW0k0O3b7vI20ulpGOVqBAKBQEdpOgqhATKRjG1FhW1x\nbrTDRFTuMyIqd3L5XAqv+Q7U1EY9fTJRrFmzhjVr1vDmm2/y17/+NeIPHgzV0YXjNX3YSOolQtWO\nBaaymciZeiPs2bKB999/H7/fj9VqZdmyZTFZQ5KkMTu6Xes8gNakW2jk0i8gmfTGuipkITEYJKZM\nG2KznXUSWPVYxXlF21BV2LQhvuq2aLbjjHuCj2rvS0G6DbNR3+VfLawkAoFgjBAe044kYSyc3N1o\nNyWg0e5JD5VbDQYwJKVgxRr19MlE0NXVxZo1ayIf19XV8eCDD7J69epBPb2OV3uo2l8QqnYskGQZ\n68LTAejasJpNmzYB+gCb5OTkmK0TbrZramrweDwxO+9I0DQVpeIp/YOUEqRJ3ckx3RaSVEzmobWy\nkiQjF+lvVKZl7sVs8FCxv5PWZm9sCu8H0WzHGU/PZnuCe7YBZNlAcabuhxJ52wKBYKwQDG2ONORP\nQjKYRqfRDhNSubvq9+OtDimJ/SSWjBbvv/8+gUCApKQkrr32WjIzM1EUhZUrV/Lwww/T3HysCqg6\nHd2q9sVfwhBSYwUjJ2Il2b8TgxIkOzubpUuXxnSN6dOnI8syqqpSUVER03MPF61hFbhCv7fTr0eS\n9EFQXk+QuuqwhWR4KW9SwWdBNiMT4OTivQB8uq4pBlX3j2i244wnEA6Jl7CahnarY7xSkqNbSWra\ntqFpY3Nns0AgOLEIhgbamIpLezfa0xPcaPfAMGkyza//g44tqyJe7p6JJaPB0aNHI+rpsmXLmDdv\nHrfffjunnnoqANXV1Tz44IOsXbu2l8rtePUZNJcTyWIRXu0YYz3lNDRJQlZVJjvbWbFixbAG2Ay6\nhtUaSTUZC1YSLeBErXoRAClvKVKGLfJY1aEeFpKy6FJI+iKZUpDy9Tcscwq2ARrVh5001LpGXHt/\niGY7znRvjkxHDr0rm+hMCW2S9AQ6aXEeHuVqBAKBIGQjkQ1knHxm70Z75ug02tCdte3Y+AHqaacO\nmsudKMLjv3uqp1arlSuvvJIbb7yRtLQ0AoEAb7zxBn//+99pa2vTVe1XQ6r2RULVjjVSWgbtafr3\ndA4+Tj755LisE7aSHDhwYNQDDtSqFyDoAtmCXHZVr8cqD+oDfkpKUzGbh99XhSdKmpRW5kzRN09v\nXNsUl69dNNtx5kSJ/etJTkopyWZ9Y4zwbQsEgrFA8GgduRdcgzk59Fo8yo02dE+RRNMItjXrXu6T\n5vRWubftSJjKffDgQex2OwAXXHDBMerprFmz+O53v8uCBQsAqKys5IEHHmDfX38vVO04sm3bNg5Z\ndbvENHd73AbvhCMAOzo6aGlpicsa0aA5j6A1rAZAnno5kqX7zZvPq1BX7QSGbyEJI6VOgXT9az6l\nRJ8N0tjg4Uilc1jnCwQCAz4mmu04cyLF/oWRJCmible3imZbIBCMLprXQ9YpZ5M0bbb+iTHQaAMY\ncguQLBYgNElSkmBKiZ5YEo50O9oIH69DboyfnxT08d9vvfUWACUlJcybN6/f45KTk/nyl7/Mdddd\nR0pKCnhcmD/WB6yYll+KIWvkUXSCbgKBAO+++y7Vqfr3VWo+SqC+Ji5rTZ48ObLpcrQiADVNC22K\n1CCpAGny+b0erzrkQFVBHoGFpCdhddvq3cf0qfrG0E3rmlDVoanbu3fv5s477xx4neGXKIiG8PTI\neMb+jfbtnv4oCUUA1nXsRFEHfrcnEAgEcUVV0TZtjjTaamHemGi0QU+aCGd+B2qquh9ISoIlIZXb\nYAB/APOefZR0OeNmK9m2bRsNDXpcazTjv0866SS++93vcq7sw6oGCUgy/6jvYMuWLWPyb9J4Ze3a\ntXR2dtKcmglJetKXd+uG4zxreMiyzPTp+u9GzJrtunpYsxYqD0d17WpN66FL94zL5dciyb2neoZT\nSIqnpGCxjNyaK+UuAnMmoLFk+h4A2lp9VOzvHPyJPVAUhbfeemvQpB7RbMeZiI3ENLLbHQPR9uDd\n1F97Pp7N6+Jy/uESVrYDipejnftHuRqBQHBCouoDa2SHG4DOzauQ5s8f5aJ6Ex7bHuw72Cascp/V\nrXLne7wYGo7GvIae47/nzp1LaWlpVM9LlqDssN6g2POn0q7A888/z1NPPYXD4Yh5nScaTqeT1atX\nA7Dk9KUkhSIAe45ujzVhK0llZSXB4AjHmCsK7N0HLhfsPwAbPgXnwBsQtaAH9fBzAEjZC5Cze/+u\n+nwKtaEUkvKZsempJNmIVHg2AEnODZSV63eaNm9oRglGF/Cwfft22toGnwIrmu04E87Zjoey7du9\nDdc7r6B2ttNy9w/xbF4f8zWGS3pSARlJRQBUiwhAgUCQaEKNdngzZOemD3HXVSAZxtZGdWPItz3g\nFMmQyq3k6L5V44EK6IptI7tu3To6OzuRZZkLL7ww6uc5Xvs3msuBZLaw9Fe/x2bTEyP27t3LH//4\nR3bu3BnTOk803n//fXw+HxaLheXLl0dGt/t2bkYLxGfiYXiTZCAQoKqqamQnq6uHQI+GvaMD1q6H\nyqp+VW61+jXwd4BkQi7/yjGPH6l0oCoasgxTy2KX7iZPOhskAwTdLJ1zGEkCR1eAfbs6jvtcVVVZ\ntWoVoL9RHXCNWBUr6J9w9F+sN0hqmkbHP/+v+xMBPy13/wBPHN/xDpXwNMkasUlSIBAkkj6Ntqe1\njq5PP8AYnhw5huhWto+gDXAbWvX56Ni3ka6KXaAE9U2TI1UdQ/RUT08//XRyc3Ojep7qcuJ85RkA\nUi78AplTSrnxxhv54he/iMViwe1288wzz/DMM8/gcsUnTm0i09zczKeffgrAOeecQ2pqaqTZ1rwe\nfHt3xGXdjIwMCgr06YojspJoGhwJDZKaVAinLgSLRf/d3G+HT3qr3Jq7Aa3uHQCk4guQkgqOOeXh\nUApJ8dRULNbYvWmWLFlIuXq0pbVzDTPn6P3alo3N+P3KoM/duXNnZDPp8uXLBzxONNtxxuPX/UXJ\nptgq295Na/GHftmybvs5hsLJesP9m+/j3fpJTNcaLiUhK0lD5z4CytiYSCUQCCY4fRptppfj2KWL\nEKaQP3osEY7/03xelJb+N0F2PvEg7uf/Qec7/6bx+b/i3b8Ddu+NiX+7r3oaLY7X/43q7EIyW0i/\n8gZA3xy/ePFibr/9dsrLywG9GXnggQfYu3fviGs9kXj77bdRVZWMjAzOOOMMAIy5BZim6t9X75b4\n3ckOW0lGlLfd1g6OUKpH6RTIz9MtUZP1O960d6vcmqqiHnoaNAUs2chTLj3mdH6fQk2Vfr5pI0wh\n6Q+5KHTtu6pZfFInskHC61HYtXVge4iqqnz44YcAzJ49m6KiooHPH9NqBb1Q1CC+oP5OLJbKtqYo\ndP5DV7Ut8xaSsuIK8u99BENBj4Z72+g33CXZejyUqgWpa981ytUIBIIJj6rqqm+k0S6DGeUEQtMj\nx6KybSyaovuz6ce3DQSOHML51ovdHzc30PzaEzQ/ci/+T0a2V6epqamXepqSkhLV81S3E+fL3aq2\nIbu3Gp6VlcU3vvENLr/8ckwmEw6HgyeffJLnn38erzd+I7EnCpWVlZE3JxdccAEmU/cmwfA0yUT4\nthsaGobvva/Sh0iRng6ZIbHRZIL5845VudeuQmutAkAu+zKSwXLM6aoPO1FCFpLS8jgMCEyfCSkl\nAFg7VzN3vh5fvGNLKx53/3eRdu/eTVOT/gb5eG9URbMdR7yBrsi/Yxn9517zDoEjhwDIuOFWJEnC\nmF9I/n16w635fbTc9X282zbGbM3hkGzOJC9N39ksfNsCgSCuhBvtcETe9DKYMR3V40JtbwXAWFQy\nigX2j2y1YsgrBI71bWuaRvujfwBVQc6fRPsNt2OcMQcAb/VBGu/+Lq2/+wXBlsZhrR1WTzMzMyPq\naTQ4X/vPMar2MV+XLLN06VK+853vMHWqfkdhy5Yt/PGPfxy1WLnxQM8IxsmTJzO/z4besJUkUFVB\ncIA7ISOltLQ0krE+rJ+Vx9P9e1ja/WYyQh+VW3IGMbgvRJbPQspZ3O8pD4VSSIpKUrDG0EISRpKk\niLqttWzmlPlGTGaZgF9l26ZjM8dVVeWDDz4AwGazUVxcPOj5RbMdR8JJJBC7DZJaIEDnvx4BwHra\nWVhmd0+S0hvuhzEUFIUa7u/h3f5pTNYdLmHfthhuIxAI4sYAjTaSRLCuO5N4LNpIoNu33Sv+D/Bu\n/AhfSDRJ/eotBMpnk3nvI+T84G6MmTmAhnvNSo5+8wt0/OP/UF3RD+OorKxk3759AKxYsaKXejoY\nqtuJI+zVvuDzx6jafcnNzeVb3/oWF110EUajkc7OTh5//HFefvllfKM0kn4ss3PnTmpr9WmGF110\nEbLcu02zzF2AZLEC8YsANJlMlJWVAcO0koS92maz7tfufxGYPw91ih9NciNhRO4qRtq46ZjEkoBf\npeZwbAbZDIaU/xkwJIOmYOlcy/xFegrQnh3tOLp6Rxjv3buXxkb9TW409ivRbMeRcMY2xE7Zdr7z\nMkpjHUgSGV/972MeN+ZPIv/ehzHkTwo13N/Fu2NTTNYeDuG87WZHRWTAj0AgEMSMQRptgECdfjtb\nsiYhH6cxHC3CiSQ9bSRawE/HYw8AYJm3CPPpnwN0BS75nAso/ONTZH72EmRrMprfh+P5f9DwX5fr\nCSGDTLKD46ung+F8/TlURyeYzAOq2n2RZZmzzjqL2267LaIAbty4kT/96U9UVlZGvfZEJxAIsHLl\nSkCf1hn2vfdEMpmxzNfV33haScKpJAcPHhw0P/oYFAVq6vR/TynWc+IHQPO2oHa8hpL8Jmp6yF4U\n9nIfrorsSag+7EBRNCQJSqfHwUISQjJYkAo/C4DasIp5C9KxJhlQFY0tnzR3161pEVV7xowZTJly\nfHtawpttm81msNlsv7fZbE02m63LZrO9YLPZ+h05ZbPZimw226s2m63KZrOpNpvt2kTXOxLCsX8m\nQxJGg3nE51M9brqefQyA5GUXYS7tfzCDsaBIt5TkT0Lz+Wj59e14d2we8frDYXLmyciS/stW0759\nVGoQCAQTlOM02gDB0LQ9Y1FJ3MZcjxRTcWiwTY9m2/Hav/XaZZnMm75/TO1Sfj5pX/oqk677PmkL\nP4dkMqN2ddLxyP00/L8rcX/83oDDZY6nng6E6nbhePlpAFIv+DyGnLwhfZ0FBQXcfPPNnHfeeRgM\nBtra2nj00Ud54403Bh11faKwfv16Ojo6kGWZiy66aMDjwlYS77aNaEpsUmn6EvZtu1wu6uvro39i\nfQMEAt058YOgVv4bVD+YrUinnwuLTun2cu8LJZa4XJFBNkUlKSQlGYf9NUWDXLRM/4e/A6NjO4tO\n06/xA3s7aG/V78Ts27cvMgAq2k3Fo6Fs/wS4DFgChE0uTw1wrAqsBL4C1ALjaiyVNxDbjG3nq8+i\ndrSC0UjGtd8a9NhIw51XGGq4v4N3Z+IbbrMxicIMfXKbGN0uEAhiiv3AoI02QLAuvDlybFpIoDuR\nRG1rQXU5UdpbI8JKyoorMJfN7P+JZdOQi4vJXHo+hdd9j5SzLwRJQjlaR+t9P6Xpezfi3d37dben\nejp79ux+1dOBcL7xfETVTotS1e6LwWBg+fLl3HLLLRQWFqJpGmvXruXBBx+kurp6WOecCLhcrkhe\n8+LFi8nPzx/w2KTQJknN5cBv3xOXevLz88nI0O/IR20l0bTujZGFBWC1Dnio2r4HrUW/6y5PuwrJ\nmAIF+ccklmgfryetrR4JLa4WkjBSUiFS1jy9xvoPmD0vk7R0E5oGn65r6qVql5eXRz0AajSa7ZuA\n++x2e5Xdbu8CfgRcYLPZjnkLZLfbj9rt9ofsdvt6YPCwwzFIZKBNDKZHKl0ddL34JACpF12JsWDg\niJkw3Q13gd5w/+p2vLu2jLiWoRKeJlkjNkkKBIJY4fXCkZAfu3RKv402QLBe/+NvGoNJJGHCnm3Q\n1e3OJ/+K5nEhpaSScf3NAz9RkvR0B6sFY3Ia2aetoOCBJyOJFf4De2j+8U003/U9AtWHgd7q6VAG\n2KgeN46XdV0sdcUVGHMHbgajoaioiFtvvZVzzjkHWZZpbm7moYceYuXKlSOfXDgO+fDDD/F6vZjN\nZs4999xBjzVOKsY4Sdcq42UlkSQpYiWJepNkz7i/qQP/vmlqEPXQv/QP0sqQCs7sfjCcWBJSuSVV\n5fTcDi4taaKsKDEDqaSi0Pe/047sq+PUpbq6XXXIwcYNO6mr020yy5Yti/qcCW22bTZbJlACRDo+\nu91eCXQBY2uGbgwID7RJjoGy7Xj+n2huF5I1ifSrvx7184yFk/VYwLwCNJ+Xlju/k/CGO+zb7vDU\n0eUZ3q55gUAg6MWhw/rtZpMJZszot9HWNI1A3diN/QsjZ+UgpaQCen6y673XAMi45psYMrIGf7LZ\nDAvm61+/04XZFSTvrgfJu/svmMr1iY7ejR9x9Jarafrjr/nknbeB46unfXG+8RxqVycYTaR96cah\nf5H9YDQaWbFiBTfffDN5eXlomsbq1at56KGH8PvjMyFxLNLS0sKGDXrT/LnPfY60tOP7kiNWkq3x\nz9s+cuRIdJtZe8b9ZQ3c92j1H4Bbt6YYyq9DkvppRUMqd4Omq+uTkv1YN2/s5eWOF1L2yWDVG2y1\n/gOmz8ogO8eCpmm8H1K1S0tLI5tIoyG+5pdjCV9BfXfKdQBxuT8wmrudXZ52AMxy6oiyRZXWJhxv\n/AeApEu/TMCaTGAo58vKJeNXD9Jxx22orU003/kdMn5+P+a5C4Zd01DIskzDKFsJql4qGz9lVuF5\nCVk3FoSvH7FrXjBcxDUUB3w+LDU1SECgZDKKEtQnK/ZB7WxHCyV0qLkFYzrj2VA0heDBvThXvgya\nhqFoCsZzL4vUPOh1lJyEYVoppsrDUFdPID0NZs8n475H8a19H9fTj6C2NOJ7/3W+JMnsLCzjjFP/\nO+rvh+Zx0/Wirmpbz72UYGo6wRh+L/Py8rjpppv48MMP2bBhA3V1dbz00ktcccUVMVtjLPPWW2+h\nqippaWksXrw4qp+LPO9UeON5/Af34W5sQD7emzKG/lpUXFyMJEmoqsq+ffuYNWvWwAd7vVgam/Tf\nycmTUAZaI9CF4chLSICaewZB82T9LlU/BIMqb1VmMNliYvmUDkxqEPbZUesbCMyehZacFNXXMRyk\nvLMw1LyI2rgOZdJlLFiSyRuvbMPp0m1rn/3sZ4f0mp7oZjucjt43miMTXd2OORUVFfE4bVS0dOnv\n3FxdAfbsGb6vKu3Vp0jy+1GTUzgyYz7aMM9luP7bZD5+P4auDtrv/j6d191GoHTGsOsaCmmGqbSr\ndnYfWY3SenwLzFhjNK8jwcRAXEOxo7jLSYGqEZQkdju6UAd4TTQdqSDcghzsdA/7tTMRpKVkkASo\nrXrqQeuyy2no5/b9gNeRpjHdbCLDH8Cwz86Bpka8RiPkTIabf4n88UpSP16JVQmyqKEC1w9upOmc\nS/AuPHPQxAiA5I/fIdXRiWYwUjt3yYDf75FSXFzMSSedxO7du9m+fTtmszmS0T1RaWlpiQywsdls\nUfujJdlKrsGIpASpfOsVfCcviXrNobwWZWVl0dbWxqZNm1CUgd28kx0uCoGAJLGrtQWtrbXf40p8\n75GteFEws989m+Ag11J7i0wwaOFI0Mr2tHTKfC5yvD7kzi5Mn3xKXVoKTUnWfu9qjRSDlsMcDMiq\nn8bdL9FhWIDDq0/tTrLk4nZ7htTXJbTZttvtHTabrRpYBOwEsNls5eiq9s54rDl9+nQslmOnESWC\n3VuCEITiwjLmlswd1jmCddW0b9NvL6V96WsULDp1RDUp06fTccdt0NZM1jN/IfMX92OaHX8HT6D2\nTDYctuPSjjBnzpwxmwrQF5/PR0VFxaheR4LxjbiGYozPh2WDnj2tTZvK7NKBmzFvYxUOQErLYM7i\n6JuR0cC1Zzbu7fprvfmU05nx+at7PR7VdeT3o23aguzzM9vrx3/qSZFG+j92O5Uzz2BpZx1zm45g\ncHaR/vozZG1ZS8p1/w/zks/2+7qsedy03v8hGpB03qXM/syZxxwTS2bPno3b7aayspJt27axZMkS\ncnNjH9moaRqtzT6qDrmornQhGySWX1RIWnp0eeOxquGxx/SNsAUFBUNKhgHomDOfwK4t5LfUkT73\n+D3GcF6LmpqaWLNmDW1tbcwdaA1FwbJOn1otTSlhTvm0/o9zVmLcq2e7M+UKbIX9D7AJ89H7TYCT\ngklJzFukb+T1N7dgsh9E9vspcbiYLBsJzLbFR+Wu3AMt6yiS7LhTPoPbq78RTk+aT6q1lGkzUo95\nykANeKKVbYC/AT+22WyrgHbgd8BKu93e7zZkm80W3s4qA+bQxwG73R7VhkmLxYJ1kB2x8SQ8qj0t\nOXfYNbQ89zioCobcArKuuAbJPMI/1tOmY77vEZp/+i2U1mY6f/tD8u56EMuc+FpKygqWsOHwY7gD\n7biURnJTS+O6XqwZzetIMDEQ11CMqDwMqgYmE6byckymgf+MeZv0eC7T5Klj/nvvbKiN/Dvrv27H\nPEC9g15HViucsgA2bkJ2ubFWVML8eVRVVekDbIwmcr/1AyaVFNH55F9xr16JUl9N1+9+hnnuAjK/\n/h0ss+b1OmXXm8+hdXWA0UTWl7+BMQHfx2uuuYY//elPOJ1OXnzxRW655ZbIRMORoGkaTUc9VB7s\novKgA2efQSXvv3GUy64qJSU1MQ33rl27IhGMl1xyCcnJyUN6fvLiM+nctYXA9k1YzGakKBv1obwW\nzZkzhzVr1tDe3o7L5SInp5+k5ppaCAZBkjCWTev3GtE0FWXvc6HCJ2OesgJJHvhnGgyq1B5xAzB9\nVmZ3vSXFup97736ob0Du7MTy6Wawzex/WuUI0ErOR2lZh+RrorLidQDSUvJJMhexfVM7M+fkYDBE\nt95opJHcB7wObAJq0OP8rgOw2WzX2mw2R5/j3aH/ioHHQ//+ecKqHSaapkUmSA53oI3/4F48a98H\nIP3am0beaIcwTZ5C3r2PYMjJQ/O4ab7j2/j27ojJuQciL7Us8n2oEdMkBQLBcPB6oTrUlE6bCoM0\n2gDB+vDmyLE3pr0nweajeDasjnwsRTnNsV+ys/RkFoC6erSa2sgAm8LCQhYuXIixoIicH95NwQNP\nYTlZv1vq37Odpu9/jZZ7fhzZVKp6PThCXu2U8y/HmDfANMAYk5aWxtVXX40kSTQ0NETqHw6aptHY\n4GbDmqM881gFr/y7ip1b2iKNdnqGibnzszAYJLo6A7z5UjVeT/zTUILBIG+/rW9WnTlzZiT5YyiE\nN0mqHa0EDg9jrHoUFBcXRxrdfi0ufeP+kvpv4rWjH4FTT8SRp18/aKMNUHvERcCvD9OZ1neQjdkM\nC04OJZaYQ7nc++GTTeBy9XO24SGllUK6/rs0xXwIgPPOW44k6deKfXd71OdKuLJtt9tV4Ieh//o+\n9jTwdJ/Pjcspl76gC1XTf2GTzMNrtjv++RdAz2BNWX5xzGqDcMP9ME0/+RZqWwvNd3ybvN/8udf4\n91giSTLF2Qs42LiG6rZtnDLlC3FZRyAQTGAqwwkkRojCyxvO2DYVjd0kEoDOJ/4Mge70jWBN1chG\ny5dPg7Y2aGlF270Xb0sLABdffHEvm4J5xmzy7nkI75b1dD7+IIEjh/Cs+wDPJ6tJvfCLSMkpqJ3t\nYDSSHqMEkmiZMWMGn/vc51i9ejXr16+nvLx8YBtDH/QGW1ewDx/swuno3TynZ5opm5FG+cx0cvKs\nSJJESWkq775eQ3urj7deruaSK6diNscvau6TTz6hra0NSZIGHWAzGKap5Rhy8lFam/Bu2YC5fJAN\njMPEYDAwffp0du/ezYEDBzj99NN7H9B+/Lg/LeBCrXoBACl3MXLm7OOuW3lA38ZXWJQ08J2Ggnw9\n9SSkctPeDh+vh1kz9VpioHLLReeidlVgy/dhK81h8Wkn42ivp2J/J1s+aWHGnExMpuO3qeOykR0P\nhAfawPCi/7w7NuHbpvsSM77630iG2L8vMk2eSv69DyNn56J5XDT/8jZ8++JinQdgSigCsLZ9B6o6\n7mLTBQLBaNJL1S49rqqtqWr39MgxPNDGt3c77jXvACBnZgO9J0kOC0mC+SejWSzImsa1s09ijs3W\nr3oqSRJJp55BwZ+fIev2O/SpkIqC843ncDz3BBBStfMTo2r35LzzzotskHzhhRfo6OgY8FhN0zha\n72b96qM8/feDvPqfKnZtbYs02hmZZk5ZkssXry3jyzeWc9qZBeTmJ0V86lPL0jhnxWQAmhu9rHy1\nhmBwCGPKh0B9fT3vvfceAIsWLaKwcHjfW0mSuiMAEzC6/dChQ8dukqwKOYDT0waM+1OPvAwBB8hm\n5LJrjrueElQ5UqmbHI47yKanym0Oqdx798PGTeAZeWJOjTsfp09GluDihclIksTipXnIMrjdQXZv\na4vqPKLZjhNuf/eLgnWINhJN0+j8x/8BYJ45h6TPnBPT2npiKi7VG+6snO6Ge/+uuKw1JXsRAP6g\ni0ZHfG55CQSCCcoQVW2lpQnNr0dzjdWMbU1VaX/kfwEwTZuB2XYSAMHaIyM/ucXMLoNU8vO1AAAg\nAElEQVSEqmkUpKRw5ZzBVWHJYCD1vMso/NvLusCTlKI/YDSS/qWvjbyeYWAwGLjmmmtISkrC4/Hw\n7LPP9mr2NE2joc7NulU9GuxtbbiceoOdmWVm4Wm5XHldGVffWM6SM/LJzbcOuEF/+qwMPrtMb3wb\nat2890YtihLbTOf29naeeOIJfD4faWlpnH/++SM6X7jZ9u3bgRqKuYw14bxtn8/HkSM9rk2Pp3uC\na+nU/rPuXTV6rjYgl1yCZO3H892H2moX/rCFJNqpkeHpk0WT9I/b2mHbjhFncn/w4Ro2Vete+uzg\nHjTFT3qmmdnz9Jyj7Ztb8HqPLx6KZjtOeELTI2XJiMWYMrTnbliN/4C+ozXjhlvjntyhN9yP9Gi4\nb8W3f3fM18lImkS6tQAQvm2BQDAEvL4hqdrQ7dcGMBaNTc+264M3CFTo6QyZ3/w+phI9xWHEyjbg\ndrt5ec1q3q3SfbLJre1QW3fc58lWK+lXf51Jj71CxtduI+/OB0ZF1Q6TmZnJlVdeCejDVd577z0a\nal2sW3WUfz16kNeeq2L39h4Ndnaowb6+jKtuKGfxZ/IjVpFomDM/m9PO1If9VB92svqdOlQ1Ng23\n2+3miSeewOFwYDabufHGG0lPH9mIEeuC00A2gKLg3bEpJnX2JSsri7w8fchLL9/2kRq9mTWbYFLv\na0TTNNSja1F23AeoYM1DKoluYmnlQd1CUjApidS0IexfCKvc80ObfDs6oK4++uf3oaamhgMHDrCp\nJhkNCYIutGY9dWXhaXkYTRJ+n8r2TS3HPZdotuNEz82RQ2mWNSVI55N/BcCyYAnWBYmJqzKVlJJ/\nz8PImTlobhfNv7wFnz22DbckSZFpktWtotkWCARRUlk5JFUbuv3ahpx8ZGv8hl8MF9XtpPMf+r6c\npDOWYZ1/amRse7CmCm2EityqVavweDysP1pPMDN0d3XPPnBGp34aMrJI+/y1WE45bUR1xILZs+cw\n/2Q9Jm716tX8518b2L29Dberd4P9pevLuOqroQY7N/oGuy8LFueyYLGuwFbYu1i36uiIfx6BQIAn\nn3ySpqYmZFnmuuuuY/LkySM6J4CcmoZ5ln5HxLslftMkjxndrih6CglASUmvrHbN3YC68z7UA49C\n0AmyBXnG15Fk83HXURSNqkNRWkgGYnKRrnQD7D8AgcDgxw/AB6Fpkdb0SUg5+p15tf59NE0jOcXI\nyQv1a2T3tjZczsHXEM12nPCEbCRJ5qFdLK4P3yJYoysRGTfcEvO6BsM0ZRr59z6EnJkdarhvxXfg\n2MxIVdXo7BjeKN0p2QsBqO/cQ1ARE/UEAsFxGIaqDRCo0293j1ULSdd/nkDtaAWTmcyvfwcAY0kp\nAKqzC7VrYH/y8Whra2P9er3x+uxZZ2FcdApYLHqDtHWH/v/j4D+4l/rrVtD8k2+h9TOdM96oqkZ9\njYuPP2zg6UcP0nl0Jmaj7mlv6lpLarrCotP1BvvqG6az+DP5ZI+gwe7LkjPymXOybhXYu7OdT9c1\njeBrUXnuueeoqqoC4Atf+ELEmhELrAu7fdsjfVMwEOF66+vrcTqd+obEQEC3jkzR7xxpagD1yMso\nW36B1rkfAClnIYZT70XOmhPVOnXVTvy+IVpI+mP2LJBl8PvhwNAHitXV1bF/v/41LF++HHnyufoD\nziPg0JNJTl6Ug8VqQFE0tnzSPOj5Jn6z7a49/jFxIKJsD2FzpOb30fX0I/rzzliOZebwBuGMBNOU\nMt3DnZmN5nLS/Itb8B/cG3nc61V4+dnD/PuJCjZvGPzi6o+wsq2oAeo6Ym9VEQgEE4xeqnb0jXNY\n2R6LzXawoRbHK88AkPb5azEW6gpnzwSSYE3VsM//zjvvoCgKqampnHXWWXqjfUooacrp1BXuQVA6\n2mj57Q9Ruzrx7d6K691Xh13LUGlu9PDxBw3869EDvP7CEfbuaMftDiJJBmZMPRej0YSqevFoG1l4\nWi7ZufHJ/ZYkiTOXFTJ9lt7wbd/UyrZPj28X6I8333yTXbv0vVDnnXcep546suF0fQn7tpXmoyO6\nbgajrKwMg8GApmlUHDzYvTGyIB+SrKgd+1C2/AL1yCugBcGcjTzn2xjmficqn3aYyoO6qp1faB3Z\ngKHkJJhepv/7SDV0DW1IeVjVzsvLY968eUgZsyBZ/z1V6/VIZovFwClL9IFL+3d30NE+sIA44Ztt\nw57folS9jKYm9p152LM9lIxt55svoDQ3gmwg46s3x6u042KaUkb+PQ8hZ2ShuZw0/fwW/Af34XEH\neeOFKlqa9B2+Wz5pprpqaBsyUizZ5KSUAlDTti3WpQsEgonEMaq2/sdXURQOHTrEa6+9xiOPPMIH\nH3yAq0++biSJZAzG/nU89gAEA8jZuaRf1b35UE5LR87UG5Ph+rZramrYsUOfm3D++ed3TwrMzoaZ\nofzt2roBvayaEqT1vp/qf4tCdD71cNw23/XkSKWDl589zN6d7XjcuvqenWvh1KV5XHVDOdd/cyFf\n/KIeG1tRUcGaNWviWo8kSZx9/mSmTNMnBX66rom9O6JLnwjz8ccfs27dOgCWLFnCsmXLYl6nefps\n5HRd2IuXlcRsNlNaWgpA26FKcOhNsVach2J/FHXnfeA5CkhIk8/HcOo9yLmLhrRGTCwkPZlWqjfd\noL/BjFL1r6+vZ+9eXWQ855xzkGUZSZKQi5YDoDVvQgv1eHPnZ5GSakTTYNP6gQXICd9sS5qKVv0K\nytY70RyVCVu3W9mOrtlW3U66wjFL510a8e6NFqap5eRFGm4HNXf+iNeeOUBrsw9JIvKOc9XbdTgd\nQ/NDRXzbYpOkQCAYjB4JJIGiIvbu3cvzzz/Pb3/7Wx599FHWr1/P4cOHee+997jvvvt45ZVXaGlp\nQQsGCR7VNwOaxpiy7d3+aWSATeaNtyIn9Z4aaCrR1e3hNNuapvHmm28CkJ+fz6JFfZqd8jLIDamM\nu/f269/uePxBfLu2AJBx461IZgtqZztd/3lsyPUMhdZmLx+8VYem6X9fFn8mj6tvKOdL15ez6PQ8\nsrL1Nw2nnHJK5Ot67733ItaMeGEwSJx3STFFxfrP6eMPj3Jwf+dxnqWzY8eOyM9j1qxZXH755RGb\nS7ChFu/WT2Ji+5BkGetCPf/auzV+EYBhK8kkn24j1ZJklIP3oDWu1Q9InYrhlDsxlF+LZBz6Pon6\nWhe+ULLHiCwkYQwGmBPK9G6PfrPkqlWrAMjJyWH+/PmRz0sFZ4AhCbQg2lH9jZ7RKHPqUn3zaDgb\nvD8mfLOtFiwDJHDXomy7C6XyP2jK8PzGQyEc/Zdkis5G4nj5ad2jZzKT/pVvxrO0qDGXTifvnofw\n50zhk9nfpsOh27OWXziZS744FbNFxutVeP/NocUjTcnRfdtNXQfxBuKvlggEgnGI14dWravT2zs7\n+c199/Lkk0+yZcsW3G59jHN4IqLZbCYQCPDJJ5/wv//7vzz5+GM0WHU1cizZSDQlSMff9Kg/88y5\nJJ9z7DATY49NkkNl7969kebzoosuwmDoM5RFkvSkhgH8265Vb+MM2VtSL7+G9C/dSNoXrgfA8eq/\nCTbEx5bpdgVZ+WoNgYBKcoqRy64qZeFpeWRm9z81+fLLLycvLw9VVXn22Wcj10O8MBplVlxeQl6B\nbllZtbIuosAORGVlJc89p48nLy4u5itf+Urk5+Gv2M/RW6+h+Ze30vHI/TFpuCMRgLu3ofpGni/d\nHzNmzCDDYsGWqfc1qroeFCcYrMjl12I45U6ktGnDPn+4Wc3Nt5KecfzNlFGR///ZO+/wOMpz7f9m\nZnuTtKveu4vcK8YNG0NsSiihhZBQ0iv5EpLvQJJzcpKQfKQXElIIEBIgVIMhptvGDRfJtmzLtiSr\n97LSanud+f4YaWXZliXZck4O0X1de2k1807dKff7vPdzPykTSpbs7OyMS37WrFkz4h4SJANC2goA\n5PatKIp675TOTCTRfu79/eCT7bxbkeY+AMYMQEFp3UzswLdRBqov6naHZCSmcUS2Y64+PBvVwpnW\na25Bk5x2UfdtIogk57Fv5Q/wWrIQ5CgLqh8lR9OBLVHHZVdmAtDVEWDfrq4x1jSM7KS5CIKIgkxr\n/6GLtetTmMIU/hfC7XazZ88ejm56FUGW8UcibDxYQTgcRhAE8vLyuOqqq7jvvvv46le/yi233ML9\n99/Phg0bsNlsKIrC8foGXipazAtFiznR60KWL05xkonC+/pGIk1qclXiZ+9DEM98BQ+Nak40sh2L\nxeLlv4uLi5k2bdrZG+r1qj0ajNBvh+tO0P+bH6hNZi+MJ21ab/oEoj0ZohFcj/1qQvs0HkSjMm9u\nasHriaDRCKz/cM6Ydm86nY7bb78djUbDwMAAL7zwwkVLDBzepsRVN+SSZNejKPDOP1ppbzl7afCu\nri6efPJJYrEYDoeDu+66C51OJWPRrnZ6/utelGAAAO+rz+L6488ueP8N89XIthIOETpycUaN09Mc\n3D47DVEQUQiiaJrUBMiFP0TMuhJBOP+Km7I8LCEpKp2EqPapODVZsvbcyZJDUe2kpCTmz59/xnwx\nc1AGFO5DcapSWFEUWLk2A5N59OTtDzzZBhASSpEWfg8h52pAhEAXscofEjv5JEo0cFG2OSQjGU9B\nG/dzj6ME/AgmM9Zb7roo+3M+8LgjbHquEbcXRAEWnvwzac3b6fnWFwnXVVNQbGPOAjU7/HBF35g9\n/SHoNWbSbeqLYEpKMoUpTKG3t5f33nuP3/3ud/zoRz/i3c2bmTYor9jd3kZeURE33HADDzzwAJ//\n/OdZtWoVycnJ8eWNRiOrV6/mm9/8JrfccgupJjUC2WVK4Km//52f/vSn7N69m3D44o9qjoaYZwD3\nU78HwLRmA/rps8/aTpOtykhiXe3xojzjwb59++jt7UUQBDZs2HBuVw7HSP22fLKW3ge/iRIKIaWk\n4fiPHyFoVOIgGk0k3vklAAK7txI8XD7ufRoLiqKw7c12ujvV9/Ca9VmkpI9PfpCRkcE111wDqBH9\nIfeVCUOW1Q5H+QHVyu4c14jBqOHqj+RitWmJxRTeeKUlvu9DGBgY4LHHHiMYDGI2m7n77ruxWNRR\nlpjbRc9/fhnZ5UQwmjEsWQmAd9Pfcf3p5xdEuKUkB9rBcu0XQ0oiu44jV3yX3MEkwZDUiFj2xQkn\nQI6G9lYfwcAkSkhOhcmoSqhATewcJVmyu7ubw4fVKtqnR7WHIJgyERJV8wql7Z349MwcMx//zOgO\nM/8WZBtAEHVIBbcgzf9PMA/a1LS/q2bP9k+uK0Y0FiYSU2/AsSLb0a52vP94AQDrRz6OZJt4afeL\nAc9AmFefb8Q9EEGSBD50XQ6zv/FFRFsCsmeAnm99AfezjzE/x0Nahvpw3PpmG+5xWgLmDFoATiVJ\nTmEK/35QFIW2tjbeeustfvGLX/DTn/6U119/nebmZhRFYU1eAVpJIioILL/jdu655x6WLl2K1Wo9\n53o1Gg0LFizgTruOD9cfIF9QX959fX1s2rSJH/3oR7z55pu4J+hMMBlwP/0nZPcAgt5Awl1fHrVd\nPF9HUYgMJnmOhWAwyDvvqC/++fPnj8+/+VT99vEahFAYtDqSv/UTpMGy8UMwrb0KbbGqfXU9+guU\ncVgHjgfl7/dQNygdWLI8dcJJcUuXLmX2bLXTsnnzZtraxi7aMwKyrFYZbGqG7h44UgXvboN95aMS\nb7NFyzUfycNk1hCJyGze2ExfryrbCAaDPP744wwMDKDVarnzzjvjnUI5FKT3e19Tq4NqNCR/+yck\nf/unmC5bD4D3lWcumHAPl26fvCRJJeKJJ0AKHgMCBhRF5vflLqK2s3cYzwcNgy4kyakGEhInSUJy\nKgrzx0yW3Lp1K4qikJCQwIIFC0ZdlZCp2gAqA8dRfOO75v5tyPYQBGsB0vzvIubdCIIEoV7kIz8h\nVv1nlOjZh4QmikBk2B91LOu/gaf+qGalJ9qxXnf7pGz/QjHgCrPp+UY87mGinVtgRVdYSsqDjyBa\nVcI98OTv6PnyR5m95TvoCBMOybz9Wgux6NhDtrmDSZJ9vma8wYlbCE5hClP43wVZlqmvr+fVV1/l\noYce4je/+Q1btmyhq0uVoJlMJhYuXMg9t3+MZVnZAGiKizCOQbDPhlh7Czm+Pm4tSOfee+9lwYIF\nSJJEIBBg69atPPTQQ7zwwgvxbV9sRJrr8b72PADWW+5Ck5w6alspJR1Bp2qVT9VtByIxYqNUMty2\nbRs+nw+NRjP+8t+D+m05FkWUNDjWfxT7F+5HV3KmH7IgiiR9+mvqsdRV43v3tfFt4xyoPT7Agb2q\nlV7pjIR4EZmJQBAEbrzxRpKSkojFYjz99NOEQuMcDRgi2kPlxhMTVamBokCv85zE25ao4+obc9Eb\nJELBGP94qZl+p5+//e1vdHZ2IggCH/3oR8nNVfMFlFiMvp9+h/BxNWpq/+p/YZi3BEGSsH/tu5hW\nqb+Z95VncP35l+dNuI0LLwUg2toUTxA+X6gVILcT2/9/1QRIBcSYWjznSG8vnZ4ADQ0NF7SNIciy\nQsNJtdNVUDLx+31cGCNZsre3l0OHVFnrmjVr0GhGl4QIjnmgV69XebAU/VgYX3WADxgEUYOQdx1C\n8kJiNY+CpwGlazux/sOIxXciJo/eowGIxGQ8wSieUBTv4McTiuIJRjBqJYocw9ZA57L+izTV4d+6\nGQDbbZ88Iyv9fwKu/hCvvdCEzxtV9XPX5ZKVO1xuXldYSurPHsPz0t8I7t9JzNmDru0Ec4K/pnz+\nffT2hNjyi5e5dIEOw6IVSAln72xkJJQhiTpicpjmvkPMzLzin3WIU5jCFP5JiEQinDx5kqqqKo4f\nP36GPV9iYiIzZ86krKyM/Px8ddj22AmVCGk0kH9+yY1Dpdo1mTlkZGRwyy23sH79enbv3s2ePXsI\nBoOUl5dTXl7OtGnTWLlyJUVFRZNWEOVUKIqC608/BzmGlJqB9YY7ztlekCQ0WblEGmrpb27inSPt\nvH6si4rmfiQBCo5WUpJqpTjFQnGKmVRdlJ07VTeIFStWkJg4/tFR/77teDc9Qcp196BzpKPLGD0i\nrp81H+PyywnsepeBJ3+HacU6RJN51PbnQme7n21vq2QnPdPIqnUZ533ujUYjt99+O4888ghOp5ON\nGzdy6623nnt9pxPt4kIoKVaTRbt7oKMTenrVdr1O9XP0mCq/yUiHNLWAzlU35A6+LyP84fdP4Ros\ndnL99dczc6baaRn6/QO7VS1wwp1fwrxmuGy5IGmw3/c9APzb38K78SkEBBI+ee+Ez4lu+mwEkxnF\n7yN44H0sV900oeWHoPjbidX+BQYL0yAZEJNvRFAPj9pBeVNNTc3ouQETQGebP271OCmWf6MhNUX9\ndPeoyZJpqXE70aGots1mG9MHXRBExIy1yI3Po3TvQim4eUz3lX87sq0oCqGoPEiOk/CmfAWzuIXs\ngdeRwi7kY7+iWinjzdA6ukM6lUwPEushch0aI3KbYa1nTZH6vblfYHqactabZuCvj4AsI6VlYll/\n48U43Amh3xnitReb8PuiaLQCG67PJTP7zIepNisP+5e/hSLLROqqCezdjnbfdvobNlFX8GHqNdOx\nPfVbMn/5PXTTZ2NcshLj0tVocvLj50Ej6chKnEVz3wFa+g5Mke0pTOEDgmAwyIkTJ6iqqqK6uvoM\nnXRaWhplZWXMnDmTrKyskc/GUAgGHUhO9dWeCORgMO4Rfartn81mY/369axZs4by8nJ27txJf38/\n1dXVVFdXk5GRwapVq5gzZ85ZtZrni+D+nQQP7AEg8ZP3IurPXYQlHJXZl72Yd4xLKW/PJdJ+Ij4v\nqkBtr4/a3uFOy0zPETKiUWSNnsNCNsHD7RQnmylKtmDUjX4c4caT9P3iv1FCQXxNx7AUzIKWNtWP\nOyvzrMsk3vMVAnu3I/c7cT//BInnUeXYMxDmzU0tyDEFW4KWKz+cg6S5sEH2nJwc1q9fz+bNmzl0\n6BDFxcWjE6bRiLYgqB28zAz1E42em3gnO0hNT2PD1en85anXcHlVJrpy5WqWLh0uce956W94X30W\nAPNVN2G9+c4zdmmIcCsoBLa/jWfj30AQSLjnKxMi3IJGg2HeElVbXzFxsq3IYeTm11BaXoNBpw3B\nsRCx+A6EqmagC6xWzNnZUHdyuHT7BaKuVo1q25P1JCad3YFm0jBzuvobDiVLzpxBX18fBw+qktbV\nq1efM6o9BCF9FTS9DLEgStdOhKxzc5gPPNn+Py9X4YvIccLsDUWJnjEUZydbfy0PFO5ivq2bEqGK\nZOkkP+9eyvt9+cDYF7tJK2HRaxgIRtBrVBuiUNTAJ/56kFSLnksLHawocrAk145RJxE6cSTutZpw\nx+cQzuOlMpno6w3y2otNBPwxtDqRq67PJT3r3JF2QRTRlcxAVzKDhDs+i727E89LLXQHzByZ8Uls\nniYsxyoJH6tk4ImH0WRkY1iyEuPSVejL5pNrX0Bz3wGa+w6iKGfvkExhClP414fH4+HYsWNUVVVR\nV1dH7DRNb25uLmVlZZSVlY1IbDwDdQ0XHtXuGNY5a06pyDgEvV7P8uXLueSSS6iqqmL79u20trbS\n0dHBs88+yxtvvMHy5ctZsmQJBsOFVSdUIhFcf/qFut1ZCzAuv/ys7WRF4WCrizeOdbGlphu3NA8G\nlSZaSWB5YTJri5JobW0lbLTT6ApxssfLQG8XGeEOAGr0BWw93A2HVRIpAFmJRjUCnmymJMVCUYqF\n7EQjgs9D7/e/jhIKIjlSMN72CTjZBM5BIplgg8GkvlOhSc/CesPH8Dz/BJ6NT2HZcCOa1Ixxn49w\nKMbrr7QQDMTQ6UXWX5eL0Tg5NGTFihXU1dVRXV3NK6+8Qm5uLqmpp8l1TifaRacQ7dMxFvHu6YWe\nXtKAG/JFjvSk0+i1EHSVEg7F0Okl/O+9ycCgg4vxktUkfe4bo77nBEmD477v45QVAjvfwfPSX1XC\nffeXJ/RuNCy8VCXblftRIpFxcwu5/xjyyScgMCit0tsRiz+O6FgAgeDwOcvPpTQSZtt72+jp6cHl\nco06mqIoCl2eEF3uIOkJBlIt+jOORZYVGmsnsZDNWDCZoKgAauvUZMnsbLZt24Ysy1itVpYsWTKu\n1Qg6G0LqUpSuncjt7yJkrjvn7/SBJ9vlLWObzwvAAHYebL+ea8MnuNX+PknaEN8v2c5dcif7pGuQ\njElY9Boseg1WvQarQYtFJ2ExaLHoJTSDFk7BSIzXjjTT4oSorEaFu70hXj7czsuH29FJIgtzEpl3\n9C3mGpLISrNjWv2hi3kKxoSzRyXaQw/Aq27IJS1j4pIWXWo6V97h4MWn6gn4DRxe90PW+jcRLt+O\n7Ooj2tGK95Vn8L7yDILZgm3lHJgO3lAPLn8rSYOJq1OYwhT+9eF0OqmqqqKqqiqe2DgEURQpKiqK\nR7BttnG8REdEtfPOK6oNEG1rUr9odUjnsFGVJIk5c+Ywe/ZsGhsb2bFjB8ePH2dgYIDNmzfz7rvv\nsnjx4glLM06F59VnVUmLIJD4ma+f8TI+2ePl9WOdvHm8iy7PSK3xrP46VvUd4caf/4QEk55gMEhV\nuIuyslwMBgOKovCHP/6JxgEwWBNZvuQS6px+Tvb6GAhEUIBWV4BWV4BttcN5MXqNSG7ISU7CpeTp\nupl7++0YDAnY582GnbshFFYJ6aWXqDrX02C75S58b29CdvXhevzXJP/fH43rXMiywjub2+h3qoXR\n1l2dTZJj8qKYoihy880386tf/QqPx8PTTz/NF7/4RbRD19HZiHbpKET7dJxOvLu6obMLuasbEZhm\ndzDN7iCmQJuvlarNXkpyQ/T//LuAKu+wf+NBhDFGTARJg+MbP8CpKAR2vYvnxSdVwn3Xl8ZNuA0L\n1CRJJeAndLwSw5xzSyKUsBu5/u8o3buG9gIh60OI+TcgSIOdzeYWVcuu1UJmBrmKgk6nIxwOU1NT\nw5IlS/CFo9T1+DjZ6+Vkj/qp7fHhDQ1X7zZpJfLsJnLtJvLtJvIdZhIiIn6/2qZwsi3/RkNhgarZ\n9geIVB6mokIt4rRq1arh62UcEDMvJ9a1EwIdKK5jCEllo7b9wJPt2+ZnkmjWY9WrpNii12I1qIR5\niDybdBJi/EJejhK8Drn2cZT+oxSJNRSJv0fM/ihC2soxL3iDViLDFqXFCcUp6Tx152J21jnZWd/L\n0XY34ZjM+419vG9ZBJcsosAEK3c2sKIomdmZtjhp/2ehpyvAP15qJhSModeLXH1j3ritl84Gs0XL\n5Ruyee3FJlx+Dcdm3cOqex8gXHOMwN73CO7bQaTxJIrPi/HN3WjzbUQMAlWP3cecrGsxLl31L1fx\nbQpTmIIapero6IgT7M7OzhHztVotpaWlzJo1i2nTpmEyTbDDPiKqfWZEerwYLtOefVYf69MhCAIF\nBQUUFBTQ09PDzp07qaioIBQKsXPnTnbv3s3s2bNZtWrV+Fw+BhFz9eF+5k8AmK+8Hl2Rqm3tdAd5\n83gXbxzr5GTvSA17SYqF9TPSWGPywn98U13W1w+m9DPWX11dTWODWhX55uuvpaxMtX1TFIVeX3iQ\n8PjUv71eGpw+IjFVRlkrJVGbsVhd0Z4B2LMTu0nHhnQTXzGGET1eXBVHMMyfjUE7kiCKJgsJn/gC\n/b/+AYHtbxO69jb0M+cyFt5/r4uWRrWI2fI16eTknRk5v1BYLBZuu+02Hn30UTo7O3nttde44YYb\nLoxonw6NBrIyaYpGeHLTyxTbElick0uRzYYkK+RaguTSidyhIK3/GKHeNqxf+DriOEdJBI0Gxzcf\nxPljhcCuLXhe+ItKuO/84rgItyY1HU1OAdGWBoIV749KthVFQenagVz/dxgyh7AUIJXchWDNH24Y\ni0HLYCc4J5uYINLuDpCQlkNPSx0vbtvPDw9FaRsYu5COPxLjeJeH413DNsHLRF6yCP4AACAASURB\nVCtlohmPEOO7W06QbzeRZzeR5zCRbzdjN2knf9R7KFmy/ABaj5c5jmRq/b4R8p/xQLAWgrUQPPUo\n7e/AvzPZ/uKK/AkPBQqGZMRZ9w1eiM9A1I9c82eE7j2IpfcgGM4xDAoEBqtHmnQJlKZaKU21cs+y\nfPr9YXbX9/LOi5s5oMvArzHS4IeGfc08ua8Zm0HDsgIHKwodLCtwkGC8uNKS7s4A/3ipiXBIxmCQ\nuPojuSSnnj/RHkJWrplFy1Iof7+HE0ddpGeamFY2C/30WXDnF4l2tRPYt4Pgvh2ktB2hvUhDu9RB\n3p9/ycCff4kmOw/jklUYlq5EP2MOgvSBv0ynMIV/SciyTHNzM0ePHuXYsWP09fWNmG8ymZg+fTpl\nZWWUlJTEC3dMGJMU1QaItKnJkdrMiRP2lJQUbrjhBq644gr27NnD+++/j8/no7KyksrKSgoLC1m1\nahUlJcVIYzyXBp58BMXvQzCZEW/9FBsr23jjeBcHWlwj2qVZ9ayfmc76GWkUp6gEVA4GGPKSiLY2\nokkZSbZjsRibN6vJ9QUFBfFkPFA7DykWPSkWPcsKhh0+ojGZmi3bqHzqKZos6bQVzKfJkkmHWyVJ\nff4wT9WHMaaIfDZVJrG3i/98vJcq0UKhw0RBspkCh5lCh5nc1VehffU5Ig01uP70M1J/9sQ5OzZV\nlX0cPaReO7Pm2SmbO9JaUFFkcNch9x1C6TsMETeI2hEfQdCcMY3TpgmilgK9lo+vy6LqeA3Blq00\n7I+RH01G6FdHDpScJMjUqXIJ8ZTlJQOCML5gV09PD3/5y1/wh0I0RcJcvf5KBKMJurtxHW3AEvGi\nEQWMeSUY80pg3wHVZjE9HdJTx7y+VcL9Q5w/fkAl3M8/oRLuT3xhXMTTsHAZ3kGyzd1nsZkMdBCr\nfgaGivtJBsT8mxAyLx9xDgYCEfprG8gPR5CB+w70s/+N9whGZLKDWqYB0f4O2pkGg8vZTdrB5F0L\nJYOfdJuBDneQpj4fjU4/jX1+mvr8NPf7yVdUflYbC3CgwcvuBueIXbXqNeQPRcMHCXi+3UR2ohGN\ndAHBydQUIvYktH39XFVYRGWi7byeX2Lm5cjV9SjOgyhB56jtpljMKBAEASF9FULSbOSTT6I4D6C4\nqohVfAux4GaEjLWj3piBiCr2P92JJMmkY01/FXP2/Z6oINL5jYfZKyexq95JY58fdzDKm8e7ePN4\nF6IAczITWFGUzPJCB0XJ5knt3XW2+3l9YzPhsIzBKHHNTXk4ki9Mn3gqFixNprPdT2uTj51bOkhJ\nM2AfXL8mLRPrtbdivfZWSuuepb3+j/QUGCFBCwMDRFub8LT+Fc9Lf0W0JmBYeCnGS1ZhWLAM0Tz5\n0ZApTGEKw4hGo9TV1VFVVcWxY8fwer0j5ickJMQdRAoKCiYnmbB+cqLaMCwjuZAy7RaLhXXr1rF6\n9WoOVuyn+uA7WOghy3IAW91e5K4oAUxEDTkYU2aiTSpFsOYjaNRofrjuBL63XgZg++xrePipY0Ri\nwzIbm0HD5aWprJ+ZxrzsxFNGVlWIBiNSSjqxnk4iLY3x6oBDKC8vp7tbjdJeddVV43o3KG2N2P7w\nXVYE/Kx1yKR+5b8QtKoJQF2Pl5O9ahS8osdDhb+fhSaZ/8iI8Yl6H9v6/Ww72RtflwBkTv80GeYq\ncvxdTH/xLWasvJR8u/mMpMyWJi+7tqqjIDn5FpatVqU9StSP0n8ExTlIsKMjr7Mz9n/MIxxuU6qF\n0jmAIiD2uRBiqp2crD2K3HcY+s+ysGRCcMxDSFmMkDQLQTw78fJ4PDz++OP4/X6MRiP33HNPXCYl\nJ9oIbvoNB3ULkMvWUGgNkGcNIipKXOPNUWFcxDtOuP/f/QTe34rnuccRBAHbxz8/5u9tXHgp3pef\nJtJQQ8zZg+RIUWfEwqSF9yAdrRhOgExehJL/Uep9Bk4e745fB7U9Xro9Qf5aGAUjbB0Q2NE2PBIz\noE8GH2iVKJ+aY2Pu9GKKUyw4zGc/bwlGLdPTRtr6tbf5ePU59X5dsSiV/JAtTsSdPjWx2hOKcqTD\nzZGOkd74kiCQlWgcJOCD0fBBIj7eQOV73Z2sFjRYdXoucahBVEVRiCkKMVkhKg/+jQ19l4meOl1W\nkKMzKBTNaGQfnTWbgTOtM+HfhGzLskIsphCLysRiCtHo2b/HogrRmEwselr7yG0kKNPJ5RW0MR/y\nyb/iOrGdKu/1uMP2ePtoVMZo1NCfrvZuTvfYVqJRBp58BADLwmUsW72EZcBX15TQ2u9nZ72TnXW9\nVLS4iMoKh9oGONQ2wMPb68iwGVhe6GBFUTKLchPRa87/BdfR6uP1l1uIRGSMJolrb8qfVO0cqJ2V\nteuzePGpenzeKG+/1sqNtxei1Y3soOSlL4P6PxLWRNH+9mGSOkIE9u4gsHc70ZYGZM8A/m2v49/2\nOkgS+lkLMS5diXHJSjQZ2ZO6z1OYwr8rQqHQCAeR072KU1JS4gmO2dnZkzusGwpB0+REtQGig5Ht\n8yHbiiKDvx3FU4/iaUDwNLAg0syCsjOLuBjwQ6gaWquRW9VpQSERl5SN94kdmBWFdmMyv9HPJRpT\n0Ekiq4qTWT8jjWUFDnRjOHBoc/KJ9XSqRVBOQSgU4u233wZg7ty55OSMnesi+7z0fv8+lIAfMclB\n8gM/RtCqpMii1zA3O5G52cPvKyUYJLbjfUyEeXyawLNyEjucURqcfgKRGArQFlBoS55JOTOhEWhU\nK0tmJhgocKhR8Gy9nv4KL4oCSQ4969ZqoP1NYs5DKO6aOOGLw5iGYJ+HYMpU58kRkCMog39RovFp\nwx91mqKMnC5HIwju2Yiyen5k7VFk3eHR/Q5ifpTu3Sjdu9Uot30uQvJiBPscBEkfP/dPPPEEfX19\naDQa7rzzzngSphKJ0PvgN4g0nqRIrKduyTreak9GK8qsmi1RnBCEnh6QTyHexyRYMA9Szj5aLmg0\nOP7vD3E+dD+B97fhfvYxEARsd3zunPegftZ8BL0eJRTCv/ddjPPSUPoOIbmOkS6rJNZHAq/617F5\nXzqNbxwZ0RkcwhyjwvTBwe5jhiTuWmqnZDBqnZtk5Oc/U0e7CqQBlubbz1h+LAwlRibaddyyKm/E\nMXmCEZr61Cj4EAFv6vPR3B8gJquEuLlfjY5vP229SSYt2YlGJEEYQYxPJcyEA0xr3YOSm8sV+QXQ\n3MYd73VRHZj4s+1z2YXcmXUETc8OSPw3JdtP/qEeZewaK+NADgbNPVyS8w5F9uMkappYavstB9pX\ncLRrMcpgfSAXYQJGJxigv0tDKDeGXq8SY9/bm+L+rwmnWSZlJ5m4baGJ2xbm4AtH2dfYz876XnbV\nO3H6wnS4g7xwqI0XDrVh0IoszrWzosjBisJkUq3jJ8rtLT5ef7mZaFTBZNZw7U15JNovjtWO0aTh\n8quyefX5Rlz9Yba/287a9SOtvpJMOZj1DnwhJy0DlaTPvA39zHkk3v1loh2tBPZuJ7BvB6GjByAW\nI1S5j1DlPlx//Bma3EKMS1dhXLIS3bRZYyafTGEKUxiG1+uNO4icPHnyDAeRnJyceILjGa4Ok4lJ\njGrLHjeyW5VpaDPPTbYVRYFgL4q3Pk6u8TSCPEpRFG0CgrUAt+zgeLOH0EArNqmP7IQIDrN67gyK\ni4SjTSiDBTOmbzDzdM5mYtYisrJnYbAngMkxLrmCJjsfDuwh0to4YvquXbvwer1IksSHPjR2cr0i\nyzh/+h313SNJJD/w0HCkcxQIBgPSgjmwrwKrHOFTdPOpRfnIJfPp9kepd/po6PVR19JN9cGjtJpS\n8A/6DLcPBGkfCFJR38f1mkRKLJ1kpNaSlnQSsXKAU1/HiiAh2krViLJ9HsJZtOnnhSGNtqxG/7c2\nNxHIncaGtV8aQdA5haArnnrknv3grlXt3Hr2ovTsBVGHYJ+DYl/Ic29U0dbWhiAI3HrrreTn58fP\ncd8vv0eocj8A9i/eT86H5iO/0cbJE27erVTwLM9h/uWz8bW242tqw+53o4nFCO+r4NceK4cjWhQF\nYrIyGF0dLCyjKMipNxJddRnRcAilUYCfv41iMCErp7dVO4zFxl6+5LCT2t5BcMsfMVpy4n2MqCLw\nXOcMHm2dR0DWAsMjCgatSHHysATkikAHDPSB1cKXNyw6Q+NeWlrKnj17qK2t5YorJmbfqygK9YOW\nf4UltjM6D1aDllmZCczKHKkQiMZk2gaCcfLd2Oen0al+HwiqiZb9/gj9/sg5t1/iq0FE5p22dmZk\nFJCth6+lxfhso8R4HOhOxcbuUu7IPEqSNkTzKG0+8GR7vERbFEGSRCSNgCQJSBoRjSSM+F+SLDRr\n7iAQOkGp7mV0oocl2dsoy66jVXcLUW0WHa0+jmvUoZbmWoWnKmuZMSuRspkWvIPJMqbL1qMrLB11\nX8w6DWtKU1hTmoKsKJzo8rCzrped9U6Od3oIRmR21PWyo64XqGZaqoXLSlJYW5pKYfLoRQZam7y8\nuamFaFTBbNFw7c35F6cs6inIyDKxdEUqe3Z0c/KEm4wsMzPnJMXnC4JArn0BxzvepqXvIIvzb4vP\n02RkY73+dqzX347s9RCs2K1qvct3I3vdRJvr8TTX43n+CURbIobFKzAuXYlh/iXnXWxhClP4IKOv\nry+e4NjU1HSGg0hhYWGcYCckjF6Qa9IwyVHtSPvwq+70yLYSHkDxNKB46tWEJm8jRDycFZIRwVoA\n1gIEayGCpQD0dgRBIAm4dA60DwTYXNnMryurkdwtzDJ1Md3YS9mWWkRAX2DBVGzGLPRDpBwayok1\ngIwGxZSLJqlEXbe1AAypZ5CNobLtp0a2A4EAu3erpbiXL1+O3T52NNH990cJ7tsBQOJn7kM/c96Y\nywDgcMCyJXD4KHh90NCI2N1D+pxZpBc4uLTAAYtz6e/bgWfjw/Rbk/Hd/1s6IhGk/iOUBmrJtzag\nk0b6rLsiet53ZbHLlcPegUyMRstgJNxNoSNGQbKZ4mQzVsN5XgunJUPWKjHebKyHxnqKikpGLcIi\n2IoRs65ECfWjOCtQespRBk6AHEbpLYfecm7Kg7kmPbqMZUybURhfduDJ36mjr4Dttk9hWX8DAJdd\nmUUoJNPS4GXfrm6ePtTCtgFVw5Ku1fD7/ChZOviSxcN9zRJ7fefohIkmMAwmHcuAf/i8GsUIixM6\nWJ7YyqWJrSTrAvj8Cu52CDX48EUkyj2Z7HLlsNuVhTNiImfIFjLFHCfXWYnGYUlTIAjbjqnf8/PO\nmkxaUlLCnj17aGlpwe/3TygpurszgM876EIyAcs/jSQOSkZMwMgRAZc/TGOfn8Otm+jzvoEkrUKn\nvQKtJKERBSRRQCMJyKEAR17bggzkz1pAT24B2V0NLDArPHVFDq6kZLWtKKIRheFlhz6SOOJ/SRQQ\naxqg78Do+z3uI/xfirUb0jAa9SPJs0ZEkgQ0p3wXxYn0ZLJRosuQ6/6O0rUdMy1Mi/wSMePDzJq3\ngeNbVLItyVYiYZnDB/o4csBJesZNFMTeIuOOz417S6IgMDPdxsx0G59ZXkivN8TuBic76pzsbewj\nEIlR3e2lutvLH3Y1kG83sbZUJd6lqZb4A7y50ctbm1qIxRQsVi3X3pSH7SIT7SHMWeigo81PU72X\nXds6SUkzkJI2nIg5RLbb+o8QlcNozqKVEy1WTKs/hGn1h1BiUULHKgkOyU3am5HdLvzvvob/3ddA\no8UwZxGGpSsxLlmFJnWSoiVTmML/MiiKQldXF0ePHqWqqoqOjo4R87VaLSUlJZSVlTFjxoyJO4hc\nKCYxqg3DEhIxwYJAJ3LLnuGodWiU5CVBC5bcOPEVrAVgTI9Hn+VBr+DGjj6a+tXh7BOdnlM0pBbQ\nzcBpns9s5w5E3z4UQeTg3Ovw1faRIDrJSoyQlRDBqFUQiYK/HsVfH9cYy6IR0VaEYBvcB0uhGtkG\nYs5uZL8PRImjR48SjUYxmUxcdtllY56PwJ73cD/1RwDMV1yL5eoJVhRMTITly1RP4voG8Png/b1q\nwaHSYpAkbLd+ktDBN8hJA1PrQ2isYdArcMqAaUCbQTMlVPjy2d2bQF1vAFdAjTx6vWF6vGH2NY0U\nUufbTczKtDErI4FZGTaKUsxju3Wd4TpSQEFhAdkN9bS2tvLcc8/xla985ZwdSUGfhJC5DjLXoYTd\nKM4KeqvfJIEOtBLMTA+Bso3Y+zsQkmYRaiNetMZ0+TVYP/YZTvZ42dfUx57GPg61uFgjJ5Ap6iny\n6mgRDDQJIbIzEnk7wciNwXZsYpRf5su8a82gU2dBFNR3vyAISCIIqIROkGP4N79AtKEGqzlGwapC\nMrNk7JE6REaOTAnFWfBuJ0owRr14JwkL5nBFJMys5kYuWzgLu22MgNRpdn9nQ1FREaIoIssydXV1\nzJ49+9zrPAVDUe2ERB325MkZXU8wanD7n8XpeQ6AaPR5ZmVEWT3t84jC8Mj35s2bkWNR9Ho9d13/\nIYxGI5R7obuHUmcblBVMuOOvFN6KLIdglIC6cGpk44OGiooKpays7IILE5wLcv9R5JrHIaQmjwSM\nGTzqUoeSbpzzG3rqU6g65CQYHA6xZ2SbmLPAQV6h5YK0j+GozMFWF9tqe9ha2xNPKBhCVoKBtaWp\nzLNYqN7djxxTsNq0XHtzHlbbP4doDyEUjPHiU/V43BFsCVpu/FhhXF7jDfbwpx1qRPvmhT8n2z62\njdSpiLQ2EtirupuEjh1SH7inQFtQgnHpKgxLVqIrmTkuO7AhBINBqqqquNjX0RQ+uPhnX0OyLNPS\n0hKPYDudI0mmwWBgxowZlJWVUVpaev4OIheKUAi2blfv15IitbjIeUCRw+BtQfHUE6p8AyHUhmTX\njfJsFcCchWApHI4qm7MRRA2+cJTmuDZ0pGPCaFWDE4xa1k1LZcOMNGbqg3R99iaUUBDLdR8l6TNf\nB9SEuubmZpqaGnF1VCMFWsiwBslOjJBhi6AdRf0mSzbCx1oJdwaw3PAVOkyFPPLHJwC45pprWLFi\nxTnPS6S1ka7/cyeK34e2ZCZpP/4Tgu4CSI3LNRzlBhSDhJzSg+Ivj7//hhCTJdo9uQhJc8lbtALB\ncKZspd8fjstRGpx+9bvTd8Z7bAgGrciMNGucfM/KTBgpoZRlOHQYOgeLshQWwLQSEAScTie//vWv\nCYVCFBYW8qlPfQpxnO+B/fv38+KLL2LUylyxMIUlRRK4jo7QmyuyQrfLQrlpOc80pFLnHvmjahG4\nQZ+MLSaBAGs2ZFE6bZDwBwKwZ7/6VxRh4fyzarhVx5aTyD0HiNa8hWQ5PY9AAFsxon0egmMeijGT\nzk/dQKyrDdvHPkPC7Z8Z/7MoFoOt70E4op7H6aOPxP/+97+nsbGRxYsX85GPfGTM86kei8LTj53E\n644wf0kyS5ZfuEwtJkd4q+onnOh8FwCjNpFARJWUFaeuZMOs+9FIerxeLw899BCRSIS1a9dy5ZVX\nqivw+2H7LvU6ys9TK02eByoqKli4cOEZD58PfGT7YkNMmoWw6EHkhudR2t8h4Bsexky02clblkJ+\n9QtUH6ijIX8DPlMGHa1+Olr9JCbpmL3AQenMBDTnUa5WpxFZmm9nab6db6wr5UjbAFtqethS202n\nO0TbQJDt5V1oxBCSICDroHBFEibLP79apd4gse7qbF55tgH3QIT33mrnimvURCuLIYUkUw79/haa\n+w5MmGxrs/PRZudj+8jHibldBMsH5SYVu1H8PiINtUQaanH//c+ISQ6Mi1dgXLIS/fyliIYLtzqc\nwhT+pxGNRqmvr487iHg8I+URNpst7iBSWFg4qeXIzxv1jRcU1VYiPuSmjSgdW9XEOUBrASynEDBD\n6mC0WiXXsjmXLp+iEukOP01Vfpr6jtDU56PHe3aSdyrSbXry7Wby7CaW5tu5JN+OdtB+zPmT76CE\ngoi2BBI++un4MlarNZ5cClcTjUZpb2+nqamJPc2N+HtrSdS4yE4Ik5UYIdUSRRJBjLkxTLNhmGaD\nvmfJ6oNvXSEQkTXYDK8TPfQegsYIGhNIJtAYVTcUyYQiC7j//AiaJBlSU0j+5rdAUi6oUq9iBKUo\nCg1OBLcdIRhDbElE0WYj6/qIBWP0N2s4KF1HuyePvJJkLl+eNer2kkw6Fpp0LMxJGjHdFYhwotPN\n0Y7hz0AgQjAic7B1gIOtw4XqUi16yjJszMmwcnWkmyT3YHT8FKIN4HA4uPHGG3nmmWeor69ny5Yt\nrFu3bsxjPnHiBBs3bgQgPbuIJdd8Eo1GQyjooWHfK8jtu8hPC6KTZNLsPq7mLdZPFzjkSWOvp5CA\nbS5leXksybNj00hser6JfmeI7W+2YzZpyMoxg9EIlyweJtwVB+OEW4n6UPqOovSNdGyRBk255GCM\nUIMXIW0J5qu/jKAddvsQUC0AfZtfIFjxPgm3f2ZcvzOgVsoMD4Zo886dgFtaWkpjYyM1NTXjvr56\nuoJ43er6C0usY7QeG6GIl1cP/zctgzKOmZkf4vLpX+W9mt9xuPVVTnbv4MUD/Vw37/vs3LmbSCSC\nTqcb2WE9tbJkUzNkZ4HtwvdtCFOR7UmE3FdJy5Gf8NJg+dwvLv0jUjSBjk9dr0Y7br4b96pPcLjC\nSXurP76cwShRNjeJsrl2jKYL7/8oisKxTg9b93YiNUQQEXApUTbH+vAjYzfpuKwkmbWlqSzMSbww\nr8oJ4uihvrgN1KWr05i9QPWB3XL8V1S2biIjYSa3LfnNpGxLiUQIVR0ksG8HgT3biXW1jZgv6PTo\n5y5Wdd6LV6JJPrN3PRXZnsKF4mJdQ6FQiJqaGqqqqjhx4gTB4MiiEsnJySMcRMYbyfun4AKi2ooi\nqyWSG54bqbnWJRBqdBE+2U1s2lp6ln2chgFBlX44fTT1+WlxBUaNUg/h1Cp3efZhW7HcJNMZBV7i\nh3P8MN333QNA0hf+Y0JyDUVRcLlcg9HvJtqa6xH8LWTYwnECnmw+0w3l/CBCnKCrfwWNcZCsDxL2\nwelqGz146pGdleBtGF5NzIEUvARBUaOzilFHj6zjlYMmZElPsjnEdffMPa8g0ulQFIVWV4CjHW6q\nOtwcaR+gpturOkoAEgoPZse4PEH9f5NfT5U1jVlZiczKsJFnN8V1yC+99BL79u1DEAQ+/elPU1hY\nOOp2W1tb+cMf/kAkEiEtLY0rPvJxDnX52dvYx4GWfsKD7h0mMcKyxFbWOZpZltiKXoyespbBaHPy\nYoTkRfijNjY914h7IIJWK3LNTXmkDhWROyXCrQgKsv0kSqgCOO16NaarCaW2WTgf/hPB/aqGP+Hj\nn8d22ydHNA3seY/e738dRJHMp94iojOM/SxSFNj1Prg9kJaqEv9zoLW1lYcffhiAr33ta+NKpt6z\nvYvKCie2BC233V18QSP83mAvGw/eT69XLfC0tOAOlhXdhSAIKIrC/san2XXyMQASjTk0vZdK0CNy\n2WWXsX79+pEri8XU6HYgAElJaidogvs2Fdn+J0C0zyWUczXUPYoGAfHoz/GeSFGjHRYbCTd9giSL\nlbxCKz1dAQ4fcFJX7SYYiFGxp5dD+52UzEhgzkIHSRfgECIIAnq3gq4xioKAOUELBXrSGwPU9/ro\n84d5qbKdlyrbSTBoWFWcwtrSFJbk2ce0o7pQlM1NoqPVT32tmz07ukjNMJKWYSLHvoDK1k10uk8Q\nivrQay48wVHQajHMW4Jh3hISP/01os31qq3gvu2ETxxBCYcI7t9JcP9O4Edoi6artoJLV6Mtmjb5\nVaumMIULhM/nG+EgEo1GR8zPzs6OE+yL6iByoTjPqLbiaSB28knwqC9WRdTRZrmcg+Eyjrs01Fbt\npk3voL/RBo3HR12PAGQkGMhNUgtl5CUN+/SmWEaToIyyT7KM648/BUCbX4x5/fXjXhbU53VSUhJJ\nSUnMnauO6oXDYVpaWjjx9GPs7+jE5UjFbouSkWzhyrUr0IpRlGgAYn6I+iEaQIn6IRZAHuiGqB9B\nL57lOGS1WmB02C/59HDbOcNvok71oLbPhYTZ0NwL9Y0IgTDJSpjFaQJHWt3Mr3oE8c4nQHPhnUtB\nEMhJMpGTZGLDTDX/JhSNUd3lpap9gFndDcwW1PvgLz0iD3fHgA5eOqwGvSx6DWXpVsoyE5hZtozk\nhkZ6e7r5+9//zr333ovZfOa7xul08tjjjxOJREBnZIs0i6efPXxGuzx/F5fOL2HZ7EXMz05EL0ZV\n7/Ce/Sh9hyAWBHctsrsW6p9Gby3iupXzeWNnGj0uC/94qYm58xOYkd+Lzn8ExXgCKTgXQbEgOguQ\nDc0o2l6EhGmqFeFpji3JD/yE3ge/QbB8NwN/fUS1Bbz1nvh8/ZxF6j0WjRI6tA9xyaqxT3i/SyXa\nMK57MzMzE7PZjM/no6amZsznzlguJBOB09vIxoP34wl2IyCydsZXmJN9bXy+IAgsKfgYZr2Dd479\nHFegBcvcToSqMlauXHnmCiVJlY9UHIT+fmjvgKzM896/UzFFticZQZ06vmMQJIh6MeYMEMgyYrry\nTkTL8JBESpqRyzdks2R5hKOHnBw/4iISljlx1MWJoy5yCyzMXeggI9s04Yux5piLbW+1oyhgT9Zz\nzUfyMJo0fJYiGvt8bK3pYUtNDye6PAwEo7x6tINXj3Zg1kmsKEpmbWkKlxY4Ro3iXAgEQWD1FRn0\n9gRxu8K88482PvKxAnLscwEBRZFp6z9MYcqySd+uNq8IbV4RtlvuIjbQT3D/LrWE/MG9KAE/kboT\nROpO4H76T0iOVAxLViDNv0SNAE1hCv9DcLlc8QTHxsbGMxxE8vPz4wQ7MTHxHGv6F0EopA7Tgvoy\nH0cikhLxIDe8gNL5HkN0sM84l+8cm82BbgnoURvaCkYsZ9ZJceeCU4teZCcaJ+355t+ymXCN6tqQ\n+JmvT0rFW51OR1FRESnTihnY8yYShUhf+g3Nzc0oabNHLf0dKN9F78+/e6MDMwAAIABJREFUCoqC\nac16ku59ACE2RMqHCblK0P0o8e+Bwf+Hvg8uEwuCPhnBMUj0EqePLPYy3UHUkYp/z0FsUoR5Dg8z\npH5ctUG8Lz89gvhNJvQaiTkZVuZ0NYCgjugEcnLJL3Fwd6eHI+1ujne68YVjeENR9jb1s3cwAdMc\nLWaJ4MTtdvOrR5/kwzffzrQ0KzFZ4WCri/dr2mnb+TLaiI+ooKHCOA9vSL1W7CYtc3pPMKdpP3M8\njUz/7o/Rl53q7iIhJC+C5EUochilv0ol3s6D6vn01KHz1PHhInAG0nEHbWQFG9HWhuOdnJixByl4\nJYJsQgxdDmWzENKyznoeBJ2e5G/9hN4ffINgxW4GnvydSrhvuRsA0WRGP3MeocPlBCrexzwesj10\nb1otYE86d1vUZ1BxcTGVlZXU1taOmUvQ2x3EMyQhKR2/C8npaO0/zKZD3yEU9aIR9Vw1+9sUpV56\n1rZlmevRYuG1w/+NpI+QOP8YzmA1ZvOCMxunpUJqCnT3wIlqSE0F7YXf01Nke5IRCKt6MpMpCzmg\nIOrBcWsB4qw5Z21vtWlZtiqdhUtTOHHUxZGDfXg9EZobvDQ3eElONTB3oYOCEhuSdBrpVhTweNUh\nD5sVDAZOVLl47221R5+cauDqG3MxGId/5ny7mbsvMXP3Jfm0uQJsre1hS3U3RzrUB9NQBUuDVuTS\nAgdrS1NYXpiMRT95l4pOL3HlNdlsfKYBryfC1jfbWX9dDmm2Urrc1TT3HZx0sn06pIQkzOuuwbzu\nGpRImODhCoL7thPYu4NYTycxZze+11+C118iRatjYN5SostWY1y8Asl+9gIEU5jCZEBRFLq7u+Ml\n0tvaRsqfNBrNCAeRMyJzigJer2rdlZI84WHQi45To9oF546cKYqM0rEVufHFeDQ2qk/niZ6V/Hnv\nsHNKVoKBHF2U5ANbyfJ3M/eb36Ig04HDPLEo9UQh+324/qIOoRuXrcEwd/Gkrj/uSNLWQpLFfE4p\nUKS9BeePvw2KgrZoGklf+jai1gBaE6DK9SZ6JhRFPqcnuCwrvLPbQ2tDGouSB5hr96BPTCL1xs/i\nPbqHWG830lnkeReMM5Ih8zFOK2W1ILC6RN1eTFZocPqoGtJ+tw9Q7/Th01g4YZrGTN8x3B1N/Oej\nL9JpKUBAIBqNsMBdTkLUh4zA8cT5zCrMY2m+nSU5NhIf+S9C5btAEHDc//9OI9ojIYg6BMd8cMxH\nkaMoriqU3nKU3gqI+nAYO3EYO+Pt+/wpNA8U4dXMJLe4lAJnDUIwCAePwSKDWnXybNvR6Un+9imE\n+y+/BQRst9wFgGHBJYQOlxOs2I1pLNlwMDh8Tkex+zsbSktLqayspL6+nkgkgvYcHeihqLbVpiU5\n9fxGPmq7tvP60R8SkyMYtDaun/cgGaMUkxlCy/EQfRXTSZpXC7owGw/ez5Vl32BGxlm0+zOnQ68T\nQmGoPTlqsqSiKMj9TqJd7US72pE9A5B5dkncFNmeZPjDavarQTbT+3gFjtvykWxalJqHkTVfQnSc\nXf+k00vMWeigbJ6dhlo3lRVOeruD9HYHeff1Niw7u5g138GMsgR04QB0dkJHl2rFNIiIqEU/oGFu\nko6Q0col12SjN47+E2clGrljcS53LM6lyxNkW60a8T7U6iIYkdVky5oetJLA0nw7l5emsqo4Gdv5\n+p+eAkeKgeVr0tn+TgfNDV4qy53k2OfT5a6OJzn8syBodRgXLsO4cBmJn/smkYZaAvu2E9y7g3BN\nFUIkTHj/DsL7d9AP6ErLVFvBpavR5l+Y3mwKUwDVQaS1tTXuINLbO9LdwWAwMH36dMrKypg2bdqZ\nDiJDBLujS01uGnouJCbCnFlg+RfxnZ9AVFsZqCVW91fwqj7TiqinXFnF/e9n4Iuo99zsDBvfWFfK\njHQb3jdfpr/uVcREO1mlkzP0Oxbczz+B3NcLGi2Jn7x30tc/5LVNNILc3TlqOzngx/mD+1B8HkRb\nAsnf+smo0e+JYKziO/t2dtNU7wUExJnTEAoklEOVCIEg1jmXEtuxC9asUa/DycJZiDbTSs8ghpIo\nDPpIW7hujno9+MJRjnd6ONJewPEdPkRnE8X+WlzaJDySjTmewyRE1YDZksuv5vtrlqHXSCiKQv9v\nHsRXvguAxE9/DdPyy8e9y4KoUaU39rkoxXeiDFSj9O6HiAfZMoN6Zz6HGsDVpybpVjf3k2x1cE12\nD3o5DOUHYNGCsQn3979O8MAeBv7yMIgCtpvuxLDwUgaeeBi530ms6eS5dzRu96cZ1e7vbCgpKQEg\nEonQ2NgY//90qBISVaJScJ4SkoPNG9lW/VtAwWbM4Mb5PyLJfO4kzmAwyM6dO4kGzBQqH2fA9Bb9\n/lbeOPojvKFeFuXdOnJfTCY1yfZkHUpjE5FogGh/N9GuDqLd7cSG/nZ3ooRPK4L1vT+cdR+myPYk\nIxhRe21iUzux/jCud4I4bs+CYDfysd/AtM8ipi4ddXlJEiienkDRNBsdbX4qy500N3jQhfxEq5z4\nW/zodNGzLquVIxRYIxRYA8AAbG9TI95JierDLikRDIaz9lbTrAZuXZDDrQty6POF2Xayh601Pexv\n7icSU9hZ52RnnRNJFFicm8Sa0hRWF6fgMJ+/bdj0WYl0tPmpPT7Avl3dLFo/A4BebwP+cD8m3dhD\nWJMNQRDQFZaiKywl4bZP4e9oo+HVF0hubyRyeD9KKEi4popwTRXuv/4eKSVdTbBcsgrDnIXxEshT\nmMJYiMViIxxE3G73iPlWq3WEg4hGc5bHtcerkuvOzrgl2wi4XLBzN5SWqFHk/+mO4Tii2kp4ALnh\nOZSunfFp3Yb5PHC0jCrn8HD+l1YXc3VZejz5LdqmkvLzKdN+Poh2tOLZ+BQA1hs+hiYje9K3ocnI\nBlECOaYen/FM0qooCn2/+j6RpjoQRRzf/CGatIvf2ThxtJ/KCtVWcsbsJGbPt4MgIKxaQXjzq2gF\nPZLehLJ7L0JhgZoIe6EuOOMk2qPBrNOwKDeJRblJBOf9f/bOO06Os77/72nbb2/v9qqu6XSnXi3J\nKlaxLYwrBmwCBENwQk0A/yCmJIGEUEIgFBMcEicQcDAJ1RRjwBhsbEuyZMlWs+rd6Xrvu3dbZ2fm\n+f0xe3u313Tqcvm8XqOZm7Izs5qd5/N8nu/38/0L7r//foaGhrjWPEWgqILuITsc6eabb+a668bD\nIUZ+9B2ij/8SAN8dbyfnDW8751uQZBUpbznkLQdAARZXwqI1gs72KMcODdHaFGFgVObhhiCvr+wj\nRzMRzx+E9VchzVTa3eEk+PdfZeDzHyV5aB/hB/8NJImcO/8MOS+INTyIfmgfLJoh4dE0oa3DXq4o\nP6v/K7/fT0lJCT09PTQ0NMxItgf7k4yE7A5FzVmGkAhhsavh2xxotT20i3IW8carvoDXeebCTnv3\n7iUej6OqKq/Zfjua63U8cvhTdIdPsrvh24S769iU2oTV14PRmybT/b0UXnsHqj8Pa98+Bn/537Oe\nQ3J7UEtmfge87Ml2e3s71dXV0zdUFwFjyrbaYb8Mcu78S5TVV2Me/TLEurBOPQBWErlk9tgpCZjn\nt5i3LInpH0RJxLO2R1IKQ1qAnMUVdIRkGvZ3UOzSqco3KctJ2cNPQkB4xJ7Giog6nRDIHSfguf4p\nP6p8r4M7V5dx5+oywvEUuxoH+GN9P/tahtBNi+dabLP+f/lDHavLAna1y4WFlPjPTkmRJIltryll\noDfB8FCSY7sCyNUalkjRPnSIxSU7zurzLgbkvCCJdVvJfef7cUiQPPKCrXrv34U52I/Z30Pk1z8l\n8uufIrk9uK7aiHvDdjveO/fSdxZexZUNXdczDiInT56c4iASDAYz8dcVFRXThw3MRrBdTigpgdJi\nSBlw9LitJp+qg95eWHkZVe4zqNpCmIiuJ7Fafm7HFQO6cx7/1b2FHzTYISOKJPHWteW8d0v1lNA2\no8uuRKnNm13lulAIffcbkNKR84KZGNkLDUnTUEvLMDrbMDtboXYq2R79+feJ7/oDALl/fg+uq2YW\ncy4UOtuj7HrSDlcsq/Cy5fqScWVQUdBueR2Df38PuSu3oOUV2gVx+vrsUZZzVbnPk2hPhsvl4q67\n7uKBBx4gHgkTb7AV7c2bN3Pttddm9ov84VeM/O9/AuDe9loC77rwIxhgt4fllT7KK32MhHWOHxnm\n1LFhftVWlCHc5v6DdBUvpnRNxbROL7LTRcE/fG2ccH/3fkDCte4aYk88OjvZ7u4BPW1/WXX2HdZF\nixbR09NDfX09t95667T7jIWQ+HI0Covnzhcme2jPD17Nbav+EYc6ez6VEIL4QB+7nn4agNX5OZj/\n+wDJ3k62DPSwZ7VJV7XC0chOhhqeZMPvYigTjH+Gd/2awtv+DFdZNZ5l69GjQ6hF81CL56EUz0Mt\nLkUtmodSXIqck4skSXQeODDttbzsyfZ3vvMdFAlKc3xUlpZQVVNL9YqV+POnH445X8TTZNsZt+Pm\n3FtvQJJllNWfxDz6FYi0YtV/B8wEctmN2QePxWBPChEZo8KW00kfuRxslWkPq4AEdWMFK5yoBXls\nuKUSySHbsVfDIQiFbXUrPGK/rJJJu7rWWIUtSQK/H/Jyp1W/c90ar1tRyutWlBJJGjzbZBPvPc2D\nad/TEIc6Qtz3xwaWleRwfbp6ZWXe3CrRaZrMa19Xzs9/0EQ8IuNM1RBXT9E2ePCKINsTITtduDds\nxb1hK0IIUo11xPfvJP7cTlKNpxDxGPE9TxHf8xRIEo4lK3Fv2I574zbUygWvhpu8QhGLxWhpaeHF\nF1+ksbFxioNIWVlZRsEuLi6e/jmZK8EOBLLJx/YtcOIUdHbZ74PLqXLPompboZNYp/8XYrayJhQ3\nu43t/MPuYpKWfZ3rKwN87DWLqCnwTfvxqXT1SHXe+VeiPBMSR16wf+dA4O4PIXsuXgdGLatKk+02\nqM2uQZA49Bzh/0nHjG9/LTl3vuOiXccYQsNJ/vBoO5YFgTwHr31d+ZR8IklV8d55F73/9HH8G28g\n56ptSJEo7NlnD8+frcp9gYn2GMrLy7nlllv49a9/DcCyZcu4/fbbM7/B+IG9DN//BQCcK9YSvPcz\nZ1UU7Vzhz3WweXsx6zcXcvpUmJ1HHGzP6SBHMynpqePJ7w+Tt2gey1bl4cvJ7rRmCPfn7iV5eD/h\n734D9/W3AJA69SJSMjH1hEJAS7ojXFxke3+fJRYuXMjOnTvp6elhZGQEvz9buc52IcmZc3s4nYf2\nDUvvRZGnp69WIkH0sYeJPvkbjO4ODviKiJUuRLYsVjzzKyLGeNjHplY4fL2LplVOOhdq7MoLcv3p\nWrzBygyZtgwNOZYg/+a3Im3fds7Jki97sg1gCugYidAxcpo9dafht7/DbySZJwvKczxUFhdRUlGF\noyTdWyksQTrLUp1jiEXtYShn3CL37g9lfpiSloOy6m8xj33NrgLV+H9gJpErXpeOtZwagw3YxLek\nGEpLkAO5lEgSNxoW9SfCHD04SGjY7onOq/Bw8xsq0TR5/LjSEnsCMC0YHRkn4MMhm5ALAeGwPU1U\nvzOhJ7k2GVcUfE6Vm5aWcNPSEhIpk73NQzzV0MeuxkEiSYMTPaOc6Bnl33c2UVPgZceiQq5fWERt\noXfWH1Ze0Mm2G0p56nddGIM1UHyKtqFD5/T9XypIkoSjdgmO2iXk3vU+jIE+Es/vIr5vF8kjzyP0\nJPrJF9FPvkj4e99EKS7DvWm7XUxn+VXn/Hy9ipcGQqFQJv66ubk5y0FEkqQsB5G8vBlGQM5IsO33\nwhSCPRGaBqtX2vtdTpV7BlVbJIewmn6E6N+X2bXLuZ5PHF6SqcJXlOPkI9fVcsPiohnfI8I0M8r2\nxQoj0XWTrvYYnS0jFDz4RTxAqnQhvZXbCIZ0/LnaRelQaxXzSezflQmTGYPR08ngv3wKLAttfi35\nH/70Re/QJxImv/tlO8mkhdOlcPMbK3G6pifNrqu34li1jvCe35EM9VFw2zuQYvGzV7kvEtEew5Yt\nWzAMg0gkwk033ZQZTdJPn2Lwi38DlolauYCCv//q+VXgPAdomszSlXksWRGgr6kQ9dQR3HKKHYV9\nPH7M4vDzA1TX5rBiTT4lZePOZTbhvs8m3Ef2E3/qMfv7Mk205jpYuy77RKEQjIWxnUOBKYD58+ej\naRqpVIqGhgbWrcs+x9BgknCar1QvnFsIyWwe2pNhJRNEf/szRh5+CCtki5ApSeZwumO/bKSXQKlN\noJWitCpdXMZNRSUctp5jb8cPGSgweLIqxh1X/Tl+d7H9wdEY7HoWKanD6dOw9NwqS77syfZ7c6Bz\nOExnQqdbdjDgzsGSZEZUJyPAqagFTT1oDR0Ux8OURMOUxEeY59LwFhWjFpXaQwZFpaglZahFpSiF\nJUjThKVYhkHcGAEFfEULcK3dlLVdUj0oKz+BdexfEUOdUFeHqFeQ9EkvqwzBnkapAlRVZtmqPJau\nDNDWHGE0nGLJysDsBQQU2f6siS+3jPodguEwjITBEnbD2NM7/nKTJDvcZEz5DuTicrvt8JFFhaRM\ni+fbhnmqvp9nTvczHEvROBClcSDKt/e0UBFwZ0JNlpX6MzGWE7FoaYCezhjHTi+G4t8wkughFOsi\n4Lk0iU7nC7WgCN8tb8J3y5uwEnGSh/bZxXT278YKDWL2dhJ55IdEHvkhkseLa901uDdsw3X1FpSc\n3Mt9+a/iAqCvry9DsDs6OrK2jdljrVy5kqVLl+LzTa/Ozolgl5TYv8OzIRtFhZdX5Z6kagvLQHQ+\njtX6CFi20pR0VvCN9k38otkeFdMUiT+7upI/3zgft2N2FdTs7wHDthO7UGTbsgR9PXE6WqN0tkUI\ntfZQ0r2Xsq7deCJ2x+H5sj8l9Nsu+3o1mfwCJ/kFLoKFToIFLvILnDic5xenPO5IMl6d2EokGPin\nj2ONhpF9fgr+/qsXvRquaQr+8Ot2wiEdWYYbby8nNzBzjookSQTe89f03nMXiRMHGd20Ff+yjdDc\nYj/bGZW71m6fpsNkol09/4IS7bHrvO6667LWGb1d9H/mw4h4DDm/gMLP3o+cc+42decLSZIorglC\n6WasvfvRkgluLhvgsc4CmhqgqWGUYKGTFWvyqV1iV6SWXS4KPn0fA5/7a5JHnreFNcDRcHzqCcZU\nbd/c7P6mg6ZpLFiwgLq6Ourr66eQ7aZ6m8x7fSrFpWd+Vs/koT0GK5kg+tjPGXn4e1jD6ZF+RcF7\nw+0czi0hfvI0sixz6z9/nfz86eO7N7GCnNwKnjjxNYaibfxo/z3csfaLFObUgHc8WZKWdGXJnLOv\nLPmyJ9tlH/0MNemsbKEniXW20V5XR1trC239A3RGE8QFpBSVDl+QDt94eEleIkJpfQslhw9TEgsT\nSMZs6yRZRgkW2rE6JfMyMTuJwU6s9OHBG94ytfc1GkHq7kEOXYMUj2VtEk4nUukMQ8EzQJIkqhac\nRznR6dTvkRGbfE9Wv0Nhe2pJqysuZ4a8a3m5XFMZ4JrqIH/72sUc7gzxVH0/TzX00zeapD0U56H9\nbTy0v42iHCfXL7SJ95ryAIo8fp/XXFdCb88iOkwXKAlOd7/A+prXn/v9XSbILjfuzdfh3nwdwrLQ\nG06Q2L+L+L6dpJobELEo8V1/sOMsZQXnstW4NmzDvXHbuPvAq7gosBJxsExkzwxk9ywghMhyEOnv\n78/a7nQ6WbJkCYsWLSKVSrFmzZrpq7ZlQsemIdhOp/1OOBeCPRmXS+WepGpbo6ewGv8X4ra7hlC8\nPJnczmf3F2AIm3RtXRDk3h0LqZhjONqYqg2cc6KiEILwsE5HW5TOtihd7VGMeILi/oOUdz/LmqGj\nyGK8ml9oxc0oC1cgDyaxLEilLHq74/R2Z+fX5Pg1goU28Q4WuggWus5KBR97J4jRMFI0YjtjfPML\npJrrQZLI//g/XZTkzIkQQrD7j910tdvt1rYb5jGv/MzPi2N+Ld6b77AVxx9+B+9/vw6lpBhePGor\nhhmVe6WdSzQRlgVHjmYT7SUXlmhPB3M0TP+n78EaHkRyeyn87P2oRSVnPvBSwONG3rwB9u1HjSe4\nrXKQXeFSTnXLDPYneeYP3Ty3q48lKwIsX51Hjt9Fwae/zsBnP0LyxRcAcB17PmukLdvur/K8vt+F\nCxdSV1fH6dOnsSwrK+dkLIRkLi4kc/HQtpIJor/7he0INIlk+9/6LkR+IXu//GUA1q1bNyPRHsPy\neTfhcwZ59MhniOqD/OT5j3D76s9SGVxrl3Hv7LJtlo+fhI1nX1nyFV+uXQjB4OAgra2ttDQ10dbS\nTO/g0LT7Og2dkliYkliY0liYolgYbcLLN+qXeOxddu/37mseJN9bOatSJRQDIZ/GUtuQSpciL37X\nGa2WLjlmUr8nQ07Hfk9Qvy2Xi5M9o/yxvo8/1vfTEcpuhPI8GttrC7h+YREbqvLQFJlwSOehpz6B\n4TuKN3k177n1i8jyRVbdZsGFLrVt9HUT37+LxL5dJF58IaPGjUGdV5m2FdyOc9nqC1Ig41XYVf6i\nj/+S0IP/BoaO/673kfPGt087QjUbTNOkubk5Q7AnO4j4fL5M/HVNTQ2qqk7/DE3MzYhEsk9yIQn2\nTEilxlVuAFmGxQvPylt3zjhVB00tCEXGmlePGN6f3iDR4tjAJw4tpD1iq7/lATf37ljItpqz87If\nffTHhP7zKyiFJcz7n1/P+bh4zKCzPZpRryOjBgiL/FA9Zd27Kel9Hs0cf29JLg/uLTvwvuY2nKvW\nI0kSpikIDScZ7E8w1J9kcMCex2LTu0YBqJpkK+BzUMHNkRBdb7O9gIff/XHKrSTRB+8HIPfuD160\n5MyJOHJgkOd22oRszfogG7cVz/lYMzxM93veiIhF8d5yJ/kf+qTtfFF/2la5xzBR5R4j2t1pu8Pq\n+ZeEaFvJBP1//0H0E0dAUSj87P2XJOH0rBGLw779EE8gZJmh+cs52GjR3DAyJmAjSVC1IIcVV+VT\nUiDR/zfvI9V4CgC5oBj3xu14tt6AljSReweQnE7Ycd15Ocb09fVx3333AfChD32I8nK7Ezg8mOQn\nDzUC8Pq3zKe0bOZO9Jk8tIWeJDJGsofSFqmygveG1+F/67tQS+wCQM8++yyPPvoosizz0Y9+lGBw\nbnl6vSP1/PLQJ4npw8iSOu7F3dtnV5YEWLMKUViAGR7CGh7CDA1iDg8iEnHqyxZOW679FU+2p0Mi\nkaCtrY3W1lba2tpoa2sjmUxO2U8CimQoTUUoHu7DKXez780OgiLI2yo+jdYfmnUoWAT8WA3/g+jd\naX9e4Qbkxe9HmiHw/4rARPV7LP47MU3CBWSp3yKQS2NK4Y+nB3iqvp/TA9nfi8+psnVBkB2LikiG\nHudk+EEwfGz2/iebts/d7/NC40KT7YmwYlESh54jvm8Xied3Y42EsrbLPj+u9elwk3XXZFUgfRVz\nR6q1kaFv/rPdgE6AVr2QvA99CueSFbMer+s6DQ0NGQeReDy705ifn5+Jv66srJziIDL2DK2YPx/n\n0PDlI9jTobcPjp2w1Wewz71qBUxTwvqckEwint6JZFpYjuNYDvv/IO6az5ebN/C7Nns42anKvHvz\nfO5aX4FTPfvGfvg/v0Lk0R/jXLOBoi/8x4z7GYZFT2eMjtYoHW1RBvvH313eaDdl3c9S1rsHd3yC\nz7ks41qzEc9rbsO96do5h2vEYwaD/QkGB5IM9ScYHEgwnFbBZ8JMKnjX22/ECg+TWLUB17EDYJm4\nt+wg+Hf/ctHjtFsaR3n8V/bIwfyaHG68vfyszznys+8T/u43QJYp/rcf4JifLvwxPAwvHrNVbrBH\nV1ausEdQLzHRFqbJ4Jf+NpP4mv/Rz+LdcdtFPed5IRaH5/bb7a8sw/q1RJx+Trw4zMmjwyTi47Ya\n+UEny5a68X/+TjCn6wRKyF4fSkERciCIkpePnBdECeSjBILjy3lB5NzAjCKQEIIvfelLhMNhbrzx\nRnbssE0OXtjbz4Hn+vF4Vd7x3oUzPj+zeWgLPUnk8V8y+tP/wRxMjyLKCt7X3GaT7AmjO6lUiq98\n5SuMjIywbt063vzmN8/pKxWGgRkaYqS3jmcPfJ3UUD+umMUCxwoKzCBWW6tNsONRrERs2s/o+9x/\nvUq2zxWWZdHX10dra2tmGhwczNqnyOPhqko/q4oKCTJJlZmlIRXCwmr8AaLLtm6S8tcgL/tgdknc\nKx3xxATynU60OIP63a+5ebo/xW+aQhzvzlYHC70DvHahbQzvavhbbr150/mFy5wHLibZnghhmuh1\nx9Jx3jsxWpuyd1AUnCvW4t5gq94Xe9j45QChJxn50XcY+dlDkHYAcW97LbLHR/TxX9g7SRK+2/6E\n3Ls/mBVaEovFOHXqFMePH6e+vp5UKnsEorS0lOXLl7NixYqZHUQAIhFS7R0YbR24TTN72+Ui2JNx\nEVVucWgXUncMgY7pfQRLc/Hb6Db++XABIl3P8IbFRXz4utqztg6diP5/uIfEwb34bnszeR/4m/Hz\nC8FAX4LONlu97umKYZrj7yZNH6Ws7zmqBvbiHcgu+KFVL8Kz41a81918warGjqngQ/3JNBGfmwqe\nE+3E13cKRyqCbBmofj/+178Z1eVEliUURUJWJBTZnk9cVhQpa59p95eZ9hke6EvwyE+aMVKCgiIX\nr3/L/PEk/LOASOn0/NVbMLo7cK7eQOEX/n38fKYJ9Q3Q3Dr1wOr5l4ZoC0HoW18j8qsfAZduxOC8\nEYvBc8+PE+6r10IwiGFYNNWPcPTQEAN94x3Kyv49LGh+BGc8hJyKn3VFUQAkCdkfQAmMEfIgcp5N\nxJVAPnuPneRQUwsF1TX8+T0fRlIUfvpQI0ODSZavyWPr9VPFs9k8tEVKJ/L4I4z+5EHMwbSLmqzg\nfc2t+N/67iltYX9/P0888QRHjhxBkiTu/chHyFfltPo8ZBf3CQ2LPFMuAAAgAElEQVRihsaWhzCH\nB7FCg1gj4XP5RkCWkf15KMFCOu/+61cm2S5/9Pto+YV2jywvP907K0BO99Ikt+eclIFIJELP6UZE\nVzdBPUX+pIpu4WSSYwN9HB8awvTnUFVVRWVlJVVVVeRMCq4XQmC1/AzR/igAUmAZ8vIPIykXj9xd\nVIyp32PkOxSCxNSRAQBcLuK+HE4mZB7vSfLrtgi6gDuWfwO3FkXrvgN5+HpKNuVy/coi8jyXthNy\nqcj2ZBjdHTbx3reL5LEDdoM0AWpFtU28N23HsXgl0vkWi3iZIXF4P8P//sVMLK9SVEreB/4G99V2\noYrk8cMMffOfMdrsTo0SLER+5z00eQKcOHGCpqYmrAkSpCRJVFVVZRTsWeP/JroLTadgj7mIXE6C\nPR0uoMot4r1Y9T9C7qxFQsXSjlHn9fLxQzX0xuxntTro5eOvWcjVVWcuSnEmdL37DZg9nQTeey/s\n+JOMct3VFiWRyP7tyKbOAv04Fb17cDW9gGSNb5fzC/BedwueHbfiqJ6+MMfFwJgKPjSQzKjhw0NJ\nLPPStc+yzCSSLpNMmKRSFh6vyp13VeP1nbuLUmzPUwx+4eMAFHz6PtwbJ9WaGBrGevFF5JhNDrvy\novSUChyaB6fqxaF6J809qLLzvJV9YZqM/PRBRr5ve2l7b30TeR/425eOVesMhBtsbtHbHef44SGa\nGkayRlUky+CNxc0EzCG6BlMc6wanHsahh3Elh3EZIzhTERzJEFpy9NyuTZKQcgKMmB6EJOPP1aZ0\n1gSCSKKfhGG/Kx2KB7+rCAkJa3QEMzycpcZLvhyU3Pwpjl66rhONRkmk31+yEORgoemJTHLo2V67\n7A8QdRmMOOMkPBLuwgpqczeiJlIonhzkLVtRyitsj+10G3zgwIFXJtku+vT7Z91HcjrTwyZ2r0zO\nIuPpYZP0dtntmTWZKSEbnOQwp61OGg6XT4nnHEN+fj5VVVUZAl5SUoIsy1htj2K1PGzv5K9FWXEv\nknqFlFk+X8xR/RaSxJDmoj55ikH1EF0RH6LtL+gTOr8xh6jI97C4OIfFRTksKfaxuDjngpSPnwmX\ni2xPhBWNkDi4l/hzO0m88CxWJPu5kv0BXFdvscNN1m6+qJ6/VzrMcIjQd75O7Mnf2CtkhZw3vA3/\nO94/ZfhfpFI0/9+3ObrzaZp8QXo92QlaiqJQW1vL8uXLWbZs2cwOIjArwRYOB/2KTO7SxTiLi68s\ngj0Z56lyCzOJ1fYoouMx5MQK5NQyhGTwj8PwWKf9/XsdCu/bUs1bripHncmF4iyQiMQ5es9fM5C3\nnOGF1zGamNrx9HgUah3tlHTsQju6ExEdJw+S04V78/V2HPbqq6+YjqtpCsLDSQb7k3TvPchAYzem\n4kIqX4Dk9WOaAssUmJY9n7hsXkCSrqoSr3/LfAqLz8/tRAhB/9/9JcmjB1DnVVLyHz/OEKZwvJuD\nrQ9zquMJlhvL0KUkR6UjnEl6lSUFxwQC7lS9OBQPDm182SbmPpyqJ4uoOyQ35vP7if/oIawOO4HX\ntXE7BZ/6yhXzDMwZsxDuMUQjKY4e6qexYRBNdZMr4txUaP/OH20rpCs+c/smWQaO1CjOZBiHPoJT\nD9tTMpwm6OPrHKnIjJ9z2TFRlR/jdRNU+SwumA6XsYTJU6e+yYsdvwKgIncVd0begJxI2s4tk5Il\nX7Fku3L3b5FGw5jD6SGE0ABimvjruUDSHMhuL4onB8XtRfb4UHICKKXzkCuqOMZhDkafIlixhjdf\n/XVCoVAm7KStrY2urq4stWwMDoeDyspKKisrWVnYR+GoHVKCrwplxceQHJfPcuiiwTRhZHRO6vdo\nSqEv7uBIXOLRaJK6hERKjD/LpX5XmoD7WFKcw+LiHAq8jguiTFwJZHsihGmQPPkiiX3pcJOOSUOv\nqopz5TrcG7fb4SZFly/e/VJCCEHsiV8T+u6/ZoYCtYXLyL/nkzhqlmTt19nZmUlw7Ovry/oczTSY\nHwuxYu1aVv3p3bhnU3UjEZtcd/fMqmAn3C6OnzhxxTxDc0JvHxw7Dsl0RbkzqNxCHyHevge553eo\n5jBYTpTYG5BQeaTfwa/6PcjA4qIc1pUFcCryjCTRmrQ847qx9dPEQGuaTGm5h0pfmGDzLqznHsfs\n6RzfQZJwrroa745bcV9z/RXfQbVGRxj4ty/QX1xBzdvfc8bnSAiBEIwT8mm+t8lkffL3bJoCIQQV\nVT78s1j8nQ30xjp6P/wOEILAe+8ltmM9L7T8mIbenQjs/0hNcVGSu5SUESdpREkaUXQjhmHNkBt0\nAaDqAp/hYeHi26ktvY5i/6KXjrI9himEex0Es0eNstqzk3XQ3YPw+UhevRE9aZGMpxg9dpzRQweI\nNjaRkp0YqpeU5sHwBRFFVRi5RaSEip40SSZNjFQ2h5Qsg+G+R1AS3RTIhRSqpWipCCWlbubXjo/q\n66kox7oeI5q0DSkq89ZQMugmeeSF8c6wJKEtWIxrzdXIEyoyG4ZBR3sHzS3NJCbk0Phzc6murqa0\npARJUVH8gQnCacGs8eazQQjB8y0/4NnT3wVgtWMzO6Lb7I1rVsG88Xb2FUu2JzdwQghEPDYhXmdS\nHM/wIFZoCHNoACs0iJgUqzkXGC4Nb+1KtPm1aAsWoVUvRKuswZBlOjo6MsmXra2txGJTg+zXlsd4\n48owsgQJKY9EzYcIlta89H78Z4t4PGM5aAz1I42MojBVYTAEdCZV6qMKp2IKx+MSXQbEhUUckySC\nfI+WUcAXF+ewpMhHWcB91t/hlUa2JyPV2WonWO7fSfL4EbCyh8y1+bVpW8HtOBYtvyTVzy41Up2t\nDH/zixlrK8ntIfedH8B325uRFAXTNGlpackQ7HA4Oy7P6/WybNkyalJR8h95CCmdqKrVLiX/nk/h\nqJ1QxGCMYPf02KNcEzFDiMiV/gzNCF2Hk3WTVO5FGXuw+GiUUONzKMP7CMj1yJLdllhCZmj4Jkoc\neSRNiR82lZK0Lq5SKFkmuaPNLHjtBsoKwVe/m/jTv0U/+WLWfmrlArw7bsVz/S2oBXN31LgS8JJ9\njiZh8Bufo6nut9Rv8NBXNv4+9jjyuKryDlaVvx6XNjVHx7QMdCOKbsZsAp6KkjSj6BMIuT0fW45k\n1o/vE0VwZs7jcxZSW7SFmqKtlAdWIcsvEaX7DIQ78wzV1uLas88Or1ixDCorpnyUORom9szviT35\nKHr9iaxtzuVX4bnhdXi23oBwetCTZpp8W+hJkz17n+bg4d14vbnceP27kCSJVWvzcbltojvZQ3uL\ntZ2yH+3H7Ou2TyDLeLbfhP9t786yww2Hw+zZs4d9+/aRmGDMsGTJErZt28aCBRe3UvOJrt/zhxNf\nxbJM3iTeRqVZYb/3r91q1xDgVbI9twMmDQULIRCpJGYsgpVKYjoUTNnCSsYxQ8OYwwM2MU8H2ZPS\nZ/5sWUadV4FWvQhH9UK06oWo82sZRqG9vT1Dvvv6+hBCsKI0zptXh1BkGIoq/PBoGblFNZnQk4qK\nChyOl1AS5Tnge7vuxhmz2JT3BhzdpeQSx6uZ0+47pn73Jpx0xzQ6EioxRJqA25OlCAJ+J8X5LiqL\nPNSW5rCwzIfLMXNP96XUwJmjYRIH9hLf9wyJA3sR0WwyKAfycV+9FdfG7biu2ojsciMibVh9exGD\nh0DLQS7ahFS4AWmaxu5Kg0jpjDz8ECM//m7mt+fedC2Bv/w4IhDMchCZ3KnNy8vLxF9XVVVlHETs\nMJR/JfZk2j5OlvHfeTc5m16DPDA4DcF2jJdKz8ubNtTipfQMTYtJKndUlhi0TlHofhFNGRcjUqZG\na2gRR3s38sbyJJos2Dvg43g8SK5HQ1GmSdI7Q+LetH9PWk7ufRL1R1/FGfDhXLKS+P7dWZaaciAf\nz7U34d1xG1rN4pesaPFSf45My6Cu5ykONP2Agfh4gZ48Tznrqt7C0tLXoioXvk0TlkV89xOEf/jf\npNqaMDVIOSTk9etx3HI7VmkhSSNCT/gkp/ueZSTRk3W8S8thQcFmaoq2UBVcj3al51LNQrjHnqHV\nbi9qS6tdevz6azNEcSboLaeJPfkbon/8baY6I6RDsLa+Bu8Nt+NcsTYj5rS2tvLAAw8A8LGPfYyC\ngvEE44ke2opQ2bxToeRQeoRRkvBcexP+P30PWsX8zDHd3d3s2rWLw4cPZ6IDFEVh7dq1bN26leLi\nS9dxbh18gUePfAaP4eRu4922IFg9H5YuBl4l2zPvdIGSmYQQPLzrr4i0nWItG6iMFZNqqifV3DAl\nxnYiZJ/fVr7Tk5hXRTcqrd3dWIOHuLb4OKoC4bjMg/uDDETtH4Usy5SWlmbFfgcCgZdsQzIdnjhx\nH0c7f0NZYBV3rPkap0+G0EdiOKIjeFJRckSMXDmBMs0tGxYMJB30xp30xu15zJxenTAlAaqE063g\nz9EoCDjxejU8HhVVsxgKt7F23bKXVAMnDIPk8UPE9+20Sz13j1c0lHM03Cvz8V5VhOKbZgxeUpDy\nViIVbUYKXoWkXNoSxXNB8tghO8GxvRkAJViE690fodVfmHEQ0fXszm9JSUmGYJeWls76W0m+8Bz6\n03/AWVSJo2BSQYs5EOyJeKmSJMOw6O2K09kWIdlbx3Kth3zVjmsXGFiOI5hqPZ2xag5FlvKbgVKO\nRlN8sNjk7gKLJBKJrVvJ9c+tMM3ZQJgGRmc7qeZ6wj/878xzMAbJ4cS1aTveHbfhumrTWfupX4l4\nqT5HuhHjaOdvONT2c0YT42FbwS6DRQdTrL33IRxVtRf8vMKyiD/7R8I//FaWu5NrwzZy73ovjoXL\nph4jBP2RRhr7nuV03+5MmfAxqLKL+QXrqSncyoLCjbi0KzTEcwbCnUgkOHHsGFcNjyClUlkkcS4Q\nhkHi4F6iTzxKfN/OjMsTgFJchveG2/DuuA2psITPf/7zJBIJ3vCGN7B582Yg20PbmYBrfhkh2GPa\nJHv7jTbJrqy2zyUEDQ0N7Nq1i4aGhsx5PB4PmzZtYvPmzVPMJi4V+kYa+MWhT7I6voxN1jUIQNq2\nBXJ8r5LtLFwkt4AHd7+TULyT6xZ/kKsq7wTsB8Yc7CPV1ECquR69pYFUUwNGVxszGq7KCmpZJY7q\nhSglflRxEK1QRXd7ePhEFXUd0WkP8/v9Wa4n8+bNQ30JNzJ1PU/z26OfR5ZUPnD9L9GUaRJ0TBPC\nI5hDw1iDIeSRMMoMIwwRQ6E77qAvZivggwkH1hzNj7x+lfkLcqio8jGvwntO9leXC0IIjJYT6Mcf\nQU7VoU3y9jfCOnqPiqO8CMUbQmKCDZniQgquQyq+Bimw7LIXXbJGRwg9eD/Rx38JQFRz0nXNTTQH\nSmhsaZniIFJZWZkh2GcsahCJjic/T1KwzegoscbjmG4HOe94D0qwcM7X/FIhSZYl6O+N09luV1CM\nDXRRHThGTf4Jcl3DAEhGGXJyA5Kwf4tHY4JPd2p06PbvKKAIfr3YwCkBtQvscvDne12jI+jN9aRa\nTpNqqkdvbsBoa0LoU3M8nCvX4rn+Vjxbb0D2nn+V0CsJL5XnaAyR5CCH237Bix2/ImmMtVkSNYWb\nWVd2B9In/hGzrxvX+mso/Oz9F+y8wrKI7/kjIz/4NqnWxsx61/ot+N/+PpyLls/5s0KxLhr7dnO6\n/1m6QsdhQgiKJMmU562htmgLtYVb8Lnm/k64JJhIuBUF1q8l4fXQ/cIBqkfS77frtoPn3BJfzXCI\n2DO/I/rEo6Qa67K2OVet57HCGk72DbJ06VLuvvtuDrX8jKcbbA98b8hk6y9j5IQF7m03kPu296JV\nLgDseOzDhw+ze/duenrGRxmCwSBbt25l3bp1V8Sofjjew68OfIrXj9xELrmMeFLkbL+Vg4cOvcLJ\n9pySmYqxcv3oVjwT35U9nxgTFs1K3tCNKAPRZoSwuGXFp1hSumPWa7MSCVJtjaSaGzKT3lw/Zeh/\nIiS3glbsRVq4iVBeJZ2SRsNogrbubgxjqk+rqqqUlZVlqd+Xqyd4LojpIf7rmTcBcMdVX2J+wdVn\nPkiIaapejkxr/WNJEsOymzZdpW5E5sSwxEhSxo2MW5JxIeNFQZ3U4RISaLkKRWVuli4OsKDCN6WQ\nyZUAYemIwSOIvj2IoRdBjD8jQmjoPSqRZxvRG4cz6yWHjHvNPLzrS1Fy4kgT4xsduUiFG5GLrgHf\n/Es6iiKEIPbM44S+fR9DsThN/iJaiirpUZxZEZiKolBTU5NxEDnj8z4LwbYV7GIM2WLwu/+KfuIw\nAJLHS+DP78F7y51zioG/UkmSEILhwSSdbVE626N0d8SQrVEW5J2iJnicIm931v7diVweG6hm11A1\nd+V7uCVgf/NJAU/JeYSLSrjeClHU3w2qYjfkZ9EoCtPE6G6334VNaXLdXI/Z3zvjMZLDiTBNMA38\n7/wrct/67nP7Ml4CuFKfo8kYirZxoOUnnOx+AlPY4TyKpLF03o2sq3oz+ekiJbFdf2DwS38HQMFn\n78e9/poZP3MuEJZFfO9TNsluGfdMd62/Bv9d78O5ePbiVWdCNDlEU/9eTvftpn3oUObexlDsX0xt\n0VZqi7ba1aOvBEwi3PqqFaSOHsdrGFBcBOuuuiCn0ZvqiT7xKLGnHssUZzuRN4+nypehSYLtW5Mc\ncxwFIK/XYMuv4uStfQ25b3sPWlVN+lJj7N+/n2effZbR0XG3oKqqKrZt28ayZcuuuHY2rod5Yd+/\nsW3U5ibHi7pISKtemWS7giH8YRNXIvveE7JOh7OXFkcbXXSQMCLoZpSUef4Zz+/Y9C0Kc2rO+jgh\nBGZ/r62AN9eTarYbG6OrfWafSFlBKS3H9OUQlTWGLehL6AwbgrjqIKo5iKv2ZEkywWAwo3xPtB28\nUvG/e99Hf6SRdVVvYfui2W0cZ0Ra/c6qejmDI43pdDLo8HA6pfL8iMXT3XGMCJTLTsokJwWoU0hm\nAouIy8IV1JhXaceCVwe9BC+QI8rZQAgLEa5D9O5BDLwA5oRYZUlDCq5BKroGKX8lkqwhUjrJoweJ\n79tJfP+u8QQVQPaquFfk41lbguqfFCvvLkUu2myHmriLLuo9pbo7qPv3r3Cqs5um3CKGXNmKpcPh\nYPHixSxfvpwlS5acmYjMRrAdjvFCM/njISLCsoj+/hFC370/kynvWLKKvHs+OV4NbwZcSSRpJKzb\n5LotSntbBD1hoco6VYEGavKPU+ZvySQ6AgynXPx+oJrHBxfQZRazqMjPwiIfi4t8XKXplLQ1IY2F\n6+Tl2R1b0zyjqm1FRu1RvozYUE+qtXFWpyiloDgTbmfnvSxCzgvS9dbrASj85wdwrZ5Dh/wliivp\nOZoOnaFjvNDyY5r692TWOVUfqytez5qKO/A6s50xhBD0feI96CeOoFZUU/LvPzw3pwjLIv7cM4z8\n4FukmsfDDVzrrsF/13txLll57jc1A5JGlJaB/Zzu203LwH50MzsnJN9bSU3hFmqLtqadTS5jGxuN\nwT6bcAtJQhrjEhvWQ8HcSpjPFfHYEJ0HH6Xn+JP0xNpoLMtF9cWR07lWJc0prhveSPCt78+8N4eG\nhti9ezcvvPBCJvRPkiSWL1/Otm3bqKqquqDXeKFhGAkGn/kFxcl8IoxSV1z9yiTb63rHy+5GiVAv\n19Eg1dEldSKkud27JMlpz85xU32H6hn39Zzg81ngq6Ys78L+uK1EnFRLI3rd8+gHf0aqZwSjP4FI\nzlL3dxrEFY246iA2YdJdHtzFpQQq51OwYCHzlizDW1J6Ti+9i4Fn6h7gYNvDFOXU8vZN/3VhPnSK\n+h2ybQin+S0IScIEkGQsIbAECEuAsC1gp6PSFvZgo4VAktKJXxLI6eWZjjvn2xk7q2WAMKfehySD\nrIKkznpeAXZok2kgDCO7kI4MyBKSOs3VZz5fQbpAdyawK7eaKR1zumqkkoSiKCiKjCwrZ3fWyaNA\nDsd46Fj+7DHY5tAAoW/fR2zn7+0VikLOm96J/0/fjeycngBdTpIUixq0tIxS1xBmoDuOlbC/SwmL\nMn8zNfknqAo0ZCU6xkyV5yMLaJJXouQtY2FxgEVFPop80xQQ0XXbl7trggo+QdUWloXR3WGT6eYG\n9DS5ntipmwLNgVZVg6O6Fq16UYZgKzm5U3bVG0/R+//eAUDp935z1g4jQghMkcK0xiYd00phTFg2\nLR0js5zCsHSEMPE6gwTcZfjdJSjyxX9fXolkWwiLxv49vNDyY7rD444VOa4i1lb+CSvKbsGhzhyz\nn6w/Tt9f3w1A4K8+Qc7r3nIW5xbjJLupPrPetXaTrWQvXXUOd3T2MCyd9qFDnO57lqb+Z4npoazt\nPmcBNUVbqCncQnne6kvyrEzBBMINYHk9yNu3nrPnv27EGYq2MhBpZjDSzECkhcFIC1F9cMZjavqD\nvHbz53FX2zHi7e3t7Ny5k2PHjjHGQzVNY/369WzZsiUrqfJKhxUZhZ27kZE5UFzwyiTbS3pbaVZb\naHd2E3bG0DTPlEpUGZP7KRWqvDhVD6rsumISD0W8F/PFLyMS/ZgjFqbzOsxRZ9oVZcC2NBwrPxoe\nPqfKSQIwXG4kfx6OgiKchcUo+QV29c1AMF2iNV3w5xx9K+eK5oF9/PLQJwGJv7z2Z7gdUxvcC4Ip\n6ndo3GP4Vbz8cBYEezrEX9jD8H98CbPXtsVTSsrI/9Df4bpq05R9E4kER48dY9GSZagOB4YpSJkW\nhiXSk4WR9jvOWj9heab1Y8uplIUZMzHjAhG3ICEgZuHQJ96XoNDTTXX+MarzT+HTxv1pLSHRqy7C\nCG6ksHITvrP1ne7pxTpwkFRPO7pskIoM24p1y2lEcubRQiVYhJYm1RmXprLKOb1ToskhGvc8RNu+\nhzFdKs4bbsayDEyRwjD1DInOLGfW6Vlk+nwhSwp+VwkBT1lmykvP/a6SC2YbdyWRbcPUOdH9ew62\n/pTh2HjydYFvAevnv5VFxdfNmVQO3vePxJ78DbI/l9Jv/QI5Z/akQyEEieeeITyJZDuv2kjuXe/D\nuWz1ud3UBYAlTLrDJ+04777dhOPZnUqnmsOCwk3UFm2lKrhu+jyki4VoDPHcfqRkktTSxWjV8894\niGHpDEfbGYy0pIl1CwPRFkbis3SWAa8zSIGvmnCvRWv9EHmu+Xz4/f+AZVmcPHmSXbt20dLSktnf\n5/NxzTXXsHHjRrznULH2ikDDaWhofOWS7eXLluFyX8IH+hJAJAYxj34Z4j2AjLzo3XYC26ShKmGa\nWCOhce/wMTI+bC8n+ntJDvRBeBg1ETs3TXKsIlNe0DaPn1iVKasaZxDZHzjryly6EeeBp9+AJUxu\nW/VpFhVfey5XefYQAuIJ9MFBOtraKC8vx6HNXqnSMAWhoSR9vXEG+hPo8akjD3FhMiQMBkkxLAwm\nBmd4HApFOU6KfE5cmoIsYX+/2MNqsgQaOoWik0LRSq7Vn/XZScnLsFrFsDYfXQ4gSSBL9rHS2OfI\nICEhSxKSZGvUY2q7U1XwaDJuh4pTlbOeB2EYpFob0RtPoTectB12JNAKXTjKPWilbqSJtjCyhpRT\nDf7FSL4y7LNPhZ5K0dXVRUd7O13T5B749ASlfh/Vm7YSLC29MLq5y3VBSqVbiTjD//dt2n/7KEOa\nj0Gnn8iKzUTXbGUgJdM3mmQgmqRvNElUn96y8mwgAV4UciWFXNQJcxUf8oyCgM8xSGn+UZYWnKLQ\nme0xTk4NcvE1SAUb5lw8S1gWZm+XHVfd3ECqpQG9qQGzt3Pmg1QNrWqBTarH6g/MX4iSG5jj3UMi\nNUrH8BHa+p6nffAgQ3rXnI+9EFBkB6qsocgaEgpRfQjO4NksSwp+dwkB9xgJLyfgmUfAU47fVXxW\nRPxKINuJ1AhH2h/lcPvPsxTcyvy1rJ//Virz1521MGUM9NHzvjsRyQS+N95F3nvvnXY/IQSJfTtt\nkj0hIc+5ZgO5b38fzmVrzu2mLhKEEAxEmmxnk/5n6R89nbVdlZ2UBpbj1vxZlS2nLU2veHBq9t+q\nfO7JgYnRUVqPHadqzeosXmQJk3CsK61QNzMQtefDsQ6EmHkE3anmUOCrpsA3n6CvmqBvPgW++RmX\nlrq6Oh588EEAbr31Vvbv38/AwHi0QVFREdu2bWPNmjVoZ2hfr3gIAaEQB5qaXqFk+wpQAS4GhB62\nCXc0rSpIGriLkTwl9txdguQuAXcJaDlnfAEK0yDW201X3Un6TzcQamsh1tuFMxnHk9JxGzoeI4nH\n0HGb56YGCSSSDidJp5ukw03S6SKRWU5PDnud7nDazBAwKnYiPIPIoWqU3kv7QrUsi3g8jtvtPuvY\ndtMUttm/bpHSzWnNZ0xJkBQWuhAYMzTcqmyxojDK+tIRlhVGUCdcRlSXOdSTw/PdfppDbi5YgIoE\nqmyTclW2fY4VWUKR0p7HloGcTCAlYsjJOC7ZZOG8FEsqU1QWW3ZHIY1YSuV0KEhDKEh/3JO5Rsuy\n6O3txTSziWhJNET1SD8LfU5qPvAJnMsvfSMqhCCSNOiLJBmI6PRFkvSPJumP2NPY30MxnemiXM4H\nTqQMic6TVHJlm1TnoHCmgBlJ0lHdERyuGMU53azMO0WBMomUZuLtNyG5Zw+7sGJRO1GxJR0C0tRA\nqvU0Ij61GNcY5PwCHPPTdqYLFtnFvcrnz9l+z0rEMfu6ifc009F/mM5EHV1KN0Oe2JTHWzYEeb0m\nHk8hniVrUNJkWJEdKLKGKjsyy+N/T10e38cx7T6yNDVXw7B0RuI9DMc6CMU6CcW6CKWXRxJ9zJWI\n2wS8LEPIbUV8KhG/nGR7JN7LwbaHOdb520xekyTJLCq+jnVVb6bYv+i8Pj/8g28z8n//BYpCyQM/\nQSsbj9MVQpB4fjfh//sWqdMnM+udqzeQe9d7ca64MEl+FxvheDeNfXs43bebrtCxTMXMs4UiadOS\nc3vZN81Ivb3eoXrBVKirq6Og3MWo3pkJAxmMtmFaM4/kqq+Vq0gAABdNSURBVLKLoK8qTaxtUh30\nVeN15M/KLXRd53Of+9wUEaWmpoZt27axaNGiKzpn7FzwqvXfyxAiFcE8/nUYOT37jqoH0uR7jIBn\nSPksBv2WZdHT05OpeNnW1sbg4CCysHAZqQz59hhpMp7Sp6w7V2JuAQnVQdKhofsF8bwUKaeKI1FE\nQnOQ0BzENDvuPC47MISEYdmTaUJqbNmSMCy4sFHSFx8Sguqgzup5cZaXJHBp47/TlAmnel0c6XLT\n0O/EFFfWvXkdJitLE6wui1MRyP7/748oHOly82KXm6HYuGd8CRbzupopjwzjlQT+N96F//a3Imma\nrb6nFXrGlkkr89KYUg9MWJ6tAUiZFgORJH0RPUOe+0fTBDqSTG9LkkhZIASqMHFYKTTLyEwOy0Cz\nUum5PblFikAiTK4+Sm4qSq5DJr9sHl6XSjwaJbdyPmqwEDkQRPgC6JqfRMpJImISGzGIjqQYDeno\nWbkYAk3WcWtRe1JjuLUofm+CXE8crzOGS43hkCMo1iiSNUOCoZaLVDSzk4wQwlarx5IV07HVE/3Z\np0BV0SoWoC1YiDZ/YSYMRAnkz3wMYCUTmH09GL1dmL1dGL1dGH3d6P2d9NJNbyBGX4XKUImCmGSi\nL1k2uS5qNyjssChKBXEVVxL4i/+XXenzMsOwdMKxbpuExzsJxToZjnUSnjMRV8l1Z4emeNRCOlp7\nWLCgGofj0njfp8wEJ7oep673qYzCqcouVpTdwtqqPyHXXXKGT5gbrESCnve/CXOgF9fG7RR++r40\nyX7WVrIbxuPBnavW43/7+3CtWHtBzn05ENNDNPXvYSDSPMHxbKzSZSTjfDYbAb4YkCWVfG8FwTG1\n2msT61x3yTkneX7ve9/j5MmTyLLMqlWr2LZtG2VlZRf4yq8cvEq2X6YQwoJYJyLWA/EeRHoi3gup\n0TN/gCNgE3BP6TgRd5eAqwBpmpi70dFR2traMpUuzwjTRIlFUGOjKLFRnNFhtGgILR5GjY6iRCPI\nsRhSNA6Jc4yflED2qMheFcVrz2WvguxRUXwqskdF8jjA60S4HQhJxULBQkEg28tCyaybuN6wJGKx\nOB6PB0m+cKRWWJBMmugJi2TSxDLHv0tVMagJ9pHjHCdOloD2UJBT/WU0hUowhWO8sp6aXWFvbN3k\ninyZ5QkV+6R0CIklBClTkDBMEoZFImWSnDRPGBZJwySRsuz9Utb0yYsTUOKOs6W4jy3FfZR6smN3\n68M5nBzNJya7EekXuZQOOJEAWYBsWaimhWxaKKaJYglk00Q1zfQ6C9kykU3TXjbN9N8WUnof2TTT\nk70O0wRTgGnZy4a9XrJMe26ayKaBbBko1vmHf8wGS9EwnB6E24XwOJE9GopXQcuRcOQIXH4TzSfZ\nz7Bj5lCRaTHmkV60GSlvGZJkK6V2wvXpLMvRVPNpRHx6/34AORBEq67FMZawuGARWlkV0jRDv0JP\nYvR1Y/R2Y/Z1YfR2Y/R2Yvba68Yq0FkSDBcr9FWo9FeoDMxTsNSp95c36qA0UUCZuoB5eSvwFFWj\nFpeiFBS/JIvVGKZOON6VUcKHY52E4vbyaKKfMxHxywWPI8CaijtYVX77RcmdiT71GENf/QcAct/5\nAeLPPYNefzyz3blyLf63vx/XynUX/NxXKkwrlSHeYyR8shXxlPXmZIviGFOfKYmAZ56tUnvnZ8h1\nwFN+wRM4R0dHqauro7a2lkBg7mFjL1VcMWR78eLFCvAl4G7ABfweeH9dXd20aayLFy++GfgaUA00\nAvfW1dX9YS7neiWQ7dkgUhGI99oEPNadJuO9dqz3GXvMMrgLswn4mCLuCGR6ucIyIDUCqVGEHgZ9\nBFJhRHqOPoJIjaTXjzBbQyJMCytqYsUMzKiBlZ6MqEHD6CiOmIU/JqHFLJTEuQ3BCRkkjwIeFcmr\nII2Rc4+C7LWJjpqeKy4VJR3vfLkwEC2mcWgZTcNLiaUujke6okhoDhl5YmdCCCRhIpspZCs9mRPn\nOpJlIJs6kplKT/aybKaQrFR629g6Ha88gl8dxqeEUSwDYVgIQyBMgTAsMIX9t2EhTAHGlUk6poUi\ngSJnT6qCUBSQFRAWUjwBMZ30UMvZQ5VQvCqSS0F22uQbRUnnQUgIISMsGWGASEpYSQssEwwDYaRs\nhxkjle0yM+29qEiqBpqKpKTnc4wtFrqeVc45axsQLpTpK1fpq1AZKFMxnFN/WwGlkIrclVSWbKai\ncN3FS4q+AjFOxG0lfKIyPrH64qVEnqectVV/wrLSG1EvYjVZYVn0fexd6HXHstY7V6y1lexV6y/a\nuV/OEMJCN+PoRozR6BANpxtYu2IrOd6XP/G9HJiJbF8OWeBvgdcDG4Ah4LvA94FbJ++4ePHiBcDP\ngPcCPwHeAvxi8eLFy+vq6lov2RW/RCFpPtB8SP5sz28hLNBDWWr4+LwfO4jDShP1XuBINkWWHeDI\nAyMCxsxq2BmhekDLtWPKHblIDj+KlgsOvz3s7fCD5gdHLruOfIaWwf3jl2AInHGBK2bhjAlc0RmW\nYxaOCSPrkgVETIiYCMYs+qaHJUPSLWHJQDpsYSKkKf9O3CZNs296SZrD/pICkoqgg3kcYN7Y9vR/\nhBDjf4vMeiljPiPExG3SJFOaqQRHQiBZJrKVQkmTa+kiKWxGerpgkCW7Qpoig2oTUNSxZZv0jq2T\n0usUzVb/JduxMO1cKJAVgaSCrAokVUJSZFCl9LJkHz9hWVIk++85dsiEEAjdwooZWFETM2pghnXM\nkI45+v/bu/cgycryjuPfvszMXtjdmVlYsoQRgqyPC7i7uIVG0AJCpCJErtmKCfegrBFRguWikcgl\nWkFQtIQkggkCSWGQCBFCXJCrpUSLS+QaHmpFw30v7o2d3rl0n5M/3rdnz/TObWenu2fG32erq/u8\n5+3T7051nXnOM895334q2yqk28skPRXSvmTwtWk5pbKlH7bs/gwaI6qUSStl6N29HGuay1Hafz7r\n3zGHdQth7dxt9OZ3vsifM2MBb+t8N12dy+jqWDb5VuJroGKhNdbD7r/Tvu7SWzz3/DMsXryYtmGm\nmayHlkJjZuPK5fO0f+wi1q36KCQJbQcfytzTVtK2ZNdvupQdqlMXtxVn08Ic9ihuo2WE8lGpj2YE\n2+cBl7n7rwHMbBWwxsy63P2Vmr5nAY+7+61x+1Yz+3hsv6JRA55ucrk8tHWSa+uEjoMG7UuTMvRs\nGByAl+JzX1xpMOmDnqFWdctByx7QMpdc67wYKM8lNxBA17Tnx3738RGLzqWQb6GvUiJJyiRpmUpS\nIUnL9KUVetIySdzO7kvSMvSVaS1VmFFKmFFKB4LwGd2Z16WUtu6E1kwskE9gZnc13JhCWdYGSvKQ\nFHIkhRyVYuY5vs62J8U8lQIkxTxJASp5Qr+WUD6QFHNUCjnSYuhbbUuq24Ud25XM8ZnA8p7Baq5c\nwqSYmbbYJ43bA1c9g/elSShdKeaKFHJF8mmBwswWCjPbKMyfTYEWChTIUxj8L81T7IPWUpmW7n6K\n28sUSn0US30USr3kS33kSz3kSj1Q2h5KZIaSy5Hr6CS/5wLye+5Ffv5e5Pfci9ys2RMexPQU+lg3\nZxuvF17n1e0vxnl3Nw7qM6u1g67OQ+nqWEZX56HMm7lQwdQYFPItFHJttBRm0lqcnsFS2+Il7H3N\nTaSVCq12iL4XMm00NNg2s3agC3ii2ubuL5nZVmApUBtsL832jZ6M7VIHuXwRZsVykRpppSdku0tv\nQt/mwYF169w468nEzClba8GcAzlh2fivr9I0IUkrgwPxpJxpK5OmFcq9JZLNm0g2byTdvJH+jRvZ\nsH4dHR3t5Au5sEIjCUmaDBwzJSFNqu0VUlLSpEJC6FN9JFR2vK62kzlO9dhJQkolZEFJSJJKpl9C\nGj9jooXAmRjIDn4OQXJ8zuxLJyTQHWdddPwDzJSQB4gZ6eyPbLQf38z4GHGhtwKksyn2MegislBJ\n2Tq/wNbOPEmxDLweH3VWu+p9cY+YtT6Urs5ldM7eT0GUDKt10UGjdxKZYhqd2a4WndZM9spmYKhJ\nXvcYou8W4OCxfmDvCMv/yjgU94a5Q0wXlgC9/QwEFJNWDiiSp0i+upmDgWmgWwjfun3DZm9vL5vW\nrGHBgQfS1taYGQDGIk3TGKBXBi4YwqMSF/aoDGyn1dfxIiO7L3vBoex9fZTLZdaufZP5e3aQK6Q7\nVitMB69amF3JsJz0kVQXZUn6SeL+ctIXXsftAbkc5TbY1lZgW0fz/q8QZqtYOO9g9m1fyu+2L2X+\n7N8jn7kI1zl5fKo/N/38ZLz0HWqeRgfb1ekxau94aQe2DtO/toq/nZ0D8GGtWTPKtHgiYzA9vkd5\nYPwLIsj45IGFM/YfyPiOWjyVA+rzB6LG2gLrtvSyjheaPZJpZXqci6SZ9B1qvIYG2+6+2cxeBpYD\nTwOY2dsJWe2nh3jLU8DRNW3vJsxgMqqh7ggVEREREWmUZkz999fAmcAfAZsIs5HMdPfhZiN5BjgX\nuANYAVwPHOTuLzds0CIiIiIi49CMdTKvBO4GHiPcEJkCpwOY2WlmNrASi7u/BJwCXEKo6/4ccJIC\nbRERERGZCqb1CpIiIiIiIs3UjMy2iIiIiMhvBQXbIiIiIiJ1omBbRERERKROFGyLiIiIiNSJgm0R\nERERkTpRsC0iIiIiUieNXq69IcysQJjP+yxgBmHFyZXu/pumDkymDDO7CfhzoDfT/Fl3/1ZzRiST\nnZl9BDgfWALMcveWmv1nApcCv0NYrOsT7v5kwwcqk9pI3yMzO5uwEFx35i13uftpDR2kTGpm9hXg\neKAL2AbcA1zs7psyfXQ+aqBpGWwTFr85AXgPsJFwcvoXYKdVKkWGkQI3uft5zR6ITBkbgeuAWcAN\n2R1m9n7gH4CTgEeAC4H/MrNF7v5W7YHkt9qw36Nojbu/o7FDkimmDJwGPAt0ALcANwEngs5HzTBd\ng+3zgMvc/dcAZrYKWGNmXe7+SlNHJlNFLj5ExsTd7wMws6OG2P0x4Pvufn/cvtrMzgdOJvwiFAFG\n/R6BzksyCnf/QmZzg5l9E7gt06bzUYNNu2DbzNoJfzp5otrm7i+Z2VZgKWGJeJHRpMCpZnYKsAH4\nAXC5u3eP/DaRIS0BvlPT9gvCOUlkrFKgy8zeAPqBnwKfryaWRIZxDOF8U6XzUYNNxxsk58TnLTXt\nm4G5DR6LTF3XAubu8wlX+0cC327ukGQKm4POSbL7fgwc4u4LgcOAHuBHZjarucOSycrMTgVWAp/O\nNOt81GDTMdiu1hvNq2lvB7Y2eCwyRbn7k+6+Pr5+nlDT9idm1jLyO0WG9BY7n5M62PkXnsiw3P1X\n7r4mvl5LKAdYCLy3qQOTScnMVhDq/j/s7tnMts5HDTbtgm133wy8DCyvtpnZ2wlXbE83a1wybahe\nUsbjKQafk3LAobFdZHfpvCSDmNk5wLeAP3b3R2p263zUYNOuZju6AbjYzB4CNgFXAavd/eXmDkum\nijj91g/dfYuZLQK+BvzA3fuaPDSZpMwsD7TGB2bWBuTcvYdQgrTazG4m1Nl+GmgB7mzScGWSGul7\nZGbHEwKi1wiZyCuB9cDPmjRcmYTM7FPAF4Fj3f2JIbrofNRg0y6zHV0J3A08RrghMgVOb+qIZKpZ\nCbxkZtuAe4FHgXOaOySZ5M4ESsBqwrl1O9BtZm9z958CnyD8ktsEnAIc5+7bmjVYmbSG+x7tR7h3\n5OeEMoBnCeWRH3T3UpPGKpPTNwh12Q+b2VvxMVBGq/NR4+XSNG32GEREREREpqXpmtkWEREREWk6\nBdsiIiIiInWiYFtEREREpE4UbIuIiIiI1ImCbRERERGROlGwLSIiIiJSJwq2RUTGwcwuMrOTmz2O\nejCzfc3sajNbUIdj58zsUjOrXS66Lsys1cwuM7OZjfg8EZFaCrZFRMbnU4Qljic1M5tnZjeb2Voz\n22pml43hbQcCnwH2qMOQPgmcT2N///wp8OUGfp6IyIDpuly7iEi9TZUVwS4DjgYuICztvbZZA4nZ\n5b8BLnH3TTHwP9fdu2r6nQ3cSFhC+p8JqyoOyd3z8T0LCEtUnwDsDfyGsBT1xcCFwF1m9lV3f32C\n/1siIiNSsC0iMn65Zg9gDI4CbnX37zV7IMDphN87t2TaRrpoSYEvATfE7fOADwIrsp3MbB/gZ0AF\n+ArwHLAncCyw3d3vNbNfEZaovmT3/xsiImOnYFtEZHxywBlmtpJQbvEQIUv7ZrWDmX0c+CywD/AU\nsMrdfxz3nU3I3hbdPYltDwOvuPsZZtYe9y8nZGo3AO9y903ZQZjZEuDrwPsI2dzrgS+7ezWI7QBW\nmdmquH22u99Sc4y94vuOBTYDXrN/OfBdYF+gG/gn4AvAkcADwDvd/cXY9w+A+4G93X19zc/sw8Bq\nd++p+TkOy93XAGvisY8D+tz90Zpu1wKzgcXuvi7T/u+Z1/8RP1/Btog0lGq2RUTG73lCtvYs4BDg\nO9UdZnYGIQi8GTiZEDDea2YHjHC8lB2Z3nbgJOBfgQ8Bnxki0O4gBLv9hGzvV4HPAZ+vOebNwPvj\n44c1x8gB9wKLgY8Syk1KNeN6lVCicTxwOaEsYwWhTKNEKFOpOgJ4ZohAG+ADhAz0hIkXJScA19UE\n2rUeBd4Vf2YiIg2jzLaIyPikwOPufh8MZIevNbM2d+8llD/8o7tfEfuvNrOlhIzwucMcc6gs7wPu\n/tAw/S8klE6cVM0Wm1kLcKmZXZPJIL8yRDa46hhgGSFr/lw8xiZCYA2Au68F/i1uPhSz1+9z99vM\n7P7Y9/q4/wjgwdoPMbNZwDxgomumFwEF4Bej9HstPu8DbBqpo4jIRFKwLSIyMV4iBMsLzKwX6CKU\nlmQ9zOAs8O46DPh5TVnGw8BVwMHAE2M4xsHAlmqgPRQzWwZ8DXgP4S+ifcCdcfftwA3x5sd+4PeB\n64Y4THt83jqGMe2K6l9oK6P02xKfldkWkYZSGYmIyMSoBrwtI/TJsaNMpD8+z8js39UZTlJ2/ybN\nNkZIvJhZEbgn9jkV+EPgfzJd7iIEuicQylRmAo8McahqsDsn07aVHUF41nygu1rLPopfxuclo/Sb\nG583j+GYIiITRsG2iMgEi7XDr5HJYsfa6COBx2NTtZzCMm/d1cD5SeC9ZpYN2I8i3MT4/BiP8Rgw\n28yOGGZ/J7AQuMbd73P3/wb+rzpWd3+LMLvIOYTa8gdj2yDu3k0IrvfJND8XP/uwmu5Hx32jcvcN\nhGz+J81s/ghdq5+rqf9EpKFURiIiMj6jBcaXAN82s/WEco4/IywWc1Lc/xPgTeCbZvZ3hBsN9wJe\n3oUxfB34S+BOM/t74ADgUuAqd98+lnG6+0Nm9gDwPTO7lHAj5wcy+9eZ2RvAhWbWB2wjlMhkx3kd\n8CzhJtEvjvBxPyGUmVwbt+8j1FrfbmaXA28AJwLHAaeN8n/PuoBws+aTZnYFIds9l5Bpv9HdXwAO\nB5539427cFwRkd2mzLaIyPgMVfIx0ObuNwMXETK+dxAy2B9y91/G/f2EoHIGof75DiAhZJpH+owB\nMXA8Jh7jdmAVYUaS7GqJYylNORG4jXBT52pgJWGWk2p99QpCecj3CQHyfsD/ZsbxAqE+vSOOYzj3\nAMeaWVt8XxrH/yBwNWF6vsOBM9z9u0O8Pztby4BYb76cUL7yJeBHhGkTlxHKZCCUufznCGMTEamL\nXJpOlUXQRERksoqZ9Znu/hcj9JlFyIivcvcbGzi2YwhTHh7g7q826nNFREDBtoiIjJOZdRGm8zuc\nkJleHhehGek9f0VY6Oed7j7RM5MM9XkthNr2h939gnp/nohILdVsi4jIeH0E+FvgRWDFaIF29A3C\nUuqFeg4sowDcTSgvERFpOGW2RURERETqRDdIioiIiIjUiYJtEREREZE6UbAtIiIiIlInCrZFRERE\nROpEwbaIiIiISJ0o2BYRERERqZP/B4vlQebm6/cKAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b5525c0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df['hour'] = df.created_at.apply(lambda datetime: datetime.hour) \n",
"for language_code in top_languages:\n",
" lang_df = df[df.lang == language_code]\n",
" normalized = lang_df.groupby('hour').size() / lang_df.lang.count()\n",
" plot = normalized.plot(label = language_code)\n",
"\n",
"plot.set_title('Tweet Frequency in non-English Languages by Hour of Day', family='Ubuntu')\n",
"plot.set_ylabel('normalized frequency', family='Ubuntu')\n",
"plot.set_xlabel('hour of day (UTC)', family='Ubuntu')\n",
"plot.legend()\n",
"plot.figure.set_size_inches(12, 7)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that English, French, and Spanish are significantly flatter than the other languages - this means that there's a large spread of speakers all over the globe.\n",
"\n",
"But why is Portuguese spiking at 11pm Brasilia time / 3 am Lisbon time? Let's find out!\n",
"My first guess was that maybe there's a single person making a ton of posts at that time."
]
},
{
"cell_type": "code",
"execution_count": 88,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of tweets: 446\n",
"Number of unique users: 407\n"
]
}
],
"source": [
"df_of_interest = df[(df.hour == 2) & (df.lang == 'pt')]\n",
"\n",
"print('Number of tweets:', df_of_interest.text.count())\n",
"print('Number of unique users:', df_of_interest.user_name.unique().size)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So that's not it. Maybe there was a major event everyone was retweeting?"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 'Desabafo de garoto homossexual com medo do futuro comove Hillary Clinton http://t.co/7I49RkKtSm via @UOLNoticias @UOL',\n",
" 'Hillary Clinton eleva tom contra a China de olho na Presidência dos EUA http://t.co/qwgr57UsD0 Governo chinês tem discurso bem menos ácido.',\n",
" 'Desabafo de garoto homossexual com medo do futuro comove Hillary Clinton - Notícias - Internacional http://t.co/pSCrQgO8aQ',\n",
" 'RT @elpais_brasil: Facebook censurou o sofrimento de um garoto gay e Hillary Clinton saiu em sua defesa http://t.co/3R2XyiXrtr http://t.co/…',\n",
" 'RT @ReutersBrazil: Hillary Clinton diz que Irã continuará a ser ameaça a Israel apesar de acordo nuclear http://t.co/4gmjpI7sSQ',\n",
" 'RT @folha: Jeb Bush diz que foi atingido por críticas de Trump a mexicanos. http://t.co/qMt7QbaTVJ',\n",
" 'RT @jr140797: #betacaralhudosan Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-can... http://t.co/d6uUMIFiIV #betac…',\n",
" 'RT deigmar: Jeb Bush diz que foi atingido por críticas de Trump a mexicanos http://t.co/XbRXsyhyOi',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/J93xGpN13K',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos http://t.co/smxaTooY0M',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/duz9LU8NvY',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/EVtHvSInRr',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/yZspQsrNSF',\n",
" '[FOLHA S.PAULO. BRA] Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candi... http://t.co/VM0QWlH5b9 vía J.A.M.V',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos http://t.co/yZspQsrNSF',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/hnEO3nSYHu',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/73eDAWXsCu',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: O pré-candidato republicano à Casa Branca Jeb... http://t.co/JK8c6w68aP',\n",
" 'RT @thiago_beta51: #SegueSigoDeVolta Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: http://t.co/Vhyb281I5c',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: http://t.co/CMjD1e5sgP',\n",
" '@DREWXAVECAO @EXFLOP Jeb Bush diz que foi atingido por críticas de Trump a mexicanos:',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: http://t.co/mgTTwptBKe',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos http://t.co/Fct3cKj5f1 #folheando a @folha',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a mexicanos: http://t.co/iGnO3AnT1W',\n",
" 'Jeb Bush diz que foi atingido por críticas de Trump a\\xa0mexicanos http://t.co/tMUUI5Dkpw'], dtype=object)"
]
},
"execution_count": 89,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_of_interest.text.head(25).unique()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Seems to be a lot of these 'Jeb Bush diz que foi atingido...' tweets. How many? We can't just count unique ones because they all are different slightly, but we can check for a large-enough substring."
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"440"
]
},
"execution_count": 90,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_of_interest[df_of_interest.text.str.contains('Jeb Bush diz que foi atingido')].text.count()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's it!\n",
"\n",
"Looks like there was a news article from a Brazilian website (http://jconline.ne10.uol.com.br/canal/mundo/internacional/noticia/2015/07/05/jeb-bush-diz-que-foi-atingido-por-criticas-de-trump-a-mexicanos-188801.php) that happened to get a lot of retweets at that time period. \n",
"\n",
"A similar article in English is at http://www.nytimes.com/politics/first-draft/2015/07/04/an-angry-jeb-bush-says-he-takes-donald-trumps-remarks-personally/."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since languages can span across different countries, we might get results if we search by location, rather than just language.\n",
"\n",
"We don't have very specific geolocation information other than timezone, so let's try plotting candidate sentiment over the 4 major U.S. timezones (Los Angeles, Denver, Chicago, and New York). This is also be a good opportunity to look at a geographical map."
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"candidate user_time_zone \n",
"Bernie Sanders Central Time (US & Canada) 18.694226\n",
" Eastern Time (US & Canada) 20.221507\n",
" Mountain Time (US & Canada) 13.683829\n",
" Pacific Time (US & Canada) 16.496358\n",
"Hillary Clinton Central Time (US & Canada) 3.302260\n",
" Eastern Time (US & Canada) 22.731770\n",
" Mountain Time (US & Canada) 0.196556\n",
" Pacific Time (US & Canada) 5.486306\n",
"Jeb Bush Central Time (US & Canada) 14.766734\n",
" Eastern Time (US & Canada) 28.625515\n",
" Mountain Time (US & Canada) 6.356858\n",
" Pacific Time (US & Canada) 16.676979\n",
"Rand Paul Central Time (US & Canada) 6.798783\n",
" Eastern Time (US & Canada) 15.359912\n",
" Mountain Time (US & Canada) 10.780279\n",
" Pacific Time (US & Canada) 12.918267\n",
"Name: influenced_polarity, dtype: float64"
]
},
"execution_count": 97,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tz_df = english_df.dropna(subset=['user_time_zone'])\n",
"us_tz_df = tz_df[tz_df.user_time_zone.str.contains(\"US & Canada\")]\n",
"us_tz_candidate_groupby = us_tz_df.groupby(['candidate', 'user_time_zone'])\n",
"us_tz_candidate_groupby.influenced_polarity.mean()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's our raw data: now to plot it on a map. I got the timezone Shapefile from http://efele.net/maps/tz/world/. First, I read in the Shapefile with Cartopy."
]
},
{
"cell_type": "code",
"execution_count": 95,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"tz_shapes = cartopy.io.shapereader.Reader('arrows/world/tz_world_mp.shp')\n",
"tz_records = list(tz_shapes.records())\n",
"tz_translator = {\n",
" 'Eastern Time (US & Canada)': 'America/New_York',\n",
" 'Central Time (US & Canada)': 'America/Chicago',\n",
" 'Mountain Time (US & Canada)': 'America/Denver',\n",
" 'Pacific Time (US & Canada)': 'America/Los_Angeles',\n",
"}\n",
"american_tz_records = {\n",
" tz_name: next(filter(lambda record: record.attributes['TZID'] == tz_id, tz_records))\n",
" for tz_name, tz_id \n",
" in tz_translator.items() \n",
"}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, I have to choose a projection and plot it (again using Cartopy). The Albers Equal-Area is good for maps of the U.S. I'll also download some featuresets from the Natural Earth dataset to display state borders."
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbIAAADaCAYAAADDo8efAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXecXUXZ+L/nnNu3b5JN7wmTAsEkhCYlQKiCFFFQFFFA\n8FVUUFHxxVd9X1RQRH+ICiJFehcISEvoJAGSQEhIThLS2ybby22nzO+POZu9u3t39+7u3Rbu9/PJ\n52bvPWdmzpyZeWaeeeZ5NCklOXLkyJEjx2BF7+8C5MiRI0eOHD0hJ8hy5MiRI8egJifIcuTIkSPH\noCYnyHLkyJEjx6AmJ8hy5MiRI8egJifIcuTIkSPHoKZPBZkQ4gghxJNCiFF9mW9vIYQoFELcIIT4\nbC/nM0UI8YgQYk5v5vNpRAjxSyHE5/u7HAcqQoiLhRBX93GeY4QQNwohZvRlvjn6j14TZEKIC4QQ\nq4QQjUKICiHE2cB04Bwg1Fv59jFlwM+Ayb2czxjgi0BxTxMSQqwWQjyd8vdJQojZPUxziBDiPCFE\nQU/L15cIIXzAL4DP9HdZOkIIcZsQYocQItLfZekG3wL6eqIwBfgxMKKP8+0XhBALhRCr+rsc/Ymv\nswuEEPcAJ5mmOTbTRIUQhwAPAvcA13j5rARO71YpByneTP+fwBBAAvWACTwB/Nk0zUQ/FOt0IJ7y\n98vA/6HeT3c5C7gLNYDU9yCdAYUn4J9BTVh8QB2wA3gJ+INpmrv7qCg/B/5omma0uwkIIa4ErgAm\nATawDXjMNM3fZKeIHTLovS4IIVzgBtM0r2/1/QJUe5hvmuYb7dzbrboXQlyC6lftscU0zUnApYA/\nw0c5IOlUkHl0tSGeAGjAVamdTwjRxWQGPaUoIfZVVOMtBU4GfuN9ntzXBTJNc3uar7UsJZ+tdAYK\nRcBo1GTsXaAAOAz4IXCGEGKGaZq9PkibplkD1HT3fm8gvQ24BfgREAamcgBNOtoh2+2xy++6h3X/\nHHCM938NeBO4F/iH910cwDTN8q6W60AjU0G2v0EIIc5HqdNGogbmRuBF4Pumae7zLiv1PhtShNfE\n1okKISYAm4DLTdP8Z8r3LWY/QogQ8L/ARUA+8BHwE9M03/J+nwbcAUzw8taA94Afmqa5PCXd8cBN\nKAESAjYCnzNNc3tneXj3zwFuBo4AqoFMl/NLTdPc5P3/GSFELXCdEGKaaZrrhBCHAr8FjkXN2F4E\nrjVNc1t7CQohvodSnwxDrRTuAX5umqbl/X4zavU1EggC95um+S0hxGuAYZrmsSnJ/VwI8XPv/7cB\nu726GGaaZpWXXr73zNeapnlLO8XakPK+DzNNc4X3jm8ETkG1tzeAn5qm+ZEQYh6wDLjANM3HvHzm\nA4uBOaZpfuB9dwXwV2C4aZoV3jMcjBIs61Hv6Xnv2knAX4AZwHBU+/yyaZovCyEmowaUE4Col3cm\nrDJN8x3v/y8KISRqFTsEqPDyPQTVto5FCZ2XgB+l1N/Xge8C41Aq4o2mac7MpD8JIX6JUoH6TNN0\nve/O8b6bDmxHvf8bTdN00pT/dGCNaZo/au8BM2hPd3rPNhTVP7YDfzFN808paUS8OvgSqn+t8p53\nY6u8LkdNBsYBm4E/mab5j5TfHwDmoVSDuvdc/yuE+CZwLTDeK+O9pmle294zAT/1yj0C1Z+vM03z\nFSHE0cBbwBdM03wqJd+lwF7TNLOpCu207tvDe/9NY2rTQmB7Slts+v4eUrRmQoj/A85DaRIKUWPs\n74DjvfIUA6uB75qmuTQlnXbbcMpY3ZrXTdM8wbv/eNS4cRjQAPwb1deb+sBxqLFgLKrvJFHC+fum\naX6SSTnaq6vu7JEdDMxG6b5PBq4HzgT+luba41EzimNQg2N7pJvppH73IHABSsXyRdTg8aIQYoz3\n+wgvjzuAU4FLvO+eFkIEAIQQecDrwKHA94HPoQa8nZnkIYQYCixCzdK/AfwXsLeDZ+qImPcZFkKM\nRg3uBcDXgG97ZXxNCBHuII13vDKchmqk3we+k/L7F1CN4MuoPYq7U35rXd/30vyebgaeRU0GUleM\nxwIG8J8OynRBSjpmSp0fDFwJXAyUAG8IIUYAy4FK4LiUNE5Iya+J44AVpmlWeH/fBnzFey4TeFwI\nMdL7bRyqTh5EddpLgQ+FEEFUhzgYJVC+QasBtgMMIYRPCFHgDYJfBlY2lcebIL0BJLw6+BlKcP+r\n1XNN9urhNOAn3veZ9qf978zbb34cpRb+PGqG/j9Ae0YVH6vbxHkdPGNn7WkBsAfVrj7nPe8fhRBn\nplxzB6pe/wCcjxrIWuybegLz/6Ha3Nko1e3tnkBv4svAWtRg/AVUPz4MuBMlgM7xyvpaB88DalL4\nY1RbqQOe8ya9S1D9+5SUchUAc4DnO0mzq2RS99kgtU8fgxrbL0C1pc0oFWU+6v1ciBrHHmy6IYM2\nvIvmvt00TgDc590/G3gFqEKNnz9FtZOFQoimhdAk1CLgl6j2dBWqzh/uQjnSkumKLB3Pe7PDN4UQ\nBwHfFUL4TNO0U655u2kG6RWyy5kIIT6DarhnoCoKVGMuR62ebky5/B3TNN/27rOAJ1GVvhjVMUcC\nB5mmudW7/tUu5PFdlFrgNNM093r3rUYJn87weQNpCWpA+wFqEF2FGrCSwOmmaTZ46S5DDdA/QK3U\n2mCa5vspf74mhDgWmA80zZAlatb/QgblSzfL24AaSB7xvpoPbDVNc10H6SxPWXkihLgONaGY2rS6\nFEIsQnWsX5mmeYUQ4gXgpJQ0TkYJt5OAW71OsAC4PeXZH0vJYxmq8xwOPJ2Sziumab6Wct0lKK3A\nbNM0P/S+exFVx53xYqu/a1ADfhNXowbKC1GDJ6iB5G4hRFlTewEaUlcAreisP6WqyX4FPApc533/\nKmpldilKiLTmV8Ao4DEhxDrU4HOPaZp7mi7IsD1tbapTIcSrqL3RC1CD1USUALrGNM0/e/e85Ald\nvHsMlMD9E2rG3VT2I7yyP55Shg9N03wl5d4mgfmoaZovpXnGdPzeNM3F3v3PA1tRq8yvCSH+jRKk\n3/auPQY1HnY0UesOndZ9lmitRt1rmuYiACHEVtTE4EXTNP/jfVcG/L1JK0Rmbfgd795ZqHr7vWma\nTXt4NwIbgHOb1O3eGPK6l+ZDKWVb7I0TbwshSlETokned5n2pRZky2rR9NLqDSuhed7n86gBP4nS\nL4dJo65sVSZQjQjgs8D6FCHW1TwOAT5uVZGZ6uDXoVZhu1Aro7eBkz010NEo1WPD/oKb5maUyuyo\n9hIUQnxFCLFSCBETQtSjBp3CDMuTCfcDnxPNlnIL6HonPxpV5/tVpKZp1qFmxEd7Xz0NTBNCjBVC\nlKDUEtcBJwhlVTgHpe56CpT6SghxqxBipxDCRqlIQM0wO+IQoLZJiHlk+v7+yytX02psFbBYNFt7\nzkOpS6I0t5+7UYP/pG7k125/EkL4gVmojm6l5HcJSuXWNjHTjJum+XXv97tRk69PhBBNg3iX25PX\ndj9BTQ5BrSybBFMqqc88CTWZ+0mrss+n474MajLxHPBvIcSd3so4YzzDqiU09/X7gRFCiCYNwAJg\nXTvjQ7fJpO77gC3eZ+qxp6bnHOZ9ZtSGhRDFqAXCm6hVVxNHA4tS94xN03wTpSpvdxyj7TidaV9q\nQU9WZKk0qcoCXbwv6X12pEJrsrA7n+YX0kQF7dO6TBrtb9ZmkkcItdfUHc7x0q0Cypv2HTpBo52B\nTyhLqftR+xg/QNXjDd0sW3vcjVJzXSCEeAWl/rq+nWvbq9f2Bu7U7/+DarTnour6Y5Ta6WbU6vU4\nYLNpmk1WlXeg1Gk/RllaFtF2xZSOEN237FpvmuYK7/9Lvdl8DcqIZyWq/axGCZM293Yjv476k4sS\nAg+gVOMZY5rmDtSK7Q9CiLuBvwgh3kbtpXSnPcVTyth0pKajMaCpn/0WZbmbSocWvF6fOUuoM5vf\nRqmnHzFN86IMytmED1V/oAbidah39ipqdfZkB/fW0bz3n8pQ7zOe5rf9tFf3pmn2utm8aZoJTxuW\nOt431XdTn8i0Dd/l3XNRGkOndONAu+OYR+u23q2+lC1BlilND9q0EixHdcqZHdyzxvsca5pmRw2t\nM5YDJwkhxqUxomia1XeUx1LgZCHEVNM0N3Qx79WpKrc06Z4thMhPUS1ORFk2PeBd07remlYC13gW\nbQghttHOjLwTamnujPsxTXOHEOIh1KCRjxLC7QmMWu9zKC03hJcAC1LrXAhRBByJN5CZptnoCYYL\nUfuoT5ummfRUjl9E7bM+kJLmbJRqYr+qMUOV9VLg20KIE0zTbL1q6CpNq9Qmw4rVwGXAbrNjk/we\nWziapul4KqpDUft03U3zWeDrwDSa201P2tP7KCFxlvf/dOxAtZUZpmn+vJ1rOsTbOnhbCPEW8Fch\nxA2maX7c2X3eav9o1J4cpmlKIcTvgduEMpaYREv1V2vWoMaP1tsnp6KEQqdlSCG17gfK+a9O27BQ\nFphno44atDa8WIrq61qKavFYVF9Zks1ypKOvBVmT6fc3hBA3maZZ6w2WXxdCrEfNbluszkxl+fY8\n8BtvWbsUNaDPME3zZjLnNtSG+itCiN+izOFHAm+Yprkygzz+iJolvCiE+F/UPs/0rlZAGn6JsvJ6\nXgjxR9TM9hcoI5Sm/Ykd3ueXhRAfoSwyAW4SQjyK6khjaDlQdjQLSv1tGfBFoSwBa4D8FGH+e1RH\nGwE83I5FHKiBywZ+6T3DEO++P6Hq/HmvzpIoE2QdtVfSxN0owwUL+G/vuwdQ+0AGaoXWxHvAuUKI\ny1AztExXWQ+gVISPCCF+jRqYSjK8d5YQIgnkAcJLx00p159RA9PL3uC4DbXKaTRNc2FKOtkyB/8/\n1N7l00KIe1GTjCnAEtM0V7e+2CtTFfAhagY8HrWJ3oja92hSl3enPWmg1OHeu/+ZUAZWr6Lecxle\n+/WExw1ePneh1Mr1KLXk46Zp7mrvgT017mdRAsOH2ku1vedqj+OEsoAeibJ2NGi553w/ysruXtS2\nQUdnKX+HMl55QQjxN1Q9nokyYLopZRL6G5RBz4mmaX7QWd0LZey1HLWn+9UO8u8qXW1rHbZhr5w3\nomwIXCFE07GAuLe/+hPUuPmk926Hoer2XdM0HyRzMu1LLchkj0zSskG3/jv1+w6v8TZe70ANbgd7\nX38HZZFyPcoq8EHUi/0o5dYvoCydvo6aUd0NnO5tHqfLvw3e5upsL+2bUSqt/0F12E7zME2zEbUp\nvZjmF/p/qNnGftPRNHRWrh2oVUcM1bH+jhpk55veGTzPNPVXKCu8k7wN96u8+55DrZQmAh9kkG/r\nd/MdL79/oQb7/UYM3qD4PKqO7ujkGS5FvdOFKLXUZK9zH49S4dyO2uiuB45PnW15m9ImauW61vv6\nOdTs/WUzxTQXtRn8DOos3iLgMVRb2ZlyTbq256L2Qf6FGkheQqlJWre1VGpRg/CNKEuqp4DvoTrs\nEaZprvHS3oQaZD9Bmfc/79XB1FZlaq/fdKk/ecYuZ6MGi3+hBMJ3ad7vaE2ld/0DwAuoAWY5cKxp\nmjt60J5al+taL51zUO3gSZSweSPlmj+gZtxN1mpPoPaNOptUlKEmEM9794xDHdtIZzSxy8vzMu95\n/4oyrvqMaZr71VOeuvJPdNK+vWufRRmD+VBjwxOod36VaZo/S7m0dT11WPcp9/RktZ7pGJ3uPiCj\nNrwAZYG6AKWWfcP796h3/3LU6nSY992NqOc9o708u1mOtGhSDvpD9zl6EW+WPdv0zorkyHEgIZT3\nnXuB8Z4hUo5BSF+rFnMMAoQ6kKijrMmu8D5z5DggEEI0HcidiDKY+WVOiA1ucoIsRzp+iTrM+DFw\nvmma73V8eY4cg4rzUXteu4BbUs695Rik5FSLOXLkyJFjUHNArMg0TYugTFlz5MiRI0fXWCel7HZk\nhYHAASHIgGn333//8unTs2EN3/s4jsPChU8SCvk4+ujD2vz+7LOLCAQCHHXUZygs7N8QX5Zls3Pn\nXoYPLyUc7t0wchs2bGPq1HG9mkd7bNy4nSlTOo9U9EiFzd/3uW1Mr/zATeMMZucZ6W7bT2VlDfX1\njUyYMLr7hR0APPbYc1x88WX4fJ0PIY8+eh+nnz6/9wvVRziOw3vvfcjevZUYho8ZMw5m5sxDMYyO\n331PuP/+f3L22ad0fmEGbNu2gzVrNjBv3iwqK6u54oofzQVWdHrjAOZAEWRMnz6dOXMGTwDlefPm\ncdttN3PooW3Pgn/wwcdceulV/O1vN3P55V1xXNA7zJ7tsmbNRmbNOqjX8kgkkoTDeRx00IRey6Mj\nDCPIwQdP6fS6Q6RkpWmxtLGlKLOAZaU6l0xs/1jbrl37+vUZs8nQoaWsXLmar371m51e+/bbi9K2\n88HG7t3lvPji60hpcO65F3LQQc0TZ9u2uf32/4eUqUctVRtxHBfQGT9+IieccDJFRV2Lj7tv315m\nzJiatTpcsWIN//M/v+Hvf/8Tc+YM/vcCB5AgG4xYloNt221mtXPmHMyKFe8yc+ahrFjxEXPmHNJP\nJVQYho7juEgp0bTeCTlWU1NPcXE2XUX2Drqmce1Ig69vsql3W/62otEl6UoCevo6qqys4ZBDOjwO\nM2gYPXokr766hA0b1jF1amdafbeT3wc+b765jMrKKFdeeQ2hUFvNxGuvvcKOHds544wTOOSQGWnT\n2L59F489dg8VFTWcc86XmDYt/XWtefLJhznzzBN7VP4mLMsiEAgRDkcwjANn+M+W0+Ac3eArX/k6\nt99+P60Nbg4+eBorVrzPGWecw/vvr6G+vqGdFPqOgw4aj2lu6bX0lSDrXzVqppxQZHBCYduusz4B\nj1W1P2j31iSgv7joonNZvPh5nnmmtdvEZuLxOD5f76nc+ooNG7ZwySWXpxViAAsWnMYNN9yM40S4\n667HeOihp1m3bgM7duympqYWy7IYO3YU55xzGhMnjuXVV1/OOO9t27axa1d2nOW//vpSTjlFnVEu\nKCgkGo11csfg4MARyYOQsrLhXHjhxdx33xNcfHFzOCZN03Bd5c7tqquu4ZZbfst//dfX+6uYAOTl\nhXEcl717qygrS+c7tWckkxaBwOCJ1n7DGIMVjS47Wrl/fr7G4aKhg3/gzgRN07jggs+zfPkq/vjH\n3/Ld7/6QQKClz+B169YweXJ3XIAOHPbtq6SsbGSn1+m6zvz5C5g/fwF1dbWsXPk+FRUV1NfX09hY\nj2XZSOly8smnZ7CKbebXv76R//znGV577YFOtxqklLzzznuY5maCwWaha5rr+fWvf8y2bbs4/3yV\n95FHHssLL7QXVWhwkRNk/czkyQdx5JHH8dxzi/nc55rVB/PmHcyTTz7Eeed9mTPPPI+FC1/hzDMX\n9GNJYebMybz33upeEWSDbbUyJqjzhVKDP5e3dD/5QVRSZbmU+j89yo65c2cxadI4fvvb/+GSS77F\n+PEqIsvq1R/x1FOPceWV2XQh2Pe88MKrXHrpVV26p7CwiOOPP6nzCzPAMAyKi0uYObN959hSSl5/\nfSnr12/mhBNO5nOf+8r+3yzL4tZbbyIajZGX16z1EGI6f/hD2nCHg45PT28bwBx++NFUVta2+O6Q\nQ2ZgWY288cZiZs2ajW3rbNnS2ml/3xOJhKmqqu38wi4yGM8zXj/aYEFhSwG8y4J/7Bv8e0JdpaSk\nmKuu+gbPPvsYL764kL17y3nssYe44oqLet3atTeRUpJMukQieWl/b2xs4N5772TZsrd7rQyu6/Lm\nm4vTWjjv2LGb++57grvvfpwJE2Zw7bW/YN68luG/nnrqUU455TgWLXqLM888d//3uq63+Hswk1uR\nDRD8fn8bw49TT53PQw89zdChw7j44su44YZfcOWVF+H3958KbsaMSSxb9hGzZ08jGOxq+Ln09KYR\nSW9iaBr/nOjj3A02K6LNgvitepef9GO5+gtd1/nqV89jyZLl3H33X1mw4BhCoe6G8BsYPP30iyxY\ncFqb7z/8cAWLFr1IIGBwxhknsGHDFv7wh/9l3LhJnHvul7LaR9evX8fIkWX7/963r5JXXnmLRMJi\n3LiJXH7599vduwNYsuQt9u6diONojB7d8ohJ0+p5sHNAePbQNG3O8uXLlw8m8/vWmObHLFz4BN/4\nxgXoevNCWUrJHXc8wGWXfQfXlfzrX3dw6aUX9mNJobq6jk2bdjB3bmZWV50Ri8XZuXMvU6b0zxky\ngNWrN2Zkfp+OzXGXL2202OiFKizQ4eVpfkS4pcKjJ3kMRnbsKCcvL0xJycC3Rk3H448/x0EHHcJx\nxymVv+u6PPzwfezevZ2pUydw7LFHtJmAbd++iwcffJIrrvgeEya0G9C4y/z1r7fgukkcR1JWNoqz\nzjqX/PzOjaNc12XRohc49tgT0wq7FStWMHfu3LlSytw5shw9R4gZhEJhbr31di677Cvk5anYjZqm\ncd55p/Pqqy9z/vlfYfbsebz11nscc8y8TlLsPUpKChkypIja2gaKivJ7nF519eAwvW+PiSGd34/z\n8e3NNntsqHfhjr0ON4//dGvuS0oKKS+vHJSC7L77nuCoo47jsMOUms51XW655XecdNKRnHHGZ9u9\nb+zYUZSUlDB2bHYNXK688vs0NjZQUNC1utR1nZNPbh1J5cDj093TBhjjx0/kxz++nrvuepRt25rD\naw0bNoTycmV+e+zxJ7NmH/zwkY384dF3WfbRJ7hu3+/JRCJh4vEOo9NnTG1tPcXFPReI/cn8QoPj\nUkzyl0cHv6ajp0QiIaLReH8Xo0tIKfnnPx/ixBNP3y/EQK2I5s8/nAkTOtYa7Nixm7FjJ2bdy4eu\n610WYp8mciuyAUYkksd3f3g99997Owft3ssRR8wG1Iwwbjms2V1H2fgZbNkdx8ofyXM7YjyzfhNB\nu5FiI8Yps8cxbfKoXi9nKBSksrImK2k5jpuRq6OBzuyIxqNevOK9liTuSkLtHI7+NDAY9z0fe2wh\n5557IZMmNR9c/8c/bmP27GlMnjyh0/tfeOFVfvCD63qxhDnSMfhHjwOQW1/6iK3OeGpWrGLlyo+I\nRCJUVdWxpy7Bn9/YhgQMNPLRyMvPg3xlUVVvuzywrgG5cj1Bp5GykM0ZR0xi7IghWS9jdXUtpaVF\nWUnrQNinBTi7ROem3Q7VDlTZsC0hOSg8+AbzTytSShoa4i2E2H33/ZPJk0d1aPrexN69FQwbNvKA\nmJQNNnI1PgApr6xk6LiJVDcOY/ied7jyyu8RCARwXcnIoiA7axM4GLQeIn0+nfzCQihUKoh9ls3f\n3qtHTyjBVuJPMv+QUcycMqbHs+X6+iijRpV1fmEGDMaZezpGBnQmBDWqo5KEhDUxyUHh/i5V/zKY\nJilLl67guOOaA6E/+ugDDB1akLGLuGeffZnvfvfarJXHcZxedUR8IJHbIxuASD2ArmkE8vJpmHwi\nV931Es8s/YhNVVF+c8ZBFPrAh4vRidrK7/dRVFxCwfCxBEZNo7ZkJg+vD/LfT27k14+u4qZHlrF4\n2VoSyWSXy1hdXYdh9Lz5DKaBLhOmhprfyerYgfVs3SEYDJBIdL199Qcff7yBww47EoBnn32SQMDl\nqKMyt4Q++ujDeOml57JWnm9+82vYtp219A5kciuyAUhAJsA7W2Xjp2TUOJ5fX8szn6yjrDCMLUFi\ndPn8lc9nUFBYAF5oGNd1ea06wSvP7cJvRwk4USYU65w4dxIjh3Xsobu0tAjbdggEeibMGhtj5OUd\nOMuWLw/Reaba5fB8jUuH5eaJJSUFVFfXMWLE0P4uSofU1dVTVKQ81rz88vPEYtWccsrxba6zbYfq\n6jqGDStp89v06VP529/u44wzzu7xSsqyLIYNK2Hhwqc455wv9iitTwM5QTYAKTZsYq5EN5SQ0jSN\nkpIiKitr2NfoJ+k4BHWJ5UKgB/1F03UlRDxBIqXk4/ooa5ZE0a19BNw4Yd1l1giDeTPHU5ri1Hfq\n1HGsXr2R2bOn9Ug1OJicBWfC8QU6Pxtl8J3hBsYBojLtCcXFhXzyyfYBL8heeOE1zj//a0Sjjaxa\ntZxLL/0yoAyRdu3aS1lZKcmkzcqVazniiFntpnP66cfz+OMPccEFPXPLtWrVSk477QQ++GBtj9L5\ntJATZAOQRkfDl0Zt6GoafkPHTiQpzAuTBc1eCzRNw+83CBeWAGrGadsWWwMBNn7YgExUoVlRdDvK\nyHyNSSOK2LZtN+PHd99Ksra2gZEjh2XpCfofTdP43ohct2rC7/dhWQNfPdbQEKO0dCh33fV3zj33\nNKSUbN68k/LySiZPHsOGDdvw+QyOOWZ2C4cFrZkwYRwvvvgGlmX1yLvHihXvcdZZ86mpqefjj1cz\nY8bB3U7r00Cuxw1AXCmh1WzedSW2FkBzXFzNIOFAvi+7M37HdvClqEQs2yXs85EXDkI4CAzxygIV\nVpJdVVHsnXUYH5vodpwin8WhU4YjJo7KOHSH67pZ2WvLMXAZ6MY8a9aYzJo1B9u2qawsp7S0BMdR\nKsQjj5yFpmmUlWVu+fv5z5/Mgw/ey9e/fhkAd999B3PnzmPWrNkZpxGPRwmFgpx44mf55z8f4vXX\nX+Hss89n1KgxXX6+TwM5QTYACbgtDxpLKamOSwzXxpESR4LdC2egbdsmkOI/MWk5lBW03b/SdQgH\nA4SDASgp9soICdvmjYoYi7fvRbPj6HYM3Y5T6LOZNm4oM6eOaeOfcaAPcjkOfJYuXcnVV1/HE088\nzKmnqn0xwzAIBPzdap8jRw6nouJVGhrqCYcjVFWV88orz5GXl8fkyS2jrFuWxQsvPMtbb73JjTfe\nsv/7pkjTuq5z+eUXEYvFefnlp6msrOfqq3/ag6c9MMkJsgFI1Mgn3MqQw3LA0QPoEgJukoJg9p2x\nuq3y1DVJXiizJqJpEPD7CPgLoKB5z6tJwL3XkOCdd6rAiqM5CXQ7QUhLUuSzGTq8lOFDS3JC7QDG\ndd0OVXL9RSwWJxxW5zA3bdrAyScfDqjJo+M4Hd3aIRdccBa3334r8+YdyaxZ0zjssM/w97/fx+TJ\nBxGPx4m+lURuAAAgAElEQVTFYsRiUcDh+OOPYPjw5qMs9fV1hMMt+3c4HCISiTBzZlsP+DlygmxA\n0mgUEItJ8vwQ8mu4EgwdHF3DjTcwrDS/U9P7bJBun66rNAs43/6D203Ytsu+RIIn1iVwk7vQ7CS6\nm0CzExhOnLJ8g8ljhjBl/Kg2HTvH4KGgII/6+mhW/HJmm6effpEvfeliXn31JY466jPc/bLJLDEW\nvXIbm2pcbv7LcqYUO1x34Vz8XYh0nZ+fx5QpY9E0ePvtFQgxhSuu+CqVldWEwyFCoeD+g9MffLCa\nww9vdof17rvvcOihLR1y19XVs3PnPs4//4jsPPgBRk6QDUAMaVEc0tA9QWLoGkUh0PFh6AW9s3KR\nEq3VEWu9l4Wlz6eT72uymmxp7u+6kgrLprwmwet7asGKg5NEdy00J4nuJinwOYwojTB2eAmjRwwj\nEhnYca827qikvKKCE49v6zX9QKakpJDq6toBJ8gSiQSJhMPQocNYseI9zj3/TG54bQNvrlvF8HCS\nHYygoGw0W5M237ztXf7+rTlqvzhDjj/+KP72t39x9dU/5c47byMQ8CGlw8iRwxFiEmPGjKKysprF\ni9/hl7/8HRUV+3j44X8hpc1FF7WME/bww89w1VU/znYVHDDkBNkAI2HZWFoAy4VgiiYmYGjQxpdH\n9rBtB5+/5YzTcvrvQK+ua4SDfgj6Ib/tAOi6kHAdPrFsNuxJYG2rBXsfOBaaa6O5FgnLoaa2liK/\nw/CiICNLIowYUkjZkEJKSor73GvCC7vC+IJhJmzaxuTJ2fWOPpApKIiwbdvu/i5GG5555iUuuOBr\nfPjhCqZOHc+dz6+icMgEDJ/OXtuhMKCsDsNBP27JaJ5542O+fGrmBhsAF174eW666X8544yzOOyw\nI/H7/WzfvoXVq1fx1lsrCYVCXHrpt/nzn28iHPbzhS+c2iYQ6bJlK5k37yjC4UjWnv1AIyfIBhgv\nfbAJxwgSzLJFYmfYtkMo1NIQw5EaddEkhZHsBNDMJroOAd0g4DM8i8q2nsG37GugWsapMzQ+Sbho\nuxzYYSOdGqS9D006+KSDjosuHXwr3keXLjoOPs3Fh4OBQ55foyBkUBDykx8OkBcOkBcJUZAXJBIO\nkR8Jkp8X6dTHXtAH/oISlqx4v9cFmSslD1e6fDZfY3yof/emBuLq07Is6upijBgxkvvuu5PLLruQ\nh/7+HoGh6h0arQ76R0IB3t0S5ctdzKekpJirr76Mjz82+etfb0HXNXRdZ+jQ4cybdxRvvLGYxYsX\nctFFnycQaNvPEokEH364jmuvvb67j/qpICfIBhiL1ldQFAwTS7qE/FqfDQKStib/uq4TSzoUDtKJ\nYCLp4vfpGLqO3zCAjs/1SMDx/iU911mulOyVEseVuFGJFnVBuuC6SOniug3g1uG6DtJx9qtjNSQa\n0vu/R6AIv66zsbH3PZn8eJvNPRUu+TpMDGlMCWqM9KsSWVJyXqnOEfl9tyIdaK7IFi58hQsu+CrP\nPvsk48ePYsPWPcT8RbR3NF/TNOpl996bz+dj1KhRDBkyjNGjlVFHZWUVGzdu4ZJLvtCuZqC6uoZ7\n732cH/zg0xhvvGvkBNkAI79xK7XBGTQkIeiTuI6L0YVN5mxiORLLHXiWZpni9MBSrmkCYWgaBkDn\ncpBoLE4k3Pk+XSxQwjvvr+GIOTN6xWhnXczl6RoXF6hz4cOo5MNW8dH+Xe3ytwlwYtGnzymt4zi8\n/fa77N69j/nzj2TGjOP573++QSR/aof3xfUI28trGDu8Y/dt6SgtLWoxKR0ypJQhQ0rbvX79+k94\n7bVlXHfdr9Ou1HK0JCfIBhh1Rgn5QZ38ICAlMStJ0FNH9BbSddHTrPwKQjrRhEVDzCA/3H0vBf2F\nK120PvSLnalIcgrH8K+N9Tz88Rr8WMyQG9kZmkr+0BGMHprP8RNDjCjsetdMupJbyx2eqHKp7MSZ\nxl4bbtvr9Jkg8/t9JJMWgUD/t6Ndu8o58cRjOf30E/YLl3on0OnB/HBePo+8ZvKjC7puOdiV/vvG\nG0upqopy7bW/6HI+n1ZygmwA4biSpB5kv5G6phEI+HFsB72Hznk7wrJt/P62TUHTNMIBH3tqE0wZ\njILMpTftY7qNrmkUFhQChbhItvgmUB+32bk3xkc7y3nxA5fjhtZy9gmzKQrraScZrbGl5PPrLZY1\nZq7CW9ogeb3O4fjC3hdmxcWF1NTUU1bW/iqkrxg7dhRjx7Z0q2Zoks4caQUCfrZW9Z6KVErJY48t\nZOJEwSWX9MxX46eNnCAbQLy5djv4Wnm+QOv1/QXHcdtVX2i6hiOhpjFJcd7gUnHYrmSgh3PS0UjY\nEPD5CBQ279CstfN49bGtTAlU8d2zDkZ3kix+bQnvV0UYL3cyqqyUY489kqIiZeTy+91Ol4QYQNSF\n3+1y2GPB9BCMCeqUGL1jnJGfH2bv3qoBIcha47iSCje/3f2xVGrcCI4rM1YJW5bFG28sZcmS5Rx9\n9FxOPPHYdq+7886HOPvsLzJjRmbxz3I0kxNkA4gnlm+hIL9ld9I0ZVHoD3QtZEs2iQQMKhqsQSfI\ndMPAciX+Pjg8DpDN6YZjhCgbEmKfVcBPntjK2EAdxtA5RDWDivxZ1Mkki57bSSSxigafn1dGT4Ki\ntpabnbG0UbK00cYAin2Qp8PVI3xcMiy7M4BAwE80Gs9qmtnCccGVmWk8tECEB1/dwOePnkxROH0d\nJZNJXnttCTt3lhMMhjnyyGNYu3YjJ5xwTNrrq6qquffeJ/je937IkCEHjgPtviQnyAYIriuxrQQ+\nf8s4R5quEw6HSMSTyrKwCQnBUKBP3P5oukbSkeyujjKyZPCYME4dGmTtviTZFTHto2karpQZqQI7\noymNUMBHcMgwahmGntTwG1ATcwEfWuFwNiTKqDI0anpoEOAAlTY4OpxUmH3BHwj4cV23yzH0+oKA\nT8u4heQX5PPcxnoWbdnIPZeKFr9t3ryVV155m7y8Ak455Qy+9CWB67rccMMvuPTSC9M+965de3j6\n6Vf4+c9zRh09ISfIBgiPvPkheii95wNN1wi19iggJfF4K+fCTde3+rsJwzDw+3xo3VihFIZ91MVt\nGvY0MHXEwPLQ0B66rhEOGFQ1WIT8GnUJSUFAQ9ckrgS/TlaEThM+n085Xu5B+I50aFpLnyuOlJQ7\nsMens3mIj6qC7OVnA49UufxoZPYnSBMmjMI0tzBt2sSsp91TIlqi84tQ72JIaSGN0Ti/u+1hvv/N\nc9iw4ROWLPmAqVMF11zz8xbm9HfeeRtnn72ASKSt6X5tbR1PPvkiP/vZL/v8cP6BRk6QDQBcV/L2\nhnIKy0ZmfpOmEcrA1DsVx3FIJpMqTAyqU/p8RsYLFl3XyO9JJM8+RO0raojheTQUOxRHVFOvbLCo\nqE8yvjSAIZPUJVzilqS83umxKbzfZxCNWVkXZKkkpcsWTWfZsCDxYOfvIqKrvbBMaXDhj7sdbAk/\nHZXd4aGwMJ/a2ga2bdvDuHEjspp2T1i5oRzLyKMr66FwOEht8Xy+8dflfPuIEn784+vbaEdefvl5\nRo4sZdy4tqFX4vEEd931KNdd96ucEMsCg/eQ0AGEuaeGhBFpcyA52xiGQTAUJBwOEQ6HCAYDSFeC\nlBQElEDtCNdxKSscHOoP15VouobP0PYLMYAh+X7EyDyK8/x8fW4e3/tsIaeJEKoaeq6C7M03mHBd\nNhoGbwwPZyTE5kY0PhPpeoliErYne0cdO3bsCGpr64nFMlsB9QX3vrWHYF7XtAy6plGX1CgYOZF7\nV8XbCLFPPlnP+vVrOPbYtqb6juNw++33cc01PyXYC1EsPo3kBNkA4JHXllNYkNf5hVlG0zT8AT+G\n32BeaZSiDlwZSVeiGcagCYIppdvhCkvFLlW/zxge4KSpIUYUDNyZcdx12YjOO8NCyE4mPEN9cGWZ\nwfPCT2M349ZNCvaeSJ4xYzIffbSBRMLqtTwyZev2XeyIBdC7uSoK+A2qnCBOyiSwsbGBBx64m698\n5Zy09zz88DNcdtl3KCrq+sHqHOnJqRb7GduVlMegOIv7HF0lEAjw/s4YMX/7s3CXwTXrcV3ZoSGM\nhP2GGT5d48zpEZJOI3vqEwPOGCHuumxyNN4fEURqGoFYknDSIRoJYLVy9Dw3onHDWIMj8g3ea3Aw\nY91bWT2+N8FuS/L7sb6s14dh6MyZM53167fiOE6L9MPhIBMmjOp1dZvtOPz9yXdZWpHPiGFl3TIH\naky47KuLcdHhE1pMmh588B4uvvj8tPW2d28FoVA+o0eP7UHpc7QmJ8j6mReXr0MG+9cS0LEdSiM6\ndQna1Y3FEjYjigd2mJRUXNdV+3/t/t72u2wM19lWyMVdl09cnfdHBLF8OhP3xhlSmcSRsHpqs5q3\nWIdzS3V+O9ZH0BtUp4Y0fjTSYFXUZUWjZEc7C6CQBuMCMCGkMcKnsbDaZZ3tI9LoqkPCUuLPsjDz\n+QxmzJjU5vv6+kbef/9j5syZTn19IyUlhe0K0kQiySef7EBKycSJo7sUxue+597jnYZRBCNtA8pm\nQm3MYm+DzbmTAvzXqYe2+G3+/AW8//4SFixoe2bsySf/ww9/+N9dyitH5+QEWT/zyoefUFw2rt/y\nl65LoVvHiTPLeGGjTV5AY3e9S9yC4QU65Q0uCVs5FC4M+YlHY+g+P4HAwG46ysy7/RWZK+HlTTC6\nUDK1BAIGHDEuyGubEmSw/dQnOK7LVjTWDvdzmGVRVuESdl12GbC50Ifl0zGAw/M1fjjC4KRW7qaK\nfTo/9KwPP4m7/GCrzdsNzYc4JgXhxEKdS4YaTA9r+y04dc3iyQqLxNq1nLszn0BeHk8e1dZgoTco\nKMhjzpzprF27iXg8SV5emJkzJ7e4RkrJxo3bSCQshJgAwMaN25g+va1gbI2Ukg2bd/Lm+jryR43D\ntu2MhJjlSHw6JGyoaLBxbItLpjhccs78NtdOnTqNhQufbPP9Bx+sZs6cw/H3ojHQp5WBPRod4FQ1\nxIjqEUL9qMpykgm+MLeIYfk+vvYZ1RzqEy51CcnoQoN3d1i8s83m9Akaa8prOHligMWb4xAY+Cb4\nHVWrC1TEYF8UPtgDZ0yBkQUGh40JsHJnMivRsXtKPJagLOTny3UWsYTEp2tYmsbwgE5+nkEoGePy\nKQVcOszodDCeHNJ5+iA/N+xyWFTncmKhzjUjDPKNtvfdPM7HT0b52Bku4j6G8Ei9wefMJEN8MMSn\nEdQ06h1JnSOJuRDSIaRrRAwY4dM4tlBjdkRPm3Ym+P0+Zs06CIAtW3axdu0mwuEQDQ1R8vMjVFXV\nMnny2P2BOm3boaEhmjataCzO4mXrWLqxmjo3RKMbwvEX4A4VBA0NMLAtG18aF21NJGxJdaONIyFp\ngY7FGSPr+a8vndfuPT5fAMdx9qtIpZS8884Krrvu192qkxwdkxNk/chfFr5DXkFRv+Vv2S6T85OM\nLG3pNqggqFPgGVMdPsbP4WPUDHK2F0IrsLWuj44Y9z6aptSM6ysle+vilNc7PVIx6noWD0XrGiWG\nD8tiv2D1aVAY1MhvsClOJJlUYKOVZeYNQtc0rh/t4/rRnV83wg8jZkxhLuB8sIdHanQsn5/2lafN\n3/9hD5T5YExA4/aJPib3IB7ahAmjiEbjWJbN6NFlNDbGmDChpZ9En89g1iyBlJIP1m7l5RXb2BPV\naXSDxPUwWrCEcMEIdF2jSfkYi6m9UL/fRyyW6FCQBQxwJEQtAIuDwi7XfaN9IQZw3HEnsXTpCo4+\n+jD27q3gP/9ZxBe/+JVu10OOjskJsn5iy54KdkQ1hgzrH/NbV7rk2fWcO7frLnFCuk2jK/fH3hrs\n6Do88VEjjm1haPToPFkgECCRSBIO9c573R9eBoiEgrywKc77O7ZTGnSZMzbCIRNK8fu7rht1pWRR\nrUtIh/FBneF+qLIlT1W7xAqHMLzRZUcys7QkUG5DuS25ZJPNo1N8jOyB0+vUva/i4pYu3Bat2Mpz\n7+0ghp+YDCKD+QSCUwiUGFixOPntnLUMBv0kExbBUIDOdjZdCYUhjahlcVCxn//70rxOy3zIIYey\naNELbN26h+HDR3L66V9g6tRpnT9sjm6RE2T9gOW43PTcCoqHDO+zPDXvny0lGhCyGrjis8WEunHA\nee64CIu2JAn20mCdDRzHJRbzfPtpav9H13V0XUPTdOUtw5NX726uw3Zs8vw9t8vUtd538twCX4gK\nF/ZGXT5a4xJcXc6YPAsxLMCQPB+HTizucE/GkZJ7KlwernBYGZU4QL4OhgaahJpumu83sTomuXSz\nzb+n+glkeeJz78treWkTFJVMRtc02h5gaT+/RMIiGFT1omm6Ol6SpnyW7bKz2mGYvYVfnTqPow6Z\nSnEGEdN1Xeeaa37WhafJ0RNygqwfuG/Re2ihgj47kxXywVkiQFm+zoMfJqisT3KW8HfJyiuVkjw/\nUg6cA63pMAzloxLU/oTrusqfpe0ipd1C2AwJSRoT4LoOjiuJWS4+UkZwTdsv+DQ07+/m1VGzUNSy\nZvkYjyfQu9A+dE0n6NcBH1uTQTZsddEl/OvDvfzguEImDW9eySRcycu1Li/VuqyKSlbFWnjxpMGF\nE/I1iv0amxKSrXHZI4G2pEHyg202f52QPSOHl97bzEuboLi0fW/6hq632KdqIh5P4Pf79h/PCAT8\nJJIWoVCzgJJSYjsuO6ttRrGL337rHGrjTkZCLEffkxNkfUxNQ4x3t1ZTMqKTjYosIaVk7ig/k0pV\nZz5rmp+VWxNEqyphTPdCahSEdIr1BA2Wjs/f8aoskUii6zo+X+cGCb2FpmkYhtFuSJfJrdRPH+2o\nx7bt/ftcEomUEul5/5BSglTqWSUPZYtPN51tfxeIxeIEgwGMbjqENjSdsLe6dHw6t71Tz/zxMc6a\nU4aUki9usHirQXaoUPtOihXkjoTLr3c5vFTrUut0nr9GW2Xdv6tcDg3bXDG850NOLGFx37JKiod3\nfBbLH/CTiCcwWnmpl5IWRzN0XUNKN+V3yaYKG40kokhy66UXkB/M/nm6HNljMJ1xPSD4/eOLye9D\nlSKAGNr8mkcWGJxxcBGO43RbBaZpGl+YW4LfaX9V5rpqQHAcNUDEE0misTixWHz/ZzyRxLbtrKvi\nepKc40ridktBpKGhazqGruPzHC/7/T4Cfj/BgJ9gIEAoGCAUDKJpWo+8mNuOg67r3RZirTF0Hd0f\n4qM9aoPriSqXpQ1u+oN0HuMC8Jm85vzHBHXumOjnnkk+5uV1PpiP9kNrz1gxCX/e47CsIQNJ2Ak/\nu/d9QqWZ+GqUXTgc2Hxh3HJxaeSWz0/knu+cSkHInxNiA5ycIOtjfMlajA4O6mabgqDG0EjL1+y6\nLoah97hzalJiJZMkEhZWIkE0niRpO1iOJN5QSyyexOcz8Pt9hENBIp6Px0g4RCgUwu/z4bqSeCJJ\nzBNuzf8SJJMWtt11gSul2+EZso6wXYmhdd8rvuM4BDqwgOsMDQ3X6eHGVCtcKdlZ67ClvIG/7U4Q\nrktyyLbGtNf6gJvG+hjia/v88wuV26vDOhFmloQFRW2v2W2rAKA94d5X1rFTlmXdMbPfZ2BZKka0\n7cLh4WqOPHhqVvPI0XvkVIt9TEzP69PZw9BIW4H1ySc7mDSp5wdc540LsLsmRklYPVFeOMDmffXU\nxFzmTAnx0voYRkH6YI+apvax2tsnbNrXchzXG2DSCTNlwGEY6lMZcTS5p+qeIAr6dArDfuqjiW4J\ns0DATzQWJxwOdWu/zDB0NF1DIrO046aEsi8Y5N/1kj27LQ6tTLJkfFtvMuMDylP+MQXtt1CfpjEl\nqPF+B9Goy204Ml9nV9Ll/WjzdRpwalH3JnG1tqSmJsrjJowckpknHE3TlFPsDPB5Zvh+v4/6aIJr\nLkgfBDPHwCQnyPqYqJFHQR+pKaSUDE3j/TweT5Cf33O3WFOGR5gyvGU6E4c17zcN3x6jrpsro+Z9\nrfYHvlQjjmTS3r/PYdtO2vhPGdMD1WTTKtNxHHzd9BcoZfaEGHjGKD4/CzckmWzo+IMGdivPLGMC\n8KfxPn6y3SGvk4PMs/N0Hq7qeNW4Jia5dYKPW8sd6h1JraNUvt8Y1vX2sKzB4aotNtrKakq1/C5N\nMCRKA5FJAFoVjd1mqKxh0oQJXS5njv4jJ8j6GNmH6zHHhYkl/edvyUanNwNYpxpxpGqaYrF4ty1C\nE7bL3vokef4Da0+kwtCJ+Q0mN1isKGq7h3dBqcH8QoMbM/BlO7YTrZ4fOLVIZ1pY57YJXX8PMc+q\nckGRjpRw9VaHDQkoLQlTFIt1aQ804K208vI6n9iEQkEq6xKM9GVXtZuj98kJsj7GcBLYto3P1/tV\nHwlojC1qOZDYttNnZv9JBojTwgzZVZOgNmaTjdihPVlRZVuERh2XDXkBpkctGnWNjYUtJdFoP3yn\nTLWJ+YWdP3y0E0EyK6JxZnHX29iGuMutexyWNLhsTMDEAAzza6yNqwyrhkcYnXTR7cz32Xx+H1YX\nro8YNt86euBFsM7RMTlB1oe4riRhhAhIuf+wrq7rBPz+tIcxe0pBQMPfSk1UUVHNsGElWc+rNVJK\nkq4xqBpYQchgS0U0C6uxrljLtcWVMrt7ZFJjesxiiAbrQkYbJ5SfiWiUdOEw+D6rY0l2clHXDIne\nrnf4S7nDsgZJdYrM2ZyEzakBPjWNuoifeLVDpAsNy2cY2LbTYTQEgERcGS5peUM8p9MH1qr8QCZn\ntdiHVNXUENAlfr9/f5Rmv99HItlstWdZds/sx1MoDbftiBUVNQwZ0vsB/arr4zj6YBJjEPYbWK6G\n3dP67+Ht4XCQWCxBIpmdwJMBA0olWC7s8rXt8qmm9p1RZbn8q6J91VueDhcMyWxJuz7mcv76JBdu\ntHmhtqUQS8eU3VFEVZxwF1fMPr+Bbdtpf5OuJJm0iMXiaJpGJD+Pny3cwtbK9E6IcwxMBtdIM8h5\n641XyC9sGWpC13VCKa6ebNsmHk8gUeopv9/XLXN9KSVl+W0HKCk7DjiZLbZXRNH0/nOI3B18hsZB\nwyNsr2ykJyckJB173u8MXdOJhEMkLYvGaIxIJNSj1Zmuaega1FsuDa1+K9ThS6WZtQcpJVdusVkb\nl5Qa8NNRBjuScF+Fs18INbrwVr3LhE5i4ayKulz8icXWDPw3GrbLQbsamRi3Ke7Galnz3IY5joNt\nOdi2TSwq97su8/kNAgGlbq2Pu4zRy5kwtO8jtufoPjlB1ods2rad0NRpxNNPDgHw+XzN+2dSYlk2\nyZiamWuaRsDvyygsu+tCbVxS3uAwLE/Pijf2rrC7zsbXR3txPcVxJeaeRgIGNCQcL7xHT1DTkJ4S\n8Pvx+3xEo3EikXCPU7QMjcZWAmZ0QGNcMLP39HiVy+I6iQFcMszg8jLVTlc2urzZ0LwMXdHo8tWh\nHbfRv+xxmoWYlIyot5jYmMRvuei2xAcEQwaO7WLHHcISCnqg8lWWpBJ/wO85Ck5PbdSh0cmjoqaO\nocWFbN26mbFjx/fJ5C9H98kJsj6kPDQGrC6E+NA0/AE/ftRsUUqJZVk4SQvpSnRDVyu2NILNMDQ+\nKrdZtccmP6hREtLJ8zlM7cSlVLaIOQZ6mkO1vU13tILRpEN93CJkZGlXKouOSjRNIxgMEI3GCASU\nYOsuTsgg1kqQdUVmz83TCGpwbIHGf49qTufwfJ03Uzx2VNsdV0DUlbzToNSTea7D1PVVjNN95Ldu\nL00zviy0I13XMwoGO6LIR308n4v/upjnfnY2v3j8fXbXvsM/Lz+GsWPH97gcOXqH3DSjj3jrrddw\nCkf3aGXU5P4oHA6h6WqAa/LyHovFiccS2Cl7bJqmoesaUQt21rt8XG4xfPiQbD1Sh1j9NEdSXj26\nVscf7Yxm1VKwp6rF1vgMg7xIGNt2cJzue8aIpTkc3BWZOzGo8Zzwcdfkli6bLhumMzTldUc6kY5h\nDR6c4uPXow0WTg8wuq6qrRDrY6TEO/unUZLnJ+or4id3PMVtV5xGMlTMnU+92K/ly9ExuRVZH/H8\nu2vwTzk2K2lJ10X3PLIr3b5nTi0ltu3s32MD5SnC71NWkSEshhan97SRbZKunnUz8kxQXj0yn5+5\nrsSvuQR6rE7sfYLBAMlEssND4h0RS2OjsSMhWRV1mRXJ5MCwxmfy2uY9IqAzMQAVtjKZ/+rQjtPS\nNI1ZEYOZYcmz1S57xwxFVicpDveNZ3kp1V607ZnlKw/5Oq4rCYeD6LpOSZ6P92uLOPcvb+HzBzHj\nfTMBzNE9coKsD3jghddJjJ5LIEvTdMuy8QfSnErVNHx+X4tot67jkEwmcaUkIB0eXbKbQ0aHmTq6\nEH8v+XyMJ21szUd2veFlRqZeHJqw3J6ZyqdFZmePrDW6pqJPdwdHSurSWCzWunDLboe7J/dMOVMY\nrWEcEe6alNepFWR50uW3ux3ea5CYcZeiQoNplkEPFpud4jgOsZhycu26LsFgQAU/1VTsOsdxsNDZ\nWWUzvMRPY9IhEPATjzocG9zAgtPO6b3C5egxOUHWy1iOy5vb45SM6F7IlHQ4rksgw8FaNwyC+2fw\nITZbLuZGB/+GWvIMm3zDZWjY5eDReYwfnt/t2X4qO/Y14Oo9d4HVHVxX4uuCmsr2vPRnS/BIUAdw\nm4J6Zhk3Q9+BrYk6ku3tHL56u8Fla8JlfIZGH+kYt2UtvzrlKGZ2IMRcKfnlTod/Vzls904WBB2H\nzyf9xO1krxokGYZBOJx+f9gwdJJJC1fq2GiUV8cpkrXUkMeskRGuOOdifvLExxw/fWSvlS9Hz8gJ\nsl5m8Vtv48/v/XNbmaLpOsGADviJATFgT9Rl1VoH/8c1hA2HPMNlSMhh+ogwE0YUEEy3+uuA7VVJ\nDKNvVJitcV0X23bQdZkSDbr96y3bpZuyIS0aKtZVONy9oKWdEU8ksLvhx1ECejvHv/bZcPMeh/83\nvmP+N3cAACAASURBVHuCzLIsZlTvZGZBS0FRabn8Y59LvQPjgrAqKnm40k0NWcqJdUmcOqsH0QZc\nbMvGlbJdQZUpSdvG78a5/uQxxAPTuXvJDubPGs2Lq8uZNaYod0h6AJMTZL3M6NGjkdt3AtlZoUi3\nC1aPGWLoOkYr4bY35rJ6o4u2IcqkIghoDkHNZniexsTheZQWhtv1MF+X1PAF+6/D67ruCTTZImBi\nOqJxh3jSwbUlfqMp2nOrf13MP9vx1VqmTbdcjEV0jYlJh+p2VmUVnXjr6Ij//GcRp59+YovvdiRc\nzttgsyHRfrrzamKUVidwMqhhKaU6A9ZK/2gYOoGAHwk0NsaIeIZQrTF0Hddx20TdthzJrmoLV1oU\n+3Ue/f6JlOSHcFzJgpkjCPkHl5u1Tys5QdbLHDxlEsHFK5GFRVmZzVmWhT/LsZjSoes6jgshv4Eb\nChNHhfjYF3P4aKONIRsJaA4BzSGk2wzPN5hQFqG0INSvPhY1rSn6b2ZlCAYlpQUh1uyoB+ns96gv\n3aao0Okt/cLhYLuHlHtz1q7rKl5ZV1XAPl2jxGpfqKczBMkEKSW7d5czenSz2i3qSr65uX0hprmS\nWbsbGFWfQLYyiZeewZJjOy0sKjVNUytdfzCtFlgDwuEQyaSV9pyY4TOwHYeAoWPZkqjlYMWi5DkN\nzCiK8MNzj2ZzVZK6hEtJPhi6hqHnhNhgISfI+oCJejU7pMyKTbbjugT6yumv7TA0v1lFpusQ0A2U\n24sgLngCTlLe4LKqVgk4y/XTQy1Pn6HrGiHdwEFL2UvsGFe6+w0HtP3fSUKh4P5VXG8R8Kt4Z93x\n9hHqQIca76YgW7duIzNnTtv/99aEy7c227zXTryysOVw6NoaxoQ0kskksVYrrCaBFQwFu9xddC+O\nWywWJxgMttAYGIZOIpFE6j5q6xo4PG8vM8Yb/GXTCPbU2vz4sQ956qrjMXrB52mO3id3jqwPOP/M\nz5GorezvYnQZTUKk1Yw56bZ1GqvrGkG/GnyMUB4MMh+LAMEuTA6aXEg1RbwOh0NEIiEsy9rvDLq3\n0DSNUChINBrHcZX0kaQGInWwbIekZZNIWir6djxBLBYnmWzfpUy8m5rFZcuWc+SRc/9/e28eJklV\n5m3fJ/bMrL16p/emG7pZmmbfm1XZURbZRBoHUVBRR9RxdBZn3nlnvplxnPHVGUFRVFARBHUU3BER\nFRBkEVCWppveq2uvysxYz/n+iKrqqq4tMyuzspa4ryu56KiMiJNZUfGL55zn+T0APNQZcekrAU+M\nIGJCKlbtzXLq1m5WZDQsQyOdTpFK2UNejmNhGHrJz3z9dm+e65HPuQMp9r4f4EYara3tLO58iq5c\nnm/uWkjK0qnXI07XnklEbBoz/e4405AoCsticTPZi82GFjuEDEYTsCdQpLV43WX/4UgZoU3DKRmh\ngZpA+rdA4Ng2YRSRz7koxyprc8zB6JpGOu3Q3Z3FNI34LCOs7emaQGhxsotAMFb6yaoS1jSVUnxp\n6XF8d7PEFD5PZxXtI3yHS9tdVnZ7NLghBhLRlzxUahfv8QcGqXT8aWND4IBA6rT3+mRMi21zTqbW\n0WjvDqhTXXzxHRtYvPi8yowlYVJIhGwS+MUfXkKkJp5+HwQBljl5v7KRghSdeIZ0q6/QUBycGt7v\nbLx2GVMRQXmcpQxdx0nZBEFU0d+VQFBTk8b3/IIzJB2lSPkR+f0arjXp8NGFxf/OvrYjz0u185E9\no3xzSrFuR5bluYAGQ4Clk8+PYTRaBlzXw7b3rZFZlkkUaezqkKTSDnNrdbp6PTq6PG7Y0MA790tS\nSZieJEI2CTzX4mM0TzxBI4okljU57gdSyhFTvIWIL5qchJHKjuKC5MkZ4/7EeRmlPeWHUfl6dxuG\njuv6UOGHDl3T0A0d1/Nx7PG/8zpgQ7vPbxYM7ZZ8Yq1gTWr0T98/E6CUoq0zx6s7u3lxl8vXghrU\nnFoML6Km06Vz/lDH+MP35lmeDybVfkoTGlIN/V3uanfBy+OqGl5vCzikXvI/t7w5yUicQSRCNglo\noY+YZu7ZbiCZWzPyzXGxJdjiq1G9XKtValOKz+LAvpSvvb0gvumXsznmaFimWfC6nCYETaHECCVh\nn8vHat/nzR09vPBCftSygfteDPE0h2wg8GScGGMaKRYEETUdneRcSRRIuuekafRDVrfkmadBOpBo\nk2z9FUURlr3voVEphSOzrFu1mFvPOZgVczKJk/0MJBGySSAUOhONUSZ7fUxJRW1q5MsjowuWWNA1\nwnqIlIp83kPXNXRdR9PGLkguJ7HPYuEn29vj05MPQcQOH+VMBrUsE98Piy4mL5ZiLavm6HDkjiw7\n51os6QlZ6kX80bK59Oz5pKyRI5SvvriVnHLAiG8Y/VdFsw2NSrFHKTI1Ois2d2IIsERlSxDGwrRM\n8nlvoDhaKoVhWWx5Yyur5h1TlTElVJ5EyCYBqcSEhSgIQsxJXB8zNMbsJ1anC+pGuO9lMqm+JoaS\nMAzjmiwGT/iJPpHT0LTSs9NGolifxa5cQNaNvZJMUV5/REPXCfwAKuw46Xk+tlN4rYMpBCujkDXt\nGrYOwtSRfb+T0XB0RW6UgFUTgoV1U+c20r8+G/dwc9A1jYbGBmRHvsojS6gkU+cKnMFsXObwaLeL\n5aTGf/MoRFE00MV2MphIdNJfCzRS0odSimzOxVQ6UgYj7qtp/dFccTVZUsqiEk2CSBFJha6Jivj8\nlWrwWwiRlPiej6YV3zTVEIpU37ywVIpNR2XGdP9PGQoK6ORcCNooDhvlpP8aGByZuSq51c1kksni\nSeCCM88g6NxT7WEUjJKqYq4GUipMQ4/dxwfVYfW/LMtC0wRhGOK6Prm+Xmv5vDvw/67r4fsBYRjF\nEV+fXsRRb+GX9PK5aaLKaU180x7HIqsUXM8nCEJsxx6SoVcsUimOX2ZzyIKxj2GX8VLQNTFQ21VJ\nfD+I3e2Jr4suWfpDZMLUJ3lMmQQMw2BBbgs5sYxIlfDkryqfNDAYN5Q0juLJN1Hi3k+j3xk1TaBp\nBmM1QpYyLv6N/RTlQJKClArX3T/xQfQdUxtoNNo//RhFqqJCZhh6LDhlzjSVUuI49oSjSAGkzPGP\nkTJB5cqzRuv5waQkW6TT+0oShBD4Knlmn8kkQjZJHHfoar7b6lOTLs27qRJP9qOeS0rqnEoJmZzw\nWl8sRoX5KcaOF7F5sJQS1w2oqYkNnIUQVNLMwTAM3Ao4fTiOjef5AxFHqSigzhr/Bj8noxO1F9ce\nZzRM0yAIKlNLlsu56LqObQ+dgs/mA9J6BZ9YEqpO8pgySWzceBaie3dpO/d1gva9Mi1UjIOOwqpY\njc3kZl8KEScyGIaBZZlDkhqkUlRwGatiMXRUQhuXwegaLG7QOXKxxckrxhfDxY0WYVSeB6lyZN/G\nTvghruuRz8evXM5DKWgb4blhZ6/PiQcvmNA5E6Y2SUQ2SXR7ktCsJQxCNEMnbQjcIpYKDMMgH7go\nqUZsU1FOjFniObe9Pc8ITZPLSrl1UhGv/6TTpa/5mEJxy0mF94ub3+Cgid6SzzcYKQsXMqVi0Q7D\naEiNW9zhwMC2rXjaMJR05uM+eoEf0NGZp7Eh/nx+KAGNT1xwaFnGnzA1SYRskmjKWPzNRUfwie//\nkXRNTUlikXLsOBMrXZmmjRA/7c6WglEhVMVFW0pFLu9OODqTSmFZJoEfxi77EzhWqAR+EBUcdc9v\nTKPTPYEzjo2UcesWGfW1bunrFNHfykXT4hmJkaakvUDS6Uq0vlXkRY0Wrbvb6A7y6LZDh2fwmQtX\nYk5Sx4iE6pAI2SSysKmeuflt9GTWkvMVTgEL7UMQAsOM65PMCqXiB5Eibc6OP/oyzZaNiWUZaEIr\ni/9kLu+iUOgTfNBQQtCd85lTX1hUl0mZGEKVLbo0dJ18zh2wgNH6MhnT6RRCxA0yBWBaBroel3Fk\ns3kMwxhSdxhKRaeraEjp+KHCMuJ6zYa0yf/ccAb/71v/y8/cBZx46KoyjTxhqjI77lhTCF+zaUxp\nWCU+QpimOWyqpZyEoaTWqYxISlm6hVQlmIyRmKYR98Eq07HKURSv0OjKFr7eKoRgFNOP4s4r1YBA\npdLOQOsW27b61i4V2Wwe27biYmZdx/N88rk4os3nXcJBiSL9pW8tLa30uLFZdRhG6LVz+fDn7+GM\nk07gHUc2T6lrLqEyJBHZZKMbcbt6Ufr6iZOycSs1xagkToUisqiEzsblJO9HPLOtl5SZRROCrB8h\n5L6FSiEEQhveDkUMWC4VXwQhEFi22de5YGIPCPGM28R/N5ESdPQWlzhk64pRGj4XhFJxRJkZZW1P\n1+KoK512BpVHRKRSDkLEDiaObZPPuwR9D3LptEMYKVwvIJ1i4OHOMnXcOev4zP8+xf/+zRWlDzph\n2pAI2SQTP3fCROKBfueMIAgwJ3hz3B9DH9uuaCLE7v3Vu+RyfkQgFWnNQAFpW6PfQqq/OeXgV1xs\nHWc2qvg/JZ1XsU/EJzItaBgavh9gTnCa0tAFe4sUMkeH7hKz5l3XQ8lYeEa77A1TRzecIeuzUSSx\n+/qk9TfMTKUdpJT09uZjb00iGusyRCLCDfd9L0IT9BiN7O3oYm5jfWkDT5g2JEI2yUhhlCUF2bRM\n8jkX0zDKajdfSbNypYrzQiw3QSRHLSIW9EVdFZqGUihc10dKOWpUMh6a0Iii/b0ri8fQBW29xblr\nOIaCEoQsDEKE0HDSYz9w9Ue//eTz3uiGyyLuxaZpgua0zhLVw7M9go6cwdyUTi7nIoQgEjr/9v2n\n+Nfrkp5jM51kjWySObwxJPDDsqxxOak4i7FcRKP0IJspZEyNhfUOtWkLKXTCShaR7YcgjqInmqhh\n2xb5vDuhNTdNaOSCwo/w69dytORK6CAtFX4QDitQHo9czsU0DfRRIk8vUOTD2CfTsgy29AhCpdGY\n1oiEPrD2FkjFaYcniR6zgUTIJpmNRxzMgfI1msdoZFgo/VOMYZmcErxAkXZmrpDZhmD53BQr56Zp\nypiTfvFHUTThqWBD17Esc0Jilg9CMkU4tzy/y6PdFeRzLvm8V/BDWC7vEobFXZtKKbS+63o0HFMj\n6yt6vFjMovQcbFx2dubp9SIiGZcr2EScfsjios6fMD1JhGySWbZsJcGe18qWMmdaJn4QlLx+Mxgl\nK5exCOUvDi6WwVmTfjj6NGOlsG0b15t4BN0vZl6JTi9KKhY1FZ4oFEbx5WU7Fo5jFTQLIKXC0HXq\n6moKOofnBWR783E0Nm5piaI5rSG8XrbsaKGt1yf0fS5bP4/OfI4dnT5t7VmkZozaYy1hZpEI2SSj\n6zp/yhxD+2gNnkrAcWxcd+L2VeP1IJsIapKNj0cdQ1/WX3d+eAuZSiOIG27m3fKIWdzrrfjHA8vU\n+f3WXMHvX3+AzYJaDS+I4lT8vvXZfN4jCEJ8P8D3A3I5F9+Pv9e4Q3bhyCgiU5Mik0mNm2wkhEDX\nBHX1tSxeMJcGM6LZjjhsUS0HzWvGknmyEi5cv6iIESRMZxIhqwIasqxJBf1dmGU0sfYYlTQ/iLP2\nqn+5CRFHC9WKD03DIE79mPj5bcskm82Tdz0iWfiDkaFpdHrjX39SKT7yrc1894ldtOQETl/GqWHo\npNIOjhO7+muahqZppNPOQIdwN+8N/HxcSsxeEUKQDRSp2npU3QJ++sTz/P3FhyCFgYbio+euLf6g\nCdOS6t9ZZiEasuwFzfYEozLVNxVUKcZr3zKZdObCPjGrFuV5iNF1nUw6heNYuEVGeboY//P7no+P\nhmfWkHLMYZm2QghM0xjSRNVxLKSUpDOFT13G3c9Lm9JuTGmEErp9jT93akgpyUmBV+HO3AlTi0TI\nqsCJcwICv/xO9rZtlbxu4oYKp4CWHqUiZXVT7wfTkQvG7Ig8nRAirqwv5rv1gpAWz+SNjrGnV//z\nJzvwteKL7jVRXGfvIAxLtvBSxFPiNbagM7L58/YWCALWz6+cH2nC1GNq3FlmGZeddw5+R/k7RuuG\njpISVcQ0Uz9KRtQWmSZdLFPFKahS9l7VwvMDrAK9NxWKIAhIOyZ3PpUd9X1f+sU2duZLa95p2YVH\niGEYTciHUhMCN1RICYZQ7G1tBcNm47pkfWw2kRREVwHDMMiofEWiFMexyeXdott8aBXtQTa1CCev\nR+noTLSqeRBSyoLr01zXx7EtDE3Q6yv+4WedpEzB2nkmi60c//HLbr6yaRmvtIZEWrqk8ei6RhAU\nti4aRXJCQhZJRdaL0DSNJfWC5TURB83LcNERSdr9bCKJyKrEFRs30NVTnh5PQxACyzQHsscKJS08\nMn4bhttFlM/iuS5eEFV5LakyVDvnRFDeVBNd1+MSjAKQcpC4KOj1FLu6Ap7e0sO3nsmB5XDLt7bT\nKwtM1BiF/i7WYTh6AlLghwRBMKEkIF0TzK8zMDVo8VN8+sd/ZrHcQV0qWSObTSQRWZU4Ys1KnF8+\nj6qrLbs7t2Ea5HMuyjQKPvZcR/LWo+YN/Ls757N5Vzc7u0PcwMBTOr7SiYQBuoGpa2gF9vKaajN5\nVZ9aLPMUq91XU5bPuzgpe9wyh2w2TxCE2PY+sWpXBkqzqa/RyeU1nDKsIabTDr29OXRN22dwreLp\nzd7eHI5jU5MpLeobjCYEjWkNhUCkV/NCd5YfPfYE55x07ISPnTA9SISsSgghOHqe4IXQA7P8C9PF\nOORHUjInM3S+rS5tccSqJo4YtE1KRXuPy6t7eni6M4NSYGnxE7cmRGyKq+vDBG4qJHpEkeK1vS6p\nlKTHlRhTZL2uXNi2hVSSXM7FcexRpxqVUti2RSadQoi4fxdin/S5fhQn/hTbK28EPM/Hti2iKMJ1\n/Xj9lvjaz2TSBT8IFYIY+AyCSLP5u0daOeeksh0+YYqTCFkVufLC8/ngV35C7YIlZT+2EALd0AjD\nEMMY+9cchRFrF2bGPaamCZrqHHbvdqhxIFJg6fEUjpSKKIrwfH8g4um/TcXrIEbsVl7hjsyj4YaK\njqxPpOL1wMnpRjYa/ZOL5R2DJjTS6RS5XH5UY2JN0/pq2fpGsl/EbhoC3dTozEu0vlZDdXZxWYgQ\nm/4auj7QQ62/dq+cDzRRJOPO0vslNxm6hgX05Dxq03bZzpcwdUmErIoYhoEjXQQKVYEbq2VZ5HL5\nuD5svxtREEqkVFimhqECli1oKOiYv90OXV6c8jx4iV7TBJo2cuPHXM5F0wT+IJFjyL4auq6hacOj\nuXLhBdHAutRkW1NNJoLY9WP/RAupFK7rjZtYoWsaC+r2TTnm/JBdHQG2IaizY0eN8fC9YKC+rJ/4\n91qC8bBSA4K1/7Wj6xqmoaPpQ9fDIqnQcg4f+OpjfPmmxPl+NpAIWZVZJHfTJlZXbB2p377KSe17\nMlVSUh91cuBcmyd2a8y3vIKKoQOpeKM7FrFiEIJR08Pjvl8KKaNRhQ5En1BqA69itciPohktYIPR\nDZ0wCtH1fYLkuh6pAtbP9idtGSxsEJg67O4KqHdAH+N7lFISRhHpIko5VF80H0bDjQKEEBi6hm0P\nL8ge8Vh9/eMOaLbZ2tbNG21ZljaPP9uQML1JhKzKdOqNhFJV7Cbbf9Mf7KyhhKDBEZy7fg4HNPZw\n4Pzawg62n8YoFU8vZiyQMk5rL1aPhRDofc08RzN32Cd2kjAMh00l7XdENE3Q60ssQ8c24qf2IJAY\nU6kIuoKzm/1rX2EU4XsB9P3+o6i0Nj1pW0cpxcp5NqsbNZ7Y6o34IBGFEZ4fxA00ByFlXLs2Wgas\nJgS6oRcsVmPRmNZZ3mQSRIrOVp933/UMD95yYtkTqhKmFomQVZm8cDAq/EdmOza5bJ50Jl43iSLF\n0ro4SePwpQWKGGDqgpShyAbgRyAVHLkANiwQvNiqeGoXVGJmcLDYjUe/6L2wuQ1di+MPAUiAKCQf\njdFWRAji3ppi6It4+8DPJ6hA5U6/3x9d0/BknBlYX1+DQCDL0Mx1/UKbYxZb/G6LN6QBaxhG5HMu\n9LVf2d8dX9MEhmHg+z6pVOUcN2xd0JmTPJ1z8SNQlsOSWrjrd9u49oSlFTtvQvVJhKzaGA5+Ec4M\npeI4Fp7rYTs2KEV9TWmL4EFfMKSLOCI7dB48uVPx+11QO7HSo7IQ36wVhsYIPbfGvtwV8bRUPD2l\n+kRRDmyj39F9gvPAYSQxRlhLLCfplIOmaSipEJoYM+JX9EW8kez7vGrEKd6nXnd5+IUIL1BDIjJN\nE6THca13896QJJNK4EUKBGgINKHQzBRm11b+uLO+oudNqD6JkFWZv7rsdP7P3T/ET9VgNixAVChN\nXdN1VBAiI4lAkTKLP08QKcK+KURdQGMKTE1w6FzFohp4dBu4IQw2CBncA2yyyAd94kNxs3eDI69K\nUqofZjEo+r77/ULk/pYrmq7t+27EvjVIwzRi0RPD404FKDtEypAau7DrRykIwxDRd+xKopQiUvG1\nqQtYWKM43vb501SaUk6oCImQVZnmWofPvOdSdu/exZe//xNaZC1W8wHozsQLRffH6ZtiFLqObhUf\nkXkRODoc1AR/3As1fUFkyhQcYMLyesWrHUP3ibPnJtf6andHHpTEzbvjv3m/aUTD0NBEhWveynRf\nVX3/VUqhJGh6PA0aRlFciKzruPtN8/U3yCw1OurKhtRahSVdRJHE83wMQx9SfF0Jgkjhh/GDVhAp\nNA3WRU/zputv4KH7/lTRcydUn0TIqsyP/7SXY5fUs2DBQv76xuuQUvI/37iP19RS7FT5s61sxyLI\nZVkyd27R+9ZYgrceDJ2u4qXWOA3/2T2KQ+ZCPoTXu+KMxmjQrFQURRWfNt2fMJKkU1ZBCTRqQAgU\nUsVehOkKruP0nRTX9cqT4DMgwhD5knTKQUpJyrGxbLOszUyljLN5xstajSIZfz5Ni+vZJiEgMvX4\nk3ZnIy5dX8Mlh6X4zF0Z7vjtDj575eGVH0BCVUmErMoctbierz65A0ODlmzAUYvrefdVl/GB27+P\nuWhF2R0xdF2nOS2xi82hH0R/8kQ+hOdb4KXWODoIouE+hkqVtwi2EGQRWaDxdKIAPa6LCwv0LJwI\nmq5hahpWGafaFIp8Lo6+Aj8klXbK3pFb0zTm1Zv05EJGszJUUuHmPdKZ1KR3OzB0QZ2j8cx2nxdf\neIXmxUfw8XMPSjIWZwGJkFWZOTUW1x1zAH4kac0G5ALJ5tZebr3wWD774JNkzXoyNTU4TvkcCnoj\nA6lKT/lvzUMk94lWfwRWbTPefiSSUvywFWpSes3ouo7v+VBGIcvnPZyU3Wc5Vbmiby9QjLbkFEUR\nnheQyUxOFDbk3FLR5UocQ/Bam4/vNfGLS49KRGyWkAjZFKAxE68fzK8bPKVVx2duvJiurMvffeke\n5IoNZbs5ZZXNn7Z1sm5pY0n7L6uHzCpodyEXxK98CPkgTvYQIl5Ly1Y+uBkRKSnpRqomR8fQ+j0O\ny4zneiBExToW5IMQP4hI7efDGAQhYRiiadqwGrLJQtcEDY5GTz4g70Vcf2QT1gTawyRMLxIhm+LU\nZxwabEGvVAhtuDdeKeiGzh939JQsZIYmWFADC2qG/6w/szFlCl7rUDzy6uQ3/4qkQivhHqbKUGtV\nLfrX9Vwv7jdWCfZ2hTSlhhtCR2E0an1Yf9KHlAolJXKQgPcbGE+kjUs/WTekuydHkwMHL5jLjecc\nPeFjJkwfEiGbonTmAhrS8ULE2846idt+/HvM+UvBHkE9isTQNV7JpnljdxdLF5S3xsbUxUD6/eKM\nLPs6TSHMRiHrR0pZESGLpMQxhj5I9Sd1jBaFea6PVLFhtK4LNMMcUg4gB/aPpyL3iV788FNoklCu\np4cVchv/8P4rqK2tm8CnTJiuTJFVjQSA7z6/h/ZsXGNk9i1EfP3JHVj1C/iv917BIncHQX709vQF\nE/rMt1yaG8qf4j+Y3e1ZlDb5z0qlzqxNdyGLoqhipsu9boS93+KY78frYQOWWGGE5/nkci75nIth\nGqRSDqZpoOv6sJo2TdewHZt83iWf9/C8AKVUXysgjVxu/PKJKAw4KtPKZ259VyJis5hEyKYQp69u\nIm3FoUTGjgXg+OX1PPD8HgDe//bLYPefJ7S+EoUhRzfluOHUhWScyqbF7+jw0Ca5hiyKJGGJ3890\nFzLPD7Dt8iQFKWLH/CiKyHsBvbmAMPDJ572Bl5Ry4P8HREiLG66m0k5BU4a6HjfdTKVsHMfqEz0N\nw9BxHJtsNj/qmp8fKYz21/j4DVeV5TMnTF+SqcUpRP1+wiKlYvXcGj5yxr7pxGs3Hs49L+xF1c7b\nf/eCMKTHmesXTmichdKRB30Caf6l4Ielu/EqqRDT2AVitAccxT7brSiSBEFQUOKQEAKhaXT0eDiG\njm1a4wp9PufGNmhlQNMEmUyKfM7FtMwhbWGUUuzp9Pj709ZNesF9wtQjEbIpzG+2dBAp2LiqaWDb\n+vUbuO/h/8HPzCmpPislonIOcUx8pTHZjaHdMCrZkHc6R2S+H7vLj+ZmIrT+wmkNpSioc3g/lhki\nVWGJRqmUQ971EEKUxc0e4rF6nk8URQMOIWEkUTLijJNOmPDxE6Y/ydTiFGbD4noefa192PZ3vvU8\nst3dRR1LKUWQz3H2msquiw3GZ/KflL0gKvnmOV2FTKEIgpCamhSplDPiy7FtbMvCMo2CmmMOpq7G\nJAgLzD4VkErZWJYRO+KXiTi7Uaerqwfa36Dea+HwJaVl3SbMPJKIbAqTsXQ++aYDh22vb15AEG4p\n6lhBIDlqARy8uPC2LRMlUPqk5yy6QYRRYsJDJVurVJL+xqmVyhC1dANNFCdKmqZhOxae62M75cmi\ntPE4cU4nH9iUrIklDCWJyKYhu3t9ZNHGtpL5qcmTlSiSBGryLy8/iAYyPovFskxyuXzc1qS/Zcs0\noD/JopIIii/i1nUdqSRhOPHpbBlFLOh6kQ9sunLCx0qYeSRCNg05eF4NQU8bvb1ZXNdHjdkxjNgl\n4QAAIABJREFUOcYwdH78ejSkILWS7O3KVyX1PppAt21D1+M1nrxHPu8W5p5fZfwgmBQvS8PUyfnF\nF7enUs6AC/5EkB07+ccPvWdCx0iYuSRTi9MQTRMcGrzEUctreWV7G9v3uPjKJBQmkWYihUEoTKRm\nopk2mmFg6CY2k2eBt7M9D1rDJJ1tH3GqdumfUhNiwCUj73rk8u5ASnjF27sUSf/aWCadqvi56jIm\ne9tdsItf97RtE98P8LwA2y6+5CPvR6R0UbbSgoSZRyJk0xTbNNmwdhkb1i4b9T25vMsbuzv5+WNP\nkGqYw5nHrJ20ZIY9PRKzCi7CccRZns+YcuzY1T8I+lwq4hR2x7aHpIJXC98PMCrcdbkfU9fRtNKj\necsyCcMI1/WKNsAOQknKSEQsYXQSIZumFOLgkE45HLxiAa07Gtm8eTOLmtZPwshiPKVXzGViLKI+\nT8pyIQDLNMGMIwmFIpvNowUaSipSaRsl1ZBoo7+uqd/tQiqFEHG0aNtW2aLiMIwmJRrrp3+drNSH\nIcPQ++rYQswCnf/9IKS11+fbt55X0jkTZgdTa64koWAMwyIosHfWyScfx/nnn8Xtt3+dP/zh+QqP\nLKYaiR4QC1klEQjSaQfHsUmlbTwvoLs7i2kZBEGI6/m4rkc2l8f1fBT7bvyGoZPL5ZFq4kbKYRRN\nep830zLIeRNL3LDtODLz/fGv3Z58QEt7Lw9/5HRSFe4wnTC9SYRsmrJs2Qp27NhV8Pubm5t473vf\nSXd3D7ff/jV6e8vg2TgGgarO1Fs0CWb7mtDQhEATGinHpr6hFtMwcBybTDqFbuik06m4S7NpYpkG\nlmli6DrptIPnBYSRJAhDwqg0YQiCcNI7b9dlDIIyfMGpVDxNGAbhqO/x/JC2Ho+vv/tknEn+nAnT\nj0TIpilr1hzE5s1vFL3fxo0ncs01l/GNb9zPL3/5WAVGFk+hVSMiiyJJWOGIbCT2z5I0DWPU6UOB\nIOXY1NSkUErheX5Jaf6WGUeAk4mh6WVrnmpZ5qjj9/yQno52Pvf2o1k6t7zdGRJmJomQTVOWL1/F\ntm3jR2RbtrzBli1DBS+TSXPjjddSX1/H5z53B7t3t5R1bN05Hykmf/nVC0vsqFkFBALLNPumB4uX\nMqFVpjnnuOctY+NOTdcGxKzfC3JnV0i2vYW7b3kzG5Y1l+U8CTOfJNljmqJpGqKArIaHHnqE+voG\nurp6WL/+kCE/27DhMA4/fB333fcDgsDnbW+7GMua+FrEjrYcSpt437RiyXvhtCliniia0OKW1kWi\nmFgbbNsx6MqGNGYmPt1n2xau66FpGm4IgVS4vs933nsGTXWTZ6WWMP1JhGwao+smURSN6v796KOP\nc+aZb+bYY0/k7ru/wubND7F06SJWrVpOQ0N93zF0rrjiYtra2rnjjrtZu3YNp5120oTGtasrwKiC\nI7kXqEk3KS4H+bxXUhxZSnG7mpiO0ZC26ektLMmoEBzHJp9zcRybrk6PK1cbNDUlkVhCcUzDP/uE\nftavP5IXX3x51J9v3ryNY489EYBrrrme008/j6amZXzjG99n1649Q97b3NzETTddT2NjA5/97BfZ\nunVbyePKhRp6FdqhuGFYldq1iSBEfDMfzex3rFcp3opKqQl7MtZlTLpy5RMzoWnkcy5LtDY+cPnp\nZTtuwuxhev3VJwzhmGNO4NlnXxr150KogbbxEK+rbdhwNB/72N/yve/9jO3bh6+xrV9/CO9//w08\n88wf+fKXv0Euly96XH6VMhb9QBbt7F59BKXaFZfiBlkOh/+0Y5IPyjeJa9smbXnJx686u2zHTJhd\nJEI2jbFtm2iMdOhMJk022ztsu67rfPSjf8ODD/6SN97YMeznQgguvvhcLrvsQu666z4efPDnRSUW\n7J96r9TYyzl5t8/b0PUJgpAoikpKZJCqdJ/F6YgQomgxUxOdWwS8MKKc/VJzvuRAu5O1i5vGf3NC\nwggka2TTHG0MY17LsnBdl9rauhH20/jQh/6Kz3/+39i06W0j7l9XV8uNN17Lyy+/xv/7f1/i4INX\ns3r1CpYsOWBMa6RAaUM6ke3e+hq1USdSt1C6hdQsNCuFmcqgmw5RpHBsC03rS6EPI6QMGRypvNLi\nYmhxqrttajiWgWPppEwdU4+nMuNC42n4bFaiq5bj2OTz3oA3ZKHnmqjW+57ELqOStfb4/PM1p5bt\neAmzj0TIpjnLlq1g27adLFmyaNjPOju7x1w4f+GF51i7dni/s/1Zs2YVq1evZPv2XWzevIXHHnti\nSCQohOCAAxaycuVSmufNJ0QfImQpXfLuC44ecsze3ixvbNvJlh2t7Oxw6a1bRv2iFZjm8BtkGCk8\n6aIAqSS9foTf7aFk3/1fKHQhUEDKml5CVvrEIn2JPsV9XqXUhB1BvCCipgTz4NHGYxOwZvH8shwv\nYXaSCNk05+STT+O73717RCEDRs1oBHjxxT9y/PHrCjqPEIIlSxaNeJ4oiti5cw+bN2/h0cd+T67p\nEHK6idJtpDCoMYeHADU1GdatXc26tasBeOinv2anOx8nNTzt2g1l31SjiB01dDHtkjpGpcToSBGb\nBhfrtTjYMqtUUrZO1g2pTU88BT8MQxbWaNNwbTNhKpEI2TSnqamZnp6R7abGu2EddNBaXnttC01N\nE2sZr+v6qCInlSKS4z9tn3v2yfznvb/DWnMUmj70snQDSRUMOyYF0zTJ592iBcnNu0W7yENcfyal\nnFAjzoYam5358mQtuoFkYU31OwkkTG9myGPt7EaM4qIxXr7EoYeu589/fr0CI9qHJkTBHZvfc+EG\nWv7wMGE41LrIC2RZkwumEpoQmKZBUEQXZdX3KkWMNF0bkslaKuUyFZFSsaY5adGSMDFm6O1hdrFo\n0eJhdWExit7enlH3Gy/rcbJxHJtbrjmdtlefHeLs70eSKpSlTRq6rg8T77Hw/aDgNij7o2kTt5iS\nUlK2q0ZFZFXibJ8wMRIhmwGcccab+O1vnxq2/cILz+Kee+4ac19Nm1rTOqZpcstbNtC+YwthX5Qi\no5mdVq9rWuw1WGDaRxRFmCU21BSIkq2tpIwd+4MwQtcUXlC6nPX25sjnXWQkSekTaw2TkJAI2Qyg\nqamZPXtah9VeNTTU096+d8ynfcdJk83mKj3EojAMnes2LqNtz27CSCJngYOiaRoEfmFRmSrzgmEk\nJW5fLd9oL9f18YMQFBi6xpyGFHmvwPGqWASjKCIMwniNTtdJpRwa6mt46s9by/p5EmYfiZDNEN7y\nliu47ba7honWhReexde+9sVR97vookv5yU8eqfTwiqa51uYdx9bR9sarfa72MxvTMArqTaZQSKXw\n/GCgiWd+BBHK5vKjRnj7b/U9H8s2ccayxHJsHNvCNA10XccyDISukct55PNjvzwvIAgioiguYsvn\nvYFRCCFoC52yrNslzF4SIZshrF17CJs2vYfPfe7OIU0zFyyYh+fl2Llz+4j7zZ+/gM7O4e4fU4E5\njXWcvkzh9XRWeyhTBoEglbIxdA3TNLBsC8exhvswCsFouf39W9/oCmnLRdiO1ScucZZpoa4quq6T\nTtukUmO/HMfCtk0sy8AwdBzHxrb3JXjoqRoeeuQ3E/laEmY5iZDNIBYsWMhHP/o33HXX/UO2X375\n+Xzta18adb+VK1dPyCS4kmw4/GDo3l2V3luTiUIVXFJm6Dq6rqNrcafq0UyAxzuerUNjSkMTcUug\nKJK05STZII769mYjAqnodIdHS2Ek6fVKi6J0XUMbVDeWTqf4zhOvlXSshARIhGzGkU5nOOaYE3jy\nyWcGthmGwZFHHsIvfvGTEfc577yLefjh307WEIvmsJouUDM7IcDzAiy7fNl7uq7jD8r89CJFjycJ\nlSSQih7XZ0WjTq2tEUlFd6DRmouTOdp6fVrau4m8LO0d3eSyWfKeR0s2YmdP/Hvozkdk9it039YR\nkveK98kUQtAmGtnbWt4Grwmzh0TIZiBnnnkOTz75/JD1smOP3cDjjz9GNMI6jGmawNTKXhzMlRee\nQm9nW7WHUVEmWqTcj20KTB0s0yAMI7pcya5OF69zL35vJ7mOVrIB2EGeLXt62LG7jd2dOWToMSds\n453rDH7wnuP5/i1n8f33n8n3bjmLB246hTPrWvFzWQSKLi8i50vMQZfMtnafmmAvR5pvIDt24OaK\nSyBy6hr59Ne/O+HPnzA7SZw9ZijXXXcD9933ba688uKBbaeeeiy//OVPOfPMc4a937ImbjdUKVIp\nh0jO3PT7cmHqcM0RaSxdcM+zOZ7u0HHCDjYurafXXsE5h8ynpTcg64Ucu6yBprSJaehkLH1MFxjT\nNNl02Vu4Ip/n2s8/RIuYw5xagyCIrcO6OzpoMGy+cvMFNNfGBsZ//cUHeK4H6msL6/Rs6BqvB410\nd3dRV1dflu8jYfaQRGQzlAMOWIKuO+zZs3dg2yGHHMRjjz1CW9veYe/3/XBKZ441ar1ERYwviKbn\nmloxyRb7Y2qC53YFPLHN55W2gKaUwNNSPLQTjjqglr09ASevauKqoxezam4NjRmbGtso2HsxlUpx\n9/vPJ5VvIZvz6cmHtLS0sW7ZfL77l2cPiBjAP93wFg5OddHdU3g/O1U7n3/6ygNFf+6EhETIZjCX\nXnolv/rV74Zsu+aat/Lzn/942HvPP/8ifvjDn0/W0IrmlIOayBcwXaVr0NXeSqrrNbJtO+ls20tb\newduGCGnaMKIG0pCFf8ptuUkpa4G5gLFk9s8ntruMS+js6jeRPUVvJ9w4Bwe29zG1rbiG6UOxrZt\n/uryU6iJusmoPBccv47/74pjhhWsCyH4Pze8lXqRK7g5q2novJyvo60jyVJNKI5kanEG8+ijD3P8\n8UcN2dbU1Mju3cM7Q69efTA//OH3yOddUsX0t5okzj9mOX948WE6zIMw7JGnq6RSzG1/nps2HsjS\npasHtm/Z3c1X7v0J7QecSsqu7hSqUopQxdFTPx15yYomi/ZeH9dXdIcB6UwaZ5DBZCAlGUujNSsx\nNXAMMWIk1b9NKni5NUAiWFwDzTUOZx88h/WLh/emK5ZTD5rPqQddNO77HFPnrg9dxOn/8hO8yKU2\nY2OM43JvNczhvV/4Ad/6+NsnPM6E2UMSkc1gNm9+dZgjvRCCefMa+dznPj3s/Zs23ci99/5gsoZX\nFEII/mbTGSxTO+jp7h4xuhJeD8cuNlm69IAh25cvqOPv3nsJmew2enqrVzMXyVjEljbEUVIQhvR0\ntGF7neRadnBmQzt/fVITf3nSApyeHXTv3U13NofnB7R1uezZ00rU20bQsZNdXT7ZESyiQqlozUVk\nfUkQQRqXjxyb4Ucv7OGUA+dWxerrjutPoN5tIeuG406bGrpOkFnAv3wtSfxIKJxEyGYIUsqBLEUp\nJV/84udZs2bZiO8955zTRnyab2hoZO7cRbz22pZKDnVCfODSY7lyZS/ZljfI5t2B7XkvwO7dwcaN\nJ464n6Zp/Mu1R3FEXTdd3V2TNdwhuJFiaYPOq7t62NHWS5O7m3+9dAP3feBcvvS+t3D9JRdyyoZ1\nnLh+Lbe/7xK+9t5zuXiFyUqji+uOWciHLjyOBQuX8A9Xn8Vix6e1xx8i6FLFXh49nqKlV6JroFlp\nPvmjN8i6LlaVWgisnF/L1z5yGYdlH2d75/gTp04qxW92aTzyzJ8mYXQJM4FkanGG8OUv/w/t7Xsx\nDJve3l4uvPAMVqwYWcgAlBo5ceKKK97OP/3T33LzzdeO2ZSzmmw87hBOOUZy2w+e5Xd766itrUG2\nbubjm44bd993n3sIn/ryL+jMHI45yZ8vbQie3Jqj1tT49rtPJGOP/ednmQZXnT1UmE9c0QTAv7/9\nVK6540neaHMxLROp4ulES4tfnp/FlIowNBGayd1P78FVOm8/ZknFPt9YmKbJSevX8tgfIwq57dQ2\nNfMfP3iGjUccXPnBJUx7kohshnDeeRdTX1/H9ddfxk03vX1MEYPRhUzTNDZtehff/vbUnGLsR9M0\nbrpoA5+6cDELg238/aUHkbELE6ZbLjka1bWzwiMcSigV2zs9NAX/etnR44rYeNTYBv915XoOml+D\n60f4UUSjfAPCHpqCFu7ddDTf/8DZfPOdx5Kua8IxDZY2FpYKXykuOP8iFsjdBb/fcSyy2alpn5Yw\ntUgishnCokWLUUqno6OzoI7PmiZoadnDvHnDuzcvWbKMxsZ5/PCHP+Oss04Z4os31VjebPOJK48u\nap/Ghjqa6aEtDLFKbIdSDEopdnT61Bpwz7tPRh8n4aFQljel+ewVG/jVyy24QcRRy46ixrFwBlUq\n19WkufjwhZx/yDwa0tXv+6XphY/BSWd46aUXOPro8SPthNlNEpHNIDZtejf33fdgQe9929su4Atf\n+OyotWNXXnktJ554Fvff/1Nuu+2uGed1+IFLjiLbUXm3EKUU7V09NNiCe99TPhHrRwjBxoPm8+ZD\nFzGnNjVExPq55pjFU0LEIqnwVOHTua5Icf/vXq7giBJmComQzSAcx2Ht2sP49a8fH/e9pmly+unH\n8fDDI/svAqxYcSA33fRBVq06iNbW9nIOterUZRwaDI+giM7M49Gai70Id/dGZANJWzZgV1sP16zR\nuefGkwouPJ6p7OjI0hmliArsp2YYOn/sSdPRM7X65SVMPRIhm2FceOElOE4zd9zxLXzfH/O9hx66\nlueff3bcY65Zs3ZKZzKWynUbl9PZXZ41mEgqbEPQnNaotxS9Xd0sF3u5/6ZTuOTs08pyjumOClwC\nYdDtSvb0FPYA4dQ388mv/LDCI0uY7iRCNgM566xzuO66G/nCF+4eYlG1P3GEIOkeJx199eo1bNky\ncj+z6czaA+qwotyoDSiLocOVZF3Jzk6PRr+Vb7/nVD79rouxrOpP6U0V5jbUYqgQIaDOKWyK0TRN\n3sgadPYkSR8Jo5MI2Qxlzpx5fPzjf88DD/yIlpZWgkEtPQbztrddwGc/++9j+iymUmmCoHxTcFMF\nXRNcfWQ9bnfp06ZSKXb1RGgqwvVzXH3MEj777gundIJMtUg7NgcaHWhKUkxJW6qhiU/cUXwW7ac+\n9UnuueeuUa/9hJlDkrU4gzFNk2OOOYEf/ejXdHe3c/PNm9D2axWSTqc455xTueuuL/OOd9ww6rGC\nQNLV1U19/cQtjqYSGw9fzG+ff4ydXg1OCeITRKAjyedd7n/3KdQ4SQQ2Fp+49iyu+cqzLEsVfusx\nDYMtXSl27G3ngLlNo76vt7eHP/3pRbZt28ru3btIpRyeffZptm9/nUymjiuueDuNjc3l+BgJU4wk\nIpvhnHnmOdxyy61cd927uf32u0fMPjzwwBVYFjz55Ojt5m+++UPceee3p7RDfql89KoTyHa0FuWu\nD7FBcU8+oMfzuf/mjYmIFcCKhXM5c2FIe7c35vt8BTt9RX8T6pr6Rv7uayMnJj366MN85jP/zNe/\nfjvd3TtYu3YxV1xxLo5jcuON76OnJ8vxxx/GHXd8jiefnLoNZBNKJxGyWcKSJcu49NIrufPOb4/4\n83POOY1HH3141P0dx+G6627kG9+YeR54mqbx3rOX07q3laiIMgPbEGTdLB9/81psM5ncKJR/vP4c\n5gc7CKNo1LY1gYKWENrD+GeGobMnsAmj4Q8bv/nNr7j++su56qqLOfLIw+no6OKrX70X0Fi+fCWf\n+MQ/8rOfPcbGjSfQ09Nd6Y+XUAUSIZtFrF69ltNPP4dvfvN7I/7cHOdmvHz5Sg466FAeeugXlRhe\nVTlyaQ0fOilDbxE+jG3dLhnL5qyDhxeVJ4zNv73rArraO2jLxubG++MImGNAWt9XsuArk91dw1vC\nrFt3GL/85WN89av3cued3yGbFbz//R/jlls+AsRT7LadwnU9UqnqupskVIZEyGYZRxxxFBs2HMcD\nDzw07Geapo2bsn/22eexatUh3HbbXeQHmfbOBFYtW0hUQFLLzu6Ibk/S2evymSuOGvf9CcOZP6eJ\nk5bXIX0PyxB05KIhkZkuYLElqB+U3Ch0g627hmfhvvnNF5DJzOXmm2/lgx/8GGeddQ7Gfo4tmiZw\nXTcRshlKImSzkOOPP5nlyw/i179+Ysj2pUsXsnnzq+Puf+yxJ3HTTR/ittu+XqkhVoW0pWEz9toN\nAAKUglAzWdZcU/mBzVA+cdVpeJHHlrYAe5T+aoMxDZ3Xdwz3yLQsi7PPPg/THL3X3GGHHcF99/2A\nVCo14XEnTD0SIZulnH76m3j99W1Dtq1YsYxXXimsdYau68ydO6cSQ6sauiYwdG3cpI9FtTqhlFiM\nHb0mjI0mBKevXY4W9tCRGz/RxjBN2lpbSzrXqaeeyac//TlWrVpT0v4JU5tEyGYx+z8AL1o0n23b\ntha07/e+9x3OPvuUCoyqurz54DT53PiWSPkA0oVEbwlj8g9vPZTbLlnOIfbuEZulDkbXBTu7S68J\nq6mpHTblmDAzSIRsVjP0169pGq47fDF9JHbv3s68eTMrIgM496hlmNk9476v3hG4JOn25WDdusNY\nnXHZ0RmMaU4tlcafupPvPGE4iZDNYqQcni5WV5empWX8G/lMdPqA2LZrQZ1F3ht72tDSBXlssv7M\n/B4mm1uuvxYZ+GxpC9jdNXLUZWshB9SNvg6WMHtJhGyW0tXVSSYzfOH73HPP4P77vzXu/qtXH8Tz\nz79YiaFVnZvOW0tPeythJEeNEHp9hSDi+88V3igyYXQ0TePhj53JLSt2MMffShAOXzPT3U42nba2\noONJKXnqqSf49a8fIYpGyO9PmFEkQjZLefzx37B+/bph2zOZNLnc+Aatl1xyJdu3d/DAAw/NuF5l\nDWmT/7hkEfNan6C9o5NghCLcOlug0Hl5b7YKI5yZmIbBlVe+ndtuvgjZsxcvHHpd7c0bPL+nMFHa\ns2cXDz74AD09u/jWt2ZWdm3CcBIhm6W8/PJLrFy5bMSfHXjgMv74x+fGPcZVV13Hccedxuc/fydd\nXT3lHmJVaWpq5K/eeS7/fkETC9qepLW9Ey8I8SJFKBWmrmET4o0zBZlQPA0NjRxtbqGlJ6Q9G9eX\nuYHEw+Dak5YXdIxXX32ZM888hRNOOJqWlh10dXVWdtAJVSURsllKLpenq2tku56TTjpmzIabg1m3\n7jBuvfVvuPfeB3nuuZk31djY2MDHrj+Hfz2/iYNzf2Bpy69oVh24oaS2JsNL20dvk5NQOldf/jZE\n6JLL5dnemqWjo436ujqsAm3zX331FZYtWwzA2952IXfeeXslh5tQZRIhm6V88IMf5d57f8QLL/x5\n2M90XUepwtcVHMfh1ls/weOPPzdj1yPmNNVz09Vv4sM3vIWLVng0drzAvK4XWPrKvdUe2oxk6eLF\n/Oxjb+KRv34zn736SA5ZsZxv3nhcwftnsz1kMrGLRyaTpqmptuAayYTpRyJksxTLsvjoRz/J1q17\neeSR4Y7gmlZY48PBXH751fzwhz8rx/CmNIcdto5PbTqVc9bVcdVV11R7ODMSpeLp25d2dfOzP7fz\ndxceRNoqvAbshBNO4b//+6u0tMQF1BdccBYPPJA8dMxUEiGb5Vx99SaiyOCxx54csn08u6CRWL58\nJS0tnbOmkeGzz/6J448/udrDmFHs6sxx2ed+xYn//AgPPr+Tzz28mb980xrm1BZnLXXUUcfykY/8\nLT/72W957rkXEEJg2+aMbEOUkAhZAnDJJVfR0xPw+ON/GNjW0dHOF7/4eZ577pmi/vivvPJavv/9\nwtbXpjNtbe3Mm7eg2sOYlqgRWrc8tbWDrpzPX37zafb2Sj514RrOOXQhn7/6CLQSHqogdr2/+eYP\n8eijTyGlZO7cJnbvHu7VmDD9SYQsAYArr3wHLS3dPP308wC8733Xc8EFG9m8+VnuvvsrBR9n8eKl\n6HqKF198uVJDnRI8+OAvuPzyq6s9jGlJKBVZb2gh+dKmFAL4yg0n8MhfncabDltUsoDtz9VXv4Pv\nfvdHHHroGp555umyHDNhapEIWcIA1177F7z44mZ27YqdPVIph9NOO4m2tj10dnYUfJxNm27kiSee\nZ9u2mfv0G4aQTmeqPYxpialr1DhDHTrm1jrUpS0cs/i12fFYseJAokjjpz/9NQcccEDZj59QfRIh\nSxjCTTd9kHvu+QFhuO+JuZT05Vtu+Qj/+78/p6Nj5tXvvPHGDg48MHFRn068613v48Mf/iTr1yf9\n42YiiZAlDEHXdW666QN89av3DWxLp1M0NdXy2muFTxdqmsatt36CO++8j1yuMCPi6cKTTz7Dqaee\nUe1hJCQk9JEIWcIw5s9fwLHHnsQvfvHYwLYLLjiL73xnfA/GwViWxa23/jW33XbXkAhvupPNutTX\nN1R7GAkJCX0kQpYwIqeccjpbt+4a+LemaaxatZRnnnmqqOPU1tbx3vf+JXfe+e1yD7GKJH82CQlT\nieQvMmFUGhub6e7e56F42mkn8Oijvyz6OPPmzefII48bkt4/XQnDENNMemIlJEwlEiFLGJWTTjqF\n3//+WQCCIOCOO77J2WefW9KxzjjjzTz99At43vTuqtzZ2UVzc3O1hzFrkFLS3t7GU089wf3338Nj\njz2C7ydGzQlDSfp+J4zKqlVruP/+b7J8+RJ+8INfcNNNH2Du3HklH++GG27mG9+4g+uuu7yMo5xc\n2ts7J/QdJAwnn8/x5S9/AaX6+78phBAD/66vr2Hx4oUccshSWlpauf32/0RKhRA6a9cewoknnpqU\nQsxyEiFLGBVN0zjllDPZvHk7n/zkP6JpEwvg586dx4IFS3jllc2sXr2yTKOcXNrbO1m06KBqD2Pa\n09nZzs9//hN27NhGGPpceul51NfXjrvf/PlzOeywuLmmUopXX32d//7vT3P44UfxpjedP/C+KIr4\n/e9/xxNP/JZMJsPVV1+P4zgV+zwJ1SURsoQxOfHEU8t6vMsvv5r/+3//lgMPXFGSn2P/0nZqAAAB\nqUlEQVS1aW/v5IgjkoisFKSUPPjg9/jzn1+goaGWE044ijPPPLrk4wkhWL16JatXr+Q3v3mK//qv\nf2Xx4qVs374VpSIOO+wgrrnmIjo6Ovn85/+d5uZ5XHPN9ZimOf7BE6YViZAlTCqapnHVVbFl0Fvf\nWtp6WzXp6OiiuXlutYcx7Xjmmad48MHvceqpx/IXf3ElEEdUjz32OHv3ttPTkwNicdqzp4UPf/g9\nRR3/xBOP4uCDV+K63jBxbG5u4i/+4kp2727hP/7jn1i37nDOP/8tE55hSJg6zBghe/rpxENtOvHS\nS6+xaNFT0266Z+vW7Tz//PPVHsa0IQxD7r//Hhoa0px00tFEUcSzz76AUorvfe/HbNhwLCtWHE4m\nk0HTNO677xusXHkAzz77Qsnn3Lu3bdSfHX/8Bl5//Q1uueU9HHPMcRx22IaSzzMTeOmll6o9hLIg\n9nehnq4IIY6s9hgSEhISpiF/Ukrlqj2IiTBjhCwhISEhYXaSTBInJCQkJExrEiFLSEhISJjWJEKW\nkJCQkDCtSYQsISEhIWFakwhZQkJCQsK05v8HRoDvIb1xxtsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b9beda0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAawAAADaCAYAAAD6xHbEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4HMX5+D+7e11dcu8FM8YGg00JJYAB0xMIJUCAEBLI\nF1JIAklIQn6kk0JCSEIIIQVCJ9QApoViuu0ANsWUdcHdxrZ6ubZlfn/MnnSSTtKddKcC93kePafb\n252Z3Z2Zd9533nlHk1JSpEiRIkWKDHf0oS5AkSJFihQpkg1FgVWkSJEiRUYERYFVpEiRIkVGBEWB\nVaRIkSJFRgRFgVWkSJEiRUYERYFVpEiRIkVGBIMqsIQQnxBCPCCEmDCY+RYKIUS5EOIqIcQhBc5n\nNyHEv4UQCwqZz8cRIcRPhBAnFSDdE4QQDwshdO97lRDidiHECfnOKx+MxDomhJgkhPiNEGLOUJel\nyOBQMIElhDhTCPGWEKJNCFErhDgZ2AP4DBAqVL6DzBjgB8DMAuczCfgsUDnQhIQQq4QQD6V9P0oI\nMX+AadYIIU4VQpQNtHyDiRDCB/wI2CcPaX1PCLFLCDHdO3QA8Km0UyqAs4FxA82rQHSqY0KIUiHE\nNiHEn7JNQAjhF0IcJ4TYvVCF7MJuwHcZvs80rwghFgsh3hrqcgwlvr5OEEL8CzjKNM3J2SYqhNgL\nuBP4F3CZl89K4Ph+lXKE4o3c/wnUABJoAUzgfuCPpmkmhqBYxwPxtO9PAb9AvZ/+8mngJlQH0jKA\ndIYVQoiFwLPAItM0n+3y209Qws5nmqYLXAc8ZJrm+sEuZzYIIcLAt4CzgFmAA3wAPG6a5ve7nm+a\nZqsQ4lBgVw7ZTAQeAy4EVg+40EOAEMIFrjJN88ouxxcB/wUWmqb5Qg/XXgxcBMwAbGATcK9pmr/s\nI8/zUe2nJzaYpjkDuADwZ3krH0n6FFgeuYbDOALQgEtM04ymDgohckxmxFONElbnoipvNXA08Evv\n8+jBLpBpmpszHNbylHy+0hkptLcLr56/P4Rl6REhRBWwBGXh+AvwPSAJ7AX0OBA1TXNdP7Mc7HqQ\n7/xyDv/jCavrgWuB7wBh1MAgmwHco8Anvf814EXgFuDv3rE4gGmaO3It10eNbAVWe4UQQpyOMoON\nR3XAbcCTwDdN00yNxqq9z9Y0IZUylbQjhJiGGuV92TTNf6Yd7zTKEUKEgJ8D5wClwNvA90zTfMn7\nfTbwN2Cal7cGvAp82zTN19PSnQpcjRIUIWAtcKJpmpv7ysO7fgFwDfAJoAHIVj1fZprmB97/Dwsh\nmoArhBCzTdN8XwixN/Ar4FDUyOxJ4HLTNDf1lKAQ4hsoc8hooBmlzf7QNE3L+/0alDY1HggCt5um\n+X9CiOcAwzTNQ9OS+6EQ4ofe/9cD271nMdo0zXovvVLvni83TfPaHoq1Ju1972ea5grvHf8GOAZV\n314Avm+a5ttCiP2B5cCZpmne6+WzEKXVLDBN8w3v2EWojnasaZq13j3sCZShRvLfM03zMe/cGcCf\ngTnAWFT9/Jxpmk8JIWaiOpQjgKiX90BIbxfn42mZae+6V7y29FuvnHHgAeAy0zSbvd+/ixrsTETV\nyeeALwFbUHX72rS07gbmmKY5L0NWf0Q9r4Xp9Rn1nHsr3wbgRdM0P+99fwzYHRiF6pDXotrpnV0u\n/bsQItXZfsc0zd8LISLAz4DPodroO8AvTNP8T1p+/0C1gVHe/W4G/mya5h96Kyfwfe/acah2e4Vp\nmk8LIQ4GXgJOM03zwbR8lgE7TdPM59zl8cA7pml+J9cLvX6zXZP12tBm0zRfST+vq7VLCPEL4FTU\n1EQ5qi/9NXC4V55KYBXwddM0l6WlsxeqHzwUaERpjt8xTbM+rU/uyvOmaR7hXX84qn/YD2gF/oNq\n06m+4jBUm5+MGrAnUUL4m+mDoN7K0dOz6s8c1p7AfOD/UB3/lShb/Q0Zzj0cNXL4JKoT7IlMI5r0\nY3cCZwI/RNnZa4EnhRCTvN/HeXn8DTgWON879pAQIgAghCgBngf2Br4JnIjq2LZmk4cQYhTwDGou\n4ovAV4GdvdxTb8S8z7AQYiKqEy8DPg98xSvjc54Zpyde8cpwHKqSfhP4Wtrvp6EqweeAk4Cb037r\n+rxvoeM9XQM8guqM0zXAQwEDeLyXMp2Zlo6Z9sz3BC4GzgOqgBeEEOOA14E64LC0NI5Iyy/FYcAK\n0zRrve/Xo+aDTkKZWO8TQoz3fpuCeiZ3ohrtBcCbQoggqkHsCXwd9Q7X9nIv6RhCCF/6H/mZ/10F\nXAqcgNJ6TkN16ilORAmG871zrjZNcxvKfHtMl7QWosxxnRBClKPMgHd0EVbZIOlcV47z8v40ai56\nHXCbEGLPLtf9mo56cJd37FbUu/gVcApKsDwghEifJlgEfIh6Diei2sXvhRDpc4GZsFGDt7NRg7dH\nvUHsUlQ7bn9W3jzrAjI8qwHyrkpenJrndLuS/j4+iaqHZ6L64PWoQVMpqn6fheqv2gcU3qD9BSDh\nXfcD1PO51TtlGx3vLtUfANzmXT8feBqoR/WT30e9q8VCiNQAbgZqUP8T1Du9BPXM786hHBnJVsPK\nxGOe7f5Fb5L160IIn2madto5L3vnpAqZcyZCiH1QjeME1IMCNWragdKGfpN2+iumab7sXWehRqyf\nRI0kv4nSNnY3TXOjd/6SHPL4OqrzOM40zZ3edatQQqYvfF6HWYXqkL+F6izfQgn6JHC8aZqtXrrL\nUR3xt1ANvBumab6W9vU5b75hIZAajUpgrWmaT2RRvkyjuTWo0du/vUMLgY2mafZm9no9XbsQQlyB\nGjjMSmmLQohnUA3rp6ZpXiSEeAI4Ki2No1FC7CjgOq8RLAJuTLv3e9PyWI5qPAcAD6Wl87Rpms+l\nnXc+Ssufb5rmm96xJ1HPuC+e7OH4gCJHe88y9TyfE0LMRT3ndD40TXNxl2P3Az8SQlSYptkkhNgD\nNcrONJgQqHa+dCBlTeM90zRfhPZnvxPV4axKO2dten3yNJ1TgXNM00wJsCeEEFNQGm+q3BJVx57z\nrluCEo5nAl2fQTq/Tc0xelrgRpS14fNCiP8AJ6MGgqD6Ax+9D7z6w0+BCcC9Qoj3UR38v0zT/DDP\n+XQ1f+40TfMZACHERuA94EnTNB/3jo0B/pqy5qAGSM0oYZbqq3XgZiHEGK9ve8W7dh7quf3WNM3U\nHNtvgDXAKaZpSu+8NaiB6Vl0DFAAnvX6g5eFENWowccM71g25ehGvrwETS+tQnjr7O99Pobq2JMo\nu3CYDGbGLmUCVYkADgFWpwmrXPPYC3i3y4PM1nb+Pkqr2obSdF4GjjZN0wEORpkMW9sLribuVwMH\n9ZSgEOJsIcRKIURMCNGC6ujKsyxPNtwOnOiZckAJjVwb+cGoZ95u2vTMXUu930AJmdlCiMneXMt+\nwBXAEZ4mswBl9nwQQAgREUJcJ4TYKoSw6egoK/ooy15AU0pYeWT7/r7qlSv97+85XJ8RIcQxQohX\nhBAtQogYanCUzTu8HTX5nhrNL0LV10waVKqMeffM9Uw3taiBYG+k3vV/uxx/Atjd68ygy/P02se6\nLNJPvyaBql+pNn07ME4IkdLcFwHv99AP9BvTNOOmaX4BmIpq458H1gkhvtL7lXllg/eZvmwodZ+j\nvc/9Uaa6KB193c2owcKM1EVCiErUgP9FlBaV4mDgmZSwAvAGMG300l/RvT/OqhxdGYiGlU7KxBXI\n8bqk99mb6Svl0XY6HS8kRS0907VMGj2PiLPJI4SaC+oPn/HSrQd2pOaZ+kCjhw5RKI+l21HzVt9C\nPcer+lm2nrgZZe49UwjxNMoMfGUP5/b0XHvq0NOPP46qtKegnvW7KBPlNSht9DBgvWmaKS/Gv6FM\ngd9Fmacq6FkDSidE/z2sVpumuSL9gBCiNxN3n3ha0WJUp30Kai7gm8CBfV1rmuYmIcR/UabCm1H1\n60mvg+/KWsBFvb9CEKOjjfVVD3KtJ6DaZq79ig91z6A63PdRz2oJStt6oJdrm+mYg09nVFp5esQ0\nzS3A74DfCSFuBv4shHjZNM2Cu6ObppnwrFjp/XrKEzlV9+OoQd75GZJI9+y8ybvmnHTh5JHpPfbY\nX3l07Y+zLUcn8iWwsiV1oynNbgdgAXN7ueYd73OyaZq9VbS+eB04SggxJYMzQ2qU3lsey4CjhRCz\nTNNck2Peq3qZiF8GnCyEKE0zCU5HeRjd4Z3T9bmlOp/LTNNs9K7ZhBrd5UoTHY2xHdM0twgh7kKZ\nBEpRwrYnwdDkfY6i84TtUmBR+jMXQlSgOuX7vXzaPLPNWah5zodM00x6psLPouZB70hLcz7K1NBu\nIszS1LwM+IoQ4gjTNJdkc8EASX9nLt3f4Z6o9vejNOeS48hCYHlcDTzjmYIPRZnNuuFNpD8GfE4I\n8ad0J6Reyttf0utBOilz5LF0NhkdhzIf1nUpQ7/xtPSDgYcBTNOUQojfAtd7TgszupShK++g+omu\n0xvHojr/d3MoziPAF4DZZO+gVWhWoZYdbDdNM+OgSyiPx5NRTjpdHSCWodq0lmYSPBSIkJvZuc9y\nZGKwBVbKpfqLQoirPfv7XcAXhBCrUSPmTtqW52n2GPBLT01dhmpUc0zTvIbsuR7lKPK0EOJXKDfz\n8cALpmmuzCKP36NGA08KIX6OmofZI9cHkIGfAGcAjwkhfo/SBH6EcgZJzUdt8T4/J4R4G+UBCXC1\nEOIeVEOaROcG39toJ/235cBnhfK8awRK04T2b1ENbRxwdw8jeIDXUHbon3j3UONd9wfUM3/Me2ZJ\nlMuvDvw47fqbUevBLOD/ecfuAO5BOXrcknbuq8ApQojUWp9staY7UKa9fwshfobqmKqyvLY/pOr6\nRUKIm1CDMxtV9qeAFai1UD8WQtyI0rBmZUgn43s0TXOJEOI11IR6M8o1uie+hjJDvyCE+J33v43y\nqt3bNM1v0qWOmcqFOhuTZ/s5pmk2CiFM4P+EEO+hBHXS89B8CCU0alCDmtNRGvSn+7rXLMpxmFCe\nxeOBy1F1Jn3u93aUV9stKLN+b2sOf43yentCCHEDSjP4FMph6Oq0QeUvUY5ER5qm+YYnFOuBN71r\npqIcCdqAV4RyrnodNbd6bh/3kwu5mqX/iBKiT3ll3oSa/2wzTXOxV87foObyXSFEyt0+7s2bfw/V\nPz7g1evRqGf7vwzeov0uR08XZTOa6uop1PV7+vFez/EmRv+G6sRSnkVfQ3mGXInywrsT9WLfTrv0\nNOBPqBt8GNXBHS+EMHrIvxve5Od8L+1rUKaoH6M6+j7zME2zDeX58iwdL/QXqFFFb+tV+irXFpQW\nEUM1rL+iOtOFpreGzXMF/SnK6+0ob1L6Eu+6R1Gaz3TgjSzy7fpuvubldyuqUz8urWyrUPN6k1Dv\nrbd7uAD1ThejzJMzvcZ9OMokcyNqIroFODx9VOVNGpsoTfQ97/CjqBH7U2bn9UCXot7PL1H15V5U\nXdmadk6muuei5i9uRXUk/0WZPbrWta5k+xy7nnsnyvT0C6DGNM04ynFnL+Bs757OQY34H0DVp0Po\n7GrfU1tLcTXK5f1W0zSTPZ1kqrV381GDtjNRz28x6jmUCCGCXetYhvvpia7nnIsSoPeh5vlS81fn\noATGFaj73Qf4rGma6YK2p36lp3JsQ3maXYgyrf4FZQLdxzTNdrOSZ4L/A33UY+/cR1DOVz5UH3A/\n6r1cYprmD3opax1KK7nDK8vPUXXrUK999HUv2ZBtX5zpOgA8S88hqD7rWlT7voqOwdIilMfyIpQ5\n9QXv7x7v+tdR2uZo79hvUPfbNeRYrzIii3JkRJNywFp4kY8wnsY03/TWYBQZPnheXK8Ds83+L/L9\nWCBU1JlbgKme40+REchgmwSLjACEWtCnozwPL6K7q3WRIUKo9YBTUfNE16IW1haFVQaEEKmFq9NR\nay5/UhRWI5uiwCqSiZ+gFgO+C5xumuarvZ9eZBBZiDKtNnifP+j17I83p6PmpLYB15qm+cchLk+R\nAVI0CRYpUqRIkRHBiNWwNE2LoNxFixQpUqRIbrwvpYz2fdrwYsQKLGD27bff/voee+TDs7zwOI7D\n4sUPEAr5OPjg/br9/sgjzxAIBDjooH0oLx/abaUsy2br1p2MHVtNOFzYrcvWrNnErFlTCppHT6xd\nu5nddut715x/19r8dZfbze3JD1w9xWB+iZHpsnbq6hppaWlj2rSJ/S/sMODeex/lvPMuxOfru9u4\n557bOP74hYUv1CDhOA6vvvomO3fWYRg+5szZk7lz98Ywen/3A+H22//JySd3DRnZPzZt2sI776xh\n//3nUVfXwEUXfWdf1NKKEcVIFljsscceLFgwYjZIZf/99+f6669h7727r5N+4413ueCCS7jhhmv4\n8pfPGYLSdWb+fJd33lnLvHmF24svkUgSDpew++7TCpZHbxhGkD333K3P8/aSkpWmxbK2ziLLApZX\n65w/veelYNu27RrSe8wno0ZVs3LlKs4990t9nvvyy89krOcjje3bd/Dkk88jpcEpp5zF7rt3DJBt\n2+bGG/+ElOnLE1UdcRwX0Jk6dTpHHHE0FRW57b26a9dO5syZlbdnuGLFO/z4x7/kr3/9AwsWjNz3\nMqIF1kjEshxs2+42Sl2wYE9WrPgfc+fuzYoVb7NgwV5DVEKFYeg4jouUEk0rzPZGjY0tVFbmM/xh\nYdA1jcvHG3zhA5sWt/NvK9pckq4koGd+RnV1jey1V69LS0YMEyeOZ8mSpaxZ8z6zZvVljXf7+H34\n8+KLy6mri3LxxZcRCnW3NDz33NNs2bKZE044gr32mpMxjc2bt3Hvvf+itraRz3zmDGbPznxeVx54\n4G4+9akjB1T+FJZlEQiECIcjGMbI7vLzFfy2SJacffYXuPHG2+nq7LLnnrNZseI1TjjhM7z22ju0\ntLT2kMLgsfvuUzHNDQVLXwmsoTV/ZssRFQZHlHdvLqsTcG99z51zoYT9UHHOOafw7LOP8fDD9/d4\nTjwex+crnKlssFizZgPnn//ljMIKYNGi47jqqmtwnAg33XQvd931EO+/v4YtW7bT2NiEZVlMnjyB\nz3zmOKZPn8ySJU9lnfemTZvYti0/gd6ff34Zxxyj1vWWlZUTjcb6uGL4MrLF7QhkzJixnHXWedx2\n2/2cd97p7cc1TcN1VeiySy65jGuv/RVf/eoXhqqYAJSUhHEcl5076xkzJlM80IGRTFoEAiNnx++r\nJhmsaHPZ0iV08WONDueMGvkddDZomsaZZ57E66+/xe9//yu+/vVvEwh0jk37/vvvMHNmf8JaDh92\n7apjzJi+g8Trus7ChYtYuHARzc1NrFz5GrW1tbS0tNDW1oJl2UjpcvTRx2ehlXbws5/9hscff5jn\nnrujzykCKSWvvPIqprmeYLBDuJrman72s++yadM2Tj9d5X3ggYfyxBMP9pTUsKcosIaAmTN358AD\nD+PRR5/lxBM71P7999+TBx64i1NP/Ryf+tSpLF78NJ/61KIhLCnMnTuTV19dVRCBNdK0j0lBndOq\nDf64o3NIxTeiknrLpdr/8TFY7LvvPGbMmMKvfvVjzj///5g6Ve3Cs2rV2zz44L1cfHE+w+UNPk88\nsYQLLrgkp2vKyys4/PCj+j4xCwzDoLKyirlzew7sLKXk+eeXsXr1eo444mhOPPHs9t8sy+K6664m\nGo1RUtJhxRBiD373u4xb7I0IPj4tbJhxwAEHU1fX1OnYXnvNwbLaeOGFZ5k3bz62rbNhQ9fA8oNP\nJBKmvr6p7xNzZCSuAbxyosGi8s6CdpsFf9818udscqWqqpJLLvkijzxyL08+uZidO3dw7713cdFF\n5xTcu7SQSClJJl0ikZKMv7e1tXLLLf9g+fKXC1YG13V58cVnM3oUb9myndtuu5+bb76PadPmcPnl\nP2L//TtvRfXgg/dwzDGH8cwzL/GpT53SflzX9U7fRxpFDWsI8fv93Rwwjj12IXfd9RCjRo3mvPMu\n5KqrfsTFF5+D3z90prM5c2awfPnbzJ8/m2Aw162JMlNIZ45CYmga/5zu45Q1NiuiHQL3pRaX7w1h\nuYYKXdc599xTWbr0dW6++S8sWvRJQqH+bhs3PHjooSdZtOi4bsfffHMFzzzzJIGAwQknHMGaNRv4\n3e9+zpQpMzjllDPy2kZXr36f8ePHtH/ftauOp59+iUTCYsqU6Xz5y9/scW4NYOnSl9i5czqOozFx\nYuelGylteCQyYiNdaJq24PXXX399JLm1d8U032Xx4vv54hfPRNc7lF0pJX/72x1ceOHXcF3Jrbf+\njQsuOGsISwoNDc188MEW9t03Oy+nvojF4mzdupPddhuaNVgAq1atzcqtPRPr4y5nrLVY622PV6bD\nU7P9iHBno8VA8hiJbNmyg5KSMFVVw9/7MxP33fcou+++F4cdpkz1ruty9923sX37ZmbNmsahh36i\n20Br8+Zt3HnnA1x00TeYNq3HzXJz5i9/uRbXTeI4kjFjJvDpT59CaWnfTkqu6/LMM09w6KFHZhRq\nK1asYN99991XSllch1Uke4SYQygU5rrrbuTCC8+mpETtRq9pGqeeejxLljzF6aefzfz5+/Pyy69y\nyCH795Fi4aiqKqempoKmplYqKkoHnF5Dw8hwae+J6SGd307x8ZX1Nh/a0OLC33Y6XDP1421lr6oq\nZ8eOuhEpsG677X4OOugw9ttPmddc1+Xaa3/NUUcdyAknHNLjdZMnT6CqqorJk/PraHLxxd+kra2V\nsrLcnqWu6xx9dNfdPj4afLxb1zBg6tTpfPe7V3LTTfewaVPHlk6jR9ewY4dya114xNEk0Hhz8zqe\nf/VVzLUf4MrBnzOJRMLE44m+T8yCpqYWKisHLviGkoXlBoelubq/Hh2Z1op8EomEiEZ73UV+2CGl\n5J//vIsjjzy+XViB0nAWLjyAadN6twJs2bKdyZOn5z3qha7rOQurjzpFgTUMiERK+N4PrmTpsjdZ\nvrxjM1TXdXGlQ2u8mblz51JVU82c/fYkNK6CVZs3sHTVWyxZtpxNW7YNSjlDoWDeOiPHcbMK8TPc\nmR/pMA/ttCRx9+MttEbivOS99y7mlFPOYu7cee3H/v7365k/fzYzZ07r8/onnljCZz97dp/nFRk4\nI7/H+IhgblvFtL2n8cbzb7Jy5dtEIhHq65tJ2Am2JzdDGWg2aBqUlpZQWqo8mBzXpbWljZXr1xBt\nacNNWMyeMYPRNTV5L2NDQxPV1RV5SWukzp125eQqnau3OzQ4UG/DpoRk9/DI67Q/rkgpaW2NM2NG\nRzSS2277JzNnTujVpTzFzp21jB49/iMx+BoJFJ/yMKG+sZ6ZYjpjxo3mxUde5uL/+waBQAApJX4t\nQFJLZgyrYug6FRVlVFSoyVjbdmhqaWHr+rW0tbRixZJMGz+eqZMnDXj029ISZcKEMX2fmAUjcSSe\nifEBnWlBjYaoJCHhnZhk9/BQl2poGUmDkWXLVnDYYR2bad9zzx2MGlWWdWi0Rx55iq9//fK8lcdx\nnIIG1B3pFE2Cw4RA0I+GRllFKceeuYgX3noac/0q4k6UaaWzQIIrXTR67+h9PoOqqkomT5/E7Hmz\n2WO/PZGVId7a9AFL33mbJf9bzpvvvEfSSuZcxoaGZgxj4FVmJHVo2TAr1PFOVsU+WvfWH4LBAIlE\n7vVrKHj33TXst9+BADzyyAMEAi4HHZS95/HBB+/Hf//7aN7K86UvfR7btvOW3keNosAaJiSiqoFr\naPj8PqbtNplWmvigYTXrW1Yjkeiajuy2yUXv+Ayd8vIyJk2dyO5zZ7Hn/vOomTGONbUf8urq93hh\nxWu88vpK6hsb+0yruroC23b6PK8v2tpilJR8dNSQz9XohDQ4rEzjgtHFJlVVVUZDw/Dfib65uYWK\nChXB5amnHiMWa2DhwoO6nWfbDrt2NWRMY489ZrFq1Zs4zsDbhWVZjB5dxeLFIzd0UqEptq5hQjKa\nxHU7PP80NCqrKmhracNBxSPLhxFN1zTC4TDjxo9hxu7TmbNgLhNmT6XOjfPmxnUsf3cV/3v7Pd56\nezXNzZ0D8M6aNYVVq9YOWEMaSUFvs+HwMp0fTDB4YJafCYFik6qsLKexsWWoi9EnTzzxHKeeegbR\naBtvvfU6xxxzOKAcgjZv/pBEIklLS5RXXnmD8vKePVqPP/5w7rvvrgGX5623VnLccUewdu37A07r\no0pxDmuYoPm0TouHUxi6jq7pJJNJIuH8ayUaGj7doKy6kupqtWePbvupCFbS3NzC5u3NtLW20tra\njOtYlJeWsGnTdqZOndDvPJuaWhk/fnS+bmHI0TSNb4wrNqUUfr8Pyxr+Zq3W1hjV1aO46aa/csop\nxyGlZP36rezYUcfMmZNYs2YTPp/BJz85P2PbTDFt2hSefPIFLMsaULSLFSte5dOfXkhjYwvvvruK\nOXP27HdaH1WKrWxYI/GHArjSxfAZaBp9zmHliprk7WiMjisJ+0MEgwFGj65h9OgOb0PLsmlpaaGp\nsYnVH3xIrK2NRCLK2DE1TJo4NuvJYtd18zIXVmT4Mtydat55x2TevAXYtk1d3Q6qq6twHIeGhmYO\nPHAemqYxZkz2nrYnnXQ0d955C1/4woUA3Hzz39h33/2ZN29+1mnE41FCoSBHHnkI//znXTz//NOc\nfPLpTJgwKef7+6hSFFjDhGSs84JcicQFbMtGhiW4uc5eZYdlOQSDHaNC6biEg5ljlPn9Pqqrq6iu\nrmo/ZtsOsWiM+qZm2qLNxGNRom1tJOIxRo2qZOqU8d22nxjunVmRjz7Llq3k0kuv4P777+bYY5Up\n0DAMAgF/v+rn+PFjqa1dQmtrC+FwhPr6HTz99KOUlJQwc2bnXbsty+KJJx7hpZde5De/ubb9eGrn\nYl3X+fKXzyEWi/PUUw9RV9fCpZd+fwB3+9GhKLCGCaVVpajttTsaiwSCIdXZJxNJwgUIKto9CK1O\nwJ99gFufz6CsvJSyLjZ+x3aIxRM0tzQTrW0iFouSiMeJx2NKwNU3UFVVWRReH2Fc1+3VlDZUxGJx\nwmG1jvElryvbAAAgAElEQVSDD9Zw9NEHAKotDMR54swzP82NN17H/vsfyLx5s9lvv334619vY+bM\n3YnH48RiMWKxKOBw+OGfYOzYjiUiLS3NhMOd23c4HCISiTB3bveI7R9XigJrmFBWVYYDaEh0T2hp\ngKZrtDa1UFZWmndzYCb0PPnhGD6D0tIIpaWRTsdd1yWZtIi2xdhR39YuxOLxGLHWNjTNZdSoSiZO\nGDfio35/nCkrK6GlJZqXuJP55qGHnuSMM85jyZL/ctBB+3DDM/czf9YcgnUaq5s28aMb/sXcikn8\n9IyLCPiyn5MqLS1ht90mo2nw8ssrEGI3LrroXOrqGgiHQ4RCwfYFxm+8sYoDDujwSPzf/15h7707\nB5Zubm5h69ZdnH76J/Jz4x8BigJrmGAlLYw0gaShoSPxaT4qysoKoolIqSJnpOPTC7uNia7rhEJB\nQqEg1TWVXQoEluMQj8WJtrVR19RKIh4nkUyQTCSIx+PYVoJIOEhNdQWjR9cM+32X6hsaeeml5Rxy\nyAEfK22yqqqchoamYSewEokEiYTDqFGjWbHiVU45/TgeevEmnjVXMilUxTqtjtIx5ZjJWs746//j\njgt+TEk40nfCHocffhA33HArl176ff7xj+sJBHxI6TB+/FiEmMGkSROoq2vg2Wdf4Sc/+TW1tbu4\n++5bkdLmnHM671N1990Pc8kl3833IxjRFAXWMMB2bAKhIG6adgVKaBXSN6HrXlwAjhxC7y4N/D4D\nf1kJZWWZN89zHBfbtonH40RjcRpa2kgmk1hWkmQyiePYNLc2YSUSBPw+IuEQ5aUlVFaWU1lZMehR\nBEZPHU9pSQnr129ixoyRvW18LpSVRdi0aftQF6MbDz/8X8488/O8+eYKZs2ayvWP30PZqAoMQ2eT\n3UJZQC23CAeDtFU53P/i05x3zEk55XHWWSdx9dU/54QTPs1++x2I3+9n8+YNrFr1Fi+9tJJQKMQF\nF3yFP/7xasJhP6eddmy3gdfy5SvZf/+DCOcgLD8OFAXWMGDjjg8IhoOdhNVgYDtOt3kxV3OIJxKE\ngsPTHGcYOoYRIBgMUFHRPZJ1NBHDkkk0TcVZtC0b27JIJJNsqmvAthwc21KCz6ez8r21OLaN4zq4\ntoNlWdiWpcyxmobfm4gPBAKEgkHCoQDBYNCbXwj3HUNOSmpG1fDM0lcLLrBcKbm7zuWQUo2poaGd\nOxqO2qRlWTQ3xxg3bjy33fYPLrzwLP7+9/8SGKXquhHoPJiJhMK8vPEdziM3gVVVVcmll17Iu++a\n/OUv16LrasnKqFFj2X//g3jhhWd59tnFnHPOSd0ckkBpgW+++T6XX35l/2/2I0pRYA0DGuN1lATC\nuEjVUQ6W4MrgdqjpkHCThBieAqsvHOmi6xqapjoJv88HWZoNZdp/0pVetHyQroPrujiOi+M4uI5L\ni+PQ2NSCbbvKrCrVpL1U/6hUJFTX1KD7DMprqgtxu5347iabf9W6lOowPaSxW1BjvF9DApaUnFqt\n84nSwdMwh1sIrsWLn+bMM8/lkUceYOrUCazeuIFWv0VpD3Vd0zQaifYrL5/Px4QJE6ipGc3Eicq5\noq6unrVrN3D++af1qOk3NDRyyy338a1vfRz3r+6bosAaBmxavZE9D5yLC+gSXHfoAmBKSc7hn4YT\n0nXRjf4J/E7GWD19IXfPzUR5nPUtEMeMG8Nbq95jrz33KMhw5P2Yy0ONLi7Q7MKbUcmbXfbn+k+D\nyw3T4MiKj19wVcdxePnl/7F9+y4WLjyQOXMO59s3/Z5wee+L8dt0m407tjF1bO4L5aurKzppmjU1\n1dT0MnBZvXodzz23nCuu+FlGzatIUWANC6rGVqGjKf88DWJJm2BQR9cLp2lJKdEypK/r0Ga1EjZC\nBEdgo+k6D1h4sstr+u4zaW5qZs3m7crks/x19j5gAZMmT6C0JILhOP3yz0y6kut2ONxf71LXx/Tj\nThuu3+kMmsDy+30kkxaBQGEdebJh27YdHHnkoRx//BHtQqTJjWPovT+LUEmI259/nB+ecUHOeebi\n0v/CC8uor49y+eU/yjmfjxNFgTXESCkJlXQ2SQQCfmzbLmhDtyxbmcu6oKGh+1wa4vWMC4wrWP4F\nQ3ZeyzZc0ICKinIqKsqRwO6zZ2E7DtFojJ31Tbiuy/b1G9lv/p5oWnZGYVtKTlptsbwte414Wavk\n+WaHw8sLL7RSMQXHjCm8ObQvJk+ewOTJnbUkQ9PJaBdPIxgIsK6+cM4jUkruvXcx06cLzj//3ILl\n81GhKLCGmG11m/F3cXAYjPlqx3F7FIgaGrZmE0vGCQeGt9v4SEQD0DR8Ph/l5R1BgEtLIuxoi7F9\n42bm7DaNRDzBCy8uo2rsGNa9t5qa6koOPfTAdmeT3253chJWAFEXfr3N4UML9gjBpKBOlVEYJ4nS\n0jA7d9YPC4HVFcd12eE2U0LfQZjr3DYc18XIUmOyLIsXXljG0qWvc/DB+3LkkYf2eN4//nEXJ5/8\nWebMyW7/rY87RYE1xGxt3ERFVddGoykNyO8bMm8rw4DmZPOIE1iG4UOSn8j22ZG/+b5wSYRwSYTy\nslJ27KyldsdOFh6/CH8oxAEH7U88FmNXbT2r1qynVhosDU6BfjjHLGuTLGuzMYBKH5TocOk4H+eP\nzq/WFQj4iUbjeU0zX9iug4Pb94mADOrc/PwjnHbQUVSFMq8rSyaTPPfcUrZu3UEwGObAAz/Je++t\n5YgjPpnx/Pr6Bm655X6+8Y1vU1Pz0QkEXWiKAmsIkVKSSCTwGZ0X0Oq6RiQSIp5IdukPJcFgsKBz\nWyk0NGwsGmKNVIUr+75gmGBIA6mBlNl1RgNF07QM4a36mZb36fP5GDthHGMnjGs/JjWNYCTCuMlh\nGDeBxqjkw40xsPovMB2gzgZHh6PK81+nAgE/ruvm7fnkk2COESzuW/cyj258lQfP/0Wn39av38jT\nT79MSUkZxxxzAmecIXBdl6uu+hEXXHBWxvvetu1DHnroaX74w6JzRa4UBdYQ8s4Hb1LeQyQATdMy\nxg6MdQmS2xeGofdbUzN0iFqtJOwE48rG5nz9UKChoWsGtvc/mudu7u3WLL2lA/nC5/Nh2/aAtpXI\nRNcySmBLwuW1Vod7dtosacrfAm8b+He9y3fG53/t1rRpEzDNDcyePT3vaQ+UErITFpqmUVNdRVs0\nylXXX89lX7qANWvWsXTpG8yaJbjssh928ur9xz+u5+STFxGJdPdAbGpq5oEHnuQHP/jJkHkCj2SK\nAmuIkFJS17qTSTW5uct2DZDZF47jkkhY7WtiNI2+F7uml1ODiG+ErLb3lI2gHsQv3XYPMNtxcDQb\nA52kHUWqSSTcLJ0besPnM4jFBrYPUl84UvJSs8vlH8TYmOhbo4roaq4qW1pd+P12B1vC9yfkt0so\nLy+lqamVTZs+ZMqU4ePE89rad0n4XXKp2eFwiG2VDqfd+EO+t98X+O53r+zmCfjUU48xfnw1U6Z0\n3xIkHk9w0033cMUVPy0Kq34y/EIpf0xojjUR6SH8UD4xDJ1QKEA4HCQcDhIMBpFS4jouuqdx9Ibm\nQllweMWD6wlXSnRdR9O0Tu7KPsMgaAQxdAO/YxOwbQxHaSj5mYEqnLnLkpInGmzOfT+albDaN6Kx\nTyT38sQkbE4WZv3d5MnjaGpqydk6UEhueOUhApHcBn+6ptOYbKNkfAV/fvfebsJq3brVrF79Doce\n2j1YreM43HjjbVx22fcJDtMoMiOBosAaIt40X6OsbPA1F01T62N8fh/x2jaMXqqAROL3BTOu1xqO\nqO0seimr7PhNl1KtfRqkua7+kHAlS5tdLloT73OqapQPLh5j8Jjw09bPW5oRLNx7njNnJm+/vYZE\nwipYHtmyYfMWNsZ2ofczUGfA72eX04zjdmxF0tbWyh133MzZZ38m4zV33/0wF174NSoqRs588HCk\naBIcAqSU6AGtoGakvggG/TQ2Rwn2pWMMs/A6veG6stedjDWt4140wO86WJqBqw2/lVsJV/JGm8s3\n1sWwJUwKaEwOaqyLS3Z2kV77RjSummzwiVKDV1sdzFj/3tl9OxNstyS/nZx/71TD0FmwYA9Wr96I\n4zid0g+Hg0ybNqHgZjLbsfnTg3expP4dxo0Z06/QUa3JKB8213PRfqd30uLvvPNfnHfe6Rmf286d\ntYRCpUycOHlA5S9SFFhDwrotJiWDYA7sDcdxMdB6FVeurVEZ7h5gdrjiui5+X8+dXn7dLTqnnE8S\nrmRFm8vFq2PUWpJLJwQ4aZSPpAPnmLH28yp1OKVa51eTfQQ9zXJWSOM74w3eirqsaJNs6UGhCWkw\nJQDTQhrjfBqLG1zet31E2lxsACnx51lo+XwGc+bM6Ha8paWN1157lwUL9qClpY2qqvIeBWYikWTd\nui1IKZk+fSKRSPbLLm567EGejr5DMBLAdd2chXJjrJXtbfWcM/0YLjv6y51+W7hwEa+9tpRFi7qv\nuXrggcf59rf/X055FclMUWANARu2r2ParClDlr9E0lTbzLQxo4lio6NjocwbBho2KoirofkI+0O0\ntcYIBgP4/MN7orincFMpNDR8wXJcx8K144DEcFzcPsLzDCZSSv7XZPPtdVHOqjY4e2IJo/0ajTbc\nsitJnS0xgANKNb49zuCoLmGWKn063/a8/dbFXb610ebl1o6ZyhlBOLJc5/xRBnuENXSv09Y1iwdq\nLRLvvccpW0sJlJTwwEHdHQcKQVlZCQsW7MF7731APJ6kpCTM3LkzO50jpWTt2k0kEhZCTANg7dpN\n7LFHdwHYFSklq9ev59k1KymZFMGxshNWlmPj0w3ijsWulgYcx+Zb007lgpPP73burFmzWbz4gW7H\n33hjFQsWHDCk1pSPEkWBNcjEk3Ei5SVDui4l1pZgXGkFfs2gAtXhORi4SPwYxLCJYeNPSGrjdRgk\nsJ0yKir6jgowrNFAM/wYegDDH8GON6JJB911cfTB3twlM9FonGl+nef2KSXsU1t6SiAcgL1KNA70\nJzl1XJgLRht91qGZIZ2Hdvdz1TaHZ5pdjizXuWycQWmG4MDXTPHxvQk+toYruI0a/t1icKKZpMYH\nNT6NoKbR4kiaHUnMhZAOIV0jYsA4n8ah5RrzI3rGtLPB7/cxb97uAGzYsI333vuAcDhEa2uU0tII\n9fVNzJw5uX1DSNt2aG3NHEk9Govx9P9e4YW1b9Eg22iRSayAxBltUKIbaD4N27Lx+Xvu/hJ2krpo\nM450iVtJDOCzYw7nG2d8pcdrfL4AjtMRuFpKySuvrOCKK37Wr2dSpDtFgTXIvPbuK1SPH7qJV8eV\n2G0JysZ0LoOBTmqsHsZHGB8dPr9B2uIOHxk0CVJD8wWxnQRygIOHfC4e1nWdyT0sXThxVICjSkux\nmlvQtOxMtbqmceVEH1dO7Pu8cX4YN2c39gWcNz7k3406ls9PzybPjuO/+xDG+NRc243TfcwcwH5c\n06ZNIBqNY1k2EyeOoa0txrRpnZd/+HwG8+YJpJSsfO9dHlv5CltitTS7CWK6hQwbhCuD6JqBnzB+\nIB5LqD3O/D5isUSvAitg+LGlS5ulInXMCU7lZ+df0Wu5DzvsKJYtW8HBB+/Hzp21PP74M3z2s2f3\n+zkU6U5RYA0i9U116GGNYHBoVrdLJM11zUyrGZXztYlEHCkHJ87hoKBJLF3H8cT0QG4rGAyQSCQJ\nZVjonQ/SyxYOBXFth+2NLdgJi6BhUF1Vhq8fHm+ulDzT5BLSYWpQZ6wf6m3Jgw0usfIaxra5bElm\nl5YEdtiww5ac/4HNPbv5GB/ov9BKn5uqrOys2T+x4hX+8/rzRDWLVpnADWr4g34C1QHiMUkknHkZ\nRiDoJ5m0vPbX+7yjKyWVgRLarDh7Vkzn96f1vZniXnvtzTPPPMHGjR8ydux4jj/+NGbNmt33zRbJ\nmqLAGiRc6bJq00rGeZu5DSapGYzmulYmlFbg64c3Vjiok4gnCOW4cHkwcV23fa2Ppqn5GU1X27So\n/zu6/pgTx5F2XsyAKQ1rsCgpjVBSGkEisW2XplicWEOzctXXoLqyLGMk/hSOlPyr1uXuWoeVUYkD\nlOpgaEr5bBygp/+qmOSC9Tb/meUnkOclEX9/5kEeWr+c8upyNC2lO6XTc36JhEUwqM7XNb1HrTjp\n2Gxu2MHkZBl/OPY7HLrnQVRl4Xyk6zqXXfaDnO6nSG4UBdYg8ab5KuVVZVlHfB4oGhql+PCh00yS\nWDJJiTSIZLn7blf8fh13mLu467reHglESiXApCtxHAfLlZ2Eio2D4zrqmAYuLq7T0VNrWkcEc03T\nvD8Ardtv+SIeT2DkMAekoeH3GfjLSigpjeBKtUtyUyxBKBmnNE1LSbiSp5pc/tvk8lZU8las85Lx\nVheOKNWo9Gt8kJBsjMsBCa6lrZJvbbL5y7T8ORs8+vpLPLRhORXVFT2eYxh6p3mkFPF4Ar/f177Y\n1x/wk0xYBEMd1g4pJZZjs7lxB9Oo4Y8X/oL6eHNWwqrI4FAUWINAPBGjKdHE5HG571raHySSMAYB\nz9xVig8rmeDD7XWMHdW/rR58hkZjSzO6oRHqY6V+Mmmh6zqGYQyZCVHTVOelHkEmjbLzPcScOLZr\ndYzPpfS2vE/FIpTekjQX1+3Y/l19SBxnYGpJLBYnEAj0uo6sNzRNw9A0DF3HV6LTFo0RbWxhTGUZ\nUko+u8bipdbe45p8Lc3rcEvC5WfbHP7b5NKUxfRlyjkknf/Uu+wdtrlo7MC7mWgixt+WP0LFuN7n\nf/1+H4lEspvAklLNe6XQdQ03bdG4lJI1dZvRgHmlM7npS7+jLDi0zlFFulMUWIPASyuXMHm3wRFW\noEbegbQIFj4MRpeWs8XeNiDngMoyg9a2aK8CS0qwbRe/XyORSHYzlSlBNrTCrCtKMHXpblNaVRbX\nJxLJAc1LOo7T/lzygabrlJSW0BhXE1D317ssa3XxaVqPETOmBGCfko78JwV1/jZd57lmh19uc3i1\nj323Jvqh3oZo2mkxCX/80GGfEo1PlA5s6cA3b72WQE2+I8OkmYitBA5w+4m/4OC53UMrFRkeFEMz\nDQLNDU0YvSxozTc6WreQS67rYhj6gEeMKphuEivpEI8nSCZtHEdtIVFf30gimVRmKr+vUwzD1J/f\n7/O2VUkSiyU6/cVjCZJJC8d2cw6w4boypy3Ju9P/ZcWO4+LvxeOsb7QBa2jdkBKp6zS3xrhhe4IF\npQa3iO7Rw0GNWq+e7KPG1/0JLCxX4Z72K+n96VgSFlV0P2e7rTaaHAh/f+ZB1mt1BPz5dVby+wws\nS8WUtF2HIwJ7FIXVMKeoYQ0CJRWDG9XCQKOrbrBu3RZmzBj4QlC/YdPUUIvu6SShoJ9Y3MaVGkG/\npLXZpbqmqsfrdV1D131kWkeZmndyHBfLtjM6Mmia5qWhe3/qPl3XbV8EmyuapmHgw8Hpl9AKBHzE\nYnHC/ZwfTA0k8rpvlKb2VLtnewxRGuC708Ic82Zbt9OmBlRk90+W9SzsfZrGbkGN13rRsnbYcGCp\nzraky2tpapYGHFvRv8Faky2pb9zFLWueYXxNds5KuTjA+Dz3dr/fR3O0jStO/0a/yllk8CgKrEGg\npKKkmwApFBKJkSGveDxBaenATSqRkI9IqHO1CQU7OqTahni/N5hMzTv1ZhpLCTXXdbEsG9dVmolt\nO5TkEKYnQ8r9vtLn8+F6zh39j4eX300ONcAfCOAEHD4R1mm2JbV253ucFIA/TPXxvc0OJX04e8wv\n0bm7vnct8J2Y5LppPq7b4dDiSJoc9b6+ODp3zXd5q8MlG2yib91Dia5haNk/11QdyUbj1jSwbJvx\nspyZ03bLuZxFBpeiwBoEtEHyDEzhH0JLr2EUtkr1JNRisUS/o29LKbH7qV0NZ8y4yy7X4CvjAvxm\nc/etPc6sNlhYbvCbLGKyTu7D2c8PHFuhMzusc/203N9DzPNiXFShIyVcutFhTQIiFXMIxjfhSrfX\nnQXSCXiaU0lJZhNoOqFQkF3NjUwzanIuc5HBpyiwBoFELIFtO528lAqFht5NYNm2k7cJ/b7oLXrA\ncCTpWEhcpJuPOaSBiLz8isuEK7lvl8WXxgWotST//LBzFNyJfvjaGFUnFpb3XS+jfSig8yIan6rM\nvY6tibtc96HD0laXtQmYHoDRfo334irD6JhPIK2tGM7mrNP0+X1YdvbzZmVGkG8d8oWcy15k8BlZ\nvcsIREpJuDSElLJ9UauuawQC/oK4zBrQzfxYW9vA6NE9zyvlCyklfv/wXVicCUPTiblJBhpxXc0/\nDez6fIYSCega540LMDGoc++uJF3F8T4RjSp/9gJmVx8bch1dkZtDz8stDn/e4bC8VdKQJlvWJ2F9\n+kaSmkE0PIFY00ZKchjw+XxGVoPEREKtUXRLfPmdQyxSEIpeggWmqbkRpFof0uEp5yeRsNq941Ke\nSvkgk9mktraRmprCxy9UE9hDE3aqv+ia5/AwxOUIhwJEPS/JfDE1qGNLeCXDQqp0F/a+qLdcbq3t\nWQMt0eHMmuyEyeqYy+mrk5y11uaJps7CKhMTdjzJlMalRHK0ECiBlbldSSlJJi1isTiaphEpCfO1\nx6/ig/rstbgiQ0NRwyowzy15GnFQ560SdF0jlLbC3radju3DNWWD78/kvXK4yHBcDtTlOztao0lK\nK0dWldI0jSAB4qjtRoasHLpOJBLCsiyi0TjhcHBAo/3UlXG3e8SKch3OqM6uPkgpuXiDzXtxSbUB\n359gsCUJt9U67cKmzYWXWlymBXuvs29FXc5bZ7Exi/iEmhNj0vbHmJzYQGU/trVJeQs6joNtO9i2\nTSwmAeVl6vMZBAJqYq45EWWGNoqZNUO35U+R7BhZvcsIZOu2zcwLzum+MDUNn89oN11ICZZlkUyq\n0WEqunS2c1AuYOHgQx80z8T2vGX+Fr8WGiklcTeBBrjSIR/CKh/mJL/fj8+n3OQjkb6dBvqi3pas\niXZWYyYGNKYEs3tP99W7PNusBkLnjzb48hjVZaxsc3mxteOZrWhzOXdU74Llzx86HcJKSmpa1zAx\n+i6G3Qp2FB8ukVAlthUjmWgiSIJyX/9DO7muxHVc/H5/rwu7G6IttDmt1DbWMqpyFBs3rmfy5KmD\nMsgrkhtFgVVgpsyejIubtfDQNNpHfuDFN7NskkmrffGv3+/PKBg0NOLYJNDQvT/Xcgj1c31Qrvh9\n/uG313wPuNLFcW3ypVXlM/itpqmI/tFonEDAh6+XQLZ9sTXusi7euWy5bFm1b4lGUINDyzT+34QO\ngXRAqc6LrR2CsMHu/f6jruSVVqXqlUiLcWtvZoLRTFnXehz39rjyAd0C2+aGruv4A32nMaG8hpZ4\nlJNvvIiXLr+Pyx64iq3Nu7j3S39i8uSpAypDkfxSHEIUkJdeeo5JMycNSNPRNOWgEQ4H0XWdYDCI\n4zgdESLiygOx/XwvLxeJjUvMsRg7tn/xA3PFFxiibVPc3CfLk9LqVesdagzDIBIJYdsOjtP/SBGJ\nDLeYy11PD2o8KnzcNLOzk9CFo3VGpcnRSB9SMKzBnbv5+NlEg8WzQ4xv3tpdWA0yKZOh3/BRXVJO\niz/JN//xQ2758rVEQzY3PPjPIS1fke4UBVYBMTe8R3medulNbf+e0sDawx2Fgu0eiKm/ZNJqH/Fb\nCYuyPCwYzgb/AMw3AyHXsExSSlw3/+uuCqFcBoOBATnlxDL4SmxJSN6KZufGr2ka+5QYRLosBh8X\n0JnujU+mB+DcUb0/f03TmBcx+OpYgw1JjaYJh7THOhwMUpaKuNdGWlujxOMJ4vFk++Lz6kgZLzSv\nYuENn8fn9/OmtXHQylckO4omwQKx9PUX2G/hgryll0zaBDLFM0J5IKbHsnMcl0TSUltruC4fbP+Q\n0mCImsryfu2FlQ2WZeMPDI5g7Ior3Zyja8hM4cUHgJQUZHfLgey1JYE1se7aWZML1253uHnmwMar\n5dFGphDhphklfXod7ki6/Gq7w6utEjPuUl42n8OcdVhObEBl6I2UJQJU5Itg0N++n5vjuDiOQ0JL\nsKthBxMqR9GajBEI+EnEEpyg78ORxx1fsLIV6R9FgVUAXOmS9CcYU5o/U5wKNZNdh6giQajhbzgc\nxK1Upo/tsWYcy8FJ2mC7lEdKqK4oxdAHLsRaWmNUj8l9J+N84LoSfw6eZGpHkPyaA5UXWl6TbMd1\n+1fWhCtZXJtZO3u51WVjwmVqls4XmZiy4T1+esxBzO1FWLlS8pOtDv+pd9jseewHHYdFzsu02NF+\nx3/MBsMw2vdH6/6bruaFkVi4bGuspUZGqKON/cbO5SsnfZWv/OenHD37kIKVr0juFAVWAfjfqy9T\nNannTeYGG13T0H0+/KUdr9uVEtuy2RptwrVc3KSNtF1Kg2GqKkp71OZ6ImnRr23a84HjuOiag9R1\nNF3rU7BL6aIcnPOHz9dz5zhQEolkv+IUSqAnebTLhms+dPjT1P69M8uymNOwlbllne+5znL5+y6X\nFgemBOGtqOTuOrfTwuWDWp8l3ryh38Iq5aouXTngHbAtyyLoGPzuyEtpDTlcv/wuFu11KA+/+ywL\nJs4tLiYeZhQFVgEYP2EiO+PbKInkx0RWiEaje84c6R6JrpS4jkOzIwlGNSwriWUlka5DWUmASKTn\ntUGGz99pC/rBRNNA0zUVFNd2+9wZWWoSRzq4rjKX6XpqR+GOv1zJp5dgprT742Id0jWOr/bxWlvm\nuaLaPqJX9Mbjjz/D8ccf2enYloTLqWts1mTy9PDYq3kpJY3v4GRhj5VSKqcTu/PZhqETCPiRUtLW\nFiMSCWV8Z4ahZwyCm3RstjTuRLou1YFynvj6TYwqrcJxHU7Y43DC/sHxqi2SO0WBVQCmTprBqhfe\noKq6Ii9roZKWTSBQ+FelaxpSNwj7S6hM2xbccVwsyyKRtLCSSohZySSGLolE/IRDAXw5amT5Jpc4\njVdf9z4AACAASURBVFJKQjJI1IniOJbnLeZ22Vm421WEQ8Ee56kKOQrXdd1b0pCbhqUBe/aycWIm\nh4xskFKyffsOJk4c334s6kq+tL5nYaW5SWbueILq1veRXepyu2BynE7PXtc0DJ/RoxalaRrhcJBk\n0sq4zsowdGzbIRDQSToW0WQCO2ZR5gbZp3Q3rvzMN1jTuInmZCujqMLQDcJ5MI8XKRxFgVUg6jbX\n486VGLkseukB13HRs1hPkg+kKwkHO48w1ZxYkFAoreOQ4Lhq36pEIklo4GtcBw2lRYEmNYyMsUG6\nI12XqDeBnxJOUkpCoUC/tbJs8ftTC4lD5GrIzLQpY4p4PwXW+++vZe7c2e3fNyZc/m+93eOuxEGr\nlamrf8+UUJhkMkmsi5t+SjAFg4Gcn6Ou656XbJxgMNBJmzIMg0TCQuqSxuYWjgjvybxJu/HzTXex\npaWeix/4MUu+elte5nCLDA5FgVUgjjnqRNbvfJ8x40cPdVFyQ2oEurinWxKabBiVfljrcO4IBQMd\noaVGEDo6DtmtcUqFTuqMJJGwCh4NXy0kDhKNxgkGg+15dWiESitM/55y1LB6CU0Y76dFcPny1zn3\n3NMBeLzR4cotNusyvX7pMKluGZNb3qCypARN0/BFQnmPIBEKBYnF4iQSyvSpooUYJJMWUTdBvDbG\nXq1jaKxq5K/uY4QDQcKOn8/IfYrCaoRRFFgFwnHsvOyDNdiTvjrdo25rwIeWJKJrhI3uY3zHcUdM\nSKbODHTeSUWk8PkcotG4Fx+yMO/KMHTC4RAtLW3eEgZPS+wy95bajVm9Qo0SHCDzHNbMYP/m6v4x\n5RP85wMXv5ZkRZukPoPMH9u4konNKyhP7MKHhuZZCAoZ7ii147MKbGuRlDb1rU2U+EK8M7aBilCC\n2uZmqmWEe8++lkmTirEDRxpFgVUgVq9/n7GzBu7Wbll2pzVWhUbPsLOrTwNdg41JiQbMDnfu6Bzb\nwRiEvb6GKyn3actyCvquNE2jtDRCImFl7ZFY5dOZFNDYkuwsnKsNuHx87u/s1q0x3isbi9vSg7CX\nLlO3P8LE+FoqDQ0CAeIF1r7j8USnOaxAwI/j6GxurCUUDjG2rIaGthbqG5r51vyz+Mqx5xe0PEUK\nR1FgFQjLlyDQS8DNbHEct5MnXyFxpSSoZy6zT4OoC4EMg3LHdQkYQ+t00R/y6den5kuSBR9c6LqO\nz6eTSCR7DeiaYpRf4xfTQ5xvdl4kdnCZxu7hnrWdlGYvpaS2qRFz2ybe+nA9t1mlyOpPoCdaCDW/\nT3T0gZ2u271uCePiayhN07gLHQBLOaVI0pW3rQ270OMusVCCNfVbmV++G3d89Q+ERth+bUU6UxRY\nBcJKWoMeLX2guI4k0oP3xES/xsakpJc5/CEh17BM6UiZj12GFZqm4bpyUEy4fr8/6zlDDZhXolNu\nQLNnujuqVPL/2zvvMDmqM92/p3J1Tx5pFEajnCNCIJAEQkgCy8S1SQKMAeNlLWyzxmC8u/b6mvW1\nr6/X4S4LLGBjgwk2IJNMsskG2QiBQMhCQkIjCcXJoVPFc+4fNd2a0DPTobp7eub8eOZBU1116nR1\nT711zvm+97tRDWHHjo5+w/F/u+tlRAULYScGg9mw4UKRJJTZLua1v4+IGYJjGYhVLUaZ3YwJza9j\ntGBBt9tA8jw97LpuH8PooCtj4bTZ+N5ZX8OMUdx5fbjABStHSBnU8OmNjwVoUzwhoErJn0CDIjBB\nIeh0+97g4l6GoihCEgUIebxhpeMAAgC264DCRS7WmhRFhm07OR8Rp5vzNUYW8KvpGu4+YmB9jYIz\nKyQEhSAUpwpiPzfyzo//iBAMQALErv8AYJQigDIbR40ISkvKMPXAf0MmBDLJbWj/QMiyDCNmJsLf\nKaMQFQn7DtRjVs2UgvSJkxu4YOUQBpbVKMu2bch5zG8iTBjw5l8mAmVJwvQDAa1bmLsL2qtqLgEg\niAJEUfQ9OINS1u9NNxkuHDjU618u3C5iMf+qR/eHYVg9CoAOhkiAJRrFg3NLEf94CQCB9h8hqYsq\nQtRI+ppACGpLC2PDlYx4Dl406oX+i4KIispykLbcfxac/MIFK0eojo5YNLsifPlcvwKQXYhvIsy9\nr3gwBkSjMYAhaQl4QghEUYAgCJ74pKEijFIIaQZ8xIUqF+OBuPN3LqCUwjTthDNHOgjoXgeLQXKc\nAd9/QFQAn96KKCR3nPCTuGh1H2lFWf7c4Dn5gQtWjjht2Zl44/0/YfKM4igAx8AgC7kRR8YYJEmC\noiZvP+404TouLJo8ccgL2fYETRBIwgaKdpVdSRVFUOH4WLixN/3ZAWVLPMconqicKQyASCnEQaYV\nNUkFBsjhSgdBIAnHiVxiWXYiV44xhlYWyen5OPmHC1aOkCQJe/++L2PByvf6FaWAJuXGrsIdJLGW\nEOI9IQ8wUmKMgbqsa9qRJtZxKKV9AhB65CSRngKX65g1SRJh205KEXzpQCmFpvXv5ZgOJIVLEBRV\n3wJITMvOS9BD98RuQghM5pPicoYMXLByyLSJ02GYJjQ1/VBaQjIvK5EJzM3e+bo/XEqhytndwAkh\nECUCMYWao4x5U4WUeQJnGDaCJfnxjpIkCbbtf96RpqmeBZaW3WdEwJCKaI8JVsLtcCGJ2d8iZFnK\nqgjlQESjBiRR7DN6D8eiCIrcxHa4wWM9c8gZZ6zFsYMNGR+vKHLSNZ+cwEjOijt6T+o5aTophHhB\nHpIkQlGkvEYt5grP/inzz4cxCsIoBEohprDOVldZA9tNzbZq8HNnP1JjXeVwDON4Ze1o1ABjDI1G\nR5/9D0aasXrm8qzOyRl6FP9f8hCGEYqS8lI4XX/46UYMSpKYcBHPNQIZGV8Fi1pgOU9l9b99L2I0\n89EOdSkUx4Hsuil9C8dVVEP0KSyF0tQFK+7cbhhWQphiMdNbwyOAqirQdRWiLKCTRgBCYNsm2tuP\ni5bleA95PzznJl/6zxk68CnBHCKLCuaOX4jdLR+hrKwko6eDuLFnX+NV/2BgkPpxuBhuMNCcp3NT\n6rmHZxuHyBiFLMtda2JZTgUKAhyXplxkc2xFFaQUnewzgVIvyMaltKukiBe7GS8xIghevbZkIm04\nFtpiIW+dEkBtRQ1aj7Yi7BAIiohmK4TfnHMbZB+mMzlDi5HxWF1ASoPlOLDzABgAmsGTNyG5XQMA\nvDWf/hKGhxv5WBWUZQmyLEPX1ax+AgEdjuOAMZZ1/pokCrDM1MO8S3QdUhJfyYzPL4mIxYzEiMm2\nHVhdwSm6riZcQmRZgq6rCAZ1WJbdZ3bBoS7ajDCq9FLokgpZkUAYQVWwFI9++Q6cpE6HyWysnLfM\nt75zhg78ESQP6CUaxK7l7kyQZQnRmAFJknKyFkQpg67kJiiBpTEdlA9SiZDLFlmWvGAAH6IuZVny\nZUpYEASYtoNUa2ATQqAJCqL9OL2nSnz90hPx3oUbveCUSCQGVZUhSRKcrvpqtu250cdiJhRZgtR1\nrNg1dX2ssRlCUEK5FvRcVkpl3HDXrfjK+V/CuGOThtR3juMfXLDygCR5lzmbPyFdU2EYRqKEgq9Q\nkrPpE6/0SOGc3BlliLkxGOGYF3kJr/RLnN4lOjynD+I5QmRYmNGrXyX74lTipTdkPxFCBAFWmqN0\nTVKySr5ljCEaNRAMJv/OiqKQKHEfD3t3XQpd98L341GRsZgBx3FBGUMgoMF2HZiWCS1wXMwVWUZn\njYUfPvffeOPfNmbcZ87QhgtWkeCFdUs5KTciQEgr+TYdXNeFnEe3jt44jAIC63XNjgto76KHlHpB\nLk6iIGKmZ2YJsc4mB0kSBZiWnXByyBRBIHDTdOHQBBkp1rfsg2GYYF0C09+jmiRJfa6P61Koqvd7\nPIRf1zVQShEOxzwrLkZQVVoBm1DEHCvROiEEbbKBxrYm1FQWWeFUTkpwwcoDoiRl7SsIAEpiqsnf\nqUGJ5O5rQBlLy5zWbxgbOMiie3l7/weCDIZhgVKWcdAM6SqdkS2EEKTbjC6pGQmWYzsQiABFG/hB\nhfQawcZiJtR+3FBAgGCJDkEgGBUsx0xnHN6O7EJLrBNj9QpEowYIIXBA8R/P3o47rvpB+h3nDHl4\n0EUesDsc2LbjSzi1rntTg37BwCAWYS2rVGGMQZN0yIIKUZDzEnRxHM/BI1vBVlW5K+owi54QApbG\nU84r+97HsVhr2udhjMGynX5tuPojGjUgy1K/08eGYyPmmIkk9D2Rg7BBUa2XwQVLBKrYzMbahSvT\n7jenOOCClQdmTJ6FA9v3QvLhcntGsSIcx5+oQdcFAnJ+XCAKAWEEiqhAFZWUXDL8xnFo1utYoihC\nUbITLdd1IUmpv/+tR/egyehMRPalGvgRjRppfzdZ1yh8oGlPXVYQtmLoMCNwKYUZZAgwGYc7GtBp\nRuFQb41Lg4Kz55yW1vk5xQMXrDwwadJU7NnxiW/teQ4YPoW5UzasQ9oZZRC6RhZ+lxNJBU1TEsa1\n2SCKImRZzrgtlzLoafgbOtQFYwyqqkDTlJQKRlJKIUkiyspKUjqHaVqIRGJdo6tBRJ0BowMVECyG\nfYcPoTnUAceyceWCC9Ae68TBjiY0t7aBEiCQo4hXTuHhgpUHRFHEiWuWwvVxQkrTVBhG9p51g9XA\nygbG8i8Qvenu5u6wwtRHkmXJl89KkkSvfEkGkSCyJMKwU1+QOmncTNSWjoJpWyCEJEZ4iRwqy4Zl\n2YhGjYR9GEvNpjABpRTBoI5gUB80z4wQAlEQUF5WignjxqJKKcFotQJLxs3B3DHTobsSwiyKixas\nS70DnKKDC1aeoK6/dZLi4ddulu1mVQNrEKhLIRQwpL07LN27qY94uVTISGh6oygyIlFPONKpvUUI\ngZhCtCZlFF95/Bd47N3XcDTWAk3xRt+SJELXtUThSEHw6pcFAlqXs4cJwzChplxYMrNrQQhB2IpB\nK9HhlBE8/85L+Ol534ZDKAQI+I91X8+oXU5xwAUrT1DKfPewy3a6KZc1sADAcQcuK5JPKKV58BDs\nH7+iOkVRRCCgpTxN1x2WgsBZpg2T2YjKNnRV65OHRgiBLEuQJDGx5qRpCiilaUVC2rab8dpetV4G\nh7potyLY0bkfLqWIUhMx8ArDw52hcTcZAZgtli9rGb1R1czXNSgFVCl3HoWU0iEjWA4cX0Y42eDX\n2Y+H4ad+bV3XhR4MwB1EOX/08sMwxfRv/OlWQbZtJ+PcMgZAEkSUqQE00xB2HdoDagOn1MzPqD1O\n8TA07iYjgNUrP5NVqZH+EEWxK+E1/dshc7sqy44ACjm6ygWWZUNJOSGbwTRtyIoER+o/5+6O15/E\nAaMpI3cPRZFTXqdzHDerRGiBEBiuBZdRyEREQ3MjIAFr5vByIsMdLlh5QpIkxEIx0Bw85Xu5WRks\n6rPjtlGc4oJSmrKDRixmQVVlEBAwEJiSDEuSYYsi3t27Cxfc/124rouPWg7AETJbE43nT6Wypupm\nOVXsUoqQGUXIjGJy2RjMDNZi3pipuGQhD7gY7nDByiPzpp+AUCick7YVRUq72KMZjeHY4SNobmpG\nR0dnl2cbLVRsAicNRFGEbaf2eTN2fGqWAF4NKZciEjPR5pooLy/D1Y//BB00llWf4lWRB8rDsm0v\niT4bf0lREDC+tBqyKOGI1Yb/ePkuzHBGo1wvzbhNTnHABSuPTJ4wFY0HG3MyPSVJEpyuWkKp4pgW\nqitVlAcJArIN12xH09GDOHTwIBqONqC1uRWhzjAMw/SenItYyIbblKCiyInovFQ+9EjEQHu791AS\njRqeMa+q4JTpJ+C2z/wTgqUB+FH+KhDQuoov9kxyZowhFIoAAEpKUvWM7x+BCKjWy1AVKIM+oQzv\nRffg2U0vZt0uZ2jD54PyCCEELEJgxkxoOXBd17tys3R98HUpyhiY0/NGpyoy1Oru6yIMjBmIhTvR\nbrqorqkFCOB0PdkTQiCJIkRJ6LPu4bqpT1nlCsYYHDgw3aEgWP5npKmqAkYpIlEDuq72e73jCcCB\ngBf1171kvSQBAaqh04xA8KGPpmlBVRW4rlc1mDGvQKNACILBgK85f4SQRFVkizB8c9PPcN4KPi04\nnOEjrDxz1upz0HC0KSdte7ZNAhxn8ARR13FQFhj8SZcQgkBAxZhx4yHLAmRJTPi2qYrnzWeado9y\n5vGcHICB+WDcmikMgEVN2NSCSzO0HfcJQpCTKEUiCAgG9QFD3AVB6DJMJl196SkaAUXDObNPgyTK\nUCQZkphZDS4jZkIQBMiyBE1ToShSQig1XfVFrFyXwkryfVMkESokdMZyM+XOGRrwEVaekSQJsbB/\n5rW9URS5y9G97/yOS1liPcMyHdSWl6XUpqiUgCQSjI/fyIhAIAsiZLnvuaJR7+ZlJqkaC3g3UVEU\nIAq5K21CKU045BfacSPXSJLYVc7k+DMoYwyGYQ66XqSKMi5dtBaXLloLANjbchi3vXQvxpVUoyHU\nDCGFelyWZUOSxR5BPJmOsBljcF0XjkP7fHdEUYAki1B65Q861AWLCvjSg7di4/V3ZXReztCHC1YB\nOFZ/DLMXzshZ+3Hbpng9IcCbEutobIcuKzA1EWbYgFhSmVJ7gpi6B12c41Vmk7zIPDFxKe1X0ABv\ncV0QhS5XhfQlh4IOKaXKpZehJ1g9o+9iMTNRDDEdplXX4v+e+3WUqyX49z/fjZZw24CiRSmF47hp\nJQ4zxuA6LlyX9omc9aaaBS+yMYW+x+uZTawag/qWw6hvOYip1XUp94VTPHDBKgBV4yp9qY/VH/Ek\nzt5P3IQBE6qr0dIZwrjRo9JosXc/CRhzvTBpksG7IPCESBSSCxrQTdQYbNsZ0IYoUVdJ8ESOwJsa\n9UZYIwNCiHe9XBemaXvVlSntSt5OP5piXOkoMADfX/tlPPXhK3i1/v2k4hE/X2+xopR6JXVo8tVD\nQfA+IyVFURqIqkAZpleOh0UdvN7Sgct/fzPevuHRrNvlDD24YBUALaDlTKziqKqCaNRI3EgYA5jp\nhRtXl6UX/suYC0JEeMJF4FoRUCcKImmQlKDPPe8iIWrAYOFrjHm2Q+1GJ4jgCTNl3ijPtp1B1/QI\nIRCE+NoOSQggIUj8f0gN1ZIgCAIYYwiHoygvL4H3UMGyvmmXKzrOmLgAL+/dCrFbW47jdkUCemVB\neq+hxcuFWJYNPQcBRnE0SUFrtBObox0wXQdMBqaUjMe97zyGfzrlspydl1MYuGAVAC2g5aTUfW9U\nVYFhWMe93jK9cfS66VEnCkEOQlKCYKywwQxAV/cIAYjnSt6dZOtrPWGe4HVNK3k/FJ4pevz37Pvo\num7OP29d1yB0VSge1CqJMbiUJUZh/b1P13Gw8e+bYBpWj/YEgSAQGNhl3TBMyDlOTDccr18ExBNU\nRUSgneKDo7tyel5OYeCCVQCWLVyFlzY9h/LKUoyrG5ez8h6iKMC2WaIkhZjC4nkyjo8GWUKgqB2F\n7VqQ1FKACOgejEG71aDKF5RlVnbDG1H1jZzzm1z4SCbDc8Do+V7ipUA8cYlHCnqiE4/q612u/jgq\nzl10Bj5s2Zty2DtjDI7jemtRORZpxhhcRiESASIRURcchTOlE7BFOJrT83IKAxesAqDJGs5fdRGO\nHTuKN954CWWjyzBh8ngEfEio7HMuTfWiBmURqp5+8ASIN9VEHQOirIMlwsMZGLXhOiZESesxY+at\nneW3rEjMNkGpi1gstRFffAQSTwUodM5YOnQf+R1fr3QRDkchiiJiMavP/pqmZGzD9cC7z3rpCYM8\nWHnRfRSmaUGSRKhpFIzMBMu1YbkOHOrCcm0IRMQp9gScdc15eOSp7+b03JzCwAWrALSZzSiRyjF2\n7Dhc9rkvglKKZ17ciKkLJyOYA9FSVQWhjjDGVKYTaNEFo3CMNoAIECUdhIgQpACoEwVAIEhqnwAS\n13WhpmzM6g+MMqiamuoYAIwyL3maeaOfXK6zxDEMEyTDUW53jq+tEViWC13XQCntyn3KPoihO5Qx\nxGxj0BGz61IYhpfKEAxqyMeanyJ6/ojtRgRfWLAaX5i/Bj9+5AHcvvlhPHDx/8n5+Tn5hwtWAQhK\nZWgwDgOMwIGNUqkMF6y7GH96+4+YPmeq79NpoigADk0pn2YwiCBAVHQIspbwpesN61blN18wuGk4\nNRAQgSRCOWw793WU4qM4P9ex4lNvAGBZTsLJwk8EQvC/zr4et/3pHnQYyZNy4/leuTj/YMiihAot\niC1HdmPHzt2orqvFDz/zDR4hOEzhglUAFFHBGK0WlLlw4IAyFxE7jBOmn4xtO99FxegKlJWXQFX8\nm1KRVDmrUHoiSHG7Bu/3IXZDoCxT25b8OHGIogjTtHwVrHieVTwaMFefyV/2bkXESm6MGw9rz9eo\nqse5KUWbEYIuqdjdegimaeGDf/jFkPtucvyDC1aBkEUZgIzurn+lNWUYV3MBTMvAU39+DEtOW+xb\n+LsaUNDY2oExVRUZHc9cC47RDggSCBESP+j68ZyHqC9TXpmRWVouY/kRX8/Dz+82AcOwEjlXueBA\n+zE8u/NNOL2srbx0AQeCIKSVMOwnoiCgUitFKBZG1DDw9cWXQZVyu27GKSxcsIYgqqKBUO8m6leC\nsShJ6IiFMAaZCRYAMOoA1Ek+JiEEYAxEVEHd/ItWJt538eOK9YE8vu4WN5zNBb/a/BRsx+4h6vEE\n5f7W/eLBF4x6Lhbdi4t6RryyL0E5ITOKUCiM0WolRo8bg6+f/aWs2+QMbbhgDSFs1+4aeQFLF6/A\ntq3vYsr0iQiWlWTdtkAItMoAmts6MKqyPOv2+tAlGLYZBcQC1CXKUHQYYzlLK8gXlNKcCJbp2miN\ndvQQq3hwRX+jKtO0QCmFJEkQRAGSIPQRO+94HcBxcYuPEFOtohwNRzHfHof/u+H7KC1NzROTU/wU\nTyzvMKXFaIDtemHI8T/shtgRjBk3FheuvhT7PzqESDiS9XlM04IZNlBW6n8UYnciERNyv35LuSPT\n2TZKs3eDKCSu6+ZsGvbZj95E2Ij22GZZNoJBPVGmxHEcmKaFaNRALOaZLuu6BlmWIIpin2srCAJU\nVUEsZiAWM2GZnpekKIoQBIJodHBjaOq4WKnNxV03/5yL1QiDC1aBKZerIBBvekQSvAFvmVyBFrMR\nAHDBuoux8/1dWdVzcmwHZksU02rGQpFyKyaG5SR1is8llLKsRljFLFiWZUPT/BtdxZ3SO6JhfHh4\nD2yrZykPSmni357YdJkUCwS6rqU01SeKnqjpugpVU7rEzSuBomkqIpFYv2tylmtDbwa+d92/+fae\nOcUDnxIsMJLYU0AYY9ClACZIkxPb5kxaiKYjTagZX5PROcyYhSnjx2bTzZQhRMr7FJsX7JHpscUt\nWAMt3bGu9SPPiNZOaSTmOWAIeHDL89jbcgiqqgx6fWIxw7cpSUEgXfW9DMiy1CPZmTGGox0t+JdV\nN+U9MZ0zNOAjrCFGp92OdrO1x7aFCxdj59aPMw4scKzc5xnFEXNsxZMMNwvRKWbBsiy7x4in949p\nWnBdL7qPMSQKbw70E08+PqF2lhfwk8K10XUNpml3VRj2JxRS17WEa0Ycx/Xc39csX+vLOTjFBx9h\nDTFK5DIcjhxAhVrVY/tZq85BQ9tBVKYRls7AEAnFUKHofnezX6QcTzkmw6XuYK5B/ZKvsHa/Ycwr\nu1IS1JMmb/cmlSrU3VkycTYC72pwkdpxuq52iaeRCKjIFlVV4DguOjpCqHZ0lCslGDMhPzMFnKEJ\nF6whhkhETCyZ2md7zZixOHLgQFptuQ6F7ABVlfmL2iuEYDFKs3DWyE/isN94dlJqSmKVCbqiYkxJ\nFY5EmlI+Jh5Q4WeYvQ4JZ1ctx81Xf8OX9jjFDZ8SLBIc2AOWckgGYwxCHqt/eOHMBRhhgWZ841YU\nGZFILGEoWyx44fi5/fOtqxyT9jURRbGrAnH209DUpZjSXsnFipOAC1aREJCCaG5sRTgS8dYuUriR\nSLKImEyzijBMh0jUgpxn01sAAGUZp1aLoohAQINhmF2h2ebgBxUY27bz4i6/ZMJcWG76TzzJ1p8y\ngbTZ+PE//++s2uAML/iUYJFACMGuv+3A6FVBHGluQdQ2IckyJEWGrMqQZRmSIkFWFaiqClmRIEtS\nzisbdydm2Civzn/0FgWFmMX7JIQkXBsMw0xEqAnC0Cs7El+78mudaCAW1k5HUNLgIP3RkqoqXh0u\n04aipv8QE7UMlAved5nDicMFq4gQRRnTJk/CtMmT+t3HMA00t7TjnffexeiaUVgwd07eRIuhMDd4\nP2fyNM27Qdq2DdO0u6oPM2iamvf8smTYtpNxXat0USQZY0uqcSjckNnxigzHcWAYZuK6portOmAS\nFytOT4bW4yNnQFLJb9JUDRPGj0VNZSX2fVyPoI9JpYMhiXJBfPkY89/4VZZl6LqKQEBHSYmecHOI\nJ7W6roto1IDruonQca8v3gjIsuwu0fO30rDjuCnbF/lBbcXorNb2JMmrZpxOCRfTttAYasfvNtyZ\n8Xk5wxMuWEWEJCmwbTulfU877RSce+5a3Hvvg3j//e057plHrsuh90fuV+gIAl15SgFdhWna6OyM\nQJYl2LZnTeStgcW6BOp4/pIkiYhG+3duSAfXdfOelL2kbi6sLAMoVFWB67iwrMG/u52xCBrbWvHh\nN59BQM1fOganOOCCVURMmjQFhw8fTXn/6uoqfPWrX0JnZwj33vtbhH3wJBwIsQARggDyUoaJdJm4\nEkGArquoqCiFLHtWQoGADkkSEQjo0DQVsixDliXIspywIbIsG67rdpXlyCx007advI6uAGDB+GkI\nSNmXD9F0b3rPGWCkZVgmmkPteOa6e6ApfDqQ0xcuWEXEzJmzUF//adrHnXHGclx55cV45JEn8Prr\nm3LQM28qLF9rKz3Om4WPYDb0TjYe6L0TQqBpKoJBHQCDZWU2TRgf0eUTVVIwtrTal7YURYbd782F\noAAAHZdJREFUz2jNsExE2iL47eX/icmjJ/hyPs7wgwtWETF58jQcPDj4CGv//k+xf39PYQsGA7j+\n+qtQXl6GO+64D8eONfraN9N0CuLSThkDKZLkX0IIZFn2AlMyWBeKO6Tnm7qKmpTSKFJBEISE6MZz\n3w52NMFojeLZr96Hkyct8OU8nOEJjxIsIgRBSMnA9IUX3kB5eQU6OkJYtGhej9cWL16AhQvnYuPG\nZ2HbFi699EIoSvaBGZGoiVFl+RcsB24WLheFI5P6yIIgZBgRmZ3YLJ+6GG/sex+qDw8kqqrAMEwI\ngoCYa8J2XZi2ide/8htUlVUN3gBnRMMFq8gQRRmu6/brVv3mm5uxZs1nsHTpcjz88G9QX/8CJk4c\nj2nTJqOioryrDRGXXXYhWlpacd99D2POnJlYtWpFVv1yXAJRzL9wUJfmNdfML2IxMyMPw0yCNzy/\nxLQPSzB/3FRMKKtBU6wt80a6oWkqYjEDuqqiPdKMa6eei6oqf6YdOcMbPiVYZCxadCI++mh3v6/X\n1x/E0qXLAQBXXnktzjzzHFRVTcIjjzyDo0d75tNUV1dhw4ZrUVlZgdtv/yUOHDiYcb+EJMX68gGl\n+Y+cyxYvUXlw5/RkP5lcYz8c6a86+bysowW7IxAB0ZiB6aQG/3Lxjb61yxnecMEqMk4+eRm2bdvZ\n7+uEsB5P4ZMnT8PixSfh29/+Hp5++mUcOtR3DWzRonn4+te/jA8++Dt+/etHEI3G0u6XVID1KyBe\nvLG4BAtAxtnOmaxh+SFY00bVQpX8y+lTVBnNsXZ8/7Jv+9YmZ/jDBavIUFUVrtv/tFAwGEAkEu6z\nXRRF3Hrrv+P551/Hp58e7vM6IQQXXvhZXHzx+XjooY14/vlX0ro5phshaBiWV7PJsGDbjveeMriH\nM9AinBDMfFVJEEjaYueHYLVHQ3Ay8BXsj4gVw1xpAhbUzvStTc7wh69hFSGC0P/HpigKDMNAaWlZ\nkuME3HTTv+DOO/8T11xzadLjy8pKcf31V2H37r347//+FWbPnoEZM6agrq52QFHq7dL+8a49aGlq\ngKpp3o+qIhAIoLSsDJqugTGWKEFBKfUSS2nPxFIHNiijECBCEAhEQYQgiBCJV5KdEAIKBqEoJSsz\nNE1FzDAT3oepkO0aFgA0hztgUQu66E9+VGOoHXet/74vbXFGDlywipBJk6bg4MEjqKsb3+e19vbO\nARewd+z4EHPmTB/0HDNnTsOMGVNx6NBR1Nfvx6ZN7/QY2RFCUFs7DlOnTsTYsWMh6cEex7uujZOX\nzOmxLRyO4MDej9DU2ArTsjFt5hzMnDUDgiACvXz6GGOIug4II2CgoIzBoTaYy7rCodEt1G7kfI09\nt4sMysxk6fH49oHtvk0JMsagQ8HsCYN/Dzmc7oycv/RhxGmnrcJTTz2cVLAA9BtBCAAfffR3nHrq\n3JTOQwhBXd34pOdxXRdHjjSgvn4/3n57KxaffCpURYGq6VAUOemYp6QkiNmzpmP2LO/3117/K2pr\naxEsCfTZl+F4fSridaYgUYi5ItO0Jsuy03Zq92NKcN64KXij/l0oPqxVOo6DupIaiELhzYQ5xQUX\nrCKkqqoaoVBym6XBbkyzZs3B3r37UVVVmVUfRFHsV8wAoLq8ZtA2zly1HH97ZwtWnHYaxF4jLMo8\n0Ro+EnUcRZEzKiUfi5kZldsQBAGU0qxGWcunLMLvt/4ZYSeacRtxDNtCXXBM1u1wRh486KJIIST5\ns8ZgT+7z5y/Cxx/vy0GPepLqE/3ihTPw7DPPwO0VMk3hvwP7UMFzvJAy8BRkaVedBgBRFAYM1EkV\nl/oTdOFSirnVU31pizOy4IJVpIwfP6FPXpUHQzgc6ve4waIM842mqThrzTK8s/mdHj55uSgZMpQQ\nRTGtMvKWZUPO0A1fEIgX/p8FlDHfHiEIA0LM8Kk1zkiCC1aRsnr12fjb397rs/3889fi0UcfGvBY\nYYitHciyjMULp+OT3Z90E9PhOR0Yx7NZikeODI7rulmYC2d6Jb2cPsdx4NgOVkxalFVoezgcRSxm\ngLoMQYG7sXPShwtWkVJVVY2GhuY+uVIVFeVobW0a8Old0wKIRLJfi/ATURRRN74Chw8f8aIAi8TQ\nNhtkWYJlpTbKynaE1BvXpTAME7HYQD9ejhxj3rTi5xatQlBKbd2NMZYodOnYDiiliVIrFeWleGf3\n+76+H87IgAtWEfMP/3AZ7rnnoT7idP75a/Hb3/6y3+MuuOAi/PnPb+S6e2mjqjICioOdH+0aEYIl\nSVKPasX9EXc1tyw7USwymcBEo7EBFjF7brcsG6oiD2oFpaoKZFmCKIoIqjqmjapDNGoMKHRGzIRl\n2nBsF9SlAPECRuJ9IISgwW33paglZ2TBBauImTNnHq655iu44477exRnHDu2BqYZxZEjh5IeN2bM\nWLS393XDGAqUl5XCjLShtbWl0F0ZMsS9B0VRgCxLUFUFuq4k9xnsN9jF286IV4xFVWXEDNPbhtSd\nN1qMdgQC2oAip+kqVE2BosqQFRmSJEHTlESiOACIuoxn//JcxteEMzLhglXkjB07Drfe+u946KEn\nemy/5JJz8dvf/qrf46ZOnZGV2W0umT9/Fg7uPzgCxlipFxkRRRGiKHaVmCEpH5f8nF4icWIdrUvk\nGDxBi/+7N1HbxKcdyQJ9Bife9zh6QMMjW/6YUVuckQsXrGFAIBDEyScvw5YtHyS2SZKEE0+ch1df\n/XPSY84550K89trf8tXFtGk6fASubQ++YxFjmravJe9FUYTd7Zqx7j+Meq+5LgjztkmKDEYIHNuB\n5Tjo6OhEZ0cIbe2dCEeiMC3LG5F1idjWw7v62GDtbz+GmGWkbcpLCMExoQNNzZkJIGdkwgVrmLBm\nzTps2bK9x3rW0qWLsXnzpqTrJF514KEVLdidM04/FU1Nw3ta0AtE8ONPkAGMQVZkOI4LBsC0bRw9\nfAzNTS04evgYiCiioy2EznAUTc2tiMUMGDETB/cfQtvhdowL1GHW+PmYOW4uZtfOx6TKadj13scI\ndYbAGIPh2Nh6aFePNbIDbcdQaao4XZgDodWBETXT6rVaruPHD/3Ch/fPGSlwp4thxNVXfxkbNz6G\n9esvTGxbuXIpXn/9JaxZs67P/n4+3fuNrmtAeGhFMg5JGIPkeg8prihB0TU0N7WAuBIm1E1CUCwB\nCIPLXIwvr4PARAiiAALPPHhaP4Yksizj7LXnIhaL4YPdW3DfJy/gzGknoinSikNtDQi1hlAll+EP\nX7sTo0u9SsE33/c9bA7vQnlJaUpdlwQRO51D6OzsQFlZuS+XgzO84SOsYURtbR1EUUNDQ1Ni27x5\ns7Bp0xtoaWnqs79lOUM6UquzrT2tqaZiXfNKJ+gh6fFEABW8H0IpSspKUT2+EgIEUFCoko5SpRyK\nqEKSJAhESNmJRNd1nDj7FOzcvRv3bX4aHzceQGNjMxZOnovX//nhhFgBwE+/dBsWqVPQEU49oMcp\nE/G9+3+U9nvmjEy4YA0zLrpoPf7yl7d7bLvyys/hlVf+1Gffc8+9AM8990q+upY2ZQEd4X48E3vA\nGBobmrDjg+04eOAgGo41orW1rSufa2jC0K2GWDbGtITAEUW4ggjCKARCIMkSwICgUArDjcCh2a0F\nqqqK2y66GWpUAKIuPnfKObjj4u9DID1vH4QQ/OxL/4FRKEUkmtroWJYkbDcPoLmtOas+ckYGXLCG\nGW+++RpOPXVJj21VVZU4dqxvpeEZM2ajpaUTsdjQtMmZVDsWH773PsIDPLEzAH97YxNYOIwl82Zh\n+vgxmFhdgQCAp3//JJwhELiRdARFCCRJhGXbsG0H4XCkz2iSAQBjYKTb70k4HjNIwLqi/2zTgaqo\n0IUAFB9cJdbOXI4Xbvot3vjmo/jO6q/0O0LTZBVP3fgrtMciaA11wEnBf1CqUHHtvd/Muo+c4Q8X\nrGFGff0nfRzUCSGoqanEHXf8rM/+11xzPR5//Nl8dS8tCCFYfdopqN+5Bx3tnUlv2O2tbSCOg4kT\na3tsLy8N4pLPn4NPdu1BKJzCKC1HxPssdImR67poamxC47FG1O/Zhz0ffAK73YVoyPhkVz0OHTyM\naDQG27YRMww0NDaj4Wgj9tcfgO04Sa9B92hAAIiEQggdDSFihRBQSrMuLZIJG6++HaPMAMJGdNBp\nXUmUEC1xcduDP85T7zjFChesIibu8xb/9y9/eSdmzpyUdN9161YlvXFVVFRi9Ojx2Lt3fy67mhUn\nnzAPDfv2o37PXhjG8Ug027axb089zjhjedLjBEHACbOno/nwYbS3d+Sru337wRg6wxGEI1Hs3VWP\nseUTsXDqEixfvAqrV30GUydNx5RJ03HaSWfihBlL0dkYxqH6I9BoADMmzsWE2ok4Yc5ShNpCfUQr\n8W9CEqlZJaWlMKUYTMcsiFgBwPSayXjipvuwLFyHAx2Ng+6v6RpebdiKVz74Sx56xylWeJRgEfPr\nX/8PWlubIEkqwuEwzj9/NaZMSS5YQP8O6Jdd9gX88Iffww03XDVg8cdCsmD+bFDGsG3HxxgzcQJK\ny0qxc/tOLD1h3qDHzp46Ga++tRnLzliRdeXdTDAcB4IgYdKoaZhWM3vAfUVRxKJ5Pad09S7/vtmT\nFuBo6CBMy8vf8sTISz5mjCHUGYbrOFB1DaquwmIGwnYnSuSyHL2zgZFlGasWnIYXdu1Kaf+SqlL8\n7xfuwJoTVua4Z5xihY+wiphzzrkQ5eVluPbai7FhwxcGFCugf8ESBAHXXPOPeOyxoTk1GEcgBIvn\nz8bokgD27NiF6bVjIKYoQEsWzMW+PI8iGQDLdsAoMKFqctYVdgUioCY4HqrslYhxKcXOD3ehtaUV\nn+79FGOC4zGnbiHGBetQVVUNUZIg9lM3LV+cd+7nMMlJvViorqmIRIambRin8HDBKmLGj58AxkS0\ntbV3JQIPjCAQNDYmdxaoq5uEysoaPPfcyzDN9BJA840sCDhx3qy0qiaXl5eio6UlJbNZP2AAHNeF\n67iYWDkViqQMekwqyKKMMcFalMhlCIplWHHSKsyuXYBTFp6G8rIKAF4oeolShmplNHQp4Mt5s4Gk\nMWrXAhp27tyRw95wihkuWEXONdf8EzZufD6lfS+99Dzcffft/eZerV9/FZYvX4snnngJ99zzUNp2\nO0OdxfNm98hRyxUMQGdHCK5DMbl6uu/rSIQQVOhVqNAroUhK0mnOErkMolD4GX+XujCQ+gNQhNj4\n/TvP5LBHnGKGC1aRo2ka5sxZgLfe2jzovrIs48wzT8FrryX3FwSAKVOmY8OGb2DatFlobm71s6sF\nR9NUxMJhX0dZca+9uAu6SylCoTDaDrdjUtW0ggU9DBU+bTuKZhqBm2KCuiSJ2BLejdZQe457xilG\nuGANA84///PQtGrcd9/vYVnWgPvOnz8H27dvG7TNmTPnDOnIwUypGzManZ0hX9qK50kRxuDaNtrb\n2rHv4/2YVDUdp5y8wpdzFD22CwsO2s0wjoZS84ZUynXc/MD/ynHHOMUIF6xhwtq163D11dfj7rsf\nHnDay3vip+jsHDjMe8aMmdi/P3k9rWKmJKAjHAoPUOgwDQgBZQyW4+LT+kOYMnoWVpy0Coriz3rV\ncKCmYjQUiBBAUK4FUzpGkWXsjR5BW6gtx73jFBtcsIYRo0bV4F//9ft48skX0djY3KPURHcuvfQ8\n3H77Twf0EdT1AGw7tfLtxQQBoAsETU2ZWwHF60a5to1IJIpStRzLFq+EqmbvKDHcCGoBzCETIIBA\nTmNNTavQcfNvvp/2+W677bt49NGH+v3uc4obLljDDFmWcfLJy/Dii2/hnnseTCpKgYCOdetW4qGH\nfj1gW7ZN0dHRmauuFozaMaNxYM++jKMhCTzHikgkhinV01GhVQ16zEjmh1/4NpoiHSmnIACALMnY\nbR7GoabDA+4XDofw7rub8eSTj+F//ue/oOsatm3bittv/zHuvvu/0NY2vEvUjDS4YA1D1qxZhxtv\nvAVXX/1PuPfeh5NG+02fPgWKAmzZ8td+27nhhptw//2PDWlH90xZdvIiNBxrzOC9MdiOA9t2MG3M\nbEjS0C3RMlSYNm4Kzh97KloGmYa2GXDEYjC7vq7B8iBufegHSfd9883X8Itf/B88+OC96Ow8jDlz\nJuCyyz4LTZNx/fVfQygUwamnLsB9992BLVuGbqFSTnpwwRrG1NVNwkUXrcf99z+W9PV161bhzTdf\n6/d4TdNw9dXX45FHnspVFwuGQAgmjKpCY2Nzeo7uDOjsDGOUXjNkXUGGIj/94vdRZ1fAcR1QxpI+\nRFmModEBWh3vNUmScMhuge32nZr+61//gmuvvQSXX34hTjxxIdraOvDAA48DEDB58lR85zs/wMsv\nb8IZZyxDKDT8ZglGKlywhjkzZszBmWeuw+9+93TS12V54HWFyZOnYtas+XjhhVdz0b2CoisyRNNA\ne1vqIdSmZUPTNJTohbE7KmbuvO5H6GwLoSnSDov2FSFNIBglAYFudyUTNo529vUinDt3AV5/fRMe\neOBx3H//HxCJEHz969/GjTd+C4A3Na6qOgzDhK4XPnma4w9csEYAJ5ywBIsXn4Inn3yhz2uCIAwa\nCn/WWedg2rR5uOeeh4ZsKZJMGT9+LJwUgkvieVaGaaK2YmLuOzYMGVs9FqsnngJqu1BFGS2xzh4j\nLRHABIWgXDyeu0YkAfuOftqnrc985jwEg6Nxww234Bvf+DbWrl13vL5YF4JAYBgGF6xhBBesEcKp\np56GyZNn4a233umxfeLEcaiv/2TQ45cuXYENG27CPfc8mKsuFgQCIJZisUEAUBQFqqzlrkPDnB9c\n9i3YroW9rUegicqgidWSJKH+UH2f7Yqi4KyzzhnQkmzBghOwceOz0HU9635zhgZcsEYQZ555Nvbt\nO9hj25Qpk7BnT2pu2qIoYvToUbnoWsEg8HLTBgu+IIwBBMNuhJlvBCLgrNkrIdlAS2zwtSVZktHS\nkpmd1sqVa/Czn92BadNmZnQ8Z+jBBWuE0fuBdvz4MTh48EBKxz799B9w1lmn56BXhUUBQyScyiiL\nIFrAYpDDhZ9f8K947MKf4CR5Emg/FQTiCKKAg6Hkhs2pUFJS2meqkFO8cMEacfT8yAVBgGHEUjry\n2LFDqKkZXiMsAKgbNwaHD6bg6sEY9ACfXvKDuXMXYL4+BZ+2Nw5oskzBsC3Ud0qQMzLhgjXCoLSv\n8WtZWaDfsiPdGY7OF4A3JSgSMmjwCQDowUDSa8hJn5uuvQnMptjbehhHOpI7j2iQMLFsXJ57xhmq\ncMEaQXR0tCMY7DtC+OxnV+OJJ34/6PEzZszC9u0f5aJrBWf21IloaPASiQfKy3JdFxGbFxj0A0EQ\nsO2WZ3Bb3RdQa5ckzbdSDIINK69IqT1KKd577x289dYbeat7xskvXLBGEJs3/xWLFs3tsz0YDCAa\nHfwm/PnPr8ehQ2148skXhl2tLEkUUa0qeOW5P6OttQ2snyAMSZLggPvU+YUsyVi//io8dP0dIJ0O\nDKfnKPeY2Y53mz5Oqa2GhqN4/vknEQodxe9/P7yiWTkeXLBGELt378TUqZOSvjZ9+iT8/e8fDtrG\n5ZdfjVNOWYU777wfHR3+lOkYKlRWVuC8dauhOTZeeeEltLd3wHVdz+wWXkShZZqwHS5YflNRUYlV\nwmwcC7eiOdoBxhgM24LBbFx/6qUptfHJJ7uxZs3pWLbsJDQ2HkZHB6+pNdzggjWCiEZj/ZrZrlhx\n8oCFHbszd+4C3HLLv+Pxx5/Hhx8OvynCysoKnHv2mdAcG2+8+Ar++OiTaDx8FABQEgygo5PfCHPB\nlZd8EYLtfU8/bWlAW2sbyssqoEqplWv55JM9mDRpAgDg0kvPx/3335vL7nIKABesEcQ3vnErHn/8\nRezY0XeKRRRFMJb6vL+mabjllu9g8+YPh+16QXl5GT579ipc8vlz0dHQgM1vvo0tb23GHT++vdBd\nG5ZMnDAJ793yFLbf+hx+c+mPsWDqfLx43S9TPj4SCSEY9FwtgsEAqqpKU84x5BQHXLBGEIqi4NZb\nv4sDB5rwxht9HawFIX0z10suuQLPPfeyH90b0ixYMBcrTz0RuiTi8suvLHR3hiWMMSiijO1HP8Zz\ne/6C/zz3WwgoqacRLFt2Ou666wE0NnoRh+edtxZPPvl4rrrLKQBcsEYgV1xxDVxXwqZNW3psH8wm\nJxmTJ09FY2P7iCmYt23bLpx66mmF7saw4lDHMaz9n2sx6z/X4antL+Enb9yH763dgJqS6rTaWbJk\nKb71re/h5Zf/hg8/3AFCCFRVHpblcUYqXLBGKJ///OUIhWxs3vx+YltbWyt++cs78eGHH6T1R75+\n/VV45pnU1r+KmZaWVtTUjC10N4oSlqSkyNufbkN7rBPXPfpdHIs04+fnfBsXzF+DB9f/BALJ7NYk\nyzJuuOEmvPnme6CUYvToKhw7dsSPt8AZAnDBGsGsX/9FNDZ2YuvW7QCAr33tWpx33hmor9+Ghx/+\nTcrtTJgwEaKo46OPdueqq0OC559/FZdcklpOEKcnNnUQtnraX02trAVhwFPX3oG/3/JHnDd/dcZC\n1ZsrrvginnrqRcyfPxMffLDVlzY5hYcL1gjnqquuw0cf1ePoUc/pQtc1rFq1Ai0tDWhvb0u5nWuu\nuR7vvLMdBw8O36dZxwECgWChu1GUKKKMUrXntaspHYXyQBn0HLjfT5kyHa4r4KWX3kJtba3v7XMK\nAxcsDjZs+AYeffRZOM5xp4FMwoJvvPFb+OMfX0FbGgURi4VPPz2M6dO563cx8Y//+DXcfPN3sWjR\nkkJ3heMTXLA4EEURGzb8Mx54YGNiWyCgo6qqFHv3pj7NJwgCbrnlO7j//o2IRlMz1C0Wtmz5ACtX\nri50NzicEQ0XLA4AYMyYsVi6dAVefXVTYtt5563FH/4wuMdgdxRFwS23/BvuueehHiO2YicSMVBe\nXlHobnA4IxouWJwEp59+Jg4cOJr4XRAETJs2ER988F5a7ZSWluGrX/0m7r//Mb+7WED4nwqHU2j4\nXyGnB5WV1ejsPO4RuGrVMrz55utpt1NTMwYnnnhKj7D5YsVxHMhyavZAHA4nd3DB4vRgxYrT8e67\n2wAAtm3jvvt+h7PO+mxGba1e/Rls3boDpmn62cW8097egerq9JJYOZlDKUVrawvee+8dPPHEo9i0\n6Y2UapVxhj+8djSnB9OmzcQTT/wOkyfX4dlnX8WGDf+M0aNrMm7vy1++AY88ch+uvvoSH3uZX1pb\n27O6Bpy+xGJR/PrXd4Mx2pVQzEAISfxeXl6CCRPGYd68iWhsbMa99/4/UMpAiIg5c+Zh+fKVPMVg\nBMIFi9MDQRBw+ulrUF9/CN/97g8gCNkNwkePrsHYsXXYs6ceM2ZM9amX+aW1tR3jx88qdDeKnvb2\nVrzyyp9x+PBBOI6Fiy46B+XlpYMeN2bMaCxYMAeA55jxySf7cNddP8PChUtw9tnnJvZzXRfvvvs2\n3nnnbwgGg7jiimuhaf7neHEKBxcsTh+WL1/pa3uXXHIFfvSj72H69CkZ+RUWmtbWdpxwAh9hZQKl\nFM8//zQ+/ngHKipKsWzZEqxZc1LG7RFCMGPGVMyYMRV//et7+K//+gkmTJiIQ4cOgDEXCxbMwpVX\nXoC2tnbceedPUV1dgyuvvBayLPv4rjiFggsWJ+cIgoDLL/escj73uczWwwpJW1sHqqtHF7obRccH\nH7yH559/GitXLsV1160H4I2QNm3ajKamVoRCnlUTIQQNDY24+eavpNX+8uVLMHv2VBiG2UcEq6ur\ncN1163HsWCN+/vMfYu7chTj33H/IesaAU1iKWrC2buUeYcXEzp17MX78e0U3TXPgwCFs37690N0o\nGhzHwRNPPIqKigBWrDgJruti27YdYIzh6af/hMWLl2LKlIUIBoMQBAEbNz6CqVNrsW3bjozP2dTU\n0u9rp566GPv2fYobb/wKTj75FCxYsDjj8wwHdu7cWeguZAzp7aBcTBBCTix0HzgcDqcI2cUYiw6+\n29CiqAWLw+FwOCMHPqHL4XA4nKKACxaHw+FwigIuWBwOh8MpCrhgcTgcDqco4ILF4XA4nKLg/wP1\nRu+P316h9AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b965b00>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAADaCAYAAAC8ctVuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4XMX1sN9btqo3997GNjbGphoIGDDEFGNqaCH0JLSQ\nQgkQfgkJKUDgCwGCAwEcWiiBYHq1KbYBg21w5eKGbdlykay+9Zbvj1nJK2kl7UqrYrPv8+iRdPfe\nubP3zsw5c86ZM4rjOGTIkCFDhgzNUXu6AhkyZMiQoXeSERAZMmTIkCEhGQGRIUOGDBkSkhEQGTJk\nyJAhIRkBkSFDhgwZEpIREBkyZMiQISHdKiCEEIcKIV4SQgzozvt2FUKIXCHEH4UQR3TxfUYJIZ4T\nQkzpyvt8FxFC/E4IcWoXln+tEOLSriq/owghcoQQfxFCHJ3CNYcLIf4uhFC6sm4Zeg9dJiCEEOcI\nIZYLIeqFEOVCiFnAOOA0wNtV9+1m+gA3AyO7+D6DgLOB/M4WJIRYKYSYG/f/cUKIyZ0ss0gIcYYQ\nIqez9etOhBA68H/AAV14m18B07qw/I5SBNxIam33BOAaYJ8XEEKIbCHENiHE33u6Lj2J3t4JQog5\nwHGGYQxOtlAhxETgGWAO8MvYfZYBJ3aolnspMc30UWRndIBawABeBO4zDCPcA9U6EQjF/f8ucAfy\n/XSUmcBjwCjkd9wn6UhfQL73VO/zNTAY8AEBYCfwEfCAYRhfpFpeb0UIMQ2YB0w3DGNes8/uAG4x\nDCOhEiuEyAZuA84EBgBVwHrgbsMwXmnnvnOAH7VxyhzDMC4VQnwP2JXct9k3aVdAxEi1kR+D1DKu\nNQwj0HBQCJFiMXs9hUjh8ENgc+z/44E/xX4f390VMgxjS4LD6dII93nNkg4M+B1gDPAk8E/kbHsM\ncC3wkRBigmEYG9J4r468s+56z209638BM4DfAKuQ/WwCsDuJcu8AHo79PQX4O/BzoEH47gAwDGN9\n6lXet0hWQDQ2CCHEWUizSn/kgFcPvA1cZxhGg7QtjP2uixMKw5sXKoQYBmwArjAM49G44zbwR8Mw\nbov97wX+AFwAZAMrgJsMw1gQ+3ws8oUPi91bAT4HfmUYxpK4cocCdyEHZi+wDjjZMIwt7d0jdv0U\n4B7gUKASWJ7MwwM+jevUrwghqoFbhBBjDcP4WggxCfgz8D3ARD7PGw3D2NxagUKInwE3ACVADXK2\ndqthGNHY5/cgZwv9AQ/wlGEYPxZCfABohmF8L664W4UQt8b+fhAoiz2LEsMwdsfKy4595xsNw/h/\nrVRrbdz7PsgwjKWxd3wn0jyhIzXhXxuGsUIIcTDwGXCOYRgvxO4zDalVTjEM48vYsZ8A/wD6GoZR\nHvsOE4Ac4Bvke3ojdu4I4AFgPNAX2T7PMwzjXSHESOD/IRWYQOzeqdJkcBRCnIY0U40DtiDfw52G\nYVhx5x8khPgCGIscwOYAvzMMw27jPpsMw1gU+3ueEGI5sAA5oG1IpH03708xE9qdwLlAMbAN+eyf\ni7vPTUKIO4EsYDVSa3+7nWfwohBiKuCP1eEXhmFsEELcQsfaTWu0JYhOBP5tGMYDccf+m0yhhmGs\nQ/Z9hBDu2OGVcc+b2GffAh8bhnFh7P83AIF8lh7gE6Sg+iFwONJkPx/5/HfEldNqGxFCXIycfTfn\ndsMwbo9d/2OkABsBbI3d886G9iOEuAa4AuiHNENXAS8hx794Bb29ttqCjvggJgCTgR8jB9rbgFOA\nhxKcezRwZOynrI0yE2kK8ceeAc4BbkXa4suBt4UQg2Kf94vd42Hg+8DFsWNzGxqAECIL+BCYBFwH\nnIwcSLYmcw8hRDHwPpAHXAJchZz6d4Rg7LdPCDEQOWjmABcCV8bq+IEQwtdGGYtidZgB/CX2na6O\n+/xMZEM5DzgVeDzus+bP+9/seU/3AK8iO2f8DOd7gAa82Uadzokrx4h75hOAnyKn9QVITbgfsASo\nAI6KK+OYuPs1cBSw1DCM8tj/DwLnx76XAfxXCNE/9tkQ5DN5BjmIXAZ8JYTwAO/E6nIN8h2ua+O7\ntEvMr/ZfpJnuVOAR4LfAL5qdmovsjGcATyAVrNvbKV4VQuhCCF9MAfo50nz3aRJVa3i/18V+/gac\nhBwcvm527iKkADkHCAMvCSFK2in/W+TzuwaYCLwjhHDR8XbTEVYDpwohJqS53HgcmvaVGUhT7CnI\nfjUEOdP7HDgduB44DimUgaTayOvs6TPfQwqYWuDl2PXXIJWj14BZyH78W6QVooGDkH7KC5HP/l5k\nu/99CvVISLIziES8EZNgHwshxgDXCCF0wzDMuHMWxmtJHTExCSEOQDq2TwLeix1egJwGXkDcywAW\nGYaxMHZdFClFj0RqOdchtekxhmFsip0/P4V7XIO0Cc8wDGNn7LqVyJfSHnpsgCpADoA/Rw5Oy5GC\nNQKcaBhGXazcz5AD38+RM4sWNLNFfxCzl05DDgYgG/Y6wzDeSqJ+WxJoT2uRA1qDtjkNqdU2H2Di\nWRJv/ohplP2A0Q2zISHE+8BGpIb0EyHEW8hO1cDxSKFxHHB/LGJmOtLc0vDdX4i7x2dIrfwQYG5c\nOe8ZhvFB3HkXI2exkw3D+Cp27G3kM+4otwPPA7cgB8b5SO3sMuCvsXMcYF6cpvtOTKv+pRDizoZ3\nnoBbYj8NOMCVhmGUplC//kh/0yOGYVS1cs5HhmG8ByCE2AwsRQ4gj7ZyPsAv47TXr2LXXGgYxmMd\nbDcd4YdIxeYrIcRHsb+fMwwj2PZlnWa1YRgfAwgh+iD77xOxWcm8WFRYvK+1zTYSs7rsipV3GVKp\nnmUYxlcxBfGPwKOGYdwYK+/tWJ+4TQjxQFx7qDcM453Y3x/FZnjnIIVWu/Vo7cumK4rJiJXVL03l\nxXNw7PcbyIE0gpSwPhKYrZrVCaQDC+AI4Js44ZDqPSYiG0f8rCFZW+zXyFnDNqQGsBA4Pja1Oxxp\ngmocKAzD2Ig0nUxtrUAhxPlCiGVCiKAQohbZEXOTrE8yPAWcLITwx/6fTupa4OHIZ95oKjMMowY5\nNT88dmguMFYIMVgIUYDUhm4BjomZSKYgzWj/AxBC+IUQ9wshtgohTGBlrJy8duoyEahuEA4xOmxL\nj2nM+yO17yh72s3FwNB2Lp+PbFv7tXHOo8hncQhSY30cmB0ztyXL/cg2t0YIcYcQoq3+Anv6TP82\nz4q/QJoBq9jTh9LRbpK573rDMI5EPqPFSNPxN6KLQ86b8W3sd3zY/iakPySlNiKEOAhp0fg/wzBe\njx3eD2lZeIemvIVU7g+JO9a8LRvExuPOtNXOzCDiaZDa7jbPakkk9rstU0pDxM1Z7HkhDZTTOs3r\npNC60yuZe3iRdseOcFqs3N3AjgY/QTsotDKACSGmIzviHKQGHEFqGunkcaT58BwhxHtIs+JtrZzb\n2nNtbQCOP/4m0h9wOvJZr0Zqg/cgZ1tHARsNw2iIsnoYqeHegJzu5yF9Nu3hBVxJnNcWOtJHBGAj\nO9vTyI6dajnQthO2zDCMpXH/vyGEGAX8BDmbarfvGIaxSQixH7L9XQvcKIT4hWEYD7ZyfjA2y0+1\nH+vs+S5zSL7dVMd+Fyb4rJim0XYJibWLZUKIPyJn/S8KIQY1s2R0FQ1RiHqzY6oQQiXJNiKEyANe\nAN43DCPedNTQT1LtXyDHPy2VeiQiXQIiWRq+aMPMZQey4m1pUqtivwcbhvFSJ+69BDhOCDEkgfO3\nQQtt6x6fAscLIUYbhrE2xXuvbCPy5FNglhAiO87ENBwYjXyh0PK5Naxb+GWD6SBmHmhPc01ENbIz\nNsEwjFIhxH+QPpFspHBrbSBu6OjFSCdpA58A0+OfeawzHIYM9cUwjHohxMtI7aYMmGsYRiRmejob\nOeV+Oq7MyUiTTaPJKUnT5afAlUKIYwzDmJ/MBQkYg9TIiTkYv0b6i5YZhpFKJz4Z6TxfkeyNY2YF\nD3sEVEM02n5IO3ZCYsrIC8ALQojngN8hfThpQQhxFLJ9fBa735YU2s03yP4/gzgHc0zjPQb4Mtl6\nGIZREwteuAYpcDrqH0wbKbSRhmi15qG3q4A6pF81flyaAVhI30cDrSobKdSjBd0tIBoa9SVCiLsM\nw6iONaaLhBDfIDXCJhpRLBLmDeBPQoh8ZEdXgfGGYdyTwr0fRDrW3xNC/BkZdtofaYNdlsQ97kVO\nyd4WQvwBaUcfl+oDSMDvgB8gNcR7kQ3l/5DO8wZ/QoOd8TwhxAr2NIy7hBDPI7WWQTRtJG1pF/Gf\nfQacHetcVUB2nJC8G+kn6Qc820a0wxfIget3se9QFLvub8hn/kbsmUWQNlEV6SBr4HGk8yyKDFsE\nKRSeRzo4/x137ufA6UKIy5EDTLKzgqeRTv3nhBC/R3a+gtZOjjmG/4R0KgeQduWDgF/HnXYH0tY+\nVwjxb+RgOAr4xDCMBqXDAYbHZn0u5OznIuA37djLhwohjkQKhUFIX9ihwOXQOBB/BFwvhKiIPYtR\nzb7Dmcj+tCX2XfcjPQPnLCFEVay825CC7pm4z5NqNzHl4O9If0wEKei8SOEykjj/kBBiAXJh6kSk\nRvwM0rfYoKxNQvbP5YZh7BRCnIx8N7+KVyZSJB3hvG22ESHETGT/vwsYH6fsbDcMY50Q4jbgntjz\nng8ciDTB/q2ZotteXZNpqy1IxgfR3JPf/P/4422eEwvHexg5aDREH1yN7IS3IaOEnkFq+/Ha1ZnI\nWOWLgFeQA8qJQgitlfu3wDCM7UjtcwnSfPEmcpBqiIRq8x6GYdQjO+g8pNP6PeRD/wS5QKc12qtX\nKVJLDiLNRrORg9e0hhA1Q8Zj344cpI6LOV+vjV33OlJDG05Tjau1+zZ/N1fH7vcEchCdEVe3lUi/\nzCD2xI239h0uQ77T15DmrpGxGdHRSB/MP5ERH7XA0YZhlMVd/z7SZrrSMIw1scOvI2cm7xpN49F/\ngXw/f0K2lxeQbWVr3DmJ2p6NtIc3RBG9gwwvbN7WGlBjP/+KfadTke3l7rgyX0BGlpTEyp2L1GDj\no4DeQYbbvoj0oxwK/MAwjITBBzHWImdPHyHb6Z+QSsAswzDiQyLPRrbHe2O/70K2x4borFHIIId3\nkT6NLUjHZUdZjnRI/xPZ5n6N/N6Hx5tNk203sXNvQL7TI5GziMeRz32GYRjxvov4dpsFbEc+67mx\nnx8jI3PiI6hs2ul/cWWncrytc5r0ryTayOmx829Evu+Gn1ti198H/CxWxlxkP/tj7PyE9+xgPRKi\nZLYczdAWsRnBZMMwjmn35AwZYmTazb5Bd5uYMuwFCJkqRUVGRv2E3plLKEMvI9Nu9j0yAiJDIn6H\ndKSuBs4yDOPztk/PkAHItJt9joyJKUOGDBkyJKTbZxCKoviROWkyZMiQIUNqfO04TqD909JDT5iY\nxj711FNLxo1LR4Ro1xOJRHjppWcZOLAvBxwwvslnjuPw2mvziUajzJx5LC5XZ9dhdY5IxGTz5jKG\nDeuPrnfdqzVNk9LSHQwbNrDL7tEW69ZtYdSo9jNu/327yUuVLfPh5WvwyHCdElfbQXxlZbuwbYeB\nA/t0uK49jeM4/Pe/b3DppT9N6vznnnuCk07ad/zKkUiETz9dSnV1Lbru5oADDmLUqDGoatftlfbU\nU48ya9YJaSlrzZq1lJaWcdhhU9i2bTs/+cn1ByIjybqFHvFBjBs3jilT9p7N0Q477DAeeOBuJk1q\nuZ5v2bLVnH/+pbz44lOcf/5pPVC7pkycOJaNG7cybtyILrvHrl2VDBw4kH79Wqyv6xY0zcOECaPa\nPe/+iQ5fr4myOtTUjFoFLOir8btBrTf/jRu3kp9fyNChSWed6LU4jsPu3TuZPn1Gu+cuXPhewna+\nt7Fhwybmz1+Ex+PnkkuuZNCgIY2fBQL1PPTQfXg88QqdbCO2bQMaY8aM46ijjsHvz0rpvsuXL+Po\now9L2zNctmw1N930W+bMeYj99+9+w0vGSZ0koVAYx3FQlKbrUfr2LSYcDpGVlcfmzaUMGTKolRK6\nB6/XQzDYtfsQVVXVMnhw3y69RzrwqwqXlmjcvMWkeW6TT+rayrQNdXUBJk4c3XWV60YmT57I7NlP\nMmHCJPr1a13gWZaFXDqwdzN37tvk5/fluutuTjiTfvHF5wgE6pg27VhGjhzW4nPHcdiwYRNPPDGb\nnTsruPrqX1BU1F6CW8l7773FxRef2dmvAEB5eQXFxX3Jycmlp1zF3bon9d7MrFln8dRTL7Y4Pm3a\nVN5++3UuvPAyXn75XUyzO1LAtM3gwX3ZtKmt7OqdIxQK4/V2NC1V93Jpicph2S0Xma4IOHxR12oa\n/BaKwN7O5Zefx9NPP8pHH81r9ZwNG9YyePDev118RUUNs2ad1aqZ9cILL+Xmm39PWVktjz32PC++\n+DrffLOerVvLqK6uwbIsRo4cxumnz6BPn0I+/PD9pO+9efMmysp2tH9iErz33gJmzToLAEXR6ImA\noswMIklGjx7L7t3f45VX3uXUU/cs1vT7fdTX16CqKj/5ybU8+eSjXHJJZxardp7i4gKWLfuagoIc\ncnOze7QuPY2iKNwyQOP89SaVcfIg6MCccpuDsrXWL96H0HWdyy47l/nzF/Hww/dz+eVXt7DDr1y5\nnHHj2jfd9WZWrFjN5MkHtXueruuccsrpwOns2LGdNWtWsmPHLmprN1BfX0s0GkXTdGbOPIeBA5Pf\nYfauu/7Oiy8+y0cffcZ557VtcrZtm3fe+Yiysp243VLhUhSFrVtLueGGqwgGI+TkyATNI0eOoaxs\nW9L1SBcZAZEChx56BLt3l7No0RIOP/zAxuPDhw/io4/mcdRRxzJhwmQ++WQJU6ce2EZJXYuiKEye\nPJYvvljFwQenfz+VvU27PixH44Q8m+d2NzWfLK13MB0HfS/7Pp3hmGMOZ8uWbfzhD7/hmmv2mE6+\n+OJzli9fyrRpk9spoXfz2Wdf8ctf3tr+iXH07duPvn3Ts1OB2+1G13UOPbT152hZFm++OY9t28qZ\nOfMMzj13j79i166d/O9/T7NlyzaGDt3jRzziiKO46abr0lLHVMiYmFLkxBNnsW7dt02OHX30VFav\nXsbq1Ss4/viTMIxvqaxsbX+W7kFRFDRNo74+/fun7I1rZ+4dqnNwVlNBYIQcXk4Q5bSvM3jwAK68\n8oc89tg/+OyzhaxbZ/Dmm69wzTWX7HXCP55gMERWVk6rEUoVFbv4178eZNWqpJPodqAOATZvXs+I\nES0TK69bt5E5c57niSf+x9Spx3HjjbcxblxTZ/Z///sMJ598HB98sIiTTprVeDwvL59jjz2xeZFd\nTmYG0QFUtaVZ4pxzTuXhh5+moKCQq676BXfeeTvXXHNxj3a4SZMEixev4KCD9sPlSs+rDocjzaI/\n9g78qsJjw3XOWhfFiO0yYAOvVFqcVfjdMDPF43a7ueKKC3jnnQ9ZvLicadMOR9P27ufw9NMvccEF\nlzU5Zts2n3zyMZ9+upDcXB8zZhzD4sVLePPNuYwfP5EZM2amNeT1448/YNKkPSH8mzdv5cMPP8Wy\nYOzY/bj66htaDYc3TZMVK5YTiQTJzS3A6/U2+XzUqDFpq2eydPtKakVRpixZsmTJ3hTm2pxFiz5i\nzZplnHnmyU2OW5bFAw88zs03/56NG9ezYME7Lc7pbnbtqmTr1p0ccEDq270mYseOChRFoU+fRHu8\ndA8rV65LKsw1EYtqLa7YaLItFtY0yAUL93OTqzUV5J25x97ImjUbGD16KLq+9wkJx3F47LFn+f73\nT2XChEmAXP/w5JOPUllZwZQp45k8eWILZc0w1vHss3P54x//mnI4a2vYts1dd/2enJwsTNNm2LCR\nzJgxE4+n/aCOQKCexYs/4cgjpyV0sC9dupQDDzzwQMdx9u11EHs7hx9+FFlZ2cye/SSXXXZuo0ag\naRpHHnkwK1Z8yYEHHsKyZV/w9ZpvGDuu+yV/AyUlBezcuRvTNNOyeK6qqpbhw3tmgVw6ODxH49YB\ncEupSbUFpVF4dKfFL/p/t7tCfn4OVVU1FBe3ukVGr8S2bWbPfpJzz/0RI0bIsGTTNPnzn3/HD394\nGkVFrSsyQoyiX79+aRMOAKqq8qtf3Uo0Gkm5XL8/i2nTpqetLukg44PoIJMmTeHSS6/igQfmNPE3\njB07muXL5bYMPzjxFNY9/xJlv/g5X9zzN7asXNVacV2Kx+MiGm09pDMVIpEobvfeZ2KK5/xirYk/\n4uPa754fojkFBblUVtb2dDVSIhqN8uCDc7jooh83CgfLsrjrrj9w/vmz2hQOAF988SVTp34v7fVy\nuVxpFTo9yXdbbeokffr05eYrr+X+fz/G944+mLFjR5OV5ScQqMXevYvoutXs17cv/QO7GFRXQd1T\ncyhFpdrrp65vf0acchIlg7t+YZ3P5yEQCOHzdX7twt7sxIxnlFflvRopNHf0/NKVHsfr9RAOR9o/\nsRfx5JMv8dOf/pySEpkKxbZt7rnnT8yaNZ2SkqJ2r1+yZBU33fTbds/7LpMREJ2k4k83MLU+xLuh\nMB9/vBiPx4tpWkQ+mY/z5EMMty0Ulws1J4fcnGxyY9dZZd9S9eDf2aRq1Hh8RAYNYfTMU8jtk/70\nFZWVtYwfn9xK0PbYGyOYEnFinsIjO+XGvpWmQ9B28Kn7hvD7LhAMhvD5shqFA8D99/+V448/nIED\n20+PsmLFGiZPPrgrq7hPkBEQncCxbUL19UzOy2ZAxQbe73MYl/3kWlRVxQ4GCD//GEoogJpg50LN\n46HI40HqOQ7RjQbVd69gk8tNjcdHqG9/hpwwnb4jhne6ntGomZZIjUSpRvZWpuaoDHbDtxHYbcKW\nsMMY377x3TrK3iT83377A0477ezG/2fPvo9DD53I8OEtw0sTsWjREm644f/SVh/Lsvb6KLBEZARE\nZwgF0B0HNI2+is3p337JVz8+g4EXX0tR3354Hn6Z0OWngqqgtjOwunxein1e5PzBwdy2kbp//oNS\nRaPG46UuJ5eCqYcz8rCDUVNoiI7jUFNT16mv2UAwuPek2GgPl6IwyqvwbcQh7MCqoMMYX0/XqufZ\nW5SA3btr6N9fBkvMmfMw48cPZ+zY5HNnjR49nK++WprUqutkuPjiC3jyyWfTUlZvIiMgOoPXT9AT\ni1VWVXy2yei8LHY/di/1to2rpB+K46CSeofTPR7yPR7yY/879ZUEXnuJXXNfpNbjpdbtRRs7juHH\nHE1Ocev2VkVRyM/PwbbtTs8iqqpqKSjI6VQZvYkT8jQ+qjGZnq9yXG7vHxS7Gr/fSzAYxu/3tn9y\nD7JhwyZGj5aZTZ999gkGDixk//3HtzgvHI4QCIQoKMht8dkxxxzO7NlPpUVAlJZuJi8vm2XLvkib\nwOktZAREJ1BUlSp/LoOJNDlWVFRI5a7dFG0vxbItdE0Fy4JOTEEVXScrW6cxNsKOUPvZQkKLF7JF\nd1Hv9mIPH4kycSJDx47Bn+VvvHbYsIEYxredTgFeXV3L6NHJTeH3Bi4sVok6Glf20fYKrbmrkZFM\nNb1eQHzwwaf87Gc3UVq6mbq63cyYcTggw1vLysrp37+Empo6Vq9ez9SpkxKWoSgKBxwwngULPuDI\nI6d1qj6ffrqAa6+9jNdeeycjIDI0xRcJgrflwK/bFrg92KEQSkE+pHmDEhtw+TzkeD2UAI5lY3s1\nFJ+L6tWr2BYKUxeJUhs2UXNzULNz2b27msLCvA7f0zStvXIhVWt4VYWr+ma6QAN5edls317eqzdI\nkut5ZL6jF174DxdcMBPLslmzZgORSJRBg/ry9dcb8fk8HHHE5DYF/9SpB/LQQ092WkBs376N6dMP\nISvLw+7d5RQW9sw+KV1Bpnd0EiWRYy8axW1FARvVscG2Ic0aqhm1mqTPsKMRXEOHovu8eH1eGnZr\ncGyHSCRCTSBI9aqVrI9GqYuYmG4P/UcNp//ggRntOQMgF3radu92VL///kJOOulUqqurcLkU3G43\ntbUBNE1lyhSZ4iKVVf6HHz6Fd955nRNOkBkP7r33Tn7wg/OabDDUHrYtw6VPOWU6//zn/fTp04/T\nTz97nxAUGQHRSYIuDzJYMoZloVRXEdZc+GwLxbLANCHNvl3LtnCrcQLC5UEtbhnKqqgKHq+HEq+H\nkoZ+4zhEoyaBynIqt5YSiEQJmCZ1kSiW20PJkMEMGjYYvVnOmIwgydDTbN26nXPOEcyefV/jtp45\nOX5Ms2MLQSdN2o+HHnqC446bQSBQj8sFjz8+u8n6igaCwQBz577IunVr+c1vfg80bLIkhWp2dhZX\nXnkh1dW1vPDCE7jdfi65JLmtXnsrGQHRSQrqayDH19SEFIngt2wcIOT14/F2UXhM3IDtZGehJmv+\nURRcbhd5bhd5uXuczo7jYJomwWAttUuWEohGCURNglGLsKIQVN1UDyohL7/jZqoMvZveHOpaVraD\n/v0HEw6HCQTqyMmRe51Ylt2pes+adQJz5jyMrruYPv1IiosLefDBe5gwYRL19QGCQfmj6wpHH30o\nFRW7Gq9ds2YVI0c2nW3k5ck+NX1692dfTTcZAdFJckL1KOE6nLx88HggGgVNQ7EsajQXucWFafc/\nJNp/UMnufHSRoii4XC5cLhe5OU03GrJMk3AkSmD9OsrDEcKmSdC0CJoWgaiJlpNDycAB9B/UH3cS\nicky9E5UVe21Mf1vvDGfa6+9keeee5KTTz6W1/7wdw446VjKbNg672Peu/pWBk07lLNu/2VKEXsD\nBvQDljBp0iE899zzXH31xVx99cVUV9fg8/nwej2Nz+P1199j5swzGq/9/PNFHH/81CblbdmyDa83\nh8GD9/6AjoyA6CQK4BQWQUMiPK8XRy0ERSFH19PuewCwbBstrgM4poman9/GFZ1H03X8uo7f76O5\nZdWxbaJRk1B9NfVf7qQyGiVk2YRNk7BlE4xa2C4df0EBhX1K6NOvpNcLkYp161hcU8khh3+3Vtvm\n52dTU1OfMDS0Jykvr6CwsARd1ykrK6Xi2xyMF95i7afLcOVmo20spSQ7m6r3P+Vviy/il28/mVL5\nZ5xxEg/0WkQ2AAAgAElEQVQ8MIerr/4ljz/+MD6fG3AYPHgAY8aMoH//vmzatIXS0h0MGTKMLVs2\n8cILz1BYmEN29p68S47jMHfuO9x88+1pfgI9Q0ZAdIKa9QYu2wbL3CMgANxuulL/MqMmrriEeYqq\n4lRUdOEd20ZRVdweN26Pu8XMA2SnsUyLqGkSrionuGMbVVGTqGURtmwilo1TVUnNtlLMrBz0omL8\nxcVk9ymhoKSY3LzctObsT4b9ln9MUHcTnDwRn693h32mk/z8XHbsqOh1AuKVV97lqquu5/XXX+aY\nY6by7h0PUFJSiFUXhNogrhw5g/Zn+TGravlmyQrGHDgx6fIVReHkk49l9uz7OfHEmUyaNAVFUdi4\ncR2rVq1g/vzFFBYWc9ppZ/PXv/6RkpJ8fvSj01tkSH799fc544xzeuUMrCNkBEQnKP/PI/RxLPB0\n7wBiO07TAVNVYecOzPp69Kzel0VSURR0l47u0vH5vCSa64SW7sClRXDqd2BVbcVcDxEHIrbDbsvG\nVBRMVcVUNDyOgvG2hqmoWKqCiYqpaUQ1HdvrQ8vKRvX5cWf58WRl4fZ58WZn4/X78Wb58Wf52+3A\njsvDgGw/S75cwSFTu3YWEbYdnq+wOSFPoa+7ZxMs+/1eAoFQj9ahOZWVVeTkyA101qxZyRFHnMsb\nm8tQdReq293ifL/Py0ePPZ+SgAAYMWIoP/7xeXz11Sruv38euq6iKBoDBw5m8uSDWLDgQyDMpZee\nnVBhqajYTW1tiPHjU7tvbyYjIDpB1jcroagYggHw+rrEnJQsihmF2jrohQIiGZxoFEVVUFQXqsuF\nC0jOte+AYwImOCHsumrsahvHsbFRsADbdrAcB8uWe1DX2jaWIwWXo4CDghO32t0BCt0qWVjUfLkM\nulhAXLbR5PUqmwINRngURnsVinUFGzAdhytKNEb5ukdwKIrS6xzVc+e+w+WXX8vjj/+TKVP246MX\n38AbikJ24rTzustF7ZZtHbqXx+OhpKQvZ501htxcORvetm0727fv5Iorzm01km/z5q3MnfsuN92U\nvvxOvYGMgOgEG4v7MzFQCYEAttuDA10/tWyl8yqmiRMOd+29uxKzEzm3GzqtoqCqKmoS21UEg+H2\n0587Dv1rK9m0+muGjhNdogC8WWUxr1ruR1FpwZKAw5JA03f8VpXNi2NcjPJ+97ZvqampjWn0d3Py\nyccxZMhAHrj7EfKy2p612+VVmNFoi1DtZBg6tH+TGcKAAf1ijuzEfP75l6xbV8qtt/6+202hXU1G\nQHQQx3EorKuGvBzIyUFxHEKBkExT0IUzCbmaueVrU/1+oos/QykoQM/dC/MlRXvhXgSKwkHZGpVz\n/0Ppa24CmovPigZzbGAX/YoK8A4chLn/FJzc1MN+6yyHu8ssXqu0CLajsG+Owp3bLB4ZsW8NPsmw\naVMpP/jBqUydeuCeg/X1KErbz8Jj2Sx68Q2OOndWyvdMZZB/9dV3yc0t5sorf57yffYGMgKig4S2\nleKLhiGWHanBzm7ZdpfOIkzTwuNtaXdFVdFCASKffYJ+/Alddv8uozMziK5EUSjIz0VuxKmwv1mO\nGamnfkMF1cYaovPnseWwaUyceghOkqHG1abNSYbJ6lDyppyPam02hW2GerpeSHi9bkKh3pG5d+LE\ncS2OKboO4bYXxvmzs1j1+vwOCYhksG2bxx9/nqOPPo6DDpra/gV7KRkB0UG2vfosuc06kEKrFqC0\n4dB6OmZF03DKtmPW1aFnt4wm6s0oZi+cQbTAQYlGcHnc5HtiQtpxyF75GYFF77Fu2FjG/+AHVNTW\ns3D+xwzduoGv8voxaMggDj/8YLJiCRR/U2qlJBwAdprwy80mFxRpCC8Mcqvkal2zuj0ry0ddXbBX\nCIjmBCurMbfuhHYWa6qqSnTrjtTKDoaYN28BCxcu5oILzmS//UTC82pr63jssWe5/PKrGThwcEr3\n2NvICIgO4DgO2uKP8DVLfKeoCtFIFE1TeywthUtxMBd/hn7scT1y/46ien0QqE3/osKuRlHI9rih\nTzGTK0rZfu9f2N1nIGe5bNwui6n+KHVla6n4x0JWuvyUu7NZOuZYKBiY8q3m1TjMqzFxAfk6+FSY\nPUxnak56Z6xZWT527aqiuLhr19Z0hGgwBEmm1VACIb569X3GHHEgvsLE36W+PsC8eQspL68kKyuX\nAw44kB07ylsVDg3O6Btv/D98Pn/Cc/YlMgKiA0Srq7Bpqb3puo6qqIRCYRkK0/CxA16fp9NCw7bt\n9svQNNj0LeFv1uIZk/wGKj2JA1hTDkVf8H5PV6VjxN6Jy+dlsNfD4GgNmAroGmpVBbmAN8uDFgpT\nqeZR5e7cwBIFdpkwzA2Ts9IvUPPycti0qSzt5aaDrOJCkt1eJc/vZ95t9/DFwH5c9vpjTT5bsWIN\nn3yyjIKCIk466VQGDpQpPP78599y7bWXJCxv1SqDL7809klndGtkBEQHMP7xFwb6E0+/VU1tsbDK\nsR1CwXD7DTtOqOiahu7SmwiEZAWM6nJhfbKAwJbN+I/r/TMJx3FQXG4Uvx/q60B3oQQD2B7Pnky4\nDT9pQqaUsNG0NHf0ZnW0bIdvHTeLsvvxyKgDWFyUvvQL9Ta8uNvmguL0+7z69Clk06Yyhg5tf3/n\n7iRqmqg5yYVyq5pGSUkx9TV1PPrQHC664od89tlSVq5cy5Qph3D99b9pMtDfd9/dXHzx2Ql9iFu2\nbGPJktX87Gc3pO277A1kBESKOJEwng0GnhR2VlNUBV8qm7A4DqZlEw5FcGKZIhVFkaarZNQnVcWJ\nRnGLMcnfswdxbAdV01AOO0pGM+VI051SuhkqK7AHDsbetgUlGkGpr0Oprem0sHC7XYRCSYS6doKI\nZfNm9iCuHnMC5Z72fUJ+FQJ28uXvMuG2LSam43BRSXq7cr9+xaxdu5mdO3enlD67q/n4P3Pxpujn\n83s8uN5fzJ+ffIVz5szmppvOb3HOM8/M4cgjp5CfwLdRWVnFq6++z69//duOVnuv5bsxT0ojFW++\nSLbdxRE3ioKua3h9Hnw+Lz6fF4/bhW07RDUN/H6pWbeBk5ePPmjvcKDZto2iqnKxYc6eDqoMGoIy\ncTJK3wFEZp5F+IzzMcdNlN+9k9EAXe0iClkOTxSN5dwJp7UrHFTgyGyF/X2pV6rShnVdtPB59Ogh\nlJbu6HAq7a5gzX9exZtg9XRbKIqCWV1Hf0Vj/u1/afH5Z58tRFVNxo9vqVAFgyHmzPkv119/63fG\nrBTPd+8bd5LSeW+RU9D96a4VVcXjcaM5DpXTTwRfG+uMIxG0BHtD9FZs20FVkxsczYmTiU4+BCen\nd+UKiqfecnjT349rRh+P0068/kAX/Lq/xrOjXGyPdkzoHZ7TddJuv/1GsWzZ171CSCxb9AX2jooO\n+/JcHjd1y1c1OVZWtpUFC+YxY8a0hNc8+eSLXH/9LbhTFEr7ChkTUwqYNVXk1uxGLS7osTr4dJWa\njz6CUKhVNdiBHk37kSq2baMqra94bZL6wePFPGIaak0VWl1tN9QuNeoth0V6AZePnwmKwuiqbQwL\nVLKwz2gC+p5BRgGOyFb4f0N0RvlU/r3L4tuORPo6NvdsM1la73DrwPR3Z4/Hxf77j+brrzdKX1Gs\nXTmOQ25uNoMH9+1yzTpYV89zf7iPmnmLKerTsV3agpXV1Oyq4IzHZzc5/vTTc7j44rMTXrNqlcG4\ncRPJ6cXKSFeTERApsPax+ylpxTndXURtB3dJCZSXNc0gG4fl9eEe13KBUW+mLXmmkECzVhRpZupF\ngrDetFnkKuTcA84irLm476u5HFu6il2eLGb03RM22VeHC4s1bh6gocbqf3yewvX9NFYFbb6od9jV\nihUzS4UhboVhHsjWFF7d7bAkCAUum5Dt4FHSvzbC43EzYcKoFscrK2tYsmQ1Bx44nsrKGoqKWg+L\nra8PsnHjVlRVZdSowbjdyafA+Pf1d6At+xqv29Wh9127o5zA9l2c+MQ/mXzGaU0+23//yaxf/y1C\nNP1+juPwwQef7jNpuztKRkCkQPTr5fhyei722bEsdgwYRr8DJ2MHa8Hnk45c04I+fVG2boVoBKWk\nEK2wiNr6EH6PCy3ZneZ6KYpl4922FTM7GzMrGzQNa/gotG9Wg6t3TP1t0+LtrEHcMvZ4bilfznmb\nlpJrRajXHO4cNZWIpuNV4PBshdsG6hzQLDx1gFvl1oHy2Od1FjdvsZrkZBrnVTghT+XCYpURHqVR\nCPzQhg+qooSWL2faxiIO7ZvHfZOabpXZVRQU5LLffqNYsWItwWCYqqpaRo5s6veybZs1azaiaSrj\nxo2gqqqGXbt2M3Bg31ZK3YPjOKxZtpLda9YzOCebYCiclPAzwxE0t4tIfYC6HeWYlsX3/nkvh559\nZotzjznmeP7xj7+2EBBvv/0hs2ad9Z30O8STERBJUr1iCQWRENBzewPUqC4KLzgPx+/DGhlr0Lt2\nyt8lfdDeeBVl82Zqjj+RmkAIfcgQ2LKZnL1dQDg2WiiIGg7hrqggMHQY1uhx2Cu/RN2+rVcsrgsG\nwxzgquSrr1/AE6wDVQMUsjw6k10m34bKuXRcP04vbP9dHJyt8bpQuWmLyYqAw8wClSv7aHgS+Gnm\njNDZHtEo03O5T+vLC/Ww0YhQ5IIiXUEDaiyosRwiDnhV8KkKPgUGuRWm5SpM8Kv4kvQBNcfv9zJp\nkpwdGca3rFu3GVVViUSiuFw61dV1jB07XOYoA1wuF9u3VyQUEDXVNSx69T02fvgpdkU1VlUN7nCU\nQtNGcXtQFVWaI9t435FAkGB5JbZlEglFQFU48O7fccIlidc2uFwuHKdpeaFQmK1bd3LuuZM69Ez2\nJTICIkm+/dd9DM/rufQVZjBE8NgT8PubOafjNla3TpoJQHwtrdLeY4LpFIoM8HUAvXI3yvKlKMFA\nrzExqbrGCCcEYWLCAVBA8fu5avPnXLz2E4L9z4PC4UmV51EV/ja0fTOMrigM8igMmjSeJxyHHywu\nY36Njq1qkMg0B02O31kGfV0yzfgTI3QKXB0XtkIMo64uIOula5im1WJGkZubxahRQzBNk68WfM5X\nr71PsHQ7VlUtal0Aj+2Q7ffKZHyaC/yuxv0p3G6dSCTaZgoQ3eMmGgpjBeU1Q849jdN+cmWb9R42\nbASbN29l0KD+lJXt4H//e5Orrvplh5/DvkRGQCTBto/fp7CuEq2V5fpdje1AeZ8BFB59VMrXhhzI\nIenFp70exbbwvPwsdjAgZw6dEBBut4twOIrHk3pK6KSI1U3RNLJ8Ktab/6M6t5BwbgGu8RPIGzEM\ntQOJHaOOw9tVNsU6DPao9HHB1rDDfyttsoqLKapr3YfRHAvYFoVtUYfzN5i8MFInW++4kMjObt0E\nO+/RZ1nz7gKcunrs6jrcpo3X4ybP5SIQDOFvJTLP5dKJRi1cLh27nfBmMxRB87ixolFGzjqJ0+/8\nc7t1njFjJvfddxc5OTkMHDiYCy+8gsLCjjnD9zUyAqId7Krd1D72NwYWdVNoq+PIgc92wJFrHbbn\nFlFw1VUoHckSm59PtL4mJadgd2NZFsGg3MtCURQUVUFVVFRV/q0occsD33oZ27ZbddCngqZJU0i3\noCjkKg65dRU4NeVEv11DQPdQ12cgzoDBKEVF5I8a2aa/KGw7PLDDYm6lzYpYjvBcVQp/G6hNYZFd\nIj6tc/jxtxZPj1TS7uh+7td/oXz+p+TlxiKCvE2FQet3c4hEo/hj2QlkQszECSsj9UEqt5bBoZM4\n4+prGD/9WDxJbKDl9Xr3uY1+0kVGQLTDqvv/RH9/5/MoJYXjgN9P9IcXg9uNPudfBOoD+C/8EXoH\n/QiK14NT27t2CGuOpmn4fHLDJcdxcGwH27YxLRsn6jQNc+0/BGprwLZQzChObQ123PCiKEosK4cC\n7Pm74f3t+Q3pmFc5jrRZp/J+FFXB7XbhxiZvxyacreuxVIX6N4Arf4YWlwSu3nJ4pcrmoxqbrwIO\na5plga2xYVa+jPNaF4JNEYf6TgiKd6pt7thmcVsaQ2Zf/evDVMz/bI9wSISiJPQvBAJhvB5343tz\nuXRM08QVtxGQ4zhEQ2Eqt2zFe+Qh/Pj++6gp3ZaUcMjQNhkB0QZVa9fg+/abFllbuwzLwjxpJvSR\nfgVr1ukEV33NzopqRnfQvOXNz6OqbAcFURO3q/XX7QCRsMxEq2lat5n247VBhdgArimt50iafNCe\nv20bZ8H7OIH6uPJiQiYmVBr+3vMD4DQuxLbbWZHeHsFACK/Pk/RCv+YomoqiuVGBHM2m/pEHCUz7\nPjn770/EdjjJiLK8jR2FclW4Y7CLQW65Veg3IYfbt5p8UOO0uxER0OjXacAC5uyymJKlcHJ+54Mb\ndmzczPoX36K4nU2s3C4d07RwN9uTW1Ga7tKo6xqBYLhRQJiRCBXGBnDpDDv9ZM7/+9/w5edRMmpk\np+ueISMg2mTdfXcgutEx7Xh9OMNH7Pl/+Ejyho9k/dI1HS5T1XWyJ44nuGp1qwLCcRxsWw6gdkwb\na1GOqnaJ8LBtB6WDgyvRqFwwGEf87KE9gsHObYoTjZq43K4OC4fmaKpKjmNTv3oF7L8/9203WR6w\ncdkmUS2xiXCgW2FA7CNFURA+hWdGuXmhwuLvOyxWtiMl+rtge1SaqBrYbcFvS00m+JROb1D09E9/\nQ1Fbq/5jJJ85pemzDlbXgc/DFQvfZ8j48alXMEOb9Hx8YC8m5PV1yInYYYoKwdN0wAqHI2lJKGc5\nEApHMKMmwVCESCiCZVrYpkVFdT3RSASXS8ft0vH5PE1+vD4Puq5h2w6hUJhgsNlPKEwkYmJZdsop\nkuQq6o41QycSlunNO4jjOJ3K5qooCpaV3hQUthlF3b6Nmrp6nt0R4afrFvDgly8lPLdQgydG6o2L\n7eI5u0jj7bEuRrXTdLJVmJbb8vr1Ybhja+e+29O/uB339vKkdlhMRelQVbVx5ufYFsOvuSwjHLqI\nzAyiDbLDQRk43k04RS3zJ61duxkhhnW6bDs/n0oAy0Lz+1GBaGUVdjiMb8QI6tevp9CXeI2HArHZ\ng0qiJuM40tFsWVarTl9FUVBVBVVVUVVVOp+RMwi9g1EzSk4uTl4BlKe2c1gDuq4TCkXwJtrCNanr\nNaLR9CZu1Nxu/Cb8brvNKd8s5hfrFzBm+q9anDfULbW7UW20T7+qMNKjsC7cutTeGIbfDtLYGrEw\n4vwbfgXOL+rYe9ltOpQv/Yrtc+dRMmxQUtdomkY4HG0WTJG43m6XDHf1eNyEwxHOu+WWDtUzQ/tk\nBEQrOKZJbrAOvN2Uh8WysAcPaVkPx8HVhu8gWXyDBtB8ou8rKWr8u9bj6bDLVlGIOWlb1xQbzFiW\nZWOa0UYfgbQ790yEldutN0ZP9RoUBbdik730U74XrmBj4QCielMBNtoDDw3T+fnm9jX8kV5VrpRr\nhSiwuM7h7sEaz1bYVFkO1Rbk6wrH5KU+O3u10uLWLSbTf3UPQ0gt7YeD08RRLc2PLYWUnEE4RANB\nPFMP/E7s7NZTZAREa0QjqF29wXQ8moozpmm6Yacb79/VhjS5n0VL53MwGO64T6O6CnaUQbo3/elh\nlvmLKcbksF3rOXe/prmDFOC6fjoHZmv8IQnlvL3dSPNVOK9IRfhUvpebeiuoNm0+rnX4fr7K9ojD\nLVtMSqOw9sDD6Fu+M6WyXLEZXcOqa0VRcFoJIvD5PFRu3kb/mS1zRGVIHxkB0RpuN0FNxzKtbsll\n5OTlQ27TaKna2npyc7snVK93ZDRKHufrFRAI4GCzL7nSaqI2T/Yfyx1bFrI+u5j3SpoOgOO9CufE\nTD/TkhjQ28sgflC2gvCl/vy+qLf45w6bz+pttkRAeKVJqzRmYfzkrAsYs3MrA3eVJl2m2+1q4tNp\na/ahKApa/2JOv+G7tcNbd5MREK1ghcP4o2Esy91oV1c1Fbfb1SVrIpzclqG027dXMGRIv7Tfqzmh\nQJAOjBE9S34RfLMa3D2bXTfds7wcO8p1FSvJVx0eLm4ZqjklS0FPof3VWa3XTwPOTiI3VAOO4/B6\nlc2juyw+r2+63sIIQbzPwHa7qSjqg7VjM1oKubIURWl1IVw8wWAI0zTRQh3JkZ4hWfa2YaHbMFYs\nw53lx+1x4fN78fm96LpGOBQhGAjJBho1O72zGQCOg1Pccml/OBzpVBhmstRXVOLey8w0Sk4uiu2k\n5/l3Ao/HTSAQSpuzWtF1xoSqCJg2zxe0NJ+ckJf8e/omaPNWdevrPPq74LSC5MpbVGtxyjdRLt9g\n8kFtO4vxHIczH/4bBy9fnJJwABk40NqztG2bcDhCIBBC13XcpsVDhx1DNNRFW+plyAiI1ljw5TKy\nPU0NL5oW2wbU78Xn9eDgEAyFCQZDhELhjoc8WhbO8J5b2GPV1SUVitiryMrGGT8RrE7ml+gkmqbi\n93uxbSc9Dm9NA1Wl3mnZNYe6YXqSAiJsO1yzyWRzBAa54J/DdC4qVpuYDHZGYXWw/ef3RpXFZRtM\nFtU5tPcNfTXV/OjPv2HK2pXkuVM3UGiaimlZmKZJKBTGNC2CQamQRaMmuq7h93tk4EYojO+kabi8\nPZdheV8nY2JqBb26XK6BaE1DVRRcLlfjik7HdohGo0TC0hylqApulws1Gc1c11B2bMcp6QNFRRCL\nr++uXPQuy0JRu19AdEj5DwZxln+B4/ZARTn0klTmHo+rUUikY91KuS+H7d6mq48HuRW8SS7Ku3e7\nNAP5FfhVf50fFGmcVaiypD7auHguArxb7XBAO26ux3dZbI8p9YplcdDnC5i4+kuyqqpw19WiOzYM\nHIC6qxxt925yrCj+DggHkCYm27JxdAe3293mDDoaChOYt5BIKITb62XTpo0MHZpcttwMyZEREAkw\nTZOJWzeAK/kdyxRVwR0347Btm2jUxA7b2LEFWS6Xq5WFWQraxx+iffwhTm4uTmERQbeX4qOOS9M3\napueSuPXXm7/RDiVFTg7t4Or9yUfVFUFl0snEAjJ/cM7YbYz8vtT4Wm6il9LwfU1yaegAmcWqlxc\nIoWoqihM8itNVldvN9uW0t+GbD6vl+f0ra7g1Hv/xOi6SnyuZoJ5nRGrJKB1blhp6CvtkdO3mHB9\ngLu/dyy3fr6IR048HSXbz6/eeZ38/J7bFnhfImNiSsD/nn+KUYrZqVTSqqri8bjxxfL0eNwuTNNs\nnC6HgnL63KhGqyqoKkpdHermTShrv6G4uHvSi7t6KBe47TippakwTZRln6Ulk2tXIU0gXsLhSKfc\nI6EEzuVUyjshX+XdsTr3Dm36rM4vUvHEPfKsdp7/II/CC6N0fjtAY+6EbPqXbWopHLoZx3GwLAuX\n30d2SRHmxi08/6c/cvkbL+Fs2ML7LydeeZ4hdTICohmmaeJduhBPmsw7pmmh6zpKo8Dw4vN58Xjd\n2Lbd6MMIBkNEInsWkIWz89C6QUu2TKvnBESqM4hQENuh12wS1BbumELQERwnsRN4Y9ihIpqcz0VX\nFKZkaS0inqZmqwxQZb328ypcVNz289cVhYOzNa7qq7FYzWL1IUcSCndTinTks4hEoo19pLaunlA4\nQjAYbuwrvtxsjIefYM7U43DpGmVvz++2+u3rZAREMz6553aOsOrStvgqapoJU0Erikz53CAwfF4P\nmqoSDkcIBkModTXseOFFqr5Z3+pioXRQt7sKTyq2izTi2CnOICJh6MJnkU40TcXqoAM9Yjl8kd1y\nS87SKNxV1rn8SIqikFVXzQS3xbOjdbnSug3WBm1+sjHKkasj/GxTlKXfPwVvF+/Lblp7HNOBQAhV\nVfF6PVKxcrtx6TrR8grK128iEghimxZKMIRl25RcdREzr/tZl9bvu0Tvnav3AOGKXfT75ks86dw5\nzkky3YCioOla46I8HzbOmq+IrlhG2O0mnJ1LNDsXs/8AfPvvT+6g/mlZjxGuqkbvoQimZOLdm5wf\nNdO6NZ5tO1im1WXpNjq6RqJW0Xm579iEn71fY1NvOWR1QqiP27GePx56BCVtbC8ath1u2GzydrXN\nzthEKM+K8rM3nsUJR7p0fxRd0/C1khfM5dIJhSOoug7BMNVlO3GGDsBZvxlx5mnMOO9HPHfexVz9\nxcddVr/vEhkBEceHTz/KIelcd+A4nRrQFE3DrWm4ccipr4b6auzSDUQXLyTk9hDJyiaanUukT198\nE/Yjd8ggtBTt83okguLvmWZg2w7RqImiqqixneTafFyhkPTVpAlVlUI5HVFHiQgEQrIJpNoGHAeX\nnXimsD4M9++w+PWAjr2zysoqjo1WtBAOpWGbR3bZ2A4M9yi8X2PzRtwaCs2xufrph1A3buqQcGjw\nG5im/F4yQWLq5SiKAo5DJBDCKSnkvGfnUPrWPNa99R4TT5jO5488zthTTky53AyJyQiIOEoGDCLy\nzZK0RfWYlpV27Vx1ufAAHiyICQ2ndCPRLxZij59IYMIBRIEICmRlkV1SiC+79ThGndS0+HTSsHeD\nbVmYttOuxq3W10HUwo6aqJrWuFPcnp/U6+DYXbfQrqN1KnCifL96M09590v4eWmk43V+9dV3OOus\nmU2OfVFncclGk9LWFiU7Dj98+Sn6rVqOkkRqdtu2MU2rxbogTdPweKTvrb4+iN/va6XtJV5NHakP\nUFlaBqpGvhjJdQvno7tcjJp0AMfccgO6y8Wk885ut34ZkicjIOKYdMb5LP3gdcalqbxo1OpwKulU\nUFw6atDEO2gQuVnyfo7jYEUDRLfUEbEh4sjMnVFFRcnOJqsoH292Vo+FuIIcQNvLAhuPI8bB8BHY\n89/GjmWHtW27yY5xiWhrhtDhzYqSIKbspiwkNJfO9ys38lTfxAIiibVtCYlEIkSjUfz+PXl9t0ds\nrt1ktSocPHW1nP3vh9h/wxqUJlmF5fOXgsAmPs2GoqromobbrZNolqBpGm63G9O0EmYq1jS534Om\naenL6eQAACAASURBVETqA5jRKEHTwsnJYsCM6fzwwftY/szz2JEIuFyZhXJdSEZAxKGqKuuLBzGu\nZmunNqLZQ/dp57auo5bs2U9CURR0l47uokmab8d2sMJ1RLfUELEdPK3k3O+NKJoGHi+q46BoalKv\nyLJsAoEQDftTgxSePp8H23a6dDGiy+UiFOrYwrkSs/X0EaEOzno++GARxx9/dOP/S+ssrtts8XUo\ncXn9d2zjopuuoaQwl2jUxGoWldUgCFwuPeV27nLJrUNN08Trbbrnu65rhMMRVDNIrWnS94yT6Ttm\nOOuuuY1tpdt5eNoMfrXqi5Tul6FjZAREM4YdfzK1z88mp7MCortzBPmzUJvtq1BnyT2G49P6K6qC\nrkrB4bZtzGh6d0TrchwHsrIhFEjq9IZUGM2LCIcjWJaNqwtj+rVYckdpTvE2DoLx+2Y3/7Fjg39U\nbz2UtKMziC1btnLCCdMAue/0X8tMtia4jR4KMf31/zL1y08p6FvYuN+HjDhLl8Kj4Pd5qa8PyiAB\nBTxul5w1RKJEdldR4/fgPmgClZs3U/XsXFxZPpTB/Sn5+RVpqkOG9sgIiGZETAs1DWknTMvu3vxG\n2S33zlaA0rCDz6fgUlp2bcu0O7Xat0fQNDo7SCmKdJJGo2aCXczSi6ap+HxeamsDjeaU5n4Tudue\niqoqjUIkV2/9O47rQOrdoO0we9RRvPaNtCU1z8YKgONwzDuvcNDijymp2InbpctZG6Rt3+2mt5Mz\nOJ/P07jeIRI1CVfVUF9dix9wfbgEV5aX2opK9LEjuea91ykoKGq37AzpISMgmhH6+J20pL42oyae\nbvA/AGDbqFktHdEuVc4g1occNAXGeJt2csuycLl6Jl12qiGuTS9Oz1oIl0tv9GN0palJVRX8fi+W\nZePxJCeMiiP1ZEVD1Luazn6GueHG/qnX9U/r61iX3Yd1tYlntlokwjmz72Hi5rVk6xqWS8c0rS5V\ncuLzVimKgsfjJhIKESnfTV5xIb6ifGrKdxOsCzDz2cc4ZObMdkrMkG4yAqIZJTu3ono6P1g43eh/\nsCJR9P79WxzXAV2B0P9v77zD5KiuvP1W7OruiRqNchYSEiCBhEBICAkFQCSDCcbghI0xYMBgDBh7\n19jetb22d8Fh/bFLMMkGG3AAAyYZMBmxSIgogoRynjwdqivd74+aGc1oemY6T6De55kH0V1163a6\np+4Jv+NBtIffeX8VJfvtJHO4uOsWzECA7zrx254Wdyelqgqu62FZTlvwtncmOQl+vv5pLp15cpfH\nl1bIVPbSw7vd8AohqN+xh61vf8j219/m7bIJSAuXMnrdO6hJky1HHNVxjuR5nHPPzczd8hGhtjoc\nRZF77C9eKNJ99xo2b0eURYjvrSe+t54Jp67kgj/+zhfODCg5gYHYD7sQK2aJ4w+eLKGPGdvtcVmC\nMZrENksMuA/a8zzkDFImu+HYiJRZMMumKH71ein6YodCWltRXt+fhiJLLGrejiw8PEn2eyy0buai\nVAvvtKYXohOexxv/eQuKbWO3xBCmibBsVF1jSfJZDnv0Qby9dXimyU13/4WD3lvLMU89whjHpLJu\nD3KXiv/i3zmI/YpIPddBHlXL1FmzOOk//o3a6dOKPoeA3hlo60a/ozk25LlYuCWOPwgjjBJNL39Q\npYKDhJPGaLmuRzKZQlEUVFXpu1CtgHieQO3lTnh/xMb1iNYWJM/z5TYK+P62390XOx7jeV5Wu8qJ\nXpI//N8f+OPkw/nS9jc5tnUHamUl1vkX9zjO6roGZMfxf9iKAmH/faotCzPMjhMzY0jl5fz8+5cj\npUxC7e9jiaTlO6Npfg/q9lRwTwhUT7Bx48eBcRggBAZiP6QCaP3YpYw/AJSV9/r0cBXS3RGWlYUR\nwo9F2LbdkUHTGUWRUVQFWZYLajx8v3/mhljs2QWNdX5SboEXM13XCtbHoTdM0yYSyfwahqqwPL6T\nUz98zJeW0FWE5/ZqZNRoGJpb0z6naBqV48f4/+PYBTWyuaBpKkL4QnzhsIGqagyrrqS1qvfvc0Dp\nCAzEfmybNpvJ295FyUPTvpTxBzwPqQ8D0RvtKYzpBAVd1+uQrfa87v5oSZJQFBlZkXMyINm8RZJl\nIVzPF1EswnubzjgWCj/2YOeUUqvIEnJ7UypFJXXaOb0fHwnj9mAgciGvZIIM0HWNVMrPYNJ1zU/1\nbYkV7XoB2THIchyLz4LzL2FnKo/agFLHHxwHZURt3wfmMrbnoesaoZBGOBzq9qfrGkgSju1iJlMk\n0/yZpoVlOTiu3zgpV6QZh4BXmL7Paccv0hqYTPqtaA0jlLZqOGMcB3vhEsTw3j9rtQdXYy5IkoRX\nZPVcX6PJ6wjcC9fF3rarqNcMyJxgB7Efw4bV8EzNWMYl9kAOQVTX87Ju1J4PniBtgLoQ9JWWKcuS\nXzPSQ9tPgV+57Xmer7dk75PD8Dyvm4pqe22ALEu+gJ8sIbcXl1mpnD6PTFEUpa13R2HdLkKIwgTA\nJclvs9oHaiTcZ9/oTLEdp22XWAxXlOgIUvtuN/9zlhQFL9FzFXlAaQkMRBqSk2bg/d8m5DTFZ30h\nSzKWW7qGKp4eQq4ojs82X/eChF+57Rce9r3ItFcSe0LguS4p0yEabRMK6a0/eAHQdZVUyi64gdB1\nDdt28ts9gN/GMwPNIS0aKZhbSFWUouwghBDEE0l0TWsznvvm2lzfSNmY7r0wAvqHwMWUhpNPO5Od\nOdpOSfb98o5dPHdIF6LRohZ5lZL2mIamKui61vV12XZRdxDttQOFJt/sKFfR8EaMwpk1B2/C5D6P\nN2qqitpgKlt8SXe7zeW4rwmQcF3MuoZux6e272bZdVf3w0wD0hHsINJQuXcH9VYK4elInocIGUhu\n5gu+HtJJxJP+3WiRg9VSNPtdzqBk0/qCdflLRzE2J+0ZYplWT6fDDodJnfm5jI+vnjSOLZaNHi5t\nhpIQokPiu7OhbVfsNQwdSZJwLZtYXR3qsEpisTg0t1JR6e+AEy2toKkc/vlzSzr3gJ4JDEQalBmz\nqbzwaszf/DvhsgiSln3KqhEOkTRTPXbGKgTCcZGrKos2/kBC5NR5J3MkaV9dSL54nodhhDBNK+/U\nWdnJLmGiavxoRNHeJoHr+o1/2iW+2z8W23F9l6IkEQ6H0sYtUq0xUq1x9IoyhCxTNXEse1vj2LEY\nIVUlXtfA1Rvf67f+JAHdGRq+iSIw4qjFfFwx3Jd2sHvqpNIzsiwjSzJulj/wbPAcB238+OKMXeT0\nxr7Y/4ZecouvOtt+p5suYyubv2g0jGlaHQH3fJCzzNwaNroWKcuugr1eX5Y7XEPJNnlu27Y73id/\nx+ArsUYiBmVlYUwzxf6foJM0sWIJjIoyv7WuLKNpGuERNVy76kW8KRPBdqgsUkZeQG4EO4heiLiW\nX4SW40IZCmkkEiYRxShO7r6uIQ8fXvBxIX/feb4Ir6uBEiXoW6HrakHu+sE3NoWQEpc9F6dNLiMT\nKmqrQdXobmKzw3FcZFkmFOq+e24PXMdivoy5oiiYpkXKsjvCzfG4iWHoHTsJWdNACOrrGwg5HlWT\nx2NZDlHL4oYLv8bC448nfHbQDW6gERiIXhCKAqrqSzvkgiR1uBqMIlTpinDUr7AtAq7romv9129O\n1O/FW/MaSSMMioLUGuvSwrJLSux+0tmdmwNlgy+5LRfEOBYqk0hBYLa2otYMy+x4VUUNhyCZe6qo\n53mkLItopCf3qEQ8niQa3dcyVAiPSFsTpnZBQn8X5QACwwhhpywcz0UX/nsthEc4bCC/+yEvbN3B\n919+Puc5BxSHwED0RnvWTB5ZQrIigwSu46IUOIVSivTcazpfRK5qqwXCa2lGNROoos3Foqt0/rp2\nbrDjV3p7bcFR0dGQJ1eSSYdo1MhrgW9Xic03vVXxXOyWFsjQQIBfTS1yMhCCRDKFBETCBj0J9vlB\nd62TcRBtQX7fYLdrK/kS5y6xeBLDCOF5HpHyclTbwetk7IXj4K3fXHTZ9YDsCQxELygFShc0Qnrh\nXU2eh1Sk+od2+jNUKJIJpF7u4vftIIpwbUGbH733fta9oaoKiYSZt4GQAKepEZiU+bUjYez6xqyv\nZaZsdE1F7WNX2nURFySTJoaR/n2SBFSURfyCuFG1VB+/lO33PUjz5u2Ex4wkmTQRioKwbd57/nkO\nOfbYrOcdUDwCc90Lm0ZNRNh2/jmQkkTICGGmsg9294TXQw+IoYI3aizK1BkwbhKSEe77hAIiSW0i\nhXlWEPs9qfP7zGVFRTQ1ZXz82/c+RCoH49Be7d6XcdifWDxJKKT3eOefqG/ETpoITxCOhNnx4it4\nKYuyUbWoEhhGiEgkjEjZjJs2Pet5BxSXwED0QujoZWw98mhEHmJ47bT7tN0CZeN4ioI8alRBxhqI\niGg50sxDkA85DFFd+syWQvSr1jQFRZHzMhKO6xEqz/z7t+3lN0jurSeZNDHNVEauNiEEiYTZlrqa\nCb4rz3VdNFXt1ZAaleWYTS04KRPheahNrUiVFTRs3k6irgnhuri2jVwWoWrsmAyvH1AqAgPRCwcf\ncihrPKVgHcyMkE7KtApSleUZBmqkcMJsnSmx3mCPtLu4JLtQ6kKZYxihgtREaJra1p0tt8p6z3GI\nTMg8ldm1bRAQCunoemY7GMdxCYV0ysszi2klkxbxuJ/22pfOlKJrlI2qpSWRZPv6jZj1jbiGzvil\ni0nGYzRt303dnjrUIPYwIAk+lV4YMWIUi575O1KsQPLDkoQe0kgVopVjAXY1PeF6/Zvi2gXXgT2l\nV/dsl0EvRNtNTVNxnNwMhKapxF9+OePjJx5zBHpVBY5lIcsyqiqTSJokzRSWZWPbNqmURTyexOmo\n0RFkkxYrhCAaDVPWFlvoDUmWkRWFYdVVjJw4Dm3EMPTqSg49/RRGHTgTR5bATLH0O9dkfP2A0jFA\nVoGBiSRJfrvHAt7dqKqK53r56eV4Xk5CgpniusVtVp8VllXEyuDe0XUtC7dL72iaSiJhYppWVhlW\niq6h1u/u87h4fSN3nn4xr//pCbyWVrRQqO26GpGwQUjX2or2fOmLaNTo0EiyLActw5RmP9Mohw9E\nkjDrmqiKRNDqGtjd1MgZv/0NwrJBD7Hoiq9nP2ZA0QmymHpDeNh5NA7qCSPsuy8iPeaZ945wXOTa\nEQWe1T481+toUtPv7NoJjgv5qqH2M1qn7KBk0sz8sxcCN4PvoOUKRCyB5ueodnu+vcajM+GwQSye\nIJrm+B6v09bYJ1skSaJ87EiS9Y2IlMX7z/6TsGnhxRIoZYG0xkAl2EH0giQrfHTAIbg5SG30Oq4k\noakKdo7uCw+BOqa4Ab2BIofj1e8Z9MahHUny78Cz2Z3ZqRTDGvdAIt7rcY9f+1MUL/sECFmSs6j3\n8OtOcq1VEK5LqKKcUHkZ8bXvsvH11XjAwaednNN4AcUnMBB9sPArl7IzVXj5ZE3XsB03p4IuVw8h\nZ5HZMqgpgQZTKcnmDlwIsF2BqimEHv5Tj8f97bqfY+/cjZyDW1DTVCwrsxugVMrOS5lWUhSSjc1+\nfYvn4WoqKjD/wi/nPGZAcQkMRB9UDx9JgxrKXW6jF8KGjplLpky0zK/Q/gRQCpG+UpPpDXsyaWKE\nDVBUpKZGjLv+F+P3t6G8+xav3vM3fnviVxBC0PD2h8g59tT2A+heRo2B8q10Fp6LnTRJNjQROWAC\np/7sR4yYM5vx84/IecyA4vLJWGXyJHrUEpKx3rf4ueBneMhZZ7i06gY74hZ74xbNiRRJ08LJcTey\nPwMkw7UDMcQMoSxLnbKHekcIOgLCkuciJeI49fVYa9dgvPI8oVgLd6z8MnIqv3TccFtMzJ9Xum+A\nIJWycD0vL/kRWVGpGDsS1QjhfryNm7/4FcqXLhg4CREB3Rhav74icfA557NFLrzYHvj56lYqi2pt\nzyMxrJbKQ2YSOWQm6sEHER83gR2qwdaEw664RX3coiWRwkzZuFkajoGgh9NltkNsBxEK6TiOm2Hx\nnCAeS9LU1EoymSKRMPGER6h+D/Om1XLKkgMJW8mOvt254veFNkgkkqRS7XGxdq0rj5aWOIoiZxXM\n7glF04gMH0bZiBpGJFNseejvbN2wPu9xA4rD0Ij+FRlF1dg68UCmNG1Fy6KzXKa0y3D0pGfTGce2\nUQ7sKkkQLo8S3q/ISXgeLS2t2PUNjDQTeIDb3hi+rcuXonQPULrOAKiBSMSR33kTLxJBSsQH3K4m\nXwxDx/M84nGTSCTU4125EIJw2CAih5GkdAqxAiuRQqnI/+bFNFNEImFs28ZMWbiO26GWW14eLWhv\nEEmSkBTFF/lraOGWBcv49z1bCjZ+QOEIDESGLP7K19l7/aWMKS989bKiyNhWW3ppH4uzpWhUTp/W\n55iSLBMtLyPc3IAshdr9FYDfJ9h1XV8bar/V13FcDEMvmFx1LnhNTbBtM0TCRe8k11/IskwkYvSY\n8iqEQFXVLsZ6/8+jpqac6WPL2VKXAM/Fk1XcUHZ3+UKItopoFVVVUFUF1/XQNbVgO0khBK7r4bpu\nt1iHUR4l1tzar9+3gJ4JDESGVA2v5WNVZ4znFbRwrh3DaFN8je73AxcC17JAklB0HSscIRrNzEgZ\nu3chuy5tjRI6HpdlCVlWuymNCiAR92WiUyk7rWtKVmQUWU67+ygUwkxAu196CC8akuR/FvvbQM/z\nME2rz2wn3dBZdtxhHf//0fqd/POf6yiviNAih5Ay+J6aZgrD6Cq2l+sO0vO8DkOw/3dHURQ0Te0o\n1mvHVRRidQ387V9/wGk//mFO1w0oHoGByBBJVtg4aiIzGoq0FW6X4UhZXbp4ebbNtskzCEcMyte+\nTuvMA8hEMUeyLOSUmdUCK+EvWJqmkq5Orr3vgut6OE56AwL7jIgsy0iylL1seDKZ0eI2FJBlpa02\nYt/rNU0rpyLKA6aMZMSwCIqq8ddH3yCphpF6CQD7QWkpi52CaNt9pjcC7a7LUEjP6OZBeB4IQfWY\nkay9615OuO5qjE9K+vYgITAQWTC6cU9Rdg/tqKqKbZtdA8VCII8aRfWJxxObNo2Rh87ObDC/a84+\nAyH8pp1CVZH8lT7rhXufDHbP70G7EfE8D8u2Eb2kX0qShCQESrwVyTCQ9BCSruHZVk45/YMRWZY6\n3q/27CY/Iy37zZMky1QOqwQh+NQ5i3m1TmbTs68ipyk0tG0Hx3H263fhL/627fRs/Nt2j5kagXS0\nu5PKx470W4/GE7z39Mvcsug4vvHmqzmNGVAcAgORBYZjgV5cl4evImoSacsY8RQVpkwFoGzunIzH\nEboOcpsSreuCJJOqrcWtqESr24ve0lwU901nI9JXSZUQAjdp4j7/lB+0lGWErIDnYfeR+tveXnT/\nP/+5fS1IBzqqqhCPJfE8j/IKf29oGHp+cxcekfnzGVNns/HZV/Y9LAS27WCaqY6Ffn/F2vbHPU+0\nFcUV4U0UAi0apmXrTlq378aOJ5E8QfX0qbx135+Zfc6Zhb9mQE4EBiILNNPEk7Wi9YGGNhkOTeuo\nuHWAaFVF9gMJsU+mXJL8tqcVlRg7d6DGYmnrCzyvtIFCSZKQHAtkBbWTWw1FgT56MbS3Fd335/dF\n3vdvUZC6EDfDmoV8iJaFuyzUvX0GnXdofrvV9K/Tem0V655+F8txfS0rf2RkWepQYU1/HUE8bra1\nDS3Od0GSZeyEue93pMiojoNz0FTe/fNDgYEYQAQGIgsO+Ob3ee03P2UMgjGS16t/Nx80TSWZMBGq\nipBk5AzSX/dHcpw2FWcPJAk35Pu0UzXDscvLCO3d67uaOi0Srlv6FFcRiyPnoCHUvoModmPUQvSE\nyOfa+2f3tKeeyrKMpik97pTCuBw0wqBxTzOykVk8w/MEtu3LaRS7eE0IgXBdJMV/DTVHHcbkpYvZ\nvWF7Ua8bkB2BgciCyIxZHPube9i4cT3P3v4bRjbuYaouYRRhUW1XfEVVCak5/Fg9D6FpOKEQWqwV\n0Xa3JnQdV9NwW2MoyUSX5dV13ZyUOvPB2bYZT5KwMliI93crqaoyqFIjO+9s2g2xZfmS24qidDNG\nnicIh3tu59kbnuOy9q2tSEbfsvDtiQe2baMoStZtR7PFSVnYiSQIgZ00CZVHaZlzEAeNmcg76z4o\n6rUDsiMwEFlg/+lO1NPOY/LkA5j877/EcRwe+eE1LG7dRajAiqPtiq8tskpFDp3jhGGQHD8BJR5D\na21BSSZRWltwy8qQUikUs3uGkxAiN63/fPA8X28oAzovsJ7nkUrZba6Q4lKoXURnt45tO20Fc4JI\nJNxm7ApyGcAPdLtIfW6wbNvBth0kibbMqeJ//mpIBwkSu+s59c6fE546nkd/cgurb72TC597vOjX\nD8icwEBkgbzgWFI/vRYqa6BuJ+rRx3HK9T/j3UvO4YDKSMEznDRNJTl6PBX5rBwCkCQkz8Oo24uo\nr/Mf8zykUhuDdGShQ9XZrSRJEl6OAnXZ4Lty1IIaTiFEh9RGe2FiodENnU+deCgPPr0OR03vonRd\nD8uyMq6rKSSqrhOqLOeln/wPeyvCzJ11OCf+x7+VfB4BvRMYiCxQxk5CuvAahKbBxo8QsoS3eQMV\nl1zDB7/9NTVmM5VlkY5uXnkjSRgtzXkNIafMtnRXQHS6PxwIxgEQOUqXlKryVlFkXNdFlgv3U0km\nUoQjRtF3bO9+tAtHpL9psW0H23GI7l+YWQJc28ZsbEYvL6P+gw1YmsaJf3u45PMI6JvAQGSJPGqs\n/4+afR3dJgOT5i7ArN/D/11/JYfrhZOHiDY1kGxqJlxVmdP5dvUw3HAY2bKQHAfZdZEcB8l1kVwX\nIcsggVSg1prZTzC3pkm+gSjwXNKgKDKplJ22cDAXhAAkv4LZ///i7II2btzN+5sbQet6s2JZNo7r\noioKkQxde4VG0TTCw6qJNTVjtsY5+2/39btAZEB6AgNRICRJIjx8JCISBZEsmIHQ8ahb/Qbh5cfm\nNoAs40WieJE09dee26bRpKA0NiCSZl5zzQVpgO8gJEkq6CK+z9fvxzYyEWjMhVdf/QgR6lqV3F4A\n15Nh6Jw+63lel9cthMAwQgVZyOP1jcTNFNXTpjJiylRmr1ie95gBxSEw2wXAa6zr+PeIU89htemR\nFIVZvBRdp+Kl5zBbYwUZrwuyAooKkkSjC2qpU1whqxhEl3OHiLhbMdKKW5tixL2umW+O42BZVtqO\ncO2CfamUhRD+nHRdIxwOEQ4bhMMGoZDeKVgv2iq/HVIpCzuLXWBzIoFx+kr+ZeM6vvncU3z16Ufz\neakBRSYwEDli/e4mvGTC/x/dvwtM/eoHHHjwbBb99z28HKrGynHx60AIEkImMXEyoQJo8feG1dKC\nUuJtvrBsJO+TaSBs2y1arcHrb2/HC3XdJdi20xGM9jyvo6I6nkhimilCIY1w2EDTVBRFadsp7Ht/\nFUVB1zWSSZNkMoVlOQjhy8MI0Z7p1ftOy/RcZlx+IVfc+AtChYrTBRSVwEDkiHrSWaD72Sdy1N/K\nK/MW4dx/O7Isc9IPb+AtV8mrVanpQdOJpzL8S18sWlFeB8lUyduYeqbpF+vlwGA3EI7joOuF8/C2\nS2q3NsfYtasJ07LbFnP/z/O8fYu77RtlWZbRVJVw2MjIdaRpaseOwjD0NmPi7zZ0XSUeN3t0x9mm\nSWLyOM68+NKCveaA4hPEIHJE7hSkBr/frnr0Cjh6BeDfWSWPP4Pmlx6l0smsKfz+JMrKqT38sL4P\nLAAapV9wRSrZVkWdfQR4sLeJ6C2u4dd5+D07nLbGPX3hV1jL/OP5D2hyJIwMxPTiiWTBAtWKorR1\npfNlOjrvjjzXoWnHHi545M8FuVZA6Qh2EAXCvudm3M1dWyeuPOUMVltSTrsI4XnYkb6rYAuF2g+L\nrReP+3GQTximmepwy6T7sywb13XbAuS0xQJ6/zMMHV1XGVlbjqxkVmEeCRudYg/5B+IlSSIaNbAs\nB8vaF5ewUjbIMhMmTs77GgGlJTAQBUJZfgrOfb/t9viIY1eSTCSzGku4Ls1CJnLaaYWaXp+UVmCj\njUTsEyPr3Y6fISSIRo0eF/tQSEfXtZwK9KZPHoFIZVb53d6LWlW7y3zkjkQ4HEIIQVNzK00VUcSY\nkcw4blmBxg8oJYGLqUAoYyagXPsf3R4fX1nZofOfKVbKQjrnPIzRowo1vV4RnofaD52fhZkaMAV7\npSKVsvbrwVBYamorCBsq2Tg1ff0lr0NBOF+EEEiVZRx6zeWc+oUv5T1eQP8R7CCKTGTPDjyRnYtJ\nKArSyNIYB4BESxy9xAFqAFwn50CCpqkkEn7dRrGKzYpFMWM9kiwzrDL7jDdd17BtB9fNX97ckyWM\nE5cGxmEIEBiIIhM64dM0JlPEW2PYpplRPCKkKth33lGC2fmYzc0o/XAnL5zcqqjBb7RjGCESiRSJ\nhEkqlVsiQClJpeyiy2gDjKwO4+WQYh2NGlh21/hBtgghaIqGufi67+U8RsDAIXAxFZlweQVPzlrA\n4jkzaPpoPe6OHYSsFLrroDuO/1/XIeR5GDJosuTLLRuls90iHkcJ9UMsIM86EVmWiER8d017gLc9\n9XKgpcC2VycX073UzvQptaxetxu5LNskB4mwEcI0U9i2jZaDvkiirpHwwdMC6YwhQmAgSoAajTJ1\n/hEw/4gej0m2ttKweQv//OujzJk+lUnHLi7Z/BRP9I+yax47iP1pX3gty8G2rY66gGg0XHoJ8zSk\nUlbJem1U1VQSjWjkGnY2jBCWZZNKWYRC2SnNOo7N2GHDc7xywEAjMBAloe+7qXB5OeFDDqZqy07e\nS5rMGFG6H5km9Y8PX7IK7xbyi8/amiMJSMSTHcbP1z3ypbZDbXUC7cZDCDr6IrTHNAq5oHduElQK\nqirC7I7lXqTpV02ncBwXNcOGVbGGRsxkii/813/mfN2AgUWwDywB2dzBnnTSCo44Yg6//vWtIJrX\nRgAAH0VJREFUrF+/sYiz2kd/3CX4OkyF20GkQ5IgHNmnJWRZFk1NMUIhHdt2SCZTmKbVEcOQZb/u\nQJZlZFkmkTApRPzbcYonq9ETo3KMQ3QmHNaxLDsjraXmHbtJyDI/2LO55K81oHgEBqIEaFoIK4u7\n5QkTxvKNb1zIunUfctdd92UlhpYL/ZLiattIBciY6QtZ9ns2K4qMYYSori5v+7dONOrXAEQivnSE\nqirouoqqKqiqQjjs++P9dpwubo6S6JZlpxXJ6wu/Wjw399j0KbV4Znb1N93x6yRc1+s1uykZj2Mm\nknx37WuBcRhiBAaiBEyZMpUtW7Jrxi5JEqeeegKnnHIcN998N2vWvFWUuVnJJFp/ZDAlk5Bl+m8h\n2H/B7c19Ikl+0Vc0agAi50wpVVWzroXxyb3nRVVNJZFwYTrV+buv9DcpyVichCe44vUXMaJpJOUD\nBjWBgSgB8+YdxVtvrevzuLffXkddXX2Xx2pqhnHZZRfQ2hrj5pvvorm5paBzizc090sNhIjHkfvB\nQOSCJElomprz3bws59Ye1Xdv5W68q3Ooh0hHe5vXdiMnhEC4Hg0bNhM3Qnz3zf9j+NQpBblWwMAi\nCFKXgKqqalpb470e47ouL7ywGkWRWLlyMRMnju/y/JIlC5k//3Duu+9BysvLOP30EwuSSui2tiKr\npTcQXrwVWflkfP0URcHJQbAxX8XaibVRtu3ciVaev6ZXOBwikTCRZYnE3gaUkI7tOFz/2ks5pcMG\nDA4+Gb/QAYAk9f5WP/TQE3z+8+czbtwE/vd/f8W6desZMaKGGTOmEWnrBWEYIb70pXPYunUHN910\nBwsXHsHcubPzmpfiuMg5+MfzRSTixZcwLzDtjXVyOS+XhT7ftqqzZ0/ijXW7KFQEy4/JWBhV5TTt\n3MuyX/8sMA5DnMDFVCKqq4fR1NTc4/OxWJIJEyYhyzJf//o3mTv3GCoqxnHzzffQ0tLa5djx48dw\n2WUXkEgkuemmO9i7t76HUftG7acUV2Hb/VN7kQftMYls/yIRIyc5kHx3EJIiM2fmaJwsxSJ7HE+S\nAEHStBh++gksPf/8gowbMHAJDESJWLx4GatWre3x+f3XgenTZzBv3pF85zs/4Le/vS9t7GHRovlc\neOHn+cc/nuMPf/gLTg5pjf21hRT5dtsbZOSSLptPFlM748dWIVmF6zUe0jWSdQ18+ac/K9iYAQOX\nwECUiIkTJ7Njx+6szzMMg+9+94fccccDaXcgmqZx7rlnsGLFEm699Xe89NKqrMbv5iAQotfVrF3S\nwu9F7OB6Xm61AkWugRho5LLOF6JrXkvcQhRQ9iLZHGPUWacSrRlWsDEDBi5BDKKEKL0EZUUvGT2h\nUIgLLriY559/jJNPXpH2mNraGi655MusXv0m//3ftzFr1kymTJnEuHGjewxmO5aNKndd3d94fwNx\nScZQFUJtf2WhEGURg7CuI9r0hAQSruvh2C6e12mxd2zkN19H6CHQdKRoFKWsHCJRZCOMpGtIspy3\nDtNgIxTSff+9kXnqab4xCIC9e1uQwoXrZx5vaOTKX/2iYOMFDGwCA1FCQqEwqVQqbcP2vjKSXn99\nFXPnzurzGocffihz5sxi8+atfPTRxzz33MsdRU6SJKEoMuPHj2XKlEmUayq1na7reh5yNMKcJcd0\nGbO5uZX3t26jbtMO3FiM2aNHMHFkDbKmAPsFmpsSeE31oCogBJ7rIhwHIcm4koSQFVA0ZM8BZXDF\nIPLBdd2spTYKsYPY3ZBA0QpTD+E4Dlp1FaECGpyAgU1gIErIkUcuYO3ad5k/f26aZ3tfPLZv38rS\npenOSzOSLDN58kQmT57Y7TnHcdi6dTsffLCe5j17mTN6OLqiYKgysicoq6zsdk5lZTmVlTPhkJkA\nPP7XRxhTU5k2g0Ukk4AHKCBJyKoK6v5fM/cTZRyE8OU2IpHC9H/OhpE1ZWyp34tWgEXdTKUYfegh\nBZhVwGAhMBAlZPbsOfy///ePHgxE7wvmqFFj2L17LyNH1uY1B1VVezQewvMyumM9/rSTeP3vTzL/\noAOQ9z8+3jpk+0yHQr6AXbaS3cmk2SYUmB1+T+r8dhFzDpvImvd35nx+Z5y4ychZBxdkrIDBQRCk\nLiG+Tk1uP/bDDz8io2rsfJBkOaNoqizLjD/6KP7xxrt4+zVAEmYy5y5xAx1ZljsW7UzZJ/6X/Xui\nKHLO+k/tuI5HoaS2PNdl2vHpY2ABQ5PAQJSYnoT7TDPZqyDaxIlT2L59VzGnlhXV1VXMPm4Zb3y4\nseu882gjOhhQFAXbzlxXKZ8+ELIsdzPA2dN7VlrGYwCeJOE0NOY5VsBgIjAQJeaooxaxZs3b3R5f\nsmQ+jz32tx7P8+9CB5brpryinIlLjmHjtl377qqL0ONhIKFpSlb1JkKInBsW5WMgPE/gOC6SIjNu\nVHke43jEYkkSSRNJlvEGWXFjQH4EBqLEzJ49h7Vr3+32+LRpU3jnnd4VW4WQc6rILSbhSJjyg2ay\nY9def26DRIAvHxRFycj1k4tAX2f85kVdH3NdD9O0OupRevqzbQch/LkePW8qJBN9Xk8Ivy2q63o4\njts2hvAl0cMGFdUVPPP7e/J6TQGDi8BAlBhFUVi8eAW/+92fuy32Rx89l0ce+WuP5x5zzBJeeWV1\nsaeYNWUjakmMHcem7buRkoWRdRjIhEJaj/LX++O6Xlv7TrvHhT2RyFzfye8tofcp7xEKaWiagqLI\nVNWUU1MeIpk0e/0zTQvLsnEcp2PHYZpWh5HSNI2WD9dn/X4FDF4CA9EPLFy4mJUrT+Omm+7q0gxo\n1qyZrFv3FolEeuXXuXOP5P33N5RqmlkxZuJ43mtuJdnD3D+JyLKEYegoioKmqYRCWtrFPJOQjbx7\nJyST6LqGabYZlAzdRp7rkrRcwmGjj78QhhEiFNLRda1jzp2L+xTLYvP6D3N5OwIGIYGB6CemTZvB\nV796Gffe+2CXx88551P89rf/0+N55eVVxGIDcxFetHIFm1qG/g7C8zJPPVVV/y7e72yXo/9eCIQe\nQoQMv9jOL6xAam0BKwWei9zUCI6LlMaVtGdHPbHm3L4zqtq1D0ZU1fjTj36S2+sIGHQEBqIfGTly\nFMOHj2bz5q0dj1VUlFNdXca6dd3jFACnn342TzzxzxLNMDtUVeXD8uF4AyxOUmhSKYtQqDDVyeDX\nO3TpOJdK+X+ui2fZuKaJM36SL4/ueRjxFqSWZhzLwm5ooKW+kXpH0NTYRGssgZNKITU1IjU3AbBx\ncz1SONIxvBCC+o82YeWg8qpqGrG172TVQjdg8BIYiH7m3HO/yMMPP93lsZNPXs6DD96f9vja2hG0\ntvYdcOwvDjrpJJoH8PwKRd6ZvEIgNA2hqBiGjm07SC3NWHv3sithsSdmsrM5geJYNLoyTZu30lRX\nj1lXR0JIvFcxim2nX0z4xj9Te+MDjLrhPkbeeD+RH9/Fy6MPIW5a4Lo48QR79rYiaWrbZQUNH29B\nzJiKtnwRjbKEmcqux0WlonD3L2/I8w0IGAwEldT9jCzLnHzy6Tz11PMcd9xiwL+jnDJlAhs2fMjU\nqdO7naOqA7dJy9hRw4lZFhD0J+4NEY6Q+tRnkJoa0P/5JOGdO9iqhCk7dBFjVeCIY5G2fowQgvLZ\nR+EZBooRAd1AkiR60lINhyMcd9FVNNR9nrp/v4THH3qZ+QtnknxvF02OS2MiQXj0KL71/NOour8L\n+tlJp5DYuIVIWWad5xRJZsfDT+B+69q24s+AoUqwgxgAzJkzj82bd5LotOVftmwhd955K6k0d3ed\nA9sDjnCEBj0L3Z82f/qgJA9XmlBU1LfXoH70PvKeXaRqRzLaTVKz+mk4/izY8hHystNRjzsTeeRY\n1MoapFA44zjGsOEjiPzwNjYmPJ568SP27m6gbncdcz91Kt9+d3WHcQC4+m8P4o4djZlhBpokSURb\n49zzXz/P6bUHDB4CAzFAWLr0ON58c1/cQdM0li1byFtvvdHt2Llzj2TVqu6PDxSSo8elNWz748kK\nOxubed1R2dIcZ09DE42NzWDbBaj+LRKWhdJW6yG1NEMv1e+9IcdbUd97C+XjD/GGDUcvK0NuHzdS\nAa8+Czn0se5MVVU1K//1OlrLy7Gi5az89rf41M+7B5gVVeXS399NQtcx45m5B0OaxscPPISVpXsq\nYHARGIgBwurVrzFnTlc578mTJ/D+++91O3bJkuWsWdNdB2mgMOXc83gppWA6vS2eEn8wdaTLruHg\nb36L2uuup/xf/p3Ws77Ag3EZdyDskoToZgCk1hbU8jKsRAI7lSLRGuveHc+2EVrIzyjqLZgrSSBJ\nSJ6LsnWz/2OcMRc5EoWVn0HS81d/PfriC/neG6/x3ffe4OhvfL3H4ypGjeQ7r75A8669JFrjeL1+\ndm3nWDa/OOfcvOcYMHAJDMQAIR5v6ab4WVVVSSrVwl133dbt+M985jweeeQfpZpeVmiaxlHXXsta\nQsTjie67ASHYmnKZtmwplZUVXZ6qnT6NZVd/kw8SDskM72aLgusiFBWvxlfPdSyLHc1x6j2ZtabK\nm4etoPmL11J//Od4LyWzraEFM57ASqWwGhvZtqeB7abH1uYEXkM9kpmm7afr+ZlGZhIcm02ygXP+\nNbgvP4kyb0mJXzBous5Zt/0PraNqMPfrg54OPRTCW7+RR265uQSzC+gPAgPRD7iu2yFwZ9s2N9zw\nE+bNS98M6KyzTiEe7/5jnTp1Oq2tJg0DVDxNkiQOvfwK1hw8n00NLdjmPldEKh5nU9UIZs2amfZc\nTdOY/O1/4eOK4f1W8yGlUnjjJ2Fu/JjEnj28Vz6GEdf9ktE33seC63/JojO/wJg5R3HA8pOZ+6Ob\nmfhvt/LxQYvYUjsV96yLmXz2BYwfOZJJV/yQXaFK7JbmroayTZZESsSRGhsQRpgJIZlt/3oBZBFr\nKDSHnvEprvrrA4hlR9K4YUufx5eHw7z+y5vY/kFQPDcUCbKY+oH/+q8fo6oyiqLR1NTE5z53OrW1\nNb2ckd4ff+GFl/Gf//lvXHrp+UWZZyGYd+LxuCuW8s7ttzFx11bKKstY7erM+/znej9RlpnytUt4\n42f/wULXhRJny4hwGG/VS1Azkqrv/DdHpGmO1Bk1HGHOeRd2ffAIfxcw4bLrSf3sSuxdO9E1Dcnz\nfJkVVcVTVOodG8X2UCUIex7eg7fjlVUhzzysWC+vV6qra6ieeRA7xZOZHW8Y/PbLX+X6l58v8swC\nSk2wg+gHTjjhZCZOHMsXvnA6l19+fh/GgR5jDbquc+KJn+KJJ54rxjQLhqJpzLjoErTPnc9qvZKZ\nV16VpstceoaddQ477BLHWmwLa/duUDQqrvwpUh/GoS+UUeMJXfETpJqReFYK17F50wvTaAveqxjJ\n8Bv+zMhfPIB+5U+pLStDVlSoya8xVL585RtXweRxGR2rKErW7VQDBgfBDqIfOOyww3nqqcdZvNhF\n1/uuyDXNJKZpYhjdg5Z+RtPLPPfcKyxadOSAzktXD5jOYQd0r+vojYlTp/CODaN1z29oVGyEwKmr\nxxo5gWHf/VXBXD3KpAOJfPf/4f7fC1AW5fBxk6FiGCM7Gcqy0RPwlp2GdORy5PLurV9LiaqqWd09\nqopEU1MDVVU9VWgEDEYCs99PfPGLF/DAA49mdOzZZ5/Cb37Tc+XqJZdcydSph3LvvQ9zzz09q8EO\nVsacdQ4NTX0HTfNGCGJ76/BqRlDzL78ueBxA0jTUhctQZ89HHjbC79e93/PK8jP63TiAH5T34plL\ncahNMZ64887iTSigXwgMRD8xcuQoIpEK3n33gz6PrawsZ8yY4Xz88Uc9HnPIIbO5/PKrkSR1wPWM\nyJdhkyfRKKmIPPsrdEZqbECur0NqqIeUidvUyN699dSfdxXl37+lYNcZrKx74im8phZEhqnUIU1j\n3Z1/wA40moYUgYHoR7785YvYtauZP/7xoT5rGpYtW8RTTz3W55hjx45n587dhZriwECSiCw8mlhz\nc2HG8zyQZbzKKqxwhIbmGG9PmsOYG+5j+hELC3ONQc6W9euRbIf43gZie+oyOieSsvj9t68r8swC\nSklgIPqZM888j5UrP82vf31HF6mN/TGMEE1NjX22u5w+fSYbNmwq8Cz7n+oFR9PqFmYHIcVieLaN\ns2c362smMuK//sj8S76NXIoYxyBh1onHIxQZRdcIV2fm8oqURdn0zPNZtWQNGNgEv4gBwKRJU7jy\nymt54IFH2LFjV48uojPOWMlNN/2i17GmTp3Gli07izHN/iVksOeQebSk8qiw9jzkhjqSkkzCcgh9\n7goOu+KHAzqw319MmDETb+pEpCx7oZe7Hndee23W17vmmit49NEHB6w6wCeVwEAMEKqqqhk/fhJP\nP72KO+64L+0xtbU1HHjgJB577KEex9F1ncbGliGp13/gp0/nbVvGyfG1SWYS2xMkLYfqX/4Z9ajl\nBZ7h0OLEKy6jZddekDMP1hthg62PP4OVrnK8Ew0N9bz66os88MA93HTTL6ipqWHVqhe58cYfc8cd\nN/fYVTGgtAQGYgBxxhnncvnl32L58pO6dZprZ/78OXz88Yds2vRxj+Nccsk3uPPOB4o1zX5l9qWX\nsbuxJWstP6GoWIkElpVi5M/v8ZvvBPTKwnM/S9ncWSSaeo/9JDzBDkvgtH0oFbLEbZdenvbYv//9\nQW688Sf85S+/w7LqmTPnAM499xQiEYMzzzwP0zQ5/PAD+clPrmfHju0Ff00B2REYiAHIoYfOZc6c\n+Tz44ONpnz/vvNP561/TNxQCqKmpZdmy4/n7358p1hT7DTUSwThuJfV19dkpvmoappWi7Lpflaae\nYohw9TNPEB9ejee6CCHSuj/jLux2BK1t+n6hcJi6tW+lHe+tt9byla98hrPOOoVZsw5i8+Zt3HHH\nA5SXV3DooXO56qrv8uyzrzBnziFYVu+7kIDiE/xSBigLFhzD+PEH8Pjj/+z2nCRJqGrvH928eQuQ\npBCvvLK6SDPsPyJHL2Hz4ceQyELML7FnD8qI8ahjpxRxZkMPWZY591c30lDXQGznHtw07r0KBYar\nEnonT5Roa326P8OHj+C1197g9tvv4667/kI0OpIrr7yOL3/5YgAikSiyrJBKWYTDQdOp/iYwEAOY\n5ctXUlY2jH/+85U0z/Z993zuuV9CUcq4++4/dYgDDhUOmjsb0+y7F4FcvxcpmcBLJqm69sYSzGzo\nMXP+fMoOmAxGCOF6JOoaujwfkiXG6xJRZZ+FELZDsrml21hnnnkOhjGMK664jiuv/DZHHbUoTfaY\njGmmCIezaDwVUBQCAzHAOeWUM0gkPD74YH2Xx1VVwewjEAhw/PEnc/bZX+C22+4t1hT7h5rhJJQM\nNJIkGTwPSZKQQvn3V/ikcvF995LYtYfWHbvRIn0v3Ios0bi3ez1OdXUNixcv7zVzbPLkKTz++DOE\nw5G85hyQP4GBGASsXHkKH3ywoctjEyeOZf36zCSWU6kU48ePLcbU+g891PcxgDesBlImMS0wDvlQ\nVjucUYfNxg4bxHbt7fN4VZHZtTO3dOtTTjmDW2+9Ey1PkcSA/AkMxCCgsrKK5uZYl8emTp3Ehx+u\ny+j8Rx99kBUrFhVjav1K/YSpfbe8FAJcj6SamUEJ6JlLX3qG5ffeQtXRh/cp5yK5gvotffeT6InK\nyqqczw0oHIGBGASk246PGDGczZs39Xmu53kkk/GMVGMHG5PO/gxbk30XzomKSsqtfuxON4Q49tgV\nJGqH0bB+U69GQrguW54Yell0nzQCAzEI8KULuv4YfaVRp8+COL8ydWiJ97Wjh0IkQ2Hc3vonSxIo\nKlE7NeREDPuLb/7PzdieYO+69T27m8Ihhk+ZXNqJBRScwEAMAt55502mTev+Y1ux4hgefvjPvZ6r\nqirl5dVs3z4E5TeA0aefwe76RoTbs0SD3FhPXJJx179dwpkNXXRd5193b2TCL3+AWVuFm0Z7ya2p\nYvEFX8loPNd1eeWVF1i16uVCTzUgTwIDMQhYs+Y1Zs8+qNvj48ePYcuWjX2e/9Wvfp0XX3yDp59+\nsRjT61ciUw4g+dXLedpSaGxqQaRJ5/XKyykXLqx5oR9mODQxwmG+euGlfP7+3xNPWbh2VyNhbdrO\n3gz7VL/66ou8++7rbNjwNk8/nb44NKB/CAzEICAWayXSQ2phWVmYhob6Xs9XFIWLLvoGY8ZM5ZZb\n7iHVV2B3kDFm3BiOvuoq6r9wEU9aOi0NjQjbBtv2pb2NMHFFhZam/p7qkOOAAw7EO3ouTZu2kWho\nQghBsrEZyfWYedIJGY2xfv1HnHDCUk46aTmvvfZyoAY7gAgMxCCgsbGJZDJ9zcNxxy3m4Yf/ktE4\nCxYcw4UXXsatt/6RTZtyzzAZqIwdN4bFV11J0/lf50FjBH+Qq2nUDCTLolJXaf647+ZMAdmz8otf\nwpUg3tLKng2baWmNMenwuRl35IvFWigvLwPgtNOO5/e/v72Y0w3IgsBADAKuvPJabrnlXrZu3dHt\nuaqqSlqyuDOurq7hu9/9IY899nwhpzigqB07hpVf+wqnXfo13pi1gNccjceio/iFMqq/pzYkmXfM\nEq7fvYkf7t3KeffdzdR58/jSQz1rhe2P5+1zC44ZM4rW1gYaGjJrUhRQXAIDMQiorKzie9/7ES+8\nsJo333y32/PZ9jOQZZklS5bx6qtrCjXFAYkkSSxYMI9DvnU18YkHcPHFl/X3lIYkQghUXWfzK6v4\n+PF/cO79d2fVfOngg2dz66330NLi9x0/++xT+d3v7ijWdAOyIDAQgwRZlvn617/Jhx9uTdPHOnO9\n/nYWLlzM2rXvfWJSP/fsaWTcuAn9PY0hxa531/HjiTP4QfVYXvr1/7Dmjt9z8o0/JRTNTmRv2bIT\nuPTSq/n97x9k+/adGEYISQoaBw0EAgMxyLjwwstYu/YDPvxwn/TG5s2bueOOW/joo/ezGmvFipW8\n8MKqQk9xwPHuux9w6KGH9/c0BiWe53W7ifj4uRdo3LqNu8/4LJ5p8tk/3MHCyy/m07f8d87XiUSi\nfPvb1/PQQ08CIEkiCFYPAAIDMQi59NKreOWVN9m4cTMA3/nOZSxffgQvvPAkTz75aMbjzJt3FBs2\nbGPHjl3FmuqA4JVX1rB8eWYZNQFdsRPdZbuHT5+GHo3wzbWv8r3dm5h54gkZB6R7Q1EUli49nhde\nWMXkyeP56KMgqaC/CQzEIOXyy6/msceeJxbzWzNWVJRzxhknsXr1a9h25n2bv/GNa/jznx+nOY00\n81DANFOUlVVk5RMP2EeorAzN6Cp0WDF6FNFhw9CKIMe9YMExfPDBJt57bz3RLF1VAYUn+NUMUmRZ\n5sorr+WOO+7r4gL49KdP4He/+23G4yiKwrXXfo/bb78/o/4Kg43Vq9eyaNHS/p5GQBZcffW/cO21\n32fChEn9PZVPPIGBGMREIlHOOutz/OUvf+94bNSoEcRiTTQ1NWY8TigU4qqrruN///fuIddYaP36\nrRx00CH9PY2AgEFJYCAGOTNnHkx19Ygu6a9nnnlSVrsI8FNpL7roG9xyyz1DKrNJkuTAvRQQkCPB\nL2cIcMYZ57JmzT4DEY1GCIUUdu7cntU4o0eP5YwzPsv99z9c6Cn2C7Zto2lDT+Y8IKBUBAZiiKCq\nepc7/2OPXcBzzz2d9TgHHngQ5eU1HRlSg5kdO3YxceKU/p5GQMCgJTAQQ4Tp02eyYcMmAGKxOPfe\n+1eWL1+Z01if/ewXeOSRZwa9q6m+vpHa2hH9PY1PDJ7nsWfPblatepkHHriH1atfC2oZBjlqf08g\noDAcffRibr/9N8TjCVatepNrrvke0WhZTmPJsszZZ3+Ohx9+kk99avDWDzQ0NDF16mH9PY0hRUND\nHXfddRuaptK5EZUQHkJ4DBtWxfjxYzjssAPYvHkLN930DCAhyyqHHjqXI49cSCgUtH8dLAQGYohQ\nVlbOgQfOJpn0uPba6/Meb8aMg3j22Sepr2+gpmZYAWZYehobmxk+PNhB5MuuXTt55pknqa/fgyQJ\nzj33VAyj70W+traGefN8A+26Lu+99yE33PAjjjvuRI44YmHHcbZt89JLz7F27RpGjhzF2Wefh6oG\nS9NAIPgUhhAnnHByQce74IKvc8MNP+KSS75Y0HFLRTJp5ryL+qTjui73338PO3ZsobZ2GIsWHcGw\nYUfnPJ6iKMyaNZNZs2by+OPPsnbtG0QiUerqdiNJgnnzZvOlL32abdt2cuONP2by5GmceeZngwy0\nfiYwEAE9ous6S5as4IUXVnHMMfP7ezpZI0nB4pILzz33NC+//Dwnn7yUE0/07/Qdx+GZZ16kqamF\neDxBu0BkIpHgoou+kNX4K1cuZceOXYRCOjU1i7o8N378GL72tc+xYcMmfvazH7BgwWKOPXZFQV5X\nQPb0i4FYs2Zoy0wPJQyjjH/840XKy6MF0dspJdu27Qi+a1mQTCZ54IF7mTJlHAsXzqWxsZnGxmYc\nx+GBBx5hxYoTmTZtCuFwBCEEd999G4sWzUsrQZ8p27b13Ct94cLDeeed1fzpT/dz7LHLmTJlWs7X\nGQqsW7eu5NeU+iNTRZKkuSW/aEBAQMDg530hRKJUF+sXAxEQEBAQMPAJnLQBAQEBAWkJDERAQEBA\nQFoCAxEQEBAQkJbAQAQEBAQEpCUwEAEBAQEBafn/HywSVmgn5CsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b786780>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAADaCAYAAACxbKUpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnWeYHMW1sN8OEzcnSauIYksgkUTOGAMimWQTnDDRGGNs\nsMHXcB2ujcHm2r4O4IA/kgEbEw2YnE0QCIRAEhKtsJJQWGVtmtihvh/Vszu7O7M7szubxLzPsxpN\nT3d1dag6p845dUoRQlCkSJEiRYrkijrUFShSpEiRIiOLouAoUqRIkSJ5URQcRYoUKVIkL4qCo0iR\nIkWK5EVRcBQpUqRIkbwoCo4iRYoUKZIXgyo4DMM42DCMRw3DGDuY5x0oDMMoNwzj54ZhHD7A55lm\nGMY/DcPYfyDP82nEMIyfGIbxuaGuRyYMwzjCMIw/DIN6XGAYxj09/H6KYRg3DmadigwtAyY4DMM4\n1zCMxYZhRAzD2G4YxunALOAMIDhQ5x1kRgE/AKYO8HnGA18AKvtbkGEYSw3DeDzt+3GGYezXzzJr\nDMM4yzCMsv7WbzAxDEMHfgTsO9R1ycI84JtDXQngWOAzPfz+BeCCQarLkOIpcdsNw/jeUNdlKNF7\n28EwjLuB40zTnJBroYZhzAH+DtwNXOOdZxFwUp9qOULxNNk7gBpAAK2ACTwC/M40zcQQVOskIJ72\n/QXgRuTz6SunAXcC05DXuFtgGMYBwJPAaG9TG7ACeBT4jWma8WzHDgaGYdwLfB4IADawDXgP+INp\nmi8W+HS9zRQu2ExiwzC+hvc+mabZ0OW3+4DDTdOcnOXY0cBPkEJ3DPKerAB+ZJrmW72c91XgqB52\n+Ylpmj81DOMIYF1OF7Ob0qvg8Mj3pTgWUIBvmaYZTW00DCPPYkY81Uih8WXgE+/78cBN3ufxg10h\n0zTXZ9isFKj4QpUzXChFCo1rgbeRI77PAP/jfX526KoGwARgJXJUogF7AJcAzxuGcYFpmvcW8Fy9\nPdvBfPY99UePA+OAHwMNyOc3FylAeuNKoNz7/8nA9cC5wEZv2ycApml+nH+Vdy9yFRztL4VhGJ9H\nmmfqkR1hBHgO+LZpmqmHU+19tqUJi24agmEYeyAf7qWmad6Rtt0Ffm6a5g+970HgZ8CXkI15CfB9\n0zTf8H6fCdyObDjVXn3fBb5rmubCtHInAbcgO+wgsAo4xTTN9b2dwzt+f+DXwMHALmBxLjcPeDtN\nc3rCMIxm4HrDMGaapvmxYRj7ADcDRyI1x+eA60zT/CRbgYZhXIXs0OqAFuTo7gbTNC3v918jRxf1\nSI30PtM0L/O0Ks00zSPTirvBMIwbvP/fBjR696LONM2dXnml3jVfZ5rm/2Wp1sq0532AaZrve8/4\nl8AJyPftP8B/maa5xDCMA4F3gHNN03zIO88xwMvA/qZpfuBt+zrwR2C0aZrbvWuYDZQhtcnvm6b5\ntLfvFOBWYE9kpxEBzjdN8wXDMKYC/4dUbKLeuXNhkWmab3r/f8q7xqsNwzBM0zQ9H9ddwFjABZ5H\nKk2NXp2uBC5FasCVQBNy1PLdLorVt4FveeU0AAl6V9qaTNN8Pa2M+7x7ciVwbw51e5Uu70NfrAxA\nmWEYzwEHpu4TcI1pmtsMw7gd+Lxpmql+IdVmlwFnm6b5WB7ngSxCyjCMKuAg4Humad6Z9tM/cynU\nNM2laWXN8P67MMOop71/Mgyjxit/GlJJ1JD3+DHgYmB/wAL+DVxummYkrZxLge8CE4E1wG9N0/yr\n99tPkGbUrnzNNM2/GYahAd9HKgpjgdXpx3tl3AiciTSpVwBbgL8hR19OLvXIRl98HLOB/YDLkB3w\nD4FTgT9l2Pdo4Ajvr7GHMjM1jvRtf0dK/huQ9tTtwHOGYYz3fh/jneN24ETga962xw3D8AMYhlEC\nvAbsA3wbOAXZwWzM5RyGYdQCLyEfwIXAFcDWHq6pJ2LeZ8gwjHHIzrQM+ArwDa+OrxqGEeqhjLe8\nOswDfuFdU7o9/GxkB3U+8Dlk55Gi6/2+h47n9GukeUah84joSGSjeKaHOp2bVo6Zds9nA5cDXwWq\ngP8YhjEGWAjsoLN54Ni086U4CnjfNM3t3vfbgC9612UCDxuGUe/9NhF5T/6OFJwXAx8ahhFANujZ\nyE71QqTi0BdS9Qh4n2uR2umpyOd3EJ3bwwFIP9VXkPf0N169fprawTCMS5BC7XngLG+fvH2Bpmna\ngJN2bG91g97bXy4EkYL4fGQbmoc0yYJ8nyoNwzg4bf9jkR1qIU1qTcBm4EuGYUwsYLmZSN2fMuTo\n8ynk+3YpcDjwZ+AJpBn3ZuR9uTZ1sKf4/R7Z9k739v2Lp5iDNHGn2tJRwEfIvupl7/dfIvve/+cd\n/yzwZ8MwLk+r4xHIPv5cZL94P1Lp/0Ye9chIriOOTDxtmqYLvO5J5ysNw9C9FzfFm94+qUrmfRLD\nMPZFOtRPpuMlewMpPb+EvIEp3kpphoZhWEit7gjkzf42UvueYZpmyj75Sh7nuBIIAfNM09zqHbcU\n2Rn0hu51XFXIBvMdZKe1GNmIk8BJpmm2eeW+g+wQv4N86bphmuZ7aV9fNQzjSOAY4LfeNgGsMk3z\n2Rzqt76r/dcwjJXIDiylrR0DrOtlmN5JOzMM43qkAJ+eGj0ZhvESUqv5H9M0v24YxrPAcWllHI8U\nJscBfzAMQ0GahP6Sdu0PpZ3jHWAnskN8PK2cF03TfDVtv68hR737mab5obftOeQ97g3NU0DKkALt\nKuBjYKlXn43Aw2nnqkPa2dOJmKb5vPf//xiGcSiyQaecrP8NPG6a5hVp5UxBdvo9oXjaZwhpuroU\nGazxkzzqlrHcHPZJZ6tpmu0asmEYjcCjhmF8BulHa0W+T6lR3jHI9lown5hpmsLzK94FrPKe7z3A\nv7r0SwPBQs868YZhGLORz/UPnh/zFcMwzkAKlp94z+vHyLZ6C/Jev4K0ZFwMPOyZlNcDGIbxM+Qz\nPcI0zQ2eUPw2cuSQ6h+eMwyjEviFYRh3mqaZ9LZvM00zJWxeMQxjHvK9uzWXemS72P4IjnRMpGQb\nA2woUJkpUkPfp7tsF2Qwf3WpE8hhHEgtYEWa0Mj3HHOAZSmh4ZFr40rvbJNI7eDbpmk6hmEchjRl\ntbVX3DTXGIaxAjg0W4GGYXwRqcHMRJq3bPrn4O7KfcD3DcMIe+aUz9LzaCMThyHvebvJzTTNFsMw\n5nu/gezsv2QYxgSk8/kA5MjpV17U0z5Ic9xjAIZhhJGC/CykKWqzV05FL3WZAzSnhIZHrs/vuS7f\nHwWuSilFnsntJuR7FEJqvl0jzLqey0SOejFkNNpE5CgjXw5Hau4ptiAFw4151K0QdL2+V7zPA03T\nfNkwjIeBc5DvlIpUoH7Vx3NlHQ15CtUcz4F9PtLJ/lPDMM40TdPMdlyBWYscnY/G84sgnempEdcU\npBL5fe8vnRXpXzxBeD3wFdM03/c2H0SHSSydZ5Ej6dnA+2TGRLaxvOrRlUIJjpTpxZ/ncSmp2JNJ\nJhW58nnkA0lnO9npWieF7C9cLucI0mGayJczvHJ3AltSfoheUMhuy/0ssmO/G6kxJ4Gf97Fu2bgL\nORQ+1zCMF5HmyR9m2Tfbfc3WMadvfwbpbzgTea+XIbXEXyM7l6OANaZppoTi7UgT1bVIQVlB9449\nE0HAl8N+mbgCWIAUPncA75mmuQnAMIxq5Ch1KdJ8th04j95HMjHkSEalw6yUb/sB+ABp544C29PM\nebnWLUmHT7In8jVdpfqW1HG3AxcahnEsUsmpRdr9M9HsfVYjfT3p1NI5KjAjadr/z5H+zr8jneSD\nQSpaUu+yLfX+pep/Mx3mvK7Hpnyy9wB/MU3z72n7pNpPvu0O5HuXes9yqkcmCiU4ciV1oSnfyhak\ntrRXD8d85H1OME3z0X6ceyFwnGEYEzM4nVNOsZ7O8TZwvGEY003TXJnnuZd2dbB1Kfd0wzBK00xV\nk4HpSJskdL9vqXkX15im2eQd8wkwKc96gWyktV03ekPifyDtoaVIoZetg0419Fo6N/T5wGfT77lh\nGBXAIXgvqmmaEcMw/oXs0BqR5pqkZ8L6AtJPdn9amfsBL5um2W66ytEE+jbwDcMwjjVN85Ve9+7M\nCk/be9/zzfzcMIyFpmm+gDQhlAH/m+ag3zNDGT1pydsMw1iD9EPkq4W3pWmiXcmlbp8ABxiG4U8z\nb3RFIDXcfDjF+3wHwDTNdwzDeB35Pq0HlpimuSzLsak2Pw8ZXoxX9yrkyCkXRQHvvJsMw1jI0EfA\npbMB2Wb2NE3zhkw7eArFP7x9uyohC5CBDifSeWQxD2kS/Ijc6LUe2RhswZEKBb3QMIxbTNNs9jqn\nCzzTzCK6jD68yJyngZs8G97byA50T9M0f53HuW9DOvRfNAzjZmSDqQf+Y5rmohzO8Ruk0/05z+a4\nBjmhsb/8BDmEf9owjJRD9EdIR1jKX5Ey/51vGMYSpAYFcIthGA8itYPxdO6cetI60n97B/iCIaNr\nmoDSNOH5v0g/zBjggfRIjC68h9Qif+JdQ4133G+R9/xp754lkbZfFWlbTXEX0g5uIW39IIXFg8gO\nK33W8rvAmZ4zeQW5jyLuR44c/mkYxk+Rjasqx2PbMU3zl57d/h5Dzlf6GGliu8YwDBt5D+dkOLQ3\ns9hVwJOGYTwE3IuMBtuT3jX9nspdnkPd7gMuQl7P3UgtdFKX864HRnkO08eyvAdhwzBORr6LByLN\nK8+bpvla2j63AP9ChsZmNcuZprnCMIxHgP9OC7CoRkb+hPD8ml7wyIfIUfyRnv/mT0iT81pk/3Y4\nskN9xjvmcqRwPtc0zaey1WEg8XwxP0e23zuR5tpWpInpYW80+02kgnUNcFCacrTONM11hswo8ENv\n+yKkT/ACpAk8fUSW9f3IsR4ZySWqStD5Jer6PX17j/t4TprbkZ3JbG/zN5EhYj9ERi39HTk6WJJ2\n6NlIz/8FSK//XcBJnnMn0/m7YZrmZqS2uhBpBnkG2XmlIrN6PIcXRncw0tH+S6QJ4EakVr26h1P3\nVq8NSK06hmzEf0Z2asekQjVN01yNnDtwEjJM8lVk2ObRyGiO55C+mA9yOG/XZ/NN73x/Q3au89Lq\nthTZCMcjn1tP13Ax8pn+G2k2m+qNoI5Gdq5/QXaIrcDRqXBQ7/iXkLbXpaZpLvc2P4XUhl7wrj/F\n1cjncxPyfXkI+a5sTNsn07vnIrXOvyEjS55H2r+7vmtdyXQfL0Vq8jd7zt0zkMP/B7w6nQe8mbZ/\npvbQaZvXiR2L9Mk9gLzv+yPvQ09162kk09Zb3bx36ctIM86TyHYxDinIU9wKvIrslDOd7x2kcvM3\nr96XIc0fp3apz1PId6EKaWbtiS8iowXPRnZotwGbkA7idD9V+j0IIUPTf4C8bw97x9/klZfa381y\nHV3pz6TG3p73r5Amxv2Rz+YRZKBNSpk509v/N8ioy9Tfhd7v30Pe48uQ9+dU4ErTNG/Lds4+1iMj\nSnHp2CI94Y0g9jNN89hedy5SpBcMw3gUGaRwYa87Fxm2DLapqsgIwDPBqMiQya97n0WK9AnDMOYi\ntfyzkO/ScM0NViRHioKjSCZ+gnRuLkPO+H23592LFOmR25H+wPeR86CyZkQoMjIomqqKFClSpEhe\nDOmIQ1GUMHICW5EiRYoUyY+PhRDR3ncrPENtqpp53333LZw1qxBRrQNPLBbj0Uf/wfTpezBr1vRO\nvzmOw3PPvU4kEuXss+ehqkO7uGIyabN27UamTZswoHWJxeLs2NHM+PGje995AFi1aj3TpvWei+8X\nG22ebXG7ba/T4a4pPkq1nqNlN2zYgq5rjBnTbcrLiMFxHB5//HkuuOCynPZ/4IF7OOWUnpbhGFnE\n4wnmz19IW1sUn8/P3LkHM2XKtAE7n+u63H//nZxxxokFKW/JkuVs3bqdQw6Zy4YNm/j61783l+wz\nxAeUoRYczJo1i/33HzkL2x1++OHceust7LNP9zmLixebnHHGubzyylOceebQLz0yc+Y0tmzZwbRp\nA5fvbcOGLRjGdKqqynvfeQDQtACzZ/fe+P+4p8vxpsXqLvNhtwEL6jWurs/eFFau/IR9961j3LhR\n/azt0BONxrGsGAcf3PuilW+++ULG93ykYZqreP31BYTDZVx++XcYM6a+/bfm5iZuv/1WwuEgHWZ7\n+em6AkXR2Guv2Rx22DEEg/nlnHz99Zc5/fQTCnYPFy1azre+dR2PPHIvs2YNnMDLhSEXHCOReDzz\nbPyysjDl5RUkEi5bt25n1Kih1U7LykpYuXJg/ZAtLW3U1w9/LbzKp/LFGo0bNzndAttfa3W5uj7j\nYYB83tOnD3Sy1cHhiCMO4tZb72b6dIPq6uzPLRJpIxDoSwaU4cWDDz7JhAlTufrqG9C07pPfH3jg\nPlzX4sgjj2TixHHdfhdCsGLFau6881a2bdvB9753AyUlpTmde8GC+Vx88bn9vgaAdevWM2XKdOrq\nRpFI5JKxaGAZWnvKCOX440/hoYe6p9k55phDefrpx7nkkm/yj388jut2N40MNqNGVbN5c08pvfqH\n47gZG+Rw5NtjNA4o6W6S+jAiaIhnf1aKsnutT3Xppefz17/eyrvvZl8Q76OPljB9+h6DV6kBQAhB\nW1uck076XNZ39Otfv5Krr76B1au3cOedD/LEE8+xcmUDmzZtprm5FcdxMIxpnHHGiZSVhZk//42M\n5XTFdV3WrFnD1q2FaXuvvfYO8+adBoCiDH17K444+sA+++zPzp3beeGF1zj++KPbt9fUVLN9+1Z0\nXeeCCy7ln/98jPPPP30Iawr19XW8//5yystLCYd3l6Xe+4amKHx3jMbFa2wiaXKiyYXbt7r8YuKn\nQ48KBAJ8/etf5tlnX2XZso/4ylcu7uYH++ijJZxwwiFDVMPC8OabCzj22N4X2fT7/Zx55jkAbNq0\nAdNcRmPjFlpbW4lEWrFtG5/Pz5e+dCmjR4/J6dyqqvKrX93KAw/cCyQ444x5Pe7vOA5PP/0yO3Y0\n4fN1jPS2bdvKd75zKY4j6wlQWzuKpqbmbEUNCkXB0UeOPfYEHn30HyxatJT99pvdvn3MmFoWLnyb\nuXMPob5+AosXf8Teew+dnVjTVPbffxYffPAxc+dmyr3XP0aaNn5ipcax5S7/buo8wlgQcRFCjLjr\n6Q/z5h3DqlVruOmmH3PVVd+jvFxmpp8//00aG9dTUjKyHeMff7yGU0/9Ul7HjB07nrFjx/e+Yw4E\ng0EUBQ46aL+s+9i2zb///SLbtjVx9tnnMmVKR9DNunVr+M9/nmXZshXsvXfHnMnDDz+K3/wm4zI9\ng8anQ8UaIM4663yWLOm8rtG8ecfw+usvs3ZtA2eccQ7z539AW1skSwmDg6oqCCGy+mb6ykidA/SH\niRp7hzoLiGVRwWutQ29aHGymTZvMxRefy623/ooPP3yfJUs+4NVXX+Tyy3NZn2z40tTUTE1NXdbf\nt2zZzF//eiurVg3cEh1NTbtobt5BfX33iMPly1dy110Pct99T3Dccadx7bX/3UloADz++MPMm3cM\n77zzAccc0zFymjRpMoceenTXIgeV4oijn2SyN15wwRe47bY7uOKKq7nyyu/yu9/dwhVXfHUIaidR\nFIV99jFYuHAZBxywF7peGBtpa2uEsrJwQcoaTCp9Kn+drHP+KosGL5F4AvjHDpdjyofefjzYhEJB\nrrjiAp544nkSiSRHHnnwkIeT9wchBPfd9yhXXXVdp+2u6/LKK8/zwQcLqaoq46STjuaNN17nX/96\niH33PYDPfOaEgl73888/xSGHdIw2GhrW8frrCxBCZc6cfbjqqu9n9b3EYlGWLVvG/fdbjB49ttt+\nM2YM7RSGIZ05rijK/gsXLlw4ksJxu/LSS8+yefM6TjnluE7bk8kkf/zjvfzoRz/nww/fZ/ny9zn5\n5KEd+m/ZsoMtW3aw994zClLeJ580UlFRSkXFQCwolxtLl67KKRw3E883OXxrnc1Wb1HRaQF4Y08/\nAbXzaKQ/5xiJLF26ir32mjoizXau6/KXv9zHOed8malT5XsejUa49947aG1t5uCD92XOnO6d7pIl\ny3n00af51a9uLViwh+u63HjjD6mqKsdxYPp0gxNOOAWfr/eVAHbt2sFHHy3h0EOPzFif999/n7lz\n584VQnw653GMdI47bh7vvPMmd9zxABdeeE67xuL3+9l7b4O1a1ez334HsGjRu6xbt4FJkwpjP+0L\no0fXsGXLjoLZ8ltaIkM28a8QnFCpcXVC8LONDlEBqxJy1PG1uk/fqCOd0tIQbW1RyspKhroqeWFZ\nFn/609+4+OIrGDdOTgpNJBL88pc/46KLzu1RwZk9eybz5y8qaISgqqp8//s/QgiR9xyQqqoajjji\nmILVpdCM3PHoMOLggw/n3HO/yu9/fwetre1Lh7PnnjP44AOpEHz+8xfy5BPv8eQTDfzrXwtYs6Yx\nW3EDiqZpBfNNCCFGtEkD4PLROvulhei+0JxtrapPD1VV5eza1TrU1ciLeDzBbbfdzTe+cXW70LAs\ni1/84n+46KJzeh0Vv/rqfE488dQe9+kLgUAgb6ExEhjZrX4YMX78RK666nr+9rfHWLtWTrobPbqO\nxsaNtLUlaG6OMW36LKqqxzBm9BwaVuv8+8lVPPboBzz173fZtnXnoNQzFAoQjfa6ZHNOjERTRiam\nBjuuY8vQz60acsrKSmhtHdqAjny5556HuPrqH1BXJ2f3O47DLbf8lC996XQqKnrParBy5Vr22Wfk\nmswHm6KpqoC88vJyamr25PHHX6K0NIjP50dVdRoadrB61U58ej1WEgKlChUV5e0vtGXZfPBBC7H4\nCmw7QlkZHHTQDCoqCm8qiERilJSEet8xB0ZqVFVXjipT+dt2GVG1wxafurDcrqiqOqKebVNTM6NG\n1VNRUQlI38KvfvVzzjzzRGpra3o9/q233uPoo4/rdb8iHRQFR4FwHJdkMsGUyXtRVVlHPNHAV75y\nEaqqkkhYrF2zE8eBTEsA+3w6VVXVVFENQCJh8fb8ZhLJjdh2hGDQYb/99ihIag/bdgrSKTqOO+LN\nVClOqFCp90GjBc0ObLNhVK4rme+mjCTB8cwzr/KlL13S/v13v7uFefOOZOzY3CbrLV78Mf/1X+cV\nrD6O44yYbAp9Zfdo+cOARMJGUXVUVaG6ehR1tftyz93PsHbtRiIRixPnGSgKqGrv2mwg4KOmpoax\n9ZOYOGFPKitm8dFSh38/uYp/PfYhjz32DkuXNuA4+dnjHcchEilMFuaWljbKy0eW8zQbZZrC1IB8\nJrscWN1D+pEiw49YLNk+efFPf/othx++H5Mm9Z4xOcW4caMLNp/DcRwuvPDLBSlrOFMccRSIYNCH\ncOWkAEVR8PtDjB03iflvNRAOVxAuCQAKqpq/tu/36/j9lYAcijuOYNvWKOvWrce2o9h2lFF1Afbd\nbxplZdnNUJqmUVpaUhBTTFNTK3V1Pa5nP6I4qlzl3YjDqZUq+5YU9Sld17BtG10f3l3Ehx9+xIEH\nHgzAnXf+mdmzpzBjxtRu+8mswFZGJ/kppxzHX//6D77//R/3uz7Lli2loqKU1atXtIcD744UW0iB\nUFUFy+7sUNRUhbq6auLxNqIRG9d1cV2l32YATVMoKyth9Kh6xo2dyoTxs7Gscbz15i5vVLKEp55a\nyqJFK4jFOs8WHzduFA0NG/p1fiisr2Q4cNkojRvH6/y/KT5CfRDuuxuVlWU0NQ3/yKr33lvC4Ycf\nw8cfLyMYVJgzR6bVsSyb9es347ou27bt4oMPPs4aXqyqKlOmTGDx4kUFqM98rr32Cp544rF+lzWc\nGd7qxAhDUwMZt6uqjq6rJJOCQOZd+oUQgkDA75mOarBtgapJYfb+olYSic1YVhQrGaG6OoDfr9LW\nFqW0tO+zvnc3B3KFpnDJqN3bLp0PVVXlrF+/hdra4TuqjEZjlJSUoaoqTz75KBdffA627bBkyUp0\nXWP06Go++mg1ZWVhDj10nx7f189+9kj+/Of72Hvv7HmlcqGtrY3y8jI0TRCNRgiHdw9zbleKgqOg\ndH8xU4vBOI60mytq4cNYLcvG7+/w5tq2Q3lpkGDQRyjcMSpwXUEykSQSbWXBuzuw7Q1YySihsGD6\ntHrGjx+9WwmDIn0nGAyQSCSHuho98txzr3LGGV9g06YNVFWVoqoqO3c2UVFRypQpcqLtqFG9R1WB\nbJN7723w9ttvcMghRwBw880/5ZJLLm8P8c0FIaTf8dRTj+P3v/9fxowZy9lnn0dZ2dAsdDZQFAVH\nAXHczmYh1xUkEuC6FkIEUBQQLgU3EMqJeB0dvkDg93d/tKqqEAwFCIYCQK13rJwotXlLlDVrt2BZ\ncWw7hpWMEgzB5D1GMWnS2G75rYoCpshQs2tXK2PGjOX3v/9fzj33ZABqaipobNzWp/IOP/wgbrvt\nHg466DC2bdtKdXUpt932a6655vp253uKSKSNxx57kMbGRq699gZA5pfy+WQ7qa6u4vLLv8yuXU3c\nffcfqasbx3nnjezEkekUBUcB8fnKuplwXFcub+q6IITNYETpqWruTnhFAb/fh99fQUVFR+NICZSm\n5gSb3t6BbcelULHiaLqNrrlMmNA6pHmqigwswzkkd9WqNcyYMZPW1hYUxSHg2YBTI/u+ctJJx/DP\nf97Hzp07OO20Y/H7/fz61zcxe/beRKMxYrEo0WiEQEDnsMP2Jx7vmEy7cOEC5syZ2am8qqpKhIDj\njivMuuPDhaLgKCCaGiAWg2BQjgAcR3bMAMlkG1VVpQXX1DO1bVXr/zk6BIqPsrKOpTKFAMd2SCaT\nLF8eJZFsxLETOE4S205g21EqKvxMmFDHuHGjO5nQiow8hqsv65VX5nPNNTdwxx1/4rTTTuDVlxuY\nPWcMqxsa2LHd5YOFixhTr3P8iXPyKnfKlEm89dZCjj56Hvfc8wBXXHEB3/zmBbS2thEMBgkGA+1z\nNB566EnOOqsj9Hbx4kWcc85JncozzVWMGzcxL3PXSKAoOAqE4zgoikowSLu2r+ugquD3a2h6WQYP\nSP+xHbsrL1kuAAAgAElEQVSTGcm2XXy+gXusigK6T0P3hQhniKpyXYFl2ezcGWPjpiZsSwqV1J/t\nJAj4BdXVpYweXc2YMTU5ZQsdShobt5NIRJk7d++hrsqgUlISIhqND7vouU8+2cjEiVNwHIfW1l2s\nWLGJxk0669YtRVFcKsonUD8mRDQa45673uaCC/NbyfC88z7HX/7ydy6++AruuOMuQiG58t4ee4xj\nxoypjBpVy4oVq2lrS1BTU0dDw0oeffRB6utrO4Uvu67LCy+8yfXX/09Br384UBQcBcI016JqWqcR\ngKIonmlq4OxTtuUQDHaEaqmqgmXZA3a+3lBVhUDARyDgo6y8u0NQCLnqmW3bbN6S4JNPmrDtJI5j\n4bgWrmN5gjCKgkMgoFFaFqKiooSqqgrKykoHfcb6xAl709q661MxIzidqqpymppahp3geO6517j6\n6ut58MH7OemkY3nphbWMGT0D265AVWjvvEvCYZKJOrZvb6K2tjLn8nVd56ijDuTee+/ihBNOYs6c\nfRFCsGrVCpYuXUJj41uMHTuW4447kVtu+RnjxtVx4YWf7/ZuPPLI0+3ZI3Y3ioKjQJgfN6Kp5WgF\nMBPlS7olQVUVEkmB47ho2vB7YRVFpljx+XRCoSBQ0W0fn65QXVWC67o4juMJGovt2xNs2hTBdWxP\n0DhYVoB33l6D6zo4roPrOthWEse15OhIV/DpKv6An0DARzDoJxgMEArJrKXhcLB3YaAIRo0ezcqV\nDcycOb3nfftJxHF5dKfg5CqVGn1oTUTl5aVs2rSNceOGT+r8TZs2U18/HlVV2bBhLccffxC6thNV\nUfBnGGmXlJbzxn9Mzjjr4LzOM2fOLKZPn8LChYt59dXn0TQNRdGYNGkye++9H2+//QZCJLj00vMy\nmvI2bmzE5wszadLkPl/rcKYoOAqEbfspL1exbIFviBu8goJjD0/BkQuKIv80TUXTVM9PkpvWmxrx\nCQTClQkL5cRLF9d12j8jEZfWFgfbSeA6rox4w3MICyFL8MqqqqohGAyyePGmARUcQgi+strmlVbB\nTzfBlIDCtIBCjU/BEeAguHKUxvjA4DxXTVNx3eGVfuXpp1/myiuv449//C1HHXUQL734IWVl2de4\n8ft0du7q2/0KBgPU1dWx//5zCIWCCCHYsKGRnTt3cdllX8x63KpVa3jppbf43vf+u0/nHQkUBUeB\niMW2ES6ZhGODqrogGPCO2xWCTH5Lx1VwnOEbEdMb/XHGpg5VUKB99NfTiEIQiyUJhXqemSkEhEPV\nbNy4lXHjBsbR+fcdLm+0yue23YbttmBBpPNzfKHZ5ekZPkb7R6ZS0B+2bdvBsmUr+O1vb+b000+g\nvn40772zgPoxPT87Vel7mp1p0ya2m5oURWHChLFMmDA26/5vvLGArVubufbaH+6WJqoURcFRAIQQ\n+HwlBPwK+MEVEIvFCZeEBsQhnsK2MucSCgUVWlsS6D61Pa58JNGXfF59J/ew5blzD2PXrl18+MFW\nYvE2Vq58nwMP+AyjRtcRDun4/Ek0LX+B3WS5/GKzw7NNLr0tB9KQgJs3Ofx2j923U8rGunXr+cpX\nzma//ToipTS995FoMFiKaW5k5sz8V9/Mp/N/+OGnmDBhKhddlH00srtQFBwF4JNPGtF9Hat8qYoi\nV9pzBcoAdoKO4+LLEO6qqgo+n0prS4Lqmr6nFRkq1GEY/glS46yurqa6uhoQ7LnnPiQTNm2tUZqb\nk1jJBInkJvbaazqqmpsA2ZJ0OWWFxepE7/umeLnFZYflUuMbeOGhaeqwCQo44IB9u21T6N2UFg6H\n+fCD1X0SHLlgWRZ33PEAp556FrNn7zMg5xhuFAVHAViyeDWhYGmnbdJmLshVo+0r2UrXNIVY3MZK\nOvj8Q9/o82EghW3hkE6R1ORJkOasSKSMNQ1xduxYzdwDZrBly1bmz3+futo9WLX6AyZPnsghhxzg\nBQbAf21w8hIaAOstuHKtzXm1GjMCCuMCCuUDFJQRCgWJRhOUlQ0/BSQSsVGU0l730zUNx85v+da2\ntggvv/wGb7yxgG9846tMnjwp435NTc3cffdDfPOb1+x2czV6oig4+okQgrY2hZpaf6ftiqpiJS3U\nQCCjH2Iw8Ps0WtsSVFcPv0bfE66j4LpyDszgUBh/kKJASUkJJSUllJeXYX68lVg8zmc+cxaq6mP/\n/Q+kra2VhoZmGjctY2v5KN7XqkDJvxk+2yJ4tsXGD1TqEFLhgWk+ZoYKe9NKS8Ps3Nk8LAWHZeWu\nmGlqiDUNOxg3rgp/luCClpZWXn75TZqaWiktrWDWrNm0tkazCo2VKxt46aW3uP76n+L3+zPus7tS\nFBz9ZNeuFlBEt9fX79NxVJWYl5JASdsjGOy/MMllBT5NU4jFHCJtCUpKByAt7wAghKCpOUJJiY+B\nHq21n7OAZaWeayDgZ9y48cD49m2uqxEOV6IGKnDrJrI+ZtGyoyXz9P8cSQJbbZgZhOnBwt+vuroq\nFi9eAdQXvOz+Eg7nPpKuqqrhnflNlJe3cfJpnQXBwoUfsnDhR9TVjeKkk85mzJh6IpE2fvObm7jy\nygszlrdw4WLWrt3Cddf9aLd2gmejKDj6yYsvLKC8LPMQVdNUwqHOQ2TXFcTi8U6CJBMC0b6Ppmv4\ndL2zsFHkXr0RCKi0tSZJJJwR4e9wvRDaZFKg6YAA11Xw+QBFgJA+nEKO4lRFwRUuqlLYDqBrHW1X\nsCbpsiBucW9zjOUFnKjZ4sCTu1zOqC68WbKqqpxNm7YxdmxdwcvuD9FoFEXN7R5qqkpdbTWtbS3c\nf//DnHfembz22tusWrWOgw8+nOuu+1H7vq7r8n//90suuijzHI2VKxtYvXojl132rYJdy0ijKDj6\nQTJpY9u+jJlos6GqSjdh0hMCmRsqHu8whCuKl8Qwh94zFaEkNfjhj3BdVE2luTUm/USeNu7z6eia\ngqY6VFT6EQKEq+K6ar+FSCDgJ5FIdpqBX2jijuCZSJIfbmulNYcRRliFaB5TKDZZcN16Gxc4q8DC\nY8KEMSxf3kAoFKCqavikB5//1gpKS7KHxmaipKSM0rIj+eOtr3L6mQdx1lkXdNvnzjv/zCmnHENJ\nSXdFa/Pmrbz22rtcc80P+lzv3YFP3xirgCx8bwWBYH5Ot3xRkMt4hkKB9j+/3+dp5g6a1nMWU1cI\nVBUCwZEhONz2FPGi03VZlk0sbmE7DiUlUUpLo+g+Gbza3ySuiqL0u4yeiDiCe5tjfGdrS69CQweO\nLVPYM5S/NNxmw+r4wFzIzJmTaWjYMGwmBAohaNoZIODPT9irioIi/EzeYy8WLljf7feXXnqW2tqy\njH6NlpZWHnzwKa6++r8+leapdD7dV99PVq1eT3lZ71EdhUZVFYJBP8KF+rFOj2lOHBv0PEZEQ43r\n9u67SREIJAkEEnLC5TCl1RE83Zbgxp2RXved5Icfj9f4f5N11ifyFwAaguMqBsYvpCgKs2ZNYdGi\nj4eF8Hh3wTJ8et/bns+nE4t1bhdr1qxi2bIPOeaYQzMec//9j3HddT8cFqHJQ83I6VGGGS0tUXx6\neEhTTgcCARoaWtH1cnqKYB0Jwa0phOh55ni6wq6qgmAogeNoOM7w04FaHMFbEYvrt8u1u6drKqN0\njQUJq9NEPx04qkzhd5N0xgdUftNos6UP7g/huly/3ubECsHV9YVv2uFwkFmzprBsWUOnmdhCCKqq\nyhk3btSAt4fW1hj/fnIhPm0c5X1cCyYet2lti3Pq6Qd22v7QQ3/n0kvPz3jMggWLOOSQIwkOsIVh\npFAUHH3kpZfeobQ094ybA4HtWFRUBIm0iaz+DsdxKavYfV72THq49IXk5PLJs+S+kxIa39rajAvc\nVFPOgX6dRsdl/tam9v3G+eDiOo3vjNHaO92zq1VaXVgedXk3ItjpZD5HqQoT/QqTg6ArCk/tErwT\ngVE+l5grCCqFX6kxHA4ye/a0btu3b29i4cJlzJ27Jzt3NlNTk71ttLZGWLeuEV3XmDZtYrfVJXvi\n8cc+oLrKwLFttD7M92mL2MRjFp/57B5MnNjZ2T958lQ2b95KfX3npI6u67Jw4Uf84Ac/yft8uyvD\nT00bAQghiLTZBINDF7vtOAJVbaV+TJjyco2KChVVlXMfwiUKQggcV6BqKrqu0dYW7ffqaMMB24ZP\n1iu0tkLqcjR96NLIZ8JxXJ5piXPTtp3cUBPkrUm1nFYeoEzXuLsliguEFTihXOHh6T6urtc7dfCT\nAio/HqfzwHQ/d07R2buLv2NOSOG6eo03Z/l4Y08f9031c9dknaPKVUKujbt4IYe+2MDPzCYGi9ra\nSmbOnMzixSswzbWsW9fYbR/bdli6dBWNjdvZc88plJeXyHD2HHBdlyVLVhGPKfh9Ws7DaMfxovQs\nl+Zmm0Qizv4HljN9xh7d9j355NN55ZX53bY//vhznH/+V3M74aeE4oijDyxfvoZgcPB9GymEECSS\nEQ47bBS6rlFdIzW2tjYXXYdgUGXVKgsrKdD0OLFYnKlTwqxdmyAUHl5rK+SL6yrEYhCLKaiqYNpU\ngd+fxEr6cBxtyCZbphBCEI8nOCiocPaUUWio7SOisE/hwKBC0ra5clKQEyt717SPLtd4ZqbKd9fZ\nNCQEZ1apXDJKQ+9yoYqi8MA0H5viKlu1Mm7Wa/lrEyxckaRWh2pdQQWaHTkasoScNBhUFUq8kcvR\n5Qp7hVQCfZy5X1oaZp99DAA++mi150wXOI6Dqqq0tUWZNWtye/RaIOBn585m6uqqupW1a1cL7y74\nmK1bkihKCFUNEg6VU1c3EUVRUBRFBlL08MAt2yUek9qFbYMghjHLx4EHdU9dAlBSUkoy2TlbWEtL\nK5FIkj32mNKne7K7UhQcfWDhwhWMHjUweW9yIZm0GT9e7ZbgsLS0YwA5bVoqiiptVKTE2R1I7yt2\n7YJQMIgQw8eTo2kakzOMRjVFcHl1GV8NaZTrMXJd4CusKvxpcu9RcT5FYVJIZ9L+s3lQCD73diP/\naQl4NyybKa5ju74JxvhgRlDhnik6pXrfDRJ77TWVlpYImqZ6UWui24JQNTWVlJaWYFkWixc3sHLF\nVhzLDwQJ+EsIhScxepSvk3CIxuIIZKoXK2kRCGQf9WuqzEDguuA4McZNDHF0Fsd3R51GsXPnLior\nK9iwoZHHHnuGa6/9YZ/vw+5KUXDkyXvvLiUYrBjkDK4dCCFAaWPy5D4sriN6y706snBdBcsqbbd1\n92e04fPpJC0Lf0GWse3eSbene1cUwuEwzU0uO3bEcN0E5eUaVVUlfXqnEq7guWaXMT4Y71ep0wVr\nE/DILpfqulqq27L7SLpiAxss2GAJvtJg88A0X59HHwDl5SVZf3vt1Y/ZuKEFhB9NDRIMlVFdWYOq\nqsTjSUJZ5tSkki7qmkail+gu15XPwbIiTDNqOfKovXqt82mnncntt99KWVk5EyZM4pJLvkk4nP06\nPq0UBUcetLTEWb58C2PqxwzK+VKRK0J+QQhIJndy6GFj+uT0LC0TxOP2gK5J3l8c2yEWk5MdFUWm\ntZYzxVOfHdddVVGK399fp7hE13VisTj0U3CkzFI9oSoKZWVlQBmuK7Btm8ZNMZJWG36fg8+vUFNT\n2uN6LlFX8H+NDk81uSz35m5UqPL8loBIP91Zr7YKrlxr89cphZ3/I4TgiX99iGNXM7oui/KT5QYK\npJ/En5YROlu2qnjCJhYV7GhaxNlnnsHkafU5rY9TWVndaRZ5kcwM3x5kGPLMM69TVVU7KOGtQgj8\nfgVjpg8h4OPlFtFolLkH1PR5gSi/T/oHhitCCHRdI+gtqtSxep/AdRws4XbqU3QN9LgKikwpoetd\n7f7yH0WRyVukbbwj0qjrZyHqH4sn8hLMqqp4GXZ9uG5Z+zVv2hhh3HjRaRTS4gge2+nyZpvLhxGX\nFV2y6ra68PlqhYgLDXFYmxDE+hEs9uQul99ttvn2mMJ1E888vRhELRU9jEYEZPRfRKMxmefNa4G6\nrrWPPtqPFYKk5RCLWsAWvv71rxGNWiN2NczhSlFw5Mjq1esRrn/QIqmEgClTdYJB+cJPnqKzYYNL\nY+M2pkzpm39l1Kgw27a3oqplGReA6ji3IJm00DSt3UY9GHRdv0Tx1jXJNt/KdsD2QquEcKmqDBNM\ny3wqhIyo6RixyVFbagJbamZ66jNl2ugr0WiccDjY5/slhYSCpqmUlpbSuClKSWmMysogEUdwwscW\nZg8zw2t1+NVEH2Wa9Cksibr8dJPD6y2CZA7n7+oJSQB/3OKwf1jhyPL+T3rbsGE7LU1B6mp7Nv34\nfDqO7aB2EcCqoqClTQ71+XTisQR6SNbNshza2gSOE2fchCDHn3AGgaCPyu6+9yL9pCiGc+SN1xdT\nU1MzaOfz+VVKSjoeT2WlxuzZNTQ1tfa5zEBAY999yrGs7N2IEOA4juxEXJdEPEksFk/7S5BMWDi2\n02Oqk77gitxnjXdFUZRuGqrM6aWiqSqapqHrOj6f3q7hBwJ+AgE/wWAAV4h+5apKJJMEgv6CCVlN\n0wiHS2htlULu5k1SaPRkOBrnVyjTOkZRe5doPDTNx/9O1DFymMozOkPhW234/nqHbVb/bF9CCF56\nYR3V1bU57ExG+1PXt01B6bQtGhNEo1s5+5x9OfVzh46YNDsjkaLgyBXFGtRZ4sFA9yVUI5FYv9dF\nUFUFhEsikcCybOLxOImEjeO42LZDc3MTlmXj8/nw+X0EQwFCoWDaXwBN13DahUqi0188niCZtHCc\n/AWL64o+Bx1Is1TfBJk3JumXOUNVVGw7Ry90jriui5VU2RG3+dc2i6vKS7imMrO2Xu+Dv0/tPopU\nFIWv1mk8Z/gY30s/OkpXOLy0+/1fHhfcuKl/1/bowx9SXja204ghKz0FgXXd1QvLBUA4TJtRSm2G\n8N4ihaVoqsoRTRu8+Q9CCEKh7qaBhoYN7Lnn1H6XX14uCATixGIulVV+bMth584EiYRgxvQwK1Ym\n21eoy4SmqVk7WSEEruPiOC5W0s4601s6veVoIGWecl23z457IQS27eLvw3KqCgq6phFPJAn2EN7Z\nEz6fjh0rbLizrusEgyF+tj7KKaWlnFsR5oj127rtN8EPFZrCGH/2a6/QVaYEFTZY2Xvk1QnBvVN0\nGtfbNKT5TypUuKi2b6aqHbZg68rNuHYN5ZW53dtUoEL6u+CmpThJx+/TsbxoONtOcOJJx/SpnkXy\noyg4csCyHHRt8NayEAIqKjNr3oVw8k2e3F1rHT26QzAGAnmuZZqGoihouobWwxyFdqe345JIM3nZ\ntt0vc1F/xoN+v09GVQ0jFAW0YBin1eGEygCrLKubIN4zpPD7SRrXfdL7iGBKQOE/rdkFR8SFD6OC\nm8brPL7LpdkRNDtQ71PYpyT/9+4f2x1u3Ghz6XKFCVruvh9pJhWdHOSu62YcrWiewAeNhL2umIBw\nkCgKjhywbbcwMZ85oukKZWWdG4nruoNoKhtYC2aH01vrZLPvT8SXpqno/Q4zHj6TCEEqEB8kXfYM\nBZjh83Pe1l2dfvcDPxyrMbdE44fjei+vtJd1yUfpcG6NSr1fzWlWe1d2WC5vtwlOrFRZERP8z0aZ\nrHFpuZ9R0fxMXbpPJx5PtK9do6oqVpaFr8LhIM1NSSZOHJww+SJFwZETfr+GYydxHHdQwvoCfqVb\naOmOHU3U1g58UkUZWTSyXotgwI+mKQx9xGVhBc9OR/BYS5z/ritlZcJiWZeOc05Y4cQKedHH5BD1\n5PTiNzioVKG+B3NXNt5odbhjm8uCNpdGC/YMKugq7Rl+n6wNMnNHnNF5KD4Bv49orEPYqD1MkFFQ\nsJ0mTjjxM3nXvUjfGFk9xBARi8XR9QC27ZBIyogkTdPw+3wDMhDxB7oXum3bLmZkSMxWaJqbo2ja\nyFifPIXjuJSVBhnqtXWEKGwSyUpV4RvVYUpUhafbupsPDyhV8hqFtvUgOQIKXJiHH0MIwUM7Xe7d\n7vB+RBBNK/qjLiHDtqqyTdcQrpuXaPWW8+p1meVoLI7rCBDF7mywGHIdbSTw3rvvEgoHCAR8hENB\nwqEgmqYSjyeIeiGqtu0UJDG3EIJQsHtDcRw3r/TTfWXHjhiqOrIaoO24OE7/VwLsL4GAn2g0jm0X\nJluvqsAePo0WR/BUpLPg8ANnVuXefN9rc3ixJbtgm+CHY8tzK+/FZod5psWVa23eaOssNLqiCMEV\n2+Mcajl5j8c0Xe8UqSbSPh3XJZFIEonG8Pl0AsFSHnlwUb/n4hTJjaLgyIGlHy0kEOgcVaVrcjnX\ncCgo5wG4gnhaSGpfU5gLAZVVQ2drj0YL44DPm370+q7rEoslC7yiRv7IuRdBHMctiKNd8ZaVj7rd\no1MnB+DAHB3WrbbL9z5xaLRgsh/umKxzTnXnY7dYsCHZ+x385w6Hb6y1WRAR9Jj5TAjKLIcfbI5x\nkOu0zy/JB13XsG0Hy7aJxRM4tuMpanFsy0b36YTDIXy6jqYGcWgYshxynzZGlmo5RGhqEFXNlhVH\nNm6/Xyd1O11XYFkWiaQUHqqi4vf7cnqpNU2hrVXg87kEAtIUkUgkO+XnGUgEQ5OavGOt8dxRFIWy\n0oCXnkXrcRXEwSQQ8OM4DrF4ImuyvnzY6Tq0dNGkJwS6T3jMxs2NDh/GBBUa/Pc4nbOqNU6tVHk/\nkmSVN5BpdeGFZsFFo3ou697tDtu9AZUiBMfFLPZLupQ6gpAj0AArrBFIOPgslyoVAn1URFRFaU8p\nEgj4e7yXrguRSBDbdtB1jXXr1jBp0uQ+nbdI7xQFRy9EoxHKyidnz6aWAVVVOqV7dl1B0rJwXRfh\nChlN5NczhhcKARs22GzYqOD3KwQDEI+3MXHSYM1aH5pwxr5M/vPpGsGAPuS+jUxomobuCqLROIGA\nv1+juBVJi2iXEVk+Cvz0oIqCyxdrNM6qls/XryrsE1ZZlegYGTf0ss75oojDoojcZ1IywQVbYxg+\nvUMwpC4x7pmX+pGWPYWmqjnN7QmFVDRtFPfc+SwXX3YKjzy0EF17i4svO52SkqFbO2d3ZRg2ueHF\ngw8+QE312H6FwqqqQjDgJxQMoqpy9GFbdqfZ1uk+klRSPispaG0VtLVBZeVgvfxDo0u4rouq5P46\nCgGh0NA7xHvC59MJh4PE4wn6szRtLMNaI/mU9sUalZdm6tw4vrNS8LkqtVMH0Ftg1l4hlUem6/x4\nrMajs0LUt7X2eTRRKFwhF4ry+VRKSvwgynjpxTc5Yd4MdK2O995bOKT1210pjjh6IB6PY1mhgjml\nLcvC59O7j0iEwLZsrFiHU1XTNHw+zcu35AzKHI5YLImiDM0rIVyBmoeGqqoqg2S96zc+v45t9y24\nwRHQmiEaqiEuiDiCkhyGHgFVYb+S7uc+sUJlFBab8bFvWOHLtT3ff7+qcEiZxj4lgvu3uzSUhjnK\nFfgGyEbY9apdIVPQO56S5TguPl3DdhxKSkIoyHa1ZnUbDauS+P0BdmwfXssK7y4MY31t6Hn4oWeY\nMH6vgnXajuOiZeg8VEWm1g6FAoRCAYKhAKqqEE/IXFDJpOD9hZvZvLmlPbPrQLBtWwRNG6IRh+ic\nGbc3VC9F+khAU+XiQ30h7grmx7onpVyVgN9u7l/+qICqUBJtYW4IHpqmM7aXORxLoi6XNFgcsSzJ\ntett3iwFvQ9O79wR2E6HQzwWi6OqKkEvstHn0/H5fTiOn6ZdNpbtgiLQtRKEcNGD6zn66IMHsH6f\nXoojjizs2NGMqlX1mH48X2RMeu8oyIiSDg01gGULGlbbrFrVjKraaKpDKCQYP6GMqqqSggi3lhYb\n3TcyUjaoBe6wHNeVDu1Y39OtZEf0OWisycksOACeaXK5tl7g74fGv8+2Nfzm0DFU9DDaa7Ndrlnv\n8HKzyw5PVtU4CX6gl4DlDFhWhVQOsWx503w+HcuyZUZlodDWGsdydqApNUyeWsP+cw/ijf+s4fSz\n5gxI/T7NFAVHFp566jnqamcWrDwh6HUiU09oqoLm94GXpEMIQSwGy5fbCNGEqtqoqkso6DJ6TJja\n2pK8hZ7r6kMWzui6rtcJyFTovQlCTVUL2l+pXo6tQkRBZSIS7Vs+FQXQssya/iguuHObw+Wj+9aM\nN25s5HS9tZvQaIi73LXNRVVkfqsnmhxebuk4f1C4/Dgm0ON9M6EKBLbtYNvy+L4mltRUlbjjYluC\npNXEKZ/bl42fjGfHjhhTpo1h2Udb2GNyMVPuQFAUHFmorCjHcWx8BdLAZarywt1ume8JNK1DmADE\n44KVKy3Wro0TCruAg4JNWZnK6NGlhMPZO0YxRBFVkFqdT5FZdS27Vw1dUxXicQVVlSYuNbXSX9pf\nfhWQfpaBIh/Hfzo1usoBAZ3X45lnTazuJRKqJ5555mUuuOCcTtteaXG4Yq3N5iyTNBQh+HbEYkys\nd6EhkAqBbTu4TufgD80LsXUdl0gkRrgklJdalbRcIm02jmNRXhng4i+egqIojBvntC83PHVqDmt/\nFOkTRcGRhXknfYZ/PvAi9fWTClKe4zj4/AOfykPTFBRLIVwSIugtZCNcQSzmsnq1hSuigA04qKpN\neZlObW2YkpIAQxWKC7Izkaa53OpgO4Lm1gTVlWE0VcjlZV23Y9W/bv2pTMudLfuugjLcchwC4Ffg\n5NJAVsER66PLq60tQiDgx5e2xnpD3OW6T7ILjRLb5fIdEfb1FshKkRIQju3geM8ghaqq6LqG3+/L\neHtVXcNx9W5LwKZQVFVG3KkqluVi2zaRaBuOm2TUqApOOe1wVny8Xa4eqSmDkl2hSFFwZMXv9xOJ\nbsF1JxbMfDNY/ZIQqQmJ3nlVBV3VuvkvXFfQFnFpbrEQIspIeh1S1htFUb2RV+/HOI5DNBpHygj5\nNASCUDCQteMqFD4v22u+aeMVBUb34H/oq+B4/vlXOfnk49q/v9HicO16p31CYFemWw7f2RSl0iew\nbAvURm4AACAASURBVAvLe5lT77Sqqmi6nJ+Ur0k2ldLeUqxOa4qDnKuTTFqoqk5T83ZKyiL4QxHs\n+Ax2bLf41yOLOf/LB+Z1viL9Z+T0FEPAxIl1WFaSQKB/I4XBzqEk/QSdG2+zN6s3PbW23E+G/dq2\ngxjAiK2BwnFdfDkGB8qUIJ2FgxCCeDyJ67oDOjtfasLCM8sEvc5Rjow6RknyzxVylJjS3LOlEwcZ\nddUXdu1qoqamGoDbttj8YbPTns02nYDjcnZznGMdQVWJhgCErvZ5id9MKEA4FKQtEm0PTggE/Giq\nSiJh4TgajVs+RlGacUQ55aUzQVeIxbfgC24GioJjsCkKjh6wrCR+X//HCbZtF2CtiNzJ1KaFgE8s\nwYygdLZ2vSo5iWqI5nCI3KLNulII57iiKIRCAZJJi0QiOaD3QNd1FEWhtSXSbiKS+ajSfTMqutbh\nswEoyzABMMU+4fw78CbL5Y/TjuHfK5K4wLttglgX+aMIwVltSQ6PO9QmkgT9OnjvjTIAsy5d4aJp\nMjhBIEgkLCwEySTEE1Hqavcg4A+iqBCP2VjOFr564QmUlpYVvC5FeqcoOHpg506LceP6r4XatkMw\nNDipyh0vpUlXAiokXVgVB58imNolA2/KjjwUiDzncKRTqMgqv9/X7iMZyMmWmhdeKvNr5fZu1Woa\nfqBrUK4RhKvG5G9e+/HqNhpKa2nIshqg33G5ckecfYVLWFOxdBXbcfEP4PsRiyUIh2XYrYKMtEok\nZZBEZaUfn67Q2hbDspIc+9nJGMYRA1aXIr1TFBw94PNV5pxIrjcGy79hWS6lZd3DG/2Kgk8VxF0x\nwJO28qevQqvQJsBUNtaBHnlJf0cy50i7KT6V71WXctPOtk7bT6zQCPYgcFNC0HEcdu2KsnlzK1u3\n26xXy1HCglltSdpU+KSkQ6nRheDK5gQH4OL30olomkYikYQBvC+Z/CJNuyKoqiAaCSOEzeh6P587\n46hBXAmzSDaKgqMHhNv/dAWD7d8Qrksg0P2xaopcO3pjUqBnbHdD1xhdV/QpCaCqKugFzJWk6zpR\nb32HgSYY9BOLJXI6l09VODzsh53yuwqcGVY5L7GLpUubMx5j2y4bP9HRfQEcW0FBQ1H8aHqAc5IO\nx7dEUeIOwoEbpvo5JG7z2YjFRE2h3O68vndPq+8VDKWz8LAdB9Q4U6buwcGHTaWiItTDwUUGm6Lg\nyILU1vp/e2zbHtQQQVXNvp5Gta5gi8wiwnEc4rEEmq6iadqgmq1c182rsw4GdDRNRYjCh9CqqjYo\nZjvHcfKK1ttDV/h1dSmvxuOcUxrioLCPgFZOeUU0owbuOC4bP9mMrobQuwxA6wJQ7QhiqoLwwb27\nYqi2NwPdEQxFfnpdl6OaVA43IQQ+PcDq1Ss44aTZ/7+9946Sq7rzfb977xOrqqPU3UqtVkIoZ6GI\nhBA5GBswngsMGcPYYxzGnjte47l37ty33r3X971Z707ACRsGnDEYGAawRwzRZEQwCiAhUOqkbnWs\nqhP3fn+cqla3urorh27tz1olmqo6++xK+3f2L3x/JZ+PZHyk4SgynudnnYKZD+liBY1jBPsjkRCE\nEEMFeEEntVNa8oScyskv9KIapNVmvlgZugrDYInjCjoVaLoCx/FyrmbOFNt2h3z6mRBmBJeGGD5X\nVweW2ABQNnahI2N0XOVgxggiSeFDjrIYi+FoqgrbcYd6mKiKgvq6Wpzo7i3rvCSpkYZjDAghcN0u\n+P5MsDxjAqVyyXIuQPOoRUgW4aXaIXmeB9f1g3TRFCmglBBQRhMLVnGv1gVIUYwGELhLeI7dGzPB\n933Ytpu1O4wQAirEkNEgRCAUio57DGXl7omYHbqmwrLsodhPkG03QSSQzzCk4RiH83duxhtvHEVd\nbW5NlEod33A9ATNUnI+U+0Gdw1huMM45+IjdynCCnQslQX0JTRiXXIOcsbgTpGYWw3AU0crH4lYg\n2hfSsy6SGwERMENxsDSGIehaWTh8zlM2HysUXHBwIaAnjGpgIGW6bSUiDcc4tLTMxTPPPI/amvqc\nFhTPL218Y6zAeCHwuRjKsklFoA9Ex/1CCS4SKrQj9aiCnuEjS5aTrjGSNDbDDA0lxZUHoZQUJ84h\nUJgiQ0FASHqjwKiAKNDmyfV8MKU4hkMk/qWEwjSNUx8tAeQSVZnITyUtcXgeoObwe2eUFb2obARE\nFEyUsRgkpU8y0aNKusREwtDYloNQOMisEVxk1co3W1RVgef50NL0p8gWJVGhn+/FRGA00hsOygQK\n5XVTGAP3/YKn5IpENb2uaVBVZcRH2tcbRXV15nEgSemQjZzScMkll2JwsCenYyklIJTA8/JruJPN\n+SYLgYIqhaIqgUDesCtdwoq946BFaZjFfZ5X73HOfTDmQ9McKEr6+VEaNMgqCAQjxAtzgQsBx3WH\nmjLF4hZiURsAQypVFc4Zzt1WuNYGksIhdxxp0NQpsO1DCb89ybrHta5riEXjYEp2stG5kGv19UTD\n1FMrrRYKUYTIe3IHlU8MxfdthCOZ1xaZIYJ4TBS86VU6uBDwPR+e7w8Zm0CqhEBhClQzEEL0fB9W\nXADEQyxqgXOKSDgEABiMOqCUYGaz7KdRiUjDkYbpM6qxbPlMfHwwBtPUoGlANpe7BIBh6LBzUEbN\nBs8XZ4ykNGXFzVSjlMBzPcQL0J+Dcw7T1EdIauRKthpR1dUaujo5UIAiydPf7lO9NhLJEEIMOc+C\nBk1BhpoZMlLGRRyHw3UFdJ3A9YBwWMGJrg7E4iZCZhi2JXDz7VvynrekOEhXVQasWrUI0WhnQsk0\n++OT7gm/mGmenh8I0RVjbJ+X1Q0mTrtSL/5MgkZDhqkN9YHP9RYOG4jH7cBtmae1yzYTq7rayNu9\nBARxCJDA7Zp0M1lxC57nwXN9GIYGwzSGXLK6riIUMhGOmLDi9qhojOdx+D6gaqey63RDh6r6uO2O\ni9A/0ApC2VAxoKTykDuODHBdF4qiQ1VJoqI8+zF0Q0csh05nmSKEgFqkjCpe5F4Vac8vRhquUmQ5\na1qgJ5V/K9kgVlOIRZAQiqBaLzOqawxA5Naydjie54MxCi1Fhgj3LQghEIvFEQ6bYJQiHrfg8KAb\nlAAQjcYQMo2hLDVCCDj3MdA7CNOIwAwFvcNra2fgRz98CKtWr0NjY23e85YUD7njyADGGITwso5v\nDIcA0A0NtnW6xmlhICl6cBQKn3PQAmpCZQtjDNURHYZOoas0cCPF7aGbZTmwHQeO68LzPPi+f6ob\nYI5mhjEGgsBo5Uu2lfFjQSmD62aeaGGaKkDym7/POVzHS2k0gMAwxGL2kNFI3mcaOjRNhaIEasCW\n7SBu2bBsG5Qi0XPcBefBe+37PkzDwJS6xXj/vf04e9HsvOYtKS5yx5EBw/P581mcFcbgOl5RCqmK\nWaxdqIUvVxRGUFWlp5SLTzZD4slGSMNbyCIR6M5xixJcSVsIh8y8Xj9jFF4Bdm2UMti2l3HKdVBb\nk9u5BIB4zAKhQZxiLHRdC/qIDOuomIRRCpbYaYVMA57vIxaNw9B1+NyHrutQFIzw/wpBoTLZK7zS\nkYYjQwgpjKvGMHTEYoV1WeUrNVLpBIv2WO8WASFBcyoABW+bHnQItAFCcnZbqZqCeNyGYuZrOIKO\neJFI5vOgNLcdh2XZ0HQ1rbEbfgEkAMSi1piGhhKKqqowAEDTBHTTwmA/g4gaYAyIW3Yie5Ghp6cP\ndXU1Oc1dUnykqypDLKsDvi/yDjYSElylFdJl5bocepEC45VANGZjYNBF/6CDuFWampgkQeU6zWu3\nQECG1F/zmgslsO3MDcHBA3H4fvY/cZ9zCC6yes0CQHQwBsPUx+xhY1kcXuI3FA6F0H3CBucEukGh\naToMQ0M4ZAAgqKqKZD1vSemQhiNDqmsE6qfEoaRuZpEVisLGFAvMBS4EdGPyGg7f57BsF7GYU5TC\nvHRwzvNOddZUFYSQvIyH7/kwzcyD7F2dDhxHIBa3YNmjs5tSwRPuuUzf52QNu+d50HR1XBesqlG4\nTtBTHQAMvQaEuBgYiAUGUSRSeWn+1fWS4iINR4YsWbIC7e0HCiZcaBh64AIpAJTk1ggpEzjnBeuC\nmC/lirUYho54AT4rTVMBQuCmKpPOAN8XWUlwBNnfQU91RVEy+r65rgfT1BGJhDI6RzxuIRaNZySt\nozDAMChOdnejtbUbnkdh2X2oqdExGB3E4KCL3r5+aKqUGal0pOHIkAULFiIWbYHvF8ZyEBJoIjmO\nm/dYxayx8P3yZlQNhxACTSv9lSghBIzSgnxWuqbmbDg0TUFHR+bptU1NGijlwY4p0ZwrFrdgWTZs\nJ2hda9kOBqMx+H7SBZi9OzYcNhEJh9LWmSQFK6dOnYKGxlqAWGAMWLhoFhob62HbFgCGjZvnZXV+\nSempjBVhAkCpAiF4Qa94k2J6+cRNOBcgRQyM+z4vaw3HSPISI88LXdeGLa75oSgMsViwgGfz2SsK\ng++ld0n29MTw5BNHsX/fCTCmg9Hg89M1FSHTgKqpQxlqqqIgHA4NNVHyPB+qkpnbMygMzW0JcR2C\n+vopMPV6eH4fNmyeA0IUEMJx9uKmnMaUlI7J6xgvMIQAXBQ+MJt0g4TM3LbnnidgmMX7GIUQFaOB\npeusrGnBhapZ1zR1yK2TjRQJ5yLxHRxfqjket8CoBk1NHQ8ZikMMux4ImQYGozGEw5n39nYcB4aZ\nfaYZIQShEIVlCTBm4I/v70dnmwMuBDRVBsUnAnLHkSGMUVhWa8FcVUkoJWCUwc1RQZcXsQdHpWHo\nrKj1KqWEEALf97OSwXddF1WRKWnjbO+/E4WiZN8HgFKa8Z4uWVqZ6x5QCEDTCRSVwrGq0NU1CO57\nOOvs3JqmSUrLJPkZloYLLtiKvr7ugo+r6yocx80t8E4E1DL4/ctB+RxVxSFokZrZAh9k4XEwxhCL\njh24/o9dR0GJkVNCg6IwOG5mcRzbdvOSUSEEsC0OSgACBT63oCg6VqyclfOYktIhDUcWzJ49G7F4\nf1HGNgwtpyyrydSDIy1n0Es9nVjcgm5oIATwfYaB/ggG+iNwXYY332jFU/96BJxzWDEGxnLbgWqq\nCs/1M+rhEXRIzP0D4SLIEnMcAYF+fPbqDaifEkJ1deauMkn5kIYjS+rrzYKkZp4OS6iEZhuA9f0Y\n4vFuxON9iMejsG0nEXDPf065CjoWjRL3cC82WX3eIqi8ThwJISgcx0dfrwBBDRQlgqefbIM6Rlwj\nUwxTRzxmjTkvAcCyneC7kYclZ5QgFGJgCoGhN+L+H/8WTOsqcwxLkilnhnO8gFx66Xn45S92wZze\nXPCxdUNDLGYhFGIZ/SR9LlAV8bByRQOAwG88MBBHR2c/4jEBAQVBBFQBowooU8AYzdgY+H5xekxn\nw3DjRSbZZY5hBH06CPVhjOv2CSxmNBqH67rQdC2o7FYZAA1z5zVg6lQbBw90g+RpXSkhCIUN9PdH\nYZoGNFUZ0p/iPGjzGgoZ0PX8e6czFjRG03UV4fASdLZ1oa+vDzU1Umqk0pGGI0tUVYFld4CQWRCi\nsFdHBEHKpG07aRaSAN/z0DT71NaeEKC62hy13edcoKcnhq6uQVhWNQJp7qAymFIKxljCoIx8Pb6f\neWpmMampDiXUaieZ5QBgmjp830c0FkfINFJecQd9YARCIQOhUPCcwKCeei7ndiJ1Or/vpECQ6RUJ\nm7AdF4LzRDU3ASUEVVXp6zWyIfkaBBFgtAa//sVruPPuiws2vqQ4lH9VmIBcdNF5eOP1I6irqy/4\n2IrC4LpBV7V0PmTOXTQ2Vqcdk1KCqqowTvYQGAaBEKfUdDnn8H0ftu0NqykIzut5XrBgi/xanuaD\nwijCIRWaphSsar/SYIwhZBpjpuYKIaCqyoiaidM/j+pqA7W1YUSjFgQnEOBZ7z4EArkRXdcScwrk\nzlVNLZh6gICA7wfGiHMOgsBYBcWdFHFr8l0cTEak4ciB5uZmvPjCXghRV5QFNXBhWKMWESEEPC9w\n3SgKBaF8DKlxnHYc0NZGwHmgJDt8yoH0NkWq5J5YlEMInjAqQ6Mhmd9EGQWjFDTFbqVQDO8zMpnd\n34QEHQIFRsYOAqPupnUNaTrD4qUNQ//f1tqPTz/phWEocBwno4U/HrdhmiMzsjL5fqWCcw7PDy5K\nhreVJSRobKWqyig3qO9zOI6Kd97+GKvXzs/pvJLSIA1HDgTy1icgRHNRFrPhciSadmrB8DwOpvSA\nUQ3RqI5QOLMgvWUDlk2yniuhFKqqpjQqyfRQ3+dwPS/lboCQU4aJUpJTlTERZ07mGKUkaJM77PXa\ntptTr/KmaVWoqTUhBLD3gw5w7o1rPFzPCz6jDL8kyZ7j/jDjkLw/eC2BC9QwtIxcWyIQIkMopGP3\n20exYtXcoumvSfJHGo4cUbWaoi5oqqogFrOgqsopPzCA2loNCxc24PDhfjQ3T8toLH5agkxykVdY\ncCXIfZJ1qmtw5cjGvSJNGhfOBVxn/DRPQgACmgj4ntI1Aimfm6zUBC1VAzeO7/sJ1dncCkMpJQiF\nVAgBLF85FceOdqPrhAuW4jvruC58n4/oNyIQ7HYCXa3UzbAopaAs6A2eqysrmfwQijCEwwyuK/Dx\ngQE8+dgHuOqaFTmNKSk+0nDkCKP595BOh2HqI/zehHDU1gaX/y0t6WMbQ+MYACXJxQCgVGD6dIHq\nKqCtnaC/P4XdKEBA4ZRxQTqVDAgR+L7ra0OBvEvC4ACAla53CUkYmsD6DPs7uNZNuoEqHU1TMTAQ\nBYChhkfCyP9zqKkViMUUdJ04VdwnIOA4LmzbCXYHCQFE4NR3gbJgt0gIxmwdWwiYQjE44CM26MPz\nBUCAUFjF0SM9aJ5dV7TzSnJHGo4cCK6kaUYB7HyghAwFy1VVge/7iESyd1twEdxIIhJJCUF1lcDh\nIwSxGEkp4+FzUdJUXEIIGKFgLHsFXJFQdE1mHwkugmZEQOBfTzyWL4USORyPqqow4okFHBhfRn74\njm6oXW6K1xmNejh0MAZneC+QxI4uHA4lpEZSjA+BaNRCKAc9qkwhhMD3xNBOiADQtDBs7yg+3E+l\n4ahQpOHIAUIItm1fgd898yKmTp2GqqopRTMgmqYiFrOgKAoIRFbaRkm8xIUm5wBlgGkGq8u0JoG4\nJdDZSRO9Lk4d4/t+yX3MhObWO50gsaNIzr9ICizxeOELP09HjJEJFYsldgPDPqThMaSkSzO1odHR\n1MRx/HhPSldVKrjgcGwXhqHlrICbKUmDl5y6bvRh1qwmnDxR+bvEMxVpOHJkzpzpuOvuL2D//r14\n8cXd0PUaNEydBU0rvAsrmWUVLKzZ/4g5D3o8axowOEigKMHipOuApgED/QKx+MgfKfd52sY8hUZV\nKVzXy6xfBQl2TsnFUlHKrZybHWJoJySG4kSW7cC2HDCFjjJSyTqOXF6j53K0tw9klBzhJ9KzPS+4\ncCi2pL7nn8oU9DwBw6Boa30HF1/yNRw+dKio55bkjjQcObJvbwfOXtSIRYuWYNGiJXAcBz++7+eY\nM3d1wYvmKCVgCoPrxnJKjwyHgblhgZ7ewHAMDBJEBgXCYSAaBeLW6BhHMre+lFAadKvLBIHAJZWM\njThOfqJ7GZ1TiILtOgg59f66XlA5zn2OSMQM0psLWGTnJ96ndAFs1/Xgeh4IkLPMf7YojAwJHu7Y\nWYOe3hNw3JU49HEXrrhqaUnmIMkeaThyZPqMKrz04iGEwyosy8esWTW4/Y7r8atfPo9p02YUfNHV\nVAWM5tmBLuEF4ZzgeCsBYwKCA0Jkn6pbFLKYAwEZkbbql6AXOaUEuq4V9LPlnMO23aG/c62bGA9d\nZ1i0tAEf7unEWIJfnu/DcV2EQ6UXGWSUQFEJ3nhtEMdbD2HTpvOwfkNLyechyRxpOHKktjaENWtn\ngTGC3p44GCOIDjpYumwaPvjgKHStCtXVVQV193CR3xW17ZARvmTOK6uwLteUTs5Lk7JLGYXPC9sR\nMR63EQobwY6gSLEEzgU62wfBRer+8cl03FAZjAYXArYloGoEgwMedK0J6zfMKfk8JNkhDUceVFUF\nbpVQ6NSCXle/AqtXL0dvbz8effRZtMw+uyDnIoSA++qoosBsaJgqEIkIODbguoDvE7ge4HmBEaFU\ngADw/PJYknxqAUqRAcYYg+d5BTMcSb0pK57MdiqOpkpn5yC6T0RHJXDYthMYQoWNqOEoJZQQ6DoQ\njVpwXIrLrlhZlnlIskMajiJACEFdXQ0YY6PE6PKBMRVHjvRhwYKpOR4PRMIAwsl7Ti1Uyc6GlAJt\n7S4sa9ThRSfX96mQ7/F4MErgFLADZNBCNYglxGIWjCIt3seP9I/KVnNcF4QShPTUsQzOOfxEqq9I\npPoCiW+MCGqMCqFfFYu5iEYHUV1roLGxFs2zZ+Q9pqT4SMNRQIQQsG0PhhHsCM46qwl79+7DrJkL\n8u6TAATV5MePE7S0eAXPeBp+Ee17A2CstNLW+dTElMpwFLOTVDK1ttAMDjjwPG+E4XC9IHMtVTwj\ncB3ZACFQEqrJNJnqm3iO5/uIxy2EQyYEAJE0Mj4HZTSj5BAhBHp6T4LQNtx+140Zd0KUVAZSDKYA\nvP9+21CVc3Lxe/21I1i7di1uu+1qfPLp+zlLRyQRQsBx4giHvaLXVwwM+EUJ0o5HPj7+IG5TIYGa\nHHAcF0qR5OuPH+sNBL+G4SWMhkCQVOC6HizbRjQWh2XZ0HQNpqFDVRUojAVpz8OOVxiDqiqIxy1Y\ncQuO6wECUFQFnHPELTut0y0aH8CChSHc8cVbpdGYgEjDUQAWLJgylF6pacEC0NgUwf79J8AYw223\nfQFt7YeGyZZnj+s6aJ4tsG5dU9ELsjyPFLUifizOFDHD0/F9v6A7yCBF2UcsaqO/34JtO4jHraGb\nz8XQou+63pBMi6qqCJlGRvEiTVVhmgZM04Cha0Nqt7qmJXTW4mMWM3o+x8mej7Dj/G0Fe82S0iJd\nVQVgeHAcCH64c+ee6tVhGAbC4Th8bkNhOebHEwfNzbnFNrJFlOFrQUnQEe5MZOzrCQGekFAJhA95\nRjurpEDk/n2d8DwvI4XaaCyOUKgwV/4KY6CmMRS3GW6IfM7R1xfHTTdfW5BzScqD3HEUgXffaUU8\nPlKY79prv4BPP92X066DcwHGMqimLhil/1okq8DPNAIpkaCwcPTNgeN4IwyGaeppb4ahQdNUhCJa\nQocq/ftqJhZ623HG3ClkAyUEoZAJx3bguKfqj2zbBSUUU6Y0jHO0pNKRhqMItMypwwd/7BhxH6UU\n06fXDRV7ZUrgVhjEsmWlFHsrbXwDACg78wyHz3kgKR4yxzYCemAENE3N+v1pbIjA9zIrjKSEIBwy\nwRgrXHU8AoPEOdDT04uOzkNwvUHMWyCNxkRHuqqKQH19CPXnhEbd39gwAx0d2QXJHdvBipVVCIdL\nk2dv2x4IKb3hCDSncj16YvaUtS0HZqh4n2tNrQmapftPYQw+8+F6XkGkc4QQcN1+LFwSwbZtX8h7\nPEllIHccJYQLHUJkZzgIETDN0n1MJ0/GQGnps1xIHi9RUZShXhL5JCCUmkDQt3i7LMYoDCP7xV/X\ntKHiwHxxPQtU7cC2bVvzHktSOUjDUUJmz65Cf/8ABgdjcBxv3I54SVRVx1tv9ZZgdgH9/W5ZWnbm\nU0ymqgp0TUMsbgV+ejtN46cKwLadoqXgDicc1jP6no0+LpSIT+QeWxNCoPPEp7jppptzHkNSmUhX\nVQmZPn06urofwtx5a9HW1oPBQR+EqKBUBaUKaOJvRVGhqjoYU6AoahGvSUdj24BulN5w5BveYIwO\nKbrGYhbicRuapiQ62FVW7MT3gza6eglk6xsaI+jsHISWZR+XZHwibtlwCXJyW8XjPsLhibMDlGSO\nNBwlRFEUaBrDihXzsWKcdsqDg3F0dJzEk0++gHPO2YgVy0spw0DLInpYCPmKJKGQAQEB1/FgOy4g\nkOieGKoII2LZTsm0oapqjIybN6XCNHTYjgPbcaFnqZHmui7mzluY87kllYs0HCUn/dV8JGIiEpmJ\n2bNr0dV1AOHw3BLMK6AcNRxA4eU2CEiQjZRodi6EQDQaD4LwlMBI9O6wLAe6ro7YmQRV+oHLzvc5\nCCUF7blNQHJ4vblduTNKYZgKXCf3eEXSDehzlrGY5MCgDY872HmBLPKbjMgYR4khWUSBP/e5y7B4\n8UL8wz/8CEeOHC/irIZT+oyqYvduB04JCobCBnRNhW076OsbhK6rcF0PsZgFy7KD/9oOmMLgJ/pj\nEBDE4lZBAu+u60JRsn+PT2/tmw3hiA4u8gt0m6YBy7LheuljHv39Nhy3F3fetTOvc0oqF2k4Sgwh\nJKsFaMGCufjKV+7Am2++g1/84lH4fn6aV+Ph+xzl+EoIURq5kWQxHGMMpmmgtrYKjDEYho5w2ISi\nMIRCBkxDh8IYdE2DogS6TIauwbJs+L4P1/VyzjhyXS8nWfx8hBynNlbBy7CeYywIgHDIhOd64OO8\n9mjMgud5uO2OSyvCLSgpDtJwlJjGxiZ0dZ3M6hhKKa655grs2LEV//zPP8EHH+wvytz6+uJgtPSu\nKoLiKMOmPe9pC9t4WU6UUpimMSSDblu5ZW4xxnIy/vkYjprqzPSnMkE39CBulIJozIJlDeKGmzfn\ntKuSTByk4Sgx55yzGbt3f5D2ee+88wH6+gZG3DdtWiPuuedOtLa24777fobBwWhB59bTY4OWWBUX\nCHqATBSdKkop1ITMeK7HJ5WUs0EAOau6U0pgmIW5IKCJHbOXMH5CCHAu0N/vIhrtwh13XTJKu00y\n+ZCGo8S0tMxFe3vnuM+xbRtvvPE+HnzwEbS1dYx6/KKLzsOf/Mln8atfPYYnn/x9wYreYjFekk56\np0PpmSM3whgd19UzFiLP9rjVNSG4eUr7JzFNA7btgAuBeJzD9ThsO44v/tlnzliF4zMNmVVV96tz\ngAAAHGRJREFUBtJJevzmN0/httvuRn39FPyf//NdtLRMQ319LZYsWQhdD9I4I5Ewbr/9Bhw6dBj/\n9E8/xo4dW7Fs2aK85iUEAynDD5/Q8si454MQIidNJyF4Tm45AQGWR3l9y5w6dLT153z8cJI1Hrbt\nQNNV9PXFsHlrc8l7uEjKh9xxlAFdN2FZYy86vi/Q0NAIxhi+8Y1vY8mS9YhEpuPeex9EPD6yp+u8\neS34ylfuQEfHCfzgB/+C3t6+nOclyvR1mGA2A0AQH8lEqfb0Wyhk5FTJLQTyqpJkjKJpehXcPIPk\nSZIuq1g0jpq6KFaskvUaZxLScJSBDRu24N13x45znL4+LF68DOvXb8Q3v/nX+P73H0I0Ght1zM6d\n5+KWW/4ETzzxO/zmN/+aY/ZVeTag+ehUTTTE0D/ZHijyLsysrw/nFF8ZC8PQ4bgC11x7acHGlEwM\nzqCfbOWwfPlKfPjhoTEfH2uBqKqqxl/+5d/ghz/8ecrAuK7ruOmm67Bp0zp8//v/gjfffCfjOQUL\nykhXgxDjNRk6Je1h207aNM3xoGfQ1zBXUUMhRN6CiLGYXdDdXSzmoKHJkRlUZyAyxlEGGGPjFgKO\nd1UYDkdw9dVfwLvvfoCtWzekfM7MmdPx5S/fhldeeRP33ns/li9fjHnzWjB9+thtZ6NRG3R4Kq4Q\n2LvnfWiaB0XRQJkORdFg6CGYZgiqZkAIAdPUE61Kg97Vw+dOCEFNtQnu++AC4DzoLxKMH8Q2CAEI\nPbP0jHRdhWXZMLKQHSlEX/XBQQdMKZyRti0Pf3rLhQUbTzJxkIajTFCqgPPUgdJ0wdN33nkLO3eu\nT3uOzZvXY8OGNfj006PYs+dDPPvsSyMysBSFoaWlGXPnzobr6qD0VLMo1/PQ0BDB1q2n5E6EEOjr\n68eRI4dx7Gg3+gc4Zs1ajPr6Jqhq6tdRXW2C0WDh45yDczF08zmHEIBSwMVsIuB5flmu0uNxt2Ca\nYI7rQlFFWepvJOVHGo4ysXTpcnz00cdYtOisFI+O/+MeHOxDVVUko/MwxjB//hzMnz9n1GOu6+LI\nkePYs+dDdHfHMbVhARjToCgaPFdg2rSR5yCEoLa2BrW1NUMijQ8//CxqanakLJ5T2CnBREKCAO3k\nSbzJbZeU3J3peulrHUJhDbFBuyBGKxazMHPmlALMSjIRkYajTGzcuBUPPPC9lIYjnUsiHI4gGo0h\nHB7dZTAbVFUd06j4fmb6UZ/5zLnYtWs/Fpy1dHQlNitmm6Lyomkq4padtcptPG7BTMi/Z49AzlWA\nAJqba9HZPpD+iZnMRBBMm15dkLEkEw+5zywTphmCm2OTnJUr12LPng8LPKORMJZZK1dd17BuXQP2\n7nlzVGwmUJwt0gTLDGMMEAIii50HT4om5vCmUEryzojivHAdEjkXmLdgWkHGkkw8pOEoI4SwlD/k\nWGx0uu1wli1biY8++qRY08qapqYGbN++AJ988iG4fyqzarK7vxlj8LOoxrZtNyeBw+BcNCFCmQdE\njJsllwnJw4XgcJziCW5KKptJ/tOubJYtW4H9+w+Oun/NmiV4+eXnxjxO07SC5uMXgvr6WmzaOB2t\nbceHcnjLUYVeSjRNheNks2vMXTaEMpqTIq+AAOccrueBUaCqWsupABEAPN9HNBpLSMxzuBOgRa+k\nOEjDUUY2b96Ol19+Y9T9a9euxB/+8OK4x+ZYMlFUamursGB+CJ2dJxK2Y3IbDiBwIWWyoPu+n1c6\nLSUU4rSLBc/zYVk24vGxb5blBC5REfRmnztvKjw3/U5BQIALDp9zeAkpeSEEVFVByDRQXRXGc8/9\nIefXI5nYSMNRRnRdx5o1G/Dww0+OemzlysV4/vldYx67fPnKosc5cmH27Do0NMZw4kRbXi1LJwqG\nocHJ8Mrb9zkcx4VtO+Ms+NY4I4w0HI7rQte18WVODB26rkFVg/7rNTUmDFNDPG6Ne7MsB47jwfNO\nFXY6jju009V1DX290lV1piINR5nZufMSbNiwHT/60c9GyIRs3LgGr776Ilw3de+DHTsuwmuvvVuq\naWbF2Qtno7dnHwg5ExaWzIwjZRS6oYGxoDHUWAt+JufyfQbOAU1VYSWMVqbeJ8/j4JzANI3xb4YO\nQ9egaxo0VYWqKtA0FYZxKo2YMg09Pb2ZnVgyqZCGowJYsWI1rrvuplE7j2uvvRz33/+DlMdQSqHr\nxpiGpdzs3LkRbW3Hyj2NouP7fkZFcAQECmNgjI7ob54tgYHgIEQE9RgiyOsSgg5JxHCe/Hv0OU6e\ntODmGNRWFWWE7El1pA6P/faZnMaSTGyk4agQWlrmgjEDnZ1dQ/c1NEwBIS6OHPk05TFXXPE57Nr1\ncolmmB2maeDwkY8Klv5ZqdiOC03PLVMqNWRE9hTnBEIQ8EThoO/7YIqbaEEMKIoB7hO4rod43EV/\nfxQ9Pd3o7RtAf/8APM8H5xScBwt+X08clJ36TIQQ6O/3curVoWkKYoNaUdsZSyoTaTgqiFtu+SIe\neeSpEfddffVl+OUvH0z5/Dlz5qGjoyvlY5XA/PnTEI0WtkthpUGQu3BhEjEkmRtofzmOA84JolEb\nXV2d6OrqQldXFwhlGByMorOjF729A4jFbFhWHJ8e/gg+78PCs6dj+Yq5WL3mbKxcOR9z5zVgz963\nEIvFIQSB53FEo+5QbU0gIeMgZh1F/8BBdHQeg2Vn12Okvq4Rjz/2WF6vXzLxkJXjFYSqqtiy5Ty8\n8spb2Lx5HYCgVqChoQ4dHe1oahpdcKUohbzaLSwLFszDkSMOIpmpo5yxUMoRCkfh+wxW3ARjBo63\nHsOM6Q2YMmU2QmEVnhsUG0bCGgQCnbFkZf9StKQcNxKpwpVXXonW1uPoaD+Jjw9EMW9BHY586sG2\nHXR3n0B1VR1u++LnQQgB5xzfv/dRoHo6jAwlUVRVw7Gjzpi6a5LJifykK4xt287He+/tHxG7uOii\n7bj33v8Pnje6ZsB1KzeXXlEEBgcyD56mk3GvZPKaNxFwHA2eq4JzBs8bQGPDDAAh1NeH4DoctXUm\n6upCUDUFmqZk1TFxxoyZmDmrBp2dHTiw/wQG+i2cPNmHNWsW48Zbtg7FWyiluPOuz6K3tx22k1ns\njBCC+rqZePrffpfLK5dMUKThqEDOOWcjDhw4VRkeDoewevUSfPrp6B4eZ521uCLTcpNYdl9Kgzec\nIKDro729DXv3vYPjx4/hxIku9PX1V7QxEQKglCX+pjnPU3AGx9bhuioo9REOR4Zk97ng6OsbL0U3\nMxobm7D+nAXo7euCz13s2LkSG7csGPU8VVVw402Xore3E7admfEwdAOHDg3IWMcZhDQcFci+fXuw\naNHIH/Xcuc3Yv3/PqOdedtlVeOGF1ys2CL18+SzsfudVOOPsjAgR+O1vH0DzbIpNm+Zj8ZJqzF+g\nQaAdf/jDrpwbRBWSVAaMcwpNY7BtB47jIh63Rn0OyfiFEGRcw0JIsoEXgecFelaaHizk9fXZCSmO\nxfoNC3DXly7FLbdvx6LFY+tM1dSGcPsXL8fAgA3b8dKqFCR3HQ/85NGCzFNS+UjDUWFwzuG69ih/\n8axZM/Dxx/vw+OO/GXE/pRSXXXYVnn22UrOrdJx//nJ8uP99xOLxUYunEMCRI59g2/b1CIXMEY/N\nnj0NO85fgU8PHxq3R3uxEUKAUA7KAgPmui7a2trQ39+LPXvfQ1v7QZghDsftw8GDH6G9vR2WZcO2\nbViWh2PHjqG17Tja2zvgujylATmVRhuE248d24empmr091uorgmX9gUjaDa1ZdtZON66B66b/qLE\n0DVA1OKVV94qwewk5UYajjLj+/7QFbVt2/jud/8OW7euG/U8xhhuvPEatLW1jnps1aq1OHy4LWU7\n2UqAUootWxfiwEevobX12AhV4Lhlob+/NaW0OxCk9a5a1Yijxw4iFouXaMYjEYJCYT4G+h0MDMRx\n9NghLF+xACtXLcBll12MbdvOQ3PzTKxYsRw7LzgXq1YvRueJo+jt7UJdvYFly5eiZfY8LF++EN0n\nu2Db/gjjkfxbCJJIm+WYNWshXn/9/YK2es2WZctn4YY/vQQDsQMYGEyvyVVbU4vdbx1Db29/CWYn\nKScyq6rM/I//8bcwTQOqquHkyW7ceut1qKlJ3eeAMQbOU/uR7777HvzTP/0/uOuuG4s53bw4d9ta\nOI6L997bi4apLYhETOzbtxvnnbdi3OMIAdasacarr+zH0qWrSy7VTohAfz+BolCctXAmCEmdxZRE\n01Rs3bp5xH3V1UEPjhXLF+LYsR5Ylj9KKVcIju7uLmiaBkoJdC2Ekz0WNF2FrpfnpzpjxixwEYXI\n0FvYMKUJP3/od/jSVz5f3IlJyoo0HGVm+/bzMTjYifXrV4JSmjalUYzxCw6HI9i0aRtefvkNbN16\nTjGmWhA0TcX69XMwMODjnd1v4txzF2dkCAgBamp9nOw5gSn1DcWfaAIhgFjMgaapaJnTlHffb8PU\nMHNWHdrbeuD7gdvq8OF9aGiYie7uVmzbvhmKouBEZxdiMQpKCBgrr+bXrbfejPvv+z2qMT3tcxlj\nk14VWSJdVWXn3HN34N1394EQklEe/MDAwJgyI9u2nY+DB4/ilVfeqoiA8nhUVTFs2748ZcvZsVi6\ndCHa246XLBFACMCyfCiKwPwFTQXrE26aGma3NKCmVsX06VXYvn0Llq+Yh/N3bht6P+qn1KOuzsT0\nGVVl6U8+HMMwhrK80kEIASEUjlO5aeKS/JGGowL4T//pJjz+eGZ58Ndccyl+8IN/GPPxe+75FqZP\nX4CHHnocv/71aNXdic6s5ir09xffhy4EEI3aUFXgrIXNBR+fMYqGhjpEqkyomjLqooExiuoas+xG\nAwgaUBGSuYEPh+rx8kuvFnFGknIjDUcFMGfOPNg2x8cff5r2uQ0NU6DrFJ2dHSkfp5Ri9ep1+OpX\nvwXPq8wU3XyYNasBvb0nCzom5xQ+p0NZTY7jo729HabpYd789O6Zyc47uw+AMTPjnZ5hhLD3g66K\nTRGX5I80HBXCXXfdg337juDRR59K+4O78MJtePrpf007ZjhcVbGZVrlCCBCJMAwOjt9eN1OSbzWl\nHK5r4eTJHhxv/Qjrz1mGufPmFuQcE53W1hOgVIFlcdh2ehcoJQRVVVPx9FPjNyOTTFyk4agQKKW4\n8cbbsGXLBfjHf7x/XLn02toatLYeSxvHWLjwbBw69GmBZ1p+ZrfUIRodzHucpPS47/uw4h46Oo9i\n5aoF2L59u9RdGsaixTPAfQ9MIVC1zALfkXAIhw7KXcdkRf46Koyzz16CL37xK3jkkafQ2to+5vOu\nuOJ83HffP6cd69Cho4WeYtlhTKC39wji8dx3HUIAXFDErRgsy8bMmfXYunWTNBgpWLLkLMTtNgiR\nXTPg6uqpeOLxZ7M+3z333I1///enKz7B40xGpuNWINOmTUdVVT127XoNigJcf/1nRz2nuXkGDh78\nFC+++B/Ytu38lOPU10/B4cPHgx4OrPxB1kKybv1ZeOmlD7B82dqcXpsQBJ7rwbEdrFi5IO8028nO\nkqXz8clBG1ptZqq5ABAOhXDsyHF4nj9ukL+r6wQ++mgfjh49jK6uLjQ1NeLll/8D7777FqZNm4Hr\nrrsRul4Y2RVJYZCXVxXKDTfcinvu+SbWrNmIxx5L3WVtx47NeOutV9De3jbmOHfc8SU89NAjxZpm\n2SCEYP36+YnGV9m6QwRs24HrudJoZMjOC9aDow+2M34F+SAXaHUFkmWq1dVT8NtH/z3lc3/721/h\n7//+/8YTT/wCvt+L9esX4frrr0BVVRUuu+yz8DwXK1fOx9/8zbfQ399X4FckyQdpOCqcjRu3orl5\nAZ555vmUj99007X41a9+OubxM2c2Y/XqDXjuuVeKNMPyYZoqqmuA7u7e7JRpiYDruliwYJo0Gllw\n6+0Xobv7GLgQEInb6Qz4QIcrEE8II4ZMA12dqaVi9u/fi9tuuw5XX30Zli5dhI8+OoT7738YU6c2\nYMOGLfizP/s6XnzxDSxefJaMlVQY0nBMAHbuvAThcD2ef350bryiKEjnlt++fSd6e+N4993R6roT\nnenTTXR0fgTbzrzgrL8vDtPURkl+SMZHVVVsO28J+nqjiMdTizXWMmCKQkb4wCnVUy781dU1ePPN\nd/DjH/8KDz74GBoa5uBrX/srXH/9LcFYtXUQQsCybJhmqDgvSpIT0nBMEK688mo4DsVrr+1O8Wj6\nIOKtt96FgQEfP//5Y5Mu6Lhs2UJY1vg9K4QAfJ+CCwLOhazPyJFVq5cBsAF4EAKj0nNNSjBbIzBG\nyI7QlNLs1157PSKRafj617+Nr33tL7F27YYUyQkUnudlpTAgKT7ScEwgrrvuBhw9egJHj45UyBWC\nZ2QMrrzyalx++TV44IFfF2uKZcE0FVhW+gyrpFeKUiJdVHlw9XVbEY06iMV8KEom7yNJ2RSqqWka\nNm06d9xMthkzZuLVV9+U2W4Vhvw0Jhjnn3/RqArzhoapaG8fLbeeit7eHixcOLkK2yhN7/8mJCjy\nE5xgIIt2tpLR1NdHUFUdgm33Ix5Pf8GiKAwnxlA6SMc111yP733vxzkdKyke0nBMMKZObUBPz8gM\nk/nzZ+PDD/dmdPxzz+3C5s3rizG1skEI0NfXDs9P36IWADwvs5aokrG54aaNmDUnBt1MX4jJqIKe\n3tyzompqanM+VlIcpOGYYFRVVY+SEZkzpxl7936Q9ljP88C5Oym3/YuXTENHx9gFk6fwEInUFH0+\nZwKXX/45dHQew8CAN27WkwBD2/H8K/0llcPkW0EmObFYdFQxlKZpiMcH08Y5HMcue2+HYhGJhBCL\nDsAf5z0I3FUEum6O+RxJdtx2+9WwbRu9vT7i8dQ7Pt+30dBYX+KZSYqJNBwTjLfeeh3Lly8adf/m\nzeuwa1fqQsEkoVAYlGro6uou1vTKSsucGpzoPDFuTQfnDPF4FE6aQjZJZlRVVeNPb10PjrcxGD0B\n/7TsKSEEXK8HixaP3zUxieu6ePnlF/D2228UY7qSAiENxwRjz54/YuHCeaPuX7JkIfbseS/t8Xff\n/VU8/fRL+MMf3izG9MrK1KkR6EYX3nrrRfT29aU2IEQgFKpCdFA2GioUoVAYX7z7z3HOpmmIRWOj\n3FaU1CIWy+z9fuaZf8Xx4x/h3XdfxZtvyp4elYo0HBMM33fH1GZSVZZW+E9VVXzlK9+EadbjJz/5\n5bgqvBORlpZm7LxgFYQ4hjfefAH9/YPgXCSUcAFGBSwrBtuWO45Cs2bNOegdOICBAR+24wfFe7YP\nQigaG6szGuPYsaO44IJtuOaay/H73//bpKs5mixIwzHB6OrqGrMt53nnbcJTTz2R0Tjnn38xbrjh\nDnzvez8dV4V3otLS0owLL1wNQtvw/AuPY9euRxCLD0CIwL3S3d1V7ilOStauXQLXczA4GEf3ySii\nUQtnnz0r4+M594YujC655Dw88sgvizVVSR7IcswJxle/+i384z/+Pa6//io0Nk4d8disWdPx/POv\nZzxWU9M0fOc7/x3f/e7f4e67byz0VCuCmTObMHNmEzjnePnlV2AaM3D48Ifo6OzA0mX/rdzTm3Sc\nu20LNm/hYIzi4IE2HPyoB9t2LMz4eN/3h/6eP38Onn/+VcRiUYRC4WJMV5IjcscxwZgypQHf+c5/\nx5NPPocPPzw46nFKs5MYp5Ri5co1+OCD/YWaYkVCKcW2bZuw/pwWeH4cX/rSPeWe0qRECAHGKFqP\n9eBEZwwXXrIoqyr9BQvOxo9//EvEYoEw4uc/fwX+5V/uK9Z0JTkiDccERFEUfOMb38brr/8Rhw4d\nznu8iy++Ai+9NPmC5akQQmBw0EJd3ZRyT2VS0dnRh/u+/yp+8qPXsPutIzhyuBebtswHY9ktMZdd\ndhXuuOPP8aMf/QInT/aguroKrju+Dpmk9EjDMYH58z//Czz33Os4cuQ4gGBRPHjwIB588D588sno\n3chYUEpxzjmb8M47fyzWVCuG117bjfPO21nuaUxITpdSF0Kg9Xgfek5G8fSTe0EZcPGlZ2P12mZs\n3JK7rE1NTS3+6q/+K3796yeHziOpLKThmMBQSvH1r/8Vnn76BbS2toMQgv/yX76O7dvX4KmnHsVr\nr72c8Vg7d16C119/D93dJ4s44/KzZ88BrFu3sdzTmJC4rj9C5ZYQgupqHYap4sZbNuC2OzdhVnN9\nQQQkdV3HmjXnYPfuP2Lq1NqMtdgkpUEajgkOpRTf/OZf4+GHn4Jl2QCAmppq3HDD1Xj22WeySmf8\ni7/4azz00G8Rjebey7uS6enpRUNDU7mnMWHRNGWU6ylSZcA0taxdUplw0UWX4/XX38OxYx2TrvXx\nREcajkkAYwz33PMXo+TSL7tsBx5++OcZj6OqKr71rb/GD3/4s0lX3wEAr776NnbuvLjc05Bkwbe/\n/bf4z//5v0qDX2FIwzFJqKubggsuuBRPPfUfQ/fNnduCY8c+SVsUOJxwOIIvf/kb+MEPfjrpfMtd\nXT2YNWt2uachkUx4pOGYRKxbtxG+z3DgwKGh+66++lI89FB2/QwaG5twww234ic/+VWhp1hWCJHu\nDomkEEjDMcm44YZbR6TW1tXVwraj6O3tyWqcuXMXYOfOS/HEE78v9BTLwsDAICKRzGQvJBLJ+EjD\nMcmglEJRtBH3bdy4Bq+99oesx1q1ai0cB2hry617WyXxySeHsWjRknJPQyKZFEjDMQmZNm06OjsD\nLaa+vn488cS/49xzz8tprFtu+SIeeeTpAs6uPHR3y4yqUsI5R3t7K1599SU8/PDP8O67b4+QE5FM\nbKRW1STk3HN34MknH8bs2TOxZ89BfOc7/9eo5k+ZoigKLr30Suza9RIuuODcAs+0dPT09KGxURqO\nQtLR0Y6f/vQn0HUNwPDiQAFAYMqUOjQ3T8eqVQvw8ccH8cILvwchwY549ep1WLduI1RVLeMrkOSK\nNByTkOnTZ2LatNlQ1Qi+8Y1v5z3e2rUb8NJLz2NgYBBVVZECzLD0DA5GEYlUlXsaE57jx4/i2Wd/\nh97ek1AUiptu+lxGi39DwxRs3LgWQNDC+IMP9uN//a+/xVVXfR7Ll68aep7jOHj++V3Yu/ePmD27\nBVdd9XlZw1GBSMMxSbnyyqsLOt6dd34Z9977/+LOO28o6Lilg07KXuulwPM8/Oxn96OrqxPTpk3B\n9u3noKYm90QDRVGwatUyrFq1DI8//ju8/fYbIISit7cblAps3LgGN998NT755Aj+9//+OyxduhKX\nX/5Z+flVENJwSDIiHI5gxYq12L37j1izZnm5p5M1lE7OXuvF5ve//zfs3v0GPvOZCzFjxg4Awa5g\n164X0dc3kFCxJQkdK46bb74uq/GvuupiHD3aiurqyChjNG9eC+6++0+xb98B/M//+bfYufNibNiw\npVAvTZIHZTccu3fvLvcUJBnS0DADDzzwg6LISxSbo0ePy+9aFgwMDOCRR36OJUvOwqZNa3DiRDdO\nnOiG4zh4+OEncfnlV+Hss8+CYZjwfR8PPPBDXHjhuXjvvT05ne/kyfHTxbdsWYtXX30OP/vZg9i5\n8xI0N2fWw3yysm/fvrKen5S7OpgQsqasE5BIJJKJyX4hRFmE5cpuOCQSiUQysZh4PgeJRCKRlBVp\nOCQSiUSSFdJwSCQSiSQrpOGQSCQSSVZIwyGRSCSSrPj/AXx6+xySHZAwAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b9875f8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
}
],
"source": [
"albers_equal_area = cartopy.crs.AlbersEqualArea(-95, 35)\n",
"plate_carree = cartopy.crs.PlateCarree()\n",
"\n",
"states_and_provinces = cartopy.feature.NaturalEarthFeature(\n",
" category='cultural',\n",
" name='admin_1_states_provinces_lines',\n",
" scale='50m',\n",
" facecolor='none'\n",
")\n",
"\n",
"cmaps = [matplotlib.cm.Blues, matplotlib.cm.Greens, \n",
" matplotlib.cm.Reds, matplotlib.cm.Purples]\n",
"norm = matplotlib.colors.Normalize(vmin=0, vmax=30) \n",
"\n",
"candidates = df['candidate'].unique()\n",
"\n",
"plt.rcParams['figure.figsize'] = [6.0, 4.0]\n",
"for index, candidate in enumerate(candidates):\n",
" plt.figure()\n",
" plot = plt.axes(projection=albers_equal_area)\n",
" plot.set_extent((-125, -66, 20, 50))\n",
" plot.add_feature(cartopy.feature.LAND)\n",
" plot.add_feature(cartopy.feature.COASTLINE)\n",
" plot.add_feature(cartopy.feature.BORDERS)\n",
" plot.add_feature(states_and_provinces, edgecolor='gray')\n",
" plot.add_feature(cartopy.feature.LAKES, facecolor=\"#00BCD4\")\n",
"\n",
" for tz_name, record in american_tz_records.items():\n",
" tz_specific_df = us_tz_df[us_tz_df.user_time_zone == tz_name]\n",
" tz_candidate_specific_df = tz_specific_df[tz_specific_df.candidate == candidate]\n",
" mean_polarity = tz_candidate_specific_df.influenced_polarity.mean()\n",
"\n",
" plot.add_geometries(\n",
" [record.geometry], \n",
" crs=plate_carree,\n",
" color=cmaps[index](norm(mean_polarity)),\n",
" alpha=.8\n",
" )\n",
" \n",
" plot.set_title('Influenced Polarity toward {} by U.S. Timezone'.format(candidate), family='Ubuntu')\n",
" plot.figure.set_size_inches(6, 3.5)\n",
" plt.show()\n",
" print()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"My friend Gabriel Wang pointed out that U.S. timezones other than Pacific don't mean much since each timezone covers both blue and red states, but the data is still interesting. \n",
"\n",
"As expected, midwestern states lean toward Jeb Bush. I wasn't expecting Jeb Bush's highest polarity-tweets to come from the East; this is probably Donald Trump (New York, New York) messing with our data again. \n",
"\n",
"In a few months I'll look at these statistics with the latest tweets and compare."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What are tweeters outside the U.S. saying about our candidates?\n",
"\n",
"Outside of the U.S., if someone is in a major city, the timezone is often that city itself. Here are the top (by number of tweets) non-American 25 timezones in our dataframe."
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"user_time_zone\n",
"Quito 1719\n",
"London 967\n",
"Amsterdam 571\n",
"Athens 368\n",
"Bangkok 249\n",
"Beijing 201\n",
"Brasilia 192\n",
"New Delhi 182\n",
"Tehran 164\n",
"Jakarta 164\n",
"Sydney 134\n",
"Chennai 133\n",
"Paris 133\n",
"West Central Africa 130\n",
"Casablanca 129\n",
"Baghdad 119\n",
"Dublin 118\n",
"Tijuana 117\n",
"Caracas 103\n",
"Bucharest 100\n",
"Berlin 99\n",
"Rome 96\n",
"Madrid 89\n",
"Greenland 86\n",
"Belgrade 79\n",
"dtype: int64"
]
},
"execution_count": 100,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"american_timezones = ('US & Canada|Canada|Arizona|America|Hawaii|Indiana|Alaska'\n",
" '|New_York|Chicago|Los_Angeles|Detroit|CST|PST|EST|MST')\n",
"foreign_tz_df = tz_df[~tz_df.user_time_zone.str.contains(american_timezones)]\n",
"\n",
"foreign_tz_groupby = foreign_tz_df.groupby('user_time_zone')\n",
"foreign_tz_groupby.size().sort(inplace = False, ascending = False).head(25)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I also want to look at polarity, so I'll only use English tweets.\n",
"\n",
"(Sorry, Central/South Americans - my very rough method of filtering out American timezones gets rid of some of your timezones too. Let me know if there's a better way to do this.)"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"foreign_english_tz_df = foreign_tz_df[foreign_tz_df.lang == 'en']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we have a dataframe containing (mostly) world cities as time zones. Let's get the top cities by number of tweets for each candidate, then plot polarities."
]
},
{
"cell_type": "code",
"execution_count": 102,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAxYAAAIlCAYAAABIJ24QAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYJFW9//F3z+zCLjBkkAwL4gcJIhhAAQURRVDgxwWJ\nEiSKBC8qwSUIlySIRBVBkLQYQIIogiAgXAQElYxfLmEJy7JkWGCXTf3745yBonfy1Gx3T39ez1PP\ndFfVqXOqp3rmfOuEqlSrVczMzMzMzAajrd4FMDMzMzOz5ufAwszMzMzMBs2BhZmZmZmZDZoDCzMz\nMzMzGzQHFmZmZmZmNmgOLMzMzMzMbNAcWJi1GEnrSLpS0lL1LksZJM0v6XhJ6w1xPh+W9FtJaw9l\nPmbNTNIBkr5Z73KURdJBknYb6jRmw4UDC7NhTNJ2kh6Q9LaklyVtCXwU2AoYVefilWVx4HBgpSHO\nZxlgW2DBwR5I0kOSrim831jSWoM85k6SXpG0/mDLV6ZGLVcZJB0q6SVJYxqgLB/4nCUtI2m7Lvb7\nvKRXu9pWku8CGw7Rsevh+8DnACTNJ+l5SWf2NU1flPH9N2sUI+pdADPrnaQLgY0jYtl+pFkDuAy4\nEDiY9H3/N/CVIShiw5K0BXA+sAhQBSYDAfweOCMi3q1Dsb4CTC28vxE4jvT7GajLc/pHB3oASRsB\nfwW+ExGzVZ4kjQYeASZERF8DhUGXqzv5rvAF3Wz+cEQ8WXaeNc4CromIp4Y4n87P/jvA9sDKwEzg\nSeDPEXEYs3/OewJHSbo8ImYVDnU7sAHw2BAVdUieuitpB2Af4OPA3MDzpHM5LCJeGIo8s/fOJyLe\nkrQB8FJf0/RRGd9/s4bgwMKsefT3n9VGQAU4ICLe6VwpqdRCNYGFSUHFzsAz+f0mwAn55yZzukAR\n8WwXqyuDPOY0UqV/MDpbfX4oaVxEvFKz/RBgeWAWfVRSuXqzHTChZl3t+9Ll79V/hjofSQsBt5Ba\nG38GHApMA9YAls1l6e5z/sB1lYOMh4eyvGWSVAF+BewCXAN8E3gFWAHYmHSjYCjVfn5P9DfNQPIx\na1YOLMyax3v/eCRtQ+r+sySpovw2cANwUER03k1bOP98qxBMzNZlQ9IKpDufe0XE+YX1s4DjI+LI\n/H4U8D/ATsB8wIPAoRHxv3n7KsC5pH/4C+fy3gN8NyL+WTju8sDJpAr9KOBxYPOIeLa3PHL6tYFT\ngXWA14AH+vLhAXcV7mD/QdIbwA8krRIR/5G0JnAi6W7uDNLneUhEPNPdASUdSOr2sBjwJql1aGxE\nTM/bTyW1TixJust6aUTsLelWoD0iNigcbqyksfn1T4GJ+bNYLCJezcebL5/zIRFxWk1ZNgRuBr4Y\nETdL+hzwI1LFcxFSRfR20jXSXeVoDKmi9ibwA1K3ls7jLwZ8D3iIdMe8mPetwOpAB+lO+KERcV1X\n5crrevysJa0InA2sCnyIdH3vGBF/6abc/+yudWIweeUK/SnAlkA7cC9wcEQ8lNPuRmoxea91JHdF\nOoZ0fY4EXgDuj4gt8va+fHdrnZE/3w2L34X8uXae54bUfM7Z9ML3f1Fgfmq+75KWA34MfIn3r5Pv\ndAbAklYFTsvnNILU4rdxRLzeRVkrwCcl3QusArxK+l78MCJmSXoMeDQitiyUfV/SNb94F8Hs7qSg\nYmxEnFhY/zfgosIxTsr7LUJqUTgzIk4ubL8O+Ej+DEaT/u4cHxGXFfZZLJ/nZnnVvaS/QxT2GQ/c\nHhHf6EeaHv9OZMXv/9kRcWBOuxfpe7gc8BRwekSch1mD8hgLs+a0OrAWsDepgn4k8FXg513s+3lg\n/bxM7OGYXbWIFNddRrozPJY01uBl4AZJy+TtS+Q8zgW+DOyW110jaS4ASfOSKgRrAgcBm5MqdRP6\nkoekRUlddRYgVTj2A17s4Zx6MiX/HC1paeA2UsX4G8C3chlvzV1QuvP3XIZNgZPyOX27sP2/gNeB\nHYAtSHdeO9V+3hfx/u/pVOBaUiWt2KKyAamC++c+nN+KpIrgD4EvAgcAawO/6SHNMqTA4Ghgv/y5\ndDoMmEQKOObOle5OPwV2JJ1jAFdIWrKrDPr4WS9H+kwvIwVmewD391DuEZKKS2WQed0nqR34C7Au\n6bP7BjAPcGO+jrs6t4+TKvcVUiX3S8B1pO9mp/58d5E0P6n707iaoKKvit//Nwrrq4Xj30YKdHYD\n9iUFBNcW9v0tsDSpK9I2wIXdBBWd5idVnrcGLiYFUsfkbdcCG0oaWdh/I+CeLoIKcp5PkYLknlxP\n6v71FVKwd5KkrQrbNyV1NfoaaYzZE8AlklYv7HMl6Xc2lvSd/Tuzj0Wr8sHvbl/S9PZ3Aj74/f8J\nvBeQnJm3bQn8AfhFDk7NGpJbLMya23W5a8Ptkj4C7C9pRETMKOxzR7GP9UC6QuUK01aku3I35dX/\nS6po7sQH/+n/PSLuyOmmk/7xrk+qcB1EqsB8JCKezvvf0o889ifdbdw0Il7M6R4iVfp6M0LS3MBC\npIrMd0h3LR8gVeqmAV+JiLfyce8mVZK/Q7rjPZuIuLfw9tbc/3pD4PS8rgo8HhHX96F8z0bE34sr\nJP0fqXL227xqQ+DpiOhP95ub8930OyQtDPxE0ord3OFfihR8XkIKIA4FDpS0OKmC923gubzv0qTW\nEyLi8kKZ7ybdpf40qetKraPp+2d9U0Tc2odzrP08zgYOHExeuVL6CWA14P/y6odJd/u/yvu/k6KT\ngGeBL3V+B/PA7n262Lcv310Akf5X39nt2fest+//N0kTIKxNupsO6fd3s6RPR8Q/SDcIboyIznPu\n6Xqukq65s/P7v+SWtoMl/Yj09+C/ScFuZ4D8eboJrEiB2LU140RmU3Od3Czpa6Tvy9WF9Y9GxO3w\n3nXwIvB14KHc4rMe8P8iovO6vUHSHjVZFVuO+5SmD38noOb7nwPbo/M+J+d8byHdLNgDuKKbj8Ks\nrhxYmA0fQWqFXIL3K39l+VT+eV3N+ipddK+qKROkCiukf8KPFYKK/uaxBvBIZ1CR9bVvcrHyOY1U\nOTooImZK+iypq9Rb7xU84qncbeMz3R1Q0o6kLg6rkLrZzKDcAZiXAodKmif35y9Wxgai+PvoKrBY\nCHg5d1k5FjhP0vGkwf/PkwKOznEYCwBImocU9G1N6kr0QnF7Fwb0WfdiKz54zXdeH4PJq/N6rB2P\n0NM1vx5wcRfBQW96+u52Xt9DNYvbp/KxX65ZXyW1ev2DFGD+VNIdwHnAbyNiCn13CynQWy0i7pD0\nJKkV5s9Kk0wsTs/Xda/nLukgUovUGOAd3p+soksR8aqkl3n/b9MahbL2VZ/SDPDvxIqk7+OheSka\nqoH3ZoPmwMJs+Oj8Rz9XP9NNyz976vLTOYPRNsD4mm21FZKeylSh+0HofcljFGmswkBslY/7KjCp\npn9zdyp0E7hI+iKp4n8h6e73NOD4AZatO78idZXZTtJNpC40Rw7ieL1dI/MAnZ/Lb3JeJ5G6dB2U\nA47O7Z3Xy7mkLlDfJ1WWFiCNGeivbj/rPnionzNA9SWvqaRrdQM+OIMXdN+lcASp0thfPf1eHicN\nlu/vdKR9nexhKuk78aUuto0HiIgLJP2Z1LpxInCspI36OJAZ3q9rdJbpPOBISd8mfS8n5ZaRrgTw\nMUmViOjynCTtSRrncAqpu1AbcE4fyjWF9z/zzuClP38/e00ziL8TndfciaQZ7IrqMZOdWZ84sDBr\nPZ3/nDvHWE0iVSZX6yFN513bZSPiykHk/U9gY0nLdTEo+qE+5HEXsImklSPi/7rZpzs9VT7vAraU\nNF+hy8wY0iDlcXmf2s+ts6J3cGd/c0nPkGZN6q83SINKPyAinpP0a9Kd2PlIFcCBVNr76r07w7kl\n50ekqXqfJvWV72rftUhdX37RuaGX7nZ9+azLMpi8HiIFH4sVurn05kHS+IFuK8H9le+sXwfsIOnM\n4kQIvegcT7EoPY9Deog0XmlWRNzXQzkmAsdL+jmpu9e+pGCyVlcB2+akQeoP5vfnkLra7UIKLH7X\nQ/kuJQ0sP5A0iL0rawGTI+K9O/uS+jv26u7882t8cCxUreLvtbs0xc+gL38nuvr+P5fXrxoRYzFr\nEg4szFpP51Snu0s6OSLeyJXXXXMXkX9T03oREf/KlZsTJC1IqrC1kf7pndqPvH9KGrR6k6QTSdO/\nLgncFhH/7kMePyENML1B0v+QBnV+tL8fQBd+SOprfZ2kn5AqzUeRBpV39oPu7KKyg6QHSTNeAZws\n6Xeku4jL8MGKR093xYvb7ga2VZpd6XVgvkJwdQppHMgSwG8iYma/z67vaif0uITUp/uGLvLtvEbu\nAf5fvmv8GGkmpJ78kN4/67IMJq9rgfuA8yWtRPodjAaWKgZRNY4kden5naRfkQYx78ngn+3wbeAO\n4DZJP86vZ5BmYFszIg7qIs1d+efJki4mzQ7WVVB6IWnMwzX5O/kYqdVpdOeMSZKOIH0Wb5G6/8xN\n98FKFRiT79SPJLVm7Qoc0dl9Kv/NOZcUXCxF12NQOp1JGpB9mtJD5K4kVbg/RBqbcRzpGvyWpONI\nkzvMJFXUe3u+yHvfwYi4TdIVwJmSPpSPOYrUitffNMW/n335O9Hl9z93QzxZ0gWk8UqTSWNOroiI\n53s5N7O68KxQZs2hdiaS2vfF9T3uk6eiPJdUwe+cEeXbpDvSR5L+MV9Gal14sJD0v0j/5HcldTf4\nFfCVPMiwq/xnE+lBVmvlY59KqoQdTfpH22seEfE2qaJ7M6lf/02kisWdpFleutNbuZ4jVVKmkO6Q\nnkNqpdkwj23onL/+GFIlZ+M8WPSAnO5PpErbGFIFrLd8a3833875XUy6k75poWwPkcadLEP6vfWk\nNr/erpEet0XEjIjYNyKu6mLfzhaL/yb9rk4gXTuXk66b2udIVPMxe/2s+1DObstcU/4B55XHSWxM\nupt+MOl3fA6zP1G5+AC1G0h34VfK6Y4jVURn1Ozfr99LnvZ1LVJgvh3p8/4jabalefOkBLVluYvU\nN3/TXPZDef97Vjz2a6SxIbcDx5KutdNzfp0P5tuI9PndQJpy+ExS16Ou/IVU6f89cBXp+/r1mqli\nyekXBf5dM7i5tnwz8jkcRJoSeFzO4zTSBALzRcSFpKmZd85lvI7UPam3hzLWfuY7kroe7UMag/Ub\n0g2Ffww0TR//TnT5/Y+IH5MC087Z3H5PmqiiOCObWUOpVKtD8pBMMzMrSb7bvlZEbFTvsvSXpP9H\nqhCtGREP9rb/cJPvom8dEavWuyyNJAdDTwI/iIiLetvfzJqDu0KZmTWgPFtOG2layn3yz6ZRGMtw\nCGmmqOg5RfOT9CnSTFSPkwbprk26035CPcvVSPJUq9NJz0WZyOxjd8ysiTmwMDNrTD8kDXp9BNgm\nIu7pefeGsyPpoWGPANtGxLRe9h8Olgb2Ig3MnYt0R/6kvLQ8pQddXkvqTnQjsHlZg9zNrDG4K5SZ\nmZmZmQ2aB2+bmZmZmdmguSuU1dWUq09zk5nNZuSYnh6pYa1q+lO1D8E2gxFLdvcgdGtlI9fZaqAP\n3CzNvpUVSq3jnFMdX/dz6o1bLMzMzMzMbNDcYmFmZmZmVrL2hm9fKJ8DCzMzMzOzkrVXWi+ycFeo\nFidpfUmz6l0OMzMzM2tuDiwGSdJYSbMk7TKEeewm6f+G6vhmZmZmVq72SrlLM3BgMQiS2kgPQ7oP\n2LvOxemRpBGSmuSyNDMzM2tu7ZVKqUsz8BiLwfkysAiwGfCgpNUi4mGA3L3oQGA3YBVS8LEd6Wm0\nBwKjgXMi4oi8/0LAucBGpN/Lc8C+wEzg58BckibnfDePiNskrQ6cCqwFTAHGAUdFxAxJK5Ce+ron\n8D1gDLC8pAWA84C18/YLiyckaXvgsLz/28AfgIMj4p28fXxO/0Xgk/kYO+UyHA0sClwO7BsRMwf4\nuZqZmZlZk3GLxeDsDVwZEY8AtwP71GzfEdgCWAx4F7gNmJdUaf8C8D1Jn8n7fp8UbCwXEQsCWwHP\nRcSdpADjyYjoyMttkhYH/gZcASwFfAbYBDi8pgw7ABsCHcAbwB+BB3OZtsnHLs6z/DqwQ0QsAGyQ\nlyNqjrlLTrcQ8ABwLbA+sEZetiAFUWZmZmYtyV2hrM8kLQVsDlySV10C7Cxp7sJup0bE8xExBfg9\nsGhE/DAiZkTEA8D9pLv+kAKPRYBVJLVFxOMRMT5v6+py2gW4LyLOy8d7Hjgpry86JiJejIgZOa/l\nge9HxLsR8Tjw4+LxI+L6iHg0v36C1FqyceF4VeDcSGYAv87H/EFETImIZ4FbC+dlZmZm1nLcFcr6\nYw/gJeDm/P4K4Cxge+CivG5iYf93gBdrjvEOqSUB4BRgZE67pKQ/AodERG2aTmOA9SS9VlhXYfZg\ncXzh9TLAixExtZvtSNoEOAoQMDfQDkyqOWbtec2MiFe6OS8zMzMzawFusRiAPGh7D1ILwwRJE4H/\nkAK12u5QfRIR70TEERGxBrAasDQp2ADoajrY8cBNEbFQYVkwIuav2a+YdgKwuKTRhXUrFM5rLuBq\n4DJg2dwd6jAGdp2U+hh7MzMzs2bSil2h3GIxMJuS7v5/ilRZ7/Rx4HpJa/TxOO9dJpK+BjwOPEYa\nNP0uMCNvfoEUEHREROcA7ouB70randQdaRopSFg5Im7oJr87gaeBH0k6hBS8HFzYPldeXo+IdyWt\nCuzfx3OpPa8m+QqYmZmZla9Zui+VyS0WA7M3cFVE/DuPX+hc/kKqvO/N7Hfsq92s67QiaQamN4Cn\nSMHFoXnbzcCNwFOSXpO0QURMIs0gtVXe/1XgSlIXqa6OT56laQvgY6RuWVcAv+jcLyLeAr4FnJxn\noDqLNNNUb60PfTlXMzMzMxvGKtWq639WP1OuPs0XoM1m5JjV6l0Ea0DTn3q43kWwBjRiyTG972Qt\nZ+Q6W9W9ueDY0R8utY5z1JTH635OvXFXKDMzMzOzkrkrlJmZmZmZ2QC4xcLMzMzMrGTNMpNTmRxY\nmJmZmZmVzF2hzMzMzMzMBsAtFmZmZmZmJXNXKLM5bMJNd9a7CNaAlt1m8XoXwRrQtE32rXcRrAG9\nMGVG7ztZy2mESYjdFcrMzMzMzGwA3GJhZmZmZlYyd4WyYUnSLGD9iPh7vctiZmZm1grcFcqahqSx\nkmZJ2qWwboW8bql6ls3MzMzMWo8DiyYkqQ3YC7gP2LuLXVovRDYzMzNrIO2Vcpdm4K5QzenLwCLA\nZsCDklaNiEeA+/P2kFQFToqI4/O6NSWdDqwCPAzsFhEBIGkEcAiwK7B43n5QRPwzb7+QFIROBbYF\n3gaOjYhz8/YVgF8AnwaqwFPADhHx2JB9AmZmZmbWUNxi0Zz2Bq7MwcTtQOccjB/LPz8SER2FoAJS\n0LA1sCjwLHBWYdsxwNdIAcvCwAXA9ZIWKOyzDfCHiFgIOAA4W9KyedsJwHhSULJIzuu1Es7TzMzM\nrCm1YouFA4smk8dPbA5cklddAuwsaW567gJ1SkQ8FxHTgIuAT+bjVUiBwiERMT4iqhFxATAR+Goh\n/V8j4o8AEXEV8Drw8bztXWBJYKWc/qGIeKmM8zUzMzNrRu2VSqlLM3BXqOazB/AScHN+fwWp9WF7\n4G89pJtYeP020JFfLwrMB1ybu091GgEs3U362mN8HzgyH2PeXKbDI+LtvpyQmZmZmTU/BxZNJA/a\n3oPU3WiCpM5NI4B9eD/Y6I+XSUHCxp1jKrpQpYfWkIh4GTgIOEjSGOAa0piNowdQHjMzM7OmV6/u\nS5KOB3Yg1RenA/cCh0XEfXn7LqQ62hLAg8B+EfGvMvJ2V6jmsimwDPAZYM3C8lVgXWABYBbwkb4e\nMCKqwBnAqZI+DCBpPklflrRk3q3Hr4ak7SSNyd2q3gSmATP6c2JmZmZmw0kdu0JdDKwZEQuQ6o0P\nA1cCSFof+BnphvSCwO+B6yR1dHOsfnGLRXPZG7gqIv5ds/4vku4kXSRHAr+WNAo4OSJO7OZYxW5P\nRwMHAtdIWobUgnEnaexF575Vuvdx4GRSZDwZ+ANwSp/PyszMzMxK0TnrZ9ZOqsNNyO/3An4fETfl\n96dI+jbw/0gByaBUqtWe6otmQ+vx/b/uC9Bms+w2W9a7CNaApn5q63oXwRrQq1PcQG6zG7NoR91H\nO/928VVLreNs9+IjfT4nSTuSWibmJ7VYbBIRL0j6N/CriDizsO/VwBMR8d3BltFdoczMzMzMSlbP\nWaEi4rKIWJA0a+fDwFV5UwfwRs3ur5MCkEFzYGFmZmZmNgxFxCRS1/Z1JK1G6rK+YM1uCzF7sDEg\nHmNhZmZmZlayBnqo3cj8czJwP7B254Y88c5apEcFDJoDCzMzMzOzktXjoXY5UPg28NuIeClPynMW\n8L8R8Yyk84DrJV0E3EF6XMBI3u8qNSjuCmVmZmZmNnx8BXhI0lvA/wLPA1sDRMQdwH7AecBref1m\nEfFWGRm7xcLMzMzMrGRtdWixyM8n27yXfS4BLhmK/B1YWF0tc8pF9S6CNaB/bb5pvYtgDWitP3m6\nWZvdkvO6KmONqdJAgyzmFHeFMjMzMzOzQXOYb2ZmZmZWsrYWbLFwYGFmZmZmVrJKe+t1DGq9M24x\nksZL2qmfaR6XtOsg8rxJ0tEDTW9mZmZmzcctFnUm6VZgXWB6XvUCcHZEnFFSFtW8DHWaMtObmZmZ\nNTUP3rZ6qALHRkRHRHQAOwPHS/pinctlZmZmZgPU1l4pdWkGbrFoMBFxt6RHgNWBmySdAGwHLA5M\nAs4qtmZIWgf4GbAy6THtNwK7R8SYwmGXl3QTsA4wHtg7Iu7M6UcCPwJ2AmYBpxfLk5/Y+EvS49/n\nAh4AvhMR/yrsczjpYSvzABcBlbyYmZmZWYtwi0VjqEB6DLuk9YFVgDvztoeB9XJrxl7AiZK+lPdf\nELgOuAxYCDgA2IcPdkOqALvnbQuQAo/iwyMOIz1I5TPAGGD5vBTTnw0sB3wI+BdwpaT2XIZvAN8B\ntsjbXwY+h7tCmZmZWQurtLWVujSD5ijl8FYBxkp6DXgLuA24FLgHICLGRcQL+fUtwJ+AjXParwKT\nI+LUiJgZEfcB5/PB1oIq8IuIeDQiZuXtH5bUkbfvApwUEU9GxFTgexSCgoh4NiL+GBFTI+Jd4EhS\nkLFyIf05EfHviJgBnEgaJ2JmZmbWstwVyuqhChwXEScASFqa1AJxAbCbpAOBPYFlSAHDaGBcTrs0\n8EzN8WrfA0wsvH47/+wAJudjjO/cGBHvSHqx872kRYGfAJ8HFiR1lwJYDPhPF+mrkp7u/bTNzMzM\nbDhxi0WDiYgJwOXA1pI+C5wE7A0sEhELAdfyfovEBFLrQVHt+95MIHWBAkDSvKSgodOJwBLApyNi\nAWDZvL7STfoKsEI/y2BmZmY2rFTaK6UuzcAtFo3hvatF0hLAtsB9wPzATNK4hYqkzYCvAL/Lu/8R\nOEPSwcBZwGqk8RTT6btLgO/naW8nAifzwYCzA3gHeF3SfHl7bfqTJV0FPETqSvWhfuRvZmZmNuz4\nAXlWL0dKmixpMimgmAjsCNwAXAz8A3gJ+C/gqs5EEfE6aeD1TsCrwJnAr4BpveRXHFh9Ys7nLuBJ\n4GkKXZuAo0gzUr2Sy3YHMKNQhotJQc21pLEViwF/6+uJm5mZmdnwUKlWPXnPcCLpRGCtiNi03mXp\ni6lTpvgCtNn8e/OmuHxtDlvrT9fXuwhm1iRGjR5d975Dt63z2VLrOJ+7++91P6feuCtUk5O0CakL\n0iRgfdKUtN+ta6HMzMzMrOU4sGh+q5O6S80PPE8aA3FxXUtkZmZm1uIqbQ3fwFA6BxZNLiJOA06r\ndznMzMzM7H1tHrxtZmZmZmbWf26xMDMzMzMrWbM8e6JMDizMzMzMzErmwMLMrAGseq2nFbXZtU+e\nVO8iWAOa2eFnspo1CgcWZmZmZmYla8XB2w4szMzMzMxK1opdoVovlLLZSLpQ0nlzOq2ZmZmZDR9u\nsWgAkm4F1gWm51UvAGdHxBlzqAjVvMzptGZmZmbDUlsLPiDPLRaNoQocGxEdEdEB7AwcL+mLc7AM\ng7n6W++bY2ZmZtaDSntbqUszcItFA4qIuyU9AqwO3CTpBGA7YHFgEnBWZ2uGpBWAJ4FdgMOBZYE7\ngV0j4oW8zxLAecAGOf3J+f0KEfFMbf6SjgC+AWwGjAfGArsCCwH/Ag6KiIe7KnsxbUQ8MdjPwszM\nzMyaQ3OEP62hAiCpIml9YBVSgADwMLBebs3YCzhR0pdq0n+dFDgsDcwLHFvYNg6YCiwDrE+q+Be7\nL1WAqqQRki4ANgU+kwODQ/L+XwGWAG4HbpQ0XyF9d2nNzMzMWlJbe6XUpRk4sGgMFWCspNeAt4Db\ngEuBewAiYlxn60NE3AL8Cdi45hjHRMSrETEZuAz4JICkZYCNgO9HxFsR8RIp6CheoVVgQeB6YD7g\nCxHxat62O3BSRDwWEdNy2pnA5oX03aU1MzMza0mV9kqpSzNwV6jGUAWOi4gTACQtTQoOLgB2k3Qg\nsCepxaECjCa1QhRNLLx+B+jIr5fOP4tdnmq7P1VIrR3zA5/IAUSnZYCnOt9ERFXSeFKXq97SmpmZ\nmVmLcItFA4qICcDlwNaSPgucBOwNLBIRCwHX0vcB0xPyz+UL65ar2aeaj3kocIukjxW2PQuM6Xwj\nqQ1YIa/vLa2ZmZlZS2rFwdvNUcrW8F6gkAdbbwvcR2oJmAm8DFQkbU4a79AnEfEccCtwkqT5JC0G\nHNFF3pWIOJs0APyvktbN2y4EDpG0sqS5SAO520ndsXpLa2ZmZtaSPMbC6ulISZMlTSYFFBOBHYEb\ngIuBfwAvAf8FXFWTtvY5ErXPltgRmAd4jjT4+nd5/bu1+0fEhcC3gD9J2gg4Bfg18BfS8zU2BL4U\nEW/1Ia2ZmZmZtYhKtepnm7UaSV8Gro6I0fUuy9QpU3wB2mzenVXvElgjmuftSfUugjWgmR0fqncR\nrAGNGj267rf4H9pp81LrOKuP+1Pdz6k3HrzdAiStSWpVeJA0XuI44Dd1LZSZmZnZMNbWJOMiytR6\nZ9yaFgKP16NLAAAgAElEQVR+D0wmdYW6DzioriUyMzMzs2HFLRYtICJuBVaudznMzMzMWkWzPHui\nTA4szMzMzMxK1ixTxJap9c7YzMzMzMxK5xYLMzMzM7OSVdpa7/69AwurqxGvPVPvIlgDGjlzWr2L\nYA1o1twd9S6CNaD2N1+odxGsEY0eU+8SeFYoMzMzMzOzgXCLhZmZmZlZyTx428zMzMzMbAAcWLQg\nSddJ+l7h/WRJ6+TXG0h6rX6lMzMzM2t+lfa2Updm4K5QTUjSrcC6wPS86gXg7Ig4oy/pI2Kzmvcd\nhde3k57UbWZmZmYD1IqzQrXeGQ8PVeDYiOjIQcHOwPGSvljncpmZmZlZi3KLxTAQEXdLegRYHbhJ\n0iLAycAmwCjgFuCAiHgR3mvxuDEijs/vZwHrR8TfJW2Yt43M2y4kBaBTgW2Bt0lBzbmd+UvaA/gB\nsChwTd5/ekTsPsSnbmZmZtaQKu3t9S7CHOcWi+ZVAZBUkbQ+sApwp6QKcDUwE1gNWB6YDFxWSFvN\nS19tA/whIhYCDgDOlrRszv9zwFnAHqQuVNeRApD+HN/MzMxsWGnFMRbNUUqrVQHG5kHWbwG3AZcC\n9wCfANYG9o+IyRExBTgU+IKkpQaY318j4o8AEXEV8Drw8bxtF+B3EXFrRMyKiN8Adw/0xMzMzMys\nObkrVHOqAsdFxAkAkpYmtUhcAPwRmBuYJKmYZgqwHPD8APKaWLPubaBzwPdSpICm6Glyi4qZmZlZ\nK2prwcHbDiyGgYiYIOly4ATgp8DbudtSWXoKEiYAK9SsWx54vMT8zczMzJpKs3RfKlPrnfHw8V5l\nX9ISpHEN9wH3AvdLOkvSwnn7YpK27y59X/PpxiXANpI2lNQuaTtgnT4e28zMzMyGCQcWzevI/GC7\nyaSAYiKwY0RUgS1JAcE/Jb0J3Al8riZ9T4OrqzWvu903Im4DDiJ1w3oV2Iw0eHxa/07HzMzMbPho\nxcHblWrVk/e0MkntpAftfToi7i3pmHcC10TESb3tO+P58AVos6nMdFxqs5s1d0fvO1nrcT3GujDy\nQ2PqPtZzwjH7lHpxLn30L+p+Tr3xGAv7BGlq2qcGegBJ2wDXk1opdsvH3LmMwpmZmZlZc3Bg0cIk\nHQgcAfwgIl4ZxKG2Bs4D2oH/A7aKiCdKKKKZmZlZU2qW7ktlcmDRwiLiTODMEo6zYwnFMTMzMxs2\nWjGwaL0zNjMzMzOz0rnFwszMzMysZG0t2GLhwMLMzMzMrGQVP3nbbM6asdBy9S6CmZk1sWcP/ka9\ni2ANaOWfX1HvIrQkBxZmZmZmZiVrxcHbDizMzMzMzErWioFF652xmZmZmZmVzoFFE5N0q6Sxdcj3\ncUm7zul8zczMzJpFpa2t1KUZuCtUHUm6FVgXmJ5XvQCcHRFn9PEQ1bzMafXK18zMzKwptLW317sI\nc1xzhD/DVxU4NiI6IqID2Bk4XtIX50TmkkbOiXzMzMzMbPhzi0UDiYi7JT0CrA7cJGkR4GRgE2AU\ncAtwQES82FV6SesAPwNWBu4HbgR2j4gxeft44HzgC8AngT0k/Qc4C1gVaAfuAvaPiCdzmpHAj4Cd\ngFnA6V3kuwFwIvBR4DXgZxHxk0F+HGZmZmZNqxUHbzuwqL8KgKQKsB6wCnBnfn818CiwGjCDFABc\nBszWoiFpQeA64ARS5X8N4E/AuzW77glsERH3SxpFCkKOAv4OjAZ+CVwKfDbvfxiwOfAZ4HngJ8Dy\nhXxXzfnsBPwR+AjwZ0kvRcQlA/1QzMzMzJpZPQILSdsD3wY+BswTESML23YDLgDeLiT5Q0TsVFb+\nDizqqwKMlfQ9YC5Sxf4c4B7gE8DawMYRMQ1A0qHAS5KWiojna471VWByRJya398n6Xyg+OSgKvDL\niLgfICKmAg8Wtk+XdCzwgKRRefsuwAmFFozvAXsU0uwHXB4R1+b3IemnOZ0DCzMzM7M551XgbGAe\n4Nwutj8eER8ZqswdWNRXFTguIk4AkLQ0qUXiAtLd/7mBSZKKaaYAy5FaD4qWBp6pWVf7HmB88Y2k\nlYBTgE8DHbw/MHsx4Nl83PfSRMQ7kopdscYAG0naurCurZu8zczMzFpCPWZyioi/AEjasJtdKkOZ\nvwOLBhIREyRdTurO9FPg7YhYqI/JJ5ACjqLa95DGSRSdAzwHrBERr0laHXiA9y+8CaTg4RYASfOS\ngo5O44ELImL/PpbTzMzMzOa8KrCspImkGUnvAA6PiPFlZdB6o0oaz3uRo6QlgG2B+4B7gfslnSVp\n4bx9sdx3rpi2M/0fgQ5JB0saKenjwO70Pi1sB/AO8IakRYFja7ZfAnxf0oqSRpMGkxevm58B20v6\nas53hKRVJX2u7x+BmZmZ2fBSaW8rdSnBbcDqEbEk8ClgKnCjpHnKODg4sGgER0qaLGkyKaCYCOwY\nEVVgS1Lg8E9JbwJ3AsUK+3vPk4iI10mDrHci9a87E/gVMK2X/P8b2AB4E/gbcC0fDEZOBG4gzRb1\nJPA0H+wa9TBpfMd3SN2zJuV8F+3HZ2BmZmY2rDRaYBERT0XE4/n1JGAvYElgnUEfPKtUq37O2XAl\n6URgrYjYtN5l6c7UKVN8AZqZ2YA9e/A3et/JWs7KP79iSMcS9MVb444ttY4z305H9fmc8hiLG4uz\nQnWxzwjgddJsoTcPvoQeYzGsSNoEeIjUarA+KRL9bl0LZWZmZtaC6jF4W1IbaabRufL7uYFKREyV\ntDnpOWcTgIWAk4CXSL1SSuHAYnhZHbgYmJ/ULenk/N7MzMzM5qBKW3s9st2FNLsopK7tU4CqpBWB\nz5OmoF2A1AX+f4FNIuKdsjJ3YDGMRMRpwGn1LoeZmZmZzXkRcSFwYTebD8nLkHFgYWZmZmZWtvq0\nWNSVAwszMzMzs7LVYYxFvTmwMLOG03bfdfUugjWgEYssUe8iWANa9ieX1LsIZpY5sDAzMzMzK1ml\n3V2hzMzMzMxssFpwjEXrdf4yMzMzM7PSObCwLkl6SNK2+fUKkmZJWiq/30nSffUtoZmZmVkDa2sv\nd2kC7grVJCTdCqwLTM+rXgDOjogzhiK/iFi9h23jgHFDka+ZmZnZcFCPJ2/XW+udcfOqAsdGREdE\ndAA7A8dL+mLtjpLaJDVHaGtmZmZmw4JbLJpURNwt6RFgdeAmSbOA75Ae5b4qsKGkDuAEYGVgBvBX\n4MCIeAlA0vbAUcAywDvA9RGxW942HhibWyc+QNJuedvKheMcBowB3gb+ABxc5iPizczMzJpKk3Rf\nKpNbLJpLBUBSRdL6wCrAnYXt3wS2BeYF7gOmAvsBiwJrAEsBZ+RjzANcAuwXEfOTgoLzCseq5qUv\nXgd2iIgFgA3ycsQAzs/MzMxsePAYC2tgFWCspO8BcwGjgXOAewr7/DginsqvpwF3FLZNknQKcH5h\n3TTgo5IeiIhXa/bvs4i4vvD6CUk/B74xkGOZmZmZWXNyYNE8qsBxEXECgKSlgcuAC4Dd8j7jiwkk\nfYLUFepjwDyk4GRegIh4R9JmwMGksRpPAqdGxK/7WzBJm5C6VAmYG2gHJvX3OGZmZmbDhQdvW9OI\niAnA5cDWhdWzanb7DXAvsHLuprQjuTtVPsbfImJLYBHgOOBSSWP6Uw5JcwFXk4KcZXM+h+Fry8zM\nzFqZu0JZg3svKJC0BGk8RU/Pk+gA3gTelrQcqcLfmX5x0liImyLiDUlvkFpFZvazTHPl5fWIeFfS\nqsD+/TyGmZmZmTU531VuLkdKmixpMimgmEhqhejO3sCepODiCuB3vD8gu400sPspSW8CZwO7RsQz\n3RyrWvO6ChARbwHfAk7O5TqL9IyLvg78NjMzMxt+WrDFolKtuv5n9TN1yhRfgDabtvuuq3cRrAGN\nWGSJehfBGtC0ZdeudxGsAY0aPbrS+15Da9rtvym1jjPXBtvX/Zx64xYLMzMzMzMbNI+xMDMzMzMr\nWwvOCuXAwszMzMysbE0yLqJMrRdKmZmZmZlZ6dxiYWZmZmZWskoLtlg4sDAzMzMzK5vHWJiZ1d+s\nj29W7yJYA3rnylPqXQRrQCM83axZw3BgYWZmZmZWslbsCtV6bTRmZmZmZlY6t1iYmZmZmZWtBVss\nHFiYmZmZmZXNg7etkUj6JHAE8FlgbuAF4DrgRxHxQj3LZmZmZmZW1HqhVJOQtAlwO/AosGZELAB8\nHng5/+zv8UaWW0IzMzMz606lvb3UpRm4xaJx/QwYFxGHd67IrRTHA0jaHjgMGAO8DfwBODgi3snb\nxwPnA18APgnsIek/wFnAqkA7cBewf0Q82ZmHpL2B/YHlgTdIrSM/lbQmcGZ3aSV9ETgFWBGYBtwX\nEZuU/qmYmZmZNYMWHGPhFosGJOkjwErAZT3s9jqwQ27J2CAvR9TssyfwnYjoIAUeVeAoYClgBeAt\n4NJCvt8Cjgb2zcddC7g7b57VU1rgYuD0nG4p4H/6c85mZmZm1tzcYtGYFss/J3S3Q0RcX3j9hKSf\nA98o7FIFfhkR9+d9pgIPFrZPl3Qs8ICkUXn7AcBxEfH3nOYV4JX8ure07wIflrREblm5bUBnbmZm\nZjYctGCLhQOLxvRS/rk0EF3tkMdgHAWINLC7HZhUs9v4mjQrkborfRroIAUfVVIg8yyp+9Nj3eTX\nW9otgR+Qgo2XgHMj4ow+nq+ZmZnZsFJpwVmhWu+Mm0BEPAY8DuzY1XZJcwFXk7pKLZu7Hx3G7L/P\nWTXvzyGNm1gjp1kfqOQFUiDykW6K1WPaiHggIraPiMWBfYATJW3UpxM2MzMzs6bnFovGtR9wraRJ\nwNkRMVHSh4DdSS0EcwGvR8S7klYlDbjuTQfwDvCGpEWBY2u2/xT4gaR/A/8AFgZWiIh7e0qbZ5za\nEfhTRLxMGv8xC5gxwHM3MzMza24t2BXKLRYNKiJuIrUKrAo8KOlN0vSziwE3Ad8CTpY0mTTT0zhS\n16Se/DdpkPebwN+Aa4tpIuJnwImk2aTeAP5JmlGq17TA14FHc3muAY6KiNsHcu5mZmZmTa/SVu7S\nBCrVam91UbOhM3XKFF+AZtYnM648pd5FsAY0Yuvv17sI1oBGjR5d6X2voTXriX+UWsdpW+nTdT+n\n3rgrlJmZmZlZ2ZqklaFMDizMzMzMzEpWbcHAovXO2MzMzMzMSucWCzMzMzOzsrVgi4UDCzMzMzOz\nslUafqx16VovlDIzMzMzs9K5xcLMGs7Ilx+vdxGsEXlaUevCuKXXqncRrAHt8ep/6l0EaGu9+/cO\nLMzMzMzMSuZZoczMzMzMzAbAgUUTknSrpLH1LkdPJD0kadt6l8PMzMysLipt5S5NwF2hGpSkTwJH\nAJ8F5gZeAK4DfgRU89KwImL1epfBzMzMrG6aJBgoU+udcROQtAlwO/AosGZELAB8Hng5/zQzMzMz\nayhusWhMPwPGRcThnSsi4gXgeABJ+wILS7oC+BLwInBwRPyhc39JWwFHAisCE4HjIuKyvG03YCxw\nJnAIMC/wO2C/iJglaQXgSWAX4HBgWeBOYNdcDiQdBOwLLA28BowDjoiIWXn7eGBsRIwr96MxMzMz\nawJusbB6k/QRYCXgsh52qwC7Aj+OiPmBs4GLJI3Kx9gE+CVwYEQslPc9W9IGhWMsDyxOCjw+BWwL\nbF+Tz9eBDUjBw7zAsYVtzwKb5vy3BL4J7FnY3vDdtczMzMyGSrXSVurSDJqjlK1lsfxzQg/7VIHf\nRMRd+f15wALAyvn9QcAZEXEHQETcQ2pR2KVwjCnAURExPSKeAP4KfLImn2Mi4tWImEwKdN7bHhFX\nRsTT+fV9wKXAxv06UzMzMzMbNtwVqvG8lH8uDUQP+03sfBERb0sC6MirxgAbSjq4sH87cFvh/YsR\nUWxReLuQfrY8gHeK2yXtAByc8xoBzEXqLmVmZmZmTdLKUCYHFg0mIh6T9DiwI3DzAA8zHrggIk4t\nrWAFkpYltVBsBfw5ImZI+jHwiaHIz8zMzMwanwOLxrQfcK2kScDZETFR0odI4xiezPtUekh/OnCh\npLtJrQjtwBoAEfHPbtL0dLxa8+X9XwZmSloX+AbwcD+OYWZmZjZ8VfpTtRoeWq+NpglExE3A+sCq\nwIOS3iRNP7socGverduB0RFxI7AXcAqpa9XzwKmkAdidaWvT167rdntEPAocDVxDmhHqUHoebG5m\nZmbWWlrwAXmVatUT91j9TJ0yxRegzWbky4/XuwjWgKYv+uF6F8Ea0Lil16p3EawB7fHqf+reXDD9\npWdKreOMXGy5up9Tb9wVyszMzMysZM0yRWyZHFiYmZmZmZWtrfUCi9Y7YzMzMzMzK51bLMzMzMzM\nyuauUGZmZmZmNmgtGFi03hmbmZmZmVnp+jzdrKSHgZtIT4O+NSLeGMqCWWvwdLPWlbap/vNis5s1\naoF6F8HMmsSo0aPrPjXrtDdeLrWOM9cCi9b9nHrTn65QvwfWIz39ebSke4CrgSsi4omhKJyZmZmZ\nWTNqxelm+/2APEkjgLWBzYCv5Nd3A+cC4yJiZtmFtOHLLRbWFbdYWFfcYmFmfdUILRbvvvlqqXWc\nuedfuO7n1JsBP3lb0pLArsABwDzAc6QxG1+LiCdLK6ENaw4srCsOLKwrDizMrK8aIrCY/Hq5gUXH\ngnU/p970a1YoSQI2B7YkdYt6FDgWuASYApwF/ALYpNxi2lCRdCEwPSL26mb7hsCNETEyv/8BsG5E\nbDHHCmlmZmbWbCoNHweUrs+BhaTngSWAV0hjK46KiL/V7PML4K5SS2jdknQrsC4wDZhF+t38HTg9\nIv7Zx8NU89InEXFCP4tpZmZmZnOIpHbgJFLPolHAX4B9IuKVoc67P6NKzgM2AJaMiL1qg4psFvDX\nUkpmfVEFjo2I+SNiQWAjYDxwp6St6loyMzMzs1ZWaSt36bvDgC2ATwPL5HWXlH16XelPV6iFgQkR\nMaO4UtKWwKYR8a2IeJh0IlYHEfEMcGQe/3IWcLWk8cDYiBgHIGkF4ElgmYh4PiedR9LFpC5uLwH/\nExEXdZWHpB8C60XEJvn9eFL3t42BdUiBzd4RcWfpJ2hmZmbWJOo4K9TewA8jYjyApEOAxyUtGxHP\nDmXG/TnjbwNLdbF+OrBdOcWxkvwWWDqPiemtq1MF+DpwPbAQsA/wc0mf6Ud+u5MG8S8A3Ah0GZSY\nmZmZ2dCRtCCwLPBel/g8qdKbwJpDnX8ZodQYYGQJx7HyPJd/LtLH/e+MiMsiYlZE/JX0zJLd+pi2\nCvwiIh6NiFnA+cCHJXX0q8RmZmZmw0l9ukJ11r9qp1d8HZi/tHPrRo9doSRtDPywsOpnkiYX3i8I\nrEYaf2GNo7M/XV8H6Tzdxfu1+pHfxMLrt/PPDmByF/uamZmZDXvV+swK1Vn3qp2fe0FSq8WQ6m2M\nxdNA51O1a5+uXSVFQz8idb2xxrEd8FxERA4E5yts66o72wpdvB/SPnhmZmZmVq6IeF3SM8AngAcA\nJK1Eaq14YKjz7zGwiIjH6XuXGKuP98JhScsCe5KmF/t6Xv1PYAdJ40gPMjyyi2OsK2l74HLg88DW\npMHYZmZmZjYAA3wGdRnOBQ6VdAvwGnAycH2e5GdI9dYVagPgjoiYJWm5nvadE4W1Lh0p6VBSC9Ir\nwB3AZyLi3rz9CNJg6omkFqhTgC8V0ldJLU6bkWZ3ehnYr2ZWp2rN696+Kn6atpmZmbW0WfWLLE4i\nTchzDzA36TkWO8+JjCvVHk5a0svA5yLiEUmzejhONSLaSy+dDXtTp0xxEGKzaZtaO+bMDGaNqu0y\nbGbWtVGjR9f9sddvvVNuHWe+eep/Tr3pbYzFNsB/8uu9mH2QL6T++B8qsUxmZmZmZk2tFe+c9jbG\n4tbC2+8Cp0XEB2aAkrQjsAdwfOmlMzMzMzNrQrNaMLLoz3MsxpCe2FzrJd6f3tTMzMzMzFpQfwKL\nl4C1u1j/CeCFcopjZmZmZtb8qtVqqUsz6G2MRdFPgOPzIO5bgJnAF0jTlx47BGUzMzMzM7Mm0efA\nIiJOl9QBHEOashTgXeB00vy4ZmZmZmZGa46x6HG62a5ImhdYFZgGPBERbw1Fwaw1eLpZM+ur9jfd\n69ZmN3P+JepdBGtAjTDd7CuT3ym1jrNIxzx1P6fe9KcrFAAR8TbpgRtmZmZmZmbAAAILMzMzMzPr\nWSt2herPrFDWRCRtKGl6vcthZmZm1opacVYoBxZNRtKtksbWKe8LJZ3X+55mZmZm1mrcFar5VJnD\nT4mXNAKYNSfzNDMzM2tmrVhxcmDRxCT9CtgYWBB4FjguIn7dzb6fBK4EjomI8yWdAGwHLA5MAs6K\niDPyviuQnrK+J/A9YEXgeGDHvH17UnCzAPAx4EzSTGHtwF3A/hHR1VPazczMzFpCk/ReKpW7QjW3\n24E1SRX8Y4ELJX20didJWwDXAntGxPl59cPAehHRAewFnCjpSzVJdwA2BOYjBRbjgAsjoiMi5o+I\nKikgPwpYClgBeAu4tMyTNDMzM7PG5xaLJhYRFxTe/lbS90iBwKOdKyUdCHwX+HJEPFBIO67w+hZJ\nfyK1fvylcMxjIuLFwrEqwAfmUI6IBwtvp0s6FnhA0qiImDqY8zMzMzNrVq04K5QDiyaVK/nHAF8H\nliB1TZoXWLSwWxtwOPCLYlCR0x9I6uq0DClYGE1qkSgaX/N+tq+IpJVIT2L/NNDB+2NAFiN1zzIz\nMzNrOc0yk1OZ3BWqOVVI4x32ALaOiAUjYiHgfj7YojAL+DzwTUmHda6UtB5wErA3sEhOe21N2s70\nPb0HOAd4A1gjIhYA1s/HafinQ5qZmZlZeRxYNK8OYAbwsqQRkr5JGm/xARHxGLABsGcesA0wPzAT\neBmoSNoc+Eof8nwBWDG3lhTL8Q7whqRFSWM9zMzMzFrarJKXZuDAojnNAi4C7gYeB54DPgrcVrNf\nFSAiniYFF1tIOhu4AbgY+AfwEvBfwFVdpa3xS1J3q1ckvZoDjP/Ox34T+Bup5aP12v7MzMzMCqrV\ncpdmUGnF/l/NTNK/gJ9HxLB4UN3UKVN8AZpZn7S/+UK9i2ANaOb8S9S7CNaARo0eXfcu2U+/8lap\ndZzlF5mv7ufUGw/ebiKSPg6sRnpWhJmZmZk1qFktePPegUWTkPQbYD3g8JopXs3MzMyswbReWOHA\nomlExP9v787D5KqqhY2/DSRMCYgGZJI5LHEAB+QyKlO8DlzkOisiMoj3U0QuKgrIKDMyisplElBA\nRFFBvAgIAQTBAQPKxYUIYQyjDCEkQNL1/XFOk7LpdCfpSu+q1Pt7nnqqau9zdq0KFVKr1t77fLx0\nDJIkSdKcmFhIkiRJLeYF8iRJkiQNWxcusXC7WUmSJEnDZ8VCRb108TGlQ1AbGr3a+NIhqA19casD\nSoegNnTyVQeXDkHtaNtdSkdAbxcu3zaxkCRJklrMqVCSJEmSNB+sWEiSJEkt1o27Qlmx0CtExMyI\neGfpOCRJkjpVo9HaWycwsegQETExIkZq5WKHfHwlSZLULpwK1Tka+IVfkiSpI7grlDpORKwOnAJs\nCkwHfgrsl5kz6v5e4AvALsDrgTuAz2Rm1v1jgVOB7YBngUMGeI3/B3wJWBG4E/hqZv627jsE2AK4\nGdi9PuV7mfmKcSRJkrTwcipUB4uIxYDLgYeB1YCNgc2Ab/U7dGfgg8A44AHg2019JwFrA+sBGwAf\nABZteo1PAIcBOwGvBs4AroiI1ZrG2AK4D1gJ2B7YPyI2bcmblCRJ6kDduMbCikVn2whYB3hHZk4H\npkfEN4CfA3s2HXdcZj4IEBHnAj+oHy8CfBJ4X2Y+VrftC+zQdO4uwGmZ+Yf6+dkRsXt93tF1W2bm\n6fXjWyJiErAhcFNL360kSVKH6O2UbKCFrFh0ttcBj9dJRZ97gCUiYlxT25Smx9OAsfXj5YHFgclN\n/c2PAVYF7u3X9o+6vc8j/fqnAWOGiF2SJEkLEROLznY/sHxELNnUthYwIzOfmIvznwBeBNZsaluj\n3zEP9OuHaurUA/MWqiRJUveY1dvaWydwKlTn6AFGRcQSTW1/Ae4Gjo+ILwPLAd8Ezp6bATNzVkRc\nABwaEX8FZjB7elOfc4CTI+JS4M9Uay3WBz42F/FKkiR1JadCqZ01gIOB55tuzwC7UU1Luh+4Bfgd\n8JW5GKvPl6imOv0NuA24FJjZ15mZFwKHAj+kqnB8jmpNxgNNYw30N6f7/jZJkiR1sZ5GF2ZTah9T\nzzvED6BeYfRq40uHoDb0pa1G6hqh6iQnX3Vw6RDUhhbfdpfiMyduvu+fLf2Os/Hqry7+nobiVChJ\nkiSpxZwKJUmSJEnzwYqFJEmS1GKdspNTK5lYSJIkSS3mVChJkiRJmg9WLCRJkqQWm9WFFQsTCxU1\n6iNfKx2C2tAtW25TOgS1oZOev7N0CGpD3ffVTZ2itws/nE6FkiRJkjRsViwkSZKkFpvVhSULEwsN\nKSLWAO4BVs3MhyPiEGCzzJwwh+NXA+4AxmfmIyMWqCRJUpvoxl2hTCwWoIiYCLwTeFdm3tDUfjfw\nzcw8dwG//pbANcA0oBd4CUjgp8CpmfnignjdzLwfGLsgxpYkSVJ7co3FgtUAngS+NUD7SKWxszJz\nbGYuC6wMHAzsAkyMiFEjFIMkSVJXmdVo7a0TWLFY8M4Ado6IT2TmhQMdEBFvAo4H3gpMB84HDsrM\nmRFxCrB4Zn6uPvZ6YLXMXKN+vi9VReT9QwVSVyiujoj/BP4C7AycWY+zBXAUsB7wFPDdzDxhkOF6\nIuIIYPf6+fcy85B6rDVomjo1VFySJEkLm26cCmXFYsGbBhwEHDlQhSAiVgCuA35CVVHYBJgA7Fcf\nchWwbX3sGKrkg4gYX/dPqI+Za5l5N/AnYJt6rDcAlwPHAOOA9wN7RsROgwzzTuA+YCVge2D/iNh0\nXuKQJEnSwsPEYsFrAN8HngP2HqD/08CkzDwjM2fWv/AfXbdDlXS8LiLWBN4F/B64ApgQEYsDmwJX\nz1lYYKIAACAASURBVEdcDwGvrh9/Hrg4My/LzEZmJvCdphgGkpl5emb2ZuYtwCRgw/mIQ5IkaaEz\nq7fR0lsncCrUCMjM3oj4KnBhRJzVr3tNYLOIeKqprYc66cvMZyPiD1RVi/WAK4F/ADtSLcSempl/\nnY+wVqWqOPTFsFVEfLCpfxHg/kHO77/b0zRgzHzEIUmStNDpxqlQJhYjJDOvqBOEg/t1TQauzszt\nBjn9aqopT68HPlOfczpwF/NRrYiIdYC3UVVS+mI4OzP3nNexJEmSJDCxGAk9TY+/QjWVaUZT23nA\nlyNiF+BC4EVgDaprQPy6PuZq4L+BGZl5K0BE3At8joGnVw2onjq1OXAi1dSlvu1uvwtcFxFXAL+m\nmr61LjAuM6+fh/fZM+RRkiRJXaBTdnJqJddYLHgvf6wy83bgApqu8ZCZjwJbATsA9wL/BC6hmp7U\n52aqL+3XNLVdXY8zWMWiASwaEVMj4hngYeCbVMnMuzLzpTqGO4DtqJKUh4FHqaoZ4wZ6Hwy8XW7/\nti786yRJklTpbTRaeusEPY0OCVQLpxnTp/sB1Cv8fsttSoegNrTRxN+UDkFSh1hiySWLz6L40W0P\ntfQ7zsc3WKX4exqKU6EkSZKkFuvtkJ2cWsmpUJIkSZKGzYqFJEmS1GLduHjbxEKSJElqsU5ZcN1K\nToWSJEmSNGxWLCRJkqQWm9WFFQsTC0ltZ7Mff690CGpDL5UOQJLmgbtCSZIkSdJ8sGIhSZIktVg7\n7woVEXsBOwJvAh7OzPH9+g8BvgFMb2o+NTP3G2xcEwtJkiSpxdp8V6iHgKOB9YBd5nDMNZn57nkZ\n1MRC8ywitgAuzczlSsciSZKkeZOZPwWIiGUHOaxnXsc1segSETER2Jhq/eMs4B7g8My8ZF7Hyswb\nAJMKSZKkOejwXaEawMYR8TgwFbga2D8znxjsJBdvd48GcFhmjgVeA1wIXBQR4wc/7V9FxKgFEZwk\nSdLCZFZvo6W3uRER50RE7yC3w+Yy/IuB9TJzeWBrYBXgF0OdZMWiC2XmrIj4HnAM8OaI+CEwHpgJ\n/AbYKzMfh5crHX8G1gS2Ao6IiN8DV2XmqPqYbYHjgLWAF4FJmTlhZN+VJElS1/sCsM8g/dMH6XtZ\nZv5f0+PJEbE78FBErJmZ987pPBOL7tIDEBGjqT54LwKPAJ+nSh6WB34MnAx8sum8XYEPZOYOEbEk\n8G/9xj0P2C8zz60rGpss0HchSZLU5ua2ytBKmTkNmLYAX2LQdRcmFt2jBzggIr5ClVD8HfhQZt7U\ndMyjEXEccFZTWwO4ODMnAmTm9IjoP/YLwDoRsWJmPgJcv4DegyRJUkcokVjMrYhYFBhV33oiYnGg\nJzNn1P0fBG7IzMcjYhXgu8AfM/OewcY1segeDarF2kc2N0bE24EjgfWBpagSkKX7nTt5iLE/AOwP\n3F4v8jk9M09uRdCSJElquQOBg+rHDaopUg1g0brtg8D3ImJp4J/AlcAeQw1qYqEfUU1/+lBmPhcR\n2wGX9jumd7ABMvN24OMAEbE5cGVE3J6Z1y6IgCVJktpdO1csMvMQ4JBB+j81P+OaWHSXgebFjQWe\nBaZFxGrA1+fyPODlXaI+CVxeb0H2NFUiMnP44UqSJHWmdk4sFhS3m+0uA33C9wB2p0oufkJVveh/\n3EDn9bX1AB8F7oyIqVRbkR1UX+tCkiRJXaKn0dkX71CHmzF9uh9AvcKox+4qHYLa0EsrrFs6BEkd\nYokll5znq0a32mFXZUu/4xw0IYq/p6E4FUqSJElqMadCSZIkSdJ8sGIhSZIktVg3VixMLCRJkqQW\n68bEwqlQkiRJkobNioUkSZLUYt1YsTCxUFGNq84oHYLa0NStdy8dgtrQpC22Lh2C2tDmZx1aOgS1\now3eXToCZnZhYuFUKEmSJEnDZsVCkiRJajGnQkmSJEkatm5MLJwKJUmSJGnYrFhojiJiC+DSzFyu\ndCySJEmdZFaj+yoWJhYLsYjYBDgY2Jjqv/XfgFMy87y5OT8zbwBeTioi4hBgs8yc0PpoJUmS1Mmc\nCrWQioh3A9cANwJrAuOAY4CT6gRBkiRJC8is3kZLb53AisXC6zvABZn5zaa2iyNiKeDMiDgbOAx4\nKTM/23dAREwGDsjM8yNiS+CqzBwVER8D9gMWiYipQANYPzMnR8SHgIOA1YHJwCGZ+fMF/g4lSZLa\nVKckA61kxWIhFBHrAmsDPxyg+0KgB3g3VXLQ/1M/UBuZeRFwJHBtZo7NzGXqpGLT+nX2BV4N7A9c\nGBEbter9SJIkqf1ZsVg4LV/fP9S/IzNfjIgnqKZGQZVkzK2eAY7/DPCTzPx1/fxXEfEzYFfg9/Mw\ntiRJ0kKjGysWJhYLp8fr+1WAu5o7ImI0VVIxBYgWvNaqwB/7td0DvLUFY0uSJHWkWb29pUMYcU6F\nWghl5l1UX+53HKD748As4NfAVGDpvo6IWAxYYZChB/ob8gDV4vBmawH3z0PIkiRJ6nBWLBZeewI/\nj4h7ge8B04H3AycCh2bmIxHxJ+DYiFiDqoJxGDBqkDGnAKtFxKjMfKluOxe4OiJ+APyGau3GfwLv\nWgDvSZIkqSN041QoKxYLqcy8AtgGeCdwL1V14iJgr8w8sj7sfOBS4Fbg78B9wIP9hmr+W3ExVYXi\nkYj4Z0Ssnpk3ATsD3wL+CRwN7JiZrq+QJEldqxu3m+1pdOFVAbtRRCwLXAfcAXwqM9viP/z0S09p\nizjUXl7YevfSIagNTdpym9IhqA1tftahpUNQG1psg3fPy+Y0C8THzvl9S7/jXPSZjYq/p6FYsegS\nmfkM8O9AAm8qHI4kSdJCbWZvo6W3TuAaiy6SmY9SraOQJEnSAtQp05dayYqFJEmSpGGzYiFJkiS1\nWDdWLEwsVFTPhM+WDkFtaOyjWToEtaGNb7imdAhqQzNLB6C21A5fcLsxsXAqlCRJkqRha4eETpIk\nSVqodGPFwsRCkiRJarFuTCycCtWFImJmRLyzdBySJElaeFix6AARsRZwDLA5MAZ4Cvgj8LHMfGk+\nhuy+FFqSJGkENaxYqE39CngIWDczxwKbAFcAbX9pd0mSpG7U29to6a0TWLFocxHxGmBdYIfMnAqQ\nmQ8Bp0fEchHxDLBJZk5qOud64MrMPDwixgKnAtsBzwKH9Bv/EGAL4GZg97r5e5l5SNMxbwKOB94K\nTAfOBw7KzJkRcREwJTP3bjp+V2C/zBzfsj8ISZIktTUrFm0uM58E7gDOioidIuINEdFT9z0F/JjZ\nCQERsS6wMXBW3XQSsDawHrAB8AFg0X4vswVwH7ASsD2wf0RsWo+3AnAd8BNgZapqyQRgv/rc04BP\nRcTopvF2B84Y9puXJEnqUI1Go6W3TmBi0Rm2BCYCewN/BqZExAF13+nAJ5u+2O8G/G9mTomIRYBP\nAgdm5mOZ+Syw7wDjZ2aenpm9mXkLMAl4e933aWBSZp6RmTMz82Hg6LqdOq4ngf8EiIj16nPPack7\nlyRJ6kCN3kZLb53AqVAdoK5aHAAcEBFLAB8DzoiIhzPz+xHxMPCRelrSp4G+y1kvDywOTG4arvlx\nn0f6PZ8GjK0frwlsFhFPNfX3UCelmdmIiDOoqhQX1feXZeZj8/NeJUmS1JlMLDpMZs4Azo2IL1JN\nbQL4H6pKxTRgFnB53f4E8CJVcnBv3bbGPL7kZODqzNxukGPOBQ6LiPHAp5hdzZAkSepKnbLgupVM\nLNpcRLwK+BrwQ+Auqq1iPwC8CTiqPuwH9eODgLMzswGQmbMi4gLg0Ij4KzCDahrTUHqYvePUecCX\nI2IX4EKqRGUNYHxm/rp+nccj4hdUFYvn+9olSZK6VaO3dAQjzzUW7e9FqilNl1CtZXgM2B/4Ymb+\nFCAzn6ZaXL0Bsxdt9/kSVbXib8BtwKXAzKb+Bq+8rsXLbZn5KLAVsEM9zj/rWNbsd87/AG8Bzp6/\ntylJkqRO1tMpq8w1uHrb2I0z8z2FXn8N4O/AGvV2uHNlxvTpfgD1CqMezdIhqA299NooHYKkDrHE\nkksWv9bXZkdf09LvODd+fevi72koToVaCETEa6kWTX92qGMX0OsvBnwduGRekgpJkiQtPEwsOlxE\nnADsAZyXmf9b4PU3pNpy9h9UF+GTJEnqei7eVsfJzH2AfQq+/h+BMaVeX5IkqR11yrUnWsnF25Ik\nSZKGzYqFJEmS1GLdWLEwsZAkSZJarLcLd141sZDUdtxWVAN5fmb3/SOtoY2Z9VzpENSOllyydARd\nycRCkiRJajGnQkmSJEkatm5MLNwVSpIkSdKwWbHoMhHRC2yemTeVjkWSJGlh5QXy1BEi4jmg79O6\neH3/Qn3fyMxlRj4qSZIk9Wm4K5Q6QWa+fKXriDgDWDQzd10QrxURozLzpQUxtiRJkhYeJhadr6e+\nARARqwEnAJtRVTUuA76cmc378W0QEScBrwfuAD6TmVmfPxH4M7AmsBVwREScD5wFvA0YDdwO7J2Z\nt9bnHAJsAdwM7F6/xvcy85DWv11JkqT21+gtHcHIc/F253u5zhYRSwDXAH8F1gDeAKwKnNzvnJ2B\nDwLjgAeAb/fr3xU4KTOXrfsWAU4FVgNeC9wKXBIRizadswVwH7ASsD2wf0RsOvy3J0mS1Hl6exst\nvXUCKxYLh75P23YATZWCFyLiIODGiNg9M/uOOy4zHwSIiHOBH/Qb6+LMnFiPNZ0q+Xig74CIOBDY\nCxgP/K1uzsw8vX58S0RMAjYEXCQuSZLUBUwsOl9P0+M1gdUi4ql+x/QCKwJT6udTmvqmAWP7HT+5\n+UlEjKOaXvUu4FX1eADLMzuxeKTfGNOAMUiSJHWhbryOhYlF52v+1E4G7srMNw1zzP6zAo+iSkw2\nysxHI2IM8Cz/mtRIkiSpZmKhTtS8ePuXVIut96NaE/EcsDLwjsz8+TyO2Wws8DzwdJ1UHDuf40iS\nJGkh5eLtzteob33rIbamWrR9J/A0cDWwwVyMMdjzg4AVgCeBScCNwMyBYhhiHEmSpK7Q22i09NYJ\nerrx4h1qHzOmT/cDKGmuPD/T/13olcbMem7og9R1Rr9qheKzJl7/pV+09H9afzv5A8Xf01CsWEiS\nJEkaNtdYSJIkSS3m4m1JkiRJw9YpF7VrJadCSZIkSRo2KxaSJElSi7XzBkkRcTawLbAs8AJwPfDl\nzLyv6ZivAl+iujjy74A9MvPewca1YiFJkiS1WKO30dJbix0PRGYuC4wHXgK+39cZETsCXwG2A5YH\n/g+4NCIGzR2sWEiSOsJSi7X9TosqYLHH7y8dgtrRq1YoHUFby8w7mp72UF177KGmtj2A0zJzEkBE\n7A88BmxOVd0YkBULSZIkqcV6exstvbVaRHw9Ip4F/gmsAnyuqXt94E99TzJzGvB3hrjoshULSZIk\naSEQEecAnx7kkMMz8yCAzDwaODoi1gDOppoK9bH6uLHAM/3OfbpunyMrFguBiFgtIqZGxIr18x0j\nYlLpuCRJkrpVo3dWS29z6QvAuEFuR/U/ITMnA18DPhIRS9XNU6kWdjd7FfDsYC9uxaIDRMRzVHPf\nABav71+o7xuZuQxNGWRmng+cP3IRSpIkqdk8JAMtU09ZmjYfp44CXmT298vbgLcDlwJExBiqRd63\nDTaIiUUHyMwxfY8j4gxg0czctWBIkiRJ6kARsTzwXuAXmflMRKwLHAtcnJl92dDpwAkR8TPgLuBI\n4B7gt4ONbWLReXrq28vquXH3AKtm5sMR8RnggMwcX/dPBK7KzCOazukFNs/MmyJiA+AU4A3AosDN\nwJ6ZeU997DlU0+ZmAB+hyoQPy8zT6/5VgTOBtwGjgduBvTPz1gXw/iVJktpeiYrFXGoAOwMnRsRo\n4BHgYuDwvgMy84KIWAW4nGoK1E3A9pk56CpyE4vOMz/bAjSGOK8XOIjqQ7MkVZLwQ2DTpmM+DHw0\nM/eIiP8ELoqI/83MB6gSnVOBq+vXOQa4JCLWycyZ8xGvJElSR2vMas/EIjOfALaZi+OOA46bl7FN\nLERm/qXp6UsRcRhwe0QskZkz6vbfZOYv6+N/FhFPA28BHqiTiwf6BoiIA4G9gHWAv43Im5AkSVJR\nJhYiItamykg3oloE3lfhWJ4qYWgAU/qdNq0+logYB5wAvIuqXNZbH7M8JhaSJKkLtfFUqAXG7Wa7\nw1SgeQH4yv36T6Paq/jN9aXdN+eVazkGu+TtUcCKwEb1+a+bi3MkSZIWWoW2my3KikXnmZ8v638C\nPhYRJ1BtI3ZEv/6xwPPAM3X14bB5fM2+85+utyM7dj5ilCRJUgezYtF55rQQe7DF2ScCdwL/AG4F\nftnv+P8GtqC66Ml1wGX9+oda/H0QsALwJDAJuBFw0bYkSepa3Vix6Gk05meTIbWziNgN2Ccz31g6\nlqHMmD7dD6Akab6NnnJH6RDUhhZZa8Pi07FX+sipLf2OM+XiPYu/p6FYsVg4vQ34e+kgJEmS1D1c\nY7GQiYg/AIsDO5WORZIkqVt1yvSlVjKxWMhk5jtKxyBJktTterswsXAqlCRJkqRhs2IhSZIktZhT\noSRJkiQNm4mFJLWBRk/b76inAhZ5aUbpENSGXlyp7XdWVwFLlA6gS5lYSJIkSS3WmGXFQpIkSdIw\ndeNUKHeFkiRJkjRsViw6TER8BjggM8cPY4z3AKcCKwAHZeZJAxyzGnAHMD4zH5nf15IkSepG3Vix\nGNHEIiL2AvbKzHWa2r4InAy8LzOvqNuWBJ4CPpyZvxzG600ErsrMI4Y4bhngG8AOwMrA08Ak4ITM\nvGZ+X7/fa0wG9s/MC1ox3ly83mbADcA5mblrv+5TgG9l5mlzOj8z7wfGLsAQJUmSFlrdmFiM9FSo\nq4G16l/D+2wD/BXYuqltM6rYJg7z9RpDHRARY4Df1q/5CeBVwFrA6cCHhvn6/WMZdKubiBjVwtf7\nHHAb8NE6cep7jR5gTeAvIxSHJEmSusCIViwy8/8iYgpVMvH9iFgUeCewG1XFoM82wO8z87mIWAzY\nF9iZaurOHcCXMvNPABGxLXAcVTLwIjApMydExKnAFsAmEfF14MHMXG+AsPYGVgS2yMxnmtovrW/U\nr7MFcBSwHlU15buZeULdtyVV0vRJ4EhgHPBrYLf6PVwGrAacGRGnATdm5nvqisqfqb7obwUcERHn\nA2cBbwNGA7cDe2fmrXP75xwRywEfBt4DfB/YCfhORKwM3AUsClwZEbOAtwMHAKPqP7/tgR9FxHHA\nPcCqmflwPe4Hgf2BtYEZwFmZ+Y2IWBU4czgxS5IkLUwavb2lQxhxJRZvX0OVOED1pXYKcBmwdv2F\nmLr/6vrxocB/AP8OvBo4G7giIpat+88DTsrMZammMX0TIDP3pJoKdFhmjp1DUgHwPuCKfknFv4iI\nNwCXA8dQJQ3vB/aMiJ2aDlsEmACsD6wLvBXYq47lP4D7qRKNsZn5nqbzdm2K/9v1OKdSJSKvBW4F\nLqmTsLn1aeDRzLwe+AGwRx3Hw5k5pj5mQmYuk5l/r59/GPhV/f6+MsCfwXuBc4CDgNfU7/F/6+6e\nOcTsGh5JktSVGr2zWnrrBCW++F1N9cs/VAnENZk5MyJuAraOiKupvpTvU0/b+SLw/sycXJ9zdkTs\nDWwHnA+8AKwTESvWi4yvn8d4xgHXDXHM54GLM/Oy+nlGxHeovsD/oOm4r2fm88DzEfFzYMMhxm3U\n404EyMzpwAP1DYCIOJAqQRkP/G2u3lGVSJxfP/4hcFBEbJyZNw9yzg2ZeXH9eHpE9O//IvC9zPxV\n/XwqcGMd95xiXmceYpYkSVIHK5FYXAOsGBHrUa2r+G7dfm39fCbVNJvfUX3pHwNcFhHN6yUWA1ap\nH3+AanrO7RHxOHB6Zp48D/E8Dqw6xDFrAlvVU4H6LEJVhegzKzOfbHr+PHO3+Hly85OIGAecALyL\nar1HXx1teebiS3o9ZWs9qgoEmXl3RNxCteZiTolFo38cA1gd+OkcXnNYMUuSJC1sOqXK0Eojnlhk\n5gMRcRdVxWFj4CN11zVUv7LPBK7LzFkR8QQwDdimb03FAOPdDnwcICI2p1o7cFtdBZibyW2/AvaO\niFdl5tNzOGYycHY9vWp+zSmW/u1HUa352CgzH60Xlz/LEAu/m+xR31/TVHUYC6wfEV/KzGfncN5Q\nC90nU01/GshwY5YkSVKHKzUH/jfAPsBdTV/m/0w1P/8jwLEAmdmIiJOB4yNi9/rX9zFUOzjdDjxB\ntWD68sx8gmqb2F6gL0V8hGoK0WBOBj4K/DIivlSPuwiwLdUWuF+gqqpcFxFXUC3KblB9yR5Xr2OY\nG48w8Bfz/l++x1JVO56u3+uxczk+EfFqqkrF54FLmrqWoPrz/TTVWoihYhjId6gWdV9LNZ1tKeDN\nmXnjcGKWJElaGPV2YcWi1JW3r6ZKIl6+RkRm9lKtdXgtsxduAxwM/AL4RUQ8Q7Wr0R7M/jL8UeDO\niJhaH3dQZt5Q950IbBgRT0XEgNurZuZzwOZU6wUuokpO/kE1deii+pg7qCosewMPA49S7bY0rmmo\n/r/4N/q1HQ58KiL+GRGXD3LeQVS7Xz1JdS2NG6mqOHMat9nO9XlnZuZjTbf7gdOYXc3ob05jvtxW\nr63YjWrXqyeppji9ey5jliRJ6iqNWbNaeusEPY3GkJd6kBaYGdOn+wHUKzR6nEWnV1rkpRmlQ1Ab\naiy2eOkQ1IaWWHLJ4v+QLLXJXi39jvP8704p/p6G4nagkiRJUou5eFuSJEnSsHVjYlFqjYUkSZKk\nhYgVC0mSJKnFurFiYWIhSZIktVg3JhbuCiVJkiRp2FxjIUmSJGnYTCwkSZIkDZuJhSRJkqRhM7GQ\nJEmSNGwmFpIkSZKGzcRCkiRJ0rCZWEiSJEkaNhMLSZIkScNmYiFJkiRp2BYrHYDUrSJic+DBzJwc\nESsAxwEzga9l5hNlo1NJEbEasAEwtrk9My8oE5GkdhERK8/NcZn58IKORerPxEIq5zRgh/rxscDK\nwAvAd4CPlQpKZUXEHsCpwNPAtH7dJhZdLCKWAMbzyoTzpjIRqZAH5+KYBrDogg5E6s/EQipn1cy8\nOyIWAbYD3kj1RfLesmGpsIOAj2Xmz0oHovYREdsD5wLLDtDttObuslbpAKQ5MbGQypkZEUsBrwem\nZOajEbEosGThuFTW0iYVGsAJwKHAGZnZv5KlLpKZk0vHIM2JiYVUzrXAj4HXAL+o29YFphSLSO3g\n4ojYLjN/WToQtZUVMvOk0kGovUTEAVTTnl4hM48c4XAkEwupoM8C+1Ktqziubluban69utcSwI8j\n4jdUSWZP3d7IzD3KhaXCroyIjTPz5tKBqK1M4F8Ti1WANYDfAiYWGnEmFlIBETEKOAL4SmZO72v3\nV2oBvVSVLIDRVF8aepjDr5JaePX7NXoycFlE/IjZVc0eqoTTL5BdKjO37N8WEXsCK4x8NBL0NBr+\nWyWVEBFPAuMy07+Ekl4hIibyrwll/wSzL7HYaiTjUnuLiMWAhzPT5EIjzoqFVM6lwIeBi0sHovYS\nEWOA9wOvAx4ALs/M58pGpZE20K/R0lxYv3QA6l4mFlI5o4EfRsTnqKY59P0S6Vz6LhYRbwSuAmZR\nfS7WAE6MiHdn5l8LhqaCImJZ4KXMfL7ePW4nYFZm/qBwaCooIq7q17Q08DaqXcSkEefe11I5LwEX\nUl3saLH6Nqq+qXudDPwPsFpmbgGsDnyvblf3+hXwpvrxwVQLc4+IiKPKhaQ2cGO/20+Bf8/M/YtG\npa7lGgtJaiMR8U9gxcx8saltNPBIZr66XGQqqV6TtUJmzoqIe4DtgWeAmzLzdWWjk6SKU6Gkgurp\nDdsBq2TmsRGxEtCTmQ8XDk3lPEU1/emuprbVqb5EqnstCvRGxOrAqL5pcRGxXNmwVFo9NW48sDyz\nt6cmM68vFpS6lomFVEhEvB24gmrryDWBY6kW3e0BfKhgaCrrXODyiDgauJfqs7Fv3a7u9VfgAKok\n80qAiFgZeLZkUCorIt4GXAKs1q9rJtU6PmlEucZCKudk4GuZuT7VPwJQzZHdpFxIagNHAmcDXwN+\nSZVUnAMcXjAmlfdF4H3AOsA367YJ1EmGutZJwM+BZamqmssApwG7lAxK3cs1FlIhEfEU8OrMbETE\nU5m5XN3+TGYuWzg8SVKbi4ingddm5gt9/3bU21VPysx1Ssen7uNUKKmcx6imNUzua4iIdah2iVKX\niog7M3O9Adr/kplvLhGTyouITefUl5k3jWQsaisvMntdxdMR8VrgaWDFciGpm5lYSOWcC1wYEfsC\nPfWai+OBM8uGpcJWncd2dYffzqG9QbWwW93pVmBbqmmT1wE/AJ4Hbi8ZlLqXiYVUzrFUFzO6HBgD\nTKRad3FKwZhUSEQcUD8cFRH996Afj5WsrpaZ/7Imsl64fQTVF0p1r92YvV52H+AoYCzwmVIBqbu5\nxkIqLCJ6gHHAE5npX8guFRETqX593gK4oamrF3gEODEz/1ggNLWpiBgL3JqZ40vHopEXEbsAbwH+\nkJk/LB2PBCYWktRWIuLUzNyzdBxqfxExDviHmz10n4g4ENgPuIPqiuwHZua3ykYlORVKGlER0duv\nqUHTBY362jLTOdNdyqRCA6mnyjX/EjgG2AG4ukxEKmxn4P2ZeW1EbEM1jdbEQsWZWEgj651NjzcE\n/ovqH4PJVFdb3gf4nxGPSm0jIlYEDqP6fIxt6mpk5rplolIbmMC/JhZTgYuAE8uEo8Jem5nX1o+v\nBVYqGYzUx8RCGkGZ+fLOLhFxKrBdZt7d1HYt8BOqX5/Unc6lWtR/JtXuLn2ct9rFMnPL0jGoPWVm\nb0R4wWO1BRMLqZy1gAf6tT0ErF0gFrWPTYBVMnNq6UDUniJiFNW8+n9k5rOl41ERS0bElcyeSrt0\nv+eNzHx3mdDUzUwspHJuBb4VEV/NzBkRsSRwTN2u7vUAMKp0EGoPEbEEcCBVInED8H3gRmBdt0I2\ntwAAEChJREFU4LmIeF9zJVRd4/B+z2/s99wKp4pwVyipkIgYT7UH/epUV+FeAbgP2D4zs2RsKici\nPgV8FDgUmNLcl5kPFwlKxUTEaVRVrCuB9wDPAn+gmiq3G/CWzNyqXISSNJuJhVRQRCwG/BvVVZUf\nAm7OzJllo1JJA+wc1sfdwrpQRDwMbJiZD0fE6sC9wDKZ+VxELAU8mJmvLhulJFWcCiUVVCcR/UvY\n6m5rlQ5AbWVsX6UqM++LiKmZ+Vz9/Pl6vYUktQUTC6mQiBgD7MXA24q66K5LZebk0jGorc2poiVJ\nxZlYSOWcBbwV+DluK9rVIuIrfVfNHeBCaFDt9NLIzCNHPDiVNtTuP0uUCUuSXsnEQirn34F1M/Ox\n0oGouK2ZfdXc/hdCgzqxAEwsus9Qu/+4I5SktuHibamQiLgbWD8znx/yYEmSGHCDhwazK1gvt7nZ\ng0rwSo1SOfsDJ0fEa0oHIknqGO9suu0D/B3YA3h3ff+3ul0acVYspEIiYiazk/tZTV2NzBxdICQV\nEhFXzcVhLuqX9C8iYhLw4cy8u6ltbeAnmfnWcpGpW7nGQipn29IBqG3MzZbD/gokqb+1gAf6tT0E\nrF0gFsmKhSRJUieKiInAX4CvZuaMiFgSOIZq/d6WJWNTd7JiIRUUEesBWwLjaFp8l5mHlYpJZUTE\nOsB7M/PbA/TtBfwyM+8Z+cjULiJiEWAjYFXgQeCWzPTXwe72WeCXwGcj4jFgBeA+YPuiUalrmVhI\nhUTEJ4BzgNuBDYDb6vvrC4alcvYD/jSHvheBr1MtzFQXqufNX0o1xeVxYHngHxHxgeb59eoumfn3\niHgj8G9UCedDwM2ZObNsZOpWJhZSOd8APp2ZF0XEU5n5jojYFVivdGAqYkvgK3Po+xGw78iFojZ0\nBnANsGFmTo+IpYCj6/atikamouokYm7WaUkLnImFVM7rgB/Xj/umQZ1HNcXhq0UiUkkrZOZTc+h7\nhuoXanWvDYH3ZeYMgMx8PiL2BbzAZheLiDHAXlSfj7FNXe4ipyJMLKRyngZeBTwFPBIRbwCeAJYq\nGpVKmRoRa2Tm5AH6VgeeG+F41F7+AawMNK+z6f9c3ecs4K3Az4Hmi6269kZFmFhI5fwG+E/gbKrK\nxVXATOCKkkGpmGuAA4HdBug7gOrzoi4SEZs2PT0HuDQijgcmA2sCewNnjnxkaiP/DqybmVau1BZM\nLKRCMnOXpqeHAAksQ/UFQt3nUOCPEbE6cAHVIsxVgU9QTXN4R8HYVMZvB2g7q9/zk4BTRiAWtacn\nsJqpNuJ1LCSpTUTEm4ETgXcBi1JdkX0isE9m/qVgaJLaUER8FJgAfD0znywdj2RiIY2wiNgSmJ6Z\nt9TPVwXOB95CtdXszpn5z3IRqrR6x5/lgKcy8/mhjlf3iIgeYMXMnFI6FpUXETOBReqns5q6Gpk5\nukBI6nJOhZJG3uHAN5uefxtYlnr72br/8wXiUpuokwkTCr2s3v3nZGBHoBdYKiJ2ADbIzEOLBqeS\nti0dgNTMxEIaea+nnjsdEUsD7wU2zcxbI+IKqkXcktTseGBFYDPg6rrtD8BRVOtz1IUyc2LpGKRm\nJhbSyBudmdPqx28Dns/MW+Hlq6i+plxoktrUfwBvyMynI6Kv7WGqLWfVxSJiPaoLbI5j9jWRyMzD\nSsWk7mViIY28RyIiMjOpfn38XV9HRCwLvFAsMkntqgeY3q9tDDC1QCxqExHxCaqdBG8HNgBuq++v\nLxiWutgiQx8iqcV+APwsIo6husL2BU19m1BtO6suFRE7RsTipeNQ27kR2K9f257AtQViUfv4BvDp\nzHwHMK2+/y/gz2XDUrcysZBG3hFUycV6wFGZeX5T3xuoLpin7nU4MCUiTo6IN5UORm1jH+BTEXE3\nsHRE/BXYhVcmG+our6O6wCrMngZ1HrBTmXDU7dxuVpLaSL2d6ASqK3B/gOqXxzOAH7n1bHeLiCWA\n7YA1gPuAX2Zm/+lR6iIRcT/VzmBPRcTfgA9SXTTv7sxcpmx06kYmFpLUpuqF/DtRTW1YCbgQOCUz\n/69oYBoxEXEA0PwPdU/T40Z9ewK42Ysodp+I+D5wQ2aeHRGHUf0gMRO4JTM/WjY6dSMXb0tS+3o9\nsD6wKvBHYAng9xFxZGYeWTQyjZQJ/GtiMZBlgVMjYr/MPGEEYlKbyMxdmp4eTLVGbxmqBd3SiLNi\nIUltJCKWB3YGdgVWAM4FTq93ESOqvUb/4DQHNYuItwCXZebrSseisiJiUWCnzDyndCzqPlYsJKm9\nPES1BfERwE8zc0ZzZ2ZmRFxZJDK1rcycFBE3lo5DIyciXg+8EfhTZk6u23akqly8BqsWKsCKhVRQ\nRLwKeD+wSmYeGxErAYtk5kOFQ1MB9S+N7wBuzcwXS8cjqT3VCcS5VLt7vkC1qP8g4M3ACcDJmek1\nTjTirFhIhUTE24ErgCnAmsCxVPPp9wA+VDA0ldMAfkN14TNJmpN9gS8DZwL/D7gM+F9g7cx8qmRg\n6m5ex0Iq52Tga5m5PtUuHlBdBGuTciGppMzsBe6k2k5UkuZkDeDUzJwGnAKMBnYzqVBpViykct4I\nfL+5ITOfi4ilC8Wj9nAe1ZXZvwVMBnr7OjLzplJBSWori2TmLIDMfDEipmbm06WDkkwspHIeA1an\n+vIIQESsAzxYKiC1hZPq+/MG6LPKLAlgVETsXz/uARbv97zhltQqwcRCKudc4MKI2BfoqddcHE81\nZ1ZdKjNNHiQN5Waqa5z0+X2/5wAmFhpxJhZSOccCSwOXUy3WnUi17uKUgjFJktpcZm5ZOgZpIG43\nKxUWET3AOOCJzPQvZJeLiEWA3YFtqD4Xi1BfeTkzty4YmiRJg7JiIRVWJxOPl45DbeNwqqtu/xD4\nD+C7wE7ABSWDkiRpKCYW0giKiEmZ+Zb68d/ncFgjM9cdwbDUXnYE3lNfSXn3zPxKRPwE+FrpwCRJ\nGoyJhTSyjmt6fMQcjnE6VHdbLjMn1Y9nRsRiwC3AVgVjkiRpSCYW0gjKzPObHp9TMBS1r4ciYvXM\nvA+4F3gv8ATwYtmwJEkanImFVFBELAGMB8Y2t3shtK52GvB24D7gBODnVPvSH1wyKEmShuKuUFIh\nEbE91bUslu3f57UM1CciXgeMycw7S8ciSdJgTCykQiLibuBU4IzMnFY6HkmSpOFwKpRUzgqZeVLp\nIFReRFw1F4c1MvPdCzwYSZLmk4mFVM6VEbFxZt5cOhAVd+NcHGN5WZLU1pwKJRUSEd8CdgZ+BEyp\nm3uofpk+slhgkiRJ88GKhVTOhsAdwJvqWzMTC0mS1FGsWEgFRMQo4IPALzJzRul4VFZEvDQXhzUy\nc/QCD0aSpPlkxUIqIDNfiogzM/Oi0rGoLUwoHYAkScNlxUIqJCKuBfbOzNtKxyJJkjRcViykcq4B\nLo2IM4DJQG9fR2ZeUCoojbyI+LfMvKV+vOmcjvOK7JKkdmZiIZWzG9UWorsN0Gdi0V2uBsbWj387\nyHFekV2S1LacCiVJkiRp2Pz1SyosIlaOiI1LxyFJkjQcToWSComIFaimPG0NTAeWjoiPA+/MzM8X\nDU4jLiIOYM5X1/bCiZKktmdiIZXzbapF28sDd9dtvwEOLxWQiprA7MSiB9iMV663MLGQJLUt11hI\nhUTEY8DqmTk9Ip7KzOXq9mczc5nC4amw5s+EJEmdwDUWUjkz6Fc1jIhXA0+WCUeSJGn+mVhI5VwF\nHB8Ro5vaDgUuLxSPJEnSfHONhVTOvsDPgaeAxSPiGeA24ANFo5IkSZoPrrGQCoqIHuDtwJrAfcAf\nMtO/lF2o365QPcABzF7I765QkqS2Z2IhSW0gIibyr9vN9vR7TmZuNZIxSZI0L0wspAIiYlvgTcDv\ngD8AZwMfBCYBn8zMBwuGJ0mSNM9cvC2NsIj4EtXaik9SLeA+lWoq1P5Uv1B/q1x0kiRJ88fEQhp5\newLbZOZGwPuA/6KqUpwKfAzYsmBskiRJ88XEQhp5K2bmLfXjG4HpmfkQQGY+AixdLDJJkqT5ZGIh\nFVTvAPVi6TgkSZKGy+tYSCNvVETsXz/uobqGRfPzUWXCkiRJmn8mFtLIuxmY0PT89/2e/25kw5Ek\nSRo+t5uVJEmSNGyusZAkSZI0bCYWkiRJkobNxEKSJEnSsJlYSJIkSRo2EwtJUluKiJ0iYpd5OH6z\niPjmgoxJkjRnJhaSpHa1G7A1QESMj4gnIuITgxw/AfjM3AwcEetExDbDD1GS1MfEQpLUrhr1jcz8\nO7AF8NMWjf0N4JAWjSVJwgvkSZLaV0/zk8y8s1QgkqShmVhIkuZZROwN7AMsD9wLvBc4DdgIWAr4\nLbBHZt5bH38WsGV9/GLA9cDnMvO+pjE/BXyzPuYvwMrA/XXfOsBdwJaZeX3d9jbgf4A3AvcBz/WL\n8bPAwfV4DwP7ZeaPmg7ZLCJ668enZuZeEbFYHcOuwChgIvCFzJwy/39aktQdnAolSZonEXEgcATw\nbWA74ETgIeAs4BPAR4DXAN9tOm0b4E/A+4CdgfWoEpG+MXcAzgMuAT4E/AQYO0gMKwM3AI8AHwWO\npkpoGk2H3QrsSZX0XAqcGxGrNPXfDmxe306o244FdgK+CnwaWBP44VB/JpIkKxaSpHkQEUsDXwMO\nyszj6+bf1Pc/aTpuUapEoU8D+Ftm/rbuXx74dkQsnpkvAF8BfpqZX66P/3VEbDdIKJ8HngZ2yMxZ\n9ZhrALv3HZCZf6JKZoiIa4EdgXdQJUEAUzPzpqaYx9bjfgr4GdVUrGeA6yJiJasWkjQ4EwtJ0rx4\nA1Vl4NrmxohYHDieqtowDngSGDPIOPdQfXFfAXigHvfH/Y7p6X9SkzcCt/QlFQMdHxEfBQ4AXg9M\nreNZZpAx1wNGDxBHA1gdMLGQpEGYWEiS5sWL9f2sfu2HUU0h+m/gr8C7gGMGGWdGfT+qvl+86XGf\nBnO2ONA7p86IeDNwAdX0rM9T/Xt38RBjv1Dff4bqPTS7a5BYJEmYWEiS5s0/qL6Abw3c1tT+ZuCa\nzDwbICKWmsdx/wi8h6rq0WewisUfgC9ExNjMnDpA/3pU6wj3zcxn6pimNfU/A7yq3zl3U723VTPz\nPCRJ88TEQpI01zLzuYg4CTi8nv70J6pdl54G3hcRO1NNc9qw36mDJQlQTVm6LiLOBS6iqoi8lnpX\nqAGcCPwXcGVEfAt4imp6VF8l4i/146Mi4idU1Y3mZOePwF4R8QWqXa1GZeYvIuJk4ICIWAS4BVgO\nmJmZlwwRvyR1PRMLSdK82p8qkfgCsCLwINWC55eoKg7LUq2xuKnpnIGmHr3clpm/jYitgOOoLoL3\nQj3u7+dw/NMRsRFVgvF9qurEI8BVdf+dEbEH1ULz3ammXt3H7IXbF1FdcO/oOu6LgF9QJTgv1ucc\nWI95JtVuVZKkQfQ0GoNNYZUkSZKkoXkdC0mSJEnDZmIhSZIkadhMLCRJkiQNm4mFJEmSpGEzsZAk\nSZI0bCYWkiRJkobNxEKSJEnSsJlYSJIkSRo2EwtJkiRJw/b/Abmiky/lOycEAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b1578d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"foreign_tz_groupby = foreign_english_tz_df.groupby(['candidate', 'user_time_zone'])\n",
"top_foreign_tz_df = foreign_tz_groupby.filter(lambda group: len(group) > 40)\n",
"\n",
"top_foreign_tz_groupby = top_foreign_tz_df.groupby(['user_time_zone', 'candidate'], as_index = False)\n",
"\n",
"mean_influenced_polarities = top_foreign_tz_groupby.influenced_polarity.mean()\n",
"\n",
"pivot = mean_influenced_polarities.pivot_table(\n",
" index='user_time_zone', \n",
" columns='candidate', \n",
" values='influenced_polarity', \n",
" fill_value=0\n",
")\n",
"\n",
"plot = sns.heatmap(pivot)\n",
"plot.set_title('Influenced Polarity in Major Foreign Cities by Candidate', family='Ubuntu')\n",
"plot.set_ylabel('city', family='Ubuntu')\n",
"plot.set_xlabel('candidate', family='Ubuntu')\n",
"plot.figure.set_size_inches(12, 7)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Exercise for the reader: why is Rand Paul disliked in Athens? You can probably guess, but the actual tweets causing this are rather amusing.\n",
"\n",
"Greco-libertarian relations aside, the data shows that London and Amsterdam are among the most influential of cities, with the former leaning toward Jeb Bush and the latter about neutral.\n",
"\n",
"In India, Clinton-supporters reside in New Delhi while Chennai tweeters back Rand Paul. By contrast, in 2014, New Delhi constituents voted for the conservative Bharatiya Janata Party while Chennai voted for the more liberal All India Anna Dravida Munnetra Kazhagam Party - so there seems to be some kind of cultural difference between the voters of 2014 and the tweeters of today.\n",
"\n",
"Last thing I thought was interesting: Athens has the highest mean polarity for Bernie Sanders, the only city for which this is the case. Could this have anything to do with the recent economic crisis, 'no' vote for austerity, and Bernie's social democratic tendencies?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, I'll look at specific geolocation (latitude and longitude) data. Since only about 750 out of 80,000 tweets had geolocation enabled, this data can't really be used for sentiment analysis, but we can still get a good idea of international spread.\n",
"\n",
"First I'll plot everything on a world map, then break it up by candidate in the U.S."
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAxsAAAGlCAYAAACSgevlAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4FVX6+D9zb5Kb3ntIQkLChJBQQpcWqogiRRAVsa5l\nXXWbq35397fuumtZXddd194bFgQERUA60gkhQAjJpPfee3LL/P6YGwwhQICEgJ7P89zn5s6cOeed\nM+fevO953/ccSVVVBAKBQCAQCAQCgaC30fW3AAKBQCAQCAQCgeCniTA2BAKBQCAQCAQCQZ8gjA2B\nQCAQCAQCgUDQJwhjQyAQCAQCgUAgEPQJwtgQCAQCgUAgEAgEfYIwNgQCgUAgEAgEAkGfIIwNgUDw\nk0eW5QhZlr+UZTmuv2X5uSPLcrAsyy/Jsjy0v2U5G7Isj5NleY0sy4H9LctPDVmWl8my/PvzlLlT\nluWPeqGtWFmWX5Zl2etS6xIIBBePMDYEgqsYWZYjZVme399ydOVsclkVjSpZliddZpEGAEsA98vc\n7kUjy7KzLMvzrhaFV5blJ2RZrpBlOcz6+WxjcxDwW8Dvsgp4YQwBFgD2l6tBWZaHybI8q5vjp/Xr\nT4D70Pr2XEwDpvdCW+OAXwNOvVCXQCC4SGz6WwCBQKAhy/KHwAxFUYIv4LI/ATOAdX0i1MVzNrm+\nApKA1Msu0VmQZTke2H6OIqqiKPrLJE5nRqP130yguB/av1D+B6xTFCXH+rnXx6Ysy8uA+4HhaIZA\nGXAAeEpRlLTeaqefeAXQA1u6HO/ar32C9ffnjm5OtSmK4tDLzfVkN2Gx47BA8BNBGBsCwZXFT/of\nrKIo7cDJ/pajC0eADk+LhGYQHQP+3ulYf9Lf7fcIRVGagQtR+Ht8X7IsS8BHwO3AGuAuoB4IQZsF\nb7qAdq8qLqJfL4VyYFGXY5bL1HZXropxLxAIzo8wNgSCK4tT/2BlWV4M/B8QAHiiKVTfA79WFKWi\n0zVBsix3KARNiqK4WK+PBV4AJgO1wGbgMUVRqq3n7wQeRlPY3IFMRVGG9qRdWZYHAd+ghSfZAnuB\nhxVFUc4iV6OiKK6dvAgzFUXZbq1rOPCcVU6Tta3HFUXJt56PAt4GBlrlkYAE4PeKoiR26q+dQAzg\nAqQDTyiKsuF8Ha4oSj2wr1M9bUCFoij7rJ9fk2V5A+CuKIpqPfYhMEJRlBGdrtsPVCqKMs/6eQHw\nF7SQnALgQ+CfiqKYred1wBPAA4APoABPK4qytouIW2RZ7vh7saIoa2RZtkczhpYBzkCy9X73WOsO\nB14FotHClZqAW619/wJwC+CN5jF5UlGULzs3KMvyEuBLYJyiKAnWY3cB7wFeiqLUWo89BzwIeKHN\nir8PRCiKkm2t6owx0KmZV2RZDgLs+PF5HqZ77kIzNP6sKMqzXc592EX2EOBfwGygHdgN/EZRlIJO\nZaZa+2800AistfZD9VnaR5ZlR+BptH70BFKAf3R+XrIs64EngXuBIKAS+KuiKO/IsjwR+AAIRFPg\nNwOPKIpS0qmZiZ3664SiKMOs/X5av55PflmWpwD/BILRnk1HP/xaUZSss90j0N4x7s/SB/8AFgK+\ngBuaZ+lj4C+dxvVi4EW0cdeKZhz+zvo962CgLMu70TxULWgG/uNWw+psbffkud4C/D8gHO07V36O\nexUIBJcJkbMhEFy5xAAj0cJGZqH9E70BeKNLuQq0mflJaCE3yLIcCvwAtAFL0YyH2WiKQQfT0OLn\nHwTmoCm+PW23HPgHWuz1MjTF4jSFtYtcZ8SiW+UMssrpAiwHfommgOyUZbkjdMPfWsfbwLVoiqc/\nsE6WZbtO1b0G3AbciKa4r5JlOaC7di+QTVb5OieXTwOGyrLsZr0PR+v5TdbP84FVaCExNwLvAE+h\n5Sp08C/gD8BLaP14BFgty/KYLu3/hh/7caf12Gdoz/VPaLkolcD3siwPsJ4PQXumnwHXoSm/x611\n/Rr4DzAXzRjqbtZ8C2AGpnS5ZwnNKOxgCrBVUZSzzX6fawxsQJtFvxNt/Kzt8jw78wCQBzx/lvMA\nyLLsijaeAtDGyYNAFPCt1TuCLMsjga1ANVrfPQlcD6zvKHMWPkbrx+fQFO5kYI0sy9d1KvM82vfl\nY2udj6AZUgC5wB/Rvku/BMZy5nf5OD/21/Kz3GNP5A9Hy1f4K9pvwiNo4/OLc9wfgCTLsl6WZZuO\nV5fzk9D0hqVo38UVaL8tv+xU5gTaOJ+L9ptyE5qR1hlX4FtgMdr34G7grbMJ1cPnOgttvJ9A65e/\nIbwjAsEVgfBsCARXPhusytxuWZYHAw/LsmyjKIrJer672cjfooWZ3ILmLQBNSfhAlmVfRVE6Zvwa\nFUX5+kLbVRSlAfi8o6Asyyqa4uWmKErdOeTqylNos5TXKYrSaK3rIJqx8Bs0xa6DfYqi7LWWMaLN\nmE4GtgEoivJVJ3kOoiljY7n0nIEdaEbbDCDR2hcBaDPK09BmlePRPDwbrdf8DViJplxK1jqGoCmr\n/5Jl2QfNq/QI8K61zE5rPffwo4IK2gx3Z8/LCDTjZC6a0gmwB22WeRnajHYHWxVF2dnp2gC02eZ3\nOrwT3aEoSq0sywes9/yS9fBMNKNmBpqS5wqMQVP8zsa5xsDGTt6tM55nF2KA9ecwajq4B23WPQ5t\n/IM2DrZbZT2E1j8ZwMJOnqoMYBfa9+XzLnUiy/I1aIbRMkVROs5vss62vwxstP79a7T8kee61qEo\nShGaAdpRpw+aMdCZ+h58Zy5E/u1Wb8heWZY9gX/LshzeyfPUlSDA2OXeH1QU5e1Ohyo6nhuwQ5bl\nOWjGx6vW+0zjRwN2p3XVsfgu7RxXFOUF69+brc//JVmW/6YoSmY3cvXkuf4JOKYoytJOsjsAE85y\nrwKB4DIhjA2B4OpCQTMa/IHCc5QbgxZC0TUsQUWb9ewwNno683dau7IsR6CFSkxBm6XsCOtyA+q6\nraF7rgEOdBgaAIqi5MiynM65lYSOcK0AOOVZ+CeaQugHlHaS55JQFKVRluWtaJ6CF9BmdHejKfdz\n0IyN64BkRVGyZVm2BYZZX7d0qa7V+j4C7ff3Dc6c3T7fqkMdno+uIWJqD679H5qnJVWW5feA986R\neLwW+JssywZgMFpf/okfZ7FnoY2Jb87TZk847Xl2g8RZVoaSZbkS+JeiKM+j9Y09mlHUmY5xfwht\nzH3QoagDKIqyW5blJrQxd4axYb0GtNCnzmwC/mlV5MehPdOuZTrkHAM8a5XRAS200aW7sufhYuSH\nH/s4EDibsVGOZsR2Jv888iho4VwAyLI8G82IikXrj0ag4Tx17EB7xqOA7oyNnjzXWLS8HoFAcIUh\njA2B4OqixfreEW5ytoTyVrRwgru6OZd+Ke1a49K3Wo/9AihCm7nsHOJyqYnuEuc2hLr2w9toSvQf\n0Fa7ckPL/egtVgPvWJXKeWghIGXAC9YwjvloHgrQ4vGNaCEmr56lvg6j4xFgf5dzHYrZuZ4taCEo\nuV3OdVXGTkNRlDzrTPMCa9uPy7L8W0VRXuum+NdoBuW1aJ6FrWix9S/LshxpreMHRVHO1uaFjIGu\nz/MM0YFhsixLnZVsK56Ao/XvVrQZ79nd1NHZqOpOtnONuY7jZ7unztee4X2xjputaN/J29Ce0y1o\n3rtzyXQ2LlR+OH8fAxgVRTlyAXJ01GsHIMvyEGA9mhG2EM3Q+DUw/jx1dOgi5xrz53uuBs59bwKB\noJ8QxoZAcHVTB3h0o4SdQDMESrokoHblYowCT7ScgN91hGBZPQs9kasrB4D5siw7dwqjCgMi0ZT1\nnjISLWTkVNx3p6Rq+PE+LzZPbQ3wOlrI0FTrew1acvIf0BLlVwAoimKWZTkNLfck6Sz3n4qmlEac\nRdGHHz1E3l2On7C+ByuKsuZCb0RRFCOa0fCVLMtfos1CnyGD1UuzD00ploFXFUUplmX5MFqexTzg\nd+doqqdjoCd8ihbb/yjw33OUO4EW/29RFOXoWcocAGZ2lkuW5cloBkuH4dd1vHQcv5bTPQdz0BZW\nqJJl+UinMkld2hyE5sV4sWPRAlmWo7uUqUPzIJ2Pnsh/sVzsc+q4LgZNr/hLR/9bw6zOZ2xcb63j\nUKf6On9Xe/JcDwKzZVm2tY5xgUBwhSCMDYHg6uYAmgL2T1mWN6IlTb6PppDdibaS0YtooRC+aKtV\nre90/QUnUCqKUiHLch7wC1mW89FCL0Z3KXY2ubryV+BmYIMsy/9GC5X4C5q35D8XIFYCsFCW5V+g\neW5su5zvCDm7VZblZEVRys5R1xl9oihKvSzLq9FyTI52WhVoA9qqQLu7rPLzD7SE+XWythNyNRAB\n7FcU5YSiKJWyLL+Jlgejos16G9GMpv8qitKGNptfAzwmy3IdWuhNqaIoB6ztPivLsjtaX+uAaEVR\nXuIcyLJ8k7WeAsADGMq5V+z5AM3IsqAZXKAZVS+g5bF8dZbroOdjoCe8ghaq9rI1QXoNWux+152h\nP0TLV1onaytlpaN5uRwURfnMWuYJq2xrZFl+H20lsL8DhzqV6Vjh6G5Zll9QFGWPLMvrgNdkbTfq\nbDTP0jQ0owtFUTJlWf4U+Kssy85oeTS2aM91D9os/+9kWTahhVDFdpH9AHCjrO2ufQQY3Nl47kRP\n5L9YDLK2albX70BaJw9Wd78ZHceS0BYWeEqW5bfQ7jmym/J+sixfi2ZUTEMzWt9VFCXXer4A8JW1\nla2+pmfP9Xdoxsr3siy/ivbd6fq7JBAI+gGxGpVAcOWgcvrMYtfPnY93sBL4N1ri8Xq0FaT8rMrw\nRCALLYF1A/AMp//jP1f952t3IVoY0QdoSZqPof2j78gR6VaurvUoilKI5iloQZu9fhNtSdH4Lstg\nnm/G9bdouQPPoiUYf4W2WlCRtZ0stKTt69ASnM/F2dp6HW2C5tNOxz6yHnu9c0Frsvp8NEXwY7Qk\n9Yetnzt4BC2BfC6a8vw5WiiYu7WOFrSQGzfrvf2XHxXUm9AU8Dut5z4ArrOGuJ3rPiLQku63oC1j\nW4CW3Hs2PkNbNndDp8T/DuVuhXWhgM6cd2yeQ7azYl0MYQ5a2NFQqwyb0Twye4HD1nI1aON+N9oK\nSBvQjNaRnepKRPM++Fhl/Cda2M/cTmW2o4Xm3Y82Ww9a8v1HaM9sDVrezRJFUb7rJOpd1vO38ONz\nmWr12i1AC/P5Am2M3mKVvYNXrPU/hTZe7urkMez8nTmv/F2vOc+xzud80Pruh06vXfwYvtTdb8Op\nY9bk7mVoeRRr0IzoiWhehw52oRkkX6CFIy5AWwL4gU5lXkVbMOENtE01e/Jcj6HldhjR+nEz2vdp\nC+fPGREIBH2IpKo/6T3EBAKBQCAQCAQCQT8hPBsCgUAgEAgEAoGgTxDGhkAgEAgEAoFAIOgThLEh\nEAgEAoFAIBAI+gSxGpVAIBBc4UiSJKElF9uj7SfQ8bI3GAz23t7ezs7Ozs4Gg8HFzs7OydbW1lmn\n0znqdDoHOzs7Gzs7O1uDwWBjY2Nja2tra2NjY2NjZ2dnq9frbW1sbGz0er2N9b3js61Op7PR6/W2\ner3eRq/X2+h0uo5jNqqqqhaLxWQ2m40d72azufP7qb9NJpPR9CNGo9F46t1oNJra29tNbW1tRqPR\naFRVtclsNjcZjcbGtra2ppaWlob6+vrG2traJpPJ1Ia230Jbp1erqqqmfnosAoFAIOgBIkFcIBAI\n+gBJknRoK0t5eXl5+QUHBw90cnIKdnZ2dnd1dXV2dnZ2dnR0dHJwcHC2s7Oz0+l0th1Kf4dir9Pp\nbK2fbezt7W0cHBz0jo6ONo6Ojrb29va2Dg4Otg4ODjYGg4HOL3t7ewwGA7a2tmh2ypWPxWKhra3t\n1Ku1tbXz32pLS4uxtbXV2NLSYmxpaTE1NzebmpubTUaj0WyxWIwmk8lksViMFovFZLFYTCaTqcPg\nMba3t7c0Nzc3NjU1NdXX1zfV1dU1trS0lDY0NBRkZ2fntba2VqItT9ysin+KAoFA0KsIY0MgEAjO\ngdWr4Ah42tvbew8cODDEzc0txN7ePsDNzc3JxcXF2cnJydHR0dHZwcHByWAwOBsMBieDweDs6+vr\n6O/v7+Tr6+vg5eWFl5cXBoOhv2/pZ4+qqtTX11NVVUVVVZWlvLy8saSkpKm2tra5vb29qbW1tbGt\nra2pubm5qampqbG5ubmxvr6+qb6+vq6lpaWwtLQ0r7i4uASoAqqFd0UgEAjOjjA2BALBzxKrEeFu\nY2MTJMvyEHd39ygvLy9vT09PD1dXV3dnZ2d3BwcHN4PB4OTu7u7o7+/v6Ofn5+Lt7a3z8vLC1dX1\nqvEaCHoHo9FIdXU1VVVVVFRUtJeVlTWUlpY2t7S0NLW2tjY2NzfXNTQ01NTW1tZWVlbW1tXVFRQW\nFp4oLi7OAYpVVW3r73sQCASCy40wNgQCwU8OSZJsgYCAgICw4ODgoa6urqE+Pj7u7u7uHs7Ozu5O\nTk4eDg4O7gEBAa5hYWHuwcHBdgEBAdjZ2fW36IKfCB3ek6KiIvLy8hqys7Pr6uvr61taWmoaGxtr\n6urqamtqamoqKyur6+rqlPT09NTW1tZCoEqEcgkEgp8SwtgQCARXHZIkuTo7O0dERUWN8fT0HOzv\n7+/l7u7u2WFIuLi4uIWHh7uFhoa6BgUF4e7u/rP1QlRVVVJTU01zcxP29g44OTlZXy7Y2tr2t3g/\ne0wmE6WlpRQWFpqys7NrioqK6ltaWmqbmppqGxoaaqqrq6tKS0vLSktLkxRFOQ4UqKpq7G+5BQKB\noKcIY0MgEFxxSJKkBwZERkbG+vn5xfn7+wf4+Ph4u7u7+7i6unr7+/t7RUdHew8aNMjG09PzqjMk\nysvLOHz4IPn5uZjNJiQJTpxIISZmKGazBUkCnU6HqoK/fyALF96MTnfulcqLigrYs2cnZWWl6HRa\nfxiN7Xh6uuLu7oa9vYG2tnaam1tpa2ultrYekwmmT5/NyJGjL8dtCy4Sk8lEQUEB6enpjWlpaVV1\ndXWVdXV1FbW1tRWlpaWVVVVV2RkZGQnV1dXpqqrW9Le8AoFA0BlhbAgEgn5BkiQXd3f3wZGRkaOt\n3glvT09PH1dXV283NzdvWZa9Bg8e7BoSEnJVhTeZzWYKC/MoLCygrKyUsrJSzGYTFouJP//5Hzz9\n9P/h4eHGiBHRDBgQiF6vP6OO+voGkpNPcuJEBpmZ2cybdyMNDY2YzSaio2MoKSkmJycbHx9fPD09\nOX78CEFBfowZMwIfH68z6tu/P5ENG7ZSU1PLwIHB+Pn5UVpahqenJ0ajhccf//N5jRnBlUtNTQ3Z\n2dmW1NTUysLCwqqGhobK2traisrKysrS0tKyioqKpKysrGPt7e35IpldIBBcboSxIRAI+gxrErZf\nZGTk6KCgoPHBwcFB3t7eAR4eHv6BgYF+sbGxPoMGDdJfjd4JgJaWZpqamvD09GLXrq0cO5aIXi8R\nEOCLv78vvr7eeHt7nleR3759NzfddA/33XcHHh6eFBTkExYWSlhYCCEhQfj6euHh4Y7RaGTbtr1M\nmDCKkJAgsrJyWbVqPY8//qtz9l9GRjbl5ZV4enqQlZVLcXE5K1d+zbx5c/H09ERVzUgSWCwqpaXl\nPPXUs9jb2/d2d13VmM1mLBbLVRd61skr0nTy5MnympqaUs0GKS0pLS3NTE1N/aG2tvakqqot/S2r\nQCD4aSKMDYFAcMlIkqS3s7MbOGTIkGv8/f1HDBgwwN/LyyvQ3d3dPyIiwnf48OGe4eHh2NhcvfuI\nWiwWkpOPcejQPlpbmzGZjGzdupOwsDBsbfXExMjExcUQEOCPvf3Zl7dVVZWMjGwOHz5uVfxLsbW1\nZeDAEIKC/AkLC2bMmBF9anydOJFGXV0do0aNwN7eQEVFFdu27aG1tR1XV3fuuOO+Xn1WFouFvLxs\ngoJCOH48iYiISNzdPS+4nlWrvuDgwX24uXng6GhPZKTMvHmLek3Oc/Huu29w5EgCUVEykqTDzs6e\nuLgxjBgx6qozQDqor68nNTXVlJSUVFZWVlZWU1NTUlZWVlpcXFyQl5e3Jy8vL0lV1er+llMgEFzd\nCGNDIBD0GEmS9I6OjoNjYmJmBgQEyAEBAf5eXl4BHh4e/jExMX4xMTFOgYGBV6WXojuMRiNr135F\ncXEBoBIZGUpc3DDs7Q2kpWXw5z//k7FjR3HkyFEkScLe3kBwcCBPP/3EafW0tbVx4MARcnIKMZnM\nHDx4mLFjRzJqVCwxMVH9EiZ25MhxHnrocUaOHM6cOXNYtGgpLi6ul1yvxWLh2LEjODs7YbGorFz5\nGZs3b2XhwusBiUGDQqiurqOurpHW1jaWLbub4ODQHtX9/fff0djYwNdfr6a+voFly25n6dLbL1nm\nnrJ69WcUFRUCFjw83HB3dyE3txBVlQA9oaEDmThxKt7ePpdNpr6gra2NzMxMkpKSKvLy8spra2tL\nKioqSouKioqLiooOpKam7lFVtaK/5RQIBFcHwtgQCATdIkmSS2ho6NhBgwZNCwkJCfX39w/28vIa\nEBcXFzhy5EgHDw+P/hbxojGbzRw8uBdXV3diYoZ1W0ZRUomKiuaVV55l+fIlgBaSkpaWyYoVq6mt\nreOppx7D39/31DWtrW08+eTfGTVqBCChqhJ6vQ16vS3h4YNobm4iLy+H6upKHn303m7zNS4XiYnH\nOXYsjYce+l2vhkw98sgDzJkzlaqqWsrKKrjrrpv5+usNHD58nPr6eqs3xR5JkqioqOKxx/50UUaO\n2Wzu1/7Lzc1m69ZNNDXVAyoDBw7A09OdzMxcamsbcHFxZ+LEKfzwww5Gjx5HTMzwq35DR4vFQk5O\nDocOHarMzMwsrqqqKiwqKiooKChITU5O3tzc3Jyuqqq5v+UUCARXFsLYEAh+5kiSJBkMhpDY2NgZ\nQUFBI4ODgwd4eXkFBwcHB40bN84vKipKutrCn/Lzc9m2bTOJiQmMGzee5cvvxWKxUFCQx/btWygp\nKWDs2OF8+ulq7rzzHpKTj5KWlsaLL/6XjAyF7du/x9HRwKhRsZSUlLFu3fc0NDSi1+vx9fXh2mun\nMmHC6FMeHFVV2bPnIMnJGbi5eRAYGEhRkeYNUVULYCEoyJ+oqAgCAvz63fOzc+d+VNWOhQuX9nrd\npaUlvPnmf7j77qW4uZ1uRGzbtpuPPlrJu+9+iLu7x1WV+H8uzGYzmZnpHD58kJqaKkCloaGerVt3\n4e/vi8ViISIiDF9fH0CHweDAvHkLCQgI6m/Re4Xa2lqSkpJajhw5UlxZWVlYVlZWkJ+fn5+Tk7Mj\nOzv7oKqqDf0to0Ag6D+EsSEQ/IyQJEnv4eERExsbe31oaOggf3//EE9Pz+DY2NjAUaNGufj7+/e3\niBdFZWUF+/b9QEFBHqmpqWRn5xEfP4UxY8YycuQY3N09SEw8xNNP/xUHB3smTRpPbm4Bu3btxtvb\nixkzphERMZgFC27mxRefQa+XyMzMIjR0IGvXruPdd18mKCjgVHtms5mEhKNkZOSgqhKSpMdkMmM2\ntxEZGcbgweH4+/v2u1HRHS0trXz55Xf85jdPnL/wRdLa2so777yKvb2e2bOnnjI6PvxwJY888gRL\nly5i9OgRGAwOTJo0lTFjJvSZLFcCRqOR1au/ID8/By8vNyoqqjl5UuHll1/Fy8u7v8XrE0wmE4qi\nqAcPHiwrLCwsqqioKCwoKCjIz89PSEpK+l5V1bL+llEgEFwehLEhEPxEkSRJsrOzGxgXF3dDaGjo\nsJCQkIF+fn4Dx48fHxwXF2dwcHDobxF7RGNjA4mJh0hJOY7JZCQxMYmjR5OZP38eTz/9HIcPH+Sx\nx37P2LGjCQkZgCwPZfLkaWcNDcrLy8HZ2YX33nuLzZs34+TkxMqVX2MwGKioKGfNmi9obm5g6tTx\nfPvtFm69dQG+vt4UFpZw4EAiDQ3N6HQ2TJ48jWHDRmJjY4PFYuHgwb0899yzVFRUYm9vx6pV7/dr\nmM/Z2Lv3IH5+EYwePa7P2yopKeKhh+7nvfdepqGhiRUr1vHHP/6VdetWkZeXRWtrG0FBISxbdlef\ny3IlYLFYqK2twdPzx+WJq6ur+H//7wlkeTAWC9x66x34+V2dRn9PKC4uZu/evdWpqan5ZWVlOTk5\nObnZ2dnbFUX5QVXV+v6WTyAQ9D7C2BAIfiJIkuQ7fPjwWQMHDrxm4MCBoX5+fmEjRowIHj9+vMvV\nkl9hNptJSUnm0KF9tLQ00dTUSE1NDe3t7QwYMABbWwPjx09k5MgxnDx5gm3bvmfgwHAWLbr5jLpK\nSopITj5Kbm4u06bNZO/endTUVOHh4cK3325mwoTxzJx5HenpqRQV5aHTSbi5uTBt2jWnhf+0t7eT\nkJDEDTfczkMP3cdrr719Wjtbt27i6NFDDBgQiCyHERjof0XG5n///S5KSsrR622IihrKrFlzL0u7\nJ0+eYOPGb9DrJTw9fbjjjl9clnYvlu+//w5FOYnJZGLYsJHMnDmnT9szm828//6btLU1ER8/gV27\nDmCxWLBYVCRJj8Fgj8lkQpIkXF1dGTFiNFFR0Vf1ym6dsVgsZGVl8cMPP5Tk5ubml5SU5OTk5GQp\nirKxqKjosKqqbf0to0AguDR+Gr9WAsHPDEmSHCIjI6eGh4fPDA8PD/Pz8wv7/PPPgydNmuQdFBR0\nRYbvnIs33vgPe/fuo6ioGH9/P6KiZAoKCmhtbcPd3Q0/Px9cXNy4664HWLHiA95++w02b97BhAlj\nuesuTXk9eHAve/bsws5O8zS0tDRRUFCCl5c3YWGD+PTTD3B3d2b+/DlUVdVib++Am5s75eVl2Nra\noaoqTU1trF+/07qnggmdTo/B4EBc3Bja29u7XeI0JeU4BoMdFRVVlJdXodOBqmqv6OgIRo8efrm7\ns1t0OggODuWmm267rO1GR8cQHR1zWdu8ECwWCytWfEBNTSWSBOHhIdxxx0Kampr5+99fJjJSJjQ0\nrNfb3b9/N0lJh7FYLLS3G60hVu4sW7bwNNm2b9/DxIljcXCwp66unhMnTrBjx0a0eUIJd3dP4uNn\nEhIysNdpNaf4AAAgAElEQVRkKy8v5f3338bV1QWQCAgIJCJCJiIiEgcHx15rB0Cn0xEZGUlkZGQA\nEACMMxqNJCcnP7Fnz56iJ598Mq+wsDAnNzc3LSUlZW1tba2iillSgeCqQng2BIKrAEmSfOLi4uZF\nRERMCA0NjQgNDQ2Lj48PHjJkiO6nsPNzUtJhEhMTqKgox8HBDldXJyZNGouvrxbP/sor79DSYsLL\ny42JE8fw9NP/wtfXlxtvnE98/AxuvPEGAgP9eeWVZ9i8eRfJyWk0Njbh4GDPrbcuZ//+3dja6li6\ndB6trW0899z/GDIkCpCwWLQEbklSUVWoqqrjr399tseym81mJEnqduO+V199mZEjBzN0qNxLPXXx\nNDY2sXHjHu6771f9LcoVg9Fo5IUX/sGcOZMZNGggAHV1DaxduwkbGwO33LIcL6/eX8b2P/95gYaG\nOuLjxxETM4S8vAI8PDxwc3O54Lpqa+vYty+R0tIKfH0DWLp0+SXv+9HQUM8XX3xCY2MdPj4eREcP\npqSkjPz8YtrbTeh0OlQVfHz8OXDgAP7+fowePYagoBBCQwfi5OR8Se13R2NjIwcOHGg6ePBgbnFx\ncWZmZmaGoijf5uXlHVBVtb3XGxQIBL2GMDYEgisMSZIkJyeniJEjR94UGRkZGxQUFBEVFRU2Y8YM\nn6s1gft8JCYe5L//fZmamhrq6xtwc3NFVS3Mnj0DVQVJAknSYTZb8Pb247rr5p2Ke//znx+nsLCQ\nuLjhKEomrq7OODnZo9PZkJmZw8iRMSxdeuM5Vz5qampm9+5D5OQUsGDBzQwZMrRX7uvxxx/lyScf\nPu8O4n1NQUExb721gr///Vk8PLzOf8HPhO+//4709GRuv/2mU97AN9/8lIcf/j3Ozheu+PeE5577\nG/7+Hixc2PthbIWFJSQlpbN8+b29Vmd+fi5btmygqakJVTWj1+uIigpHVeGHHw6wbdsPmM1mIiMH\nYTQaKSoqQZIk/Px8iI+P58EHH+2TkC+z2UxycrJp586d+QUFBVk5OTlZmZmZO5OTkzepqlrX6w0K\nBIKLRhgbAkE/I0mSbUhIyDhZludFRkYODgwMjBg7dmzYNddc4+Tk5NTf4l0UbW1tfPnlJzQ21qOq\nqjVEqQlPTy8cHZ2Jj59BUFDwqfIJCQd4/vlniYgIJzg4GF9fP2JiRhAZKfdoltZisZCdncGxY0dJ\nSUlmxoxZTJgwmaKiAr79dg0mkxGdTjoVeiJJ2stsNqPTSTg5ORMfP5OwsIhe64PCwnzWr/+KW26Z\n32t1XgwbNmyjqqqGmppG/vKXf/SrLFci//3viyxefC1OTo7U1TWwdet+7r33oT5rz2g08tprL6PX\nq0yffs1pq5xdKhaLhRdffJNFi25m8GAZN7fez9Vqb2/n+PEkamtrmD59NhaLBZPJhF6vP/VdbWxs\noKAgj8rKSsaOnXDZcpjy8/PZunVrSXZ2dk5+fn5GZmbm0SNHjqxubW0tuCwCCASCbhHGhkBwmZEk\nSR8aGjouOjp60eDBg4eEhITI8fHxocOGDbO52pM+c3Oz2bx5A/X11cyffy0+PqfPojc0NPLaax/w\nu9/9EV9fv27ryMhI49ChA9jZ2bJkyTIAmpub2LFjC5mZ6bS2tmJra0draysjR44iLS0FSbIQEhKI\nwWDH2rWbcHZ24Z577ufEiWPk5uZQU1PDffc9SF5eDsnJxxg2bARZWRkYje2oKsybt6jX4/KfeeYv\nPPjgsn5dkUpVVV5//UOWLr2DiIj+D+W6EnnmmacYNCiYOXPiUVWV99//it///o+93k5BQR7vvfcW\nXl7ugERbWytZWdk89tgv8fLy7LV2GhubyMjIJje3kIaGZlpb27BYzLi4uOHq6kZ1dRU2NnpAh6Oj\nIxERg7nmmino9Xqqqip49dX/4OPjQ2BgEPb2Djg5OREXN6bHoVFHjiTw9ttvEBMTjaOjE8OGxTF8\neNwlh3ZdDLW1tfzwww91R44cycrLy0tTFOVwUlLSly0tLcWXXRiB4GeMMDYEgj5GkiTJx8dn+IgR\nI5YMHjx4aHBwsDx9+vTwuLg4uytxadQLwWg0smvXNk6cOAaY8ff3ZfLksTg5OVpXcTrKtm27KSkp\no7a2jqKiEv73v/8xefI0WltbqKqqxNHRkZUrV9DY2EBjYwvJyccZNiyGoUNjWbJkGZ999iFVVaVM\nnjyWkyczKC4u58SJVAYODOb662dgb29PYuJxamrqqaqqxc7OFhcXJ9zdndmxYx8FBUXMnj2NwEBf\nhgyJZN26zZhMRm6/fTGuri5UVVVz4kQud9zRe6En27ZtQqdrYeTI2F6r80JYtWo91dX1ODo6IctD\nLtvKU1cr//vfiyxfriVmf/rpGn7xi0cvaFd1o9HI119/SWhoOJGR8qkQv/b2dmxsbNDpdJjNZlau\nXEFxcR6LF19/xoaHfY3RaGTFijVERoYxceJYQNtzJSMji8OHT6DX22Jra0tFRQXbtu3A0dGBO+9c\nSnBwECkp6bS1GZEkPe7uHsydO/+c+4Ns27aJ1NQTtLS0kJJyktraeh555FFmzLj2ct1ut9TW1rJ1\n69bqY8eOZebm5qYpirIvISFhlaqqVf0qmEDwE0cYGwJBLyNJkuTh4RE5bNiwW2RZHhYSEiJPmTJl\n0Lhx4xx+CjsmNzU1smnTegoKcpEklbFjRxAVFUFLSys7duxj9+4DVFdXo9frCQ8PZfbseNLTs8jI\nyCU8PJR33vmYW29dzMqVXxMRMYiJE8cyYUIca9ZsxMfHn5kz5/Dtt6swGGxRVYkxY2KJjR1CUlIy\nGzfuwt3dBX9/H2prG7C1NRAYOIDS0mKam5sYNkxm7NiRGI1G/u//nmHq1InMmROPnZ0dOTl5fP31\n9wwaNJg1a9bg4GCPLA8mOnooixff1mseiJKSIt5447/87nf390p9F0JaWgZ79iQwbtxIUlJyePDB\nRy+7DFcjL774DDfcEE9AgB9paRk0NsLMmdf1+Prq6kqee+5vzJ07nfz8Iiora/D09KWwsJCVK1fz\nhz/8nttuuxOdTmcdH6/g5ubM4sXX4+Hh3od3duGoqkpraxsNDY0YDHZnGEU1NbVs376XhoZmnJxc\nWbz4lvPmAS1bdjMODgaGDRuKJOlOvQB0Oj0+Pr74+wfi7x9AQEBgnySYd0d5eTmbN28uP3nyZEZ2\ndnaaoig7jx49+o3Y70Mg6F2EsSEQ9ALOzs7esbGxt0VHR08ICQmRx48fHzFlyhSXq2XjvJ6wfv3X\nZGUp2NnZMnXqOAID/cnPL2Lz5l2cOJFGW1s7UVER3HjjLMLCQrutQ1VVvv9+F6+99h7x8RO55Zb5\nbN78Az4+Adxyyx3Y2NiwevWXDBs2EB8fL1RVZc+eg+zZc5iSkjLa29uYMGE806dfy9ChsXz11WcU\nFuZy442zzgjZ6kxmZg4ffPAFQ4bIDB4cRlxcLDY2Nrzzzuf84Q//r1f6p66ulo8/fhd7ez0LFszp\nl7CR5OSTbNmyBz+/QBYsuOm0vBjB2Tl0aB/bt2/kwQfvRFVVPvlkNTExI5k+vecz8YWF+Xz55Ufc\ne++tAJSWlvPll+t56KHf8NhjvyYsbCCVlZWMHj0MJycn8vOL2LfvEIGBftx551IiInp/ed2+prGx\nia+/3oTFIjF+/ERGjx6PXq+nrKyU8vIyoqNj0Ov1WCwW9uzZSVJSImazkeBgfyZPHoe9vQGz2UxV\nVQ0VFVWnXi0traiqhCTpGTZsJBMmTL4seR8FBQVs2rSpKDMzMyM9PT315MmTa9PT07erqmrq88YF\ngp8wwtgQCC6CJ554xFans3lEp9PdnZ9fEG4yqTavvfaWnadn78Rem0wmTpw4RmLiQWbNmtura+hf\nDO3t7bzwwtMsX34TqanpZGXl09rahrOzO++88y5BQf7cd99yJk06967U9fUNHD16grFj4/jmm80Y\njSp33nnfaSv/LFmygMmTx1FT00BqahpBQQFMmDAai8WCn99Apk6dQUZGKn/721PcffdSRo26uH0s\nEhKSeOWVdxkzZhQTJ05hxoxL27zto4/epbi4AC8vD26++YZLqutCycnJsxp7kZjNZt555wuefPKp\nyypDX2KxWCgrK8HPL6BPVvayWCx89NE7NDTU4OTkwLhxcWRl5ZKZWcCkSVMZN25ij+p57bWXWLbs\nxwUBCgtLWL16Iw0NDcTHj2f9+q0kJ5/kyScfYfLk8YC2mEJZWQUhIQN6/b4uF2azmWPHUjh+PA1J\n0uPg4EhamsLu3Xu57rpZODg4Ymdng52dHe3tRj744FMmTRrH9dfPPNUP3aGqKqmpGRw5cgKLRQV0\nuLi4Ehc3lujomD416FVVJSUlxbRhw4bs48cTDa6uzrUGg839L7/81qE+a1Qg+IkijA2BoIc4ODgE\nTJgw/m5PT5c/6nQ6Q1hYqH7AgGApNDSMGTOuvSjXf2VlBceOJZKenmbdJRgsFjOSpFJcXMJnn60h\nJmYI8+bd0K8hMX/842M4ONgzcGA4w4aNpKqqgmPHDgNgMrUjy4MYNy6ux7OPr7zyPvfd9ysCAoLO\nOJeTk81XX32Gt7crc+fOwN7ewMGDSZSW1nLnnfexe/d2Nm/eiJubC4sXX4+7u9sl3dumTTtpbjax\nbNndFz172trayscfv0t7exvJySf45S+XM3BgyCXJ1VNUVeW11z5Akmy4/faFGI3trF27hcce+/Nl\nab+v+PTT96mpqQDAYlHx9nanvLwaSdIzdOgw4uNn9omyWVdXy7p1qygrK8LHx5OMjGxycvKJiYnl\nj3/86zmv3b17BydPJrFkyQ2njCKj0ciWLT+wfv0WQkND8PR0Y8iQiPMa5lczHXt/FBYWs39/ApMn\nj+eee27tlbobG5s4cSKNjIxc67LYOiRJQlUtgGr9G2uYlsTQobGMHz/pkjYjtFgsfPnlJ2zbts1S\nU1Nt0ettc06ezHgiJSVlg9jhXCA4P8LYEAjOgiRJdlFRUbOjo6PnybI8NC4ubsjs2bM9XV0vPLHT\nZDJx/HgShw8fpK2tBdCWg3V3d2bIkEjCwkLOWIu+sbEJR0cHNm/+gaKiMkDFaDQTERHJ2LHXUFNT\nQ2trc49nXTtoaWlGUVLJzExn+vTZrFu3iu3bt/Hww78mOjqWrKwMRowY1e21FouF/Pwc/va3p0hL\nU7BYLDg7O2OxmLn77lu58caehZ18+OFKfvMbbcWf8nItPMrd3YP3338Tg0HPwoVzsLOzo7W1jQ0b\ntuLi4sOSJdrO1++++zqNjXVERIRwzTVjup3prq9voKysgsjI8B7JU1paznff7byoVYgU5SSrVn3G\n7bcvws3NlZycPHQ6HaGhfR/C1NDQyIMPPk5oaAjR0dGsWbOWuXPncOuty6+6ECqz2cyWLRvJykrH\nbLbg5GTLTTddf+p8RUUVJSWlDBs2lE8/XcXJk5m8/vq7fSpPQ0MdNTXVVFdX4+rqSmRk1Hmvy83N\n5vPPP2bs2GGMGjXs1HGj0cjKletxdHQlNzebX/3qznPu/SK4dCwWC+npWSQlnaS1tQ0XF3fmzVuE\nn1/P9iuqrq6ksrKSoKABZ0wmZWRkqN99911OZmZmampqalJSUtLH1dXVGX1xHwLB1Y4wNgSCTkiS\n5DFhwoQ7hw4dOnnw4MGxN9xwQ3hUVJS+Y8OvCyE3N5stWzbS3NyATgeyPIjhw6MvKfbYYrFQVVXD\n/v2J+Pl5s29fAvb2Ljz66O9O+2fY0tLMkSMJVFZW4O8fyLFjR2hra0FVzdjZ2WIytXPs2EnGjRtF\nRUUV27b9gNFooq6unilTJhIREUZoaDjz5y85VefBg3vZunUjshxOeHgoAwYEYGdnh6qqnK9/zGYz\nmZk51NTUkZ6eQ0uLEV9fX2prq3Bzc6a0tApZHkJkpD8hIQNQVZU///l5HB2dePjh3562LK3FYmHt\n2pXs37+XgoIiVNXCmDFjMBi0WW5J0mFv70hmZgYLFswmKiryvP164MARDAYPpk2bdUHPo7i4kA8+\neJOHHrqT1NQMtmz5gdbWVp544uELqudSKS0t55tvNiNJNixffi/+/r23d8PlYOPGdZw8mczkyWMY\nPHjQGec3bdpOU1MzgYH+HDyYyNy5M9i+fT8Wi4QkQXh4BIsWLb3seTKrV39OQUEetra22Ns7EBkZ\nxZgx43FwcGTz5u8oKspmwYI5p30/jhxJZvfuw1gsJh544HYcHX86eV1XOg0NjWzfvpfq6jrs7OwJ\nC4tg+PCRbNmyiebmJvR6PYGBQYSEhOHl5cXx40l89dVXpKUphIYGM2bMj95bTXeSrJuNmqmsrGkr\nK6vMqaqq2p+cfOKzjIyMHaqqmvv3jgWCKwNhbAh+9nh7e0fGxcXdPWTIkFHDhw+PmT9/fqCXV892\nWVZVFZPJRGtrC2lpJzlyJIG2thYsFjP+/j5MmTKu15WJ5uYWvvtuCzU1dYwYEUN7extNTeDo6Eh2\ndiZgwWCwZejQwXh4uFNeXkF0tIy9ffdGzrFjKdTW1tHY2ExkZBiRkeFIksTbb68gNnYks2dfT3Ly\nUZ5//hmmT5/SbT5Ca2sbaWkZpKVl0d5uwtbWhhtvnIWTkyMVFVV8+ulqpk6dga+vPzU11Xz00Xvc\neutCZDmCr75aT3T0cBITD/LQQ3cCWo7I229/yoEDiSxffjtLly4HICcnkxUrPmLGjGsYMkQzIrZs\n2cXAgUMZM+bH2O+SkiJeffU/3H//bbi5nX0n6MrKKvbsSaC2tpnf/ObxC34Wra2tvPPOqwDY2tpR\nXl7Cgw8uvywz1haLhd27D5KRkUdgYDA33XTLZds8rTf59ts1tLfXM2PGJPbvP8yaNd8xduxIFi26\nHp1OC5H56KMvue22Rdja2lJaWs5LL71BeHgIY8fGMWrUcAoKitm6dQ82NnbodBI6nQ1xcaMZM2ZC\nn+7eXlJSxOeff4yDgx1z5kyluLiMY8dSMRpN2NoacHPzoK6uhtraaiZPHkNsbDQA5eWVvP32p0iS\nnsjIgYSHBzNq1PDzGu2C3sNisVBQUERKSjqjRw/H19cbo9FIWVklRUUl1NY24OfnRVVVDQUFpaSn\nZ3L06HGGDJEZOjSKCRNGnfoNUlWV0tJysrNzyc0tIi+vSM3MzG5tbGyqs7Gx2RsTM/iBF154VSyv\nK/jZIowNwc+OJ598VK/T6R/Q6XQPbd++Wx4zZoz5n/98ydDTdfUzMxV27NhKS0sjqmrB1tYGOztb\nwsKCiYmJ6jOFT1Ey+eGHAzg4GJg7dyaentruwDU1tezZk8Dw4UN6Pcn05Ml0EhKOcvjwMRYtuom3\n3nqLuXNno+lEEpWV1ShKOjY2NgQE+NHc3MJrr71LTU0Vq1d/SXNzEx4enixefCt2dgYSEw9x9Ggi\nshxNaWkxRUWFtLQ04ePjyfz5szEYDCQkJPHuuysYOXIYJpORG25YTEBAEF988TEuLvYsWDAHnU5H\nZWUV33yzhZCQcBYvvu00ud944xUqK0u5//5l3T4Pi8XCH/7wNDNmzGLWrOvw8fG9qP5pampky5aN\n5OZm4+npzLx5s/tUYWxvbyc9PZvDh4+jqnpmzpxDbOzFJchfCaxZ8zmSZESnA5PJzOHDR5kzZxqb\nNm2noaGJiIgwzGYzBoMdt9/+o5ftzTc/5sEH7zhrvWazmaSkZI4dUzAY7Jk790bCw0/3cB07lkRu\nbhZDh8YSFhZx1qWP09JSWLPmSyoqKvnTn/4GQE5OFg0NdezcuQ0XFxeGDh1OdnYqt99+06nr2tvb\n2b37IPn5Jej1tpjNFsxmI+PGjSA2Ngqj0ciGDdvJysrD3t4RR0c77rrr5kvpTkEfYzQaOX78JCkp\n6ShKJs8883/nLK+qakd5U21tfVVjY9Px1taW3/7732+kXCaRBYIrAmFsCH4WPPHEIw42NnbP2dnZ\n3ujk5BQQEzPYfvv2vYwbN5mbblpy/gqsHD58gB07NrFs2U2XJfyhvb2d77/fQUlJOYMHhzNlSt/O\n1HbQ1NTM5s27qKtrRJJsmDRpMrGxcWRmZmA0tjF8eBwfffQuDg4S8fETsLOzw2Qyce+9v2PGjGk8\n+OCvT5vdT0o6zHffrWXChJEkJh5n27bdzJkzG3t7WxYunHOa16WhoRFFySIh4Tjjxl3D0aNHcHa2\nP2WMAHzyyWrc3LxYsuS2U4mf2dkZrF27itraaubMmUdUVDSffvoOd9zR/fNNTj7J3r1JXH/9gotS\n2NetW0VmZhqzZk0mJOTMRPdLpa6uge++24aqasqzTqfHzs6eqKhoxo+fdNXH+3/44dv4+blTXV1F\nSkoat956E+XlFadWFzt2LIXduw9w7bXTzsi9SUhIIjHxGHPmTD9vIn57ezvbt++juLgMDw8vbr75\ndpycnGlqauSZZ54CLAQE+NHY2MKCBTczZMhQAOrr63nvvTfw8/PguuumcfRoCkePplJRUcHs2VMw\nGAxERUUgSRKHDiXh4GBPbOyQbmUwm80kJBwlJSWT5uZGHnnk9A0kDx1KYuvWvXh4uDF58hhiYs6f\nGyK4+mhoaGTHjn2WkpKy+rq6hixVNf/1uef+u76/5RII+hphbAh+sjzxxCNONja2/7SzM8xzc3Px\nnzp1nF1YWChpaRls336AX/3qt7i59WxDraamRj766B2cne36fPYaID+/iK1bd6HT6Zg9O57AwJ4l\nNPYWHYqu2WxBkjrik1UUJZOamjpGjRpBREQoU6acuWxlVVU1X375LS4uzqiqBUmSCAoKwN7ejoce\nepwbb7yOJ5985KzGWk5OHq+//glRUZF4e7szd+70U7H4qqqyatV6YmJGM2HCZEDzUrzzzmsYDBIu\nLk5kZRXx6KOPsWHD13h7OzJs2NCz3qfJZOLll9/mmWf+3eO+qamp4o03/sfkyXGnwmJ6E1VVWbt2\nE21tFpYtuxsXl8u70/Tl4Lvv1uLgYCEsLIRt23afCpnqiqqqvPPOJ9x//5leDIvFwvvvf87kyeOQ\n5YgetVtbW8fq1RsYMmQYc+dqS9T+5z/Pc9ddi9m0aSfbt+/h1Vff5sCBPRw+vJ9bbrnxsuVUbNiw\njZEjJ3HgwB6iokJOhegIfpqYTCb27DmkKkpWQ319Y7bZbPrL88//99v+lksg6AuEsSH4SfH44w+7\n2NjYvWAwGOa6ubn4T5s2wS40NJjW1jY+/nglK1asIjAwgPnzb2TGjNk9Wl3m+PEkNm1ax9Kl888Z\n/3+pmM1mtm/fQ05OPsHBgcyaNfWMFar6m8rKKjw83C9qt+1Nm7YzY8bk8ybx7t2bgKur02mKfFVV\nNTt27KO6up7585cgy0M6ld/FN998TWBgEDNmXIskwYYN64iOjmDixDHnlev11z9i2LA4YmKGM3Dg\n+VeveuqpJ/nlL5efNQfmUqipqeXTT79m8eLbTs2w/9QwGo289NI/ePDB5axZ8x3Tpk085y7aO3fu\nJSDAr1uD4qOPvmTJkjMNgvMtWvD99zsJD49mzJhrSEk5ztq1Kxk/fiR79x7hl7/8NaWlJRw8uIPF\niy/ffikmk4nPP1/PPfc8yEsvPcsjj9wtcjh+JphMJvbuTVBTUzOaGhoas1VV/duzz768pr/lEgh6\niytLkxEILoLHH3/YxdbW7iU7O7s5gYGBftOnX2PXkbugqioLFtxJXV09d9yxlK1bV6EoWezadQhP\nzx+TwI1GI2lpJzl2LJH8/Dw2bdrCXXfdhV4v0dRUy/33395n8peXV7Jx4zZMJhPTp09i1qypfdbW\npeLt3bPE+e6YM2f6ecs0NDSSkqIwefI49u49RE5OIWazire3H4sX34G7+5mbJk6cOJWJE6dy9Ggi\n3323lvDwAfziF7ecpqg1N7eQlZULcEaoy7Jli/jXv97o0caJ3367hoiIgb1uaOTnF7J9+z4MBice\nf/wvPc77MRqNpKamkJmpMHPmHFxdtT1HWlqacXBwxGw2s3791xQU5NLW1s4NNyw8zVDrDz755F0W\nLtQ2UKypqT2noQEwZcoE3n77426NjRtumMUbb3zIAw/cgbOzEwB1dfXcc89vmDhxAl5eHhgMtowc\nOZTBgwedGhNhYcHk5ORgb+/Irl3bGTt2Ivv37+O++25l3brPUFWV+PhrevnOz42NjQ1tbS20tLRQ\nX1+P2Wy+4iYbBH2DjY0NU6dOkKZOneBsNpuH7d2bsOqf/3yqqb6+MVtVLc8+++zLX/a3jALBpSA8\nG4KrknvvXeag0+k2KUrm5Ly8Aun662fx7LN/OqOcqqpUV9dgb2/P4cPHSE/PJjR0EKGh4Rw9mkh7\neyuqakGnkxg0KASTycTKld8gy4NxdHTguuviCQjw65N7OH48hQMHEvH19WHOnOl9MlN+tdDU1Mzq\n1RvQ6Wy5445fsHv3DsLCIhg0KPK8ind9fR1vvfUq4eFBTJ8+8YzZ4MTE4xw9msaECZPYu3cX992n\nbS5msVjYuHE7xcWV3H//w+cNqTt6NJGUlASuv37mpd0sWjjPgQNJVFRUYTSaCQ+P5PrrF1zQ0q11\ndbW89NKzTJgQR3BwEKtXf8ekSfEkJiZgb2+D0WhGVVWmTZvAoEEDWbnyWxYuXHbRyfC9QXV15ak8\nmsrKKnbu3MfixfPOeU1RUQmffLIaBwcHli9fdGphhA5aWlp5440PWb58CT4+mjHc3t7O2rXf09pq\n4u67H+DQoX2kpqZgNhsB8PLyJT5+Jl988SH33nsrJ0+ms2HDNv7wh4f65sZ7SFVVNXv2JGAwGJgz\nJ75fZRH0P2azmQMHEklJURrr6hqzVdX8f88++58N/S2XQHChCGNDcNXw5JOPSkaj6aXc3IL7W1tb\n7U+eVPQxMdEsXDiXRYvmniqXn1/Irl0HrUqnhMWi4uzswjXXTCUhYT9VVWWMGBFNdPTgfkmy7Uhu\njY2NZuLEsZe9/SuJmppaVq/eQEJCEllZuTz//LPMnHldt2VNJhP79++mtbWF9vZ2qqoqaWhooLi4\nkDw2QA0AACAASURBVF/96q6zxta/9dYKnnjiKQBeeukZ7r57CZs27aSwsIxFi24mIkLukayZmekk\nJ+9n2rQL20Sxg9TUDA4cSEKvt8Xd3YP4+Jk98qacjVWrPic3NxNbWxsWLLgWZ2cnjh1LYeTI2G7D\nb/bsOYStrSvXXnv5QoO68txzf+Wee5ZgMBh4770V3H774nMakxkZ2ezbd4x77nkAvV7PypUrkCQj\n8+efvnlkXV39qdyPzhQVlZCQkMZdd913Rt2PPfYI/5+9Mw+oKX//+Ou2ryqJFMqSsreQQpEthBDZ\n992YfZ8xM76zmzEz1rFGJPtOUbYkpUhElihp3/f9du/5/dFPM02iKIX7+q9zP+d8nnO6y+f5PM/z\nfr744h1Z9EDGa0FZWRn+/leEe/eicvPzC24VFxctkqlayXhdkH3Lymj0GBgYdO7Zs+c7Kipyc8zN\nzRW//voH+aZNddm92520tGRsba3Iy8vH1/ciubmFtG3bgYULP6zkSNy9G8Hhw3txcLBl1Kh/0pTS\n0jIIDb1J//59UFWtmfTtiyAIAoGBIdy6dRcrqx4sWjSr3uZ6HSgsLOLw4VM8ehSLjo4Wv//+Lffu\nPSQwMAAHh6FVakJ8fE5y/fpV+vXrSbNmasjLq9O9uzEaGurPzWuXSqUUFOSjrq7BoEHD+PtvD8aP\nn8yUKbUr7r5/P4JmzaqmcdWE3buPoq9vyIcf1r5DeXWoqqpSXFyKWFwGiJCXl8fSsnu1442NW3Po\n0KkGcza8vI5gY2OOsrIyOTm5qKqqPDdqde7cZT777LuK4nEHhyFs27ahyjhBEMjOzqly3NCwJX5+\nV0hLS0FXV4+vv/6EFi1a0LZte5YseY9169yYN29yRQqWDBmNFQUFBQYO7CcaOLCfVkFBYT9f34vh\ny5Z9khkcfP3w2bMXPhYEIb+hbZQhozpkkQ0ZjRI1NbUWffv2fa9Hjx79HBwcejg6Omr9ewcyKiqS\nFSt+pHdvK3JzC9DU1MbZeXy1KSKrVq1ATg7k5OR5+PAhrVu3wt19N/r6evTsac4HHyyol/4YgiDg\n53eZ+/cf0qdPr2cqI70N3Lv3gMuXr6GoqEJmZha2thb07m1R8XpsbAKnT1/is8+WVRzbu3cnaWkJ\ntGvXhszMXLKzc4mNTWDgwH7Y2lo+d86cnDx8fAJYsODdF7Y7OTmJ/ft3MGPG+Fqf6+t7EROTHlhY\n9Hzh+Z9GQUE+hw7tJTT0Gl9++W61aXgFBYX4+PghFsP8+UtfiXTyf3nw4C6nTx9n+vTyPhRFRcVs\n27abd96Z88zzzp71p23brlhZWRMd/YD9+3excOG0pzqYly+HEBUVw/TpEyq9Xlpayl9/bWXs2PEE\nBwfSvn1rDA2b4+8fTElJKa6uo2jSpP6EH2TIqA8OHTrJunVulJaKcXGZkBgfnxAYFhZ25MaNGwcE\nQRA3tH0yZPwbmbMho9EgEomUe/fuPcfS0nKUra2tpYuLSws1NbWnjr116yZ5ebl06GBC8+Y1l4VN\nT0/j6NED5ORkMHbssCr533WFIAj4+vrx6NFj+vfv+1bKWAqCwOXLIURGxqCsXB41MjBoTWZmOpmZ\naUycOBp5eXlOnTpPWNhtfvrpCzw8DvDoUQJ//rmu4jr5+Xlcv34VPb3m6Om1QEenKfLy8mzcuJo+\nfcwr9bjIzy+oskt94MAJRowYj6Fh6xe+l40bVzN27OBaO6ShoeHExaUxa9bCF577WaxY8QNRUQ+Y\nMGEUnTuboq5e/nkpKCjk/PnLZGRko67ehBEjRr/U/b8MV68GEhR0kenTxyMSibh16w4BAcF06NDu\nmWIIKSlpHD7sw2effUNs7CMOHNjF/PlTn6MydQEzsw4YGVW+V6lUyvXr4YSH3yc8PIJVq76vs/uT\nIaMhyc8vICgolPj4ZNLTs4TU1IyUrKxc37CwsPVRUVEhDW2fDBkgczZkNAJMTExsLCwsFvfs2bP3\ntGnTTA0MDKodGxUVyejRo9HSaoK1tQVGRu358MPPKo0pLS0lJycbZWVlfH29SUiIBcr7RGhra2Jv\nb/NcBZwXRSKRcPr0eeLjExk8uD/t2xvXyzyNnfv3H3LmzGWcnJwrdvQLCvL5/vtvCAy8wrRp4yks\nLEFVVZ1x4yZx/rwPSUnxiERyGBq2YcKEKc+ZAX777QdsbHrQvfs/6VDffLOC/v1tGTzYHoCkpBTO\nnbvC0qUfv9T9rFu3kmnTxtR4fElJCUeOnEZbW49Jk6rvdF0XlJSUcPv2TcLDr1NQkI9UKkVNTYPh\nw0c1mIMB5UpZe/bsQCIpYuzYf+pwtm/fw8yZE58ZYXnwIJoLF67w8cdfIxKJ+Omnb1i6dNZzU+Ye\nP47j+HEfpk0bX2+fcRkyGiuCIHD79j2uXQsnOjpWkpKSlpCenrX72rXQ33Jzc7Ma2j4Zby8yZ0NG\ng6CpqdnU2tr6fQsLi4GjR4+2sLOzU6+Jpny5HvlF/P0v0Lx5CwYPdqR9+45kZqZz7NghsrLSUVYu\nV/RRVFSkX79er6QhXllZGSdPniE1NY1hwwbyRHr3beLOnUiuXbuJRCLQsmVrJk2aXmVMXl4uGzas\nYeDAIVy/HkJ+fj7t25vg7Fz79KQNG1bTq1dnOnRoW3HMw+MQZmbduH07DGPjViQmZrBo0fsv1Bfk\n32zevI4xYwY+V1BALBZz9OhpCgpKmTJlFs2b14+SWWNGLBazf78nSUmxjBw5GH39yqmN27fvYfbs\nydWeHxAQQmpqDrNmLUROTo6wsGskJT2gT5/n90wBKC4u4fDhk2hqajBqlOPzT5Ah4w0lKioGP78g\nQkNvijMzs5Ozs3N/Cg6+ukUQBGlD2ybj7ULmbMh4ZYhEIvkePXqMs7S0nGRra2s9efLkVhoaGi98\nvUePHnLmzGmKivJRV1dhyBB7tLRebbfl0tJSjh07TVZWDiNHDnnlnb4bGolEwpkzl4iPT6Z7d0sG\nDx723JqATZvWcv/+HXR0dNDR0WXixGlcuXIZPb3m9Ohhibv7ZkpKihCJ5LG07EWrVq3x8zuLsXE7\nHByGVlxHKpWyd+9OMjJSGDrUnhYt9PDwOMjixZ9QVFRIREQ4Njb96uQ+/f3PIy9fRJcuz1au8vQ8\nwtixkzEwePucTSjv7/Hrr//D1XUkhoYtnzpmx459TJ8+odr3yc6dh3nvvX+ilYGB/mRnJ9KnT+1q\nXtzcPJk7d2qtzpEho7EQG5vAn39uoksXM5ycBr7Ub8vWrbspKirm8OGTKCoqlOjp6e8KC7vxS2Ji\nYlQdmixDRrXInA0Z9Y6Ojo5h3759P7e0tLSbMmVKVzMzsxdWQYuPj+XEicMUFxdiaNgCO7ve9aoi\nVR3FxSUcPepNfn4ho0c70rx5s1duQ0MiFos5dsyH3NwiRo8eV2P5WIDdu3fQrJne/3f7FvHJJ++S\nl5fHnDnz8fHxZu7ciWhqaiCVSrlzJ5LExBRsbCw5eNCLhQs/QF29soOanZ3JmTOnSEyMJzc3j6+/\n/r7Oi6A9PNywszNHW1ur2jGCILBpkydffLG8Tud+nVi1agUuLo5oala/iXD5cgg6Otp07tzxqa/v\n3n2cJUs+qnTst9++Z8YMlxr3ogkNvUlBQSH29rY1N16GjEZATEwsBgb6KCkpERFxnwsXgsjJyUdf\nX/eF6gylUinu7of46KMvgfJ0Vnl5Bby9vTPPnTt37dq1a4dCQkK2y4rKZdQnMmdDRr0gEonkevTo\nMcbKymrGoEGDbMaPH9/iZXpapKQk4+b2N61bt2TIEPuXboAnkUh49Ci2UgpOTSgoKOTIES9KS8WM\nGTO83grMGysSiQQvr7OkpmYzefKMl64JkEgkeHq6M26cK6tW/caUKaOrfaZ37z4gN1fSINKtf/31\nK7NnV5/qJQgCW7Z44uo6A2Pjdq/QssZFTWpbJBIJ69a5MW3aeHR1q0oJ79hxmPffr1yHFRMTTXDw\nBRwdqy8of0JeXj67dh1g8eLZtTNehowG5PLlq4SG3sbCworHjx9RUlKIra0VnTt3xNv7HNra+iQm\nJlBQkMO4ccOf6dD/m+vXw4mIeMS77z69bi02NlZwd3ePuHbtmv+VK1d+S01NfVyX9yVDBsicDRl1\njKamZlNbW9tPrKysBk+bNs28S5cuNW+J/BSKi4vZv38XaWnJzJw5/qUacCUnp7J1qyf+/oGUlJQy\ndep4Zs50JTIympiYeEaNGlLtubm5eRw5Ut64dcyYEWhpvX1SmWfPXiI6Oh5X16l1uqCWSqWsXPkz\no0Y5PLNb+/37DwkKCuP27bt8883/MDKqnaP4Mpw/78u1a4Ho6GghJyfHsGEOFcpPADt2HMDR0Rkz\ns9r17njTcHffwqBBvZ67EIqNjScqKgYHh6ppbp6eRxgwwJEuXf7pGSKVSlm//jemT39+bc+6dW7M\nnTu1QSKeMmS8KCUlJWzc6MGiRR/QooU+EomE8+d9uXUrDDU1ZWJjE1i27AekUim///4TCxZMqfQd\n9Cy8vc/Ttm0nbG3tqh0jFos5dOhQ2rlz566EhobuCgsLOyir7ZBRV8icDRkvjUgkEpmZmfW3tLRc\nbG9vbztt2rTW6uq1b5JVXFzMnTu3uHs3AnNzS7KyMgkJCWDUqCHo6em+kG0FBYUcP+6Lh8c+FBUV\nWbx4Fv3790EikbB//wmUldUxN7ckMDCASZOcqiySCguLWL/eDXV1dWbMcH0rm38lJiZz+PBpRowY\njaVl3Xc837NnJ+3aNcfUtMNzx165cp3cXDGurlVz8aOiImnf/umpOXVBUVEhUqmUwsJCdu7cxNy5\n5UXO+/efoFcvuzrvo/E6cvXqFfLyEp/ZXBDKC1eTk1Po27d3ldcEQWDPnqN06NCZoUP/6Qju6bmd\npKQ4JkwYWVGbJQgCERH3CQ29hZycHBkZWWhpaTBr1sTnKlfJkNHYKCsrY8MGD2bOnE+bNsYVx3Ny\nstm9ewedO3elf/9B5OfnsX79HyxcOO2Z11u9eis6OtpYWHQmIOAac+e+UyPRinv37ol37twZfv36\n9XMBAQG/5+fnp7/svcl4u5E5GzJeGJFIpGJnZ7fUysrKecKECZa2trZqL/MDP2/edFRVlVFX12TQ\noCFs2PA3Dg79UFdXY9y4ETW+TnZ2Dn5+gdy585ALF/wZMWIIrq6jyMzM4t69KAoKipCTU2T27IVo\napYvWoqKClm16jc0NdWRSkFVVQEXFyfKysq4d+8B588H8MEH//RKyMnJfeXF6A2Br+9FcnKKmT17\n4UtFlaojIuIWly+fxdV11HPHxscncflyGAsXvlfpeExMNHv27OTx48ds3Li9zm18Gr6+XkRG3gXA\n0tKaPn3sX8m8jZ2Cgnw8Pbc89//p7X2WTp1MaNvWCEGApKTyHdqWLQt58hXi7X0WY+POlZ5tSUkJ\nv/yynJYt9SgpKUUqFWFubomd3cAKxbHw8DB27NjKN998WD83KUNGPSKVStmyZTfOzq7PjJTeuBFK\nUJAfkyc7A+V1hEFBV1FWVsbT8xB9+9ogFktZsuRDgoMvExISxIULF5kxY0aNpMUBCgsL2b17d/zF\nixevhIWFrbl9+/alOrlJGW8dMmdDRq3R1dXVt7W1/bpPnz4D582b17l586d37a4tgYH+mJiYoafX\nnMzMdPbu3UV2diZOTg5VmnT9l5SUNHx9/REEEXJyikRG3qe4uJCOHTugqKiMqqo6Xbt2p1s38woH\n41lERz/Aw2Mb778/l5MnfWnTxpCsrBwePnxEfHwSRUVF/PrrN3Vy340RiUTCjh0HsLGxr5eFdHZ2\nFu7um2naVINRo4Y+dxe6PM/fnWXLfqxYVEqlUvbv9yQnJ40JE0aya9dx3nvvkzq3VUbtWLXqF2bN\nmlDluFQqxdf3Ira2PTl06ARz5kxBEMDLqxmLFpUX3m/cmIOTUzoiEezde4xp0xagoVE5ZVEsFlNa\nWkJeXh4nTx6huLgQqVSCnJw8IpEcd+/eY9Gi6bRq9XQ1LBkyGoKSkhKio2ORl5dDR0cbbe0mKCoq\nsnHjTjQ0miAIUuTkRIwePQQNDXVOnjxLenoWTZs2Z8yY8WhpVe0bExJymfDwa4wf74RUKuXAgZOc\nOXOR2bNnM2DAYHJysqso40kkklpLgQuCQEBAQP7+/ftDrl69ujc4OHibIAiSl3ogMt4q6n6rUsYb\nS6dOnWwsLCw+XLlyZd8pU6YY1rab8vPo08ceqVTKsWMHuXDhHHJyIgRBSvPmekilUjIzs3jw4BG2\ntpXTVR4/juP06Ut8+OEXKCkp4ea2kV69emFu3pPOnbu+UI8FQ8M2aGs3ITw8gsOHvbCzs6FvX2vs\n7W1Zu3Yr3377ck3iGjOCIPDee8tYuHBJnTsaEokEDw83cnIycHUdiZqaao3Oc3ffx6BBwyr+l2lp\nqWzatJYhQ/piampLSUlJjfOXZdQ3cgiCUMmBlEgk/P33Dmxs+vG//61k+fJypzApSY1Fi7QoKCgf\nu2iRFiEhhUgkD0lPz67iaEB5/xypVMoPP3zDV1+9V+X/vmFDBoaGb5cEtYzGiVQq5Y8/NmFgYICS\nkgqmpp0oKZESFxdNZmYGYrEYdXWtiqaj+fl57NixBXl5AXv73iQmJhMcHMa8ebNYu3YD+vqVHWhr\n676UlUk4dMgbF5cRTJw4mpEjB+PhcQh9/ZZYWVVNU3yR30ORSISdnZ2GnZ3dwJiYmAFubm6Lhw4d\nejokJGRFdnZ2zos9HRlvE7LIhoxnIhKJ5Hv16jW9Z8+eU8ePH9/bwcFBsz5zoc+dO83Zs750726O\nu/sOkpKS0dNrRlTUI0aPHsa0aS507Nie7OwcfH39KSgopk0bY5ydJ9Rpms+xYwdp3lwdE5O2yMvL\nVyycwsJuUVZWRq9eFnU2V2MkKyub5cv/wM3No06fa1zcY86fP4mzc+2arZWWlrJpkycDBw4lODgQ\nVVUlXFyGVzTZi4tLJDY2Eyenmnf5lvF0pFIpq1atQElJEbFYjKqqGosWvV/j8wMD/QkLu4Kr6ygU\nFRUrCl8XLnwfff2W7Nmzk86dW2Nk1JrERDWsrVtWOBvq6gKnTkVw9aoX77zzAc/a0PjrrxVYW3el\nVauWlVIaN2zYLlOiktFo2LLFk6VLP0VVteabISkpyQQG+mNk1JbOnbuhovJssYPg4MvcvBlSKX3x\n+HFfdHT0GTVq3Avb/izy8vJwd3d/dPHiRf9r166tiImJuVsvE8l4I5A5GzKeikgkUh80aNCnvXr1\nGjlv3jzz9u3bv1wL5hcgPPwGp0+fQF9fl2HDBhAXl0hwcBgJCSkUFhbx4Yef0aaNUb3MXVJSgpvb\n3wiCFEEQuHXrNu+8MwsvrzMsWjTrjS8+3bHjAGPHTq5UpFgXlBdArqyRqtB/OXcugKZNtTA371rl\n+V+7doOmTY2wtKxZl2kZ1bN9+yYsLTtiZNQaN7e9zJixgPz88jQnY2OlGr33ExPj2bvXA3l5EYqK\nykyaNJ2mTct70UgkEn7//XsWLZr+1DSqbt1ukJxcgKOj07OmQCqV4uV1lLt3wzExMcba2hJ1dTXO\nnvXH0LAlnTqZvOSTkCHj5cnOzsHb258lS+qvhkgikfDXXyswNGzG8OEDK46HhIRx48ZdHB1H0q2b\neZ33H4Lyz+Hx48czTp48GRQaGrrpxo0bXoJsYSnjP8icDRmV0NDQ0O3fv/+3/fv3d1ywYIGptnbV\nPNH6pLCwAF9fbx48uIeiohwqKioUFZUQHh6BqqoqbdoYkpubS25uPt9//0vFAqa+KCoq5I8/fsHC\nohO3b99lwYIZb7yjERAQgoZGcwYMGFzn1z516gS6ukp07Ni+Tq97/LgvTk6u6Oq+Xc0V65ri4mI2\nbfqTmTNdiYi4z+7dR+nY8Uu+/rpcZnjr1mImTlR5oc+ARCJh27aNKCgooKWlhZFRM9q3N65SIJ6e\nnkF4+CNcXCY99Tq3bt3g8OF92Nr2Y+hQJz75ZCmTJ4/h0qUryMnJoa6uRkFBITNmuL74g5Ahow45\ncOAEjo5j63zz5gnZ2Vn89NN3DBhQnu77bwRB4NKlYB49ikckEqGkpMK0aXOemqL4soSGhha7u7tf\nCQkJcQ8JCfGQSefKeILM2ZABQKtWrYytra2/HTJkyMDZs2cbPS9sW5fk5ubg43OSuLjHKCiIUFJS\nJD+/iLZtO9CsmR4+Pt40b66LVAoKCkr06zcAc3Oretml+TdSqZT//e9LRo0ajK+vH4sXv/kRDalU\nyrvvfoWNTW/EYjFKSsrMnDm/RkX1z0MikfDzz9/y7rt1n+KyY8d+3n33i3p/T7zpHD9+iPbtW5Ke\nboZIBBKJiLQ0eb7/Xo2ICAXU1QVu3Sqlbdva1Wu5uW0gJSWJkSMH4ud3laVLP+ann75h6dKqn6n8\n/ALOng1h1qz5T73WypU/MG/eZHx9L5KRkU9c3GM++2wJUC5VnZubx8GDJ3BxGfnMvi0yZLwqJBIJ\nbm77+Oyzb+t1ngsXzhAbG/nMNNXc3DwOHfJGW7sZU6fO5mWa7VbHgwcPyjZv3hx65cqV/QEBAWtl\n3cllyJyNtxxTU1MLS0vLL0aOHNl/4sSJLepD3vS/SKVSbt26yeXLfpSWFnPnzl2aNdNFX18fZWVV\n+vTpT7duPQBYu/YPNDQ0GDTIsd52harD2/sYysplBAQE8+67897KhWx+fgGbN3vy4Yefo6PzYr1O\noPx//tdfv+LkNAB9/bpRL3vCpUvBZGYWMnPm0xenMmrOrl3byMhw5euvy/vJfPttIRs3qvDee8Vs\n3apMTIx8rZ2NsLBrJCZG0revNTk5ubi57eeLL74hMTGJyEhNlJWVsLTMqJC8vXXrDnJyWvTt+/Ru\n4atW/cysWeVRi5ycXJSUlKo08BOLxWzZsoslS2S1GzIaBydOnMHOzrFOG6I+DR+fkzx8eJeJE0c9\ns94uNTWdY8d8MDY2wcVlUr38viUnJ7Nhw4abgYGBJ86ePfurIAgFdT6JjNcCmbPxltKjR4/BVlZW\n77u4uPQbMWKEdn3v2BcWFvDoUTQXL56lqKgQQ8PmpKVlUloqwd7eAUtL6xdSyagvrl8Pwc/Pl8mT\nx3Do0AmmTasq5fm2kJSUwt278YwbN/GFzo+Pj2Xbto04Ow95roRxbREEge+//4s//lj3VjqDdY2/\nfy4jRmhWKtj+4osifv1VlW3b8pBIFJk0qXZpVOfP+6ChAR07tkcQBJYvX8ns2fPx8+vEsmXl6VM/\n/liItXUAoaE3iIi4x+rVG6stDv/yy4/Q0dFAWVkZkUiEIAgIgkBmZjZ2dr0rxBv27TtGZmYWo0Y5\nymRwZTQ4YrGYXbuO8+GHn9f7XAkJcbi7b6F/f2u6djV75lg/v8usX7+dffsO1ltack5ODps2bYr0\n9/f39fPzW56fn59RLxPJaLTInI23DEtLS8eePXt+NHPmzL59+/att3bYOTnZeHkdIzU1idTUFO7c\nuU+7dkbo67dARUWNJk10cHYe91K75fXFnj07KSsrYNSoIfj4XKCkpITRo4c1tFkNhkQiYe/e46iq\najBnzuIan5efn4en53akUjGuriPrzZmMiYnl+vX7tbJNxtMJCMhn2DD1pzobu3blIRYrMH68aq2c\njaioB4SHB+Lg0Bcvr3NYWPQlOlqXSZP0K82zb18KTk76SKXSZzqOq1f/hqvriCrRDIDg4OsEB4ci\nCNCxYzvs7W25cCGAe/ceoqOjRdeunejd27KWT0WGjLrBw+MQc+a8g7q6xiuZ79ixg0RF3WPKlLGo\nqDzdeS8tLWXXrsOYmnbByWlsvdpTXFzMtm3bHp8+ffr0+fPnl8k6k789yJyNtwQLC4thvXr1+nD2\n7Nl9bW1t69zJKC0tJTj4MuHhYcTHx3PjRjhWVuY0b94CA4NW9OljR2FhIe3adWj0O9A///wNAwbY\ncv78Jfr370O3bp0a2qRGwa1bdwgODkdNTQ1BEFBRUWX8+ClVmk0lJSVw7NhBSkuLcHZ2REur7gsR\n/4u7+366d7ekb1+HZ8qlyqiKWCzm5MkjKCsr4+g4krVri1i2rO7SqMrKyli58gcWLZrOli2efPjh\n1/j6ZuDq2rySs3HoUCaOjs/ffAgODuTo0f1MnjyG1q0Nqzg+hYVFeHgcYOHCGZWOC4LAiRM+mJp2\nwNS0Q43tfx05ffo8ycmpQHmPBAeHvrRp0+o5Z8mobzIzs7h48TqzZy98ZXNmZWXg5rYRAwM9hg93\nqHaj4MaNCIKCwhg4cAi9e/etV5tKSkrYtm1bjI+Pj8/Zs2dlTsdbgMzZeMOxtLQc0bNnzw/mzJnT\nx8bGpk6djLi4x5w5483du3d58OAhzZrp0rlzZ1q3bsPAgY6vpTLQzZvXWbPmD5ydh2FnZ/PGF4S/\nKOnpGXh6HuPLL5ejpKREUlICR47sp7S0mKZNtXBw6IOm5qvZvYPyheT9+w8JDAyla1cLhg59tmyq\njHLS0lJZv/4vxOJihg1zIDj4FnPmLOLixWzU1FRRVFQlPf3lC8Td3Tfz+HEUeXn5DBs2kgEDhrBu\nXUmlNKqlS5Ur5ZhHRUXi5XUMEGFp2ZN+/Qbwww/L6NixLVZWXbl58w7Xrt3g88/frTTX2rVbGTfO\nCUPDqqlT5cWxJ5k9e3LtH1YjRiqVcvXqDe7ejUQQBNq2bcOAAeULRkEQ2LrVk8GD7Wjbtn6kwmXU\nnE2bdmFs3B4Dg9a0bduOVq3avJJ5796N4Pjxg3TtalJFseoJgiAQEhLGmTOXWLlybb3b9P9Ox+PT\np0+fPnv27DcFBQVp9T6pjAZB5my8oVhaWo7o1avXB7Nnz+5rY2NT562VY2NjmD59KiNGOGJm1plu\n3XpgbNy+0UctnlBSUoJUKkFRsbxvgLy8PIcP76GoKBcnp0ENbV6jJiMjk717T/D5599VLA737NlJ\nr16mNGvWsGlxUqkUT8/jvPvuJw1qR2NHKpVy4UICmZmZ2NkpsmfPIWbPnsyePUdxchpPq1ZtS3+K\nlgAAIABJREFUiIt7zK5d7hgZfcCiReXRq19+icHQMKRW9TuCIHD9eiKxsdHY2TVn//4TZGXl8u67\nHxMQUIxUKtCiRQy9etkglUrx9z/P1atBGBq2YOhQexQUFPD2Pk9mZg5JSYk0b16+iSESiXjwIBoT\nk3ZMnjwWRUVF8vML2L37EAsWzKjWHm/vc6irq9K/f5+XeoYNiVQqJTExhejoGGJj40lJSWfQIDu6\nd+/81O/gJw6HsXFrYmLiaNpUmwED+qCr27RiTGpqOps27eSbbz56lbfy1iGVSsnKyiYlJZ2YmDji\n41Owtx+IjU0/srOz8PX1olkzPayt+1TI027atJb+/QdhZtb5pecPCQnk3Dlf+va1oHv3LlVeLy0t\n5c8/t/Lrr3++9Fw1paSkhO3bt8d6e3v7BAUFLUtLS0t9ZZPLeCXInI03jB49egywtrb+av78+X2t\nra3r3Ml4EwgLu8bp08fJzMzkxo3bbN++k1at2rBmzQpmzHBpaPMaPevXu/PZZ9+hqKhYceyPP35m\n6lTnavOCXxXh4REkJeUyceL0BrWjsSIIAo8elRAYWMrHH2tQUCDi11/zgQ3k5+dRViZi2bLvK8be\nuJFMTMyDirSjli0L2b59Lx99tKxG8xUVFbFnTwHvvVfuhG7cmIOTUzo3b0Zw9+5D7O2tMTRsydWr\nYVy+fB2RCOztrbGw6Fbje0pPz2DNmq20b2+MVCrF1dUZdfVnf/UFBl4lPDyC2bMnv3ZpdytX/k3z\n5s1o2bIF7dsb07q1QaXPYnUIgsDt2/fo2tWM7OwcLl4MoqCggKlTxxMbm8CJEz7Y29sSEHCF7t27\nVLv7LaPuCQoK5d69KAQBbty4ydKlc7h6NZziYjFDh46gpKSYjz/+GC2tJmzZsp0WLfRfek5fXy9C\nQ0MYNsy+SsTr1q07XLoUyvz576CnV7fqgc/iX06H98WLF7/MycnJfmWTy6hXZM7GG4KZmZl5r169\nvp8zZ05/BweHl2+K8IZy/XoIISGXkEoFNDS0mTp1NvLy8pw8eRiptBB7e5uGNrFR4+t7EROTHlhY\n9Kw4duNGKJGRNxg69OlSpa8SsVjMgQMnsLUdWMlGGeWLzX37ipk3r7ywesGCYrZsUUEQ4OzZdDp2\nzGLfvlMsXvw+e/d6kJLSj6+/NkZdXeDvv3Pp1KmQli0LuXgxkA4dzOnatXuV68fElFJWVkZIyAEy\nMlIoK2vFt99OqVSbERKShIFB4b/OK2/ql5mZyePHATg51b6Z5I4d+xgzZkSt6oPi4hI5fPgkI0cO\npX1741rP2RAIgsCGDe7Y2fWmW7eX3+X29w/i0aNYlJWVmDhxTEXa6I0btwkMvIqdnY2sZu1fXL8e\nTnj4HeTk5HiydjIxaUf37p3R0Hj5LGVBEMjNzUNLq/wnXCqVculSMFFRsRgYtCE6+gHa2k2Ql1di\n1qyFL+0oS6VSjh7dT1RUJKNHD6FFC72K10pLS9m9+yht23bE2Xn8S81TW4qKitiwYUOUj4/PIV9f\n3+WCIBS9UgNk1DkyZ+M1p1WrVsZ9+vT5derUqYNGjx7dTFZjUD1SqZSPPnoHbW1tFix4BwODVkil\nUrZsWUebNvrY2spUap6FIAhs23aAjz/+quKYVCrll1++Y8mSxtNZfd++4zg7T0ZfXyZ3+m8ePSqh\nWzelSgv/ESNK8fZW4uzZdBQVbxIdncqECVPYufMUS5YMQySC+fOL2by53EFZtSqfceNS+O239Qwf\nPpJevWxQU1NHIpFw6lQBt24p4OmpxHff5dKlSzExMY9xdbWp1tkQBPDyasaiRVoA/PBDFLNmQW3f\nSsXFJezadZB586bW+Jz33/+aHj264OrqXCcLxVfJX39tolcvc/r1612v8/j4XCAtLZ3Jk8c1Kmny\nhmLNmi28++68iu86iUTCw4ePuHkzgry8fFRUlBk0yL7OewkBJCYm4+l5mKioR3z00SIuXrxChw5m\nODtPeOn0ZbFYzO7d7mRlpTF+vFPF58HNbTdSqRwff/xVg6RIZ2dns2bNmgg/Pz/PCxcu/C4IQtkr\nN0JGnfB6JNjLqELz5s31xowZ4/bzzz9f3rNnz0RnZ2eZo/Ec9u/3pLi4mC+/XI6BQbkyi1gsJj4+\nFhsbiwa2rvFz82YEvXtXznPfvHkdw4cPaDSORkFBIaWlUpmjUUOUlGDFigJMTLLx9vbDxWUSABKJ\nFIAxY0rZvFmFggIRBQUiPvhAA2/v5nz66TsoKpbw55+/IJVK2bChmEmTNPnpJ1Xmzi1h6VJtrK1b\nEhXVks2bs1BXF1BXF9i4MYeWLf+JaiQlqbFokVbF9b/5pj0xMU9f1AoCJCaqkZioxn/3yO7cuY+a\nWlUp3GcxadJYOnXqiLp6ubpaTk5erc5vKKRSKXFxCa8kzcnR0YHBg/uzZs1WYmPj632+xo6RUSu2\nbPEgJiYWAHl5eUxNO+Dq6szcuVMZN24kly+HsH37HgoKCp9ztdphYKDPp58u4YMPFvDjj3/RrJk2\nBgZa/PjjNyQmvtz/RlFRkZkz5zN37lKOHj3LgQMnKCsrw8lpMEVFhTx+HF1Hd1E7tLW1+fbbb7vs\n3r37588//zzI3t5+oUgkkq1bX0NkkY3XgKysLM2rV+UXA1y+/MeOa9eufT58+PCxCxYsMFZSUmpo\n814b3Nw20L59BwYMGFJxzN//PEFB/ixYMLXRLJgbK9u27eWDD8p3uMrKyli9+jdsbc3p3LljQ5sG\nQHx8Env3HuPTT5dVkeOVUTWNatWqfLp1KyIu7jTR0TFMnTobQ8PW7NvnQWJiHHp6C8jOVuGLLyr3\n3RgzphQXlxI6d76Ln18wPXvOo39/1SoRkwMHlCsiGU9o2bKwUtQiMVENa+uWlc7dvNmXESPa/8f2\nyhGQJ7UfT66VkZGJt/c5pk+fQGxsAqWlpejpNaNJE42nfq6lUil79hzm5s0IdHS0MTDQR0FBHnl5\nBSZNGlM3D7yeyM7OYceOfbz//oJXNqcgCBw4cBwlJSWcnYc1yHelRCLh8GEvHB0daNKk/uW0q6P8\nc3QMI6NW2No+PVUzLy+fffuO0by5LqNGOdb585JIJHz33e+oqamxdOlsjh3zoXXrdowZ41on109I\niMPT0522bQ0ZNKgfBw960ayZPuPGNayKW1RUVNnq1auDQ0JCVl25cuVggxojo1bInI1GTlZWlubO\nnUpnv/pKxVoiOciECQmF69fPU2vSRFaW8bLs3LkVHR1V7OzqNxXhTSEgIBgjo65oaWmxfftmJk8e\nXaEM1JCU5957k5CQjKPjcFxcXqzT+duAIAgEBcUQFRVJXt4diouLGT16HB06mFaMWbPmd5o0UcXQ\n0Im9e1vSpYuEb78tL7hesKAYT09lPvigmHbt7jNmTGdu35Y819n4d41GZXuqOhGpqWuYM2dKpXFP\nc0r+e90//vgbBQUFzMxM0NBQIzU1g+zsHARBQF5eHl1dHUQiEcOGDeThw0fExiYwZEjlOiMvrzO0\nbWtU7w60WCxm+/Y9FTn3YnEZPXp0pmdP8+cuTMViMSdO+JKamoaNTU/MzbvWq63/5uHDR3h5nWHa\ntPGVlKxeFStX/k3r1obk5+cjLy+Pvn5zevbs0SAqeG5unsyd++y0vZiYWLy9z9G9e+c6T3kTBIG/\n/tqMmpo6zZpp065dG4KCbjBt2myMjNrWyRzh4WF4eR3FwqILiYnJDBs2riIroCEJDQ0tWrNmjV9w\ncPBX9+7du9HQ9sh4PjJno5Hj65v7mbPzzRXFxdcAF9TVW7+Qzr2Mypw5401RUaasILwWlDdn20jX\nrqYMHdqfhoqqSaVSzpy5RFJSKiDHvXv36dzZhOTkVObNW0K7diYNYtebgiAIrF8fyxdflOv/f/55\nAa1aCZw7p8SZM4p8/HERGzeq8Mcfd9HVTSUq6iE5Oa4sW1buMPz4YwG//KJGQYGoSgTi6fOVp1MB\nKCrGsX37bnr3tqokTVsTZyM5OZULFwKYPHncU+dJTEwmIyOL69fDUVJSxMzMpIrqVXZ2Djt37kdd\nXY0ZM1xrpPJUW8qf7zamTnVBR0e74lh4+B2uXr2BSAR2djZ07Fge3SkoKCQ8/A5lZWUoKCjQq5c5\nCgoKCILAlSuhhIdHsHDhzDq3szrEYjG7dpVvKkdGRtG1qxkjRgxGR0eblJQ00tMz6dy5Y71EP9zc\nPJkzZwoikQhBEEhOTiU09CZpaRloaTVh3LhX11/n+PHT9OjRBSOj1s8de/NmBP7+QYwaNRRj47rr\nq1FaWsr69Ttwdh7PuXM+GBrqUVRUTFFRGXPnLkZVtW4EKQMD/Tl3zoeiohJ+/nllnVzzZREEgaNH\nj6Z5eHicCggI+CQ1NVXWo6MRI3M2GjEdO3bs1LfvyEN797p2Ki4uXxS/aFMtGeWdVN3dt2Bj05cD\nB/Yyffq416rJlSDA/fvlCzpT05xaF9G+CYSF3SYo6DoTJkxBV7cZa9f+wYgRDpw8eY733vsEXV29\n519ExjPZt8+PuXP7V1rYz5hRzKBBYqKi5P+/o3gevXvfwtv7OCNHDuTcuSB6956Duro6pqY5xMTI\n4+vrx7x5fZGXf36KdXlqylFKS8X07GlOZORDsrJyMDfvioVFtyoRkEWLirGyKmbYsIxKn4MDB45j\nb29bSVXnRcjOzmHPnsMsWjSrzhfNu3YdwN7ettqO3hKJhEuXrvDwYQxKSork5OQyZEi5c19cXEJQ\n0FUUFRVJS8ugWbOmpKWl88kn79SpjTXh2rUbaGtroa/fHG/vs+Tm5tOiRTN0dZsSGnoTB4d+dO1q\nVuPr+fhcIC4uEXPzLlhZ9Xjqc3/06DHHj/swdapLlWjG3bsPuHjxMvPmTavUHLK+kEqlrF+/jaVL\n59boPfKkg31WVg6TJ4+ts82asrIyPDwOYWlpQ7Nmehw8uIcxY4Zy5swl2rY1YezYiXVW3B0fH/vK\nmhDWlNLSUjZu3Bh98uTJvWfOnPmfIAilDW2TjKrInI1GiJaWlvaAAQN+nzx58khXV1f9/ftLKvKs\nt24tZuJEFVl9QS0pKyvjxx+XsWjRdMLCbhMREUlkZBTTp7u8FtKOggC7d+vz+eflKiErVhQwZUry\na+9whISEcf9+9P/fR/nNSKVSdHW1ad/eCB0dbRISkoiPTyIhIRUrK2uGDnUiLS2Vv//+k/HjnVi/\nfgd//rkOFZXaFQjLqMr69X9iYGDF9On2lZyNL74oYts2ZebPL8HOTkqfPmqkpaVy+vRBnJ2HAbB1\nqycODn0rZGQ3bfJg4cLn9zt5IkHr7Dys0q6vIMDhwxHk5RUglT5k+PB5/PSTLqWlcOqUEoJApehG\nQUEhGzZsZ8aMiXWS3hcZGcWlS1cq/lZTU2XixDEvvHBzc/NEVVWFvLz8GkciioqKUVFRrvJ9X1RU\nTFpaBm3aGL6QLa+CU6fOEReXgKVl92qdByhfhG/Z4kGfPtZ06WLKzZsRhIffQSqVUlhYxODB9hVR\nHij/Ll+1atNTHaz09AxOnPBFEAT09HQxNm5DaOjNSnOrq6sxfPig5/ZiecKFCwEoKSnRu7dlFScm\nOvoxp06dY/HiWTV+X2RlZePpeYj+/fvU6W+Pn18QKSlZzJy5gA0bVtG1awd0dLQ4c+YSAwYMwdbW\nrs7maoxkZGSwcuXKMH9//3WBgYHbBdnitlEhczYaESKRSM7BweETR0fHue+//37HJ4unJ/r1AMbG\nSjJH4wV4+PA+W7ZsYNasCbRs2YLHj+MIDb2Pjk4XTE3bVylcbWzcu6fF4MHNKi0Az55Nx8wsp4Et\nezEKCgrx9DxCr159cHAoL9j/+eflqKoq06JFS+ztBxEVFUl6ehpGRm1p27Y9OjpNkZOTIyUlmU2b\nVjNrlivff/8nenq69OhhyaRJ1XeNllEzvL2PkZWVhZzcRObPL//+WbGikO+/L6/J2Lq1mEGD8ti3\nzwOJpJQJE0aipqYK/FM4m5eXT+vWBvj4+DF9+ngsLbs/a0qKioo5cOA4M2b8U9z630jG6tWpqKre\nYMGCodWmUm3fvofx40ehqalRp8/kyW9kQkIyXl6+KCkpoaSkiK1tL9q2bVPj7+MdO/bh5DSY1au3\n8OWX71c8tzeZ8u7x4QQEBGNl1YP4+ETatGlFnz69KsYcOnQSc/OuT+11IggC585dIjExGUEQEAQB\nkUhEQkISX331wTPnTk1NJyoqBmtri0qyvVlZ2Zw6dY6CgiIGDbKjXbvqo9s5OXmcPOmDlVUPLl0K\nRiQSoaioQFJSKn369MTGxort2/cwb960WksD+/r6ERubgK1tT0xN29dJNCY+PokjR3z47LNvOHvW\nm5iYh0ye7ExQ0DXCwyOZNGkabdt2eOl5GjP37t0r/f333y9dvXr18/Dw8NCGtkdGOTJno5FgaWlp\nb21t/cOXX37Z18jISCZoXg+sWbMSZ+eBaGk1YdeuI+joLGHhwvLdrZrkljckT3M2Dh9+RGlpUL1r\n7dclSUkpnD17ibIyEXPnLkJRUZH8/Hz09JoTEnIZf/9z2NlZc+rURT7++Es0NZv85/wEtmxZx5Il\nMyt+nLds8UReXpmSkiIMDVszY8a8hri1N4p/b3AYGSmyY8dpBEFCTk4EampKjB49FFXV6iNJt2/f\n4+jRU+jp6bJgwfTnLsj37z9GixZ6FXUaT6vRCAqKw8srjx9/LG9m9+OP0SgoHKSoqAhT0/bcunWX\nd96ZUxe3/1yKi0u4cuUaSUkp1daI/Jd169x45505b+VmkUQi4cGDaIyN23DzZgQ3btyibVsjEhKS\naN3akMGD7Wt8LalUSl5efkXjuxdFEAROnz7P48dxdO1aHmEwNNSnTZtW3L8fRXBwKMXFxUybNqGK\nA7tv3zEMDFoQExNH27ZtXvg7uLCwiNu37xEZ+ZCyMgllZRJ697Z4qYaNOTm5bNu2n48//pKsrEx2\n7tzCwoXTSElJ58gRL7S0dJk1a8EbrdgnCAJHjhxJc3d3PxoQEPBxZmbm66Fr/QYjczYaGE1NzaaD\nBw9etXDhQqdhw4a9enmPtwgfHy/U1CR07dqZ69eV2L69BceOKZGfL/r/HgCnycwMa2gzAaosSFRU\n1CgomPmvItwc7tz5gLlzJ2Fq2vh3qpKTUzl8+BRGRu0BgZSUROTl5VBRUSY7OwdHx9GYm1uRk5PN\ngQO7yc7OYuHCdys5G2fPnubGjRBmz55YZRdRLBYjEolYs2Yby5f/2iANqN4kxGIxN26E8vhxNFZW\n1ty6dZN27ZrTqlXt+pdERcUQEBCMWFyGsXHrZy4qAwOvEh0dw5QpLvj7JzNtml0lZ2P16hOYm6uj\nqtqJrKxsjI0lqKgoIS8vT2joTX7/fT17925+qfuuDYIgsGPHPmbNmlSj8Tdu3CYrKxsHh371bFnj\nJykphR079qGjo8X8+dMb9PNaVlZGTEwcAAkJScTFJdCypT6DBlWfdiSRSNi8eSeLF8+uU1sEQSAw\n8CoREffQ02vG8OGDUFGpfX1mUVExmzZ5sGjRBygrK7F69e8MHz6AH39cRb9+fYiIuMs333yHiUnN\na2peRwoLC/njjz8ifH19/w4ICNggS61qOGTORgMhEonk+vfv/9GIESPmv//++x2fSCDKqD+iou7j\n5XUCE5N5lJTIERAgj4KCiPXrVavkfzdG/lsgHhR0lcjIKKRSKb16mb/Ublh94ut7kVu37qOrqwtI\nGDSoH61bGwBQUlLCvn0nMDPrxtCh1SvJrFnzO2ZmxlhbV998cceOfVy6FMLu3QcaTCnrTSA3N4dl\nyz5lzJhhtGplQHj4HaKjYxk4sC8dOryYpObx46exsuqBoWH1zkpWVjbu7vtQVFSgZ08L0tOHsGhR\n+e7rd9/dZ9iw1Ir3DZTn5+/ffxxNTQ3U1FRp3doAa2vLp167pKSEwMCrGBjo15lzLggCa9du5b33\n5tdofHDwdTQ01OnSxfT5g99gkpJSOHrUGwuL7rRubcD+/cdxdh72zHSmxoi/fxA6Olr19r2bmprO\n0aOnMDPrgL29bZXXMzOzuHXrbiXVtn9TVlbGpk27mD59Hs2b67N27R8YGOgSH5/Kp58ue6s2ZCIj\nI8W//PKLf0hIyGcRERHXG9qetxGZs9EAWFhY9O3du/fPspSpV4uHhxsZGZNYtqw8derbbwspLRV4\n9EgBB4fiRp1G9SwEQcDP7zIPH8agoCCPWFxGkyaaFBUVVaQcLF48i1ft0Obl5bN1627i4hIZMKAP\nw4c7VJISffjwEefOBTJv3pJnqkhduRKAt/cxPvpo4XPn3LnzEO+993md2P+2UlpayoYNK5k5s24a\nhAG4u+99bgRg1apNLFo0q2In99+SuFu3/sj7789HS0sTb++zxMcnoqioyNSpLkgkUgIDQ7h/Pwot\nrSYoKCigr69Ht26dkJeX5+RJX2Ji4jAwKE+RefQots6arfn5XUZfvzlmZs+XW87NzWPbtt2MHTui\nRnKpbyp5efns2nWgIirw73SmTp06YmNj9cq/q16U1as3M3nyuApBgqysbIKCrjFwoN0LRSSeRmjo\nTUJCrjN16viKZoY7duxDU1ODFi2akZOTz4gRg556rlQqZdu2A3zyydcAHD9+iODgyzRpov3WORyC\nIHD48OFUd3f3IydPnvxEEIT8hrbpbULmbLxCRCKRmpOT058LFy50GTVqVMN3Q3uLOH36BCKRDS4u\nlesevv66iD59iunePfO1dDSehiDA48cKKCoqYmBQRF5eHlu27GLBgul1XjxbHZcvX2PXrgOYmLRn\n7tzJaGlV7fjr5raPDz/88rk/eK6uYxg8uD9KSorIyYnIzc1HRUUZR8cBqKgo4+FxCAuLrlhYdMXD\n4wjvvvtpfd3WW8PRowd49OghqqpKjB/v9FLFq1FRMWzbthsjo9bk5ZXLo7Zp04pWrQxITEwmOzuH\ntLQMgoOv89dfP1SpBdm79whFRUUoKSkhFpdhZmaCjY1VpTFPogxWVj3o0aML6ekZBAZeRSQSYWvb\nE2PjNly5Ekpubh5Dhw7g9u17xMUlMHz40xdpNbknL68z6OnpMnLk0Bp/rp504i4qKkZOTo6pU13e\nqgXfE27ejCAlJY2hQwdUHBMEgejox1y5co2iohIsLbs9V1ygoSkrK2PfvqMUFhajqKhAenoG48eP\nIiAgmMLCIoYPH1wpGveiFBeXcODA8QqxAhOTdhXdy48c8aZLF9NKil3/5ujR0wwaNIrWrcsjRzEx\n0fz443e0bKmPg8MQBg4c+tL2vU4UFBTwyy+/hJ8/f/7nwMDAfQ1tz9uCzNl4RdjY2IwbMGDAsq+/\n/tpCU7PqwktG/SAIAiEhcURHR6Kvb8WoUdpVnA1n5+xGnT5VG57WkdnJKZ2SkhL+/ns7c+dOeeHC\nyn/vNFen3pWTk8e2bXsJD7+DlpY6TZpooqmpztKl8yotIsViMfv2ebNkyYfPXWyJxWLE4lLEYjFl\nZWVoaWnj73+OFSt+xc6uHxKJlOnTx3D16k1at+5Inz41LzaV8WxSUpLZuHEVixfPeKHUtKysbP78\ncyOLFs2sSKGKjY3nyJFTKCoq4OjogLy8PGVlZcjLy2FsXFXdadeuA0yYMPqZu91hYbcQBOG5i9MT\nJ3wwMNDH0rI7bm67sbPrXeu0KrFYzN69RykuLqFpUx1cXF6skVxCQhIHD55g8eJZlZ5tcXFJne2K\nNyY2b/ZAWVkJNTVVunbtREBAMPPnT6t2/Pnzl4iLS2TqVJdX0jejrpFIJHh7nyUpKYURI4bUut6p\npgiCwLp1btX2+xCLxXh4HOWjj76sOFZYWMDvv/+EiYkRsbHJ9O1rj52dQ73Y11gJCQnJ//33330u\nXry4WNYQsP6RX758eUPb8EajqanZNDQ0dPvy5cs/nTNnjtHrEh5+ExAEgV278nB11ePEiXb0719C\nv34S/P0VUVIqT6Nq166UHj1y35ioRlKSGs7O5dEbsViEr68ykyeXoKMjYGXVna1bd1XZFa4JT5wY\nZ+dmbNmiiampPCYmlR2OvLx8li//HTk5OYyNDfnyy/cYMqQ/Dx5EY2ravtJiMSjoGjEx8Rw7dgRH\nxxGV5tqxYyvXr4dgYVG+cycvL4+iohIqKiqoqamRk5PF33+vZezYcbi4TOLCBR/U1FQpLoYRI5xf\n7MHJeCoaGhp0726Ou/sOLC27Pf+EfyGRSPj7b3c+/3wp2tpaFcdVVVV4/DiOx4/jiYyMIjc3j+jo\nx2RkZNG0qXZFlCAtLYPbt+9x4UIAvXpZoKZWfV+EEyd8cHIa8ty0KFPTDvj5XUZbW4sBA/rg4XEQ\nE5O2KCgoEBFxD5FIrtr+C3fvPuDmzQhOn/ZHSUmNrKxsWrRoTseO7Wr1XJ7QpIkmhoYtCQ4OxcSk\nHZmZWWzfvp9Hj5K4fj2c27fvERQUSvfuZrWWVW2MJCQkYWdnQ5cupsTGJtC6tQEtW7aodnzbtka0\natWSLVs8sbGxeu1UvK5cCSU5OQVBgLVrt9K/fx80NNTrfB6RSESzZk05efIMPXp0qfK6vLw8qalp\nFBQUVTTkU1RUws5uABcunMfKqgvXr4dy/PhRunbtjobG27EZamhoqDR27NjOioqKY7766itmz559\nVbYerj9kkY16QiQSiezt7RcOHz78g48++shUVrD6apFIJPj55eHsrFVFlz8pSRWpVETr1oW0aNG4\n+2vUJJrwb54mGfrvwvehQ1357bdvMTfvWis7nnfdJzx4EM21azcq5EATEpIICrrG+PGjKo3bvn0f\nGRlZtGzZAolEyq1bd/jmm/9x9OgBbt68yapVf1eRva2OBw/ukZGRjo2NTOWnvrh48Rw5OUnY29vU\n+JzS0lKWLv2Sd96ZU2kRdPDgCXJz8xCLxZWa22VlZXPlSij+/kGYmZmgrKyEmZkJAQHBpKdn4uIy\nslITtJKSEhQUFAgKukZqajrjxtUswlAeVTtKZmY2CgoKKCkpUVpahoPDUI4ePUT//r1ivYm8AAAg\nAElEQVTp0aNLhdNRWlrK5s2e2Nj0w9i4Pe3adcDL6yiJiTFMnDi6xs+jOnbtOkBcXDJmZp2YMmV2\nJac8LS0VT8+tzJpVd/UzDUVpaSmenoeYPXtyrc67e/cBSUnJDBz4+jSl8/G5gLa2FlZW3VFQUKC4\nuAQ5OVG9CleEh0fw4MEjXFxGPvV1N7e9TJs2jxYt9CsdP3HiMLt3e6KsrExUVDRr167H3Lz2G1Kv\nM5GRkeIffvjhQlBQ0NKHDx8+aGh73kRkkY16oGXLloajR4/es2LFiiVjx45t8SbsSr1OSCQS1q0r\nxstLmXv35BGLyxfISkowf34+pqa5GBoWoqEhbvSOxr+jCe3aKWJmVvBMm/PzFZGXVyQ8XAElJVi0\nqBhLy2I0NcUAWFh0w8/vMr17//Nj8sShyctTrPaZ5OUpsmWLZpVn+eS6UN4J+swZP2bOnFixC+nh\ncYDp0ydUSZVSUVHm0aM4CgqKSE5OwdjYiJCQKzg5OaCurkpaWiYmJjVT7dHVbVaxYyejfjA2bsex\nY8ewsqp5dENeXh5HRwe2bPFASUkJb++zBAVdw8BAnwkTRtOzp3ml8aqqKrRrZ0RMTDxz5kyha9dO\nRETcp2tXM1xdnQkLu8X58wGUlUnYu/cw0dGPuXDhMunpGcyY4VrjnW95eXmuXbuJgoIiCxfOoFOn\njjx+nMzYsRNxcBhMSYlAQEAQJ0740KNHZxQVFXnwII7Jk2fStKkuIpEIU9NO+Pmdw9Kydk770zAw\n0Ccvr5S5cxdXSRdSV1fn+vVrmJm1e+2jG/Ly8ly/Hk737p1rVaeip6fL6dPnn9mFvLERGRlNp04m\nFQXdCgoK9f7/a9GiOSkpqWRmZmFgoF/ldVPTdnh5+WBp2es/xzvRq5c16emprFu3icePH9GmjXG9\n2trY0NXVlR87dmx7TU3NMZ999lmTmTNnXlq+fLlsJ74OkTkbdcyAAQMWz5s3b/Ovv/7au0WLFq9f\noukbwKVLecydq8H9+/IsWFDMrVvlC++NG3OwtMxp1A7Gv/lvStTZs0pYWspjbFx9hCMvT5GPPtJm\nyBAxJiYSjh9XYubMf5wCdXU1rl69Qc+ePZCXl0cQ+D/2zjw8pvOL4587k0z2fU+QlRASEhH7UltJ\n7Hvtu2jxa1VLSzdF6aJFKbXvW+0SSlA7sYdUIog1iQjZJ5OZzNzfH1Oj0yTEVtR8nqdP5S7vfe+d\n7Zz3nPM9bN7sTKdODqWmRwFYWqrw95eya5cJMhnMn5+Fq2sRubnGmJsXsnv3H8TF/cnAgT11BoEo\nisTFXSQ0tLreWKIo/tX1OwC5vIBatYIIC6tOtWqViIqKwcbGmXbt3szC2VeZc+dOERj4ZLKtUqmU\n1NR0LCzMaN68CY0a1S1VPnfLlt85cuQMGzZsJTX1DqdOnSM+PoFu3dojCAJ+ft4EBweSmZmJRiNS\nvXpV2rdvRW5uPnfu3H2iQtz4+ATS0tLJzs7hyJHT9O07GDMzcyQSCS4urpw7dwonJxuqVvVHKpVy\n8+Ytjh07RlzcWQoLC7h16wZqdQEVKz6dFPAD5s9fSXZ2IZ06dcfERL8wvrCwkOPHD2Nra8eVK0l4\neZWsYJWbm8f27bs4dOg4oiiWaGi+KsjlBaSn33ukBHJJlCvnzuLFq6lSpdIrX8+yd+9BLl9OJiSk\n+r86V6VSia+vF5s2RVOzZlCx70+ZzJgTJ86UGAG2tbWjXr2G7Ny5DXt7e9zcPP6tab8yCIJAcHCw\nTZMmTRrev3+/0dixY4+MHDny/sue138FgzH8nHB2dnZq0qTJ/FmzZr0dGBhYemtdAy+EBx2Pc3Nz\nyczMBazJyxOYP9+UDh2UDBggJyTk3mvjaACkppoV25aQIMPf31yXvvTPNCs3Nzk//JCjVyDu5vYw\n1cnCwhwnJwcUikKMjIzZu9eRkSOtdOlRkZE2xMbKi6VHXbhwEbjF4sX+SCQCqanehIVp1U0mTrxM\nkya+vP22foGhIAhkZmazYsVmBEFCSkoqe/bsY9SoIYSHN8PMzJTg4Kr88cdRzp69iJ2dI//73yeG\nHhmvKE+bcmtmZoqnZ7kSFcn+Tna2nA8//BSZTEZeXjYg4bPPRrNgwYq/pdypMTY2xs7Ohp0791K1\nqj9NmzZg795DrF+/la5dy5bW1Lt3V06dOoeVlSWnTl3Azs5Bb7+trR3JyZc5dCiWRo3q0KZNc06e\nPMvZs3+yYUM86el3+PHHiU/1PB6Qny/HxsaB3r1L7no+duz7dO7cmrt303FzKy4NHRcXT2zsWSwt\nzWnZsgn29nacOHGGefOWUqVKJRo2rPNKRAJycnLZuXMvubl5ODlpJYefFDc3FyIj+7FpUzSFhUrd\ndhMTGVWrVtZLr/u3mTdvKa6uzgQHB5GZmYUowrvvPt9mf4+joEDBjz/OxcPDjcJCJRcuJJRYvyEI\nIiqVSk+C/O/Uq9eQ3r170KhRA1q2DCckJOxFT/2Vo0KFCtIlS5Y0nTdv3p6mTZv+vG/fvu8NzQCf\nHYOz8Rxo2LBh3w8++OCTMWPGVC7tQ2zgxSGKImvXKhg82BRwYOlSKZMnyxk/3hxRhFq1ivQcjSet\ng3hx8370PGQykchIBXPnan3XyEgFly9L9M4vSXkqIiKD2Fh5iePK5QWo1WqsrCxJSTFn06biDs3F\ni+a68y5eTCImZj81a1anYcPaCILAvXu29OvniSBA69ZKTp+uQOvWFsBDByU7O4etW3cRFBRMjRqh\nbN26AX9/Lz74YAX5+XJWrtxEUZEGV1cPevQYiLW1TbF5GPhvoFAU4ujo8NjjNBo1AP37D+XEiWPY\n2tryxx/HUKvVjBgxSE9e9saN2+zefQDQOrXNmjVk/fqtbNwYRWFhoa5m6FHUrFmd99//jHHjPiu2\nr0MHbY3ElCmfERpanRUrNlKtWjCjRo1DJpNx+XIiX389A29vD3r37vJUUbj9+4/SqFHTYtvVajXL\nli1EqVRRsaJvqU3jbty4TatWTfVUjmrVCqZWrWDi4xP59ddleHqWp2XLJi81SpiensHdu/d4990B\nz+T8mJiY0KNHR71tCkUhp0/HMXfuEnx8vGjevNG/fq/GxsY0bFiH06fPk5p6h969u/yr19fOwQgH\nBztCQoIe6XgFBFTk3LnThIbWLnG/vb0jc+b8yvr1y7l16xK7d++gadOW1KpVvKngfxlBEIiMjKzQ\nvHnzyZ999llTT0/PodevX7/5suf1OmNIo3oGbG1tbU6cOLH066+//qB79+7ur3tO7evKtWtKWrc2\n0aUbRUWZ8t13GbRvX0SvXgpatryr52g8TlXp36As83B2LuD2bXMsLKByZTX29hrq1lUQHJxDaqo5\nKSnmdOtmX0x5ytpahZWV9r9/3tf69Vtp1641mZl2XL9uTkCAmsaNFVhZCQQFqWneXMnkyRZERGSz\nfv1SpFIpPXp0pEIFD0xNTTAxMaGgwIxVqyzp37+QNWu0dTG+vhICA/M4ceIMO3fu59atDPr0GYKv\nb0WWLfuVIUN64uzsyJo1W0lJyaRnzwE0atSMatWCiqWPGHg1iY09TFDQk68gOzras2DBCqpUqcS+\nfUfZt+8oGRn38fX11DM+z52Lp1KlKtja2uHt7YubmwdLly5h4MCeLFmymtq1Q3TH29hYk5FxH3Nz\nMxwc7ACoWtUfExMTfv/9D+rVq4WxcfG1NLm8gAMHjmFuboalpQX37+fRunXp0RArKxt27Ihh8OD3\nqFatui7v3t7ekRYtWpGQkMR3380kKekq9evXKnWckvDwcGPJkuVUq1YdC4uHKkUSiYRNm9YSEOBH\n5cp+peb6+/h48ttv20uU+3V2diQ0tAZSqYSlS9fh6VnuX+ux80/s7e2ws7Nh8+YdBAcHPtdoi5GR\nEeXLe+jqfzZtiubUqTicnByeWuL7SdFoNOzZc5A2bVq+tLoSiURCaGgNTpw4Q2Li5VLlnB0d7dm7\n91CpzgZoo3r29k6cOnWCgQO7c+lSAtu3b+X06RPIZDLWrl1JdnYmfn6VXtTtvDLY29tLO3bs6CcI\nQrtx48YVDRw48KTBZn46DGpUT0nt2rVbtWzZ8tvx48cHmpoajKWXyZ498bRvH/BYpSQou6rSi6as\n8xBFiIuzp6hIwN29AFdXOVFRjnz4oTXvv69g8mQzvTFiYjLw99fWpYgiJCZqIwb+/tncvCnjypUs\n8vM9OXtWpouYfPddPrNnm3LtmpTISAXLl5swdWo0rVt7F+vmLJPBlSvmaDQSYmMFvv/ekrw8AQsL\nkfXrs3BwuEhoaB3d6uLs2dNp2/Ytdu3aj1otoX//Ya9Nd+D/Onv3/o6ZmTk1atTEzKx0WVmAxMQ/\niY3dT9u2LZ7qWufOxbNu3Ta6dOnGW2+15M8/z7Nq1TL69euCk5M26qFQFLJ8+W+EhNSmWbNWgLbP\nx7x5M2jTpjkxMfsZPLi37r0liiILF65i8OBeeteaOXM+SqUSe3s7TE1NsLW1wcLCnMTEy1hbW1Gn\nTk1iY8+QnZ1LTo6cr7/+9qnu6e8sW7aINWvW8MMPXzxSzvWfqFQqfvllOf37D9UrytVoNGzcuAYz\nM+GRTszy5evp1CmiVLneB2OtWPEbvr5e1K8fRmZmFikpd8jOziEnJ5e6dUP/FcP86tXrxMQcYMiQ\n3i/UIBdFkSVL1hAaWuNfS6/Kycnl11+XM2RI73/NySmNU6fOcetWCu3bty5x/7JlGxk16uPHjhMX\nd4aDB2Po1UsbTVKpVJw8eY6UlDRcXV1JTr7N8OHvv/bCBWXlwoULii+//DI6JiZmYFZWVvbLns/r\nhsHZeEIEQZC2atVq2qhRo/q3bt368bkBBl4YGo2GZcsWYG1tilzerlg6UUm/Z6+Ks5Gaas5339nj\n46MhMVHCrl0y9u1Lw91drudgeHgU4OIi16VbSSTw3Xf2eHtrmDXLlD59CvXSrJYvN+Gnn7KpXr2A\nxEQLrlwx4vJlCYGBasaOtaBDB22+8+bNMr1nMGtWHp98YvFXnUsGrVrpOyzp6cZs22ZM48YqZDKt\nsVdQIJKVBRMmWCOKsHFjLi1b6v/Q/v77di5dSqRdu054ej5bMa2B50Nq6m0WLZpH/fohSCQC8fFJ\nFBUVAaBWa5BIpAiCBNC+PwQBEhMTmTjx48caideu3eDw4VNoNGo8PctRtWol5HIFW7bsZtSoMXrp\ncjk52axZs4hu3fRlkX//fT/ly1fUNWdMTb3N4sXzsLGxJC0tjZEjB2NsbMzChatIT7/LJ5/8j/T0\nDOztbTE2Nub8+YvExyfQo0dHCgsLycnJIz8/HwcHe73V/djYMxQWSmnb9vEpV2Xh3r0MBg7sh49P\nOTw9y2NiIsPTszyVK/thb29X6nna77FNvP/+2GL75sz5kcaNQ0stqM7Kymbnzr3F0otK4sCBo1y5\ncg07O1vKlXPDxsYaCwtz9uw5iImJjE6dnq5TfFpaOnJ5AT4+no899saNW+zYsYehQ/u+8AjAhg3b\ncXCwo0mT+i/0Og+YO3cJgwb1KrUe4t/k8OHj5OcX0LJlE27cuE2FCg8LvhcsWM2YMcVTB//J/v17\nWLt2Nc2bN6Bp0+JF5ampd1i1ajOjR48rVvP0X0WhUPDVV1/FxcTEjDlx4sTulz2f1wlDzcYT4OPj\n4923b99F06ZNa+zq6vryK+/eYOTyfH766VtatKhPxYo+iGLJdQolFVDPnZtdagH1v4EowqlT5qxb\np13hj4xUMHFiPm5uWkdj2TI3xo/XznnKFGNMTa0YPdryr7/lmJiI3L0LM2fmUVAAgwaJuLrClCna\n+ou4OBOGDLHVjb1pkwnW1oUIAiiVWtnaf7Jnj4wRIxRMnWpG9eoqnaOxapUrY8dqUzy+/z6frCwj\nxo3T/j1pkpygICXt2ysJDS2iSZPiEb63327D22+XrPtu4N8nNzeH77+fwiefjNQZlkFBxQtJ/8n5\n8xf55ZclhIQEERYWDKAr1n7Ad9/NpW7d+gwaNPIvudhETpw4RWGhgk8//UoXkVAoFCxfvpAhQ94j\nMzMHURT1DM+3327MnDlLqVOnARKJBDc3Dz79dCJJSQksWDCPSZN+pGvXdtjb29K0aQN+/HEed+6k\n4+TkQK9eXahWrTJ79mjrOUxMTHByMtFFT/5OYuJVRo4sbuA/LQ4OjmzZEsXmzeu4ejUJLy9PHBxs\n2bfvMPfuZeLv70vDhnWK1RRIJBKKigrJzs7CxsZWb9+wYaOYN28mBQVyQkICCA7Wlx62tbUhJycX\njUbz2FqFRo3q0qhR8dz7Pn26kpaWzowZ8xkwoMcjHSPQqh4lJ9/Az88bqVTKwoUrqVs3lH37DiGR\nSBAEQS/6JAgC1tZW+Ptr08Lu3MmgoECBuXnxerHnSefObTh+/DRz5y6hT59uj4z+PCsPiq5fBUcj\nJyeXjIz7HD9+GgsLMw4ePIWdnQ1Vq/phZmaKi0vZVNtUKhWdO4dTs2bxND1RFFm1ajO+vhUxNn5z\nBD1MTU355ptvgurXr7+yZcuWi3fv3v2pKIrqlz2v1wFDZKOMNGrUaFCXLl0+GTFihK9BkvPlM3Xq\nl/Tq1eGRecilFVDDyy0QLym60qGDkj59CgDo3Nmm2L6VK010fy9fnkVBgZToaBN27zZm3LgCrl8X\nmDHDnK5dC4mO1o9ahIcriY6WMWGCnJ9+MmPgQAVKpVAsIvL++wqsrTX07JmGIEBCgg3Nmzs+ci7r\n1+cgkQi89ZapQUXqNeHbb79m6NAna6wGWgPjwoUETpw4Q36+/C9D3oG6dUNJSrpKUtJtRo9+vPE+\nefLnCILIRx99TkrKLVavXsKwYfqpNTdvphAd/QejR3+iZ8AVFRWxZs1yfvvtNzp1ak1AgD/ffTeb\nAQPeoVatGnz++TRGj45kz56DdOv26G7yCxeu4cMPJzzxcygrO3ZsJSvrDq1ba1XaEhKS2LFjL1ZW\nlkgkAuXKudOyZRNAm0L2yy/LGDnyQxwdnYuNpdFo2L17B/fu3SY8XL+o/MqVa1y9ep0WLRrrts2a\ntQATExleXhVo1qxhmVJdCgoUrFu3hX79uj/yuMmTf6RJk3pcuXIdtVrN+fMXmT5dq8ylVqvRaDR6\nr5koiuTk5HLmzHkuXrxEfHwi3377xQt3Nh6Qny9n8+Zo1GpNMcf2gf3z4P9SqZS33mqgV3RfEqmp\ndzhw4BiFhYVoNBoUCgXdurV/rKP2byCKImPHfo1GoyYnJ4+ff/4VZ2cXzpw5SWbmPZo0aVHmIvop\nU76gV68O2NhYsW7dVjIyMmnevAGVKvmWOULyXyUlJUUzbty4P/bv39/fUDz+eAzOxmMQBMGsbdu2\n8z777LNOtWrVsnj8GQZeNHv37kKlyqZ27eBHHveiUqb+WQvxpM5Kac4GQNWq6mJ1GH838KtWLSIy\nUqGLLgwdqmDlShMWLsyjRw8rOnRQFkuReuBsTJ2aT0qKBGNjkUaNlGRlSYmKkhEVJePzz+V/GZNG\nDBig7cuRk2P8WGdjw4ZsWrSwNvTEeI34+usJFBTkEh7egqpV/Z8pneX27TtcuqTGwcGO+Pi9DB/+\nv0cer9Fo+OmnKfj7+1ChQlUCA6uTnHyZlSsXM2xYbz0jNSPjHitWbKZPnwFYW9vi5PTQCC8qKmLB\ngjn8+ecFPv98NN9/P4dy5dy4du0mHh5upKSkMWLE4BLldu/du0909B6uX79F3bqN6Nz50cZ1bm4O\nx44dorCwEJVKhaenV5klQWfO/I4OHZrrmrv9ndjYMyQkJNGtW3tMTU3+qt9YxuDB7+HuXq7E8X74\nYRJyeR6JiVeoVq0yFSqUIzy8GfPmLWXYsH6Iosjq1RsJDKxCYGAAV69eZ+PG7fTv36NMimCLFq0i\nLCyk1PfFoUPHdY5clSoVy/QM/o5Go2HLlh1IpVLatWv1xOe/aFQqFbt3HyAlJQ0XF0datmyiV2OW\nlHSVffsO4e7uStOmDTEzM30l5IUfkJmZxdq1m6lWrQoNGtRm6NAx9OjRi06duj7VeAqFgu++m0Sn\nTm9jZ2fL8uUbqV69JhcvXuD06TOMHTueatWKRz7eFLTfZz9d3rx588QDBw4sf9nzeZUxqFE9gipV\nqgR06dJl07x588K9vb0Ny7avAFeuXOLgwRjatGn+2GMf1/X6QW3EnTtmuLgUlMlpeJBa1LevLcuW\nmePqakJgYF6Zz01LM+fQISt8fTWcO/ewy7e9vYZly0w5fdqIr7+Ws3+/sd6+M2ceNCbMJzLSUqdA\ndf68ERERKmrVUqJQSBAEkdatVZw69XDsrVtlDBhQyM8/m+HoKNK7dx7VqmXi7Z2Pvb2MiAgliYlG\nTJpkQVqahCZNisjLM6aoSEqDBkXExMiQyWDatHzKldNw4IB2bpMmyalTR4ODw7+zQmng+bB79w5G\njx7GunVbOHv2PDt27CUwsDJmZk/2OooiHDjgxaBBlVi50plWrbyoWdPikcaXIAgcPnyA/Hw5zZq1\n+qtnhj1VqwYxa9YcKlXy1q14m5ubU716AMePH2X16pUEBtbAykpbE6RV36lNfPwFjIwEnJ0dKSpS\nM2xYX4KDA6lVK5itW3cSGBhAYWEh2dk5mJubcf36LT7+eCIffBBJo0Z12LFjFzVrhpUoWpCWlsqc\nOT+SmHgeX193HB2tcXGx5caNZDZv3kReXh4+Pn6PvF8XF1d27IgGtP1GTEwe/ox4eLjh7u7KRx99\nSVraXWrUqEZYWA3GjZtAtWrVsLd3LDZeVNQ2bt1K5aOPPuHWrWtUqVKRqKjdVKrkS16enKNHT+Dj\n40mNGtp0Kzs7W0JDa7B69SZq1qxebLx/UqmSL0lJVzh37k8qV9Z3Jg4fjiU/X46RkdFfal9PljJU\nVFTE8uXrsbGxJiKixStlpD9AKpVSsaIPISFBWFtbER0dw5kzF4iNPcPp03FcuZLMsGH9qFTJF2Nj\n41fmHgoLC/nqq+9xdHTgypXrtGnTEpnMmIyMLAYOjHzqcY2MjGjYsAlr164nLy+HzMxMXFzc6NNn\nEK1ahWNlZf1GqwkKgkDdunXtK1eu3GzYsGEVevfu/fuXX36pednzehUxRDZKoUmTJv26dev25fDh\nw71elS+UN5179+7yyy8zeO+9fmX6ki8tjepBPcLfayMmT5bTt2/qY52GklKLYmIyqFz50eIUogi7\ndzuQl2fMnTsS5s83oX79IgIC1ISGFtK7tw3p6drowKhRcipW1HDsmDG7dxszaJACa2uRS5ekdO2q\noGtX/TSrX3/NpXXrdN29WliILFyYg0wGa9eaIorg769GoxG4eVNgxIhMvaaAe/c60q+fDZaWIuPG\nybl1S6pLsfrmm3y8vVWIYhETJ9oyZkweFhZS1GqQSjVERNi8Mj+4BsrGTz9No1+/TrrXbdeuP7Cw\nMKd+/Sdr4JWSYkZYmLvee/H8eSXe3o9WG0tOvsyCBfOYPPk7ve0qlYq5c2cgiioqV/bT1YYAnD59\nntjYc7Ro0ZqaNR/Kdp4/f47btxOwsbHm/v371K9fm/x8OcnJN1i1agMVK/pQVKTGysqC7OwcpFIj\n7t27zzvvdKJCBQ+ys3PZtm03UqkJbm7uuLq64e5ejvv37/H779sYNKhHqUXTFy4kcOTIaezsHAgP\nb4eHh7bDd2FhIcbGxqSlpbBgwS/4+Hjg6upMfHwipqamNGxYm+Tk6/zxx1GcnR1xcnIgMzOL+/ez\nMDKS0qZNSw4ejOWtt1pRvXpIsWfUqVNbNm3azunTsezfv5vGjeuwfftuMjLu4efnjUqlYtiwfnrn\nHT58nIsXL2NqKkMUISKi+SNTftau3YKHhyv29nY4Otrj4GDHvHnLePfdAcTEHODq1es4ONhx924G\nYWEhJcrv/p3s7BwOHz6Bra019eo9mUTwq0JBgQKZzPiVVV9avHg15cq5c/PmbUJCgqhRoxqXLl3h\n5Mk/effdD555/LNnT3HvXgaxsUeRSqUMGhSJg0PxZpNvKnfv3mX06NH79uzZ0zslJSXlZc/nVcPg\nbPwDQRCMwsPDZ4wfP753vXr1Xq6GnQEdt2/fZOHCOQwf3veJVtRKa5x37pw9ERF2eoZSVFQm1avf\nL3WcxEQb7t83YcQIC5KTpbrzyuJspKWZs3WrDRMnaufy+edypk83Iy9PICYmg2PHzJkwQbtv6tR8\nHBxUREVp/65QQc3ChaZ89pkcNzcVN2/K9I5t1KiA8uW11//7vSYn25CWJqOgQOCjjyxIT5cwaZIc\na2s1HTum657FnTvmHDlihaurhrNnjYulca1fn4soFlKlijUg8kClyMtLZnA0XkNmz/6Rnj3b6F67\n+fNXMGRI7ycaQyuneoZPP+32RM7Gxo1ruHQpAVFUU69eExo3blbsGKVSyYEDe0lKukCXLhG6z7so\nihw8eJz4+Mv07j2A8uU9uXQpgcTEkzRsWIcFC1aQl5ePmZkpVatWplatGpiYmBAfn8jJk3GIolbN\n7caNW4wf/z5Hjpzk0qXrmJiY8OefFxk8uAc5Obmkp98DBJo3b1imZ5GfL2ffvsNkZGQhlUqQSiWo\n1WpMTEzo3Dlczzi9c+cu338/m2HD+lFYWEhMzAEqVfLFxERG48b1uH79lk7VaeHC1XTu3AsvLx+9\n6929m87Wrb9Ru3YD8vPz2LZtA2PGDH/sPFUq1V/F6EXMnbuU3r274OBgX+KxGo2G+PhECgoUXLx4\niWrVKvPnn5eoWzeUI0dOkJ+fT/v2rXF3dyU29gx//HGIfv164OJS3PjcsmUHBQUK/P39CAoKeGWN\n9VcZhaKQhQtX07r1WyWqfqWkpHHo0PES65Ti4uK5eTOTXr36P/M87t/PYPXqxXTr1oalS9fTqFEz\nwsL+HbWv1wG1Ws3UqVMvbtu2bcyxY8eiX/Z8XiUMalR/o1y5cm69e/deMX369KZOTgaP/VXh8uUE\n1q1byXvv9X/iHypBoMQajaKi4kZySdtA62gcPeqAIEgRBJgxI4f//c+a9HQJ3x2sMkkAACAASURB\nVHyTj7//4yW379wxZeJEc51hNnGiOePHF2BtrcHfPxt//2wCArRpE7VqaYvY3d1FYmNNkMk0TJ0q\nJysLvL2LcHGBDRtUaDTw009mjBtnwdSpZvTqlaYXsThw4KED88C5mTBBe90//7RHKlUjlcLhw+Z8\n840Zo0YpuHix5Ocrk5k8dsXawOuBUlmoczREUdRL7Skrv/0WRXh4a5ydFQwerI2CLVigwMvr0SkV\nXl4+mJpCvXqh/PLL8hKdDZlMRvPmrfDx8WXWrAX06dMJJycHBEHA1NSEihUrsGrVImrUCKVRo2bE\nxGwHwN/fD4lEoovQREfvpXnzBixduo5Jk77F2Vnb/+Lbbydy4sRZ/vjjKN7eWjlmW1trvLwqPPFz\nALCwMKdNm7L1H3FxcSIwMABv7wpIpVLu3cskLy+fpk21js3fDcmBA3uwYsV6lEo1Q4a8p5MNdnJy\nJicni2vXzpOdncuHH5YtTeaB0yaVSnnvvYHMmDGf//1vSImRG4lEoutRERYWTEzMAerXD/tLtrYP\nGzZEIZNpxwsIqMTRoydwdn6Y9nXzZgo7duxBJjPm8uVk3n13AO7urmWap4HiLF/+GyNHfkR09FbO\nnv2TTp30e2hER+9h4MCSRR+ys3MJDKzxXOZhb++IqaklV69eZ/Dgnvz++x8kJFykd++Bhro9tJ+t\n8ePHV6lRo8aSFi1azI2JiflCNKzoA2B4d/xFnTp13o6MjNyzZMkSg6PxihEVtZXhw/s+1xUxD48C\nPv9cjoWFiIWFyOefy/HwKCjx2Js3bbh0SUbXrlZ07WrFlSsyli7NYfz4AmrXLluth4lJcXW8sLBC\nnfKTIEBYWAa1amWQmmrO3r2OLFtmzi+/mFJYKGHkSAs++8yC/fvN6dzZhs6dbUhIMCYpyYj8fIFx\n4yw4eNCRB19rsbGOTJigdW7y8wUmTjRnxAgFALa2RSQnG/Pzz9ZcvGjKhAnmNG6s4ptvzNiyRcbQ\noQrdc5kyJZ+CAjWNGxvqMv4rCMLD376YmAPUrRv6ROfHxcXj7u6Fn19lunc35fx5JefPK+ne/fHF\nsjVqhHLlyjUALC0fLUXq41ORzz6bxMaNOzl7Nh6A8+eTCA5ugFoN0dFRmJmZI5OZc/jwCS5eTNJL\nBYuLu8js2UupU6cmP/wwVbe9T59BJCRcx93dhZ4929KzZ1vGjHn6vPYn5a23GrBw4Sq2bt1Jw4Z1\nuH8/k9TUO8WOEwQBd3cXNBoNt27d0NsnlRpz40YKzZo1fKroopGREf37d2fmzAXk5eU/9vjmzRvh\n4+OJpaUFO3fuJT8/n3HjJvHTT7+ycuVven0zrly5xu+/72PIkN7079+DSZM+MTgaz0BeXj62to5Y\nW9vQo0cf5PJCvf0ajYa8vLwSjf3MzCxOnIijQoWnc6RLYtCg4Zw7l8Tp0+d5++0mBAR4MnXqRBQK\nxXO7xutORESE06+//jquS5cum+zt7YurQ7yBGJwNoFmzZh9+/PHHSydMmFDFEOJ9tVCpVBQU5AMC\nCQk2JCTY8DzWCVxc5Hh5KRk/voDx4wvw8lLi4lKySlVqqrGe4T5hgjl5eVKsrTVUrFi2RqL+/tlM\nm5aPs7OGXr0KmTMnj9xc/WO09RNObNliS3S0Ke7uGiZNytdFRPLzBT77TOsYPPj3p58+dJDi42W6\nNKqSkErh11+zkEgkREZasnmzjOxsCRYWDx+otqmfKR06KNm4MZu6dVW0bWv5SujHG3h2du2KIiDA\nD9CqMh06dBw/vydrtnjixHnCw7XpGoIg4O2tjXqVxejVGkRlN46NjY0ZO/YLjh8/i0JRyN27d5FK\njRg37gs6d+4GwODB75KYeA17e/0eFcHB1WjZMpyIiG5Mm/ajbrubmwc5Odn07v18mvk9KeXLuzN0\naB8EQWDgwPcxMTFh5coNnD//J6Bt1Ldv3yEA7O1taNKkOQEB+v01Ro36iOrVw0hKuvrU83BwsGfo\n0D6sXbuZ7dt38agF2KtXr7Nly46/0tTMsLS0JCgogCpVKtKnTzfMzB5GtDIy7lO58qML5w2UndTU\nO/j6+un+1mhEbty4DcCGDdEsX76F4ODaLFiwhmXL1nP16nXdsUlJyTRu3BRb25LT5Z6WoUNHcudO\nDgcPar8/evVqz7RpE1GpVM/1Oq8z3t7exsuWLWvfs2fPPVWqVKn0sufzsnmj1agEQZCeOHFi3rRp\n0/731ltvvXyBbAN6iKLIunX7CAxszcmTdgwYYMvChRZPpABVGoIAPj4FeHioqVxZQfXqOaWOd/u2\nOevWmeqpWvXooaBVq/THzuFBzUh+vjFyuYTQUA0//2xGVJSMwEANHh4aLC1ViCKsWePKu+9acfCg\nMQ0bFiGRgL29hqgoE921y5XT0L9/Ia1aFTJsWAFWVpCbK9Knj5ING2Q0aKDhzh0zPD0LKFdOyqFD\nWuWoyZPlNGmiJD3diFGjHqpZHThgzIIFeSxdqu1GHhenTamIjFTQpYsVHh5mhhzr/xAbNqymXbuW\nAMhkxly9er1MKkV/5/TpeOrXb/z4A0th//49KJVFHDx4jDZtOpTpHC8vH7Zt28bQob1YsmQ5jRo1\n1etIX6NGKHv37qZWrYf34ufnxbp1vxEcHKpTsXrA4cMHsLKqhkplhaWl6l/vtQMQFRVD9+7tOXTo\nOEZGUjIy7uPi4szKlRsICPDnyJETVKtWmaSkawQEVCt2vrGxMWvWrKVKFT89Y/9JkMlkhIQEYWRk\nxPLl63B3d8XGpnip4tatvxMaWoN69Wrh7++Lk5MDjRvXw8zMjJiY/Zw4cZa4uD+Ji/uT1NQ0MjOz\nizUgNPDkbN8ew4ULCbi5eeDjo3U4atWqy7x587G1teTevXwiI0dRuXIA9eo1IjS0HitWrKRyZR9k\nMhkeHm5s3RqFRCLFw6P8c3UAAwNrcOjQIezsLHF0tKdiRU8WLVr6TN8N/zWMjY1p3bq1h1KpbDV6\n9OirgwcPTnrZc3pZvLHOho2NjW3Hjh03z507t6uvr69B1vYVIycnh5iYQoqKyjFihB1r15oyYEAh\np08bsXu3jIgIDY6OhY8f6BEIAlhZqbCyerSx4eEhx8HBVGe4T5okJyKiZEfjgXORm2uMpaWKqChH\n2rd35O5dE6RSCZ9/bq4z9I8cMSYiQo27ewGJiTb06WOr2xcXZ4Sbm0jFimoaNizCzk6kQQMV4eEq\nPv7Ygt27Zdjba2s/+vRRkpws8tZbGgYNsmbVKjOcnaW0b6+kRYtCuncvJDw8ncuXLdi40ZSEBKme\n4wQCXbsWEhKiIjhYzaBBCurUkWJnZ/hY/JfIyrrP9etJuv4IEomE06fjSuwQ/CguXkzC27siFhZP\n13ZIJpNx/342H300vsznWFvbsGuXdmXdyMiE4GB9RSNjY2PMzEw5cuQolSo9LKg+ceIsVatWx9b2\n4VqSKIrculWHbt1cmT/fCn9/KRUr/vvNPQVBQBAEqlatTEJCEqdOnePcuXjGjRuFmZkJiYmXuXbt\nNk2bttLVa/wdKytr6tSpz+zZ86hSxRdT06eXILWzs6V27RBiYvZz8uQ5vL0r6MkBV6rky9GjJ4mN\nPUNoaHUsLS2QSCTY2FhRrVoVgoMDqVGjGtWrVyUkJIjU1HSUSpVeHYeBJ+fgwZOMGfOZztEA7fsm\nNfU2RUUSunbtpedAaGttqjN//gLCwrR1GjVrBnHzZjLr1q1HJjOmXLnnl1IVGFiDJUuWEBoahLm5\nGUlJVwkIqP5GdRV/HH/J4zo4Ozs3HzFihKRv376HX/acXgZvZBpVtWrVqg0cOHDv0qVLWzo7Oxti\nva8Yubm5LFokpUcPawYNsiIyUoGlpcivv5rSurXyX5+PIEC/fqls2JDNhg3Z9OtXskTuA6ndsDA3\nwsLc2LzZmQ8/tCY/X0BZyrSNjB6dE+bpWYSNTRGbN8soX17US+eaO9eUxo1VTJhgTtu2RYwf/3Df\nDz+YsWOHTFffsWqVNmd6925jvZqMoUMVbNkiY9w4C86d06pLSSQSvLwenU9v4PXDysqGxMQrpKdr\nBQiys3MxN38yAzUzM4vMzBzs7J4+LaNWrXp07PjoRnr/JCsrEysrC65dS2HgwJKVl0JD62JiYs2F\nCwm6bcOH92PjxlXs27dLt+3aNSVDhpjqPiuRkTaPTD98UdSpU5PY2DNUr16V8eM/YPHimUyfPhFT\nUxMcHOyxsbHm3LkLFBSU3oTU3NyCwYMjOXLk1DPPRxAEunRpS+fObdi+fRcLFqzk8uXkv65jRocO\nrWnYsDbR0TF650VHx7B69UYUioeLP+HhzThzJo5ff11OdPSeZ57bm0qNGpX57rvJxeoh3nmnL23b\ndiqxTsPGxhYzM0s0Gm27B0EQCAmpTu3a7dm3L5Fvv51EYeGzLdQ9wNjYmCpVAklI0C7Yh4YGcfjw\ngecy9n+Ndu3aOU+fPv3LNm3aLBQE4Y0TZ3rjnI2GDRt2Gj58+Nbp06cHy2QG7/tV5MgRdanFzTIZ\nZVaAep48KOC2sVGRmFhy3UhqqjmRkTa6eY8caUWLFtoc1h07ZCiVol5R+pQpclxcFKSkmOPvn83k\nyfoF602bFuLoqGDnTjPCw5VPtPLaooWKTz7RPkNBgORkKR9+aMm4cQWsXGnC+PEFdOigZP58U/Ly\ntAM3bFhEmzZSIiIsDfnW/0GkUilffDGF7du1xp+1tSUZGSVLPZdGdPQ+xoz5tNTeE8+DsWPfZ9as\n75g163tmzfqWGTOmMnz4IA4dOkqdOo+W2ezatSexsed0f6vVakJCqhEbe1hnfL1KGBlJdbUS/2wS\nFxHRghEjBrJmzcpHjlG+vCd37mTo/j558izLlq1jzpzFLFmyhrVrt+g5Ao/DwsKcnj07M2BAD27e\nvM2CBSt1NSSVK1ckJUW/mD0l5Q5NmtTnxx/n6tV99O7dlaFD+5Cdnc39+5llvr6Bh9SsGUS3buHM\nnDmNWbO+58CBvbp9Go2G1NTbJZ4XHt6OuXOXk5CQxOHDsWzebE27djWYNGkALi6R/PTTN1y4cK7E\nc5+UFi1ac+rUeQB8fb04dGj/c3Nm/msEBgaaLV26dOA777wTbWNjY/v4M/47vFHORvPmzf/30Ucf\n/fLee+95G4ypV5nir41UChMnyqlRo4gWLUqvr3hRPOgc3ry5I82bO7JqlWuZCtU7dizAwkJEFKFS\nJSXt2mWzZUsWUVGZuLoqCQ19GAWZMcOU8HAl4eFKfvjBDEdHNceOaQu5o6NlyOUiX3zx0CGJjFSw\nf78xkybJWblSxpQpD/c1a/YwlNK6tZK5c02Jjzdi1ixTvvlGTkiIigYNtLUiFhYi8+cXUL++Fd7e\nj1cUMvD6Ym5ugbGx1lE4dy6estYtqtVqoqP3IJcXYmr64pTJVCoVCoWCDh1a0KdPB/r06US/fl2o\nW7cOy5evo169Ro8dw9LShtzcPECrurRgwSqysvLIzc0BtP1hFix4GN2bOzcLN7fSowcvggdGeatW\nTVm58rdSj/PwcKNZs7p8881XnDlzslSHydzckvv3M8nNzeP8+Yv06dOV4cP7079/D1q0aMSqVRtY\nunQtJ0+epaCgbKpBUqmUt95qwP3794mLu4harVXUeyB5C7Bs2Trkcjlubi5ERDTn6NGTun3nz18k\nISGJunVDmTNnySML0A2Ujo2NFUOH9qJ37/akpSXz++9aqec9e35nxYr5TJ8+mdWrl3HkyAGKiooA\nqFw5gLFjv+TGjfvI5eUYOdJJtwj23nsOtG07hNOnD7Fs2YJndsKPHz9CcLC2pkgretCNadMm6t4v\nBvRxcHBgyZIlLXr37r3bx8fnydQ5XmPeiKZ+giAIb7/99tQvv/xyeJ06dQwyZK8woiiyY0cWiYky\nPvtMm9owaZKcGjWUdO9uww8/5Oi6gGuPh5MntZKv3t5yHB1fTO51WTqHl9axvKSmgikp5oSFuemN\n16GDkpUrTXR/jx9fUKzB3urVWahUUtLSBDw91UgkEjZulLJmjTk//pjL3btGqNWwaJEJnTppnYwO\nHZRs3iwrdq369Qtp2dL4r7QpQ4O+N4H8/DxWrPiVbt3aMnPmfFq3boafnzeCICnxffqAZcvW07p1\nRypWrPxE19NoNPz+exRpaSmYmJjStWtPANauXU5a2m1UKhVdumi3PRg7KyuTNWuWIZfnUadOMFWq\nVGTRorV8+OGEMl0zNzeHJUvm0KdPFzZt2kF+vop3331fL+VEFEWuXVOSlZXJ6dPr6Nw5/Inu60nQ\naDQcPXqC/PwCUlPvcO3aTcqXd0cqlVJQUPBXH4QAwsOL9xx5gEql4tSpOGJjz9GzZz/8/Pz19isU\nCsaMGYmfnyfdu3cosWBcoSgkKekqR47EUrNmdUJDH9174c6du2zbtgsfnwrcuHEbQRBQq9WcOxdP\nkyb1uXHjFs7OjrzzzkNVr7lzlxAZ2Z/ExMucOHEGPz8f8vPlxMdfJC9Pzscfj3ihUbE3gSNHTpKQ\ncIWcnBzef38IAHfv3uPWrRQOHz7NuHFf6D3j5ORCAgP1v/9jY1Nxd5dz+XIye/ceY/ToT574dRkx\nYhj9+w/g2LHD9OzZVu/zlZaWTnT0fkaP/uQ53PF/E1EUmThx4sWtW7cOOnXq1NGXPZ8XzX/e2RAE\nwaht27aLpk+f3t3Pz8+QN/WKk5xcSJ06xrz/vhwXbQ8uZDI1tWvno1LpG0KiCEuXuuka102aJMfX\nV0mDBveeu8ORmGjDrFnWKJXalChRpMTO4aKo7Raek2NMXp4RRkYiQUH3i82nJGdj8eJcBgzQ+sKR\nkQpcXDR89ZW53jEbNmTTubON3raFC3PZsMEES0uRdetMdPucnTW8/76CihVVpKdL+fhjbUHv0KEK\n5s83RRRh//4CatY01Ge8Kdy8eZ3lyxdhbm6Om5sHTk5OHDy4H1/fj3VO8vTpqbi7/4EgiKjVIikp\nd6hQwZfw8OLKUXfvphMff44rV5JQKLQyzKIoIooaVCo1hYUFvPVWXTw9y5OdnUNU1F4SE5P44IOh\nuLm5cO3aDX75ZTkKhYKlS1frja1UKjl0aC9HjhxCpVLx1VfTynyfK1YswsbGhKCgKuzadZQhQ94r\n9djFi+dhaWmMkZEUH58KeHqWB+DWrVSSk69jYWFOjRrV9IwpjUbDsmW/UbmyL76+XkgkAlu27MTe\n3o6MjPtoNBosLc1RKlUolUoaNqyLtbUlNjbWbN4cTe/eXXXP6sKFBE6ePEu7dm+X2tH7AaIosmnT\nDvLyFEgkEoyMZCiVhYiimooVvalXr2aZns/evQe5fTuNXr06l9qMLT4+kfx8OWFhwXrbi4qKuH07\nVfec/nnO5s3RlC/vgZ2dDffuZaJWq3F2dqRGjWps377rr/qBkDLN00DZKCwsZMuWXaSl3aVLl556\n6mWiKLJ27cPmm1OnXqdXryLdb9KdO3dZty6KTz/96omUB6dP/wY/v/Jcu3aTvn27Ftu/Z88h/PyC\nqF7d8Fo/ivnz519btmzZhwcPHtz4sufyIvlPOxtOTk4Wb7311vo5c+a0dnQ0qGK8DjxYhREEbfqP\nTAbjx98rMc3hxAlHOnbUN7xXrsylYsW8EruGPy3/jFhERiqoWLGIbt3uFHMiRBF27nTg1ClT5s7V\nfrlPmZJPnz5peseWFgXZu9eRqChTXF01LFyolaN9MM7QoQrq11fSr591MSdl504ZLi4alEpBd/zX\nX8txdy+iZcu7AJw+7cDixeZs2SIjL0/AwkI0OBsGiI4+RbduIXrvqX37UrC0zMTIyBhTU1PKl/fU\nO+f48cMcPrwfe3trqlTxw9OzPKamZeswv3jxagYMeNjt+OzZCxQVmdK8easSj9doNNy+fbPYHB7H\nkSMHOHr0ANnZuUycWLqjolaruXw5EZlMxrFjR8jISKFNm+YsXbqenj0HcP9+Bjt3buedd9rj7OxI\ndnYOW7b8Tvv2Pbh37y6LFy+ke/c27NlzkF69uuDk5IAoihQVFSGVSnXGvEajYdq0Wbz77kBsbPQD\n7CqVijlzFjNq1JAnijCqVKqn7oGTmnqHnTv3kp6ewQcfDOOfNYyFhYWsXr2J/v17PNG4W7bsoLBQ\nSZMm9UtUo9q4MYqqVf3x9/cr4WwDT0Ny8nVu386hTZuOJe5/EMlLTr5CcnJMsUheauodYmKOMnLk\nmDJf8+TJY9y9e526dUt2cEVRZObMRXz66URDn6bHsG3btvQZM2ZMjomJmfmy5/Ki+M86G87Ozk7t\n2rXbPHPmzHrm5gZj6nXhn6swD4zwkn5/Y2Md6dRJ39lYsyYXH5+yORsPZGqh5NSRB5QUhXgQhi7p\n2ClTHIqlLW3cmMWDRaOQEG3kRRS19wDa4vMH2+Li7ImIsCM/X8DSUqR9eyVNmqj44AMLKlcuolcv\npS6aM3VqPhUrFqHRSPj8czMSEox0TpqpqciaNSa6CMyDupOxY7URjmnT5AwfblbqyqaBN4OrVxUE\nBZnovV/Pn1fi7a3vPGg0Gq5du8Lu3TuxtzenRYun09NfunQt/fo9VKOKjT2DqakDjRo1ffqbeI6k\np99hx45tNG7cFC8vrYxuUVERy5cvpKBAjq2tPdWrh1C1qraPRHLyZX75ZQa1a4fQrFnDR469YMFK\nBg/uVeK+y5eTiYnZT9++3TE3f3F1Mf8kLS2do0dP0rGj1gAVRZHNm3dw61YKvXp1xt7+yVpQff/9\nHD78cHipTpMoisyevYgGDWoTFBRg+P55DsTEHMTHpyohIWGPPTYu7gy7d0cxcGB3vdcoNvYMCoWE\ndu06l/m6338/icGDS3dG7927z/Llmxg79jPMzAx22KM4fvx43ldffTUrOjr605c9lxfBfzJ50tPT\ns3yPHj02TZ8+vaYhP/T1QhAEunc3Ra2OITi4Km5u8lIdAm9vOZMmGeulUZmaaovSUlLMH+lAlBZZ\neBFlCxYWIklJxjojf9IkGf36pf4jBcxYJ6lrYvKwsC4vT2DzZhlVq6oRRfjf//IJCFCxYoUaExMN\nSUlGdO5so7v/BQsE1q83wcJCJDxcX29XEODtty/i7m5OhQreBAcbHA0DUKGCEZ9/nsjEido6gPnz\nCzAxuY9K5aJbkdy3bxfHjh2iUiVvWrasi53d8xNSCQsLZvbsJS/U2Th8eD979uxiwIChZGVl4ejo\niIuLW4nvf2dnF/r1G6y3zcjIiAEDhqFUaus8zp8/w7p1K/jqq2l4e/vh6ur2WEcDQCot/fPm5+eN\nk5MDM2fOZ/ToyGKRhheFq6sz8fEJFBUVER7eHIlEQm5uHiNHDn78ySXQo0dHVq/eSM+eJRutgiAw\nfHh/zp2LZ+nStYiiiL29HR06tH6W23hjEUWRK1du0qXLgDIdHxQUjLW1DStWrKdPn4evUVhYMEuX\nriMr636JHcd//z2KS5cuIopqRFFEEATOno1DqexU6nvVwcGed95px/btm+jatWQn24CW2rVrW37/\n/fejw8PDrXfs2DFS/I9FAv5zlnjlypX933nnnfVTpkwJNBhSryeCIJCZeQ5BqMqBA87s2GGMSiXQ\nqpUlgYF5uLhonQhHRzm+vmasWKE1ziUSNWlpAh06uAGPdiD+LlMLEBlpQ2ysvMRohZubnLlzs/Uc\nk9LUa9zc5EREmOHqqtGlM/34Yx5Dh1rprjVhgjlVqjjq5H3/vq127Qz8/bOZNs3sb85J/l9RiWwa\nNsxgwwYX3n/fkkWLcvn0Uwu9MRYtymXgQG1vkuXLTZg27aFM8PXrN9m58wAffjjeUKRpQEdU1Gaa\nN7enTRtrsrKyiYvbwf79VmRk3EOj0Uqb1q9fk+HD+z6X65X0G2ptXbxr9fNEm84kMHjwADp1ikCt\nVhMVtZsvvviKsLB6ZRrj4MF9/PzzLIyMJGRn5zJr1mzdvrL+1jwuJ97Gxpp33unInj0Had269ILx\n50358h40b96IzZuj0WhEWrV6esevXDk3VKoicnJysbYuWY9FKpUSEhJESEgQ2dk5zJ+/gl9/Xcag\nQb2eqG7AgPb30tLyyRpsenn5YGVlR2rqHdzcXHTb/f19OXz4ABERxeuzTp8+RmRkX71oSN++j4+C\n2NnZcPXqlSea35tKQECAyezZs4eOGjXKQhCEQaIovnp63U/Jf8riCAoKqtmrV6/lEyZMqGJQ1nl9\nuXQpAVvbnsTGWpGSIkWpFAgK0qYGXb1qydWrZtStq01FatDgnl5Drr+nOz3KgXgSBAEiIjKIjdWO\n86iIiSBAq1b38PW1ISxMRX6+gEnZUtn1xujZM41q1ew5ccKE7GwJ332nTauYMUPK+PFaB6OkdQ+Z\nTFu4LgjQpUse/v7ZXL16jcOHT2JiYsFHH31miGYY0KFWq7l48TyNG/cB5Li7GxMQ0E7vmHPn4snP\nf341UP+UxCwsLCQv78VKz9ap04A6dRqg0WiYP/9nzMysiIwcTlBQ2YtXZTIZ9eqF4uLixKlTF3Bw\ncNLtc3Fx58CBYzRsWPuZVd1iYg7QqVPEM43xpEilEqytrejVq8tzGa+goAArK8ti29et24KFhTmB\ngVUoX96De/fus2LFb0RG9kMuL2DGjPkMG9YXCwtDys2TIJMZMXfuDHr06IutbdnS3nr3HsjXX4/n\nvff6IZPJWLRoLb6+/rRuXVyZ7c6dNJydHYq9t0VRJDs7B1vbhx3us7KyuX79Fnl5+eTmyklMvMrI\nkaOf7QbfILy9vY3nzZvXd/jw4RaCIPQURbHoZc/peSD98ssvX/Ycngu1atVq1Ldv3+Vjx471Nzga\nrzfXrim4csWG5GQply9LMTICV1d47z1L1q83oXp1DeXKabCwUCEIYGWlwtJSRWKiNfXrq3Fw0HD5\nsnZ1bMiQPKysVMWuYWmpwt9fyq5dJshk2mhFSIg2AhAXZ8+dO2a4uBTonIoH17GyUj021UoQwN6+\nkIQEM957zxpHRw0dO6o4dMgYmUxbuF21aiG+vui2TZokJyIiXe96Go3A7mNyPgAAIABJREFUkSNm\n/PSTVv5WpRLYs0dG9+6FnDplzMWLUsaMUeiNYWtbRM2amTg6FiKRpLFgwWpsbFzo1q0PtWvXM8jb\nGtBj7doV1K8fjI1N6ZEFV1dnYmIOEBwc+MzX27fvEK6uLpQv76HbNn/+KoYPf/+F9u94gCAIhIbW\nJji4Jv7+VZ4owleuXAXKlfPEzMyavn0HYWLyUF725MljiKKKixcvlVr4XFhYyK5df9CwYZ1HXufC\nhQTq1CmbqtTzIiXlDtbWVk+8Ql4aCQlJ+Pl56/XkuHbtBtnZuYSFhXDxYhIHDhzl3r1MmjVrhKOj\nPRYW5lSvXpW5c5cSFBTwr6WR/ReoWrUSnp7ubNiwgZMnT1CzZthjv+slEgnVqwczd+4CEhOTadCg\nCU2btiwxsjR9+jf07t0JqVTbhHLdum1s2rSDTZuiuXEjHRApV06bUbBs2QYqVgzC1bUCfn5ViIjo\ngIVFccfTQOlYWVkJLVu2rHr58uWQHj16bPzyyy9f+6Yl/4nIRu3atVsMHjz412HDhnm97LkYeHYy\nMqw5fdoIOzuRzZtldOigZPx4/ZSjgAAVTk7a1VBRhJUrXbl2TapLXRo5soCgoMJS051KilYALFvm\nxvjx2lW1yZNN6Ns3tUTnQhQhPd2cGzfMkUhEXdF3SePn5Rlz8aKMmTPzAZBK1Xh5ZePllU2VKvoF\n4v+cY5MmRcyerb+9TRsVK1aYcu2aFC8vJVu2KNFoBDw95Tg5ybl58zb79x9DpdIwbtyXhh9tAyWy\nbdtGFIocKlTweOyxzysalpR0laFD9dOxZDIZSqWylDNeLbQOR4Vi27Oz7+PgUK7U8+LjE9m37xDv\nvjvwsddQKBSo1ep/NZ3IxsaanJxcXF2dn2mc69dvsmzZeoyNjYr1+ihf3oNNm3bQqlXTUutbzM3N\n6N+/O7t379cVrBsoG1ZWlvTs2YEbN27zww/f8OGHnzz2c2tv78iECV8/dmwzMxnr12+nqKiI+/ez\nUKtFFAoFX345hu3bY9i+PQY7O2sqVfLFzMycsLC6z+u23lgcHBxYvHhxG2Nj462CIHQQRbHgZc/p\nWXjt8ylq167dbNCgQfMNjsari0qlIiYmh5iYHFSq4lGG4oj4+WlrHvLzBUqyQ/5umMfGOnLsmLHu\n+Px8gVmzzHB3Fx8ZhRAEcHfXplkJgjai8cCpyc8XGD/enLi44oVy2v4UDuzYYUPHjja0b2/L0qVu\nJaY1nT5tTtOmjnz1lSWOjkUEBBTQrt1dBEF7/dq1M6hdu+S6ElEEtVrbKfzvXcPNzNTExqYSG5tK\n48b3qFnzHrVqZeDsLGfbtl2cO3eZYcM+YPToTwyOhoFiJCdfZsqUz7GyktKxY8lys//kWbsMP6Ck\n92NERFNWrPiVo0cPPpdrvAwkEglXr16nUSN9I0uj0bB69UauX7/JiBGDiknelkT79q1ZsmTNi5pq\niXh7V2Dr1p1kZ+c+0zienuVxc3OhX7/uxQxdqVRK9+7tWb360e0EHBzsyczMem7vuTeNChU8ePvt\n+kyf/s1zeYaxsUewsrLE0dEehaKIoUNH4uTkwOTJ4wBtl3s/P29u3rzPvHkrkcmKN5Q08HRYW1uz\nYMGClt27d98sCMJr/WBfa2cjLCysycCBAxcMHTr0yQTYDfxrqFQqZs9W0qGDFR06WDF7tvKxDkfj\nxib4+DxMU9yxQ6ZncE+aJCc0NOOFzdnSUqRr10I6dFBS0sJQWpo5KpVUV+Cdny8wYYI5p0876B33\n9yL05GQpPXvaUFgoJTHRpkTH5J+4uckRRQ1eXmo6dFDSoYMSLy81ISH39Jwk0Bo1a9dupUKFSvTp\nM8jgZBgokW3bNvLHHzv4P3vnGRDVtbXh5wwMM/TeBQHFRhcEERV7b7FgxxKiaIzJzU25iflyvYnp\nzWgSC0bF2EtibLHG3ogaEQuKAlZA6b3OfD8mjiJtgKGYzPMn8ZS992HaXnuv9b7h4ZPw9nZT+T5z\nc1MePUqrd/82NlYcO3a6wrHp08dz4sRhFi78guzsrCrubp6kpaVy4sSpChP13Nw8vvlmGenpGQwa\n1Efl9qytLfHz82bHjr3qHmqV2NhYYW1thZ6eeuYzaWkZlR63s7PBwcGekyfPVnv/wIG9+e67HyvU\n92hQDUfHFvTrF8Snn/6PoqKiOrdTWFjI8uVLGD16MP36BTNt2mh27drCw4ep/PHHRTZv3om9fWtK\nSmSMGjWeN9/8P8LCZqvxSTQYGBgQERHRLyQk5BdBEGpZAdp8eG5rNjp16tR92rRpq2bNmuXc1GPR\nUDWHD+cxY4aBsubgxAkxgYF5uLhU/ZnR1tYmO7sAfX24dEmR6delSwkDBpQwZ04+Wlpb0NXVUa4S\n2tvnk5GhR+vWMi5d0kZHBz77LI8+fR6pLGUrl8OVK3oEBJTRurWMDRskxMZq0a1bMa6u5QvC4+MN\niY7W4fhxhUoWKAqzQ0KKsLd/kraVkyMmIsKw3DX5+Vq8+64hNjYSPDxya9x5cXQsIDZWH0NDsLKS\nY2Agw80tj6QkPXJyxBgYlHD27AV27/6d4cPH4OPjp9oDa/jHcflyNHFxMYwcOajWtTuWlubs2rUf\nb2/3mi+uhtatnbl5M5EHD5JxdGzxzDknbt68wZUr0Zw4cZQzZ05w9uxpZLKyWhn6yWQyfvrpR44e\nPUBU1GnOn49CS0sLW9ua08Xqwu+/72PQoO78+WcM3t7uSCQ63L59l40bfyE8fApxcQm0adOqVsZm\nNjZW5OcX8OuvvwGKSXpDc+fOPSQSSb1kjQsKCklMvEuvXl2rvKZlSwfOnr1AVlZ2udqdpxEEASMj\nQ6Kjr9C6teYnvi4YGxvRpo0Lixd/R4cOHnWqm9DW1qZz5yC+/34pbdu6oK+vj5tbW65fv4VEYsTl\ny1do164948ZNBhSvm0aARP1IJBL69+/f+tatWx1DQkK2Po81HM+lqZ+fn1/XqVOnrp4zZ06rph6L\nhuo5eDCbESMMyxmGbd+eQ58+1UtdnjiRy6hRegQHK3ZBjh4V8+WXeTg5FZCbe5iYmKuMGzfirx8k\nM6RSgexsgdJSEVKpDB0dGW5u6SqP87Fx36RJhaxdK63WwO/6dWPGjzcjPLyQDz544vERFJSPq+uT\nVdnKnMeXLZMq3bsfm+1VR2Uu6Vu2ZDFmjKLNDz64RadOd+nWrafKz6rhn8nXX3/M9Okhtb6vsLCI\nuLh4zp49R1jYZLWMZeHCZYwfPxJr6yeKTpcuXSE5+RH9+vVQHpPL5Zw/H83Fi7G0bOnCmDETqm1X\nJpPx+ecfMGhQT2UtSllZGVu27MLDww9//y5qdzPeuPEnTp06homJCba2lmRlZf+VPz8KQRDIzMzi\nt98OMX78yDq1/8cffxIdfbVKM0B1IZfL+fbb5cyd+1KdJ4zp6RkcPnySUaOG1HjtH3/8ydmzF3jx\nxYkV6juSklJ4//3PGD/+BXr1qtm/REPVlJSUsGrVZnr16o+fX/XiBFVRWFjIunWrSEt7SGjoaB4+\nTOXmzSRGjqydu7yG+pGVlUVYWNiurVu3jpLL5c9HodtfPHcF4j4+Pn5TpkxZpQk0ng+Cg3VZsCC/\nnPFecHDNqjOBgbq8+26Bslj7iy/yiIiQcOGCAR99NIRJkzzYunU7YrE27du/SO/epuUm5Lt3P9nG\nLy0tVeauCoJQ7WQjPb3mH9k2bbJ44w1dvvxSl3nzCnBxKaWkREbr1uUDh6eLxB89khISYkJubv3V\noIqKRMpnff/9VsTEONS7TQ1/b0pKSqo1lKuMgoJCli2LxMbGCldXFyZNqn2gUhWvvBLG99+vZO7c\nlwBF4XhMzLUK0qsK9Shv/Py82bfvKFeuxCiduyvj8OH9BAX5lit6V9QKDOPkySgWLvwEPT199PUN\nCQ0NU8sqbE5ONpaW5hgaGlQIKJKSUjh06BipqemsXLkegO7dA2u1Wt+pkw/6+vrs2LGXYcNUq7Gp\nC4IgMHhwXw4fPqmSQWFlmJmZ8uiRaimuHTt6cvz42XKKVY+xtbWmZ88g3N3b12kcGp4gFouZMWMi\nv/12mMuXL9XpfS+VSnnxxVmkpCSzY8cGxowZysGDJxpoxBqqwtjYmIiIiCEymWyzIAij5HL5c7PD\n8VwFG25ubq7jxo1b89prr1WuLaih2SEWi3n5ZXB3V+QzBwfrqrSyqKWlxZw5Upyd7yCVGhMebkhC\ngkKdZd48Pdq3NyU0NISMjEwOHFjLggUv8t57CtnGjz7Kx9NTsauRkvKIH39ch4uLIg3jypXr/Pvf\ns8rpgsMT475//9uI8PBCpapVVQZ+PXtm4+5eTEmJgIFBKW3aZFWaEvW4CN3WNp/339dRGvU9bbZX\nHX5+qRVc0r/++rmuE9PQBOza9Qs9e6q+qrlt2y6ys3N46aXJDeJ5oKWlhZWVBQUFhcTEXOPKlVim\nTq1+lbRfv+5ERGyoNti4fTuBvn0rKuEIgkDXrgF07RoAwPXrt3jjjVdo1aoVcrkMPT0DBg8egbV1\n+XSl5OQkdu78maKiQoyMjBkyZARmZhblrklPTyU1NZ2Skid1ZocOHSc+/ja2tlaMGjVUuXIvl8vZ\nv/8IBw8eZdiwASqnR3Xo0IYTJ6qvc1AHrq4u7N59AJFIIDCwE1KpainiyckP2bp1J3p6urRoYafS\nPTEx1wgI6Fil6lZIyHAWLlzOnDkvqjwODVUzcGBP4uNvs2zZYmbNerVObVhb25CdXUBxcTE2NpYk\nJNzE2VkzHWtMTExMWLZs2fCSkpLVgiCEPi9O489NGpWjo6P16NGj93711VfeGq+Afw6LF3+Op2cY\ngweX37lYuzaRbt2KlT9UqamZXL1q8df/7yI3NxsAkUhg3LgXlHr62dk5bN68o9KUBLlcUdQtCCgL\nuB8b+MnlCtUrgOJiOePHK/Kaq3Ipl8sV6VYAbdtmKdu4ccOYwkItLC0LlUFMUpIeYjEkJCgmdZ06\nlW9PLodz5xR9+/mlsmqVnPffV3zBr1hRyNixUo1/hoZqWbjwU6ZOVd2wbc2azYSGqm8nozKuX79J\namo6ly9fY+bMKSrdExsbx5kzFwERnp4+9OjRp9wqbUpKMr/9tpURI6rfAdi+/Tc6d/ZVSr1mZ+dw\n6NAJMjKysbFpwYgRo7ly5RIHD+5l+vQQJBIJWVnZLFmyBh0dHdzdPfH1DSA19SG//LKF/v2DOXv2\nPOHhUwG4eTOB48fPMG3a+Er7Lysr49df95Kbm8fEiaNUkrldv34bgwf3rdYTRR3I5XISE+9w8OBx\nXnppUo3Xf/vtcgwM9BkypF+5tDhV+vnxx/XVpodlZeWwadMvtG3bmuBg1ZzeNVTPjh37CAzsjatr\nuzrdn56eSkTE9yQnJ/Peex+UM7fU0Hjcvn27dPbs2ct27949p6nHogrPRYG4mZmZ4dChQ3cvWrTI\nT1N89M9BJpMRFXWcfv1csLCQcPy4wrzuo4/yyctbi5fXky12PT0pLVvKaNlSRvv2rfHycsPLyw1P\nT7dykxGJREJy8iO0tbUqFEI+bdz3tIGfXA6RkbaEhxuyebMUHx8ZSUkCaWkitLVFtGolYG5epAwQ\n5HJYv96G0FAT1qzRUxaDA5w5Y8iECSZERBjStq0W8fG6zJ9vgra2mJkzDdm0SYq5uRQvryfF44Kg\nKIK3t8/n6NHTeHsb8PrrFsyeXUbXrhJNoKGhRv744wxeXjVPLrKystm6dQd6enp06NCmQcdkbm7K\n77+fQFtbW+XCcwsLc7y93fD27kBqajLbtm3j4sXztG/vjo6OhNjYGPLzs5U7mVXx6FEagiBgaalQ\nkJNIJLRv74qPjzvGxnps2bIFkaiE0aMHKxcqpFIJ1tYW9O7dFRMTPa5evURhYTalpaV069aZmzcT\n8PJSKHyZmZkilUrZt+93PD0rqn6JRCLat2+DnZ0NERFradXKqcYdJBsbayIi1ip3ZxoKQRAwNTXh\n4sUYvLzcqk25SUi4jUikxZgxw2ptCCgIAufPX8LX17PKa6RSCb6+XmRkZPLzz7vR19fDysqiyus1\n1Ex8/F3kchFOTnXLRNfV1aNr1x74+wdibq55LZoKExMTkZeXl+fkyZMlkydPPtzU46mJZp9GJQiC\ndPz48b8sXry4c2OaHGloepKTH2BpaYEggIFBJHv2TEYkEuHiksmRI3V3uu3SxY9jx07j7Kyawk1U\nlIVS5hbgk090Wb06F5kM5s/XpU8fC5YuFSt3OK5fN+btt/WV17/9tj6+vsYYGZUopXABwsONGTGi\nmNdfL2TSJMNnTAst8PdPVe62gGKX5c6d+4wYoZ4iXQ3/HESimgPSq1dvcOLEWSZMGKk2J+nqEASB\nu3cf4OFRt7x8D4/2eHi0Jycnl+XLvwW0kUi0mDjxhRrvNTExJj+/csNPKysLJk8eVek5V1cXAHR1\npcpdEQ+PDkrVqKdp396V3bv3k5OTi6Fh5UpAlpbmzJ0bxpo1m2nXzpXAwKrV5CwtzenUyZuoqD8x\nNjbE0tIcMzPTap+zPijqfKr/zbWwMCcq6mKd2r91KxFn54oGiZXh4+OBt7c7R4+e4ocfTtG2bSuu\nX79F377BytdEg2qYmBjz6NGjerdjZmZe80UaGhR3d3fp/PnzX+3Tp0/awYMHv23q8VRHs94mEARB\n9MILL2xYunRpb6lUk6f+TyMh4RYODrYA5OXl0b27EV27GnDx4gXc3Oq+6pqdnVNhMiWXyyv4f8jl\nEBtbvrbDwEDO5MlFjBljyNixhkycqPC+CA83JilJr1pd+NLS0irPPUtZmZxfftnH7t0W+Pvb4u9v\ny+7dFojFNRfXa9DwLEVFVXvbyOVyTp6M4siRk8yYMblRAo3HuLq61LkY+TGGhgZMnz6O8eOHqBRo\ngELm1d7etk79yeVyMjOf1FsZGxuSn19Y7vOdnPyQtWu34OrqUmWg8RgtLS2mTRtPSUkJa9duqdKI\nbevWndy8mciqVRvZtGkXBw6cZsWKDSxbtrZOz1EdUVF/4uZWcxBoYKDPw4d1m7geO3aanj2DVL5e\nEAR69Ahi6tRxnDlznvDwKdy9e5/Fi1dw/35SncbwTyQwsCOGhtp88cWHXLt2pamHo6GeBAYGGr3x\nxhvvBQcHVy/V18Q062Bj0KBBixcvXjzMyKhhc1Q1NE8ePXqIRKIwp5PJnkziS0qK6yVfee9eEhYW\nZn+1K2P58p+IjNzEqlUb+P13hYvx41SoPn0sCA01YsGCfPT15QwfXlzOqfy99/T4v/9TrJBGR19j\n3bqdnDsXyYIFWUoTwsfF4LGxh/juu0zl8YiIQoYPL+Prr6XK9h+bFvbsqYuenptyJyQvTyA83Bhj\n4w51fm4N/0yuX7+KRFJ+hbq0tJRt23axevVGVq/eiJGRAbNnT2v0sfXt252DB4+ppa1n5VOro0eP\nIA4dqlu/eXn5jBhRvsZk2LD+xMRcU/57+/Y9jB07guHDB6rcbvfugfTs2ZVvv40gIyOz3Lni4mJy\nc/OYMWMynp7ufP31d8ycOZc33vg/goP78PvvJ+v0LFUhFmuxevVGIiJ+4o8//kQul5OenkFMzDWu\nXYtj/fptbN78K8uWRdK/f91kt0UikUq1Ks/y22+HmDVrKiKRiF69uvHyy9M5deoP1q/fRnZ2/RzQ\na0Iul5OVld2gfTQGnTt3JCxsHNu3b9I4tf8NGDBggMWUKVM+6dSpU920jRuBZptG1adPn39/8cUX\nU+3t7Zt1QKSh4Rgy5AU+/PA9XnvNGTMzI5KS7mNra09OTjZSad1N4zt39mXZskjy8ws5e/Y8ISHD\nsbW1BiAiYi29enUrlwqVlyfwySe6bNumWM3cvr28O7cgwLx5+WhrB/LKK70QBAGZTEZAQCYJCbco\nKDjNsmVp3L//gM8+CyE4WCGP7eSkmBz5+RUDcjp0UPxQ9ughRVtbG2trr0pGr6nP0KA6KSnJbNmy\nnpdffjI5Pnr0FNeu3eCFFwbXqqC3ITA3N2uSyZu+vh5FRXWTqTcw0Mfb24Pffz9Jr16KlfmiomJi\nY2+yevVGCgoKCAzsVKcFEXt7W+bMmc6qVRuRSHQQBAFtbS1u3kygUycfsrKyMTExIj09VamK1blz\nVxYtOk1mZlYFlb264uPjyf/93784cuQUOjo6rF69EXNzU2xtrUlMvMuoUUMoKChUW3/PUpnAxmN0\ndaWUlT2ZIItEIsaMGUZ6egZ79/5OSUlJBQnl+nDvXhK//LIbS0tzcnPzyc7OYdCg3rRr56q2PpoC\nQRDo2TOQ/ft3M2DA0KYejoZ6Mn36dMfbt2+vcHFx6R8fH3+/qcfzLM0y2OjSpcuId955520fHx/1\nay5qeG7Q1tame/cexMbexNOzPWfPnmLEiDGkpaXWK1dZJBIxa9Y0zpw5z9Sp45VO5EClmu8AeXkC\nxsYltG2bVUGKtrRUxrffGpCbK+DnV4yzswSRSERgoCmBgX4UF3uio/MkQHF+RmLf2VkCSJTHi4uL\n2bs3l4ICLd54I58vv1T09dFH+ZSU3AL61PnZNfxzOHLkANHRfzBz5kSliMCKFesICPBRqiY1B5pK\n4EBbWxu5XF6n/l9/fSazZ/+HHj0CEYlEXLsWR8+e3WqU71UFhS/Ck7qskpISMjKySEl5yOrVGxk6\ntD+rV0fw+uvvKK+ZOXMuX3zxAS+/PFVtf08nJ0fc3dNJTLzD1KnjlO126uQDKIrqq+PZerOnh/Xo\nURpGRoZV3rd+vc1TMuG6TJiQrLzf2tqSgwePMmbMMGXxPiiK8kNChhMTc40lS1bh6tqK4ODAeu2C\nJyWl8OuvvzFnzovk5eWTkZGFg4MdixevwNGxBXp6z3daa7t2rqxatUUTbPxN+O9//+uWlJS0WRCE\nvnK5vPKitCai2e0aeHl5eY4fP/6roUOHavTUNKCvb0BGRhaGhgZcvx4LgL19C5KSUurddufOvuUC\nDXgy8WnbNovPPssrlwplZ/eANWu24OS0m23bsti2LYfcXBkzZxqTklL1R+npQKMmSktL+eGHEkJC\nDJkyxRBTU5g5s4D//KeAjz/WxcBAI//4T0Eul5OQUERCQhG1lSg/deoYiYnXmTIlpNxkS0dHjIeH\nJhUPwMzMpEK6kqo4OrbA19eLyMjNgELFy9i4YVb5xWIxVlYWeHh04JVXwjh69BT37t0lNvaq8hqJ\nRMLo0RPZvHmnWvv28/OmVStnli5dzcmTUSrfJ5dTod7s6bfwrl37GTSod6X3Prur/Pbb+spdDgBf\nXy+CggJYvXoTP/20hfz8gnL3e3i0Z9asabi6OrNq1Ub27DlY7edHLpdz/frNSq/5+efdzJqlCOAM\nDPRxcFB4iNjYWLF1606OHj3F4cMnSUy8o/LfprmhrS1QVFTU1MPQoAZEIhHffPNNl1GjRq0XBKFZ\nze+b1c6GoaGhWXh4eOScOXM08hIaiIu7xpEjBwgPn0x2dg5WVgr1l8GDR/Dhh/N48cXxmJubqbVP\nAwN9MjIyMTU1YcKEZHx9FT9ycvk5Nm78gzlz/o2env5fx+RkZBQilyu8P1asKFSmRtWV48fzee+9\nJ8pU8+bpsWpVDteva9O3b8lzv5KmQTXkcjmbNhUSFqZ4P6nip5KXl8uyZYsRi7WwtDSr0WuiudBU\nXk92djbcv59c513SN9+czdy587CzsyEvr/Cv12wnY8c23CqxSCRi2rTxyOVyliz5iXff/UB5rl27\nDty6dZ2TJ6MICvJXW5/u7u1wd2/HqlUb8PX1UslgLylJr4Ly3pYtsdy4cQgjI0MEQahxZ6Q6HB3t\nCQubSFZWDhs2/IyBgQEjRgwo12bLlg7MmDGZhITbREZuUu5iGRkZYm5uSlxcAgEBPkRF/UnLlg4c\nP34WsVgbfX09hg7tx6FDJ/D396lU+nfMmGGUlZURH3+brVt3ERd3iyFD+qls0thciIm5RnZ2QZN9\nBjWoH319fb799tuhhYWF3wKvNPV4HtNsfDb+Up76+bvvvuv69Naohn8mc+fOpKwsn4kTX0AQBFJS\nUsnPL6V9e3fEYjHu7t5s2bIFHx/V9PlVxd7elr17D+Pu3g5BAAuLIlJSLnH9+l3mzPk3YvGTXQpB\nEHBz02bChGK1eV4kJhaxYYOEkhJFOzo6MGFCEa+9ZkBsrBZBQTJ8fPQ03hp/cxITixk4UEJenkBJ\nicDevYr3malp5d+NZWVlfPzxf5kyZRR+fp60bu1U4Zr09AyOHz+r1omoOrh48bLKPhvqRCQSERcX\nT+vWzjVfXAk6Ojro6emRmJiEvb0D4eGvUlYm48KF87Rq5aTewT6DIAhIpWJ+/vkX3Nw8kEgUQWmb\nNu25ffsu+/f/zq1bibRr11pt3xXm5mZcuHBJpWfLyRETEWFY7nusZ88YQkK6Y2dng6+vZ5XF4ebm\nRdjYSDh6VOGr9NlnefTsmVbBOBUUPhwdO3piY2PJtm27uHTpKi1btignFmBqaoK3tzs+Ph54ebnR\nooUtjx6loaOjw8WLl9HX1+OFFwbRsaMn3t7umJqa8OGHX+Ps7EiPHlWrZYlEIkxMjDh3LprZs6ex\ndetOHj1Ka/DXXp0kJNzB378bdnYtmnooGtSIkZGR4Ozs3D40NDRl6tSpfzb1eKAZpVENGDDgq6+/\n/rpvbVJONPx9cXR0ZNCgXsofSkdHe+7fv6s8n5KSTNu26t8A09WVUlr6RCZULpdz7NgfTJs2s9Lr\nBUHA2VmCs7N6zPW6ddPj44+fKFOFhxdy86YWBgZy8vIEXnvNgsTEJ4WtmhUpDQAbN/7E6NGDqzSG\ny8zM4ujR05w79yf37jUvmdCmCpwtLc159CitXm306dONsrISxo0LBSAgIIicnGJu375bw531x8Oj\nAyEhg1i06MtyikJ9+w7iX/96h759h7F48UqysioqNMlkMi5cuFSr53d0tOfBg2T27v29xmttbfNZ\nuvSJIt9HH8XTo4cdgiBgbGxUbR2FIMCECckcPJjKwYOp5eo1qsKvMHfTAAAgAElEQVTCwpxp08Yz\nZswwDhw4SmTkJiIjN7FixbpyqXKPdza6dg0gMfEODg72FUQSbG2t+fLL+dy9e6/aPh89SiMi4ieu\nXbtBSUkJ06dPoKCg4LmS4RWJRBo1qr8pgYGBhuPHj3/f09OzMqWZRqdZ7Gx069Zt4vvvvz/Pw8ND\nkyOiAYDWrdvy7bffYW39xLjqzJnzdOnSHUEQMDQ05MCBfXh7P3Hnlcvh3DkLHjzQw84uv8YfqMqI\ni4tHKpXi4GAPwLFjZ+jUqRs2NnXT5K8tIpGIgoJ88vNFuLiUsXOnDlIpvPVWAQYGMhIStJg0KZ81\na77mwoWzfP75Z0AZ7u5Vu/BqeP4wMdGiVatC9u7VRkdHkUZV1c5Zfn4eR47sp0ePQOWxQ4eOc/z4\nGc6di+bSpatcuXIdb28PpFIJ8fG3kclkzSblIzr6SpPtbERHX1G6fteFx8pzSUkPadlSsUPi7e1L\nRMSP+Pi41UnatTbo6IixsbFk+fIIWrZ0xsTkSUqYiYkpnTt3ZeXKVaSkPMTe3haxWMyJE1Hs23eC\nVq06EBV1gdzcHFq0UO37zdvbnb17f8fHx6PaZxMEcHXNZ/z4Il56KZfz57+nfXvXGl3Sn77fwqII\nC4uiWn2Pi8Vi3Nza4e3tjre3Ox4e7Vm7diu5uXkYGxuV2/GQyxUeKRkZmRw5cpLbt+9x9ux5Ll26\nSnT0FW7ciCc4OLDS57x3L4mtW3cQHj4FPz9v9PX10NLSonVrZ7Zu3UXHjs/H93Fy8kPEYgPs7Oyb\neigaGoCOHTua3Lhxo9PEiRPXv/3223WT31MTTZ6v5Obm1n7WrFkfBgcHN0x1nYbnEisra6ZPn8GW\nLRsxNjbC0tIcPT0ppaWlf6Uv6NOmTQcOHjxOnz7dkMshMtL2KZUoMVOmJNU64BAEgcLCQuW/b926\nw/DhjevYXVoqYvt2HQQBXnqpkOXLpWzfrsOHH+bh5ZXHgwcZZGVlYmFhyeDBg1m1ahWjRo1Dk374\n90EQBMaOlRIQ8EQmubJAIz4+jp9+WsnUqSHPHL/NSy9NKndMLpdz7txFQkND2LPnELt3H2Dw4L4N\n9xAqUFZW1qTFqerYGQwI8GHJkp8ICgpGJBIhEomYM+dfREYuY9q0sWoYZfU4OtozZ85UVq5czxtv\nvFfunFQq5a233ufOnUR27dpFVlYG/v5deOutCWRkpGFmZs7PP2/C39+7xh2mxMQ7/PbbIdq2ba3S\nd40ggJ2dQhDnlVdeZNWqjfTsGdSoaUZisZiZM6cQGxvHsWOnSU/P/Gtswl+vlaJ2ZOrUceTk5GJh\noZor9tatO3j11RkIglDOHFJbWxsdHTGFhUUq1bY0NTo6YkpKNMXhf1cEQeCTTz7xvXfv3k+CIIyU\nN2EqRJPubAiCoDt69Ojt8+fPd9fkoGt4FjMzcwICurB8+XL8/b25dCmWLl26K88fPLiXLl06oq+v\nx7lzFsycaajMcT9xQkz37lrY29dO/c3c3JSLFy9z5sx5XFycuHnzNgEBqrvcqgMHBxGGhoUYGclZ\nt05S7pkGDCjCzk6fKVMGExAQxLFjh3F2bknXrsGNOkYNDY8gCJiaamNqql3pRLCoqIglSxYyd+70\nchObhQuXYWFhhkgkIjMzi9zcXPLy8snKyiEpKQV393a4urqQl5fPb78dwsvLrclSmXbu3EdgYCdM\nTU2apH917aro6Um5eDGGdu0USl+6unokJCQgkYgwNm54U1pBELhy5ToBAV1Zu3Yl2dlZODo6Kc8b\nG5vg6+tPUFAwTk6K9NOPP/4f8fE36dt3IDEx0Tg5OVTbx8qVG5gz50Vat3au9ftFJBLh7e3Ozz/v\nxte38Vf9LSzMadfOFR8fD3x8PPD2dsfLyw1PTzf27z/C1avXiY+/g4GBvkqCAUVFxRQVFSvNYZ/G\nysqCEyfO0LZt64Z4FLWSkZFJSYmg3JXT8PdDLBbTqVOn1teuXRNPnjz5cFONo0lrNoYPH77k888/\n99cEGhqqQiwWY2j4+Me6/Ns1KysDS0vVVqJURRAERo4czJgxw4iI+Ak9vcq14BsSsVjMyy/rMHly\nQYVzLVuCnd2TVcUxY8YTHj63MYenoZmwYUMkEyYMLzfxu3cvibi4eNq0aUVubh4PH6aSkHCHq1dv\nEBNzjZ49nwTOPj4eDBjQi2+/jSAvr2kk2fv27cG+fTXXADR33NzakpBwg0ePHiqPjR07ie3bD9RZ\nXre2WFiYcenSn6SlPeT48UOUlpZWuOaxnPLFiylYWJiQlpaOr28ADx6k8dNP21izZgsnT0ZVutv0\nOICtKyKRCHNzU65di6tzGw1BQUEBY8e+wIQJI9m//4hKu10mJsYUFBRWei4/v6BWcudNjabu7++P\ns7Oz9uzZs2f4+vr2aKoxNFneRbdu3aZ8+eWXow0MDJpqCBqeAx4+TEEqVRQTPhuTduzoz7Ztexg1\nahB+fqkVzPb8/FLr3G9ZmQwjIzNefDG8zm0AFBYWcvSoIhUmOFgHqVQ1aVyxWIxIBOHhhSxdqrgn\nPLwQLS0ZLVuK+e23nfTtO1CjIvIPJjc3u0Lax+HDJ/D19cLHx0OlNuzsbJg5M5Rly9YQEjKsXEpI\nY6Cnp0u7dq7ExsY1iSOzOhe6JkwYwerVEbz55jwAtLS0ePvt91m48BNmzpxUw931Z8CAHvzwQyRl\nZaUEBHQkJuYiPj5+yvPl5ZStWLo0HFgOwKxZrwGKwvErV2L49dfDFBbmAzJ0dSW4ubWlsLCQ2Ng4\nbt9+QFpaOmVlZYAAyP/6rwhBECguLmTatLGV/m1HjhzM1q07yc7OISCgYwP/RVTj9ddnsWxZJEOH\n9qd3724sXLgcT88OtGhhS2lpGTY2lhUk1hMT79C9e2Cl7e3ff7hZmWZWx927SQQE9Cp3bN261fTu\n3b/R6hQ1NA7Dhw+3Onny5Dfm5ubd0tLSchu7/yYJNlq2bOnw2muvvRcQEKDfFP1reH7YtOknxowZ\nCIBcXl41o1+/wXz//dfIZDJEIhFTpiTh5mYBgJ9fap0KxB+zfv12/vWvd2q+sBoKCwtZurSM995T\n7I4sWJBPeHihygFHt25Srl8vZcSIx3n7ZXTvLmHPnl85ffo4Hh5etGjhWK8xang+kclkFBWVX1mV\ny+UUFhYhkai+qrpjx14yM7MxNTVm8eIVhIQMb/TiVm9vdw4dOt4kwYaurpS8vHyVC5erQ0dHhw4d\nWnHo0F5691Z4nEgkEqRSPeV3VEMiCALTp4+jV6+RBAcHUlJSUu58YmIxYWHSp7wvTPjgA3uOHfud\n7t0VE06RSISHhxceHk8EbHJysvnzz3Po65tRWCgmKKgvVlY2aGtrV/pMCQk3WbIkkpkzJ1VaXD16\n9FCWL1+Dv79Ps5DwlkollJSUYm9vg0QioU2bVty9+4D795PQ1tbi+PGzZGfnEBr6pC7K0tKC5ORH\nlab/icU6zeK5VCE5+SH29k/S57KyMklPT+GHH77m9dffwcREvT5WGpqW//3vf95xcXERwPjG7rvR\n06gEQRAFBwevfPXVV5t/QqOGJsfGxo4LFy4jk8mQyyt+gbu5eRITcw1Q7Hx06pRKp071CzTOn7+E\nv3+gykFBVRw9Wsx77+kpnXDfe09PucuhClKplLAwbSZPLmLy5CLCwrTR1dXl4sXz+Pv7lCtk1/DP\nQSaTsXLlEjp39lEeKysrY8mS1fTv37NWbWVmZhMaGsLUqeP49NP/Izn5Ebt27Vf3kKvF1FSRzrNi\nxTpOnDjbqH1bW1vy8OEjtbUXFOTH1asXuXMnUXlsxIgx/PLLb2rrozp0daUsW/YFu3cfIDX1YY3X\nt2nTijNnjpORUbUErqGhEd279+Lll1+jR48+tGjhiI6OTpXBU8uWLvTo8RpHjhQpXcNzc/OIi4sn\nLi6emzcTcHCw5+DBY3V6RnVTUFBIcXGx8nkEQcDR0Z7AQD86dfJhxIiBFVKNPD07cPnytUrbE4Tn\nJzUpP7+oXEC4a9d2Bg/uRUjIMA4fPtiEI9PQEOjq6vLf//53eHBwcP1SNupAowcb/fr1W/DJJ5/0\nauhVHg1/D8aMmcDt20ncvXufgoJc9u3bVe589+69OH78D7V+uV+4cEW5MtnUSKVS+vc3on9/I2Xw\n07Ztey5fjsXS0qqJR6ehKVi3bhVubi64ubUFoLi4mMWLVzB69FAcHesnYTloUG8cHOyJiFj7V5pM\n4zB5cgiTJ49GJBKxfv22RuvX2tqSlJS6p1tWxsSJI1m1apmy7qFlS2esrR1ZsWI92dkVPS/Ujaen\nG++++xpbtmzi888XsGjR5yxe/CX79i1l/vw4pffF99+nc/LkJqZMGc2iRV8SH1//WgqZTMaSJQX0\n62fGlCkerF1r9ZdS4CYePUrj0aM0UlIeYWRk2CQ7WZWhqytl2rTxLFy4rNLze/YcKieZu2fPIZKS\nUjAyqryer1271ly4cImTJ89y82ZCg4xZHRw8eJzg4N7ljmVnZ2FmZkqLFrblfK00/H3w9vbWDQkJ\neatNmzaNuuDfqDN+Dw8Pv7CwsOn29vaaSEODysyY8Qr79h1j5szJxMZeLXdOJBIxduwk9u5Vj8iC\nwnW37rr7TxMcrMOCBU8M+hYsyCc4uP6Fg05OLmRn52Fs3DQKPhqajsuXo4Fi2rdXTNTkcjnffbeS\nadPGY2VlUev2tLW1KqTbeHm5MWxYf779NqJRJsegqN2QSCR06dKJli1bcO7cxUbpV907G6D4TmrR\nwqbczsKQIS8wZ85brFy5udH+piEhw3B3b0Vo6EgmTx7BuHGDefFFEVFRSURFJSEIG5k8eTQSiYS5\nc6dz4sR+Fi36jO+++4q4uNg69fnnn4W8/faT3dx33jFk795s7Oys6dKlE126dCIoyJ+gIH8cHOzU\n/MR1x9bWGisry0oXrR49SiUwsBNJSSkAXL16nXPnLuLm1q7StgICfImPv42lpQX79h1u1KBdVe7f\nTyItLYfOnbuWO/708z8vuzMaas/s2bOdAwMDlwiNmO/XaJN+QRC0u3Tp8s2YMWOsG6tPDX8PtLS0\nMDQ0obCwCJmsosKKq2s7Hj5MV0tfR46cZdCg4WppSyqVEh6uxbZtOWzblkN4uFaNqVmPHj2sMPl7\nFn//Lnz++bdqGaOG54u9e3cxZEgf5b/v3r2Pl5cbxsZGbNmyg8jITZXKcVaFsbERWVnZFY5bW1vy\n8svTiIzcRELCbbWMXVWkUin79h3mxx/XERNztcKkJzHxDosXr1DLuIyNjcjMrPj89UUs1kYiKf9Z\nl0qlvPnmPLZu3a32/iojMNCP6OjL5Y499r54bHr6OIVGEASGDetPaOgoxo0bzKFDu4mKOqmWcbi6\ntqGkRMShQyfU0l5D0bNnV7Zs2VHheHZ2DmvWbGLz5l//MsO0ZsSIQVUaIWprazNmzDDatGnFiBED\n2b699il0P/+8m8zMrFrfpwrZ2Tls27aXsLCXK5xzd/fkjz8eB/oaZ/G/K4IgMH/+/B49e/Z8q7H6\nbDSfjVOnTn24aNGiCQYGBs9H5ZSGZkVU1Gmio2Pw9e1My5YuFc5HR1+gdWvHehnb5ecXcOvWXQIC\nutRnqOXQ1tamdWsJrVtLKh1bUVERmzev4/Dh/Zw+fZTbt29w5swJzpw5zqlTxzh37ixt27ZHKtVV\n25g0PJ8UFRVx8eIZvL2f7Lzt23eYHj26cPnyNYyNjRg0qA+urhU/H1Xx6FEq2tralXoLaGtr4+/v\nw969v5OdnY2jY8Mqn5WVlbF27VakUgmhoWPx9nbnzp37bN++BxMTY8zMTNm6dQcPHqQwdeo4Tp6M\n4vjxM7i6utSqKP5pBEGot4t4ZZiYGLNx42Y6d+5arrZBR0eH+Ph4dHW1MTZueFltuVyR9nPnzj2k\nUh1MTIyVxcunT5+ja9eACveIRCLc3duxY8du7OwcyrmS14SNjRYmJgUcPSpGRwc++yyfYcP08PPr\nTGZmNr/8sgMvrw4NXixfF4yNjbh5M6Hc5yEzM4sOHdpw7lw0o0YN4ejRU3To0JZ79x6o5LpuZGRI\nSspD9u37HWtrqxpf8/z8AjZv/pX27V05ePAYMTHXKCwswsbGSi1/s8LCIiIi1vP22/+tVJ63ZUtn\nNm3aiK+vBzExV/HzC2yWr5WG+mNqairKy8tzHTt27K+vvvpqg+tzC42xVdahQwfPd95557fJkyc3\nn31TDc8VDx+mIJfLsba2qfT8xYvnSUm5VS85xXXrfmHChOmYmqrXu6MqDh3ay8WLf9C7dxAHD55A\nLJZw8WI0X375X+WKY15ePhER6xk5chw3blyjV6++mJnVPl1Gw/PPnTuJHDmyh2HD+imPrVq1gWnT\nxhMZuYkpU2rvVn35ciyFhYX4+XlXe92RIydJTn7E2LHDG0Rp5969JLZs2cGECSOxtrascH7p0tUU\nFhZRUlLCm2/OUR7Py8tn06btmJmZMmxY/zpNjNas2VxOaUhdJCWlsHnzbt58cx56ek+EF8vKyvjm\nm48JC2s8QZjMzCyio6+QkHBHeezChUuEh0+lQ4c2ld4jl8tZtWoz3t5+9OrVX+W+ZDIZf/6pEK/w\n8ZGWe01SUpKJjFzGjBkT6/gkDYtcLmf58jXMnDkFgB9+WI2NTQvu3r3DiBF9OXr0NK6uLhQXFxMc\nrPqi1MOHqZw7F82gQeVrJO7evc/WrbswNzdFLpcjlUrx9/fG2bkloPhb/vHHRdLTMxg4sHdlTVdL\nYuIdRCIRp09foLRUjlgsYfTocdX+hty9e5sNG1ZhbW3B0KHjMTNrnN9DDY2PTCZj0qRJezds2DCo\nod3FG1z6VhAE0bRp0xZNmjSpWQcaOTnZfPjh+8yZ8yqOjho3zeaGlVX12XcODi2Jjj5drz5kMqHR\nAo0DB/Zw7Vo02tpa7Nt3nFmzXiM/P5+UlC/YvHknLi6OeHm5oa+vx4QJI4iPv46bmyOLFn3JO+/8\nD4lEUnMnGv42lJWVsXLlcl55ZYry2KNHaejoKDxoRCJRneRVTUyMiY2tWbWoR48gbt5M4PvvV/LS\nS5PU+v7bu/d3MjIyefXVl6oc/8yZU5DL5axZsxm5XK4MePT19Zg+fQJ37txjyZLVdO7si6+vV6Vt\nVEd09JV6PUNVBAR48eqrs/nqq0UYGRkDitQliaRxdypNTIwJDu5SboI8adJoli6NxMWlZTkH+sco\npHTHsmbNz7UKNkQiEb6+lUsJSySSZlnD8BhBEGjRwo5Ll67Qtm1runbthEhkwtSpM/jssw8YNWog\nK1b8hIWFWa2CDVNTY27fvlPuWFZWDsuX/4SRkSFjxw6v9DMlEonw9/fhyy+/p3//nrX6fMvlcn77\n7QgWFla0bt1BZdETB4eWDBkyinfffZtBg9QfhGtoPohEIubPn987KSnpVWBhQ/bV4GlUR48efXvR\nokXTjI2Nm3X6VHFxEZcvR9O//xDS0lLJzc3m0SMdMjPLMDHRem50s/+p3Lx5A5ksv15FhzExsfj7\nqy+Fqiqiok4RGbkKExNTZs9+nR49+iKRSDEwMKRXr36YmHhTUmLML7+sB2S4urrg4GCHoaEB7du3\nJiLiR7p06a55T/6D+OGHbxg2rHc5BZzIyE1MnToOkUhEQsId7OxsK500VocgCFy5EkuHDm1rvNbM\nzJR27VxZtmwNzs6OGBjUzyZJsWv3Ex4e7endu/r3syAICILAgwcpGBsbVujb2NgIf38fEhJus2vX\nARwc7FUeX3T0FWxsGkbZTSzWpk0bFw4fPlLuuyUq6hSenm2b9DMsEokwNjbi1q2EKlPksrJySEpK\nx9vbVy19CoKIY8eO4OzsoBZvE3VSVFREdPQV8vLy2b37MFeuxHH16k2GDRuJgYEBvr6dWLNmDSYm\nRoSEDK9V6t7jnepff92LtrY2OTm5nDoVhViszZQp41i+/Cc6dfKuNJgQBAEXl5asXr2RtLQMbGys\nuHv3Prm5+RgbG1Xa36lT59i9+zBjx06iT5+BuLjUTnjI0tKaDh3csLOzr1dqsobmj7m5uVZqamrr\nfv36rX/33XcLGqqfBk2jMjAwMJ8/f/6ZN95447ny1Jg7Nxwnpzd4//1WAKxYUcjYsVLN5K4ZU1hY\nyI8/LmLChJEkJSl+xGxt82vlt7FmzTbmzn27zmNISUnm0KF9pKam/PVeEZDLyzA2NmXKlBk13l/e\n4VfxvnNxuUhU1CmSk5N44w2FNPbNmwlER99k2rSZmnzafwgzZ05DJnssHKB4U9vaWuHm1u6vuoPL\njB8/SqU88qd5vFtQmxQsmUzG6tUb8fZ2r7MB4ONajLCwSejpqb7Kf+fOPa5fv0XfvsFVXlNaWsq2\nbbspLi4mJGRYjbswDZVG9TQ//riR1157RznpPHx4PxJJaZUpTI3F2bMXMDIyVKqbPcvPP++hb9/h\nODi0VFufpaWlfP31J/TrF4ST0xNTUrlczuXL1/Dw6KC2vlTlm28isLd3wMfHD0NDQxwdncqlvj3m\np59+5I8/ztC5sy+DBvWppKWaOXv2ApmZWVy8eBlvbzfMzExxcnJk1679TJtWfWpdUlIK33yzjIED\nh6ClpUViYjyFhfmEho7m9u27nDlzEUEQ4efXmS5dutdpfBr+eRQXFzN+/Pi127Ztm9xQfTRoyNqv\nX7+Fc+fOfa4CDYBJk+bRq1cLpdNqWJiUgIBinJ01qSvNlZ9/3kRAQEd277YgPFyRrrB0aRaDB6tu\n8CcIdZu4379/l3XrVmNpaUJwcGfMzIKU58rKyli/fqdK7Tzr8BsWJiUmpiNz5gTy9defKNNHWrd2\nJjc3n4ULP8bU1IJp0xrdn0dDI5OTk8P8+W8olZme/a+7eztsbWsv9FeXBRSRSMT06RPYu/d3du7c\nx9ChqqfYAPz5ZwyXLl3llVfCat2/g4M9u3cfwMvLrUqpX21tbcaOHU5GRiaRkZtwcnKkb9/gJl0s\n8vBoy+nTx+natQcAXbv25LPP/kf79q5NOq60tHRatao8kMjKyqawUKbWQAMUr88bb8zjhx++ISMj\nC29vd27cuMXBgyfR0hJjbGxcb7+Y2mJkZEhY2OwaF29GjRrHL79sr7SwXlUCAjqSnPyQ5OQUUlJS\n0dfXx9LSnDZtXDh58ixBQVW3fflyLOPHT6Jnz6frtpZRXFxMQsI9Ro+eWM4RXIMGVdDR0eGll14a\n7OXl1S06Ovp4Q/TRYMuiXl5e3WbMmDGoMsWD5o7GLO35Ijc3h7t349HT60B4uLFS4z083Fi5y6EK\ndd3li4yMICxsLC+8MLCcqo9cLmflyo0MHz66Tu0+zdChL/Djj5vYsOFX5HI53t5uTJ8+jjt3Evnq\nq4+4cuVSvfvQ0HyZMGECcXEJWFtbYm1tiY2NFTY2VtjaWmNra42dnU2jT1oHDOiFk5MjkZGbVL7n\n4MFj3L+fxJQpY+s0XkEQGDFiEAcOHKnxWlNTE2bMCMXR0Z7vvvuRq1dvVHqdnp4ueXn5tR5LbYiP\nv4On5xPHd7FYzAsvhLBrV9O6NKenZ2BqWtGvp6SkhFOnzjN4sHpkwJ9FJBIxZ86/KS4Ws3btryQl\nZfPOO//j9df/0yQSudbW5iqZ2Onp6TN9+ots2LC9Xv3t2nWASZPGEBoaogxcgoICSE/PZM2azaxZ\ns5mNG38pd09cXDylpeJygQbAiBGj2bZtD7a2lty927gy1Rr+PgwYMMA0MDBwgVDXVdcaaJBGBUEQ\nBQQELBgwYIDqgu/NCCcnHVasKFSasf3wQzZOTs9f0PRP4eOP5zNunGo/inI5xMYaExtrzLOxRUlJ\nMaWlFX08qiM+Pg5nZ4dKV8QiI7cwcuR4HB2dVGrr2ffdihWFyvedq2s7Xn/9XdLSMrl/P1l5z6uv\nhjF9egg7d24lIeFmrcau4flhyJCRXL/eMG7E9QlSPDzaY2lpTmLinRqv3bTpV/T0dBkypF+N11aH\nra01xcUlZGWpZo7Xrp0rc+a8yIMHySxbFkl6eka58xYWZqSmptVrTDXh4+PGuXNnyh1zc/NER8eA\njRt/bbKiaZlMrkztepoVKzaQn19Cy5YNK5bSv/8QXnnlDUaMCEEkEqGjo4NIJG7QPp9FLpdz716K\nyjs4Q4aMwNu7E/v3H61Tf4cOHSc1NY2TJ6MqnBs6tD+hoSGEhoZgb29LVNSfynPHjkURElJRxcvU\n1BxX1/YcO3aW4uJiZDKNP4aGuvGf//wnKDg4+LWGaLtB0qi6des255133gmq+crmiSAIjB0rxc4u\njpSU+1y7dpCysv9pCqWaKTY2VhgbG2FklM/SpVnl0qhsbZ+sWMrlsH69DW+/rcjF/ewzXSZMSFam\nWfXo0Zn9+/cwaNAwlfvetWs748YNrnBcoWbiTqtWqudkP37fBQQUA+DkVL5O6N1336C0tJgjR878\n9YMi/0uFCExMzHF0dObQob3Exl5BLJbg7u5FVNQptLS06Nq1Bz4+fiqPRUPzQyzWKafEpC7qW7fX\nv39PNmz4mZMnoxg+fGCFwuyysjJWrFhLjx5BtG2rvqza2vhUCIJAnz7d6d69M1u27EBLS5uioiIE\nQaCgoEClAvn64Orqwvr1OyuoOo0dO5n79++ybNlyZs0KbbTdqbKyMvbtO0xhYVGl5w0NjXnxxdmN\nMpanKSsrw9V1IufP69CxY1atau7qwsOHqWzcuIPx42uXqt6//xD27t3BqlWb6N27q0ppX+npGZw/\nfwktLRH/+c9c1q/fRnp6RqUeNwBBQf7Mn/8F/v4+lJWVIRZLKg0Mr127QlzcDUxMjLl16wpnzpzg\nrbfer9XzaNAA4OTkpNWvX7+XzMzMItLT01VbzVERtc+eBUGQzJs3b5qzs3PFT8VzhCAIXLiwjalT\nx3DrlhaZmRlYWFTUf9fQ9OjoSCkqKkIikTB4cCpRUYoA49kC8evXjXn7bX1lTcTbb+vj62tMu3YK\np1ZHR3v+/PN3lfu9cycRXV3tSs2RTp06z1tvza/1swiCUDTiQVgAACAASURBVGVt0Keffl3j/efP\n/4GDgw29enVh6dJIJk8OwczMhIMHj7Nnz07GjfsPIpEIJycdjeDBc4f6Aw11oKWlxaRJY8jKymHd\nuq1Kj4Li4mIOHDhKYuJdxowZVmWNRV37rAs6OjpMnDiahw9TWbQoggUL3lHbmKpDJBJRVFS50Iu9\nvQPjxoWyYcN2Jkx4oUHHkZOTy86d+8jPL6Rfvx5VFjmXlhY36Dgqo6ysjO++K2TePIWi4Ecf6REa\nmtRgAUdU1EVu3rzLO+/8D7G49rspAwYMo1u3Xnz11SfMnTut2mvLysr4+uuljBkzTGkgOWzYABYt\nisDFxYlx40ZUuGfVqg2EhU0CFMptVZkrbt++iVmzQpX/XrFiPSUlJXV6Jg0a5s6d2+7kyZMfAmrd\n4VB7GlWfPn3m/etf/6reIeo5IC0tlatXY1m+fD19+gzSBBrNmBEjQli2bC0FBYUIAtjZ5WNnVzsl\nKkApSagKUVEnWbduFSNHDqpwTrFSrNUkSlFvvfV/PHiQjEQiwcjIEDMzRT52797dsLIKx8tLioeH\nDps2FVZY0ZbL5SQkFJGQUFTv1W4N6kcqlTZIu+oKYIyNDUlKekhk5CY+/XQR69f/jLe3Oy+/PF2t\ngYY6sLKyoE2bVo3ap4uLA1evXq7inCsikU6D1I6UlpZy+fI1VqxYx44dexkypB9hYROrXI0vKSmh\npKSYgoKGrWN5ltOnC5g3T09Zczdvnh6XLjVMJrZMJuPixWvMnv2vek3K9fUN6Ny5CydOVEyJepr8\n/AI6dvQs51RvYKDPu+++hkxWRnFxxeBOLBYTE3MVmUyGoaEB6emVp/rp6EieuU+qCTQ01BkDAwMG\nDx48wlLNxctqnQ2Zmpoa9e3bd6y5+fPvOGliYkpo6DTeeut9/Pw6N/VwNFSDtbUNY8b8hx074igp\nqbrmom3bLD77LE9ZE/HZZ3m0bZulPC8IAubmhnz33VfExcVWuD8h4SY//riEhQs/4f79W8yaNbnS\nFdb9+48xdGjDrlA+TWzsVf788xwlJQppVLlcRFxcPGVlT3J3k5L0+Ne/bJQ/5GFhUhITn/zAPZbd\n9fDQqTIY0dC0VPferg/qfJ3ff//fTJkyFnt7W6ZOHYe9fe2keFVBXePV0hLVukarPnTv3pn9+3dX\neX7kyHHs2XOoXn1kZWWzZ88hVq/eSGTkJiIjN7Fx4y/cuBGPo6M9EyeOLufV8ix37z5gyZK1ODu3\nQSJpmOC2ObB79yFGjVJd7rk6+vUbTFJSBgkJVRdnZ2fnVCnxbGtrTXJyRWPN0NAQ3Nzasnz5Gs6e\nvYCurpiYmIsVrhOLdZQ1PzKZTFOzoaHehIWFtezatetn6mxTrWlUQUFBC15++eWmFQ5XE4/z3DU0\nb554UxgBIygoiGfKFHmluxqCABMmJOPrq6jpaNu2Yk7wsGH9KCkpYc2azXTt2ofo6AsUFuYhl8ux\ntbVkwICgKs2otm//jZUrN9CtWxfGjn1RLc8nk8n45JP5GBjoIRKJ0NISM23aTHR1n4xhw4ZIgoL8\n+OCDjVhYWGFq6kFGhhk+Ph6cPHmOO3fuYWLiDVSc+P3wwzeUlRVjaupNeHg/jdxzM0YQ6uYSrgrq\nqgVpjN287OycaifMqmJiYkxmZhYWFo2zOKalpYWrqyNLlixkxoxXKixUWFlZk5+vKHyvTT3KY/bt\nO8yDB8kMGtQHKyuLCq/n0qWra3z/HDhwgvfe+7BJdmUDA3X56KN85s1TfLctWJCHp2e62vspKSkh\nKSm1VvV0NfHii7P49NP/MWnSiErfmytXbuD11yuXKG/Z0oGEhDvljBVjYq5y924Snp4dCA+fyu7d\nB3B1dWLv3l8xNTWjRYsn/iRDh77AihXrsLe3Ij7+ToNJob/++su0aGGHjo6U+PgEPv3060pTiDU8\n/+jo6DBmzJgBrVq1anPr1q3KZfxqidocxC0tLa1mzpz5VZcuXYzV0qAGDSqQmFjMwIES8vIESkoE\nTpwwpXXrKM6cOYQgUMEZWBDAwqIIC4uiKtOstLS08PLqwNmzZ+jXrxudOnnh7d2BVq2c0NFRbE8/\nfJhKVlY2ubl5FBQUsmxZJGZmpjg4OPLmm++pTUxALpdz9OghBg/uhZubKw8fPmTv3n10795TeY2Z\nmTlHj57Aw8OTnJz+vPmmP5s22eHjo49cHoe3tx/t2jni4yNl715tdHQUhoFdu0rYseNnDA310NW1\nYdeuVpSUKP4oOjowe3YZpqYaUYTmwoULf9CunXOd6xWqIj7+Ni1a2NZoflcboqOvlEsZUSeJiXcQ\ni8W1NjB8lrS0jL92MxtPNNHR0R5zcyM+/PBjBgwYXCEg8PT0ZuXKlfj51c4s8dSpP5BIdBg2rD8G\nBvqVBo5WVhYcP36m0iL9tLR0oqL+5N69JHr0qJtZXX0RiUR06qRFjx75TJpUQkbGKtzdKzcbrA+r\nV29h6tSZ6Our5jCvCoIg4OcXwLp16/H2rmhKaGZmwuXLsbRuXVHdy8TEmN9/P4G5uRkREWu5evUG\nV65cZ+DA3hw6dAyZTE737oHs33+EXr2C2LhxE97efsq0SlNTM7p27YGBgQk9e/bDyspGbc/1NHFx\nV5gyZQytWjkik5UC2tjYqH/nUkPzwM3NzeDs2bM2o0eP3qKO9tQ2kwgMDPzv9OnTHWu+UoOGhqV7\n9144Ow/k228/x9raCplMIWlYG0dxLS0thgzpW+m5tLR0Vq/egI+PJzKZjDt37tOhQ1skEgm+vt3V\nmlsvEol4993/sXXrBnJysgkO7sXQoeW/4L28OuLl1ZGEhCJCQ3WeKoB35NKl8bi4KMbj4CCvoHS1\nYMEXgCKo0dIq717u5PT3TaN4HikpKWqQXGwzMxMyMjLVslvQGBQVFSOV1j8wMjMzIT09Uw0jqh3p\n6Zk4Odmzb98uBg4sr3ynp6dPv36DWb58HS++OA65XM6JE2fp2jWAgoJCiouLMTQ0qLCifPnyNWbM\nCKU6HB1bsHfv75UWDysm4DPo1athfDVURZFRYABAerodiYl3yrmM15eDB4/RsaN/g3hp6erqoaUl\nVoqVPI2HR3uuXImt9HkUimiFHDp0jH//e1a5QHHSpDFs27aL4uISQkNDWLx4BWPHjuDrrz/lvfc+\nLPc6urioPzB7msfZi/r6enTu7Muvvx7Cy6tjg/apoekQiUSMGjWqh4ODQ5u7d+/We3dDLXulJiYm\nxr179x6gzpUxDRpUoTpvipdffp3ffrPC398Wf39bdu+2qOCtUVvu3LnPN98sY/r0CfTtG0z//j3R\n19elR48g4uPv0rZtezU8VXm0tbUZN24yL730Mm3atMfYuKIJV1U8/cP1WOnK2VlSYeXzsexuTEwx\nMTHFjB0rbZbKR/9kZLKG8WJQBBtZNV/YTBCJBLX4UpiZmVbw3GhIkpJS+O67H4mLiycsbCIXL56v\nNL/ex6cTvXsP5Ny5aP6fvfOOi+pK//97Zui9SVOUDiIWFLGAFTWKERULSgTU2FuKSdzNN7u/ZDfr\nxsRsqiV2Uey9IBZs2Csq9gaiggIivU35/UEcnTDAUDXmvl+v/MG95557rrkzc55znufzOXHiLOnp\nmURFbWD//iOcOnWe6OjNynqMqKgNJCU9wNpaMwGTQYOC2LZtj/Lv0tJScnJyMTe3wMXFDROTNycx\noV+/YA4fPlV1Qw2Ji4tHT8+8nCleXTJ48HD27Tuq9lxo6CBiYuJ49Ci13LkJE8IZM2ak2u/cIUPe\n5eLFMtPWSZMiWbVqIyNHBvO//81u0PqMV29lamqCs3Njjhx5vaaUAvVLSEhIo06dOv2jLvqqk52N\nTp06fTFu3DjnuuhLQKA6VOZNkZIi4x//cFau9E+aZMqZM2VKVTXFwcEeS0sLlZXFoqJidHV1APFr\nVQF5EXjVdHeiMtldgdfLvXu3MTc3qZe+zczMuHPnXp32WVJSWm/1JWKxBLm89tKs5uamZGU13M7G\nrl37mTJljPLfpHv3jsTG7iQoqPxugo+PL//+9zY8PBxp27YVLi6Oavu8desu589fZtCgfhqNwdra\niuzsHO7dS2L//mMYGBgjEomYMuWjGj9XfaGtrY1cLqqzeqL79x/zySeVS9TWFltbe54/Lx+4x8Ye\nxszMhEmTIpk3bxnh4cMwM3sZ2FX1u+Hj04orV67RqlUL3n8/jNWrN9GvXyBLlsxjwoTpdf4c6nBw\naMbjx2nY25elaQUE+LF69Xa6dXs9aXcC9Y9YLCYoKKinnZ1d49TU1Ee16qu2gxGJRAYBAQH96zL/\nUUCgOlS2Yv9HTp9O4OTJ87W618SJEaxduwUoWxnU0tIiLu4Y3br1rHG/dYGwO/H2cuLEMeRyGWvW\nbGbhwhWsXLmexYtXKxXIaoOFhRmZmXW3wp+V9Rxtba16K2SPjz+pUkxbU7S0tFQU2+obXV0dlX+T\n5s3duHnzmtq2YrGYceMmc+DA0UpradzdXRgy5F2N63jOnEmgsLCUe/fSmTLlY6ZPn8m0aR/Xm6xy\nbQkI6MbZs+UVmKrLvXvJDfJdqO7/w8WLiYjF+ly5cpvCwiImTYpkxYp11VJV8/VtTXz8aQDMzc0Y\nMKAPBw4cwd3dgdmzv+T58/rfoXN3b86JE+fq/T4CbxbvvfeefYcOHb6sbT+13tkIDAz8bMqUKXWf\nOyIgUEvUrfSHhvbjwIE9/Pbbavz8WtOmjTcikQi5XE5MTByZmdnI5QpMTAwIDu6jsuK0a9c+ZY73\nC5fks2cTyM3NR1/frJxE8oULZzA0NKaoqAhbWztsbOqncO9VhN2JtxUFEomYgQP7KdXQMjOfsXz5\nOjw9XenatVONezY0NODJk/S6Gijbtu3hvfeG1Fl/L5DL5SxYsILg4L5vnG+HJqibXGprSygoyMfA\noPxiXePGDnh7t6h1Ifyr3Lhxj3/84z911l994+vbke+//xo/P59qXyuXy0lOTuHgwRPY2zfjo4/+\nVg8jLE9KymOkUilaWlqcPZtAaupzIiLGkZeXy6JFPzN2bCjvvNOTI0dO0L27v0Z9isViunXrzJo1\nmwkLG4KjY1MGD+5PdPRmxowZyeLFP9Oz5zu0a1d/Mv0LFvysopJ2+vRFwX/sL4C2tja9e/fuZWxs\nbJGbm1tjebhaBRsikUj8t7/9rb+5uXpnSwGB10lFKVa9ewcRGNiXEyeO8ttv0ejqaiOTwaBBQ3F1\n9QDg8eOH/PrrL0ydGomOjg7Hj5/GysqSd99Vzfe1sWmETKZg/fr1XLhwDh0dLfT1DVAoFDRtao9C\nIUdHR5vz5+MpKChl2rSZDf7vIPDnJzX1EePHj1Q5ZmlpwYQJ4axbt5W0tKfllNc0RSqVYmpaNyla\nMpmM0tLSepHEXLJkNUOGvFvj53yVw4eP8+hRaoPWbKhjwIBefPfdf/j8c/Uu1nXpgaJQKBp0J6cu\nEIvFeHm15MKFK7Rt27Ja1x48eAypVJspU2aqSIXXN5Mnz2Dt2m3I5VKsre2IiBgHgJGRMTo6epSW\nlqUYViShXhHe3p4AyoDDxqYREyaEs2bNFiZMCGf58vVYWlrj6Fg/Ge2Bgb1xc3sZ+F6/focPP/x7\nvdxL4M1izJgxjjt27JgFzKppH7UKNnx8fIZGRka2rk0fAn9u5HI5Fy8WAeDjo/da9Nkro6KVfrFY\nTEBA9wq9VOztmzB16sesX1/mEn716i0mTAgv187W1hotLRETJ4bTooVHpWO5ffse3377Lz7++PM6\nk8YVePs5duwwXl7l5UpfMGxYML/+upQZM8bz4MFDtm+PxdbWGnd3F86fv0Ra2lMcHMrcol9MXl9N\nKVEoFPTrF1ijsR08GM/Dh6nKfkQiEQEBdb+6KpVK0dfXr5NAo7CwiOTkh4SFhVBSUvs0NE2QSqVI\nJOW/G01NTRg1ahBff/0PPvpoFmZmqgt36vL/a8K5c5c4c+YSQ4aMrLrxG0b//oP59tt/4e7urNxR\n1oTU1HQmT57Z4N+1Tk6uTJ/+idpzvXsHcfToaTIzM/H396t2397eniQkXFEqXhkZGWJjY8WDBw8Z\nPXo4v/66hJkz/0/tTllt6ddvAAsX/sDo0aGkphpgZdW2zuppBN5sDAwM8PX17SUSiSQKhaJG6hy1\n+hT6+vqGe3p6vr6KWIHXSllaQyGzZpWt0MyZU8DkyfpvXMBRU6ytbbCwsOX8+Us0aWKvts2CBcuZ\nNGl0pT+C6emZWFlZoK2txf3799ixYwshIcPra9gCbxHJyfc5ejSOKVMiK2xTJtPchy1bdlNUVMTE\niRFkZ+dy//4Dxo4NA6j1hODx4zR27dr/u2yqFgUFhZiYGNOsmQMREfX/Licm3lCu7NaWXbv2ERz8\nDtra2g0m6JCS8kgZ8AFs3ryLkJD+Sp+PKVPCmTfvewYOHIa398v1O21tHUpKSmq0U5SV9Zw9ew5T\nVFSKr28HPv/8X3XyLK+DqVM/5qef5lT6Ofgjuro6FBYWYGxcP8IKNcHDozm7d2/h2bNMhg2rWVqt\nt3dzrl+/TZs23gAEBfVi48YdhIUNYdSoENavX82YMRPrcthAmbRvo0Z2bN1qzIwZ1oAdJSWZjBlj\nKQQcfwFGjx7dau/evSOA6JpcX+Ngw97e3uXnn3+uvwRBgTeeixeLmDXL4BVfBwM6diykXbuG27Ku\nb0aOjCA8PJQffyz/Q33hwhWaN3evNNCIi4vnwoVLmJqa4OTUDE9Pd4KDQ+pzyAJvEfPn/0xERNXv\ni4uLI6dPX0BLSwtdXV2srXXrrK5hy5bdALz/fpiyAHblyvVERobWSf+acOXKdUaMGFQnfeXm5mFu\nrrl8dF1gamrCo0fnUCgUpKY+ISMjk++/n4+BgQElJSWYm5vxzjvdOH36MMnJ9+nfv+xZ33svkri4\nQ/Tr16OKO6hy6NAJ0tOzCQ+f8EZNtmuKoaERvXr15ejRU3Ttqtm0o1u3jsTE7CA0dFQ9j656mJtb\n0aKFKzt37iU4uK9G1ygUCjIynmFmZoKhoQGpqU9QKBRER29iwIC+SKWy3/s2IyPjSb0pwXXuHEar\nVrrK3/wZMyzp0aNEqBP8C+Dm5qbl6+v7Hg0ZbGRlZQWGhMzca2jYU1LTVRcBgT8DYrGY7777gUWL\nFjJhwijS08t+uFNSjhMffwqRCHr37lbuM1BcXMytW3dJS3vCp59OUx6fP3+lkEIloDGzZ8/lu+/+\nzaRJVU+YmjVrjK2tTZ3e//Dh4xgZGdKnT3eV4w2p7w/QqJElly9fo1272mft5uXl18GIqoeFhTk3\nb95lxYp1pKdnMHFipEqdjEKhIDb2IJmZmejoaHP48H66d++Nk5MrW7eu1+gecrkckUjE2bMJlJZK\nGkwStaHw8/Pnf/87rHGwYWPTiLQ09Z4Xr5Phw99j2bJ52Ntbc/z4afz9O1TY9t69ZPbvP4yuri6N\nGlny/Hk2SUkpuLo6ceXKNezsbImJ2c+TJ0+V13Tv3pE9e3YoA9a6RN0OxvHjh9m69RylpVICA98p\nJ5Qi8PbQt2/fDk2aNPF4+PDhzepeK/nyyy+rdUFWVlbgsmXiA999d1O8eXMAxsbFtG2rXvJN4O3G\n1laCmVkhR45oo6NTlkY1YID+W7elamxsgpubB+vWwciRDixebEz79iZMmOCDl5c7P/zwG8ePn8Hf\n34/Hj9NYt24r+/YdQU9Pl6FDXzoEX758FVtbJ5ydK86/FxB4FbFYzMOHKRga6mBoaMCJE2eJidmP\nvr4+iYnXsbS0UEqjlpZKefQolWbNHOrk3tHRm7C3t6VLl/KTh6ys5+Tm5mFjo76GIicnlw0bdpCQ\nkMjZswloaUlqVW/h6upETEwcbdu2qnEfAAUFhSQmXsfXt02t+qkucrmcR49SiYwMxd+/QzkHdJFI\nhJubMx4erhw6dIz8/BwMDU1o1MiGGzeuY21thoGBfoX9FxYWMW/eCu7efYipaSMGDRpW34/0Wrh5\n8wZ2dpYaO8hfunSV9u07v1GpvTo6Opw4cZwBAwI5ffoiJiZGFQo0bNy4k/HjR+Hj0xJ3dxdatfKi\na9dOWFlZsGPHPoYPD6Z16xakpT3F3NwUY2MjLC3N2bcvjs6du9X52M3MJLi4FBEbq4WODvzwQxpS\n6RECAzvTrVtHrl9PZOPGjXh5tayXuhGB14ubm5v+sWPHtEeMGLGrutdWO9g4erTk+vjxx7VKSjpQ\nWmrBsWPadOhQgIuLsI32V0MkEuHrq0XfvkWMGSNlwIC3p17jj2Rk6DJ0qBX5+SJKS0UcPmyCu/sZ\nXFxM6dWrGydOnMPHx5vdu/cTGRlKjx7+eHioBhUxMYcZOTLyrQvGBOoXXV1dFi9eyoMHj0hPzyQ/\nv4Br126SmvoEuVyBs3MzoMykbteuffj5ta3xvdLSnhIVtYErV67j6upEx47t1LZzcmrGpk27aN3a\nS+1O3fLlaxk1aijt2rWmbduW3LuXzJYtu/Hx8UYikXDt2i0aNVLN9c7MfEZW1nNiYuKQyWTY2lrz\n9GkGCxasIDk5hZycXHJz83BwsK/x4pZEIiEx8QY+PtVTNqotDx+mUlhYVKE53wt0dHRo0sSeixcv\nc+vWDTw9W6Cvb0BaWorSTA3KdkJOnDjLiRPnOHv2Eleu3GbatI/p0qUHbm51U9vyJmJv34T9+/fi\n6anZgk1hYSFFRfIGkR2vDo6OTqxeHU1Y2GC2bo3Bx6clW7fu4dy5y0gkEqytrZDJZFy+fFXtbp6R\nkSGdOvkqf2/d3Z3ZujVGWceRnZ2DQqFFo0a1F1R4FZFIRIsWWri4HKZnzytkZcUyduxk1qxZz8WL\nlzAwMMDPrzVJSQ9xdnar03sLvH7EYjHXrl3T6tmz5+Ivv/yyWlJ5NZoZKhT3AcEwXKDs5WvXzoB2\n7Qze2kCjIvz8/Nm9+wjR0dspLpbyxRffUFoqrTBNSktL5y/3byRQe06ePI6ZmQklJSXY2FgzY8Z4\n+vfvxaBBQfTq1VXZTiQS0a1bZ/btO1zje+3cuY+JEyMYOTKkSrWcNm1aKJWo/oiurq5yx0UkEtG5\nc3tGjx7JkiXRLFoUxZMnT1mwYAUnTpwFYOvWGPbvP8KlS1fp378XxcUlLFy4gq1bd/PRRxMRico8\nRpKSUigoKKzx892+fY9mzWpvCFhdTp06V2Hg9kcaN7ajd+9uNG5szbx5/8PS0oq7dx8ozysUChYt\nWo2ZWWPGjJnGRx/9Hx9//HdMTEwr6fXtwNrahuzsPI3bt27dgnPnTtbjiGqGnV1jOnfuzqlT55W/\nCXl5xUyfPosLF64AZYGxXK7ZfE5LS0slcPf1bc2ZM/Xz3CKRiDZtbID7+Pm15MCBPcyc+XdcXb2Q\ny7V5/DiN+PjDPHuWWS/3F3i9DB8+vEWLFi36Vfe6aiePGxtfHTp0qM7O7dvLPgRff11A9+5vpvuo\ngEBdoc4g0N3dGA+PGQCsXr0Ma2ujSleVxWJhR0Og+nh4NKdJE3NMTU1ITLzOunVb0dHRQU9Pl5s3\n72Bt3Qhf39ZIJBJatmzO+fOXanwvbW0tJBIJ+vpV7xx4eXmwdWsMR4+exN3dWZl7fvjwcbVpSqam\nxkydOlb5d8+eXbhw4TIrV66nXbvWKmpTfn4+KkZuISFBLF68mmvXbhIQ4FdjX5AjR05WubtQH2Rn\n52JiYlx1w9/x8HD9fQfGi9mzv8LAwJCNG3dSVFRMQUExPXq8g59f53oc8ZuLiYk5z55lYWFRtb9X\nTk4upqZvpg9Yhw7+zJv3LaamJr+bapbVQd24cZtVqzbh6OiAvr4uhYVF6OtXb45lbGxEfn5uPYy6\nDE9PL+7cuUlhYTGpqY8Ri8XK1L24uFiePcskJmYnzZt7YW1tg4NDs3obi0DD4u3trd2mTZswYHd1\nrqt2sDFr1izPDRs2EBlZ9iJ3764nFIgLvPVUZBD4grCw0cyZ8y9cXZ3U/gheuXKt3r9wExLOs2vX\nFlq18iE4eCgymYyiokIMDY3q9b4C9YunpxeffrqQd9/tTceOvlhamlNUVExJSQnLl6/DyakZy5at\npaioCENDAwoLC7l27RZeXu7IZDK2bo3B1NSE3r0rz+E+eDAeL6/KvWJexdzcTCmtu3jxalJTn9K7\nd3eSkx9q7Izctm0rjeowdHR08PPzIS8vn0OHjuPpWbMUjYiI4WzevJOcnOpN/jXhwYNH3L17n+7d\n/VW+G2JjD1bpwaMOLy8PDh6MZ8CA3ty8mUxY2HiAv/znOSxsND/++F8mTqxaNOHixat07aqZ4lND\nU7ajIWLAgD4sW7YGPb2yGof585cCcPbsSY4fP8fatVuUn7OKKCwsIi3tqcqx+hZxePfdwURFLaGw\nsEjleGBgXzp08Cc6egWHDu1BV1eXDh264Oen2XeCwJtPmzZt2otEIj2FQlFUdesyqp3T0bp160A7\nOzv69DGhTx8TIdAQ+MvwwiDQyUm3XN2FWCzmk0/+j61b96q99ty5RIKDh9bb2A4fPsDx4weJiBjK\njRs3APj++/+wfPlv9XZPgYbB1NSMpk2b4evbBhubRmhpaWFkZIiFhTlmZiZ4e3syfvwopk8fx9ix\nYVhZWXHr1l2WLInmxx8X0amTLxkZmWRlPa/wHklJD3j6NFNlN0FTFAoF16/fokcPf5YtW1Nvak/t\n2/vg5NQUhaLmkyg9PV1cXZ15/DitDkdWVqOya9c+bt68g0z20vPqRR1Kp06+1e7z0KFjTJkyBjMz\nU7S0tDA0NKpRoHH37i1mz/4nmzevqfa1byK6urq0atWWy5evVtk2PT0DO7vGVbZ7XRQXlyISibCx\naUROTo7KufbtOzF79vcUFkqRSqUV9nH8+BmiotYzefLoP5ypf8W4iIhxTJ36EVevXuLBg/vK40ZG\nxkycOB1DQ1MCAtpz6NCBeh+LQMMRFhbm1r59+/Iux5VQrWBDJBKZtmzZskX1hiUg8NdAW1sbR0fn\ncj+CcrmcoqLierlncXExP/zwDfn56aSnP2Xq1L8xhromVQAAIABJREFUcGCZL4OBgR45Oc/ZtWsr\njx8/rJf7CzQMkZHjmDdvOffuJSOTyYiK2sCvvy6lY8fyk9jQ0IEMGtSPMWNG8NFHE2nc2I5Bg4KI\nitpQYf9xcfGEhg6s9riuXbvFokVRTJ06FktLC2bMGEdGRv3lamdkPMPCwqJWnycnp6YcPXqqDkdV\nliPfpo03BgYGKjVbsbEHNfZSeJXs7BwsLS0QiUQcPnxCxeiv6mufc/XqZbZt28iPP35DXNxuJk8O\nJy2tbgOs10m/fsEcO3ahyvfAysqCJ0/U1xW9CYSGhrN5c8zvqVLl1cbEYjGRkePYsmWP2uujojag\npaXFxImRKjt1CoWi0sWF2iCXy1V2TXR1dTE0NOKzz2by009zmDfvf8pz5uYWbN++n1atPDl79s2r\nnRGoGfb29nh7ewdW55pqpVH5+fm9N3jw4LrRVRQQeAsZMiSMr776nEOHjjNoUD9yc/PR19ejdWvN\nikOroqAgn5iY7Vy6lIC1tRVFRUUMG9afpKQUMjOf88MPP3P69El2795K69bNad7cjczMLJYtW8D0\n6Z9iatqwZmYCdYODQzO++upbli6dz7p1Wxk/PpxGjSwrveZVxSZ9fT20tbVRKBTlduUUCgUlJSVq\nVdKkUilFRcUUFRWhq6tLauoT8vLysbW1RiwWs2dPHDNnTla556tO2XVJTMwBOnRoy507SSgU1RJC\nUUFfX4+bN++Qn5+PoWHdyHN6eXmwevWm312rX+bYl5SUYmhYfZNTU1MTUlIecu5cAtbWlpw9exy5\nXEbv3kFq25eWlrJjxyYePEhGR0fCrVu3GTduFN27V3+n6s/C1KkfsXLlQiIiKt4xdnR04M6dW2/s\n7oaDQzOKi0spLS1CV1f9e9KkSVMUCgnp6ZnlPvPdu3fm+PEzdOigWiu4atUmwsPHUh/s2LGZoqIi\nRox4ubDt6OhC584diIgYwtKlawHYvXsbly9fwt6+ESdPnicr6yDt23eqlzEJNDyurq4tRSKRRKFQ\nyKpuXc1go0WLFt2tretWSk1A4G2joKCQqVMjOHXqIvr6nXjwIJ87d44QFBRc9cWV8PTpE+bP/4HQ\n0AEEBLRWas2fPXuR5OSHTJwYwcSJ41mw4FusrQOU1xkY6DNuXBgrVizigw8+A8p2RLKyMrG1tVe2\ny8nJ5t69O2RnPycnJ5vS0lJkMil5eXmkpT2md+9+gmHTa6RsBXMGy5Yt5NGj1CqDjT9y714yjx+n\n0bixncrxtLSnar05vv32F+ztbdHT00NfX4/CwiJMTU24cOEybdp4Ex9/mk8+mVzuOiMjQ7KzczE1\nrbuaiKtXyzyk2rVrTXp6JunpGTRtWn1VqRs3bnPo0DFCQoK4dOkanTu3r5Pxbdu2B39/PwoLC0lI\nSKRTJ1/i409hZ1dzk8WQkHfJy8vjzp0kPv/8A+bPX0nnzl0xNDRCKpVy7Nhhbty4hlRaQnFxIX36\ndCMwsOx51qzZjK1tI5X+3jbF7bKFEwmVGQs7Ojqwd+9JunSpngN7QyGTyZDJStHR0UYkqjjR5P33\np/D11/9g0qRR6Onpkph4g+PHT6Onp4eOjraynVQqZcWKDXTrVmYIWR88eJCMTFai5oyI5OQULl++\nxpQp75OdnU3Pnr1IS3tIkyZNmTbt7fR++asyYMAA91WrVvUC1OeO/wGNgw2RSKQ9e/bs2jkqCQj8\nBbC1tcHY2Jj09OHMmlW2cvr1165IpRXL4mpCdPRypk0brdKHVCrl3LkEJk8ew969R2jTphXW1lbl\nrtXT08XYWI9ff52DXA5aWmIUCgUODi4EBw9BJpPx7bdf07WrHyYmRjRubMr8+SsYMGAgz57dx9fX\nG7FYMO58Exg7dhI///yNUlNfU8LDh5GQkKis+1i3bhvZ2dl07+7P3btJ5drb2FgzalT5CULjxnak\npDzC3t5GbZF1Xl4+RkbVX82vjFOnzimLZHv37saSJauZODGyWn2UlJRw4MBRpk17H4VCwS+/LPk9\n9aksfSUjI5OjR0/h6OhQadG6QqH4XeWoTBHrwYNHiEQiXF2dUCgULF++FjMzU65fv82ECdVKa1bh\nhX9KfPxpACIjh/Hjj99gbGyCTFaKn18bhg7to/Y7xdzcjKysbOV3QX5+AVpa2uXa/dkJCQklJmYH\ngwapT1W7cOHyGy3BKhKJSEl5TM+enXn2rOJaWy0tLWbMmMmmTetIT39KaWkRH344QaVNfn4Bixev\nYdKkD7C1taugp9ojl5eUqy8BaNy4CQkJd2jf3pfi4nwsLc0xNbWgtLSYR48eYGb2ZqqCCdQMb29v\nrRYtWgylroMNT0/PPsHBwYL1sYBAFZSUFHPjhjGzZhmSn1+2nPjFF6Y4O98kOLhmhltlObLychOL\nhIREAgI6kJX1nNTUDJo0caCoqFitw25ISPkUjOPHz/Hzz3MoLCxk5MhglVVvB4cmXLt2lYyMp+Tk\n5PLZZ9WW1haoJ/T0jLh8+SqtWr0soXv8OI2YmDgABgzog42N6sq2nZ0Ne/bEkZb2FG1tbVq2bE56\neiZ37tynQ4e2bN0aw+DBQTx7llWpH4yXlzsnT54lJKQ/K1asK6eUU1paWmPTvYp4keK1bt1WTExM\nSEi4yuPHaSpGd1WxfXssw4cPVPb3/vvvsXbtFt5//z0A1qzZQmRkKOvXb8fNzRljY/XF2L/9thKx\nWEzr1t506NCWPXsOMG7cKGW/Y8eG8cMPv2lsPFcVnp5uXLlyjZYtvZg6dbRG11haWpCR8UwZbFy8\neIWAgDdzdb82NGnSlGfPyk98AW7duktBAUyfPrOBR6U5YrGYp08zMTDQx8KiaaVtLSysmDBhGgCx\nsTvZvDmGIUNefqevXbuNTz75P4yM6lZl7VVOnDjKvXtJvP/+pHLnhgwp+x6YM+crhg0L4ujR03h7\nt8LbuxUXLpwTxITeMkQiEZ6enhpvQGhcIO7h4dHfy8tLWNoUEKiCESMiuH37frnjUmkpJ07Eq73m\n4MF9xMbuqrDP+/fv0LRp+dWqhISreHl5cPnydXr3DsLJyZknT56q6UE9/v6+REQMYeLEUeXSa0aP\nHo6fnzd2djb06zfgLy+5+SYxYcI07t5N48aN20BZIfLRoycZO3YkY8aMYOvW8hLoGRnP6NKlA++/\n/x4REcPx8WlJnz7d6d+/N35+bZFIxMydO58DB46yb99hzp1LqPD+2tra2NpaY2xspFKI+uRJep1L\nyj57loWxsRHnziXg6NgUHx9vfv31v9VKUSopKeH58xyVXT9DQwNlUPTgwSM8Pd0wNTUhImI4S5ZE\nc+3aLVasWMeuXfuAsh2NlSvX4+3dnAkTIsjNzWPJkmjatWtdLrhKT8/Ay8u9Dp4eAgO7cOTISYqL\nNS+Kt7AwU/n/8uDBY1xc3k5HZzc3T+7dSy53/Pjx84SEhPL8eRbjxkVQUFA/Kmm1pWNHP6ytG/Hk\nieYF/H37DiA//+X7cPnyVby8WtVroCGTyYiL24ujoxOtW6v3k3r69AkGBrpYWJiTk1OIm5snbm6e\nhIaO4uef53LmzPF6G59Aw9O2bVs3fX19jQqiNA42XFxc3NUVEAoICKjSrJkTgwd7MWdOAYaGCgwN\nFcyZk09i4hr27t1JaWmpsu2DB0l8//1sCgszycx8yE8/fcPcuf+hqOjllvrRowfZtGkN7dqpLiLk\n5uYhk0mRSCR06NCW+PhD3Lp1Q23+fU0wNTWmXbvWjBsXxsmTR8jISK+TfgXqhjFjJhIXd5KcnFyS\nkh4wYsRgxGIxEokECwtzsrNVTb28vNy5fv1Ohf0FB/flk0+mMHz4QIYPH/h7DULlMuqurk5cv14W\n8MhkMqKjNyt3D+qKrVtjGDSoH02a2HPt2k3s7GyQSCRqC9rVcfPmHRYuXMmQIf1Vjr8qUZuQcEX5\n+dLT0yU8fChPnjwlMjIUZ2dHli9fy8qV62nbtiUBAWXmhb16dWXcuPfUGhg6OjZVqy5UUyIihrNg\nwQqN3dMfPUpV8fuRSmVKR/e3jX79gjlypLy6mImJAadOxXP//l1CQvrxzTdfvZEBh0Ihp3FjOw4d\nimPDhtUq72VlyOVlvyOPHqVy5kwiQUGD6nOYzJ//A2IxDBw4pMI21tY2mJpacfToKYyNVY03tbW1\nSEq6wfLlC+t1nAINR8+ePc19fHyGa9JWo2BDJBLpO9VXtZGAwFuIsbEJkyfrc+RIIcuXXyYsLI2i\nogL8/HyYO/droqKW8OOPc4iL20l4+CCSkh6SkpJKUFAPhg0L4vvvZyOXyzlx4ih3715l4sRRmJmZ\nqtxDIpFgamrKvn2H0dPTxcREj27d6qbg9Y94ebnx6JEgn/um8d57o5k9+ydGjx6pctzCwpxnz56V\nay+RaK527uzsyP37Dypt4+PTkps3ywKYM2cu0qdP9zpPoRKLxWhra2NnZ0Pbtq1YtCiK3Ny8Sq+Z\nO3c+UVEbWLlyPffuJTN9+rhyZpsSiYSsrGwKCgq5fv02lpYWynNWVpb06BGASCTCy8udMWNGMnr0\nCFq29NJozC1aeJCdrT69pyaYmBgzZkwYmzfvYsmSaB4+rFjOVaFQcPXqTZo3f3Uno9qWWn8atLS0\n0NLSVXknli1bj0RiQJs2viQn38PDw4Vx40by22+/vMaRVkSZsto///kRTZpYsH37Ro2uMjQ05dq1\nW2zffoCPP/57fQ6QxMTLXLlyhXbtOuDiUvmOXUTEOHJySnjvvTHKY0uWzOfJkzTatGlBbu5zlQU3\ngT8vZmZmuLu7ayS1qdE3UPPmzXv16tWr8oRCAQEBFcRiMe3aGXDz5iays3OwtbXB3789kyeH06qV\nMyNHvsugQX3ZvDmGjh27MnPmF6xfvxMTEyNcXJowe/Y/uX//BoMHq6+VMDDQJzR0IHfulKVsBQX1\nxMOjftYEHBzs2bZtAwsW/KTxyptA/ePo6EyLFs3L1ej4+/uxdWsM69ZtU3oRlJSUcP/+A41Xx11d\nHbl7t3w6IJTVf7x4714EF7du3a2z1KEXxMTE0bz5yz7btPEmLGwIO3bEVnhNRkYmhob6REQMJzIy\nlH79AivcBRk0qC+fffYVYWEVr9ZWl5KSEp4+zUBPT6/O+oSyncbw8GGMHh1KQsIVFi2K4uzZi+Xa\nbd8eS//+vZR/5+bmYWxsWq7d28S4cVNYsmQtxcXFPH2agZ2dA6NHT8DIyJiMjHQsLMwxMTHGwcGG\nixfPve7hluNFnZOXlzu3b9/QyP179OgJHDx4ik8//aLSGqu6YOnS3xgwYCB9+2qmqBgaGs633/6L\nnTu38OBBEtnZmXz44Tisra3o2NGHQ4f21+t4BRoOBwcHjb70NXpDXV1d+3p4eAg5VAIC1UShUBAS\nMpOYmHucOXOJJUvWsm/fERwdm6Krq8t33y2kR48g2rXrgLa2Nk2aNOXUqfPY2DTC378d/fv3rLR/\nkUikVNOpT+ztbRk7NpS7d2/yr399zqNHKfV+TwHNUGc5UVRURErKYzp08GHz5p0AJCbeIDj4HY3f\nFyMjQ54/V78636tXV44cOaFyTCQS1emk5/HjNAoLC+nYUXXhzMjIkIIC9eldmZnPiI7ezPjxmqlA\nOTk1Y+7cr4iJ2U9i4o1aj1mhUPDDD79hamqMg4N91RfUAC0tLd59tw8TJkQgFotZtCiKHTtiSU/P\n5Pbte+Tk5KqkUsbHn6FXr+obC/6Z0Nc34KOP/sbChavYtGm3isy4QiFXBpuBgQHs36/eIO91kZLy\niKlT/65cBOjSxY+4uKoFfrS1tfnii3+hrV3/KmMzZnzEgAEhGrVNTLzEnDlfMXJkMPn5zzh0aDeR\nkS9V7dzdXbh+PbG+hirQwLRu3dpFX1+/yi87jX4ZXFxcnIV6DQGB6qFQKFi/vgg/P1M++2wI/fsv\nZ+bML3j2LI/Nm3fz/Hk2xsZGODm5KK8pLCzAy8udu3eTKC5Wp2VeHqm0/ncaioqKWbRoFZ98MpUZ\nM8aydOn8ahWsCtQfJibmpKW9FAVQKBRERW3gm2++wMmpGUVFxWRn53D69MVqrbbv3XuIwMAuas89\nfpxGkyaqvy+1MdpTx8mT5+jZM0DtOVdXR27fvkdKymPOnr3I8+fZrF27hc2bdzF16thqSUzr6eky\ncWIk589f4tGj2rlN37lzn7y8/HozNvwj7dq1ZsKECHx923DmzAXmzVtazgn+yZMMHByaNch4Xidm\nZuZMnPgBoaGjVMxL9fUNlLVHIpEIR0d7rl+/+rqGWY5u3XrwySez+O231ZSWltK8uRvXrl153cNS\noTpZ9Pv372bq1EgsLS1IT8+gZ0//cp9HuVxa10MUeE10797dwtvbu8otryqDDZFIJLK0tBRcwwUE\nqklSUgnjxumRny8iP1/E+PH6JCWVMHbsZMzN7Th9+gJyuYwHD16mqnTp0oNvv/0VJ6em5VZ0K+L5\n8+cap8bUlCtXrtGjhz96erpIJBIiIoayePGv9XpPAc0YNWos69a9FB7Yu/cQ/foFKguCZTI5ixZF\nkZ+fR4sWHhr3++RJRoXSslev3qRFC1UZ57pekHr27Dnm5uod758+zWDHjr3Exh4kJyePffsO079/\nbyZMiKixl03v3t2Ii1OvFqcpbm7OfPXVZ5w4cZb798srJNUX9va2yGQyJk8eo1IIXlJSgp5e3Xqe\nvMnY2trh4qL6jrdq1ZZr124q/+7VqwsHDrw5uxtBQQPx8+vE1Kkfs2zZekQiEVJpCfn5ldclvYnI\nZDIkEjFHj55i6dJ1uLh4sWzZBjIzX9aPZWfnYmlpytOnT17jSAXqCisrK5o2bVqlBG6VwYaurm6T\nli1bVt+qVUBAQC06Ojq8++4g5HIdxoyZhJvby0mbt3dr3N29cHQsi+8VCnj82IDHjw3UpssAjB8f\nwbff/srKletZuXI9y5at4cKFy3U6Zh+flhw8+HIiVlasXrcr2QI1Q0tLi6lTP2LBgtXcu5dMcnIK\n7u4vd8siIoYTERGKlZWlxgFBaWkpenoV6+IbGxuRl1e3k6HY2IOsWrURqVTKs2dZ6OtXrJ6Uk5PH\nzJmTGT9+FIGBXRg+fGCtJXft7W1p1cqLdeu21aofsVhMRMRwYmMP1qqf6nD/fjIlJaXlarYOHTrJ\nO+/0r+CqvwYtW7bh5s2XCzovFNveNKytbXB39yI5OYURI4L59tuv34hC6tzcHI4dO6JRrV5hYQGJ\nideRybSYOfMLgoKCsbW1VSqzPX6cxgcffIGtrTX379+t76ELNBAODg5V1nRXGWx4eXkF+vn5vd3V\nZQIC9YCjow5LlhQp5W+XLCnC0bFsAqejo8PIkZHY25eP4ydOnMauXQdRKGD3biv8/Ozw87Nj924r\ntQGHqakxX375KZGRoURGhjJ2bBhXrlzn+fPsOnmOPXviiIrawHvvDVU57uBgw1dffU5JiWbpXgL1\nR6NG1nzxxb+5fTuVoiLVCYqeni42No0oKdF84nL79n3c3FwqPN+yZXMSEsryrqXS2qdEHD58HBMT\nY/r378WPPy5i9+4DFUro3r2bpHTXrmvatPHG1dWR/fuP1KofkUhE585+LFq0qt4FFUpLS9m+PZYh\nQ94td+7hw1Scnd9Ofw1N0dXVJS+v4HUPQyPefXcwmzfv4ciRE4wcGcz8+XOZO/c/dfIZqylRUUso\nLs5g7tyvqyxcNzIy5quvZhMS8lIdTyqVKmu5DhyI5+uv/8v8+cvx8vKu13ELNBxWVla1DzYcHBx8\n7ezKm4kJCAhUjkgkIjRUjytXSrhypYTQUD2NVpb19PQQi8WkphowaZKpMg1r0iRTUlM1S4kYMWIQ\na9Zs4eTJc5w5c5Hjx8+wceOOGq2UPXqUxtixYeVM1Lp160R4+GB++OG/GqmnCNQvYrGY0NBRdOsW\nyP79R8udz8nJ5ckTzbxSrl37o3Sq6i6boaEhubllngWFhUXEx5/i6tVbrFq1iaiojaxatZmEBM3y\n4leuXA9A587tsbAw55NPphAePqxCx+Ft2/bQvXtnjfquCb6+bUhKSql1DUrr1i3o27cHe/cerpuB\nVUBU1AbCw4eV+24pc1gXRCQB2rfvxNmzCRQWFrF69RZ8ff1e95DUoq2tzYcffsbly9fZsmU3bdp4\nERwcyJdf/v21pFVJpVKKigpo164177zThS1b1lV5jZ2dar3SkCEj2bGjzBgzOLgPJ0/G4+3tXc6H\nQ+DPi6enZ2ORSKQ+5/Z3NAk2GqbSTUDgLUQkEuHkpIuTk261ctprO9HR1dWlZ88ATE1NMDIypFEj\nS5ydm3HixNlq9ZORkYlYXPG4LSzM6dbNj5kzp/Pbb7+wefM6fvhhNr/88i0//jiH7ds3qRgUCtQ/\n3bv3Rl/fjC1bYlSOT5oUyfbtsUrJ2spo27YVZ868lFUtv8tmiVgs4eefl9GokT3Ozq2ZN28J06f/\njRkz/s706bO4d++x0oOjIl7sinXv7q/Rs5WWlmJnZ13vaTAdO7Zl48Ydtf4cNm3ahJSUh3VePP+C\nkyfP4eHhquIR8oK9e48wZMiIernvn40ePXpz/fp9duw4yKBBI/Dz0+x9ex1YWFhhZ9eEKVPGcPHi\nFQoKCtDX1+bbb//d4N+lCxf+RFBQD6DMqPLy5QQuXy4vt1wZtrZ2NGnixKJF0chkMnJynvP119/W\nx3AFXhPt27e38Pb27lpZmyor6czNza3rbkgCAgJV8fTpE3R0tLCzK2DhwmwmTSrLYly4MBs7O83T\nATw9VVemly6NJjx8WAWt1WNlZUlBQSHFxcUVOhCXlkoJCupO69YtuHMniZ49X66yLl0azdWrl9DX\nN2LgwJC/fEpHQ/HuuyFcuZLA4sXRjBsXhkgkwsjIkPHjR7FkSTSurk6VXu/s3IwDB17ujry6ywYw\naZIZcXGRdOhQ8cr52LGT+c9//oGrqxMSiQSFAuXOnJ1dASIR7N9/hN69u2n8XNnZOZia1v+KaMuW\nXujp6fHTT4v44IMJtSp+b9++LUuXRhMZGVqnMqXPn2eTmHiD8eNHlTtXVFSMlpZuhbtDf0VmzPj0\ntd4/O/s5sbE7sbW1x8OjOdbWthVKRWtrlwXT7u4u3L2bzLhx71FUVML//vcNn3/+ZYOMd/Pmdbi5\nNVXZ0f7oo/EcPnySfft206qVD336aFYPFBQ0iMDAfqxcuYjmzYX0qbcNBwcHrK2tWwMbKmpTabAh\nEolEc+bMEYINAYEGxNjYGJFIhEgE/ftncOZMWYDxYoJWE4qKipFIJDWafISHD+Prr3+gcWNbxo8P\nL7eqfP78JYYPH4iOjo6KqVtxcTEymZwpUyKRyWSsWbOFgIBAfHx8a/YQAtWiZcs2GBoasmTJGmXA\n8eK/V3nw4BGJiTdJT89EIpEgEono3r1jle+atbVN5Q2AwYNDOXLkJD16BLB7t5VK4Ny/fwZPnqRX\nqHilDhMTY41rkQoLi5BIxFW+8wqFglOnztOuXSt27dpPTk4uUJaWlpOTS2zsQfr1C9R4jH/s++jR\nE/Tv35uVKzcwbtx7NernVWQyGfn5BaxcuZ7Jk0erbbNtWyzDhtX+XgJ1h0wmIzU1mWbNrIiL20Fm\n5nPy8wsZPDgUT09VZ3p9fUPS0zPp3Lm98piuri7+/j7Exu6kb98B9TrWNWtWEB9/hP/+9/9UjotE\nInr06ExAQHsWLIjSONiAsvFPmDC9rocq8AYgFouxtbWt9Aehqp0NW1dX1/L7swICAvWGvr4BxcVl\ntRUiEdjb1764MSnpQbmdDk15UWBsbm5OQUEhxsZGynPLlq3B1dVJrVFcXFy80slYIpEQHj6E1au3\nIJFIaNXKp2YPIlAtnJ3dGDBgGPPmrSA8fChGRgbo6ur8PsG+wOXLN2je3Jvu3YOUYgUFBfns3bsb\nfX0Tli5dj7a2GJDw3Xej+PTTsvq9MrGDqj07vLy82bp1PZ6evf+wM2LKjh1J1a710dLS0qjQ/c6d\n+8TGHkRPTw9TU2NCQvqrBMmlpaVcunQVhULBmTMX6dChLatXb6JVKy98fduo9PXbbyspLCxCX7/6\njuDR0ZsYMmQADg72nDxZO+fq48fPcOnSVUxNjdHX12fo0AFqA6mMjExEIm1sbYVayzcJCwtLcnOL\ncHRsqvwuVigUzJu3kunTP1HxBnnvvTH89NM3jB8fptJH69YtWLx4bb0GG1FRS2jWrBGenhV7a3z2\n2b8JDx9db2MQ+PNhZWXVqLLzlQYbzZo1a9G8eXMh2BAQaEAKCwuQSOrOiRkgI+MZtrbV26QsLi5m\n795DpKQ8Jjx8OBcvXubEibO8804PZRuFQkHXrp3UXq+lpVUuTWDUqBAWLIgSgo0GxNPTi48//pzl\ny38jOzuLx49TWbJkHV279mTWrNBy7Q0MDBk8eLjy76KiIvT09FAoFPTtW1Zj4eiomdgBQGjoKM6c\nuQqomgBKpWIyMp6jUCg07kssFlNQUEheXj5GRoZq28hkMmJjDzJt2vsApKY+4eefl+Dv74eXlztG\nRoZs2RKDk1NTRCKYOnUsQLkg4wUjR4bw00+LcHNzJjc3j8LCQvT19Rk9uvJ6iLi4eFxcnJRO4q6u\nTixZEo1CoSAkJEhtnQWUfaZkMpnSLyQvL59z5xLIzy9gypQxVf4bbd68hw8//HuV7QQanunTZ/LL\nL3OZNm20cpdx3LiR/Pjjt3zxxb+VAbGOjg76+urfbz09nd/9LOq+bunKlQQuXbqAs3MQyckPefYs\ni7t3k4AyuWt3dxeys3OwsbGhZ88+dX5/gT8vpqamlU4wRJUVrgUEBPz9wIEDs6vjOisgIFA7zp8/\nw82bFwgK6lVnfaanZ3LmzAX69+9d7tz//rcQExNjjIwM6du3B1ev3uTmzTtIJBL69OmukrO7aNEq\nJkwIByAz8xmHD59QK7kJkJycwvXrt+nbt6fK8SVLVpOXV8g//jH7jdS7f5spLS2ltLQEAwP1E5n6\n4uLFs5w4YcesWWV6I0uWFBEaqkd8/EFkshzT2fXzAAAgAElEQVR8fFpq3FdhYRGbN+9k1Cj19UfH\nj5/BwsJcRU1LLpeTmHidGzfukJubh0wmY8KECI3vWVpaytOnGTRuXLZbEBMTh6WlOR06tFXb/tix\n08TExPHPf85ET0+11kkqlbJ0aTT+/h3w9lY1RkxISOTYsdMUFRXTp083zp+/jJ6eLq6uTrRvX3WA\nfvZsAgqFfrXSWwQaljt3bhIbu51Ro0KUx1JTn7BjRxyffvqFcoFmy5b1NG/epJwK4JYtMQwZEqGy\nE1JX/Pe//4/WrT04ffoio0YNZdeufXToUGYu+/x5NhcuXKagoJR//vNrhHmhwKt89913dz/77DM3\nRQVBRaU7G+bm5o2EF0pAoGFp06YdO3duJiio7vps1MiS27fvqV1FDg8fRkzMAfr370VMTBz29jaM\nHRtWrg+ZTKbiqWFhYU5GRmaF92zWzKGcsVlOTi5aWlr06tWFo0fj6NFDWB1rSLS1teu0SFlTfHza\n06aNgqAg1Z2RgIAerFixiIyMLHr3rlTMRIm+vh65uXnI5XLlxCwuLp7k5BSaN3fnxo3b5Tw6xGIx\nrVq1oFWrFjUav7a2tjLQAAgKCiQmJo61a7fw9GkG1tZWSKUySktL0dLSomnTxsyaNZ0NG7YTETFc\npS8tLS0mToxk+/Y9XLhwGQsLM3r16sbVqzd48iSdadPep7CwiOPHT1NcXMKYMSP/OBy1FBQUcvHi\nNT777J81ekaBhsHV1YN27ToRHb2VsLBBiEQi7Oxs6N+/B3PnzmbmzL8jkUjo128A33//H6ZOHa3y\nnZ2fX4ChoVEld6gZW7eup0uX9nh7e9K5c5k0sEgkUqnDu3XrPp988rEQaAiUw87OzhgwA7LUna80\nV8OktpasAgIC1SY6ejkhIXUYafyOlZUFubnltdqtrCwQiUQYGxsRGjqQLl06qr3+zp37tG3bSvm3\nSCSieXN3li6NrvCeL1JBXrBp006GDQumRQsPEhPr1uVc4M1GnQy0WCxm7NhJpKQ8qZZx2bvvvqP0\n5zh16jxSqZTRo0dgbm7K7dv3KkyxqkuCggJ59uw5M2aMJyioN8OGBTN2bBgREcPp3t0fU1PjSmtS\nBg7sx+DBQfj4tGTLll3cuZOk3M3U19fj1q171Sooj47ewqRJH9T6uQTqn06dutCzZxCrVm1RHmvS\nxI7+/bsxe/b/o6SkBH19A4YMCWPnzgMq17Zo4c6FC9WTMK+KtLRUUlLuqey0KRQKFcnmss+nRAg0\nBNRib29vDFRYt1FpsGFsbCwEGwICDcizZxk8f55B06Z1a29z69ZddHV1Ubd+oGnO/NWrN2nRwkPl\nWNeundDR0VHrkiyXy1XSpKRSKSKRCENDA0QiEQpF/TorC/x58PXtyPXrtzVu7+BgT6dOvuzYEcul\nS4m8804PxGIxnp5ueHi41kqqtjoYGxshEokwNTUuly4FYG5uWunun7GxEY0b2xEWNoTQ0Je7MSdP\nnsPXt025YL0ijh8/S9u2HTAxMa3+Qwi8Fpo3b0HTpk7cunVXeaxxYztGjRrEr7/OVbZ5/jxH5Tp3\ndxeuXUus9f1TUpL55Ze5/PzzHDZujCIsbLDK+Y0bdxAQ0EH5t0QiIS8vt0bGsAJvP7a2tvr29vYV\nTlwqDTYMDAyEYENAoIFYuXIRK1YsZNgw9TUQtcHMzJTHj9PUmouJxWKSk1M4fvw02dm5Ffahp6en\ndI1+FX9/P6VL8sGD8Rw+fJwtW3Zz8GA8fn5tlYHI/v1HVJyfxWKRSlqWwF+XpKS7NGvWpFrXeHq6\ncfLkObp2fflOyWQypNI3J4jt0SOAuLhj1b7u1q27+PlpJqJw8WIiGRl5BAb2rfZ9BF4vwcFD2bcv\nXuV72dzcjDZtmrNjx2YA2rbtwKpVm5VtjIwMychIJTm5anPOipDL5Sxc+DMjR75LRMQQwsOHqAS2\nCoWCvLx83NyclcdEIhEjRgxg8eJfa3xfgbeXRo0aYW9v71LR+UqDDX19fSHYEBBoAORyORkZTxg7\ndkSNJDarwtraiq5dO3HkyAm15z/5ZCppaels3bq7wj569+7KoUPlJ07Ozs1ISXlISUkJCQlXadq0\nCV26dCQx8QY7dsTyz3/OYdeufaSnZ+Lk1Ex5XevWnpw9e7L2DyfwpycpKYlt2/YQFbWBVas28tVX\nc1m2bA3Ll69lwYIV/Oc/PxAVtYGVK9ezevVGsrKeA2BoaKBSCH769AWV1dj6xtbWmm3b9lR43sTE\nmLy88qmLVaHpzsylS1dJSnpCZOT4at9D4PUjFosJC4vk11+XU1RUrDzetm1LUlOTiY5eTkZGOp6e\nLfnll2Xk55fJoI8ZE8rWrRurda9Xd5/T05/SvLlrhTtnt2/fw929/LyxzOQ1t9qS1VVRpnxY8W+P\nwJuPhYUF+vr6Fbq8VrpHq6OjU148X0BAoM45d+4kOjp1V7h75sxF8vPzkUgkSCQSkpIecO3aLZo1\nc6B7d/9y7Xfv3o+dnU2FylJQViT7x5qPxMQbHDwYj1gsZvHiVVhbW+LsXBZQfPjhRORyOUVFxeTk\n5GJjo5rO6eXlwS+/LEOhUBAQ0L32Dy3wp8XMzJiIiCHKv6OiNigLq+/fTyYpKYUePQKAMinYmJgD\nZGfnlqvNuHXrLpGR5eV86wO5XM7du/cJCal8J1Iur1jxsTYcOBBPcTGMGTOxXvoXaBicnd2YMeMz\n5s79Dx99NF4pejB8+AAyM59RWirl2LEz+Pn5s3jxWsLDB/8umyylpKREI6PW4uJihg4dSKdOfvj4\ntOf06RMMHlyxOMfZsxcZOlS9l0dpqRSpVFojg1i5XI5CoSinQrhs2QLS09N55x1BRe3PikQiwaiS\nYrlKgw2JRNLwsiUCAn9B1q1by8yZEzRqq1DAzZtludkeHtlqnZ7PnUtgwIB3kMmkSKUymjVzoF27\n1nz//QKldG1ZX2XuyZmZzyoNNF7Qs2cAixatwtvbk8uXr+Ls7MiMGRWvqorFYgwM9NWa/kkkEj78\ncDzR0duFYOMvTGFhAVpaFUsgOzo2ZfPmXTx/nkOTJna0b++jVJv64wqrOof0+mLt2i0EB/ctF0S/\nyh+LbOsChULB6tVbaNmyLd27l5eyFvjzYWpqxvDho4iPP023bmW+RSKRCCsrSwCGDRvAjh376dmz\nN+vW7WTgwD5YWppy9+4tmjf3rrL/xYt/5f33R2JoaIipqQ4ffDBW+TmJjT1IauoT9PX16N27G/fu\nJZOR8Qxd3fI1SAAjRgTz3/9+yd///qVKwFFSUkJubjaWluo/D1KplLlzvwZE/O1v/0/lXGlpMe3a\ntWTmzGn8+99zGlyaW6Bu0NHRqTCmqDTY0NK0Ok1AQKBGZGams3TpbwQG+rNy5XoCAvwqledUKGDN\nGltmzSr7Mp4zR5+wsLRyAUdBQSE3btymd+9ur1yroHFjO+LjTynTnI4dO0WnTu019hzw9HSjUSNL\nbty4zcSJkbWe2CkUCoqLhbqNvzIZGencu3efqKgNymOvFluLRCJGjx6BtrYOq1dvVPGb+KNpZEOR\nnp6JlpaqHK46Dhw4Steu6tXdakJpaSkLF64mLCwSFxf3qi8Q+NPQsmVr9u/fpQw2/khwcG8WLFjF\nzJn/x8aNazA1tdX4HVAopHTt2okFC1YQEtKfpKQHPH6cxsOHabi4NKNv357k5uZx4MBRXFyaVbqA\nZG5uRkRECP/+9//xj3/8RykQMmfOv7CyMqOgoAQHh6a4uLjj6OhMaWkJubm5rF0bhbNzE+ztncv1\nqVAo8Pf3RV9fh6tXr9C+fd19ZgQaDm1t7ZoFG2KxWNjZEBCoJ1JSklmyZB6TJkWgr6+Hv3974uLi\nWbZsjVqfCyjb0Zg1y5D8/LJJ/qxZhrRrZ4qnZ7ayTUFBIU2bNiY+/pRKsCESifjyy0/Zvn0PK1eu\nRyQSMWnS6GqP29LSAn//usmL37RpNwMGDK66ocBbi51dY5o1cyA8fGiFbV6s8KpTfHod7Nt3iMGD\nK0/5KCoq5v79ZJXPoKaoC+KlUinz569k8uSPsLa2UXOVwJ8dAwOjSlOjBg9+h+jo5bz//uRq9atQ\nlAXmkyePZvXqTdjZ2dCsWROsrRspi8CNjY0YPLhyyXWFQsHPPy+lUSMb3N09KS4uQkdHhx9//Iah\nQ/thZ2eDQqHg2bMs7t9/wNWrZ9HS0sLQ0ICwsGC2bNnLqFHlx/7idZfL5RorsAm8edQm2BD+rwsI\n1BOlpSW0bNmCrCwLsrLAzq6AwMAuHDp0jBUr1lFSUkJpqZSxY8OqVTS+f/9h/P39CAlRPxkaOLBf\nXT1Crbh69SYWFta4uXlW3VjgreXy5Yu4u5df7fwjqalPsLW1rrRNXacsVYRMJlebGvgqGzfuIDR0\nUI36/+NzKBQKFi5czaRJHwqBxltM166BnDx5vsLdDVtba2xsTPn11++ZNOmDakzMy9INxWJxOZPJ\n6pCQkEhgYF+VtNfExMtkZ2dx4MAxQIxIJEYkKguYpVIpMlkpWloSbty4z/jxUyroWcKJE+fZu/cQ\n06d/XOPxCbxeKsuGqirYqDiRVkBAoFbExu7G2DgCPz9zABYuzKZ//wxlIaxCoaCgoJClS6MRicQM\nHNgXD4+y1KmXaVT5eHhkq/Qrk8kxMjJ641eIrKws2LfvKFlZWTRu3BQHh2a4uroLplF/MU6fPs6Q\nIVU7yd+//wA7u4on2oWFRXUqslBbpFIppqYmddLXpk27CQ0dhY2NbZ30J/Bm4unpxZYt6/Hx8Vbr\niQQQEOBHaekxLlw4i5+f+qDkj9TVVO7y5RtMnz5L5dihQ/uwtLQqd/wFcrm8yoJyiUSLmzfv8tNP\nC+tknAKvB8kfK/9fodKEV7lc/uYIlgsIvEXI5XKMjDyYPNmc/HwR+fkiJk0yJTXVQNnmhQHetGnv\no6urw759h7h27SZhYWkcOJDBgQMZaus1unbtSFTU+gZb5a0pNjaN+Oij8QwY0J3GjY158OAqCxf+\nRGlpKQUF5f08BN5OiooKNFK26dTJl2PHTlcou/nkyVPs7et/Ml5YWKTWxPKPVPK7Wy2uXLku7AD+\nRRCLxXzyyf+xdOm63x271XP3bgq+vpqnstaVIppYLCpXJyWTlVLZVFKhUPx/9u47oMnj/wP4OwHC\nnrJlC+LAiaLiHqiAoohbcQ9wdg+t39pqq7WtddWtCAioOMCJAwUEEVGQKYqCbGSHTdbz+4OfVGQl\nISGg9/qP5J67Q8m45z73+bT5+h45cgzCwiJQUVHearsrV87jn392IyjoOqnR1AlxW3ljbPXWJ4/H\na/mvnSAIoT179gRaWup8t5eWlsKyZfNx+LAHeve2aHRG42Oamt3Qv38fpKVloEcPExHMVrxkZWVh\nZGQAIyMDpKXlYNeu7dDQUAWHw4OFRS9MmTKt0+/SEMKJi4uFmZkhX21pNBr69u2FnJx8GBrqN3qO\noihcv363Q9Levnz5GoMG9Wv2OTabjaqqalRWVqOmpkboMSiKakgbHRHxDD/8sF3ovoiuRU5ODu7u\nX+DSJT/Mm+fUbJuSkjJUVJRDVVWNrz41NXWRl/eu1Z1BfpSVNf7cKSwsgJqaMsrLK5CRkQ5jY1Mk\nJSUgIiIUtbXVKCwsAI0mhV9//aPVfgcOtIalpQXOn/fGqlXrGx6vra3FzZuByM3NApfLQf/+vbB8\n+Wykpqbh6NG9kJGRh7v75nb9ToTocFpZIbe12CB16QlCDC5c8MEPP2zE0aNMuLnVp7E9epQJPb3q\nJm0pimqoijxrliMOHDiB5csXQlW15ZqbAwf2w717oV1isfGh6Oin2Lr1C2hrawIA3rx5i/37d0FN\nTRPz57tCUVFJwjMkRKm4+B20tLrx3b57d13k5OQ1WmxQFIUTJ7zh6DgJysri//uo/zyl4a+/DoPB\nkIGammrDczIy9YdhFRUVIS8vj8DAW3Bymipw1rYJE0YjMDAIXC4Pq1evb/sC4pOiq6uHyspaUBTV\n7N/Opk0r4OV1DOrqWli8eEWb/c2evQAHD+7BypXzhZpPfbrlS5g0qfEB8jt3bmLMmGFQU1PFwYPH\n0KNHT9DpbEyfPg4xMYngcHiwth7C1xi//rqnyQ4Il8vB8+fP8NVXjdPCW1iYwcLCDOfOBaKqqpJ8\nLnQSbDZbuMVGa6sUgiCEZ2jYHVJSdDg6FuHJk/oFhp5edbM1M0JCIjBiRP0btq6uNtauXYrz5wOw\nbFnrHxwdVW9AlPbv39no5x49TNCjhwnKypg4ffpfdOumg4ULl0lmcoTIjR1rh7//3ok+ffhL4cnj\nNf3ydfVqEMaNG9moOr04RUXFQEqq/qBtQMDNVg/cpqam4cCBE3B1nQMNDf53Mg0N9XHz5l2w2Wix\nbgHxaZs0aSrCw6MwenTTNLBycrJwdXWBt3cAX30xGAwMGTIcfn4BWLBA8KQFFy5cg4PDrCapdktK\nihr+rlesmI9Xr9Jgbd0fT57EIi0tG1999QPfYzQXaqWoqAQHByd4eV0CjQYsWDCj0S63gYEusrIy\n0KtX03TxtbW1yMx8CwAwM2u5WjohOq0tNlo9s8GtD8YjCELE3oed02iAvn419PWbX2hkZeUiKysX\nfftaNjwmLy8HOp2OysqWzzUUFRU37A58CtTUVOHq6gJ5eToePQqT9HQIEZGSkoKengHy8wuafb68\nvAKJiSkNP798+RoWFqYNP7NYLBQXl6Jnzx5in+t7yspKcHNbBm1tzRYLn71nYWGGdeuWIyDgFkJD\nH/E9RlxcEng8OjZv/ra90yW6qAEDBuPly/RW23C5LNTV1fHV39ixk8DjCXcDisPhNlvTg6L+C9FX\nVlaCtXV/HDvmDTm5bti48RuhxvrY8OGjsGnT95gxYx6uX7/X6DkdHS3k5mY3uebevSDs378bKSlP\n8eJFNPbu/Q3nz59t8bwXIRosFku4xQaLxRI+6JQgiBbl5eWBySyHl5d/i22qq2tw6dI1uLrOafLc\nzJn22L//OO7dC8Px4944fNgDZ86cg6/vJXC5XOTnF7SZJrQrGj/eFo8fR6Curg4PHtxBSUmxpKdE\ntNO8ea64cuV2k8dZLBZu3gyGv/9VPHoUjczMbOTm5jfaIQgOfgg7u3EdNte0tAxoamogISEZ16/f\nRVlZ6wdaAUBGRub/01fL4+jRM6ipqW21fXV1DZ49S8aPP/4CZWXRZLMiuiZLy7549epNi887OEzA\n9u1bcPfuTb6SFgiruVwjWVkZUFFpWulbX18X+vrdRT4HIyMTyMgowscnEPv3n8a2bXugoaGGnJz/\nFhs8Hg9//vkbeLwKrF27GGPGDMfYsSOwZs0iWFrq4/ff/4ewsPvkcLkYcLlcVLZyB7TVxUZNTU2F\n6KdEEMTy5Wuxb99JVFQ0Xc/zeDzcv/8QJ054Y/Vq12bDoVRUlLFlyxfo2dMMixfPxrp1y7Fs2XxM\nnDgGe/ceQVZWLnR0Pr3wCzabjcTEJBw7thcMBhtXrpzFP//8jjNnjjdaePB4PHIXq4tgMBiwtR2D\niIgnDY/FxSXh9Glf9O5tge3bv4WCgjzevHnbpHZMbm7Tw+Li9OhRNMaOtcWjR9Hgcjmwt5/A97U2\nNoOwaNFseHj4IT4+qdk2794V4tChM1ixwk1UUya6MEfHmQgObnlHTFtbE19/vRqysmz4+Hjw0aNw\nOxvNZbPy8/PC9Ol2//88D4GBQYiPT4Kj40RcunRO4DGqqiqRnv4aCQlxSEt73eR5Fov1/0kTamBq\naoBhwwZBWVkJxcVFDW28vE5iypSRsLEZ1OR6ExMjrF+/FEAFjh/fh82b3XD16iWRfk4cP34Q27Z9\ni/j4WJH12VWUlJSgpqYms6XnWw1iq66uJosNghCDXr36YNeuvTh0aE+jx1+8SMWDB+GwsxuLCRNG\nt9oHjUaDkZFBo8d0dLSgrKyEurq6Djks29FkZGSwd+/2hp/fh5eVlTFx5cpZVFfXAqj/YCwtLcec\nOYvQu3fTeF6icxk7diL++us39OnTE+rqaigvr8CoUcNhZVWf7nXgQKtmr5OR6di6GrKyDBw75gln\nZwdoa2vh/PkAgUK4lJWVsG7dcty9G4qAgFuYObNxgc34+BdYs2Y91NT4P99BfLrodDpGjRqHsLDH\nGDOm6dkNAJCWlkb//n3x+PFZcDicVs8mDBo0BF5elwHwwOXyMHhwXwwY0BfFxSXIzs7DgAFN3ysr\nK6ua3WFjMKQb0jt7eV2EoWEP1NWxQKfT0a+fJR49CoOt7Zhm51FTU4MnTx6hrKwUgwYNgZGRCf76\n6zf0798L8vJyKC+vRGDgBaioqDdUS2ezWXj58gWWLp3TKKlE9+6aOH36CIYPHwUajd3kM/FDNBoN\n/fv3Rf/+feHldQE6OorYs+dX9Os3EPb2Tk3S+grKwWEGzp3zxvHj/2LiRDs4O4s/O15nUVhYiNzc\n3Ba34Vr9l62oqCCLDYIQk19//QkzZ05p9Nj9+w/h7r4MFhZtV1RuzuvX6TA1Ne6Sh8PbQ01NFS4u\njnB1dYGr62y4us7Gxo3L8eRJCE6dOiLWEANCNDZt+haenhfB4XAwYsQQ3L//sM1rOrqWzKxZjujW\nTQOmpsbg8eq/sAnDzm4smMymIVipqekwMjJp5yyJT8no0ePx9m0eSkpKW23HYMi2eQja1nYMNm36\nDps2/YAvv9yCBw+i4OFxAY8eJaCigodjx87Czy+gUajfo0dPMW7cpCZ9KSur4cqVm6AoClJSUpCS\nosPAoH6XUUVFCZWVLX99zMvLRlRUGMzNdeDpeRJMZtn/L3jykZqagYKCEsjISIPH+++Qt6KiErZv\n343z568BAEpLywDUv5asrXvh6tWLcHJquzjohywtzeHmthgaGrLYu/d3nDp1BExmmUB9fMjAwAjf\nfLMVw4fbIikpDteuXRa6r64mPz+/Jjc3N6el51v9yywvLyeLDYIQA0/PE1BRkQeTWQFNzfq7NE+e\nxMLGZlC7FgoxMfFQUmoaR/s5otFomDFjCrKycrFz5zb88MPPbR7oJSSHwWDA3f0LHD16ECxWHZYu\nbTnLE1C/sG6pyrK4fFioz8fnIpYtWyB0X926qePZszhYWw8AACQnv4K19fB2310lPj1ubpuxf/9u\nrF69sMU2wlQJ377990Y/T5vmjMLCAly86I3hwwfi3r0IhIU9wty5K5tcu3z5Wnh4HEVVVTVoNBp6\n9uyFsLC7mDfPCcrKisjObnpw+z0zMwtoaekjMPAuJkywg6qqGg4cONaoTWVlBfbv/xNBQdexZs0G\nAPW7OMrKyigsLMaRI14wNTXC4sWzYGxsCDc3V4F///d697ZA794WYDIrcO7caVRW1mLatJmwtOwj\nVH+LF6+Ar+8ZBAXdRM+evYTupyvJzc2tAFDY0vOtvquVlpYW1ta2fpiNID41XC4X4eGVCA+vFMsd\n8djYp1BSkgaPx4OR0X8H6V68eIWhQ5vGmgrC0LA70tMzkZT0sr3T/GQYGupj2bLZ2L37l1ar8hKS\np6Oji5Ejx6F3757o1k2jxXaZmdm4fz+8SRhSR3n48DEGDLCCnJzwi9dp0yYjP78A9+7VZ1d79iwe\nEyYIdmeW+DwwGAyYmJgjJSW12ec5HA5kZFqv0s0vLS1tKCmp4e3bInz11Vb8/nvzBfnodDo0NbVR\nUVEJiqLQp08/9OkzCPfvR8DY2BDZ2emoqWlaN+q95cvXYsuWXzFy5Nhmn1dSUsbWrb82LDTe699/\nEK5fD8Hu3f9g2jQXHDrkgaqqlsdpTks7oqqqypg3zwkrV87FrVsBSEqKF6hfAKiursKePTtRW1uD\nHj1McevWNYH76Iry8vIqALS4LdTqYiM7Ozs6Pb311GsE8Snhcrk4dKgWU6cqYupURRw6VCvyBUdE\nRAjGjbOFubkp/Pyu4MSJs+ByuQK/Yb7H4XBw/nwgPDz8QFEUHBwmYt26ZSKdc1enqqqChQtnYM+e\nHSSkqpMbP94OublFqK6uwZUrN+HrewklJaU4csQDAQG3UFlZhcDAIKxevVgi4YKvXr1BRUVVQ+2b\n9nB0tIO8vBwOHToFBkOxw8+gEF2Hi8t8JCamIyIiuslzWVk5MDOzENlYrq4r4ew8D1JSUujXb0CL\n7bhc7v8XHqz/KqmoqARZWWk8fPgYJSWl8PQ8IbI5vTd+/GR8+eX3YDAYMDU1x1dfbcGFC7fg7X0Z\n584F8pUKuLy8ss1d0aVL5+D69UvIz88TaH5sNhva2mooLy8FjwewWJ9HBYmKiopCqpW41lYXGxkZ\nGUkvXrwoEf20CKJzioyswdatCqiqoqGqioatWxUQGSnaDNAcDg8URWHy5HFYsmQuxowZju3b/8Sc\nOU4C9/XuXSEOHjyFiRNHYfnyBbC1HQpTU2MYGxuKdM6fAi2tbpgxYxJ2796OsLD7JFtVJ7Zq1Trs\n3PkPtLU1kZKSCg8PP6xatRh0Og379x/HqlWSWWgAQM+ePeDgMFFk/Y0caQMGQw5r124UWZ/Ep4dO\np2PVqnWg0xVw+fLNRs/l5RXAwMCow+eUkZEOfX1dvM9yZWU1AHFxr/D27TuMHWsLNlv8KWYVFZXw\n5ZffY+PG7+Di4gpv7wAEBYW0ep6rsLAIWlot75wC9WG4K1cugJdX2wum+Pjn4HK5YLFY8PA4BkvL\nHuByeRg/fhLWr/+ioV1xcYtRRl0ek8lsvljS/2srODT/9evXZLFBECI0a9Zc3LwZ3PCzpaU5duz4\noVGGDX4UFBTh4sVr2LRpVcO5D6J13bvrYf36peBymfj33z/xxx8/4969IElPi/iIqqoaevfug7y8\nd9i0aTW+/nodZGRk4OQ0FVu3fgl5eTlJT1FkKioqoaHx6aWpJsTD3n4GzM2tEBIS2fBYfn4hDA07\ndrHBZrPB49WHpb5f+DMYDGzZ8gvKykpgZWUp9rv6tbW1jW4aaWlp45tvtsLKaigOH/ZqsUZJYWEx\ntLTaLnorLS0NObmm4Wl1dXWoqKhP8Po2eEYAACAASURBVMDhcLBunRvKykqxZ88OODlNAIvFQt++\nA2BtPQyKiv9lhZw2zYHvIoxdTVFRUasrqVYXGxRFURUVFa2uVgjiUzJihDx++60aiooUFBUp/PZb\nNUaMkBfpGEZGJnj3rv1r+PT0TIwbN7LRoVWCP4MG9YOrqwvWrnVFXFzTsARC8oYPH4nw8CfQ1OwG\niqLA4/E6PPtUc0Q9h/v3IzBtmrNI+yQ+bWPGTEBOTiHy8wvA5XJRVlYOFRXVDp2DlJQU5OQUcOaM\nf5MQrnHjJsHP7xpWr14v1jns2PETbt262uRxK6sB2Lp1ByIinjV7XVFRMd839wYP7oc//vgFEREh\nDY+dOnUEZ88ex4EDu3H48F/48cdN8PM7DWfnyfD2voSsrGJMnTq9SV/Tpk3Bv//u5e+X60J4PB7y\n8/Pftdam9TxpAEpLS8lig/hsSElJYcMGOVhb1xfCHDFCXuRf5jkcDjic9t/xiYtLwsqVLWcnIfij\np6eD7OxMiYQhEC2zth4GeXl5eHj4gcvlQVaW0eSLPo/Hg7KyElxcpklolu1XVlYOXV09SU+D6GLW\nrt0ET8/j4HK5qK5mY9eu/0FZWQkcDhe6ugaYO3eRWDOb0el0rF//VbPPjR49HqNHjxfb2ADw+HE4\nhgzph4KC/BbbqKlpgMmsgKpq4/MZpaVMqKo2rR3SHCsrS1hZWeLJk1js2rUd8+cvhrPzHJw5cwJ9\n+vRoqH9SW8vC9ev3sWbNRujpNV9BXUFBESoqCsjJyUL37p9OqHNWVhYKCgriWmvT5mIjKyurxby5\nBPEpkpKSwqhR4iuIR6fToavbHZcv34Szs73QsecMhgzZ1RABW1trhITcw+LFKyQ9FeIDdDodRkYG\nWL689fSyHh5+HTSjehRFgcvliuy1x+FwUFdXR9IyEwKRlpbGypXrUFFRjsOH92Lt2v9Sv75+nY69\ne3/DgAHWsLNzaHicxWLh1q2rsLOzh4JC106R/uxZNKSkeLC3n9VimxEjxiAu7hnGjBnR6HGKogRe\niNnYDIK1dX+cP38N69Z9iR9/3I7nz5/B07O+lsaECZPh4rKs1T6srAZCRqYOx48fwnffbYO8vMIn\nkeo6Ojq6JDExMay1NvwsNp7m5eVBT4/ceSEIUaDT6Vi+fC2SkxNw8qQvVq1aKPCCIy4uSejsVURj\namqqKCkpkvQ0iGYMHmyDmJgEDB7cr8U2NBoNbDa7xUxOWVm5UFNTgbKyaG4gODhMwpkz57By5SKR\n9Ofi4oDdu3+Gu/uX0NbWEUmfxOdj586fMWCAJfLzC6Crqw0AMDc3hbm5KY4e9UZqagoAGmRkZJCR\nkQk7u5Hw8DgMNpsLAwMjTJ/u0iUXuqmpbzBhwngYG5u22EZdXQOVlaL5nDx27CyUlVXQv//ghscG\nDrTGwIHWfPcxceIU7NjxE7hcDhIS4nDo0H6cOuXdJf/9P5SSkpJDUVTLW0zgY7GRnJwc/OTJE+aM\nGTM6NiCQID5xffr0g5ycHDw8LmDFinkCXRsTE4/168mdeFHh8Ug63M5oypRp2L9/d6uLjQkTRuHe\nvTDY2zfOEBUeHoXU1DTweDzk5b3DjBlTwWAwYGlp3q456ehowcqqd0MRzvZSU1PFiBHWyMx8SxYb\nhMC2b/8NOTnZ8Pf3hbv74kbPfVjojsVioa6OBWVlJQwY0BcAkJ2dBy+vk2I/WyEOe/ceaHNXQEVF\nBRUVVU0eF+bclaKiEtataz5sjF90Oh1fffVDQ386On743/++x65de1FXVwt5eYV29S8pRUVFmW21\naXP/pq6uLjshIaHlUpAEQQjNzMwChoamyMzkP1qRzWaDySwX46w+PzQaRVLhdlI0WuvhSkZGBkhP\nz2xSP+XFi1QsX74Ay5cvgIPDJHA4XAQE3BLJnGxsBiEx8YVI+gKAhISXGDx4qMj6Iz4f8vIKMDfv\nibFjx8PT8xI8PM4jJiYe1dU1ePYsDiUlpQDqM0V9vLtnYKCH/PwcBAVdR1ZWRpd6D2xroREZ+RAH\nDvyJUaMav67Kylo/r1FSUorU1LQmj8vLM5CcnCDcZD+grKwCZWUV0Ol07Ny5ByYmpmCxWNi8eR32\n7PkVXbGQdlZWVpuLjTZ3NiiKor788sssAH1FMiuCIBpxdp6LP//8Fe7uS/hqLyMj067KxURTdLr0\nJxE7+ynS0tJBUVFxq+mdnZymwtPzPAwNuyM9PQMVFVUNBzfpdDoGD+4PoD78sL4IWftqdLy/XhR9\nAQCDIUv+/oh2sbUdC1vbseByuYiOjsS1ayEYNGgIHj9ORm5uFnR0umHq1HFNwg3XrVuKzMxsREbe\nQ05OPhgMeaxevQEMhvAVyUV5pkkYVVWVePQoBGvXLmrIYvf+dZqamoaePXs0uebly9cIC4uGtrYu\ntLS0ERp6Dubmxhg3rv68x6xZ9jh50hdKSsowMjIRyTzl5RXg7r4ZAPDDD1tx5swJ7N79M9au3dTi\nIfPOpqioCJmZmW2WWqfxs53k5OT0b2Bg4DpJFVEiiE9dZORDZGa+xJQp4/hqHxERBSWl/7bDifbx\n9g7Axo3fSHoaRDNyc7Px4MF1ODpOarVdSkoqFBUVYWCg1+IB0OfPE8FmszF0qODhTzweD5GRT5GW\nlgEul4vk5JdwcJiEceNGCtzXx3x8ArF+/dft7ocgWpKRkY7r16+Ay63PhEinA6qqKmCz2ZCXl4ed\n3WhIS0ujpKQUx4/7YOnS1ejdu/7zJT8/F5cunUdOThb09btj5MgxGDRoKJ49i0JERBgUFZWwdOlq\nVFaW4/z5s7h9+w78/QObLDg4HA5evkxGQUE+nj+PwbRpM2Bh0Vvkv+vOndtgYWEEBoOB2NgkaGpq\ng8WqxdSpYxEe/hgzZzo0umF3924opKWVMGPGnEbvGz4+ZzBgQA8YGNSfWaYoCl5eV7B583cinzMA\npKWlwsvrJGRkZLFmzQZcunQObm6bxDKWqFy8eLHE1dW1X01NTW5r7drc2QCAV69e3Xr58qV7r169\nyGqDIMRgxIjRiI5+jNraOr52LWxtbXDw4EmYmRmL7ODr54xOJ29tnZWMDKPZuOuP9er1X67/lm6M\nMZnlMDQU7o7h6dN+GDFiCBYscIa0dP1HZ2DgLZw96w9HRzuoq6sJ1S8A1NWJv9Iy8XkzNjZtlKqW\nzWajrKwUcnJyKCoqgKfnBUhJATwehT59rGBkZAwACAi4gIKCHAwd2gczZkxAYmIKrl0LRL9+g3Du\nnDe+/34DiopKsH//buTl5UFbWwuTJ09utNDgcDjYt+8PyMjQYW5uBCazEkxmGWRkxLNDv2jRUtTU\n1EBeXh5Tp86BvLwCuFwuduzYClVVxSafsfn5Rdi4cWWTfmbOnA1v72OYP38GgPr3lfeFDMXBzMwC\n3333P4SG3kdBQT6ePHkMV9cVjQoDdjZxcXFv2lpoAHwuNl6+fBl87969zF69ehm3f2oEQTRnwYKl\nuHTJu+GNrTU0Gg1r1iyBh4cv3N2Xd8DsPl25ufno1k1b0tMgWuDjcwYLF4qmjsbbt1lN0mDyo6am\nFgyGDPr2tWz0+IwZ9igvr8Ddu6EoKCjEwoUufOfv/5CsrDQqKyugpKTcdmOCEAEZGRloadW/7ykr\nq+Drr7egtrYWcnJyjdrduHED/fr1xuPHcVBSSsPgwTbYssUFdDodo0ePh7//bfB4HMjLK2L69Fmw\nsRnRcNCZx+MhKOgaQkNDMGLEQKioKCM6OgG9evXFtm2rxBZqZWraNAmElJQUli1bg6+/3gwjIwOo\nqalg4EArvHnzFkVFpc32o6ioBCazslEYlpmZIf74YwfGj58AG5v272p+TEFBEfb201FezoSUlBRe\nvEjCkCHDRD6OqGRlZb3ipx1fiw2Komq+/vrr1wDIYoMgxERLSxt1dVy+dzfk5GSRlpaJiIgojBz5\n35tRdXUNyssrGtIgEq0LDLyLb7/dJulpEC2g0WgtprUVlKysLGpr6yAvL9d244+0tPuloqIMF5dp\nqKurwzffbIeVVW8YGurDwaH1sK8PjR8/Anfu3MSsWYJlpSMIUfp4oQEAJ054Nvq5sLAAvr5nUFRU\niKFDh8PJyaXZvrhcLnbu3IYpU0Zj8OC+ePw4DtOnz8C3326T2PkkExMzeHicRXFxIQoKCnD2bCB6\n9LDAzz//3uI1Li7zERAQBGdnewDA2LEjYGzcHc+fJ4llsfHTT99CXV0VU6c6wdzcHKGhwZ12sVFW\nVoZXr141X6b9I3z/j7958+aVMOnCCILg34IFSxEQEMR3+99/3wKAhuDghwCAqqpqHD7sgXv3QkFR\nQG6uAnJzFfDxSzczMxtXrwbB0/M8wsOjRPgbdC2hoZEYOXJsQ1gM0flYWw9FfHyySPqaNGk0Ll68\nJvB18vJyYLNbD5+QlZXFrl0/QU5OFhRFIScnj+/+9fV1kZ3dZkIXgpC4kpIiJCcnYs4ce2RkvER4\neEiz7U6cOIS5cx0hJSUFJrMGu3fvxciRYyWeCEFFRRWmpuYYNswWmzd/h2nTnFudk7m5JWRkFPHq\n1ZuGx7p310Nubib+/nuXyOdHUTx066aGAwf+waxZ89p835Gk+/fvl8bGxl7gpy3f/+svX768kZyc\nTJLRE4QYaWvroLa2vqIwP2RkZDBypA3q6ljw8roAX9/LWLduOeh0ady4oQkbGz3Y2Ojhxg3NhgVH\nSEgEoqJiMGrUMCxdOg9paRli/I06r+zsPOTmFmPMmAmSngrRihEjRiMmJkkkfWlqdhMqxz6/WaeU\nlBRBURSmTp2AW7fuCzSGrKw04uJiBJ4bQXQkS8s++N//foOf31XU1NTg2bMnTdpUVVUiOzsToaGP\nERWVgFWrul4djw8tXLgMkZHx8PT0x927YSgoKMLixS6g0bjw9T0j0rF+++1vODrOxe+//4nc3JyG\nuhydUUxMTGpNTQ1fefv5vp2XkpJy59q1a6/7fhy0ShCESC1YsBSXL/tgwYK2z2685+DQuKCZiooV\n3NxUUVVV/wXJzU0VYWEluH37FPr374s5c5wa2n5cn+BzwGazcenSLfz00w5JT4Vog5SUFOTkFFBa\nWtauQ9jtkZf3Dnp6/BXc43Dq037KyAi2W0aj8eDhcQL79h0RZooE0WEUFBTx3Xf/Q3FxEVRVm74m\n5eTkYWs7FmPGjO+055BKSoqgoaHJV1s6nY7Nm78Fj8dDRkYa4uOfIyLiEvr1s0RKimh2XT/0/izN\ngwfBePDgLubNc23IDNZZUBSFlJSUNlPevsf3uyFFUewVK1bEAyCLDYIQIx0dXdDpMu36clVT03Rn\n5MmTGKxYsRCyso3Pg3yO4ZFeXhexbt0XEs0FT/BvxQp3nDixD4sXNx8fLoi0tAzcuhWM/PwCUBSF\nsrJybNq0qtVQulev3qBXLwvk5tYffNXTq0ZzGx1cLrfZx1vz5s1b3LhxF5Mnj0NdXecNmSCIj3Xr\n1vyXdSkpKTg4ODX7XGeQmBiHX375H44cOQlNTS2+r6PT6TA1NYepqTns7OxRVVWFRYv4W7AIY+LE\nSYiLi0FaWmqnW2wkJiZykpKSLvLbXqBbL0lJSSEFBQVztLXJwVOCEKelS9fg5MmDGDJkGQDA0pIp\n0JcYW1st7N6dgR9+qM/psG/fO0yebN5koQFAZIdvu4r8/ALo6Rk13D0iOj9ZWVmRVTdesMAZamqq\n0NLqBhqNhl9//RunT/uCwWCgTx9L2Ng0rcGRn1+IykonuLnVL/6PHmXC0bGoyWsyIeFFQwFBoD6L\nVVkZE7q62o3CsEJDH+Ht2yywWGyYmhphw4aVoNPpePo0USS/I0F8Cvbv/xMlJYVQVlbF6tXrm91F\nEUZQ0DW4uS1BevobgRYbH1JQUISCgqJI5tOS0aMnYPTozhnme+3atVcpKSn3+G0v0EmdJ0+e+Fy5\nciVL8GkRBCEIBoMBHm8tJk3SxKRJmvD11W1yyLs13bvrYNEiDp48ycP+/dfg7FwOFZXmc3WrqCgh\nMTFFRDPv/O7cCSNZf7qYkpLiFv9+BWVpaQ4dHS3Q6XRkZeVi5EgbrFmzBMuWzUd8fDIyM7PB5XJx\n9qw/XrxIBQAoKvaBm5saqqpoqKqiwc1NFXl5Ck36Tkh4gf79+wCoD6e6fPk6YmMTcfq0L06d8sHx\n417w8roAOp2OpUvnYfXqxZg0acwHB1RJvReCeG/NmvWorq7F4sUzsW/fHlRXt11vpy0JCc9hbKyP\n9PQsWFj0FMEsP0+vX79OoCiK7xhsgXY2KIpibtiwIQmAocAzIwiCb7GxtdiyRbnhzMX33yvC2loV\nvXox+e6DRgP09asxfLg6AgJuwsWl+VoFM2bYw9//KiorqzB8uLVI5t9ZURQFLrf5FI9E5/X8+VOY\nm5uKvF8NDTUUFZU0/Lx48WyEh0fh3r0w2NtPhLf3BejqakFXl7/zGqqqyigvr4C6uhp4PB4WLZot\n0Hz4OYTOj4yMdLx7lyuW1JwEIW7v3uVDU1MLRUWFUFCQh5ycLJYudcGpUwfBYnHB4wGjRo1BeHgI\nWCwWtLS0sWbNxjb75fF4CAy8iPXrlyIrKxdXr17BkiVNi/kRrcvNzUViYmKwINcInO8xLi4uuLi4\neGq3bt0EvZQgCAno3l0PZWVMVFVVQ1Gx6d1YAJgzxwm3bgXj5EkfDBjQB71794SSkni3iCUhMPA2\nnJxmSXoahAA4HA4ePXqIDRuWibzvuro6MBj/hRHKycli0qQxDT8vWTIPISGPAACHDhlhw4b6+Oyj\nR5nQ06tu0p+qqgry8wshLy8PRUV5gecjqvNT3t6nQKfTMGTICImnGiUIflVXV+Ho0QNQVpZDVVUN\ndHS0sGLFfACAmpoqXF3rF++VlVWIi0vGqlXzQaPRcPiwZ2vdNrhxIwBTpoxpWNSrqUkm4URX5+fn\nlxodHe0tyDUCLzbCw8OP+fn5rd+wYYOJoNcSBMGfQYPk8Mcf1fj++/rFwe7dlbC05H9X42Oqqipg\ns9mttrG3nwgWi4XU1HRcunQd+vq6sLMbK/SYnU1JSSlqajjo0YNsnXclx48fxOzZDiLpKz09A+np\nmaDT6aDT6Xj7NguWlk2rDb+nq6sNZ2cHnDsXgIkT0/D4cS3i45Nhb9+jyXkNiqIQG5uAzZvXgEaj\nSSw/PpvNhoaGGvr1s0RIyD1MmDBZIvMgCEFwOBz8+edvWLlyXps3upSUFDFy5FAAQFRULKyt+St6\n9/JlCgYPrt/hNzTUx4MHTdP2Em2LjY2NpiiqVpBrBL7lQVFURWxsLF8VAwmCEA6dToe7uzxCQ2vw\n4EEVWKyDAme5+VBVVTXU1FTbbMdgMNC3ryWWLq1/wz950gehoY+EH7iTqKmpxcGDZ7Bihbukp0II\nIDo6Erq6GtDVFc1h/uDgcJibm8HU1AiGhvoYNWoYBg5sO8uLi4sjTpzwRlTUJZSXxzf7WoyJicfY\nsbbtCoUSRRhVaGgw+vQxR79+vZGczHdmSoKQKG/v05g715HvHfW6ujrcvh2C3NwSTJnSfIjwh7Ky\nMqCpqdJod19Kiuz6CSohIYH9/PlzX0GvE6psbkxMzOU3b9449+jRg/xPEYSY0Ol0WFvXvzFyuWMQ\nERHdcDdHUFJSdHA4HIEqZY8YMQQjRgxBdHQsTp3yAZfLhY3NYAwcaCXUHCQpNjYBK1asaTYbF9F5\nhYYGY9Wq+SLrT0ZGGkZG3YW4TgbffLMOtbV1UFBoPjzq+fNErFixsOHn0tIyhIdHYdQo/u66Au1b\nbBQWFqCsrARxcdFYuXIBAIgsgxdBiNPjx+F49y4HWlpj2m78/+7dewhT0z6wteXvmoAAf8yb998O\naUrKa/Tq1bnSyXYF/v7+SUlJSbcEvU6oxcLz588v+Pn5vRDmWoIgBKeqqo6qqqYx4vzS09NFXl6B\nUNcOHToIK1cuwpo1SxAXl4T8fOH6kaS3b7PRs2cvSU+DEACTWQYVlc5zbojBYEBFRbnFBbuiogL+\n/vtww7mLL75Yi8LCYrx9mynAKMIvNp4+jYKvrweWLPnvUDqdTrJbEZL34kUSDh78Czt2bEVqauPM\nh5mZbxEdHQE3N1e+b4bxeDy8fp0BGxtbvudAUVwwGIyGn58+jcP48XZ8X0/U1xGKj4+PoihK4LsY\nQi02KIriPHv2LILDIQWICKIj9O7dF+np2UJX+zY2NkBGRvuzVtvZjcWzZ3Ht7qej6elpIztbkC99\nhKTduBGI8eP5/zIhCdnZeTh71h+nTvlARUUZDg52OHbME1FRMQAAJ6cpCA5+yHd/7dmJyMxMx5Il\ncz67ujlE58Xj8bB9+4+4evUCFi6cjg0blsHf3welpcUA6s9peHgcw6JFzgL16+19EUuXruZ7cVJV\nVdkkZEpeXg7+/j745pu2s1gR9a5du1by9OnTf4S5VugwqKioqD0BAQFFwl5PEIRg5s9fgjNnLgiV\nsSY1NQ0GBnrtnoO+vi4yM7Pb3U9HMzDQQ0ZGmqSnQQigpKQQWlqdL+theXkFvLwu4NQpHyQmvsDs\n2U5YuXIRHBwmoU+fnnB2dkRJSSliYuIhJSUlUGgUlyvcDbwHD+5ASUkO6uqNs+uIKrsVQQgqLCwY\ne/f+jtmzHbB2rWvDa2HJktnw9vZAeTkTTGYZTE0NBMqYdvduGIYPHwsTEzO+r7l8+QLs7cc1esza\nuh+MjbUwZcpYhIYKlMW1U8jISIePz5kOHTMoKCgqOzv7pTDXCr3YyM3NfXPnzp3Hwl5PEIRgjI1N\nYW8/E0eOeLWZWepjGRlZMDIyEMk80tIyhd5hkRQDA31kZKRLehqEADgclqSn0KzExJSG0MKpUydA\nTq7xOSAdHS1YWJihoqISAPi++5qTkwcdHX2B5+PrewYlJblwdGyu0jAPdXV1AvdJEO2RlBSP+Phn\nWLVqfpObXEpKiujTxxT+/mfg5XUMZmbGAvWdm/sOlpZ9BLqmsPAdNDTUGz1mamqM3r0tMHToQERE\nhArUX2dw/foVpKW96rDxUlNTOU+fPvUR9vp2HfB++vSpd0pKimDfegiCEFqfPv2wevVGHD3qg5SU\nVL6vMzU1FkkYFQBYWJhCSkpKJH11FHl5OVRXC3/mhehYWVkZ0NLSEHm/7c32xGRWICkppc3zU2Fh\nkRg50kagvoOCQgSubO/j4wFdXVVMnDiqyXOBgbfBYDBQVydQhkqCaJf7928jIiK41dCoIUMGwMXF\nEcuXz4OVlWBn6ebPd8K+fXtQU8Pf+3laWirU1Fo++/Xq1RsMHNj1itlWVVVARUWlw8bz9PSMf/bs\n2Tlhr2/XYiM2Nvaip6dn1wvgJoguTEtLG1u3/oqsrFKcPXsZ/JydYrFYIlsg9O1ricTElLYbdjok\npKSruH37BsaPF231aw6H064D09ev38HVq0Ho3dsC167dxpkz51oMKZSWloa0tDQoimrY4WhNTk4e\ntLX1Gx1gbQmHw4Gvryf27/8DKioMDB7cr0mb0tIyXLt2F5mZOVBRaTvlNUGIApvNRmzsE8ydO10k\naZybIysri+XL5+LgwT8RFRXRZns/Py84O9u3+Pzz58kYO3aiKKfYIdTUNKGsrN52QxGorq5GdHT0\nPYqihA5pECr17XsURfEmTZp0vbS0dIi6esf80gRB1KfFnTNnIXJzs3H06DHY2Y1stTiZo6MdDh/2\nwIYNK9s9tq2tDXbs2IuEhGQwGAzIyjKgr6+LwYP7t7tvcRLXhx8henV1tS2mmBUWj8dDTY1wIUUx\nMfFQUVHGtGn1BfJGjRoOHo8Hb29/mJubYNgw60bhUrW1deByuTh1ygdTpzYX3vQfDoeDCxeuY9u2\n31ptFxsbjYiIUNTV1cDObgyMjFpejCkqKmD8+LGYOXN2i20IQpT8/DwRHv4Q7u5LxT6Wqqoy1qxZ\nBG/vS9DW1oGpafOffUFB1zBmzNBW3/tra+ugqKgkrqmKTW1tDaqrq8Q6Bo/HQ2RkGP79919WYWHe\n3+3pq911MoKDg/ccOXKEpMElCAnQ1zfAli2/IDeXiZMnfVFaWtZsOzqdDmNjA+Tm5rd7TBqNhm3b\nvoKLyzRMmTIetrZDER0d2+5+xY8sNroKHk/0mQ4ZDAY0NNSQlZUr0HWXL9/Ay5evMXr08EaP0+l0\nLFkyF7Kysjhw4CTy8t41POfkNAV79x6Bnp4OevQwabFvDoeDI0e8sX79V22e7QgLe4DFi2di5coF\nbdYKYbHYUFCQR/fuhm3/ggQhJC6Xi6++2oBTp45CWpqLH3/cKJJEJPxatMgZPj6ezWZxKy9nIi7u\nGfr1a/18B43WNcvFGRoaCnSwXlCHD/+Dv//egUuXzkNJSSEtJia+XTnv2z1TiqJqHj58eKOqSrwr\nLIIgmken0+HsPA8bNnyHO3cewc8vsNkD5IWFxdDT0xHJmDQaDQwGA0pKitDQUBeoWCBBtIVGoyEj\nIwuenufh5XUBISFth0vww9nZARcvXuM7xeytW8HQ19fFggWzmr07SqPRMGTIQKxduwRhYf/lS9HV\n1Ya9/STY2zcfnsFms3H58k14el7GqlXroK3d+uuSySwDjcZ/WtwLF65h8mRHvtsThKB4PB7+/HMH\nJk0aiYqKCkhJ0fmu/i0qdDodjo7j8Mcf2xEW1jij1JEj++Dq6tJmH+Xl5QInXOkMnJ3n4bvvtoml\n7+LiIkRFPYGcnCJ0dIwKL1681u44M5F8Q4iMjNx54sQJ5y+++KKHKPojCEJwcnJyWLt2E969y4en\n5ymMGDEQfftaNmojrlCiXr3M4e9/FbNmOXbKw+NcLhd0euebF9G8zMwcJCerYOHCWZCRkUF4eBT2\n7TvWJKPMx2RkpDF/vnOLf+d0Oh1z5zrh9GlfaGl1Q0lJGSiKwoQJo2BiYtSobWTkU8jIyGD48LYP\njxYXl0Bbu3Ga3uYOvnI4HFy/fg8lJRWYN28x3zsPHh7HMXcuf4uH8vIKqKtrkV0NQqw8PI5h2rSJ\nUFNTwbNn8RgyZJJE5mFqagx3uVPbCwAAIABJREFU9yX455+TGDp0BBgMWXh6nsCQIf34CsVUVlYm\ntWkAVFdXISDAHxwOF3Z29vD09AOPx8P8+fNvl5SUCLYd3AyRLDbKysqYTk5Ot93d3dfJysq2fQFB\nEGKjo6OLb77Zil9/3YKePc0gIyODkpJSJCcLlR6bLyNHDkNubj68vf2xbNl8sY0jLBaLDfLe1HWY\nmBg12hUYNWoYbG2Hthk2kJ2dh337jqNnTzOoq6tBQ0MNGhrqUFVVxosXqXj+PBE8Hg8cDhe2tjZQ\nVFRASkoqdu8+CCurXjAy6g4rq94Njy9fvoCv+RYWFkNLS7PVNuXlFTh16hxWrVoHQ0PB0n1KS9P4\nPsOSmJiCIUOGt92QIITE4/FQVlbcEDK1cWP7zwK217Jls3H48N/gcLiYOnUsjI35W2y3p5Dmp4LJ\nLMPevbswZ840pKdnICwsGPPmueLy5cuFkZGRO0QxhshiHyIjI385ffr0NHd3d6O2WxMEIW5r1mzE\n6dPHYW1thYSEZDg5TUVg4C3MmNFyZo720NfXBY1GQ01NLeTl5cQyhrBCQiIxfHjT9KBE58RiscHl\nchvtkvETn2xgoIdNm1ahtLQMJSVlKC1lIinpJd68SYeCggLk5ORAp9PA5XJx48ZdsFgsWFsPwIED\nv8HP7wpGjRqGmJgEFBQUYsmSuXzP9+3bLEyaNKbF56ura3D69AX8+OMvkJMT5rXBfya1lJQ3mDx5\njhBjEAR/goKuY9iwgZKeRiPq6mpYuZK/mwPvZWRkQVdXNPWnurKbN69i2LCByMjIRExMMrZt2wke\nj4dLly6FZGVliaSYh8gWG4WFhQXTpk0LXLJkyUZFxY6N2yMIoildXT18//3P8PHxgLq6GsaMGYHT\np33B4XDEdsZCR0cLTGZ5p1tsFBWVonfvvpKeBsGn2bMX4OLFi5g3z0nga6WkpKCp2Q2amvVhTUlJ\nKZg8eTx0dLQanVl68+Zto8PbdXV1UFNTbXXR0JKyMiZUVZvPeV9XV4fjx33w7bc/CbnQ4L8SOJvN\nhpQUg5yhIsTG398XNTVlsLWdLOmptFtYWBTWrftW0tOQuNmzF+Dhw2Boa+vD3n4B6HQ6fH198yMi\nIraKagyRHmWPiIj46d9//+24koYEQbRpwYKlKC2tAACMGTMCISGPxDbWx3ejOwuS9bZrMTAwgqys\nErKz89rdl7S0NAYOtGqSHOHjLFFTp07EzZv3hBqjpb/5ly9fw8PDH1988X0702vy91F9924YnJxm\ntWMcgmjZ+fNn0a2bPJycuv5CAwC4XBJCBQAyMjKYMGEqrKz6g06ng8Viwd/fPygzM5P/ysFtEOli\no7S0tPzu3bvniouLRdktQRDtQKfTQaNJgaIomJuboqioGI8eRberTx6PhxcvUnH3bihCQiJQXFwC\nAHj3rhDdunW+mjukxkbX4+q6EnfvPuyw8YyMuiM7W/BzkExmebO7Grm5+YiIiMUPP2yHmlr7XhMU\nReNrdyMnp6DFmgME0R5hYfdRW8tstohkV2VvPx47d24Dk9l8yvjP1cmTJzPCw8O/F2WfIk/Se+/e\nvd//+eef56LulyAI4Vlb2yAhIRkAMH++M1JShLthcedOCM6cOQdvb3+UlTHRu3dPmJoa4fbtB/D3\nvwoul9cpv9iz2aKv20CIl5SUVIdnEBs3biSuXg0S6Jr6O4GNU2cmJCTj+vUQbN78nUjmJSUl1eZB\n1oSEFxg4cIhIxiOI996+TcO+fX+guDgbM2ZMkfR0REpHRwtr1y7C3r27umT6W3GorKzEjRs3AgoL\nC9tVV+NjIg/spCiqbsyYMR7p6el/m5qaksBRgugEbG3H4NChPejfv/7cgrAx3Tk5ec1m6DE2NkRO\nTh4WL3aHk9Nk6Ohot2u+olRUVAwVlc6320K0TV29G8rKmFBTU+2Q8Xr1ssCLF6lITU2DhYUZX9dw\nuVzIyDR+PUVFJeC7734S2bxYrJo2wxMjI2PwzTfiybtPfD7Ky5k4deoIZGSkwWLVQU9PG3PnOvCd\nDa2rkZOThavrLBw5sg+bNknu/AaPx0NQ0HUMH24LDY3WM9uJ04EDB1IeP34sujev/yeW8oMPHz48\ntGvXLvEFhhMEIZD6Lyr/vdzr6lgC98FkVkBFRbnF57t314ODgx2UlVtuIwlXr97FwoXLJD0NQgj2\n9k548KB9HyX8Hq5+b+ZMewQHhyE8PIqv9lev3m5UXZzFYkFJSXSvgeDgIPTpY9Fqm8LCYujo6Iu1\nojDxaQsLu49//tmFkycPYf78aVi8eCZWrJgHe/vxn+xC4z1NzW5QU1PE8+fPJDaHtLTXyM1Nw8GD\nf4PL5UpkDunp6dw7d+6cKC4urhR132J5Z6IoihcVFfVTUFBQiTj6JwhCcAoKSqiurgEA9OnTE0+f\nChbtyONxIS3d+t1VN7eluHLlhtBzFLXS0jKoqGgInQWIkCwtLW0wmSL/3GsVjUaDm9sypKamtdn2\n/etJS+u/gn7S0tKorq4SyVzYbDaioyMxbNigVtvdvHkfc+cuEsmYxOchNTUFf/31G/bu/Q27dv0P\nLFYJli+fgxUr5nW6bIIdIS+vAP37t/46EyctLW3Q6XRMnz4J165dksgc/vjjj4jQ0NB94uhbbLdB\n4uLiHh4/fvwmiyX4HVSCIERv9OjxiIqKAQCMHGmDqKgYcDj8n2VQV1dDWVl5q22UlZXA4Ujmrkxz\nXr58g2HDRkp6GkQ7aGrq4N27QqGupShK6DNEFEW1uSty+fJ1ODhMbPQYnU6HlFT9Dkd7cDgceHuf\nwpAhrR/IrY81l4K8vEK7xiM+DywWC/v2/YHo6FCsWFG/uHB3X4IhQzpX3YyOpqmpjvJyyR0UV1VV\nA5NZCTMzY7x6ldLh49+6das0MjLyJ4qixJKiS6x7rnfu3PniwIEDIkudRRCE8Hr27IWMjJyGn2fP\nno7LlwXbheiMh79bQ6fTIab3TqKDzJmzCDduBAt1bXl5JZSVhUs5a209ACdOeCM0tPkwrvDwKBgY\n6DfU8/iQpaUZUlKShRr3PX9/X1hZmbb5JfD27RDMmDG7XWMRnz4ul4urVy/hr792wMlpAhwcJpKw\nuw+w2RwwGLISnYOsrDyqq2vQv38vREZ2XCY+FouFkydP3oiLixPboGL9S6usrCy+cePG6aysLPJp\nTxASRqfTwWDIITdXAbm5CtDW1gKTWdGwu8Hj8fDPP8fg4eGHK1duorCwPoX19et3cO3abYSHR4HB\nkGlzHBqNhrq6OgBAbW2dxOJPgfqtcQaDIbHxifaTlZWFnp4RX2FN72Vm5mD//uO4dOkaBgwQrpjj\ngAF9sWbNEigqKsDX9xJKS/+76/nq1Rvk5uZj3Ljmd8309XWRmtq+u5P5+dno2bMHH+2KYWLC32F2\n4vPz4kUSvvpqA379dQu6d1fFunVLoaFBEmZ8jMXiQE5OsmdTFixYAj+/AAwfPhiPH0d02LgHDhx4\nffv27S/EOYbYs0WFhITs+fnnn6eeOnVqbFe7K0oQnxKKosBmz4SNjR4A4OhRJhwd7XDz5j04OU3F\n7dsPMGPGVJiZGaOsjAlf38twdJyE0lImHB0n4cWLVBQVtX0My8FhIi5evAYWiw02mwMajQZDQ31M\nnTpB3L9iIwEBQdDWNkCvXqRyeFc3b95i7N+/m+8MUVlZ2XB0tIO5uWm7xuXxeEhPz0RdHQsPHkSg\nqKgY0tLSKCgoxA8/bG7xOnV1VSQl3YWLi/Bjt3U+CgCSkl5iwABr4QchPmkFBe+wc+d2cDgcHD68\nu1MWXO0sUlNTsWXL11i1yg3m5pYSmYO6ejeMGDEW//xzHHp6Bh0y5qtXr9g3btz4t7KyUqwF8sS+\n2KAoite3b9+NPj4+txYvXtxd3OMRBNG8t29Z2LrVFFVV9Yt+NzdVPHliiry8IDx8+BjPnyfA3r4+\n/lxNTRVubkvx8897MGPGVGhoqGPkSBtoamrg+HEvrFq1uMUteE3Nbli0qHFYx82b95CWlgEzM2Px\n/pIfqKysxbJlMztsPEJ86HQ6pKXb3lV7r6SkDL1792zXmAkJLxAa+gjOzg7o3l2v0XOenudbvVZO\nThY6OjqttmkLP1m0Hj+OxZdfbmnXOMSn68KFs/j2W3fo6GiThUYbduz4AYGBQXj0KFxiiw2gPk29\njY2t0OnpBcHj8bB9+/bgkJCQ/eIeq0PqYCQlJSVMnjzZa9KkST/o6uqS7Q2C6ERmzZqGsjJmk9hz\nOp2On3/+ptGiwtLSHCoqyjhw4ATc3ZdBVpa/GFc7u7E4dy6g3YsNigLy8uoPwurpVeP9ZmlJSSnu\n349AVVUtGAxZUBSFAQMGt2ssonMRZGO8pare/AoPj0JxcQk2bFgp1PWvX7+FpWVvocfnR3V1DRQU\nlEjcPdEsHo+H6uoqmJgYSXoqXUZpaTnc3VdLehodstAAgKNHj76NiopypwTNDy6EDnuXunv37rbt\n27eHd9R4BEE0ZmLCwL59hVBUpKCoSOHoUSb09KqhpdUNFhZmzS4cpKWlm3yZ0dPTwfLlC3Ho0Gkw\nmRV8jS0jI9Pu7DwUBdy4oQkbGz3Y2Ojhxg1N8HgUTp06h/DwOMya5YrNm3+Au/uXWLfuK4we3bFh\nW0TnweNRQt/JffAgHNXVNZgxw77FNlJS9FYzuYWHP8GoUeOEGv89Gq31LxxBQQ/g7DyvXWMQn66z\nZ09j8uRRkp5Gl8Lj0fi+gdbVpaency5evHj0zZs3bztivA5bbFAUxY2IiPjK39//XUeNSRDEf2g0\nGlxcpOHhEYInT/Lg6FjU6G6xIDc3VFWVsXHjSnh7X8CVKzeRnZ3X5jXdu+vhzp0QnDhxFpmZOW22\n/1hengLc3FRRVUVDVRUNbm6quHIlBXPmLMaSJaugodE0KxDx6RDk71PYG3XV1TV4+zYLkyePa7Wd\niYkR0tMzW3xeTk4W5eVMoebwHp3e8lYORVEoKmJCV1evxTbE5+vOnRtQUZEluxoC+lw2CSmKwvbt\n20MePHiwp6PG7NB/2oSEhKcnT548nZOTQ7JTEYQEqKtrIDc3Cvr6/4UgURSFwMBbUFJSFKgvBoOB\nDRtWYvz4kYiLS8Tx416orGy5mNmUKeNhaNgdixfPRlCQcKlMPzZhwmQYGZmIpC+isxN/BK6//1XM\nmuXYZrvevS2QktJ8Vvfc3Hyw2VS7F7+tLZgePozCxImT29U/8Wmqq6tDXNxTjBs3QtJT6XK0tTWQ\nkZEu6WmI3eHDh9MjIyM7JHzqvQ5fx925c+enH3/88T6PR9YbBCEJH2eFu3btNszMTODiMk2o/tTU\nVOHoaIdFi2bD1/cSHjwIb/aLEo1GQ+/eFpCXlxNqq1pPrxoHDhQ0hIGdPFkLExOS1vZzIUg2Q0GK\nVQJARkYWTp/2hb6+Ll9nPSoqKqGoqNDksbNnLyM8PBabN38n0PjN4fGaTxlNURSSk1/D2npYu8cg\nPj1MZhl0dbUlPY0uaeLEUQgKui7paYjV8+fPay5cuLDn1atXrzty3I45hfIBiqJ4xsbGK/bv33//\nyy+/NO/o8Qnic0enN45lHzSoP5KTX6Jfv/YdaFVUVMCaNUuQkPACJ054o1s3Dcycad9s7LwwabB5\nPC4KC48hPv470Gg0mJjIdbkig4TwaDT+742lpWUgKioGw4bxlyTg9u0QrFnjCqDlJAQfevw4BtOn\n1+8s1NbW4dKlmwCk4Oq6BqqqanzPszVKSipISHjR8LqkKAqPHz9DfHwKJk92EMkYxKenqKgA6urC\nJ0f4nMnKyoLNrpP0NMSmpqYGv/zyS2BoaOjRjh5bIhFqGRkZWVeuXNkZFRXVcswFQRBiQadL4cOd\nRUNDfeTktH3mgl/9+vXGmjVLMGTIAAQGBrXYjt/D5e/dunUfc+cuhJmZHExNZclC4zOjoKCA6uoa\nvtpaWpojLi6pyePnzgXg+HEv3Lx5r+GxzMxsKCvXhxBSFBAQoN0oCUFzgQY1NTVQVFTAkyex8PEJ\nxNy5S7F+/VciW2gAwIoV7igrY+PUKT9ERETj6NGz0NIywbff/g+DB9uIbBzi08Lj8Uia23ZgswXb\nFe1Kfv7559iwsDCJpNvq8J2N98LCwjxnzJgxwcfHZ4mSkpKkpkEQnx0Tkx7IzMxudHiQoihQFCXS\nL/DGxoYIDn7Y7HOVlZXw87uEnj17YMKE0Xz1l5dXBFNTshn6uRo4cAgSE1NgYzOIr/aamhooKipu\nSOkcGfkUPXuaYfDg/khMTMGZM+dAURS0tTUxZ44TKAq4f18TGzcqf1SLphr6+tUAgOjoWMTExCM3\n9x2Kiorx6lUWvv5afHUupk+fhfLyiUhOTsCPPy4Q2zjEp2H37l+hqqoKIyMtSU+lS3r9Oh09e/aS\n9DTEIiAgoCA4OPir4uLiSkmML9Gz91evXnX77rvvnnTgGRWC+OzZ2o5CTExio8d69DBBWlqGSMcp\nLCyGpqZGs88pKSnBzW0ZiopK+N5VUVAQ7AA78Wnp128gXr5Ma7NdXV0dGAwZ0Gi0hnz1UVExeP06\nHYMH9wcAWFn1wrJl87F8+QI4OtpBWloaeXkKuHJFvsV+uVwuHj2Kxtq1S2FmZgwpKSlUV4t/c15F\nRRXDh5MUpkTrQkLuobKyHCEhIXwvyInGgoMjMHly2wkiupr09HT24cOHjz179ixEUnOQ6GKDoqia\n0NDQZf/++++nf/yfIDoJNTUNVFZWN3pMWloapaVlIh0nPDwKo0Y1f4hVSoqOmppaTJ48Dk+exPLV\nH5dLkkp8zqSlpfnaeSsqKoGmZjeUl1dATk4OwcEPUVxcClfXOW1ee/euDNasqW1IQnDwYAX09Opf\nK48fP4Od3TgA9QuPyspqEq5CdBoxMdEwNTXE/v07ISMjI+npdDkJCcno27f/J/dvV1NTg2+//fbG\n3bt3f5bkPCSeVTgpKenF+fPnt4WGhrYvKTlBEHz7uGDYqFHDEBLySKRjFBeXQkNDvcnjNTW1KCsr\nh7x8/QFvJrOcr/5YrGpwuc1n6CE+D/xsghcVlUBLqxvs7SfCz+8yNDTU4OAwsc3r9PSq8fff5fDx\nkcXMmSx4ejIxc2ZBwwFxY2NDxMcnAwBKS5l48OAhjIxM2/PrEITIyMrKwsXFEXJyn0dROlGqqKhE\neHgMpk2bJempiBRFUfjxxx+fPXjwwLUj09w2R2JnNj708OFDH3t7+yEWFhab9PX1Jb4AIohPnaqq\nGpjMCqiqKgOoT/1pbi7aL05WVr1w6tT/sXefAVFdWxuA3zND7wLSREClSlFAmijYFVEUNbaosbeo\nUdOLyZd2k5imxpuosdfYFQVBKQoqRXqR3ptSlN5m5pzvh5FcYkMdGMp6/tzrZM4+75iIs87ee+1j\n4PF40NXVhoWFCWpq6uDnF4i1a5egtrYO+/Ydx7p1S9s1nqWlKZKTEzFkCC0R6K04joFIJHrujEJ5\neSUsLEygpaWJJUvav8+BYQBPzwrY2T2ayfh3Jyp9fV3o6PTFwYN/YcaMyQgOvo0ZM2a/8mchRJxo\n5vfVnTnjh3feeV/SMcRu3759+cHBwcsktU/jf3WJYgMA/P393928ebPF4cOHJ8rIUO98QjqStfVQ\npKVltrYGDQoKw+LFc8V6D2dnezg724PjONy7V4a0tEwoKCjg3XfXoK6uHvv3n8DatUvQ3j/vmprq\nqKwsE2tG0r2MGTMRoaERGD3a9ZnvebSM6ul7hV6EYdC6GfxpRo16dF+O4yAlFUvLqEiXIRT23Jat\nHY3Pl+pxewLDw8Nrjx079lViYmKCpLMAXWAZ1WMcx7F+fn7zPvnkkwTaME5Ix2pubm4z3c4wDHi8\njvlxwDAMdHW1MXr0CDg52UFKSgpHjpzG+vXLXmrKv08fVVRWVnRIRtI9WFnZICMjDw0Njdi9+9BT\n9xkJBIJXOjTyZWRn58HCwrJD70FIe927VwJ1dVVJx+iWCgqKoaWlK+kYYlVcXMx+8803B0NCQvZL\nOstjXabYAICampqHV65cWbhz584XtxwhhLyyuroaKCn98ySnM8+sCAgIwZgxI196I15l5UNoalJL\nx95uzZqN+PzzHzFx4micOdP2tN+qqmqUlb1+QVpZ+QDNzc9+UhwcfBvu7i/eB0JIZ9DS0kFlpXgb\nfPQGLS0tuHDhKmbPflPSUcSmvr4eGzZsuOTn57dR0ln+V5dZRvVYSkpKkqur62ZDQ8M9Xl5eWpLO\nQ0hPJRT+c3hRR81q/Ft9fQOKikowceLol7qO4zhcuxaGd9/9tIOSke5CRUUVjo6O0NLqC0NDfezd\newx9+6qjrq4ezc0tWL9+2SuPzXEcTp/2AcuyKCm5j3feWdFmqRTHcTh50geuru4dPntCSHulpqbA\n1NRI0jG6FY7jsG/fX1i3blOn/f3X0ViWxcaNG2+fO3duHsdxXWoTT5crNgDg1q1bF8eNGzdIX1//\nKzs7u561kI6QLsDdfRx27PgBZmaPDsn73xPFO9L587544w2vF76P44DSUgUAjzbqXr0aCm/vOZCX\nV+joiKQbmDJlOgIDL8LLayIAoKysAkpKilBQePY5Ge2xf/9xjBrl2nruzKVLVzF9ugeAR+1ud+06\ngpkz58PcfPBrfwZCxKWsrBQ6OvRstr04jsP+/X/B23su1NU1JR1HbL788suUoKCg2RzHNUo6y791\n2XIuMDDwl88+++xgcXFxl6rOCOkJpKWlISsrj6amR0tFWloEHX7PhoZGCIUiqKgoP/d9HAf4+mrC\n0VEXjo668PXVRHn5Q1ha2nR4RtI96Onpo6Lin2UjWlqar11oXL58FY6Odhg0yAgAEBh4A5MmjWn9\n5wcPnsKyZW9ToUG6nDt3ImFoqC/pGN0Cx3HYu/c4vLze6FF/lvfv319w6dKlZTk5OcWSzvI0XbbY\nAIArV65sWL9+vU9NTfv68BNC2m/mzLm4evU6AGDIEEvExyc//4LX9OefR1FXV4eSknvPfV9pqQJW\nr1ZFfT2D+noGq1erQk2NCg3SlpaWHsrLK8U23v375TAy6o+HD6tw6NBJmJoOam1gcPt2NBwcXKGj\n07M2kpLuLz4+BmZmRu3u6tebPZ7R8PJ6AyYm5pKOIzb+/v4Vhw4d+jg2NjZS0lmepUsXGxzHsefP\nn5+7evXqoKamJknHIaRH0dXth6qqWgCAo6Mt4uKSOvR+ioryWLNmCQIDQ3Hr1sv9TFRQUOqgVKS7\n8vZ+AwEBN8Q23rx5M7BnzxH8+ecRzJ07vbXNbUNDI5KS0uHmNuYFIxDS+W7cCIabm7OkY3QLp09f\nhofHdJiZ9ZwZjfDw8Jqffvrpmxs3bhyXdJbn6dLFBgBwHNfs7+/vvW7dugg6PZgQ8Xp8EFRjYxMU\nFTt2P4S0tDT4fD4WLZoNjgP27DkCHx9//LvVta5uA3btqoaiIgdFRQ4//FAAJ6f+HZqNdD+Kikpo\nbhaKbb+RgoI8FiyYhY0bV7Vu/n70JPQk1qzpUo1dCGnFMGyndhPsrmJiEqGl1Q+DB1tLOorYJCcn\nN/7f//3f9sDAwO2SzvIiXb7YAIAHDx7UXrx4cdr7778fT2dwECI+MjJyqKurR2npfWhrd15b2REj\nnLBy5UJYW1vgt9/2oqDgn2Wmj09yjooqRWRkMRoaDqNfPyo2yJM8Pafj2rUwsY2nrd23zXKUo0fP\nwdt7NlRU6AwD0vWIRCIwjGS+E3Ec98SDoq4qNjYJhYUVmD59tqSjiE1+fr7wgw8+2BcQEPC5pLO0\nR5fsRvU05eXlZaampm/06dPHZ8uWLRaSzkNIT7BgwVIcPrwb8+ZNQ0BACNzdh3fYvaSk+BAKhZCS\n+ufHzoABhli/fjlOn/ZBQkIypk591F3o8UnOJ0/6YM6chR2WiXRv5uaDceXKhQ4Z+8iRM3B3n0iN\nCUiXFRsbBVPTgR16j6amZty6FYWCglJISUn/3QqaAccBLS0NWLJkTofe/3WFh8eirKwaixevlHQU\nsSkvL8f69ev/unLlygZJZ2mvblNsAEBGRkaWra3tImVl5RMbN240lnQeQro7VVU1MIwUmptbYGMz\nGLGxibCz65gvV3p6OigqKoGRkUGb1xmGwezZ05CWlonffz+AVasWgc/n486deGhp9YOBgVGH5CE9\ng7S0eDfGchyHw4fPYMwYD1hbDxXr2ISIU0hIIFasmCu28QoKigAADMPD7dvRaGpqgZycIsaMGY+Z\nM5/cUH3nTjgOHz4HoVCAxYvf6HLnVVy8GAANDV289dYKSUcRm6qqKqxevfripUuXFnPdZWoJ3azY\nAIC4uLhoBweHxVJSUofWrVs3SNJ5COnu3nxzMU6dOoTZs71w9mwytLXloafXCHEvA3Z2Hobz532f\nKDYeMzc3gbp6H+zadQhr1y5Bamo2Nmz4ULwhSI9SUJCHlpZnn/T9sh4d9HUCkyd796i13aTn8fU9\nj6FDzV97v4ZIJMLVq6EoLr4PY2MzyMjIQigUYP785VBWVnnutQ4OLnBwcEFRUQH27TuAFSu6xknc\n9fUNOHbsHMaO9YC9vZOk44hNdXU1VqxYcencuXOzOY7rVpuYu12xAQB37ty55ejouITH4x1au3bt\nAEnnIaQ74TgOeXktAAAjIxn06aMBlmXg66uJjRunAQB27aqGp2eFWAsOeXk5NDQ8v6uclpYmjIz6\nIze3AAzDf+57CYmLi8a4ca5iGevhwyocOXIWCxcux4AB9ByLdF2FhfnIy8vCm296v/IYN29GISsr\nHzyeFDw8pmLevFdvBcswDITCp3/3zc7Og7S0NAwM+r3y+O3V0NCIs2f9wONJY+XKd6Cm1qfD79lZ\nampqsHz5cr8zZ87M4jiuRdJ5Xla3LDYAICoqKszR0XEpn8/fv2rVKio4CGkHjuNw8mQTli+XAwDs\n3duEOXPkoKJihVWrHp1tAQCrV6siKqoBenoNnZ6xqKgEbm4unX5f0v2MGzcJR4/ugYHBqx9o1tDQ\niMuXA9HcLMKHH/5faycU+HVaAAAgAElEQVQqQrqipqYm7N37OzZsWPrKY1y5EoK+fftj48b5Ysmk\no6P3RDdDkUiEkycvwcfnCg4f/k0s93mM4x6dxwQ86l7IMEBBQTEuXryG9evf7VFFBgDU1tZixYoV\n/mfOnJnRHQsNoBsXGwAQFRV13cnJaQXDMPtWrlxpKOk8hHR1eXktWL5crrWoWL5cDk5OLWCYzllr\ny+e/+D5vvOGFzz/fip9/3tEJiUh3JhQKIS39/L/GmpqaIRQKkZmZAzMzY8jLyyE9PQsiEYvo6ETw\n+TKYM2ch+vbV6qTUhLyaP//8LxoaarB06dy/N2o/W319AyoqKmFgoN+61EogEODYsfOwsbHHmDET\nxZaLYZg2s+BJSXcREhIJlmXx2WebxHrgIMcBvr6aWL36UYe4Xbuqoa0djKysAnz66Vddbt/I66qr\nq8PKlSsDTp065c1xnPjWjHaybl1sAEBkZGSQk5PTCo7j9qxatcpI0nkI6Y6UlKqwc2cF1q3TBAD8\n+GMR6uvTAIh30lBHRxunTyfD1dUBurpP3xeirt4Htra2UFfXFOu9Sc/D5/Nx7NgZzJgxuc3rHMch\nPj4ZUVGJUFXtA1lZWVhYWOLKlZuoqamBpaUVCgvz8c47H0soOSEvJzg4AP36aWD48GcXCZGRcUhK\nSoe8vDwUFBTRt682QkKiICXFB8PwwefzMW/eUmhr64g1W1CQP8zMBiEzMwfBweGth+Z5e0+AoaF4\n25aXlipg9eq2s/CnTxthzZoZYr1PV1BTU4OVK1dePXnypDfHcd36ZOtuX2wAQGRk5DVHR8dF9fX1\n+zZv3mwi6TyEdFVGRjLYu7ftMiojIzncu6cFDY07iIp63H2nACkpBTAxEV+x8ahV4gxs2qQBAPjm\nm1zo6oZg/PiRbZ5GBQffgrl5zznhlXQcJSVlbN36I377bT8WLpwJhuHh1KlLkJdXxNChdvjwwy/a\nvN/ZeYSEkhLyekxMzHHo0B4MHz6szetNTc24dOkqKiur4ODggvfe+6xTczU1NSEi4ibs7YcgMTEb\nq1e/g59//g+kpXlQUOjYg2IfMze37JT7vIqiogL8+efv+PDDLVBQUGz3dZWVlVi5cuWlc+fOvdGd\nZzQeY7pR56wXGjJkiN3MmTOPbtmyxYJO1CTk6f69QZxhGOTmZiE+/hZGj3602TYzMwdlZRVwdXUU\n231LShTg6Kjb+kRKUZFDSEgxbtw4BCkpPgAONTW1cHMbjVGjxovtvqTna25uxvbtP0JRUQHLlq2F\nnJycpCMRInZxcdEIDw+GlZUZVFSUER2diPr6Fsyb9xa0tLQllmv79q0YMGAQ1NU14ONzDnw+HzU1\ntfj224/Efi+OAy5eVG2dhX+877CrfufbuvUr8HjA5s2ftXuJV0lJCbtmzZozPj4+b3IcJ+zgiJ2i\nRxUbAGBubm7m5eV1+vvvv7fuaWv3COko9fV1OHbsT8yePRUAUFRUisTEu5g8eazY7vG0YuPkyRh4\nev7zpI5l2R635pYQQsQlJSUJNTVVqK6uhpWVDfT1n95KvLPduBGEU6dOwMrKBuXl9+DtPQn9++uJ\n/T5hYZEoKqrAhAkrwePxWh+YdUWJiXHIzk6CqqoS8vMrsGTJiw8WzM3NFaxfv/6Yr6/vMo7j2E6I\n2Sl63N/qaWlp6SdPnvTcuHFjjFDYIwpCQjqcoqISmpr+manV19dFUVGxWO+hq9uAXbuqoajIQVGR\nw65d1SgouNnmPVRoEELIs1laWsPFZSQmTZrSZQoNAHB3H4v//ncvqqsfgmEAZeX2LxlqD4FAgD17\njkFNTQ9r1ryDQYPkMWCAbJctNAAgOPga3N2dERERh2nTXryn5O7du83r1q3b4+vru7QnFRpADyw2\nACA/P7/w5MmTk1atWnW7oaHzW3cS0h39uyOVgoI86uvF9+eHYQBPzwpERZUiKqoUnp4VUFFRgJ/f\nBbHdgxBCiOR89NEX8PT0Rnp6ttjGrKqqxs6dB7Fs2VqMHDlabON2JJZlwXFC+PhcxdSpM1/Y8CQi\nIqL2vffe+8XX13dddzoZvL16ZLEBAPfv36/w8fGZsHjxYr+KigpJxyGky/t3sdHQ0PhE7/TXvweg\np/fo/I5HxccYyMsDx48fFOt9CCGESMaNG8EYOlQ8m7YLC0tw/LgPPv30a2ho9BXLmJ0hISEWiopy\nSEnJhIqK6nPf6+PjU/bpp59+6ufn90knxet0PaIb1bOUl5fXMwwzrbGxcd+vv/4619jYWHzNngnp\nYRiGB47jWqelO+vhiq2tFRITz3bKvQghhHScmJhI6OlpiOVwzPT0LISHJ+Cjj77oVktsa2qqceXK\nRRQUFKGsrByFhfkwNHx6Z8c9e/bkHzlyZHNYWNi5To7ZqbrPv71XxHGc8PLly4vXrVv3a0RERK2k\n8xDSFTU3NyM8PLxNgaGl1Rf37pV1yv1fdEAVIYSQrk0gEMDf/xImThz12mNlZ+chPDwBGzd+2K0K\nDZZl8fvv2/DWW29AUVEec+bMwYgRo576vi+//DJ1165dc3p6oQH08JmNx/5e//bR2LFji995553P\nvLy86KhYQv6HrKwshg8fjvr6BigrKwEApkwZjz17juDtt5d26L2rq2ugqtqnQ+9BCCGkY+Xn58LS\n0vS572lsbIK8fNvW1BzHITo6Hrm5RWhubkZjYwsGDTLB+vXvdWRcsWNZFtu2/YBx44ZDUVEBKioq\nGDfOA1FRt3H9ehByc3Pxxx/70dLSgk2bNkX7+/u/kZ2dnSfp3J2hx7W+fRFXV1fvefPm/fT2228P\n7MpdDAjpbHV1tdi79zcsXjy79bX4+GRUVDzAuHFuHXbfM2cuY+TIiTAzs+iwexBCCOlY+fm5OHRo\nD956azZUVZVbXxcIBLhwwR8+PgGYP38GPDzGAAAqKx/A1zcYIhHg6uoGa+uhkJWV61YzGY/V1FRj\n+/Yf4e09Efr6ugCA2to6BAaGgcdjkJtbhCVLVkFRURkbNmwI9PPzm1VVVVUt4didptcVGwBgZWVl\nNX78+MM//PCDrYwMbeMg5LHTp4+jXz81DB78z9Op7dv34O23l0JKSnwToRzHIT+/EFeuXIeLixtG\njRontrEJIYRIRm1tDc6dO4Xi4nx4eo5BcnI6SksrMWnSVOzevRNfffU+amrqcOGCPxQVVbFgwdJu\nfwhnQkIsfH0vYMmS2U/M2gQGhqGsrAorV65Hampq48cff3zC19d3VU85rK+9emWxAQBqamqqHh4e\nJ7dt2zZBW1ubpjgI+du3336OpUv/+aH52297sX798lcer6KiEt9/vxNDh9qAZVkwDA8Mw0P//obw\n9Jwu1iKGEEKI5LEsi7/+OgIHByeYmJgDAGJjo/DXX0dhbGyC+fMXQ0lJ+QWjdF1CoRD+/peQkZEK\nXd2+8PB41JKX4zjU1tahpqYOFy8GYOLEKRg2zBk+Pj5lO3bs+DkwMHCrhKNLRK8tNgCAYRi+p6fn\n7998882CoUOHirfHJyHdVFXVQxw/vg/z508HABw4cAJLlsx7rTEPHTqNBQuWd6vWhYQQQsSLZdlu\nuUzqf1VWlmPHjp/g5TUegwYZtb5+924Grl+PgJ5efygqKsDbew74fD5++eWXzDNnzmwKDw/3lVxq\nyerVjxQ5jhMBWDVu3Lj0tWvXfjBjxgxtSWciRNLU1PpAJPpnhpdhmNf+C2Ly5DEICgrA7NkLxBGR\nEEJIN9TdCw0AaGlpgaqqcptC49atKFRU1OOTT75qfa2xsREbN268ExQUtCA1NTVDAlG7jO7/b10M\nAgMDf9m6detbX3/9dapIJJJ0HEIkrrn5n2LD1tYaMTEJrzVe374ayM/Pe81UhBBCSOfhOA65uc3I\nzW1+6tlTeXkF+OOPw1BU1MJbb61ofT03N1ewcOHCiydOnBjT2wsNgIqNVhEREQG7d+8e+9ZbbwWX\nl5dLOg4hEtWnjwaqqx8dS2NjMxiJiXdfegyWZdv82szMCKGhwWLJRwghpOsRCAQICwtBY2Njm9eF\nwu63H/ru3WRs3ZoGa2sZWFvL4OTJJly96ofDh//E9OkTsXfvcaSmFuGDD75o0+TE19e3fNWqVd+d\nPXvWu7Kysk6CH6HL6NV7Np6GYRipyZMnb/v0008XDh8+XEXSeQiRhOrqKvz1137MmeMFADh27Awm\nTRoDDQ31do/xzTfboKurCy2tR9dkZORg/fr3oKVFqxUJIaSnaWpqwvfffwk3NweEhUXBwGAAamur\nwbIi3LkTg9Wr38bIkaMlHfOFsrLScfr0cejoOGD9ek/U1z/qIaSoyOH8+VhkZoaAYaTw1lsroKCg\n2HqdSCTCd999l3b58uV3IyIi/CSVvyvq1Xs2nubvdmTr3Nzc7syZM+eLtWvXDqDzOEhvo6qqhrq6\nptZfz549DX/+eRRr1y5p9xja2n2xdu0mVFZWQEZGFgsXUpFBCCE91f79f2Dx4llQU1PFkCGWqK9v\ngIqKMq5fD4eh4cAuX2g0NjbgxInDAFqwevUCXL1a8MR77t2rwMyZC6CtrdPm9fLycmzevDk4JCRk\nQVFRUWknRe42aGbjOSwtLS3c3Nz2//jjj85KSkqSjkNIpwoJuQY+vwE2NpYAgDt34tDSIoCrq2O7\nrq+uroGv7w2sXbupR3QgIYQQ8nQlJUW4dOlU62z4Y4GBoZCTU8OUKTMklOzFmpubceDALjQ3N8DD\nYzS0tDRRUVGJS5eCoKi4FJs3P3pQ9uefjZg7Vx7/fgB9+/btmm+//faon5/fO73t/Iz2omLjBRiG\nkffy8tr92WefeTs4OFDFQXoNlmXx66//QUtLM2RkZDF8uB2ioxOwcOEb7R4jMjIOCQmpuH+/DIMH\nW2LZsjUdmJgQQkhnq6+vw9atX2P9+iWt5yYVF5fi0qVAuLiMhLt71zy0lWVZXL58HmlpyZg1azLU\n1fugqqoa58/7Q0VFHQsWLIWMjAzy8loAAEZGMm0KDZZl8csvv2T5+Ph8FRoaekRSn6M7oGVUL8Bx\nXCOARW5ubktmzJjx6YYNGwbRE1rSG/B4PCgqKsPExBAaGga4fTsMdXU1EAgEkJaWbtcYTk62cHKy\nxb17Zfj990Noamrq9qfFEkIIeYRlWfz883dYufLN1kLj9u0Y5OeX4v33Pwefz5dwwieJRCJcunQO\nGRmpcHW1x8qVb6K6ugYHD56CgoIyVq3a2GYvxoABsk+MUVxczH700UchoaGhS/Lz8ws7M393RDMb\nL2HgwIEDRo4cue+HH34YpaOjQxs5SI93//49HD68GxzHg4yMLDw93XDp0lUsXTr/pcb5738P4YMP\nPm93kUIIIaTrO3v2BAwNNWFg0A/nz/sjICAYy5cvx+TJ0yUd7Qnl5WU4f/4UamoeYvRoFwwaZITC\nwhJcvRoKJSUVLFiwFIqKL17A4uPjU75z5879165d+/Tv89rIC1Cx8ZIYhuFPmjTphw0bNiz28PDQ\nkHQeQjpaUlICUlOTYG1ti9TUaMjLyyIvrwBz5kxv1z6M3Nx85Oc/wPTp7V9+RQghpOtbvHgehgyx\nAssyePPNJVBX14CMjIykY7USCoUIDPRHSkoCVFQU4OExBkpKj2YtgoJuoqGBxdy5C9v1IKypqQn/\n93//lxAcHPxeVFRUYEdn70mo2HhFTk5OkyZMmLD1008/taZlIaSnKy8vg4aGJrZt+w+WLp2LwsIS\nRERE4403vF54LcuyOHjwLDZv/rgTkhJCCOlMXW15bH19HQID/ZGbmw2OE8HV1R6mpoPQ0NCIkJBb\nKC9/CCkpGfTr1w/e3nPbNWZycnLTF1984RsUFLSsqqqquoM/Qo9DezZeUWRkpL+amlp4SkrKro8/\n/niqg4OD4ouvIqR7+uOPHZCSYhAXl4g33pgCPT1tlJdX4tatqBd2p+LxeJCSYtDY2AB5eYVOSkwI\nIaQzdJVCIzc3CxcunIWUFIdRo4bD3X0oAKCurh779/8FRUVVeHpOg76+QbvHFIlE2LFjR/bFixd/\nvn79+h8dlb2no5kNMRg5cuQiDw+Pj99//31zWpNOeqKysvu4ePE4Zs2a0qYbx08//Y63314Kefnn\n/2WTlpaJxkY+Ro+e0NFRCSGE9BIsyyI0NBjR0RHQ1dXExImjWjeqcxwHX98gVFbWYNmyNVBSUn6p\nsTMzM1s+//zzoOvXr68oLS0t7oj8vQXNbIhBWFjYYW1tbb/4+Pg/t2zZMsna2rprlPmEiImWljZq\nahrBcVybYkNLSxM1NbXPLDYEAgF+/HE3jIyMMGHCpM6KSwghpAdjWRb+/peQlBQPJ6chWL687XKo\n27ejkZSUjunTZ8PMzOKlxuY4Drt3784/derUbyEhIb9w9FT+tdHMhpi5u7uvnj59+rsbNmww7oot\n3wh5VenpqUhIuI0JE9xbXxOJRNi9+/AzTxYPDAyFpaUTLCwsOysmIYSQHiwk5BoiIm7Czc0RlpZm\nbf5ZWlomQkIi4O4+FsOHu7302AUFBaItW7ZcDw8PX52RkZElrsy9Hc1siNmNGzd26enp+URHR//5\nySefjLW0tHyyQTMh3ZCBgSFCQvzavMbn86Gvr4vS0vvQ1dV+4hpbWytERNyhYoMQQshr+/XX76Gq\nqoDVqxe0zrI3NDTi2rUbePCgBiYmFvjwwy/a1Snxf3Ech/379xf99ddfewMDA7/mOI7tiPy9Fc1s\ndBCGYZiRI0eu9PDw2PTuu++adaVWcIS8ivj4GKSlxWDSpDFtXm9ubsaJE+exePHTu3ocO3Ye/foZ\nYvr02Z0RkxBCSA+VlJSAgABfyMnx0LdvXxQX34OCghK8vGZCT0//lcbMyMgQfP3118Hh4eHrs7Ky\nMsUcmYCKjQ6nrKysPnHixP9u2rTJ09XV9eV2JxHShTQ1NeHKFR8UFxegqqoKCxfOgKqqCgBg795j\nWL78zWdem5KSjuDgcIwdOwEODi50uB8hhJBXIhQKUViYBx6PB0PDga88jkAgwPbt2zMuX76888aN\nGztpb0bHoWKjkzg7O88YNWrUZ59++qmtsjLVHKR727ZtKxYt+udQv3PnfDF27MjW4uNpWJZFUlIq\ngoNvYe7ct2hpFSGEEImIjIys//nnn69cv359bVlZWbmk8/R0tGejk0RERJxjGMY/JSXl5xUrVszy\n8vLSlHQmQl4VxwnarIm1s7NGaGg4pk6d+MxreDwehgyxxODBpjh92p+KDUIIIZ2qvr4e3377bcL1\n69e/u3379klJ5+ktqNjoRBzHNQBYY2tre/Ty5cv/+eSTT1yNjIyoZRXpdmRk5NHS0oLHe5GMjAwQ\nGRmHwsIS9O+v99xrm5tbUFdX3xkxCSGEEHAchzNnzpQdPnz4/OXLl9/jOK5O0pl6E1pGJSEMw/Dc\n3d03e3h4rNi4caOprCw1rSLdR05OJm7evAYvr38O6WtpacHJkxexcOEbz732t98O4L33PqXTxAmR\nsIcPK3Hw4D5s2vSBpKMQ0mEyMjIE//nPf25ER0d/kJycHCfpPL0RzWxIyN9t1X5SUVHZFxkZuW3F\nihVTPDw81CWdi5D2GDjQBIGB/m1mMh48qIKs7Iu7rqmqqlChQYiENTc3Y9u2rZg0aRR+/vlb6Osb\nYs6cBZKORYjYNDQ04Mcff0wJDAzcefPmzd20AVxyXq4RMRG7mpqah+fOnXvro48+mr569erQ/Px8\nkaQzEdIey5e/jfPnA9DS0gIAzz1J/H+xrAgsSy3MCZGkXbu2Y+JEdzAMUFNTgzFjJrz4IkK6AY7j\ncPbs2fK5c+fu2b59u0tYWNguKjQki4qNLiIhISFs9+7doxcvXvzRDz/8kNHY2CjpSIQ8F4/Hw7p1\nm3Dw4GkAgKnpIAiFImRkZD/zGo7jUFtbh4YG2rNBiCSZmJihvLwBTU3S+PDDL9C3r5akIxHy2lJT\nU1uWLVsW9Pnnn0/y8fFZ9eDBg1pJZyK0Z6NLUlVVVRs1atTWOXPmeM2bN0/78SmZhHRF0dHhuHPn\nNubO9QIA7N59COPGucPYeMAT701Ly0RlZQs8Pad1dkxCCCE9VGVlJX788cfYmzdv7rx169ZBmsno\nWqjY6MJMTU0tHB0dv1+7du2Y4cOHK0k6DyHPkpqagnPnTmDp0rmQk5OFn18gsrPz4ORkDycnu9b3\nVVY+gJ9fGNavf/e17seybJvWu4QQQnqflpYW/PHHHzm+vr7Hr1279jXHcS2SzkSeRMVGN+Do6DjF\n0dHxw/fff9/F0NCQWuWSLqm6ugrHju3F/PnTW1/bs+cwZs+eBjU11dbX4uKSce9eNebNe+ulxmdZ\nFjt3/gxpaWmUlJRAQUEeU6Z4w9p6qNg+AyGEkK6P4zicP3++/OjRo363bt167/79+xWSzkSejYqN\nbuLvVrnvjB49eunmzZut6BRy0hXt2rUD9vbmMDEZCODRU6d9+45h1KgRsLAwaX1faGgEamuFmDdv\nUbtnKLZv/xHu7vaoqqpBnz6qMDDQx9atv+O7737tkM9CCCGk64mJiWnYsWPHjaioqI9TU1MTJJ2H\nvBgVG90MwzCKHh4eX0+ePNl7xYoVRnQ+B+lq/vxzJ1RVFTBu3IjWQiIgIAT37pW1vufhw2rcuhWJ\ne/cq4Ofnh/79DV84bnZ2Bg4f3gd1dU20tDSDz+dj5MhRcHBw6bDPQgghpGvIzs4Wbt++PSIyMnJb\nZGTkWUnnIe1HxUY3paSkpDlu3LjvvL29Jy9YsECPz6fVVaTrSE9PxZkzf0FFRQHTpk2Aiso/M3EP\nHjzEnj3Hwefz0NjYjAkTPDBpkqcE0xJCCOmq7t27h19//TX61q1be2/durWHNn93P3SoXzdVV1dX\nAWCFvr6+kZ+f33fz5s0bP23aNA3qXEW6AjMzC1hYWOL99z+Er+9V2NnZ4O23l0BRUQGxscng8/lY\nuXI+FBUVsGbNB6ipeYjZs+lAMUIIIY9UVVVh+/btyaGhoceCg4N/4jhOKOlM5NXQzEYPYWFhMcTe\n3v6rZcuWjRo9erSKpPMQAgACgQCHDv0Jf/8rEIlY9O2riTfemIKQkHAYGvbDnDnTUFRUisOHT6F/\nf0OsXbsJNEtHCCG9V2NjI37//fesa9eunQ0ICPiS4zg6eKybo2KjhxkyZMgoR0fHT5YtW+bq7Oys\nIOk8hABASUkRjh49gJaWBjx4UI38/CK4uNhj+fI3AQCBgaEQiUTIyyuBoeFAzJw5F9LS0hJOTQgh\npLM0NzfjwIEDBb6+vr6hoaGfVFdXV0k6ExEPKjZ6KHt7ew97e/tNS5YsGe7i4qIo6TyEAI82eV+4\ncAbKyvLw9BwLRcV/6uHduw9h7twZqK2tQ0DADUhJyUBHRxeuru7Q1zeQYGpCCCEdpbm5Gfv378/3\n9/f3v3379ufl5eVlL76KdCdUbPRwtra2kxwcHDYtWbLElYoO0lVUVpbj9OnjqK+vweDBJhg82BRy\ncrLYt+84lJQUUVdXBwUFRUyaNBqHD5/Bf/7zi6QjE0IIEaPm5mbs27cv39/f3z84OPizv/eikh6I\nio1ews7ObqK9vf3mJUuWjBg+fDgtryJdgkgkQnJyIhITY1FWdg/KygqwsDBGYWEpAFlUVpZDSUkJ\nS5aslnRUQgghYvC4yAgICLgSFBS0hYqMno+KjV7mcdGxePFiV1dXV5rpIF1KTU01kpMTISsrA3t7\nJ0nHIYQQIiZNTU2Pl0tdCQ4OpiKjF6Fio5caMmTIODs7uw0zZ84c4enp2Yda5hJCCCFE3Kqrq7Fr\n1670sLCwq9evX/+yrq6uUtKZSOeiYqOXMzY2HjJs2LBPpkyZ4j537lxtKSk6eoUQQgghr6e0tBR/\n/PFHQnh4uE9gYOAPHMfVSzoTkQwqNggAQF9f38jR0XHL+PHjxy5evNhQXl5e0pEIIYQQ0s1kZmYK\nd+3aFXPnzp2TYWFhOzmOE0g6E5EsKjZIG0pKShpubm5b3NzcJq1evdpMTU1N0pEIIYQQ0sVFR0c3\nHjx4MDI6OvpAZGTkUY7jWElnIl0DFRvkqRiGURw7duz7w4YN81y+fPlQY2NjWl9FCCGEkFYsy+Li\nxYuVvr6+t2NiYnbHx8f7cfTFkvwLFRvkuRiG4Ts4OLxpb2+/YNasWc5jxoxRps3khBBCSO9VW1uL\nAwcO5IaGht6IiIj4vqioKF3SmUjXRcUGaTcLCwsnOzu7TWPHjh355ptv6snKyko6EiGEEEI6SW5u\nLrt3796EO3fuXImKitpaVVVVLelMpOujYoO8NA0NDR0XF5dPXFxcxq5YsWKwlpaWpCMRQgghpANw\nHIewsLC6U6dORUZHR5+IjIw8yHGcSNK5SPdBxQZ5ZQzDyI4cOXK9vb39tFmzZtkNHz5cgZZYEUII\nId1fQ0MDjh07VhwaGhoeFxe3Izk5OUzSmUj3RMUGEYvBgwe729nZrRkxYoTLwoULDRQV6XByQggh\npLtJTU0VHDlyJDEmJibo1q1bW+kQPvK6qNggYqWiotLH2dn5PVtb2/ELFy4camVlJS3pTIQQQgh5\nNoFAgDNnzpQHBweHx8TEHI2LiztLrWuJuFCxQToEwzCMjY3NtGHDhr01evRol9mzZ2vLyMhIOhYh\nhBBC/lZQUMAdOHAgJTo6+kZUVNTW+/fvF0g6E+l5qNggHa5Pnz79XF1dP7S1tR05f/58KwsLCzqz\ngxBCCJEAgUAAHx+fB8HBwXdiYmLORUZGHqBTvklHomKDdBqGYfg2Njbe9vb2c11cXJzmzp2rr6ys\nLOlYhBBCSI+XmpoqOHr0aHJCQsLNiIiIbRUVFTmSzkR6Byo2iEQoKyurOzo6bhg6dOgYLy8vOzc3\nN0XqZEUkoaqqCvLy8qBzYwghPU1NTQ2OHz9eGBERERUbG3s8KSnpAu3FIJ2Nig0icSYmJs62trar\n7ezsnBctWmSmp6cn6Uikl4iPj0doaCikpaVha2sLZ2dnSUcihJDXwnEcbty4Uefj4xMXHx8fFB0d\nvaOmpuahpHOR3nBK8HEAACAASURBVIuKDdJlMAwj6+zsvNTW1naqs7Oz3axZs7QVFBQkHYv0QE1N\nTTh48CCSkhKwdOkSREfHwNV1JKysrCQdjRBCXklWVhb7119/pSYkJNyJjY39Izs7O0rSmQgBqNgg\nXZSCgoK2q6vrehsbmxFjxowZOnHiRFUpKdpXTl7fjRs3cP36dbS01MHd3REcx0FDoy+GDRst6WiE\nEPJSysvLcfz48dz4+PiYhISEc3FxcWdoszfpaujbG+mSGhoa7gP4DAD69etnYW9vv9bS0tJ5+vTp\n1o6OjrK0v4O8qsTERHzyySfYtu0/cHS0BQDw+dSWmZCeoqamGkpKyuDxeJKO0iHq6+tx5syZ+5GR\nkbHx8fEB4eHh+ziOq5N0LkKehYoN0uUVFxenAljPMAxz4cIFdxsbm8XW1tbD5s6da2FsbNwz/zYh\nHUYgEEBaWhp6ega4cyceDg5DwbIicBwLhqH/nEj7sCyL+/dLUVtbC0PDAT2+wQDLsrh+PRDR0RGY\nM2chDA0HtOs6kUgEhmE65Yt/Wtpd7NjxC27eDEd8fFKH368zCYVC+Pv7VwcHB8cnJSWF3b59+7f6\n+voySecipD1oGRXplhiGkba1tZ01ZMgQb0tLy6GzZs0yNjIyoukO8lyZmZnIycnBxIkTAQC+vheQ\nnByPVasWQElJH1JSchJOSLqytLS7CA4OgFDYAo5joaWlCUVFeRQX30djYws2b/5Y0hHbqK+vQ1DQ\nVXh5zXjlMVJSkhAU5A+BoAWOjjbgOBYcpwh393FPvJdlWcTHx+D27VAAHFhWhLKy+7C2tsWcOQtf\n45P8M35jYwPq6urAcSxKS0uQl5eD0tISFBUVIjo6FqtWrYS395weMashEolw/fr1+qCgoKSkpKTo\n2NjY3/9++EZIt0IzG6Rb+ntN6gkAJxiGkT1x4sRsa2vrKRYWFkNnz55tMmDAACo8yBPy8/Nhamra\n+uvw8JsYPtwBACAUNlKxQZ7q3r1S7N37OywsBmH2bA/8e/9YTU0tTp70k1C6J9XX1+H48UMICAjA\n/PlvvvT12dkZ8PPzQUtLM4yNDTB//tTWz7x791G8994WCAQC5OfnIjMzHfn5uWhubgTHsTA3H4h5\n86aAz+cDALZt24OcnGxUVJRDU7Nv6z2ampoQEnINGRmp4PEAgUAIKSlp8HgMHj0E5cCyAJ8vBY4T\ngWVFADgoKMhBQUEeDMOgb191mJv3A9CEuro6/Pe/u8CyIsTG3sGDBxVgWQ5CoQAsy0JVVQ2mpubQ\n1e0nht/hjiMUChEcHFwXEhKSlJycHJOUlLQ3Ly8vQdK5CHkdNLNBehSGYWRtbW1n2djYTB08eLDt\nrFmzTAYOHEiFBwHwqNi4c+cOZs2aBQDYseN7LFr06P/LyKhAQUFLkvFIF9HY2IDTp4/j4cMKMAyg\npKSAqVPHQ1pa+pnXbN++F6NHT4Crq3vrF20AqK6ugrKyiliftNfUVCMoKABFRQWQk5NDS0sLWJYF\nwIHjWEhJ8TFpkjuCg2+juVkIjuPAcQCP9+hHIcuyUFJSAcChsbERHMdBJBJCJGLBcSL066eDMWOG\nP/Xz+vtfR3l5BXg8Hvr104GRkT769+/X5jP/W0FBMS5fDoKqqhoADgJBC6Sk+HBxscOgQUbP/awc\nx+FFe/TS0jKRmpoFZWVFyMrKQEFBHn36qIHP54HH40MkEuL8+SuQkpLDli1fv+B3t/MJhUIEBgbW\nhoSEJN+9e/dOfHz83sLCwp61Doz0alRskB6LYRgZW1vbmTY2Nl7m5ua2s2bNMqE9HsTf3x+lpaVY\ntGgRfvnlO8ybNxVKSoqQklKAkhKd8dIbFRcXwtf3IhoaagEw4PEAD4/R6NtXo91jCAQCxMYmoaCg\nDDNnzsPt26FIT78LBQVZ1Nc3QVZWDsbGZujf3wA6OnptnvK3R319HUJCriEtLQXKygpwdXWAvr4u\nWlpaICPz8g0OiopKoa6uBgUF+Ze+tjvx8wvGgwe1mDLFG0ZGAyUdp5VQKMS1a9dqb9y4kZScnHwn\nJibmz9LS0hRJ5yKkI1CxQXoFhmGkhw4dOsPKysrT2Nh4yKRJk8wcHBxke8K6XvLySkpKcPDgQaxe\nvQoHDuyGtnYfeHp6oE8fI0lHI6+hsbEBsrJyL5xFqK2tQXR0BFJSkiAQNENDQw1jx46AouLrn+uT\nnJyGzMwc2NpawcjIoPV1juOQn1+Is2f9MGrUOIwdO+mFY6WmpiAoyB8sK4CsrAwcHYdgwADD187Y\nm+zefQybNn38SgWZuNXW1sLHx6c8Li4u+e7du/EJCQl/0h4M0htQsUF6HYZhmAEDBgy3sbGZb25u\nPtTFxcVy4sSJqnJytF6/NwgI8IWh4QDo6xvgwIEDWL9+PbKy0nHx4mlIScnA2dkVDg4uPWKDaW9y\n/vxJ5ORkIi+vANu2/fHEsp68vBwEBQWguvoBVFQUYWVlBlPTQZ367/nevTIEBoZj3bp3n/u+69cD\nERl5C8bGhhg1yuW5S5TI85WXV+Ly5UCIRIC8vAIEgmb4+QXg1KmzUFNT7/D7FxUV4fz583lpaWlJ\nKSkp4VFRUfv/bu1OSK9BxQbp9TQ1NQfa2dkts7CwGGZjY2M1bdo0PU1NTUnHIh3k4483YehQK+Tl\nFUFb2wDW1jawt7eHQNCAurpixMQkIDY2BaamFvDymkVFRxdXUlKEo0cPwsnJGkOGWOL+/XJcuhSI\n2to6LFiwBH37amHXrh0wNOyHESMcoKysJJGcN26Eo6DgPtas2fjEBnORSIScnExERUWguLgAdnaW\nGDZsiERy9mQcx+HIkdPg8+WxfPnaDmlXzHEcEhISBJcvX87IyspKSE5OvhYTE3OK47gGsd+MkG6C\nig1C/gfDMH1cXFwWWVpajjQ1NbXx9PQcaGFhwadDBHuO7OwMHDt2EPPnT8ONGxG4dSsa7u5jsXDh\nAtTWFoLjRACA9PQsXLt2CwsWLOlSa727usrKcpw8eQzDhjlBTk4ONjaPDk6sqanG+fOnwXEcPD2n\nITDQHw8eVAAAGIYBy7LQ0OgLBwcnGBubPXP8pqYmXLhwGvfvl4BhOKipKWPixFFPfHFkWRbHjp2H\nvLwsJk4cJZEiIzs7D2FhUWAYPhwcXDB8uBsAIDo6AmFh1yElxQPwqPNS//56sLY2h4ZGxz9t782u\nX7+NuLi7WLPmHejo6IplzKamJgQHB9fevHnzbnp6ekJycvKpjIyM69zjHyaE9HJUbBDyDAzDyJib\nm48fPHjwVDMzM6uhQ4eaT5o0SUNFRUXS0chramlpwX//+wusrU1gaWmGnTv3IysrH2+/vRQ2Nv98\n0WVZFhcu+KO+vgXz578FDY2X29TbWzQ1NeHqVV/k5uaAYUSYPHk08vOLkJiYhlmzFiAjIxUxMRGY\nPXsqWJbF3r3HsWjRG9DR+af7F8dxePiwCsePX8CIEaORmprc2gKVYRgIhUJwHAsej8HYsa7Q1dWW\n3Ad+gaamZnz//U64uAzHzJnzWmcy4uNj4O9/CVZWJnB1dXxhlyUiXmfP+kIk4mPRouWtezheZeaS\n4zhkZmayly9fzs3JyUlNTU2NjYuLO/rgwYNMcWcmpCegYoOQdpKXl9d1cHBYaG5u7jhgwADLSZMm\nDRo6dKg0fWHonh48qMCHH76HiRPdMW7cSNy7V4atW3dCQUEeK1cuhIGBfut7GxubcPasH1RVNfDm\nm0t63NKq5uZmNDbWQ0VFDRzH4ZdfvoeiogJWr34HPB4PVVUPkJycCJFIBHt7R0hJSSMk5BqyszPA\nskIwDODu7tTm9wx4PLtwDhYWxhg2bGi7sjQ2NiErKxeDB5t2270KYWEROHr0HH7+eRv69FHH2bN/\noaLiPgYONIC7uzMVGRISF5eMwsISNDQ0QiAQgOM48PlyePvtTS+8tq6uDgEBAQ9jYmLSMjMzU9LS\n0vySk5P9OI5r7oTohHRrVGwQ8goYhuEbGxu7DR48eKaZmZmllZWVxZQpU7TV1WkJxKuqqalGdHQE\nBg0yga6ufod3j/n2288xaZIbVFSU27Q4DQy8gcDAMAwaZIS5c6e3WX6Tm5uPy5dDsH79u1BT69Oh\n+TpLS0sLvvzyE5iaGiEnpxA8njTs7Myhp6eDsLA74PEYKCkpwNR0IPh8Pi5cCICurhbc3JwwYIAB\nfXH+HzdvRuLu3Ww4Og7HkCG2OHHiMITCZnh6jqHlUV0Iy7JISEhBVFQCJk6ciqFD7Z94D8dxSE5O\nFvr5+WXn5ubeTU1NjY6MjDzc1NRUJIHIhHRrVGwQIgYMw2g4OzvPHzx48HB9fX0zFxcXYzc3N2UF\nhddvpdlbPHhQiQ8/fBf37pVCT0/3705BfAiFIjAMA319A8yYMVdsRcjDh5U4cGAPpKQY9Ounjby8\nIgwbZgMbm8H4/fcD0NPTwb179+HmNhyWlv8srWpqasbRo2dhZmaFqVNniCWLJO3ZsxPDhw+Bvv6j\n9etCoRB8Pp+KiJckEonwzjtbMHy4C4RCAaSl+ZgyZazENqSTfwgEAiQlpSIlJfPvww2lMGyYExwc\n2nb6KiwshL+/f3FWVlZGRkZGWmpq6vn09PQQjuOEEoxPSLdHxQYhYsYwDNOnTx9jGxubuWZmZjb6\n+vrmbm5ug1xcXOS7Qq/3rm7x4sUoLCyAnp72318MHrWslJOTxcCBA/HOO+899brbt2/jzJkzmDFj\nBpydnZ/o+PMsLS0tyM/PwaBBpjh9+ihKSwvg4jIMZmbG4DgOP/64Ex98sP6J65KT03DjRhSWLFkJ\nPT39p4zcdbEsi9u3Q3Hz5nW4utrD2tpC0pF6hEcndXM9bpldd1NXV4/o6ATk5RWBx5OGjIwM7O2d\nMHSofZtT0cvKyuDv738/NTU1MycnJz09PT0kISHBh+O4WgnGJ6THoWKDkA7GMAyjpaVlY2Nj84aZ\nmZmlvr6++ZgxYwba29vLdNc16Y+xLAsvLw9YWlrC03MK7O0dcfLkccTHx2LqVC+YmJhBWloGiopK\nL7XsKCMjA0FBQeDz+Zg8eTJkZGQQHR2NgoICsCwLKysrmJqaor6+HteuXWt9Cn/z5k04OjpCUVER\nQqEQLMuC4zhoaGhAT08Pffv2haGhId5++20YGxvD3t4e1dXVGDx4MCwsLABwqKnJh5/fVdy/Xw4A\nsLe3gY2N5VNzCgQCnD7tC13d/vD2nvPav5+dob6+Dj/88BVGjXKGra01zWCQbq+4uBTR0Qmorq4D\nwIOKihpcXEbCxMSsTeFXVVWFa9euPUhISMjMy8tLy8zMvB0VFXWW47hKyaUnpOejYoOQTsYwDL9/\n//4OlpaWM83MzCwMDAzM3N3djYYMGSLV3qfxXUlZ2X1ERNzElSt+SEpKQVNTEwYPHgx1dTXk5OSi\noaEBUlJ8/PTTNlhaWiMoKAjq6uqIiopCVVUVDA0NMWHCBGhoaDwxdktLC65cuYKSkhLIyspi6NCh\n0NPTQ0VFBXJzcyEnJwd3d/cXLq168OABysrKcP/+feTn56O2thYaGhpwcnKCmpoaUlJSkJz8qPtR\nfX057OysYGdn0+7fg1u37kBKShkTJ0556d+/zpaamoITJw5i2bJ5UFWlzmqke3jcrSw5OR25uYVg\nGB54PCkwDIN+/fpjxIhR0NRs2y2uqqoKN27cqI6JickuKChIy8jIuBMXF3eysbGxVEIfg5BeiYoN\nQiSMYRhpAwMDRzMzs6kmJiamOjo6Jo6Ojkaurq5KSkpdb713RkYGjh49iv79+4NlWfB4vNalIwKB\nADIyMnj8c4XjOIhEItTX10FOTh5SUlJ4+PAhxo8fj+zsbEybNg2NjY0ICAjAw4cPwTAMMjMzYW1t\nDXt7e5iamrYWEo2NjUhJSUFJSQmKi4vBMAxsbW3h4OAg1mUrdXXFEAobX+qa27ejcfduNt5771Ox\n5ehIly6dg5SUAC4uT26MJUTSWJZFdnYe4uJS0NjYDB6PDx6PD3V1TdjaDoOpqfkTf+Y5jkNBQQEC\nAwNLcnJycgsKCrKysrJi4+Lizjc1NRVK6KMQQkDFBiFdDsMwjKKi4iBbW9uZxsbG1vr6+ibm5uZG\nY8aM0dLVFc8hVC8jJycHaWlpcHFxwZ49e6CkpAQ3NzdYW1uL/V4ikQhVVVVQVFRETEwMsrKy0Nz8\nT2dJjuPAsiykpKTAcRzi4+MRFxeHLVu2YPLkyWLJUF9/HwLByy3ZLiwsQXx8JhYuXCaWDB2lsbEB\nBw/+CU1NZYwf7ybpOIRAJBIhMzMHKSkZqK9vBMCHlJQUTE3N4ew8AkpKys+8LjExURgSEpJfVFSU\nk5ubm5WVlXU9OTk5gOO46s79FISQ56Fig5BugGEYTTs7u6mDBg1yMTIyMjYwMBg4evTo/hYWFryO\n3oxaUFCAP/74AxERETAxMcE333wDLS2tF1/YSUQiEaqrqyGutsONjRVobq5q9/tLSu7h8uUguLuP\ng5OTq1gyiFtRUQF8fM6iubkB06ZNgLp6z2jbS7qf+/fLcedOPCoqqsDj8SElJQ0LC0vY2TlCVVXt\nmdfV1dUhPDy8PioqKre4uDgrOzs7MyMj41JeXl4Ex3GCTvwIhJCXRMUGId0QwzDygwYNGmlsbDx+\nwIABA3R0dAaYmJj0HzlyZF99ff0O2/RbVlaGmzdvoqysDOnp6XjzzTcxbNiwDrmXpLS01KGh4d4z\n/znLsigvrwTDMODxGGzd+gf++GNflzmA7u7dZISFhaC5uRE8Hg8sK4S6uirGjh0JeXk5SccjvYhI\nJMLduxlITEyDSCQCjycFHZ1+cHV1g65uv2deJxAIkJiYKLx582ZRSUlJfnFxcV5eXt7dlJQUn6qq\nqnSOvrgQ0q1QsUFID8EwTN8hQ4ZMMDIycjE0NDTS0tIysrW1NXB2dlZ+1af+H3zwAUJCQmBjY4OF\nCxdCV1cX4eHhMDExAZ/PR2hoKLy9vWFiYiLmTyM5LCtETU0BALbN6xzH4auvfsGtW5EYNswOFhYW\n0NTsiwEDBsLZeYRkwv5LUJA/MjOT4e3tAVlZWUnHIb2MSCRCbGwi7t7NAsPwwOdLY8gQOzg4uDzz\nv0eWZZGVlYXQ0NDS/Pz8/NLS0tzc3Nzs9PT0K8XFxdEcx7V08scghIgZFRuE9FAMwzAyMjKGtra2\nnkZGRkMMDAyMtLS0Bjg7O/e3t7eXlZeXb9c4HMchMTERR44cQWlpKRwcHPDgwQPIyclBU1MT2tra\nmDZtWgd/ms7DcRxqawvAsk9fmSEUClFUVIK0tBzcu1cOjmMwaJAJpkzxFutG9ebmZsTF3YGV1ZBn\nrlt/LDs7AxcvnoWBgQ7GjRsptgyEPI9QKERCQgru3s0Ex/EgJSUNR0cX2No6PHOmr6SkBGFhYZXp\n6ekF9+7dy8vLy8vNzs4OzsjICKXzLQjpmajYIKQXYRiGr66ubmllZTXFwMBgkK6ubn91dfX+VlZW\nesOGDVPR0dF54Ri//74De/fug56eLtTV+0BXVx+6unpQVVXDwIEDYWpqCh0dnW59fkNtbTFEohd3\npGpqasb7738JDQ0NvPfex9DXNxBbhlmzvLB27WJkZeWjvr4RamoamD9/8RNPiAMD/XH3bhzmzZve\n5sAyQjoCy7LIyMjGF1/8CDs7W3h7z4KdncMTh2gKhUKkpaVxkZGR94qKioorKiqKCgsLCwsKCqLj\n4uL8OY4rk9BHIIR0Mio2COnlGIZhZGVl+1tZWY3R19e309fX19fU1Oyvr6/fz8nJScfc3Jz595fY\n5uZmREbeQmxsNNLSUpGWlomHD6ugpqYKDQ11KCkpo39/Q/Tr1x/S0tJQUVGBuro6+vbtC21tbaiq\nqkJeXr7LFiT19fcgENS1671JSakID4+Fjk4/TJ487Yle/6/Kx+csFBUZ2Ns/Ou/jwYOHOH3aF8OG\nOWPs2Emt7xMKhfjuu//DrFke0NXVBgBUVVWjvr4Benrdu+gjnYtlWRQUFCE3txANDY2orq6FSMSC\nYXgAmL//Fxg82ApOTq5QUFAE8Og8i9jY2MbY2NiSioqKorKyssL8/Pz8nJyc4Ly8vDs0Y0FI70bF\nBiHkqRiGUTYyMnIYMGDAaAMDAyMdHZ3+mpqa+ra2tnq2trby/94HwrIsSkqKkJAQi/T0NCQmJiI1\nNR0eHpPw7rsftTlYr6amBg0NDW3O4wAALS0tmJqawtTU9P/bu7/Ytqo7DuDfc+71tevE/53a+dcA\npkmqJG1SAiqb0BB02iR4ogi0J4Q07YUJ0IZQhMZ4mYToKoQ0tAckQAihbeKBhz2NDTGNoSpja0bT\n4CR2ndZxYifxnziOHfvec8/Zg5PSrkChNE1afh/p6kT+l5zIsu/3nvM757IrpdfTN12RCgDy+QI+\n/vgTlEpr4NyBe+/9IQYHD15xalUqlcCJEy9hbOxX2Lfvlkvue/nlF/Hwwz+G1/v5NKrx8QmcPj2L\nJ554+sLJnhAC77zzJqrVCqRUCARCcDh0pFKzePzxR6l+g1ymXF7DmTNxpFLzUIpt1ljouPXW29Hb\n2w+Pxwufz3/Je0dKiVQqhfHx8XwqlVosFArzmUxmPpPJfDY5OfnXWq2WUErZO9gtQsguRGGDEPK1\nMcY0t9u9f2ho6GgkEunr6OhoD4VC7T6fLzo4OBgZGhpq6ezsvKqr6UoprKysYGZmBrOzs7BtG0op\nhMNh3HfffQgErt9yraZZQa22dNXPF0JgfPw/SCa3djrWwBjDvn23YGRkFF1d+/DBB3/B2NgY7rnn\ne5idTeDIkVE4HE489tjPEI22Q0qJRx99CC+88Et0dX2+v0q93sAbb/wRDz74EA4eHPnKvyOZnMEz\nz/wCJ078GuHw5Tu0k5vfxkYdyWQKs7Nzm/tYcAAcgUAAhw/fhb6+A5cF+0ajgUQigYmJieV0Or1c\nKpWy+Xw+t7CwsJjJZE5OT09/rJTK70iHCCE3HAobhJBvjTGmGYbRc+DAgbuj0ehIV1fXVghpj8Vi\nbcPDw6FYLPa1Ryuq1Sruv/9++Hw+OBwOZDIZuFwuPPDAA3j++ee3uTeAlNbmilTX7vNRKYVMJosz\nZ2awtJQH5xxCSJTLa7AsE4GAH7qu4/TpKbz44m8RjbajVqvivffeRaGwDMYYlJLQdQPHjv0Ekcil\n9TWZTBq5XBZzc0lkMmloGofX68Zdd42go+PKtTjkxmdZFqank5icnIEQNjRNx549bvT3D2Bw8BC8\nXt8ljy+Xy4jH42JiYiK3vLy8VCwWc0tLS9lsNps+d+7cP9Pp9KdKqeIOdYcQcpOgsEEI2TasOcSx\nNxaL3dHd3X13V1dXZ1tbW7vf7492dHREhoaG2mKxmB4Khb5wNGR1dRVzc3NIpVJYXFxEIpG4sHO5\nruvo7OxEf38/uru7r2ltglIKa2vnoZS4Zq/5Zb9ncTGHdHoBudwK1tbWL8yPNwwXBgcP4vDhOy9M\nlwKAer2O11//PZSSUEptjpxwvP/+3/DUUz9Fe3sE0eju2XSRbA/TNDE1NYPPPkteqKswDBcGBoYu\nec9YloX5+XkkEonq1NTUcqlUyhYKhVw2m80uLS0l4/H4P1ZXV+NKqSuviEAIIVeBwgYhZEcwxjyt\nra239/f33xkKhXojkUg4FAq1eb3eNq/XG+7t7Q329fX5enp6YBjGZc+3LAsLCwuYmZnB/Pw8Lv4s\n6+npwcDAADo6Oq46hFQqGdh2/ar7921tXaWemppFvW6CMQ1HjnwfH330dxw79iMEAp/vtiylRCaT\nxb59X75RGrlxbY2KTUxMYnW1AkCD0+nCoUMjGB4excbGBs6ePWvH4/FCJpMpVCqVlXK5nM/n8yu5\nXC63vLw8MT09PQngPNVUEEKuNwobhJBdhzGmAeiMxWKD7e3th6PRaEc4HG7z+/1hj8fTFo1GQwMD\nA+EvGhVRSuH8+fOYmprCwsLC1utBKYVIJIL9+/dj7969CAaDX1m8/U1WpLoepJQ4deo03n77Xbzy\nym9olamb1Pp6FXNzaczNpTeDBYNtAy0tHni9wWoul1spl8v5tbW1fKlUWsnlcvlCoZBMJpP/LhaL\nCaVUaaf7QAghF6OwQQi54TDGvK2trbG+vr7RUCjUG41G2/x+f2BycrL/ww8/7P3/xx89ehSPPPII\nTNNEtVqFpmnQdR1bGxtefOLu8XgQDofhdnM4nRIOhw6/33fJilCEXCtvvvkHvPba25ieTgAAhoeH\nxB13jGb27HEvCGFnS6VSPpvNLm2OTpwGMK+2e34fIYRcQxQ2CCE3HcaYA8Dtra2tI9FotE8pNTQ6\nOrpiGEablDIihAgJIXxut9sdjUZbAoGA5vc3C7Sr1Sry+TyWl7MwzSreeutP8HhaMDBwAD6fB+Fw\nENHoXhw9+gOMjh7a0SV6ye7VrPupYHFxCdnskspml6VpWkIp1RBCbFiWqDYa5nq5XDaVUv89derT\nk2fOxP9cLlfyir6YCSE3EQobhJDvpM3idZ+u6529vb39gUCgPxgM7g0Gg36fz+dvbW2JuN38UKWy\nrrvdLhaL3cKdTgdTiqFWq+HkyU/g9Xrw3HNP73RXyHVimiZKpTKKxVUUiyWUSmtydbWshLBtKaVl\n27IhhKiZplmt1+tlAGkhxEnLsv5lGI5Pjx9/lTa3I4R851DYIISQK3j22Z+HLEvcatt2rKWlZQhg\nvbZttxuG0epwOPY4HLpL1zUX55qhadxgjOmcM83r9fBQyM8DAT+CQT+CwQBcLtpgb6dtjTo0A0MZ\nxeKqKhZXZa22IZWCUEpZUkpLCLshhGgIYddM06zZtl3WNH7Osqx4o9GIOxz6nK7rcy+99LvGTveJ\nEEJ2KwobhBCyDcbGntSEEN2WJW7TNK3X5XINSilv41wLGobh1nXNreu6U9M0J+dMB8AZY5w3q9a3\nDsY54wDgcDiYYRjM5XLC6XQwp9NghmHA5XLCMAw4ncaFduswDOOGKSS3bRuNhgnTNNFomGg0Gptt\n87Z6vQHTcNTPOAAAAUtJREFUtFSjYaqL7ldSSqUUZHPqkVIAkwBk83ZlK6WkUsoSwq4LITZM06qb\nprnOOc8CarZarU5qmnbW4dDnjh9/tbDT/wdCCLnZUNgghJBdbmzsSaaUcksp/VJKj5SqtdlKDwCP\n0+kM6rojyDkPAsoLwCOlbJVSujnXdM65rmnNlnOmNVuuNUdguMYY44xBY4xrjDVDz+ahoVk/z5UC\nYwwMzVAEpSABKKWUbDaQm8uqys0TfKkUpJRSKKWklMpWSgoppZBS2VJKu/mzFLZtW0opS9P4OmNs\nHcCaUqospSyaplm0LKvEOV/nnFc4ZxXOeYUxXuGcrdGoAiGE7G4UNgghhBBCCCHb4ssXmSeEEEII\nIYSQb4HCBiGEEEIIIWRbUNgghBBCCCGEbAsKG4QQQgghhJBtQWGDEEIIIYQQsi0obBBCCCGEEEK2\nxf8AshvOOouzrekAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1b648cf8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df_place = df.dropna(subset=['place'])\n",
"mollweide = cartopy.crs.Mollweide()\n",
"\n",
"plot = plt.axes(projection=mollweide)\n",
"plot.set_global()\n",
"plot.add_feature(cartopy.feature.LAND)\n",
"plot.add_feature(cartopy.feature.COASTLINE)\n",
"plot.add_feature(cartopy.feature.BORDERS)\n",
"\n",
"plot.scatter(\n",
" list(df_place.longitude), \n",
" list(df_place.latitude), \n",
" transform=plate_carree, \n",
" zorder=2\n",
")\n",
"plot.set_title('International Tweeters with Geolocation Enabled', family='Ubuntu')\n",
"plot.figure.set_size_inches(14, 9)"
]
},
{
"cell_type": "code",
"execution_count": 110,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqsAAAGVCAYAAADZg7ixAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd8VFXax793ZtJ776GGSyChhN5BUEEUEURFXVkQbNjr\n7svrFre5u667r7h2RBEFXFCwIYoiK713uHRIIQHSe2bm3vePm4QEUibJJDOTnO/nk08y955z7jNz\nM/f+7nOe5zmSpmkIBAKBQCAQCATOiMHRBggEAoFAIBAIBPUhxKpAIBAIBAKBwGkRYlUgEAgEAoFA\n4LQIsSoQCAQCgUAgcFqEWBUIBAKBQCAQOC1CrAoEAoFAIBAInBaTow0QCASCjoAsy72B+4GXFUW5\n6Gh7Woosy8nAHOCPiqJkt1YfgUAgEJ5VgUDQIZBl2U2W5YmyLPdwkAmDgCcBXwcd394MAZ4AfABk\nWX5BluVLsix3sbVPY8iyHCvL8p0ttlQgELg0wrMqELRjZFn+CTAqijLqqu0moAL4vaIov6+n73XA\nAiAZ8AbSgO3AA4qilDdwzM7A6UZM66woynkb34a9iAG+AeYCx9v42K2GLMuxwK+Am9DfYzFwGHhX\nUZQlbWjKQmCNoihn7DjmXOA3siz/R1EU1Y7jCgQCF0KIVYGg/dPQMnV17pNluQ+wFvgOfdq2HOgE\ndGtIqFaSAYys/FtCFzEG4JEabTIbN7vVkBx4bLseX5blAcD3gBn4G7AH8AQGAx72Oo4tKIpSAhxr\npeEdfc4EAoEDEWJVIBDUxXjADZilKEpOUzoqilIBbKl6LctyAWBQFGVL5evngE2yLEcoinKpctvv\ngMcVRQmu0W8ZkKQoSnLl61HAn4EBQBbwGfC/iqKU1ugzD3gGiAfOAP9SFOXdq0x8V5blqm3PKory\nqizLBuAF4EEgDFCAlxRFWV05bgDwPtAPiEQXh08pirJYluVfVfaLArKBvyuK8q8GPqLXZFnuCwQD\n2ypt2CPL8t3AUmCAoih7a7ynC8B/FEV5vOYgsiy7AyvQPan9rooBXVujXTfgCyAW/ZxuBh5VFEWp\n3H878OtK+4Mrx1sHPFF1firb3QW8CHQFUoFacbeyLP+y8jPqrijKaRv7+AH/RX8Q8gb2VR53+1Wf\nmVmW5aq/QxVFyZFlOR54BbgBfZbgZ+BJRVFSEQgE7QoRsyoQCOriSOXvZ2VZdrPz2N9W/h5dY9s4\nIKAyAaeKUVVtZVkeBKxHF5G3AX9FT1b6e1VjWZYfB14DPgRuRRdob1eKsZq8jO75HQksq9z2CvAc\n8A9gKrqHclXlcQGCKo+7AbgFuAf4ryzL09EF9ArgZuBpYFcj7z8XmI/usQ4E1suyHIIuMK3o4qvq\nPSUCEejhC1czHl0E/qaRZKWLwB8r39c9leOtqLE/CegPPABcjy4ubwberGHH9cAnwCFgBvB7GvF2\n2tJHUZRC4FXgDmA6UAaslmX5aq/wGK6cs3xZlv3RRW4U8EvgIaAn8KUsy8ILKxC0M4RnVSAQXIOi\nKOtkWX4e+C0wR5bl5cAiRVEO2mHsg7Isp6GLrVWyLPsCw9C9kuOBg7Is9wKiueIhXADsRvdgVomR\nCHRv6KOyLBsrbf0X+nS4hC4sh6CL2pU1TDhZ5eUFkGU5DHgUeAx4r7LvT+gCaQ6ws0bfLYqi/Fij\n76TKP99XFMXWONjf1PA8bgDOoXsEX6x8PQ1djAOMRRdwG+oYJ6ny99aGDlYpCKtEObIsa8BnsiwH\nKIqSX6PpN5VxoT9XJqE9KsuySVEUC/rnv19RlDtrjOOFft7qw6Y+iqJ8VGN/OvqDQk9gf41mm2vG\nrMqyPAcIB1KAgsrNOcCP6CEQV3tmBQKBCyM8qwKBoE4URXkF3XP1PNAb2CfL8qLKKfOWsga4sfLv\ncehTxO8BEyu3TUIXHz9Vvh4EDEWffq+o/Pkt4CHLciS6hzEIXbzWbDMWaCg7HfSpfRO6J7GqbznQ\nzYa+S9HF7A5Zlv91lWe4URRFyUL3Yg+s3PQRMKhGRv0E4Kd64oSrRLtnQ8eQZbm7LMufy7KcLcuy\nGXijcldAQ6ah3x8iK18nU7dgbohG+8iyHC7L8hJZlrNkWbYAX9tgG+j/D57AZa6c6x/RY7AbO2cC\ngcDFEJ5VgaB9kw90r2N7aOXvsoY6K4pSBCwBlsiyPBtYhB5XuLCFdq0C5lcmct0CfFn581Slp3Uq\n8EUNb1operLX/9QxVjZ6LCbAXyrHrkmV0Ksv0azqM3iMa72UhQ29CUVR8mRZHoouvB9BF/R/UxTl\n1w31uwq3GratAv4J/FKW5b9Ujvt8Pf2qkpn6o5+Ta6j0OK9H//zmAunoAv7lRmyqigN2r/ztUeNv\nW7Glz2fo4vJp4AS6R/WDGvsbOmc51AiZqMHZphgpEAicHyFWBYL2zSFgoizLXa4qKVTl1axT5NTD\nGnSxmmgHu/6LXgrrHvT40rvQk43y0OM5h6F7Tqs4jO59PFozoaqKyrCCfKCXoigL6jlm1ZR36FXb\njwIqemLQv5v6RhRF0dBja7+VZfmvwPOyLP9RUZTixvrKstwd6EFlmIKiKCWyLP8bPXRhP7rg+7Se\n7t+jx6P+ryzLn101pV9FMHqy2dOKonxeeUzvJr1Bne3ADbIsuymKYrZjn37Ae4qifFxp29WLJdQ8\nZzX3HQJmA6qiKE35HxYIBC6IEKsCQfvmLfTkk+9kWX4ZOI+eTf9rYKuiKN8ByLI8GT3p5hlFUd6u\nzOxORs8cz0EXPQ+ge7q+r+yzCT1uMNmGclZXJ9aosix/iO41zEaf6tYqY2NfAlJrxoaiewI3At/L\nsrwQvRpAPHBGUZSfK/v+CfibLMvvowvrQvS4zpWKomRUekEV4AFZlqsEaoWiKN/LsvwWeoymhu6J\nNKN7LP+vkZqy49E9gyfRs9mHVh63IY/1DbIsH0MPXViALsJer7F/IfAsevztOkVRLtc1iKIopZXn\n6XP0ON8/o0/fu6GHbVgVRXlNluVzwFxZls9XHmtgXeM1wtPADmCdLMuvoyeJNTaOLX12AbfLsrwD\nPRSk01X7t1X+/pssy0uAOPRKBR8ATwFrKj3Qx9FDB7wURfmk6W9PIBA4MyJmVSBox1SW8RmGnrTy\nF/SYwAeBd7l2ClXlyrRrHrrQexN9+v1N9Ifb6VUeusq2DdVwraK+dm+jX4OWVXonQc/kd0MX2TXf\nx1b02NayStu/RhfcsTXavII+1Z0CLEefUv8FeixrFfeiJ+SsrBxneOX2x9BDDG5Cn5peBkxBz9Zv\niBj0gvzr0DPfJWCKoijWOtqeRBdfv61s/zJ6nGX/mtn8leJ0ceV7e6ehgyuK8i26ANwI/G/luCsr\n33dVRv1t6OJ+ceXxnkUXkSWV++s7P9XbFEXZjx4nakY/R9+hfz7fUztUoql9fomeOLew0rZ/AnvR\nH2BQFGUbehzyRPRz/gIQqyhKLjACvVzVS+jVEv6F/oAhEAjaGZKm2XKvEQgEAkFbUVmG6zGgRw0h\nLxAIBB0SEQYgEAgETkBluSgvoC/wB/QFGYRQFQgEHR4hVgUCgcA5eAg9uewM+gpTqx1sj0AgEDgF\nIgxAIBAIBAKBQOC01OtZlSTJG73mnUAgEAgEAoFA0Noc0zSt5OqNDYUB9Fy6dOnuxER7lFQU1MW2\nbZtQlMPcdNN1eHo2uAhNLc6dS6WoSGPw4GEsXvwWd9xxSyta6VoUF5dhNEqkp1+kS5cYDAbXL3iR\nm1uA1aoSGtpYYnr749SpVLp2jUWS7LPc+0tpFn4sVBtvWIP/jTYyIcBol+MDlJSUce7cBWS5U7v4\n/3RV0tMvcP78ZW644Sa7j/3FF58xZEgS3t5edh9bYH80TePs2VQOHz6OqkJAQCDDho0iJOTqksyu\nxeeff8rQoX3w9fVxtCk2oSgnefDBZwegV6+pRYMxq4mJiaSkpLSaYR2dlJQUCgryefvt10lJSWTA\ngD429evTpxdLlqxm4MCBWK2zuXjxLKNGDWlla12L3NwCcnLy6dYtztGmtJgTJ84TFxeBp6dH443b\nGUajB717d7ObWH0jUeVGxcy5Ctv77A+UeKZbUxdvqpuCgmJOnjzPnXdOttt7EjSPvn17s2jRMnr2\nlPH2tu/NfOvWDQwb1pxytoK2QtM0tmzZxfHjZzAY3EhOTuaeex7Czc2t8c4ugKqq/Pjj14wYMdjR\nplxDfn4BS5d+RkREKCkpyXTtenV55WsRCVYOxt8/gOeeW8Drr//dZrEqSRKaZgFgyJAR/O1vPzBs\n2ABMJnE6qwgK8uf8+Quoqury3qvy8ooOKVSrsKeoi3A3MCPYyCuZdZVBrZu9xRoFVg1/Y8vsyMsr\n5OzZDPr37ymEqpNw++0388EH7/DII0/ZdVxVbZr3XtB25OXl8/XXP1JebmHs2PFMnjyz0T5Wq5X0\n9FTMZjNmcwUWi6Xy75qvKzCbLVgsZrp3l5HlRIfeezZu/IEhQ/o67PgN8d13G3n44acwGo18+OF7\nSBJ06dKwYBXqxmlo2s0rJCSQCxfSiYqK4d5757Bq1afceeeUVrLNNYmLiyQ1NYtOnaIcbYrAiXg+\n2sj6ApV9JbYll6aZ4b2LVp6Oav7lMicnn7S0LPr27SGEqhMREOCHyQTp6anExNhzFkaIVWdC0zR2\n7drHvn3HCAkJ4777HsTPz9+mvhcvZvHGG/8iMbE7Hh5uuLkZMRpNuLmZMJn0H09PI35+7phMXhiN\nRk6c2Mu6dWswGEx4e/syatQ4EhLkNhWve/bs4P7772yz4zWFoqJSgoNDAJg1ay7/+c8HQqy6Ck29\ngY0ePYR1677ml798gOjoWMBEdnYOISHBrWOgCxIcHEBGxiVHm9FiRMUO++ImSTwaYeTRsxbKbPxo\nNxaqPN2CZ56zZzNISRHx/87ItGmTeP/9D3j++RftMl5xcREeHvYJGxG0nNWrv+Xy5XxGjBjNM89M\nb5Jg3L17BytXfsLTTz/YpPCAmJgoRo8eCkBxcQk7d+5k7drVGAxG/Pz8GTVqHN27y01+L7aSmXmB\noCC/Vhu/JWRmXiQq6sqDYUBAIMXFpY32c+350XaEqmqUlTW2vPoVAgL8ycurXqGR2bMf4uOPVwth\ncxVlZeVYrcLLIajN9GAjI/1sf0A8UKxxuqz5/0fu7u0jDq49YjKZ6NWrG59/vsIu4x0+fJCEhM52\nGUvQMs6cOUdgYATPPruAYcNGNdmz2bNnL3r1Suajjz5j/fqfsVptDx+qwsfHm7Fjh/PLX87gvvum\ncf31w9i/fwsLF77S5LFs5bPPljNp0nWtNn5LWL9+E1OmTKu1TZIa95sKseokzJo1j7ff/qhJsU7u\n7m6UlBRX/u3OzJn38dln37SWiS5J797d2L9fcVkRX1ZWLrw0rcQfY02E2zi3lKfC2xebfqMSuAYj\nRw4mMNCDV175E+XltjsN6uLw4YP06NHNTpYJWsKGDduYPHlqs/v7+Pjyi1/cz9NPL6B378EsXfoF\n77+/nDNnzjV7TF9fH8aPH4XBoJGfn9fscerDarVSWlqEl5ftFYbaErPZek1Co79/IAUFhQ32E2LV\nSfD3D2Du3Pm8++7HNgurUaMGs27d19WvExJ64ucXytGjJ1rLTJfDy8sTHx8vzGaLo01pFnl5hU47\nnePqyF4GJgfafgncUay57EOPoHH690/i9tsn8vLLv+Ps2dPNHqekpBAfH287WiZoDhaLBaPRzW7Z\n/YmJvXniied47LEXSE3N4/33P+Xzz9dSUtL4FHZNNE1j8+ad5OcXkJ6eahfbapKfn0dBQRFbtuxy\nuuvVmTPn6gx/GDZsJHv2HGywr4hZdSJiYuKYPHkay5d/wcyZtzbaPi4umh9+2Fpr2x133MOf//xb\nOneOc9onq7YmLCyIEyfO06tXV5dLbsnLK6Rr11hHm9Fu+V2MkS1FKkpZ422PlmhsLFQZ62+/mqsC\n5yIwMIDHH5/DsmWf0aVLApMmNX4dvhpRCcA5WL9+E5MnN/38NYabmxtTpkwH9NjQr776HLO5AtAf\nZqt+dK781jQNi8WCphlsrkLQHIKDQ/j97//Kzp1bWbToU0JDA7jpputwd7f/DF12dg5FRcVYLFas\nVmv1b1VVsVgsWK0qKSnJ1ZWK/vvfHTz88DPXjJOQILN27ecEBQXUeywhVp2MpKS+5ORks3btBiZN\nGmdDDysWi6VW2ar585/irbf+xYMP3tt6hroQwcEBmExG9uw5SkpKoksJVrPZIuIdWxF/k4FZoUZe\nTLPS2CR/OfBJthCr7R1Jkrj77qls376X1177Ow8//GQTvXNCrDoD6emZ3HVX6yUxAURGRjF37iOt\neozmMmjQMAYNGsapU8d5990PmT9/tt3GPnbsBBs37iA6OpawsAhMJiNGoxGTyRuj0YCHhxsmk4ll\ny5aSkpIM6B5lq5U6RbPBYMBgaPi6KsSqEzJ69HWsXn2ZLVt2M3z4gAbbDhzYhw0bvuf66ydVbwsI\nCGTMmAmsX/8zEyaMam1zXQJ/f1+6do3l1Kk0und3nYUCXElYuyoPhhv5Kk9lS1HjU2Z7i1XKVQ0P\ngzgv7Z0hQ/rTrVs8f/7zb7j//oeJjY2vt21ZWRmenp7s2rWVsLCQNrRSUBcZGZlER9d/vjoS3333\nDffeO90uYx08eITNm/fQp09/nnvuxQYT1kpKiomPj652pB06dIyUlPoXyjAYTA3OSoiYVSdl6tQ7\nyMzM4fjxUw22S0rqyb59O0hNrR3wPXToSLKzC8nIyGxNM10KPz8fCgqKHG2GwMkwSBK/ijYSbIPD\n9GQ5LMsWnrOOQmhoCI8++ktWrfqYH374tt52hw8f5ocfvuXAgZ1MnDi27QwU1Mn33//Mbbfd4Wgz\nHE5GRhoGg0pAgG01Zetjz54DvP32x5SVufH887/hpptubbSywn/+8wk33XRldnjnzgOMGlV/hYKk\npL6cPl1/4poQq07MnDkPs3Xr3kbb3X//TBYvfuuazMK5c+ezcuU3zSq30R6pKmHlbEHn9eEqdrYH\nRvkZeSjciC3rhH2bL75PHQmj0cisWTMoLc3hjTf+Wef1dO/eXeTkpDNt2k0OsFBQE1VVsVrB01Pk\nbCxduphp0yY13rAOVFVl06btvPPOJxiNAbzwwm+5/vpJNpX/UlWVS5eyquu+q6qKJJkwGuv3CAwb\nNoqzZ+t3rgmx6uRIUuOnyGAw8MAD9/Lqqy9jNpurtxuNRubMeYhPPlndmia6DB4ebnTtGsuRI6dd\nQgiWlpbj5dVxl1lta56LNjE9pPHv275ijctm4V3taIwcOZhx4wbzxz/+L1lZV26qH3zwDm5ucP31\nYxxonaCKTZt2MGHCxGb3z8/PZdGiN/nkkw9bXMbMkezbt5tu3eKaFG+taRp79x5k0aIVLFmympgY\nmeef/w1jxoxv0rE3bvyBwYOTq1/v2LGX0aPHNtjHw8OjQW+4iFl1cgwGI5qmNRq76OnpwaxZ03nl\nlT/xwgu/qX76iY2Np2vXHuzefYABA/q0hclOTWCgH0VFJaSmZhIf79zLsOblFRAY2LLpG0HT+L9O\nJi5UmNlQWP/DTJYF3r6osiBGPOt3NKKiIpg/fxZLlrzHoEEj2Lt3FykpiRiN7lgsVkwmkXznaE6c\nOMuUKU1PLt6+fTObNm3E19eTSZPGUVxcwhtvvIK7uxe33343ERGRrWBt67F27Rc89JBtn8ORI8fZ\ntm0vkmRkyJDhPPXUr1u0NOzVS70ePnyCp56a0ezxQIhVp6d7d5kzZ87TtWvD6+YCBAcHMWnSaN56\n6/945JGnqrdPnnwbf//7n0hI6IK/v6jZGRDgR1ZWtk0PAY4kP7+IhASRrNGWmCSJxV1NTD1hYV9J\n/YJ1c5HwrHZUTCYTc+bcxcaNWxk7dhDx8bFkZFwiL6+Q0NBAR5vXoVm9+lsGDRpmc/uiokJWrlxG\ndvZFkpNl5syZUX1P8Pf3Y/bsOyktLeOrr1aQm1vEhAkT6dev4aRnZ6G8vAKLxVKvZ/X06XP897/b\n0TQDffr044knftXgNL2tnDt3hrCwIHbs2MuhQ8cxGt0YPnxMi8QvCLHq9AwdOpyPPnrHJrEK0Llz\nPDk5+axYsZQ777zyVPXYY8/wj3/8kUcemeXUAq0t8PPzJi0tk717jxETE05EhHMKQqtVFZ4aBxBg\nMvB2ZxMzT5k5Xc8s4MESjYMlKsnewrvaURkz5oooCgryJz09S4hVB7Js2Rr69x/C0KEjG227d+9O\nfvzxezw93bjppnEEBdV/3ry8PJk+fTKaprFp03Z++GEt3bv35Oabb7OLuGst5s9/isWL3+SBB+6p\n3paWdoENG7ZgsWj06NGT+fOfs9uiCVXs3buL7OwCEhP78+ST01ssUquQ6ovdkyQpZffu3btTUlLs\nciBB81m7dg3p6We5/fbJNvdZv/5nQkJiGDfuhuptBw/uY+/eLUyZckMDPTsW+/Ydo1+/no42o04O\nHTpJUlJ3R5vhUBz5GazPtzL/rIWL9Sx+NivUwL862XahF+ey/XPw4AmSkxMcbUaHQ9M0PvjgU667\nbhJ9+9avV0pLS1i5chkXL16gZ8+uDB8+qNmOm1OnzrJu3Sb+539+10yr24Y9e3awZcsGDAYjFRUW\n4uO7cNNNtzpt8tmePXsYMGDAAE3T9ly9T3hWXYBJk27l4MF9vPnmEubOnWnTk9CECaNYsuTzWmI1\nObkfe/fu4pBynm05erzmzBQTPh4d19MaFBRATk4+wcH1r5wh6JhMCDDybJTG79OtFNcx67+rWEPV\nNAwdfKZCIHAUqqryzjsfM336XSQkJNbbrrCwgFde+RP33juNsLCWJ8IdP36GGTPuavE4rU1KymA8\nPLzo1Kkzvr6uHQIo5rBchOTkfjzwwGP8+99LyM7OsamPJF17h506YxbzVxt49ScLr/5kYfaycorL\nnT8zvrWIj48kPf2io824BleoVtARmBdu4t4QQ50XSqVU45s8Ebsq0Ono4VVtjcVi4d///pC7757d\noFAtLS3hlVf+xEMP/cIuCzZomkZaWiYJCc45I3c1vXsnu7xQBSFWXYqQkDAWLHiJzz77niNHjjfa\n3mAwUFFRUWvbR9tyuaRe+cIeuqCxbE8985wdAEmSnPImU1xcio+Pl6PNEAB/iTPR3+fa/xELsCpH\niFXBFcRDZttQXl7O668v5oEHHiM+vnO97SoqKnj55ZeYO3cmXl72mfresGELEyfeYpexBLYjxKqL\n4ebmxnPPLeD06UzWr/+5wbbdusVz9OjhRsfctWsfn3yyilOnzoqLrZOQl1dIYKDrPw23ByRJIqGe\nUJmDpSqq+M4IAC8vD0pLXbcup6ugl5RawpNP/qrBclIWi4WXX/49s2fPwM/P1y7H1jSNEyfOkpzc\nzy7jCWxHiFUX5d575xAaGstHH62qV2AmJvbgwIHaccqzhofQL/aKxy4pSuIfDwzkttsmk5aWwQcf\nLGfx4mWsWvUVFy5ktep7cBacUaDn5xcREGCfC6yg5QzyqftSmW2m3gQsQcciKMif3NwCR5vRrsnP\nL+Tdd5fx/PMvEhgYVG87VVX529/+wF133UJgoP3yETZv3sH48TfabTyB7YgEKxdm7NjriYvrxMKF\n7zNv3j3XTHMEBPhRUFB7CVZfDyOfPtCFD7dks2XrRv42s19lgpUnY8YMZ8yY4QDk5xewefNO1q79\nAYCIiDBGjBhs1y++oH40TbNbyQ9By5kSZODPFyD7KmGap8LxUpVIN+ctYSNoGwICfMnMvExMTLij\nTWm3rFmzjhdeeBEvL+9626iqyquv/oUpUyYQHh5q1+MfOXKKm2++p/GGArsjxKoLs23bJs6fP8eT\nT/6Kf/7zr8yYcRPR0bWnRVT12pg6Xw8j88eFox0+i49H/zrHDgjw56abriyxlpV1iR9/3ER+fgGa\nptGlSzxDhgzA29u14yqtViuq6nyeVYFzEeom0dVDItty7f/K/hKN0WKhsQ6P0WgU15JWRFVVrFYa\nFKoA//73q4wfP5TYWPuuULhz5z6GDRtl1zEFtiPEqouSnp7Kli0/MWzYABYu/AePPvo0H3+8GKNR\nw2q1IkkGwIDJ5G6X40VEhDFtml7nVdM0zp49z5o1ayktLUOSJHr1kklJSbZ7geHWRtPA3V18DQSN\n081DYmfxtWIkrUIIFIGgtdm8eQfXXddwjfB33lnIwIG96dLFtkV0msKePYd54YXf2n1cgW2Iu7SL\nsmTJezzwwN0YjUa6dIln0aJ/M3z4GPr06Y+vr1+rTiFLkkSXLp2qLwiqqnLkyHGWL1+NxWLBaDTS\nu7dMnz69nF68VtnrTKiq6pQVCjo6A30MLK8j+z/H6gBjBIIOxvHjZ7nllvrXul+y5D1kOZ7ERPsv\nzHDgwGFSUgbbfVyB7Qix6qL4+vpWiyxPTw8eeOAeNmzYwkcf7eHBBx9v03hHg8FAUlJPkpL0unMW\ni4UjRxRWrFiN2awH+cXGRjN4cH8CApxrvvTMmXQ6d45xtBm1KCwswc+v4akuQdtzS6DEX+qIW80x\nC8+qQMdgkLBaVYxGEW9uT/Ly8gkODqt3/4oVS4mICKBv396tcvxt2/by7LO/aZWxBbYhxKqLUpcY\nHTduOFlZl/jTn15k1qx5dO7c1QGWgclkok+f3vTpc+XCkZqawfr1/6WgoBBJkvD19WHQoH7Ex8c6\nzItYlbnr5eXhkOPXR15eIUFBomyVsxHubqCL+7Vxq8KzKqjC39+XgoIigoKc66Hc1Vm79ifuuWdu\nnfvWrFmJt7fEkCF151/Yg+uvH8Xnn69g+vSZrXaMlrBkyXvcd1/dn097QYhVl6VugRcREcZjj81m\nxYrPiYiIZto05/hyxcVFExcXXf06P7+QXbv28eOPmwA9OSE5OZHk5ERMprb5t/T39+XUqVSys/MI\nCQlsk2PaQmFhMfHx9dcPFDiOnl4Su0quEqsWDaumYRShGx2eoCB/srKyhVi1I5qmUVJSjr//tZVo\n1q37CrO5kAkTWjfxqUuXTnz//SYsFkub3Z9sJS8vh08++YRbbrmNoKCWr9DlrDjXpy6wGQ8PD8rL\ny/HwuNYRleSpAAAgAElEQVQraDAYmDnzVg4ePMrLL/+O+fOfxs/PuS6eAQF+jB9/5QJjNps5dOgY\ny5Z9jsViQdM0OnWKY9Cgfvj7t46X0Wg04OPjhb+/c9Uz1TRNxKw6KfPCjKzOVSmqDF31lmC4r6Ge\nR0dBR8Pb25OSkjJHm9Gu2L//MIMHD7tm+08/fc/ly+lMnjy+jl725+abx7N8+RLuvXdOmxzPVrZt\n28KCBU+ycuVy5s2b72hzWg0hVl2U6Og4srIuER8fW2+b5OREunXrzOuvv8Ltt8+8Zv1kZyqG7+bm\nRv/+yfTvnwzotp0/n8Z33/1EYWERAP7+fgwa1J+4uGi7iTlfX29ycwsIDw+2y3j2QAhV56WPj4F+\n3hKbijTi3ODJSCNzwsVlVKAjvrv2Z9eugzz99IJa27Zv38yZM8e47bZJTR4vL68QVVUJDm5azfDo\n6EjWrt1AWVkZnp72WbrVHpw8qXDPPVPYvn0/VqvV6RKG7YW4yrooMTFxXLhwokGxCuDt7cXcuTP5\n/PP1Ti1Wr0aSJDp1iqNTp7jqbfn5Baxfv5kff/y52vYuXeLp3z+52YlbcXGR7NunOJVYFTg34wMM\nlKgqr3c2keglEmkEgtaipKQUH5/a1W1yci7z888/MHfu3U0e79KlXC5fzqVnzy7Nsmfq1Bv5+OPF\n3H//w83q3xqoqhVJkhg1ahDfffc1kyZNcbRJrYIQqy5KUx7g3dzcMJvNtbZlXMplT3kPKraamZli\nqlzFyrnx8/OlZ88e9O7dDdDF9rlzqfzww88UFBQCIEkGevToSlJST5vXgw4M9CUzM5vISMfH+1it\nVgwG5z8XHZn5EUYeDjfiIc6TQNCqrFv3E7fddmetbStWLGXmzKkN9issLMZiUasTVTVN48yZdDIy\nLjJ8eL9me8BDQoIpLMylqKgQX1/HJ8HqThvdcSPL3XnvveVCrAqci6KiwiauHnXFi1pUbmXmonOc\nyO3Odz9Z+E6xsnimh9ML1uzs/FpTN5Ik0blzPJ07xwNQUlJGWlomVquZdes2UFxcUt02NjaaPn16\nERZ2rSDt1Cma06fTOH26lK5dG/ZUtzYFBcUEBDhXDK2gNm6SVF9+o0CAh4cbZWXleHo6V5URVyQn\np4DIyCsrUZWVlVJeXoKPz7Wl/dLSssjN1VdY9PPzoaSklNTUC3h5eVJYWEyXLjF2ub5PmzaJjz5a\nxMMPP9nisVpKauo5IiOvLCkbHR3OqVPH6dathwOtah2EWHVRiouLCAmxvRZnzWUAP9ySzYncK3Et\nhy5oLNtjYe4w5y7gf+lSLj161L8ySVZWNlFR4fj5edcqDK1pGqmpGezYsYfLl3OqQwiCgwPp06cX\nnTrF0a1bHPv3Kw5PbsrNLSAiwvEeXoFA0DwCA/3JzS0kKkqI1ZZw8uQZZLlXrW3Ll3/EzTfXTqjS\nNI3c3ALOn7/A8OH9rtmXl1dIQkK83ezy9/dDVc3k5FwmODi08Q6tyJYtPzNwYFL16xtuGM1HH33O\nU0+94ECrWgchVl2UoqIi4uKaUm6p9so7bsYyekbqZaOOZY4EnN+bZ7VaMZnqDx4vKiqhc+foa7ZL\nkkR8fAzx8bWL/2dn53DgwBE2btyKpmlYLBqHDx+hb99eyHI3h5QoKSkpw9vbeYL3BQJB0wgK8uPE\nifNERTlWyLg6Gzdu54knflX92mq1culSJqGh19Vqt2fPUSIiQhg8OPmaMSRJapUyYtOmTWLp0sU8\n/vhzde7XNA1N01p9cZ7Ll7MIDb1SKcFkMmEyaezdu4v+/Qe26rHbGiFWXZTmhgGcP32Rin99zLOG\n0+QmH8Psp5IYfYDpfZ8GnNuzagtN8YqGhAQzbtzIWtuKi0s4fFhffcti0au9m0xGevToRu/ePZv4\nmTcPkVEsELguJpOp+tohaB5msxk3N49aDoMvvljJhAkjrmnr6+tNWFhQg44Me+Pl5YmXl4mMjDSi\no68NLfjHP/6C0Wjgqad+VUdv+6Fp1y7/fM8909i6dTc//vgtfn6BTJ06g/DwiFa1oy0QYtVFKS4u\nrjNupz40TReqK6YsJb8oDAgl5FQMhb/+AT+/85zI3shg74mtZ3ALqagw4+ZW/7+rvSob+Ph4M3hw\nfwYPvrIaitlsRlFO8eWX31FWdqWGopeXJz16dCMhoWuTzkVDOHOFBoFAIGgL1q/fxOTJt9baduKE\nwrhxA65pGxMTTnr6xTbPN5g6dSIffvghzz5bu6yWxWLBYNAYOrQv7777OvPmPdrsY5SWluDh4Vmn\nh9ZisVAzF6UKg8HAiBGDGDFiEEVFxXz55XLy84vp2jWByZOn4ubmmk4pIVZdFFVtWj01SYJVTy2v\nFKo62QUxxH/ehdT7TrWGiXbl4sWcBmM5CwtL8POzj2C8Gjc3N5KSepKU1LPW9uLiEk6ePMM336yn\npKS0RnsTXbp0Qpa7ERwc1KRjCa+q81BUnse6Ex8CcGPCLHw9nGeVM4FzI77HLSMjI6tWktBPP61n\n0KBrp/lB96yePp3WVqZV4+bmRmRkCIpypFZs7TffrGHcuKF06dKJ0tIyPv54MffcM9vmcVVVZdOm\nDezatYNNmzazbNmqOhf/OXz4IAkJnRscy9fXh+nTJwNw8OBRXnvtFZ555tc22+JMCLHaQQgODiBT\nK69zX6RvZ/pFjW1bg5pIXl4hMTHh9e7PysomNrb+/a2Bj483ffv2pm/f3rW2V1RUcPr0OTZt2k5u\nbj5AdfxSfHwMPXp0Iyoq4pobmtlsadOpLEH9FJXnsWj3i1jUCgAW7X6R+wf8QQhWgU1IkoSqqq0e\ns9geuXAhi+jo2glRu3ZtY+7cu+rt46jr5uTJ43n99Q9YsOAP1ef65EmF0aPvACAlJZnNm3eyZs1K\nbr319gbHOnv2NF9/vZqyslIGD05m9my9fV1CFWD37m1MnDiyzn11sXXrHh57rO4YW1dAiFUXpa5Y\nlYYIDQ0m4pFo9j67o9q7GuSXSegDPRmZdAPuJudO6mksS7+srBwvL+d4D+7u7vTsmUDPngm1tlut\nVlJT0zl48Cjff7+x+j1pmkZERBhRUVGEhIjFCZyBdSc+rBaqABa1gnUnPmR60hMOtErgKvj5eVNY\nWCLK0DWDdes28tBDT1e/PnRoP127xtXbvqysbidMWyBJErfeej1Ll77PfffNJScnGze32g8oI0YM\nYv36/7J8+RJiYuIpKSmu/CmhrKyE0tIyzOYyIiJCmTFjIu7u7gDs2rWPYcPqF6MlJcU251Bs376X\ngQOH4uXVOrOPbYEQqx2EsLAQsrMLiPtVPNalp3F3d2PiH64julPTlpwTNB+j0VirLmwVmqaRlXWJ\no0dPcOjQYazW2g8ivr4+dO4cR6dOsYSEBIspRoHAyQkK8ic7O1+I1SZSXFyC0eheaznTtWu/qNer\narFYOHjwBCkpiWiaxoEDR+jTp1ebXiPj42PZsmU358+fJT6+MyaTJ4pyElnuXt1mwoTRnDx5hoqK\nEiIivPD0DKpM0vLEzc2tTnv37z/GU09Nq/e4tjqsysvL2b//GM8//2LT35wTIcSqi6KqTfOshoWF\n8M9/vszUqRN5aHn9XwBnpKioBB+f+p8gXT0pSZIkIiPDiYysO4yhoKCQc+fS2L5drxNbV9/OneOI\nj48VhcjtxI0Js2qFAZgM7tyYMMvBVglcBV9fb86du+BoM1yO1avX1YrvTE09R3h4cPUM1KFDx0hO\n1pcNLywsRlHO0revTEFBIUuWfErfvr15443FDB06gAED+raZ3TNm3Mwbb7zHggUv8fDDT/Kvf/0V\nT0+PWsuFd+9u+xKvZWXleHv71htGUlJSjLu7bfJt2bI1zJv3iM3HdlaEWHVRmhoG4Ovrw7x5M+nT\np3fjjZ2MzMxsoqPD6t2fl1fYKrX0nAV/fz+SkxOrL9I1UVWVzMyLnD2byp49Bykvrz0l5uHhQadO\nsXTuHEdERJiIobMRX49A7h/wB5FgJWgWVeJKYDtlZeVYrdQqtL9y5XLuvVdfPnT37v3s3LmXnTv3\nMmHCWAoKShgwoBdbtuzk6NETPPzwL3F3d2fs2BFs2bKTN95YzC233Ehc3LW1t+2N0WjkhhtGsmrV\ncmbMuJvHH3+OV175E+PHD6Nr105N9vR+991PTJkyvc59J04cY8WKj5kyZUKj4xw+rNClSwJBQa6/\n0IwQqy6IxWJBkpp2IZQkySWFKkBpacOF8i9dyiE+Pqre/e0Zg8FAdHQk0dGRDB8+6Jr9paVlnD+f\nxsGDR1m//r913kA9PDyIitI9u1FREfj5ialL0AWrvWJUCwuLOHcuFbPZQpcu8U2q5CEQdATWrFnH\nXXfdV/06Ly8Xd3dDdamlvXsP8dBDvyQnJ5ePPlrFzTdPYNGiT0hMTGDu3HtqjTV8+CCGDh3Ahx+u\nYPToYXTr1rnV7Zfl7mzb9ikXL2YRHh7BM8/8D19++Rnbth1A01RU1YqmqYSHhyLLXenUKfaa64Cm\naXz77QYsFgMxMbXjdPfv38O6dV8TFxfJI4/8olHHg9Vq5aeftrNgwUt2f6+OQIhVF+TYsSN07Wq/\n5eNcnaioMNLSLtK9e/1B+B0VLy9PZLl7rfipqyktLSMr6yIZGVkcOnSMoqLia9pomoa/vx9RURFE\nRYUTEREuQg6awLp16xk7dhj5+QWkpWUwduy1xc0Fgo5KRUUFxcXltYrXr1jxEbfeegNQtUiACUmS\nCAkJ5okn5vLll+uYPn0yQUF1z3gYDAbuvnsaK1d+2SZiFWDmzKksWvQmv/717zAajUydOqPWflVV\nuXAhnUOHDrB9+1qsViuqakHTNHx9vbhw4RJTpkynT58rdb63bv2ZTZt+IiGhM/Pm3WWzl/Y///mK\nWbPm2vX9ORIhVl2Q3bt31FkcuT3SWBUAAD8/H06eTLWpreBavLw860z8qommaRQUFJGZmcXZs6ls\n3bqbioqKWm1UVcNgkDCZjAQGBhAYGEBQUCBBQQEEBQXUW4KlI9C1azxjx45A0zQ+/HCFo80RtAFu\nbiYqKsy4u7tmEfa25IsvvuOuu35R/bq8vJzi4gJ8fX0A2LBhM+PGXXnAkySJKVMaX8TGw8ODigqz\n/Q2uB3d3d4YO7cdf//oSI0eOYeDAobWuewaD7jG92msKkJeXg59fAEajEVVV+eGHdezZs4N+/Xox\nb97MJtlx/nwaPj6BxMa2H6eWEKsuSGFhHv7+fo42o03IySmwKR41JiacrKxsIiPFetytgSRJBAT4\nERDgV6+X9tChkyQldcdisZCXl09urv5z/nwaubl5jd40DAaphsDVRa7ZbGmNt+MwxMNUxyEoyJ/c\n3IIGFzMR6GFt+fkltZYt/fTTpUyePL769fnz6dxww9hmjW8ymSo9s23z0NC/fxLJyT05evQ47733\nGhaLXm83NDSCESNGEx/fuc5+gYHBqKrKmjUrUZQjDBvWjwcfvKfOtg2haRpr1nzPggV/aOE7cS6E\nWHVBVLXjrDt98WI23bs3/nQYFhbEgQPHhVh1EFarisGgCzGTyURoaAihoU27Ses3rYJKkZtHWloG\nly7lcuDAfuCK0KuKu61L+BkMEl5eXtVlYa7+29vbE09P/bUjk83a0yzAZbPKd/kakwMNBJjax3uy\nB0FB/pw5ky7EaiN8/fUPzJhxd/Vrq9VKZmY6ERFjAL0aiq9v8+uDDhjQl1279jNs2MAW22orJpOJ\n5OReJCf3wmy2cOZMOsHBvmzZsp7Vqy8DBoxGN/r27c/AgUMxmUz85z+fkJp6huuuG86YMXc3eoz6\n+PLL77n99rvbXTKtEKsuhqqqTa4E4MpYLFbc3Br/N5UkSSStOJCysvIWx7CaTCZCQoJbtDCC1Wql\ntLSs8qe0+u/Ll3MoK9P/LikppaysvMFs7ZqC2GpVMRobv/DXFJ9Xj13zdWxsNGlpF9okS7m1yTar\n3HnSwp4SjZfSoYuHRIKnxCg/AxMDDfgZO654dXd3a9MpaFfEarVy8WJuLW/j11+vZty4YdWv163b\nwI03jmv2MRITE1i8eFmbitWaHD58ksTEbnh4uDFx4tjq7RaLhaNHj7No0ULKy8u5/vrRTJo0vEXH\n2rlzHwaDJ4mJrplM3RBCrLoYZ8+eIjY2st79FcVW9n2aCUC/OyJx9+k4As5q7TgeZ2ejpKThig1t\nhdFoxNfXpzrWzR4cP36WTp2i8fBwb1b/q4VrSkoyP/+8zeXFqqZp3HdaF6oAWRbIsmhsK9b4KFsl\nyg26eUh085TwkiQsaFg1sGhg1SDeQ+K5KCOGduJhFjSdb775kenT76x+vX79t5w5c4LRo68sTZqX\nV1BvEpUtOHIGw2y2YDQa8fC4NgShpvfVHnz55ff4+4dy771z7DKesyHEqouxe7cecF0XFcVWPn3g\nCJmHiwA4vj6HO97p5bKC1Wy22Lzms6qq7S6+0ZUoLS3H399+AtGZCAkJ4vLlPGJi6l60oTGuvlkG\nBweRlub6BeOXXFbZXlS/d/qCGS6YNTbV00YCthapvN7JRKxH+5qyFDSOnhl/ma5dE1CUo3z22XKG\nDu3HrFlXhGpGRibR0RENjGIbfn6+5OcXEhDQtrkeBoNEz562LwbQHFRVZfHiTxkzZjwDBw5rvIOL\nIq4QLkZW1gXCwuqOgdr64blqoQqQebio2svqily6lENYmG1TwpqmYbWqTV7ZS2AfGquF68oEBfmR\nl1do1zGvu24Ub731ARaLaz5gWTWNjy5baclchgZsLNR47Jxrfga2IhYHqJt16zYyduwE/vnPv7Jr\n10Yeeuhe+vdPrtXmhx9+Zvz40S0+1siRQ9i8eUeLx2kqRqPRpjC25lJYWMTChe9z112z2rVQBeFZ\ndTkaEmPl5RX17nNFcnIK6NWrq01tjUYjSUndOXLkNElJ9dcUFbQOZrOlVS/KjsRgMNhdcCQmJhAR\nEcprr71Hv369iY+PJTY22iVq1xZbNV5Ms7C3xD6fyY4ijQ35VsYFuOYMUEP4+npTVFSKn1/zE4Ta\nI5qmsXLlF4wdm8Ndd03Gy6vuB12LxWKX70RUVATffvtji8dxJs6fT2fNmu95/vnf4OXV/v+/2ufd\npR3TUHLV2AcSyNx5iItHSgCI7O1Lvzvqj291djRNa1JGo4+PF0FBfhw/fpYePTq3nmGCOmkv2e1t\nRXBwEE8++QDp6ZmcP5/Grl37q2vXqqpe7iYxMYE+fXo5RY3aIqvG3y9Y+TbPyvHyxtvbSokG/77Y\nPsVqVfkqIVZrI0kSf//7bwgODmqwnUiarZudO/dx8mQaCxa81O6y/utDiFUXIjMzg9DQ+gPN3X2M\n3PVuEmtfO0RUZKjLJ1g1R/zExERw5kw6OTn5BAcHtIJVAoH9MBgMxMVF15lspWcLn2DVqq+qs8oD\nAvwZMKAvcXHRbfpw8Kd0C6tzrZy0o0ityfYijU2FVkb6ue71qi78/X1IS8tytBlOSWNC1d7ExESR\nmprh8omNX3zxPQEBoTz88JOONqVNEWLVhdi1azvJyYkNtnH3MdLtFh+SkmLayKrWoaSkrNnTP507\nR7N37zEhVgUujZ4tnFjrO5+Xl8/u3Qf44Yf/YrWqTJ48gaioliegNMSqHCv/zrJS2oqhl0UqLMxq\nf2K1o3i9XIHhwwfx1Vffc9ddUx1tSrOwWq188MGnjBkzod3Hp9aFEKsuxNmzpxkxIsnRZrQJ+mpU\nzSumLUkS4eHBXLqUS1hY2z69CwStSWBgAOPHjwL09dK/+WY9Fy5kMWrUMHr3lhvtr2kaZrMZd3fb\nynCVqxoLM1tXqFaxrVBjZ5GVQb7tS7AKnANfXx9KSkra9JiapnHo0FG6deuCt7dXs8cpLCxi0aJl\nzJv3aJ1LtXYEhFh1IVRV7TBxgUVFJXTp0nzvcExMOPv2KUKsCtotbm5u3HrrJDRN4+eft/H22x/S\ns2cCo0cPq3WdKCoq5ueft5GZebGynwmz2YLBYKB//ySSkhLr9QD+KcPK/rZQqkCBCi+lW5kTBrIn\nxHgY8De4fiy0qFDiPEiSVB0P3lpomsb+/YfZs+cwVivs3buHhQv/3Ozxzp9PY82a9bzwwm87RCJV\nfQix6iKUlZVBiwrFdCwkSSI0NLBJ5a8EAldEkiRGjx7G6NHDOHLkOO+8s4SgoEDKysqxWCz4+Pgw\ncuRgJk0aX6uf1Wpl796DLFnyKZqm4ePjzciRQ4iO1pMyz5SrrMpp22vOpiKNTUUW3IBAE/gbIcAo\nEWCEIBMEGiUi3CSeFYsJdAjsXYUjOTmRQ4eO0qePfVd40jSNPXsOsH+/gsFgZPDgYTz55K955ZU/\n8+c//0+zE8V27NjL6dMZHSqRqj6EWHURVq/+D9dfP6re/VmXivjk9e0ADJkUzalTqXTuHGPTMpHO\nhr3WTY+NjeDAgRNCrLYyHcHj7yq1Mnv16kGvXj3IycnFz88XN7drV86pwmg0MnBgPwYO7AfoU42b\nN+9g3boNWCQDH3YZToZv8xZCaClm4JJF/9Erslah0ddbX/nKVQgM9CMz8zKRkaGONqXD079/Mm+8\nsdguYlVVVXbu3MehQycwmdwZOnQ4Tz55W7Wo/OSTDxg5MoXAwOblTuiJVGE89NATLba1PSDEqouQ\nnn6OiRPrDqrOulTEB3M2YUzVvxQ/7znHjIUDOXz4JJIk0bVrLO7ubpw7d4HS0jIkScLd3URcXBRe\nXo4viXM1eXmFBAT4tnicqvdZXFyKj0/z44UEDVNaWu6U/0f2xl4PUW1BczKt/fx8ufHGcbx/SeWj\ny1YOt9H0f1Pp7Sm5zHkAiI+PYt++Y0KsOgFGo5EJE8bw+uuLmDPn7ibHkaqqyrZtuzl69DQmkzsj\nRoziqaduv8bruX37ZgwGC7169WiyjVarlcWLVzB27A0MHDi0yf3bK0KsugCnT59ocMm5T17fXi1U\nAYypAaxZvJ+nfj8ei8XK2bMZWCwW4uIiq0VbWVk5589nUlxcSkxMOOHhzuN9zMi4RI8enewyVvfu\n8ezadYTu3eNE/Gor0RHEakxMOGlpWcTFuW7d4sZYl2fl/7Ks7CzScNY1pSRgYqDrzRb5+vqIh+Zm\n0BoPJYmJCcTHx7B48TLGjx9Fz54JjfYxm8189dV6Ll/OY/z4G5k48c56p+UvXEhn06YN3H//XU22\nTVVV3nzzQ2bPfrjDJlLVhxCrLsBXX61m5sybm9XXZDLSvfu1//Senh7VgvDIkVPk5xcRHOyPwWDA\naDTi5eVxzYpEZWXlZGVlU1ZWgcVirZ4aNRgMBAX5YzQauHQpFz8/H6KiQlu0opHBYJ+LlJubiQED\nEjlw4DhZWdkEBwcQHR1ml7EFOqWlZfj5+TjajFYlKMifjIxLxLXD+8ehEpU/Zlj4uVCjxMlzgQIM\nEOCCd62YmHDOnEm3eUU+gV5n2F73gavx8fFm/vw5fPHFtxw7dpKpUyfV2a6oqJg1a76jokJlxoyZ\nxMbGNzhuRUUFb7+9kMcem90su95/fzn33feAEKp14IJf+46FxWLBbC5vMPbs7keH8MGeK2EA1rh8\nfvHoSJuP0atXN0pKysjPL8RqVbFarWRklGOxXEmu0DQNDw93IiND8PT0wGQyVj9ZWixW8vIKsFhU\nZLkTRUWlnDqVitlsQdM0vLw8iIoKw9fXtkzG0NBALl/OIyKieaWrrsbd3Y2BA3tjsVhRlLNCrNqZ\n0tJywsPtc66cFUmSsFrbV4JjVoXKb9OtrC9QyXZWV+pV5Knw6BkLf4uHiYGuE7fq5eWB0WggN7eA\noCB/R5vjEuzff5g+fXq16jGmTJnI8eOnWLjwPWbPnomvr/7QfflyNl9+uR5PTx/uvnsOQUG2Xd9e\ne+3v3Hff9GYlVK1Y8QU33jiF+PjOTe7bERBi1cn59tsvGDNmSINtIsJ8+eX7I6sTrH7x6EgiwpoW\n8+nt7Ym3d93rMzeGyWQkNPTKFHtgoB+BgX7Vr0tLy8nMvMyZM+lAVaZ+EGFhQXUmgKlq68QGHjt2\npk4vs6BlVFSYcXdv/5cSDw93yssr8PCwrUapM/N5jpXfp1s4V+FoS5pOqhmeOmchzwJ3hbqOYO3R\noxMHDhzHZDK2+5kIe3Do0DF+8YsZrX6cHj26ERenhwXIcjdOn04lLCyKhx9+Bk9P2++Jn376MUOG\n9GlWvPjatRtITOxHcnK/JvftKLT/O4yLoyhHGTnyzkbbRYT58tTvxzfazhF4eXnUqplqtapkZ+dx\n7NiZ6hqEnp4eREWF4uvrTXZ2HklJ3e1qg6ZpWK1qs1fFEjSMKyW8NJdOnaI5dy6DHj06O9qUFvH+\nJQt/ybByuRW8qX4GsGpQ0sq5WZkWWJBmQQNmuohglSSJPn16sGfPUZKSEvDwqH+2zFEUl2ss26P/\nY8xMMeHj4bjvdWvXQ62Jl5cnjzwymzfe+IB77rmfTp26NKn/rl1bMZuLSE5u2LFUF5s378TXN4TR\no69rct+OhOtFqncgMjMzCA5uf1NGRqOB8PBgevfuRnJyAsnJCcTEhHPxYg4HD57g8uU8zGb73kkv\nXLhst7ACQcfEy8uDigoXmS+vh1cvWHgpvXWEah8viVuDDK0uVKvIscKZcuesWFAfkiTRt28Pjhw5\n5WhTrqG4XGP2snJe/cnCqz9ZmL2snGIHfb5ms7lFOQ/N5cEHf8EHH7zTpJCfrKxMNmz4jsmTm+4s\nOnjwKNnZxdxyy7Qm9+1oCLHqxKxe/R9uvHGso81oE7y9PenaNZbk5ARSUnpy/vwFu45/6VJus5dv\nFQhcHU3TeDHNwj8uWMm3c+htoAHuCzGwtqdbmyZoGYCx/q7n0TeZTERGhpCenuVoU2qxbI+FQxeu\niNNDF654WduavXsP0a9fcpsf12g0Mm3aJBYvftum9mazmTff/D9mz2589vNqzp9PY98+hfvum9vk\nvh0RIVadFFVVKS4ubNF6wq6Kv78vRUWllJaW22W8goJivLxcP85QIGgOqqbxxDkLb2dZ7e717O8t\nsbEVJ00AACAASURBVLibif/r7IabBAfaUK1GukF/H9e8hUVFhZGTU0BRUduuVe8KaJrGli07mlWj\n1B7ExUVTUJDDxYuNP0wsXPgK9947FZOpaV7g4uISvvpqA/PnP91cMzscrvlN7wBs2vQTAwe2/ZOl\ns5Cc3J1Dh07YZeWgvLxCsYqVoENi1TTmnbGwNFvFbMdxQ4wwL8zAWtmNsf56zOhXuSqn7PN8aRPR\nbhJerVTaqC1ISuqOopx1GsE6M8VEUtSVzzMpSmJmSttOxauqyjvvLGHy5OsdtrxoRkYmkmQiPLz+\n2uYAq1Z9woABvQgNbfqM3aeffsnjjz/b4ZdQbQoiwcpJ2blzG/fff4ejzXAYBoOB7t3jOXcug86d\nYxrv0ADl5eXtMvZXIGgIq6Yx97SF1Xn29XYO8Jb4Q6yRYX61E5u+yVNpywjHErOFr3ON3BhowOSC\nCX6SJJGSksiRI6dRVRUvL08iI0Pw9vZ0iIjx8ZBYPNPDYQlWZWXlvPXWB8ycOY2ICMeUFywoKGTl\nyrUsWPBSg+32799DcXEe48cPbvIxzp1LJTIyDl9fv8YbC6oRYtUJyc/PxdtbZK0HBvqRmprZ4nEi\nI8O4fDnP5jqvAtupquYgcC5aQ6gGGOC2YAMvx5nwuMqjadE0DrbxigJHzEZmnbaQ4AlJXgb+Gmck\n2M21PFWSJNG7dzcAiotLycrKprS0vM4ZJVVViYkJJyQksNXs8fGQmDusbasUaJrGd9/9xIkT55gz\n5278/R0j4sxmM4sWLefXv/5do3VSMzLS6d27eWEK33yzgRde+F2z+nZkhFh1QlatWs5NN41ztBkO\nJzU1i6iolj1h5+YWcOZMOrLc2T5GCWpRVlbR7pdadTWsmsb9py2ssaNQ7e0l8WK0kRvrKcRfocEg\nXwOBJo2T5VqrLDLgJUG8u162qipJzAocK4NCq4q7wbVvZz4+XnTtGlvvfk3TSE+/yP79ChERoe0i\nYdRsNvPKK28wY8YU+vRJorzcMQldmqbxzjsf8+ijz+Dp2XieyPjxN/LWW6/SrVvnJh1n06YdjBt3\ng5j+bwau/e1up+TmZhMQ0LGnrTVN4/LlXFJSEls0TlpaVovHENRPaWl5hxKrzu5JbkyoukGTYld9\nDDApwMA/4o34m+q/wXobJBZ21j1ylypUVudpbClS+W+BSk4zqw+EmSDeXaKzh0RPL4mbAw3InhKP\nnLWwPKf2++vpJeFrdL1QgKYgSRKxsRHExkZw6NBJfHy88PPTZ4uKi0vx9vZsUb3jnJx80tMvVo8R\nGxtRa3GX1qCoqJikpJ50794FVVU5cuQ0YWFNL6rfUpYuXcWdd/6CsLBwm9q7u7vT1EuBxWLhyJGT\nPP/83c2wUCDEqpOxe/d2EhPtWxDfFdFXm2p4HWZbuLpea9X0WkcoYt8WlJaW4ePTcSpWuLmZKlfs\ncr6C7gDz6hCqwUZI9pYY4Wegl6fEHzOsHCtrPLq0t5fE4xFG7ghpWtH9MHcD88JhXriRDflWfptu\n5WCpbdGsvTwlBvtKDPM1cH2AgSDTtd/Tl+OM7C1RUcqubOuhlQHupFWoPHq0gM/6BGBox9/xXr26\ncuDACQIDfenUKZrdu48QEOBL375yk8cqLi7l+PFzBAX50bt3NwwGA1arld27jzJ4cFIrWH+FkpJS\nvLz064fBYHDIw+BXX61n0KCRdO/etM8uPr4LaWkXiI2Nsqn9Z5+t5Z57ZjfHRAGiGoDTsXHjjwwb\nNuCa7cXlGu9tNfPeVrPDCjW3FZcu5eDh4Y6/f8uXJLRYrrh1VFVl167D7N17rMXjCnQ6mmfValWd\nVqhaLFb2VsaNemNlsDc8HmHkp0Q3Vvdw57koE5ODjHzZw8Q4P4n6pFwnd3giwsj6nm5NFqpVVFjK\n2JH6LT4F37Omu5U7gw3UV2XKgF4C6/cxRjYkuvHPTvpx6xKqAAEmA/PDTfw/e+cd31Z97v/3OUd7\n2fIecezsPSGh7NFSKBRKC6QJo5TR0hZISy/tBTrhtr33ttxS6PpBgbDDbstq2WHPmIQkThwnsR3H\ne8iWtaVzzu8P2Uq8JVmyZFvv18uvROucr6Sjcz7f5/s8n8fWtz2jEuJs0Ymqqlz43iHeDOq5pTHB\nZrJphiiKrFy5AJvNws6d+1i6dC75+Tk0NrZFvQ1FUdi9+wANDS2sWDGfiorSyPK0JElxt9+OltbW\ndl5+eQsWy+HW4P0tjSeKd9/9hOzsAj73uRNifu2ZZ36ZN9/8IKrnOhzdqKpEaWmm3Xe8ZCKraYTH\n40arFYZE/fo7i/QbNr9cLbNpgz6lrfCSRTAYoqEhcUv3ZWWF1NQcRJJEnE43S5bMxe8PsHdv3aRv\nm5kO+P0B9PqMh22qaWxspa3NgUkp5iKzxPdmmlhiGl4d5mlFnpqn5aeHZB7plHH26bo8DXzBJnLr\nDIn8cRQqBUI+ntx5Oy2uOgBqOj/lzqXXc5pNy23NIWr67K10wGqzwPpciUvyRKQYIqGX5kucmiXS\n4FfY0eig7sMP2PaBiGvxGaCKPNgeJF8Dp2eJlOsFDFFYXLlkFQWwiEyaqGxOThY5OVmR25WVu8nP\nt485oers7KaurokFCyompPA0GAyyc+cedu3aEwkgFBTkccIJx6LXHxbFZWVFNDS0JGRVbSx27aqm\nvd3JN7/57bhebzKZCQajmxQ9+eQLfP/7N8a1nwxhMmI1jXjmmceH7Vg1UmeRia7anAh27drHsmXz\nEra94uJ8Wlo60Om0keIFo1GfEJeBDGGmU0pFInx/E01HhwOHo5dVqxbybpSvEQWB35RpOMoscEut\nh0U2PT8r1bB0BIEbC9uat0SEKkCLq45tzVtYV3Ymp9oEvl8fwqPAN/MkvmIX4z5+ZugEZugkjl1Y\nBAsvAOB4t8IV+3zUhiR+1ijzqyaZHA3kaARyNWFBbtcI+BRwyipOmb4/lV4ZVEAvhou5jKKAUQSD\nCEYR8jTh/NlTbQKLjWJUAniiWb58HpWVe5g5s4i8vGycTnckD3XevJl0d/fS3NyBzWbmqKMWj7ot\nk8lAXV0TFRUlMY+jra2Djz/+lPb2TgA0GomlSxfx9a+fh1Z7+Lrl8fgGRINNJgMej2/I9hLNu+9+\nQltbD5dffvW4tpOfX0RHR+eoXqu7dlWzaNEy9PrpswKVDDJiNY1obW2ioOCkVA8jZbS0dJCbm53w\nntBFRXkDbguCkKnGzBAXNpuFnp5esrLSxyMxEAjF7Zpxfo7E0X4/nc2HKPYWgyl5tkgA+VqRR+cm\nLxK/0izyyHwD6z7r4ZDGhF+F5iA0B4+cZEQ74Rj8vPDt/24Kd88q1gqU6KBYJ3KKVeDMEZwSJhKN\nRsOaNUtob3dQU3MQi8XEkiVzUBSVPXtqyc3NZsWK+VFNEGbPnkFrayeyLI9q5RQMBtm1q5qdO3cj\ny+E0lPz8XNasWUVBQd6IrwNoaGihvHxgzqcgCKiqmrRJ8LPPvkJOTtG4hSrAOed8lcceu491684Z\n9nFVVXnzzQ+58cZfjntf052MWE0T3nvvLRYunDPsYxtWa3i5Wo5EV1PRWWQiaG3tjKtAIEOGiSIn\nJ4uODkdaiVVJChfExEt5cR7lxXl8+umehHh4riw+hZrOTyPR1SJLBSuLTxn3dqNlkVHkHyuyOP8z\nJ/VS4ov/ZKAxCI1BFTzhex7pgJtLVL5bmPrzsiAIFBTkUFBwuGufKIY7ZsVKYeHAiKGqqtTXN1BZ\nuQOnsxdBEJBlWL584ZCoaTSYTAZ6ez0YDIejjnl52XR0OBLedVBVVR544EmOO+4U1q49LiHbtNmy\nRmwLrqoqzz//Kueee34mOJIAUv/LykAgEGDLllf43vcuG/bxVHcWmQjq65uGnBiTSbpbEGVITywW\nI/v2HUz1MAYgSeKAQsJ4KSrK5bPP9jJzZjFZWZa4I1s6jYELl17PtuYtQFi86jTJLdYZzByDyJ8W\nWvlOXYjGRPaZHQGXArc1y2RJAhflpT7Cmig6O7uorNzBoUNNCEK4nqK8fAaf//yJEXvF1tbwUn+s\nQhXC9ljbtlWTn2/H7Q+nt6lqFiuMBxMqVv1+P3ff/QiXXnoVFRWzE7ZdAJvNzltvvU9TU1uf+4yA\nIIgIgsTChYtYunRFQvc3XcmI1TTg3nv/wrp1Xx71OanoLDJRdHX14PX6KS+PPTcqXsIRsm7y8pK7\n7JlhaiEIAtnZVhwOJ3Z7enghS5KE3z9+RVZcnE9ubjYtLR2RnG5BEMjLyyY/PwdJij46pNMYWFt2\n5rjHBOEI1U6vgkUSKdKGc0mHoy2g8IxDYatbpcavcsCn0juBc9IuGW5pDGGV4Bz75BSsbreHZ555\nIRKpz8nJZvXqFXzhCyeNOHmx223s398QV7BBEAQ0GmlIEfGcrDweW6wmJCjT1eXggQee5vrr/5Ps\n7MR7uK5bdzH79tXwhS/Mx2Qav4NNhuHJiNUUU129G5NJO2qC9lTG6XTR0NDKihXxta6Ll5KSfLZv\n35sRqxliZubMYvbsqU0jsTq+NIAj0em0zJx5OIdQURQ6OrrZs6c2shoxZ05Z0m2NABRV5ZFOhUc7\nZLa6VbQi2CSwiWCTBLIkQACNqtKlCOz3qXE3IEgUbSG4uSFEiRaOskwuwdrZ2cUDDzzBd75zGSZT\n9OkTOp02kqsaK6GQjKIoQ4qI9/foeegjH985cXxpHAcO1PPyy2/zk5/cik6XnFxps9nCihWrkrLt\nDIfJiNUUoigKjz/+ENddNz2Ngv3+ADU1B1PSYUoURQwGHX5/EL1+akask42qqnR19bBz574B9wuC\ngNGox2jUYzCE/9XrdVPGNUCSUmNePhJhE/fkjEcUxQH5j7IsU1NzkEAgSG5uNlarCUEI/5YSVRgp\nqyqb2hUe75T51KPSrz+DCngUCMd8w8ImW4Ju+fDtdOBQEH5wUOb5+QJZo3T9SicOHjzEs8++xMaN\nV6HRTIwsUFWV7durWbp0Lh9XDn28u9sFxC9WX3vtHRwODz/+8c8zOaNTgIxYTSGPP/4wX/7y56fM\nRTxWdu3az4oVC1L2/g0GPT6fPyNW48TvD1BSkj/EE1GWFXw+P16vH7fbS0dH95hG36qqotFI6PW6\nI/606PVhEZRuv5F0Go/L5Um4g8ZISJLEwoWzCIVknE4XDkcvqqrg8wUIBMKpCAsXzhrW57M/JxGG\nz7v3KCr3tck841DY5lHHlJ92CYq1oBegNTUt5Udkp1fl27UhNs/VDvBsDYR8Kc3lHY7q6n28++5H\nXHPNFXEf1xqNhMfjizri7nZ72bOnljlzytDrdWxYrQ4pIj61tBuI3eXC7/fz4INPcfzxp3L++dPX\nXWeqkRGrKaK1tYX29ka+9KXEVCVONjweH1arGY0mdUtlTqeLWbNKU7b/yU64e9XQi5MkiZjNxpjb\nsIZCIfz+YJ/wCeByufH7g0Na5o6FIAhotRq0Wg0ajRT5V6M5fJ8kSUhS/B6f6UAoJLNr1z7MZhNz\n505sZxyNRhpiSB8eU4g9e+qGVJ4P19jkvvU66hV4okthp1ehxqvSEEPq7UydwJbFOnpCKi/1KLzv\nUtjvV6n1qTQGUx9rfdWpckujzC0zwpfZ4ZolXLj0+pQKVr/fzyuvvMm11145ru3Mm1fOzp01Ubu5\n7N/fwKpVCyMRz+GKiA/sJWYLq/376/jXv97kmmt+gN0+PVPrpioZsZoi7r33r1x11ddTPYyUEQqF\nYirYSAZFRXkcOHCI8vKSlI9lMuLx+BLaalWj0aDRaGIWuYNRFIVgUCYUChEM9v/JeL1+QiG57y80\nrqVzt9szrjGOl66uHurqmliyZE5adRCTJIlAIEhV1X7mzSuPRHyHa2xyyksBmsoEvHGqyvy+4G2W\nRmBdrhRpDetVVN7uVXioQ+ENp4I7RRkbCvBgh8wqk8B5OdKIzRISVYgWDw8++CSXXnrhuLcjSeKo\nXqyDEcWhE8XBRcT5+Xba2x0DLLhG47nnXkEQ9Nx88y2ZZf8pSEaspoBXXnmRNWuWJS3hezJgs1lo\nb3ewY0dNQjtWxUJhYS5NTe188skuVq5cMO6Lvs/np63NQU6ODbPZOKmjdtHg9fqGRNbSAVEU0evF\npKV3KIpCVdWBpGw7GlRVpa6uKSW53mMhCAKrVy8iEAhSWbmbo49eMuJEsCWo4lXj/40UaId/rVEU\n+GKWxBezJJ53yPxfi8w2T2LjrALRRW67+xwClpnS71zw4YeVLFw4N2JBlQhkWYlq4q/VaggGQ6O2\nhS0oyGHXrv1DxOqHdb3c+c4WADaecApL8kQeeOBJzjnnfJYvzxQ6TVUyYnWC8XjcVFZ+xNVXX5Lq\noaScOXPKOHDgEC6XZ0L6Uw9HSUk+eXnZ7NvXwOLF4/Pfq6trIi8vm/Z2B3V1TZElLFVV0em0ZGdb\nyc62TZkcWZ8vgMEw/SZce/fWD6iYn2gOHmxm5syilO0/GnQ6LSUl+TidLux225DGJgEbeMrGJ+AK\nNGO//st2idOzRP6rUebpLpmWBOW25mvClf/RUBeA79aFeGrOySltlnAkLpebbdt2cPXVw3t7x4NO\npyEYDCJJY6+2KIoyZvRTFMUh7Y0/rOvlmao7WV0R9jp+pmo7L9Qv43+uvyljGzXFyYjVCeb+++9m\nw4avpHoYaUNXV09cvacTiU6nTUh1dzAYIi/PTl7eUC+/QCCIw+Gkrq5xSA6mXq8lK8tKVpZ10gnZ\nqR49Hkx1dR02mxmbLTUXRlVVcTicE+pJnAj6cxJ/90GQhztkumYIqFGIzZGYpYfz7NEt9epFgV+V\nabg0T+TmQyHedqqM15V2tl6gTAdbo4zYfuxW+Y8GDX9OcbOEfh566Akuu2x9Qrfp9wcHdKIajfBE\nfuznGQw6fD5/ZLt3vrMlIlQBCmwNVNpWZoTqNCAjVicYVVWw2dKnVWMqURQFg0GfFvlF8YjVYDDE\n7t0HKCrKo6AgZ1ThptNpKSzMHdY42+8P0N3dS319I4HAQCErimKfOLJgsRjT4rOarnR19aDVaigp\nKUjpOILBFJuJRonT6aao6HBveLNeYHcJdFrGdwwvNwrcM0vDPGNs21lgFHlqrpbbWmR+0zS+z7DW\nr3LPbA3fqY2+Q9ZzDoUlJg0/SGGOKsCWLe+ydu3qmLxUoyGWiWs4XWDsHNeysmIaGlqYN698PEPL\nMAXIiNUMKaO2tjFtljNVVUVVVZqa2vB4/JSXF6PTaampqScQCFFcnIfNZhngXrB3bz3z55dTXV0X\ndRHAcOj1uhGFbCgk09vrpqurh4MHm4c8rtFIWK1mrFZzRswmmawsKwcPtqR0DIIgUFFRQmXlblat\nWpjWke1wodUBzGYDc+fO5I0emXdd488dPd4qxixU+xEEgWsKJR5ol8fVhrU1BHu9cF2hxC8bZXxR\nvC0/sCPBubOx4nB0c+BAPVdccVHCty1JYtS+1dEet0ajHq/XH7m98YRTeKbqMwps4ehqm3MmN5+R\n+PeSIf3IiNUMKUFRFHp73cyZM7GWOyNRXl7C229XUlFRQmlpAfv2NeD1+qioKCUry0JrawetrZ0E\nAqGIKbzH4+szvTfgciWnOlyjkbDbbSN2SwoGQ6OKWQCTydAnZk0YDFPHnH+ikSQRu91Kc3M7xcWx\n+z8mivx8O35/AIfDmZYFbv2sXLmAUCjcREBVVe5olXEroEXlKLNItU/FEUeAc75hfMevSRSo0As0\nBscnHD9wKdw9W8vHbpWnHWOvzNgl+I+i8GR3LM/ZZPHww09x9dXfSMq2Z8+ewYEDDSxaNHrufzAY\nivkc1J//f0yFFdjIne9sQVEUfnrWpRw/N7UrHRkmhoxYzZASmps7KCtLj6gqQHa2lRNPXB05iQ4u\ntiotLaR0kCVrf4vL2bNn8O6725g1a+LzCLVazbB+l/2oqorH46O3101jYys+3/Dm/Hq9ts8b1YTZ\nbEyp/206U15eQn19M9u2VbNixfykCP+AW2bbE+EI7sp1RejMQ78LQRCS1rUqUQiCgNPpxmYz80+H\nwvu9CiBwolXkG3kSV9ZGX+200BBur/qpW2VNAtITZ+uFcUd5q33h1Zg7KzQc8Af5dIyo6bEWgcUm\ncVjP2U0b9EMEa6IbCLz44mt8/vMnJc2FRq/XReWJ3NHRHdNKVFaWlZ4eF9nZ4fS5Yyqs/KdzNmDJ\nCNVpREasZkgJDoeTJUvmpHoYA4hVePTnXGk0EiUl+WnTK/5IBEEY06BfVVUCgSAul5eeHhdNTW0j\nCiFJEjEaDRiN+oT1o59slJcXY7db2b//UMLN+ANumSe+XUXLLhcAe1/tYt3di4cI1o4OB8uXz0/o\nvpNBTo6NT7Ye4o86CwE0zNTB7eUafn4oRLRHzzw93DdbwyMdCgf9MrMN4091WWsReahzfGJ/v19l\nr09lgVHk/2ZquPxAkLYgw/rGWkS4tjD8HQ7nObu5MjTAYzQRDQR6QwpX1IYIqbAQL4sdDs466/Px\nvdkoiSYNyeVyxxSomDGjgM8+q2HVqoWR+7Zu3cnGjTfGNcYMk5OMWM2QEgZ3JokmmpTO+P2BlNlv\njRdBECItTnNzR19WDoVkPB4fdXWN48rTnezYbJak5K9ue6IlIlQBWna52PZEC2svHxjWlyRpUqRz\nCILA+zMWsL0xhAaVK/M12DUClVHmbs7SwV8rNCwyilyYo/JCd9hHdbycnS1ySyN0jMPKyq3AJ26V\nBUZYZRZ5b4mOlgDs9ytU+1RaAtAjq/TIKjZJ4Fhr9Oe08TYQaA8qXLI/xEfu8Oe8RdXz3RPPjen9\nxcuR1fvD4fcHR/VXHYwkSZSWFrBr136WLJnTZ2clxdSEIMPkJyNWM6ScaKNJ6c5kEA/jRaORsNnM\nfcI2O9XDmbYM9p9MV5oDCpvaZWQETrMKXFcocUerTMPw2SgD0AI3l2o4yhI+Dyw3iSw0JuY3ZtcI\nWEToGMc25uvhgpzDkUSTKDDbALMNEqePMucb7Dm7tFhgw+rEXYoDisqG/SG2uo84RgSBzZ0qX7bL\nHBeDaI4Vs9nIhx/uoLS0cMRVB4vFhMvljcn+raAgB6/XT0eHg/b2DpYuXZ6oIWeYJGRKhzNMOC6X\nZ8Cy9EjRpMnEZBEPiSIYDEVaaWZIHCvXFVG0xBK5nTffQMPbW3llw9/wbH4IvOFCPkWZHMfbjxpk\n6gIwUwf/V65BEAS2OKNbfl9sFPjaEV6qgiDwt1mJ8SFWVZXx9gc43iqijyPK2+85+8NTNPzwFM2w\n+aori0+hyFIRuT1cAwGXrPKmU0YZdO75dZM8UKj20a3A413JzXOeNauUk08+Gq/XN+JzsrOtdHf3\nRr1Nd4+bT/76CO0vvsb+6oN8+GElp556eiKGm2ESkbnaZJhwWls7B/gvTgWmQ1R1MNPxPfczOI0l\nUejMEuvuXsy2J1rwOv3UPLmLWlc+kE9bfQPrdvwY7c9+G1VLy1TzeKfM6z0KGuCKfIkKvcgBn8L2\nKFMATrSJiIM+Y4uUmM88BMjj0Pt5Gri+KP4IpVkvDMhRHYxOY+DCERoI7PQo/LlV5gOXwqFAWNSf\naBXZWCjiVuGprpGzgXcPl1CbBPo79w33GzEa9bS3d0W1HXePm7af38CxvXsB2LtnPruXnYpGM7ma\np2QYP+l/xptiBAIh2tu7pl0k7kg8Ht+AyOrgaFLREgsr16WPU8BYeL2+adl2dDoTbheZHLGuM0us\nvbyUjqoqul2HJ3XNnjK2b8tFeOPZpOw30fy5VcarwolWgY19xUV3tSl0R1FZVaSB6wqSd3kKqjCe\n4PRas0CZPrmXT53GwNqyM1lbdiaipOeBdpmv7Q1wdnWQx7oU6gJh0f2ZV+XPbTIn7Q5yyb4QTaP4\nx1Z7Vep9yXeRyMqyjBg9lSSJUGjsgyAQ8rHj0d8xv0+oAszv3UvuwaaEjTPD5CETWZ1gVDWELCvs\n3LkPVVUxmQyUlRWh109fsXNkNAkmX4FVV5cTuz19/S4zJB5FSU5kNVomw2T3PLuIIyRHlv9VVeUj\nV3RCabVZoECXRLGqELUbwWB0wCV5E3N+6goq3Nai8JZTocqnMtq33hqC1tDox4VTgUc6FW4uTa7Q\nzs+3c/Bgy7AOKRqNNLrtWnMD4p03E/Q50M4YWqhlsWQ6QE5HMmJ1AmlsbKCgIIeiorzIMrjb7aWu\nrgm/P4AgCBQW5pKfb5+yS6yKogz73vqjSZORnp7eYbtPZZi6qKqatMhqP6f98iSeWbcFR2+4AUGx\nqYEVKztRTz2XQFVdX8vK9F0c+2GxhvNzRMr7IpCvOxWqolyGXjPOlqxj0RJUiTfAuMIkcGZWkscX\nUPifJpk3ehUORlGMFi0mARLg/DUmBoMevz+OgTc3oPnp5QiqSjawqF3ikYZLkRSVs8v/QXNOMZ0z\nJ+d1IsP4yIjVCeT111/mhBPWDLjPbDayYEEFEBZybW1dkairXq+jrKwIk2l8ZtDpRFdXT1p33YkH\nRVEzJvrTjPCkK7lXfXuxja89cQpbfv4GFlcbx59rQHveb8FoYsmSOVRWVjF/fgVZWZaxN5Yiyo9Y\nKv+7QyEa+WKX4EJ78j7bkKryHwdDRBnkHcLns8SkBRPq/WGR+lavMupyfjzYJNhYKPHD4om57I/0\nGcny8AELAOnOnyL0rRr0Biz8rep6gko4uvr/qn7Ihofn4/nk/eQMOENakxGrE0hXVwd2+8h2P6Io\nDoi6+nx+Dh1qxeMJV1ZmZ9soKcmf1MKovd3BvHkzUz2MDBnGRbIKrAZjL7bx1b99Zcj9BoOeo49e\nQm1tI/v3NzB3bhk2W/qKVoDWKNubzjEIlCYxH/SmhtC4ulcl41sPKCo/3B/k1R0yLgU8ZQJoEren\nPA3cVCJxRf7EXfJVVR32d+Lxu6gLfIy7oWbUzlwv1J8XEaoAIUXHc9ftQVqf3p3bMiSHjFidQBQl\ntiwpg0HP3LlhYaeqKt3dvVRX10WW0gsLc8nLy55UKQOhkIxGkznsJjOyLKf18vNEoCjJTwMYXtFf\nvQAAIABJREFUC0EQmD17Bqqqsm1bNdnZVmbOLJ7w7ybahh7tUUYKFxiS97k+2SXz+KDOVTN1cL5d\nZJ9fpcYHdX4V3yhadp8/sfnCh/wKV9UE2femgs4JNsDQqtJ1NKgJEKwlWvivGRq+ljOxQY5+P1Wr\n9XCzlEDIx7N7/0SLu549bqjuqOS04stxOryEQjK6M7/F4gd+iThCdm53pwHd3wtov7iD/JKp5SiT\nYXQyqmGC2LevOqYWc4MRBAG73RZJWFcUhdbWTnbu3AeEk9ZLSwvSProy1QiF5KhaDE4lvF4/RuPI\nHWqmA+kgVvsRBIFVqxbidLqorKxiyZK5E5Y6FG1DD7+i0jFG8U8/J1uT83uq8yv8d2OI3iO0qlmE\nHxVrIgVTqqpydW2IJx0jR+8aAokTqwFFZf2+EHV7FGzOw/frnGBqUHHPGt8xVqGD35drONU28atx\ndrsNh8OJ1WpCVVVcLi/v1T5Pi6s+8pw2dz17HO9z8rxz+4IY85Dnb4I7f8qJ+n/T8OEsQsrAc02g\nScs/fvsG3/rDhRP8jjKkkoxYnSDeeut1zjjj+IRtTxRFiovzKS4OF18EAkGamtqoqwvbehgMembM\nKEyrfNdAIDjljOS7u3vJzp5e1akejw+jMX2Oq1SgqsnPWY0Vm83CUUctZuvW3axYMT+mlpbxEm17\n2P0+NarIaqkWzspO/OcaVFW+VxeidlDS7LoccUBlvyAIrM8T+YdDYaThNvhVfIqKIc7JSqCxjW0/\n+TshlwPpZBfNR10LRJ/HLwFZEhTIHi7b8QIS8OyqLxPUm9AIIAnhC7skwH8WS5EOYBONzWamqmo/\nPT1hCyuLxYTRZATnwOdZLaaBq23FZXh/eh/Vj9ai6N9AeGsBqjLwWO7sbE/28DOkGVNLOaQxLlcv\nZnPyesfrdFoqKg5fILxeH42NbXi9flRVxWw2UlpaMGrP5mTT1tY15frJOxxOZswoTPUwJhSv1zes\nJc10Ip0iq0ciiiIrVy5g9+4DLF8+P9XDifCJR42quMoqgTlBxv9HUutT2Taoq9MJFoHfzhx6CTzF\nGm7rumME54LmIHzsVjgxjralgcY2nlz3Fs3ucLvQ4qYG3th3Laed/0cCrdno+oRcwBbOWzUJcKxV\nYL5BJFcDcw0Cc/RQLPsouP0niHXVAHyn4T3kG24DY/KuMbEiiiI2m4WlS+dG7isN5dLg2kmLqw4Y\nvjPXwGj90mG2rCLn9XLo0EFmzBhY/+By9WasraYoGbE6ASiKgqKMt7lfbBiNhki+K4Qtsg4ebInY\niZjNRkpK8idUvDocTkpLCyZsfxOB3x+YdkviXq+f0tLpHllNrc/qaGi1GvLz7WzfvpfFi2cndTVj\n5boi9r7aFYmujtTQo3qCOieNxDyDQIVeYHdfMuo8Pdw1S4NmmO9QFARWmkYWqwrwplPlxDg00faf\nPkuze0nkdrOnjLaaJfyk6v/xH0ffhKkhvM9gmcCx2SLXFUqcmT1UFAsvPhcRqgBibTXKG8+inrU+\n9kElCVePm4//vofqVw5yxhXHYMkyj9qZC8I5rc/d/R4tu4wjbBVAwPuPAu4x38VPfvFLtNrDUddb\nb/05BQV5fO97P8BkMifpnWVIBRmxOgHs2rWDefMqUjoGs9nI/Pnlkdsul4eDB1tob3dgs5kxGvWU\nlBQkPW0gXS/wGaInUySXvpHVfoqL88nJyWLPnlpEUWThwllJKbyKtqFHW5T5qslCEATmGmC3D3Ik\nuGWGhpJRmg5cnCfyZJcyYqFVMr55VSMQnCVQHnLxNYOX/5xfOmnPl64eN/d+8x2Ctbl0Ave+9Q5X\n3n9CRLCuLTtzyGsCIR9P7ryd5m4LcPToO1A1rDAcz1/+cjvf//6PI3dfd90P+Mc/NvOnP93GUUcd\nw+c/P3Q/GSYn6ZV0NUV5442XWbNmZaqHMQCLxcS8eTOx2cwsWzaPkpICGhvb2LGjhh07aqiurqO3\n153qYWbIkJaoqpL2hXV6vY5ly+Yxe3YpW7dWxWfSHgX9DT3WXl46ihNA6jtuXZUvcX2RxP+Va/jS\nMNHKI1lrFllkHFkoFmvjE5ErfnUuxebGw9sxNVAyfxevHfs9zs4SuH+Ohg/W2Mn9aMuoQlU99VyU\nWQsit5VZC1BPPTeuMSWDl+77kGDt4VShYK2Nl+77cNTXbGveEk4POHEPzDyck2qbKRGOZw/EbDaz\naNEsXnzxH5H7ysrK8flCXHXVBiorR99fhsnF9A6PTABtba3o9RI6Xfq1U+3qcpKTEz6hmEyGAf6n\nfn+Apqb2SMGWJIkUFuaSk5MV12y/t9eDxZI++VSJYDK0vMyQHFLdbjUWjEYDRx21iKqqAyxbNi8l\nY2hNsMF9PJxkkzgpylRrQRBYZRL41DP8b7w0xtP5kfZeX7n/BKp+/U9CLgczTneTd/HdPGwZmMuv\n0UgEg8EBS9wDMJqQb7gN5Y1ngbB4Tad81fEgGEKoG1+CtxcyK3sJX/7WSez65BCvX98Aaliy9Keb\n6MylPPLI36mrO0BFxWwAzjnna7zyytsprc/IkHgyYjXJbN78AOvXn53qYQxLS0tHpHvWYPR6HbNm\nHS7YCoVk2to62bVrf0Sk5eTYKCzMHXZJ2O1X2VwZztPdsFpDa2sHJSVTK1/V5fJisYyWW5VhqjIR\n7VYTiSSlrpFIdyh626qOUNhiqiKJTQGi5Vy7yKYOZYjj5yKDwFHm6L/7ofZeFtbdfdWIUWiAk087\niX89+BzBzeFo+Bl/OAbL0lkDn2Q0pVWO6pGcccUx3PPW24Rqwy4H2llOzrjihFFfs7L4FGo6P6XF\nVYdgCGE7s4PZ5kL21tbi07nZ+M5xw6abXHTRedxxx13k5uYDKqqqUFpaiCAIhEKhaZ+yNFXIfItJ\npKWlGZNJi16fnjM8RVGi7oal0UiUlBREBKeqqjgcTmpqDhIKhZsdGAw6CgvzEHVGrngswM7m8Gn+\n5WqZG1YEmJtGNlqJwOHomfZV8dMVRVFTKgDjIVWR4O0ehY4o60s7QvDbZpm/VKRerK61iJRoofGI\nqPByo8BDczTkaaMfX7T2Xqqq8olb4YEOhc4dbo75c07EY/Teb9Rz5YMMFaxpiiXLzCV3reXFv72P\n2WTkjCvC+aqD8fsDtLZ2ReytFovnkmPZiVYrMUO3koXzwk4CLS0dNLQ0sfbysiHbEASBjRuvRBCE\nAcf43/72CF6vB6s1c46eCmTEahLZvPlBLr74nFQPY1jGu4QtCAI5OVnk5Bz2B/R6/bS0dPDINic7\nmw+3ld3ZrPJylpm1q8a1y7TD6XRPO9uq6cLglQGzfqDQUxRlUkVWIfybDY97YoXghzG2Nn3LqdAR\nVGIShMnAKArM0Ak09uXbrjYJPDpHQ+EohVnx0OhXuKtd4QOXwk6PileFO35fSZtyuCA2qOh56Qcf\ncv6rk0OsAugMOk6+ZDXl5cWoqkpPj4vOzm7cbi9OpxubzYxer6WgIJeyssIjhOYSVFWNNLwBKCrK\nY+vWKrze4T2ejzyme3p6eeyxf7JmzbEZoTqFyIjVJNHY2IDNZkjLXFVIjpm90ahn1qxSilqCsGdg\nKCUUktmxowatVkNhYS7Z2dZJk/M3EuGl4NRHgDIkFrdf5fLN/gErA5s26AcI1nS2rhoJs9mA2+0b\n0P5yIjgUY8enxiD8b7PM72am/rc1UwcfuuFzZoHNczRkDxbQXg/CEXmjAa04xJZpOHuvFRcW8nSX\nzKMdMtu9Kp2DIs+pf+fjR6vVcOhQK06nC0EQsFrNFBTkYDYbkeXRHUWG+22tXLmQ+vomZs+eMeLr\nXnrpTVpbu9i48ccYp0gOb4YwGbGaJB577CG+8Y2vpnoYI9Lc3MH8+TPHfmIcbFit4eVqOXKxX1os\n8KNzSzHrBQKBIG1tXTQ2tkWiu0ajgcLCXCwW46QSAJNprIkiGAxFnToyWdlcGYocuxBeGdhcGeKq\nY8PFLqFQCLfbiygK6HTayPKjIDBgKfLwv/1b6v+PSv/Chqr2/1/t+7+Kogz8v6IoqKqKLCt9ns3h\n+/pvy7Icud2fkjMcLpcHnU474WK1NQ7bqjecCi5ZxZKEBgGxkO1ysFzW8MRcO1bNUKEq3XYDYm3Y\n71T+5E3+fmYJhwKHAKjp/JQLl16PzmwYYO/lPyuf9U0KH7jUYa2xckWViv9dQ+d3Ggj2pQFoRT9n\n/OGY5L3RJGA0GiJuM4OJJo9UFEVkWY6k20iSOKJQbW5u5Zln/sXZZ3+Vr3/9qPENPENakhGrSaCh\noZ6cHOvIlZxpwFgz2/Fg1gts2qAfdhlVp9MyY0bhgOVzt9tLW1sXdXWHLV0sFlNkFp4hfRhpGW46\nsWvXfiwWEz5fAL+/a4jA7Bej0aTa9ItcCItcURQigrf//6IoIor9/4potSKSpIvcJ0kSkiT2/Ukj\nTqKCwRA1NfVxFzoGQr4RzdxHoy0OJ4D9fri9ReZnpam9RFV8+hY3X3juUKEKCG88GxGqAFLdXko/\n6eTQcjsALa46tjVvYW3ZmejMEuUXF/OjBpk3mxScQ52YwtsArijUcELJHFY+KPLSD8L2S8MWWEXJ\nWCktyWQ8E/qCghza2roiLcX7kWWZV155m9bWdkRRQhQlcnLyufHGWyZdHnmG6MmI1STwxBOPcNll\nX0v1MEZkIiyXzHohEoka87lm4wDnAVVVcbu9tLR04PH4BjyvX8CmOqoZCAST2hkoXfF4/JhM6Vkw\nmCiGWxnYsPrwd11WVoTb7aWsbGinpnRGq9Wg0+lobGyLuZNcv2F7f5vMSNRwBMHaL5BUVaXbpBCP\njf6/uxV+XKyin4jcYEcH4qbbAFAuvwHsefh8foxKiOwEHO+9IYVLD4T42D36ufc0m8BNxWHBZVk6\na9w5qtGktCSbeFNmcnOzqKo6MECsVlbu4IMPtrF+/SXMnp0aG7YMqWH6XW2TTFdXJxaLIa3tMnp6\nXGRlWVI9jBERBAGLxTTAl7VfwLa1deF2exEEAVVVMRh05OXZJzwH1uFwTksngN5eN2azAb8/iE6n\nSfmkIRmMtjLQj6JMTo/d2bNL2bVrf8xiNWLY3seRUcPBuP0q333IwarqFwAwVZyFcLQZVRPbsVLl\nU9nULvOdwiSfSx0daG76BkLAD4B40zcI/feDPP/a+5xzzhdHfJl66rkoW9+KRFc9M+fx4fJiIOxN\njb6cTvOJ1PpVflg/tlBdaBD4a0Vif1NjpbQMpv88297uwOXyIAgCCxfOijv1x2Ix4nJ5sFpjb30q\nimIksNLT4+Sxx55l1ao13HzzLXGNJcPkJn0V1SQlKysbt9ub6mGMSnNzO3PnJidfNVkMJ2ABfD4/\n7e0OGhvb+jr0qBiNRnJybOTmZict+ulwOJkzZ6iNylTH5/Oj02mor28iEBh9fVev12Ew6DAY9BiN\negwGXVpP4o5krJUBt9szgaNJHF1dPeTmZo/9xHHw1AdObtx6Myv8NQCc4XqXr+b+mrZ5sU+Qa/19\nQmtQIVMiDfDFTbdFhCqAEPAjbrqNLsti8vJyR35hnzF/4PV/8niXzK/nn02HJLI69A4AlcIJBGo1\nmMQAnhGW/fvJkeDWGRK5E+iAIMsKDkcPHR3dBIOHK7zMZiP5+TlUVJTg9wf45JNdlJcXD1mOj4bs\nbBsOR29cYhXC4vm5517B6fSyceN/YjRm0sKmK5PjyjGJCOeMSWldLRwKyVNmCdtg0FNWVkRZGdTU\nHGTGjEK0Wg0ORw/79h0cUHBiMhnIy7Njs5nH/d1Mpc8wFgRBoLy8ZMznqapKIBDE6/Xj8/np6HDg\n8wVGLQDqp79wSafToddr+/4f/tNoRs7JnChycrJobGxL6RjiJRAIotfH7lBypGE7QJGlgpXFpwz7\n3CVVz0eEKsAKfw3frH+R385bF/N+fSpDCpmUrW8h33BbwgSrrEBI1lHZvhaA1fkf4ejs5sQvHTvm\na1WDkSsXXsA/uw+r0Q+0XxjwnLGEqoDKJXkaTs9KfL7l4JSWOdkBlhsa2bEj7GSSk2Nj9uwZ6HTD\nT8wMBj3HHLOM2tpGDh1qjdmqz2Yzx/VbCYVCvPrqO9TWHuJrX1vHggWLY95GhqnF9LvaTgDHHXci\nW7du5+ijV6Z6KNMKn8+P0RjOL8vPzyE/f2ALQ7fbS0dHNw0NLQPuz8qykJubjSmGpgWZVqujIwgC\ner2uTxjFZpEmywqBQJBAIEAgEMTt9uJwOAkEglGJ3eGQJBGNRoNGI2GxGIccG7Eiy2MokDTFZDLS\n2+smd5SA4XDoNAYuXHp9VAVWK0tF+HjgfcYY99ePTxlayCTWVqO88WzCujc9snAjyjPv0eYJ581X\ndS9j53wbv100dk7kzxtlnu8e37FwtODjF6VZYz8xCnw+P52dPXR390bOUTesgC352ZhMRr55rBWL\nIbZ9CYLA7Nkz2LGjJmaxeuRSfjQ0NDTx2mvvIIpazjrrXNavXxDT/jJMXTJiNQmsWXMst9/+m7QU\nq06nK+4lmXRnrIib2Wwc4i6gKApOp5vm5na83vBSYL9/alaWBbvdhslkSHk0bzohSSJGoz4y8Rgv\n/bZPoVCIUEjG4XCyfXs1S5fOQ5LiW3aN93WpxmYzc+hQK2VxZLDoNIZhc1QHozn9K4Q+fRtNfVhg\nhsoX8NEx50Ag9n16JyA3uPuTED7P4QLPNk8p5taxo7b3t4d4oF0mvukTGAX4crbI1e5ORCG21Ayv\n109XVw89Pb2R/GlVVdHrdeTmZrNwYd6AYzQRDVn6LdMS7S3d0dHJK6+8g98fpLx8Nt/73g1p60+e\nIXVkxGoSEEURjUY3wCMuXWhqah/VVHkyE0+0UxRFsrOtQxokKIpCT4+L1tbOSA5yv2A1GvWTtsBm\nOiIIAhqNFCkSsVhM5OXZqaysYu7cmWRnW2lt7aSzs2fAMWQ2GykrKxpSXNLd3YvNlr4FiqPR712Z\nVIwm1B/fRuiIHNOCNi10xB6B9CtDC5mUWQvCeasxEHDLw/aVB1hmdw0OBHPa0tFDwY90yPxvk0xv\nnEHVUi18v0jiWwUadu4c/lyiqiq9vW4cDie9vZ4Bx6bBoCcnJ4uiotwJu8bMmTODXbv2D+ubOhoj\nnZfffvtD9u2rJz+/mEsu+RZWq43eXidPP72Zs876CllZyc2tzjC5yIjVJHHKKafzwQdbOf74take\nygCCwdCI+UmTGZ/Pj8GQOEslURSx221DKv5VVaW5uT3tJiEZYsNo1HP00Uuor2+itraRkpJ8Fi6c\nFYlGhYWCh08/3c3cuTMHHAd1dU0xX7DTiby8bOrqGqmoKB37ycPg7nGz+9F/ALDoovMwD9PzHaNp\nwDK9VojDbBXwKkQKmZQ4C6wCbpknvl0V6SC199Uu1t29GJ1ZItDRyLGf/YhDpsto9oTDzb05Aksv\nGN6WTFFVbmoIsblTiVuorjYJ/KFcwzLT4WOtpaWD7u5egsHQgFUcq9WE3W5j5szilK/uWCwmSkoK\n+OyzvagqVFSUROUqU1SUx759DcydG/58FUXhwQefYtWqY7j++osB2L69kldf/TdGo45TTvkc99//\nV7Kycrn44svT2q88w8SREatJYsWKVbz22otpJ1anKu3tDvLyopuJ94QUsoYx+Y4GQRDw+4Pk59vj\nen2G9EEQBCoqSocVbYIgYLOZOfroJdTWNlJf30xBgT1iqD9Z0wAASksLaWnp4LPP9mI2G2NytXD3\nuGn7+Q0c27sXgL173qHg1tuGF6xHEO86RKTD0yDxGwvbnmiJCFWAll0utj3RwtrLS/Hf/QtyVB8b\n5m2KFFgJ81p4uvoorhpUX9UdVLiqLsTrTjWu96NH5Ry7xJ0VGoxHeMfOnj0Dj8c7aqHTRDFaBBrC\n3qe5uVn09rr57LO92O3hAq3RAgXd3b2RrmkORzcPPPAUV131PfLzC9m8+UGamg4yf34FV1xxYUSQ\nX3bZhezYUcW1136bu+7alKR3m2EykRGrSUSS0mtG2NvrmbIdoXp6XFEn/6/fH+LuCg1l+vgEh9vt\npaJi7Ir4qcZ0LCrrLy4BaGnp4KN3q2h/V6HnvQMce1n5kIt5smltd/Hon8JdjS669hjsdk1cXaWK\nivLIsdp59/46drt38MVrFkf1XnY/+o+IUAWY37uXtx96mvkXfaWvKC785/cHBxwvncFsYi20g3CB\n1USglwIcWxS2nPpEUz7k8a0umesPyuzwxvcbWGSALwUd/Gx28ZDHhsulTwWjRaAHs39/A8cdt5Jg\nMMSBA4fw+wPk5WVTUlIwIAJcV9eE0ainKMtE6313UFvfhvZz1/LrF/4fJbouzl1zIV/60nEDtu3x\neHn66RexWLL505/uTu6bzjBpyIjVJJJu0ZemprYpK7JisQqzS3B1XYh/zteijWNpLZ1tyZJJIBBM\neeQnleRY7bz4h4N01fiBXurfcrH+3iUTJlhb213cf8U7SA3hau77K98h/z8/xUEdMHZXqSMZLEya\nPqhk7U1ZaIyjn7N6e4f6y/ZblOl0WrKzDWi1YZsxWQ1EhHSZcgJ0xPBm+5iZgDqbleuK2PtqV+S9\nFi2xsHJdeJlf/+1bCN78TbShsCr2SyJ3zvspNy2T6AmpmCR4tEPhd80hGuPIZKjQwbl2iRtLJPZX\nucf/ZpLIaBHoI3H5FJ6vzeITb4gNqzUsXBjustXe7qDyw2oa3/CTk5vN2otnUJhlxPnEJgLb32SG\nz8UMYHXTxzx0XindWTrebHuE9UU/RKcxoCgKzz33Ct3dbi677NtkZ2dWrzIcJiNWk4iipJe9Tbwe\ni1MNmyTwrx6F/6gPcWfF9BVfseL1+hNWoT8Z+eThpj6hGqZtj5tPHm7iuKsnpjnEo3/6MCJUAaSG\nLLpesSCcHr49WlepwQwWJs4DIfw7zKy8YvQ8VndZMXt/Xsn8/jQA63yOunL9kDSAwe1Zs/WV6IRr\nCAjR28PZxHAR0njRmSXW3b142OVtXV4pgd/cT89dv6DTq3DxwpuonV/CqzVBdCJoBegJgSeKgKol\n4OGqHeGuXU+vPJvTCi38okTCPoFG/8nG7Ve59EE31Z3ZsCc0oH2r4jex5UYXancQ8PDBvc2UmA/x\ntZI3MesOH2tmWeaqvx/kr+sqaKeebc1bCNTbqaraz4UXXsSsWXNT9wYzpC0ZsZpU0kusTtVl3LDr\nQvQXBEvf9e/JLoVibYhTbQJ/a5e5d3ZGyI+Gx+OLyYt2qtH8WW9U901WmpragNHFqjnLTMGtt/H+\nGAVWg9uzqv56VmveGWKYPxrHWATWWGIXq26/OqRVrs4sDYkQ9qPLK0X3k3u4am+APb3hc6RfIabT\nt93Zy+//+hgzXO2szv+IHzS+R9aNt8EkKg4aLQLdz6Nbg1R3HpYN/e1bvzQb7lu3A6PniPCzX6XJ\nX8pd3ddz9eLbsR4hWDUKfOntVp46o5QPPqjkjOVX8uMfX5zcN5hhUpMRq0nC7XalVRTT7famRV5U\nMujqcpKTE73RtaWvuMGnwl/aZP7SBmYR3LKKWRp9ed/r9SXUdWAy4fX6hlh8TSeKl1upfbdnyH0T\nxUXXHsP9lYfTAOSyHvJPd+Hoe3y0rlKDGU6YLPlaNg6Hc4gDxmDMWWaO/u7wwqJfKPoGrSppOnSc\ndV+Ik3mbTd9dTlvB6L9XkwDfLYhPqF6+2R/p2HRk5G80PuqVed8ZAiH2feq8Mlf/Zgf72o9iH1Dd\nvYQNbEIY1LhAEISk+JQmitEi0P20tnYBA7+7QEjl5z9tYpFn+DyJoKLnhfrzWD/v4SGPGZR8fnjZ\nnRh1k9MKLsPEkRGrSWL37l3MnTs0UT9VNDW1MWPG8HYsk53Ozu6YKpqLj5hDuPquqUaRqMy9w8J4\n9Iv5VMXnC2AwpM8EbKI5+pIS9m3pom13OG/TViFx9CUTlwNemG/hm/edECmwuvTaE7DbT4mrwGo4\nYaI1iXz22V4CgSCFhbG3nHL7Vb77kINV1S8giiH8p5Sgtzah6dCh/tcF+GUdGuDqn+7hrl8tHFWw\nrrEInBpH+9HNlaGIUIXDkb+rjh05wqmqKv+1twe3EF+zlNVvtCO1H/7cmz1lVLavZc2g51mtJnp7\nPVHZPaWK0SLQAN881sjHbUFqusKf59Li8CSg1z/iS4bFL0l0XnQdN6y5HL0mMW1zM0xtMmI1SVRV\n7eDkk49K9TAi+HyBKZtvGArJaLXRH8pn2ETu0Mo0HxEIEPr+xqKnx0VRUfpMQiaS/s5e0xWdWWL9\nPUsjAs+00oeqkYGJcwQozLdw/S2fH3BfNDmqwzGcMFmxYgH79h0M7ysKwXrkkrvqdXPj1ptZ4a8B\n4LPn5vLWhV/CtEmkVT48yVFkLZf/9TP+9xcnDj8u4Ir85H2miqLgcnkiZvt7/So7xbK4s7aGG6ma\nkz+kcUF2thWHozetxepYlBbauHnNPnb4K4BwmsXmyhB75uYx61A3+V3eYV6lcHZ5OG0kJGmRlhxD\n9sbfc1pObK1bM0xvMmI1STidPWRlTd8l04kk1lzcCoPIf83QcGNDiI7wdRaLBKYodJiiKJmGANOY\nIwWe3x+gpuYgS5emX0GIoyvEI3c2AXDxxhLsOdGf6ufOncnOnfvGFKuDl9x/6H4uIlQBlvv20fOZ\nh49aZsY09uOsAudkj/1jlGUFr9eHx+PD7fbi9fpYYYTZtlwOOMMT8wW5IVaamtm5Uxng4mG1miNm\n+6JP5dRmmR0ehX0xRAhLtHC0WeDrVxbTtauTlj3hFxeVeFjxh8uGNC6wWEwcPNgS/Q7SkN27D7B0\nwQyOMR+OVG9YreHRrSH+dcpcvv7ue+hbB173VuZ8FM5XFQQsd7yMVDJ7ooedYQqQEatJIp2cADwe\n35SNqsZbNHZ+jkR3SOXWJhmnDHP1AlIUdlRTtUgtQ+zo9Tr0eh1Opyut2q86ukLcsWEnltZwlOuO\n97v4/ualMQnWaBi85D7cUnD3jiwC/oGTO0GQ2fTd5cNuc7kBbrf7aGrqxuv14/ONrB5Vr7F4AAAg\nAElEQVRFUcBoNGA2G8nPt2M0GpAkkT/ldXHvO21YrWYuOlpHcV75qBPMxUaB+2aLBBSVZ7oU/t0j\n85lHpTYw9Lk6YJlJ4CSbyDUFIrlaERwdyNZb+bRkBQCrSrcjSfcw2Fd2KqxKqCpDcvbNeoGHL3Dz\n/qY/4iopoL119YDHtVlOvHm52H/5VEaoZoibjFhNGknuvx0DjY1tlJYWpHoYScHl8kS6o8TKlQUa\nHCH4fYvM/DH8JfuZjv6qGUYm3n7pyeSRO5siQhXA0urlkTubuPaXI0c4HR4vj3z6BgDrlp0Yl7B6\nNPssviG8R1FH2NaqwXoMO97MGZJec+hL2cPkq6osEwLcqnGiDWgxGg3k5NgwGPQx/+by7UauOMbL\nrFl5Mb1OJwqsz5NYnyfhU1T+3aPQElDxKeFizKAKa80CX8wSB4xJ3HQbWrk30lQAGeRNt6H88H9i\n2v9koKAgh5qaehYsqIh8BgFXF6Y/fIv1bU78io4HbIV0OvvSS2a2c+gmG9bT3kHK5KZmGAcZsZoE\nZFkm/gaDicfn809Zy6H2dgcFBTlxv/6GEg0dzhArn2/mI704bAXskXg8Pnbu3IcgCGRnW8jOtmEy\nGTIidpoiimLf733y4vB4ueO932M1hHNV//zBVq4+6toxX7dhtYaXq+VIdHVWqRnDtbcRevc5AB7+\n1SyEwYmgQohFn9/Kzz79lF5F4MkVZ6MxmTgnW8MvZujRCOMvXjQa9Xg8vnFtwyAKnGfPpPsMJj/f\njiDAnj21LFoUjpK2P/dHKtqcQLgT2GWz7uV589m0l+UTnN/EVaf9LlNElWHcZMRqEhAEgWAwfdIA\npjLjteQKuGUW3bqX2io3tUD1UzV8/YGj0OUNn2+8du1SIDwh6elx0dLSgdc7cKlSp9OQlWUlO9uG\nXj95fBYzxEdWlpXeXjdWa3zV5P1UNYe46rFw1d8967UsLo7v9HzxxhLueL8rEl3V2n1cseQ98OaB\n0UQg5BvgIPDIp29EhCqAzXSIZ/a8z7XHnzXqfsx6gU0b9EM8TSN2Tb/+aOiLDEEueOlpCjvC3Zx+\n1vweyo9+h8aUuDQlURQnNF1HufwGxJu+gRAInwdUnR7l8htGfP5k74CXl2enp8fF7t0HIt2r+vHL\nOirb12LMtnLpxgt46p8vZoRqhoSQEatJQBRFtFpdn1l9amfnXq9/ytsNjefE/9GjLbQf0QaxtVHP\nto0PsPbeK4YUSByJJEnk5GQN6+/q9wfp6emlvr6RQCA04OKk1Wqw2SxkZ1sxGHST5qKVydUdGYvF\niNvtG5dYrWoOccH9h+0pLrg/yLqVQX50mmFMj9DB2HM0fH/zUjbfXs/iPf/iJNML6P8VQNnzFt7r\nf8WT++6KGPbXdH4K6uK4x23WCyPaQp3/l0U8ddkOhEgigMrSM5+ksP7w701fX01oy3MD/EgnHfY8\nQv/9IOKm24CweMU+fAqCxWLqS10a38Qm1cyZU0ZPTy/bt1ez6MvX0r59G7ZmH5trLqfZUwZN0Prt\nKvjC5Di/ZUh/MmI1SZx00ml88EElxx8/2G1vYmlqaqOkZGrmqyaCbY1Dl3DF7vYhht6xoNdrKSjI\nGTY9IRAIUlV1gM7O7iGPCYKAxWLEZrNgtZrRaCZoouPoGPNCG/ZYnZpFeuMlEAiNu4CxP6J6JE9s\ng50tfh64aGxT+8HYczRcc+zHaBr/HrlPrK2m/bk/0lLWFLmvxVXH0SVLeePAzEh0tdc3kyuOOzXO\nd3KYWSusnH1vBS9u3BO+45qXsPV0Q/24N51+2POiylHNzrbS3d076cUqhFcUZs+ewa6aBpb85B5e\n++nzYaHaR8suF9a8qZl+lmHiyYjVJLF8+Spee+3fKRerHo9vynauCgSC6HTjW2bXn1yA7/X94Ayf\nVItNDazO/whYlIARDkWn06LRSCxZMmdIVDXs/+jF6QynF8jywFSSfjFrtZqxWs0xecuOiKMDzRFL\nmOJN3yD03w8OEaxe79R1lBgvVquJ2tqmmLqoRUtVy9im9uNFkFW+kPUV3u/Zi9Fo4IrjTsVuSsw5\nY/FRJcx83cRLNQ8AJSwv+wFy+61IdeEiLGXWgiF+pFMZq9VMY2NbqocxfpobkO78KXbA+MUr8coz\nyFr5BXjz4JgvzZAhHjJiNUmkUyrAVKWjw0Fenn1c27joOD3XrF/G+f/eTHGog9X5HyHNnpX0C+hw\ny/+iKGKzmbHZho+69IvZ3l43bW1dhEJDo8JarQaLxYTVasJsNo557ImbbosIVQAh4EccppJ5Kk96\nxovNZkGv19Ld3Rt3O9p71msHpAEkAvXUc1G2voVYWw2EhWH+OddRdEQagE0qokhcytyjKjhBXJrQ\n/fdj0Wdz/tLvR24rP/o/WjbfR2FRXvh3Nkq6zVRDksQRbQ27uzrZ8/gfAVj49evIzom9i1gy6W8A\nYWk9yJy7H0KggtX5H7H0oVtxzrmPletKh7TwZWVnikedYaqQEatJJBGpAAG3PGqv5tHw+wPjjjym\nMw5HL4sWxWZPMxizXuDPV+by1JJvUFz1PErpQsTTv5KWF9CxxCyEo83h7jy9HDrUNuyFURQFTCYj\nZrORPEWJqv+S1+sjP398E4OphKstwEu37APgjF/MpaKihIaGlrjF6uJiDQ9drHLZoyGUI9KDFxcJ\nbFgd52naaEK+4TaUN54FwuJVZzRx4dLr+fe2p8nNyWLNzC9E3aI1YRhNtK09k4I0bKYwEQznHtHd\n1YnvN1dyYlcvAA37t9F9871pI1j7G0B07ejkrNcOcYgzAKjuXsKGeZvo/Z+fYL39wSEtfJ/6Z10K\nR51hKpERq0lkvKkAAbfME9+uisxU977axbq7F0ctWKeyvyqEI42JMNo26wUu+JyNzbp1bAM2iBom\na0aZTqcdsfCrH1lW+rr+eKj/wiXM3rsDKRR2QJc1OqqOu4DQzrAQ0+t1mEwGHA4nZWVFk76SORG4\n2gLcc+6nhHzhicA9537KZc8sw+l0j/HK0TlqppYPr9fwwEdBtjUqrCwVuWytNuZ81QEYTUNyr3Ua\nA7P0a1k2O328YRONJImEQvLE5X1HyZ49tbjdh221XG0BXvz5ProO1vDNHDXcdQAo6+rl7cf/yOe+\n+8vUDHQQj251kdX5Gmtfy0fhcMFus6eMyva1FOgPRNJVBrbwnd7nigyJIyNWk8h4UwE+ebgpIlQh\nnLC+7YmWIf28R8Lt9mKxpF+EMN0Y3Dby5WqZTRtiL2qJhnSoqpckEas1nCpAUR7K/z4ERxRYLezL\nV1VVlUAgiMfjo7g4j4aGVvz+Ydr6HIFer8No1GMw6DAY9BgM+rQTDOPlpVv2RYQqQMin8Pqv65jz\nrcRMnL53YvLdOwwG3bjSFtIdk8mAx+MbdRUiFfj9QSwWE6qq4mjp5f7zdqD4RaCAu1qu5+rFt4db\nk6YRgZAPt3Iny/+5Aj9Dj3EVgdcsx7By2xOw8quRVanJ7j+cIb3IiNUkE28qgKMrxPubW8e1b1EU\n8fn8U7KKW1GUhEX4BreN3NmcvKIWl8uTfhOIESqZBUGItBS128c2a1dVFb8/0NcmM0BvrwOfzz+g\nUEyWZVasWJDQ4acPwqSJPM+dO5Nt26pZtWphqoeSFNJVrM6dW8b27dU4nA4e/vG7KP7DaUxBRc8L\n9eexft7DNORYWfj161I40sNsa96CzEEkVgx5TCRAVlED3+5+Gz4GpeVN5Bv/AEYTr7zyNqeffmYK\nRpxhKjL5mxWnOcuXr2LPngOjPifglvloUyMfbWok4JZx+1V+8fNG1O6BBReWQh0r1xVFve+FCyuo\nqhp935OV7u7eqARUutHT4yIrK336yCcSQRAwGPTY7TaKi/OYNauURYtms3Tp3MjfVCg2POMXc9EY\nDp86NQaRM34xl+xsKy6XJ4Ujix5BEKZcxPtITCYjHo937CdOMP1Fj1sPvU5AHjq+RlMOzy05AUMa\n5auG+iKk8jWvwYCOZAprztrPEuoi94gN/5+9M4+PrCzz/ffUvmZfKvvSSXe2XpJuQBaxcUQQxFEZ\nWkBcWJQ7yiKO43VBEWUcZ0blIjpzRVa9LDYiCrYCgk032EBDd9Jb9nTS2fekUvt67h/Vqex7rcn5\nfj75VFJ16py3KlXn/N7nfZ7f04aw72kAurv7KS1dn5MhicgjidUwMz0VYDZum49Dv+zisU/UcfCB\nTg4+0MneL9bz1CEX/RNzl4u3fTJjRQVWcrmc7Ox0urvXFqGNRYaGxkhLSwrJvq6rUVCVNRUNq8pa\nQ1HLEkxMWGMu2iOxMgwZKm55oZqiCxMpujCRW16oxpChQq1W4naHtqJfYnVoteo5neViAZ/Pj06n\nweV0w/V/B9XU58Wn8PP2VZfw/tu+F1WhKooiExNWTp/u5sSJFjzdaaTr8vHl2FF883doE8dJSnVx\n0zNl7BYPzHm+7MhBGhpaqKraEYXRS6xXpDSACDCZCrBj165ga8IP5Io888V6tH0zZ9f9p6xoDgzS\nWJJGUfc46aOBx+UFOnbdkL3iY5tMadTVNZKZmRoaX84Ywe32oFaHJrdvobaR4cDvF2Muujhmd/Bk\n7X4APl0dOo/N9cJ8jhyGDBVX/2Jm5yeFQoHH443GEFeM1+uNi3SF1RLplqvLxWazk5BgIHdiB+bc\nM/R99zl46kJAS9INF/CrfzCG7dwzH263h9FRM6Oj5hnpOgkJejIzU9HrtYyMjFPoyGZAPAUFsOPq\n3UEHCTE1Awa6Z+xTTM3gzTff5V/+5e6IvQ6J9c/6US8xzLZt1fxh3z4eaNkazI38a8MA5/TNv0y1\nI0dOmVLBX3aXUNY6jClB4N7v56woqjqdiopN1Ne3reNcwbWzWNvI9cyY3cEDh34a7F70wKFa7rzg\nq5JgPcvKHDlE4qX6ua2tm02bcpe9/aTHJoRuMhcv+b2hZHh4nIyMFCwWG9dU3UVd6uuwHXZk7Q6r\nhZjP52d83MLIyPiMIkmlUkFqahKbNxcumBaSkpJI36lhzq26nKamVgRxajv/zf8b2bSmIl6lgrc+\nuJ3E9sSQOLVISEwiidUIIJPJcOZ/hJMnp2b6C835TZUGzr3exGMKGU8flcOlOWu+OKhUSpKSEhgY\nGCEzMzbyoCRigydr9weFKoBR08mTtfu57cIrojiq2KFub/+yHTksFvuam1REAofDicvlRqtdnjgK\nh1uGUhmIQq9nH+j5mO7QolJoODcvtAVIfr8fs9nKyIgZh8OJIASK/mQyGUlJRvLzTSsuuJ3cB8Dg\n4DD33/8Q//qvX2LTpkJITsP7779GePQ/6bN08IcLjNjsb2AqKcHltaNWxFgxqUTcIonVCJGXWwAn\np3JHZy/zuw0Kdn/GxK4bslHp5aggpJG+goIsjh5tIC0tGbk8vme8NpsjLrspxeKyZCTxen1x/9lb\njIQEPWazJWI5yaIo4vP58fl8eL3Tf7wzfs/LMwVF4cDACN3dAytyAQiHW4ZarVr3TUuWYi2RZa/X\nx9jYBGNjE7hcbgRBwOPxMjg4SlpaEuXlxeh0S09G3DYf7/2/XvqOW8jaZgxef2YzKVgvuug86uvb\nOHWqgxMnGvnHf7wMITmNd/Z8kDfOPB/cvt/SyjsdL3BxybVz9iUhsRoksRohPndBKm/85V0q/9iO\ny6XHplXw8kWl5A5YUcrhP3+UQ05meE/c5eXFNDScpirOO8cE2qyGprgqkrhc7pDl2YaKT1dfwgOH\naoPRVYszn5suuCQsx4rF178UO/aYZrSQVBnkdLwzTsWV6RgyZr6WtLRk3n77OOPjlogtb8vlMhQK\nRfBWoQjcarUBf1uZTEZdXRO7dlXg9foYGBhh586KpXccZjQaFU6nG6NxbcJ+0OLn7n2BZe37rlSR\nYYztyZAgCPz4J99B/dTF7Kcd1/UH+dq//GDebUVRxG53MDZmwWy2zpjsymQykpONFBRkoVaraGxs\nB+BDHzqP0dEJ2tq6sNkcnHfe1gU/i26bj2duOclgQ8DBov3vZlr3j3HtI5VzBGtKSgIjI2bS0pKo\nrCzBZNqETqfniSd+j0wmoM3q4byWMQBqyxNxK2P7/yARf0hiNUL0HW2gZO8wLgKdhfQO+MRfW2j/\nXCnfuyUlIidZrVaNTqdhdNS8aIejWMdisZOfnxXtYayY8XErSUnRta1y23zUPdkJbfVUv89K8uVX\ncecFXw0WWN10QfgKrOJRrKr0cvY8VME7j3bz7hN9uK0+Ot+e4OGP1QZdAKZTUpKH0+kmNzczSiOe\nS3l5MXV1TVRWblqV5/J1NQpeafIFo6uhcMvQaNRYLGvr+DVo8XP5L104zxbUX/5LFy/dqo5Zwepy\neXjp5cfgN1fimsxt/s1H+DHf4TM3fIXxcQsej3dGxHV01MzWraVkZaXPWJUYGBihtbWTtLRkxsYm\nUCoVlJUVAZCenkx6ejJms4VTp9oWDE7U7e0PCtVJBhtt86a5ZGSk0tzcQVpaEhdeeC6/+tXTfP3r\n36WiYiuiw0r7rR8g0zoCwJYOKwc+tZvzCj8WkvdNQgIk66qI8dwt+5n9dgvApieb0Pkj5wdYVJRD\ne3vPvD3j44V4Lcwwmy0kJkavY5Db5mPvLSc4+N/9HHw5hb3/JeD992+QLIjcduEV3HbhFWEtrAo0\nqIgvsQoBwTrYaMPvnYpseZ1+Xr63dc62k+IhljAadRQWZnPsWNOqvFUn3TK+ulvBV3crQtLdbTKy\nuhbu3ucOClUAp4dglBUmW67GjjvDxIQF9VO7mVmEJ6B+6mIEQaCoKIeqqhK2bi0N+hKnpCSSlGSc\nIVRFUaSrq59t2zbT1tbFyMg4RUU5DA+PzzivJyYacbs9uFxTb5LNJfLwWx4efsuDe4G3xuuf+4BC\nIQ+6BQiCQEXFJt57720APC/9hkzrcHDb7GEX149VSfmqEiFFEqtRRvTK+H8/fx6317n0xiFAEATK\nyopoauqIyPEkpoh2QUnd3n76G6YmRn32POreS0bY/0JEju90utdlN7XZxOJEMCUlEbVaRXHx8h0A\npjPplnHL+cqQOAGoVOH3pA00BojMeXU5LJaynpGRMu+5Qa/XYrNNfWfb2rp4992TlJTkYzTqKSsr\noqQkH5lMxunT3dTVNTEwMBLcPj8/i3ffPUljYzujFhc3Pu3ip697+enrXn4uJqHbNEuY5g5j3voO\nDQ0ti76WCy88l9dee3nBxxXyjZuLLBEeJLEaIa5++BJmdv+Ywuoeo67v9Tn3T58F21yhK87R67Uo\nFHLMZkvI9hkpvF7vuu68s56JxzSASRbqWjUf2dkZHDvWFHOiNZashELhg3rflSo00zSRRhm4b5LJ\nlquxQk/PIK7rDzLTC0Y8e9/8JCYagufpgYER5HI55567laSkuSs0Op2GmppyXC4PdXWNuFxuxsYm\nKNtaxuvDyXzv5X0Isr+ilDvR++2c1/J7tl38OvLLj0BFF1xxFL7yEoPmAV5//dCc/RsMOk53DHH/\nPa/xf773N3bUVPPDH36PiXM+gqxkqhWrrGQ7yss/s+r3SUJiPqSc1QhRen4VH/xhB3/71iAw7Qyb\nPQLvb2TMPjPiEQ67mOmUlORz5Eg9O3dWxNWS+vCwmdTU+CuuigV27DHR/MpQMLqapetix64xxEsi\nk1vmdnuw2x1oNGqUSkVcfe4mu1ZNLv1fdk/JnHzVSdLTk9HpNLS0dLJlS2EER7k48fR+L4cMo4yX\nblUvWGCl02lmRBmjyenT3ZhMaXztX37AjwkUWAGLFlgBJCQY6O8fIT3dQ2/v0IIuDj6fLzgZyc83\nkZ2dTkPDaboHzDxxKIGC9F9QYOqkANiSeJTrXu5li62To6fOpcZg4diNp/AY/ZgMhXhOpKPTzY2M\nKlQanrz1XRTdgXqH1492csNDV/Dkc89Q9YEbef/5gcYZyss/g6Bdny2lJaKHJFYjiOKcCbjvOfiv\nq8B8tgpWHhCjb3W2cdk0z/5w2MVMRxAENm8upKmpI5iYHw+MjprZvLkg2sOIS1R6OXse3sqvbzvC\neK2HPnsOf0z6IldrI5Nb5vf7GRuz4HQOL7vTkyAIKJUKVColKpUCpXLmrVwuj5gIm69r1ULo9Vqp\n9WoEyDDKeOja+S2aZrdcDUdjg+XQ1zeMKIpkZaUBBMTpv0w+eumiz1Uo5Lhcbo4da1rUbsxmc6LV\nqmc8b+vWUt6acCMKL5ORMOWl/MGGNt47eiX7nLlMLq6m/Gycsv8jsGvTbn574s+YsnPo7x/EZMoI\nPu93D9UFhSqAvCuRvf+3lrvu/Sd+/evf8w93fH2Z74iExMqRxGokEWTwbsmUUAXoSoM3yuCiyBcC\nJCTo6esTzvarj4+ZsN/vj8s0AK/XGxMeoy882sJ4rZfJi1T7ryd4pL6WzzywbdUd0paLUqmkoGBl\nLg5+vx+Px4vb7cXj8eB2ezCbXXg8HjyegJ/oWpHLZcjl8rO3gd9lssDvMpkMmUw4exv4XRAmb4Xg\n7eTvICAIAZGt0agYGzOTnBwbzhvx6PPrHu7B9dA9AKi/eC+qtLnNGBZieqpBuFeqZuP1emlv70UQ\nAp/hzZsLV70vhULOtm2bFz1/dHT0UFGxac79gc/kFPIeHUeeuQFx1qV/tC8JxaF8VFs0gMBll32U\nZ555lD17rlrWGNVqBXa7HZ1OKqqSCA+SWI0g5xV+jFc9tXMyV30+OZ+v+fSM+8JhFzMfmzcXxFU6\nQDxecAHMZhuJidGfEHQ8MsLMVHWBsfec7P1i/SJtRKOHTCZDrVaFLdd1urF+4Dbwu9/vP/sj4vH4\n8Ps9wb9FcfJWDN7O/CH4e2trF3l5Xkym2OgctxonjWhFJN3DPai+9Xn03sAZ0/Otz+P+4eMrEqyT\nhHulajb19acpKMhGJhPW7CW7dWvpoo+73R5kMtm8k/jrahS82vx+BieOk67qxf/jj80RqrORyWQk\nJCTOiEoDXHPTLp7cfwT5RMAxxJdn5jO3XQTAjh0VHD58iN27P7SSlyYhsWwksRpB1AodKaWpOEu9\nWFsCb70vz8Inb91DYWrKjG0n7WLCfZEIpAMU0Nx8Jqby6+YjXi2rIGBbFcutbhdrI7qeEQQBhUIe\n1mj9ZJU2iJSWFkSt+1pKSiLDw+Okpy+/JWwkIpJurzNYYLojazcqRWBZ3/XQPUGhCqD0+rE8dA+q\nbz0csmOHg4aG0yQnJ0Rkcup2ezh2rJkdO7bM+7heLfDItYk8deQOLC+9g9+zUFcrPzv2mICAxRyA\nSqXB7XajUqlw23y8/q3OoFAlycenf34+mekGRFHEZMrkj398TRKrEmFDEqsRJjcvj/L/KqBnfyCf\nbcce04LRrEm7mHCTkGCgt3co5tMBzObYHt9i2O3OZbU/DDeFN6fS8cgoM70eJcJJcXEufr8fQRA4\ncaKFbds2R2Uc2dnp1NY2rkisrjUi6baOMvTigwCkX3U7KsPMSbnb6+TZk/fTb+0AoGWklmuq7goK\n1lARqZUqvz8Qnc/LM4V83/Nx4kQLVVUlKJULvxa9WuALFxg53FTOQTrn2ULkintSg9ehxEQd/f19\nXHzxP/D220e5+OL3BWzvznZxA2BczpGnOhj7aGDZ32jU4fPFjqetxPoj+kl0G4yKiq20d7dz7o05\nnHtjTswsu27ZUkhz85mYXmYfHh4jPT1+nQBiISr8T7eXUXhzCgEbtamolanSEIysSIQemUxGT89g\nVH12BUGgoCCLhobTETme2zqK/b6bKfzrQQr/ehD7fTfjto7O2Kau7/WgUAXot3YEo6zqL96LRzF1\nifIoZKi/eO+qxhKOxgbz0dU1QGZmytIbrpEzZ3qpq2uisDB7RmHVYuzYY8JUOX2y70eGm4/9MJWK\nT0wVb330o5fy7LNPUl5eSVvbfOI2QJYpja1bS9m6tRSDQUNaWvpqX46ExJJIkdUIU1q6hdde28dF\nF50X7aHMYDIdIJbdARwOF1pt9KOT8c4/3V4Gt59tvbo3YDezWIRfYu24XB7GxiaWzD8MN6mpSbhc\nHlpbOykpyV9y+7VEJIdefJDCwaluXumDE3S8+CA51wUKpgRBWHRyrErLwf3Dx7GsssBqNuFcqZp8\nHWazhfz88E76vF4vFot9waX/hZhsHbzod95hR7v/BSo7juMcH0EmUwS3bX51NBhdnT25ffnlg3zu\nc/9rDa9KQmJxJLEaYZTK2O3sMZkOYLHYMRqlqs71jkov33A5qtGiq6t/1d2jQk12djq9vYM0NXUs\nmaceztx5URSpTL+I1tG6YHTVZChkR9bu4DaqtJw15agqFHLcbk/YI9q1tY34/X6USgXj4xaSkxPC\ndqyhoXEyMlYXvV30O++wI//x15C1N3EeMPy1q9j6T9/gwIG3+MAHzl9U6LpcXgyG6LWSllj/SGI1\nCohi7GZfbNlSyNGjDezcuTw/SYmlibVORtHA5/PPsdHZSKSnJ9HdPRAzRYzZ2RkMDIxQX3+aiori\nRbddbUQy/arbGTpWR/rZ6OpQRgLpV90efNzn82HQGrmm6q55C6xCgUaj4ujRhmBFvigGitzU6tCJ\n17GxCVJTk9Bq1UxM2MIqVAEGB0fZti30EXph/wvI2puCf6eO95Hh6OFQcgmPPPI0N9zwyXmF7qlT\nTWzbVh3y8UhITCd2VdM6RiaT4bb5OPxYD4cf68FtW7tXZKgQBIH8/Cw6OnqjPZQZOJ0uNJr4bNVp\ntdrXbF8T78Rzq9VQkJhoRKNR0dc3HO2hBMnMTCU9PYm2tq6w7F9lSEF39yN0XHoxHZdejO7uR2YU\nWE12XFIpNJybdznn5l0e8sIqi8XOtm2llJTksWVLAWVlhRw71oTXG7pioK6ufvLzTWRkpFBSkhey\n/UJgkldX18jg4FSu76SPbyg5cOAQQ0NzP5tNjfV88IOXcdNNX+Lhh3/LyZONMx53OFy88cYR0tNX\n5p8sIbFSJLEaBYyaJJ66+TgHH+jk4AOd7P1ifUwJ1vT0ZMxmS0x14BkaGiMtbW+0n/QAACAASURB\nVPlVzLHE+Lg1JjxWo4nL5Y7byUaoKCjIpr9/GBx2hD8/g/DnZ8Bhj+qY0tNTcLs9TEzYwrJ/lSGF\nnOvuIee6e2YIVbvdGZFis+TkBOx2F2q1CoVCgUKhYPv2LTQ2doT0OOEqnhwdNWMypTEyMs7x480c\nPdpAVlboC5lSUpK4//gATd6p/8mQMYO9o4Fc3OTkVL797e8zMGDhySefx+v18t57p+js7EOtVrN9\n+/aQj0lCYjpSGkAUUJ3JYbhxKPh3LHpcVlRsor6+je3bV5bEHy7MZiu5uZnRHsaqsFhs5ORkLL3h\nOsbpDPg1bnRS9SrEf78LZXcrAP4jB/F97ccQoZa381FWVhTx1B+dToPN5gj7cbRaDf39w6SlTbmI\nqNVKDAYdTU0dFBZmo1IpFxWboigyMDCCVquZd9I52SkrHILVZnOQkpKIyZQWVp/prVsr2PqTHzAx\nOMiRRx7E7faS9Mlbue+if5ix3dVXX0dX1xl+9atHufHGPbS2tlNTsyssY5KQmI4UWY0CGRmxL7qU\nSgXJyQkzlp+iSTw3BBBFMSZarUYTKbIaoKD1MKqzQhVA1t6EsP+FKI4oEBVMTU3EbD7roxmhyG9m\nZipDQ+E9v+h06nlXiAoLs8nOTufMmT5OnGgJpgaYzRbq69uCQnpsbIIjR+oRBIHW1s457gV+vx+L\nJfAeWQfdPPflep77cj3WQXdIxj82NhEsdo3E+S8hI4Nt3/wBO7/7Q0bso/zkJ//G3/9+YMY2eXkF\nGAw6NBo1R46c4MILPxD2cUlIbOwraJS46MYqFKapk1mselzm52fR1dUvFQhJrJmNnrMKMDbq5Xd/\nNPBW/0W4fLH1XuTlmejq6g9WhCt+9ysUv/sV8h9/LWyCNTs7PaQ5vKIoMjpqZmxsAq/Xx6lTbbS1\ndbN9+/xNGIxGPZs3F7Bt22bKy4s5daqNwcFRNm8uoLt7gBMnWhgft7BzZwWZmamUlRUFq/4n6ekZ\npKysENuQh4c/Vkv73820/93Mwx+rXbNg9fkC7gLRmKQLgsB559Vwyy3XcuTIOzMe8/v9iGLgPRBF\nAYVCWqCVCD/SpywKqA1Kkq8Zo1x2DhDbHpdlZUU0NrZTUbEpamPw+XzBYgyJ+MTj8S7aZWe9M9Dt\n4uFrT6C2ptLO5TSNV3J18ZOc4FLE7vPYYfNF5Rww3WtXvVVkZO/jmKZVhMvam/DvfwHximtDfmxB\nEEIqxNrbe4JL8m1tXVRVlaDRLM8wX6VSzkh5ms+1Qa/XBt1SMjNTSUoy0tc3xK5dlTx/eyNe55SI\n9Tr9vHxvK1f/ogKbS1yV9VdLyxmKiqKfGub3z6yn6O/vJT09jf7+QbKzY8OOTWL9s3GvHlFGroZz\nb4j+iWgp9HotCoU8qq1YR0cnSElJjMqx10osdwSLNPGaxrFW3DYf/++GE6itU8vRffY8Hjr9Vdx2\nFZzsp/mAlT0PVURUsLptPvZ+sT5o9J5eocderSGSazx+f+i+HyqVEq1WQ2pqYlDktb/ZxYt3BdIu\nrrq/hKKL1latr9dr2bmzgoMHj5CXZ6KmpmLRibTNJXLj065gU4VXmnzL7p7l8XjR67UA9Ax4+NkP\nAw4td3wrm5zMyPl1JyToGR0dISUlFYDm5kaKi/M4cOBtrr/+loiNQ2JjI4WrooROp8fhcEZ7GMui\ntLSAlpa5+VqRYmRkfEaBRDzhcLiWHd2RWJ/U7e1HHJ+bN+m2T6UCTBZZRpLZ/d6H6m2MvGGdsY0t\nPQ/xko+F5fhjYxMkJYXOSH583IJON/Vda3+zi+du68Lt0eD2aHjuti7a31y7TVcgxzeJ4uJcFIrA\n5OKye0pQaKYupwqNjMvuKeHpo96gUAU42TcVZV0Mr9cbFME9Ax4evP4U6Qd6ST/Qy4PXn6JnYOVO\nLau1S9y5cytvv/334N9tbc0UFOThdLoxGsPrKSshMYkkVqNEWVklzc1t0R7GshAEgeLi3LD5MS5F\nPC8hm82SbZXEXDyq2Dz1mrwjM/52bD0/bE4FAwMjZGev3YbJ5hL5yUujvNydil82JVYDEdXpEUyB\nP9zRHhKbwNkTd0OGilteqKbowkSKLkzklheqMWSsPi+5qelM0LP1Zz/sJW1kyjkhbcQRjLIul8ko\n+mrsEvPzczl9uiX4t9PpwO/3o9NJHaskIkdsnjE3AOeccz5Hj56M9jCWTXJyAk6nOyrR4HhePjab\nLZJY3eDs2GPCVDn1GRCSlFz5swJSN08Jq2gUWc4eFwlOatIPz9hmX7sOmyv0Kyo+nw+bzbHmSejk\nMvsjtVoeqdVw49OuRcfr8ytD4ms9X9GpIUPF1b+o4OpfVASF6nU1Cqqyps5fVVkC19Us/ppdLg+i\nKIa0IHF2FL3/lJXDTy0vki8Iwoy8VZ/Pz4EDb/PhD18RsvFJSCxFfIar1gFKpRK5XIXH40GpjFz+\n0VooLy/m2LEmamrKI3ZMURTjOu/T6/VFxPxcInZR6eVz+qqP28xc+h959L7uDt4X6QKr6eNye+Fh\nj5rGEwVsdwWiaMfUpdwvuwL7Ue+q2q0uxokTLUu2eV0OTx3x0Nrm4kPvdgLw5jn5PH1Uzi3nK7nq\n/hKeu62LmdHV0Pha5+Zm0tzcwebNhYtup1cLPHadekUFVs3NHZSVFQX/vuNb2Tx4ciwYXR1O1XLH\nt7JXPfZJ9h7zUu0Sl5U/K4o+/H7/2dQEPwMDwxQUFC35PAmJUCGJ1Sjy0Y9+nL/+dT9XXPHBaA9l\nWcjlMnJyMujs7CM/PzLt9axWBwZD9AzTJSTmY6UV3iq9fIY4EuwCCq0Q9UYg08dV7RL55rM/pOjY\nPgCeSroCmyz03z2v14tCoUCrXXtr1aG2Qa75czdKX2BCe82fG/BfsBVQUnRRHlf/HP5wRzs+f2jF\ndmpqElarg4GBETIzUxfdVq8Wli32A7ZQ4oyIc06mktufqlxTgdWOPSb+/odhfGcCNmRDKVpez0jl\n6WVORIqK8mhqaqC8vJKhoWFMJqm9qkRkkcRqFCkuLuX5538b7WGsiMzMVI4da8JkSotIxHBoaJSM\njJSlN5SQiBBrqfCeRBAg1hYM9GqBf78mmRu91wRf23KWrVfC6KiZ06e72bp1fu/TxZiYsOHz+UhO\nnirqyXylnzHf1Bup9Ikk/fEMfCTQjavoojy+/Eb2DNeDUKVc5OebeO+9U6SnJ4fMWm9szEJi4txc\n0JxMJf/xQMGq96vSyzF8ZQt/fSwQ3W8sScOrXH4kv7q6itdeO0R5eSU/+MF/Sd7bEhFHylmNMkVF\nJXR2dkd7GCsi0Ir1dESOZbM5gvYtEhKxwGorvGciADGmVplatr6+bJyv7lasWIQvxciImbKyItTq\nxSe6syvXHQ4XJ04009x8JiiUXC4PCtncsclnabDJdIeL78zn4jvzQ2YRJggC5eXFNDa2r3lfk6Sk\nJDA2Zp77QAi6il1/gRo+aOJkeSZepXxFExGj0YDFMjUuyfdaItJIkdUoc9VVV/Pzn/8nN974qWgP\nZdkolQrS05Po6xsiK2vt1byLYbc7OXmyFbVaSVpaMklJxrg5UXo83qC1zUYmnnOOw0UsRlYn0asF\nri5zUFDgQ7eEqFwpcrkMl8uDYZGaw9n+r82vjrLzG0bKy4vRaNQcPdpAenoKQ0OjfPTfyvjNP50M\nGvJPWkbNZnYaRqgwGHTo9bqQnQuHh8fmriSd7SomO9uswX/kIL6v/XjFLg2ryZ+FqcYR1iMaXDd6\nUBukHHyJyCOJ1SgTj4VWADk5mdTWNpKRkYJ8digjhOh0GrZuLcXpdDE8PE5v71BQ/AiCQFKSkdTU\nJLTa2PMylZwAArjdniUjaZFmeuemlRY3XVej4JUm35qWygMOFzGqVgl0cHrvvXqqq8tCahs3MmKm\nuHjxrkfzVa43/8lP+TcLAdi1q5KxsQnS05PR6TTc8kI1L98bMP6/7J6SNVlGrYaCgixaW7tobGxn\ny5bCVbmXjIyM0909iNfrnVPAKux/IShUYW1dxVaSPwuzJw6J/PuHfk3KnnEyczL51KduWPHxJSRW\niyRWY4B4K7SapLy8iIaGdqqq5kYyQoHL5QnmxWo0anJzM8nNzQw+7vf7MZutdHcP4HJN9eFWKOSk\npCSSkpIQ1b7VZrM17JHneMDpdIfUhmetzBe5W8nS8GojVLOJ1cgqBJZ5q6vLqK1tZOvW0pBNBmfv\np76+DRDw+/0UFeWg12tnfJcnkctnrqZMz1udtIyKJiUleUxMWDl+vBmbzcEFF+xY8jlOp4uGhkAK\nQVKSkc2bC9BoVDFl1Td74uDtV1HWpMBqstDQcIry8soojk5iIyGJ1RggUGi1N9rDWDEajRq1WsX4\nuCWknWgmGR4eIy0tecHHZTIZyckJMy5cEFh+Hx0109LSic8XWB4URRGVSklKSiLJyQkRWZ53OFwx\nGfGNNC5XbInV+SJ3K7UyWmmEajaCIMR8eoRSqWDXrgrq608jCAJlZUVzRONKsNudiKJIY2M7Lpcb\nl8uN1+tj165K5HIZra1duN0elFUuTJV6+k/ZADBV6vnwl6MrRpfDZDtqjUa1rM+82WzFZEoNTGgd\ndoT9zwMEOoZNW+IXL/kY/iMHp9IAiraEravYcpCdOMyl+iEe7x6UxKpExJDEaoxQVLSJzs5u8vMX\nXyKLNUpK8jh6tIGamvKQRwTGxy2Ul6et+HlKpYLMzNQ5ljIul4exMTMtLWeCIhYCkdikpARSUhJC\n7nAQS1GSaOFyuTEa9dEeRkwRL58LmUxGVVUJDoeL2toGNm8uCIqylaJWqzCbrQgCXHDBDkRRZGLC\nFvzObdlSGBS0NQ+pVp2mES3q60+Tl2ciIUHPiROtVFeXBR8TRZHa2kYSEgxoNCpGRsZRqZQBP9Wl\nclK1Onxf+zH+/S8E9jVLzIaTHXtMNL86GpzcZem6qEk/jKzDzTZFKmbzOImJ8dkKWyK+kMRqjBCP\nhVYQuOhu2pRHa2sXpaX5Id33lAl1aFCrlZhMaZhMMwWwx+NlbGyC9vYePB4voigGxYTRqCc5OQGj\nURc3AiPWcLncpKcvHCGPNLMvwNHoHgXxVXim1arZuTMQZU1JcawqvcXhcJKSksDmzYG8zsmc8+no\ndFPeq9H2oF2M2T67fV3dpKQkkJKSCARsrerqGklOTiQnJ4O6ukbKyorw+Xy43V62b98S3NeyclK1\nulXlqK6VYOOI77+E7MRhatIPo5YH0jRKSwp56qlf88//fEfExyWx8ZDEaowQr4VWEMi36u4ewOFw\nzjH67j5q5tkvNYAIld8bJ6kKdmTtRqVY2hA8UuJQqVSQkZEypwrX7/djsdgZHTXT2dk34zG5XEZS\nkpGkJCMajVoSsoswPfc4Fpivo1SkI3ex7AawEIIgUFm5idOnu+npGSQnJ2NFz+/q6mfz5sK4d8iY\n7bP7Qp2dn3xENWMSnJqaRGpqEsPDYzQ2trNt2+aY+g6sBEElUvCl7aT88veo+wNC1WYqpK/iIhyH\nj0V5dBIbBUmsxhDxWmgF87di7T5q5pmb6oN/H/9mAty5j5bqWq6pumtRwerz+aMuAGUyGYmJhnkr\n+r1eL+PjVnp6BnE6ZxaEyOUyjEYdbrdnRpR2oyKKYszZjYXLymi5xEPO6kIUF+dSV9eIyZS6IicQ\nvV6HxWKbk2Meb8z22W0dV3GgT0dp4dxt09KSF827h9jJSZ3M9R8bm8Dr9QXGdrabVkpKIsK37sd7\n8M8AqC75GJu0Ok6dPkNfXw9ZWbEbBZdYH0hiNYaI10IrmN6KtZ/8/MCS6rNfapi1lQD//WH673+K\nur7XOTfv8gX3NzpqDi6pxSIKhYK0tCTS0ubma3m9Xrq7B/F4vJw61Tbncb1eS2KiAaNRH1JbIIl4\nIratq5YiOTkBm82xovxVr9cbFEES04hwTqrd7mRsbILxcQt+/1RQYNJFZdOmvAXPS7NTEXbvPp+X\nXvoTN954a9jGKyEBkliNOVJS0rFYrBiN8efPmZmZSl1dE1lZaYGT3TKvxV6vD7lcNiMCOTIyzqZN\neWEaaXhRKBTB6unZUVlRFLHZHJjNVgYHR+e9eOv1WhIS9BiN+rhdOpRYnHhMA5hOVlY6LS2dVFYu\nfZ7q6xtiYGCUtLSkmMpdXi3X1Sh4qd5D/WDgfBWSlrQhzkn1en1MTFgZG5vAbnfOOLdqtWqSkxNW\nHBmfj4QEI2bz6FqHKyGxJJJYjTE8HvecvM94orJyE/X1bWzfvoVrPtvDM7/KIhBFAhApv+x3jBsK\n2ZG1G5vNQWNjO1qtBq/Xi1KpoLy8GAj0AY/nqKPVaicvL3PO/YIgYDDoMBjmj5z4/X5sNicWi43h\n4UDB12yUSgUGgw6jMdA9Zy12QhLRIk4jqw47wv4XUANkLm1b1NLSiU6nYceOLUtuGy9olSJ3VHTQ\nVF6CIAir9tldK36/n4kJG2azBYtlqgWrKIrI5XISEw1kZaWj1YY3p16hkONw2NFGyKFAYmMSv2pg\nneL1eqJqZL9WlEoFycmJDAyMkFfk4dMlv+SZts8DcO2mx/FXFpN+Nl+1qaGFHTvKgmKrq6ufwcFR\nxsYm2LQpviy8ZrPaPE2ZLJDvajTqgPkrrt1uD1arnbExC93dA/j9YvCYkxcluVyGXq/DYNCi12tR\nqZQbPnc2lojLyOosi6WSjAKo+PmiS9ZOp4uSkvhcIZkPURQ5caKFHZUFXJwQGu9gt9dJXd/rwNzi\nU6/Xi9kcEKR2u3PG8wRBICFBT3JyIvn5WVH7fl900S5effUlrrrqk1E5vsTGIH5V0bol3q5gc8nP\nN3H0aANpH/gouUcO8vWE+4BA4YDv4/8KZ0/GSqUCn88XFKt5eSZaWs6QmGggNVXy7luIyeYGi+X0\ner0+bDY7NpuDkZFxXC7PvNvJZAI6nQadTotOp0Gr1YQsUms123j50XeYsNopzMvCkCh5rU4SjwVW\nsy2WDINn8E6zWPL5fNjtTmRuJ4Z3/gpAXvUldHb2U1CQtaZjr6U9bqjw+/0cOdJAWVnR2cnk2nF6\n7Ow9/lOGHF0AHOt+i3MMn0IhBISwXC4jIcFAZmYqOp0mJiechYX5vP76u9EehsQ6RxKrMUa8XcAW\nory8mIa2LqoWKRyYL/pYWloQ0XGuVxQKOYmJRhITF+8s5vP5sdud2O0OhobGcDicwUjtfKjVSrRa\nDRqNGo1GtaC4tZptPPL5N/G0JwBaHjn6Jjc/fpEkWNcZXq8X+dnbI0cayErWkf3Ev6PoC7QRNR56\nje6P3w5rEKtrbY8bCtxuD8ePN1NRUYxer13Wc6xWO+PjFiYmrOj1Wux2Jz6fP7gCIooi7a7DDDm7\ngs+Z8PXjTupkxyLFp7GIKPpC7ostITEdSazGGOtFrGq1arRaNaMODykLFA74fP6491ycj3j6H07a\nbC0nUiSKIi6XG6fTjcPh5PTpbhQK+bxFYO8+34infaqDmKc9gT/+zxtc/oX3oVarUKtVKBTymIwU\nRYJIR1ZDEZmcbbHkK9zMiYxK5Cda8Hp9VFeXoX71uaBQBdD0nqa89wSwbdVjD0V73JXg7m6FB74B\ngOe2++hyqPF6fXO8UkVRxOl0Y7XasFjsc5bp1WoVaWlJDA2NkpmZSk5OxpwUL0dXGy1nwvIyIkp5\n+Sbq6o5QU3NOtIcisU6RxGrMET9CZymKi3M5cqSepCTjvDPueBJ1K8Fud87oxLNeEAThbERVTVKS\nEbPZSnFx7rxitemvnYzMuk8mk+FyeZiYsAX7wgPL8qKVy2WoVEqUSkXwdvJHoVDEnfANiNXIHCtk\nkcl5LJYKnF56egYxmy0LVpYrFPK4Oau5u1vRfvdWJs9W/nu/jPzm7+JLyqW5ea6qVKtVGI36RZfp\ne3oGF0xr2pG1m5aRWvqtHQCYzhafxhvnnLODp5/+kyRWJcKGJFZjDKvVFu0hhIxJ+6ampo5glf90\n1qtYNZut8zYSWG94vb4FHRsuu+k8Hjk4mQYAyqIJrrp1dWkAoiji8/nxeDy43d6ztx6sVgderxeP\nJ7T+nYIgIJfLkMkmf4RZvwsIQsBqLfC7gCBw9r6pzmtTt8E9MzkZdbnc+P3+kI15MUIamZxlsZSs\nDXiujo1N0Ns7SF4YDO5D1R7X7/fjcnlwudxnf6Z+n2TTI//K9Gm1DCj4/c9Q/Nezq17iXuw8p1Jo\nuKbqrgULrOIFuVyO1+teekMJiVUiidUY48MfvoK//GU/H/nIJdEeSkgwGALWShtFwAFMTFjXVQX0\nYiwUzTQk6rn58Yt4+dF3ALjsptXnqwqCgEIhR6GQo11euuCa8Pv9+P0BgRz4PfD39N9FMZB7GLhf\nRBRFRNF7VpiIiOJMkTJdrwhCZMVqJNBo1IyMjIfF4F6ll/OJX2zmvacCVm5Fl+np6u9d8SRFEATU\namUwDSUxUY9anYxarQp+jt3zpSWdnaysFK/XR11d45LesiqFZsEGKYs5BUxn0OLn7n0BsXjflSoy\njJHPHU1NTaK3t5vs7Ph2cpGITSSxGmPU1JzL8eN1tLa2U1JSFO3hhITS0gKOHKln586KGeJmvSbj\ne72+uLYfCxWGRD1X3xV/rYMDEVTCmk/tcrnp7OwL2/6nE6rI5GLY7Y6p1JdFDO6dThcNDe2o1Uqy\nstLRaNTBAj+bzbGg+FQo5BRfpUOjUU9LB1Egl4c4/ePOH+GfngZw9r7V0NraSWXlplX7Zru9Tp49\neX8wRaBlZP421YMWP5f/0oXzrOHH5b908dKt6ogLVoVCgdPpiOgxJTYO0hU1BvnsZ2/h6ad/zcGD\n77BpUwHvf/95cS3sBEFg8+YCmpvPsGVLYbSHIyGxoVDp5ex5qCKs1k+Dg6PL6jg3mWe8ZUsRHR09\niKKITqfBaNRjMqVFvRGIKrcEx/d/GSyw4s4focotWdE+JiPqTufaGrzU9b0eFKoA/daOedtU373P\nHRSqAE5P4L6Hro1sOkFv7yDFxaURPabExkESqzGITCbj05/+PADHj9fyxBO/Ry6Hyy77AJmZ8xvF\nL8jZjjMQ/p7Ti5GQYKC3dwiLxR6sPF+vOasbgUDLWAsnT7bOuD+w1KpCown8qNUBi6t4K4CKBJH8\n+Kv08rBUzw8OjtLbO7SgK8RsJouw5HJZzLZTVuWWwH/9bsXP8/v9nDrVht/vx+PxUly8cZbDW1pO\nU1a2dEczCYnVIonVGGfbtmq2bavG4bDz/PPP0tf3GoWFuezeff7SfZ1ndZzxHzmI72s/jppg3bKl\nMJgO4HS60WhC0wFGIvJYLDY2by6ck483WcTidLpwudxYLGMzKv+XYlL0TP5MVv+rVMp1JnjjtN3q\nNF588XWSkozk5ppwuz1zJi4LESpD/VjBarWj12s5ebKVkpL8kDmBLNcp4L4rVTPSADTKwH2R5ODB\nd/jKV74V0WNKbCwksRonaLU6rr/+cwDU15/kwQcfZ8+eK8nODuSe2VwiTx8N9JGf7FU9u+OMrL0J\n/7SOM5FGEARKSvJpbe1ELpeTlbXCKHEc4HZ7or6UGQnsdieZmalz7pfJZEGP3ZUSqPr34XZ7cbnc\neDxerFY7Ho8Xt9vD4OAoO3dWLNuUPZZZa7vVqeKuQNGXzzf545vnNvC71+vD6/WtuLDLarVz3nlb\n50wU0tKSKSzMxmjUBycW0ZxMLLcYKZQ0NJzG7fZisQRs3EJpWbdcp4AMo4yXblVHrcDKarVhMCQu\nHTyRkFgD6/+qug6pqKji7rt/wI9+9D1uu+3z2FwiNz7t4mRf4Or3SpOPx65TE4u190lJRvr6hoIe\nnesNs9myIVwPnE4XGs3KBeliBKr+A76p8130FQp5XOduT0cmk9HfP4zH413DPgTk8sB7Mmm1JZdP\n/gTcEzQaVfD3wG1gu5WIyokJ25x8c6fThU6niZkJ53KLkUKFKIq891492dnp5ORk4HZ7lpUGsVIW\ncwqYToZRFvEc1Un27XuNa675bFSOLbFxkMRqnKJQKLjyyo/zyisH6DReEBSqACf7RJ465GJ793kI\n7mF2yvehlrtD4nkYCsrKinj77RPRHkZYMJut5ORkRnsYYcfvF+dtsxpOPB7vuolaKxRyUlOTqKpa\nWfFONEhI0NPR0TPjPrPZuqDRfShwW0cZevFBANKvuh2VIWXR7ZdbjBQqLBYb6enJ5ORkAIRFqMYD\noihisThISUmL9lAk1jnr48y/Qamu3sXBg3/DqXQBcvR+O9eP/xnRK2C7v5KDnU5gJ025VXzq5gGU\nl18VtXzV6QiCgMEQ/0u58yHl4oYPn88fcYEcTuKlwHBwcJSEhJmrBadP97Bjx+awHM9tHcV+380U\nDk4AMHSsDu5+ZEnBGim6uwfo6xumpqYs2kOJOocOvcsHP3hptIchsQFYP2f+DcoXvvBlLO89Q7lu\nhCe6v83XRx7n4qYWvJ1Tfar7u9XUvm3A+9c/8sQBM7/a7+TNX/Vw+LEe3LZA4YvNJfLwWx4efsuD\nzRUfF9FYZf0UAa0Nt83H4cdmfs7Wynp6b+PhtZjNVgYGRigszJ5xv16vWZMt02IMvfgg6WeFKkD6\n4EQwyroQO7J2YzIUBv8OV9vSU6fakMvlnHNOZchzNOPxHNzQ0EZNzbnRHobEBkCKrMY5Op2e//i3\nH9H8wLfJcbUsuJ3sxGG0Q29Srfg7T7fchHnMBQT6hF/5YDm3vuCdk/OqV4fvYjrZ9SceLtgSKydk\n/ehjHLfNR93eflwWK7bmd5DLRc7/9pUYMuJ/WVQURVpazrBzZ8Wcx3y+2Oq+Fe62pR6PlxMnWigs\nzCYlJTF4/5jdwZO1+wH4dPUlJOtWt2K0UN1BOM/Ba6W3t5+cnIJoD0NigyCJ1XVCYX4uk77QNemH\naRqvpM8e8DHM0nVRk34YAHd3KqlnhSoE+oQ/+bNeTqqnCiVO9gWcBW45P3x5WDk5GfT0DJKbu/7z\nOzciIe1HH6PMFuQQMETvqTvAPz37gSUFqyAI+P3+mC0aa2/vwe32cOpUC7FeTwAAIABJREFU24z7\nwz3JTL/qdoaO1QWjq0MZCaRfdfuSz1tuMdJK8Hi8dHcPMDY2QVVVyYzc1DG7gwcO/RSjphOABw7V\ncucFX12VYH36qHdO3UG4z8Froa9vgCef/APf/e6/RXsoEhuEdS1W27paOfZo4CS3/aYH2ZQX+8UM\nq6UhYyu9gxej9PupST/MpTV/omPbvdBWz67+x1DL3dEe4gzS0pI4dqx5XYlVn8+HTBa7kRCJ0DJb\nkE8ybM7mrX/bx6UPfG7R5xsMWqxWBwkJ+nANcU0UFeXM69gxODjKyMh42I6rMqTA3Y/QsYICq1Az\nPDxOd/cAarWSnJwMiormTrKerN0fFKoARk0nT9bu57YLr1jx8dzeucv+890XbVwuF88+uw+DIYl7\n7/2R1FZaImKs209aW1crvu9fyWUjgdzNnu9fSdt3961LwVr37hHe/MJB+u0fBqBxvBLnHjdszUUs\nSWbTS3/CNNwMgCp3hBGHOhhdNVUauPKObA5OSwOoyhK4rib8H41wCLvJZVkIT1vJxZiYsGE0xqbw\niDSR6Ecf7yQkGJiYsMasWF0oetrTM0h1dXiLi1SGFHKuuyesx1gIs9nCwMAIO3ZsCf/B+rqQ/+xu\nbrD7eTHlu5xRxa6d32uvvUl7ew+f+9wXSE/PiPZwJDYY61asHnv09qBQBcgZcfLyo7ez6Z6/RHFU\n4aH+7l/Sb39/8O9+ex5lh97g6w4voOahxPu4XvwzGUawX3QVxYKG8tYRVIopQffYdfI5TQXCjVwu\nw+FwhqxQI9p5kmazdUY+23rF6/WiUCz+nkaiH320mS3IJ0lL7OX8b1+55PONRj39/cPhGl5YqK8/\njck0txnEeqKtrXtZYvzT1ZfwwKHaYHTV4sznpgsuCT7u9XpxOFzTfpwzOrmpRgcof/wePD4lzUPn\n8n2e5N6a6zitzw88roiNVZq2tg5eeukAH/nIVVx99eejPRyJDcq6FasSU7h8at7pvZCMERulbjO3\nftOI6pKZy1p6tRDx/KgtW4qorW2gsrJkVR2PZhPtPEmr1U5+/vqPHtrtrmX9v8LVjz5WmC7IV1Ng\npVDIY65QaTEmu1/FSiOAcOB2e9DpNMvKyU3Wabnzgq8GC6w+c85FdLZ00qdU4vf7zzZlCHRzS042\nkp2dPsMnWP7NH+DxKXm65cZgfcEnxht44PIcyvIVEVndWgyr1cZvf/sieXlFfPOb98ZsbrXExmDd\nitXtNz1Iz/evJGcyDSBVw/abFrc/iVcq7ruV0c+9TP/ZE55J18V/V30UAIXHxxX7W0gbC7wPrj9Z\neaZtnGsfrkKll8/bpnWS7qNmnv1SAwDX/Hc5uTWhjRrK5TJqaso5frwlMktuESCUJ/RopjQsRiij\n4fHOTEG+Pj7DC6FQyFfcqjVe8Pn8nDzZiiiKlJUVLvt5yTotX77gIzQ3n2Goe4jy8uIVNQg4OnRu\nUKgCjNkzudE9yBevK5p3dUsURdxuDxaLHas1kHYUjuYMr7xygP7+UW699U4MBmPI9y8hsVLWrVjd\nlFdC23f38fIGKLDacc5OeCKQDgBQ/L0v8uf3kqDbQVnrcFCoTjLYYKfuyU4qP1e4oF1K91Ezz9xU\nH3zOMzfVc+2jFSEVrG63h4aG06SnJ4dkf+spTzLaKQ2L4XC4NkS6g8RMxsct6zYne2hojKysNDIy\nll/I5fX6aGk5g8/nJzc3k6SklYk63x33Id78yJz785Rj9HUpcDrdQeeF6Q4MKpUSo1FHamoyg4Mj\njI1ZKCnJm7Of1dLY2IJSaeCOO24O2T4lJNbKuhWrEBCs6zFHdT52nLOTHS8/FPx7b42PJw6NMO61\n4jg+d3vh4D5+t+UznOyb6rY03S5lMqI6nWe/1MBdb78vJOPt7R1keHiciopNIWuhuZ7yJKOd0rAY\nDocTnW79uDhILI3f76elpZNdu+Z6rq4HPB7PooVufr8fq9XBxIQVi8WG1WpHo1FTUpK/+hSmrDy2\nP3gjzTfV0mcOfJ9MlQbef0suCSlaNBr1kukIRqOOwcFRjh1rYuvW0jWv7IiiyKuv/p1vfev7a9qP\nhESoWddidSNjUMv58iUZuM5J5uGmUfpOjgYfM2m72Snfh1CfDHwy4mPr7R3C6XSzbVvo2zVGK08y\nXlpnhgKfz79kgZXEwkxPvanWyfD5fCHvhhRq+vqGKC7OXbdNPFwuNzabjImJgBCdnUssCAJ6vZbE\nRAM6nQalUkFJSf6c/bi9zhU1JlBtKuCaP+euaYKdkZGCwaDjyJF6tm4tRaNZff7/iy++wqc+dYOU\nnyoRc0hidZ2jNii55ZkPc/Brj9P59w5y9N2cm3kItdzNjhwZVVphXsuqa/67fEYawOR9a8XhcDE8\nPBYWoRpNbDYHOl3o8jjXU0pDKFgvk4HZnYo2p6Tzf3OdmFJje3l9fNxKWVn8FFb5fH6czqkqfIfD\nhdvtWXB7QQClUkFiopGsrPQFJ2N+v5+jRxvm7erl9jp59uT99Fs7AGgZqeWaqruWFqwhmGDrdBpq\naio4fryZvDwTaWkrz2MdHzdjsbgoLQ2vLZmExGqQxOoGQG1Q8qH7r8N5z/X4W48B4C/aguLSf+Qx\nmXreAqvcmkSufbQi5AVWp093U1m5/nKHzWbrinPWFmM9pTSEAp/Pj1we/9Ge2Z2KmkcVPHfCz5d3\nR29MS3H4TA9/6n4UoUfgyi3/zLkFkVu58Pv9uFweXC43Tqfr7K0bj8e76PNGRsbJyzOh1WowGvVk\nZKSgUinXHBlua+umrKxo3v3U9b0eFKoA/dYO6vpeD3lXrYWQy2VUV5fR0nKGiQnrvA0dFuO3v32R\nO+/8RphGJyGxNiSxukEQtAY09z6F56XfcPDA39j+lW+g1OrQw4KWVbk1iSHLUZ1EFMV1ITpmMzFh\nJTMztP6T6936aSV4PF6UythsPblWBGFt3wdrZxe1d/8egOr7PokhPzTFNjazjcOP/RqFcj/pFYm4\nlTIOnPkB8J01Cdbm5g7c7sXF5iSCIKBWq9BoVKjVSpKTE9FoVCiVikWF5/HjzSsWa8vB4XDGvCNC\naWkB/f0jHDvWzNatJcta0j969ATV1eeg0UguHxKxiSRWNxCC1oDqE/9M1fkf57k/PMW11/5jxMcQ\n6yf61SLlcYYXj8cTskK8aHJdjYJXmnzB6GppsoePV/k43HUAWF6e43SsnV384dq36befC8CZa9/m\n48+wZsFqM9sY/O7X+LAl0Pmu7IyVZz6Sg1spY1/T/1Cs/xoejwe324vb7cHj8eD3Ly9Vw+VyYTQa\n2Ly5YE1jXAyjUc/EhC3k3cG2bi2ltbWTzs5+KiqKZwjBHVm7aRmpDUZXTYZCdmTtDunxl4vJlIrR\nuLw8Vp/Px9tv10pFVRIxTfyf/SVWjMmUhVf0c7Dlj2g06hVfIFfLxIQNnU4b9uNIrD8CkdX4P13p\n1QKPXTeVelOd0MNrZ37LoD3QBWm5eY6T1N79+6BQBei351J79+95/6/vXNM4G576A+efFaoA2cMu\nqhvMvLMtGVEU8Xi8qFRK9HotKpUSlUq5oqKckydb1zS+pcjJyeD06W4SEopCul9BECgtLcDhcHLk\nSANFRdkkJycgl8tRKTRcU3XXigqswolerw3msebmZi5oEfjss3/is5+9JcKjk5BYGfF/9pdYMS6v\nHVlFG+8OtAArv0CuBlEUaWrqWLfWNxLhJSCO1sfpanq3uH217wWFKkQ+z3Gl+P0CHy37EllZS3fo\niiYqlXJOXutiDVBWilarYdeuCnp7hzh2rJmCgixSU5NQKTQx9b+bzGNtbe3EbLYEHQzsdgd/+9ub\nDA+Ps2VLJbm5c50NJCRiifVx9pdYEe90vECfpSX4d7gvkCMjZjo6eigvn78wQSJ+8Pl8UbG1cbu9\nIWnJG2uI4trSYqrv+yRnrn2bfnsgP9Ok66b6vrXb0ZVf/3GaTh1kiz0QAe1MMXCgcBOXFtwW0QKr\ntTJppj/bhWF6A5TVIggCOTkZZGenc/RoAykpiTF7fispyWdoaIxXXnmDnp5edDojV1zxj+TlhS8V\nQ0IilEhidYMjDhjglx/isEJPyX87SCkM/TJ9T8/AvFYv6wWXy71uon5L4XC4oiIaAzmr66/AqkBT\nzZjQwaDtDLDyPEdDfh4ffwaOfPt3uH1O7F+QQ+alax6XKBcYvv7LjB47AQTE67cTY9teazYJCYag\nS8dsF4bpDVDWiiAIFBfn0tbWNa/3aqwwMDCAzyfnrru+He2hSEismI1xhZWYwXmFH6O+7yDdzT1w\n3ydBlOEEHv1EHTc9vyPkgjVSkbhQLvOtBLPZSmLixuifHT2xun7SAKYjE1VcU/UVjvcfBFaZ55hp\npO6fT+P1uwHoOPIdbt75Awzq1feM7+joZdf7qpBdsG3V+4g22dnptLZ2htRSbiGSkxPo6xvCarVj\nMOjCfryVYjZPcOhQLV//+neiPRQJiVWx/jyEJBalr9PCf3zidQb/4wr4+ZUgTvsIiPD8nXPbrMYD\nk8t8P33dy09f93Lj0y5srsgYyZvNlohcEGMBh8OJVhv5opGkJCMnT7bhcrkjfuxwIooiGqWOc/Mu\n59y8y1eVN/5yyxNBoQrg9bt5ueWJNY8t3rsYKZUKvF4fEJi8VmVNTV6nN0CZjtvm4/BjPRx+rAe3\nzbei45WVFdHY2B5zDSz8fj+PP/4sd9759WgPRUJi1ay/UIXEgvR1WvjZB19A7g3kyfnRRmS2Eq6T\n954fdXLR/loA/nxuNWa5lptPvg3A76rex9NH5SFZ5lsKl8uDWq0K+3FiAYfDhckU+eIakymN9PRk\namsbqaoqWVNLSYmliTXBtRZEUZzjwjDfyot10M2TN5zAMhgQ/s2vjrLnoYplN+OQyWRs2pTHe++d\nYufOipgR+7/5zXPcdNP/Qq2WvjMS8UtsfJskIsKvvvxGUKjCPP98AT7xwNpbqs5Gr9fS0dET0n3u\n+VEn5+9txz2QgXsggw//qZ0bX3kbsTUNsTWNm159C/mEJaTHlIiuhZRcLqe6upyTJ1vp6uqnq6uf\nuromjh1rXlfiaqVcVvo5FLKpyZJCpuKy0s+ten/j4+vne5OSksDY2AQw5cJwy/nKeYXqo5+sCwpV\ngP5T1mAHueWSnJxAZWUJR47UY7M51v4C1sj+/YfYvn2XVEglEfdIYnWDY8sErUkgIVfJjc9vD0uB\nVXFxLhaLHZ9vZctqi3HR/lp8/qkLtF9UMWGfiviZremUv/pWyI4nMUU0K57lchk7d1ag02kxGHTk\n5GRQWJhFa2tX1MYUbQzqJG7e+QMKkyooTKpYU77q6KiZ3t5BKis3hXiU0SEzM42+vuFFt3HbfDx5\nwwnc1tCcn3Q6DTt3VtDa2sXw8FhI9rla2tt72L177QV3EhLRRkoD2EB84Rfvn5EG4FUIVH7eyaay\nVLq6eth38E+IBwIRKkEQEEWR5ORE8vNzyc/PITk5adVCRalUnO3vHrkuTzGyCicRYgRBIDU1ccZ9\nnZ0ri4CtNwzqJK6uWlsjAICurn4qKjbFzBL2WlEo5EtOkuv29s+IqE5izFCxY49pVceVyWRs376Z\n48eb0Wo16PWRb4YS6BSWEPHjSkiEA0msbiCy8o3c8beP8asvvwHAzT85h1f2/4bq6t1UV2+ds70o\nioyPm+ns7OHQoXcZHR1fcN8JCUbS01PJyEgjIyONhARjUNiKoojd7kSlCl3+6JuXVHP+3vZgdFUm\nuDFoJ4LRVVPSMDv+dXfIjrcQXm90fEclZpKUZOTEiRZEUSQpKYG8vMyY9byMVVpbO8nMTF0XncKm\nMznxXujz4PbOvc+pELjiweXnqy5EVVUJ771XT3l5EUZjZK2/Wls7KC+vjOgxJSTCxfo6K0ksSVa+\nke++eEXwb9dLngW3FQSB5OQkkpOT2L594ZOeKIpMTFgYHBxmcHCYU6eamJiwUFt7kk9/+lMolUq2\nbCkM5ctg7zfy2QPBAquDu6u5ssZA0e8PkZMgUPO/d6NKC3+F/sSElcQ4859cj+TlmcjLC0TBhofH\nOXGiBZlMhtvtYdu2Ulpbu/B6fYiiSFZWOmlpq7d1Wq/YbI6I+IT6/f6ITiTS05MZGhojIyNl3scb\nSlIZShkifTSQY2rVKnnhQ6X8fT/8Zcvaji2TyTjnnEqamjpQKhVs2pS3th2ugKamNq6++rMRO56E\nRDiRxOoGJxQXDUEQSExMIDExgdLSYgDGxsYRRZFdu8I3s9/7jXz4RuDiesfknZd9NGzHmw+z2bpg\nz22J6JCWlhQUo263h1OnTlNQkEVSkhFRFDlxokUSq7OwWOwRswXzen0oFJFLB8rISKG+/vSCYlXQ\nyPnL7hLKWgO5rY0laXiVoRufIAiUlRXR3z9Me3sPRUXh7wAmiiK9vQMkJkqfc4n1gbR+ucERhPB8\nBJ599kUuueTCsOw7lrDZHFHJR4sGo/YBDpof5pH3vsOofSDaw1kWKpWS7ds3B31wAxMrIy0tnQB4\nvV5OnWrD51tb29N4xufzc/x4c8S6zEVarMpkMvz+hf+/19UoKDTJOVmeycnyTLxKOQLwP9eE1o7O\nZEpjfNwS0kLThXjiiWf5xCc+FfbjSEhECkmsbnDCJVZvvvl6/j979x3X9LU/fvyVQSBsZMhGEBQQ\nq+Cqs2pdVeuiWke14ra2tr1ddve233vb3729tdZZR9171VW1ddW6FdSK2yqKCoiA7JH1+4OKIisJ\nCUE9z8fDhyb5fM45QZK8cz7nvN+HD8eybt2WSj8ongRPw9rI9LwUFsZ9Tr4ug3sFd1gY9/ljE7A+\nKiDAi7y8fDIzc4iLu4CPjwcnT54vSSBfUFCITqcjOzuPw4dPl6RySk/PrLLtnJw8zpy5TF5eAVC8\nTOTEibNV7ki3JJlMiqOjXY1tflSr1cjlNXtRTyqVVhgk2llLWPmqDSNbSHC2AX9n2DZOQT1X0/88\nQkMDiY09b9b3xMWL19KlSy8aNXp8q48JwqPEMoCnnL29Izk5udjbm3bdpUwm4+WX+3LzZhIzZiyg\nR4/ONGjwZKTDeRptPDcDeDiXqY6N52YwuvlXlhpStQQG+nD37j1atGiERCKhUaNg4uLOYWVlRXZ2\nLhERwZw/f41nn23M+fPXuHr1Jnl5+UREhJSqVpaenkliYnHQrtFocHCwo2HDepw/fxWpVIpMJqNZ\ns3Bu3brDqVMXiIgIqdFZRX2oVOoa/cJV0zOrAJ6erqSkpOHt7VHu43bWEt7vYsP7Xcw7DqXSmrCw\nIM6du0pERLDJ21+yZB2dO79AREQTk7ctCJYkgtWnXHBwCAkJiUREhJqlfV9fL954Ywzbt+/m8OET\nDBnSH4Xi6aj2JNRejo72ODral9xWKq1p2bI4I0Zy8l2uXr1J/fp+yGSykqBCp9Nx8WICN24kUb++\nH5cvX8fR0Z5nngkpE+w1aVJ6Z46vb108POoQF3eexo1DUCprRzUhtVrDyZMXaNq0mjuJDOyzpjMO\nuLo6Ex9/pcJgtSY5ONiW/C7Uq+dNnTpOVZ+kh6VL19GxY3caN25qkvYEoTYRywCecsHBDbl+/aZZ\n+5BIJPTs2YU+fbozf/5yTpw4Zdb+asrTVDWpf/jrwMMBmeTv+548np5uBAb64OnpWur++xtlGjas\nR3z8FRo3DiEoyFfvWUmFwoqoqDASEm5x+vQlMjKyLP47lJOTR506jiZNK1cVlUpd4zOr99NX1RYe\nHnWIjAzl1q07ZGfnVbu9pUvX06FDN555JtIEoxOE2kcEq085d3cP0tJqpsqKi4szr70WQ2FhIXPn\nLiE7O6dG+jWXnJw87O2fjs1VdWzr0sllHE7W7jjbeBAT9U/q2Na19LDMxtW14l3U1tYKWrVqbNQa\nT7lcRlhYEBER9cnJySMnJ5esrBzUag2FhaoaD6gKC4uwtq7ZKx2WWAYAxYVJVKpykqpaiEQiISIi\nmMuXr1ernWXLNtC+fReaNIky0cgEofYRywCeclKp1GybrCrStm0roqKasHz5eoKC/OncuX2N9m8q\nmZk5ODmZP5drbaHQOTK6+VdPxYYyc5PJZPj5eeLrW5fz56+i0WhRKKzIysqhceMQbGxqZpmAi4sj\nZ8/+VZKjtiZYYoMVgLe3O7dvpxIQ4FXjfVekODuFPdnZeTg42Bp8/vLlG2nbtjNNmzYzw+gEofYQ\nM6sClvg1UCptGDNmGO7ursyYsYA7d2rvbumKZGXl4Oj4dBUEEIGqaUkkEsLD69O4cQgNG9bD09ON\ngoKayXcKxUsTanqW0xJrVgGcnBzIzMyu8X6rEhDgzfXrtw0+b8WKn2nd+jkiI5ubYVSCULuImVUB\niaQ4D6ElyoY2bhxOWFgD1qzZhFKppF+/Fx6bgEir1dVYuh/h6VBVTtBH5RbqWBlXfGl7SJQcO2vD\nXzs1/XqzxJrV2kwul6HRaNBoNHq/n6xcuYlWrdoRFdXSzKMThNpBzKwKNGrUmEuX/jJJW7m5efzy\nyx6DzpHL5QwdGk1kZATTp8/n/PnLJhmLIBiqKFfDsYW3OLbwFkW55k/e/ihDgtXcQh0xKwv5bp+a\n7/apiVlZSG6h4WtepVIpubn5Bp9XHZb6Qmpra0NOTvU3NJlagwYBxMae16uK2Pbte2nW7FmaNXu2\nBkYmCLWDCFYFnn22HSdPnjNJWxs2bMfNzZelS9cbvFmkXj1/3nhjDDdv3mbu3CVkZmZVezwJaRpe\nmJPPC3PySUir+eBDeHwU5WpYM+4c+6fdYP+0G6wce5Z5ewuYf1hlVBBoDKlUglarX18r49TEJz04\nNj7pwSyrITw9Xbl3r/qvtcdBYKAPCQmGX3I3N6XShqioUP7883Kl75uJibfJzVXRsuWTXx1QEB4m\nglUBpdKWoiJVtdu5ezcNW1tHunXrSdeuL/Ljj8sMLi0okUjo2vU5Rox4mZ9/3s6GDduMrvaSkKah\n17wirmfA9QzoNa9IBKxChU6tSSb57IMMFanncvltYXK1Zi0NZegyAFNIT880Wa7P2k4mk6FWa2pV\nGqv75HI5oaGBnD9/tdzHNRoNGzfuYNSoCTU8MkGwPLFmVQBAIqner0JKag6z/28/Li51SLqTTmho\nOCNGjGXGjBmMHz/c4N3NNjbWvPrqyyQm3mbWrIW0adOCqCjDygdOXFvEw59JOl3xfdsnVD/dVEFB\nYY2n/BHMqygnt8x99triS8b3Zy3HtDZvPlKpVIpKpd8Xx8GRMn69oCE+ufiXPNwDeoUUkpGR//ca\nSC1qdfFayOK/tajVajSa0sFwWto96tf3M/lzqa38/T25fj2JevW8LT2UMhwcbJFIJOTnF5YpHLFi\nxc+MGjXBInsLBMHSRLAqAODr68ft28l4exuewiYlNYeFMQewv+mJCvghdiWT1w/B29uXt9/+kP/9\n72sGDeqFs7PT37uP5XqvWfPz8+b110dz4MBRZs1ayMCBfXB3d636RDO7dy8HZ2f7qg98QtTGmShT\nyi3Uoby8CC/bpiTlFQduXraJtLLfxBE+r7FxSKUSrl27RXq6fpflpzSTsTPBDqlUSq+QAopyZWjl\nxWVeZTIpSqU1crkMmUxW8rdMJi31+ktPz+TKlURCQvzN9bRqlTp1nLh+PYmAAK9auZkzJMSfS5du\nEB4eVHLfqVNnCQgIxtf36fg/EoRHiWBVAKB9+0788ssa+vbtYfC5K2YcRX7zwWVEWaIj877exGdT\nY3B0dOLjj7/k55/XkJ9fgEpVyN27aTRqVJ/27Vvp3Ue7dq1o1SqKdeu2ADBwYJ8qczXOHqig17wH\ns6sSSfF9ppCZmU1goI9J2nocFBQUYWPz5M4kLz6moolGzZCQhcSlFu+wjnI/xl8u9jiRwRvq3QxK\nlUN+X1Aang9TXxKJBH9/L4Pynhp4waEMZ2cHbt26U71GHjNBQT5cu3aLoCBfSw+lDLlcTnp2IfMO\nFSGRSOgTquLo0VN88EHNfWkShNpGBKsCUFzJKiPDPDkIFQoFgwa9Uuq+jRtXs2/fYTp2bK13O1ZW\nVgwZMoDU1DTmzVvKM8+E07ZtxQFvPVcZ28YqmLi2eIft7IEK6rmaJmWOSqWu0RKVlpafX4BSaWPp\nYZjNqVtaVntOZvf10bT2PABAkVzC/nb2bPn9PbzuJsM10J7+A82735otYJVIoKYnse/dy8bJ6em5\nSgDFOVdr40YrKJ7ln3rGn/Opxevrl/2RzvZ/vGnhUQmCZYnFL0IJqdS4QG7o661Q+94rua3xy2Ls\nh30rPad//5eRSJTs3n3A4P7c3V2ZODEGGxsbpk+fT2JixR869VxlbJ+gZPsEpckC1adReWvoniRN\nfaTkSZVs8YnkrqOcq95KfnwpgIbXc4sD1b9Jr11Esnez2cZhiRr2Tk4OJCU9fkU5qksqlRr9sz6f\nnMaUX6Yy5ZepnE9OM+m4VsapOZ/64KP5jsaVDWdqrlCEINRGIlgVSjg6upCVZfjsal13e4JHKZD2\nyUfRX83k9UPw8qhT5Xl9+76EtbUju3btN2a4NGvWhEmTRnHsWByLFq2ioKDQqHaEqj06s1qkLuBY\n4g6OJe6gSF1gwZGZxqvPqFid8jGDEo/jlqXGpkiLykqKg8KlhkdS82soMzOzcXev6edpef7+nly4\ncM3g884np7Hpwhe4O17A3fECmy58YfKAVRCE0kSwKpRo164DJ06cNurcAL869I+J4rOpMXoFqvf1\n7j0AOztXdu7cZ1S/UqmU6Oje9O/fk8WLV/Hrr/ue+M1AlvDwmtUidQFr46fyx/WN/HF9I2vjpz72\nAav9wS00zHlQjML7biEDkn0JG/w12sCGJfdrAxui69THbOMonlmt2dRVdeo41cpE+eZWfLXA8KUt\ni+OWYCV/MNNpJS9icdwSk41rSJScCK8HX1qa+ip5tY3lN5UKgiWJYFUoERQUQmJictUHlsPNrQ53\n7qQYde4LL/TF2dmT7dv3GnU+gJOTI+PHv4qvrzfTp8/nyhXDZ0z/JluuAAAgAElEQVT0pVarkcnM\n+9I5fjye+PgrxMdf4dKlBG7fvkNWVo7BeWtN6f7O6VNJ+0jOSSi5PzkngVNJ+8o/KT8PyS+rkPyy\nCvIfr4DI16khCvs6aN79FvVLY1G/NNas61WhOBuAJb5r6XQ61OqnKwdxSkparUxfZWctYeEQa9rb\nxTOlmztrxgViby2WMAlPN7HBSighlUqRSIx7U3R2duLChVtG9929e2/mz59JcvIdPD09jG4nPLwB\nYWEhbN++m717DzJ4cD8cHEy7eSQzMxdHx4rb1Ol0/PTTCuzs7PDz88LPzwcvr7pYWem/IcvaWkGj\nRvWRSCQUFqrIycklIyObmzfvlJs0XiKRYGtrg52dEjs7JUqlteXzMebnIfv2XaTXLgKgjd1v9mDP\nWLpOfdDG7n8w1odnUJW26HoOrrmxWCBaDQ0NJC7uPE2bNnxqNg4a+/p4NWoEmy58UTK7qlIreDVq\nhCmHhio/i67eGYx53vBUgoLwJBLBqlCKQqFApVIZFFgBZGVl4+xcvXVvhYWFeHi4VasNKA7cevbs\nQm5uHqtWbcTJyZHmzZvg6+tdZborfWRmZlO3bsWX5e7dy8Td3ZWuXTty8+Zt/vorgQMHjpbMXN0P\nRmQyKZ6edfHz88bPzwdb2wfFClxdnbl9+w4+PnWxtrbC2toZV1fnCvvUarXk5RWQm5tPSkoa+fmF\nFQY9VlZy7OyU2NraoFTaYGOjMCjfZFOvjlxOO1kyu+ppX4+mXh3LHCfZu7kk+IPizUnavZtrNPDT\nm9IWzbvfov1785SuUx+LBNWW2GAFxV+OIiNDuXTpOo0a1S+5/062lk+2FQdl/9dLgYfDk3ExrqhI\nZXRQHubpCnxRcun/1agRf99nOps3/8bo0a+btE1BeJyJYFUoJSqqJfHxF4iMbGzQeampadStG1Ct\nvjUajUlnA+3sbBk9ehipqWmcO3eRgwePlbrUKZVK8fb2pH79AIMC2by8AmxtK17rlpCQSL16fiiV\nNoSEBBESElTucWq1muTkVBITb/Hnn+fIzy9e96nT6dDpdMhk1vTt2w1HR7sqxySVSrG3t8XevvIA\nS6fTUVSkJi8vn7y8AtLTMykoqHynsbW1otTmNYXchoERb5dc+m/q1RGF/AlIa1XDM6jlKQ5WLdP3\n3bsZpQpd3MnW0uPHQgr+LqjV48dCdoy3fiIC1rS0e7i6Gl9iNszTlW96vm3CET1QUFCIRCLHzu7p\nSicmCJURwapQSmRkc+bM+c6IYDWD8PBnq9m7edbMubu78txzbcr2ptFw61Yy165d58CBo6XKUEql\nUnx8PAkKCsDPzweZrPTyiMpmIhMSEuncuX2V45LL5fj6euHr61Xu42fOnOfIkeN069axyrb0JZFI\n/p6ptcLFxbHK43U6HYWFRfj7l74cqZDb0NKv8gISlV5aF8pVnGe15qPVrKwc0tIyiYgILrnvk21F\nJYEqQIGq+L65g43/YlJbNj9qtTrLL5OpwJYtv/Lyy8MtPQxBqFVEsCqUYmVlZdTMTnp6Bu7udY3u\nNzn5NnXqGD/TYQyZTIa/vw/+/mUrUd0PZK9eTSgTyBYV6bh9+yb16vnh7++LjU3p/KNZWdk4OTlU\ne3yNG4dx4sQp7t3LxNm5Zn8290kkkjLPT2+15NL646T4S1DNB3Q3biQTFlb+FQBTUqs1yOWW3yxU\np44jN24k1/h7jj4KClR4eBj/XioITyIRrAplSCQydDqdQesYtVqdwetcH5aRkVHppqWaVlkgq9Vq\nSUpK4fr1m8TFnaGwsHR+14SERJONY9iwaObNW8akSaNM1maNqgWX1h8vNb8MoKhIRVGRqkyGi//r\npSi1DMDGqvi+6tBqtUilNZ9L9lFKpQ35+bUzL7NEUjtnfAXBkkSwKpQREhJKQsINAgP1X4NqSGBb\nngYNQtm1a0u12qgpxUsEvPDx8aJNmxZlHjflpU6FQkHbti3Zu/cAnTq1M1m7Qu1kZSXj3r3sGpuB\nzM8v5OzZKzRtGlrmMQ8HKTvGW5t0g5VCYUVRkbpabZiKk5M92dm5ODhUvSZcEATLEl/hhDLatu3A\n8eN/GnhW9YJVmUyGTmf5GRdTqG7g/qimTSO4fv0mt24lmbRdofaRSqU0bdqQ06cvVn2wCZw/f5Wo\nqLAKA2MPBylzB9swd7CNSTZWWSrbQXkUCitUqtoROD/M1O8fgvAkEMGqUIaDg6MRl8iq/wZrbI7X\np8GIEYPYuvVXEhJuWHoogpkpFFb4+3tx44ZxBTr0lZ2dh5OTfY1vNKotwZihS51qTm0ckyBYlghW\nhXJJJHIDZ0Cq/wZrY6MslSJJeEAqlTJu3Aj27DnAhQuXqz5BeKy5u7uQmZlt1j6Sk+/i7W18AY7H\nXW3NCFAr42dBsLDa90oVaoXQ0HD++itB7+MLCqpfSvOZZyJFIFYJiUTCqFFDiYv7kz//PGvp4Qhm\nZu5Zv7y8fJRKIzM9PAGsra0oLKw8x7BliGhVEB4lglWhXO3bd+TYsdN6H9+oUQOOHTtUrT6feaYp\n589fqVYbT4OhQ6O5dOkqx46dtPRQBDPSaLRm27GelHTXommbasO6VVdXZ+7ezbD0MARB0IMIVoVy\nKZW2pao9VeXZZ6PYv39PtfusjRseaqOXXnqRmzdvc/q0mGF9UjVuHMzFiwlmafvu3Qz8/CxTd16p\ntK4VaaPkchlFRaqqDzQTjUbD6dMXiY+/wp076Wi1WgoKCi1WwUwQajMRrAoVkkhkaLXaqg+k+JKl\nm5szt25VL8eo2GSlvwEDenHqVDzXrl239FAEM5BKpVhbW5Gbm2/poZiUnZ0tubnVXzZkjPsV2dLT\nM0lMTCYvr4AbNyyTZePcuauEhgYSFhaEVqvl/Plr3LiRjEpluQBaEGorEawKFWrSJIpz5y7pffwL\nL3Riw4bV1epTKpWj0Zin7OqTaMSIQfzyy25SU9MsPRTBDPz8PElOvmvSNlNTMyy6C97BwZbsbNMF\nq1qtltzcfO7ezSAxMZmLFxOIj79S7p+zZ//ixo0k8vMLcXCwo0WLCO7evWexZQnW1gpkMimenm40\nalSfBg0C0GpVek8SCMLTQhQFECr07LPt+P77fxMRUTZheHmsra3RalXk5uZgZ2dcNapmzVpw8uQZ\nmjdvatT5TxuJRMKECa8ybdo8xo0bjr29SHD+JLG3t+XSpesmTbN05046YWGBJmnLGEqlNXl5BZUe\no1KpuXMnnYKCQgoKiioNJiUSCUqlNUqlDQ4OdtSt64qVlVzvn5efnyeJiSn4+5t/WYRWq0Wt1qBQ\nWOHoaM+9e9k4O5cuzdy8eQQHD/5O+/adzD4eQXhciGBVqJBCoaB589asWbOFQYNe1OucAQNeYMGC\n2Uye/J5RfbZs2YapU/8tglUDyGQyJk4cycyZP/Hmm2OrVfZWqH1CQgK4dOk6DRvWM0l7Xl5uJCXd\nxdfXMvXn9UkXdfXqTVxcHHFxccTGRmHWFFPu7i6cOnUBT09XNBotGo2m5G+1WlPy9/0/928bQyKR\nkJOTR4MGAdSp40RaWkaZYLVx43AWLVovglVBeIgIVoVKde7cHQ8PT+bOXc7o0YORySpfU+rgYI+r\nqwPnzp0hPLyxwf1JpVJsbe3Jzy9AqbQxdthPHaXShjFjhjFr1kImTx5bS5OdC8ZwcLA1aYqllJR0\n6tRxJDs7t1QAplKp/76tRqXS6HUpurCwCC8vd7y93U02PihOK2Vjo8DWtmbeAwICvLl27RYymRSZ\nTIZMJkUulyGTyVAorFAqbZDLZSV/ZDKZ0a8xnU7HmTOXcXNzxs5OWeZxiUSCVAoqlUp88RSEv4lg\nVahSREQTXF3dmD79B8aOHYadnW2lx/fs+TyzZi0hNLSRUTMiffpE89tvm+nTp7uxQ34qOTs70a/f\nC2zb9hu9e3ez9HAEE9HpdCZdU+nkZEdOTh75+YWlAjAbG2vkchlWVnLkcjkyWdWv3Rs3kswSUPr5\neRIXd55mzcJrJHH//VncmiCRSHByKl4CEBYWVO4x7du34Ndft9GrV78aGZMg1HZig5WgFy8vH957\n71Pmz19FSkpqpcdKJBK6dWvP+vWrjOrLx8ePu3czjTr3aRcQ4Mft2+Yt0ynULK1WV+UVDUN4e3tQ\nv74f9ep54+tbF09PN9zcXHB2dsDe3rZk048+7t3LxsnJuPXplZHJZISH1ycu7rxJNlymnEtiWdeN\nLOu6kZRzltn9/7CAAG/Cw+tXODsbFBTApUvna3hUglB7iWBV0JudnT0ff/wlq1dvIS+v8nQ6ISFB\nJCZeJTPznlF9+fvXIzHxtlHnPu2CguoZVH1MqN2ysnLKrGusTapzObwydnZKgoJ8uX274i/HuYU6\n5h9WMf+witzC8ttLOZfEylcukZzqSXKqJytfuVQrAtaqWFnJyMvLtfQwBKFWEMGqYBC5XM7kye+x\nevXmKo8dPLgv8+fPMqqfF1+MZs+eg0ad+7Tr1Kkte/eKn92TIjn5Lh4edSw9DJOytlbotQ63oKCo\nwmUGuYU6YlYW8t0+Nd/tUxOzsrDcgPW3N4+g1ipKbqu1Cn5784jxg68hzz/flk2b1lt6GIJQK4hg\nVTCYs7ML3t4BVc7e2doq8ff35OTJEwb3UZwGS1IryjI+bmSy4jWIhYWWrxL0JClSF3AscQfHEndQ\npK489ZKpFFc1KkKhqJ0bbXQ6KCw0PIm9g4MtOTlV51qVSIrLzpZnZZya+KQH7w/xSTr+ueoiavWT\nUQXPy6suN25cFTlXBQERrApGGjhwKNu376symOzatQPbtv1s1Btux45dOHTI8EBXgB49OrN9e/XK\n3woPFKkLWBs/lT+ub+SP6xtZGz+1RgLW69eTCAryMXs/xmrUqD6nT1+sMKCsiL29foUBcnPzcXd3\nKbmdnp7Br7/+zqJFa4mNiy9zvI9PECtXbmXBglVcuHCZInUBAZ/okEsffHGTS4voOu1Zg8ZrKZ06\ntWbbtp8tPQxBsDiRDUAwilQqpV+/gezcuY8ePSrPB/jii8+zcuUShg0baVAfkZHN2bt3J23btqjG\nSJ9Onp4e3LlT+UY4QX+nkvaRnJNQcjs5J4FTSfto6dfDrP3m5OQRGFh7g1W5XEajRvW5ejWRkJCA\nco/RarXcuHGTc+euFFdaU8vJP22HVqvDoVksEistoAO06HQ6FAoFrq7OuLu7olKpWLbsODodSKUy\nXF09aN26EwEBgeQWaRk09xqnbhavn2/qq+SdFwOxtw5Ho9Gw47fN7Nj7CRplNsoPrXCb2xpQ0nVa\na+qGexn0PHfvPsDlywkoFFb4+XnRsWPrGkkr1aBBffbuXU6vXv1qJCuCINRWIlgVjBYR0YRdu3aQ\nk5NbaeWkgAA/9u49TE5ONvb2hm0UsbKyru4wn1re3p6kpKRSt65pc2AKwsPs7JTk5ZVechIXd4bT\np89jZaVAKpURFBRCp069cLZzY9Hw3aSeLi4P7JLtyqjlXbG2fxD45efncedOCikpydjZSRk/vg8K\nhYJH2VvLWDMukMWHitt6tY0r9tbFWRNkMhkOwYVoLmQXt+mlIv/z/bQP6E9dP/0D1aysbJYt20jn\nzt2Ijh4JwOXLF1iz5hcKCnJ5+eU+eleNK8rVcGpNcaaOpoM8Udjpl+Ghdeum7N37K88/b94vRoJQ\nm4lgVaiWMWNe48cfpzF69OBKj+vd+3l+/nktr7wyyqD2TZmy52nTvv2z7Nq1n+jo3pYeSq1w+cgt\ntr55CYDe0xoQ8qz+M5ZNvTpyOe1kyeyqp309mnp1NMMozSsnM5edPx0FoPuoVtg7maY8r1JpTU5O\nHrduJbNnzyFat27H229/VOa4/XPiufV3oApw63QaR5ddpMOEiIfasiUgIJCAgKpLwtpby5jUyUPv\ncaal3wM//Y49dCiWc+eu8NZbH2Br++DnFBISSkhIKPn5eXzzzZeMHz8MW9uyyf0fVpSrYc24cySf\nzQHg0q50Bs0N1ytgfeaZRvz443IRrApPNXFdQagWe3sHgoJCuHjxSqXHubm5kppqTP5PscHKWE5O\njmRlZVt6GLXC5SO32DThOppCGzSFNmyacJ3LR27pfb5CbsPAiLdpH9Cf9gH9GRjxNgq5+asrmXKD\nYU5mLgtGHuDaYiXXFitZMPIAOZmmSY0UFOTDwoXrSE0tYMqUz+nYsYtJ2q2OVvX64OPUsOS2j1ND\n7pyRc+nSX5WeV1BQyPz5K7Cxcebddz8uFag+TKm05b33Pmbu3OUUFFS+mfHUmuSSQBUg+WxOySyr\nPp55JpQjRw7ofbwgPGlEsCpUW9++A9m162CVH6zu7i789delGhqVcJ/IqMDfM6oP5wOVlMyy6ksh\nt6GlXw9a+vWokUAVMOk6xZ0/HUV17UGVJtU1x5JZ1uqSy+VIJFpeeKFXpXlXW73SEJ8mriW3fZq4\n0uqVhhUeXx3WcltiWn9L19CxdA0dS0zrb3nz9SmcOHGOc+fK/78/deosS5asZ+zYyXTuXHUFPXt7\nB95+ewpz5iylqMh0JXEf1bp1M/bvFxsmhaeXCFaFapNKpURHD2Hbtt2VHtez5/Ns3ryWY8cO6d22\nSqVBpTI8NY5QrGHDYM6fv2zpYQhGepy+aPTr152lSxdUeoy1vRWjlnel25RIuk2JLLNe1dSs5bZ0\nCB5Mh+DBWMuLy0S/9trbnD17lTNnzpUcp1KpWLRoDTk5Gt5//zOcnJz17sPJyZk333yP2bOXVPhe\n1XSQJ56NHlT68mxkT9NBngY9l+DgAP7886RB5wjCk0IEq4JJhIaGc/t2aqUfrlKplJiYlzl8eL/e\n7Q4cOIQNG7abYohPpRYtmhIbe9rSw7C43tMaUHpJie7v+2ovnU6HSmW6nKHdR7XCKjCr5LZVYBbd\nR7UyWfu+vl4UFGRz8+aNSo+ztreiw4QIOkyIMGugWpmxY1/nxo00Fi9ey5o1W5g7dyVDh46md+8B\nRrXn4uLKa6/9g9mzl5RbHlZhJ2PQ3HA6vOlPhzf99V6v+rBOndqwc+dWo8YnCI87scFKMBlra4Ve\npRelUv3LM3p7+6LRSMjMzMLJybHqE4RSrKysTJ4kPSUllXXrtuDgUHFNeIXCiv79e2JtXTuyOYQ8\n60PfORi9wcoQReoCTiXtA4o3Zhm7ZKCoSEW9et4mG5e9kx2jF7V7aINVO5NtsLqvd+8u7Nq1k5Ej\nx5q0XXMYNiwGgIyMNFxcXKs4umru7h6MGzeZWbNmMGnSq2WWcCjsZLSMMf53TiKR4Ovrydmzf9Ko\n0TPVHa4gPFZEsCqYjE6nX2JwnU6LVqvVez1eTMx4Zs36H6NHD6nO8J5a4eENWbduCy+99GK121Kr\n1axYsYHJk8dUmqkhKyub2bMXER39In5+pgu4qiPkWR/ePmrenKX3iwfczxpwOe0kfQMnc27DPcCw\nlEXW1gqsrcumbKoOeyc7ot/ubNI2H6ZQWKFWm2/tpjmYIlC9z9PTi5iY8cyZM4+JE0fo9eXdED16\ndGTmzMWEhISWm85LEJ5UYhmAmWzevJm+fftaehgGOXHiBKGhoUade+3aFby99Ush4+ZWh5SUJL3b\nVipt8fUN5OrV60aN7WnXqlUUjRqFMndu+ZcoDbFw4SpGjBhYZUoxR0cH3nxzHPv3H2L//sPV6vNx\n8mjxgKS7N1k+Jo79026wf9oN1ow7R1Gucf8HBQWFnDt3ia1bf+PKlWsmGrFpWVlZUVT0dK8x9/X1\nZ9iwUcydu9zka44lEgmvvNKfOXOmmbRdQajtnvhgdfjw4TRu3JjIyEgiIyPp1q0bixcvNnu/ffr0\nYdOmTUafr9VqmTlzJt27dycqKopWrVoxZMgQjh41ze5dU9u3bzetWzfT69iIiFAWLZrLf/7zf+Tk\n6JdaaeDAoezYsa8aI3y6hYWF0L9/L6ZNm0d2dk7VJ5Rj5869NG/eBFfXOnodL5FIGDbsJeRyOYsX\nr35ia5xf2X+FH1rs5ocWu7kX98jv8x+hZF9+cAFL35RFSUkprFy5iaVL17N06UaWLfuZbdt+R622\noUuXfty5k8/ChWtZseJn7t5Nq7K9++7dy+T33w+zdetvZtm8ZeqZxMdVQEAgL700lAULVpr85+zs\n7ERwsD979uw0abuCUJs9FcsAJk2axIQJEwA4ffo0I0eOJCQkhDZt2hjVnkqlMnupvXnz5rFt2zZm\nz55NUFAQeXl5xMbGYmNTMylzDJWdnYlSqd/Y/P19mDhxOEeOxHLt2lUaN25S5TlSqZTnnuvCoUMn\naNOmeXWH+1Ryd3fltddi+PHHxURHv4ivr/6VfK5cuUZ2dg7du1deWrc8bdq0oF49P6ZNm0dMzGCc\nnZ0MbqO2urL/Cj9PvgMU7zT/83MlbpNDuHu9eK2uvaQO+n41SEtLZ9euA+TnF+Hr68/IkRNRKm3L\nPbZnzz707NmHnJxsfv55Lampybi6OtO1a4eS12FmZjZ//nmWa9duAhIkEhl16rjRsuWzaDRaZs5c\nxKhRg6tMaG+4xyeDgTnVr9+AHj36sm3bbnr3Nm3e2TZtmvHTT6to3DgSd3f9iyIIwuPKYsGqWqMj\n/nY+tgoJIR42NfaNvEmTJtSvX59Lly6VBKsZGRn897//5dChQxQWFtKqVSs+/fRTXF2L1zJ17tyZ\n6Ohojhw5Qnx8PP/6179YuXIlERER3Lp1iwMHDuDq6sqUKVN4/vnnAdiwYQNz5szh119/LX6+ajXz\n589n48aNpKenExwczMcff0xERES54zx58iSdOnUiKCgIAFtbW9q3b1/qmA8//JDDhw+TlZWFl5cX\nEydOpHfv4mpFR48eJSYmhm+//ZapU6eSkZFBu3bt+Ne//oWdXfGmioSEBD799FPOnj2Ln58f/fv3\nL9V+VWOeMmUKKpWKxMTrXL58heTkZCZOHMG///0DsbFn0Gg0eHi48cEHk2jatFGZ5+jmVoc7d5KA\nqoNVgLZtn+Prrz+nWbPGtWbjzuPGxsaayZPHsmLFeqytrenX7wXk8srfBnJz89i+fTevvz7a6H69\nvT2ZNCmGhQtX0qZNCxo3Dje6rdrkl3eucz9QLSbh7g+tuP/WatPQBtswKXfO5wFlUxZlZmaza9d+\nsrPzcHPzZMiQ0Tg66h/M29s7lFSFu3UrkU2bNlBYmI9MJsfR0ZkWLVrTs+eQcpdtvPnmB3z//X/o\n27cL/v6+Bj/3imRkpJOSkkzduoalZnoS3S9JnZeXb/IvBcOHR/Pjj9P56KN/mjQfryDURhb5Dc9X\naRmy4BovzvqLHtP/4h9rb5o1n+D9tnU6HSdOnODq1atERkaW3Ddp0iRkMhlbt25l79692NnZ8c47\n75RqY926dXz88cecPHmyJCDduHEjo0aNIi4ujmHDhjFlyhQKC8uvZDJ9+nT27t3LggULOHbsGNHR\n0YwZM4asrKxyj2/RogXr1q1j7ty5nDhxgry8vDLHNGvWjE2bNhEbG8ukSZOYMmUKf/31oDqLVqvl\n0KFDbN68mZ07d3L+/HmWLl0KFAei48ePp0GDBhw5coQffviBVatWlfrSUNGYs7OzS9r/5ZdfaNMm\nkj171jJ58miWLl1PYWERmzcvZPfuNfznP5/g4eFW7nN0d3clJSWl3McqMm7c6yxfvtGgc4TS7l+e\nb9u2JfPnL2P79t0Vvv50Oh0LFixn9Ohh1f5CqVAoGD/+VeLizpCcfKdabdVuD4L/uxcLCO5Yp0zK\noiNH4li0aC179hyjX7+hvPXWh7zySoxBgeqjfHz8mDDhTd58cwqvv/4uI0aMISysUYXrix0cHPn4\n4y85cuQMf/xhuuVF48cP48cfp5GSYkzFuifPyJHjWLvW9CmnrKys6NmzIytWLDJ524JQ21gkWP1h\nzx0O/pWLRgsFKh0bTt3j4F+mKftXnjlz5tCiRQsiIyN55ZVX6NOnD40bNwYgPj6ec+fO8emnn2Jv\nb4+NjQ3vvvsuR44cKRVIDRw4sGTz0f1ZvV69etG0aVMABg0aRHZ2NgkJCWX61+l0LF26lPfeew9f\nX18kEgkvvfQS7u7u7Nu3r9wxjx49mo8//pgTJ07w2muv0apVKyZNmkRy8oMPgJdeegknJyckEgk9\ne/akYcOGZda0vvPOOyiVSlxdXXn++eeJj48HipdD3L59m/fffx+FQkFAQACjR48uFdgvXbqUMWNG\ns3TpfBYt+pEuXTrj7u7O3r17uXMnhdOn43jmmTBGjnwZiUSCjY01CoUVmZnZJCTcRKvV4ufnjbd3\n3XKfo6OjA/fuZVT131eKq6s7ISHhnDoVb9B5QlleXnWZMGEkwcGBzJ69iEOHjpc5Zu3azfTu3c2k\ns0LDhkWzaZNpc+fm3Cli/aRzrJ90jpw7Nbcbvef/Ang0f+uj5AopLWN8aBnjg8JOxm+/7UelkvPW\nWx8SEzMeV1f3Ghvvo6RSKePGvYFS6cry5RsNnjRQqVQsX76RX37ZU5IiTS6XExPzMtOmfWuOIT92\nnJ1dcHFx59Yt/TeV6isoKACNJp9z586YvG1BqE0ssgwgq6D0bliVBlJzTJsL8mETJ04sWbOakpLC\nO++8w0cffcQ333zDzZs3KSoqom3btqXOsbGxISkpibp1iwMtH5+yKW/c3R98yNjaFl8KzM0tG3Rn\nZGSQl5fHhAkTSs1OqdXqSmcW+/TpQ58+fQA4e/YsH330Ee+++y7Lli1Dq9Uyffp0tm/fzt27d5FI\nJOTn55OR8SD4k8lkuLi4lNxWKpUl40tJScHV1bXU5fSHn+P9Mf/jH++gUMgBCVOnzkSr1bJt22bO\nnYslLCy4zNrdV14ZgFqt5ssvv+Pu3QzatWvB66+Pok6dshVhin8Whs+ov/jiAP71r88JCwsRywFM\nICQkiJCQIGJjTzNjxgI6dmxLREQoJ06cwsXFmaCgAJP2J5fL8ff35cqVawQHB1a7vZw7RczvcxJ1\nQfEGrvl9TjJmcyT2HuZP7RPcIZh+P9xfDgBd/+VH7OLCklfufc0AACAASURBVDrwj17237lzHw4O\nbvTs2c/sYzNEly49CAqqz4wZi4iJGYS9fdX5Vy9cuMyuXYcYO3YSubnZLFu2EYlEQ9u2zdmyZRdT\npnxaAyN/PAwdOpL//vdLJk4cofc5OYX32Hm5eDNw95BXsbcuv6pWnz7dmDFjEaGhjcRyAOGJZZFg\ndWCUCzvOZpGUWRyghnla83xDhxrpu27duvTo0YPvvvuOb775Bh8fH5RKJcePl51Velh13gRcXFxQ\nKpUsWrSowjWqVWnUqBEvvfQS33//PQBbt25l3bp1LFy4kODgYACio6P1nhnx8PAgLS2NgoKCkk1b\nt27dKjPm+fPnsWfPNsaOHVbyWGpqGu7urnz55dQyl4ZtbGyYMGEEEyaMIC0tgy+++Jbp03/i88//\nUe44jF3+MXHiGyxaNIdRowYbdb5QVrNmTYiKeoZ9+w4ya9ZCFAoFY8YMq/pEI/To0ZnZsxeZJFjd\n+c8rJYEqgLpAy85/XiF6Zs2siw3uEMzk48Elt+u31ZTs+H84r+ovv+zBzc2Hbt161ci4DBUUFMI7\n73zE99//l3btIvHwcEcqlSKVSv7+W4pEIkUigS1bduHh4cMnn3z199mevPXW+xQUFLBt2898+OE/\na+1mUEuQy+U806w9X6y9ga+vF0Oi5NhZV7ysJqfwHgtiP0WtLb5KsCD2U0Y3+6rcgFUikRAcXI+k\npFv4+PiZ7TkIgiVZ5GtYUz9bZg/15+Xmzgxr6cLyUfVwVBpWes4QDwdEqamp7Nixg7CwMAAaN25M\naGgoX331FffuFSfuTk9PZ9u2bQa1WxmJRMKIESP4f//v/3H9evEMTG5uLn/88Qd37pS/dm/hwoXs\n37+/ZH1oQkICP//8My1atAAgJycHuVyOi4sLarWadevWcfHiRb3GA9C0aVO8vb359ttvKSws5MaN\nGyxcuLDMmL//fhpOTq5cvnyVvLx8jhyJfShALfv8Dxw4xrVrN9BoNCiVNlhZWSGTVfxrpm8hgUfV\nqeNGw4YRnDwplgOYkkQioVOndkycOJLRo4eatZ8mTRoRF/en2fqwlPuViu5f9ofi4K5uXf9aG6je\nZ2trx5Qpn6HRKLl48TZnz97g9OlrxMZe4siRcxw8+Ce//x5Hv36DGTiw7O+HjY0N0dGDRaD6iJxC\nDTMvBrLmijvf7VMTs7KQ3MKKPz92Xl5cEqgCqLVFJbOs5QkJqcf58+K9UHhyWSwbQMt6drSsZ9pS\nfxWZNWsWc+fOBYov17ds2ZIPPvgAKP7QnDVrFtOmTWPAgAHcu3cPV1dX2rZtS69elX+wVLbhRCKR\nlHp88uTJLF26lNdee43k5GSUSiWRkZF88skn5Z5vb2/PrFmzuHbtGkVFRbi4uNChQwfeeustAAYM\nGMDRo0fp2rUrSqWSPn360Lx56ZROj47v4THJ5XJmz57N559/TuvWrfH39+fll1/mm2++KTPmNWvW\n8MMPs3FyciQiIpR3351wv8Uy4755M4mpU+eRlpaOtbWC5s2b8PrrMRX+nLRa45PU9+rVj3//+wvC\nw8VyAFOriewcbdu2ZObMn4iMbFyt/rp/HlxqGYDcRkr3z4OrOKvm/PzzDgIDQ3nuOdOmLzIXqVRK\np07dLD2MJ8riQ2mcTcqgsc8BAC4kt2NlnIwxrU2TAjEgwJfY2F10eTx+xQTBYJKKZgclEklUbGxs\nbFRUVA0PSaiNjh8/zK1bV+jYsbVJ2z1w4Bj29u507NjVqPPT0+/yv/99TXR0T5OvrRTMLz7+Anfv\nptGxY9uqD65Ezp0idv7zClAcvNbEelV9rFu3jdDQJrRr11Gv4wvVeRxN2AxAq3p9sJaXn2dVeLxM\n33Od+OQv8HC8AcCdLH+CnScztk35y98eXQYglyoqXAZw3/Llm5g06Z0KHxeE2i4uLo5mzZo10+l0\ncY8+JlZjC3pp0aI1ly5dQ6UybSnFdu1aEht7hPT0u0adX6eOG1988Q1JSdksWrSepUvXc/Om6Xfd\nCuYRERHKuXOXql3dyt5DQfTMcKJnhteaQHX16s1ERDQzKFBdePhdfrswj98uzGPh4XcpVJdNWSc8\nfsK8D5YEqgAejjcI8z5Y4fH21s6MbvYV9ZzDqeccXmWgCjyxFeIEAUSwKhjglVdGsX79LyZvd/jw\naGbNmmb0m62VlRW9evXjrbc+YOzYN7l06Tbff7/A6LKiQs3q3bsr27b9ZulhmNSKFT/TrFlrnn22\nnd7nHE3YzK3MB+vOb2VeLJllFR5vCnnZj1pFFds07K2diY54k+iIN6sMVAEUChmpqU9y/mLhaSaC\nVUFv3t6+SCRWpKcblhu1KgqFgu7d27Nx46pqt2VjY8OAAS/Tu3c/Ll++aoLRCebm7+9LUlKKWQuD\n1JTi/MTraN26I82bm3bJjPD4alWvD85WD6qEedrXo6lXR5P20bdvd1EgQHhiiWBVMMjIkeP56afV\n5OSYtohDSEgQiYnXTdZew4ZhXL16o+oDhVqhQ4fW/P77IUsPw2g6nY5du/5g3ryV9OjRl8jI5lWf\n9IhW9frg49Sw5LaPU0Na1etjymEKFlKYBqrvOmM/bzAt7fszMOJtFHLTZkywsbHG1taKpKRbVR8s\nCI8ZEawKBrG2tubDD79gxYotxMaaNu2QUmlNVlamSdpycHAkP7/80rdC7RMaGsKlS39VfWAto9Pp\n2L37APPmraRhw0jef/8zQkLCjGrLWm5LTOtv6Ro6lq6hY4lp/a3YYPUEyErJY2rHn8m5KCX7tA2x\nE1woSjfPR2+/fj1YuXKJWdoWBEsSwapgMDs7e95//xMKC6UsWbKupMxidXXq1IZt2zaZpK1i5k+/\nJJhOYGAAf/2VYOlh6EWn07F37yHmzl1JcPAzvP/+ZzRu3LTa7VrLbekQPJgOwYNFoPqE2Pj+YVT5\nD1L0qQu07PzknFn6srKywtXVkevXr5mlfUGwFBGsCkbr2bMfAwcOZ9aspVy/nljt9jw83EhJuW2C\nkRWTSMSv9+Pk+efbs3v3H5YeRqV0Oh2//36YuXNXEBjYiA8++IwmTUR6P8FAF09DhnEZUKrSu3cX\n1qxZbpa2BcFSxKe5UC1eXsUlF0+evMz+/Yer3V6dOo5cvGiaWQepVPZEbNp5WkilUhwc7MjMzLb0\nUMrQ6XTs33+EuXNX4OfXkA8++JymTZtZeljCY6D/f1pjJX9w9clKWkgvvw1IF35rlv5kMhne3m5c\nuaJ/RUNBqO1EsPq3yMhITp8+DcDRo0dp1KhRyWPTp08nJqbiKkyW8ui4xo4dy4IFC2p8HFKplJEj\nx5GQkFztjVcvvtiV1auXkp9f/fySHh51SUtLr3Y7Qs3p3bsbW7futPQwSlGpVMycuQhv72A++OBz\noqJaWnpIwmPEsa4tE186SKDDBQIdLjA+fCoOCjOl1cvPQ/LLKnpzhy1rl5mnj/K6NcH7tSBU5okP\nVocPH87s2bOrvP/kyZM0adKkJodWpYSEBN59913atWtHZGQkXbp04aOPPuL69fJ3zc+bN4/Ro0fr\n3X5FPxtjxcSMZ+3arQCo1Wqj1rJKJBJiYl7mhx/+W+3xNGgQzpUrCdVuR6g5Dg72FBQUmjzbhLFU\nKhWzZi1m/Pg3ad78WUsPR3hMub3/LwZHrGdwyDIcFDnoFNZoY941bSf5eci+fRf5unnI1y9g4F+7\nOBd3xLR9VGDgwH78979fERd3rEb6E54+T3ywChXXOa+J+udarRaNRlP1gY+4ePEi0dHRKBQKVq1a\nxcmTJ1m/fj2NGjVi//79Zhhp9Tk4OOLu7sWpU/HMmLGYmTMXGRWwOjjY065dc1avrt7MQIMGoZw/\nf6VabQg1b+jQaObNW2bxJRz3A9XXXvsH7u4eFh2L8HiT1qmLcubvSCOfI8HJB/XXS8DFzaR9SPZu\nRnrtwaV/l/Tb3FxsnqUGj+rUqSPdu7fn9u3L/Oc/X7Jp0zqjPvcEoSJPRbCqj9DQUOLiypSjLdfi\nxYt54YUXiIqKolOnTnz33Xelqi+FhoayZMkSBgwYQFRUFGfOnCEiIoL09AeXpHU6HZ07d2bz5vIr\n1Hz99dc0btyYf//73/j6FieTdnJyYtiwYQwfPrzccx6eKb158yahoaFs2rSJXr16ERUVxejRo0lN\nTQXgyy+/JDY2llmzZhEZGckLL7wAFM+Izpgxgy5dutCyZUtGjhzJ5cuXS/qYMmUK77//Pp9++ikt\nWrSgQ4cOrF69uuTxIUNe5dKlRD755CsmTnybOXOWGVWZqlGjhhQUZPLnnycNPvc+Gxsb/P0DOXPG\nPDtvBfNQKm2Iju7NsmXrLDYGEagKpiatUxflp0vQvD2TbYdO10if7m4uJp3tVKvVJCZe5+DB31m5\ncgkzZ07lu+++pnfvfhw/fp6cnHzGjRuKr68zU6f+i/nzZ5GTU/vWoAuPH4sFq3/e2sOyY5+w4vhn\n3My4YNa+TD1D4+Xlxfz584mLi2PWrFmsX7+etWvXljpm/fr1TJs2jZMnTxIeHk7Tpk3ZuHFjyeMH\nDx4kJyeHHj16lGk/Pz+f48eP07t3b4PH9uhs8fbt21m+fDn79+8nLy+PH374AYDPPvuMZs2aMWnS\nJE6ePMn27dsBWLBgAZs3b2bevHkcOHCA5s2bExMTQ27ug8uyO3fupHPnzhw/fpxPP/2Ur776itu3\ni3fxy2Qyxo17A7lcjodHXUaMGMP8+SuN+j/o27c7W7ZsIDs7y+Bz74uOHsqRI2e4d880+VuFmuHv\n70NQkL9FCgWIQFUwp2eeiSQ3t4ikpBSTtqvr1Adt4IOiEtrAhtQb/Tq//mp8iWyVSsWmTeuYOvVr\npk//f8yZ8x2HD+9Cp8umdetGDB3amxEj+rN7905Gj55IcHAEs2YtxsurLmPGDKVLl1YsXDiL7777\nWqTTEqrFIsHq5TvH2BY/nYt3DnM+5SBrT/6L7ALzbYSZM2cOLVq0KPVH31nU8nTr1g0fHx8AwsLC\n6NOnD4cPl94JP2rUKPz8/JBIJCgUCgYNGsT69etLHl+3bh19+vRBoVCUaT8rKwuNRkPdunWNHuN9\nr7/+Os7Oztjb29O7d2/i4+MrPX7Dhg2MHTuWwMBAFAoFkyZNQiaT8fvvv5cc07p1azp16gRA165d\ncXBw4MKF8r9w+PvXo0+fgSxdur7cx6sSEzOIadP+a9Ts7H2TJ7/LkiXrq9WGUPPatm3F7dvJJCTU\nXCUyEagKNWH06NdYu3ZbtSdSdDodnyaq+OymmoU51mje/Rb1S2NRvzQWzbvfIrG1o0mTMA4fNiwl\nXGzsUaZO/YaZM/9LQEAdYmIGMnx4NK+8MoBu3Z4jIiIUZ2cnJBIJcrkclaq4AEvz5s/yxhvvsXjx\neuLjL+Ds7MTw4dEMH96PlSsXV+u5Ck83iwSrF+8cIU/1YLYsPe82f92NNVt/EydO5Pjx46X+REUZ\nnxtx69atREdH06pVK5o3b86KFSvIyMgodcz9YPa+7t27k5aWRmxsLBkZGezevZtBgwaV276joyMy\nmYzk5GSjx3ifu7t7yb+VSmWpGdLyJCcnlyw7gOKZWh8fH5KSksptU592Q0PDadfu+ZLNV4awtVXS\no0cH1q5dYfC591lbWzNy5DiWL99gdBuCZQwe3J9Nm3aQm1szu41Xr94iAlXB7GQyGUOHvsqGDcbP\nekLx+/P2TC3TUzT8lKoBpS26noPR9RwMyuKiEq1bN+PAgX16t6nValm9ejkjR0YzcuQg6tXzr/T4\n7OwcLl++UrJG1cHBkQ8//IK//komPr54EsPKygp7e3vjnqQgYKFg1dHGnYerC1nJbHC18634hFok\nKSmJ9957j0mTJnHw4EFOnDjB0KFDy8zaSaWlf7TW1tb079+fdevWsWnTJsLDw2nQoEG5fSiVSlq2\nbMm2bdvM9jzKGyOAp6cnN2/eLLmt1Wq5desWXl5eQPGbozGzAVFRLQgLa8rWrbsMPjc4OJDU1OoF\n7v7+9QgPb8offxytVjtCzZJIJIwdO5x585aafcNVYWEhWq1EBKpCjQgOboiVlR3XrpWf3UVfDrLi\nz9Jsja7C14i1ddkreBWRSqV4e/tUugE5P7+ALVt+46efVrNjx0E++eQrZDJZqWMGDRrKmTMPrrjV\nxIZm4cllkWC1Xf1BNPLqgJ3CGQcbN1oHDsDPxbh62vqo6AVszIdfXl4eOp0OFxcXZDIZp06dYtOm\nTXq9EAcNGsSOHTtYtWoVAwcOrPTYKVOmEB8fzyeffMLNmzfR6XRkZWWxcuVKliypuPazIc/Jzc2t\nTBqsAQMGMH/+fBISEigqKmL27NloNBqee+45g9t/VLt2HfHw8GP37gMGn6vTVf8S/vPP9+D27TRu\n3kyq+mCh1rC1VdK/f09WrDBuKYm+tm7dxcCBQ83ahyA87JVXRrFly55q7Zx3kYGvAgp1kF3B26RM\nJqGoqEjvNsPCIrh06a9S9xUWFrJjxz5++mk1mzbtpmPHnvzjHx8zduwkPD29yrShVNqiVj/8vESw\nKhhPbolOpRIZg5t9Rn5RNjKpHIVcadb+jEld9fBjEomk5Hb9+vV54403eO2111CpVLRq1YrevXtX\nuGbzYUFBQURERHDu3Dl69epV6bENGzZk3bp1zJgxg8GDB5Obm0udOnVo06YN48aNKzOuisb96GMP\n3zdy5Eg++ugjWrRogaenJ1u2bGH06NEUFRUxatQocnJyCAsL46effsLOzq7CPg3RrVsvNm1ay8GD\nx2nbtoXe55lqVm3s2Nf55psv6dXrOQIC/EzSpmB+AQF+7NlzAJ1OZ5YZGq1WS0ZGDl5ePlUfLAgm\nIpVKGTVqPKtWrWbYsP5GtbGhgQKdTkeRDqyl5b826tZ1IynpJgEBQXq12blzN2bN+pagoAD27z9C\nQsItbGxs6dGjN0FBIQaM7uHPIwNOE4RHSCoKAiQSSVRsbGxsddZ2CmVNmTIFhULBl19+aemhWNSq\nVUtwc7OjeXP9CjGsXbuFIUPGYG/vUO2+tVotixfPw9paQs+enavdnlAz9u49QGCgf5Vr6Izx66+/\n88wzrQkNDTd524JQlfXrV+Dl5Ux4ePlLw6rr7NmL6HT2tGv3nN7nzJs3g8LCQp5/vgdhYY2qPqEc\nM2Z8yyuv9ANgxYrNvPbaP4xqR3g6xMXF0axZs2Y6na7MDniRZ7UGXb16lZ07dzJixAhLD8XiBg8e\nQWLiXc6cOa/X8YGBfly6ZJoUZ1KplJiY8YSFRTFr1pIa27wjVE+zZk04ccI8+Slv3kwRgapgMdHR\nQ9m79wiXkvPp/UMO48cnsPP7q6g2rkbyyyowopxpkbqAY4k7OJa4AzcPJxITDVsbO3bs67z++jtG\nB6oAEonsoatiYmpVMJ5FlgE8jSZPnsyBAwcYP348wcHBlh5OrRATM57Zs7/HxsaakJDKL08FBQVw\n7NgFoqL0XzpQlcjI5jRoEMrMmd/RunVTGjcWwUpt5ujoQHa2eWqq29jYmKVdQdBXj4Hj6T8nhRf2\nXcU9PZ8zR+GurYQhIYuwit2P5t1vS3b4V6VIXcDa+Kkk5yQAcJBYHNMizDf4Cvj4+JKQcIPAwIAa\n71t4soiZ1Rryww8/EBcXx4QJEyw9lFpl4sS32LGj6vKxdeq4kJaWavL+7ezsef/9zzh40Hyp0wTT\nMd+OYjHrI1jWmz/nEHolHff0/JL7kvL8iEttifTaRSR7y692WJ5TSftKAlUALTc4LCkip7BmS6D2\n7NmXEyfO/51nW7zGBOOJmVXB4tzdPdBqteWm0nqYKTIClOfMmdOEhxuyaUCwlOKcvnnY2ek3wyQI\nTyuFSkvk+eLKfSfDnMjW2LD4UBqTOtVcajaFQsHYsa+TlpZKVpaoIigYT8ysChbn5ORMZmbVJVXN\nFazu3r2Tdu1amqVtwbSiohpz8uQZk7ZZvKZOzPoIlrU4JoCLIW6k1nmQHcfLNpEo92NoAxui69RH\n77aaurRk8PZUOp1Io9OJNKK3pnLjVjNzDFsvrq7uBAaK5W+C8USwKlicu7s7GRlVf+s2R1J4jUaD\nRlNU5ayuUDsEBwdy5Yppa4yrVCoUCiuTtikIhqrvbsOeKaFcGBDOpRae2D1XwKD3dMheftWg9aoA\n1vt/xftudsntgIxsRmdu5dU2ruYYuiCYnfiEFiyuTh030tMzqjzOxkZBXl7l5WINtXv3Ttq0sdyM\ng2AYiURSplpcdeXnF2JjY95cz4Kgj/ruNvz+SThr1nbFs6OW21FtSpVO1ZuqbAGAKGUC9taycg4W\nhNpPBKuCxbm7e5CeXvXMalCQH2fPmvYScHz8acLCxHrVx0nduu7cuHHLZO0VFBRga2tnsvYEwRRe\nfXUsmzbtQq1WG3V+oUbB4eR2HE5uR6FGgVxqnmVUglATRLAqWJyrqxv37lW9ZjUysjEHDvxusn5z\nc3NQKMRMw+OmR4/O7Nixx2TtFRQUoDR05koQzEwqlTJ27GusXPmzwecWaa1ZeTmGfbd7sO92D1Ze\njkGVbVzQKwi1gQhWHxEaGkpcXJniCRYzfPhwZs+ebelhmJVMJtdr9kAmkyGRaCgsLDRJv0ePHqRp\nU5Fb9XEjk8lwcnLUa+mIPtRqDXK5+NIi1D5eXj4EBTUkLs6wK0onU1uSlPegnHRSnh/aeDtunDxk\n6iEKQo14KoJVcwZ806dPJzw8nMjISCIjI2nXrh2fffaZyQIqMGduydrh5MnjeqeO6tatAxs3rjFJ\nv+3b///27jyqqWv7A/j3JiEkzIiigjhUFIqijAoWB0RalVfBARUERLFOVbSPJ8/62r6+ttbfetW+\nOlcrVRzQCk5gtbaKIFbEiNQqIqIFZRAcEIQwmeT+/rAFozJpkgthf9ZiLXLvuTmbKeyce87Zo5GW\nlqGS52qpvNx7WB14DKsDjyEv955G+9YmEya8g/j4Eyp5LmNjQ5SVqSbxJUTVfHwm4vffcyCR/Nby\ni3SELxxiAAj/b5bqAiNEgzpEsgqoN+Fzc3NDRkYGMjIycODAAfz222/YtGmT2vrTNpcvZ7S4JraF\nRTcUFraubGBjdHR0YGLSssVdqpCXew+x064D10yBa6aInXadEtZXJBaLwDAMqqqqm2/cDGNjI0pW\nSZu2dGkkdHRMsHnzLly5cq3Z9g5Tu6GrXkH947+2wNJRPFFnmISoDWfJKiuXQZ5zGfL8HLVsSdSY\noqIihIeHw8PDo34UVCpVXmF+5coV+Pn5wcnJCSEhIbhz506Tz/ls/F27dsVbb72FGzdu1B972cju\ns9MNrl27hoCAALi4uGDo0KGYPn06Kioath0pLy9HeHg4nJyc4O3tjVOnTr3y198W1dXVQCh8cSSg\nMVZW3ZGdnaWSvgMDZyIm5rBGfgfj/nURTF3DFklMnQ7i/nVR7f1qK1/fsYiK2gO5/PWq8ujo6ODJ\nE/onTtq2UaPGYPnyT1FVxcPmzbuaXGQo1OfDJ7gQoyx+wiiLnxDQbzt0+XWQj/RXeVxyuRxVVVJU\nVDxGWVmpynfrIATgKFlla2tQ858g1KyYiJplf0PdhmUaSRZqa2sxc+ZM9OvXD4mJiTh27BiKi4ux\ncuVKpXaxsbFYv349UlNT0a9fPyxYsKDFf4CFhYU4e/YsXFxclI43NbL72WefYfjw4ZBIJDh37hxW\nrFgBgaChuNihQ4cwe/ZsXLp0CTNmzMDy5ctVOs2AayzbumTDy8sDx48nqKRvsVgPU6bMwIYNO1BW\nRhVW2hMTE2NMnOiDqKg9OHLk+GsmrZp7w0zIq2IYBu+88zf885//xvHjSU227RQ6F06DbsO921no\n8utQ1/UNdAn7WOUxrV69Ert3b8X+/dtx8OAubNu2UeV9EMJJslp3YAMUV1MBuRyoq4HszGHIr6h3\n4jfLsjh9+jQAYPHixRAKhTAyMkJ4eDgSEhKUkuVZs2bBysoKurq6WLZsGe7cuYPff/+90eeWSCRw\ndXWFs7MzvLy8oK+vj0mTJrU4Nh0dHRQVFaGoqAh8Ph+DBg2CWNyw76OPjw8cHBwAAFOnTkVFRQXy\n8vJa+R1omx4/LodYrNuqa/h8PuTyJyp7B29ra4fIyE9w8OAJXLigvjmsU1a6gBU2jOCxwieYstKl\niStIc3r06I65c0Pg5DQYUVF7EB//0yslrRq8uUPIa+PxeBgwYBBu3LjVeCOxHnj/3gTZlPdw4Q03\nmHydAEZsoPJY9PTEmDr1XUye7INJk3wgl9ehuPiuyvshHRs30wCkz21TJH8ClD1Qe7eFhYW4e/cu\nXF1d6z9mzZoFHo+H+/fv17eztLSs/1wkEqFTp04oLi5u9HmHDBkCiUSC9PR0pKenw97eHgEBAS2+\ntbhq1SooFAoEBgbCy8sLa9euVfqH26VLl/rP9fSebrHz/NSF9koiScXgwa1fke/gYIu0tF9VFoeu\nri7+/vcVkMuF2LUr7rVvLb9M7z7m8P/BFrB7BNg9gv8PtujdR3N1urWZlZUF5s4NgaPjIERF7UFC\nwolW/Qxra19/7ishmjR+vC+Sks433UisB3b8dGT2dlVLovqU8qDBlCnjsXPnNjX1RToqTpJVgedk\nwKx7/WOmpy34zp5q79fCwgK9e/eGRCJR+rh8+TLMzRuShoKChonp1dXVKC0tRbdu3Rp93mdHZfX1\n9eHv74+8vDzk5OTUH6uqqqpvU1JSonR9jx498OWXXyI5ORmbN29GbGwsjhw58tpfb3tw/fo1WFv3\nafV1Tk6DkJam+tH4ceN8MXFiIDZs2IG7d0uav6CVevcxxz9ixuMfMeMpUVWDv5LWwYMH1o+01tW9\nWM3neba2fSGRpGogQkJUg8fjwcqqDwoLmx7FfPiwFCKRevYRVigUYFnlZFVHRwf9+vXCxYvNJNKE\ntAInySrfejBEf18P/mh/CMZMh+jjnWD0jdTaJ8Mw8PT0xJMnT7BlyxZUVlaCZVmUlJTg5MmTSm2j\no6ORn5+P2tparFmzBj179sTgwYNb1E91dTXi4uKgTEnh1gAAEjNJREFUp6eHnj17AgAGDhyIkydP\norS0FJWVlfjmm2+Urjl06FB9AmtoaAiBQKBUq16TC9A0TS6XKX2tLcUwDFhWrpYR0B49euKjj77A\n6dMXkJioutFbojk9e1pi7twQODsPRkzMQWzbtqfJW6bu7s5ISjrZ6HlC2qIpUwIQH/9Lo3fxTpxI\nxk8/nUVIyBy19H/vXjE6d+70wnFPz2E4ceIoLbYiKiNovol68N90Bf9NV431xzAMRCIRoqOjsWbN\nGowfPx5SqRTm5ubw8fHBmDFj6tv6+/tj0aJFyM/Px4ABA7Bp06ZGF0gxDIMLFy7A0dERwNN3lTY2\nNti6dSsMDJ7edgkNDUV2dja8vb1hZmaGiIgIHD7cUJUkLS0Na9asgVQqhZGRESZMmAA/Pz+lPrSV\nXM7i1q089O3bu9XXurgMxLlzZzB8uOpH5fl8PhYu/AApKaexdetuhIZObdWOBaRtsLTsjtDQ6VAo\nFEhJOY/k5FSYmBhh3DgvGBg0lFhlGAaWlua4desG+vZt2TZqhHBNR0cHPj4TcfDgSchkdWBZFiwr\nB8sqUFEhxbhxEzBt2hC19X/z5g306tXjpefeeWckDhzYB3//QLX1TzoOprFRO4ZhnNLT09OdnJw0\nHJLqTZw4EQEBAZg6dSrXoZDnKBQKREdvhampPkaNcm/VtSzLYufOQ1iyJFJN0T1VXHwXBw/uQWCg\nX/ONSZtXWvoIP/2UiMrKKhgbG6GmpgYA/rzT8girVq3hOEJCXs/T2/Ms+Hz1VmbbseM7jBkzROmN\n37O2bYvBwoUR0NN7+XlCnnXp0iU4Ozs7syz7QhlRzkZWNSUrKws5OTktvo1PNIvH42HWrPk4ffpn\n7NoVh6CgyS0eSWYYRiNlMrt16w6FgkFlpbTRF2XSfnTqZIrAwMlgWRZVVdXQ0xODYRhcvpwJlqWf\nL2n/XmVq1auQSiuafE30938X33//LRYtitBIPER7aXUFqw8++ADz589HREQEbGxsuA6HNMHT8228\n++5UrF+/HRUVlVyH84KgoNk4dOg412EQFWIYBvr6evVvjiSSKxgxYjTHURHSflhYWCA+/kSj6yqM\njQ0hFgtw+3auhiMj2kark9X//e9/SE5OxqxZVA+5Pejd+w0sW/YRoqJ+aMUG/ZqZz2tiYgqBQITy\n8ormG5N2p7z8MUxNzTQ2IkWINpg4cTqGDh2NjRujkZPzx0vb+PmNRWxsjIYjI9qGXplJmyIW62HF\niv9gx444PH7cdGLIsqxGF5+FhMyh0VUt9eOPiZg6dQbXYRDS7tjYvIkVKz5DXt4DbN/+A6qra5TO\n8/l8CIXqn65FtBslq6TNEQqFWL7834iK+gFSaVWj7WpqaiEWq2f/wJfR1zeAgYEJSksfaaxPon4s\ny6K6ug6GhurdPo8QbcXj8eDvH4jQ0Pn4/vt9L5wXCnVQVaUdhWwINyhZJW2SSCRCZORH2Lp1zwvv\n1P9SXv4YxsYmGo0rKGgWDh8+odE+iXqlpKRhzJixXIdBSLtnamoGL6+xSElJUzpua9sXV65c5igq\nog0oWSVtlr6+ASIiVmDLlt0vrUKkr6+HnJwsrFv3FXbtikJu7k21xyQSidGpkznu3VN/eWCiGTdu\n5GLw4Pa/RR8hbYGbmweysv5Qes22sbFGZiYlq+TVUbJK2jQjI2MsWbIM3367GzKZTOmcoaEB5s0L\nQkjIRAwf7gCJJBnffLMKe/fuUGtMgYGhiIk5RNVZtEBRUTEsLXtxHQYhWiU0dC727z9a/1gsFqG6\nuvEpXYQ0h5JVNbh48SJsbW056bugoAC2trb15Vu1gampGRYsWIrNm3c2Wl7VxMQYb789EqGh/qis\nfISCgjtqi0coFCIsbCG2bYvR6lK4HcHPP5/BpEnTuA6DEK1ibt4VhoamKCy8W39MoVB9aWzScWh9\nshocHAx7e3s4OjrC2dkZEyZMQHx8PKcxrV+/HnZ2dnB0dISjoyO8vb2xceNGTmNq67p0Mcd77y1G\nVNSLk/efN3HiOMTE7FBrPFZWveDjMwkxMYebb0zapCdPnoBhBNDV1eU6FEK0TlDQbBw58jOAp+sL\ncnNvcxwRac+0PlkFgPfffx8ZGRm4cOECJk+ejOXLl+PWrVucxuTm5oaMjAxkZGTg888/x9atW3Hg\nwAFOY2rrunXrDi+vsTh2LLHJdgKBAHZ21jh//qxa4xkwYBAcHYciIeEXtfZD1CMpKRU+Pr5ch0GI\nVuLz+Rg9+h2sW/c9Tp1Kw6effsl1SKQd6xDJ6l/4fD78/f2hUChw82bDYpwPP/wQo0aNgpOTE3x8\nfHD0aMNcm7S0NNjZ2eHYsWPw9vaGi4sLli5dCqm0YRuOvLw8BAcHw8nJCb6+vrh69WqzsTx7+9jN\nzQ3W1tbIyspCSUkJwsLC4O7uDhcXF8yYMQOZmZn1bdevX/9CkYPg4GBs3rz5lb4n7Y2z81AoFIJG\nN6D+i4fHECQmnlD7vNJhw0agc2cLJCenqrUfonqFhSWwtqbKdoSoi5ubBz755EvMnr0ARkbGXIdD\n2jHOktXLR3Kxe85p7JmXhILL6l1Z/VdiWFdXh71790IoFGLAgAH1552dnXHkyBGkp6fj/ffff2Hk\nVaFQ4Ny5c4iPj8eJEyeQlZWFXbt2AQBkMhnmzZuH/v374/z581i3bh327dvX4s3qFQoFUlNTkZOT\nA3t7eygUCgQFBSEpKQnnzp2DnZ0dFi9e3Ohczb9ocnN8rgUGhuLnn39FVVV1k+3Gj/fE/v171B7P\nuHG+qKpSICOj+TcppO3g8Wij8vbifNpVrHDdhBWum3A+jf7OCOloOElWc5KL8OOnElw/WYCsE/nY\nH34WFfebTjxex7fffgtXV1c4ODhg3bp12LJlC3r06FF/fsqUKTA2NgbDMBg/fjxsbGyQlqa8T1xE\nRATEYjHMzMzg5eVVP3p6+fJlFBUVITIyEkKhEL169UJYWFizC28kEglcXV3h7u6OlStXYsmSJfD1\n9UX37t3h6ekJXV1dCIVCLFmyBEVFRcjLy1P596W94vF4CA+PwPbt+5ts17t3TxQW3tbIZtQBATNx\n/Xoebt6kGtjtgVRaBQMDQ67DIC1wPu0qEqang3ffELz7hkiYnk4JKyEdDCfJ6vVTBah6VFv/uPR2\nBW6lFKmtvwULFkAikeD8+fMYMWKE0mImlmWxdu1ajB07Fi4uLnB1dUV2djYePWqoUsTn82Fqalr/\nWCwW108DKCkpgZmZmdIiDUtLy2ZjGjJkCCQSCdLS0nD06FGEhYUBAEpLSxEZGQlPT084OzvD09MT\nAJTiIYChoREmTJiMI0ea3qB/yhQf7Ny5TSMxzZsXjsTENBQX39NIf+TVXbx4GcOGjeQ6DNIC8YvO\ngGEb/lUxLA/xi85wGBEhRNM4SVaNuusBz9y11tETwKyP+uezGBkZ4YsvvsCNGzfqdwRISEhAXFwc\nNmzYgIsXL0IikcDGxqbFWxKZm5vj4cOHqKlpqLJUWFjY7HWNPf/XX3+NBw8eIDY2Funp6UhKSlJq\nr6+vj+pq5VHoe/c6ZnJkb+8AkcgYmZnZjbYxNjaETFaLhw/vqz0eHo+HiIgPsX//jygvr1B7f+TV\n5ebmo39/braXI4QQ0jqcJKvD59ph4Phe0O8sglE3MdxDbWHl2Flt/T2bGBobGyM0NBQbN26EXC5H\nZWUlBAIBTE1NIZPJEBcXh+zsxpOf5zk4OMDCwgKrV69GbW0t7ty5g+3bt79yrFKpFCKRCEZGRpBK\npfjqq6+Uzg8cOBCZmZnIzMyETCbD7t27W5Qca6tp04KQkiJBRUVlo22mTPHB7t2v/jNpDT6fj8jI\nj/H99/tQW1vb/AWEEzyeADxeh1pf2m5N2DACLNOwUJJlFJiwYQSHERFCNI2TV2sen4fpG0dg6akJ\nWJroi7cjHdXa3/OLj0JCQlBWVoYjR45g0qRJGDRoELy9vTFy5EjcunULLi4uTV7PMEz9MYFAgM2b\nNyM7Oxvu7u4IDw/HtGnTmlzw9Oz1zwsPD0dpaSmGDh0KPz8/ODk5QSAQ1J8fMmQIZs2ahTlz5mD4\n8OF4+PAhnJyUS0V2pMVWALBkSaRStZTniUS6MDQUIT9fM/v8iUQifPDBcmzZspuqXLVBtbW10NUV\ncx0GaSG3oQPx7j5nKLpUQNGlAu/uc4bb0IFch0UI0SCmsdvRDMM4paenpz+fCBHSFq1b9xVCQiY2\nel4mk2H79jgsW/aRxmIqLMzHwYMxCA6erLE+SfPOn09Ht27WcHBw5joUQgghf7p06RKcnZ2dWZa9\n9Pw5ug9GtEKnTmYoKytv9LxAIIC5uYlay7A+z9LSCl26WODWrTyN9Umal5OTB3t7B67DIIQQ0kKU\nrBKt4OExChcu/NZkG6m0BmZm6psb/TJTp87AsWOnW7xgj2gGn097rBJCSHtBySrRCr17v4GiosZ3\nRVAoFHj8WAqxWE+DUT3dISAgIKTZLbaI5nS0Od2EENLeUbJKtEZjFYlKSu5jw4YdCAgI0XBET1lb\n26CmRo4HDx5y0j95HiWrpGOQyWTIz7+NM2cSkZJyWmmLRULaE0HzTQhpH4RCEerq6iAUCuuPJSWl\n4u7dh1ix4jOlXRU0LSxsIVav/hwLFnCTMJNnUbJK2h+ZTIbq6ipUVVWhuloKqVT65+dVqKh4jMLC\nAjx58nS7PIVCDuDp1KOuXTvDysoCcrkcUVHrIZcrwDB89OtnCw+PkVTJjbQLlKwSreHsPAS//34N\nLi4OqK2tRXR0HIYNGwk/v2CuQ4OOjg48Pd9GcnIqRo505zqcDo2mAZD24I8/crB3704YGRmAZRXg\n8XgQi0UQiXQhEulCLBb9+VgEKytTuLr2V3qj/jIDBz4thMGyLPLy7iAmZhuqq2vBMHxYWfXCiBGj\nNT6vn5CWoGSVaA1HRxesXZuIrKw/UF1dg/feWwRTUzOuw6rn5uaB1auT4erqAD092ueTK5Sskrbs\n8eNyxMXtBcvWYuHCELX8vjIMgz59eqFPn171x4qKipGQsA/l5RUwNjZDSMgcKpxB2gxKVonWEAgE\niIhYwXUYTZo7dxG++249wsKmcx1KB0bJKmk7ampqkJJyGllZmWBZGfT1RRgxwg3m5pod4bSw6AY/\nv7EAgDt3CvDFFx9jwYIl6NLFvNlrS0sf4vjxBNy/X4y6ujr07dsPfn5TadcNojKUrBKiQUZGxrCx\nscOVK9dgb2/HdTgdztPqVbpch0E6MLlcDokkFenpFyCXPwGfz4Or6yAEB/u2mVH/nj17YP78GYiO\n/hZubiPg4TFK6bxCoUBWViaSk0+irq4GBgZijBrljs6dPQAAubm3sXr15+jXzxa+vv6UtJLXRhWs\nCOHAypWfYP78GfQirmF375YgO7sIfn7+XIdCOqCkpJNITT2DoUMdMHjwgHbx93/q1Fk8ePAYM2fO\nRVLSSVy/ngmFQg5r655wc3Nqcp7sH3/cxi+/pMDe3hFjx75L0wpIk5qqYEXJKiEcKCzMR0LCfkyf\n7st1KB1KZmY2AAO89dZIrkMhHcj169dw6NAPcHGxh6tr+6ueVlBwF4mJZzFsmAusrfu0+vrMzGyc\nOSOBt/dYuLi4qSFCog2aSlZpGgAhHLC0tIJYbIT8/CJYWVlwHU6HUVr6CP37t/6fLSGv4v79e4iO\n/g4WFp0xf35Qk7f56+rqcPt2AcrKylFWVoHy8seoqqoGwMPTy5j6j19/PYd1675odvW/qvTo0R0h\nIa9+N2LAABsMGGCD5ORUnDp1AtOmBaN37zdUGCHRdpSsEsKRoKDZ+O9/P8OCBdxvrdVRPHpUjs6d\nm18wQsjrio8/gNzcGwgO9mt2nnRNTS02bYrGqFFe6Ny5D2xsOqNTJzPo6ekr3TqXy+VYs+ZLfPjh\nYo0lqqo0cqQ7PDyGICHhGMrKpJg5c06b2rGFtF1NJquXLr0wEksIUSEDAxMcPnwcffr05DqUDuHq\n1Wy8+WYubt++w3UoREtVVDxGbOxeODjYwMHBDtev32yyfW1tHWJjjyI4eDYMDAzBssCDB6V48KBU\nqZ1MJkN09DaMHu2GsrLHKCvLVOeXoVZ9+lihpqYWq1Z9Cl1dffj4+LXL5JuoVlZWVqPnGp2zCjyd\nt6qOgAghhBBCCHnOdZZlq54/2GSySgghhBBCCJdoHwlCCCGEENJmUbJKCCGEEELaLEpWCSGEEEJI\nm0XJKiGEEEIIabMoWSWEEEIIIW3W/wMD0sFBWOUhZQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7ffb1ade86a0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot = plt.axes(projection=albers_equal_area)\n",
"\n",
"plot.set_extent((-125, -66, 20, 50))\n",
"\n",
"plot.add_feature(cartopy.feature.LAND)\n",
"plot.add_feature(cartopy.feature.COASTLINE)\n",
"plot.add_feature(cartopy.feature.BORDERS)\n",
"plot.add_feature(states_and_provinces, edgecolor='gray')\n",
"plot.add_feature(cartopy.feature.LAKES, facecolor=\"#00BCD4\")\n",
"\n",
"candidate_groupby = df_place.groupby('candidate', as_index = False)\n",
"\n",
"colors = ['#1976d2', '#7cb342', '#f4511e', '#7b1fa2']\n",
"for index, (name, group) in enumerate(candidate_groupby):\n",
" longitudes = group.longitude.values\n",
" latitudes = group.latitude.values\n",
" plot.scatter(\n",
" longitudes, \n",
" latitudes, \n",
" transform=plate_carree, \n",
" color=colors[index], \n",
" label=name,\n",
" zorder=2\n",
" )\n",
"plot.set_title('U.S. Tweeters by Candidate', family='Ubuntu')\n",
"plt.legend(loc='lower left')\n",
"plot.figure.set_size_inches(12, 7)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As expected, U.S. tweeters are centered around L.A., the Bay Area, Chicago, New York, and Boston. Rand Paul and Bernie Sanders tweeters are more spread out over the country."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's all I have for now. \n",
"\n",
"If you found this interesting and are curious for more, I encourage you to download the dataset (or get your own dataset based on your interests) and share your findings.\n",
"\n",
"Source code is at https://github.com/raj-kesavan/arrows, and I can be reached at [email protected] for any questions, comments, or criticism. Looking forward to hearing your feedback!"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
flaviocordova/udacity_deep_learn_project | gan_mnist/Intro_to_GANs_Solution.ipynb | 1 | 218986 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Generative Adversarial Network\n",
"\n",
"In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!\n",
"\n",
"GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:\n",
"\n",
"* [Pix2Pix](https://affinelayer.com/pixsrv/) \n",
"* [CycleGAN](https://github.com/junyanz/CycleGAN)\n",
"* [A whole list](https://github.com/wiseodd/generative-models)\n",
"\n",
"The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.\n",
"\n",
"\n",
"\n",
"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can foold the discriminator.\n",
"\n",
"The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"import pickle as pkl\n",
"import numpy as np\n",
"import tensorflow as tf\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting MNIST_data/train-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/train-labels-idx1-ubyte.gz\n",
"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"from tensorflow.examples.tutorials.mnist import input_data\n",
"mnist = input_data.read_data_sets('MNIST_data')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model Inputs\n",
"\n",
"First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def model_inputs(real_dim, z_dim):\n",
" inputs_real = tf.placeholder(tf.float32, (None, real_dim), name='input_real') \n",
" inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z')\n",
" \n",
" return inputs_real, inputs_z"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator network\n",
"\n",
"\n",
"\n",
"Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
"#### Variable Scope\n",
"Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.\n",
"\n",
"We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.\n",
"\n",
"To use `tf.variable_scope`, you use a `with` statement:\n",
"```python\n",
"with tf.variable_scope('scope_name', reuse=False):\n",
" # code here\n",
"```\n",
"\n",
"Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.\n",
"\n",
"#### Leaky ReLU\n",
"TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can use take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:\n",
"$$\n",
"f(x) = max(\\alpha * x, x)\n",
"$$\n",
"\n",
"#### Tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):\n",
" with tf.variable_scope('generator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(z, n_units, activation=None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum(alpha * h1, h1)\n",
" \n",
" # Logits and tanh output\n",
" logits = tf.layers.dense(h1, out_dim, activation=None)\n",
" out = tf.tanh(logits)\n",
" \n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator\n",
"\n",
"The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def discriminator(x, n_units=128, reuse=False, alpha=0.01):\n",
" with tf.variable_scope('discriminator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(x, n_units, activation=None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum(alpha * h1, h1)\n",
" \n",
" logits = tf.layers.dense(h1, 1, activation=None)\n",
" out = tf.sigmoid(logits)\n",
" \n",
" return out, logits"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Size of input image to discriminator\n",
"input_size = 784\n",
"# Size of latent vector to generator\n",
"z_size = 100\n",
"# Sizes of hidden layers in generator and discriminator\n",
"g_hidden_size = 128\n",
"d_hidden_size = 128\n",
"# Leak factor for leaky ReLU\n",
"alpha = 0.01\n",
"# Smoothing \n",
"smooth = 0.1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build network\n",
"\n",
"Now we're building the network from the functions defined above.\n",
"\n",
"First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.\n",
"\n",
"Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.\n",
"\n",
"Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"tf.reset_default_graph()\n",
"# Create our input placeholders\n",
"input_real, input_z = model_inputs(input_size, z_size)\n",
"\n",
"# Build the model\n",
"g_model = generator(input_z, input_size, n_units=g_hidden_size, alpha=alpha)\n",
"# g_model is the generator output\n",
"\n",
"d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, alpha=alpha)\n",
"d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, n_units=d_hidden_size, alpha=alpha)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropys, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like \n",
"\n",
"```python\n",
"tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
"```\n",
"\n",
"For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`\n",
"\n",
"The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
"Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Calculate losses\n",
"d_loss_real = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, \n",
" labels=tf.ones_like(d_logits_real) * (1 - smooth)))\n",
"d_loss_fake = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, \n",
" labels=tf.zeros_like(d_logits_real)))\n",
"d_loss = d_loss_real + d_loss_fake\n",
"\n",
"g_loss = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,\n",
" labels=tf.ones_like(d_logits_fake)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So we need to get the variables for each part build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.\n",
"\n",
"For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables to start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance). \n",
"\n",
"We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.\n",
"\n",
"Then, in the optimizer we pass the variable lists to `var_list` in the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"# Optimizers\n",
"learning_rate = 0.002\n",
"\n",
"# Get the trainable_variables, split into G and D parts\n",
"t_vars = tf.trainable_variables()\n",
"g_vars = [var for var in t_vars if var.name.startswith('generator')]\n",
"d_vars = [var for var in t_vars if var.name.startswith('discriminator')]\n",
"\n",
"d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)\n",
"g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/100... Discriminator Loss: 0.4509... Generator Loss: 3.0922\n",
"Epoch 2/100... Discriminator Loss: 0.4521... Generator Loss: 3.3643\n",
"Epoch 3/100... Discriminator Loss: 1.1145... Generator Loss: 2.0269\n",
"Epoch 4/100... Discriminator Loss: 1.2234... Generator Loss: 5.3097\n",
"Epoch 5/100... Discriminator Loss: 0.9824... Generator Loss: 2.4857\n",
"Epoch 6/100... Discriminator Loss: 0.6849... Generator Loss: 4.9342\n",
"Epoch 7/100... Discriminator Loss: 1.3959... Generator Loss: 1.4954\n",
"Epoch 8/100... Discriminator Loss: 1.4697... Generator Loss: 4.1061\n",
"Epoch 9/100... Discriminator Loss: 1.3477... Generator Loss: 3.5981\n",
"Epoch 10/100... Discriminator Loss: 1.6315... Generator Loss: 1.3647\n",
"Epoch 11/100... Discriminator Loss: 0.9667... Generator Loss: 2.9019\n",
"Epoch 12/100... Discriminator Loss: 1.7558... Generator Loss: 1.9616\n",
"Epoch 13/100... Discriminator Loss: 1.7716... Generator Loss: 1.9058\n",
"Epoch 14/100... Discriminator Loss: 1.6518... Generator Loss: 1.5656\n",
"Epoch 15/100... Discriminator Loss: 0.9880... Generator Loss: 1.5790\n",
"Epoch 16/100... Discriminator Loss: 1.2666... Generator Loss: 1.7686\n",
"Epoch 17/100... Discriminator Loss: 1.0612... Generator Loss: 2.1832\n",
"Epoch 18/100... Discriminator Loss: 1.1171... Generator Loss: 2.4456\n",
"Epoch 19/100... Discriminator Loss: 1.0664... Generator Loss: 2.0049\n",
"Epoch 20/100... Discriminator Loss: 0.9786... Generator Loss: 1.6016\n",
"Epoch 21/100... Discriminator Loss: 1.3682... Generator Loss: 1.6308\n",
"Epoch 22/100... Discriminator Loss: 1.1557... Generator Loss: 2.6635\n",
"Epoch 23/100... Discriminator Loss: 0.9550... Generator Loss: 2.0002\n",
"Epoch 24/100... Discriminator Loss: 1.0305... Generator Loss: 1.7659\n",
"Epoch 25/100... Discriminator Loss: 1.1000... Generator Loss: 2.0710\n",
"Epoch 26/100... Discriminator Loss: 0.9630... Generator Loss: 2.4943\n",
"Epoch 27/100... Discriminator Loss: 1.0380... Generator Loss: 1.6416\n",
"Epoch 28/100... Discriminator Loss: 1.0275... Generator Loss: 2.0813\n",
"Epoch 29/100... Discriminator Loss: 1.1164... Generator Loss: 1.9739\n",
"Epoch 30/100... Discriminator Loss: 0.8892... Generator Loss: 2.2403\n",
"Epoch 31/100... Discriminator Loss: 1.0110... Generator Loss: 2.0343\n",
"Epoch 32/100... Discriminator Loss: 1.1000... Generator Loss: 1.6957\n",
"Epoch 33/100... Discriminator Loss: 1.4025... Generator Loss: 1.0932\n",
"Epoch 34/100... Discriminator Loss: 1.0098... Generator Loss: 1.9229\n",
"Epoch 35/100... Discriminator Loss: 1.0641... Generator Loss: 1.7733\n",
"Epoch 36/100... Discriminator Loss: 1.0345... Generator Loss: 1.7005\n",
"Epoch 37/100... Discriminator Loss: 0.8535... Generator Loss: 2.2726\n",
"Epoch 38/100... Discriminator Loss: 0.8591... Generator Loss: 2.0769\n",
"Epoch 39/100... Discriminator Loss: 1.1413... Generator Loss: 1.4235\n",
"Epoch 40/100... Discriminator Loss: 1.3984... Generator Loss: 1.1456\n",
"Epoch 41/100... Discriminator Loss: 0.9506... Generator Loss: 2.2071\n",
"Epoch 42/100... Discriminator Loss: 0.9823... Generator Loss: 2.5504\n",
"Epoch 43/100... Discriminator Loss: 0.8836... Generator Loss: 2.0873\n",
"Epoch 44/100... Discriminator Loss: 0.9042... Generator Loss: 2.0568\n",
"Epoch 45/100... Discriminator Loss: 0.8294... Generator Loss: 2.0742\n",
"Epoch 46/100... Discriminator Loss: 1.2781... Generator Loss: 1.1468\n",
"Epoch 47/100... Discriminator Loss: 0.9042... Generator Loss: 2.0545\n",
"Epoch 48/100... Discriminator Loss: 1.2619... Generator Loss: 1.7359\n",
"Epoch 49/100... Discriminator Loss: 0.8223... Generator Loss: 2.0187\n",
"Epoch 50/100... Discriminator Loss: 0.9064... Generator Loss: 2.0313\n",
"Epoch 51/100... Discriminator Loss: 1.0697... Generator Loss: 1.7297\n",
"Epoch 52/100... Discriminator Loss: 0.8376... Generator Loss: 2.5357\n",
"Epoch 53/100... Discriminator Loss: 1.3334... Generator Loss: 1.3655\n",
"Epoch 54/100... Discriminator Loss: 0.8523... Generator Loss: 1.8732\n",
"Epoch 55/100... Discriminator Loss: 1.1794... Generator Loss: 1.6913\n",
"Epoch 56/100... Discriminator Loss: 1.0819... Generator Loss: 1.7088\n",
"Epoch 57/100... Discriminator Loss: 0.9776... Generator Loss: 2.3128\n",
"Epoch 58/100... Discriminator Loss: 1.0706... Generator Loss: 1.6848\n",
"Epoch 59/100... Discriminator Loss: 0.7647... Generator Loss: 2.4860\n",
"Epoch 60/100... Discriminator Loss: 1.0917... Generator Loss: 1.3422\n",
"Epoch 61/100... Discriminator Loss: 1.2628... Generator Loss: 1.2969\n",
"Epoch 62/100... Discriminator Loss: 0.9957... Generator Loss: 1.3618\n",
"Epoch 63/100... Discriminator Loss: 1.1555... Generator Loss: 1.1670\n",
"Epoch 64/100... Discriminator Loss: 1.0881... Generator Loss: 1.8223\n",
"Epoch 65/100... Discriminator Loss: 1.1534... Generator Loss: 1.9852\n",
"Epoch 66/100... Discriminator Loss: 1.1387... Generator Loss: 1.5949\n",
"Epoch 67/100... Discriminator Loss: 0.8727... Generator Loss: 2.5177\n",
"Epoch 68/100... Discriminator Loss: 1.4540... Generator Loss: 1.6328\n",
"Epoch 69/100... Discriminator Loss: 1.0361... Generator Loss: 2.0942\n",
"Epoch 70/100... Discriminator Loss: 1.0027... Generator Loss: 2.2991\n",
"Epoch 71/100... Discriminator Loss: 1.0430... Generator Loss: 2.3470\n",
"Epoch 72/100... Discriminator Loss: 1.0126... Generator Loss: 1.9801\n",
"Epoch 73/100... Discriminator Loss: 0.9988... Generator Loss: 1.9687\n",
"Epoch 74/100... Discriminator Loss: 1.0168... Generator Loss: 1.6237\n",
"Epoch 75/100... Discriminator Loss: 1.1100... Generator Loss: 1.6345\n",
"Epoch 76/100... Discriminator Loss: 0.9052... Generator Loss: 1.7472\n",
"Epoch 77/100... Discriminator Loss: 1.1249... Generator Loss: 1.7241\n",
"Epoch 78/100... Discriminator Loss: 0.8936... Generator Loss: 2.0298\n",
"Epoch 79/100... Discriminator Loss: 1.0929... Generator Loss: 1.8513\n",
"Epoch 80/100... Discriminator Loss: 1.0809... Generator Loss: 1.9343\n",
"Epoch 81/100... Discriminator Loss: 1.0059... Generator Loss: 2.1882\n",
"Epoch 82/100... Discriminator Loss: 1.1598... Generator Loss: 1.4602\n",
"Epoch 83/100... Discriminator Loss: 1.1491... Generator Loss: 1.4668\n",
"Epoch 84/100... Discriminator Loss: 0.9658... Generator Loss: 1.7634\n",
"Epoch 85/100... Discriminator Loss: 0.8389... Generator Loss: 2.3250\n",
"Epoch 86/100... Discriminator Loss: 1.0300... Generator Loss: 1.7529\n",
"Epoch 87/100... Discriminator Loss: 1.0931... Generator Loss: 1.5098\n",
"Epoch 88/100... Discriminator Loss: 0.9472... Generator Loss: 1.8881\n",
"Epoch 89/100... Discriminator Loss: 0.9540... Generator Loss: 2.0735\n",
"Epoch 90/100... Discriminator Loss: 0.9209... Generator Loss: 1.7510\n",
"Epoch 91/100... Discriminator Loss: 1.0731... Generator Loss: 1.6584\n",
"Epoch 92/100... Discriminator Loss: 0.9268... Generator Loss: 1.8312\n",
"Epoch 93/100... Discriminator Loss: 1.2169... Generator Loss: 1.1970\n",
"Epoch 94/100... Discriminator Loss: 0.8167... Generator Loss: 2.0158\n",
"Epoch 95/100... Discriminator Loss: 1.0919... Generator Loss: 1.4955\n",
"Epoch 96/100... Discriminator Loss: 0.9238... Generator Loss: 1.6834\n",
"Epoch 97/100... Discriminator Loss: 1.0673... Generator Loss: 1.5553\n",
"Epoch 98/100... Discriminator Loss: 0.9863... Generator Loss: 2.0410\n",
"Epoch 99/100... Discriminator Loss: 1.0105... Generator Loss: 1.4941\n",
"Epoch 100/100... Discriminator Loss: 0.9665... Generator Loss: 2.1574\n"
]
}
],
"source": [
"batch_size = 100\n",
"epochs = 100\n",
"samples = []\n",
"losses = []\n",
"# Only save generator variables\n",
"saver = tf.train.Saver(var_list=g_vars)\n",
"with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for e in range(epochs):\n",
" for ii in range(mnist.train.num_examples//batch_size):\n",
" batch = mnist.train.next_batch(batch_size)\n",
" \n",
" # Get images, reshape and rescale to pass to D\n",
" batch_images = batch[0].reshape((batch_size, 784))\n",
" batch_images = batch_images*2 - 1\n",
" \n",
" # Sample random noise for G\n",
" batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" \n",
" # Run optimizers\n",
" _ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})\n",
" _ = sess.run(g_train_opt, feed_dict={input_z: batch_z})\n",
" \n",
" # At the end of each epoch, get the losses and print them out\n",
" train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})\n",
" train_loss_g = g_loss.eval({input_z: batch_z})\n",
" \n",
" print(\"Epoch {}/{}...\".format(e+1, epochs),\n",
" \"Discriminator Loss: {:.4f}...\".format(train_loss_d),\n",
" \"Generator Loss: {:.4f}\".format(train_loss_g)) \n",
" # Save losses to view after training\n",
" losses.append((train_loss_d, train_loss_g))\n",
" \n",
" # Sample from generator as we're training for viewing afterwards\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\n",
" feed_dict={input_z: sample_z})\n",
" samples.append(gen_samples)\n",
" saver.save(sess, './checkpoints/generator.ckpt')\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll check out the training losses for the generator and discriminator."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x1247f6e48>"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAEICAYAAAB/Dx7IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4W0W6/78jWbbcHXc7dmI7vTuJkwAJvQcILAtL2QUC\nS7u7wAWWhb2/LZctlwUW9lKXcpfQ2ya0JRBaKmkkdroTpzl23HuTi6wyvz/eM9JRl2zJtpz5PI8f\ntXOksXTO97zznXfeYZxzSCQSiSR80Ax3AyQSiUQSGFK4JRKJJMyQwi2RSCRhhhRuiUQiCTOkcEsk\nEkmYIYVbIpFIwgwp3JJhhzGmZYwZGGPjgrmtRDJaYTKPWxIojDGD6mEMACMAi/L4Ls75u0PfqsHD\nGPsLgBzO+fLhbotE4o2I4W6AJPzgnMeJ+4yxCgC3c86/87Q9YyyCc24eirZJJKcC0iqRBB3G2F8Y\nYx8yxt5njHUB+Blj7HTG2HbGWDtjrI4x9hxjTKdsH8EY44yxPOXxO8rraxhjXYyxbYyx/EC3VV6/\nlDF2hDHWwRh7njG2hTG2fAD/0wzG2Eal/fsZY5epXrucMXZI+fxqxtgDyvPpjLEvlX1aGWObVPvk\nMMY+YYw1McZOMMZ+qXrtNMbYLsZYJ2OsgTH2t0DbKxndSOGWhIofAXgPQCKADwGYAfwngFQAiwFc\nAuAuL/vfCOD3AJIBnATw50C3ZYylA/gXgF8rn3sCwMJA/xHGWCSA1QC+AJAG4AEAHzLGJiqbvA7g\n55zzeACzAWxUnv81gHJln0wAv1PeT6O8304AYwFcCODXjLHzlf2eB/A3znkCgIkAVgXaZsnoRgq3\nJFRs5px/zjm3cs57Oec7Oec/cM7NnPNyAK8CONvL/qs458WccxOAdwEUDmDbywHs4Zx/prz2vwCa\nB/C/LAYQCRJTk2ILrQFwvfK6CcB0xlg857yVc75L9Xw2gHGc837OuYi4TweQwDl/THn+GIDXnN5v\nEmMshXPexTn/YQBtloxipHBLQkWV+gFjbCpj7AvGWD1jrBPAn0BRsCfqVfd7AMR52tDLttnqdnAa\nia/2o+3OZAM4yR1H8itB0TJAvYtlAE4yxjYwxhYpzz+ubLeWMXacMfZr5fnxAMYpFko7Y6wdwMOg\nqBwAbgUwHcBhxtgOxtjSAbRZMoqRwi0JFc7pSq8AOABgomIB/AEAC3Eb6gDkiAeMMQa72AZCLYBc\nZX/BOAA1AKD0JJYBSAdZIB8oz3dyzh/gnOcBuArAI4yxs0EXk6Oc8yTVXzzn/Aplv8Oc8+uV93sa\nwEeMMf0A2i0ZpUjhlgwV8QA6AHQzxqbBu78dLFYDmMcYu4IxFgHy2NN87KNljOlVf1EAtoI8+l8x\nxnSMsfMALAX53NGMsRsZYwmKHdMFwAoAyudOUAS/A5QyaQWwDUA/Y+xXymdoGWOzGGPzlf1uYoyl\ncs6tyn5cvKdEAkjhlgwdvwJwC0jYXgENWIYUznkDgOsA/B1AC4AJAHaD8s498TMAvaq/w5xzI4Ar\nAFwJ8sifA3Aj5/yoss8tACoVC+jnynsAwBQA6wAYAGwB8Czn/HslNXIpaKC0QnnPVwAkKPstBXBI\nych5CsB1nPP+gX8TktGGnIAjOWVgjGlBtsc1nPPvh7s9EslAkRG3ZFTDGLuEMZakWB6/B2Vs7Bjm\nZkkkg0IKt2S0swSUS90E4GIAP1KsD4kkbJFWiUQikYQZMuKWSCSSMCMkRaZSU1N5Xl5eKN5aIpFI\nRiUlJSXNnHNf6aoAQiTceXl5KC4uDsVbSyQSyaiEMVbp77bSKpFIJJIwQwq3RCKRhBlSuCUSiSTM\nkCvgSCSjFJPJhOrqavT19Q13UyQq9Ho9cnJyoNPpBvweUrglklFKdXU14uPjkZeXB8fChpLhgnOO\nlpYWVFdXIz8/3/cOHpBWiUQySunr60NKSooU7REEYwwpKSmD7gVJ4ZZIRjFStEcewfhNwk+4a3cD\n1SXD3QqJRCIZNsJPuL97FPjmt8PdColE4gdarRaFhYWYMWMG5syZg6effhpWK60JUVxcjPvuu2/Q\nn/Hyyy/jrbfeCmifM844Y8Cf98Ybb6C2tnbA+weD8BucNPUB5t7hboVEIvGD6Oho7NmzBwDQ2NiI\nG2+8EZ2dnfjjH/+IoqIiFBUVDer9zWYz7r777oD327p164A/84033sDMmTORnZ3t9z4WiwVarXbA\nn+lM+EXcln7ALBcDkUjCjfT0dLz66qt44YUXwDnHhg0bcPnllwMANm7ciMLCQhQWFmLu3Lno6uoC\nADzxxBOYNWsW5syZg9/85jcAgHPOOQf3338/ioqK8Oyzz+LRRx/FU089ZXvtgQceQFFREaZNm4ad\nO3fi6quvxqRJk/C73/3O1pa4OFpPesOGDTjnnHNwzTXXYOrUqfjpT38KUTH1T3/6ExYsWICZM2fi\nzjvvBOccq1atQnFxMX7605+isLAQvb29WLt2LebOnYtZs2bhtttug9FIVYPz8vLwyCOPYN68eVi5\ncmVQv8vwi7gtJhJviUTiN3/8vBQHazuD+p7TsxPw31fMCGifgoICWCwWNDY2Ojz/1FNP4cUXX8Ti\nxYthMBig1+uxZs0afPbZZ/jhhx8QExOD1tZW2/b9/f22ekiPPvqow3tFRkaiuLgYzz77LK688kqU\nlJQgOTkZEyZMwAMPPICUlBSH7Xfv3o3S0lJkZ2dj8eLF2LJlC5YsWYJ77rkHf/jDHwAAN910E1av\nXo1rrrkGL7zwAp566ikUFRWhr68Py5cvx9q1azF58mTcfPPNeOmll3D//fcDAFJSUrBr166AviN/\nCM+IWwq3RDKqWLx4MR588EE899xzaG9vR0REBL777jvceuutiImJAQAkJyfbtr/uuus8vteyZcsA\nALNmzcKMGTOQlZWFqKgoFBQUoKqqymX7hQsXIicnBxqNBoWFhaioqAAArF+/HosWLcKsWbOwbt06\nlJaWuux7+PBh5OfnY/LkyQCAW265BZs2bfKrnYMhDCPufsAsFzCRSAIh0Mg4VJSXl0Or1SI9PR2H\nDh2yPf+b3/wGl112Gb788kssXrwYX3/9tdf3iY2N9fhaVFQUAECj0djui8dms9nj9gANpprNZvT1\n9eEXv/gFiouLkZubi0cffXRAudfe2jkYwjDiNgEWKdwSSbjR1NSEu+++G/fcc49LLvPx48cxa9Ys\nPPLII1iwYAHKyspw4YUX4vXXX0dPTw8AOFgloUaIdGpqKgwGA1atWmV7LT4+3ubBT5kyBRUVFTh2\n7BgA4O2338bZZ58d8vaFX8RtNcnBSYkkTOjt7UVhYSFMJhMiIiJw00034cEHH3TZ7plnnsH69euh\n0WgwY8YMXHrppYiKisKePXtQVFSEyMhILF26FI899tiQtDspKQl33HEHZs6ciczMTCxYsMD22vLl\ny3H33XcjOjoa27Ztw+uvv45rr70WZrMZCxYsGFCWS6CEZM3JoqIiHrKFFJ7IA/o6gP9uC837SySj\nhEOHDmHatGnD3QyJG9z9NoyxEs65X/mR4WmVcCtgcfWqJBKJ5FTAL6uEMVYBoAuABYDZ36tCSBAZ\nJZZ+QBt+To9EIpEMlkCU71zOeXPIWuIPnKuE2wggZlibI5FIJMNBeFklVpU9IgcoJRLJKYq/ws0B\nfMcYK2GM3eluA8bYnYyxYsZYcVNTU/BaqEY98UamBEokklMUf4V7Cee8EMClAH7JGDvLeQPO+auc\n8yLOeVFaWlpQG2lDLdzOEbepF+huCc3nSiQSyQjCL+HmnNcot40APgGwMJSN8ojFpLrvFHFvegp4\n/ZKhbY9EIvFJQ0MDbrzxRhQUFGD+/Pk4/fTT8cknnwxLWzZs2DCoyoAjBZ/CzRiLZYzFi/sALgJw\nINQNc4uDcDtF3F31gKFhaNsjkUi8wjnHVVddhbPOOgvl5eUoKSnBBx98gOrq6pB9prtp7YKBCLe3\n9xsu/Im4MwBsZoztBbADwBec869C2ywPeLNKzH2Owi6RSIaddevWITIy0mE24fjx43HvvffCYrHg\n17/+NRYsWIDZs2fjlVdeAeC91GpJSQnOPvtszJ8/HxdffDHq6uoAuJZ6/fzzz7Fo0SLMnTsXF1xw\nARoaGlBRUYGXX34Z//u//4vCwkJ8//33qKiowHnnnYfZs2fj/PPPx8mTJwHYZ0cuWrQIDz/88BB/\na77xmQ7IOS8HMGcI2uIbb1aJuU9WDZRIPLHmN0D9/uC+Z+Ys4NLHvW5SWlqKefPmuX3ttddeQ2Ji\nInbu3Amj0YjFixfjoosuAuC+1OqiRYtw77334rPPPkNaWho+/PBD/Pa3v8WKFSsAOJZ6bWtrw/bt\n28EYwz//+U88+eSTePrpp3H33XcjLi4ODz30EADgiiuuwC233IJbbrkFK1aswH333YdPP/0UAFBd\nXY2tW7cGdQGEYBFeM1i8RtxGShfkHJALpEokI5Jf/vKX2Lx5MyIjIzF+/Hjs27fPVsCpo6MDR48e\nRWRkpK3UKgBbqdWkpCQcOHAAF154IQBaVSYrK8v23uoSqtXV1bjuuutQV1eH/v5+5Ofnu23Ptm3b\n8PHHHwOgmtvq6Praa68dkaINhLNwu4u4AYrKIyKHrk0SSTjgIzIOFTNmzMBHH31ke/ziiy+iubkZ\nRUVFGDduHJ5//nlcfPHFDvts2LDBbalVzjlmzJiBbdu2uf0sdQnVe++9Fw8++CCWLVuGDRs2uCy2\n4A+hKskaDMJrAo7aKnGuyS0eW6XPLZGMFM477zz09fXhpZdesj0nyrRefPHFeOmll2Ay0Tl75MgR\ndHd3e3yvKVOmoKmpySbcJpPJ7eIGAEXvY8eOBQC8+eabtufVJVkBWjT4gw8+AAC8++67OPPMMwfy\nbw45YSbc/e7vA6qIW/rcEslIgTGGTz/9FBs3bkR+fj4WLlyIW265BU888QRuv/12TJ8+HfPmzcPM\nmTNx1113ec3giIyMxKpVq/DII49gzpw5KCws9Jgh8uijj+Laa6/F/PnzkZqaanv+iiuuwCeffGIb\nnHz++efx+uuvY/bs2Xj77bfx7LPPBv07CAXhVdb12Frgnavp/rLngXk32197YSHQfBh46CgQlx78\nz5ZIwgxZ1nXkcmqVdfVqlfS5biORSCSjkDATbi9Wibrcq0QikYxiwku4rTLilkgCIRRWqGRwBOM3\nCS/h9jblXWaVSCQO6PV6tLS0SPEeQXDO0dLSAr1eP6j3Cd88bnXEzbnMKpFInMjJyUF1dTVCVmZZ\nMiD0er1tctFACV/hVt+3mmkdSkCuRSmRKOh0Oo8zBiXhTZhaJcwp+u5TbSMjbolEMroJM+FWRDky\nztEqUd+Xwi2RSEY54SncUXGeI26rtEokEsnoJsyEW7FKdDEy4pZIJKcsYSbc/YBGB0TopcctkUhO\nWcJMuE2ANpLKtnqMuKVVIpFIRjdhKNw6QBvlWI9bWiUSieQUIsyEu5+EOyLSqeCUtEokEsmpQ5gJ\nt2KVaKM8WyUyq0QikYxywky4lYhbGykHJyUSySlLGAq3r8FJWWRKIpGMbsJMuFVWicPgZJ/jNhKJ\nRDKKCTPhVg1Omj1UCpRWiUQiGeWEoXCLiNvTlHcZcUskktFNeAm31ax43E7CLWwTbZS0SiQSyagn\nvITbllWicx2cZBpAFy2tEolEMuoJP+HWKDMnrSbAqiyeYO6j+iXaSBlxSySSUU+YCbfJPjgJ2KNr\ns5HsE61OCrdEIhn1hJlwqwYnAbu3bYu4da6Dk4ZGYM/7Q9tOiUQiCSHhKdwRinCbnSPuSFePe/8q\n4NO7gY7qoW2rRCKRhAi/hZsxpmWM7WaMrQ5lg7xiqw7obJX0URSucWOVmHrotuXY0LVTIpFIQkgg\nEfd/AjgUqob4hXPEbbNKvHjcIvtECrdEIhkl+CXcjLEcAJcB+Gdom+MD25R3HT02qyJuW1aJk1Ui\nxL3l+NC1UyKRSEKIvxH3MwAeBmANYVt8Y8vjlhG3RCI5dfEp3IyxywE0cs5LfGx3J2OsmDFW3NTU\nFLQGOmBbuszd4KSHrBIp3BKJZJThT8S9GMAyxlgFgA8AnMcYe8d5I875q5zzIs55UVpaWpCbCcBq\nAbhFsUrE4KRTxK3RubFKlMdtlY6FqSQSiSRM8SncnPP/4pzncM7zAFwPYB3n/Gchb5kzwgLRRqgi\nbuc8bjczJ0UBKm4B2iuHpq0SiUQSQsInj1tEzg4RtyLSaqvErcfN6L60SyQSySggIOHmnG/gnF8e\nqsZ4xRZxu7NK+lSDk052iNkIjMmj+1K4JRLJKCBiuBvgN7aIW+d5cNLc57pYsMUIxGUAxi4p3BKJ\nZFQQ5laJOuKO9BBx99NrKROBZincEokk/Akj4VZZJerBSauFUgAj9O6zSsR0+JSJMuKWSCSjgjAS\nbpVVoq5VIjJLbEWmnK2SfnotZQJgqCfLRCKRSMKY8BFuq4eIW9glEXpKFXQXcUcoETcgp75LJJKw\nJ3yE221WiclNxO3O49arhFvaJRKJJLwJI+FWWSWaCACMom0xwUZMwAEn39u2n5GeT86nfWTELZFI\nwpzwE26NDmCMImyz0THi1kQ4bgvYp8ProoHEXBlxSySSsCeMhFtllQCUKWLpdxNxw3H2pBBugAYo\npXBLJJIwJ4yEW2WVAJSb7Rxxi9eEcHOuWCVCuCeSVcL50LVbIpFIgkwYCre3iFvnuK24jVAJt7ED\n6G4emjZLJBJJCAgj4XaySlwibpVVYlUVnwLswh2bSre9baFvr0QikYSIMBJuJ6tEpP6JiFsbSQOX\ngGPVQIBEHaABSgAw94a+vRKJRBIiwlC4I+23DjMn3VklRsd9RORt6gt9eyUSiSREhJFwK1PZ1SLs\nMjjppk63eA0AIkTELYVbIpGEL2Ek3M5WibfBSQ/CrVMsEyncEokkjAlD4fY0OBnlxSoREbci3Cbp\ncUskkvAljIRbZJWoI26nKe9icNJTVokQbvG8RCKRhCFhJNz9ANMAGi09FutLuvW4VSvjiNcAmVUi\nkUhGBSNXuBvLAEOj/bGl3y7MgGpwUlkogTGVVaIMZJo9WSXS45ZIJOHLyBRuixl4/VJg/WOq50yO\nwm0bnDTaBdmTx+1ilUjhlkgk4cvIFO7aXUBvK9DdZH/O0m8XZkA1ONlnF2ZfVokUbolEMgoYmcJ9\nbC3dGjvtzzlbJQ4RtxBuMTjpZJWI1zUaeg+ZVSKRSMKYkSncx4Vwq9aHtJrdR9wWlXBrfKQDAjQJ\nR2aVSCSSMGbkCXdvG1BTQvf7vEXckSTMpj6Vx+3DKgFoEo7MKpFIJGHMyBPu8g0AtwLp0x0jbndW\nCQD0G1ytEuesErVwR0TJrBKJRBLWjDzhPrYWiEoECs518rhN9qXJALJKANrGY1aJmG3pbJVI4ZZI\nJOHLyBJuzoHj64CCs4HoMSSwZpUIu4u4+zpds0psMyf7AKYFtCrB1+mlcEskkrBmZAl302GgswaY\neD4QFU/PCbvEOY/bXcTtrh632iYBaFuZVSKRSMKYkSXcIptkwvmAPoHuC7vEOY/bXcSt0VCErR6c\ndCfcMqtEIpGEMSNLuI+tBVInA0m5biJuN1PeASUdUG9/Xhtpj7jVCwULdNEyq0QikYQ1I0e4Tb1A\n5RaKtgEgyjnidp7yrs7pjnJ83maV9NstFfW2MqtEIpGEMRG+NmCM6QFsAhClbL+Kc/7fwW+JHrhr\nk12E3UbcbqwSl/s6lVXS5xiNAzKrRCKRhD0+hRuAEcB5nHMDY0wHYDNjbA3nfHtQW8IYkDbF/lif\nSLd9HiLuCDe2CUADlCKrxNLvxiqRWSUSiSS88SncnHMOwKA81Cl/PJSNAqCKuD1ZJercbA8et7oA\nlXpbaZVIJJIwxi+PmzGmZYztAdAI4FvO+Q9utrmTMVbMGCtuampyfZNAcfG4nasDRrm/72CV9HvI\nKpHCLZFIwhe/hJtzbuGcFwLIAbCQMTbTzTavcs6LOOdFaWlpg29ZRBTZHh49brVVoo64dY5ZJc7C\nrYum563WwbdRIpFIhoGAsko45+0A1gO4JDTNUcEY2SWePG53qYGAU1ZJn6vHLbaVUbdEIglTfAo3\nYyyNMZak3I8GcCGAslA3DABNwvEUcUd4irgjVVPe3aUDinUnVcJttQA/vCK9b4lEEhb4E3FnAVjP\nGNsHYCfI414d2mYpRMWTcHNOYuzP4KTGRzqgzs0qODUlwJqH7TM3JRKJZATjT1bJPgBzh6AtrkQl\n0uCksD78HpxUpwM6R9xiwWDV7Elhx3QHYVBVIpFIQszImTnpjqh4RbhFeVZPHreHwUmz0c0EHL39\nNUG/ku3Y0xKcdkskEkkIGdnCrU+gaFh41p4GJB0i7kjvRaZ0wuNWRdxCuLulcEskkpHPyBZu4XG7\ns0o0ftQqsRjdWCXKtuqByP5uupURt0QiCQNGuHAnkFUibA21CGs0dvF2N+XdaqEFht3VKgEcBydF\n5kpPc3DbL5FIJCFghAt3PImvEFZP0bPLlPd+1XqTTvu4yyqxWSVSuCUSychnZAu3WExBRMIapyQY\nIeQuVomZbBLA8+CkOqvEZpW0Dr7NEolEEmJGtnCLeiXCe/Yr4tY5Rtye0gHVWSVGkVUiI26JRDLy\nGeHCrVQI9CTctojbTXVAs4eI21tWiakH6O8ZfLsHSv1+4L3r5QxOiUTilREu3ErELdL01FklgCri\nVg9ORtDgpE24PdQqMbnxuIHhzSwp3wgcWQO0HBu+NkgkkhHPCBduPyNurZs8bosnq8RNVonwuNWf\nNRz0Kh57Z83wtUEikYx4RrZw63143NpIirC1EY7PWc2erRKtDmAap3RAAxCrlKIdTp9bDI52VA9f\nGyQSyYhnZAu3y+CkG6vERZgVERcphM7pgIwpq+CoPe4uIGk83R/O2ZO9bXR7qkXcXfWOvR6JROKV\nES7cwipRomB3Ebcn+0T41s7CLp5zqFXSDYxRhHskWCUdp5Bwcw68ei6w9s9D/9kWM7D2TzINVBJ2\njGzh1urIkxYnlrt0QJeIW9lGpPg57wNQZok6q8RoABKyAaYdZqtEibhPJauk5TjQVQvU7Rn6z67f\nC3z/NHD0m6H/7MFgMQNvXkGD2ZJTkpEt3AD53GJGo7NVoo10zRoRk3RsEbfT6+I5kVViMdFAZlQC\nEJMyzBG3sEr8FG6jAXhpMVCxJXRtCjXVO+m28RBF30OJoZFue9uD+76V24D9q4L7nmoMDcCJTUDF\n96H7DMmIZuQLd1S8KkPESbgnng9Mu9zxOVvELTxud1ZJtH1wUgh8ZBwJ93BOe7dlldT6tyZm/T6g\n4QBQ5bJ2c/hQvYNu+9qHvh66oUH57I7gvu+2F4Bv/zu476lG9ApliYZTFp8LKQw7YoAScLU9im5z\n3V6Ie783q0S10ruwVCJjgdjU4Pqd3/yeTq4fveR7W1MfTQCKywQM9XRyxqV736ehlG7D+QSu3gno\nYgFTN9BU5vt/DiYi4u4LcsTdVR/891Qjfm+58McpS3hE3ALniNsdzh63p8FJYZWIbIaoOCAmOXge\nt9UC7HoLKFvtnwUgou3MWXTrj8/dcIBuuxsH1sbhpr+bLj4zf0SPmw4P7eeHKuI2NFLgIMoLBxth\n54XzBVsyKMJMuN1Ez844R9zO6YCAklXibJXEAzGpwTsZqosp6jJ2+pfeJ/xtIdz+7NNwkG4NYSrc\nNbsAbgWmLaOe1XAJdzA9bs5Dd0EQyIj7lGfkC7c+0X7fH+EWNbq9edw6dx53LHncvW0ULQ+WY9/a\n7zce8r29sGgyZ9Ktr4jbagUaFeEO18hLDEzmLADSppBVMpTYrJIgCmxfh31MJtiDngLpcZ/yjHzh\nVkfczmVd3eGcx+1O7COi7BNwhKUSFUceN7g9+h0MR78B0qfTfSGw3hBWScpEutj4Eu72SvofI6LD\n1yqpLqb/NyZZEe7hskqCKLDq3k+ofG4h2MYOx/kInqjfD7y+FFjzm9C0RzLkhIFwK4OT2kia9egL\n28xJg+d9IqLtB7xzVgkw+JTArgagbi8w6xogPiuwiDsmBUgY69sqEQOT40+n9gajlzCUcE4ZJTkL\n6HHaVLoADdVkGM4HH3Ef/Q6o3Or4nLgYACGMuFXHp7eo29RL2S2vnA1UbgH2rxz6lMuB8O/7gA9+\nOtytGNGEgXArEbc/Nol6u36De5sEULJKeu3bAY7CPdgu6LHv6HbSRUD6ND8jbiXKj04GEsf6nj3Z\neBAAA/LPIp843Gb/tVeSR5tTRI9Tp9Bt85Gh+fx+A2XxMM3ABfbr/wLW/cXxObVwhzriBrz73O9e\nC2x5Bii8ATj3d2SxdFSFpk3BpOoHoGrHcLdiRDPyhVsUmvInowRwzCrxJPbqrBIXqwSDzyw5+g1F\n2hkzyS5pOuw7Iu5tpXZFxgAJOX5E3AeA5HxgTB49Hk67pOU48OIioLXc/32qi+k2ZyHdpinCPVQ+\nt4i2k8ZTrRqLObD9OQfaTwLtTkI4FMLd0wzEZ9vvu6OxjCbonP8H4MoXgYnn0fO1u0PTpmDBOdBW\nQcezrF/jkZEv3IFG3LaZk12eI26HrJJuAAzQxQTHKrGYgOPrgYkXkE2TPo0+q63C+349bUD0GLqf\nOBboqvMuJg2ldFGIVfKe/c0sOfARcCTIU7xPbiPBLV7h/z5VOyh/W4wDJObSbzBUPrcQWHHBMHYG\ntn93E/2unTWOF2VDA5VOAEJnlXQ3A+lT7ffdse8Dasfcm+hxxkwauK/ZFZo2BYuuevu52VY5vG0Z\nwYSBcCtZJZoBRNzuUgEBskq4hUS230A2CWMqq2QQwl21gwaNJl1Ej9On0a0vu6S3jWwSgDxubiXx\ndkd/D0W3GTPtE1b8SQ2zWoDVDwKr7/dvZqa/iIvS3g/8z12u3gmMnWcfk9BogNRJQxhxK8KdOolu\nAx2Qbj9Jt9zi+DsZGqm3FREdmojbYqL3TVOOK3e/u9UC7P2QggdxfEREARkzgNoRLtzqAKddCrcn\nwkC4RcQdoHBbTY4LLKhRLxjcb6BUQIAO7sj4wUXcx76lqL/gHHqcpkRGjT4EqbeVsisAIDGHbj3Z\nJU1lJOyeOQktAAAgAElEQVQZM+z2jj/CXVNCJ31nTXDrXLRVAGDUhiNf+d6ec8p0yC50fD5t6hBG\n3EoPRXjrgQ5QqkVFbZcYGoD4DCA6KTQRtxjLSM6n49vd735iExXuKrzB8fmx84DavcG9aPtD6Sf+\nV7xUC7evXuopzMgXbr0qq8Qf1IsquCswBagWDO6jyDwqzv5abMrgPO7yjeTbinZHxpIP7Svi7mm1\nWyUJY+nWU0qgyCjJmAHok+i78ccqOfotDcZFxgH7PvS9vb+0VQDjF9N0/V1v+97e2EkX1rhMx+fT\nptBFpS9A22IgCEsjOZ8eBxodi4gbcBzwMzQCcRn0u4Qi4hbHZkwKLf7hzirZ+z7Nf5h8qePz2fOo\nNxjIWMRgaT8JrFwOFL/m3/ZtJ2CzLsNNuBsPDdmg6sgX7oFmlQCehVunWr5MWCWCwVQItFpIoMfO\nc3w+fbrvlMDeVkePG/AccTcepAN7TB5ZPLFp/kXcx76l9LsZPwIOfha8wZ+2CiClACi8kT6j04PF\nIxBRo/h/BaJ30nw0OO3yhqGBbARhTwUccZ+0HzdqEbe9b4gibiHUsakUZDj/7sYu4NDnwIyryRJU\nkz2XbofSLjnyNd36OiYEbRXU40wuCD/h3v4S8MGNQ/JRYSTcflolai/cV8Rt6iPxchDuQUx7bzlO\nF4OMGY7Pp00FWo4C5n73+3Fl0o+wSvSJlL/uqXvZcIC8c40yCBab6lu4DU2UUTDxAmDODXTBKvvC\n///NE/3d9Nlj8oC5PyMLZ+973vcRfrL4fwWpQ5hZYmgkgRUzcwMV2faTyuShFHvPyGKmYycug943\npBF3qvsL9sF/U5rjnBtc902bSt77UA5QCuusq9a/7VtP0LE0Ji/8hLuj2t5bDjEjX7gjA424VcLt\ny+M291KE4mCVpA484m7YT7cZMx2fT59O62B6Wr3d2EWvR6uELGGse6uEc6D+gD0bA6DMEmerpK/D\nMdvh+Dq6nXgBMO50IGkcdakHixj5H5MHpEwAxi8Bdr/jfaKHLWfdKeIek0e/c+2u0E8UMTSQwEYn\n0eNAI+62SvoOE3PtVkl3EwCuXBCSgN4Q1CoRA+exQridjtW97wPJE4Dcha77aiOArDlDlxJoNJDf\nDgQWcduEuzI8JgwJOmvs41MhZuQLt0ZD4h3o4CTgxSoRwm1UIu5Y+2sxySTcAzlg6g/QwKRIMRP4\nyiwR093VEWjiWPcLKhgaaHv1xSEu3THy4pzyqj+5y/5/HPuWorSsQvpOZ18PlG+g2t+DQURFIp98\n3k3koYo6JO7wJNzaCGD8GcDOfwIvnQH88ApQ9iXw7R+AFZdQmVx3DOS3EhG3LoZ+s0CiY85JrJPG\nAUm59sFJkakiLgihjLijk+09LfH/W8w0eWXqUs+zjLPn0qzeQPPWB8KJjYClnzJguup9b9/fTfnb\nQrjNvf6N3Zz8AXjnx/a5GcNFR83IibgZY7mMsfWMsYOMsVLG2H8ORcMc0CcMLOL2aZX0uvG4UxXv\newD+b0MpkDrZ9XNTJ9FAmCef253nm+Bh9qQY/FBnZDifwB3VlKK2fyWw718UeR9bSwtPaJSffM71\nZGvsXxn4/6lGCHdSHt2OO51uvWWHeBJuALj+PWDZ8/QdrnkY+OAGYNs/6Ls9+Jnr9jv+D3h+nvdM\nCYvZ0QqxWu2DiIwpA4kBRMeGRjpGksYDieNIxNVT6MXgpLEz+KUIupvpe9NGUMRt7rUfq20VJJTq\n3pgzY+fRPsGyo7xdNI98RZbfzKtpUNTXOSWOpeR8++Ld/tglm56k2cregoVgUrWTLhZq+jpo7kji\nCBFuAGYAv+KcTwdwGoBfMsa8HBkhQJ/oWYSdURei8miVqAYnjQbHQlaDmYTTcMDVJgGo7SkTPQu3\nerq7IDGHoivnKKJyC7U/WzUAGptOJ6wQH/E58VnAlw8Bh/5NUfrEC+37pEwAxs4HSj8N7H90pq1C\nKYkrctCzATDvRbK8CXdkLDDvZuDODcDdm4FbvwL+q4omkrj7Ter2UoTv3JtprwI+ugP4xxnAY1nA\nkwX2Qc/eVsq/jsugx/rEwDxuMRiZNI5+J1MP/U+2iDt94BaML3qaKbgASLgBe29LiLFzj0+NOG6C\nMUDZWAY8lg2c3O76mtVKA5MTz6fvCfAddat7b6IH50u4W09QUAK4b4c/HPwssHGtNb+moEKNCLJG\nSsTNOa/jnO9S7ncBOARgaFonuORx4KyH/NuWMXt07ssqMfXQyitqq2Sg0957Wsnjch6YFKRPAxpL\n3b/mbrDOU0pgxWbyL9WTi5wn4QgRu/FDiog+vhMAAyac5/he+WfT8memXgyY9kp7dgtAPZ74TO/r\nZva2+Wd/Zc6iIlq6aMqg6De4XsiEmJ/c5vj8rjeBA6soApp/Kwm1OMHVAgsotkYAAityuIVVApCY\nq60SvRDuQdolLccdo9ruFvsxahNu5VgVwp062fP7JRfQpLZg+NxHv6ZzaOvzrq/V7aHvY/IldDwA\nvm251hN0OybfLva+hLvkDUpxjc92PQb8obcd+NfN1HPzB86BpiPUVvXvIjLAEnMDb8MACMjjZozl\nAZgLwGWRQ8bYnYyxYsZYcVNTkAu8F5xN0aG/iMwSX1aJsCic0wHVr/mLyK3OdBNxi+fbKux1wtXY\nrBKVcIv/t3y943YNpUDemY77ixNYdNUbD9GBnDUHuOwpisbHziPxU5O7kAZFB3MSt1UAY8Y7Pudp\nYFXQ2+Y+2vaG7XdxuqAK0XI+acs30Hf405XA0iep6y0mHakFFgg8A8QWcefaT9SOKvr+oxLpQiMi\n7sGkBB5fTzaQKFoG0IVKfBfOk6+aDlOdG3UP0hmNhmy2kjeBFxYA799AKzUNBLFI9eEvXWu2HPka\nAKNenqir4mkmsKCtgr6/6DEUXMVnexdus5EGwqdcCky+mGzEQK0pcSx4ShxwprOWgj1jh6NGiON9\nBFklAADGWByAjwDczzl3mSHBOX+Vc17EOS9KS0sLZhsDR+uncIuTXh1xJ+bSFXzdnyna8RexjFjG\nLPevZ85WtnMTdYvBSXGyA9TdTZlENofg5DYAHMhb7Li/c5e58aB9QHT2dcC5vwXOcuraAfaSqgOd\nNCAKAolurSAxx/tMud42x//VH4Q94NylFf9z5TZ7BNTbTrNEC861b5d3JtlMwt8GVMIdaMR9ki6y\nUfH2yLC9yp7DLd4TGFzE/f3TdKv+fXqa7YId4yTczYe92ySCS/4KLL6Ptq3dA3zxkOdUVU9YLXQ8\nCvvNeYLNka8oMIhNARKy6Dmfwn0CSM6z997G5Hmf9n7oc/o+im6jQe3+LvfnlzfEseCvcKurV7ad\nsN/vqCbdcJ5UFiL8Em7GmA4k2u9yzj8ObZOCgBBuTx63mIAjojd1hJKQBVz3DqUivXI2sH+Vf59Z\nf4BOJE+L3Yolyer3u77W20aDOGrrgDFg+jKKakTKV8Vmuug49z7UVonVQpGXEG7GgLMfBqZc4vq5\nsanUdfYm3NUlwNe/dT/4Z2igcQK3wl3teeBKPUvUXzxZWD0t1GPqqrWf5BWbaeC14Bz7dnlL6Htu\nPOjeKgnU4xaCHT2GimV1VNlTDMV7AgOPuGtK7D2Eur10a1XK99o8bpVwW63UhReTmLyRMQO44FE6\nzi/5K63Y0+DmuPRG/T4afJ1zPTBlKUXwwsY6vIaskinKzM2oePqNfKUEOgcBY8Z7j7iLV5CtUnAu\nMO40ei5Qn1scC63l/mUnqQVePQO1s4bGlNQzt0OIP1klDMBrAA5xzv8e+iYFAZvH7amsqyLotog7\nzvH1qZfRwFjGdOCjn1OtBV80HCA7xFMaVnwWdXHr97m+5knIpl1B3uzhL+lxxWaKkp17EjEpABhF\nD60n6ET05LU7k7OQFjTwdNCWfgxsewEo+9z1NedUQEFiDmUueLKb1JON/EWIlfo9zUYSD1HQq1Kx\nS8rXk5iKHgVAwg2QGBoaKQ1Q/O7CKvE3rVAt3IwpF6ogR9xbniXbYOrl9mOmr52OByHYumh7bZ2O\nk/Sd+xNxqxHfkSiz6y/CJhm/GFh4J/UaSz+m32DlchoEXXCHffv4LO8Rt9VC36uDcOcp1oSbNL/G\nMupBFd1K9k9iLll0gfrcIuI2dvo3QNl8hI4tMLsnDwzp5BvAv4h7MYCbAJzHGNuj/C0NcbsGh80q\n8VTWVYm4RRdTbZUIknKB5V+QDeGrDKrFTL6yu4wSAWP0utuIu9W9kGUVUrrZoX9T5Fa/39XfBmgG\nZYwy/VkMTIqI2xe5C2g/T5GNiEg2PO4adasn36ixFcny4HMPxOMW/rzDIgLK/bwlJHLipC3fQHaS\n+sKdlEvtrNhsF1hxkdUnkddv6qHHnAPf/dG996/O4Va/d3uVPcUQGFzE3XKcZkAu+DkJY1cdraok\n/l9xEQPsqaAi/dKfiFtN4ljykgNNpavYTL21hCxazCNtKlk7719HIvrTlY4T2+IzvQt3Zy2NxYzJ\ntz83Jg8Ad7/4w4GPKMW2UFkphzGKuk9uCyyvX13HvtUPa7T5CF0cE8Y6WiWdNUPmbwP+ZZVs5pwz\nzvlsznmh8vflUDRuwGh8WCUaDUXlIiMhKs79dlodRSTVPjzglmNKlOtFuAGySxoOuk5+UJd0VcMY\nRd3lG2hxBnf+tkBMwmk8BIDZp4/7IncR3Xo6cQ2N9H02HgQOOqUOiqqAziPp3opkien9gQq3PolS\nPdVWibgflwGMW0QnbXsV/R5qf1uQt4QEp6veLrCA67R3QyOw+e/Ad4+6voc6h1uQmEuf2W9QlVHV\n0zE2kIh763O076K7gSxlbKR+n/3/VQ8yi2nvtlRALxklnsgpCky4rRbg5Fa6qAB0nC68g74DXSxw\n08f2XoEgIdu7cLvrvXlLCazdRcGJ+nPGnU6foa4d4wtDo71+uj9jWs1HKWsnOd9ulXBOF54hmjUJ\nhMPMyYHgKx0QoBPLk1WiJmcBHZDeskzEwKSnjBJB5mwS+BanIkrePN/pyygSWfcXuhCNLXK/XWwa\nHYSNB+mgiozx3hZB+nT6/z353N1NNE0+dQqw8QnHUfu2CjohnYsZ2TIt3Ai3sZO6+4EKt6iX7i7i\njk2lk7b5CKUAAo7+tiDvTBLS6p2OYxHOOdfCxyzf4FrwSoiCOpMmKde+BJ5IfRMTewKNuA2NwJ73\nqSRrfIZ9bKRur4eIW6kQ2HSYBsYC/V4BOsbbKqiejT80lNJ3pe79zbkROP0e4KZPHHsjgvhMumB6\nioZF9JrsHHHDVbg5p0HVLKeywN587tZy4JlZrj1eQwNZokzre4DSaKDIOnUitU1YJT0tdDFPkMI9\nOHxllQAk3CLi9ibcouaDt4ikQZnq7i1/FvA8QOnJKgHIg47LoIG3nAWuIikQkVfjIe8z55zRaClV\n0FOvwtBAJ905j1BUp/b72yocI09bW1LpIuNOuN1NNvIX58qNaiEbfwbd3/o8fV/urCIRIZr73Efc\nIjpWn8A7nbIl1DncgkTVfecLQqAR98ntdHGfe7O9bWPySbjVJV0FNqukLHB/WyB87ho/fe6KzXSr\n7v1FxgAX/499ZR5n4rMpAPE0sa2tgs4htfjFZdB56izcnTX0XTjXc0+fToP87nzubf+gi67zeWxo\npB7imPG+rRJxXKROJpuou5HSe4c4FRA4lYVbrIIDuFglnHNUtfZg9b5aPHcoDpxpvWde1B+giNTX\n7M7USSRo6gFKi5miF09CptHQABXg2SYBSDC66ung8tffFuQspP/BeUqyxUy9gbh0YPqPqObEhsdp\nBR7AfSogoAzYecjl9jZr0hfOEbfaOsieS99tTwtF2+4GiYXPDTgJt5uIWxtF5W/3vOf4vYiIW20P\nJTqJjfp9A505Kb4zdeSZNYeOGXWBKYE64g7U3xZkF5Jo+muXVG5RpvsHEGGKnognu6Stgr5TdVYG\nY/Q5zsItxh6cI26NlgIt54i7tw3Y8y7dd1kjtJG+w5SJQIuPOuWi9yWsEtFu8ZuNsMHJ8ENYJZ48\nbsBx4FJnH5zs7DNhyRPrceaT63HPe7vx9401OKHNA/d0UPf3UGGfsXP9aJeORFUdcYsT21uWxeyf\nwDaZwROibgW3BC7cuQtpP+dynz3NsFW702iAC/9EovbutSQiXbXuhRugk9pdPfHBCHdsqqPH3d1M\ngqNPooumSJN0528LRHaJOjJ29rhbjlNEtfAummihrufSfpIuIOqLfZJKxNXCPZCa3J01NHiu/n6y\nZpNAtB6nLBJ1gBCbSr9dv2HgEbcumnqDno7xzlpg/WO0SIjZSMItvkd/SVAm4XhKCWw64nixEqgt\nCUHtHrI23FmT404Dmg45Tq/f9TYNPOtiHIMJq5V6K3EZVFHRV0pg8xHK1U4usA+itp5QzZqUVsng\nEPVKPKUDAnbhjoh2uMqXN3Wjpr0Xty/Jx+f3LMFfr56FzX0FMJ/c6X5WVuknSj6rnwXUMxWfzTZZ\nxMOiAmrGnQY8XE4ZIJ6IVU16CsQqAVQpYU69CpFRIhYknnwR8ON/Ulf0NeUi4km4E3JCEHE71Urv\nbqLnRHSdtwQAo5m2nsg7i24dBFZpizriTplA33vGTKpWKH4vdSqgID6LjjmmcbQxBrIKTkcVCYC6\nx5A1h27LN7jOflX/7gONuAE6Bmp2uR7jViuVTNj4BPDWMqr50ttmt538Jd7LJJyeVrIbc09zfS17\nrpJ7r/Lf6/bQ/yrmY6iZtozO7VW30fqcFjOw41Xy47PnOWaoqGvWpEygGZHe6qk0H6HjPSLKfpFp\nLafjXBvlOPYQYkancNsGJz34wYD9R3dKBWzqMgIAlhVmY1ZOIq5fkIuu1LnQWXrQcmKP6/uUvEEz\nHIXH6ovM2dSdFwewu+nu7vCV9ywiSI2OoodAiEmmrmKVs//X5PjeADDrGuAnb6oG6fLcv2dijvuV\n6j2tfuMPsakkhOI9e1ocbYMz7gVuXWOP7twx9TJgyQOUwiaIUpaZ62sn4Wotp++DMUrJq98PfPUb\n4J1ryN91Fm6Nlj4zNs2+uAUwsIi7w01aWaYi3F11ruKg/v8HK9z9BteqgcWvUe77pX+jyo3Tr6IB\ncpE77y/iQulOuCu3AuBAvptU16lL6TWxIIMYmHT2twVpU6i6ZOUWYM0jQNlqEuvT/sM+MUxgm4iV\nRlE04H2AsuUYnesA9dJiUmhQtbOGfn/N0Mnp6BZur1aJ8pqTv93YRcn+afH0OmMMV1x+JQDgm6+d\nJqE0lFKUOn+554k3zjgPUNpqcQ9AyNSIyCt1kveehiey57kOmoocV+fZoNOuAG74gIpWeZrok5jj\nfqV6IWQD9bgB+3fW3ewoXPoEKkrljag4mjWovmBrI8iC6OugC5LVRMINALN+Qm394WUSgDnXuy8f\nMCbPHlXa2qN43IEszttR7drljkuz1/twTrMTv3tMqms0Hgg5SraS2i5pLada6BMvoHS/qZcBV70I\n3LGW2hQIEZHUVneFpk5sop6vu4ypzNnkfYvVmsTApLO/rWb2T4Az7qOLzhcP0m8z+RKytDpr7Rd+\ndemDFCXYEQOUnANvXkHZXABd0FuO0fklGKOkBHYM3QIKgqGZnznUCOvDa1aJiLgdC/KIiDs1zr7v\nuAkz0KMbA11dCTYeacLZk5WDtuRNukgUBrDOnBC6+n1UGGcwWRZqxAkcqL8tSM6nVDpzv134na0S\nNZMuoD9PJKpyudUecG8bZfEM5OJim+LdbM9bTwqg+Jg3RGlXkcsrhDsqDvjlDrJCvPV6LnmCskHU\nRCcB4GSl+VObxdxP37m7tLKsOTSm4BJxK7/7YKJtgEQoJoWEe/5yuth8dg/14K54zv/AxBsiJdCZ\niu/JlnJ3TDBGU+p3vUmDxLVKrzfbx5jSBY+SxXLsO+CsX1NPKDGHrJGuOjom1cKdmEvnsvj9K7fS\nBaViC63fGRlD2UjqzLHkAmUglAduHQ2S0R1xexHuHk6ZJ6YIR5+sscuI5NhI6LSqr4Yx6PMWYb7m\nKDYcVn7s/h5g3wfA9CsDm76tT1DSu/ZRPYoDH9HzA4lA1cSl00XIU563L5LGUYSsHlA0NNGAjqcJ\nSt7wlMs9kMk3AucKgc5WyWAQpV1FV1kIN0Dfra/fOGO6q5gEOu29qxYAdx+9iYk4zlF1dDJ56wOZ\neKOGMbJLDq+hSPOZmWQ3XPJY8NLc4rNd157sbiaBdWeTCKZeRqJ5fB35254GJtVotMA1K4DL/k5l\nfQHHSo6AKjBRLC4RQQNAyes0G1efQLW3m5TiUg7CnU/v1Vk7pKmAwKiNuH0Ld1WnFVMAdFr1UJ8K\nTV1GpMe77qcZtxD5R79CZ0sDgBlUfL2vg6KTQMmcRZXNDv2bIv8Ft9szGwZKRBRwb7Hj4Fgg2Krc\nnbQPvHQ3Og5+BYJIjXKe9t7bGnhlQIG6QqCoUxIs4RYDiS3H6IQNxvuqp737c63q8JKdIAYonSNu\nbQSw7AX7DNjBMP0qSrUz9dJAb+4i+5TyYBCf6bqAgyiklXeW6/aC8WfQ+VH2JfWyPA1MOqNPpDEK\ngXMw0d1I558oMpcygSLu7hY6v+cvp8/64kEqiQC4RtzgFMUPYSogMFqFW2SVePG4qw0cUwB08ygH\n4W7sMtr8bQdyaCLOoob3gfXbgX0fUlQ2kC7S7J9Q5DnjRzTYN1jRFohc2YGgFm6BuvZGoETFkRi6\njbgHaAvZKgS2uJ9FOBj0iTS5RmSUBMMacJ7Y4wvbRA43wj22iHo/7qywuUES18Ib6C9UJGST8Krt\nuBObqKfozfrQ6sijPrKGou3JFw/s88X3Ko5xQyN59eK3Ti6gxTb2vEOThebfSoOdJW9QJlX0GMce\nj7quyhAtoCA4Ja2Snn4zqrsovavD4ph50uxJuMfOg4lF4ie9/wI2/Y28v4sfG9gJPu0KYPlqigaC\nJdqDJWEsdbldhNtDmVp/SMwNrlUiBL+7WTX5JohWifC41TbJYNCrIm5/EF14d9FbfAbw8AkaKAxX\nRGAhLAoAOPE9DSj7Koc6ZSkdO74GJr0RGUM9UnFMOgcmKRNonGLLs9TbyJhOFsrSv9HrzjOj1Xnn\nQ2yVjFLh9j5zcmdFG3oVj7vNYh8Q4ZyjyZNwR8biX3PewGXG/4Hx4SqyJQZ65R+JaHUkGGrhHoxV\nAiizJ50m4QxGuLURtK864h5M+9ToEyka7KhyzBwYDNEBetydNXRx8lRnRqcPTk9guHBeCaezjur2\nuKt46czE8+09aE+pgP6QmKvyuJ2FW7lg97TYfXGABk4veJTK16qJTbOXyxhiq2R0C7cHq2TLsWaY\nGAl2S7998YL2HhP6LVakx7vP/9blzEYpz0dDz+j82pA0zi7cFpMy3X2AVglgr1MtGGhlQDUxyuzJ\noFslSUpWCLenhgXjPQH/p727SwUcTYiVcERKoKh5ku/F3xZExSulDDS+q3B6IzHHPu3d0OB44Rfz\nH/RJwIyrHPdb8gDZmmoYI7skMm7Ie86jU4EScqhSmjYCRrMFJ5oda3B8f7QZKUn0RTcZ7cLdZKB0\nLrcRN4DsRBoQqe0YxOK6I5mkcfYiSt1iuvsgItqEsRRtGpXKecYuGuQZjHDHpjpZJYPIXVajPvGC\nZZVExtJ4i99WydDnAw8pttmT9XRMHPuWvncxt8EX5/+eBmL9rXzpjqRxdIG0mCmyVgcm8Vn0eP5y\n/wY/AWp72tQh7wmNzsHJotuAwhvQbTTjtjd2YkdFK1bdfTrmj09Gs8GIQ3WdyJ0xBugC6vu04JyD\nMYbGThJud1klAJCVRJF43agV7vEUDZn77ZNv3OVw+4sYsOmsoUEed6vZB0pMCqVsqeuUBAN1pkug\nM089IUq7BjI46a2QmAde33ICpxWkYFpWQsD7DikxKTT+9PV/AV89Qs9Nvdxxtqk3Mmf5L/KeSMyh\nqe0tR+ESmGg0wD07HWoX+WTp32ggc4gZnRG3NgJdXI9bVuxAcWUbkqJ1+O0nB2CyWLH1OFVYy8uk\nLnaHRY/WbvrimwyOsyadsUXc7W6WUhoNJI0DwCmFzzbdfZBWCWC3SwZTp0QgKgQ61ykZLCLijs8a\nWN66J/yd9t7XSQWtAvRKe/st+OPnB/HGloqBtW8oYQy45HHgtF8AF/wRuPIfwNKnhrYNIpioKaFb\n5+NbnxjYupFRcYMLRAbIqIy4O3pNuGXFDhyo6cDzN8yFhjHc/U4J3thSgWONBiToIzA2jcTDAD3q\nOvqQEhflM+KOjtRiTIwOte2jNeKmlMDqE4fRWluO2cDgrBJRx6SxDJh4AQ5XnMQUYPBWiRicDFZG\nCWCP3INlk6jf15+Ie4AV5qrbqMRuWX1noC0bHtR51cOB+H7FGpuDCUyGkVEZcb+xpQJ7q9vxj5/O\nw9JZWbh4RgYumJaOv397BGvLGnDGhFRolAUJeqC3CXFTlxF6nQZxUZ6vZ1mJ0ajrCF7EbbVydPWZ\ngvZ+g0IR7nXbi/H1DqVuyWCskoQsEsLyDahq7cHzq5Xqg4MdnORK3YiBTjZyh4i4gzUwKfA34vY2\n+cYLJ1tJuA83dMFiDWCtxVMVMV9BRNzBykoaYkalcFe2diMrQY+LZlDeKGMMjy6jGiHNhn4snpRq\nq1HSyWNsQtzYZUR6vB7MS/c7O0kf1Ij73R8qccbj69DeM/Q+mQsJY8GZFsamExjD22GJGOB0dzUF\n5wKVW7C+tApJTBmkHExdFhFlt5YH96QTFwFfqxgFiqeIe8f/0dRyMXAr7KQAhbtKEe4+kxUVLd0+\ntpYgJoVmS4pFtQczT2EYGZXC3dDZh4xEx5S+nDEx+NVFk6HVMJw9KQ0oOBvWK19CmWaiLUvEYw63\nimBH3NtPtKKrz4wv93upAzxUaCNgjs1CiqUBaawDvZFB8O4mnAeYelCzfyMSoQjLQKe8A3aB5Zag\nWiXmmDS8k/9XHM/9cdDeEwAJQ3sVsP1lymSwWoA1vwG+fIhmDZZ+TNt11tCswLjAZr9WtdmDiLK6\nrpGFlrIAACAASURBVGC2fHTCGF0crWZK44sMYCByBDEqhbu+ow+ZCa652D9fko/t/3U+xqXEAFod\nNHNvREZijG2wsbGrz6O/LchK0qOj14SefrPX7fyltIZyfD/d42a1mGGgRZeBHNaENNaBNhaEjI28\nJeCaCIyp34xkjQHdPApmpvO9nyfUYh3EwvXHmgz43aHx+LwsyF7xGfdSAaWvHgFePRt47yfADy/R\nAF3qZFqdBaCMkviswAbGQBH3+JQYaDUsfHzu4Ub0asI02gZGqXA3dBqR4Ua4GWMuEXVWoh517f5H\n3MHMLOnsM6GipQcpsZHYcaIVNSNg0POEORXjtc3I0RlQZ473vYMv9AloT56DM7APs5KtaEccKpXu\n/YBwXig3SJQ3UW/geFOQ7YaEbOBnHwM/eZu87uPraFGCS/4KzL2J6rk3HR7w5JuTrT2YkBaHgtRY\nHKqTwu0XosxwmA5MAqNQuLv6TDAYzchM9LL6jYrsJLI++kwWdPaZfUbc2UlCuO0iu/z1HfjL6oMB\nt/VQLZ1o951PU6z/vcdNkfkhxGrl2NuVgDTeijS0oLwvDtYgDHgVa+diJqvA9MhGdPA4HG0YRJde\nFWVbnQYnd1a04p73dg1okK68ibzm442GgbfNE4wB05dh7QVf4P+NfR3WBXfQ83NuoFz0XW8pwh1Y\nKiDnHNVtvRiXHIOpWQk4JK0S/xApgWE6MAmEoXC3GIxoNhg9vt7QSZFwlp/CnZWoR31nn20/3x63\n4yScpi4jNhxuwvs7TgZsnxxQhPvSWZmYNy4Jnw2zXXKksQtH+1OgAUe0xYB6S/ygB7w45/igZQI0\njCOuaRfaeByONAxCHHV69IAunnUmx4HTj3dVY/W+OlumRSCIiLu82RCUi5UznHM8/l0l3jumw37F\nHkNcGjDlUmDvB0pN58Ai7vYeClJyxkRjWlY8atp70TlSMpRGMoky4h5Suo1mXP3SVvz8zWKP29R3\nkKi7s0rckZ0UDYuV46Aiop7qlAgyE/VgzG6VbD1OU6+7+y34prTB264ulNZ0ID0+Cunxelw1dyzK\n6ruG1afcfrwF1dwehTTzRJTWDq49B+s6scGQg34dzerrj0zAkUFE3P1mK5o5WTgHOx0vsnuqSBAP\n1wf+/seVsgh9JmtILKtNR5txVInmNx5RLXw792aavm8xul/5xgtVSg53bnIMpmXS9ysHKH1j0NMA\n8Mn+IE60GmLCSrj/8sVBVLb0YG9Vu23igTP1SuTsbnDSHdnKNPY91ZSy5Svi1mk1SIuLskXc3x9t\nRlKMDjljovHRLjermnuhtLYTM7LphLtsVha0GoZPdw+fXbK9vBUmlXi0sjGDFu71ZY2wQAurUiif\nRScPSrgrWrrRqgj37mb7VOmefrPtfQN9f845ypsMmJpJ73u8ybFHsL6sESdbBuHLA3ht8wmkx0dh\nRnaCfRUlgKreiap5A8zhJquE2i4HKH2zvSMJFs6wu2uElwjwQtgI93cHG/D+jipcNpsK1Xx70H10\nKywPfz3uLGWwcZ8SrfnyuAEgS/HFOef4/mgTFk9IxdVzx2LLsWbU+5kq2Gey4FiTATPH0sSPlLgo\nnDUpFf/eUxOSrrovrFaOHRWtmFAwidLSAMSMyUJprZ+V7TywrqwRc3ISoZ9yPgAgKj4FJ5q7YbIE\nsICuiiMNXWjhCTBBi+J6+3uU1nbavO3DAQp3s6EfXX1mXDidus7qAcrefgvufLsYP3vtB3T0DMyG\nONLQhU1HmnDz6eNx/rQM7Klqt+fta7Ton0WLFxhjHVenN1msWLO/Dj+Ut7idpFXVSsFDbnIMMhP0\nSIrRjXif+7m1R/G7T/fjn9+X47uDDegzWYa8DWtrInBZ/1/xkfG0If/sYBEWwt1iMOI3H+/D1Mx4\n/P0nczA5I86jLVHX0YukGB30Ov8K14gskf01HWAMSI71vYhtdiJNwjnWaEBDpxFnTkrFj+blwMr9\nT+srq6eZbjOy7VXprpo7FrUdffjhRKtf7xFMjjYa0Nrdj4UT0m2DZKmZOSit7QTnA7uQtHb3Y3dV\nO86dmk753ABiUrJhsnBUNA/MOz/SYEA9ktGlS8eBOrtY762iHlNhbhKOBGiViIHJorxkJMXoHCLu\nvdXtMFk4Trb24MF/7RnQRXXF5hOIitDgxkXjcc6UNFg59dQEz/Vegt+bluPmL3rQ0UsC3dlnwq2v\n78R/vLsL1726HbMe/QbnPb0BB2rsF9Kqth6MidEhLioCjDFMzYwPeWaJ6J0MhOKKVvz92yNYWVyN\nv3xxCLe/VYz7P9gT5Bb6ZuvxZpTxcThQ3z3gY3u4CQvh/vPqg+jsNeOZ6wsRFaHFRdMzsaOiFW3d\nrrMN6zuMftskAJAQHYGYSC0MRjNSYqMQofX9lWQlRqO2vQ+blJNvyaRU5KfGYv74MfiopBqcc7R2\n9+Out4tx3SvbcMxNpoI4AYVVAgAXz8hEfFQEVpZUuWyvpqq1x+8DrrffgrveLsbb2yu9bre9nIpv\nnVaQQlUCAeTm5qG1u99mPwXKlmPN4Bw4e3Ia1S1Z/gV0828CgAEPUB5t6MLKhFtQvPhV9PRbbCKy\np6odY5OisWRiKsqbu2E0+x/JlSsXkYLUWExMi3PILCmppMJYD1wwGWvLGvHSxuMBtbfFYMTHu2vw\n4/k5SI6NxJycJCRG62w+d3tPP1aUtKI4/RrsqmrHT17ehpLKVlzz0lZsL2/BX66aiddvXYCHLpqM\nmrZerCqx23FVrT3ITbaXOJ2amYDD9V1B6bEdquvESxuOu7zXl/vrcd7TG23fSyA8t+4YUmIjsfsP\nF2L37y/E8jPy8PXBeo+2ZyiobutBZUsP8lNjB3VsDzdhIdw7TrRi6axMTFUGYC6akQGLlWNtWaPL\ntg2dfX4PTAKU2y0yRXz524LsJD16TRZ8sa8WBamxyBlDJ8/V88biaKMBb2ytwKXPbsL6siaU1Xdh\n6XPf49VNxx3S1EprO5AYTd64QK/T4vI52Vizvx4Go2uGCuccT35VhjOfXI+3tnkXYoDsj1+t3IOv\nSxvw8objHsW+q8+Ed7ZXIjc5moQgaTwQGYep42kQp7RmYFHclmPNiNdHYHaOMpEnbwkKcrKgYYH7\n0IIjDV1IzxiL/Gm0RuG+aroA7q1uR2FuEiZnxsNi5bYsEX8obzIgKkKDsUnRmJAW52CVFFe0YmJ6\nHO47fyKWzcnG098cxmZVtCzgnLv9fj/YWYV+sxW3LaZlrrQahjMnpWLjkSZYrRxvbq1ET78F/3vd\nHLxx60LUtPfixy9tQ11HH968bSF+dtp4nDslHfecNwmnT0hxGNisbut1EO5pWfHoNVkGlFWjpqGz\nD7es2IEnvirDzgrH3t8nu6lHuXpfrcs+Zz65Dpc8swm/fG8XnvnuCJq67Nlfe6raselIE+44qwAx\nkREYExuJO84qAAPw/o6T8EW/2YrffrIf172yLSCbTfRgBKI66M+X0O9xUDWGwznHzSt2OFwcRyo+\nhZsxtoIx1sgYOzAUDXLGbLGivrPPJo4AMGtsIrIS9fim1HWaeH2n+1mT3hC52f742+rtd51sx5JJ\n9rziy2dlIzJCgz9+fhAxkRH45Jdn4NsHz8LZk9Pw2JdluOm1H2yeXmltJ2aOTXCpi3LN/Bz0miz4\ncl+dw/MWK8f/+2Q//rHhOBKjdXjmuyMuB6UzT397GF/ur8dpBcmoae/FnirXmhlmixX3vLcbJ5q7\n8fjVs+nJJQ8AV/8fpmYmgDHgQG0HOOf4ZHc17n67BCuLq3ymPpL/34wzJqRAq7H/j3qdFuOSYwYk\n3EazBRUtPZiSGY+CtDjERGqxv6YDLQYjqlp7MSc3EVMyaJDO0/uX1nag6C/fOVgK5U3dyE+NhUbD\nMCE9Fs0GIzp6TLBaOUoq27AgbwwYY3j8x7MwIS0O93+4x0GUTBYrbl6xA3e/U+LyeZuPNmPm2ARM\nTLdnMJwzJR1NXUbsOtmGN7aewPlT0zE1MwGLJ6biw7tOwxVzsvHRf5yBxRMdJxidPTkNJ5q7UdnS\nDYuVo7qtB7lj1MJNgc1g7BKj2YK73ymBwWhGTKQWH++yW38dPSZsPELB0lcH6h2i8VUl1ahq7UVG\ngh77qzvw7NqjuO6VbbYxp+fXHkVSjA4/O228bZ+xSdE4b2oGPtxZ5bWH1Nrdj5+99gPe/eEkfjjR\nipXF/gnrhsONmPunbxwutFuPNSM1LhJXFtJ4glq4DytjEU9/c9jl4vDwqr149N+lwzL+5A5/Iu43\nAFwS4nZ4pLHLCCu3L2IAUJR80fQMbDrahN5++w9usljRbDC61CnxhfC5/Y241TniZ06yp88lxuhw\n77kT8bPTxuHze5dgRnYi0uP1ePWm+Xj86lnYerwFD63ci36zFWV1XZiZ7brc0bxxSShIi3W46hvN\nFtzz3i68v6MK95w7Ee/evgjtvSa8tMHebTcYzfj9pwfw0Mq9eGHdUTz9zWG8uP44bliYi1duKoJO\ny/Dl/jqXz/vz6oPYeKQJf75qpl0oUicCU5ciNioC+amx2FnRivs/3IMHPtyLLceb8etV+7Dwf9bi\nj5+Xeox+Klt6UNPeiyWTXCc5TMqIH5BwlzeRYE3KiIdWwzAjOwH7azqwV8kImpOThPzUWERomMeU\nwBfXH0OzwYiPVRlA5c3dKEijmhUT0khgjzUZcLTRgM4+M+aPp5otMZEReOHGeejqM+GhlXttJ/Gf\nPj+I7482Y/3hJofBNpPFit1VbSga71jz5azJ9D0/tHIv2npM+MW59oqEM7IT8fwNczE5w3XW6jlT\naIr2xiNNaOjsg8nCkZts77FNSo+HhgFflzr22EoqW3HTaz/g2pe34l/FVQ7njBrOOX73yQHsPtmO\np6+dg6WzsvDF/jrb9l+X1sNk4Vh+Rh7qOvps3zvnHCuLq7AoPxlv3rYQmx4+FyvvOh0NnX24/tXt\n+O5gA9aWNeL2JfkulTdvOn08mg39+OqA+1o9x5sMuPLFzdhT1Y5nry/EvHFJeH7dUZ+DmpxzPP3N\nEVg58Levy2w9oi3HW3D6hFTE63XIS4nBQdVF7vsjJPB1HX34QhU4bT7ajH8VV+ONrRX40+qDI8IX\n91kYgXO+iTGWF/qmuEek3YkoV3DRjEy8ua0Sm4424WKlCmBTlxGc+z/5RiAuCoFG3FoNw2kFjifl\nvee7LjTLGMP1C8ehvdeEx9eUwWzh6LdYMT3bNR2JMYZr5ufgya8Oo6K5G1lJevzinV1YW9aI3102\nDbefWQAA+FHhWKzYcgI3nT4eidE6LF+xA7ur2pEaF4lVJRQNLpmYij9dORM6rQZnTUrDl/vr8f+W\nTrNF+W9vq8Cb2ypxx5n5uGHhOLf/68zsRPx7by20GoZfXTgZ/3HOBOw62Y63tlXg9S0VmDtuDJbN\nyXbZ7/tjzbY2ODM5Iw7ryhphNFsQFeHn6iewR9GTM0hcZ41Nwns7KlFS2QYNA2aOTURkhAYFabFu\nLwwVzd1Yc6AeWg3DmgP0XYiBx8tmUbaSiIyPNxlsF6Wi8fYytFMy4/G7y6bh95+VYsWWE4iJjMDb\n2ysxd1wSdp9sx+6T7Th9As3oPFjbiT6TFUV5jmVs0+P1mJGdgNLaTizMT7ZdGHyRnxqL8Skx2HC4\nydazGKeySqIjtbiycCw+2V2DtWWNuH5BLk409+C7Qw1IjYtCYnQEHl61D39efRAXTs/AjOxETMuK\nR6RWgx0Vrdh2vAXfH23GfedNxKWzspAUE4lVJdX45mA9riwci8/31WJccgweuHAy3v2hEmsO1GPu\nuDEormxDRUsP7jnPfuwX5SXjrZ8vxC0rduL2t4qRoI/AzWfkufxPZ05MxfiUGLy7/SSuLHSdOfrb\nT/aj22jBh3eehrnjxiAtPgo3/h9F38LucMf6w43YX9OBMyel4vujzfj2YAMK0mLR1GXEGcrvMz07\nAQdUNuCmo0223///vi+3ReV/+7oM2Yl6XDwzE69vqUBCtA4PXjgZJ1t68HVpPXRaOr/9TYgIBiN+\nIQUx0UVExYKF+clI0Efgm9IGm3CLqn0BWyUBRtypcVGI0DAU5iYhXu9/waS7zipAZUs33t9Bg48i\nFdCZq+fm4KmvD+P9HSdxrNGAtWWN+MtVMx26mb+6eApW76/D/3xxEA2dRuypasfzN8zF/2/v3uOi\nrPMFjn++MzAIA8IwDKDcQUTxjigS6dp2MbWOJ1tLKyu3U3u2zsn2tN1e1Xbas7XntJ1Otbt2ssup\nU7vVrt3vF6s107xV3vICghcEUUTACyCX3/7xzAwDMsAoyDD83q+XL5kLw/Odmef7/J7v7/LMGjOE\nupPNlNXUkWq3ussUs8YMYfn2g3y/r5oJyTb2VZ3goQ+2MT3Lwd0zR3rd5tljh7Cn6gS/uiSbic4E\nNjktmtwUG5v31/DS6t0dJu6VhYdIiAol1X7q9QGHxxl16JLK46TarXy2rYJRQyNJi+l8pbbCimOY\nTeJ+3tjESJ7/uoW3vitjeFwEVmdrbnhchLs16GnpV8UEm00sPj+T3328gy37awm1mGluUe4Wd6It\nDIvZxK5DxzhU20BMuIWUdjFcMyWFFYWV/NdH2wGjhPH4lePJ+c2nrCk57E7c650deO1b3K7f2VpW\nyy3n+XbhhunDHby2fh/njzRa356lEoD/uXI8C/NTeG5lCc9/vZuwYDN3zMhiUUEqocFm1pZU8ee1\ne1mxs7JNGQQgw2HllvMyuO0CY2nbvLRoEqJCef3b/RQMi+Hrokp+Pj2DyNBgCobF8MHmcu6ZOYK/\nrt+H1WJm1pi2KxtOTDGS909fWMfN0zMY3MG+YjIJV+cl8/AH29l+oNbdjwVG38M3xVXceXEWE5KN\n7945GTGck2FnyRdFzJ+U5P7MPSmleOKzQpKiQ3nm2lxmPvEVj326kysnGTMmCzKMxsSooZF8sPkA\ntfWNWMwm1pRUsXBKCsNiw7nnjc2sLj5MbV0TG0treOTysczLTeREQzNPLi/kvY1l7k5tgOe/3s29\ns0dyUXZcp8tC95QeS9wichNwE0Bycsett9PhanF7lkrAmAhz3ohYvtxx0H3NSFc9zZfOSc/X7mrW\npIvZJFybn8qkVN8uCCAi/HrOaEqP1PFDWS1p9o4TVXzkIM7NdPD0imKAU5I2GPXBG85N46kvdxFk\nEv6wYAIzna3GUIvZfcrvckF2nLtcMj4pivvf3oJZhN/OHdOmBt3ejFHx7gOjJ5NJuCYvhYc+2Ma2\n8to21ztsblGs2nWYWaOHdPgldpUBHnp/G1v213DkRCMJUaG8f+u5RIV5H465s+IoqfYwdyt9TKJx\n4NtfXceVuUnu52XFRfDepnKONzS5d+xDRxtYtqGUy3MSuWpyMo99upMPtxjvBUC68/1yHRh2HTzO\nzoqjTEyxnRKDiPDI5WOZ9eRXDAo28+T8CUSGBTMyfjBrils78zbsqSIhKrTDOQU3nJtGhiOcaZm+\nLZT1oywHL67ew+sbShE59UwUICfZRs5VNiqPNRASZGrTuMhLt5OXbne/J9vKa6lvbGZiig17eNuG\ni8kkzM1J4I9fFPHC17tpUXCp8yA9a/QQ7nx9E+t2H+H9TeXMHjuEMMup6SQn2cb6ey/odLTWvIlJ\nPPrJTl5ctYffzm29puRr6/YRZDLOQD39ckYWc5esYumKYi6bkEDlsQYUMDHZhskkfLnzEBtLa/jP\nuWMYFGzmtgsyWfzq9/zh8yISbaHG6qBA9pDW2ab1jc2cbGphamYMU9LtPPrxDp7+WzFl1XVkOKzM\nzUlARHh47hgURqPjqrxkZoyKZ2/VCR58dys/e2kDUzNjWLowl1BL77a+eyxxK6WWAksBcnNze6wI\nVFZdT3hIUIdH64KMGN7+voydFcfIio9wT37p7uQbl0mp0SwqSG3T0diVX12a7dPfcAk2m3j++klU\nn2jE1EnCXDglhZWFh/j1nFOTtsvPp2dQWHGMK3IT3ReN8CYyNJipznLJuKQovtxxiPsvyXZPQDod\n83ITefSTHfz/6rY73KbSao7WN3l9P9MdVgYFm1i16zAXZccxbbiDX729hdv/spFnrs31+r4UHmyd\n3QiQZrcSHhLEsYYmxiW1LkE73PmcwoPH3In5hVUlNDa3cOPUNGxWC/npdj7acoDBocHubXLJiLWy\netdhjpxoZKGX995mtfDh4qkEmVuvmDQl3c6f1uyhoakZi9nE+t1H3K3v9uzhIVw+0ffVAPPTY7AE\nmfh2rzH80RLkPSHGhHd+BumICMER0flCS5dNSOD3nxex5MsihseFu1vEF2bHYX5TuOv1TRw/2cw8\njwNne10NsbVZLVyRm8gra/dx3TkpjIgfzMmmFpZtKOX8kbGnNKhykm2cPyKWJ5YX8sTyQvf9qfYw\nFhWk8cZ3+0mICmVujvH+Xjp2KEu+2MWOiqNcMbL1PXeVKreW1VBWXYfFbCIvzc6gYDML81N4/DPj\ntZdcneOOwWwSHvnJuDbbkxQdxvu3TuXlb/awubSm15M29IPhgGXVdV5r1q6dYrVzvZCK2nosQSZs\nYb6t9zwo2MwDl44iMvQM1on2QbDZ1GVZ5sLsODb/+wyvSRtg8KBgnr0ut8uk7TJrzBD2V9dx17JN\njBo6mOvyvb92d0SFGb3zb323v83iRq5e/HO8JK2QIDNv3lzAyrvO46lrJrJgcjL3zc5m+faD/O8K\no8NVKUXRwaPuGYb1jc3sOXycTI9OO5OzgxJgXFJr2ck9ssTZQXmsoYmXVu/h4lHx7pb1xaPjKXbW\nvGPCQ9o0DDIc4RxxzpKc2MlZVVSYpU1nW156NA1NLWwqraH0SB0Hjza0qY/3hFCLmbw0o/TiOZS0\nt6Q7wpmQHGW0tse2lsRcB7+SSmNEzpnGefuFWUQMCuKBt7eilOKzbRUcPn6S+V76Xn5z2Wjumz2S\n/543jhd/Opkn5o/HZrXwwDtb2bivmlvOG+Y+qJlMwr9dZJR/pg1vPVDFRoQQE27hh7JaVuysZFKa\nzZ10F05JISTIxJiESGaO7nr/CjabWFSQxmNXjj+j96G7umxxi8grwHQgRkRKgQeUUs/19oa5lNfU\nM6SD00EwjnQJUaGsLj7M9QVp7qGAZ6PGdDZ0VL87Exc6yyUnGpt5+LIx3Zps1JVr81P5y/pSXt9Q\nyiLnWOWVRZWMGjr4lFNvT56lFeN1Uli3u4pHP97BD2W1rNtdRUVtA3arhT/fOIXG5hZaVGvHpEte\nWjQ7Ko62GYWRFB3GoGCT+zqMdy7bSG19E//8o9bRGzNGxXP/21vYuK+ayWlta9CuDqqQIFOHI3+8\nmZxqvM43uw6T6Bzt0d2OR19Mz4rlq8LKNmO4e9OCycls2V/jLpO4zBwTz8qiSn4yMfGM9zmb1cId\nM7K4980tvLupnL+u30dCVCjTOhiVBMYkOFdHvcuc8Ql8u/cI3+45wrzctmczM0bF886/FLT5PEWE\nkUMGs7KokvKaeubmjHA/Zg8P4eV/yvPbfNKdUSULzsaGeFNeU8foBO+LweRn2PlsWwUtLYpyL1e+\n0QyRocHc5JwA4VlaOBOjEyIZnxTFS6v3kGq3cvj4Sb7de8Q94aS7jHHSY9lZcZSVRZUUDIthcmo0\nS74sYsEz37h3xKx2w+Ru+fEwrslPIdjjIGQ2CZmxEew4cJQH393KB5sPcN/skW1idkSEMCk1mrUl\nVWQ42vY1uPoHxiVFdVqKaM9mtTAiPoI1JVWU14YRERJEVnwPXIyinelZDv7jPUg5S4l73sREzsuK\nPeUscc74BEoOHefqvJ7p05o/KZlX1u7lwXe2cvj4SX5xwfBO+186kpNsIye549a/eyKYh+yhg93L\nD0xtd5CYlNrzB92e4tejSuobm6k8drLTOmx+up1lG0rZdqCWitr6Dj8crdUdM0Z0/SQfXX9OKre9\n9j2LXlgHgEmM2a2+Cg8J4sPF0xBw17mnDXewYOk3PP23YoLNQmq7kSchQWZiI06tKQ6Pi+DN70pZ\nWVTJjVPTTmmdAcwaHc/akirSY9q24tMdVixmE1PSfN9xp6TbeW3dPspq6hifHOVz4umODEc4Ty6Y\n4LUU1dM6unIUGJ/XfZecXl9PR8wmo/N+7pJVmASumOR7H4CvXGsFxYSHtOk/8Xd+nbhdnY2djctu\nrXMf5kBNPRdld29In9Zz5owfSnzkIEKCTNjCLNjDLT4Nk/TUPtGlxVh57WdTWLD0G2xWS5uWdWey\n4sNpUca23eNluOPssUN5bX3pKTMUwyxBvHVLAakxvrdo89KieWHVbooPHWfOON+uaOOLjoZgBoKc\nZBs3T8+grrH5jDrOu8s1smRaZkyngwX8jV8n7jIvk288DY0KJcUexsdbD9DQ1EL8WfiwtbZExFic\nqpek2K28f+tUGpq6v0bFZRMSMYkxbNPbDumICOHDxVM7fKyjyVHd4Vkvbz/xRuueOy/u+bNCb9Ji\nrMybmMiCHir3nC1+nbjLq7t3GbL8dDuvrjMmtegad2CydWO5XU+OiJAOyyO9zR4eQmZsOMWVx91D\nETX/ZTYJv5s3rusn+hm/Hg7obbp7e55jZeMjdalE61tX5SVzRW5ij48K0jQXv/5mldXUE221dLkG\nQL7HabqvsyY1ract8nFEjab5yq9b3J1NvvEUO3gQGQ4rIt2ftq5pmtZf+XXiLq+u73bP8oXZ8WQ4\nwn0ad6tpmtYf+XWWK6upc1+FvSu/vGg47/3rub28RZqmaX3Pb2vcxxqaOFrf1GXHpEuQ2YQPSztr\nmqb1W37b4i6vdi7n6uNKf5qmaYHObxP3/uruDQXUNE0baPw2cZd3Y7q7pmnaQOS/ibu6DhE9LlvT\nNK09v03cZTX1xEaEdHtRIU3TtIHCb7NiWXWdrm9rmqZ1wK+GA17y+6840dBMU4uivKaOi7K7d0ku\nTdO0gcSvEvcwRzhNLYpgswmzKZr5k7xfgFTTNG2g8qvE/fj8CX29CZqmaX7Pb2vcmqZpWsd0I+WG\nrgAABApJREFU4tY0TetndOLWNE3rZ3Ti1jRN62d04tY0TetndOLWNE3rZ3Ti1jRN62d04tY0Tetn\nRCnV8y8qcgjYc5q/HgNU9uDm9AcDMWYYmHEPxJhhYMbta8wpSilHd57YK4n7TIjIeqVUbl9vx9k0\nEGOGgRn3QIwZBmbcvRmzLpVomqb1Mzpxa5qm9TP+mLiX9vUG9IGBGDMMzLgHYswwMOPutZj9rsat\naZqmdc4fW9yapmlaJ3Ti1jRN62f8JnGLyMUiskNEikTk7r7ent4iIkki8oWI/CAiW0VksfP+aBH5\nVEQKnf/b+npbe5qImEXkOxF5z3l7IMQcJSLLRGS7iGwTkfxAj1tEfuH8bm8RkVdEZFAgxiwiz4vI\nQRHZ4nGf1zhF5B5nftshIjPO5G/7ReIWETPwR2AmkA0sEJHsvt2qXtME3K6UygamALc4Y70bWK6U\nygSWO28HmsXANo/bAyHmJ4CPlFIjgHEY8Qds3CKSANwK5CqlRgNmYD6BGfMLwMXt7uswTuc+Ph8Y\n5fydJc68d1r8InEDk4EipVSxUuok8Cowp4+3qVcopcqVUt86fz6KsSMnYMT7ovNpLwL/2Ddb2DtE\nJBGYDTzrcXegxxwJTAOeA1BKnVRKVRPgcWNcEjFURIKAMKCMAIxZKbUCqGp3t7c45wCvKqUalFIl\nQBFG3jst/pK4E4B9HrdLnfcFNBFJBSYAa4A4pVS586EDQFwfbVZveRy4E2jxuC/QY04DDgH/5ywR\nPSsiVgI4bqXUfuBRYC9QDtQopT4hgGNux1ucPZrj/CVxDzgiEg68DtymlKr1fEwZYzQDZpymiFwC\nHFRKbfD2nECL2SkIyAGeUkpNAI7TrkQQaHE7a7pzMA5aQwGriFzj+ZxAi9mb3ozTXxL3fiDJ43ai\n876AJCLBGEn7T0qpN5x3V4jIEOfjQ4CDfbV9vaAA+AcR2Y1RBvuxiLxMYMcMRquqVCm1xnl7GUYi\nD+S4LwBKlFKHlFKNwBvAOQR2zJ68xdmjOc5fEvc6IFNE0kTEglHEf6ePt6lXiIhg1Dy3KaUe83jo\nHeA658/XAW+f7W3rLUqpe5RSiUqpVIzP9nOl1DUEcMwASqkDwD4RyXLedT7wA4Ed915gioiEOb/r\n52P04wRyzJ68xfkOMF9EQkQkDcgE1p72X1FK+cU/YBawE9gF3NvX29OLcZ6Lcfq0Cfje+W8WYMfo\nhS4EPgOi+3pbeyn+6cB7zp8DPmZgPLDe+Xm/BdgCPW7gQWA7sAV4CQgJxJiBVzDq+I0YZ1c3dBYn\ncK8zv+0AZp7J39ZT3jVN0/oZfymVaJqmad2kE7emaVo/oxO3pmlaP6MTt6ZpWj+jE7emaVo/oxO3\npmlaP6MTt6ZpWj/zd4YHML02MRFiAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11b427668>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator samples from training\n",
"\n",
"Here we can view samples of images from the generator. First we'll look at images taken while training."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def view_samples(epoch, samples):\n",
" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\n",
" for ax, img in zip(axes.flatten(), samples[epoch]):\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)\n",
" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" \n",
" return fig, axes"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load samples from generator taken while training\n",
"with open('train_samples.pkl', 'rb') as f:\n",
" samples = pkl.load(f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnWeUFNXWhs8YEBUwDEFAZEAUQZSkKGAWRQxgFjNeDPea\nMGK6BgQFc07ANeecEFRABQUVUMGAiCRBBUFAzJHvx7dq+7TUYaqmu890D++z1qz1WlZXVVc67Lf3\n3qdk+fLlTgghhMg3q1X2AQghhFg10IAjhBAiCBpwhBBCBEEDjhBCiCBowBFCCBEEDThCCCGCoAFH\nCCFEEDTgCCGECIIGHCGEEEFYI83KtWvXXv7tt9/m61gqxGqr/T1m/vXXXyv8/7XWWsv0r7/+GruN\nJk2amP7hhx9ML1y4MNWxlJSUmE7SwaF9+/Zu0qRJi5YvX14n1Y7+QSFeFxKdl7RdLTbeeGPT8+bN\nK3f9ddZZx/RPP/2Ual8kF9eldu3ay8vKytykSZMqfBxiBar8s1JRNtlkE9NffPFFsP2mfVZSDThl\nZWWOF2v11Vc3/eeff6bZlHegKG8AcS7zxc6XzI8//uicy3yx8aU1Y8aM2G1cccUVpt966y3Tt912\nm+kk35WD2y+//GLa950mTpzoSkpK5sRuLAX/vC75IMlg6vue0XnhOUmyvT59+pju27dvueu3bNnS\n9MSJE2PXSXK8ubguZWVl0Xay2YzIpCielbSk/YdqHOedd57pU045JetjSkraZ0WWmhBCiCCkinD+\nCUdjjtK+EbtWrVqmO3bsaHrEiBHl7mvNNdc0/fvvv5uOi4IYjfBf1fXq1TP9zTffmJ4yZYppRjX8\nHtzP2muvbZo2nc+y42dD/Is3SZTow3ftkvzLy7cvXoM02zv33HPLXYcwqknyr8a050YIUr16ddNx\n93hSctFAOZuoplq1aqZ/++23rI9lZSjCEUIIEQQNOEIIIYKQlaVGS2KNNf7eFC0nZn199913ppPY\naGS99dYz3bZtW9OLFi0yHVkwI0eOtGXPPvus6R133NH0iy++aPrGG2807bOjaNH8/PPPpvm9//jj\nj3K/R4j5h7Kxinw2aS6Oe9111zUdJXj8cz/t27c3zQwvn73pQ/M8iXyTjY1WSOTbRiOKcIQQQgRB\nA44QQoggZGWpEVoY33//fU62SbvqgAMOMD158mTTt9xyi+moOHDbbbe1Zcccc4zp+++/33TNmjVN\n0/bj9+D+mclBaK/5MvVI6MyotLZYkgy3xo0bm2a2H89FHLTRWMs0YcIE09ttt51p3ke0Yxs1arTS\n/ayMXNuEQojkKMIRQggRBA04QgghgpDaUvNZErRIfOswu+z999+P3T5tHH72nnvuMc1CTWbERXYM\nrTDaaLTaPv30U9Nz5vzdmeGrr74yzawzXwYav2vr1q1Nf/DBB7Hrh8ZnG/my65JYfjxfSQpZL7/8\ncueccxdddFHs52ij8Vh4bRs2bGiaGYu02nxk04JpVYMF1szw7N69u2leuySZmYWMr6C8srZT1VGE\nI4QQIggacIQQQgQhtaWWJLOHdg3DS1phzIby9eyi3myzzUx/9tlnprt162Y6sk5oCx166KGmWRDK\nAkNmQy1btix2uQ8eo89Ga9OmTbnrhCZXVkiS+2GfffZxzmVec8LrNWDAANPXX3+96WwyH302mjLW\n/p/Zs2eb5v3J+5ZFjh06dDBNa7q8LMVCJFf2V662E92T7DU5btw407SHec8WS19ARThCCCGCoAFH\nCCFEEFJbakmssBo1apheunRp7GeThKC0PFj4SYvk66+/Nh3N8sjZ72bNmmX68ccfjz0WFnWyCDRX\nFMokXBtuuKHpxYsXx67jO9a0llPdunVNR9M2LFmyxJaxeDRXhcJpWZVtNNKsWTPTCxYsMM3JDflc\n3HrrraafeOIJ04MHDzadzYyrqxpxBePz58+3ZXw/8b255557mmafwueff950Eus8pLWsCEcIIUQQ\nNOAIIYQIQmpLjdkQnGWO4XQ2NhphRgYLRU8++WTTL7/8sumrrrrKOZdpFzFzhpluUeaUc86NHj06\n9nhzVSToK3INDS0tXzFkrkJqhvVRwe2bb75pyzj7a2VZauL/4fXv16+f6auvvto0n3tmtXGaEd5T\nLNotxuy1fEMbi89CNMUKpwz46KOPTF9wwQWx23jrrbdM83niu833PgtpLSvCEUIIEQQNOEIIIYKQ\n2lJbf/31Td9xxx2mk/RYSwK3w6wq7osh6JAhQ0zPmDHDOZcZ2teuXdv0XnvtZZp9z5K05M8VLIrN\nF8xY8RXhMouI2Ugs8Et7LgYNGmSafeuizCcWCfqKQEXu4fMQZxn37t3blvksmyjT0Dnnhg0bZpr2\nOe+XYrTRkmRr+WatTUL16tVNH3bYYabPP//8FbbfoEEDW8Z3KK8lYWYwr/H48eNN85mvrEJRPfVC\nCCGCoAFHCCFEELLqpZbvsKxVq1am69evb5rh/aRJk2KPLaJOnTqmaS/RCmB4++ijj5r+4osvKnLY\nKyVEO3eGzrQJeL1YeMnpBkhaq5H9n7jfevXqOeec23TTTW1Zly5dTHPqiXzDe4rZP1UZWjJxFjez\nN1mw67PURo0aZZozvtLWKUaSZGultdH4DPEc8t7jO+zggw9e4XPUvsJs2uK0Rbmcn62szFBFOEII\nIYKgAUcIIUQQUltqnGGRIXSuepCttdZapmm10NL5/PPPYz8bZXA0atTIlrHYMbJ2nHPu8MMPN81Z\nPocPH246m1n8fBkvIfqqffLJJ6ZbtGgRu87cuXNN+65jEhuN3+fdd981TXst6nfXtWvX2G3nu5fT\nBhtsYLqYbLRc9bXzET0vZ555pi3z9UqkHcR+a8o2TA7P59SpU01zupXoPcP+ab77gPYoZ2Tlclpn\nhZA5qLtFCCFEEDTgCCGECEJWVYgMs8kWW2xhmsV+SWBxFDO6aGnNnDnTNMPHKPRk0RTDSGZJcT+0\nXPbee2/T2dgvzIirWbOm6RB91Xw22kYbbWSa7c+zsUMZ7r/yyiumeb0mTpzonMu0Lps0aWKa91GS\nQmFeOxaq+mCxHLOwmGFViNCC8fW+y4bI1kxi0b333nvlHsuq1hMvSRanbznv22+//dZ09L5KkvHH\nbfPZysY6KysrM82eeblCEY4QQoggaMARQggRhNSWGrMn2EKby9PaaLRlSktLTbOA6T//+Y/pE088\nMfazkWXE3lCcqoBZUrQCnnzySdNTpkwx7Wux7ss643LagTwGhqyh+xnRRssV/A4jR440feSRR5p+\n6KGHnHOZVhhtPN5HW265pem2bduavummm0xzWoxnn3223GNctGiRafbnI7Q9CxHer7nq/Rfdu77+\nfry3zzrrLNPZZMntsssupl9//fUKb6cQ4LlPa3nys7fffrvpKJP24osvLncbzEblPZ4WWu35sNGI\nIhwhhBBB0IAjhBAiCKktNdofDCMPOugg0wwRaZH5wn8We7Zv3940+159+OGHphnSc7qEqG8arZvm\nzZubpkXAY+c6ffv2Nc3vSmhpsFcR+yz16NHDNK2sjz/+OHabxQrPKa0ZzsQaza7K68LP8fpPmzbN\ntK+okBYoi3OTWD20N0mhZFgNHDjQNC1lkisrNprmw2cR8/7n9CCHHHJIhY+rEGw02qdJrjvva18v\nRJ+NlqSomX0Njz322JUeCzM6+e6h/c8MUV4T37Hz/ZRNsXsSFOEIIYQIQuoIh5EBR+xHHnnENDsu\nc33fv4C4Dv9VtfPOO8eu/+CDD5pmvnqzZs2cc86tt956scfIf21w9GYePH9U5g9x/NcBvwejGv7r\ngDUpTDjIV2ubfLeH8cF9cXIq1kIxyi1vG7wujHzIl19+GfvZqoAvqskVjBqjyJ41IfyXMs/t22+/\nbTpJ2ybfdUkSLeQbuiJJIpxsjpOTRbItGM/Dm2++ucL6vohp8uTJpvv06WO6YcOGptm2Km2Uko+o\nhijCEUIIEQQNOEIIIYKQ2lKjncSaklmzZpn21aNk7BghJa0obpMJBLTduD7D+Mgu8Fl3PJYxY8aY\npkXDEJj76dWrl2nWhBx44IGmn3vuOdPMbWcYnC8LqLKsJd9EUY8//rjp6Nyx5RGvJ5MA+vfvb3rs\n2LGmORneiBEjTNMe4aR6xQprxVjXxHs67bXmfUy7OUqQ4bNI+5dtgGh1+2yXJHZxrtryZAMtp3zA\n88DJEHnuzz///NjlkS3ts+1Zg8iO00yECGHhVxRFOEIIIYKgAUcIIUQQUltqDOdpo/nqMXzhN7Nh\nrr32WtNvvPGGac71TQumdevWsfuNrAOuy/9/1VVXmR49erRpdlplZhoz4AYNGmS6U6dOpmmXsV1L\n6E7E9evXNx1NeJYvaAHQRuPyzTff3HRkNbIG46mnnjLN89+lSxfTbN1x7rnnmr7//vtX2LZzzr31\n1lvJv0SBwvqlbGDNE2EWZlS3RruM9zOtmSQ1NkmsvqqUVeirE+O5Yo0fs9F4HpiNuWzZMudcZqsw\n2pCnnnqq6TPOOCN2e3wOacclybbLdxahIhwhhBBB0IAjhBAiCKktNV9bCIZ01L7u0lE4/8/tsNjz\npZdeMk17jZ2IaYEddthhzrnMokNaarRiaDuxYNFnB9IiWrJkiWnaaAylfW10mDGUS/JtoxFer3vu\nucf00UcfbZr3QNTR+ZhjjrFlzAbksdNeo73EDDS2H/JNApgWnz1SrNCGoeYEg9OnT3fOOffiiy/a\nMmZvhu5mXgwk6QrNCR1pyzPrku+tnj17mo7el75i9NNOO80036d8Dnjd0l7DJDZaNs9K1XrKhBBC\nFCwacIQQQgQhtaXm6z3UokUL05yAjWEnM2eGDRtm+pxzzjE9ZMgQ0y+88IJpFsHRAuDEbJE15gv5\nnnnmGdMHHHCAaWbjMOy97LLLVti2c5m94mj1bLfddqYnTpxomucgX1k6IXupMUzfZJNNyj2GKPNw\ns802s2WRneNc5vU66qijTHMyvBkzZpj+/PPPTdOaJUkyiAi/R1WAdjCLYy+88ELT0fP4wAMP2DL2\nTFvVSPIMJSlcpeX+7rvvmua9veeee5rme7F79+4rbIOWGjtE0/5ngWmurFDf+chm+4pwhBBCBEED\njhBCiCCkttR8vXnY18e3/n//+1/TvXv3Ns1iPxaEMuyMMtCcy8zwiOYA52dp+zHbg3YBLQfuk5lR\nLIIbP3686bvvvts0Q02Gz77+VbnKqvonIQvqaFdxjnrfOldffbVzLtO2uu2220zTonz++edNM2OG\nVkK7du1M33vvvbH7Z6YQ7wEf+Z7LvSKktUl5zvnZbt26maY9E63PAsJVmSRTKtx1112m+Q5LC7Pd\n9t13X9PRNdljjz1s2ZVXXmma77Z8TyWQj3eKIhwhhBBB0IAjhBAiCFn1UiMM52lRsZcPLTVmZkSF\ngf9cXrt2bdO+vk5c/+OPP3bOZfbgYk+zUaNGmeaUBCeccIJpFnKyIIvHwu/K/XO/W221lemLL77Y\nNDPyQpCP7DVfnyfaBCRazrnTCbP7WJhI+4dZO2zRTluD9l4SG63Q8c2mSbuWxX+8R2+++WbTO+20\nk2neu7SAhR9au7zf+BzQ8mXmKq9bjx49TLds2dI0r+d5553nnHNut912s2W8lpU1S2quUIQjhBAi\nCBpwhBBCBCG1pcZMI86c55vlzkfTpk1NM0uDWSATJkwwzRbetAK23npr01FhJ4suab/xuHxTGMyb\nN8/0uHHjYtePWoiv7Dtxv6FtNJKPTBNaAL/88otpFscy9I+yfLiMVisz1ubMmWPaV2DWsWNH07vu\numvsPqsanH6CNjEzPAcPHmyaz6mvCPa6665zzuU/26kqwXcF7eTvvvvONPun0ebt06ePaZ+1+dBD\nDznnMn9C8GW2hiz2zhWKcIQQQgRBA44QQoggpLbUmMVFGF4yXPSFeszoIrvvvrtphqalpaWmP/zw\nQ9OcLiEKa33TBLAlPjPp2GONM/SxeJDZQMxIoTXE701NO65YQt9/wu/D4rODDz7YNDNromJP5/4+\nX8xS47VgRpnv/PTq1cv0Rx99ZJp91dLC65jEBg7BNttsY5r95nhPt2rVyvRNN91kmtM8NGnSJHb7\ntM+efvrp7A52FYG2Le0vPvuEBeN8z7Vp0yZ2fRY7RxY1reok/duKBUU4QgghgqABRwghRBBSW2qL\nFy827ZvNk+E/W6OzICrJ9hlWMjOHtgsLAiNoo1HTTqBdt/HGG5t+//33TTNkZhHiggULTNOaY+v3\nadOmmX7wwQdXOMZiw5cxNmLEiFhdHuyHlwRfz7S00N7MV1+7bGCGJaGNefbZZ5t++OGHTZ911lmm\nmbHnm04i11ZNktkwC40kmV6vvfZaqu1sscUWpvv372+a78J+/fqZ5tQrFT1GH6NHjzbdtWtX03wX\nhsx2U4QjhBAiCBpwhBBCBCG1pUaSFNolsdF8VDRziGEhNbdHTYuMBab8LK0zZmzR9rvkkkvK/SwL\nugoFZgBWhR5kK6NYrJ5/wvuJ1i37E0a9BJ3LnM6Dz2A+779iPLdJLCSf5eSbDsI3szF7KubCuuLP\nAr7sYWaO+gg6tUmwPQkhhFil0YAjhBAiCKkttR133NE0M7poRdGWYdjJdSrDWvKFxrQGqXnss2bN\nKnc7PvhdfX2tcgn34csuIz4brdCtwKqO7z5jhtGll14aq0V6jj/+eNNDhw41zXOfJOuWGYVjx47N\n+rh87xjaaGmf+cpCEY4QQoggaMARQggRhNSWmi9EZJFk1I7eOef69u1reuDAgWl3l1PSZmNwfbbk\nZzZONtvMF76QOokVeNppp5m+5ZZbcntgBQzPTaFQrH33ihXaaL6ZOjk7cT7h/mmX+TIBs7HRVPgp\nhBCiyqEBRwghRBBSW2q+Vvuc7bFOnTqmr7322nK345vaINfZFp06dTI9Y8YM08zGmj17tmlfJhvX\n9xWn1qtXzzRnCA2d7cUiNBap+hgyZEg+D6fCsGhuwIABpmkHpL1finHGRJE9tPyTFK+HstEI78ck\nBbW+93KSZ0KFn0IIIaocGnCEEEIEoSRNOFVSUrLQOTcnf4ezStJ4+fLldcpfzY+uS17I6rromuQF\nPSuFSeLrkmrAEUIIISqKLDUhhBBB0IAjhBAiCBpwhBBCBEEDjhBCiCBowBFCCBEEDThCCCGCoAFH\nCCFEEDTgCCGECIIGHCGEEEHQgCOEECIIGnCEEEIEQQOOEEKIIGjAEUIIEQQNOEIIIcKwfPnyxH+l\npaXLnXP6y9Ff+/btlzvnFqa5BrouxXFdSktLo+3oL3d/elYK7C/ts5IqwikrK0uzepWipKTE/nLF\nxIkTncvBZFBJr0va75CP71wM5OK6lJWVRdsRuSPYsyKSkfZZkaUmhBAiCGuk/QD/tVuos4XWrFnT\n9Pfff296tdX+Hl957Em+R6F+1zQk+Q4bbLCB6SVLluTzcIQQqxiKcIQQQgRBA44QQoggpLbUaMvQ\nXlt99dVN//nnn7Hrh4I2Gvnrr78CH0nxIRtNCJEvFOEIIYQIggYcIYQQQUhtqRHaZX/88UfWB+Oc\nczVq1DD966+/lrt9n8UXUatWrVj95Zdfms631VaImX3VqlUz/dtvv1XikYhi4P333zfdqVMn0//+\n979N33DDDbGfZXaobO1VG0U4QgghgqABRwghRBCystR8ZGMh/fDDD6bXXXdd07///rvpxo0bm16w\nYIHpqG3F1ltvbctYBNq8eXPTpaWlpvfaay/TEyZMMN27d2/TixcvNu2z8XzftVBsNCIbTZSHrzh6\n2bJlpt966y3TPktNNlp28GcGFmbPnTvXdPXq1U3/8ssvYQ6sAijCEUIIEQQNOEIIIYKQF0strYXk\ns6VYQHrkkUea3mqrrUyfeeaZpqPQnVkxLAKl/vnnn00zY2v77bc3vdlmm5meNm2a6aVLl8YerxDF\nDp85wvucxcHPPvus6bp165r+5ptv8nB0VZ8oG7B169a2jD8n8F3lszlfeukl0+edd55pWnCVhSIc\nIYQQQdCAI4QQIgh5sdSS4Ou9NnDgQNOXX365aWZVdevWzTRtsqiwk9vecMMNTa+33nqmaeP99NNP\nphm+3nTTTaYvu+wy02+88UbsZ4sV3wRrlWEX+uzNsWPHml5VbEyf1dyzZ0/Tjz76aNb74bmlHe07\nls6dO5uePn16udsvxMLnQuL44483PXPmTOdc5s8GfCYIi+H5bmvTpo3p2bNnm+Z7sbKy2hThCCGE\nCIIGHCGEEEGoNEuNofUaa/x9GAMGDDC9ww47mD700ENNr7XWWqZZFBXZAcxAY9EZl7OvGm2Etdde\n2zSzblgQuqrYaFyH14i2oy8052cjW3O33XazZQcddJDpKVOmmGZWDbexaNEi002bNo099qqGz37K\nxkbjOY2sbN+9QE477TTTSWw0Ihvt/2nVqpVp9nLs06eP6S233NI559y7775ry5ixxudtzTXXjN1P\nixYtTPP9d9RRR5l+8MEHUx17rlCEI4QQIggacIQQQgQhtaW2zjrrmKa1lDYTxVfg2axZM9Psicb2\n6CzIPPvss02PGTPGOZdZdPbtt9+apkV22GGHmWY2HK0j9i1isZsvw64y8R2TrzV8kmtUr14908cc\nc4xpniPaO/Xr1ze9xx57mD7uuOOcc841aNDAlvEade/ePfZ70DKgjVqI5z8f9OjRw/Rzzz2Xk21y\nOoEoy8lnzcyfP980iwlFctq3b2/6888/N80ekLT6v/76a+dcZlbu5MmTTXfo0MF0EiuUmWwPP/xw\n0sPOG4pwhBBCBEEDjhBCiCCkttRoo2VjbfgsnY8++sj0nDlzTNNeY5g4fPjwFdb3WUdRuOpcZnh5\nzTXXmPaFqY0aNTLNYqpCwXf+07aG33zzzU0zk4bXgsW01113Xex2mFX28ccfO+cyC9jOOecc07fe\neqtp2pi8FjyWVSXrKVc2GjniiCNM0xqN4HP26aefmmZmolg5tChp3V999dWmee459Ul0fSZOnGjL\nBg8ebHrbbbc1ncRS47Hw3dqyZctyP5sPFOEIIYQIggYcIYQQQciq8NNn42TTO4nb5DQAnFnQ1/up\nPFuPx0JrgcdLTRuJM5EyHP3kk09Wus9iI+rl5FxmBhpD/KFDh5rmrKzsPcc+aG+//bZzzp/1x95P\nffv2Nc3r+c4775heVSw1ntsff/wxJ9vkdYlgIe2sWbMqvO1VrWcaZxOm5cj79tprrzXN9xmvJy21\n6LmIbGjn/p7JuCLwmtCa82Ub5xtFOEIIIYKgAUcIIUQQsrLUfFlq+Qinuf24flBJYGbIoEGDTNOW\nY2j8zDPPmKYFxBA4LTxnlUkS+2O77baLXZ/t8VnYxmsxbty4FZb7ZoG89NJLTZ977rmx+zzllFPK\nPd60sG8ei+8KhSQ2GrMnOaMjs6MeeeQR0zynkR08b968VMfF54ht8dM+F8VuwXFqFJ4TZnEyW5Pv\nmRdeeME0C3yjYmvanHwncZ+1a9dOdbzXX3+9aRZms69hvqcqUIQjhBAiCBpwhBBCBCErSy1tUWGu\nSBN+M4zt2LGjado/LCRlZhqzrnLVs6uyzplzmUVgvkI+Zt5weoj33nvPNEN5bpPnKM35uvfee03z\n2rI4lJZmrihEGy0JvoJYWqA+G41E2ZZPPPGELTvxxBNN77///qZZ4MtrzmeH90USa6YYbTQfPA88\nP3z/3HbbbaZpS991112me/fu7Zxz7r///a8tY2H0BRdcYPrCCy807cu05TkeP3587Gc146cQQogq\nhwYcIYQQQcjKUst3SJxkVsryPkeL6OSTTzbNbDEWdTK8ZaFWrsjXOSstLTXNKRlIkn5Y3333nWnf\njJvM7tpkk01Mf/bZZ6ZpHUbb4Tlnm/UDDjjANK04Tj1x4403lnvsqwq8hy666CLTzPZL0mcrgllS\n1En2z2kjHnvssVTbqUrQRqPNOXr0aNPM6OzcubNpZrg1b97cOZdZdM3CzIEDB5rms3r//feb5rQS\nfA5pkVeWnakIRwghRBCyinCYg8/RNh9wRPb9QBZ1I+a/wDl3984772x62bJlpvmvhieffDJ2n8S3\n/8pMCPBFNWnhv7buvPNO04xk9ttvP9P8zjVq1DB99913m95tt92cc86df/75towTgfkmAGN36fXX\nX990PhIIihX++FvZNV677rqr6SQJKsUOn30mDZAuXbqY3mWXXUyzDqdbt26mH3jgAeecfxJFRjtM\n5OA6jHRZb8j3Ga+J7/nLB4pwhBBCBEEDjhBCiCBkZanRlkoLw1GGg7RoaNnRXtl7771Nb7zxxqaj\nycPYEbdx48amacXQ/hk1apTpL774otxjZ2haFWoJeC1oR9IW48RPtMOOPPJI06+++qppXpevvvrK\nOZdp+fCaE1oTvEZvvvmm6S233NL3VaostDppgXA5n50k9lp076ZJMHAus36J+2d3a1o/tEPZGZwd\n4AsZHj9bNkVtaJzLnLiOSQOvv/66aSYn0V7+8MMPTaexH/nuYXLUyy+/bJqtomiv+Wy0fLcbUoQj\nhBAiCBpwhBBCBCFndTgVrZlxzrm2bduaZnsMWiqsN6hVq5bphg0bmo7CRIaltBZo0bHGZsaMGeUe\no48kISi/B8PqQoHHzW60H3zwgWlOOte9e3fTtCDLy+rznStqXi/aNbTo0uLbL23a3377rcLbDwGt\nxsiidC6ZTUn4bESZpbTCeH4WLlxomnU1tGPOOuss02zXcsIJJ5hm65RisdEI3xV8DnjPsGs3J13j\n+6lJkyam+Qz5Mtzi4L08YcIE0/yZ4ZVXXondT5J3cb5/IlCEI4QQIggacIQQQgQhK0uNMBRLUvR1\n6KGHmqYtwImBqlevbvrXX381vdFGG8XuN87W82XAPf3006YZ8ucqS6N169amJ0+evNJjLCR4jtgi\nY4MNNjDNLJjHH3/c9IgRI0zTjqlbt65zzrmDDz7YlrEVD7tys0UHLa+LL744xbdIZmMWuo1GeN9w\ngi/e37yPmUk2duxY059//rnpqF0QzwMLDtnOiM8oNTtU83kZOnSoabZ08bWXKkZYMM6O2z7719eh\nvjx4L0+hVXkCAAAgAElEQVSZMsV0WVmZ6a+//to0rzcz5gphwjtFOEIIIYKgAUcIIUQQsrLUfHYV\ns4toqXH9bbbZxjStFhYw0QrhNqkZlkdhKv+/b3Khe+65J3Z7/B4MO30ZQHFdkZ1z7qOPPopdP0km\nUSHColn2VTv22GNN++zT6DuzCI6939jvzjeJ280335zqeAsxGzAbaMu++OKLppk9xvuY7LvvvqZ5\nX/bv3985l2ljP/XUU7Hb4LVg5hWtU1o8fO7Y9Zu934oFWvv8XuyOzsxZH2nsdL4nmC3KTDdfb7S9\n9tor9ngLgeJ8+wkhhCg6NOAIIYQIQlaWGu0khoC+ueKfe+4501HLeucyMynmzZtnukWLFqanTp1q\nmj2MGErOmTPHOefczJkzbRmzN2jjffPNN6YZpjJMZpYUs0poXTDrhrYPLQhfSF6sJOk3R6L7JLo+\n/4TXy1fISF3VetkRn6XMCbt233130127djXN+4xZhSzmveGGG0xH2VQjR460ZUkKpXn92WeM+5k+\nfbrp3r17m77jjjtcscFnltYypxjgdfPBd8LcuXNNb7rppqaj7E0Wo7O/IfFNk1LI7xhFOEIIIYKg\nAUcIIUQQclb46WuN3qlTJ9Mnnnii6VNOOcX0mWeeaZpzpNNG2WyzzUzTRvnxxx9X2D6tM2bOXHLJ\nJabbtWtnmpYaLT0WXDEzZ9asWaYHDx5smlYbj71p06amP/nkEycy7Z+OHTuaZtEwiz2rso1GaEvR\nJhkyZIjpAw88MHYd33nh89inTx/TUQEpsw75HI8ZM8Y0Z/PkvU3b7f333zfNaQiK0UbzwYLlY445\nxvTRRx9d7md5bzdo0MA0p3KIzm2S3pTvvfeeadqWhYwiHCGEEEHQgCOEECIIObPUmEnBvmfsx8R1\ndtppJ9M+O87XSp6ZaexnFNlrLOpkFg33w+UMdZndQzuQs1kuXrzYxeErOK1MG60Q+ifFwV5znE2U\nPPzww6aZsZiP81noPe44cyOn6mAmG60uThvAglvalJGVxvuCmVSPPfZY7LGwf16rVq1M066jBVfs\n8N447rjjTHNGXL5zkpCmAJzXh30HWTDNHmuFjCIcIYQQQdCAI4QQIgg5s9RY7MnMsE8//dQ0M1o4\n89+oUaNM0y5gsSXDSm5z9OjRpqMCQlp6tPF22GEH0ywkHTdunGlad+wr5euxRjsuTcvxUBSSjUbq\n169v2ldA3KxZM9MTJ040nY8ZVAvxPPGYWChIaE2yTxotuGh6COec23zzzVfYPs8hM81oxfG6nHTS\nSab5rB111FGmmRFa7HA6lC5dupjeeeedTbMYfcGCBRXeV3RNaOPx+aDNOWnSpArvp7JQhCOEECII\nGnCEEEIEIWeWGkPA2bNnxy5n6D5t2jTTtMjYY439iXxt8NmHLSqaY6bblltuaXrYsGGmmVG2bNky\n0+uss07sfnwkWUesSM+ePU3TlvH1qTvkkENMd+/e3TRnbl0V4bQFPtg3kLOFVhROLUFY4MzniIWN\nxQj7MR5++OGx6zRq1Mg0bS8WOG+11Vam2T+QNl30vnz00UfL3WcxoghHCCFEEDTgCCGECEJqS81X\nSOjL8uFyZnHdf//98QcES2X77bc37Ztd9LffflthGyxeY8FmEtibTeQWzjwZtcZ3LvPa8v46/fTT\nTV9xxRWmhw8fnq9DFDmi2G20tDCLkHaxyEQRjhBCiCBowBFCCBGE1JYas1yYreKz2likRz1//vzY\n7XNmw0KFWXC07wqxb1k+jolTNTBL0Ed0vmiFLVy40DSLdzmzZK9evUz7CoKFEMWDIhwhhBBB0IAj\nhBAiCKktNV/Rl8+uYdYXW/YXM7TRSJIW96GtNu6Px3f99deb5oyrSUhio5HofLEIjr3R1l133VTb\nE0IUJ4pwhBBCBEEDjhBCiCDkrJeaD1/hZzHjs85YkFqI8FqktdFyQVWxVIUQFUMRjhBCiCBowBFC\nCBGEkjRZUyUlJQudc3PydzirJI2XL19eJ5sN6Lrkhayui65JXtCzUpgkvi6pBhwhhBCioshSE0II\nEQQNOEIIIYKgAUcIIUQQNOAIIYQIggYcIYQQQdCAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04\nQgghgqABRwghRBA04AghhAiCBhwhhBBB0IAjhBAiDMuXL0/8V1pautw5Z38lJSX2x+XZ/CXZJtdZ\nffXV7W+11VZbvtpqq6XeZ82aNe1vrbXWsr+021lzzTXtL8l3at++/XLn3MI01yDJdSm0v4pel+hz\nFflsNn+5uC6lpaXRdvSXu78q/6zk4q9atWr2l+99pX1W1nApKCsrc4sXL7b/XmONvz/++++/m159\n9dVjP//nn3/GLi8pKYnd5l9//RWr11xzTdPrrLOO6T/++MM559wPP/xQ7rFwe9tuu63puXPnmp4+\nfbrp1Vb7OxjkHELUtWvXNj1//vzY78RzMHHiRFdSUpL1ZFBlZWXu22+/zXYzeWPdddd1zjn3/fff\n2zJec9+cTNHnnHPup59+Mu27j3JFLq5LWVlZtJ1cHZbIwcRphf6s5IL69eubnjPn71PG91D0rsyW\ntM+KLDUhhBBBSBXhOOf/l36NGjVM//jjj+V+tqyszPTMmTNNc+Tl9hmpMJriv5qjqKVRo0a2bNGi\nRbGf42g/btw407/++mvsPhkRVa9e3TT/tb106dLYY+d+eQ7yhe9f1SFnd+X35DVKcyxxn1vZfniN\nqhobbLCB6SVLllTikawaJInACxVGNSRXUU02KMIRQggRBA04QgghgpDaUmN4yR/sf/75Z9Nrr722\naf7YyzB11qxZsct9P2xxv5tssonphQsXmo7sFf5g77OzuD2fFcPjov7ll19it/nbb7/FbsdnzeWL\nfFsASWysUPZWVbbRiGy03JHELqssGy06Nt/+8/HDf0gU4QghhAiCBhwhhBBByMpSY70LbRbaa7ST\nfPUrhGFirVq1TK+11lqmFyxYYLpr166mp0yZ4pzzZ2kxi4zZZb7vwfCV2+Qx0rIj/CyPnRZjMcHM\nvNatW5v+6quvTH/99demeY5q1qy5wvbGjBljum3btqY33HBD06z58tl4PC5anT58NumqYs2JZHYZ\nfy5g5iprAJPcb1zf967gfRjd54cccogte/75500X6/sjQhGOEEKIIGjAEUIIEYTUllrGh2EbMUz1\nWRV169Y1zeyyatWqmWb4umzZsthtbrPNNqYbN25sul+/fs455zbaaCNbdt5555meNGlS7LabNm1q\nmu1saLvRGqRlGNdax7nMjDVuJ0ThZz6gfcDC2vHjx5t+6623TJ922mmm33vvPedc5nlr2bJlrP7k\nk09i98/7iOeQx0X7YuuttzY9e/Zs02xrUmwFfSIcvFd5n6Rtq+Sz933WffTeqFevni378MMPTbdo\n0cI0n4liyVgrzrefEEKIokMDjhBCiCBklaXGMI6hIws/2VeNxWvcjq9gkuy7776m33zzTdO9evUy\n/emnnzrnMjOd2KeNdgqtMGZRsaj0yy+/NO3r6+XLGuH58FmJIcim1xitM3bRbtKkiWleR1qdEyZM\nMB2dC55zwmvEe4f3hS9LkDALiPap+Bva1//617+cc85dfvnltoz36qpMruxW3sPdu3c3zcwzdkWf\nOnWqcy7zXXXSSSeZ5r3ve54POugg06+88orpJL0J840iHCGEEEHQgCOEECIIqS01huS+Xmc+K4SW\nh6+fES0V7ouZGrR0aN1EGSS0U2bMmGGall7Hjh1NM9PtoYceMh039UFSfNZj6MyoJMe90047mea5\nmzdvnunLLrvMdP/+/U3fcMMNpt99913Tbdq0MR19Z2b40KJL0stOGWW5gdfgzjvvdM45N23atJxs\nm/Ztu3btTH/wwQemfZMqFjtjx441zQwznodXX33V9HbbbWd69OjRpo855hjnXDIrjFNWMLv3qaee\nSnXsIVGEI4QQIggacIQQQgQhtaVGu4xzZ3/zzTex6zMDgxlrvuJQ3zQA7KvGLDT28orCShYgssCT\n26Bdxx5gzZo1M83ea0ky6Xww46RQ5rhnkST7mtGC3HTTTU03bNjQNIvP1ltvPdMM/WmBRdfxzDPP\nTHWMstFyD/vWjRgxwjnn3HfffWfLmHVJq/X00083fcEFF5j2Tc/B+4j9Dn3viWJnxx13NM33Inv9\n8Xw+9thjpvn+izIHk9hi7AGpwk8hhBACaMARQggRhNSW2qmnnmr6jjvuML3++uubZjYYwz7CbBlf\nC29aOuy3xV5pkS3g3N/hOnsTMaRl9sgWW2xhmjYCbTx+p1xZAezJli+StOzncfCc87zQ/jvxxBNj\nt3nKKaeY7tChQ+w6Ua86ZtL07NnT9MMPP+z7KrEoe618mO1JS5fZntH9XVpaGrsNZin6inYJr2+U\nAedcptVWCJlpvPf5HkpyXyUppKa1/OCDD5reddddTbNXW+fOnU1//PHHKz12wuec+yzk50MRjhBC\niCBowBFCCBGE1JbaXXfdZZrhKMP2tC34mWHh68NWo0YN0+xxRvsumlmTITwz2rbaaivTO+ywg2kW\nkjK75rXXXkvxLZIRIpuE1obPwvNZbQzBuR0WqjHT6fjjjzfNmU35PaPCQt4vzBhMYqnxnmLBG7fJ\nrMJVEVop8+fPN02LmbZnedBq9U0/wgw32t7M/KRlXgj4phjw2U+04jkLrc9So0W/yy67mI6m6XDO\nuT322MN0mncCzz1tND7ntWvXNs33YzaZtrlCEY4QQoggaMARQggRhNSWGsNRFnUy6yJtJgpDfoaG\nderUMU17Z86cOaYZ7kZ2GAuvOB0AM7DYSp+hJrNEeFxpoY3AkDlElhrD7iQzFDIbkN//iSeeME0r\nIWqh7pxz48aNi12H90CUqcNMP1pkPCc8b/wezI7kLK60cZhVSLsh7SyNxQpnrk3yDEZWJ4udmVU1\nfPhw07Sj+Vz++9//Nu2zpArBysmGBQsWmGZmGC1HwikebrzxRtPXXXed6Ypa60my5/jcsNj6mmuu\nMV1Z2YKKcIQQQgRBA44QQoggpPaMfO3FGcaxSMw3IybxWU60epj1QhttypQppqMsKfb6YrYOC9l4\nvDxGZqbRIkoLzw2tR84umi984TKnYaAtSc3zPHDgQNPsA8U+dNdee63pTz75xDSz4KJwn1MS8PwP\nHjzYNGcZ5XExA46fpQW3aNEiV1E402uxQjuUWaNPPvmkaU7LcdVVVznnMi0y9iHk88Lrz95ohVZY\nmA98/SB9MNP1kUceMZ1Pa5eZm3xvRtMdOJf5rGZD2izkjM/m5AiEEEKIctCAI4QQIghZzfhJ24RW\nGDPKkkCLhJbTyJEjTe+5556mOUMhrYPo2Lp37x57vHvttVfsMfbp08f0m2++merYfdDWYhhemRk7\ntKh800OwCJZZerTLaBP4sm0Ydt99990rbM93XJxBlFlyZ599tmlatpx+ghlERxxxhOmhQ4fG7pfQ\nei0meE4333xz0ywy5PU644wzTEfPAFvlH3744aZ79Ohh+oADDjDdoEGDbA+7IOE96yuATsKVV15p\nmu8nZvLmGj6Hzz33nGlmpuXK0pOlJoQQouDRgCOEECIIqS01XzjVpk0b0+x1xqwnH75ZMFu1amWa\nPdHYM6t58+amo+K0Ll262DLaWb5ZPlnY5ZtOIQn8Huz9xnA3bXieS3xty9menr2xLr74YtPvvPOO\n6WHDhpW7L9p0//vf/5xzmRkzDO95LIcccohpTn3gW5/Xi9lEL7/8cuxx0Xbj+rQ+igneWyxmHjBg\ngOnRo0eb5nP00ksvOecyM9B4Pjt16mSaM35WVXzZnZztlvavD54rFtLyncDC5IrCnzG4T/Yp5LW9\n+eabTWdj72XTD1IRjhBCiCCkjnD4L3T+i5k/Uvo6y/py9hl5MIJiOw3+y4JRDf8V3K5dO+dc5r/i\n+C8J/mDPiajYooI/wvpaV/i+EzW3w381hmht48N3/vmve3aXZYugtP8i4r/m3njjjZUeC2tpTjrp\nJNMvvPCC6dtuu830ZZddFrsd1lPxHvAdVzZ1O4XI008/Hbuc9ysTBHbccccV1mXUd+GFF5qOnq2q\nBp9HRjjrrbeeaZ8DQ3wdtOn8+KKauAkofRO9cT9s5cRrxWQuJg3w/ZdkIjnC88SauLQowhFCCBEE\nDThCCCGCkFXSALXPfkq7HU6MxhY2rLegjcY2NtGPZfxRi+EiLRr+qMwu0kx4SDJJGWG4y2SFJDZd\ntjAsZy1TkvY8/D6sVfJ9fx/8nlHtDeE1ZF3P66+/bprdp1kfRduV15Q1OZwkbubMmbHHWNVstCTw\nHHHyvOh+5fVncsaBBx4Y4OgqF19tChOTaJH52nbRquX9SSvS182cSU7R9jt37mzL2HaJCU48Lr7z\nnn/+edNPPfWUaSbkMJHEB4+X5yNJuzIfinCEEEIEQQOOEEKIIFR8hjHnz+7ydZTO2DHWZ9jJbLe1\n117bNHPLOZEXs0mibDCGtwyZ2RKH+enTp0837aszSmKj0dbyrZ+vLDVeC5+NxnNOi4pZf2+//bZp\nHmuSthhcZ/fddzcdZcdcdNFFtoytUk488UTT559/vmlmrLE9DSf94mfZlmfy5MmmO3ToYJp1OKsK\ntEAmTJhgun379s4552rXrm3LeD/vvPPOpmfPnp3HIyxsfJmQfFewJRbtdFpwfC59mW/RM0SLjPvn\nTwF8DpihyKxT7p/vpyTQRssVinCEEEIEQQOOEEKIIKS21BiWUSdp2eIrNmIIyOyMzz//3DQtNS5n\ntkWUpcTO0rTXmIHGjCkWRCXJwOD3oO1EW4sZdsyMyqZoKlt82XsffPCBaV8hXBLYIocZLtF55wRw\nu+22m2lf5t7jjz8ee+xcn1YGs3bYMZyTjiUpRK5q8Jp269bN9D333OOcc65Xr16x6yZpYVTs0FpO\n28mdBch8P9G2ZGdtWpe+zunR+edEeLxPmZVL9tlnH9O8xzmJIieX5DvMNwMAjzGbdjZEEY4QQogg\naMARQggRhNSWGu0MhnrHHXec6fvvv9+0LxRjMRMzKQ466CDTG220kemo47Bzzn3xxRemWUAVWTe+\nieGuu+662O2xmIqTWH300Uem+b1pNfH70UaiTch1GL7mEna0pXVIaHn5uiNnM0kTM8/iJnijHbBw\n4cLY4+L+aZERFrDtscceseswI8jX4462AjMiqxq+ZzB6Tnz9ANnLkHZMVYLPdVp77d577zXN7vMs\nXt5///1Nn3rqqaZ5z/PniKuvvto5l2nL8T3E4nUWTDMTkz8jcCLCCy64wDR7DTK7kwXTvsLvtNlu\nRBGOEEKIIGjAEUIIEYSseqnR/qCNxuW0tJiZxALDrbfe2jTbebMlPjNCxo8fb5rTFkRhIq0ztmBn\nHynaDNtvv71pWjEzZswwzeJIFhXSgmDmGyev4nfNVy+1+fPnl7tO2knGkhR+ct77O++80zQttUaN\nGjnnMi21aPIv5zILDGk1RJ9zLjMbkdluPP+8X3g+aJMSWqMs1isUkpx/FrL6LBBeC2ZJRjYQMzNp\nY06ZMiXlEVecysoe5L6S2Gg8TtpPnPaB1jqn1eCUKCxwZyF7dA19GaIjR440zXXYP43XcNCgQaZ3\n3XVX08xAPPTQQ1fY/8rI5h2mCEcIIUQQNOAIIYQIQmpLjaF9kj5ptK5effVV08x0OOqoo0z7Zm1k\nGDdmzBjTzFKKskb2228/W0abiy3zp06dapp9v+rWrRu7f2aKMJuFx9W0aVPTzDJhtt3cuXNdPvBZ\nLr5ebyxU87Xsp31KK4Z2Ieds9/Whi/pw8XyyGJMzotIuY98oFs35CoiZabbxxhub3nTTTU2zaDht\nYWtokmQMJrFAaBsxgynKiOrbt68tu/32202ntWCzoViKcH3HyfeMr5ehb0ZWEt3bnGKEGajPPfec\naU7xcfPNN5s+++yzTbN/4fDhw02zMP2qq64yfeaZZ8YeV64sT0U4QgghgqABRwghRBBSW2osEmIB\nJmHIxUwb2mu0OViEefTRR5tmdhFtqXXXXdf0kCFDVtjvqFGjbBmnL2DWDTPjmAHF41qyZInpDTbY\nwLSvzTiX02qjjcYi1xD4snB8Nhq/j6/YlZlRvoJJWqOR3cDzScuRGYC0EnidfQV6PF7abtxXsdg1\nuaSsrMw0C4F5XXr27Omcyzyf/fr1Mx1Zbs7lL7uymPH9dEDL11dU6yOabuPTTz+1ZZwFme8wZrcd\nfvjhsfs5+OCDTbNolBY5s+d85OoZUoQjhBAiCBpwhBBCBCG1pebrEUZ8BWu0Pxgy+mbcZHYGi6mY\nvcSeXNHxcBvsU8QsKYaI7KVGW4w2HrNQ+FlaTbQrfP27kkzjUJn4Qme2WacFSatl1qxZplu2bLnC\nOrwv2H6dM76OGDHC9MSJE003a9bMNG0f9ofyZQcVE+y99eyzz6b6LJ8vFsHecccdpllky3Ma9zna\nv76+dlWJtJlYfLfxGWeB5dixY03z2fdtP3ovvvPOO7aMGbV8VxFuj9Zyly5dTLPAnZmh9913X+w2\niW+G0rQowhFCCBEEDThCCCGCkNpSW7p0qWm2L6ctRpulTp06pplVQRiasscPbTRu06ejsNI3mx7t\nAmZpcbmvqJBZTzxeZvhQ0z5i+FqIJLESmGnHc0TbpTwbgv+fffUIs95o//gyggYPHrzSfa7ss4VI\nWhuN8PzyfmWfOPbiigqBWQTI/mCFfq5yQZSp55xzjz76aKrP8nzzXPEcp83u4pQDEXw/JYHvNhaE\nDhgwwPTQoUNN85r7UJaaEEKIokIDjhBCiCBkNT3BtGnTTPtmAmUWWVpo36XBZwVwue94aRFxFj/a\nTtS015jJxvOUdibB0KQNlyvag4yf4wyFPhuTZGPvrArW0D/heWT2HmeA/Oyzz5xzmb0EWcy9KhR7\nprXRCpVzzz3XNO/3G264wfR5550X+9kLL7zQ9JVXXpmHo/sbRThCCCGCoAFHCCFEEFJbarScWOjI\nnmW0wmg/sdCMWW0k1Mx/voJUX0YZj8U366lv+7Q3fC38KxPfNU1ideWCQp8moBihrcJCWeooO43Z\no6ti37nyYCGlrwchqYxzeM0115jmNCRJSGKj8R2ZTT/Iwnv7CSGEqJJowBFCCBGE1JYai8gIey2x\nff3ee+9tmrPV+fqtVUY46tsnj5F93WhBcMZFX78hLq9MS81XAEkbjcjqqtpEz6wvA1PX///hrMKP\nPPJIJR5JMphdmCtbnO9C3xiQBEU4QgghgqABRwghRBBSW2rsdcV228xc4EydzzzzTOxnff3LOBNd\nkh5CabLaOIMkCzA5yyenTaDVN2/ePNP8Hr6QleeD+/JlteULHoevkI/hMr+Db4qFyiik9BXPZmMZ\nhMqILFRoBws/PhutGO6fbGw0X/ZqNijCEUIIEQQNOEIIIYJQkiYULCkpWeicm5O/w1klabx8+fI6\n5a/mR9clL2R1XXRN8oKelcIk8XVJNeAIIYQQFUWWmhBCiCBowBFCCBEEDThCCCGCoAFHCCFEEDTg\nCCGECIIGHCGEEEHQgCOEECIIGnCEEEIEQQOOEEKIIGjAEUIIEQQNOEIIIYKgAUcIIUQQNOAIIYQI\nggYcIYQQQdCAI4QQIgzLly9P/FdaWrrcOWd/JSUl9sfl2fzlepvVqlWzP986zZs3t7811ljD/tLu\na/XVV7e/JOu3b99+uXNuYZpr4Lsu+bgW66yzjv3laptprvlqq61mf/ncfz6uS2lpabSdgv2rjHOb\n5V9OnpUC+B45/0v77snVX9pnZQ2XgrKyMvftt9/af6+11lqmf/nllzSbcqut9ndw9ddff5muXr26\n6Z9//jn2syUlJSvdNieV22ijjUx/8cUXpldffXXTgwcPNn3YYYeZnj9//kr3809q1aplesmSJeUe\n78SJE11JSUnWsw+WlZW5ZcuW2X///vvvsevxOKh5/knLli0zjjUN3H7cJH+8/mus8fdt+Ntvv5le\ne+21Tf/000+x2ytvPxU5xlxcl7Kysmg72Wwmr0TPGs9tgZOTZ4XvMOK7H3zvKsJ7+I8//kh1TNl8\nNiLJu4fvvCT7SfJspX1WUg04zmWefN+LjfCgOZi88847prfeemvTvkFmnXXWMc0HhCcxOilrrrlm\n7PFy3T///NP0WWedZZqDjO+Eb7DBBqa///570z/++GPssftekLnEdwMleYhI586dTb/11lupjqG8\nB9M3yFWrVs00Bxzf+SRJBhnfOS+m2W579uxp+tFHH83JNqPnKJtBOy0h95WEtm3bmn7//fdN++5V\nvkMOOOAA008++WS5+/J9dz670bPA5yDJ9jjIEO6H77wk5OP66DccIYQQQdCAI4QQIgipLTWGl7RQ\nkvw+QLuMNloS+BsRPc/S0lLTV1xxhXPOuf79+9uyL7/80jR/c6ItN3ny5Nh9+kJKX/iahHzZCGk9\nZ4bXvF7jxo2r8DFwvzyeSPu++w8//FDhfSaxDLmOz1Yo5N9anMudjRZHSGurEGw0QhuN8Dj5UwDf\nQz4brXHjxqbnzPn75w1uk+8f/lwQ/RzA+5Sf4/Ncr1692OPi77m+dwF/H+Vnfe+LXKEIRwghRBA0\n4AghhAhCakuNMNRLm3KXlgMPPNA0w+Crr77a9EMPPeScy7RHxo4da/qCCy4wPWHCBNO+bChmuzEj\nz5ft5iPt+tmSxB5iSO3LDORxM9T22SIVve7ZZC751k9iDSSxHkXVpl+/fqYvvfTS2HVoOfnuGd7D\ntPF9NjNttBo1apiOs5f5HHbq1Mn0448/brpXr16x2+O7ktm1/BnB977wZY/6MlyToAhHCCFEEDTg\nCCGECELOLLUkdkpZWZnp2bNn/30QCSptn3nmGdO+qvOoEIsh4ksvvWT6xhtvND18+HDTzOq45ppr\nTPvsL9/yhg0bmmZYHQKewySFpj4bjYSw//5JyCJNX0FfvqClkU2mo8gdAwcOjF2eJOs2SSGnD36W\nNr14tasAABPOSURBVFpk49PC53P4+eefmx40aJDpV155xTQ7qrDTyssvv2yaRas+O9lXfJqN/awI\nRwghRBA04AghhAhCVpaaD19217x580wz04FZFUuXLo3d5rvvvmt67ty5pps2bWo6zo7p1q2badoY\nxx57rOkRI0aY3mKLLUx/+OGHscfiw2ej7bbbbqZHjhyZaptJySYz0JeNkg1xmSzrrbeeaV4L373A\nPnUkib1Gi6xmzZqmv/vuO9NJCkJzSWXZaPyezLjidY+oX7++6bTNa4sRX9PhuMLlla3jgzb7119/\nbZrvpSeeeML0UUcd5Zxz7pZbbrFlLCTt2rWr6Ztuusn0r7/+aprv2VtvvdU0nz/fsb/xxhumd955\nZ9N8nrIpklaEI4QQIggacIQQQgQhtaXGbChfv58NN9zQ9MKFC8v9LG002isMAWnN0QpgtlUU9tHS\nY8j86quvmub8EY0aNTL98ccfu1xDKyVfvaT4nXlufRklDIuzsePWX3990+w5tckmm5iOMmt69Ohh\nyzi/zqJFi0zzejVv3tw0zyFtCha20TpjJuO6665rukuXLqZHjRplmlZbVeDQQw81fd9995nmfRKd\n99q1a9uyr776ynQ2BX6FTJJC4yZNmpjm/emzeQnPMc/n8ccfb/rOO+80zWc0KgiltbzDDjuYZu9I\nHhffue3atTO9/fbbm+b7tG7duqYXLFhgmjYa4TuF7/G0VM07SgghRMGhAUcIIUQQUsdGtF+uuuoq\n0+xT9s0335j2TRPsw1e0yN5ntAvuuOMO09dee61zLrM3Grd3wgknmG7Tpo1phsm019haPBvSTs9c\nEWg50uaiVeQ7t0kKuXgdmbFy2mmnmaYdxhkqo4JH3zZGjx5tmuE9i9xatGhhmlMoMLynvTZp0iTT\nt99+u2n2n6KVW2ht85PCbMunn37a9COPPGKadgiLnGn9xJGk354P2nS05vhuqCySXOtZs2bFLvfZ\ncSyw5BTWLCQ//fTTTTPTljrqicZ12Sdtq622Mu2bYoRWG21m6mwyELOx4BXhCCGECIIGHCGEEEFI\nbak1aNDA9HnnnWfaF2omsdF8fYtoDf3rX/8yzZk7r7zyStOLFy9eYRu0BWht0V575513TOe7p1aI\nzB9fcSPx2Wg8Pp7/bbfd1jSL0s4999xYHRf6M4uNYfmee+5pmgVsvHa02mh7XnjhhaZpkx588MGm\nafUxO6cqWGrMQGOvtlatWpmm1cgspPfee2+F7fF+4TnntaP23Ue0dZglmM1UFPnGN40I33k+K2q/\n/fYzTdv2iCOOMM3ssU8//TR2+5HlyOkLaE8y043WHTV/UrjttttM83r6ivPzjSIcIYQQQdCAI4QQ\nIgipLTVfCJ1NeOz7LPukMYynFRLZaIS2ELfRrFkz07TlDj/8cNP77LOPadovuSLEzJK+bDSeQ2Yd\n+WwOtk2nlcCpHQ455BDT7PnEaxRZPewZ5eulxsy0U045xTSt2ddffz32eNn7jj3xPvvsM9O+aRyq\nAjyn1CwWPP/8802XZ+/6MjyT3MO8p2jxZlM0mG94zCwuZ/EmoVX4v//9zzStOU7J4utTyOkEIrv6\nueeeiz0uXrMhQ4aYpnVH7StkT2uj5coKVYQjhBAiCBpwhBBCBCF1fEtrJR9t7Zk98eyzz5pmCMjs\nmrgMN2Z9sHgzKgx1LjPUJbQifFkrhY7PKklSvMfvvPHGG5ueOnWq6ccee8z0ZpttZnrMmDGmL7nk\nEtMHHXSQcy4zc4mt2mlvMhtu2LBhptlPitecrdhp6fkKDH1Fa9m0XC90mLXUunVr05E1xvuFdknn\nzp1Nf/TRR6n2STuaffUKjQ4dOpjmFCg+aE8yM4z3T1q7ijbnjBkznHPO7b333raMzxUz3U466STT\nLF7fd999TU+ePDn2GGltJjneXNnPinCEEEIEQQOOEEKIIGSVMuKzJ4455hjT999/f6ptsuCJBXuc\niY6z2JEo7KP9Mn36dNPMXKKNwKwbhsnZ2GgMXyNLybnMWfryRdpMOIbLvKa0I2l10kZjxhgtGBYb\nRjYlLQtm+NBS45QEBx54oOkjjzzSNLN6eI9wOQtIaf367tkQ2YOFwK677rrS/89+bNlM1cEeYuyr\nx2vB6/vCCy+YDlmImMRGYwEy3w8kbRYXz8OAAQNMR+8lbu+MM84wTVuczw3v37jtOZf5bH3yySfl\nHmOSY0+LIhwhhBBB0IAjhBAiCKktNV/mFkPAtDYa2X333U3vscceptlPiPYa9xvZcf3797dlnOWO\n2yCzZ882zZ5t2RQ7cf0nn3zS9FNPPWU6lzYOrwu3y+PwZSP5vhu3w2v90EMPmd5pp51M00a54YYb\nTEeZN9wPM6d69+5tumPHjqa//PJL02effbZp2mu0zgi/K220VcU688HMwyib6YEHHrBl48ePN51N\nZhKfXVowfKaYncVCx3zjy0jk9/VluvqmdMjmviqvfyOn2uDPArSTP/jgA9MDBw40fdFFF5meOXNm\nhY+RZJORrAhHCCFEEDTgCCGECEJqS43WCm0L9slilli9evXKPwgUIbH1PLNDGMoyk42hb7du3Zxz\n6QvNmGnFrLYkloLPyuI5YEYW95VLkmTUZRP287PUzPJhIRqLPKPrW6NGDVvGVvq77LKL6YYNG5pm\ngS8zE3k+WajL61Uohbpp28Bz5shsZmXk1BK0L3leonuXtuQ999xj2pfJmQQWKBJeIxZdhiTJc+1r\n5Z8WnsO2bdua3muvvRJvg5lxd911l2n2GmTRM7d99dVXm2bm6IMPPljufvmeTTLNTBIU4QghhAhC\n6gjH968e1pqQJD+8818QI0eONM2oiT88XnfddaYZBUV56Un2yWPnyM/c9iSjOv/FyH8RsHMxOyeH\naKGSq86u/KwvEYHniOeRUevChQudc841adLElp166qmm+S8ytlBhCx12kWb0lKuWG/m6LmlrSrKJ\nagg7NLPbMes4Zs2a5ZzLvFZdu3Y1/eijj6ba56abbmqatVpsY1Ro+JKgkkTISVpfMRpnqy5G8iR6\nnhjdsyXXNttsE7tPJkfxPTRu3DjTrLFKEr363n/ZTCKpCEcIIUQQNOAIIYQIQlZ1OKzB8P0Y7rM8\nGJbRFmP4SAuGtltFQzqGjkOHDjW9+eabxx6Lb5Iyav4QTjuOk5eREJN+5WMfvkndeE75nVn7Ev2A\nzVCfbU14T9ECoL3EH765T599mLbTd1WbjI3JOjxftF6iNjf8/6x9SntOonqrf+pCxldL6PvutB9b\ntWplmq1iTjzxRNODBg0yfe+995pm+y+eq9NPP90559zYsWNj98n7ev/99zd9xRVXmObPElwnSe0d\nSVLblxZFOEIIIYKgAUcIIUQQUltqzLrx2WhJQlOuw7DznXfeMU2ri9lLzGqivRZntfF4+/TpY5oT\ndzEbg9k9vhCUoSbbPDA8Z9uJYsVnIzLE53nhJFC0F6OWQmwbxDZDDNdpqUVZVM7522n4rD6fjZbE\ngqsKcAI61qXRJo7OKTNAn3nmGdNbbrml6VxlzxUCvgwtLvfdP506dTJ93333mWYLGdbEsM0Ma2j6\n9u1rmjVT0XuDE72xfufoo482zYw1HjuPhfVEtFOXLVtm2veObtmypWnWJ2aT0akIRwghRBA04Agh\nhAhCakstbbsDX/jKbDB2UGbWF7M9aKkddthhpmvWrGk6Klpj2EurhF2beey0HHwZUMRn3dBGY/hK\nmy6boqmkJOmGmwRmBtaqVcs0vw9Df1/7m6jNDzNmeB5ob2644YamacvlKtOM38lnh1YFeP4vu+wy\n08cdd5zpqF0QzzPPP58XtmoqdnyFjr57gEXct9xyi2laTieffLJpdjZnJ/pzzjnHNAtCeR9G1hVb\nP7HD97Bhw0zzJwfe+5dffrlpduT+z3/+Y5pZdXxvMbt06tSpsctlqQkhhCh4NOAIIYQIQmpLzWej\nMTOCRUiENspRRx1l+vnnnzf95ptvmp42bZpp9t5iOMiwNlpOS437ZE8pdlHlPs8991zTzCRhBhZh\nOJwkCySEpdalSxfTr776aqrPMnuMxZbsKLz99tubnjJliunWrVubpgVz7LHHOuecq1u3ri1jkejj\njz9umgW5zDDM1cRp2UweVRFonfB8ZsMLL7xger/99it3fVpqvAa00uLo3Llz+oMrMpihR9uInc95\nDc8880zTtP9px7F3HLvfM7uT0PbfeuutnXP+DNGoI75zfvufGYXbbrutaf50wHfElVdeGXtc/NmD\n7z8VfgohhCh4NOAIIYQIQmpLjWEhtS8sY/g1YcIE05zOgHPUM0uGFs1nn31m2jcJXAStGIaaLHpj\n2MmCRK5TVlZmetSoUaaZQUL4WfaBo5VCqy1fsJdSEhjS01ag5nVp1qyZad/0BLTgaFNG0NIcPny4\n6Wwm/UoC74c6deqYZqFkLsmVjUZ69OhhOu1UFNFUEc45t++++zrn/LYrzz9737HNfbFDi5Xnks87\niexh5zKzx/r162eaxZ5JCor5Pouz3XiMvkJVPm/UN954o2nae773NWFh6WuvvVbu+klQhCOEECII\nGnCEEEIEIbWl5rNcWFBHTcuFIRozP9hLjWEtiw19WRvUc+fOdc45V716dVu2ePFi05MmTTLNOb1p\nqfF4WcBF+4XZKT7LcOeddza9xx57mH7ooYdcPvC1Ek8CQ3oWdRJm+DGr8IADDojdLzPPomxDzgj5\nxhtvmGZhHe+pfEwZQBsiXzZavsnGauQ5HT169Er/Py0YFjZWJUvNB2eYjesL6JxzDz/8sGla5exf\nxsJ09kzzTYswZMiQFfbDc88sw+uvv960z9ru37+/6RYtWpjm1AosqiczZ86MXa7CTyGEEAWPBhwh\nhBBBSG2p0QpjGEdLJ0mPNWYusd8Qi5Nor/j6ajHbLCoOZb83bvuDDz4wTduPWWdbbLGFabbK79Ch\ng+m3337bdFzRlnOZmXL5stFIrnqBMUvGV1jGddiKndYk12nfvr1zLrM3F/un0ebKh42WxI7l/bCq\nENk2vnPCqQqoix2+E5iJ6rv3aC3R/mexO/uXcZu8t8844wzTfG/xPbNkyRLnXKa1zWtCG/jwww83\nvWjRItPRTwvOZVrbLJhPUoA+Z86c2OXMME6LIhwhhBBB0IAjhBAiCKktNV+hGVtcswcPiyH5WfZ3\nor722mtNs519w4YNTe+zzz6mmzdvbvqll15yzmVaQTzGevXqmWZYePvtt5tmDyVmmnEm0o022sj0\nl19+adrXKynfxYzOpZ9l1bfcd3w855zplVYUsxBJVFhIa5H3Sz76m/nOB21aErrHmg9aI8xUyhXM\ncho/frxzzn9fsGdekp5tafFN4ZFvOnbsWO46zCjj+WFR5VVXXWWa1jrfA7yvbr75ZtN8nmiBxVnj\nvplpec6YDcfsQsLv4csw5k8BPmiNp0URjhBCiCBowBFCCBGE1JYa28r7sltoo7HYb8aMGeVun7Pi\nvfvuu6aj2Tydy8wqu/POO01HoSfDTh4Xs9fatWtnmtlrnBWP22GGB220zTbbLPbYGRqzcCtfJMnu\n8q3jmz6B527y5MmmaU3uuuuuppmdyHPdoEED51zmeeM+02ampbUPmeFIK4/Xt1Bm/KSNxgJjPne8\n/5kxyZbz7JkWZQk6l9kjLLJSfP25+LzS6ssVIW00wukDaEWxBX+ULeZcpp2/dOlS075ZMHm/Rfe+\nc5mZaSwS5zFE58T3HHKfvGd9VhgtQK7De8v3Wf6k8eyzz8aukxZFOEIIIYKgAUcIIUQQUltqPnzZ\nTUlsNB8sWqIuD1+fIhZw9e7dO/azzDDhdljwSrto+vTppmnH8Xywh9HUqVPL/wIVIK09xOI0FsL5\nbFJfZk+bNm1i1x82bJjp++67zzmX2W/q22+/NZ3WUvMVrfmmraCN5lu/EKGNRmi7MUuTcOZU370e\nnXcWE7Zt29Y0bbmqBHst+mbyJb5CdmarspB57733Ns0+gezPxgxYWnzRNfFlDnKmZPZy4/uG7wJm\nAtJeI74s2lzZaBn7yvkWhRBCiBg04AghhAhCakvN1/cqSeYQi6mY7ZFP0to1vsJAn71BfLZivmw0\n4rOHfOEy+yT5Cj/r169vmi3XTzjhBNOcObBnz56mWRwWWTOzZs2KPUZaANWqVTPNbEd+D591Rs3r\nSJvUd30LEd8zRRvXx/HHHx+rhd9a8t0nzFhr2bKlaWaukhdeeME071XOEFoe/ByvPadVIVERr3PO\nderUybTPTibZZImmRRGOEEKIIGjAEUIIEYTUlprPNmLmB2HBJmeKLDbYH45haj7a6ecSX1EfrStf\nMSSzZ6hZsMcZVdlbijOkRutw/5yGgllyPJYkoXuSAtK0FlyhUOj3VrHiO6++Qk6u77PRSC6yH9Ne\ne2aR+jJNkxR++/AVIadFEY4QQoggaMARQggRhNSWmq9PGdtts+iPNlqS0C2frfwPPPBA08OHDzfN\ntuHMwCK0eljwRauJ0LIiIdrgl5aWmmaBJc9nkmJI37WYNGmSaX5Pfje2XI+2w22wCNeX+ePLnkti\nE5AkFkohkvZ7imT43gM8x8xk43Vg78TPPvss1X5zZUtF+LLqatWqZZrF1j581jXPRy6O1zlFOEII\nIQKhAUcIIUQQStKE6iUlJQudc3PKXVGkofHy5cvrlL+aH12XvJDVddE1yQt6VgqTxNcl1YAjhBBC\nVBRZakIIIYKgAUcIIUQQNOAIIYQIggYcIYQQQdCAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04\nQgghgvB/xVT6G8KI428AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11cce2e48>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"_ = view_samples(-1, samples)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAKhCAYAAABkTRjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3WecZFW5NfDVE2BmGAeQDKKiV4aoKOEqqKBIFgNiFjGQ\nRFAxAiIqCiqCoiBcAREVFANRggEDgooC5hwQ8KJXclCSzPT7Af+1u/dM0VU93TWj715f+tfdFc55\nzrPPWetJe2h4eDgNDQ0NDQ2TjSmL+wAaGhoaGv7/QHvgNDQ0NDQMBO2B09DQ0NAwELQHTkNDQ0PD\nQNAeOA0NDQ0NA0F74DQ0NDQ0DATtgdPQ0NDQMBC0B05DQ0NDw0DQHjgNDQ0NDQPBtH5ePHv27OGH\nPvSh+dvf/pYkmTLlgefVtGkPfMzMmTOTJKYXDA0NJUnmzJmTJLnllluSJPfcc0+S5OEPf3iS5P/+\n7/9Gfc706dOTJLfeeuuoz1l22WWTJHfffXd9XKM+d7nllkuS3HnnnaOOy/vmz58/6jjvv//+JMkd\nd9xx0/Dw8Eq92GKZZZYZfuhDH5qbbrppof93TOC7ll9++STJjTfemCSZN29ekmTNNddMkvzv//5v\nkmTWrFmj3u972MY53nXXXfVxjTrXVVZZZdT7fe69996bJPnnP/856vh85r333jvU5dQXdq4L9Yup\nU6eO+s7aL1zPm2++edQx8Yu//vWvo86Zf/Aj3zOWX/j7CiuskCS5/fbbkxS/4DeuBf+YP39+7rrr\nrtx3332LzRb8whqZKFs89KEPTZLccccdo2xRr5GJsEW9vpdaaqkkydJLL52k2N3/H/KQhyRJbrvt\ntiRlHfML58yGPsfrHHN9X2Bra4SN2ewf//jHKFv8/e9/H/U9Pvf+++/PPffcs1j9ol4jbOrzJmuN\nuFeOtEk/ftHXA2fGjBnZZptt8r3vfS9JcsoppyRJvvOd7yRJHve4xyVJvvGNb4w6iRkzZiRJNt10\n0yTlwp566qlJyk34+c9/fpLkmGOOSZKcf/75SZL3ve99SZINNtggSbLhhhsmKSd/ww03JCk33513\n3jlJ8vGPfzxJ8t3vfjdJss466yQpxnczdlFOOumka3u1xezZs/O85z0vp512WpLkggsuSJJceOGF\no2zhu10gF/KpT31qkuIo73znO5Mkj3jEI5Ikr33ta5Mk733ve5MkV155ZZLk4IMPHvX56667bpKy\nOP1kkz322CNJ8qEPfShJ8pOf/CRJsdXmm28+6ryGhoY659IrZs6cmR122CEXX3xxkuSzn/1skuRb\n3/pWkmSjjTZKUvzCorE4nvjEJ476+wknnJCkXKeXvOQlSZKjjjoqSfL1r389SbENv/DT53iou3E8\n73nPS5Icf/zxSZLvf//7SZLVVlstSbLGGmskKf44ZcqUnH322X3bYrvttssll1ySJPn0pz+dJPn2\nt7+dZME1YiHzg80222zUOZx44olJCsF40YtelKRcz6985StJkiOOOGKUDayR++67b6G2eO5zn5uk\n2JotVl999STJqquumqQ8mKZOndq3Ldwvfv/73486Zuf+3//930mSc889N0nxyYc97GFJit+4SfNL\nN1/ncOyxxyZJjj766CTlvmRtzJ07t3MOSSF1HnBPf/rTkySf/OQnk6Rzf3vyk5+cpKxZnzNv3ry+\nbTFr1qzstNNO+epXv5ok+dznPpck+eY3vznqXP3uusGTnvSkUX//2Mc+lqQ8MF7+8pcnST74wQ8m\nSWctHn744UmKX6y33npJFlwjHtbuwfUaWXnllZMkj3zkI5MUETE0NNS5fr2ghdQaGhoaGgaCvhTO\n7bffnvPPPz8vfelLkywoNS+66KIk5Sm44oorJimyHeN49atfnaQonbXXXjtJkYH7779/kuRrX/ta\nkvJ0Fv4h0T11sbbf/e53D5zUv5jLa17zmiSFpZGfmBEWijH1g1tuuSVnnHFG5zswBqBshESc+y9+\n8Yskhcm+6lWvSlIkdB1CYSvskCrDBq+++uokyVprrZUk+cMf/pAkueaaa5Ikp59+epJkv/32S1IY\nt8/faaedkhQGftttt3WuZ6+47bbbcs4553RYlhCJn1g4v6AohPnWX3/9UeeKbfELr6P6zjnnnCSF\ncWJ9f/nLX5IUdu5z+MV5552XJNl3332TFCXDL3bdddckRZndfPPNnXPoxxbnnXdedttttyRlbfgc\nDJctHGttC8rUOTzmMY9JUtYIW4gC8C9rhC34izXIFl/+8pcf1Ba77LJLkuIXt9xyy7hscc4553Q+\ny3ViE9fxUY96VJISsRBeoraof6EzNuPDzuHaax8IUGyyySZJyn2BbX2eMJE16n6xzz77JCn3reuv\nvz5JYf2XXXZZ57z6tcWtt96as846K7vvvnuSBcO37nUiHFSec6RY3S/qNUKpsMWXvvSlJMl//dd/\nJSlKml9Ygz6HCqVW3NdEGfiFKMF4/aIpnIaGhoaGgaAvhbP66qvnbW97W84888wkJfnmqfzb3/42\nScnpbLvttknSyXNg49id18tnUCKPfvSjkySXX355kuSkk05KUth4zVzq5J6n+Y9+9KNRf3/2s589\n6v8Y0Ytf/OIkyRe/+MW+bPH2t7+9E/fFVDCOH/7wh0kKY2CrT33qU6O+G9vCqpyjmD3lIu598skn\nJymsy7n8+te/TlLi1D4XK5QDwh6f9axnJSk2xHz333//XHHFFT3bgS0OOuigfOELX0hScnaO3XWn\nHJzjZz7zmSTJH//4xySF1f3pT39Kkmy11VZJSiITE8ZM5TecC8XMFvxCjg6Dvuqqq5IUVckvsD3q\n8OUvf/m4bHHggQd2fKm2hXNlix122CHJgmuELfz+tKc9LUlZI2wh38AvnvnMZz6oLZwzJcQWwBbe\nz09f9rKX9W2L1VZbLQcccEDnfiCvQKH85je/SVKUg3OkiP/85z8nSR7/+MePOlfH6HPkZq05Kn7r\nrbdOUq67+4FiJGtFhEO+AigztqIitt1228539Qpr5POf/3ySsi75BZ9nIz5tjfADyoSqkH9yv3Dv\nZFP3znqN/OpXv0pSIiX8ol4jbCQqxI+skd13370vv2gKp6GhoaFhIOhL4dxwww059thjO/kKjOTn\nP/95kvJUxL697k1vetOo/z/lKU9JUuLLWJt4tKf0FltskSR561vfmmTBvMNHP/rRJAtWXojJYmee\n7gcccECSkiNyPOLf/eBvf/tbjjzyyAXKGj3tVVJhnMpZ3/KWtyRJfvnLXyZJdtxxxySF+ao6wWyo\nx+c85zlJCpPBulSvqMzBjNkCe2MT10a+4sgjj0xSqtcuvPDCTlVOr7jhhhvykY98pBOjxyx/+tOf\nJilK1Xc6dn7hu7fccsskhcXJK9Sxfq878MADkxSVRlEfd9xxSQrzrXMHmDPWJl7t2riGc+fO7TDC\nfmzx0Y9+tGN/DJQtfvCDHyQp16G2BRZujbCF604xWyNeZ41g4dttt12SUsHFx+tc43XXXZek+Jfc\n0Bvf+MYkZY2MxxY333xzPv3pT3fYs4pIbN4akPvjdy972cuSlPuKvJZKPjZREarqzH3AsfseOWdV\njWwmD0FBY+3bb799kpI72nPPPZMUBbT22msvYMexYI243pQvv/DZciSUxpvf/OYkxS+ofrlafqFq\nzhqxBvmF3N8222yTpFShicjUrQH1Gtlrr72SlDUnYrL22mv35RdN4TQ0NDQ0DAR9KZxZs2Zl4403\n7sTQPYUpD7kZMVcxdkwTw/3whz/8wJf/i3Xrw8Bg1HhjASo0vB5jxfLUy1NKelA8teWcXve61yUp\nMVxPazXt/WD27Nl5ylOekksvvTRJyRNQKqpDxOj1BOn1kDf6n//5nySF6WJf8k5eL+ZL0ah2o5x8\nH1uI0apO0stAOb3jHe8Y9f+3ve1tSR5Qjf0qnFmzZmXTTTftxI0pCRUxWJe+C37hmLF9ihUjdq7O\n0fXlJ4997GOTlDwFdlazfwyWEsLI5JwoXz1Mep2OO+64zt8W1RaqfNhClSK/UIXGFh/5yEeSFL9i\nC+dO/XWzhbXJxrUtKCExfDkntuAD1sh4bDFz5sxsuOGGHfZu3VqfcjDyGPzC+nS/UKFZ9/P5XaOo\nNbLSSg/0bos6uA+wsfsTW1ALflfBp6LM/Y3i+cQnPtHJ9/WKbn6hEo5fUIHuC93WSO0XIi3OgW2c\nq/uB7/W5ogVsZo04PzknSotfHHTQQUn694umcBoaGhoaBoKhkSNNxsIKK6wwvNNOO3WYiXyD2CeG\noXZbbBWzxWwOPfTQJKXu3WSAbk9pT3PMVUwfU63HRKj0oLh8nsotLB9L9L4LLrjgquHh4U16scXy\nyy8/vPXWW3cUCJYlb4SVy1OJJ2O2FMcHPvCBJCWGj4liIvU0BMfse3UsU38Yq2shtisfVo8VUWXn\nmt5111350Y9+lDvvvLPnsR0rrLDC8I477tiJravIq21BoYgPU7Zs8a53vStJ6RkSS6/9wrE7Z+zQ\nudbjO7xfD4z+HfFvfqG6yXEmD1TE3X777RNmC8fuu9miXiPYtL4Kub6xbGGNnHXWWUkKuwd+JMeI\n9de2qNfI0NBQ37ZYeeWVh5/3vOd17Gk9yxuxjfuF6IA+Giwbu5Z7FTXw/vpzrB1+4X5ATbCV+5cc\no8iKtWWtqCz1/xVWWCEXXXRRbr755r78Yvvtt+/4RX2/cEyuKxvVa+Swww5LsuAaERWgVHwem7sX\nivaIqLCV16sQrKey+BxrxHHOnz8/3//+93v2i6ZwGhoaGhoGgr5yOCuttFL22GOPTmxTZQtWJC4o\nniwWqqJDbFZ1yBve8IYkhaFgQuLLOoOxOk95DMgAO1Bd5H0U0I9//OMk5amOBXp6q+DoB6uttloO\nOeSQThWaShisCqt/whOekKTEidlK7sR0Bp3pWJe+HMfGNhgqJizm63vFyZ2z6hIMSC8DhlLnx268\n8caOvXvFSiutlH322adTXaR/ASN0nfgFJeJ68AtzpLB6tsCyxZexxNoW/EJlH/WuooZfUEAqsLBN\n/uv3W265ZVy22HvvvTvXU5WPc5GvYHdqvbaFPh2svraFNcIWjpMt5DnGWiNsoQqqzv2wxa233tq3\nLebMmZMddtiho1DcL6jwjTfeeNR3YdtUmfUuZ6ziiq9av2zBto5T3kz1Wq2Y5ZbqQZiUlpwgdUAF\n9pvLSh6YirLffvt1crfyUz6TqjJrT07NMfAL/XjWiDxVnZsTsaj9gpJ2zvUaecUrXpGkXANrxFpW\n1eZ7+10jTeE0NDQ0NAwEfeVwll122eEtttiiw4r0eHj6eRpj21ic/+sFwPbFSNXZ/+xnP0tSKq2w\nMDFWT2dMBMMVm8VEzMzy5MX25UOwx2c84xlJCuu76KKLes7hzJkzZ3jTTTftKBXVG86VwsFcnKM+\nGbFz+S/MEkvH9uW3KBwKRX+Hc/d9qpRUp+htYgsMybWgsHRv/+AHP8g3v/nN3HrrrT3Hp/kFRUmV\nsQXmWrN7bF28GLPEYL0O+1ZRg73xC5U6/MK5ioNTtBQ3v3HdXRO20c9zxRVX5NJLL81tt93Wly02\n33zzDotnC2zcGmELqs//XRe2cC5swZdN56Bw9PeI+asQ9H65IrawRtgCw+Wv/E/fxhVXXJHLLrus\nL1ssv/zyw1tttVUnwqHai2oC8wPlNx2TNaPL3rnIwZmOIYpAKcnZ8Bfs3uc6DvcXlVjWmL4wLN7v\nvufHP/5xLr/88txxxx19+4W8FMVijQC/cO5yMpRFtzVCiejTsUbcL+Rwu60RtuMX7idUoKiBmW/U\n4pVXXplLLrmkZ79oCqehoaGhYSDoK4ez4oorZvfdd8+73/3uJEXJiEO+4AUvSFI6hD2VVcx4yor1\nq5DC6s1Ww7ZUbKnkEN/E6j3tsQBzg7BFDBbTwYioCyqhnnbdC1ZbbbUceuihnRyJc8UMxEKxo1px\n2P9CTPcTn/hEksJYKBXMhbpTT48NUplsjqWZPOB49AuJHevjUeWEvd19990LzJQaCyuttFL22muv\nTv8KFo3JOkcKVkydX1Ao8mD8wjHxC7bgRyr/2BJ7c535hTljjsccLNff52Nx/OX+++9fYNZYL7bY\nc889c8ghhyQpa4RPvvCFL0xSrhd1xxZycvYAYgv5jtoWogFsYY3UtjBZXa8LZm2NmBri9aIFbDFv\n3ryO0uwVyy23XHbZZZe8//3vT1JYtEiD/Cdf93csWwRCPkrlHH+hfNiC71NUflJ7ZrfV/TZso0fG\nWmMLa1el4IwZMzrrp1esvPLK2XfffTt5KLaQm6vXiAn58p3We7c14tzcO/kFG3kddefc5Iqtkbpy\nj9r3+dSoe/O8efPaLLWGhoaGhiUPfeVwlllmmeF11123wwBUkWAS8g3yGeLXnqLi056icjhYoKeo\nHA+WhQVSAXY9FIf0FHc8Pl/tOMaEoYkBY05iu/vuu2/POZyZM2cOP/KRj+ywbbFQas8sKzbws95R\nUcxWzB9DpYwwEbF+LJyaYwvX0evZou4HOeOMM5KUmD+1IfY7e/bsHHzwwbn66qt7jk/PmjVreJ11\n1ukwTyxKvgKTVd0jfs0vKM66L8rfzdziF9ghVYmdsYXryS+wfddGbJ6qwJD5Gf+ePn163vve9+aa\na67p2xZ1/4QcHVtYIxRqHat3rHV/DTXAFtYOn65tUa8RtqC42AKTHjk7baQtpk2blsMPPzzXXntt\nX9sqb7TRRh1bWANyKhSD6kNrgB94H1jPbGEOmYiHdU8NuL7yk/UsPT8pHtdI/srnszGlc/fdd+eY\nY47Jn//85778Yu7cuZ01QnWpHjUfcqw14ljBdaK4+l0jokTWLNurpmVDysk9nBKfNm1aDjvssJ7X\nSFM4DQ0NDQ0DQV85nNmzZ2fzzTfvKAUsXbxRDgQb91QWfzatVR4BM5FHEJ/29MSIsDNPezFDjEYM\nnyJS+eU4sQK162K32CJ20Q+WX3757Lrrrp3OXKzLOat4wjTqvebNMhO7xWgwWzvwyW9hQmxBKcnp\nYLJsrZJQbJ+iEa82z841kVPYcsstO+ynVzzkIQ/JVltt1cmNODaKQYe/yhuszHV7z3vek6TkAPkF\nRku1YYcqfdjCOWHnWDtGiqHyC6/jT/pETG1g0x133LGTA+vHFltuuWXHRylM158t/M4WjrVeIxQJ\nW9RrhFJiC0qJ77MFW1PU9RphC71xdoy0RnbcccdORKJXzJgxI3Pnzu34hevk3E17puqtFVEDthA5\nsSas17rnSA8Kf8HS7ccjh2eN6EWxRuo9o+TRrGVKe5tttuncs3rFnDlzsvXWW3fyo9aI66/6S8Sh\nXiMmDMgB8gvHyjYUqYpRfiE/JnJSz1pz/+q2RsxOM3WBotp+++37WiNN4TQ0NDQ0DAR9KZz77rsv\nf/7znzsM2FO+rmgQt66nttqbQ4WMennsXUcxdiengwHplxCLlTcRD/V+DMjcH0zF0xobED9XOdYP\n7r333vzpT3/qxH3ZhOLRVY0hUn0qacRU2cb7MFZxZJ3qjlF1iPdhcWxgfh1Fgx1iJvYewTYpLsc/\nnv1w/vnPf3bi4UnJzamME6unXFTMUKj2r+EX5nxBXWHHb3wOpQ1s4Pv0IsifsIVpAPwCu3T+559/\nft+2sEaALVRAmQPmetW26LZGoF4jdd8VRQWOpV4jbGGNqByt861yCl/+8pfHZYs//elPHV/FqlVi\nydHI3YhQyP198IMfTFJUP6VBqfAT6x3rp+IobJ/PBn5aY2yB3duTxvfIMcmPfO1rX+v03/Vji+uu\nu65z7+IX1Be/cL2oMMdg/xp+4tzZ6pJLLklSpnzwG59jvVvnvmesNcIvvN8asfNnv37RFE5DQ0ND\nw0DQl8KZOnVqll122c7TXcxVzFR1iDgzJVFPLPZEVGfvaf+qV70qSXLUUUclKU9bDKWesQSYkUoL\n8Wdd0qrbVOaoJbcrnoqvfjBlypTMnDmzw77EWtlCjwdVhj2ZkeTYMEjHUsePjznmmFGfJ6+leokK\npLTEYtneuauaM53atXN88hynnHJK37sZTpkyJXPmzOkcm/gzP8Bk2QZTVAFDtfErtqCga7+gmORy\nnDvmClSlv+soZ4sTTjghSVGdYvp6T04++eS+bTF16tTMmTOnk5NTJeTcxdjZpl9bvPKVrxxlC+we\n4zSTDdtXvWiNsIW9gEQl7L/CFtaI6sXx2GLppZfOox/96A6b5nNyvXI58gymKMipjKwKS8p18fur\nX/3qJCW/Yc8Y9wv3g7oyjwq09i644IIkpRdJvw+bswW/OfXUUzszC3vFlClTMnv27M76pr74hZyc\n361f9zLn7pjdO6lGfmHvIJMAxloj1CClo4qVX9grjMJhC8q8X79oCqehoaGhYSDoS+EMDQ1l6aWX\n7rB5T0UVEOLJGK7Y/JFHHplkQWUi9yOuqYpJ9z52Vu8NQS34PO9XIebp6/vFu7FILEGVS13b3gso\nHCxalZcYOLYm/3TaaaclKTs8mp6A8YgnY2EYqcncKkF8D4ajbr7ufVHdxma6ve1BRPlQSpTOKqus\n0ndl1pQpU0b5hesjh6fqC6tTIYeNYaD1RGuVd963xx57jHqd71G9xna1X3i/eLbdNFUIYvsU2sge\nCPYZry34rjVS24KCrW0BtS2sLWsEFtUW+jMocLkCec4VVlihb1sApeLcKEm2oXTkk1Qtur9QE6rI\nqD+qQGWd11kL7gNUG3bvPLB1x0fxul9QYiq+vH+llVYal1/MmDGjcz+g4viFCjg5EgrWWqlnoMkJ\nWqv8whoB38NW9f2i9gsVf/xSDofycb+yRvr1i6ZwGhoaGhoGgr4e09OmTcuKK67YeTqqkALsW/cq\nBoFlYSAYhdyNp6z4swodtenyF2KzqpAwF/vriFuqxxc7VvuumqmeK1RX9vSCadOmZZVVVulUsDhm\n5yq3whZyJGKzWBNVJkbr79Sden09Iipo2JLNMSXMx+dhZY7T/71eLokie/SjH913jwG/cO78QkVM\nPSnAtASsTQy49gtqTfzZ9cY8qTwxfaqRYlUBJB5N0WLOKrbEp+VX+M0aa6zRd+9JtzXCx9mCX4xl\nC9eCLawRucNutnAObKaKSR6CLfgHJcUvMF1rbY011uhb+cr5OhZrRC5WRMT/rU/r13UfOfkhKerL\n55iiwYepe5EMtnVueqGe9axnjXodW7hfsB31MNIP+1U406ZNy8orr9xZI5SC6zqWX9R7CPFL/uDY\nKBh5KdebreqeRn5Rr5G6qpHtKGiKes011+xrjTSF09DQ0NAwEPQ1S2327NnDG264YWcSKVaEAWAe\n2LynISaj/l6+QIWFp72KnrqyCzxJMSAszOQAbMHx1HuBUEzyIxg45n3aaaf1PUuNqqIcxEIxIDFZ\n+5dgMn5iDq6DvAfl41jFu8WvMVwMSHUTW2CDWKNrw6YqB+WgMOvrrrsuF1xwQW666aae50Qts8wy\nwxtssEHnHGu/cH1VKYkn135R7yWvB4EtKGZKxvXmR/WuhmzBtir42IZN9UA5Pq//4x//mAsuuKCv\nvetnz549vMEGG3SuB7/Q11Lbol4jFCtbUDiuX20L15OCqm2hcrS2he9nCzbF/tkKxmML+yTp9TJx\nQA6HgvBdVB1byHc51jrXKjLh/yr/2Bj7pypU3MnlquyTQ7JmrSmTEBw/FfGrX/0qX/nKV/qyhTmU\njoFyqNeIe6A1wga1X4y1Rvg2G1Da3dYIqFrjdz6HYnJ8/O3qq6/uyy+awmloaGhoGAj6CkTOmjUr\nm2yySSe+JwbqqYlp2LOBovA68Ul5A09tLLzeyZMK0IehfwfToWA85cU5sTydySpt5Efq+Lb4Zj+Y\nM2dOtttuu06sXgd/nRfSK3DuuecmKRMIVI/oozDjCIPBXDEZKsD3qKgSs8VIVCfJU2BnqkywOExX\nTkkc/B//+EdHOfSK2bNn54lPfGLn+pmOwC8oXhUvFEXtF+LItV/Uu1f6v94DfuF6OkeqAJPFIrF4\nalHeg83Z9O67704/EYDkATtuttlmHVvo/O5mizqf0G2N8KfaFtaI/Ze62cIaqW1hjcpjTKQtll56\n6TzqUY/q+GKdP3K/UCGne14/jUotERWRCH6hx8Tf/WQL5+R+Yf3LJbGRtUOZszF14Jp4/bx58/q2\nxezZs7PFFlt0/EIlHPVFWZh+YY2YdC33woYmWbtfdFsj3fyCsnW/YCtrpq7QEwFx3xJh6dcvmsJp\naGhoaBgI+lI4M2bMyNprr91RCNiT+KG+GowAW/K7uKSno2oSsVJd1di2p/7pp5+epDAbT3Gfg43J\nIXjiYn/YnfwKRYPZmGOkq7dXW6y33nqdJ79jUlVmCu9rXvOaUceEecj9YBRsIbeim141CZVmJ0+M\nlwLCYNhCXNo1oJAcX12ph/HsvPPOfe9yaSow9sMvsHmxezF2NqOu5DuwLbYwPw7bdx1rv5AHcw56\nBOQl+F1dKeb75NmwOX7xzGc+s9P70SuWXnrpzJ07t3Md+IU8hRl3OsprW2DzfFueUgzdGmELOb5u\ntqCEHY9pH2xh6i9byDWJFrDFTjvt1Lct3C/kXPmFvOG3vvWtUcfIx1XG8QNrhE9TZda7iAh/U9Ep\nF0yxUzryEvzKdXefcs78TO6GTbfZZpvOva4fW8ydO7fjD37Wa0T+il9YM6pOqbM6fy064P8Ui/4/\nfuF+YY1QTnKJ9Rrhh2xPVbJFv2ukKZyGhoaGhoGgL4Vz00035ZRTTlmgUgGTFEMVW8csPA3r3QU9\nPVVqeDrrOMbyMQ3xZ30T2Dvl4neMyFMbw6onLHu9nE+/tjjxxBMXqJfHYH2n/JN4MJaHwehyx4B9\nHlvoBLcPhv+zBaWDkfoc78fWzImiTl07tvX7tGnTOp38veLGG2/MSSed1PGLejdBP+WzfJfXYV38\not7lEJs3wdaMvbH8ou6fYIvaL+pqSQp4qaWW6tsWN910U04++eTOsdf7GLEFv7BG+IVjYQusXL7D\nde3XFtYIP2RzttCnZW2whfePxxY333xzTj/99AV2dKXu9M2omKq/27nLZ7CRvKR1zlbUYb2fFqUj\nZ8cv6h1dMXBRAAAgAElEQVSCVcmxIT9gM6ph+vTp41ojJ598cuc6sj8FQ4FaI3zWOVNEztX19XnW\niAiI3A8FTJmIErlf8AsRGN/HhiIgjtf3un/16xdN4TQ0NDQ0DAR99eGsuOKKwzvvvHOHiXgqY6pm\nU4mRYmNqyet91j1lVa1gNhiJnhSVGJ7e4tBY3dFHH52kPOW9T0zY7ov+L05KDaiJ/81vftNzH84K\nK6wwvOOOO3Zi3z6TLd70pjclKaqvZrqYKXZVx/TlsRwjtqeH4cQTT0xS4thi7/YQYXvHh92xBbYv\nt2P219e//vVce+21ueeee3qmLfzC9ZPLYQvz4PzdObOZnT7r+DKG6nP1GNR+YS6cXFDtF2zBhj5X\n7Jmt5TMw4EsvvTTXXHNN7r777r5s8cxnPnMBW7j+qgxFBfikNULJYpquG1+ubUENWjNsge3LEaj4\n4g9s4XPZwrWpe2Auu+yyvm2x0korDe+yyy6dc8GW+YUKTTkbx6YCa88990xS1gSfdb+gDvkB9o6F\ns4XeF68zt865ym+o9JJ/FYGhSr3/qquuytVXXz0uv+Br7gNA2binusdSQCr3rBHXjerqtkb4hf23\n+IX7ClvUlXvWiPuFz7dmRTO+/e1v93W/aAqnoaGhoWEg6CuHM3369Kyxxhqd6hJ5C4pDBZQ8BjZe\nM9j6aervJhtjWxgMBYKpUA16VzAbLNJxiD9jVH6XB8Gc/G7+WS8wMwsrxkzMOhKLFyfGCNhCXgtr\nMykbo2VTtnAOZh+ZL+casJE4OdthVM5dXBqDwmCxxoc97GELTCweC9OnT8/qq6/e2ZlT34U4MLZl\nRpXqI7Zgg1qVOXZ+oXrOuenil5/CGrEyTJdfYLJsQd3zA2qA8l5zzTU759KPLdZYY43OdWJLuRK+\nqsoJA61tQfm4nq6Xz6nXSG0LrNzrnHs3WwD/EPv3//HYYqmllsoaa6yR8847L0nJEzlGthg5xy8p\nvSjmBbqOrpccizXifuO6uf7WiDVKOfmeeq8guUXqz7m7j4nMrLrqqqN2de0F06dPz6qrrtpZA1Qd\n36ZU/d99hF+4n1Bl9W6k/MIacS7WJJu7T/ELaxP8zpb1nMs6h7zWWmt1lGsvaAqnoaGhoWEg6Evh\nzJw5s8PEkxIjVaOtn0a8EVvCvjAFjAKD9XfxbspH/JJi8ZTH9sHfPZ3t2IfJqNvfeeedk5SKDexS\nPLQfzJkzJ9tuu22HaVBdKm5MFsBQ5CUci3iw3Akm4ZjkdOpZV5gQ22EemKvf2VjHMJaIWYuf60GQ\nt7jyyiv7rsCZNWtWHv/4x3eui1ybaiI9JCZdY46mObv+rhc27++Ui5g6W2PpdZWh46cWvE5/hhyP\nSRS6/F0j33vLLbeMyxYbbbRRxxbWiN4TttBpzhaYqBj8WLagfPTvqFZkC8ftpyhCN1tcfPHFo2wh\nN+B4xmOLpZZaKg9/+MM7vUP8QjUYZWIyifsFdYhNY9uuv2OWK+br8k7uF5Sy46Zo5CPcLxwXta9y\n1JQIPW4jd03t1xYmUFjPvtP613NmjViXbOH6i5S4nmzEL5xzvUbqyf5Qz1x07j7XPl38wr2TLayZ\nXtEUTkNDQ0PDQNCXwrntttty3nnndZ6G2DQG4qmqjwZ7023v6ahiAvPB6vVFiEuq5DIBoI71Y3Xi\n1dgj9o4xvf3tb09S4pfip1icPoF+cOutt+aMM87oHLs8AFtgnp/85CeTlKqP173udUlKfPrwww9P\nUmYkySNQXSpnqDO2cA3Y2PtUnX3+859PsmBO6YgjjkhScj6uoZju4x//+E6su1fcdtttOfvsszvX\nQw+BY+MXekewt3333TdJsZkdF+3tgmXxC3mm2i8wVj+pRypRH4dubMd36KGHJilKWlyeDddZZ52+\npy7UthhrjdS2EBu3M6w1guFaG3KDtV9gshQwts8fXQOTLhzfIYcckqSsJbYwGWPu3Ll92+KOO+7I\nxRdf3IkCuD7WQr1PEtauOs11t67lO0QDrGO2lbPRq4K9UzJUoe9nY9W18m3veMc7Rr3O97DNqquu\n2vfeQLfeemvOPPPMzvXotkZOPfXUJMUPXvva1446x2OPPTbJgmtkLL9wDdi4XiP8kb+x8bve9a4k\npTqNv7pHrLvuun35RVM4DQ0NDQ0DQd+blM+bN69TVy8+KMapxlv+QgxfVZuKGvtuYyJYvBirfb9V\nt2B34pzimGLwmInYsKcvlmkKrH0wxNUxZhN7+7XD3//+946Kwlyci1ll55xzTpKiusTqnevBBx+c\npMw8UgkkByC3IpYqX+ZcsDbnKNfj+yklORxTox3XZz/72SSFzX34wx/uOy47PDycf/7znwtUQPlM\n1Wq+U5WanVqxKUr4zDPPTFKuK1vxJ34glm+elN/5G5ZO5alCpA5dC7bE/vnF2Wef3WF0/dji/vvv\n71w/PsimKqv4vmNjC2tk77337ssWmK7f5YD4Db+0RqgLxyfPyhaYNluce+65fdtiaGgo06ZN6ygM\nFVZUlR4yfkGlu39QafJd8p982n2H8uHb8k5swVYiHJSK+4z8lWgF9e84RGSoiMsvv7zvierd1ohz\nsUb4hXOq18h+++2XpORa6vtFnU/nB87FvdTnWiPuFxSPNcIv+CElRH1+4Qtf6MsvmsJpaGhoaBgI\n+lI4999/f26++eaOkjFlGWvyUyWVp7mnrRpzLM+EVHs2YDCewjp+PW3rnUbVnovxYkrYnhwNZktZ\nqWZR0VHvLNqrLW666aZO9YacjBlGlIlzxdZ0vzuGmv0fdNBBSQprVw2i50g1is/Fzky+xfIwJe+n\nCsVbTX3AdGE8e33wC31SjgVLwyQxT/0M4sv8gC2wKrF8CtR11beBtbMFxeJ3Cplt2cLnuAbmmunX\nEO/+61//2mHj/djipptu6kz3ZQvTfa0RyqKekaVyiy34Ot9li3qNULDWCBt2WyNsQYV2s4V86fXX\nX9+3Le67775cd911netP5VMSjo2/iRY4FhWWFLE8lHPHxvmVyAZVxg+8zhpwzrWykU+hZN74xjeO\nOh5RjKuuuqpvtWeNyDPJwThGVYx8U75aNaE14vUUihyPe6z3W+fUJb9QGWoqB3/gf6IE/EM+0z2a\nX7if/e1vf+vLL5rCaWhoaGgYCPruw9lggw068Uvxf/0zasY9bffff/8kJf6oSghrq3tTKBGdq+Kc\n4oXyEyotMA7xbizABFQsRFzT52F/mI3/96N09FtQNmKkzkFu5Ytf/GKS5LDDDktS4tjYv10OVb2I\noatKOe6440a9T0xW5Qzb6lF4wxvekKRUnTk3rA7Dpu68DjNaZ511Oq/tFTNnzsyGG27Y8QsqS6xc\nlZiYOuZIAauMcV1U6Hif63L88ccnKdcR6r1nqAeVX/zCvDnVkmL71IHYPb9Yf/31F9kWGCpbuN7W\nyOtf//pR78d82cKxUjaqmVRYYbBsqTdFnlU1kvwYBVWvEQzb57GF92+wwQZ95/b0Z7me4v/YNrVO\niVJXXq+HTaWcakLs30QB9wXKh1KSy8PG3X9EH7B9+yGxmf/zC/c1rH/zzTfv3LN6hXun6jRVpPVu\nomzx1re+NUnJzVgjjtk5WlNyMR/72MeSlCgT+D8/cW71GtFnKT9Gnfq8RfWLpnAaGhoaGgaCvhSO\n+WGewnI4uut1sWNLYu3YPlYl7uyprdLizW9+c5KSr9DbIpb/zne+M0lRSJ66WL8Yr+/BoDBix6NX\nod49D1voBWZmqd7AnlTeYKg6h+tpvGL8XofdYU5UG1thRgcccECSUq0ipoqliWdjhfJfbLHZZpsl\nKeyQjdloo4026ti/V6hEEg/mF2L0rhdV55yoLErDMXk/Nk8FOC6qko30WdXVifwCM/Y7VokR8wvK\n2XFtvPHGffeejGWLelaW7/adFCl/0Z/l+rn+ztX122uvvZKUHhL/d11VgMln6KpnC6qOjakIa3eT\nTTbp2xZTp07Ncsst11Fzen/4IFs4Nr0efqe2+Li8FvXvflD7slls73nPe5Is6G/67rB+9yvRCfcH\n38sGck3rrbdeJ1/YK8xSkythC+fEFtSf6++YTSRwrnrR+Da/cK7WCAVz4IEHJik5Gdebres1ImpF\n1fFTKlBEpd810hROQ0NDQ8NA0Nd+OENDQzcmuXbyDmex4xHDw8Mrjf2y/3hb9GyHpNliJJotCpot\nCpotHkBfD5yGhoaGhobxooXUGhoaGhoGgvbAaWhoaGgYCNoDp6GhoaFhIGgPnIaGhoaGgaA9cBoa\nGhoaBoL2wGloaGhoGAjaA6ehoaGhYSBoD5yGhoaGhoGgPXAaGhoaGgaCvoZ3Dg0N/aePJbipj9E2\n/9G2GB4eHur1tUuaLYxgn6gpGv3aYmhoqDNu3uh220jYQsH2BYYhGs5qgKjhi/Xrwdh6n+uc/d3r\nDV+0hYPX1T99j++tjwv+nf1iotFsUdCrLfp64AwK3W4YE30jWQj+U2cdLRFw/WBRr2/9er+7Wfa6\nE+FYx9UPhoaGMn369M40X7uamnBsyq59dlZYYYUkD+ycmJR9RkzrrV8PJhqbkOxBY7dSr7cPk2nk\nbGP/Jb+biGw/HQ9Mu196sDUsXgzgHjip6Hd45/C/fib59z3pB8FVw8PDm/TywsZYCsayRTe2/CCf\n5xhG/T7i2B70/W6+9evG66/jsYVjtgWGc7ctgDHxXmdLBZsPAuVhjLwHgnOhSDwQ/N0GWzZw8zq2\nsRGfLT1sx17bfsaMGUkeeLDNnz+/sfoR+He2xeKKArQcTkNDQ0PDQDAuhdPD65KM/+lJ7guJdItP\nTwLGrXD6ZfH9ohvrnyyVuSisfsRn9PWdY52TDdNsr21zKhsA2rzO+8drm5HnMTw8PK4cTq1c/vKX\nv4x6HX+x0ZmtnoXKrAF/r3NAT3jCE5Ikf/3rX5MUvzv99NOTJLvsskvn+JOiYEYqlpHHYU1RZLZ5\ntmHgvffem3vuuSfz58//t2X1E40lUeHUuT2/z5o1K0m5rhONpnAaGhoaGpYoTIrCWVR0Y7qe1lAn\nMieA9S9xOZyx8hHdqpgWFf2yt5HXpt8Ec33dbIvtp62AVXBh9bZPVgm27rrrJilbA9su1/bMtY16\n9ZN+bDFlypThpZdeegFF4qfiAair0iT3P/vZzyYpWwF7v9e/8Y1vTFK22bYdM0Vka/PPfOYzSZLT\nTjstSfKiF71o1OfUx+XvQDkNDw/n/vvvXyJZ/eLC4rRF7VeiQRTs3XffnWTB+wfFKrc3UfePpnAa\nGhoaGpYoLBFl0eKLWFYdd8TasC/x54kqs12cVXc1w6iPpe6zqI/R+zEbYMtBndO/ch0L/V+3Y6+v\nu5Jg1/tTn/pUkmS//fYb9TvF8t3vfjdJ8rSnPS1J8q53vStJ8R8lvb0eT42pU6f2zfyGhoYyderU\njo96v++Ss6FovO7nP/95kuSJT3xikmT33XdPUhQKNXfDDTckSTbeeOMkyZve9KYkRYn85Cc/SVLK\nob/61a+O+lzf7/PklubOnZsk+e1vf5uklFcvs8wySZKNNtooP/jBD/qyxWRhUddr7Xc1JitqMBFw\nbO4Lqgwf85jHJElOOumkJMlZZ52VpPjVVlttlST5xCc+MerzBl3u3hROQ0NDQ8NAsFgUTl1JgWms\nt956SZKPfvSjSZJnPOMZSZJvfOMbSZInPelJSUpVkjj2XnvtlaSwtN/85jdJCgMai6kszn6ibnkF\nTKbOSzz72c9Okhx//PFJii3f9773JUne8IY3jPr7brvtliT53ve+t9Dvmyj0YkPHhKGqxBJXdt1X\nXHHFJMnBBx+cJPnWt7416v0nn3xykuS9731vkuSee+5Jkuyzzz5JCoN1zmzwyU9+ctTnjIXx2Grq\n1KmZM2dO55jYxTlRImuttVaSonD4ttfJW1FxFM0LX/jCJGWtHHHEEUlKzL5WIdbG5ptvnqQooM02\n22zU99cNnqIJFNW3v/3tgVVgjgWvcx2pNjYY63ucB/VWRwOWJGVTV7++4x3vSFKUzIYbbphkwSZn\nr6OAnKP+L/4lH8ofNRxPlsprCqehoaGhYSBYIqrUPMX1IGCHP/3pT5MkW2+9dZLC3v0Ub6Z4VOp4\netf9Oz0wtCWmSq3uRar7Jdhmgw02GPW+X/3qV0mSyy+/PEmy//77j3pfzYS6Xf9FqcCpGWsdd/Z/\nfTQqsdZff/0khZ1RrPXneP/vfve7JMmFF16YJHn5y1+epORy/ud//idJsuOOOyZJLrnkkiTJHXfc\nMep4xsJ4KvZqFu735z//+UlKbF0+qh7Ls/baaycpNjrjjDOSFEVCFWKwzlHu5tWvfnWSwmD/+Mc/\nJik29T4jdVSv8adf/vKXSYrNh4eHM2/evMVambXFFlskKWuD2nvLW96SpKi2b37zm6PeRw16HzVn\nrciDUc7G/Kh+7IZB2IL9HZN7mNwbJdptRh6/Oeigg5KUXjWqnyKmgL///e8n6T/q06rUGhoaGhqW\nKExKDqfbEEVVSFhX3RHuaY2NP/nJT05S2JjPwUzEJTERlVpYISbr88yXEpdeEoER1z0omA02hiFj\npOrqqYTHPe5xSZKXvvSlSZKvf/3rScqsLmqyW6XOoqBmRyqewBwvKuyKK65IUipoHvGIRyQp1xUz\nxc5U4MjJXHrppUmSD33oQ0kK0+UH559/fpJk++23T5JccMEFSYqf8gtsf1GqoKZOnZrZs2d3rgdY\nCz6b/fXHvOxlL0tS+me+8pWvJEnOPPPMJCXf8LnPfS5JUbhf/OIXkxSlROGYxmDygGGiogFssuuu\nuyYpuSPXRGWg45s6derAK5rq/MWPf/zjJMkrXvGKJMVmFO3tt9+epKyZNddcM0ny2te+NklRfXI+\n8h8iI75PlSRFJY82CPAPw1NvvvnmJOWe+fSnPz1JmRhgbbnHnXfeeUnKWqHaDj/88CRlQoU16J4s\n39mtgs+9VfRpvGgKp6GhoaFhIJhQhVMzwzpnYq7U9ddfP+rvqtFUI22yyQNpFE95SsWcJ09ls7XE\nOakDPQwU03HHHZckufHGGx/0eBcH6mP4whe+kCTZY489Rv0fy8fi2Ew82jnKZ6js22ijjZKUCh6K\nqB53PxlwXczx8jt1RsWpLlORd+KJJyYp+Q4VWpQPdod9O2efd+655yYpTBbkcLbZZptRv1M2E4F5\n8+blzjvvXEC96xUSUwe5E777wx/+MEny61//Okly1FFHJSkVeZjpe97zniSFjfMPa4XCoYT0MLkG\n1sLFF1+cpKgG06xFE9jw3nvvHfg6kXdyXZ1j3X+nKlWeY8stt0ySbLfddkmS17zmNUmKMpbvYhP5\nMq+zBsfK4UwG6nun6yUq4zqdffbZScq5vPKVr0xSzp1CPuSQQ5IUf3rqU5+a5IGqw4WBgnFvpRYX\nVdlAUzgNDQ0NDQPBhFSp1dVgdX18PaG0ZvXikFgVVqZ7Vre0ajVsT8WOGK1qFLscyvWIPfcw0Xmx\nValhMquvvnqSwlCdC0VCqVANbFgzUvunPPaxj01S4tAYMUxUldrQ0FDXzxL/dd2do257bMo5uF72\nfnHd3va2t406p/e///1JSu8A5YvNUTKf//znk5Tr7ji6TXeo0Y8tllpqqeEVV1yxw0jryjyVVVg0\nxiqnQqGI1avEE8vHaE844YQkyZ577pmkVJUde+yxSUr+s1ZAL3jBC5IUW1N31gqbyOk4j5kzZ+ae\ne+7JvHnzJrwyq9tkbeeuSx7btu6ds59sCSPnwCXFj+o1I6/lcxwH/+uGyahSs1bk0ChQubt99903\nSfET6g7M4qOA5XRVgoouuN/If1lbkz1vsCmchoaGhoaBYJEUzlhTnes4dv167F1c+93vfneS5Jhj\njklS4pSgRlx3tSoTjNa8KPFGDLqPbtmBKZxaDWKgYrGqSzBkbE3llWqTegqDKcMmE6jkAbYZa/vl\niWRvzlFlFoXzhz/8IUmZGPHxj388SclPYeNi6/ot5K3E4OWl/F1/lpyPaiUqb2Re4l/nmqT73Lp+\np0VPnz69a/+U3ymcl7zkJUlK/kGVmIq7D3zgA0mSa665Jkmy6aabJim9SiZO1PmGH/3oR0lKTB9T\nfvGLX5ykrBnXxuuuvPLKJKUqzuf6OZm9J9YAu1PzbFfn5Oqek273IfkqOSFrh59Qge4fY923YDJt\nYetxypbKk+NTfSjvSclY75Sr6lTKSdTIxAlrR15d5ASawmloaGho+LfEIlWpdduBs9uOi3Vfjqew\nn9i3yh1xbTXh4poqdcQhMRMVXLVqWJJmI0G3fSzOOeecJOWY6zwDW6izV5//4Q9/OElRhz6HLai9\nsZTNZKBmotg6di9mT/mooNFDpDfgYx/7WJKSb5Bf0FuEDVI0zpmyYXN/n4yqKx35KqtUfV122WVJ\nyjQEFXhYu6nQcjB6hfzUb8MWhx56aJIS09d/QbmwjVlq1J7/18rZNZAbMJFgZG/SZFep8U09ZPVE\nbetZTnesnKzP837q0LlbO3Ukpd6NdbJ2yVwYKEu+7Lo95SlPSVJ8X0+RCEfd16Wvxjl6/Vvf+tYk\nJW/uulOw1gj0mufsFU3hNDQ0NDQMBBM6S63bftoYA8ZSV7V5vaevrtiPfOQjSUoVGobiqatqxfux\nSVVudRx0xHkkWXDq7Pz58ycth9Mtr1XnoepY/9vf/vYkpeqECnzzm9+cpFTYYHGve93rkhRbqkIx\nK6nXqdHjiU93Y0GYqXPSZ4VNO3d7tIgnU0Iqs0wkEJOn9pyjPEWtbMXq6z1lTCSQS+rWST+eir16\nfpxzxyzl4vQgYZqUropLlVfU/bXXXpsk+dKXvjTq3PVbUEgUFiVEGalSYgt5Dd9HLdbXcqmllso9\n99yT+fPnT1rewnw4nf/yD3ZuVZ2qOlHupZ5sTCVQZ/VUaP5hTVqDpnio/Bvr3jgZORx2V5Hr2PWW\n1T4sV2cqghyMXI/3135G0bC5KQ4qPfmZateJyvk2hdPQ0NDQMBBMyrToWrl0+78qNewPQ1UTrmpJ\nrbk4JAbs6a06SVWLeOZY+2MsBJNepSbfhImYE1dPtHZupiuI/atCUY2mJ8UEbdMVqL/6Wkx01UlS\nbNHtumOg2JLrZ7KE3hSsHwPFuuUhzDzDwjBTPSMq87D/U089NUmZHozBHnnkkUmKwhKrr3ecHRoa\n6ntCsio1Nqh/1oyTije115QMeSez1ZZbbrkkRcmwiZi9WWkHHHBAkhLzp+6w/4suuihJmb3nd+fM\nxhgu29555525++67J6UPpwYVLz+lYpM/mBtX5zmBv1n/7i+ugZyMykCYrAnJSe+2oERFLL785S8n\nKftgWSNUIFuJXJgvqLJT/43rSOFQNO4bckG77LJLkpITpGzGuqc3hdPQ0NDQsEShb4XTT7VKHQfG\nSMXMP/jBDyYpTES8GfsyBdjudu985zuTJHvvvXeS0mGuC7+e0NvtOB4Ek65wHItOcHOc9JTIK+h6\nFqvF2uyKKVejb0OMV/9GzfrqHoex9gaayEkD9THUkG/C4lSrmZR89NFHJyksjDr0erlBuT6VOfIh\nWJrKPb1OKvr430RNXVjYjqK1D6oy3GGHHZKU/KOqNGpLf4Vc3bbbbpuk7IZqbdj7Rz+NPAf1Zi4h\n+N3nWEuf/vSnk5S8J8a92mqr5dprr80999wz6Tkc11MOhrrD5uu+LhOy9SZh9fWkAJ/LJvWeU0CF\n1lM5akxmH06d85XLlbt1zPKZ7q0mlHidNaRPT/SIMpYT0uOoD0v+2/1nonK+TeE0NDQ0NAwEE5rD\nGWsfbCxPHb3qI30TZl6JW2Mo4tp6GVQvYYVmLvm/iahitHWV2oNgwhROzWjrCbcYBNaut0is1TlS\nMDqN5avkH9hAJY+qI9VKlJBqJipxLEwEe3PO8lD11G/Xnd/ItZhwbcYav3CuztEEZnFpcW+sj/9Q\nkfq7xLnlEOs+i4X0lfVli5F7x7ABtaV6zPXlH+Z3Uf3Y/imnnDLq9RioXIu+DNPFTWdw3U1x8DpK\nmg3kelTBqW6inKjG22+/PcPDw5MygYKi4PsUrP6Yet8afkR91flPkQ7KqO4toup06cuLsrHPHWSV\nWn3vHJlHTIr/8G33DzaRk/F3a8FkAe/z+fKdbM+f9ECpCOWHE2WLpnAaGhoaGgaCcSmcsXIi3fps\nPE1rRinuKA5tphqWhvWZ+4OxqCXHhFXWdJt00C1mOwITnsOpu+zZggqjytZaa60kpaqonkCgK19s\nVuxfrF+8uVu/T22LsdToRORw6l4UCsV3yrWoOlpnnXWSlFg726hWMmNNBZfKLorJZAJVb5SNKiWV\nO/o7KCR9W/Xk3fHMUps6derwjBkzOtWDmKJjkYegruRsMEs9SWzFhhQKBUO9y0uZXGDaBtYuimBS\nAdtYC9i8vYFMPFA95zx+9rOfZf78+ZOSt+CzzpVScV9wrmymV0guWARDnsJ1c59x35HflJcwnYMt\n6irFbmsHJnNadF3dSKFQgdaQc3FvNKPPdad42MI+Oe5HVB/bH3TQQUnK7rvyXY6Df9VoCqehoaGh\nYYnChOz4uZDpuknK0xr7xu6wKU/heu9wDEYeoo65q0rDbFTY1BCXxAIWxxwxtsC+TcamxuRwxMqv\nuuqqJKUb3/v13ahuw3hU6tTfV9fL12pzIufLDQ0NZfr06R1lAvV3UDKuqx4A7B+Ll6dQcYVtY2+q\ny+wZgwFTf/psVC05d/kvs9owYoq5ZrLjmR+2/PLL51nPelan2st3yw+wEQXDl+XgVFjJY1I0+nas\nBUoEE/3Od76TpPiRGVx6V0zadlyYq8kD9g6SH3PeYv0HHHBAp7JpolH7qvsJm7iPYOPyXVg59e9z\n3ve+9yUpFVnOQeTEfUgOkV8uQv/ehMGxyVu5Pio35beoMz1p1LsKTP4m+qO6lRLiJ/yM2pcvpbTl\ngOq1PV40hdPQ0NDQMBBMyn44NTBQTNJuhXoB1IqrHsHysH/9OBiI99dzhTz9MaKx9uFeyPFPWh8O\nNr1PROwAACAASURBVOac5GBqpVLvRom1qaih5hyzz1XRs+uuuyZZdEayKPHpWk05RhVa/KCeFEDB\nODf9OVi9WLv3g65oe9jXFT5YIrYmF6QCsK4oqxl3P7aYNm3a8HLLLddRLo4Zm1Y5J6+gosoUBrF2\nOzfqTbPvjWrFZz3rWUlKLtD1p5zlpahAx0MdyFd5v1l7Ottr/1l66aUnfZZaPRHAT3u36Emy++WB\nBx6YpFQpAj+T46FY5DNECXTnjxeLska6VbGqCrP+3RdU3FFr/i9K5B7J31w/a4FioRrrqdAqgSlm\n/tnrfaTlcBoaGhoaligsUg5nrJ0+YeONN05SqkDMgfJU12sgLukpi9GYnCpe6Smu/6bu7B5L2XQ7\n/omE2Kl8lGogMVSM0wRsMdc6n+Dc6go8oPJ03ddVcTXjGQRqhSD2Xu8NY78jx2gO2IUXXpikTO3F\nUM3WM1PP3Cfd92wlV4fFyf2J1f/sZz9LUubO8Zduc6L6wbx583LLLbcskEtzvVWLUXPmvpksAdaI\nGDv1RuE4F9EAioj6V7Wm+s1UYf8/7rjjkpRufiqiVqf86L777pu09eI7+bKZd1j8zjvvnKTMB8T6\n68kDjpkfmTtmzhy/qqdsPOc5z0lSKv4GgYXlC5Oi8uS95TUpH0qUatdH5fPk/ORi5CutPd9jjbCx\n3A8/G2u30/GiKZyGhoaGhoFgQiYN1E9BFRV1bFUcUexevFgPihg7xqKyhrI58cQTk5QuWiyv21O4\nWw/Mg2DCcjjYNaUjv2QmFrZFpVEBNbPQAW63yxHfn6SoP5O2sf6zzjpr1OvHmvZaYzJ6DMTM5VDq\n2n6szLnI8YnVY7QYqeo1CknVmbwIVVnviqnaCnOmoLrtdrgoPUn13jz+TnHqPfJ3uRcMVi+KPJfK\nPROU999//yRFrfm/akh5DJWBmK5KLgxaLkAfmA52fTgXX3xx7r///knJ4ci5gvXN500mkf90TO4n\nogL17pTmEvInexHJi5nBNuJ4k0zuRPWxID+l8s6x1P1blCulIsJh/yRVipQz/+EnKnypQD/Z3nR6\nVY1tllpDQ0NDw78VJnSWWj0vTDzSU3i33XZLUhimuU3ih2LrmK+nun4KMXyMFAP2tMaUPKXHEXec\ntFlqKq1GzqZKStWSKqW6g1iMvtseM87Z+9hsrP3ex8JkzMxyzKZ9yydgqlgd9Se/pfJOrwiViK1R\nET6f7alKuUNz5MwTY6Oxcn79Vqktu+yynSkYrj8GiY3zXb0ieo/k+OT05DNVEcnpmMphRh6lJFck\nB6T3RK5IfkTfht43VUkUlT4dfvUvdTMprN51wML1S7l+VJl9lGolSsm6z7hf8A/z5OQ7TKiw5uRH\n++1Nm0hb1PdOCoUf8Cd5Lv16lA4FK8ej/4qt6qpW32fygMq9o446Kknxm15VX1M4DQ0NDQ1LFCZl\nx0/AbM260lFuvpRZWqpOxFjlH+xGqIpt5P7qSffKq/qpPNbcsBGY8D4c3y0/hXk+4QlPSFIUiFwM\nti1u/dznPjdJd4bRb26mV0yGwqkn3/pdtZpqM3moF7/4xUkKw9WLYk6YPIeeJrlDakEOkO1157O5\nfg25xrra8V/TkceVw6FgKA65PApGP5Xv1BdDjdWxdirQPjdyMzvttFOSkt/0fzF4Cobfvf71r0+S\nHH744UmK4vrABz6QpExrsCatsc022yw//elP8/e//33CFY7+GOcqH6GSj7+oWjTJup69puKOMpIX\npQpcC+/rtZq1GyZD7dVKh9J0P5CjMxmAbeqcnojKEUcckaTks9jW2mA7a0cvZF0lO9b9pSmchoaG\nhoYlCpOyH05dw+879BCIP+t6xUDEEVXYYFlivHUVylhP3V4nDozApE2LriGGLvbKRnoBMA2sTFy7\nZhwYsw7ksY5jMitwep0iDhioPBYlrHpM/oKCwXjlArE45y6XYyKy664Xiu2oh15nZvU7LXrWrFkd\nn8W2QS6H4qHSMFP72sjdURiYKhaP5VNpdmw00UBew0/5MHlTeQ7KyaQCa7juVF9qqaVy7733Tuqk\ngRqma1gDekr05zk2OUFVbXpY3C/079Tv6zbDbXFWqdWolabrQ5HqOaJQ5KPkp37/+98nKUrWJAv5\nUtGAOtc7WbZoCqehoaGhYSAYSA4HMAq5GgxUn40qE6wLG6wVTbenb7cZXn1Un0zaLDUwV06vSD2d\noa6cMkNJlUoNHcj1HkOLismMT481/YACqXtX2EAfhvg2W4pTm2Tg+9iSjXr1HxhPDgdqle075EpO\nPfXUUeeCnWOkeoiOPvroJEUFUk5UAGargs8EdsrFzDRrgjqsO8/93/FQgVOmTMn9998/KZVZY92D\n5H4dk2pVfVXUoRyfakYVfKbTT/SkhMlUOL1GC+q+vZE5t6RUrelhohb5l9ePtfcPLOoaaQqnoaGh\noWEgmFSFM+J9SUo8Gduz94bKCz/Nm6rjyAPYz2bSFU6dx+i3GsTr/KxVwERhEPHpbqCAKZduELem\nCry+VtIqv2ql241F1sq4X1tMmTJloQph5E+x+bpCy7F7n4nWGKs15POpPj1Netl0iFtDqpP0XbAZ\nG9h/SX8HFao/56677pr0adELef+o3+WhzIXrtqutik95LfkvFXqL2qMGi3ONiHzUOcIa9gSTA65t\nNVFVrk3hNDQ0NDQsURiIwukGbK1WMmK2qo/qPEcfs9H6xaQrnImCPIfu7Hpu3aJicbK3bug2jdwe\nL6Yz9MpcJ7qL+l/HODxjxowOA7XfUbcpHPV0YGvC79SW2WYq7kxNkANS6ae/B7s3WbueRuzz5H7Y\nzP9978g5c/PmzVssfjHeqrK6KnERJpAsFEviGhlrruRkTfxuCqehoaGhYYnChCqcyep6n6zPXQj+\nbRTOZGNJZG/jZbqLyu76tQU1kJS+mtNPPz1JURLykSoxqXw/5VBMUqdE6jmCcjjd8hJ1rF7eC9v3\nfsdLDah+lCP4l7pZIv1icaHZoqApnIaGhoaGJQr9Kpwbk1w7eYez2PGI4eHhlXp54X+4LXq2Q9Js\nMRLNFgXNFgXNFg+grwdOQ0NDQ0PDeNFCag0NDQ0NA0F74DQ0NDQ0DATtgdPQ0NDQMBC0B05DQ0ND\nw0DQHjgNDQ0NDQNBe+A0NDQ0NAwE7YHT0NDQ0DAQtAdOQ0NDQ8NA0B44DQ0NDQ0DwbR+XvyfPoAu\nyU19jLb5j7bFZG4x/e823aINaSxotigYjy0W1xqoB99O9HH0aou+Hjj/qRhh/P/UWUeTjqGhoV72\nlUnS+/Rv16XeS6bbovH7g+y7/qDfU/9/xowZnanKk42xbNJtp9humOh9UaZNm7bIO2T+/476Go78\n21jXqX5vvTb4Tb0T8Hi/r9f3TZ8+vS+/aCG1hoaGhoaBoG+F0wuT7RX2/PCErJ/O42Vj/e6fsySE\neCZqn/XFgSlTpmTWrFm55557kpTr182uY12XmTNnJil7ttjR85ZbbkmSLL300kmSv//970nKHi72\niqn9hz/YxdJeNPX+7v0eZzdMmTJlzM+GsXav7bbbrb9bQ2zV62649dob6ziXBL981KMelSS5+uqr\nkyx4f3B9Xf9HPvKRSZJrrrlmgEe5cAwNDY1SiQtTOyNRnwvUflBf/1rp+L1X5ex7vb6OStTHc//9\n9/d1/2wKp6GhoaFhIJjQHT97xaKy+V7jjWPFMxeCCdvxs1d11o3JLG70mxCdMmXKAgqi1+vkJ6WC\nXa244opJim0onGWWWWbU3/nRnDlzkiQ333zzqP/7fMcHjnMs9GuLhUUB+lXrNfPky/X/naNz68Zs\nfS9GDN7fq/8tjqIBfnD77bcnKee0uNfMRBQNjKXSxvodXHf3VjvHjvj+UT/HUsBjFRnUv7cdPxsa\nGhoaligsUpXaeFlbvX96rXQ22eQBkXHVVVclSTbffPMkyQorrJAk+cpXvpJkwbg1OJ76KT6ZJYk1\n8+j1O8ZiabUa9D32nL/jjjt6+r6asUy0shoeHu5Z2dTHBOuss06Sck4bb7xxkmS55ZZLkvztb39L\nkjzkIQ9Jkqy88spJSqz+8MMPT5Isu+yySQoj5jc33XRTkpIDmujcISzsfb3mcqC+XjNmzEhSmKu/\nU3t33XXXqM8ZK1fgc6xB39drTmcy4XpRtBSrY+L7cni1H/EL/ii3x0aLC0NDQ51jra+TdV77oN+7\nRYW6KZbahx/72McmSX79618nSf7rv/4rSfLXv/41SVlz3mcNsZnjqPOf/eb0m8JpaGhoaBgIJiWH\n061/Auqn9ZOf/OQkhXm+7GUvS5I89alPTVKeshjP8ssvnyR56UtfmqQwnD/84Q9JkjvvvDPJggqq\nh8qhCcvhLOT1Y313knIuNROSn9hll12SJN/97neTJM985jOTJF/60peSFBttt912SZLPf/7zSRbM\nj4xVvTKevEW3nJnr7dyxJwp10003HXUszmnttddOkmy22WajXi+m/6tf/SpJMnfu3CTpVMnts88+\noz6PIqbqsPtu/rCQ3ycsb1GvibpazBqoq5DYltLB7ikc/7/tttuSlHOsv69WdXU0YKwKz8nM4TiX\nf/zjH6P+7pxd3xr864UvfGGS5IorrkiS/PSnP01Sqh4nGpOR26sjD/4/a9asJMU2/u7craHrr79+\n1Od5H2Xy2te+Nknynve8J0ly/PHHJylras8990xS7qHUoeOqK0F9V8vhNDQ0NDQsUZgQhTNW16sY\nvNirpzK2/vznPz9Jsu666456XV1h432Y7k9+8pMkyYc//OEkhclif9gihdRD3mKRFc5YbKybrR76\n0IeOOla2uPjii5Mkf/nLX5Ikv/3tb5MU22EuFI+8F+aCNf7ud79LUpgv5tytUmtRmGzNqilS1wXj\nfPGLX5ykXI+99947Semb2GabbZKU681GbIu93XrrraPO7ZWvfGWS5Gc/+9mo/9c5pprF1/4GE8Hq\n6+teHwMbYZDOjTJ1vbxObxJ/kLegYP785z8nKbH5OrfY7Ti69X2M+H3CFM5LXvKSJMmVV16ZJPnT\nn/6UpEQqHvGIRyz0ff5OzVnn/MN1l7N7whOekCT5v//7v14PvSeMR+GMeG+Scn27rUPXWz6SX7iX\nuQduvfXWSYq6P+OMM5IkH/rQh5IUW+2www5Jyn3GGtx5552TFH9573vfm2TBPh9rb2R/zrx585rC\naWhoaGhYsjCQPhzM40lPepLPSVJY+MMe9rAk3StrfvGLXyRJ1lprrSTJ//7v/yZJLrjggiTJdddd\nl6Q8jT3dVTX1cY6LrHDGytU4Rq/DbOQ1vvrVryYpjObRj350kmTVVVdNUs6ZwqlZOZbv/ZSS2G8f\n0xcWOT5N4VI0daUVVuXvFOxuu+2WpORufC5bUSy/+c1vkiTrr79+kuSQQw5Jklx77QMj8fgVlVjn\nN+oeA1hIrmfCYvXd+mkoFOoeo6xt5dgwX/mrn//850mKSqB0rTnq33HxhzqPVXea18poIhUOdi9f\nsN566436+3//938nST71qU8lSd7//vcnKfeBN7zhDUmSyy67LEmy5pprJkm+//3vJ0m22GKLUZ/X\nrXel15l+i6r2HmyN1L5Y57ldb+qOCqREVGqussoqSZL3ve99ScoakLMB9xuKRr7rtNNOS1IU8je+\n8Y0k3RVy68NpaGhoaFgiMaHTouunHmbhKYp5fPCDH0xSWJw4dD235+STT05S4tVf+9rXkpS442te\n85okyemnn54kOeKII5IkN9xww0KPZxDoNhGZLeoOYD0lfh533HFJyrn/+Mc/HvX/pzzlKaM+lw3F\ndv0d65c3wZBUsU00hoeHu060dYzyE87lxhtvTFJYODamIs/MrBNOOCFJUTiXXnppkuRpT3takuTQ\nQw9NUlQgVch2Ps9x+Flfk4nqYH8wf/M/qo76q2PlWLweNP0S8pV1zk6eFKvHjH2+yj+28z11ntO5\nj3eOXC+o7a4a8fe//32S5NRTT01S2Pob3/jGJOV668vh866zSitVr1QA29STCnrt05uM+0etYBy7\n9VlHe+q8pejNueeem6T0LloL73jHO5KUKlX3WAra/eB73/teknINVPjxR8pbDrlG68NpaGhoaFgi\nMaEKp37S1RVRu+66a5JkjTXWSFIqqORkzjvvvCTl6X3JJZeM+j+mIlb75S9/OUmZIosReX0dLx8k\navbEFs4ZY/nsZz+bpLCxDTfcMElhojqCsf1XvOIVSZIjjzwySbLVVlslKYzI9+osxoQpncnClClT\nFjjneqJE3WMi7/CYxzwmSWHxrtt3vvOdJCWeLHcjz0A5sxF8/etfT1JYu++t54nVXdyL2kUND/Y+\nf6f2XDeKBoMVk99oo41Gncspp5ySpNhUr5rcnrWD8VL78l0qt7pNVZhodr8wW1gLrrMcjOvqnL/4\nxS8mKcrEOVkrbLfTTjst9Ludo/c7DqxdHst193OsuWXjxfDwcNe8ketSw+vl6l7wghckKdeVmj/w\nwANHfY7frSG5H9Eh58qmVKLKUFEFyqtWpeP1i6ZwGhoaGhoGgglROGPlSjARzESMVncshqJqzdMf\nq8NAsXlVSHIAqlkwGYy23q2xZhf97pszEcCqsCfVI2L1uqWf+9znJikVPBSKc9xyyy2TFNtQRBjL\n/vvvn6Qwl7EUzlh9OeNBXR3kJ3Unt/LEJz4xSXLhhRcmKX04K630wG7f3/rWt5KU3I/3UwmuIxXo\ne6gF6kElju/FBl2Lbt3e/eLB2F+3CdlUuflxcjH6p170ohclKaredVfB9fSnPz1JUdD6M5y76IA1\n98Mf/jBJ8QtroJ42vLDekX6wsPewr/yBnIyqs09/+tNJyro++OCDkyTf/OY3k5SqVwr31a9+dZKi\n/kDPiWNwPZ2b+4trUB/rZEyj7la92O3/rouq1Fe96lVJyrGLDsh/yenVCpaKZCt/p2DkhuXLRA2s\nmTpaNHL2W8vhNDQ0NDQscZjQHE6Nen5XnZdQd3/YYYclKSxMtZLKine9611JSj7CDDUM+Oijj05S\ncgB1nBEzphZgkMqmBoahK1o3tMo7FTn6KsTmMdR6JhaGstdeeyVJPvOZzyRZ8By7TUJYVGUzf/78\nBSbe1lVfmO2zn/3sUefw5je/OUnxCzm+s88+O0mpUqwruMx9+shHPpKkVKn5v+/F4qgIlUB1dVQ9\noXdR0K1ir1YSbOKnnjPAaFVoUi51zL+eqiAPwo9ED0wLdr3rGW61X0xGhZZzVInp+lEscrS+W08J\n21kLKq4++clPJik2tM6xf316bC6aIOLCHyhtcwlNrZ4ojMxn1XnEep06Vj5q3VKmlLDr7vPq2Xiq\nFOuJ6e6x1oRKX9EjCsr31pP5x7uXWVM4DQ0NDQ0DwYQonJoF1XFgDNVTWAzW0xU87d/97ncnKR3i\n+jT89Pl//OMfkxRmrCKjRq1sBok6v1VPg8YsnYtqFBV7piaoQhJjraveqEEdxN12/us24w0WVm3W\nK+puZCyI0pVfuuiii5KUPJU5UM4dy3IuKnLkKeRmqD/vl8Nh21/+8pdJFuw851f1PvATyea7VXvV\n153SsEYoWEqXUpXvoGDqPWH0SYjRP/7xjx/1d9emztlM9F5AvcD0izpvyGf5iXxlNzYtH2q6PF//\nwhe+kKRUK9ZQ6anii5/JFVIDlJPZfIuKkTbtFlGod26lSPTNUPHnnHNOkuTEE09MUpRPHU1QdcYf\nKBu+z8YiJM5dfnRhlZsj0e/9oimchoaGhoaBYEIUTl3BULMlM6w8JeUrPF0xVE9jrGzbbbcd9blq\nzsUX9WeIY3bb6XOQqPcZ6cZ02QjTxWCwKQxDPmLHHXcc9TkYbp3LoYhqZdMrFsV24r2OHYN1jvav\noVDEzuXiKF6VdRQJ5uuc690tsXZ+RsWZxeb75T8cpyrHug9nIvovuu0BX+dKqD+/qwpSceWYtt9+\n+ySFvWOibIGh+nxr4wc/+EGSwmidW93pPhkVWWNBT4h8E7gu9W6Y3Xa7tEYoWjkaa4pfyBFbY/WM\nPtVxJi4fdNBBi3J6C0W3aSz1JHPr3etUI+q74h/ufd4nSkAJv+Utb0mSrL766qO+xxq1FkQb6skk\nKgi7zRvs12+awmloaGhoGAgmNIfTrcYc28a+Lr/88iRF0aha8XpVaEDZyFOId9tHQ8d63Q27OFjb\nWLFv/2cLMVoVNXI1bAP+j1lQB9QCNbios9LG212fFNZUM9J6fyIsTAze/Caxe69TUaXniCLG8lTg\n2OdEPktljzlTcj/Yfp0zqNXgROQvuk3Vrb+rvp6Pe9zjkhTmSQWYFICpsomeNrF9XfR621RofvSj\nH01SbFbPk+uW25vMXjWTifVdUbRyc9Ath8O23/72t5OUvJfcjFyRc3a9qT+5X1WKL3/5y5OUazLR\n++eMVAnUP3+oq0eds59Um/yjGWmOWWWfPLfKPOpP75ljMHn7c5/7XJJkjz32SFIqfq21brs2j6y2\n7KdirSmchoaGhoaBYEIVTh3Xq3Mqnt46iM8888wkZW6U/4s/HnDAAUlKHb79uDFjuSA/KZ5BToce\nL+pO4WOOOSZJYfdYmqolLE0eQzya6sNUTModLybCdvWkW+wK+1Z1pp9CldDDH/7wJIXhYmt6UHbf\nffckxRbyHT5PDohSOuqoo5IUds8/fZ9cIcUzGWy+m+rHtn2X6yoP4TqqXvQ5WDsGqxdJTkfFFv+i\n7sTize5jMwqnPt5uu6JOJFwHFVeu31g+WFfWmT4vV+P3fffdN0lZW3XOjrLZYIMNkpRISx0ZmaiZ\naiMnqtf5Qr9b147l2GOPTVLUvh42vu/ex1/YTlShVjaUi7wZP9DDqKK312rFfvtxmsJpaGhoaBgI\nJnSWWq8MwFwfDAcz8fQ1P0qlhFiq3I844/Oe97xR34u5eCrXcelB7o/T63dgWfJSYq6qzbA5++TI\nk1AHbCAOviSpO/bGtl1f54CV16yasqlzdj/60Y+SlHwGG5iwrX8Hm/c+igjjNYW4nl5dT6iYSFt2\nWyOODbt3LmeddVaS0j9hlprqJNPAMVNrCWO2w6fv09d1/fXXJylryzWpj7NbDmoiYd2/853vTFLy\nkSIYNepjoWTlH+Q19HnpXaojK3I+1hY1wSb8U55rInPBdT9WnUPjg/JMZi2KdFA2ZqaZPycHpBeN\n36j4NJlAH59J/NaQ75dD9D1Q90yNnAnY+nAaGhoaGpY4DPXDXMbao7wbPM0pEBU1GKbYvqezOKZd\n6/zufZ6ucjye0mL/dW9KvVfMg7C2q4aHhzfp5ZzGa4sR7x/1U4UViOmLuYvVYsQYELZmhlq3rvl+\nmWq/+7U/WMcxFidXh8WpSqJIVA3Jxam8o2zYQNwZE/YTy9t7771HfQ+/0Vfhd9OHqYR6mvDUqVNN\nw+3LFg/2/3rSBLiuWD6bmQOHnevDWWeddZKU/IOdQOv5dfKf8lWiC9aM19f9OJTSyHzc8PDwhNpi\nxOuSLMj+uylNytXaoIjrfNTrXve6JCWnY0afnhYTmLF2LN418FOEZSE9dX3bots6dP2du9dZ19/4\nxjeSlLwktW4vMMrkbW97W5JS9eh6qmY0jUX0wL2Vf7jebCMa0G3Cfr9+0RROQ0NDQ8NAsEg5nG5P\n63oSar33h/3VMVvxRO9TuaVL9iUveUmSUrklNqsSQ9xbbF+1k0qeen+cyYhPj0NBJCmxd3kOc+Zq\nlqejWCxWNQkbjRVnHuucF9UW8+fPH5OpYlGUjf4q54R16/g2RVhfDaVDAZnuazfDZzzjGUlK/Nr1\n9z65AtWOphNTNN3mi00EunWYUxIYrlg6f9BHg+E6JqpM1MBa8Ds1Jx9qrfGbek5drSbqSsPJzA3W\nPSndlLJ9ccyXM+FYXxalIpfHH0zcZqOdd955oZ/v/arm2JCtFxVTp07tmsvzu0gHG8jdmv/GN9mA\niqPa3OPcR/TpiJjwN1AR7H3Pec5zkpQK4joSU6+Rfv2iKZyGhoaGhoFgUnI44s5YlVjorrvumqQ8\nPSkPsXdPW+yr3vcEkxXLV4nj/yahUjri23obeqimGFgOhyozJQEwHHkte4ZQAxirWCwGhK13y1N1\nm0fVDRMRn64rcUwYcI7Yez3niV9g486pnnxsPyWszI6w9bwyFTeUNAZsEgE14fW1n0xE3qJbxzZ2\nX+/ZhIlaOyqn6snbqte8T7e96iZqXz6Uiqj3N3HuY1XoTUYOp18454997GNJSnVZfczyGir+5L3G\nug/Uk7i7oV9bDA0NLRDtqXNncjJ11alc7YEHHpikrHdriS+b2mEigapEOV+TTeRH5QR9Hj+sqxe7\n9SYNDw9n/vz5LYfT0NDQ0LBkYVJ2/FQhoQICi/PUfPvb356ksCv9GJ/4xCeSFJaGeXrae/qqGhHD\nN21YtRI2T9l4n/+Pd7e6RUHdI+RY2MY5YJ4f+MAHkhSVpmNYXb34tc+RA/B7zfacs+/DUMbaH6cf\ndNuPHTtyHfkFlYehUnWOSbWZeWJ1roeCwuLZmF99/OMfT1IqbihrCofNuqmPRZkr1w3d8kPWDHXv\nelkD9Qw+alE/jgoseSp5Toy27inxO9T78yyONdINrs8qq6ySpOxbQ/0B2+rDcb9hq/pa1tPH+Stb\njKVwxoO6KpAPWgP1GjEzT7WYe6doj/4qkwO22267Ue83iV8+ykQC0ztqPxBlAveJevK285g+fXpf\nuwU3hdPQ0NDQMBBMqMLBMLF18WIMRaxe/LmOU5uUDLrwzY/CSOQvDjvssCRl33Z/l0MSl/QEHuT0\naOdMUdRVP1QaFu/c1NFTNI7dpGM44YQTkiQ77LBDkgVzNzVrr+fa9cNK+kW3ChbnxBZ6QjBX/RVU\nndlXcn+qkbAz1YveJ49BBVK22B32x0/Mp6qro1yz+fPnT5jP1LmReqZWPevKWpLfdC7yEpSN2L3p\n0PIb8lU+r2ay1lzd4V7nNyZzWnSvYDMVdSYjsw24Vq6rOXQUS41awfhcVWmTce51Ba/cnDWh9RoS\nLwAAIABJREFUIpPSEbGQ66Xm+bxokFwORSNCcumllyZJjj/++CSlJ8k9VZ69nloNjouygZHVjP1E\nAZrCaWhoaGgYCCZU4WACmKldCuv9UMQD9duM3FshKU91T3vv85RXJ08xYTJyQX/4wx+SFKWFGXWL\n1Y8XI2P83bqjMVg9AaYpHHrooUlKlYjeE0y2PlZ5C+rQbpZ1XX3NUDCoyegt6YbaBlgd5qiakGL5\n7ne/m6RcT/uzUyz1sdsvyfXlDyZNsDE2yGbvfve7k5TcUR27r1XHoqCbr3WzTe1HjqnePZVvm71G\n2VD1pguzBX+w5thQbmcsv1icyqae0ux35y5voTLL60we4E/detD8roel3g9nMs69jnTU+96I6vBZ\neNOb3pSkKFJz49xHRDrsquuexy9EUvi+KIHqN3lOkZd6J9I6B83WDzZhZGFoCqehoaGhYSCYlD4c\nT0dPQRUTGKc9Ojzl9QiI8Ys3e5rrPdFtqzrNxFTKZwKm/E54Hw5mANiAPcR32223JIWVYST1HDix\nVjOz7PEi/4H11XsR9XAeC339eHoMxmKS9cRZFTr11Gb+st9++yUprEzOx0w2CkWljr1CTCJQ2WNG\nm2kNtW0f7Lgnen5YnWMbawIE2/ipN00M39QG5yS3x48wVrmcuu+jngbSw461i70Ph1Km2pzTPvvs\nk6TsJAq1aqx7n1Rm9XvfWJQ1MrKPZeRP6p2CUbXoelIyrrsqNkr2pJNOSlLuD6JLfto51OT9ekL6\nWP7QrZ+v9eE0NDQ0NCxRGMi06DoWq6JCDF6dvKe7LmlVZhitjnFPX0qojiEuwvynSZ80wBbUHJYl\nl2OiAEYjH2GO1IUXXpikqL96L5du3zdW7qa22WQwWcdS5zfqGH3dE8I/5Aad+/rrr5+k9LCIW1M+\ndZVkN/W3sAm4I183may+W1UhqCZz7Powzj///FHHbK2wndeLDtT9H72ukUHaoldYI1i+/Kf7hAov\nOV1qcP/99x/1k3+NNyIyEdM46vXp/3WPmXNwz1OJxwYiJKI+/m86h88RCal3YQb3HTm+XtEUTkND\nQ0PDEoWBKJxuqOdE9RFHXujfe33/g9TXD2yWmmPQIa5OXnXRiSeemKTETDETysjrFuFck0xcDqfH\n1y30u2rUceKa9fm9niyAsdY5mlrhdKsoXBJtQQFjoqIDzl2+FANWpVRPRp+oiQmLU+GYNIHF177N\nFn73k20oZK8zVVyvSr9YlD2juq3Ler8k/6+nqegpo2xNVVHZ6d7q/3W+khJ2762Pq0ad/7LW+t0z\nqimchoaGhoaBYLEqnCUFI9jmwHf87BbLrZnEoDCRlVljsfh6mnRdMQO1Aqk/H7Cw8eatFvb/ia5S\nG+tYYKz9RrrZqP48SqieaDDIvMVEoa74pP5MVzBjTV+e6IGczkRjPAoHuuWdR3z2qL9TLPXvVJtK\nTH089ef2mresMZafNIXT0NDQ0LBE4t9K4XRjAROICVc4g9gxcTIwHiZbx5977Qnq1pMy4lgW+nqo\nWXy3z+31+0f+fVEVzmT77HiZab+fvyRVqfUKfTr1BOSJwkRUqXXzj267JtczEbuh7vOpP99PSkll\nZ6/HN16/aAqnoaGhoWEg6Ffh3Jjk2sk7nMWORwwPD6/Uywv/w23Rsx2SZouRaLYoaLYoaLZ4AH09\ncBoaGhr+H3tnHm/bXP//p3MvXZEkGUJEiMwUMmSWWSpTVCKzBmTWYJ5DITORIZIhMoQoEclUoZAK\nkSGKSt/r3t8fet7P2e9z1tl77bP3Ppvf+/XPfuy91/hZn7XW6/UeE4l2kSa1RCKRSPQE+cJJJBKJ\nRE+QL5xEIpFI9AT5wkkkEolET5AvnEQikUj0BPnCSSQSiURPkC+cRCKRSPQE+cJJJBKJRE+QL5xE\nIpFI9ATjmy9S0KmmY80Kz3UbIxR1fK5GaZvJgwvb1S0QOVbtByJ62XTsjYoci4Ici4L/H8ciPrfe\n9ra38Z///If//ve/LY1FrRcOVFenhfLQqnqxxK5yI1QeHXb7cb0JEyYApRuiXez8HrvXxf27X7so\nvvTSS7VqHY30kqnq3eI6sT+Jxx57wniOduaLFZnt5Df99NMDpSNgrNjsdoT7if0wBgYGmvaRGSuM\ntvqzqOqqGMciyz51B632KxKxA6zwOvlZ1T2zVYI744wzAvDiiy+2tHwnULeidafugbpzPHbVFS+/\n/HKt+yRNaolEIpHoCWr3w5lqqqkqGUcVo4hKJiqRTqGqB0SzrnauN3HixNr9cKr6R1Sxr3hsVWM5\nWtRlkaKXXS4H7xM6ryjsCGmf93aPp5tjUTV/qnoA1WWkzbZbF90cC+es8Hkiq44WjmZdLOPzwN9n\nmmkmoDx/7AXTDP3QG2jWWWcF4G9/+1vDsfj7M88807D8zDPPDMDzzz/fsHyV9UdLiJ8vvfRSw3oR\n73znO3nxxReZOHFi9sNJJBKJRP+gtsIZGBgYwjCq+mNHdt8r23jV/ltg/bUUjmpgpGMQVb3l43Ld\nCqiIY1/F/kQn2Vur171qHlWtN8888wDw5z//ueH3xRdfHIB77rln2PXqBmz0gslOO+20QPHVDfap\nwdA5e/DBBwNw5plnAnDssccCcNFFFwFw6623AoWhdsqa0It5YRfKeMyLLrooAL/5zW+AMib6L199\n9VUAFlxwwYblZOtaEaLPznuhygoxgrWia/OiSsn4HPHTefOPf/wDKGOx5ZZbAnD22WcDsNRSSwHw\nxz/+sWG7Sy+9NAB33303AB/+8IcB+PnPf96wXzHNNNM07F91mB0/E4lEItFXqK1wxo8fX9mrXgYw\nyCfS3kEF5iNDcbux/3aVj6aqL7ffZVJu/7nnnqulcIZTe1X7ale5vOc97wEKi49jU+U3a1VlRrv4\nbLPNxnPPPddymOP/tlmLvcmSjJQTsb96VCLao2MUkec0wwwzAEX5vPDCC0AZu8hom83PGWeckX/+\n858t26f/dywjjoX7nn/++QF4+OGHgaG2eFm6SmXvvfcGipJx+ZVWWgmARRZZBIA99tgDgHPPPReA\nL3/5ywC8/e1vb/UURkQ7rL5d/5Nj5XyJEZ4qnvvuu6/hf+fBpz71KQAuuOACoPj0nn32WQDe//73\nA+Ueu+qqqxr26/zwu77nuqweYGBgYPKECROmKNgYYVul7kXV/b7GGmsAZb5svPHGAKyzzjpAGSvv\nNe8px+biiy8Ghipsz9n1Z5llFqCM3WDFNXHixFQ4iUQikegvtKVwfDu//PLL/g5U59dU2UYjXP9L\nX/oSAI899hgAjz76KFDeujLW2WabDYAzzjgDKG91o1CefPLJhu3KJkZgXLWj1GRNjkVkIo6V+zRP\n5p3vfCdQokeEtlHZvMt7TrI9bbEur/3anKKYmyRziUrI7aoGuhmlVqW6mkXqVc2rk046CYCvf/3r\nACyxxBJAUQWyNnMcYv5N9KdV+Ut6EZkVFc/ss88OFFu7Y7X99tsDcMIJJwBFwRxxxBFAuf5HHnkk\nAA899BAAd955Z8N3bf3O21bRzbFQcTzyyCNAOWfZu2PhPLn88ssB2GmnnYASoeWc957wOaHy2Wqr\nrQD4yle+AhTV+I1vfAMoqkFl1Mnk6BhNVmWhiGpfbLLJJkDxzTz99NMA7LrrrgD8/ve/B8oYnnXW\nWQB87nOfA+BPf/pTw3JrrrkmAEsuuSQAV155JVDmo8+bqHy8R+o+L1LhJBKJRKInqK1wwnegfg6B\nrNq3pjZ3o4s+/vGPA8Xu7Po/+MEPgMLSllnmdTFihMZcc80FFJvuT37yE6AwG5mudkzXG8Ssayuc\nqnOUucgQ3Ief0e/gmHzzm98ECks/5JBDANh3330BOP/884HCTPRnuJ9f/vKXAHzgAx8ASqSO5x7Z\nvIzriSeeABjsn+sak5WFq96q7NVV6zlvtt56a6Ccg2Nw+umnA8XeHO3REc3yOzoxFs1UXPzfY5Kt\nzznnnEBR+7LytdZaC4CFF14YgE984hMA/OUvfwGKwvaecM63GynaDR9O/H+77bYD4JxzzmlYTgVk\nJN6mm24KlDEyMsvoxNtuuw0okVeqgT333BMofq8bbrgBgBVWWAEo947zyXnTCeXbzOdaNUZWJIhW\nJZWq98QHP/hBoEQxfuhDHwLgd7/7HQALLLAAAOuuuy5Q/Fbvfve7gaGK6qtf/SoAhx9+OFB9D6XC\nSSQSiURfoa1KA61G+WiH9K0oE1lttdWAws5kDp///Ocbtuvb1vVkIrK05ZZbDij2blnib3/7WwCW\nXXbZhv+16ceIr0EMuG2F0wwegwzlox/9KABXXHEFABtttBFQFM/+++8PlHOX2cp0VHP33ntvw3dt\n9SuvvDIAc889N1AYsn4tr4ksTgyq5db13JNWa125nLb43XbbDYCdd94ZKIpVP4ZqTrXnd+3adSMH\nuzEWw9nCAX784x8D5foceOCBQFGgqnyZqX4Hz8VzXXvttYEy1/Xpvetdr9emVfk8/vjjrZ4a0N08\nnKh0VTSe04orrgjAeuutBxTFe8oppwBw++23A7D88ssD5fp7L3iv6AfTr/GRj3wEKNFqPkdUhT6H\nYl5QJ8bCOa36EvHe8JicL5/+9KcblncMvM+97/UVX3LJJQDsuOOOQPHR7LLLLgBsscUWAGy44YZA\nedaaj+NzIvqc04eTSCQSib5EW5UGIjOULRkVEhmkykJFIyOVvWurjW9zWZ0szrex0SpWd51vvvmA\nwhq1a95xxx1AiWZx+/pBfFsPYpstK5xx48ZNnnbaaaf4IYSsS1YU1eA111wDFDUnY/nkJz8JlMzf\nzTbbDCjM50c/+hEA1113XcM5eQ5ux7H5whe+ABQ/yf333w+UePq//vWvALzvfe8D4A9/+APQnTpR\n0c7sdYix/VXVfvVv3XXXXUBh6c6fGKmnCtD/pbLx3KKfxP3qMzQ7X3RD4URm6z3jsep/UNl6vf1f\npRyrfrs9/RF+Vw2q/o3oPOaYY4Ayb5qhzliMHz9+8tve9rba1Ze9Lvql9NVqGTnggAOAEln5mc98\nBigRWVHFOT+MetUv4ViYu+I1UV2qgJy3RpaZq/Z///d/tebFYAVXFRE5zHoNywufqUadGWWmhWOh\nhRYCil/Lc3WOa1nRCmWkp8rpO9/5DlCevR7He9/7XqAo47o+31Q4iUQikegJavfDmTRp0pB8Cpll\nVfVW/Q7XX389UJip0SZVVacvu+wyoLA1s2NlOEa3aaeU7cn6VU6+1WWJ+oAGn1NdTJo0iVdeeWWI\nHygqHvN0XE77s1EhVjI2YkZfzK9+9SsA5p13XgB++tOfAiVHyTGQmcTqCUahmEnsOcZ4+sj+u4GY\neyTjjbkIEbI4FY6M1eWjXduxdH/Oqxg5WFVjLyqbbkLl4THpb1C1q+Y9N9m9x+i5xSx8o5BUMNrg\nrUAQKw7o1zDnpJN47bXXaqkbLR/6O72PvZ7bbrstUHw7Tz31FFDmtH4rx1RrgEra6/6LX/wCKNFr\nt9xyCwDHH388UPwf7j/2kor+llYx+B5zm/F5UbVO9PWZp+d29GtqTdAXowLyOsfK266vb2exxRYD\nyvPJ/ZuzpCIeXBEh++EkEolEou/QkY6f8Q0nQ/B3WZkRFPpctDOaKzLHHHMA5a174403AvDcc88B\nJeLm+9//PlBYnPvRb6LvR7vm1Vdf3XAcUVGNht1Hv0CE+zQeXj+ENnNZvz4bfTVmnGunVvFok33w\nwQeBoaxdf4h+qsjOPJ5YIbebcIwiY4zVe4XnZCSN6k+25nfPRVZnroCq0moMMVs6Xm/ZY7d6Ew2G\n56afwUoBnpNMUx+NrP/aa68FSk0182y81/T1eOxmjKuEzzvvPKBEP5rDYs5JNxHzWapqlXkdnPMe\nmypNi4aRnCqa7373u0AZU+8BWbrzRpXo/95Le+21FwBf+9rXGo7La6Hy6QR8xhktGuEcFB7Lcccd\nB8DRRx8NlEg7/eI+N4zUMx/L54pz3zHyWenvP/zhD4HyXPrZz34GlOeW+x0mR63ZKTcgFU4ikUgk\neoLaCgcKQ429O3zbGcHg79rgfavKNLRfare+6aabgGLb1/djxI62XePs9VfIkGWPbs9eIUZoiZjp\n3g3/RfQTqGxidIosXh+NttZLL720YXv6fqoirPRfOLZC9Rghc45j0U04zs16szh2RtDdfPPNQIng\ns7ZW7OgpezML3zGOyiZGVUY7eTcRu07ut99+QFEizm3h9XZ5la0KR7/kNttsAwydy/o1DzrooIbv\nJ598MlCiJmXe+kU6eU/EquCeU6xQrBLyulhRxOWd2/p2tZjol7JCiVYD/VKem9n2jrXqwPpkqkgV\nl/Xq2u0cOxyqlI3wXH22eS9YHeFjH/sYUM7Je8PaaM4fx9L5scMOOwBDoxE9Z58T+ret3uG5G/X6\n7W9/G2j/XkmFk0gkEomeoC2FIwOJTLEqc1xmIGO11pUZwCobo0msA+T2ZUgyly9+8YtAsQnr4zFL\n24gco+GEbCFWyB1NJ9IRKsk2fI9RJrI7bfeOhfHx2peNh5epaJtVmcScJW2tZqhXHWeVyqgbdVK1\njcH7imhWU8toRKOMtEPb40UWZoXc733ve0CZP2amV+0nVg1vdlydhP5LfS6ydfOwtMF7LKp8/Roq\nHe85a+9FX52+IXORVERuT2uD2zOarNNdeQfPp1ihOj43hJFSHrMKyFwSz8FcMrdvLpnzxtqM3iMu\np3/Te8/niJUFPB7v0U4om2aIvZ+c20cddRRQqn/rt/T5oBozmvXCCy8EinLxOkefjdByYs6RFheV\nks+bz372s8BQi8jMM89cKxIxFU4ikUgkeoK2qkVX9QCPUT6+tf3dHAGjRzbYYAOgRGT59jY6RT+G\nnf2MGpGZuF/toieeeCJQFFTMwhYjVLOu3fEzRtg0i/rS9iqTMZs6di+UvRmpZ9UEGYnsyzFTJe6z\nzz5AidDyWsgKY9XoEVRI29n17XZ4FLJ1o5FkZ+YUWftK1q+Pzsgdx67qWmgfr4pai+hEpYE4Jqox\nKyPLyvVbRJ+a62uLNw9DG75Z9LJNf7eXvfdgrNCt3yNGJelTjKg7FoMVTsxZ87tzVHbt/ewxex87\nL7RcaOkwSk0fr748a6PF2nrWZHOsHCP9E0bDWp3Bvkti3LhxvPbaa7XHwvWg3L+em79HK5F+J5+l\nZvr7vzlEnpPVolVlWjqMblRBO5ZajbyXfD45th6XtdpG+7xIhZNIJBKJnqC2wpGdwND8Bb9r54u9\nG8yil0UZjWb9HpmJkTNGkXiMvr3djz4b8y9cToYrmp1jO7XUVDhV3U0HLTfsMcR+NDJe1Z+2dSNz\nrLYga3MM/DSCS2VT1QOmVfXRCVbfajVoEeeROSZG3NiJ0Wxn59fmm28OlDwNa2p1Ct0YC79b8Vzm\n6b2jujNqzLHxf/1Y5mfI3lWB+kfMqjdyU/+I29GKYKa6voFDDz3Uc284j06MRVWlbMdEBSqspabf\ny0grq27I0h0z7xH9GG7XGnvuV6uBVgbHTEuKyqZKfXSyxp7bNsLXfVjxPj7TVKoqJevJGcFpVJkW\nE58j9ghze0a9qaCMVnOe+FzSTx59OE888QTrrrsu9913XyqcRCKRSPQP2qqlFllPzA2RecrKfEvK\nRGLFZPtzmyugb0fWJ9syCkVba8wZsMZRzDGJPe0j4243pnzwdlqNyIrdJfXBmIWvynOsZO0qFRmN\nY6E/S1Yok9UmK3uMWdh11Uc7GFxvCZqrqpjhL4v3nDxHM89XXXVVoEQjmTcxWnRjbNyWilZGqg9n\nlVVWAYof4u677waKutMHZ+6J11P/g/XFrK6hf0qmahTjAw88ABTfgepQdq9S6kXEnvA+VWk4BlbX\niBWuvV9V/SpfoX/CSsfC9axwYkSnY6XvWIWsYnIejiZP6y1veQtzzjnnFJUWofXHZ6CKQv929L3p\nxzIHScVi1QTvGSN29fnps/Pe0WdoPpjzxehGo2Sdr9G36HxsFalwEolEItETtFVLLTLAGGXkd6NO\nfIuqQGQO/m4khtnPKhSjRGRnZr0aXaK9UZtwrICgshFV/pVWe1MMhxh5EyP3hIwk5oDEag3a3PVv\nmbtgBJbHaI6CKtIxcexijTXt3s26XXYiDyci5lnEcY4KKOZfWTNLm32M5FLhuF7sy161n6rr303V\n53U1qszoH/f9rW99Cyj+S6+/ylSfj/UEraC80047AcUXY36PnWWdfyuttBJQ8oGcj0ZmuVyn83EG\nw22rWFRza665JlDysMwxcu5q0VC9awXwenn9Zfmrr746UCpPqBK9BloHfB75u2rP7Q43X+uOy6uv\nvsrjjz8+peeOCsZtW+/N+9/cs5hLKFQ0Kmbz+HwmOhbOJ33C5tfYATRWgRBGu7p9ox71KdXtmitS\n4SQSiUSiJ2jLhxP9ELH6q/8bMRW7xclYZFUyDO3H9nixhprRaVZzNUfA7chImiGyNj/1DdTNKB4c\nV1+1bREz+wdH+0GxyWsv9tyM4NMm67lutNFGwFA2H/tdRHbmcWknj9Ev0047bdNaZ80QFW8z5Rj7\n1cTcBG3u99xzD1BYu2NljsFwlcyH2088zl5UzBba1FVpXl+ZrL3kvc5GEVkXTFu/LF+rgctrDdBG\nb20+M9Hdj32QXF/mbWX1biocr7OsWdZtBQBVu/eIvhxZ/7777guUfldGvTpv9e3or3A7novPHfen\nH1VVGa9BRLtWgMH3QfRXOt6egwojKiKfCyoWLSRaPOxm6qfwXvEeisfv8ub9aZ3y3nCMxWArQfbD\nSSQSiUTfoa1KAyP8DwyNxDIKxQgaI3KOOOIIoLB33+radM0glmn49pUlGvER/SbRZzCSv2LwekCt\nPJw6+6rqteL6RiMJ1aFRaY6hUStGJ1XZYLX9q4BUl263SomJblYaiP1RqnwqsnH9HdrsHUtZm71d\nZKatKpZe5iQJo4q8LuaCWB3DmlkqD9m5Kk/Vv8QSSwDFZ+f6W221FVBYvPeSUZD6weyPo78kjkXV\nfG1nLOIcl8X7PHCfPgfMRdG3a9SrFZGNetUn41zXQqF6dzlVvH4NrQNGw1oBxbFRFXpvDadGJk+e\n3NZYxJppjrvX13M2x9Bnnv4oI/L0rein3nrrrQG48847gXKvxHngmHmPeJ2tdGLFC/1e5jKpyKuQ\nlQYSiUQi0VdoS+FUsR/fujIN7Y9GxhhJZTSKce9G1MhEzJbVNm83O/tqux2Vj6wx5p40Y/HDoJbC\nGewzqFs3zPwHo42MGjrssMOA4s+yiqs1jlSBRvRFxOq/MXKvGYMddD612NvAwEDbvhCvn7Z0v5tv\nYw6BDFjGbOSWuUrd6mszGoUTe8ebg/brX/8agKuuuqrhd8cwRl55TjJjWb3wdxWSqs970LGLvsOo\nOppdw3bGIvrWPIbotzQK1ZwiLSGyd/1XqkMVret77EZ0Rh+zKsKIMH1ARvqpuFQZjrn+k4hOKl/P\nXWWjj00fn9fH+aClw+ry3t+ek9FqKhujGx0jr/utt94KlHN2zFU8WlicX7FyiUiFk0gkEom+Qm2F\nM1JUQqxAq/3R6A/74WhjtUaS3TCNVrMisuxQVm/lAWEGcqzNVBU9J6ryiOpWi25xuYZj8rufMop1\n110XKL3FrabgMWqL3WKLLYCi7mKklXHyjqWVlFV/rdZW6yR7q7EdoPgnVMCqOa+n18+q0WbPywJH\nqAbe1nF1Yixi1Q0jr6xtpeo3O151b10wrQDeW1E16G8wJ0nbu+pP271jZJWPWC+sGUZTLVo4Fs5Z\nfSeqMP2MKlwjq5zD5l85lqoAI+wG7R8oFhP9J/aM2XDDDQG46KKLgBLZF+dRlerrZBVx1Z6+u1hX\n0GOyzptqzwg/fSzmEql0XT8qWxWP1igj+7QmGQloTTYx3LOzjj8rFU4ikUgkeoLaeTiTJ08eoihk\nDtoXZekqG6NBVDhWRDbiRjuziifaC2U25hLYA0J/hYwnKpwq/0S0j7eax9MOotoS2kiFdaT02ejH\nML7eczRaTWbksVuTy3yNyNKqjiMy23Z9MaPx4YjIfM0NiNWD9d3YNyV2MYyoqmcXKzd3Mx/HuWge\nhR0+rdulWtN/ceWVVwKlz4nsW3hO+ur0W3guRiU6n4z49DjMNI9jIDo1FsOpSo/BuWiF61gJ20rW\np556KlCsAZtssglQ/BU+RyJUyA8++CBQxkoLit0sVY8xulYFJOsfzOpH6yeMPZl8FjkmKlbve5WP\ntc2sYeY5qXz0U0W4H302119/PVDqD9pPSz+6qjNaB3xWx26rrSIVTiKRSCR6gtoKB4ayH5WIzEWm\n6ltVu6KRWEaJWEFARiN8e8pcVEpWGJANGtHhfqtqpVXlGKgCIrPpBOI+VYEeo7Z4cwxktpHly3TM\nstb/JcMxZ0GmE8/JaCb/j31yYn+LdpntcGNX13cia/T6ei6Ogb09ZKaOnRE3VTlJQvYn4xV1q1qP\nBs5Va2Z5TFoBvDe8J/S9eN3OPfdcoKgCa6epBpxnnkNVbyAjR12vm+ou+pucm1o6rI7gclYu9jlg\nnThrn+2yyy4ArL/++kB17Tz9mPoh9JuZu+IY6sdwPglzUmLkYLuYaqqpplwf50GsfuD/5qA5Vj4X\nVG37778/UKId7YuksnUMtQKoCo1+c341q3If/1dptXuPpMJJJBKJRE9QO0ptYGBgSmx2ZBb+HpWO\nEROyLSMr7Edx2mmnASXe3qgjo9BkJtY+isfcqj01KpkYOdZOlJo2TVVcrHZQlfeisjCCxogc/3cs\nZX/amc04Vh06JiqgGJmnwlHBxLGL/jjRyQic2AG2Ch6L9mTt3B67Cldmak+g6BOInWijLy9me3c6\nJ6nF5dw2UKLRZLrmHlmJwMg9fXbOg1hdoep+rvJTNetIG5cfTR5OvDfctipOBWPVBKPP9HfKyo1+\n9R6JfbHMsle56N/w+WN9OnOgnGduJ6KTVRdaWM5tA+UctRb53Srju+++O1AsGD4HrETYZaqFAAAg\nAElEQVSi705VH/3cNY6/4bPdeZEKJ5FIJBI9QVt5OFW9X3z7yQiMFZdRapO3X4XbcT3rOxnBY601\n1zMTvVk/FdEsGmmYt3YthTNu3Ljh3vQN24zZ8dqP9WdpwzcXwHON7N36TzIZq7lGf0SrMComVoYe\nTZ2oGssDQ9Wf88SIKyP0jEqzdp7M1c8qldZsv81+F73ISWphbraz2SGIPsK62+2k8q3Kz4mfQr+T\nOUaDjmnY/cd50ey5VfW9Cp0Yi3gfNpvLzSIqYy+pVq9vVP0+t3zeVMGK+alwEolEItFXaKuWWlXM\nfqwC7FtTpmKtIrNi3bcs37o/1mTTnj3aqKEqG7K2Yyvp0kYttaq6bTFyyryaWIFW/4ZRSjILo0ns\nGaLtvsoOHhGvUbQJuz2ZlHZvx6KTrL5ZtQXhsZlTZM6AdaNivk1USKLKF1OFsfDhDFrefYx4LJ2K\noBuhykZL63djLPSh6BOu62/qFJop4OhT7ERFddGqump3DFROPpfivVRl8ahCnKepcBKJRCLRV2jL\nhxPRzBYafTWyahmtisaKAr5lI6sfdBxANVuLzKhGJnnHaqk1y9yuisdXaTgW+mrMt4m5JvF6NKuU\n3aq/o5esvlVG2y6764daahGtzsl47NYPs2JBXbQ6FlW5TZ0YC+e+c9CxiM8Hx6bVOVsX/TgvIqwS\nbz5NM0RfTKtodT7qlzd6dtBzJhVOIpFIJPoHbflwqhhHtOvFXJQqVu9ybi/a+CPbqsqjEVXnFH1M\nwyxfS+EMVjF17c2R1bl+zHFyOZmOzMLf49h5DVplOHH/3YhS67QyacbGOm3rb2cselGfbSzQCb+F\n18UcsZifVdefIFqtkdfqcTSzUtQdi+EqZ7f67BpmeyMuH//feOONAbj88stbPeQG6IM2F8qq5HZH\nTYWTSCQSib5CXYXzLPCn7h3OmGPuyZMnv6uVBd/kY9HyOECOxWDkWBTkWBTkWLyOWi+cRCKRSCTa\nRZrUEolEItET5AsnkUgkEj1BvnASiUQi0RPkCyeRSCQSPUG+cBKJRCLRE+QLJ5FIJBI9Qb5wEolE\nItET5AsnkUgkEj1BvnASiUQi0ROMb75IQbsltt9AeK5GaZs39Vj0ovT6GwVjORb9VgS0H+ZFs4Z5\nvUI/jIWFlJ0nddsSRLQ731odi1ovnP8P8GatdZToE9StZG1H2H/+859A/zxsxwI+XGeaaSYAnnvu\nOWD0L+NudxLtJmaYYQagVJl/6qmnRrU9t2NXU9GpMapVS21gYGDy1FNPPaQpU6/QbnvcGg2cOtaA\nrdfoh5L8vUa7zabq4o0wFr16aPZyLMZK3bU6lp0cC4mEz6huXcdvf/vbAOy2227D7qfdeZTtCRKJ\nRCLRV2irAdtooWz797//3db6kfnYlvn5559vaf0Rmh71XOHstNNOAJxyyinD/v/II48AsMACCwC9\nY3tvBFbfK/TjWIyVGWgsxqLfTF6dbFIYTaQ2g3v11VeB7qv3TiEVTiKRSCT6Cj1ROM18KP6/2Wab\nAXDBBRcM+7/s/v3vfz8Af/vb3wC49tprAVh++eWB0kraNs010DWF04ylRaaz9tprA3DdddfV2c2o\nMTAwwKRJk7rKZLfccktg6HUe7ligtBZXGTuPVl99dQBuuOGGOruvjU60Eq7CGy0IoJvzot8i8pqh\nzljMNNNMk9daay0uvvjiEZdrt+X0WCMVTiKRSCT6CmPiw1GhbLjhhkBhNGeccQYA8803H1CYrMvt\nsMMOAPz5z38G4NlnnwXgS1/6ElBCAmXEdaPZGAMfzlvf+lagqLEqNTjXXHMB8MQTTwBvrmgksfHG\nGwNw5ZVXAvDiiy8CsOeeewJw+umnA8WufdFFFwGw1VZbdWL3lUgfTkE/jkUVuq2Y3khjoZJ+73vf\nC8B//vMfALbeemsAzj33XACefPLJhvX2339/AA499FAANt98c6DceyIVTiKRSCT6CqNSOLPMMgtQ\nfCnNoG/Ffcritc3rg/nRj34ElMQul7/88ssB+NOfXs/P/MMf/gDAT3/6U6CoBCM9/vGPfzTsJyK+\nvRmFwrnzzjsB+NCHPtTK6lPQqn/L+PlddtkFaJ21mTgYE7kiImMeDXurkffUAOfHxz/+cQAuueQS\nYKhiNYLn7W9/OwDzzz8/AA8++GA8LqCcU91oRjGasZhxxhmBotbeaIjzZyzmRauQxTuPZPGD5nRH\ntq+/bTRj0Wkf7YQJE4Byztdccw0AH/nIR4By7H767DvppJMAWHXVVYFiXWgGn7VaaFLhJBKJRKKv\n0FMfztve9jaglOnwrSy0zc8666wAfOITnwCKApEh+Zb+1re+BRTGu99++wFwzjnnAPDXv/4VgJ//\n/OcA/PjHPwZGVAc99+FEpvP3v/8dgJlnnhlgSlTLKqusAhRVueiiiwJw3333Dbvd0bLJXtinP/Wp\nTwHwve99D4Cll14agHvvvReAOeecE4Alllii4XcVbpVikZXPMcccAPz+979v5/CmoBdjUVUTS7Ye\n/ZFjlZ/RT34Lx8rnwVve8hageu6r0qru/7p+sX4YC58HK664IgCXXnrpiMs7BlqFHAufte3Oq1Q4\niUQikegr9KR4p8zh5ZdfbviuvVGGsv322wOF7W+00UbAUN+Pn3vvvTdQmI32RBnztttuCxRl43pu\nrxc14WRh7lM1Zh2wu+66Cyhq7eCDDwbKub/rXa8Xrz7qqKOAonyeeeaZYfenz+DMM88Eij+kH/HQ\nQw8BhZHefffdDf+rZPyM0C8Sx1iFM1plMxpUseX4u9dZNn711VcDJVLTczziiCOAoTWwtBosueSS\nANx///0Nvxt15FxvNXJLX6S+ydGgrtquGju3I77yla8AZc6vv/76QPGxfOELX2jYr/PL7eg7ViG7\nv7j/fqt0ALDyyisDZQw89wiP2ettdZeTTz4ZKFFnWpvqKpw6OWeQCieRSCQSPUJHfDijjXd3/R/8\n4AdAsUdahlyW9u53vxuAbbbZBhiaqS4TcX2jnIx6+9znPgeMyDpH7cNpNhYyWqNB/vjHPwKw0EIL\nASVHSaZqBNbTTz8NwBZbbAE0r70mU3G7ddEJ+7RRgpZQ7zRUiX56XR9++GGg+O6sbNAuOjEWV1xx\nBVCuv9dZFeZ8WWSRRYCSY+Y9YI7ZD3/4Q6D4v/baay+g3BNaDa6//noAjj322IbtLb744kCpzjHo\nHFs6v06MhQrUSKdmykILiGNhFOrvfvc7oESzqli0dOivOOSQQwD4xS9+AcDjjz/ecDxG2XrvtqrE\nOjEWa6yxBgA/+clPWtqOY6Ffe/fdd2/43bEzp1GFvOCCCwLluaHVQHXXaqSxiBHK6cNJJBKJRF+h\nIz6c0WbyalP95S9/CcBKK60EFMahjdZKAzHazLe6TFdVsNZaawHVPgDRSdtsHAtt7ioaWZjnEJXN\nPffc07C+fg5RpWze8Y53ACXCTxbZbu5JJ9AtZSNkd/q5VLLmGMw999xd3X8dqGyc66p2Wfw888wD\nFHbt3F9vvfWAMo/MPZKl33HHHUBRkw888AAAH/jAB4CSZ/HYY48BsNxyyzV8vvDCCx06w9ah8pCV\ne89E32r8f9dddwVg3XXXbdielg/Vneree0y/xWKLLQaU54MVS7w3HPsqn003Khe0qmy8Xuussw4A\ne+yxR8MxCX3Ezg+3/5e//AUofnSvgb4bVaP/N4PKJn04iUQikehL9EWLafMtvvrVrwJDqwL7Vr/t\nttuGXV9G4qe+nU022QQoUWyywYjR9ucZCUafqdrMq7n99tuBwsqisqkLVaBjKLsbC2XTLcjePvvZ\nzwLFNm+Vcdncd77zHaCogrFE7ErqnDYXzVwhfXRLLbUUUOayPjkVissZXeQ5WznbqEfHyBp8RjWq\nkFVEraIukx0Os802G1DOIVbIVtnIur0fVTp+V6HI0l1P1u2YeK76frQi6N+affbZGz5VAVXopLJp\nVS2piH/7298CcOuttzb8Lry+3hNWJnE/G2ywAVCi2YwI1t8lWlU4ou6cSIWTSCQSiZ5gTKpFC3MF\njjnmGKBULlWR+L/HWKVAVCj6DL72ta8BJUZdJiTbG4HJdLzSgOxMxnrjjTcCpQ6cuULtwu3KpDfd\ndFMAzjrrLADe9773AcVe3Sr6IYu6Cl//+teBcn3Nml5zzTWB4gvoFDo5FjJO57RM1Tnvp2ruN7/5\nDQD77LMPUKLajFpzOaOQnG+yfCtRaNNXaXsv1GXt3ZwXkbUL7+8LL7wQKBUn9Onqz3Ae6C8zF83t\nyuadJ46hFUn0l7bak6YX94i+FX1+fnceGXlnpJ4V1/Vr+uwzqtHngupSH7LPh2Y1F4U+4ldffZWJ\nEydmlFoikUgk+gtj4sORQVgjSxu8tlvt2818Kr5lZWna7L/73e8CJc7fbHvzfHoBe7io3rQ7649q\nl4V/+MMfBgqzkX1p2zWa5fzzzwcK4xWnnnoqUNjhGwmOpdFpzqPVVlsNKHk3skH9I1WQ5cUx6ibM\nCfL6DKo8DBR/hErHXDJZuD4/FYps3zp0n//85xu2Y8UAo928t6KyiX2ZegF7s9jjST9XVBiOkRF1\n+mZVND439D84Zm5P/6ZVPFREPl9iZKDoZedRKwfos/M6GJWogtEXc8sttwDleaBVx3P3epvnp+/Y\n383HsoJFq1VXHKOYQ9UqUuEkEolEoieo7cPpRLSKzMRs1chctLkaYSXDMdpE9qdKMIfBng4HHXQQ\nUGy/sroWajp1zIcTK2PPO++8QIk2irH+Vb3tPWaXM9fEXAQZxwILLAAUVvZGqJBcF7I47c76q8w1\nkbk2Y2uyxpdeeqml/Y7FWJx44okAfPKTnwSKQlbhRFau7X677bYDip/C5VTE9lMyS78uOjkWze5H\n7xHVl+xcdu/vXke343PFSDz9mFpUrLUoYq+ibvhwxo8fP3mGGWaYUg2+VWjF8dyMsFt22WXdLjA0\n6i1+V/V7jxjVpmUkPp+aId5D6cNJJBKJRF+htvG6FXUT2bv2ZaPIZFe+nc2Gt9KAbM63ur0arKRr\nxrBs3+1bMVdfzcc+9jGgfo2kTkBmIQOQEWy44YYAXHXVVcDQ7GrPXaVjXobrWSPJaq9WxP3iF7/Y\n8PubCbEHjBUktF/Lylq1Q7eqbLqJeI84R/00qij2hvIeiDkq5t04NpGlW1OtXWXTDdSoWQaUOnJV\nvl59NVpArO7hmOkzOv3004GhPpu4v07itddeG1HdxOeA1y9GjR1++OEAfP/73wdKjb6PfvSjQIli\n8/mjlejAAw8E4Bvf+AZQohqNbm1V2Yh276FUOIlEIpHoCboSnhMZgnWdjj/+eKBEOPh2NbLCt6y/\nm29x9NFHA6WfheubTWtWvTkG73nPexqOw0/rjdW1o7YDmYnKJkZ3WPPqgx/8YMN65gipzqxIcNFF\nFwEl6kiGYpTJDTfc0LDdNxMcu8suuwwodmgrZ6vuWkU/9jeRkcrerWzuuWu7128huzfXRJ+e52bW\n/c033wwMZbCqgei/6Cd4ffRb+T1mw/u7kV728Il+hssvvxwo/k6z96v8p72A1yuq86q56bNuxx13\nBOCmm24CyhjptzJa8ZprrgFKxRPHRMT6cXWx7bbbTlFZrSAVTiKRSCR6gq5UGtAeaWSMb2+7Vp53\n3nlAscnam8N+3Nrq9fkcd9xxQGG0sjVrIMkOZbraN2M16RbOtWNRajECRya57777AsUXE3MP4jHa\n78T4e3v9CM/RsVEtjrZbYT9GqS288MJAOWeZbKtVqWX1jqXzsFnUWi/Hwut12mmnAYWpRji/jDo7\n4YQTgDKftOWrhGXA5nm4n36qNFA1V7V4+FyJfo3oizEPz2hYq8VrIfGeVA20q3TrjMVb3/rWyQsu\nuOCUvKl270sj7KzKUvf66dPR2uNYWon73HPPbWk7RhZPNdVUrLrqqtxzzz0ZpZZIJBKJ/kFHFY5R\nICqMc845B4DDDjsMKG9X+1dYy8gY8GH2BxQfjjkGMlrrSFkV1rwb83DMzhZmnhuTPgw6pnAcVyNm\nZFV+aluNvT0iZp55ZqB0bIzZ8bJy2Xun0EtWb6SdPjmhTV6lLEt3XsjiW63/1C7GUu1VVTJ3Xlh5\n2bHRd2PuiQw4VlRvN4u+k2NRl+VXLe+9YMVs2buRflamcKycLzUsH8Oik2NhjmGz/kSjvY4++3yG\nqh71DXZ7XqTCSSQSiURP0FGFY1asMeFnn302UN6q/m9OgPWkfKt7LObl7LzzzkDJMPd/Wb42XaPO\nfFtrk6+KvKhiSBMnTqylcFqpuuD/Mgqji1qFXSutiVR1TkbeWIV6tOgFq4/Z0F5Xf9fmrnJ2/hjJ\nZSXlRRdddMT9NKvy0AxjoXCaRU5pJTCq0XNyvjTr7dIuujEWVRFzzoN4vaJq05f74IMPAnDkkUcC\n5fmiZcXnQrR81FU448ePr1Uh+X/H2tJOnNsq1giViP+3qkgcS+eTY2c0pD4h6xJWIc7LV199leWX\nX5677747FU4ikUgk+gcdzcPRzmxctvW8jC4yWiTWMjrggAOAkgG80047ASXCxmrPRrX5tjb6zbpC\nVlQVkRlFJmOkT7vx960wI4/V+k/6JVqFfi59PzIacxGsI1albPRvOab9ALPnjajyusvullnmdZFp\nDlKE1YXvv//+Effj9Y11oz7ykY+0fey9QtWcdD7ZJdfoNKMXR/BPNmAsc5GiStcPGSM7Xc7v/q8l\nw+eDuWxWUTDa1XtEX68+nNGecyfzdby/9S83q5ZhHl+V+quCeX1aBRZZZBGg3BNao5ohnrs+6laR\nCieRSCQSPUFHFE7M4NfWbv0ebavWvpKhytb9tIOjdkIjdKwjFe2P2nxlSDIa/7e+lF3uIrpRW017\nsmrPWP9HH320re1pq5XR2Iv8Zz/7GQAPP/zwsOutsMIKQFE2v/rVr4CiHnqBqggrFYew0rHX1xp5\nKqDYNdUILaOQRLR/W3HCbpeqy8iY30iQyZovoX/LfJxo03fMPNd4z/VD1QX37XzxPvZ3/RZ2sfR/\nI/GsHm6k13zzzQeULpb9VFEiwh5ezSLmnLv6rbUKNIvwtfup3VJVhyopK/QbCdxtpMJJJBKJRE8w\nqii1ZuxIViXTNHvammfa/yIrUykZVRJrKrldIyzsZtfqcY2AjuXhiBiJVReei1WkY5+buufaat+L\nsYjMir199E/pn7D6rz1iahwfUOahvsRWx66fqi6oUL137GKpL0f/acx16xS6MRbN7hEtI/pgrBbv\nORvFak7bBRdcAJTnhL7AfhqLqDxV3XEuxjmqojWy19qKKhVrKvpMdGy1Mmh90hfkd+eVlpC6yDyc\nRCKRSPQVRuXDqWKGvpVlWeaQyECM+baemIwzVoE2Q9jKqEabGI1SVfW5n2y2o+2L7rnEGljC76pB\n/Vr+bh8dmW/0n/QTHKuHHnoIKJnj7ULfn1FLzjPRT/OkVZhzJLM1h0Xbvn4QK1O0irH05XjdPXbZ\nvj48a+bFHCOrPQtZ/GyzzQaUnlNWX2gVjoW+Q4+jk3AfVRFvsRuyy5mjaFV4r7u+Gf3WsQeYSsbr\nq/9LVCkbt+M885nb7jxJhZNIJBKJnqAr1aIjtFNqdzZCItotY7a0jLSHHTs77sMZLaJtNdrm7XZq\nVn4VYkfBZugnv8VYYyzHQpZt5WMj7vRj7bnnngAsscQSAOywww5A93q7dLOWmtFlWkR8XjgG+vL2\n3ntvoHS3PeSQQ4BiOfFeiZUJWjjehvWaoe5YWKFgOOjXNvpUqPr0Xxuhd8cddwDNKwNoFfIZ6tia\nw9SuslWBqR7Th5NIJBKJvkJXOn5GqEz00VTBt6wsLq7/ZoY+GBnMOuusA5ScFBWK9mtZXzNlI1pV\nNomxhdfZnBMVrp/a3o3EsrKAPaU6pWx64dOJ2465arJyIytj3Tg/F198cWBojcWY/1X3eDqNwduP\nFoeobLQKeQ7mGFmJX5/uKqusApRnpGNmvUpz1Yxui/6ouufs9lU2AwMDtfzUqXASiUQi0RP0xIfz\nBkLf+XDMso7qMDJQ65MZ0WPXQ6s91EX6cAp6WTnb66lPRmZ62223AaUOofXgZL7bbLMNACeeeOKw\n27XLqYx30003becwezIWscOnLN9IKa0A9kOStVuJPY5l1TNutDly7YxF3KffrRdpx966aDeyzjF1\nvViPslWkDyeRSCQSfYWuKJzRMocxxJgrnGZ9UHqFVDgFY9kPx0gtq3Qcc8wxQOkVZa28Ts+Xqr4s\n3aw0UKVIYu6ZVTeskN7NfJmRkPdIQSqcRCKRSPQVeurD6YfKtE0w5gqnX5DsrWAs68o1sxK0ek91\nyuowlvOi354fdceilQ7B7WKsLSOpcBKJRCLRV6ibh/Mc8KemS1WgX5jJCJi7xrKjGos+R51xgByL\nwejIWLSqRFq9pzrkTx3TedFnz4/aYzF58uSu3SNj7PNteSxqmdQSiUQikWgXaVJLJBKJRE+QL5xE\nIpFI9AT5wkkkEolET5AvnEQikUj0BPnCSSQSiURPkC+cRCKRSPQE+cJJJBKJRE+QL5xEIpFI9AT5\nwkkkEolET1CrtM2bvUgjr5efeFcrC77Zx2I0RRqbFVlstQhj3e3EMvZitNU0ulGw0sZqtk0e63YU\nEVXFILOoa0GORUGrY1G3ltqbHW3XOpplllmA0uv7/0dYkdgHv33Z7VPy9re/veH3559/HigPN+t9\n+Vn1QrFXi50gXd++7vaQsZeL+4t9391uPG4fsuPHjx/1iyDuW/zxj38E4B3veAcAf//73xv+b7cy\nst0yY2+Yqu1VHV+/vQATbw6kSS2RSCQSPUFP++EMsz2gr6rAdq0fTlUHRXHjjTcCsMYaawBlTGab\nbTYAXnjhBaCw/0UXXRSAe+65p85htIzR9PqQZTdjyVGZuP5b3/pWYKhCGXRsQLUS8veoYKJS8vfB\niiZuZ/LkyW2ZTmaaaSagXLeoJA455BAADjjggFY33RcYSzNSv3USzrEoyH44iUQikegrjKnC6UP0\nvOOnTGW77bYD4IwzzgAKc5ERR5bf7n5q9Flpmb0NDAxMnjBhwhRF4r6iX0BlET8H7bPhU1+M23H5\n6aabDijKRH+Fy/k57bTTAkUpee6O5QwzzADAiy++2LDfwcf7P5XT8liMGzdu8nTTTcc///nPlpbv\nN6Ya8eyzzwLwrne9HkuTjvKCHIuCVDiJRCKR6CuMSZRau6yuKqLmjQijk2Ttm266KQBnnXUWAD//\n+c8BeOc73wkU9v3Xv/4VgDvvvBOAjTfeuKX9xbF2O7PPPnvD7+30XZ88efKwvinPrSrEdvrppwdK\ntJn79frKqj12x+zVV18F4L///S8ACy20EMAUVaHf5NFHH23Yrn4013/ppZcatv+2t70NgH/961/A\n674ol20VkyZNGlHd6KP7yU9+0rDvfoXXINEfcI56L33wgx8EyvNihx12AOCCCy4Ayr3k3Dca8t3v\nfjcATz75JFDmYdW92imkwkkkEolET9AVhdNMwcRoIZXLnHPOCcAHPvABAG655RagvI1lpL6lZbhv\nRHgOe+yxBwBrr702UKLPTj31VKCw9GuvvRaAtdZaC4CPfexjo9p/VDaiExGDMd/FeRB9KioBfTUu\nP+OMMwKw5ZZbNmxvkUUWAeBPf3o9XcqxuPXWWwF4//vfD8Bpp53WsN6yyy4LwKWXXgrABhtsAMBV\nV10FFBX5j3/8Ayjz8tVXX21rPEbK31HZjBbrrbceALfddhsA++yzDwD77bcfUK6j5+Z8q2sdmGuu\nuYCSoNoNNItWjfPI7zF/ynOril58I6Aq98zvn/zkJwE477zzgKKYherce8Hnic9Ot3PFFVcAZaz0\ni2ptaHYc7SIVTiKRSCR6gp5EqclE3ve+9wGF2Rpd9N3vfheAvfbaC4CVV165YXmzsl9++eWG7V59\n9dVAR7P7ex6lFnHuuecC8OEPf7jh95lnnhkoNlZtud1CO3k45p5YQWDJJZcE4N57721Y3nOIUWcq\nINXXkUceCZQKBc7V+eefH4AbbrgBgPvuu69he3PMMQcAyyzz+qX8wQ9+AMBNN90ElHmn/VpW6PZf\neeWVKdtrJw9nYGBgSETcaP2OK6ywAlCiGBdccMEpx9gKHCtVYauIzLYbkVlVCmbuuecGSqScFo0l\nllgCgPvvvx8oOU+qSpWq1zlaWjqleLoZpRbH3UomPgPNVbv99tsBOPjggxu+f/7znwfgwgsvBODo\no48GirJxu2effTZQrA5uV4uLVoFmyCi1RCKRSPQVOqJwmrE4IyT0xahoFltsMaBkpj/zzDNAeZvL\nWLTxu9yhhx7asJ1HHnkE6Ahz6brCqRqrHXfcESiVA/z/a1/7GlBs9k8//TRQxjJCdiib1w8iy3OM\nm41V3Tyct7zlLUMY5TDsGCjXUTalepNlHXTQQQCsuOKKANx9991AsUM//vjjQJkn+hkeeOABoLA8\n2bz+B9maCtvjkTkPV6mgrsKZYYYZJi+zzDLcfPPNra4yIpwPsvp24TmpFlVxzeaB/rRBuUqjZvVV\n/gHnhc8FFagRnM4vx0If79JLLw0U357fF154YQA++9nPNvzfao5UM3RiLGIFklgLz3vEMbLyyIYb\nbggUNe/1vP766xuW89n5jW98A4BNNtkEgDPPPBOAk046CShj/pWvfAUYWgexGVLhJBKJRKKv0BGF\nExmLb8dYG0tbrCx8mmmmAYZm02un/PWvfw0UW7zbMTdCpaN9Mmact4GOKZxVVlkFgJ/+9KdAiS65\n5JJLgHIOHrNRZ0ZiGX0iS3dsHnvsMaD4t8Sss84KwA9/+EOgRPypAoT71e5dNVZ12dv48eOHMFZ9\nMzJKf4+RMa5nToG+HMfCXBB9QT/72c+AUuJf7LzzzgD89re/Bcq5/+53vwPKfFIJxbwf52WcR3XG\nYplllpl81113TTk3x7tuvo05Ss3YuNvV5i7Djb4dGfBOO+0EDM3TaBWdYPWx1mcPJqgAACAASURB\nVF7Mx/K7Kt1j93qff/75AHzoQx8Cig/P3LQvf/nLQJlP+nSM2FI5RUVbF9304US/1nLLLQcUv5Zz\n3bFYfPHFgRKNaF7ORhttBMCf//xnoKg+t+dYWOlEFVg3DycVTiKRSCT6Ch3Jw4lVec38/v3vfw/A\nuuuuCxS2Z4SV32Vjv/rVr14/qP9FMWlz1yYr85QJ6cPx91YjdnoBlY1Q2ehv0Ma/+uqrA/DNb34T\nKAxEf4VjIap8Ny4vk1EVypC1zd5xxx1A56s1TJo0aUgNNY9J+L8M1ugwc0WcL46Jtc6MUpTpqh5c\nXzX44x//GIB55513yjFBifAyl8njiLXfhAx83LhxLduwxd13392wvQUWWKDh3ERVXoOqrlkVcFWc\nywuVtf4NYT6XynaeeeZp+L2XkD3Hat1aPMwhca7GyhL6Jb/97W8DpQLFe97zHqCMiddf1u+9FaNa\n3X4/5evEiD0j8o4//ngAHnzwQQD23XdfoESfrb/++kAZqyuvvLLhdy0jjoHPUJ8b3e6DlAonkUgk\nEj1BRxROtM3LSI2Q0Hbqd9+mu+66K1DyNnyLy1xlY6oBY831Yyy//PJAyRiXjfZTBd7Y88VMc5mE\nrMrqCp7T1ltvDRSbu2Msi4uQ7W222WZAYe+O4be+9S2gRPzIkDrB6qaaairGjx8/RRl4/URUEPro\nVDqyMZWNdmqj19Zcc02gsLtof37iiSeAYqtXYcvmHPPoY6zqm+PvEydOHPX4/OEPfxj2d7cb++bo\njzAqzP/Fb37zG6DcUxGORYTLH3fccQCccMIJrZ1AFxAtEV5vxypeJ+fLZZddBpSoRa+Xc/kTn/gE\nUPLz9OGcc845QLGsOO9il9WxQLNnlWOg/9pjNhfN58pqq60GlOfHSiutBBRrkNd7m222AYoVwGdr\nXSXfLlLhJBKJRKIn6IjCUbnEiBxj+GXdJ598MlAY6KqrrgqUCgPxLS9L1/5tJI7+EX1D2u4HZ4jD\n2FSXNsLKsVDJ7L///kBh3fpi9OkYSSW7++UvfwmUDHGz5Yfr2QJFCX3pS18C4KmnngLKtZHdeXz6\nTZ577rlRnC1TjmnSpElDMvaj8hWxIq0sT/UlG5flq2hVPNqfVYVG5MnWjNiT6cYoOVlf9DnFz3YU\n8qyzzsqnP/3pKZGT+hf0HxlZJVQ2Xg99KjEKURiNFOF+nEcR3//+94fdv+rC6KSImBfSCeir8R4x\njy7eE6effjpQckjMObF2nusJnwteX1m/OWxGyXpOUeGOBarmWLQKOP4+C60k4Bjqp3RsfbbGqFXv\nGbdfdd1Fp5+hqXASiUQi0RN0ROHEXih+l6nK9j7+8Y8DJSKrqidIjCLy7ayPxzpjRuoI3+4yYXu+\n9BKyq9ih87DDDgNg9913B4ofy0zjyLIcAysfy85j5JfrWZHglFNOAQqr117tcv4eGdRoq8G+9tpr\nQ/rOeF1llDGb2n3Kuq+77jqg+Gi87nfddRdQqiyYX6MC8lyswWc+htnTF198MVCUkQrL9WJOlNeu\nnd5AzzzzzJT5DkXBRGURoR/TiEzPTThfov/D7/HcIrQyeI+IZgy3G3AeRP+m88Xr53PCCKzos4k+\nQOe2atEx855Uzan6Y7+mXvkxWoH3kDjiiCOA4sO9/PLLgeK/9llndKrLafUxX8d59dWvfrWl4+i0\ndSgVTiKRSCR6go5GqcXokj333BOA3XbbDShMpFlvDhmH2zPj2LwMf9dmb80t4/Z7pWwGVwUW0ebp\nucjejQ6xs2cVg3a7+jXM41lqqaWAwvrd3yGHHAIUn4y5Kkb0xGz6eJyj7nMxaCxifpXM0bFwHsQK\n2C7/8MMPN/xuzojKViar4nG/KiL9V0Y1ea6xZlock+ivaCeva9555+XII4+cUllCyLL1oVXBc1O9\nG42kX8Njt5aW90CVsjE60XlRl8V3w//puEYfntfPSLyLLroIKHUGt99++4blVLT6ctzeFltsAZRs\ne/sf3XjjjcDQyK9YhX4s++hE1e0xzDfffA3/ey4eq4pHf7jfrUhg3yStTg899FDD9iOinyt9OIlE\nIpF4Q6GjlQZiVJIRU7IxfTgyFW2q2lplf77NjULzdyNwtIebxa0vSFYf38bRHt4pDBdhEvdtNInK\nRJZeVTEgwmquMTvaMXcMHSMrCrj9Aw88EChRSmZhqzJVg53IWfL66yeIuUbx2I1qM3fAGmfa2GVl\n9n7RdyMDtsKA1aGtleZ2ZfUqHs8xMtt4zUbDcB977LEh6gaaK5sI/Vhef/MnVDpuz8razg/HyGPX\nytBud9xu5LJV5UNZaUT/g9dXFWf9N3PUZOGOjdtRxal8jNCU1esHdZ5EJdsPUWtG+OqD8b790Y9+\nBJReUVZlcD74aVVo575q0XllxJ6wTp0+PSOC3V92/EwkEonEGwpd6fipndFKxzJKK5da0TbW0PJt\nriJRCX3uc58Din3bnANZnXka2i+NZouZyi28pWtXizaqSF9JhP4H8ypk48suuyxQ/FNVkMGYx6Hd\n2kifWCfKTHOz8GV/LmeNLRlvp6pFw9DIt6pxtleHbEyFY47Apz71qYZjtnKFzFUW7zz4xS9+AZQs\nfZWS88NP7eIep2NQFfk1ceJEJk2a1NZY6FMxd6TT0WCOnedmxJYwF6lZN9zYj6UK008/Pf/61794\n7bXXulYh2bmuclHJqEysJGAejtFsWj7WWWcdoKg6Fa5jZR8l/WNWmxfRn9nsedHJatFxDjoG9v7R\ncmHVDRWKzw/919ZO85j1HfosdV64nn5QnxveE1onWlXGWS06kUgkEn2FjvhwIrQHGkmh/2KXXXYB\nSh9tbbbmmtiNUDum7MtcButKyQa09ct09eHI1mTMxu2LTkbeVCkboZrTpyK70o5szaMTTzwRGFrf\nSX+Vdm2Zc2Susnv9X46FUU5f//rXgeLniDbc0WJwzorKUpYU815iz3nHUBZm3owRNi6vL0el4nra\npVUR5t8YGRjzLCJri1Fsnag6bi6OeVedsoGbj+H1jcpGNFM2okrZxByqcePGda0auwrE6EQtH1ZC\n1kqgL8fjsE+SY2ouk/da7HrpnI+5bc4Lj0NV0EvEeeFctPKEXUu13liBROuQvj3vFcfQ54lVXvRn\neS+qIq3KYXdcn5Ex16ldX6BIhZNIJBKJnqAtH04ztub/2guFPhjzafRrWGdM27yRV3vssQdQInFU\nODE737pjRlzpA/D/mAcyQs+HjnX8jLbxJZdcEigVcbVH279EVq8qlEkYpWSttDPOOAMoakAYDWdk\nl/k7ViDQT2L+TjOVV9c+PdVUU01hkpEFeR1i1QOZq9FIzg/PVf+YUYyup4/G+eXv9vbQ3+U805b/\nzDPPAIXl6SuUzTs/BleJePXVV5k0aVLLYzEwMDB5woQJHWfJ2tgdI/0dcW6riLUedBrt+C3qqrtY\ngaDKxyacV97X5t+4nNvZdtttgTKf9O06hnXVZzc7fsbq8PE54jxQ5av6q2qfuT0/3Y7+LueL1cRj\nzqP3SFUH2vThJBKJRKKv0JYPp1UmIHPQXxE7+xlZYQ9yGYg961VA1lQymz6+xWXCMle3H5l2t7vZ\nQWEQMhJtq+aO+F0GYSVbFYmfxr/bA0Z/hjZXFY5+Lz/dj5F70Y7drcrZAwMDlUwxZpZ7DNqLzRXY\naqutgKJk9ckYhWR0kvZpFY5RTPoAZGH6H4x+jHkf2rE9Xo/P/2M9vFYwefJk/v3vf0+JBvzIRz5S\nexuD4Vx2TIx6E56jaDW/qy5mmmmmIXX8WkVd5RDv01jVW3h9zKfRZ+v65q4Y5WiEp3l7zqt+6hQs\nYpSZzwlzD/VD6XfyeRPHyO34aSSvOY5WHjj33HOBkjvp9kXscdUuUuEkEolEoifoSpRajBqJMHJC\nhiIztXeD9mojMHzL69OJlVSNwNh8882BklXbajx9JxG7R8riN954Y6DkjMSIGtWevX1Ua7E3fVQq\nRgDGXi4y4e985ztAYXf6yTqtdF577bUp1zOOgZCly5Tti2QUompM34qqzegklZDRZ9qd9d3NPvvs\nQPENeY6qBJWLkTxVx2vU4wsvvFB7zkw//fQsueSSo1Y2wsoUziNVf5zbjlWzfJp2Mcsss3SM5dZF\n1Vz1enoPec8YcaVf1HtE9e9zZSz6ZbXq/47PUJ+NQmXiszJW94h1Cz1XfXzm7TnnVTjOW+dRM6tQ\n3YrqqXASiUQi0RN0ReG0Ct/msnHt0TJcme+xxx4LlLe20UYqpfPOOw8oMeoi2i97gZgjpDqzemvs\nc2N9KP1QIvor4vb9NNLGMZKt2SHU6LXoPxnpuI14qYPBakY2pRJ1DMxqttqvvhX9Wl5fc4esdOx2\nzC3xXMzLESocfTpWW4gVb6OiiUrHqLZ2bPv//ve/h/RpagcqUcfAMfHcjcyU4erjO+qoo4bdXqsV\nBURk2o8++mhPfKB14Dn5PPBesWaj0YwnnHACUBRO3YoCnUSzfcT/PVb9kubZqUS8/p67+XjOba0G\nRgJb1zJWpTa/S/Xf6rWuO2apcBKJRCLRE3SlllqrMH5eBmzUkezOyAyZ8DHHHAOUt68+m9gXRxtu\nG6idh2NMv/HyEbFKcKv5GeYi6duRqUQ4NsbVm6ejz0Y7tj1CRAtMq1aOwcDAwBQfjXZnFYsKw7GI\nfgj9W8LrbldCFZEKyegj2foOO+wAFH+Vy5uXY+6TMJouVrSI3VqnmmoqJk6c2NV8i2aIbNxjNtNc\nZRNrtcXePsMcZ8N2hfeg8yr2iulFHk6r8By9N+x74/XXF6cC0k+hP0y0q9zaGQurQLdbwd57yIjO\na665BiiVCDxn739zkowEFt47/q+VwSoddSsKZB5OIpFIJPoKY+rDkUWpdLSd+/a3I+Rqq63WsLz+\nEdmb2fR77703UJ2H0w1UKRvRbsa5tlnPOUK2aCXu9ddfHyj1p7TxR59NzD3pFCZNmjTFp+b1kY37\nKauSYTp2kZHKsg8//HCg+Ke0N1tDKypkI7XspqrScoy0g8eab9GWL3oZvVQFr5cs3E/7lVx44YUA\nbLbZZkCZN1U5K806vKoGOolOz7WomHxemG/jp9U8zM/RB7j44osDpa5gL9GusvGcnetaD6wc4nPC\nyE2j2PQNe92dB+bjWF/uiiuuAKqfmS1UaWkJqXASiUQi0ROMqcKRocg8I3ORMVtrK7I6ezqYq9Lp\n/tujwWgZgedg3LzsTIZiLS2ryVbVToroRgdH9xf9DCrQ2B9dpSITNePbqKLoj9A3JDM1Gs1eIbvu\nuitQaujJ0s338bhUQEbixKoQMbpuNHknbtttWFmiyqci5p13XqBUVPfYnU9++vsXvvAFoOQi+btj\nbg6KvsBW4f7tp9TPUPEKfbtWibdeoWNjJFcvo9PaRdUxGuWqz1Zr0HbbbQfACiusAJToNS0gVi/3\nGaoSUjlV7a9TEYqpcBKJRCLRE3QlSq1Zj/Cqt6jMUhZoJrpRSSoaI670+Vh3TOZatd8W0LFq0Z2G\njFX/iJFe9957b1f2VzcCZ9y4cVNUVsxvkZULKwFod/ZcVHOyL23wsjdt7s4HfT4HHnggUMZIttZM\noVSpQH//X7fPWmMxMDAwefz48UOUzD333AMUm3pUmlbINurMvBtzSux/Y95W7OHjGFsV3G6Y8ZxG\ny+Z7USG52fPC715/x9Kq8vaY2nHHHYHSXdfIT6MfY3fLfqoWPcJ23DdQ/JOeg/PO/lfm/1lb0XtE\nP7fVO0aLjFJLJBKJRF9hTPNwRIycUukYX7/lllsCxa5snoYVBvQJdCBzuJbCGa6OULftwp2OwDNe\n38oGU089NRMnTqzVAyaORVQ4QhYWxyj6J1RKsU9N/B6rU7vf+HsVQ47fY9RaOwon3iP6lfS1GT0Y\n54fnpH9Kv5X+BuH1N3JPH46s3us4WqgeYgfaTrB6r1Ndf2JUyqo+oxpV/1pG9FsZwefzQh/faJ8X\nY5mf1QyxMnrMkWsXVdcuFU4ikUgk+gp9oXBG2B9QbdMVHVQTfefDGatImnYqDUTWY/Ve2VaMRox5\nOsMpDCisKlbEjesPOp6G7YhYNTr2tI/1xvRL9YLJ6pcysir6w2So+i1bhWNqlJL5Fl6bqg6Oqgf9\nbCussAL33nsvL7/88pj7LYRj43VT9UfFG2sqdiqKtR8VTqy1GO+tbkXwpsJJJBKJRF+howqn02x8\nDNh93ymcQfsDejcW7bA3I2ZUCLFWmUoi9qqvYq6yMteLPiG37/oqGJePDDf6fqrgetNPPz0vv/wy\nEydO7DiTjXlakZnqv4z5NdbQOv/88xu2p5/C2nlVsBZXuxUw+pHVj7B/oHv3TD+PRTx3ewZ1Kiot\nIhVOIpFIJPoKdRXOs8Cfmi74xsXckydPflfzxd70Y9HyOECOxWDkWBTkWBTkWLyOWi+cRCKRSCTa\nRZrUEolEItET5AsnkUgkEj1BvnASiUQi0RPkCyeRSCQSPUG+cBKJRCLRE+QLJ5FIJBI9Qb5wEolE\nItET5AsnkUgkEj1BvnASiUQi0ROMb75IQVXTsTcRnqtR2uZNOwjQ34UJe40ci4LRjIUN0myY2C9o\ntyFczouCrhXvHO5lM9VUU1X2hx9LDAwMTJlMLWLMax3161i2Ao+92bg3+7/uGEwzzTRMM800U7Y7\nfvz4hu6Qdbc33XTTMd1009WdO13Bs88+y7PPPlt7vZdeeomXXnqpC0fUOmaaaaYp1a3h9RdNL182\n66yzDuuss07T5SZNmsSkSZOGzJP4vY3nSVPEuRq/jxs3rqFKusfUbE7HY222vPuZMGECEyZMaLq8\n90hdjP0dlUgkEon/L9CTjp+xN0O7Ena0aKE/Rt/2w+kVNJnWMRcMDAxMfstb3jKlD46wP86//vWv\nIfuAodch9mGPPecH7W/Y9avm09RTTw2U3jPd7l1vp9DRYKw6vTZDJ8xIzXryNOtG2uz/Zthpp50A\nOOWUU9paX7QzFlVdbasQO3XG9e0BZbdTtzfrrLMC8Pe//71heT9nnHFGoHkH2Vaf3dkPJ5FIJBJ9\nhVEpnHaVim/N6ERs9Vi6yP7esAqn02PSSYdoVCjxGKuOPf4uu1M5vfzyy8OuJ6rmZ+wMWnVcg37v\nmXN49tlnB0qnz9H2on/7298OMMSfs+yyywJw9913A0M7j/ZyLFp9jqywwgoA3Hbbba0eAjD6LqfD\nzcPXXnutthVg6qmnnqJEqtR/9BHNM888AHzsYx8D4C9/+QsAW2+9NVC6637yk58ESifZ6aefHoAX\nX3wRgC996UsAnHDCCQ3Led21AngN4nzzeL1nPA+RCieRSCQSfYWe+HDaRXwLzzzzzMBQthaZ6re/\n/W0AvvjFLwJDfQIjoOsKZ8MNNwTggQceAOCPf/xjw//vfe97AfjTn14PmFt00UUBuP/++4He2fQ7\nwWRlWSqR0SIyTVmZn5EtxvUioo/Iz3bt0//bRq2xiHN8jz32AODYY48ddvtzzz03AI8//njDOcww\nwwxA8Wt861vfAuBzn/scUKwIs802G1CUU/S7CcfUe2tgYIBJkya1NRb6EfSdXHTRRa1uYthjGbR9\nALbYYgsAbrrpJgA+9KEPAbD++usDcPjhhwOwww47AHDEEUcAhf3PNNNMALzwwgtA6z6iumMxOPIr\nzjF/V9E888wzQJnTKpSTTjrJfQNFiSyxxBJAea74u9tdcMEFAXjXu17P+ph//vkBWHfddQH4zne+\nA8A999wDwGabbQbAOeecAxR16H61Tv3f//1fLbWXCieRSCQSPUFPFU5kqNpWY/SQ9sill14aKAzp\nxBNPBAor0xYf376yONnBP/7xD4ApceMjMO6uKxwZ7fLLLw/A+9//fgC++c1vNixn9IhMVlb27ne/\nGyjn6Hqysr/97W/tHNYQtBOZJWuO9t1mPpwWtt/wXTu3ClbG/MEPfhAoLFE/hczW/Tr2MmLZYIz4\nGXS8tVl9FStvFWussQYA119/PVAUyoQJE0ZcL+5vkUUWAeD3v/89UO6tH//4x0B99dkPyY4qD+e6\nVgFVg/4Gr+sPfvADoCiaz372sw3LGbH11FNPAdXXbnB0ZDuRnOPHj6+MlHSOe1+be+X1dnnV2AUX\nXADA6aefDsAjjzzS8P/vfve7hnPabrvtgKJgfv7znwPlGel+XF4F5LP2ne98J1Cexd7rjlEqnEQi\nkUj0FcbUhyPb1/68wQYbAOVt7dtYu7V2Q+2Z1113HQCHHXYYUOye2iW1Q373u98F4DOf+QwAJ598\nctUhjVrhRBXn94UWWgiAVVddFYCrr7769R3+L0pIluV6d9xxBwCXXnopAE8//TQABx10EFB8Oo6Z\nNloV0WgxmhyDGOHSrsJR/Xnu2p/f8Y53APC9730PKD69m2++GSjK+aGHHgLgRz/6EVBUogxXRqyi\nGW2OAXQuV00lK5tXpcsoHesq/5Pn5Jz//ve/385hDcFYqD3h8+Liiy8GSuSWqkEVqB/De85IPcdW\n9u+8sRpB9Nk0i55rZyyqng9+OndnmWUWoEQrCp9xntN73vMeoKi9LbfcEii+3x133BEoykXlpPoX\nMUpRte/3ZlGSqXASiUQi0VfoqMKREfjpW1PIUFQqKpHf/va3QLEny0xkttraZbaRzenDefDBBwHY\nfPPNgcL2tU/6lq6KzKEDCqeK5avCZCLbbrstAB/4wAeAwv5kX46NvhzPVRu8qlD2+Ktf/QqAu+66\nq2H5dtEPtnrZmupt4403Bso8cqwuueQSoFxvI/zmmmsuoLA655fz5/nnnwc6l0X9v213xM+pCleN\nec/4v5GYsnrnmxFZ+ividvVz3XnnnQ3/x2i5KnRzLKqUsD6Ygw8+GChzPUZqeQ/F50zcrs+LnXfe\nGSiRWHVRdywG+3DmmGMOoCgY51xUPJ6jfknv9yeffBIoz7IPf/jDAJx22mkNy99yyy1A8dk4dvvu\nuy8AK6+8csNxqox91lZFfvpMdf+pcBKJRCLRV6itcNppT7DaaqsBJUt2zTXXBAoT1UcjK/vKV74C\nFPZmtJo2VyMxhMcjezCmXMZ7/PHHNyw3AjoWpRYzhl955RUAdt99d6AoHrHrrrsCJfpEJhPj6bXt\nm5GuH8MoFH0/I6i4ljCWCsc6UM4Lo9D00dx4441AOdc///nPQIlWcsxURLK6X/ziF0Bhl86/iKh0\nejkW+p30X1XVi9OnY/RQhDlrKhkj9Yx6azefq85YLLbYYpOvueaaKX6Gqn1W1TaTRatcnNODqylD\nue8POOAAoDw/9IsOrrYMcOWVVwKw0UYbAb1rT2AuUx2stNJKQJnjWjyMItM6tPbaawPFV+ez8wtf\n+AJQnhNeA9W/VRu8J1Q0jl2V4o0KLBVOIpFIJPoKtRqwQWvMKPpylltuOaAoDt/C2ljvvfdeAD76\n0Y8CsPDCCwPF5u5bXbujkV5Gocl4ZLZzzjknAHvuuWfLx9xpyGRUKkafyNpPPfVUAJZaaikAfv3r\nXzesHyOn9GPI0mWuMpX11lsPgJ/97GedPpWeQyV7xhlnAGXeHH300UCxe8vGvO6uZ+6JdugnnngC\nKOpQu7Vq0vVHW4V4ODSrTRZraqlsnDeeq4rW+WDE3oorrgiUqEVVwCGHHAKU3LP99tsPKOrRyM1u\n4oEHHpgyP0eCysYcFH23nku8z4W+GNm4Y2Y2vtUa3ve+9wElcssIUa+N2435V51GK+rG66tav/32\n24Hib9ISsvjiiwNFBcbIO+e2Ua7D+CWBEsV2xRVXAOVZ3MyXN7iyex3VlgonkUgkEj1BbYUDzVmb\nbzyZx3333QcUhiGDNM9G2/y8884LFKZy5JFHAoXh/vSnPwWKTd7saSunaivWT1J13DHKrSrDvBPQ\n/mzcvPHwRqdZW02GIqszUk92tummmwKFjS255JIN52J0moyyU/k4rWLcuHF1atZVbgNg9dVXB+Ds\ns88GSh6NkTnapyOzMurMSCzVpErZ62tUW4wkrIrIGQ2ajUXcpzXXZJgqG7fz2GOPAUW5qGj937m/\nyy67ALD99tsD5d77zW9+0+6pdAyxIrZQ2URoEdl7772Bck/I8n3OGAHqPeHYzDfffADstddewNCo\ntGb3fXzefe9735viL6qLZtGAzmnPxe/6cFR1PrO0EunDtX6cdeFihWwVkfk8KiCVjT6hZrlTzRRQ\nFVLhJBKJRKIn6GgeTowqkUFefvnlQLEzm2OgvdKckhtuuAEotnQja4zD963q292KA/p2ZA+uH6NP\nWsh4bjtKrdV+NNqpZRhGJRmNItOw1pWq7uMf/zhQMoRjTlJkxqP1W7VTS62qi2GrYyMLN4PcMVEF\nqmxUQjH6yKoL5ippxzYPRxXovKyqiBCPs5NRajJR/VPDrA8M9TsJ2bpKJ8JoSBWQvgCrkuvDcf41\nQ8wrG8voRa0EHpMsXvhciPeA/s/FFlsMKIop5pLURSfGIuYIed1U9d/4xjcAuPDCC4GiClVYPg+2\n2moroNw7sbq8Y2bE7jbbbAOUZ6RWqE984hNAscRU1XwTEyZM4D//+Q+TJk3KKLVEIpFI9A/a8uFU\nITIFGYfZ0tpUjchS2RhpY76O9Z9EfMtaE8u3usxH35AZ6jJc6xLJdLuBVhWFdmqPXWViTTUZqOdg\nPxPtzI5pzD1yDLXpXnvtte2eSlsYqdZSs7GRZcnqVXnm33h9zT2JHWNVNrJD82scW6tK2zcl+gpG\n21WzDlQ29myJGf/mnBlpGdXiueeeCxT/lH5LoT/DqMjYb6lVZSN6MSatIiobLRrOHy0Xqn8/VZXm\nojTrBdRs/+2OyeA8nCo1rb9Rn81aa60FlBxFK5Co9r1XVC5VUYHOB+8Zz+G8884DYP/99wfKM1T1\n5zPaMY5+t7pdVFPhJBKJRKIn6KjCEbEvyqc//WmgRIfEas0yW2PBr7rqKqBErwkrDMgOZDD6QWQP\nRiEJezjECq1jkZ8j9E9oo4/HJhPxd5WNcGxlecss87rr6bjjjuvmYY+IDQ3izQAAIABJREFUVutx\nCc9VNv/www8DxWdj/SfPzTH54Q9/CJRIvD/84Q9AqSdlHo7K1sxzjysyVeeNLLAua2sHUdmIWCfM\nczaaTSUrE9VnY3TS+eefD5TMcfN8Ys+osYSKNXbubQYVbrx+Vi7R/+D8Oeuss4By7kZ2Gh1bF6NV\ne5MmTRriV473jNfL6MIYhajlwgg9t+eYeC+4XS0pVtA2X08/ltYiny/6in2Gul3nm9v1+OtWTkiF\nk0gkEomeoKv9cFQk1nU64YQTADjwwAOBYp/ULujbW9v7o48+CpS3vbWPjMzQXi3Lk4H4exvoesfP\nQesDQxmCTEfmEqNC4nKec4zAsxPoZZddBhTm3CpGE4ETFWRVdKBs7swzzwRKdJm+tpj57/fYbdBz\ndH3ng+fs8ah0rCrejLFqc+9kZFbd3jCqLpml94pjN2i/QJn7jplKxzqGo8VoxqKuAm4GqzKYw+a9\n5Pywr5aKSr/ZWPaMGvTdbQBlbuvD8Zj1yVgRwOvvPeP32FssRicusMACQLm3jJa1HmFVDl18/qi4\no/8ra6klEolEoq/QVYXj21HG4VtchnPNNdcApTeMiiYyTyMmjKfXvmilXLdvvwz9GG3Yq3umcIRR\naKo2fTr6ubT1Owbm5RjBZQSOjEXI4lZYYQWgxNW3im7mW3guMk7rynl9vW76qVQFUf25nDkL+sWc\nD2Zrr7LKKkBhgVYsiPb06Buwf0knOjt2Co6dx2oFCv0V+jmsHvzLX/6y1nFUVU62SnwvKiS3ilhJ\n3ZqLPme8t8wD7JRvbsMNN+SWW27hxRdfbPseidVN4txTnVn53q6kxxxzDFCiWl1vt912A0oUm7Xy\nXG+fffYBii9QpRMrcBv9pi9Hn5A5bIOqQzecXyqcRCKRSPQVuqJwYhSKDDV26BOtHoM+IWPOrUem\nnVN79Sh6p/dc4bQLI/Rk91bkFrI5bbrd7vURvruNYZe3KrhMVBbn9a2KJox+L9Wfdm9zFcznsvuh\n+Rfm5+jfqOqu2IlKA+1GYrUKma39TKwf57HLXP1dZmw0W13lNRq1F9Fu/xnh80R14LlYo03Vf+ut\ntwLdq6A+mrFQ4fis8hxiVJlRh85RfXrLL788UHLPrrvuOqDUo1TBOFb6/JyP5m9Zl85I30HnFo8f\nSB9OIpFIJN4g6IjCifkLfh/U79r1Gz7bZThGG9nX3WgkmW2zbOqY/zEogucNo3CElQnMONavZc0t\nI3msUxfRi/phEdqLjTo0T8t8iqiIzbrWT+Ux69OxMoVqzk+VjVFrssmq+TcWY1GFWB3aHCPVnOdk\n9QR9OKp97wF9glZXcH7EOmQ1jqvtsRitslEBWxXcMbJyiSo/RsG12ueo6vpX1YjsxLxQqapM9N34\nuzlFVsS3P449guyLpHLx2PSHCtWg111l4zVxzMxhc945Js47YeSxfrNUOIlEIpHoK3Sk0kCM/vAt\nq01VtjWIGbS03cg49NFYQVXWZgaxzFlWZ0SGtn3h9jqVmzAWkAHFqCWj0VQ8ZhKrcGJ0zFhknsum\n9D9YCUK7svZnlY8+H9XaTjvtBJRztdKtETZGp4lYvypGpcUchMG5B50eH1W5nRsjvvzlLzd8l/ma\nb7HJJpsAJfLKaMVYGdvjjnXjvBdVkRGjVSEjwW3qd/B+lT03y4uy7le8Tvo5zN/zflf56uuzf1bM\nXXNe6TeJaLeadIR+sMGIlc8dG49R34qdfu0R5Tl7H+ufPOqoowC46aabgOLrOeyww4ByffXlXXnl\nlQ379ThU0FVQ2Uw99dS18qpS4SQSiUSiJ+iID0cbqUxAG7qVBC6++GKg2mau3VCGa36O8C3tW9v+\n7O7PasHGnOu/MK+nCsP0Bum6D8dzVpmoOJpFM8lAZB6yM1mi/XM23nhjoESTmM+jrT92N6yqgNsL\nv0VVX5sYueN1UhXsueeeDcdsFrb1oVrt4CjcT1XdsW6OhVWf9VN5TtaVk31XHbsqL/q3qmB+hrW4\nNt98c6Aw6arut+3k4YwfP37yjDPOOMXnIqzebeWRZjkpoqrSsizd7pUqIWE2vRYNVaFqwB4yKpyq\n+RHRTs+omDsUK4p4PxtdqJq3mob/WzfO54AVJrT+OK98Fqqcfe5cf/31QMnj8rnicWg18NlrFXPz\nAAf34XrllVd47bXX0oeTSCQSif5BR3w4Rn/4tpWtyyR23nlnoNT/WWqppQC48cYbgcJwtMGbLe1b\nW2aiPfrQQw8F4Ktf/SpQqr/KUGOERRVDqdsbpB1EtmZFAbuZ6qfwd5mFKtGxjIzT7c0zzzxAydp3\njOIYV2Es+53EzpuOVbxeCy+8MFDGLPYzMUqxmbIRVfNhuLyfbvm49FvodzCjO+ZnCO+NCNdT4agC\nYjUGz+1rX/saUF1PLPr2RlMxYdKkSVPu5cFQvQnVuPs2Aurqq68Gio82Kg+/648woivC6LWFFloI\nKLX0VI/6IKrOtVP9kgav7z7sQqrP1e7GqnnngxaOU045peFYrQDw/9o790DLxvr/v86ZYSSSGiWR\nVC5dpojkEkLJJaGLKKKLJEWRW1RSUtFFkdxqpKIkUZLCUKl0ISKJQldFpb4/GV8z5/z+4HWevT/n\nrNl77dvZM9/P+589s8/aaz3rWc9a6/3+XF1PsaupnT09tkrGHMaDDjoIgOOOOw4odemsvabqs2J7\ntLS0ivyLSIWTSCQSiYGgL5UGZN2+dWXp+mBiZQDtksIxxbweIbM1o1gfUQ/Yet98ODJZe5GbUWxe\nhKrN6CMZhpF2ZhLLZI3EUv1ZH0x/mEpJxmPme7tVGKYj96SKwX7kIx8Bij3b62w9KX04sv1u64Y5\n90Y19XIuWkWBHXPMMUCxleufcP10msOm9UHFEatNRxjpGWvwdTIX3ueu0XYRfTYRKpU111wTmPwc\nET5HYiRYzEHxHjziiCOajtsrH07j/2PVcFWcikLlYp6N1RL0zbidfqsbbrgBKPe51hvP2erRc+bM\nAco6O/roo4GSw2jEqLXZ4hyouJyzhgjP9OEkEolEYnjQkcKp6lqn38Fs1s033xwo9mL7ZqtM3E+E\nY3L/vk214RtXL8PpIXqucGTLkX0bkWeEnRE7qrc4t9bCsu6YfisZkJFAKiYZjfkbkZG0wnQoHCED\n1cZu1JHZ0fpsjC6SlbXy4cR1G/0css7oW+rlXHiseGwR/QXveMc7gDIH5tmYB6G/o0oF+L0+IP0l\noioLv5/RizEiK6pur7v3uWoszplZ+SqcOAcnn3wyUKwBsnq/P/jgg4Fyz9X1V3VSOTvW69PSYbdj\nr4PXVeuNz1atR97nhx56KFCUq9Fn+oTtjmtOpL3I3L95YXbX9ZpoWalSmVktOpFIJBJDjb72w5GN\naXc0EkNlYp6Ob09zEYw2McLK7pWy/D5iYLXUjCozp8Q4e22qKhdttUafyerMRdLG75wZhWTUSafd\nFaejB0zMTbDTqzkAsjz9G9aV6rRHvf4wbfwxF6rTHjAjIyPsv//+QGGQvUbVHMtQq/yZ7dYVW8Rx\nu+746dhUstHXa3SqOSIqFP2TsnSjVK2mYY6JrLyVn6pdVPndupkLx+r9qfI0+svngz2erCygElGx\nXnXVVQDMmzcPKD4Wo9RUf+5XK4FzaeSwSkkVGHPTvEbOhddIa1YqnEQikUgMFfqqcITVXLfYYgug\nRGJZAdWsWiMz6nan7CH6rnDsbqk/6kUvehFQmIt/13Yv+7aemDZamYzMpcoe3irHoArdsLdYOaBu\n9KC/N7pJ1SazVe11W++rak4ac2E6UThdDWpIIAO//fbbgeIDqDMXo6Oj40sttVRL35pKM+bFVUXk\nGeVqFGGsujEodLIu2s3pcf633HJLoNz3zpWf5hyqDqPPxU+VrUpKn2+sfNAqRy1uNzo6ysKFC1Ph\nJBKJRGK4MBCF0/D7pv9PR6XiFljs+uFE9Krabze969vtpLmI/TVt388KxlNB+7RVh6fDnzWs6GWU\nWlVXycVlzuqqvVmzZk2KiGvYV9P3fkYfSsP+gPbvCaPaVE7mRMU5j362eC1ipOAyyyzD/PnzGRsb\nS4WTSCQSieHBQIyeK664IlDyJURkkoOCb/FOI7h6iV7VaRKR8QxKHTTuf4oY/Vr7itv3auyRzcn2\nYr8T1+OcOXMmogLrYtAsvdvr3G30Wh3EuTE7vlXF9EGjqkNx3R4w8NA5N66zVuouVlsRVl1pVVk7\nQp+NXVOrxtFuz7LGa1ZnrafCSSQSicRAMFAfjoh1hKpQpYx6hSlsxou9D6dXmM7ILOuGRbt1jfE0\n/b/dNV6leAY5F1ZSjj3phwW9nAuz5q0HGFl6VfWEquup6qiKVovPHSsgW7lCtKsauvFzdop2/VzR\nijNVJfR29mO16blz5zZtHxV1RqklEolEYqhQV+HcDdzZv+FMO1YfHx9fqZ0Nl/C5aHseIOeiETkX\nBTkXBTkXD6HWCyeRSCQSiU6RJrVEIpFIDAT5wkkkEonEQJAvnEQikUgMBPnCSSQSicRAkC+cRCKR\nSAwE+cJJJBKJxECQL5xEIpFIDAT5wkkkEonEQJAvnEQikUgMBLXaE8RifLEAnK15LZ3t3y301qoY\nXmzu020VhA4K3d1To7TNIndqGfFYCLKqba5wDoRz+sADDwCTzyUWGpyuBmwt/u4+F7mfquKZ043/\niy2mq1B3LkZGRiqv+3Oe8xwArr/+eqDcM7EkfxvHcWxT/r1VOxKLenrPtNt2OddFQbtzUbsfzsjI\nyMRDLT4M7Xv+hz/84aGdP3yhH/WoRwHwz3/+E5j8Yon788Jb1TU+PH3I+n3VC80HmAu4qvqsPSL+\n/ve/16p1NFX1V895rbXWAkrf9Tj2qg5+3nTOzeqrrw7A7373O6Cco5/2FLLfRbxpq15wsdeH+5s5\nc2bP+wQ5J62qg1s9+De/+U1Pj5/oHjNmzKjds2lkZISZM2dWkqHLLrsMgJVWeojjWSH7hhtuaNqu\nCu5v1qxZwOQ17z3kPXLPPfcAk19AHt/fW53e/UYC1MlcJB5C7fYEIyMjE21PvUD+/7777mva3gVh\ne9P//Oc/QHm4uaCqXiiRacQFEBeWL7y//vWvTfvz7+43PoQbFFWt9gSNL1/3tdNOOwHwjW98Y8pz\nii1jPSdVof93O5tSxZdAnKM5c+YAcNNNNwHl5V2lFqrUpIz0/yJ7W3PNNQG49dZbm77/vzAX7arL\nTubiiU98IgB/+ctfAPjYxz4GwEEHHTTl72IbAe8Fv5fges9UvZhaNZVbb731ALjuuuvaOp9OS/LD\n4rsu2kW2J0gkEonEUKGrBmzRtBWb+zT8run/bhcVi1L3uc99LgDXXnstUNiXjEamIdOJqFI0sRnR\nxhtvDMA111wDwMKFC2spnEVJ66r22VVmvf322w+Az3zmM03f77///k3fr7rqqkBpWlVlZ65qwKTJ\n7b///W/T949//OOBh5TRXXfdxQMPPJDs7WEMI5Odrjbpg5iLqjVd9b0WFM3K7foMq447hZJp+n7G\njBksWLCAsbGxoVsX7SK6IY4//ngADj30UKD+HKbCSSQSicRQoZbCGR0dHZ85c+aEbbUqQqphe6DY\nXt1OpeLvJwYTHNk686PTWd+RCic60qMDPtp63W4Khda2wpk5c+b48ssvP6FgIiNwzFUO02233RaA\n7373u03bnX/++QB87Wtfa/p897vfDcAVV1wBwJ13PhTfoK/o8ssvB+CII44AiirUV+RcRMe9DNm5\nGB8fZ2xsbChZ/XRhmOaiFfOsy0zrRjXWmYuVVlppfKedduKss84CmoJzgGoLhOhWqfi7733vewCc\nccYZQLE6eM943FZzsfLKKwNw1113uf+hWRft4sc//jFQrDs+D3xG+9zQH3777be3td9UOIlEIpEY\nKnQUpRYjnGJobYRs3+2iQvKtusIKKzRtv+GGGwJwxx13AMVGK0Mx6q1hfEDxR9x9991AYS4qnejH\naLBn1vLhNCq6dnOHPNcPfvCDABxyyCEAvPzlLwfKHGywwUPDOPDAA4ESQvq0pz0NgG9/+9tACSX+\n4he/CMBLX/pSAFZccUWgRAi94AUvAEokoX6zpz/96QDcfPPNQAn5XBzZW7/QzVx4HQy17RZGH77n\nPe8Byj1w0kknAbDzzjsDJdTXdeF2/t61Xxd152KQIcTOtee62mqrAbDOOusA8JKXvASAffbZB4Cv\nfOUrAOy1115Aee487nGPA4oSe+QjHwlMjsJdnO4RnzvOzfvf/34AjjvuOGBweXupcBKJRCIxEHSk\ncGKkVVVSYdx3Y5QHFPbt9x//+McB+MIXvgAUhvK3v/0NKDkmf/7zn4GilIzccjsTTWfPng2URDKP\n96c//QkojEZf0NjYWC2FA8X2qR04nrNjMOms4fdAidRbd911gZJD9LOf/QyAZz/72UBhZ3PnzgXg\nyiuvBIpyede73gUUu7Rq8Otf/zoAxx57LADf+c53gMk5TvEaLk7srd+YzrnQb2DStArl9NNPB2CX\nXXYBioJyHarijX4877zzejKeOnMxOjo6PmvWrMoqGaLqHukUb3nLW4ASffqjH/0IgN122w2Aiy66\nqGn7GIVW9TyLkV2Lwz1irpFzYHSrCeWqwk4Vr0iFk0gkEomhQlelbWRTxsFHO3WMWouZv3vvvTcA\nv/rVr4Die5G1G5FlxIQKZo011mjajwrHyK+f//znE2NtPK6KRtbo276TGk4jIyPMmjWrke0A8NSn\nPhUopWickzhHz3zmMwG48cYbgeKbUcVtvfXWQLEbn3POOQB89rOfBeBVr3oVALfcckvT2H/wgx8A\nJTptzz33BMqcxbycWBZkcUJU0jFbXv+WGe768IYZ8Zz0I3gP/PKXvwTgq1/9KjBZ3cvOtSKowF/z\nmtcA8OUvf3nK4/QD4+PjzJ8/f5IPJCoJ1+Ryyy0HTC771ApRgejPUuk4F9Zu03rg88BSXFV+DOdo\ncSxn84tf/AIoVhx9e1tttRXQWtn4d6s9dItUOIlEIpEYCGornLGxsQnG0CojN+ag+P/dd98dKCzN\nbHrfotqpzTWRkWyxxRZAKYjpfmWyZvfLaI2XN3JLNeB4ZUadsHvZm2NwX0bEqHA8lj4VIauShZ16\n6qlAsWdbyFAbq/Hz+qeMNtGWr2/mta99LQCf+tSnms75+9//ftM4vVZV1RoGgSc96UlAmYtVVlkF\nKNevCjLTN73pTcDk6gzWn9OvZURfrLE3jDBCyrEefPDBAPz6178GynU8/PDDATjssMOAohK8d4Rz\ns/766wODUTaNGBkZmaRsdt11VwDOPfdcoKzlKoVRVVvRiM5jjjkGgIsvvhiAHXbYASj3xFVXXQWU\nyFDVor7ciFjLbdBz1g1e/epXAyU6UWjJ8ByuvvrqtvbXK2UjUuEkEolEYiDoqNJA9ANoo/X7WM1Z\nyEiElZX32GMPAC699FKg+FyMJtGOLcN55StfCRRF8+Y3v7npUxZoiwChz0bI7mXEQK0otalK+esf\nUtFUVWWIeP7znw+UudT2ql9C34+Kx/36fyP6zjzzTAA233xzoNj2VQXuPyquiGGIwNEnJ1NV/anq\njNzTB1cF15X7q4tBzIX+BdWYivd1r3sdUNaqvj/hGj/hhBOAouZl829729uA4sNTTXTK1nsxF/o5\nVbat2laImLenH9Pq0+bVWPVba4C+YatTv+997wPK+vEeidaKVnXqhuEeEc6N6yRWcRE+F/T19goZ\npZZIJBKJoUJH1aJlyzINIxnivow60Q4ogzC7Xeahotl0000B+P3vfw/A2WefDUyuobbddtsBxV9h\nvTHZm/Zu1YT+FG3HKq3TTjsNKHbv++67r3Y/HM9ZP5JVEYRz9clPfhIoUWnWdYqVrZ0j2ZsVBvRH\naeNXobzwhS8E4OijjwaKT8hIH9mffhF9Atp0tVeroKyE20/2Fn1/MZrRirXWj4vrR1+PNnj9GR/9\n6EcdD1Dm1u2dw7oYJJP1XtBK4HWWrUe4bmIldX//rGc9Cyj3gOuxqhdVK3QzF96X+pOi71TfrvUB\nPYdY0cQo1m9+85tAUcAbbbQRUJSwlUpUi+a0bb/99kC5Z/00b8d7zv34XPE51FBVZNoVTsz/8/pG\nxKrzvUYqnEQikUgMFTqqNKDNXAYSo75EzI+QVZuTYq6JzESWrR/C/7t/++SYlS/8+09/+lMAfvjD\nHzZ97zhk80apWLHAcdVRODNmzBhfdtllJ1RUZGNVqGrPreqKFaxlV86t5/DpT3/aMQOl6rQsUdYX\no1WE7M3x68daa621uOOOO7j//vsHxt6qauxFZmuukrX0XFfa5K2RVbX/dsfhca+//np23313brrp\npoHNRStfX4T1AvXl+XuVtr6bXqETVh+rLE+xnfte5Peeoz5cfTDWI/T6b7bZZkBRQv7eyse2MH/j\nG9/YNK6ovM3S93lntv68efPYd999ueWWW6ZN4fjs8llWtca1pBjl+rnPfa6Xw5hAKpxEIpFIDBU6\nUjix26D70Nbu97HvjPZpc1WOOuoooPgbzLex5pk2Wm2/Mg73p1LSh2TNtNtuu61pXJEt+vsYbVen\nH46MxR4f1roSsiV9LPPmzWs6lhF2Vks48cQTgWJrFbKrpzzlKUCZC6OaZLIqpte//vVAqbmmgjJC\nxyrDIvbt6ad9uhWTjXkWbmd2tIo3Vub2HGMOSswL6xTDYKuf4jhAyUlzHXovWSur3f30urPjw/se\nh9Y1yoxWVUEYlerfvV9dq/qGve+tvqACsvK5Csc1b/1BLSSXXHIJMDkPzP8v4rwYHx+flnWhWvS+\n1zoTYbSiuUntotNqD6lwEolEIjFUqFVpQHUjE/Xtqu099pcRbicDVcEYC25ugW9lo0X07ey7775A\nYcAXXHBB0/6NdlFl6Ofw+5gvpKrweyOAGvJx2sLo6OiEP6HxOyhsTiUjPKa+GdWedmhZnD4W2Z7+\nCn01zpn5O+Y2GJXm3BmdZhSbWdjmpLz97W9vGteKK644qc9Qr1DFoo3g8/o6Byper2uM6IuRWRGq\nxiUJMVJLJeOcVUUpVaHf2fON/XAcu34lo1EvvPDCpt9E1aUlwnvK58lPfvITAD784Q8DpXK2UazR\nN+inUWsqZ4+jsjES1B5V1i8UF1544YTFYNDweVClbKy+0UrZOBc77rgjUHy+PiPrKpx2kQonkUgk\nEgNB7UoDs2bNmmCWsUprrD0Uba/6XKx8rM1Udm6m8HXXXQcUNm5PcivjWkXaKDfrhnncmIcTGVNV\nbaY6PpwZM2aML7PMMm33kYiVsp0To9vmzJkDFD/Ytdde2/R7c5aMxLFOmErmlFNOAYrPSEVkvbJY\n2y36sSIGYZ+WTcnSzVFyHWmvdn3oozPyxv4mKtoIFXW7mexVGCYfjusoKl/XtpXX9fH1GnX74Sy1\n1FKTnhdVzxyrKtgPy+2/9a1vAWXN6+uxAraq3yrR3hNaAaxA4pyoTuK6iYpZ/+nGG28MlPycpZZa\nigULFjA2NjawdeGYPFeffRHRJxuh5cToRj+/9KUvAfDOd76zo/GlDyeRSCQSQ4WOKg34to0VSGUI\nsmjftrIy6z7ZkyP2L7Hjn8rHyK64PxmH/XSM4NLmr204jkfErH7ZQCcdP6MfSJ+N1X4dg2O3yoJM\n9BOf+ARQsuudU8doXo3qziqvsn/nwmx7s6itvqCN9vzzzwcmR3hNpf4WLlzYV1bvMf3UFv+85z2v\naSxeF31KznHMq4pwzqvs3HXRzVzEysPdQvX/jGc8Aygqzjkxi9/teo1u5iLmiugjcW0aZaYPxueE\n/gijVmXp+lyPO+44oNxz+m6tSyeL179pRROtCd5T/s65rOqTZQ3FQSpfoxD1tXivCCPwzE3yHvAZ\n26oivlYG57SuPzsVTiKRSCSGCh0pHCFrb8jUByZHDcnC3vCGNwAlbl5Wrx9B/4YdO42X1ydj7TTr\nQ2l3NJteBqUyajdrWxb6v//7v7UVTkQ8pnHtzo3zbd0vo8f0tRi1pr3ZSL6TTz4ZKCxNJuPcaXtV\n+WjjN0rtrW99KzC542Ps0rrMMsvwwAMPDNQ+LfvSh6ct33NznVXl70TmrCKK1ck7xTD5cGKPKeF1\nNAfF3lGtKh7XRS/mQhWmn1KrgBYQLRVm02+yySZAUUJWxvYcjXKU/evnsJ+W9cP0t+oD0jfoOjE6\nTSuBFhd9SBGDXBc+o7yPPWcRFbSV8X2utIpetBKBc10XqXASiUQiMVSo3fGzkU3KtmTv/i1WAVYB\nybq1F5533nlAYRjWNNLmKuMxXl5GIvN58YtfDJToFLOuq5RN9Nk43k573TdWixbx3GM8u9/7acSV\nvX+MuDMiR7YXa7U5F+bhxGqwsWab3+tPq4qz9ziDhJngdm7Ufuy68PpbOTnWoYvXU5W4JEE/RVXO\nkXNlvbleK5tOMGPGDJZffvlJuWr2ejIfx2gyoxb14dinxu1V7/ozrSqtcvH/Po9e8YpXAMUq4LqS\nxRu56dz53DnrrLOA4erwqcLx3IRjtLOvvj1zHdvNyzISuN9IhZNIJBKJgaCjjp8ykdg9MOa5yPbN\nv5GZaitde+21gaJMjE4zesSeMNoh3V72ZsUBo1GsEi2jcjyOI0adxHyhBx98sHY/HKNFrFStgpCJ\neM6qKKPKnDtZnj4aI3BkNGZF26vcCgEymmOPPRYo6sAcA+dYm6/jUNmorMxMnqI+3rT5LWLPlth3\nSSVsbpJz7dz3mpn2ci5c2+3mbzWMYZF/1/9pVKPrRX9Yr9DJXNiNVr+CisKoNKsmqGS8l9773vcC\nxcfjfbvVVlsBJbpR9adf1DpjrgtzVvR72GfpyCOPbBqXzw0Vs0pIn0/EdNwjrhufZTHaVHgOVm0x\nP0+rgOvFZ6e5kVpa6iJ9OIlEIpEYKtT24UBhArHSgKjqp23vBiOntNFGH44qIEav+TaW4RiFYiRX\nZI2Ow3H6do+KLNaEaxejo6MTbEzIquwuGPu2u73RYrI4I+6MzLv1RxlHAAAgAElEQVT++uuB4quR\nsViRwMg9cwr0ZxnJYwSQuSsxgtD6dMK5XnbZZafFjzPVWES8rqpAYTRRq+oJw4C6ysYox1ZQ3Xn9\nq35Xtzp0L2BnVqHK1qdrrTx9KubXeU+o4rWUqMp9Lmhl0Bdkfs+tt94KFAVlHxxVv+PSR6hVQWVd\npWwa68P1G6q7yy+/HJhcET0qG5+JRgTrm4nRqK4X6w3qK+43UuEkEolEYiDoKA9Hm7qsPVb5jX1I\njJyQ9ZsxHCvcmntiFJuRFubdaJv104oCvp1l8TJ0lYuMJdZ0EjKb+fPnd1xpIM7jVVddBRTl4TFk\nTTKV97///U2/UwWaV2NkjSzNXCQVjipRe7hzImuU9asircpgLpRz5TiOPvrovlca6BQxylCoeIxi\n6zV6ORdWANh1112BwsIjXCeq/XYR/ahV93fdzqIN+689FzFfyvvRtW1UmMrE+96x6+80clO273PD\nc1Hpem+o9qzR53PH54JRaT43ojKO603LirUcB3mPeK6trDDRb+05VPl4fCY7Z50ifTiJRCKRGCrU\nVjgzZ86ceItqU5UpRGgb1W4djyUz9e0tszE6RAakMtEG61v7pptuAopakOHI5mW8bh9ZXWQBdWup\njY6OTuzDirSnn366f2/aPo7VbGujR7QrO2dG0tgjSJ+P6s6IHVWhviLP0ci/GH1mhKFMKeYgLb30\n0jz44IMDrTTQLlSNm2++edP3nlNd/0i76CWTrep+qV/Ue6pVr58quLbNVdEvGuE6ke3HOmJVqDsX\njfeI/kmrflvV2XNXdTsWIy/1R1h/0Aol+mA81yc/+ckAHH/88UB5jhix6XMq9suK94gRYF6DKhU4\nCIXj88LqCVZX6BTxWjin3SIVTiKRSCSGCrWj1BYuXDjBEGJ0kG9PP42MMCJCRB+Qfgv9CbIylYos\nzL/LaGMmuln3VpeN+RwymBi9FtlmuxgbG5uIGvv85z/ftG/HJjsy8sbuhKovvzcCz78Lo9puu+02\noJy7+zVKzfpz9ojxe+vMrbfeekDx7cgOI7vrtOpCP+F1ispGuH6MchpmVK01fXDeU+aeWclYv6bX\n3XUma//+978PFD+Hvj3nzuutFcH99EsVirGxsYkK6dFP4Lm+7GUvA0pelcrGe8tIKtm+7FxVb9Sr\nfk6rRrs/nxvOvefuXFi5RMVlPTrvhZhLN0h4X2oJ0TJizqHP0iocdthhQPEZmpNUtxp0r5AKJ5FI\nJBIDQW0fzowZMyrt0BEqk2iHlnWZK2CsuTkjMgqZkfsxN0WGo4KyhlKsrRXHF8cd84gWLFhQ24cT\n58//ew6qO3MHrHRrV0MrCchgYw8Xt4v1w1RQ5jRYPVqlY+SNuQqx3li8Jv59tdVW46677uJ///d/\nh8aHoxKuqgtlrsE222zTk+NFX98go5FUOrFmlrZ2lYwVJWT3rrOq/jvu13smKlvR6t6u2/HT3jEP\n/7bp71Zd0NeiL2bu3LlTjrnq/hVaOoy41Fqgktp5550BOPfcc4Fq30xVtXuV0iB6RrWCzwWfhSrh\n/fbbb2KMUD8KsVOkDyeRSCQSQ4WuOn5GhiE7l4UL7dHam2UMsjFrLWlzNTLLemGyNZmN2ffWA9M+\nrY3VKBPj92VSRqXEismO5/777++4H05kYyoQO/WZASz7+tCHPgTABhts0PR751Z/xJZbbgnApz/9\naWCygtI2a4dP2aSfnqvszLk68MADgdJDRJvu3nvvzUUXXcQ999wz7QpHlqafIWZZux6qKlv0CtPB\nZFt1Co3rrVPUrTzQzVxYK1Efi88LfXC33347UGokWu25ql6Y/7fauPeUa9/q0t5DVi5YxHiB8vzS\nAqOlRQuLmI51YX1JK+33C6pDOwm3QiqcRCKRSAwVOlI4kRUZOaWCkLloP5RlW+so9q1Zc801gZJT\nohpQqVhFVqWiX8I+F0ZmVdUAixUQqj6Brjt+VtmZHcOee+7ZdA7mllhXynN0TFW9yN1vVHPOdfxd\n9N3I/ozQiRiGSgOem3kURuo5l/vssw9QOoU6p73GIOaiV4qlFbqtpdaLuTBfxpwy4fV2jKq7KpUX\n8+s8J9dHfB4ccsghQHlueI/6/FLZxPy8Bl9e0/6G4R4ZFqTCSSQSicRQoSOF08Z2wOT8HJmqLPyA\nAw4ASuawaPCpAKUigQzW/ep3iKwt1nITfq99PKqD8fHxjhVOtC/HY2oPjhndsjHj4y+55JJ2Dj/h\n71IZeU7OnX4P595IwDhnVpW24u7MmTOZP3/+UFQacMzazvUF6quL1RP6hWSyBYOci07VmP5TUZVz\nEiP14vF8PtizSsV0xx13MDY2luuiAalwEolEIjFUqK1wRkdHJ5hAzHqWXcsYZNf6dGSmfm8ElzZd\nayz59xidEiuhiqhozL71/7J/azbFaLqGigNtK5zR0dHxWbNmTfSQtyJtu4jsykgaM4id01a9aaKy\ninPmXDTmEDQed6q/T3eOgZBZmqGuj8/Ojdtvv31X+6/KRYkYhrkYFnRTLTrepzHKsFXOSLu/ixF+\n0eLS2PsJStSrFQZU0kbNqaCNap09ezb33nsvDz74YK6Lh5EKJ5FIJBJDhY58ODEqJDIObe8x4iZG\nbrm9jETFYcWBVvV+PL4+If0WMiEZjsrL/8fjup9O+uGIyL5UDp5Tp90ojV6SXcWIncgeI+vbYYcd\nALj00kubtosq0f3suOOOXHnlldx77709Z28bbrghwKQuqcOOVDgFvVA4wvwWc85c251G0LWrWOP2\nPj+0gFQdX5/OCiuswD333DOUCkf/1aBrpaXCSSQSicRQoa7CuRu4s3/DmXasPj4+vlI7Gy7hc9H2\nPEDORSNyLgpyLgpyLh5CrRdOIpFIJBKdIk1qiUQikRgI8oWTSCQSiYEgXziJRCKRGAjyhZNIJBKJ\ngSBfOIlEIpEYCPKFk0gkEomBIF84iUQikRgI8oWTSCQSiYEgXziJRCKRGAhm1tl4SS9MCNxTo7TN\nEj0XWbCyIOeiIOfioWKk4+PjteZi5syZ40svvfREG5Cq1isRVS0YYnPJWBjZ1i//+Mc/mr4Xvaow\nU3cuar1w/g9gSa11NBC0W623006OrdBuX5VOt0/Ux8jIyKR5rrruVnX34Vm3srrweI1jmGp/cb3G\nDsWiF+t04cKFE5XjAVZZZRUA7rrrrimPsdpqqwHwxz/+ESi9ofy/Y4xjFf/85z+b/m+l69irzBeX\nc2FHYufCStq+KL2G7qfu3KRJLZFIJBIDQUf9cJZgdNwPZ0lDL/ueLO5IM1JBL+ZCJWMH4CrzUF1U\n9YYSfh//HpVP7IIrHOfDJqTaczEyMjLRPfS+++5r2mc85/h9HHNVV+RoOnO7qObi/u27ZU+g2PNM\nZaOpzl5nj3nMY7j33ntZsGBB9sNJJBKJxPAgfThLONZaay0Afvvb3/b9WJ0qmyVVGU0HIjv/n//5\nH6DY4l//+tcD8PnPf34g49Gp3IjYtbaqE3D0rcV1Ikt3+wMPPBCAk046CYCNNtoIgF/84hdA6Qjs\n752rxz/+8UDpPKryEh7Hz058S0svvTQrr7wyf/jDH5r2VRU8EBVM3F7F4rn7d7stP/nJTwbguuuu\nA0rnYX8X5zbu12u0+uqrA/DnP/8ZKApo1qxZwENKp44iTYWTSCQSiYEgfTjNSB/Ow+iFrb5XUWBG\n6BjRY8SNkThVdvBeYXHw4egXeec73wmUKKeXvOQlAMyePRuAVVddFSg+hLroxrcnvJ633367+2y1\nH6Cwaq/zVlttBcCRRx4JwDOf+UwA/v73vwPw//7f/wPgRz/6UdPxLrjgAqCsS9n8f/7zH6BEakUl\npGrsJCx6ZGRkfObMmRNjX3bZZZv2udRSSzUd23P2e8fq79/3vvcB8Kc//QmAY445BoAvf/nLALzw\nhS8E4Prrr2/6+4477gjAT37yk6a/O3dGwalkHvWoRzXNjevnr3/968QcLViwgLGxsfThJBKJRGJ4\n0BOF0yuG6X7uvvtuAJZbbjmgMKK//OUvXe2/DfRd4VTZof2UyVRFqQwKvWD1O+20EwAXXXSR+5zy\n90984hOBomDWX399AD7zmc8A8KxnPQsobC/a0mXrBxxwAFDY26233rrI47aLxUHhCG33+iNiBNjb\n3/52AE477TRgsr+iFTqJzIrzr2KIEVeye6FqMzJKdr3xxhsDcNRRRwGFbavqokqQtfu55pprAvCN\nb3wDgC233BKAXXfdtem4+i3ivdkQ7VZ7XUS/U/ThRP+W3xtFpk/Oc/Bcb7zxRgB23313AD784Q8D\ncPHFFwNFDX7hC19oOq7X4pxzzgHKtfj3v/8NFGXkp/CeW7BgQS21lwonkUgkEgPBUPhwtt12WwCO\nOOIIADbffHOgvIXXXnttoDDWKcbVtH0X6LvC0ZYuW9pwww0BmDNnDgCXX345AJtssgkAp556atP2\nkRUuzn4Lr5uRMdtvvz0At9xyCwBf+tKXgHL99d1E1i6cI+3ORiV1i2FWODHqaN111wXg2muvnXJ7\n53a//fYDYN68eUD791A3cxEjrRr2GX/X9L3XXUuH98RTnvIUAH7/+98D5d665557APjlL38JlHvG\nOVEpG7mlb8i5eMITngDAVVddNeX4RkdHWbhwYVf+rKootarIPD/33XdfoESfGUXmmleZ6CPyHjBK\nUaWiitOapC9n//33B4qCuu2224DJc7XFFlsAcPXVV/OPf/yDBx98MBVOIpFIJIYHQ5GHY9bqs5/9\nbKDY5v3eCIo77rgDmGznXJzyNzwnFY221ssuuwyAr371q0CJtPnud78LFLu1zEVb7XbbbQeUaJd+\nKZ5+QHbuOcnSZKzHH388UOzORsq4necqg3VdGIlz6aWXNv1ucZqbCOfK6y5Ld1187WtfA4pfogpP\nfepTAXjPe94DFCX9oQ99qMcjfggjIyMT7Lwqm75K4Xhd9V885znPAUq0mQpH9m1UmlFosvPf/OY3\nQJnDddZZByjWBefOe+imm24CYOuttwbgiiuuaBpfJ1GXo6OjLLvsshO+DxWGx1TFO9ZYFcFcIRWM\nRTlVfyqYH/zgB0DJx/GZ6Tn/+Mc/BpjIB/K4zrXKRjXpc8h15zU74YQTgIfmvs7zNxVOIpFIJAaC\noVA4vqV9e/v2N0P4jDPOAIo6MHt+GJVNVcSeNZTe+ta3ArDLLrsAJRLrb3/7G1DYk7Z2I3CMJjnu\nuOOAwmCM3DNC6+yzzwaGY25aRS+qSLzuX/ziF4HCcL/5zW8C8NjHPhYoUYsqluc+97lA8XtdffXV\nQGGo7ncY5qJTuG6+/e1vAyV73nUiY37Ri14EFBt7tBKoIo1yetrTngYUhdRPhROvv2zcsUREdu/n\nyiuvDBTF435/+tOfAnDzzTcDZR24nepAC0qsnKxaMGLP9fa9730P6E0+2djYWFNtNlWZkXeOPSL6\nK70HvEd+/etfN32q4oxSVAl7r5144okAvPGNb2zajypO39DPfvYzoDx3VDReize96U3AQ9aHGF24\nKKTCSSQSicRAMK0Kx7erDOPrX/86AK95zWuAElcvy5ONDTNjjXWhYry75yiT2HvvvYESB2/OitnR\nMhptu/o3jEaSdT3vec8DSmTXMPR4qesziddV9h7t1EYhWTvLigPOlbb7YV4nVZChev032OChoMnI\n9mPvGNmzc/a2t70NgG9961tAUb7HHnssUBSTv//Upz4FlDydXmGqNVClbESsJ+b2RlJpJYh9bMyb\nUdk+/elPByZXKFhppYd6LDrHKhqj2rwG3rOPe9zjgJLH0zjGOpiqBpuVAqrgcfRPeR09p+c///lN\nY9a/qS9PZaMvRqXrs1UF9LnPfQ6YnJcVIz3NWZo7dy7w0BzFqtqLQiqcRCKRSAwE06JwYoVT82us\n/+NbWmWjzd7ILplMrHk0TIhM1HOwRpG29fi9cxHzbWRlbi9bkukceuihwHAom24RqzB4TkYnee5W\nJpCJ9irvZpCIeRauA5lo/Htk/86FzPfoo48GSi6J0UYy2Be/+MVAUYvOrXk5vVY4o6OjHUcHeq76\nO1Sw5sfok/nVr34FFL+nrF0l/OY3vxmASy65BChqwCg3I7Z83qgmZO4qm6pou3YwOjrKIx7xiIlz\nUklUVZ6O/Wsci3PgWK3+bTTaBz7wgYnjNf5eRaM6tHr8mWeeCUyO/BVx3V1zzTVN3//nP/+p9cxJ\nhZNIJBKJgaCWwvEt3WmlWeHb0reqn1Ya0O4sQ/HtrN9CP0jsHNgpIpvoJRybx4g1k1772tcCJePX\nvBy3075sxNbHP/7xpv0bjdKPsbeLRzziEayzzjoTfqleQaUr45SRqmzNKbnzzjsB2GeffYDJnRrr\nop/rQcToIdWb/irh+nH7mJFudr2s2zlzTvw0ou8jH/kIUPyk5l30y0rQjcIR/l4lYn6MvpqYj6Ol\nxOg11d7LXvYyAFZYYQWgRHzqA3SdVfWKUXV28vwbGxvjv//978T187rpW4lw7cVKElo+9tprL6Bk\n/K+33npAyVnzuWFtPat4eM+ccsopQHl+VF3/qu9VSkavtYtUOIlEIpEYCGopnLGxsa7VjfuZCtpm\nfYsboy5jNYPc6JLvfOc7XY8FBqMO4jHMKTCa6IYbbgCKH+Lcc88FSiUB8yasrCyMrJnOLPr7779/\nkepGtmU0YrswAidGD5kjYO+PZzzjGUD3SlcMYj2obMyzcj1EqOKF0WQHH3wwMHms+oAi7PD56le/\nGijKRpjz1mtMtS47rX1o9XF/b/a8uUl77LEHUNbLe9/7XqCsCxWMNdX8v5FirXwRPvumqoDdLvyd\nkXdR6Ua45vXZqGBjXxvVn9UTPvGJTwClKvhuu+0GwEEHHQTAhRdeCBSfcLvQunDyyScD9RVsKpxE\nIpFIDARDUWnAiApzTWKHQCOx9Hdo716coV1ZyNZe+tKXAqWjnwzXSCwhk5WZDnOdsLrKRph3IRvT\nTu33Rh+dddZZQGGDixOMPqyC11UmWqVsImJ2vJnkm2666ZTbW3VYa0Jcb51ifHx8kqLpVB24jozU\ncm702bhf82ZUNioTu5+ef/75QFGXdSM7Oxm//m/nN/bsqUL04amMVlllFaA8R1Q2+rXMxzvkkEOA\noua8R3beeWeg3DutEK9hp9aEVDiJRCKRGAimhRLGt6VVfbVHVrEta2TJ0vTltNp/q++nA/ohjKyx\nxpG+HPMpZLTWhZIRG21i1JHRJnb4WxJgno0RNtaNcz2ojK2tZ0TW4oSq3j7C9SFrb6VsjEoyL0PE\nKDehSrDemFXLe4XGey0eu9370Jwhq8bL0v29/7cKh34OLSMeV/9orNIwiOfC2NgY999//8QxVSau\n8Srou1Gxev/rdzJy12fhNttsA5S6hCopFYnPCWs3VuV5VSFGSTqudpEKJ5FIJBIDwbQoHN+ivn2P\nPPJIoEReGGViZJaQHVQpm7j/qu9lyN3ma3QDz93YflmcbE0G9K53vQsoNvwXvOAFQImDl90b1SYD\nms5z6zWsyqANPypfq/oOsx8r4uc//zkwueOj8HsrAFQpm9hTJiob2XyVf8t+S/7dHJd+QMXRam3G\nuXBNe894L7idPh3P1e2MYlUl+nfz+7zn3J+svV+KpzGiS2XT6hhGeJprZJX5xzzmMUB5fpjXo7/K\nfD7n3PVmZQJzGV1X+kXjtYlzESugLL300llLLZFIJBLDh2kN6/GtbV0f39rmVcS+7L1i7cPI/o0i\nkUnI6mUYMhWrSZufY8dGo1e0Xw/jOXYK50Tf3g477ND0fzPHFyfYmXH99def8u9GbLbqb9RK1dn3\nRP9HhJFb/fJnNLL6VmtS9uwYVCSOUdXvGtcno0XkSU96ElA6fpqbIus3N0W/x+abbz4xRphcp26q\nc1nU39uB59huxJ6+FrezbpxKVIWiqjPvxj5bPlf0b1lBW8vJtttuC1QrYK9FrGvo93V64UAqnEQi\nkUgMCH1VOK1qUhkHry1VaJOPETxG2iyJaMV0jDKRIdmbXLYvu9tzzz2BUh14SUCMUpLpytaM6Ivs\ncZh9OtrihWN1zVsRvdtzsLJAVV6N/o1uc2SqMDY21rZq8lytJ2fknBGaKhMVjBYSc4zc3qz9tdde\nGyj9kVQHqkuVsfXMWs114zWqe11GR0dZZpllJhSH17nV3LidVb5ViVaO8L53zl75ylc2nZPX13so\nRugZ1eicOb6qytgxqm10dDSrRScSiURi+DBSh9GMjIwMNIEljk2l1Eel84vx8fEN2tlw0HMh9HNp\nv5aZVPWB7xTj4+OLToFuQNVc9MofIDuPfVG0zauk9XNFf1i36MVcCG3m9maZ4lhAYeExiz4i2t71\nd5hvcfPNNy/yOPoAzYFrhbpz0Vh3LFo8ZNsyZBWHOUfmmLnGVfPvec97gOLLsSuqdcKM3NQ/ZqVs\na67tv//+wOSumHGOY52zKSomdD0XwjmJEXpWFHCtv+IVr2ja3h5Aqj2j3+wAbDSa98YBBxwAlHvE\ne8uajvH40XcTny/LLrss8+fPZ+HChW3NRSqcRCKRSAwEffXhGDFhzat28YY3vGHK743EGkS/kulG\nZFOyLZmMjEXmc+ONNwLDNSfxHFpF+bi9DNd8Cc9VheM5y5CdG3MP7FrZqcLp5/q6/PLLgepMbXNC\nVB7Wwjr11FOBUk1BlVc309s51Obf76objbXUIouPysFP/RVWFrFKdIzcNEpRpWONNOuJqQ48juvI\n3lNeA1l+VcRVZP2dVoseHx+fuG4ey2PHteZ1NUdRBXr11VcDxf+txcPaihtvvDFQ5kolYw6bdQmt\n2aj/y3ye2GHUccQKFvrHfvvb32a16EQikUgMH4bShxPthsK3rxUI+lA7a9p9OLKpqk5/sndts7I1\nfToRVXPZCr30W1TBPAgj7hyjbM4IK/MpYg6AnWDtXimD/ehHPwoUljYM/qyGvwNl7XoO/YZzcthh\nh3W1n7pzMWPGjElrUEZs9Jmf1g0z6tBIK3sFWeHY/fj36IMxO18VZw7K3LlzAfjkJz/ZNA4jQCNT\nV0H73IlRanXmYvnllx/fYIMNJnp+6Veyj1Rj5r7HAHjVq14FlOoqqnvPzXNVeVhR3W6nWgtUQlbc\nN5rVaLczzjgDKJX4nVPP3YhQfUaNeVvj4+Ntz0UqnEQikUgMBEOpcKyEbPx8RMwM7iGmXeGoZMwp\nkMXJaGQaZlfLDmX3MiJZnHNV1VGwCoNQOELWdcwxxwClR4d+qVtvvRUoc2MlXFlb7Cnj9yqcVufe\nymfTj7mIUWpGr01xbPfb7hCaYO7JFltsARTbfqfo5VzoF9CfseWWWwJw+OGHA4XVW/8r+oL08emr\ncT+xK7GVTE455RQArrnmGqCozFZWgGht6DRKDSbXIlPVaaFw33YvXWONNZrGLKIyUim71vVr6ts5\n6aSTgOL3cu58rlh5wOfIlVde2bR/4fjd7v7772fhwoWpcBKJRCIxXBhKhWM0mhEdwoiLWJmgh5h2\nhdOwf2CyipO9q4CMn7eKtHZqcxq0h9sRUNtuKwxC4Wivltmec845QLm+ka3JRKPC1QZvxdsDDzwQ\nKLX4qvIs2kU/5kLVZp6N/U3ahcxTNi/jPOqoo4DCaOvWumqFbuYi1gWM1yX2vZKdq2BVASoa8cc/\n/rHp08rIdsPVv+E6UTk3nFPT+Py/7D/OYSc+nKWXXnp89uzZEwozVqxXtelz8ZjHH388UHxw3t97\n7bVX0/Zrrrlm0379vc+BXXfdFShRiuYkqXjMXVI5uZ3rzOeHfbwaexItWLAgFU4ikUgkhgsdKZzY\nL73XMEvanJP4VtZ/0QdMu8KJLEuGorozCmXevHlAYRq77bYbUDo2yga9VnVzSgbpw/Gc7exp/pbR\nSVVdMV0XMllzWKyk3SmiT2cQc6GKM5Pc/kbDhl4oHHM+ZOGudf0ZZsmr2lWqRmQ6V15/7w1r7Flp\nu92eM62gVeGf//znxHnUicx6+DfjIyMjE5YJ1ZtzIfzeCE4r5/u9z1xzlczr0hpkV1yVi2rPOfUe\ns5+WPiKj52KunNfMa6Mi8x554IEHaqm9VDiJRCKRGAiG0ofj21O7pFEm/VJUDZh2hSPD0DarvVvb\nqlnV9smQeZx55plAyUD+2Mc+BgzOb9FYQbduf/Sq7XbffXeg+CUuvfRSADbbbDMAXve61wHFRt/K\nX9FpP5NBqr1hRzf1w0Ss6i3Llz1Hn53fxz45KtBufXSLGH/T/xsrZtT14XiPRIuDqkyLhErGc9fC\n4Zo1SlXfnQpFhXPxxRc3fW+FAf3i+qWsFGDejRF7VRVOqmq9Paz0UuEkEolEYrgwlApnGjEwhROZ\nRPQb6JO54YYbmv7/jne8o2l7mcmcOXOAybkCnaITVt+vXvANx2n6f7/rgDUcJxXOw+hmXQhZs1Fj\niyt6kYfz6Ec/Gij5UbFCdcPvgWLh8P/uL/qzqu5Fnxsev6q6fIzQixXb4zVMhZNIJBKJoUIqnGb0\nXeFU+RGqGInby2y08cow3I/Kphd91x8ex2LP6rVbW7fK3JcYddQKS8Jc9Ar9nIt+K2ShqrCqdMzr\nqsqub7zHOvHhTOXPUnFUVdCusoDUvc9nz54NlAoDQuXicWPVBX3IjsO50Oe03HLLcd9992U/nEQi\nkUgMF1LhNKPvCsdoEm2tw4pe5Ft0G6XWL9Rlh6lwCurMxejo6PhSSy1V21djFFrV76pqKXa6jtyf\nFS7M56qqQNBwvNpz0SqiLq5N82msmF4V2ef3KhK/F1P19Gn8XYxK22abbQD44Q9/CEzuomv1h3/9\n6188+OCDjI2NpcJJJBKJxPCgrsK5G+h5E5ohwurj4+Mrtd5siZ+LtucBci4akXNRkHNRkHPxEGq9\ncBKJRCKR6BRpUkskEonEQJAvnEQikUgMBPnCSSQSicRAkC+cRCKRSAwE+cJJJBKJxECQL5xEIpFI\nDAT5wkkkEonEQJAvnEQikUgMBPnCSSQSicRAMLPOxkt6YU9NrxwAABmdSURBVELgnhqlbZbouciC\nlQXDOBexZP6gMIxzMV3ox1z0qr1Iu6hbQLeq+HC7c1HrhQMPDXBJKYdjP/G//vWvftX3WkfrrLMO\nAL/5zW86+v10VVhOtA/7pcDk61V1/byR7ajoi6RqP/7d72MfkyrEvioivsDsk+J2cft+YK211gLg\nt7/97ZR/b/UwXhLuDc/NytX2dBKdnuMiKl4Dk3tEfehDHwLgyCOPbNqu2yr3aVJLJBKJxEAwlP1w\nBi0rG9D3fjjixS9+MQDf+973FrmdcyFD2WSTTYDSpyJev16xvF50Mxx2xLmqWnd152J0dHSSomnV\n4dUeMK985SsBOPfcc+MYmj7j71Uon/rUpwDYf//92x1v0+9VMvH7sbGxjrpcTjXWuui1sqnbdbcK\ni7N58aijjgLgmmuuAcpzqNNnb7tzkQonkUgkEgPBtCqcVVZZBYArrrgCKP6NQaPBft1zhdOKNVX1\nGhePfOQjgcJcf/WrXwHwyU9+sp3D1x7f8ssvX6tH+cP76GguYhfCKqXhdnY5fMQjHgHACiusAMCz\nnvUsoHQhvOSSSwD4y1/+0vR7r3PsH9/qHqjDZGfOnDm+wgorTNjCRfSRtPLtOAe77bYbUNbBEUcc\nAcDHPvYxAN7xjncAsPXWWwOw4447AvC4xz0OgJNPPhkoviF9M3/729+mHH/VelXB9oLVx+vbilW3\n6gDaLrwGzo2+26c85SkA/P73v2/reL2ci17Be+L+++/v52GmXLd15iIVTiKRSCQGgoEonB//+McA\nbLzxxlP+vVWI57rrrgvAL3/5yym372GIaN8UjlFIj370owH44x//WGtgsnvZ17///W+gfxE5g2Bv\nRkw5N/aSj8pG9iZ7P+ywwwB48pOfDMCf//xnAC677DKgMFjnTFV43HHHAYVRv/SlLwXgK1/5yiLH\n2Y+5OPzwwwH49Kc/DcBPfvITAObMmQPApptuCsBHP/pRoPhkXvCCFwCw4YYbArDeeusBsMYaawBl\nTv10nYhXvOIVAFx55ZVAmYsf/ehHAGy00UbxfCb+3W9Wf8cddwDluvYa3/72twH46U9/CsCWW24J\nwBZbbAGU9fKkJz0JaB1JOkwKJ2K77bYD4KqrrgKK8qn7vHjGM54BwK9//etFbpcKJ5FIJBJDhdp5\nODNmzKhUEvoZDjjggKbvb7311qb/GyFhjPeKK64IwDbbbAMUG/wNN9wAlMgZbfV/+MMfAFh77bWB\nycqmygfg293jyaj7kTz3mte8BoB58+YBsPPOOwNw+umnd7S/o48+GoBvfetbQGEcVb4f/WP6MfqJ\nkZERlllmmZb2Y1l3zDGJLFyF4nay8qc+9alA8Xvp15Dd77LLLkBRRKeddhoAs2bNAuDiiy8GYKed\ndgJaK5tOsaiIvcc//vFAyXdwTW+++eZAuW7vfve7ATjnnHOAYh246aabAPjud78LFNWvP0qWHv1e\nO+ywA1AUzHXXXQeUuYvKRqg+Yz5Iu2jMSRJaJByb+47K5qKLLgJg7733BmDNNdcE4IILLgDg6U9/\nOjB5/VTB9XLKKacAhfW7n5tvvhmoVjbTGD1bGz7jnEOfR3//+99r7aeVsqmLVDiJRCKRGAgG4sOR\nbalU5s+fDxQmak6Jdmwjb5ZaaqlaxzHyZuWVV25re5mR0U70MQ9HP9SNN94IwGqrrQbA7bffvsjf\nyYiroop65b+KKrAf+RZVWfH6pcRjH/tYoDBg/RT6MVRKKqFTTz0VKAxW34xKyDl8wxveAJTcgzvv\nbK+wRDe2+pgx7lrz/7JlfTLiZz/7GQB77LEHUPIkjFKTpbsfI67c3qg0r4VK5dJLLwWK32uK8Tf9\nzvE2+AwH5rfwOv7iF78AilK99957gRJF1so/4TmplFWDrrMvfOELQP1qCsPow9Fq47rzXB/1qEc1\n/b/XVp304SQSiURiqFDbh7MoqFhkHr5FZR533303AO985zsBOPvss4Fin95ss82atpelyWyqIFur\nm8fToGy6RmSGt9xyCwBvetObALj22msBePvb3w7AJz7xCaCoOJmHrPwf//gHAP/6178Wedy6TKVV\nTaVu0EY+CzDZt+b/VS7+3/VkNJFzokJR0aiQVSyuG+daFWiUmr7GE088sfY51sV///vfKf+v70S/\n5Zlnntm0nXNjZNWqq64KlHXk+opzLltXRVoTS1u8cxhRpT7b9Y/UQVUByFhVQ/+k6yDmLEUVN1V1\nBCh1wjyukX4qp0HUiesX9AEaCew94bk7Fyoc/WBaWGJFi34jFU4ikUgkBoKB+HAOOuggAL785S8D\nkyOnZKjWCZO53HXXXUBRAUbw+NaOMDJDH5GfNdAzH45qzXM1gkpWraIRMhO/f+ITnwgUJmzehNFM\nMtWPf/zjAGy//fZAYTZ+dqpcBmGfjqza66xt3e/Nv1HtWU1YBqxNX1a+6667AiXHxf36d7d3PfWy\n0kCVPyv+31wPo9XMBYmsXhYer2u0IkT4eyM6jdDTjxUjrYwQMxemqlrxINaFuUj6O72vVcBaSlwf\nfsZ7yuu+5557AvDe974XKJF+Riu2q3Aa1+vChQu7motYtdtzcH2svvrqQLkeEW6v/9PrrIUk+s1j\nBQvXjc+jQw89tN1TmRLpw0kkEonEUKGnPpwqyMJl+75tZV1WTrY+mG9bWZhRRp/73OeAwubdj/Zp\nbcLTaZPdaqutgFKXSca6/vrrA2XsMhDzId7ylrcAJV5ehrn77rsDJXLPzHNVXmTn2267LVB8BWbZ\nqw6++MUvNu13OlDlR/J6q3C1uf/85z8Hypyq7mRrzoWs8WlPexpQGK4s3d9/6UtfavpdP9ZLVb04\nYaUJ/QlGpbk+zBHyHL2erdSYfklzS8477zygRKdV/V4/qHPonE1HjxnXrEpXP1JUNFH1VfmGDjzw\nQKBU+VAVdBCVBvQmwstj61OJuYoqliolpALyOmnNiXOiv9N1JpxT/y763dgvFU4ikUgkBoLaPpyR\nkZHK3hmNFYehvH1lHtqtZRqy7EMOOQQolWy1sceok+uvvx4o9X2EjMVoti660nXtw3HMsmsVjozB\nMZpDol3ZPAtVn5nm1rjSlitLdz9z584FSjScMLLr6quvbtreuW2Fftrqqyoj+33MGTAfR9t91Zp1\nOyO49NG4Ds8//3ygVFpuN4u6m95A8VxlrDJUmajrwUg7/ZeLOA5QfH/Pfe5zgRKl5n6MzFM1VOXf\nCK+FPiCV1cyZM1mwYAFjY2N964cTz6mqcoXPCdWB97++GdeNlpNvfOMbQFEBRna1m4dVhV7cI56L\nY/PZqI/O+XdurIhuxQCfrf5fS4bbVeUyei38+6B8vqlwEolEIjEQ1PLhzJgxg6l6fcS3oowysqS9\n9toLKBFbZpBbGSBGZLjfJzzhCUB5+8e/q4Duu+++pr/LCqq6LnaLqWpmyc600RthI3Pcb7/9gDIH\nKhCVystf/nKg1EwTRhHJ5vRzGHXkOJxz+6AY6WMnySo79yBRpXBUYZ6bCrrVWN2fNv9of1YZqaRd\nj/2wV6+66qocfPDBE7lm0YfjOclgXS/68lRAVZCRxnVm/S/vEa0Mqjxrr7WC90jsFfRwt8+29hHR\nrrKJ27tWva/t+WO+ndaD73//+0CZO+fGHBOvswpI/8gwQGVjBK8+3AjnKNZCc2422KDZMON9XwXn\notXa77UPLxVOIpFIJAaCnubhtOqU97KXvQyAyy+/HChv11b5MjIUWZeVl41qMxLn/e9/P1AYcnx7\nx6z+KVDbh1PFAGTtqjdrXRklZiSebEy78te//vUpj/eiF70IgDe+8Y1AsfnL+uJx9enoN7PadKz+\nUIVB5Ft4XVVlXjfZucqm3U6Pdm60Jp+MN+bxGBEUcxSq0M1cRPbu9ZaZer1E7AhqhKaVKU466SRg\ncpSR+Tra7s844wwAPvvZzwLFH9Kuyq9Sf4NYF86Rx1bp2MfGOXjf+94HlKhDa6/FfC7PZa211gLg\nd7/7XSfDmoRezkWsWVcX/t617Tqowp/+9CegPB+6VTDpw0kkEonEUKGneTgyRm3kRg0J83B8u+rf\naAVZoJ0er7jiCqD0RxGx34q9QqzUvAhl0zGqmIGsynOVveuPOuGEE4DCQKuUjeeuvVqmK9uL2+27\n775AmXtt+9p4Zf9tqL2eoyonxbmJzLZd34pz/eY3vxkokXgf/vCHgcL6VDjdRuS0M54qJamyif1q\nop/K6CXhOamUvcfe9a53ASXqLVoLVAcqHK0Qjqvq+rudv1tUH6x20a4/wDlyDowuNIv+gx/8IABv\ne9vbAPjIRz7S9DvnJvZVco56pXB6idgjKNbgq4Jz6nXSOtAK3mtWWzCSrwqf+cxnAHjrW9/a1v6r\nkAonkUgkEgNBTxSOSkUGGZWNb2E7eJqNHyEDsfeLLPz1r389UNh97NxpVFxka/bzHgRi9JdjkaXZ\ni0PmYp2vdnNB2o0qsRKyas98DtmeLFGFtc8++wC9ieBrl8HGjqtGHRmB45z596rjGLn3gQ98ACi5\nR9rBnWsjtdx/9Jv0MlptdHSUWbNmTWKoMTveOarqpOn6cXsrBXgO+jGNPot5O15//RhaH6zM7v6q\nIGN2P4OoJi68HlaMsGqC95jXybXuWH3+uJ5cJ6q+2267rbsT6AM81xj52y5e+MIXAuU6G5FpLcZo\nVfD/Khbz//SjVuU+datsRCqcRCKRSAwEtfNwlltuuQn2JYtr1bNFZqNd2MgIcw9kvOZh+HdzVLS5\n6u8wakm7dhU7t4aS6GVM+ejoKMsuu+yEook2+BiFpG3VygFWxK3qyeNYjcs3h0R/VIRzq69G/5VR\ncuZnOE6ZcS9zk6rmVSZqZJ7RikZYqWSsICGDtTK268Aoo9e97nUAvOQlLwGKopbFqxqdQ32HVflY\nvczDGRsbm5Ilxh5AraoluL3K+PjjjweKj07W7j3ovSO718cng3adGSHqepRZxwoDrt9e1g9rF577\ndtttB0xWxJ7r6aefDpTup+ayxOtrr6HYYbbd6MeIqfLvOoVjMqrU6MKIWEFbvPa1rwWKindduJ15\nfVbfcD14PJWQVqR+IxVOIpFIJAaCvvbDkTVddtllQGG4HtO+JiqVaFsXMhFt9KqEKsSYdrPsjXZZ\nxDl3XEutKuorRit5jp6zTDP+PbJyGYiqINr+N9poI6CoAX9nryEjuIxau+CCCwC45JJLADjttNOa\n9teLHIPY70b2ZnfC6IeQzZ966qkAzJs3Dyhz5LnpV4hqwOhF10vsduk46uY6DLJ3fVS29vYxm16b\nvXkW5qDIVI3Ycn21qizhHLp+9fVpVYg+p170BmoFx+R6sdK6XU+9/ipex6iScXs7ferf2nvvvYEy\nl1X+inbRj3Whr8R7INat1L/pOerv1jerkonWIp8DDdcRKPl/PovrYnR01CoUmYeTSCQSieFBX/vh\nyDysfLz22msDpU6Y7F+2rjKpytqXGbeKKooM1r7w0ZfUqQ13KlTlM8hIZZxGznlOjsFzkmnac1xb\nrBUKjNgR2re18cZoKPtgGAG46aabAoU5x4jCXiLa/63vZi6QY3RdqHRk41aNtuKxcxSjj2SqKhwj\ndczSN/fpwgsvBAaTgxT7mLSC1817wwoSMtgddtgBKP4rc5f22GMPYLIiFs5RXBdu57XRZ+OcxCz/\nTmvvdZK/4xgOOOAAoOSMmHejEjY3zXP85je/CZSqHMJ1pB+zVb26fmBkZISZM2dWrrkYPRb7XZlz\naKSd/ZOsP/mc5zwHKD65GHXmcybWt1TZdOrfrusDToWTSCQSiYGgq1d97OVQBSNmzKa3a6WMw7e5\nb2EZ6EUXXQQUFm6EltFtkbUJI7qM7DnqqKOA0jnS/aoirLjbDaLqMoLKc/YcjLx5/vOfD5QaZxEy\nFeuDWQ9ss802Awqb00YbfTAyFo+nr+aYY44BSjSTfVK6QYzYE7IpowuNmFHRyjxlabI3z93r/bzn\nPQ8oLF4Fqz/Kdfi1r30NKNf7yiuvBEqknuuqlbKN/ZzqQrt2Hbh+jDZyrPpmtM17Hb3+Kh9zVlTS\nUV06Ho/jnMl0PZ7Kyb+rLjpVOI3qpup+jVAFqGA8J3OHvL9F7KMjPI4q05yTuufSi+jW8fHxJnVj\nLqJr1Otijx+72qpwb7/9dqA8R7wn9O3GHCR/b/+sWGXe4zaObxBIhZNIJBKJgaAvUWpVjEAWpY1d\n/4Nv/sMPPxwoTEU2LtO89tprAXjVq14FTM4c99MIG+uYbbLJJkCx/RqtNgW67vgprFyrTT52fNRf\n5VwYYfPqV78aKEzEczFD3N+rDvy9TDX2ArGrqqze6JVWmcV1I3CmYvVej2c+85lN52iETfTFqGxU\nMrI15062Zr6FylRWqBpU9bmuvvOd7wBFFdj1spUyF3XmYnR0dLzRVh+71lb5dFRVrmm3P/HEE4Gy\nXvbff/+mT318+q8i3I9Kyf2rDvWLuE7jNYz38iAj9tqF68xITKvIm7fzgx/8ACj9uFzz7fqWqp5n\n/YjYU9V732oNUrFEqER9HtjrxzmJHT+9t4z465WyySi1RCKRSAwV+hKuESOwYsSO0SduJ0u3z4W/\n8+0rM5Hly4T9uxnpRiGZS3D22WcDhdHay34QiB07tcFalVU2JgMVfh8Rq/zqx5DNq1ycG3MNovpz\nP0ZuqRq6xVR2eb/T7yCz9FN25vrQ1yIbj34IqwRbRcHKyW5vDoMRe+btWMPPrGwrH7jOrM4wVQXu\nur6YaKsXraLVPHfPTVVoh1iZqWtcP6Tq3+svjGISRjk5J+ZhmaPitVABGZ3WGNnZbVRf3ci9dqFq\nUCV633sPeDz9HdYxbBdRBay77roTPrW6iPsyV8j71uuvclW5RFhFxWepEZ533nknAGussQZQ1rjq\n3n5a04VUOIlEIpEYCPqicGSFMhpZvNFDsrWvfvWrQMmS16YuY9GG73ZRObk/c1uMevP4RvD4/XRC\nRmSklsym3QgYqyx4buayqN6c61122QUocflmpGvP1jfUK2XTDvTZmPmvutK3JjOt6pcTa2i5TvRr\nyLxdV7J0FYtRjVYuiHMd1YDops6cOUCqd2E+lEzUe8MoI+uCycaNSjQKTaWy7bbbAkX96evzuCqU\nmM/hulN1XnzxxUBRWFXXotOctcY8nH4pGz+1bBj1qCK25poWlFjdPt6DzllV3yRVSC9QVSXauYo5\nhTEiz+otXkerqpx11llAuTe87zvtKNorpMJJJBKJxEDQ11pqvoVlGEZeRNi1UPYmW5Oh+JbW/+D3\nxx57bNN+Wp1LG2qiZ1FqVdUQZOHmAPW6Cq9x+qqBVpW8q9DLaCSVqWMyQkZla06BKk5VZg0+/Q3a\nqVU47s+5Vt2piFS+srtYAblh/FN+L7qJRvLcW11nI+2MvFMFmq9lzTT3G303Rilq8/ec4zqQCcuA\nHZf+MH2NUY2oVHqxLnwueD26hWrOiC7P0VwXrQD6bmJdMq0D5ue0+0ycjog9o0tjvyQ/Vb5adZwL\n/ab+vtMcM9Fp9GIqnEQikUgMBH1ROOaSnHfeeUCJzDJb3rdxVX0n4fayPJVNrD+m3Vr1YCy7tta4\n314qHKuwWrOsXXRbo6oKrezTMljVZJWfoh/szbGYGxB9fX7KzuN2ItaFku3JXN0+RgB1ik7mQoZp\nlrxwzcdM/1ZjjfkU+lqcC+fW6MivfOUrQMlFk+ka0Wd0WvTNRB+Tinn+/Pm1qgI/PKZxKPetPtde\nIc7l3LlzgRKdZlSiOWl+mr3fCq2i6np5j+hzvf7669vdZavjAaXvjdUZ/DTaUVjvUj+r8Dklqp5X\nqXASiUQiMVToqw+nCjITWdZb3vIWoEReaavXHi0b923brl/CvAwrsLaBnvlwZBiyr257b7RCFRtz\nHEalGZ8vZLRGdjnObthbLzurDgM6mQv9UfqRWmXw96qCtfvVd6OPxvXh31VWVb5GIwC19TdEbNWe\ni3Z9NnXXjds7Vi0bWh0OO+wwoPh2vDfcf7QGtEK0yAxT1YWqOnUqbatCu858LmklaBfxGq288src\nc889PPjgg6lwEolEIjE86EjhRMZivacTTjjB7YBS16cqrr1VX5uIVtVme5DJ3HOFYy8eqzYPCrGC\ngXPcLovsB3ure72HBXVrqS2zzDKTFK1rM+aStUKnajH+rt2abq0qwPdiXTz2sY8FSn2w2KG3V4iq\nsdP1Z+WKWFm9H1aATnt1eW7mU9lN1/w/OwXXjcRrF+nDSSQSicRQYVp8OO1CNhhZWlQ4PWRIPVM4\nRvdoK+819tlnH6DkOAnt1va2jxiEwqliksPu2+lVVeAZM2ZMsOsqpVClQOrmCLUxnqbP2BcnKt+4\n3eJQLbouWvlu2rWUDMNcxOtj5QH7cR100EHA5Oi3Xnc9ToWTSCQSiaFCXxROr9+eA0QthTMyMtI1\nI41RQ0aNdOvvaLe7YhWGgb0t4nhA/5RSt6x+UVWmVb727rEqsIrIfBxzRWbPng2U7pexj1HM53L/\nDdGGTcePVgM/43qJ/589ezb33ntv29FID491fI011uDmm29e5Hax867z7xxZeaSVMqla83XXi3O6\n9dZbA5NzVkQ/7pF2n52tInA7vUc6ncNUOIlEIpEYKtRVOHcDd/ZvONOO1cfHx1dqZ8MlfC7angfI\nuWhEzkVBzkVBzsVDqPXCSSQSiUSiU6RJLZFIJBIDQb5wEolEIjEQ5AsnkUgkEgNBvnASiUQiMRDk\nCyeRSCQSA0G+cBKJRCIxEOQLJ5FIJBIDQb5wEolEIjEQ5AsnkUgkEgPB/wfzCMuiOYA8WwAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11c9304a8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"rows, cols = 10, 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling from the generator\n",
"\n",
"We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXeUFFX6hu8oKggIOkQDjAoqBkQHRMSAYc1ZgmFdI4qo\nmCPrsgKGhd01gBhQAcUlqohiAEEMJAEzCIKKIjmLgGKY3x+/U5/PSF+na7r7TvfM+5wz57ynqK6u\nrlvVl/v2F/KKioqcEEIIkWm2KusTEEIIUTHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEII\nIYKgCUcIIUQQNOEIIYQIgiYcIYQQQagUZ+datWoVrVq1KlPnUuEoLCx0M2fOXFlUVFQ7leNoXNJL\nOsalVq1aRQUFBW7mzJnpPLWcZ/vttze9cePGuC8v82elevXqptevX1/i/vvtt5/pWbNmJdyncuXK\npn/88cdSn1tpKSwsNB33fo37rMSacAoKCpy+2NLHjBkzXF5e3jepHkfjkl7SMS4FBQXRcdJ1WuWC\nJk2amC7FZFzmz0qLFi1MT5gwocT9R44caZqfnTRq1Mj0Z599tsW/8x7KRCmy6dOnm95qq3imV9xn\nRZaaEEKIIMRa4QghRCrkosXIFUYyqxriW9WQRKsakukCy1zVVKtWzfQPP/yQ/vdK+xGFEEKIBGjC\nEUIIEQRZakII8SdkwtLiMTMZWLJkyRLT9evXT7hP1apVTWfCRiNa4QghhAiCJhwhhBBBkKUmhBBp\n5C9/+YvpcePGJdwnVH6Wz0YjGzZsSLid0Wu//fZbWs5HKxwhhBBB0IQjhBAiCLEttUqVfn/JL7/8\nktaTKQ3bbLON6Z9//jlj75OJ5WU6YQ0m1mbKBFtvvbXpX3/9NaPvlYgaNWqYXrduXfD3j8O2225r\nevPmzWV4Jn5oqTRs2ND0ypUrS3wtI5x81kxFw2ej5RqZ+J7TCkcIIUQQNOEIIYQIQmxLLRtstJo1\na5o+/PDDTb/77rvOOefOOecc21alShXTL7/8smlacYsXLzZ94IEHmp42bZpp3/Iy05VckyXTNhqt\nVN/n5LXg/pHV2a9fP9vWvn170/PmzTO9evVq0+3atTNNyzDbbTSSbTYa7++orhkt0vfff9/0Tjvt\nZHrMmDGmL7jgAtPbbbedaVpqBx10kOkPP/ww1dMu19AijloeZKNtnw60whFCCBEETThCCCGCkBWJ\nn7S32BGQdX3OPPNM05deeqnp1q1bm4668dH2o77mmmtMs0w6O96xi9/o0aNN9+zZM+G5l6WNli4a\nNGhg+ttvvzXNqD8u8XlNGb1HG41E22mFMbptl112Mc2oLtaBou3Aku+ff/55wvcUv0M77KSTTjKd\nKPlw9913T3iM888/P6F+7rnnTPO+6N+/f8L3KQ/PS2mh7f3TTz+Z5nfOSy+95Jxz7vTTT7dt5ema\naYUjhBAiCJpwhBBCBCErLDVGwzCqhzWJzjvvPNNHHnmkaVowUa/yAQMG2LZ69eqZfuONN0y//fbb\nptu2bWv6+OOPN01bgJE8XOKWh2iSRYsWJdxOi2zt2rWmGSX4/PPPmz711FNN0yaNrhcjBmfMmGH6\nyiuvNM1IpzVr1pim1SobrWT+9re/mT755JMz9j6MWONzcdFFF5keOHCg6SuuuMJ0JhO1U4VWMa1C\n2ry0gmkb+pLEaSPz2eL30tFHH+2cK24h85nI5muWDFrhCCGECIImHCGEEEHICkuNS0YuTbl8nThx\noukhQ4aYfuutt0xHUW3NmzdPeLyvvvrKdNOmTU1zyT9q1CjTjKri0rg8RY04V9wCYMIeoY3GZT2j\nBOvWrWv6qKOOMv3qq68655x77bXXbBujpWhZ0Lrk2JUH6zLTfPTRR6aZ4FkSvLaMmOJzyTL3vtL6\nvu203WipZQO08/nZeY/z+aD2Rd9R77rrrqa///5707znDz300C3Oa9asWaavu+460yNHjjTNZ2WH\nHXYwTSs629AKRwghRBA04QghhAhCmVlqjGJigiejzmbPnm2a9hrtnd122810ZO9w6TpnzhzThxxy\niOnPPvvMNJe3XP737t3bNJfSZVGSP5PQPpg+fXrCfRg9yAQ2n7348ccfb7E/o6V4jB133NE0LTrW\nuOP7RDXzRHFLORkbLVGE5bJly2xbFCXlXPH7nAmhtKGGDRtW4nvyWWftw7lz55rmWGcafscw0uzT\nTz8t8bU+a9fXtmXhwoWm+f0zZcoU04nGhNfYd204PtlsoxGtcIQQQgRBE44QQogglJml5mtz4KvT\nRdutc+fOps8++2zTUXJgnTp1bFuXLl1MM3mRnQ2XL19uesGCBabLcw0oJl7ecsstpmmvMTrmoYce\nMn355Zeb9tXM+uabb/70/fk+TOocPHiwadoXF1544Z8er6LSpk2bEvfhvbv//vub/uKLL5xzybUc\nYYQnj/fMM8+YZqsCH61atTJNOzAktIeTsdF4f9Jy572fzDVkmwY+K4w2u+2225xzzl1//fW2jT8R\nZEMH2csuu6zUr9UKRwghRBA04QghhAhCUEstrkXF5T+X676kqKgr5KZNm2xbr169TF911VWmE9X6\ncs65N9980zQjWGjH5UpEyJ/RokUL02PHjk24D60zXqOOHTuaZrQNI/8SwVpqLJnPEve8R1jCndFQ\ntCDKW8RgMuy1116x9mdkGKM24yTTcvxp63Tv3t30PffcU+JxWOcwV9i4caNp2mhxYTQmv8/YBiXq\nMswkatYovP/++0v9/unilVdeKfVrtcIRQggRBE04QgghghDUUvPZaLS3CLtP3nHHHaYbN25smgmE\nkWXD9/nyyy9Ns+PnE088YZrLW0bR0DqjpZYNkSKpwmvENhBMOLvrrrtMP/zww6aHDx9umlFSJVlq\ntMJo51x77bWm2c2VVhvx2Wi8FyJ7tbxAq5Hdan0wemzy5MlpPRfe8zfffHOs1zJqtGvXrqZzpVYe\no8cefPDBWK9lNCxr0/H569Chg3OueIdhJqBnQ+QsE4XjohWOEEKIIGjCEUIIEYQyS/xkxFKtWrVM\ns2YaLbATTjjBtM/qiiyVqlWr2rY999zT9HfffWf68ccfN82oi3Hjxpk+7bTTTN96662mc73r3h/h\nMp0dTxk9w7YFtFTi1DVjnTS+jpGE7NDKZDpfohyjeULW4woNIwmrVatW4v4jRoxI+tip2DS0l33Q\nAr399ttN0ybPFeLaaISJ7EwgpRX8wQcfOOeKf8eMHz/edDKJvtmMVjhCCCGCUGYrnJYtW5rmj5oH\nHHCA6Xnz5pmOfkxzrnjZFK6Uomqs3JelUpo0aWKa/2Nv27ZtwvOqXbt2wuNMmjTJdHlY7fB/WPyh\n/ogjjjC9dOlS01xhsORQSbB3O//XxpXM119/nfC1+fn5pvnjK/93zpVXMmVWsh1Wfz722GNL3J+r\nE1YvZoOvKM/D97q4MCdo0aJFJe7P/+VnG5nO7+J1ZkNJPlsNGjRwzhXPQWQzQ8JxZcBOnGcyNNk7\n+kIIIcoVmnCEEEIEocwsNS4pa9SoYZp2GZeMDCagdcIyNq+//rpzrngVWu5Lu4bv+Y9//MN0QUGB\naVo37BdfHmw0wmtIK4o/TjOfKZncI1oniXIskqmuS+bPn2+a158/WtNe4/v7+s1nO2xid+edd5q+\n7777SnwtSwdl8n595JFHStyHJYp22GEH0+vWrcvIOZWWTJdJ4r3Hau3MyYlsPdrPtFMZ7OQrA3Xj\njTea7tevX6qnnVa0whFCCBEETThCCCGCUGaWGpeDtLcYpUYbjfkZUeMo5xJbJL6yJmwiNWrUKNMs\nscHzWr9+fcLt2VBeIlPQ6tpnn31Ms5wFSxHRIlm1apXpdJcqqV69umlfpJOvAjitQY5pLnHvvfeW\nuA9z0s4991zTzz77bFrPhdeftreP9u3bm2YF9rKy1Fg1/tFHHy2Tc/ARfbf4ohL53UNohSeTG5UK\nvnNIBq1whBBCBEETjhBCiCCUmaVGy6Nhw4amO3XqZPrzzz83zcZopbVr+J4sj7NgwQLTTGRj1Apt\nOiaErlixIuHxywM9evQwzZI3/Jy00dINE1LjJgyyaRZtv2yHCcmMPHrqqadMszEeqVmzpulM2mj/\n+9//TC9cuNA0ywyRvn37mt59993Tel6lIdtsNBJZ2kyMPvroo037ngN+V6VSfof4fjpI5XtOKxwh\nhBBB0IQjhBAiCFkRpfbee++ZPuaYY0zPnTs3Y+/v6wvPSJ8rrrjCNJMjqcsbtGXYGKosKCwsjLX/\nnDlzTDN6KpcSdT/88EPTjBL02WiEzxQj9uJ8fh5j9erVphkFxRqH++23X8LXMgKtUaNGSb+/+H9Y\nFTqZqDDWzksXmfiJQCscIYQQQdCEI4QQIghlZqlxic4IqKefftr0OeecYzqZ+l2J8EVasJQ6o5hY\nvyoqFe5cybXByguMjGKyJUueh4rGY729ZKAFlW11upKlTp06pmkp0+ql7Uk4LnfddZdp1gpMBBsW\nsn7g9ttvn/DYLJ3P54JRpbTGc+V5yaZnnOfis9RatWoV6nTShlY4QgghgqAJRwghRBDKzFJjohIj\nc2ijPf/886bjlrOPYBc/1nFq3ry56eHDh5umFTB06FDTZb3EDgXHhfYO7RXWVUs3tA/iRt6wc2yu\n1rtjgjO7nN52222mWaKe8DNfe+21pplMzTpbkWWaTFKtr5Zgx44dTT/55JMlHiebyYZnPBqLZCLT\npk6dmunTSTta4QghhAiCJhwhhBBByApLjRE4Xbp0Mc3ES0bdjB492jSttsg68dlo48aNM12rVi3T\nrLt14IEHJjzH8gyTBNn6gQl7jFLbcccdTTMJ1tdlM+KSSy4xzcjEtm3bmo5b+pzv6YuqyiWaNm1q\nms/CY489ZprWj88O80WylRZeT9Z7YydWIUpCKxwhhBBB0IQjhBAiCEEtNdolPivk7bffNn3iiSea\nvu+++0z36tXL9DXXXGM6ss/YNZRRNLTImFTH4/m6hZZnWGuLNebYiZXXhR1S77zzTtOl7QToG5cm\nTZqYpqXTokUL00888YRpjnV54OGHHzY9bNgw061btzbNCEufvVbacaHVzOTQXKd+/fqm2VU4G4js\n0mnTptm2li1bmman4lxEKxwhhBBB0IQjhBAiCBm31Hz1iRhddsQRR5jeY489TFepUsX0TjvtZJpR\naGPGjDEdWQe0X/iejLRi8uLIkSMT7l8RYc06dvPceeedTbNOmS/B8vvvvzdNay7RvhxDjnMyVpDP\nRuO9Ux7aSfB+feGFF0wzwpB6w4YNpn0JtNEYsGsn66StX78+hTPOXpKx0WjLf/rpp5k8nWL36skn\nn+ycc+7ss8+2baz7yFYumYD3SmmT7f8MrXCEEEIEQROOEEKIIGTcUkvGopoyZYpp2gW0VNasWWOa\nrQ1o70RtBl555RXbxq6FM2fOND1hwoRY51jRYcQSrZtkiMaxdu3ato32Jo+dLsqDjZYMtCZph3KM\nKleubJrtJ3I1OTYEPhstEy0MeK+yfmRE9+7dTffp0yct7+kjEzYa0QpHCCFEEDThCCGECEKZ1VIj\njMLwwUgnWQG5RTRe7CYpwlERk5kzRVnY7926dQv+nplCKxwhhBBB0IQjhBAiCFlhqSWDbDQhhMht\ntMIRQggRBE04QgghgpAzlpoQQuQaf/nLX0yz9UrdunVNs5ZdeUcrHCGEEEHQhCOEECIIeXGiv/Ly\n8lY4577J3OlUSBoWFRXVLnk3PxqXjJDSuGhMMoKelewk6XGJNeEIIYQQpUWWmhBCiCBowhFCCBEE\nTThCCCGCoAlHCCFEEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEII\nIYKgCUcIIUQQNOEIIYQIgiYcIYQQYSgqKkr6Lz8/v8g5p780/RUWFhY551bEGQONS26MS35+fnQc\n/aXvT89Klv3FfVZirXAKCgri7F4h2Hrrre0vLjNmzHAuDc2gNC7pJR3jUlBQEB1HpA89K1lG3GdF\nlpoQQoggVCrrE0iVrbb6fc787bffgh/7119/Tbg9Ly/PtLqqCiEySa5832iFI4QQIgiacIQQQgQh\nJy21atWqmf7hhx/SeuwqVaqY3rRpk+ltt93W9ObNm0s8Dpe17733nunDDz881VMsNY0bNzY9b968\nMjuPbIGBHj5rVIhsJV02WsjnQCscIYQQQdCEI4QQIggZsdS22WYb0z///HPaj59uG438+OOPprnU\n5OeIu5QtSxuNyEYrjmw0kWvstNNOptesWWM6FVss5HOgFY4QQoggaMIRQggRhIxYaj4bLZNJmumC\nFpksl7LlvPPOM00bc+jQoaZ5H11++eWmn3zyyQyfXcWiVq1apmlp0z7fuHGjaT076YP3PseB29eu\nXZtwe7YlgWqFI4QQIgiacIQQQgQhaOJnXBuNFhyXhlwyMjojOn7dunVtW/369U1/8cUXptevX5/w\neNm2BK1o1KxZ0/TXX39t+u233zbdv39/09tvv73ppUuXmqallumoyYrA//73P9Offvqp6REjRpj+\n/PPPTa9bty7MiWU5/G6pWrWq6ZIibatXr2563Lhxpps1a2aa33277rqr6ZUrV5rONmtTKxwhhBBB\n0IQjhBAiCGVWS41LTVKp0u+nxCVo5cqVTTdv3tw0l6bRa3fffXfb1qVLF9O77bab6VmzZpnu2LGj\n6dmzZyf3AURGGDJkiOnjjz/eNK0w2mi0aa+66qqEx5SNVjpob+65556mjzvuONNXXnml6euvv940\nLThGr1UE+P3EJnw+G43WWIMGDZxzzl199dW27cADDzRNe5jH47MydepU0wsWLDCdDc+BVjhCCCGC\noAlHCCFEEGJbaumK6PJFnTGqjPvsvPPOpllD6MwzzzR90EEHOeeca926tW2jFUe47D3mmGNMy1JL\nPxdddJFzzrmbb77ZtrENBGvN0a7hfUGr9aeffjL97rvvmn7llVdMT5o0yXSbNm1M01b96quvkv8Q\n5ZjIxnHOuVNPPdX0Aw88YJpWDuHztWLFCtMVzUajLUYbLRkYSRZFWvL5+OWXX0yzTQr3oQXXqVMn\n09lSxzFCKxwhhBBB0IQjhBAiCLEttUwkRtI6qV27tulTTjnF9JQpU0wzabNPnz5bvPa+++6zbbTL\nuOylRfDhhx+W+txFYs4991zTAwYMcM4VH+e99trLdMOGDU1zH2pGFdICogVHa4L3CEu6y0b7nSi5\n8Pzzz7dtPXr0ME0b0wftHiZ70mpjy4/ySiq1IdnB+LrrrnPOOXfiiSfatlWrVpnmPb7ddtuZpp08\nYcIE074xLKuINa1whBBCBEETjhBCiCCUWeIn4dJw0aJFpp944gnT+++/v2nWcuLSMLJOXn75ZdvW\nqlUr01y60q6piDZLJuqL8ZoOGjTIdGTDfvPNN7atoKDA9GGHHWaa1sTixYtNH3DAAaYbNWpkOoqA\nc865vffe2zQtvb/+9a+mH3/8cdPZkAgXAl9kaWRBM2E2GRuNpfD32Wcf08uWLUvpPHOZVH5q2Lx5\ns+m77rrLOVfc/l+yZEnC93nvvfdMT5s2zTRrEKZyj2eixqRWOEIIIYKgCUcIIUQQglpqrMf05Zdf\nmvYt3S6++GLTY8aMMb3HHnuY/u6770xHCYHz58+3bQsXLjTdpEkT07RuKqIVkAk7iXYMl/ujR492\nzjnXokWLhP/O19FKqFGjRsL3oQXHiES+lu/Vt2/f5D5AOYXPFFt+RHW2kmkDQvbdd1/TFe3ZyYTN\nNHfuXNPRzws8NutBMrozPz8/4bnQgkuFTEQka4UjhBAiCJpwhBBCBCG2pUabI25XP9poXMazJhDr\npG3YsME0E8wY7bTDDjuYjiwVvg/Pl8dgolR56PLJqDBGboWE15cRgU8//bRzzrnVq1fbNpZWZ6dO\nWn1sT/Gvf/3LNEvf+xLuJk6cGOfUvbXCyhuM9ouSaRkl6rPROLbpsmySIdu68abrHOrUqWOa3Toj\nvv/+e9Ns+8DakWzTkSsdVrXCEUIIEQRNOEIIIYIQ21JL19KNVgj1kUceaZqRRrRIWG+NkRpR6Xkm\n+tHaYYLVI488YjrkUr1Dhw4ZOW7jxo0zctw40Bql7Tlq1CjnnHNHHXWUbWNNKNoLtFqp77jjDtM+\n2ycVKkoS6Lfffms6stf4PBE+F+w6GZKMRErhvkqlBlpceN/269fPNKMrI+uSLQ4uvfRS07xPfQmh\n2YxWOEIIIYKgCUcIIUQQyqyWGsuXRyW5nXPuk08+MT1v3ryE+7BmVlRi3bnfo9OOPvpo28akQtYY\nYm22d955xzSXrIzeSaXEOpfSw4YNMz106NBSH/OPMBmyrGCXR7YQiOwYn13ms8iuuOIK07TrNm3a\nlPrJVlDYtoFdURNBu+mcc84xnetdcVOx0VKx4/jaunXrJtwnquvIzsctW7Y0/cILLyQ8Hi3qbEYr\nHCGEEEFI2wqHP3z5Zlv242Zf+ptuusk0fwjjcXbeeWfTjD/n/lEjL/4vjispltZh0y/me/B/2/wf\ne9zqyvysDFaoKMycOdP0wQcf7JwrXoaI/4PjKpSVoLmq1KomPXTr1s00n41E8D5nU6+KTCqrI181\n9cLCQtPRc8EgAD4fXBmxajefj2wOINAKRwghRBA04QghhAhC2iy1ZH60orVUs2bNhK997rnnTEfN\niJzz97pn+ZuoMVuzZs1sm29peuGFF5pmjg+bsTFowVe2hSVaSEW00dhUrXPnzqajMWIJD44hq3gz\nsIM/ior0cOWVV5qOLDPaxbzPo7w253KndEo2EzWIdK546Ro+C9E9zyroDGpizhpLQrHEF4+dbfaa\nnmghhBBB0IQjhBAiCLEttXRVb2WERbt27UwzemPFihWmmYfBiDhGMg0YMMA559yNN95o21gdl+fO\nXILjjjvO9PPPP2+a9hrtONoOhBEkjMKj7Re6hEqmy3h89NFHpvfbb7+E+zAKMIKW45w5cxK+LmTZ\nkfIMnxeWjoqeAV7nhx56yPTKlSsDnF35hs8fryer2DMfKrKXab/xJ4JFixaZ5vdc//79E75n3Pyc\nTFfn1gpHCCFEEDThCCGECEJsSy0Ty6yFCxeaZuLfBRdcYPr11183fcIJJ5jm8nHHHXd0zhWvIM3k\nNlphTAKlFdajR4+E5+izwlgi57PPPjNNC5CvzUSl4z+Ddgn7oX/xxRelPiavFyPTaDsmgvcOk3dD\nUlaVgsuSU0891fTIkSNNR/cix+WWW24Jd2LlFD7jtDP5XcSITZa4OvbYY51zxb8z+H3H0l9Tpkwx\nzWR33tfJJOSTTEe1aYUjhBAiCJpwhBBCBCGlxM9UIhqYPMmmUFwOvvHGG6Z9kTZRhWjnnDvppJOc\nc8XrCq1atco0k01prbz88sumGRnHz8TPyuUubTTWT2PyFRPrQiRisbIvo+5SsdHIiBEjTDPaxkf0\nmceOHWvbaC8wii/TVBQbjfd3165dTSeyPStiknI68Nmz/G6j1cXIs+nTp5tmw8joe4MJ5UzWHTNm\njGl+P3JcOZ7ZVkVaKxwhhBBB0IQjhBAiCClZaqnYQ1wy+pamtNpoaXXq1Mk0rbbevXs754o3I2Pp\n76uvvtr06NGjTR9xxBGm+VrW9TrrrLNMP/7446ZZw4hL2ZJKv2cS2miZIJlmb1zKt27d2jlX3F5g\nMmhISy1biBs9FBdeX1q9fGajpOkWLVqk/f0rAvyuYt05JnjWqlXLNO1nNnc88cQTTQ8ePNg559zp\np59u22jJ0/5fvHix6bj3EO8/fg5FqQkhhCgXaMIRQggRhLS1J0iFZJZx3IfWVaK6ZuPHjzcdtSxw\nrnjEGusXsbMnkxpXr15tul+/fgnPhfvkKsuWLTPt67XOz+wbr3vuucc0W0tE+/vKs1dEkrFAGIHJ\nRGXC7az9R5uGyckksrLTFb0Yl2TqE+YKTF7v2LGjadrIjF6jjT9r1izTkydPds4Vt+iYyM5kz1Qi\nLssqek0rHCGEEEHQhCOEECIIOWOpkZKW34xoY8QIrQNaOtRcpjLB03eODz/8sOkuXbqUeD7Z1oHP\nueL1tRgRw+6rxFcPjl0KE31OLuOzIQGTVgXt1myhcePGCbfz+i9YsMA071dGfvruuRkzZjjnits3\njMzMNL7nONMRfJnmqaeeMs0IQVpttOj5GSMr9L333rNtfK54n6byXVJW30la4QghhAiCJhwhhBBB\nyApLLd3Qrtlnn30S7sNkQy5pGVXCpK3ly5eb5hKUNhqjUHj8bLTRuKRmQiyvBW2ZZGALCUbhRKxb\nty7W8TJB27ZtTdNKzEZ8tiPvp+bNm5umpUYrh2PNjp7//e9/nXPOfffdd6mfbBrJRRuNcNzYpoTP\nR/v27U3Pnz/fdGTzsnsu6ztOnTo1Lefo+07KdPsOrXCEEEIEQROOEEKIIMS21HIhgoTLwlNOOcU0\nE+luv/120x9//LFpRs4wqo3JkVwmsxUC68NlO74l9dy5c003adIk1jE7dOiQ0jmFINtttLjw3u3V\nq5fpqH6dc8717NnTNDtGloek5WyEFiYjDa+//nrTtDzZkTX6CYDfMTzeoEGDTPMZTpcVlunoUa1w\nhBBCBEETjhBCiCDEttTi2mhlkWDE0t+0yIYOHWp66dKlpmk58LXHHXecadY7oo1WnupBOefcvvvu\na5rRa3379k24/08//WSa5dJJomi3bEj8LA/w+erWrZvpBx54wDSTQ7MhUrC8wzp27MrJiFm2Rxk1\napTpqP0AI2Rpffq+Q/k8ZXOiuVY4QgghgqAJRwghRBAynvjJJZ1vqZfKEpCvjeqAde3a1bbROrvm\nmmtMjxgxwjRtQtYq4j6+8yoPNpoPthPgdeFyPxlkn2UO2rvkhhtuCHwmIuK1115LuP3ggw9O+hip\nWJ/ZZqMRrXCEEEIEQROOEEKIIAStpeZb6jHSi/Wg4h4z6gT697//vRRntyXl2QqqWbOm6bVr1ybc\n59577zXdo0ePjJ+TEKJ8oxWOEEKIIGjCEUIIEYQya0/A6LK4NlouE7fkf6bw2WgDBw40fckll6Tl\nvaKxzuaM9h8JAAAgAElEQVTomWzn4osvNs0xEiKXyI5vPyGEEOUeTThCCCGCkBfH5sjLy1vhnPsm\nc6dTIWlYVFRUO5UDaFwyQkrjojHJCHpWspOkxyXWhCOEEEKUFllqQgghgqAJRwghRBA04QghhAiC\nJhwhhBBB0IQjhBAiCJpwhBBCBEETjhBCiCBowhFCCBEETThCCCGCoAlHCCFEEDThCCGECIImHCGE\nEEHQhCOEECIImnCEEEKEoaioKOm//Pz8Iuec/tL0V1hYWOScWxFnDDQuuTEu+fn5RYWFhUVbbbWV\n/SXz3nH351+lSpXsryyuW15env2l65hbb721/aU6JqGelUxch0z+8Z77w/Uu8S/us1LJxaCgoMCt\nWrUqzkvEnzBjxgyXl5eXcjMojUt6Sce4FBQUuBkzZriqVavato0bNybcd+uttzZdpUqVhPv/9ttv\nJb5nfn6+6WXLlsU634ittvrd9EjmPck222xjevPmzQn3ycvLM+3rxVWp0u9fS9WqVTO9du3atDwr\na9asSXg+v/76a4nnybHi/mS77bYz/fPPP5e4Pz9von0y3bOM9yjPhdfJR9xnRZaaEEKIIMRa4Qgh\n4sFViu9/x9Q//PBDwuNw5bHtttua/vHHH02vWLEi4f6+lUq0D/+dumbNmqbXrl2b8BiEqxquEEjc\n/63zf9zpgp+R14n4ztO3SiEcE991IL/88kuJ+5SEb0Xmuw+4Gt2wYUPC1/I+40otlRWXVjhCCCGC\noAlHCCFEEGSpCREInx1TUFBgesGCBQn3oR1Cy+aYY44xPWHCBNO077p37276pJNOMt26destjjF2\n7FjT69atS3guydh1qdgujRo1Mr1kyZJSH8dHMj/8007yBUAQXhN+dt91SCU4IxG+9/EdmxaZD37u\ndu3amX7xxRdjnt3vaIUjhBAiCJpwhBBCBEGWmkiJZOwJ8f9sv/32phm95rPRfNSvX9/0xIkTTfty\nSv7xj3+Yfvjhh00/+uijzjnnLrvssljvnw4L6M+YO3duRo8f9z5lRBcjymhj8Zok80xk+hrGIRk7\ncMSIEel5r7QcRQghhCgBTThCCCGCENtSa9y4sel58+al9WTSBa0Flm2IonKcc+7dd981TXuDr/Ut\nNbNpOVzWVK5c2fT9999v+vDDDzcdRcScfPLJto2JhL7Ew3RRlrYf7RhfaZtkLA1eZ0Zu8X495ZRT\nTDOB9MEHHzT973//2/TIkSO3eP9Urj8/K6O8mFjog+dAnY6kyD97L9/n5fa455Br1nIyY86xTeUe\n0QpHCCFEEDThCCGECEJsSy1bbTTCyJ2GDRuarl27tmnaFZdeeqnpb775vfDp119/bXrTpk2mmTTF\n5KjybLV98cUXpmlRfffdd6aZEFa9enXTe+yxh3POueOOO862cSyefvpp07SIaMXQBknGsvBFbIUm\nmQQ7Xqvvv/8+4T5M9txll11M0zKeNWuWaUaenXPOOaZ79Ohh+uabb3bOpXbfXn755aY7d+5smtY7\n7T2ey7Rp00xzjHw13NL1fCVznExYeenAZz3y+mWiujTv42Tqw/nQCkcIIUQQNOEIIYQIQk4mfnIp\nySS4yCJo2rSpbWMzJDa3IsOGDTPN5ShtNEZg0WobPHhwrHPPJXbccUfTU6dONd2+fXvTtCybN29u\nev369aYj2+fWW2+1bU2aNDG98847m+bY7bPPPqa/+uor088884zpUaNGJXzPTDetShZfhBy3p1Kz\njNdl9erVpnmvX3HFFaYfeugh08m0HEgELZW33nrLdJ8+fUwzqonnQqtv8uTJCY/va5CWLtJdxyyd\nx4w+r69tAq8HNa8x7/2ffvop4Xmx7UMy9mFJTeKSRSscIYQQQdCEI4QQIghZbalxWck6VLRannrq\nKdNRWXMu530dA33JhlwucjnKSJtXXnnFdHmoJcbrxWiUBg0amD7rrLNM06bk8p3Leib+RRYYS+Mz\nCfKiiy4yXa9evYTnGEW6OedcixYtTJ9++ummadmxxD2tm2SSENOJzxJK5l7hvevr+MkotcWLF5se\nPny4aT4jjMJMB7TU+Jl4j8yfP9/0wQcfbNpnQyVT3j8VfJ0vfZFY/Cy0n6j5PeDrKMrjMBKPROeT\nn59v2ziufG74/cTPwWMvWrQo4fvEjcJLV9SeVjhCCCGCoAlHCCFEELLaUuMy9eqrrzZ9ySWXmKZ1\nEtklr732mm17//33Ta9cudI0bYnnnnvONJeptDR22GEH06WN7slWfMmJjJ5i/S5ec16vbt26meb1\nHTBggHOu+PU8++yzTdOK8VlQtFZ4nKOOOsr0jTfeaPrVV18t8ZghoBXBemhM5PTBceGz8Mgjj5hm\nKf++ffua9iXT1qpVyzSfh5LwWXr//Oc/TTNijs8gu4jecMMNpn3RXDzfTEcb8hx878ux8kWJEUbO\nMhpzr732Ml2tWjXTtJE7derknHNu4cKFto0Jsvfee69pfg/RauM9x3Hjc5PM/edDiZ9CCCGyHk04\nQgghghDbUvNFZcW1C5I5focOHUzffffdprmk59J3xYoVzrniyW2rVq0yffzxx5vu37+/aUYu8f1p\no/F9krF9ygNc1tMm4OdkmwdaPYyyiayEjz76yLa1bdvWNCOtaAfQMuA+vBfGjRtnevbs2aZ5b2ZL\n9KDPmvHdNwUFBQn1tddea5rRk7TIGBHFBOaSkhJ5Xqx3x+Tcrl27mmb0IlsfMDKQ0YnXXHPNn76/\nc5l/jnzXnteY974vYZffQ4wSa9WqlelBgwaZnjNnjmlGdLI2Ho8fUbduXdP8OaF3796m+XzQrubz\nxHMpK7TCEUIIEQRNOEIIIYIQ21Lz2ROp2GiES9wnnnjCNJeshBbBf/7zH+ecc8uWLbNtLPf+2GOP\nmWZbAcLPx5pOhNEeyZSfz1V4LVhLrVmzZqZZG6uwsDDhcaIaaz179rRtjGhasGCBaXYK3W233Uzz\nmsdtWxAy6ilZkjkPWmFsuUGrixYMbUxGFTJRme0BoutSp04d28ZEWkaGDhkyxDQtG17b6667zvQt\nt9xi+vrrrzfN55jXwFdenwnfvo6pcfFde9ZI5H3Fz0g7k98ntJwZLcn7luPDa54omZT3PseY9tvQ\noUNNMxmelh6/C5kQmsy1zMRzoxWOEEKIIGjCEUIIEYSsS/xkR1FG2nCJy+UdrYaonD5tNF83RV8C\nF4/N5CzaG9ynPNRSSwbaBLRo9ttvP9OTJk0y3atXL9PHHnusc6647crrxm6itBKSsWl9dat8tblC\nE9m8zjl30003mU6mnP2DDz5omgmetCMZkclIJd7Tp512mmlG8kWa9hfr2vHZ4TF47mwJwUjVqFWI\nc8Wjv3z4nqN02WjEV5rfZ6NxfBjp1a5dO9O0eWmX8R5mTTteTybjRnXnnn/+edvGTqqMbnvggQdM\n087mzwW+SNPzzjvPtO/58EXmpvI8aYUjhBAiCJpwhBBCBCErLDV2jWSCmQ/aC1ymRjWHaC1wSenr\noke4dNxpp51MH3300aY/+OAD075kw/IGI8lo9bRs2dL0l19+aZoJalG9NdoXPAYjkRgNlQxc3jN6\nip1Ay3JcaKMR2jS0YJYvX276X//6V8L9X3zxxYTH9FlCvhYSkcXMhFw+L4xqYvIh7eU33njDNOun\ncXsy+MaI55CuGobJdL7k9fN1u3zhhRdMs3YdW0B8+umnpo855hjTjIBlgnlkpfHnBNp4jOJkIjvH\nlffB+PHjE75PMtGdhPeQLxo1GbTCEUIIEQRNOEIIIYJQZpYal6wnnHCCaZ/txWUfLa2XX37ZdBTR\nErfWGbezVPiECRNMM3qKnSWZLOZLJi0PsGbXZ599ZprJnOeee67pRIl8jPq74oorTHfv3t00I6bu\nueeeWOfIyJ5sgdFXvM9o69BGI7NmzTJNC8YXvemDVhGjyi644IItjrH77rsnPHee78CBA01ffPHF\npl966SXTu+66q2kmKB555JGm+ZzyvZhMzRYZ6cLX7Zfwc0XtNZwrfv1o57OTKe/bQw891PSee+5p\n+vXXXzfNaLfoJwVeg7/+9a+mmYDN701f7cA2bdqYZisJ1oGjRZoMM2fOjLU/0QpHCCFEEIKucPg/\nmocfftg0/7fL/+lwxcDVBhs6Jark6vsfjC+Xh0S5PM4V/58k9+f/wv/73/8mPE55w1chmuVPhg0b\nZpr5B1GOgi9PhNfwxBNPTNMZZwdxy+0wgIL3P5+LRBWF/wiPSc3SMtGzkUyOBVca0croj/vzf8oM\nMmGTPAaZ8Md1lmApq1JEfF/+UO8rx3PfffeZptPBHBdWM+cKY+nSpQnPITrO3nvvbduefPJJ01wN\nMWeRwVb9+vUzPX36dNNvv/22aY6VL3AiE2iFI4QQIgiacIQQQgQhqKVGK+D99983TRuLceYsxcDK\n0YxtT/TjtO+HwJKaTzlXPCfIZ0vQRqqI0Hro27evaY5voiq5bBBGG40VeGmzZGOV57j4PoOvhBIr\nCtNGpkVJq9cH7bgoD8q54j/mR+PFf1+9erVpPlvMFeIPznymaCUxL4Q/Ms+YMcO0r3xMpuH7+vJR\nuJ0/4PO+ZkkmBhDQAuP3mS+PiM9NVOaG40d7jefOfEQG8vA5i5pSOud/hjJtoxGtcIQQQgRBE44Q\nQoggBLXUuHRj5WbGsLM8CmPho7I1zsWPGy8JWgTMt2HuAyskM9rjlFNOMT1mzJi0nle2whIZBx10\nkGmOL8ulHHLIIc654hYEo7EWLVpkmpYFNSPcuH3VqlWmfZYBx5SlW0LgKyvDe5g5TtS0jqOK2388\nJi0W2m6MgmLezBFHHGE6uu/ZUG/48OGmo8Z5zhUvMcOoLX4Oln9iZBptOp895Ls2mYCWJO1E4osu\n9NlPtK7YII/lb1gVmvc/78+o4jbPi9dpr732Mk2Lju/J78oPP/zQdLpsy2Ryv7yvTcsZCCGEECWg\nCUcIIUQQMm6pcRnJpTU1l9BMHmRESzqW2VwKsrkUz5GlKBg9x8q9jCApzzaar/rwnDlzTDPChvYW\ny3Gcf/75zjnn3nrrLdvGhlWPP/64ad+yn5GBTA6ljZMoYtG58Daaj7j3MKtf87W+6C7uw2rcrBjM\nqsZRsiCTOpmcSEuZkVpsisYyLt26dTNN26pp06ama9SoYZq2Os+dzx1to3RFKvoa+/kSapOppkyb\nl7boPvvsY5pjRWuMSbKff/75Fsfgd1Xr1q1NX3XVVaavv/5602zQ53ueUokATcWa0wpHCCFEEDTh\nCCGECELGLTUmIXHZuXjxYtNsJMTlGm2X0sIlfKtWrUxz+czqz1wCsyYRI9mSqWWVqzAJkTbHlClT\nTPsqINMCZdXhKPKQSZ20Xzp16mSaCYaM3qHtM3r06IT7++pTZWPSKK9hMpYNmwEyknPw4MGmeb8y\naomWIqP9Lr30Uuecc507d7Zt77zzjunevXubpgXOCu1M/GXEJqPRjjvuONPPPvusKwlaeZnAl/jJ\n75649wxtRo4tx4rWGCuEl1TfjlGht99+u2l+J/Eas0FfMonHIdEKRwghRBA04QghhAhCxi01JnQx\nuovlyBs0aGCaJbd9yWAlLQe5jGQv9gsvvNA0+4sT2njffvut6T59+phmBFa2w2V3Mg3iGMHDZT+t\nNp8NQXtn8uTJpgsKCpxzxSNzmEhLC4INunjNaSlxjFiTjWPts9fKEp8t64teY8MuPhe77LKL6SgC\n0LnikU1vvvmmaSbW0uqKGtbxeWEUFO01Wja0jxhJRxuPEYuMOssGfI3wmNzKRmtxa43RIuXY+tpN\nkGgfjkmPHj1M8zuRn4NRgb5ozWxAKxwhhBBB0IQjhBAiCBm31GjRcJnYokUL01xyFxYWmmZSJZfx\nvs6d0XJzjz32sG2TJk0yTUuDx6Bmme9nnnnGNPua5xLJ2GiE9gHHjpYW96E1cMcdd5hu1KiR6ShS\nceLEibbt3//+t+nTTz/ddBQ55Vzx+4W1pVhXjGPKBMMlS5a4bCPuWDCBj20LaNMwYoyl8BnVx2eN\nkaJRDUPaYhxz1lVjgi3tcCbzMvmQEVlsLZJt8PsjE0mmvvcqyfbidxJtTl/bBD5P2WajEa1whBBC\nBEETjhBCiCBk3FLj8u66664zzSU6EwaZhMbkQdZsYmQOLbCoJPqdd95p2xjVQfuHds3HH39s+rDD\nDjOdTEJeeYOJgUwyo6Xo65J4wAEHmGb59ahWXVR63bni9wX35bgQdjds3Lix6U8++cQ0O2RmI/yc\ntIiJLyGUUV+8zoxemzp1qmnayrzWtMzq1avnnHPuyiuvtG2MwGzXrp1ptpbo0qWL6WuuucY0k4MZ\nPciWCOPGjTPNhEfaQyFbFYSEEXEl1TLjMzZq1CjTtC0ZickE97iE7KyrFY4QQoggaMIRQggRhKAd\nP1lHiR3yGA3G5R3rbbH7Z8OGDU3TdoiigHyWD20MRjqx3H4qS/iQS9NMwWv03HPPmb7xxhtNM1GX\n9gctsyjZ07nfI8lo5zBRzWej0WbhePm6fGa7Bcpry2gxRv35PgP3ZydQwki+hx56yPT8+fNNc4xu\nvvlm51zx5+XAAw80zQi4Sy65JOF7Dh061DQj6U477TTTtNdI+/btTfNe87ViyPQzFfK9Sjo+74Oz\nzjrLNG05jjdrU8b9HL4Ospm4BlrhCCGECIImHCGEEEEIaqnRCmGESlTTyTnn2rRpY5rJY7RofNZE\ndExaMUzmatmypWlGeKTLislVG43wMzBijcmD5P777zfNCEMmZEZwrHzXnPYO67fRdioP1zlu18Rk\n6nnxurBzJ697FMnpnHMvvfSSc6540iDbiXCM2In37rvvNs2I0JNPPjnh/oTjSxvNZ+X47PFUYBJz\nMq0QkokujIvPRo4+L7/7WOON9wFr1/FZ4fXzWbeJ3tO54lGS/B5NF1rhCCGECIImHCGEEEEIaqmR\ngQMHmmb0GpfNXHYOGTLE9EknnWSa9aOicu5MgGNpdhEPlrv3cdttt5nu2bOnaSYHRhFmbA9B64Y1\n86ZPn246bu2xbMRnndDW4bVIF7TsaKuwtUNkh/GZ81l9Dz74oGlacNyftdfi4rPO4lqPycDupRwf\n31gxujJdMFqQVlfUlfjaa6+1bYwE5XXq1auX6e+++y7hPr7vU1+LhmSuN88nLlrhCCGECIImHCGE\nEEHIixPx07x586KZM2dm8HQqFkVFRS4vL29mUVFR81SOo3FJL+kYl+bNmxfNmDGjmJ3FyCN2lPSV\nnE+FZKKTcpC0PysLFy40vdtuu5n2XT+f7ZauyMno+LSfBw0aZJqWKO2vZs2amea5s9YeSSbZM5kk\n0LjPilY4QgghgqAJRwghRBDKLEpNiIoAo4QY3cOEZCbb+doTRC0enEsuqo0J1G+++WbyJ1zBoI1G\nfF1tU0k+9dl0++67r+nIao1aRzjn3OTJk02zBcfYsWNN0xosqZvoH+F7sVNuJmqsaYUjhBAiCJpw\nhBBCBEGWmhCBoF1BmOBKi4c2iS96zWd1jB8/vsT9E70uXXTs2NF0//79Y72WtcvY3ZWdeUPiS56k\n1eaLZPMlWJLZs2ebjqLNmNTZu3fvEs/RN4Y8F5+lx7qSyeCL1EsGrXCEEEIEQROOEEKIIMRK/MzL\ny1vhnPsmc6dTIWlYVFRUu+Td/GhcMkJK46IxyQh6VrKTpMcl1oQjhBBClBZZakIIIYKgCUcIIUQQ\nNOEIIYQIgiYcIYQQQdCEI4QQIgiacIQQQgRBE44QQoggaMIRQggRBE04QgghgqAJRwghRBA04Qgh\nhAiCJhwhhBBB0IQjhBAiCJpwhBBCBEETjhBCiDAUFRUl/Zefn1/knNNfmv4KCwuLnHMr4oyBxiU3\nxiU/Pz86jv7S96dnJQN/eXl59hf3tXGflVgrnIKCgji7b8HWW29tf8K5GTNmOJeG7oOpjosoTjrG\npaCgIDqOSB96VjLANttsY39bbbWV/SVD3GelUinPsVT8+uuvId9OCCFECWzevNl01apVTW/YsCHt\n76XfcIQQQgRBE44QQoggBLXURPkmLy/PdFFRUc4cW4g/stNOO5levXp12o9fqdLvX72//PJL2o9f\nWnw2Gn/T2XXXXUt9fK1whBBCBEETjhBCiCDIUhNpI5NWl2w0ERLaaLSTfvvttxJf261bN9N33313\nwn3KwkZLJQKNn/vbb78t9TlohSOEECIImnCEEEIEIScttZYtW5qeNm2a6Wjpy+XfI488YvqEE04w\n3ahRo0yeoiiBKlWqmK5fv77pwsJC05MmTTK9ZMkS07LXSk/NmjVNr1+/3jmXmYTsXI8qbNOmjemJ\nEyeaTuZz0UarU6eO6eXLl6fvBEsBbbR69eqZ3rRpk+l169Zl9By0whFCCBEETThCCCGCkHWWGgt7\n7rnnnqYHDBhgunXr1glfG1lpXNLee++9ps844wzTub7kz0W23XZb0+3btzfds2dP07TX/v73v5vu\n37+/6VWrVmXqFHMO3sc+qlWrZvqiiy4yPX36dOdccRtz5MiRpmkBMVKLFhyTAJOJXuLznc21FWmj\nkWS+K2rVqmV6xYoV6TqltLJ06dIyeV+tcIQQQgRBE44QQoggZJ2lxmX2F198YdpnoyWCiVdMsDrs\nsMNMy0YLT926dU3369fPdOXKlU0zwrBz586mx4wZY7qiW2qs89WgQQPTUdSZc849++yzpleuXGma\nkUo9evTY4nX33HOP6cmTJ5vms7jbbruZph03YsQI0127djXNZzCb6oalkz59+ph+5513TPOalIWN\n70taLaufFLTCEUIIEQRNOEIIIYKQdZZaOuBycfjw4abHjh1rmglwIv1wKR9Fp/3nP/+xbd9//71p\nJoFyec99aK9dddVV6T3ZHOOHH34w3bBhQ9OdOnUyfeCBB5r2tXSfPXu2c664pbZmzRrTgwcPNk0b\nrV27dqaZ2Hjsscea9lmgtOZ+/PFH09lscX/++eemzzvvPNOMRhs0aJDp448/3vStt95qmlbbZ599\nlvC9tt9+e+ecc4cffrht69Wrl+nRo0ebrl69uukvv/zS9NSpU01/+umnplkfrqyut1Y4QgghgqAJ\nRwghRBDKpaXGqKczzzzTdH5+vmklfqafbbbZxvT9999v+tJLL93i31mzacGCBaZnzJhhmhGLX3/9\ndVrP1bncvQd22GEH01999ZXpHXfc0fRTTz1lesKECaYXL15sOnpOOnToYNuiZFDnnPv5559N33DD\nDaYZ7cTrRhuVtlv37t1Nb968OeFrs5mTTjrJ9I033mia1/6+++4zvd1225n23WOsX8bvK17DRHAc\n+Hzwun788cem+/btm/C8nn766T99n0yhFY4QQoggaMIRQggRhHJpqTHqhhE63F6pUrn86MGhTXbw\nwQebbtq0qenIAqKlQE3rZu7cuaaPPvpo076onlTIFUvHueLWDCPJCgoKTNPG2rhxo2ne661atTJ9\n5513OueKR7199NFHphnJycinxo0bm65du7bp8ePHJ9x/l112MU3rp6wSeFnTj+dDdt99d9NMVj30\n0ENNM2KNtpgPjmEUjZYu+D3XrFkz04cccojpaLydKx7R+Nhjj6X1XP4MrXCEEEIEQROOEEKIIJRL\nX8mX6LZs2bLAZ1L+ocVQtWpV06x9F1lmtLDeeOMN00wYvO6667Z4nXPFE+EqIrx2tGaYlMhESj4D\ntNrYyTKy0pgkyigoltZngmlUg8254lFQ77//vum33nrLNK0zRriVFT4bjRFitC157V966SXTvIdp\nIZJ58+aZZl013ueJWjbQxmOiM624c8891zStUB6b58XnKaSNRrTCEUIIEQRNOEIIIYJQLi01H/vu\nu29Zn0K5g1FlxxxzjGlGSY0aNco5V9xOYSTNnDlzEm5PpptleSCZBFTftfjpp59MM6qPVs67775r\nmjbMq6++6pzz19uiRTd//nzTixYtMn3OOeeYZjTc3nvvnXB/JkuWFazpd9NNN5nm/cnIPY7Jgw8+\naJq1GVlTjvuzlQSvAy0tXue99trLOVc8eZMWIO+DI444wnSXLl1M0wqljXb66aebZmfXkGiFI4QQ\nIgiacIQQQgShQllqZ511lumBAweW3YnkOLQmly9fbppROKyPtmTJEudccWuHiZy0gtiS4Oabb07P\nCWc5ySSgch9aV74ujhdccIFptgpgJGGUnDtr1izbxuvPRF52a2WyL+u6sVYXa7bRtrr22mtNM+KK\nFlam4fn47ExGifmiAtlt1XccRrsRbqct6ot2i+D4sQ0CE085ntS0rlMhFatbKxwhhBBB0IQjhBAi\nCOXKUjvjjDP+9N9lo6UH2h/JdG2MbBrW3aIdQPuiRo0apssqkiYboY1GG4tjwc6QtMBYT6tevXqm\nI0uL0U6FhYWmWXPshBNOMM06Y7179zZ91FFHmR4yZIhp2mi+SLCywnfPso4cW2nQRmOiaNyEVkae\nlfRavk8UxeZc8Rp1ZL/99jPNDqu0PPncxiWVGoRa4QghhAhCuVrhRPkehHHoFRH+T23t2rWlPg6b\ne/FHTgYQnHLKKab5o3X0v23+T5H94PkjNMuj8H9zzEvI1cZpqVCtWjXTzJXhSoY/RPN/s8yJ4fWN\nKk1zxcQflpnbwVXoZZddZvrLL7803bFjR9OTJk0yzf9l5wp8VrjC4P2WSpkeNk8rCQZXvPjiiwn3\n4Xmx3BTfJ857ZgqtcIQQQgRBE44QQogg5Lyl5qsMHZGKjVQeSNfnpx32t7/9zfQDDzxgukqVKqZp\nk0V2TDJlW/r372+a5VlIRbHRCMeRuRjVq1c3zetCS43lh6ZMmWI6ypWhXUfLjQ0LmVdDO/TUU081\n/cgjjyTcPxusHB/J2LNlXeGaY0kLlefFSvgMzuE4ZANa4QghhAiCJhwhhBBByHlLbf/99//Tf093\n7/CKCq2HmTNnmp49e7ZplkKhjRNFuA0ePNi2MQJq6dKlpmnLpZIrUN5gpNQee+xh+sQTTzTduHFj\n007EdkYAAAXsSURBVLRbBg0aZPqdd94xHeX29OnTx7bROr399ttNs4laixYtTNevX980yxkxkjHb\nyIUoR+ZdMa+GVjWtSj5vrP4dl0xfG61whBBCBEETjhBCiCDkvKX2wQcfbLGNS0EmPorSw+U7Kz2f\ndtppps8//3zTjDCL7AGWQWFpj2HDhplmpJP4Hd7TjDyipcWINTYKGz16tGnalImq/jIiitW/aeV8\n9NFHplmBnU3a+D58bTYkYoe00eJaVJGlzIRqWtGMyqXNyoZuyUTV+cryZPraaIUjhBAiCJpwhBBC\nBCHnLTUuMaO6Tg0bNrRtZZ20VR7hspsNux599FHTTA6MqgWzNtpzzz1n+p///GcmTrNcwWvuq6XG\nSCVWdI5qpjnn3Ndff206skn5DO28884J92W9NSaeDh8+3DQTRUk22GhlRWktKtpou+66a8J9Nm3a\nZJoJu8lQVt+LWuEIIYQIgiYcIYQQQUibpXbnnXeavvfee9N12FhENaG4jGXU01VXXZWW95k+fbpp\nJsFVRFi2nhGBY8eONX3AAQc454pH7NBm8Vkx4nd47fisDRgwwDSbpzGSjTqRvUUbjdGIPuuUljWj\n0ZjsySjEikzcKLVofNgoL1E0oXPO9e3b1/Ty5ctLe4pB0QpHCCFEEDThCCGECELaLLWystFIFEkz\nZswY28aaXemiottoPm644QbTkY3mXGJL4J577glyTuWRIUOGmGZn1Zdfftk0awjSJmPtwYULFzrn\nnPvhhx9sW40aNUzn5+ebbtq0qWlaZ3Xq1DGdbaXwswGOw4YNG0rcv0mTJs654i0jCMfy/vvvN71x\n48ZY58XET5Lp6DWtcIQQQgRBE44QQogg5Hzi51dffWU6qtnFLoQVOeksBEwaZGuBRDYao3SWLFmS\n2RMrZ/Daffvtt6aZ/PfQQw+Z/uSTT0wfeeSRprfddlvTTz75pHOueGIhn5e77rrLNBNJWRNv2rRp\nCc9R/D/J2Gi0MSdNmuScK34taaOtWLHCdCotIOJaZ+lqW6AVjhBCiCBowhFCCBGEnLTUmjVrZvrV\nV181feWVVzrnnDv33HODn1NFhUvz9u3b/+m+tD+VGBgPWmG0WN544w3TTMI86qijTF9++eWmv/nm\nG9Nnn322c6543a7oGXKuuGXzyiuvmB43bpzpypUrm2a0m0ieDh06mGaduggmRrNtQdzINEa++caK\nUXU8frrsUq1whBBCBEETjhBCiCDkpKXGjoMTJ040HZXBV7RMOFi2nh0nE3URvOSSSxL+uygZWpBt\n27Y1zVYFS5cuNX3YYYeZZsfNvffee4tj00ZhPbyhQ4eaXrt2bcJzkTVaOph4yYTpaDujD3v27Gl6\n3bp1pX5Pn43GCLS4Nl1ctMIRQggRBE04QgghgpCTlhoZOXJkWZ9ChYbtCRhNM2/ePNOHH374FvuK\n0jN+/HjTtLqYhLvnnnuaPvTQQ00zem3EiBHOOee6du1q2xo1amSaXVujpGpRemhXfvjhh6aZeBvZ\nz4xK7Ny5s+nHHnvMNC0y1r1btWpVrPMK+ROEVjhCCCGCoAlHCCFEELROFinBWlFnnHGG6Y8//rgs\nTqdCsGbNmoTbaVmyE2ivXr1M0z6JLDgmkq5cuTJt55kL+BIdMwGvM63LRFYzx7igoMA069t169bN\ntM9GYzRcNkSGaoUjhBAiCJpwhBBCBEGWmkgJLtllo2UPy5cvL3EfWjwVlUzbaKRevXqm2WaARPXr\nDjnkENvWpk0b0zfddJPp7t27l/ie2WCjEa1whBBCBEETjhBCiCDIUhMpkW1LdiFCwdYMbA3hg3UH\nmRjNWmZXX321c865BQsW2LaBAweaZvRhoq66pSFd3TyTQSscIYQQQdCEI4QQIgh5cZZQeXl5K5xz\n35S4o4hDw6KiotqpHEDjkhFSGheNSUbQs5KdJD0usSYcIYQQorTIUhNCCBEETThCCCGCoAlHCCFE\nEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEYT/A/eXvFd9OFeNAAAAAElF\nTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f4e80057c18>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"saver = tf.train.Saver(var_list=g_vars)\n",
"with tf.Session() as sess:\n",
" saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\n",
" feed_dict={input_z: sample_z})\n",
"_ = view_samples(0, [gen_samples])"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
kit-cel/wt | sigNT/tutorial/approximation.ipynb | 2 | 46483 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Content and Objective\n",
"\n",
"+ Show approximations by using gaussian approximation\n",
"+ Additionally, applying Gram-Schmidt for \"orthonormalizing\" a set of functions"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"# importing\n",
"import numpy as np\n",
"import scipy.signal\n",
"import scipy as sp\n",
"\n",
"import sympy as sym\n",
"from sympy.plotting import plot\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### definitions"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# define symbol\n",
"x = sym.Symbol('x')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"# function to be approximated\n",
"f = sym.cos( x )\n",
"f = sym.exp( x )\n",
"#f = sym.sqrt( x )\n",
"\n",
"# define lower and upper bound for L[a,b] \n",
"# -> might be relevant to be changed if you are adapting the function to be approximated\n",
"a = -1\n",
"b = 1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Define Gram-Schmidt"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1, x, x**2, x**3]\n"
]
}
],
"source": [
"# basis and their number of functions\n",
"M = [ x**c for c in range( 0, 4 ) ]\n",
"\n",
"n = len( M )\n",
"print(M)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"# apply Gram-Schmidt for user-defined set M \n",
"\n",
"# init ONB\n",
"ONB = [ ]\n",
"\n",
"# loop for new functions and apply Gram-Schmidt\n",
"for _n in range( n ):\n",
" \n",
" # get function\n",
" f_temp = M[ _n ]\n",
" \n",
" # subtract influence of past ONB functions\n",
" if _n >= 1:\n",
" for _k in range( _n ):\n",
" f_temp -= sym.integrate( M[ _n ] * ONB[ _k ], (x,a,b) ) * ONB[ _k ]\n",
" \n",
" # get norm\n",
" norm = float( sym.integrate( f_temp * f_temp , (x,a,b) ) )\n",
" \n",
" # return normalized function\n",
" ONB.append( f_temp / np.sqrt( norm) )"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.707106781186547, 1.22474487139159*x, 2.37170824512628*x**2 - 0.790569415042095, 4.67707173346743*x**3 - 2.80624304008046*x]\n"
]
}
],
"source": [
"print(ONB)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"# opt in if you like to see the correlation matrix\n",
"if 0:\n",
" corr_matrix = np.zeros( ( n, n ) )\n",
"\n",
" for _m in range( n ):\n",
" for _n in range( n ):\n",
" corr_matrix[ _m, _n ] = float( sym.integrate( ONB[_m] * ONB[_n], (x,a,b) ) )\n",
"\n",
" np.set_printoptions(precision=2)\n",
" corr_matrix[ np.isclose( corr_matrix, 0 ) ] = 0\n",
"\n",
" print( corr_matrix ) "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"# opt in if you like to see figures of the base functions\n",
"# NOTE: Become unhandy if it's too many of them\n",
"if 0:\n",
" for _n in range( n):\n",
" p = plot( M[_n], (x,a,b), show=False )\n",
" p.extend( plot( ONB[_n], (x,a,b), line_color='r', show=False ) )\n",
"\n",
" p.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### now approximate a function"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3.0*x*exp(-1) + (2.37170824512628*x**2 - 0.790569415042095)*(-11.0679718105893*exp(-1) + 1.58113883008419*E) + (-9.35414346693485*E + 69.2206616553179*exp(-1))*(4.67707173346743*x**3 - 2.80624304008046*x) - 0.5*exp(-1) + 0.5*E\n"
]
}
],
"source": [
"# init approx and extend successively\n",
"approx = 0\n",
"\n",
"# add next ONB function with according coefficient\n",
"for _n in range( n ):\n",
" \n",
" coeff = sym.integrate( f * ONB[ _n ], (x,a,b) )\n",
" approx += coeff * ONB[ _n ]\n",
"\n",
"# if you like to see the function\n",
"print( approx )"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAasAAAEgCAYAAAAKZlx2AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAujElEQVR4nO3deVgVZcMG8PsAIiibrLK4IWqILAEqamigoqChQr0umQuaoZWW9fr1VlpaqWWWW2m45ZaoSKKyqLkmLoga7kYqCgjKKvt6nu+P94svE1kSzpzl/l1X1+U5M3PmZhq5nTnPzMiEECAiIlJmWlIHICIiqg/LioiIlB7LioiIlB7LioiIlB7LioiIlB7LioiIlB7LioiIlB7LioiIlJ6O1AGInpVMJrME0A+ADYBSAFcAJAoh5JIGI6ImI+MdLEhVyWQyHwAfADAFcBHAQwB6ALoC6AwgAsBSIUSBZCGJqEmwrEhlyWSyJQBWCiHu1TJNB8BwANpCiN0KD0dETYplRURESo8DLEjlyWSyLTKZzPgvrzvKZLLDUmYioqbFsiJ1cBLAWZlMFiCTyV4HcBDAMmkjEVFTqu80IM8Rkko4efIkfHx8YG5ujosXL6Jt27aS5Bg6dCji4uIkWTeRipI1ZCYeWZHK27JlC0JCQrB582ZMmjQJAQEBSEpKkiRLdna2JOslUne8zopU3u7du3Hy5ElYWlpi7NixGDVqFCZNmoSLFy9KHY2ImghPA5JaqqiogK6ursLX6+npicTERIWvl0iF8TQgqbfPP/8cubm5tU7T1dXFkSNHsH//fgWnIqLmwNOApLKcnZ3x0ksvQU9PD+7u7rCwsEBZWRmSk5Px22+/YdCgQfjwww+ljklETYBlRSorIiIC8fHx+Oqrr2BpaYmMjAwYGRlh/PjxCAsLg76+vtQRiaiJsKxIZZ0/fx53797Ftm3bcPTo0cemlZaWsqyI1AjLilRWaGgohg4ditu3b8PT07PmfSEEZDIZbt++LWE6ImpKHA1IKm/69OlYvXq11DEAcDQg0T/A0YCkGZSlqIio+bCsiIiowX5/UIjSimqFr5dlRUREDVJQVonZy+Mwc5viT3WzrIiIqEEW7b6Ab9a+jy/3faPwdXM0IBER1euXaw/Q9dsv0DX7HhC6VuHr55EVERHVKa+4AnsXr8fk8/tQPXMW4Oen8AwsKyIiqtNXW37F3MglKHN0gvaXiyXJwNOARET0VPuT0jHw6/+gTUUJdHZsB/T0JMnBIysiIqrVw8IyJH38JQbdOgfZ4sWAs7NkWVhWRET0BCEEVq7aj9lxYSh50Rfa78ySNA9PAxIR0RMi4m9hwvcfQda6FfR/2gpoSXtswyMrIiJ6zL2cEhTO+QAyHR3oblwPWFtLHYllRURE/6+qWo5Nn/6AkNO7Ye3bD1qjRkkdCQDLioiI/mLTz2cRunEBCjp3Q+tVy6WOU4PfWREREQDg8r08OPzP2zCuKEWLn3cBSvQAUx5ZERERSiuqcfKtjzDg9nlUL/kaMgmHqdeGZUVERNj8fSSmRK9FzuAA6M98U+o4T2BZERFpuOPnb2Pg4v9BuakZzLZvBmQNenivQrGsiIg0WFZBGYqmvAG96krohm8HzMykjlQrlhURkYaSywX2vLMQw5J+gd6k19ByoI/UkZ6KZUVEpKH2bDuEV7d+hUz3PjBf/JnUcerEsiKNlJqaCh8fHzg6OsLJyQnLlz95PcmxY8dgbGwMNzc3uLm5YcGCBRIkJWoeN25losfsaajSbw2rfRGAtrbUkerE66xII+no6GDp0qVwd3dHYWEhPDw8MHjwYHTv3v2x+by9vbF//36JUhI1j9KKatwZNwVDcu6haM8+yGxspI5ULx5ZkUaytraGu7s7AMDQ0BCOjo5IT0+XOBWRYhyZ9y38E2KQ9sYsGAUOkzpOg7CsSOOlpKTg4sWL6N279xPTTp8+DVdXV/j7++Pq1au1Lh8WFgZPT094enoiKyurueMSPZPj+05iwLfzkNbDA+1XLpE6ToPJhBB1Ta9zIpGqKyoqwoABA/DRRx8hKCjosWkFBQXQ0tKCgYEBYmJiMGvWLCQnJ9f5eZ6enkhMTGzOyET/WOr9XBS794RNUQ70rlyCbsf2UkcCgAZd1MUjK9JYlZWVCA4OxquvvvpEUQGAkZERDAwMAAABAQGorKxEdna2omMSNYnKajlOTZmNTtmpKFu7QVmKqsFYVqSRhBCYMmUKHB0dMXv27FrnyczMxJ9nHhISEiCXy2GmpBdMEtUn9j9LMTpuE1KmzYLl2Cf/cabsOBqQNFJ8fDy2bNkCZ2dnuLm5AQAWLlyIe/fuAQBCQ0MRERGB1atXQ0dHB/r6+ggPD4dMCW9DQ1SfxJiTGLRsLm5390C3FYukjvOP8DsroibE76xI2WRlZKPIxR3G5cVodSUJeu3tpI70d/zOiohIk1VXVSN5xDi0z0lHycbNylhUDcayIiJSUydmf4a+5w7h6vT3YResGtdTPQ3LiohIDSXtPoh+332Bq897w3nFQqnjPDOWFRGRmnmYkg7LKa8h19gMHaMjIFPy+/41BMuKiEiNVFVW4eLEt2BS/AgV23egtbWl1JGaBMuKiEiNnJ38Doac2INrH32B9kMGSB2nybCsiIjUxKU129Bv23c4/2IgPD6p/WJ3VcWyIiJSA5kXr6Lju6H4w64LnKK2AWp2ATvLiohIxZUXFKJ65CgIGaC352foGRlIHanJsayIiFSZELgUPAnW9/7AH9/+ADsPJ6kTNQuWFRGRCrv47wWwO3MMR6a8D483xkkdp9mwrIiIVNSdXfvh/M0CpDn0wIurVf/C37qwrIiIVNCjm3+gzeTxSDO3g310BHRaqPdDNFhWREQqRl5cgrwhw6FdVYmSHbtgZmMhdaRmx7IiIlIlQuDGyHFof/d3JH6+Et19ekmdSCFYVkREKuTagqVwOBaDA/+ajhffmyx1HIVhWRERqYj7O6PQbf7/4HDPoRjw47ca9eRqlhURkQoounINhpPG47ZlB7juXI9W+rpSR1IolhURkZKT5+Wj0G8YKqGF4h0RsLFT/wEVf8eyIiJSZtXVSPEfBfMHqTi35Ae4DXCXOpEkWFZERErs9rR3YH/2GPZN+QB+M0ZLHUcyLCsiIiWV8f062G9YhVjvkQj4br5GDaj4O5YVEZESKjgeD+25c3Gpy/N4PnIz9Fqo/qPpnwXLiohIyVSm3EV14AhktDSAPHwH2pobSh1JciwrIiJlUlSELN+h0C4rxcPla+Dm3kXqREqBZUVEpCzkcqQGBMEq5XfEfvwtBr8yUOpESoNlRUSkJNJD30G7Xw9hx9h38fJHr0sdR6mwrIiIlEDWyh9gu3Yl9vUNxEvrFkJbS3NH/tVGvR+AQkSkAgoP/IK0ZauR6dQbrrs3w1DDbqXUECwrIiIJVVy5BllQEIz0TZAfcQzt2xpLHUkp8TQgEZFExIMHKBzoh1Jo448fw+HxvL3UkZQWy4qISAqlpXjgOxStc7NwaFEYhgzvK3UipcayIiJSNLkcmYGvwPJaEra+9QXGvv2y1ImUHsuKiEjBHr75Ltr+Eo3No2Zg/FfvavQ9/xqKZUVEpEB5366C5ZoV+NkrEMM3fa3x9/xrKJYVEZGCFO2NgdH7sxDftRecIjbC3FBP6kgqg2VFRKQAFWcTgDGjEdftBejs3IGutqZSR1IpvM6KiKiZyW/dRtmQABS00IfOsm/Q27Wj1JFUDo+siIiaU3Y28gYMhLy8HL+u2IIhfh5SJ1JJLCsiouZSUoKsF/3Q+sF97Jz3HcZM8JM6kcpiWRERNYeqKjwcHgSzq79hXehnCJkznkPUnwHLioioqQmBrIlTYXn0ANa+8g5Cls6GjjZ/3T4Lbj0ioiaWPXcBLH7ahB2DxiNo/UK00uVYtmfFsiKNlJqaCh8fHzg6OsLJyQnLly9/Yh4hBGbOnAkHBwe4uLjgwoULEiQlVZO/fBXkK1diu9dIeG1fDQteS9UkWFakkXR0dLB06VJcv34dZ86cwXfffYdr1649Nk9sbCySk5ORnJyMsLAwTJ8+XaK0pCqKf9oBw3dn4YalPZy3r0UHcwOpI6kNlhVpJGtra7i7uwMADA0N4ejoiPT09MfmiYqKwoQJEyCTyeDl5YX8/HxkZGRIEZdUQPmBQ9Cd+BqSbLpBd/cu9OhoLnUktcKyIo2XkpKCixcvonfv3o+9n56ejnbt2tW8trOze6LQACAsLAyenp7w9PREVlZWs+cl5VOVcA5i5EjcNrFG9vYIeLl0kDqS2mFZkUYrKipCcHAwli1bBiMjo8emCSGemL+2ocfTpk1DYmIiEhMTYWFh0WxZSTmJmzdRNngIsnUNcHn9Dvh5d5c6klpiWZHGqqysRHBwMF599VUEBQU9Md3Ozg6pqak1r9PS0mBjY6PIiKTkRFoaHvX3RbVc4NDyLXg50EvqSGqLZUUaSQiBKVOmwNHREbNnz651nsDAQGzevBlCCJw5cwbGxsawtrZWcFJSWjk5yPAfCe38PGz79AdMmjhY6kRqjYP/SSPFx8djy5YtcHZ2hpubGwBg4cKFuHfvHgAgNDQUAQEBiImJgYODA1q1aoWNGzdKmJiUSkEBsl/wRemDbET+z3LMePcV3p2imclqOy//F3VOJKLHeXp6IjExUeoY1JxKSpD9gi+MkxKx5u2vELr0HbTg3SmeRYNanluYiKihysuR7TccphcTsDrkE7y+ZBaLSkG4lYmIGqKqCjkjgmEefxTfjZuDkFX/4SPpFYhlRURUH7kcOaPHw+xANDa+PBPjwxbAoCW/8lcklhURUV2EQE7IGzCL3IH1fpMxbP2XaNNaV+pUGodlRUT0NEIgZ+Z7MNu0Dtv6/wtDw1fB0og3ppUCy4qI6Cmy5y+EXtga7O71Erx3b4Btm1ZSR9JYLCsiolrkz1sA8/kfY4+HP9z2bkV789ZSR9JoLCsior/J/2wRTD77BDHOPvDYtQ6drYzqX4iaFcuKiOgv8r9cCpN5H+KQ8wC037cTz9m2kToSgWVFRFQjf+lymHzwPg459oNV1C706MBnUikLlhUREYD8ld/D5P13cLRrb1jti4RLJz7uRZnwqjYi0niPVv2AO8vCUOTgiTb798Cls6XUkehveGRFRBrt0YrvYfx2KIpkLdA6ei/curSVOhLVgmVFRBrr0fLvYDzrTZxw8ETr6L1w78rnlSkrlhURaaS8b1bA+J23cKJLLxhE74V7NxaVMmNZEZHGyV2yDG3em4VjXXvDKDqKR1QqgGVFRBole/FSmM55F0e7ecEilt9RqQqOBiQijZE9fyEerN2E37q/ANuYn+HI66hUBo+siEj9CYGsOR/D/NOPcL9NW3Q4EMWiUjE8siIi9SYEHr79Hiy/+xbRzw+GY/RO2FubSJ2KGollRUTqSy7HgynTYfVjGA4PGIUeuzahg4Wh1KnoH2BZEZF6qq5GxthJsN61Fbu8X0bfnzfxeVQqjGVFROqnqgr3R46GTXQktg9+DYMiwmDBJ/yqNA6wICL1UlGBW2NCYBMdiW0vTUPAnvUsKjXAIysiUh/FxUj39YfFxURsePXfGL1+IVq35K85dcAjKyJSCyInBxm9vNH2XDx2T3gf4zYuYlGpEf6fJCKVJ0+/j6x+L8I07Q7C/70U4xfORAtt/ltcnbCsiEilVfz+Bwq8fWCQl42I+T9g7H8mQ0tLJnUsamIsKyJSWaUXLqLM1w/a5eWIW74N40JHQSZjUakjlhURqaSCX47h4cz30FoucHFjJILHDJI6EjUjntQlIpWTtXUnWvoPQWVOLm5HxiKARaX2WFZEpFLSv1wO0wlj8btVJ5THHEC/QT2ljkQKwLIiItUgBO7OnAPbD97B2S6e0D9xDG4eXaVORQrC76yISPlVVSFlzCR03L0NB3sNhUv0TrQ15w1pNQnLioiUmigpwR2/EbCP/wUxwyfhhZ0/wEhfV+pYpGA8DUhESqvywUP83m8wWl5Owu6JczDw53UsKg3FsiIipVR05RpyXDzQ4UoiEmfNQ9DGxWipoy11LJIITwMSkdLJPnAELYKDoCsXiF+zAyOmjJQ6EkmMR1ZEpFTurfkRxsP9kdfSAH9EHcRAFhWBZUVEykII/P7eXLSfPhnXbLug6sRJ9BrcW+pUpCR4GpCIJCcqK5E0YQbcwtfhpLsvusbthqWFidSxSInIhBBPnTh06FCRnZ3dJCvKysqChYVFk3yWIqlqboDZpXD58mU4OztLHeMfkWqbi6oqlP/+B7TLy1Bi2AZGnds36ma0qrqvAKqbvSlznz9//oAQYmi9Mwoh6vqvyXh4eDTlxymMquYWgtnrMnnyZGFhYSGcnJxqnX706FFhZGQkXF1dhaurq5g/f36DPrdVq1ZNGVOhpNhf8pKuivS2HUSFto6Inf2FqK6WN/ozuJ8rXhPnrq+HIITgaUDSTJMmTcJbb72FCRMmPHUeb29v7N+/X4GpNEtqZAyMXhsDfSHD2TXhGDo1WOpIpMQ4wII0Uv/+/WFqaip1DI11bcE3aPtKIHJat8H9g8fwAouK6qGwspo2bZqiVtWkVDU3wOzP6vTp03B1dYW/vz+uXr361PnCwsLg6ekJT09P6OnpKTBh01LENhdVVUh6JQTdP3kPl7p6oFXiWTi98PwzfaYy7Cv/lKpmlyJ3nQMsANQ5kUiVpaSkYPjw4bhy5coT0woKCqClpQUDAwPExMRg1qxZSE5OrvczPT09kZiY2BxxVV5ZTh5Sh45El8QTODpkDLwif4R+q5ZSxyLpNWg0DU8DEtXCyMgIBgYGAICAgABUVlaiqUbGaqLMC1dwrZ8fLK5cwKn3P8OLsT+xqKhRWFZEtcjMzMSfZx0SEhIgl8thZmYmcSrVdH3jTrTq1wed7v2OW2s2o++Sjxs1NJ0IaOKy2rVrF5ycnKClpVXnqZC4uDh069YNDg4OWLx4cc37ubm5GDx4MLp06YLBgwcjLy+vKeM9VUPWe/PmTbi5udX8Z2RkhGXLlgEAPv30U9ja2tZMi4mJUUjuhmYHgI4dO8LZ2Rlubm7w9PRs9PJS5E5NTYWPjw8cHR3h5OSE5cuX10x71m0+duxY9OnTBzdv3oSdnR3Wr1+PNWvWYM2aNQCAiIgI9OjRA66urpg5cybCw8Nx4MCBWvfbPwkhkJqaCgcHB7i4uODChQs10562zytCfevetm0bXFxc4OLigr59+yIpKalm2tP2m4YQcjnOz/gA3ULGIKuNJQpOxMNj4qgmzX7s2DEYGxvX7AcLFixo8LLNqb51L1mypCZzjx49oK2tjdzcXADPts2fVUhICCwtLdGjR49apwshMHPmTGn28XrGtjfKtWvXxI0bN8SAAQPEuXPnap2nqqpK2Nvbi1u3bony8nLh4uIirl69KoQQ4t///rdYtGiREEKIRYsWiTlz5jQ2wj/S2PVWVVUJKysrkZKSIoQQ4pNPPhFLlixp9py1aWj2Dh06iKysrH+8fFNryHrv378vzp8/L4QQoqCgQHTp0qVmX1H0Nq9rv/1TdHS0MDIyEnK5XJw+fVr06tWrwctKmTs+Pl7k5uYKIYSIiYmpyS3E0/eb+pTkPhIX+vgJAYiEXoNEQXZes2Q/evSoGDZs2D9atrk0dt179+4VPj4+Na//6TZvCsePHxfnz59/6vWH0dHRYujQoU29jzfoOqsmPbJydHREt27d6pwnISEBDg4OsLe3h66uLsaMGYOoqCgAQFRUFCZOnAgAmDhxIvbs2dOU8Z6qses9fPgwOnfujA4dOiggXd2edZsp8za3traGu7s7AMDQ0BCOjo5IT09XSL6/q2u//VNUVBTMzMwgk8ng5eWF/Px8ZGRkNGhZKXP37dsXbdq0AQB4eXkhLS3tmdaZdvEa7vfwgOvpQzg19X14nDoAQzOTZsneHMs+q8aue/v27Rg7dqxCstWnvks6oqKiMGHCBEn2cYV/Z5Weno527drVvLazs6v5BfTgwQNYW1sD+O8vqocPHyokU2PXGx4e/sTOtWrVKri4uCAkJERhp9KAhmeXyWTw8/ODh4cHwsLCGr18U2vselNSUnDx4kX07v3/NzZV5Dava7/96zy6urpPzNOQZZtLY9e9fv16+Pv717x+2n7zNBc27kT1oMGwyMnA5bBt6Lt2CbS0/9mvmYZmr+0SA1XZ5iUlJYiLi0Nw8P9fZ9bYba5IT/vZFLG9G30Hi0GDBiEzM/OJ97/44guMGDGi3uVFLUPlFfFla125G6OiogJ79+7FokWLat6bPn065s6dC5lMhrlz5+K9997Dhg0bnjnzn5oie3x8PGxsbPDw4UMMHjwYzz33HPr3799kGWvTVNu8qKgIwcHBWLZsGYyMjAA0/zb/u4bst0+bR6p9Hmjc37ejR49i/fr1OHnyZM17Dd1vqquqcWraHPT9cRnOOvWF7obv4NrTpdmzu7u74+7duzWXGIwcORLJyckqs8337duHfv36PXY0I8Xf1YaSch9vdFn98ssvz7RCOzs7pKam1rxOS0uDjY0NAMDKygoZGRmwtrZGRkYGLC0tn2ldf1VX7sasNzY2Fu7u7rCysnps+T+9/vrrGD58eNOE/j9Nkf3PbWxpaYlRo0YhISEB/fv3V/ptXllZieDgYLz66qsICgp6bPk/Ncc2/7u69tu/znP9+vUn5qmoqKh32ebSkNwAcOnSJUydOhWxsbGPjXp82n7zV7npD5Ay/BV4//YrLvYdCvf94dBrY6yQ7H/+4wX47yUGM2bMQHZ2doN/7ubQmHXXdpamIdtcKk/72RSxjyv8NGDPnj2RnJyMO3fuoKKiAuHh4QgMDAQABAYGYtOmTQCATZs2NehIrSk0Zr21nV/OyMio+fPPP//81JE0zaEh2YuLi1FYWFjz54MHD9ZkVOZtLoTAlClT4OjoiNmzZz82TdHbvK799k+BgYHIycmBEAJnzpyBsbExrK2tG7SslLnv3buHoKAgbNmyBV27dq15v6795k/XDsaj2NUDLpdOIfHdT+H2a3STFFVDsz/tEgNl3+YA8OjRIxw/fvyxfb8h21xKgYGB2Lx5szT7eD0jMBolMjJS2NraCl1dXWFpaSn8/PyEEEKkp6cLf3//x0aUdOnSRdjb24vPP/+85v3s7Gzh6+srHBwchK+vr8jJyWlshH/kaev9e+7i4mJhamoq8vPzH1t+/PjxokePHsLZ2Vm89NJL4v79+wrJ3dDst27dEi4uLsLFxUV0795dZbb5r7/+KgAIZ2fnmrufR0dHCyGk2ea17berV68Wq1evFkIIIZfLhYWFhbC3txc9evR4bETs0/Z5Ragv95QpU4SJiUnNNv7zjtp17TdyuVwc+fgbUaLTUmQZmonk3TGSZF+5cqXo3r27cHFxEb179xbx8fF1Lqso9eUWQoiNGzeK0aNHP7ZcXdtcEcaMGSPatm0rdHR0hK2trVi3bt0T+/iMGTOaeh9v0GhA3m6JqAlpwu2WHuUV4sIrIbBNSoAwM4N1TBSM7NvVvyBR7Xi7JSJqWjdP/oZMZw/4HI5A0bBAdL10hkVFCsGyIqJ6CSFw9IvvYTf4BVjnZuKPdT/B/ceVkP1lqD5Rc+LDF4moTnl5RTg/eioGHdqBu517wGRfJBwcu0gdizQMj6yI6KmSjl/AWZ8RGHRoBy6/MhntrybCmEVFEmBZEdETquUCsR9/C/sh3uh38yzubNgO550bIGvJx3qQNHgakIgek5GejduvToX/8Sjc7uoKy70R6NTNQepYpOF4ZEVENU5EHEapmzv6HN+L36fORKcr52DAoiIlwLIiIhSVVWL31I/gNCEIJhUlyIrci65rl0PWooXU0UgNnTt3Di4uLigrK4NMJmstk8muymSyOm/VwdOARBru8vmbKBo/EcE3ziIpYDS6r1uGFtZtpY5Faqxnz54IDAzExx9/DABfAdgqhLhS1zI8siLSUJXVcuz5Yi3sfPrA/Y8LSPl0MVz3b2dRkULMmzcPhw4dAgBP/Lew6sQjKyINdOdeFq69FoqRJyKR0aErdHYfQUcPN6ljkQbJzc1FUVERABgC0ANQXNf8PLIi0iBCCERv2IuH3r7ofzYOt8e/DusbSTBkUZGCTZs2DZ999hkAbAPwZX3zs6yINERGVgH2jpqGIVNHoUvhA1RGRMJ+Sxigpyd1NNIwmzdvho6ODsaNGwcAiwH0lMlkvnUtw7uuEzUhZbzruhAChyKOwnZWKJwyknFraBDsf1oHWZs2UkcjAnjXdSJ6+KgEO8fNxoCxQ2FXmIWHG7ehc+xuFhWpHA6wIFJDQggcjj0LkxnTMPruZdztNwh2u7bAmCP9SEXxyIpIzTwsKEX4zC/gNcoX3R/cwoPlq9Hh14PQZlGRCuORFZGaEEIgbv8ZmLzzJoal3USulzdsNq6BlX0nqaMRPTOWFZEaSM8txuGZnyJ45ypoaclQ9PkitH/vbUCLJ09IPbCsiFSYXC6wf/dx2Lz/Nibcu4L0Xt5oG74ZFp06Sh2NqEmxrIhU1B8Z+Yh/ey7G7A1DlY4ucleshu1bbwCyBo0EJlIpLCsiFVNeVY1dG6LR9uuFePVWIh7284H19h/R2tZW6mhEzYZlRaRCEq+lIfmtORhzbAdKDY1RvHkbbMb9i0dTpPZYVkQq4FFpJSIWb8SgFZ/AMz8TGcFjYR22CjA1lToakUKwrIiUmBACsUcvo9V/5mBKwgHk2HRA2Y5DsPYbJHU0IoViWREpqVsPChD74TcYt/0bGFaUIuudf8Ni0QLeeJY0Ei/CIFIypRVV2LxmL/I9++CtDfORN2AQtC5ehMW3X7GoSGPxyIpISQghcPTcLeTN+RDjft2NstZGKPxuDTqHvs6Le0njsayIlEBKVhFi5y5D0LZvYVGch6wxE2C16hsOoCD6PywrIgmVVlTjp00H4bjwQ0xP+Q3ZXZ0g/zEaVn28pI5GpFR4boFIAkIIHDx1Ewf9X8X40EDYycpR+PW3ML+WBB0WFdETeGRFpGBX0/Jw4sOv8fLu72FW+gjZr4xD+xVLASsrqaMRKS0eWREpSE5ROVYv2oqqnr0xfctCoLM9xNkEWO7YyqIiqgePrIiaWUWVHLv2noXh/LmYfukwCk0tULJuIyxCJvI2SUQNxCMromYihMDhxNuIGz0do8b4wLH4IfLeng3DlFtoNWUSi4qoEVhWpJFCQkJgaWmJHj161DpdCIGZM2fCwcEBLi4uuHDhQqM+//K9PKwOmQcnn54IjAxDka8fHOIi0WbFUsDQsCl+BCKNwrIijTRp0iTExcU9dXpsbCySk5ORnJyMsLAwTJ8+vUGfW1ktx3fz1kLWqydm/Pg5dNq3Q9Wx47CM2wuZg0NTxSfSOCwr0kj9+/eHaR0X3EZFRWHChAmQyWTw8vJCfn4+MjIynjp/YVkl1q6NQdn13/HmZ9PQTpSg9MfNML98AToD+jfHj0CkUVhWRLVIT09Hu3btal7b2dkhPT39ifkqquR4f+4q7H/+RUx8IxC68ko8mjsfxim3oD/xNd4miaiJcDQgUS2EEE+8J/vLgAi5XCA2/gZyPvkcn/26Gy1ENfInTUHLC2dhvGCeIqMSaQSWFVEt7OzskJqaWvM6LS0NNjY2EELgxJU03Jz3FV4+sBmmpQV4MGwULJd9BXMHB8DTU8LUROqL5yiIahEYGIjNmzdDCIEzZ87A2NgYmaU6CJs8F5WjgjFtzypUubpBfi4RVvsjOXiCqJnxyIo00tixY3Hs2DFkZ2fDzs4O8+fPR2VlJQAgNDQUAQEBiImJgYODA/Qs7THVcRCMej6PN3LTkd7LG5Wr4mA5dIjEPwWR5pDVdm7+L+qcSKTObj0sxC+L16L/1pVwzEpBTqeuaP3lQui9HPTUC3o9PT2RmJio4KREKq1BV8fzyIrob+7lFCNm2VZ4rf8Gb2T8jlzbDijZuBlmr40DtLWljkekkVhWRP8nLbcYB5ZvhduGFeirLUP7qkIUrloN0zemAjr8q0IkJf4NJI2XnleCA8u2wHXDckxJu45HZlbAf/4D47dCgZYtpY5HRGBZkQZLzSnGL8u3wPPHFQhJvY5887bIX7ocJm++wZIiUjIsK9I4KVlFOLp0A9rs34PJV4+iwMIaed+sQJsZ01hSREqKZUUa44+MRzi1eDV6bv8Bk7NSkG3TEfnLv4NJ6FRAV1fqeERUB5YVqb2rd7JwceFK+EZtxISsNGS1s0fBD+thPvk1oEULqeMRUQOwrEhtJV65h+sLl8E7Nhzj8zPw0KE7Cr/dDoux/+INZolUDMuK1IpcLnDq9DVkLPwag49EwLOsCNeHBKN4xiRYvjSMT+clUlEsK1ILFVVyHN5/ClVLvsbghFjoVVXgrrcf9D+fC8f+L0gdj4ieEcuKVFphWSWObNgDw+9XwqQgHx73b+D+8GDYfjEXHZy6Sx2PiJoIy4pUUmZOEZJWbETbDd9jRNoNFLUyRPakaWjxYSw62tpKHY+ImhjLilTKtev38PvilfCI2oIhjx4gy8oOaZ99Bbt3psPAwEDqeETUTFhWpPTkcoGzB88gf8ky9ImPhoWOLko62CNr5QpYjAvmzWWJNADLipRWUVkl4ldvh1HYavS+eRbVWtq44zsM1p9+AIu+XlLHIyIFYlmR0klNycSFb9bBeXsYhmSnIs/QFMlvvAv7j99DV1sbqeMRkQRYVqQU5HKBCzG/onzld3A9tg/PGVlC29gId+f+gA6hk9CGt0Mi0mgsK5JUQUExzi/bCNNNa+F5+xLKdVrgzsDhsJjzDsx8vHkRLxEBYFmRRG6du4zUL1egzZlf4ZN+E5nmNrjyzsfo8sHbeM7KUup4RKRkWFakMGWl5fht9Ra0XL8ertfPoiNkuOHujduLv4D9uFFoy/v1EdFTsKyo2aWeu4x7X6+C/pl4eN27iixjc1yc+DY6fzATTt06Sx2PiFQAy4qaRXlRMa6s2gT9zRvR/XoibGRauObWD1c/3gbHia/AQpeP5iCihmNZUZNKPRKPO2u3wTVqKzxKC5HexhrnX38PHWZPh/NzPIoion+GZUXPrDg9E79/swZtdm5Dx7Q/0KaFHq709IX+65PRY/wo2OrwDhNE9GxYVvSPiIoK3N4SgYzIaPSO24nn5VW4adcVZ2bPh8PM1+HVwVrqiESkRlhW1HByOXJOnkX68h/Q/sAedC5+BJllB5zyHw2zt0LhNKQfZLwuioiaAcuK6lWWfAt3Vq2D0a5wVJaWo1thFi649kfVq+Ph9vpo2Bu2kjoiEak5lhXVSp6dg7trt0Bs3Qr7a+fhCOC3Dj1wf/x0aE0bhz4OdlJHJCINwrKi/1dSggfbdqFww2a0TziBFgamqGihi5jRb6Jt6GS49XeHmxZP8xGR4rGsNF1FBfKjopEWvged9++CVUUpZAamODzwZehOnACv4EGw1+M1UUQkLZaVJqqqQvHBX/AgbBMsD0XDpKQQoqUBfuntD63gIHi8NgL+pnzqLhEpD5aVpqiqQtnho8hctxmFyXfgnBQPC119xPd4ASWjXobzpJfxkp2p1CmJiGrFslJnVVWoOHwEmeu3os2B/TAsyINli5ZIcvHB3U9WwW5cEPy6tOVwcyJSeiwrdVNRgcqDB/Hwx+0wOhiDcrkMZhWlONmtN3ICAuEw4RUMd7SDNgdKEJEKYVmpg5ISlMcdQvbGLWhz5ABalRShjV4rHO/SCw+GBaHr2BEY6GQHHW0+goOIVBPLSlXl5qLs5yjkbdsJs/ijSGrbFV0f3sGh5/ogd+hL6DJuJAZ1t0ULFhQRqQGWlSpJTUVR1H4Ub9oK8wtnoSevhszAFFHP++FRQCCqXhmGYV2teARFRGqHZaXMhACSkvAoPAKVkXtgnnwVV9r1gHlxPhL9X8N9nyFwHTkIQZ3M+B0UEak1lpWyKSuDOHIEeTsikX/zFuzPHoMhZDhv64g9w9+A9ogR6OnfFwE2RhzFR0Qag2WlDDIzUREdi0fbd8Eo/hhalpWila4efnXojQOvfQjDl0fAu58Tppq1ljopEZEkWFZSkMuB8+dRHBmF8qh9ML1+CTesu8K8KBeRTr7IenEw2gUPg7dzO5gbtJQ6LRGR5FhWipKfj+oDB5F96BgMInehdV429GUy3LDphl2DJ6PSPwA9/L0xqrM59FrwybpERH/FsmouQgCXL6Pk570o3bsfJr8lQlteDS19Yxzq9DzujeiP1iOGoW/v5zCtrSG/f5JAXFwcZs2aherqakydOhUffPDBY9OPHTuGESNGoFOnTgCAoKAgzJs3T4qoRBqPZdWUcnNRffAg8iL3Qe/wIWS2MoFDWjIy23XFzy/8CyUD/WA/zBcvOraFSStdqdNqtOrqarz55ps4dOgQ7Ozs0LNnTwQGBqJ79+6Pzeft7Y39+/dLlJKI/sSyehZVVUBCAh7t2Y/KmDgUCm10upYIHT0DHO30PO549of+MH/07NMdIXYm0OLwcqWRkJAABwcH2NvbAwDGjBmDqKioJ8qKiJQDy6qx7t5FaXQsHkVFQ3b9OqxSb8FApoVLbbvgVr9BiB73NjoF+KJ/Nyu81IrPgVJW6enpaNeuXc1rOzs7nD179on5Tp8+DVdXV9jY2ODrr7+Gk5PTE/OEhYUhLCwMAJCVldV8oYk0GMuqPgUFqDx8BJnHTsHw5wiYpN6BPoA8Q3PscxkI+fAQGL3kj94eDgi2MOB3TypCCPHEe3//f+fu7o67d+/CwMAAMTExGDlyJJKTk59Ybtq0aZg2bRoAwNPTs3kCE2k4ltXfVVaiOuEcsnfvhfzgIVheT0ILeTW0DcyRZNURt14OhGyIH7r79MLkDqbQ1eGtjVSRnZ0dUlNTa16npaXBxsbmsXmMjIxq/hwQEIAZM2YgOzsb5ubmCstJRP/FshIC8itX8SByPyoPHoLFhbPIN2oDq4fpuGTtgKO+Y1Hxoi/shg1Ez27WGKDPU3vqoGfPnkhOTsadO3dga2uL8PBw/PTTT4/Nk5mZCSsrK8hkMiQkJEAul8PMzEyixESaTSPLSn73LjIiY5B3KgF2h/bB5FEOrAHcaWONg26+kPv4oqXfQPT06Ao3Q16Uq450dHSwatUqDBkyBNXV1QgJCYGTkxPWrFkDAAgNDUVERARWr14NHR0d6OvrIzw8nKd5iSQiq+3c/V/UOVFVVD54iLTIaJTGHoJZwklYPfjv6Z/7Bma46uCGR14vwHD4ELi84AZrY32J05Iq8/T0RGJiotQxiFRJg/4FqJZHViXZubj7cxxKDxyC2dl4oKgInfIzUKirjyud3ZDgPwZGw4egi28fDG7TSuq4RERUD7Uoq4cPcpESdRAVvxxBRUoq+icehKOQo1y7Ba7bOyOn/xCkDx0Mh2E+6GNqKHVcIiJqJJUrq2q5wO8pWUiNO4KqYyfgkHQaHf+4gl7yKlRqaeO8ywtIGDMN+kMGo9NLg+BmalT/hxIRkVJT+rLKK67A5duZuH/wBHROHEf7pAS4pl2HY3UlqmVaSHbxwrXRITAYOgjtA4fAy4TlRESkbpSqrCqr5biRUYCk2w+Re+wUWp/6Fd1unIeJqET/e9cgl8mQ2ek5pI6dDCN/P1gEDMRzJiZSxyYiomYmWVkJIZCSXYxL6Y9w6XYWSk6dgcX5M+hSmoOgC4fQqrIcAJDd+TmUv+iLUr/50B/kCxtTU6kiExGRRBRSVkIIZDwqw6W0R7iUlo9rd7MhP5uAFzOvw+H6ebyXfq2mnB74DIE8ZAqE30DIBgyAOS/CJCLSeAopqwvJD7BwwRZ43buMvqmXMTP9OvQqy1HYvhNatG4N3dBpgI8P4O0NK97KhoiI/kYhZeV0/yZ2b5sDAJA7u0Br+hvAgAEw7N8fYDkREVE9FFJWen37ALt3AwMGQIun9YiIqJEUM8BCVxcIClLIqoiISP3w+RZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0WFZERKT0ZEIIqTMQqQ2ZTBYnhBgqdQ4idcOyIiIipcfTgEREpPRYVkREpPRYVkREpPRYVkREpPRYVkREpPT+FzM58uKt6ADRAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAasAAAEgCAYAAAAKZlx2AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABFCklEQVR4nO3deVxVdf748deFC7KDsiO4wEVEFFxwSZvK1FwqypzMltHGJiezsWUms5lpmaZGq+lXfccpY2oabUzbo0UoLCs1FVFxw+WqKNtll32/nN8fCJPJclG451x4Px+PHo/Bez6c97lz4c35nPfn/dEpioIQQgihZXZqByCEEEJ0RpKVEEIIzZNkJYQQQvMkWQkhhNA8SVZCCCE0T5KVEEIIzZNkJYQQQvMkWQkhhNA8vdoBiL5Fp9P5AVOAIKAGOAykKorSpGpgQghN00kHC2ENOp1uKrASGADsBwoAJ2AYEAZ8CLykKEq5akEKITRLkpWwCp1O9yLwD0VRMtt4TQ/cANgrivKR1YMTQmieJCshhBCaJwUWwqp0Ot07Op3O8ydfD9HpdN+oGZMQQvskWQlr2w7s1ul0c3Q63b3A18Ar6oYkhNC6zqYBZY5QdLvt27czdepUfHx82L9/PwEBAWqH1G1mzZpFUlKS2mEIYUt0lhwkd1bCqt555x0WL17M+vXrufvuu5kzZw4HDhxQO6xuU1RUpHYIQvRKss5KWNVHH33E9u3b8fPz4/bbb2fu3Lncfffd7N+/X+3QhBAaJtOAQnX19fU4OjqqHUa3iI2NJTU1Ve0whLAlMg0otOPZZ5+lpKSkzdccHR359ttv+eKLL6wclRDCVsg0oLCKUaNGceONN+Lk5MTYsWPx9fWltrYWo9FIWloa06dP549//KPaYQohNEqSlbCKDz/8kB07dvDCCy/g5+eHyWTCw8ODu+66i/j4eJydndUOUQihYZKshFXs3buXs2fPsmHDBrZu3XrBazU1NZKshBAdkmQlrOK+++5j1qxZnD59mtjY2NZ/VxQFnU7H6dOnVYxOCKF1Ug0orGrp0qW8/vrraofRY6QaUIguk2pAoT29OVEJIXqOJCshhBAWq20wY26y/qSbJCshhBAWW/v9KYY/kUiD2bqbe0uyEkIIYTFTaS1eLo442Fs3fUiyEkIIYTFTeS1Bnk5WP68kKyGEEBYzldYQ6Gn9dZGSrIQQQljMVFZLgNxZCSGE0KqK2gYq6xoJ8pJkJYQQQqNMZbUAMg0ohBBCu3JLawAIlGlAIYQQWtV6Z+Uld1ZCCCE0ylRWi50O/Nz7Wf3ckqyEEEJYxFRag697P6svCAZJVkIIISxkKqtVpbgCJFkJIYSwkKmsRpWydZBkJYQQwgKKojQvCPaQOyshhBAaVV7TSHW9We6shLgcSUlJREREYDAYWL169UWvK4rC8uXLMRgMREdHs2/fvtbXFi9ejJ+fHyNHjrxgTElJCTNmzCA8PJwZM2Zw7ty5Hr8OIbTKVN6yxkrurIS4JGazmWXLlpGYmEh6ejobN24kPT39gmMSExMxGo0YjUbi4+NZunRp62t33303SUlJF33f1atXM23aNIxGI9OmTWszCQrRV5hKW9ZYyZ2VEJckJSUFg8FAaGgojo6OLFiwgISEhAuOSUhIYOHCheh0OiZNmkRpaSkmkwmAq666igEDBlz0fRMSEli0aBEAixYt4tNPP+3xaxFCq3LL1OteAZKsRC+Qk5NDSEhI69fBwcHk5OR0+Zify8/PJzAwEIDAwEAKCgraPC4+Pp7Y2FhiY2MpLCy81MsQQtPyymqxt9Ph5y7JSohLoijKRf+m0+m6fMylWrJkCampqaSmpuLr69st31MIrcktrcXfvR/2dt3zc9NVkqyEzQsODiYrK6v16+zsbIKCgrp8zM/5+/u3ThWaTCb8/Py6MWohbIuprEaVfaxaSLISNm/8+PEYjUYyMjKor69n06ZNxMXFXXBMXFwc69evR1EUdu3ahaenZ+sUX3vi4uJYt24dAOvWreOmm27qsWsQQutMZbWqNLBtIclK2Dy9Xs+aNWuYOXMmkZGRzJ8/n6ioKNauXcvatWsBmDNnDqGhoRgMBu69915ee+211vG33347V1xxBcePHyc4OJi33noLgJUrV5KcnEx4eDjJycmsXLlSlesTQm3NC4JrCFLxzkrX1lz+T3T4ohDiQrGxsaSmpqodhhDd6lxVPWP+mswTN4zgniuHdve3t+ghmNxZCSGE6FBL2bqad1aSrIQQQnQoT8VNF1tIshJCCNGh3PPJSu6shBBCaJaptAa9nQ5vN+vvENxCkpUQQogO5ZXV4u/hpNqCYJBkJYQQohO5Km662EKSlRBCiA6ZymoJUGlrkBaSrIQQQrSrZYdgNYsrQJKVEEKIDpRU1VPf2KTa1iAtrJKsahvMFFfWWeNUQgghupHpfNl6n5gGnPN/2/jzp4etcSohhBDdKLf0fPeKvlBgMdTbldOFVdY4lRBCiG6UV36+e0VfuLMK9XUlo7gKc5P0xRVCCFuSW1qLg70Ob1dHVeOwUrJyo76xqfV2UgghhG1o2XTRTsUFwWCtZOXjCsCpwkprnE4IIUQ3MZXVqj4FCFa8swLkuZUQQtgYtTddbGGVZOXj5oiHk57TRXJnJYQQtqKpSSFPA90rwErJSqfTEerrJndWQghhQ4qr6mkwK6qXrYMVO1iE+rrKMyshhLAhpvM7BPeZZ1YAYb5u5JfXUVnXaK1TCiGEuAy5pS1rrPrSndX5isAMmQoUQgib8L87q76UrFoqAqXIQgghbEJeWS2OejsGqLwgGKyYrAZ7u6DTwSm5sxI9ICkpiYiICAwGA6tXr77odUVRWL58OQaDgejoaPbt29fp2LS0NCZNmsTo0aOJjY0lJSXFKtcihFbkltUS6OmETqfugmCwYrJycrAnuL8zp6XIQnQzs9nMsmXLSExMJD09nY0bN5Kenn7BMYmJiRiNRoxGI/Hx8SxdurTTsStWrOCpp54iLS2NZ555hhUrVlj92oRQk6m0RhNTgGDl/azCpHxd9ICUlBQMBgOhoaE4OjqyYMECEhISLjgmISGBhQsXotPpmDRpEqWlpZhMpg7H6nQ6ysvLASgrKyMoKMjq1yaEmpo3XVS/EhBAb82Thfq4sft0CU1Niup9pkTvkZOTQ0hISOvXwcHB7N69u9NjcnJyOhz7yiuvMHPmTP7whz/Q1NTEjz/+2Ob54+PjiY+PB6CwsLDbrksINZmbFPLLawnoi3dWob6u1DSYMZ1vOS9Ed1CUi7v5/3yOvb1jOhr7+uuv8/LLL5OVlcXLL7/MPffc0+b5lyxZQmpqKqmpqfj6+l7KJQihOUWVdTQ2KQR6aePOyurJCpDnVqJbBQcHk5WV1fp1dnb2RVN27R3T0dh169Zxyy23AHDrrbdKgYXoU1p2CNZCX0BQ4ZkVSENb0b3Gjx+P0WgkIyOD+vp6Nm3aRFxc3AXHxMXFsX79ehRFYdeuXXh6ehIYGNjh2KCgIL7//nsAvv32W8LDw61+bUKoxVSqne4VYOVnVn7u/XB1tJc7K9Gt9Ho9a9asYebMmZjNZhYvXkxUVBRr164F4L777mPOnDls3rwZg8GAi4sLb7/9dodjAf71r3/x4IMP0tjYiJOTU+tzKSH6gtwy7XSvANC1NWf/E92+te+N/9iOl4sD79wzsbu/tRCqi42NJTU1Ve0whLhsz32Zzju7znL0mVk9vc7Kom9u1WlAaH5uJdOAQgihbbnny9a1sCAYVEhWYb5u5JTWUFNvtvaphRBCWMhUWqOZsnVQ6c4KIKNI7q6EEEKrtLKdfQvrJysfaWgrhBBa1mhuQm+nI7h/H05WQ89vFXKqQO6shBBCi0xltWSd005fQFAhWTk72jPQy1nurIQQQqMyS6oBGOTtonIk/2P1ZAVSESiEEFrWmqwG9PVk5ePK6cLKNvuyCSGEUNfZ4moc7HV9u8ACmncNrqo3U1BRp8bphRBCdCCrpJrg/i7Ya2h3DNWmAQFOSdslIYTQnLMlVYRoaAoQVEpW0tBWCCG0K7O4msGSrCDAwwlnB3tJVkIIoTGl1fWU1zZqqrgCVEpWdnY6hvq4yjSgEEJojBbL1kGlZAXny9dlrZUQQmjK2WLtla2DqsnKjexzNdQ2SENbIYTQCi2usQIVk1WYryuK8r8sLoQQQn1ZJdX4uDni2s+qe/N2Sr07q5aGtvLcSgghNONscbXm7qpAxWQ1VNZaCSGE5mSWSLK6gFs/PeMG95dkJYQQGlHf2ISprIZB3q5qh3IR1ZIVgKezA0dNFWqGIIQQ4ryc0hqaFO0VV4DKySoiwJ2TBZXUNzapGYYQQgjgbHFzowZJVj8zPMCdxiZF1luJy5aUlERERAQGg4HVq1df9LqiKCxfvhyDwUB0dDT79u2zaOw//vEPIiIiiIqKYsWKFT1+HUKoKet82fpgjS0IBlC1NjEy0AOAY6YKhgd4qBmKsGFms5lly5aRnJxMcHAw48ePJy4ujhEjRrQek5iYiNFoxGg0snv3bpYuXcru3bs7HLt161YSEhI4ePAg/fr1o6CgQMWrFKLnnS2upp/eDl+3fmqHchFV76yG+rjiaG/H0bxyNcMQNi4lJQWDwUBoaCiOjo4sWLCAhISEC45JSEhg4cKF6HQ6Jk2aRGlpKSaTqcOxr7/+OitXrqRfv+YfXD8/P6tfmxDW1FIJaKehrUFaqJqsHOztCPNz45gUWYjLkJOTQ0hISOvXwcHB5OTkWHRMR2NPnDjBtm3bmDhxIldffTV79uxp8/zx8fHExsYSGxtLYWFhd16aEFal1bJ1UDlZAUQGuHM8T5KVuHRt7Tit0+ksOqajsY2NjZw7d45du3bx4osvMn/+/DaPX7JkCampqaSmpuLr63uplyGEqhRFaU5WGnxeBRpIVsMD3ckrr+VcVb3aoQgbFRwcTFZWVuvX2dnZBAUFWXRMR2ODg4O55ZZb0Ol0TJgwATs7O4qKinr4aoRQR1FlPdX1Zrmzak9LYcUxubsSl2j8+PEYjUYyMjKor69n06ZNxMXFXXBMXFwc69evR1EUdu3ahaenJ4GBgR2Ovfnmm/n222+B5inB+vp6fHx8rH59QlhDpoYrAUHlakBoLl8HOJZXzhVh3ipHI2yRXq9nzZo1zJw5E7PZzOLFi4mKimLt2rUA3HfffcyZM4fNmzdjMBhwcXHh7bff7nAswOLFi1m8eDEjR47E0dGRdevWXTS9KERvkVmi3TVWALq25uB/osMXu4OiKIx7dgvXjfBn9bzonj6dED0qNjaW1NRUtcMQoste3WLk5S0nOPbXWTg52Fvz1Bb9Baj6NKBOp2N4gDtHZRpQCCFUk1lSTYCHk7UTlcVUT1bQ/NzqRF4F5qYev5ETQgjRhsySKs1WAoJmkpU7NQ3m1gd8QgghrEvLa6xAK8kqsLnI4rh0shBCCKurbTCTX17HYElWHQv3c8dOh2wXIoQQKmhpYCvTgJ1wdrRniI8rx+TOSgghrO5scXOyCpE7q84ND3CXhcFCCKGC1gXBkqw6NzzAg8ySaqrqGtUORQgh+pTMkmpcHe0Z4Oqodijt0lCyckdR4ES+3F0JIYQ1NTewddV0hxbNJKvWjRhlKlAIIazqbHEVgwY4qx1GhzSTrAZ6OePqaM8xkxRZCCGEtTQ1KWSdq2Gwt6vaoXRIM8nKzk5HhBRZCCGEVeVX1FLf2KTpSkDQULICGB7owbG8ijY3uBNCCNH9Mou1XwkIGktWkQHulNU0kFdeq3YoQgjRJ7SUrWu51RJoLFlFtGzEKJ0shBDCKjJLqrHTwcD+UmBhsYjWjRglWQkhhDVkllQT5OWMg72m0sFFNBWdp7MDA72cpe2SEEJYydnias1uZf9TmkpW0Hx3JdOAQghhHVka3xqkheaS1fAAd04VVlLf2KR2KEII0atV1DRQXW/WfNk6aDFZBXrQ2KRwqrBS7VCEEKJXyyiuoqbBTJivthcEgwaTVWRrkYU8txJCiJ5kzG++KTD4uascSec0l6yG+LjiaG8nz62EEKKHGQsqcbDXaX5BMGgwWTnY22Hwc+OolK+LLkhKSiIiIgKDwcDq1asvel1RFJYvX47BYCA6Opp9+/ZZPPbvf/87Op2OoqKiHr0GIazNmF9BqI8beo2XrYMGkxXA8EB3jss0oLCQ2Wxm2bJlJCYmkp6ezsaNG0lPT7/gmMTERIxGI0ajkfj4eJYuXWrR2KysLJKTkxk0aJBVr0kIazAWVGLwd1M7DItoMllFBniQX15HSVW92qEIG5CSkoLBYCA0NBRHR0cWLFhAQkLCBcckJCSwcOFCdDodkyZNorS0FJPJ1OnYhx9+mBdeeEHT+/wIcSlq6s1knasm3E+S1SWLkCIL0QU5OTmEhIS0fh0cHExOTo5Fx3Q09rPPPmPgwIHExMR0eP74+HhiY2OJjY2lsLCwOy5JiB53qrASRYFh/tovrgCNJqvhgeeTlRRZCAu01aX/53dC7R3T3r9XV1fz3HPP8cwzz3R6/iVLlpCamkpqaiq+vr5diFwI9ZwsaK4ElDury+Dr1o8BLg6tb6YQHQkODiYrK6v16+zsbIKCgiw6pr1/P3XqFBkZGcTExDBkyBCys7MZO3YseXl5PX9BQljBifwK9HY6zW+62EKvdgBt0el0TAj1Zn9WqdqhCBswfvx4jEYjGRkZDBw4kE2bNvHuu+9ecExcXBxr1qxhwYIF7N69G09PTwIDA/H19W1zbFRUFAUFBa3jhwwZQmpqKj4+Pm3GoCgKeeW1VNQ2svb7U9Q1NnGmqApFUVAARYGQAc7o7eyIDPQgKsiD4P7O8ixMqMZYUNm8VEivyXuWi2gyWQEM83Pj6yN5VNc34uKo2TCFBuj1etasWcPMmTMxm80sXryYqKgo1q5dC8B9993HnDlz2Lx5MwaDARcXF95+++0Ox1riZEElXx0xsd1YTLqpnLKaBkzFVaxOPMbkMG+yzlWjQ4dOBzqgtLqe7SeLaDo/8+jeT09koAcjgjyYPsKPiUO9Nd/5WvQeJwsqGR5gG8+rAHSd7Mqr2pa93x7LZ/F/UnlvySQmhnqrFYYQF8grq+XzA7kkHMjhcE45Oh1cHe5LoJczwwPcWf3bm9m5OwUvF8c2x9fUmzmeX0F6bjlHTeWkm8oxFlRQU2/Gy8WRBeNDuH3CIIK8tL23kLBttQ1mRjyZxAPXhvPIjGFqh2PR9IJmb1ligr0AOJBdKslKqEpRFH4wFvHlwVw+2JuNokB0sCdP3DCCG6ID8fdwaj32H/307SYqAGdHe0aHeDE6xKv13xrNTfxgLOS/uzJZs/Uk/9x6kmuH+3PXpEFcFe6LnZ1MFYrulVFURZNiO8UVoOFk5e3Wj5ABzqTJcyuhol2ni3np6+PsOXOOyWHePDgtnLiYIEJ9u++HXG9vx7XD/bl2uD9ZJdVsTMnk/dQsthzNJ2SAMw9PH8aNMUEyRSi6zYn85krrcBtZEAwaTlYAo0P6s/dMidphiD4oLfMcf//6BNtPFuHv0Y+/3jyS22JDevxhdMgAF1bMGs5D04fx1ZE83tl1hr98ns4b35/mb7eMZNzgAT16ftE3nCyoxE4HQ31soxIQNJ+svPj8QC4F5bX4/WSqRYieUl7bwKrNx8gorMRYUMmfr4/krkmDcXKwt2ocjno7bowJ4saYIL4+ksfTnx1h3us7uWPiIB6bORxPFwerxiN6F2N+JUO8Xemnt+7n+nJoPFl5ApCWVcp1UQEqRyN6u++OF/D4x4fIL69l8ZVDeXNRLG5O6ieF66ICmGLw4eXkE/x7RwZfH8nniRsiiYsJktJ3cUmMBRU2NQUIGl0U3CIqyBO9nU6eW4keVVbdwB8+OMDdb+/BrZ+ej5ZO5s/Xj9BEomrh2k/Pn28YwWcPXEmQlxMPbkrjyYTDFFXWqR2asDH1jU2cKa4m3Ab2sPopTd9ZOTnYExnoIclK9Ji9Z8/xxven+OZYAcumhrF8Wrimp0ZGDvTkk/unsO7HDF777hTfHC3gjV/FMirYU+3QhI3IKKrC3KTInVV3iwnx5GB2GeYm1ZZ8iV7q3d2ZLIjfyfG8cj66bzKPzhyu6UTVwt5Ox+IrQ/nPrycA8Mu1P/LxvmyVoxK2wljQXAlosKGydbCBZDU6pD+VdY2cLpQ+gaJ71DWaefzjg/zxk0NcEeZDwgNXMnqQl9phddnIgZ58/rsrGTPIi0feP8BfPj9Cg7lJ7bCExhnzmysBw7px+YU12ECy8gKQPoGiW+SX17IgfhcbU7K4/5ow3r57fIeLeLXO260f79wzkV9PGcLbO86wbMM+yqob1A5LaNjJgkoGDXCxeoXr5dJ8sgr1ccXdSS/PrcRlO5JbxmMfHeR4XgWv3TmWFbOGY98LukM42Nvx1I1RvHRrNJkl1dzx5i7ZuFS0y1hQgcHGiivABpKVnZ2OmGAv0jJL1Q5F2LBdp4tZ8MYuThdW8uF9k5kzKlDtkLrdvHEhrJw9nJMFldwev4vCCqkUFBdqMDeRUVRlc8UVYAPJCpqnAo/nNzf7FKKrvj6Sx8J/p+Dv6cSmJVcwIshD7ZB6zDURfvz77vFkllRzW/xO8spq1Q5JaMjZ4ioazIpN9QRsYTPJytykcDi3TO1QhI15PzWL+/67l8hADz747RV9opv5FIMP6xZPIL+sltvid5JTWqN2SEIjjPnNhWq2spX9T9lEsoo5X2QhU4GiK97ZdYa3tmUwxeDDu7+ZSH9X2y2k6KoJQwfwzm8mUlJVz/y1O8ksrlY7JKEBxoJKdDZYCQg2kqx83fsx0MuZtOxStUMRNmLD7rM88ekRDH5uvLkoFtd+ml7/3iPGDurPu7+ZRFV9I/Pf2ElWiSSsvs5YUElwf2ecHW2rEhBsJFkBjB4kRRbCMu/tyeRPnxzm2uF+/L/bYmxioW9PGRXsycZ7JzHM34073pSii77OmF9hc22WWthOsgr2Iqe0Rn7YRIc+3JvNyo8PcdUwX167c2yfTlQtIgM9eOS6CAor6rhn3R6q6xvVDkmooNHcxOnCKpssrgBbSlbnOwzIeivRnq+OmHj2i3SmhPkQ/6txNrfosSeNDvFize1jOZxTxgPv7qdROl30OZkl1dSbmwi3weIKsKFkNTLIE3s7HQckWYk2/HiyiN+9m8akUG/+tTBWElUbpo/w55mbRvLtsQKeSDiCoki/zb7EWNBcCWird1Y289TZ2dGeCH93ubMSF0nPLWfJO3sZ4uPC8/OibfLhsbXcNWkwuaU1vPbdKYL7O7NsqkHtkISVnDyfrMJsNFnZzJ0VNE8FHsgqpUk6sIvzskqqufvtFNyd9Pzn1xNkB10LPDozgptHB/HiV8elW3sfciK/goFezrjZaGWsbSWrEC8q6ho5XSQd2AWcq6pn0dsp1DaYuXdYPVMnjsZgMLB69eqLjlUUheXLl2MwGIiOjmbfvn2tryUlJREREXHR2EcffZThw4cTHR3N3LlzKS0ttcZl9TidTscLv4xhcpg3/9x6kpSMYrVDElZgzK+0uW1BfsqmktWYlsXBWdLJoq+rbTDz2EcHyT5XQ/yvxvLcigdITEwkPT2djRs3kp6efsHxiYmJGI1GjEYj8fHxLF26FACz2cyyZcvaHDtjxgwOHz7MwYMHGTZsGKtWrbL6dfYUR70dr981Fke9Hcve3U9BubRl6s3MTQqnCisZZoM9AVvYVLIK9XXDrZ+etKxzaociVKQoCo99dJCUMyX8321jUApOYjAYCA0NxdHRkQULFpCQkHDBmISEBBYuXIhOp2PSpEmUlpZiMplISUlpd+x1112HXt88ZTJp0iSys3vXlJmnsyOv3DaGytpGHtgoFYK9Wfa5auoam2x2jRXYWLKyt9MRHewpRRZ93OvfnyIhLZd7fxHKrFEB5OTkEBIS0vp6cHAwOTk5F4xp7xhLxgL8+9//Zvbs2W3GEx8fT2xsLLGxsRQWFl7u5VlVRIA7q24ZRUpGCS9+dVztcEQPaekJaJA7K+sZHeLFMVMFtQ3Sgb0v2pKez4tfHefGmCDuvyYMoM0SbJ3uwn2q2jvGkrHPPfccer2eO++8s82YlixZQmpqKqmpqfj6+lp8LVpx85iB/GrSYN744TRJh01qhyN6wAkb3cr+p2wuWU0YOoDRIV4ckD6Bfc7xvAoe3LSfkUGevDAvujWpBAcHk5WV1XpcdnY2QUFBF4xt75jOxq5bt44vvviCDRs2XJTEepM/3xBJTIgXj35wkIyiKrXDEd3sZH4lAR5OeDjZbrWszSWrMYP6sy/zHDtOSgVTX3Kuqp7frN+DSz89/1oYe8FaqvHjx2M0GsnIyKC+vp5NmzYRFxd3wfi4uDjWr1+Poijs2rULT09PAgMDOxyblJTE888/z2effYaLi4tVr9fa+untee3OsejtdSz9717ZO66XMRZU2uSGiz9lc8nK09mB6GAvdpwsUjsUYSUN5iaWbthLfnkd8b8aR4Cn0wWv6/V61qxZw8yZM4mMjGT+/PlERUWxdu1a1q5dC8CcOXMIDQ3FYDBw77338tprr3U4FuCBBx6goqKCGTNmMHr0aO677z7rXriVDfRy5pUFYzieX8GfPjkkHS56iQZzEzUNZiaGeqsdymXRdfKB1OSn9cWvjrH2+9OkPTkDdxu+rRWWefWbE6z59iTPz4vmlrHBaofTodjYWFJTU9UO47K8usXIy1tO8Nzckdw5cbDa4YjLdDinjBv+sZ3/u30McTFBnQ+wPovm123uzgqad0I1NymkZJSoHYroYQlpObycbOS3V4VpPlH1Fr+71sDVw3z5y2fpsjt3L9BSPT062EvVOC6XTSarsYP6009vJ8+tejljfgWPf3yI8UP68+D0cLXD6TPs7HS8cttofjHMh9+9u1+2FLFxB7JKGeDqSMgAZ7VDuSw2maycHOyZMHSAPLfqxarqGlm6YR8ujvasuWMsDvY2+VG1Wf1dHbnnyqFkFFWxavMxtcMRlyEtq5SYYE+br2a12d8Ak8N8OJ5fQUGFtInpbRRF4fGPD3G6sJJXF4zB38Op80Gi200O8+GeK4fyzq6zfH/CthY7i2YVtQ2cLKxkdEh/tUO5bDabrK40+ACw85RMBfY2/911ls8O5PLIjGFMOf//s1DHozMjCPdz49EPDlBaXa92OKKLDmWXoSgQE+KpdiiXzWaT1YggDzydHdhulKnA3iQtq5RnvkhnaoQv918jey2pzcnBnpdvG01JVT1//vSw2uGILko73zxh9Pkm4LbMZpOVvZ2OyWHe7DhZJOtBeomy6gZe33qSAA8nXr5tNHZ2tj3H3luMHOjJQ9PD+eKgiYS0i/smCu1KyyxliLcLXi6Oaody2Ww2WQFMNviQW1bLmeJqtUMRl0lRFB7/5CDfHCvg/24f0yt+uHqT+64OY8wgL5749DCmshq1wxEWOpBd2ivuqsDGk1XLcyupCrR97+3JYvOhPH5/XQRjBtn+w+DeRm9vx8vzR9NgVljx4UHZrdsGmMpqyC+vI0aSlfqGeLsw0MtZkpWNO1lQwdOfH+FKgw+/vSpU7XBEO4b4uPKn6yPZZizinV1n1Q5HdOLA+cXAkqw0QKdrfm6183QxZvlLzybVNph54N39uDjq+X/zY+Q5lcbdOXEQ10T4sirxKKcKK9UOR3QgLasMB3sdIwI91A6lW9h0sgK4MtyH0uoG0nPL1Q5FXILVicc4llfBS7fG4CfrqTRPp9PxwrxonBzs+X9fH5fdhTUsLesckYEeODnYd36wDbD5ZHVFWHMn4R2nZCrQ1mxJz+c/P55h8ZShTB3up3Y4wkJ+Hk6sumUUXx7K4987MtQOR7TB3KRwKLus1xRXQC9IVn7uTkT4u8tzKxuTV1bLox8eYESgB4/NjlA7HNFFs6ICmB7pz0tfn+CMbNaoOScLKqmqNxNj481rf8rmkxXAZIM3KRklstW9jTA3KTzx6WFqG5r4xx1j6KfvHdMUfYlOp+PZm0fiaG/H4x/L3lda01JcMXqQl6pxdKdekayuNPhQ19jEvsxzaociLPDmttPsPVvCc3NHEuZr27uX9mUBnk48PieSnaeLeW9PltrhiJ/Yn1WKu5Oeod6uaofSbXpFspowdAD2djqZCrQBR3LL+PvXx5kw1Ju5YwaqHY64TAvGhzBx6ACe23yU/HJpKq0VB7KaFwP3puraXpGs3J0cGB3iJftbaVxtg5mH30vDy8WRv90yyua3LBDNe1+tnhdNfWMTT3x6WKYDNaCm3szx/Ipe9bwKekmyApgS5s3B7FLKahrUDkW044Wk45zIr+TFX0YzwFXaKfUWQ31ceXjGML5OzyfxcJ7a4fR5h3PLMDcpvaoSEHpTsjL40KTA7tNyd6VF24yF/HtHBouuGMw1EVKm3tv85sqhjBzowTOfH5GtRFSWllkK9J7OFS16TbIaM6g/zg728txKg0qr6/nDBwcI83Vl5exItcMRPUBvb8fz86JxdtTzfNJxtcPp09KySxno5Yyvez+1Q+lWvSZZOertmre6l80YNUVRFP70yWGKK+t5dcEYnB17pkw9KSmJiIgIDAYDq1evbjOO5cuXYzAYiI6OZt++fZ2OLSkpYcaMGYSHhzNjxgzOnZNq045EBXkyPdKPjSmZ7D1bonY4fVZaZu/ptP5TvSZZQXMJ+8mCSvLKpCpJKzYfNLHzdBEPzxjGyIE9s1up2Wxm2bJlJCYmkp6ezsaNG0lPT7/gmMTERIxGI0ajkfj4eJYuXdrp2NWrVzNt2jSMRiPTpk1rMwmKCz00fRhBnk788ePDNEgrJqsrrKgjp7RGkpXWTTacb70kU4GakFtaw8pPDjEyyIv7rg7rsfOkpKRgMBgIDQ3F0dGRBQsWkJCQcMExCQkJLFy4EJ1Ox6RJkygtLcVkMnU4NiEhgUWLFgGwaNEiPv300x67ht7CtZ+ep+OiOJ5fwVvbpRWTtfW2Tus/peuo1HTWrFlKUVH3/OIvLCzE19e3W75XR9JN5bg76Qnp79It389acfcEtWPPKKqiut5MuJ8bjvqu/V3UldjPnTtHeXk5gwcPBqC4uJiqqioGDRrUeszJkycJCAjAza15EfKJEycIDg6mrq6u3bFpaWmMHj269Xv8/Oufxtryc1JXV9fmMbagOz8vZ4urqahrYJife5f/v+8qtT/nl6O7Y88vr6Wgoo6oIA/senBpSHfGvXfv3q8URZnV6YGKonT0X7cZN25cd367dt2/Ya8y4blkpampqVu+n7Xi7glqxv729tPK4Me+UDbsOntJ47sS+/vvv6/cc889rV+vX79eeeCBBy44Zs6cOcq2bdtav7722muV1NTUDsd6enpe8D28vLw6jcXFxcXiuLWmOz8vOeeqlcgnEpVfv53SbT+L7ZGf0f+5681dyqxXfujW79mWbo67szyEoii9axoQYNYIf/zdnThqki1D1HKyoJJViceYGuHL7RNCevx8wcHBZGX9r91PdnY2QUFBFh3T0Vh/f39MJhMAJpMJPz8pubdUkJczj8wYxrfHCkiStVdW0dSknO9c0TPPhtXW65LVFQYfDueWyeJElTSam/j9+2k4O9rz/Lxoq3SpGD9+PEajkYyMDOrr69m0aRNxcXEXHBMXF8f69etRFIVdu3bh6elJYGBgh2Pj4uJYt24dAOvWreOmm27q8WvpTe6ePIQRgR48/fkRKusa1Q6n1ztTXEV5bWOvLK4AKyarJUuWWOU8Pm79mDjUmy8Pmbql9Yu14u4JasT+z62nOJBdxnM3j7qszRS7Erter2fNmjXMnDmTyMhI5s+fT1RUFGvXrmXt2rUAzJkzh9DQUAwGA/feey+vvfZah2MBVq5cSXJyMuHh4SQnJ7Ny5cpOY/Hx8bmEq9WG7v686O3t+NstoyioqOOlr3tu7ZX8jDZLs2JxhRrveYcFFoBNNvp6Z9dZnvj0MF89dBURAe5qh9NnHMwu5ZbXfuT66EBeXTBG7XBUERsbS2pqqtphaMoTnx7mv7vO8sXvriSqh5YvCHgq4TAf7M3m0NMzsbetBrYWBdvrpgEBZkb5o9PB5kMmtUPpM2obzDzzeTpXhHnzTNxItcMRGvLorAiuCPPmj58cwtxkk3//2oS0rFJGDfS0tURlsV6ZrPzcnZgwZIAkKyt68avjpJ49x5KrQvF0cVA7HKEhHk4OzI8N4UB2GZv2ZKodTq9U12gm3VTeqzZb/LluTVYffPABUVFR2NnZdTgVYo32NnNGBWIsqMSYX9HpsZac9/jx44wePbr1Pw8PD1555RUAnn76aQYOHNj62ubNmy857q6y9D0bMmQIo0aNYvTo0cTGxnZ5fEd+PFXEW9ubm9T+ItyytReWnDcrK4upU6cSGRlJVFQUr776autrarznlrR0ysrK6lJLJ2vo7NwbNmwgOjqa6OhoJk+ezIEDB1pfa+9z01U3jQ5iUugAXkg6TnFlXbfF/t133+Hp6dn6OXjmmWcsHtuTOjv3iy++2BrzyJEjsbe3p6SkuUXVpbzn6bnlNJgVRl/mtiCLFy/Gz8+PkSPbnh1RLqFtWbfppLa9S9LT05Vjx44pV199tbJnz542j2lsbFRCQ0OVU6dOKXV1dUp0dLRy5MgRRVEU5dFHH1VWrVqlKIqirFq1SlmxYkVXQ2iVV1ajDFn5hfJK8olOj+3qeRsbGxV/f3/lzJkziqIoylNPPaW8+OKLlxzr5bA09sGDByuFhYWXPL495TX1yuRV3yhTX9yqVNc1dmvcubm5yt69e5vPU16uhIeHt35WrP2ed/S5bfHll18qHh4eSlNTk7Jz505lwoQJFo9VM+4dO3YoJSUliqIoyubNm1vjVpT2PzeX4kReuRL2+JfKH95P67bYt27dqlx//fWXNLandPXcn332mTJ16tTWry/lPW9Z15hbWn3JcSuKonz//ffK3r17laioqDZf//LLL5VZs2Z192fc+uusIiMjiYiI6PAYa7W38fdwInZwfxIPdz4V2NXzfvPNN4SFhbV2PVDT5b5nlzv+mc/TMZXV8NL8mC41qbXkvIGBgYwdOxYAd3d3IiMjycnJ6VJ83cXSlk7e3t5daumkhbgnT55M//79AZg0aRLZ2dk9Eku4vzv3/GIoH+zNJvVM541uL+d90/p7/lMbN27k9ttvv6xzHsurYOYIfwIuowIX4KqrrmLAgAHtvn4pbcu6i9WfWeXk5BAS8r+FosHBwa2/gPLz8wkMDASaf1EVFBRc1rlmjwzkWF4FpworOzyuq+fdtGnTRR+uNWvWEB0dzeLFi63andvS2HU6Hddddx3jxo0jPj6+y+Pb8vWRPD7Ym82yqQbGDOrfI3G3OHPmDPv372fixImt/2bN97yjz+1Pj3F0dLzoGEvG9pSunvutt95i9uzZrV+397m5VMuvDSfI04k/f3qYxk4a3Voa+86dO4mJiWH27NkcOXKkS2N7QlfOXV1dTVJSEvPmzWv9t66+543mJr48ZMLLxbHH1zW2d23WeL/1XR0wffp08vIuXnD73HPPWbRoUmmjVL6n3uDZowJ45ot0Eg+Z+PRvS9uNuyvq6+v57LPPWLVqVeu/LV26lCeeeAKdTscTTzzB73//e/79739fdvwtOnrPLbVjxw6CgoIoKChgxowZDB8+nKuuuuqSYyqqrOPxjw8RFeTB764N77G4ASorK5k3bx6vvPIKHh4eQM+/5z9nyee2vWOs+Zn/ua6ce+vWrbz11lts37699d+6+3Pj2k/PkzeO4L7/7mPdzrPcc+XQy4p97NixnD17Fjc3NzZv3szNN9+M0Wi0mff8888/Z8qUKRfczXT1Pd+XWUpFbSPXRPR8f0Q1P+NdTlZbtmy5rBNa0t4mMDCwW9rbBHo6M3aQF5sP5XUYd1fOm5iYyNixY/H3979gfIt7772XG2644bLi/rnuiL3lPfbz82Pu3LmkpKRw1VVXXdJ7rigKf/rkEBW1jbx77+h2G5V2R9wNDQ3MmzePO++8k1tuueWC8S164j3/OUtbOh09evSiY+rr6zsd21MsiRvg4MGD/OY3vyExMRFvb+/Wf2/vc3M5ZkYFcPUwX15OPsEN0YH4tzN1ZUnsLX+8QPPC7/vvv5+ioiKLr7sndOXcbc3SdPU933q8AL2djinhPb8gvb1rs8Zn3OrTgNZubzNnVCDppnLOFFW1e0xXztvW/HJL/ziATz75pN1Kmp5gSexVVVVUVFS0/u+vv/66NcZLec8/3pdDXlktf5g57JIXXVtyXkVRuOeee4iMjOSRRx654DVrv+eWtnQqLi7uUkunnmbJuTMzM7nlllt45513GDZsWOu/d/S5uRw6nY6/xEVRb27i2S+PtnucJbHn5eW1/lWfkpJCU1MT3t7emn/PAcrKyvj+++8v+Oxfynu+9VgBsUP64+HU80tGLqVtWbfppAKjSz7++GNl4MCBiqOjo+Ln56dcd911iqIoSk5OjjJ79uwLKkrCw8OV0NBQ5dlnn23996KiIuXaa69VDAaDcu211yrFxcVdDeEi2eeqlcGPfaH8c6ux3WPaO+/P466qqlIGDBiglJaWXjD+rrvuUkaOHKmMGjVKufHGG5Xc3NzLjttSlsR+6tQpJTo6WomOjlZGjBhxWe95ZnGVEvVkkvLL13cojY3mHo1727ZtCqCMGjVKiYmJUWJiYpQvv/xSURR13vO2Prevv/668vrrryuKoihNTU2Kr6+vEhoaqowcOfKCitj2PvPW0Fnc99xzj+Ll5dX6Hrd01O7oc9Md/t/Xx5XBj32hbD9RcMmx/+Mf/1BGjBihREdHKxMnTlR27NjR4Vhr6SxuRVGUt99+W7ntttsuGNfV9zy3tPn329rvTnZL3AsWLFACAgIUvV6vDBw4UHnzzTcv+ozff//93f0Zt6gasFe2W/q5m/+5g8amJr743S/UDsWmmZsUFsTv5JipgsSHfkFwN+0Z1ptIuyXL1TaYeWjTfk4VVvHF8ivpp7e8mlQ025SSycqPD9l6a7m+227p5+aMCuBwTjmZxdVqh2LT3vjhFHvOnOMvN0VJohKXzcnBntsmDMJYUMmb22RX4Uux9XgBQZ5ODPN3UzuUHtcnktXskYE4O9ix5Wi+2qHYrMM5ZbycfILrRwUyd8xAtcMRvcTUCD9mRQXwj2+NZJXIH5NdUd/YxHZjEdcM97NapaOa+kSyChngwrjB/Xln19lu2Takr6ltMPPQe2kMcHXkubkj+8QPhrCeJ28cgQ4df/k8Xe1QbErqmRKq6s1Mjegbm4L2iWQFMG9cMBlFVew8Vax2KDZndeIxThZU8vdbY/Bycex8gBBdEOTlzIPTw9lyNJ8t6TL7YanvThTiaG/H5DDvzg/uBfpMspo9MhAvFwc27Jauz12x3VjIf348w92Th1jcpFaIrlo8ZSjhfm48/fkRaurNaodjE7YeK2DC0AG49uvyclmb1GeSlZODPbeOC+arI3kUVlje9bkvK66s4/fvH+CGUQGsnD1c7XBEL+aot+OZm0aSfa6Gf249qXY4mpdVUo2xoNIqXSu0os8kK4DbJwyisUnh/dSszg/u4xRF4bGPDnKuuoH7p4bj5CBlxaJnXRHmzdwxA3njh1Od9vPs6747UQjA1OF943kV9LFkFerrxuQwbzamZMqOpZ14Z9dZthwtYOXs4YwI8uh8gBDd4PE5w3HS2/NUwhEphurAd8cKGDTAhVAfV7VDuSR79uwhOjqa2tpadDqdq06nO6LT6Tps1dGnkhXAnRMHk32uhh+MhWqHolnH8yp49sujXBPhy6+nDFE7HNGH+Lk78fuZEdQ3NvHFQdnpuy21DWZ+PFXMNRG+NluZO378eOLi4vjzn/8M8ALwX0VRDnc0ps8lqxkj/PFx68eGXVJo0ZbaBjO/27gPDycH/n5rjM3+MAjb9atJg6ltNPOXz9Mpq2lQOxzNSckooabB9kvWn3zySZKTkwFiaU5YHepzycpRb8f82GC+PZZPbmmN2uFozt82H+VEfiUvzY/Bx62f2uGIPsjeTsff5o6ipKqOF786pnY4mrP1eAH99HZMCrXtkvWSkhIqKysB3IFOd43sc8kKmgstFOC9PVJo8VNJh00cyilj6dVhXD3MNqqMSkpKmDFjBuHh4cyYMaPdTRiTkpKIiIjAYDCwevXqTscnJyczbtw4Ro0axbhx4/j222+tcj2i2ciBnvx6ylA27M5k71nrbWZqC747XsgVYd5d2plbi5YsWcJf//pXgA3A850d3yeTVcgAF64e5sumPZmd7lbaV2QWV/PohwdpalJ4eMawzgdoxOrVq5k2bRpGo5Fp06ZdkIhamM1mli1bRmJiIunp6WzcuJH09PQOx/v4+PD5559z6NAh1q1bx69+9SurXpeAR2YMI8DDiT99cogG+TkF4ExRFRlFVVxjI39Mtmf9+vXo9XruuOMOgNXAeJ1Od21HY/pksoLmQov88jq+OWb5Nu69VV2jmWXv7kMHrLljbLubKWpRQkICixYtAmDRokV8+umnFx2TkpKCwWAgNDQUR0dHFixYQEJCQofjx4wZ07p5XFRUFLW1tdTVyfo8a3Ltp+cvcVEcy6vgre3S6Bbgu+PNv6+usfHnVQsXLuTjjz8GQFEUs6IoExVF6XD6wnZ+K3WzqRG+BHg4sWHXWbVDUd2qzcc4lFPGi7fGEDLAtrqp5+fnExgYCEBgYCAFBRf/8ZGTk0NISEjr18HBweTk5Fg8/qOPPmLMmDH069f2M7z4+HhiY2OJjY2lsFCqTLvTdVEBXDfCn1e2nJBGt8DW44WE+rgyxEZL1i9Hn01Wens7lk0N41BOGQeyStUORzWbD5n4z49nWDxlKDOjAtQOp03Tp09n5MiRF/3XcnfUmbbW61ha5XjkyBEee+wx3njjjXaPWbJkCampqaSmpuLra9vTM1r0dFwU9jodTyYc7tNrr2rqzew8XWzzd1WXqm80lWrHzWMG8vIWIy9+dZz//mai2uFYXUZRJU8mHCYmxEvT7ZS2bNnS7mv+/v6YTCYCAwMxmUz4+V38gxwcHExW1v+KabKzs1un+Doan52dzdy5c1m/fj1hYWHdeEWiK4K8nHnkugj++kU6mw/lcX10oNohqWLX6WLqG5uYOrxv/kHUZ++sANydHFg21cD2k0XsOFmkdjhWVVXXyH3v7CPQ04k1t4+2qedUPxUXF8e6desAWLduHTfddNNFx4wfPx6j0UhGRgb19fVs2rSJuLi4DseXlpZy/fXXs2rVKqZMmWKlqxHtWXTFYKKCPHj6s8OUVderHY4qvj1WgLODPROGDlA7FFXY5m+obnTnxEEEeTrxQtKxPjPFoCgKKz46iLGgghWzhhMywHbnv1euXElycjLh4eEkJyezcuVKAHJzc5kzZw4Aer2eNWvWMHPmTCIjI5k/fz5RUVEdjl+zZg0nT57kr3/9K6NHj2b06NFtPs8S1qG3t+Nvc0cR4OnM6qTjaodjdQ3mJrYbC7lj4iD66W27ZP1S6Tr5Bd0nfnu/n5rFig8Psvauscwa2funGNZ+f4rVicd4fPZwfnu1TG91p9jYWFJTU9UOo9datfkob/xwmg2/mcgUg4/a4VjN5kMm7t+wj3/fHcu1w/3VDqe7WfQAuc/fWQHcMmYgBj83XvzqeK9fd/XDiUJeSDrG9dGBLLkqVO1whOiSh2cMY6iPKys/PkhVXaPa4VjNu7szGejlzNXD+mZxBUiyApqnGP5wXQSnCqv4eF+O2uH0mMzian63cT/D/N158ZfR0vdP2BwnB3te+GU02edqePGrvjEdeKaoiu0ni7htfAj2dn33Z1aS1Xkzo/yJCfHi5S0nqG3ofTuVVtQ28HxSc5+1N341DhfHPl0IKmzY+CEDWHTFENbtPMOeMyVqh9PjNu7JxN5Ox23jQzo/uBeTZHWeTqfjsZkRmMpq+W8vWyjcYG7i/g37SDqSxxt3jWOwt+0WVAgB8OjMCAZ6OfPYhwd75R+XLeobm/gwNZtpw/3w9+i012uvJsnqJyYbfPhFuA//3HqSitresTWBoij86ZNDbDMWsWruKCaF2XanZiGguRXT6luiOV1UxctbTqgdTo/56kgexVX13DFxkNqhqE6S1c88OjOCc9UN/Gtb7+hFtubbk7yfms3yaw3M7+PTCKJ3uTLchwXjQ/jXD6dJy+ydndnf3Z1JcH9nrgrvmwuBf0qS1c9EB3tx/ahA3tx2mqJK225c+tHebF5KPsEtYwbaVCd1ISz1x+sjuSrcl4ffP9DrqgNPF1ay83Qxt08YhF0fLqxoIcmqDY9cN4zaBjNv/HBa7VAu2Y8ni3jso4NMDvNm9Typ/BO9k4eTA0uvCeNscRVPfXZE7XC61caUTPR2Om6NDVY7FE2QZNWGMF83/nBdBP/64TRb0vPVDqfLDmSV8s/vThLq68rrd42z2VZKQlhiYqg3D0w18OHebD47kKt2ON2itsHMh3uzuS7KHz/3vl1Y0UJ+i7Vj8ZVDGRHowe8/OEBOaY3a4VjsQFYpd721m8ziatYvnoins4PaIQnR45ZPC2fc4P786eNDvWIrkaTDeZyrbuCOCYPVDkUzJFm1w8nBnn/eOZZGcxO/e3efTexUmnY+UfV3cWTTb68gwFP+IhN9g97ejlduGw06eHDTfpvvRPPu7kwGe7swWap3W0my6sBQH1dWzYtmX2Ypf/9a26vl07JK+dWb5xPVkkkM9HJWOyQhrCpkgAt/mzuKfZmlvPqNUe1wLpkxv4KUMyVSWPEzkqw6ERcTxB0TB/HG96fZekybXbdbE5Vrc6IKkkQl+qgbY4K4dVwwa7aeZNfpYrXDuSTvpmTiYK/jl+OksOKnJFlZ4MkbRjA8wJ1H3k/DVKat51cpGSX86i1JVEK0eDouiqHerjz8XhqlNrb3VXVdIx/tzWZmVAA+bv3UDkdTJFlZoOX5VV1jE8s3amc+/NP9Odz11m6uCveVRCXEea799Pzf7WMoqqzjsY8O2tQ+dW9tz2CojyuLrxyidiiaI8nKQmG+bvxt7ijyy+t4IuEI5ib1fgCamhReSDrGQ++lMXaQF8/ePFISlRA/MXKgJytmDuerI/ls2JWpdjgWySqp5p/fnSTQ05mxg/rmbsAdkdbbXXDzmIGYymp4Puk45bUNvDzf+tvBV9U18vB7aXydns/tEwbxl7goWUclRBvuuXIoZ873Dgz3d2NiqLYr6/7yeTp2Oh1P3jhC7VA0SX7LddHSawz8cc5wvjxoYsk7qdTUW6/j85HcMn63cT9bjubz1I0j+NvckZKohGiHnZ2OFbOG4+XiwJJ39nK6sFLtkNqVnJ7PlqP5PDgtXGZJ2iG/6S7BkqvCWHXLKL4/Uciit1N6vEN7dX0jqzYfJW7NDrLPVbN+8QR+PWWotFASohOeLg68ffcE9HY6Fv9nDyVV2iu4qKk38/RnRwj3c2PxlUPVDkezJFldotsnDOLVBWM4lF3KvetT2XGyqEfO893xAq57+Qfe+OE0t44L5v3fXsGV0oFZCIsN8nYhfmEsuWW1/PadVOoatbX/1ZqtRnJKa3j25pE42Muv5PbIO3MZ4mKC2LRkErmltdz55m6WbdjXbaXt+WW1LN+4n7vf3oOj3o73lkxi9bxovFwcu+X7C9GXjBvcn5dujWHPmXOs+FA7FYInCyqJ/+E0t4wdqPlnamqTZHWZYkL68/XDV/Hw9GFsOZrPtJe+5/XvTlHf2PXy9kZzE98ey2fZhn3Mf2Mnyen5PDQ9nMQHfyEf5HaUlJQwY8YMwsPDmTFjBufOtb2vUVJSEhERERgMBlavXm3x+MzMTNzc3Pj73//eo9chet6NMUE8OjOChLRcXtmifocLRVF4MuEwzg72PD47Uu1wNE+SVTdwcrDnwenhbHnkaqYYfHg+6Rh3vrmLh99LY2NKJqcLKzv8Sy49t4xnv0hn0qpvWfyfVH48VcTU4X588/ureWj6MPrp7a14NbZl9erVTJs2DaPRyLRp0y5IRC3MZjPLli0jMTGR9PR0Nm7cSHp6ukXjH374YWbPnm2VaxE97/5rwrh1XDCvfmPk433Zqsby2YFcfjxVzKOzhuPrLguAO6Pr5HZYG/fKNiYlo4SNKZlsMxZSVNn8QNfHrR8ThvTHycGe4qp6Ss7/V1RZi6ezIyVV9Vw73I9544KZGuEnVX4WioiI4LvvviMwMBCTycQ111zD8eMX9nHcuXMnTz/9NF999RUAq1atAuDxxx/vcPynn37Kjh07cHV1xc3NjT/84Q+dxhMbG0tqamo3X6XoTvWNTdz99m7MTXDXpMHcGBNk9RjKaxuY9tL3BHo68cn9U7Dv2z0ALbp4WWfVAyYMHcCEoQNQFIXTRVWkZJSQklFCVV0juzNK8HZzxNvNkXB/N7xdHRk3uD8ThnozwFWeR3VVfn4+gYGBAAQGBlJQcHH/xpycHEJCQlq/Dg4OZvfu3R2Or6qq4vnnnyc5OVmmAHsZR70d/1o4nl+/vYflm/ZzrrqehVcMsWoMLyefoKiyjrcWxfb1RGUxSVY9SKfTEebrRpivG7dPGKR2ODZr+vTp5OXlXfTvzz33nEXj25o96Kzs/6mnnuLhhx/Gzc2t0+8fHx9PfHw8AIWFhRbFJNTl2k/P+nsm8MC7+3ky4QhFlfU8PD3cKstBPt2fw85Txdw1cTDRwV49fr7eQpKV0LwtW7a0+5q/vz8mk6l1Gs/Pz++iY4KDg8nKymr9Ojs7m6CgoA7H7969mw8//JAVK1ZQWlqKnZ0dTk5OPPDAAxd9/yVLlrBkyRKgeRpQ2AYnB3vW3jWWxz8+xP99Y6S4so5nbhrZY3c6iqLw6jdGXtli5BfhPvzp+uE9cp7eSh6MCJsWFxfHunXrAFi3bh033XTTRceMHz8eo9FIRkYG9fX1bNq0ibi4uA7Hb9u2jTNnznDmzBkeeugh/vjHP7aZqIRt09vb8cIvo7nv6jA27M7kdxv39cg6rNoGMw9uSuOVLUbmjQ3mzUWxODnIvUJXSLISNm3lypUkJycTHh5OcnIyK1euBCA3N5c5c+YAoNfrWbNmDTNnziQyMpL58+cTFRXV4XjRd+h0OlbOHs6fr4/k26MF3Ls+lfTc8m77/oUVddz+r118diCXFbMi+Put0VLhewmkGlCIbiTVgLZt24lCHnwvjbKaBn5z5VAenB6Oi+Ol3wEdyyvnnv+kUlxVxyu3jWbWyMBujLbXsGjeVe6shBDivF8M8+WbR67ml2ODeeOH08z4fz9c8g7hW48VMO+1H2lsauKD306WRHWZ5M5KiG4kd1a9R0pGCX/85BAnCyqZO2YgUww+TBw6gJABLh2OK6ioZePuTF79xkhkoAdvLRpPgKeTlaK2SRbdWUmyEqIbSbLqXeobm/jXttNsMxay63QJAAO9nJk4dAATQwcwZlB/qusa2Z9Vyr7MUvZnniP7XA3jBnvh5+7ES/NjLmsasY+QZCWEtUmy6p2amhSO51ew+3QxKWdK2H26hOKqenzcHFu71AR6OjFmkBdjB/Vn4lBvRgV7qhy1zZBkJYS1SbLqGxRF4VRhJdklNVTVmxk72ItAT9k08RJJuyUhhOgJOp0Og587Bj93tUPpM6QaUAghhOZJshJCCKF5kqyEEEJoniQrIYQQmifJSgghhOZJshJCCKF5kqyEEEJoniQrIYQQmifJSgghhOZJshJCCKF5nfUGFEJ0gU6nS1IUZZbacQjR20iyEkIIoXkyDSiEEELzJFkJIYTQPElWQgghNE+SlRBCCM2TZCWEEELz/j+m023Tm6kuyQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"<sympy.plotting.plot.Plot at 0x1fca1c9ea00>"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = plot( f, (x,a,b), show=False) \n",
"p.extend( plot( approx, (x,a,b), line_color='r', show=False) )\n",
"p.show()\n",
"\n",
"plot( f - approx, (x,a,b) )"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.10"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| gpl-2.0 |
djvanhelmond/AdventofCode2015 | Advent of Code - Puzzle Selector.ipynb | 1 | 1930 | {
"cells": [
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#!/usr/bin/env python3\n",
"import random"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"You have the following options: [11, 12, 13, 15, 17, 18, 19, 21, 22, 23, 24, 25]\n",
"I suggest you solve puzzle: 17\n"
]
}
],
"source": [
"Solved = []\n",
"for i in range(1, 26):\n",
" Solved.append(i)\n",
"\n",
"\n",
"Solved.remove(10)\n",
"Solved.remove(1)\n",
"Solved.remove(2)\n",
"Solved.remove(3)\n",
"Solved.remove(4)\n",
"Solved.remove(5)\n",
"Solved.remove(7)\n",
"Solved.remove(6)\n",
"Solved.remove(8)\n",
"Solved.remove(9)\n",
"Solved.remove(20)\n",
"Solved.remove(16)\n",
"Solved.remove(14) \n",
" \n",
" \n",
"print(\"You have the following options:\", Solved)\n",
"print(\"I suggest you solve puzzle: %i\" % random.choice(Solved))\n",
"\n",
"\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
kuroniko/MAT258 | 258a_hw4.ipynb | 1 | 46154 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# MAT 258A: Homework 4"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Exercise 4\n",
"In this exercise, I test the code of 'pure' Newton (newtmin), Newton method with Armijo backtracking (newtmin1), Newton method with Armijo backtracking and two different way of treatment of the Hessian (newtmin2 and newtmin3) and BFGS method with treatment of the initial Hessian (mybfgs)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\n",
" \\begin{array}{cccccc}\n",
" &\\textrm{pure Newton}&\\textrm{newtmin1}&\\textrm{newtmin2}&\\textrm{newtmin3}&\\textrm{GFGS}\\\\\n",
" 1&\\surd &&&&\\\\\n",
" 2&\\times &\\times&\\times&\\times&\\surd\\\\\n",
" 3&\\surd &&&&\\\\\n",
" 4&\\surd &&&&\\\\\n",
" 5&\\surd &&&&\\\\\n",
" 6&\\surd &&&&\\\\\n",
" 7&\\times &\\times&\\times&\\times&\\surd\\\\\n",
" 8&\\surd &&&&\\\\\n",
" 9&\\surd &&&&\\\\\n",
" 10&\\times &\\times&\\surd&&\\\\\n",
" 11&\\times &\\times&\\times&\\surd&\\\\\n",
" 12&\\times &\\times&\\surd&&\\\\\n",
" 13&\\surd &&&&\\\\\n",
" 14&\\times &\\times&\\times&\\times&\\times\\\\\n",
" 15&\\times &\\times&\\times&\\times&\\surd\\\\\n",
" 16&\\surd &&&&\\\\\n",
" 17&\\surd &&&&\\\\\n",
" 18&\\times &\\times&\\times&\\times&\\times\\\\\n",
" \\end{array}\n",
"$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The above table shows the outcome of those methods, it is 'success' if the gradient's norm is relatively small, i.e., $\\frac{\\|g(x^*)\\|}{\\|g(x_0)\\|}\\leqslant10^{-5}$, this is a relatively high requirement and actually one can see that those 'failed' cases in BFGS and newtmin2 and newtmin3 also have a relatively small norm of the gradient. Below is technical details of the exercise."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"using Toms566\n",
"using PyPlot"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Testing Toms566\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"No. Name n f(x0) |∇f(x0)| cond(∇²f(x0))\n",
" "
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Toms566 tests passed\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"1 Hellical valley 3 2.50e+03 1.88e+03 9.82e+00\n",
" 2 Bigg's EXP6 6 7.79e-01 2.55e+00 1.30e+01\n",
" 3 Gaussian 3 3.89e-06 7.45e-03 5.10e+01\n",
" 4 Powell 2 1.14e+00 2.00e+04 1.37e+08\n",
" 5 Box 3-dim 3 1.03e+03 1.49e+02 1.19e+02\n",
" 6 Variably dimensioned 40 9.39e+10 1.01e+11 1.65e+04\n",
" 7 Watson 9 3.00e+01 1.78e+02 1.63e+02\n",
" 8 Penalty I 60 5.45e+09 8.02e+07 4.24e+00\n",
" 9 Penalty II 65 2.87e+05 3.28e+05 9.84e+01\n",
" 10 Brown badly scaled 2 1.00e+12 2.00e+06 1.00e+00\n",
" 11 Brown and Denis 4 7.93e+06 2.14e+06 6.93e+02\n",
" 12 Gulf research and development 3 1.21e+01 3.97e+01 4.65e+04\n",
" 13 Trigonometric 40 2.01e-03 5.30e-02 1.57e+02\n",
" 14 Extended rosenbrock 40 4.84e+02 1.04e+03 9.90e+01\n",
" 15 Extended Powell singular 60 3.23e+03 1.78e+03 2.27e+01\n",
" 16 Beale 2 1.42e+01 2.78e+01 7.97e+00\n",
" 17 Wood 4 1.92e+04 1.64e+04 1.69e+02\n",
" 18 Chebyquad 50 1.39e-02 2.65e+00 6.30e+02\n"
]
}
],
"source": [
"Pkg.test(\"Toms566\")"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"newtmin (generic function with 1 method)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
" #\"Pure\" Newton method\n",
" # Minimize a function f using Newton’s method.\n",
" # obj: a function that evaluates the objective value,\n",
" # gradient, and Hessian at a point x, i.e.,\n",
" # (f, g, H) = obj(x)\n",
" # x0: starting point.\n",
" # maxIts (optional): maximum number of iterations.\n",
" # optTol (optional): optimality tolerance based on\n",
" # ||grad(x)|| <= optTol*||grad(x0)||\n",
" x=x0\n",
" status = 0\n",
" its = 0\n",
" (f0,g0,H0)=obj(x0)\n",
" (f,g,H)=obj(x)\n",
" while status != 1\n",
" x = x-inv(H)*g\n",
" (f,g,H)=obj(x)\n",
" its = its+1\n",
" if norm(g)<= optTol*norm(g0)\n",
" status = 1\n",
" end\n",
" if its>maxIts\n",
" status = 1\n",
" end\n",
" end\n",
"return (x, its)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"10x10 Array{Float64,2}:\n",
" 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0\n",
" 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0\n",
" 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0\n",
" 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0\n",
" 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0\n",
" 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0\n",
" 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0\n",
" 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0\n",
" 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0\n",
" 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"v=randn(10,1)\n",
"A=randn(10,10)\n",
"inv(A)\n",
"eye(10)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"obj (generic function with 1 method)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function obj(x)\n",
" f=1/2*norm(x-v)^2\n",
" g=x-v\n",
" H=eye(10)\n",
" return (f,g,H)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.0"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x0=zeros(10,1)\n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(x-v)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Toms566.Problem:\n",
" name: Hellical valley\n",
" n: 3"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(1) # Hellical Valley"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"obj (generic function with 1 method)"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.0002073324421774e-8"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"11735.764558124118"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(2)\n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.3020078124065462e-8"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(3) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.0155390280377853e-9"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(4) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"8.68652479136446e-7"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(5) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"6.720802512276261e-7"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(6) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"9.060968995677416e18"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(7) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"9.223518288696248e-7"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(8) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"7.262191147715546e-7"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(9) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"7.083640796727696e6"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(10) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.9734314374508443e8"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(11) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"2.6556527256401906e239"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(12) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"5.50382562199281e-8"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(13) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"8.050634401598488e9"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(14) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"3.242292834706322e23"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(15) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.0"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(16) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"9.282369975556412e-7"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(17) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"p = Problem(18) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"newtmin1 (generic function with 1 method)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
" # Newton method with Armijo backtracking\n",
" # Minimize a function f using Newton’s method.\n",
" # obj: a function that evaluates the objective value,\n",
" # gradient, and Hessian at a point x, i.e.,\n",
" # (f, g, H) = obj(x)\n",
" # x0: starting point.\n",
" # maxIts (optional): maximum number of iterations.\n",
" # optTol (optional): optimality tolerance based on\n",
" # ||grad(x)|| <= optTol*||grad(x0)||\n",
" mu=1e-4\n",
" x=x0\n",
" status = 0\n",
" its = 0\n",
" (f0,g0,H0)=obj(x0)\n",
" (f,g,H)=obj(x)\n",
" while status != 1\n",
" alpha = 1\n",
" xnew = x-alpha*inv(H)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts =-fnew+f-alpha*mu*g'*inv(H)*g\n",
" while sts[1]<0\n",
" alpha=alpha/2\n",
" xnew = x-alpha*inv(H)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts=-fnew+f-alpha*mu*g'*inv(H)*g\n",
" end\n",
" x = x-alpha*inv(H)*g\n",
" (f,g,H)=obj(x)\n",
" its = its+1\n",
" if norm(g)<= optTol*norm(g0)\n",
" status = 1\n",
" end\n",
" if its>maxIts\n",
" status = 1\n",
" end\n",
" end\n",
"return (x, its)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "LoadError",
"evalue": "LoadError: UndefVarError: Problem not defined\nwhile loading In[2], in expression starting on line 1",
"output_type": "error",
"traceback": [
"LoadError: UndefVarError: Problem not defined\nwhile loading In[2], in expression starting on line 1",
"",
" [inlined code] from essentials.jl:116"
]
}
],
"source": [
"p = Problem(2) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "LoadError",
"evalue": "LoadError: UndefVarError: Problem not defined\nwhile loading In[3], in expression starting on line 1",
"output_type": "error",
"traceback": [
"LoadError: UndefVarError: Problem not defined\nwhile loading In[3], in expression starting on line 1",
"",
" [inlined code] from essentials.jl:116"
]
}
],
"source": [
"p = Problem(7) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"250000.25000099998"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(10) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.005490328480657573"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(11) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.16957718015199827"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(12) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.5779385738800985"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(14) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.45464058777161137"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(15) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.933985346920556"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(18) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin1( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"newtmin2 (generic function with 1 method)"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
" # Newton method with Armijo backtracking and some treatment with Hessian, treatment 1\n",
" # Minimize a function f using Newton’s method.\n",
" # obj: a function that evaluates the objective value,\n",
" # gradient, and Hessian at a point x, i.e.,\n",
" # (f, g, H) = obj(x)\n",
" # x0: starting point.\n",
" # maxIts (optional): maximum number of iterations.\n",
" # optTol (optional): optimality tolerance based on\n",
" # ||grad(x)|| <= optTol*||grad(x0)||\n",
" mu=1e-4\n",
" epsilon=0.01\n",
" x=x0\n",
" status = 0\n",
" its = 0\n",
" (f0,g0,H0)=obj(x0)\n",
" (f,g,H)=obj(x)\n",
" (V,S)=eig(H)\n",
" bar=ones(size(H,1))*epsilon\n",
" bar=Diagonal(bar)\n",
" bH=S*max(bar,Diagonal(V))*S'\n",
" while status != 1\n",
" alpha = 1\n",
" xnew = x-alpha*inv(bH)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts =-fnew+f-alpha*mu*g'*inv(bH)*g\n",
" while sts[1]<0\n",
" alpha=alpha/2\n",
" xnew = x-alpha*inv(bH)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts=-fnew+f-alpha*mu*g'*inv(bH)*g\n",
" end\n",
" x = x-alpha*inv(bH)*g\n",
" (f,g,H)=obj(x)\n",
" (V,S)=eig(H)\n",
" bar=ones(size(H,1))*epsilon\n",
" bar=Diagonal(bar)\n",
" bH=S*max(bar,Diagonal(V))*S'\n",
" its = its+1\n",
" if norm(g)<= optTol*norm(g0)\n",
" status = 1\n",
" end\n",
" if its>maxIts\n",
" status = 1\n",
" end\n",
" end\n",
"return (x, its)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.15069684447784829"
]
},
"execution_count": 72,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(2) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.0698683411045317"
]
},
"execution_count": 73,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(7) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"8.404388296420837e-13"
]
},
"execution_count": 74,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(10) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.22947981066293166"
]
},
"execution_count": 77,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(11) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.5231878310266746e-5"
]
},
"execution_count": 80,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(12) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.9826622874404953"
]
},
"execution_count": 83,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(14) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 86,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.834929873113459"
]
},
"execution_count": 86,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(15) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.32465019085415453"
]
},
"execution_count": 89,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(18) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin2( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"newtmin3 (generic function with 1 method)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
" # Newton method with Armijo backtracking and some treatment with Hessian, treatment 2\n",
" # Minimize a function f using Newton’s method.\n",
" # obj: a function that evaluates the objective value,\n",
" # gradient, and Hessian at a point x, i.e.,\n",
" # (f, g, H) = obj(x)\n",
" # x0: starting point.\n",
" # maxIts (optional): maximum number of iterations.\n",
" # optTol (optional): optimality tolerance based on\n",
" # ||grad(x)|| <= optTol*||grad(x0)||\n",
" mu=1e-4\n",
" epsilon=0.01\n",
" x=x0\n",
" status = 0\n",
" its = 0\n",
" (f0,g0,H0)=obj(x0)\n",
" (f,g,H)=obj(x)\n",
" (V,S)=eig(H)\n",
" bar=ones(size(H,1))*epsilon\n",
" bar=Diagonal(bar)\n",
" bH=S*max(bar,abs(Diagonal(V)))*S'\n",
" while status != 1\n",
" alpha = 1\n",
" xnew = x-alpha*inv(bH)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts =-fnew+f-alpha*mu*g'*inv(bH)*g\n",
" while sts[1]<0\n",
" alpha=alpha/2\n",
" xnew = x-alpha*inv(bH)*g\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts=-fnew+f-alpha*mu*g'*inv(bH)*g\n",
" end\n",
" x = x-alpha*inv(bH)*g\n",
" (f,g,H)=obj(x)\n",
" (V,S)=eig(H)\n",
" bar=ones(size(H,1))*epsilon\n",
" bar=Diagonal(bar)\n",
" bH=S*max(bar,abs(Diagonal(V)))*S'\n",
" its = its+1\n",
" if norm(g)<= optTol*norm(g0)\n",
" status = 1\n",
" end\n",
" if its>maxIts\n",
" status = 1\n",
" end\n",
" end\n",
"return (x, its)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.04974099571706037"
]
},
"execution_count": 104,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(2) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.003400009283027661"
]
},
"execution_count": 96,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(7) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1.789679515697544e-13"
]
},
"execution_count": 97,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(10) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"3.3822921362972896e-7"
]
},
"execution_count": 98,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(11) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.011037420345164398"
]
},
"execution_count": 99,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(14) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.001195675544522462"
]
},
"execution_count": 100,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(15) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.0407760590874033"
]
},
"execution_count": 101,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(18) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=newtmin3( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"mybfgs (generic function with 1 method)"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function mybfgs( obj, x0; maxIts=100, optTol=1e-6)\n",
" # BFGS method with Armijo backtracking and some treatment with initial Hessian, treatment 2\n",
" # Minimize a function f using Newton’s method.\n",
" # obj: a function that evaluates the objective value,\n",
" # gradient, and Hessian at a point x, i.e.,\n",
" # (f, g, H) = obj(x)\n",
" # x0: starting point.\n",
" # maxIts (optional): maximum number of iterations.\n",
" # optTol (optional): optimality tolerance based on\n",
" # ||grad(x)|| <= optTol*||grad(x0)||\n",
" mu=1e-4\n",
" eta=0.5\n",
" epsilon=0.01\n",
" x=x0\n",
" status = 0\n",
" its = 0\n",
" (f0,g0,H0)=obj(x0)\n",
" (f,g,H)=obj(x)\n",
" (V,S)=eig(H)\n",
" bar=ones(size(H,1))*epsilon\n",
" bar=Diagonal(bar)\n",
" bH=S*max(bar,abs(Diagonal(V)))*S'\n",
" Hk=bH\n",
" while status != 1\n",
" mp=-Hk*g\n",
" #////////////////////////////////////////////////////\n",
" #line search\n",
" alpha = 1\n",
" xnew = x+alpha*mp\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts =-fnew+f+alpha*mu*g'*mp #Armijo\n",
" while (sts[1]<0)\n",
" alpha=alpha/2\n",
" xnew = x+alpha*mp\n",
" (fnew,gnew,Hnew)=obj(xnew)\n",
" sts=-fnew+f+alpha*mu*g'*mp\n",
" end\n",
" #////////////////////////////////////////////////////\n",
" sk=alpha*mp\n",
" yk=gnew-g\n",
" tt1=yk'*sk\n",
" tt1=tt1[1]\n",
" rho=1/tt1\n",
" Hk=(eye(size(Hk,1))-rho*sk*yk')*Hk*(eye(size(Hk,1))-rho*yk*sk')+rho*sk*sk'\n",
" x = x+alpha*mp\n",
" (f,g,H)=obj(x)\n",
" its = its+1\n",
" if norm(g)<= optTol*norm(g0)\n",
" status = 1\n",
" end\n",
" if its>maxIts\n",
" status = 1\n",
" end\n",
" end\n",
"return (x, its)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.004652492176771119"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p = Problem(18) \n",
"function obj(x)\n",
" f = p.obj(x) # objective value at x\n",
" g = p.grd(x) # gradient at x\n",
" H = p.hes(x) # Hessian at x\n",
" return (f,g,H)\n",
"end\n",
"x0=p.x0 \n",
"(x,it)=mybfgs( obj, x0; maxIts=100, optTol=1e-6)\n",
"norm(p.grd(x))/norm(p.grd(x0))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Julia 0.5.0-dev",
"language": "julia",
"name": "julia-0.5"
},
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "0.5.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
dhuppenkothen/ShiftyLines | notebooks/ResponsesTest.ipynb | 1 | 4248010 | null | gpl-3.0 |
jsjol/GaussianProcessRegressionForDiffusionMRI | notebooks/show_ODFs.ipynb | 1 | 9064 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%load_ext autoreload\n",
"%autoreload 2\n",
"\n",
"import os\n",
"import sys\n",
"module_path = os.path.abspath(os.path.join('..'))\n",
"if module_path not in sys.path:\n",
" sys.path.append(module_path)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import json\n",
"import matplotlib.pyplot as plt\n",
"\n",
"from dipy.reconst import mapmri\n",
"import dipy.reconst.dti as dti\n",
"from dipy.viz import window, actor\n",
"from dipy.data import get_data, get_sphere\n",
"from dipy.core.gradients import gradient_table\n",
"\n",
"from diGP.preprocessing import get_HCP_loader\n",
"from diGP.preprocessing_pipelines import preprocess_SPARC\n",
"from diGP.dataManipulations import log_q_squared\n",
"from diGP.model import GaussianProcessModel, get_default_kernel"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"with open('../config.json', 'r') as json_file:\n",
" conf = json.load(json_file)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load the data."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"dataset = 'SPARC'"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"if dataset == 'HCP':\n",
" subject_path = conf['HCP']['data_paths']['mgh_1007']\n",
" loader = get_HCP_loader(subject_path)\n",
" small_data_path = '{}/mri/small_data.npy'.format(subject_path)\n",
"\n",
" loader.update_filename_data(small_data_path)\n",
"\n",
" data = loader.data\n",
" gtab = loader.gtab\n",
" voxel_size = loader.voxel_size\n",
"elif dataset == 'SPARC':\n",
" subject_path = conf['SPARC']['data_paths']['gradient_60']\n",
"\n",
" gtab, data, voxel_size = preprocess_SPARC(subject_path, normalize=True)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"btable = np.loadtxt(get_data('dsi4169btable'))\n",
"#btable = np.loadtxt(get_data('dsi515btable'))\n",
"\n",
"gtab_dsi = gradient_table(btable[:, 0], btable[:, 1:],\n",
" big_delta=gtab.big_delta, small_delta=gtab.small_delta)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fit a MAPL model to the data."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"map_model_laplacian_aniso = mapmri.MapmriModel(gtab, radial_order=6,\n",
" laplacian_regularization=True,\n",
" laplacian_weighting='GCV')\n",
"\n",
"mapfit_laplacian_aniso = map_model_laplacian_aniso.fit(data)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We want to use an FA image as background, this requires us to fit a DTI model."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"tenmodel = dti.TensorModel(gtab)\n",
"tenfit = tenmodel.fit(data)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"fitted = {'MAPL': mapfit_laplacian_aniso.predict(gtab)[:, :, 0],\n",
" 'DTI': tenfit.predict(gtab)[:, :, 0]}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fit GP without mean and with DTI and MAPL as mean."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
" c:\\users\\sesjojen\\documents\\github\\gpy\\GPy\\inference\\latent_function_inference\\gaussian_grid_inference.py:68: RuntimeWarning:invalid value encountered in log\n"
]
}
],
"source": [
"kern = get_default_kernel(n_max=6, spatial_dims=2)\n",
"gp_model = GaussianProcessModel(gtab, spatial_dims=2, kernel=kern, verbose=False)\n",
"gp_fit = gp_model.fit(np.squeeze(data), mean=None, voxel_size=voxel_size[0:2], retrain=True)\n",
"\n",
"kern = get_default_kernel(n_max=2, spatial_dims=2)\n",
"gp_dti_model = GaussianProcessModel(gtab, spatial_dims=2, kernel=kern, verbose=False)\n",
"gp_dti_fit = gp_dti_model.fit(np.squeeze(data), mean=fitted['DTI'], voxel_size=voxel_size[0:2], retrain=True)\n",
"\n",
"kern = get_default_kernel(n_max=2, spatial_dims=2)\n",
"gp_mapl_model = GaussianProcessModel(gtab, spatial_dims=2, kernel=kern, verbose=False)\n",
"gp_mapl_fit = gp_mapl_model.fit(np.squeeze(data), mean=fitted['MAPL'], voxel_size=voxel_size[0:2], retrain=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"gp_model = GaussianProcessModel(gtab, spatial_dims=2, q_magnitude_transform=np.sqrt, verbose=False)\n",
"gp_fit = gp_model.fit(np.squeeze(data), mean=None, voxel_size=voxel_size[0:2], retrain=True)\n",
"gp_dti_fit = gp_model.fit(np.squeeze(data), mean=fitted['DTI'], voxel_size=voxel_size[0:2], retrain=True)\n",
"gp_mapl_fit = gp_model.fit(np.squeeze(data), mean=fitted['MAPL'], voxel_size=voxel_size[0:2], retrain=True)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"pred = {'MAPL': mapfit_laplacian_aniso.predict(gtab_dsi)[:, :, 0],\n",
" 'DTI': tenfit.predict(gtab_dsi)[:, :, 0]}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Compute the ODFs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load an odf reconstruction sphere"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"sphere = get_sphere('symmetric724').subdivide(1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The radial order $s$ can be increased to sharpen the results, but it might\n",
"also make the odfs noisier. Note that a \"proper\" ODF corresponds to $s=0$."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"odf = {'MAPL': mapfit_laplacian_aniso.odf(sphere, s=0),\n",
" 'DTI': tenfit.odf(sphere)}"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"odf['GP'] = gp_fit.odf(sphere, gtab_dsi=gtab_dsi, mean=None)[:, :, None, :]\n",
"odf['DTI_GP'] = gp_dti_fit.odf(sphere, gtab_dsi=gtab_dsi, mean=pred['DTI'])[:, :, None, :]\n",
"odf['MAPL_GP'] = gp_mapl_fit.odf(sphere, gtab_dsi=gtab_dsi, mean=pred['MAPL'])[:, :, None, :]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Display the ODFs"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for name, _odf in odf.items():\n",
" ren = window.Renderer()\n",
" ren.background((1, 1, 1))\n",
"\n",
" odf_actor = actor.odf_slicer(_odf, sphere=sphere, scale=0.5, colormap='jet')\n",
" background_actor = actor.slicer(tenfit.fa, opacity=1)\n",
"\n",
" odf_actor.display(z=0)\n",
" odf_actor.RotateZ(90)\n",
"\n",
" background_actor.display(z=0)\n",
" background_actor.RotateZ(90)\n",
" background_actor.SetPosition(0, 0, -1)\n",
"\n",
" ren.add(background_actor)\n",
" ren.add(odf_actor)\n",
"\n",
" window.record(ren, out_path='odfs_{}.png'.format(name), size=(1000, 1000))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| bsd-3-clause |
esa-as/2016-ml-contest | ar4/ar4_submission2_VALIDATION.ipynb | 2 | 106501 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Facies classification using machine learning techniques\n",
"Copy of <a href=\"https://home.deib.polimi.it/bestagini/\">Paolo Bestagini's</a> \"Try 2\", augmented, by Alan Richardson (Ausar Geophysical), with an ML estimator for PE in the wells where it is missing (rather than just using the mean).\n",
"\n",
"In the following, we provide a possible solution to the facies classification problem described at https://github.com/seg/2016-ml-contest.\n",
"\n",
"The proposed algorithm is based on the use of random forests combined in one-vs-one multiclass strategy. In particular, we would like to study the effect of:\n",
"- Robust feature normalization.\n",
"- Feature imputation for missing feature values.\n",
"- Well-based cross-validation routines.\n",
"- Feature augmentation strategies.\n",
"\n",
"## Script initialization\n",
"Let us import the used packages and define some parameters (e.g., colors, labels, etc.)."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Import\n",
"from __future__ import division\n",
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"mpl.rcParams['figure.figsize'] = (20.0, 10.0)\n",
"inline_rc = dict(mpl.rcParams)\n",
"from classification_utilities import make_facies_log_plot\n",
"\n",
"import pandas as pd\n",
"import numpy as np\n",
"#import seaborn as sns\n",
"\n",
"from sklearn import preprocessing\n",
"from sklearn.model_selection import LeavePGroupsOut\n",
"from sklearn.metrics import f1_score\n",
"from sklearn.multiclass import OneVsOneClassifier\n",
"from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor\n",
"\n",
"from scipy.signal import medfilt"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Python: 3.5.2 |Continuum Analytics, Inc.| (default, Jul 2 2016, 17:52:12) \n",
" [GCC 4.2.1 Compatible Apple LLVM 4.2 (clang-425.0.28)]\n",
"Pandas: 0.18.1\n",
"Numpy: 1.11.2\n",
"Scipy: 0.18.1\n",
"Sklearn: 0.18\n"
]
}
],
"source": [
"import sys, scipy, sklearn\n",
"print('Python: ' + sys.version.split('\\n')[0])\n",
"print(' ' + sys.version.split('\\n')[1])\n",
"print('Pandas: ' + pd.__version__)\n",
"print('Numpy: ' + np.__version__)\n",
"print('Scipy: ' + scipy.__version__)\n",
"print('Sklearn: ' + sklearn.__version__)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Parameters\n",
"feature_names = ['GR', 'ILD_log10', 'DeltaPHI', 'PHIND', 'PE', 'NM_M', 'RELPOS']\n",
"facies_names = ['SS', 'CSiS', 'FSiS', 'SiSh', 'MS', 'WS', 'D', 'PS', 'BS']\n",
"facies_colors = ['#F4D03F', '#F5B041','#DC7633','#6E2C00', '#1B4F72','#2E86C1', '#AED6F1', '#A569BD', '#196F3D']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load data\n",
"Let us load training data and store features, labels and other data into numpy arrays."
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load data from file\n",
"data = pd.read_csv('../facies_vectors.csv')"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Store features and labels\n",
"X = data[feature_names].values # features\n",
"y = data['Facies'].values # labels"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Store well labels and depths\n",
"well = data['Well Name'].values\n",
"depth = data['Depth'].values"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data inspection\n",
"Let us inspect the features we are working with. This step is useful to understand how to normalize them and how to devise a correct cross-validation strategy. Specifically, it is possible to observe that:\n",
"- Some features seem to be affected by a few outlier measurements.\n",
"- Only a few wells contain samples from all classes.\n",
"- PE measurements are available only for some wells."
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Define function for plotting feature statistics\n",
"def plot_feature_stats(X, y, feature_names, facies_colors, facies_names):\n",
" \n",
" # Remove NaN\n",
" nan_idx = np.any(np.isnan(X), axis=1)\n",
" X = X[np.logical_not(nan_idx), :]\n",
" y = y[np.logical_not(nan_idx)]\n",
" \n",
" # Merge features and labels into a single DataFrame\n",
" features = pd.DataFrame(X, columns=feature_names)\n",
" labels = pd.DataFrame(y, columns=['Facies'])\n",
" for f_idx, facies in enumerate(facies_names):\n",
" labels[labels[:] == f_idx] = facies\n",
" data = pd.concat((labels, features), axis=1)\n",
"\n",
" # Plot features statistics\n",
" facies_color_map = {}\n",
" for ind, label in enumerate(facies_names):\n",
" facies_color_map[label] = facies_colors[ind]\n",
"\n",
" sns.pairplot(data, hue='Facies', palette=facies_color_map, hue_order=list(reversed(facies_names)))"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Feature distribution\n",
"# plot_feature_stats(X, y, feature_names, facies_colors, facies_names)\n",
"# mpl.rcParams.update(inline_rc)"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABIEAAAJZCAYAAAA+iyW5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcZFV9///XGxDFbVhEmIWZiUGMSxAwEZcorWDiFlEj\nfl0SQMjy0xiMGhUwfpmJ+SZCUAMxMdEgwQUFRYUkJhLEJm64sQhicANmZZCwiRoC8vn9cW8PRVG9\nTVd3dXW/no9HPbrq3HPPPVVT9zOnzj3nnlQVkiRJkiRJWti2G3QFJEmSJEmSNPvsBJIkSZIkSVoE\n7ASSJEmSJElaBOwEkiRJkiRJWgTsBJIkSZIkSVoE7ASSJEmSJElaBOwEkiRJkiRJWgTsBBpySUaT\n3JTkfl3ppyf5s3H2uTvJj5Pc1vH3T9ptJyf59678f53kvK601Ul+nuQ945R/eVfa25N8oH2+qs1z\nW/vYnOS8JId07XNtkp921fPUdtsRSe5q025JcmmS503wOR3U1nfsmOuSnJXkV8bbR1oskrwiydfb\n82xjkn9N8pR22wlJPtRjn7uTPKJ9fp9403Geb9e+7jyfN7X7PLBrnye2x745yY1JLk5yZLvtoCTr\ne9Tj80mO6shzd5JPdOXZt02/sMf+P0xyZY/00SQ/S7K8I+3gJNdM8Dl2xtYbknwkyUMnqGtnTFqf\nZM14n3FXemf864yPe45XN2nYTSFO/W97HtyU5ItJntS1/5Ik723bHLcnuXwsvnTk+bUkX2rbFTcm\n+UKSJ7Tb7pfkne25eluSHyR55wT1vc/5O1487dh+vyRrkny3fZ8/TPKPSVZ25funJHd2nvPtexuL\nBXd0fB63Jflcx7bbc08bbCxtRWd86jpWd5ttbJ/DxnsfkrZNkmuSPLPj9cvamPa03Ldd9U/t6+d3\nlfHXbfrh7esrO87fscf/JLmr3d7dHhk7xw9M8udJLugqf58ktyZ57ATv48i2Di/p5+ej/rETaIgl\nWQX8GnA38IJp7FrAvlX10Kp6SPv35Hbb24BHJDmiPcaTgd8B/qCrjMOBm4CXpasDqrUsycsmqcOS\nqnoo8HjgAuBTYwGrI8/zuup5TMf2L7dpOwPvBT6Wjh9cPWxs8z8UeBLwX8AXkjxjgn2kBS3JG4B3\nAX8OPBxYCfwdcGhHtuqxa6+0ifJsPZ+B/YD9geM66vFk4HPA54FfrKqHAa8Gnj3NY/4IeEqSXTrS\njgCu7s6Y5OnA7jQx7wk96n47TUwc7z112xpbgUcAuwJrJsjfGZN+DTg6SWcsn+hYY/GvMz5eP0F+\naWhNMU59rD2XHgaMAh/v2P9+NPFlL+BAYAnwZuAdSf64zfMQ4J+BU4BdgOXAWuCOtpjjgQOAX2mP\n8wzg0gmqPd75O9F5fQ7wfOBlbR0fD3wTOLjjvTwQeDFwC/DKrYVWvXosFgB/MfZ5tI+DO7Y9lnva\nYGOxY8MEdaIjf2e8+fgk+0iagfa32N8Az6mqL7TJ3e2qq2naOGP7bA+8BPj+1kxVj+uIBQ8FlgI/\nBDov3m3s0ab4aptnjyS/25H3fcDJVfXtCap/OPDfnXXT/GIn0HA7HPgK8E/AkdPYL+3jPqrqZ8Dv\nASe3nUynAW+pqs09jv2nwJ3Ab/Yo6iTgz8Z6qyeoB1V1Q1WdSvNj6aReeabgQ8CDgEdOJXNVbaqq\nE4B/BE6c4jGkBaXtNF0LvKaqzq2qn1XVz6vqX6vqLZPtvi2HhOacBz5L0xk05iTg9Ko6uapuavNd\nWlUTdSb38r/Ap4GXA7Qx6KXAR3rkPaLN+xl6N1ROBV7efTV/Altja1XdDpwHPGYqO1bVdcCXu/Jv\ny2csLSjTjVNVdTfN+b4syW5t8uHACuAlVbWu3f+zwDHA25M8GNin2b3OrsYdVXVBVY2NFPwV4FNV\ntaU9zrqq+vBEVZ/m+zyEprPnBVV1SVXdXVU/rqr3VtXpHVlfAtxM8+PsyOkcYyb124b8krZRkt8H\n/gr49bYzZjz/Ajw1yZL29bOBy4GJLgqdBqyrqp4zRjpV1f8CRwN/mWRpkj8AdqbpaB6v7quApwO/\nD/xGkt0nO47mnp1Aw+1w4MPAmfTxJKuqi2iuRn0D2FxV/9i5PcnTaK6QfYzmStvh3UUAnwRuZXoN\nlE8CD0/yqOnUt+31Pormx99109m3PeYBSXaa5n7SQvBk4P40HSFzJskK4DnA99rXO7V1OacPxRfw\nQe6JS78BXAncqyO7PeZLaH4snknT2bNDV1kbgffT/ACdlnYk0gtpOuqnkv+RwFOnml9aRKYVp5Ls\nSNOp+980nSUAhwD/VlX/05X9HOAB7TG+C/y8nWLx7CQ7d+W9GHhjklcnedy2vZUJHQx8rao2TZLv\ncJqYdRbwS0n2myR/v9gJJM2N19C0O55ZVRONNgT4Gc0Fp7ELZofTtIF6nq9JjqGJdy+famWq6ms0\nAw4+BLwdeFVV/XyCXQ4HvlFVn6KZdfHKCfJqQOwEGlJJfo1mOPTZVXUJzbC/V0yjiEvaOaY3t3+f\n1bX9CzRTGc7sse/hwGeq6tZ2+3OSPKyzejQ/xP4v8H/HmS7Wy1jDZ9eOtE931fPojm1PTnITTQA8\nCfjtqrpxisfqPGZoerWlxWY34Mb2yvlE/k97/o09bmZqU7O6fTrJbcA6YAv3TJXaheb/o+4Rh92W\n96jHU7szVdXFwC5J9uGeBlG33wL+h2ZE0r8A2wO97iv2DuD5SR492ZtrXdLW6waaqSfvm8L7uZWm\noXQx8KUpHufJnZ9Dku9NcT9p2EwrTgE/pbly/ZKOfR5Gj/jS/pC5EXhYVf2Ye6bYvw+4Icm5HRfY\n/oImHrwC+HqSDV1T2Hu5pCteTTTCcrdedeyU5t5AzwDObEdUXsDcTLcI8KOu9ti0LthJmrJDgIs7\nRiFO5kPAEe2oyaczTod5mvuk/TlNbLy5a/PyrjbFTV0XyN8G7A18cAodU7/DPaOvz8QpYfOSnUDD\n63Dg/I6T+KNM7yTbv6p2rapd2r//MbYhya7AycBf0wyT7ryx6QOAw2g7h9ofW+vp0QFVVf9G82Ov\n+35C4xm7Aet/d6Qd2lXP0zq2faWqdqXpwDmPJvBN13KaH7O3bMO+0rD7b+Bhk0zbBDirPf/GHrtw\n76tMdwHdnb33A+7u+uF2aDsf/SDgl2h+mEFztf5umnnqE9nYox7jdZp8CHgtMAJ8qsf2w2k60asd\n7vwpesTQtmP5PTRXv6Zi/7ZeDwD+HvhiOzJhovezhCaO/Q+9O6x6+Urn51BVU5oKKw2hacUpmnsG\nXUkzfWvMjfSIL+1I4oe126mqq6vqqKpaCTwOWEbTFqKNFe+tqqdxz3SID0zSGbJ/V7yaaPr5f/eq\nY5ffAa6qqiva1x8FXtG+j9lUwG5d7bH73GdNUl/8f8A+SU6bNCdQVV+iub/hnwL/UlV3dOdpL9af\nDRxbVV/vUczGrjbFrtXcImTsGP8DXANcNVFdkjwV+AWakYrQxKh9k+w7lfeiuWMn0BBqO2JeChyU\nZpWLzcAfA49P8stTLWaCbafQjPR5I3AR0Ln6xYuAhwJ/13HsZdx3StiYtwFvBR44zvZOLwa2VNV3\np1hPAKrqp8AfAr+T5PFTOE73MS/pDHTSIvIVmo6HF86wnHXA6q60R9B0EHcau1/OF4AzaGNLe/59\nhWZ0Tr98mGZI9b92TwFJs+LXM4Hf7ohjvwU8t+0E73YyzdX37ptH9zL2Hn9Oc8+xX6D5MTmhdhTC\nmTQ3hZV0j2nFqfaeYv8fsCbJHm3yBTSjlrunfr+kLfviHuV8l2YKxH3O3/Z+QX9H04E90X2/pjOF\n6gLgiUmWTZDnd2huZD8Wt95J04n1nGkcZ1s5HUyaGzfQTA99WpK/m+I+HwbeQNO2upckoRmZ84U2\nbs2msYtpl7Ux6mKaTuTJRk1qjtkJNJxeRHPl/dE0K0c8vn3+Re59ku2Q5P4dj0mnZSV5Lk3geWOb\ndAxwaJKD2tdH0txQ7Jc7jv1rwP7psVRge3+hK7jvFfatN1BN8vAkr6XpMDp2sjr20jb63g+cMEG2\nrQ2YJMuSnEBzL6Hjxt9FWriq6jaac+ZvkxyaZKckOyR5TpJ3TKOoc4DnJTkkyXbtj5i30lwBGs9f\nA8/quDr0ZuDIJG8c64hJ8vgkE5Uxrqq6lmZ04J/22Hw4zYoa+3BPHNuH5h5A95kn3059Pbmt45S0\noxaOopma8sPxsnXkf3B77O7VNu7fFce3695XWsi2JU61o1T+nXumX30I2AB8PM0yyzsk+Q2ai14n\nVNWPkzwqyRvaTmKS7EVzTn6lff26NEspPyDJ9mlW7nkwE68QNp33+TngP2hWSj2gPcaDk/xBmuWW\nn0zTuf6r3BO3HksTZ4+c5uHGix/364o3O3TkN+ZIc6Sa1T6fSXPP13d1bBrvPDwVeFZVfbHHtrU0\nN8b/vQkOOePzO8n9aWaL/B7Nwh9jceoYmotu9jvMI/5jDKfDgQ9U1cZqVta6oZ0b/h7glR0n2Vto\nfoCMPT7XUcblSW5L8uP277vaHyHvBf6oqm4BqKofAX8CvL/9YfcM4N2dx23vSfRv3NPR032vkD+l\nuedH97KGNyf5MfAtmrvZv6Squnuw/7mt39hjohvHnkJzpW+8q+5Lx94z8DWaxtNBbcNLWpSq6t00\nV4/+lObq0zqaETST3YR16/lcVVfR/Fh6B82Uhi/R/HD6s175231upLli9bb29VdoGjwHAz9IciPN\ndKp/nWo9ery3L1fvZdMPB/62qn7UFUP/nvHj2Kk0ne+TLRF/eZr7Ht1Ec9X+hWPxtMe+YzHpNpph\n1jtz7xsoFs20lp/S3Pvsp9zzY+9JHXFxLI5PZaSSNHS2MU6dDPxekoe1Uz4PoRmd+FWahStOBo6r\nqrEfWD+mWT7+q2074cs07ZM/abf/jGbkzWbgR8CrgRe3Hc49qz39d8pLaFYrPItmmvoVNCMQL6CJ\nW5+uqqu64tYpNJ3w07m34Xh1+zvu3W78QEf+m7vizR9P981JmlRn22oDTZvot5L8v+7t99qp6uaq\n+nyvcmguyj0C2NKj3bCizbO0x7YXjVe3cbyQJm58qCtGnUbT5/DsSfbXHErVxP+e7XzE59NM09m3\nTTuJZlnwO4Af0Nwl/LZ223E0Vz/vAl5XVefPXvUlqblCC/xu+/L9VXVqmtWZzgJWAdcCL21HdEjS\njPRqG7Xpf0QzPflOmqmIx7bpto0kzSnbRpLGM5WRQKfTLLHb6XzgsVW1H80Sv8cBJHkMzb1qHk0z\nP/nv2nmIkjQr2mmIR9PcBHQ/mpWc9qaZWnhBVT0KuBCn/Unqn/u0jZKM0Fwge1xV/TLNSBPSrCxn\n20jSnLFtJGkik3YCtXMLb+5Ku6BjxZeLaeYZArwA+FhV3dUOj/0e8MT+VVeS7uPRNEtp3tHejPc/\nae6b9QLuuUHeGcz85seSBPRuG9FMD3pHVd3V5rmxTT8U20aS5pZtI0nj6sc9gY6imb8MzXLbnavB\nbOSeZb8laTZcCTw9yS5JHgg8F9gL2KOqtsDWG+ztPsA6Slr49qGJRRcn+XzHPZpsG0maa7aNJI1r\nh8mzjC/JW4E7q2ps9ZZew5u35cZ4kjQlVfVfSU6kuXHmj4HLaO67IUlzaQdg56p6UpJfBT5OczNO\n20aS5pRtI0kT2eZOoHZpzOfSrOYyZgNNL/OYFcCmcfa3ASQtEFU10PtbVNXpNPfooF1BYT3NKgh7\nVNWWJHvSrChzH8YiaeEYcCxaD3yyrcfXk/w8yW40baOVHfl6to2MRdLCMeh2UVsH20bSIjdeLJrq\ndLDQcSUrybOBNwMvqKo7OvKdB7wsyY5JfgHYm2Yp7vEqNWuPE044YVbLn4tjDHv5C+E9DHv5c3GM\n+SDJ7u3flTRz3j9KE4+ObLMcAZw73v7D/m9g+YM/huUP/hgDcK+2Ec1y5QcDJNkH2LGq/psmFv2f\nqbSNhv3fYNjLXwjvYdjLXwjvYb6Yz22jYf839jwY7vIBPvLqz036ePGvHD5pnpmcK4OMRZOOBEpy\nJjAC7JZkHXACcDywI/Af7QIXF1fVa6rqqiRnA1fRLI/6mpqsBpI0c+ck2ZV74s6t7TDos5McBawD\nDhtoDSUtGOO0jT4AnJ7kCuAO4HCAuWgbrV61jOvWbZ5S3rVr1064fdXKpVx7Xc9B3JKGi20jST1N\n2glUVa/okXz6BPn/EvjLmVRKkqajqp7eI+0m4JABVEfSAjdO2wjgd8bJP6tto+vWbeb2yw6aNN//\ne++1vPXVqyfM8+D9LupTrSQNkm0jSePpx+pg89LIyMg277t65TKSTPpYu3btpHlWr1w2kPcwH8qf\ni2NY/vw4hiY27N+jYS9/Lo5h+fPjGJrY035l51kt3++p5Q/DMYxFgzfs/8aeBwu/fIBHL3v8rJY/\nyFiUQc3WSjJvZ4ol4SeffkZfynrQCz8/6Zw8aZgloebBDRC31XyORRq8ZStWsnnj+skzTtHS5Xux\nacO6vpWneyzmWJRkSiOBpuLB+11ku0WagWGPRWDbSAtbkq3385mpV7734Hn7f+ZEsWhGS8RLkrSQ\nbd64nn3/on/TY751fH9+qEuSJEnbYsFOB5MkSZIkSdI97ASSJEmSJElaBOwEkiRJkiTNa1NdvGeq\nj5ks4CMNM+8JJEmSJEma165bv7lvi/dAs4CPtBg5EkiSJEmSJGkRsBNIkiRJkiRpEbATSNLQS/L6\nJFcm+VaSjyTZMcnqJBcnuTrJR5M4/VWSJC0Kto0kjcdOIElDLcky4I+AA6pqX5p7nb0cOBF4Z1U9\nCrgFOHpwtZQkSZobto0kTcROIEkLwfbAg9orWjsBm4BnAOe0288AXjSgukmSJM0120aSerITSNJQ\nq6pNwDuBdcBG4FbgEuCWqrq7zbYBcB1QSX2R5LQkW5J8q8e2P0lyd5JdO9JOTfK9JJcl2W9uaytp\nsbFtJGkidgJJGmpJdgYOBVbRNGYeBDynR9aay3pJWtBOB36jOzHJCuAQ4LqOtOcAv1hVjwT+APj7\nuaqkpMXJtpGkiXgzMEnD7hDgh1V1E0CSTwFPAXZOsl17xWsFzTDontasWbP1+cjICCMjI7NZX0l9\nMDo6yujo6ECOXVVfTLKqx6Z3A28CzutIOxT4YLvfV5MsSbJHVW2Zg6r2xeqVy7hu/ea+lbdqr6Vc\nu27ckCxp5mwbSYvMdNpFdgJJGnbrgCcleQBwB3Aw8HVgN+Aw4CzgCODc8QrobOhIGg7dP0rWrl07\nuMoASX4TWF9VVyTp3LQcWN/xemObNjSdQNet38xPPv2MvpX3oBd+vm9lSerJtpG0yEynXWQnkKSh\nVlVfS/IJ4FLgzvbv+4DPAB9L8vY27bTB1VLSQpZkJ+CtwLN6be6R1nMKhlfepeEzyFGJ47FtJGki\ndgJJGnpVtRbo7u6+BjhwANWRtPj8IrAauDzNMKAVwCVJnkhz89W9OvKOOwXDK+/S8JlvoxLH2DaS\nNB5vDC1JkjR9aR9U1ZVVtWdVPaKqfoGm42f/qrqB5v5AhwMkeRLN6jxDMxVMkiQtLJN2AvVaBjXJ\nLknOT3J1ks8mWdKxzWVQJUnSgpXkTODLwD5J1iV5VVeW4p4Oos8A1yT5PvAPwGvmtLKSJEkdpjIS\nqNcyqMcCF1TVo4ALgePAZVAlSdLCV1WvqKplVXX/qlpZVad3bX/E2Ko87evXVtXeVfX4qrpk7mss\nSZLUmLQTqKq+CNzclXwocEb7/Iz29Vj61mVQgSVJ9uhPVSVJkiRJkrSttvWeQA8fm89eVdcDD2/T\nx1sGVZIkSZIkSQPU79XBprwMKrgUqjSM5uNSqJLGt9eKlWzYuH7yjFOwYvlerN+wri9lSZIkae5t\nayfQliR7VNWWJHsCN7TpU14GFVwKVRpG83UpVEm9bdi4no+8+nN9KeuV7z24L+VIkiRpMKY6HWzr\nMqit84Aj2+dHAud2pLsMqiRJkiRpqKxasYwkfXmsWrFs0G9H6mnSkUDtMqgjwG5J1gEnAO8APp7k\nKGAdcBg0y6AmeW67DOpPgO4lU6VFwykYkiRJ0vBYt3Ez33/zE/pS1t4nfbMv5Uj9NmknUFW9YpxN\nh4yT/7UzqpG0QDgFQ5IkSZI0n2zr6mCSNG8k2SfJpUkuaf/emuSYJLskOT/J1Uk+m2TJoOsqSZI0\nm2wXSZqInUCShl5Vfbeq9q+qA4An0ExH/RRwLHBBVT0KuBA4boDVlCRJmnW2iyRNxE4gSQvNIcAP\nqmo9cChwRpt+BvDCgdVKkiRp7tkuknQvdgJJWmj+D3Bm+3yPsRUKq+p6YPeB1UqSJGnu2S6SdC+T\n3hhakoZFkvsBLwDe0ibVVPZbs2bN1ucjIyOMjIz0u2qS+mx0dJTR0dGBHDvJacDzgS1VtW+bdhLw\nm8AdwA+AV1XVbe2244CjgLuA11XV+QOpuKRFZVvbRWDbSBo202kX2QkkaSF5DvDNqrqxfb0lyR5V\ntSXJnsANvXbqbOhIGg7dP0rWrl07l4c/Hfgb4IMdaecDx1bV3UneQXOvjeOSPAZ4KfBoYAVwQZJH\nVtWUf4xJ0jbapnYR2DaShs102kVOB5O0kLwc+GjH6/OAI9vnRwDnznWFJC08VfVF4OautAuq6u72\n5cU0HT7QXIX/WFXdVVXXAt8DnjhXdZW0qNkuknQfdgINwKoVy0jSt8eqFcsG/ZakgUuyE83NDz/Z\nkXwi8KwkV7fb3jGIukladI4CPtM+Xw6s79i2sU2TpFlju0jSeJwONgDrNm7m+29+Qt/K2/ukb/at\nLGlYVdXP6LrBYVXdRNPIkaQ5keStwJ1VNXb1PT2yORVM0qyyXSRpPHYCSZIk9UGSI4DnAs/sSN4A\n7NXxegWwqdf+3ohVGj6DvEm9JG0LO4EkSZKmL3SM8knybODNwNOr6o6OfOcBH0nybpppYHsDX+tV\noDdilYbPgG9SL0nTZieQJEnSNCQ5ExgBdkuyDjgBOB7YEfiPJAAXV9VrquqqJGcDVwF3Aq9xZTBJ\nkjQodgJJkiRNQ1W9okfy6RPk/0vgL2evRpIkSVPj6mCSJEmSJEmLgJ1AkiRJkiRJi4CdQJIkSZIk\nSYuAnUCSJEmSJEmLgJ1AkiRJkiRJi8CMOoGSvD7JlUm+leQjSXZMsjrJxUmuTvLRJK5AJmlWJVmS\n5ONJvpPk20kOTLJLkvPbWPTZJEsGXU9JkqS5YNtI0ni2uRMoyTLgj4ADqmpfmuXmXw6cCLyzqh4F\n3AIc3Y+KStIETgE+U1WPBh4P/BdwLHBBG4suBI4bYP0kSZLmkm0jST3NdDrY9sCD2tE+OwGbgGcA\n57TbzwBeNMNjSNK4kjwEeFpVnQ5QVXdV1a3AoTQxiPbvCwdURUmSpDlj20jSRLa5E6iqNgHvBNYB\nG4FbgUuAW6rq7jbbBmDZTCspSRN4BHBjktOTXJLkfUkeCOxRVVsAqup6YPeB1lKSJGlu2DaSNK6Z\nTAfbmaY3eRVNR8+DgOf0yFrbegxJmoIdgAOAv62qA4Cf0Ax3NvZIkqTFyLaRpHHN5KbNhwA/rKqb\nAJJ8CngKsHOS7drRQCtopoj1tGbNmq3PR0ZGGBkZmUF1JM2F0dFRRkdHB12NThuA9VX1jfb1OTQN\nnS1J9qiqLUn2BG4YrwBjkTR85mEskqT5wraRtMhMp100k06gdcCTkjwAuAM4GPg6sBtwGHAWcARw\n7ngFdAYXScOhuyGwdu3awVUGaBsy65PsU1XfpYlF324fR9LcrN5YJC0w8y0WSdJ8YdtIWnym0y7a\n5k6gqvpakk8AlwJ3tn/fB3wG+FiSt7dpp23rMSRpio4BPpLkfsAPgVfR3Lj+7CRH0XRaHzbA+kla\nQJKcBjwf2NKukEqSXWgugK0CrgVe2t6IlSSn0kyZ/wlwZFVdNoh6S1pUbBtJ6mkmI4GoqrVAdxfT\nNcCBMylXkqajqi4HfrXHpkPmui6SFoXTgb8BPtiRNrb08klJ3kKz9PKxSZ4D/GJVPTLJgcDfA0+a\n8xpLWlRsG0kaz0yXiJckSVpUquqLwM1dyd1LLx/akf7Bdr+vAkuS7DEX9ZQkSepmJ5AkSdLMPbxr\n6eWHt+nLgfUd+Ta2aZIkSXNuRtPBJEmSNKH0SOu5TLOr8UjDx5UKJQ0bO4EkaZ5avXIZ163f3Lfy\nVu21lGvXbepbeZLuZbyllzcAe3XkWwH0PBFdjUcaPq5UKGnY2AkkSfPUdes385NPP6Nv5T3ohZ/v\nW1mSCPce5XMe9yy9fCT3LL18HvCHwFlJngTcMjZtTJIkaa7ZCSRJkjQNSc4ERoDdkqwDTgDeAXy8\ne+nlqvpMkucm+T7NEvGvGkytJUmS7ASSJEmalqp6xTibei69XFWvncXqSJIkTZmrg0mSJEmSJC0C\ndgJJkiRJkjTkli5fQZK+PZYuXzHot6RZ4HQwSQtCkmuBW4G7gTur6olJdgHOAlYB1wIvrapbB1ZJ\nSZKkOWC7aHG6ftNGlh/6hr6Vt/Hcd/WtLM0fjgSStFDcDYxU1f5V9cQ27Vjggqp6FHAhcNzAaidJ\nkjR3bBdJ6slOIM1Ly1as7NswxmUrVg767WhuhPvGtEOBM9rnZwAvnNMaSZIkDYbtIkk9OR1M89Lm\njevZ9y8u6ktZ3zr+oL6Uo3mvgM8mKeAfquofgT2qagtAVV2fZPeB1nCeWbViGes2bu5beSuXL+W6\nDZv6Vp4kSdpmtovUd8tWrGTzxvV9K2/p8r3YtGFd38rT1NgJJGmheEpHg+b8JFfTNIA0jnUbN/P9\nNz+hb+XtfdI3+1aWJEmaEdtF6rt+XqgHL9YPip1AkhaEqrq+/fujJJ8GnghsSbJHVW1JsidwQ699\n16xZs/X5yMgIIyMjs19haYFYumIZ1/dpRNmey5eyeYqjyUZHRxkdHe3LcSVpoZlJuwhsG0nDZjrt\nIjuBJA29JA8Etquq25M8CPh1YC1wHnAkcCJwBHBur/07GzqSpuf6jZtZ+rqn9aWszad8Ycp5u3+U\nrF27ti91kKRhN9N2Edg2kobNdNpFdgJJWgj2AD7VznvfAfhIVZ2f5BvA2UmOAtYBhw2ykpIkSXPA\ndpGkcdl3Fnv0AAAgAElEQVQJJGnoVdU1wH490m8CDpn7GkmSJA2G7SJJE5nREvFJliT5eJLvJPl2\nkgOT7JLk/CRXJ/lskiX9qqwkSdJ8luT1Sa5M8q0kH0myY5LVSS5u20YfTeJFOEmSNBAz6gQCTgE+\nU1WPBh4P/BdwLHBBVT0KuBA4bobHkCRJmveSLAP+CDigqvalGXH9cpr7b7yzbRvdAhw9uFpKkqTF\nbJs7gZI8BHhaVZ0OUFV3VdWtwKHAGW22M4AXzriWkiRJw2F74EHtaJ+dgE3AM4Bz2u1nAC8aUN0k\nSdIiN5ORQI8AbkxyepJLkryvvRP9HlW1BbYuTbh7PyoqSZI0n1XVJuCdNDdc3QjcClwC3FJVd7fZ\nNgDLBlNDSZK02M2kE2gH4ADgb6vqAOAnNFPBqh8VkyRJGiZJdqYZEb2KpqPnQcBzemS1rSRJkgZi\nJjcm3ACsr6pvtK/PoekE2pJkj6rakmRP4IbxClizZs3W593r2kuan0ZHRxkdHR10NSRpPjoE+GG7\nAg9JPgU8Bdg5yXbtaKAVNFPE7sN2kTR8bBdJGjbb3AnUdvKsT7JPVX0XOBj4dvs4kuYmiEcA545X\nRmdjR9Jw6P5hsnbt2sFVRpLml3XAk5I8ALiDpm30dWA34DDgLCZoG9kukoaP7SJJw2amS5QeA3wk\nyf2AHwKvorkh4tlJjqJpDB02w2NIkiTNe1X1tSSfAC4F7mz/vg/4DPCxJG9v004bXC0lSdJiNqNO\noKq6HPjVHpsOmUm5kiRJw6iq1gLdQwGuAQ4cQHUkSZLuZSY3hpakeSPJdu1Khee1r1cnuTjJ1Uk+\n2i7XLEmStCjYNpp/VizbkyR9eaxYtueg346GlCe+pIXidcBVwEPb1ycC76yqjyd5L3A08A+Dqpwk\nSdIcs200z2zcvIVjHtefsk69ckt/CtKi40ggSUMvyQrgucA/diQ/k2bVQoAzgBfNdb0kSZIGwbaR\npPHYCSRpIXg38CagAJLsBtzcLscMsAFYNqC6SZIkzTXbRpJ6shNI0lBL8jxgS1VdBmQsueP5mJrT\nikmSJA2AbSNJE/GeQJKG3VOBFyR5LrAT8BDgr4ElSbZrr3itADaNV8CaNWu2Ph8ZGWFkZGQ26yup\nD0ZHRxkdHR10NSRpPrJtJC0y02kX2QkkaahV1fHA8QBJDgLeWFW/neQs4DDgLOAI4Nzxyuhs6Ega\nDt0/Stau7V6VXZIWJ9tG0uIznXaR08EkLVTHAm9I8l1gV+C0AddHkiRpkGwbSXIkkKSFo6ouAi5q\nn18DHDjYGkmSJIC9Vqxkw8b1fSlrxfK9WL9hXV/KWuhsG0nqZieQJEmSpFm1YeN6PvLqz/WlrFe+\n9+C+lCNJi5HTwSRJkiRJkhYBO4EkSZIkSZIWATuBJEmS+iTJkiQfT/KdJN9OcmCSXZKcn+TqJJ9N\nsmTQ9ZQkSYuTnUCSJEn9cwrwmap6NPB44L9oVuS5oKoeBVwIHDfA+kmSpEXMTiBJkqQ+SPIQ4GlV\ndTpAVd1VVbcChwJntNnOAF44oCpKkqRFzk4gSZKk/ngEcGOS05NckuR9SR4I7FFVWwCq6npg94HW\nUpIkLVouES9J0oCsXLWa9euu61t5e61cxbrrru1beZq2HYADgD+sqm8keTfNVLCays5r1qzZ+nxk\nZISRkZFZqKKkfhodHWV0dHTQ1ZCkKbMTSJKkAVm/7jo+edWtfSvvxY/xfsMDtgFYX1XfaF+fQ9MJ\ntCXJHlW1JcmewA29du7sBJI0HLo7bNeuXTu4ykjSFDgdbIFasWxPkvTlsWLZnoN+O5IkzXvtlK/1\nSfZpkw4Gvg2cBxzZph0BnDv3tZMkSerDSKAk2wHfADZU1QuSrAY+BuwCXAL8TlXdNdPjaHo2bt7C\nMY/rT1mnXrmlPwVJsyTJ/YH/BHakiWufqKq1xiNJA3AM8JEk9wN+CLwK2B44O8lRwDrgsAHWT9IC\nZ7tI0kT6MRLodcBVHa9PBN7ZLoN6C3B0H44hSeOqqjuAZ1TV/sB+wHOSHIjxSNIcq6rLq+pXq2q/\nqnpxVd1aVTdV1SFV9aiqelZV3TLoekpauGwXSZrIjDqBkqwAngv8Y0fyM2nmwEOzDOqLZnIMSZqK\nqvpp+/T+NFe9CngGxiNJkrTI2C6SNJ6ZjgR6N/Am2lUvkuwG3FxVd7fbNwDLZngMSZpUku2SXApc\nD/wH8APgFuORJElabGwXSRrPNt8TKMnzgC1VdVmSkbHk9tFp3GVRXQpVGj7zdSnUtlGzf5KHAp8C\nHt0rW699jUXDa+nyFVy/aWNfytpz2XI2b9zQl7I0++ZrLJKk+WAm7SKwbSQNm+m0i2ZyY+inAi9I\n8lxgJ+AhwF8DS5Js1waeFcCm8QpwKVRp+Mz3pVCr6rYkFwFPAnaeSjwyFg2v6zdtZPmhb+hLWRvP\nfVdfytHcmO+xSJLmg21pF4FtI2nYTKddtM3Twarq+KpaWVWPAF4GXFhVvw18nntWvXAZVEmzLsnD\nkixpn+8EHEJzw3rjkSRJWlRsF0maSD9WB+t2LPCGJN8FdgVOm4VjSFKnpcDnk1wGfBX4bFV9BuOR\nJElafGwXSRrXTKaDbVVVFwEXtc+vAQ7sR7mSNBVVdQVwQI9045EkSVpUbBdJmshsjASSJEmSJEnS\nPGMnkCRJkiRJGriVq1aTpC+PlatWD/rtzEt9mQ4mSZIkbatVK5axbuPmvpS1cvlSrtsw7qJHkqR5\nbP266/jkVbf2pawXP2ZJX8pZaOwEkiRJ0kCt27iZ77/5CX0pa++TvtmXciRJWoicDiZJktQnSbZL\nckmS89rXq5NcnOTqJB9N4gU4SZI0MHYCSZIk9c/rgKs6Xp8IvLOqHgXcAhw9kFpJkiRhJ5AkSVJf\nJFkBPBf4x47kZwLntM/PAF401/WSJEkaYyeQJElSf7wbeBNQAEl2A26uqrvb7RuAZQOqmyRJkp1A\nkiRJM5XkecCWqroMyFhyx/MxNacVkyRJ6uDNCSUNtXb6xQeBPYGfA++vqlOT7AKcBawCrgVeWlX9\nWW9Sku7rqcALkjwX2Al4CPDXwJIk27WjgVYA465dvmbNmq3PR0ZGGBkZmc36SuqD0dFRRkdHB12N\ne7FtJGkidgJJGnZ3AW+oqsuSPBj4ZpLzgVcBF1TVSUneAhwHHDvIikpauKrqeOB4gCQHAW+sqt9O\nchZwGM0PryOAc8cro7MTSNJw6O6wXbt27eAqcw/bRpLG5XQwSUOtqq5vp19QVbcD36G52n4ozU1Y\naf++cDA1lLTIHQu8Icl3gV2B0wZcH0kLnG0jSRNxJJCkBSPJamA/4GJgj6raAk1jKMnuA6yapEWk\nqi4CLmqfXwMcONgaSVqsbBtJ6mYnkKQFoR3u/AngdVV1e5Ip33zV+3BIw2c+3odDkuYT20bS4jGd\ndpGdQNomS5ev4PpNG/tS1p7LlrN544a+lKXFKckONI2cD1XV2P02tiTZo6q2JNkTuGG8/b0PhzR8\n5ul9OCRpXrBtJC0u02kX2QmkbXL9po0sP/QNfSlr47nv6ks5WtQ+AFxVVad0pJ0HHAmcyCQ3Y5Uk\nSVpgbBtJ6slOIElDLclTgVcCVyS5FCiaFXpOBM5OchSwjmZ1HkmSpAXNtpGkidgJJGmoVdWXgO3H\n2XzIXNZFkiRp0GwbSZrINi8Rn2RFkguTXJXkiiTHtOm7JDk/ydVJPptkSf+qK0mSJC0uy1asJEnf\nHstWrBz0W5IkDchMRgLdBbyhqi5r7zz/zSTnA68CLqiqk5K8BTgOOLYPdZUkSZIWnc0b17PvX1zU\nt/K+dfxBfStLkjRctnkkUFVdX1WXtc9vB74DrAAOBc5os50BvHCmlZQkSZIkSdLMbHMnUKckq4H9\ngIuBPapqCzQdRcDu/TiGJEmSNB8tXb6ib1O1li5fMei3I0lawGZ8Y+h2KtgngNdV1e1JaubVkiRJ\nkobD9Zs2svzQN/SlrI3nvqsv5UiS1MuMOoGS7EDTAfShqjq3Td6SZI+q2pJkT+CG8fZfs2bN1ucj\nIyOMjIzMpDqS5sDo6Cijo6ODroYkSZIkaZpmOhLoA8BVVXVKR9p5wJHAicARwLk99gPu3QkkaTh0\nd9iuXbt2cJWRJGkKVizbk42bt/SlrOVL92DDpuv7UpYkSXNtmzuBkjwVeCVwRZJLgQKOp+n8OTvJ\nUcA64LB+VFSSJGk+S7IC+CCwJ/Bz4P1VdWqSXYCzgFXAtcBLq+rWgVV0Edq4eQvHPK4/ZZ16ZX86\nkyRJGoRt7gSqqi8B24+z+ZBtLVeStHB49V2LzF3AG6rqsvaeid9Mcj7wKuCCqjopyVuA44BjB1lR\nSZK0OM34xtCSNGhJTgOeD2ypqn3bNK+8zwNefddi0q6Ken37/PYk3wFWAIcCB7XZzgBGsRNI0iyx\nXSRpIn1ZIl4aNitXre7bUq5JWLlq9aDf0mJ3OvAbXWnH0lx5fxRwIc2Vd0maE0lWA/sBFwN7VNUW\n2NpRtPvgaiZpEbBdJGlcjgTSorR+3XV88qr+Xfx48WOW9K0sTV9VfTHJqq5kr7xLGoh2KtgngNe1\nI4JqKvu5aqo0fObjqqm2iyRNxE4gSQvVwzuvvCfxyrukWZdkB5oOoA9V1dgKqVuS7FFVW5LsCdzQ\na19XTZWGzxCtmmq7SBLgdDBJkqR++gBwVVWd0pF2HnBk+/wI4NzunSRJkuaCI4EkLVRTuvIOTsGQ\nhtF8nIKR5KnAK4ErklwKFHA8cCJwdpKjgHXAYYOrpaRFasrtIrBtJA2b6bSL7ASStFCkfYwZu/J+\nIpNceXcKhjR85uMUjKr6ErD9OJsPmcu6SFr0trldBLaNpGEznXaR08EkDb0kZwJfBvZJsi7Jq4B3\nAM9KcjXNj693DLKOkiRJc2FQ7aLVq5b1dfXd1auW9buKknAkkKQFoKpeMc6mWb3yvnrVMq5bt7kv\nZa1auZRrr9vUl7IkSdLiNah20XXrNnP7ZQdNnnGKHrzfRX0rS9I97ASSpG3Uz8aODR1JkiRJs83p\nYJIkSZIkSTO0dEV/p0UuXdH/aZGOBJIkSZIkSZqh6zduZunrnta38jaf8oW+lTXGkUCSJEmSJEmL\ngJ1AkiRJkiRJi4CdQJIkSZIkSYuAnUCSJEmSJEmLgJ1A0pDq553nZ+Ou85IkSZKk+cXVwaQh1c87\nz8/GXeclSZIkSfPLrI0ESvLsJP+V5LtJ3jJbx5GkiRiLJM0HxiJJ84GxSNKsdAIl2Q54D/AbwGOB\nlyf5pdk41nhGR0dn/Rj/ecXNs1r+xet+PKvlb7h9VosH4I4b189q+bf/8NJZLf/Kr83uCJmrNl42\nq+UD3LHhllk/xnw1H2IRwH9+fXb/DYxFkzMWTcxYNLuMRf0x27EIZj8eDXssmov29WzHo7l4D/OV\nsag/jEWTG/Z2Ecx+LBpku2i2RgI9EfheVV1XVXcCHwMOnaVj9TQXAf4LV87uP9xXZ/uH109mtXhg\nLgLM7J6cV37ti7Na/nc2XT6r5QP874ZbZ/0Y89jAYxHAF74xu7HCWDQ5Y9HEjEWzzljUB7Mdi2D2\n49Gwx6K5aF/PdjxazJ1AGIv6wlg0uWFvF8Hsx6JBtotmqxNoOdD5zdrQpknSXDIWSZoPjEWa91au\nWj3pQhJr166d0oITK1etHvTbUW/GIkmzdmPo9EirWTqWJI3HWCRpPjAWad5bv+46PnnVxFemP/ae\nv+Rlrz1u0rJe/Jgl/aqW+stYJIlU9f+8T/IkYE1VPbt9fSxQVXViRx4DjrRAVFWvRsXAGYukxcVY\nJGk+GOZY1KYbj6QFYLxYNFudQNsDVwMHA5uBrwEvr6rv9P1gkjQOY5Gk+cBYJGk+MBZJglmaDlZV\nP0/yWuB8mvsOnWZwkTTXjEWS5gNjkaT5wFgkCWZpJJAkSZIkSZLml9laHWzOJXlrkiuTXJ7kkiS/\nmuT57fPL2m2/N8Wy9kjy0STfS/L1JP+S5JFJTklyRZJvJflqklVt/n9J8tDx6tGj/J+32y5t/65M\nslOSD7dlX5HkP5M8sM3/xfZvxqvDFD6PJyZ5X5Jfarcf1ZZxefv3N9v0zyc5YJqf/d1Jzuh4vX2S\nHyU5r3398CT/3P47fDvJv0yj7HclOabj9b8neV/H65OTvH6qn8sUjzn273Nl+2/0+iQzntvdUe4V\nSc5K8oA2fdLvzDTLvyzJN9p539P63mjmhikWtflmNR4Zi4xFxqLBMBZN+nkYi6Z+TGORtpmxaNLP\nw1g0vfc0dPFoXsaiqhr6B/Ak4EvADu3rXYGVwEZgaZt2P+CRUyzvy8Dvdbz+ZeBPgbM70pYBS6ZQ\njz17lH9bj7RjgZM7Xj8SuF9XnpdNVoep1INmKcjvAw9uXz8QWNU+/zxwwDQ//x8D3wTu375+NnAJ\ncF77+u+BP+rI/7hplP0S4GPt8wDfAL7U9W/1tql8LtM45m0dzx8G/AfNTfRm+j3tLPfDwB9P9Tuz\nDeX/OjA6ne+Nj5k/hi0WdX9vOtL6Eo+MRcYiY9FgHsYiY5GxyFg0Hx7GImNRv8+1YYxH8zEWLZSR\nQEuBG6vqLoCquonmS789cHObdmdVfW+ygpI8A/jfqnr/WFpVXQH8hOYGamNpm6rq1nafa5Ls2qse\nVXV9r8OM8x42dpT/vaq6sy3/xx15etahR1n3qUdHD/LDgduAn7bbf1pV13Xs/9K2J/K/kjy11+fU\nw78Bz2ufvxz4aFd9NnTU+8oplgnNiTdWh8cCVwI/TrIkyY7Ao4GfAVs/5wk+l2mrqhuB3wde24/y\nOnwB2Jupf2emovN7tQS4qX0+1e+NZm7YYhHMbjwyFhmLjEWDYSy6bznGoj4wFmmajEX3LcdY1CdD\nFI/mXSxaKJ1A5wMr2xPib5M8vapuBv4ZuC7JmUleMcWhYo+j6THtdjbwgnYo18lJ9uvYVuPVY5xj\n7JR7hhme06Z9ADg2yZeSvD3J3j3Kn6gOnSarx+XADcA1ST6Q5Pld27evqgOB1wNrxjlGpwI+Brw8\nyf2BfYGvdmz/W+ADST6X5PgkS6dQZlNw1WbgziQrgKfQ9Cp/FXgy8CvtezkT+M0pfC7bpKquoRmx\nt/sMiwpNQTsAzwGuYOrfmakY+159B3gf8PY2farfG83csMUimN14ZCzqI2ORpsFYdG/Goj4yFmka\njEX3ZizqsyGJR/MuFi2ITqCq+glwAE1P4I+AjyU5vKp+D3gmzRfyjTQn8LYeYyOwD3AccDdwQZoe\naWi/NOPVo0dxP62qA6pq/6r6rXbfy4FfAP6KZqjZ15I8ahp1mOzzOII2SFXV3VX1bOC3aJaJfFeS\n/9tRxCfbv98EVk3x87kSWE3Tw/yvdPR4VtX57Xt7P/BLwCVJdptKua2xnuanAF8BLu54/eWq2sQU\nPpcZ6se5slOSS2iW47yOZkWGqX5npmLse/VomuD1IZj690YzN4SxCGYxHhmLjEUYiwbCWGQswlgE\nxqKBMxYZi5ibc22+x6P5F4tqDuaczfWD5sQ5tyttN3rM8eyx7zOBi6aQ743AKe3za4Bdp1KP6poX\nOEH5fwO8fqL8nXWYwudxHnAhPeaSAk8ALm+fb51v2n5mP5xC+be1f99Gc4I8FjiIdr5pj/z/DLxo\nGv+erwFOoZlrGmAX4ALgHOB52/q5TPZ+Ol4/AvhRH76XU/l37/md2cZ6Xw88rN+fj49p/ZvM61jU\n63szTp6+xCNj0bS/P8YiH315GIt61sNYNPXjGYt89OVhLOpZD2PR9L5DQxeP5mMsWhAjgZLs0zUs\nbz9gS5KDOtL2B66drKyquhDYMcnRHeX/cpKnjw2RS7IdzXC6e5U3Tj0653FuzdrjPTwlyc7t8x2B\nx3SUPzY8bf8edbhP+ePU49qO7UuT7N+xff9x6tmzrhPk+QDwZ1X17a76PCPJTu3zhwC/CKybQrlj\nvgQ8H7ipGjcDO9MMN/zKVD+Xadj6ntuhhe+lCfYz1evffarfmWmVn2aFge2A/56Fz0fjGMJYBLMY\nj4xFxiJj0WAYi4xFxqJ7l28sGgxjkbFoFs61YYxH8y4W7TAXB5kDDwb+JskS4C6au6q/Dnhfkr+n\nuSnVT4Ajp1jei4BTkhzX7nst8O80Q/J2bPN8jWYeJdwzF7RXPX6/R/nVI+0XgfemmRK7HfCvVfWp\nrvwPB97fVYf39ChrvHp8ot1+P+Dk9kv3PzQ9w38wTt161bXn+6lmSFuvk/AJwHuS3Nm+t/dVVa85\nveO5gqbH+8NdaQ+sqpvSLNU3lc9lqh6QZjjgjsCdwAer6t0zKG9Mr89yqt+ZqRir91igObyqKslU\nvzeauWGLRZ37dOpXPDIWGYvAWDQIxqJ7MxYZi8BYNAjGonszFs38XBvGeDTvYlHaoUeSJEmSJEla\nwBbEdDBJkiRJkiRNzE4gSZIkSZKkRcBOIEmSJEmSpEXATiBJkiRJkqRFwE4gSZIkSZKkRcBOIEmS\nJEmSFqkkeyW5LUkmz61hZyfQIpPkmiTP7JF+RJIvTJQ/yelJ/qxj22OTbEry+vb1tUl+2gaQH7d/\nT52gLnsn+WiSG5LckuTqJKckWTZO/hOSfKhH+t1JHjG1T0DSfNfGkuuT7NSRdnSSC9vnd3fEmLG/\nf5Jkz3bb7h37vbVH2vFJPtM+/6ckd7Rl3Jrk60me3m57TBub9u6q3+eS/L/Z/hwkDd4E8ejzHa/f\nlOS7SX7S5v/LJDt2bL9X+2mc4/wwyZU90keT/CzJ8o60g5NcM/N3J2nQun4/bWrjxQPnuh5Vtb6q\nHlpV1dbr80mOGi9/klVt++q2jvbYpR3b35rkurYddWaSB8/F+9DU2AmkTjXVjEn2Ay4E3l5V7+7Y\n/3ltAHlI+/eYcfbfG/gqsAHYr6p2Bp4K/AD4tWnWccr1ljQUCtge+OMJ8uzbFWtOrqrrge8BT+/I\n9zTgO11pTwcu6jjWiW0ZS4C/Bz6ZJFV1FfBXwAfGdkxyNLAUWDuztyhpSIwXj8Z+KP0N8LvAbwMP\nAZ4DPBM4e6oHaDuedwcekeQJPY5zO/C2XseXNPS2/n4C9gP2B47r90FmaYRPAUs62mP7t8c6Angl\n8GRgGfBA4D2zcHxtIzuBNG1JfhX4D+DYqnpv9+YpFnMC8MWqelNVbQKoqhur6tSqmnLDaZrHlDQ8\n/gp4Y5KHjrN9vPP+C7QdPkm2o2lMnQIc1JH2ZOA/x9n/TGBXYI/29TuAByV5dZKHt69fVVX/O723\nI2mI9YxH7QWtVwOvqKqvVdXdVfUd4LeAZycZmWL5RwCfBj7TPu92KvByRz1LC1YAquoG4LM0nUHN\nhmTHJCe3o2o2J/m7JPfv2H5okkvb0czfS/Lrbfrnk/x5ki8m+QlNJ/O9ZoR0zrLoGNmzXZI/p7mI\n9p7JZnbQuz32fOC0qtpUVT8FTgRemuQB2/oBqb/sBNJ0HQj8O/C6qjp9BuUcApzTnypJWoC+AYwC\nb5rmfv/JPaN+9qcZBfS5jrQDgB2Ar3fvmGR7mh9gPwS2AFTVz4GjgT8HPgx8sKq+Os06SRpu48Wj\ng4H1VfXNzsSq2gBcDDxrsoLbaWYvAT5C0wn98iQ7dGXbCLwfRyBKC1qSFTSjCb/XkXwSsDewb/t3\nOfB/2/xPBM4A3tiOZn46cG3Hvr9NM1LxIcB14xy2up9X1Z/SXFR77UQzO8aqPU5aZ/p2wP2BR05Q\njuaQnUCaricBt9B0BPXy6SQ3Jbm5/Xv0OPkeBlw/9iLJH7b7/DjJP/S5zpKG0wnAa5Ps1mPbJV2x\nZuzH1kXA45IsobmK9YWq+gGwW5v2a8DFVXVXR1lvSnITzZSLdwFvG5sTD1BVlwGnAb8EvLXfb1LS\nUOgVjx4GbB4n/+Z2+2R+C/gfmqv//0Iz9ex5PfK9A3h+kkdPucaShsWnk9wGrKO5CLWmY9vvAq+v\nqlv/f/buPFzSurzz//sDiCJq0y4s3U03ouI6BjERomNoEBNBQ+skOGKiLE4mv3EdyUQBZwZ6/CUq\nExcwRkWRaYzKolHQYSIhcohLAJVFFAMyAr3SaFhUTAiEe/54ngPFoc7Wp86pqlPv13XV1VXfeur7\n3HVOnbur7vouVXU3TS44sr3vWJoRN18DqKotVXVDx2P/V1X9QztKsfN9T68E+EnHe7Hj2vb/A/yH\ndnTREuAdbfuCr3Wk7iwCadx9wCO6tD8CuLfj9p/TfIN+cftHPdGaqnp8VS1t/z1jkvP9I826GgBU\n1UeqainwoUni6Bpjx7dl9z78cEnDrKp+QPOhqNvc+OdNyDV/0z7mFpq1xl5M843Y+IL3f9/RNnEq\n2P9s+9gJ+FXgz5L81oRjfgDcXFX/3IvnJmm4TJKPfkrHe5kJ9mjvn87rgXOr8S/AF+kyJayqfkrz\nHuzds4lb0lBY064JdCDNF05PBEizqcWjge+2RZbbaQos48XoPWnWU53MhvkLGWhGDj2h473YB9r2\nTwGfoxlBeS3NOrLQvD/TALAIpHHrgZWdDe3K9Lvy0OGD/0qz0Nd64KIkj53Qz0zX5/lb4N9tQ4x7\nTWjbm6Y4tGmWfUkaDicDf0Az/LnTVLlmfF2gA4BvtW3faNtexOTrAdEuBv1Nun8TL2m0ncxD89HX\ngJVJfrXzoCR70uSfi6fqrN3x62Dg99u1PrbQjAw6LMnjuzzkz4CDgImLR0sabuNrAn2dZnrX+9v2\nnwK/BJ7dFlkeX1W7tFO/oCnyPGWKficuIH83Dx2Ns/ssHjtl7A95YGNtVT25qlbSTM3fVFV+XhsQ\nFoFG045JHtlx2Z5mp65/TvLOtm1nmuGG366q9Z0PbtfIOIImMV2Yjm1TZ+Fk4MXtQmfLAJI8EZhq\nmPNfA09P8ntJdmjfIP0JcF5V3b8NMUgacO1UrnOAqeajT/R1mm/XN1fVL9q2b7RtS2hGBXWV5Bk0\nU8YetlWzpNE2MR9V1Y9odhT8TJL92wVVnw18Hrioqi7pePgOE957PYImJ10P7AP8SnvZh+aLrSOZ\noGXaSHMAACAASURBVKruoikEvWPifZIWjQ8BL03y3HZq+ieAD7WjgkiyfHzxZ5qp6sckOSiNZUn2\nmaLvq4HXtJ+jfpVmPbJOnQWdrTRftk+l6xdySZaOL2Sf5Fk0RS3XNBsgFoFG0/+mqSr/U/vvSe0Q\n5JfTfMO0EbiRpjr86o7Hda6RcS/NSJ5/Ar7csdr7l9tV5McvXRd/bt84HUAzjPGaJHfRfHDbxMO3\nQR1/zE+Aw4D/D7gN+B5wB/DGWf8EJA2yid8+/Q+ab646269pc8zP238/0HHfpTTbLX+9o+1q4FHA\nd7pM6XrHeF80xeYzqur0njwTScNuunz0ZuCTNAvH/5xmh6+v8fAPV++kec81fvlb4HXAR6rqJ1V1\n2/iFprA0PiVs4vlPoxkB7Rbx0uLwkL/ldurnOh78PHQ8zeeyy5LcCVxEUyymqr4NHENTOLqLZvrV\nqm79tv4bzeLSt9Osc/aZKWI5FTgiyT8m+dBMYu/wRJqBAr+g+dz5ySmWCFEfpGPty+4HJGfQbPO2\ntaqeO+G+/0KzYvkTq+r2tu00mlXN7waObhfUlKQ565aPkiyl+WZ2Fc2OCK9uvy01H0maF5PkolOA\n3wbuoVmj4Ziq+ll73wk0C3jeR7O75kV9CVzSyEjydprdLe+nWZflGGAZcDawFLgSeN08LRgsaYDN\nZCTQmcDEBTLHt7A7hI71YpIcCjylqp4G/CHNNxmS1Cvd8tHxwMVV9XSab19PAPORpHnVLRddRLNu\nw7402/uO56Jn0YyqfSZNUfovksx0/TxJmrV2qYW3APu1heodaKYYvg94f/ue6U6aIpGkETNtEaiq\nvkEz5WaiDwJ/PKFtDXBW+7jLgSVJdptrkJIEk+ajNTTDZmn/XdPRbj6S1HPdclFVXdyxPt1lwIr2\n+uHA2VV1X1XdTFMgesFCxSppZG0P7NzupLsTsJlm2YfxpRrWAa/qU2yS+mib1gRK8tvAhqq6dsJd\ny3noVnSbePiOLpLUS7tW1VaAqrqVZkc7MB9J6p9jadaGAXORpAVWVZtpFuNdT5Nz7qKZ/nVnR7F6\nI830MEkjZtZFoHYnqHfRLCb1sLu7tLlwnaR+MB9JWnBJ3gXcW1WfG2/qcpi5SNK8SbILzYjoVTSF\nnp1ppqNOZC6SRtAO2/CYpwB70ezMEprhzlcmeQFNRXnPjmNX0Aw9fJgkJh1pkaiqfq5vsTXJblW1\nNcnuNDvHwQzzkblIWjz6nItIchTNLpYHdzSbi6QR0+9cRLNu6487Nu75IvBCYJck27WjgfycJi1y\nk+WimY4ESnuhqr5fVbtX1d5V9WSaNzfPa7e0vAB4PUCSA2iGHG6dIqh5u5x00knz2v9CnGPY+18M\nz2HY+1+Ic/TBA/modQFwdHv9aOD8jvYZ5aNh/x3Yf//PYf/9P0cfPCQXJXkZ8A7g8Kq6p+O4C4DX\nJNkxyZNptue9oluHw/47GPb+F8NzGPb+F8NzGBDrgQOSPKr90v4lwA+AS4Aj2mOO4sH3TA8zzL+D\nYe9/MTyHYe9/LucA2ONtL5728pj9V87ouG39e5zKtEWgJJ8FvgXsk2R9kmMm5ggeLBBdCNyU5Ebg\n48Abp+tfkmZqknz0XuClSa6neZPzXjAfSZo/k+SiDwOPAf4myZVJ/gKgqq4DzgWuo1kn6I013buz\nAbPXymUkmfaydu3aGR2310qXIZHmU1VdAXweuAq4huaz2uk0O6oel+QG4PHAGX0LUlLfTDsdrKpe\nO839e0+4/ea5BiVJ3UyRjw6Z5Pihzkd7rVzGLRu2zOjYtWvXTnvMqj334Ob1XUd+S5qFSXLRmVMc\n/x7gPfMX0fy6ZcMW7v7SQdMe9yefu4l3HfnkaY/b+ZWX9CIsSVOoqrXAxDcHNwH79yEcSQNkW9YE\nGgqrV68e+nMMe/8LcQ77H4xzaGrb+juY6Qevv7v2Dn7j3yyd9rht/eDl34H9D8s5NLX5/h28+Dm7\nzGv/i+F1av/9P4e5qP+G/Xfs38Hi738hzrHjiiXz2v9U0q8RyUmGbTS0pC6SUP1fAHGbDXIuSjKj\nItBM7fzKS6adIywNK3PR/DEXqRf2XLGSjZs29KSvFcv3ZMPG9T3pq9eGPRfBYOcjadAleWAtn17Y\ncurXt+n/zKly0aIdCSRJ0lwtW7GSLT360AKwx/I92TygH1wkaT5t3LSBz/ynv+1JX7/30Zf0pB9J\nGkUWgSRJmsSWTRt47p9e2rP+vnfigT3rS5IkSZqtmW4RL0mSJEmSpCFmEUiSJEmSJGkEWASSJEmS\nJEkaARaBJEmSJEmSRoBFIEmSJEmSpBFgEagPVq1YRpKeXVatWNbvpyRJkiRJkgacW8T3wfpNW7jx\nHc/vWX9PPeW7PetLkiRJkiQtTo4EkiRJkiRJGgEWgSRJkiRpkUiyT5KrklzZ/ntXkrcmWZrkoiTX\nJ/lqkiX9jlXSwrMIJEmSJEmLRFXdUFXPq6r9gOcDdwNfBI4HLq6qpwNfA07oY5iS+sQikCRJkiQt\nTocA/7eqNgBrgHVt+zrglX2LSlLfTFsESnJGkq1JvtfRdkqSHya5OskXkjyu474Tkvyovf835ytw\nSZIkSdKU/j3w2fb6blW1FaCqbgWe1LeoJPXNTHYHOxP4MHBWR9tFwPFVdX+S99IMJTwhybOAVwPP\nBFYAFyd5WlVVj+OWJEmSJE0iySOAw4F3tk0z/kx28sknP3B99erVrF69upehSeqxsbExxsbGZnTs\ntEWgqvpGklUT2i7uuHkZ8Dvt9cOBs6vqPuDmJD8CXgBcPqNoJEmSJEm9cCjw3ar6aXt7a5Ldqmpr\nkt2B2yZ7YGcRSNLgm1isXbt27aTH9mJNoGOBC9vry4ENHfdtatskSZIWhUmmyk+6606S09qp8lcn\n2bc/UUsaQUcCn+u4fQFwdHv9KOD8hQ5IUv/NZDrYpJK8C7i3qsaTS7ocNumwQ4cZSsNnNkMNJWmR\n6jZVfnzXnVOSvJNmqvzxSQ4FnlJVT0uyP/Ax4IAFj1jSSEmyE82i0P+xo/l9wLlJjgXWA0f0IzZJ\n/bXNRaAkRwGHAQd3NG8E9uy4vQLYPFkfDjOUhs9shhpK0mLUbao8za47B7bX1wGX0BSG1tAWi6rq\n8iRLxqdjLFjAkkZOVf0TExZ+rqrbaQpDkkbYTKeDhY5RPkleBrwDOLyq7uk47gLgNUl2TPJk4KnA\nFb0KVpIkaUDtOmHXnV3bdqfKS5KkgTHtSKAknwVWA09Ish44CTgR2BH4myQAl1XVG6vquiTnAtcB\n9wJvdGcwSZI0wmY1VV6SJGk+zWR3sNd2aT5ziuPfA7xnLkH1214rl3HLhi096WvVnntw8/pJZ8RJ\nkqTFYbJdd2Y8Vd61EqXh41qJkobNnBaGXqxu2bCFu790UE/62vmVl/SkH0mTS/J24A3A/cC1wDHA\nMuBsYClwJfC6qrqvb0FKWmweMlWeB3fdeV/77/kd7W8CzklyAHDnZOsBuVaiNHxcK1HSsOnFFvGS\n1DdJlgFvAfarqufSFLePpPkg9v6qejpwJ02RSJLmrJ0q/y1gnyTrkxwDvBd4aZLrgZe0t6mqC4Gb\nktwIfBx4Y5/CliRJciSQpEVhe2DnJPcDO9FMtTiIphgEzU49J9N8AJOkOZlkqjxMsutOVb15HsOR\nJEmaMUcCSRpqVbUZeD+wnmbXnbtopn/dWVX3t4dtpJkeJkmSJEkjyyKQpKGWZBdgDbCKptCzM3Bo\nl0PdjUeSJEnSSHM6mKRhdwjw46q6HSDJF4EXArsk2a4dDTTpbjwwujvyrFqxjPWberMTIsDK5Xtw\ny0Z3Q9TCcEceSZKk2bMIJGnYrQcOSPIo4B6aBVm/DTwBOAI4BziKB3fqeZhR3ZFn/aYt3PiO5/es\nv6ee8t2e9SVNxx15JEmSZs/pYJKGWlVdAXweuAq4hmbL5tOB44HjktwAPB44o29BSpIkSdIAcCSQ\npKFXVWuBicMAbgL270M4kiRJfZVkCfBJ4DnA/cCxwA00I6RXATcDr66qu/oVo6T+cCSQJEmSJC0u\npwIXVtUzgV8B/oFmlPTFVfV04GvACX2MT1KfWASSJEmSpEUiyWOBF1fVmQBVdV874mcNsK49bB3w\nyj6FKKmPLAJJkiRJ0uKxN/DTJGcmuTLJ6UkeDexWVVsBqupW4El9jVJSX1gEkiRJkqTFYwdgP+Aj\nVbUfcDfNVLDqa1SSBoILQ0uSJEnS4rER2FBV32lvf4GmCLQ1yW5VtTXJ7sBtk3Vw8sknP3B99erV\nrF69ev6ilTRnY2NjjI2NzejYaYtASc4AXgFsrarntm1LmWRl+SSnAYfSVJyPrqqrZ/8UJEmSJEmz\n1RZ5NiTZp6puAF4C/KC9HA28DzgKOH+yPjqLQJIG38Ri7dq1EzdOftBMpoOdCfzWhLauK8snORR4\nSlU9DfhD4GOzCVySJEmSNGdvBT6T5Gqa3cH+lKb489Ik1wOHAO/tY3yS+mTakUBV9Y0kqyY0rwEO\nbK+vAy6hKQytAc5qH3d5kiXjQw57GLMkSZIkaRJVdQ3wa13uOmShY5E0WLZ1YehdJ6wsv2vbvhzY\n0HHcprZNkiRJkiRJfdTr3cHSpc1V6CVJkiRJkvpsW3cHm2xl+Y3Anh3HrQA2T9aJq85Lw2c2K89L\nkiRJkgbHTItA4aGjfC7gwZXlj+bBleUvAN4EnJPkAODOqdYDctV5afjMZuV5SZIkSdLgmMkW8Z8F\nVgNPSLIeOIlmJfnzkhwLrAeOAKiqC5McluRGmi3ij5mvwCVJkiRJkjRzM9kd7LWT3NV1ZfmqevOc\nIpIkSRpSSd4OvAG4H7iW5guxZcDZwFLgSuB1VXVf34KUJEkjq9cLQ0uSJI2kJMuAtwD7VdVzab5s\nO5Jm+vz7q+rpwJ00RSJJkqQFZxFIkiSpd7YHdk6yA7ATzQYZBwFfaO9fB7yqT7FJkqQRZxFIkiSp\nB6pqM/B+mvUSNwF30Uz/urOq7m8P20gzPUySJGnBbesW8ZIkSeqQZBdgDbCKpgB0HnBol0Or2+M7\nd02duBOjpME0NjbG2NhYv8OQpBmzCCRJktQbhwA/rqrbAZJ8EXghsEuS7drRQCtopog9TGcRSNJw\nmFiwXbt2bf+CkaQZcDqYJElSb6wHDkjyqCQBXgL8ALgEOKI95ijg/D7FJ0mSRpxFIEmSpB6oqiuA\nzwNXAdcAAU4HjgeOS3ID8HjgjL4FKWkkJLk5yTVJrkpyRdu2NMlFSa5P8tUkS/odp6SF53QwSZKk\nHqmqtcDE+SA3Afv3IRxJo+t+YHVV3dHRdjxwcVWdkuSdwAltm6QR4kggSZIkSVpcwsM/660B1rXX\n1wGvXNCIJA0Ei0CSJEmStLgU8NUk307yH9q23apqK0BV3Qo8qW/RSeobp4NJGnrtnPZPAs+hGf58\nLHADcA7NVs03A6+uqrv6FaMkSdICemFV3ZrkScBFSa6nKQzNSOduhRN3QJM0eMbGxhgbG5vRsRaB\nJC0GpwIXVtURSXYAdgZOxHnvkiRpBLUjfaiqnyT5EvACYGuS3apqa5Ldgdsme3xnEUjS4JtYrF27\nduLyhA9yOpikoZbkscCLq+pMgKq6rx3x47x3SZI0cpI8Oslj2us7A78JXAtcABzdHnYUcH5fApTU\nV44EkjTs9gZ+muRM4FeA7wD/mQnz3tvh0JIkSYvdbsAXkxTN573PVNVFSb4DnJvkWGA9cEQ/g5TU\nH3MqAiV5O/AGmjU4rgWOAZYBZwNLgSuB11XVfXOMUyNm2YqVbNm0oSd97bF8TzZvXN+TvjSQdgD2\nA95UVd9J8kGaaV/Oe5cWsdnMfZekUVJVNwH7dmm/HThk4SOSNEi2uQiUZBnwFuAZVfUvSc4BjgQO\nA95fVecl+ShNkejjPYlWI2PLpg08908v7Ulf3zvxwJ70o4G1EdhQVd9pb3+BpgjkvHdpEZvN3HdJ\nkiQ15rom0PbAzu1CrDsBm4GDaD6EQbMOx6vmeA5JmlQ75WtDkn3appcAP8B575IkSZL0ENs8Eqiq\nNid5P8180l8CF9FM/7qzqu5vD9tIMz1MkubTW4HPJHkE8GOaqanb47x3SZIkSXrAXKaD7UKz+84q\n4C7gPODQLofOeF0OSdoWVXUN8Gtd7nLee5+tWLY7m7Zs7Ulfy/fYjY2bb+1JX5IkSdIomsvC0IcA\nP24XGCPJF4EXArsk2a4dDbSCZopYVy7GKg0fF2PVbGzaspW3Pqc3fZ32/d4UkyRJkqRRNZci0Hrg\ngCSPAu6hWYfj28ATaKZdnMM063C4GKs0fFyMVZLUa6tWLGP9pi096Wvl8j24ZeOk30FKkjTS5rIm\n0BVJPg9cBdzb/ns6cCFwdpJ3t21n9CJQSZI0e3uuWMnGTRt60teK5XuyYeP6nvQldVq/aQs3vuP5\nPenrqad8tyf9SJK0GM1lJBBVtRaYOAzgJmD/ufQrSZJ6Y+OmDXzmP/1tT/r6vY++pCf9SJIkqT/m\nukW8JEmSJEmShoBFIEmSJEmSpBFgEUiSJEmSJGkEWASS5smeK1aSpCeXPVes7PfTkSTNQJIlSc5L\n8sMkP0iyf5KlSS5Kcn2SryZZ0u84JS1+SbZLcmWSC9rbeyW5rM1Fn0syp/VhJQ0n//CleeJirJI0\nkk4FLqyqI9oPWDsDJwIXV9UpSd4JnAAc388gJY2EtwHXAY9rb78PeH9VnZfko8AbgI/3KzhJ/eFI\nIEmSpB5I8ljgxVV1JkBV3VdVdwFrgHXtYeuAV/YpREkjIskK4DDgkx3NBwNfaK+vA1610HFJ6j+L\nQJIkSb2xN/DTJGe2UzBOT/JoYLeq2gpQVbcCT+prlJJGwQeBPwYKIMkTgDuq6v72/o3Asj7FJqmP\nLAJJkiT1xg7AfsBHqmo/4G6aaV/V16gkjZQkLwe2VtXVQMabO66PMzdJI8g1gSRJknpjI7Chqr7T\n3v4CTRFoa5Ldqmprkt2B27o9+OSTT37g+urVq1m9evX8RitpzsbGxhgbG+t3GBO9CDg8yWHATsBj\ngQ8BS5Js144GWgFsnqwD85E0XGaTiywCSZIk9UBb5NmQZJ+qugF4CfCD9nI0zaKsRwHnd3t854cu\nScNhYoFk7dq1/QumVVUn0ixIT5IDgT+qqt9Pcg5wBHAOU+QiMB9Jw2Y2ucgikCRJUu+8FfhMkkcA\nPwaOAbYHzk1yLLCe5kOYJC2044Gzk7wbuAo4o8/xSOoDi0CSJEk9UlXXAL/W5a5DFjoWSaqqS4FL\n2+s3Afv3NyJJ/ebC0JIkSZIkSSPAIpAkSZIkSdIIsAgkSZIkSZI0AuZUBEqyJMl5SX6Y5AdJ9k+y\nNMlFSa5P8tUkS3oVrCRJkiRJkrbNXEcCnQpcWFXPBH4F+AeaVecvrqqnA18DTpjjOSRJkiRJkjRH\n21wESvJY4MVVdSZAVd1XVXcBa4B17WHrgFfOOUpJkiRJkiTNyVxGAu0N/DTJmUmuTHJ6kkcDu1XV\nVoCquhV4Ui8ClSRJkiRJ0rabSxFoB2A/4CNVtR9wN81UsOpFYJIkSZIkSeqdHebw2I3Ahqr6Tnv7\nCzRFoK1JdquqrUl2B26brIOTTz75geurV69m9erVcwhH0kIYGxtjbGys32E8TJLtgO8AG6vq8CR7\nAWcDS4ErgddV1X39i1CSJEmS+mubi0BtkWdDkn2q6gbgJcAP2svRwPuAo4DzJ+ujswgkaThMLNiu\nXbu2f8E81NuA64DHtbffB7y/qs5L8lHgDcDH+xWcJEmSJPXbXHcHeyvwmSRX0+wO9qc0H7xemuR6\n4BDgvXM8hyRNKckK4DDgkx3NB9OMUIRmkfpXLXRckiRJkjRI5jIdjKq6Bvi1LncdMpd+JWmWPgj8\nMbAEIMkTgDuq6v72/o3Asj7FJkmSJEkDYU5FIEnqtyQvB7ZW1dVJVo83t5dOky5a7/pk0vAZ1PXJ\nJKnfkjwS+DtgR5rPe5+vqrWulygJLAJJGn4vAg5PchiwE/BY4EPAkiTbtaOBVgCbJ+vA9cmk4TPA\n65NJUl9V1T1JDqqqXybZHvhmkr8GjsP1EqWRN9c1gSSpr6rqxKpaWVV7A68BvlZVvw9cAhzRHjbl\nIvWSJM3FHstXkKQnlz2Wr+j309EiUFW/bK8+kuaL/wIOwvUSpZHnSCBJi9XxwNlJ3g1cBZzR53gk\nSYvUrZs3sXzNcT3pa9P5H+hJPxptSbYDvgs8BfgI8H+BO10vUZJFIEmLRlVdClzaXr8J2L+/EUmS\nJC28ttjzvCSPA74IPLPbYZM93vUSpeEym7USLQJJkiRJ0iJUVT9LcilwALCL6yVKi9Ns1kp0TSBJ\nkiRJWiSSPDHJkvb6TsAhwHW4XqIkLAJJkiT1TJLtklyZ5IL29l5JLktyfZLPJXEUtqT5tgdwSZKr\ngcuBr1bVhTTrJR6X5Abg8bheojSSfCMiSZLUO2+j+cb9ce3t9+GWzJIWUFVdC+zXpd31EiU5EkiS\nJKkXkqwADgM+2dF8MG7JLEmSBoRFIEmSpN74IPDHtDvuJHkCcIdbMkuSpEHhdDBJkqQ5SvJyYGtV\nXZ1k9Xhze+nklszSIjKbbZklaRBYBJIkSZq7FwGHJzkM2Al4LPAhYIlbMkuL12y2ZZakQeB0MEmS\npDmqqhOramVV7Q28BvhaVf0+bsksSZIGyJyLQG6FKkmSNCm3ZJYkSQOjFyOBxrdCHTe+FerTgTtp\ntkKVJEmL0B4rlpGkJ5c9ViyONZOr6tKqOry9flNV7V9V+1TVv6+qe/sdnyRJGl1zGqXTsRXqnwDH\ntc0HA0e219cBJwMfn8t5JEnSYLp10xb2eNuLe9LXllO/3pN+JEmS1N1cRwK5FaokSZIkSdIQ2OYi\nUOdWqDy4/emstkKVJEmSJEnSwpjLdLCeboU6cXtFSYNpbGyMsbGxfochSZIkSZqlbS4CVdWJwIkA\nSQ4E/qiqfj/JOTRboZ7DNFuhdhaBJA2HiQXbtWvX9i8Yjbw9lq/g1s2betLX7suWs2XTxp70JUlS\nv7Trtp4F7A78K/CJqjotyVKaz2irgJuBV1fVXX0LVFJfzMf27ccDZyd5N3AVboUqSZont27exPI1\nx01/4AxsOv8DPelHkqQ+uw84rqquTvIY4LtJLgKOAS6uqlOSvBM4geazm6QR0pMiUFVdClzaXr8J\n2L8X/UqSJEmSZq6qbgVuba//IskPaZbpWAMc2B62DhjDIpA0cua6O5gkSZIkaQAl2QvYF7gM2K2q\ntsIDhaIn9S8ySf1iEUiSJEmSFpl2KtjngbdV1S9w12ZJzM+aQBoAK5btzqYtW3vS1/I9dmPj5lt7\n0pckSZJmZ9mKlWzZtKFn/e2xfE82b1zfs/40eJLsQFMA+nRVjW/UszXJblW1NcnuwG2TPd5dnKXh\nMpsdnC0CLVKbtmzlrc/pTV+nfb83xSRJkiTN3pZNG3jun17as/6+d+KB0x+kYfcp4LqqOrWj7QLg\naOB9uIuztKjMZgdni0CSJEmStEgkeRHwe8C1Sa6imQZ2Ik3x59wkxwLrgSP6F6WkfrEIJGmoJVkB\nnAXsDvwr8ImqOi3JUuAcYBVwM/Dqqrqrb4FKkvrGafIaJVX1TWD7Se4+ZCFjkTR4LAJJGnb3AcdV\n1dXtAojfTXIRcAxwcVWdkuSdwAm4DaokjSSnyUuS1HB3MElDrapuraqr2+u/AH4IrADWAOvaw9YB\nr+xPhJIkSZI0GCwCSVo0kuwF7AtcBuxWVVuhKRQBT+pfZJIkSZLUfxaBJC0K7VSwzwNva0cEVZ9D\nkiRJkqSB4ppAkoZekh1oCkCfrqrx7U63JtmtqrYm2R24bbLHd26DOnF7RUmDaWxsjLGxsX6HIUmS\nNFQsAklaDD4FXFdVp3a0XQAcTbMd6lHA+V0eBzy0CCRpOEws2K5du7Z/wbTcrVCSJA06p4NJGmpJ\nXgT8HnBwkquSXJnkZTTFn5cmuZ5mO9T39jNOSSNhfLfCZwG/DrwpyTNodia8uKqeDnyNZrdCSZKk\nBedIIElDraq+CWw/yd2HLGQskkZbuwj9re31XyTp3K3wwPawdcAYTWFIkiRpQTkSSJIkqcfcrVCS\nJA2ibS4CJVmR5GtJrktybZK3tu1Lk1yU5PokX02ypHfhSpIkDTZ3K5QkSYNqLtPBxue9X92+2flu\nkouAY2jmvZ+S5J00894d8ixJkha9uexW6E6F0vBxp0JJw2abi0DOe5ckaW5WrtqLDetv6Vl/e65c\nxfpbbu5Zf9om27xboTsVSsNnEHcqlKSp9GRh6KnmvSdx3rskSV1sWH8Lf3Vd73YK/3fPcgZ2P3Xs\nVnhtkqtopoGdSFP8OTfJscB64Ij+RSlpsUtyBvAKYGtVPbdtWwqcA6wCbgZeXVW9+w9I0tCYcxFo\n4rz3JDOe9+6wZ/WL375vO4c9S1J37lYoaUCcCXwYOKuj7XhcskMScywCzWXeOzjsWf3jt+/bzmHP\nkiRJg6uqvpFk1YRml+yQBMx9i/ip5r3DFPPeJUmSJEkLYtfOJTsAl+yQRtQ2jwRy3rskSZIkLT4u\n2yENl9ks2TGX3cGc9y5JkiRJg2/GS3aAy3ZIw2Y2S3bMdTqYJEmSJGmwpL2Mc8kOSYBFIEmSJEla\nNJJ8FvgWsE+S9UmOAd4LvDTJ9TSzNt7bzxgl9c+ct4iXJEmSJA2GqnrtJHe5ZIckRwJJkiRJkiSN\nAotAkiRJkiRJI8AikCRJkiRJ0giwCCRJkiRJkjQCLAJJkiRJkiSNAItAkiRJkiRJI8AikCRJkiRJ\n0giwCCRJkiRJkjQCLAJJkiRJkiSNAItAkiRJkiRJI8AikCRJ0hDba9UykvTksteqZf1+OuqTlav2\n6tnraOWqvfr9dCRJk9hhvjpO8jLgQzSFpjOq6n3zdS5Jmoy5SNIgmM9cdMv6Lfzi6gN70tdj9r20\nJ/1o+GxYfwt/dd1dPenr3z1rSU/6Ue/5vkjSvIwESrId8OfAbwHPBo5M8oz5ONdkxsbG5v0c4+8C\nNwAAIABJREFUf3ftHfPa/2Xrfz6v/W/8xbx2D8z/7+EXP75qXvv//hVfn9f+r9t09bz2DwvztzCo\nBiEXwfz/DsxF07vnpxvmtX9z0fTu2XjnvJ9jUA1KLvq7b8/v72DYcxHMfz4yF01vvvOR74v6n4vm\n+3cw7P0vxDnsv//n6Of7ovmaDvYC4EdVdUtV3QucDayZp3N1tRAvjK9/f35/cZfP9wevu+e1e2Ah\nikDz+0bh+1d8Y177/+Hma+a1fxjtNzsMQC6C+f8dmIumN/8fvMxF0/mXjb0ZYTCkBiIXff0785sr\nhj0XwfznI3PR9OY7H/m+qP+5aNgLBIuhAGH//T9HP98XzVcRaDnQ+b/cxrZNi8Qey1fMaE742rVr\npz1mj+Ur+v10tHiZiyQNAnORpEFgLpI0b2sCpUtbzdO51Ae3bt7E8jXHTXvcz/7hWzzuGS+c8phN\n53+gV2FJE5mLJA0Cc5GkQWAukkSqev93n+QA4OSqell7+3igOhceS2LCkRaJqur2pqLvzEXSaDEX\nSRoEw5yL2nbzkbQITJaL5qsItD1wPfASYAtwBXBkVf2w5yeTpEmYiyQNAnORpEFgLpIE8zQdrKr+\nNcmbgYt4cPtBk4ukBWUukjQIzEWSBoG5SBLM00ggSZIkSZIkDZb52h1swSV5V5LvJ7kmyZVJfi3J\nK9rrV7f3/cEM+9otyeeS/CjJt5N8JcnTkpya5Nok30tyeZJV7fFfSfK4yeLo0v+/tvdd1f67MslO\nSf6y7fvaJH+X5NHt8d9o/81kMczg5/GCJKcneUZ7/7FtH9e0//52235Jkv1m+bO/P8m6jtvbJ/lJ\nkgva27sm+XL7e/hBkq/Mou8PJHlrx+2/TnJ6x+0/S/L2mf5cZnjO8d/P99vf0duTzHlud0e/1yY5\nJ8mj2vZpXzOz7P/qJN9p533P6nWjuRumXNQeN6/5yFxkLjIX9Ye5aNqfh7lo5uc0F2mbmYum/XmY\ni2b3nIYuHw1kLqqqob8ABwDfBHZobz8eWAlsAvZo2x4BPG2G/X0L+IOO2/8G+K/AuR1ty4AlM4hj\n9y79/6xL2/HAn3XcfhrwiAnHvGa6GGYSB81WkDcCj2lvPxpY1V6/BNhvlj//nwPfBR7Z3n4ZcCVw\nQXv7Y8BbOo5/ziz6/l3g7PZ6gO8A35zwu/pvM/m5zOKcP+u4/kTgb2gW0Zvr67Sz378E/vNMXzPb\n0P9vAmOzed14mftl2HLRxNdNR1tP8pG5yFxkLurPxVxkLjIXmYsG4WIuMhf1+m9tGPPRIOaixTIS\naA/gp1V1H0BV3U7zot8euKNtu7eqfjRdR0kOAv6lqj4x3lZV1wJ30yygNt62uaruah9zU5LHd4uj\nqm7tdppJnsOmjv5/VFX3tv3/vOOYrjF06ethcXRUkHcFfgb8sr3/l1V1S8fjX91WIv8hyYu6/Zy6\n+D/Ay9vrRwKfmxDPxo64vz/DPqH5wxuP4dnA94GfJ1mSZEfgmcA/AQ/8nKf4ucxaVf0U+I/Am3vR\nX4evA09l5q+Zmeh8XS0Bbm+vz/R1o7kbtlwE85uPzEXmInNRf5iLHt6PuagHzEWaJXPRw/sxF/XI\nEOWjgctFi6UIdBGwsv2D+EiS36iqO4AvA7ck+WyS185wqNhzaCqmE50LHN4O5fqzJPt23FeTxTHJ\nOXbKg8MMv9C2fQo4Psk3k7w7yVO79D9VDJ2mi+Ma4DbgpiSfSvKKCfdvX1X7A28HTp7kHJ0KOBs4\nMskjgecCl3fc/xHgU0n+NsmJSfaYQZ9Nx1VbgHuTrABeSFNVvhz4deBX2+fyWeC3Z/Bz2SZVdRPN\niL0nzbGr0HS0A3AocC0zf83MxPjr6ofA6cC72/aZvm40d8OWi2B+85G5qIfMRZoFc9FDmYt6yFyk\nWTAXPZS5qMeGJB8NXC5aFEWgqrob2I+mEvgT4Owkr6+qPwAOpnlB/hHNH/C2nmMTsA9wAnA/cHGa\nijS0L5rJ4ujS3S+rar+qel5V/U772GuAJwP/k2ao2RVJnj6LGKb7eRxFm6Sq6v6qehnwOzTbRH4g\nyX/v6OKv2n+/C6ya4c/n+8BeNBXm/01HxbOqLmqf2yeAZwBXJnnCTPptjVeaXwj8PXBZx+1vVdVm\nZvBzmaNe/K3slORKmu04b6HZkWGmr5mZGH9dPZMmeX0aZv660dwNYS6CecxH5iJzEeaivjAXmYsw\nF4G5qO/MReYiFuZvbdDz0eDlolqAOWcLfaH5wzl/QtsT6DLHs8tjDwYuncFxfwSc2l6/CXj8TOKo\nCfMCp+j/w8Dbpzq+M4YZ/DwuAL5Gl7mkwPOBa9rrD8w3bX9mP55B/z9r//1vNH8gzwYOpJ1v2uX4\nLwOvmsXv843AqTRzTQMsBS4GvgC8fFt/LtM9n47bewM/6cHrcia/966vmW2M+1bgib3++XiZ1e9k\noHNRt9fNJMf0JB+Zi2b9+jEXeenJxVzUNQ5z0czPZy7y0pOLuahrHOai2b2Ghi4fDWIuWhQjgZLs\nM2FY3r7A1iQHdrQ9D7h5ur6q6mvAjkne0NH/v0nyG+ND5JJsRzOc7iH9TRJH5zzOBw7t8hxemGSX\n9vqOwLM6+h8fnva8LjE8rP9J4ri54/49kjyv4/7nTRJn11inOOZTwP+oqh9MiOegJDu11x8LPAVY\nP4N+x30TeAVwezXuAHahGW749zP9uczCA8+5HVr4UZpkP1fdfu8zfc3Mqv80OwxsB/zjPPx8NIkh\nzEUwj/nIXGQuMhf1h7nIXGQuemj/5qL+MBeZi+bhb20Y89HA5aIdFuIkC+AxwIeTLAHuo1lV/W3A\n6Uk+RrMo1d3A0TPs71XAqUlOaB97M/DXNEPydmyPuYJmHiU8OBe0Wxz/sUv/1aXtKcBH00yJ3Q74\n31X1xQnH7wp8YkIMf96lr8ni+Hx7/yOAP2tfdP9MUxn+w0li6xZr1+dTzZC2bn+Ezwf+PMm97XM7\nvaq6zemdzLU0Fe+/nND26Kq6Pc1WfTP5uczUo9IMB9wRuBc4q6o+OIf+xnX7Wc70NTMT43GPJ5rX\nV1UlmenrRnM3bLmo8zGdepWPzEXmIjAX9YO56KHMReYiMBf1g7noocxFc/9bG8Z8NHC5KO3QI0mS\nJEmSJC1ii2I6mCRJkiRJkqZmEUiSJEmSJGkEWASSJEmSJEkaARaBJEmSJEmSRoBFIEmSJEmSpBFg\nEUiSJEmSJGkEWAQaUUn+bZJvJrkzyU+TfD3J85McleTrXY6/KcnBE9pWJ7k/yX+Z0L6qbf/yhPZP\nJ/nv7fUDk2zouO8RSf6qjeMxSU5K8ulJYr85yS+T/CzJz9t/T5vLz0PS/JtL3mmPua/9e78zyVVJ\nXt5x7Hje2a69/b/a26+Y0OeH2vbXT9LvleP9TsxTE/o5M8n/mHDuSXOeJEmSNAgsAo2gJI8Fvgyc\nCiwFlgNrgXvaQ2qGXb0e+EfgqEnuPyDJr0/x+Grj2RH4IvA44KVV9Ytp4ijg5VX1uKp6bPvvW2cY\ns6Q+6FHe+Vb7974L8FHg7CSP67i/Jly/no78lGR74HeBG6fo91PAuUl2mUVc46bLeZIkSVJfWQQa\nTfsAVVXnVuOeqrq4qr4/0w6S7ETzYepNwNOS7NflsFOAP5lBP1+heS2+vKr+eaYhzDRWSQNhznln\ngk8DOwNPm+KYrwAvSrKkvf0y4Brg1ike8ylgJ2DvbYhp2pwnSZIk9ZNFoNF0A/Cv7XSJl3V84z0b\nvwv8HDgPuIhmVFCnAj4C7DNxGlmHRwH/B/glsKaq7pnkOEnDrxd5B3hgRM+xwL8At0xx6D8BFwCv\naW+/HjiLSYrISXYA/oAmt/1olmHNJOdJkiRJfWURaARV1c+BfwvcD5wO/CTJl5Ls2h7y60lu77jc\nAew5oZvXA2dXVQGfBY5sP5h1+meab8X//0lCeSxwALCuqu6d5dP40nhs7b9vmOXjJS2gHuWdX09y\nO01x5xTg96vqp9Oc+tPAUe20sd8AvtTlmPF+NwP/HnhlG+9sTZfzJEmSpL6yCDSiqur6qjq2qlYC\nz6ZZn+ND7d1/X1WP77gsBToXcd4TOIim+APNN+07AS/n4T4B7DZxcdbWT2i+oT8ryW/O8imsGY+t\n/feMWT5e0gKbS97pPAbYhSbv/MYMzvlN4EnAfwW+MsmIw/Fz71pVL6yqS7bxKcLUOU+SJEnqK4tA\noqpuAP4XzYeymXgdzXSKLyfZAvxf4JE8fEoYVXUfzeKv757k3F+imX5xXpLVswjbNYGkIbYNeafz\nsb+kWY/sdUl+ZQYP+UvgOGDdbM81W9PlPEmSJKmfLAKNoCRPT3JckuXt7T2BI4HLZtjF64CTgX2B\nX2kvvwu8IsnS8dN0HP+XNEWiQ7t1VlVnA28Bzk/ywo67tk/yyI7LjjOMT9KA6UHeeYiqup1m1M1J\nnaeZ5PDTaHYe/MY2nCoT8tAjJzuu4/qUOU+SJEnqF4tAo+nnwP7A5Ul+DnwL+B7wR1M8Znw79/2B\nVcBfVNVtHZcv0yykemTn8QBVdT/NB7WlTLLdclWd1Z7/K0l+tW1+Dc2i0b+kWQOkc1vnLyf5Wcfl\nCzN/+pL6YJvzzhROBQ5N8pypjq+qOyZM8ZrNtu/LeGge+mWSbjuHzSrnSZIkSf2QZl3fKQ5IzgBe\nAWytque2bacAvw3cQzMV6Jiq+ll73wk0u7bcB7ytqi6av/AljZJu+ajjvv9Cs1jwE9tRIiQ5jWY0\nxt3A0VV19QKHLEmSJEkDYyYjgc4EfmtC20XAs6tqX5rRHycAJHkW8GrgmTQfvP4iiWu3SOqVbvmI\nJCuAQ+jYLjzJocBTquppwB8CH1uoICVJkiRpEE1bBGrXULhjQtvF7XB3aNZzWNFeP5xm2/D7qupm\nmgLRC3oXrqRR1i0ftT4I/PGEtjXAWe3jLgeWJNltfiOUJEmSpMHVizWBjgUubK8v56Fb+m5q2yRp\nXiT5bWBDVV074S7zkSRJkiR12GEuD07yLuDeqvrceFOXw1wUU9K8SLIT8C7gpd3u7tJmPpIkSZI0\nsra5CJTkKOAw4OCO5o3Anh23VwCbJ3m8H8akRaKq+rX211OAvYBr2vXHVgBXJnkBM8xH5iJp8ehj\nLpIkSRoKM50OFjq+VU/yMuAdwOFVdU/HcRcAr0myY5InA08Frpis06qat8tJJ500r/0vxDmGvf/F\n8ByGvf+FOEcfPJCPqur7VbV7Ve1dVU+mKfw8r6puo8lHrwdIcgBwZ1Vt7dbhsP8O7L//57D//p9D\nkiRJ05u2CJTks8C3gH2SrE9yDPBh4DHA3yS5MslfAFTVdcC5wHU06wS9sXxnJqlHJslHnYoHC0QX\nAjcluRH4OPDGBQ1WkiRJkgbMtNPBquq1XZrPnOL49wDvmUtQktTNJPmo8/69J9x+8/xGJEmSJEnD\noxe7gw2k1atXD+w5Vq1YRpJpL2vXrp3RcatWLFvQ+AfpHPY/GOfQ1Ib9dTTs/S/EOex/MM4hSZKk\nqaVfs7WSjOxMsSTc+I7n96y/p57yXddDUN8koYZ4MdZRzkXSYjLsuUiSJGkhLNqRQJIkSZIkSXqQ\nRSBJkiRJkqQRYBFIkiRJkiRpBFgEkiRJkiRJGgEWgSRJkiRJkkaARSBJkiRJkqQRYBFIkiRJkiRp\nBFgEkiRJkiRJGgEWgSRJkiRJkkaARSBJkiRJkqQRYBFIkiRJkiRpBFgEkiRJkiRJGgEWgSRJkiRJ\nkkaARSBJQyHJGUm2JvleR9spSX6Y5OokX0jyuI77Tkjyo/b+3+xP1JIkSZI0OCwCSRoWZwK/NaHt\nIuDZVbUv8CPgBIAkzwJeDTwTOBT4iyRZwFiHwqoVy0jSs8uqFcv6/ZQkSZIkTWGHfgcgSTNRVd9I\nsmpC28UdNy8Dfqe9fjhwdlXdB9yc5EfAC4DLFyTYIbF+0xZufMfze9bfU0/5bs/6kiRJktR7044E\nmmQKxtIkFyW5PslXkyzpuO+0dgrG1Un2na/AJWmCY4EL2+vLgQ0d921q2yRJkiRpZM1kJNCZwIeB\nszrajgcurqpTkryTZgrG8UkOBZ5SVU9Lsj/wMeCAXgctSZ2SvAu4t6o+N97U5bCa7PEnn3zyA9dX\nr17N6tWrexmepHkwNjbG2NhYv8OQJEkaKtMWgbpNwQDWAAe219cBl9AUhtbQFouq6vIkS5LsVlVb\nexizJD0gyVHAYcDBHc0bgT07bq8ANk/WR2cRSNJwmFiwXbt2bf+CkSRJGhLbujD0ruOFnaq6Fdi1\nbXcKhqT5FDpG+SR5GfAO4PCquqfjuAuA1yTZMcmTgacCVyxopD2w18reLty810oXbpYkSZJGWa8X\nhp7VFAxJmqkknwVWA09Ish44CTgR2BH4m3bzr8uq6o1VdV2Sc4HrgHuBN1bV0OWiWzZs4e4vHdSz\n/nZ+5SU960uSJEnS8NnWItDW8WleSXYHbmvbt3kKhutwSMOhX+twVNVruzSfOcXx7wHeM38RSZIk\nSdJwmWkR6CFTMGimWhwNvK/99/yO9jcB5yQ5ALhzqvWAXIdDGj6uwyFJkiRJw2naItAkUzDeC5yX\n5FhgPXAEQFVdmOSwJDcCdwPHzFfgkiRJkiRJmrmZ7A7WbQoGwCGTHP/mOUUkSZIkSZKkntvW3cEk\nSZIkSZI0RCwCSZIkSZIkjQCLQJIkSZIkSSPAIpAkSZIkSdIIsAgkSZIkSZI0AiwCSZIkSZIkjQCL\nQJIkSZIkSSPAIpAkSZIkSdIIsAgkSZIkSZI0AiwCSZIkSZIkjQCLQJIkSZIkSSNgKItAe61aRpKe\nXPZatezh/a/sYf8rH96/pG2T5IwkW5N8r6NtaZKLklyf5KtJlnTcd1qSHyW5Osm+/YlakiRJkgbD\nDv0OYFvcsn4Lv7j6wJ709Zh9L314/xu2cPeXDupJ/zu/8pKe9CMJgDOBDwNndbQdD1xcVackeSdw\nAnB8kkOBp1TV05LsD3wMOGDBI5YkSZKkATGUI4Ekjaaq+gZwx4TmNcC69vq69vZ4+1nt4y4HliTZ\nbSHilCRJkqRBZBFI0rDbtaq2AlTVrcCubftyYEPHcZvaNkmSJEkaSRaBJC1W6dJWCx6FJEmSJA2I\noVwTSJI6bE2yW1VtTbI7cFvbvhHYs+O4FcDmbh2cfPLJD1xfvXo1q1evnp9IJfXM2NgYY2Nj/Q5D\nkiRpqFgEkjRswkNH+VwAHA28r/33/I72NwHnJDkAuHN82thEnUUgScNhYsF27dq1/QtGkiRpSFgE\nkjQ0knwWWA08Icl64CTgvcB5SY4F1gNHAFTVhUkOS3IjcDdwTH+iliRJkqTBMKciUJK3A28A7geu\npfmQtQw4G1gKXAm8rqrum2OckkRVvXaSuw6Z5Pg3z2M4kiRJkjRUtnlh6CTLgLcA+1XVc2kKSkfS\nTMl4f1U9HbiTpkgkSZIkSZKkPprr7mDbAzsn2QHYiWbR1YOAL7T3rwNeNcdzSJIkSZIkaY62uQhU\nVZuB99OswbEJuItm+tedVXV/e9hGmulhkiRJkiRJ6qNtXhMoyS7AGmAVTQHoPODQLofWZH24LbM0\nfNyWWZIkSZKG01wWhj4E+HFV3Q6Q5IvAC4FdkmzXjgZaQTNFrCu3ZZaGj9syS5IkSdJwmsuaQOuB\nA5I8KkmAlwA/AC6h3aIZOAo4f24hSpIkSZIkaa7msibQFcDngauAa4AApwPHA8cluQF4PHBGD+KU\nJEmSJEnSHMxlOhhVtRaYOBfkJmD/ufQrSZIkSZKk3prrFvGSJEmSJOn/tXf3wZLV9Z3H358BiZiw\nI6DCzFyGWZOID2iExJDoGlowiUEjIVmSIpqAWjGbTRYKrNTCbO3WvUlVKuz6hA/lFkasSSSKEd1B\n8+AUkiZEg4gD4wwgusXDPI+yPCi4a0C++0efO7TDvTM9t7unb99+v6pOzelzTn/Pt08fftzz7d/5\nHWkMWASSJEmSJEmaABaBJEmSJEmSJoBFIEmSJEmSpAlgEUiSJEmSJGkCWASSJEmSJEmaABaBJI29\nJBcn2ZLka0muTnJEkjVJbk5yd5KPJzl81HlKkiRJ0ihZBJI01pKsBP4TcGpVvQw4HDgPuBx4V1Wd\nBDwMvG10WUqSJEnS6FkE0qK0cmo1SQYyrZxaPeqPo+E7DPjRprfPkcBO4DXAtc36dcA5I8pNkiRJ\nkhYFb4/QorRrxzZe9mc3DiTW19aePpA4WpyqameSdwFbge8BG4CNwMNV9WSz2XZg5YhSlCRJkqRF\nwZ5AksZakmcDZwMn0in0/CjwK3NsWocyL0mSJElabOwJJGncvRa4p6oeBEjyGeCVwLOTLGt6A03R\nuUVsTtPT03vnW60WrVZrmPlKGoB2u0273R51GpIkSWPFIpCkcbcV+LkkzwS+D5wJfAU4FjgXuAY4\nH1g/X4DuIpCk8bBvwXZmZmZ0yUiSJI0JbweTNNaq6hbgU8BtwCYgwJXApcAlSb4BHAN8ZGRJSpIk\nSdIiYE8gSWOvqmaAfbsB3AucNoJ0JEmSJGlRsieQJEmSJEnSBLAIJEmSJEmSNAEsAkmSJEmSJE2A\nvopASZYn+ZskdyW5I8lpSY5OsiHJ3Uk+n2T5oJKVJEmSJEnSwvTbE+gK4O+q6kXATwFfp/NEnuur\n6iTgBuCyPvchSZIkSZKkPi24CJTkKODVVfVRgKp6oqoeAc4G1jWbrQN+re8sJUmSJEmS1Jd+egI9\nH3ggyUeTbExyZZJnAcdV1R6AqtoNPHcQiUqSJEmSJGnh+ikCHQ6cCnywqk4FHqNzK1gNIjFJkiRJ\nkiQNzuF9vHc7sK2qbm1eX0unCLQnyXFVtSfJ8cC35gswPT29d77VatFqtfpIR9Kh0G63abfbo05D\nkiRJknSQFlwEaoo825K8oKq+AZwJ3NFMFwCXA+cD6+eL0V0EkjQe9i3YzszMjC4ZSQd0wtRqtu/Y\nNpBYU6tOYNv2rQOJJUmSpEOvn55AABcCVyd5BnAP8BbgMOCTSd4KbAXO7XMfkiRpgbbv2MbVf/CF\ngcR604fOHEgcSZIkjUZfRaCq2gS8Yo5Vr+0nriRJkiRJkgarn4GhJUmSJEmSNCYsAkmSJEmSJE0A\ni0CSJEmSJEkTwCKQpLGXZHmSv0lyV5I7kpyW5OgkG5LcneTzSZaPOk9JkiRJGiWLQJKWgiuAv6uq\nFwE/BXwduBS4vqpOAm4ALhthfhqSFaumSDKQacWqqafFXzm1emDxk7ByavUIjpIkSZLU0e8j4iVp\npJIcBby6qi4AqKongEeSnA2c3my2DmjTKQxpCdm9cwerzr5kILF2rH/305bt2rGNl/3ZjQOJD/C1\ntacfeCNJkiRpSOwJJGncPR94IMlHk2xMcmWSZwHHVdUegKraDTx3pFlKkiRJ0ojZE0jSuDscOBX4\nw6q6Ncl76PT4qV4DTE9P751vtVq0Wq0Bpyhp0NrtNu12e9RpSJIkjRWLQJLG3XZgW1Xd2ry+lk4R\naE+S46pqT5LjgW/NF6C7CCRpPOxbsJ2ZmRldMpIkSWPC28EkjbXmlq9tSV7QLDoTuAO4DrigWXY+\nsP7QZydJkiRJi4c9gSQtBRcCVyd5BnAP8BbgMOCTSd4KbAXOHWF+kiRJkjRyFoEkjb2q2gS8Yo5V\nrz3UuUiSJEnSYuXtYJIkSZIkSRPAIpAkSZIkSdIEsAgkSZIkSZI0ASwCSZIkSZIkTQCLQJIkSZIk\nSRPAIpAkSZIkSdIE6LsIlGRZko1Jrmter0lyc5K7k3w8iY+hlyRJkiRJGrFB9AS6CLiz6/XlwLuq\n6iTgYeBtA9iHJEmSJEmS+tBXESjJFHAW8Bddi88Arm3m1wHn9LMPSZIkSZIk9a/fnkDvAf4YKIAk\nxwIPVdWTzfrtwMo+9yFJkiRJkqQ+LbgIlOT1wJ6quh3I7OKu+Vm10H1IkiRJkiRpMPoZtPlVwBuT\nnAUcCRwFvBdYnmRZ0xtoCtg5X4Dp6em9861Wi1ar1Uc60uJywtRqtu/YNpBYU6tOYNv2rQOJ1a92\nu0273R51GpIkSZKkg7TgIlBVrQXWAiQ5HXhHVb05yTXAucA1wPnA+vlidBeBpKVm+45tXP0HXxhI\nrDd96MyBxBmEfQu2MzMzo0tGkiRJktSzQTwdbF+XApck+QZwDPCRIexDkiRJkiRJB6Gf28H2qqob\ngRub+XuB0wYRV5J6lWQZcCuwvaremGQN8AngaGAj8DtV9cToMpQkSZKk0RpGTyBJGoWLgDu7Xl8O\nvKuqTgIeBt42kqwkSZIkaZGwCCRp7CWZAs4C/qJr8RnAtc38OuCcQ52XJEmSJC0mFoEkLQXvAf4Y\nKIAkxwIPNU8pBNgOrBxRbpIkSZK0KFgEkjTWkrwe2FNVtwOZXdw1P6sOaWKSJEmStMgMZGBoSRqh\nVwFvTHIWcCRwFPBeYHmSZU1voClg53wBpqen9863Wi1ardYw85U0AO12m3a7Peo0JEmSxopFIElj\nrarWAmsBkpwOvKOq3pzkGuBc4BrgfGD9fDG6i0CSxsO+BduZmZnRJSNJkjQmvB1M0lJ1KXBJkm8A\nxwAfGXE+kiRJkjRS9gSStGRU1Y3Ajc38vcBpo81IkiRJkhYPewJJkiRJkiRNAItAkiRJkiRJE8Ai\nkCRJkiRJ0gSwCCRJkiRJkjQBLAJJkiRJkiRNAItAkiRJkiRJE8AikCRJkiRJ0gSwCCRJkiRJkjQB\nLAJJkiRJkiRNAItAkiRJkiRJE8AikCRJkiRJ0gRYcBEoyVSSG5LcmWRzkgub5Ucn2ZDk7iSfT7J8\ncOlKkiRJkiRpIfrpCfQEcElVvRj4eeAPk7wQuBS4vqpOAm4ALus/TUmSJEmSJPVjwUWgqtpdVbc3\n848CdwFTwNnAumazdcCv9ZukJEmSJEmS+jOQMYGSrAFeDtwMHFdVe6BTKAKeO4h9SJIkSZIkaeEO\n7zdAkh8DPgVcVFWPJqle3zs9Pb13vtVq0Wq1+k1H0pC1223a7fao09gryRTwl8DxwA8kJMn3AAAK\n80lEQVSAD1fV+5IcDVwDnAjcB/xmVT0yskQlSZIkacT6KgIlOZxOAeivqmp9s3hPkuOqak+S44Fv\nzff+7iKQpPGwb8F2ZmZmdMl0zI5PdntTlP5qkg3AW+iMT/bfk/xnOuOTXTrKRCVJkiRplPq9Hewq\n4M6quqJr2XXABc38+cD6fd+k8bdi1RRJBjKtWDU16o+jMeb4ZJIkSZLUmwX3BEryKuBNwOYktwEF\nrAUuBz6Z5K3AVuDcQSSqxWX3zh2sOvuSgcTasf7dA4kj7W98siSOTyZJkiRpoi24CFRVXwQOm2f1\naxcaV5IWwvHJpMmy2MYnkyRJGgd9DwwtjaPVJ65h29b7BxbvhNUnsvX++wYWTwfH8cmkybMIxyeT\nJEla9CwCaSJt23o/n75zcA+K+vUXLx9YLC3I/sYnuxzHJ5MkSZKkvgeGlqSR6hqf7IwktyXZmOR1\ndIo/v5jkbjq3qP75KPOcVFMrjx/YIPJTK48f9ceRJEmSxpo9gSSNNccnW9x27NrDhScPJtb7tuwZ\nTCBJkiRpQtkTSJIkSZIkaQJYBJIkSZIkSZoAFoEkSZIkSZImgEUgSZIkSZKkCWARSJIkSZIkaQJY\nBJIkSQu2YmolSQYyrZhaOeqPI0mStKT5iHhJkrRgu3fsYsVFrx5IrF1X3DSQOJIkSZqbPYEkSZIk\nSZImgEUgSZIkSZKkCWARaImaWnn8wMZomFp5/Kg/jiRJkiRJ6pNjAi1RO3bt4cKTBxPrfVv2DCaQ\nJEmSJEkaGXsCSZIkSZIkTQCLQJIkSZIkSRPAIpAkSSOy+sQ1Axu/LQmrT1wz6o8kSZKkRWxoYwIl\neR3wXjqFpo9U1eXD2pckzce2SIvZtq338+k7HxlYvF9/8fKBxZIkSdLSM5SeQEmWAR8Afhl4CXBe\nkhcOY1/z+aevPDz8fWx+aKjxb9763aHG3/7oUMMD8P0Htg01/qP33DbU+FtuuWmo8e/ccftQ4wO0\n2+2h72OxWgxtEQz/O7AtOjDbov07FG3R97cP///LkiRJ2r9h3Q72s8A3q+r+qnoc+ARw9pD2Naeb\nbh3+H5s3bRnuPr487Auvx4YaHjgUF17DvXDZcss/DzX+XTs3DTU+THYRiEXQFsHwvwPbogOzLdq/\nQ9EW/ev2wfV4kiRJ0sIMqwi0Cuj+i3t7s0ySDiXbIkmSJElqDKsIlDmW1ZD2JUnzsS2SJEmSpEaq\nBn89lOTngOmqel3z+lKgugdkTeKFmLREVNVcxZaRsy2SJstibYskSZIWi2EVgQ4D7gbOBHYBtwDn\nVdVdA9+ZJM3DtkiSJEmSnjKUR8RX1Q+S/BGwgacey+xFl6RDyrZIkiRJkp4ylJ5AkiRJkiRJWlyG\nNTD0IZfkvyTZkmRTko1JXpHkDc387c263+sx1nFJPp7km0m+kuRzSX4yyRVJNif5WpIvJzmx2f5z\nSf7NfHnMEf8Hzbrbmn9XJzkyycea2JuT/FOSZzXb/3Pzb+bLoYfj8bNJrkzywmb9W5sYm5p/f7VZ\n/o9JTj3IY/9kknVdrw9L8u0k1zWvn5fks833cEeSzx1E7HcnubDr9T8kubLr9TuTXNzrcelxn7Pf\nz5bmO7o4Sd/jTHTF3ZzkmiTPbJYf8Jw5yPi3J7m1GQ/noM4b9W+c2qJmu6G2R7ZFtkW2RZIkSYvH\nUG4HO9SaPzDPAl5eVU8kOQb4MeB/AT9TVbuSPANY02PIzwAfrarzmvgvBX4LWFFVL22WrQQeA6iq\nN+wnjyPmiP9YVf3QxU06A9burqo3N69/Eni8if/vms3mzaGH43FEVb29Wb8KWNusf7S5uHtuj8dm\nLo8BJyf5kar6PvCL/PBjuf8E2FBV72/2f/JBxP4S8O+B9zUXP88Bjupa/0rg7+nhuByEvd9PkucA\nHweWA9N9xNw37seA/5DkZno7Zw42/i8Bfw606PG8Uf/GsC2CIbZHtkW2RbZFkiRJi8tS6Qm0Anig\nqp4AqKoHge8ChwEPNcser6pvHihQktcA/1pVH55dVlWb6fyhuqtr2c6qeqR5z73NH8xPy6Oqds+1\nm3k+w46u+N+sqseb+N/t2mbOHOaI9bQ8un5Zfx7wHeB7zfrvVdX9Xe//zeYX2q8nedVcx2kOfw+8\nvpk/j87FSnc+27vy3tJjTIAvArM5vATYAnw3yfIkRwAvAv4vsPc47+e4HLSqegB4O/BHg4jX5Sbg\nJ+j9nOlF93m1HHiwme/1vFH/xq0tguG2R7ZFtkW2RZIkSYvIUikCbQBWNxcKH0zyC1X1EPBZ4P4k\nf53kt3vsRn8y8NU5ln8SeGPTxf2dSV7etW52YKWn5THPPo7MU7dfXNssuwq4NMkXk/xpkp+YI/7+\ncuh2oDw2Ad8C7k1yVZI37LP+sKo6DbiY3n5xLuATwHlJfgR4GfDlrvUfBK5K8oUka5Os6CFmJ3DV\nLuDxJFN0fmn/UhP754GfaT7LXwO/2sNxWZCqupfOnQz99FCA5sIoyeHArwCb6f2c6cXseXUXcCXw\np83yXs8b9W/c2iIYbntkWzRAtkWSJEnq15IoAlXVY8CpdH4l/TbwiSS/W1W/B5xB5w/1d9C5sFno\nPnYALwAuA54Erm9+qYfmD+r58pgj3Peq6tSqOqWqfqN57ybg3wL/AzgGuCXJSQeRw4GOx/k0F29V\n9WRVvQ74DTqPz353kv/WFeLTzb9fBXoar6H5RX0NnV/e/5auX4KrakPz2T4MvBDYmOTYXuI2Zn+B\nfyXwL8DNXa+/VFU76eG49GkQ/60cmWQjnceU30/nSVW9njO9mD2vXkTnwu6voPfzRv0bw7YIhtge\n2RbZFmFbJEmStLhU1ZKb6FxQrN9n2bHAd3p47xnAjT1s9w7gimb+XuCYXvJolveSx/uBi/e3fXcO\nPRyP64AbgFPnWP/TwKZm/h9nt2mO2T09xP9O8+9/pXPx8BLgdOC6ebb/LHDOQXyf/xG4AriVzgXd\n0cD1wLXA6xd6XA70ebpePx/49gDOy16+9znPmQXmvRt4zqCPj9NBfSeLui2a67yZZ5uBtEe2RQd9\n/tgWOTk5OTk5OTk5DXRaEj2Bkrxgn9sVXg7sSXJ617JTgPsOFKuqbgCOSPK2rvgvTfILs7cOJFlG\n5zaDH4o3Tx7d41vs3XSOz/DKJM9u5o8AXtwVf7br/ilz5PC0+PPkcV/X+hVJTulaf8o8ec6Z6362\nuQr4k6q6Y598XpPkyGb+KODHga09xJ31ReANwIPV8RDwbDq3YfxLr8flIOz9zM1tFx+icxHcr7m+\n917PmYOKn86Tl5YB/2cIx0fzGMO2CIbYHtkW2RbZFkmSJC0uS+LpYHSevvP+JMuBJ4D/DVwEXJnk\nf9IZrPMx4IIe450DXJHksua99wH/QOdWhdmnpdxCZ3wJeGqMjLnyePsc8WuOZT8OfCidoUKWAX9b\nVZ/ZZ/vnAR/eJ4cPzBFrvjw+1ax/BvDO5o/x/0fnF/Pfnye3uXKd8/NUp6v/XBcoPw18IMnjzWe7\nsqrmGutkPpvp9AT42D7LnlVVD6bzGONejkuvntncKnEEnSci/WVVvaePeLPmOpa9njO9mM179gLs\nd6uqkvR63qh/49YWdb+n26DaI9si2yKwLZIkSVo0UtXL39WSJEmSJEkaZ0vidjBJkiRJkiTtn0Ug\nSZIkSZKkCWARSJIkSZIkaQJYBJIkSZIkSZoAFoEkSZIkSZImgEUgSZIkSZKkCWARSJIkSZIkaQJY\nBJIkSZIkSZoA/x8o2BHPKjtUBwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1125169b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Facies per well\n",
"for w_idx, w in enumerate(np.unique(well)):\n",
" ax = plt.subplot(3, 4, w_idx+1)\n",
" hist = np.histogram(y[well == w], bins=np.arange(len(facies_names)+1)+.5)\n",
" plt.bar(np.arange(len(hist[0])), hist[0], color=facies_colors, align='center')\n",
" ax.set_xticks(np.arange(len(hist[0])))\n",
" ax.set_xticklabels(facies_names)\n",
" ax.set_title(w)"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABIUAAAJaCAYAAACx9PdtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xm4JGV9N/zvT0ExKgKiScAVl/gooqC4RBBcYjRRIW6v\nJAquiSZGIy5xF+MaJD6IqIkbGnfzGDWYmAUFBBVF2cUdFAQiIjsoKtzvH1XtNE2fc/rMnJk+M/X5\nXFddp7u2u7qn6ztVv9qqtRYAAAAAhuV6814AAAAAADY8RSEAAACAAVIUAgAAABggRSEAAACAAVIU\nAgAAABggRSEAAACAAVIUAgAAABggRaFNTFUdVVUXVtXmE/0Pq6q/W2Caa6rqsqq6dOzvC/thB1XV\nf06Mf3BV/dtEv9tV1dVVdegC8z95ot9rq+p9/evb9uNc2nfnVdW/VdVDJ6b5YVVdObGch/TD9quq\nX/f9Lq6qE6vqjxf5nvbol3fU5llV9fGquvdC08BQVNWfVtXx/Xp2TlX9e1X9fj/s1VX1wSnTXFNV\nO/Svr5M3Y+v59fr34+vzuf00vzUxzX36ti+qqguq6riqeko/bI+qOnvKchxZVU8bG+eaqvp/E+Ps\n1Pf/wpTpz6iq06b0P6qqfl5V24/1e0hVnbnI9zieredX1YerastFlnU8k86uqgMW+o4n+o/n33g+\n/s5CywYbuxly6pf9enBhVR1bVfebmP5mVfXOfpvj8qo6eZQvY+PsVlVf6rcrLqiqY6rqXv2wzavq\nH/p19dKq+kFV/cMiy3ud9XehPB0bvnlVHVBV3+0/5xlV9Z6qus3EeO+vql+Nr/P9ZxtlwVVj38el\nVfX5sWGX15ptsFG/W43n00Rbk9tso2kev9DnANZOVZ1ZVQ8ee//EPtN2r+tuV72/f//IiXkc3Pff\nt39/2tj6O+p+UVW/7odPbo+M1vH7VtXrquqIifnfuaouqaq7LfI5ntIvw+NW8vth5SgKbUKq6rZJ\ndktyTZJHL2PSlmSn1tqWrbWb9n8P6oe9MskOVbVf38b9kzw5yV9MzGPfJBcmeWJNFKR621XVE5dY\nhpu11rZMco8kRyT51CjAxsb544nlfO7Y8C/3/bZK8s4kH6uxHbApzunH3zLJ/ZJ8O8kxVfWgRaaB\nTVpV7Z/kLUlel+SWSW6T5B1J9hobrU2ZdFq/xcb5zfqc5J5Jdk7y0rHluH+Szyc5MskdWmvbJnl2\nkocvs82fJvn9qtp6rN9+Sb4zOWJVPTDJLdJl3r2mLPvl6TJxoc806TfZmmSHJNskOWCR8cczabck\nT6+q8SxfrK1R/o3n4/8uMj5stGbMqY/169K2SY5K8i9j02+eLl9uneS+SW6W5MVJ3lRVf9OPc9Mk\nhyd5a5Ktk2yf5DVJrupn87IkuyS5d9/Og5KcuMhiL7T+LrZefzLJI5M8sV/GeyT5RpKHjH2W30ry\nmCQXJ/mz38y0tWePsiDJG0bfR989ZGzY3bJmG2yUHT9eZJkyNv543vzLEtMA66DfF3tbkke01o7p\ne09uV30n3TbOaJrrJ3lcku//ZqTWdhzLgi2T/G6SM5KMH8w7Z8o2xVf7cX67qp4xNu67khzUWvvm\nIou/b5KfjS8bq4ui0KZl3yRfSfL+JE9ZxnTVd9fRWvt5kmcmOagvOr03yd+21s6b0vYrkvwqyaOm\nzOrAJH83qmYvshxprZ3fWjsk3c7TgdPGmcEHk9w4yZ1mGbm1dm5r7dVJ3pPk72dsAzYpfRH1NUn+\nsrX2mdbaz1trV7fW/r219rdLTb42TSbdOp/kv9IVh0YOTHJYa+2g1tqF/XgnttYWKy5P88skn06y\nT5L0GfSEJB+eMu5+/bj/kekbLock2WfyaP8ifpOtrbXLk/xbkrvOMmFr7UdJvjwx/tp8x7BJWW5O\ntdauSbe+b1dVN+9775vkVkke11o7q5/+v5I8N8lrq+omSe7cTd4+0TpXtdaOaK2NziS8d5JPtdZ+\n0rdzVmvtQ4st+jI/50PTFX8e3Vo7obV2TWvtstbaO1trh42N+rgkF6XbWXvKctpYl+Vbi/GBtVRV\nf57kzUke1hdnFvLZJA+oqpv17x+e5OQkix0kem+Ss1prU68oGdda+2WSpyd5Y1X9blX9RZKt0hWe\nF1r22yZ5YJI/T/KHVXWLpdphw1MU2rTsm+RDST6SFVzpWmtHpzta9fUk57XW3jM+vKp2T3cE7WPp\njsTtOzmLJP+a5JIsb4PlX5Pcsqp+bznL21fFn5ZuZ/BHy5m2b3OXqrrRMqeDTcH9k9wwXWFkg6mq\nWyV5RJLv9e9v1C/LJ1dg9i3JP2dNLv1hktOSXKuw3bf5uHQ7jx9JV/zZbGJe5yR5d7od0mXpz1Ta\nO13hfpbx75TkAbOODwOyrJyqqhukK/L+LF3xJEkemuRzrbVfTIz+ySRb9G18N8nV/SUZD6+qrSbG\nPS7JC6rq2VW149p9lEU9JMnXWmvnLjHevuky6+NJ7lJV91xi/JWiKAQbxl+m2+54cGttsbMRk+Tn\n6Q5AjQ6g7ZtuG2jq+lpVz02Xd/vMujCtta+lOwHhg0lem+SprbWrF5lk3yRfb619Kt1VGX+2yLjM\niaLQJqKqdkt3+vQnWmsnpDtN8E+XMYsT+mtUL+r//sHE8GPSXfrwkSnT7pvkP1prl/TDH1FV244v\nXrods1cledUCl5dNM9oQ2mas36cnlvPpY8PuX1UXpgvEA5M8qbV2wYxtjbdZ6areMDQ3T3JBf2R9\nMf9fv/6Nuosy26Vckz5dVZcmOSvJT7Lm0qqt0/3/NHlG4qTtpyzHAyZHaq0dl2Trqrpz1mwgTXps\nkl+kO2Pps0mun2TafcnelOSRVfV/lvpwvRP65To/3aUq75rh81ySbsPpuCRfmrGd+49/D1X1vRmn\ng43NsnIqyZXpjmw/bmyabTMlX/odmwuSbNtauyxrLsl/V5Lzq+ozYwfc3pAuD/40yfFV9eOJS96n\nOWEirxY7A/Pm05ZxXHX3FnpQko/0Z1wekQ1zeUYl+enE9tiyDuABM3tokuPGzlJcygeT7NefVfnA\nLFBAr+4+a69Ll40XTQzefmKb4sKJA+avTHLHJP88Q6HqyVlzdvZH4hKyVUlRaNOxb5L/HlupP5rl\nrXQ7t9a2aa1t3f/9n9GAqtomyUFJDk53WvX4jVK3SPL49MWifufr7EwpSLXWPpdu52/yfkQLGd3Q\n9Wdj/faaWM73jg37Smttm3QFnX9LF4TLtX26nduL12Ja2Nj9LMm2S1zmmSQf79e/Ubd1rn0U6tdJ\nJou/mye5ZmJHbq/+evY9ktwl3Y5a0h3Nvybdde6LOWfKcixURPlgkuck2TPJp6YM3zddUb31p0d/\nKlMytC80H5ru6Ngsdu6Xa4sk/5jk2P7MhcU+z83S5dgvMr2ANc1Xxr+H1tpMl87CRmhZOZXunkOn\npbvca+SCTMmX/kzjbfvhaa19p7X2tNbabZLsmGS7dNtC6bPina213bPm8on3LVEc2Xkirxa7XP1n\n05ZxwpOTnN5aO7V//9Ekf9p/jvWpJbn5xPbYde7TBqyIZyW5c1W9d8kxk7TWvpTu/oivSPLZ1tpV\nk+P0B+8/keQlrbXjp8zmnIltim1ad0uRURu/SHJmktMXW5aqekCS26c7kzHpMmqnqtppls/ChqMo\ntAnoCzNPSLJHdU/ROC/J3yS5R1XdfdbZLDLsrenOBHpBkqOTjD9d40+SbJnkHWNtb5frXkI28sok\nL0/yWwsMH/eYJD9prX13xuVMkrTWrkzyV0meXFX3mKGdyTZPGA8+GJCvpCtE7L2O8zkrye0m+u2Q\nrmA8bnS/nWOSfCB9tvTr31fSnb2zUj6U7hTsf5+8ZKS6J4o9OMmTxnLssUn+qC+KTzoo3dH5yZtR\nTzP6jFenu2fZ7dPtXC6qP0vhI+luMgussayc6u9J9qwkB1TVb/e9j0h3VvPkpeKP6+d93JT5fDfd\nJRPXWX/7+w29I11Be7H7hi3nkqsjktynqrZbZJwnp7sx/ii3/iFdUesRy2hnbbl8DDaM89NdTrp7\nVb1jxmk+lGT/dNtW11JVle7MnWP63FqfRgfXTuoz6rh0ReWlzqpkA1MU2jT8Sboj8/8n3ZMp7tG/\nPjbXXuk2q6objnVLXsZVVX+ULohe0Pd6bpK9qmqP/v1T0t2g7O5jbe+WZOea8mjC/v5Ep+a6R+B/\nc0PWqrplVT0nXQHpJUst4zT9RuC7k7x6kdF+s0FTVdtV1avT3YvopQtPApuu1tql6daZt1fVXlV1\no6rarKoeUVVvWsasPpnkj6vqoVV1vX6n5uXpjhAt5OAkfzB29OjFSZ5SVS8YFWaq6h5Vtdg8FtRa\n+2G6swdfMWXwvume2HHnrMmxO6e7h9B1rrPvL5U9qF/GmfRnNTwt3aUsZyw02tj4N+nbnnyaxw0n\ncvx6k9PCpmxtcqo/i+U/s+ZyrQ8m+XGSf6nusc6bVdUfpjsI9urW2mVV9XtVtX9fNE5V3TrdOvmV\n/v3zqnt08xZVdf3qngx0kyz+BLLlfM7PJ/mfdE9i3aVv4yZV9RfVPd75/umK7btmTW7dLV3OPmWZ\nzS2UH5tP5M1mY+PLHNhAWvc00Qenu2fsW8YGLbQeHpLkD1prx04Z9pp0N9p/5iJNrvP6XVU3THc1\nyTPTPUhklFPPTXcQTh1iFfGPsWnYN8n7WmvntO7JXef315YfmuTPxla6v023QzLqPj82j5Or6tKq\nuqz/+5Z+p+SdSf66tXZxkrTWfprkhUne3e/oPSjJ/x1vt7+n0eeypvAzea+RV6S7Z8jkYxQvqqrL\nkpyS7m75j2utTVa4D++Xb9QtdiPat6Y7ErjQUfnfHX3mJF9LtzG1R78hBoPUWvu/6Y4uvSLd0amz\n0p1hs9RNXX+zPrfWTk+38/SmdJdAfCndjtTfTRu/n+aCdEe0Xtm//0q6DaCHJPlBVV2Q7vKrf591\nOaZ8ti+36Y9p3zfJ21trP53I0H/Mwjl2SLpi/FKPpD+5uvsmXZjuqP7eozydMu0oky5Nd1r2Vrn2\nDRlbustgrkx377Qrs2bn735juTjK8VnOZIKNzlrm1EFJnllV2/aXiD403dmLX033IIyDkry0tTba\n4bos3ePqv9pvJ3w53fbJC/vhP093Zs55SX6a5NlJHtMXoKcu9vI/aR6X7mmIH093Wfup6c5QPCJd\nbn26tXb6RG69NV1Rfjn3Rlxo2d6Ra283vm9s/Ism8uZvlvvhgCWNb1v9ON020WOr6vWTw681UWsX\ntdaOnDafdAfpdkjykynbDbfqx/ndKcP+ZKFlW8De6XLjgxMZ9d50NYiHLzE9G1C1tjb/R02ZUfe4\nuc+21u4+0f81SY5urX2hqp6X5J8mT90HWCmyCFgNZBGwGsgiYCkrXRQ6vLW24I2jqurMJPfqL+0B\nWHGyCFgNZBGwGsgiYCmbLT3K8uZXVe9K8vvprtXeO93lR4ene6rTdkmOrKoLWmsPWeG2AUZkEbAa\nyCJgNZBFwIJW+p5Cd0ryttbajumuff7Nk2Naa29Lcm6SPYUNsJ7JImA1kEXAaiCLgAWtdFHojNba\nqf3rE9I9knjy+jRPKwDWN1kErAayCFgNZBGwoJW+fOyqsddXJ7nRrBNW1crc3AiYu9bavDcsZBEg\ni4BVYWPOokQewaZioSxa6aLQtEbG+12aZMt0j+a9jpW46XVV5fKT9ljWNK9/5w/z8mffbubxb3LP\no6cua1Xlik8/aPZ2P3pmXr7P7Wce/8Z7H7lgu99/8exPHn7rsefmebttN/P4dzzwGwu2+9yFHva+\ngON+ktzvt2cf/5DTVuZ3ccABB+SAAw5Y5/lUVXZ6w9Ezj/+/RxyW33noU2ce/5SX7bHgd/2vp18y\n83w+dugb88TnvHTm8ZPkMXe92Yqtg6vA3LMoWX4eyaLFLZRFo7aXk0crlUVVle332n/m+Vz67S9n\ny7v8/szjn/OZtyzY7saQRcny80gWrSGLFjevLEpWbttIFi1tXttGsuja5rGfNrQsSua3nza0fbRk\n49lP2xBZtNKXj7WJ122i37uTfK6qPr/C7QKMk0XAaiCLgNVAFgELWrEzhVprP0qy09j7t0wZ59Ak\nh65UmwCTZBGwGsgiYDWQRcBSVvpMoY3S7vfeaj7t7jifdu97m5vOpd0kudWN59PunnvuOZd2b7LD\nPefS7o732W0u7bJuZNGGM68suuG2t55Lu/PKokQebYxk0YYjizYcWbTxGVoWJfPLo6HtoyX208Yp\nCiV54K7zWfEfePet59Lu/ea58XOT+bQ7v6LQznNpd8f77D6Xdlk3smjDmVcWzW9HbD5ZlMijjZEs\n2nBk0YYjizY+Q8uiZH55NLR9tMR+2jhFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAA\nAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBF\nIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAA\nGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQC\nAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIAB\nUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAA\nAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBF\nIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAA\nGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQC\nAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIAB\nUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAA\nAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBF\nIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAA\nGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQC\nAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIAB\nUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAA\nAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBF\nIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAA\nGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQC\nAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIAB\nUhQCAAAAGCBFIQAAAIABUhQCAAAAGCBFIQAAAIABWpGiUFU9qqpevBLzAlhbsghYDWQRsBrIImAW\nK1IUaq0d3lo7cCXmNQ9fPP7i+bR76kVzafe4sy6bS7tJ8uPL59PuUUcdNZd2Lz/jxLm0e9rXjplL\nu/Mmi9ayXVm0wVx1wdlzaXdeWZQMM49k0Vq2K4s2GFk0DLJoLdudUxYl88ujoe2jJfbTxi1ZFKqq\n21bVt6rqsKr6TlV9qKoeUlXH9u93rar9qupt/fiPr6pTq+rEqjqq73fXqvpqVZ1QVSdV1R3W8+da\nlmO+Pp/AOea0+bT71Xlu/Fwxn3bnVxQ6aS7tnva1Y+fS7voki9Zju7Jog5nfjth8sijZ9PJIFq3H\ndmXRBiOLNn6yaD22O6csSuaXR0PbR0vsp43bbMbx7pDksa2106vq60n2aa3tVlWPTvKyJJ9K0vpx\nX5nkYa2186pqy77fs5Ic3Fr7aFVtluT6K/gZgOGQRcBqIIuA1UAWAets1svHzmytnd6//maSz/ev\nT01yu4lxj03ygap6RtYUnb6S5OVV9aIkt2utXbX2iwwMmCwCVgNZBKwGsghYd621Rbskt01yytj7\nw5I8ZmzYqUn2TXLI2Di7JnlNkjOTbN33u32Sv07y3SR7Tmmn6XS6TaNbKlfWposs0ul0y+xkkU6n\nWw3dxpxF8kin23S6hfJk1svHasbxUlU7tNaOT3J8VT08ya2raqvW2plJ3lZVt0myU5Kjxqdrrc3c\nBjBYsghYDWQRsBqs9yxK5BFs6mYtCrUFXk97/+aqulP/+ojW2ilV9ZKqelKSXyU5L8nrl7+oALII\nWBVkEbAayCJgnVV/SiAAAAAAAzLrjaY3CVV1y6r6cFV9v6qOr6ovVdVeVbVHVV1cVd+oqtOr6s3z\nXtZxVXV1/6jI0/rHSD6/qhY9jbN/TOWp/et7VNUjZmhn/Hv4ZlW9aqz/4RPL87Oq+lFVfbyqjq6q\nXarqson57VdVh/SvX11V+/ev319VP66qzfv3N6+qM8eW+8qxf4vjqmrftfy+Tu2Xb4uJ/if2f1+8\nnPluCBPL/pnR0yHGvpfx5X9SP+zMqtpmYj77VdX5Y7+bZ4wN27uqTu6/35Oraq+xYfftv/MTx38D\nrCxZtGQ7smjOZNEwyKIl25FFcyaLhkEWLdmOLFoFNuU8GlRRKMmnkxzVWrtja23XJE9Mcqt+2Bdb\na/dKskuSR1bV/Ucr0PjKO66qDquqM/p/mG/3K9J2iy3AtB/GDK5ore2S5IAkWyR5S5J/nJjvS6vq\ne1X1rap6WN97dBrYzkn+aMa2Rt/DrkmeVFU7T8wrSa5I8m9Jnp/udNPtpoyzmJbk10meNtFv5Put\ntXu11u6a7t/o+VW134zzTvrvq7V29375njXRf+f+74GzzrCqrhn/j6iqXjAWyAf0w3cYG/78vt8u\ni8zzh1V19JRBm/XLflGSvxrr//2J5f9Q33+h7/1j/e/mQUneUFW3qKp7JDkwyaP673evJAdV1Y79\nNB9I8ozW2s5JdkzyiYW/FdaBLFqaLJpCFrHClpVFSbJK8mi0Du2Y5JAkr01y9eTvfDyPkuweWbRi\nWZRssDy6It3+Soss2pTJoqXJogXYNlp3gykKVdWDk1zVWnv3qF9r7ezW2tvHx2ut/SLJSUm2z+LX\n6Y68sP/Hv0s/3ZFVtdi9mtbler1Tkzw63eMjn5AkVXW9qnpPklekC4IPJHnHaIJ+WV6T5AnVVSMf\nX1W7VleB/0ZVHVtrri9es5CtXZnkG0nuMJrVAst0TJIbLTHONAenC5JFf4OttR8m2T/J85Yx73HH\nJLlj/3pdbpJ3VZLHLPAfRUtySrpwHHlsukeDLqYluWlVbZ8kVXWXieFfSfc7HFlo+Rf9XK21nyb5\nQbonUbwgyRtaa2f1w36Y5I1JXtSPfoskP+mHtdbat5f4DCyTLJJFkUWyaBVYyyxKVl8efTnJo9Lt\nyIyy6MCqOjnJK5MclOQRSV7XD5dFK5NFyQbIo6wpCCWyaJMki2RRNoIs2tS3jQZTFEpytyQnLDVS\nVW2d7gf6xeU20Fo7ON1N2hY7DfA3P4yq2r+6089OqarnjfV/ZV/R/mJVfSTJDfr5f6e19r10P/yq\nqlskeXq6SvrfJblPuh/52Unu2U/z6ySvSvLxvmr5L0m+lWT3vtr86nQ/tmstX1XdPMl9s2aF2b0P\nrBOS3Dhd6F2v/6yX9+PcaDROVZ2YLugWclaSY5M8eZFxRk5I8nszjDf5GTbrl++UieUbndb3+GXM\n89dJ3pUu/Kb5TLpqbqrq9kkuSfLTGeb7iawJqX3SVc1TVddP8pB01f6RO0ws/wNmWfC+Mn77JN9P\ntx58Y2KUr/f9k+4/gu9U1Ser6s+r6oaztMGyyCJZJItk0Wqw3rMoWT95lG4d2r+f/3daa0f289gq\nXRZdnOSj6Xa+npFu4/7MJDeSRSuWRcmGyaPNk3ykfy2LNk2ySBZtDFm0SW8bzfr0sU1OVR2aZLck\nv0xXfXtgv5LcKcnBrbXza/FLQhdyYpK7JDl8sZGqO11tv3SnAF4/yVer6qh0/yZ/ku6RkDfIwiE5\nWriHpdsBu0u6H+2W6X7kv7NI81sl+efqqs8t1/4d7F5V30hyTZI3tta+VVW3THfK4qP7Zf913/6B\n/efcqp/2yv40uNFn3C/JvRZZjjemW0n/Y+zzLPZZZ3WjPhiTrgr9vmnLt0wtyduTnFpVfz9l+KVJ\nzq6qu6ULnY8leeoM8/x/Sd6f5B/Shfhm6X6D5yU5Pcn/jI3//WUu/xOrard0O+5/3lq7uLof9eRR\nkN/0a629tqo+lO53tU/fPWgZbbJMskgWLZMsYr2YJYvWYfYrnUeXLDKbhyW5e5Kbpztr8er+M/wk\n3Yb3NLJo7WyIPLpBkqek2/G8MLJokyeLZNFasG20joZ0ptA3M/bjb609J12F7xbpvugvjl2f98yq\n2mkt21lq5Rj9Q++W5FOttV+01q5I8skkD+z7f6a19svW2uWZHlpbJLmmP92s0q1UL+tPj7xDknNz\n3R/UuNcm+ULrrod8VD+/kS+27lrRXcdP45xwZbrK6Atba89boq0FtdZ+kO5UzicsMY9d0lXOZ3Vl\nX3HfpbX2vL4Sv876f48PZPppki1dwDwxXdh8KrMF5YVJLqqq/y9duPw8yfeS3Kaf/jnrsMgf67+D\n+7fWRpUjKn1CAAAgAElEQVTs09L9BzfuXn3b3Qdp7czW2j8leWiSe/RHZlg5smgNWbQWZBErZENl\nUbLyeXStdak/0trSHZWvJH+d5OPp8ugOrbUjlmhfFq2lDZBHv0p3z5VvRRZtqmTRGrJoLdk2WjeD\nKQq11r6Q5IZV9RdjvW+cNT/06sf7YZI3JHnJWja1c2ZbOSZ/iKMqYE0Ztmak7jKNO6f7YSfJf6W7\npvS2/fA7pfuh/mRsssvSHbUf2TLJOf3rpaqksyz7Uv0X84YkL1xoPlV1uyRvTnfztlmt5PJNemu6\n00FvPGXYZ9OdavmjPphm9Yl01e2PZM3v8BfpQu2F/SmKyeLLP+tn+4ckL6mq0e/ldklemu4651TV\n+M3u7pzuP7uLZ5w3M5BFsmiR/sshi1gnGzCLkpXPo/F18xZJ3pnkx32v/0ryl+mK0reuqjtV1Y3S\nnbX4q34cWbR4/+Van3k02mlskUWbJFkkixbpv1y2jdbSYIpCvb2T7FlVP6iq45IcluRvM3ZaVu+f\n0t0Zfvz7WfJHXFXPTbei/+ciyzAa/4tJ9q6qLarqxulORTwm3TWcj6yqG1bVTZI8Msnm/bWJpyX5\n73RVy/f083lPki8leVU//P3pdsxOGmvzyCR3rTXXaB6Y5E39KYhr8xtomX5zt+Xc2b570drp6S5L\nGZ92h+ofd5huh/OtrbV/XubyTbNFXftazzcsY56jELgoXTg8/TqNdgHx4nQhOvM801Wr/z7dv+3o\nP5y01k5K9+84upZ1h4nlH69On1xVZ1fVWVV1UBb4DlprJ6f7zR/ef7+fSXc0YfTUhidXd530Cemq\n7X/aWluXm+4xnSySRbJIFq0Gy8qifkN16g7RhPWdR5sn2X8si/4zyY/6+bwn3VHV/dI9KfGf0mXR\n7dId5U1k0ci6ZFGyYfJoVBQqWbRJk0WyaLVn0aa9bdRa0y3QJbm0/3vbdNf7nZXuxqlnpbuJ6mHp\n7hZ+YpLv9P842y0xzzOSbNO//pt0T/E5Jclfj43zqiTfTnJ0kn9J8vS+/959+z9Pdy3j58ameWm6\nG1R9K8nD5v3dbWrd6LfQv75luhu3vbJ//+ok+0+Z5gtJdpnltzDW77ZJTpn359Wtrk4W6SZ/C/1r\nWaTb4J080k3+FvrX8ki3QTtZpJv8LfSvZdFadNV/QFaRqrpxa+2K/hTDLyZ5ZuuqkQAbjCwCVgt5\nBKwGsohN0WCfPrbKvauq7prkhkneL2iAOZFFwGohj4DVQBaxyXGm0HrSXw97g9HbdNcOPrm19s35\nLRXz4LfAPPn9MeK3wLz5DTLit8A8+f0x4rfQURQCAAAAGKChPX0MAAAAgCgKAQAAAL2qunVVXVpV\ntfTYbOwUhQauqs6sqgdP6b9fVR2z2PhVdVhV/d3YsLtV1blV9fz+/Q+r6so+UC7r/x6yyLLcsao+\nWlXnV9XFVfWdqnprVW23wPivrqoPTul/TVXtMNs3AKx2fZb8b/+kj1G/p1fVF/rX14xlzOjvC6vq\nd/phtxib7uVT+r2sqv6jf/3+qrqqn8clVXV8VT2wH3bXPpvuOLF8n6+q16/v7wGYv0Xy6Mix9y+q\nqu9W1RX9+G+sqhuMDb/W9tMC7ZxRVadN6X9UVf28qrYf6/eQqjpz3T8dMG8T+0/n9nnxWxt6OVpr\nZ7fWtmz9vWaq6siqetpC41fVbfvtq0vHtsdOHBv+8qr6Ub8d9ZGqusmG+BzMRlGIxcx8w6mqumeS\nLyR5bWvt/45N/8d9oNy0//vcBaa/Y5KvJvlxknu21rZK8oAkP0iy2zKX0Y2yYNPSklw/yd8sMs5O\nE1lzUGvtf5N8L8kDx8bbPcm3Jvo9MMnRY239fT+PmyX5xyT/WlXVWjs9yZuTvG80YVU9PcnvJnnN\nun1EYCOxUB6NdpzeluQZSZ6U5KZJHpHkwUk+MWsDfSH6Fkl2qKp7TWnn8iSvnNY+sNH7zf5Tknsm\n2TnJS1e6kfV0BlBLcrOx7bGd+7b2S/JnSe6fZLskv5Xk0PXQPmtJUYh1VlW7JvmfJC9prb1zcvCM\ns3l1kmNbay9qrZ2bJK21C1prh7TWZt6QWmabwMbjzUleUFVbLjB8ofX+mPQFoKq6XrqNq7cm2WOs\n3/2TfHGB6T+SZJskv92/f1OSG1fVs6vqlv37p7bWfrm8jwNsxKbmUX+A69lJ/rS19rXW2jWttW8l\neWySh1fVnjPOf78kn07yH/3rSYck2cdZ0bDJqiRprZ2f5L/SFYe6AVU3qKqD+rNuzquqd1TVDceG\n71VVJ/ZnO3+vqh7W9z+yql5XVcdW1RXpis7XumJk/CqMsTN/rldVr0t3UO3Qpa78yPTtsUcmeW9r\n7dzW2pVJ/j7JE6pqi7X9glhZikKsq/sm+c8kz2utHbYO83lokk+uzCIBm6CvJzkqyYuWOd0Xs+as\noJ3TnSX0+bF+uyTZLMnxkxNW1fXT7ZCdkeQnSdJauzrJ05O8LsmHkvxza+2ry1wmYOO2UB49JMnZ\nrbVvjPdsrf04yXFJ/mCpGfeXpT0uyYfTFaX3qarNJkY7J8m74wxF2KRV1a3SnW34vbHeBya5Y5Kd\n+r/bJ3lVP/59knwgyQv6s50fmOSHY9M+Kd2ZjDdN8qMFmm2Tr1trr0h3kO05i135MVrsBfqN979e\nkhsmudMi82EDUhRiXd0vycXpCkPTfLqqLqyqi/q/T19gvG2T/O/oTVX9VT/NZVX1Tyu8zMDG6dVJ\nnlNVN58y7ISJrBntfB2dZMequlm6o1zHtNZ+kOTmfb/dkhzXWvv12LxeVFUXprtE4y1JXjm6pj5J\nWmsnJXlvkrskeflKf0hgozAtj7ZNct4C45/XD1/KY5P8It3ZAZ9Nd6naH08Z701JHllV/2fmJQY2\nFp+uqkuTnJXuoNQBY8OekeT5rbVLWmtXpMuCffphT0t3Rs4XkqS1dl5r7btj076/tfbt/izG8e2e\nlVJJfjq2LbZ/3/9zSZ7Rn310syQv7vtv8HslMZ2iEAv5dZLNp/TfPMmvxt4fmu4I+xH9Sj5pr9ba\nNq21rfu/712gvZ+luy9HkqS19vbW2tZJDl5gOaYu49jRtF9dd3RgY9Za+2a6naRp19bvPJE1/9NP\n86N09yrbPd0Rs9EN9L8y1m/y0rE39/O4UZJ7Jzmoqv5wYpxvJvlha+0XK/HZgI3LAnl0Qca2ZSb8\nbj98Kfsm+UTr/DLJpzLlErLW2gXptsFeu5zlBjYKe/X3FNoj3QGobZOkuodk/FaSb/RFlwvTFVxG\nxelbp7sf60LOXn+LnKQ7s+jmY9tib+n7vy/JR9OdYXlquvvQJt32GauAohALOSvJbcZ79He+v2Wu\nfbrh1eluHHZWkv+uqptOzGfW+/t8Pslj1mIZbzfRb4d0xaJzljkvYONwQJJnpjtdetxiWTO6r9D9\nkny573ds3+8BWfh+QulvLv2lTD9SDwzbAbl2Hn0hyW2q6t7jI1XVrdPlzxGLzax/otiDkzypv1fI\neenOHPqjqtpmyiQHJXlQksmbUQMbt9E9hY5JdznYP/T9L0hyZZK79UWXbVprW/WXiiVd0ecOi8x3\n8ob0V+TaZ+v8zjKmXXTZrzVh5zWttdu31m6T7lL+c1pr9tdWCUUhkuQGVXXDse766Z4E9ouq+tu+\n343TnZ54fGvtrPGJ+3tsPD5dUP1HjT2mdRkOSLJ7f+O07ZKkqrZNsthp0f+Z5Peq6s+qarN+g+n1\nSf6ltXbNWiwDsMr1l359PMli17NPOibd0fdzW2uX9/2O7fvdLN1ZQ1NV1V3SXWJ2nUdDA8M2mUet\nte+le2Lhh6vqvv0NWu+W5P8l+e/W2pFjk282se21ebpM+k6SOye5R9/dOd2Brn0yobV2SbrC0Isn\nhwGbjIOT/EFV7dRfyv7uJAf3Zw2lqrYf3Uw63aXtT62qB1Vnu6q68yLzPinJE/v9qHunu5/ZuPEC\nz0/SHXxfzNQDdFW19ejG+FV113RFLvdEW0UUhUiSf09Xdf55//fV/SnLf5zuCNSPk3w/XfX4CWPT\njd9j41fpzvT5eZLDx+4mf3h/l/pRN/Vm0v2G1P3SnfZ4clVdkm5H7pxc97Gro2l+muSPkjwryflJ\nTklyUZK/XPY3AKxmk0en/i7dka3x/if3GXNZ//ctY8OOTvd452PG+p2UZIskX59yCdiLR/NKV3x+\nb2vtXSvySYCN3VJ59Jwk70l3I/rL0j1B7Au57s7W36bb5hp1n0/y5CRvb639tLV2/qhLV2gaXUI2\n2f4h6c6Q9kh62DRca13uLxX9QNbsD70k3X7ZcVV1cZL/Tlc8Tmvt+CRPTVdIuiTd5Vq3nTbf3ivT\n3az6wnT3SfvwIsvy1iSPr6qfVdXBsyz7mG3TnThwebr9zvcscksR5qDG7p25bjOqum2Sz7bW7j7R\n/zVJjm6tfaGqnpfkn9yDAVhfZBGwGsgiYDWQRcBSVroodHhrbadFxjkzyb1aaxeuSKMAE2QRsBrI\nImA1kEXAUjZbepTlza+q3pXk99NdcrR3kncmOTzdTfi2S3JkVV3QWnvICrcNMCKLgNVAFgGrgSwC\nFrTS9xS6U5K3tdZ2THJxuicmJElaa29Lcm6SPYUNsJ7JImA1kEXAaiCLgAWtdFHojNbaqf3rE9I9\nLnzy+rRZH1EOsLZkEbAayCJgNZBFwIJW+vKxq8ZeX51k5keTV5WnJsAmorU27w0LWQTIImBV2Jiz\nKJFHsKlYKItWuig0rZHxfpcm2TLdY++uYyVuel1VufykPZY1zevf+cO8/Nm3m3n8m9zz6KnLWlW5\n4tMPmr3dj56Zl+9z+5nHv/HeRy7Y7vdffK+Z5/PWY8/N83bbbubx73jgNxZs97k7zjybJMlxP0nu\n99uzj3/IadN/F1WV7ffaf+b5XPrtL2fLu/z+zOOf85m3LNjuTm84eub5/O8Rh+V3HvrUmcc/5WV7\nLNjuv55+yczz+dihb8wTn/PSmcdPksfc9WYrtg6uAnPPomT5eSSLFrdQFo3aXk4eyaLFrVQWJcvP\nI1m0hixa3LyyKFm5bSNZtLR5bRvJomubx37a0LIomd9+2kpl0XIdcMABOeCAA9Z5PsvNomTj2U/b\nEFm00pePtYnXbaLfu5N8rqo+v8LtAoyTRcBqIIuA1UAWAQtasTOFWms/SrLT2Pu3TBnn0CSHrlSb\nAJNkEbAayCJgNZBFwFJW+kyhjdLu995qPu3uOJ9273ubm86l3SS51Y3n0+4Nt731XNq9yQ73nEu7\nO95nt7m0y7qRRRuOLNpw5NHGRxZtOLJow5FFG5+hZVEyvzyaVxbtueee82k49tPGKQoleeCu81nx\nH3j3refS7v3mufFzk/m0O7+Nn53n0u6O99l9Lu2ybmTRhiOLNhx5tPGRRRuOLNpwZNHGZ2hZlMwv\nj+aVRfMtCtlPG1EUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIU\nAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACA\nAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEA\nAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABgg\nRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAA\nABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIU\nAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACA\nAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEA\nAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABgg\nRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAA\nABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIU\nAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACA\nAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEA\nAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABgg\nRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAA\nABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIU\nAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACA\nAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEA\nAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABgg\nRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAAABggRSEAAACAAVIUAgAA\nABggRSEAAACAAVIUAgAAABigFSkKVdWjqurFKzEvgLUli4DVQBYBq4EsAmaxIkWh1trhrbUDV2Je\n8/DF4y+eT7unXjSXdo8767K5tJskP758Pu1edcHZc2n38jNOnEu7p33tmLm0O2+yaC3blUUbzNCy\nKBlmHsmitWxXFm0wsmgYZNFatjunLErml0fzyqKjjjpqPg3Hftq4JYtCVXXbqvpWVR1WVd+pqg9V\n1UOq6tj+/a5VtV9Vva0f//FVdWpVnVhVR/X97lpVX62qE6rqpKq6w3r+XMtyzNfnEzjHnDafdr86\nz42fK+bT7vw2fk6aS7unfe3YubS7Psmi9diuLNpghpZFyaaXR7JoPbYrizYYWbTxk0Xrsd05ZVEy\nvzyaVxbNtyhkP21ksxnHu0OSx7bWTq+qryfZp7W2W1U9OsnLknwqSevHfWWSh7XWzquqLft+z0py\ncGvto1W1WZLrr+BnAIZDFgGrgSwCVgNZBKyzWS8fO7O1dnr/+ptJPt+/PjXJ7SbGPTbJB6rqGVlT\ndPpKkpdX1YuS3K61dtXaLzIwYLIIWA1kEbAayCJg3bXWFu2S3DbJKWPvD0vymLFhpybZN8khY+Ps\nmuQ1Sc5MsnXf7/ZJ/jrJd5PsOaWdptPpNo1uqVxZmy6ySKfTLbOTRTqdbjV0G3MWySOdbtPpFsqT\nWS8fqxnHS1Xt0Fo7PsnxVfXwJLeuqq1aa2cmeVtV3SbJTkmOGp+utTZzG8BgySJgNZBFwGqw3rMo\nkUewqZu1KNQWeD3t/Zur6k796yNaa6dU1Uuq6klJfpXkvCSvX/6iAsgiYFWQRcBqIIuAdVb9KYEA\nAAAADMisN5reJFTVLavqw1X1/ao6vqq+VFV7VdUeVXVxVX2jqk6vqjfPe1nHVdXV/aMiT+sfI/n8\nqlr0NM7+MZWn9q/vUVWPmKGd8e/hm1X1qrH+h08sz8+q6kdV9fGqOrqqdqmqyybmt19VHdK/fnVV\n7d+/fn9V/biqNu/f37yqzhxb7ivH/i2Oq6p91/L7OrVfvi0m+p/Y/33xcua7IUws+2dGT4cY+17G\nl/9J/bAzq2qbifnsV1Xnj/1unjE2bO+qOrn/fk+uqr3Ght23/85PHP8NsLJk0ZLtyKI5k0XDIIuW\nbEcWzZksGgZZtGQ7smgV2JTzaFBFoSSfTnJUa+2OrbVdkzwxya36YV9srd0ryS5JHllV9x+tQOMr\n77iqOqyqzuj/Yb7dr0jbLbYA034YM7iitbZLkgOSbJHkLUn+cWK+L62q71XVt6rqYX3v0WlgOyf5\noxnbGn0PuyZ5UlXtPDGvJLkiyb8leX660023mzLOYlqSXyd52kS/ke+31u7VWrtrun+j51fVfjPO\nO+m/r9ba3fvle9ZE/537vwfOOsOqumb8P6KqesFYIB/QD99hbPjz+367LDLPH1bV0VMGbdYv+0VJ\n/mqs//cnlv9Dff+FvveP9b+bByV5Q1XdoqrukeTAJI/qv9+9khxUVTv203wgyTNaazsn2THJJxb+\nVlgHsmhpsmgKWcQKW1YWJckqyaPROrRjkkOSvDbJ1ZO/8/E8SrJ7ZNGKZVGywfLoinT7Ky2yaFMm\ni5YmixZg22jdDaYoVFUPTnJVa+3do36ttbNba28fH6+19oskJyXZPotfpzvywv4f/y79dEdW1WL3\nalqX6/VOTfLodI+PfEKSVNX16v9v796jbq3qeoF/f4lcDkqYYQ1NQRBjKN5AvAWo2XHkEZUyDRoi\np7zUOakkkkctMbMw8TLwlsdLAuox1ExpO8rMvADeUu4IkigIpnlJkJuiyDx/zGe5F8v3st69X/ba\n7ufzGWONvdbzzGfOudY712+v+XtuVW9J8qfpgeDkJH892WDoy4uTPLF6NvIJVXVA9Qz8mVV1Rm08\nv3hjJ1u7PsmZSfaaVLVMn05PstMqZZZyQnogWXEMttYuS3J0kqPWUPe005PcbXi+ORfJuyHJby7z\nH0VLcl56cJx4fPqtQVfSkty2qu6UJFW1z8z6T6WPw4nl+r/i+2qtfSvJl9LvRPGcJMe11i4f1l2W\n5KVJ/ngovluSbwzrWmvtC6u8B9ZILBKLIhaJRVuBTYxFydYXjz6Z5DHpE5lJLDq+qs5N8sIkr0jy\nqCR/MawXi9YnFiVbIB5lY0IoEYu2SWKRWJSfgli0rf82Gk1SKMk9k5y1WqGqul36AD1trQ201k5I\nv0jbSocB/nhgVNXR1Q8/O6+qjppa/sIho31aVb0zyfZD/Re31r6YPvCrqnZL8pT0TPqfJ3lA+iC/\nIsl9h21uTHJskncNWcv3JLkoyUFDtvlF6YPtZv2rqtsneWA2fmEOGgLWWUl2Tg96PzO812uHMjtN\nylTV2emBbjmXJzkjyRErlJk4K8kvz1Fu9j1sN/TvvJn+TQ7re8Ia6rwxyZvSg99STk3P5qaq7prk\nu0m+NUe9787GIHV4etY8VXWrJI9Iz/ZP7DXT/1+Zp+NDZvyuSS5J/x6cOVPkc8PypP9HcHFVvbeq\nnl5VO8zTBmsiFolFYpFYtDW4xWNRcsvEo/Tv0NFD/Re31j461LFreiy6Ksnfpk++npr+4/7SJDuJ\nResWi5ItE49uneSdw3OxaNskFolFPw2xaJv+bTTv3ce2OVX1uiQHJvlBevbt4OFLsneSE1pr36yV\nTwldztlJ9kmyYaVC1Q9XOzL9EMBbJflMVX0s/W/yG+m3hNw+ywfJSecemT4B2yd90O6SPsh/cYXm\nd03yturZ55abj4ODqurMJDcleWlr7aKqukP6IYuPHfp+49D+8cP73HXY9vrhMLjJezwyyf4r9OOl\n6V/Sf5x6Pyu913ntNATGpGeh37pU/9aoJXl9kvOr6mVLrL86yRVVdc/0oHNKkt+do86/S3JSklem\nB/Ht0sfg15NcmORfpspfssb+H1ZVB6ZP3J/eWruq+qCe3Qvy42WttZdU1TvSx9Xhw+Pha2iTNRKL\nxKI1Eou4RcwTizaj+vWOR99doZpHJrlXktunH7X4o+E9fCP9h/dSxKJNsyXi0fZJ/mf6xPM7EYu2\neWKRWLQJ/DbaTGM6UujzmRr8rbVnpGf4dkv/oE+bOj/vaVV1701sZ7Uvx+QPfWCS97XWvt9auy7J\ne5McPCw/tbX2g9batVk6aO2Y5KbhcLNK/1K9YDg8cq8kX8tPDqhpL0nykdbPh3zMUN/Eaa2fK3rA\n9GGcM65Pz4we01o7apW2ltVa+1L6oZxPXKWO/dIz5/O6fsi479daO2rIxG+24e9xcpY+TLKlB5jD\n0oPN+zJfoPxOkiur6rfTg8v3knwxyV2G7Z+xGV0+ZfgMHtxam2SyL0j/D27a/kPb/Y20dmlr7Y1J\nfi3JfYY9M6wfsWgjsWgTiEWsky0Vi5L1j0c3+y4Ne1pb+l75SvLMJO9Kj0d7tdY+vEr7YtEm2gLx\n6Ifp11y5KGLRtkos2kgs2kR+G22e0SSFWmsfSbJDVf3+1OKds3Gg11DusiTHJXneJjZ1v8z35Zgd\niJMsYC2xbmOhfprG3dMHdpL8c/o5pbsP6/dOH6jfmNrsmvS99hO7JPmP4flqWdJ5+r7a8pUcl+SY\n5eqpqj2SvDz94m3zWs/+zXp1+uGgOy+x7gPph1p+ZQhM83p3enb7ndk4Dr+fHtSOGQ5RTFbu/7zv\n7ZVJnldVk/GyR5Lnp5/nnKqavtjd3dP/s7tqzrqZg1gkFq2wfC3EIjbLFoxFyfrHo+nv5m5J3pDk\nq8Oif07yv9OT0neuqr2raqf0oxZ/OJQRi1Zevla3ZDyaTBpbxKJtklgkFq2wfK38NtpEo0kKDQ5N\n8rCq+lJVfTrJiUn+T6YOyxq8Mf3K8NOfz6qDuKqelf5F/+AKfZiUPy3JoVW1Y1XtnH4o4unp53Ae\nUlU7VNVtkhyS5NbDuYkXJPlQetbyLUM9b0nyiSTHDutPSp+YnTPV5keT3KM2nqN5fJK/Gg5B3JQx\n0LL0xd3WcmX7/qS1C9NPS5neds8abneYPuF8dWvtbWvs31J2rJuf63ncGuqcBIEr04PDU36i0R4g\nngKIDe0AABgUSURBVJseROeuMz1b/bL0v+3kP5y01s5J/ztOzmXdc6b/09npc6vqiqq6vKpekWU+\ng9baueljfsPw+Z6avjdhcteGI6qfJ31Werb9d1prm3PRPZYmFolFYpFYtDVYUywafqguOSGacUvH\no1snOXoqFn0wyVeGet6Svlf1yPQ7Jb4xPRbtkb6XNxGLJjYnFiVbJh5NkkIlFm3TxCKxaGuPRdv2\nb6PWmscyjyRXD//unn6+3+XpF069PP0iqiemXy387CQXD3+cO65S55eT/Nzw/I/S7+JzXpJnTpU5\nNskXknw8yXuSPGVYfujQ/vfSz2X8p6ltnp9+gaqLkjxy0Z/dtvaYjIXh+R3SL9z2wuH1i5IcvcQ2\nH0my3zxjYWrZ7knOW/T79di6HmKRx+xYGJ6LRR5b/CEeecyOheG5eOSxRR9ikcfsWBiei0Wb8Kjh\nDbIVqaqdW2vXDYcYnpbkaa1nIwG2GLEI2FqIR8DWQCxiWzTau49t5d5UVfdIskOSkwQaYEHEImBr\nIR4BWwOxiG2OI4VuIcP5sNtPXqafO3hEa+3zi+sVi2AssEjGHxPGAotmDDJhLLBIxh8TxkInKQQA\nAAAwQmO7+xgAAAAAkRQCAAAAGCVJIZIkVXVgVX2iqq6qqm9X1elVtX9VHVlVpy9R/tKq+tWZZQ+r\nqpuq6piZ5bsPyzfMLH97VR07PH9oVV0xte7WVfX3Qz9uU1Uvqqq3L9P3y6rq+qq6uqquGf59zeZ8\nHsAtb3PizlDmxuH7flVVnV1Vj54qO4k7PzO8Pml4fchMnScMy5+8TL1nTeqdjVMz9ZxYVX8+0/ay\nMQ8AALYGkkKkqm6bZEOSVye5XZI7JXlxkhuGIvNeeOrJSf4ryZHLrH9QVT14he3b0J/tk7wvyS5J\n/ntr7dpV+tGSPLq1tktr7bbDv8+as8/AAqxT3Pnk8H3fNckbkpxSVbtMrW8zzy/OVHyqqlsl+a0k\nl6xQ71uTvLuqdl1DvyZWi3kAALBQkkIkyd2TtNbau1t3Q2vtw621C+atoKp2Sp9c/WGSvatqvyWK\nHZ/kL+eo5wPpY/PRrbXvz9uFefsKbBU2O+7MeHuSnZPsvUKZDyT5lar62eH1ryc5N8l/rrDNW5Ps\nlGTPTejTqjEPAAAWSVKIJPn3JD8aTq/49ak94mvxW0muSfKeJB9KP2poWkvy+iR3nz3tbMqOSf4p\nyfVJHtdau2GZcsBPv/WIO0l+fMTP7yX5QZKvrFD0e0n+Iclhw+snJ3lblkkqV9V2SZ6WHtu+uMZu\nzRPzAABgoSSFSGvtmiQHJrkpyZuSfKuq3l9VdxiKPLiqvjP1uDLJnWeqeXKSU1prLck7kxw+TNSm\nfT99r/lfLNOV2yZ5UJKTW2s/XOPbeP+kb8O/T1nj9sAWtE5x58FV9Z30ZM/xSZ7UWvv2Kk2/PcmR\nw2lmByd5/xJlJvV+LclvJzl06O9arRbzAABgoSSFSJK01i5urf1ea+0uSe6Zfn2PE4bVn2qt/dzU\n43ZJpi8KfeckD09PBiV9T/xOSR6dn/TmJL8we7HXwbfS9+C/raoeuca38LhJ34Z//2aN2wNb2ObE\nnekySXZNjzsHz9HmJ5LsluRPk3xgmSMSJ23fobX2kNbaRzfxLSYrxzwAAFgoSSF+Qmvt35OclD5J\nm8cR6adfbKiqryf5UpId8pOnkKW1dmP6xWRfskzb708/XeM9VfWwNXTbNYXgp9gmxJ3pba9Pv57Z\nEVV1nzk2eUeSo5OcvNa21mq1mAcAAIskKUSq6per6uiqutPw+s5JDk/y6TmrOCLJnyW5b5L7DI/f\nSnJIVd1u0sxU+XekJ40etVRlrbVTkjwzyalV9ZCpVbeqqh2mHtvP2T9gK7MOcedmWmvfST8q50XT\nzSxT/DXpdzY8YxOaqpk4tMNy5aaerxjzAABgUSSFSPpFVB+Y5DNVdU2STyY5L8lzVthmcvv4BybZ\nPclft9a+OfXYkH5h1sOnyydJa+2m9Inb7bLM7Z1ba28b2v9AVd1/WHxY+kWor0+/hsj0baQ3VNXV\nU4/3zv/2gQXY5LizglcneVRV7btS+dbalTOnhK3lNvN3zM3j0PVVtdSdydYU8wAAYBGqXxd4HSqq\n2j39+gz3mln+4iQfb619pKqOSvLGNdxmHGBNxCIAAID5rHdSaENr7d4rlLk0yf7DYf4A604sAgAA\nmM92611fVb0pyUOSfDXJoUnekGRD+l1l7pjko1X17dbaI9a5bYAJsQgAAGAV631Nob2TvLa1tm+S\nq5I8frKitfbaJF9L8jCTMOAWJhYBAACsYr2TQl9urZ0/PD8ryR75yYtqunU4cEsTiwAAAFax3qeP\n3TD1/EdJdpp3w6pyRxbYRrTWFp1wEYuArSEWAQBs1dY7KbTUj6/pZVcn2SXJkhd3XY+LXldVrj3n\noWva5i/fcFn+5H/tMXf529z340v2tapy3fsfPn+7f3tp/uTwu85dfudDP7psu5c8d/+563n1GV/L\nUQfece7ydzv+zGXbfda+S2ywgk9/I3nQL8xf/jUXLD0uqip3etzRc9dz9Rc+mV32ecjc5f/j1Fct\n2+69j/v43PX854dPzC/+2u/OXf68Fzx02Xb//sLvzl3PKa97aQ57xvPnLp8kv3mPn1237+BWYOGx\nKFl7PBKLVrZcLJq0vZZ4JBatbL1iUbL2eLSNxSIAgK3aep8+1maet5llb07yT1X1r+vcLsA0sQgA\nAGAV63akUGvtK0nuPfX6VUuUeV2S161XmwCzxCIAAID5rPeRQj+VDrr/rotpd9/FtPvAu9x2Ie0m\nyS/tvJh2d/j5Oy+k3dvsed+FtLvvAw5cSLtsHrFoyxGLthzxCABg6yUplOTgAxYzITr4XrdbSLsP\nWuRE7DaLaXdxE7H7LaTdfR9w0ELaZfOIRVuOWLTliEcAAFsvSSEAAACAEZIUAgAAABghSSEAAACA\nEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEA\nAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABgh\nSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAA\nABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIU\nAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACA\nEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEA\nAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABgh\nSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAA\nABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIU\nAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACA\nEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEA\nAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABgh\nSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAA\nABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIU\nAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACA\nEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEA\nAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABgh\nSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAA\nABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIU\nAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEZIUAgAAABghSSEAAACAEVqXpFBVPaaqnrsedQFs\nKrEIAABgfuuSFGqtbWitHb8edS3CaZ+9ajHtnn/lQtr99OXXLKTdJPnqtYtp94ZvX7GQdq/98tkL\nafeCfzt9Ie0umli0ie2KRVvM2GJRMt54BADw02DVpFBV7V5VF1XViVV1cVW9o6oeUVVnDK8PqKoj\nq+q1Q/knVNX5VXV2VX1sWHaPqvpMVZ1VVedU1V638Ptak9M/t5iJ2OkXLKbdzyxyInbdYtpd3ETs\nnIW0e8G/nbGQdm9JYtEt2K5YtMWMLRYl22Y8AgDYVmw3Z7m9kjy+tXZhVX0uyeGttQOr6rFJXpDk\nfUnaUPaFSR7ZWvt6Ve0yLPuDJCe01v62qrZLcqt1fA/AeIhFAAAA62Te08cuba1dODz/fJJ/HZ6f\nn2SPmbJnJDm5qp6ajUmnTyX5k6r64yR7tNZu2PQuAyMmFgEAAKyTaq2tXKBq9yQbWmv3Hl6fOLz+\n+2HdB5K8PMn9W2vPGsockOSQJE9Osl9r7cqquuuw7JlJnt5a+9hMOyt3BPip0Vqr9a5TLALW6paI\nRQAA25J5Tx+b+0dVVe3ZWvtsks9W1a8nuXNV7dpauzTJa6vqLknuneRj09v54QbMQSwCAABYJ/Mm\nhdoyz5d6/fKq2nt4/uHW2nlV9byqelKSHyb5epK/XHtXAcQiAACA9bLq6WMAAAAAbHvmvdD0NqGq\n7lBV/6+qLqmqz1bVJ6rqcVX10Kq6qqrOrKoLq+rli+7rtKr60XAL7QuG22s/u6pWPMVluH33+cPz\n+1TVo+ZoZ/pz+HxVHTu1fMNMf/6rqr5SVe+qqo9X1X5Vdc1MfUdW1WuG5y+qqqOH5ydV1Ver6tbD\n69tX1aVT/b5+6m/x6ap68iZ+XucP/dtxZvnZw7/PXUu9W8JM30+d3DVr6nOZ7v+ThnWXVtXPzdRz\nZFV9c2rcPHVq3aFVde7w+Z5bVY+bWvfA4TM/e3oMsL7EolXbEYsWTCwCABiHUSWFkrw/ycdaa3dr\nrR2Q5LAkvzSsO621tn+S/ZIcUlUPnkwspic106rqxKr68vCj9QvDBOOOK3VgqR/Nc7iutbZfkj9L\nsmOSVyX5vzP1Pr+qvlhVF1XVI4fFk8PA7pfkf8zZ1uRzOCDJk6rqfjN1Jcl1Sf4hybPTT8O54xJl\nVtKS3Jjk92aWTVzSWtu/tXaP9L/Rs6vqyDnrTobPq7V2r6F/fzCz/H7Dv8fPW2FV3TQ9Qa+q50xN\nVP9sWL/n1PpnD8v2W6HOy6rq40us2m7o+5VJ/nBq+SUz/X/HsHy5z/2UYdw8PMlxVbVbVd0nyfFJ\nHjN8vo9L8oqq2nfY5uQkT22t3S/JvknevfynwmYQi1YnFi1BLAIAYD2NJilUVb+a5IbW2psny1pr\nV7TWXj9drrX2/STnJLlTVr5+ycQxww/jfYbtPlpVK12raXPO1zs/yWPTb6v9xCSpqp+pqrck+dP0\nCdLJSf56ssHQlxcneeKwp/YJVXVA9SMTzqyqM2rjdVc2drK165OcmWSvSVXL9On0JDutUmYpJ6RP\nsFYcg621y5IcneSoNdQ97fQkdxueb84FhG9I8pvLTKJbkvPSJ40Tj0+/ZfpKWpLbVtWdkqSq9plZ\n/6n0cTixXP9XfF+ttW8l+VKS3ZM8J8lxrbXLh3WXJXlpkj8eiu+W5BvDutZa+8Iq74E1EovEoohF\nYhEAwFZiNEmhJPdMctZqharqduk/3E9bawOttRPSL1670ukRP/7RXFVHD4fmn1dVR00tf+Gwt/+0\nqnpnku2H+i9urX0xfVJQVbVbkqekH2Hw50kekD4BuCLJfYdtbkxybJJ3DXt035PkoiQHDXvhX5T+\nQ/xm/auq2yd5YDZOJg4aJnJnJdk5yWPSx8+jklw7lNlpUqaqzk6fAC7n8iRnJDlihTITZyX55TnK\nzb6H7Yb+nTfTv8kpD09YQ503JnlT+qRwKaem7+lO9VuefzfJt+ao993ZOIE7PP1oglTVrZI8Iv0o\niIm9Zvr/K/N0fDhq4K5JLkn/Hpw5U+Rzw/KkT5Avrqr3VtXTq2qHedpgTcQisUgsEosAALYK8959\nbJtTVa9LcmCSH6TvmTx4mDzsneSE1to3a+VLZSzn7CT7JNmwUqHhUP4j00+NuFWSz1TVx9L/Jr+R\nfqvs7bP85HHSuUemT8D2Sf9Bv0v6BOAXV2h+1yRvG/bKt9x8HBxUVWcmuSnJS1trF1XVHdJP5Xjs\n0Pcbh/aPH97nrsO21w+nCEze45FJ9l+hHy9Nn8D8Y1bew7zWP8ROw4Qx6Xvn37pU/9aoJXl9kvOr\n6mVLrL86yRVVdc/0CdkpSX53jjr/LslJSV6ZPrndLn0Mfj3JhUn+Zar8JWvs/2FVdWD6xP3prbWr\nqg/q2SNEfrystfaSqnpH+rg6fHg8fA1tskZikVi0RmIRAADrZkxHCn0+U5OC1toz0vd+7pb+I/S0\nqWsXPK2q7r2J7aw2aZj8CD4wyftaa99vrV2X5L1JDh6Wn9pa+0Fr7dosPaHbMclNw6H4lT7ZeMFw\n6sheSb6WlU8NeUmSjwzXinjMUN/EacM1NA6YPr1lxvXpe42Paa0dtUpby2qtfSn9NJcnrlLHfulH\nFMzr+uFIhP1aa0cNRyhstuHvcXKWPn2kpU++DkufiL0v800gv5Pkyqr67fSJ1/eSfDHJXYbtn7EZ\nXT5l+Awe3Fqb7OW/IH3yP23/oe3+Rlq7tLX2xiS/luQ+wxErrB+xaCOxaBOIRQAArJfRJIVaax9J\nskNV/f7U4p2zcQJQQ7nLkhyX5Hmb2NT9Mt+kYfZH+mQPaS2xbmOhfprG3dN/9CfJP6dfa2P3Yf3e\n6T/ivzG12TXpe+0ndknyH8Pz1fYgz9P31Zav5LgkxyxXT1XtkeTlSV6zhjrXs3+zXp1+mszOS6z7\nQPopKF8ZJm3zenf6nv93ZuM4/H76hO+Y4fSNZH2OYHhlkudV1WS87JHk+UleMbyevgjw3dNPVblq\nzrqZg1gkFq2wfC3EIgAANttokkKDQ5M8rKq+VFWfTnJikv+TqUPWB29MclBu/vms+uO+qp6VfqrE\nB1fow6T8aUkOraodq2rn9NM0Tk+/tsUhVbVDVd0mySFJbj1ct+GCJB9K36P7lqGetyT5RJJjh/Un\npU/Mzplq86NJ7jF17Yrjk/zVcGrGpoyBlqUvfLuWO/70J61dmH5ayvS2e9ZwG+j0CeerW2tvW2P/\nlrLjzHUwjltDnZMJ0pXpE6en/ESjffL03PTJ5dx1pu/Jf1n633YyGU9r7Zz0v+PkOh97zvR/es/9\nuVV1RVVdXlWvyDKfQWvt3PQxv2H4fE9NP8pickerI4ZryJyVfiTC77TWNueCxCxNLBKLxCKxCABg\n4cpvrOVV1dWttV2GPZn/nr7HezJpe3b6JOng9Gs4/Lckn07y/Nba11ao88tJ7t9a+05V/VH6D/qW\n5M2ttdcOZY5N8jtDe99M8sHW2t9U1aFJXpvk59P3mJ7TWnvUsM3zh7p+mOSo1tqH1vfTGLfJWBie\n3yHJl5O8bLjuxYuSXNNae9XMNh9Jn+QseS2W6bEwtWz3JBtaa5t6yhDbILGICbEIAID1JCm0Faqq\nnVtr11XVTul78Z827KkF2GLEIgAA2LaN9u5jW7k3VdU9kuyQ5CSTMGBBxCIAANiGOVLoFjJcJ2T7\nycv00zKOaK19fnG9YhGMBRbJ+GPCWAAAYJakEAAAAMAIje3uYwAAAABEUggAAABglCSFAAAAAEZI\nUggAAABghCSFAAAAAEbo/wMRC2jE9IMGiwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x114b1d7f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Features per well\n",
"for w_idx, w in enumerate(np.unique(well)):\n",
" ax = plt.subplot(3, 4, w_idx+1)\n",
" hist = np.logical_not(np.any(np.isnan(X[well == w, :]), axis=0))\n",
" plt.bar(np.arange(len(hist)), hist, color=facies_colors, align='center')\n",
" ax.set_xticks(np.arange(len(hist)))\n",
" ax.set_xticklabels(feature_names)\n",
" ax.set_yticks([0, 1])\n",
" ax.set_yticklabels(['miss', 'hit'])\n",
" ax.set_title(w)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Feature imputation\n",
"Let us fill missing PE values. This is the only cell that differs from the approach of Paolo Bestagini. Currently no feature engineering is used, but this should be explored in the future."
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def make_pe(X, seed):\n",
" reg = RandomForestRegressor(max_features='sqrt', n_estimators=50, random_state=seed)\n",
" DataImpAll = data[feature_names].copy()\n",
" DataImp = DataImpAll.dropna(axis = 0, inplace=False)\n",
" Ximp=DataImp.loc[:, DataImp.columns != 'PE']\n",
" Yimp=DataImp.loc[:, 'PE']\n",
" reg.fit(Ximp, Yimp)\n",
" X[np.array(DataImpAll.PE.isnull()),4] = reg.predict(DataImpAll.loc[DataImpAll.PE.isnull(),:].drop('PE',axis=1,inplace=False))\n",
" return X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Feature augmentation\n",
"Our guess is that facies do not abrutly change from a given depth layer to the next one. Therefore, we consider features at neighboring layers to be somehow correlated. To possibly exploit this fact, let us perform feature augmentation by:\n",
"- Aggregating features at neighboring depths.\n",
"- Computing feature spatial gradient."
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Feature windows concatenation function\n",
"def augment_features_window(X, N_neig):\n",
" \n",
" # Parameters\n",
" N_row = X.shape[0]\n",
" N_feat = X.shape[1]\n",
"\n",
" # Zero padding\n",
" X = np.vstack((np.zeros((N_neig, N_feat)), X, (np.zeros((N_neig, N_feat)))))\n",
"\n",
" # Loop over windows\n",
" X_aug = np.zeros((N_row, N_feat*(2*N_neig+1)))\n",
" for r in np.arange(N_row)+N_neig:\n",
" this_row = []\n",
" for c in np.arange(-N_neig,N_neig+1):\n",
" this_row = np.hstack((this_row, X[r+c]))\n",
" X_aug[r-N_neig] = this_row\n",
"\n",
" return X_aug"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Feature gradient computation function\n",
"def augment_features_gradient(X, depth):\n",
" \n",
" # Compute features gradient\n",
" d_diff = np.diff(depth).reshape((-1, 1))\n",
" d_diff[d_diff==0] = 0.001\n",
" X_diff = np.diff(X, axis=0)\n",
" X_grad = X_diff / d_diff\n",
" \n",
" # Compensate for last missing value\n",
" X_grad = np.concatenate((X_grad, np.zeros((1, X_grad.shape[1]))))\n",
" \n",
" return X_grad"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Feature augmentation function\n",
"def augment_features(X, well, depth, seed=None, pe=True, N_neig=1):\n",
" seed = seed or None\n",
" \n",
" if pe:\n",
" X = make_pe(X, seed)\n",
" # Augment features\n",
" X_aug = np.zeros((X.shape[0], X.shape[1]*(N_neig*2+2)))\n",
" for w in np.unique(well):\n",
" w_idx = np.where(well == w)[0]\n",
" X_aug_win = augment_features_window(X[w_idx, :], N_neig)\n",
" X_aug_grad = augment_features_gradient(X[w_idx, :], depth[w_idx])\n",
" X_aug[w_idx, :] = np.concatenate((X_aug_win, X_aug_grad), axis=1)\n",
" \n",
" # Find padded rows\n",
" padded_rows = np.unique(np.where(X_aug[:, 0:7] == np.zeros((1, 7)))[0])\n",
" \n",
" return X_aug, padded_rows"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Augment features\n",
"X_aug, padded_rows = augment_features(X, well, depth)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generate training, validation and test data splits\n",
"The choice of training and validation data is paramount in order to avoid overfitting and find a solution that generalizes well on new data. For this reason, we generate a set of training-validation splits so that:\n",
"- Features from each well belongs to training or validation set.\n",
"- Training and validation sets contain at least one sample for each class."
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Split 0\n",
" training: ['SHRIMPLIN' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['ALEXANDER D' 'CHURCHMAN BIBLE']\n",
"Split 1\n",
" training: ['SHRIMPLIN' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'NOLAN' 'Recruit F9' 'NEWBY'\n",
" 'CHURCHMAN BIBLE']\n",
" validation: ['ALEXANDER D' 'CROSS H CATTLE']\n",
"Split 2\n",
" training: ['SHRIMPLIN' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['ALEXANDER D' 'KIMZEY A']\n",
"Split 3\n",
" training: ['SHRIMPLIN' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['ALEXANDER D' 'NOLAN']\n",
"Split 4\n",
" training: ['SHRIMPLIN' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['ALEXANDER D' 'SHANKLE']\n",
"Split 5\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['CROSS H CATTLE' 'CHURCHMAN BIBLE']\n",
"Split 6\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['KIMZEY A' 'CHURCHMAN BIBLE']\n",
"Split 7\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['LUKE G U' 'CHURCHMAN BIBLE']\n",
"Split 8\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'NOLAN' 'Recruit F9']\n",
" validation: ['NEWBY' 'CHURCHMAN BIBLE']\n",
"Split 9\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['NOLAN' 'CHURCHMAN BIBLE']\n",
"Split 10\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'NOLAN' 'NEWBY']\n",
" validation: ['Recruit F9' 'CHURCHMAN BIBLE']\n",
"Split 11\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['SHANKLE' 'CHURCHMAN BIBLE']\n",
"Split 12\n",
" training: ['ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'NEWBY']\n",
" validation: ['SHRIMPLIN' 'CHURCHMAN BIBLE']\n",
"Split 13\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['KIMZEY A' 'CROSS H CATTLE']\n",
"Split 14\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'NOLAN'\n",
" 'Recruit F9' 'CHURCHMAN BIBLE']\n",
" validation: ['CROSS H CATTLE' 'NEWBY']\n",
"Split 15\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'NOLAN' 'NEWBY'\n",
" 'CHURCHMAN BIBLE']\n",
" validation: ['CROSS H CATTLE' 'Recruit F9']\n",
"Split 16\n",
" training: ['ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'NOLAN' 'Recruit F9' 'NEWBY'\n",
" 'CHURCHMAN BIBLE']\n",
" validation: ['SHRIMPLIN' 'CROSS H CATTLE']\n",
"Split 17\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['LUKE G U' 'KIMZEY A']\n",
"Split 18\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'CHURCHMAN BIBLE']\n",
" validation: ['KIMZEY A' 'NEWBY']\n",
"Split 19\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE'\n",
" 'Recruit F9' 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['KIMZEY A' 'NOLAN']\n",
"Split 20\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['KIMZEY A' 'Recruit F9']\n",
"Split 21\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['SHANKLE' 'KIMZEY A']\n",
"Split 22\n",
" training: ['ALEXANDER D' 'SHANKLE' 'LUKE G U' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['SHRIMPLIN' 'KIMZEY A']\n",
"Split 23\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'Recruit F9' 'CHURCHMAN BIBLE']\n",
" validation: ['NOLAN' 'NEWBY']\n",
"Split 24\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'Recruit F9' 'CHURCHMAN BIBLE']\n",
" validation: ['SHANKLE' 'NEWBY']\n",
"Split 25\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['NOLAN' 'Recruit F9']\n",
"Split 26\n",
" training: ['ALEXANDER D' 'SHANKLE' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE'\n",
" 'Recruit F9' 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['SHRIMPLIN' 'NOLAN']\n",
"Split 27\n",
" training: ['SHRIMPLIN' 'ALEXANDER D' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['SHANKLE' 'Recruit F9']\n",
"Split 28\n",
" training: ['ALEXANDER D' 'LUKE G U' 'KIMZEY A' 'CROSS H CATTLE' 'NOLAN' 'Recruit F9'\n",
" 'NEWBY' 'CHURCHMAN BIBLE']\n",
" validation: ['SHRIMPLIN' 'SHANKLE']\n"
]
}
],
"source": [
"# Initialize model selection methods\n",
"lpgo = LeavePGroupsOut(2)\n",
"\n",
"# Generate splits\n",
"split_list = []\n",
"for train, val in lpgo.split(X, y, groups=data['Well Name']):\n",
" hist_tr = np.histogram(y[train], bins=np.arange(len(facies_names)+1)+.5)\n",
" hist_val = np.histogram(y[val], bins=np.arange(len(facies_names)+1)+.5)\n",
" if np.all(hist_tr[0] != 0) & np.all(hist_val[0] != 0):\n",
" split_list.append({'train':train, 'val':val})\n",
" \n",
"# Print splits\n",
"for s, split in enumerate(split_list):\n",
" print('Split %d' % s)\n",
" print(' training: %s' % (data['Well Name'][split['train']].unique()))\n",
" print(' validation: %s' % (data['Well Name'][split['val']].unique()))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Classification parameters optimization\n",
"Let us perform the following steps for each set of parameters:\n",
"- Select a data split.\n",
"- Normalize features using a robust scaler.\n",
"- Train the classifier on training data.\n",
"- Test the trained classifier on validation data.\n",
"- Repeat for all splits and average the F1 scores.\n",
"\n",
"At the end of the loop, we select the classifier that maximizes the average F1 score on the validation set. Hopefully, this classifier should be able to generalize well on new data."
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Parameters search grid (uncomment parameters for full grid search... may take a lot of time)\n",
"N_grid = [100] # [50, 100, 150]\n",
"M_grid = [10] # [5, 10, 15]\n",
"S_grid = [25] # [10, 25, 50, 75]\n",
"L_grid = [5] # [2, 3, 4, 5, 10, 25]\n",
"param_grid = []\n",
"for N in N_grid:\n",
" for M in M_grid:\n",
" for S in S_grid:\n",
" for L in L_grid:\n",
" param_grid.append({'N':N, 'M':M, 'S':S, 'L':L})"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Train and test a classifier\n",
"def train_and_test(X_tr, y_tr, X_v, well_v, clf):\n",
" \n",
" # Feature normalization\n",
" scaler = preprocessing.RobustScaler(quantile_range=(25.0, 75.0)).fit(X_tr)\n",
" X_tr = scaler.transform(X_tr)\n",
" X_v = scaler.transform(X_v)\n",
" \n",
" # Train classifier\n",
" clf.fit(X_tr, y_tr)\n",
" \n",
" # Test classifier\n",
" y_v_hat = clf.predict(X_v)\n",
" \n",
" # Clean isolated facies for each well\n",
" for w in np.unique(well_v):\n",
" y_v_hat[well_v==w] = medfilt(y_v_hat[well_v==w], kernel_size=5)\n",
" \n",
" return y_v_hat"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F1 score = 0.565 {'S': 25, 'M': 10, 'L': 5, 'N': 100}\n",
"\n",
"Best F1 score = 0.565 {'S': 25, 'M': 10, 'L': 5, 'N': 100}\n"
]
}
],
"source": [
"# For each set of parameters\n",
"# score_param = []\n",
"# for param in param_grid:\n",
"\n",
"# # For each data split\n",
"# score_split = []\n",
"# for split in split_list:\n",
"\n",
"# # Remove padded rows\n",
"# split_train_no_pad = np.setdiff1d(split['train'], padded_rows)\n",
"\n",
"# # Select training and validation data from current split\n",
"# X_tr = X_aug[split_train_no_pad, :]\n",
"# X_v = X_aug[split['val'], :]\n",
"# y_tr = y[split_train_no_pad]\n",
"# y_v = y[split['val']]\n",
"\n",
"# # Select well labels for validation data\n",
"# well_v = well[split['val']]\n",
"\n",
"# # Train and test\n",
"# y_v_hat = train_and_test(X_tr, y_tr, X_v, well_v, param)\n",
"\n",
"# # Score\n",
"# score = f1_score(y_v, y_v_hat, average='micro')\n",
"# score_split.append(score)\n",
"\n",
"# # Average score for this param\n",
"# score_param.append(np.mean(score_split))\n",
"# print('F1 score = %.3f %s' % (score_param[-1], param))\n",
"\n",
"# # Best set of parameters\n",
"# best_idx = np.argmax(score_param)\n",
"# param_best = param_grid[best_idx]\n",
"# score_best = score_param[best_idx]\n",
"# print('\\nBest F1 score = %.3f %s' % (score_best, param_best))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Predict labels on test data\n",
"Let us now apply the selected classification technique to test data."
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"param_best = {'S': 25, 'M': 10, 'L': 5, 'N': 100}"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load data from file\n",
"test_data = pd.read_csv('../validation_data_nofacies.csv')"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Prepare test data\n",
"well_ts = test_data['Well Name'].values\n",
"depth_ts = test_data['Depth'].values\n",
"X_ts = test_data[feature_names].values"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"...................................................................................................."
]
}
],
"source": [
"y_pred = []\n",
"print('o' * 100)\n",
"for seed in range(100):\n",
" np.random.seed(seed)\n",
"\n",
" # Make training data.\n",
" X_train, padded_rows = augment_features(X, well, depth, seed=seed)\n",
" y_train = y\n",
" X_train = np.delete(X_train, padded_rows, axis=0)\n",
" y_train = np.delete(y_train, padded_rows, axis=0) \n",
" param = param_best\n",
" clf = OneVsOneClassifier(RandomForestClassifier(n_estimators=param['N'], criterion='entropy',\n",
" max_features=param['M'], min_samples_split=param['S'], min_samples_leaf=param['L'],\n",
" class_weight='balanced', random_state=seed), n_jobs=-1)\n",
" \n",
" # Make blind data.\n",
" X_test, _ = augment_features(X_ts, well_ts, depth_ts, seed=seed, pe=False)\n",
"\n",
" # Train and test.\n",
" y_ts_hat = train_and_test(X_train, y_train, X_test, well_ts, clf)\n",
" \n",
" # Collect result.\n",
" y_pred.append(y_ts_hat)\n",
" print('.', end='')\n",
" \n",
"np.save('100_realizations.npy', y_pred)"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda env:python3]",
"language": "python",
"name": "conda-env-python3-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
nicolas998/wmf | Examples/Ejemplo_Hidrologia_Maximos.ipynb | 1 | 595267 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Realiza el análisis hidrológico de la cuenca de Danta\n"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from wmf import wmf \n",
"import numpy as np\n",
"import pylab as pl\n",
"import datetime as dt\n",
"import os\n",
"import pandas as pd\n",
"import pickle\n",
"import plot_y_tablas as pyt\n",
"from scipy import stats as stat"
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<script>\n",
"code_show=true; \n",
"function code_toggle() {\n",
" if (code_show){\n",
" $('div.input').hide();\n",
" } else {\n",
" $('div.input').show();\n",
" }\n",
" code_show = !code_show\n",
"} \n",
"$( document ).ready(code_toggle);\n",
"</script>\n",
"<form action=\"javascript:code_toggle()\"><input type=\"submit\" value=\"Click here to toggle on/off the raw code.\"></form>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"execution_count": 97,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML('''<script>\n",
"code_show=true; \n",
"function code_toggle() {\n",
" if (code_show){\n",
" $('div.input').hide();\n",
" } else {\n",
" $('div.input').show();\n",
" }\n",
" code_show = !code_show\n",
"} \n",
"$( document ).ready(code_toggle);\n",
"</script>\n",
"<form action=\"javascript:code_toggle()\"><input type=\"submit\" value=\"Click here to toggle on/off the raw code.\"></form>''')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lectura de mapas de direcciones y de elevación:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"___\n",
"## Trazado de cuencas y corrientes "
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cuCap = wmf.SimuBasin(0,0,0,0,rute='/media/nicolas/discoGrande/01_SIATA/nc_cuencas/Picacha_Abajo.nc')"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#Guarda Vector de la cuenca\n",
"cuCap.Save_Basin2Map('/media/nicolas/discoGrande/01_SIATA/vector/Cuenca_AltaVista2.shp')"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cuCap.Save_Net2Map('/media/nicolas/discoGrande/01_SIATA/vector/Red_Altavista_Abajo.shp',dx = 12.7, umbral=470)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Tiempo de viaje "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cuCap.GetGeo_Parameters()"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"{'Campo y Munera': 0.57998596426157101,\n",
" 'Direccion Carreteras Espana': 0.46243262008405484,\n",
" 'Giandotti': 0.56255080064090079,\n",
" 'John Stone': 1.4473803735315547,\n",
" 'Kiprich': 0.59417325923551134,\n",
" 'Temez': 0.20455629037544334,\n",
" 'US Army': 0.59125843592315985,\n",
" 'Ventura': 0.23583395960988951}"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cuCap.Tc"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfgAAAFgCAYAAABXHWtRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcFPX/B/DXgoAICgqCCgIqHqAcnolpgaWopX5LvkqW\nimJemXmb0qFf/SbSYRqUt6YiWfZNzRQ1YDQIwQ68kEwuFRUKf4qgcu3n9wftFqILs8zymR3ez8dj\nHzG70+zr7Qz7Yea9M6NijDEQQgghRFFMeAcghBBCiPRogCeEEEIUiAZ4QgghRIFogCeEEEIUiAZ4\nQgghRIFogCeEEEIUiPsAHxoaCkdHR3h7ez92HkEQ0LNnT/To0QMBAQENmI4QQggxTire58EnJibC\n2toaEydOxNmzZ2u8fufOHQwYMADHjh2Dk5MT/vzzT9jb23NISgghhBgP7nvwAwcORMuWLR/7+p49\nezBmzBg4OTkBAA3uhBBCSB1wH+Brc+nSJdy6dQsBAQHo27cvdu3axTsSIYQQIntNeAeoTUVFBX75\n5RfEx8ejpKQEfn5+8PPzg7u7e415VSoVh4SEEEIIP4/rtMt+D97Z2RmBgYFo2rQp7Ozs8NRTT+HM\nmTOPnZ8xxuXx7rvvcntvqofqMfaHkupRUi1Uj/wfushigNcVdPTo0UhMTERlZSXu3buHlJQUeHh4\nNHDC2uXk5PCOICmqR96oHvlSUi0A1WPMuB+iHz9+PARBQGFhIVxcXLBixQqUlZVBpVJh2rRp6Nat\nGwIDA+Ht7Q1TU1NMmzYNnp6evGMTQgghssb9NDkpqVSqWg9ZGIogCPD39+fy3oZA9cgb1SNfSqoF\noHrkTte4RwM8IYQQYqR0jXuy6MErgSAIvCNIiuqRN6pHvpRUC0D1GDMa4AkhhBAFokP0hBBCiJGi\nQ/SEEEJII0MDvESU1teheuSN6pEvJdUCUD3GjAZ4QgghRIGoB08IIYQYKerBE0IIIY0MDfASUVpf\nh+qRN6pHvpRUC0D1GDMa4AkhhBAFqlMPvqCgAA8ePBC14KZNm8LBwUHvYPqgHjwhhJDGpN7Xop86\ndSqeeuopUYPnDz/8gC1bttQ9pQRogCeEENKY6Br36nS72AEDBmDixImi3rSyslLU/MZOaXcoonrk\njeqRLyXVAlA9xqxOPfgpU6aIXrA+/w8hhBBCpKHXefCff/45vvzyS+zYsQMff/wxnJycMGvWLEPk\nE4UO0RNCCGlMDHIe/M6dOxEREYGUlBQ4ODhg3bp1egckhBBCiLT0GuCLi4thZ2eH48ePY86cOQgK\nCkKzZs2kzmZUlHZuJdUjb1SPfCmpFoDqMWZ6DfAdOnSAr68vioqKEBgYiIqKClhZWUmdjRBCCCF6\n0vta9MXFxWjSpAmaNm0Ke3t7LF68GIsXL5Y6nyjUg9fNrU0b5Obn845RK1dHR+TcvMk7BiGEyF69\nz4N/WGlpKSwsLLTTubm5sLe3574XTwO8biqVCsbwr6MCaD0SQkgdSP4lu7Zt2yI3N1c77erqyn1w\n501pfR2BdwCJKW79UD2ypaRaAKrHmOk1wM+aNQuurq5SZyGEEEKIRPQ6RD9u3DiMGTMGY8eOrXeA\n0NBQHDp0CI6Ojjh79uxj5zt9+jQGDBiAvXv34sUXX3zkPHSIXjc6RE8IIcoi+SH6GzduIDw8HG3a\ntMHYsWOxYcMG5OTk6BVu8uTJOHr0qM551Go13nzzTQQGBur1HoQQQkhjo9cA/+KLL+Lnn3/GxYsX\nMW7cOJw5cwZTp07VK8DAgQPRsmVLnfN88sknCAoKavC704mhtL6OwDuAxBS3fqge2VJSLQDVY8zq\ndLOZh/373//GsWPHEBgYiDFjxmDMmDFS59K6fv069u/fj4SEBKSmphrsfQghhBAl0WuAd3JygpOT\nEwDg9u3b+PrrrzFhwgSYm5tLGg4A5s6dizVr1mina+vNhoSEwM3NDQBga2sLX19f7Z2DNH+5GWLa\n39/foMuXYhqo2jP3/8fPeMy0fy2vG3Jam7WRrR+qRz55aJqm5Tqt+bkubXG9vmSXlJSEvXv3olu3\nbggKCoK1tTV27tyJGTNmiF0UgKrz6EeOHPnIL9l17NgRQNXA/ueff8LKygqbNm3CqFGjasxLX7LT\njb5kRwghyiL5l+y2bt0KT09P/Pzzz/D09MQLL7yAEydO6B2QMfbYgFlZWcjKykJ2djaCgoLw6aef\nPnJw5+2ff10pgcA7gMQUt36oHtlSUi0A1WPM9DpEP2LECAQFBWHGjBmIiorCkSNH0KFDB70CjB8/\nHoIgoLCwEC4uLlixYgXKysqgUqkwbdq0avOqVCq93oMQQghpbOp8iN7d3R2BgYEIDAxEYWEh/vWv\nf9X67feGRofodaND9IQQoiySXIv+lVdeQUBAAI4dOwZBEGBpaYlXX30VzzzzDPr16wcTE71vLS8Z\nGuB1owGeEEKURZIe/IcffojQ0FDs3bsXN2/exL59+6BSqbB06VK0bdsWEydOlCywMVJaX0fgHUBi\nils/VI9sKakWgOoxZnXuwTs6Omp/VqlU6NOnD/r06YNly5bh3r17Oi8zSwghhJCGVadD9CdOnMDT\nTz8tasH6/D/1RYfodaND9IQQoiy6xr067cEfOHBA1LfkGWM4ePBggw/whBBCCKlSpz342NhY5Ofn\ni1qwo6Mjhg0bpncwffDcgxcEQXvFIbkSswcv4O8rzDU0Q+zBG8P6EYPqkS8l1QJQPXJX7z34hh6o\nCSGEEFI/el2q9mFlZWUwNzfHgwcP0LRpUyly6YV68LpRD54QQpRF8kvVPmzu3LkAgNLSUhw6dEiK\nRRJCCCGkHiQZ4J977jkAgI2NDVq0aCHFIo2O0s6tFHgHkJji1g/VI1tKqgWgeoxZnQf4Ll26YOHC\nhdiwYUON1+7cuYOVK1ciLS0NGRkZkgYkhBBCiHh17sFPnDgRO3fufOzrBw4cQFxcHCZMmIC+fftK\nFlAM6sHrRj14QghRlnp/ix4AOnfurPP10aNHY/To0eKSEUIIIcQg6nyI/tatW4bMYfSU1tcReAeQ\nmOLWD9UjW0qqBaB6jFmdB/h169bBxcUFkydPRnR0NG7evFnt9Q8//FDycIQQQgjRT5178PPmzcOg\nQYPw/fff4/jx48jKyoKHhweeffZZPPvss/j222+xceNGQ+fViXrwulEPnhBClEWS+8GvXLkSb7/9\ntnb6ypUrOH78OI4fP474+HgUFhaisrJSmsR6ogFeNxrgCSFEWSS50M3Dp7+5uLggNDQUX3zxBfLz\n8zFhwoT6pTRySuvrCLwDSExx64fqkS0l1QJQPcaszgN8fn4+Nm3ahIqKihqvqVQqdOrUSdJghBBC\nCNGfqGvRZ2dnIy4uDlOnTq3xWm5uLlxdXSUNJxYdoteNDtETQoiySNKDNwY0wOtGAzwhhCiLwW82\nQ5TX1xF4B5CY4tYP1SNbSqoFoHqMGfcBPjQ0FI6OjvD29n7k63v27IGPjw98fHwwcOBAnDt3roET\nEkIIIcaH+yH6xMREWFtbY+LEiTh79myN10+dOgUPDw/Y2NggNjYWy5cvx6lTpx65LDpErxsdoieE\nEGWR5Fr0hjJw4EDk5uY+9vX+/ftX+zkvL68hYhFCCCFGjfshejG2bNmC4cOH847xSErr6wi8A0hM\nceuH6pEtJdUCUD3GTPQe/N69exEXF4eCggKo1epqrx08eFCyYA9LSEjA9u3bkZiYqHO+kJAQuLm5\nAQBsbW3h6+sLf39/AH+v2MY6DVQN3P7/+BkynNbg/e9F0zStz7SGXPJQPcqqR/NzTk4OaiOqB79o\n0SJ8/PHHCAgIQLt27aBSqaq9vn379rouqprc3FyMHDnykT14ADh79izGjBmD2NhYnRfUoR68btSD\nJ4QQZZGsB79z507ExMQgKChIkmAajLHHBrxy5QrGjBmDXbt20dXyCCGEkDoS1YNXq9Xw9fWVNMD4\n8eMxYMAAXLp0CS4uLti+fTs2btyITZs2Aai6yc2tW7cwa9Ys9OzZE/369ZP0/aXy8OEfYyfwDiAx\nxa0fqke2lFQLQPUYM1F78NOmTcPu3buxfPlyyQLs2bNH5+ubN2/G5s2bJXs/QgghpDEQ1YN/7bXX\nsGfPHnh6esLb2xtmZmbVXl+/fr3kAcWgHrxu1IMnhBBlkawHn56erj1E//DtYx/+wh0hhBBC+OF+\nJTsp8dyDFwRBezqDXInZgxfw9+lrDc0Qe/DGsH7EoHrkS0m1AFSP3El6Jbv8/HxERUUhPT0dKpUK\n3bt3x6xZs+Dg4FDvoIQQQgiRhqg9+KSkJAwbNgyOjo7w8/MDACQnJ6OgoABHjx7VPscL9eB1ox48\nIYQoi2T3g/fz84OXlxc2bNgAE5OqM+zUajVmzJiB8+fP48cff5QmsZ5ogNeNBnhCCFEWye4Hn5aW\nhgULFmgHdwAwMTHB/Pnz8euvv9YvpZFT2rmVAu8AElPc+qF6ZEtJtQBUjzETNcDb2NggOzu7xvPZ\n2dmwtbWVLBQhhBBC6kfUIfq5c+fiq6++QkREBAYMGACgqi+/ZMkSjBs3Dh999JHBgtYFHaLXjQ7R\nE0KIskj2LfqIiAgwxjBlyhRUVFQAAMzMzDBz5kyEh4fXPykhhBBCJCHqEL25uTnWrVuH//u//0Na\nWhrS0tJw69YtrF27Fubm5obKaBSU1tcReAeQmOLWD9UjW0qqBaB6jJno8+ABoFmzZvDy8pI6CyGE\nEEIkUmsPftSoUdi9ezdatGiBUaNG6VzYwYMHJQ0nFvXgdaMePCGEKEu9evB2dnba68zb2dlJm4wQ\nQgghBkHXopeIMVzfmK5F7y/pMnmieuRLSbUAVI/cSXahG0IIIYQYB1F78GFhYXBxccH06dOrPb9h\nwwbk5eVh5cqVkgcUg3rwulEPnhBClEWyPfhdu3ahd+/eNZ7v3bs3du7cqV86QgghhEhO1ABfUFDw\nyC/a2dnZIT8/X7JQxkhp51YKvANITHHrh+qRLSXVAlA9xkzUAO/i4oKTJ0/WeP7kyZNwdnaWLBQh\nhBBC6kdUD/7DDz/Ef//7X6xZswaDBw8GAMTFxWHp0qVYsmQJFi9ebLCgdUE9eN2oB08IIcoi2bXo\nFyxYgD///BNz5sxBWVkZGGOwsLDAG2+8gUWLFkkSlhBCCCH1J/o0udWrV+PPP//EqVOnkJKSgj/+\n+APh4eHai+GIFRoaCkdHR3h7ez92njlz5qBz587w9fVFWlqaXu9jaErr6wi8A0hMceuH6pEtJdUC\nUD3GTPS16CsqKnDmzBlcuXIFZWVluHjxova1iRMnig4wefJkvP7664/9f48cOYLMzEz8/vvvSElJ\nwYwZM3Dq1CnR70MIIYQ0JqJ68BkZGRg5ciSys7PBGIOpqSkqKipgZmYGCwsLFBUV6RUiNzcXI0eO\nxNmzZ2u8NmPGDAQEBGDcuHEAAA8PDwiCAEdHx5rFUA9eJ+rBk8Zs5cqV8PHxwfnz57Fs2bIar5eV\nlWHPnj1o3rw5vvvuO0RGRqJZs2Y4evQoLl26BBMTE0yZMgWWlpYc0hPyaJKdBz937lz07t0bd+7c\nQbNmzXDx4kX89NNP8PX1xddffy1J2Ifl5eWhffv22mknJyfk5eUZ5L0IIXwUFBTg/v37Blt+XFwc\ngKqbZ5WXlyMxMbHGPKdPn0Z8fDzGjBmDoqIixMfH49atW9i5cydef/11FBQUICMjw2AZCZGaqEP0\np0+fxokTJ2BlZQUTExNUVFSgV69eiIiIwOuvv/7IPfCGFhISAjc3NwCAra0tfH19tdcd1vReDDH9\nz75OQ7yfPtNA9WvMaxI/avrvauo2v5TTGo1t/TTmevbs2YO2bdvC0dHRIMtPSkqCmZkZBEFAz549\nER8fj4qKimrzl5eXY+zYsQCAwsJClJWVYeXKlXjiiScAAAMHDsSdO3eg8bj30zwnp3/f+kxTPfKa\n1vyck5ODWjERWrZsyTIzMxljjHXq1InFxcUxxhi7fPkys7S0FLOoanJycpiXl9cjX5s+fTr74osv\ntNNdu3ZlN2/efOS8IsuRVEJCArf3risAjNXxkSBiXqkfhliPxrB+xDCmeg4fPsx27drFGGMsLCyM\nXblypcY8a9euZbm5uY9dxqFDh9jzzz/PHB0dWUBAAPvss89EZXjttddYfHw8Y4yxuLg4NnPmzEfO\nV1hYyKKioti2bdsYY4zNmjWLLVq0iH333XcsPDy8Tu9lTOumLqgeedP1eSlqD75Hjx44c+YMOnbs\niH79+mHNmjUwNTXF5s2b4e7uLmZRD/+R8dgewqhRoxAVFYVx48bh1KlTsLW1fWT/nTfNX1lK4c87\ngMQUt36MqJ7vv/8ekydPBgD8/PPP1VpuGj179nzsZ8DVq1fx7bff4ttvv8WBAwegVqvxwgsvAADS\n09Nx/PjxR57FM2nSJNjY2AAA1Go1TE1NAQCVlZXanx/WqlUrzJo1C//+97/h7u4OtVoNGxsbjBgx\nAunp6Thy5AiGDx+us15jWjd1QfUYL1EDfFhYGEpKSgAAq1atwnPPPYeAgADY29vjyy+/1CvA+PHj\nIQgCCgsL4eLighUrVqCsrAwqlQrTpk3DiBEjcPjwYbi7u8PKygrbt2/X630IIXycO3cOPXr0QFlZ\nGSwsLLTPZ2Zm4tChQwCAy5cvw87ODi1btoRKpcLLL7+svSz2559/jjlz5gCoOnTeoUMH7TI8PT3h\n6elZawZHR0ftZ1dRURFat26tc/6uXbsiJiYG7dq1Q7t27QBUDf7nz5+vdYAnRC5EDfCBgYHanzt2\n7IiLFy/i1q1b2l9KfezZs6fWeSIjI/VadkMSFHaPYQHK2otX3Poxknru37+Pe/fuAQBSUlLg4+OD\nH374AYMGDUKnTp3wxhtvAADWrVuHF154AS4uLjWWcfv2bbi6ugIAkpOTMWHCBO1rmj34h6lUKkyc\nOBG2trYAqvrnP/30E4YPH47U1FQ888wzAKrO4NEsOzw8HKWlpXj33XeRn58Pb29v9OrVCwkJCQCA\nW7du6bxeh4axrJu6onqMV50H+PLycgwcOBA7d+5E165dtc+3atXKIMEIIcYvJSUFRUVFOHz4sPaL\na02a1PzYedzheQCYOnUqYmJiAFRd9MrMzEz7Wl334AcPHowjR45g3759UKlUGDp0KG7fvo3x48cj\nKSkJABAcHIzk5GRs374dlpaWmD17NlQqFeLj47F9+3aYmppW28khRO5EnQfv4OCAxMREdOnSxZCZ\n9EbnwetG58GThrZq1SoMGjQITz/9tM75kpKS4ObmBicnpwZKRogySHYe/KRJk7B582ZJQhFClC87\nOxt+fn61zvfkk0/S4E6IxETtwc+aNQvR0dHo0KEDevfuDSsrq2qvr1+/XvKAYlR9D4DXnp8AhXWt\nQfXImQCqR64EKKcWgOqRO4nuJnfx4kX06tULAJCVlVX9LfT8kh0hhBBCpCdqD17uqAevG/XgCSFE\nWSTrwV+5cuWxC7py5Yr4ZIQQQggxCFEDfIcOHfDHH3/UeP7hi080Rv+8TrASCLwDSExx64fqkS0l\n1QJQPcZM1ADPGHtkr724uBhNmzaVLBQhhBBC6qdOPXjNZSKjoqIwefJkNGvWTPtaZWUlUlNTYW5u\nrr1gBC/Ug9eNevCEEKIsusa9On2L/ty5cwCqPnQvXrwIc3Nz7Wvm5ubo1asXFi5cKEFUQgghhEhB\n1LfoJ0+ejHXr1qFFixaGzKQ3nnvwxnB9YzF78AL4nSlqiD14Y1g/YlA98qWkWgCqR+7qvQevQXdy\nI4QQQoyD6PPg9+7di7i4OBQUFECtVld77eDBg5KGE4t68LpRD54QQpRFsj34RYsW4eOPP0ZAQADa\ntWtHV68jhBBCZErUHryjoyOioqIQFBRkyEx6ox68btSD95d0mTxRPfKlpFoAqkfuJLuSnVqthq+v\nryShCCGEEGI4ovbgw8LCYGZmhuXLlxswkv6oB68b9eAJIURZJOvB3759G3v27MHx48fh7e0NMzOz\naq/zvl0sIYQQQqqIOkSfnp4OX19fmJubIyMjA+fOndM+zp8/b6iMRkFp1zcWeAeQmOLWD9UjW0qq\nBaB6jJmoPfiEhARD5SCEEEKIhESfB3/kyBFERUUhKysLR48eRfv27bFlyxZ06NABzzzzjKFy1gn1\n4HWjHjwhhCiLZN+ij46OxtixY9G5c2dkZ2ejvLwcQNUNZyIiIuqflBBCCCGSEDXAR0REYPPmzVi7\ndi2aNPn76H7//v2RlpamV4DY2Fh069YNXbp0wZo1a2q8XlhYiOHDh8PX1xdeXl7YsWOHXu9jaErr\n6wi8A0hMceuH6pEtJdUCUD3GTNQA//vvv8PPz6/G89bW1igqKhL95mq1GrNnz8bRo0dx4cIFxMTE\nICMjo9o8kZGR8PX1RVpaGhISErBgwQJUVFSIfi9CCCGkMRE1wLdr1w6XLl2q8fzJkyfRqVMn0W+e\nmpqKzp07w9XVFWZmZggODsaBAweqzdOmTRvcvXsXAHD37l3Y2dlVO3ogF0q6MhLA7yp2hqK49UP1\nyJaSagGoHmMmaoCfNm0a5syZg6SkJADA1atX8fnnn2Px4sWYOXOm6DfPy8tD+/bttdPOzs7Iy8ur\nNs+rr76KCxcuoF27dvDx8cG6detEvw8hhBDS2IjaFV68eDHu3LmDIUOG4MGDBwgICICFhQUWLlyI\n1157zSABV69eDR8fHyQkJCAzMxNDhgzB2bNnYW1t/cj5Q0JC4ObmBgCwtbWFr6+v9i82Te/FENP/\n7Os0xPvpMw1Uv8a8JvGjpv+upm7zSzmt0djWD9WjjHoerol3HqpHWfVofs7JyUGtmB5KSkrY6dOn\nWUpKCrt7964+i2CMMZacnMwCAwO106tXr2bh4eHV5hk+fDhLTEzUTg8ePJidPn36kcvTsxxJJCQk\ncHvvugLAWB0fCSLmlfphiPVoDOtHDKpHvpRUC2NUj9zp+rwUfR68lCorK9G1a1fExcWhbdu26Nev\nH2JiYuDh4aGdZ8GCBWjRogXeffdd5Ofno0+fPjhz5gxatWpVY3l0HrxudB48IYQoi2TnwYeFhWHj\nxo01nt+wYQPefvtt0cFMTU0RGRmJoUOHonv37ggODoaHhwc2btyITZs2AQCWLl2Kn376CT4+Phgy\nZAgiIiIeObgTQggh5B/EHApo3779Iw+Pp6amMhcXF1GHFQxBZDmSMobDPqBD9IpB9ciXkmphjOqR\nO12fl6L24AsKCmBnZ1fjeTs7O+Tn50vyBwchhBBC6k9UD75Lly4ICwvDpEmTqj2/Y8cOrFq1Cpcv\nX5Y8oBjUg9eNevCEEKIskt0Pfvr06Zg3bx7KysowePBgAEBcXByWLl2KJUuW1D8pIYQQQiQh6hD9\nggULMH36dMyZMwddunRBly5d8MYbb+DVV1/F4sWLDZXRKPzzHEUlEHgHkJji1g/VI1tKqgWgeoyZ\n6Gu+rl69Gm+99RbS09MBAB4eHo+96AwhhBBC+OB6HrzUqAevG/XgCSFEWSTrwQPA3r17ERcXh4KC\nAqjV6mqvHTx4UL+EhBBCCJGUqB78okWL8MorryAnJwe2traws7Or9mjMlNbXEXgHkJji1g/VI1tK\nqgWgeoyZqD34nTt3IiYmBkFBQYbKQwghhBAJiOrBt27dGsnJyXB3dzdkJr1RD1436sETQoiySHYt\n+mnTpmH37t2ShCKEEEKI4Yga4G/fvo1169bhySefxMyZMzFnzpxqj8ZMaX0dgXcAiSlu/VA9sqWk\nWgCqx5iJ6sGnp6fD19cXAJCRkVHtNZVKJV0qQgghhNQLnQffiFAPnhBClEXS8+Dz8/MRFRWF9PR0\nqFQqdO/eHbNmzYKDg0O9gxJCCCFEGqJ68ElJSXB3d8eePXtgaWmJpk2bYvfu3XB3d0dycrKhMhoF\npfV1BN4BJKa49UP1yJaSagGoHmMmag9+4cKFeOmll7BhwwaYmFT9baBWqzFjxgwsWLAAP/74o0FC\nEkIIIUQcUT14S0tLpKWloWvXrtWez8jIQM+ePXH//n3JA4pBPXjdqAdvHFauXAkfHx+cP38ey5Yt\ne+Q88+fPx5o1a7B582YEBQXB3t4eMTExsLS0RH5+PmbOnNnAqQkhPEh2HryNjQ2ys7NrPJ+dnQ1b\nW1v90hFCtOLi4gAAo0aNQnl5ORITEx853+eff44OHTrA3NwcDg4OiI2NhZeXF1588UU4OjoiLS2t\nIWMTQmRI1AAfHByM0NBQREdHIzs7G9nZ2di9ezemTp2Kl156yVAZjYLS+joC7wASM5b1k5SUhJ49\newIAevbsifj4+EfON3PmTFy7dg1Tp04FADRv3hzvvPMOSkpKcP36dXTo0KHBMtfFqlWr4O7ujq1b\ntyIqKgozZsxAcXGx9vX6rp+VK1fi4MGDeO+99x47z/z581FeXo5PP/0UBQUF+P333/Hpp5+ivLy8\nXu/9MGPZ1uqK6jFeogb4iIgIBAUFYcqUKXB3d4e7uzumTp2KsWPHIjw83FAZCTEaR44c0V7t8a23\n3sLVq1dF/f8FBQWwsrICAFhbW+PmzZuPnO/GjRuIjY3Fhx9+CAAYNGgQWrVqhe7du8Pa2ho2Njb1\nqEJ6ffr0wbBhwxAaGorXXnsNNjY22LFjhyTLFnvUw8zMDA4ODrh69SrmzZuH1q1bo23bthg5cqQk\neQiRC1FfsjM3N8e6deuwevVqZGZmAgA6deqEZs2aGSScMfH39+cdQVL+vANIrKHWz/fff4/JkycD\nAH7++We0b98eQNVFoo4fP/7IC0JNmjRJOyCr1WqYmpoCACorK7U/P2zr1q0AgMzMTBw9ehQ+Pj54\n8sknMWjQILzzzjsYMmQInJycJK9PXykpKejVq5d2+tq1a9W+y1Of9ZOUlKRdtuaox8CBA2vM98kn\nn2D8+PHa6Xv37uH+/fswMTHBqVOn0Lp1a70z/JPiPguoHqMl+jx4AGjWrBm8vLwkCRAbG4u5c+dC\nrVYjNDQUS5YsqTGPIAiYN28eysvL0bp1ayQkJEjy3oRI7dy5c+jRowfKyspgYWGhfd7T0xOenp61\n/v+Ojo4nrLdcAAAgAElEQVQoKSkBABQVFT1y0NmxYwcqKysRGhoKS0tLnD17FqmpqVi2bBlMTU3R\noUMH7N27F/Pnz5eusHpKTU3F6NGjAQA3b95EXl4egoODJVl2XY96ZGVlITY2FhcuXMCCBQvw/PPP\nAwCKi4uRk5OD/v37S5KHELkQNcCHhYXBxcUF06dPr/b8hg0bkJeXh5UrV4p6c7VajdmzZyMuLg7t\n2rVD3759MXr0aHTr1k07z507d/Daa6/h2LFjcHJywp9//inqPRqKIAiK+stQgLL24hti/dy/fx/3\n7t0DULXH6uPjgx9++AGDBg3S7sE/TKVSYeLEidovqQ4cOBA//fQThg8fjtTUVDzzzDMAgNzcXLi6\nugIA7O3tUVZWBgDIycmBv78/kpKSUFpaqv3jOz8/36C1ivXrr78iMzMTly9fxt27d7Fy5UosWLAA\nQ4cOhZOTE3744QdYW1tX+2yR+qjHW2+9BeDvox6BgYEAgI8//ljSP4YU91lA9RgtUQP8rl278L//\n/a/G871798bq1atFD/Cpqano3Lmz9oMrODgYBw4cqDbA79mzB2PGjNEebrS3txf1HoQ0lJSUFBQV\nFeHw4cMoLCxEWVkZmjSp+hWr6x784MGDceTIEezbtw8qlQpDhw7F7du3MX78eCQlJQEAnnvuObz+\n+usoKiqCs7MzBg8ejF69eiEqKgrt2rWDSqWqdiiat6ysLLi6umLMmDHa506ePInPPvsMQNX1NZ5/\n/nmcPXsWV69e1bY1DHnU49y5c9oBPj4+Xjv4E6Ikogb4goIC2NnZ1Xjezs5Orz2GvLw87S8zADg7\nOyM1NbXaPJcuXUJ5eTkCAgJQXFyMOXPmYMKECaLfy9CU9hehP+8AEmuI9ZOYmIhPPvkETz/9tN7L\nUKlU+OCDDwAAQUFBAABbW1vt4K6ZJzIystr/Z2tri0WLFun9voaUkpKCJ598stpznp6e+P3333Hi\nxAncv38f/v7+yMrKQn5+fo3vLTxM36Meffr0AfD3UQ+g6vNFczREKor7LKB6jJaoAd7FxQUnT56s\ncQrOyZMn4ezsLGkwjYqKCvzyyy+Ij49HSUkJ/Pz84OfnB3d390fOHxISAjc3NwBVH3q+vr7aFao5\nPaKxTgPVD70Lf/1XbtMavP+9xE7/+OOPeOKJJ4w2vyGmz5w5g/3796N9+/b45ptv0LJlS/j7++PI\nkSNo27YtBEFAu3btAAA//fQTrK2ttQNxQUEBfHx8an0/zVGPFStW4OrVq9qjHs899xwiIyPh7++v\nPephbW2Njh07YvDgwRAEAVlZWdo/KOTw70XTNF3btObnnJwc1IqJ8MEHH7CWLVuyTZs2scuXL7PL\nly+zjRs3slatWrE1a9aIWRRjjLHk5GQWGBionV69ejULDw+vNk94eDhbvny5djo0NJTt27fvkcsT\nWY6kEhISuL13XQFgrI6PBBHzSv0wxHo0hvUjhrHXc+HCBZaSksI2bdrEfvjhB/bRRx+xjz/+mHcs\nSRj7unmYsdTj6OjK8Nfnh1wfjo6uktet6/NS9Cfpm2++yZo2bcpMTEyYiYkJa9q0KVuyZIlewSoq\nKlinTp1YTk4OKy0tZT4+Piw9Pb3aPBcvXmTPPvssq6ioYCUlJaxHjx7swoULjy5GBiuQHvSgBz3o\nQY+GfDyOXrtKxcXFLDU1laWmprK7d+/qswitI0eOsC5dujB3d3e2evVqxhhjGzZsYBs3btTO8/77\n7zNPT0/m5eXF1q9f/9hl8f5Hpgc96EEPetCjoR+PI+pmM3JnLDdTIYQQQqSg6+Zcoi5VSx5P4B1A\nYgLvABITeAeQmMA7gMQE3gEkJPAOIDGBdwCJCbwDNCC9rmQna7wOSAgCIPPTL4zlCIdBbhdrJOsH\ndV5DAvidzGiA2zIrav0I4Huiad3WT5s2bsjPz22APPpzdHTFzZs5dZrXONaPAX53HnEhKO1LijtE\nr5xyJNeoB3gjIG6A56lx/p4pbf0YRz1139aUVk+dlyjV/eAJIYQQYhxED/BHjhzB888/D09PT+2t\nMLds2aK9ZWNj9c+LECiBwDuAxJS2fpS2hpS1fgTeASQm8A4gMYF3gAYjaoCPjo7G2LFj0blzZ2Rn\nZ6O8vBxA1Q0eIiIiDBKQEEIIIeKJ6sH7+Phg6dKlCA4ORvPmzXHmzBl07NgRZ86cwdChQ7nfwYp6\n8LpRD17ejKOHCFAPXu6oBy9fMu7B//777/Dz86vxvLW1NYqKivRLRwghhBDJiRrg27Vrh0uXLtV4\n/uTJk+jUqZNkoYyRsnqIyutSKW39KG0NKWv9CLwDSEzgHUBiAu8ADUbUAD9t2jTMmTNHe+vKq1ev\n4vPPP8fixYsxc+ZMgwQkhBBCiHiiz4MPCwvD2rVr8eDBAwCAhYUFFi5ciJUrVxokoBjUg9eNevDy\nZhw9RIB68HJHPXj5atgevF4Xurl37x7S09OhVqvh6ekJa2vreoeUAg3wutEAL2/G8QEF0AAvdzTA\ny5eMv2Sn0axZM/Tp0wf9+vWTzeDOm7J6iMrrUilt/ShtDSlr/Qi8A0hM4B1AYgLvAA2m1mvRT5ky\npc4L27ZtW73CEEIIIUQatR6iHzlyZLXpkydPwsTEBF5eXgCA8+fPQ61W46mnnsLBgwcNl7QO6BC9\nbnSIXt6M4xAjQIfo5Y4O0ctXwx6ir3UP/ttvv9X+vHr1alhaWmL79u2wsrICAJSUlCA0NFQ74BNC\nCCGEP1E9+PXr12P58uXawR0ArKys8Pbbb+OTTz6RPJwxUVYPUXldKqWtH6WtIWWtH4F3AIkJvANI\nTOAdoMGIuh98cXExrl+/Dk9Pz2rP37hxA/fu3ZM0GCG1MYb7WQPi7mlNCCFSEXWaXEhICOLi4vD+\n+++jf//+AIBTp05hyZIlCAgIwI4dOwyVs06oB6+b0nrwxtFzA5TVEwWoBy93StreqAdf6xKlOg/+\n/v37WLBgAbZt26a9k1yTJk0QGhqKDz74AM2aNZMmsZ5ogNeNBnhelPSBC9AAL3dK2t5ogK91iVKd\nB29paYlPP/0UhYWF+PXXX/Hrr7/i1q1b+PTTT7kP7rwpq4eoxC6VwDuAxATeASSlrN8fgXcAiQm8\nA0hM4B2gwYjqwWtYWVnB29tb6iyEEEIIkYhel6qVKzpErxsdoudFSYdMATpEL3dK2t7oEH2tS5T6\nUrVSio2NRbdu3dClSxesWbPmsfOdPn0aZmZm+N///teA6QghhBDjxHWAV6vVmD17No4ePYoLFy4g\nJiYGGRkZj5zvzTffRGBgIIeUdaOsHqISu1QC7wASE3gHkJSyfn8E3gEkJvAOIDGBd4AGw3WAT01N\nRefOneHq6gozMzMEBwfjwIEDNeb75JNPEBQUBAcHBw4pCSGEEOMj+kt2+fn5iIqKQnp6OlQqFTw9\nPTFr1iw4OjqKfvO8vDy0b99eO+3s7IzU1NRq81y/fh379+9HQkJCjdfkxN/fn3cESfnzDiA5f94B\nJObPO4CklPX74887gMT8eQeQmD/vAA1G1ACflJSEYcOGwdHREX5+fgCA6OhorF27FkePHtU+J6W5\nc+dW683X9gWFkJAQuLm5AQBsbW3h6+ur/fDQHAZsrNNA1cEp/3/8DBlOa9SlHmOqqLHVo7Tpv6oG\n/3//2qb/mqJ6OOWtbfqvKT23R83POTk5qBUToX///uzVV19llZWV2ucqKyvZq6++yvz8/MQsijHG\nWHJyMgsMDNROr169moWHh1ebp0OHDqxDhw7Mzc2NWVtbM0dHR3bgwIFHLk9kOZJKSEjg9t51BYCx\nOj4SRMwr9aOu6xGAiMUm8Cqn0dYjhrH8/sh/3RhiezOObU1p9Yip+3FE7cGnpaVhx44dMDH5u3Vv\nYmKC+fPno2fPnmIWBQDo27cvLl++jNzcXLRt2xZffPEFYmJiqs2TlZWl/Xny5MkYOXIkRo0aJfq9\nCCGEkMZE1JfsbGxskJ2dXeP57Oxs2Nrain5zU1NTREZGYujQoejevTuCg4Ph4eGBjRs3YtOmTTXm\nrzrPUZ6U1UNUYpfKn3cAifnzDiApZf3++PMOIDF/3gEk5s87QIMRdaGbuXPn4quvvkJERAQGDBgA\noKovv2TJEowbNw4fffSRwYLWBV3oRje60A0vSrrwCEAXupE7JW1vdKGbWpco1YVuIiIiEBQUhClT\npsDd3R3u7u6YOnUqxo4di/DwcEnCGitlncerxDNFBd4BJCbwDiApZf3+CLwDSEzgHUBiAu8ADUZU\nD97c3Bzr1q3D6tWrkZmZCQDo1KlTo7/RDCGEECI3el+Lvri4GABgbW0taaD6oEP0utEhel6UdMgU\noEP0cqek7Y0O0de6RCmvRf/xxx/DxcUFNjY2sLGxQfv27bF27dpG+QtPCCGEyJWoAX7x4sVYvnw5\npk+fjuPHj+P48eOYMWMG/vOf/2DJkiWGymgUlNVDVGKXSuAdQGIC7wCSUtbvj8A7gMQE3gEkJvAO\n0GBE9eC3bNmCLVu2ICgoSPvc4MGD0bVrV0yfPh0RERGSBySEEEKIeKJ68K1atcKpU6fQpUuXas9f\nunQJTzzxBP7v//5P8oBiUA9eN+rB86KknihAPXi5U9L2Rj34WpcoVQ9+4sSJiIqKqvH8Z599hgkT\nJuiXjhBCCCGSEzXAl5aWYseOHejWrRtCQkIQEhICDw8PbNu2DRUVFZgzZ4720dgoq4eoxC6VwDuA\nxATeASSlrN8fgXcAiQm8A0hM4B2gwYjqwWdkZKBXr14AgNzcXABAmzZt0KZNG1y8eFE7n5wvKUsI\nIYQ0BnqfBy9H1IPXjXrwvCipJwpQD17ulLS9UQ++1iXqGPdE7cEDQEFBARITE1FQUAC1Wl3tTWbO\nnKl/SkIIIYRIRtQefExMDKZMmQK1Wo2WLVtWOxSvUqlw/fp1g4SsK5578IIgyP6OWGL24AXwu+eS\nYfbgBfCsqDHWI4ax/P7Ubf0I4HvHMqm3NwHGsK0prZ46L1GqPfg333wTixYtwjvvvIMmTUTv/BNC\nCCGkgYjag7e1tcUvv/yCjh07GjKT3qgHrxv14HlRUk8UoB683Clpe6MefK1LlOo8+Jdeegnfffed\nJKEIIYQQYjii9uBLS0sxatQoWFpawsvLC2ZmZtVef+eddyQPKAb14HWjHry/3pnqh3rwtTGW3x/5\n93gB6sHXRoAx1FPnJUrVg9+0aROOHz8Oe3t7XL58ucaX7HgP8IQQQgipImoP3sHBAUuXLsW8efMM\nmUlv1IPXjXrwvCipJwpQD17ulLS9UQ++1iVK1YOvrKzEqFGjJAlFCCGEEMMRNcBPnjwZ0dHRhsoi\nO23auEGlUsn+0aaNm+S1C5IvkTeBdwCJCbwDSIquRS9nAu8AEhN4B2gwonrw9+7dw5YtW3D06FF4\ne3vX+JLd+vXrJQ3HW35+LozhS0/5+XTtf0IIIdWJ6sEHBAQ8fkEqFeLj40UHiI2Nxdy5c6FWqxEa\nGoolS5ZUe33Pnj1Ys2YNAKB58+b47LPP4OXl9dgMUvY3jKOnA4jpuRlHNdSDlzfqwcubkrY36sHX\nukQd4x7Xm82o1Wp06dIFcXFxaNeuHfr27YsvvvgC3bp1085z6tQpeHh4wMbGBrGxsVi+fDlOnTr1\nyOXRAF/LXDTAc6KkD1yABni5U9L2RgN8rUuU6kt2UktNTUXnzp3h6uoKMzMzBAcH48CBA9Xm6d+/\nP2xsbLQ/5+Xl8YhaBwLvAJISeAeQnMA7gMQE3gEkRT14ORN4B5CYwDtAgxE9wB85cgTPPfccPDw8\ncPXqVQDAli1bEBcXJ/rN8/Ly0L59e+20s7OzzgF8y5YtGD58uOj3IYQ0PLc2ber8RdGAgABuX1J1\na9OG9z8VIQYh6kt20dHRmDFjBqZOnYr4+HiUl5cDqDp9LiIiAs8884xBQgJAQkICtm/fjsTERJ3z\nhYSEwM3NDUDVtfN9fX21V8jS7CXUdbqKgL+/PCf89d9HTfvX8rohp/+aqkM9Qh2X7m/AtLVNa7M2\nwvWjpHpy8/ORwCGd2OmA/PyqaUnXD8/pv6aoHk55a5v+a0rkePTPo1yCICAnJwe1YiJ4e3uzmJgY\nxhhj1tbWLDMzkzHGWFpaGnNwcBCzKMYYY8nJySwwMFA7vXr1ahYeHl5jvjNnzjB3d3d2+fJlncsT\nWU6tADCAGcGjbnWDf9A6PcTUI4O4kq4f/llpe2tM64d/VmlqUWI9Yup+HFGH6H///Xf4+fnVeN7a\n2hpFRUViFgUA6Nu3Ly5fvozc3FyUlZXhiy++qHEhnStXrmDMmDHYtWsXOnXqJPo9Go7AO4CkBN4B\nJCfwDiAxgXcASQm8A0hK4B1AYgLvABITeAdoMKIO0bdr1w6XLl2Cq6trtedPnjyp1+BramqKyMhI\nDB06VHuanIeHBzZu3AiVSoVp06Zh5cqVuHXrFmbNmgXGGMzMzJCamir6vQghhJDGRNRpchEREdi+\nfTu2bNmCYcOG4dChQ8jJycHChQuxfPlyvPbaa4bMWis6Ta6Wueg0OU6UdNoSQNub3Clpe6PT5Gpd\nolR3k1u8eDHu3LmDIUOG4MGDBwgICICFhQUWLlzIfXAnhBBCyN/0utDNvXv3kJ6eDrVaDU9PT1hb\nWxsim2h89+AFyP0ew2L2qATQ/eCl0zjvB994tzcBdD94qdD94GtdolR78BrNmjVDnz596hWKEEII\nIYZT6x78qFGjsHv3brRo0aLWW8UePHhQ0nBiUQ++lrmoJ8qJknqiAG1vcqek7Y168LUusT578HZ2\ndn/9w1X9TAghhBD5q1MPfsqUKVi3bh2aN2/eEJn0Rj34WuZqtD1RgHdFjbUe46iGevC6CZD7tgYo\nr546L7G+N5v5/PPPcf/+fUlDEUIIIcRw6rQHb2Jigps3b8LBwaEhMumNevC1zEU9UU6U1BMFaHuT\nOyVtb9SDr3WJUtwuVtOHJ4QQQoj81XmAb9OmDUxNTXU+GjeBdwBJCbwDSE7gHUBiAu8AkhJ4B5CU\nwDuAxATeASQm8A7QYOp8HvymTZtga2tryCyEEEIIkQj14GtZnvx7OgD1ROVOST1RgLY3uVPS9kY9\n+FqXWN8ePPXfCSGEEONSpwFe6r84lEngHUBSAu8AkhN4B5CYwDuApATeASQl8A4gMYF3AIkJvAM0\nmDr14NVqtaFzEEIIIURCet1NTq6oB1/LXNQT5URJPVGAtje5U9L2Rj34WpcoxXnwhBBCCDEeNMBL\nRuAdQFIC7wCSE3gHkJjAO4CkBN4BJCXwDiAxgXcAiQm8AzQYGuAJIYQQBaIefC3Lk39PB6CeqNwp\nqScK0PYmd0ra3qgHX+sSqQdPCCGENC40wEtG4B1AUgLvAJITeAeQmMA7gKQE3gEkJfAOIDGBdwCJ\nCbwDNBjuA3xsbCy6deuGLl26YM2aNY+cZ86cOejcuTN8fX2RlpbWwAnrSq659KOsagDlVaSseqga\nOaN6jBXXAV6tVmP27Nk4evQoLly4gJiYGGRkZFSb58iRI8jMzMTvv/+OjRs3YsaMGZzS1uY27wCS\nUlY1gPIqUlY9VI2cUT3GiusAn5qais6dO8PV1RVmZmYIDg7GgQMHqs1z4MABTJw4EQDwxBNP4M6d\nO8jPz+cRlxBCCDEaXAf4vLw8tG/fXjvt7OyMvLw8nfM4OTnVmEcecngHkFQO7wCSy+EdQGI5vANI\nKod3AEnl8A4gsRzeASSWwztAg6nz/eCNhfR3vhOzvM8lfu+6q2vdxlGNmPVoHBU11nqMoxpDrB+e\n1SirHnGf6Uqrp364DvBOTk64cuWKdvratWtwcnKqMc/Vq1d1zqOhoFP6CSGEkHrheoi+b9++uHz5\nMnJzc1FWVoYvvvgCo0aNqjbPqFGjsHPnTgDAqVOnYGtrC0dHRx5xCSGEEKPBdQ/e1NQUkZGRGDp0\nKNRqNUJDQ+Hh4YGNGzdCpVJh2rRpGDFiBA4fPgx3d3dYWVlh+/btPCMTQgghRkFRl6olhBBCSBXu\nF7ohhBBCiPRogCeEyIZarQYAVFZWck5CaqNZV0S+aIAnolBHR9727t2LEydO8I6hF8YYTEyqPpKW\nLVuGgoICzomILps3b0ZpaSl9JsgYDfAG8LgNXgl7JZpzOBMTE7Fjxw4cPnyYcyJpaNZNcnIyYmJi\nsGjRIuTm5nJOJV5xcTG+/PJLbT3G9OGrybp27Vp89NFHiIuLq/Z8Y6BZb9evX8dPP/2EXbt2cU5U\nE2MMd+7cgbW1NSoqKrBu3Tpcu3bNKNeT5ihEcXExrl27hvv373NOJC0a4A1As6F//fXX+O9//4t3\n330XQNVZA4DxHtrSfPhs2bIFH3zwATIzM/HWW2/h3r17qKio4JxOf4wx7bqZNWsWTE1NkZCQAH9/\nfyxevBilpaWcE9ZOs82NGjUKt2/fxuzZs1FRUdGgF9WoD83ee0FBAXbt2oWtW7ciJSUFlZWVUKlU\nyMvLw507d3jHNDjNdjh+/HgIgoAPP/wQfn5+2Lt3L+dkf1OpVLCxscHLL7+MwsJCHDx4EAsXLsT+\n/ftx+7ZxXefdxMQEiYmJGDx4MJYvX4758+fj22+/5R1LMjTAS6yyshImJiY4c+YMli9fjqeeegqr\nV69G69atsXnzZgDQHoY0NqampigvL0dkZCS2bduGwsJCBAUFoVmzZoiPj8eZM2d4R9SLZhBcsWIF\nhg4diieeeAJmZmbYt28fYmNj0b59+xo3QZILzR+Ld+/eBQDtdmZlZaXd3oxhz0qzDtavX4/nnnsO\nEydORGpqKhISEgAAb7zxBnJycjgmbDgbN25Eu3btEBoaChMTE0yYMAFhYWEYNGgQbty4wX19agbx\nI0eOIDk5GfHx8RgyZAiioqLw1ltv4cSJEygvL+easTY3btxAdHQ0AODLL79ESEgIpk2bhp49e2L/\n/v2YO3cuTp8+zTll/ZkuX758Oe8QSqIZvCdPnowlS5aguLgY1tbWWLZsGV566SV88803mDRpEszM\nzDgn1U9JSQlu3boFe3t7REdHY9u2bQCAmTNnwtvbG+7u7pwT6ketVqOwsBAvv/wywsPD0adPH4wd\nOxbFxcXo27cvXnzxRd4RH0kzMC5btgxhYWH4448/cOjQIVhYWCAmJgbu7u7o1KkT55R117RpU0yc\nOBEqlQqlpaX4448/cOnSJZw7dw5z587lHa9BnD17FlOmTMGWLVvg7Oys/T6CSqXC+PHjtXv5PDx4\n8AC7d+/G8ePHERUVhQEDBqBHjx7o1asXRo8ejZ9//hk7d+5EcHAwzM3NueXUhTGGjIwMvPjii/jq\nq69ga2uLt99+G25ubnB1dYWzszNycnJgamoKb29v3nHrRXHXoudJrVbDxMQEJSUlmDt3Lvz9/TFi\nxAisXLkSAwYMwNKlS2Fvbw9LS0veUfVmZWWFu3fv4sknn8TixYsBANu2bQNjDIGBgZzT6c/ExARB\nQUEAgG7duqGoqAjXrl1DTEyMdk9Ys37lgjGmHeBXrlyJM2fOoLCwENevX0dSUhK8vLzwn//8B7a2\ntujbty/ntLXLyMiAiYkJrl+/jjZt2mDEiBF45ZVXcP36dcTGxvKOZ1CabSsmJgbdunVD+/btYWFh\nAQcHBwDA+fPnMW/ePDRp0gSVlZXcBvmmTZti9OjRCA4O1n5HJS8vD/b29rCxscGiRYvw5ptvwsrK\niku+ulCpVOjbty/u3buHyMhILFmyBDdv3sTBgwdhb2+PQYMGoUOHDtpLov/z98zY0IVuDGD69OkI\nCwuDi4sL3n77bdjZ2cHd3R0rVqzAiRMn0KxZM94R9VJSUgIrKyuo1Wrs3LkTO3fuxN27d+Hs7Iwl\nS5agf//+XD98xNJkvXr1Kq5fv47r16/jhRdewOXLlzF9+nS0bdsWJiYm2ksly8k/P3Sio6Nhbm4O\nNze3agN5WVkZduzYgStXrmDVqlW8ouqkWQebN2/G999/j8uXL8PR0RFffvklrKysMH/+fFhaWuK9\n997jHdVgNOvy2rVrGDt2LJKSkqBSqXD48GFERESgU6dOOH/+PFJSUrjmLC0thYWFBQDg/fffh5OT\nE7766itYWFhg+vTpyMnJQXh4OH777TeuOWuj2eZ+++03dO3aFXfv3kVoaCiOHTuGxYsXY9myZbwj\nSoYGeIlo/gLfunUrUlNTsXHjRgDAN998g2+++QalpaXo378/5s2bxzmpOJq64uLisHLlSjg4OGDY\nsGHw8fGBh4cHsrKy0K1bNzRp0sRo/9Lt06cPunbtCrVajZKSEixbtgz9+vUDUPVhYGZmJrs/XDT/\n1u+99x727t2LIUOGoKSkBC1btsTo0aPxxBNPAKj6QmRMTIz2G+lyxBjDoEGDEB8fjxUrVkClUmHV\nqlW4cOEC3NzcYGlpKasjJ4ayZcsWxMXFISYmRvtcamoqzM3N4ezsDHt7e67boeYPj8jISDg7OyMi\nIgIAEBkZicOHD6Nly5Z48cUXMWbMGC756kLzeZaTk4OQkBBs374dHTp0AACkpaXhpZdegouLC44e\nPco5qTRogJdQSUkJ3njjDRQXF2Pz5s1o3rw5AODq1ato06aN0fbdAWDEiBEICQlBSUkJfv31V1hY\nWKB3794YMGAAXFxceMcTTfNBmZKSgq1bt2LTpk3Iy8tDbGwsvv76azRr1gyRkZFwdHSU3R8tmsG9\nrKwM77zzDubMmYPWrVvjxIkTSElJQXp6OgICAjB16lRkZWXB1NQUrq6uvGM/1m+//YaNGzdi8ODB\nWLFihfbLTZo20OjRozknNLzCwkLMnTsXGRkZmDRpEgIDA9GpUyfZ/GFTWVmJ77//Hu+//z5++eUX\n7Nq1C4MGDUKLFi0AADdv3oSZmRns7Ow4J9VN87szZcoUeHp6YuHChSgrK0OTJk20/9Z//vkn9z+m\npEJfspNQcXExLl68iMzMTNy8eROVlZVwdnZGy5YtjXpD2b9/P86cOYNVq1ahZ8+e8Pb2Rl5eHo4c\nOSvy6E4AACAASURBVIKuXbvKevB4HBMTE5SXlyMkJATOzs4YNmwYWrRoAS8vLzzxxBO4f/8+nn32\nWdl8wD5MpVLhxx9/RFxcHCorK9GnTx907NgRbm5uaNq0Kfr37w97e3u0bNkStra2vOPqZG9vjwsX\nLmDNmjWYNWsW+vTpg0OHDiE5ORlr1qzhHa9BNGvWDC+88AI6duyI7777DpmZmSgtLUXz5s21Owo8\nmZiYwN3dHZWVlTA3N0dmZiaysrK07ca3334bw4cPR9OmTTkn1U2lUuHu3bv45ptvEBgYCHd3d5SX\nl8PMzAybN2/G3bt34enpCcB4z3b6J9qDl8hvv/2GCxcu4MUXX8Svv/6Kr776Cvfu3UO7du0wbtw4\noxwEgaq/eD/77DO88847GDVqFFasWIH27dsDqPriT48ePTgn1I9arYZKpcLChQtx4MABjB49Gu+8\n8w5sbGwA/L2HL7cv1mnyJCUlYcqUKRg4cCAOHz6MyZMnY+nSpbIYDMQoKSnRHo1YsGABSktLUVRU\nhNLSUixbtgxPP/0074gGo9nG9u/fj+zsbCQkJGDt2rWwsLBAdHQ0Tpw4gWXLlmHgwIGyyFlRUYHC\nwkK0bt0aOTk5WL9+PYqLi3Hjxg3Y2tpqTzuTo+vXryM7OxtPPvkkAGDDhg04e/YsIiMjYWJigqKi\nIvj6+uLEiRPazzdFYEQSx44dY4MGDWITJ05kZ8+eZWq1mn3zzTfstddeYwUFBbzj1VtKSgoLCwtj\nzz//PFu3bh0rKyvjHUkvlZWV1f7LGGNXr15lwcHBrHv37uyjjz7iFU2UGTNmsG+++YYxxlhGRgYb\nPXo069KlC/vss884J6tdRUUFY4yx+Ph49vLLL7PevXuz1atXM8YYu3DhAvvll19YVlYWz4gGp1ar\nGWOM3b17l3l7e7PU1FTm4eHBPv30U+08v/32G694WpqcjDH20ksvsUmTJrHOnTuz999/nzHG2I8/\n/siSkpLY/fv3eUWsk2PHjrHk5GSWlpbGfvrpJ1ZcXMwmTJjABg0axGbMmMECAwPZqlWrGGPVPxuM\nHe3BS6S8vBzXr1/Hvn378N133+GZZ57BrFmzYGlpKfvDVg/T/MVeUFCAkydP4urVq+jfvz8sLS2R\nl5eHrVu3wsvLCytWrOAdVW9RUVHIzMxEp06dMGTIEHTp0gUnTpzA7Nmz8cUXX6B79+68I9bA/uof\nZmZm4tVXX4WDgwPef/997R7H119/jdzcXMyfP59z0rrx9/fHxIkT0b9/f7z++uvIzc3FihUr8PLL\nL/OO1mD++9//wsLCAiNGjMC0adOQmJiIoqIifPTRR5g/f762x82L5rMgPDwcZ8+exSeffII//vgD\nM2bMgIODA6Kjo43iu0WaI1/btm3D7t27MWbMGMyYMQNpaWm4cuUKnJ2dtWegMCP9svCjUA++nhhj\n+OOPP9CiRQvY2tqiV69esLOzQ1RUFI4fP44JEyYY3caiOSQ9cuRIlJWV4ddff0V2djYePHiAl19+\nGX5+fnjqqadgaWmpPdRtDDRZDx48iO3bt2PYsGFYvHgx8vPzcf36dQQEBGDhwoVwcHCQ3S+5Jk95\neTm2bt2Kp59+GteuXcPp06dx+/ZtdOnSBV5eXvDz8wMA2a4XzZUe7969iyZNmmDkyJFwc3PDpEmT\n0LFjR0ydOhXNmzfXnsWgdObm5rh58yaioqKwYsUKuLq6as96mDx5Mu94MDExQVlZGbZt24YxY8ag\nV69esLe3x4QJE3Ds2DF4eHjA3t6ed0ydNIP7xx9/DFdXVwwdOhQJCQnYvHkzOnbsiBdeeEF7zjsA\nWf7e6I3j0QNFOHToELOysmIffPCB9tAjY4zNmjWLnTp1imOy+klMTGRPPfWUdjopKYn5+PiwyMhI\njqmk8fzzz7Nz586xzz77jE2dOpXt2rWLtWzZks2fP589ePCAd7xH0hwqfe+991hYWBhjjLFffvmF\nbdiwgc2ePZtNnTqVXbt2jWfEWmlquHfvHhs6dCjz9vZmkydPZoIgyPbf3dDy8/NZYGAga9KkCUtJ\nSWGJiYmsV69e7PTp04wxVu0zpaHt37+flZaWMsYYi46OZqNHj652KL5v375MEARe8epEs83l5uay\nJ598Uvv8tWvX2FdffcWef/559vbbb/OKZ3B0JTs9lJWVwdzcHH/++Sd8fHwQFxeHpUuX4ssvv8Tc\nuXORm5uL06dPIyoqindUvWku8pKUlIS+fftiwIAB2LBhA3bs2CG7L57VlVqtxr179/DKK6/AyckJ\n+/btw6FDh9C0aVN8++236N+/PywsLGS39w5U7VXcuXMHv/zyC4KDgwEAPXv2hLu7O1JTU3HlypVq\neyFypPl33bRpEzp27IiFCxdCEATs378f6enp6N27N/r16yfLf3+paA555+TkaC8c8+233yI6Ohqv\nvvoqnnrqKYSEhKBPnz7VboLU0FJTU/HVV18hKSkJ//rXvzBu3DicPn0aTk5OeOWVV3D37l24uLjI\n/kuQmu3ou+++g4WFhfYUOCcnJ4wcORI9evRAq1atACjr0LwGHaIXiTGGY8eOoaioCPPmzcONGzfw\nyiuvYNKkSWjatCm+/PJLWFpaYt68eUb7bcy4uDjY2dmhtLQUFy9eRElJCYqKivDhhx+ic+fOePrp\np43ql0GTVaVSwdzcHD169IClpSWSkpKwZ88ePHjwALGxsVi3bh0A+R6ii4+PR3JyMpKTk9GqVSu0\nbdsWLVq0QMeOHdGjRw+YmprKer1ovj+wfv16hIWFwc/PD927d8f9+/eRkpKCiooK9OvXT7b5paD5\nw3jo0KE4fvw4zp07hwsXLmD48OEICwvDiBEjtBcpAvhti7a2tnBzc0N6ejr27duHoqIizJ8/Hy+/\n/DKuXbuGwMBATJkyRdaXpNUoKipCQkICsrOzkZWVBTMzMzg5OcHCwgL29vbaGpS43dGX7PTw3Xff\nYeHChSgsLMTx48fh6ekJlUqFJk2aoKKiAk2aGN+BkWvXrmHfvn3w9PTEqlWrcPToUdy+fRsbN25E\nYWEhbty4AScnJ+0gKOeB5GGaIw579+5FRkYGWrRogc6dO8PLywvr169HZmYmpk+fjuHDh8v+4hY/\n//wzYmNjkZ+fD1dXV/Tq1QsBAQG8Y9VZcnIyhg8fjv9v787joqz2B45/QNkkwQ3XrlioIK64kAub\nmIWaCpFS6L16sTRzX66YKxYuqImWomlGqKVIKqghRuEKCJcUF9xlMUVQQUUBkZk5vz+8MxfarvrL\nnhk477/smXm9+g7PM/N9znm+53tsbGyIiYnRrTnOyMigQYMGNGrUSOEInx/ttbVjxw6Sk5NZvnw5\nu3fv5vjx4xQUFNCsWTPee+89xZvFaH/DvvnmG3bs2IGZmRn169enuLgYX19f3NzcDG45Jjxeyrxl\nyxaKioqwtbXF09OTTp06KR3WcyUT/DPasGEDSUlJ3LhxAzc3N/75z3/q7nKjoqIMrt98eXk5ERER\nTJ06ldatW5OWlqZ77ebNm7zwwgtYWFhgZGRkUFP02lhPnz6Nn58fb775JhYWFuTn59O2bVvGjBmj\nt58nOzubw4cP4+TkRElJiW5kp1KpSElJITo6GiMjI+bPn6/XI6nf+vuGhISwdOlSBg8ezKeffsoL\nL7ygUHR/rfv37+Pi4oK/vz+BgYHA406X8fHx3L59W7eBk9I0Gg1dunQhKiqKli1bcv78eSIiItiz\nZw9eXl4sXbpUL78zWtqbqa+//pqUlBSSk5OZNWsWr7/+OklJSWzbtg1/f388PT2VDvW5kgn+KWgv\nmocPH6LRaKhVqxbnz58nJCSEgoICNBoNrVq1IjQ0VOlQn0pKSgpOTk4UFxczduxYrKysSE1N5Z13\n3iEwMJCdO3eSm5vL+PHjlQ71mU2aNIlXXnkFf39/CgoKOHLkCGvXriU0NBRHR0e9nJH4+OOPmT9/\nPnPmzOHixYtkZmYyZMgQLC0tcXV1pbCwkJo1a9KrVy+9jB8qz/QsW7YMIyMjjI2NmTp1KgUFBYwd\nO5ZDhw6RnZ1t0LssPqni4mKCgoLYuHEjw4cP5+OPP9Y1V7p//z61a9fWixvO4uJiRo0aRd++fRk1\nahTw+MZyyJAhzJw5s9JjBH2jveaKioro0KEDn3/+OYWFhXzyySc0bNiQbdu2cffuXYNssf3U/tqa\nPsNVsQK4b9++Yvjw4WLevHkiKSlJCCFEWlqaSE5OVjLEZ5KTkyNatWqlq/gvLy8XQghx4MAB4e3t\nLdq2bSscHBzE+fPnhRCVG18YisuXL4t27doJd3d3cePGDd1xX19fsWHDBgUj+2Pp6enC2dlZjBo1\nShQWFork5GRhb28vPDw8hK2trZgyZYrSIT6xhQsXioCAABEYGCicnZ3F/fv3dQ1FcnNzFY7u+dJ+\nZ65fv667/s6dOydGjRolunTpIhYtWlTpffoiLi5ODB48WCxevFikp6eL3bt3ix49eigd1hOLiooS\nkydPrnRszJgxYtOmTQpF9NeTRXZPSPznrnDFihUYGRkxdOhQ7ty5w5EjRzhz5gwvv/yyQa7dHTt2\nLAMGDGDo0KFoNBqysrI4evQoZmZmTJw4kU6dOuHl5UW3bt30YmTxpESFkaOVlRWOjo5cunSJqKgo\nMjMzEUKwe/dugoODMTc318sRcOPGjXn99ddJS0ujVatWdO7cmRUrVpCamsq0adNwcHCgTp06ervm\nPTk5GRMTE2rUqMHChQvZsWMHe/fupXv37vTu3Zvdu3dz9erVqv8c9D/nZunSpUybNg1LS0s8PT3x\n9vamRYsWbNq0CQ8PD73ZMyAjI4OSkhI6d+6MtbU1165dY+7cuRQUFDBz5ky9brt9+/ZtatWqxe3b\ntxk9ejTZ2dm0atUKGxsbzMzMOHv2LMnJybz55ptKh/rXUPb+wrBkZ2eL/v37i+vXrwshhLh165aI\niYkRU6ZMEcuXL1c4uqd34cIF4ezsrBs5hIWFCU9PT9GxY0fh7+8vvvvuu0rv17cRxh/Rrh9eu3at\nOHjwoNBoNCI/P19s375ddOnSRbRu3VosWLBA4Sj/mFqtFiqVSmzYsEE4OTmJVq1aiY8++kjpsJ6Y\ng4ODOHjwoFCr1WL27Nli/PjxldYid+vWTddut7qIjY0Vrq6u4tVXXxX79u0TQvz3WlWyRar2/x0f\nHy+6desmbG1txfTp08WhQ4dEYWGhePjwoSgpKVEsvidRVFQkVq5cKVQqlVCr1eL69etixowZom/f\nvmLevHli8eLFYsCAASI9PV0IoWyPgb+KTPBPISEhQdSvX184OzuLixcv6o5fvnxZ3Lp1S8HIno1K\npRITJ04UERERYsGCBcLNzU1s3LhRlJaWijVr1ogRI0aI+/fvG1RiF+K/P1Z5eXnCwcFBnD17Vgjx\nuM/5pUuXxMWLF8X69evFoEGDxOjRo/W+j7YQQmzfvl04OTmJ1NRUIYT+98tetGiR8PHx0f13YmKi\n6N69u5gyZYpIS0sTK1asEP369VMwwr9WUlJSpYQyf/58YWRkJD788EMFo/q1t956Sxw9elQUFxeL\nOXPmiEGDBomgoCBx+vRppUP7n/Ly8sTZs2dFZmammDhxokhMTBRCPL723n77bdGpUyexfPlyodFo\n9P7782eRU/T/g6gwdfvSSy8xcuRI7t69y4IFC8jJyaFnz540atTI4KrmhRAYGxtz8+ZNjhw5Qmpq\nKlOnTmXw4MFYWFhw8+ZNDhw4QEBAgF5O//4RbbxBQUF07dqVfv36sXHjRt59912uXbtG3759cXNz\no2XLljRt2lQv+85raa8/BwcH7t+/z5dffsnAgQMxMzPT2/OSn5/PyJEj6dKlCwC1a9fG0dGR+vXr\nU1hYyJo1a2jUqBEffvih4kvC/grx8fF8+eWX5OfnY2ZmRqNGjfDw8ODnn3/G1dVVb4o8ExMT2b59\nOz4+PjRv3hxPT0/s7e3ZuXMn9erVo3379orG90eSk5PZunUrQ4YMITMzkytXrnD8+HHOnDmDs7Oz\nbvnhtm3bOHDgAO7u7tWiqFNW0f+Bil+6iIgISktLadCgAV5eXmRlZbFkyRIuXLjA0aNHDW5DmYpu\n3rxJnTp1MDU1BR5Xy/bs2ZMlS5bg6emp92vDK0pNTdXVQkRHR5OUlER6ejoeHh6MHDmS4OBgWrZs\nqZcbsty4cYO8vDycnJx0xypeg48ePWLs2LEsWbIEGxsbpcL8nwICAjA3N6dr166cOHECGxsbPDw8\ncHV11X0WQ7qmnsW2bds4dOgQkydPxs7OjujoaBITEzE3N6d58+YUFxeTkJBAbGys0qHqREdHEx4e\nzqNHjxg2bBg+Pj56vfyyosTERFauXElUVBQApaWlfP/99yQnJ1NaWoqdnR0TJ07k9u3bxMTE6FYG\nVHUywT+B4OBgrly5Qnl5OTk5Ofzwww8YGxtTo0YNMjMzadmypdIhPpPfGjXk5OQQGRnJuXPnCA8P\nVyiyZ3P16lU8PT1JSUmhfv36lJSUEBYWRtOmTfH390etVuPk5ERUVBT29vZ6MWqqyMfHh9dee41h\nw4ZV2kVMCIFara7UQElfCx6zs7Px8/MjJSUFeNx97/DhwxQUFNCyZUt69uyp27WrqhJC4ObmRlpa\nGq6urvTu3Ztx48ZRXl7Orl27OHPmDJmZmUyfPh03Nze9OpdFRUVERkZy/PhxLCwscHd3Z/DgwXr3\nXdHSxvXzzz8zYMAAkpKSKvVUKCwsZPv27RQVFelNj4G/kkzwv+PChQs0a9YMExMT+vbty+HDh5ky\nZQrNmjVj+vTpxMbG0qhRI900pCGr+AOjUqk4e/YsL730kt6syX1SAQEBODg4MGPGDFJSUsjIyCAg\nIACAsrIyZs6ciampKSEhIXr3ub799lvCwsJISEgAHv9wRUZG0rp1azp37gzob1L/pcLCQl1/b3i8\nvnv//v2kpaVRUFDA5MmT9fqxyJ/h1q1bBAcHY29vT1FREYmJibzzzjv4+/srHZqO9nq6evUqBw8e\n5MSJE7zzzjs4Oztz4cIFtm7diomJCbNnz1Y61N+l0WjIz8+nSZMm+Pr64uvrq/sbFxUVUVRUxLFj\nx3B1daVRo0ZVfubol2SC/x2BgYHY2dnx7rvvMnfuXIyMjDh48CBHjx4FoFu3bsybN4+BAwcqHOnT\nqZgktJtdaI9r+7UbokOHDvHBBx+QkZEBgJeXF8OGDePvf/+77j2XL1/G1tYWExMTvRuR9O/fn/Hj\nx9O/f38OHDjAN998Q2JiIvn5+QwcOJDw8HC9ivdJVfw7Z2dnk5KSgp+fn8JRPX9qtZrt27cTGhrK\n6NGjadiwIVFRUZSVlTFixAgGDBigN9egt7c3Li4unDhxgoSEBFxcXAgNDeXFF1/UNd/RV+fOnaNz\n584EBgbSsWNHUlNTqVu3LmlpaWRmZmJpaUmTJk3Ytm2b0qEqQv+HAwrQaDR06NCB1atXs2PHDtzd\n3YmPj2fAgAFkZ2fz2Wef0aBBA4NL7trCuocPHzJ16lQCAwOZN28et2/fxtjYGCMjI1QqldJhPpPv\nvvsOOzs7Ll68SGhoKDVr1qyU3IcPH44QAhMTE0D/NpZwdXUlOTmZ69evM2nSJGxsbPjhhx+4efMm\nd+7cITc3V+kQn4mRkRHaMUSLFi2qfHLft28fly9fRqPR4Ofnx8aNG8nNzaVz584sWbKEbt26cefO\nHUC5a7DimG7//v08ePCA6dOnc+nSJWJiYlCpVLz88svs3LlTr5M7QJs2bSgqKqJGjRr4+voSEhKC\niYkJvr6+bNu2jYSEBF1y12g0Ckf715Mj+D+wd+9e1q1bx6hRo7hx4wZnzpwhIyMDR0dHJk+ejL29\nvdIhPhXtiCEwMJCMjAxGjx7Njz/+yOnTpxk6dCjvv/++0iE+s9zcXL766ivOnTvHTz/9xKRJkxgz\nZgzw+DwuXryYxMREhaP8tbKyMu7evcujR4/w9vbGxMSErl27EhISgqWlJQ8fPqRr167ExMRgZ2en\ndLjSH/jxxx/p27cvzZs3Z9q0aWRkZPDw4UOuXLlCu3btCAsLo7S0VLfiRqkR/L1793TtcRMTE7Gw\nsODChQvs2LGDb7/9lj179pCcnMyMGTP0pvnOk7h37x5jxowhOzubjRs3VvnHQE9CLpP7Ay1btiQ/\nP5/9+/cTGBiIt7c3b7/9Nv379ze4Xa+0U/N5eXmcPHmSBQsW0LVrV3r06MHf/vY3Nm/eTHp6Oq+9\n9prSoT41IQRWVla4urpiZ2eHSqXiypUr3LhxA3Nzc6ZPn05ISAi2trao1Wq9eo69detW3YYeQUFB\n+Pn54ePjo1vRMHv2bJo3b46/v7/eTOlKv61FixYUFxeTlJREWVkZn3zyCZaWltSqVYsWLVrg4OBQ\naUSs1LlctWoV1tbWmJmZ0bp1a5o0aUJBQQFXr16lffv2fPTRRzg7O+Pi4qJIfM/K3Nyct956i65d\nu+Ll5cWZM2fw9vZWOixFyRF8BVlZWZw+fRqAQYMG6Y4vXryYffv2ER4ebvCjqMDAQFavXs3cuXOZ\nOXMm8Ph5YV5eHqamptjY2BhMMdcfiYmJITY2lrNnz2Jra8uWLVuUDuk3HT58mEOHDpGXl0eLFi1w\nd3fH2dkZtVpNeHg4a9euJSEhAWtr6ypxXqqqX9YavPfee1y6dInVq1fzxhtvKBzdfz148IDr169j\nb2+Pr68vrVu3ZuLEidjY2DBixAjgcZHkvn37FI70/0cIQWZmJnZ2dtX6xlgm+Ap2797N1q1buX//\nPhcuXGDgwIGUlpbi7OxMTEwMzZo1Y82aNUqH+dR+eYF//fXXBAcH06FDB4KDg2nVqpWC0f05tAWD\nFZPggwcP2LVrF/369aNBgwZ6myArrtlVqVT06NEDX19f7t+/T1ZWFh06dKh21b+GSAiBRqPRnafo\n6GimTp1K/fr1WbNmjV7sVTFnzhysra3x9vbm6tWrJCQkcOrUKV2Fv1qtRqVS6YpvJcMmE/wvaH9I\nU1NTuXLlCg8ePCAqKgqVSsWdO3c4ceKE0iE+lYrJPSUlhcaNG2Nra0t5eTlBQUGEh4czYsQIFi9e\nrHCkT0+bsDdv3oyZmRlDhw791Wta+nYXX1BQ8Ksubrm5uezbt4/IyEg+/PBDevfurVB00v/HL2/G\nZs+eza1bt1i/fr2CUUFISAinTp1i9erV1K1bF3i8PLNevXrExcVx+vRpgoKC9HorWOnpyAT/hAoL\nCzE1Na3URMGQrFixgoiICKytrXFzc6NPnz707t2bzMxM0tPTDW53JW0CV6lUjB07lnHjxtGpU6dK\niVzfkrqWEAJPT09sbW1ZtmzZr7rSff7551y7do2goCA5ajcg58+fx8HBQZfgVSpVpeZEoFwHv7y8\nPNzc3EhMTNRdb6tWrSI4OBhbW1umTJlCSUkJr7/+evXYJ72a0L/5Sj2jXVpRr149g0vuSUlJjB8/\nnnPnznHw4EEOHDjA+vXrMTMzY+vWrSxYsACNRqNL7oZ0r6cdnc+dO5fY2FgePXoEPC5cUqvVun/r\nIyMjIzZs2IC1tTV9+vRh2bJllV4XQpCVlSWTuwFJSUnhyy+/BNCdt5o1ayIeb+ile59S5zQuLg53\nd3dsbGwoLy+npKSEuLg4Dh06xLhx44iPj+fNN9+Uyb2KkQn+f9DHZ7ZPysLCAmNjY2bNmsW9e/cw\nNTXFwcGBuXPnMmTIEK5du8aDBw9079fXhPhL2puue/fuMWzYMNq2bcurr77KV199BTz+EdX3m5WW\nLVuyatUq1qxZQ2JiIs7OzkRERHDkyBHWrVvH/Pnzgeq5dtcQ1a1bl6NHjzJmzBiKiop0x/WledQr\nr7xCfn4+5eXlmJiYUKtWLYKCgnB0dMTFxYXc3FyDG8BI/5ucoq/ibt++TWpqKosWLcLExIRx48bx\n1ltvAY83L9EuxzJEgwYN4v3336d///7s27ePKVOmYG5uzurVqw1qiY9arSY6OpqlS5fSp08fHBwc\n+Mc//qG3RYFSZdpHQWVlZcybNw8PDw/69eundFg6QggePnyIv78/NjY2TJgwodLOcH5+fri7u/PB\nBx8oGKX0PMgEX03k5uZy8OBB9uzZg7m5OWPGjKF79+56+5z692jjTUpKYs2aNWzatKnStOeCBQvI\ny8tj7dq1Ckb55zC0c1Md5efnExkZSZ06dejXrx/r1q0jLi6O+fPn611PiZycHNatW8eDBw+oV68e\nHTt2JCMjgz179pCamqp0eNJzIBvdVEHaZi6HDx/ms88+45NPPqF27dq0bt2a1157jStXrlBcXIyz\ns7PBJRBtvN988w0rV66kvLycPn366F738PDQrTvW9tc3VIYce3URHx9PXl4e3333HampqRgZGbF3\n714ePHiAi4uLXrV6rVOnDl26dEGlUnH16lW2b99Oz549mTBhAg0bNlQ6POk5kCP4Ksze3p6QkBBy\nc3O5dOkSZWVlLFy4EAsLC0xNTTE2NjboUWJsbCzLli1DpVIxa9YsvZoWlaqfzMxMmjZtyokTJ9i0\naROPHj0iLCxMrimXFCMTfBUVFxfHqlWrdB2p7t27x/vvv0+7du30evvH31NxWVxWVhbGxsbY2dmh\nVquJiIhg2bJleHp6GmQjIskwVbwmf7kcDh5vhLJr1y4cHBwUiE6SZBV9lRITE0PDhg05cuQIXl5e\nWFtbs2nTJm7evIm1tTUBAQG67VQNjXaW4YMPPiA0NBQnJyfee+89Ll68SEBAAAcOHGDcuHGAYS33\nkwyXtgDyl8ldo9GQm5tL3759ZXKXFCVH8FXMypUrWbx4Md26daNnz56YmZlhamrKrVu3+PHHH5kx\nYwaDBw82qApt7WOE48ePM2HCBBITE3F1daV27dqkpqYyYsQI5s+fj5WVldKhSlWY9jtTVlbGmTNn\nuHfvHi+99BI2Nja/ucTMkL5jUtUkE3wVUfFZukajYdq0aWzYsAEbGxsmT56MlZUVJiYmDB8+3Jfm\nAAAABtNJREFUXOFIn92SJUto0aIFpqamREZGEhkZycKFC/n88885cuQItra2SocoVWHa71hAQAAl\nJSVkZGTg4eFBr169ePvtt5UOT5J+Rd5eVhHa5K6toA8NDeXs2bN06tSJ4OBg6tSpo0vuhtQ8ZfPm\nzcTFxZGbm8vMmTPx9fXl0qVLNGnSBHj8uWfNmoWtra1BfS7J8BgZGXHmzBnS09PZtm0bp0+fxtXV\nlY8//pivv/5a6fAk6Vdkgq9itGvCNRoNzZs3Z9euXXz11VfMnTuXjz76CDCc7nzHjh0jLCyMpk2b\n0qBBAwBMTEzw9vamsLCQkSNHsn79evz9/QG5rEx6/u7evUv9+vXJzs4GYOjQoYSGhnLy5El5gynp\nHcP4pZeemnYJnEajYcCAAezfv5+0tLRKbTT13b/+9S9mzJhBhw4dKnXca9WqFf369WPUqFFs374d\nKysr1Gq1TPDSc+fi4oKTkxNRUVEkJiZSXFxMXFwcJSUlBnPjLFUfv17bIVUZFftg5+Tk0KxZM4Mp\nRDt16hTm5ub4+PjoRkbaH9Dy8nLq1atHr169dMfkxizS81CxtuXKlSu88MILeHl5sWPHDrKyspg3\nbx516tTRTdEbcl8JqeqRCb6a6NGjB126dFE6jCfWrl07LC0t+emnn3RxazfKUKlUrFixAltbW7kM\nSXqutAl7wYIFJCcnc+nSJcaMGYOXlxdt27bF3NwcU1NTzM3NZdW8pHfk1VhNGBkZGUxHLSEExsbG\ntG/fntmzZxMfHw88fv4OEB4ejpWVlUzu0nOlvQ7z8vKIjo5m7969JCQkULNmTZYvX052dnal+hCZ\n3CV9I5fJSXqrrKyMTz/9lJycHCwsLOjcuTMqlYolS5awc+dO7O3t5ahJeu6++OILoqKi2LVrF7Vq\n1dIdO336NMuXL9fdeEqSvpG/jJLeMjMzY9KkSQwePJi6deuybt06srOzWbZsmUzu0l+iqKiI7Oxs\n7t27x7x58zhy5AgApaWl5OXlyeQu6TU5gpcMlixokv4q6enpbN26lczMTK5fv069evX44osvaNy4\nMWq1WhZ5SnpJJnjJoMikLj1v2oQdHR3NyZMnyc3NZeLEiTg6OhIXF0dUVBQNGjSga9eu9O7dGxsb\nG6VDlqTfJOc3JYMik7v0vNWoUYOysjLGjx9P48aNadGiBcOGDWP69Ol0796d5cuX06RJE+Lj4yku\nLlY6XEn6XXIEL0mS9B/aGaJr167x7bffMnnyZABd7ceuXbs4duwYzZs359y5c7Rp00bhiCXp98kE\nL0mSxH93f8vOzmbRokUcP36cGTNm4OnpqVsKd/LkSTp27KhwpJL0ZGSClyRJqsDPz09XPPfw4UPa\ntm2Lq6srbdq0wdLSEpC1IJJhkJ3sJEmq9rQJOzExETMzM1atWgVAXFwce/bs4dixY0yYMAEXFxdA\n1oJIhkEW2UmSVO1pE/bRo0fZsmULc+bMAcDLy4uVK1fSr18/OTUvGRw5RS9JklRBbGwsoaGhlJaW\nMnPmTN544w3da3JqXjIkMsFLklRtaQvrVCoVWVlZGBsbY2dnh1qtJiIiguXLl+Pu7s7atWuVDlWS\nnppM8JIkVVvaEfno0aOpWbMmW7Zswc/Pj6lTp9KmTRvy8vIoLCzE0dFRjt4lgyOfwUuSVC1pE/bx\n48fJyMggLCyMjh07cv36dVxdXZk2bRq1atXC0dERkIV1kuGRCV6SpGpJm7C///57JkyYwM6dO2na\ntCmxsbFMmTKFqKgo7ty5o3CUkvTs5DI5SZKqnc2bN2NjY0OHDh2YOXMm5eXlrFixgiZNmgCPk/+s\nWbOwtbWVuxZKBktetZIkVSvHjh0jLCyMpk2b6jrUmZiY4O3tTWFhISNHjmT9+vX4+/sDcmpeMlyy\nyE6SpGrF1dWVqVOn4uPjU+m4RqMhMjKSF198ETMzM5ydneVWsJJBk1P0kiRVG6dOncLc3BwfHx80\nGg2Abvq9vLycevXq0atXL90xmdwlQyan6CVJqjbatWuHpaUlP/30E8bGxhgbG1NeXg6ASqVixYoV\nXLx4UeEoJenPIRO8JEnVghACY2Nj2rdvz+zZs4mPjwceP38HCA8Px8rKCgcHByXDlKQ/jXwGL0lS\ntVJWVsann35KTk4OFhYWdO7cGZVKxZIlS9i5cyf29vaycl6qEmSClySp2nn06BGHDh3i3//+N/v3\n7+fVV1+lS5cu9O/fXyZ3qcqQCV6SJKkC2ZJWqirkbaokSdVexXGOTO5SVSETvCRJ1Z5M6lJVJBO8\nJEmSJFVBMsFLkiRJUhUkE7wkSZIkVUEywUuSJElSFSQTvCRJkiRVQf8H2hl4B19OxkoAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa8062cbb50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Parametros Geomorfologicos de las cuencas \n",
"cuCap.GetGeo_Parameters(rutaParamASC=ruta_images+'param_cap.txt',\n",
" plotTc=True,\n",
" rutaTcPlot=ruta_images+'Tc_cap.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"No se tienen en cuenta los tiempos de concentración de campo y munera y Giandotti, los demás si, se tiene como tiempo de concentración medio un valor de $T_c = 2.69 hrs$"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"34.8"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"0.58*60.0"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#Tiempo medio y mapas de tiempos de viajes\n",
"TcCap = np.array(cuCap.Tc.values()).mean()\n",
"#Calcula tiempos de viajes\n",
"cuCap.GetGeo_IsoChrones(TcCap, Niter= 6)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAAESCAYAAADdWICBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4FVX6xz+TRgmETkA6IVQRUbDSrCD2irq6NhR7d9ey\nPyxr17VgRRRdexfXggUrqChFBREkhFCkC4RQEtLm98e5k9vvnbl3+j2f55lnZs60EybcfO/3vOd9\nFVVVkUgkEolEIpEYI8vpDkgkEolEIpF4ESmiJBKJRCKRSFJAiiiJRCKRSCSSFJAiSiKRSCQSiSQF\npIiSSCQSiUQiSQEpoiQSiUQikUhSIKmIUhSlt6IoPyuKMj+w3qYoypWKotyqKMqfgfb5iqKMiXN9\nC0VR3lIUZbGiKIsURdk/5NgVgfaFiqLcG9L+XOBZYwP77yqKclzI8SWKotwcsv+2oignpPqPkIlY\n9V4TXS/fq7VY+X81cPw6RVHqFUVpHdIm36nFWPh/9Q5FUX5VFOUXRVFmKIrSOeQa+V4txsL3en+g\n7RdFUd5RFKUg5Br5Xs1GVVXdC0J0rQW6ALcC1+q45gXgvMB2DlAQ2B4FfAbkBPbbBtYDAvfOBt4I\ntF0H3BvYbg3MAz4IecYaoL2Rn0Uulr3XmNfL9+rddxrY7wx8ApQBreU79f57BZqFnHMFMEW+V1+8\n18OBrMD2vcA98r1atxgdzjscKFVVdXVgX0l0ckABD1dV9XkAVVVrVVWtCBy+JPDyagPH/gq01wH5\nQB6gZQL9Hjg4sH0Q8AHQLvCM7sAuVVU3GvxZJEHMfK/xrpfv1V7MfqcPAzdEXCbfqf2Y9l5VVd0R\ncmo+sDmwLd+r/Zj5XmeoqlofOHU24gsQyPdqCUZF1DjgtZD9ywOW4bOKorSIcX4P4C9FUZ4P2JLP\nKIrSJHCsNzBCUZTZiqJ8pSjKEABVVZcAucA3wJOBc+cBAxRFyUG86O+BPxRF6RuyL0kdM99r5PUt\nQb5XBzDtnQbs/tWqqi4MvUC+U0cw9f+qoih3KoqyCjgXuAfke3UIsz+DNc4HpoN8r5ah17JC/ONv\nAtoF9tsBSmD7TuC5GNfsC9QAQwL7jwC3B7YXAo8GtocCy5M8fyawP/Al0ALhZF0APA5c5LSl59XF\ngvea9Hr5Xr3zToEmiG+zzQPtZUAb+U69/V5jnPdP4Hn5Xv3zXoFbgHd0PF++1zQWI07UUcA8VVU3\nAaiqukkNvAFgCkIIRfIn4hvs3MD+28A+IcfeDdxrDlCvKEqbBM//DhiBGMffhvhgPwg4EKmW08HU\n96rz+lDkezUfM99pEdAd+FVRlDLE0MA8RVHaJ3i+fKfWYPZncCivAkOSPF++V2sw/b0qinIuMBY4\nU8fz5XtNAyMi6gxC7EZFUTqEHDsJ+C3yAlVVNwCrFUXpHWg6DPg9sD0NODRwr95ArqqqmyPvEcIP\nwATg18D+AuAAoKuqqlHPlujG1Peq5/oI5Hs1H9Peqaqqv6mq2kFV1Z6qqvZAfHgPVhPHSch3ag1m\n/1/tFXLqCcAvSZ4v36s1mP1exyDiF49TVXW3jufL95oOeuwqoCnCbmwe0vYi4h/7F4QgKgy0dwQ+\nDDlvEDAncN67QAs1aGG+hBjWmwuMTNKHdojAuPNC2r4CPnbazvPqYtF7jXm9fK/efacR919OYHae\nfKfefq8I92IB8DPwDklmYcn36pn3WgKsBOYHlifle7Vu0cZdJRKJRCKRSCQGkBnLJRKJRCKRSFIg\nx4mHKooi7S+JRCKRSCSeQVXVqPxdjogoADmM6B+2bt3KrbfeyqRJk5zuisRESkpKeO2115g4caLT\nXfEnZWUwfDhs2BDeXlsr1qecwrVP7U2/L5Yy5I3omO/CPzayx+/rxSU52QDkoMCFF8KTT0adrzF7\n9mzmzZvHZZddZs7PIXEFr776Kq1ateKoo45yuiu+RFFi5z91TERJ/EOjRo0YPny4092QmEzLli0Z\nMiTZrHdJSsyfLwTUrl0xDy/fvxv3v3EQalYWc8ftw9xx0VkJcqpquGmvh+lcspac2rrggaee4osK\nMQn6MDrDscfCuHENhwsLCxk4cKC5P4/EcYqLi8nPz3e6GxmHFFGStNm9ezczZ87k1FNPdborEhMp\nLy9n7ty5jB071umu+IuVK2HYMKisFPsXXsglT/QNO6U+JwvifPPVWNa4Nxf88STZAQHVtGIXb7Q/\nh+z6eg575Zvgia+8Ak2bNuxuVVUWrl7NiBEjzPl5nKCkBJYsga5dYdAgp3vjCkpKSmjVqhX9+/d3\nuisZhRRRkrSRTpQ/kU6UBdTVwb77BgXUWWdx1YNF1Odmp3Y/RaEuV3yMb29TwBVz/0O3RasAaLKj\nkisveVqcd9xxDZfs1bEjO15/PeUfwXG2b4e99oKqKrFfUgK9eiW+JgOQTpQzSBElSRvpRPkT6USZ\nzJIlMGIEbA7kFB4/nisfLmZ3s0aGb7WCHjHbSwf3pHRwz4b9/PKdDPhuCQBZdfXsN30eOevWMfTw\nQ6nKyaYx2XDoofDBB0mdL1fw00+w//7hbcXFMG0aHH+8M31yCdKJcgYpoiRpI50ofyKdKBOZM0f8\n8dcm1IwZw4Qpe1r+2DdvPCW4o6o8OPJmBs78nSY1dVATiKP66CO+PmME1U3yOJKuwfOzsuD88+Hg\ngy3vpy6++QZGjYp97IQT4J134KSTbO2Sm5BOlDNIESVJG+lE+RPpRJnEypVw4IFBAXXZZUx4zIHh\nJ0Xh+m/upvKb39j+83K6TBjDy10uoGDLdka9MSv2NVOnwvTp0e35+XDQQZCd4jCkUZYtCxNQL916\nOi/fdgaHvfQV//j7I6Lx5JNFX/PyRMxZXp49fXMJ0olyBimiJGkjnSh/Ip0oE6iqgoEDRSwUwIUX\nctXdXdIaOos3lKcLRUHt1p6crCx2N23Etd/dS78flkSd1nvOMo59KiCe4k2Zf/xxsCNNwubNECIM\nXr3lVN76h3CcvjpjBKqi8M+zHxYHtb7+859w773W981FSCfKGaSIkqSNdKJcQkWF+Aa+cqXYb9EC\n3n0XUhRCMZ2oCy6At9+GNm3Et/4+fUzouE/59VcxFLZzp9i/4AIum9Sb2sa5ad22O2VpCanqDeXs\nWLiC1iMGsLpvZ1b37Rx1zoyzD0FRVTqUbYg6NuTTn8XG5Zez8+Z/kE8ONGkCL7wAY8ak3K+YzJol\nUkEE+N9lY3nxjjNRs0SxjfqcbL48axQdyjYw4LvFwb7ddx8z1vzI4S99ZW5/XIx0opzBkdp5iqKo\nMtmmf9i1axcfffSRFFFO8b//wYcfij84ixdHH78T0D5XT4z4fzd5MsybF/O2lVVVbNq4ka5dQ+Jk\npkwJbufkwOzZsGpI9H0zndmzxRCexgknMOG9UabdPh0RtatsA1Wr/6L1iAEpXb/P579w+zH/Jq+6\nNurYxxceyVi6BRvGjDEep6Sq8MADYggv5Pdt+vgjeGTK5Qkv7b5wBZP2u4FGVdXR/Rk+HM4+21hf\nPMScOXPoMGsWXbTPgJwckXh18GBnO+YTFEWJmbFciihJ2siM5RazYQP89lv844cfHr4/cqT4Ax46\nnHFbyPFhM8R68+awJIwpkQs8AbRFCqlQDjkEvv5abF9zDRP+09XU2W/piKjy2X9QMW8ZXS87OuV7\n5FXuJicgog5/6Wsuu+KZ+CfPmGHs5osWwVVXhTU9f9dZvH6zvi9peZW7eT9/HFmx/sbMmSNSTHhh\nJqJeqqth9my++OQTDrvnnvBj+fmwdCnssYczffMRUkRJLEM6URZSXy8+ACNLg8TigQegZUsYOxa+\n6QRvAe/pfM7kyWL984SGpu2VsGIjDOwWcW5H4Bvgy8B+E2Aq0AgppDQOPFC4UZdcAvfdx4TmU029\nvZNOVCQ51TUc+P5PNNu6o6Etr6qaS696Nu17PzL5UiqbN+H7E/anuon+VBA9f1lOn59KGvavnhBS\nBufzz6O/eHiZa66BRx4Ja3qvxwmcWDZN7LRsCevXQyPjqTQkQeKJKBkTJUkbGRMV4IMPxB9NLQlg\nJBUV0L59/OOxqK4WyQVB5PPR2PRl+Hl9gKIbxPaPQGPgTGAnsC7JM4YB7QLi6chg8/q18N4sGHhk\njGv6ACrwFVAJnAfcDbynZLaQqquDI48UAgrE8FHz5s72KYLQmCgzqM3LZeap0WkQmpXvZOA3i1K6\np5ql8OElR/HdSQcmPzkGy/fuyfK9g/myGu/azcXXPCd2jjgCnnlGDHV5nTPOgJDEqV+0GcSXRafy\n0KBrmfzNBP6+9CUoLxdfxL79FgaY884lQaQTJUmbjHaiqqvh/vth3bqERV/Tpj8itslGNm2DOctg\n7L4JTroHmBPYPg84NrCdqUJqxQroEXCJWreGP/5gQttXzH+Mi5wor3DMU9O54tKngw2XXgqtWsH1\n1wu3xmvU1DSkcdiRl8+Qkc/zR+sB0DoYWP7RR2MZuyokRcWll+q7d9OmYki1c/Skg0xFOlESy8hI\nJ2rzZhG7MWMG/Pvf4ceeflrkrAH4qJ1Y/wPYGDg+DjBaaL1Z6l1NlfKdMLc0iYi6EXgU+BZYDIwG\nMis9T2zy82HtWkuGUNJKcYD5TpRX+PCSo/iz9x7cd/hE0aB96eneHcaPj3/hmjVQWhretvfeUFBg\nST918/vvDZvtztlE1fL3YPvKMBF19NiPeGLmZVy66CnRYOSL3g8/wN13G+tTv37Qrp2xazyOFFGS\ntMnIPFH77AOrVoW3Pf64mPp/8snwYB70BbTP2VuBXxDxQwci4odcTst8GFKU5CQFaBHYng1MAq5H\nDuu1betKAQWQV9iSZgO7p98ZD/LLoXtx27SbafvnX4x48zv2+nYRT1T+xGXEEVEVFaKsjFbrUGPI\nEBGk7hRffy0mLwBV2Y2oymkCLYshJyJPlKJw0/73MLfdEJrUVUbfJwZXLphEn21L4bvvxCQVI7Rr\nJ7485GSOtMicn1RiGb5zolRV1OFK9CG5fr1YDx8uPjBuugnmHgkVwIMxzu8YWDyELicKYBQiyHwn\nsMnybmUsZggoyFwnCgBF4YfjRe29LkvWsNe3i7jsyimQNUgkDt29W8S0LV0qztf+nwPfDhxO+/KN\n9F39B8ydy7o2HelY0Fh8eTo69ZmOhnn+eVGOJ8DEo+8QG+Ul0KhVmBMFUNGoBc/3Ox+9fNjtGB6b\neQUtq8sNdWvEupmwaZMYIm0WsM6HDoX33/fXbMgIpIiSpI3nnChVhaeeCn5QRrJ+vQgST0Yn4KiZ\nYntuSFK/vmn30BXocqIAegD/hxjak1iCWQIKMtuJCqVk35Bf7ssvh5ISWLBABGBH8ObIUxk38U1y\namtYcm5fitYtp+OW9bAFOOaYqJQMumjZEq6+2lg81muvhQmoK096lMdGXglLiO1EpcCq5t04fuz/\nDF/31fujGLX2G9ixQywgPkc3bIAOHdLul1uRIkqSNpY5URs3RscimEFJib5yFQUFsCSkJMakiFwr\nDsQp2YluJ0piGr0opYhlYW2fMtrUZ2S0ExXC5+cexpriPXh4WED9P/pow7GSTr0Y8XBQTK1vLURA\nbU4u/Z5fTJuKzZzy7ds89viVUdcaoqwMLr44uK8oIt6qcePoc+fPhzPPbNgde9FHTB8QUk0gjhNl\nF4ce9yWFuzaw/8YfmfbJiaIxO1sEqfsYKaIkaWOJE7VzJ/TqFZzebxUPPxzcnnFN+LGiCnghRDjp\njSNdgi/cKN1OlCQtehH8ohApoABG8ymfMto0N0o6UUF+P7gft713Ex1WbGxoW1wykI8OOJr1bWKP\nv9fk5rG+TUcmHzOB8mYtaVOxOfbNE6QWefD968mpr4MXXxRLKEcdBR9/HN42fbrI/xbg1HPfZHr/\nkNkpfYGN5jhRqaIqWazP78i2vBbBxs8/dz4A32KkiJKkjelO1IIFMGJEUEAdcED48d9mx7+2CSJH\nUjIUYH+gMkQ4Rae6yWikE2WAhx4SbkRNTVjzA1xJrwSXxRJNsTBTSEknKpwfTgh+vpRSRNmG7tQv\nSi5GanLzePmIkDIykUUFEpSV/KbXSB6cdj1Na3Y1tPXbsJiWlduEYAottQSwenXD5rUn/Ie3B8f4\nrG1aAk1bQd/+4ouc04wa1RD87mekiJKkTdpO1F9/wRNPBMfRHwyJzD72WFEbTuNABfZMcr++QO/U\nuyMRpORElSAScB5C5szQe/ZZuO66sKa1g6uYzVjMNPLMElLSiYpNaeBt9ShcQRn6hBQQLZ508Evn\nwRx++Rdhbc2qtlN2Rw/a7twcJppCuWjcZKYcdFHsm7YrhkaBPvfFHUIqA5AiSpI2aTlRu3eLBHBv\nvRV9bMKE8LwmB+qc4bGE4AfIcca7lBY+GMbTMOREhYY9PAYMAlrjTyG1bp3IHQSwfHl45uuZM5ne\n9f+o7KzHDjWOGUJKOlEmkYJ4SsSOxs3petsq2u74K+bxqtzGbGrePv4NNgWcqA7OxERFMXcubNki\nks76GCmiJGmTlhN1/PHw6adiu6AA/vUvsZ2fD89fBgdPTq9z/8M6IeUjwRQLQ05UZ+AG4IHAfrU1\nfXKcNWtEcsba2uhj06bx7rC7EWPK1pGukJJOVDSlRjxDk8VTKJV5TVndumvyE2MR6kQ56ELVK1li\nY8cOkWNrzZrYgfI+IcvpDmQUH34oMroWFYnlvPOc7pEpaE6UIaqqRD4WTUB16iQy5N5wg1heusw8\niW98tm5i+uJ7AQVBJ0o3BwKFge1rgTKTO3TzzcH/O9py6qkiZYUdfPutKIOhCah992XrvgVsHdKC\nec/tybvHpyn4DTCaT+lOWdIlFpoTJYlPj8IVsQ9YKKDSZlMJbFkZ3Heor3PaDeW9HieInS1bxP/T\nJf4dW5ROlNVUV4ucRBs2wD33hB9bvlwkJWvenF9Cju19003h5ykKnHiiyJLrQgw7URs3wkUXiZkb\nILJ8L1kSTNCmd9jOCFY6Uj4lpZiobsAGoAq4DuFMGRnSW74c/vvfqABtIPr/j3b+oVli6BDgxJfg\nrLPi33/XLjFEvGWLvv7Ee/748fw85TugE2V0N34vExjNp0nPieVYSSdKH0WHLqL0S5cOeWqaJPTL\n3K5iqM4XxzQB9RvJY0hNpjK3KSeNeY/PPjiCI/6cITKYf/IJ9PXnN09ZgNgMVq4UlbJj8eGHwSEq\njYcfhmuuiX1+PHJyxBhzPPr0CVqmO3boy6/UsiV06yaE3uLF8c/r16+h0GUstm7dyq233sqkSZOS\nP3P3bjjttGCweLduogZdfsCGtkJAhWKGkPLnZ0EUJWvhtVkw8TQDF9UDzwCfBfZzgXsD24f9kvz6\ns8+GhQsTn7NwITRpAn17QYxRNT74ALp0iX3tyy+HT1xIhYkTqfi/e0BRKM0uckxE6SVSSJXP/oOK\necvoepmNWbZdTLKhvDAh5aQTlczMWfoqrG8FrWMU5rRZSAFk1dfx3icnctzKD8TsVaN/81yGLEBs\nFR9/rD/l/113idpC55wDBxzAnAMPTHpJCwITzWprRRK2eAwdCj/9JIY2Bg0S39D1MH06/Oc/opBu\nPEaPFt8k4mDIiTryyGBG4MJCMZxnl4AC6UgZICUnKgs4G5FC4lOgBuFIAZDg9zeSIUOE+7rolvD2\nXkDJQLF9LzA/5NirgfWxx+p7xl13UVU/UX+fALUV1Pz9Hk+VsYiMoZJOVBA9sVBhjtSeOCekks24\na1kMW+PMKHTAkarPyqa0hf8TzXlTRP3yi5gRYyQRY14e3H8/jBkT/5w77oBXX41/PBZ//BHc3muv\nsEObFywAxJfzucCaWwJ/EC6KM0U1BgqQDcQrDJAHNAeYM4dyRQmrB7sZaBPSJ60/AG20jaOC31p2\nAztCrqlesIA8gE8/pVxRqAW+B7S0dOMDbqKu2Xk7d4o/ipqAKi6Gjz4Sa7BHQGlIIaWLlPNE5QPj\nge3AmhQe3Aq4Yi40nwv9EpzXM7BoNEM4YMlM7jxgIlSccTvif5f/CRVScnaewEgwuSeEVHkJ7G4F\n+XFm54X22QFnyq94T0T9/DPss09q1x51VNgXV419Jga+jd5xR8rdmgUsCREpZqEi0u7EQwHGIf5+\nhAqtLcB7IBJXxqAf4bklK4HXgbqQa3KA0xG5K7V7H4fQIBuBZwPfxs/cuTOxE7VunQii12KgCgvF\nkIxW5d5OAaUhhVRS0spYng1cb2ZvdDAmsOig4rj4w9NGKKorhWxcP6QHQSFVUbidnQMbsdvpDjmI\nodl4AVwvpBI5UZE44Ez5FXeLqM2bRUB2KAcdFNwePz4qyd1b/aK/unYD9gtsx5RfkeJpzpxgkHOc\ne4ZSh3BwnEAF3kZ8+Q8lmUe3GFhN8Hv4LgICKoRa4A1ECqA+gOZpHRd4Zl3gOVPy8ym94opoJ2rT\nJrFce21wFl6vXkIIOymgNKSQSohfM5abJaA0vCaklm7YSunCCnqPgBkc7nSXPIVrgs1jCalkTlQk\nUkiZgntF1OrV4g9udZyEMxMmwL33hlXAfjZOnMJviNAMPZkq/gJWDx1qtLeOUgtsS+E6PcKvJnDv\n+QjRNDjQfkpg/SNiqLL6sccgNLB8yRLYc0+oC5FmXbuKGDIrZ+EZxaiQypCgcvBp7bzE34cyghaF\njeg6sHlDyZlME1KpuFAxcdKNgmgh1bIY2ubDWgP3kEIqbdwpor79FkaODO5HOkEDBnDH5Mmok4N5\nWToluF09wnmRpE4tMA/heLVDhK2AKD9XBBwAvKQo7AbGf/JJeOxZv34ijcHLL4vZeG4QT6FIRyom\nfnSiKorNdaG8yLYNu1m1cDsDRrRuEFLLKDKtwHHG4IacUaFCqrwEGrWCPfsb65sUUmnhPhH1ww/h\nAmr8eJgyJeyU2yMcp0QCSmIugbBwOgDHBLbbBpYuwCoIF1DXXitm/2m4TUBpSCEVhe+cKOlCAUEn\nSqOIZQ1iajIXO9UtWzDNhXKDgNLQhFTLYsgJBHYYdcmkkEoZd2Us37IlPObppptgcngWYCmg3MF6\nxIzydxBDoADtgbB0oE2BFx4K7rtVQGkky2yeQUN5kELGcokn0JyoWEzgaZt7Yx+mCSi3Ul4C20My\nlhsVRSYLw+z6Woq3lZh7UxfiHhFVUgIdOgT3b71VJKnMCnZRCih3sQvYCkwHPgB+DizrQAioxojp\ng20VsXjh/5PZJWI8jO+cKAkQ7URFEq9cjJfxvYAC4UQ17xbe5qCQ+uTDMRyz8iOx46G8akZxh4j6\n8kvo3TtY6uG88+C226BpsDS8FFDuZQvwCCJmah4BEdUEIaAi8aqQyjAXCqQT5VcSOVESDxPpRKWK\nSUJqzy2BG3XunDg/o8dxXkR99x0cdlhw/8orYerUsFMiBZTEXeQAxUYu8JqQykABBdKJ8ivJnCiJ\nR4nlRKXKbyFLulxwgZiZ7VOcDSzfuhWGDQvu3357VJ05KaDcTy1CFxkqj1yCQeXlAEsRNXeWkJFC\nylez8/pZOzPPS7miQmfnSXyENjuvdUSeqHRTMWjXGhwa3JmbL7I43367SHVz/vn6LmzcGDp2NPYw\nB3FORC1YIOpjadx3n3ChEsRASdyJYSfKK2hTh3s72gvHkE6UMbwipDLNicqIeCgIn50XiRk5rQxe\nf273F5i5YITYufNOsejl6adFLkgP4Nxw3qBBwRioCRPgH/8QCjSAFFDeQXOifMkShCOVrIK6D5Ex\nUcYpqiulByuc7kZCZEyUT0kWE2VzCoNZq4czotk3LMrqT1lW99gL3cKWBi6+GPbbTyzDhwdrrroQ\n5/NE/fOfIvN4CFJAeYuUnSgvDOlBuIDKoGE96USlhtsdKb87UbY4T4kEiVM5pBI5UXYT+DeYmTuC\nPVssSnzu1sqGzTF8ynROFDtz5gTPGTkSHnww+tq2beHMMyE3N80Op46zIuree+GGG8Ka9AioTJ2Z\np9X9i1VE2UlSionSkELKtbg2Jio0aaYsRWAYP8dEuWLozu5yMJEZyyNjokKxo29p3P8TRlPMAlqx\nFYDTeJfreVQcvD5ORfMdO+D444P7WVkipsomM8Y5EXX//XDVVTIGSicxCye7hLRjoqSQciWucaIS\nZRp3qaBysxvlJyfKCdGUNWAn9YuSOD52CqlYGcsTYWXfTLjvMiqA7MDtjmUzVbSlPOq863hDbFx+\nuVhCueKK8FquFuKciErBgcpUIgXUPrjLjUrLifIaGSSkXOFEGSnVEnmuw6LKrUIqmRPVi1JX1dFz\nhbsUQo/CFZTR3X1CaqkOJ8oKTPkZY/9Fq6Qx93J2zGNfM5hHmEQjahraOrNJbDz2GKiqEFIWawvn\nY6IwJqAydSjPzZgyO88rbhQEhZTPRZRrnKhUcUGtPDcKqWROlFZHbwaH29Ul/2KnkBpUDGt0xkQ5\nMFsvLq2awFbj1sCHDONDhoW1dWU9yzmNbOrh8cdFwu7OneHoo6FnT5M6HI7zyTYlSXGT6xQL02bn\n+XaKnzeRs/PMwW0z9vTOznND+Re3uVBlG7o3bGcN2KnvIrtmxW0qgZYGMpan0y83FWAOYRUd6Mmb\nwYb77xepk445BjZsCF+qqkx5phRRkrQxNU+UFFKuwRVOlIvinNLBTUJKT0xUEcvoRakrhJTbCBVS\nurFDSLUrhtbdrHXIzcpiHkmrJpgV+buKDhzCJCZxCt8ySDQuXixq84YunTrB5s1pP0+KKEnamJ4n\nygtCagm+zx3lGifKJ0LKLeh1oswSUt0pi7lITGZTCWwxoXaeD/iafbiKqzmSh5jFQDbQKmwBYMsW\n6NtXJP5OA1fERCVCxkC5H0sylnshRkqrr+fT2ChXOFES0zE6O68XQknrCTbvTlnD+ZEsixia606Z\nqwLYk5GSA2Un7YqhUSAmSpuxl+HsphHDeSqq/W1u4WS+gb/+goMOgnnzoE+flJ7huBOVKKhcCihv\nYFnGci84Uv/Dtx9WrnGifIJbhvRSyViuOVLJlngCSrtHJMkcqqIE90tEqtcZRXdcFFg/pCedKN2c\nxURe4zCxs3MnjBoFu3endC9HnSiZ1iB13JR409LaedKRcgw/OVFWFh82ghtm66WaJyqRQDJyj0hH\nKpJ0HSqfmlh4AAAgAElEQVQrBFQiF0pX3ig7CHWiJAmpohGXcR27yeNcpsP69SJB56JFhosfO+5E\nJWKN0x3wAPvgfCJOy2vnSUfKEWx1ovphWUoCtwgot+B07Tw9YizUmTIiiuwWUBqGHCmrkE6UIbZS\nwPncxGcMDTRsheJimG/MmnC1iJLDefoxU0gZFWaWOlEaUkjZjm1OVL842z7F6WE9N2QsN+JqGRVS\nTqFLSFk5pKfNzjOCzUWJ3YZKFqN5mJcYLRp27oQpUwzdwzERJYfyzMdsR0rv/Sx3ojSkkLIVW5yo\nWKLJQldKYsyJ0hJvOo1eIaXllXIqv5SjjpQXnaiQ4sNOchH/4HUtRqquztC1rnWipAuVGk4IKVuc\nKA0ppGzDcicqmVDyuZhyyo1ygxOVLC4qFkaFlFMkFVJWuT+pOFFuwAVCqopGfJniX0/XiiiJd7DN\nidKQQsoWUnai+kUs8Y4buZ/PKKpzbngqnZioZRSFCaDIfb33SBVNSGmL1aSa1sARIRXqRHnts8cF\nQipVXJ8nSmIcuwsU2+pEaXhh1t7SwNqjs/ZScqLiiSZJGKXZzrklZjhRkUJoGUWmzN7Tg5YGwcoc\nU67PCRULq/NEmZmp3MOiKRLpRPkUO2fs2e5EaXjBkVqK974VBjDsRLlULBWUVDvdhbg4MaRn1ey8\nZA5TKq5VIswMOA8VTbYJKLPdKK/ERLldQFVVgarqPl06UT4mUkhZ5U454kRpeMmRiodLnSpDTpRL\nBZRGQUm146kOSrOLKKorjXKhjAgpM/JLpepE6RFAdjpSEF0kOZ14KEfcpz0xz+HxQp4otwsogJde\ngooKmDZN1+mudKJkULk1WOVOhTpR+wD7tLHoQfHwiiMVb/lfguscRLcT5XIBpeGkI6UJJyeH8TRS\ndaL0iqNYjpOZDlQkZtTi61G4wpzOBHAk+WYqTpQVxYTj4XIB9T0DqaCp2Hn/fbj4Yti1K+l1jomo\nW1WVWw1YZhJzsEJIhTpRtgsoDS8IqUS4UEj5KWO5k5gpnMwY/rPSiYo83+whPCsxU0g5kurA6Ow8\nOwTU1srg4nIW0ZM2fMxWmomGyZPhyithe+IvHI47UZFCSrpQ1pNISKUishyLiYqkJMbiFKkM0blM\nSMnaeeljhfOUrpByOmO5mzHbkUqKmULGiBNllYAKFU0eEE6R1JLDvjxHLdmi4bnn4P/+L+E1joso\nCBdSstSL93A0JioZdgupvqQX4+QiISWdqPSwcuguHSHlhjxRVmFGoLkZQkrXcJ7ZQkaPE/WbBc81\nDTdUgoUyOnEgTweF1MaNCc93hYiCaEdK4h00J8rpGn5xsVNImTETzyWz+aQT5W5SFVJGnSi3ZC1P\nhNnpDtIVUrpLwJg5Qy/SiTJ7wkq6fW3VxJRu2MFc+vF3bhE7r70mhvbi4BoRBUEhJd2oaJzU6MnE\nUQ5wJA7GQ+nBa0LKBehyojwSVO5XUhFSfnOirMwX5SliOVFumfmrCSgPCakNtA7uXHFF3PNcJaIk\n3qQW+NnpTujBK0LKJbmlkjpRUkDFxc5ZeEaFlN9joszKHWV7fFS6xIuJ0oSUU8N4kcIprpBy11jG\nl+zLSB4TOzU1cc9zTkTtsQes9EBisAwi1V/hHGCwmR3xCx4XUgmdKCmgXIURIZWKE1XEMlvzP+kl\nngtlR0kY12FH7TyjQ3qGnad9cI+YUviWvZOe5ZyIWrcO5kcPUskhPXuI/DVN59e2FljTOI0b+BkP\nC6m4TpQUUDEpzS5qWNxMqk6UW4VUPNIRUmUbuqedfNP2NAd2ZSzfM8YSi7SG7twipOAT9kt4XA7n\nZTD7RKxTZQgwXOa+j49HhZScnect9LpR6cREuUlI6YmFSkVImZm5XHeAuRnY4UTpoVWTxAJKd+oD\nNwgphaP4D29ySNwzpIjKcPT+miY6rwZ4Z4cJnZHExiEhJWfn+RM/xEQZCSY3IqQcKzxshpBysnae\n1v9k7pMHc0eBQn0CqeSsiDrpJHj+eUe7INHPPnGWXGRMVFLSFUEOCKmYTpQcynMteuvqmTE7z0k3\nKpXZeE7GSOke1ktXSMVzopZgT1B5vP6nlXzTeTfqPW7idL6Ie9x5J2r69KimW1VVZi73EDV4ZHae\n03hMSEU5UVJA+YJ0nSgn80alk84gmZCy0oUyJKRSzR8Vz4mya1ZerOeY4jw5I6Ty2cWDPMYJzEx4\nnnMi6qWXEh4eL5NvRuGOfK7RaE7U/M1O9yQDsEtI9YOWg2HIKLEtBVRi3B5MHorf8kQZoYjSqMU3\nuCUmyieM4Ueu4w2xU1AQ9zznRFRenmOP9jJuFFKhTpTrhZQrivylyVJEeRgrxFSIYCqvgLmuLREh\nSRU/xESZiWuFlN5ZcBpOxkRF4uraeQsCCyHraPIIyQ31449xz5NzqjzIfNwwUhwkMiZq/mYPZC93\nbbE/AywN2TYrM/FiGkRUywIYYmZZCp/iJRcKvOtEZVpm8lhDgPXkxx+ea1cMjXTU7LMCT37ZChVS\ne8U/7YwzoG/8D1jnY6IkKeEmR8qTMVF+cKRACCnNmTIZvzlRFcXS/QZvOlFWCqhShAh2U4byeDFU\nWQN2xneknHKiXPkZsSBi0XN+ajjvRH32GaxfDx06ON0Tz+EWR8qzs/P84khp/A84zrzbSSfKn5jh\nRGnB5cuw3oWzQ0B5iawBO2M7UrGcKCdyzNk2jGdE+Og591f2pRGtqQBgL53DvM6JqOxssd62DQYP\nhrVrQVEc644kdTQn6ginO5IKfhRSvUP20xjm05yosSPT7ZTzSBcqiOZEDRjROubxUnpFtTk5I88q\nYgmoHoUrnMsVZYCYQmpTCTRtBR36i327Uhs4QurOUTyOYhEf82T0gZzEMsk5EXX44XDWWfDyy8KJ\nqq8PCqsA41WVZ6WwisIN7lMonnWiNMwWUk5XTl8asZ9if6QT5U9iOVGxhJOe470otcWNMhsnHKis\nATupX5Q8ZklvOoQoIRXqRNkloGwTaftgZRDLZXzN47wZbDgiYAnk5cGllya81rSYKEVRtiuKUhFY\ntofs71IUpTbqghYtRJqDLBmWZQS3CSjwaEyUlSwJWZwmlZQIi8XKbzFRVuCVoPJSejUskTFRyQRU\nMtxSBsYsrIyNMrueXkOM1J4EY6J8J6BikSAQ3CDjmRUuoJ57ToQZffYZfPghHHBAwutNc6JUVQ37\naqMoSjPgMmAC8F6q9w0tRCwTcLoTzztRVrIE9zhTRvqxGFoWSifKLxSxrEEsbSvsTc7AHZR64BPV\ningoPS6UJqS8MrQHUH9AMfyZD7NseGg8AeXatAbhNKaa/VhBW3YyhVeDB777Dg46yNC9TLeBFEVp\nqSjKbYhBy+bAUFVVrzPj3muSnyJxAF84UVbO1vOoI1X+s3Si/IQW17R9QyXrF5qb0M0rbpTRYTw3\nzdhLhqL8Bs1XwikWP8g1nwmpu1Gv8Dzf8AjvMCXY+OGHcOCBhu9l5nBeW0VR7kEMXNYCg1VV/Zeq\nqqb+b5VCyn3EcqJcn3QzFlJIhdEyXzpR8SjNLvLMUF4kzQub0GGg+YnczBZSfs0LZfaQXgM9ilAO\nbpd62Zh08YgLBdCFreENkyfD0UenNLnNTCdqJXAG8F9gF3CBoijXaouJz5FCymXEc6KkkIrAY0Kq\nfCfM/RoRI5VoySC8LJ40rHCi/IpVw3mWCKmyUvhztbh35NB9OjX59GC5gIoXVJ6aG/VjpEDv2TOl\n+4C5s/MeALSCd5anw9UrpNw/6q8fNwaVg4yJ8ist82GIHr0QkuXcrRSUVJuS5qCortTzIsoqJwpS\nc6Pize7rTlnDthOulNXxUHpn6+mmRxE0bRrdbqZwihzKs8V9SjYrTxNS+tMeXME4VtKaB7Rw7SOO\ngOXLoYfx3zMzA8tvM+teZqKJLa+LKbcKKPB4nihJXMp3wtxSGLuvjpOlkPIMmhPVc4Q7PhVjpUlY\nQY8wEeVXYgmp+kX5qTlVZaXQoiX0sek/oisEVOo8xij2YBvX8KVoKCqCpUuhl7HZqqaJKEVRWgB/\nQ/xNfUVV1V1m3TvTcbOAgthOlKtr5yXDigScTs/QC0XnbD3dTpSGB4SUxFonKlXcKKTiBZWb7VCZ\nJqRiOVGxXKg9ST843FYBZX6OqCv4ihv4nC6UBxtVFVavNiyizIyJegfxMboeQucMugOvxlG5XUCB\nT2bnRWJmbJSbBJQBNCfKEBkWI+VF3BgTFSmgNPHk1+ByPRge6gvERDWQaBgvUYxUstgp2wPIzRVQ\n5/E9k3grXEABNGsGvXvHvigBZoqo5sDywNLSxPuahteElBcEFPg4JsovRYpTxLATpSGFlKtxoxMV\nC7cKKTvTHhgSUj2KoHMX4w/ZE/2B566dgacvHmoPypnKy8GGr76CP/8Uy/r10Mn4ELeZIup04HLg\nrMAiSRPrRoPNxZdOlJm4YVZeJDpm6aXkRGlIIeVa3OhExcOtcVGuzB8V6USli+PpTfaJWMdjAXpn\n6TWhOrgzbRqMGiWEU6dOkJ9akL9pIkpV1TJVVW9QVfUmVVX/NOu+EvfjWyfKTDwopFJ2ojR8nAKh\nqM4bySVj4TYnKlntvVhCKhVxZXa9PLuElG43KlUnytXoEVCh6/gMZhULuUvsFBXB8cen1TMNUzOW\nK4pysKIo/QPbIxVFuU5RlMN0Xfzgg1BVZWZ3JDYhnSgPk0BIpeVEhSKFlKtwkxOVSvFiN7lTrhJS\nZjtR4AI3yhyGsoL53EsTakTDoEGm3dvM2Xl3A4cCWYqifA2MAD4CblUUZbCqqg/GvLCgAMrL4cYb\nobgYTjrJrC55HhkT5TM0seKRQPO0nahQ5Mw9y+nBCsronvCcIpbRrHAXhQOrGsrAxCLdosR6SEVA\nhdKdMlfES6VbZ0+v05R0xl68PFHpogkp15R7MUY7tjObB4INV1wBjzxi2v0VVVWTn6XnRoqyCDEw\n2QgxQ6+zqqoViqI0AWarqjoo5Fz1jTfeoKamhg7Ll3PYxIkAfH/xxfx5yCHU1NSQm5vbsH5j3Diy\ngHpIa90CyAbqXL7uglC3tR5Zbwe+AsaGtPduJhyqXDy+7gg1KuQqJq47QG4W1NS7ZF0IuV2gphZy\nc4Lr1Zvgx2Vw/NDw9rTXhSbfz8C6pks2tTWQk4tp6zV1heTkKtTWqK5Yr6tpQ3ZuFnU19THXfy7e\nzl+rqhh4aOLz1ta0T3g8nfWm3I7U19SRlZuta705tyNqTS3tc7fEbFdyc5Ku19e00XVeOutNOztC\nbS3k5Oheqyuyk/6iKd3rkt/nh1nQvDlK3wGoc5rB6hrIyoV6k9arauAP1aFP4tXE/4tZFqe9jrZU\ns5rXaUw9AEuPOoqfTzwRpUWLKJ2RaP23v/0NRVFQVTWqLoyZGcurVVWtA3YpilKqqmoFgKqqlYqi\n1EeePGjQIOrq6sgeMoTyOXNo+cEHdOvWjTZae3Z2w/ob0hNP9UDHNK+3c93XJf3Qu64Edkf0e2AO\n1KmQrXh43dWi+26D7CIX/HzauiNkd4e6esjOCq73aA3Nm8LgnuHtpqyLoa4OsrPtXVf2zDL9vs1p\nTFY21NfhinWvuh1kZcOquj3Iylaor1PD1vktc+hQVE2PwQUxj2vrrnW7wvZX1nVFyVZQ69S01/XZ\nexg6vzq7C2pdPW2yG8dsV7KzEq5XZ3enkam/wLHXnbOz+HNDB92/QGpZc5Qx21HLmsc8rvTZrf8X\nUVUhvxl07QZrmkNlHSjZoJq03lyHEDR22woLEYn74h2vjfmXaT9W82NItqVtRx+N+sADDFTVMH2h\nZ50IU0WUoihNA0k2G3IcB5JwRtldffr0Ce60aAFAp06dILQ9QPs0O+aOvLz6Sb2KjzNUAB8Q3u8+\n2Q51xizMTrYZyTrcM6y3DWEnRvQnS4EvF0J/K2JVq3BkeK+i2HiB0WRkZTcy/Z5m0J3NMYf3dm6t\nYV3JLrr0N1adqxNbotpSHfbbTqGh87fRORALVRjVnoxSikg/T71+evbRP7Sn9Alfp8WCXyArC6VP\nP9Rf8omssZs2+SC+MtvNjiTHy6Na9qeM2UwNNvztb7R4+WVamNsxwNzA8hFalnJVVUOdp1zgHBOf\nYwivCSgvImOi/ImpMVGx8EnAuZsDzHuwIqqtRWEjug40p7xporgqN2D2jDy9OJICwZez84wn+mkb\nGQN13XXw4osm9ikcM1Mc7I7T/peqqgvNeo4RpICyBzk7z+PESdJr2uy8RNgspApKqpOflAJuFlKR\nbNuwm1ULt5t2PzuEVKwZeXqCyotSKIhsFrYLKStm5zmKcQHVia38yS3Bhn/8A267DbJMTUQQhml3\nVhRlL0VRZiuKslpRlGcURWkVcuwnXTf5+9/hnXdM6Y8UUPYhnagUcUPuqFABFdEfy50oDelI2YqZ\nTpSG3Y6UkVl5RZSGLXbSo3BFw2L9w/zkRBkXUMNYxp/cQiNqRcPf/w733ivKuViImfLsSeA2YCAi\n+8wsRVG0j+DchFf2CwmOmDo16vCtOmcQdgpZvIpX0hqEEulEebr4cCYRy4EKEVK2OFES2zHbidIo\nYpktYirdtAZOulOW4hsnKrVaHeOYF9wZPx7++19QzI+BjMTU2nmqqn6iqmp5ICfU5cAniqIcQIzA\n8jBuugkmTRLbcQSTXiHlZbwooEA6UZ4kUZ3NgJCyzYmSWEpkXJQVTlQoeoRUL4eFjC+FVKQT5cm8\nTqkJqFxq6cd6sXP55TB5sol9SozZGcsbgt9VVf0KOBl4CeiW5EKRhj2D8aqAAh/ERBVHLBLAv06U\nVXFR4I0hPaucqFDMEFIr6BG1mInvhFSoE7UEj4qo1PiKRziMP8ROv36WxkBFYuaT7iNi0rKqqguA\nw4B3TXxOTOQQnnNEOlHz3VFRIjnxRJMUUrDE306UlULK7VjtRJlBPMFkhZDyjZjqUYT6vz7U354P\nrwfaXk94hcsw7kI1Zycf8QQHs1w09O0Lo0eb3K/EmDk771VVVWfHaF+lquqFZjyjU4LFq3hdQEFs\nJ8r1QspKoRQr/1PfOIuL8asTpZGpQsoOJwpSCza3wnHSgx+ElPrgn/DRymjh5Akhldow3oH8xlgW\niZ0OHWDBAttHtWzxvBRFuUj3yaWlGVOI2A8CCjwWE2XHkN0SPCWW4mGrE+WTGXrg/iE9O50oI0LK\n6Tp4XhZS9afmw0/FkBUnciZVIfVbyOJCFC3cukMH+OMPyE08h80K7Bo41B8iv3SpGNOsrbWwO87j\nFwEFHoiJkvFOKVG+0N9OVKYQmbXcLifKCE4LKA0vCqn62/OFyKkvgfqV8U80KqR+i1hmOpGtXCeD\nBkFBgSOPNq3si6Io+wOLQ4oO34jQCr8Ddye9wYEHwrBhMGsWrFgBBx8Mb78NXfyS9yKInwQUuNyJ\nksIpmkQz80Jo2di/MVGZjNtiotwioDQ0IWV2tvMehSt0l4MxhOYSZRWDkp/4XE8M7eljBD/zCdc7\n3Q1TnaipwK7A9qNAC0Sw+S7g+aRXt2oFM2fC4MCf459+gunTw04Z74M0B34TUOBiJ8pJAeWGRJrx\nWKrvtPIq6USlipuG9CJTHLjJiXKbgLIas5Nu1r+RHxRRyZwon3EuIfrAwdn9ZoqoLFVVtTG4Iaqq\nXq2q6ixVVW/HSE3dWbNg30D94tWro/JG+UFI+Q1XOlHSgUob6USlh5uEVChuc6LcituH9uoX5Yv0\n1hpZCWKifEgWgRK9V18dzDPpSD/M4zdFUc4LbP+qKMoQAEVReiPMCn00bQpDhojtO+8U/0A+wY8u\nFLjYiZKkhXSi0sctQirUjXKTEyUxkQxzohrYe2/Iznbs8WaKqPHASEVRSoH+wA+KoiwHpgSO6efk\nk4PbkyaJeKkxY2C5yAUh3Sh34Tonyi0ulFuH9GRMVAOZlOZAS1m5Z+Em6UT5gVMi9jPMiXILpgWW\nq6q6DThXUZQCoEfg3n+qqrrB8M2OOALKysQ4Z309zA6knxo1Cq69FoDxzz4L48bxbHNvfBj41YWC\noBN1hNMdkehjKbqEVHkVzF0LY/e1vEeCxUSk67WHgpJqKorz7H+wQ2zeUMeqhdsZMKK1012RGKT+\njUDg+NuxDpaA0gqy+9vap0zHNBGloapqBfBr2jfq3l0IqTVrYOJEmDFDxEhdc03wnKVLGb92rQhK\nb9wYgGdtKDiYCvPxr5BynRPlJrScUR7EESfKISFlJUV1pZRmu8fSa1OY7QonapnJs9+8Qqqz9Orf\niIiBikTP7DyfkEUdHXFHRmf7CsykQteuYijvxRfh5pvhqqvEonH//bDHHtCpE2zZAsihPidwVUyU\nW4byfICMifInmhNlF7ESbi6jKONm5oVidJZeUgEFGRUTNZPLOJI5TncDsMCJsoSOHeGuu4L7Z5wB\nZ58N27fD+vVCQPXpA198AXvt1SCk3OpK+Q3pRHkMGROV0TjtRGW6gNIw5Ejpia/MACeqBduZwn0c\npOV16NMHRo50tE/udqLisf/+IrP5unVw4omi7a+/4KCDYEnwt026UvbgGifKrS6UWwPMk1BeBXOj\nqmHagI9KwLgRu50oCLpRUkCFo8eRql+Ur6/siplO1NbK6MVh2rKV17iNU/laNHTsCL//LkJ/HMSb\nIiqUV1+F008X2zt3wiGHCEEVWMbX1zvbvwB+jYcC6UT5lZaNYUhnPCsCU6GgpNr3M/accKJK6WXr\n87xEUiF1G/pElI9n52VRxxTu5yh+FA1du4piw1nOSxjne5AujRvDE0/AOeeI/fXroV274DJmjOOO\nlJ8FFMR3oubbHfdXYvPzfE55Fcz9M7DjcyGVCeJJw24nShNQWiB5d8oSLpmIKZnMzXSiWjUx5z6m\noPITF3ICM8Vuly7w6afQtq2z3QrgjZioZLRuDVOniuG9efNEW309bN3akB4hUkjZFS/ldwEF0onS\nhVtm6emMh4IQJ0rDLT+DJC3sdKJK6WV4Fp4eIeXHIcG0a+uZHRPVqomjw3hH8BPX8TpNqWJfrVbV\ngAHw2WdiQplL8IeIAmHrffppcH/bNmjZMu7p41XVFCGVCSIpGa7KE1WCu2OjPCRCNCdqbJ+QRo/9\nDJJo7MoTlYqA0kt3ymwRUkWUml6IOBGRQiqsNl4yPJwn6iAWMCBCPD/DA+En9ewJv+n9x7AP/4go\nB5ACSpDIiZq/GfZpY2dvcLeQ8hBRTpSGFFKexg4nykoBpRHpWFklqpwSUrrSGoRixew8i92o5lTQ\nmq18x6XxT/q//xMz8AYNsqwf6SBFVIpIARUkmRPliJCSpE1MJ0pDi5GSYspzWOlE2SGe4mGXO2UH\nUcWFdV1kkRNlkZB6jGu4nMnhjRdeGL7fqRPccgvkuFequLdnZlFRAeefD48/Loobm4AUUOHoiYmy\nXUhJNypt4jpRoUhXynNY5UQ5KaA0rBJSdrpRpV8OiK6LpwcP5InqxTLuYSLN2MEYZgQPFBTARRfB\nAw/Ev9ileH92XjyaNAnGRD3/PMyaZcptpYCKRm+eqPmbbZ6xVxJjcRKPiY2w2XmJ8PnMvXRxU8kX\nsGZ2nhsElIZVM/yKsCl9/20pXmdlxnKTZuudyRucwrSggMrKgrVrRQyzBwUU+NmJyssTeSS6dQNV\nhdraqFNSCS6fr+OcTBNaRmfnOTq8pwkpJ1wqjw2B6XKiNHzkSJlZjNhtAgqEE7X/wJ2m3c9NAkoj\nVEj5ZYgvKS52orKooxG7aUKVaDj7bDjzTBEs3rGjs51LE/86USDySYwZY/tj54csmUAqGcttzyEV\niZOu1JKQxcXodqI0XP7z6MFMAeVWNm+oY9nCKnqwIu17uVFARZIxuadcWjuvBeWsoje7aMuN/Ec0\nFheLv829DeRccSn+FlGhnHwyzJ1r+2MzQUilmicqo4WUhouFhyEnSsPFP08yrBBQRXXuq+DcpjCb\nXgMbA6QlpLwgoDTMElJWD+mVThqgP6VBJC7NWN6bEjqxjnoUEWZTWAiHHup0t0zD/yJKswqrqkRw\nuQP4XUi5pnZeKrghXsqlwsOwE+VhrHSg3CakNCcqHbwkoDTMypBulZAq/XJA6vFQ4FonSiNr6BDY\ntUtUFTn4YKe7Yxr+F1GTJomxV4DKShEfFYJdJWH8LKRSdaJcl/ZACqkwUnKiPEgmDOGFEupEgXE3\nyosCKhGpCKoiSu0LNNeL1U5UisHl2bijfq1V+F9E5efDUUeJ7TffhLFjne2PD0nViXJ8OC8WfhZS\nBsMPUnaizPg5FptwD0lMYjlReoWU3wRUJE7V9Es5rUEoLnSiTmQaP3CI092wFP+LKID99oP27cX2\nZ59FHZZuVHqkUztPCimbSCF+03EnykdCyk1DepFOlEYiIVVKL98LqGRYJaRMEVDgypio4Xwf3Dn2\nWOc6YiGZIaJ69xa5KBIghVTqpBsTpeWPcqWg8gMpToBJKybKLFdNCinTSRQTFUtIaeIpkwWUhtlC\nyjQBBa50ohp46CFRvsWHZIaIklhKOk6UxGLSmEHsuBOl4TMhpS1OEc+JkujDLCFlqoACVzpRmUDm\niaj6ejHFstQd3wr9gKdn57kJs5NVppmCxVWz8ywSUpkWVA7GZudl+hBePFyZe8rNTpSPyRwRlZUF\no0eL7Y0bYd48Z/vjI6QT5UJMyGHnGifKpzjlRiVzorQhPSmgEpO2kLrNlG4EcZkTdSrvcA3OpBWy\nk8wRUYoCn3wCp54q9j/4AHaGlz6wKy7Kbxh1ovZpE3/JWMx0oUxKAuwqJ8oCKorzKCipjrkkQs85\nbkavEyUFVHIOCy2ia4DSEWkk1YyHi5yoIczlTc4ONhQWOtcZi8kcEaWRmyvWL78M119v++P9WFcv\nmRMVKo4yWijFw4UCCvztRGkCKh56RJJXhZSMiXIWSwQUuMaJ6ssS5jAi2PDKKzBunHMdspjME1FX\nXy2KE4PInBqBdKOMo8eJyninyQ5MLkPlSidqMbHjo+K1xyCZgDKCXvcqHk4M6ZmRsVwSxDVJN13g\nRB9yqboAACAASURBVJ3KOywOtQruvlsku87Odq5TFpN5ImroUHj9dbE9bRo884xtj/ajCwU+jYny\nWq4oC+p4us6JWhyxHbrEOicGRgSUUXHkFWcqmRNVRndK6WVjj7xNd8p0C6m0auMlwwVO1BF8Edz5\n97/hppuc64xNZJ6IAmjXLrh96aWwe3fYYelGGUPOzksDs2fkmYgrnahk9It/yEwHKh5eEFLJnCgZ\nUG4NpZPSrI2XDIedqA6s41g+FjtPPgn/+pdjfbGTzBRRBx8Mn38utuvqRNqDCKSQ0o8vnSiJ+5yo\nZMQRUFoaA7cKHLuH9GRMlPkkc6MsF1DguBP1LUfSgY1ip3Hm/H5lpohSFDj88Ix60VYinSiHsWAo\nDzzmRCVwoNIRT7HySFmRW8pOISVjoqwhnpCyRUCBY05UR9ayjAEUaz/7ySf7tsRLLHKc7kAmMR9/\nxkVJJ8pBLBJQYIITFav0ixXDlwkEVDokEktmDw2WZts3fCadKOvoThmlIUOhtgkoEE6Ukm/Tw+Bv\nvMZhfMWxTKctgZpdQ4fCm2+KvIwZQub8pBLLkE6UP7HMiVoSY0kVBwSUkXP0YKeAAulE2UXplzYK\nKLDdiXqOSziPl4MC6rTT4McfM0pAgXSiJCYgnSh/4vqYKAcFVOi5bo21iod0oqzlMGbwBYfb/2Cb\nnahGBH7vp06FnBwYO1aEymQYmSUZJZYgnagUcfHMPLDIiYrnOqXjRplIKu6S1+rv6XGielFKL7fk\nP/IqZhYX1oNNTlQ3VrKUgcGG886Ds8+GNpmZCFCKKJuZ73QHLEA6USngcgEFDjhRRob2LHCh0hFD\nXhJSiZyoMrqH7WtiSgoqY5R+OcD+h9owO28gC5nPQcEg8mHDLH2eF5AiCuDXX0GmNEgZ6UQZxAMC\nChycneeAK2WGCPKKkIrlRJXRPWmSzVBBJUWVC7HBifoX99GarWLnrLPgm28sfZ4XyGwRpaWiP/BA\nmJFaIUmJdKIM4REBBQ7HRNkkpCqK80wVP14QUpFOlCaejGYpl2LKZdjgRDXOrREbJ54Ijz6acUHk\nscjsf4E77wxuH3lkVAkYqxJu+m1ITzpR/sTxPFHxZu+ZOJTntaBwMwh1oswo8SKFlEuwc3beuedC\n69b2PMvlZLaIuvpqeOqp4P6ECfDCC2GnyMzlyZFOlD9x1ew8TUhZEAuVaUJKc6LMrJEnhZQLcEHt\nvEwks0UUwMUXwxchRRPPOw+++y4sRsoKIeUnN0o6Uf7EcSfKRuwUUsomlexv6xuW/G93kb251rbn\nb95Qx48L82WRYSt52+D5qsrg2vkMq5lJE3VXas90uHZepiJFFMAhh8C0acH9YcPgf/8LO0U6UvGR\nTpQ/cZUT5RfqVPIH15B/aG3D0nvkSvoOKrNtcsuuwm7kDPRQcJ7HeObSq+B1Y9ecXz2V+dv3ZeaO\nEby746TUHiydKEeQIgpEgrDjj4fHHgu2nXACPP542GlmCym/uFHSiXIIC0u+QGY5UWCtG5U7tY5m\n3appXlhD1nrRVjtMoXaYSE6Yt6aWwfW/MZjfLesDiBioRRvas37hZkufk2ns98pc7ulyG/d3nMja\n/3ZkbXnsZXV5Zy7cHR57+6/Kf/PcrvEN+2NqP2VteUdKtvVieM23+jthpROlqry243SOq/nAmvt7\nGJmxPJTLL4fmzUXQHMArr4i2EMarKs86mJXVjfX3pBPlTzLRiSooqTZlhl3W/HpyX6mHwPeuRpPq\nw47XHqSQMzPQlp0N9fVw111www3QJO3Hx0SLgWpeuI0OAzMzMaIV7Pvmz1xw1ssN+y2oSHj+M7sm\n0L8uKJav3v1o1Dkd1fWgwrc7RjKq2Vd8kzsqeUcszFiez05Or3lD7DRtCv0sKhfgQaSIiuScc6Bt\nWzjmGJg9GzZsgMJCx7oT6Va5TUBB0Ik6wumOSExFc6LG9nG6J/aSkpCqUsn+RW0QTU2PrEWpjHHe\n++/D0KHktG8fbGvZErZsgVtvhV274E4Vcox/UWv8+26yttVROagxatPwQYbQIPLtGypZv3AzPUd0\nMvyMRPSilGXYWwfQKbJq6uj685/k7armonH/DR547TUYOTL2Rb/8IkqjEFs48ccf0K2b+F145hm4\n7TYAvt5xCF1arOLPrC6JO1VfAkoryO6fwk+UmN51S4M7GzdCvn3lZdyOFFGxaNs2uN2rF6xbB82a\nmf4YNwqiVEjmRM3fDPvIL76CJZiTK8rioTzITCdKw6iQanJ6LbkfRg/314zLom4/hcZZD0LnznDs\nsdH1xT75BPbbT2zfdx+Dt1/Kz098Zai/Ld6poOcpawDYcXATSmZ1B2BGjBpuzQubWOZEZYqQ+tsl\nbzHsudnhja+/DqeeGj93UocO8M47sGpV9LH+/aF34D91x47wj3+IenT/+hcAK7Z1p2fBclZlJ4h5\nssiJOqxmBjN2BL4iN28uBVQEUkTFYvBgOOMM8a1ixw7xyz9rFuy9N2DOkJ5eAeUFoSWdKJuxQUBB\n5jpRGsmEVPbsehpfWIuyA7JWizY1H+r2VMhR9ocePch94QVy85KIsaFDReZnzcF48kkGl5/Jzy/P\n113QtVFZTcN2s+8qGdx1B9sbb6bkiVWsPKJr2LlWOVEaWroDN4ip5hu2c9mxU2ixXgyx7WjbjKff\nPY/N3VMUkarKRae9wL5v/xpsO+AAkXxy3LjE1yoKnKQzaLxJE7j5ZlizBp56imzqWVnRncObfc4X\nuXGKG1vkRPWoLwvuBESdJIgUUbHIy4NXX4XKSjFrb+dO+PjjBhEF6QkpLwgjI8iYKBuxSUBBZjtR\nAKyFgkeq2Z0f7Sw0Kq+HqeFt9a0ha3k5OS1aGH/WiBGwbBnsuSdUVcGrrzK46438est71DeLP/+n\n9fPlNP59N01/iigovHo1zYHTjnyfNz8/npWHB4WUlU5UKHpdKaW+nlFPzKL1qq2sGtyZOWfua8rz\n25b+xeXHPEPHJRsb2lqvLufmIQ/x/Xn7xb1OVRTmnbY3K4eEi8/GFVUcN/HjBgG1u2kejZYsgy5J\nhtlSRVHgySdFzFxgktOMHUdwWLMZfJl7WPT5FsZEATB+vHDIJGFIEZWId96Bv/9dBJjHIBUh5TcB\nBdKJsg0bBRQ45ETVAxuAupC2fOBALEm0GfXspYCWsulO4FdoRH38a0AEg19+OVlt24qg21QpKhLx\nJgUFYv/eexnU/0V+OeUuGi/aHXV63uoaup2/LrzxllvgoouEi37jjQCcdsT7PLX6PHZ0FiEJVjtR\niVDq69njt/XkVAfzYnWbs4rTr3y3YX9H23x2tsnnz732oD43O+k925b+Rf7W6NxK557zaoOAWnJo\nMX1b7AnvvUezzTs58sHEw6WHP/w19/1wdVjb8Gd+YPiUHwCoycum0fq/xPCW1UyaJITaP/8JwBc7\nDqdzi9WsyYr4hmNhTJQkPlJEJSIrC7p2TX6eTvwooEA6UX7FESfqU2BmjPa7sF5EPQo8E6O9CDgR\naH9/9LGCAvjb38yLmWzeHObOhSFDxP7Onew9uj3MjPWPEmTN/e3plH8rnHmmCFS/+mpo1AiuuQaA\nS7q+wNTfzmRz/9a2OVEQ7UYdc/unHHPHpwmvuXr00wDMPXVvprx5bsJz+3+6mKvGTE54TsmwnvR9\n6WvIzYVRo2B3tCBt4Lff4MUXya6t5+ahD8U9LffHufYIKBCO1JVXihip664DYNW2rvQv+J0/skMC\nLK12oiQxkSLKJvwqoCC5E+XZoPISoNiC+6YSXG6zCwUOOFHvAXNC9jsBawLbtwA9XhWxiktMSjHy\nEfA4QddrdcixAYF159EwdSrssYc5z9TDvvuKElSTJ4sYlM0ip1NNh2xqOuXStKFziD+wF11Epwsv\nDL9Ho0ZCSK1YIQrFqirnD3iFdz48hpVtmljqRBWsqOC406bTZLMYYqwht+FYu+XB/FQr9+1CNwKz\nFLOzRRhFZSXMmwfAkLd+oVvRvxM+K+79NAoLKX7xRWgT+BC68srEna+rg5oaWLo09vGmTeGhh8JC\nO2yhcWO49lpYuRImTSILlSUV/SjN6skHucdyTdNHTHGiJux+muuq/kNWiPtaoCZO2ZDpSBGll1tu\ngTFjYB/jcsjPAgoSO1GeFVBgjYDyELY5UTXAdwQFVDZwOVAI5NwfjMM480xYsAC4ETbfm/5zp8Ro\ny8kRTtCgQenfPx0GDhTrgICiQwdyy8rIbdzY2H0eeUQIqvuFi3byMR/S5uI92ZSTxarqOurzkg+X\nJaLtwr/o+3oJSn1wZuLA534nf1Os/A4BcnLghx/oprltkfz1F/ToATt2hImkhDzxBN0uvdRAz+OQ\nnS3iYd3Ko48KsfnggwAU1S/n6t2PsiarE9SvprVaCbWJE3T+mj2IN/JOb9hvWb+VS3Y/RXO2c1NV\ngv9X2u+kJAxFdaCciaIoqhPPTYl774WbbhLbjRvD6tVhKRCSxUT5XUABVABPA5Ehh1JAJcADTlTJ\nX/DarzAxRgyradQDXwChISr/h0g4eVPgM+KNN+D006MuNY3nn4fhw8V2q1buqU6/Zo0IMgcx7T3V\neCtVFYHJkS7MXXfx37EL2VrUgprmxvJitVi+jUYV1Zx22DSabKmKfdKxx8LDD0e3t2wZdIbisX27\niA/TQ+PG0Mn++C7HUFWRJmH3buiTmk18RLPP2Ki0Z2l2b57adQnnVv83/IQPP4S+IR9SmfZvHANF\nUVBVNeoPvhRRySgvFwF9zwSCJZo2FUIq5IM2npDKBAEFUAnMIno4z7Miyg4HyoiIckBAAWzaAXPW\nWDyc9z7wY8j+BKAbQQEFIpv3Sy/B2rXmP3+PPeDss+Pn9vEL1dXw4ouwaZOYOh9CRZdmPFN2Dmq2\nvn+D3m+VcPxpn4S1lRzfg+L9Q4YUGzUSsWIOJirOCL7+WtR+DeXuu+OfH/Huw8jJgTvugJ49k6dr\nyECkiEqH2lrxgfDmm2I/Lw+++y4Y/Em0kMoUAQU+c6LsGsLTK6IcElBgsROlAu8QnpJ/PNCTcAEl\nMZ3FDz9M60cfpbBlS/g1kO9o8GCenjaI7V0TB0sPfvxXDr8iOFy0cVBb2vcYJhJNNmpkZbcl8Zg+\nHSZOZPOWLSw/5xyGTpwY/9xHHoEXXgi+d41WrYQg22svK3vqaaSIMoNx44JCCuCnn0SivAChQiqT\nRJSvnCg3iSgHBRRY6ERVA98QHMLLBq4BWiMFlA2UlZWxevVqRowYIb4IBgK56d6dKZ8Np7y4Zdj5\njTdXstezv5O7s4aD/h2M/P/opSM4+qzP7Oy6JAFz5swhPz+f/v11BJZv2SJKzOzYIWaYrloFqeQ3\nyyDiiSife9gm89pr4QWJL7gg7PB4LwpDE9Bm53keNwWSOyygIDg7z1TqgS8Jj4G6CSmgbGTDhg0s\nXLhQ7Hz/PYweLbZXrODCY36kzaLNYcthV37LyBu/DxNQzJolBZTLKCkpYeXKlfpObt0a/vwTliwR\n4SlSQKWMnJ1nhKwsUWk9K0skQNu+PeqU8arK/DRLwngNX+SJkgIqCktm570HzAvZvxhoihRQNlJY\nWMhAbaZVXp4IrD/nHPj8c1i6lPP3jD29v6ZxNj/eNIRhfa6Bgw+2sccSPRQXF5NvpK5dixZSPJmA\nFFFGKSgQ+VcmTXK6J67B8xnL3SSgXISpeaJU4C3gl5C2CUBXpICyGc2JGjFihGjo2FFUZzjlFOFO\nxKKggNxnn2XYgAGxj0scp6SkhFatWukbzpOYhhRRRqmoELk6JA142olySkDFS7jpEhcKTHKi1gO/\nA+UEBVQ2cANQgBRQDhDmRGk0bw6fJs4kLnE3hp0oiSnImCijvPBCUETFKPWQaUN54KOYKKdxkYCC\nNGOitgF/Ac8CM4C5IcduBO5RpYByiLCYKIlvMBQTJTEN6UQZJTQOaurU+OdlEJ52otyCywQUpOFE\n/QK8GdHWD+iAcN/ulOLJSWI6URLPI50oZ5BOVKrcfHNYeoNMxrNOlIyFSkhKTtQPhAuoNgjhdCbw\npQpPSgHlNNKJ8ifSiXIG6URJ0saTTpTbBFSceqdh2OxWGXaiFgAfhOyfDmi5++TQnWuQTpQ/kU6U\nM0gnSpI2nnWivIYeoWUihpyo5cDrIfsXIQWUS5FOlD+RTpQzSCdKkjaedKK8ylJsc6R0O1FzgXdD\n9k8Fuge2pYByHdKJ8ifSiXIG6URJ0kY6Uf5ElxP1HeEC6niCiloKKFcinSh/Ip0oZ5BOlCRtpBMV\ng52Iaf6JaIpINmk1GxEOVjxN0wvoGN2c0IlSgYXARyFtZyNm4YEUUC5GOlH+RDpRziBFlCRt4mUs\nn7/ZpUWIzQ4qrwNqI9oWIerEJWIVMHMmdO8u9q/tEn48D6FQ06EGmApUJDinWTNYvFhsPx7sw44t\n8McyGNsBaAQoQFXg4BrCY6AuBTTBJQWUq4nKWC7xBTJjuTNIESVJG085UWYLqErErLR4uqENQgxp\nnHGtWD/0kFgPHx7/3jmI4bHmIW1G4qEqgQcDa+3a9oHt/a6FdetEUe0dO6BLl6jLewDXgBiyS8Rp\nSAHlIaQT5U+kE+UMUkSlyt13Cwfhwgud7onjJKqdN3+zWLvCkTJbQG0DFofs50UcH3sCvPsuxMpi\n36kTPPwwqHFEx6ZNUF0NF34Co0eLtnsMZsPfSlBA9UIMt2UTFDqqCrt2wdy5MS+vqa2lsrKSgooI\nG6tTJ9i+RkRU/uc5OP98Y/2SOIp0ovyJdKKcQYooo2hDLwAXXQSVlcH9Qw+1vTtuQI8TZcnQXg3R\nw2ixyAKMfq5UIOKaEhEaw1mIsG40fkjiyFx7rVjiMXo0fPYZTJ4MQ4ZAmzZC/CQTUlqdOgjGZHUE\nYukcRYFp0+Leqvz/27v3IKnKM4/j3wdGcOQygIKUEi5OVCAgMusiuxaFSGlgFi+ltaULtQR2TbZS\nWUKt7m50q6xsxbKybpW6lVS0SqVwDVExGm9ZoxFlABeJINcochMIlyC3wbhclMu7f7ynnTM9M9Dd\n9OnT/fbvU3Wqz73f83Lm5ennvOecfftYvnw5jYsXw4MP+pmzZunl2xVOmagwKROVDgVR+Zo6Ffr1\ngxtu8NOzZ7cs69mThj17oEsX6N0bqI536Z0uE1VUjtaXzU7Xzyfb7Q/BtGl+vLH/6dc9iQ9GcnXv\nvfCjH0FNEf+camv950svwbnn+qwVwBF8h/S4U/iAby8wr5191VDQZbZDhw6xYsUKGh94AG67zWeu\nGhry3o+UF2WiwqRMVDrMdXQ5IckvNXNpfG9RPfkkrF3rx/ftg+eea7380Ufhu98Fwg+kjgLvcuYg\n6qwyUQ6fYWmvs/a5WdPfntUy/tOfnsWX4t/3FvfXs1pP9+sHd9/dEvQUy7p1MH48NDe3XfZNYHxs\nei6wKWudv4iNP/wejB2bdxH2ZTJRjY15byvla+vWrezYsUNBVGCWL19Ot27dFEQlxMxwzrX5z1yZ\nqELdeWfLeKZvybJl/vLe55+36mfSEAWMoQZTuWaiMv2joCWg6rDPlMNnXU7EpjMBVLwauwBHTxOQ\nT5nS9rJrrmbMaLmMVWojR/pz6MYbYf9+P2/vXv/5JnAsFkVtWuQ/O+OzVNfig6iz7OT9VSZKQVRQ\nlIkKkzJR6VAQVQxm8MorfnzOnNYBVkyDc0EGUoXcnRcPqAzYdgAGxy/nn6Lldvq4zkAvYH+OAcIN\nN8C2bXmWrkxccgl8+GHL9Pvvw9VX+/FFi1qv27s3ZC4lF0mvXr246qqrirY/KQ/qExUm9YlKh4Ko\npBw86DNUAQZN2XLNRBntPyK/H9GzHjvqyL1wYcv46NFQV5d3GYMwZgx89BF8+mnbZUOHFjWAAmWi\nQqVMVJiUiUqHgqikvPwyXH89LFiQdkkSl0smqgZ/g9wZT7iuWdOv/RauvbawgoVo2DA/lIAyUWFS\nJipMykSlQ+/OK7Zx4/xzdACWLm2zuKHSO9S3I/vded2AevyjiTLDSFoCqBNZA717w8CB8N57cMy1\nHq5P/J4/6UAmEyVh0bvzwqR356VDmahiu+wy2LgRqugXQSYTVYc/oQadbuVp06iZ1959+FJulIkK\nkzJRYVImKh3KRCXp6FE4fjztUiTuFD54qqd1ALUPf+f9JvAPjnz7bXjiidIXUAqiTFSYlIkKkzJR\n6VAmKml9+8IHH0B9fdolScTl+Mt38TfA7cdfptuDD7BCvIRZDZSJCpMyUWFSJiodykQlobbWP98H\n4LPP/IMTYyo9qOiBzzpdig+gwD9w8wSwFfgDsBu40rmKP9ZqpkxUmJSJCpMyUelQEJUEM3j1Vbj5\nZj/97LM+mIqp1OCiFh881eGDKfAB1E+AtcCQKHCq1OOTFspEhUmZqDBdeumlDBp02h6pkgAFUUnq\nGt2v//zz/tUgFRxYGP45l/Gb6/cAm4GV+LvzFDiFRZmoMCkTFSZlotKhICpJ99wD3bv78Tlz4Lrr\nWgVSlRJ0XIS/+25UbN4f8ZfsMu8Avu3550tdLEmYMlFhUiYqTMpEpUNBVJJGj/YvKR440E83NbXJ\nRpVjIFUHXBIb4u/gPYW/6+6P0XSDcww/eJAlS5aUtpCSOGWiwqRMVJiUiUqH7s5L2pAhsH07dOrk\nA6i33vIPkOxUXvGrAT3xUfWQDtb5PfAlPnDqG5vftWtXxo0b18FWUqmUiQqTMlFh0t156Siv/8lD\nlnmv2aRJ/plJZaYv/o67eAC1E9gSDaxezYgOOox/8cUXykQFSJmoMCkTFSZlotKhIKpUHnusZXzy\nZHjkka8m07qk1xkYATQAA2LzD+L7O+0FPgPqnYNRo9ruIKJMVJiUiQqTMlFhUp+odCiIKpWZM+Gp\np1qms15MXMpAqjc+4zQMiPJjOPxznjYA2/B33uX6qAJlosKkTFSYlIkKkzJR6VCfqFL61rfgggtg\nypR2Fzc4x0qzRIvQjbZ9ng4Bn2SVIx/KRIVJmagwKRMVJvWJSocyUVWkFv+alozt+OAp/tulkIyY\nMlFhUiYqTMpEhUmZqHQoiErL66/D+PElewBnb1o/KHMncACfhToZzSv0kqIyUWFSJipMykSFSX2i\n0qEgqtRGjYL+0ZOXFi+G6dPh4MGvFp9N36hO+A7ig9sZsu+625u17dl8rzJRYVImKkzKRIVJmah0\nqE9UqQ0YALt3Q309bN0K8+bB4cO+03nPnkBhfaM6AQOBPmda8bXXGDBlSqu78c6WMlFhUiYqTMpE\nhUl9otKhTFQazOCdd6BPFPK89BJ85zutVsk3M/Q1WgKoU8DWrIFnnvHPp2psPJuSt0uZqDApExUm\nZaLCpExUOpSJSsvgwbBokX96+Z49MH8+7NjhL/F17gxAw8KFnJgwIadIN7POSWAjcDS2LOnHJygT\nFSZlosKkTFSYlIlKhzJRaRoxwr9bL9NHaulSuP122LsX3ngDJkygBv+PdKYBgL596bxjB8Oi5zvl\n+pyns6VMVJiUiQqTMlFhUiYqHcpEpa1vX9i1C4YPhw0b4MUXoV+/1k84f/hhVt11V6vNRh871nZf\nNTVfZbFKSZmoMCkTFSZlosKkTFQ6Uguimpubcc5hZvp0js7z59Nj4kQ6HTjQKoA6cv/9HLvjDgbP\nmMHqPn0w4IoDB2g+cqQsym1mNDc3s2DBAiZOnFgW5dFncT63bdvGkiVLGDt2bFmUR5/F+dy4cSNr\n165lxIgRZVEefRbnc9WqVfTq1Yv+/fuXRXlC+uzTp+Nbtsy50r+3zczSeVmciIiISAGcc21um08l\niBIRERGpdOpYLiIiIlIABVEiIiIiBVAQJSIiIlIABVEiIiIiBVAQJSIiIlIABVEiIiIiBVAQJSIi\nIlIABVEiIiIiBVAQJSIiIlKAVN6dZ3a+g4NpfLWIiIhIvrY75wZnz0zx3XmPFnmvVxR5f3ENyey2\nd20y+x2RzG4T3ffQhPabYF10+sbhRPY75MJtiey3ni2J7BdgMFsT2e/XEypzPZsT2e8QtiWyX4D6\nk8nURc9NXyayX9Yns1sAPk5ovxsT2m9S5QXYlMxuVx5IaL/J7BaAXQnu+99p/915upwnIiIiUgAF\nUSIiIiIFUBAlIiIiUgAFUSIiIiIFUBAlIiIiUgAFUWk63pR2CcrHpqa0S1A2jja9n3YRysaWpp1p\nF6FsLGk6lXYRykbTJ2mXoHw0HU+7BOUjmXuET09BVJpONKVdgvKxuSntEpSNo03L0y5C2djSlORN\ny5Xl3UUKojIURLVQENViWwrfqSBKREREpAAKokREREQKkNYTy/cAF5b8i0VERETyVz6vfRERERGp\ndLqcJyIiIlIABVEiIiIiBShqEGVmk8zsYzPbaGY/6GCdn5jZJjNbbWZX5rNtJTnT8ZjZ5Wa21MyO\nmdldsfkDzOwdM/vQzNaZ2fdLW/Liy6EupprZmmh418xGZi3vZGYrzezV0pU6GTnUxU1RPawysxVm\ndl1sWZ2Z/dLM1kfnx9WlLX1x5fo3b2Z/bmbHzezW2Lx7ozpYa2a/MLMupSl1MnJsO6+Nzovfm9nC\nfLatJDn8jfxzVA8rozbyhJn1qtK283wz+030/+k6M5uRtbya2s5eZvarqP1cZmbDY8uSazudc0UZ\n8AHZZmAQcA6wGhiatc5k4H+i8auBZbluW0lDjnVxAfBnwP3AXbH5/YEro/HuwIYqqIuxQF00Pilz\nXsSW/xMwD3g17eMpQV2cFxsfCWyOTT8FzIzGa4CeaR9TknURW+9t4NfArdG8QcAnQJdoej4wPe1j\nSvi8qAM+BC6Opi/Ipx4rZcj3eIApwIJovBrbzh8CP86cE8ABoCa2vJrazv8E7ovGL8+cF9F0Ym1n\nMTNRY4BNzrntzrnjwHPAzVnr3Aw8DeCc+x1QZ2YX5rhtJTnj8Tjn9jvnPgBOZM3f45xbHY3/H7Ae\nuLg0xU5ELnWxzDn3WTS5jNjxmtkAoBF4skTlTVIudXEkNtkd2A9gZj2Bcc65udF6J5xzfypNwLjF\naQAABCFJREFUsROR69/8LOAFYG9s3p+AL4FuZlYDnAfsTri8ScqlLqYCLzrndoFvP/LYtpLkezx/\nAzwL1dl2AnuAHtF4D+CAc+4EVF/bCQwH3gFwzm0ABptZ36TbzmIGURcDO2LTO2l7Ane0Ti7bVpKi\nHI+ZDQauBH5XlFKlI9+6uBP4TWz6EeBfgBBuI82pLszsFjNbD7wOZC5JDAH2m9ncKD3/uJnVJl7i\n5JyxLszsIuAW59xjgGXmO+eagYeAPwC7gEPOuQWJlzg5uZwXlwF9zGyhmS03s7/NY9tKkvPxROf/\nJODFdpYNpjrazieAb5jZbmANMDu2rNrazjXArQBmNgYYCAwg4bYz7Y7lduZVqpOZdcf/Ap8d/aoK\nnplNAGYCP4im/wr4NPp1aVTJ+eKce9k5Nwy4Cfh5NLsGaAB+5pxrAI4A96RUxFL5L6JzIWIAZnYJ\n/jLFIOAioLuZTS198Uoq8+8/GR843GdmX0+3SKm7EXjXOXcoPrPK2s57gTXOuYuA0cDPzKx7lbad\n/wH0NrOVwPeAVcBJEm47a4q1I/wvwoGx6QHRvOx1vtbOOl1y2LaS5FIXHYouUbwA/Nw590qRy1Zq\nOdWFmV0BPA5MijINANcAN5lZI1AL9DCzp51z0xMuc1LyOi+cc0vMrMbMzsf/8trhnFsRLX6B1gFG\npcmlLq4CnjMzw/f3mGxmx4Fzgf91zh0EMLNfAX8JPJN4qZORS13sBPY7544Bx8xsMTAqx20rST7H\ncwfRpbyMKmw7rwEeAHDObTGzrcBQqrDtdM59DvxdZjqqi0+AbiTZdhax41dnWjp+dcF3/BqWtU4j\nLR3Lx9LSsfyM21bSkM/x4DsG3p0172ng4bSPo4TnxUBgEzD2NPsZT+V3jsylLupj4w3Altj0IuCy\n2HnzYNrHlGRdZK0/l5aO5aOAdfhgyvCdRr+X9jElfF4MBd6K1j0vOv7h1dp24jvaHwBqs+ZXW9v5\nEPDDaPxC/CWvPlnrVEvbWQecE41/G3gqtiyxtrNomSjn3Ekz+0fgt/jLhHOcc+vN7B/8Yve4c+51\nM2s0s83AYfylmw63LVbZSi2Xuog61K/AdwY8ZWaz8Y3iKGAasM7MVuGvZ/+bc+6NVA7mLOVSF8B9\nQB/g0SjrcNw5Nya9Uicjx7q4zcym4ztOHwZuj+3i+8AvzOwc/C+smaU9guLJsS5abRLbdo2ZPQ18\ngE/Xr8JnMStSjm3nx2b2JrAWf8yPO+c+Aqi2tjNa9RbgTefc0cy2ZnYN1dd2/hiYa2Zr8D8o/tVF\nGdqQ5FgXw4D/NrNT+DtZ/z62i8TaTr32RURERKQAaXcsFxEREalICqJERERECqAgSkRERKQACqJE\nRERECqAgSkRERKQACqJERERECqAgSkRERKQACqJERERECvD/d7FctnGabZwAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa806470690>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Figura de tiempos de viaje \n",
"cuCap.Plot_basin(cuCap.CellTravelTime,\n",
" ruta = '/media/nicolas/discoGrande/01_SIATA/ParamCuencas/AltaVistaAbajo/IsoCronas.png', \n",
" lines_spaces=0.01)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Este mapa debe ser recalculado con una mayor cantidad de iteraciones, lo dejamos haciendo luego, ya que toma tiempo, de momento esta malo."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"ruta_images = '/media/nicolas/discoGrande/01_SIATA/ParamCuencas/AltaVistaAbajo/'"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbgAAAEYCAYAAAAu1uNdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXlYVNUbx7/DkhuG4IqgoICKqaCJKz+XTETKLStxDTRx\nV1xKzUxcyqUyt1LU1DTXtNxBU8HUJMoNEzU1AcFdQwEFhXl/f5wYJVlmmOUehvfzPDzOnbnL596B\n83q296iIiMAwDMMwZoaF0gIMwzAMYww4wDEMwzBmCQc4hmEYxizhAMcwDMOYJRzgGIZhGLOEAxzD\nMAxjliga4CIiIlCvXj3UqVMHc+fOfeHzDRs2wNPTE56envDx8UFsbKzmMxcXF3h6eqJx48Zo1qyZ\nKbUZhmGYYoBKqXlwarUaderUwcGDB1G9enV4e3tj06ZNqFevnmaf6OhoeHh4wNbWFhEREQgNDUV0\ndDQAoHbt2jhx4gTs7OyU0GcYhmEkR7EaXExMDNzd3eHs7Axra2sEBARgx44dufZp0aIFbG1tNa+T\nk5M1nxER1Gq1SZ0ZhmGY4oNiAS45ORk1atTQbDs5OeUKYP9l5cqV6Ny5s2ZbpVKhY8eO8Pb2xooV\nK4zqyjAMwxQ/rJQW0IbIyEisXr0aR48e1bx37NgxODg44M6dO+jYsSM8PDzg4+OjoCXDMAwjE4oF\nOEdHRyQmJmq2k5KS4Ojo+MJ+sbGxCA4ORkRERK7+NgcHBwBA5cqV0aNHD8TExOQZ4FQqlRHsGYZh\nzJ/inqpYsSZKb29vXL58GQkJCXjy5Ak2bdqErl275tonMTERPXv2xLp16+Dq6qp5/9GjR0hLSwMA\npKenY//+/WjQoEG+1yIivX6mTZum9znMwUEWDxkcZPGQwUEWDxkcZPLQ98ccUKwGZ2lpiSVLlsDX\n1xdqtRqDBg2Ch4cHwsLCoFKpEBwcjJkzZ+L+/fsYPnw4iAjW1taIiYnBrVu30KNHD6hUKmRlZaFv\n377w9fU1mmt8fLzRzl2cHAA5PGRwAOTwkMEBkMNDBgdAHg9G4T44Pz8/XLx4Mdd7Q4YM0bxesWJF\nngNIatWqhdOnTxvdj2EYhim+cCYTLQgMDFRaQQoHQA4PGRwAOTxkcADk8JDBAZDHg1FworepUKlU\nZtOezDAMYyrMoezkGpwWREVFKa0ghQMgh4cMDoAcHjI4AHJ4yOAAyOPBcIBjGIZhzBRuomQYhmFe\nwBzKTq7BMQzDMGYJBzgtkKFNXQYHQA4PGRwAOTxkcADk8JDBAZDHg+EAxzAMw5gp3AfHMAzDvIA5\nlJ1cg2MYhmHMEg5wWiBDm7oMDoAcHjI4AHJ4yOAAyOEhgwMgjwfDAY5hGIbRkkGDBqFq1apo1KhR\nvvuMHj0a7u7u8PLyUjxnMPfBMQzDMC+QV9l59OhR2NjYYMCAAYiNjX3hmPDwcCxZsgR79uzBb7/9\nhjFjxiA6OtpUyi/ANTiGYRhGK3x8fHItPP1fduzYgQEDBgAAmjdvjgcPHuDWrVum0nsBDnBaIEOb\nugwOgBweMjgAcnjI4ADI4SGDA4jk8FCI5ORk1KhRQ7Pt6OiI5ORkxXw4wDEMwxiCBw+AFi1gr2CT\nHJMbRRc8LS60a9dOaQUpHAA5PGRwAOTwkMEBkMNDUQci4P33gZgYNMrOBj78ELAoXvWHqKgovWuf\njo6OuHbtmmY7KSkJjo6OepoVHQ5wDMMw+rJsGbB1K1C+PLBpU7ELboD4D8Lz/0mYPn16nvsRUb4D\n97p27Yqvv/4avXr1QnR0NCpUqICqVasaQ1crit+3oAAytKnL4ADI4SGDAyCHhwwOgBweijmcPg2M\nHSter1iBqKQkZTxMQJ8+fdCqVSv89ddfqFmzJlavXo2wsDAsX74cAODv749atWrBzc0NQ4YMwTff\nfKOoL9fgGIZhikpqKvDuu0BmJjBkCDK79wKORyltZTQ2bNhQ6D5LliwxgYl28Dw4hmGYokAE9OsH\nbNgANGqE5G3RaNK6DEaNAqZMAVQqpQX1wxzKTm6iZBiGKQqrVongVq4csHkzps0pg9u3gTNnin9w\nMxc4wGlBie5f+A8yeMjgAMjhIYMDIIeHSR3+/BMYNUq8XroUf2bVw+rVgJUV0K2bCT2YAuE+OIZh\nGF1ITxf9bo8fA4GBQP/+mPQmoFYDw4cDTk5KCzI5cB8cwzCMLgwcCKxeDXh4AL//jqjfy6F9e8DG\nBrhyBahSRWlBw2AOZSc3UTIMw2jLunUiuJUpA2zZAnWZcvjgA/HRxInmE9zMBQ5wWlDi+hcKQAYP\nGRwAOTxkcADk8DC6w4ULwLBh4vXixUCDBvjhB+CPPwAHh2dT4WR4FoyAAxzDMExhPH4M9Ool+t/6\n9AEGDsSTJ8BHH4mPp08XgykZueA+OIZhmMIYOhQICwPc3YETJ4Dy5bFoETBmjOiKi40VIyjNCXMo\nOznAMQzDFMTmzUBAAFCqFBAdDXh54cEDwNUVuHcP2LkT6NJFaUnDYw5lJzdRaoEMbeoyOAByeMjg\nAMjhIYMDIIeHURwuXwYGDxav588HvLwAAPPmieD2v/8Bb75pAg+mSHCAYxiGyYvMTNHvlpoKvP22\nZoBJUpKIdQDw+eectURmuImSYRgmL8aMARYtAmrVAk6eBCpUAAAMGiSydL3zDrBli8KORsQcyk4O\ncAzDMP/lp5+At94CrK2BY8cAb28AIkOXp6dY7u38ecDNTWFPI2IOZSc3UWqBDG3qMjgAcnjI4ADI\n4SGDAyCHh8Ec4uNFthJAdLb9G9wAYNIkkZJr6ND8g5sMz4IRcIBjGIbJ4ckTMWIyJQXo2lU0U/5L\nVBSwZ49YtHvqVOUUGR0gBQkPD6e6deuSu7s7zZkz54XP169fT40aNaJGjRpR69at6cyZM1ofm4PC\nt8gwTHFiwgQigKhGDaJ79zRvZ2cTNW0qPpo5U0E/E2IOZadid5CdnU2urq4UHx9PT548IU9PTzp/\n/nyufY4fP04pKSlEJAJa8+bNtT42B3P4khiGMQG7d4sIZmlJdOxYro82bRIfOTgQpaUp5GdizKHs\nVKyJMiYmBu7u7nB2doa1tTUCAgKwY8eOXPu0aNECtra2mtfJyclaH2tIZGhTl8EBkMNDBgdADg8Z\nHAA5PPRySEoC3ntPvP7sM6BVK81Hz6fkmjGj8JRcMjwLRqBYgEtOTkaNGjU0205OTpoAlhcrV65E\n586di3QswzBMvmRlAb17i5nbfn7AhAm5Pl62DPj7b5GSKzBQGUWmaBSL7GmRkZFYvXo1jh49qsj1\n27Vrp8h1ZXMA5PCQwQGQw0MGB0AOjyI7TJsGHD0KVK8OrF0r5gD8y4MHotYGAHPnapdvUoZnwQgU\nC3COjo5ITEzUbCclJcHR0fGF/WJjYxEcHIyIiAjY2dnpdGwOgYGBcHFxAQBUqFABXl5eml/CnOYE\n3uZt3i5522c+/xyNZs+GysIC2LABUefO5fp8+PAo3LsHtGnTDm++qbyvqbeLPUp1/mVlZWkGimRm\nZpKnpyfFxcXl2ichIYHc3Nzo+PHjOh+bgyFuMTIyUu9zmIMDkRweMjgQyeEhgwORHB46O1y/TlS5\nshg9MmPGCx9fu0ZUurT4ODraiB6SomB4MBiK1eAsLS2xZMkS+Pr6Qq1WY9CgQfDw8EBYWBhUKhWC\ng4Mxc+ZM3L9/H8OHDwcRwdraGjExMfkeyzAMoxXZ2UDfvsCdO0CHDs9GkTzHtGlARoZIydW8uQKO\njN5wqi6GYUoeM2aICFalCnDmDFCtWq6PS1JKrvwwh7KTM5kwDFOyiIoSS3CrVMD69S8EN0C7lFyM\n/HCA04KcjteS7gDI4SGDAyCHhwwOgBweWjncvg306SOi15QpwOuvv7BLZKR+KblkeBaMgAMcwzAl\nA7Ua6N8fuHFDrFQ6bVqeu3z4oXg9caJowWSKL9wHxzBMyWDOHGDyZKBiRdHvlsfUos2bRa5lBwfg\n0qXCs5aYM+ZQdnKAYxjG/Dl2DGjbVoye3LsX+Dcr0vNkZopsJVevAitWAO+/r4CnRJhD2clNlFog\nQ5u6DA6AHB4yOAByeMjgAMjhka/DvXuiWpadLdof8whugEjJdfUqUL++fim5ZHgWjIADHMMw5guR\niFZJSUCLFsCsWXnu9uABMHOmeD1njnYpuRj54SZKhmHMl/nzgfHjATs74NQpwNk5z90++giYPRto\n00bMIlCpTKspI/mVnREREQgJCdEk2Zg4cWKuz+/du4d+/frhxo0byM7Oxvjx4xGoUJZqDnAMw5gn\nMTFA69ZitYDt24Fu3fLcLSkJcHcXWUt++w1o1szEnpKSV9mpVqtRp04dHDx4ENWrV4e3tzc2bdqE\nevXqafaZPn06MjIyMHv2bNy9exd169bFrVu3YKVAtZibKLVAhjZ1GRwAOTxkcADk8JDBAZDDI5dD\nSgrQq5cIbmPG5BvcgNwpuQwR3GR4FsZCm7U4q1WrhtTUVABAamoqKlasqEhwA4rJcjkMwzBaQwQM\nGgTExwNNmwLz5uW769mzwJo1os/ts89MZlhsyWstzpiYmFz7DB48GB06dED16tWRlpaGzZs3m1pT\nA9fgtECGpSNkcADk8JDBAZDDQwYHQA4PjcM33wA//gi8/DKwaRPw0kv5HpOTkmvYMMOl5JLhWSjJ\n7Nmz4enpievXr+PUqVMYMWIE0tLSFHHhGhzDMObDyZPAuHHi9cqVgKtrvrtGRoopcUVNyWVuREVF\nFdq8qs1anMeOHcOUKVMAAK6urqhVqxYuXLiApk2bGty5UEy6OI8CGOIWZVjfSQYHIjk8ZHAgksND\nBgciOTx+2b2byM1NLOA2bFiB+2ZnEzVtKnadNcuwHjI8C0OQV9mpzVqc48aNo9DQUCIiunnzJjk5\nOdG9e/dM4vxfuAbHMEzxhwh15s8HLl8W69zMn1/g7lu2AH/8AVSvDowdayJHM0CbdTwnT56MoKAg\neHp6gogwb9482NvbK+LL0wQYhin+LF0KDB8ukkeePAnUqZPvrpySSzvMoezkQSYMwxRvvvkGGDFC\nvF62rMDglrOLIVJyMfLDAU4LZJjXIoMDIIeHDA6AHB4yOAAKeRCJ1FsjRgBEuBIcDPTrV+AhKSnP\nUnLNnWuclFyyfCcMj6JkGKY4olaLFFwLFoi8WmFhuObujvzHTArmzhW5l9u0Ad54wySmjIJwHxzD\nMMWLrCzRcfbdd4C1NbB+vUhDUgickks3zKHs5BocwzDFh4wMsfTNjh1A2bLATz8Bvr5aHfrJJ+Lw\nd9/l4FZS4D44LZChTV0GB0AODxkcADk8ZHAATOTx8CHg7y+Cm50dcOBAruBWkMPzKbk+/dS4mrJ8\nJwzX4BiGKQ7cuSMWKj1xAnBwAPbvBxo00PrwSZPEmBRDpuRi5If74BiGkZtr10RN7cIFoHZt4Oef\nxb9acugQ0KGDSMl15QpQubIRXc0Icyg7uYmSYRh5+esvwMdHBLeGDYGjR3UKbmo18OGH4vXEiRzc\nShoc4LRAhjZ1GRwAOTxkcADk8JDBATCSx8mTIrglJgItWwKHD4vmSR0ctmwRrZqmTMkly3fCcIBj\nGEZGfvkFaN9e9L35+opmSTs7nU6RmQl89JF4PWOGGHTJlCy4D45hGLnYvVvMa8sZ079uXYFruuXH\nggWi1la/PnDmjHGylpgz5lB2coBjGEYe1q8H3nsPyM4GgoNFnklLS51Pk5IiRkveuwfs2gW8+aYR\nXM0ccyg7uYlSC2RoU5fBAZDDQwYHQA4PGRwAA3ksXixySWZnA5Mni6zIOgS35x1yUnK1bWv6lFyy\nfCcMBziGYZSGCJg+HRg9Wmx//jnw2Wcix2QRuHZNNE8CwLx5RT4NYwZwEyXDMMqhVouOskWLAAsL\nYPlyYNAgvU45cCCwerXovtu82UCeJRBzKDs5wDEMowxPn4pgljOIZONG4K239Drl2bNiQW8rK+D8\necC1sOUFmHwxh7KTmyi1QIY2dRkcADk8ZHAA5PCQwQEogsfjx0DPniK4lSsH7Nmjd3CLiorCxImi\nxXPoUOWCmyzfCcO5KBmGMTUPHwJdu4qJ23Z2QHg40Ly53qc9eVKcqnx5YOpUA3gyxR5FmygjIiIQ\nEhICtVqNQYMGYeLEibk+v3jxIoKCgnDy5El89tlnGDdunOYzFxcX2NrawsLCAtbW1oiJicnzGuZQ\nzWYYs+HOHcDPT0Sj6tVF0uRXXtH7tGq1WALnxAmxWkDOBG+m6JhD2alYDU6tVmPkyJE4ePAgqlev\nDm9vb3Tr1g316tXT7FOxYkUsXrwY27dvf+F4CwsLREVFwU7H7AYMwyhEYqLISnLxomg//PlnoFYt\nvU5JBMTHi8EkOSm5QkIMo8sUfxTrg4uJiYG7uzucnZ1hbW2NgIAA7NixI9c+lSpVwquvvgqrPFIQ\nEBHUarVJXGVoU5fBAZDDQwYHQA4PGRwALTwuXABatxbBrVEjkTRZx+CWng5ERwNhYcCIESJNpa2t\nyL08eTIAREmRkkuW74RRsAaXnJyMGjVqaLadnJzybWbMC5VKhY4dO8LS0hLBwcEYPHiwMTQZhtGX\nEydEs+TduyLI7d4NVKiQ7+5EQEKCSK8VGyv+PXNGLHWTV4tZtWpi5KSbGxAYaLzbYIofxXaQybFj\nx+Dg4IA7d+6gY8eO8PDwgI+Pj1Gu1a5dO6Oct7g5AHJ4yOAAyOEhgwNQgMfhw0CXLkBqqliwdOvW\nXFWs9HTgzz9zB7LYWDEO5b9YWwMeHiKY5fw0agRUqaKxMPBdFQ1ZvhNGwQDn6OiIxMREzXZSUhIc\nHR21Pt7h32UzKleujB49eiAmJibfABcYGAgXFxcAQIUKFeDl5aX5JcxpTuBt3uZtA2/v3An122/D\n4ulTUEAAEmd8h/ULfsWVK8DDh+0QGwv89ZfY/1lwEttVqrSDpydgZxcFV1cgIKAd6tUDfv31xevF\nxUlyv2a4XewhhcjKyiJXV1eKj4+nzMxM8vT0pLi4uDz3DQ0NpS+++EKznZ6eTqmpqURElJaWRq1a\ntaJ9+/bleawhbjEyMlLvc5iDA5EcHjI4EMnhIYMDUW6P9HSiK6FrKdvCkgignxyGkb1tFokGxtw/\nVlZEDRsS9e1LNG8e0b59RDdu6O+gJLJ46IuC4cFgKFaDs7S0xJIlS+Dr66uZJuDh4YGwsDCoVCoE\nBwfj1q1baNq0KVJTU2FhYYGFCxciLi4Od+7cQY8ePaBSqZCVlYW+ffvC19dXqVthmBILEXDkCPD9\n98DSpaKJ0e+vhVhAYijjLEzB1BszAahQqVLupkVPT9HkWKqUsvfAmC+FzoO7ffs2MjIydDpp6dKl\nUeVZw7iimMNcDoaRlc8+A6ZMydkihCIU0zADAPB94y+R3GucJqhVq8aJj4sT5lB2Fhrg3n//fbRp\n00anGz1y5AhWrlypt5whMIcviWFkZPFisQCASgUMG6LGiEtjUP/gEpCFBVQrVwJBQUorMnpgDmVn\noU2UrVq1woABA3Q6aXZ2dpGFZCQqKkrxTlcZHGTxkMFBFg+lHL777tnqNsu/foouP/qj6sEDwEsv\nQbVpE9Cjh8mdZPg+ZPIoDhi7hbDQADdw4ECdLl7UYxiGKR5s2yaWpAGAhbMf4f29vYADBwAbG2D7\ndqBDB2UFmWLDRx99ZNQWwiLnoty+fTsePXqEzMxM2NjY4J133inKaYyOOVSzGfl49AgoU6bk9Snt\n2yemtT19CsyZcBcTj3YR6UUqVhSZjr29lVZkDIQpys5Vq1bpXCHS5ZhCA9zmzZvRunVrODk5ad5b\nt24dunbtCltbWwBASkoKdu/ejX79+ukkago4wDGG5tw5kZDjlVeAHTuASpWUNjINR44AnTqJlW5m\nBv2NKUf9oLp0CahZE4iIEEMiGbMhv7KzsCT5gGimHTt2LJ4+fYrKlSsjMjJSp2tv374djx8/RmZm\nJsqVK1f0ClRh8wji4uKoVq1atH37ds17y5cvp2vXrmm2ExIS6OuvvzbEtAWDo8UtFooM81pkcCCS\nw0Nph169cuZxRVLdukTx8cq5mOpZ/PEH0csvi/ue3vV3UlepIjY8PYmSkxX/ToiU/73IQRYPfcmr\n7MzOztbMX37y5Al5enrS+fPnc+2TkpJC9evXp6SkJCIiunPnTr7X2LRpU65YQkS0du1aSklJ0Wz/\n888/tG7duiLdQ6HJlj08PPDxxx/j0KFDGD16NJ48eYI+ffpgzpw5qFu3LurVq4d58+bhvffeK1qE\nZZhixF9/AVu2iLRRLi4id3CrVmIlaXMlLk7U3B4+BD71CcfUg+2gun0b6NgR+OUXkcKfKRFokyR/\nw4YN6NmzpyYzVaUCmjgaNWqENm3a5DpHRkYGUlNTNdsPHz7Ew7xyt2mDNlFw48aNREQUHh5Ofn5+\ndPHixSJFUyXQ8hYZRiuCgkTFZfBgopQUorZtxbatLdEvvyhtZ3iuXCGqXl3c4/wG35LaUmQnoQED\niDIzldZjjEheZefWrVtp8ODBmu1169bRqFGjcu0TEhJCI0aMoHbt2lHTpk1p7dq1BV7n22+/pdGj\nR9OoUaMoMzOT0tLSaMSIEVSnTh2qW7cujRgxgtLS0op0D1plMrG0tAQA+Pn5wdvbG2PGjEGHDh0Q\nxPNcmBJEQgKwbh1gYQFMnCiWaomIAPr2BX78UVRoNm0CundX2tQwJCcDr78OXL9OWOU8A0F/hooP\nPvoImDWr5I2wYbQiKysLJ0+exKFDh5Ceno6WLVuiZcuWcHNzy3P/smXLYuHChYiIiEC3bt2wcOFC\nLFmyxCAuhTZR3r59G+Hh4fj666+xa9cuPHr0CN9//z2ys7MxZMgQpKWlGUREZnISkJZ0B0AOD6Uc\n5s0DsrKAPn3Eep1RUVEoXVo0WQ4dCmRmAj17AitWmM7JWM/i7l0RsBOvZuGnSsEISggVkf2bb8SS\n2f8JbiX59+K/yOKhK1FRUQgNDdX85IU2SfKdnJzQqVMnlC5dGhUrVkSbNm1w5syZfK/7fAXq+++/\nx4wZM7B69Wr9bwgovP1uxYoVdO7cOc32zZs36fHjx0REdOnSJerTpw/9/vvvRao+mgItbrFQZOg0\nlsGBSA4PJRyuXycqVUq0zuX8OTzvoVYThYY+SyI8Y4Z4z9gY41mkpBC9+ipROaTSYRt/cUNlyhA9\nN9DMFB66IoMDkTwe+pJX2alNkvzz58/T66+/TllZWZSenk4NGjTIFUOe59atWxQUFERLliyhnTt3\nUmJiIhGJuBMcHKxJql/keyhsh+XLl+faVqvV9ODBA812VlYWzZw5k9avX6+XiLEwRIBjmPHjRTn/\n1lsF77d0KZGFhdh3+HCirCzT+BmK9HQiHx+iyrhFZ0o1FTdSsSLR8eNKqzEmJr+yMzw8nOrUqUNu\nbm40e/ZsIiJatmwZhYWFafb5/PPPqX79+tSwYUNatGhRvtcwdgWq0HlwV65cwejRo2FtbQ0AaNy4\nMaZNm/bCfllZWbCykm/9VJ4Hx+jLvXuAs7NYnPOPP4BXXy14/x9/FM2YmZnA22+LTPvFIWN+ZibQ\nrRtwZd8l/GzpB5fsv4FatURHY506SusxJsYUZeeKFSswePBgzTYRITU1FS+//DIAkfZx9uzZqF27\nNvr06aP7BbSJgtnZ2XT27FnNvIbihJa3WCAyNDnI4EAkh4epHaZOFRWZzp2194iKejZvrH170exn\nDAz1LJ4+JerZk6gZoumOqpIQf/VVops3TeqhDzI4EMnjoS+GKDsL4/Lly+Tv70/dunWjbt26UWho\naJ77PX36tEjnL7TKdfjwYbRt2xYNGjTQOmjmHMMwxZ0HD4BFi8TrZ8vCFE7btmKKmJ8fEBkJtGsn\nMllVq2YUTb1Qq4HBg4En23YiEgEoS4+Bzp3F6BkbG6X1GDPG1dUVu3btQlxcHOzs7F4YsJJDUVsH\nC22iHDduHEJCQrQ+IRFh0aJF+PLLL4skZGi4iZLRh9mzxaj4tm2BogyOu3pVTJK+dEm09u3fD+Qz\nWloRiIAxY4Ani5fha4yAJdQik/KyZWI2O1NiMUXZWZTKkC7HFBoWfX19NcNetb3Zjh07arUfw8jM\no0fAV1+J1x9/XLRz1KoFHDsG+PuL/rtWrURNrrB+PFPxyVRClcVT8TE+FW+EhgKffMJz3BiTsGPH\nDtSqVUvr/YkIO3fu1DrAabWaQGhoKPz9/dGsWTOtRWTBEP8LkWF9JxkcZPEwlcPChUBICNCsmUiY\n/98yXxePtDQxR27/ftHqlzMxXF/0eRZfznmKipMHIxDfQW1hCYvlYcCgQSb3MBQyOMjkoS+mqMFF\nRETg9u3bALSvQFWtWhV+fn5a7atVw2ZaWhqePHkCAFizZg0CAwO1OjnDFFcyM8XEbkD0velbobGx\nAXbtEq1/69cDb7wBrF0LBATo71oUVi1MRcPJPeGLn5H1UllY/fSDqGYyjAnx8/MzagVKqxrc2LFj\ncffuXbz22mu4cOEC5s6da3ARY8F9cExRWL4cGDIEaNQIOHVKJPEwBGo1MGHCs6bPhQufrYxtKn78\n+gZqjfRHY5zGI5vKKHtoD6/jxryAqcrOCRMmoHv37vDx8TF4BUqrAJednY2tW7di37592L59O9Rq\nNTw8PODl5QUvLy80adIETZs2hUrCdnsOcIyuZGWJaV9Xr4rckr16Gfb8RMAXXwAffii2J00CPvvM\nNN1eh765gNoj/OCCBNyv6A7738JF3jGG+Q+mKjuNWoHSdV7BrFmzKCMjg06cOEGrVq2i0aNHk4+P\nDzk7O9OwYcMKXPtHCYpwiy8gw7wWGRyI5PAwtsPatWIaWJ06BWci0dfju++IcpLzBwWJuWi6oovD\n7wuO0l3YEwGUUL050e3bul/QAB7GQgYHInk89MUQZac2ZGVl0aZNmygoKIjs7OzI1taWWrRoQUOH\nDqVly5ZRTEwMqYuY907nyQVjxoxBqVKl0KRJEzRp0uT5QImYmBgsWLAAs2bNMlwEZhgTolaLqQGA\nqFn9mwfWKAwYIFYDf/ttYPVq4M4dYPNmoGxZw1/r4uwf0eCjPiiNTMS6dEXDPzcC5YxwIYbREUtL\nS/Tq1Qv7LIPzAAAgAElEQVS9evWCq6srJkyYgHPnzuHMmTM4ffo0vv/+e1y7dg3+/v6YMWNGgevL\n/Retmii1pUqVKujRowfCwsIMdUq94SZKRhe2bRMBp2ZN4PJl00wFi44Wg07u3wdatgR27wbs7Q13\n/uRJi+EwdwwsQDjkPgTt/lwCi5fkS6vHyIUSZWdaWhps8kgukFOB2rVrl04VKK26zpOSkrQ62alT\np7j2xhRbiMRKMIBY781U85xbtACOHgVq1ACOHwd8fIBr1wxwYrUa99//EI5zR8MChPX1P0Wbc0s5\nuDHSkldwA0Sw7dKlC+7cuaPT+bQKcM7OzvDw8MDo0aOxa9cuzRpwDx48wDfffIPw8HAAYq2gypUr\n6yRQHJBhfScZHAA5PIzlEB4uRkxWqyaG85vSw8MD+PVX4JVXgPPnxYTwuDg9HDIzkd6jH+y//RxP\nYYV5r3yHt09+BCtr44xkMeffC12RxaO4YMwKlFYBLjQ0FDt37oS7uzvmzZunWcRu8eLF8PT0xIkT\nJ3S6KMPIxvO1twkTgNKlTe/g5AQcOQK0bg0kJYma3K+/FuFEDx4gs0NnlNu5EamwwYf192DEbwOK\nxYoGTMnDmBUonfvgFi1ahH79+iE2NhYHDx7Etm3b0LdvX0zRJROtCeE+OEYboqKA9u1F31dCgrI5\nhh8/FhPAd+4EypQROY/ffFPLg5OSkNXJH1ZxZ3ED1TCu7l4sjW6MChWMqsyYIaYqO2fOnImAgABE\nRERgy5YtiImJQfPmzeHr64v27dsjMjISHxcxV57O01dLlSoFe3t7tGvXDjNnzkRMTEy+GaAZpriQ\n0/IREqJ8Av0yZcRgl0GDRLDr3l2MsiyUP/+EukVLWMWdxXnUQ7/ax7HoCAc3Rm6mTp0Kd3d3jBo1\nCu+88w5u3LiBGTNmIDMzE4MHD9ZrfrXOAS45ORmLFi1CZmYmANEpWKZMmSILFAdkaFOXwQGQw8PQ\nDr/9Bhw8CLz8MjBqlHIez2NlBaxYIdKEZWeLPsE5c0RTap4Ohw+DfHxgkZyEo2iN3jWO4bvDLjBV\nl7g5/l4UFVk8iiOGrkDpHOCmTZuG2NhYVK5cGf7+/hg0aBAOHDhQZAGGUZqcvrcRIyBVbUelEjXL\nRYvE68mTgbFjxVy9XGzeDPL1herBA2zDWxhQ7Wdsi7SHk5Mi2gxTZAxdgSryPLizZ8/iwIEDsLOz\nQ+/evVFK0h5s7oNjCuLMGcDLSzQLJiTAZDUeXdmyBejXD3j6FOjdG1izBnjpJQDz5wPjxwMAFmEU\nZtp9hagjlnjlFUV1GTNAibIzOzsbQ4YMwZYtW+Dj4wMHBwdYWFhgxYoVRTqfzgHu0KFDGDt2LO7d\nu4eOHTti+vTpqFmzZpEubgo4wDEF0auXCB5jxgALFihtUzAHDwI9egCpqUDXdg/wQ83xeGnttwCA\nDzAPYTYTcChShaZNFRZlzAIly86cCpS9vT0CAgKKXIHSuYly165d2LJlC9asWYNKlSrB19cXZ8+e\nLdLFiwsytKnL4ADI4WEoh4sXgR9+EDWhCROU89CWDh3EaM/+tjvxddQreGntt3hqYY0+WI8lpT/A\n7j3KBTdz+r3QF1k8iiMrVqxA27Zt4eDggLFjx8Le3h4PHjwo8vl0DnBNmjRB3bp18frrr+Pzzz/H\nkSNHsGrVqiILMIxSzJ4tBm0EBqJ49Ffdvo0m8wKw9kE3OCEZx9ECXuowbLXugx9/BNq0UVqQYfRD\npVJh/PjxKPtvQtYuXbpg165dRT+frk2Ue/fuxePHj9GjRw9Y/LtI1saNG9G7d+8iSxgTbqJk8iI+\nHnBzE6//+guoXVtRnYIhAtatEyNM7t8HypbFw8mfocOPI3HmT0usXw+8847Skoy5oUTZOX/+fIwb\nNy7Xe+vXr0ffvn2LdD6da3DffvstvvrqK1SvXh1du3bFxx9/jLjncgr9/PPPWp8rIiIC9erVQ506\ndfJcA+jixYto1aoVSpcujfnz5+t0LMMUxLx5Yvh9nz6SB7f4eKBzZ+C990Rw8/UFzp3Dyx+PQfTv\nlrhxg4MbYz5YWVlh3rx5ePr0qea9R48eFfl8Oge4li1bYt++fUhMTMQHH3yAUqVK4fjx46hWrRpe\nf/11TNCyM0OtVmPkyJHYt28fzp07h40bN+LChQu59qlYsSIWL16MDz74QOdjDYkMbeoyOAByeOjr\ncP068O23z4beK+VRINnZYrnvBg2AffsAOzsxdDIiAnBxASCW8jl71ogOOmAOvxeGQhaP4sjo0aPx\n999/w8nJCb169cLAgQMRHx9f5PPpHOCGDx+O7du3IyMjA//73/8wdepUHDhwANeuXcO0adNQpUoV\nrc4TExMDd3d3ODs7w9raGgEBAdixY0eufSpVqoRXX30VVlZWOh/LMPnx5ZfAkyfAW2+JJMfSERcn\nElGGhADp6cC774oMzO+9Z5plvxlGQZYtW4bdu3ejWbNm6NixIz7NmahaBHReN6Ns2bJ5todaW1vj\nf//7H7766iutzpOcnIwaNWpotp2cnBATE2P0Y4tCu3btjHbu4uQAyOGhj8Pdu8CyZeK1vulTDf4s\nnjwRI18+/VRMeKteHVi6FOja1XQORUQGDxkcAHk8ijPe3t7w9vbW+zwGXxiqQYMGhj4lwxiMhQuB\nR48Af3+gcWOlbZ7jt99E8slz58R2cLDoKLS1VdaLYYoxiq186OjoiMTERM12UlKS1jnHdD02MDAQ\nLv/2W1SoUAFeXl6a/2XltJcXtH369GmEhIRovb8xtnPeU+r6OdsLFizQ+fkZeruo38eDB8BXX4nt\nKVP09/nvd1OU8/0SHo5aq1ahxrZtABEeOTri4oQJaKzl/cnwfTz/DJT8/TTE96Hk76eM28UeUois\nrCxydXWl+Ph4yszMJE9PT4qLi8tz39DQUPriiy+KdKwhbjEyMlLvc5iDA5EcHkV1+PRTIoCoXTtl\nPTTs30/k4iKkLC2JJk4kevTItA4GQgYPGRyI5PHQFwXDg8Eoci5KQxAREYExY8ZArVZj0KBBmDRp\nEsLCwqBSqRAcHIxbt26hadOmSE1NhYWFBWxsbBAXFwcbG5s8j80LngfHAGKshouL6IM7cEBkBVGM\n+/eBceOA774T215eYlhnkyYKSjFMbsyh7FQ0wJkCc/iSGP356isRU5o3B44fV2gwIhGwdSswciRw\n+zZQqhQQGiqSJVtbKyDEMPmTX9kZERGBkJAQTeVi4sSJeR7/+++/o1WrVti8eTPeeustY+vmic7T\nBEoiz7ftl2QHQA4PXR0yM4EvvhCvp0wxXHDTyeP6dZEp+d13RXD73//EUgaTJukV3GT4PgA5PGRw\nAOTxMAbazkFWq9WYNGkSOnXqpIDlMzjAMWbPmjUivnh6Am++aeKLq9XA8uViwt2OHUD58mLof1QU\nULeuiWUYRj+0nYO8ePFivP3221rPizYWHOC0QIYRRTI4AHJ46OLw9KlYCRsAPvrIsE2ThXpcviw6\n+4YMAR4+FNE1Lg4YOhSwMMyfngzfByCHhwwOgDwexiCvOcjJycm59rl+/Tq2b9+OYcOGKd49xAGO\nMWs2bhTpHOvWBXr2NNFFs7LEHLaGDUVNrXJlIbJzZzFZtoBhik5ISEiu/MBKBjkOcFogQ5u6DA6A\nHB7aOqjVIjEIIHJOWlqawOP0aTGSZeJEICMD6N9fpNkKCDDKyBYZvg9ADg8ZHAB5PHQlKioKoaGh\nmp+80GYO8h9//IGAgADUqlULW7duxYgRI7Bz505jqueLYhO9GcbY/PgjcOGCmB7Qp4+RL5aRAcyY\n8WyZgpo1gbAwwM/PyBdmGMPQrl27XM2r06dPf2Efb29vXL58GQkJCXBwcMCmTZuwcePGXPv8/fff\nmtdBQUHo0qULuhaQbs6Y8DQBxiwhEqm4zpwBvvkGGDbMiBc7cgR4/32xsJxKJaYBfPqpGFDCMMWU\ngqYJFDR/+XkGDhyIN998U7FpAhzgGLNkzx4xpsPBAfj7b6B0aSNc5OFD0RSZk73Zw0NM2G7Z0ggX\nYxjTYg5lJ/fBaYEMbeoyOAByeBTmQATMmiVeT5hgpOC2Zw8y3NxEcLOyAj75BDh1yuTBTYbvA5DD\nQwYHQB4PhvvgGDMkMhKIjgYqVhQj9A2KWg1MmwbMmoXSANCsGbBypRgxyTCMVHATJWN2dOgAHDoE\nzJwJfPyxAU+ckQEEBgKbN4t5bHPmiPxfhh6eyTASYA5lJwc4xqw4fhxo1Qp4+WUgIQGoUMFAJ759\nG+jeXVygfHlgyxYeIcmYNeZQdnIfnBbI0KYugwMgh0dBDjmr248cacDgdu7csyzNNWsCv/4K+PlJ\n/yxMiQweMjgA8ngwHOAYM+L0aTF6smxZ4N/1JvVn/35RJYyPF/1tv/0G8Kr1DFMs4CZKxmx4913g\nhx+AsWOB+fMNcMKwMGDECDFx+513xPptZcoY4MQMIz/mUHZyDa4YEBsLfPaZWKyTyZvz58VSay+9\nJKYG6EV2tlijbehQ8fqjj4BNmzi4MUwxgwOcFijZpv7rr4CPDzBlShReeQX46SfFVADI0b+Ql8Oc\nOWL+W1AQUL26HidPSwPeektUAa2tgdWrRcdeHtn/ZX0WSiCDhwwOgDweDAc4qTlyBOjUCUhNBezt\nxUC+t94C+vYF7t1T2k4erl4F1q8Xo/XzWVxYO5KSxEKkO3cCdnai/y0w0FCaDMOYGO6Dk5SoKOCN\nN4BHj4B+/YBVq0SX0MSJ4r1q1cS2QjlMpWLYMJFQZMAA0U1WJE6dErm9rl8H3NzEaJU6dQzqyTDF\nieJadj4PBzgJOXRIlLWPHwPvvSfSG+bMJb5yRTTDHTkitvv3BxYuFBWOkkhyMlC7tljYNC4OqFev\nCCfZuRPo3Vv8z6FNG7EMQcWKBndlmOJEcSw7/ws3UWqBKdvUf/5Z1NwePwYGDhQ1N0vLZw6urqJ2\nt2CBGPOwbh3wyivA7t2m8ZOhf+F5hy+/BJ48EYuZ6hzciERfW/fuIrgNGCCaJbUMbrI9CyWRwUMG\nB0AeD4YDnFRERABduoiMUIMHAytW5Dm2ARYWwJgxYimY1q2BGzfEcYGBQEqKybUV484d0UwLAFOm\n6Hjw06eibXP8+GfZmdesAUqVMrQmwzAKwU2UkrB3L9Cjh6iNDBsGLFmSd3D7L9nZoolyyhQRGB0d\nRWDs3Nn4zkozZYqYPvHGGzrWYB88EPPafv5ZBLS1a8UkOoZhNBSXsrMgOMBJwK5dwNtvi+A2ciSw\naJFYN1MXLl4UNbjoaLE9cKBofbO1NbiuFKSkAM7OYkm2X3/VYZWaq1dFB2dcHFC5suh/a9HCqK4M\nUxwpDmVnYXATpRYYs019+3bRf/TkiWh2zC+4FeZQty5w9Cjw+eeiUrJqlcgotX+/YX1l6F+IiorC\n11+L4PbaazoEt+PHRU7JuDigfn2RdkuP4CbLs5ABGTxkcADk8WA4wCnKtm2ipezpU9EV9NVXutfc\nnsfSUmTxOHVKpE1MShLz6IKDRTAwFx4/Fs8K0KHvbfNmoH170XHn6yuqfbVqGc2RYRjl4SZKhfjh\nBzEyPTtbzG2bPVu/4PZfsrLECMNPPhG1w5o1xXSD11833DWUYv588R+CFi1EnCrwuRGJTCRTp4rt\noUOBxYvFKtwMw+SLrGWnLnCAU4CNG8X8tZw0h7NmGTa4Pc+5c6Jv7o8/xPaQIaIZs3x541zP2GRk\niHlvN26Ivss33yxg58xMMRx13TrxgOfPF+3AxnrYDGNGyFh26go3UWqBIdvUv/9eZCbJzha1K22D\nW1EdXnlFdD19+qlIrRgWBjRsKCaTFwWl+heIRLAePx64cSMKnp5i9GS+3L0LdOwoglu5cqKzMyTE\noMFNhr4WGRwAOTxkcADk8WA4wJmU774Tc4nVamD6dPFjisqElZWoKZ44ATRpIla67tBBjNhMSzP+\n9YvKw4ciuXRwsBgx2aAB8M034rNPPing2V28KNovjxwR8yaOHOGcZgxTAuEmShOxahXw/vvP5hTr\nPDHZQDx9CsydC8yYIV7XqiUS5rdtq4zP8xCJpYEiIoDwcODYMdGXmEOVKoCfn5iylm/tLSpKZKT+\n5x+gcWPRjunoaAp9hjErZCk79YEDnAlYsULUQgCxrIteGe8NxJkzom/u9GmxPXq0mDRdrpxpPVJS\nxHzriAjxc/36s88sLcUUAD8/MXHdy6uQye+rV4sHnZUlamzr1wM2Nka/B4YxR2QoO/WGzBxD3GJk\nZGSRj126lEjUTYi++EIZh/zIzCSaNo3Iykr4uboS/fKLcT2ys4lOnCD69FMiHx8iS8tnzwcgcnAg\nCgoi2rKF6P59LR2ys4kmTXp2kvHjibKy9PLUBmN8J8XRgUgODxkciOTx0BdzCA88VtqILFkCjBol\nXn/1lRjjIBMvvQSEhgLduolVC86eFU2VY8aIQSllyxrmOvfviwnnObW0W7eefWZlJa6ZU0tr1EjH\nfsmcJMnbtokq39dfi6GiDMOUeLiJ0kgsXPgsoC1eLAZ0yMyTJ6Jv8LPPxAhPd3eRe7hVK93PpVaL\nAS3h4SKg/fabeC8HJycRzPz8xGCXIqcTu3lTNEX+/jvw8svA1q1i5CTDMHpjDk2UHOCMQM5EZECM\n+hs2zKSX14sTJ0Rt7tw5UZMaNw6YOVMszVMQd+8C+/aJgLZvn0gYkoO1tVgoOyeovfKKAUaPnj0r\nJsElJgIuLmKB0vr19TwpwzA5mEOAU7SRNTw8nOrWrUvu7u40Z86cPPcZNWoUubm5kaenJ508eVLz\nvrOzMzVq1Ii8vLzI29s732sY4hZ1aVOfO/dZV1BYmN6XLpKDvmRkEH30EZGFhbiPunWJjh/P7ZGV\nJd775BOiZs2IVKrcfWnOzkRDhxJt30708KFh/c7MmUNUvry4UIsWRLduGfYCWiJDX4sMDkRyeMjg\nQCSPh74oHB4MgmJ9cGq1GiNHjsTBgwdRvXp1eHt7o1u3bqj33KqV4eHhuHLlCi5duoTffvsNw4YN\nQ/S/6fItLCwQFRUFO4mWsv7sMzH8X6UCVq4UGf2LI6VKiT647t3FSMu4OLHu3PjxopsrLEz0qd2/\n/+yYl17K3ZdWr54R5vidOwesXImGixaJNs9evcTIycKqlwzDlEyUiqzHjx8nPz8/zfbs2bNfqMUN\nGTKENm3apNmuV68e3bx5k4iIXFxc6O7du4Vex1S3OGOGqFCoVERr1pjkkibh8WOiiROf1eae/6ld\nm2jECKJdu4jS0owk8M8/Yiiqt3fui0+dKkZPMgxjFBQMDwZDsRpccnIyatSoodl2cnJCTExMgfs4\nOjoiOTkZVatWhUqlQseOHWFpaYng4GAMHjzYZO7PQyRGIs6YIeZoffedSMVlLpQuLebu9egh8hVb\nWj7rS3N3N1ImFrUaOHhQ1M5++kkkoATEQJKAADFj3tvbCBdmGMacKLapuo4dO4aTJ09i7969+Prr\nr3H06FGjXSu/3HJEotDPCW45eSZN6WAqmjcXzZITJ0Zh9GigTh0jBLcrV8QDdXERS9ps3CiCW4cO\n4uHeuAGEhSEqPd3AFy4aSn8nsjgAcnjI4ADI42EsIiIiUK9ePdSpUwdz58594fMNGzbA09MTnp6e\n8PHxwdmzZxWwFChWg3N0dERiYqJmOykpCY7/Sank6OiIa9eu5bmPg4MDAKBy5cro0aMHYmJi4OPj\nk+e1AgMD4eLiAgCoUKECvLy80K5dOwDPfhkL2j59+vQLn7dt2w6TJwNz50bBwgLYuLEd3n1Xu/MV\nZTsHY51f2+3T/6Y+MdT5fgkPR+XDh+ERHQ0cPvzsRl1cgKAgHK9TB5nVqhX6fZTUbUN/H8X991OG\nbXP6/fwv2oydqF27Nn755RfY2toiIiICgwcP1oydMDlKtY1mZWWRq6srxcfHU2ZmJnl6elJcXFyu\nffbs2UP+/v5EJPrsmjdvTkRE6enplJqaSkREaWlp1KpVK9q3b1+e1zHGLarVRBMmiK4gKyuirVsN\nfgnzRq0mOnKEaOBAIhubZ/1qZcoQ9e9PdOgQ968xjMLkVXZqM3bief755x9ycnIyip82KFaDs7S0\nxJIlS+Dr6wu1Wo1BgwbBw8MDYWFhUKlUCA4Ohr+/P/bu3Qs3NzeUK1cOq1evBgDcunULPXr0gEql\nQlZWFvr27QtfX1+TeBOJuWELFogsHFu2iP4pRguSk4G1a0Xf2qVLz95v1QoIChJZlF9+WTk/hmEK\nRJuxE8+zcuVKdO7c2RRqeaNYaDURhrjFnHktajXRqFGismFtTbRjh96n1tlBaXT2yMgg2ryZyM8v\n91BMBwcxPPP8eeM7GAkZPGRwIJLDQwYHInk89CWvsnPr1q00ePBgzfa6deto1KhReR5/6NAhql+/\nPt3PL6msCeBclFqiVot0W0uXijlfP/5YyIKbJRki4NQpUVPbsOHZhDlra7GUTVCQGERixb9+DCML\nUVFRL/Sp/hdtxk4AQGxsLIKDgxEREaHoXGVO1aUFarVIt7V8uZgEvX27GCbP/Ic7d8QSNatXi4Xd\ncvDyEkGtTx+gUiXl/BiG0Zq8ys7s7GzUrVsXBw8ehIODA5o1a4aNGzfCw8NDs09iYiI6dOiAdevW\noUWLFqbWzgX/F7oQ1GqxxNi334o5YTt2iMoH8y9ZWSIB5apVwO7dYhVVAKhYEejbVwQ2Ly9lHRmG\nMQjajJ2YOXMm7t+/j+HDh4OIYG1tXWA/nVFRrHHUROhzi1lZRIGBREAklSlDdOCAAcV0RJZ2fY1H\nXBzRBx8QVav2rF/NwoLI318MK83IML6DwsjgIYMDkRweMjgQyeOhL+YQHrgGVwA7d4olY0qVAvbu\nBfKZGlJyePAADrt2AZMmiTVwcqhbV9TU+vcHqldXzo9hGOY5uA+uAIhE0uE2bcRPieT2bRHpt28H\nDhwAMjPF++XLi7RZQUFAixZGytnFMIxSmMNyORzgmBe5elXkgNy+HTh27NlqpSqVqMYGBYnRkOXK\nKarJMIzxMIeys9jmojQlhQ2dLfYORMCZMyJrtJcXULu2WBvnyBExlL9zZzGE9Pp1RH3yiWiKVDC4\nyfB9AHJ4yOAAyOEhgwMgjwfDoyhLLtnZwK+/PqupXb367LPy5QF/f5GipXPn3NlFLlwwvSvDMEwR\n4CbKkkRGhliG5qefRL/anTvPPqtaFejWTaxy+tprYmQNwzAlFnMoO7kGZ+48eADs2SNqaeHhQFra\ns89q1xa1tB49xEARS0vlPBmGYQwM98FpgQxt6jo53LgBLFsm0q1UriwmXP/wgwhujRuLBexiY4HL\nl4EvvgBat9Y6uBW7Z2FEZPCQwQGQw0MGB0AeD4ZrcObDpUvP+tOio8XAEUCsxNq2raildesm1llj\nGAlxcXFBQkKC0holDmdnZ8THxyutYRS4D664QgScPPksqJ079+yzUqVEPrEePYAuXTj/I1MsMNu/\nVcnJ77mbw/fBNbjiRFaWGLqfE9SeW+0ctrbAm2+KoNapE2Bjo5wnwzCMBHAfnBYo2qZOBPzyC276\n+YmRjq+9BixeLIJb9erA8OHA/v1iROT33wM9exo1uMnQvyCDAyCHhwwOgDweDPM8XIOTFbUa2LUL\nmDsXOH4c1XLer1tX1NK6dwe8vUUfG8MwDPMC3AcnG0+eiEVC580Dzp8X79nbi5panz7Ac+suMYw5\nUez+Vv9l9uzZuHr1KpYvX660SpEw5z44DnCykJYGrFwJfPklkJQk3nNyAiZMAAYN4j41xuyR9W+1\nfPnyUP2bTDw9PR2lSpWCpaUlVCoVwsLC0Lt3b4UN9cOcAxy3b2mBUfsX7t4Fpk0DatYExo4Vwc3D\nQ6zTc+UKMGYMYGMjTR+HDB4yOAByeMjgAMjjYQxSU1Px8OFDPHz4EM7OztizZ4/mveIe3MwdDnBK\nkZAAjB4tAtuMGcA//wAtW4olw//8E3jvPeCll5S2ZBjmOYjohVrN9OnT0b9/f812dHQ0WrduDTs7\nOzRu3BiHDx/WfNa+fXtMnToVrVu3Rvny5dGtWzfcu3cP/fr1g62tLZo3b47ExETN/hYWFli8eDFc\nXV1RpUoVfPjhh7lcZs2aBRcXF1SrVg2BgYF4+PAhACAzMxP9+/dHpUqVYGdnh+bNm+PO86n5SgpG\nX1JVYaS7xbNnifr3J7K0fLYStr8/0S+/EKnVStsxjGIU9Lea86diiB99cHFxoYMHD+Z6LzQ0lPr3\n709ERElJSVSxYkWKiIggIqIDBw5QxYoV6e7du0RE1K5dO3J3d6erV6/Sw4cPqX79+uTu7k6HDh2i\n7OxsGjBgAA0cOFBzbpVKRa+99hqlpKTQtWvXqE6dOvTtt98SEdG3335L7u7uFB8fT+np6fTWW2/R\ngAEDiIgoLCyMunbtShkZGaRWq+nkyZOUmpqaz7PN+6FIV3YWAa7BmYqjR8Wk64YNgXXrxHt9+4pl\navbsAf73P140lGGKOevXr8cbb7yBTp06AQA6dOiApk2bYu/evZp9goKC4OLigvLly6Nz585wd3dH\n+/btYWFhgXfeeQenTp3Kdc5JkybB1tYWTk5OCAkJwcaNGwEAGzZswLhx4+Ds7IyyZcti9uzZ2LRp\nE9RqNaytrXHv3j389ddfUKlUaNy4MWxKYD8+BzgtKHL/gloN7N4N+PiIALZ7N1C6NDBypMgD+f33\nQKNGxnUwMDJ4yOAAyOEhgwNgfA9D1uGMSUJCArZs2QJ7e3vY29vDzs4Ox44dw82bNzX7VK1aVfO6\nTJkyL2ynPZ8QHYCTk5PmtbOzM65fvw4AuH79OpydnXN99vTpU9y6dQv9+/dHp06dEBAQACcnJ0ya\nNAnZ2dkGv1/Z4XlwxuDpU2DTJjGHLSeFlp0dMGIEMGoUUKWKsn4MwxiFGjVqYMCAAQgLCzPYOa9d\nuwaPf6cHJSQkoHr16gCA6tWr58rdmZCQAGtra1StWhUWFhaYOnUqpk6disTERHTu3Bl169ZFUFCQ\nwTIWZHcAABCLSURBVLyKA1yD04J27dppt2N6OrBoEeDmBgwYIIKbo6MY+p+QAMycWeTgprWDkZHB\nQwYHQA4PGRwAeTyUpl+/fti1axf2798PtVqNjIwMHD58WFPrKgqff/45UlJScO3aNSxatAgBAQEA\ngN69e+Orr75CfHw80tLSMGXKFAQEBMDCwgJRUVH4888/oVarYWNjA2tra1iUwKQQXIMzBPfuAUuW\niBRa9+6J9+rVAz78UPSz8WhIhjELVIX0kzs5OWHHjh344IMP0Lt3b1hZWaFZs2ZYunSpVsfnRbdu\n3fDqq6/i4cOHCAoKwsCBAwEAAwcOxI0bN9CmTRtkZmbCz88PixYtAgDcvHkTQ4cORXJyMmxsbBAQ\nEJBrpGeJQelRLsbGELcYGRmZ9wcJCURjxhCVLfusib95c6KffiLKztb7ulo5mBgZPGRwIJLDQwYH\nIsN4lIDiSGdUKhVduXLFqNfI77mbw/fBNbiiEBcnUmmtXy8y/ANicdFJk4A2bXg0JMMwjARwqi5d\n+PVXMXBk506xbWEB9OolmiK9vAxzDYYpoZhDaihDY2lpiUuXLqF27dpGu4Y5p+riGlxhEAHh4cCc\nOWItNkAM9Q8KEnkijfiLxzBMyaYkDu03JCVvWI0unDgBeHoCb7whgputLfDRR0B8PPDNNyYNbiVl\nvlNxcQDk8JDBAZDHg2Geh2twBVG1KnDhAjIrVkSpSZOA4GDg5ZeVtmIYhmG0gPvgCuOXX4DmzYFS\npQwnxTDMC5hDn09xhPvgSjJt2ihtwDAlAmdn5yLNE2P04/l0X+aGon1wERERqFevHurUqYO5c+fm\nuc/o0aPh7u4OLy8vnD59WqdjDYUM/QsyOAByeMjgAMjhIYMDYBiP+Ph4zXI0RfmJjIzU63hD/cji\noe1PfHy8Tt+TPuW2qVEswKnVaowcORL79u3DuXPnsHHjRly4cCHXPuHh4bhy5QouXbqEsLAwDB06\nVOtjDYmSX5BMDoAcHjI4AHJ4yOAAyOEhgwMgj4cx0KfcVgLFAlxMTAzc3d3h7OwMa2trBAQEYMeO\nHbn22bFjBwYMGAAAaN68OR48eIBbt25pdawhSUlJMdq5i5MDIIeHDA6AHB4yOAByeMjgAMjjYQz0\nKbeVQLEAl5ycjBo1ami2nZyckJycrNU+2hzLMAzDGJailNuOjo6Klc/Fah6cUiN6dG2jNlcHQA4P\nGRwAOTxkcADk8JDBAZDHg1FwFKWjoyMSExM120lJSXB0dHxhn2vXrr2wz5MnTwo99nkMMTLru+++\n0/sc5uAAyOEhgwMgh4cMDoAcHjI4APJ4GBp9ym1FyD8Ps3HJysoiV1dXio+Pp8zMTPL09KS4uLhc\n++zZs4f8/f2JiOj48ePUvHlzrY9lGIZhDIs+5bYSKFaDs7S0xJIlS+Dr6wu1Wo1BgwbBw8MDYWFh\nUKlUCA4Ohr+/P/bu3Qs3NzeUK1cOq1evLvBYhmEYxnjoU24rgdlnMmEYhmFKJsVqkImh0XXC4qlT\npzTvu7i4wNPTE40bN0azZs2M6nHx4kW0atUKpUuXxvz583N9ZiiPwhw2bNgAT09PeHp6wsfHB7Gx\nsQZ30MZj586dmms1bdoUhw4dMriHtkkEfv/9d1hbW+PHH380uIM2HocPH0aFChXQpEkTNGnSBLNm\nzTK4hzbPIioqCo0bN0aDBg3Qvn17gzto4/HFF1+gcePGaNKkCRo2bAgrKyvNcH1TPYt79+6hc+fO\n8PLyQsOGDbFmzRrNZ4Z8FowOKNY4qjDZ2dmatuQnT56Qp6cnnT9/Ptc+e/fu1bQlR0dH52pLrlWr\nFt2/f98kHnfu3KE//viDPv74Y/ryyy9zfWYID20cjh8/TikpKUREFB4ertizSE9P17yOjY0lV1dX\ng3po45Cz32uvvUZvvPEGbdu2zaAO2npERUVRly5d8jzeVM8iJSWF6tevT0lJSUQkflcN6aCtx/Ps\n2rWLOnToYFAPbRxCQ0Np0qRJRCSeg729PT19+tRgDozulNganL4TFokIarXaJB6VKlXCq6++Ciur\nF7tMDeGhjUOLFi1ga2uref38vBZTPouyZctqXqelpaFSpUoG9dA2icDixYvx9ttvo0qVKrneN+Wz\nyLleXpjqWWzYsAE9e/bUjJIz9PehrcfzbNy4Eb179zaohzYO1apVQ2pqKgAgNTUVFStW1PzNGupZ\nMLpRYgOcvhMWVSoVOnbsCG9vb6xYscKoHgVhCA9dHVauXInOnTsb1EEXj+3bt8PDwwP+/v5YtGiR\nQT20cbh+/Tq2b9+OYcOGvRBgTP0sjh8/Di8vL7zxxhuIi4szqIc2Dn/99Rfu37+P9u3bw9vbG+vW\nrTOog7YeOTx+/BgRERHo2bOnQT20cRg8eDDOnTuH6tWrw9PTEwsXLjSoA6M7vJpAETl27BgcHBxw\n584ddOzYER4eHvDx8TF7j8jISKxevRpHjx5VzKF79+7o3r07jh49iv79++PixYsm9QgJCcnVB/N8\nkDPls3j11VeRmJiIsmXLIjw8HN27d8dff/1lUo+srCycPHkShw4dQnp6Olq2bImWLVvCzc1Nkb+R\nXbt2wcfHBxUqVNC8ZyqP2bNnw9PTE5GRkbhy5Qo6duyI2NhY2NjYSFNelDRKbA1O3wmLDg4OAIDK\nlSujR48eiImJMZpHQRjCQ1uH2NhYBAcHY+fOnbCzszOogy4eOfj4+CArKwv37t0zmIc2Dn/88QcC\nAgJQq1YtbN26FSNGjMDOnTsN5qCth42NjabJtnPnznj69Cnu379vMA9tHJycnNCpUyeULl0aFStW\nRJs2bXDmzBmDOWjrkcOmTZtyNU8aykMbh2PHjuGdd94BALi6uqJWrVqaRMSGehaMjijT9ac8+kxY\nTE9Pp9TUVCIiSktLo1atWtG+ffuM5pFDaGgoffHFF5ptQ3lo45CQkEBubm50/PjxXO+b+llcvnxZ\n8/rEiRNUu3Ztg3romkQgMDBQM8jE1M/i5s2bmte//fYbOTs7G9RDG4fz58/T66+/TllZWZSenk4N\nGjSgc+fOKfI3kpKSQvb29vTo0SPNe6Z8FuPGjaPQ0FAiEt+Nk5MT3bt3z6DPgtGNEttEqc+ExVu3\nbqFHjx5QqVTIyspC37594evrazSPW7duoWnTpkhNTYWFhQUWLlyIuLg43LlzxyAe2jjMnDkT9+/f\nx/Dhw0FEsLa2RkxMjMmfxbZt27B27Vq89NJLKFeuHDZv3gzAcN+JNg7P83waOFM/i61bt2Lp0qWw\ntrZGmTJlFHkW9erVQ6dOndCoUSNYWloiODgY9evXx9WrV036LADRN9upUyeUKVNGc6wpn8XkyZMR\nFBQET09PEBHmzZsHe3t7gz4LRjd4ojfDMAxjlpTYPjiGYRjGvOEAxzAMw5glHOAYhmEYs4QDHMMw\nDGOWcIBjGIZhzBIOcAzDMIxZwgGOYRiGMUs4wDEMwzBmCQc4pkQRFBSErl27Kq3BMIwJ4ADHmA0W\nFhawtLSEhYXFCz+WlpYYOHAgFi1ahO+//15pVYMSERGBcePG4fDhw0Y5/6pVq/D+++/j9u3bRjk/\nwxiLEpuLkjE/bt68qXm9a9cuBAcH4+bNm5rlbMqUKYPy5csrpWcwLl++jNu3b6NVq1YARL7FkJAQ\n1KxZU7M9fvx4REdH4/Lly3pfb+DAgbCyskJGRobe52IYU8I1OMZsqFKliuYnZz2wypUra94rX758\nnk2U8+bNg5ubG8qWLQtPT0+sX78+1+ft27fH8OHDMWHCBFSsWBFVqlTB4sWLkZmZiWHDhqFChQpw\ndnbGxo0bcx0zbNgwhISEwN7eHvb29vjwww9znffJkycICQlBtWrVUKZMGbRs2RLHjh0r9D7nzp2L\n8+fP5/t51apV0b59e3Tq1KnQc2kLp6xliiMc4JgSzZQpU7B69WosXboU58+fx+TJkzF06FCEh4fn\n2m/Dhg14+eWXERMTg8mTJ2PMmDHo2rUr6tevj5MnT+K9997DwIEDczXjbdiwAUSE6OhoLF++HMuX\nL8eCBQs0n3/wwQf44YcfsGbNGpw+fRoNGzaEn58fbt26VaDzzz//XGg2+v379xs0wDFMsUTBpXoY\nxmhs3bqVLCwsXng/MDCQunTpQkRirbAyZcrQ0aNHc+0TEhKiWQeQiOj/7d1fSFNtHAfw79RtJiOc\nzinVqOWFMFA2BvkPZVNiClJBspsgUduF80IFcTDRC6uLwD8gXsdxBJFdRUGkMigvLCIUiXXhhQki\nIU5HTBm67elC3tHR6cVre9+c3w/s4nnO8+c8u/lxnj/n2Gw2UVVVJStTUFAgbt++nUjv7+8LlUqV\n+DaczWYTJSUlsjqPHj0SBoMh0bdKpRLPnj1LXI/FYqK4uFgMDAwkHdPr169FZ2enMBgM4vHjx2Ju\nbk4IIYQkSWJ1dTVRLh6PC71eL54+fSpevnwpWltbE2NcW1sTY2NjoqamRjidTtHf3y+0Wq2IRCJC\niINvIE5MTAhJkoQkSYk2D/dBdBZwDY7OrUAggEgkgoaGBll+NBrFtWvXZHllZWWytF6vR2lpaSKd\nlZUFrVYre4KrqKiQ1amsrMTg4CDC4TBWVlYQjUYT62jAwSaZyspKBAKBpPfb1NSEYDCIWCwGr9d7\n7Li+fPmCCxcu4M6dO9Bqtdjc3MSLFy9QXV2Nr1+/oqurCz6fD3fv3oXT6YTL5YJarUY4HIbX68Xi\n4iKCwSDu37+PlpaWY/sh+tsxwNG5FY/HAQBv3ryBwWCQXVMqlSemFQpF0rx/2jyN3z+ietj79+/R\n2Nh4Yv3p6Wm4XC5otVoAwOfPn2G1WgEADocD29vbWF9fh9PpBABcvXoVwEGQ/vnzJ8xmM27evAlJ\nkk49FqL/E9fg6NwymUxQq9X4/v07rl+/LvsdDnj/xqdPn2Tp+fl5XLp0CRqNBsXFxVAqlbJNJfF4\nHPPz8zCZTMe2+eHDB9jtdgghEAwGk5aZmZlBfX09ACASieDVq1dobm5GKBQCAPj9ftTW1h6pl52d\njW/fvmFoaAgLCwuy9UKis4hPcHRuaTQa9Pb2ore3F/F4HLW1tQiHw/j48SMyMzPx4MGDU7W/vr6O\nnp4edHR0YGlpCcPDwxgcHAQA5OTkoKOjAx6PB/n5+TAajRgdHcXGxgbcbnfS9ra2tqBSqaDT6eDz\n+RJB7He7u7sIBAK4ceMGAODt27ewWq3QaDR4/vw52tvbMTs7i7q6Olm91dVVWK1W/PjxA7du3cLe\n3h7PvdGZxwBH59rDhw9RVFSEkZERuN1uXLx4EWazWbalP9mU4XF5v+ffu3cPsVgM5eXlyMjIgMvl\nQnd3d+L6kydPoFAo0NbWhlAoBIvFgnfv3qGwsDDpvebm5sJisUCSJFy5cgWXL18+UmZpaQkOhwMZ\nGQeTM0ajEXl5efD5fGhrawMALC8vw+PxyOrpdDr09fVhamoKOzs72N3dRVdX10l/HdFfTyEED7gQ\n/Wl2ux2lpaUYHx9PeV+Tk5Ow2+2Jg95ntQ+iP41rcERElJYY4IhS4KSdkKnAiRiioxjgiFLA7/f/\nJ9OTwMGrucbHx1P6suW5uTlkZ2enpH2iVOEaHBERpSU+wRERUVpigCMiorTEAEdERGmJAY6IiNIS\nAxwREaUlBjgiIkpLDHBERJSWGOCIiCgt/QK1TSfPxtflZgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa8069f05d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cuCap.Plot_Travell_Hist(ruta=ruta_images + 'Histogram_IsoCronas.png')"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Curva hipsometrica y cauce ppal "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/wmf/wmf.py:482: FutureWarning: pd.rolling_mean is deprecated for ndarrays and will be removed in a future version\n",
" Y = pd.rolling_mean(Y,window)\n"
]
}
],
"source": [
"cuCap.GetGeo_Cell_Basics()\n",
"cuCap.GetGeo_Ppal_Hipsometric(intervals=50)"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/wmf/wmf.py:1811: FutureWarning: pd.rolling_mean is deprecated for Series and will be removed in a future version, replace with \n",
"\tSeries.rolling(window=10,center=False).mean()\n",
" elevPpal=pd.rolling_mean(elevPpal,ventana)\n"
]
}
],
"source": [
"cuCap.Plot_Hipsometric(normed=True,ventana=10, ruta=ruta_images+'Hipsometrica_Captacion.png')"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAGICAYAAACQmJPYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8U2Xa//HPydKNlpZFKLbYshRosVBAKAhiWQRaFRxh\nkJHlQZwB5HGAedRx43EZBGRQoKwDPrggKoPjCMxgRf1BizBAlVKVTUDWRoqytLSFrjm/PwIVBApp\ncpLc7fV+vfKSnCZ3vonQK+e+zrmPpuu6jhBCCCG8yuTtAEIIIYSQgiyEEEL4BCnIQgghhA+QgiyE\nEEL4ACnIQgghhA+QgiyEEEL4AJ8oyDk5OfTu3Zu2bdsSHx/P/PnzAXjhhRdo3749CQkJ9O3bl5yc\nnMrnzJgxg5iYGGJjY/nss88qt2dlZdGuXTtatWrF5MmTPf5ehBBCiOrQfOE85NzcXHJzc0lISKCw\nsJBOnTqxZs0aIiMjCQ4OBmD+/Pl8++23vPHGG+zZs4fhw4fz1VdfkZOTQ9++fTlw4ACappGYmMiC\nBQvo3LkzKSkpTJo0if79+3v5HQohhBBV84k95PDwcBISEgAIDg4mNjYWm81WWYwBioqKaNCgAQBr\n165l2LBhWCwWoqOjiYmJITMzk9zcXAoKCujcuTMAo0aNYvXq1Z5/Q0IIIYSTLN4O8GtHjhwhOzub\nxMREAKZMmcLy5csJCgpi+/btANhsNrp161b5nIiICGw2GxaLhcjIyMrtkZGR2Gw2z74BIYQQohp8\nqiAXFhYyZMgQUlNTK/eOX3nlFV555RVmzpzJ5MmTeeutt1x+HU3TXB5DCCGE+xjVPQ3TNPJdHCMq\nKoojR464I06VfKYgl5eXM2TIEEaOHMmgQYOu+vnDDz9MSkoK4NgjPn78eOXPcnJyiIiIuO72a/GB\n1rlTXnrpJV566SVvx3CKaplVywuS2RNUywvqZTZyJykfeMnFMV46etQNSW7MJ3rIAGPGjCEuLo5J\nkyZVbjt48GDln1evXl3ZZx44cCArV66ktLSUw4cPc/DgQbp06UJ4eDihoaFkZmai6zrLly+/ZnFX\nkSe+nbmbaplVywuS2RNUywtqZjaSxcWbJ3N63ZYtW3jvvfeIj4+nQ4cOaJrG9OnT+b//+z++//57\nLBYLzZs3Z/HixQDExcUxdOhQ4uLisFqtLFq0qPIb1sKFCxk9ejTFxcWkpKQwYMAAb741IYQQXmb1\ndoCb5BOnPXmapmnKTVmnp6eTlJTk7RhOUS2zanlBMnuCanlBvcxG/k7WNI2ZLo7xNJ5pc0pBFkII\n4VVGF+TXXRzjCTxTkH2mhyyqlp6e7u0ITlMts2p5QTJ7gmp5Qc3MRrK6ePMUn+ghCyGEEEZRpdDJ\nlLUQQgivMnrKepGLY0zAM1PWqnxxEEIIIapFlaOspYesCBV7QqplVi0vSGZPUC0vqJnZSHIeshBC\nCOEDVNlDlh6yEEIIrzK6h7zCxTFGID1kIYQQwmWqFDrpIStCxZ6QaplVywuS2RNUywtqZjaSnIcs\nhBBC+ADpIfsw6SELIYTvMLqHvNbFMQYiPWQhhBDCZaoUOukhK0LFnpBqmVXLC5LZE1TLC2pmNpL0\nkIUQQggfoEqhkx6yEEIIrzK6h7zZxTF6IJdfFEIIIWoNKciKULEnpFpm1fKCZPYE1fKCmpmNJGtZ\nCyGEED5AzkP2YdJDFkII32F0D/kbF8doj/SQhRBCiFpDCrIiVOwJqZZZtbwgmT1BtbygZmYjqXIe\nshRkIYQQNZpRB3XZ7XY6duzIwIEDr/nziRMnEhMTQ0JCAtnZ2TfMKT1kIYQQXmV0D/mwi2M049o9\n5Dlz5rBjxw7OnTvH2rVXrpidlpbGggULWLduHdu3b2fSpEls27atyteRPWQhhBDCSTk5OXzyySf8\n/ve/v+bP16xZw6hRowBITEwkPz+fkydPVjmmFGRFqNgTUi2zanlBMnuCanlBzcxGMqKH/Kc//YlZ\ns2ahado1f26z2WjatGnl/YiICGw2W5U55TxkIYQQNZqzhW4L8J8qfr5u3ToaN25MQkIC6enpbptu\nlx6yEEIIrzK6h3zaxV3PBuVX9pCfe+45VqxYgcVi4cKFCxQUFPDggw+yfPnyyseMHz+eXr168dBD\nDwHQpk0bMjIyaNy48XVfR6ashRBCCCdMnz6dY8eOcejQIVauXEnv3r2vKMYAAwcOrNy2bds2wsLC\nqizGIAVZGSr2hFTLrFpekMyeoFpeUDOzkSwW1243a8mSJSxduhSAlJQUmjVrRsuWLRk3bhyLFi26\ncc7qvkEhhBBCBVazcWPffffd3H333QCMGzfuip8tWLDAqbGkhyyEEMKrjO4hl4a6NoZfvmfWspY9\nZCGEEDWaVZFK5xM95JycHHr37k3btm2Jj49n/vz5APz5z38mNjaWhIQEBg8ezLlz5yqfM2PGDGJi\nYoiNjeWzzz6r3J6VlUW7du1o1aoVkydP9vh7MYqKPSHVMquWFySzJ6iWF9TMLHykIFssFmbPns3u\n3bvZunUrCxYsYN++ffTr14/du3eTnZ1NTEwMM2bMAGDPnj2sWrWKvXv3kpaWxoQJEyqnEx577DGW\nLVvG/v372b9/P+vXr/fmWxNCCOFtZhdvHuITBTk8PJyEhAQAgoODiY2NxWaz0bdvX0wmR8SuXbuS\nk5MDwNq1axk2bBgWi4Xo6GhiYmLIzMwkNzeXgoICOnfuDMCoUaNYvXq1d96UmyUlJXk7gtNUy6xa\nXpDMnqBaXlAzs6GMurqEm/lEQb7ckSNHyM7OJjEx8Yrtb775JikpKcD1lySz2WxERkZWbo+MjLzh\nUmVCCCFqOEUKsk+1ugsLCxkyZAipqakEBwdXbp82bRpWq5Xf/e53bnut0aNHEx0dDUBYWBgJCQmV\n3yov9V986X52dnZlT9wX8tzM/UvbfCVPTct7eVZfyXMz9+fOnevz/95UzpuuwO+L7Oxs8vLyAMdO\nmLhI9xFlZWV6//799blz516x/a233tLvvPNOvbi4uHLbjBkz9FdffbXyfv/+/fVt27bpJ06c0Nu0\naVO5/YMPPtDHjx9/1Wv50Nu+aRs3bvR2BKepllm1vLoumT1Btby6rl5mI38nA7re3LWbp2qGz5yH\nPGrUKBo2bMjs2bMrt3366ac88cQTbNq0iQYNGlRu37NnD8OHD2f79u3YbDbuueceDhw4gKZpdO3a\nlXnz5tG5c2fuvfdeJk6cyIABA654LTkPWQghfIfR5yHrMS6OcaAWnYe8ZcsW3nvvPeLj4+nQoQOa\npjFt2jQmTpxIaWkp99xzD+A4sGvRokXExcUxdOhQ4uLisFqtLFq0qPISWAsXLmT06NEUFxeTkpJy\nVTEWQghRy/hEpbsxn9lD9iQV95DT09MrezCqUC2zanlBMnuCanlBvcyG7yHHujjG3lq0hyyEEEIY\nRpFKJ3vItciRjAxO7dtHs169aNCqlbfjCCEE4IE95AQXx8iWPWThRpkLF5L2+OMAWOvU4ZEvv6RJ\nhw5eTiWEEB6gSKVTJGbt9vXXPzJx4iJyc2+hokJH13WKi8spKSlH0zQCAy34+5vRdSgvt1NRoWOx\nmDCbNXQdSksrGHlqOqFACKAXFZH9xhs0uYnrc7pCtT6WanlBMnuCanlBzcxCCrLP2737J7p3X0Zp\naQ5gveZj8vNLqhyjLbuoy1nC+eV/+NnVq7HPm4fJmatvCyGEihT5NSc9ZB+XmrqNyZNdu0DGb/gn\niXxLI6AQKMfx93Pkvn2EtW7thpRCCFF9hveQu7s4xhbP9JB9bi1rcaU2bRq6PMYpGlIOFAEXgLKL\n//3mzTddHlsIIXyeImtZS0H2cf37t2TWrL7UqWPDZIKL659c5dfbL7+/he5spTPnsOAHNAAaAj9+\n8olBqR0uX2dZBarlBcnsCarlBTUzG0qRgqzIzHrt9uST3bnjjjIXD9L4C9umTWPvlClogAaU7NpF\n3t69hMW6eNa8EEIIl0kPuRYpOHyYj5o3xw/HNbd1oOXjj3PH/PleTiaEqM0M7yH3d3GM9dJDFm4W\nHBVFg/h4zDj+xwcCxxctoqK42MvJhBDCQGYXbx4iBVkR7ugJaSYT7V98ETOOPnIoUM9uJ2fePJfH\nvhbV+liq5QXJ7Amq5QU1MxtKkR6yFORaJuL++2lw222YgCZ+EBMI5fNe83YsIYSo9aSHXAsdmzWL\nkv/9M9EBv2wzvbYQ8+8neC+UEKLWMryH/KCLY/zTMz1kKci1kL2khHOtIwkuOYW5KWAFPeQ2TOsO\ngdmDDRMhhMADBfm3Lo7xoRzUJS7jzp6Qyd+fkFGPYI4AzR+0+mDyOwZrF7vtNUC9PpZqeUEye4Jq\neUHNzIaSHrLwZabnp0JIAEQBkUAE8OVfoLjQy8mEEKJ2kinr2mzRJPhuHgTjuOlAz2nQ+zkvBxNC\n1CaGT1mPdHGMd2XKWhjtkakQYIW6OKZl/IDtf4GKUi8HE0IIN3LzecglJSUkJibSoUMH2rZty3PP\nXb0Tk5GRQVhYGB07dqRjx4688sorN4wpBVkRhvSEAutCv/9x/IWzcvFvQwnsetctw6vWx1ItL0hm\nT1AtL6iZ2VBu7iH7+/uzceNGdu7cybfffsuGDRvYsmXLVY/r2bMnWVlZZGVlMWXKlBvGlIJc2/V6\nBvwCoBTIA/KBT56HMlm9SwghricoKAhw7C3b7Xbq1at31WOcneaWHrKAf4+ALe85rstYgKOXfP/z\ncP+Np1iEEMJVhveQx7s4xt+uLq52u51OnTrxww8/MH78eP76179e8fOMjAwGDx5MZGQkERERzJo1\ni7i4uKpfRwqyoCQfXroFTpRBBY69ZX9/WHAM6jbydjohRA1neEF+3LnnpOdAuu2X+y9/df293XPn\nztGvXz9mzpzJ3XffXbm9sLAQk8lEUFAQaWlpTJo0if3791f5ujJlrQhDe0L+oXDXs45inAvYgEMl\n8OaLLg2rWh9LtbwgmT1BtbygZmZDOXkQV1IUvHTnL7eq1K1bl3vvvZevv/76iu3BwcGV09rJycmU\nlZVx5syZKseSgiwc+jwNhMIFoBD4Cfi/JVBwzru5hBDCVW4+qOvUqVPk5+cDcOHCBT7//HMSEhKu\neMzJkycr/5yZmYmu69SvX7/KmDJlLX6xZiG89LijGAO6DtrDY+C1Zd7NJYSo0Qyfsn7CxTFev3LK\n+rvvvuO//uu/0HUdu93OyJEjefLJJ1myZAmapjF27FgWLlzI4sWLsVqtBAYGMmfOHBITE6t+HSnI\nolJ5OdzTEn3fUcqLAR20wADMu46jNWjo7XRCiBrK8IL8tItjzJSFQcRlPNITsljg8amOdUF00PyA\nimLsM6rXS1atj6VaXpDMnqBaXlAzs6HcvDCIUaQgiysNHgnRLTHXBUuI42ba8CGUlXk7mRBCVI8i\nF5eQKWtxFfvSuZhm/gnqAY2AcuC5jyHpAS8nE0LURIZPWb/g4hh/kSlr4SWmgb9FDzZBMxwFOQZY\n/ScvpxJCiGpSZA9ZCrIiPNoTCo9A+90ICAd6Ad2A+CNwdrdTw6jWx1ItL0hmT1AtL6iZ2VBSkIXS\nRj0PrTVHUb4DuBM49oyXQwkhRDXIQV03Lycnh969e9O2bVvi4+OZN28eAP/4xz+4/fbbMZvNZGVl\nXfGcGTNmEBMTQ2xsLJ999lnl9qysLNq1a0erVq2YPHmyR9+HkZKSkjz7gre2ghZt0GNg9y2t2HDb\nnXwXeQh7xambHsLjmV2kWl6QzJ6gWl5QM7PwkYJssViYPXs2u3fvZuvWrSxcuJB9+/YRHx/Pxx9/\nfMX6oAB79+5l1apV7N27l7S0NCZMmFDZcH/sscdYtmwZ+/fvZ//+/axfv94bb6lm6DCJPaGtyGzQ\nge/rxPBlgy5sYbm3UwkhhHNkyvrmhYeHVy47FhwcTGxsLDabjdatWxMTE3PV0W1r1qxh2LBhWCwW\noqOjiYmJITMzk9zcXAoKCujcuTMAo0aNYvXq1R5/P0bwSk+o0QhOBkZTSDBm7NThPAdMOzhL7k09\nXbU+lmp5QTJ7gmp5Qc3MhpKCXD1HjhwhOzu7yiXGbDYbTZs2rbwfERGBzWbDZrMRGRlZuT0yMhKb\nzXatIcTNMNUhJOAhrJQRSj5h5NFQ+5mvmObtZEIIcfMU6SF7sPbfWGFhIUOGDCE1NZXg4GBDX2v0\n6NFER0cDEBYWRkJCQmXf5dK3S1+7f4knX7+DaQQfpa/kDKfpmBSChXKy09MpZC4PJk326uch95NI\nSkryqTw3c//SNl/JU9PyXrp/eXZfyHP5/ezsbPLy8gDHTphw8JmFQcrLy7nvvvtITk5m0qRJV/ys\nV69evP7663Ts2BGAV199FU3TePppxwKlAwYM4OWXXyYqKopevXqxd+9eAFauXElGRgaLFy++YjxZ\nGMQ5+/iUw7yKP6WYqcBMBRBIIp9gJcTb8YQQijN8YZC/uTjG+Fq2MMiYMWOIi4u7qhhfcvmHMXDg\nQFauXElpaSmHDx/m4MGDdOnShfDwcEJDQysvdbV8+XIGDRrkqbdgqF9/6/WkNgwggEaYqcCfUvwo\nxZ88DvG/VT7Pm5mrQ7W8IJk9QbW8oGZmQynSQ/aJKestW7bw3nvvER8fT4cOHdA0jenTp1NcXMwf\n//hHTp06xX333UdCQgJpaWnExcUxdOhQ4uLisFqtLFq0CE3TAFi4cCGjR4+muLiYlJQUBgwY4OV3\nVzN0YTY7eRAz5ViooAQ/TrOJM2RQn7tvPIAQQniLB/vArvCZKWtPkinr6jnEXznLOxRRh0KCKcEf\nPyzcwwr8CPV2PCGEogyfsn7XxTFG1rIpa+H7mvE/+BFBAcGcpDG5hHOERnzJEm9HE0II5UlBVoQv\n9IQ0LLTmXYoJrtxLPk8dsjjOT/x41eN9IbMzVMsLktkTVMsLamY2VE3pIS9dupTc3JtbCOLXwsPD\nGTt2bLWeK3yTH42JYjBHyAQ0QMeEnb/zOuOYhh8B3o4ohBBX8omjpW7shj3k4cOHM3369GoN/vzz\nz7NixYpqPddI0kN2jZ1yFvA0JZRgpQwLFWjoNKUDA3nc2/GEEIoxvIf8TxfHeNAzPeQbfm/o3r07\nUVFR1Rr8zjvvrNbzhG8zYeE3PMYqZuNHGVbKMFHBT2wlj8GE0cTbEYUQQjk37CFPmDDhhoNs3ryZ\nzZs3V+u54ub4Wk+oKS1px51YKMNKKQEUE8o5vuTFysf4WuYbUS0vSGZPUC0vqJnZUIr0kKt1UFdR\nURH//Oc/2bRpE2VlZfTo0QNN03jjjTfcnU/4sD78DisWrJRRn7OEUIiVA+xhgbejCSHELxQpyNU6\nDzk5OZkzZ85gs9k4f/48Q4YMYfDgwWzbto0XX3zxxgN4mfSQ3ed7/h+7eJ06XACgHDN2zHThJcLp\n5uV0QggVGN5DdvEqvFp/Hz4PuX///mzfvp2cnBwyMjK45ZZbePbZZ92dTSigNX0Ix3HpzGL8KSCE\nfOqSTirF5Hk5nRBCqKNaBdnPz6/yz/Hx8UybNo2srCwl9o5V5cs9oW68jD+3cIEAzhPEeYI4TR1e\nS/8fb0dzii9/xtcjmY2nWl5QM7OhFJmyrlZB7t27N++//767swhFmbDSlflU4E8ZVs5Rl0KCOUY+\nmWzwdjwhRG2nSEGuVg952rRpTJ06laioKPr06UPv3r1JSkqiYcOGRmR0O+khGyOLD/mSL7hAIOWY\ncSwcAiN5jChaeDecEMJnGd5DvvokIOfG6OHDPeScnBx27NjBnDlzCAkJYcaMGTRp0oS+ffu6O59Q\nSAcGU48mlGPiUjEG+DtvUk6p94IJIYQCqlWQ27dvT9u2bUlJSWHmzJns2LGDkydPSg/ZQCr0hDRM\nDOXP+OE4xuBw+nH8KcGfU3zALC+nuzEVPuNfk8zGUy0vqJnZUIpMWVerIAcEBHD8+PErttWvX5+7\n7rrLLaGEugIIYii/B8BKKWHk0ZTj1GcDX/Oal9MJIWolNxfkkpISEhMT6dChA23btuW555675stO\nnDiRmJgYEhISyM7OvmHMavWQN27cyLhx45g4cSL9+vWjVatWzg7hVdJDNt6nrGY/nxDNERrxE4Fc\nQEPnVqbTkCHejieE8CGG95BvXAurHiPh6h7y+fPnCQoKoqKigu7du/P666/TvXv3yp+npaWxYMEC\n1q1bx/bt25k0aRLbtm2r8nWqtYe8ZMkShg8fzrp16+jYsSORkZGMHDmSjz/+uDrDiRpoAA/QlFhC\nKCCUfOpyjrqco5A/UcYxb8cTQtQmZhdv1xAUFAQ49pbtdjv16tW74udr1qxh1KhRACQmJpKfn8/J\nkyerjFmtghwfH8/QoUNJS0vj7NmzfPDBB7Ro0YJVq1ZVZzhxE1TsCYWmtyOApvhTjIVyLJRjpphT\nPISO3dvxrqLiZyyZjadaXlAzs2rsdjsdOnQgPDycpKQk4uLirvi5zWajadOmlfcjIiKw2WxVjlmt\ndvXzzz/PunXrOH36ND169OCuu+6S/rG4igkznXmD47RDo4xyLOiYKOcwecymHk96O6IQojZwstKl\nZzpuVTGZTOzcuZNz587Rr18/MjIyuPvuu6ufkWr2kFUnPWTPOs+/OcUYKjBjoRwTOjomGrMFKzHe\njieE8DLDe8gHXBwjpurzkKdOnUpQUBBPPPFE5bbx48fTq1cvHnroIQDatGlDRkYGjRs3vu441Zqy\nFsIZQdxHIIMwU4EJO1ZK8ecC+QxEp8zb8YQQNZ2be8inTp0iPz8fgAsXLvD555+TkJBwxWMGDhzI\n8uXLAdi2bRthYWFVFmOQgqwMFXtCl2duwDzMNHTsIesV+JWV4Fd6kPMV47wX8FdU/4xVoVpm1fKC\nmplVcuLECXr16kWHDh3o2rUrAwcOpE+fPixZsoSlS5cCkJKSQrNmzWjZsiXjxo1j0aJFNxzXg6c8\ni9rMRCC3sII8euNfVoLJbsdcoUPZ25T7/w6L5R5vRxRC1FRurnTx8fFkZWVdtX3cuCt3MBYscO7a\n8G7rIeu6TnFxMYGBge4YzlDSQ/aeQn0KWsl0rGU6pov/C3QaYAk5jqb5/t8dIYT7Gd5D/tHFMW71\n4bWsr2Xs2LHExsa6azhRQwVrr6ARdVkxBjiNXrrEi6mEEDVaTV4681oGDx7M5MmT3TWc+BUVe0LX\nyxxg/Tc6GhUmKPXTKPU3UWKf4fVZi5r0Gfsy1TKrlhfUzCzcVPsrKioYMGAAAwYMcMdwooYzmdtS\nYU6m3JxGudlKmcUKFII+nUDteW/HE0LUMPp1VtvyNW7pIW/fvp2NGzcyZMgQWrZs6Y5chpIesvfZ\nKw5TVBFDiTUAtIuXatRN1NMOYaaBd8MJITzK6B5yWb5rY1hDfbiHvGrVKjp27Ejv3r2ZNWsWkZGR\nPPPMM6xZs8bd+UQNZTI3w2we9ksxBtDsFPGM90IJIWqkCotrN0+pVkH+5JNPmDp1KkOHDmXr1q20\nadOGbt26sWXLFnfnExep2BO6UeZA899A9wfAjnZxpet/Yue0B9JdrSZ+xr5Itcyq5QU1M4tq9pC7\ndu3KvffeCziWBzt37hzp6el06NDBreFEzaYRjL/2KBdYTBlWdDR0NPJ4ifrM93Y8IUQNUW529fhl\nz1wMp1o95DfeeIPf/OY3NGzY0IhMhpMesu/QKeIk0ZQB5ViwYwJMNOUL/Gjt7XhCCA8wuoecX+7n\n0hihllLf7SHHx8dzzz33sHLlSk6dOuXuTKIW0ahDAKOpwMwFAjlHKHnU5RhP3PjJQghxEyrMZpdu\nnlKtgvzaa6+RlJREamoqt956K/Hx8UycOJENGzZUK0ROTg69e/embdu2xMfHM2/ePADOnj1Lv379\naN26Nf37969czBtgxowZxMTEEBsby2effVa5PSsri3bt2tGqVasadV60ij2hm80cylR0GnKeIE7S\nCBuRfM95zrLD2IC/UpM/Y1+iWmbV8oKamY1Ugdmlm6dUqyC3a9eOp556iq1bt3Lq1CmmT5+OyWTi\ntddeq1YIi8XC7Nmz2b17N1u3bmXhwoXs27ePV199lb59+/L999/Tu3dvZsyYAcCePXtYtWoVe/fu\nJS0tjQkTJlROJzz22GMsW7aM/fv3s3//ftavX1+tTMJzNAJowCzOUZdiArhAAAXUZRNzqKDU2/GE\nEMIjqtVDLi8vZ9WqVdx222306NHD7aEeeOABHn/8cR5//PHK60fm5uaSlJRUWag1TePpp58GIDk5\nmZdeeomoqCh69+7Nnj17AFi5ciUZGRksXrz4ivGlh+x7dHQ28xAnKAbAj1I0dOqTwF3M9HI6IYSR\njO4hn9BDXRqjiZbvkZpRraOsLRYLDz/8sLuzAHDkyBGys7Pp2rUrJ0+erLx+ZHh4OD/99BMANpuN\nbt26VT4nIiICm82GxWIhMjKycntkZCQ2m82QnMK9NDTieJETPIc/xVw6O/ks2RzhE6JJ8Wo+IYS6\nKhS5sKFPpSwsLGTIkCGkpqYSHByMdvmiEXDVfVeMHj2a6OhoAMLCwkhISCApKQn4pf/iS/ezs7Mr\ne+K+kOdm7l/a5szz2zCEf6XPw45Gs6Sm2DHxTvpr9CSQXkm9fC6vt+//Oru389zM/blz5/r8vzeV\n86rw+yI7O5u8vDzAsRNmNE/2gV3htssvuqq8vJz77ruP5ORkJk2aBEBsbCzp6emVU9a9evVi7969\nV01ZDxgwgJdffpmoqKjKx0DNmrJOT0+v/Autiupm/oIx5JJPASGcpw4adnpwD1140P0hL1ObPmNv\nUi2zanlBvcxGT1kf1Ru5NEaU9pPvnvZ0Lbquc+HChWo/f8yYMcTFxVUWY4CBAwfy9ttvA/DOO+8w\naNCgyu0rV66ktLSUw4cPc/DgQbp06UJ4eDihoaFkZmai6zrLly+vfI7qVPrHdUl1MyfyEiX4c45Q\n8gnlFA35hK8pvthfNkpt+oy9SbXMquUFNTMbSZWjrN22h/yHP/yBzz//vFrTD1u2bKFnz57Ex8ej\naRqapjF9+nS6dOnC0KFDOX78OFFRUaxatYqwsDDAcdrTsmXLsFqtpKam0q9fPwB27NjB6NGjKS4u\nJiUlhdSMMMqMAAAgAElEQVTU1KteT8U95NpmDa+ykzyKqEMx/lRgJo7GPM4Ib0cTQriZ0XvIB/TI\nGz+wCjFajkdqhtsK8qeffsq+ffuUOPdXxYKs2hQUuJa5kHPMZBanCeNnGpFPKDoar9CeRG5zb9CL\nattn7C2qZVYtL6iX2eiCvFePcmmMWO2o7x5lfS1yPWThTsHUpTN38iE5HOM2csvDOXehLg9QzvY6\nFdxmUuMgDSGEuFk+c1CXJ6m4h1wbVWBnLCvZYO9AzqkI7BevMm5G5+PQAO4N8KmTBIQQ1WT0HvIu\nvYVLY9yu/eC7B3WtW7eOESNGUFBQwKlTp/j4448rzxEWwl3MmHiKfpSWWSuLsV4BZXn+3HdY5438\nCi8nFEKoQJWDuqpVkPfv389dd91FUVERd9xxB9OmTWPMmDF8/fXX7s4nLrr8fFNVuCNzGxrypCUM\n0NF10H8OhFwrHLYydrOJN3NcfolKtfUz9jTVMquWF9TMbKQaXZA1TWPcuHFs376dn376iS+++IK1\na9fy4YcfujufEPzJ3JB5IX5g16DIBHnAWeC0xqMbYME+bycUQgjXVauH/NRTTzFs2DBeeeUV8vLy\n2LhxIwALFizg8ccfd3tId5Mespo2FJfTZ6cZjmhQhuPrpBXQYEosTI33ckAhRLUY3UPO1G93aYwu\n2i7fPcr6mWeeYfz48Rw5coSlS5cCjtOegoOD3RpOiMv1DrCwtrXOwKM6oIEfEOC4vZIL35TD2g5e\nDimE8DmqrGVdrSnrBg0a8OGHH7Jz5046d+5MXl4eQ4YM4ejRo+7OJy5SsSdkROb762ss76qBhmPv\nOADH10oz/OsMxG+t/tjyGXuGaplVywtqZjaSKj1kt3xtCAsL4+effyYwMNAdwwlRpZHREGaGgV/x\ny1fKcqAIdp2CRj/BwRSoa/VeRiGEcJachyyUlX0WunwNZWbg3MXbRSbgne4wwrXTD4UQHmB0DzlD\n7+LSGHdrmb57HrIQviChHhT0hvoWHAd5XVIB9kIYuR7ar4IKu7cSCiF8gbunrHNycujduzdt27Yl\nPj6eefPmXfWYjIwMwsLC6NixIx07duSVV165YU4pyIpQsSfkicz+ZrB1hzb1L9t4AUePORC+vQBh\n70N+6Y3Hks/YM1TLrFpeUDOzkcoxu3T7NYvFwuzZs9m9ezdbt25l4cKF7Nt39fmXPXv2JCsri6ys\nLKZMmXLDnD5z+UUhqivADHv7/Gp6OgAwA35QaIFGH0NOkZcCCiG8qgKLS7dfCw8PJyEhAYDg4GBi\nY2Ox2WxXPc7ZaW6fuPyip0kPuebKPAV91kDhxWKMGQgGghx//K4LxNbxakQhxK8Y3UNO05NcGiNZ\nS79uviNHjpCUlMSuXbuuOPU3IyODwYMHExkZSUREBLNmzSIuLq7K13HbyVmDBw+mbdu27hpOiGrp\n0hAKHoXWH8L+MiAQqAeElWMPKqP9SY2DTf25zap5OakQwlOcPXXp2/SzfJd+9oaPKywsZMiQIaSm\npl61DkenTp04duwYQUFBpKWl8cADD7B///4qx3PblPWAAQOUuBayqlTsCXkz8/e/haRbcPwND6nA\n0qiIsIgz1I0+TRf7SS7Yrz7SSz5jz1Ats2p5Qc3MRnL2IK62SQ0Z9lJM5e1aysvLGTJkCCNHjmTQ\noEFX/Tw4OJigoCAAkpOTKSsr48yZM1XmdEtB3rx5M5s3b3bHUEK4zcZ7YFg44GenTsh5TGYdf4rx\n8zvH3Rz3djwhhIe4+6AugDFjxhAXF8ekSZOu+fOTJ09W/jkz03HaVP369a/52Euq1UMuKipi/fr1\nNGzYkG7dumG1WtmyZQt79uzhD3/4g7PDeZz0kGuXR3IqWN34JHUs5wnWCvGnGDMV9NAbMU+79rdf\nIYTnGN1D/khPdmmMwVraFfm2bNlCz549iY+PR9M0NE1j+vTpHD16FE3TGDt2LAsXLmTx4sVYrVYC\nAwOZM2cOiYmJVWetTkFOTk7mzJkz2Gw2zp8/z5AhQxg8eDDbtm3jxRdfdP7depgU5NpncOkZdlhP\nUl87SwjnsFCBrsMTWjvupam34wlRqxldkFfp97s0xlDtX767MEj//v3Zvn07OTk5ZGRkcMstt/Ds\ns8+6O5u4jIo9IV/K/JFffaKwEEAxVsrxo5Q62nn+xlecwnG6ni/lvVmS2Xiq5QU1MxupRq9l7efn\nV/nn+Ph44uPjmTZtmttCCWGENK0Z9+k2rFoZ/pTgOM66gidZz1Jc+wYthPBdniyqrqjWlPW+ffvI\nysri4YcfNiKT4WTKuvY6RAF/5DP8KEOjAjPl6JhoQyNeob+34wlRKxk9Zb1CH+zSGCO0j3x3yvqj\njz5izJgxtG7dmgkTJvCPf/yDU6dOuTubEG7XnBAeohWgY6aCIkLIJ4z/UMbf+d7b8YQQBjDiKGsj\nVKsg5+TksGPHDubMmUNISAgzZsygSZMm9O3b1935xEUq9oR8NfMo4rmDWynFnxL8KSCYUzTi2fQN\nZFD1eYK+xlc/46qollm1vKBmZiO5e+lMo1Trldq3b0/btm1p27YtKSkpAJw5c4bdu3e7NZwQRnmO\nnoziX5zGjzN6fQr1EC7Y6zHCfpatWjCRmt+NBxFCKKFG95Dffvtt+vTpQ9Omap4uIj1kAXCCIn7L\nVxzRI7HrJgK185g1O0G6lR1aG8zI8ppCeILRPeSl+kiXxhirveu7PeSoqCj69OnDggULbrg2pxC+\nqgl1mEt7dF0jUDuPn+aYxLZrBQxnr7fjCSHcRJXTnqpVkJcsWcLw4cNZt24dHTt2JDIykpEjR/Lx\nxx+7O5+4SMWekAqZ76Aek7V6mLFTkr6dAIoJoohD/MxSjno73g2p8Bn/mmqZVcsLamY2Uo0uyPHx\n8QwdOpS0tDTOnj3LBx98QIsWLVi1apW78wlhuKe0+iQQjJlyLJRTij9l+LOYH1nJCW/HE0K4SJWj\nrKt9PeR169YRGhpKjx493J3JcNJDFr9mR6c3mRRRSjlWNOyEkYeFckbQhlG08nZEIWoso3vIr+sT\nXBrjCW2RR2rGDY+yLisrw2q1XrX93nvvveHg13uuEL7GhMZ7tGMIWZQDt/Az9TlDA07xFftoyN2k\nUPXC8EII4YobTlmPGzeu2oO78lxxJRV7QqplPpC+nXdojxWNAC4Qzo/cyo805xC7WcERfvB2xKuo\n9hmDeplVywtqZjaSKj3kG+4hnzhxgr/85S9OD6zrOidOSP9NqKUVwfyDdjzBccLIJ4SCi8tsnmcj\n83mEud6OKIRwUo05D/nEiROUlpZWa3A/Pz+aNGlyw8c9+uij/Pvf/6Zx48Z8++23AHz77beMHz+e\noqIioqOjee+99wgODgZgxowZvPnmm1gsFlJTU+nXrx8AWVlZjB49muLiYlJSUpg799q/PKWHLG4k\njwss4i/Ux0YJgZTiB+j05n46yZrXQriV0T3kqfoTLo3xv9rrHqkZ1T6oy502b95McHAwo0aNqizI\nXbp0Yfbs2fTo0YO3336bQ4cO8Ze//IU9e/YwfPhwvvrqK3Jycujbty8HDhxA0zQSExNZsGABnTt3\nJiUlhUmTJtG//9W/PKUgi5txiD2k8TqFBPMzt1BMAGZ0nuVRwqnv7XhC1BhSkB2qddqTu/Xo0YN6\n9epdse3AgQOVR3D37duXjz76CIC1a9cybNgwLBYL0dHRxMTEkJmZSW5uLgUFBXTu3BmAUaNGsXr1\nas++EQOp2BNSLfOv8zYnjnpEcY66FBCCjVv5gWZMZCP5FHsn5K+o9hmDeplVywtqZjaSKmtZ+0RB\nvpa2bduydu1aAFatWkVOTg4ANpvtiiU7IyIisNls2Gw2IiMjK7dHRkZis9k8G1rUOPfxR8DKWcIo\noC75hHKMBozkK8qRWRYhVFBjDuryljfffJM//vGPTJ06lYEDB+Ln597F/kePHk10dDQAYWFhJCQk\nkJSUBPzy7dLX7l/iK3lqw/261KNlejQZHMCU1IQCgvk5fR+HdDO9kprwmdac7embvJYvKSnJpz6v\nm7l/aZuv5KlpeVX4fZGdnU1eXh4AR44cwWg15qAuTzl69Cj3339/ZQ/5cgcOHGDkyJFs27aNV199\nFU3TePrppwEYMGAAL7/8MlFRUfTq1Yu9ex1rEK9cuZKMjAwWL1581XjSQxbOepdvWMQZTtOAs+X1\nuFAcQHmpP1Fmnd1162LR5EIUQlSX0T3k5/T/dWmM6drU2tNDBsdpUpe/4Z9//hkAu93OK6+8wvjx\n4wEYOHAgK1eupLS0lMOHD3Pw4EG6dOlCeHg4oaGhZGZmous6y5cvZ9CgQV55L0b49bdeFaiWuaq8\nI2lPV+pRqlu5UBLA+by6lOQGs/9IXSK+t3PB7rmcl1PtMwb1MquWF9TMbCSZsnbCww8/THp6OqdP\nn+a2227j5ZdfpqCggIULF6JpGg8++CCjR48GIC4ujqFDhxIXF4fVamXRokVoF/dOFi5ceMVpTwMG\nDPDiuxI1zRwSOMUR/lFmRS+wQrHj++xP5800/EZna2uNdkFeDimEuIon16N2hdNT1u+88w4ffPAB\nx44do7j4yiNNNU3jhx98bzWjX5Mpa+GKHoV5bDlcF8ouTjBZAT8dTDpTG2hMqS/T10I4w+gp68n6\nDJfGmKs96xtrWV9u6tSpvPjii9x+++0kJCTg7+9vVC4hfNbm4DASQ8rJPGNyNH0CdPArJ7BuEX/1\nK2XnBT8+DAjFJH1lIYQTnCrIy5YtY9KkScyZM8eoPOI6Lj/KUxWqZXYm77YoCyPsOu8XaGC2E1i3\niLDQMwRqF8gGhpLPP4gyNC+o9xmDeplVywtqZjaSKkdZO3VQ1+nTp7n//vuNyiKEMjQN3muu8W4k\nmO0aVv8SArULaJrjZ9laIdPkWspC+ARVDupyqod833330adPH/70pz8Zmclw0kMW7pRTrnPn+TP4\n1c0FoAwLZbpj8uk9GtNLC/ZmPCF8ntE95LG6axeFWapN9r0e8ty5c3nwwQdp0KABKSkp1K9/9Xq+\nJpPPnEklhEdEWjQOhdSjs/4TZzWNEt2fct0CaAwjj+/0QBqZ1JgyE6Im8uTyl65wqnq2atWKXbt2\n8cgjj9C4cWOsVusVN3evpiV+oeJ5hapldiWvRTPxhRaDhka5bkbXNcrKLBQV+dPxwhnKDfp2rdpn\nDOplVi0vqJlZOLmH/MILL1Se8yuEuFIDLLzBrQwjn4pyM8Ungym11aEoD2LqlrOvqwV/2VEWwuPc\n3QfOyclh1KhRnDx5EpPJxB/+8AcmTpx41eMmTpxIWloaderU4e233yYhIaHKcX1m6UxPkh6yMNJz\n9rPMK6ygaE9DOAgUARVgNcPbveDhVt5OKIRvMbqHPFJf6tIY72pjr8iXm5tLbm4uCQkJFBYW0qlT\nJ9asWUObNm0qH5OWlsaCBQtYt24d27dvZ9KkSWzbtq3K15GGrxBuNt1Uj86a1VGIi4EKwB/KwmD4\nt9AvA+zyfVAIj3H3Udbh4eGVe7vBwcHExsZedXXBNWvWMGrUKAASExPJz8/n5MmTVeZ0uiCfOHGC\nJ598ks6dO9OiRQs6d+7Mn//8Z3Jzc50dSjhBxZ6QapndmXdDcF3a1CsHHce/smAgAPCDz89A+Do4\nXeL666j2GYN6mVXLC2pmVtWRI0fIzs4mMTHxiu3Xu1RwVZzqIe/fv5+77rqLs2fP0r17d1q2bElu\nbi6pqaksX76cL7/8kpiYGGeGFKJG0jSNPR0sPFQEH+4BzIAGlDr++7MO4f8PNneFxKtPVhBCuJGz\na1n/lL6Xn9L33fBxhYWFDBkyhNTUVIKDXT+90ake8m9+8xt27drF559/XnktYXBcOrFfv360bduW\nf/7zny6HMpr0kIUnfWmDvlug1B9HQa4LhAFBOpoOO1tqtJeLUohazOge8mB9hUtjfKSNuCpfeXk5\n9913H8nJyUyaNOmq54wfP55evXrx0EMPAdCmTRsyMjJo3LjxdV/HqSnrjRs3MnXq1CuKMUBUVBQv\nvfQSGzdudGY4IWqFuyIg70GICcLxLy4EqG9Ha3gerfF5OuWfJ6fCS9dvFKIWMGKlrjFjxhAXF3fN\nYgyOSwUvX74cgG3bthEWFlZlMQYnC3JpaSkhISHX/FlISAilpaXODCecoGJPSLXMRuYNtMD+e2D4\nbYAFtMASNBPopWYqivxpccjOngvO7yGo9hmDeplVywtqZlbJli1beO+999iwYQMdOnSgY8eOfPrp\npyxZsoSlSx1HdKekpNCsWTNatmzJuHHjWLRo0Q3HdaqHnJCQwPz580lOTr5iRS5d11m0aNENz7ES\norZb0RmaHIbXNR293IRe5A/5GqVFcPsRndRW8Efjr0khRK3i7vOQu3fvTkVFxQ0ft2DBAqfGdaqH\n/Omnn3LffffRokULHnroIZo0aUJubi4ffvghBw4cYN26dfTr18+pAN4gPWThbf99pozFhXb00/5w\nGjiLo79sgQci4ePuXg4ohAcZ3UNO1j9yaYw0bbBHaobTC4N8+umnTJkyhZ07d6LrOpqm0alTJ6ZO\nnUr//v2NyulWUpCFLxh/towlhy1g06AAR1+5ZTHWuiXcrlvIbBSMWVbGE7WA0QW5n77GpTE+0wZ5\npGY4fR7ygAED+PrrrykoKOD48eMUFBSQmZmpTDFWlYo9IdUyezrv3+pZebeZhgbgB1rzYuo1PUOj\nRqc41fhH+lTk3HAM1T5jUC+zanlBzczChZW6goKCiIiIIChIztcQorpG1IPvksCqgV9oCXX8z+NP\nKVbKybGc48/cuCgLIapWY66HbDab2bp1K126dMFkMlV5cQlN0ygvL3d7SHeTKWvha34qhoQfC/Bv\nfhwzjr+bGnY0dF7gVkbQ0MsJhTCO0VPWSXqaS2Oka8m+cT3kF154gcjIyMo/y9WehHC/RgHwY/MQ\n7rD7kWcqwXTxu7kGTOc4DTCRjCzpJUR1OLtSl7fI1Z4UkZ6eTlJSkrdjOEW1zL6QN58KurIPnVJM\ngJnyizc7qcTS41dF2RcyO0u1zKrlBfUyG72H3E3f4NIYW7XevnlQlxDCOKGYWUkzTGiYqMBKGSEU\nEEAxfyabTE57O6IQwiBO7SHPnDmTnJwc5s+ff9XPJk6cSNOmTXnqqafcGtAIKu4hi9rlP5xjHPsJ\n4RzlWCgkmGIC8KeCDFrTCD9vRxTCbYzeQ+6iZ7g0RqZ2t+/tIb/11lu0a9fumj9LSEjgrbfeckso\nIWq7O6nLXFqgoVFEHU6VNyDn1K3st7Wgw+nz8oVSCCeocpS1UwX52LFj1728YvPmzTl69KhbQomr\nqXheoWqZfS1vH+oxl/aUYSUvL5Sy/BDseUH8mBNGzH6dYrvvZb4ZqmVWLS+omdlINbIgBwUFXfcC\nyzk5Ofj7+7sllBDCoTP1+T23UFHiDyVmKAFK4YfTJm7LArlIlBA1h9PXQz58+DDbt2+/oviWlJTQ\ntWtXbrvtNtascW2JMk+QHrJQzR0/n2dHbpCjIOcDFwA7NAiA3L5gkcMzhcKM7iHfrme6NMYurYvv\nrWX9zTffcOedd9KwYUNGjBhBREQENpuNFStWcPr0abZs2UL79u2NzOsWUpCFauw6tPnBzoGfTY6L\nUdgBP8AM9c1w4m7wU+NUSyGuYnRBjtWzXBpjr9bR9w7qat++PRs3biQqKoqZM2fy+OOPM3PmTJo1\na0Z6eroSxVhVKvaEVMvsy3lNGuxvaeL2IH4pxn7Ad+mcAW75Ek4WezXiTfPlz/laVMsLamY2kio9\nZKeuhwzQpUsXNm3axIULFzh79iz16tUjMDDQiGxCiF/5rj00PwOHy67cfs4OEf+BTR3hzjDvZBNC\nuEZW6hJCQTGb4ODly8YHABpQBm+0hN/f6qVgQlSD0VPWLfRdLo3xg3a7b6xlfS3ffPMN33//PcXF\nV8+RjRo1yunxHn30Uf7973/TuHFjvv32WwC++uor/vu//5uysjKsViuLFi3ijjvuAGDGjBm8+eab\nWCwWUlNT6devHwBZWVmMHj2a4uJiUlJSmDt3bnXenhA+70BP6PYVbCvA8a+4AsgBzsAfvoPC7jA5\nwbsZhfAVqqxlje6Es2fP6nfeeaduMpl0k8mka5qma5pWed9kMjkzXKUvv/xS37lzpx4fH1+5LSkp\nSV+/fr2u67r+ySef6ElJSbqu6/ru3bv1hIQEvaysTD98+LDeokUL3W6367qu6126dNEzMzN1Xdf1\n5ORk/dNPP73m6zn5tn3Cxo0bvR3BaaplVi2vruv6/e9s1PlS1/lY13ld15mj6yzVdZbrevdPvJ3u\n2lT7nFXLq+vqZTbydzKgR+oHXLp5qmY4dVDXc889x+nTp9m0aRO6rvPxxx+zYcMGhg8fTvPmzcnM\nrN6h5T169KBevXpXbGvSpAn5+fkA5OXlERERAcDatWsZNmwYFouF6OhoYmJiyMzMJDc3l4KCAjp3\n7gw49tRXr15drTxCqOJ/boM3WgCXpq+DgQZAKGwpgRbrQbozQqjBqSnr9evX8+KLL9K1a1cAIiMj\n6dSpE0lJSTz22GOkpqayfPlytwR79dVX6d69O0888QS6rvOf//wHAJvNRrdu3Sofd+nUK4vFUnmZ\nyEvZrreIiYpUunLLJaplVi0vODInAf5dYNRxIBDHv+pSoAIOFUPTtXDoXvCrVoPK/VT7nFXLC2pm\nNpInj5R2hVN7yCdOnKBZs2aYzWYCAgIoKCio/NmDDz7IunXr3Bbs0UcfZf78+Rw7dow5c+YwZswY\nt40tRE0z8jbY8TD42XGcFlVx8b/FYDsKIQsh7aB3MwrhLTXytKfw8HDOnDkDQFRUFFu3bq38Jnbw\noHv/tW/fvp3PP/8cgCFDhvD73/8ecOwRHz9+vPJxOTk5REREXHf79YwePZro6GgAwsLCSEhIqHwv\nl87h86X72dnZTJ482Wfy3Mz9S9t8JU9Ny3t51kv384fBLbPSKSwGYpLgZ+CbdEp1SDmZxLB4GNfE\nu/nnzp3r8//eVM6rwu+L7Oxs8vLyADhy5AhGq7CrsYfsVKd65MiR+jPPPKPruq5PmzZN9/f318eO\nHatPmDBBr1Onjv673/2u2s3sw4cP67fffnvl/Y4dO+rp6em6ruv6F198od9xxx26rv9yUFdJSYl+\n6NChKw7qSkxM1Ldv367b7XY9OTlZT0tLu+ZrOfm2fYJqB2nounqZVcur69fOXFah67eu0XXe1nVe\n0nWevXh7Ttd5Xtcbz9D1b370fNZLVPucVcur6+plNvJ3MqCHlpxw6eapmuHUecg//PADP/74I3fd\ndRdlZWU888wz/P3vf+f8+fMMGDCA+fPn06BBA6e/FDz88MOkp6dz+vRpGjduzMsvv0y7du2YMGEC\npaWlBAQEsGjRIjp06AA4TntatmwZVqv1itOeduzYccVpT6mpqdd8PTkPWdR0dh2SN8Jnm4FiHOco\na4AVx0FfgfB4G5jf3ZsphXAw+jzk0JITLo2R79/E99ayrimkIIvaYuU+eHg5VJ5P0fTirYmOKaCC\n31hN/KOlXJlCeJfRBTm46GeXxiisc4vvrWXdoUMH5s6dy8mTJ43KI67j8l6hKlTLrFpeuHHmYW3g\n0FMQ6g+YgRAgyk5AdD5+TQr4V/1zTCz07CLYqn3OquUFNTMbqaLc7NLNU5wqyE2aNOGpp56iadOm\nJCcns3Llymuu1iWE8B3R9eDsFHiuB1AB1rAS7LpGaYkf5WVWFhaV8+S5Em/HFMIwqhRkp6esf/rp\nJ95//31WrFhBVlYWISEhDB48mJEjR9KrVy+jcrqVTFmL2uqHc3D7mQuUBlbgaCr/4n+CLMwK8b/2\nE4UwkNFT1n6n810ao7RBqO/3kPfu3cu7777L+++/z/Hjx4mMjOTo0aPuzGcIKciiNvuxwk6L00WU\nXmwsW/zKMJsr0O0aSwLrMMpfirLwLKMLsim30KUx7OHBV+W71jUYLpeRkcGgQYNo3rw54FirY8qU\nKVW+jktHc8TGxvLCCy8wbdo0br31VnJyclwZTlRBxZ6QaplVywvVy3yr2UR2vUCsgMlcgdlsp/h8\nAMVFQTxySiertMLtOS+n2uesWl5QM7OR7BUWl27X8sgjj7B+/foqX7dnz55kZWWRlZV1w2IMLhTk\nDRs28Mgjj9C4cWNGjRpFZGQk8+fPr+5wQggPam218H2DQCwmndJiK3qJH+T6Yd/pzx2fmvj3CZlB\nEjVIudm12zVc6xoMv+bsXr9TU9a7du1ixYoVvP/+++Tk5BAdHc2IESMYOXIkMTExTr2wN8mUtRAO\nG0vL6HumFPvpANhjhoM4Vvcq1flTksbsId5OKGoDo6esOVrm2iBR1mvmO3r0KPfff/91p6wHDx5M\nZGQkERERzJo1i7i4uCpfxqmlM9u1a0doaCi//e1vGTVqFD169HDm6UIIH9PLz8rcEJh4Ejhx8ZYH\noDFnLbzxBawYB4M6eDWmEK5x9kjpbemwPd2ll+zUqRPHjh0jKCiItLQ0HnjgAfbv31/lc5yasl61\nahW5ubksXbpUirGHqdgTUi2zannBPZn/WMdKaqQGFTpcfvZTIBT6wwMfQsxsuODiTsYlqn3OquUF\nNTMbqlxz7nZHL/jvl3+5VUNwcDBBQUEAJCcnU1ZWVnktiOtxqiAPGTIEfzkCU4gaZ2IDE28na46l\nNcGxiEgAEA40g4O3Qt218P7x648hhM8qd/F2HbquX3eq/fIFtDIzM9F1nfr161cZ0+nTnnbu3MnU\nqVPZtGkTeXl5ZGZm0rFjR5577jl69uzJgAEDnBnOK6SHLMS1HfwZur0Mp4qAW4AooDFQFwgGLNAr\nFNbHgFVW3BRuYngPebeLY7e9Ot+1rsFQWlqKpmmMHTuWhQsXsnjxYqxWK4GBgcyZM4fExMSqszpT\nkDdv3kzfvn1p3rw5ffv2ZcGCBXz99dd07NiRKVOmsGvXLlavXl29N+xBUpCFqNqSDfDHT6CsJRCB\n4zcxy+0AACAASURBVIIUdXDsQZuggQkOtYC6ilzVTvg2wwvyNy6O3d4zNcOp77jPPPMM/fv3Z/fu\n3cyePfuKn3Xs2JGsrCy3hhO/ULEnpFpm1fKCcZnH9Ybiv8LddQE7jsM/LRf/fBJOH4CIDXC6Givn\nqvY5q5YX1MxsKIOmrN3NqYKclZXFY489hqZpjm8dl2nYsCE//+zaFTWEEL7DZIL0h2FbDwiuwPHb\nIg84CXwHhR9Co8dgrXwPF76uzMWbhzhVkAMCAjh//vw1f3bixAlCQ0PdEkpcLSkpydsRnKZaZtXy\ngmcyJzaA/K7QzR8oBX4EsoBssH8Dg34PMYNgz6GbG0+1z1m1vKBmZkNVuHjzEKcKco8ePZg7dy4V\nFb8kvLSnvGzZMnr37u3edEIIn2DS4D/N4a6GOIpyLr9M5elw8CC07QfRPWGb7DELUS1OFeSpU6eS\nlZVF+/btmTp1Kpqm8c4779CrVy+2bdvGiy++aFTOWk/FnpBqmVXLC57PvKkd/FdnrvzNUQYUAeWO\nBZG6TYGwEfCvndceQ7XPWbW8oGZmQ9XEHnL79u3ZtGkTjRs3Ztq0aei6zoIFCwDHMmGtW7c2JKQQ\nwne83QsWP8svvz0qcBzs1QDHectRkN8EBq6EZjPh2xPeSirERYoU5GpffrG4uJgzZ84QFhZWuRqJ\nKuS0JyFcl3cOfvtn+GIzcA5oCjTHcd6yH47FRfzg/7d373FR1fkfx1/DRRFR8RYoCHiBFRQEFDSX\nSmxNRcU0L4QtRliZteqWu2n5c7OLtr9qzfKSZZnubqJdVrzhHUwtREOULQpRAZnUX14wC5XLnN8f\nA5MocnGYmXPg83w85qFzZvjOG7bl4/l+zvd70MFTobAsynZZhbpZfNnTdjPHHmqdmmHW/ZC1Sgqy\nEA2n6GeIfQ6SvwaCgc4Yl0i1BHSAApSCfwc4/AQ4N7NhWKFKUpCNap2ytrOzw97evk4PB4d63atC\n1IMWe0Jay6y1vKCOzK6tYesHcD0D5kSCYynGQlxZjH8BCiA7BVpNhLmLUm0Zt97U8DOuLy1mtiiN\nTFnXWkHnzZt3y5pjIYS4WbNmsCABXjXAnG3wv0cw9pYvAeeND8M1eG05rN4DO5dAT2/bZhZNhBWL\nqjlkyloIYRGnLkHAe3DtBJAHXMQ4J+cKtAFaQoAX7PkruLW2YVBhcxafsv7czLEfUsmUdV0ZDIZa\nby0lhGg6uraFK8/D/X1vONgcYzHuALSD7xzAfTnM2mubjEKoSa0FuV27dlX2qFYUhejoaE6erLot\nz6FDh+jYsWPDJxSANntCWsustbyg/swOdrDrKfhoNugcMPaUL6UaC3N7jDeu6A5v/QxBu0GNE1dq\n/xlXR4uZLaqxbJ1ZVFREWdlvE/AGg4HNmzdTVFRk0WBCiMYj/g/w65cwJBTjTl9gvJ1jO4zLpDwV\nsjob8M0xcF2NVVlom0a2zqy1h2xnZ0daWhrh4eEAlJeX4+joaLrtYqWDBw8ycODAKttqqpX0kIWw\nneJrMHYZbC8HAoBOCrQrQ9esDAWFDtjxY6fmOMrFpE2GxXvIq80ce7LGeshCCFEXzk6w7Vn4bjK0\nMADNFGMxNthBUXPOn2mG7/fq/4e9EA1NCrJGaLEnpLXMWssL2s7sfxcURYGHokMBuOwAp+wh0478\n3Q70SFTHLJaWf8aiQmNZhwyg1+tNF3FVTknr9XpcXV1N7yksLLRAPCFEY9bMHk731hF8zo5jV3TG\nu0gVApfhxEkdrbIg+y/g6VrbSELUoLGsQ7azs7tlYxBFUW57THrIQog74ZVZzul99sY1y0rFowQo\nhyd+D+89AtJWbpws3kNeaubYT1unZtR6hrxq1SqLhxBCiBNB9rgfVbioVFTd60Ax8DO8/yms3ghJ\nc2BoaE2jCFGNxnKG3Bhp8Qw5NTWVQYMG2TpGvWgts9byQuPLXGYA79fhx58wFuOLGAuzA8YlUh3A\nozN8NgEGuNs+r1ppLbPFz5AXmzn2jCZ0lXVCQgJubm4EBQWZjsXExBAaGkpoaChdu3atssRq4cKF\n+Pr64u/vz44dO0zHMzIyCAoKws/Pj5kzZ1r1exBCmM/BDvQvwGP9Md6corziz1aADxAM+iC4+wQ8\n/IMNgwpt0chFXao4Q96/fz8uLi7ExcVx7NixW16fNWsWrq6uzJ07l+zsbGJjYzl06BCFhYX84Q9/\n4Pjx4+h0Ovr378+SJUsICwsjKiqKGTNmMHTo0FvG0+IZshBNTc45uG8+nNVj3DwkFOO65WbANeA6\n9HaBb+6GZqo4tRB3yuJnyK+bOfbsJnSGHBERQdu2bW/7+vr164mNjQUgKSmJmJgYHBwc8PHxwdfX\nl/T0dM6ePcuVK1cICwsDIC4ujg0bNlglvxCi4fm5wZll8NokcLiG8c5RzTBOYV8EzsF/T0DH9VDw\ni02jCrXTyE5dqijINdm3bx/u7u5069YNMC636tKli+l1Dw8P9Ho9er0eT09P03FPT0/0er3V81qK\nFtcVai2z1vJC08j8wgS4/jH8zQ/srmG88vpXjFdhX4affwTv9+GdjBqHuWNN4Wcs1KFO65Btae3a\ntTz88MMNPu6jjz6Kj48PAK6urgQHB5sugqj8j1lNzzMzM1WVpy7PK6klT2PLq9XnmZmZd/T1L/1h\nEH8pgy7LU7n0I+A9yLjx/7epUAwz9INYvRcWBqbSzMH2eeX3Rc35Ku+HkJeXh8XJVdb1k5+fz6hR\no6r0kMvLy/Hw8CAjI4POnTsD8Prrr6PT6Xj++ecBGDZsGPPnz8fb25vIyEiys7MBSExMZO/evSxf\nvvyWz5IeshDaZVBgwE44lIvxTPk8xiuyLwM6sHeE1VNg0gCbxhT1YPEe8v+YOfYrTaiHDMaNRW7+\nhnfu3Im/v7+pGANER0eTmJhISUkJp06dIjc3l/DwcNzd3WnTpg3p6ekoisKaNWsYPXq0tb8NIYSF\n2ekg/QGYFYpx2roc+AWwB1yg3AUeSYQhy2waU6iJRq6yVkVBjo2NZeDAgeTk5ODl5WXajGTdunW3\nTFcHBAQwYcIEAgICiIqKYtmyZaZdw5YuXUpCQgJ+fn74+voybNgwq38vlnLztKoWaC2z1vJC0878\nxgD4+hFo1hxjYXbEeNEXQAns+i80/xNs+9a8z2nKP2NhXaroIX/yySfVHr/dLmFz5sxhzpw5txzv\n27cvWVlZDZpNCKFeAzrDpXkw8E04mo9xzXLJb6+XlMPwpRDRDfbMBEdV/MYTVlfa8EMmJCSwefNm\n3Nzcql2uCzB9+nSSk5Np2bIlH3/8McHBwTWOqZoesjVJD1mIxmf1AYj/DJQSjGfMlSrOnB3sIf0Z\nCPG8zQDCZizeQ/6zmWMvujVfbftnJCcns2TJErZs2cLBgweZMWMGaWlpNX6MKqashRDCXJN/D0UL\noOtdNxx0AFoY/ywzQOib8Ng/oVQjV92KBmKBHnJt+2ckJSURFxcHQP/+/bl8+TLnzp2rMaYUZI3Q\nYk9Ia5m1lhck881at4CTf4O3xxlnr7GreJRjvAo7B1atgBaRMO99qMtJmfyMxZ243Z4ZNZGOihCi\n0ZkxGOLvhvA34YdijAX5HMYdvoDyzvDKIfjfTNgzCwZ2s2FYYXn1nRHRp8KPqQ2foxbSQxZCNGr/\nsw1e3Q18B/wfxn2xuwJOGE9JFHg2At4aacOQTZzFe8hTzBx7ZfX5qts/o9LUqVOJjIxk4sSJAPTs\n2ZO9e/fi5uZ224+RKWshRKP2yjA4MRt8AzDOYzfHeKGXI8b9sUvhHweh4xuQccaWSYXFWGgv6+r2\nz6gUHR3NmjVrAEhLS8PV1bXGYgxSkDVDiz0hrWXWWl6QzHXVrT3kvAGfvwEuJVQ0mDFOZbYxPs43\ng77rYf7XVb9WfsaNgAUu6qpu/4wVK1bw/vvvAxAVFUXXrl3p0aMHTz75JMuW1b5TjfSQhRBNxtj7\njI85/4HX0zEWZieMZ82lQAm8tAeO/ghfPGTTqELlbrd/xo2WLFlSrzGlhyyEaJKyz8E9y+FCC4xL\no36teBiMr3drBz/MBAc5bbE4i/eQHzZz7LVNbC9rIYSwJn83OP8SvHI3xo1ESjEVY4CTF8HlZTh0\n2jb5RAMqNfNhJVKQNUKLPSGtZdZaXpDMDWHuvbB/HNjZ3/RCGVz/BcL/nMqDH0K5odovVyW1/Yxt\nzkIXdTU0KchCiCbv9x6Q/ydwcqw4YMB4MY8BKIGkr8F5Gnx6yHYZReMnPWQhhKhQVga9F8MPP2G8\nScW1iofpDeDlChufhT4+NonYKFm8hzzKzLE3SQ9ZCCGsysEBvn8OXh8GOt1NL14HzkPBQQgeCkFD\nDWQe1dA8dlMm90MWDUmLPSGtZdZaXpDMlvL8ILjwCvh1As6kGg8WA+eB08Cpa2Tt+D9CgrPR6dJp\n23YXQ4bsZe7cLDZtOkNxsW3vXqGFn7FVaeSiLrmgXwghqtHWGX74H5izFN7KrPi9XAJcMUDpr8AF\n4GegkKIiA7t22bFrVznGxvNloBl33eXE6NHOzJ3bEi8vx9t+lhAgPWQhhKhVaRk89294dxmQbYAr\nFwA9xrtV/FTxrpZAZ8AFaIZxcXMle9C1wM+vGX/9iwMJCTfPhzdtFu8hR5o5dor0kIUQQhUcHeCd\nyXB+B/w+yg4cnTBuhn3jWqnKez3qKl6r5AC0AlqSk+fIlD/psHOGkAGw/jOrfQtNm/SQRUPSYk9I\na5m1lhckszXcmLd9G9ifCEpJK95+2wd3944Yz4jB2GS+inHK+saLvewAR2ONrviNqwCZx2BiHNg5\nQ+hA+GKDZTILpCALIURjNmNGS86cCUBRRlBePp7c3KG8954bI0YY6NTpOnZ25RhLr6Hiz+opOjjy\nHTw0CexbweTHjcuvRNMjPWQhhLCQy5cNvPnmL6xcCWfPu4CD3W93mqrUHOOSKgXjRWMVJ9e/84cF\nCyF6ROPfT9viPeR+Zo592Do1QwqyEEJYycbN8Nrf4ZtMKK/ckrEZxkJcxm9LbOwBV4zXhblAnz6w\n+Hm4L8T6ma3B4gU5xMyxj8hFXeIGWuwJaS2z1vKCZLaGhswbPRIO7oOyK7Dpcwjvd8Mv4Rt/37tg\nvC1kO+AuOHoFBr0E7pOh8IJ1MzcK0kMWQghxOyOHw8EvobwIlr8Lzq1ueoMjxqLcsuLPcjiXD11G\nw31Pw0m91SNrl0YKskxZCyGESnz1FTz6KJw4DYb2GJc1u2Gcwr7Eb1PaDkBz6OEJX78NHdrYJm9D\nsfiUtb+ZY2dLD9lipCALIdTucCa8uBh2ngGlOcZtOxWMxbhySrtiGfRAP9j4PLRvbau05rF4Qe5h\n5ti50kMWN9BiT0hrmbWWFySzNdgqb79g2L4KyrbC8L78tteIPVX3JHGArwqgw9PwdrLxkNZ+xhYn\n90MWQghhLjs72DoP8tZDZF+q3XOEcqAY/rwcXMfDzm9sElW9pIesXjJlLYTQqpJSGPoipJ7EOH3t\niHGDsGsYNwur0KIZLJoGT0bbJGa9WHzKuouZY5+WHrLFSEEWQmjdz8XwwKtwsABjQf4V43rmm2x8\nFUYNtHK4erJ4Qe5k5thnpIcsbqDFnpDWMmstL0hma1Br3tbOkLYANj8Hzi2pugPYpVTTX1MyrZ1M\nhTRyP2QpyEIIoWEjQuDXNfD+s9Da5dbXQ3pYP5PqaOSiLpmyFkKIRmTHIXhpNRRfh0n3w19ibJ2o\ndhafsm5r5tiXmtCUdUJCAm5ubgQFBVU5/u677+Lv709gYCCzZ882HV+4cCG+vr74+/uzY8cO0/GM\njAyCgoLw8/Nj5syZVssvhBBq8UAYfLUEMj/QRjG2Co1cZa2KghwfH8/27durHEtNTWXTpk1kZWWR\nlZXFrFmzAMjOzmb9+vVkZ2eTnJzMtGnTTP9yeeqpp/jwww/JyckhJyfnljG1TK19rJpoLbPW8oJk\ntgat5QVtZrYoKch1FxERQdu2bascW758ObNnz8ah4r5jHTp0ACApKYmYmBgcHBzw8fHB19eX9PR0\nzp49y5UrVwgLCwMgLi6ODRsa8I7fQgghtEku6jJPTk4OX375JQMGDCAyMpJvvjGudNfr9XTp0sX0\nPg8PD/R6PXq9Hk9PT9NxT09P9PrGs/v6oEGDbB2h3rSWWWt5QTJbg9bygjYzC+OyclUqKyvj0qVL\npKWlcejQIcaPH8/JkycbbPxHH30UHx8fAFxdXQkODjb9R1w53SPP5bk8l+fyvOGfZ2ZmUlRUBEBe\nXh4WZ4Erpbdt28bMmTMxGAwkJCTw/PPPV3l97969jB49mm7dugEwduxY5s6dW/Ogikrk5eUpgYGB\npufDhw9XUlNTTc979OihnD9/Xlm4cKGycOFC0/GhQ4cqaWlpypkzZ5SePXuajq9du1aZOnVqtZ+l\nom+7zlJSUmwdod60lllreRVFMluD1vIqivYyW/J3MqCAYuajar7y8nKle/fuSl5enlJSUqL06dNH\nyc7OrvKe1NRUZdSoUfXKqpopa0VRqlxW/uCDD7Jnzx7AOH1dUlJC+/btiY6OZt26dZSUlHDq1Cly\nc3MJDw/H3d2dNm3akJ6ejqIorFmzhtGjR9vq2xFCCNFIpaen4+vri7e3N46OjsTExJCUlHTL+5R6\nLpVSRUGOjY1l4MCB5OTk4OXlxapVq3jsscc4efIkgYGBxMbGsmbNGgACAgKYMGECAQEBREVFsWzZ\nMuM6M2Dp0qUkJCTg5+eHr68vw4YNs+W31aAqp3u0RGuZtZYXJLM1aC0vaDOzltx8LdPtrln6+uuv\nCQ4OZsSIEXz33Xe1jquKHvInn3xS7fF//vOf1R6fM2cOc+bMueV43759ycrKatBsQgghmprUised\n69u3LwUFBTg7O5OcnMyDDz5ITk5OjV+jijNkUbvKCyO0RGuZtZYXJLM1aC0vaDOzugwCXrrhUZWH\nhwcFBQWm54WFhXh4eFR5j4uLC87OzgAMHz6c0tJSLl68WOOnSkEWQgjRyDXsQuSwsDByc3PJz8+n\npKSExMREoqOr3ufy3Llzpr9XXtvUrl27GlPKXtZCCCFsyuJ7Wd94o+g74nxLvm3btjFjxgzTsqfZ\ns2ezYsUKdDodTzzxBEuXLmX58uU4OjrSokULFi1aRP/+/WvOKgVZCCGELWmxIFuCTFlrhBZ7QlrL\nrLW8IJmtQWt5QZuZLUsbe2eq4iprIYQQwnKseIcIM8iUtRBCCJuy/JT1WTNHcZcpayGEEKKpkIKs\nEVrsCWkts9bygmS2Bq3lBW1mtizpIQshhBAqID1k1ZIeshBCqIfle8g1b1lZOz/pIQshhBBNhRRk\njdBiT0hrmbWWFySzNWgtL2gzs2WVmfmwDukhCyGEaOSsd2GWOaSHLIQQwqYs30P+xsxR+lqlZsgZ\nshBCiEZOG2fI0kPWCC32hLSWWWt5QTJbg9bygjYzCzlDFkII0ejJOmTVkh6yEEKoh+V7yClmjhIp\nPWQhhBDCfNo4Q5YeskZosSektcxaywuS2Rq0lhe0mVnIGbIQQohGTxtXWUsPWQghhE1Zvoe80cxR\noqWHLIQQQphPG2fI0kPWCC32hLSWWWt5QTJbg9bygjYzCzlDFkII0ehp4wxZeshCCCFsyvI95H+Z\nOcoj0kMWQgghzKeNM2TpIWuEFntCWsustbwgma1Ba3lBm5mFnCELIYRo9LSxU5f0kIUQQtiU5XvI\ny8wcZZr0kIUQQgjzaeMMWXrIGqHFnpDWMmstL0hma9BaXtBmZssqNfNhHaooyAkJCbi5uREUFGQ6\nNn/+fDw9PQkNDSU0NJRt27aZXlu4cCG+vr74+/uzY8cO0/GMjAyCgoLw8/Nj5syZVv0eLC0zM9PW\nEepNa5m1lhckszVoLS9oM7PWbNu2jZ49e+Ln58ff//73at8zffp0fH19CQ4OrtP/JqooyPHx8Wzf\nvv2W488++ywZGRlkZGQwbNgwALKzs1m/fj3Z2dkkJyczbdpvc/tPPfUUH374ITk5OeTk5FQ7plYV\nFRXZOkK9aS2z1vKCZLYGreUFbWa2rDIzH1UZDAaeeeYZtm/fzrfffsvatWv5/vvvq7wnOTmZEydO\ncPz4cVasWMHUqVNrTamKghwREUHbtm1vOV5dEz0pKYmYmBgcHBzw8fHB19eX9PR0zp49y5UrVwgL\nCwMgLi6ODRs2WDy7EEIItWvYKev09HR8fX3x9vbG0dGRmJgYkpKSqrwnKSmJuLg4APr378/ly5c5\nd+5cjSlVUZBvZ8mSJQQHBzNlyhQuX74MgF6vp0uXLqb3eHh4oNfr0ev1eHp6mo57enqi1+utntlS\n8vLybB2h3rSWWWt5QTJbg9bygjYzW1bDniHfXIeqqze3q1U1Ue1V1tOmTWPevHnodDrmzp3Lc889\nx8qVKxtsfOOl8NqyevVqW0eoN61l1lpekMzWoLW8oM3MluDt7U1+/ktmjeHm5tYwYWqh2oLcsWNH\n098ff/xxRo0aBRj/lXH69GnTa4WFhXh4eNz2eHVkDbIQQjQNlpgt8PDwoKCgwPS8unpTn5pUSTVT\n1oqiVCmUZ8+eNf39iy++oHfv3gBER0eTmJhISUkJp06dIjc3l/DwcNzd3WnTpg3p6ekoisKaNWsY\nPXq01b8PIYQQjVtYWBi5ubnk5+dTUlJCYmIi0dHRVd4THR3NmjVrAEhLS8PV1bXWM21VnCHHxsaS\nmprKhQsX8PLyYv78+aSkpJCZmYmdnR0+Pj6sWLECgICAACZMmEBAQACOjo4sW7bMNP28dOlSHn30\nUa5du0ZUVJTpymwhhBCiodjb27NkyRIeeOABDAYDCQkJ+Pv7s2LFCnQ6HU888QRRUVFs3bqVHj16\n0LJlS1atWlXruE1y60whhBBCbVQzZW1tn332Gb1798be3p6MjAxbx7mtuiw+V5vqNnpRs8LCQgYP\nHkyvXr0IDAzknXfesXWkGl2/fp3+/fsTEhJCr169eOGFF2wdqc4MBgOhoaG3TO+plY+PD3369CEk\nJITw8HBbx6nV5cuXGT9+PP7+/vTq1YuDBw/aOlKNcnJyCAkJITQ0lJCQENq0aaP6//9ZlNJEff/9\n90pOTo4SGRmpfPPNN7aOU63y8nKle/fuSl5enlJSUqL06dNHyc7OtnWsWu3bt085cuSIEhgYaOso\ndXLmzBnlyJEjiqIoypUrVxQ/Pz/V/5x//fVXRVEUpaysTOnfv7+yf/9+Gyeqm3/84x/KpEmTlFGj\nRtk6Sp107dpVuXjxoq1j1NnkyZOVjz76SFEURSktLVUuX75s40R1V15ernTq1EkpKCiwdRSbabJn\nyL/73e/w9fVV9RXXdVl8rka32+hFrdzd3QkODgbAxcUFf39/1a9hd3Z2BoxnywaDQRM/78LCQrZu\n3cqUKVNsHaXOFEXBYDDYOkad/Pzzz+zbt4/4+HgAHBwcaN26tY1T1d2uXbvo3r17lbW7TU2TLcha\nUJfF56Jh5eXlkZmZSf/+/W0dpUYGg4GQkBDc3d0ZNGgQAQEBto5Uqz//+c+88cYbmtoDQKfTMWTI\nEMLCwvjggw9sHadGp06dokOHDsTHxxMaGsoTTzzB1atXbR2rztatW8fDDz9s6xg21agL8pAhQwgK\nCjI9AgMDCQoKYtOmTbaOJlTol19+Ydy4cSxevBgXFxdbx6mRnZ0dR44cobCwkC+//JK9e/faOlKN\ntmzZgpubG8HBwbcscVSzAwcOkJGRwdatW1m6dCn79++3daTbKisrIyMjg6effpqMjAycnZ15/fXX\nbR2rTkpLS9m4cSPjx4+3dRSbUsWyJ0vZuXOnrSOYpS6Lz0XDKCsrY9y4cfzxj3/U1Pr11q1bM2LE\nCA4fPsx9991n6zi3deDAATZu3MjWrVu5evUqV65cIS4uzrROU606deoEGDcqGjNmDOnp6URERNg4\nVfU8PT3p0qUL/fr1A2DcuHGauRA0OTmZvn37VtkQqilq1GfIdaXWf63XZfG5WmnpLAjgscceIyAg\ngBkzZtg6Sq3Onz9v2tv96tWr7Ny509QDV6sFCxZQUFDAyZMnSUxMZPDgwaovxsXFxfzyyy8A/Prr\nr+zYscO0QZEaubm50aVLF3JycgDYvXu3JloZAGvXrm3y09XQhAvyhg0b6NKlC2lpaYwcOZLhw4fb\nOtItblx83qtXL2JiYvD397d1rFrFxsYycOBAcnJy8PLyqtOCeFs6cOAA//73v9mzZ49pCcaN999W\nmzNnzhAZGUlISAgDBgwgOjqa+++/39axGp1z584RERFh+jmPGjWKBx54wNaxavTOO+8wadIkgoOD\nOXr0qCaWxBUXF7Nr1y7Gjh1r6yg2JxuDCCGEECrQZM+QhRBCCDWRgiyEEEKogBRkIYQQQgWkIAsh\nhBAqIAVZCCGEUAEpyEIIIYQKSEEWQgghVEAKshBCCKECUpBFk7F69Wrs7OxMDxcXF7p27crYsWP5\n9NNPb3n//Pnzsbe3r9dnJCUlsWjRooaKbJY7yX87Z86cYfjw4Tz22GOUlpY2yJjVWbZsGZMmTeL9\n99+32GcIoVZSkEWTotPp+Pzzz0lLSyM5OZlXX30VJycnHn74YYYMGcL169dN73388cf5+uuv6zX+\nhg0bVFOQ7yT/7ZSUlHD33Xfz0Ucf4ejoCMDLL7+Mm5sbc+bMaZDPAJg2bRoLFizg7NmzDTamEFrR\nqO/2JER1+vTpQ7du3UzPJ02axPjx4xk3bhx//etfWbx4MQCdO3emc+fOtoppNkvnnzdvHmvWrOGe\ne+6x2GcI0ZTIGbIQwJgxYxg9ejQffPAB165dA+Cll17Czu63/4scP36cMWPG4ObmRosWLfD29mbi\nxIkYDAYA4uPjWb16NXq93jQtXln4T5w4QVxcHN26dcPZ2Znu3bszbdo0ioqKquSo/Mzc3FxGjhxJ\nq1at8PHx4ZVXXrkl89GjRxkzZgwdOnTA2dmZnj17Vrnd3s3565qhrk6fPk1+fr5qb0cohNbIulZF\nogAABgRJREFUGbIQFaKiokhKSuLw4cNERESg0+nQ6XRVXm/fvj0rVqygffv26PV6tm7disFgwM7O\njnnz5vHTTz9x+PBhNm3ahKIoNG/eHIAff/wRDw8PFi1aRLt27Th16hQLFixgxIgRHDhwwPQZlZ83\nduxY4uPjefbZZ9m0aRN/+9vf8PLyYvLkyQCkp6cTGRmJr68vixcvxsPDg+PHj3Ps2LEqY92Yv64Z\n6iolJYXAwEBat25d768VQtxKCrIQFby8vFAUhTNnztzy2oULFzhx4gSLFi1i5MiRpuMxMTGmv3ft\n2pWOHTvSrFkzwsLCqnz9PffcU2Vqd+DAgXTv3p17772Xo0eP0qdPH9NrOp2OWbNmERcXB8DgwYPZ\nvXs3a9euNRXkWbNm0aFDBw4ePGgq+oMGDarx+6tPhrpISUnh3nvvBWDnzp18++23HD16lJUrV2Jv\nb89rr71GVlYWTz75JPn5+Vy7do2jR4/i6enJQw89xJ49eygpKWH79u189tlntGzZsl6fL0RjI1PW\nQlSovBPpjWeVldq3b0+3bt2YPXs2K1euJDc3t15jl5aWsmDBAvz9/XF2dsbR0dFUHH/44Ydb3h8V\nFVXlee/evSkoKADg6tWrfPXVVzzyyCOmYmyJDLWpLMh79uzB1dWVPn36sHbtWoqLi9myZQtjx47F\n39+fJ598kvvvv5+pU6fyzDPP8Morr5CRkcG0adOYOXMmFy9eZPv27fX+fCEaGynIQlQ4ffo0Op2O\nTp06Vfv6rl276NevHy+88AJ+fn50796d9957r05jz549m5dffpm4uDi2bt3KoUOH+M9//oOiKKae\n9Y3atWtX5Xnz5s1N77t06RIGgwEPD496fX/1zVCTU6dOUVBQwIULF3B2diYsLIzw8HAOHjxIq1at\naNOmDf7+/qSlpTF9+nS6dOkCQH5+Pt7e3sTGxprG0uv1dOjQoV6fL0RjJFPWQlTYvHkzTk5O9O3b\nt9rXfXx8+PjjjwE4duwYS5YsYdq0aXTt2pWhQ4fWOPa6deuYPHlylSVCV65cuaOcbdu2xc7ODr1e\nX6+va8gMKSkp9OvXj7Zt25KSkoKXlxedO3c2TXtHRERQWlrKvn37TFetA+zdu5f777/f9DwrK4vi\n4mLuvvvuO8ohRGMiZ8hCAJ9//jmbNm3iqaeewsnJqdb3BwUF8dZbbwHw3//+13S8efPmXL169Zb3\nFxcX4+BQ9d+/H330UbXT47Vp0aIFERER/Otf/6qybro2DZkhJSWFqKgoxo0bR6tWrZgxYwZAlYvK\n0tLScHV1xc/Pz3Rs165dDB482PQ8MTGRcePG4ejoyP79++udQ4jGRM6QRZOiKApHjhzhp59+oqSk\nhIKCAjZv3synn37K0KFDWbBgQbVfl5WVxYwZM5g4cSI9evSgvLycVatW4ejoWKXABAQE8MEHH/De\ne+/Rr18/nJyc6N27N8OGDWP16tX07t2bHj168MUXX5i1acebb77JoEGDGDBgAM899xyenp6cPHmS\nzMxM3nnnnWq/piEzpKSkkJCQABg3Daks6hs3biQoKAiA3bt3ExkZafqaixcvcuzYsSoXnyUnJ7Nw\n4cI7uspbiMZGCrJoUnQ6HRMmTADAycmJu+66i9DQUNavX8/YsWOrfT+Au7s73t7eLFq0iMLCQpyc\nnAgMDGTLli2EhISY3j9lyhQOHjzIiy++SFFREd7e3pw8eZJ3330XgLlz5wIwYsQIEhMTCQ8Pv+1n\n1nS8X79+HDhwgHnz5jF9+nSuX7+Ot7c38fHxt/2a+mSoyaVLl2jevDkDBw4E4KGHHuLAgQO8/fbb\nTJw40fS+H374wfSzBvj222+57777qvSLR48eTVpaGp07d+bxxx+vVw4hGhudUnlpqRBC3EZ+fj6r\nV69m3rx5jeqzhFAT6SELIYQQKiAFWQhRJzKZJoRlSUEWQtSqWbNmpKWlWeX2iy+++CLu7u4W+wwh\n1Ep6yEIIIYQKyBmyEEIIoQJSkIUQQggVkIIshBBCqIAUZCGEEEIFpCALIYQQKiAFWQghhFABKchC\nCCGECvw/kbVZejNORZsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa805fde390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cuCap.PlotPpalStream(ruta=ruta_images+'Perfil_cauce_ppal_Capta.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"El cauce principal presenta un desarrollo típico de una cuenca mediana-grande, en donde de ve claramente una zona de producción de sedimentos entre los 0 y 10 km, y de los 10km en adelante se presenta una zona de transporte y depositación con pendientes que oscilan entre 0.0 y 0.8 %"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAgUAAAGDCAYAAAC7nWNVAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4VOX5xvHvZGELSJDNLJgoW6JoAhJARIzWoFBlcU3F\n2ig1VkWkrrRa91axtXXBBUFJq5VFUcCFoEYiiECksgmiwo9ForIpyCKBMOf3x3FCIgmZTGbmnHlz\nf64rV+ZMzsw8d4fpPJ73Pe/xWJZlISIiIg1elNMFiIiIiDuoKRARERFATYGIiIj8TE2BiIiIAGoK\nRERE5GdqCkRERARwuCkoLCwkLS2NLl26MHbs2Br3++STT4iNjeX111+vuC81NZWMjAy6d+9Or169\nwlGuiIiI0WKcemGv18vIkSMpKioiMTGRrKwshgwZQlpa2hH7jRkzhvPOO6/K/VFRURQXF9OqVatw\nli0iImIsx44UlJSU0LlzZ1JSUoiNjSU3N5eZM2cesd9TTz3FJZdcQrt27arcb1kWXq83XOWKiIgY\nz7GmoLS0lA4dOlRsJycnU1paWmWfb775hhkzZnD99dfzy4UXPR4POTk5ZGVlMWHChLDULCIiYjLH\nhg/8MXr06CpzDSo3BgsWLCAhIYFt27aRk5NDeno6/fr1c6JMERERIzjWFCQlJbFp06aK7c2bN5OU\nlFRlnyVLlpCbm4tlWWzfvp3Zs2cTGxvL4MGDSUhIAKBt27YMGzaMkpKSapsCj8cT2iAiIiIuFNCl\njSyHlJeXWx07drQ2bNhglZWVWRkZGdbq1atr3D8vL8+aPn26ZVmWtXfvXmv37t2WZVnWnj17rL59\n+1pz5syp9nEORgyqe++91+kS6s2EDJalHG5iQgbLMiOHCRksy5wcgX73OXakIDo6mnHjxjFgwAC8\nXi8jRowgPT2d8ePH4/F4yM/Pr7J/5f/i37JlC8OGDcPj8VBeXs7w4cMZMGBAuCOE1YYNG5wuod5M\nyADK4SYmZAAzcpiQAczJEShH5xScf/75fPHFF1Xuu+6666rd98UXX6y4fcIJJ7Bs2bKQ1iYiItLQ\naEXDCJGXl+d0CfVmQgZQDjcxIQOYkcOEDGBOjkB5fh57MJbH4wlssoWIiEiECvS7T0cKIkRxcbHT\nJdSbCRlAOdzEhAxgRg4TMoA5OQKlpkBEREQADR8I8PbbcNFFMGUKDBvmdDUiIlJfGj6QgL30Ehw4\nAP/8p9OViIiIk9QURIhQjXNZFnz0kX37o4/g669D8jKAOWN1yuEeJmQAM3KYkAHMyREoNQUN3KZN\nUPk6VK++6lwtIiLiLM0paOD++1+48kpo0QJ274asLCgpcboqERGpD80pkIAsWGD/Hj0amjeHTz6B\ndeucrUlERJyhpiBChGqcy9cU5OTAkCH27alTQ/JSxozVKYd7mJABzMhhQgYwJ0eg1BQ0YDt3wsqV\n0KiRPWyQm2vfP2WKs3WJiIgzNKegASsshIED4fTT4eOP7dMS27e3m4XPPoOTT3a6QhERCYTmFEid\n+U5F7NfP/t2oEVx8sX07VEMIIiLiXmoKIkQoxrl88wnOOOPwfZWHEIJ9gMWUsTrlcA8TMoAZOUzI\nAObkCJSaggbq4EFYvNi+3bfv4fuzs6FdO/jqK1i61JHSRETEIZpT0ECVlEDv3tC1K6xZU/VvI0fC\n00/D7bfDo486U5+IiAROcwqkTn45n6Ay3xDC1Kng9YavJhERcZaagggR7HGu6uYT+PTtC8nJ9hLI\nixYF7zVNGatTDvcwIQOYkcOEDGBOjkCpKWiAKl8EqbojBVFRcPnl9m2tWSAi0nBoTkEDtHYtdO4M\nbdvCli3g8Ry5z5Il9oJG7dvbF0yKjg5/nSIiEhjNKRC/VT5KUF1DAHDaadCxo900fPhh+GoTERHn\nqCmIEMEc5zrafAIfjyf4yx6bMlanHO5hQgYwI4cJGcCcHIFSU9AA+Y4UHK0pgMNNwfTp9hLIIiJi\nNs0paGB27IA2baBJE9i1y17a+Gi6dYNVq+Dtt2HQoPDUKCIi9aM5BeKXjz+2f/fqVXtDALpyoohI\nQ6KmIEIEa5zraKciVsd3auKMGfDTT/V7bVPG6pTDPUzIAGbkMCEDmJMjUGoKGhh/JhlW1rmzfSbC\n7t0we3bo6hIREec52hQUFhaSlpZGly5dGDt2bI37ffLJJ8TGxvL666/X+bGmyM7Orvdz7N8Pn3xi\nn1lw+un+Py5YQwjByOAGyuEeJmQAM3KYkAHMyREox5oCr9fLyJEjmTNnDqtWrWLy5Mms+eWVeX7e\nb8yYMZx33nl1fqxU9b//2WcRnHwytGrl/+Muu8z+/dZb9hEDERExk2NNQUlJCZ07dyYlJYXY2Fhy\nc3OZOXPmEfs99dRTXHLJJbRr167OjzVJMMa56jqfwOf44+3hhp9+gjffDPz1TRmrUw73MCEDmJHD\nhAxgTo5AOdYUlJaW0qFDh4rt5ORkSktLq+zzzTffMGPGDK6//voqp1b481g5Ul3nE1SmsxBERMzn\n6omGo0ePbhDzBfxR33Eur/dwU1DXIwUAl1xiXyipsBB++CGwGkwZq1MO9zAhA5iRw4QMYE6OQMU4\n9cJJSUls2rSpYnvz5s0kJSVV2WfJkiXk5uZiWRbbt29n9uzZxMTE+PXYyvLy8khNTQUgPj6ezMzM\nijfed6jI9O327bP5/nto3bqY9eshNbXuz3f22VBUVMzDD8Ojj7orn7a1rW1tN+Tt4uJiCgoKACq+\n7wJiOaS8vNzq2LGjtWHDBqusrMzKyMiwVq9eXeP+eXl51vTp0+v8WAcjBtXcuXPr9fjnn7cssKzL\nLgv8OSZMsJ8jJyewx9c3g1soh3uYkMGyzMhhQgbLMidHoN99jg0fREdHM27cOAYMGMDJJ59Mbm4u\n6enpjB8/nueff/6I/T2VLudX02OlZvWZT+Bz0UUQEwNFRbB1a3DqEhER99C1DxqITp1g3Tr7tMQe\nPQJ/ngsusK+D8PTTcMMNwatPRESCR9c+kBpt2WI3BHFxcOqp9XsunYUgImIuNQURwjehJBC+oYM+\nfezD//UxeLB9hcX582Hz5ro9tj4Z3EQ53MOEDGBGDhMygDk5AqWmoAEIdNGi6hxzDPz61/btadPq\n/3wiIuIemlPQAPTuDSUl8O67kJNT/+d77TW49FL78suLF9f/+UREJLgC/e5TU2C4ffugZUt78aKd\nO6FFi+A8Z7t2sHevPVfhxBPr/5wiIhI8mmhouEDHuUpKoLwcMjKC0xAANGsGQ4bYt6dO9f9xpozV\nKYd7mJABzMhhQgYwJ0eg1BQYLpjzCSrTWQgiIubR8IHhBg60r1cwZQpcfnnwnresDI47zh6SWLUK\nTjopeM8tIiL1o+EDOcKhQ/Dxx/bt+qxkWJ3Gje0VDqFuQwgiIuJeagoiRCDjXKtWwY8/QkoKJCcH\nv6bKQwj+NKSmjNUph3uYkAHMyGFCBjAnR6DUFBgsVPMJfM4+G9q2hS+/hGXLQvMaIiISPppTYLDh\nw+GVV+CZZ+D660PzGjfeaD//HXfA2LGheQ0REakbzSmQI4T6SAHUfQhBRETcS01BhKjrONfmzbBp\nk71w0cknh6YmsCcwJiXZr7Vo0dH3NWWsTjncw4QMYEYOEzKAOTkCpabAUL6LIPXtC1EhfJejog6f\n6qg1C0REIpvmFBjqpptg3Dh46CG4667QvtYnn9jXQTjuOPsIRXR0aF9PRESOTnMKpArfkYJgr09Q\nnZ497esffPcdzJsX+tcTEZHQUFMQIeoyzrV7NyxfDjEx9n/Bh5rH49+yx6aM1SmHe5iQAczIYUIG\nMCdHoNQUGGjRIvuqiD162BcvCgdfU/Daa3DwYHheU0REgktzCgx0773wwANwyy3w2GPheU3Lgm7d\nYPVqeOcd+5oLIiLiDM0pkArhnE/g4+8QgoiIuJeaggjh7zhXefnh9QLC2RTA4VMT33gD9u8/8u+m\njNUph3uYkAHMyGFCBjAnR6DUFBhm+XLYuxc6dYL27cP72l262PMYdu+G2bPD+9oiIlJ/mlNgmCee\ngNGjIS8PJk0K/+v//e/2dRAuu0yXVBYRcYrmFAjgzHyCyi67zP795puwZ48zNYiISGDUFEQIf8a5\nLCs8F0E6mpQUe2nln36yG4PKTBmrUw73MCEDmJHDhAxgTo5AqSkwyIYN8O230Lo1dO3qXB06C0FE\nJDJpToFBXnoJrroKBg+GmTOdq+O77+wrJ0ZHw5Yt0KqVc7WIiDREmlMgjs8n8DnuOMjOtlc2nDHD\n2VpERMR/jjYFhYWFpKWl0aVLF8aOHXvE32fNmkVGRgbdu3enZ8+efPDBBxV/S01Nrfhbr3As8O8w\nf8a5fE2BU/MJKqtuCMGUsTrlcA8TMoAZOUzIAObkCFSMUy/s9XoZOXIkRUVFJCYmkpWVxZAhQ0hL\nS6vY59xzz2Xw4MEArFy5kmHDhrF27VoAoqKiKC4uppWOTQPwww/w2WfQuDGcdprT1cBFF8ENN0BR\nEWzdCu3aOV2RiIjUxrEjBSUlJXTu3JmUlBRiY2PJzc1l5i8GwptVuprPnj17aNOmTcW2ZVl4vd6w\n1eu07Ozso/594UL7d8+edmPgtNatYcAAOHQIpk+376stQ6RQDvcwIQOYkcOEDGBOjkA51hSUlpbS\noUOHiu3k5GRKS0uP2G/GjBmkp6czaNAgnnzyyYr7PR4POTk5ZGVlMWHChLDU7GZOn4pYHZ2FICIS\nWRwbPvDX0KFDGTp0KB999BG//e1v+eKLLwBYsGABCQkJbNu2jZycHNLT0+lXwzdiXl4eqampAMTH\nx5OZmVnRDfrGj9y+7buvpr8vWGBvH3NMMcXFztebnZ3NkCEQG1vMvHmweXM2a9dWzeJ0fYFuL1u2\njNGjR7umnkC3f/lvy+l6Atl+/PHHI/LzXNfPdyRsm/DvKZI/38XFxRQUFABUfN8FxHLIwoULrfPO\nO69i++GHH7YeeeSRoz7mxBNPtLZv337E/ffdd5/12GOPVfsYByMG1dy5c2v8W1mZZTVpYllgWdX8\nz+Ooiy6y6/rnP4+eIZIoh3uYkMGyzMhhQgbLMidHoN99jq1TcOjQIbp27UpRUREJCQn06tWLyZMn\nk56eXrHPunXr6NixIwCffvopl156KevWrWPfvn14vV6aN2/O3r17GTBgAPfeey8DBgw44nUawjoF\nixbB6adDejqsXu10NVW9+qq99HGvXrB4sdPViIg0DIF+9zk2fBAdHc24ceMYMGAAXq+XESNGkJ6e\nzvjx4/F4POTn5zN9+nT+85//0KhRI+Li4pj68xV2tmzZwrBhw/B4PJSXlzN8+PBqG4KGwo3zCXx+\n/WuIi4OSEli/Hk44wemKRESkRkE8WuFKpkQ82iGtoUPtQ/QFBeGrpy6uuMKu79pr5zpdSlCYcnjR\nhBwmZLAsM3KYkMGyzMkR6HefVjSMcJblrkWLquM7C6HS2lMiIuJCuvZBhPvyS/viR+3b2xdD8nic\nruhIZWX20sc7d9pzHipNGxERkRDQtQ8aqMrzCdzYEIC9mNJFF9m3f54WIiIiLqSmIEJUPge4Mrdc\nBKk2l18OUMyUKfaQRySr6b2INCbkMCEDmJHDhAxgTo5AqSmIcG6fT+BzzjlwzDHwxRewfLnT1YiI\nSHU0pyCCbdtmX2ioWTN7vD421umKju6GG+DZZ+HOO+GRR5yuRkTEXJpT0AB9/LH9u3dv9zcEUPVa\nCIb2aSIiEU1NQYSobpzLN8nQ7fMJfMrLi0lMhI0bI3t1Q1PGHE3IYUIGMCOHCRnAnByBUlMQwSJl\nkqFPVJRvwqGunCgi4kaaUxChfvoJWraE8nL44Qf7diQoKbGHOxIS4OuvITra6YpERMyjOQUNzJIl\ncPAgnHJK5DQEAFlZ9vUPvv0W5s93uhoREalMTUGE+OU4l5svglST4uJiPJ6qEw4jkSljjibkMCED\nmJHDhAxgTo5AqSmIUJE2n6AyX1Pw2mv20Q4REXEHzSmIQF4vtG5tr02wcSMcf7zTFdWNZcHJJ8Pn\nn8Ps2XD++U5XJCJiFs0paEA+/9xuCJKTI68hAIwYQhARMZGagghReZwrEucTQNUMvlMT33gD9u93\npp5AmTLmaEIOEzKAGTlMyADm5AiUmoIIFMnzCXy6doXu3eHHH6Gw0OlqREQENKcgIp14IqxfD0uX\nQmam09UE7tFH7esgXH65hhFERIIp0O8+NQUR5ttvITERWrSwFy2K5MV/Nmyw1yxo1gy2boW4OKcr\nEhExgyYaGs43zuUbOjj99MhrCH45VpeaaufYtw/efNORkgJiypijCTlMyABm5DAhA5iTI1BqCiJM\npF0EqTY6C0FExD00fBBhsrLsJY6LiuCcc5yupv6+/RaSkuxLP2/ZAvHxTlckIhL5NHzQAOzZY08u\njI62LypkgoQEyM6GAwdgxgynqxERadjUFESI4uJiSkrg0CH7jINInJRX01hdpA0hmDLmaEIOEzKA\nGTlMyADm5AiUmoIIEqmLFtXmoosgJgbefx+2bXO6GhGRhktzCiLIeefBu+/CtGlw6aVOVxNcgwbZ\n10F49ln4wx+crkZEJLJpToHhDh2ChQvt26aceVBZpA0hiIiYSE1BhJg0qZjdu+3FfhITna4mMEcb\nqxsyBBo3hnnzoLQ0fDUFwpQxRxNymJABzMhhQgYwJ0egHG0KCgsLSUtLo0uXLowdO/aIv8+aNYuM\njAy6d+9Oz549+eCDD/x+rGlWrrR/mzafwKdlS3sIwbLg1VedrkZEpGFybE6B1+ulS5cuFBUVkZiY\nSFZWFlOmTCEtLa1in3379tGsWTMAVq5cybBhw1i7dq1fj/UxZU7Bb35jH1p/7jm47jqnqwmNadPs\n6yD07g2LFjldjYhI5Iq4OQUlJSV07tyZlJQUYmNjyc3NZebMmVX28TUEAHv27KFNmzZ+P9Y0pp55\nUNmvf22farl4sX3BJxERCS/HmoLS0lI6dOhQsZ2cnExpNYPJM2bMID09nUGDBvHkk0/W6bGm2LQJ\nNm8uJj4e0tOdriZwtY3VxcXB4MH27WnTQl9PoEwZczQhhwkZwIwcJmQAc3IEyvUTDYcOHcrnn3/O\nrFmz+O1vf+t0OY7wXQTpjDMgyvXvWP3oLAQREefEOPXCSUlJbNq0qWJ78+bNJCUl1bj/mWeeSXl5\nOTt27KjzY/Py8khNTQUgPj6ezMxMsrOzgcNdoZu3p04FyOaMM9xRT6Db2dnZte7fpEkxcXGwbFk2\na9bAd9+5p/7K2z5uqSdU74fbt333uaWehrxtwr+nSP58FxcXU1BQAFDxfRcIxyYaHjp0iK5du1JU\nVERCQgK9evVi8uTJpFc6Pr5u3To6duwIwKeffsqll17KunXr/HqsjwkTDTMzYfly+3S9M890uprQ\nu+YamDQJ7rsP7r3X6WpERCJPxE00jI6OZty4cQwYMICTTz6Z3Nxc0tPTGT9+PM8//zwA06dPp1u3\nbvTo0YObb76ZKT8fU67psSbatQtWrIDo6GJ69nS6mvr5ZRdek8pDCG7s5/zN4XYm5DAhA5iRw4QM\nYE6OQDk2fABw/vnn88UXX1S577pK59vdcccd3HHHHX4/1kSLFtlfjF27QtOmTlcTHuecA23awJo1\ndkOUkeF0RSIiDYOufeByf/kLPPQQ3HYb/P3vTlcTPjfcYF8HYcwYePhhp6sREYksETd8IP6pfOZB\nQ+L2IQQREROpKXCxgwcrr+xX7GAlwVGXsbp+/exrPGzYACUlISspIKaMOZqQw4QMYEYOEzKAOTkC\npabAxZYtg59+gi5dID7e6WrCKyoKLrvMvq01C0REwkNzClzsX/+CW26xT9F74QWnqwm/xYuhTx9I\nSICvv4boaKcrEhGJDJpTYKCGOp/Ap1cvSE2Fb789fO0HEREJHTUFLmVZVS+CZMI4V10zeDzuXPbY\nhPcCzMhhQgYwI4cJGcCcHIFSU+BS//d/sGULtG0LnTs7XY1zfE3Ba6/ZEy9FRCR0NKfApf7zH/jd\n72DoUHjjDaercY5lwUkn2QsZFRbCeec5XZGIiPtpToFhfEMHDXU+gY9bhxBEREykpsClfJMM+/Wz\nf5swzhVohssvt3+//jqUlQWvnkCZ8F6AGTlMyABm5DAhA5iTI1BqClzo++9h9Wpo0gR69HC6Guel\npdlXivzxR3sIQUREQkNzClzorbfgwguhf3/48EOnq3GHsWPt6yDk5sLkyU5XIyLibppTYBDNJziS\nbwhh1izYu9fZWkRETKWmwIV+OZ8AzBjnqk+G1FR7dcN9++wjKU4y4b0AM3KYkAHMyGFCBjAnR6DU\nFLhMWRl88ol9+/TTna3FbXQWgohIaGlOgct8/LE9bHDyyfDZZ05X4y7ffAPJyRAbC1u3QsuWTlck\nIuJOmlNgiMpLG0tViYlw1llw4ADMmOF0NSIi5lFT4DI1XQTJhHGuYGRwwxCCCe8FmJHDhAxgRg4T\nMoA5OQKlpsBFLKv6SYZy2MUX25dQfu892L7d6WpERMyiOQUusmYNpKdDQgKUltpL/MqRBg60FzF6\n7jm47jqnqxERcR/NKTBA5fkEaghq5oYhBBERE6kpcJGa5hOAGeNcwcowdCg0amSv9vjNN0F5yjox\n4b0AM3KYkAHMyGFCBjAnR6DUFLiI5hP4p2VLGDTInoPx6qtOVyMiYg7NKXCJLVvguOMgLg527oSY\nGKcrcrepU+1hhD59YOFCp6sREXEXzSmIcB9/bP/u00cNgT8uuACaNYNFi2DDBqerERExg5oCl6jt\nIkgmjHMFM0NcHAwebN+eNi1oT+sXE94LMCOHCRnAjBwmZABzcgRKTYFLaD5B3eksBBGR4HJ0TkFh\nYSGjR4/G6/UyYsQI7rzzzip/f+WVVxg7diwALVq04JlnnuHUU08FIDU1lZYtWxIVFUVsbCwlJSXV\nvkYkzCnYt8+ePOf12vMJWrRwuqLIUFYG7dvDrl32Gg9duzpdkYiIO0TcnAKv18vIkSOZM2cOq1at\nYvLkyaxZs6bKPieeeCLz5s1j+fLl3H333eTn51f8LSoqiuLiYpYuXVpjQxApPvkEysshI0MNQV00\nbgzDhtm3p051thYRERM41hSUlJTQuXNnUlJSiI2NJTc3l5kzZ1bZp0+fPrT8+VJ4ffr0obS0tOJv\nlmXh9XrDWnOo1DafAMwY5wpFBt8QwuTJ9imK4WDCewFm5DAhA5iRw4QMYE6OQDnWFJSWltKhQ4eK\n7eTk5Cpf+r80ceJEBg4cWLHt8XjIyckhKyuLCRMmhLTWUDvaokVydOecA23a2MMHK1c6XY2ISGSr\n9eS3rVu3sn///jo9aZMmTWjXrl3ARf3S3LlzmTRpEh/5/pMaWLBgAQkJCWzbto2cnBzS09PpF4Gz\n9Lzew6cjHq387OzssNQTSqHIEBsLl1xiXwdhyhT4ecpJSJnwXoAZOUzIAGbkMCEDmJMjULU2BX/+\n85/p379/nSYszJ8/n4kTJx51n6SkJDZt2lSxvXnzZpKSko7Yb8WKFeTn51NYWEirVq0q7k9ISACg\nbdu2DBs2jJKSkhqbgry8PFJTUwGIj48nMzOz4o33HSpyarugoJhdu+D447NJTna+nkjcticYZjNl\nCuTkFOPxuKs+bWtb29oO9XZxcTEFBQUAFd93AbFq8cILL9S2S0CPKS8vtzp27Ght2LDBKisrszIy\nMqzVq1dX2Wfjxo1Wp06drIULF1a5f+/evdbu3bsty7KsPXv2WH379rXmzJlT7ev4EdFRzzxjWWBZ\nV1xx9P3mzp0blnpCKVQZysstKzHR/t9x8eKQvEQVJrwXlmVGDhMyWJYZOUzIYFnm5Aj0u6/WIwXX\nXHNNnRsNfx4THR3NuHHjGDBgQMUpienp6YwfPx6Px0N+fj4PPvgg33//PTfccAOWZVWcerhlyxaG\nDRuGx+OhvLyc4cOHM2DAgDrX6QaaT1B/0dFw2WXw+OP2EEKvXk5XJCISmQJep2DGjBns27ePsrIy\nmjdvzqWXXhrs2oLC7esUnHCCvUzv8uXhGQ831eLF9hLRiYmwaZPdKIiINFSBfvfV2hRMnTqVM844\ng+Tk5Ir7XnrpJQYPHlxxuuDOnTt56623uPLKK+tcQKi5uSkoLYXkZDjmGPj+e32R1YdlQefOsG6d\nvWbBZZc5XZGIiHNCtnjRqaeeSv/+/ausIbB//352795dsf3jjz/y448/1vnFGzrf0EHfvrU3BL4J\nJZEslBk8HrjjDvv2Aw/YZ3WEignvBZiRw4QMYEYOEzKAOTkCVWtTkJ6ezt13380HH3zAqFGjOHDg\nAFdccQWPPPIIXbt2JS0tjUcffZTf/e534ajXKP4sWiT++93voEMHWLUK3njD6WpERCKPX3MKpkyZ\nQm5uLoWFhTzxxBM88cQTdOnSJRz11Zubhw9OOw0+/RTmzoUGfmps0DzzDNx4oz0/Y+lSiHJseS4R\nEeeE9NoH0T8f2z7//PN5+eWXeeCBB5g0aVKdX0wO270bli2DmBjNlg+mESMgKQlWrIBZs5yuRkQk\nstTaFGzdupXZs2fz9NNP8+abb7Jv3z5efvllDh06xHXXXceePXvCUadxFi+2x7179IBmzWrf34Rx\nrnBkaNwYfBfbfOCB0FwPwYT3AszIYUIGMCOHCRnAnByBqrUpmDVrFrfddhs33ngjF154IY0aNWL/\n/v38/ve/5/bbb+e6665jyZIl4ajVKJpPEDrXXgsJCfbwwVtvOV2NiEjkqHVOwYQJE7j22msrti3L\nYvfu3RxzzDEAHDp0iIcffpgTTzyRK664IrTVBsCtcwpycuD992H6dLjoIqerMc/jj8Mf/wg9e0JJ\niX12gohIQxGydQrWrVvHqFGjiI2NBaB79+7ce++9R+xXXl5OTEytCySGnRubgvJyiI+HvXvhu++g\nfXunKzLPvn1w4omwZQu8/TYMGuR0RSIi4ROyiYYdO3bkzTff5KGHHuLpp5+utiEAXNkQuNWKFXZD\n0LGj/w2BCeNc4czQrBncfrt9O9hzC0x4L8CMHCZkADNymJABzMkRqFqbgg8//JCoqCi6detW7VUM\na3qM1MyRuQCqAAAgAElEQVQ3nyACr/QcUf7wB2jb1p7U+d57TlcjIuJ+tQ4f3HLLLYwePdrvJ7Qs\niyeffJLHHnus3sUFgxuHDy6/HKZNg+eftyfFSeg8+qh9NkLfvnYzprkFItIQhGxOQWFhIVu3bgXw\n+wXat2/P+eefX+diQsFtTYFl2dc7+OYbWL0a0tOdrshse/ZAairs2GFP7PzVr5yuSEQk9AL+7vPn\n+sr33nuvtTgcF6oPAT8jhs369ZYFlnXssZZ16JD/jzPhGt9OZfjrX+3/zc8807K83vo/nwnvhWWZ\nkcOEDJZlRg4TMliWOTkC/e7za0XDPXv2cODAAQAKCgrq3nlIBd9FkM44Q0vwhsvIkdCqFcyfD5ru\nIiJSM7+uffDHP/6R7du3c84557BmzRrGjh0bjtqCwm3DB9dfD889B488cnjlPQm9Bx+Ee+6xrzEx\nd67T1YiIhFbI5hSAvUDRa6+9xpw5c5gxYwZer5f09HQyMzPJzMykR48e9OzZE48LZ3G5rSk49VRY\nudKe9KbVDMNn1y5ISbF/f/gh9O/vdEUiIqET8gsiXX755bz44ovceuutbNmyhaeffppevXqxevVq\nbrnlFk444QRuuOEGtm/fXuciGoqdO+Gzz6BRI/sKiXVhwrmzTmZo2RJ8J9E8+GD9nsuE9wLMyGFC\nBjAjhwkZwJwcgarzikM333wzjRs3pkePHvTo0aPifsuyKCkp4fHHH+ehhx4KapGmWLjQPvsgKwua\nNHG6mobn5pvhX/+yz0L4+GP7NEURETnMr+EDf7Vr145hw4Yxfvz4YD1lvblp+OCuu+Bvf4M77oAI\nmpZhlL/8BR56CM47DwoLna5GRCQ0QjqnYPPmzSQnJ9f6ZKWlpTRq1Ii2bdvWuZBQcVNTkJ1tj2fP\nmgUXXuh0NQ3Tjh32ugV79sCiRdC7t9MViYgEX0jnFKSkpJCens6oUaN488032bNnDwC7du3imWee\nYfbs2QAkJSW5qiFwkwMH7OV2IbDD1iaMc7khQ+vWcNNN9u0HHgjsOdyQIxhMyGFCBjAjhwkZwJwc\ngfKrKbjvvvuYNWsWnTt35tFHH6V169b079+fp556ioyMDP73v/+Fus6It3Qp7N9vr2DYurXT1TRs\nt9wCcXHwzjuwZInT1YiIuEed5xQ8+eSTXHnllaxYsYKioiKmT5/O8OHDueuuu0JVY724Zfjgscfg\nttvg97+HCROcrkbuvNO+LsKFF9rDOSIiJgnp8EFljRs35thjjyU7O5sHH3yQkpISv6+e2JBVXslQ\nnHfrrdC0Kbz5pn0UR0REAmgKSktLefLJJykrKwOgefPmNG3aNOiFmcSy6n+5ZBPGudyUoV07e3VJ\nqPvcAjflqA8TcpiQAczIYUIGMCdHoOrcFNx7772sWLGCtm3bMmjQIEaMGMH7778fitqMsXYtbNtm\nfxF17Oh0NeJz++32ehEzZsDy5U5XIyLivIDXKVi5ciXvv/8+rVq14je/+Q2NGzcOdm1B4YY5BQUF\ncPXVcNFFMH26o6XIL4weDU88ARdfDK+95nQ1IiLBEbY5BR988AEZGRkMHDiQFStWcM455wTcEBQW\nFpKWlkaXLl2qvcjSK6+8QkZGBhkZGfTr148VK1b4/Vg38Q0daD6B+9xxBzRubDdrn33mdDUiIs6q\nc1Pw5ptvMm3aNAoKCmjTpg0DBgxg5cqVdX5hr9fLyJEjmTNnDqtWrWLy5MmsWbOmyj4nnngi8+bN\nY/ny5dx9993k5+f7/Vg38U0yDHQ+AZgxzuXGDImJcO219m1/V+d2Y45AmJDDhAxgRg4TMoA5OQJV\n56agR48edO3alXPPPZe///3vzJ8/nxdffLHOL1xSUkLnzp1JSUkhNjaW3NxcZs6cWWWfPn360LJl\ny4rbpaWlfj/WLbZvhzVr7Jnu3bs7XY1U58477YtUTZsGq1c7XY2IiHPq3BS0bt2a6dOn4/V6AWjb\nti29evWq8wuXlpbSoUOHiu3k5OSKL/3qTJw4kYEDBwb0WCd9/LH9u3dviI0N/Hmys7ODUo+T3Joh\nORlGjLDPEvnrX2vf36056sqEHCZkADNymJABzMkRqDo3BS+88AL/+te/SExMZPDgwdx9992srvSf\nV++9915QCwSYO3cukyZNcv3cgepoPkFkGDPGbtqmTIEvvnC6GhERZ9T50smnn346119/PbGxsSxe\nvJji4mI+/PBDjjvuOLp168a2bdtY7sf5XUlJSWzatKlie/PmzdUugrRixQry8/MpLCykVatWdXqs\nT15eHqmpqQDEx8eTmZlZ0Q36xo9Ctf3OO/Z2v371ez7ffaGuN5Tbv8zidD2/3L76anj++WJuugne\nfbfm/ZctW8bo0aMdr7e+225/P/zZfvzxx8P6eQ7Vtu8+t9TTUP89RfLnu7i4mIKCAoCK77uAWHW0\nd+9e6+WXX7Z27dpV5f4DBw5Y8+bNs84991y/nqe8vNzq2LGjtWHDBqusrMzKyMiwVq9eXWWfjRs3\nWp06dbIWLlxY58f6BBAxaH76ybIaNbIsj8eydu6s33PNnTs3KDU5ye0Z1q+3rJgYy4qKsqyvvqp5\nP7fn8JcJOUzIYFlm5DAhg2WZkyPQ776A1ymoyWeffUa3bt382rewsJCbb74Zr9fLiBEjGDNmDOPH\nj8fj8ZCfn8+1117L66+/TkpKCpZlERsbS0lJSY2PrY6T6xR89BGceSaceqoWx4kUv/89vPAC5OXB\npElOVyMiEphAv/uC3hS4jZNNwSOPwJ/+ZC+n+8wzjpQgdbRuHXTtat/+8ks48URn6xERCUTYFi8S\n/wVjfQKfyuN1kSoSMnTsCFdeCYcOwd/+Vv0+kZDDHybkMCEDmJHDhAxgTo5AqSkIEa9XV0aMVHfd\nBVFR8O9/w4YNTlcjIhI+Gj4IkdWr4eSTISkJvv4aPJ6wlyD18NvfwssvQ34+jB/vdDUiInWj4QOX\nqXypZDUEkefuu+33bdIkqHT2q4iI0dQUhEiwhw5MGOeKpAxdu0JuLhw8CL9cMyuSchyNCTlMyABm\n5DAhA5iTI1BqCkIkmJMMxRm+owUTJ8LmzU5XIyISeppTEALffQcJCdC8OfzwA8TUed1IcYvLL7cv\nlHTTTfDkk05XIyLiH80pcBHfUYLTT1dDEOnuvtv+/fzz8M03ztYiIhJqagpCIBQXQTJhnCsSM5xy\nClx8MZSVwd//bt8XiTmqY0IOEzKAGTlMyADm5AiUmoIQ0HwCs/iOFjz3nD00JCJiKs0pCLK9e6Fl\nS/v2zp32vAKJfEOHwsyZcOut8I9/OF2NiMjRaU6BS5SU2EvkZmaqITDJPffYv599FrZudbYWEZFQ\nUVMQZKGYTwBmjHNFcoYePeCCC2DfPrj55mKnywmKSH4/fEzIAGbkMCEDmJMjUGoKgkzzCczlO1ow\nYwZs3+5sLSIioaA5BUF06BC0agW7d0NpKSQmhuVlJYwGDYLZs+1LYtd0FUUREacF+t2npiCIli+3\n5xKccAL83/+F5SUlzBYtstefaN4cNm6EY491uiIRkSNpoqELhGo+AZgxzmVChj59oGfPYvbsgccf\nd7qa+jHh/TAhA5iRw4QMYE6OQKkpCKJgXwRJ3Omqq+zfTzxhL2MtImIKDR8EUUqKfZndlSuhW7ew\nvKQ45NxzoagI7rsP7r3X6WpERKrSnIIahKsp+PprOP54iI+HHTsgSsdgjDZvHpx1lv1+b9hweMEq\nERE30JwCh/mGDvr2DU1DYMI4lwkZwM7Rvz9kZ9urVj71lNMVBcaE98OEDGBGDhMygDk5AqWmIEhC\nOclQ3Mm3bsE//wk//uhsLSIiwaDhgyDp3h2WLYMPP4T+/UP+cuIClmW/1x99ZK9Z8Kc/OV2RiIhN\ncwpqEI6m4Mcf7UWLoqNh1y5o2jSkLycu8v77kJMDrVvbcwt0vQsRcQPNKXDQokXg9cJpp4WuITBh\nnMuEDFA1x69+ZS9mtGMHPPOMczUFwoT3w4QMYEYOEzKAOTkCpaYgCDSfoOHyeA6fkviPf9iXzhYR\niVQaPgiCX/0KPvgA3ngDhg4N6UuJC1mWvdJhSYndGNx6q9MViUhDpzkFNQh1U3DwoH2u+r59sGUL\ntGsXspcSF3v7bfvSyu3b29e9aNbM6YpEpCGLyDkFhYWFpKWl0aVLF8aOHXvE37/44gv69u1LkyZN\n+Oc//1nlb6mpqWRkZNC9e3d69eoVrpKPsHy53RB06RLahsCEcS4TMkD1OQYNsueUbNkCEyaEv6ZA\nmPB+mJABzMhhQgYwJ0egHGsKvF4vI0eOZM6cOaxatYrJkyezZs2aKvu0bt2ap556ittvv/2Ix0dF\nRVFcXMzSpUspKSkJV9lH0HwCAXtugW/dgrFjYf9+Z+sREQmEY01BSUkJnTt3JiUlhdjYWHJzc5k5\nc2aVfdq0acNpp51GTEzMEY+3LAuv1xuucmvkW8mwX7/Qvk52dnZoXyAMTMgANee48EL70tnffgsT\nJ4a3pkCY8H6YkAHMyGFCBjAnR6AcawpKS0vp0KFDxXZycjKlpaV+P97j8ZCTk0NWVhYTHDpea1m6\nMqIcVvlowSOPQFmZs/WIiNRVxJ6SuGDBAj799FPeeecdnn76aT7yHccPo/Xr7f8qbNPGnlMQSiaM\nc5mQAY6eY8gQOPVUKC2FF18MX02BMOH9MCEDmJHDhAxgTo5AHXlcPkySkpLYtGlTxfbmzZtJSkry\n+/EJCQkAtG3blmHDhlFSUkK/Go7h5+XlkZqaCkB8fDyZmZkVh4h8/wAC2W7VCm67rZj9+8Hjqf/z\nHW3bJ1TPr23/t5ctW1bj3+fNK+aii2DFimwefhg6diymUSN31W/S9rJly1xVjz7fkb99tM+3m7eL\ni4spKCgAqPi+C4RjpyQeOnSIrl27UlRUREJCAr169WLy5Mmkp6cfse/9999P8+bNufXnE8D37duH\n1+ulefPm7N27lwEDBnDvvfcyYMCAIx4brmsfiPh4vfbRglWrYPx4yM93uiIRaWgicp2CwsJCbr75\nZrxeLyNGjGDMmDGMHz8ej8dDfn4+W7ZsoWfPnuzevZuoqCiaN2/O6tWr2bZtG8OGDcPj8VBeXs7w\n4cMZM2ZMta+hpkCcMHUq5OZCSgp89RXExjpdkYg0JBHZFISDKU1BcXFxxSGjSGVCBvAvx6FD0K0b\nrFljn4kwYkR4aqsLE94PEzKAGTlMyADm5IjIxYtETBUdDX/5i337r3+1V74UEXE7HSkQCZFDh+Ck\nk+DLL2HSJMjLc7oiEWkodKRAxGWio+Guu+zbf/0rlJc7W4+ISG3UFESIX566FIlMyAB1y3HFFdCx\nI6xdC1OmhK6mQJjwfpiQAczIYUIGMCdHoNQUiIRQTMzhowUPPWQPKYiIuJXmFIiE2MGD0LWrvQLm\nK6/Ab37jdEUiYjrNKRBxqdhY+POf7dsPPqijBSLiXmoKIoQJ41wmZIDAclx1FRx/PHz+OUyfHvya\nAmHC+2FCBjAjhwkZwJwcgVJTIBIGjRodPlrwwAP2UsgiIm6jOQUiYVJWBp06webN8NprcPHFTlck\nIqbSnAIRl2vcGP70J/u2jhaIiBupKYgQJoxzmZAB6pfjmmsgMRFWrIBZs4JXUyBMeD9MyABm5DAh\nA5iTI1BqCkTCqEkT8F3Q84EHQCNbIuImmlMgEmY//QQnngjffWcfLbjwQqcrEhHTaE6BSIRo2hTu\nuMO+raMFIuImagoihAnjXCZkgODkuO46aNcOliyB2bPrX1MgTHg/TMgAZuQwIQOYkyNQagpEHNCs\nGdx+u31bRwtExC00p0DEIXv3QmoqbN8Oc+bAgAFOVyQiptCcApEIExcHt91m377/fh0tEBHnqSmI\nECaMc5mQAYKb44Yb4Nhj4eOP4YMPgva0fjHh/TAhA5iRw4QMYE6OQKkpEHFQixZw6632bR0tEBGn\naU6BiMN+/NGeW/DDDzB3LmRnO12RiEQ6zSkQiVDHHAN//KN9+4EHnK1FRBo2NQURwoRxLhMyQGhy\n3HQTtGxpHymYPz/oT18tE94PEzKAGTlMyADm5AiUmgIRF4iPh5tvtm/raIGIOEVzCkRc4ocfICUF\ndu+GBQugb1+nKxKRSKU5BSIRrlUrGDXKvp2fDzt2OFuPiDQ8agoihAnjXCZkgNDmuO02SEuDVavg\n/PPtMxNCxYT3w4QMYEYOEzKAOTkCpaZAxEXi4+H99+GEE+yLJV1wAezb53RVItJQODqnoLCwkNGj\nR+P1ehkxYgR33nlnlb9/8cUXXH311Xz66af87W9/45ZbbvH7sT6aUyCRaP16OPNMKC21r4kwaxY0\nbux0VSISKQL97nOsKfB6vXTp0oWioiISExPJyspiypQppKWlVeyzfft2Nm7cyIwZM2jVqlVFU+DP\nY33UFEik+uIL6N8ftm6FIUPg1VchNtbpqkQkEkTcRMOSkhI6d+5MSkoKsbGx5ObmMnPmzCr7tGnT\nhtNOO42YmJg6P9Y0JoxzmZABwpeja1d49117SGHmTMjLg0OHgvf8JrwfJmQAM3KYkAHMyREox5qC\n0tJSOnToULGdnJxMaWlpyB8rEkkyMqCwEJo3h1degT/8QddHEJHQial9l8iXl5dHamoqAPHx8WRm\nZpL98wLzvq5Q26Hfzs7OdlU99dn2CdfrvfVWNuefDxMnFvPDD/Dqq9l4PHo/fPe5pZ6GvG3Cvyen\nPt/B2C4uLqagoACg4vsuEI7NKVi0aBH33XcfhYWFADzyyCN4PJ5qJwzef//9tGjRomJOQV0eqzkF\nYorCQhg8GA4ehLvvhgcfdLoiEXGriJtTkJWVxdq1a9m4cSMHDhxgypQpDB48uMb9K4er62NN8MsO\nNhKZkAGcy3H++TB1KkRHw0MPwdix9Xs+E94PEzKAGTlMyADm5AiUY8MH0dHRjBs3jgEDBlScVpie\nns748ePxeDzk5+ezZcsWevbsye7du4mKiuKJJ55g9erVNG/evNrHiphu2DAoKICrroIxY+y5Bjfe\n6HRVImIKXftAJAI9/zxcd519e9Ik+8wEERGfiBs+EJHA5efDY4/Zt0eMgGnTnK1HRMygpiBCmDDO\nZUIGcE+OW26B++8HrxeGD4e33qrb492Soz5MyABm5DAhA5iTI1BqCkQi2F/+ArffDuXlcMklUFTk\ndEUiEsk0p0AkwlmWPdnw2WchLs5eBbFvX6erEhEnRdy1D8JFTYE0BF4vXH01/Oc/0LIlfPAB9Ojh\ndFUi4hRNNDScCeNcJmQAd+aIioIXXoCLL4Zdu+wrK65adfTHuDFHXZmQAczIYUIGMCdHoNQUiBgi\nJsa+PsLAgbBjB+TkwNq1TlclIpFEwwcihvnpJxg0CIqL4fjj4aOPoNL1w0SkAdDwgYgA0LQpzJoF\nffrApk3wq1/Bd985XZWIRAI1BRHChHEuEzJAZORo0QLeeQcyM+Grr+yhhB07qu4TCTlqY0IGMCOH\nCRnAnByBUlMgYqhWrezTE9PS4LPP7Asq/fij01WJiJtpToGI4UpL4cwzYf166NfPvgRzXJzTVYlI\nKGlOgYhUKynJXukwKcmedDhsGJSVOV2ViLiRmoIIYcI4lwkZIDJznHCC3Ri0awfvvQeXXw7vv1/s\ndFn1FonvRXVMyGFCBjAnR6DUFIg0EF272g1Bq1YwcyY88ggcOuR0VSLiJppTINLAlJTYpynu2QO/\n/z08/zx4PE5XJSLBpDkFIuKXXr3syyw3aQITJ8If/2hfVElERE1BhDBhnMuEDGBGjrPOgvvvLyY2\nFp54Au65x+mKAmPCewFm5DAhA5iTI1BqCkQaqF69YOpUiI6Ghx6y5xiISMOmOQUiDdzLL8NVV9lD\nCE89BSNHOl2RiNSX5hSISECuvBKee86+fdNNUFDgaDki4iA1BRHChHEuEzKAmTny8+Gf/7RvjxgB\n06Y5U1NdmfheRCoTMoA5OQKlpkBEAPsshPvvB68Xhg+3z1AQkYZFcwpEpIJlwZ13wt//Do0bw9tv\n22saiEhkCfS7T02BiFRhWXDjjfDss9Csmb0KYt++TlclInWhiYaGM2Gcy4QMYH4OjwfGjbPPSNi3\nDwYNgk8/DW9t/jL9vYgkJmQAc3IESk2BiBwhKgpeeAEuuQR27YIBA2DVKqerEpFQ0/CBiNTowAH7\nUsvvvAMJCTBvHnTq5HRVIlKbiBw+KCwsJC0tjS5dujB27Nhq9xk1ahSdO3cmMzOTpUuXVtyfmppK\nRkYG3bt3p1evXuEqWaRBadQIXnsNzj4bvv3WnnS4aZPTVYlIqDjWFHi9XkaOHMmcOXNYtWoVkydP\nZs2aNVX2mT17NuvWreOrr75i/PjxXH/99RV/i4qKori4mKVLl1JSUhLu8sPOhHEuEzJAw8vRtKl9\nqeU+feyG4Nxz4bvvQlubvxrae+FmJmQAc3IEyrGmoKSkhM6dO5OSkkJsbCy5ubnMnDmzyj4zZ87k\nqquuAqB3797s2rWLLVu2AGBZFl6vN+x1izRELVrYQwiZmfDVV5CTAzt2OF2ViASbY01BaWkpHTp0\nqNhOTk6mtLT0qPskJSVV7OPxeMjJySErK4sJEyaEp2gHZWdnO11CvZmQARpujlat4N13IT0dPvsM\nzj8ffvwxNLX5q6G+F25kQgYwJ0egYpwuIFALFiwgISGBbdu2kZOTQ3p6Ov369XO6LBGjtW1rr1vQ\nvz8sWQK//jUUFkJcnNOViUgwONYUJCUlsanSjKXNmzeTlJR0xD5ff/11tfskJCQA0LZtW4YNG0ZJ\nSUmNTUFeXh6pqakAxMfHk5mZWdEN+saP3L7tu88t9QSy/cssTtcT6PayZcsYPXq0a+oJdLs+70dR\nUTb9+sFHHxVz1lmwYEE2jRuHP8/jjz8ekZ9nfb7dux2pn+/i4mIKfr6ame/7LiCWQ8rLy62OHTta\nGzZssMrKyqyMjAxr9erVVfZ5++23rUGDBlmWZVkLFy60evfubVmWZe3du9favXu3ZVmWtWfPHqtv\n377WnDlzqn0dByMG1dy5c50uod5MyGBZyuGzZo1ltWtnWWBZQ4ZY1oEDwamrLvReuIcJGSzLnByB\nfvc5uk5BYWEhN998M16vlxEjRjBmzBjGjx+Px+MhPz8fgJEjR1JYWEhcXByTJk2iR48erF+/nmHD\nhuHxeCgvL2f48OGMGTOm2tfQOgUiobNiBWRnww8/wG9+Ay+9BNHRTlclIrr2QQ3UFIiEVkmJvX7B\nnj3w+9/D88/bSyWLiHMicvEi8V/l8bpIZUIGUI5f6tXLvppi06YwcaJ9CeZw9eF6L9zDhAxgTo5A\nqSkQkXrr3x/eeANiY+GJJ+Cee5yuSEQCoeEDEQmaN96ASy+FQ4fg4Yfhzjs1lCDiBM0pqIGaApHw\nevll+7LLlgXdu8PIkfYkxKZNna5MpOHQnALDmTDOZUIGUI7aXHklFBRA69awdCmMGAFJSXD77fB/\n/xfc19J74R4mZABzcgRKTYGIBN1VV8HmzXZz0LOnfcriP/5hX3b5ggtg9mzQpUtE3EfDByISciUl\nMG4cTJ0KBw7Y93XqBDfcAHl59nUVRCR4NKegBmoKRNxj2zb7tMXnnrMvwwz2XIMrr4Qbb4SMDGfr\nEzGF5hQYzoRxLhMygHLUR9u28Kc/wbp19pkK554LP/0EEybYl2U+80yYMuXw0YTa6L1wDxMygDk5\nAqWmQETCLiYGhg61r7j4+edw003QogV89JF9pkJKCtx3H3zzjdOVijQsGj4QEVfYvds+nXHcOFi9\n2r4vJgYuusgeWjjzTK15IOIvzSmogZoCkchiWfDhh3ZzMGOGvRASwCmn2M3B8OHQvLmzNYq4neYU\nGM6EcS4TMoByhJrHY1958bXXYMMGuPtuaNcOVq6EP/wBkpNh9Gj48kv3ZqgrE3KYkAHMyREoNQUi\n4lrJyfDgg/aZCv/9L/TtC7t22ddX6NrVXhDpzTcPH00QkfrR8IGIRJSlS+Hpp+0mYf9++77UVLj+\nenv1xNatHS1PxBU0p6AGagpEzPT99/Dii/Dss4eXT27c2D574cYb7ZUURRoqzSkwnAnjXCZkAOVw\ni2OPhZ49i/nqK3j7bRg4EMrK7KWVs7KgTx/7bIayMqcrrV2kvxdgRgYwJ0eg1BSISESLioJBg+Cd\nd+Crr+CWWyA+HhYvht/+Fjp0gLvuOryCoojUTMMHImKcffvglVfs0xqXL7fvi4qCIUPsoYVzztGa\nB2I2zSmogZoCkYbLsuDjj+3m4LXXoLzcvj893b4Y01VXwTHHOFujSChoToHhTBjnMiEDKIeb1JbB\n44EzzoDJk+3hg/vvh8TEw0srJyXZRw58Kyg6pSG8F5HClByBUlMgIg1CQgLcc4+9INK0aXDWWbBn\nDzzzDJx8sj2k8Prrh48miDREGj4QkQZr5Uq7KXjpJdi7174vOdleOfHaa+2VFEUikeYU1EBNgYjU\nZtcu+Pe/7UWRvvzSvq9RI7j0Uvtqjqmp9pUb27TRBEWJDJpTYDgTxrlMyADK4SbBytCyJYwaZc81\nePddGDzYHkb473/txiAryz5qEBcHaWlw3nmQnw9//at9lGHePNi4MfChB70X7mFKjkDFOF2AiIhb\nREVBTo79s2EDvPCCfUrjxo32RMWdO+GLL+yfmh6flGQfVUhJgeOPP/J2XFxYI4nUiYYPRET89OOP\nhxuEjRsP//i2v/3WPg3yaFq3rtos/LJ50BCFBIPmFNRATYGIhMuBA/D111Wbhl/ePnDg6M/RtGn1\nRxh8t5OTIUbHeKUWEdkUFBYWMnr0aLxeLyNGjODOO+88Yp9Ro0Yxe/Zs4uLiKCgoIDMz0+/HgjlN\nQXFxMdnZ2U6XUS8mZADlcJNIy+D1wtatRx5l+N//itm7N7tiiOJoKg9R1NQ8ODFEEch7YVn2PAzf\nz6FDVbd/eX9UlJ2teXP7d6NGwT+qEmn/pmoS6HefY/2m1+tl5MiRFBUVkZiYSFZWFkOGDCEtLa1i\nn9SHukMAAAw7SURBVNmzZ7Nu3Tq++uorFi9ezB/+8AcWLVrk12NNs2zZsoj/h2pCBlAON4m0DFFR\ncNxx9k/v3ofvf/zxZYwenQ0cHqKo7iiDb4ji66/tn5r8cogiKcl+7Zq+bINx/zffLOPYY7Pr9Dxe\nb/3+94yJqdokBON3Sckyzjoru8EO4TjWFJSUlNC5c2dSUlIAyM3NZebMmVW+2GfOnMlVV10FQO/e\nvdm1axdbtmxh/fr1tT7WNDtr+8+HCGBCBlAONzEhA1TNccwxcMop9k91yspg8+aa5zVs2gQ7dtg/\nS5eGKQAAO/nmm7o/KibG/omOPny78k/l+w8dsteT2LPH/ikvt08n3bUruDnGjAluo+H73ayZ3Zy5\nmWNNQWlpKR06dKjYTk5OpqSkpNZ9SktL/XqsiIiJGjeGjh3tn+pUN0Tx7bf2YfajfeHW9/6JE2Hk\nyLo9T1RU/Q7/HzhwuEkI1u+dO+3mY/du+yfYmjWzr+r56qvBf+5giKjpKibMDQjUhg0bnC6h3kzI\nAMrhJiZkgODmqGmIItSefnpDjUc3QqVRI/unVavgPWde3gYmTrSbhGA3HPv22T8HDwav3mBzrClI\nSkpiU6ULnG/evJmkpKQj9vm60sCZb58DBw7U+tjKPIYMDv373/92uoR6MyEDKIebmJABzMhhQgYI\nfY6ZM9172qljTUFWVhZr165l48aNJCQkMGXKFCZPnlxln8GDB/P0009z+eWXs2jRIuLj42nfvj1t\n2rSp9bE+DfnogoiISF041hRER0czbtw4BgwYUHFaYXp6OuPHj8fj8ZCfn8+gQYN455136NSpE3Fx\ncUyaNOmojxUREZHAGb94kYiIiPjH5SdH+K+wsJC0tDS6dOnC2LFjq91n1KhRdO7cmczMTJYtWxbm\nCmtXW4ZXXnmFjIwMMjIy6NevHytXrnSgytr5814AfPLJJ8TGxvL666+HsTr/+ZOjuLiY7t27061b\nN84+++wwV1i72jLs2LGDgQMHkpmZySmnnEJBQUH4i6zFiBEjaN++PaeeemqN+7j9sw2154iEz7c/\n7wW4/7PtTw63f7ah9hwBfb4tAxw6dMjq2LGjtWHDBuvAgQNWRkaG9fnnn1fZ55133rEGDRpkWZZl\nLVq0yOrdu7cTpdbInwwLFy60du7caVmWZc2ePdt1GSzLvxy+/c455xzr17/+tTV9+nQHKj06f3Ls\n3LnTOumkk6zNmzdblmVZ27Ztc6LUGvmT4b777rPGjBljWZZd/7HHHmsdPHjQiXJrNH/+fGvp0qXW\nKaecUu3f3f7Z9qktRyR8vmvLYFnu/2xbVu053P7Z9qktRyCfbyOOFFReCCk2NrZiMaPKaloIyS38\nydCnTx9atmxZcbu0tNSJUo/KnxwATz31FJdccgnt2rVzoMra+ZPjlVde4eKLL64486VNmzZOlFoj\nfzIcd9xx7P75ZOzdu3fTunVrYly2sH6/fv1odZRzztz+2fapLUckfL5rywDu/2xD7Tnc/tn2qS1H\nIJ9vI5qCmhY5Oto+SUlJrvrQ+ZOhsokTJzJw4MBwlFYn/uT45ptvmDFjBtdff71rzw7xJ8eXX37J\n999/z9lnn01WVhYvvfRSuMs8Kn8yXHvttaxatYrExEQyMjJ44oknwl1mvbn9sx0It36+axMJn21/\nuP2z7a9APt/u+k8C8cvcuXOZNGkSH330kdOlBGT06NFVxrcj9f88ysvL+fTTT/nggw/Yu3cvp59+\nOqeffjqdOnVyujS/Pfzww2RkZDB37lzWrVtHTk4OK1asoHnz5k6X1mBF8udbn213CeTzbURTUJ+F\nkNzCnwwAK1asID8/n8LCwloP4znBnxxLliwhNzcXy7LYvn07s2fPJjY2lsGDB4e73Br5kyM5OZk2\nbdrQpEkTmjRpQv/+/Vm+fLlr/o/DnwwLFizgrrvuAqBjx46ccMIJrFmzhp49e4a11vpw+2e7Ltz+\n+a5NJHy2/eH2z7a/Avp8B3HOg2PKy8srJlSVlZVZGRkZ1urVq6vs8/bbb1dMRlq4cKHrJvH4k2Hj\nxo1Wp06drIULFzpUZe38yVFZXl6eKycj+ZPj888/t84991yrvLzc2rt3r9WtWzdr1apVDlV8JH8y\n3HLLLdZ9991nWZZlfffdd1ZycrK1Y8cOJ8o9qvXr11vdunWr9m9u/2xXdrQckfD5tqyjZ6jMrZ9t\nn6PlcPtnu7Kj5Qjk823EkYL6LITkFv5kePDBB/n++++54YYbsCyL2NhY110Iyp8clbl1CWp/cqSl\npXHeeedx6qmnEh0dTX5+PieddJLTpVfwJ8Of/vQnrr76ajIyMrAsi0cffZRjjz3W6dKruOKKKygu\nLmbHjh0cf/zx3H///Rw4cCBiPts+teWIhM93bRkqc+tnG2rP4fbPtk9tOQL5fGvxIhEREQEMOftA\nRERE6k9NgYiIiABqCkRERORnagpEREQEUFMgIiIiP1NTICIiIoCaAhEJkgsvvJBrrrmmYvvss89m\n1KhRDlYkInWlpkDEMFdffTVRUVFER0fTqFEjOnbsyO23386+ffvCWscbb7zBww8/HNTn/Pe//02L\nFi2C+pwicpgRKxqKSFU5OTm8/PLLHDhwgPnz5zNixAh++uknxo0bF7Ya4uPjg/6clmW5eqU8kUin\nIwUiBmrcuDFt27YlKSmJ3NxcrrzySmbMmAHA6tWrueCCCzjmmGNo3749V1xxBVu2bKl47NVXX82F\nF17Ik08+SXJyMsceeyzXXHMN+/fvr9jnp59+Ii8vjxYtWpCQkFDtEYFfDh8cPHiQO++8kw4dOhAX\nF0fv3r159913K/7+4YcfEhUVxQcffECfPn2Ii4sjKyuLpUuXVvz9mmuuYe/evRVHQh544AG/nltE\n/KOmQKQBaNy4MWVlZXz33XecddZZnHrqqSxZsoSioiL27t3LkCFDquw/f/58Vq1aRVFREdOmTeON\nN96oci32W2+9laKiIt544w2KiopYunQp8+bNO2oNeXl5zJ8/nylTprBq1Sp+97vfMXjwYFauXFll\nvz//+c88+uijLF26lNatW3PllVcC0LdvXx5//HGaNWvGli1b+Pbbb7ntttvq9NwiUovgXatJRNwg\nLy/PuvDCCyu2Fy9ebLVu3drKzc217rnnHuvcc8+tsv/3339veTwe65NPPql4/PHHH295vd6Kfa69\n9lorJyfHsizL2rNnj9W4cWNr8uTJFX/fs2ePFR8fb1199dUV92VnZ1s33XSTZVmWtXbtWisqKsr6\n+uuvq7z20KFDrRtvvNGyLMsqLi62PB6P9d5771X8fcGCBVZUVJRVWlpqWZZlFRQUWC1atKjyHOvW\nrav1uUXEP5pTIGKg2bNn06JFC8rLyykvL2fo0KE89dRT5OXl8eGHHx4xWc/j8bBu3bqK66yfdNJJ\nVcbuExMTK67Yt27dOg4ePEifPn0q/h4XF8cpp5xSYz1Lly7FsixOOukkrErXYDtw4ADnnHNOlToq\nP09iYiKWZbF161YSExOrfe5PP/3Ur+cWkdqpKRAx0FlnncWECROIiYkhMTGR6OhoALxeLxdccAGP\nPfZYlS9QgPbt21fcjo2NrfI3j8eD1+sNuB6v10tUVBRLliwhJqbq/+00bdq0ynbl1/Y1Jkd77bo8\nt/x/O3fMa0gUh2H83RCEXqJhBIWEgk5DRKXQKCRUZAoSUc+HwHfQi29wOpGIREc9pUqhmNCI28hN\n1t297CbbrOdXnsz5T/vMycwA3yMKgP9QOBxWMpn8sl4sFjWfzxWPxz9D4U+lUin5/X6t12tZliVJ\n8jxPu91O6XT6l3sKhYJut5sOh4Mqlcpf3VeSAoGArtfrP5kNgBcNgbcyHA51Op3UarW02Wzkuq6M\nMer3+/I876UZkUhEtm3LcRwZY7Tf72Xb9rdP85lMRp1OR91uV4vFQq7rarvdajqdfn4VIenL6cUj\ny7J0uVxkjNHxeNT5fH55NoDniALgjcRiMa1WK/l8PtXrdeVyOY1GI4VCIQWDwZfnTCYTVatVNZtN\n1Wo15fN5lcvln655/J/AbDZTr9eT4zjKZrNqNBpaLpdKJBK/3fO4ViqVNBgM1G63FY1GNR6PX54N\n4Lkft2dpDgAA3gInBQAAQBJRAAAA7ogCAAAgiSgAAAB3RAEAAJBEFAAAgDuiAAAASCIKAADAHVEA\nAAAkSR8jeyDnw4hAYwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa8061347d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cuCap.PlotSlopeHist(bins=[0,2,0.2],ruta=ruta_images+'Slope_hist_cap.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"El histograma de pendientes muestra que gran parte de las pendientes son inferiores al 0.6, por lo cual se considera que el cauce ppal de la cuenca se desarrolla ppalmente sobre un valle."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Mapas de Variables Geomorfo "
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cuCap.GetGeo_HAND()"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlwAAAESCAYAAAAopgsxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4VOXZ/z/PTBKWSAJuuFV0cGMoGkOgRaqkBVuXUhFj\noRpaLbaQVqs0QFsUIqCIQOpS3xesovxKtKKR0mKrfcEKWio1EFOpQcVEqXUBBcwIJJlkcn5/POfM\nnFkzy5nMkudzXXPNzFmfmTNzzn2+z/18b6FpGgqFQqFQKBSK5GFLdQMUCoVCoVAosh0VcCkUCoVC\noVAkGRVwKRQKhUKhUCQZFXApFAqFQqFQJBkVcCkUCoVCoVAkGRVwKRQKhUKhUCSZbgMuIcQ5QojX\nhRD1+nOLEOJnQogqIcR/9en1QojLwqxfKIR4RgixWwjxphDiK6Z5t+jTdwkhlpqmr9b3dYX+fr0Q\n4jum+W8JIeaZ3tcKISbF+yX0RpJ1XCOtr45rcknmf1WfXymE6BJCHGuapo5pkknif3WREOJfQogG\nIcRmIcRppnXUcU0ySTyuy/RpDUKIZ4UQBaZ11HFNJZqmRf1ABmgfAV8CqoCfR7HOGuBG/XUOUKC/\nLgX+D8jR3x+vPw/Xt20H1unTKoGl+utjgZ3ARtM+PgROjOWzqEfSjmvI9dVxzdxjqr8/DXgBeA84\nVh3TzD+uwDGmZW4BHlHHNSuO6wTApr9eCtyjjmt6PGLtUpwANGma9oH+XkRaWI+sL9Y07XEATdM6\nNU1z6bMr9APdqc/7TJ/uAfKBPMBwZf0HMFZ/fRGwEThB38cZwFFN0/bH+FkUPqw8ruHWV8e1Z7H6\nmN4HzAlYTR3Tnsey46pp2mHTovnAAf21Oq49j5XHdbOmaV36otuRN0ugjmvKiTXgmgL83vT+Zl22\nfFQIURhi+TOBz4QQj+vS6G+FEP30eecAlwghtgshXhJClABomvYWkAtsBf5XX3YnMFwIkYP8UfwD\neFsIcZ7pvSJ+rDyugesPBHVcU4Blx1TvcvhA07Rd5hXUMU0Jlv5XhRB3CSH+A9wA3APquKYIq8/B\nBj8Engd1XNOCaKUw5IH6FDhBf38CIPTXdwGrQ6wzEugASvT39wML9de7gAf016OA5m72/wrwFeBv\nQCFSIZsOPAT8ONVSYaY+knBcu11fHdfMOaZAP+Rd8gB9+nvAceqYZvZxDbHcL4DH1XHNnuMK3A48\nG8X+1XHtoUcsCtflwE5N0z4F0DTtU00/WsAjyKApkP8i74x36O9rgWLTvPX6tuqALiHEcRH2vw24\nBJl30IK8CFwEjEFF4Ylg6XGNcn0z6rhaj5XHdChwBvAvIcR7yO6JnUKIEyPsXx3T5GD1OdjMk0BJ\nN/tXxzU5WH5chRA3AFcA10Wxf3Vce4hYAq7vYZI8hRAnmeZNBv4duIKmafuAD4QQ5+iTxgON+usN\nwDf0bZ0D5GqadiBwGyZeBWYA/9LfvwF8FThd07SgfSuixtLjGs36Aajjaj2WHVNN0/6tadpJmqY5\nNE07E3miv1CLnNehjmlysPq/epZp0UlAQzf7V8c1OVh9XC9D5lt+R9O09ij2r45rTxGNDAb0R0qe\nA0zTfoc8MA3I4GmwPv1k4DnTchcAdfpy64FCzSejrkV2Le4AxnXThhOQSX83mqa9BPwl1TJhpj6S\ndFxDrq+Oa+Ye04DtN6OPUlTHNLOPK1IVeQN4HXiWbkajqeOaMcd1D7AXqNcf/6uOa3o8jH5ihUKh\nUCgUCkWSUE7zCoVCoVAoFEkmJxU7FUIoWU2hUCgUCkXGoGlaRH+07khJwAWgujKzh0OHDlFVVcWD\nDz6Y6qYoLGTPnj38/ve/Z8GCBaluSnby3ntw8cWwb5//9M5O+VxWxhcP/RH737rIfboraHXbO2Bv\nlOdRTT+TC3LgRz+C//3foOUNtm/fzs6dO/npT39qycdQpAdPPvkkgwYN4vLLL091U7ISIRKKtYAU\nBlyK7KFPnz5cfPHFqW6GwmIGDhxISUl3TgGKuKivl8HW0aMhZ3eOFhx98o9gE3R+107nd+3BC7Vp\n5F/YgX0PiE7vmrByJe6WhwHIE9+DiRNhyhTvaoMHD2bEiBEWfyBFqjn77LPJz89PdTMUEVABlyJh\n2tvbeeWVV7j22mtT3RSFhXz++efs2LGDK664ItVNyS727oWvfQ1aW+X7H/0I14Nr/JfJAbq7o+4r\nONKYC3qwJVxwzMkdiC7Ie9JQxJ6AJ56A/v29qx3SNHZ98AGXXHKJFZ8mNezZA2+9BaefDhdckOrW\npAV79uxh0KBBOJ3OVDdFEQYVcCkSRilc2YlSuJKAxwMjR/qCrfJyXPeugdw4uyuEkAY7gHYcHPln\njrebkcPQ76ce+fo73/Gucv7JJ3P4qafi21868MUXcP750NYm3+/ZA2edFXmdXoBSuNIfNUpRkTCG\nwqXILgyFS2ERb70FJ58MB3R/55tuwvXQOihIPDfEoOtCGx3X2+Vjhp22u+10XCnk4zK5n5yPP2bM\nhHFo/YVUvr79bciUnNrXXoOCAl+wBXD22fDHP6auTWnCnj172Lt3b6qboYiAUrgUCaMUruxEKVwW\nUlcHX/mKL7C57DJcq34HWBdshcL9Czug539pGuLrneT8XSO3A1mJj1b485/pmJqD1g/yxPd9K9ts\n8MMfwtixSW1j1GzdCqWloedNmgTPPguTJ/dok9IJpXClPyrgUiSMyuHKTlQOl0Xs3QtjxviCrZ/+\nFNf9vyXZwVYQQnD0pRx2bu3ijQaNG39s55gzOrAdxDQKco3/Oo89Bs8/H7yt/Hy46CKwh0jmTwbv\nvusXbG1DxoulC4EqfeI118i25uXJHLm8vJ5pW5qgcrjSHxVwKRJGKVzZiVK4LKCtDUaMkLlbIBPk\nF/+2+4R4EwUNbjrGQ24RuF5MMIgQguOG2DjHpkF/wdGXc7FvD7acsO/QyFulTw9nM/DQQ9AT1hIH\nDoA5iDgd/vkfvVLzt6D1DDv9fqB/v0Zbf/ELWLo0+W1LI5TClf6oHC5FwqgcrjTB5ZLJxIWF8nH6\n6ZBADlbIHK7p0+W2HQ54++0EG5zl/OtfcPzxMskbYPp0XPetiT1nay3c1wJbtsrgK1E+3afR+G+p\ntnWdJ+i4wR70aLvfjnuGjc5viqCHl5tvRisU8vdw0knwwgsJty2Iv/9dfocdHQC4f2KDKvj541C6\nA1wleXRcb6ftTrt/2+69F3d5D6lvaYLK4Up/UlJLUQihKePT7OHo0aP8+c9/Vl2KqeJPf4LnnpMX\np927g2Y/CVxbCK0H8iiwt/vPfPhh2Lkz5GZb29r4dP9+Tj/9dN/ERx7xvc7Jge3bcRVdFLzd3s72\n7bIb0WDSJFy1f4l7cwXj3VAErurEu8nef0/jww80xl4S3/22fVMX/a/qRISI/dw32cgT030TLrss\n9rwqTYPly2U3oun35p5uo+3hyJ0ytl1d5I/pRLSFaM/FF8O0abG1JYOoq6vjpL//nS8Z54Ac3QT3\nwgtT27AsQQiRsNO8CrgUCaOc5pPMvn3w73+Hnz9hgv/7cePkxd7cpXI+HFkuL1b5dl2JOHDAzxAz\nHrQ+cPjtXLTThAq6zHz967Bli3w9axauZQ/F1I2YTOq2d9FQr/GjnySgALVqoAdcuTVd9LvVE37Z\nzZtj2/abb8Ktt/pNaltsx/2rKNvbqjGgoIOQBeTq6qQtR5ocC0twu2H7dl584QXG33OP/7z8fHjn\nHTjllNS0LYtQAZciLVAKVxLp6pIny8DyL6FYvhwGDoQrrsB1zBn0uctDn+XB+TkheVg6k7NiBn/d\nA+P7waGFdv7zvoZzhP85pussQe4TXeStkdvWBsAXH+VCPxV0eRkzRqpcFRVw7724+h+f6hYBUFDp\n5p3H4L9d8I0SC3LCANwaOX/SEId853TRBn1nRQjCoqR1pR1tAHReZYN+0V/rbA1d2Ot87elXYWrL\npk3BNymZzKxZcP/9fpM6rhLk/lH//AMHwiefQJ8+KWhc9mBFwKWS5hUJo0Yp6mzcKC+wZo8gMy4X\nnHhi+PmhcLt9OUDf+IZ3cqf2kt9injGC9lm3m6YI2u+yI1rAtifyzU3HVBsd028BoKARvoXsuvrv\nHo31T3Vx9o+ClQXPGAFdkPe7LsQXMODkDo68nIPr/D69O+jyeOCb35TBFsgurAEDIPHYwxI61sAD\nX8CHgG0rlDa4cRUlGHTlCTrLQlyHPoecl6MM+AOxgXumnc6r4+v27Cqy0VXkey+OQt9K/SBcein8\n9reyuy3T+d73wGRiu/98QUGZDfcsG1qFh7yaLvj8c3nT9vLLMHx4ChurUAqXImF6tcLldsOyZfDx\nxxELBidK59cER7fkJm37ofjsU436Oo1vXhH+otfv6g5yN8r/clu1HfetMjjrtUHX++/DmWfK18ce\nC2+/jWvQqSltkpl+x7mZ3wKfA6tutSYnLFPIXeWh382myPcnP4FBg2D2bKkCZRodHV7rCy0fXnvU\njhhu4zynL/jt9+0Ocl8wXWt/8pPott2/v+zWPe00K1uc0SiFS5EW9EqF68ABmWuyeTMsXuw/b9Uq\n6QkEfOGRuRP5X+3A9r6c3bbATsdPYrtz145NtMGx0/I5vL5T45sRbLha1+eg/cBD3pNd2Ld1wQwb\n9M2i/Jh4yc+Hjz6S3Thpom6BtJY4fSt8qbR3BVsAHTPtdJ0tyP+WXnzSuEE64wy46abwK374ITQ1\n+U8rKpKO96mksdH78otPcvn3hi4G7tX8Aq7WjTlot3h8Fh+x3BS++iosWRJbm4YNgxNOiG2dXoQK\nuBQJ0yt9uIqL4T//8Z/20ENw3HFwzTW4bMfoE+XJ78gLueRs6oIB0DHZBv3TPygpHAgXjuymnUKg\nnShf5q7XwOah9akcXJ5e3rV4/PFpmTPjejGPy//s5q0BvfPU7/mG4Oj6HMR/NXKf6SLnFY3WIzPp\nR5iAy+WSpYOM2pcGJSUyAT9VbNkiB2YgB67QT+A4S5CfH/B/FYK8EV109oOcr0Dr5O4HHuQ95MH+\nDrBtmxyAEwsnnCBvNHJ65++rO9S3okiYrFO4NA2uuiryCfWTT+TzxRfLk8uvfoXrG9/WZ/4geJNn\nCTrOyixfoGgULoCOcht5a7oQn4Ntr0oVSHeaj8uhsV5j7CWpbkkKEILO78igxP62Bq9o9LvNAzn/\nI01c29tlDt4778jljf85sltffKphfxvYsYOukwW2vmfIG60rr+y5z/D447Lkkk77nfK80vyuxsCB\n+ClcADwNv26FWa9Dx+buz0GdV9roe2sn4vPYmpXzdw0+/VR20x6j33COGiXrXGbTqNAEUAGXImEy\nTuHSNFi50ndSDeSTT2QCfDd4RgqOvPRP/d23Iy6biUSlcCETlI/+OYf8sZ090CpFopwwWOD8cqpb\nkXo8xf4mruzZA2+8IZPLA+gos9H6VA50aBwzvANbM9g+AXhfFv8OsLGIioED4bbbYssf+/3v/YKt\ntvvsuG+RQVRIhQugGuZWAjdAa/DcILQhgtYNseeL9v9GBzkva3D4sHyAPI/u2yeNcRUq4FIkTtIU\nrv37g3MnrGDPnuhKkhQUwFtved9+4RniN9voSstWolW4FJmF4TTfKxUuEx0/sNN1liB/nH6j8MAD\n3nmes+DoS76gQzPihVzB4X/nIg5AzrNdUh0LWDcm3nsPZs70vRdC5of17Ru8bH09XHed9+3RP+XQ\naRrQEk7hchXlwYvxNS8Wjm7OQewD+2sa/a/Rv1O7XSbgKwAVcCksICkK15EjcNZZPkuEZHHffd6X\nbV2z/WZ1jj9K14lnmKb0Llk8WoVLkVkohcuHZ6yNo8/mYHvf1BUuoOMKG9rJYX77eQLtZOj4sQ0G\ngjgQ+377zPUgPMDvficfZi6/HP4SUJXg+efBVET+6FM5dF7u376wCldPYZPfi1Zg+i43bUr94II0\nQgVcioSxXOF64w245BJfsPXVr/rN7tT+GWKlGBHQUWGj4/pfmCZmVo5VslEKVwz8+tdS5dBr/hm4\nPOmXOB+twlVQKa3ks300Y+dVcZYUzhN0xFmvsfMSQd+5Hjjqm2Z/S0O0IIMrczktgA8+8L5sW26n\nsyy4zWFzuCJQsNYNDUk6xqWl3sR+hUQFXIqESVjh+uwz+J//8fX7r1jhmzdxoqwVqCMvYD3rR9Vb\niUfhstdp5P7OQ8f37b1npOKjj0Jlpd+kd/bu5SMhZIHlRI1FLSYahatgrZtlei/ZXNxZH3T1NF0X\n2ji6KSBo+kLjmLM6sB3AL8Ay07rSTkcII2KIXeEqaHCz5UZ4DZjb4Lam6oAiIirgUiRMQgpXe7s0\n43vmmeB5M2b4+cako1qQzcSicGmFJrPFH3rovFR2yWRl0PXxx9KbCaC52d+x/JVX4LGL+ehxGFuY\nfsEWRKlwjYDRxuuiCMsprGOA4PB7uYjPwszvC9qJ4QOqWBUuV1EeYwvd0ALcEHNru2fHDjh4UBoA\nKwAVcCksICGF66qr4K9/la8LCuCOO+Tr/HxcU28D7fG0Mo7sTcSicHWdJzj6dA79v6snyx6NvHzG\n8uGH0iizM8SIzA0bcI0ZT0E/KP1pegZbEJ3C5SrKo3SH2/ta0UP0F2ind79YKOLJ4Wo9kGdNeScz\nhnB3+LD0MPvww9CDAHohcXZeK+LiueekE+/QofJx442pbpElGApXTLS1Sb8bI9g69VTpbDxnDsyZ\ng2vGLChUCdupxFC4oqVzso0uh3x9zMgObA1x1tELx7x5vv+O8bj2Wmnz0RO8/LIsdWIEWyNH4hkp\n8JQIWh+x4/r2dwEZoKRzkGIoXN2R7p9D4U/zuxofxOGDZ/Ux9owSdFyln7sPHpT/U9No796MUriS\njdstPZ/27YN77vGf19wsDeIGDKC9617v5D62X/gvJwRcfbV0N05DYla49u+HH/9YjmAB6c7+1lte\nszzVdZgexJPD5fmywNasIQ7DMSWdHP5nDq6RMXQrNjfD//t/QcnnQPD/R1/e/YMcNFlBiT5f/n9Q\nXh5++0ePym7qgweja0+4/d90E65VvyMT8wnVKMXsJOWjFA36C1qfzUV8q4OcFzXpPP/CC3Deealu\nWcpRAZcV7N0rK7KH4rnnfN1kBvfdB7NmydcPPQSAf4gR4sKybJnsEw/Huef6ZNvDh6Pzrxo4EIYM\nkUHh7t3hlxs2zFskNRQx5XC1t8ucFyMRfsgQWZMwPx9QwVY6Ec8oxdbaHLSbPeT9Vqpb+Zd0cuQf\nORwml2PsEX6/BtOmwa5dkZfZtQv69UNznoVwQ95as5I2Tf6uv/Sl0OvW1PgPyoiHBQtwzb+HTLUJ\nUT5c2Uk8oxSTydG/5NDvmk5yn9N6ToVOc1TAlSh/+Uv0ZR3uvlvWmvrBD+CrX6Vt89e6XcX2jiYv\nKJ2d0hAvHKNGwWuvyR/2BRdIpSAann8eqqtlEeZwfOtb8g4lDDEpXN/8ps/JefBg2aWogq20JC4f\nLpug7R47CMh7uAvRDseMNPKdYsi+LimBq6+mrWuB32TPSIFn2Ei5q2055LzgO5H3na8n+02cGN0+\n7r47aPvdoQ2Cju/fk9GlSmJRuAoq3XSsgdz7wTVNdS+mM2mjcBnYBV0OAahgyyAzA66GBqmSxGKK\nmZcnVaLLLgu/zKJF8OSTsbXl7bd9r88/32+WB/1OPQ/aFtrxfGuhPudmGAWMisLDxaMh3GDbHfpH\nKz7XsP0HqKvDc55AdIJNj7U85wvsjPAuu/+NNwA4MR84ok+8/HLvfK0Quob41tGa30AcBv76Vzzn\nCegvaHvAjucimfpndBNFpXAdOSK7RY1g6+yz4c9/ls+oYCsdiduHq1DQ9qAdcRBsb8d+stUGQ2vN\nv9COe4NI3mhdF9pwX2habxDkPdLlPb/bD2nQCp5TAi5CfaBtmR3PxQsjbj9biUXh6lgD97XA3DXA\ntCQ3TJEQPaFwJdW3qxeQeQHX669DcXF8615+Oe13BI8T6GPTu/wWLYq7Wa3/a6fjx4GJgRbkd9gF\nrU9EOEydGsec3YHtA2RRVR3PCMGR+lwKKt/w+ukYzH0IWo/Y6Xezb/hf1/FwuDkX+gtA/xxHcjnm\nzA5sB41ta7KL6JUcPGNs3iCpT59DkRWujz+WAwSMnK3Bg2W3UB+5vgq20pOEnObtgtbf9+zppWOm\nnY6ZMoAqaHCzpUT3GLpe8wYLKglc5XBlK8lUuAoa3LALn2+X8maLi/QOuA4ckMnmZi66yPf6ppuC\nDAcPe/xVJoCcP3XRd54MLvrcFWrkVECgVVfnq3YeZptmtH6y4GdKyJG1vWwBPnldZ/pejzZNL33c\n1zXQebkNoVcz7ToVPdgykS843JSL7UPIfcxDn1/reTkXd3L4jVy0vqCdCZ8eHcgrr8wMVrg+/VQ+\nfv5z32jEs86SQbMKttKeTHaa9/MYKoIt+niTYlVfOyaFK7cIRm9FeXFlAMlSuAoq3Wwx3bSPDr+o\nohvSN+D64AN5cXa7Q8+fMQOWLvWrtC4v3sE/NrfDhjYAxKfd77arWNB54diAqWnULx6KfEFXmAEg\nruo8Sqf5vkPzHb42RHTfuz5Abru9yg59oM89Mug65nw5iqxtmZ0+M22MHLsSeNC33ltvwZe/DB6T\nidbpp8ucNzUaMSPI9FqKrQfyKF3rpuM2eVc+Gnmn3ttVrlgULteLSfBpUiSFZChcBZXu4B6SW1WX\nYrykZ8D18sswbpzv/bBh/vOHD8f14GNgj9IUM0/QUdH7cjUMLDlZ5gvaF9kRH4K9rgu7Pqix71wP\nxz7uYfRhcH0jD44VFGz+k3+u3LBh0vqhpgaGDFGBVoaQyQqXQcdtMgdpViHk3gCspderNbGOUlTB\nVmZgtcJV0OCvbHnp5f+fREi/gOvVV/2DrZtugkce8VsknJKlSDJC0PaY/MnYt3aRP172z+TthmGA\n54pOOibaoMoUbP3853IUpI4KtjKHTFe4QI6um6UHXajagIDK4cpWrFa4XEV5lN7q5jVT0DV3nBqt\nmgjp5TR/8KB/jtavfgUPP+y3iLpgpweecTa+eD+Xw6/n4HbKafYdGn2rfJJj2z12XPf+xvteHbvM\nIlan+XTENS2P3Ptld6Lx6O136NE6zSsyi3id5iPRscb3elYhsRW47tSwvat+Z2bSR+HasweGD/e9\nr6qCuXPB5osJ1QU7vdBOE2inCVp+n8OHi7sYdrZp3okC949tIIQ6bhlKNihcIIOu0hGh8xh7I0rh\nyk6sVrgKGtxsaYl//f5XdJLzNz3gymDfOitJj4Drb3+D8eN972+8Ee68028RddFOX46eIlh1Eixb\nnB4/J4U1ZEMOl0FvD7LMZIvTfLm9xvt6Ehso89SmsDWpx/JRimvlYBOQynDuDZC71h11l6LtTT3Y\nOu20yP6XvYjUXyG3bfMPtn72M3jAP1NPBVvpTZ8+MOZr6dU7rUicbFG4FP5kg8JVbK+nqdnpfb+R\nMnDQq4MuKxWuwNGJpbfifT+X6IMuAKZPlyPUFSnO4Tp0CL5mKm+zcKGsM2hCBVvpT3s7vPr3UP5m\nikwmG3K4FMFkQw5XDeVMdPgHV9Oba6i1l6WoRanHqhyuQN+tuMnXnxculIXf33svusfHH1uw8/Qk\ndQHXG29Ix3GDe+9VOVsZilK4shOlcGUnUuHK7OPq9DQyjyUwQ8iHTjKDroLxbgrGh/GFTAMcZwm+\nZIUBd4PsSpxVmNhmWlebOtDuugscjugep5wSNFguW0jdVfKCC6BDmmcyY4YMtvr29c5WwVbmoBSu\n7EQpXNlJNihcXh7WP0eJkA+gkWERVoiPgrVulm2FZVv1eoJpiFUKl+vFPOaO061UkFYQ8eC52MaR\nv+XgcQq6ziCqh5eZM2H0aPm4+GJfDd4MJ/U5XL/4hXSMN6GCrcxCKVzZiVK4spNsyOECqXINdTTS\n9LBTqlybF8LKKlhu/b5c0/KYdZvb+zodsTKHy/ViHrOOc7OtRQaZc+O0UvFcYuPIG9FfG3Ke76L/\nRL3+Vl2db8a4cbBiRfAKxx8P110HuRbULe4BUhtwLV0Kc+b4TVLBVuZhKFxXl6mgK5vIplGKCh/Z\nMkoRoN5TTKPDyZibXofNyd1X64H0DLQMrBylGM4SYjTAiIQ3H5bOy20c3p0Lh6RSl/tMF33u03tP\nZs8OvdLhw3DVVb73NhucfHJaWlGkLuBatgxuvVXlbGUBSuHKTpTClZ2kWuEqaHBDJVBkTU0+p6eR\nlrI+FM5uT7xxaYyRPxbOfNQqhcs4PoYlxNxxwDRd5RqRfIuVrrMFRiWZ9i8LtOME4rPgrtI+9+uB\n2M03y4eZW26BBx8MWifVpO4qOWcO5PkOnAq2MheVw5WdqByu7CSVOVzGxXzZVtjygP7eIlqWymvI\nO5xr2TbThWhyyCxzmtePz6xCqWgt2wqslV2pPe5n11/g/qWd9hU5QY+jf8ihywFdp8oHJ5rW+81v\nZNClpdf5S2gpaJAQQjPvVwVbmc3Roxp//YumuhQtoKDBnTYmnZ99qlFfp/HNK9RxzSbef0/jww80\nxl7S88e133FuXzHxohhLxURJ4d42Wob07X7BDKPfcTLQCte1ubOui/x84delGGrEZiPDWOBZHHY/\nBWvddNymF3tvgI4GyH0xM8yDC8a60f5pqrQ8d640Xr3ySjkCMgGEEGialpCEmPqkeUXGo3K4rKHf\ncTJvovTxGI0Fk4TK4cpO0iGHK1nBFgB1AoYkZ9OppLscssAcrlp7GdOba4KWq3TcHXE7rml5MA1a\nzfuOubWpwbUtD7FXY8BQ3QFh2TL5vHIlvPSS/8KFhX7OCD2BukIqEkblcCVOQYMcEfQawJro1yu3\n11Bsr6fYXm95m1QOV3aSSh+u1gN5zH08icEWwKOwyD4/edtPU8w+XOGCLYDq5tuz+vvRhgiObMqh\n/WYbnV/Tf+e7d8NJJ/k/Tj0VDhzo0bYphUuRMErhShxXUR6lj7spbYg+kbjcXsPGZl+XQaPDidPT\naFmbepPCVVDplkncaaAsJptUK1zJ/I4X2efDTtjA1SwgfLdZNtL8rsZfjvseZ444h+rm2yMua+S5\nFTS4ZX4GtBrdAAAgAElEQVSWfs7pLhCL1BWZTni+bsPzdRu0afT/Zie2d/1Tp2z7gYMH4bzz4MUX\n4fzze6RdKuBSJIxSuKzBkPKjodZeJoOtOgE7gBIgsRSFIHqLwmXUjRsNlI5Inxy6ZJHqUYrJYpF9\nvjfQaGp2Uuvw3Yxka41Fc47WS+cOYP3BW8BUYxLwnSNMNC53SuuHEqmqz21ws31LUbeBGg5wsjtz\nvs++gqMvB3t09bu2g9w/aPDZZ3DRRbBzJ5yb/MEWKQ+4VMJ85qMUrhRRJ2DqemAXALVTrmEBSuFS\nRCbVClcyMAdbBuYutSWOedR7inu6WUklqNtw25NQsBfO1gOuOv1myXSOMGhqqML1Qh5jC9281gIU\nQSMBgVoIjO94g2MSNZ5yCz5Famj9XQ7c5CF3XRccOQKlpfD++1I9SCIpDbhUsJUdKIWrZwmXn1Et\nPKDNt0z27y0KV28j2xQuv2Br6H4YNDhomaZmJ8WO+owPusy5mk2BStYZZ0M/vWL0SgEr1usz/IMt\nM60H8pi71s1jN1wXNucrFBubyyh2+PY/iT9kTHcjAP0Erb+xo/WBvN91wSefSLPUN9+Uz0ki5QqX\nIvNRClfP4q0VN0qDQZPh0FhgFWBt0NVbFC5XdR5zG/QcrizvToTsUriCgi1WwSFkiZ8K/7wdp4Xq\nb7QUNLhhly9vLfB9LBTb64ODLJDB1WrA/S6IQZA7HA4tjLyxnaZ8rRvovisxBOa2VOMMm9KQtoHY\nsYK2R+3YPtLI2azBoUNw9tmybmNxcgLzlPpwKYUrO1A+XD1LqO4TeUfrO8lWavaET3TKhys7SaUP\nl5U02p2MadYVHyPYMjO7yve6Qutxby6/HKlxQDV+72MZqRn2Pw+m//2HQC7+DqARmB0clAaxshuF\nu7v1gYmOWuaxJOIyVg72iYe+P+gk7wndvHvmTGkjEUBG+3CpYCt7UApXGlChAb4LTPWxwMHgu8tF\n9ujVr96icPU2sknhAkIHW2AKRGZCRZRBiIW4inw5Ulu2QmkljC3EmzMVCws8i8FhUqJKRAgV6wDQ\nj6gDrhXrmbjcwzyWUE5NsHoWcBMXmu6Dto3NZWwk2IDVzERHbUpzwtpW2REdkPt0F3g8SduP6lJU\nJIzK4ep5QpoXLpcn5ErH3WxYfjXVx97hF3QZXRIbHFfjpLHbE5zK4cpOsi2Hq1sGDQY0b/7TPJYk\nfZSdUfeQIpiLLI8ztsGXMxVPl2IZz1JNpK6/45AKV/TUeMopGO+m/sViih1huiwjsWIhrJgJEwbD\nw+lVRicm+gk6vy7IfTq5u1EBlyJhlMLVs5TxbFgJvswh5y1gMeUHa6iecwfVJXfIYeENwE5oYjhN\nI4dTvomIQZdSuLKHgrVub+HhbFG4yok+yRt8OUeNjmHJaA4gFeQVO+fL+oM6cx+XQRc3SMf2x264\nzpuHGUltjkWNlsSocKFbomyFuePd1GwpZwzxGCivgs0z/fdbJ6AizOI7MjgwSxAVcCkSRilcPUuk\nfAfzvBpPOSzVAypd0fcm3q4UbLz0WgofLgub2xJJ4Wq0W2uyqkgefj5jO9ycMDg3KxSuGuILEJJl\nimrkWa0g2DzUyNdqtDv9RwM6Qgdd3v+pQ95gAdRyTTctiF3hYhrMWgPcENtqwazyH6hQQfjE/aEz\noannu3jTAXWVVCSMoXAp0p96TzGvOop5dfmFVG66i0rH3RRe1h5yWUPhCqTcXsOY5noa7TF2PyjS\nAkPhynScnkZedRSHtIGIRFOz0/JSWOak9nAjXf2S/HVCldkxj0asbr6dMc31jGmuj2Ik4QGgJbaG\n74Jt+ire79OgQvMfeNAdKxZ2n2QPwCo9785HWnl6tbVBkgYTKoVLkTBK4cosDGXKMEld8MJiCve2\nBSldgQqXcZGKOc9DkVJc1XnMLfJ1KZ7wnpYVChfov+UdGrAAZgjYHEJVObQQSqqS0pUV6j9RuLeN\nSs2XY/kdzqURZ9j/TVSK20oRxYjAOBSuBjlqsnQNME1+n0Mdjb62lgCMIJKXlx9GTleoQQx+rJJK\nFzBRe5mCUjfcENouo9xeE9KUNZo81LhYuxZcLtiwwfJNq4BLkTAqh6tnKYgz6TYSoboVWz6HmteH\nsX3id9nA1d6uSFYDI4FNyWmLwnrMxyhbcrgMZajScTcLPItZtGk+1ZeGUWR2+r9tanayyBGfX12j\n3Ukt1/j+EyGI2teqRNA0fTiNyyN00RujBRuqAhLTZ+rPRnATaw7XLsQYjZbqPrjCLeL1+osm4JrZ\n/SJ+yHbPYwPLtsKsBkKWNgsXrDbhpNwB5/C23/R47XA8YwTaABBfAH/8o7SH+PWvoX//uLYXipT6\ncIGyh8gGlA9Xz1EwXia5ziqUI56spthezzyW4KSRf37q4LY//RC+rmfN+w0Tn4k27iSZcHtr9AW3\nFaknG3y4zIXbhzoaqaE8Yk7hIvt8qufcEaQSGcFatITqFowbw9phggykjJHH1evu8K99aLZmmFAl\nLSXMn8NrixGjD5fBU1W0lPmuwyENVkPaUJgJyMvqdnkflZqdewbOJ/eG0OeRsIavYQj0/TL/Low0\niLC/lQ6NASd3ID7X30+fDvfdBwMGWOLDlfJ/XIE9dP6IInNQOVzZxfRjn2BMcz23vXEP/Fs/80fl\nyaPIBDI9h8scbIFUq6IasVihBeUYhcqhCkdSgi1zW+bcIStFTN0Xfr3NC+VoYzNNJ8pcq/xSYs7h\nAnhUfqcR2aHBoBjyuaJkqFbGAs9iWg/kWXbTtrG5zJv3Nqa53lvgu9bumx728+YKDr+Wi2bX369e\nDfOj+31EQ8oDLlBBV6ajcrh6DteLecx9PDnqFkiPIlYi82GuGQT3nyXvoIOCrW1s31LE3MeVupVp\nSB+u0Dfq5fYa7wUqW/BzaTeCrhLf569uvp1ie73lifQhGbpfPszB1uaFpv+YrhRVaL5HNInrFRrU\nnAUF82Jv0+aFbBSXUHhZO4V728KrSdNj33RkRnTrQG8F05trKLbXR10rUnMIjvw9xxd07d8fcflY\nSJurpAq6MhelcPUsseZMFax1R71smaeWyil3yVyROz8HNhIyAXb2ZJyeRpW/lYEEKlyNdieL7PO9\nypG3VmcG0dTsDKtUvcO5/hMqNBk8lAjvo+nY4TQdOzxi0BVSRTO2Ec3ovJUC+V8KlVC+CiZUMVT7\njKGOgO4ub9A1Uz7CudS/vwfue9+kRM00PbpjlQz8ohplGIIJASNFQwZnM5EJ+BazUvgdS+9jhu+z\nxDrQp2uUjSd/p994/P738PDDljQ1rZLmC+ztKqcrA1EKV/rizfm6zR27KpY/EBgaPH12FS1L1f80\nUwl0ml/CPL8uukyluvl2r/GvQaPdGfqzVWhAcDd507FVFB+sp97jX7x4kX1+6NI3hlK1AqIpcxOW\nCVW0vNAH9KoyixwBtRMrNFN5ojD7OONs6Jcvu/8CR2WWVEWXUxXYXRll24Nc5o1SY+bySk0nQt1k\nmArGqMcNTKKMYNf/Yns9NZRHHN0JSIPVFesJOYpyMzAjRM4bMhG/0e6kEScbmBSktJVTwxDPx1xv\ntO2WW8K3IQbUVVKRMErhyi4WeBbLBN4jnwNNwEy0x++kpTP58r8i+QQqXDWeciY6klvqxkqibW+3\nOVeGcuRVj4BDC7tVusIStQ9V9yzwLJZ+eY7ioHkTHbXeeX7z398DH+6VrwMtMIwcrAnG5w2jNG1e\n6KcMdUuoYMvA+H4nVFGpPSKVu1EaPDXZu/+N664N6sI2kuTHNEffDRiWzQvlcQnw/TJvPzDna0yz\n3P/fLvoG4558Sa7Q0ZFYO3RSF3Cdcgrs3Zuy3StkV1PBeDcFDZG7nArGu72PUCiFK42phrnjIPf+\n2FZb4FlMxfWPcdKfx9HSeTrLboRVOW5aOpcwdPmbyWmrokcIlcNV4ymXF8S6zKidGWgFYGAkRBvm\nvN1i5El5u8Rk4JVQ0GXkaZkv8nEMOnF6Gr1mpJWOu71djefwtneeef6pY+1w6pDwG9yhyeCoQrd6\nCEfUQdcIuKmbRSo0Wl7owwLPYp+K5A26gKnrmX7sEz2TPxcrQvDyaGu9U1JnCwGwfj1cfXXQfNWt\n2DP0O87NfS3ygmyUngjE6JIyCLXsoUMa9yz0sOz+tOqh7vUUNLjZUiKNDeOxkWjao1H7VBd3f+5h\n2QO+6XNvhdn3L47b70aRWuq2d9FQr/Gjn9iD5hVe1s7ETc/0iPN3uJyraH5Xlo4YBD0g2hdccqZO\nyAAh7DrdBVF6YedQhqxmjC7FbjC62kLZGjzzew93HPcQn5w7o9vtRGXzEJiXtXkfwfln4cv0THTU\nBv2O/Cwe6gRMNXUHNi2I/H2HImr7iTjLCWkaz994BZe98lcEJGwLoQKuXkzBeDdbtkJpGB8lIyAb\nbZr2GsFBl/LhSj/MwRbEF3B99qlGfZ1G2SmdbCnxTS99XBbgXcI85rGEMk/mdEcpuvfhKqxt9/Nl\nSgaB1g6BhKvvacbyoCscQ/eHvliHc7aPixGs1p5N6L+0s66L/HzBdSNe7z5JPFKgYnQTRqvKhehW\nDBVsGUQMugCYCbNDlGsqwT8Yi8HrC0ZIVS2WYM5A01j3s6lM+cszCQdcSpLoxbhezKO0wR229pdB\n6TigGjrGw2shbF6U03x2YtRS/OYVeZTu8HUnu4ry5IXBDtPXPcGGKZPSqxaaIiLdOc2nOtgCqbQZ\nik/BWjcdt0FuUXglPiRGPlU3ieyGcapByCAuMOiyNNgC2MX0OU/AcuIOuprf1Rg4EOqdxTQ6ggOu\nWq7xJeIbifWRApagxPfIaD+0QRF85/6noz8fGN2LO0J0ca4moH2moCmmYAtgl0zW7y7oqhPwKP4B\npBB0CWuubakNuCZPhscegxtvTGkzejORgq3WA3nMNZVu6YfK4coUXEV6kGRSuWLFXEsx1O+kzFML\nU2D6pU9QWHStGrmYIQSOUgxHsb0eJ768oR7pQjbynswFqdcglfatRHWDCASoM+FHDw51NAaNSJzo\nqPUFhF4X9wBrhYBSQYkzEyo0pjfX4HQ0RnTND4fjLEF+vvy/hlp/AY3gMJUdmo4+ujIC0dRS3Lye\nliHfY9lWeYz+NO27UEnY2ohBjNJgVIjpFcigEPTgSg+aGAusimzEGlMwpmNW24bOlL/BHRp/mHE1\nkzb/ke/FvsUgUq9wPf98UMCl7CHSB/MfJvd+mLsGqPZfRilc6YkRdJXqJ7/WGNf3KVzhlynz1DL9\n4RoYup9C2pm4/BmZ1Mtuvzv1wHydwPmKniPaWorzWOI/SswhnxIJvGrtZcHqlqEqmHOEDski0Noh\nmywfNQ4oinyD6IfZ3mDFQsIFXWZlKwivbxbyeYbpAh90QY+mYHN0jGmu51VHccxBl6FwnecM3+u1\nwLPYF3SFC6bC+XyFYbX2LKuEvBkvvRWoJGJtxJgwRlvWVckADODQvsijIyF6GwyDoK7NVeQfameh\ns51J7X+Mo+GhSV3AtXYtTAt/NDIt6Oq2RlMW4JqWF/IPpBSu9MVVlAcvxreuWeGKRKXjbqqbboc6\n2Hjstd6T5AbHJCaxIfzQbgc4ie9uXhE/0SpchrrFSgEVmk8ZccQXdDXancG/hZA5PDpDF+HqzGM0\nbhlsxVLRYHNAeRwj6ApkefSbDNuFOEj3vFoZffdbdyxhXuRgMARmhSsS3qCL22UXm8kXi9kJeImB\nd3DNaGQXcKw3eaGodNzNgiGLocyctxdPG3fBo5NhR4jvKISX12W8S2X7M/JNQQG4wpb4jprUBVx5\n2eNQXWsv855IYi2Gmg0ohSs7iUbh8mOUqWzKDo2NzWVsnHFt2DtR4z8TKcFWYT3RKlyG5cCYivrw\nieOJECnY0llkn8+KHfOjV7bA1A0YQIhgqHb5NbKrLSYCkrqNACXGnCeriUbhMggKuowcqhiDrdXa\nO3wmngyaXhph5HusONnte+1pZKijMWbneC+bF0pD1CjIM1xoAf75TxiWeAUGdYVUJIxSuLKTaBUu\nwyi10nE3lVPuYujBN32B1078PX0CSm4APVJPTeEjUi3FQJyeRmkyOmGw9R5dOyBibhBQLZyIQV1R\nF5iOlWrhCV87siJMweZBg/1rHQauM7tKXy+akjo6AaPyNjaXef3Eoq1v6ThL8KUh0R+jMp6VL0Zp\nVC6/K7S/3igNZofz7BrBD28LDraAmLsl/SgRfl5mG5jknWWMcDT7koVkJfIYWFFw+3vfg/POS3w7\npEMOV5ZRve4ONky5mkn8wTutjGezuttEKVzdY9QzzKTag7EoXGZVdwGLYSkUL9eHf8/Qg6ydyLwK\no+QGMHHTM1n930hHolW4DLwmoxXASME7m86NuLylzJ4M6N2Z0XRlzjDnXUXH9OYayoaEySfcockE\navM2Dy2U3Yfh1KAKTX5XdYNhqpEjFSH4mj045LbMuW4bKQNH5BGMsShc4FOLDF+vMvuzjCHECE2v\ncmfuppXfh6s6j7khjLMjdf86aaSJMApVyNGHTgpMg7eM/DanfTfTQ9W3BBko7kBXUbtJ+u9BUh9w\n/d//wSefwEknpbol1jB1H01T36b6qTu8w083OK6mnuASDdmCUrgiU7DWzTJ9XMhc3BkTdEWrcIWj\n3lNMsaOepof1oMt8It28HmZPZhIbLGipIhaizeEyWOBZTPXDt8PQRbAZNh5bBZ/2UBewKfndCLoM\nZaYx8KK90mqrhgis2GeqbRgGw/KgYnJwqR0/ouvGm95cEzHoijaHy0zgCM2w+NVyRE9KX0+tvYyy\nF2Mb/FLjKafcQfDgiZWhgi2pgC+7UdaDrT+QzOuoxkg+4lg98+x89nWzfOykLuCy6y7HLS1w4YXw\n0UcgMqOsRCBlnlrvCB40WZBzY3PPG8qmCqVwZScx53CFoN5TTK2jDDbh1zWwcc5kfZSUoqeJVeEC\naZ/QNKFKBjSH9tFod/aMMrl5oVRD9TzA6ubbZd5RTzJ7MKwIztta7ZBBZ8R6f6M0SOCmJZBIQVes\nClcgTk8jqx3l0dUv3KFR6WiMe6RxuNJM3dHvOHfMBs7Rcjl7+AshukhzrAuTUhdwTZgA5eVQUyMV\nrq4uXxCmk0kjFc0/vDJqYUg5hXvbAFkos9gRXIE+W1AKV2Rc0/KYS+Z1KSaqcBkY/40yTCfnpeUU\n/rKd6UjjVEAlzvcQsSpctfYy2TV8E7B5Jq9qlyUebNUJfWRYFAQEXd71RwW8j3Z7sVKhQclgv/1N\ndNT68pfujxB0Dd0fXCInQRoJnbx9/nMe8nOBy+M/xxjiQeA+vCNUdeKxrYiXJczjT+O+6y0xN3et\nm+03FCVe2NrET/knD/G8b8Kll8rnvDz4yU8s249lAZcQ4gt82qhxltb0feRpmua/r8JCaQ3x5JMy\n2MpCWob09Qu6ah1lWek9pBSu7smkQMvACoUrEq8uv5Axl77OxlGya6HRsSRr87kK1rphRGQfqYIG\ntzfVJJm/l1gULvMIbCqwJtgC6bvVbV7NCN9LI+jyvl8PEyb7v7cgTyekTxgEuZPXeMq9Fghzi56E\nG0IEXV4fLwsSt014k91NFKx18+t10A94bHxiaQuhrlFOx26WMA8gbC3HZLFRXMJ2rYi5pbJ/2TUt\nj1qusWz7N7HTP9havRp++EPLtm/GsoBL07QB5vdCiGOAnwIzwJRB3svwBl11wtftGIEek+otRClc\n2YlVClc4nJ5Ghm56k6Z1wwFkORJ79nnZFVS6WfaA9CYq3RHaKT2w9uXcNW6/YfVW+vxFq3D5BVsz\nBK8evDCh/QflXEVEL+NiUDE5ID9rhFTcAKbuI6Fga4agdlOZTAVZd62cFqH8S8uQvtTnuH01Zkf4\nlKGQqsvmfYA1lhphlaURMA7oq7+2mjJPrb9C3aOsYsyc12l50brerr50MJoPOZ6jPMJG34xt2+Ci\niyzbTyCWdykKIQYCtwHfB54ERmmadsDq/WQSLUP6UkgbG5gU8UdrDHkNVW4inVEKV3aSbIXLSwVw\naD3TeUIOUe+FXnbsCl+CyVx70IqunGgVrsBupUT26xe8dUuIQsMjhck/KWB+04ly1KCB2QdrUJUs\nYROI2ehy80KmC0MxWQ+DJuuWFZKhjkavdckPdz4JD8pjNatQX2AX9Bvv5of3P8n0S0J9xlVypGOM\nPmZGjphBJJNgV1EeBXe5GTQgBjf+XswTPMtk3vKf+NxzMGZMUvdrZZfi8cgKSlOAx4ALNU0LUeq4\nd7LaUe6XNByIt4L6SkFTRWblfCmFKztJtsLlZSW627XkHXrQdqAHcFX7cvhYS7ceRbMKw5tGxlv2\nxUy0ClcZz/olqBfb4z8n+QVv4UYTGp5JKwlWmB7WfHX1Qs33s1XQzUcNB/hQlAQ4rHufR8jtI02s\nwd+KomO8rOs4dxy+nKI1+rQ1wCXoha33AdtMO/QPuoxtG1Q33+43LR4roZPH58Q8SjFVLPAsZoPj\n6rgMTBfZ5wfllIVllCa7njf7K6BfIsA1/uGH4corY25LrFipcO0FPgUeB44C04Vp1KGmab+2cF8Z\nxxLmyR/XkODE4GJ7PU2Xym4VeSKq8gZd81iS9uVPlMKVnfSYwmWYK1bgpyxkFdPwdhnOxR3Rpyj3\nBl9JlFA5RYkGXTGPUqwTsHk9TesmUzvFgjzUCg0aqgKCrpnSMDcMTc1Ov+DJbHoZdNE2fKMiuaYb\nlg1+QRfydzhKjkCM+DmL4Pgt1wHwHWQJq7OYB5dGsqbwBV2BCq7TkXht0URHKfY081gS3kcrkBUL\nfb5+YQjrQG8E6ybLiX9yKqP4yLeMI4p8HwuwMuBaji9pfkCkBXsjNZQzhnoK97b5ScXTm2uCzd5W\n+IKu6dTILsY09vFSCld20mMKl8GhhVBSReNBpzdnKZB0vvGIhKsoj7GFbmghahfuoNqDK/VjUaEl\nFHTFOkpR5kjpbQozQq47glTLnQELDBpMvef0sOsvcvhUjcAu52JHiAtxNCVqwgRdrzqKaRMN9Csk\nyIIg9waYtQYeu/86ps95Qj9XN7KRc4Ba/RGJVbIQ8xD/qVYMporHhyuVxPpbahK1YWs9GuXBGh1G\nrcXI3MKV7GUgy9kkJ1x6KTQ3w5lnxtSmWLHsKqlp2p2api0M97BqP5mKUZfMCLY2MEl2MdYJWf08\nkBULYaXIiHwuQ+FSZBeGwtWjHFpI07HDGdNcH/IRTYmTdKX1QB6lO+IcgbhSBNXoG9NcHzYwjYSh\ncEVN04nAWEB2fcVaZsecgwaEcROPjomO2iB1qN5THLnMi85qR3lQXpQ36DJlmjs9jbwGbGvRR46a\ncFXncc3nTwfko42QgYDxiMSgKhilUW63ztLAoPldjQ/2Zob/Y0zdgmb062I4DPf8aPgNo7mPr/om\nDB0K774be5tiwMocrkLgeqADeELTtKNWbdsKCip1H6RYKs5bjNPTiFMvlGokz5dPQQ6LDywfoTPJ\nogGexh98HtYPvVcKV3aSbIXLm7cYyKHwo7q6c9vOBAoq3TCt++Rmp6eRSsfd8sJUocHqKlgNILx3\n+fEoXTErXCC9pKbug6YTqW6+nXcc/orVObwd/UCHEDeYEw8+g7lWsJlae5n34hyu7qa3qkGYLqeh\nZpPOwNGE5jyfFespLGlntXY9zzGMX4fIJ9x46bX+OVoTJgfnkK0O/VmMbtGNzWUscsTwnUVBpilc\nfoS4oQjLioXSiNbExqaykOk64biF7czhH/65XJoGH3wAZ50V9XZixcouxWeBu4FjkKMTw2eI9zAF\nDW62PBBd/kRP43XcfWpwcM2nFft4Z3niCcTmPJBzHG+zAGsDLpXDFRvmumDREknZSVbwkcwcLq+Z\nZhzE262VDniTrhuAF7tffoFnMe84zpX/XyOHaeh+wFd/r5ZrIv6nA39v0eZwGb5LgOwG3ezLQQrp\nVRV1rcNtSEVJP9c9VUVNGIPrWEY3hgu6hjp8N7og/y+NjmFhFJZdMBXviNmQ7e+ufJBRSzECyRiJ\nm2k5XH6EC1DDEiBOlFRRe7CMRoYFn1cCSgbdSD0P8kLwJo85Bs45J9aGxISVAdcAoBkZcA20cLsJ\nE0/+RE+xwLMYHFBdd0fwzAmD4y6BYKaRYcHOzBaiFK7oMTyZZt0WfYmK7uT3DY5JSXFp7/EcLi/b\noG5yyN9rpltG5BbB6K0EnYdc0/KYdZubbdGeo/Q8z+5ylQrGu1m21d/XKxqFKyhZ31vAeKEMup4K\ndk+vrruDd6acG/RbbMQpzz+P6hMMf60dkyOqGrFZSUgCg65uk99DIoMuPx8wg5uAzYkVQ07Wbzij\nFa5EObQv+LdSJ+QgHNNv7BRcPMaffMu89BKcfbZ8PXAg5OcntZlWBlxTgZuBTiDtanS0HsijtCG0\n6WCqcbLbN1JrhemPbFFwuIGr4VGYOCU4/8EKlMIVA3ox3vtaYFYS64JZQY+NUgQmLn8GlsuL5MZ1\nk2X31VPB5VQyOdgCafcQ7jwU8znKCLqW+08uaHDTMV4Gdx0NwavFU0sR0GtfjgBW6Wp8MBun2ils\naqNlSF/vtKY5+gjsIvwDxFFAxQJahgSrW/EEWwbe+p0kov7u8rMq8fP9CjW60YTZtysUyVKkM0nh\n8lNuk0GJgEPB1Qf60eF7s2EDlJYmZ/9hsNJp/j1gjlXbSwbpGGyB/AMuccyjqcKJ9y6SmbAaqrkD\nlkch1YfAyNtqmjOciZueSVqtOqVwxcd9LbIuWKTuRT91a+h+34xBg8N7DEVJwVo3NITPa0y2wjXU\n0cgk/hDkOeTNayxBdgfoF7pIF7FMItJ5KNS8eSxhI2EuTCsWsmF5GQswnR/Wyt8WW6Vf1Nwi/2Mc\nVw5XnYCp5gtYBIVn6C4KZ7f73pdA5ZS72IC/75IxsiyQcMHWREet3+8kUl6uNUGN/hn1RHcvRqJ9\nha6A6Y73oXy7ehIrFS7ju4Xk5T1PYoPvd72S4JSamNC7u83vB1UB+jE6tJAL+YhtPCbfDx0KV10V\n57/+rbQAACAASURBVL7ix1KneSHEWOCQpmmNQohxyFNmg6Zp3WcrrFgBt94Kfft2u2g2YthG+HvI\naDBDUD3nDjYsv7rb0YrmPJ8NTPLdPTQktzCwUrhioBpGl4R3FQ9kA1fLF966bDqHkMPLR2lxdTsX\nNLjZcmPkvMZkKlxOwo++PYe3pafODv3irBtJLtHmUZN+4nnScXoaWe0oD6v4NK0bjnHdKljrP6pu\n2VZk4NXg61KMS+GKqvahiRXroUn+do1uvQUsptghh+w7aQx7TjLK5JhzyAKXL1jrNtUyTKx2YFyM\n0vw849JBfbVK4TK6oQ165PsN54sWE8b5cUSQ6e2oqZfzWt1XfItecEGc+0gMK0cpLgG+AdiEEFuQ\nnrt/BqqEEBdqmrYi5IoFBfD55/DLX8q+1Mkh+s17G7rsXum4m7JNz7KEeWxcdy2Fo/ylejPdSfDJ\nrNGoFK4YWCufzHXY4uZRYFR8d9TR5DUmU+GK9Ftc4FnMAhb7PHV2Amxj47prqZ2yIaNHKCaFR4Ey\n6Hecmy0tUPp4iGVMxzguhStOAnOoorW46bZ23wiL/kNZRDJyuEZDz32/VgRds6ukzGNSJE/4bD/b\nd5jsH265Be6/P5GWxo3QNGsSqYUQbwLnA32AT4DTNE1zCSH6Ads1TbvAtKy2bt06Ojo6OKm5mfEL\nFgDwj5kz+e/Xv05HRwe5ubneZ1f7deTkQmcHWf2813Mqdx5cxo+OfQB7ro2R7du983f2+Sqeji4e\nOXgrjwy83m+9f3hG88jBW8Nv+OFOmJHDncfOZYj9Q8vb3fK5xnMbNKZcb0uL7zGdnwvu8fCH3TCx\nH2jzoOMse8Tl7+hzL/s+HAx/y4MzOhh58Q52vlICDx0B/srgdRdxV/sv4m/Phx5cp9pDzv/wA40d\nr2lc+Z3UHddP+pzG/A/vgp8fhZvzmXnxSr//RW96/odnNPZcG//pOJl9uafR1eHhK7n1jGzfzo+e\nfpJ5z03hfeCb/aDfDfCHldJo8YpvQccNvt/Z27s1/vuBxrivhz+uO/t8lVUfzvRNeDwPdq1DbrGr\n++f8KdT8cgq5H4FrTOjfV6LPue96yM0h7O830vMf+1zDcx9O7P7z5U+Bxe5uNzjy1J3MbP9NSn8f\n27Z2MaBQ4BwuEvteF3r4y1twBnDBMHD9KjnHL+TvLCcX3umEh+qB96P/vWEDToVbL4Ih8nj96NgH\nONJ6AqsrnqdvZwcA71x+Oa9ffTWisDAozoj0fP311yOEQNO0hCJaK7sU3ZqmeYCjQogmTdNcAJqm\ntQohglwxL7jgAjweD/aSEj6vq2Pgxo0MGTKE44zpdrv3ucVtw24Hj4esfnZ6Pua8vDs5092kT/d9\n7gvtr+HxwPi8O5n6/r/Y8aULvev9l2PhowtCb/jpHHjzBei8DPuFIxjBx5a3+8hhjbZWjfOLesdx\nSui51sb8ezqwT4KWc3IjLj+be3HabQz78qeIK2wsdc/Bbod3vjyU6676A1x6HnkXuDg/kf/HSFvY\n+SefrHHMgNQe1wvtH/Hilz9ly5gr4AwPX7pgUGKfN4OfnZ4dQdP7X9TB44dhx5vllJS+yVtnDOe3\nZfDjHfDlu8D+DrTM9v+dDSzUcAyNfFz35w2CwgvlhCe6YNdK4CTCXvAKfgauF4B35fvzL6Bjvhwj\ncuOpHlqvzrX+exke/+/gH3kn+T6fxwPH5ABb/T8PHr70WjNDPR8i7Dbe9ZzJBx+dE3KDk89Yl/Lf\nJRrk5wuGnCkS297TNhZM7+C3dVC3G278T5KOn0de10798kDmf7TCN+McD/yuBFwPhvi9XQcFgwA7\n4Al+ftwOT3fy1BllfHnHHob/yOONOVquvBJt+XJGaBrm+CKaZ6uwNOASQvTXDU9HGhN1Q9QgGe3c\nc03+UoWy7Pqpp54K5wb7Trk86T/qwirOoxkI/3nPo5nV5y6hpLmdSsfdONnNGuZB3+Dvbaijkaaz\nz4H/nAt/gVNmFXJ2Er7LQ4fgybVdVGTA6Ji0YI3Mhzi5m8X+yC8Dpsjv92yaedX5PcY01ZPnaOS8\nJP0/bDZ4+SUt5aOeRtqPsGXsuXA3PFa5lJs9/5fS9qQTBb+BpbdB67mC1c672cZ1LC18ktyf+Bzt\nA39nnx/SaHo3cq7PdfalkKvn0K3ZDxwfvhFGvkzduTBVH4Kffy43jJOjJFt/mR6Dlcw5ri/zY9/n\nA8gXwHj5esJkWX8PeNpxvV/3d7FT5qA1NZ+rO5p7mMcSyjz/R6TzdjQYrvbxDu5qqJf/WUv+r6/m\nsfQ4N7lF4ErS8TM+79lFmzjFuVivN6xfx+ym4+FlrLf4dyRWO8r59rZ3yS83BUrXX09hTQ2F1jQ9\nbqwMuC7RNK0dQNM0s6KVC/zAwv30eoyk0unrngieWQHs0Lzu08WOepoYDpsXsoFJkfMi4kTlcPU8\nRqmoMc31QXXZrCJ1Plz+LPAshuVyxG7TpcMp31ST1EEgmYRrWh5M873fwCTKDtR6i1+HorscrnJ7\nTdymtF52guvT9Ai0zHjzXGcI7+hCQL6+Sc8fjuBXaOSglTus/Q0WrJWDWABKd8RnX2R1DlfrgbyI\nv6NECPy8ZUUyZ8+bt7kSvCMMDaL0kez7aRv5X+v0TaishGXLLGl3olhZS7E9zPTPNE2L3yVOEZIy\nTy2rp1wvA6yp630PdGdl/a7MSaO8WxvUTY2vBFC1FFODEXQV1ob86yVMSmophsHJbt0HqncRT63E\n7jDXUiy218dcG9Gfmb7RYKM0mbQ8oSphy5Jk4Ax04zfOmRXIthsPndWO8rCDOywNthrcdNwmRwy/\nBnHni2dSLUUafJ93S0lwzUq/4xFwXMxUOu72q4956sf/ZcppG3wLzJ0Ld94ppb80wMpRiucDvwVO\nBZ4HfqFp2iF93muapo2OtD4A3/8+9O8P11xjVbOymjJPLdN31MBQ0z/00C6a5lTB0oCFV8LGdddS\nPsU3yaqThlK4UofT08jqKddTuK6dlrLQ5VHiJV0ULj82r5d2JzHUTcsUAgsaN+KUtU+jLMU1vbmG\niY7uFWxD4TJqWVbj9KuNGJMZ5ezB+GWM6COshzoaCVcbMVWUY1K3/MrzBI+Mj8+hPk4qdd80YO6t\ncRY3J8Oc5k2GvK8BpWuBIlkbNBLmMk3m+p1ORyMbXrmapZeYhIXvfx+WLgWRPt+JlV2K/wvcCWxH\nCrR/F0J8R9O0JmS3YniGmWqjPfZYUMBVYG/HFabWVm+n0nE31bOrfOULBkkPr0X2+TjZ7Tt5VgDT\ndUNJnVqHNUPslQ9XbBRYXPGgzFNL45Rh1FJm6UWiJ53mu2ODtzTrWJghqN0UOihItWVEo90pS9no\nRNuesIW8HdHtt9heD3VCGkl2E4x+uk/j+42/4LMhvv1tbC6TgcjDAUpCoP9bD2H1f2SRfb7v+90c\nUDz70Hq/UlI9GmwFsOyB+H2vetJpPpHjY/h8zTInVE2Tv2GZF+fD/J8Y6gjv3ef0NFL81Bu+CTfd\nBI88Elf7komltRQ1TTMqQq4QQuwEXhBCTCNE0rwfv/oVDBgAP/uZrNgdAhV0hcaX36IHXYf2AScG\n196bjryrSEJNRaVwRU9BpSykXjrOZ0RpBU52W56jly4KV7m9Ri/ejCz3U0FYz7lGx7CUGVA22p1B\nd+jRtMcbbMX53/TLuVopKF8eOb/oh6c8x2cf6H5+dfrxrUAW+J1R5cttCqhD11MY/5GxhUkofVVn\nFM82MSjFwZZRX9MgTt+rnlK4Ej6H6Z83twjv+nmXtdPyQvD13cjpihRsAeDWsO3W/zs33wwPPBB7\nu3oAS6+S+ohEADRNewm4Bmn1GDmtVwhptR8n/Y5zex+9ESe7pZQ/uwpZ4mB/8EJG/svU9aHnJ4DK\n4YoOo3D1a4SucZcoG5vLgrqlEiGdcrhYKYIMDUNR3Xw7xfZ6qfj0EIvs8ym214fsDjHaE9RdaHd6\n29nU7JSfb+p6XVFKjI3NZd5th3r8p74A3t7lK9czdb0MtkB2tU1dL81UG5D5WBOqiDUKSKgigJ7f\ns60lRG5PIgSVJwom2u5bK3FV51G6A+8jXuWox3K4GhI7hxmf1wi2CsMEW+DLU+3OMLf/+E5yXtI/\n+7BhaZOzFYiVCte9wDBklyIAmqa9IYQYDySSlRmRgko3y1p87+dWhi5Tks341WJcMVPmVcxAd+jW\nWYnsLhg6FqPu1PSmGpymBPt4UQpX9xQ0yLvCZLOxuYxyhzX5eemgcC2yz5fqVgOwYp+sIXloIZSE\nHwTSNH04lcvvinufjXanX1kZM4Hfq1+tS5BFc0O0x1xg2k8JM5Y3Ap4Q+USR8H4/gfuMNMrw+Pfg\n3BGyQHio4GP2ZP8i0yC73Cp8dekiYYyQjhfXi3nMrXRDkS/4KKh0w7T4gpFae5k8Rjsg+POO0EfE\nScqpoZ7o3PCtxIru055SuLzHZxpxj2I0Pm+j3cnQTW9GzPeL+FtyafS7rpOcV/Xf63nnwbe+FWer\nko+VxaufDDP9P8CPrNpPJEaD3xDp3oS3FmPTibQMkXcLxl1+05zh8o71USMfY4TsmkGjlmtYkOBd\nncrh6h5XUR6lt7oZu0a+z70h/pNVKMx35hsvvZbyTYkHXemQw+WtJbl5H7BK1pCEyBf9kqq4uhUN\nn6ZIJbLKHbLoLkAjw4KDrVDtWjGCJiZTvLweJ42+ACnU8iv2QcNgWYqnQmN6cw1lQ0J3cQUFexXI\nlIKGwZE/aMt+qPsHsCV43uyq4GAL/GsHllTJvCcIGjmaaLBlYL5pNnJ+Rj8Qu2WCX8mz1SEWmD05\nSDWttVubC9lTJDOHKzBnyypRwzuQIU7sr2rkvqAfv5NOgjfegNzIKeOpxNLi1eEQQvxY07TfRrVw\nUxO0tUVfxLrIV1MrETk2G5joqPW7yBoybONyJ7VcQ/W6O2Cz9YWxlMIVHa7qPKiWr632t/Hz5XpY\nY+Ol11K7KbFBEalWuBrtTqnUlMSQuD2oKq48qKDgpS70595ImUxMN1Mn5A1NqGBrgi8nqmnOcJoa\nhsv3FWGWZxVsRv+fToYSKJzRzqubLvRbyqiv6sW8vc1hP6bOIWQRzTO6WzA0OzSpeIHfd21VsBWE\nnvMztjC283uj3envu5VkZS7VJEvhSlbeabG9nqY5ianR3uzwk06Ct99O62ALeijgIhYL3nfekX2w\ne/ZATvfNc03Lo3REYg692YDT0xg2b8LpaaTMDtWjbteLg663dN9K4UoPnJ5GWV2g2Rm2IHUs9JTC\ntcg+P0iRCpWAzqAqUw0LE+Yh/vr8cnv4xPFF9vk+5UzHrwtuhoDNYf4jgd1tQ/cjk7ADuqomVMHD\nGkMdb9LU7GS1o5zGKcOonnOHHpx19x/cBSt8r8eIFwLmb4MJprfdbs/MYWA/IQOuCs3P1wjCKH4B\nQW0ygxVXdR6l06wdtQjIY6Qfy0wPtiCJCpeeszU2hpyt7lRCI9iiQpM5yIlywQVQUJD4dpKMlT5c\nXwF2mwpW/xIoBhqBJd1uYMyY/9/emYdJVV17+91V1QPdUAwOqIlT8Ymx44AEjAYHDGi8RiIiBoyN\nQxyQ3CQORJJghIsKSRD0Sm5EjSiRViE2SsK9JigmEDUaQWxFWsWAA0FFhJZm7u6q/f2xz6k6NXZV\ndc213uepp6vOuOv0GX7122uvBaefDi++CB98AEOGQGMjHH54p6uWs9BKmWBFdhMPs2T7RUyha6O6\nxOEqHEbyNLPJTLLMbDtc8QL8w8RW0JmwYm1iuVdzp5quODDia+5Ulk6IjmWz95cwz1RUjqYIZq2F\neVb8WIudXiBCbPWeSr/n1hmH2W9GWgUf5neZQHrGj4LlnWW4dM6/H7je2n5fmDuKEWOeDH2fqO1d\nT0whCEB3ILJEitn2RN/06Aelz6TlaKYuZmxYLsRKl+7xc2P8Ty1BDKUhtiB7DleqMVt2N268EbpO\nsdUV3CsD1F7Q0fmCBUQmn5IPA3us9/cCPTGB9HuARzpdu3dveOEFONmyzl99Ff7857BFvO7sZNQu\nB2z3A7BElwk+3rDoq13etoxSLBym+O9gom96RraVjVGKze46Gt2jg6keIsVPmNhalcBpcjJBmxpr\nGw4GrodZZrTf0lsuoWfjfurdDfT8cJ/Z3y2XmAdwv8/Cuw3nqs7Flk3LU0Zs2fuMrOIQcV05H+ZT\n/HeY5KQDwIz8i9XFH2fawr6w4WAmbr+THaOraPDX0+Cvd2zPovdU066Fo+Jsy3a4rO0Onxr8LrHc\nhtF+E6qwxj8wKk9SIYuVRqx8jrYYt493kYotb1NbwlGb2Ryl2Dq7MinR64yZc47QtV/BUbldFFsA\nFY86njldyHKQSzLZpejSWttyc5DW2h7q8aJSKnkz8sUX4cwz4bXXYNMmk5fLkSlW8nGlzxr/QJp9\n5hdqo+9iZo/NTDyXOFylSaYdrpjdhCnMt+nni+4+tx+uddoWDIsBU280GOsUmVdq9VRAWaP1UogR\ni+e0Bbm+8ziyCRoGWXFQYyHoRNnbnzCq05ijqO3Zufhsgm62Y/tA0OH6ydSkUm04cd5DoJMRZHnk\ndvdtJmYVME7fCZYAJfh9i01srbAGKMQbOJDvTPNhAxQAxis2LG9kAxA8/oNDlQjsazjt/4Gtt268\nEWbNSrhooZBJwfWWUuoqrfUjwBtKqUFa69VKqf5Ae9JbqamBQYOM4LrzTmhtLdgkZsWIfXJPoZn1\nuoGli7q+TYnhKk26EsPV7K6LGoEUL1XB0nMuYeBzsburglijyeIlQIw30rZuTHNIxE2IeBjNsroq\nnWLHGSP2GuGip3ecGoFzgbH2dq6HDQcnLG3T4K+n0beEZp81ynHhKHjIEgN2pvevqYjg97UwYRQj\ntjdGddM0+OsZ6KszaWGIGGVoi66HRjm+zy4YNiimy5BM8txiEClLuMjEytksHJWbAP9ssdaqswgw\nKLboymWm+Uhiia2QWxwttjrLq5USAwaA25257WWRTAqua4B7lVK/AD4HXlZKbQI2EV6XvXMuvhge\neMC8nzPHdC/27An33Qc+n7hcGaLBX0/9GOi5cR8jfI30592w+ckOrReHqzRJ1+Hq1KlapcyoOpuW\nLYnFVu+QiJicRDiok7DRm6u1ldLA6RzZzk+cGLFBU033Ye++YWJrhK8xFNMUdJKGWN2aRlzW++IH\n7gfjpHwwm1thcMQC1wDLrZgt7g+KPTslRSRr/AOp9zXAXSamK6p99vYHTYWL34dhH4Wtb9dgzGRR\n5nwQLOQ+WIfEq1W2x/6Ok5lRXGIrgleBoROB58On59Phaua48AnOHJDDsyi2ioxM5uHaAVyplPIC\nR1vb/rfWekviNWNwzjnw/vumXzYQgFesXKpDh8LNNwPg7XEfjBlDa7cDMvQNypMGfz31vtiBxOt9\nxyZ1AxaHqzRJx+GKElurVCh/k82syGzf1xOTh6InLWEkuE3esWQfmnX+Zub56s0v8JiiC9Oeh0ZF\nC5/VGhNgHhJbE33Tgz9GBvrWhETNhlAgej9fc/DaSVR3bor/DiO6IktxObc3KOSsJXKg7P3d7ns3\nun3O7/P6p/DWWjjlzKjvU8wEqwtEimZLbBWzmGwdV8lNN7YFi1zHIp8OV9io31Uq5qjZchdbkIW0\nEFrrVuCNLm/oqKOM6Nq8GaZMgeXLTUzXTTeFllm/Hu+NH5iAeytvlzhfqRPskohwGZZuHB12846H\nOFyFxRT/HSy566LoX50pko7DFdaNmEQplbBlI7kGuCa8K2jpxtE0++q6duOOJ7qswPPIGLF6TK3C\nl31mn06ht8Y/MFrUOPAOa2PFShh6Q/wKGFP8dzDatzhsWiMXh0SYw1mLdKHjbc/ZvmZfXdj2hg1c\nw8UH3cvJvnlR36dYud19m3GuxkR/lxlMLmqxZbN3WyU3HWCJrhhpX/LlcIUVXo9zzWdcbPk1rk8K\npOxYCuQqD1d6HHGEeT36KPzP/8Du3Wa6HdM1c6Z59elj8nb16RO3u9E7zMrVlcHEbaXEZGZw9arH\n0koaWUwOl7epDSZiyoaUcAmoOpqZvegXjB6zOO0Hau4yzd9vxUBZ9B4VO1bKIiP17oKi6ynT5WFl\ndo/1YFjDwPDUDhHEEl22YGu3cxjNJ5j0NhaR255CM3W+2CMGU6XO3xy2vSNf+gNNb2jqhhRH3Etn\n3O6+jTrejntsulTXscDYu62SSQvaaB0Xfe/Kh8PVqdjqbUaEZrpGZc1ZHXheEcGVHQ49FKY7hrpf\neimMGwc7d8Knn8L27XDssfD883DiicH0Ebbw8jaZX5mvUp61FpPh6o0NRmytUimLrqJyuCbCzJVw\nUxMJH4DFjj0yr5m6tG92mRulGKvLMHJUoOMm3TKE6DxR5ldyHc1x45gSEaw3Gtm9FhHfE88J6Uy0\nBmOoCI8RqngeJi0grbpzmS4vY2/vg76KuuMzuum8YY9G3DG6fHo2YoktyL3D1egeHX49DdbAEMIG\noST44ZQWX2i6jXeIrWOPhbPOyuw+skiRPCUj+PrXTUb6Tz6Bi6y+488/h298A955J7hYUHgNqGTo\nWXBTT8q21mIigrEPYC6aucqUUxmkWM+xna7/ZMeFLHjJF6xFV9Bcac6DiiujZ+Wr/Y3u0VGvZnf6\nyUsHutcE46biFWFOhs7ycNltTcjwUaF8Vc7XT+IXn46F7Tw1+OvTFiKx8kgxWDPRNz2Y06or2Ntw\nirPWAZVJ5zDKFVu3aJrfKj53IJLb3beZzP0CkN08XLFYwsjoiQv7AidEia2lG7t2TwNQWzU1l3VQ\nsdja7qGHQnOzCT8qEorD4UrE44/DVVfBwoWmy/Hss2Ft6Ney94B9tAaqg12Jma5hVwrU0cwGZ3by\nCRqazLDepYumwuj4D6KB7jVs+Pgo6P9/PL/xkrjZhQuF1nGVMd0Gu+5artsfZslHkM7Q9bDtrYYN\ng+sY6FuTVvxEIofLOQx8hm+yiRVyd5LawUmsvFFxyGT8R2QeKSiNGKZUOKgEHK56d4NJYjtrGixM\nTbyXKrl0uG533xa/YkNESMAIX2PXR4b6NdXjO/Ass7Z7xBEmdZSruDyj4hdc1dXw29+afq3f/950\nMR50UGj+uefiXSZpJBIRMxB3ACYP0EMwcIxxwCIfesGHe1sLrHoBzr/EBOb6kk8pUSjU+ZuZ6JvO\n7I23ssRnXNNsjahpdI8OOk9JC5R0tjdrGjCVDROM6AITz5LsjS/ZGK4NG+voyb7wiXY8x/BR8Ve0\nRVdkWuRrAIzzlCg2J13KTWBFYjtcQ87Md0uSI7L25YZzvgrLtwBGrPcbsw7v0LaSj8vsjGzFcAXj\nXq+M350JxLzmMzI6VGtqT+vAvcYSW4cfDsuWwYEHdm27eaD4BReYoPmHHzZdjK9ZCUACAWhpCaaU\niCwLJAIsxBT/HSzxXRTxsLayebwWeogP9K1hJE8DZhhwcPnKKhh8RnDVJXS9PmM+CB6HRV+FwTot\nZ6jRPZpmjmMJF8UUNzETBDpz1sSJebjdfVvcfUalFHDiEF1g1fVLMqYrlsPl/H5AqP0tTwFDTL4q\n7M9rYcCoYHyUk+Cv4zglPkolVUEhUmwO13qODb83LQ+vDDCSp5m5Ek5ZSXaKXBcJWXO4nHGvsUJy\nwu4Ba4GQ4Eo1b54T97MBqu7xwx5CYuurX4Vnn4XDDkt7u/mkNAQXGGtx2bLQ5x07oFevuItL8tRw\nGqjnNBwFg+0bWstTMNdcQBsm1IUKI891XNj72uClF+HD78IEzYaNdTT6EleLL2gmAFcrNkyo43bf\nbUk/+KPElK+T+bGK6va7Hn7SF+bBaavXMMLXGNu6t4+/U7DMVbEFjCW6mKCTyiRuE8vhmoEj8Dwy\nmzQvQQs4A+D73bUu5i/cZt+MuMlRRWxll2JzuMKY67g3WSzhIt7ueRsVA7pY5LrIybTDVe9uoD/v\nMuX5O4LFqxdYMZtLuMj8L5pIrv5oJ7hfCuBqDr93dZsQUarB54O33uryvvJJ6QguoUuEZeR+QMP4\nqdaFtBZm2Q9Qq/baBCJyGLUBn8Lr02CeCZa8emMDdb7kk1MWHLZIuSu5xaPEVGfz56o48Uv3g10W\nrB8stWvrOXEe/3nW/Icw/6+mqaZLLrKbzvo+SyeMpt6XXEbxhKMUI8XWTxxdh7OG0FltQvt8izdP\nyB7F5nAFiXPNbFj0VfZuqyz7+Nx0HS570JTTzXfGaM3mVvixNWOj9XeQil3r01EYPClaNWo71J7V\nEX+Z224zIxFPOin57RYoIriEIHX+5pCjYsdwOZm1BYb3terNWYGqy6dhisZ9CHy1y21odOfPGUsU\nwB4PO74kar1VKth9l7zYikHLUzDYkcV5vAodf7s23lhHPcDl02C547OTBCLSzlMHoVx1kQ5X8PiE\niS2AIeHO2oSDjWAHYF3crybCKj8UtcMVi7HT6Llwf1mlhohFVxyuDRvTH1wTJEWxVf3jDirvC4RP\nvPba8M9f+hLceit4SkOqlMa3SERrK3z/+yZxak1NvltT8IxkCUsZbR6gsxz5k4b3tS6miAuq3/XA\nHOBI87llmkkoCdRvb2ANyV/At7tvCwbd51p0xRxhN2sLsyfcGuwajOzmCrY3Eit49OrBDaECxU7m\nJduqE5inFzPaf2lon89F7NOu9ceQiHXjZHefNY2lTVPpeY3J07VjdBXeiW3MXBlaxM5V53S4wnLu\nvBa50RhYN94NG+sSJg0Vck8xOVxho+FmJagSN3ZL2YuudB2ukTzNbKvuZr3PdCMmjAsdr6x7jqPW\nZwyxNcLXGHXdu97TVN3agdoFnmcdy3u9cN11cFeSXQpFSukKrm7dTAzXF1/AI4/A2LFw7rn5blXB\nM9rfCD4rEapVy80Myz8CsIZjR8UURThcltW8oc9U6reHCvg687A0crHZH4uDn+2L/OqNDSzxjSyA\nchz3w/ipzH7Auvn4Yrc3DGe25bmjjGCLnB+jzlg0ttgKF55RtfeCtf4imJsg5cLyaUH3sufwuyIR\nFwAAIABJREFU/cx77jIm8Tgz7w1fLPlM8/eb/cUJgD9t45q0Ulxkk0T1DUudYnG4mt11ofPcGVca\nSTDnk2agu4suTRGTrsPlvKeE3dvnxtiOHargqBvK+NhiK9b92/NEgIqnHMu6XPDvf5ucWmVA6Qqu\nykp480048kjQGjqi+4glcD42TtEVmQOpwV9Ps28GzdSFRNmcKfDXr8HaiAdqSyiPV7wYp9nE/iW1\n9JZLqL8ruVijTNBM512JszfeGre9QHK1A8duiTE/IgZqEMwbc1nXXL5Yea6GTw3VYJuHEcbLp3G1\n6s/VLEbfcDErHKIrpUzzs56CQaPiVikoJNHlXdDGiqtgSM829m4rP9FVTA5XqmzYmNpAl1Iio6MU\nU4nRSkZs+TXsB7XXWnbcOPje90wgfJmILShlwQUmX8d558Gf/5zvlhQdtuiK9dCv85sSK/igmeOY\nfcUPoOXv0Pc30RsaO42evfcbC3phnLJBkaPrrM/JFs/uKnbSUyD+jSaSVcqIp5/0NW1PpVBzFOEx\nUCN8jQnFlv2LFIwInOibHrXMEi6yUkHYousEE0wfPP4qFJwPMHwU6lENG3RwlOCOL+AXr4/iZyOm\nhLoT496Ijdjq52sOpg5xUsfbBSG2ALDqG7IDhpah01UMDlezuy7uKNZwro9KpTJ7462M9qVfQ7RY\n6UoMV8zUQJEkEaMVU2x9oel+Yjuujx3TjjnGPJvLDKV17ks8KKV0zvZ7/vlGcFVXwwsvwKBBYbPF\n4eo6a/Z/hbMfvhXOvyQ6jcEqZUbQ2cSK/2mZZroFbFZrdhxZDTiGJmdRdIXFYvX7jKiuC2fbbFoc\n4qr31PDPQa4Pt97jbd9xIxvha2QkS5J2t5rd8eOjgkHuc5WJf4nXFueNdJCCq2HiXXeyduuhPPun\nQ+Bsq08xnqh0rD/Pl37pnVziHVa+iTI/eF+zeZNmyJn5y9LtXdAGJ8RP4xAVH2n/wIkk8pwmvQoN\npcBrqwLU1qq000KEidyogT0x7mUOEtUidb0aoPs3OtAKVHU3E6+1eDEMiYw7LWyUUmitu2QhlrbD\nBSG7ct8+Ezg/f35em1OKHL3nbS5Z/5/c/MNfUudv5nafCbp82TeQuiObwaG/gjFgkRe07ZpsmBIU\nWzbZzl7vzGIdE7ttP3HEKc0dFUqXEdcRuz+UV8s5zYlDrKTzoEi0/Br/QAb61hina0KMm+WGg6Pj\nL1ZrGKSYzS/gvPXw1hMhwfUQJBJbxYQ9ErMcybfD5R1mBmmcAgxdnaTDOFgnfODblKvYggzn4Uqh\n9FayP7LUoMHw6qtdb1sRU/qCa84cI7Yefxz27jXxXCp0QkocV9epqoJvD/mCOn9rcFpaN74YYstm\n9i2/gLsyL7qSTgXhFFvQeYyUk1nhmbHDYrYmpC+2kiEouuJ9x1hiyRJd7OkNAy1HOFaSVkts9fM1\n04D5ZVuuD7tiIu8xXAOAlZ0ulTLlLLag6zFcYbkYIeY9bp6vPqpSRWfHXPkTzi4rSr9LEaChwQTp\nQcyYLhFcXaOlRfPLaX5m/nfn+j1oW0c6XHHEVrO7jkYuZj3HsvScS4IPeCcjeTotIRYltmJ190G0\n2HISq1suFuMdN8KwWKrcPCicpYEiR1dGxoAF54/7F3z6BGwcT6adOSF/rHolQNMazbU/cOd8394F\nbTDf+tBJl27kiOhYsYo2oym/mK1InnzCT69einP+o2tdxVHxc3NV2gN5PE8HqLnEGrA2uLgdrkx0\nKZaH4Fq/Hs44Az77zAxD9UdLbhFd6bNnj2bZM5qLRid3oQfjM2yx0nsqO7Z2fvzr3Q1GdA0gTABF\njqRMhqibSjyx1ZmQ6veZ+evo7rDjGZqJkdsrgnyUsXGOGI3VHRD8/2zbCm+ugne+HZ4DKZiTrbzE\nlrepDdZ2UsC3CMhnDFe3A9q4Z4d5b7oUE5fjqXeb8zTbcZylQFdjuJw0u+uYweSwaemMGK+6uYOq\nOVZy09tvN1njixSJ4UqW/v3h448TZquVrsX02b8fXn4xkLTgCrLhYBPj1DKN292dD+Vu8NdT/xxG\ndDlyxGyYYJJrRpJICNh5wID4YgtMody5VgxWpMsVrOsWShAbKaASduflibBca4lo/QLeWg0/Oj8i\nBqw8xdaKQWZ046SmtqIOts93DFcq5D8XX/GQyRiuOn8oTADCHfK0uPtuuOmmLraq+CkPwSVklaoq\nOO305MVWWPLODQfD3KnMvgXq7nq7U8u6wV9P43NLWMJIlt5yiemWnHU9p22IHkIeTxB0OioxDEdt\nQ5xB88mV50kUQ5XPIs226IpF8P+z7To4PnxU7whfI5OZAZRPvJZTbAHMvBcmUbyiK+8xXEJWyGge\nrgjEXcwM5Se4AgHo2xf+8Q/o1y/frSkJ0nG4RrM4lETUEjGRwZhx1/U3UuduZumE0ZigzgQlPyKI\nW44nGSxxx3DL8RpupYsYAKAZ4WuMeWOyS2c4scWWt6kNJgJX5r6rqrNcXy29tvHO5jc5zfd62PSy\nY0FIbNm0zwdm56EtGSCfDtfebZVMWmDV7UyQFkJInYyOUhSyQvkILpcLvvUtWLbMxHK99lpRCy6v\nddNqHVfZaU6bTGBbyrEeuKk6XBAqlO3M8J6KYxKML5igoakvDCIqAWIswlJADEpQLiQedqLTGNjO\nTySjWcwSX2i/YUH+E2HmSripCRiXWlOyza09fsuakzXn+l/Md1MKilOAiudhb74bkib5driKPQau\nUMmmw5UOnif9ofgtASgnwaUU/OUv8N3vwpNPwtKl8O1vQ21tcJFiiePyLmhj5lXm/aSmNmbem2JO\nmyRw1j2cweTQaKEY+bDSjeFKNz4jrKAtmDgr7jeFnK8OTa6/q4HJ7hlhzlmnGdMTkWi0YgLq/M3x\ni3hfacRWxYDCe4AnX0uxvBh6Q3E7M8UUwyUkTyE5XK5VAWoudQxO69s3/sJlRPkILpuKCvO3oQG6\nd4e5czO2ae/ENtrnQ8WV2ctg7RRbQFTB4UyQardbOg5XxnDGYLVMCytXs2EWXD38sehRhonqhEXm\n0bLjtNIUW53ROq4S7wmFWV4mpVqKJYp9TZcS+Xa4hOxQKA6X621N99MctYsfewzGjMlfgwqI8hNc\nN94IjY3Q1gaffho1uysuV/t8uGcHTGrqdNH0yea2MSkDEomtWFnf0x6l2FU6DXjHJOsc5CjN07IF\neveNLtfzNRjx3JP0592wybOxlptgYrQi5ztJN4i8EMUWiMMFoWv6pp4E0xkUO+JwlSaF4HB5nvSH\nO1szZpgi1QJQjoJr8GBYuBBGjYIlS+DBB+G66/LdqqRpnV3JpKa26BkDMvPgbua40Id+n4UCxCHo\nFC3hIqYQElyZcLiSSQsBpqtz9sZbHSkZOiEyj9bc6BgsO5FqzC7Ou8z3raO57Iaoi8MVzilEB88X\nI+JwlSaF4HB5ljvurXfcAT//ef4aU4Dkr3ppPjnooND7H/zAWDQOvO79pEPFleamHLO8SwZpfb4y\n+pWhLswp/jtCGZ03HBwSK8unWUHm0dgOV7rUuxuYvfHWTnO9hGWpT9fpixBbE33TWeMfGDdx6hT/\nHazxDyw7sQUhh6ucsa/piithSE/r+i6wwQ2pYjtcQmmx8V+aTR/m7/+qPtF4/td6Dtx3H/ziF3lr\nS6FSfg4XmCrlzz0H55xjss4HosVCOl2LrbMrGTquMONxUiEsT5aTlmkwdyprfhUuTpJxuOwg/Mhu\nN2f5jkRFqoNiK1H5HZuo2oUhnHX/YrVHCCEOV8Q1PRuGNhX/9S0OV2HS7QDTc7F3W3rnV74drpqz\n23HZGXqqY9fELXfKU3ApBcOHm5Ni376MbrrYb8Y2YXmynAyKnhQvhssuywEERZUzGWlkrTQwomu9\n79iofSzdONo4bL37AhHxV1cTUVj64FDc1gM6rAZbWeaRSpNMx3B5J7ZBk3FoiwnnNV0K17fEcBUe\n3gVtzLRiBCctaEsrdUa+YrjUx5raoe24NloTLr4YRozIaRuKhfIUXEKn2HmyIgVRLGI5XLHEFMBp\nG9cw0TfdFKN2zreLOz+gQ9MdBZ/7PbcOtiff/g2rjaOWz2zuxU4mHS5vUxsr7rVK4wxrgyuRxJd5\nQhyuwqN1XCWT5odyK6ZDrh2uisf8uP9quhFd26yJgwfDH/5g8l4KUYjgEuLS4K+n3gdLuSThcpEO\nVzBP1ioFY7eYZKF2zNUAmI3Vt2+7UuOViREDU1vRXn75NOg9lX7b16VenNoXUZxaSJlMOlytAyoZ\n0rMNdphEr6zMfO44ITnE4SpMuur85trhqr7Wj3KO3/rud82ANFXeYQiJEMElJMSuXRgavXgn+MOX\niRnDtUrB2KeAtWG5sVjuXChWbiurduFPpsKAqfS7K3WxBcahK6fiyl3B29RG+zDz3hk/kukYrooB\nMKQJXrW6Tl4Fhq4l64NMhHDE4SpNcu1wBcXWww+DxwPnny9iqxNEcAmd0llBaafD1egezexFvwiJ\nLYjOeQUmH5Zdm5D7w5e5GibedSfQtZgrEVtJsiCUY8oZP5JJh8vb1MaKlVaX4lmYLkWkzEs+EIer\nNMmVw6U+0NSc1x6acNVV8RcWwhDBJaSNnTvLdrga3aO5emMDPARhYitWjcO5fS3n6/6oZfr5miXu\nKoc4c7s5BVAmHa7WAZUMvaGNoUUYNF9qiMNVmuTC4XK9GaB2WAeqxZpw+ulZ3V+pIZFtAG+8AVry\n0qTKFP8d9PxwH092XMi0l4Zz9aLHTI6s5Vs6X9kmniATcoqdz81JpvNwtc6O3oeQeyQPV2mSizxc\nVTMCIbFVXw8rV2Z1f6VGeTtcbrf5e9pp8OyzJi+XkBI7jqym5zvb4eFn4DcR9QkTiakJmlgxXP18\nzWnFbAmZR/JwlSbicJUmOYnh2mfdry+6CO69V0Yjpkh5H6077wy9P/dcU+bHQboZ58HkHPJOjFGC\npwT5z8NmwMV/D4/Dcoitib7pwVcYE6Lni9gqHCTTfGmSSYfL21Q+97lCJ6eZ5q+8Evr0yc2+Sojy\ndrhuvNEkP50wwXwePx4qK83JZJFOxnnvgjZm3mveT6ItY2V3ChV3lRsGnwFTtUnr0Lsv/bavA2Ay\nM8KD7n2mNqFN1HyhYIjncHnTTMxYqHgXWIIhx3nBvE1twVDHXO4/kw5X+zAz4GJSU5t0F+eZfGea\nFzqnvAUXwPXXQ//+MMwaF3/VVXDMMfCNbwSHuKYqulrHVXLTjW28tIOir7sWD7tUD8C7+4+G/3sR\nDvpuUGwlqk3oLHwtFC6xRil6h7UxcyXcdGNb2iVICgn7+0Du8oKprZoeS9t5/Tp425r2OXBijvYv\noxQLEK1xva5Ru8H/NQU1qQunfGWaF5JHBBfA2WfDkiUwcqT5fPrp5vOFFwYXSVV07d1WWRJ112IR\nHI1oc81e+Ns6+CcSAF9ClHoMl1Ns5Qy/pvbkdvgUTsa8AHYCr+WoCZlyuOzaf0JivAvaaL/RFECP\n19tR8UiAbteZBIcd5yr2PFOR8n6y7XB1O6AN9+6sbb4sKO8YLhuljLj6zW9C00aOhP/5n7DFUonp\n8k5sgwUR06x4B29Tcd+oQklQLQL7gRdMTUOhZIgVw9X6fCWTbki/wG6hYOcFczL0kex16VU87Kf7\nkW306NuO61NrYn/gMPO2BzC0owO+lv0fLJmI4fIOa+OeHVZ34lmS6sPzuJ/uR7XR/cvRL8bD/h2g\n50D3I9uo+F145ujKO/1BsQXgeVabdY9tw/33QNJtyGYMl/fmNv61A1wdWdl82SAOl5Mf/hB69AjF\ncD32mJnmIBmnK14MVyjeAbyzi9f9iips7aoCzggWtq5DEo6WAvEcrlKISXTmBQPgyswmYXWtCVDx\nWACs51/VnPAHZ8c3FJ6XrGluNwQCMH063HILZPnwdtXh8k40zuApwFARW3ie9FNzuT/hMt0BNKjN\n0G2CH9fbIWEUeW4AQVFe+80Odi/34B/auTeSTYer9fYKjptjJTutqYHjjku8ghATEVyRXHEFHHgg\nXHABvPIKbNkCffumtImwGC5H2ZKKAXDKSlNL7pRBxVtHzi6bE6xVuGY/nNcGgzUjfI00+Ovz20Ah\nI2Qy03whklHhuE/jbtJBgVVzbgdqb4zl/vhHGDwYz8EHh6b16gXbt8PUqbBnD0zT4En9welq1qgd\nGv9JiWOAuhzDNcCIrSE9y1hstVsxV3ug5lKH2HriCTjrrNjrNDWZ8jfEFlm8+y4ceaQ5Fx58EP7r\nvwCoHd7Bzvcr0IcnPieyGcPlWu9wzj77DGprM76PckAEVywOPDD0/v/9P/jkE+jePaVNxIrhan2+\nkqHD2ng1ibgROz6i4LtuBimYUwWtp4vYKjFKPYYrk3Qb20HF/0Z357SPceE/RVHtmgVf/jKMGBFd\nb+4vf4FTTjHvf/1rvDt/QOuch1Lav+epADXfNf09Hd9Q7Pl7/BigrjpcreMqGXpCcf5YzBTV/+mn\n8uEI0bRwIVxySfzcVIccAosXw0cfRc+rqzODtwAOPRQmTTL1CX/xCwC692tn13sV6CPjX4/Zcrjc\nywPUnmf1JfboIWKrC4jgisXJJ8Oll5pfK7t2mQvlxRdhgLGrkg2gj3VDan2+kkkT22BA/HgR74I2\nZtq17SYWZlqJZuqM2JoL9N/H0Y88QoP/r/lulpBBSt3h6iruVwJUX9uB2gWuTWaargX/8QqP+joc\nfTQV8+dTUdnJ9Tt4sMnYbTsj992H94vv0fr7J5MuBux6PyT2PP/QeI/ui796E/vmePCfEy4AMjFK\nsVjEltqiqbmwA7XFHB99oGLPkx70UWkKE62NuF7sENennmoSgY4Z00ljFIwaldx+unWDyZNh82aY\nOxcVgB792tn9Fw/+4bEFXbYcLtcHju9qCUAhPZTOQ0kbpZTOx35T5qKLzGhFMPEVkyeHzU41P1cq\neIdZte0K1LLv+bP9MAj6jVlH/z2vM2bpVVw0WsZglBKfb9WsWaU59/zy/L+qjzSVv/NDnLEyVXeH\nOxyBPuDa+AX07JneDjdsgOOPh337zOef/YzWn82G7vEfoBXz/XRr9NOxW+F5IfY9NfIh/cH7ms2b\nNEPOLJD/a0BTcV8A10ca/8mKjkvdGdms2qCpubAd9zsRuzsA2q9I8N0VtF/iIjAoYplWTdV/+YPd\ngboG1DsfweGHZ6S9cfnRj8IGcO1e5sE/LLr9r60KUFurMi64Kh7y0+16P1xzDfzudxnddjGhlEJr\n3aWDKw5XIhYvhssvN8HzMUgnKWqyFKrQAujZaMTWvDGXMdrfSMsezS9fDIjgKjHy4nAFNK61GtpD\nk/SBKn1Hogv7rr7Bj+efSfwwvOUW+OEPcR14oAkoTpd+/Ux8jNdrPv/qV3jrHqX1oqtxrYtuh+vf\n0O0aEz/ksYPHbr0VrrvOuPM/+xkAted1sPODCvSXzTHMax6ugMb1lgbHQG33ak23G0NxULsPUOgD\nIHCigorO/+9qg0a1RB+fbt/3B8VWx9kKT6+R8PTTuLZFi+VIKu8NsPvF8Mdj5UMBKh+yxFYlqE9b\nTRdbtpkzx4i6n/4UgNpvhf8/bSQPV+EjgisRLhcccUS+W1FQ1LtN/i1bbAFUVcFpp4vYKjXyEcNV\n9TN/zIfh7hUe/Fk+x6pu81P16+h9+4+D9ivcVLt+Gb2S1wuXXZZyjGdcevSA1athkDXkd/duvOef\nCi+8kHg9HzDxt/C975kg/BtvNBfmTTeZzR7dwa43PATqVF5rKVbd7qfqzsRip/Z8Ey/UPtrF3oWJ\nH1HuZQFqv504V0HHEIWn4d9QUQFDh8L+BOl93noLHn0U1QHdT42/XfXP13MjtsB0Rf74xyama+JE\nALof3c7utRUEvhK6PiXTfOEjgktImnp3A0sXXUK/MevCyvHs3w8vi8NVcuTa4aq+viPoIIDJuO22\n8oDVDu2Axx+HSy+N6yp7F7RBU/KjDz2L/FRN86Os56prY2ie3xKa7gPPxf3ww7gPOyyNb5QmX/ua\nKTP2wAMmZmbbNgACh4D+ksKNo4qDUsbRuvba8G1UVRnR9cEHpsiw1nQ/sZ09f/Sw9QCy6nCpDzQ1\nYztQ22O4chHHOPhd3G5TVm3vXnjNpICtaAzg7p84Z2Hc7dn07Yvn0UfhgAPM5x//OHHj/X5ob4f1\n62PPr6mBu+8OxvPmjOpquPlm+PBDmDMHpaH78e0EfNB+gYv9d3sy4nBVPOCn8h4/yqmJW7vefMEg\ngitZbr0VzjsPBpZnceVmdx1Lb7kEJuioPFvicJUmOXO49moq/9vRXVMBu1d7CHzVhffuO82ILTDu\nzZtv4uVm9gdmhm2i6rMAH86HT4BTX2pj/zc7Px+rZsZwWjweWL0a90kndfFLdZETTjB/LbHFIYfg\nev998+BNhf/+b3OBzjTHq+bCDk4Y7+IwN9CmobJr/1/X2gAViwLgOJQVjwRwbU2wkscDL7+M23bx\nIvn8czj6aNi1K0xQJeS3v8X9gx8k2+z4uN1G2Bcq995rhOmsWYARnFVzAujD/Jy1SVOzT1P1QmIH\n0X+SomOMI06uRVN5fwC1U8e+Jmzsc1JIGwma74xf/Qp+/nPzvroaNm0KSxuRzcD5QqLe3cDSWy5h\nxF1PRqV+aGnR/HKan5n/Lfq9lNjwnqZxYYCf3paZIOaYBDRV0/xUTQ/d6Fu3VkBvFarssGgRjB2b\nvTY88giccYZ537s39OmTvX2lwubNoQD6Qw9NPz5MaxN0HenuTJ/Orm9NJdBPQY/UhJfaqFGtmppz\nO3Btj7PQiBFwzz3R03v1CjlO8di508SzJUN1NXzpS8ktWwpobVJL7N8Pxx6b1iZ2/9mDPhgC/ZVJ\ncfFohND63/+Fr3wl9LncjnEMMhE0L4KrM774wgQrPvig+VxTY0SX46Zc6qKr3t3A0nMuYcRz0WIL\nYM8ezbJntHQplhi5GKVY/aMOKueGbva7/+7B/w1XeBmtQAAWLICPP858Aw47DMaNi587qVRoa4NH\nH4WtW6NGWwcOh13/qgB3cs8ST2OAmrHh8U3t31FUnDo9NKGqysS2pZg0WkiRFStMLWAnM2bEXz7i\nfx+GxwO33w4+X+cpLsoQGaWYC3r1gt/+1givP/zBZII+9FB46aVgYGs2Ryvmm0b3aJYuii+2QGK4\nSpWsxnBpTfXV4b+sdy+PIbbAiKErrshCI8qIykozrB94u7qaPvfeS99eveCNN3BtAu+px7Nz8Vvo\nIxI/Typ+66fbDaERhf6TFO6jL6Ri4UIjsoTcMnQoPPMMTJnCtu3b2XjFFQy2e2Ri0a0bzJ8Pb7wR\nPr13byPeTjwxi40VxOFKhTFjjOiyefVVk7TQohRF1+3u21jPsQkzyIvDVZpkzeHaran6tZ+qGaGY\nrV3rKtA+lVKBeCE93n//fTZt2sSZZ55pfjRaQeocdRS7/ryZwDHhoktt01TMC6B267Cu372/d9Pt\ncqlmXCisWrWK2tpa6urqOl94+3ZTRmjXLjPS9qOP0s8fVyZkwuGSJ2QqPPFEeDHrq68Om12KD4sp\n/js6LddjO1xCaWE7XBkloKm6IyS2AHZuFrGVS7Zs2cLatWvNh3/8A771LfP+gw/ofuHRuNYFwl7V\nN/qpnhweZ8eLL4rYKjDee+89Pvzww+QW7tMH/v1veOcdEyIjYisnSJdiKrhcJuO8y2WS0e3cGbVI\nKXcvxkNGKZYm2RilWH2dn8r5jm7EFz3QR8RWLunbty8n2CPOKivNoIErroDnnoP16+keZ4Cmrob9\nP3VTfdxjMGRI7hosJMUxxxxDbSp1Dnv2FKGVY+QpmSper8lvIwQRhyu3eCe24W1KnJ8oE2TU4dKa\n6ss7wsXWSg/+U2PEbAlZJczhAhOTungxnHuuKaIc63XqqajVb1H9Xx0SUF2gpORwCXlBHK5UaW01\nuVCEIOJwpY+3qS2lQsDeYW3MXAk3zQe2Za1ZQGYcLtdbATx/1Lg+0lQ+HiqLsutfFejDxNnKB2EO\nl02PHrBsWX4aJGSElB0uIefIUzJV5s8PCa4Y5TzKrTsRxOFKl24HtLFikHGskmYAnAJU5CDRdVcc\nLrVZ41qvqRneQfVUP5XzQufHro8q6HF4m4itPBHlcAklgThchY84XKnijNt6+OH8taOAEIcrdbxN\nbazYAa8CQ5uSX691diVDx6XmiqVLug6X5wk/NeP8YdPav6MIHK9ov8BFj77Z7w4V4hPT4RKKHnG4\nCh95SqbL5MlhKSHKGXG4Uqd1QCVDH4FJN0Dr84nFU2TMVi7EFqTncFXcFy62/MdA+7cVexd5qJru\np/tp7ZluppAi4nCVJuJwFT7icAldRhyu9GgdVwnjEi+Ty5itSFJ1uDxP+un245DY2vO4m47vmrJA\n0n1YOIjDVZqIw1X4yFNS6DLicGWRHMZsRZKKw+VeEaDm0pDY2r3CI2KrQBGHqzQRh6vwEYcrR3iH\nRcStDDDxOKWAOFzZI5cxW5Ek63BVPOKn27UhsbX392781vkgYqvwEIerNBGHq/CRp2QO8C4w3ULO\n14p7yUkupVwgDld2yYfYguQcrsp7I8TWb920XybOViEjDldpIg5X4SMOVw5oHVfJpPlGdNkMPSt/\nD9JMIw5XNK43AnieTyxWAscoOkZk/7i53tF4/hyAOM3pGK4InBjdjoQOl9Z4GgNUT3TEbD3tCX4f\nEVuFizhcpYk4XIWPCK4c0fp8JZOsAOhJZ3U+Mq2YsB2usi1evVOjdoRPqj2zA7U7iXVfeAGOOsps\nxu8Lm6V7Ad27WFpnr6bmW+24NidYpnt3ePvtqDbseV+z4W8B1IkK7QUUwe/pfk2HxWztetlDYLCI\nrWLAdrjOPPPMfDdFyCDvvfcevXv3Tq54tZAXRHDlkNbnK5m0oM2MTishytnhcr2nqT25HbUv9vz2\nS10E+oY+V7msslB3323+nnFGcF6PiHV1Dex6swJ9VJqiq0XTo387qsVqy3mKwFdUqB1waUY7AAAS\nDUlEQVSffGIKsu/aBYcfHtWG460X9yTuLt6zwC1iq4gQh6s0EYer8BHBlS4zZhhn4tprU1qt1MQW\nlK/D5V4RoHZ4R2jCwcAe8zbQE1yDR1Lx2FOgYgimL30J7rkHdJx+vq1bUXva6PGvpdDvW0DqVQxc\nH+qg2OoYpti7xAMeRzkdrWHPHli9Oub67R0d7N27F29ra1TbA2wGN7imzqOm/vsptUvIL+JwlSbi\ncBU+IrhSxer+AeC662Dv3tDnb34Tjst5i/JOvhwu9z8DuF/tPG2B7g3tl7igKnmnyL0ygPvNxNuu\nvsmRTf27sOIPJnP8pLPAtaKTdt18s3nF41vfgmefhQcegEGD4IAD8Lr3dyq6PH8K4PrQ7Fv92/z1\nn6TYs6wiemGlYMmSuNv6YutWVq1axfl//zv8+tdm4o9+BHPmyGibIkYcrtJEHK7CRwRXqnzve3Dw\nwXDuuebzDTeE5nm9eNd/BJWV0Ls3UB61FXPmcLVr1HbrvR9qh3QkXNxJt20z4bLLANjpPzzhsqoV\naoclv21+/nO4/XaGLvIwNPm1EtOtm/n79NNQXW3cMACXhj4RwjGgUVvBtU5TMyq63bo6va6+L774\ngtWrV3P+9Olw8cXGERs4MOXtCIWFOFyliThchY/S8bo0srlTpXQ+9ptRHnoI3nzTvN+6FRYuDJ9/\n330wYQJQ+qJrzx7Nsmd0dgWXX1N7Yjvud6Nn7f9h+H6r1H+GPvzmN13abcJtgxHfEyeGBFKmWLsW\nzjoLWlqiZu2b4aZtkjv4ueY/2vE8F349BdutoOp7L8Gpp6bchK22w3X++SmvKxQu77//Pps2bRLB\nVWKsWrWK2tpaEVxZQimF1rpLo5jE4UqXa64JvbdjYV55xXQx7twZFhdjuwulKryy4nBpTdVEP+4m\nq3vsC4JiK3BwaLGO77io+o0/xgYsLrgguus3Wa68kiq7Ky3XnHCCOYdGjIDPPzfTPvsMgOrJfqqX\nnR5adqXJN+IH3D1h7x1u2n/g7nIAe9DhEsFVUojDVZqIw1X4iODKBErBH/9o3s+bFy7GHCQTg1OM\ndDmGa4+m4qkA7ApNcn2sqZoTPTrOf6Ji95qKoJjodAjCuefCBx+k37Z84vPBunWhz6++Cl//unm/\ncmX4sr174/70U6ispBuQCb+tV69eDBo0KANbEgoJieEqTSSGq/ARwZUttm83zlesEWolRtIO134N\nMXJTVd3rp2p6gtQDf/tb8K375JPxunum2dIi55RToLkZtmyJnveVr5jYwQwiDldpIg5XaSIOV+Ej\ngitbLFkC55wDy5envKqz7mIxJEhNxuFSn2q6nxDKCRWPtvHh26m8+C8wdGgXW1hCHHeceeUAcbhK\nE3G4ShNxuAofEVyZ5owzTI6lzZvhH/+Imt1Zt6J3YngJoEkT2wq+yHWkw+V+OUDlDD/KUSrSvVKj\nrAF0unf4+ore0KMHLFpEZRrB3UJ2EIerNBGHqzQRh6vwEcGVafr3h/XrId1fGuPgpvnhnwudqio4\n7RsKz9IA6jNNt/EJgtgvuwzV0JC7xglpIw5XaSIOV2kiDlfhI4Irm+zdC+3tUBEj6WQ81sJLjrp8\nQzPeqAwT0LRt0+xdEKDmz+GpCdrGu2gfaVyvWvcz4HbDaaflo5VCGojDVZqIw1WaiMNV+IjgyjYH\nHQSvvQb9+iW3fJPJVm4zdAEwIBsNywABTe1pHXhf01zvmNz2fRf6INg/2Q21SurrFSnicJUm4nCV\nJuJwFT5SoSMbdOtm8icB7Nhhklg6SCRAWmdXMuksgq9CjN9yLw/Q7cJ2aoZ14H7NuFr7KiDQB/Y8\n6mbfgx72T/fg9baJ2CpibIdLKC1sh0soLd577z0+/PDDfDdDSIA4XNlAKfjTn2DkSJOf64kn4Oyz\noWconUGi4PlCHpnoWhOg9rzw8jEdPlg0w8NFo10isEoIcbhKE3G4ShNxuAofcbiySZUlqP7wB1P+\npZjLGe3XqM813U8Jia39P3Wx508ePlnq4eUXAyK2SgxxuEoTcbhKE3G4Ch8RXNnkZz+D7t3N+3nz\n4JvfDBNdxSJQqiZ34K1tp8ch7cFp+3/uYv80Nx3nu6g4XDHszIUJtiAUI+JwlSbicJUmxxxzDEce\neWS+myEkQARXNjn5ZFPg+ogjzOcVK6JcrkIUXZ4/Bug2qp1uF5lX1cxQFnhdBW3Xudh/hwc8JiC+\nqmMLL7zwQh5bLGQDcbhKE3G4ShNxuAofieHKNkcfDR9+CC6XEVvPPWcy0LsKTOvu13iWaditqRkX\nO4/Wzn9VoI8yIssZZVZVVcUZZ5yRm3YKOUMcrtJEHK7SRGK4Cp8Ce+qXMHadu/POg2efzW9bnGgN\nfk3l/wSoGdURJrb2/drNnqc87HnKA01N9OgXe9Th/v37xeEqQcThKk3E4SpNxOEqfMThyhVz58L3\nv2/e/8d/wN13w003AZ2X+8kaLZruA9txbQqf3D7Whf9YRdvNLlCd59ESh6s0EYerNBGHqzQRh6vw\nEYcrV1x1FcyfH/ocUdQ6l7Fcnsf9dPtuO91PDIkt7QLdC3av8LC3wUPbbW68nuTyaInDVZqIw1Wa\niMNVmojDVfiIw5VLrrgCDjwQLrgg5uxcOF3ulwPUXB4eo9U+UrG3MVR+KFXxJw5XaSIOV2kiDldp\nIg5X4SMOVxnheiNA7RmhPFp7H3Sz50kPe38X0t3pOG3icJUm4nCVJuJwlSbicBU+IrjyxTPPwFln\n5SwZqudxP92/FhJb+2a6af++m46LXNBbAel3a4rDVZqIw1WaiMNVmkgersJHBFeuOekkOOQQ8/7v\nf4fLL4ft24OzuxTLtUNTdWMH3S6Lfjm7Eff9yk3bze6wVbuyX3G4ShNxuEoTcbhKE3G4Ch+J4co1\nX/4yfPwx9OsH778PDQ2we7cJqPd6gTRjuXZpqn/kp/LxQOLlli6l+oILqE6v9TERh6s0EYerNBGH\nqzSRGK7CRxyufKAU/PWv0KeP+fz003DddWGLpOo4Vd8QElu6G+xpcIe9ePxxk//r/PMz8hWciMNV\nmojDVZqIw1WaiMNV+IjDlS+OOgpWrjRZ5z/9FBYtgk2bTDej23T3eV9YRuDis1G7Ot+cajN/dQ/Y\n/VcPgZNDWjrbKSfE4SpNxOEqTcThKk3E4Sp8xOHKJ8cfb2ot2jFd//gHjBkDn30Gf/kLnH02ru1G\nTHX2AuCgg1DNm+g+qB2ve3/wlW3E4SpNxOEqTcThKk3E4Sp8xOHKNwcdBJs3Q10dvPsuLF4MBx9s\nMtPb3H03reN/Graa170zelseT9AdyyXicJUm4nCVJuJwlSbicBU+eRNcLS0taK1RSslfrXEvWkSP\nYcNwbdsWJrb23HEH+8aORe2/kh0dfVEKerg+pUXtKYh2K6VoaWlh+fLlDBs2rCDaI38z8/eDDz7g\nhRde4NRTTy2I9sjfzPxdv349b775Jscff3xBtEf+Zubv66+/Tq9evTjkkEMKoj2l9LePHW/dRZTW\nuckDFbZTpXK/U0EQBEEQhDTRWquurJ8XwSUIgiAIglBOSNC8IAiCIAhClhHBJQiCIAiCkGVEcAmC\nIAiCIGQZEVyCIAiCIAhZRgSXIAiCIAhClhHBJQiCIAiCkGVEcAmCIAiCIGQZEVyCIAiCIAhZRgSX\nIAiCIAhClslLLUWlemnYkY9dC4IgCIIgpMqHWuujurKBPNZS/K8c7OmEHOwDYEiO9gP07pub/Xwt\nN7sBYECO9jMoR/sBGJy766qfrzkn+6kjN/sB6M+7OdlPHW/nZD9mXzn6P/lz93/yNrXlbF+szdF+\nmnK0nxzuqz2H3+mlHHkpr+ZmN0F+StdrKUqXoiAIgiAIQpYRwSUIgiAIgpBlRHAJgiAIgiBkGRFc\ngiAIgiAIWUYElyAIgiAIQpYRwVVstK/IdwuKm3Ur8t2CoubzFevy3YSiZc2KnfluQlGz4p18t6C4\nWdmR7xYIIriKjY4V+W5BcdO8It8tKGq2ieBKmzUrduW7CUWNCK6uIYIr/4jgEgRBEARByDIiuARB\nEARBELJMvjLNfwrkKGW6IAiCIAhCl9iitT6kKxvIi+ASBEEQBEEoJ6RLURAEQRAEIcuI4BIEQRAE\nQcgyGRVcSqnzlFLvKKXWK6V+GmN+L6XUU0qpN5RSryil6pJdt9RRSs1TSm1RSr0ZZ/53rOP2ulJq\ntVLqm455Hzjm5bqIekGQxPE7QCn1Z6VUk1JqrVLqSse8cj/3vqyU+qtSap11bH4cY5nvWefYG0qp\nF5VSJzrmlfX5l+Tx+4l1fNZYy3QopXpZ88r9/KtSSv3TOj7rlFIzYixzrFLqH0qpfUqpmyPmle35\nl8yxs5Ybai3zllLqb47pZX3u2SilXNa1+ac48+copd6znh8nO6andu5prTPywoi3fwFHAhVAE/CV\niGVmArdZ748Flie7bqm/gNOBAcCbcebXON6fAPzL8Xkj0Dvf36HAj99U4JfW+wOBbYBHzj0NcAgw\nwHrfHXg3xrV7KtDTen8e8IpjXlmff8kcv4jlL5B7X9QxqbH+uoFXgCER8w8EvgbcAdwcMa/cz7/O\njl1PYB3wJftYWn/l3Asdo5uABuBPMeb9B/B/1vuvd+Xel0mH6xTgPa31h1rrdmAhcGHEMnXAXwG0\n1u8CRymlDkpy3ZJGa/0i0JJg/h7Hx+7A547PijLvHu7s+AGfAj2s9z2AbVrrDuTcQ2v9qda6yXq/\nC3gb+FLEMq9orXdYH1+JmF/W518yxy+CS4EnrPdlf/5B2P2tCnMutUTM/1xr/RoQK31nuZ9/CY8d\n8D1gsdZ6s7W8/eyQcw/jUAPnAw/FWeRC4FEArfU/gZ5KKTvLQkrnXiZP0i8Bmxyf/030TecNYBSA\nUuoU4Ajgy0muW/YopUYqpd4GngGc3RYaeE4ptUopdW1+Wlfw/A74qlLqY8x5eIM1Xc49B0qpozBO\n4T8TLHYN8GfHZzn/LDo7fkqpbhiHcLE1Sc4/gl06r2N+GK3QWjensHpZn39JHLv+QB+l1N+sYzTO\nmi7nnuEe4BbMeRSLyOO0mdBxSunc83SllWnwK+BepdQaYC3wOuDPcRuKFq31EmCJUup0YAGmWxaM\nhfyJ5RY+p5R623J8hBA/B97QWp+tlOqHOU4ndrZSOaGU6g40AjdYTk2sZc4GrsJ04drI+Udyxw8Y\nAbyotf4idy0rfLTWAeBkpZQXeFYpdZbWemWSq5f1+ZfEsfMAA4FvArXAy0qpl/PQ1IJDKfVtTH6t\nJqXUUIxjlQopnXuZdLg2Yxwrmy9b04JorXdqrb+vtR6otb4COBjTB9rpukII6x/qUUodYH3+xPq7\nFXgaYxUL4QwBngTQWm8A3ge+gpx7ACilPBixsEBr/cc4y5wIPAh8R2sd7LaQ8y+542cxllB3Isj5\nF4bWuhX4P2BQCuuU/fkHCY/dv4FlWut9WuttwN+Bk5BzD8xz4TtKqY2Y6/JspdSjEctsBg53fA4e\np1TPvUwKrlXA/1NKHamUqsTcWMIi/pVSPZVSFdb7a4GV1i/BTtctExRxFLblytjvBwJorbcppWqs\nX9YopWqBc4G3ctDWQiTu8cPE1QwHsPrf+2PEvpx7hoeBZq31vbFmKqWOwHSDjbMEqz1dzj9DwuMH\n5v4HnAU4BVnZn39KqQOtY2N3uZ6DCeCOu4pj3bI+/5I8dn8ETldKuZVSNZjA77eRcw+t9WSt9RFa\nax/m+/9Va315xGJ/Ai4HUEqdCnyhtd6SzrmXsS5FrbVfKfVD4FmMkJuntX5bKTXezNYPAscBv1dK\nBTCjJq5OtG6m2lYMKKUeB4YCByilPsKMqqskdOwuVkpdDrQBu4Ex1qp9gaeVUhrz/3xMa/1srtuf\nb5I4fr8EHlFKvYG5YU/SWm+31i33c28IcBmw1ooF0cBkzOgl+/jdBvQB7lNKKaBda30Kcv4le/wA\nRmKchr32unLvA+BQzHPBDkBeoLV+3vnssH4krcYMeAkopW7ADMI6iPI+/zo9dlrrd5RSy4A3MSE8\nD9pxXnLuxSbi+D2jlDpfKfUvzLP3KmuxlO99UtpHEARBEAQhy5TtUFpBEARBEIRcIYJLEARBEAQh\ny4jgEgRBEARByDIiuARBEARBELKMCC5BEARBEIQsI4JLEARBEAQhy4jgEgRBEARByDIiuARBEARB\nELLM/wf86J6jQXB06gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa8061216d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cuCap.Plot_basin(cuCap.CellHAND_class, ruta=ruta_images+'Map_HAND_class.png', lines_spaces=0.01)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAAESCAYAAADdWICBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXmYHUW99z+dSRiyTwIhIUBYMlnYJyEYAQOoiCwKiHpx\nAZV9EVzhetUriq9eEbmigoZFRQVBuKCoIIgCAiKEwGQIsmSBkARCQiAJCVkmyaTfP7r7nOrqWrv7\nzCShv89znnNOL1XVVdVV3/ptFYRhSIUKFSpUqFChQgU/9OrpAlSoUKFChQoVKmyJqEhUhQoVKlSo\nUKFCDlQkqkKFChUqVKhQIQcqElWhQoUKFSpUqJADFYmqUKFChQoVKlTIgYpEVahQoUKFChUq5ICV\nRAVBMDYIghlBELTH328GQfC5IAi+GQTBy/Hx9iAIjtLcPzgIgv8LguC5IAieCYJgsnDugvj400EQ\nXCoc/0Wc1zHx/98HQXCccP75IAi+Jvy/LQiCE/JWwtsRjWpX0/1VuzYWjXxX4/NfDoJgUxAEQ4Vj\nVZs2GA18V78dBMFTQRB0BEHw9yAIdhbuqdq1wWhgu14WH+sIguD2IAgGCfdU7Vo2wjB0/hCRrkXA\nLsA3gS853PMr4NT4d29gUPz7cOBeoHf8f/v4e+847SbglvjYl4FL499DgSeBPwt5vALs4PMs1adh\n7aq8v2rXLbdN4/87A/cA84ChVZtu+e0KDBCuuQC4rmrXraJdjwB6xb8vBb5XtWvjPr7qvCOAF8Iw\nXBj/D0wXxwx4ShiG1wOEYbgxDMOV8elz48bbGJ97PT7eBfQHtgGSSKD/Ag6Jfx8M/BkYFuexG7Am\nDMPXPJ+lQh1ltqvu/qpduxdlt+kVwEXSbVWbdj9Ka9cwDN8SLu0PvBH/rtq1+1Fmu/49DMNN8aWP\nES2AoGrXhsCXRJ0E3Cz8Pz8WGf48CILBiut3B14PguD6WCx5bRAEfeNzY4FDgyB4LAiCB4IgmAQQ\nhuHzQB/gQeBn8bVPAnsHQdCbqKH/BcwKgmC88L9CfpTZrvL9LVC1aw+gtDaNxf0LwzB8WryhatMe\nQanvahAE3wmCYAHwGeB7ULVrD6HsMTjBacDdULVrw+AqsiKq/KXAsPj/MCCIf38H+IXingOADcCk\n+P+PgEvi308DP45/Hwi8aMn/YWAycD8wmEiSdTpwFXBWT4v0ttRPA9rVen/VrltOmwJ9iVazA+Pj\n84DtqjbdsttVcd1XgOurdt162hX4OnC7Q/5Vuxb4+EiijgaeDMNwKUAYhkvDuAWA64iIkIyXiVaw\nT8T/bwMmCud+H6c1HdgUBMF2hvwfAQ4l0uO/STSwHwwcRMWWi6DUdnW8X0TVruWjzDYdDewGPBUE\nwTwi1cCTQRDsYMi/atPGoOwxWMRNwCRL/lW7Ngalt2sQBJ8BjgE+4ZB/1a4F4EOiPo4gbgyCYIRw\n7kTg3/INYRguARYGQTA2PvRe4Nn49x3Ae+K0xgJ9wjB8Q05DwKPA2cBT8f+ZwDuBUWEYZvKu4IxS\n29XlfglVu5aP0to0DMN/h2E4IgzDPcIw3J1o8J4Qmu0kqjZtDMp+V1uFS08AOiz5V+3aGJTdrkcR\n2S8eF4Zhp0P+VbsWgYu4CuhHJG4cKBz7DVFldxARouHx8R2BO4Xr9gemx9f9Hhgc1kWYNxCp9Z4A\nDrOUYRiRYdypwrEHgL/0tDhvS/00qF2V91ftuuW2qZT+i8TeeVWbbtntSiS9mAnMAG7H4oVVtesW\n065zgPlAe/z5WdWujfsketcKFSpUqFChQoUKHqgilleoUKFChQoVKuRA757INAiCSvxVoUKFChUq\nVNhiEIZhJn5Xj5AogEqNuPVg+fLlfPOb3+QnP/lJTxelQomYM2cON998MxdffHFPF2XrxLx5MGUK\nLFmSPr5xY/T9kY+w/dipvPeF+zhpwS3wJrCC6Hs1jOMp9uZFADbQBECf3gGceSb87Gfo8Nhjj/Hk\nk0/y2c9+tvxnqtBjuOmmmxgyZAhHH310Txdlq0QQqOOf9hiJqrD1oLm5mSlTpvR0MSqUjJaWFiZN\nsnm9V8iF9vaIQK1Zozz92NDJHLz/LYQTe3HrISdxa9sJ0NEcmRBfD8yFZh5lJh9jLAvoQ1d040Zg\n6lRunPoSACd/cih88INw0km1tIcPH86+++7b0Mer0P0YM2YM/fv37+livO1QkagKhdHZ2cnDDz/M\nRz/60Z4uSoUSsWLFCp544gmOOeaYni7K1oX58+Fd74K1a6P/Z55Jn+tOByZGUbn2h40Te8OEeOXb\nJnipz6j/7OQgxvESvYkkV4NYyWvsQBObODkKUg2/BX77W+jXr3bf8jDk6YULOfTQQxv2iA3HnDnw\n/PMwahTsv39Pl2azwJw5cxgyZAh77bVXTxflbYWKRFUojEoStXWikkQ1AF1dcMABdQJ18skMuu5k\nNjIZWoE2YEL8rcNc8U/ARvoAsIztmMQT7M1dAAxgDVdHO7nAccfV7thvxx1563e/K+mBegCrVsF+\n+8G6ddH/OXOgtdV8z9sAlSSqZ1CRqAqFUUmitk5UkqiS8fzzcOih8EYcU/iMMxjw8ytYzYAsgRKl\nTx3N8Xf8oV2bRXRJvb1aWMUhPAUMpokujuFuer/6KpMOO4I19KZfX+A974E//xk0Nh+bFR5/HCZP\nTh8bMwbuuAOOP75nyrSZoJJE9QwqElWhMCpJ1NaJShJVIqZPjyb/xKHmqKMIfn5d9NtEoBJ0EKny\nalKoaUTbnZnxfa6s/xkd8uArh3HouofpxwZgA6wF7rqL3/U6irU0c+pnhJ23evWC006DQw7xedLG\n4cEH4fDD1edOOAFuvx1OPLFbi7Q5oZJE9QwqElWhMCpJ1NaJShJVEubPh4MOqhOoz36W4KenRr9F\nApWgozlLpGYgSKHcCFQGQcBhOz1I37UPwqIZwNksZBe2Yxkf497oml9J9/zyl3D33dm0+veHgw+G\npib/cuTB3LkpAvUtjuESPsDJTOMGfh0d/PCHo7Jus01kc7bNNt1Tts0ElSSqZ1CRqAqFUUmitk5U\nkqgSsG4d7LtvZAsFcOaZDPrpfwAHmG2gRBXe9cDchDyBO4GS9hmeC7QGrO2zK1Gc5X4cwiMchGgf\ntSsABw6aznkrp0aHdC7zV10F3REm4Y03QCAG3+EoLuNIAG5mEiFwY0KkkrJ+5Stw6aWNL9tmhEoS\n1TOoSFSFwqgkUZsJVq6MVuDz50f/Bw+G3/8echIhpSTq9NPhtttgu+2iVf+4cSUUfCvFU09FqrDV\nq6P/p5/OttedSicHqSVQIjJbAU+0/Ie0rZTqPLE6cAnRlqUDmAXM4jjpooncMOwUAkJ23zgPalEY\nVgJwFI9Gf88/nzfP/wqDBzVB377wq1/BUUdpHign/vnPKBREjKs4jIv5AGG82UYXTfyWyezOGxzC\nixyV7G///e9zw/ef5pTwrnLLsxmjkkT1DHpk77wgCMIq2ObWgzVr1nDXXXdVJKqn8Kc/wZ13RhPO\nc89lTk/hS/yTyHspDM9Nn7zmGnjySWWya9etY+lrrzFq1Kj6weuuq//u3Rsee4xgUkAYaibttyse\neyxS4SU44QSCO74BTITEkcxEomZojneQ9s5rlf7TTo1AJfmkzgP8mYhIqdrMdG9E0o7gMe7kCzSz\nIXP3tRzCWWcKk/hRR/nbKYUh/OAHkQpP6G/XcQhnIQb0zUrm9mEOj/Np+tIZl+dMzjozPjllCpxy\nil9ZtiBMnz6dEf/8J7skY0Dv3lHg1Qm6TlbBB0EQKCOWVySqQmFUEcsbjCVL4N//1p8/4oj0/8MO\niyZwQZ3xXqbWft/39zHRjzfeSAVhzIN1bEMrL/AKr1VESsS73w3/+Ef0+4tfJLjik8AB0f9ECgVq\nElWzfyJLtJJzc6kTnQRzoUaiWuXjCdqJpFDPAf+hyFwgURnyVZd0bcs6tolJ1Cn8jKu4VZFWjL//\nXX9OhWeegc9/PnXoa3yW73Ga5oZ0v9uWtaymP71QzDHTp0chJrYET0RXrF8Pjz3Gfffcw3u/9730\nuf79YfZsGDmyZ8q2FUFHoip1XoXCqGyiGohNm6JggvLWICr84AfQ0gLHHEP/nQbzDUL+i+8DcB+C\nBOoIxb3XXAPAWWcviA/MA3YgCoGdRLeOzs3hvZzCDZzG9WzLep5lL4azhCCo206/7ZHEMDr3XLjk\nErhiYPRfJFCgljiJJMlbiOBCZIcC6zEaqGcIVBrr2JZ1bAtM41rexRIGMYQ1wO4AbEsnP+Hy6GKZ\n5HvgLL7OKvpxB4cLR83PuI6+TNylnXese7x27NqlZ0c/DjwQ/va3QmXa7PCVr8CPfsR7hUN/4AQ+\nxB2RKnnvvWHxYmhu7rEibs2oSFSFwqhsomL8+c/RpJlMoDJWroQddtCfV2H9+ii4IETxfGLcd794\n0Sr+xfu5+KILU7d+ne/SwgrGMAdYpUg8mthv5uP84uxkYhLtpxYAM4GzMnc+ykH0GriJz6z6NYNY\nxWvswCE8QhDs9/YmUl1dcOSRkToPIvXRwIH186ogmhn7J+qSpOulezqk815IJEkPA4uAMXkSyWAD\nvbmNczPHW1jFYbQT9TNV/xMxMPVvE72Yyvv5A++RrnMgia3wFG08Nblecf3mrOFHT30x+vO+98G1\n10aqri0dH/84CIFT72Ms9/MpfsiXuGbg2Xxq1Q2wYkUkiXrooYhQVSgVlTqvQmG8rW2i1q+Hyy6D\nV181bvpaFA8xgcP4OXZ7F9Lnldckk6ltQloKTAcheKM8ed/x6vEcv/pPAHyBK/gxXwDexhKpl16C\n3SNpDEOHwqxZBMO2j/63AqcK14pqOxnJ/N8h/Zch3i/bSmWOJ+1+F7CciETJkihdn9AF+PT1GFSh\nJDWwTCylOjvnwalMXXpe/cB558GQIXDhhZEEd0vDhg21MA5v0cwkLmEWHwRim7RWuGvRMRyzRghR\ncd552XRU6NcvUqnuvHO5Zd6CUanzKjQMb0tJ1BtvRLYbf/87/L//lz539dVRzBpg+2HRoekcyO68\nBMA3OZufIteVtP9XPA8zL/paxlBSM2Zb/Fdlu2KVUgiTluraWnorgCeAY7QT1AnhHdyw5BROfuu3\nvKv/P7l69Tl0sq2tAFs/+veHRYvqKhRZjZcgqWtVO3Qofpu2g3HGKiJJ1MkF05lmvyQFC1ky9VuL\netEFVw8+l9l9xnLfoliVlyx6dtsNzjhDf+Mrr8ALL6SPtbXBoEHFC1UEzz5b+zmM+1nHS8B8YK/a\nuHAsd/FTPst5iU2kz0Lv0Ufhf/7Hr0x77gnDhvnds4WjIlEVCuNtaRM1cSIsWJA+dtVVkev/hz9M\nsE2f1Kn38TeO5Oesoj+38x7W0pfMpKKaRFISJ0kKlRAp3b02WO9pASaZrwsClvQeDsBHVt/OpgG9\nOOmtWyv7qO23d7NB0dWtLGESr5uA3ntPRop8TCSSKE0BHnBMAEzbzJQGW19UGrpLUBnbS7i/73s4\nfsQd7Lz4Zf6DWzmMh7jgzNlcqeNQK1dG28okex0mmDQpMlLvKfzjH5HzArCO3rF92hhAjhMV8FVO\n4glW0bfmTbmbMenP8TvGMR8eeSRyUvHBsGHR4qH324davH2etELDsNVJosIw2ofLNEguXhx9T5kS\nDRhf/SrBke/TXv4CrUzlUjKqNIsKAtBLnBK4TEAJkolGTEskY6nzK2BoLIlSlSnGDQNP4bSVv2TI\nphXsumG+24RXwQ1zhW8fIqWt/4lE3nku0bxt5MlXhSeEX8gDVyKVXNtB9n0KAv404HhohfFzn+cw\nHuJKfgA/3TUKHNrZGdm0zZ4dXZ+858BDTGEHFjCe+fDEE7wabM+Ouw2MFk/HHpv/uXxx/fXRdjwx\nLuYD8a85wBBq6rwYKxnI9Rwc/0vaTG6HelvfyRSu5DJarHZsaRzKDFi6NFKRDhgQHTzwQPjjH7cu\nb0gJFYmqUBhbnCQqDGHq1PpAKWPx4shI3IInOIADH34o+iMu7JWu5wkMqjSbqsaXnMh2NWKeOuIl\n5rF7C6yzB+p8qrmNo0bew7SX3wmdnmV8u2EGbh53KTumskNHDCVq6CRdVR4ygfLZaiaReKmgeR6T\nWlOEzRZQTE8kUgrbsyd3OABei/+cfz7MmQMzZ0YG2BJuHfBRTnrrVnqzgefZndG8wo68AS+9AR/4\nQCYkgxNaWuALX/Czx7r55hSB+hwXciUfj/91kUScB6TxQmw7Q3wwYAHtHM8VmgLo+8wDHM7hPAhv\nvRV9IBpHlyyBESMMD7VloyJRFQqjYZKo117L2iKUgTlz3LarGDQInn++9nfHZDH3ErAbvNa0A8gL\nLNXg7kJ+8tq6nErkweWbnul8MlGtXwGdT0B/h73zXrZf8rZHMqGrJEhGyZECSRoagmAmX8ukDG0k\nzcX2yUScZBjK5qCSc4ZIpBT49aDPMKfPGB555V3RgR//uHZuTp9WDj0yJlPPwOKmETACNs7tw57c\nznas4CPcF0mxpHu9MG8enHNO/X8QRPZW2yrsCtvb4ROfqP09hru4G5GcLAC2h9a96u93G8DEdJBW\n4yLPlbRnr3kP9zOcJUxmGnfwoehgU1NkpL4VoyJRFQqjIZKo1auhtbXu3t8oXFFfcX3hi+lTfx98\nBM8cumP9QPK2iDZJCUTbJNVEYJoYTIRG570lqiq0E2kOiGVvaoFlkyLBhe2eCm6Q2ylP3ckkLNP+\n7cK3akIcilJFm7k/QRHPOxVKkKxZgoHW8rCQsn/1PYQTRvyB3Ta+FB14HcLtA+6adCyL+8bvvjRL\nbqAPixnGNXyHFezLdtu/kb7gdfHPy4Dg4RY7al7++oX0pgt+85voI+Loo+Evf0kfu/tuELZf+uiI\nW7l78dGkO8MoUpKoBInk0zpOFLN9C+nFYnbkTQbXD/7tbz1vgN9gVCSqQmGULomaORMOPbROoN75\nztTpRx+Tb1hN1qASMNj1hkHAz9adx2+/eLKZ8LhKiGQjbxXBUt3jA9WEK0awtt3nusKXvfPmOkii\n3u744Q8jacSG9FYoQWBRX4nQtY94rcrOJwWXiXAZsABaD9WXxRkTFb91ZSjgnae73qXsFiL1xwEn\n1P+04PBeRs+xAbixNd5GRn7fdeEm4useXH4Yl8+8kH4raxsTsueG52jZ9GZEmMStlgAWLqz9/NJ2\n/8ttA5KxVqzzWBIl2kRNkL4z5VO1VUkq5MMPrxm/b82oSFSFwigsiXr9dfjpT+t69Msvr5/74Aej\nveFieNkn7mI4Z5vEfAmOaYWnWwF2SNeY0nOe6OIB0BT2wJZXDbF3ngcm8zif4tf8hk+/fTz0fv5z\n+PKXU4f+ML+FE4OpKKU4urYxORXIx6z9M7FhUk2IQ4Hd0+Ra2b9sdlA2OyrddUK+3QXXMCCqelW9\nv6o2U9m6adqpY8gEjjjsvlS6AzatYt5Lu7P9pjdSpEnEWcOu4brBZ6XLUPPcfYaaJEruI8oxKGkv\nOdaXjUDZNrrW2JpupahIVIXCKCSJ6uyMAsD93/9lz519diquiXZVr4JrzBnVdXkJVLLiVe13ZhOl\n+5Am2Wi2Bo0aRyUZc3pGIU5UBmkvQ1GE/2s+w70cyWJ2JAjat7499V59NYodBPDii+nI1w8/zKgp\nD/IyLUST0kR9X5SJbdJnEg1NYRWtjgTFkigOLZCGa5t2V9vLBM4yVuiksy7vhon0ivAcR97qNZBR\nuy1g+65YHzg/fX4d27J08A7q8swFWACHbA877lXvO66ODM4ESoZqw+ux0fcTT8CyZVHQ2a0YFYmq\nUBiFJFHHHw9//Wv0e9Ag+O//jn7378/gz+7NymvKMvZRoEwClaRXRjBEVxXFR+SDknGvaqNb0wSd\nyVcnicpGPJ/FeD7MbdweF6ofayhqY7FZ4pVXouCMGzdmz91xB8GUfsDR8QHDhFRE6gma4Juu9R1L\nooyYJv22eXcZoIue72pErvIyLQuqMshESl4kgbrNRPMkm4RKE55iba9+LOw1KqeB/Sjov2uUn5yn\nsu6S8cKXQInjTPaeTfSKfrz1VhRj65VX1IbyWwkqEtWduPNOuOiiaKsQiOx+rle5Vm1ZyCWJWrcO\njjsuMjwE2GknuPde2CvS56elTuLkoFlh5lUN5CU98qBkGzRFmAbIjK2CQ0DOFIRVoSwR0+alyy+R\nRI2Qjou/6/f9nt15gT0YzYt00MYUruUpxtkK7I6vfQ1uuSV9bOJEuPXW7olD89BD6eCDBxzAE0+u\nISRgKh/h+hNE/bEmDph8rCjpFif4FExquGHAk9glUUka00gTKZtE2BIRX4RJKmyrm7IcGlSqvg7F\neXmRJC9MVLCNBToJta6PaIlkbBO1WrCJktNW2k+WLymczoH1DZCXLYPRo+G++2D8+NLz2hxQkahG\nY/36KCbRkiXwve+lz734YhSUbOBA/ud7daLwta9KHTsI4EMfiqLkbobwlkS99hqcdVadQG23XRRK\nIA7QFs2HbhuNGqFbwepWk65qLh2B0g2YYmDEudJ3Ju6NQS2het4kT3kicCZQqvwSLCeSRknlSCFN\nrp5mX0bzIgN5iw4+wQHcSBBMIwyzG9Qq8eKL8OtfZwy0gez7E1//614H8Upczq/dcDKcbNjOZM2a\nSEW8bJlbeXT5n3EGwc/PxVnapEJ3SS0zGA7sq0lDbH/HbV1cQ3h0WK6VFxcmyVMmDZtRuwd8jP5F\niOOHkwoNf+maUSoXS6LE69qoh0Cx5aWMweVfn2vpx4n8gXt5J+9jWhTB/J57KhJVwYD586OdslW4\n8866iirBFVfAF2N/+quuAuBr4vnv/TWbzmWXRTpmHcaNq4tM33rLLb5SSwvsumtE9J57Tn/dnnvW\nNrpUwUsS1dkZ2ZAkxuK77hrtQdc/8q4LAhRxTMziYyXy2Cv4TGplTIBgGbA0K3pxhZmsLl0Gee1K\nVDdQrgKeBd7lkHiEE/k9P+M8zuEaAB7hdCbzK/YPfsdTHXvaEzjlFHj6afM1Tz8NffvS2TqeZjby\naXGyP+WvUb/eReNVcOONaceFPLj4YoJvfwtaJelXkRhHrhJDpWrM15tqCVHUclkSVaL6Na+0zcWT\n1EjYSpasuKrvOoRv3fPKEquy1JM1w/LnYXW8d55KJem640GN6Nr6g1TXUvpHcSV/4EKO46Gt2sOk\nIlFF8Ze/uIf8/+53o72FPv1peOc7+dpB90fHhxLZeiowjll8mt9ENhhthtHowAPh8cejzrr//tGK\n3gV33w3/+7/RRro6vP/90UpCAy9J1JFH1iMCDx8e2UOZCJQLZLF1yQafhe9PyAvo7UMArwnAZKgu\nl89qqKxSzwEMpO4u7Va2sLUXX+n6PuEbAeeuvJpt6eSpJKKyT71NmgQf+hBf+/o0RDfLJ9iTv+27\nHlhPGxdxNM/Uzv8PP40u+uAH3fL47nf52tcXxX9GSicXZY8NheVNQ/j1jZ/OEigw28SZJkwVgdJN\neqpte2pt4yqNkSRRSkzGWRLlKg2zOVfkSbM7oJJYm9CBmUz5kicxLZPqb92YaCxNjMlFYqczE2ig\nh+QmmnhBjJG1lWLLJFEdHZE0wycQ4zbbRNKco47SX/Ptb8NNN/mVZdas+u/99kudempmtGnlevrw\n35zLvV8/GJgIZwG8E1qF+EeiA4MwgPSii21Yz148K1xQ3wyzhU52ZQFMn87zwXh6s5FWIgL1FGPY\nf7++QnmSoHD92J850c+jj66dX8EA5rNj7Z5VM+cykDXw17/yfLAba9iW8/kKj7I/UFfROEmiVq+O\nVJIJgRozBu66K/pGQaBsxqTyCjEZoHUSJhdVndJYtwBs5EUlPvdRAdkGd9VKObXC1KnnkvP+kiiA\nlU2DOX/YVQzdtIzxbyUR39ca7xGxmO34xBPfZdkTLYD+fe3gI3QI1vXLGcjZ/J6A1Zo7osjJ69jA\nhZzIP7+epF1S/CJTv9ERCJlAZexrNAEkjZDJlCyp0kmiXKOOO9pDOSGP9KvBHn9l2ayVbQhvS2/D\nHFg9BA4T4kRl+pNCemTt3yKZLjvw6paPLY9EzZgRGZPmwdFHc8mQiyNTDwHfvDj+8e1v5y7W2VzN\ntTPPdrvYZjQonN9EE5/g5voBaQBtYiMvsgejWMh46oRuJq208TuYKa8mI7frc5jKVM6rHV3K9uzK\nfNbSD2ZGx/qxmgWMYjuWRZtuAv/iNA7iXzzGubHxN6xePd4siXr1VTj11LoN1PDhkUom3uVeaRPs\nMgDJA5xtEnOFinC5GJEm0JEXV1d3uSymc6rnUonykzI4IXm/diHaqNY/rMSmoImPjbhFyjevukgV\njyh77Go+ytWIRN4kSdFMBr77E7pAZ6SsiySd6vsOxEZbZvFeMY2l6CVR4j06aVSOYIy5CYUcwyhn\n/i5QvYdyqBIZTkbfJcCW9lxgZ0ESJd6XW+2r6nuueyhuhZ65GmzeJOqNNyKDbBEHH1z/fcYZmSB3\n40Wzizjo6/Gr/8j33/gvAL65XEGU5EPTp9d3oQbG7/mMdMHeqX9r6cuCVincvo3hlyTt6KI3e/Ic\nu5AOzjaPxEZL3eGv5lz+wjH0jSUEr7BTRKCgVu419Ge3TS+x08ZXOH3lL7hoRWRL8igHsxfPsI4W\n5rGc/v0f54ILFJKopUujz5e+VA9j0NoaEeEagZJebJdBSaxX2yDnCld1i2gkLkOOyaIjUDqpRGIM\n7vIc8v22/zZioJyIV6CPEyXd65R2Dts2Mf1a+SYq1KI+e7dp3PVbhW/ZNsdFNWNSu+jqX5akKpE8\nm2ISbJW+M3mpVHw+caJ0E6ZqQs6jIjK1m4pAKdqrKOlVeQWKBFeE6CCSCEGTd1ZsQ5Ntl6ySld+9\nvPZgL8+BriHQX5BEuXjiedvy+WxGvfVj8yVRCxdGE24SDkDG2WfDpZemdsBOSTSETnHFpD1YNW8g\nwzqXwmKy9keJKm0ZPMkB3HVgL2CNcEESU8XD3bxRBEox2a2hP7OQPR/sRsoLVPssSXir10BmvWM8\n32r/Fp1BM/+9/LsAPBsTyS9zOT/kXK68cho/+Ylw4/PPwz77QFdX/dioUZENWc0LTypjUWIpEhAf\nGynd5GVEHYIOAAAgAElEQVTzsJHvayNt/wTmyVMuo7hFg5yOrpw6KYcpb1ME6dQ9LfhGLLejQLBU\nncQlRdLAnUwZXPHz2opoyZNAHl3iiSnt5aTnMkk2jfcPJdq0RAUfCYKjZKOQhKZAfCrQkxgXmNoo\nSVc1RuhiYcnHdeVxeo9V7TQGXpW3v9JEFzfZZmaIl0qbkaStapO3jxQKNlcSJcdj2VPy6tl7b5qu\nOZ1N17yIy4u1odc2TB0dq67WkyZRYmcaikb1YBhsXSZ+X1sbnYpGVwYR4mq9KIRyrJnYn2+E/4+d\n732Zd6x7nL02RN58/8uFfIZfsJi3GBqcyXJeIrxnadr2bM89ozAGN94Iu+4qkSdp9aqVxEirHxfj\ncRcD0AS6WDAyTHZOrtKHMsT+8srVNCi7ptcqp+UoiSrileYD0+o+VW4xiKCjcbQNOhWpqVwmAj1B\nkZ7sgGByPMhV38n9T8eJ55AKqsriUyYjsbdtfCxN2mKf9YFK0phA1TY6uEqo80rKtPfpSMocYAiR\nM4hhES3DqMK2ESKdRPLtQ6Q2PxL16KNpAnXGGXDddalL6pOwYUWdF5lVrZSe6uWy2cuUobqzkQLT\niyquaIoYyQYBp77/VwAcuvRBHnzwcAD25Tn2Be7hKP7EcXDUN+r3fOlLkfdfPQmUEj2VJKYGMaqu\nB0z1bpMWmaRQOhsj3erON16QKhSB88qxADLpeEiiXOtCBdOkJqfh/G43iEjJMMU8Uk1koi2UCS7v\ncy67t3ai1WKrdEynalVNhjk9uzLhPESvQld3+pLsoWxlV6lmkzFJ5dxhW+SWamenshEEGEO0EbsD\ngXEqTxEi9PYhUpsXiVq2LG3z9NWvwne+k7okowLynaBkqIiFKk0xHVNQRRFFbHR84BP/Iy+kZ3uI\nw9h58kKGrF3Ob3/1MfZb9SzvYDrvYHrtmv/k+/zghxcRxhwqo241rfrk4JSAcR8yS3lTaaqQp250\nKzgfAgV6A3Exfa1Iv5GeSo6SqFweZDFUdkgyfNOq3aMiUootLmxtpFPJmK7Tlc9lQeVLoFzuA+rt\nNIzIJsql78iToSOBMi76dMSsqGdgSZBDBHTHOO6z6Mggqbt7gUHAISUUKAcBkt7hJjYyhgUllGXz\nxuZDoubMgb0Fg+1vfhP+8z+hV6/aIaUayARXCZBtlStKSYogkbCoRL9a75wcsEnObOmb6k049wo7\n8wo7c0JwK6f8/hL6rB5b83x8jR24ZvTZEAQEYzTlSghUW6dUvub0ICYPsC7tqjPwVR1TtbtsJO4y\nkLoOfrr+5rzxbHet8FwkUZ4bv9ogE5G8K/iMMbvFOBnMEe6t6g4VeVTUQ9LnO6R8lIsGBzhLoMTy\nzEPtnWcwYM+jSrSq1F37SjcQJx1k20TV2NPWGY1ZCcrqw6Cua216o4C+iuOu9acaVzyi1iffcfnu\n4WscwT+jP92xLVMPYfMgUfffD+99b/3/qafCt76VusRoR+ML46CI3r09DyGR09CqrBwg56/K2+ZN\nZDrnQ64S4tPRzLyDR/Lt6SNgp+/owwPIzyoQqLEjo9AMsxcJ+6yp4puIK3mTCnWCUD6a8we3M6ln\nXdL0GQB9VEUpNFIapZNE5bGT0ED2VILiZBThuMkrUPeuqNRkWkmUh0mBrAaSJR0+/bTQQksXJwrS\nREo8FsN1zHWyDyyh3/pKfW3QvfsmlX9CoGQTAZ/y6BwmVFD2xYnA3USSqD0MGfkswIqpwffh39GP\nnXc2x2fcwtHzJOqRR9IE6nOfgx//OHWJtwQqgU5NAvZBzvWcbkK1ucHL512IjUpPD+rJwEVy5loG\nuSzydX2aYdcp0eJWJpzJPXJ5VBIoiAYkHTmUCVTye4Z0PEP2mrOryaLSviQNGyGXobpeVR5jmgrV\nR+JufZtHWUxoBbpaYJ4oiXJ5D1VxiSzvrNX7SGFMLN8vS5QyBtoaz9oy7BVV6YoQ+22RhZgzKbcY\nFe86HObr4kTJ9lGK/F0Wc8byqfLKS6iEe73t5jRQvovtwu94QSeOnypJorcEymDrqxojMmPJkUQ2\nUXuRha/0ugw7wo3R1+mnR57ZWyl6lkQtXw7velf9/yWXZPaZy9hA+UApeo2/5Q6pG0xllZMothXv\nldPTSZqKSKJQ5COWQUzfdI34X6VSUEEeME4V6mFDJ6x+GNo+miVGtfpW1JuA2YvG1QmUbpsUUD+f\nTJ500i1dnatWszJhtU22NuN9ua6dPCxNKOqp5YAuk02UbsAvQypmeed1dmhWiRRZsgX530UxfV25\nbBDz9ZXA5UWXae882di7oNTfijJU0xqvvdKQlDHxEG6HuROzY0LudvEgrMb8RO+8RsHVwaed1cR7\nuV5ySRTq5rTT3G7ddlvYccdcpesJ9ByJmjkz2h8rwfe/H0mhXGygXF4Q26TnsgItagcl2kA1Cr7S\npyIwSaL2npIiUAmJgZjIyHYDwrVaAiXCtT1V0q28kKWAOrRqfssoQwJmg69kTIe5kLWJUkkoNFKE\nhnsoadJvxazmTtBGVqKZwEa0VWm2YW9fOV3lhtAGONefxUj7ZdXeeZ7BM3XPWSaR8L5fIlLgTqZU\n3qWpY9OEb4FIyEbopoCoqnx0sEn7lOkk3nlJOVyhCmrqCv2i6TNcwsOcEf35zncyTmJGXH11FAty\nC0DPkaj996//PvvsyIhcQCaMQcNWQgbYCJDLhOjrJWaCSVpWFKYy6chTgvEr4a5/AMfVDqUkQJCV\nRCX/E3JlIlAJPJ4zkz+obU9MEopaWd3zzUBlX5Pk26o5nkIOVUdZRq0pmyjToKyRWMjP7iyx8VHx\nKAy7XTzHXPpS0i6m8A026W6STnKdqM6vESiDvZayP4jII/mTJVFiXUv1LktEOtC/Pw0jyZr+pa0b\nBZnyhfG+hHTE+dTGTlmVbWsbjZeik5RadW9ZkihXVZ6unqOy/ZMJHMp1TOV79GOdU4q7E28Ifs45\n8ItfRL+bm+G734VDXSLsdz963ibqK1+JIo8LSBEom1jTd4LLS2pEEiAbhJrSzpOXnE9Z5MlFLaWC\nfI+Yb1snrG2GdyjcauU6U9qDeBh+60it6Zlc0rd5MybQGbG6qv1skgrjAKmAWIaakauQViv6Adlp\nckkkUZ7l0anRvcmoD4F0tI2xESiZaOtIDsJ1rkQqOZeJgSbAiSQkMNWNHOtJ/C9KotqlazRpqtqu\nkP0P5No+xElV1+jQH5M16fvERvKQFGXIvHivWIcecaIysLWDHG/NzavyYSayD2c4l+kolnB3Yj4w\nvR4uh8MOg8svz96w/fbwiU9Anz5O6TcCPUuiLr0ULroodUhpA+U78eclHTrSIg8guq1FZANnF6gG\n4TJUPjqCZ5ro85Kszk5anrmTHc7epy4BEqVLSf66Z7V5J4n3uKhHVfZXysnRkI9YvtT18QCtGsxV\nz+Zl0+Ax+BW2qXJBIom6WDiWY/UMWXswq8Gx+NtmxI76Gl/bGLGPmAitnK7cznKfcSKytjosIoGS\nr00kUQMU1zpCXlA497l2Sgt+2nCIdV7mXnE5SE6mP6rqMG+cqLL3wdMRTBnZeriHoxnDbIbEsXL+\ngyu5kBujkxdeqM7urbfg+OPr/3v1imyquimsQs+RqMsug89/XmMDJYhuG02gbBO4Ll6QSWTvApu9\njU7dg0M+KmmX+Bw6UqhKVxdKQHze5mb6ThFeEpHEJKqLjO2AIj0ZJgmY7pqM2hAzgXKZZDMDmDCx\ni/mr6kruF8lvLYFysE/QxbWSkds7KMFysnGiJkrX5lzxqzzslGUoKFGQ29plHEhJnyzpOqlkBST9\nIddCybcuxDYSn2cpoHL0MKjDEqIkt5uTVKhEZPIrIzK2qi+XWG5VGA8lXNV/MoFKpFG6OFE+6CmC\nW3/2uYyp/f431/AGe7E9r8dHltTOfZnfRj/OPz/6iLjgAtKbuTYOPUeiMhKoqaTEpDKBsm2tAm6T\nrgjX+CymwJhivq5Eykmlg34lm+Rjs2OSy+IbQNK2N1QHQDPstpxX75nHq4co7JDEdHzaTlcO13tk\nlasvgfKZ5FTlc1EhGtV3Je2U7myHpCrDKOBm1N55BRw9ypC0ZlCCCsdIoDRp5/EEyzy/FANNWT95\nCZT8G6LNQ+dKaZrUf9T7j/MCxIWEuPbv7gi2aSNQjqpc1fXKehLJiqUean3SRnAWYI8TZYNpmySx\nnGWqTPXprKUfl/JV5bl/cBI/4lyahc20d+a16MeVV0IYRkSqwRKpnreJwkKg5AlKNyGrCJcKspTA\nhjzX+HjkuUgLdC744B93RkcIdfUtQpYqJfevGwQ7HG4NY6AtY171qy1d2VDdVtdGuw/Fqj6xr9FN\nfqW7WlvSS6mhhDJYoZvwFlCTROlsdXzUeCZk4jn5DNIO1+nK6SSByhPnyvX6RhAEG4EZSrZCVF6X\nCRy9L53yTlDSAkEVA8z1Xmz3y1JXBVSEWJVPDUUkXEmd6aTVZUiiVOnKMNS3V7iPYn3/Tj7InXwQ\nsU5H8Sov8kGaCOGqq6BfvyjY57HHwh5FyKUemwWJSjWaiUAlaCSB8lkxmyQhKiLlO6mrYLPHkMtl\nioHjQ6BkiM83oxOeeRimfNRdGpdH8iRDZYuia+O8dV2DQm2gCp7o4jhgVec4bFEiQ0WgnKFTiWgk\nUUWIk0vf8HLlN0A1oKf6LRr7J4V3YN5YULIaTLatE9MuBS6TtEoS5ZJmD3pK6+ATSkN1rbJdHWOf\nKdvVkh9QXGWmIjkTgeephziQz5WsVrVBq65vLBawI3vwZ+bzgejAZZdF31OnwgMPpC8ePDiKSVUQ\nmwmJgoxI22UzX3mw9pl8fa/xtc1S5VGWGkN8eV1UmC62Oq6EVbw3Obd3M/SfUn8+1XPm8WQEO6mV\nJU+q47oX2CQpyrjsJp5L8e8yVIE+BrnehuS+4nZ5oJ1IZDszSZ+3SgLnOoGZVLytRMEMi0A1iFul\nJxoVqpfdj4b0KvuTS9o+cJ0oVZKoAvCeIAtKoRqhGvYN0WCqvjKqNvVciSpPR54SJN55e+H//rua\nDzhKZbuVaKfHrgXsyLu5mg/xAG3M5lBmwHPPwYgR6duGDoXZs2G77QrlvpmQKIlAyTDFD8ojRRGh\nkuzo8rBBvldXZq9Vi+EeX4hSKbnefMiK+L+NSBL17MOw70ez95mittugkrDpSJOqbKXGsJHCbrQp\nyucaPDFVPpNBucNEqyVQeSAPkCtgqC5iOX5kEbJelqa05DbzlQSpSNNcoQyZbTpk6YCm7o19yUVq\n6DC55TY8d4UoiXI1pjZIY5zuN8FRUqKaI3zqyjbBF4mv5jR+ly0NkttEjhPlmp8LgfJc1JQiefIN\n6VG//h8cyD84kGY6+TvnMoaFqauHswyWLYPx4+G++2C//XKXcvMgUaqXQyVV8PWqcs1bhPxSmkia\nTq2YZ2Vug2rw9pWOibBtDyM+g2mQ6gD2aYbtpxTbOsMXLpLJVum3qi10EgrTZGmyQ9P1UatxvTyI\n+QxaOex4nNACyyZFcy649VldbCYTdP1LRZzyEGLxHh9yIpM/7b0+Rvaaa1V1VAr5VyGRROXsI95l\nstkWeZIL07vkamNadP5wDXFSK5PtGSWPSFeynoIYsVyHvKpEi42cL3Kp+1yka+lFQScHMaXWEPVn\nuI2L+DD3w+uvw8EHw5NPwjiNY5QFPU6igjG4eVnZKtmkLtKpeXT5yoOmr5TLtDqyDZymQd5lNW4y\nahfPiXnLW7KI1yfXmsr1VCcsexhe/6h9wnTxmNSFYpDLJaOMFbw2DUkyYfTIc3jZU22Y0xOvjNWt\naTJZvwIWCJKoPJOPrj/kITN5oXtfbO+aTuqhm+DyllNeqBkXIzrC7NMPlgElbo8EhvxlD8CC/VXn\nMZzHuL9MlZOun+clwUbPXR0SSZQuOnhZ4QsKeub5LlozeYvQeZia/5/MnaznND7O72D1ajj8cHjp\npSg6uid6lEQFAcU7ss52yTUsgQyVyssVshG3qVOIA+cM6bhtghE99FRllIN+6oKAivvMiURKNtAW\ny5ucFxE0Q98p6nOq+1VQ7YhuilGlS9M0aede2QsvYxtqkjcDgdQobKaM4TQ8pFDawV8mYg5xnGzv\nXlMLqThRPUGgZFjVl4oYR92BRtiAaGOJuR5XYSLRRLvQdiHFw2zogi76lpc0qfVaLDXI29K0GM6U\nTRVh3IXQ+JZ9DDBfcdwlL1Vbm9o/J5Eq7T0pJg1bR18+y0/ppJnP8GtYvDgK0PnMM96bH/e4JCoD\nkVS4SqFEyBOs68umW+G4SqFcrpPVAxOEb18ipYNIrFQbnpaxz55ct2EnLH4YUNhEubw0upW3zZtS\nRyJtkMlUQkxsaZnc5H3ay7jKdLA90b4PhkFPJcW0GtavoL53nuV6FWx14mqEanz/da75hkHWS83i\nAGe1ny9ykI3Uvbo6kPfO0+VVNoHKCZNUsGaD6FpXmkCivuVRQW73TLmmSd8+9Wu7tp16xHLRld9V\n+iRuZdMuHLPlCV5tXciDuFwsZyin8UtGsogj+RssXw5jxsBDD8FE9/x6nkSJL4eKVKQ6osbYUzV4\nFR3ITKEBUJzTTfimF9Ql+KTpOUSpiKs9Ukpd1pyWRon5qZ5fVpEmA1nQDCOmwGLpetWz28qpIkYy\nmS5jNSMSKXmQVpFYG4HyHhw8Jkht2vJE6WgcLaettU+QJFHiOd82MNVPQyRGGrG/1t5kcv06HaG2\nLepMKvxCsaTywDQJiHvngVe0fGt+Bu/VPLZUOo9tZV27lF/RL4p6yCrJk4xGRQIXnyeJE9XdUcdL\n3mWglqZnOj6LsfidDOnF+7mX33AKp3BjpNq77rooJIIjeoxEWVV5uhWGzaYoD3TSGZNtkUqlpJt4\nbWqNPM8hEihdusl18v8U4TPogE1EMjnXBjzZCWs1kigbTKRJhE6CIt/vskVPAttLZzMcVRIoBwmI\nFjnj9ijv9VwdKusilkS1arzzckmSyjRQ9ZHUCINymaTNlUz6EKlaP3ElNb71aNo7Lw+BEic8Fy8+\nFxjCiCT1k1Khi/BRQ+aQpuig7ecyqXEpm4uUWr7mAaAfsLdD+j5QkTIbUbWVVfYKdfUSLQDDu3oW\n19KHDXyMW6CryyvZnpdEyeoncXKGdLyYMglUXlWQzdYqb1nAvTw+5daVz2fLFxuCZnhzSva4anLW\nqeVMcLEtAz+VqgkqlbCYj+t2QXJ6UIIKyeaGntNWQVnHLbCjvHeeABsxsNr0lDiBZVBEqoLb+FC2\nh62zd2ue+hL7xXCivfNc1De2vBT9USvZzKFyU0mhQKFCV+0nJ6IBqikRSgLlSz7yQMxjGOo9EV3h\nMy7Z3i8VaWo3nG+ggwyo5yLBxGEdfbmf90QkyhM9S6KSBxMnLdk2CMN/Eb5kxpWIuLjSJ/AJwSCn\nYVIfqK4zeYf5qFxkKVUC3SbGKoSdgEUSlZds+nhB+bSV7TpZvaeDjkTIx1NlVhnXugzeLgONJRCo\nNS2xHCug8wnor5FEQQGvGlfIUcTl3zqoBvcSV7h5Vcqm+kr1QZUxMuQnUOL303EhPNzuS7nOAzo1\nHmhMPeQtUWSYpFPiOYfAqSKcyZMJNqmNK5YSSaL8DKOLwWWfPTA/k24fQQux9bWlzBPOxgE9L4ky\nqWZQ/FdBXumb9PHyOddtYsS8VGmZGkwlaSpCCE1RyTuodwpVOcU6lvPJS3R0NlEoyuBrnCwbRKsk\nWzZ1qW98MZWqtKgEUivqF4+ZJiPHgTWZfGwqUSe0QLNBEuWVXg6JhvZ8g8T9PYGk/2aklSIkey3t\ndSaIkgOXiOVlE6gcUigTMlKopI5MZMqH3EjlMNoOQj5SL95ri6UlX6dCUUmUiCLhKBLvw7KkbgVD\nKogoO7QFmwOJguyDqUiCOPHbAnE2oKJqeRm9pKSo1qr7wY9AlfUsJrsjG/FUQbw+dLCJKqN9VPeY\nCFRKjSAZFqvK51qmMlS4SpQQf0VXH04TrpT3qBXwlkYSVboxuC/J0q1e5fRUq1kHKZzNTq/Ieymv\nfI0ESgGxbGJYDWcsi2/UhSDICdVCqSjR1qnxyvKsBJwn+9x9XhXCpGR1FlBMElUm6RHTTKAK6yDn\n52lnJb+Dru+k1rlkQfS1bh2EYWy4bUcPkihHHXQbkgdZzLRtXlE+aiAVyrB9Mkl8XCRsc4XvpOw+\ne9xBfWKVvfjE1W+e1a1YJp1NlK48eVDYtd4w0YjPUqbKuOGQnklVdm17ygO5QnXRJUminFbejbBv\nUkG12nUlBYZVdiMWXzqoJoEMStjPLJPOUKKwFQ2IPJ0g8ywmyYZUDt1iQEmg5LABCVxjMbnY9PgQ\nfBtREA3w8xAn+R7xPXgJd0mUrX5snr8myPZS0xT3u7aPiKlk6lPeY7OMxd0NN8DKlXDHHU6XbwaS\nKMPkFhOosSNn1Q7NZlzkUZaRNIhwmCx1sMUmcoWsunNJy7QiTcou70Jvuq8VOBX9gCSWK0/nq93T\nCYMfhmEaSVSZoQls5DPzPIqBSrdSdjFibYg7fhEUcSlXGKKL6XQJNlHOxsEWqYgt3IIWqknHQqCM\n0hADicxjA6c7b2sXY3oqu5KixGcisB54knScqBzwfp9zOD4Yje1N9jgiwXa129HBx3tMzNMn1IIL\nTAExp1GuTZSLelEFsXxF20eESJYd7aZs5jYS/sV+rKQ/g1gNf/wjnHMO/PCH0K+fsWQ9RqLCMHro\nIGgH2iNGKRqZnwpjj5nJ6PhpXxBrRI4OnWnwnG7UNjWhERZVngjZ60ulKtChQ/FbpbaSCVRNmhcT\n0CJbJsjYoxnWGCRRplABKrWiiuy6kqckHcA4AMhk00cyWBhF7A1UaWmgM5hMHTeIyBe0AMLeedoV\nt+Nk7xJSwptIJccd0rel9xHf+yWoyq7zCnIiuA55OKcltMmuw2HjvvCK7T4Dci+ICpJAJzWei2rK\nV3Xl8r6qbLNU6agkPC4qaTmP5L4kDR+bKFfvRZ+xyrVOfaK2m+4XoVH3GZF+rmdoZTvu4zXexxBW\nwTXXwMaNcMUVMHCgNpUel0SF4cQskZqQJlApJFIo5UCtWV2qQiOI0hxZ8pBLAiXkpVKf6eBKoGTj\n8NT17dlrXb0PM8ix2n0xlkQNyBEnSkYeomK0KVEMAnkmABVR7XGUZL+iPbaCesRyX8+jEuy7tBIk\nxbW50hLSk9XlvhJpU79VSWJ9PYvkc3JarqSsFVi3BDqfhtZDDffJxs4ebVno/XKFT/iAIhO2L3wC\nfpZFIopKonSerBM11/hEQfe51geOREoLNTHcSB8O4EZmcyK96YJf/AIGDIAf/UibUo+TKBCJlBov\n0MrsRSo1ngqSasKFTJgGzNoA5aCmcCUuvsTJeaWpyasNMvviKSVtyTP6xkyJbaLelA7bDMF1k5OP\nUb5xgstpfyDGK0vlIUo6PQlCpi11ZXI1hHZ1v7ZIZY0TXkv8MQ36JqNZj3qySswaCHnhI8KmYvdB\nUbW2Tj1RO+7oEt40HJrliOWq/maR5OZ5Dt37rzK2t77rPuogeUIvy5A6T0gF1X0q+z4fabXJJiov\nidTl70uOdJ6Sru0nX2vK3/QOqCTpWZOAecBBXM+jnBoRqddeM5ZusyBRkBAp9bnRzI1soRK4DK6J\nOkuFGXgEtktgUdPp7GnKUJs5GW8aJitx8DHa97i8uKpO+jhwO1rvPB251NlkmQZom1TAJsFw9fCz\n9g8PlbFWaqBa6TtMYDpoFwCeqN23AngWeBfuBMrw32fi3dxsz7zK47sI0aBRddUVS6L6qmyiLIRd\nzte1jC4LTJPXohI2D00ZvjY4tjSLSJJsULWDrTw6SVRewmJCHimTLSCqqiy6tHyDp+rGU3WMsCfY\nm09xCTfx33DzzXDYYdqcNhsSBbFX4Zj0sXHMjr5HzmbWyLHc3XYs0AzXTzR74LUJ3zKJAL2HnMpG\nyXXiVa1kvclaQdi8+LQEyiQVUUE81yebocvgahoki7iQ2+Cr6rTaYZSh4rORphyqlVQbJwOS4l6d\nFyktwF7YBzudWj2PnYIHcpEMgyG9DN274hwvqACZKmw/hl5ylUiinLwtxXOK5zCVwcXjVXePFSrJ\nUnJchTzeZT0JV0N2Ee8m2jtvqXRcpfoT6y8PqfStI1/ylqcNVHZevrZsdSxhu/qfCy7Q3r1ZkSgg\neilnwOxF4xg9Mv2GjmM2L4xsZXbbfsK2MPG3bPekkkKpNtR1US+p4LMtSkYF2QC7GtuAJT678+Bp\ngjipb8DIFm1kyfWc6wDrIjE0oVtDGfjWf171mGZykb1IQQjYmkiizkJviOri/t2gvm6CcZEgeTS6\neuNZ83VoyzIXBikiZbH7S3ldxpKoot55NpS5ECpEvhtBoHw8ysBNuqOTArkSqgXAIOAQQ1quZVGh\nCLn0kVzZ1H9l3YPx/P0cyGFcy4OcBRs2aK/rORI1ciQ8+ijsuqt0oh06JkJHMy+MjN7ARBrlBJ1t\nw/WK6+IQCkBkM6SSQunIkks8oQyvUK1SZRQw4HR20VflrVrJuRpvKiRRTjFwPFDm5KPbWDk3ebK0\nmTKkQlneeb4QHDh0qL0HLcBxigvKDsoXlytvaIQEefqYKR5R2WiEZDUjkXIYPxJJlIvBfU/DSIZV\nE7MPcVFNsrKEpixj9bKkWyZbn1FEkihozDvqow7dXCBK3eTy2+oo4CGH96DnSNSrr0J7e4ZE1Wyj\nrofZ7Bc5BqkwAfV+Z7po5yJB0l0npm1CavUuBAJNjLe1caFcbY48BzAdeZKRIlBFDCLl8xpJVFmq\nG5V3JegnOhfjc5lIyaob5wkvj2SoBALl7HQAykEjIXaiWlv2TBu1AhY8AXxAk26ZKswcXnfg6F1m\ngPj8siOBS936hCpohIpaFarClofRJipBTgmiTc3oE84lVRYdinre6YiUy3154VJmn/pPrrubSBK1\nh0c5IDs+5FWt2eYO23OXZa9lS9cvjXs4iKN4VHt+81PnJeiIPgmRUoY7aCP9Ek4QjstpaW2EmtPX\n2UOOPRkAACAASURBVJBJW+EN0aH5DZSywvOxMdBGdi9qPCjbRH3YIb2crtIuhum+cHVhd/UELRWG\nQJDg4Srfjrr94nZQESkRTS1AErFcXs3Znt1lwWAJviiTDmfVuyNJFZ9fdU6Ou+YFS5ynPARRdY9M\nWuR3RvVsGe88GTn7taszSNkLityGy+K9efJspGF5HhwJ9AfW5SxLHkNv1TVFiFTR9E355kHA0VzJ\nLZyFrq9upiQqVjkkE51JGgXpScAkhRClDzoPPdlOSkxDNdHoBvO8BuV5PKpcDNpr6eZxnbV1+g2A\nae+8HAOlakD2ib0l2/ronAsSyHGgylI/5k7HQJxscApIGJ+Xt00Q+1LXCqI4UYkkqhEqgrKJqIvK\n3AKn+qNYH7HZWukCd5rucYWTJKokFFZlq9QxOnRXPKiywiPIcA3QqcMcYAhwtHBfAvn+RpoTNJpI\nqfIrE9kwCpvQ76PXsyTqxBPhl7+EUzWxCGIJ0uxF42BkHOpg0bj0NeKgL9s4uahxdGmJ0Ek8VMdU\nEzSYB0qTEaiqLDa1XVlb19Rgi7HSB9BFLC/4sqpUlaY2TCAT36QNtVIH8Itv5Gi/402Kc5AKrXTD\nNLho8hHrtSaJskjGtG7xJbv4W/uyZ18zkhdLeAajrU7BwJRlqBGThYRqQaj0zisBuvSM+ZjsU3y8\nxxIUsdsx9WtTXKdGETffsXMMkSQqgWnBnJxrFPFsBNE09REbXMuT7XN/4GpOYCYf19zR85Kou+/O\nkKhMzKiOZhgpbf0CWelTaqPiEiAP2jrSJEs+XImLTlVRFpSSFvCXRoF6NZgMOsuBW8hKonISKHli\nsYVrAL29ia0tctlk5DEk16XlmKYpL9XvGlSDpCYvuR/XJFGJKNgWwK5k2GyIcquFLKo2p/x0eTu2\no1PsN0+4Sqe6lsAriXeeZ9+uQRH2wCR99VpMdKfhcpF4UGWW0yXuka1tEknUXsIxVyKVYHMwGi8j\nmKcKfh5+/VnHJdzFCcw0ptpzJOqGG+CUU7SnazGj4o1yaxIonYQpJlBjR86qX5usqnWTsCzFSqBS\n/UxQHEuuLWtF5xM2QQfbpsQ1+MYdSl421bXN6CVRBWAK12B6vlzt4ToJF4jAXYRAqQiFrILMwER8\nNRDrNWUTpbtPFeG+RGJlfO4EOdUWRrLrA4ttlyucy6B4Xp2nrgpNwwGVTZRLuAoDChnOlym5cLWF\nKpsENYqAJHVjI+uyJMp0rXjO5vEonsNw3hdFbNlMnuNZdVz6PjfSeBTP8mXui/4MGgQrVyqv6zkS\ntc02+e5r60xvYyJIn8aOnKW+R94fT6U9FElY2zj4VXM9LEKbkIbSg6c9a1siQjdQJ9tNlAFn8iTD\n1wNEhU6yNlEekY99IKvxrJKYMlGk/CVIoIzErOAkrpoAM5IoV+ji2pQgbcugQJwtm9rVi2B5Plvh\nECA56jIZG+YvAZ4GBjik51m/3iq97rJjagRM4RHKgMroW46uLbabShIlQdnn8mgmykQjCK0JJpJV\nxzZ0CbdMgz33VF7X8+o8D6SkTABtnYwdOYvRzM2q+hLIhuUa1V+SDgAjiQJ6QtTRZDskpfTJIBbX\nibd1oQlsBuyy501uAlUAqZfRRRLlYCgtltlELn1c0HOrKwz3mCY/pdqi4ACVd/sWwM2bTmNMv3sL\n7DgJXjWl7/NsZbRFHtKkuKdR0fB9UOY7Khud69TYcyGKaC16FRdR05YZTFXniu5i2+fbL3ztrHzU\nS675iM/namNlktjpJFFFkTx/I8muSx37SCtt9enxLB//OIwfrz29RZEoHYGCegiEGpkSJ1rDgJlI\nr0Yzl3HMZhyz+BMfjKRRys0cVVC9yIatEsTy+BIoFzRcIiPnoZJEGVDGBJYxBi/ifeJxransxudS\nBQHUBL10Vk+KMb/yqkIMBGP9Cug0SaJc6s00yRnekVz5uagcKbBdjC2f7oJcpxYjePE4AMviP3ml\nTypjcIeQHN7jki1wZhH1se/7Ik/yrvf72Fvp0je93yKJdZBEOZkZiM86WfqWy5kXRaOmbz4SzJ4n\nUffeC4sXw4gR+ms6AJqtqrs6gZLIj9xxEnWgxhC9tr0M+xkGXNUKTLXq1QwuonSrDJVeKV54eeFh\nE5WHQClt0FT13ODJzVZ25eSlGqBAS6Bs+WiNx5O8VHWgmNRcJrSmFmiepDihm7Rc2sA1WrAKRdUO\nefuHI4HKRRZMz+Mai8uHjLYDQ4H1mntc6jenEbS23+WdEIv0BVs/VKXdqLAGBSUltfo2SaJs76bP\nu+VCqFRErDsxWfrtUp8hB7CAoawGYD9eccqp50hUU1P0/eabMGECLFpE2iWP+guXeA1NiLZmGXvM\nTHXwTciGQEhe3Lmx3VItLYBmZjNOb0t1Kll7qhpKCkiXh0CpDN8TdIcUKgOVJEoyti1j3zvQEKge\nkgzYYvmkJEXgHqgyLxxW5q3Ct8l+pZXIJurVRBJVlnqn6ApS5RDhYhdmUa83HHkmfNdQG75pLwMW\n5ShPI9ComEu++fekVKOs/B0kUUpMlL5ljz0Tyqy7ngrEGeFonuEv/Cx7oreZJvUciTriCDj5ZLjx\nxkgStWlTnVjFCMOYVyU6fov32uxF49QRxIFaB8kMoBGRkjc7Hs3cul2UCU7GoRKR0MV6MkmTTF6C\nXjZCFBCv66CTRAnPrSOL4jPbCJSyfnwIiavth8EFXmvzlDO+k9x/vKRQOq8weWK1kQtFHcyFaO88\nlSQqD8R8ypg0Jyp+l20cayGjOrVrIRs2XRk8pAjWBcsC4Ai/NI0osqhxmTgbTbLE2EA9Seh0cClT\nO9AFrEYtOS06Tsp5idDFb2pUXer6TP78Pss/uIpb6wfe977oe5tt4LzzjPeWRqKCIFgFhMnf+DuM\n89gmDMN0XoMHR2EObropIlBaxBKkVmrhDmSkjMrbOrNESh7UFETqhZGt2Y2O2zrJ2EVZI5FbbKAg\na6TunLbiGlcCVcgTyAaDTZRtQHfdusVbXWmYWK0k0kA6nGMTyW7DcrkUUMUNk0mmkkiR75msk31e\n7zwdVBNzmVK5MtMykGsXaZ4WeVUcLuoYA1LlXAWxykLvrZV8l+AUYYTKxqWIKsjVkNt0fx7vrqI2\nPkXSSLCA7N55jTBz8O0XtjrNk155OIN/pgnUL34Bp53mfH9pJCoMw4Hi/yAIBgCfBc4G/lBWPjKU\nXnk5iNTstkgaNYuxtWNjR85iNuNqvyHey+/zoJ2UVOmLK1TX2EcmyBOsbiDvNg8kQRIl1rNK8pZn\nOxztc7oMDo1QnZUk8TC1T4/auCUoUxKVoDtVr3mNwS3SSZ1EUhsyQVbrmtDIFXxSjinAYE3/K9o+\nmhASSuh2QSi7DmTyVFRtpLrfVGbTOZfndJG0TgNWEi1oVfd6wrrothEflZeiyTmge7Et63kHL7E9\nq7mOm+onHnkEDj7YK63S1XlBELQAXwA+BdwEHBiG4Rv5U8xWcrINjIwa0Vk0rh7bSYRp5djRzN0c\nm7GPSjwAEymV1WsvkazoxP0qEqXbJFg3COUNZdAwW5BYEtUaS6J8yNtmQRa6CwZjcsihzjOd06n6\nfJBXEtUNRv5OZTD9h8JxtUznci1gZLWSp5rSOQr6MOBJoojleeEpVbSOPbIhcF6YJESq3y4BGV1h\nI1JyGUzQOYio+kKS9lKgn2P63QmfumyUfVo63d9yPSfyVPqSO++Egw7yTrlMdd72wJeBk4BfAhPC\nMHyzlMSTwaG291lzRkIE9TAHo0fO5W6OxTlEQY1sqdNNMI5ZcTDO/dSDgrxPW2Y1qngxTBIoVURl\nH2/BIqTJZxLY1AwvTlFPHkU9D4uQLF2ka+f4Uj7xc+TrPUmMV9lcochbO8FLZW0FulpgXsmSKO0K\nd3MgXuAvZRRslow2UbqJQTUxypNOCWq1lG3VPNhJFbFcdb0KDuq+Ho3DpYrUD2pSaoqarbP1McFE\nljwJlHL8Et8R0cZwGhE5dg3LY0DuBUAe4lm2HaMbdmF5+sA118Cxx+ZKq0xJ1HwiKnw9sAY4PRC8\n7cIw/GEpuQiEh7ZOZi+qe9cl0qJZjI3IzgTBMNw2GdeMtCMPQBOZYgLQEQ+a4sCZeP4p7ViEzq9S\naaW8zvJ4EkkTYHcRKICwEwY/DMMUNlHyfmzyue6EV72UMaEb1L0irHGgSiYXrnZdXStg6BOwrCSb\nKGu/0pWlEeSqTENbCarFTwq6+Eq2PA39wSXeWIKdl8C6p6GvThLlUyaHujF6rCL8b4QKT5W3K1Rl\n8pWU5JR0qdrT2qeWEdlEFYAuX2WfzuPQ4bd/XaMwjd05kAX1A3vsob/Ygl4llCfBD6hvlDJQ8ckP\nsdN0EJGQ60nZPSVSqHHMqhuIa6UgYmwVATOoS4Z+1QwdzamQCbMYF+Xzmc4o/MFHhPTkcAziR+yY\nqk2NawTKswOJBE78QPeuBINm6GuJE5XULQgSRQ/kIYWqezL1Ik8CtjYoaUKfS5qE19COtn92N7Rx\nomxwrKNaW9ietV3xsV2/mSDV3yaTnyioJBACjAFapeubhkOzJInK2G+pUFTqZGuXzSN4Yhp5y6SK\n8C1HJlehyPgyCtixWFou42yqvW0SS7EMLnVZ5B1xxwWcxEV8qH7gfe+DefNypVWmYfm3ykrLipTE\nJxuiYByzmMXYyH5pQnN98rZ1EOXGxobrJwC3Cf91qhIvldY0tJ1fTtukOuvAsnIxwNemI+yEtQ/D\nAE3EclEaJdexzg4sr5SqkBROfMlLVi8VCivRQ6quLlvEcgO8vEFFtVAZEgnbCrmsunQlFar8GmBA\nboxGLeTXtQQ6BUmUE4ESr/GVPqlgk+jIqkJNxP9UuRqFMttK5amrIcW2YLxz5fsXkCUuOSC2nfM8\n4Op910iC5NdOV3I4I3mTL3J/dGD0aJg9G1r9JBBl2kQNBj4JbAB+G4bhmnJS1ry0ySQrEIdICjWL\nWYIqbnbbfoL6TPLWmZtNo5Z2bdJPhz+oeQOm7J4m6u9PIKr5jPGOpgFTSRuWOsCUXx5YbbAEuEii\nfGNZGaGxxZBdz02DUKocSXryC+hDXhxVLN5pa9ItVI9y3SWDj1CmuUR759UkUQXscpLyOpe5rEjH\nm5NnpkwUHZAi3nnyVeTXCmwQJFFlvI+l2fHJ5CipM5cwAEXtxlzVdK573CVp6qCKcybAZdzNmIp0\n0Zi983xgeudc3ufukUZewANcxN/YhRX1g2EICxd6k6gy1Xm3A88Bi0H0GWwARNVZrNaTQx2MY3ak\nemvrjCRGmUlTgE69JNguzWJsPfxBR3OaxIlqNHlAmYB9e5da0eUOWECt00h7o7nSJ5FE2a5TEjPh\nGZ1thqQ6EevflL98jxNsXl6alZ+VQKnSEtMzrCiNEgdfiJOCbFieRCzvKXS3esfkNFCGitVG6hJV\nRhnkz0DY9oglUcrry0K79FuVvspbziRd6unI5i6SjsmYVVKOkqJcxHQOkWlyETj2de2cpUtTRs85\nkZzKv/gJ/5cmUAADBsDYseqbDCjTsHwg8CIwgCjATGMgejGJqp9jqEmgRESxnhIDc8VL4OBRNntR\nXV2Y2VZGhG7iFA3JrRKiZEVUQIScNwSCCi73z4vjRJXji+kASywaXZmNBr8qAiv+9rXz0ZVLRcqK\nDigiKStxcGpqRJwoX+R4D0x9orAUzwFWdXied1yWtJja2iLx2la2iZLVZjn3xsuk50LM8gS2dC1H\n2VAZmetQ0PhfdY3J2BxgrmnvPBcoxiZZy+KUhq/0vjtsGKP+M5IV/JIb64cfeADGjIl+t7RAf//6\nK5NEfQw4H9gInFxiumnIg2C8HczsReM4ZuRfLPedi1KKoYMQWTwT1NMWNDJR6XkFl5RdVj0GWZMX\nXMMhRyy3rDxUUkExMCe4SdLyGM97eefJk5bqmjzlKKKukj20XAegHBNO2d55mfIkEMtVUNpgsyOR\nfyvVuqpygbVfy+k6E6nkvwRrXxXb1GMiWifZROVShen6U5EJUZZCuajxXPMrczNc07icUzWnw1zp\ntymt4XNgSZ6988DNWaNRhLWMEB4JzHNm39rG28Add8DhhxfOsUzD8nnARWWlZ4SmI4nRxiEiPrXA\nm8nkPNcixZARk5NaKAVRled4rztUBniKjisbkKt+N3q1nUISsVyc4HVqMMOLWAYJ9PYuMd3j8HK7\nDpCu7WE0QHckdVqobKEMcPLOsxEPl3L4DqCOjhcu0Lptm/KVJhSTW7gRcjwjW92Z3isRhnadS9om\nSlkmE3Qu+zoUCS7pKqVygSlati8Rc8xbp+FwnT9U/cckleozBkb1R/TcN5ZHl0fqOQ19MmWTZRrf\nyyRJeTGZCfwfj/C/0d/Ro+H440tJuUxJFEEQHAIsD8Pw2SAIDiPSBXSEYXif9ebLL4fPfx623dYv\nU83EKxOq1H51csexde6OekyqWogF+VqVcXry7UIOlIOuZVBVlbdR5Mn4AqokUR4DVJHJT1keC7qV\nYNrgSup9PKdUA1oOiUXGO09HmHpwkBRJkG2lbnrPVe+flmznkUCq6k10Zsi7ys9hNyZ752lh6zN5\nbdZyOlTUYFM/ukgQVXAxLndU4cmSdRFakw6VvaV8zlAvG+ZAL40kysnTT5b+JfmW2V6m+8X3IW/f\nUrfPgfybx7m0fmD//XOmn0WZ3nn/A7wH6BUEwT+I9hS4C/hmEAQTwjC8XHnjoEGwYgX8139FuskT\nT/TPfAbQFnnRJahJoRIkqrWaREo4Ll6TdG6RdEF2Lz4ZedVp2hfKMrkaCZTpZcwBq5ebsHdeJj9L\n3qbBZrPGxKjsOvIsQtkuFgNirWeWTcWhk1bJbSJ7Iyr6m1ISVbYKR0ZSNt0ELuUvEicbqbG9o7b7\ndeeTd1hL0mzt0B0ESmjrTJyoRhr+qkiO5pnFPm9cJMmkXZFHq+n6IvCQQNnGNNegtylo6q4NeGwM\n9FLY9LiUx7iwbE9fI6vGvUKYyOnqFnp5tn9Rk+lh/J3H+Ez98AUXwI9+5Jm2HkEYhuUkFATPAPsR\nzaiLgZ3DMFwZBEFf4LEwDPcXrg1vueUWNmzYwIgXX+S9F18MwL/OOYeX3/1uNmzYQJ8+fWrfJ520\nAYb3IYqe0Ad23QBBHwiF7/f0gZ3WsOMOSwk3bGTxqlGwcQP07gMvEH9vgAV94KU4HTbAblI6yfce\nfWDnDfX7mvpAV3x/cp2Yjiq9lwzpz5eeY34fWKJIb7gmXfG62n2ziXjxRul7l2y6Pt/DDeeX9CHa\nY+0PRKZwnumrni+pj1r64nONTd/nko+qXr2+5XrdpV4vunI7tY/ULsOF64frnv8lIlfmpvh7nKK9\nVd9xvbFQyFdRr2I5Ni6EddNg9fGG+lmofp7huvpfCMzSlNvUTxdmz4v9comln7p8q8YVVXuaxg3x\n/dT1u+FJu2res0x97YK6vmcJ/cD2ndT3WBjyHGxcAKveo+gHiv5QO++Tn/i9myV9j/d5iVwPLynS\n30V6f+R6k/ub6v3SvVfJedVz7WKfp5T9Qzduy++tYvwR++NzD0KvQdC8T/Z9EPvrqA3Z+aw2/4j1\nKteDIt9Mu7iME4Z+oG0PXX9StX+9vNuzloWcx7ZsAGD20Ucz40MfIhg8OMMzTN+f/OQnCYKAMAzr\n27DEKFOdtz4Mwy5gTRAEL4RhuBIgDMO1QRBski/ef//96erqomnSJFZMn07Ln//MrrvuynbJ8aam\n2jc8DUv2hVFxJbZ0QdAEofC9rgl6d/HqiC7Y1AW9murf4+PvZ5tgVhMMVtwvfo/vgr2E+9fGx5/t\nghbhuv274PkmWBCXa1QXvBrfn5wPhP+hkM4QKd8hTfBcFywQOkvyvPL9+wv/n4+vW9BEFLHi38Am\nIpHupvjYJmBf/Ae/+HtJF4yK/y9QXfcWsJZIfOeZfrPi+cIuWCzUK72yz9HsmY+x/LbvfYDnhfoc\nHx1vlvrDc7Zyic8hpCPWc/J/SXL8+fi65L6Nwv37SOnZvnsBH9I8l9A/muPv3iOh10BYbWrXvurn\nUdbD00SDZqumfOMN+UyK71eUU2zfXJN8F+ypGQ+S91K+vkVzfSCVS9cPxf44ylS+vkK9JPWX1Nca\nj/ZP7tsX+rbAxtGwKmlXuV/K40UvS377UB93VOfXkx6PFO3s+j6PSsaFpD/I41yc/hLxPrneVP0u\n+a9Kb5Pj+fHp51iseY5meRxK6rdDkX7SDpOy9SD+f7UJ+obQawD02T06L4+rqnF2J6mfL0jqNRln\n1pEeZ/ZV92/T+5dqr3+THbf2EdpJbg9xvNtEJE5za493sJ5pnEmCN489lvAHP2DfMEzxC5dvE0ol\nUUEQ9IuDbB6QHIyDcGbEXePGCaq2wYMB2GmnnWCcKoTAamAcbINeJDmMKOr9W0SxoVRoJVLLDcPs\nNbcDsLPw//X4+kHx/0TVN4OoTEnaCV6Mv5Oy7iD871CkI6YlikeTtFXXJ2lfj6A+GAeo9gCSxL9G\n42UNEmNFpfh2OfBr4PMeCcbYhvR2TxNI1yvtpJ9pXP0+cI+uvoB6PCkX0TWQrre9hHN71cswUCqz\nsTxi327HzYtmnfR/D9w3V5WhUtEk6QtlS+pqfS/ouh9a9zLUmVg+4Xkyxq1yO6pgqw9pbNhGfZXb\ndj8STBtTqfJxvV722JPTsvZdsd/J9bdE+O1qYD0OFi0niimUpK1ql6SuxfNyfmI/XGrJdzfht9TO\nYh3oxndRRVobv8QyihD75EQy/cZZdeZrW7WXvk+C4R0aF6e9JP5Mls7FsPWVzidhj16wo1C/qjlD\nhR2I+vQ2xPWajDOQGX+T8UGGzuGpNuauJuonS0k/Y9Jeqn4olsNk+5Zum8k8nVbhffKTDL7xRgYr\nciiKMknUoWEYdgKEYShKnvoAny6evKA/FUkMpBusjbT9UltnahPh2YyLzss2Ty7Q2VToOrd4vfwt\nIymPzXOjDcYeMzM2cpfttHT2Iwo9eqnG1bJNlAQlcSnoMpvHiNxIcFyNH5NrLWX39cTxgusWCzJU\n5TY8k9U7rxExrxzh64xg8mpqBFR9rfS8fd31k7YZTiThcL3HNd6TzobFo5w9GqrFBlNdaPq99zgr\nOhp42nH1GZMrzpEfHN9xHaGqwTf+m815oF5f27M8TaC+/GW47DKPvPxQZogDpfgnDMPXiWQ5jYFq\nKxXbSygac6sMg1X3y1IjH/iUByweRp0cw18YPXIud3NsRKSUQRwNxt1FCJTyXtk7T4EMkZqYTq/I\nwGk1RLUcq5XHlRRIx0z9oU3M05d0+AyiRQmM4t7EO6+/Kk5Ug73xZAlOWdD1Fd17byPBZXrIWsNa\n6OAS2kK8ZgmR6sTknSffo9pMd7LitwyHiVJ87lZyLDyKGI6byt6NiwIlPMPxbJgDTw+BQwRJlDg2\nzcC+e4YqFJAKrhoAZZrThG8XImUjUPXjO3E3LyCELvjP/4RvfAN6lbk5SxpleuftB1wL7ATcDXwl\nDMPl8bnHwzB8hzWRT30K+vWDD39YOjENOFd/n9igcnRwCVEE83FE0hMFTC6pidrGF6bVlUpCJQ8i\nwv1jR0b7AwK8MLI12htwbjKANGBT0xpMHjzNRM2uUYV1R0iBUvKQVWIGV3ZbfrK0NFcwQ7FcriEO\ndPCQoiVwihPVDVBJMp0HcQfX8ATye2qazHXnfIIjWlEGgVJd4yqJsuWvU7O4RDxP0EgJuQClNNw0\nmesn6joU9SO2udL7zoOUufadJM8+Y2AvgyRK9DwvJCGPx5DC/RvcAqqK0Nffu3iYh8XN0j/1Kbj0\nUggytuClokx13s+AbwGPAWcA/wyC4LgwDF8gUunpseee9d+//GWGRIXhuel6SAY6kdCIHTYZDGcA\npzYzm3EplV6dSFFXiSV2VLr/MmxxolTX2GBKIyFxAkYzl9kT9oPbxEnWtrIC/9WVST0EsJKost+X\nP6+GiPFLDvUgIhk8XMpdG8A93L0zsAzezvd6uNUnkqhXZUlU3np1fAbfyUN1vxzTyTXtIpOLTvLp\n8jxaaaUJefuziyQqD4pE4HeFzzPnieeVF8I7ZSOCVilrznZVSaJUC/IEVu2Kg2mA2L+dxnBZGiXC\nMxK8hJO4pf7njDPguuus95SBMknUwDAM74l/Xx4EwZPAPUEQnILCsDyFr34VBg6Ez30u2klZgTCE\nYAzphk8x6va0CDJp3OuBU5thZDq9hFTNlo0OZaP0ts442Cb5pFFlEqkYqT0C24CPEBMp0NslyPGD\nyhRT90FtZOYQB0lGHkmfEi5xSXTwrBuvNvYlUjp1Yh7JVpJWmZKoPARK/K8h21qJkHS9ytapu4Op\n2vJztsdSxQPLP6nosRS9JKqR0mwX5wexHCjKIr8rDjZKSiLrEm+tB1V5eWz+dh4TxYlyWeCD41jr\nMNa4LhScYkqZoG+TPqxnT56L/px/Pvz4x0Uy8kKZJIogCAaHYfgmQBiGDwRB8GHgdmCo5cYoDHtu\ntEvfUGPJAB0wuy0tjUowduQs86bCIkQilcB1AhX10SJU7F20kUruuS1KI9kjMBORvdZBXQdAg0jd\nGxvISqJypFmqEbYpwJt4jSdMwTWdxdsqe5JGDto5bKvmQhT/S4xYnqCBk4ux/gwLAZ/Vvw2yjU5Z\n8OofUD6BSupvGfAI0V7xqnxVyBP8UESZfcbXAxWDpM9kyO2bT1HJtyUArwo1e9iJ8PIcYAiRt9tE\ndTDgBKp5x3n8FccsSM21GPKEeJ5S2dr5qICzeIB3cwj/iv7suWdDbaBklEmivg/sSaTOAyAMw5lB\nELwX+EaJ+WhgWEHFEc1ltV4C1TEtsRI7SBIB3aXzqVxNRVWdikiJ1yToaGbWyIhA1TZFrknk8hpY\n2iZwW7qyJMoyEMgTiWzo30GJNk4FDKBV5ZQhll28XrnKEycizw1R84SlyAWx7VqI4rsYYCMFRcsr\nSpozMNnpCTD1NxEujghyWkq7F4cyZdIQ1fEIv/NISWx9fijZB3EhSEWJlA/kDZrF4zq4EhDVzv/O\nZAAAIABJREFUMxSxWfQsi0ima4tfx7FKS8TbieIyrcaJQInfRqjKpNmqSFTrJdASquR5dX1KVR/Z\nOh3ISn7Hx+oEavx4eP/7dZk2BGV6592kOb4AhIhXZaNma5J8K9h8R/whTaRGa0b4F1yWi7Jdlk4f\nrCNHye/rdecStWJzPf0ORfnaOqNrUl5geKo3XFVcupd8A/BKOh1TFcoDQYfmtxK+EpsitkQSCttt\n+UwIPY12ooAwM8lKonCX0DiJ8BW2K7KEzxma/mEyGNelr3qHcnnQSfYyqTpRqfASmPqH6jld+/ey\nuAATFXnaYCJSuvfSR6IjXivvo2aSzOVxvJDJQF77rCKmA0hECvU2LeLCUvs+NMGO/aE/ZgJVWAXu\nsFAR87NCtf2UW/0dxKMcw93RnxEjYOZM6GM2wS4bparzdAiC4KwwDK91uviFF2DdOv1GxOL+dxkY\nBp2aZCBrH6WCs5rPFG9K65EnGK0nNlYzbPfE37FqsobE8D2RRomiUlcpmTN0hOQd1ILtdVccnlzw\nGNR08CVSKamaaSd5FXwnpRIJIxBF35MkUaW2r2sZ2/GT3AlqhiKSMif1m+oZLHZFTkbkvgTbp70T\nSZSKDPnm6+pR5Vq+ooQmRkZyq5L0yfeZ3p+y1JEacuAi9TZiIuzcFdlEmexqRfWfU9mS/1NResjr\n3g/53XFeyPstkgPmRD9GjIBZs7qdQEE3kSjA3cdw9uxIpzlnDvTWFC/pEDOIWbzmRZYZfUxUaiRE\nIlOJZGo0c+vSHpV3niglcjU2V9lEJVKk5LxIpDqa6/m0kU5f5zEoS7nE77mmgSzPgCFesxx4GFoN\ncaISuKx4vFVAlhfP+DI7eBHKKzdR9ahDhry6iae157ylia7tbTJonwPcDBzTQHLsUO/eMIRE+f/t\nnXmYHUW5/z+dbRKykI0kDCEQMkkgQJiMgYAQFpEtsglEZFGCIq4o6PWngMu9oojoBQGBq7K5sBhB\nEa7sXIJB2UIyJCxmMhCykhCyELJNtv790V3nVNepqq7uc2YmOVPf55lnzumurqruU131re/71ltZ\nFS4nc51atopyB2AXAil+7zRi9CIwn0hlPMqSzoaUyYBWfbT5KKY9nzQzYh7zZpr/kcugbpvMqP57\nCrKEB7BOhKW8t8yDTv0wRv5X23KzbpJh6htyqOaZiJN8TPZxdnx3DjoI+vTJULnKoZJxoiYAb0qb\nDn+X6Am8AVydmsFhh8ERR8Bzz8E778Dhh8P998OeexbTWAMlgraxqgPdLBDmL7EyT+cTBZjJSiHv\nmASlESmbjVgmUjrTnlgdKOevDuK61RgqYctsEhFwacQpEct1dcgSILMENv+YFJNiiSnFxV9F+mwy\nOanQ/jaVmM2WM0POukIv9okydfY2E5mA9ffMShRdYvnM1KSLkZiNi7Q2ZPRbsxGoivi0yQpXg8NM\nXzWHCfQmOYMs16ysMcc6E6lWXKRghEKgrM8xb/3yKmoKtO+V4Rl2lVbnaU2Baf26/PtoJmVpbdjY\ntl18bnX1sz+7I/ktj3GJNU1boJJK1B3AQfHnG4h2q/wZcCwRPTjDenW/fjB9OjQ0wKxZ8NJL8Oij\ncPHFhSRhKMXNKsc3RTbtgdbhvMSUp13NIGJKYR5EShzDNfnIfk3q6j9xXrdVjZy3jsCVvEhlOlqb\nMLwFVqVELIdix9pqy9GVjjF19Ynhxa5EnSpqRnWE00Cd5fdfA/11q/Nwe/8yEeK02b6GQGlJuCEf\nK4HSmd90EboFdKTDkXAlfiP1fayE47YLIfoQWAqcbzifgzhUXKnUPZsMMLa9mEBVpL4upFCXRloB\n6+pL5EL8hRLVbYxGcdVcpyW9jsqwSO/c17iq3yJtmho1kyk8XPxa1ur+8lBJEtUpDMOt8efxYRiK\nO38uCAL3IeW55+DII+GVV2DRIoU5SfGiXHI0/cCySpDFJCPSqwqVK4EqHC+a6pLxquItXCS/r4Jv\nlkrU8sRTKiwvrQCRkl/A7TXQw6BEqaawzJ2Xa301Tplq1HDxDMuJV1KRKL0xUs2MefylcLg/10Gy\nrz5OVCo5TStfQNfJuszglUFQN4kxqpwmR26bH5NL7CQLATIpokBhMEWuW8YtVFJN9mrdJpLcTDiu\nRx6U9T6nlVmpSZ/IR6OYmdR8GVbFvMw62voTo+uBBnXApliJKrleQ2DS3h8bSlYWZqhn4XxeBb2Y\nfyfiLXovvRR+8YsM+VUWlSRRrwVBcGEYhncCrwZBMD4MwxlBEIwiWr7lhl12gfHjIxL14x/D2rWl\ngbOyDGTOge40MBEVE/ESJjen1T+SzxMiivpYqYyWUjOjaOyijLTBTDUjlrwoLoODQ4MPW2DjdOhl\nUaJMv1lFzBwWAgX5t+sxoZw25Yy02ZqCXHVJ+23XwLszoE63d14M15VuiTLLOW+ATJB1KKlXmuKT\n9l6oz81iRsyEjFtflPRFJhIq5zuH4uo8JT8X7JCLR9KImXLc1Ier/ZHpXhMEosJk0EpMVEVUKltW\nokrKl6Bb/ac7b61PFmTZ2sXVb1dCfT107pyxTpVDJUnURcANQRB8j2jD4eeDIFgELIrPuePMM+HX\nv44+33hjZNrbdVe45RbYZx9VnJJgkk4pSpV1aFfUNS0dzYjaqLW8RZ3ZHyrrYKz61EDU2V9IaSN2\n3dMoq6lIXflXmLFmDcwpvYxyJxNolKisL56RTGXwzzIRNdWXrFImxLQYQmlllVuP1MHMxdxgI1Kx\nT5SKzKbKVjAhy+0vc31cTGY282KaP4mSXufAq22rNiXJVieSfUnCLKPLr79UuCOBKps45XUqz+pb\nlGGRiQx1kqkzV6nXlqNop9VHCwuBgqJPVFp5NutLqh+pDaaVqgJZ98ZrhX6jFVDJOFEfAFOCIOgD\nDI/zXhyGoaobp+O442D+/MjOuX07vBDH7zz6aPjmN6PybusNZ59N0FuOumsgUCYojekt6kpjR+mc\ntsWgbApvIF5I2yAbBwBN+HfWU1BRjM7uiVV66FfkqelS4brVg6aDaibyido4HZal+ES5KIglZCrD\nLDktNEEiX4Gs0rJjuS6djsmcl9vhXk3raiIzzeLXoI9YnlaurSwZJjKTQR3VPbdU84TO9KaJVaMl\n9nnayky9r5b2NzU5yzuUqzVX667bTLQ6rxWdup2d913fP9UMaFsZZ0BWIqiSB13/5ax8tqL/pUDt\nPOjaD5YbVue53L/uHtU6Otc5K4GSkWdVZPug4iEOwjBcC7xadkZ77x0RqSVL4Ac/gKeeinykLrus\nmKapiXDppZFTevfuQANBIDulqYg7MzncQGw2E47kb1EXfbb5OQmyopKpHCajpqWjkzGpxmGeKbSK\ns3IFIhAHNfCBrERlXd3XijBtUl3ij5NFoUlBOR2jzXyQGTonV9t3FQYlSofM92xrd1n2b1MIoO7d\nKSFBQoVVncENK7acZ+I6svqi5nxWVPodGox57zxH6HyJsvjwtDXyKmkuRCqrT1FmyL5ylvem10jo\nkqJEqcjtzyhD11eaCJRtQtdg+FyKTmxjd953rWCrou02mMmDYcOi0Ae//z1ccQV84xvRn8C110Jt\nLeyxB6xaBUDRn90CqeEIxUcQmYhApYQ2aEzmkYjxJCNtaXgj0FiTXAlYDyWbICt1LokBZVLEUl/s\nrEu4DXi7BZheXh4yKjk70z6bDI7qLmhW/myok/7kayF/R58VzuUIJcqCknt2HTjT2pxuyw+1HENZ\nzgPaBIpmEQOBKhvyfWYgFWo7McF0r9brlxP5RalwqJ9Qy+XvZcH2ntkmxAJqO2kF4qYSahmufkVZ\ny0v8dnL7FG1WU9a6ebB+QXr+jSTHsMQ7bFOrUwSKBCYo/yELSbKjgelcxPFttgWRHRVXoloFu+8O\nP/lJ8fs558BnPgMffgjLlkUEavRoePppGDu2QKSC4Fa0G70KNSp+AYQJT8SNSkBnmhON1ra6Tzc7\nkWcxYnBvhEKcKCgQqIRCpQ34iZvztHUFYqX2wpLjRKV0YlkWBThL5RqowU21K7PUAa6VVTPrKq0Y\nLs+nkisEC9D9bntiVaKM5qhKDWQ5yL0TgTI42lYENp8mcT6jycnkLyjaQdo9l7QxWYmyuUBoFmyU\nDSXWVS5kbF+6Z2p6ZmkLYCB9D035miwTwlR/pJSVjUtjn6huGcrUkifRRrOa/1Vk2VDZ4Z1shl1Z\nw2/5Ah9ldnRs9Gg4Sg0a27bYsZUoEyZMiCKbv/sufPKT0bH334ePfhT+/e9CsjD8MsmZivg/s6TB\nl+yXp5IUGfKLkbUDUyGv5otNi4WwB7ptZ8ZJf6Ke6uzQCWJ2U4kVRUKJcuzcVOUmi5KjRTxDkh33\nodShvAATccwz+LvMlh0g37vtmaQRqLQZZSbC4KBElcBkytJhgvI5LVZTTthMpGeR8R1K+71dBo0c\nig8o9yEvmMmIobIS1VoTB/Uedaq37TmU805J12ZZxZ32LNPaSEVIpiafElVKOSewZR5siZWotHtJ\nVZ9Mv5+appx3IVvbG8gK7uUcJnN/dGD33eGNNyLXn3bEzkmiZNxzD3z609Hn9evhmGMiQhX/hdu/\npFwgNYbGiKgIAlVw5pa3W9H5KKkvpolIievkuBqyP5WiHI2qnVtQxQp1aaxJz1+gJEinVD/VBFlR\n1AB7aI6X0UE7D/aGl1gQTa2fWmts/FtmrBiXNDLJsuYzU/nvUpbOX6ov7G5QohJlWcpLLUslTxOU\nP9218p+anwGyieSs+O9CkhMSyDAQpg0eunpWGhKRyuL829nFJ0oTT0gHpz4lDxl2eXZqnC9NOZnI\nRDvCpb8rkCnDb9N1JHTdSzqgkBztRLVSqnHeCY/mN9Y8i07hNn7LFziJx6IDw4ZFmw13an8Ks3OY\n82zo3h1uvhlqauB3v4vMe7vtVjx//PGE4eOxaU9CM9EAOyVjeabGbjWbKdepg7t1U+UyYZKZoUKd\nx0xgLdFNHBcf03R8qSEMHAYaF8dVZ1NXuSYFHVJMNWrdUp+/JT85L2unaFhRqTU1qBL+GmiZAT1d\nVudlJVBZlq7bfiMHk1Ojck5MjOSNwMV7It5FIznIa650bGc6E13q7xvnbzL3qVgglKgj7fV0nSzK\n6UvalG1wVZezuygX4n7T9gh0yM8lRImM1pqEpj1nnRO/Dto4UW25wi3LgpAYch9m7BtDXuIQPiLq\nvOee8PjjMHBg3opWFDs/iQLo3x/uuCMy773ySnRs+3ZYvboQHiEy7RURBDOhsQHuqqFpStFsVowQ\n3pL0RXIZmOXOOq3Byyv6DHGrEipUWlgFOV9VfXEeFNIGNtMLeQiwwnLeBMMKOesSf5uZQMrDaaVk\naygEqj+BhsCUpHfJTwPnvAx1SQx6umv7wqrxUVgha7k6uM5MdasiTefI578kEyuJQCV2CxBECsyL\nRLS+KQZkIssKcvm8aX5j3QDVDKWr88T9OKpPmWAbVCvth6iaDNvAzzENWfyiZLKkI05p48r+8eq8\nt7NVsbJwJFIOoSKO4wm+xX+zCxuKBGr//eGJJ6IFZTsIqoNEQSTrPf548fsHH0DfvsbkYdgQBewU\n8ZqkTjURckCFOtPVNWqb+U02DzaSCLXQtHR0MW5UY01yQ2IBmXSZ1C8b0ZLrZownIzpV107pJeAB\nYIThPNnIQ6ZBJ69zfJbO1VUt053PG+8k68pJXV6uzvOmesQ+Uc2TUlSvSoUrwFA/7MRad05+BwwT\nEO3+mLoyZHN8W5l+MsXiMfzGqi9dAZISVfhdW4NAqdBN0lozDEKKKiyjte7bZbWuQKPhs+4aXb7r\n4jhRaOJEWa0PORQkIxzzUSYKH934T/bf/Hr0ZUX07zd8MXnNPvvAa6+VXcNKo3pIVB4I2VyskGtr\ncjulJbGPHigKlM4Moc6S08yITkgjB/JLplu50ZXiCOVCOPI6cJtQxiCdato0qGUleaY5yZoUl7y+\nBC7PUBcLSfjRpKmOM0mszquYH0WO1Wmm38Z14NP5NZr2v1S3bdKWIfuAGUxSrUa21Lama/tpCsxg\n2ONA6CEdcol9pFuhbDqfWQHK4gJgg+Z5qGQ7C4GSTd9ZiVZauS5Q2634XXR1yRQnSm5H5RIoXR/m\n5p7Rm7X0ZxX/5Ahzuu9/P1qBd9BBuWvYmujYJAoSqlBT/ehkpHDTbEBVerLYymVfDCgJ9lnALPQh\nEcQ5+XurOYwLpL1kLwCPUfSJgky+TsZ0WQdrTR6J8BRZlrbbyIUu3omNSNlMVi6ohFkiz2xTrM6z\n+USVuYLO1aEW0gfxvBC+UM7vkfxbpy0Hbw24+JOp5+T2sxxa5sBhOp8oA2yO622p0AH2aPMCmvcl\nr/qkLuhwWh2rSetCplzKMKV/PfaJ6mmIWC7SZTFLp0IXVNNtAn0TP+NrTE2e/sIXkt/32AOuvBK6\n7LhUZcetWaWwdi187nPwq19Fmxs7oKAGyaqPzR5tc2a1QCZsiZhQLivpbD4/cviDRumY7ZqSWDJZ\nnDy7xBnoBmrdbN0FWf2yJLh26MbZZR6So0MlZXIVeTpA1X9MHFNjqQn0xR6xPM25NwVZiZDOzygv\nmTKFwdC1HXUgzOzXZsjLBGdCkqUNyJOawVBzYE4VW+OzZvottPehq6/rBEF2MagAnMOFSMiaXgdT\nHur1ab+Nmr5k77wU03izSJPWhtQQQbp33G1j4ToW8lN+RS82cCLPF0/36QMXXww//3lKPjseqpdE\n9egR+UStWQN33hmFQTj+eH1aoew01tDUODY65mqfNkEmMLI5LoZ2bzxBoO4k/YXUdYDi2Cyi5dtq\nPXSwxdApIVI6FWYmcBDwYPzdRKSyIIVAuXZCaUidGbr4JdkIlA2m2XSFosgn8rXVRT0v/34uSpSa\nVwbkcqBG7+sj8pHfAZtaa4wh5lp2BgIj36P8zqaRGKf2nIdMOyhR1oUoUFw+b3knSwhnxnq2hbqV\niQBib7OmlWaZUIbqLFbnLbQoUW2O5G9+Lo9xFk8XD3TqBIsXRzGfdlJUL4nq1i2KI7HXXhCGsHVr\nSZJwHgQjpQOi480i7asKj/xdtypIgYgL9RZ1pQRKfhHVjYfl//XKsUqFSyjpCHQrzRqAfwInkhxE\ndWTKxWSnW30n5SPH2hJolM6lwblzMxELSNZRR3rStiuxmSOy+neZzKaq30yeGfxCzEqUi0nFBMV3\nqBKmOTkfE5GS32vdO5Yaf0tFhjANundS7R9y7L1ZrIdp1aqA/PvESlQWVCQsSjnmoyzX5SAhlSRs\nOv8yHUxhLGx9nAnNACMBjU+Uyd8ttxlW7g9N27ok0Ylt1LCZHmyKDnzmM3DuuZGz+E5MoKCaSRRE\n8SROPBEefTQ9rdzxCpjs26q6o/pI6YiVArGtS26og4bumAuZ0g1irubJQsc6BviTcjLPrt06ONjZ\nbWqbzeyjHcDzdvKqb4C6n5ep/pVQnEzO7qJsuU5ZooIPA+4lqUTpno9bR9rqfkMmIoV0rFmpR6rZ\n2gUpjvIqWQI9Yao4kRJQf/NYidLGiSLfyrB2Q2uZyw3ISvhd+2Agkwql/Q3mAYbVeWp9En2myd2i\nMoteduVDXmcye4hldwAjR0ZjcxWgukmUjDPPhOnTYbwys5YH2bTOQ4QogHQzmW0lnVgZVKvZbkat\nmy0Qm3rellZV17J2hDZitU8NvD0Ru+9TBeO1qGbSNAJlQy5zg8uM2qVzTyMfrisDFRh9HmwESqca\nrsDuE+VKnsD6vLKulirJtyF5Xp1cpNbLFoKijHar3odtr0udeTGz+qP+1gafvL0Gw9YD3dX2tGde\nNrKE3qgUacrhm5VGoNL6a1u+4l3VlaGbJGvJrEGJciq7XOjcPCKMYgF7sILtBHTq0T3yf/rYxypR\n6A6B9o+Z3toQUuGmTZFzuQlpq08qZSJrLP7JK/IKn+tJfxF1PiG2F0Elc7Z71ZWXhlDsnSdDt4LN\nhBelPxUNlAySAjYH/MwrudJmYOU6tAofEgEXAtJgOWeASqrrbPmnDUjCJ0pAmCLVwVkJ8Cj/5UGz\n9KceL0ElBnPdgCqvvkshzOo9y/cu+0PWo1elBHKtsrXFXDKY07cJJcqCkt9gpvSX4Zm3Vvylwruh\n/rkghyLqQqDEf1NfXG/4E/mrbcaUv1once3gecCClIpqkLg3+TmaHMjVd99tctfp4PGwYUO0q8jh\nh2ev5w6K6leibrwxIlD33AMbN0b+UUFQOJ34KscEEUizT7vYu00SfX0NTRjMellmCDoS5LJ5su24\nyQymU3+CGmCiIWPF8TTTrMfQKVbKj0aLrGTJMuO3XgOVnc2nwaSe2ZaHy6vzTCujDLPnzDAMzrp3\nMg/SlGMBWRVwUgIrAF291H7FGlJA9YuzqCx1wBbFJ8r6bB0VZdukpaS+5SzYsNQh9VwaDL+xyRXA\nhjx9lGkssZUll9F1JAzrGbkymuoiu3nIfXmJb6Bo/7pYcwJuz7oz253S7ayofiWqZ0846aTo89Sp\nMCllpVGagqGGPahvYdSk2VHsJzn+UwaUxIiyqV46pQrlWKVUMyidWenUH60SBdqVOyV1dyQtqrLR\nrPyhnLN9L4FL4Evb7vNpG+XqkKWzd0yrtoF69bjLjF0+J5QoVUGrNAlUVR9F/cmydNw2cBXeCzm2\nl/Q85Jl9Ip1cT83g7lo/9d0xTq4seZTUMQ2a+3NRoox56eCg7GQm2qqSnVVtMiGjClXJxSq6vlN1\nTSgn/y3zYMuCfORN/ivpL3SbgbuZ7z/J//F8Yal4daL6lSiAQw6BQYPgvfeifXcUKOKUO+JAmSNo\nhlr0e+7Z0AigpJV9JWR5V3ZItc1SbWVZ/X9S/EJsDtpBDQyZCMsM16pIzExNMx1bOANLrBodnDoV\nuQ4mc15efwydCpRV2VDSunaUxpU4tpV9ArISBdH9p9TDWTEqYzDL4kOly6cw03aB6bdT8pBn+2kO\n7kjnZMjXpe2Raa2ffE6DzpISpTrauyBNVRb3keazmArFTGyDU7srJ0aVoaw0UpvFT8q26CAtT0jG\niZLf96wTbDlNpndFoPicJ8o3c8opGfPZOdAxSNSoUbB0qTXqaQmRstmn4+MFAgVJIlUO5PAIupfN\ntILHRT42mkUyyOO6DiRsgY3Tgcnma60dqmGWY3r5m+WBo9yOMSWkQqvvy+eIVjFfptVTKFEnl6Zt\nNXOqBq1RlkoEcpmgNE7t6mfdgpWsph413lUJMRbvg6iPYeIi3qEXYiVqSYaI5dZJjaYsJ+i2k7Lk\nI/cBqcRMnWg5+LWVQ85tKHuCR7pJux5YGO+dt9ywOs80lqmEXTdRx1C+q5vGddfBZZelJNo5Uf3m\nvEpD2gV+BM2MponRNOXPT3I010KoUKpTqg6iIeee+blAY2YJauADk09UGhwk+kqaJwW0A2QachAq\nYydpMhVpzFmV6sxN+ZQcF+ULJUoaQHM7jGcllhkG7TTkbT/astU2oJr4NKbIEtPzTPuAZIPxXizP\nV81XVqKcVCiX3y6LmqWLMVQGjBNDuW+R78HwHlvdDjJAa0o3QFf3cWRQIiX0Ggk990q2kUpOQGx5\naZ3T29Lns/3Q8UjU9u0weDC89Vb2ayUCdVLt3zmVhxlN5BReIFIi6rgIKWCzg6uKkvo9QaA0Plem\nlSDyS5QadyaPaqMMEm/LPlEaItCM21Y2LijY7G0vqaZ8ub6p0r9utaDwCzCtItTAuQMzDUBl+N+Y\n4ESkxLNdA/1nROfOQr+qyFQ33Uo15441hUBlMWXanHVdnqUTkQI9mXKEro7qe6sOrMZB2lKueAe3\nLYclwicq52BXYhpOKRuU99aBQJn8MRtRSKmhrJI2KK86sxApF0VfB7W9pRKplOclh9NRoXs26+bB\neml1nqsZMUtsMp35XlZdS575oAyZ75zoGOY8iMLLn3ACPP545Bv1yiswYoSSSCMpy6sZAOpbuLT2\n+gJ5AhjNXOYimfEEgVJ9I3RQoypnhuSfIUv2Ti9GOWYvGWJ1nuPAUdLx6Ry7G/Q+IpmCEbo4P7aS\nClXScZpMCuq9p+xCb+vgXc1EaaYBgeF9YdP4pE+eCrVdpxGfhI9FRl8c3XMol1TKyOTDk2WFmdoO\nJT8+1dyXRTXTmvUcsHgwoEYs1ymjmuPGNqYp2/oc5fQp7UD1N7Nel7ZaVF11lmF1qWk1m3zOhJJ3\nTqPom0iTqc9T67A09olabqmHOp7JZaQFe01bdCWjHiYvmsplzb9MSbjzo+MoUUEAjz0Gk2O/nYcf\nhvXrE0nC0ODfIK2giBSohxLXzWU0cxlF0yNjo21bZCfuNKUIooarRji3SbqF/JUBuDXMXi4YLpQo\nw2ABlpmjZWWcIIW5SabGrFI4buu4Jxj+5POOKJmxywRCV4cMSpeuHNmka1P/dKY59fu2NdAyAy3U\nrY1ykRmdCqKoUKppQue7JMOkXKQ9i8zvjqxMpmFmsZy0wSevWqvL11jeckC3Ok9jSs4LkwroSsBU\nlPQd5QTLlBWpVobRtCfavnQfasDVrG2hdh7sqYkTlaYgq+Wr1wpkMOePf+Flpr54dvHA4MHpF+2k\n6DhKlEDXrtH/P/4RevWCW281p9XMukbTxKj4D+AX/AePMClyKFcJlA5qI25UjhuJU7yKb5bIX9Rb\n6Qh0ik3Jy+jaSdpWb0mqXWJ1nkOHKD9T7bYbDY4ESg2QqesU02Lo5Inv5AArqdCpUmV26K7qkg5q\nOxeft/WFmnh1nqyY6szOlYRKoEyLLGSoJtssDtC2+qc+07TfLWV1qmn1Vj3ZVerEe6WcS3zXKVEZ\niFMWfy6duqetp9uSeTMcfegKipajapd1EYAJchvTmUIFSTQpRSp0StiqkdClZ/J9cX03Xct1wL6b\n3+TlxYcUD9x9N5x9tvmCnRwdj0Rdeincfz9s3hxFTlUQrdKTCIKmw9hj/koAlgwfEJvyRtEkzHnN\nhuX3cqM3EZ1MjVhRRtSXyirNOqxWSUA2cyrX1QHbpNV5ug7HqSMSdVLMkk54UfkvQ17gEZ9oAAAg\nAElEQVT9Yysbcx0raTJSy8wdVFCDvJ296bqCEhXHVrNJ/ZlMYTI070vZmJkcJE0qDTi2s7ybLVvq\nkEZ65eco/CKzKhTG/IUSdSTpkwyHUBzlkAyrWda1j1LqZ5qo6sqVr0lLZ3vuuv5b3fxaztP1txff\nXSbm6+LVeX3GJI+Lulgn1oZjGTH5w6lMXS4RpquvjjYarmJ0PBJ18MFw331wxhnw4IPwm9/AxRdr\nEpo7jyXDByS+j6aJt2rraBo3Fu5vIFKJNB2tqqyMw63hNiqfhZOkywzdeD7rzM/SoQU10GMi7GY4\n79zJKnXSLb0FyZTpYkqxxXdS/CHKnYllXXFl9GMxPOssPgk2yKTW1IbqgZa+sGq8u89OWQQqRiZy\nE6PEzGMJyyFDfh9NYUOcSG6KacllhZbOLKkb6NUN0nO1A1mJyuCblAUyqahEuwD0ez1azL/lQn2+\nafejEimbkmibsKl+cq6TuF6xEmWqjwwd0ayA6nbc8ieLX666Ci6/vLwMdwJ0PBIFsJs02n/lK3DB\nBVBTDHoZhg2xGiX71DRAI8ydFBnzhDlPOJjPZRRN9WPjWYbsK6FxXNS9jGkvvxopXfdyqjMf08yq\n0srKAS3wRqxEuRA7LTSDn0uAwhK4+qk0mDtedWB1HQx0z9bWMVXaOdrUhnQdsq6zVq/ZvAbWzYD+\nk5LHTeXJv31ewifXS80/tZMvgwSoM/XEbyIGbGXhQwKGSYnrvbu2AdE21eec5iuWKEdWomTkVAJN\nv0tuZSNNKZeCvqrvsEn9SYPuHbH9dqY+QTWj2dSfeuWczcSrQpdGVaJEvqZ+Qe3nRP/l0mY19z9k\n67uc0vlh2Abccgt8+csOGe386Jgk6vDD4ckn4bjjYNu2KOyBgohIQWJZ/6wG3qIuuRJPRT3u9nbh\n6KfrbFw7gDxO106Dd4YZaqcaGDgRhhrOpw4QcuiEuFx1JlvSEahOyXId5UEvJZBnlpmrLq362+Uh\nqbZrTH4ueWaNpjJMx4dLPlE6pPpdxL9nqkNwCpxn5baQF2lppLKMy/dTFM0sv7vRfJWVyGiesa1d\n1BHtnbdA9YkqE6b2WNEJm/L85Xe4rBXOElzq69JnuBJIlRRr3xkNVDNjPaVKFJjzUS0ich1MKmgK\n/rHkSIZsi5cGdu+efkGVoGOSqCCAj388+qE3bXK/rjGKSD63NkmiCqSqvgXGxXGiClG1Y/8M+YWX\n4z2NU7Z9cVVfhFQs8hPxqcQ5k4lGh3I6unpgcwu8Px2GKhHLnfK1+JCpZkw5z5IOW/Vhkwc9jWnF\n1ilkmcGa1BeX6wSEiTbr76A+C9us03S9bcAVPlE9U/abVMstcRbOqRDlMWkkYCAlpnu2+p7I96Lk\nWSf9d6mncYWq/DkeSNV2IiCOF0yOGcjXNoMSVWllNM3MaoVNjZLyMbV3daWbXCeT6dRGRF3eK9tz\n0+UnhzSot5Tv+nsIJertMcnr5Osrae6M89t9xlKmL57IiK1vR8fOPLNqt3jRoWOSKGcoA3w90FjD\n3NpR5kvECwGlykF8fFRtZAKM9tqLz6sDtzqA6BzHYwI1qnZu5Ngu79mnyq31yrUitL9pxuTSoYo0\nQonKDJPflWUm5urDpFMDbdI/6DveSnc6OiR+BxfCYVs1GUO9t/sN6Wx+XPLqvDRYZ94ZFjKkqmsW\nValk4DE8H9375EycHRzWK0JCYtKhe67aRSOaxTCmZ9lZtzqP4nPJqyjJz7UkfR5Toa7dSEqyK4FK\nU+nqDOdc3n1jH6qQRtOEJVGG4R3RPVM1v0ZgUxwnqpsmD93E1Kbe6SZoSn3Pm/5Hjt3wNKesf5iB\n26PFVhx8MEydGsVl7CDwJMoKZcVYjLc0b0PiWMFhXFKj0joR25544r9crLK/0ajauZFPFoY0Qi0Q\nL06JjGxAHTEhUUMqSPezXaNEpTrl2mAYKF0IlOjUXExdtmX7AlnVHVcY883gkCxL/5VYhq1i2xro\nNwPGWJQonUKom+kXkHOlW4GcyANr6btZUaQ5/2a9Tj6fUExzIuE6oFk1a8K25TBwDvTNsHeeCzms\ntJIFaBVA3b3ZJqEynMhMDB3JMJWj/T2VOqvExPT+23wobURqyzzo1A+6jdHUpyFZfiP5TKCi32qE\n25d/nho2F8996lPRoq3EJrTVD0+iUiENalKjk0lTYdNhnRKkUUSalo5mVO3cSJGqhaZ6SUVyjRgr\nyIJMpCbNjvIX+Yk06oaSOl+j1I7PMtilKlEu0Z11cHAelaE6grtApz7pZnm6fF39oVyWJ2eCOnBK\nJmMTOdPVLW3QO6hvtDqv1VBusMM8BEqZ0OTZMSCPL1ouopfFBJZB6UnsnbezICWMgYyyzcAZ4UqI\nxTuommkLsCx2sZHCAkYCsk+UZZVvHfl3y4jrUiBQd9wBXbrApEkdjkCBJ1FuUKRjQYLEZ6DUJ0m+\nVjT0RrSDXMEch+IfJaC+pDIxmxL9GyG/TbUU41bhQM7SUFCjDGYkoUS9r/hElagOtnADMiw+TJVy\nIBUw+TPpTAAuzqKF39tkdlKOp5lTrXAwk7n87ibyt3kNrJ4Bu09yv3cB1ZxcUleDw78zLOldHNlF\nmnqU0BmaNGm/hclvyQTtwG5oI2pauf3byrI6eptW50mwqYnOk4VKxQDLQCZtBMr2O+omSuX0maZy\ntSpYS9E31qR+yQq7kRjOA/oBY3B+9lrfMUW9Uuq815Z3eHLpccUDF15ozr8DwJOoNKgmNABqiiSl\n0eAYLjdKBym8QKTESzyFIjG7Mz6mqlqNwF01NE0ZDbWa/JZaVhGq0NWxZCAE7QsplKj3RT1BP3hl\nUB5MHZ7r7MllqbOJQKXVw2lwVc1OmvM2HxK180p1eJagDq4uA7uu7Ka+0d55WQmUjFSl03FwTEwk\nyg3KqVkFqh1ERNlZTKwGaEmNzXHacK6cgb3wDNMiljeUtnGXtmhVNh38+IzQTODKaZPlQCZbJXVI\nmdTo+lOxyKgemCItOBLjiuqfaXJVaIZSJSojtKtSkziwZTbTlhxN/+2rowNHHJG/vCqBJ1EAr74K\nEybYpUhVQZLJk6xAuSgLjREJG1U7N6EgjaiNPo+mKYo/VQvXT7os8nW6Ez3uBIiIlFDHADcCpc6g\nBZHSOW0W1CgFjcCYFnhzOuw2WSFQaaRJZ+Zz6GTTBhIXkqWSXBvUzs/Z58UhTITNmVebZyvAlK9p\ndV7aDN9oanGMrWSFJpBmpsHSgXSWoAzipvqwOENxShZwNf9an4kuYrkMuxLhVHaJ/5qcd5mqlLza\n2QTTREc7MXSA08TE0b9N9xvGC4RALDgShEqxJJgc2euAZlmJEnB41rYJBCTawPdW/7hIoM4/H373\nu/T8qxwdm0R17hz9P+wweOKJKG6UC0wvoM7JVoXqn0REmuYyqvD5VB4qBPME+HL9/wA15iizgkgJ\nx3I5hIIrbLOcNCn5tThiuXa5dVrQPBkGx1FTxyGfd0XWzlP1Jct6vRGawcTZLGRZZq/WUau2aczC\n8sAp8urcN7k6z0QCXM1eCVhW1mVBqjOztDhERVZSWlFlIye5MPm8ZYJQolKisVfkfitFpDKs8JRR\n7qIL03toVOntJKQ075oEgTJCXngkv+OJeshKlMPzKjF9WtLH70p34pBAn/wk3HBDh1qFZ0LHJlE/\n/jFcdln0+fjj4de/TmwBE4YQjJTSi0ZnWhqvwjS4iJcnNsEJAgVRBPRRNBX25xs9fC4n1f6dR8ed\nYS5TEKmCadrgW2WCS8gDAZlIic4hbIFlccTyVLUhZYsME9S6qStNRJqs+eiuy5KfCVbzh+Z+1bLU\nTlrrb2J5brlmysrAKStRWudZQ/nyQK81ecTIMrjpVjeZzpcgrX2lDeqWc6Y2UgnVUG1DWXzzVCTq\nI5Sor+L0Php/S4MJMC2/3Mhq+pW+256dy7OV06gTq0SZKnlRTMfydQXXj5rSldU6qERKxeB5sFxW\nogyTUuHcbn3/Ut7zKVOgf397fTsIOjaJuvTSKOCmCE//xS9Ct25RA4kRzkshUjoCpToXGyKYN9WX\n+jI9RBSk7JThDxeOjaaJR1WVQiZy4gW+k+LLZSMAptlsmtpj6oCoASZi9HtIDAY5OlSb75JKpkTn\nZPt9TKRJnHMhT7pOyDiIWPxBXIlEgiRkfIbaDl6zNF6ti1CirPdl6KgrodjplLm00AKZyYvJby1F\nKbO9P6l1kMuSF1tYnqfNN8+WRgvd3nmWEAm6yUuaumSqS6XJpTF/pZ27EnDT5Efn4qBFitleQH0/\nVF9PkwIuEyl1Mv/CSBhmiBNlqlMJdJNe8duWEY6jitGxSRTAl74Eo0bBscdG3y+8EEaOhI9+tOAj\nFc6T3KXEi2AanEUjLzRQZb+tRMONncIFGmtoYiyP1n8CapP78iVNdDXJl9D2cqoQL6uarqxVby3A\nA8D/Kz2VNhikdV4F6IiIJTinShTT4kFhSC/D2anXMiC7DHRq2TKB0D0b599f7gw1HaJKWoQShfCJ\nEte4rrKMkXuwt8BEhG3PyLp6zHJPpmXnatkYylYwkNXsx3zgjfjIPF7nZFbRN5lPVqXOGXGcqPfl\n1XkOg2QJQVE3BHYw06UR3YqTL03QSxvS3q9y6qD7TUXbCUPGvTCLnuF6Xjn4I2xkF3uWuv5JjhOV\nC7bfTvzmH+TMu3rhSRTAMcfAgw/C6adH3484Ivp+2mmFJGEoESnVXCE+a4mI3DFLL1MBNaVyeWMN\n119xGZN4JL3uMnETeeRVAUwBP+WySpwQG4gGA83Nu3Q+qWl0M15dGs2M08V/JI+PlMl3zFg/Q3pd\n3dLIrDoIletUrZ6T24DqEwUYN+G1rTS0oVJ+ZvI7ZHpGieMqgTLARKBy1rkT25jN2ezOysTxxdzJ\nnjxFSVt2Ud7kNC713GswbD3QQGgMbcSoQBnqpdbHxU3A5bzJFFVpU6LtmeaCZJXQPPfPDbqD29+7\nCIDHVp/ASV0eK5503VS560hYHPtEZW031omrhw2eREHEjk47DW66CS65JDp2+unR9699rZCsQKRk\nPxwnyJK5wcSnvBxNj4wtCABNS5UtXRpJyr/iJVd3DDe9/CY5OBdmAlviTI+jbP8H6wBs86/SzDhV\nE58K9TeUn1nZMWKEsiHVyaUzzlKuOsA7tUmDD0wdpeaEl9bAu0KJssV4iuFCnnSDk2ng1yk8auev\nKoxqXql1ciBQrrCU9Tlu57/4IT1ZTz/WAPCPuIAjaWYoawi31kPnzgRBRiIlkNq+4ny3LYeWOdBD\njRPl4jsmYHlutvq4tBEbERQEILPp3BZOQkGa8qjWrRnO5W6u4bt0YStRfyggf+7KNjrzo+ar+C1F\n39vv8WWueu9/Ct9P3PA4S+/fnfVde/K5QXcw3RbPS9RzFpESVbI6D30bsn0vebYvAiH3cgen8oq9\nLh0QnkTJ+NrXoHfvok/U3XcnSBQoRAqKSpAR6ksqBteZpURKzudOaGocq/cLkQdaeSCyDcCpipnD\ndUZ0jTMtY/l56kxI18FbOv0sJk4ZprQ6Z1JjeoVACX8Ksd+hfJ1tv75Gw3dbvUymJa1KZCDyon28\n0hdQlSjNtj9GVCjYYkIFUeI7yZMJlVCV63+jOhyrv4Ml/3HM5Hz+SCe2A3ApNyTOP8dBHBnGGXXu\nDNu3w09+At/+dpwixwo207sqr5qtA7akRCx3UnkmUBqiRBPHTpe3ybxbEcUnKzS+XK7kKcZkpnI3\n5zuX+Bu+yBimFb5fyr0laXZnGWyBfyw5iqP/9QzP7nJ0aSBQuT8ZR9EnaqGUTn3Wpr5EO/kQJt4J\n9GQDnxYEapddYL/9bLfYoeBJlIoLLoCBA+Hkk+GFF2D5chg8WJ8210svOh9pNt+ItLJOOiY6RVc5\nF4odv1q3PARKrov1XrcAS+z1yYVKrerJCVMHpB4rGSyk31b9LXTPUqeIqVBn46JsU9vIs+RftENx\nT9vWAEKJktVU198lJZ36LHT3XWJG0sQJyqUaFgcIZ5gIKlDDJuppJCAE4GmOYRc0oUb+9jc4+GCO\nGDSoeKxvX1i1Cn74Q9iwgc4MZRsfxepLI+ogHd9v8xvs+vwHvFpzEBs77aKtJ2BRorLCEN/N1Qzp\nilSTr4vZyeTzpTjyO5r/u4RbGNcyi10Wb2AqZxfP33svHHWU4drGaGsU9MSJuXNhr72itvCb38B/\n/icA05Yew54sZDF72utYOw8W9YO6WImSn7GqzMvQ5Vf4/aL2N4q7i+feew96lhHUs8rgSZQOAwcW\nP9fVwbvvQq9eUoK4I7e9cHW4r0RT8ynMpKUBS93uQVe28AexqWO6AV2ncOmUkRKI+9sArDAlciNS\nuVZWGfLJAtuqHRVOqpxmVmtyFLfVR65TJtOxDEM8KVMEbvXeFuqUKF2blstJiUydtkpJpEmDnCbL\nZMa4UtQSS8pBmZnKpziVh0uO38sJvEhvfnn94TB0KJxySmlQ38ceg0MOiT7/7Gds/cpXCG7pjJbg\n6ZbvA2cMeYAHlp0FwHPdD2fipufQKoHNRD5RNQdW5n2T81brlZVIOb1fKirgt6MSKNPERGqrt674\nMhetvT2Zz333weTJ5thJQ4bAAw/AwoWl58aMiRY4Aey+O/y//xftR/e97wHwDnuzT/PbLKzbyxxC\npNdI6BqTG9ff1jYxjM8du+EpnloaK229e3sCpcCTKB3GjYNzzolmFevWRY3/ueegPmpVYdgQ9YPq\nS6/OiI3EYELxvLheXeIq+4DYOhadLCvLvDZk7bCMg3kL7BpHLJehzoTyoBIruVTYQiVkgel5iDrr\ntpRy3WBa993W2ZdAXrrvENhSboeF/7ISlYYKOaEm7jljnmmKlDqBSJg4LRMeQ9uYwAvcwefoxTqG\nsQiAdfRgDnUcdmhPGD6cc+66i3O6paw5P/hgePbZooJxyy2E555LcE8YJ1AWTWgwfNn8wucjNv2T\ncM9hNC0K+Crf4SkOTSZeoEYsr5CyqCJtglL2xCm9fQxiOQ9zCkNYBmzmffpyBr9gAbVo/RVN71TB\nhBsylU8xmfuL5w49NAo+efbZ2ksLCAI44wx7GoEePeCKK2DJErj1VjqznQXszcc3PMnTu3w8SqOG\nclk3D7ZYVufZ1CgV0vnhQ+bD0vhLTOo8ivAkSodu3eCee2DjxmiV3vr18MgjBRIFmkCcagcuN9KC\nT4IM6QWWXwT1Ja4znBMvtW7pfj2kRi1X9/xTIc90LGYM6oDtNbBhYmke5XSSechTmpkM8tfHhXC2\ntm9HM3AWDh29JY9MdZOUKOvSc8cYMmm/qdNvo4mjJO5bNztX09VLaRs1aaQ67MlCLuY31OjMcsC3\n+UXi+0p2ZcCaBRy26672W9DhyCOhuRkOOAA2bYJ77iH87jB6XTOW9Uq9ipjJFB5iDG9zCAuSpxYt\nYhTwJF/l49zC0wkCpNs7rxVhM0cCQfN2vjrwZoZtXcis6eO4t/e59rwAl/a2D2/xv5zMfvy7cGwY\ny5nB+dzJqUTPgWjPz6eAQcBsCAcHTO36KV7pH7f9xqjc3qzlR/ygQKDW052eC5tgzz1T65ILQQC3\n3BL5zP3qVwA8tfQ4jq19iv8jDskj9/tLJSXKBJlICZisGuL4MKLHfdFFkULmkYAnUTY88AB89rOR\ng7kG4TwIJlO53b5B2X/PvoIvcUx+KRpBbCcgQ7s3k45MmWYqpqX1YQtsnA69JqtXSMjgZOxCoBx9\nF4x528IE2OIaqSbQLLDtrSjKybJ6yUgSK6QKDVsDC2dAnaJEae+/Mv5rAds5kDl0ZU7h2Pv0jZWD\nGKb2odZJl05u27JSOAuCcDsHtsyha7gFFsNNXMJhvJBe6W9/G772NQYMHBg53ebFiBGRv0mfPtH3\na65h3e/H0OOzndi/JILiv9mTZdzJfyUPX3lltOvCvffCd78LwFN8haGcwhKGxomEEiVcFDI6secJ\nZSEIE9s5gNfoxubCqYN5mZve/3rh+/vLB7Jy6ABm14xla9BVU06yfe/DIvrxoZJmO7/jggKBepqP\ncewnd4W//pWBfMC3+UMx6RrlfxNcxvUcNvR5WFxMdjG/4WJ+C0ALXem59r3IvNXauPHGiKh95zvR\nvSz9OENnLGJJl/j3FO9j7Tzo2g+Wj7H/Ri4mdYFxwMtl1r/K4UmUDZ06wbBh9jQu0mjCD8VxgHNR\nNXQKUUkMqogsyXszjaqdW7pBsW7Fnwwb6QjivfN0aQtQwzxkHHRdFRRXcqPGSkm75xKSqkmrW8kl\nkEag5HqpZcvn1DAEOn82HbJI+XKcKNUnSlVyKuXLFufxM75TovAAHMFt/JNxRRO4TWXMaQL+8Wvf\n44pFPy05/gbDuZNT+fm1e5Re1KcPnHee4jNZBnr3hhkzYHz83NevZ+PE78L06dbLvs03+PnNo+Dc\ncyNH9UsvhZqawrZWi4NhjAmn8ib7ECkwGbeG0iH1ty/1j/sh/8UP+ZE12yc4ARbDVCZzNlMNeUY4\nnn/xOJdY85vOERy75A/QtSscfTS0WFT6116D3/+ermxlxuKDjclqZr3UNgQKIkXq61+PfKS+9S0A\nFr4zjDHD3mBut32L70KvkdDF0V9JFydKfW8aqVAYnOqGJ1FthUKHk2L6UE0TpvMCOnn7/gZpZV8N\nTCntNLREylaOgG6AclKiBOSI2Y7Ox67Iqg6ZCJRMEPIitzN4jCyz/RIClVMVUtve/Cw+UQ5IMev8\nmosLM32AGezHeN4E4Dkuikzs5zRE6q9KpGQFTl69J5epEMmzH7qP/3r9h3QJt0ILjNj6tlT2R4AN\njD9hGGPuuIOf1yr7M7UmPvKRaAuqX/868kFZGQXmfJcBLGEQ4z8iqV1BABdfzM+/8IVkHjU1EZF6\n551oo9gw5A0m8wl+ySP0JXoYKX5gLu1fQ6T24h2m8ikGFBxpioRtBPIz3q94L507R24UGzfCK9FS\n+k/xZz7CCKXAlvivJs5viT4/gcGDmfj738OAAdH3r38dK7Ztgy1boKlJf36XXeC66xKuHW2C7t3h\nm9+EBQvgxhvpRMi/F+7HW+zDw5zCZXW/hNfjiOU9TRHLU/Y6bIYv7vY/fGvNf9Npy/aIHfw39Nm0\ntnXuqUrgSZQrrrwSTjwRGjSxkMBMelTfC5MTq6xUCOdw+RzolSdAG9VbLqe+pmSPvkxIm+GrSlQq\nHAZ5neScwRkyNQ4KlLm1iwQXolMuqTJBbRt5lSGd0ja8L8wfn66yZYGmbt3ZyGVcXyBQm+nCOO7h\nDUYQXvt00Q/j3HNh9mzCOvjpX4HORJapApZJ5QzRlykptpdzTWllunSBGTMYf9BBmW+tojgw9lmK\nCRRDhrD7/Pns3r17tnx++cuIUF17LQB/51J+ypkspwu3sIUtdI0TaqL+m8za0vEDmMOnua8QDwuW\n8Xn+xiBWm+vUpQs8/zzjx6srP2O8/z4MHw7r1iVIlxU338z4r3zFLa0NnTtHZH1HxQ03RGTzF5Fa\nO4K3uZQbWNK8B7CI/n02wsZ/aC4svhuvMoo/SWf6Mpwvcyu9+ZDLV0jvxFZglZTwwDb0o9uJ4ElU\nGoR/AsDhh8OiRckQCHLQTHlwkR2+ZR+WrH4vAndKn12dK9NW9plgcyTXIU2JyqLo6GKbyPVyvR9T\nOvG7yOpcY00piTARMtvzsJkHTSYokc5EmlWzowzVOdSVSLk+x0KcqCHFNq46pepgUZtUBGzncn7K\nD7iqcGwwT7KGPoRhA9AQmdQ//eno5DVRJ3+5Q/WdceedMDGeBPTrt2PsTv/Vr0a7JmzaFH3fffdI\njciDa66JwivEKszlPADAL38ylvorh/MWQ1lHhmXrdTB8y9v0WbCWpzmWAYmRVsIpp8D115ce79u3\nqAzpMHAgLF0a+Ye5oHt32ENjaq1WXHttFAS6pQVGR9aEn4t9Sx1Fo5Xsynv0p4lhXM9nmcL/JhP8\n7//CvvsWv3e0Z5wBnkSl4Utfgvnzo+BnmzZFwdAWLSp0tFG4AwORguReZDaHZFfbc8lg5OBrVd/C\niPjCt7IwGldFQyhRJj+eQj0seZgIQJoTpEp2VFIiK0vqNjkq5N9Jd305sVdsUH97dQ9DlZiZ2lCl\niVTCJyqHH5sDbuLTfJU/F75/lDskAhVj8uTo3Vu6VJNDmaithc98xhzbpz1RqUErCCLzYI8esGJF\ntHQe4MoraQQWMpjhPFzQkoyI29NZQ/7Mn5d9KnHqQU7j9KuluFY1NZGvmClQcRp69247n6OdDUEQ\njUMAzzwT7f0q4+qrzdfGv/2TfLX0XJcu8KMfwT77wCc+UaHKVj88iUpD375w882wZg1MnQobNkSz\nwn/+s+D8mZlIpQ3GOkJVQsDUQU0TidqyHL7gD9WImwnLxr3CFlg2HVCUKNM1prAMrkRKvsb2XVem\nLk19iznkg7jufv3pshyrs5gnBdTYMDYfuqyEVEVBifpBMg+Rt/xdhtPzCLmTC5kiEaij+TXPc1CS\nQEFEcC64wCVTDxO6dYuWqANvdu9O/xtuYHDfvvDqqwxjOdvGfZFhs65iEbtrLi7+Hl/lV/xqWdGR\nu5GDqD99OKffd19EnDzaFkcfHYXf+cEPWLlqFW9fcAEHX27RaXv0gLvugldfTR7v1w+mTYOxY1ux\nstWJIAzD9FSVLjQIwvYot2ycfXZEpAReeikKlBejsHGoGqlaN/CJAU2kUxUTVWER5ryEKc+gDMj5\n1sOoSbMTSlSRQNXoSVRW/53tG2DD32FZColyUaJk6HyxBNnKY6ZUV7bJZesUK4FZ6EmUidjpSKLN\nlKeWadogOuvvlEZmrLGfIIpC/zIVcyyPsQvr+S7X8H1+DEQ+UPvyAPMZWkqgPCqO+fPns2jRIo48\n8shoIhg7crP33ox853qaSa5I7s8aLuJBerKRH3Bb4fj5XMUfQx98cUfByy+/TM+ePRkzxuRYLmHV\nqkjNWrcucllZuBDyxDfrQAiCgDAMA/W4V6Ky4N57YdCgQuAzPv95mD27cLpEkbV2P4kAAB7bSURB\nVLJBHsBcnZkTg2KZg41MoFTfGlX1sjlsQ9En6qzJ9oFdkB+ZBNnSZ1F5dMRFxSzls07F0UV7n5VS\nlzRCJ8qRSaGuDBm6etRTJNOCiIv8ZLg+M0HkjSuxhBKlkqj8pr2A7fyAH/Edri0cG8ITrGZXT6Da\nCMuXL2fOnDkRifrXv+DUU+Hxx+Gdd5g36jvs3/QpYCwQ9W1X8DjnqcGCnnuOPx5+eJvX3cOMefPm\n0a9fPzcS1b8/LF4My5ZFlhXZ99cjEzyJyoJOnaKd1jt1igKgfagGeJOIlG2QsakpeeJypLg5NS0d\nXVid17R0tJlA6erogqAG9pvodl2j8j8NOp+qclaHmZzE00yBukUBMvlQSZzsHJ5l9Z6kIFrTFpb0\nazaodSGfqjlOm172iVKRIXiqhNu4iM9JqyQO5S5PoNoYgwcP5kCx0qpbt8ix/oIL4MknoamJ12OF\nUMVGuvJTTuBH950fLbLx2KEwcuRIembZ127XXb36VAF4EpUVffpE8VduvNGeTg19YNsWBtxNTSoc\n/cSNJjxVzdCRmzTCE7bAm9NhaGzOy0LAXCE7jMsExfR8VdjqowtTkYj2XpMeO0pVuUSZWXyG1NWU\n9coKwsT1ElHXOZ6biJRaf2s8qjXQfwb0l5QobbqUTYcBCPkDn+F8aTf4w7mdFznQE6g2RkKJgkiJ\neOABOOusSJ3QoU8fetx2Gz/af/+2q6hHJmRSojwqBk+ismLt2ihWhwvSYkiBnTyZkCVkQCMkohPL\nBEqnyqiDap3lnDimixOVZq7LEl1aXXEniFSlyVoiL2XbHN2+habvAmnhEFSIiOSFZ2dz1G0oJU9I\n32UiZfNNk5351XoN7wubTErUixQ20i6gVIHdn9c4nQfZiwUFAtVCN4bzEO+ymydQ7YCEEiXQu3dk\n0vPYaZFZifKoCDyJyoq77iqSKM1WD5EpzxGq2UZVP9JMbmkQDu2NyjFQTEJg3CleZ75SVY6wBXpp\nVufp8nElgFlNdqbAgDbI9+ESoVlnalX9nTJhJgUyUtdQ3MvN5jgvyJHr83HZPsiEbWugZQb01DmW\nqwQqSYZqWUJP1vMMx7Ab7yfO7cEjvB8em6NCHpVAiRLlURXwSlT7wJOorJD9oO64w57WNNipg6Sy\nv13B9GYiULYBX/Xz0Zm5tKTMwVlY9bsRCGpg4MRi3jYVSiZilUA5/lFgr0dj6SbOgD6QalYUIspL\nz1zNS31+U1o4ad7fGU0TcxkFwKNLPwF31djNmVnqKCtSnftCjUmJkpFsN+dwD/dwXuLYgxzFHOp4\nmCM9gWpnaJUoj50eXolqH3gSlRdXXJEIb5BEg3lwlv1kxgH1LYnNgVORZcWaUygA015+Gp8bAdUc\nJHyi3p9cPCYjrb7lEiFdncrNo5BXTWl+upV1Wcs3PVNB2hprkqvxLoRba7/Elx6+C+4FDoQllw/g\nF7X/wdwrRvHo1WckSXfe/Qfl+m02KVGamGQxvsLN3MzXCt+bGMZc9mIyP2NLOIHvl1Elj8rAK1HV\nCa9EtQ88iWpLaByNR9XO1UcT1w3E1uXoAsrgZiNStr38TE7LOtgiltuQhTzZVi2qMZby+ErZzGci\n3xLza3xeXZmXlpeuzJhQF8+JzxGJGzVpNl96+C5WnQE3bYVD7oWT5qzk1HseYi6j4QoiIqXGs1L9\nyQRcouh37gv7jU/uT2dpM5OZmiBQZ/NTpnI8gPd92oHglajqhFei2gc74F4HVYbG+O9+JB8ks99U\nIQSBCTYCpSMxugG93nBcV5ZLWhEnSjbT1WH/XgmMI19IiCwQJtE0UpZn42JNniWq5DjgBriM6+E1\n6L8fHAJM6AIcCKNo4hQe5lQeji+wt69MdR21BlbPKG0Dmt/yKKYxlbML34/gNk+gdlAIJcqjujBv\n3jwWLFjQ3tXocPBKVMWhMeUlHLhfjI85DixpfjK68kWZaYTFRI5M6gXoo3Crq/NMy+hdkRapW02T\nh8CoEPdiI4y6cvJEe5d/G5Feuh+ZSI24oplTeZhTBEk6AE76CSw5ZQBL4jR7zF8Jw+O61zXoybSL\nb5zaZrr1hX6ST5ROtaqDC5vv4A4+Xzh0Plfxz/iGPIHa8eCVqOqEV6LaB16JalO8KH0uVQsSgTDB\nvIce5N+vTeRr2ktOJlD1yp8MeTAVSlRrwaY2lUugmqU/SA8UOkv5a1T+XMrTlSthBM2MoJlJPMK3\n+QWn8HBElD4NnAPPnHIYv+A/aIqdy5cMH1C8uJ6kSiTXqVH671LXV2MlyoJvrPllgkB9iVu5m2gr\nEE+gdkx4Jao64ZWo9oFXoioNreqSHvYg4Q8lr25zUWXywCUf00o7dQCeXwNMhN0ylF8JZ/JKECj1\nex1JR/E0UqVeG2Nsy6t8fNFT1uLnMZKHObXkuGgL0Sq8aKVm0/D45HD42NJnGFU7l9EUFSuRTofR\nL/2bSesfISCEZ+KDK+P/A+DJXY5jTo2y8WgzUZyo1eMNW/2ETF73Z375/mWFQ6fyt8L9eAK148Ir\nUdUJr0S1DzyJam0kBmo5tk40yIgtWQphDRLOxRT9o+SBLNVRPAVZyIcaY0olDgC0ANOheXJ2E6KL\nGU2HtHtwWS1ne17yNeOkY5q8ejV/yK58kMjrnxxOL9anVBKYPh323huAoTfA+v37F05NO+No5vYa\nBZxSOPYWdQVzn0ycRMgDIHHv3bdt5KmHPs7QbUvQYiXQ0gvefDOqw57Sufnzoe/TUDOWtZ36EBKw\n69sfADB+yAymLi/6QB3MS8wgWq26M+4t3pHgV+dVJ/zqvPaBJ1GtiTRCMwuor6FJURESzsW10PTI\n2ORKMN0qMDG4qwEk1XQybKvFbL4+JfcVK1G6c7q970x1cSVSuojrLtfq/MSyhIwQeYjrgLrmecxm\nLD3YpE1+NyeyjC2F79/65kHRh+uui/5PLPqSqRturJ+yC/sPe50FXfeODlwITCmGxHiESTwSbw4c\nmYKT1/fdvJq3Hh1B/22ro/S7nMSbG/aL6wG8+260qfa6dbDnnto6sAZYc13pjS0rfjyXu2MCNdMr\nUDsBvBJVnfBKVPvAk6i8uPrqSEH4whf05xPO5FCyJLwOSdmQVuPFStQIeWSfpCFSKmxL1VWCknXb\nFGuamcBa4AFgBLYYQqn5inoKkmQzZZquNZXhSpTkdGroAiXdUUxjGscUDi1mUCLJ0NM/ynl/+QsE\nQen1e+wB119vlm1WrKDn5g288+u5cMLeAASTAWpomqJZwSn8tSTstWEB/bdEBOpJPs6pGx5iG12K\nRYYhbNgAM/R+T1u2bmXjxo30Wbu2pO6Ll2xhG53Y6/afcM/nzuUeIMtGxB7tB69EVSe8EtU+8CQq\nK2LTCwAXXwwbNxa/f+xj0HxA/EX1gzJs0non0eBfIAw1UFs8PZqm6IMgUmA2ZckkQpC45oYiYdMR\nKZFWpHFBiXrTVboBhUCpK9HSfI3kNCkryg7Z9CITFsfO+gOBafGJPaT0zbCafkzlU2ymxo1MNcOR\nG5/loHmvFo+VWMMWcSO/KHy7ibP5OkcVvofhl+1lfPOb0Z8JJ5wATzwBv/41jB8PAwYQ/hmCq4ki\nlAsoqtyp6/7GXoMj59KhCxbHpw7ieJ6kpA0GATz4oLEKa1as4OWXX2bSP/4BP/tZdPCSS+DGGxlq\nvzuPHRheiapOeCWqfeBJVFacey4MGgTHRzFw+MY3iuf69CFc1gTdukG/aKDS7qUnm5TUVWH10MRY\nmJRUo0bQHBEpxhZ9k1RSJEO3550Ksa+eSooyhSRoIGIvs4Dj0pPnUb5ixaxLuIX+21YB0PmdbbzI\nocU08vZsya3aAPjDf6+A86KtSAYPmQ2MLU0Uow9reXbJ0RriZMDll3PJj37EJV0q+Dr16BH9/+tf\noXv3SLUC+r3YldXdin5TNEIQbme3t1awP6/zN05PmNoANrI9Vp+yKUVr1qxhxowZTPrJT+DMMyPl\nqsGrTTs7vBJVnfBKVPsgCNvBCzQIgrA9yq0obrsNZs+OPq9YAffdlzx/yy3w5UiNSBKpBj2JEqij\n4PtyUm1ynzSQ9koTCpaAHLKgkeh8s6Q8yJHH1RhLjZhJVFq8qWaADcDfKZrzDCgj0GancBuvL9yf\nfbeUbpFzI5dI397j65dIZrWbbspfqJz3rtG/r39WSTBoEHzrW0XSUynMmQNHHQWrV5ec+s4B13Dt\nvt8p/G6PcQIn8IS23iEr+Mbz34BDDy3JJw0rhBI1SbcBscfOivnz57No0SJPoqoML7/8Mj179vQk\nqpUQBAFhGJb4ZnglKi8uuqj4WfiWvPBCZN778MOEn4lwtjWqUqpqdCdQX8NbtcWl7gJv1dZFapQO\n9cQ+VfG+a4WAnpJZzwTTOXXbF02wRZrj1XlMds9XhtbEFnId32RcbK/qx2r2jZf0L5d8j/7G4Xw9\nvNGc98knl5pdXTFlCl8XZqy2xoEHRm3olFPg/Vhae+89AH722nf52YBHI7PlHsCzzwKwmc6spC8/\n5iJu4VNlO3kXlChPoqoKXomqTnglqn3gSVQlEATwt79Fn2+/PUmwJIRhg9bHuEA05FV1dxbNeqNp\nKsQEEquxUiFMdRCTqZlFUqVzmLY5ZcvQOaPvUwMbJkIvt6pFdSp+7MEGzuQBerGucKyWpVzGL0su\ne5WR1HNfgSBcnFbO8cfDO+9kqNgOhH32gddfL35/6SWYEIfJiIlTAf360W3ZMnbv1o2bgZsrUHzf\nvn0ZP358ekKPnQreJ6o64X2i2geeRLUWVq2KFCota3JAvJFsU/1oRtQ2JwIrOkMQnjqS28zYVrmp\nkJ3OTWEERMTyXholSkK3sIWe29fDfPnoq1zKPfyA28wXPvNM4eNB48YR7rprSqWrFIccAm+8AcuX\nl57bd9/IF6+C8EpUdcIrUdUJr0S1DzyJai08+CAcdxw8ZY9aXUBJSATg/gYYVwNX5ChfjSElzIau\nS/115MpEuNS98zQYvHUZbywcQ//tpT4+Mm7lzMT3Lz/xRTj6aOs1HQr77Rf9tQG8ElWd8EpUdcIr\nUe0DT6IqjYkToxhAS5bAv/5VcjoMIRhpuvhFoqjm0h57sxp4dOknGF1b9IvS7mUnkBbh3CVCt5o2\nzblcUaIO3fg831v9Y7qFmwtJjt44ja5sBWAVfaSLt9K/Xw307g1/+hNfzuEA7dE68EpUdcIrUdUJ\nr0S1DzyJqjRGjYKmJsg1I5igfH8RGhugsYZHajWRqVUTm87kZtu8V8AxdpIZNQQczsm7PMSgre9x\n2wpDAFKA886j/x//6FCgR3vDK1HVCa9EVSe8EtU+8CSqNbFxI2zZAl275s+jGWjEvCJPEKpxyncZ\naU7jqmN7BgRsp+de73Pcgt/xl3cfTZy7tc+X+MvaMwB48gmgc2c47LDshXi0C7wSVZ3wSlR1witR\n7QNPolobu+0Gr7wCI0YUj+liMqnO3wXTHsUtWkC7vUchjWk7GLGpcT1QX6PfMkWui1pHAwK28xKH\nMH7BK4njt/F53mMQP1l7JRvo6Tek3UnhlajqhFeiqhNeiWofdGrvClQlevSI4vsAfPBBFDhRQjqp\naCAiUHFsJx050u0JZ9oOhmhT41G1cyNCJQJuygE6VVh8oI7lKR7a5RSe6X4M44kI1Id0ZSX9OY8/\n8gVu40rOYn3oCdTODKFEeVQXhBLlUV2YN28eCxYsaO9qdDh4Jao1EATw0ENw+ulR/Kh774VjjgFp\naX569INYlRIER6hJ1CTJkhysU2ze6+IHZdvMWFamFEVqHDN5iuOiIOUx5jGCUfwUmEwYwt1y/T12\nWnglqjrhlajqhFei2gdeiWpN1MQr5aZOjbYGySrL6NSg+pZoW5gLKVWQBPmxKFLJvKQ/VZkSeddF\nf91GtDBg+PvM5COFy6/udzmT+DtH8HdguledqgxeiapOeCWqOuGVqPaBV6JaE9/9LjzyCKxbF0Uy\nf+st+L//K0hQBTXKtgGwTi0SW7vooK7cmwWMq6Gpfmx0XaPhOlmZmiUdA66eczmXz70mkfzH/a7k\nP/v/J9tWdwE2MHWqPU6Ux84Hr0RVJ7wSVZ3wSlT7wCtRrYlx46JNiocNi75Pm1aiRoUh6U7csygl\nP7Jvk6pIifxUZcpEoOS0wGk1D/LXf53Og/88jQf/eVqCQG0KavifPl/k+wN+zLa3uhCGsGpVC9On\nT0+5CY+dDV6Jqk54Jao64ZWo9oFXolobw4fDggXQqVPEmJ58Mopk3snCX3WkqhGijYVbisdURUq3\nyk4oUinbu3Tb2sKJTY/Rc8t67pl6njbN3nvNZ0HXvQnnwZek4zU1NUyc6JWoaoNXoqoTXomqTngl\nqn3glai2gtjX7MQT4YknlJMzpT8VMwsbEtOIWU0aR9FPSucrNUvzBxCGdNq+jUuev4m/3X16gkD9\nx4E/57QhD3LakAehsZF33okIlIqWFq9EVSO8ElWd8EpUdcIrUe0Dr0S1FW69FT73uejzSSfBddfB\nZZcBEIYNBIEgUOL/i8nrmxuS8aJkyEqT8GkyqU/Ssb6bV/PqkwcxbOOiRJJ79jyHf/fel/8e9S0Y\nHRD+2X5rXomqTnglqjrhlajqhFei2gdeiWorXHgh3HVX8buyMXEYqiEBJkh/MRrRq1EpprrEtcC5\nH97Nn989i9f/vn+BQG2jE6s79eWIo6dz3oR7uGrMDwjvTydQ4JWoaoVXoqoTXomqTnglqn3glai2\nxAUXwMCBcPLJ2tNJRUpAIlfNSOELNBsNC8gr7MR1sZ/Uoc3PczfnJ5L/pecnOXP3v0RfFkP4TNqN\nJOGVqOqEV6KqE16Jqk54Jap94JWoHRqagJX3E6/Ww02BEmiGsc2v8jwfLRz6PLdxBg/w+fW3R0Sr\nGa3PUxq8ElWd8EpUdcIrUdUJr0S1D7wS1V545BE46qgo7IE2dLku4vfM6LhJfTKhDs5tvjuhQH2L\nS7mjcFE/IHssUAGvRFUnvBJVnfBKVHXCK1HtA0+i2hoHHQRDhsCyZfCPf8BnPws33AD9+wOySU+Y\n9VQyNVPZqLiIPvt9wFVPfZ/dFq+IDqwunjuH+wqfv821XMe3i/kxU+OT5Q6hRE2ePDl3Hh47HoQS\nNWnSpPauikcFIZSoI488sr2r4lFBzJs3j379+jFmzJj2rkqHgidRbY2hQ2HpUhgxAubPhz/+Edav\nj5zO+/QBTL5REBGq+LgSS6rn9nXc/NJXOX/h3fbyH36Yn598Mj9P5FkevBJVnfBKVHXCK1HVCa9E\ntQ88iWoPBEG0/ctHPgKrVsFf/xrFkbqvqBZFRCotoyLRuuntmzg/3vp3Q+cefH7g7YmU915P5NR+\n7LEVuokivBJVnfBKVHXCK1HVCa9EtQ88iWov7L03PPtsFL182TL4059g0aLIxNe5MwDhM9NYecyZ\n9GJdfFEIyMyq6MRUwxYA1ga9Oar2WRprik5SeZzFs8ArUdUJr0RVJ7wSVZ3wSlT7wK/Oa08ccEC0\nt96QIdH3f/0Lzj4b3nsPHnsMjjmGAayihs3x3xbps/i+pUCg2G03+ix8g1kLxxHOo/DX2vCr86oT\nfnVedcKvzqtO+NV57QOvRLU3dtsNliyBMWNg7lx44AEYNCiKcC5w3XXUfPOw+EukMLVs0uTVpUtB\nxWpLeCWqOuGVqOqEV6KqE16Jah+0G4lavXo1YRgSBIH/H4Z0/tOf6H3ssXRauTJBoDZcdRWbPv1p\nlk3pTv/+jcDzrFw5ltUbdox6B0HA6tWreeqppzj22GN3iPr4/5X5/8477zB9+nQOPfTQHaI+/n9l\n/jc1NTF79mwOOOCAHaI+/n9l/s+aNYu+ffsyZMiQHaI+1fS/f7x6XocgDHMGByoDQRC0faEeHh4e\nHh4eHjkRhmHJcq92IVEeHh4eHh4eHjs7vGO5h4eHh4eHh0cOeBLl4eHh4eHh4ZEDnkR5eHh4eHh4\neOSAJ1EeHh4eHh4eHjngSZSHh4eHh4eHRw54EuXh4eHh4eHhkQOeRHl4eHh4eHh45IAnUR4eHh4e\nHh4eOeBJlIeHh4eHh4dHDrTL3nlBMCCEVe1RtIeHh4eHh4dHViwIw3Bv9WA77p13SyuWMKEV85bR\n0PpF1LV+EdS3QRkA49qgjLa6l/qWVi9iVO3cVi9jBM2tXgbAaJraoIzWf15tUQbAqDZ4XnvMX9nq\nZfBa6xfRZuXMaYMyoE3uZdWbrV/Gi1tbvwyAl9qmGP4T/d553pzn4eHh4eHh4ZEDnkR5eHh4eHh4\neOSAJ1EeHh4eHh4eHjngSZSHh4eHh4eHRw54EuXh4eHh4eHhkQOeRO0M2DCtvWuwc2H2tPauwU6F\nldPaaglVdaBx2gftXYWdCtPaalVblWDauvauwc6F+e1cvidROwM2TmvvGuxcmDOtvWuwU2HVtNfb\nuwo7FRqnrW3vKuxU8CQqG6atb+8a7Fx4p53L9yTKw8PDw8PDwyMHPIny8PDw8PDw8MiB9opYvgwY\n3OYFe3h4eHh4eHhkx46z7YuHh4eHh4eHx84Ob87z8PDw8PDw8MgBT6I8PDw8PDw8PHKgoiQqCIIT\ngyD4dxAETUEQfMeQ5sYgCOYFQdAYBEF9lmurDa73HATBwUEQbAmC4Azp2DtBELwaBMGsIAjaaiPr\ndkXa8wqCoG8QBH+Jn8sLQRCMcb22GhEEwe1BECwPgmC24fypUhuaEQTBx6RzHbF9pT2vAUEQPBr3\nXXOCIJgineuI7WtoEAT/FwTB6/Hz+LomzblxO3o1CILngiAYK53rUG3M8Xn9R/w8ZsZptgZB0Dc+\n16HaWBAENUEQvBg/j9eDILhak2Z0EAT/CoJgUxAE31TOtU37CsOwIn9EhKwZ2AvoCjQC+yppTgL+\nHn+eALzgem21/bnec5zuaeB/gTOk428D/dr7Pnak5wVcC3w//jwaeKqjtq/4vo8A6oHZhvO7SJ8P\nBJo7avtyfF4/BH4afx4IrAS6dOD2NQSojz/3AuZq3slDgV3jzyeKPr8jtjGX56WkP9n3YVEfBXQG\nXgAOV84PBD4CXAV8UznXJu2rkkrUIcC8MAwXhGG4BbgPOE1Jcxrwe4AwDF8Edg2CYLDjtdUG13u+\nBLgfeE85HtCxzLEuz2sM8H8AYRjOBfYOgmA3x2urDmEYPgestpzfIH3tBbwvfe9o7Sv1eQHLgN7x\n597AyjAMt9Jx29eyMAwb48/rgDeBPZQ0L4RhKEK8v6Cc71BtzOV5KTgHuDf+3FHbmOijaojaymrl\n/PthGL4CbNVc3ibtq5IF7AEskr4vprSBmNK4XFttSL3nIAhqgdPDMLyVqEHICIEngyB4OQiCL7Rq\nTXcMuLSRV4EzAIIgOAQYBgx1vLZDIgiC04MgeBN4BJDNCx2tfbngt8D+QRAsJWpr34iPd/j2FQTB\n3kQq3ouWZBcBj0rfO2wbS3teQRD0IFLuHogPdcg2FgRBpyAIZhFNYKaFYfhGhsvbpH11aa2MHaES\nA48kfgnItm/5eR0ehuG7sdLyZBAEb8Yz6Y6Ma4AbgiCYCcwBZgHb2rdKOzbCMHwQeDAIgiOAPxCZ\nQcG3Lx0uB14Nw/CYIAhGED2XsWkXVTuCIOhFpJZ/I1ZYdGmOAS4kMpkKdMg25vK8gFOA58IwXNN2\nNdvxEIbhdmBcEAR9gCeCIDgqDMNnHS9vk/ZVSSVqCdHMX2BofExNs6cmjcu11QaXex4P3BcEwXzg\nLODmIAhOBQjD8N34/wrgr0RybzUj9XmFYfhhGIafC8OwIQzDC4BBRHbxjti+MiHuXLoEQTAg/t7R\n2pcLDgf+DBCG4VtEe5/uSwduX0EQdCEiBH8Iw/BvhjRjgd8Ap4ZhWDDHdMQ25vK8YnyaoikPOnAb\nAwjDcC3wd6Ix0fWaNmlflSRRLwN1QRDsFQRBN6JG8JCS5iHgswBBEBwKrAnDcLnjtdWG1HsOw3Cf\n+G840Yv3lTAMHwqCYJd4NkMQBD2B44HX2rj+bY3U5xUEwa5BEHSNP38BeDae6XXE9iUQYFB8YzVF\nfG4ACMNwZQdtXwLG50Xkw/JxgNiXcxQRSe/I7esO4I0wDG/QnQyCYBiRSeozMfEUxztqG7M+L4j6\nMeAoQCZZHa6NBUEwMH4Wwrx5HJFDvfES6do2a18VM+eFYbgtCIKvAU8QkbPbwzB8MwiCL0anw9+E\nYfhIEASTgiBoBtYTybvGaytVtx0RLs9LvUT6PBj4axAEIdFveHcYhk+0ScXbCY7Paz/gd0EQbAde\nBz5vu7ZdbqQNEQTBPcDRwIAgCBYSrS7rRvF5nRkEwWeBzUTv49nxpR2ufYHT8/opcGcQBK8Sddj/\nLwzDVfG1HbF9HQ6cB8yJ/VZC4AqiFWTimX0f6A/cEgRBAGwJw/AQOmAbc3xeAKcDj4dhuFFc20H7\nsN2J+nPhIP6HMAyflvv8eDIzg2ihx/YgCL5BtMBoN9qoffltXzw8PDw8PDw8cqDDLC/18PDw8PDw\n8KgkPIny8PDw8PDw8MgBT6I8PDw8PDw8PHLAkygPDw8PDw8PjxzwJMrDw8PDw8PDIwc8ifLw8PDw\n8PDwyAFPojw8PDw8PDw8csCTKA8PDw8PDw+PHPj/HTpLhXl+THMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa806665450>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cuCap.Plot_basin(cuCap.CellSlope, ruta=ruta_images + 'Map_Slope.png', lines_spaces=0.01)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"El mapa de pendientes muestra como las mayores pendientes en la cuenca se desarrollan en la parte alta de la misma, en la medida en que se observa el desarrollo de la cuenca en la zona baja esta muestra claramente como las pendientes comienzan a ser bajas."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAAESCAYAAADdWICBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXt4XVWZ/z87Lb2kKbQQCCCFFAg9KW3R2HiBaQF1GNoR\nTIvoTH9cFUVAGAdvLTOCdNRWdHBELiLjcNOigDSjYhUBsRVlbEEgwSRGSCAiBFKoJfTenN8fa6+z\n3/2etfbZJ2lJW/b3ec5zztl77bXWXtfvet93vSvI5/NkyJAhQ4YMGTJkKA8Vw52BDBkyZMiQIUOG\n3REZicqQIUOGDBkyZBgEMhKVIUOGDBkyZMgwCGQkKkOGDBkyZMiQYRDISFSGDBkyZMiQIcMgkJGo\nDBkyZMiQIUOGQaAkiQqC4KggCP4QBMFj4fffgiC4JAiCK4Ig+Et4/bEgCE72PL9PEAR3BUHQFgTB\nU0EQvFPcuzi83hIEwVJx/bthWnPD//cEQXCquN8eBMFl4v/dQRA0DbYQ3ozYWfWa9HxWrzsXO7Ov\nhvc/HQTBQBAE+4prWZ3uZOzEvro4CIIngiB4PAiC+4MgOEQ8k9XrTsZOrNerwmuPB0HwoyAI9hbP\nZPW6o5HP51N/MKTrr8Ak4Arg0hTP3AKcG/4eCewd/j4BuA8YGf6vDr+PDuMeAfwwvPZpYGn4e1/g\nUeAnIo3ngQPKeZfss9Pq1fl8Vq+7b52G/w8Bfg50Aftmdbr71ytQJcJcDNyU1eseUa/vAyrC30uB\nJVm97rxPueq89wFP5/P5nvB/kBQ4ZMCz8vn8zQD5fH5bPp9fH96+IKy8beG9vvD6dmAcMAqwnkB/\nCxwX/j4W+Amwf5hGLbAhn8+/VOa7ZIiwI+vV93xWr28sdnSdfgP4rHosq9M3HjusXvP5fL8IOg5Y\nG/7O6vWNx46s1/vz+fxAGPQRzAIIsnrdKSiXRH0YuEP8/2QoMvzvIAj2cYSfDPQFQXBzKJb8ThAE\nY8N7RwGzgyB4JAiCXwVBMBMgn8+3A3sBvwauD8M+ChwdBMFITEX/FugIgiAn/mcYPHZkvernJ0BW\nr8OAHVanobi/J5/Pt8gHsjodFuzQvhoEwZeCIHgOOAdYAlm9DhN29Bhs8RFgBWT1utOQVmSFKfyX\ngf3D//sDQfj7S8B3Hc+8HdgKzAz//xdwZfi7Bfhm+LsReKZE+quAdwIPAvtgJFkfBa4FPj7cIr3d\n9bMT6rXk81m97j51CozFrGbHh9e7gP2yOt2969UR7vPAzVm97jn1Cvwb8KMU6Wf1OoRPOZKoOcCj\n+Xz+ZYB8Pv9yPqwB4CYMEdL4C2YFuyb8fzfQIO7dE8a1GhgIgmC/hPQfBmZj9Ph/wwzsxwLvJmPL\nQ8EOrdeUz0tk9brjsSPr9AigFngiCIIujGrg0SAIDkhIP6vTnYMdPQZLLANmlkg/q9edgx1er0EQ\nnAPMBRakSD+r1yGgHBL1zwhxYxAEB4p784FW/UA+n+8FeoIgOCq89F7gj+HvZuA9YVxHAXvl8/m1\nOg6B3wHnA0+E/58E3gUcms/ni9LOkBo7tF7TPK+Q1euOxw6r03w+35rP5w/M5/OH5/P5yZjB+235\nZDuJrE53DnZ0Xz1SBG0CHi+RflavOwc7ul5PxtgvnprP5zenSD+r16EgjbgKqMSIG8eLa7dhCvtx\nDCGqCa8fBPxUhDsGWB2GuwfYJx+JMG/HqPXWAMeXyMP+GMO4c8W1XwE/G25x3u762Un16nw+q9fd\nt05V/M8Q7s7L6nT3rleM9OJJ4A/AjyixCyur192mXjuBZ4HHws/1Wb3uvI/Vu2bIkCFDhgwZMmQo\nA5nH8gwZMmTIkCFDhkFg5HAkGgRBJv7KkCFDhgwZMuw2yOfzRf67hoVEAWRqxD0Hr776KldccQXX\nXHPNcGclww5EZ2cnd9xxB5dffvlwZ2XPRFcXzJoFvb3x69u2me8PfpDqu/+J9/IHPswfzLVgdCHY\nlHwHR4f7dLaGQ/leI4GPfQyuvx4fHnnkER599FEuuuiiHfYqGYYfy5YtY+LEicyZM2e4s7JHIgjc\n/k+HjURl2HMwevRoZs2aNdzZyLCDMWHCBGbOLLXrPcOg8NhjhkBt2OC8/QgNHHv3NeSp4E724U5O\nAKbDiBqoN2FGD2ziyadmcBSd7EVIvLYBN9zA975tnM2fsQA45RT48IcLcdfU1DB9+vSd9moZhgd1\ndXWMGzduuLPxpkNGojIMGZs3b2bVqlWcfvrpw52VDDsQ69atY82aNcydO3e4s7Jn4dln4e/+DjZu\nNP8/9jH2+p/rYkG2MRK2Wy8SlvC0ADWFMJsrxjBlRAcj2Qb1sPf29bzUdgAjGOCM/PdNoO8D3/8+\nVFYWnns1n6elp4fZs2fvlNd7Q9DZCe3tcOihcMwxw52bXQKdnZ1MnDiRqVOnDndW3lTISFSGISOT\nRO2ZyCRROwHbt8Pb3x4RqDPOYO//+Trbgr1SPDzdSKGmhH87gCBgG3tBAK+M3I+ZR67h6E1PAVA1\n0M+3/3qBCXvqqYVYZhx0EP0/+MGOeqM3Hq+9BjNmwKZN5n9nJxx5ZPIzbwJkkqjhQbY7L8OQYSVR\nGfYsWElUhh2E9nY46CBYG/oUPu88qu64gdeCvePhtvWaj8bImohA1WPcY9bHgzz+1rfx/Yln8P13\nncGN+32ChdOW8JPx7+cn49/Pz6qMrczIF15g5vHvY0NQaSRU738/7C42qr//Pey9d0SgAOrq4H//\nd/jytIugs7OTZ599driz8aZDJonKMGRkkqg9E5kkagdi9Wp45zsjsnLyyQS33ARuW9U4RkYqPDow\n5Kkp/J8Dloe/69U38NWOhfAP4XP5PL9uPZ7ZrKKSrcBW2Ajcey8/GPHPbGQs554t0q2ogI98BI47\nrrx33Vn49a/hhBPc95qa4Ec/gvnz39As7UrIJFHDg2FxthkEQT7bnbfnINudt2ci2523g/Dss3DE\nEUaVB3DRRQS//ha0JzAoK4kaGRmScwtU5fpSJ9vfXg1LMATKIp9n7B9/Dfk/QMX59GyfxH68khzR\nihXF18aNg2OPhREjUudnSPjzn43EKcQXD7iCK2d/kTOevZ3bV58VhVuxAkaNMjZno0a9MXnbRZDt\nztu5CIJg13JxkGHPQSaJ2jORSaJ2ADZtgunTIwL1sY+x96++AiPEWCwJk4UlT00YaROGQNVWdsWi\n794wOTn9RcSJVBCwse4w2FoB4yo5btPDvHvD7+CF+GON+dVcmL/B/PFNytdeC2+Em4S1a0EYS39p\n/3/jqv0/B8Adk/6ZPAHfW32muWnz+vnPw9KlOz9vuxAySdTwICNRGYaMbHfeLoL1680K3NpF7LMP\n3HMPDJIIOXfnffSjcPfdsN9+ZtU/ZYo/gjc7nnjCqMJef938/+hHGfPba9g8Ygy0OcJv642IlDUg\nz5lPVa6P/vZqWpuro/BtFNlEFZCDqiYjteqfV21Ufh1hnGt74dUW2D6bjjE5OsbkYF+iPNXD7X88\nk2Agz2S6YBzmE77Gyf2/MD8++Un+9snL2GdvYOxYuOUWOPnkckspGb/5jXEFEeLafS/i8prF5HMV\nUA/bGcn3jz6DyZVdHNf+MCf3hnn76le5/arnOXPg9h2bn10Y2e684UGmzsswZGzYsIF77703I1HD\nhR//GH76UzPhtBXPzrMOX8lvxpmJKP+kunnjjfDoo85oN27axMsvvcShhx4aXbzppuj3yJHwyCME\nS99O/q6hvsQehkcegXe/O/rf1ETw0+WG9MgqkgbkmkDNC6+3h99tRESogxjpASKjc4vw+aqmPvqb\nqyPbqQO7YH0PbAhdHEh1n47TYkp07X3P/JKf3vF+Rg9s0W/NdyZ+jI9/UFw4+eTy7ZTyefja14wK\nT7S3myaex8cPuSluXC/RBtOeaOH3f34HY/PG8Pw7nMHHPzbW3J81C848s7y87EZYvXo1B/7mN0yy\nY8DIkcbx6tveNrwZ20PgU+dlJCrDkJHZRO1k9PZCa6v//vveF/9//PFmAhfqjPdOvr/w+wE7L61d\nG3PCOBhsCkZz5Jw/83zPIcUE7c2ME0+Ehx4yv//1Xwmu+U+wHo81kbLXIFLf5YjI01Lc5KZFqQFd\nUilphA5GtTf+ERh4FE66KCJWlkj5SBTEyMuYrRsZtX0L3Atnjrqdax+/2PFAiPvv999z4amn4F/+\nJXbpsoovs+Toy+J5cZAoOmDMwEZef2ocFTjmmNWrjYsJj/fp3RJbtsAjj/DAz3/Oe5csid8bNw7+\n9Cc4+ODhydsehMwmKsNOQ2YTtRMxMGCcCeqjQVz42tdgwgSYO5dxb9nEF4I8C/NfBeCBLkG03ud4\n9sYbAfj4BcBBGJ+O216Dlm4IQmePB5mvzlF1nLnudj7y6s2MyW/mjz+bSs2IXoIZYzMiZWG34F9w\nAVx5JXwrYdL2SZIgIlBWYtVW4yZhPrRRUO31t1fDIqgcsxc1fSN5eWYf/cur42m3qW9JVJqj/5vq\nx7Jpr7FwGnznqY/TO6aGiVteNTd7YczAJq55ISRCmuSXgY9X3MhrjKe5vimeL5k3pdbc1DGWhhGP\n8Y7872FgPVTszXcGzjc3Gxvhl78cUp52OXz+8/Bf/8V7xaXlezcxb32zUSUffTS8+CKMHu2NIsPg\nkZGoDENGZhMV4ic/MZOm9GEjsX49HHCA/74LW7YY54IA73lP4fIDD26BINp99FuO5fJFn4meGwn/\ntu0SJgTrqKvshEpAnzDyuonjjuCf+e6155lrFRj7mMOB1zqh9Q6o+Li5J3jc7/LvpiIY4Jz8rezN\na7y0/QCO2/gwwYwZb24itX07nHSSUeeBUR+NH18cTpITrZ5ajt/WSUIaomsiJlV0y6GfaqqajGF6\n1SMPsL7laWpnN9A6rzquLtQETZIpm4aNO1QXbs2N4u720+PPdMCE7es4/vVfm2uy7VWK3+5Tbxig\nghuCC1heEaoCrUdDmz+bLxfxrIcn2t7KE8FbC89VsoH/GvhX8+fv/x6+8x2j6trd8c//DMJx6gNj\njuHBLadz9euXcmNwPmflb4d164wkauVKQ6gy7FBk6rwMQ8ab2iZqyxa46ip44YXEQ1+HipXM4viR\nK6ML0gi5FLSXawufSokw/OaX4cnV8Lz/2Jfm7R/gA/kfA/Cpg77BN6s/BW2Q35oua3scurthcrhj\nbt99oaOD4KDq4nC2TmyZW/WdrBNp9+SrbxcZcyHc6VeV6+Pg3t8wsaeFfWebCXXFsvnxtG26WtKj\nVWjCeB1ClwpgJFYyLgmXMXwaqZrrGdmuLbRaUuATAzdww8CF0YULL4SJE+EznzES3N0NW7cW3Dj0\nV4xj5ltupmPM0TAmMiy/t2suc/uFi4oLL9SxuFFZaVSqhxyyI3O8WyOzicqw0/CmtIlau9bYbtx/\nP/zHf8TvffvbcNppAFQfaC6trmhk8tZuAK6Y+kWumxNuDf+ZivdP7uReYV/ywSAPGEhLonTY1zrh\nD3fAK5f7VUj5PLcPnMkZ+e9z996nccak77G5Y0xGosaNM21k9GiKTnTRUiNJVlyG40lwGYC77uei\nS2MP/jkTnnqQ/S6KL3q6N0ym/+yQCGnyo/OagzkL7okFWbVhtjFgh0i6BX5Cpe+XQgk7LcAQuIR4\n3zPwAA8MKFXeTTfBeef5033+eXj66fi1t77VeE4fTjzxhMkHMPboDWxavxxGTITxoZuHKUA+z3Xd\nF3HhozeUH/9xx8FXvlLeM/X1sP/+5ae1GyCzicqw0/CmtIlqaIDnnotfu/Zas/X/tNMIKsOZM1wU\n/v3mX3LSuPt4beR4fvSW09j4bKWZVEYSH+x9pjNyonXdSzsRlYNRE2CscI/gSicI6A0Pxf3g+h8x\n8JcKPsydBEEv+XxKSdmeiOrqyAallNTQkiefywL9vPQrleTmwEGgADY+PoWNVZW88Fhjse8p61dK\nkrEwnqqFxY4+J9MNQBe11FZ20d2E+d4w2UimrB1VGxE5LIckSrje1cZn4VosCDwYvIcPVDRzCH/h\nQwN3cjwrufjyjXzLx6HWrzdOPu1ZhxYzZxoj9eHCQw+ZzQvAporRbKofC6/UwchxILnd1IBFhy9h\nzT/OZOzvN4JWtb8ofocLvkv+eg1T+BM8/LDZpFIO9t8f/vpXszPwTYI3z5tm2GnY42yi8nn4wAeS\nB8kXw9Fn1iwzYCxaRHDSDDOx2V3UYsB/evSR3HDEkXEyNJQVuO/eYAmVK40t62DjGmBuYtjbN57J\nR575HyYOrOOwLaGPqrSqxjcDdFlI422XcbRW48lvV3yloG2s/tILL7TAc7Ppz1XTmjPSo2kNq6Gh\ni9Z5jSacIF+WbE2ip3Cth0lGFRiGm9awmlmVRuU8qbKHnoZJtGKIWv/S6ohIuSDz52u/rrIq101Z\nEPDj4AMA5PLtHJ9fybdeuASuqzCOQzdvNjZtfwpFwi9GLGMlsziAl8jRAWvW8EJwEAfVjjGLp3/8\nxzIzMgTcfLM5jifE5UcvNuXR0gkvT4S9p8bKc/0/7cPqhum0PtZoSK2U1u1HETn96fj3860/XcyE\nseuS86Hs2WazCl5+2ahIq6rMxcZGc67hnrQbUiEjURmGjN1OEpXPww03RAOlxosvGiPxElgz9u00\nrltpBqFVRL3JR3o6StxH3C9XlZMkjfBNNKUkJFYSVSKdJ8a+lZMn/5z/e/pdUZidIRnb3aEPFXYZ\nhkO87EoRJp9NlCYc0kD8xRrYOD0i8mHYVgx5mrYgWjxI0gSGOMWkTM0UbKVaaSzEUZXrY1blSiY1\nmOdXLZwdqQp9+fdd021pWy+E0s+CJMralJVhb/Vo8HYKXhA++Uno7IQnnzQG2Ap3Bqfz4Wl3MjK/\nlfY/5ThiyzMcxIvQjTnAWblkSIUJE+BTnyrPHuuOO2IE6pKDvsm3plxi3nN9nVEjQ7y+m6O6pYlI\n8okII/DcqMP4wLQfJ0s5LUT5/mrbCZzAr6G/33zAjKO9vXDggenfcTdDRqIyDBk7TRL10kvFtgg7\nAp2d6Y6r2HtvaI+MOw46+GXzY8T+UAcvjTzA/VzS4NMh7jURXxW6nk/ybO1LJy2JGVkTJ1KabFlJ\n1N5+w/IijEkf9E0HFyHSdVjKkLxcuEjFn3phYwu8Mrv43jzozhnD+NrKLnqYBBgy1cMkI83Q5/HZ\nZ0Wb66+vpmfxpML/WZUrWXVrSKTS7DxM8x716p70rSWf86jAb207h86gjoe3/5259s1vFm53MpnZ\nNJu+DrzIgdAG2+r3or6ujf22r+WDY+7mW49fUvRsWejqgk98IvofBMbOaYyjIz32GCxYUPg7t+Je\nVrw8N6qLsZ2wVyiJstfsdzOwMPw9j8iD/VAhyvc9Ix6khl7e+Zb/o/m5cOvmiBHGSH0PRkaiMgwZ\nO0US9frrcOSR0fb+nYVvfKPw81NXEdvGf//r7+Opg6UxdzipbSccrPuiM860+qVNTYDa3451gOiy\nDUmS/NQDLeK/S7XRoa4NVjI0agLUzYT1JcJNAdYCku8OZqJ8M8FVPtIfVFoClVZaYNtAB9BdA0yH\nlxxhl2J8R9VTUPMBdDdNjg40dkHbdHVAa1so/VgEkxp6qK3sonVRdbRwsLZRpaDfT/a5NO0sYUHy\n2+A4mriZWnqgYjwMvEaegHt5Hy9SA0FxPWytGMWL9Qdx48D5rNtrAvv9Za0ZNwbCsapCuLSwj0sh\n5MBrfJ0rGcl2uO0285GYMwd+pnacrFgB4vil0yvuZMVAQ+T6AaAqtIny2ZudjbF5yxF3WWGliRZp\nJeYS9ZBvq+DF+oP4W/8+0fVf/nL4DfB3MjISlWHI2OGSqCefhNmzIwL1rnfFbv/uEfFnrPitbD+L\n7gvkg4Drj76Q7z98RnTxOIoHINlD5AQnbVWsA0SIyJO2YdEDvh24tJNDSX58E4yWINnw8rd+Vqad\ndgW6ZR28ugZGOCRRPhVhGS6w9ihcfbWRRmyNb0sMZlBMYn0Eakehnsieyaq4pPE6vZBvgWB2lLYr\nT+1EjjqtTRM4CVMhXShWKzbDCuYzp+EeJjX0sIL5UbpDgTRYl8bz9rernTsI1f+OPMf0pwFHeNnn\nVRltrRjF9w4707T5l4EBh/QwFF7HyE4F/Dr/fr4+8Bkq89awaCv1dDKB9YYwyaOWAHoiteqlfJG7\nK043ccoy/79OszvvL+LsPK1CXlJjFnDzxLWFRJ7rbVylxgiPf64YTjihYPy+JyMjURmGjCFLovr6\n4LrrIj36178e3TvlFHM2XIhgL9y2R3olZQfJrY6wFoc5rlkJkWuAlwOky1jYru7axH05iOnJyg5U\nlkzJFbr91ruPfIObDCcnNz3B6YnPwjUojpoAE0NJVCmD4N+Yr3du/D1nvXort008m2CG46y+PRH/\n/d/w6U/HLi3f+jbmn457QkqSoKSRQGlplY1PtoGQAJEjUt3YNn1kDWydbg4VlpDtJxfZRrUuayx2\nHeDLv24nNmwzrMoZ0jatYbWx0dmRxNGq8nIJYcqVjrr6sIUsa/vdUhys8Lyq18eDt/G+EQ/EwlSN\nqKRr+2SqWRsjTRIf52vcNPIzxTc6gFF10D3Ov8NXhhUEubayy9RHuwrj2+mopdsldkTu6chIVIYh\nY0iSqM2bjQO4uxwn2J5/fsyBZZG/HR+0dEf+TpLITCG+g2gwg7yNw6Icu5YmR5580PFKR4hycLOT\nn0tFOAVo9uSvHli7Dp5eA1NL20T9LbcP/Mr8vvUv53DfMSfx4nMHEey1BzrefOEF4zsI4Jln4p6v\nV63i0PMO5S/ThJNCl52TJiJJKld9T0/uPvs4Oynqw4o39MKmFhinbKIUujdMNu4PXD6f5H+XytmB\n/qXV0ATduZBILWqEcxKz4IZP3S1tomw/lgsVbUyt38VHmnx1JuMGmC7qwWUMr/us6q/9wXgOHfEc\n1RS7kgDYxBheDjx2mFOA5zqhayJs3y8uLdfvIdNsr6ZbOE0tbBiQCzhJkuQiM8luE2DNGnjlFeN0\ndg9GRqIyDBlDkkR94APwi1+Y33vvDf/+7+b3uHHsc8n/Y/13K9Lt4JEDpFxRt6iBRNoq+eJwqdlK\noV6lW+o5OTDZwUkSuHJWzfI5G6eNz+alDWMPIfNrw+prFmNCSVQp5KCjPcdph97Nj577IACV2z3n\neezueP55qK2FbduK7zU3E5z4d6YcXRs/XdJLO7lKKaZEUtuXamSIt9l5GEIhvYfLfIyZ7oi4GN0b\nJsfz6/qt009CM/Q3VUNDl3F9cEv14IiUhI88ariIFLjLRxKQUn1R+r6Sz9h4bXySSBURaBNm48ga\nejg0OX9QvLmkHuMnKtDixQSE40L/vOoCiarK9dGfE+4oZB5cuz+hyARiIB/qLvv7jY+t5593G8rv\nIchI1BuJn/4UPvtZc1QIGLufm28e3jztAAxKErVpE5x6qjE8BHjLW+C++2Cq0ecHe1FwVFmk3vJB\nEpNCh68pnqwgIhbadkmqRdIQqaSVadJzeoWsV7lWLaHj0JIumwdpTA5xmyv7ntYewtrMtKs4NDaF\nNlEHpdudd88+p/H0qMM5YsszPH7fW5l1+CqeqH9rqmdT4bLL4Ic/jF9raIA773xj/NCsXBl3Pvj2\nt7PmUcgTcEPFBdz8QeN/KHHXpL1vYSfYNjG5uuoczIIg6bw8mabcfWXjtPe3OSRRcoIM1YD97eJc\nPV+7K/V+HrS2Nxp1YUMXrbc0xg3Wd6RayKcK13WkxwaLNDaKrrSGCtkOSkrNwt/9nWbTS+woYqtj\nnB7FBfF3WSqO7LEq4LSLOEddr6aR5UET8/LNRhJ1xBHwwAOQS9K17r7ISNTOxpYtxidRby8sUVtb\nnnnGOCUbP56vLAXCdnyZ9p4bBDBvnvGSuwuibEnUSy/Bxz8eEaj99jOuBEIHbcEMIrEx+CVGWkXn\nEt0XCE2N+5lwBei1L5GEKO3Aoicv1ztIyHfV40wZE1MMMnwT0FFTHEcOtw2LNTp9dALMmAkOoYsT\nU6Bl7XSO+OszjB/o5/E/v423H7mG4PS3k3doa5145hm49dYiA22guP+E4W/d9xye3+stAFx29VQ4\n44zicBYbNhgV8SuvpMyQJ/3zziO45ab4CKoJuryG45qUVMgwkvTI+ilISJREy7bVNnVNQubjqBrY\nMB1cp3PIcO3EHXXqfOv3SWM3JfLZGnpML6j2rNRML4Z0X5b3bFq6D+m2rstDq85dkiEbt8y7Ky57\nzS5QXG5LwC2F0vdd0iqfitA+Y/NVVUdhd01hcTg9nnZSXBBJn5ow9W9JtH1GbljQZDP8vzGoZP6I\n5dw35u/5+/77jQfzn/88I1EZEvDss+akbBd++tNIRWXxjW/Av4Ynil97LQCXQbSTw7WN+KqrjI7Z\nhylTIpFpf386/0oTJsBhhxmi15YwS9fXFw66dKEsSdTmzcaGxBqLH3aYOYMudBIXzAjD6UFSDuT2\nt1VZ6UFLkh9IlgzJAdMHG1+aFbKeWJLIUxqCJp0IyvxLyZovbz7JgR7LrBRL52PTOnhhDew/N52K\nsgPmv/serv/VhXzilRsBePjp43hn7f9xzN/DE18v8TzAmWdCi89CN0RLC4wdy+a6qYzOb+HsdWKL\n+JmYdj1pkvvZ730vvnFhMLj8coIvfzH5iB5NNEqFc91zSTZc9k8+yZUPm3rhby2wv7KJ8rXBcgi8\nzJuv/dnvdujHqPamNaymOzc5vgtQqpPkc5Zo6U0XFq7+IiH7S9p3S4rLF3+pPqNdkrQRl0zK8nKN\nETru/k6omBjuMmwBpsclVpJIaTikb1VNfZE00qci9ZVjPZyc/znLn53Hqa/9xDg43kORkaih4mc/\nS+/y/8tfNmcLnX02vOtdXHbcg8Vh1OpwyksdnJ2/zdhgvDVBNdLYCL//vWmsxxxjVvRpsGIF/Od/\nmoN0ffiHfzArCQ/KkkSddFLkEbimxthDaQIFxStAO4iUUkNZL8rSD5PLVimNhEgjDZHyrb7lYOOS\nrNkzxpooJjnynX3p68FcGx3b8vBJ9az6T6Y9ZgIcNBPq1LMJE0q+o4LP/+2r5IOAC/LfZkx+M0/c\nH7bbcjRp/0hRAAAgAElEQVR7M2fCvHlcps60XjN2Jr9cMM1Ed8QjzHlthZHg9sFXev/NBDrllHRp\nfPnLXPYFz739iRY1Aq8ykVu/fHakPnRNTr42pSUL9pouT1cb0QsBXxyliFA98NcaOLCETZRdmMwT\nLg6SJKw2P2nItkS78aY9rcHsBKxaKNwppFmINBPZ+tnJ3uV004VyCa6ulySy6iJSaZ91pedTD8s8\nViXYRJWzwcXW/cLQRgqh6kuDMK8DwQieHnVE+nR3U+yeJOrxx400oxxHjKNGGWnOySf7wyxeDMuW\nlZeXDjGrzZgRu/VEuL17C6P494ovcd8V/2AuXAjwLqiI+z8CQG2+qOjbzqiBLUzN/9FcUPZ5E7av\n47Ctz8Hq1bQHOUaymSPpNukzg2NElp54Nvp9zN/CzM2ZU7i2rmIfnh11GMccZf6/9uQzjKcffvEL\n2sfk2BBU8smDr+V3DccCFFQ0qSRRr79uVJKWQNXVwb33mm8UgQK/vYXcfeMLa4mUlNLIQatN/faR\nA9dKN61ESobX6sYklaElPNKPi0RBHF8Tj7fUoKzDpJlorCSqbm58IkiaKNtgfbAPn6y4ln0HXiGX\nDxMZA4wOw2zG+NaRbVnce3HkgSx4fRmv/GC/ov4g8fjYt/H42LeZP7Pg1acncv4zNxLgWfVuNuls\nqhjDZ2Z8nd/8YBYc7XgXW64HJLwnxH2FOXY+OeO0v8tRDycRLihuP/IaFLfXbb3QqTyWS3WgUPlM\nW7ya2azi+qZLo8lV9x8XXLvRXGHDibn1sYhIdS8Uu8REmBhcBvOlsCO24rvUrOCWmNm0tLQ7yV1I\n2neSJM2ivxPyE2Hk1LgKXo6DpeIXdd/fXG3cIOT6YnXQ3xySKu3mIXNxsJvgD38wxqSDwZw5XMml\nEFTFLl9hV6OLFw86W+dXfJvv/PF888cOIGlK1+fzJfw9MHUEC7gjavx14tk2GJHbxjOth3MoPeZg\nzBBPjpnOW+ueMGdD2YYekiM64BNrb+CGv15YCP8y1RxW/ywbKyrhjyZflSOqeG77oezHK+Q2m7h/\n+8xxvJvf8si4dxeIz+uPlJBEvfACnHtuZANVU2NUMuEp90UEyrVy05KoUioDOwBr8uAiU3IVrWGf\nd6kSyoElTa74bb6sS4K7e4Ga+Ptag087eUibDpunpLRdsDZRvncZMwG2zYzisJN0EpEKrw8EI/in\nET+Mrm8jart6QK8X10nITwl8+4gL+PYRFzjzU4CNO61JVNLE5tpG7noe3JOvT5rjQpIE1kWi9TWZ\nxhE1ZneebzFh2+GU0EfUgjBte13CKyFxqJFk3jRykUuFWZUrocH4lbITeRHhdxm6+5Dk88j3DhJp\n30HGI4lfM8VtXEL2QVt2pY52csVVVQdHjIOu8H9an2OucB0Ye7h5RuVaILgbJkfv1qSe8fW1PRy7\nNolau9YYZEsce2z0+7zzipzc5er7YET8oMsP5P+Xrw6Yg4Ou4GqKFqqaO61eHZ1CDeSmAYerMEJb\ntpGxPBcIz42+xisbmSZPcpArY4W1PRhJ/Yi2+EGhh0PXqMnuB8KG/e39LuBnvXMZGxoiPj/lLYZA\niXfYANSO6OYtPM9HJ36Xz/YZW5LfPXMsU+ueYlPFGLr2msy4xs1c/F6HJOrll83n0ksjNwZHHmmI\nsI9AyR1ILnG2SxKlJyM7yfsMPPUqrlR5u7YupyVSaaQNkgTZQVQOvFI9uYjyj81Igj5HSzos3LQO\nOtXuPJdKVcNFPJLUEVp64rNZqXfct0iSxtnt/jZcKWhCofORBvp9tSGzK95yVMuDRROwvNd4LK/w\n+ImS+WyH1ssbo/8+dbXveUk0NSmQ4XKRzyIqzVl9sypXwgJYsWx+unPxfO3S1S7KrU+9u1fGoW2Y\noHjhUwq6TfvmENe72HT37oStE6F+KrHdnlPUs+WQz/A9CvNLJbRS7X9GLzY3Yo6E2oOx65Konh4z\n4Vp3ABrnnw9Ll8ZOwC54s1Yd/RsDh/Paq+PZf5sycnD4NHuUt3Pvu8XqG6Kt9hLl7qjWg49vFZu0\nKvX83zB1HB1tYukj1SQJRscx4jfCne3+YDwd2ybyxZovsjkYzb+//GUA/th5NACfrvg6VwcX8K32\nWVwj7Vfa22HaNNi+Pbp26KHGhkzuwhP5Afwn29vXW0ryICAneUs85NlQUoUmV38abcTrpwX4YE1x\neL1zyLWTSOfHRTAkaXLlZwnRuVdasuay1WhztC81ORbsryyRQt0fMwHGzvQTFN+EmkRUXOome02q\nYF3x6PcspRKTRNnWgSveUmqypDClpFG6rrQKBJJtoGy6WqVVjjrQhrft78ga+HMKP1HWh5mUxMry\nKyX9dPVpX97CsP311bTmqmnNNXJhw9WAMHD2ESkJ6aFd9jdfm/SVYUwjoOrYSuTs/RaKXYhI2IPG\nteQmCaVUe3oBmAP+WgdHjYMXHHlIetZCSr9kHppgMt10Ucskeox386Hmfw/CrkmitD+WetUijj6a\nEQ9fx8DsEalWclsrRnHDfhe6V0xJFe0aqFwT4GAbSznGfmkHzKRBodQzvglwZA0bKuALNf/BIVv/\nwjs2/p6pm02E/znwGc7hu7xIP/tOfS+vjtyX/Nd+Ebc9q683bgy+9z047DBDdl0ruiToSd4FKb2Q\nNkVy8nKp9nwkQQ+ed/caIpVEdnQ8cpDT9zXxslI4SyTkxCkHaftupcrE5YPI5skSN7talkTKTlSb\n1sHGNfD83PgkvFzkIY0Br03T9du3Ok7aou+6pkmHknIUbckeDGzcuu36PFFrNTBEE2qRCodidV85\nJEm3YVc/thP/wb3wWgvsNzu5THx2hDbvrvGzXtzX7+6qLxdC1wrXz7uUqqY+ZlWujM7bS2s0niR9\nSuq/NpysEysd1rD9Vda/rFMrjfLZN/pQTr3LsKM7Yb+J8M6pg2vrrvmoPrSJCrFqw+zi3XpJab06\niHzsZtj1SNTvfhcnUOedBzfdFAsSzMAtCXJVppYa2IFNqlDKJVI67nKIlGsV4CIx5Yr2h6oKSLNb\nJAg4d9ItAMzu/zW/7joBgOm0MR34edvJ/LjmVDhZbHm69FKz+89GYY9ucZVX0plgaSDjlJ1cem+G\nZGPxIulDTVyUbycHfeCpnKT1JCvz5ZL6uOCSXLrC+NqdvSclJXYicEmvXLCSqDRwOQf1rXjtNVue\nLmKZJNHSNi56si8ldfDZs+j608RbG/LKsPpZO85o2xgbp85DOUf+WOg6TCpvee+IGqibbuzC5HXf\n+7vilkTJRZCTysxeR4WVz4ebQ/pvrWZV02zmNNzDqg2hjVSTIw4othmzbcH3Dj641HNJYV2bCuyz\nNk960RGTdKk4XSS0VF7agc11sM+4ePquuCEqO5fkXxD6aYtXM4kebttwVuTuQI9fpSTGezgqSgd5\nA/HKK3Gbp0WL4MYbY0Fi56cldQbrZt8ODvYjSYpdNZWq8KGuYG0+XJCD7s7AYLbkp+gAK6uO55AR\nPUwf8SRPhvrOd7CaL/VGBOpzFV8l+GbkkycIeqN6kR+IS3zkPV+5yWcl1CAce94nTtcSAH3vg6EE\nSE6odjCUK+MkgmyvWaN4VxmnNVT2OeSU/2W7lqtln0TIFbeVROn45co6p57xLQKS2lRSG3WVlUuS\nJeMq1V+T6nqQ/aEAnbZsJ77JX+arnuJ8JKXvqs9S7fnPvWZ3HsQJhotQlSsR1Hny5UOGsVItV5xL\nzW6wHozfr2kLVkcSnqT+LMf6tORU9m+tvktqzzZsQWqF3w7K9pXBSptctoL2/9pO+NuzUZ/0eR6X\ni/8U9TmZbkNe9QHFUhopP2F+RuS3UbelM+HF9gzsOiSqsxMOPDD6f8UVxkllRZTF1AfQQtzJmJ6Y\n9CTXhFuXLZ/TEoVyICdHuatkONl6qcnaByG9ez44hNZgOk0Vd3JFcDpfCv6t8Lmk4pt8M/gXCAKC\nvUrUnSsvWkxuoetAkzEbRpLm5USDStKKX0uktPovCXJwtAOpHsjaRFhJPOQ7laPitelJyLblm2RK\nDfA2DimJqqf0tnKfxKlUXsG/a0n+9tllScmJGMRj8J0jVy587UK/WwcRkbcrd2vP5sqDT2Jjn5NI\n03dluRSVW43ZnZfWzs1HTJNUj1rSJMvMpeZ0PWPb71KzS7C2sssYOEuSkOTt31VPacZe14LD5jlp\nPNDpyX4mCUhOfCf5XiqnrXYA6+tgn8Pi1zWRkr9d5SPrqgPO4nau5IrC2XqxY4BccQr8vOtk3v/a\nvebPG3Es0zBh1yBRDz4IRx0VHfVw7rnwxS9CZbRbrDAJu4iOb1CxE3E521Nl/GkmtMFKkHYmgSon\nT3qS06LvFPnsCg5mMQfyhRFfKny+VXEJW4LR7gdKlavcsajVBSBcSKSoH0ukpCM+TS70YFlq5Sql\nShAdkSAHd20H4StHawCbVN6++pSDsJwc2sR11+LApgtmgm8OT3HXA7qVRCWlbSVxliikIRgSUuIh\nn5uHe9Kyk5lns0QsTVvPS4i7vHCpH8olV0nG1S7p93LiUkiXJMGSriT4JCLaNCHxDLRe6G6JG47r\nenORIi2hSpJSabWqzKdM0ycJsR+bp5BIrdpgVHuFd3QtFHQe09SttPNqwu1AVaeVNP5oMq9tuWRf\nk2UjVZCudgLutj8FeKgTfv6s46YDScdqiTDncjPVn+o3OyWXUzxWJmDa5lbz45BDkv0z7uYYfpuo\nhx+G94oDEy+5BL75zVgQL4GqJzpfsRT0zgOIGpLLB0ubem6wkHG19AI16cT69n6aSd0Xh+85H+m0\n+dQ6ed9AVyjL0RDMisedhij5JFBpROcyvL3ui8/mU5IdKCYeMq2kMtfSBLnzTsMab0vI9mbbhFj9\nxQYn164sSZ5sPHLyrSc682weZkejXPnLd0waCMdMgLqZsF7E62oLpdwd2PeSafsmB5ctkZzsobh9\n2nRkGrKOfAbQGm2e677wPsNrF2R7krvGXETRXtd2d/aez69P6sVTDQRqd56esHVZuKS0Ml2fGtfe\nl/FZqaaNp1k9J9/f7rbDfPcT2Uj1MInuDZPpz4kt9zkRv41LQ+fRVY9SYq3rQoe1YbREVKctfb65\n8tQmviWx1eXjq+egDnrGxTd+yPhlPmR7sqYKejdmDn7FiZz+Lz8x6lTpKsTVn3R5PIPxD/fRj5qd\n2XsohlcS9eqr8Hd/F/2/8kpzrpyAl0BZpCU4dtK2n5beqKNJiYIPeoLWg58cIOSnXJTB9L3P60lH\nw+VJOI1Bu9d+bDMM/KLYrsmXbhLhSQsXmYo932I+rvqGYmmRrC9Zt22YZ6VkwRoI2/s+SOmUTFcj\nTZ1ZWKmaxrZe98rfEjxfvElkcdM6eFVJooaiDvOpFUrFqY1h5TUdTvdLnwovSc1IynuuuJLuS8mI\nVFdBevXxrSJfafLmlEb1Gj9RGnrRpCVPOH5ryZILWmql3XRoe0PXIsp+2uM2UrWVXZGqSULbNqUd\nS6Udps2TlCbJY5nqgekpxixb5z5JlMvGUS+KZJ58yHdCXkmi5IYafV2OgbbfyEVMDm7mHC6a/J/x\nZ1OOAa8TGrlfeaU5vLurK93nhRfSJbCLYPhI1JNPGs/VFl/9Knzuc3EbKO2IUcPXoPSEaOEiD3qQ\ndXXktNKoUoNaWg+yutGXS6bsIJ0W2oDbteLU+ZHht68D3llWFmNwqeZ8aadVBTKdwgnm9rqt76Sz\n93RbsANlKTuUZscHShMoiMpftr0kWwkX7HtbWxwJPZG6VEmusGMmwMSZRXYSLDfbnu2nCGkIpoYv\nrN5RqUmfJqk+mxSLwdg5lqqLekq3D92/bBkn2SXJdioN1Bd50pDlrgm8TOfIGqid7n531/jX0lsc\n1kdok8adpDhsmjJd38G37eaYmEn0MIkeQ6Rc7RD87idsXnXeZT9SzxS1d/v89FCSLO20tMTVJQ3V\ndpGaOMndnHoBIiV1FpPrIHDYRMk02jCSaWknquMNYb2UQ+ipvBy0wTk1t0T/v/QlOPzwdJ+DDy7a\nULYrY/jUecccE/0+/3xDoAS8BEqrI5qAjhr3gFCvwgNF/j6kGidHcTxSgmX/Q3HnG4zKzYWhqA4h\nPeGTYVzhW3phSk28rL0kcQvwf8CpZWRUnTLug1QFEebB5UhSwqUqlOpcW3d2wJM2PVosXahnB8mD\n+Co7SS3jUulZgtYi8qrF7qWwnLg43qZr86MnDY8arX+p2ToeO3DUSqKkx3KXNFL2G5mHbb0UlZuE\nLGupxnDkL0biZLo6D3oVD8V9wrUtPY1UR0toZF5tm3NN2m3iuXr12+X3SJellH64nLZqKdEUktvO\nwb3Q0QL1s+PvlYSkbf96nPWZIcj/VjWkpXSaxPl8fLXBikXzmdZgtuBTifF2jlH5FY0ZqDwlLcA1\nuQ7rqbbSnKfSSnXcZYGrP8g6smXTEd2vynkciBbNVyq/rvK3bX9LeHaeyzt0G3H/cnaxZfPqWHjN\nZhWAcW/QnOCl3EKNnb95bhazR/yaG0ZeQOXAhuRnQ3PoyXSbH5/4BHz3u+b36NHw5S/DbI+H/WHG\n8NtEff7zxvO4gJNA6cHW/pYdz0ek9H/XSrxcb7KDgZ5UfORLStHaSoR1QU+cmgClKaeRNdFKyGWc\nbPO2rRcYRUES5ZpM5MRRIDgOj8kudY+rriyRSkLSpCYGMyD5LD4L3+ReSpJh01oYpWlXs/1NdmCq\nSVCVJsBni6QJiZRKSHsN3SZ0H7CSKBtfKZWvJnEugqzbsT4jzEXWNamVfV7XYZt6xqc2TkOkpHTB\npoEnjzreNG3ZQpe7a2KV+WiGqoXhJHyOJ04f2oj8RO1fIqwtT1892jAyLJj38RFiKWWzu6KXqDgh\n8vCt3YcQD9OdmwyVZsKfVNljnEHKuHzSNtc8oPMgiG5Vro/Wx0JP3dbe0PW83HnnIlICBSIVvkss\nXRekhNq2Edu364E/hGfn+fqn9FkVbigp5NGWdbtpW7MqV7KSWcbmzEegXBs0FFZNnc00nvJkqPj5\nkwdWsGIgXLStjiRhHH88fP3rxc9UV8OCBbBXOVv3dyyGl0QtXQqf/WzsUjADv+h+R8HXAVyritjE\n74nLohySo1cYSfFa7EiJlw928JtCdBCuvCfzta0XI1GaBPwfjPyYue47usVClqdr0nHlSaPUxKTz\n4YIkF0kOMF1puQiUXvlKLKVApPrbqwuqgYhICfikCGlIlquN6MHS5tUngbED9KZ1MHINtM0tNgwP\nUVvZZVbmpdqlNFxNK/mRkM8kqYxc+bDtq01d80ltZfxSjZaj9O65pDZXT/EkretapmfDOPJRcHy4\nENO2SkG24YN7YXQLkLCy9401SXVXqk59UlZ5fqMtH22MLtMX8fU3V9PdBJMqzdlusypXsiI3P3kx\nJBcF2kAe4nUkpYBgCJ9v11+HCp8jXj/S3kjC3rfvKs8PdUm5LLSN1fROeNkhiZKEUpJe2Sdy8e/J\ndNPDpDiB0n6iLEotJJOg8vRz5lD3xz8xkVehFj70tzv5TF9ok/WZz7jj6O+HD3wg+l9RAQcd9Ia5\nVRg+EnXVVfAv/1KeDZTEYKVB+nnbAJYQnU1mIRuKyyuty7BcPycxsia+gksjEdKQafomDNczWsev\nVQsyPruSTGM0yXRgA06bqCQpYBrHkvI538HE5cL13lbSJsvBJT6vx73rx+VpXT8LZrC0A2lIqApE\nStpQ+XbvyHcoJTm1g6SFbN9aHaRh018/AV6ZaXbYyDy0Qf/Z1VTdqnzHyLR9q3xNQkoRXU36bDwu\nuNLUhN6ec6bt8DRB02odLWHQ7+F751Lkr118W/vMJuKbHqSN3SKRviTGSeROT55jamD/6abbloKW\n/Ft0iG8tRfW1YXEtJoWxBs5WOiLJpuyTikDZPPS3V7Nq4WzOqrzNnX8f7ILRxmXL1EH2+pur42RV\nSjr13KClRcqXlbSrqsr10T+lupjgS9g8NolnmsWYYYlbQx38dVws3zHpqSWmbUTqVC1BJFJbTqKH\n1lxjRBy1cEO3d1kW5YzPajz/89S6wu/WMdNYO2I/ql9SNm/7waf7zNmKfPKT5iNx8cXED3PdeRg+\nEuWSQFm4dhmVw3aTJAIaMozddmsbWKnJRqs3BiOV0vnQO7R8gzMUN2pX3lyrK9f2cAvphsGlHnFh\nxAQYSOtrwgGXvUVRHda4iZSrfNLUu942LFULLrsMcLvBcO1ITCJ74Sq2n8gGqSrXBwtDu6QwncKh\nq82YidPnQ6icwWoJ0QRtibLMY7NRMU5rWE13bjL9314HL6yBV+YWx9UB/e+qprWp2qiWctWRNEFC\nrvybSWezJwd1bRhrMVgSLW0c5YDv6nNSamDtR+x/W36o52w+Zfu00FI4qW6V/zuIJJc59eyS8HsR\nkTpHj1NJkqIOYFMvPNkCpyRIonw7RZOkgAmbKCRxsJN0d464pCPpjDkrHdeLmLCu+turocGddhHJ\ns21RQxCzorrznb3oasvt6ttRLoUysAbbmqzqtt4kzACaq+OSc0v+1nbC+ImQE5IoLRTQKn4LRaQA\nswNSG7vLuDQGQ6BKzG8bqWRpxyI4QOV1HTx02An81wufYvSWzYbJ7AWHbHzehPnWtyCfN0RqJ0uk\nht8mCpIPpJUEpRSRGqzBqITdQq53LSSF12HqHfdK2fBYlLsTTz7jsn0aTHzWqByS392WdX5D5Ceq\nFORE49otaSc0udK1HdvH0wZDtG2c2lDZEhZ5zYU0aZVaBYeTcmFAtUTKqmtsPu0EblUD2ijUDvCS\nMNswU4gMz33SE/ts+E6tNDKtYTXbznyV9hdnQhd+1Q4YAmXLzq5afe/uI1A6vF7Ry9W8tmmTccT6\nnCcduTFBEijdjvTzPtJSjupLSxBdKhZ73dre6DYp69+qGC3h9KmlpZ3VmBqYMd1/X6YD7k0UqHuu\nshKk06qwIb7Tq6qpLyJStg1BZCelYctPl8cSWHmXGYPmNNzDikXzo7Yo389HoOw7DJacy7xo6Zzc\ntBLmZRI9BTcNBWjpJ1H4guROO7a179cMvKMOBsaly6eUZKbZwCKh57xyxl0f0pa9SOunz5/CT+tP\niS5MgUNff5ZnVhzOCAbg2muNw+5DDoF//Eez828nYNfwWO4jUBYuI8YdgSniI1HK7kHDpR935TFp\nhehCTtxP8876PbS7BBtPGmLlmnBlHmJxbIb8qigcDL6O2vBvn5Z+pmxYTbhd6brqWE8IbcQNNSX0\n/6RBI+3uyg6M88Dm6sKkUlvZxbTFoTGlz6eMaxKRcUK8juW1RUVPRPekiD5M+7kX9mHU6JXJddnS\nG1dzLKJ0+yqlxrV5sV6+oZhIlQPrJ8yiHqOqtuXkkhhZLCEu/XARN4iPJaXGMwlLiJLGD5enfR/R\nd9Wxrr8/9cJLYkUiyWpSXfs2V2hi5TLGRywM1O+YkbT9WI/1PjhU8K2nN7rD6rpNOza56qTUwsg+\n0+z4v4TCWYAxyD7jid8utBLt324Oz86D4gPYdd2JRRNQpILtojb6k8KAvIChzM0yXt0vfeYVKi/P\njTuMw6c8E1246irjwPv974fe3vhn06YhZDbCrkGikiBXe2mQdE6ehKtRuVRfEB+AfZBESor8ByMJ\nko22FKErNShoJ4ylUI4/rEK6o40kKi2Bcqk6ZNxWMuIrO2lPVSqtKeq3q941gXDZdLhWaz7v6eWg\nPZpQrN+b2ARk8yN/l2MTZK/bOJM8GQvy0rqskWCffah42zHJaYLpH+eYn1W5voic6GcGM8A2Ux6R\nStqVpUm3JDxadSjJgUt64dqEkiZfHepj47dkSpI22xf02Y8WS4l7rNe2OIT1odvuyBrY6Ngda5+1\nE6ytQ5eEW5elHv/kx77XEiNp7W+uLkhW7G8gTqLss1qqLyFVxSFK+jOSebZjY5u6bwlQuYteDdcC\nVrXLgoTOJRHV+bXwST2DOrjzMLc6UUv4pRRJSSBtGXZvmFyc/o6Q1kF586JrXtZzjX23Dnhu1GGc\nOPtBrtnvYlZWhhqStjZzNq/8vOUtsHbtEF7CYJdQ56VarVm1RJv4b+/tLNhBq60mvZ2VJlIaLibt\na5hJx2no9FzqKR2mPsxX0mRr1R1pO0o9sH0z9K4CTk/5EJF9kx5YdFkkkUSXLZUcKHwdVduH6cHL\nR6QQ4XxlmLbcZB7azVbtbszgNafhHlblZsdspAp5sUc6aEmVlCZZtInrVjWUBLlgWQ6vPzwCejup\nui30HWVXwXrDRamdq1q6WI60TrZvSSTSSotdNliyXMJ8FvxjLRf3dbuE4tMNmh1hUddsH9cqyTZH\nWBtersTtxO56f6uytTZSxO3p+nPV0X+rzjqsF/7WAm2zTfyyfUnpt+0bUmphF4Y+abEsI6t2kqQw\nfL/+9upCnfY3V8dsfoDIh5LMT5KWwgcXkS/VdwejntL1beOy7cNhQ9e9YbIhlvNCu0Jp6yTzrW2X\nfMQy3wlMhOapxYsCC5dE3jEuFKkaXfG4jP3TQOYhTVnrenGlo8b8hzpO5KGDT2T0wCbu73ofdVs6\nzY1wk0wNL8Err0AuBw88ADPK2dUWx65BotLAq0oS16yE2mcblYZ42cahB0ufjl7CZ4xpYRu27/yh\ncmHthdIQST2Iu+5rUuJqrC7biWA0jEuwiSqX8GppgQtJk3e5qxxfvsJBqGCPoFffMg9pD0OWA6Aw\n8rS2UOSgp2GSEd8v7qL18sZCmMIuJkXynDv8XAN6G8nk0IYhzFvPBMjNjOJE3LODb1uKd0+q9zQD\nr14oJEmkNJnUeSuogsX1MA8xR6M+SZbNRxo7Els+9lsO9NpQWk/uUmJg61yr9WR4QYT6m0Pi5HKf\nAdBdA4dNj6Rh1q4urbrUJUWW5SF3Gkr4FoxhutJuKmYD5FNj+jQHpVCq3aZpkzaMyx2BfE8579i8\naolneCZgzCZMIOYl3bdgBCOJOjy0iWom8k0H8TFBx+FY+E+ip7Coi0GOX2kIlIu0JUEucOyiX0P2\nI7KLB+EAACAASURBVE3mpXQX2MwYZvGbKEwogL372dM4bf090NcHxx4Ljz4KUwajNtoF1HnBUH1k\nyYr8YI27Y2jmnjRx2vtWjWAJg23caaRmWqztgl6dJ+WlHAxWhTgU5DfD66vi15LUcRZaKpckxq5X\nH4hIjGvyKQd2ILE74JbglgLauCV5k+0tqez15KHDtWEkPc1ETv1snBqiXU1rWM2sypVmoNXibj0g\ny8VBEmzb3LIOnhFn5yXV545ucy6pmrYDKtcgVsJBwPvbq02ZpZXYgbt+fGoHO7lqNY9vTLFjiWuX\nVxMmr/aTEzs9S5ZLL2wSNlFJY1ra/qTbldUcuGDbl0OaKG2lqnJ90bl4clGrj6HxmQb40rbP2HwO\nBdYNTBpC4cunlRRbePpoVa4PblEXpRQ93wlbny16p0KbkGnr/7adibRrK7vcqnl7LYk4+cZ/17XB\nqAddc7giUEk4Y9L3uCP4J/Pn9dfhhBNg8+ZBZGSYSVQqAiWZfI6IodqC16L9evy+kvSKIC2R0vYI\naSQlrviSoKUcaWAP1ZUrWg2rMtsRemxwd/BgNNTNKjauTUrT55DTJV2yk4KvDDWRGgxs3dr0fUQK\nFQ7izkLlarSlNxrwXQTKrrSshMnW4xJjk9S9YbI5v8q2vTBsVVP83LrJdJvzw27ti3xBSbs8H2HX\nk5weVJ+bAIfPjK5JA1UXUUgDuTovdwKzBMRXL5I8aMJdIl5r7Bsjo0kG8OcQhZcopUp2hZNESudZ\n7i4TkGcXes8wBLfa98gaGDM9PuZo4qVV3hZtno9NS3oYt2osCfl+dvFyTvixdlNhXdRWdpmJ3O5I\ns+16ek0Ur+hDBb9l+r3l++mFm+t9S0FKbyRcREra6Nl8+s6bDN+f5US2cc2GWFo7pQKRcqlTJ9fB\nUeLsvKUmfMEo3ebLpbq1+VW7O6sW9iX3Id1eByMVlN9p4nGNQWnGI3F9U8dYLspdxy0TzjYXXnzR\nOOgcxOHHw6vOs4OH9tkiJx07yMhO3kx88LEqLbv6celrXaq2Ujp2O6lNwUwg1ijXiqqbRDjXDhX9\nnjsD23qho6a4EQ1GIuM6FzANjtgMf1wFhzhsorSNkiXB1h+VLjstGrertHlEW7ilKknCpSooB01A\ns0h/KcUrP+0XSvqE0uUmdxO2iXhdbdESKft+oYi/NbRpsYgNiCFWMovZrGJ25aqCr5zbcmcZFaFt\ns3qVZklZkkR0+zq4dQ39Y+aawTQH/cuVimiwq8ik67Z8pEpL1rWY+J1nkDnE+pH6Bbc/m+VEkrt6\nokVJCb9WsV1mpdT58j1cCzGpStXjoJzc6onUjnoXXFNUJlYCUVDv2We2hZKo+tlFfagq10d/fXV8\nUeZTw7ny7iKEeiy28BHO5aadtdZXFxYN/e3VkbNax9b8qqa+grPN65ddGnds6yKIss2XMz67ysL1\nvG6/4XsVbeyQ4Ww5Ocq5v0mpOm8RdWTT3tIJr0+EvadGcWvonZOutM6uZsWi+cxpuMccpbNQ2Gf6\n8j4YiV5SPVhV80L9kCMOG75MvNq5Lx/J/Q8Hb/srJ/X/El59FerqYOVKaGgoHUGI4SVRtsD0ICVX\nGVDcCXzkRzdaHVYPclaKpVd+LomVPHcI4ids6/STkEadUi70RGElF1Zi72qsOq960C4HFaOhuoSf\nKF1n2hu6HoRdedG7depx+47Sq7RyBkkt2XS5PNCQ0lJLrqV00OeB2MYvv/Ugq9J37T6KORoMMaty\nJSyGFZfPL1ZnJ0FK0kZMgLqZxfYV5UIPsLo+SpEqCYcqLeb92sYP7vFAh7HhphDtlCzYQdYUS6Nc\nq+DBQtp/uCQ/si2UslcSbcQSqJhHcImRoSRKwSvNkvm10GUs278kofaeazHlgmx/4QLWOqYlh3uL\nf84sLk7gIQCuz10aj0uEi+VJG1UPpU5d8UgSJwhLf3s1q3KzzYLori7jmsHVVlUZWRu32JFRcv56\npQ6OGhediSjjkrZlvjnILqjCsaunwRiXz6pcaYiUdc2gPZ0PBvJ519yd1EZ8/aVUeg7k2yv4h/r7\nuK3nTM5c9z2j2rvpJrjhhhSRGgybOq+kKk8TKMugFxJVgC48XfBJelsLx64JZ7xaZbhIhbWi61ID\nv453R0HbWgB8QUzeOq0daTs1sBn6hE2US2QuVW5aZ67ryaeGsYRCDrSunVcu2GfS7OpytQkX0h5Z\nIlVLusytHRZ4yVp/c7XZDi4+QGGLOEuMj5zWy8PPMmNT1cMkI0GS+fFJE1xEZ/s6eHWN44FBwKVe\n8w1+KdtlyUnfhaSjjKRfKjB9PMnG0iKtQbbrWZcEQ/aHIdp+OVV9VhIloXeASbjajDY/sJIDC6my\n9rV9CSk51JOrlMItxPSXu3vj7iCAbmrpppYLG66OHfgdk7yUqwLywbeQ1+9t01WbEWK+ohZRXDZW\n4ma1LGJ8t/2/KtdH1cI+41tuHtAf+omyUu1cJLmW0uyYKwmtkhX5KGxqwRCpQhxSDajHDlc/1/AR\nTlf7cBG+cubYUnkJ8fG3fIcfHPJh82f79tIPCOw6u/PKacTWc7Oj4guER28nlr9dhCINm7XxSnsT\n36SsJRh61aMhiUFSGHlfH2EhVUoyj/adbWeR5yZJQjpY1cw2IYnyxZF2W7tUz2p1hlXpQbx+tTd4\n+ZwrP7p9uGDz0K6uSW/XMn7ZrprF71J2Rw7VhBPKtqUgZZDnjYl4VzCfaQtWRweyinxIO4nWeY1x\nj+exiXCCOTtvvbhmVY44wrve0/VeUqVVqs3JvuroG7WVXZF0Tu56TerPrkHc1UcguY+fQzTRDUWN\nrMexpLJbIn770swJdR+qjKYAr9fAhunwSkIcGmnGJ6mKcU10pUi0i4TZNraEaOHaBFBTpKpbvOFy\nZlWu5Fxu4YQFD/Ghx34cHZWytDo57zZ/8j18kOOtT8qp1ayI/yGpal3WCDmzOaR1XqP72CSIykAY\n4/c3VXPV4ktC2thF94LJ/LDucGrH9fHhqZ+jsasVgD6quIIroRJzULhtPynrvfXyRlgMs1kFlZix\nRL5LWrLku+9aRMjfug/oOvKpisvpj22wqX4sDx7wHv7pLz8s40GD4SdRUnxnYRuMHdRsOL07BdxE\nSl53qTJcndyl33WpHYQ9RlEeZP5K6J13CKwNj8sA1k50rhPSJcGT+RuMHRVEkiiXTZSFHHggXv6l\nysfm3fo6suUu1bG6I0mCIlGPscfSdmQuhIS8n9CPixWf+46fcdkHJEx0RdvCSxFo+5wNbwkUxFeT\n9cBSaG1vpDXXyLQFqwvRTKInFm130+SIkEkSbnfnvboGRsw1k1ATkW2N73gRm8dSalBbby4JmM2L\nC4Ic11Z2RVuxZTm47Cz0OCMXD1LdZO/btibV9y4sCeNZRNQeh6LmsO9QT3EZLqF4HAP32KckEbWV\nXeasOqrN2Xl/a4Eps6M42sN2rqVWehz1SdLkgkyig+KFgh5zXOOxS2WzhJgWILYYeKwRmmHy4m7z\nvnRxVcMl3MaZTKKHFU1i8rflK/OaVtpXT9T/XWTczlNSg7JE/LZ9YwmFxWxre6PpVzmHLZpMR9Z9\nE5zLzVTf1w9AI61sfRAmrofG++HqThuwn3PyN1NLN5+jsXgR54NOO8S0htXmyJqGyI9U94bJcZsp\nV1nqHaZyA4Kuj3riC1EfBjtfyXQlDhpcVMNvWK47itSty0K192QjlZOkXuFYaYOtIK0CTCJSsuO7\n0EbUGXS4JiI/KfJ/OSin8TRhCIG0r4C4KFnaVlhnghZaWqbT1o1e6feBdDZRpSRRto5Kqdts2du8\naLs23WYk+bb3RtbEDduTIImzRTmeyX2qEde29VJkUtaFbGOuNMVA1N0U2VFZ3y928plVuZKehkm0\n0lic3+cmwIaZ0BilVXDemKuOH9bsy6srb67BT7+7HuT0ql/cK/jwskhjT6HHBfmcft4eQeIq7229\nZiFjpaR6YeWCawCXeZOQjit1+q7JVZLAeeYcxKqcMbqeVNnDCubD0TWwfjocRlE5xWzLkvLqu2//\n6wlRjpO6bfgkUr7ruSivrbmQ+IXk9bYNZ0ElwAnU0s3l/Adg7Hta21Ubd+XNxp+kRnI5I5blEOZv\nWoNZvLTWNxafVddGbAwobARYSJwYWpKu67odaIC+k6oAc0zLsxMnMmLcC9D0Zy79ZhhuLnBfK420\nUntSNx9q/nG8DDQcxLx7w2QmVfZwIg9RSzdgSGrjda2FMHMX/4gVj82P8ibKoch5sSxb+25yjLYL\n4LaEZ102vRpyQehCWsljCQyfiwPXS1u9b1IF23vS8ZwceHLhf31unE3TJfGScNms2OuSoOitwxo6\nn0krHV8lD9YWIo0qQxMpPZnPU9f06kpiYDN0ripvZSDD6gkQzz0LKQVJItMyjL5npWJDWc2AWxyt\n47R2Tx3itx0stB2OL95y71t0QP+7qs3n7PCztDpm7zCJHuY03GNsK2QZbV8HG4VNVBLB1eXuGzB9\n4vek9ynVR8uFUIsAcTsOqdrXeZVqO/m+23rdBs9J+fQRZmkbZMmy3JEqIcmfyzYlJNqSGE27azWH\n/79fQRCKU9Lac5VLpNI8b+0bk0ivhH2/peKzRKjqwrZ+/YxLzQ49F2yatn1aQu1yieBTJfkgx0xt\nBmDNTGRcskyEmjbmzmARcYS2UtLG6UQe5B3LWrjsK5/gn750DUF1nun3/p7xd73M6oumFcLV0sXv\nF4sNBSnHvv726pIezK/kCl5uGM/LDeO5c8Gp3Lng1AKJtDssndBlmpQnvTHAF4cLrj7ie37TJsjn\nU0RqMPzqPDlouLCtV6lPauJHWEgbJfs9j0g6oyUzSTp5C1nQMdsbFYfQb8egPZIPhgxpAiMZuFY9\nyDxJGwI76NtVbBOmbGy+pFQHisXu4N6Wa8PYeJ4eneyx3AfXytu1utZqJqnac9mnudREMi45gPnU\nwY48VeX66J9SHV8ZWjIk09T10qHC+aBJik9dI+P29RudliOO1mWNsCBS8U2ih+6FQjS/eQI8ObOo\nnmoru4x9hUq/SBUk220SgUqCfEa+k3w3PQFqezr9rH1e2zi6XCRYw+Z5Iox9rynEXSZYyL6hF20a\n2oO6lLrbOMol+vI9w7xe334pcxbcw2xW8VTNWF5YMImNfcQlXXrCLjdNV/uWEnLfWKL7fClS5esP\n8rml8Dmu4aoFlxSkJ95FoEzLZ4e2iLh61SfBsvfajJquQMZsGVg1lSXt0tj8XdWFd2udV23U8A1d\ntC5qLGrjsypXxi+0Aw11MNp4LO/eYNT072hugRzMWXAPP7vuNKgzvp/6z3a4LNDjjZD8tdJo1IFh\nGcxpuIef1Z0GwNdOupjP3vetQjSn1/0EgIcmn8DshlWFXZM3N5zDimWhtEpLoKRkXc/ZElazo+cE\nmW95zQVX+5oCbAx/3347rF8PzWl2Ie0KJCoJ23qJM6jpcSKTcx+w2U+18e9jdegWshP5xII2bhvO\nPmMnbTk42nBhJ6vK9RVsR8gRX53aa8orbAxa7aRhO67UF8sByCVFk6pJ2yasYbmVhNgVuCwXueVe\nExaN/GYYtQqmnF6aKOjBVudbTlCS8OgBVtunQVx9i7iWlL6Fq/yS3kEjibTJlahPjQPxtu1L0yW1\nc8XpI1Dy/dtDp55C3TercmVkP/L7dTBuDUyZG+8TiCNSVF4LBEvCJfHztRFb/z7SJQdPiTREwzfJ\n698uIi83NsjJdHqNv/zTEMZS5/r58urKp6s9CCK2gvkm3y2PMLX/u1RcdFDkHb+UlDHNIkD3O11/\naYiUzYtOR493MqwOp4hUVVMf/1P5ETOJPzbfvyi1cJEtSZpcqjw7uVsyMIU4YZKmBzYtKbmydS7y\n0bqs0RDfBuP/rYtaVjw2n2kNq7mNs7mZc/kVJxR24/JiJ4ybCEx157vOfJ1VeRvXc2n8/WXZabs7\nOSe0wYV3Xc11XZ/mayddzG2cSevljfxq8QlA/My9lq53mB+hfVbtSV30LJhkpOC2DKVWQS9ebLmE\nsJKt7tzkuF2mazxIM5arev/tIceyftR49t7yGvzv/8InPgFXXw2VlYnRDBuJyj9pvgPfuX9FBEpe\nr4n04s3VRZN7weDwLvPf61vHQg5CmizYDjcPQ4rsgKInpubQXsQeJAnRLkJIPutLQx4wqwdT1yQi\nSRHEB9OWXphSE+XBDlCWIFpPwBY54ifCt+NWJVh0AEeNhhdnJa8gZP7tt54EfGoAOfG7Bj2bb7tT\nKkRhZ440nE5SX/iIlFZ1dqj/cqJwrVDluzY7rum49D09qMkVWLmSHS2BI77delXT7OgA5C9MgP6Z\nRfmcRI/Z7ZMTfmMkXCv9tCobHySJFPGUPCjVBVl+umx1ejbMFOImBPadZR/H4bNKp5vUdixKkb2k\nay7Y+Gw+D6mh61OncAThzjAa/eo42TdLESmXZMA+IyEXZdr+yDXW6EWWhXRZ4Ou7S03/v3nxOZzI\nQ5zY8BCLN1we1ZFelLq0B4uIe8rXC04JKT10xbmQ5EXpFKNy/RXviV2u7jIG5EwEuuBrk0MCs0wc\nEXVgKImSJD/Mw4rH5nPXSadQSxfX3fdpVt41y/inknnV0n9XPas+bM0CVlw+P+qb4Tx61+JTAKid\n3MVkumm8r5WWuncwfuHL/t2SPrtEDHmyXuy7m0JhSakNOT44tAZPHTCN/T6zlpeWHsDEgXVw442w\nbRt84xswfrw3qmE/Oy//JFGFFVXadPMZ+b7wUxN3+Q+Ri3z7UQ3bRaAKsOqtheFnEYUOUtXUFx2v\nEf6OddK0u3DS2hy4Vj9LVBhpr+F63hrASoysMT5VLKwaIwkyzzoPOo9TiHbnpSkPuZNQr1JLqT21\neiNJEiNQkFbaFXDSKsVTvgVP4ZbEJunkk8iCVbH6JiLfPU30XbDuLmw+00DZg8gjN+o+sZJRJ4Zq\ng3DCq8r1MdmqRzzw+m8aqi2TQmLflihlM6EnD9m3k/IsJaD6+mDtGdPAtRvXJ3l0SfLu62XjudEu\nzWkNq93SIR3XYGHb5bbe6KgqmS+frUsCqpr6istdk2KL5nCSD3FW5W1xGx2XHabWGOjx2ZLptPUs\n33ceBc/y0xpWm8/i1dz55KncedepnMXtdFFLF7WFR/omV8WisxKgmL+nFzuh71l3+s3wodN/XPg7\nm1X+hZprjBFkReYraZz50LIf86FlP+Ydj7VwFrcWrj9YeaLfBZGEGt/lYq+2sisuxdPjZjnjq7i2\nbcRevL3uUbYxwlz47nfhC1/wRGawS6jz8lsdEikt5rYvPoVoFWBXVlIML48MsPdc6pKFxAa7JMd9\nBT8riyicmQXEbXAweeo/uzrSn/tE1/IZCanus+SlpReW1sQ7rFTRtVHckbWEYmSNf0u5QExyk7T7\nS7/HPaPhmVmGkg9WJeayjfJJbVwSJSvaFfYw/VTDQoqdxCHCuuBZ1dZWdtHaUR1fxZSSrmjVo+u5\npHh8NmPyno1b+w3Tz0kS6lKphqvjVRtmM6tyJZsnrGfvd4+g44S+gg1GTPIjV9TtxsC3tamaaQ2r\nzXZ6n0QmLXwDtJbGuiQCPimfhC13KS2x4axEUbc7C2n/kgvjWgL988QRKzJNKcF2qat0XpPahK1n\nlyd8CZdaD2B7BfRON5KIRca+pTXXSCJ0XEn91zUG6LzKsVNv/NCkVqYXjqkFtbFLau8quzb43OXX\nMGfxPWaXWWUX3QtDo3RX29B17dB22Hv9zdWRetuVB1seapORddEBcC63cHqXsSXqm1zFiTxYULUW\n0qoRO/eWNRbXw+Y6GBhHERz9qJbuuBQuyf6ylBrXhkmotxXMZ+5JP+JKrqCxq5ULG67m+nmXRnO4\nazzUwpL6UPLVFKn2iqCJlDbmd/2WJjsd0DXqcN59xO/43dPvZiTb4aWXvK8NuwiJAiOR8nox1xUo\n9ahykHKtDGxlytVbC7C8JhavdE6n42jNmYmBhi5aFzbGyZsUP9sGuYTorD0XkXKJgrX+XUJux7d2\nP1LfLjtnkjsFW1aO3WxO/zC2E7jE6dZYsg1jE5VfBXj8REkSIc+ac9WrHFStGF0PpFKt50rLxg9w\nNvTfGp0/VxAB27CliJTOo8vuyoa396UKSIqnLfQKMImI6We11Na2P02kZFiZrpQCuFSqmIllRdN8\neK6TUY92cN7c20Knft0AfGTD/0TG56VUPBpJK0Tdd6UaV08EYX5TS6NsfKVIvkzPpWZ22bnY/g7J\nO7p86rs00M8mudnQiyhd5n8cgJoW6Jid3uu7tHGS9TIUyLGzTf2GeDtXpLn1scZwTA4JRdKCT4wJ\nK5bNZ1XTbC6vXEx3ZS23LTzLSDisilb7P3PZsIbjp11YrGqaHU9LEynXQipHnEDd9xPuOukUFmOk\nHoWjYKZgzjIM0ZpT5iu23DqAIzphrLKJUmPLOx5r4cKTrua6+z5tXB7cEkmnOKc4fBJq6S5ulwlE\nfkW7KfuzJt9m0l/QzeeWXuOOXJeXImit84z/u+5cuBHGNf9JdS/qvrRttCYsIo01lY2cNek2lvX8\nP7jjDjj+eHc+2YVIFIQSKReRcg32epCwxEA3+ALBCQcdu4Jrxu93RSKshO5bzWA9bUFoQ7BUhZOr\nWWs/ATECVVit+PLoyr+MX4a3jdeWjdwp2IYhXq6B1krypM2ThqtshDqnIKkCUx/BaJg0C/bx5F0i\nzUQiG/dgbJg0QiJVpH6xkoGkgSPMq52s5yy+x+wwkfUry8KVJ9dKT5aDa+CVE0mS+rJJ/NdE1fMu\nRdd8EoBDJ7DlsNl0sQkwx2oAXF65mNsWn0nrDLf0opXGaNHR3uivozR151o9WvF+u8M55GCg26Sv\nTOw4Y/uHlTgvioJYe8wi43qdnoYdl9IQPfkMxJ3Y2vwn4aQa47F8fyNFsXZwPUwyu7pceZeLglKS\nNMT9ZtJLzpKg+1W7sZGBcEzONUZaAm03KPPUbt75VwtO4EQe4vLKxbAgvN8ALDASq0SE41MPk5jN\nKk6sfIhuas2h3/XV8TQ948u0htX8rOu0wn9LoFpnNLrtk0T+C3nQ99fXwQYliZLjST1wDlx/y6Wc\ncNJDnN71E/ITg0LQrz15MZ+bUeLdLTqByUQ7UXX9aJswqx1YWk1twSFqtzuvFrK/68XoUmjNGR9o\n0xYLqZQl1RDfqCXHaam90Zu5RLvple314ovxYdhtooogO6fWpcuPRCm7o3rMQLeI+NlZhfjvj9Kw\nFS5VHx1GTRc70HOhiL9NxGd/SxKS82z/lt+UOAvMxu1qZDYPehWsjyeRKzuZN5cPDxm2noJ9WAHS\noC+/GV4Pz86z+dMicF8duQY7LUovRaR0fiXstbMptnFwrXJ1vkJIj7xVTcU7Qr2TX9qVnUttp/Nn\nJ2+X9MolNXOponziehc2rYN71rBi2Xxu23AW1z92KSuZRS3dcc/nVjJqkSQNlfm1eXRJodLkLyle\nbbfmkwSWituSBpfNiMteMIQ91yy1zYyUIMp0NHztvBxYj+VgzB+ErcmsypXuPCdJtqB4XNIqOnAf\nl5QE11hs0R5XF1tHlUWQ7UxspilstXdgzuJ7mLP4nvjkrNDfXl0kBS3YTWoyUMoOEgyBOl0tOHyS\nGLl7VQoV+jvh9Wejsmn3pHmOsVdy4cInry6+aElYmJbTJlITKB9U27rqyUuK46mnYDdWsFuWcdv4\nPf1v2oLV0Ritn/f1dz1+T4EHx72H449/yPzfuvX/U/f2UXJV14Hvr2iEoGhA4CLiq00VILpaI4Gp\nqLEdWx3JGZOITJyWHNlxOxYfk2TmQRxnxDJPWutZhPYk0rNj3gQHZTKeSKhJlMRyUAcnlseTIEVt\nJxgRxUZtdwsZupzGYNltg3HRGEui3h/n7Hv33XXOrWpox5m9Vq/qunXu+T777O8defHHKYm65BL4\nx3+Eyy9v/S1XWuEP/0kc4tlMVkynEbpsXnuZyybPOP+pes0jB4tdote1/anNg6ibIF1YiWAsEoIJ\nWuOvWLGjFc9qsMhVqHIZl1WnyMHJQ8rKDqxcm8oUSUTjRgxq0ytkCLqjC6G5Er5HqjLSCE2vZ54a\nQB++vDhQofc6Qco3AbsIcyExuwBVr6i51tQeZGxwIJtEVJfVHJPloGRMWqVox9Iph64JSBmDhhhn\nGDpfVprVB3xlEVywwl20k06S11NTxJPxTAsmUo54ICVt2N+tt00MD9jnMYIpb12taiqvTsiq8gS2\nquf+nNdnK4kdZfeg99aNEZYhKRhkJYy6rIVYguQJ0vN/xJRvLgaWwykSqfm+w25f54K2q5wLczBB\nGB9BeH/YOdHMhPxv3ltZPOjOZCglkZ43xTzdebhV6rKm5mymAPazysVNu6k1lId4Y2+vbmRN7cGU\nsJCLfyvxs+zVkZzvvt5e+Vgm+G1GEh2a54hqm+8sgbefnbWthbBN5l44Z/DbCV7vYZrPTL2TmUo3\nU4+Xgaz9ozBN0/RkopYDWYmR7m/EzmqE91G+oc76z30alsD+x1ex75p12bo0iFNQ4Aw1trmo9WuG\n3Bqs4oDLJVissLN2M2OzAylBqe8eCWArz0Ie1dUCB5sDtINCcw6ROecLCoWCa/XBB2Ftq+V1i0ov\nOXxHcB57uEMZMvz8lBEbawpTX2BCbIUOdghE1A6JUXoSF0o2j0jIpG8Cm5XRtoRkULrZREWmiRO9\n6XUfZWx67PriQ43xw2ou9DwNuoBr2rBxmp40zYCGtU7yIvr/fYfXtar7vvocvHIXdCmkZAlYMVTX\nlwSEEY01KrR1aNBrC9n50yoS+Q1QjiJpvaHLWiMBNbd6PoCsek8jv5gkQRsy2vYs0WURkXVmsP3T\n49ABInW/YoSJVg8BXHEMTv8zeOeWxJtIYENxBMBFhr7JjM9fJIlqa3d/eI7t0ddIUjsV6Lr1sy/6\nszOqLk6LD/ScCtj5Cl1Uuozs29Blrn/zhJSep3Jxyp0rfamFmAE7TiGiYsSKLR9iTrSEXOPEchev\ncAAAIABJREFUk58Bvgyne6rPc+trhhwRNTY7kA3GGLKxChFSlkjV+9wa+PbSih8ENJ4weKsFlJlB\nxuha7wdD1C+rHcpIkUIOEN3VGafqwyU2DganVPV3D84kZwJg++GNrXEKBSage9cM3//8hbAEzln8\n7ZTQ1kIAe8Yt2HW5eDe89Xy4ak22nNRncSVp38vFKTbwAKvYnyQvBmfkXppqJLGeJNbUocoy7ueW\nNDK8xTEabN83pzn4xND8xopJG6O0N4mEjzSIqL4/P1L7TT44lQb75DO+77d3s4FdDj/rAN2hcyXE\nr9Qr5b/aZN/n1/Bzx/8XBaDZbBbMm/+2bKLyQRFQyxeHDdjEld/aCmgEU1V/QDSBr4WTx0lyJm0D\nNqnEtKOlcNoHaD1E2tA8ZASv38tTNYTUWHlSHgHPlQgBJdxGfbbSQkB17wp4ZYUuw+pC+P5KeMb0\nL68vES4lGYe2W4KsjZRGyHJJWqlSL6kdnEAfjtC9aXFKSIU4YZEsRLhIsSMRWDZ0KJXQzUXVYtc4\nJoEK7Ys8sbS5WBJPnjzpQchmpWsRvLjC/T+ZSqOYhINDLkL9mqEHXRDHkEQqpF7RoC9QS4Tq/+08\nnTyeVcuH6tWqjJAdpUBIzaL3hNgZaqJBnz3921GSC0Au5nGU55ZASPURO+8hdbeWLFiisRNpVVcf\noFzm/b6VM76yeJB9m9el+CBkixci9AN2S0CK70L7T+8B+V/GFyOgtOTQ/9+olqj7Mondqs4T6s/E\nJ2vvYDX7uat4tyN0dD8F9jrcPrLHJS/eUBxhZNcGR0hF8FZjtMTUUBlw87im9iBjuwZapVi+Pwnh\ndgwazwViFmro1HbwwiXwnbPhqkgZuz7VtC/1KgyzhXqxTL1yIPtexcV6EqhT4QCrALht6J6UkLJ7\nz54XAa/RGaefylCdeuWAsw/zkjnejCPadvrvS0iIt5lKNxfy/WS/yHruqfxCUn35dheXqnRfg88s\neSeFarM90zRB0AuTpQXWHN3HX/zg3fC9PYEX/y3aREFEj64kUBrkILVzx5fJ09x/H04E/6HF8EuL\nXd36z4K2edpG9vD10vpe7ELdRtxWolMxuYw5ppYBNy7djwAnkgnWpsGqIPEeI9agcYKsTZSpH0g3\nZ0ydFOIK9G8x6VM7iNlSnTyelZ4IcWb7GYIJXAC/80ruT2cvD3g9ZiCkvoqV1e3pT11ebPoi+184\nuO7BmfQiixFfof0uufMmyEZjJg2yV6Hu6rcEk25H5lWP0ybFFuhk//u+ttgQxuZX+qMJpk7PWSc2\nTVra7SHpW0htH1tv6V9IYtBLlrCP1ZFHYCdwHJpH0vb6gFEyKqVg3jbdhoa88yJj1vH4AmYFGbDq\nFet1LTjhqPrf2HZ1D87Qvcv/bZqJq1Nvdu8mufjUXhxf358hLLt3zbSMd9nwoSRX3C3czy3cn4Qm\nKBen3Dv+gv7ksIsD9eie5TxaUznsID9wp4yZyHfZM2ITlbcHQpJozyA1Jkts372Rd61/yP1d4z+3\nPMT1u48kf7fO7gDgvs/dwX1Td6RmJTgNx7I9h+L7U+bOE0Hbd29MCLJO4SO134QJfEqfKUpTDYb5\nUNLf67dk41I9Wlue1XxAeI78GnRXZ7L4qVDglRxS6ccriVq3DnbsgFtuaf1NLtqYp1HMA0Mg7z2d\nwkFAkLy+kPK8nKye3fa9nURCcV4ZcfJc7A0gy8lK/2PxqXRZPOepD6+8vzaNw5GoqnKlYgvh0pVw\niSkn1D2kem2th5Y+aRWWXQP5bRtZZCrlZEwifpWwEnpMMfASxZCRf0fxRSZwXBX9iRHq+GRrnqsW\nsDZxeaAJTj1vfQBmf+p9U/UEcpXUhgsvMW17yXroWgRnrWg1ZPfrNL6ln/HBfm6r3cPI4AYaEsH8\nZhJnjPHNEjeq4i45GYPM9VbSNRulVU2dGW8OhFRD7aRvcgFbYsX2UeoPqc303tlLIsVInDW85DIJ\nsSHSPOmffEoIgbmAnRMtTbT9zKz5YiioS1zhnPHdTkKwZuhBpms9Lm/bVtpLo0KEVMw2TuxbtPRJ\n5k8MiqV+ywhZZkHP4VEfI1DyzikYH3TmEu/iIRelXVR+Ft/q/dDr9nh9U8Wp9oqwr3cd9Dnj82l6\n2MADSXwnUXmtucHZ59zC/VCEA3tWcTd3UfpcI23nGHAjToJy2IwlJJWMSew1fGcJnHY2XByZH61G\nFRyrcarGSTl7sTFach6Nx/zfm0nmbGXxIBXqjA8q6XdIQqrWffuWjWyvbsw+L0H3W1sdnh5mNbew\nk5E97+MWdjJF2alD15cye3Tf+nUs3/Mo+3kb/Z8b57Yb7nGpbvJwglIharOfvV8fZPCFv+I9kdd+\n/Oq8fftaiKhozKiQuHCCztRxWhrTR/YAQ1Zd1Eeu5w0QVw10ekEJ2H60A6t2se3pPljuPwRVpWf2\nBFT34ExqxyFqmpD6VKD3ZZgYg2fWZy8aS7BWSY2RQ4SUhl7zm1x4vaRIWNqA7MHQaXCsbYmNo+QJ\nKe2h2FhbyiJrGWtIzSCEVNURLMuGDqU2QKH9UDXvCkdt1Zcx0O3nSSWU/c1YdSBNlRAKgBlrUyRR\n596YXQ9NjI/CdjZyW+0e5yKOc6FODGu3qpgugz5OlzZ87aPVZgZVfwiUtCYJJ6DtGWRMMQSe14be\nT7ImIWIgdGaFGNybjlOngWobfHSuDJSGPpy5QYyQ0uOcPQ4vHQFMfCOBbS444rKhQ6ypPehUe6Hz\nAK1nN6TaE3wLrSoTLwXpHpxJiXApZ1WDViobYlY9wzWOkrB7RoKaYwrHR9UFL9K9PFtBnDv+ag4w\ntssFotXhCW6s/KX7p+JiPunfANYf+7QjNrRa6oZudnILdcrZsUlf7Lhid4uchaPAD49B1/lwdGmr\nMblI9zSDKt/nwtThyo7MbuC+G+9gptJN92yqrt53eJ0jRGJMqMy5bk9MNMz4QqE23rZrPxuKI+zn\nbdzF3YzMbkgDppozOb6ln8qmKTbcMMJ9U3dQrtW5s+/eFmFCAtVUel+vQrN8Jnf/77sYfOGvcqfj\nx0dEPfAAvO990Z+DMaNCCDFkdK7BcpmdEDpVnM2MtvPQl4jiVDMZ7dvZAVmwgcE0SB87IRD1AYRW\nKVsIyXnoHlRG7ZtNHKht5r2Y5K+wEAor077YObAcZ0jNZpGuHZMlsvTBD6loBFmLhErXaVMy7vV5\nDz0X0j044+JK3UQYAdi+QUKMjdOfndM8iaU2ntZ1hbjOkM1SzHgdMtKYxrYSda9u697kEV4Iydlz\nIZIoDZZwExup2sqkSMYeRPclBp0SDnmSZwHt/q37CeG9OREoZ4l2C6FLR/abEFLabjIUQkS3NRcI\nMR5tCIAWOH0xnBnAlZDagO2F+mCFOpU0l+K2Uv7cdyKB95BhWrwqSRuH16uKsRMIramdP5kXLY3e\nnLrlJzY8nczX0bR/9VqZrsLHuZuPs/EDsOe/pTY4+9annmWV4XrGfqh/ajwhnFjiJE91ygzPbkkM\n0ZcNHXISbH0mQwS1vbu09HICuNxLovQ86PqsVEo+Y+dT7kuFr5fVDjHAGGXq3F75GFOUnc2YBC01\noScyEjA9DkjvBfkUfJ0DjZtKjOzawKriAUdAaZuzwJlsbCvBcGBc8mn2VA/TVKhTp8LPffmz3PGI\nD/lw7rnwwgvBPv34iKgzzmhfJnRxaESYbChDQIU80uxh0x5mupy20m9jGCuXbqKuIJJUUYOWnlhk\nbFVRMQjNC6ZegZiER4OIdQUsAQX542q+DOePwfciEcvlXc3Zx0IWhC46S2DFIHQh6su+ihtXiBjZ\nCo3NAULKzkMIOcm8+4uzXFPSkVHinJ7ex3YNLORFqM4jDvz/jW2l1MNOJILW29Ei6Seeh9d5SVQb\nSOxpBmGgNsZ0sQf2ZMNniDQMFKKNeWJpaENoJEQrtFfh2bmSMcf6oCVvIZWWvGPV1oqQCkqtlB1J\nBuZKVFnIw5cClxyH547AVQO5ZZMUVjXSNCkTrzGVTwBs0uYepqnjvefyGIUQBPDEnAOyGtVXd3WG\nMnUdGY2d3Jy65at2t+9OVVPd1Rm2VIZZxX6owAFWc+fuexNCdapWTl5fNuyN4S0hZUHvVy1Fg1QS\nNbU0LsmK2Q5bqaX8r7xsLWRy6EFWHYZX+4XMSvI0LzaUgZwRtQ8aN5V4V99DaV9DoM5jS1DPCF2g\nU8k0Jkuc8S8/TH/84hehL9zYj1+dlwcZt1wlkZmwF0qEqxKwEg69kU4edzSYFoF7tZbeFFYUrzeL\nZLVPcjGJiBTCl6c+HNY+SxNZrwaUh1BSn0XWo1DfVMkcjEwIhjwCKsQdvbIQzvZxojTocWoVo/Qt\n5mlnCWXLMWiiJKZm1IbiVnQcGheuL41BQ0gRIaR027p/e72NlLfJGKe/5ZIIwlwkmALCKUKYeAjM\nf0OnjdC2OZbLnwBYBDMrnOmVlnboPWq51UkYqW7IuHuDE/+DijdmpWF5Yww9C0k7JfZLO7AEk5wR\n8cDV7WpbvTywavlIXBsg6z1opZC6X3mgcZqWgMs4LCOp23hxMZwXwZl2brbCvs0+hlQRxjeXUlWt\nQEilHiN8/NluVEsJMbGsdohxnDSqp+ZsaijCvqoJiGnVbhZX2nVS6yEX/r7D67LrEtovZv43FEdY\nP/VpDjWdW/+NlDMJjVva8/u6QYn6cBnxZtu+e2NGdbdvdB3Lhg+lXtKCs7bRer4srrJSKIBnlgBn\nQ4sTvhmrlgzlMceKgNKhcLYf3piGFlF3pCW2ouYDHixxm7EX1FoGe0bypPshMx0PZeppxgnIjL17\n00wyxpHZDVnc9J73QDVO+f3bJqIgrM7KU3GFkIfl+EN16LAIUmZtfBOIvnacEvWqI0hWFg8ytskE\nYTTUeXJhbSO179lL3BNGj6kT1Z4QIX7NE5uMgAt5MO9YTK2o67dqy8Q7b336Tugi0AQqpBdvjJCy\n7WqwxrmhtqSctpfRUrCI9EYTUhk7LgvWsFakFntTtZ7EQ5mu9bTGpumN9CMEGpHK/IYusphExdpe\nydgEcVsCpA848jU47TGYuDGsqokg4sZoiZHBDZlnG4ojTFFOUmXUBytZz8ZOiUiZhxBOixFQeXtE\nE1IszkqlhNPvBEJeeFWSvV0uTrmkzDeXUml3J/3sxPygpXyEgJLvTx+HZ49An5JEhdoQJkQRUgO1\nMbZv3thKSNlLLtZnq3oZTdMEiSpFJAdrhh5k3+S6VmJb43M7RnkmZ16tS+JIE5ICxvDNhCPAZird\n1KmwfcvGbPkJUjvaAI6dokyZsruYdZJ0P0f12Qo9RXd5J3ZbrAvHubLqZavyax4DzoeCyp1nx2dV\na7E5UM5F9dkKFN1jsfdMtC5rs7ZL43nMoiFwMnerMerODVCrxxJSq5s27+Re9tdW8ZnPvZP1Sz7N\n7UMfc+vo9073JhfKJ0l7tG1u0tYfPxH1uc/BN78JF10UL2NF1DFiIsZ9yaSHOF8bSVf+P7o4rloz\ni9fA25wUfdqEIR+80ntHRUGkRiGRp+5fqK/tuM12HnpzhZPHSbzB7OEteEnUJf57O6QvfZNDFZNI\nWdAIRT8LgVVtag5Ht2klDoqQSiCPkNL96CMdh9gG1KYSwmGg6MJAbD+8MeutCPmXtZWYCAiDEJPo\nyJi07ZVuS6StYtRrL8a+q2D2ORIb3TxCpxpJH+RhijIVnHFumTpTxbLzdMrbj7E56aPF+4pJsmsZ\neAfI35taPWLnqlNCxu7PwaxN2rLHD7lQIUKgeCIlE4JCEweaWbBSRyHEYuPWxLaW8F6zGC5d3lrO\nqIATWIvbQ7XoqFvb7QTUmaxX3UUttksJITXs45DFHA9CUrzBbJ7SxmiJ6aEeepimZ8gRLPuq69L9\nHmI8/Fze9vg93MxO9rOandwcn6O8ZxoMs9OYLDFdc/hBYM3Qg0wPpdHChflKcNLWwJgngIKXRMk4\nQuegHZ7xe7K7OpO2O+picGWC2kr91q5X9mY7Qu0oWXMZT5glse2qOUSUvG+lxBbHq7r3sY5DNyyj\nf2qc++67A4ad6nXZUCoJrL9Ypvf/q3PB/sPwerjmW4/ndCCFHx8R1dXlPr/3PbjuOnjmGSgE5JB5\ntiCdQkeGlyYaurxnIbI5BFEKVwHGVgNlhK4R4ihh26tOkH4I5EDNhViKEXrSdswGS0AkUeetz/YB\nwvPlpTWZoKMhQkq/H7BxaJEShuoIhbOQNjeRjWQrIBfZ5kD5TmykFLc9PukkUkJASf8T0XXMNmy+\nIGSMa2y4krnZTBZxffN5+IfHYHPcJsqK5CXdiYVpejJSBoBlew65hKtzlcSptQxG2dcQk4pasGto\n952cqbzzKHZtal93V2doDLp4Yt2b/FxtxvVZ9lco+K62kbN7N3ZJWeZG+i2fQuh/7zicOALXDGSD\nkloJj5Yat4NObZcC67Fs6BBb+DAAq9nf8srU8F1cXz0SdvQxsGzY1VVmCmpQr6V7UdKUVKgzVbuL\n+/fcwvb1G6Ndve3xe5L9upObW1V4QsS1Y+Tyvm91ye01foA0zQrgTEX0mQrZzvYBXzkGrz8fCEii\nQuvTZs0ak6Usga/f0e+G1KPW8cHOU2jOJknSkCVEcOy86fMZc9jRzCJw/eEjScLlMvUM0zd+uJ81\nH/0Mn/nzn29t6/R8MunHR0T9+38Pv/Ir8Cd/4iRRr7ySElYemiegcA3ZiWwnhYIs4hCwREmLimw5\nGUIqxJ1orlQ4QeVd0Bgtsa/qXDxXFg8yUBxjpJpVa7T0sY9WdV4IGQrEMqJb6KXj0Am53kPSptQZ\naufkQmiszD6PEVL6EOr8eEJQxAhAUcXalC05XGTSrqiqQka+9j3dV2vsrQmpmPoigBwa21yOLdkn\na4aUt1OVzi6fUFsa8i73PCLCxjWqKuJ08SI4fUWuYa5NyZDJASYXZtWpvcer/YxUNyQpJuqUqT9S\nofGmDu3FQqo8S0CFbPYEjkTOTWh/2jnT3y1e0YSB7Gv/W6Oauu+7+DpTrKk9yPSeniTQrWW2tKqr\nxbZP9otmljrdP2JbctFiuHZ5vsNDO3VXCGJ9CRnmiyplcIYBxtJYSwLH0n9LjGekM+Pr/R7b3Jpi\nx8Zt6senMFmS1scxKB0bp3L7XUztcSrm8Wv6MxfzsuFD3OxDZt/KjrRNDbIO1qtsLo4NpB5nkh0i\nk++tqpgu7cWmbe6kvVVLYPrs8P0RIqBywEqdMvtTmAkt3cxrS75b3Gvj+XlcmzgWiNq1z3xKeVun\nSMIitnHd1Rlmit2Ulrh4XYK79u1ex+0P/AF/8Nn3p++8/e3u84wz4LbbyIN5I6IKhcL3AUnEJyKl\npm/jjGazmW3rvPNcmIPdux0BFYNBsiqJEFjEGCJ8NGiEkHk3QpiEjNp0XjL9idtwY4MDTBd7MrrW\n+mwlzimG2pSyOs1FTDokfRTE64mOBImLy32EQEsO6VykItLmKy/DGcomSkNofCFDVG1wHirTS2ss\nIFtW2+3oZ+IBpokfQX7aPiqm0ggRUrYfEc4qeUfNrcTgYXjKER2hHHd5ELvQ9e8h5BZiKiCNa2TB\nS6IapRtbEKBcXhKdObE/0RIbLW0F6HXtjK8tMTIEA4w59+hHNjhCao72R/XZSnbNYuos2fMxPKH3\nmLZt0/2xEhk9vhiRKiobH2xTE5wDjDEwNMYU5TS2DqRu2YPp+xkCStrLO6d5NklHge8ch68dgeJA\nWrfdL1byp8c/SfwS7kQCrtrZUbyV9VOf5sbKXyaqvCnKVCr1zCsjKsXA6j0PU5+t8HBxdZr4V8FH\nK+93EqQKXvZZzvxertThBvjg5z7OZ3AxnW5//GNJGpg1tQcZ4SZ2cgsjvC9MQKlLP8mRF2EAW7zD\nIIvfNrkLfWzW2ahl8ujh49ZBa6wtwV/CSJw8BivOh/GAJCrUth2PBr3GOhRBDK9ok5KQdEjq0ftS\n44mj/h2rMtb70LZtjdDtHaIg5GEosRB/dfcnsgTUH/8x3HpruKIAzBsR1Ww2z9HfC4VCN3A78J/o\nzHE/DHpjdposOA+0qD4PEWkiRSPZdpeT/130yBSV956IZCOSpO6qCjiXd5mGEiy366MGP/6M6sWG\nNbDt53Ebpy2E0kp4MdJerD+aM7W2SxA+7NYgV0TbIUJK6tb/y/dRnPSvaozvY8jQtyti5gxhGgOr\noxcp1jYXg6cx6XMvikRKj11L8eZq2wDh+c7bEyHi9MVFsCDNnZcxChXnCcuB99JKjFjJ8FEf2X2Y\nNDfZIybmSx4hkEeY55VpIzFMQO8xuSBtTLIQY2XbNW3IWatTcSEgPKypucS/CUEw7O3mrNRNgzCW\nIQmsbttecABHFsOJ5WE1TEDl0l2dYWXNMYPT9LwWbJ7tkxlbVLW2GVbVDiRf9/M2porO6y0JhaDg\nzt33phHit5VaL25/0a8aTlWH903dwX0zd7gvUy6e035WpQSUNaKPSfEMhIi8DJhzbAmojMQesgSD\ngKjhH/aSKAHNRAjkEbkaX+XdP5ZpCeGiUD9FmwBh4sjHJtMmMdG29XxoSa1+pvrSwNmnCpz+0kl+\n9tt/xdl7T/KJv/n1tOwXvgA/9VPx9gMw7+q8QqGwCPgtYAOwG+hvNpvfedUVxrzp8sCK10PGhxM4\nZPmpiIj/9MXpBhwl6/6sjTp1nBuBgA1OD9P0FKedMe0RWgipoMoktJE7UeV1AJoqbzEY1PMXu7D0\nnF71MoyPwVmROFG6ntDlFbKRCrWl3m2xh9LERl6eOC2lkRhOmoDRiFETeZAhpJLPTTgpiiXuNFFo\nQyyM+nfu93Zyg6U40rF9iSHBmPTptcAPnodnHwMiNlHWRsXaSuRJkL1XFsPuoikXp6jvor1nTIjL\ntfYXUs7O39HA81g9ArHYXbF5jjy3+3VcJL+D0FNrvTS6qzOJ6rpteAzIXmghYkrDJcfh6BHYOpB6\nlun3cvbQ+Pr+uLo9r03pY54NkS2LL78VFxeo6vKlAUlARMnjluAwtT+SeYvYJl2//gisdQE4+4/d\nkVEh7qzcnAbR1H3RaiTj/ZeUMe2JLRYQHrvdz5pICTGzIU9QgO8cgxfPh4mlrW11wojJmDRTKvek\nhU73v/ZItL9HNEbT9LQal1siFtLAsKjvoThbfs7G6U8kXbe993/wX/b+Ybavf/3X8OY3h0aVC/Op\nzisBdwDvBnYA1zWbTRs56NVDyM2/E2JiAmcLAS7JsDwDN7nLF7de8JqCFwJK2j59cavHkw6PsDm1\nMRJCZZqexFCwe9cMjU+pvltOQTZynk2UgH5X90mkUVKfBSWab0yWWg+NhXZI7/SFcO1KeEI9k3mJ\nrVFv4H9rI2VBxNteRUnVBwTMi8kTqiOgykrqE4PvELet4khpInR8U84lJ4SaJc6OAjfD+Kb+NOu8\ngOakRMffCYTWyY7XXnZysYXW/eVFcHJFlsOLqc70d43I8vbORJqbbENxhIHimMtvpcGK76s+rtDh\n/jRgbozAzEP0ebYcGh+E9lZIpZAH1aw6oT5bSffaqIsXpPd8d3UmCQkB3uXd2n6EoJ1pgEiuLlsM\nS5bD68iGvggRmHnjizFGsecWz1mPvxDO088m4M7JexkZfl/iUZVIL2UfWOmdSJ9jZ2AbbJ/cyMHh\nlfTc4HD02OwAjS2GALNqKss8a2mISPA2GcbYElh559oSUKFzavFKbQk8czZIYG17LkJSSUjHJURh\niHizECOuNIRwWBtiThy0NhRHXABrnQpIE+FV55CgPQhb+myN3KtQqU6x44ZbWf9+Y4P3R38EPx8w\nKu8A5lMS9XXg28BOYBb4jwXlbddsNu+Zl1Y0MdUJQTUIHF2cihJFly3ftXpPQKv7QhIwy12LvdIm\nbyTqg5CNezuT7upMIqJcWTzI2IsDNN5EZkNkghDqPkz4sckByJMQ6eexA7rZR1iXfHlbySeg2sFR\noPwyfHkM3rA+y3HY9CrShuWQ9HoIaEKqXb9s8mHtkRcihmwfJlO7FRf4rz/X7qRRLTkuyUOLu72H\n+mwlTX0iY9GieS+BG6/2Z6LlJikvQuOPGY22k1ANBspoewSN5OT5y8/D84/BCzdm3+kE8lTeevxI\nKAj/TMf3McRKEsBUCKh2yBmyRth5l4rt+4T6i40pROy3i1vjQXCElm5qwlzsc8Cn0ZlNYzo1qjle\nS5oBDEl+JnC5887xufP03OgzpN5piVZt99urwRu+DWuvFBwLpGMZ9A4Mo/3phW8vy7mCJ+bHq8q+\nT0CPdSL7jpZKyd6US12M3AHux+eG1V51xu4uGLMPUg2InNM8+M4xOOd86FU2UZogaqeKDsS5Sr4L\nwSSMscUbtrx86j2l246NZSKNMyfhgvbtXtfCTC4bOsQObqVe9NLIEGNh++YZ5ndVH6L5xkKW6b/i\nikiH2sN8ElEfJTUsPyev4LxALL6T/Baiui1CbCfazxBQ3nNPS53ASZ42pQgwSdyrDc2rztBcvC/K\nxSl43JW3AeZGajgEYTeZPkzS/xjCiEgvpJ8ZAkq/IxATucbgdG8TFQIrjbL1DZqyR31ZayNlLrxE\nVL+ZdBzapsmCvCseWpqAiEEep6XWt14NI8DGZMlJHm8qZblUTRCPkrg5C5SLU/TUvKeOePG9movK\nQkziBK0XxQTQXATNFfBd0vkTYqwTTjW0jzRhIs8m0xQYt9XuYaS6IT/YXshmI0RI5klmdF/sRW37\nnidZaycBVVLFhGuebB1bgxL1ajhEhKg3dB1BOKn2NmQJKL3X64vh8uVwtvlNVEU6hpuP4ZRrpzIX\nEKnHIHy75q6JPZVfcJHEtYmEgCIKl+1RRHSeE8ykmuOYCjekfZC2Bt0+PMhKp74MqUiVNH/N0IPc\nzV0A1Iti95YatI/Mbkjxle6L4GlrwxNTl1rm0+7Fi5bAwrPhs3RmSxkioCycPA59EQFFjGG3cyV7\nCrKSvFFTXqnpJLYX+KCrZCPNjx/up15zN2cGP+pxWyLP92XZ0CH2jPwC6xd+Gv6n/+3wkb6pAAAg\nAElEQVTtb4ennoJKzvmKwHwalv/2fNXVMVhCSiCETDwXkxG7an1riCBZrjaPTjUj0ixfV4ZT0wdb\niZgbe0uM7RrIhNAPwQBjjA/2t4qLZVwxD0L5XQgW456fyWlkCSgNnRBNLe2+DKe8d57exHp9dL2h\nue7DqVtl/mI2UgJeTdY9OOO8VzT33MkYtI2bfUcjtQ7UhIm0ycJmb/Ok+2fH4tcosQUaJCGgQOUs\ns4hC97sTgiJU3jIZFjGLJGrA2ESFmBJdfx6Eft/rgh/eVnNxeZJ4agLVuLSvbVvSR00Qy+VlOWYI\n224EbPJs/3P7MElGLZEENw1AiEiqz1YSL9+VxYOt6VAEQt6HwX18HH5wBM42ufMisakyksK5QEzS\nB3yk9puUppyr+a2Ld6QG/PpdgV5gcxo7KUnWG1MbhvBFSIJv3/PfRSrcwzTjff0ZprR710zCDENq\nOK4NyOtUKFOnTtlJFENE0oT630OIuO44pM0EzjvvLB8nai7ahRDDI++F2s3DnZawNRK7DISYVEVI\nj2/pZ9mwW4tlQ4eSgKSi5n7X4Ycy+2DZHq9h0SFTDIGm07vc8/H/i43f+cP0/F55JTzxBFx1VaBj\ncZhPm6jzgPcCJ4A/bTabs/NVdwKhA9mSRy8CJhceVSVSzwPZ1CHDYcthin2O2BgZTrdxU4nxvlIi\nNha352l6mKLMag6wigMcrK1kfFO/M9wNcVChDX+U1gN3NO2/EG/7Dq9LCahXK/7W0IuTRL1+ZfZZ\nnnpF+m1BnmlCSghWaEVGN/mkwZt8YLa9ph79vybs9Cckc9wY9B4cnYYaaAdbYXxtf3pp2pAH8r+G\nSWcDo3NW1amkcxC7BEIq6Xbif/uereMri2DJinB7sTZyLs7oXhNutebcwXuYTlUrAFUSG5jxw/2t\nRItWQYb6EJLMSLv2spb6RiPvqD4l0pA89ZaYECjVfSbwpoKMnd1kup8ba7OS7GW1Q+5yj0lirJS6\nxZNsMZy5PB2fBum7Ir4yceQ2k9pR5UnypR8CvY4AkTHewk72VH6BA6xK7Y9sXTIOn4JkbNZLZWMX\ndWytYn0S0I5COfeBEFCrOQCkoQvKTLGBXc5zUUGidoasF1keE0LObyFmScPrlsCCswmC3RP63tDP\nLYMRApspQ+Y/JGUWtaUOTxOzeVX3s9ie1mcrbCg+wC0+ajzAKikvKXImgLVOAJE4b2mc4Inw7uoM\nW4rDlKnztXuv5gMfvQ+eVu03mzA9/eMjooC/BH4H6MZ55bUzO5sbhPS5evPnXRgeeSVJEyGVYrTz\nfMlzZfUHI6nDutsL6A0pm3aze09yDdUHndtzD9Ns4cPUh8rcyb1wE62cSOiiko1vOQe/WRPpV0zf\nD+FLuROvjpMvw7+MweXGO68PR+Ravb5WmViDWUtIxbgY0nINvHecVu0JyHvt9oeFPCJwLgSWMVwv\nF6cccq36voa46ck0lVAdL4Wo9ThbrZidVx6I6jCm0ojBqefhmLeJknGH7GzsHgoReu2kOcBBHCF+\nN3c5BDmZNajuYTq1V5P+hwioEIRU3DGJKKTET8xY3RrZx9qNEGCZ/JoeEjs7uXA3p79JepAepl3u\nwU2VYB2ZdmNhMzgO9SPw7wayZbVNjFKnZ9Km1KazaVhiEh49t2sdrn24uDp5dBd3JzGygvMo9frL\nT3K2tahWbbta8tZOimyJB9+m5LMbmx1InndvchcwwPDslgwxdYBVaVJbaVvX+1qhEweqo8CVx+Db\n3ibKzqW1kZOzo/upCZ9258mea6kvdC/p+mOe0MqjclntEFtqaZym9fd9Gn4fVj+xn9U8nDBUW/gw\nq2sH3D25DUYGvdrU4ITuXSnxVKfM4zuu5cMf+K+tY+ruhquvjgw4DvNJRJ0DPIUjohbNW612UTTl\nrAPShS59eaYRiRA593fgOtyJvYPUH/JssKrGIzgV4WZSROnVVo3RkktmPFhhdfEAAJ8cegfvmnwI\ntgYOkeYY5FB493kLGXVjaEx5B91eNKHL2Eqi5L2EW12c344NB6APsyB0rYYN9V2IaeGUtdRKDHg1\npxSBoM2JRTCWkG8He71HoeesJC4Qe2jhXrW3iQRdnK65MonReyjtQydgiYIYQSPj7VoEZ61onTON\nLK2kL69eXXcAxnf3w5Dj8FdzgMpQne27N2YlISHj17mooCfIqq0s3gip9vTYZP1jF1AIrORB7+Vt\ngXLQGtyz6iUbXq22sniQsUcGUlWyxgV5Er8JgMVQWJ69ZAOxdfT38cP92VAMMQZMn7FeWLMntRc6\nwOpEejNF2REe1oU9T7qapz620uq5EFCm3cZkydkieptGIZjExqmxrcS+wXXJWmTGoftpccUo8bWx\nfWtHfIVMO15YAmcbSZTeD5bgEdCMLeRnjjhd4XLLSOWJTdo5YHj4SO03WcX+1BgfWH37fko02Mkt\njK/vZ7yv30lyfVJkwWuNm0rpWPxY1+x50IfDKAPw3DfO53f/43Da4P79sMSHs1+0qHX+OoD5JKJ+\nGfgN4CTwK/NYbxg0Eu+Q2s8QTVYHH4M8StzaV1kpiGy4QfMepJIIzdniPROG3pfkf1o2fIjxiYjo\nXl8GmpDq5GKHMOcH+UjY/j9BXBIVUveEJBheHNsC8r5HjEn6AwsTwM2kaV30mlgvv5jdBbReJKE+\na7ASiBj35hFSo7fkiLxaaxA+IaYSB4VqqmoeP5x672W8B2U8sTOQJ020ZXQ5Gcep5+Glx6Dvxmxd\nvbSmxOlUfQhxomPSxSG6c3M/n6y9A8i6MUuZlv5KnSGIrUmo/+1A+t2JYX2nsImUsdOqvxCR3JfG\nuhlgjOlij7Md03tBJA25eoDj0DwCBS+JssQdZM+PfPdEw7LaIcbX9mc9zQS+6IyyNcheP4C3Y9H1\nWybYjzPpD4Hn0mZMumkJ7XZErgJte6PtwMrU2c8qlz9vkIw3baYt6Vvo/9B3Cxofd6JS09A4BgvO\nh3MDcaL099BdIv2y+0akOdWAHZ9eu146tyMN/e7VxhJC9SArXTaHCdje5xO2R8IQrhl+kOnhnoyt\nsWVOxdv1ygNf43fxRNToKKxa1aaz7WE+DcungA/OV30JCHIOcYga8gxprVu5FePO1TYoRkBptZts\nRk0c2BgjWoyuCInxLf28q/oQa4YeZAsf5tZdO1JvJUuo6YsvhGS0PYnflJn3LLwaGymRRHUqAtYg\n/bSJgE3ZvPxtSZvbcBncdQTyPOhUgmGJkZjRpkWAWhIp0ritsG9zmuYj1k8xqAQnoRmnP5Fg1asV\np8LUl2doXBrJWe7czrVINvVZeHkRfHcFXBxoQwipkB2KnR8tAbNnT0DXNQrv4iFuq93DBh5gpPi+\ntJxIb2MEVOzysX08eRxGF+dLbqRuK3ULtWOlz9puRI9dJDWa0NGSxQnzGdij9apKWCtSba2urJow\nJi2ebF4SFSM+7F6ZdH0dm3V2WZKy5uBQq0fuBh7gg1MfzzxbXnk0TQ8EYacZ2xdF0GUYJ7sGVnqm\nJfPQqk6KaSz87wOMscqr6TQM8yGHPz0zl7HRC0nHY2dTlwmBPovtylkc3r0ETleSlBDjY+fH1qkh\npMnRIQ6kjPwv5zIk5bMEud7fqv46Zfaz2jFO+izo8oNuTwzXPsQGHuAW7gecbZpEsBfJU2LcvxWu\nW3SYL9z/FlfPlVfCL/5iYBLmDvMasbxQKLwFeK7ZbH61UCj8NLAC+FKz2fy7ti//3u/BBz4AZ56Z\nfR4SE4c2EKqcPixCJNnyeZ5f7UATTzECaq0pC1kOSedLkwtENppXOexjHdNDPWwojsCQK769uhGV\nRspBSBfdCeQg6jmBSKKWrk/rCyGxGOLMk1Z12jfFZTVEitOJWP+1QEyqlSDPxeGLdqvKhxVyHugj\nY1gtnmnC0U8Xe9JovnbtYwSVTfYZI2b08x8+D889BhffmN0rOr6aJeI1MdaHCykhBGTeuQ1cGjZZ\nsXjltIBF7O32TB907JAyFwh5CscIyQmy6mb9e2jPqN8b20qMbNrgApTWxpwjymR/ljETmMStvV6T\nr3pJFMY7T8pDa75IsT0chpvZSf/UeHgOcLnrBPazyhEf2rDYMnJWfWWk81EVrsXd+tKN7bNOpaXA\nTm5O/h9f359NEi9gpTp2DfOIFgFvN7ls6BDUVILlTtSZ+rfnj8HrvSRKn8129WiCKELcJBBS5+l3\n9NkLqfDs2isCqzFZYri6hXJxii3FYUb2mLyFfWmYHpE6aWLpIB9y/yvJdWO0BNug/8JHefRTb0zr\nuvbawOBeHcynd97vAm8DTisUCgdwJ/RvgLsKhcJ1zWbz94IvnnsuPP88bNrkdJPrIu67Ap0gSKui\nsMSCVR0FDNyCl6/9TUuGNOdpk3Vq8NKShGDSsTLspbzNie97hlIxZRIz4yZa5yLm9WAhZH/Qicjb\nHhz5P2QT1QlYpBiTCMb06dqQXPdnG3jmZM5Ecobr7VQql4fcQghUpKN59cn6DqZIQWL1bOHDDA99\nKL2cQtLUkAFnngTXjvUoUF4E56+gBUK2iAJ2vJIlwEqTdTuaY1YqSoleXC+Ws0lcLcGhCaj5gJCE\n0dYfWnMbDy1IWJP2XcJ4CC6wHpiWgdSE1E0lpvaUASf9Gd6kArtOprHLkmj4mf3mJVExCOE+37db\nuJ/+qXEOVZZFX79z971pPVUlGZYxW9DrbgmqkOopdC5Dat7QPGKeSXlf5xRlypRd4uHd/WmfVfnG\naClhapN685wr8vCDtK/7r/GaZVR0fXZfnhGwidJtCISCVGuJkscdibQ8z3bYEsK6P/ZetfOgCXWx\nDZ50gYz315wDRc+e6ST9zrLhVLUv6rppepzqb3d/2KkLuPDkt3jk4TelD97/fvhv/y0+pjlCodls\nti/VSUWFwleAa4CFwDeBy5rN5guFQuEs4JFms3mtKtv8i7/4C06cOMFFTz3Fz2zZAsA//Of/zNOr\nV3PixAkWLFiQfL77PSeABcAJuHQBNE9AIefzYv/5jRPwjH+PBXCJf/8nT0DXAvjiCXjWv9dpvact\ngFf856iq93r//FlV/yn1+c0F8LSv5yf990dN/T95Anp8vx5r7e9lbzzK0gXH+NwTPwvfWgB71fuX\nqvenT8A/+edrF3BNzz/w3IKfYPrPLnf9+0ZgfM+o9vLm4TI1Dnn+uufh6F5Y/ivp/DyrftfrcKlq\nT9ZFr4/M82W+np4F8BMnWHj5S3DiJC9/6QI3P5epdg6Z9818LPyJ7/Lyty5w8/Vszvh+Qc2/7X+o\n/DcC7er914y095MnsuvwDTMPep4uzb73hp8+zMoT+xlbsJqJxpJ0Ph7z7/X79nvU/rP7Kbb+dh1+\nOA0vfRGqv5hd94sj49Lnw/7+rJkX/dyO36zjwl//Lr/U/VccP3EBf/vFX3T7W9b9lRfhtLNfHV64\n5ETretn1tftWz9crM8Dprv3Y+oX2ufx+sWpf1svihUsD+1u994b3pPth5sQinn6wN8FPl607SmnB\n83zpiRr8s6r36QngX+DSt7XUl1m/b6h+vtGdoy3dv8vlh6fZV/s5/vTPfiXb76ddueT7Rer8/c0F\nrv1LF7Seq+kZOK0Uxj/Pqnm05zs2b6HzFDqn+nxdls5X9cQ4X1jw00z//eVpvdf78Xh8/oafPszM\niUV8+5WLefkPzmrd77I/TiuF1z9wzi97/1EKC7qYfuJy+OvIfrTj0/P14t/DhefCecvC51Pes/v2\nEjWfp2XXjQWnO7z7LY9nHoqf00w7Fs/o+mV/yXc7v9NuH/1yzx/z3QWL+dzHfhbWLuCyHj8/f3+5\nu9/0PavvVzVPpYteYvqZ2ziTEwA8sWYN/7x2LYXzzmuhM/I+3/ve91IoFGg2m2kaFg/zqc77YbPZ\nPAXMFgqFJ5vN5gsAzWbzpUKh8IotfO2113Lq1Cm6Vqzg+UOHWPTpT3P55ZfzOnne1ZV8cuUpKHTB\nk6dg+jngFHQtdp90uc8ru6B5Cq7ogqd8+Wf9p/xe9p9f888XnYLz/XvyfqHDz090QeEU/PsuqPj3\nXzkFp/l+Vvz3ui+/uAve6H//3/75s6bd2VNwsgueOwVX+f6+PS3/9NFlPP32Lt667rMc77qUY5dd\nB3/sy9W74PJTFG94gdnPnQt/654Xf+4Fzj3jWV7quhT2L4WXuuA81S89X2edgkU54674z4bq91QX\nXNyAky/BRdel5V9S731XrcNZ/vlV/vOpLrhCtXOF/3zRt/d6N46uq16AU6fgsRLUfLvNU1Az45F6\nnvPr/DNddF0+A18vufV+Xs2XlC/7z9WnKF71ArOnnQsP+9/rfl50P5/047/SzE9Zfdfz85QaV70L\nvuK/S78Lfh+H5kHP+yun+NKOFTzxO+u4rfu/8zOnjvOHtd9g9ui56fw+1wXXnYJVav+dUOPW6yHz\njzkn0u7pl0DXOfDcde6c1NT4a2p8ev9Kfy/25f7Oj+s/qHJPqvl/Ro1fzvOzaj6e6+LlmVNc/JYv\ncOrUxfDstW48L/n5l/6f1RXft/K5yIz/LDPP9lPKXRH5vesUnHoOCudn+6/LX+XHq3/nlMNjz5zv\n8Iec++YpeLM/X3W1XgU1L1d6/FBw++dLB1bQ+I3r2dr1IR45dT1/+O/ezuwfnQtTXTz9+WU8fWUX\nxTUzzJ5Zgp845fZ1YRFwJTx7natP5mVW9XuR35+FLrjoFBzo4uXKKa7+rXtY+jjMXPsyf1q/Lj0n\nV3a5+p/w6//mLoqrZ6CrC05d6s7tWX5/yvzJuepS+07jn6f8uj6pysv++Xdm3l5Uv9v9ZPe1Pqd+\nvxb/0wu89YzHuKzrW2xvbGF2f8mdnxe7YKn/vPxUgt+fuPpKLjnj67y+q4tjH1wK/7ML/la1J/vD\n9oMuOHU8vb+e8ful1sWZ1zUpdHU5PP1Latxyzr5rxnfqOJy1OB0HTfhBN1xeceddnzf8e6eeAy7y\n389P99Wzat8eOQW/3kXXtW79Zr92rluXrxs88aSaV7uuzwXO10WnWu/Jh7vgP5xK77knffmru7i0\neiGFrkvgg9exZPlXOXbkna78k36ffE21/6I53091cf2l/8wXp38toTm+9/M/T/OjH2V5s5mhLzr5\nzIN5JaIKhULRB9n8SXnog3C2iLt6e5VM9rzzALj00kuhNyCrvRYnpisEeqz1ufhyZ+JEh6eUndK7\n/e8TwLO6I/7z25FRhdQEW33dv7Q4qzsW8eVKVbZh/p8AHvbfC7igENLGuUDJ93+Tf7bXP7/Gf/8i\nfOm217GyeJCr7pxk32XrXJlrgMvgtKtn4KslJw98FmZfgXOWPsPz9MDKpTDj52ihr+8c395S2quv\nLvSf3/b9lGcvPQeP74ILP+CeTZBN/HOmHyuqXYGl5vszpKJlmdcr4Io3HAK6GN/mO3k9aVtv9H9W\n9H8u8AM4re91UChl5/EaWuEKNX/S/4W+jQIkydhl3QRk/Z4lu5/6cPNzjikzgZsT6YfMSUg1BlmV\n5K/BLL18tvcMepjmZv6B7Vs3Ou9EfN3XQGI+9EPgi76/MmY5HzIWDXpczdPgdQ/DmUvdusicKNMC\nLqTV7mPGfy/h5hzS/SKqSrEFXEpc3THl67kMfqL3fGa5CH7Q6xKszpDuq9AZDaknpS/y3plk96lV\niepyFmTfTuDUIzqR+Zlk1TAtvCspHvs7nFpD9ssLpPNj18jiOtx7X/vzXnYML6BCnd9mN3euvBe+\ngFuzGZi9pJfu27xn6wzuIp06Bkv9IM4lHy4EVjrvqcuLC1k6AH/TuwwaS905HPV1yH6fcJ+n9b0O\n8OogwWsW7Po9o/6XfSrjl/1QIMUTMm8zZO8JCxrv6PEeBX4XfvsNv+nst+hhdkt/Ou4v+HITpDjn\nQodXv1l2QRmX9U4x/sN+16d2qjuA083mnAJKsGTpV5ya6sKlbh8Ivp3w47XzwSJ4SqmyX/onKJwG\nzy7NnmMpf/I4Luu0B00bnL44xW9+H57W9zq3do/j9uiFZPe9xd0hswVZz17//gvq9xngLlKzlhlf\n/n7n4flHs07l1t0DC4svwotLEce6lnv7GfXsTHhj+REeefI9aVvvfS/n/cmfcB7zD6fNY10DEqW8\n2WxqydMCWk2h5w4hL6AYyGKq/HYtBm2o73l/1iB6ArehfmlxWP9rjTptv2JRhm39OQbRjW0lpl3o\nO2eMuJnEDqsldcBoqj9eNnQoa6+VRzRZI8E8WGpsovLe6wTJyBqpcdRnK9RnK3TvMl56uq25uqzn\nwVzGr/eI3TtSl60bVV6MtDsB78wwvrufsdkBpig7r737c97RY5mT7dAimAnYREE2dpfsqdCchex6\nrPFyn/kbVH/e4WI/q5ii7Nzn29m5heZSu8PH5jr0PDRfMdsa6b/U0+maCk6QORIbKT2veTCBc70P\nwVGc4bLghbXA1YuhvDxbJgaKkH+4uNo5NyyBEd6XzkMknEJjspS1pwlF3cc8azd3IePx0OWdZ8Om\nHI3WPP4gH6k5AmqaHmfI3AmOmgwHTKWPsINBCPSetzCh/jo1hj9jCUxf3ln/Lej0XH7uc22hOrER\ntHhRl6m6IJiZ8DNHofuRGdbUHmSKcrJ/GpMlZwtl7d70n4LSyW/zyJNvTh/ccQeMjMTH8hph3oio\nZrP5cuT5TLPZPDJf7URBX1x6E2tEHXKtFdCbVoNFcAL6cggZS1qiagL41PH8AyabQd6xGb8VjG/p\nd5F1mWZN7UFuG7qH24buSRM7Sn+3urI9nuwCWhFUJ8SUvSw0iHeefa9dPXlg5lsOdLk4laTwSS5a\nfanKs/k0NI5BO2SpEYcQHK+GuJs0f5IOZLTEvsPrqFB3RqD3E3Y2EAhJMixk3n8eSo/l/G7akb+Q\nMX0sJEEne3HUEAmhMc0VXk0+BU3s6jFog/JOCLHQvhHHEpm7UIwkSwgYmJKkt5OBsltJ1+ei4y53\nnm0/BlUXBLFCndJUg49W3p+GLAgZUNsLc1SNJ+aIECI+58I4h8aQ965vo4JLFTw2O8D4Nf3xfdoO\n9NnWOVc7gV5cUF0d20jj/E5xxtQxaH49/FunhJ0GHfU9z8v51RBtfj90V2eSO7b7Eed5V6HuItmr\nNjMEXU57l44/zdOTl6UP7rwTfvu34bT5lBdlYT69864B/gdwKbAP+L+bzeZz/rdHm83m9XnvA7Bh\nAxSL8M53Zp+HkLIGEZ0LASXeOr205rJrV5cF7QkkbUErQRXy6tMxoD6Vs4k1EumjNYidSKekLU+1\nNyZcUuMdxTRE/simDa0cUmi8r1VSo+H0hfDmlfHftWpDQ7t16CX1YPIusOOSQkVBwySr1f9LfsJ6\nFRp9pVd34PP2jI4LZL1TNEi/bGqgPFdkgQlTRvaIb2s7G7mtdg9TtbKLpBx6X/cjxLlrDl/GcHIR\nzBpJlJUm5XmESlk95qOk3n2aqJbxScBJLcUzHlvd1Znsmmtot68lyOZETtlOcIROZSQBbtsRp7E6\n8y5747GYPIvsm2gYCCGk+oC1i+Gp5am6yNZnYNnwoSR32c7Kze6ZBH3VnmNW8iAMqMT2kjFYIkv3\nca54KdRnfR9osMRaKGSBhZA0OUTk2rY1k90O+lJPuMQ9X5unmLJRqU9hCaC889oSTkcAL5HUoQtC\nYAlz3W679o7Q6rlqAxtvhi3FYVqSNscCIEvbal3eeniMsadU2I4NG2DbNiiE9LvzB/NpE7Ud+G3g\nEeBXgc8XCoV3NJvNJ3EqvTj0qZnYsaOFiGoOQ+Ea4gusD4zYJohNkQ0w2MmmtgSSPkj2oFsCSlR2\n+oC2E8cKIpa2bXmRrAQCDTZuKjG850OAC6q5o3grtz6yg8Z5kUsmJimw/YmBjr0k4/7nl2FyDG5a\n/+rmW8ASJJANxGku7MakS6XSXZ3JPE/S3HSaeb4dxxpbP0n4HANLvHiiLkmWbCWMdm/FVNC6z5O0\nEJXBslLeugHnjf2J5+F1j8G5N2b7p8+D5lYFtJRHyopqai9hYjM0bv1/L+w7vC5JIprEkAkxOHn7\nrpds+o3QeZbPUN0WrBoqD3S/QkELbR/y1Jad4JTYO08fhzcdgWsG0hhSEUnzbcP3cDd3JQl267OV\nNDH2rkqaaiPUp1BGBUijtNv8e3ljCRH+AnY/xYg0DWtJouIP8yEab2qjutJhPUIwGejDHKAxWaLe\nTk2tz12oL81jwPlQsMZKMTAEVKidTiEPD2qhhsLjIl2SvIQjvC+rtgtJwUJCDP/93ef+Rfr9V38V\nPvGJOQzg1cN8yrjOaTabn202m8/7mFC/AXy2UCi8iYBheQY2b4Z7fWyRSMiF5uO4hZI/DV4cymbc\nAd2lfsvTnUN7at2qByHLfVVN2XY2T3bD2gMaI6Cg9bLyZcev6Xei6LnAq1GDVCP/L10I53hJVN7l\nFYJQzBL9TK+dv7ATW4vJsN5e7Kc0lIsuhU5UpeiRfWOyFE25kQvS55Ba2NulSP3dgzPhNDdSNu+7\ntKGgMVlKJBBrhn1evlDsM2hN4Br6X+BqnztPwK6hHusoaUJlTWTreu1Fo/umCUpbRsa71eSB1CAI\nWklqM9CpOlH3KU9SFTrHoTmMOQvkwWAHEfot5F3Adi9+czEs8BfoWlWmD27bcw+PDi/n0eHlfHL4\nHaziAPtZ7dRdu7M4JrMWeWowG6dM9kEeoWelbKG9KnvPElTtJH5r4bahe7wir+zircVAzAMsYx1i\nHvTvsX7nMQ8WYupJ6Yvdg4UlULg8Lbt8cWfJi0PQqURQ+mTbOX1x+hfb85NOormhOOLWYrbi8oXO\nBfxcLGj+kL6X/Zff+A34oz+aWz2vAeY7Yvl5zWbzewDNZnN/oVB4J/CXwAVtXnRh2F8t9LnLo0I9\nyZGT2I7EOAKbniEGOhK5PrBaZCuH6VOmzk7SjujDpm229G8C+iAfkUs77b/WqXd/L0XCmtBIxPCi\nNpF658JRQ1b6JjZR29bHbUI6lUjp9QghSGmT9P+Yame8WkrUeYk92DAtl4G+tAAW1S8AACAASURB\nVBo3lbJzA/nSqFC/NegxjKYRd8dtHiopa9+xyFtLTtQa7GMda2ruDGSCG+q6YwRUDCR3nkiiQmDr\nkTY2kxXJh2wENSFp19pKgAPQvWvGIV27t0QSIYRVSIphc+flgd7TIZVTzM7H/i57SAfm1b/7Oemu\nKhV0TG2ZB5YItMTGE8fh2SOwdiDtx6CzeypTp39qnJlKNxXqTFHmVtK0U43JEtQU8aRT1ljVXujs\nahCpZkiSFAK7D0L7Itamet49OMPN7OR+bknvCw0at2t8ryUpNk2VNt3o5GwFyiR42jL+sXOBKgNw\nyTHoOh/OWWrKLw4zqxAWImjcMxdmWyTzMVyo1fkAk057UqbOnYfvbU0NIxB6ZuZh/6nVvOXFf/C/\n9f1IbaAszCcR9f/ihvaIPGg2m48XCoWfAR+PfT5BFqvX6exHuInSVIPtbEyJEdn4VjrUTvoU+91e\nrBoiBzbzm91cGslbby6pX+cUk7JJW0dcumdP7Y+v7+fWXTvYUnR+oBISn5qzlRibHXApZGq4NBF2\nU86VgBKQiOV/Zeqwh12IEW03cIT4wRO7E0u86vpCoOa/MVqiPphG++5hGoY8ISURlaue6NAqBj3v\nciGHxgT5SEn/5ueth+k0/13IfqMd0tRzoFSc+w6vSzi7g0MrU+NfkQi1k5Lq/dUHdBlJVAikzsHA\ns5C0LWbj0O5C9N/rsxXqxTJb+DAUYefwzYzNOmKgxTNVQ0h9J4SUnmPbt5j0LY8AE7uzza0SJUlD\nkdlTEF5ncJL1bTn96QRs3VcvhtnlyfhvG3YJgz/4OZfz7sYb/jKZU/CMhZK612crUPSf2jzAEoua\nkIXWcxQjlqwUxzIUIRsuOy+CXywh0JtK0MrU07tC1yft6DW20bVjYOe6HfMo/cyTasWIGUvszC7x\nATRNuzECyn7Xd4AmdvS8tyOsQoSUZYbkDOVlDtHt5NhFndN8gT8f/2XegiegqlX42Z/N6eD8w3wm\nIN4def4vwK+FfntNYLi5DeyiUqmDzSnYToIQJai80Z3lGjXELtQQIaFVVacvziJva6MSMirUXoIn\nj7f2zyOCxmiJ/UOrktemcdmtV3OA1cUDDM9uSXLxBcXYdpzaBkpAb+oq8Gcvw5fHgPVZOwd7KXcK\nSdnFWemM/T0Piap2G9tK7BtclyTwBZ8Ow0qkpO8nj7vpRa19DBmGiL8YJxZClJZ7l77rfRCSUMl3\n/azq0gRRc4lUB2pjjMxuyHdVhuwFotfsCiOJ6sSIVxCv3geWSw8hxdD6msv0k8PvYDX7AccUVKiz\nmv2UjrtgbIdqy7h+MuAIbPeJXMIhImaS1ssDU+7IcTi6OEsgyBh9W8v2HGIHtyb5DhOD7yG4vnok\n67GmYVI5UFRnsjZ0ui0D3YMzSVuZvgpoSfN3jkP5CAwO8MnaO1g/9Wk4BoduWMYBVrPvGuWcYPdg\nTG1ocdlcpM+2LTtOYXQmA1Jirf7T69lGWlj3fnnRvrYjlLW0Kva77LGYjZachwny1bGWkLLMtDz/\noZdETRmbKEsoWQgRoHkmJu3WtROJ1P0uFtSUT7HTlsET3NlHZo+9+fv/yI31fe77RRfB44/DgnwT\n7PmGeVXnxaBQKPx6s9n8Hx0VfvJJ+MEPWhMRawgQNmOzA+zb1sYzCbKL246AikFM2iL639imlzLW\niDwkgbIGx5Cq8CDtn4xh+eKkvX27s/MwXu2nUqsDOAJK9z2GCLQI1ao+LIL52kJ4amVqYWfVRqFD\n14mKTN7XEEIekEWi8vso6fxuhX1fdJIage7BmZTACCGxI8cBtaYWcdqLPw+5+LE6dUhOOVu35eRt\nnb2tz+vVCgPFNOREd3XGJWWWfgrkSfImgCcXQXMFfDenXKgvdg/nefBBypHGEGkVPjn0DiTDu4Up\nb/5Wp8Inh97BuyYfyhKeeq/Zy1Zf+krakguxy6Hq4g6N+LB4O7mFuiVs8GqzmkupLP0Gku/X7z7i\niKnBlJCS87ahOMIqDgSbFwJze9WoqBTTsWzPIT48dRPHp09Qq/13KtSZqXRDxfXjzvX3Zt/Vtkme\nUGygjKA1cxdTQdl+xEDvIUNsJ1JGS6TnSeZkTUn7vmz4EAOMcYBVHMTYcYa0FhoC0jMxCE/OmLb7\ny3PgsHOkVd8xR5IQ3tNwxhKonx0ONmrbjZld2LYs0dopcRw6I/LeLmdWIozF+Jb+/LsoIE2UOSr8\ni7ehvugiOHr0X52Agn8lIor8Zc3CE084neaxY3C66V4EeSWqGUgPQmhBLHWc8a7SHKzxWsi7eKxo\nWf+uvYBCEqiQd0pI7TJBPmVv25XEyIqj3963kTXDD7LaI+Apyk5qYdu3IERLjCubBF55Gc4fg++t\nT59bz5w8yOOULLEVIyg0xLjhN8L4rn4XdBQn1h8P2ZzEvO4GyScQ+8huI4Ejx1MJ5SSMVQfcpRCT\ndECWWNTqzzxu29Q3RZnGqAoJYSU8GoJE7fPAY0DAJkpUrfpdfQY0IaXCVGRsoybVb7LvA3ule3CG\n1exninJCYISInU8OvYMyU6wZ9km68y5avXYhqUKV1MPWq3yW7TmU2tZ5EOlPWX2W7mvAElh1w37X\nXyVFWjP8IHdzV/JuaarhJOgKPjL0my6J71ZobC4lHonShsyFhdKUk8jdVrvHRZmOwJnHpzm5/yX6\nvQnl7ZWPOYnlNmWTY3Ge/j4KbPKETcBjOKkD87wTVWSIMbDBWQW0x6cF3V+/V5YNH0pscIZnt2Q9\nC7UULCT9jsEoNKollg0doj5I1jDami/oOi3DLERjJxCSmgG8kuOd1w4H299D0rN2jG8n2ppd7jz3\nMM3Y7EDYpjEEISJLv3fttXBuu9D7PxqYzzhRbwQmVNLhTTie+6vA77at4M1vhre+FT7/eajX4S1v\ngU99Cnp64u+EuHWRGMik59k/zQcBJZ95CFnqswSUsutK2tpq3s8joPSlqNUmUrcMa2IxHHXGx5Xh\nesrJSgZ5W99c4bSFcPZK+J6qJ0YkWuiEMIxJDiyEvDCtPcBNTjInqr2EkLQIzKhJE4QdQiS6LyFR\ntvyv3wshTEtMS/uWiLUXmuYuJwJZ5l81LAIiNlE2rkxM2iPPhfCxhGjMS1GdiZXFg+lzuTBtmALg\nXTzEmiEnCbpruM72wY3pPOuL1uIKLf2AxEBfYKrm7Am38OFE2gOpis6q0W683dkUNXaXXK4GRSDu\nm1jH2K4BysUpBhiDiqtHwgfsKN7KB+/7ONwOd1bvTQioVeynf2rc1V/5SxeMUEF3dYYNFSelum/q\njuT5TKUbSAksgN7Fezl/9RG+WnH2M9sPKztSmRf5X+87HfwwFK0bNY/6DGpCIkZI6UtSG3HLbxD3\nDg5JR4zUZtnQITbwAOCirScElH5PE//tLvYYYyn7W/oUIqT6zHez/1oEAZqJsuPTYONE6bYgi38s\no24ZGKlfM0vSx9B8x3C8lO0DNrl1GGAsJdpj89xOXdoLA42/57NTa3IK/evAfEqiduCyFwH8PjCL\nMzb/GWAnEMlL4OH882FsDGo1+Od/hkcfhX374Nd/PSkiSaIzkLfZrapNQ4a4Mqq7Tgko23ZerKfN\nZLk2ybdlLx+76e2FbDfWIFkPKC3B0OCfba9uZGqo7GykhpyNVItbadV8hjazlga88jK86G2idD87\n4TCgvZRN9yGmjhGwbYZUt6PEVWqhfmsEY4NlzpXDs2EZbLyg2PsxDjDPfsdCnsg81O5XcyRRMYkZ\ntM7NUVLJpKhkxCYo5HmjQCQ3TjVWbjUM1+t1E+ybXMeGYbibu7i5tpN6zanKhoc+5NQGMcNx39fb\nhu5JJEVCeMxUuqEI+1nNXdydeX0Kd5acs7xTx+07vC7NZRiQbDRuKjHeV2J8UBHwfk/d+sgOuP1W\nbmEnt9R2ZvpxqGJslhSh0OgtsX3zRkaqGzhQyaa4KFOnXEn798TdF8HUN/jKinen7edJRU1byTvt\ngiBaQipULgbWnKGXlBAWhlFgkCiBJZ6OA4wlNlDjW/rz8UaexMz22bc1frg/iVnXGDS2W1pK2+n5\n08SYtlGy9ej+2DhRcpfE2ozNf+jelPXUhFQ70IzUWidhrVPmICsdER7aH+20IqovNz9/f/rba/Hu\nf40wn0TUac1m86T/f0Wz2ZRr6vOFQuFLHdfy+c/DwAD80z/B9LSLG6UijkYJqdjG1xeUSHXyIORB\nB+3VSJorsQhAuXQmxJcQULpOq6450qavUlYuoHbGeQB7vURqyEVJ2VIc5s7Be1vLtTN01O1aSVSo\nrk7CPeT9Zi9q1PcQQRuTBnXSh9DloYkAkeCF5rsPEpfidulA5gpWzSCINYd7bhuIU0OLlC1HEiXt\nhYhOO1a5ELwa6NVC4o6u+2jb3ur29y3D9wOph+oGHoDhB5TazbvpD6U2SB8Zdi7+iarMq9nke50y\n26/xfVBztW9wHd2bZlhZPOikUrLXY0SrPT9awnNTiVt37eDhorP9SmyWgAOs5s5r7g2P29fTmCyx\nfXJjujc3AVVng5KoImcWQ8/yueVGg1bCo9PYVKHf8qS5ofetzaPMbSD4b3d1Jiu9JJX2JR6roTaO\nHM9P2WLNCibSNjMqTumLNjGx4w3ZvFqwUi2tvgy9E5JECeh+hlSXeaDx4hEvmbLrlSNp7N41k8SC\nAm9+k+fhKPW1gdMkRe9v/Rb83u+1f+FHBPNJRI0XCoVbms3mTuDLhUJhRbPZfKxQKFwNnOi4lmIR\nVqxwRNR//a/wwgvw+7+fLRMiaPJExRq0vUvexRq6UHVbE4Gy+jctitVqNikfErHaZzEJlOYudN1a\nBGvf17DXpwoZuodVHEi5p5iKqZ0BuEii+tZnRdi6zzFCSogOAXvx2PmXg29F/vKuQJ6HyITJU5UH\nmgODdD2hVTUVgjzpz2Zg6+K0Xsg3zrX7XhCsVUOoeS4XpxzS2qbebzd3CUQkUVpEr7/rceg6NUds\npZw50JJsWupvRzSPwrsmHkra7t40w47irQnhJOo3kfAIh7yK/VSos4FdLeoyJsmGGrDn3MOU5K6j\n9Tf6iKrHdL2NN5W4fvBIElMssR+5qY36Q0f2Vxd3d3WG8cP99NQ8EbXiOPy5ihMF7c94CELSqE4v\nZmv3JDBh/m8n8Qj0IRSQdWx2IBuHKbR/BI6aT3uvaPxtjd8hy3BJ+U7mN6bGtEICqc+OwUqi9Dh1\n7LAQMWhVjBb0bzrlkfymP9XdJHH6VnGAA6xyjJAQge3u63aSyvNwKOoNb4CurjaV/ehgPomoXwV+\nv1Ao/D/ADPCPhUJhGpj2v3UO73xnGnH03nudau+882D7drjiCpqP+zQwIZFxaMNbCEUbDoGtSy5v\nS0DpC1Bv/EGywehCBpoT5ruuz+rNdZtyKHRewDziyV6gk46zP1hbyY7irRyorXIcbAjabXaRROl2\nQiDxc0LQiZhYvO0GzfeYLUNsHvpIuPLEJqoTryypWyPukM1DrG1dh6gg7B6wRqgxSYaVSuk5sGDj\nr9i6dJ16L1+9CI6uiJcPPY/1Udk+Je7q2nVd3vHtL9tziC18mDJT3MXdjM0OuLJrS1liRsDGpZG5\nO+rsd951/0OJaqeHaUdIVZyq64P3fRyWOBf/1Tzs0smEGDWxVQlAi9elJTJhbsE9q67f49WS26Pi\n9WUdG3RbeXYzkzBd84zDBSVYsTzzW2ZslimMXa5WxZenagqBvsDb4QXdl9Bv4n2nbW60pM16GFsQ\npiuPcLN4WWsYtFRKmCv5fSup1Djm9KQh1AexK7R90fOmJVF2DW3uwhgIcZtnYhGSsFuGmdQOrUyd\nYT7kpIBbSe+rEL7qhHCWdw+1KfevBPMZJ+p7wM2FQuFcoOLrfrrZbLbRSQXg7W+HqSmn53zlFXjE\nx+9ctQo2uou++YFz4N3vpnC+E3VnEAl0prO16rM8yCOgQgbNm/2nFVuGkIVNmmzVFXpcVoV3lFTt\n1wlxqMebZxvUCYh06aqXnT3becomSo9DEx2dcKpCgFrQ74qRvr5UQohFv9PJnsjjxqRuLY3S7WoJ\nXJ46Yi7QKSFluUEPNv1Npl6pB1L7JL1fT+XYRFkI2V5odYuJQCwekoCLzD1Yyvy2n7cxRZm7uDvJ\nmZd4g8XswPLWd6tzzR9fW2K82p+ofKYoc8vtO5PI3OML+sMXWGxt9XnUZ8niFm1AH1P3acZLx9XK\nC04qF572lBTw8yTEhOS947vH4TEjiZL6tKNCCGJElVzQIe/VvHWx82kl7nnvQYaQuW3IBQ3NGC3H\nzo7F5W2T9ao+hYg5TahIv2SdN5N1GAoRwgK2bi0JDxEsGvJy5+n1CnkZY75rXyvdn1AQTSG81F7t\nHpxhAw+QpNY53J8NOWNBz2vo95DG5t8IzHuIg2az+QLw5ddcUbnsCKlvfAO2bIG//VtnI/Vf/kta\n5oknaP7LbzmjdB9XqnCN/02Qeswl3UqQNIRUEnbx7SUv+vR2C2wJrlhevthG0yBlYnr8WF/UZpcI\n0OCQ0PbdG8NIOxIYkCpwZCEsWQkvks67FctbNY4ghVejRrBEw1FaiYgYYjaQiSgdIkRC/dPP9IWn\nIUZI6f5M0hqROgR5l4H8rjnf0FrlqU5CBGsv8JVF0LMCvq640lBfQvtMB0ocdOo0C4l6rVh3BIgn\nQqYoM0WZOpVErZaRKsSIqHbEsvEETAPRPpyqPC1Y1Y6Gzer/ybS+Fs8xLbGwoJkkYQzkecj42V6A\neZ67MWblgsXwE8tbVWHtCKmYhMQSblZaF1qX0Hx2wuRoUH1fM/RgYruWcZTRkq4Q4/NqJGCxd/WY\ndFvajhKyaxM72zFCwhJSMUlUCDSRYnGvZoKOkt1TWuoWw6uKGVtWO5Qx5G/x/oxB7L4K2JOddvUp\nLv7Os20q/NeBf604Ua8OXv969zcyAn/wB/Dii+652Eh95CPu74ILXFypCy5wqr4FZC8GvUHsQoWk\nS3qz5tk/CZGmDRL179qIT+qCrOoNwt5ZeQglhGA1zIFSb4yWGB7cksShGRnsIMK1cEZyKV3xMnxq\nDN6wvrWc9Efba1TN73ncqAWN6AdpRcwWyViuDjIITuwngvGi9HsWAYRiH0l71ubAglwyMheh9cq7\nBGNtxKRdnUj+QpJCyZ13eo4kKm+veXXdhuJIasjtwdolcSz9rbRknNsrH8vmwYRW4jB0YYfsNewa\n+ICR45SyIS5iXHAINH7Je8f2OZT/Sy41TVyHjOfbESEhYlgHccRLJr/7NfjWEWCgtXyIkMozitbf\n20lMLXQ616E6IWNIXqHOQVamHph5KmwB2bsSx00nEbeQJ0kOEbuQNTvQ/1sizBJSc2EsNTElkqil\nAUmU4AypO+YIJWXzvsekhYNuLSQW135WucDPMe/PELQbu5+rsX0r+anZf+yw0h8t/NsmogQuvhh+\n53fS7+95D7zvffD978M3vwnf/S709sLf/R1ccw1Nb8aeSKUgKwnR3myxxQ0RPCJpsohGP7cETuiA\nWdslK9LXYImBTg0U9TsxEINIT0itLB5kS3GY4eqWpEhLAlThqtT7nL4QSivz+6MvqNAB1uOMjVEj\nGyFgNZckEDr0RhImeeYGGHMcbA3G+/rzJYD6t1cjQdOgPdU6UXG28xzSUKU1GGOojXacf+8i+JsV\naST6ENi9rue+6iJs38zOxK5Jw4biCGUJNFmB/axKfstE3TeEgNSdrKlmdLRaHFrVYbYurTbT5zpm\ne6NVbtDeSDbPKzXGOAhhZRm6UD8Fh1gpVh8pkW/xnJZEybs6REpI3dUOtD1WTN0Xw2GhfZgnRYdk\nXMuGnd3NnYfvbY2xp/e8VrdZabikl7ISvddC3Mg+CYHGeXOVSOURPDp3XkjtKHZvgjtt//T+0neZ\nnrOQ+QQkDBM4iWzde0NmHKr0mWynsrPgy5/XfJ5PfP3XUgKqtxd++qdzXvzRw/8ZRJSFN77RRTYH\nWLcO9u6FmRn4qZ+Cxx6DqlvxxAAdWpGZICpL0Gjxr4BGzHqjD9LKkQryCYnCdX0CFnlaCVWIGwxt\nwE5F4UYa1F11ubkakyXGqgNQhC3FYeqUGZnd0MpJy+HTz0++DDNj8Pb1af/aca9Shy7bztAwhmRk\nXTpRP3iQ9C9CbPQwDcMB91stTbOXg76E5GLOK98paPsb6YPeC/qSi4yvQj1OSEmMstj7Uu6HyiYq\npD6QvkLrpbsWPllzue42sMsRRdvInJntbEyMvROj0xDRI582ppREFd8a6ZOtQ94RCLmKhyQvApqA\n0jaJyWUcgVhMpdi+1wxcn3kWWi8rkRUVovXaFfjucSeJmh2Ie9eFTAdOHifJJ2l/60R6HMIBcwHd\nhj9r4iCSOB3Yful29Zmy9cX2cbuxdQqxcAeWkAqBqGztXWAJpJPH4Kzz4SoVJ0pAM7B2f9mgy9b0\nIhaQWYi0tWkKLQlUexCfAF32UsghoxPcqOak1Pw2I69sYM0Ln3UPLr4YvvpVOC2Py/vRw4+39fmA\n3bvhl3/Z/f/ii7B6tSOo/F/zy023WKOkCCV0yZ88nhIwR45nv0NYLWAhdLFJeyGw9Vn7KC1ezqsH\n85tc4NKG/hPwB6MxWUqCxAGJtEBiSLVToXRXZ1olURoRteNmNYc6V9AERQykfUNE12cr1GcrmVAH\nPUw7g+cYN2thlOyFbi8z3b6FkLTMIvXYvAhiEo8fXV7VISqz6L5tt5/P8DZRut3YO9If3Ocnh96R\n/LTvsCegfMwiDY3RkiNcNSE0qf4IPJe+xCAk/bX7YC9ZfBDxusvUYUFU+X1pOIaE+5Z+6HY7UTEJ\nhFzuQ2D33ATZOZZx6TpEEiXQaboRCxYntcNRutx8wFp8GuF6Ni6UMDOivrJ9jI1Xz5Ge/7lK5Gxd\nul/zQZDptrSK7nVL4LzL09+r6m+t+tNnNVTWzo9lmjWsTX/TCd4TpkigE2m7QOC+O615ik+88mus\naXoC6vWvd8mGf8wEFPyfKonScOaZcN99sHAh7Nrl1HsXXpj+fsMNNB//X6lEyoo4bZ60kJeGveBC\nRJg8t987icadcHmB9DO2HxlplUqUrDkVXV6DDYsAwYttP6uSKMxrag+yb3RdawyabcD9/gWRRGFs\nokJguUGRRoUMN0MQ+k2I5DzoI40M3efVlBMwvtalSNE50bo3zWRTEti1j3F4Mh5N3ITeQZUNgd2j\nIW51UJU1oI3lVxYPsq+6LqsS0ntFnoeQ59Hn4ezH/n/23j2+iurc/3/vJHIJAUGj8YYmWiRB0Yqg\nbRUKvVih2kZa9BhbEdt6erOn2p89cGzxW2wrrefYVo/0tKdVtIotVqH1nFIvrWh6O4K2ChIiaoLx\nhiKghnDN3r8/ZtbMM89ea2Z2RKOb+bxeeWX2XNasua31WZ/nWc8DTdPSqw1neU6+xgfqCr4VRimX\nJgHXu+q6v7Z1YPcfsqnD5pmY9yANTLlxUeX9dE6Bb90jE4qflax/KcqGS/kx34whUPLZGTNj3DUa\nJapmkt3EBXbl29WO6XomKQw2ZSrNQEreO7/DN5HigwFDkvnUXIvL0Tv4ndBmJ9XPwKakutQoW1+R\ndtZgOzB4HewzAg4e41Z0odgdQy7r+yctFs21VjXYtDdTWE4n9aEjuakXFJukJcw6F8kqFHio9yRO\n5BHv98iRcPfdUJvgu/sW4Z1PosBzLL/hBnjhBS9IJ3ihETZvDsIjFFRCzkicKVtqEMR67R/x6w12\nfya5LKONxwR9tJ5X5++T+9vS1egGPs4cIbePpjgNyVq8TnecN8qbxUJaZ08KZ7zIeCOmYagaCMfH\n+ETJjtD4RvmNYE2zZ05MlXpCKi1aeWu3rHdBEq6ZsHrtBDpnNwQxhKiGztn+LJ9SJGfpp2M7l6W+\nkezvEG+61Oc0ZhtFNLqX1vJgy8QgHpKR2iPvm82kXGSSHA6bxsPBFDf88rffYNc0bwx8oJYzBTM7\nJ3jOa2tDRVieWzeirobWwJBM8/5Jc4EeYUt/PFnfdizfXZ19IKSRxlE2rWqcFvKeSMJkfJ6gOJCn\na9bnfnWwbSw8R7Ezva0zS1IRDCmP6yjjkFaJNqqLJP4a8tyudqEduyrYV/O7CzqUhf7GtUqmAwTr\nwb1toCzxiu8TdTDFiqT5VgQpMuheWhsObM7Ce4+kijRHHKOV5LW11Fd3cD6/4H4me5YMU5bNN9hl\nvrS8Xx/O38PXCv9BdaEnJFDHHAP33AOHHOK4CW89yoNEgSfr3X13+PvVV2H4cOfuwSw+sCQiViqQ\nVE9MgyVfaih+sdM6AY8G2ut80iXOq3MWReqp9gH7xyXJkm5M5L5LKRphtDZO8qae40e9bquNKnLC\nKX3IaU+yc8U97IpTomTDYTpAPEUo6GBd9bP9lijF2d6cQ5KVpV49OmcD1QREajW19oZVqzhmnSEh\nNllcPx9DYPEzwPc0eI2ZnA6ty9EE0pSpR5Zrfd8uPwnx3Op53Dzv02HOMFtMIRt2boHNK+HgacX7\nm3ehzXPuvZ8PBJuu4Fvc3HN+kAbl2HErvPpIJ1ONNOQlCUaZMccaJ1pI57sEIcGSz9ylQok6jqTL\nHgU/zTm1OmvOKYM/aiVLK06aQMWl1di0AV71Z+dpRcTURyPu+7MNEl2dfVI7ZVtvttl8a0RYjMBc\npgeLNhKYRllNoybL7UmQbZttMAjFlpFSsHMdVI4AfJ+oJcAcFcaFaET3kXQF7URrjz9YXusdFwx4\nloo4bj5MmcYHyjiSBznxkgbyCu8r/JljCo9H1v00/8/RnY48ElavdhTcfygfErVHIcxkEI7WXB9R\n3MflMj9pjK2Lz5UXR6AM4kbwRSpWXfQYJePKCMyTaGXS7a3WatXTyc6eXfx6yr78wyT30eTCBqne\nGGgzmNyexo8hLWzPSxCpkdWeae/YeSu86NVSAbPNWjLEUJtGjGnPRRzWegrNXK6EaoLGTMMErLPB\n5IKLYJyXqX71IxOCZziSrnA6v75+l9Nz/XAYMd5+jA8TWVw6sQehCXQgczu80wAAIABJREFUV9t9\ncN1L128bjLlOnytRDVHmcBfivvvRuM2ycdDvkSv2lVlnq4NRxOao9TaH+YVieXMd7DsWNqn6aJOp\n7Zy2GXaGZNoImYaLPOjjXRDP+YvzrqGTepYzpWjmZ5/aBdskg1LIkcRsxz5xEwQMSnkX5bexaRRU\nDQkVageCoKsWBK4MZhCn22R/YGecyA06qHcH9jWw3KehhdfY712b+HP7qe7jvvlNbwbe8cfHl99P\n2LtJVNEIaixFBEo3LJAumS2kk6lNJ9FOdBQSOJVbRiZpzy/NJLIMHRTUjBwMWfA/oJt7zodquIAb\n6ST8QGSHXk8n3Tt20tu6lanXeh/VsrXT3Y2YvidLobuxNkiU231WrdcJGGnZQCoyukGS65LgmoXj\nNxbdS2tpbZ7E+dU300G9O+yBhjQbNYaJf7uptTeYfkNXX93BFO6PLTpMgFvcSOn4Swb3M5mR47qY\nxULq6fCemfTJkHWWkI1m+xbYshJemxa9BvMsmr3EvjM67uLqhou9aeYQPidBomqaN9K9xGEe7Qtx\n0pCdsyYENuILWP0OXeVKyO8FikmUMRUaNdqmNNnO4XrPpHlKmvT0N2LWS/izp8xs1NWLJsBvn4R1\nq+ClScXnlwprm9qmO2abr1haU16cuVYrtnq9H4+o3h9ezOObxT6M8pkL1TQ4lzZjxtWzFFU0zQSk\nN1K+PpdE9zo4agQ0jwlmvYJlxnFTGBdvdWOYkHlqy51ekubG2kDFAuxuCoQzgG/uOT8kZXE+aepa\nrxv2Zb686fpom/C5z0WPOfRQuPxyqHr7UpW3b832FF57DS680AvWWV1dvL3IBj02akrT5hwdggDc\nDYfuDGwjcTkCawKrX4YrabLLt0XWqU3tp81Qpp4aPrlZ0HgpCwhz6tmk4UMGPsm5E/+VD3EFAF3z\nRrK6bUJYDxeECta9tDY6k0RPC5cEymZeSwtpOjD3wcSb8tWk7sbawCcscOJFHCfPKWfJieddX91h\nH5n5jaxJijuF+5nCHyO7SCd38OOu9DQEMynrqzuYhFEGJ0dUIGNSugEvQrhxuK2nk2NbVkQaTQOT\nAiU4z1m1MBMYNRwGjw/vkam/r34cO25FVAkzfhT+e7hs0XRqmr2yqYbVc2q9fWwqkYtcmf+lTjaQ\nsL0fowmt9y5znQ02tcIG7byviReERMtmpjJlyPpqspXGiRyKO8BBdbBhLOREeTYiJzs9006Z9rAN\nO4HS5Y0Wx8uytauBi0zIwR1AM3xx3DVBQtt5PXM9AiUnLcj73Ia7fdbnccHULY0J0CjRcc/E5lDf\nFyKl36exo+B0L05U91ovmGxg2k1S5hrD73Vqy52eX+xSIkmwDZY9Mp0vjruGB5kYqFqrH5kQnRXp\nwLsK67gqP4eaId2cvkm43wwbBhddBFdfXdIteDugfEnU4MGeT9SWLXDjjV4YhNNOiz/G5ixukPSS\nxxEpg2Y8p/TIcXV2YqPPa4hUZPSXoEgVmfAsdTP1tgVesyg+3cZPCIIRzeqR7+KFVQt4dobXqs/l\nSpbfPpkFcy8tOt5aR2lOFCpOcE7pL5VWpi+l0YyLV9NI2IhKXwbZOZj/qm711R3RSOj+MTWzN9JR\n7RGsG5lVNFJc3aSIjnj3us+qpbPZc4YPIBtsf3nhvFleHXySc1nHdVy27jpv4yjY2FATkK8GQYQa\n6AjJ1rlbvIjlw6ZZFYEbuJAJHau5veFM5vXMjapxfr0NIQ1gRrc6oKVG0jsjzWhxo3mb2cgQY9vA\nIu13Xqri0K7+g9tvUg589LkkGdOxszRZGu2FXphY/WCQPgeA7RugsApywgRmGyiAm/xAdIaovm/m\nPsl3Qqta+nuWZAWxvyFZjZ4PTr3vgwP+7FPE7GFjPtdms1LVpBJ9emLfBdsgQK9Lo0jFmfKagIHr\n4IURcKTvExU3ucCB7rW1dI0b6Znq/O/WhJEwmDJueeAuUNO4MRwsumJhGbRBS2ERnyzcAX6iAioq\n4NlnvZhP71CUL4kaMMCLI3HEEVAowO7dRbsUCnXkcjEkA4qnOceZ0vTHr9dFTHa+2dCkqZCdsvmg\n9AgtopilMOnFRUZ3ESgdXVbL4mYfWdaqgayq/AqrFs3g2JYVTGY54PksGNzccz7d7xHmHG1OFGZE\n8KNZ+x/u/eMmew1lu9rfLL8RmA7ZwC/XnPv7477C17k2eow5t+60ZjvWS9VqjufobfD1R64tjnqt\nOxezXsRkAaLpY+SMsSZCAtvmdaSXcR2M8lZJAgWeudBI8zdUX8g8vultWDAc7h4PP6CoE1g8LowD\nNY9v0j3TJ4uWxtMoXAGaKFYMDNKoBqWQF4gqsW2EaqephzYluuB619YSJYraj0RP6gD3t2iQRKBk\neYYUynfDRlBNJzeoDnJj3bOGpeJkoL85WxtnuzYbtLnO5UulrkEmrZaome1PTDGxuOJIkIRrH5dj\nfVJbk2Qi1M+5Lz5Yuq2S/pePj4LBfsRyPQvWBn28j86ehsAv1IYgobAm8ZqIi+urWNPLQHYwuLDN\nW/HpT0NLi+cs/g4mUFDOJAq8eBKnnw7LlqXbP+7jTzPbzowgtZlAj67a6igiQSYSOEQbQ1sD01YX\n33Bp0iW3Szne/JZ10OeVo2J5TrncsANWt0JuBquXTODCm24oSjjbUV3PsoXeaNiYBLvX1oZRqoV6\nUX97R+DvAIQzvJonhHWMa2xkVnsJ0ylJEigVJKVImRg0x45bEXSSkgwYmVsqOfJYgPtv72LZPtOD\n8xw7bgWzuJEbmeWpN4ZMuEby5nn58bxqGjd6pk/pxK4bMEWEu+fXMnT2y2FH81dvfeC35TuJfosr\nmNFxF/MavklN40byTz5Nz2sroXlatAOYA1O4nw7qGdvwkOd8r+ttcBWsPmuC1wGO82V/KH5fSzWn\nleo4bN5hc2/mEJIPOWhx1Ud+v5rYNFI8My9uQoHrHLquLr9FDVssIih2ODfbt2+AOt8nKimOne07\nk+9lKQTK7GvM9UmmMYNGj0AZk5JJD2TIeX11B4zroLPRn+GKo24Ssr3tixN6XJ1tg+k9UbZWPxUB\nGrj7EXa8cDg8Nqa0waXF38k207SDepbNnR7ZP7ASSDXcvKf+O7Jv7xYe7z2GQ3k+3GfUKK9vLgOU\nN4mS+MQnoLUVxo+3b4+TSjX0Rzda/A/CFVCcDNWQqTQfl2vGj/blsSGufHlMM16DlsZmboO5lqcG\nws6JQRndM2u58KYbIjNAzucXTBm3PHr8OJh309zQH4pwtprxd5hY/aDvHN3JzfMIZ5jpekho8miI\noCGfMvWBo1P6OtcG/kdzuRLwZ8lV10d2ncxyZnTcxcaGmmCdVHkmcz+tr04KGnfpWxBMB5b1lPWG\ngECZUXhg+pPOyjYCpcyLQZyvNgJfGhNSoWb2RpYtmk5r8yQmNjzIDVzIFdXfYtlNE2H1eLiWULFp\nCp2Ug/pIgqWvI42DuOyU5XE2heaNwPggmfL0lHgs59PPZLQ6xvcNC0bmksjI+pv9tSpmuzbpa2TU\nMii+l1qhkmUJZ/LWnklhvZYAx9RBfizsTzS+bylIIik2yPveTHi/XM/XJznHjlsR+W5aeyZF2ozV\nfkd+bMsKaOnw3knTTsYR2T1FnkqFTUl3qVBy8CuVIwt2VI2DNUPgzwnnNyTHDMBk1gV8f6rG2ohz\negf1xTMgofh9F+TJLB/99yc4lOfJk6Ni8CDP/+kDHygu6x2K8idRRircvt1zLl+40L6fbtBsM4Zc\n+xeZXurCzOASaeRaKdFLnw8bbOvjypemOynDatleIs1ItbAD8q3wfBgnqnum79jo1/H+eXZ5eG71\nPG5u+XTgCA0EyWq731PLstnTocWLhns+vwiJlC1go6t+TRBx2JfPVpIpaVYkbEyWj5sMeA2JHqFN\nZnlAoK7gW9Yq3FB9IbSEM+mMzhbc+7hnNtsjloGCo01/NgdW/V5I/xBpNjXTlX0y1f2eWpYtnE7D\nOC/I6umf/0/+5feTYek0amZ7qtXc6nlc1nEdX2r4D48s6jyDaQiPvl45CCmlY9bKS5wDugyca43O\nLs5tI7MWx+6amzaGEwiM/4n01dKQM29tREoSUW2ys/nUKKItSYmJPVZf3RGqM4aw/GkDDF4Foydh\nncgiYb4tmzKX1qSun4s/uy4SAFafk2gaERATLIzpWMZHW0rwjRzbssLzGdQDJo04xUhvs9VTukuk\nGSyYY7SqbytfmzVl2y3bPtmO/+c6eGkEDB0TXwdTnnYEV0pXN7V0NhI17dkCeNp8oSz3o2LCeHjo\nofi6vQNR/iTq2ms9ArVoEWzb5vlH5XLB5kKhLgy6qRtP7cugnbRX4Z4dN7Yu2ig3WfbRkE6YFlt1\nAFvHWeqo0JQhP0hbGXGzAQMMhJwjYrl/7cvmTi/aNHWe10jO5Uo6afCn4jcEBAqAJbCM6UxpWQ54\nMatwEam46zD7GDUwoh5SbOIzWAsL1l4aLEd8aJrgxnkXUE8HC5nFguMuLSLeNX/byOTq5ZFqLGeK\nFz6i1Gd2Ffbs6xJpTAqSqENUibwAFiy8lMnjlvPK8KP46NVdvH/aVyKOpYY0LjtuenFjKc2/uzd4\nyqyASXjtJFxJ30cSbKTU5hOoZ3tqc11SnZrCoIWBedWFSH2EL6QkUhLaxG4jxYqURL5nEaNo9SKf\nfMs2Y1AdHDAWenDHp0q615JcpiUQEFE7gMDPT8/61ehiZHE+tiUUESmafZN7XNwtAxdBKsXUXMrM\nThfi0go1U0xcTLsnY1EtwYtYvs+Q+HPJtqON4oC0ECVSfmL6otyEtmUoVpTbobKzN75O73CUP4ka\nMgSmTvVI1OLFXsgD7SPlirhrYDrfpGiytlGjjUjZSJk+vw7caIOR511kIgk2BcoWSsFVx+C+7YCC\nnzvP1gmZNACqfsvapsPt8LuOT3B7w5mctMi3LcxXZSzxzGtTW+5kCss9BWSeH+PEZorUjaCtITSN\nx2iKOwJzjIZ2uJ2jfAe0M36Tp+6cPfu3gBeHpYFOz8l+Zm1xh5/G1GNTPzUkkZHqhtlm/jeqY0z5\nF8DZs39Ly4Q5DFm5hMnT9kHiCr7FgkWX2k1uNrMVYUTv+uoOL9SBuQZNCGxOwa5Ru+wQXPfD9m3H\nESgJFwGVqkBaBN96THBPaS4034zrvZV1Me1AO0GnG3Hk1z5zB22Av6+CM33zTFoSpJV5ORnGIG4A\nI+tj0j755MkW/FF+WwGB0qq/nJUHcJU3g/XYlhXeQMu843qWmm1ga1Mi464prs9wwdWG6uesn4kh\nicaHVJIrM7jKrwNGwDEOJUpaIWS/Ie+FVDh9ZbO72ZuxF6zDcpxZVvfgrFfv5M7eT9jrUyYofxIF\ncNJJcOCB8NJLXt4dhUCNcjUGspE1Dss6KCZEZVrZMWsiZSRmE0jTlr7F1pGYdUa6lyOxpRQ7tUvY\nytTXaTvOhqKEzT1QMTHq22IhFBH4ncWyRdOZ1nKHNwVbNnS6rr4i1dUykvP5hWcOa/EVqSUxx2lo\n84TphHQgTxskabjJi1dzATfygZ77wzx70iRl/q8NVbebe8535+TTqqbNhCPrItfJfeXzievgtDlM\ndXS/OWUmk8dvZDmD6aSeB/HUxiCFi1ZrDVkz34gpb4mXj9H4tnQ2NtA9pzY0gdmuIckE49rWRPqk\n3/K/vHbX7Czzv9kzNXUxMrwXrvJtAzBX3TSBktckVQLbIM0QKGkqs5ksRwMv1sFxItCo9ovU36v8\nrm3lpSEPgvBJXxvwCPayR6ZH66tzvMmwBfL8BoYgNAHzvXbBm8zgrV7NhCiZtBFH2/uXRslyIe5c\nBpJAyf006TQKlOk/zMQFoyYB5EYBDiVKmrHjBt6yDuZ++epeJMeqjXAalb45XJ44QGS6OPNMe93e\n4dg7SNTRR8Pzz8dGPS3sIkqkLKw6WA+KTCmJvo2ouUg7OEoHvF8TP9XYRqZ0XrVgunZCx6EbiTSN\nnwuyvoXNMNxXorSyYFPiJNb6pj5bXfQIyW8c72/xInFPZjnzWr4ZJVKaXEgTnny2muBK82mcaQbg\nJnioZSydNLCcKWFiXX1eC4KGSM7ekvWRCtkc0SHa3h/UOhfiOjrpEyeVhWY4ZOfjrFhZwfppnw6V\nAE3K5H10KTrteMfertY3Eg4IDJLMywZm5plWWeIIi6mvJB6mvpIkuN5ZPdsNQiXEQL5j8vmaMtOQ\nO5cSYhukmO3NBH5rgNvnqw2YuAFeWgVHTAr3NQRYmw9dgzqwkwMdQV3BEGkzozVwWJbEUZTTTW1I\npOR2/Y7J6x2N11aIwLJydh/4zuk2omnKMs9MtydSaZWps+R+tvui2yN5HbZj5T7y3DcRnZErv5eC\nr0ShlCijWpl27deO/kYTKLlsU63joO/BNdfAJZekOPCdh72DRPUVSRJr8DJZ0kdo3xWXg6MtdEJc\nB9mE1yHdJOrQKJbTmPO0fB23j9xPjqrlPvmB8LrFJ0rPjJHlSIKoR7k2FdAcNz/0kaqn0/ORsilS\nukw9U1KW6RPSqeM8c6Erhx2EKW9MCpab+XRy2AVb5HV5fv17tOe0HCAp5ouW1cFuInARXF2PZq+z\n2/3yUAaPbyo2pbi+CxcRlvskwaZ46Lhoce94kgoV53wO9nsyGjir2NG5CLpcTZRtTtxx/jBp4PBj\nAdzq6oN1cKpos2RbZTPRGNjum/l+3gAiKVtMmaVCTxZoAy7wl2dTlMexKBBuX2AjOno5DjaTsHQZ\n0M9Nq1PmPOYdsilR+plpAmVTweL6EVcbZ2u/24HNjv3LCHsficrnoa4O/vIXOOqo4u3yBYprbIOO\no87uJ2WIgpHo5WjFQH4wpThn2l5wSaQMdLoXm0NqUkA21/nkusIO2NoKJ/mz89KqXK599GjN3F/j\nyD8fvr7kWqbefiez/Myqnc0N0cjmEO2Qdccq/EcgTCWRNo/dcqZ4KSfMzCepcDSpZR8R/yl97ZJQ\nzgl9RFbPtShAErZ7qE0EuoG3jXzN/zmhCaV3y+usv+E1Lz1I0jPVipSFwK2eO4HVzRO8kAAmJYU2\npUrlMQ5pBwxxkNeedH2N0cjuHSbgoDYPS9gUHPlu6HZDk34D+Tx1J2sz+yZiA7y6ClA+Uaa8tAq1\n6/7bnieEvlrVvhIkyZO5dunrY4vCHlcP8y5Jv542YCasXjLBywTQHJoTA5V3vtjXpjbqQawcSPYV\nWr3UapYJk5PmPGYfrUSZvgeKTXhJdWsjfb/kIpBtwL4pz/kOxt5Doioq4CMfgbvv9nyjHn7YTqIk\nbDNjDCI+TwlqkqUxCRoa89IlnUvb/03jIk0+GnFpbKTs7vq4tJRtytImh8JAODSME5XYCNvMFa5r\nd+UqBJbNmE7X7SOZy5VeME+mR+so6yzhExUI88Z9y8/7dz43FQXPNKENrLFqXP4w6pwBgYrLqeXX\na+q4O0NzQ9qGT0KbCDRsjZ7yV+nsaaD7mXp4cTC8ZjneRcSkKQyss9BW4xGpzsYGryM1s8u0ecIc\nr6/NQHbAUoEr8tkT2zS0qd0FPyp5PZ3cz2SWLfKCDgZZ780zN9+2+T5l9PIkPzgbZMBec+0RdYvA\n/Oo0T4H65upg37H271QPBsw6U39bp6rP6VKS20waID/sgo5/5TIn9QWaqC6tC+5/d7MXfqWmcaOX\nGNt8Z9IEm4Y8pJkI4qqXJDiSvEoCJc8R1z6aOkglSpffTrFKqwm43h+SBzMxvosz8ou55JUfJhTw\nzsfeQ6JyOfj97+Hss+H22+Guu+CjH/Vm7/kI/KLMSx33UUi/Jtu0UZuzrIH0adKBE+POBUGDOXXc\nndGR8ThBIsx+GjazS9LI37Vdlr9mB3S1wr4zwm1pRrNxpNHU0zYjUhy3eu4Ebpx3AbNYyKx5Czl7\n7m+jqpxttD7HS1ti4jaBl8MOfP8s8zzXRv9HZvuY9fpetqn/s8OYPUGdbCqRf87IVG+Xf1DcMzPX\nmtakYBpb24j/zi2weSVUTovWw6awSLhmu5oOupHQvGJ+m7rjKFubmUzd5X9JpEw9bNAkUO5rm+Rx\nFnyx5Ro6fOf61TP8AKOzfeJiHH1l4EIVwNCpGNqu02Cs6vDMdhM0FEKHYXNOre7J403Z9b4SdYAj\nd55LOXcRC5eq6oA1MbeE8sfpptYjq821cLLaVytXst6uNkg/G+ObZ7ZdhUdk5D2GqPon26Y4IqXr\n4FIsbQQKogRqoeN6DIwSNXpM9Dy2cm0EKo7s2xCz3/jCChbnzwlX1L1B5e5tjL2HRBns40/XvuUW\nqKmBH/94z5YvZ8vZRs0GaToOGxqjEaMlal51KFIUx2GJqBySMKo4SAHilI1Gi0+U69rTzJxywXHs\nskXTmdWyEPBmwRmVwCQPljn8XOikngUzLvXqHRcHRftdGCQ8vyDFjT4OijqnQLWSikAadc/WgLsa\nda2MynqO6/D+DyrAiPGeEmU676Rca024o2CXaraGKIl2dda6THm/XHHctGqaKh4aYYqb0djDkEin\n31LMjfra4tJMycChtnI0IdbfYpWvRMXBFj5CK1La5CNJhq1eN2E30ZnjTDmSBPozkOvHeT5MNa9u\nDGPIyTpKAmsg30WdoxScbSVzgKvq7Nci1T/bN2kj+y7IfV0EykBfqxkgSth8omz7JQ3YJVyhPGIG\nOo3b21jRe1K4/tZb4ZxzLAeUB/Y+EvXVr8Kvfw07d8KLLxZtDtQoF0xnAqEZT049bcQjUiY/lD7W\nwIQnkLPsriI6IrZ9wH4D1NoziWXzfeXJzy01sfrBMJ5HDEbSRde4kUEKFUmwupvDhiXIcaeDCcoG\npInQJ2rfGSRCdorGx0lfp2lU42JyGfj348IeL1/fLBYyq2UhN/pepV2M5AJuDBzBDTqpZx7fDKfu\nSsdpiaSGME41SYolpP0H2n1zR0uHu4G3HSs7/Tj/HhuBMstLCFOYmGn7j2+BdSuhzleikhy2bYg5\npr66g9VNtVFl1tRR1j+JdNsc3puImtldHbttu5mA4Kt0JscgEP2u24h2UuZ71ttlHdMotFDs92Sr\np1nWxEQ7lGuz3JoNXsTyAyxpPDRs/nQ2855852zXKO5j9/za4tl4cRAhC0bSxbLmsN0DiuN+QXj/\nZHvjIg820jtHlGcjkaY8W5gaUxcDGXxW50w15zDk1mVBkAFVXdA+Ufr+yjrqgbK8dxImZIbNf01f\nBzBjy2IWdwnC9N3veomGyxh7H4maMAF++UuYPh2WLoWf/hQuuijdsYGUG9+omzxnRraOTGsHazyU\nMHCaxZwAQadc07gx2vH7WL12gjel11a2WK5p3EgnDUysfpCR4yypWMYVr2ptnuRFmV5CVHEwnURh\nIBQmwiFiu4ZsaFzqgLxuTaCkf5cxnxD68Mi0MQDf4orA3DmFP9LZ0xCJuhtEQDaNuR4Nm3rEQV+n\n7LRGe/4y9dUd0VhCcT5KbcBaYe6YQzG5s80ylI2va0akgU1d1OsNBgyHwePd2zWSFEfb/TQmbfmu\nJpljzDbXu6NVgiQCpcuTMYeaPbIXRGyXSpOBeT468KOrY4qDVqaDmHJETTCy8ytFWRgN7EyhRLlU\nJak6yvKTvhWXAmneE3OdWgk20OviYruZdqnZP+9Sn8BoB3oNG2FNqyrpcmywKYiSkMlnq4l5Gr+9\n3Cg4ckhxHXTcuLQEKq1qLM714e57wx9XXglzbJ765YW9j0QBHHBAuPzFL8LMmTBwYLCqKGaU9L0w\nL7P2oRAdcFGS3LgRhM0J1WKmkDFgAlOc/DiupFj+lY2CX4duvMSdrc2TiqIEBxnRFSZWP0hXy8gw\nYF2R0rEDRjjiRAWESxEnebzLVGhzjF/ozaSTaUi81bOCZS8zXWegPpnksMuIZiAvIlC2Ouh1LhMK\nap/20DRm3cd1rAvSD8O2zcBGXsx7Ik1EaRrIkVvgf1dChfCJcnXYcaNeeaztvLrjlB2LyUEZZ9LU\nnV/SPU17z0VE7fuZXLxdEwhTjzjCHHcdLvO5rdM3763NH8tWT3nfD9kAmy1KlFZGzX8bkUqL3Rvg\nk3XU3CQCgEpCYJ6tNBHazK4+iiZo2AhAk1rfTHEMvTaKB7CGfLlM4FrlCs5lUaNsz1m//7LdMfdg\ntl8fOeDWSpmL9ByyDnZZ4kSZekllXNZPEzQzYJ/tPbNIovQYHFR4gTM33+X9WLAAvvCF5IPKAHsn\niTrlFLj3Xvjwh6G31wt7oFDYBbnjHMcHATaB3f66qrroTDvZCOoYLNonQBIpHaxO7RsQqKsgCPKp\n4eroTL3a/OS6ljgpwTqjXDVvDBJQTm2505oDDwbCEN8nSqs5ssHRIRfM9iZxnKOBPvax0A9MEyjw\nZtAtO86v2+xQDQzUJj1tOo7YxjVWLvVJH9uckA8sTUcuY8GYss1xUhE00D4VBtpM4CCCkWCNAIOG\nw8jx8Byl+bIlKY1rwzQwRcEqNbRztbxvcSqMfIa6A4qDuTfqOwxmSxro98B2f1whRFwdrK4D2EmF\nGcxJp2qzL2pfG8Ef5CtRNgf7UhF3P5sA6jyfJhOXSadfkfWKgzaN2wY9kpCY33HvlnSpsKUzsamN\nNiSZjs33ZyNQMkDzTdhh0mAl3eueUVAxxO576HItMIPxuJncMum57X77eLB3Egfht0GDBsVUtryw\nd5KoXA4+9CHvQW/fnry/NqcEUATGNNjG9m1s2ToatiZRclq02hbxVzIjucjL6yBSWm63rXc1XKYD\nWev5Q7U2T+L86pvD7UUf8w545m6omhGOqJrVvjYzqG12SLCuLhKKYBJh+oCb+XRIjgzk8hIvbpS5\nhsh/CX0dNp+FtNCdaFx8G5vUrjrgIGyFbrhsREqXqZFEoFx1fH0LbFsJTEveN+6c8rztwFlhzKWI\naluKyUQfI4/VJpk05TuO6V7rZbIvCh+gn4t5fpLc2Hwi05hFEWXbVBFTjh6Qmd9xEffbgdoNsG4V\n7D+pb36AafYxpME2aEyjFMr3fKFyY9DH237HKX4aadoG+f72RWEhWqggAAAgAElEQVS0EShDMiHa\nTyQF15WQ7cbOdfDcCKgQcaJM2bIu+OeX1gztVymfma0vEdd6cOF5Wnvfx1Gs91Z84hNlm+LFhr2T\nRPUF5qVxJSHW8WhGE5IR06g14ZEC6VRp5H9HpxsZ/cZJ9nokoUdlGjbpWjd6tjrJ0XXwIQ0ETg79\ndWwfrfajstVLNbjHtqwIyFOQHgLh6O4a5dsQdz8C4mtBmnABb2TGoSxDqC6JjuXE1MuWz1F2ahqu\nd2rAcNg4HiqSqxKBi7SZ+vrPWIboKNrHhlJJls2snLS/eQfXEnWqTVMnOQPMvMdFph+xrI/XqpDt\n3ul3zdV2xN3H5+tgkGXgpa9FxfeKIEm9EB14TePGwKReBPNeukzmoi2JENm4wYP0G7TNNE5C0vdu\na7+kv5Um9Dbne02sUCmedBmuQa8pZylQGAW5IcXbTb3MpAhNoMxA3JR1FtH4WY72+rz8LXyw8AfO\nLPyWWjZ5KydMgMWLvbiMewkyEtVnOLKxy49DNnBzxDrzEkP4weocYhBtHLXPyO4NRBQoKQtLxDXa\nBobw6dkuPrqppWNcPeD5Iy1YeGmYUgGAHZBbBZWfC+tnzmcb0UhiJaY1T23x064IGF+UIMJxGswh\njCRepNwRrjdoBtrr7LFUkjruNxqywaCqLvCHcKoeUoEoxfyiG2xt3nJ1MDu3QO1KeOlE+7Hmtz6X\nqbNe30QQ48wEMI2U47qmvihUEL5f8n1zlSuVHfPOaDVV7pt0XvP84s5tzilNU9L/UqONYh/MvqRc\n2b0Btq+CITGz89IGAbVBEJeISVsrZEnT533V0ro97p1wzYSTx9vaaJvPkwvyOzD7m5mLpm2XExTk\ngM//DvQ1OAdOrm/UlG/q2rsS2BfGjom6SUAxgQLxjMWznCOemfZfU/h5/jMMZGe44uyzvUlbuZz7\noDJERqLSwtah2giUhE11MQqK7nx1CAEJPdocDWDp9OOyxCeZMnRjrOqzbO10prbcST2d3jT4hRM8\nItUGMBByltx5zWFEcIlI5wlBJHCbMrHsken26dABkfRhm/myRO3vX0sRgnV1pcUxKrVzLdpXdIha\nzrd1juYdTHOeJAf0NrWsJ9G0A7v92XlafS2V1JjzNnshFBro5Oae80NSbCuvr8TJpqya9eb+2ToG\nC8mM9WmLg6m77EQhHfE15kAJTRqUalkyqnwlSpNpG2Q7FTdgsM30jAvxYYtDhVqnVShXvWxwxTPb\nE0ijqNsgibmBjCcYF5jVkGYD2yClZ7znE2XbZsqIMxOK44oGcpZ3JSBQN9wAVVUwbdpeR6AgI1HJ\nSNtpSciPVc+e0bPq2sR/l6nJNCg6QKcrb19SqgutFpjRd9yMF7xo3suap/PFcdfAOFg9ewLMBNgB\nhVZomhGUWzM7JE+zRKhdk8DXhfuZ7IUfkGEB0nSoaRWhNor9SGz/9yRswQ/1xAM94tbKY5ySZJB0\n/bb76HfaJoDr6kUTQuff3i3Q5c/O09GZk84jFdD28Bwj6QryDwbb41SoUhD37PQz1+c0xyon3sAh\nOo0qCcWKsFF5bYqwTY1Kev9M+WnVElcZ20XuPHNevb/2l3GZ72wmMzGzMRLYV7dzSy3HyjLj8ue5\n3ke5Ps73U0Jee5p3URIpiD4PfT+0ScwoU6s2FA+kbf63RvXTBFubQJ9ZB/uoOFFmgJw2M0YKHFHo\n5N7eD4crZs1y77wXICNRaaAbO5dflIb+eCWBcqlF0lQjR6CGiGkThItIGbjyJcmPyRX3BrFeNEYL\nuJSp4+5kZEuXFzbg9oHw4kQw31UznF99cxBqYB7fDIqTKR+0QgUiJ53pzNKSGu0nItGuluWsHD07\nzKZ4pYEsQx9jG9HJBlcqgS4fBN1Ap1XB4vxsxKg0MlvOoHI4MD78nZZA6d+qbl2MLFYW0pACF2zX\nLu9TE8UTN7SpXI/QJam1Kcxym/ltU+xkh2qbIBD3rG3nG1sXnZ0nr0H+N7ARDaNEaWhinqRmgt3h\n2mZmNIFUmwkJgVZD5eBOtU+Bj05wzrrid81Ap2FxKV2lqM422IiUrWxb22r6EQ2zry2EDrhzrLYD\nB4yCKuETpX1yk643RVs7dttjLO+dzH5s9lacemryQWWOjEQBPPoonHxysRQpp5XaiJSBrWExjYrt\nxXSlmNCdeaRBrgsbBOkjI8tzkSkZJ0jaymWjGTdLR+/bBq03eaPYY1tW0Dv1NTZc8WtOnlcZObzT\np1GrF00oMg/WzN4YOIobdK/1koJGcmClGf0bzMHp15WIpPO4lELtGyI7bRu0Cihhrls/C0kwZAOd\n5t64HHYtz3skXV6m+8DHYguQYnaehkMJ7expgGr/fykqo0ZcY+8yZUjEJen1v3ETXbsoz9ue6Hxt\n5wU3GdTPzaiX5jnFves2/6DdG6BzFVQon6g0z0J/B9rBW9y/gPTETYgxcBEoXzkOyjIZIWTg37T1\nj7vPLrKVBEmk4r6vuEGWXq8TaKf1uVy3Dg4fASf7SlRcvDKJuPdZ3tPR8I17vx0SqE99Cm5yxWXY\ne7B3k6hKv9N/73vhnnu8uFEacqQpiZQN2mYtnbXN8WlH87vvEyvGhuuhbx+7JFAGSdGt9QcsOpDu\nmbXU3LSRkXSxfuABHD7Rnm5mwaJLo7FhdGwbH8YRvNsSuyoC8zxGE+bFqqqLEigZ1yQNLGqbdbsm\nk7Z9SoVRoXSDp+uiFSWIn0HlUgxMGVpN0fu2U6xEmX3jrtWmfNrqJ9e9UVOe6znr69Lmats9E9Hw\nAftkBlsHqdUoSa7loMCmRtnqCvbr0utcueg05Hmq6iDnUKJcz1YP6Gyw3L/imbwx0NdmjpHKcZq6\n2hC3bykDLtvzMnVxvceS8Lq+06JjReiatERqlFCipAlPn9emfI7G7sOm7vOgvB8S6Kyz4Ec/2qtm\n4bmwd5Oob38bLrnEWz7tNPjJTyIpYAq3+wE3S/1gIegcaxo3egRhpmM/W2gCV8oTs93sL+sVOUZm\ngB0b+lBo5SmpM5SQ0rhfVvf8Ws+ct20zPHA7/zhqesTvZdmM6cXHgzeyXFob3h9t2nE1lk1q3Vhf\n0p+D228iDrbGM8lsJq9DP7O0Od7MsjR7GJOSvNYkIhh3Ppdy1m7Z5tehi5HRzsAoUU0WJcplAnUp\ntMI8FjitGrNOGmjCGKfo6XPboJ+vIQDynXSZhV33NukcaetpI+36OuW7ZEtFI6Hbj8IGKKyC3KTi\na3GRXptLgFY5faIThIWQQYdNnW3qsikvjnAbNSsu5lTc8UmQSlIaUp/2HdDH7IlwKLZrlj5RbWPi\nBwpQTJikD9tS0R7LGaryvlxwAey3Xx8voLywd5Oor37VC7hpwtP/8z/DgAHeC+Kj8FgfiVQbQd6t\nkhxTXdAKhBwNFpnxRPgFWwNl+7jiiBu4G4xGYMdAqJ3I1HF3RmdeuUZfBmuF8qRz/unZYhJSEXQo\nW7GQU9DTwOafoBtsSYaTpp777wYQ7Rhs90kSqXb1X9Yv6XlpBUT66jQWz5gEPCVq5Pji9S4CZTsv\nBM/IBK7ssynPRqRsHZ6ro9bLsgPyY+PUV3eEMY1kfDfXSF4TfKM2SxJsI8M28udSkGzXqWdzxikh\nBsH9E0qUvBatfNrMyvIYMSgynXB9dQer504oDuESB5fvo810rb8rHbdOWgpc75ft+5W/XWRKlqdz\nWMYpvxJJ0fwDJOQ2lHUy74eJWP6apb7yfFot9BEMZo2fqExHlsGJvZtEAXz+83D00fDBD3q/Z83y\nZNH3vS/wkSo8BrkZJDu/yo/eJwER/w+w+yNZFaWUHxEkx2zR9njdGNjKk4j72NcCI3dwxHMLaeCD\ndFDvjWRsCoNpoGxpb/Rv8+EaR8q0HW5fFCkbbM85KQChISdnqSTUOn2LKT/J3Bg32k2j/hjod0Dc\nI0Mcinx/wFOitq2EYUKJSvCrKoI2j+nUKWkdym2TOWymFdc9VUpogNnePZhY/SBdjPTug83p2VVH\nG8GSvy3H1e5+maaX/Z2O8P49fsAxbGL/ZFMchCRRx2BLUkeC98RXosbExIlykQPlmG+UZ/AmhQT3\nT9dfmq3kM2rGTnpc91urUdo/TF+DJFalkPY076QtGbguI8nfyBxbKHDC9r8zpLCVhytPZFuuOn4S\nki4H4OB1UDkCBo0pVr30gNOV0NmsX4oXt85sM3GtOuOrsjciI1EAU6bA0qXQ7Lf2p57q/f74x4Nd\nCrcLIgWpPrKaxo10zxSKjK1hkstxjuFGeSp1VqAsX3cOfVGfLGaQIWe9zujhXufY2jMp3rRgykyS\n5mVjHadcyO1J6o+NSLjqaevck+6PT1ZqmjcGs90iz1+fS048MOqUmcGp/U5cDrRpzVYGjY5lPD+3\nyOyfSj9OVF9nzjlGvEC8SuBCUmdSKiltDEM7NPi9w+r5Ig1NKdecRGD8sioKvTy27jgObnsxsvnZ\noYcy8rQuIGfv8LVZT6qpmvAlos7uE6WR8G4ZAtVAZxC2ontmbTHpk3WT65rVNgP5DsY5aGvy7Hpe\nWqEy+9v2s52zLxYEl4rnKO/CzTfw8+c+C8Dvcx9hauXv3ROQ5DqDqjoY4CtRNnVcK/bSb7SJKHky\nsLXRNcDrxfXfm5GRKPAUp49/HK67Di6+2FvX3Oz9/vKXg90CIgVvbIZOXOiDNNCjcpnaQyLOhBcX\nSyqNrd/fp2b2RkbuWMcLrU/zrhnHxx+jO9S4GDBJMNdb6iy8UjAad1Jfl3yfljSY+hu/EeMz1E7U\npU2aF2zlxEGbXxRJDcwvOg+hqZtRopgWnXEqO6w45ct2L/R5zP6yvFKucfcG737J2Exx5B+C966m\ncWNAAm7uOT/MVm8zn6UhrvL86nu8cNPP+daGKxiS38qI/BYAHqz2AtRO6mnlsNefo/CrPFRWFrsP\naCX5jWD3Bq/gig5om+T2uUphpjUK1M0953sK41XYFWjboECWaVP64p6lTdkHu9+Y6zu1mcltcL2L\nsg1ug5aDbmX+s7Opqtod3a+NSC/bm6tkXn4u/11xUVC3b2y4kitfmhvsc3rhbp7ffTBbGcKFlTfQ\n2utXNKmP6FgH+Lnz5HM1pjlJug1RTfvdFQrc9rdz+dgLd8XXYS9ERqIkvvxlGDo09Im69dYIiQLh\nbB6HNATLvOQyBH9SvCfbsvntGqW7CFSaGDAa8rp8P4j66g7eywpWTDyZB5kYOiVKXwVXh5r2/KV0\nqnGkKkktsMH1XHSn2o5nGvKJSWvPJHuUZVmuhjFjxqlQSfXQEM6+BvXVHcFyxNxsOp02/2/UcBg1\n3q2CxYUTsD1v4zyfRArTEinXN2Hun+xIdDBT30ertXESrfixybSyo03tNji2nVB4hE89fwsV5GET\nfLXwo8j2P1WfwqStfpy0ykrI5+E734HLLgMGx5yQ+PfYfNsuU1BVHRSa8CQFH7KjNXCloBLvUiSX\npTRZJ7VH5pz6OmyDPG0uixss6vOk9TuzbU/z/vnXOCO/mFuf/ZS3brdlP7Xup/wzYwpr4Hnv91df\n+VHRIQfjKZUP9r6fyRX380A+RcOVGwVHDoFB/m/bc9Vx6KRlQZqEjTLuvwdDdm3ln579lfejuhqa\nSm1IyxcZidKYORNqa+GMM+Bvf4MNG6BONQhxH5h4t4JOVL+0smGWZcmGx3RC5sVOMr3ZYEYcGqWY\n7WzwP0wj5/9pxwSevP+X7No1IbqPaZCMPR0CspEasoNPq/4lkY5Svv8mcDrxy1QzZ4WxhUBFabbB\nlttLjhZtsL13srPU75moUxCDi2jso6ADtL2PvVtg80qonBZuc907SVJs6mJacmtUKZcS4/peJGxk\nTk9c8H9bZ+GZeujz6fqK/wML23k3/yBHAbbCH/IfpPqVbcXH/uY3MGECpx54YLhu+HDYtAmuuAJ6\neqgsfJveXJWbHNjQBk2FNexb+SqPFoayTfvJRY7bEM7Ok/5yaVRdfzJIZAajNt8nRRHX15NEbOR7\nEKeA6v1tsJn9SjaHQlVhFyfwd6oLPSzOnxNuuO02eP/77Qf94x9eahR8Uv2K2t7eDkcc4b0LP/0p\n/L//B8Dy/BRG8jDPcqh/csd7f8g62OX7RNmeqxkcSZIUnJviNkDci6OHPxH+eOklGKISHe/FyEiU\nDbVCQXjXu+CFF6Cmxr2/rYHQDZLugIwpB7VOL9samDgCJYlGUoR0fc408FUl40sC8EzvKHbtc5r3\nQyfOlTBOoH2FnlKtOzODZjzTwhsxuboadhsBVfcwMI/JDsKQsTRmWxeBSKqPg0ABXufnh5WIDTYp\nUTkcto6HYZZtur4u6HNJE4oeTMQRKX2upPtjm/Eln4eesSrPJQm7S4lS6xbnz+ZjBd/U8XS4/rZ9\n/4n/qz6ZH34dOOwwOPPM4qC+v/89nHSSt/y977H7i6+Ta70+eq+04qgc/Kfn7+CO/CcB+BOnMLHq\nT9FzyHuxsw52jYVxluvR35g+FmApdDcmJPjWgwT93ehBkev9KjUkgCxHK6guH6y48zvw4/wX+Gzh\n59GVv/wlzJjhjp100EFwxx3wzDPF28aM8SY4ARx8MHz9614+um98A4BOJnBk5dM8kzvCXakBo+Co\nId73KpE0cIwLhQB88OH7uK/Dj6E4dGhGoBQyEmXDCSfAued6o4rubu/l/9Of4N3vBqCwC3L7iP11\nrCc9hV430AauTt6sl7MiNLQiYhpWQ85syYnjUs2kga9AGV8S8CT9rUsqYW0rnDwj3Nd0WHomjgkC\nZ0IYuJJcStgIjS3mjPSxMjN2ZOMpTQlpzhEHLYevVRHXDWRnr4mUud64mV+yjLT1ERJ+4PME4b0H\nO6FtIszn1QTssMzOM3XWHazLuV+ut8WGsqmyoykmUmlMOAY2/x6XSRLi3y/XMcDJhb9xw6oLqaGb\nw/3vobtiCKuGj+W9RwMNDZy7cCHnDhgQU1lgwgR44IFQwViwgELLFnKP3RKf0FXUqYHQRHsqf6Zw\n8OE80TWIL1Vcz30mH5O5nlc2wGaRO8/WNmnIcA+aiNtIp2xrdLuT1Oa43BVcx9nW+9dy4JoN3NV7\nJgfxIvwaNg6qZfoRd7K+qd5uPkwibIUCi/NnM6Pw63Dde97jBZ885xz3ceA9y+nT4/cxGDwY/u3f\n4Lnn4Mc/ppI863vr+VDFvfwhLyYFyPruXAdbRcRym8Lm+p4MdG7GVRtoODR8twypyxAiI1E2DBgA\nixbBtm3eLL2tW+F3vwtIFPhEKqc+PDmidY0ioTT1xxAp8c0WZVaHKIFqg9A7eWz0OFlfA1cjpGf5\nNYbTwQN/iLW18HQPDJ1oV9+S1KC0zuVJDa/ZrpUwfe+b8UxPNjXGdo44AiNISM1sz7wRmDhkxy2n\nQjcDSxWR0mTG5muURKRk3YXfSiR0gQ61oMscTUjy2uo8n6jB492jdq0Gythe0swjn0vaEb+Oa6Wh\nOwXbvpocxJEnC4EYueoZLsr9lIH5HXAksCm6/bKN/x75/Urlfuz/ytO8d999LRVOwKRJ8OSTcOyx\nsH07LFpEYfbh1Pz2crZWWlRw//u8oPNGxrywhpPyD0W3d3VxNHBv/jQ+9Pi9/OGYD4XXuLMODhpb\nXJ4LWvXT6pNrZlzcsxZtQ66Q50v56zm88Ax/z53AbVUtdiIF3nupya2j7kfueIr/6T2DJvGxH769\ni5VPjufGEbOg119Z2CrOAwVyLK6cxcO5aIy0oYXXmJefGxCorVQz5Jm1MNKereENI5eDBQs8n7n/\n/E8A7st/mA9W3McfKz4Y3bcJL07US0OK/Q4NtCk0afBm8IL//7Of9RSyDBFkJCoOd9wB55/vOZhb\nUCjURRUpcDcccvTuasz1i28IRhPwyTr4tcUUNLau+LjdGwjJkyJTffWHiknVwu4d8EwrjJlRvJNt\nhkwaxIVASCpPNiLaRCo7dKOI2BQHfQ5bzBWDOIdcebz2gdLncZlGbHWyEb4kU2mbKksTZaNOLfXr\nKWfn2ZRMqQbOIXxmNj8ZeYyGIEK5NXnGblvFPoVdweaNnbWsz9W7r8mUAcXvbtIgRmzLFfKMZRX7\n1O+CTrhuwMW8d9vf7OeVuOwy+PKX2b+21nO67SuOOsrzNxnm22Pmz6f75jEM/t4nOeaIx8MYPWuA\nehj5XBc3rrwwWsbll3tZF267DWZ7zof35T/MYase4bmqE7x9jtgA61bBAb4S5epM5XpbKhfXACmG\n9OcKeY5lNQPYGZDSCZtWcF3+K96PAmyklleAxyqnsNs0sFpphYBAHbnjKUb83c/nZqxdPXDTszMD\nAvWH3Af4YPO+sGQJtb2vFBFgjUt6f8p7K/8aWXdR/qdcVPhvAHbkBjDk1Rc989abjWuv9Yjav/4r\nAH/If4jDcl08N+aw6H47/ThRHWNKszAYyG/8jc4C3YuQkag4VFTA4Yf37di4l9DWsBtIoqWVFZPm\nxMClmkRmlDmk31KQ6JczEA6faD/O1tCW8nG7SEWpDUScaSbuWQWdR/y9K5qJZzuPPpe8P0nJQpPM\nWeo+F9XH5aMnQxboZ/XUcDjMH427AnpKs2AjpeVKk/A73u/l/5XLnizu4E6tbOXPuVPdypNr5O0i\nUJb6fTv/Df6tcBU85a/Y5v1bM7CJG0fM4upLLecYNgzOOy/eZ7IUDB0KK1fCeP++b93Ktv0+Aq2t\n0f2eIqwncNlB3+fqbw6BlhbPUf2rX4WBA4O0Vs/mTmTM7uW0VU3ynuWgsW71KO7dkqbYuO/GcZ+v\nyH+LKwrzvB9/tB96T/4jACzOz+CcysXuctvhtNfv5u7O08PtT1GEVk7mg8/+AvbZByZPhh073PVe\nvRpuvpl92M3K3gnO3QY+8n9vDYECT5H6ylc8H6mvfQ2AZ3oPZ8z2NbQPEiO4AaOgcwhoC3Bf2kuJ\n/GvJ++zFyEjUnoTNXCYbEWlWsI2G24jvfIyviE5zYAtIZwvOaZvhZ1M5tPOt/50aU96yR6Z7dTDf\n75od8IJSoprE/zbC2VtmGr8ts3uSn0RaEhhnQnT5f7Sh7k+d3TlZ7i/NG3EmSVuYBK0g2vwXXOfV\nkB2L9Fmx1cmVg06Xt2oDVL4GXSuhYlp0256GX4+fDL2Iizb/d7B6JScynocB+FPvRM/Efu65nhnd\nFqVff1NxClQTnPP4L/lW/gqq/DnoRwmP8JWcCMD4j9Qy5oYbuPqQQ97QJZaEE0/0UlD95CeeD8or\n3jSuFwYdxHPbD2X8iWLfXA4uuoirP/e5aBkDB3pEqrPTSxRbKLCG9/PR/P/wu937w/ZVMERFLHcN\nWGwKekzHfMTOThY/czb7974CFcDOcFvkHo84kfFH+j8qKz03im3b4GHvmZ9duJ0Td9cDlZ6gPgD4\nHrAP4AuVR+0U5Q0+kfFjVGXq6ph4882w//7e7698xV5pg95e2LULnnjCvr26Gq65JuLa8ZZg0CC4\n9FJYvx6uvZYKCqxd18RTHMlduTO5pPKHkPfjROUsPlFpUFXHP+f/i6+1/wcVO/P+yl6GZdE1Y5GR\nqLS4/HI4/XQYN869j4s86d9pnWRtfklym6vcNB9PXKoQaQoz6R1avHAGAYEy52gEKnwlyjXzyyhq\npfjHaAJgiIhOu+JSIEYnbJdl6OsfWxdNO2MrQ5JCG1nRJE0TQJvZSdZJIs4nyqX2SSSpXNboynWw\npgIQfiE24q/NkXKb3DeGfA0avY1LHv8BF+U9ArWTfTih8u+syR1D4btXh34YLS3w2GMUZsNV87fC\n6iGY1IvsJIi7wyt4pqJecZJaIBoknDn5+cWVqaqClSsZf3xC4Ng3G2N9BdknUBx0EAd3dHDwoEHu\nY2z44Q89QvX97wPwv/kzuGrz59kwoooF+Z3sqhgQb0LWkzLU8rHbV/FPW35JxcZ8sO4zFT/nwN6X\n3XWqqoK//pXx48fbt2/cCA0N0N3NUawP1+9U/yWuv57xX/yi+5xpUVnpkfW3K370I49s/run1h7F\n03y18COeyx8Kw7vYr7ANtjwYPUa9+48OOp5fDf+n4Pfw3s18If9jhu7/OnNenm+/vxC+kxkiyEhU\nEoaJ+aKnnAJdXdEQCHHQ6kmc6SEJ2rcHitOGyO1W014KWNSXY1tWeA7K1RSnjgHI74CeVsDiE2VD\nUvgHG4y6llaRcvmZJTnAmpkpNgWx1Jg6YK+vjs9iq0dcUmFNYAxplCqUa7Zc3L0rMultAXyfqLjn\n00b60BXKCTlXyDPn5auYm78yWFdXuYEtuRF4blGXeSb1f/Ib/fke8ZkDUABMXx3TZyduv/FGmOib\no0eMeHtkp//Sl7ysCdu3e78PPthTI/qC+fO98Aq+CjNn03/BJvjhdw7m3XOn8RRH0Z2zmKb0Mxfm\n0YbC0wzb9hp/6Pgg+/cqj3tDXs88E37wg+Jyhw8PlSEbamvh+ec9/7A0GDQIDj003b7lgO9/3wsC\nvWMHjPY+2KvzXy+a+BDA8u6/Urk/L1UdyBMdR/OD/CVcULgput///A80isZjb7vHJSAjUUn4/Oeh\no8MLfrZ9uxcMrasraGiDcAdaLdDExWU2KVVyVQlAg6nHBq6ZMhppzDqNYR64Thq87Oy2+lYMhEaL\nT5Quu0n8bsNNdCRs5so0cJk65XZpfjX3Q94HmcNLEqikfH2S5Gjipx259TFQ/O7o52NTDoVqGKh+\nLhNjHBGVRKp3J1SMD9Uul1qWxsTneM+ve/5ivrRpQfD7fUf+mS1DRlB4TOw0Y4b37T3/fHEBbxSH\nHAKf/rQ7tk9/Yk91WrmcZx4cPBheftmbOg9w+eX8g8t5hpE0VHaQH1PprU8Y1Hwyfzu358+GJ8N1\nS3Mfp/k7J4crBg70fMV0oOK0GDr0rfM5eqchl/P6IYD77/dyv0p897vuY/1nf2/nacXbqqpg3jw4\n8kj46Ef3UGXLHxmJSsLw4XD99bBlCyxeDD093qjwz38OnD8LuyjOd2VgOkST30vCFkQvDrITNzgL\nj0jJkApOrMI6S08rZH4jWtPspTDpYmS43ob8juI4UX2FNDD0e8IAACAASURBVBOa/9IPTJv1oLRo\n5jZIAmXIQhy5tRGoteq/QRPhBEltgrSdIy4MhYapryZQrkjpwXnTdmyvASuhTUQsl+eGMMmwzcfN\nBvOs1ha48dlZXLDlpmDT5En389cD30fhdnVMRYWXSSBD3zFggDdFHWgbNIj9fvQj6oYPh0cf5XC6\n6D1uAoc/tpSu3OGx7dCX8v/Jf+YvDn7/g+N5d3MDzb/8pUecMry1mDzZC78zdy6vbNrE0zNnMmHO\nHPf+gwfDwoXw6KPR9SNGwPLlcFxSTrMMGhmJSoOqKvjVr7zlxYth504vQN5DD3n/gcJjKqeejuNk\nlnXQuFJnqmm/o0ZCIgUJSlQKAuWvq5m9Mcix1tnTEIYzsKFiYHGcqFIVNhdMmValr65YzUmr7kly\nI528NYEyZernJEmLDfI5jK0Lg1imRZIJ1pgd/dx4AYmJSzWTVtUz+1S+Cwr+1HEbgRqNOwyFC21Q\nnd/K7JfmBwRqZ24fGj+ylo6aI4sJVIY9jkHNzbSfeCJ1kyZ5A8GHH4a//51n6t/PqK57eLJtVOR9\n32/HK3y242cMeWlrxOz6qYpfcEvvp/rhCjJEMHUqTJ3K0ytWMCQpmvhXv+r9bdrkqVnd3Z7LSkcH\n9CW+WYaMRJWE226DAw8MAp/xmc/AY6HdISBSpkOWHZqOam4z67hMPdLRWxMoA0OkpN9MqSkT/HPU\nzI4GagwCSLrMb+/aAQ+I2XmmI41TiHSHnpb4tBHv51UKkRrr3xsZFd7mMK2vQd53bfqQ59VEyuZn\nlRa29yeOQJn8hFohkiqYK3aVQe+TUOH7RBloBcp2DhfaIdeYZ+6L8/jXjd8PVh/U+CKba/bLCNRb\nhA0bNrBq1SomTZoEf/kLfOxjcPfd0NnJuqPP4Jin7gTfFYtX4d/WfpfzupSz9Z/+xC2nnPKW1z2D\nG+vWrWPEiBGMGaOnKFqw337w7LPw4oueZWWYzhWTIS0yElUKKiq8TOsVFV4AtNeLp34WHoPcXOwk\nxqU62YiGK3aPhE6poSNx28hGnArVBDR7qUI6exrCWENJHWTVQKicuOfUpzeCvvpQQbyKo8mVTtqb\n9Gx10FHjvK7fkTQTAQyBMpAEytTFED2dtV0iLpUG4CXhsszO0wqUfj9k7Cmzv4+fPfdZLtx8Y/D7\nPUf9lc1VGYF6K1FXV8dYM9NqwADPsX7mTLj3XnjiCR7nWFjn77wuPG5bxSCuapzDvLmjvUk2Gd5W\nGDVqVLISJbHvvpn6tAeQkahSMWyYJ4dee617H9Nxufxa0nT0xvwjOznrVHQf2qzi8iFyKSxnhT5Q\nhkDVNG6ke35tWLaL0O3eARtb4bA94BNlgzSxNVGcFxCxLahTjMpi7mlRqhxVjk1VkudwkVxbLjGb\nz5pxPHedU0abl6bg0d6z6l5b69Vd1l9etyZ6SdBEsXIA7L8S6oQSJRUw27EuFAr8ouvTfGpLGP3/\nlCP/xP+tfw8iOHmGtwARJQo8JeKOO+CTn/TUCRuGDWPwz37GvGOOeesqmqEklKREZdhjyEhUqXjt\nNS9WR1popcHkJYME9aKuuGPSfjtmhpstBckchDoRY7LxVQsTB8rkxDO514pmedmIQ9VAqHXMzusr\n4mIO9TXyehJcZjmIXreeEWkro138N+ZCvc5FaIMkxZZo83O8Y7vn+yqhIVBavdIJYvV5tMnTtnz0\ncNhvPBxsuT7beST8cx6zfTXNbUs5omd9QKB2MICGyg5eeOaQjED1AyJKlMHQoZ5JL8M7FiUrURn2\nCDISVSoWLgxJlCXVQxDuQHZScf47GkalMtHJzTq9T1xcnkbCxMXg9KOqaQydx4FgFl4kZYiL6ElV\n5o0qUWln16XNtD6a5BloUh0CN4FyXf9SxzYX8XXBKFxaZRxbV7yfxlUJZdtgC1PgClmwYwtsXgkH\nT4uuh+hsRIuv1yG7nmNIfiv3Pz2FA3o3Roo/tPI5Nu5OGWstwx5HkRKVoSyQKVH9g4xElQrpB3XD\nDfH7yjhBaaF9VGwddULCW6MiBWSosXgbeL5PI+kCPAJlZuFFTEXG30orKRJvhhIVB5fDfCnhImzH\nuMrQz6RdLbuCc8oytUnSFgndmHBtcaBkfa4iTEZt86FyETdJ6rWju8ZoYMdweMwRVdqWYNi/7nO3\nLGJR13mRTUsP+TirXhjLXRVnZgSqn2FVojK845EpUf2DjET1Ff/2b0F4g1SwhTww0AqLS6EysJlQ\nxLrutbXuQIsCnT0NdNIQ+kEZAjVfkK8lJPtv9UWJMuZIsEdG1mYxGZIgCWmDjbaL0AbSJCaJjCFQ\nOv2FMcsmkbU4lc02O1Gae6FYIWsHVt3nr/B9pWT8r7F10cjlunzXb1tKnR1bYJuYnWfuhe3986/l\ni69cz/XPfzlY/UTNKNqHjmbGfrez67l9+Kbl0AxvLTIlqjyRKVH9g4xEvRmQyoVRo4JOWXXQtjhS\nEnKmlYsYqfxtNY0bw7AEBv522/rVS2uhmSiBMuXaVBVNHOKUKO2MXSqaiTrqy/tVSjgDiThl0EWg\nzDnaKXZsl0TJlpfPlWrG9R4gtknnd/AJ1GNYUVVXHPxSx71ykXibslc5HEaNdyS4pmgW3owtiyME\n6pyTf8nikecAZLPv3kbIlKjyRKZE9Q8yEvVmQXaSRsUohVCYYxJMd5FtkijJ/aUqIZUlE0tII0m1\nMOtMHV1KVOz0eeLjWBlzl+t4OVutFMTtbzOlpTk+zu/JRvRKmTEn9wsUqOOwEintJ2fLc6gRRyh7\nt8C6lbBpWvE2Zdp9f/dyFnedE2w+9chW/jzyVCAjUG83ZEpUeSJTovoHGYna07BOVffXnwXMJz7t\nBxQTKJv/SZPax+xnWzYkaj7R6f0KAfkqNQjmG/WJcoUAkOfvi+IkyyhSzyyKn+28erkU/7Y0cF2X\nPn/kvAkqQhrypKHDYIwGHh8OG8eDTiunntGsTTdww3OfCX5/6rBf8Ochp0I70Rx4Gd4WyJSo8kSm\nRPUP3oZZN9/hkL4+Es14ZGY24ey9Zjwflir/b2xddOr7Ev9vKeEMLk0yzD5r1Z8871KKCZQJ1pgU\nSDMNaTBKlITLhCWRFFjSXO8byYtnexZScZIBIbWD+FsFTeB2bwjvi41AVdURS6TMNdjum0v5s+V1\n7N0CrLSX7eNfNv4wQqA+X/Fjbh3hpQLJCNTbE0aJylBeWLduHevXr+/vaux1yJSotxg1zeHsuMA/\nSRMZ01GZafRSSbGpWDbCYnJQGlXCRqAgVLm0KchGJmy5/8CuRJl6Sn8iXVeXs3icGdBGvGSASRcJ\nspko5T2VDuxJJj/tl2XKEGUdV3iUDxV889vLQC3wUrSodSNHcRcfs5cLFoI51rFeQRHP0YW1TCv8\njhwFb0UFkDdbX+feyumsoq5YRS0MJxKxXGJNgRmF2/lh/pJg1ccqfsNdFR+DNrL4T29jZEpUeSJT\novoHGYl6s2H8enyfpUgMpjjINB7mv20Wmw0m/Uujf5whY5pAmXJt6yRcTs8mHtXfd0BvKzTNiB6b\nRtlJmmovtxmCowlHX4Nvmnvarn7bzh+TA7Cm93X2PfRV7/c6YBf8ufcUatjqrXvRcex6oLUV6usB\nOGzky5HNWypHsTXnxyIrIk6SfY61K0nAoNHbuO/xD3EYzzkqAQz+D2jzLvSwDwPv8q+j0AGFP0Dh\nOF5jGAVy7MursAbGF1ayOB/6QE2ofIiVOT8Zd0ag3tbIfKLKE5lPVP8gI1F7Gi5naeOTJJHG30dO\nu5eKEmrZqA9yevtVhM7sxpwo67NUrHdFCJdwmoIGwuET3deiTXK22V5pkcaHSCIpCXMaJ3oDU29R\n3rt2rOOxdccxeM126yG3jmzhxUMPgleAzfC18/0N11zj/Z8YKng64cbW3mqOqXyc9bl6RRxFOhhT\nH60itcHwozfzVPtR7MdmAH6Xm0qbv+PXLgFeeMFLqt3dDSNHWusAQO811mszaKm4NSNQ7yBkSlR5\nIlOi+gcZieorvvtdT0H43Ofs23V8H/lfI4lAmWUdx0eewxAoGRJgKfEEygVTrgn+6DIfGbVr9w54\nphXGpIgTlTRjz3WMrJsJG5FEkPaUE7jDqf/93ctZ/sSUYPWzQw8Nv6jX4bAzJnDenbdALldc5qGH\nwg9+AIWC/Zwvv8yQnT10/m87fKQekMUI8iTqo3HEzvXs1+sRqHtzH+JjFb+lN1cVEp1CAXp6YOVK\n6/G7du9m27ZtDHvttaK6P7sBenOVHPFfV7DowhYW2auQ4W2ITIkqT2RKVP8gI1Glwje9AHDRRbBt\nW/j7Ax8ADrAfZxQhG2GyEa64oJxQnBbEmORkQlrjpC79nYxC9UZiN0kitJaoEpXGMdulprngSPdy\nUmUnJ+d/FXOgF11+c/5wFufOZmduYIrKeZhUeIDjC496P+qAjcAGsXwgXNvxL8H+1034MssemkID\nnSx45FIK4xJOcOml3p8LH/kI3HMP/OQnMH487L8/hUIduZy4F5b79rHnf8MRj6+H/Osc9pRnYvwH\nx3Pasfd6O8jnk8vBUjeb3vLyy6xYsYJpDz4I3/uet/Lii+Haazks4fIyvH2RKVHliUyJ6h9kJKpU\ntLTAgQfCaad5v/8l7EgZNozCi0/AgM0wYgQAueP6cI4kBUWrLzLekyFQcgYghOa6mf5/F3kxPkJt\neERNB5a01jdGiUoTPdwG2dn711tV2MV+azbBKKgs9PJ/ve9JV1YefvEfL8N5XiqSukMt+4wKF4fl\nX+OBJyaHK16geFmumzOHi+fN42L/c7o+iUClweDB3v8lS2DQIE+1Akawmc2MiOyaK+Q5YPfLHPPS\n4/zmL4Ix+yLXNgb3aabcli1bWLlyJdO+8x34xCc85Wrcnri4DP2JTIkqT2RKVP8gI1GlIpeDD38Y\n/vu/4TG/Z3r5ZfjlL+G11+Cgg7x1CxbAF75A4TGRlNgGmwoVlyJGKxCSJJmEtMaJXEc4nym2G/8q\nuZ8xz0n/paQwBOApUZUT06lQaeI9WfapKPSyqncsjbQXzWa8dv+LYVP4+ytfFhuvu877/7WveX94\nglIRHKEern3XxbCZoPxI2eAR6q99Dar28Kd05ZXw4IOwebPnt3TbbeBX41+5nO/z7YAIL+ucyke6\n74lcw7W5iwEokONf/nJun6owfPhwxo8fD5WVpaU4yvC2RqZElScyJap/kJGovuKznw2XjW/J3/7m\nmfdefz3iZ2J8UHL7qDLiAnMC1uTFMmeb8XUysaR0wESVDsZ5PglNJqT/kS4nqFOK3HlJ8Z50gM9C\ngWvyl3JC4e+Ap8A0+jtt4EDvza2E34z5OF955Fp3uWecUWx2TYsLLuArxoz1VmPsWO8dOvNM2OiH\nxXjJi5HwPb7D9075U7jvqgcA2Jnbh1cq9+fb+W+woOJLb9jJO1Ciplkilmd4xyJTosoTmRLVP8hI\n1J5ALge/+Y23/POfRwmWQGGXIlLS7GZ+6/UBgRFJZpsITXiaQGlfI0mkZDwkG2zxqJLMcWuBJwfC\nzonufXUoAUXCBq/p4RMH30FNvjsIB3BI4XkuKfywqKhHBx3Hu3c/GhCEixKqx2mnQWdn0l5vTxx5\nJDz+ePj7oYfg5JO95QceiO47YgQDXnyRgwcM4Hrg+j1w+kCJylBWyJSo8kSmRPUPMhL1ZmHTJk+h\nss3MssFEzIaYgJSroOpDUUdxG4HSZTSKdVKFktHRpQJlU41sM8EMOcrvgK2tsG/87LwB+R0MWbsV\njhYrC/DV/A+Z++yV7gPvvz9YPP6EEyjsG3ua8sVJJ8GaNbDBYpBsbIQBA/bo6TIlqjyRKVHliUyJ\n6h9kJOrNwtKlnu/Uffcl7wvRAJZGXTLrqupg96pwPxPXqQ07gTIwMwJt/j5G6ZJllQJJsioGwhBH\n7jy/3Lo1L7Kmd4wXsyjmXD/OfR5GgB/aiC/cPR0mTy6xcmWMpibv7y1ApkSVJzIlqjyRKVH9g4xE\n7WlMnOjFAHruOfjLX4o2O016fuTwmuaNdGOJat72oeJ10jxmU7Ek0UlDlLQpz7bNNqtPKVHv2fpX\nvvHytxlQ2Am93i6TC8vZh90AbGIEVPrHVsB+NcDQofCrX/GF96SccZfhTUemRJUnMiWqPJEpUf2D\njETtaRx9NDzxBJQ6IvCJSffaWi+/XjPUV3cA0NnTEObZA0+pgjAMgYtANYn924mqVuaYpATEom7B\nsiy7DXhqILnqUzjjtd9y4O6X+NlzjgCkAOedx3633JLipBn6G5kSVZ7IlKjyRKZE9Q8yEvVmYts2\n2LUL9tHT8gQsM+a6qaWmcWN0v7XifzthNHEbJMlB7J+EuMCXtijpQG5tniFtG/lw9U3c2b0ssu3H\nuc9zZ246APf+Hm+q/Hvfm1yPDG8LZEpUeSJTosoTmRLVP8hI1JuNAw6Ahx+Go46K38+oSL4TePfa\nWlZfVRtuk5HMq+qKFSWwz75rwydQYnafPF8a9xpJoAxBa/MI1EOrT2I8D0N3uPvPRnyGl7YcyHcq\nLqcnNyTLp/YORaZElScyJao8kSlR/YOK/q5AWWLwYC++D8Crr8KqVZHNEVLRJv7AU5pMbjsTFmDV\nBo88SXNcM8VJfdv99e1qvcTuDfFJd11+U4KwfXD5ffz27jO5f/UUj0ABr7MPr1Tux3mH3cLnXv8Z\nl1d+l627MwL1ToZRojKUF4wSlaG8sG7dOtavX9/f1djrkClRbwZyOfjtb6G52YsfddttMGUK7BvO\nzS9yMAd7nCUXqdH+TybsgcmZl+REbqKVm/1MeUbNGi32E/9POPAR7mv9cKSodRzF0RVXwZgZFB6D\nWxNOneGdgUyJKk9kSlR5IlOi+geZEvVmYqCf8HbxYi81SKGQ7rg0BKgtYT8Z3LKqjogpzyAukGZ7\ndPuAwg72X7ORR/5wYrDuu7k5TKv4X06t+F8otPYpP1uGty8yJao8kSlR5YlMieofZCTqzcTs2VBT\n4y3//OfwgQ9EiFSfTF3GrCdhQiQsLaEcV2BOC77bO4cdvYPY2HtAsO7bucuZW/gSyyqm8VJ+AIt/\n5YgTleEdi0yJKk9kSlR5YtSoURxxxBH9XY29DhmJejNxwglekuLDD/d+L19epEYFREqHEbAtS0gi\npUxuRcsSY2Mim/v4+ONLWbK+maWdH2fp7tOZU5gfbNvOQP6L8/lm4WJ6qaKwCzZtGk5ra6vjhBne\nqciUqPJEpkSVJzIlqn+Q+US92WhogPXroaLCI1D33utFMq9w8FcTZdygGRhdF1WZDIHavQGoC4+z\nHS8x1hESAS8ly+ndv2fI/21lUf48eK14n3oeYj2HUyjU8XmxfuDAgUycmClR5YZMiSpPZEpUeSLz\nieofZErUWwWT1+z00+Gee4q3u3ycGi3r9HFx5ZjUMC4CVShQUejl4leu4zfrm1nUdV6w6f+ruJqP\nVyzl4xVL4R//oLMwgUKhuJwdO3ZkSlQZIlOiyhOZElWeyJSo/kGmRL1V+PGP4cILveWpU+Gaa+CS\nSwDHTD0XtD8UhCqUCYGg4SBQw3s38+i64zl8V1dk/aLcuazNNfIf+U8BOStxksiUqPJEpkSVJzIl\nqjyRKVH9g0yJeqswaxYsXBj+VomJrU7mbYSRyqWJzgTblITJFlHcEYG8ZfOt3L7pkzz+9DEBgeql\ngs0Vwzn1yFbOq1zElfl/plA4KJFAQaZElSsyJao8kSlR5YlMieofZErUW4mZM6G2Fs44w7q5sAty\nx/k/2rDPmrMpTYZAjVX+URYC9Z6tf+XWZz8VWXdn7iw+ceydkXoEvlYpkClR5YlMiSpPZEpUeSJT\novoHmRL1doMMgAlF8Zqc0ITJ4l913LZH+evT7wt+f+bQnzH98Dv4TNPPg3V9ifWUKVHliUyJKk9k\nSlR5IlOi+gcZieov/O538P73FwfgbCIMlKmJkNmmYdYZAmYJedCy+VYeffLdwe+vHfTv3LDfZ1iy\n73S2VI4A+kagIFOiyhWZElWeyJSo8kQWJ6p/kJGotxrHHw8HHeQtP/ggnH8+bNoUbC7M8xdk2hVN\njCSZEnn0hq15lR/t/iyLes8N/1Z7f9KEd1nF97lm49ciJOuNRBvPlKjyRKZElScyJao8kSlR/YPM\nJ+qtxmGHwfPPw1FHQUcH3HILbN3qOZ0PGwZ4RCo3gzASuYFcHu3/+fsMWdPN9c9/iU9xK8Rll7nr\nLq4+4wyu3oOXlClR5YlMiSpPZEpUeSLzieofZEpUfyCXgz/+Efbbz/u9ZAlcdFFkl8LtJZTXDte9\ncDGf2uKl/u1hMOdWLIr8sWiRF59q2rQ9dBEhMiWqPJEpUeWJTIkqT2RKVP8gU6L6C/X18MADXvTy\nF1+EX/0Kuro8E19lJQCFa5fzypRPUEN39NjV/p9BAQayE4DXGMr7Kx/gH7kTgrhRfcrRVwIyJao8\nkSlR5YlMiSpPZEpU/yBTovoTxx7r5dYzPlJ/+Quccw689BL8/vcwZQr7s4mB7Iz+FdSfT6A44ACG\nda3h77tPoLALCoU3n0BBpkSVKzIlqjyRKVHliUyJ6h9kSlR/44AD4LnnYMwYaG+HO+6AAw/0Ipwb\nXHMNAy/7orfsp4HZ8bClrKqqQMV6K5EpUeWJTIkqT2RKVHkiU6L6B/1GojZv3sz/397dx8pRlXEc\n//7gQhQKLQWh0tIWggUj0VJBGouCXmOKJtgQ/qgkIvyj0aQSorwZjYmYgCb4FomJQsuLL1QKgYoh\nkEpvqESgQOmtUNsCbSnF1nC9hmBFaXn8Y6ZkO925XcaZPbuX3yeZ7OzeM+c+Z2bOmWdnZ3YjAkl+\njODgpUs5YnCQg0ZG9kmgdl17La8vXMiOS3Yx+T0BIUZWBaO7eiNuSYyOjrJixQoGBwd7Ih4/1vO4\nZcsWVq1axdy5c3siHj/W87hx40aGh4c57bTTeiIeP9bzuGbNGiZNmsSUKVN6Ip7x9Dh57/XLbShi\nrFu5miGp+//UzMzMrKKIUPG1JEmUmZmZWb/zheVmZmZmFTiJMjMzM6vASZSZmZlZBU6izMzMzCpw\nEmVmZmZWgZMoMzMzswqcRJmZmZlV4CTKzMzMrAInUWZmZmYVJPntPGlywGiKf21mZmb2dm2NiJnF\nFxP+dt4NNdb4wRrratXAL50PHFd/nQDvb6DOUxqoE5qJ9dQG6myo3gmnvlJ/pcDMwzbXXucJbKu9\nToAT2VJ7nTP7pM6s3vq3VRPrFOCYza/VX+mm+qtsrF7Hys4G6l1Xf5UADDdU79dp/9t5/jjPzMzM\nrAInUWZmZmYVOIkyMzMzq8BJlJmZmVkFTqLMzMzMKnASlcKbQ6kjSGvLUOoIktv98COpQ0hq+9Bz\nqUNI6smhBu546zNDa1NHkNbQSOoI0hsPu4CTqBRiKHUEaW0dSh1BcntWvdOTqOdTh5DUk0P/Sh1C\nckNN3YveJ5xEOYkyMzMze8dyEmVmZmZWQapvLN8BNPTV3WZmZma16p2ffTEzMzPrd/44z8zMzKwC\nJ1FmZmZmFTSWREm6WdJOSaU3sko6V9IaSX+RtLKpWFKRdJCkpyQtL/n7TyVtkvS0pNndjq9pkiZK\nulPSeknPSDqrpNyZkt6QdEG3Y2ySpGvydg9L+rWkQwt/P1rS/fn2XyfpkkSh1qZdv5d0Yd7H90ia\nU7LcNEkP5etrnaSvdS/q+pS0/7uS1ubbeYWkaSXLdtRfel3Z2C9pUd62dZKuL1l2vqS/Stoo6aru\nRFyvkn3gTEmP58e7xyWdMcbyYx43el1ZX5Z0lKQHJW2Q9ICkiSXLjzlu9pyIaGQCzgZmA8Mlf58I\nPANMzZ8f01QsqSbgcuBXwPI2fzsP+EM+fxbwaOp4G2j/LcCl+fwAcGSbMgcBfwTuAy5IHXONbZ8B\nvAAcmj9fClxcKPMd4Lp8/hhgBBhIHfv/2e79+j1wCvA+4CFgTslyU4DZ+fwEYANwaur21NT+CS3z\ni4CbSpY9YH/ph6lkHZwLPLh3/2433udjwXN53zkEeHoc7QMrgU/n8+cBK8dYvvS40Q9TWV8Gvg9c\nmb9+FXB9m2UPOG722tTYmaiI+BMwOkaRi4C7ImJ7Xv6VpmJJIX+3+RngppIinwNuA4iIx4CJksbN\nHYuSjgQ+FhFLACJid0S82qboImAZ8PduxtcFrwL/BQ6XNAAcBrxcKLMDOCKfPwIYiYjd3Quxfu36\nfURsiIhNgMZYbkdEPJ3PvwasB6Y2GWsTStrf+vXkhwP7jXVvo7/0vJKx/ytkB83deZl24/1HgE0R\nsTUi3gDuIBsn+0pJ+/9GduIAYBKwvd2yHRw3el5JX55Gti1vzYvdCixos3gn42ZPSXlN1CxgsqSV\nklZL+kLCWJrwI+AKoOz2x6nAtpbn2+nDg8YYTgRekbQkPzX9C0nvbi0g6XhgQUT8nDEOsP0oIkaB\nG4AXybbtPyNiRaHYL4EPSHqZ7Mt7L+tulL1J0kyyd/KPpY2kPpK+J+lF4BLgujZFDthf+tws4OOS\nHs3H/HYfZxXHxJcYP2Pi1cAP833gB8A1JeUOdNzoKy19+VHguIjYCVmiBRxbLN/huNlTUiZRA8Ac\nslOb84FvSzo5YTy1kfRZYGeejYtxliB0aO/2vTEi5gC7yAaSVj8mO62717hZT5JOIjstPwM4Hpgg\n6aJCsWuAtRFxPHA6cKOkCd2NtLfk7V8GXFY4g9PXIuJbETEdWEK23xd10l/62QBwVETMBa4Efpc4\nnm67GViU7wOXA4uLBcbbcaNNXy4mhvslih2Omz0lZRL1EvBARLweESPAw8CHEsZTp3nA+ZJeAH4L\nfELSbYUy24ETWp5Po+QUb596CdgWEU/kz5eRHSRanQHcIWkzcCFZEnF+F2Ns0hnAIxHxj4jYA9wN\nfLRQZh5wJ0BEPA9sJrt24B0pP32/DLg9Iu5NHU9DfkO2bxR10l/62TayPkBErAbelHR0ocx2YHrL\n8/E0Jp4VEfcARMQyso8uizo5bvSFkr68c+8lK5KmGlG0XAAAAgJJREFU0P4Sjk7GzZ7SdBI1VjZ9\nL3C2pIMlHUZ2cfX6huPpioj4ZkRMj4iTgIXAQxFxcaHYcuBiAElzyU5b7uxyqI3J27JN0qz8pUHg\n2UKZk/LpRLIO99WI6Ms7UtrYAMyV9C5JImt/cf9eD3wKIB9cZpFdVNnvxur3Y727Xgw8GxE/qT+k\nrtqn/YUz7AvILpjeRyf9pc8U94F7gE8C5G08JH/z3Go1cLKkGfkdWQvJxsl+VGz/JknnAEgaBDYW\nF+jwuNEv2vXl5WQfZwN8kSwHKOpk3OwtTV2xTvaO62XgP2Sfb14KfBn4UkuZb5DdoTdMdqoz+ZX2\nDayHc8jvsmjT/p+R3Y2ylpK7lvp5IjuzuJrsoHE32YWV+6yDlrKLGUd35+VtuqJl/76F7I6jt9pP\ndkfe7/PtPwx8PnXMNbS5Xb9fQHYm4t9kF9jen5d9L3BfPj8P2JPvK2uAp4D5qdtTU/uXAevydt0F\nHFtsf/58v/6Suj01roMB4PZ8PTwBnFOyDuaTHUg3AVenbkuN7f8w2TV+a4A/A6e3a39LHW8dN/pt\nKuvLwGRgRb59HwQmlewDrePmrWQJd/J2lU3+2RczMzOzCvyN5WZmZmYVOIkyMzMzq8BJlJmZmVkF\nTqLMzMzMKnASZWZmZlaBkygzMzOzCpxEmZmZmVXgJMrMzMysgv8BEUuECMX/xW0AAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa805dd27d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"IT = cuCap.GetGeo_IT()\n",
"cuCap.Plot_basin(IT, ruta = ruta_images+'Indice_topografico.png', lines_spaces= 0.01)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Precipitación \n",
"\n",
"A continuación se realiza el análisis de la precipitación en la zona, de esta manera se conocen las condiciones climáticas en la región.\n",
"\n",
"## Procedimiento para Desagregar lluvia (obtener IDF)\n",
"\n",
"Lee la estación de epm con datos horarios "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Caudales \n",
"\n",
"Calculo de caudales medio de largo plazo mediante el campo de precipitación estimado para la zona mediante el uso de las estaciones del IDEAM \n",
"\n",
"- Q medio por balance.\n",
"- Qmax por regionalización y HU sintéticas \n",
"- Qmin por regionalización y análisis de serie de caudales simulada a la salida de la cuenca \n",
"\n",
"### Caudal Medio Largo Plazo"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlsAAAESCAYAAADKehBIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeYHVX5xz9nSzbZJcmmbkJC6m4ahBAInQREQIgiICLS\nRKQKqFQVkfJTUZpSRBCQIkIQFEVpQbERSiAJQkJM2VTSC+nZZLNlfn+cO3vn3p0+Z8q9O5/nmWfu\ntHPOvXN353u/5z3vEZqmkZKSkpKSkpKSEg4lcTcgJSUlJSUlJaWYScVWSkpKSkpKSkqIpGIrJSUl\nJSUlJSVEUrGVkpKSkpKSkhIiqdhKSUlJSUlJSQmRVGylpKSkpKSkpISIo9gSQowQQvxXCPFBZr1V\nCPFtIcQtQoiVmf0fCCFOtLi+uxDiD0KIeUKIuUKIQw3HvpXZP0cIcbth/2OZuiZntv8khPii4fh8\nIcQPDNt/FEKc6vdD6IiEdV/trk/va7iE+beaOX6tEKJVCNHTsC+9pyET4t/qj4QQHwkhPhRCvCGE\nGGi4Jr2vIRPifb0zs+9DIcQLQohuhmvS+xoXmqa5XpDibDWwD3ALcI2La54ELsi8LgO6ZV4fA/wN\nKMts986s982UXQo8l9l3LXB75nVPYBbwkqGOVUBfL+8lXUK7r6bXp/e1cO9pZnsgMBVYCvRM72nh\n31dgL8M53wIeTe9rUdzX44CSzOvbgZ+l9zX+xWs34nHAYk3TVmS2hd3JGUU9UdO0JwA0TWvWNG1b\n5vA3Mze5OXNsY2Z/C1AFdAL0jKvvAEdmXh8BvAT0ydQxBGjQNG29x/eSkkXlfbW6Pr2v0aL6nt4D\nXJ93WXpPo0fZfdU0bYfh1Crg08zr9L5Gj8r7+oamaa2ZU6cjfyhBel9jxavYOhN41rB9Zcaq/I0Q\norvJ+UOBjUKIJzJ26CNCiC6ZYyOASUKI6UKIfwkhJgBomjYfKAf+AzyYOXcWsK8Qogz5hXgHWCCE\nGGXYTvGPyvuaf301pPc1BpTd00w3wwpN0+YYL0jvaSwo/VsVQvxECPEJ8HXgZ5De15hQ/T9Y5xvA\na5De19hxa4Ehb9IGoE9muw8gMq9/Ajxmcs1BQBMwIbN9L/B/mddzgPsyrw8GljjUPw04FPgn0B3p\njF0IPABcErdFWKhLCPfV8fr0vhbOPQW6IH8dd83sXwr0Su9pYd9Xk/O+BzyR3tfiua/AjcALLupP\n72sEixdn6yRglqZpGwA0TdugZe4U8ChSMOWzEvmLeGZm+4/AgYZjf8qUNQNoFUL0sqn/bWASMs5g\nK/IBcARwOKn6DoLS++ryeiPpfVWPyns6HBgCfCSEWIrskpglhOhrU396T8NB9f9gI1OACQ71p/c1\nHJTfVyHE14HJwNku6k/vawR4EVtnYbA5hRD9DMe+BHycf4GmaeuAFUKIEZldnwX+l3n9InBspqwR\nQLmmaZ/ml2HgXeBS4KPM9mzgMGCQpmnt6k5xjdL76ub6PNL7qh5l91TTtI81TeunadowTdOGIv/J\nj9fs4zjSexoOqv9Waw2nngp86FB/el/DQfV9PREZX/lFTdMaXdSf3tcocGN/AZVIm7OrYd9TyJvy\nIVI41WT29wdeNpw3DpiROe9PQHcta53+DtmdOBM42qENfZABfhcY9v0LeDVue7BQl5Duq+n16X0t\n3HuaV/4SMqMR03ta2PcV6YbMBv4LvIDDqLP0vhbMfa0HlgMfZJYH0/sa/6L3C6ekpKSkpKSkpIRA\nmkE+JSUlJSUlJSVEyuKoVAiR2mkpKSkpKSkpBYOmabb5z+yIRWwBpN2XxcPmzZu55ZZbuP/+++Nu\nSopC6uvrefbZZ7n55pvjbkpxsnQpTJwI69bl7m9ulusvf5klD71N5T8a2eu5hrbDVXt2yxeLQCyQ\nL7XMf3JBGVx8MTz4IFZMnz6dWbNmccUVV6h6JykJYMqUKfTo0YOTTjop7qYUJUL41llAjGIrpXio\nqKhg4sSJcTcjRTHV1dVMmOCUDSDFFx98IIVWQ4Pp4S2HdmXjc+9CSSk7zqxkx5mVAAzftDJ70m7Q\nJoFYDKJZ39kMDz2EtuEhAETFOXDyyXDmmW2X1dTUMHbs2DDeVUqM1NXVUVVVFXczUixIxVZKYBob\nG5k2bRpnnHFG3E1JUciWLVuYOXMmkydPjrspxcXy5XDUUbBrl9y++GJe/9WCnFOGly0Gp1/SnYH3\nQNOF1nZgJIhWEH/UT3oGnnkGKivbLtusacxZsYJJkyYpeDMxUV8P8+fDoEEwblzcrUkE9fX19OjR\ngzFjxsTdlBQTUrGVEpjU2SpOUmcrBFpa4KCDskLr3HP5+93z0Mqz/4prWYTZ1Hg5rpaOQCbRATmN\n8D9Am5/Z3gniuszrL36x7ZL9+/dnx+9/H/CNxMj27bD//rA7051aXw+1tfbXdABSZyvZpKMRUwKj\nO1spxYXubKUoYv586N8fPs3kbr7oIv7+0DJauuULrfaYCi0z9ge+klkuAO0m0D6XWY6Tp5StWcPh\nxx2NVimk4/WFL0ChxNC+/z5065YVWgB1dfCXv8TXpoRQX1/P8uXL425GigWps5USmNTZKk5SZ0sh\nM2bAoYdmRc2JJzL10UW4+RfsWmiZcZXhtQbaySDehfIm5Mx67IJXXoHjS6AC6Pv17PklJfCNb8CR\nR/qvXyX/+Q8cc4z5sVNPhRdegC99KdImJYnU2Uo2qdhKCUwas1WcpDFbili+HA4/PCu0rriCqb/8\nmPyuQjNXK5DQykeAuBPe/y/8dyFceipyMphtwD/0k57Mvebxx+G119qXVVUFRxwBpaXq2mfHokW5\nQutk4BTkRDOPZfadfrpsa6dOMiauU6do2pYQ0pitZJOKrZTApM5WcZI6WwrYvRvGjpWxWgAXX8zf\nf/oRiGj/9Yp5+gvo0w9GlyAD7B/CfPbSeciJYgCsUgk88ABEkT7i00/BKCA+D5yYeX1IZq0LLr2t\n3/se3H57+G1LEKmzlWzSmK2UwKQxWwlh2zYZONy9u1wGDYIAMVemMVsXXijLHjYMFiwwvzBF8tFH\n0Lu3DOgGuPBC/nb//JwYLZ0wXa02oZVh3SaYszizMRgpXvKXq5BTUx9isuhceSVUCvl96NcPpk5V\n0t4c3npLfoZNTXL7M0hHqyJzvBQ4PLNvX8N1d9wBhwfLi1RopDFbySaWuRGFEFqa1LR4aGho4JVX\nXkm7EePir3+Fl1+WD6Z589odvv7NHzN3onQGXiUvpuXhh2HWLNNid+3ezYb16xk0aFB256OPZl+X\nlcH06Uw+aHn7cjs606fLrkOdU09l6p+3mJ4aOCjegXyxtXQ1rFgPkw7wUdh8YC7wS6DZ5PgkYOTF\n2e0TT/QeR6VpcNddsuvQ+H2bCJzvcO1K4DYy8Wh57Zk4Ec47z1tbCogZM2bQ76232Ef/H1CWSXA7\nfny8DSsShBCBMsinYislMGkG+ZBZtw4+NuvryXDccbnbRx8tH/SGbpQb3ril7fXPyHT5fvppTrJL\nP+ypKOfCRb/i04G9UsFl5DOfgX//W76++mqm/vwD07xZVkJLJ6jgyhdaANM/hlkL4IrTfRSop5XY\nQ1ZsTQem2Fzzxhve6pg7F77zndx9pyEdNzfsAa4AzB4xM2bI1BsBs4Enij17YPp0/jF1Kp/92c9y\nj1VVwcKFsPfe8bStiEjFVkrspM5WiLS2yn+U+VO6mHHXXVBdDZMnc1r3f3PWj//AV+540fk6kA4X\ncD8ftO1q3r6LXcs20HXsoJxTV9f159jfvckJT/wTgIauXTh73WPs6VKRCi6dww+X7tY3vwl33MHU\nrl80Pc1JbOXjVXyZia3AzlY+zcCHwE7DviZARSqv85CxZeMBL/HunwBLDdu/M7z++9/b/0ApZK6+\nGu69N3dfJaBPTlBdDWvXQkVF/pUpHggqttIA+ZTApKMRM7z0kny4GnMAGdm2Dfr2tT5uxp492Zif\nY49t2/0uO3JO++8R47jvuhMyWxsZTmeeuu1s9trSwN71a2yr+M9ZR/H6Rb0zWye07d9Zv5rVz75F\n3SUntLtm3uEjEa2tHP/bf1O5fRdT+n6D696+jcn7/6ljC66WFjjhBCm0QHZbde1qeqpXoQWwuOdA\nIJjjpcdseRZbZkIL5FPEbBzFLsBvWJ8AjgEO8nn9oMyiswd4LvP6+OPhkUdkF1uhc9ZZYEhQu7ET\n9K4CugMbgR3Ali3yB9ubb8K++1oUlBI2qbOVEpgO7Wzt2QN33glr1thO/huUGRMP5Nw3n3B17nAf\nD3EzGjdsZeuMRfSdbP3Eu+mU2zn8rzMAePieC/jLVV8ATGLDOgrLlsHQofJ1z56wYAFTe5v/XfgR\nW0bcCC6lzpaV2CoU/gU8Y9i+/HLo0QOuu066P4VGU1M2vYWAOb2htALGGB3ANUjRq3P55e7KrqyU\nXbkDBypqbOGTOlspsdMhna1PP5WxJW+8AT/+ce6xX/9a5vwB+q6XfSvvnXg0Q1fIkUL33/pNplzh\nLVZqS8/urs5TJbQAmrfsZOvMxbZi68cvfo/rzrufY595k33fmserl51AU+eOld/IlKoqWL06kV03\nvpytQhdaIEcy9gN+ntnWfxwNGQIXXWR93apVsHhx7r4DDpCZ7OPkf//Lvh4McxqgR3Oe2OoH25ZC\nW0u9/CB891346U+9tWn0aOjTx9s1HYRUbKUEpkPm2TrwQPjkk9x9DzwAvXrB6adTummP3NerCwCf\ne/6vnPPBc+zsWsnrpx/H7souypukUmgBlFVX0X3CcPuThGBLjRSCR70wHa1E8LPnr2MyHbw7sXfv\nRAotgJqeMNbhthYto5DB85uBmcBC4J8XW4utbdvkdEC7duXunzBBBtvHxb//LQdhgOxyLYG6MqjK\nS+a0bKk8vAez2TbN6UZmus2335aDbbzQp4/8kVGWSot80k8kJTBF52xpGpxyiv0/07Vr5XriRPmP\n5YYbKN3/CLlPF1oGFg8dzpTDgo38s0K1yAKoZTEfbeli6mzVkvsrv/684TQ83oXKLbvou3yj8rYU\nK4uoDdyV6AfPzlYxuFo6AhlsD7AWKbaeBY78lUzQ2tgoY+4WLsycszZ7bR2wPXPdzJlQLaDHEPkj\n6/Nuh0oq4Ikn5DRKOj3kqr4ZepTkOVvIQZm5EZ72NAC98J6EszPAhg2ya3avveTOgw+W81YW0+hP\nn6RiKyUwBedsaRo89FD2H2o+a9fKYHcHZu4/nkP/YDKVSYSoFFr5ImpE9Qa6T6hkSN7+fFYdsDcP\nTb2Qaw97gAp2tysnxZpF1ALB47es0Ea3j9sqSmfL+B5Hu7xmsOH1lVdCfT3Mni0DyfOZAFyGHHl5\nE7AB2ApsXSYn8s5PVeGG6mq46ipv8WLPPpsrtHohg+Exd7b80AKs93FdPzKCa8cOuYD8P7punUx6\n28FJxVZKYEJzttavbx8roYL6enfTjHTrBvOzP+v7v5V7eOOR7qfGqK1R/z5UCS0rcdS4ZRfrZ65k\nyGS3T68Uv4QpuvIFl+/RiEklfxCAvu30tT0S6Avckdm+777ssb7Adw3n6iGTZcA5yKDzhcig+/xr\nvbB0KVx2WXZbCBkP1rlz+3M/+ADOPju73Q+Z4iGDmbM1ZBgsW+KvaV5Zi0zoX4H8+AA5d2ZlpeU1\nHYlUbKUEJhRna+dOqK3Npj0Ii3vuaXt5VX3uoTcOPI658/pnd/TKvizZdyduKUShBVBR3YW+E9LR\nSMWGZ2drFMnsSjQZadnuuJPgqkPGcBl7vwUwFrAynEqBvYBxSCtnl8V5dvwH2b/31FNyMXLSSfDq\nq7n7XnsNjBPC9wXywj6tnK0hw+Q6CtHVArQad/z97/EPJEgIqdhKCYxyZ2v2bJg0KSu0Djss5/C7\nXv5pWPyo0hA8eNTlPFNyLuyX2bm/uyK9CC2/hBWH5YXU2fLAL34h3Q19Dr8M93EpI2NqkhGju+XL\n2RpleB2H8HISVnbXOX19vcxmY2xHKTDG6kQHBgJvIpO/6mJtB7Kb8rXX5LymRlasyL7uiRR7eVjF\nbMXGMcdkg/hTUrGVEpzAztbGjfCrX2X7+e++O3vs5JPl3H8ZxMVkxZEbxvpvlhlehZZXVysMkQXe\nhRb4c7aGvL+CQ347k/fPn8C3uYv7ud5zvQXHb34D116bs2vReMErXBpTg+wJHLOlCy9VosuvkPJS\nvorfCyrbWUP7/2PNyG7JJnLFlZH9yGaGz0NVzFZKOKRiKyUwgZytxkaZaO8Pf2h/7NJLc/LCCK8J\nn1OhFQgvztau7tkYk3O//jzzTxjBtv7dilNwrVkjcy8BLFmSm4l82jQeH/QQ2wfKeL6RWAzCMMFL\nvFYsGeRVErbAMqsvKQat1XsvA45F5mkwowQZEGUhchPnbM2cCZs2yeS+KanYSglOIGfrlFPg9dfl\n627d4Ic/lK+rquj+5DlsO6oEYp5hwk+3YZKElt/RgV6crfWj+vLYH8/jwi/LSeg6NTQ5XFGgrFol\nk2A2N7c/9uKL3HfU79D7eMISWkFRNhrRbyxX1ELLWK9fwaWizW7KKKVdLJZbkuJstc0Ns2OHzFG2\napV5wH8HIwG3pgPx8ssyw+7w4XK54IK4W6QE3dnyxO7dMp+NLrQGDJAZi6+/Hq6/HvH05Wwrc5c1\nPUwKXWgFQXe23PLR6WPZOEz+iv3uAfcw4MPVahv0gx9k/3b05YwzZCqPKHjzTTl9iS60DjqIdQf1\nZt2EPvz9sUncd0o2qNmL0PJKEFcLss5WLMQltILUH7TN8xSUAVLY2ojb+mZYbvIbIGr2YJiTfNMm\n+Xc6P4kjLKIldbbCZs8emdNp3Tr42c9yjy1ZIpO/de3KT3+WHdLygxvyftoIAaedJrMWJxDPztb6\n9XDJJXKkCsis6/PntyXCE0coaJTbLkQv8V8O+Bl1GLbQCpLzyk/M1uqx/em9ZBOdd+zhe+Pv5a6Z\n3+bbB3noSlyyBH7723aB5kD7v5/M+f/7+kh2DpDddgePuRbOPde6/IYG2TW9aZO79ljVf9FF3Pdo\nCf5nSs7i1tUKKrJ0lObZSupIRTvcpobwU2YYuPx8k+RsbUA6OV1AZpSfOhVGjbK9rthJJ6JWwfLl\ncmZ1M15+Ods1pnPPPXD11d7qKCuTfeBWjByZtWp37HCXn6q6GgYPloJwns1/i9GjsxOemrB582Zu\nueUW7r//fuc6GxvhK1/JBr0PHiznGKySD0tToeW1G1GR0HLravlN7ZBkoQWwpX4DC5/9kENuPt71\nNaK1lTMu/zNHPfweAE0VZfz8vSsB+D5fdy7gvPNgzhz7c+bMgS5daB4zgrI9re2Pv/QS7LOP+bVP\nP507AMMPN9/MfbeuscyKrbL7UJXAguxoxOkfw6wFcMXpigp2K7bidrXMcBJcbtqcAKEFMGWHjNk6\nyWIEttfUDx84HD/QRRl9yQwI/8UvvD/zEkY6EXXcvPqq+6kabrtNzh11/vlw2GH84PCXHS8ZySLO\n5znZdXGATUTrwQfD++/LLpVx46RD4IbXXoOf/1xOqGzF5z4nf5lY4MnZOuGEbIbmmhrZjWgntLyi\nOCjeiTByaPkhjKztfpwtraSEv94xGYTgqF9Pp7yxme8fcG/m6L221+YwYQKcdhrv8GLO7nUT+vDJ\nfr8EoM/0UxnyWnbU1hE3ZqZXOvlkd3Xcdlu78p3Y3aOCeeevBNH+X6fqrkOVQstIUWaQ94tZ5vkk\niEIfbqGVsxVVUlMzijRy0xeFKbY+/FCOAPKS8LJTJ7jzTjjxROtzfvQjmDLFW1sWLMi+3j83UdNH\ns1sA2EM5P+RG/nbjsfLAJTuAEcA1jsWX0EInmhjDAtPj1WxlMCthxgzmizrKaKGWpbL+kv0ZZ3Bv\nPvo4+3pc62z54qST2vZtoTvLSwa3XbN99hK6sgNef535paNooJIrOz/Au6VSFWnb5HmuRiPu3Cm7\nQnWhVVcHr7wi1xRe16EXkZV0B8sKs9GIdu9lcSYL+u7uXfjDA6dSuamBmvkbXNXVica21w39Kpk6\nZQy7ey3HLgnShvG92TC+d9v27h4VjH14nmMMV0vnUqbdfRirJ9qX7wU/QsvO1QpDaOm5thIxGjGJ\nxBHPZSRgd6zZaMQwhdYHuHO3UiSF14343//Cgf5v8f/RPp7jlpszKXZ/9CPf5V7Kd3iEL2S2ovsK\nltLMEg5kEKty9s8uGcu4qtmW11225yEeary8bXuD6M3gquXsElkPulLbySc7BtGL3PiWwyvfYXrp\n4W3bO9c28Morr1iLrTVr5GAAPRi+pkZ2vVZUAC6ElttuRDdiy6XQsutCdCu0kpQzyw+7Nuxg3YwV\nDJk82tN70UWXW5I6QMANQdwsK7EVlqMFUmwtXQ0r1isSW14EQhIcI9V4fU8hxrfN2C2drTGd1Igs\np25EcH7S9SAz01HajZhwZ+vTT2VguZEjDE/miy5ql0xw1OjftCvmFLZwB48BcAtPt68nX2PNmJGd\ntRwYNfod22buooJPqMlsRav1WyhjNO+yT2WuOFhaMtT2ul93+iavlk2miyYD81eVDMgRWgANoooh\ney1jQOsqLmx6jOubZKzLuw1HMKZyLrtFZ5aKoVTVNPKtC0ycrQ0b5HLNNVmhVVsrBbNboaWSCB2t\nJGSAt8NN+zZs2crKmYsYPrncV9leRVfSCHNEYdRCq6jnRiwEQhJZRlH1DlLYRDkTYepuuSe5YmvF\nCvlg3mOR4e3SS+H223NmTBfiTgxTYGY4kHtoYjuV9GGrY7WzqOOVg7cAxoD3QVanE8lXrat9UrgG\nelp0MtrzSclgx3N2iK4sKB3FrSW30igq+OGe2wD4X4O0m66tuJtflH+TXz46kZz4+PnzYb/9oKUl\nu2/QIBnj5mXUYQw5toJOx6NaaKl2sty2r0t1JwZN6BOoHifBlVRXq5CFlnBwW5TFbEXparm5PilJ\nS/OJQGgBDCFaoZXijWSKrTffhKOPzm6Pzvsr2ndfSh8eQuvDj7gqrolyHuKLChsIoYgsB1EVJw2i\nips6/ZiBrSs5pPV9xrTK/34/b7yOrzc9xlptBz27fpbNoifaH17PjY0bPVqmd3j6aRg8GNENpSkX\nXBFh96EKouoqtGPXlj18MnMDYybb/diwx87lSoWWOpwElpGCc7bcvjezYPco688nxC5Ds27CZUhn\nqy68atuRulruSZ7YevfdXKF10UXw6KM5p0gHKy46lsjKQQgu6PIkAJOa/8N/dh0DwNjWeYwFpjac\nyF/Lvggn3pS95ppr5GhHvYg4JoCPUNipEBBhCi0v7QvqbOXXaxRcHVFo2RFmnFY+gZ0tryIijlgt\nFbm0EhpjZhWPNQR1zpabeK0UbyQgBZqBTZtyY7JuuAEefjjnlKIRWl17Zpcks5/58mbZ0QysWsHY\nytnMLhkDwCGtM/jJnqzQ+m6nOxCPZHMa5Qgtw8hISyLuQkyCq5UUoQVZZ0tl/fqSRMJ2tJLgakHA\nDPJRJzCNK3t7kHodMr0HwS7wfRnkDZOKH2/RnsVNcpyt+nrY1/B0veUW+O53oSSrB70LLVXiSLHI\nSjJuXaD9YNXHA1nFQE7t/Dzn7fk/yktGtB1eL/rycPmlIIS5m+VUT4KElluCiIgkdBvmo9LZCouR\nLGQBI5xPjJEwE5d6FVoQwNkqpHkQ8/HidCWw2xCcRxgOQY2z5dbVcnoq1mCY5tEiAXBHIhli65//\nhM9+Nrt9wQVw6605p4TraMUf5B47frra9gM+hqUle/Mj0Q8qfqKmLpVCS1GWeCf8Cq0oRJbftqmI\n2QoLowtlfO1XeIXlaoU5wbQfoQURxmxFERQftExViUxjFlqgJmZLZfdhW7qvgQPt81t2EOIXW2+/\nnSu0vv1tuO++nFPCdbQUCa2kiykrgsYz7QfMqYBSmwzybusIIrJ8ZI5XJbS8kmSBZSSpzpadMPLj\ndMUVpwX+XS2/QgsiyiCfRKEVVj0RB8JbMYSEjka88EI5Er2DE6/Y2rwZjjoqu/1//9duHsFEC61C\nEVhGsfMx6gPGRzfCimmw05Bny2sdqdBSgsp4qCQ6W26EUVK6FsPoPgwisnR8OVsdPXlpDHhNTLqM\nYM6WF1fLzZOzFSgF+VxvaYFvfMNd4Z07Q//+HlpTGMQntmbPlvOf6dxxh3S1fMdoeRVOAYRW0kWW\nndAJY2SeqIBuE8E+j6o1foWWk8iyeK9ehZaq4PhCElqQPGfLiwPlVnA5lWkmmBa5SNaqWmipEFk6\noTpbKtpZSGIt6gEDNgzBv7MVxujDjUCbZPrJT+Till//WubSLCLiE1vjxmVfX3qpDIY3kEihFYXI\nijr/lFf2Bebm7dMaYds06GUzN6JdeX6ISGi5ZTG1sY6yC6PupDhbfrv57ASXmzKtBJOVAAszPksl\nnp0tt4KikERSzLRLSDrM/rirMvHnbIWV5qERWAP0AtyGx7eNXrzsMnhMzvpCRQXcdhtMmqS6iZES\nf8zW974nM8EbcC+0/IimmIVW0sVUPmZiSN+niy7d2QparlsiFFpJdrXCFndxOluq4qj0chYwwlOZ\nXoWTl/PjdLXAwdny69SkQssVViJq2RIpuILMaTgE785W2Pm0GoHVHs7vAm0T3zFjRvbA0UfD3Xe3\nv6B3bzj7bChPfpKJeMXW7bfD9dfn7HIWWkHirHxcq9LNKiSh5UYM6ed85OBsqRpdqHCiaTdEmTHe\nLWEKrHwxsmpLA/NnroeIna0wAtbDFFqFRo6zpaIbLBVaSgg6efQyvDlbSUxcugtYSTYBaBWZiawB\nrrvO/KIdO+CUU7LbJSUy5ith6SbiE1t33gnf+Y6LGK0YcmX5FViFIKbCyF+1bwV0nQjDnE/1hdsA\neJvP34urlUSRBdEKLYCq6jLqJnRVIn7cBqzHOTIwiSJLtavFfKjZDGPLSVS8URtFLNyCiiknhuDe\n2Uqi0NJpNrxuQgbam2VfbxNhV14pFyPf+ha5k/XGT3xiy9LRCiPnlcsyi1VkhZ0gtKUR1k6DYT5i\ntqzwOsIw4UJrEcMDdSVGLbQAdm5ppn7mdg6Z3EtZHUFiqMIiiSILFAstg7Batw3mrIRJ8Q/YVIuT\neBwVSStW+ztgAAAgAElEQVRiYxnunC0VQusDopkXUQO2WhzbDfQkNx6sTdD88pegaVJwJcThij9m\nCxDiDcK7dR1YaEWVhb20Avp5jNmywkcah6QLLQgWsxWH0IKssxVVfXEQtdCKcg5EK/FR0w3GDlRU\nh0pBGHSKHLfnqBJdHpzBsF0tcHa2kuxmmWHWXuPTfBftpycqBQaSEWAPPACVlTKp6uc/D8PC6npx\nRyLEVnh0IKEV8fQ2OahwtvyILEjMPUjqfH/5eBE7Kp2tJJJURwsCuloOIqDonC2v3aHzcSe4ktjN\nasMycp2tsMVVWO6WXbv1Y1b1tiBjvvbRd9yZ6TF76CH4179yT+7eXeb0iogiFVsdKD4rCpFlJoTm\nGF4HcbZCFFlxJS5ViQoR59dNCsPZ6shE4mq5EAhKnS1V+BGXQcSQnculWGRF4WpB1tmK0sEy1hVF\nt2J+vWZ1tgBrkZ9FJ6AzwLx50K9f7ok9e8LChdArmh+TRSa2PN5uP0IrCSIrLoFldbyhEZZMg7EW\nztacvO0IXKwoE5eG5WrFKbSg+J2tKPEitHy7Wi5FQtE5W0FIwJyGyuoCNhCt6DGiIgO9V6Fo5a7t\nziwCmUoiPzFEKcCmTTBqFPzjH7D//h5r9k4RiK0I82bFIbSi7h70I4TKKmCYjbPlV1yBr8+8GBwt\nFQSNj0qdrWBEGp/lAWXOlqp4rahdrYiIQmgZxUkjkJz5HuxR6b7ZuVwa0uXKpw8yrQQbN8IRR8Cs\nWTBypMJWtSd2sSWD492gQK8HyZmleq6//Czsbq4JQhDB40Rzxtkar3A0IkQmtIrR1VIRiJ50Z8vv\nVDpW16ogqMAK29WC1NmKgjCFlpVQWYMUEPtYHC92vMSQbUQKsb0Adu6EY46BZctktvqQiFVsyXQP\nbj6eGIVWWBMqR+VYhSmydJycLa9E6CBGIbTCnhMxH1Uj/pLsbDlNpeNWdPkhqY6VWxIVs1WEebXC\nElpOblB/IDypUBi4FVwasAn4FBgMsHatTIQ6d25ok2DH7mzZo6j3OYouwzhHA5oRhcjSUeVsBRRZ\nxRCnFbRslakV7JwtVc6QH1Hkpm470RWk7YUutKAInK2EdiFGGZ9lRkd3tnScRiwazwEZQF8DsHkz\n1NXBm2/Cgeoj32IWWxGE8oUptJImsCBakaXj19lS5GAlueswaldLJfnOVhhdb/llOokvP3MW6mUG\nbX/YQkt5tngLEuNsFZGrFbbQchPjlDpbubiNC3sbmAAMAtml+OijMlWEYmITW+67EAPgVWh5efgn\nTWipDkL/2MP1Xp2tGEWWHwolh5ZqdGfr7MmbI6vTTnz5FUsqRGIxOFo6sTpbQQVWwlytuN0sI6mz\n5Z8PkCMX9wFoaQmljoR3IwYgFVr2OL1fN5+HLsjcOlsKY7Gi6jIMIrTicLUWMEJJV2Iti+hR3YI2\nYQ/QJXjDArQjbqIQWmEmMc1HibPlp71F5GRBsoQWpM5WEFqRaTPCFKoxiq2QXK2029AZVaJHL2d7\nI7xk42wpDniPagqejuRomYma7VtamTOziWMmxye24qaYHC2dWJwtFUIrIa5W0kSWTupsJZuEO1se\nBnOGPdowytGD+UlArc7zQxgj/cor4JiJoY8ijHKew6BCq5Bitazco67VJYydkJ8OMKXQCexsxeFQ\nxSy04hRYbmOPUmcr2SRcbIErwRWW0FItsNwKJKvpceIIfndDUyPMmQZHK86zZSApE0q7qr8IhBak\nzpYfzLoDtdHerwmTQM5WkXUF2pEEB8tL8s/U2VLE7t2gaSCE0mILQGzZECRJqRMqhZYKkaSijLCc\np/IKGKswz5aBKNM56Ph1tQpJZLmhoztbqqbYMR5zEl5R4NnZiltgRexqJUFkgfcs66mzpYjf/Q62\nbYMXX1RabInS0kIjhKk17YRH0oRW0tGdLQWU7LszZ4kaP0KrlsVFJ7Qg62yl2OPFmRLzsovXa1Wh\nO1umzDNZOhBJEVp+WIMM8k7xxyag7b/dX/4Cl10GDQ3Kyo/N2dK04wC30/VEOLVmMQqtsDOyK3C2\nVAirsOO0ilFQ2dGRnS03rlZQoRSH0AKDs1UIQipCV6uQhRZ0HGfLKaTZ72N3G/Ay8HmgE8DDD0Nz\nM9xzD3QNPpNG7M6WLrqKjiQIrf2IZuqbgM5WEoSWY/kdTGhBx3W2ohBaShnl7XRbZysMkvRZWVDo\nQgtSZ0tnTt7iBQ34JzIVBACPPQY33aSkXYmI2dK04zxMSG1g+6ZopuLxSlKEVlQEcLaCCq0oYrQ6\notAC/86WmVhZ3DMJKctTIONshZO3UaJKXEXkahWD0IKO42x5xa3g0h/bDcBjwIVk3Kj165W0IxFi\nCyIUXMUqtHy+LzOx0zq3ylshPkYjJsXNSlouraDt8ZrQdBG1liMS/YxGtHKF7NyiJAmxgnO1fLBu\nG8zZAJNUf+wF+LkkWWgdSDoaMUryRdmfgdMBnn0Wjj46cPmJEVsQQHC5IQqnJw6h5eN9OQkd/bhr\n0eXB2UqKyAJ3wiYqVytpog+ii9kyCpw4hVcxJjA1o6YbjO0TdysciMDVSrLQ8kPqbKkl50n1rW8F\nLi9RYssah1xbTu5WGEKrQLsKvYgd166XC2dL1cjCKIVWWIRVt4ppeox4dbZUiBW9DK+iK0jXpaoU\nD6FiFB8eY7TyWTc7BGfL7+cSU7LSQhFaXtytjuJsuc37HZSlwJPA1wGagseuxie29t4b3n0XBg92\neUFAwaWKJIgsn6gQPCX77mwvuCycLdWpGwpdaIVZbxChZdWV6MXZUu0KuRVddvW6KSORbpaTAAko\nUGqqFDtbfoRWjBnhC0Vo6diNxTcKsdTZUs9yhWXFNxpxzRr4oL1mj3V0olPaB9VCa7+8xeu1Hgg1\nZ5XJaMRUaCWjXrcsorbdviSMRhy+aaWpILLab1VGkOt1Qne15hOJCFm3UzpbsRDRe7Si0ISWEweS\nFWPpaMRwUPWfO6HdiFYuVkjulpvcWl6Flp+uS/2aj9WWHXpy0DxnK2lCK+6M8EkXWla4cbaicoaC\n1jN808o2h8tPWcqEVtyTKc9T7Gx5+Vw68PyGYXMgUAosi7kdxcgzwJcVlBN7ni1rfGaN376p/T47\n8aJSaPl1qazKCUhYWdjblWlwtpIgtIazKGeJkyjqVxWrle9uJcHZUokfN0sZMTs6QJswUuZsFeDo\nw2JmGdA9b5/R+SoWoojXykdTUEa8ztaXvgSPPw4XXBBrMyxxEllhj3Dcj/ZC0UWdkU9zE8LciH5F\nVlKIqi2qg+KNODlbiYx3CoFArlbcAkvH8B6UOFteP5MEulpDhlkfK0SGAJVAnckxr2kkUrKcSeAx\nKUASnK3XXmu3S9O+a3OBw1dGVZB83ELLWI9LxyzK+QRz6sk4W6rSOngVWqodrKBzHSZJ9AXBztlK\nhZYDSXCyLPDtbBXRfIm60Mp/XcgsA1bZHC82hytsyoETUCO0IE6x9bvf2R62F1whkxSh5YE4Jm3W\nxZ3Yvxlx0sGByyt0kQXRCi3Vrlb+iMSOPDdiIJImsvLEkWdnq0gElh3FILiGAAMczkkFl3tqgcP1\njW7dApcXn9jq1MnFSVYu1gc2xzoecQitHPY0or33TqAivAitMGKxOuqUPDpmqR+KLWbLK75crYQL\nLfDgbBW4yFq2JLt0BJZh72zppILLHaXGjffeC1xe/N2IjtiJKgWCa67H8xPmasUutAA6VSAOPcL3\n5V6FlmoKcdShSlfLarqe1NnySAEILXDpbBWwyAJngVWMAmwIzs6WTiq4PHDWWTAqeGdiAYgtUCK4\n7EYkehVcCSERQguUOFtuSLLQipIohBZ0bGer0Oc/tMPR2Srw9+5WSBWb4FqGO2crJR7iz7P1t7/B\n2rXQr5/DiQ45ttygC64Ccqes5idMjNCCQM6WW1cr6UKrkFI86NgJLbB2too9OL6YhRY4OFtF/t7z\nKSbBNQQ5GtEt6QjF9vQH9MnJahSXHZ/YKs30iG7dCuPHw+rVIITDRQoElxVzyebcmkNk0/K4nRQ6\n0WScLfHFL3m6TFVWeD8UitAKM7WDE17nRiwGEiW07Noy2v+1urPVbm7EJL33FM8sQ+bZMkv9YEXS\nBFd+Dq0oZ8erBc4xO1CmRibFJ7aOOw7OPReeflo6W62tWQGWQdO+ixB35l2oyOGK2d0qCBHlFh/O\nVtxxWqpQ1bY4RZUVYcZsBRE1mpPQiAMV8VpePhP93PzPwkUZyudGTEkEQ/DmbOkkTXAZyfc9wkpo\nejAw2bjj+OPlulMnuPxyJXUoE1tCiO1kE63qFpWWqaOTpmm5dXXvLtM/TJkihZYq3EzZYyW0InC3\nohZZZqJm0brhaivx6GzF6WipJMkiUAVJdbaMQk2l8IrV1fJbt4/rTJ2t1NUqeJbh3dnSKSTBpZoD\nyRNajz0G3/iG8nqUiS1N07oat4UQewFXAJcCf1ZVT6SY3WUfrlgcLpadoDEeUyK8XDpbSckKr6IL\nUWW7kuhqQWGMRhTzEuB0JW0UogPF7mwNGVZcsVhuGYI/Z0unIwmuMuTIzUrgZOOBt9+GI/yPrHeq\nUylCiGrgKuBrwBTgYE3TPlVdj2+8dh8GvMtJcLLcnB9IdLlwtpIitJJGUoUWJNfZykeF4CpIV8sn\n7ZytsOuPQYzaJSktViG2DP/Olo5VgE4SRJjKLsQvYRL2+PLLcPjhJmerQWU3Ym/gWuRUQo8D4zVN\n26qq/CwhZwgxdiUWGEG65wKJLhtny2+bwhJaSUr1kGShBdbO1uKeAxM3IjERDleBkONsdcDuw2Kb\nE1FnCMGcLTuMT92whFeUE0y3ywf/8MPw+c+HWqdKZ2s5sAF4AmgALhSG0YWapv1CYV15uAya9xsU\nH8HoxHxR4lb0qI5/8tOOYdUL+HTOa/S9eFzg+lWJrCSJKjOSLrTA3tkKIrgSNeKP5LUnbNqcre1x\ntyReiq27cRnBna2OwiryEsAOC3++JpVi6y6yAfJd7U70TwBXS+XoQ8WjGf0IpqiCzN3U09pQTpeJ\nwRzHjiKyoDCEFhRGzJaR1N1yR00VjG0AOsfdkvgpJsE1hPCcLSNJju1yy2vAVuB4fcfxx8OSJTB0\naGh1qgyQv1VVWebEPMFAhLm3QIocK1cpaaP5tMYmdk37gK5nnOD5WtUTSSedQhFaUDgxW0HoaK4W\nZJytbTDJYdB2RyHJgsss9syqrcuQztbxedck9b0ZibILUec9pCt0mL5j+HBYuBBqa0OpT2XMVndk\nTrAm4BlN0xpUlR1YaHl1odzEbbl0t1rnVikNkk+a0AIQFf6crVRoxYdT9niwd7aS2oXoxd1S1pZR\nFNSIxJoqGNsuaCUlaVgF+VvtP2I3VJlMwBeGmCx0d+sQ4AikOG1D02DFitDElsq5EV9AhluuRY5C\nVITbh3jh3nq3DlYShRZkna24iENoLcbbH2QU8xnWssj14oZCnRtRzLMXUk7Hix3d2UpJLnajKa2o\nb4blzdbl+SkzCqJ2tQ4ATiJPaAHstReMGBFavSpjtroCS4C9gGqF5XrHTWJTFSh0txatG+46N1bS\n8OtsqSBOR2sxtZGlp8gXSG4FUxAKfW7Ejiyo7KhZkzpb+SSpK9GvKKorM3e28stW9T4L0d3qCpxi\n3PGvf0FdZkhBdTVUmc9FrAKVYuurwJVAM3CuwnKTjWLBBbnCKskiSydIzJZfCqHbUBVRCCszzGK2\nggitVPwkg3WNacxWElDtNNU3Q48SGNPJud6kCMuoyRE8L74IxxwTT91B0DRtKXC9qvK8Y+OshD0X\nouLynVyupBG2s1XowipJsVpeKLTRiAVJDAK0piJiZ6vAYtrCJMyuPDfOlrEdKgRXIblb/YC2SXiG\nD4dTTrE5Wz0qY7YQQhwphBiTeX20EOJaIcRnXV18992we7fJAUW38mM1xURVvtfkosNZ5LiERZgx\nW4UutIISl6sF7WO2CqX7MHL8ComYnD7d2fLFfJPFDaN81leg6DFS+UuY2MVsmaGqPUF/ZkcxyH9v\n5LyBbT8dxwXPCekVZWJLCPFT4OfAk0KIO4E7kGk/bhFCXGd5YbfMT6zvfx9efVVVc8z5mHBFl0PZ\nrXO99QernjA6LOHlx9ly04ZiEFqF6mpB6mw54kVsJIV5AZytoO+1AwiuOAPR68pgsMe+qqQEzYcp\nuCqBi4w7vvUt+MMfQqzRHKFpmvNZbgoSYi6wP1CBHJE4UNO0bUKILsB0TdPGGc7VnnvuOZqamui3\nZAmfvflmAN657DJWfuYzNDU1UV5e3rY+88w/A7XIcLAyi3UdMutEuVx37pG7nb/epxy0JhAW60Hl\n0NoEJYb1gCYoLYcWm/WQcmhugjLztRjSAs3NUFbmat2v96doTc2I8jLLdZ+mVZSUl9La1OJ5vaF8\ngGP5TuuWLdvZ8ed/0u3cz7s630179y7f6Ov9RLnu3bSa0vISWppaLdf7lK+juUmjrFx4XvdqWkt5\nOTQ1Ect69YoWZr+3h8+e0oWBjZsClddpHTS1QHlpga7DaP8KKC+BptYI12tg3nb4ZDcc28vj9Suh\nXECTZlgPDNAes/JiXm/eYP+UsVv36BNv+/+zC7qVwH6dvF23er2/95u/XgSUAi0B18uQLlCrgnU1\n8BCgh7EtPOkk/nvaaYju3dvpDLv1OeecgxACTdOy0+J4RGWA/B5N01qABiHEYk3TtgFomrZLCNGa\nf/K4ceNoaWmhdMIEtsyYQfVLLzF48GB66ftLS9vWMv3YMOw/1n3JuW27S6GyK4hS0Frar6ss9uvr\nnib7G1pgpMN1w0uhpQVKzddaaSli1HbL4/nrtaWlDOqxDFFaitbS0m49qHQlWstQRGkJWkur53V3\nw/YnLQMz5Vmfv7J0aLt2tOxoQNvVSMX4UZbt9Nre3qXlaC0aolQEWg8qXZHZbvW1Xlk60LL8gS17\nbOsf3LKU0tK9aGnRKC0VntcDWsrdfk1CWffdu5S9ugrGjC9n6PZg5ZV1i+99eF4vgtISaBGG9T7Q\n0prZVrFeCi19oVRAixbRehGUdoXqMhjeCOO7eby+wuTh2DVAe0Zl1kvUPKSVrAdaH/9kpfXTZ5DN\ndVGtNWAvAUPLvV2330BYszK4uBmJND+DljMos57v4/pRhu0+yFF7Ols//3m0u+5irKbl6As3axUo\nFVtCiMpMMtOD9J2ZZKft7LORI0dmN7rLjBcDBgwA4/42aoB9HKrfTrve4wasU0Asxj6o3Sp5RY1D\nM7Y6lAtozVAy0n2i04qaUtP9situgOkxP4xBcyxvNHpQQHbdtHkP9b/9mDHfOTRnv/naub2y+7Cv\ny1abk+2mDJaFpB/bLHNq9cM+8GUwwYYR12YjDGKhpKSJd//ZSt2YcoZv8l+OmIf8DxqU/G6soN1S\nVt1iewcs14l5QJQjAfXYsMwkapuboH4njPE6qVr+KDdV3YL7Z9YJ75IdaehyW7YkAV1weZ//rFVQ\nss55NKIZYxQFzNehLmDe+KTQc3GNNdmXvx+gB/AZ445zzqH700+3z60VISrF1iRN0xoBNE0zOlnl\nwPkK6/HG9sxTwkx0hTVK0UW5XjLLJ310YklFOT0mJmNSujAGAuhlGkVXVPm14iRRMVtmD2K/4ivq\nh3qcKS9M6o58NKJbnO5fgsRY0oQWQF0VVNXhbmZik88yySMUzWK6rOK8OpEntK69Fu68U3GLvKMy\n9UOjxf6NwMZgpStIK+A10ambKXvsUCy4kkxrYxObp82j/xlHxNqOsAVQRxBYRvTRiBce9qnvMpTk\n1nL7kE3CwzguYeWhXiV5tuIIdtfrTMJ9jhOLz75+J/Qod+lYhpyOI66UEF2AnGyP3/0u3HQTlChN\nvOALlaMR9xdCTBdCrBBCPCKE6GE49r6rQr72NXjhhQCt8HF7vY5O9DK3wMc4joB0O0JR9chElSTJ\n2UpRRyKcrUJ5sM4jHqHlo17fztYowxIncdcfJzbvva4KBgecMz52xy4AvZDT8LQF3Xzta3D77XIa\nngSgUu49CNyKdPcWAm8JIXSFYP8fe7ThQf344+0Oa9pxalq43SLwxEoMzVVTrW0deE8JkTR0ZytO\nitF1WuRx/kXVBJ0bsUNkjI9LZOl1+yBQnq2k0BEFl8N7rt8Jy3cFryYp+be8MtC4cdFF8NvfgvA9\neFA5KsVWV03TpmqatkXTtLuRU/dMFUIchkmAfA433AD33y9fW6SiiE1wmeF35kwHweUkupLqbqXO\nVnESu7OVZFcrTpGl1++TxMZseaUjCi4bVDhbOoXmcAkMoWpXXgkPPxxja8xRnUG+Ldhf07R/AacD\nvwMGO1wo0+dHxfZN5qLLTAxZuVshCC7w5nJZjZKLmiQ4WynqCeJsFbWrFbfIClh/UThbOh1FcLl4\nn6qcLZ1CElyTMIxfHz06ETFa+ahs0R1Ajr2hadps4LPAnxTW44CHuC23gsuKOfgTXQGy2Oe7W0kQ\nXCqdrWLIGg+FnTleJ1ZnKw5Xa57LpcApGmcrJQdPzpbLv6+ggivsrsQy4AhkvBYAo0bB5z4Xcq3+\nUCa2NE2bomnadJP9n2iadrGqetzxAa5Fl1W3ohGn2C0/oquIYrhUOVvFIrSKBb/OVsG5WnEHt7ut\nW1Ebi8rZ6gi4dO9cOVs+ppiKcwoiJ3oiJ5gGoF8/mD072l4yD0TitQkhLnF98uLFFhNS++GDvMWC\nfMHlpTvRiFfR5VNwJc3dUuFsFZPQSpqr5XcC6a7VJZww0v1TWcyLONVDUJIU3G7XDsXtLCpnK8lx\nffn46fL0cI3KmC0zkii42sLf+/WDBQvk/GAJRWVSUzvcDwlYuFD2udbXy/kBlaILLhNz000eLre5\nt8zS3RYxQfJsFbLICltU1QYYYZkvsPTtxT0Hmp1uSo9la5j6IUw+3vlcZW5WFA/PQnLeQmirkjxb\nKf4IMb+VbZ6tQhKlfhg3Drol+xeEMjUjhDgUmGeYfPr7SFXzP+CnjgUcfjgcdRS89RYsWwZHHgl/\n/CPs4zRNjx8+wLE32SopqZdkp3bzCTjVg7ekp4upjS39gZOzFYWgCvv9R+1WBRFadnhxuTZ0hwkH\nOJ9XMEKrkERWiBSVs1UojDJ5bfd99+GC1VXJKX/boeDvym9m+TATm/YGjgyxfNWo7EZ8HDkbIcB9\nQHdk0HwD8ITj1T16wLRpMH683H7/fXjttZxTlKV/AAJ9DebiPQeXXRdjgIB5I4upjaVL0Sxmq7at\nNcl0rkaysN1id15U1LIosNDy222Yz5atMPNDJUWl5JP/2yTCzClFE7NV6G7NKJvFB6YxW0UqtCAv\nxUFC47SMqOynK9E0TZ9teIKmabp19JYQwv2/7LfegkmTYNYsWLFC5t0yJCbTtOMQ4g11rTYSxZQ+\nc/DUvehnSh+3Lo9bIbQI+y+y0dlKqrgyYies4kKVk6VKaAFUu3C2ArtaUcZnJY2YUtOlzlbERJSe\nop2zFaMYjXSqnquugrvvjrJGX6gUWx8LIS7QNO0J4CMhxARN02YKIUYA7oc0VVbChAlSbP3kJ7Bt\nG9x3n8JmesDNRNURCC4/OAkuL6LI6dzdjQ2snTad2jNqXJepGjfiMmmB6xBed6EKdGfLKmbLt9Aq\ndEciTowCLWAG+TRmywVmQsnL9zfCPGCe5kZ0iR9XK/I5EQ84AErN+k+ThUqxdRFwnxDih8iJp98V\nQqwAVmSOuef007MZYO+/X3Ypdu8ODz4Iw4aF627lE5bg8lNPQimtKGPviUNjq7/QhFYS4rHc4MbZ\n8kwqtLwxGimqzFww/ZhHInO23Dh3SXMc3YgjN0HuMSRbzXG2Av6d+e06TLFGmdjSNG0r8HUhRDdg\naKbslZqmrfNc2PHHw9Klsh+2tRWmZ9J3HXMMXHONrO83XeHMMxFd26X2Uk8Ygitkd0uVq+WGlsZm\nVk9bSt0Z+yst1wm3AfFJEVphuliqhRbYO1sFl0urkLETLT4EVyTOltsuUp+CUTlexZFdkHtMWe3b\nnK1V/q5XIbDculpmw9O8XtvL9qzkoTz1g6Zp24CPAhc0ZIgUXKtWwc03wxtvyBiuq6/OnrNwIdrq\nq2RwfefOAB4dLxejEnWicLg8uFuL1g2ntiYZ8VFROluFOOF02F2FYQgtsHa20u7DhKELG5f3JY3Z\nyiOIOErQdEF1VVD1CdDJ+7VROllWT1zj/g8s9htJfsdhLsmbQMjIoEEyJcRTT8EPfgDf+Y5cdO68\nE/beGwYMgE0yManaEYs+8DpKsQjQna2wGM6itsUrcQe9F6rQggIZjej2YecnGN1sxOBok/1JwWW7\nQh2NmOTPx4wEiaWg1O+E5c3O5+WTBKFldp6+mNEPCDF/ayhEldQ0GP37w223ZbfPOgvOOw+2b4e1\na6XQGjkS/vEP2H//NsGlPK5LdVyVWVdiAcZuBXG2CtGpsiLKYPcwRZaOmbOVyO5Dt4ki3XZZjbZ4\n7aesqHHhcrl2tgpJNPmhiIQWQN0GqPL4RFcttA7EvDtQ1RyJJcjuw876jpEj4eijFZUeLsl2tqw4\n9FCZaX7NGjjtNLlv40Y44giYn/2v687lyvtqOM2V6CYnVkTuVv60PXHh1dkK4lQlDd29ikpoDd+0\nMhKhBe2drcBCS/XDTWV5flyrJLs4Nu/HlbOV1PdlpEi6/1RR3+zN2QrL0TrQZFFBCTKRadtEdv37\nw//+J0OOCoDCFFtGpkyBr35Vvt65Ez7zGSm8MovW+tl425dAnPJmecWLs1UMAksnaicrKpGlY3S2\nlDlaqh5yfssZbbEEIenCJO+9OjpbUb6fKAV8wKShkeD3s58PdWUw2KWzVYijDXsDlfrGoEFy0umS\nwpEwhdGNaEfnzvCrX0FFBfz2t7JbsU+f7PETTkDTXnfoUswLlHdKbqoqWN7laES7xKZJCJSPazRi\nnBRbl6EZurP1effTKbrD7/xwdg/JEOecc0VSuxVNWNcf5qyDSUkXiW5Jsnhyg9NsAi6/V/XN0KME\nxj485SoAACAASURBVDgEyBei0OoPVOgb++wDr78OvXvH2CLvFL7YAujZEx5/XHYrzpol97W2wubN\nbWkj8rsUI8vTpQg/meSjwq2zVSyuVkcQWgA91sHBYY2vDuMB6WbOuTDx+ZCMmpoqGNvH+bwU7J0m\nFffXjeB1I+RHQd2HUFU4Ro8jnZFz/gkMQmvffeFvf5MD4wqM4rk1JSVS7epdiEvtY4gc47kSGLvV\nOrfK+aQMTnMkquxKDHs0YhIo5tgsK7bsgJmFmK4hKU6HVVelyi5MH6zbCXM2RF9vQeHm3gTtjlZ8\n773GbCWJCmCvvEUfcdgWDD9sGHz8cUEKLSgWZ0sJHnJuhYnCkYhu50gMihtnKy5XawEjPKd/iHMK\nnagFll0sVvVeMCEpwsUrbrsVo3TD7EY2WhGCO5YYZ0tVvrYkfUfdTKfkNw2Jw+dVV1Z4zpZA5svq\nb3fSTTfJEYfjxkXTqJBIxVYbPoRWQtI0+I3bWsRwJdnknWK2Cqn7MBVaWXRna/Lh0bRHOcaH8HyT\nfWbnJs3J85iw1A26szVJdSyeF5KcGFeV46TSuXLxebmN2RoyLBlxWz2BduM0Lr44d3vAALjxRigr\nfKlS+O/AiW3b4BvfgAcekJNcm1IYjpafmC0nd0uF4LJztgpJaMXN4p4DY+86NFLQzlY+bt+HmUBL\nAgoD8GN1toK8h0ISWjFQCM5WGdADGb+Uk5S0Wze45BK4665Y2hUFCb81AejSBaqr5esnnoC33rI4\n0UZoOcVtBSHEeRG9EjR+Kz9mq1DzaMXpauks7hmn3ZBLwcZsqSJpQlOREAgcs+U3TimhAwbaKGCh\nBYURs1WVWdqEVkkJrF4NW7cWtdCCYhZbnTrJPBxCyO3m9t/C0Kf2CTJPokfsEpw6BctDMMEV5dyI\nXknKJNReWNxzYCJEV1E5W35J2vtXIAhcO1th5CRLKkXwvupq3efZGjIs3LaYITAIjvPOg9deg3nz\nZHLSDkDxii2Q+ThOPDFYGX7dLcVCK4q0D34FV1JHI3oRWklwtfKJW3B1eGdLp8gEV46zZSWokig+\nzO6DinuTxPfqA79zI4ZNCTAQGIxM5QBAXZ18No8YEVu7oqb4Y7Z0Tj8dpk2DCRPibkmiuhDz8RPD\nle9shTUK0ko8LaD9H2whOlpmxBnHlTpbBuJOmppPgBiuNmerEEWGqu9jIb53B+qqoKoOWOXu/KgC\n5csyiwaILl1kfNaxx4ZfccIofrGlW5S7d8sg+SefDL9OO1fLh9CKOpmp0eFyI7yiyCBvJ56CCqsk\nulpJIO7RiJqiB2KiJs82Ewt+RZxPwbVuJ8wphUk+q/VFku6BCkIYJWqJ2wzyO6FHOYxJ6MhacfDB\n8P77cTcjNopfbN1/vxRaU6bArl2gadk4LkDTeiJEiIHwBY4uvOxEl1nMVlQ5vjoCcblbcThbqgRW\nfplKBFcY0wzlH/davpu8TnnU7A9jN3usx4piE1FOWE2t4+Zz8JtPzaWorquCqlLDDhff1yjcLeF8\nSoeguGO2AKqq4KST5Ovnn4fJk71dbzdHolm6hgJ3taywi+eyitlaTK2r4Pw4KRRXSw+aVxnHpY3O\nLmZEGbNl1w5V5SvBz8THYZWfj8upX9ZtgznJyTBSHNglrHWbjT4g9Tth+a68nS6+T2EGy1fikLC0\nA1H8YgvgkEOgb1/5+m9/a3dY02wElRcUCy0vRDEZtZXgchqNmFTBVShCK5+oRitG5WyFKbJCwWlC\nbD8iy235Tth9lpljNd1gbPyDXQuPOKfvcVFWXRUM7mJyIEbBVWHcOPnkcCopEDqG2BoxQubysMFU\ncHl1tfwSsCwnoRV2d15SRyMWO0a3K6j4MhM8xTYaUamoG2WxqCzfLw6jC1Nni8Ls/nQQcKbOlk7M\nDhe/+IWcdqcDU/wxW1ERg6sVhZsFzkHySc6zZUWhulp2GAWXihgvP85WvqBxipWK2tUy1peowHkz\nQgp0Tp0tHyTJfbWIE2sXs5WPyxguSMZ0PsVGx3C2jLS2Qk0NLHYQKnauVj4hCS2reK3amsWRCK3a\nTNSVE26craBdiWbpHVKsUdHN6MXZsoq5sovFirv7MOw4MWUo7spNna0E4+X7mOd02TpbOi4d2CHD\n/Dtd+rVDhkH3dpMfdlw6jrNVUgKf+xy8/jqsXw+zZsFwn1nT3Xb7uRFaHrsQk+JmGSk0Z6sYXS0z\nvI5izB+158bZcitWCkLUJBmFeb6UOltu008onNvRM0G/e1F/d71+VpnzHZ0tIy6/T/mCy+h4OYqx\nHcA2l+3pAHQcZ0sImDoVzjhDbr/0EuzMdY7a4rZUuFoJSVzqJ17La1LTNGarODE6W8aRi06jGAuN\ngnkfihyu2JytOERLodzbfHwE17tytoz4+D4ZXStbdgPrDds1Nd4rKzI6jrOlU14u108/DXvtBQ89\npLZ8LyJLZZC9IrwKLYjG2SqWjPBR48fd0uneBw4SBSRGMuhdqG7fd5yxW55zgClwuJTHbHlxYvK/\nS2F99qq+swX03a/bD6o+8XhRGDMj7AGM49GeeQbOPFNxJYVHx3G2dK66Sk5SDbB2bbvDgdJAKHSz\nzOK1oupC9IobZytNcBoffuO3tmyFmR8qboxP3Iy8TMoE3m7RRaxntzCgwxWKs+XXRQrDfYpaIFmN\nTFU9QtWB+s2w3M0E4/mobOMOwPjd+ulP4eyzodRt/2bx0vGcrYMPht//Hr70JXjxRXjkEbjkEm9l\nfEwsrtSidcNDFVx+XC0wd7ZUiivVrtYiak3jthbZBPFbxXnlX5PUeDA/Weiru8OEA0JqkAfMBJST\nqFKecX8+Sh9KdqJKPxaW4xbqaES/sVk+MuE7lhMFbr4T+eeElE6lrgdUlQNDyX6Gbu+HKofL2I35\n4x/DDTcoKLQ46HhiC6CPQf5ffjmcfz5UZNOvadtA+BlFMYfExGpFSf7ciIXgYtkJqyDn6+eFKbr8\n1uFVcOnO1uTjPVVTnEQktPLPsxRcAR6OurM1SR/gq1oMBA2GN/t8nKazCQOncv1+J9zeO4+fY/1m\n6NEZxvQit+1RzePYDDRkXj/4IHzzmyFXWFh0TLF15JHw97/D8cdDS4tMB5GHa8E1F/vUDz6wm6Jn\n0TrzEZRxdjEanS3VQqtQY7XCEF35gs+4HYa4S4Kz5adbMI55JN3iNf5N2byOOqMyztYArMVCEicy\nLqDYKVeEECvV5mxZ4STegt731UBL5nXnzj4LKV46XswWyJGJxx0XzhdijvoigxDFVDlhjUYsVKFl\nZBG1touXctzU44QX8eIlZqvQ4qXiwO9AA8vr3DorefFD6zbBHDe/zSKehDxRhOVqecVDTFv9Zlju\nlGohjJjAZuCTzBrg9NM7/NQ8ZnRMZytsEtaduJjaULv2dGerELoPk4ZqB8wqHs0P+c6WGzHlJzas\nIxDaiE4fD/2anjDWbYrBJLpcYZNEF82qTQanytHZMpbl5Ja6+V6tAjYiUzzoQuvgg+H552Vey5Qc\n0k+kSLDqXtRx43BZTTTtRJpnK1xUx5e5daB0Z8ura6XK4SqWLsSkpc5w7WwZ8SrqkvCevU4K7fY8\nVa6WinKMGeTdOFsm1/lmDlJwNWW2v/IVeO+9VGhZkDpbKjCL23LjbkU8qjEsh6u0oowDJ5pNN5/i\nFj8jJIPgxoGq7g4DJvYKpf6OgEqRpTJ2y5OzZSSMnEyqsfvMVdyPBHetuna2VKGHOj/+OJSVweTJ\nMkQnxZRUgvrBrUCKOH5r0brhgR0uP+5WS2Mzi6et8XydEwsYkbNY7S/WeRPDElo6TjmrZosa5sxs\nMj0eNoUa/1UI2fV9OVt+iCNjfJgkVWhl3rcnZysIDcC/DdsXXADnnQe90h9mdqTOllfMhJbdaERd\ncFm5XCbuVuvcKtsRiU4Ezce1iOGecm7VVXxC08T+vutzi52o0o95DaoPItTCyP8VB0aXyyhyulaX\nMHaCv5/KQWK3ClFoJVlc5ePb2fKDi1ijUOtRRVhCS6FbGImztQ14j2zX4VFHhVxh8ZA6WwAffQSa\nFm4dc7B2uj5uv6t1bhWtc6t8V2fncKkeodjc2BKKs+UHM9fLblFRVzFg5nJt39Iam7MVJUGFUlRC\nS1U9kTlbdhTSvIVhO1r55fvMPh+Js7WIrNA691z4z39CrrB46NhiS59C4PDD4Y03nM9XEV9lJbpM\nBBcQmuByvNZld+JwFlFWUcrwCJytpJJEwaXCJQvibIE/h6rQXK1CcrR0InW2nEiy6Ipyuh0rgeW2\n/tHS2RrsJxm3F/Q4rdNOg/vuS4PhPdCxP6mf/CT7+oQT5NQ9BjT9V8J+qA9ktxJcxiWD0eXSX5st\nZlgJLpXuVpKcrRR1RO1sFZLQSnpclh2+na0wg+ODfJZh3AcfIit/jktl3w+XbYksZgvg61+HngHm\nEe6AdGyxddVV8NBD2e1LL4Unn8w5RQvzy+sUQJ/ndgVxucxQJbg6urMFyXS3ghLU2fJCnELLyyi/\nuEVWkMSo+uLL2YpiFGKBile774Qy8eXCZasbH4GzleKbji22AC67DP7xj+z2BRfA22/nxHBp74RY\nf8IyzvshdbYkxSa4VDhbbhOhxoVXoaWEjcA7ecsmRWXnYfaQX9stATFbVnj9jGN0tfwIKMvzNWAB\n8BGw26YAm7bVr4fl3b21JyU6UrEF8JnPwIsvZrePOgr++tecU2wF19yA9dsJLotYLi+EHSyfOlvF\nSdjOVtxT/LgVWkrdrBZgEoiTcxcmIR+4CrFqc01fj85W1Lm1vCQhVY0HoeUX02tfAS4ErgB+4FCA\nRRvr+sLg/Emo7ShQJ7FQSVM/gEzEdsop8Mtfwre+JfedeqrcvvLKttO0d0AcEVIbAk7xEyRVRFB0\nZ+uAM4bF1oYwyBeiQRPCOqWncOuMRTVnpO5sHTM5WMJao6Aavmmlb4HlZioiFdMFhdJN+DRwO9AA\nYmumnsPlWrwLYg1Q3QylpWib7BND2iU4ddP2deulszUp5knGHTG+l/z3q/IeeYzPMv2M/wD8iOxE\nzFaUANeDdr7hHj4J/MZwzvvAKUBn4AbA7D6ZpIyoXw89KmHM3g5tMOJm6h6QPwQ+RE7Nk+KLVGwZ\nufJK6NpVBv8BPPNMjtiCkAWXFbq7ZROk75SbK2juLTusnC3VYsULYUzA7ScDv5mAUpFyAsIXXWE4\nW0GElr5WNfejGcqE1kfIB3Bm9JZ4OK+eQ0G8k7GySkuhtRVuuw2uv95TO8U8722u6Qv7HevtmtiJ\nUVw58iKIyzycfw1oC6R+EZuQ35N8Ps2srwTuBw50LrauL1RVeGiHjp2o1WkB9EiRykoYndpiXknF\nVj7nnw+9e8MXvgDTp8O6dVBTE3erJC5EV9Qsppb+jXPbnC07kaMfC1N0hSGyvLCAEZE5T3Z1qRAk\n27e08p+ZXRk4eYiyMv2Qn8ZCleAyOkSBRdZucsIBtNMEJbtM+gX/8hc4+GBE377ZfdXVsGkT3HIL\nNDTANbj+z5zT7vnAdmSS5Urra9athzn/g6OPdFdHURFAaOV81k3AbGAXiAsN+599Fo4+2ryADz+U\nU9rQXnwDsGABDB4svwuPPAK33ir3fxt4Ach/DOW5W76crXyshJfxd/z69VCldrBWRyAVW2b07p19\nXVsLa9bAXnvF1x5FhOVufVJRR9XEFtdCJ25BFDbFECi/iFq2VO+hbsL2nH1RC66ws+orc7IuBDE1\nuykyAVjbv9qF3Yd2og+3wsCBcPLJ7eePmzoVDjlEvr7jDsT2y9F+/KC3+v8K4gL5UjsUeNX61Jq+\nsH/Yz8p8UZP0ORUdaPc9uQ7E03n7fv97OOMM69xT/frBCy/AJ5+0PzZmDIzI/N/o3x+++1053+AP\nfyj3nQE8D/SzbqNvZ8sK/T1PQ3Ztguz5SYWWL1KxZcb48XDWWfJXyo4d8o/krbfgANl5HkpXYoB4\nrbhpaWxm9bSl1J2xf9xNCZ2wJvNWTRBhpAucnVuaqZ+5nUMm98o5FpXg8iu0VMRtuWIG0nXYCWKV\n3NVaJdgztpzOHAhDh9L1ySfp2qmTfTkHHywzceuOyIMPIracjXb/FHA7r6/h+S3eAw7YB63TCrgD\n+EzuqZ5jtrxOKWPmHun7ohZdW4FfIqeZKQOqgdsAD+N5coSWBnwDhHH81GGHySSfZ55pX5AQ8KUv\nuau0Sxf4wQ9g1SqZnqgV+DJwD3Bw5hwVMVtuMI5w1MVfimdSsWVGp04wZQrs2iVHKe7cCa++2ia2\nwERwzcV+jkRVOMRtGYkqaL60ooy9Jw6NpK6ULE7dlbpY8SuOqqrLqJvQ1de1QYhrjsh2rAR+C+wx\nPyweyN1u6VlC6ZJNdO7uY/z9pEmwaBHstx/s3g1TpiAGfR/tm7eDnan+DLAQ+CBv/4oVUqd9GbQX\ngGOyhzyPRgT3gsupm86snFbgX8j0F4OAQz22zYr1yHintXn7LgIm21wngGNBOy1v/zbg9qzQ0ipB\nzP8E9tlHUYPz2yHgwQdlTN8DmS/b1cC9wIT2p+c4W24D371w0UXScUvxRSq27HjhBfja12SgvAmR\nB8t7jNUyC5oPoyuxIzlbhYhRvFgJLzOBY+Zs6eeG4W4tohZaNbrO2YFoam3b39S7nF1Dgo2IdEUr\n8D+yc799H8RMF9ddfz1ceSWlvXvL4GG/DB8u42G6ZTJT3n47YsxTaMd+zVzorALx7bx9N94Il1wi\nXfnvfx8AcTpos4EB8hTfoxHt3Cm3sVCtyKeO8euzFHjWsD0aKbwG4u4JtR5oMNn/OFmhNQoYfRr8\n+c/S7XrW5HwD2vPAkLydT4F4KnO8E4i122S3Wtjcf78UdN/7nty+CvhT+9PaOVthCK4U36Riy46S\nEhg0yP35UblbHnAapWjHIoZTi7MwS50tdxhj1eLqivTiGtk5W6oFl96ukd9bwtC7V7Q7Pn3aAWw5\nqhpw59Tpox49dSfeBuLe9ru1EcDZICrvbH+wWzc45xx1MZ1du8LMmTAhY13s3Ik4ayJMm2Z7mXYr\niD6/grPPlgH3V10FFRVw9dUAiHEC7S0NRvl0towEGc33RGax45rMegLgNMrvY6TTY0cd8I9VUF4O\nxxwDjY025X0MTz2FaAaOsz5NvPffaIQWSIfr29+WMVzXXiv3nY5MNWHoDjWN2XIz0jAlElKxpZqw\nBFeCRiDm09GcLT9xW/mDAgoh9svK2VKJUfzte8kC9nk0OxPB1oP2ovusHQAcNvFD2bV/1lkswn23\njW381p+Qua8yuZHEsuwhbVxmX7/PIR5/HPZWHQhjw0EHyanDHn5Yxsh8KvMAaDVAPxBlB2XPFQIu\nuQRx8cW5ZVRUSMG1bJmcMFjTEEeC9iys6wGzd8o8qqGwBrgZ6SDls9rweiSwV+a9lJbK8I1du2DW\nLLlvJjLPlB0bDK8HA70Pyj1eUwNPPQW9Mt/hb+dbgXm0tEBTEyy06KKvrIRf/CInpCQSOneGa66B\n5cul06UBNwF9gHHAV13EbOUH+ZuJr4+Qn7txIK1FN3qKN1Kx5ZYbb4QTT4QDXSQ80TPKqxJdAYVW\nEHfLDUl2thaR/QnvxqULA6vRl0lwuuxwitkKGhOmX1+yq4Uh96xsE1qt5YJ3/juBHftWceJdk7Nx\nImefDbNnU8u5bOZXruvZQleqd21vt1/cZ3JyWRnMnIkYN87z+1HK2MyImYzQol8/xNKl8qHrhXvv\nlcLrTunKibNg1AXQpxS0r4EI+iexGHiD3Ifzy8AWm2vKyuDdd7PuXT4bN8LQoXJw0gbzU9rxq1/B\n5Ze7PNmG0lIp6pPKffdJUXr33XJ7A/Lzr4aJm6BLEzhmntkHOISs+NoJ/BtYRXbUoRljC3gUVwIQ\nmqZ4jgg3lQqhxVGvL26/HW7I/Lzq3BlWrMhJDeEqZsuN6LL7HitwtYxiKz9my+lB7yRSdm9u4L1b\n/s7R95/iv4EeMYqoMHAjzNwIpKBpLpzqCDOn16r6Bv797HrOuXmIq/O9iK42R6tVo/bWZdT+eHnb\nsTc2HUlzj3JO5F9yx3PPwVe/6rpszzzxBEycKF/36AE9e4ZXlxdWrZLB8iDTAfiNB9M0GWCd7+rc\ndhvakTci9mCbl8u8bcg4qe8gA8fNOPlkuOee9vurq7NOkxXbt8v4NTd07gwDBrg7txjQNJk+orER\nRo70V8bVQDdk7q6nkfNzGnn5ZRhl6C/uaJ+xCUIINE1zOz64/fWp2HJgyxYZmPjII3K7slIKLsM/\n5NAFV8xiC+zFR1PDHpa9Mj/0bsSwBZYRty6Y1WenMpeY3f0JU2xt2bCHhTP8dSOaCS+zeLHRVyxk\n8IPZvqXpb49nyxHds0ILZHb13/0OVq9ud31g9t4bzjvPOjdSsbBnj+xO27BBphQwoA0AMQUodVnW\nP5HdhEYmAif9NLtdUSFj2ZKSELpY+fe/5dy+Rn76U9NTgXb3PoeyMvjRj2DYMOc0Fh2QVGxFQXOz\n/Mfx/PNyu1MnePvtHBvcUXDFKLbyuxD9iC07mjbvoP6W5/ji/ccEKseOKIWWjl/BFUbS1jgEl1dn\nyxOaxtgL5jPgt+vadr3/r3FsOqZHrtBKUc68e+6h5333UVNdDR99JHeOHw83/tc2aSYgM5kbzapa\nYL9TZULPCpUZNVNc89prcPPNfLppE0vOP5+Db85XwgbuvReefDJ733V69JDCbf+OEXfrh1RsRcmZ\nZ2YFF8D778uEhBkCC64QxJZZrJZqsdXS0Mj6V2bR/wx/eTDsRE0cIksnrhgvM+IQW0GcLTtKd7Yw\n9PZPqP2J7DpsLRdMm38Iu4Z1SYVWBCxdupQVK1YwadIk+YNRD0gfMgR+tox24w+2Ai8hpyR60rD/\nJuBHBfh/vEiZMWMGVVVVjBkzxvnkTZvk1ED/3965R0dV3Xv8swNJCAmQBAhRLA8xqDxUKCK2RQRU\nHsVAUS8CihZaq7ciy3K9FR+1VytVq2h1+WgFq1VeWnl1iYoogVhAiSAvBYIC8pAQIOGVmECy7x/n\nzGRmMjOZmcyZOZz5fdaaNTP77LPPnh8nw3e++7f3PnnSmFH73XcQyfpwCURjxZbDvfMoM3eu98bU\nkyZ5Hda+497RIEyhldT9lNfDF39rbDXWiamtOk1ZYeTzinfSJeBDaJjtdI14iyDXuf7acM1GjCq1\nmi6P7nYLLYAVB38iQiuGlJSUsHmzuZHj6tUwZIjxevdueKQrfIv34zngFbyF1qefitCyGcXFxezZ\ns6fhimCkwezbB9u2GWkxIrQsR2YjhkNSEjz+uPH8/PNGEqcPMV/o1NW1GK0W7/faqclk9XfeLvCh\nrjNmF8LdBNufQPMsO5lZSV6fyqj0zUWPX23nvH/ULem9Zk0vTmcni9CKIe3ataOna2ZZSooxQeC2\n2+Cjj4wlDyYEODEFuBW4dh78NBF3sbY3eXl5pIezb2GrViKyYoiIrXBp2dJYv+b558M/N86LngZb\nOb4x6z65nK1IhxGtIBS3Lt7LLfg6d9EQdqEKrlCcsMryar4oSqFvsK1NQkVrLrn1a86dXTfDbO2n\nvTjWr5UIrRjjcrauuspcaeucc4zdMm680XA7/NGyJcycCd1ttmqz4Ka4uJisrKzQhhGFmCNiK1yO\nHzfWOrERobha0d6ix+v6cXS2GjMEGso6V1a4W4GGRwNdK1xRGExwhTPcmJaZQoc+bTGSdSIjY8tJ\nchYdJm1PlVto1aYoVu7qR9W5qSK04oCXs+WiRQv48MP4dEiICmE7W0JMEbEVLq+/Xie2/GzREdUh\nxBivGh+puxVrZ8uK2X7BPnu0BFcsc9AizeHypLK8mu+KSmF4+NuSpO6vosmpGvoO3EjK4dNex1bs\nv5LBbf7T6P4JkVHP2RIcgThb9kbEVrh45mm99lr459tw/0RPIhFcsXS2rBBanm0HE1wQ2VDf2Zro\nH6mzdc6cEi4d7z1homRka070zKD0+tYitOKMX2dLOOsRZ8veyGzESHngAa9lH0LGxkLLRbiCprGz\nEUPFSqEV6jVCnSnphBmVbmcrDDq8uN9LaJ3KS+PQiNZ8+U53LnhsN1f2/SLa3RTCxGs2ouAYwpqN\nKMQccbZiyVkgtFyEI2xqUyup7j+w3jnRSkCPhcjyd72G+h9rIRUoDlYl+rucre10CCnpPvftQ3S7\nu9j9/st53Tg4JgdAcrNshDhbzkScLXsjYisWnEUiKxJ01WkqC9fT4qbrvMoDJaDHWjw5Ac+Y+Q5p\nNmYmaTBczla34R0anOWYXVDGZWO+cr9fW3gZ5T/LBERo2Q3J2XImkrNlb2QY0c5siV5TO0usc2FU\najJp/XsHrfMNF7gfZwvx6Ks/t8yf0ApUNxQ8/y2Cfca6nC2DQIuntn/te/oOrNv+Y+ObF4nQsjHi\nbDmTvLw8OnbsGO9uCAEQsZVAWCW4XM5WrNlZ0sXrITRMOAIyUM6W54rzac9V0XPSdvexrS/n8f0t\nxgZ7IrTsieRsORPJ2bI3MoxoNY0dQtxCVJeA2FnSJeprboXibEWTQMIqVMFl5ZpjLjpv3M1lyzcF\nrXMg7xw+y68/ycLfzMfG5IdlbSun09LvOKJb04H99Y5vv7YraZfUX6vN19nyQmvy3vmWAfeucRct\nWXwdu/I7ATCFv0XcX8FaxNlyJpKzZW9EbJ0NNCC4aremh7VdT7QFV6CcLSuIhoPlaiOUGPjmQ/nL\nj0o7UUnzYxVeZU//9EHSToWwZEJhobEBMHAr73sd2pd5Lj9kpAU81VOMBcrbalJ5hl9c8x4t9ge5\nPzJWwtfGDMJZ/N5dXLXrBBUf7yfjkmyqW6agFaQeqwYgp+gww8d87K477/NRlFxuJMOL0LI3krPl\nTCRny96I2LKacNbV2gzE6AdnOIKrIXFitbNl1RBhqDHwHXrzFDbnFh/gxUumkvpDtd9zV4zrT1lu\npvv9aPKMFzNmGM/9+7uPvelz7g/NU7lz63Mc6pTTYB/9kVpWxa1d3ia9zNjfcOuwCym52GhriMGz\nYgAAEzpJREFUEJfD998bm6ufPAk/+hEAk/w1NCP4kNMHsweJ0DqLEGfLmYizZW9EbEXK9OmGI/Hr\nXzdcd6ufskACzPX/mu93YQjuFoS3IXUwseFP4ASqH01nK9a5V41x+XoWbOHJgY+43x9un+11vM3l\nVzHwrQWgVP2T27eHZ58Frf03XlpKs4oqXt/eGToNAWA4C9yH/S2u6isK2+854BZa267J49Ult1Pb\ntAnPc59RQWuoqICiIr9dOH3mDJWVlbQ8frxe309Qjm6iaPnIXxk6biJD/X8KwYaIs+VMxNmyNyK2\nwsUc8gHgjjugsrLu/aBBRC3BKkKXK5IhxXDwJ04a62xFKrD6rl9H3/XrGqxX3iqLt/NHU52aGvD6\nvp/p8pVFXLRxu9/6Lh6a8pT79ZK7h/HKC79yv1/K6OCd+t3vjEcghgyBZcvgb3+DPn2gdWuWMprh\nLAi6in3PxVvJ2lMGQOa+YwDsu/QcXvrIz48CpWDRooBtlZeWsm7dOoavWgVPPmkUTp4Mzz9P+Bv4\nCHZBnC1nIs6WvRGxFS7jxkFODlxnujhTptQda9kSvWMHpKRAVhbQyL0SfQVXlJPlI8VXnITrbEUq\nrpqePk12+VEAmtTUsmb4wJDPfaP6OIwfD8A5pfXF6PHSDDq3NWbyZBw/yVtX+x1Q88+0aeQ/+ij5\n0fxzSjNztRYuhGbNDBcMyEg+Ad4GGqq2lozSU+RuLeHXo96o19TptOQ6NysMysvLKSoqYvjjj8MN\nNxhOWO/YTYQQrEGcLWcizpa9UTrQMIaVF1VKx+O6UWXmTNhkzjYrLYV587yPv/QS3HUXEEBwhTNL\n0fdHaAiCKxx3K1Jcgqu2opJT7xU2KLYaM0SYVFPD5gF9uGhncb1jL0y60+v95ObJHgdfiPiaAP+c\nPNbr/QTaeFfIyYGpU+vEUbTYvBkGDICysnqHljwxjOW/rxOadw2ZycXLvBccXTn5pwBoBVePfRr6\n9Qu7C6UuZ2v48LDPFezLrl272Lt3r4gth7Fu3TrS09NFbFmEUgqttZ+ckNAQZytSflU3ZOTOfVm7\n1hhWPHHCKw9GrzaeG+Vy2RCXwxXI2WpU/pXWPPPI/Vy22VgsM+tYuVtolbSpW45gydCfM3nmy4Hb\nGTGi/nBvqNx+OxNcw2expmdP4x66/no4fNgoO3QIgPz73yf/fY/ZjysNoXUmuQmnWjdn2UODKfzt\nTyJyszxxO1sithyFOFvORJwteyPOVrSZNcsQYhMnGq99cAuucNff8pdiYROHS1dUwPIPUPkN5CkF\nIK2ighveW0zGqZPusnNKvuehZ5+qV3djtx70/mQtNe0SMDfh88/hiiv8H8vKgoMHjSHsKCHOljMR\nZ8uZiLNlLeJs2ZWjRw3Hy99MtEgWOvWXMO/azieEWYouLBFf1VXoz1Y3KLZSqqpIr6h//Sl/f5GH\nnw3iIK2oW4n80l69qGmVgEILoG9f+OorKCmpf+yii6IqtECcLacizpYzEWfL3ojYsopFi+Daa2H5\ncuuvFUbifLizFUMiJRV1RfAx0naHSthyVR+yy+vnIHnyygTvxPQ7bxkDV1/d2B46h4svNh4xIDMz\nkz59+sTkWkLskNmIzkRmI9obEVvRpn9/Yw2l/fth9ep6h/VqUCEszRU28RRcPs5Wv6LPePDZp0g5\nXbfQ54DVhSSfOQPA0cwsr9OzFdCiBcyfz50RJHIL1iDOljMRZ8uZiLNlb0RsRZuuXWHHDojHL4x4\nCa6UVJIu78f1H75HzuFS/j717sB1x48n+623onNdwVLE2XIm4mw5E3G27I2ILSuprITTpyE5ueG6\noRDKQqdhCi7wn8flmesVTJSp2lrSjx7hmnfmsODjZV7HXpkwiYU/HwnAh1nNoEkTuPLK0DonxB1x\ntpyJOFvORJwteyNiy2ratoUvvoAuMdyGJszFT32T6P0d9ye4VG0ta4cOoM+mDV7ls8bdxqE2bZk+\n5T4q0tMTc+agAxBny5mIs+VMxNmyN0nx7oAjSUsz1kcCOHbMWKDSA/1qI9oOvidwHVs8HlHAU5AN\nXrWCxbfexMejh7mF1onkZI5kZXPri7O4Y8aLPPTAHzlxfo4IrbMYl7MlOAuXsyU4i+LiYvbs2RPv\nbggBEGfLCpSCJUtg1ChYvBjmzoWBA6FVK3cV/apFifL+CGGJiFCo3ZpOrx3rWXbX9V7lxR07c+GD\n/4fKH01Nu3TebNxlBJsgzpYzEWfLmYizZW/E2bIS18bHb79tbOkSrYVcI/1R2ginK6W6itbHDrP+\nrh+7y6aPncbw6e/Rf/a76M9Wi4vlMMTZcibibDkTcbbsjYgtK7n/fsjIMF7PmgWDBnkJrpgMJ/oj\nTME1feY0qoY14/Doum1y/jT+Qf7wy0d5/4rhlBy7kLeHDGpEhwQ7Is6WMxFny5nk5eXRsWPHeHdD\nCICILSvp1cvYrLpDB+N9QUE9dyuugiuA0zXy00UsfHgUix4eyaKHRzJt7hPuYz8kp/LKiN/w8MQ/\nUdOkKXoQHL2yisLCwkZ0RrAj4mw5E3G2nIk4W/ZGcraspnNn2LMHkpIMofXRR8bK8klR0rmhLAfR\nEFsg5UwVQ099QPoPp5gzfbzfap1m72JPbif0ILjTozw1NZX+/fs3shOC3RBny5mIs+VMJGfL3ojY\nihUpKVBVBUOHwvvvG88utobYRqA9FT1/pIb7Hao1SbqWyate4OnF93kd+p/f/IXi9nkALM7vxO5L\nO/ltoqrKcLZuuummMC8u2BlZZ8uZyDpbzkTW2bI3IrZixcsvw8SJxuthw2DGDLj3XsDcwif41oIG\nLlEWbCNrf6MDAQRYZkUZG5+8lA7le73K5/Qey7Z2F/HMTVNBKXQD6VjibDkTcbaciThbzkScLXsj\nOVux4pe/hNdfr3vvs0G1rr+NYmBCdcJcbMZLhI0rms07r93I1j93dwutGpVEWVomP7unkPG3zeGx\noX9AD25YaEGdsyU4C8nZciaSs+VMJGfL3oizFUtuuw3atIERI/weDtnhAkNwBXO4AtBv1xpmv3mL\nV9mCS37BDZMW1PXjnvDaFGfLmYiz5UzE2XIm4mzZG3G2zmbCdLguKdjImufq1Nykm2cyeuK7TBo7\ny10WrtACcbacijhbzkScLWcizpa9EWcrXixdCgMGGMtBKBV5OyE6XON2zmZ2QZ2jNXXk07x25SSv\nOpEILRBny6mIs+VMxNlyJuJs2RsRW7Hm0kshNxcOHoRVq2DCBPjrXyE7GwhzKNGF6XC1zDvGY0UP\n0/aH0npVxn47z/36vvynmDFoqtfxSIUWyGxEpyKzEZ2JzEZ0JjIb0d6I2Io1550HBw5Aly6waxe8\n9RacOmUkz7dsCUQmuNJrTvLi0t9yy+HZwSv++9/8ZcQI/hJZ7/0izpYzEWfLmYiz5UzE2bI3krMV\nD5SCTz5xu1ksXAh33OFVJazZicALuya7hVZFkzTGDpzj9WDOHFi2DCxwKSRny5lIzpYzkZwtZyI5\nW/ZGnK140akTrFxprCZ/8CDMnw979xpDi02aAKCnF3Dk2hvIqDnZYHOpuhqA48ktGPDzlXzZppf7\nWKO2BAoBcbaciThbzkScLWcizpa9EWcrnvToYeydmJtrvF+9GsaMgUOH4IMPYOBAWp85SqqubvAB\nQNu2tPz2KzYs7IV+FffDasTZcibibDkTcbaciThb9kacrXjTti3s3w/dusH27fDuu5CTY6w472LG\nDFLn/7fXaVUr/bTVtKnbFYsl4mw5E3G2nIk4W85EnC17EzexVVZWhtYapZQ8a02T+fNpMXgwSUeO\neAmtisce44ebb+bg7RVkX6dBKY58oCmrsEe/lVKUlZWxfPlyBg8ebIv+yHN0nnfv3k1hYSH9+vWz\nRX/kOTrPO3bsYNOmTfTo0cMW/ZHn6Dxv2LCBzMxMcnNzbdEfJz1nu/KrG4HSWje6kbAvqlTsLyoI\ngiAIghAhWuuIF8WMi9gSBEEQBEFIFCRBXhAEQRAEwUJEbAmCIAiCIFiIiC1BEARBEAQLEbElCIIg\nCIJgISK2BEEQBEEQLETEliAIgiAIgoWI2BIEQRAEQbAQEVuCIAiCIAgWImJLEARBEATBQuKyN6JS\n2RrK4nFpQRAEQRCEcNmjte4U6clx3BvxSQta7m1BmzFqv0XjN7oMSA/rmqa7hW0D9LSwbQvjktT9\nlGVtX9DuG8vaBujCTsvavgDr+m5lvy9kh2VtA1xgYd+7HN1nWdvqa8uahm0Wtg1gZd/P0rjs/ta6\ntgHWW9j2ZgvbBvgjjdsbUYYRBUEQBEEQLETEliAIgiAIgoWI2BIEQRAEQbAQEVuCIAiCIAgWImJL\nEARBEATBQkRs2YUzBfHugT0pLoh3D2xJRcG6eHfBlhQXHIh3F2xHwafx7oE9Kdgb7x7Yk7Xx7oBD\nEbFlF2oK4t0De7KzIN49sCUVBUXx7oIt2Sliqx4F/4l3D+yJiC3/iNiyBhFbgiAIgiAIFiJiSxAE\nQRAEwULitYL8QaBdzC8sCIIgCIIQPiVa69xIT46L2BIEQRAEQUgUZBhREARBEATBQkRsCYIgCIIg\nWEjUxZZSqqtSaoNSar35fEwpdY9SKksptUwptV0p9aFSqpXHOdOUUsVKqa+VUtdFu092IEhcHlVK\nbVRKfamUWq6UOs/jHEfHJVBMzGOTzc+9WSn1hMc5jo4JBL1XLlFKrTbvl8VKqQyPcxwfF3B/zq1K\nqU1KqdlKqVSl1FPm5/5SKfWuUqqlT31HxyVATB5RSu0z76H1SqmhPvUdHRPwG5cUpVRfpdTn5t/V\n50qpPj71EyEuU8zv1c0e37c3KqW2KKVqlFK9feonbFw8jk1VStUqpbI9ysKLi9basgeGmDsA/Ah4\nEvhfs/z3wBPm627ABqAp0AnYiZlL5tSHT1wyPMonA68mYlx8YjIQWAY0NY+1MZ8vTqSY+InL58DP\nzPLbgUcT6V4BOgLfAinm+/nABOAaIMksewL4c6LEJUBMbgMeAX7np35C/A0FicsK4DqzbBiwIlHu\nFfNzdgc2AalAE/N79nzgQiAP+ATonYD3i29cPgLON4+dB3wA7AKyI42L1cOI1wDfaK33AiOBN8zy\nN4BR5ut8YJ7W+ozWejdQDPS1uF/xxh0XrfVJj/J04Ij5OtHi4nmv3Ikhxs8AaK0Pm3VGklgxAe+4\ndNVau9YDXw7cYL5OlHvlOFANpCulmgLNgQNa6+Va61qzzlqML0dIjLj4i8l+85jyUz9R/oYCxeV7\nINOsk0ldrBLhXgFDJHymta7SWtcAq4DRWuvtWuti6t8ziXK/+MZlJTDaPPYscJ9P/bDjYrXYGgPM\nMV+301qXAGitDwI5Znl7wHMt3/1mmZMZA8x1vVFK/Ukp9R2GW/FnszjR4uJ5r3QFrlJKrVVKrVBK\n/dgsT7SYgHdctiil8s3X/0WdqEiIuGity4BngO8wPmO51nq5T7WJwFLztePj0kBM7jaHVmd6pG04\nPiYQNC73A8+Y37dPAdPMUxIiLsAWoL8y0nqaA8MxXPNAJHRczO/bfVrrzT71w46LZWJLKZWM8Wvh\nHbPId42JhFxzwk9c0Fo/pLXuAPwDeC5efYsXfmLSFMjSWvcD/tejPKHwiMu/zKKJwG+VUuswXNDq\nePUtHiilzgfuxRgiOhfIUEqN8zj+IHBaaz03QBOOI0hMXsIYBrkMOIghPBIGP3FJV0qNB2YBk83v\n23uB1+LXy9ijtd6GkdLzEcaPkg1ATVw7ZQMCxKUZ8ADwh2hcw0pnaxjwhccQUIlSqh2AUioXOGSW\n78dbWZ9HnbXrRFxxKfVzbA7gSthMpLj43it7gQUAWut1QI1SqjXG5+/gcZ6TYwI+94rWeofWeojW\n+nJgHvCNWS9R7pU+wH+01kdNq38B8BMApdTtGL9Gx3nUT4S4+I2J1rpUm8klwKvUDXEkQkygflwW\nYtwrfbXWiwC01v8CLjfrJ0pc0Fr/Q2vdR2t9NVAO7AhSPZHjsgUjH2ujUmoXxmdfr5TKIYL/i6wU\nW2PxGCoDlmAMk4GRqLjYo/xmc6ZIZ+ACjERgp+IVF6XUBR7HRgFfmq8TKS6+98oiYBAYM/MwklyP\nYMRkTILEBOrfK23N5yTgIeAV81Ci3CvbgX5KqWZKKQUMBr42Z9rdB+Rrras86idCXALFxHOl69EY\n/3FAYsQE/MflK2CnUmoAgFJqMEauDSROXDy/RzoAv6AuTcFdxeN1IsflDa11rtb6fK11Z2Af0Etr\nfYhI/i+yKLO/OVAKtPAoy8ZI6t2OMQMi0+PYNIxs/q8xZ4o48REgLv/CmAWxAXgXyEmkuASISTLw\nJrAZKAIGJFJMgsTlHvPvZxsw3ad+osTlPmCr+TfzunmvFAN7gPXm46VEikuAmPzTfP8lxo+XdokU\nEz9xecOMSx/gM/P7dg3Gf56JFpdVGOJ7A3C1WTYKY0ShEmMSwfsSl3rHv8WcjRhJXGS7HkEQBEEQ\nBAuRFeQFQRAEQRAsRMSWIAiCIAiChYjYEgRBEARBsBARW4IgCIIgCBYiYksQBEEQBMFCRGwJgiAI\ngiBYiIgtQRAEQRAECxGxJQiCIAiCYCH/D+HZGtMye7/HAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa805cb7350>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Caudal Captacion: 0.181601\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlsAAAESCAYAAADKehBIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXecHGX9x9/PlVxyl0su9RII6ZdGQiihBEgCSI0iCEZ+\nNOlFBKUIqChgQWlKEUFAQBCDDUVpkWIhlEAKkESTcJdGSO89lyvz++PZuZ3dm5md8kzZ3Xm/Xvva\nnZlnnufZnb2bz36e7/N9hKZpJCQkJCQkJCQkBENJ1B1ISEhISEhISChkErGVkJCQkJCQkBAgidhK\nSEhISEhISAiQRGwlJCQkJCQkJARIIrYSEhISEhISEgIkEVsJCQkJCQkJCQGSU2wJIYYJIT4UQsxJ\nPW8VQnxDCHGbEOKz1P45QoiTLc7vKoT4kxBigRDiv0KIww3HrkntnyeEuNOw/4lUW5NT238RQnzR\ncHyhEOK7hu0/CyFO9/ohFCNBXVe785PrGixB/q2mjt8ghGgVQnQ37EuuacAE+Lf6QyHEx0KIj4QQ\nbwgh+hnOSa5rwAR4Xe9O7ftICPG8EKKL4ZzkukaFpmmOH0hxtgrYD7gNuN7BOb8BLkq9LgO6pF4f\nA7wGlKW2e6ae90/VXQr8IbXvBuDO1OvuwGzgRUMbK4Hebt5L8gjsupqen1zX/L2mqe1+wDRgKdA9\nuab5f12BzoYy1wCPJ9e1IK7r8UBJ6vWdwE+T6xr9w+0w4vHAYk3TVqS2hV3hlKKeoGnaUwCapjVr\nmrYtdfhrqYvcnDq2IbW/BagCOgB6xtV3gaNSr48EXgR6pdoYCOzSNG2dy/eSkEbldbU6P7mu4aL6\nmt4H3Jh1WnJNw0fZddU0bYehaBWwMfU6ua7ho/K6vqFpWmuq6AzkDyVIrmukuBVbZwHPGbavTlmV\nvxZCdDUpPwjYIIR4KmWHPiaE6JQ6NgyYKISYIYT4lxBiHICmaQuBcuA/wMOpsrOB/YUQZcgvxLvA\nIiHECMN2gndUXtfs82sgua4RoOyapoYZVmiaNs94QnJNI0Hp36oQ4sdCiE+BC4GfQnJdI0L1/2Cd\ni4FXIbmukePUAkNepPVAr9R2L0CkXv8YeMLknEOAJmBcavt+4Aep1/OAB1KvDwWW5Gh/OnA48E+g\nK9IZuwR4CLg8aoswXx8BXNec5yfXNX+uKdAJ+eu4OrV/KdAjuab5fV1Nyt0MPJVc18K5rsAtwPMO\n2k+uawgPN87WKcBsTdPWA2iatl5LXSngcaRgyuYz5C/iWantPwMHG479JVXXTKBVCNHDpv13gInI\nOIOtyBvAkcB4EvXtB6XX1eH5RpLrqh6V13QIMBD4WAixFDkkMVsI0dum/eSaBoPq/8FGpgLjcrSf\nXNdgUH5dhRAXApOBcxy0n1zXEHAjts7GYHMKIfoYjp0BzM8+QdO0tcAKIcSw1K7PAf9LvX4BOC5V\n1zCgXNO0jdl1GHgPuAL4OLU9FzgC6K9pWru2Exyj9Lo6OT+L5LqqR9k11TRtvqZpfTRNG6xp2iDk\nP/mDNPs4juSaBoPqv9WhhqKnAx/laD+5rsGg+rqejIyv/KKmaY0O2k+uaxg4sb+ASqTNWW3Y9wzy\nonyEFE61qf19gZcM5cYCM1Pl/gJ01dLW6W+Rw4mzgEk5+tALGeB3kWHfv4BXorYH8/UR0HU1PT+5\nrvl7TbPqX0JqNmJyTfP7uiLdkLnAh8Dz5Jh1llzXvLmu9cByYE7q8XByXaN/6OPCCQkJCQkJCQkJ\nAZBkkE9ISEhISEhICJCyKBoVQiR2WkJCQkJCQkLeoGmabf4zOyIRWwDJ8GXhsHnzZm677TYefPDB\nqLuSoJD6+nqee+45br311qi7UpgsXQoTJsDatZn7m5vl85e/zJJH3qHyzUY6/2FXRpGqvXugAcQi\nua2l/pMLyuCyy+Dhh7FixowZzJ49m69//euq3klCDJg6dSrdunXjlFNOiborBYkQnnUWEKHYSigc\nKioqmDBhQtTdSFBMTU0N48blygaQ4Ik5c6TQ2rXL9PCWw6uZ8Yf1DC0pZcdZlew4qzLj+JBNn8Ee\n0CaCWAyiWT/SDI88grb+EQBExblw6qlw1llt59bW1jJmzJgg3lVChNTV1VFVVRV1NxIsSMRWgm8a\nGxuZPn06U6ZMiborCQrZsmULs2bNYvLkyVF3pbBYvhyOPhp275bbl13GP365KKOIVibA4pf0kE2f\nyRcdgfdB04XWdmA4iFYQf9ZL/w5+9zuoTIu1zZrGvBUrmDhxoqp3FD719bBwIfTvD2PHRt2bWFBf\nX0+3bt0YNWpU1F1JMCERWwm+SZytwiRxtgKgpQUOOSQttM47j9fvXYBW3v5f8VAactcnkEl0QC4j\n/CZoC1PbO0F8K/X6i19sO+WAvn3Z8fvfe3wDMWD7djjgANizR27X18PQofbnFAGJsxVvktmICb7R\nna2EwkJ3thIUsXAh9O0LG1O5my+9lNcfWUZLF+dCq83VsuIA4Cupx0WgfR+0k1KP42WRstWrGX/8\nJLRKIR2vL3wB8iWG9oMPoEuXtNACqKuDv/0tuj7FhPr6epYvXx51NxIsSJytBN8kzlZhkjhbCpk5\nEw4/PC1qTj6ZaY83YPYv2LPQMuNaw2sNtFNBvAflTciV9dgNL78MJ5RABdD7wnT5khK4+GI46ij3\n7QbBf/4Dxxxjfuz00+H55+GMM0LtUpxInK14k4itBN8kMVuFSRKzpYjly2H8+LTQ+vrXmfaL+cgx\nQGd4ElrZCOBFeP9t+HAeXDkeuRjMNuBNvdBvMs958kl49dX2dVVVwZFHQmmp/345oaEhU2idCpyG\nXGjmidS+M8+Ufe3QQcbEdegQTt9iQhKzFW8SsZXgm8TZKkwSZ0sBe/bAmDEyVgvgsst4/ScfgzD/\n12vmaikRWjoCeu+FUd2QAfaPYL566QLkQjEAVqkEHnoIwkgfsXEjGAXE54GTU68PSz3rgkvv6803\nw513Bt+3GJE4W/EmidlK8E0SsxUTtm2TgcNdu8pH//7gI+bKNGbrkktk3YMHw6JF5icmSD7+GHr2\nlAHdAJdcwmsPLjSN0QoDsUA+1m6CeYtTOwcgxUv241rk0tSHmTx0rr4aKoX8PvTpA9Omqe/022/L\nz7CpSW4fi3S0KlLHS4HxqX37G8676y4Y7y8vUr6RxGzFm0jWRhRCaElS08Jh165dvPzyy8kwYlT8\n/e/w0kvyxrRgQbvDN771I/47QToDr5AV0/LoozB7tmm1u/fsYf26dfTv3z+98/HH06/LymDGDCYf\nsrx9vcXOjBly6FDn9NOZ9tcttqcojdXKQhi+FktXwYp1MPFAj5XNBG4Emk2OTQSGX5bePvlk93FU\nmgb33COHDo3ftwnABTnO/Qy4g1Q8WlZ/JkyA889315c8YubMmfR5+2320/8HlKUS3B50ULQdKxCE\nEL4yyCdiK8E3SQb5gFm7FuabjfWkOP74zO1Jk+SN3jCM8p03bmt7/VNSQ74bN2Yku/TC3opyLmn4\nJRv79UgEl5Fjj4V//1u+vu46pv1sjmXeLHCY5iGFF/FlFFsz5sPsRfD1M11XI1kI7CUttmYAU23K\nv/GGu/r/+1/45jcz930J6bg5YS/wdcDsFjNzpky94TMbeKzYuxdmzODNadP43E9/mnmsqgo++QT2\n2SeavhUQidhKiJzE2QqQ1lb5jzJ7SRcz7rkHampg8mQO7Pop3/3RXXzlrhdynwfS4QIeZE7brubt\nu9m9bD3VY/pnFF1V15fjfvsWJz71TwB2VXfinLVPsLdTRSK4dMaPl+7W174Gd93FtOovWhZ1I7SM\nOBVdIsvs9O1sLczabgY+AnYa9jUBKlJ5nY+MLTsIcBPv/imwNPW6D3CP4djrr7f/gZLPXHcd3H9/\n5r5KQF+coKYG1qyBiorsMxNc4FdsJQHyCb5JZiOmePFFeXM15gAysm0b9O5tfdyMvXvTMT/HHde2\n+z12ZBT78MixPPCtE1NbG4BKnrnjHDpv2cU+9attm/jP2Ufzj0t7prZObNu/s34Vq557m7rLT2x3\nzoLxwxGtrZzw9L+p3L6bqb0v5lvv3MHkA/5S3IKrpQVOPFEKLZDDVtXVgTS1uHs/Ty6XHrPlWWxl\nUwaYzaPYDXgN6xPAMcAhHs/vn3oAjAAaAd14P+EEeOwxOcSW75x9NhgS1G7oAD2rgK7IfwM7gC1b\n5A+2t96C/fe3qCghaBJnK8E3Re1s7d0Ld98Nq1fbLv7rl5kTDua8t55ydc4Qj46JTuP6rWyd2UDv\nydZ3vO+fdifj/z4TgEfvu4i/XfsFwCQ2rFhYtgwGDZKvu3eHRYuY1tP678Krq6XjRGwpdbayXa18\nYQTwV+Bnhn1XXQXdusG3viXdn3yjqSmd3kLAvJ5QWgGjjA7gaqTo1bnqKmd1V1bKodx+/RR1Nv9J\nnK2EyClKZ2vjRhlb8sYb8KMfZR771a9kzh+g93o5tvL+SZMYtELOFLr9xu8y7ab2bpEdW7p3dVXe\nr9ACaN6yk62zFtuKrR+9cDPfOv9BjvvdW+z/9gJeufJEmjoWV34jU6qqYNWqWA7dKHe28oGFwEjg\nBtKCS/9xNHAgXHqp9bkrV8LixZn7DjxQZrKPkv/9L/16AMzbBd2as8RWH2AjMpcauPtB+N578JOf\nuOvTyJHQq5e7c4qERGwl+KYo82wdfDB8+mnmvocegh494MwzKd28V+7r0QmAk/70d07495vs6FzN\nRxeNYU9lp8C6pkJoAZTVVNF13BD7QkKwpVYKwaOfn4FWIvjpH7/FZIp8OLFnT0dCq4Ghvt0tt9R2\nhzE5Lqsp+epqGRmBDJ7fDMwCPgH+eZm12Nq2TS4HtHt35v5x42SwfVT8+99yEgbIIdcSqCuDquxk\nTgLoDhu2OU+h24XUcpvvvCMn27ihVy/5I6MskRbZJHm2EnxTcHm2NE0u3Nu3r/VDF1oTJsh/eq+9\nRumUCyk97tS00DKweNAQfnXR5cz4+mF5IbQg7Wzl4p/nT2J7jUym2Hv5BmXtFwsNDKWB4BZS1kZm\nbmfk2So2BDLY/jhAHyF7DvjlL+XrxkYpMPS/865d00KrDukUgcxfVyPkkPHLL4f4BoCnnkoLLYBu\n8qm+GZabpONYtkyGbm13+FiDjK3f4/IBwPr1cmhW//y++MX8WXczYBL5meCbvHO2NA0eeUROiTZj\nzRoZ7J6DWcMO4fA/myxlEgEqRZaOnbM1FMPd+kB4bNpF3HDEQ8r7UAgsYhjDsfiuGdAFVxBOlzYy\nHbvlydkqBFcrmwGG11dfDfX1MHeuDCTPZhxwJXLm5feB9cBWYOsyuZB3dqoKJ9TUwLXXuosXe+45\nuV6lTg9kMDwWzhYwcDAsW+K8iRZgnfPibfRBThxlxw75APl/dO1amfS2yEnEVoJvAovZWreufayE\nCurrnS0z0qULLEzfZfq+nXl4XU1vDL/pIkOl0DKKqC1b1rNz1kcMnez8ZlDBnkwhlgA4F1xh4Clm\nawTxF1wLkHFZTjkK6A3cldp+4IH0sd7ATYayeshkGfAjpFX0MvAvk3PdsHQpXHllelsIGQ/WsWP7\nsnPmwDnnpLf7IFM8pKhvhm4lWTFbKQYOls9uRJdb1iAT+lcgPz5Arp1ZWWl5TjGRiK0E3wTibO3c\nCUOHptMeBMV997W9vLY+89AbBx/Pfxf0Te/o0f50N+PwQ3urFyGqhJaZQKqo6UTvcclspEJBd7c8\nx2yNMLyOm/BakPXsVHTVIWO4jKPfAhgDWP3GKEPO8huLtHJ2W5Sz4z/IpKvPPCMfRk45BV55JXPf\nq6+CcUH43kBWNIKVsxUmLUCrccfrr0c/kSAmJGIrwTfKna25c2HixLTQOuKIjMPvuf11ZvLDSkPw\n8NFX8buS8+SO0cAB7qotGb0zd6EU+Sa0ABq37GbdrM8YONmNXVCk/Pzn0t3Q1/BL8QBXAMTG1QJF\nsxF14RW16Gq/OlV6v9OvrdfVbEqBUTlLmdMPeIv0skIghyabkcKqf2YiYVasSL8egcySn4WdsxUJ\nxxyTGVtW5CRiK8E3vp2tDRtkgKo+zn/vveljp54q1/5LIS5H/up0w2jvXbPCjdDyipmYWsxQXyLL\nzRCfF2dr4AcrOOzpWXxwwTi+wT08yI1uu5h//PrXcMMNGbsaDhK8nBJaccOzsxU1VsLKrnwQvxPc\n9sOMWsD423QBUmj9CynAjOLKyGhkslYTkevE2XIbv5WgjkRsJfjGl7PV2CgT7f3pT+2PXXFFRl4Y\ncbmPTirErdBy62rZiamwhBa4c7Z2d03HmJx34R9ZeOIwtvXtUpiCa/VqmXsJYMmSzEzk06fzZP9H\n2N6vKpq+OUBpni1VsVwqBIxVvSoFl+p+GusrQ86SNHGtABmzYJNNJHbO1qxZsGmTTO6bkIitBP/4\ncrZOOw3+8Q/5uksX+N735OuqKrr+5ly2HZ36qebVnVLsakUptMLGjbO1bkRvnvjz+Vzy5d8C0GFX\nU44z8pSVK2USzGaTOfYvvMADR/8W6Jyx280QYtALUkOMnK2gBJZZO3EbCbd676W0i8VyihNnKwxX\nqy3Rw44dMkfZypXmAf9FRpJnK0xeeklm2B0yRD4uuijqHinBU56tPXvkGnK60Np3X5mx+MYb4cYb\nEc9exbYyd1nTg6Rk9M68FlpeZgjqzpZTPj5zDBsGy1+xNx14H/t+tMp1m7Z897vpvx39MWVKeHl8\n3npLLl+iC61DDmHtIT1ZO64Xrz8xkQdOe6XdKUEJLT8oz7M1IneRdoQltFS2p6qOgN67VZ6tsNmL\nYU3yTZvk3+nCqIP7oidxtoJm716Z02ntWvjpTzOPLVkCnTtDdTU/+Wl6Sst3v5P100YI+NKXZNbi\nGOLa2Vq3Di6/XM5UAZl1feFC+VkA4sgAOukDL/FZcRJaXvESs7VqTF96LtlExx17ufmg+7ln1jf4\nxiEuhhKXLIGnn24XaA60//tJlf/fhcPZua8ctjt01A1w3nnW9e/aJYemN21y1h+r9i+9lAceL8Fu\npeQgg+K9uloQA2crbKFlbNerw+W3z6res41micNsRJDO1nqkk9MJZEb5adNghBdVXjgkC1GrYPly\nubK6GS+9lB4a07nvPrjuOndtlJXJMXArhg9PW7U7djjLT1VTAwMGSEG4wOa/wciR6QVPTdi8eTO3\n3XYbDz74YO42GxvhK19JB70PGCDXGKySN0tLoeVlONDpOTnKBT3rMGih5TXv1Zb69Xzy3EccdusJ\njs8Rra1MueqvHP3o+wA0VZTxs/evBuDbXJi7gvPPh3nz7MvMmwedOtE8ahhle1vbH3/xRdhvP/Nz\nn302cwKGF269lQduXy1/BNkQhKvlR2SBTP0wYz7MXgRfP9NXVZm4MS6iEltG3IouJ30O8n05+Hyn\n7pAxW6fYpLUKOzi+N6nJ4D//uft7XsxIFqKOmldegc9/3lnZO+6Qa0ddcAEccQTfHf9SzlOG08AF\n/EEOXRxoE9F66KHwwQdySGXsWOkQOOHVV+FnP5MLKltx0knyl4kFrpytE09MZ2iurZXDiLmElhdC\nFlpeUzvEVWiBN2dLKynh73dNBiE4+lczKG9s5tsH3p86er/tuRmMGwdf+hLv8kLG7rXjevHp6F8A\n0GvG6Qx8NT1r68hbUmvVnXqqszbuuKNd/bnY062CBRd8BsL+X6dKoeVXYBnRRkLtqgidrTgILXDn\ncuWB0IJgnK05FvsPdnh+gUZueiI/xdZHH8kZQG4SXnboAHffDSefbF3mhz+EqVPd9WXRovTrAzIT\nNX08twWAvZTzPW7htVuOkwcu3wEMA67PWX0JLXSgiVEsMj1ew1YG8BnMnMlCUUcZLQxlqWy/5ADG\nGsTEx/PTr8e2zpUvTjmlbd8WurK8ZEDbOdvnLqGaHfCPf7CwdAS7qOTqjg/xXqlURVpqJXlHsxF3\n7pRDobrQqquTa4rV1QHxFFpOCSKHlhd0YdXAECVZ3L3m2drTtRN/euh0KjftonbhesfndaARgF19\nKpk2dRR7eizHLgnS+oN6sv6gnul2u1Uw5tEFOWO4WjqWMv3eI1g1wb5+L6geOlQptHSUzkbMZ4wC\nKfsrHgdR6DLMyW42YpLuIXrybxjxww/hYKe6uj0/oH08x223ptYy+OEPPdd7Bd/kMb5g2OO9j24o\npZklHEx/Vmbsn1syhrFVcy3Pu3LvIzzSeFXb9nrRkwFVy9kt0h50pbaTT3f0pweZ8S3jK99lRun4\ntu2da3bx8ssvW4ut1avlZAA9GL62Vg69Vsh5zI6ElmoB5bCcnbPlRmTF2cGyYvf6HayduaKd2LLK\n/+WXOMatucGL0LJztYIQWgDL3oQV6xSLLafCIA4iRjUq35OPOPKZe6SzlS22/AgtK2cLnN3hupFa\n6SgZRoy5s7VxowwsN3Kk4c586aXtkgmOGPnrdtWcxv+4C7lg8G08276dbI01c2ZbsLas813bbu6m\ngk+ptS0TFC2UMZL32M8otiprWFoyyPa8X3X4Gq+UTaaTJgPzV5bsmyG0AHaJKgZ2Xsa+rSu5pOkJ\nbmySsS7v7TqSUZX/ZY/oyFIxiKraRq65yMTZWr9ePq6/Pi20hg6VgtmN0FJNiEIrKAERxvqD2c6W\nk/xfXkVXPgutIALhgxJaEICzlUw0c0dAn1e2s5W4WfEivmJrxQp5Y95rkeHtiivgzjszVkwX4m4M\nS2C2cR/d2c5QerE1Z7OzqePlQ7cAxoD3/lbFLQjH1dLZRRWLGAbV7pLHfVoyIGeZHaKaRaUjuL3k\ndhpFBd/bewcA/9u1PwA3VNzLz8u/xi8en0BGfPzChTB6NLS0pPf17y9j3KKcdahg6DBKoaVSZOXq\n346a3XQaV+rqffgVXXEjyBmFVq5WUEJLpByYyGcjFisBiSxdVFUhb+jLgmkmwSfxFFtvvQWTJqW3\nR2YNqO+/P6WPDqT10cccVdfEYTyisHvtCUFcuRRSqtklqvh+hx/Rr/UzDmv9gFGt8j/3zxq/xYVN\nT7BG20H36s+xWXRH+9M/MmPjRo6U6R2efRYGDEDo65KGHFvlBr/L8agWWqqdLCf9271lL5/OWs+o\nyW5/bMj6nQquuLpa+Sy0hM3QllJnK8xZiHbnxy1paTYBCy2QIqsrcm3thPgRP7H13nuZQuvSS+Hx\nxzOKSAcrDgQgsiIWVbYIwUWdfgPAxOb/8J/dxwAwpnUBY4Bpu07m72VfhJO/nz7n+uvlbEe9CuMC\n8PMJV0iFHKfllzCGCu3oVNOB/uN6eT7ficuVCC112AksI3npbOV6b3bB7mG0b0WAQ6zZw4QDSaVZ\nSIglMUiBZmDTpsyYrO98Bx59NKNIPITWwSgXWtXd4y20snirbBL9qlYwpnIuc0tGAXBY60x+vDct\ntG7qcBfisXROowyhFTYhijoVAiJIoeW0f7qzFVR7xSi07AgyTsuIkgzyC4lvbi2VWdoDzPjuB7N4\nrGWQNU3KH36D4wHKVXSkQIiPs1VfD/vvn96+7Ta46SYoSevB+AgtReSLuMoWKqkUEitL+rGSfpze\n8Y+cv/cHlJcMayuyTvTm0fIrQAh/IivkIcQ4uFpxEFrg39ny2m6U5KOjBc5dLVDgbIUdEO9V7Ojn\nRZE1PkRHS2cg8XK2ajEs85gjAXAxEA+x9c9/wuc+l96+6CK4/faMIt6FlipxVEQiK5fAGU2b4AJY\nWrIPPxR9oOLH6tsJEb9xWuBPVEQ9bJiNn5ithEyCTFzqRmiBz5gtLyIiamfIi+iK4bAh2M8wXIa6\nmC07V8spbRko+vWzz29ZJEQvtt55J1NofeMb8MADGUXCcbQKP8g9J27ETYbgqoBSF2sjOmlLpdBS\nuByPHV6FVhgiy0vfVDpbQZDtQi1imEVJb/WpIi6Olk6oMVtxWVPQrC7ViUwjFFqgztnKJbRc3ykv\nuUTORC9yohVbmzfD0Uent3/wg3brCIbjaCkSWnEXU1Z4FTZtgqsRWqZDuU0G+TBmHno4V5XQcktc\nBZaRODtbZsJoOJ94FlxRxWmBd1fLi9CCEDPIx0loBV1/BMOG7coRr9mIrUApyPt6SwtcfLGzEzt2\nhL59A+xZNEQntubOleuf6dx1l3S1lMRohSi08kVgZQ39KXOORgMtFTDXxNly20aeC63FDHUkcIIW\nWqrio+LqbNkJIz+CKwiCGD70KrJ0PDtbcQ2IL2DcJCYdiH9nS8Xwoc4GoE0y/fjH8uGUX/1K5tIs\nIKITW2PHpl9fcYUMhjfgTWi5FU4+hFbcRZaZ+AgqBkprhJrpMMjG2cqFH3fNw3G3QktVcHy+CC2I\np7PlxIFyK7hy1WkUTA0Oc4c5GTp0K7T8iiydwJ0tFf3MJ7EWkwz6y/DnbKkUWgCNwGqgB+A0PL5t\n9uKVV8ITT8jXFRVwxx0wcaLiHoZL9DFbN98sM8EbiLXQCkNkuRUeumMVQfJPAEQFdHEZs2Uk5kIr\nX1A94y9OzpbbYT4ngstJndmiyUxEGQVYkPFZqvDkbBXz2ocBobtWAwfbH3fKQLw7W6qFlk4jsMpF\n+U6QXvhu5sz0gUmT4N5725/Qsyeccw6Uxz/JRLRi68474cYbM3a5F1peRFPEQku1KApaZJnVbxyS\n1Bph23To4dLZCnLYUKHQirOrFWRKhaidLb9xVPr5RtHlpk6nwsmLwIrK1QIHzpZXpyYRWo7IFlHL\nlmQKLq9rGi7Dm7MVlNDywm7gM9IJQKtILWQN8K1vmZ+0Ywecdlp6u6RExnzFLN1EdGLr7rvhm9/0\nGKPlJ87Kw7kq3ayo3Ccv2PVVPzYfZ86WyhgxFWUcojK3VgNDlAiuIAWWUYzU1uxlfUTOlsqAdS91\n5YND5ZV2zpaKYbBEaPlCxaLRA3HvbMVJaOk0G143IQPtzbKvt4mwq6+WDyPXXEPmYr3RE53YcuVo\nRZAry6vAygcxZedUeQlqb2yE2dNhtI+YLSft+CznxtXyKrKcBsl7JSyhBbBzSzO7Zi1k+OQ9vup1\nG7Ae5czAOIosla4WwNoPYd5ymNhRbb3KKGDhpkJUWdaNO2crjkIrGw3YanFsD9CdzHiwNkHzi1+A\npknBFRPRv/M+AAAgAElEQVSHK/qYLUCIN7L2BJHzymGdhSqygsxrVVoBfXzEbFmhcDZjGEILghVD\nYQotgKqaMurGVSurW0UMVVDEUWSBYqGVcrBqu8CYfgrrjRNWLt2IUHsRCQNx7mz5EVpzCCUrZU52\n0355olKgHykB9tBDUFkpk6p+/vMw2CI4LiRiIbYkQV6+IhZaYfStpRHWTIfBipwtL32OgdDKWbeP\nIcSwhRZIZ6t+1nYOm9wj0HaiJmyhFdYaiICp+Fi7DeZ9BhNVZcgIMvGoG+yGQ/VjqkWXiyHYIF0t\ncOZs5YObZcTYXyd38RZkzNd++o67UyNmjzwC//pXZuGuXWVOr5CIkdgKiiISWlH1RZWzFdSsxJAo\ntPX/VDlbcSaujhb4dLVsREBBOltORc9C3AmumKR1cMJA2jtbQYmroN0ts37r+3K12wKsQX4WHYCO\nAAsWQJ8+mQW7d4dPPoEean5M5qKAxVYRxWeF0Q9jG/Ozjvl1tgIUWYWQ5kGFiPPiKql2thJCcrVy\nCATlzpYqvIhLL2LIiculWGQF7WpBprMVhoPl1nVS3a5dm3tSD4FMJZGdGKIUYNMmGDEC3nwTDjhA\neT+zKUCx5fKyexFacRBZYQssu/17K6BkQu4UEU7q9tonE8JMXBqUqxWV0ILicLbCxI3Q8uxqORAJ\nBelseSEk1yoMoQVpZyuKoUI3bea6Qzuty4m7piFdrmx6IdNKsGEDHHkkzJ4Nw4c7bNkbkYut9sHx\nbgk5C3wUQivsNt2219wIS6bDQSbOloq+x2ApnnzFT5xU4mz5J9T4LIcodbZUxWuF5WqFTBhCSxcn\n05ECIg7B63aoFINOhxaz2YAUYp0Bdu6EY46BZctktvqAiFRspdM9OP2oFHyN/OTMUjU7zsrt8dKG\nG4Kqu6wCBgcwGxFCE1qF6Gr5DUjPB2fLy1I6ZueqxK/ACtLVgsTZCosghZaZYOkLBCcV4o3bGDIN\n2JR63RlgzRqZCPW//w1sEezInS3nRCi0VC+oHHenyi12zpZXQvyMwhBaQa+JmI2KmX9xd7asltJx\nK7q8EEfHyimxi9kqwLxaQQktO1doNdLZ2s+mTCHjVnC1Ih2unaSWCNq8Gerq4K234GD1/mAeiC1F\nbzqMIcM4xHLphNkXlc6Wz34XQpyW37pVpVjI5Wz5dYb8iCK7tp2ILj99z2ehBQXibMV0CDGs+Cwz\nitnZ0nEzrGgUruOA/iCHFB9/XKaKUExkYsv9EKIPghRacRJYOmH3yY+zpaivcR46DNvVWsSwwJwt\nlUNv2XU5FV9u1izMrtNv/4MWWqqzxZsRK2ergFytoIVWrlinYne2jLiNC5uDnLm4H0BLi/L+QF44\nWz5xK7Tc3PzjJrRULexsF1NmhhdnK0KR5YV8yaGlEqOzFUY+Kifiy20/VPY73x0tncidLb8CK2au\nVpRulpHE2fJOK7CeYIVqHogtH+nTEqHl7RwndRkFmRtnS+Hn5mXIsGHdENeOlh+hFbarpZKeWxbz\n3qzdDJ28OZL245RwNAyhFVQS02yUOVte+ltAThbER2hB4mzFnYjFllMR5VJwJcOGwZxjdf4cB86W\n4s/N6xI8YQqtfCNb3GysKWHMuOx0gMVHoThaOpE5WyqEVkxcrTiJLJ3E2Yo3eeBsuSDo2YZxE1px\nWd6mrhHenQ6jp6Qdr4A+qzDXOfQrtPLJ1TJzkbZvaWXerCaOmdwpgh4lBIUSZysKhypioRWlwHIS\ng5Q4W4rYswc0DYRQWm2EYsvt0GAOdysooaVaNHipzzhkFzfBB1BeAWNSzlaA/YvLgtKO2s9zoQVQ\nnThbnjAOB2oj3Z8TNL6drQIbCrQjDg6W02DvxNlSxG9/C9u2wQsvKK22RGltUVDd3V+iUjtUCofR\nPuobjb/zs+tSTVMjzJseQMWSktE7QxdaXl2toSzOK6Flh+5sFTNul9jJFk36vjDFVC50Z8sVCwyP\nKAjZ1Vq2JL+EFkhna31QHSkCNgFt/+3+9je48krYtUtZ/ZE5W5p2PKBiuR4f2AkP1UKrkDE6WwqI\neqkdL0KrUASWkcTZco4TMWXleCkRYiNQl0E+RsIwCuIgsryQOFv+2Aa8BHwe6ADw6KPQ3Az33QfV\n/lfSiDxmS9OOdyi4LIYQt29S72wVotAKsh+6szXJXwZ5FSIr6DitQhRVVhR7zJYTV8urUIrS6cqI\n2coHYRWiq5WvQguKK2ZrnsX+MT7r1YB/AieSGvZ74gno3Bnuv99nzTEZRtRdLs9s35S7TBTEQWip\nGn60Q4GzFQehlbP+AhVaVslEi9nZClJoRU0ksxHz4LOKo9ByE9ncF+gVVEfyhHlZDy/sAv6DzL0F\nwLp1/jtGDJwtHecOlyKCFiBxEVph4NPZ8iu0wojRKlShZYcfZ8soVhZ3z/e1YQqLNmcrmETZElXi\nKiRXK45Cyy3F5Gw5xangynbENgN/Bc4EeO45mDTJd19iI7Ygl+DKMRvRzXBioQotj+0axU7r/Cr3\nFXh0tuLiZsUtl5bf/qhaG9Grs5XtCtm5RHEUYoXsaoHB2QpCbOXh5xJ3oXUwzgLliylmawzenSsz\nzOoaZNy45hrfbcRKbOXGp+AKQwRFIbQ8tGkldPT9rkSXS2crLiILnAmbsFytKEVfA0PbpYAII2Yr\nbg5YoSUwNaPN2eobdU9yEIKrFXehpWM3nKgLscTZUstS4DfAhQBN/mdlRye29tkH3nsPBgwIp70g\nRFCeDhU6ETtmZSwFmENnS9UswzCFVlAE1bYfVytbcHlxtvyIFf1cr6LLj3Bzm+IhEhYiZx36pLYL\njImTqxVRstJ8EVq50IVYA8XjbIXFcoV1RSe2Vq+GOXPaiS05lHh3astMzyscTvRKHESWR/wInpLR\nO80Fl42zpTqNQ74LrSDbVTV8qOPW2VLlCrkVXWbtuqkjlm6WlQBRIEzWboN562GiSiPRi9CKMCN8\noQgtIxVA16g7UYA0gMUUInfEfBjR4yLUZoJrPs5EUlQZ5efblrI/1yGB5a+ycLYSoRWPdt1gdLei\nno2YSzA5EUlDNn3m6/xsAne1QhAgtV1gTJTT1op42Z0gGQhUAnWY3zndJEhNSPM74MsK6om52AoR\nFULMT3m3oisuQgtMna24CS0/GeFVkA9CKxunzlbQzpDf+s0EV6RCK2KxsXauYmfLzecSE6E1cLD5\n/nxmGdLZqsPconAaaJ/QHk1BHdHm2TrjDHjqKQ8nKv7KqBRafpfWUZwXy+1SN07qa0eWsxUHoTWE\nhoxHlITRvuohRIje2VKJUVxFNmy4kMjFBgugtkqhs5WHsw+zhZbVvnxjILBvjjIexoliicqZiLk4\nCzW35OiTmr76artdmnZTBB2xIJf4GY1/gWVVr5djKVSLLFsCWhtxaO/FroVWHMSVTlh9CUJogbO1\nEWMZ72TBkE2fee6vL1crDiIL2oTR2p3S2VJVn2Ni4mpZke+Caxmw0kG5QhFcQVOOzCSvYE4KEKXY\n+u1vbQ+nBZeVizXH+piqAPmw47fM6h9ts21CGCKrXf0GZ0tVWoeoRZbfBaXjIvj8kMvZyieh5QfP\nQisuIisLX85W1AtSJ1gykNzOlk4iuHIzFBivb3Tp4ru+6MRWhw4uCtsNGyoYUjSLk4paaGW35dDN\nCgtd1JWM3okYuglW/jOS/FlxE1kQrtBS7WoZUz84cbYSLIibyDKII0/OViKwYs8ynDlbOongsqfU\nuPH++77ry6MAeY8zE43YzUh0OlsxpoQptNrRoQJxxJG+q3EjtIIQNMW4JI+R7KSmhRSz5RVPrlaM\nhRa4dLbyXGAVQuC7UwYiZyMmKObss2GE/8HE6GO2XGE3pOiQ+XhLs2AkZqIsUqEFsLcRbca7vqoo\nFKGVj67WUBraCS1InC1PxFxogQtnq0CFVqEKsGW4c7YgcbfCJHqx9dprsGaNixMCnLw63+J1jIlc\naIEyZ8sJcRZaYRJUULyRYne28nn9QzscOVt5/t5zCapCFFwDcR6zZSQRXGn6AoNTj1rFdUc3jFia\nGhHduhUOOghWrQIhHJ4c8JBiBLhaHsfmnEhIOVvii2d4Ot2pqxV3oZWPMw/NHC0duzxbhR4cX6hC\nC9LOlmWerQJ+70YKTXAtI51nyy1JDi4ZEH+u2YEyNTIpOrF1/PFw3nnw7LPS2WptTQuwFJp2k2Hp\nHhf4WbLHKMJCEmS5FoWOPT6cLVVZ4T21nSdCKwwXy4xidbZiJbTM+jLSx7nkcLbi9N4TXDEQfzFb\ncRFceg6tMSG2eSgw2bjjhBPkc4cOcNVVStpQJraEENtJJ1rVLSot1UYHTdMy2+raVaZ/mDpVCq24\nYia4FImwvBFTufDobEUdp6UKVX2LSlRZ4XZtRLd4ETWaU6ERBSritZx8JnoZq88iRx05na0CYODg\n9tniC83JymYZ3p0tnbgILpCiy0xwqU5oejBZQuuJJ+DiixW3olBsaZpWbdwWQnQGvg5cAfxVVTvK\ncCOWFDtcYYsso6hpWDdEfQMenK0oHS2VxFkE+iWOzpZRoAUhvCJ1tdy27bGvls5Wgbla2UlKjduF\nKLwGomY2olWAThQizEpw+aUMGd9WCZxqPPDOO3BkMPHHygPkhRA1QojbgblANXCopmk3qG4nUAII\njjfmpQoLs+Sg+j6lYsfFbESvCUtVo2IIUWW/4uZqgf1sRKvFncMkVsN9cZuFaIOyDPJ5zMDB+Z8x\nPptluJ+N6IaDiSaYPoilec4ALgS+Ytz50kswfrxpeRUoE1tCiJ5CiJ8iBXAzcJCmad/TNG2jqjbs\ncaG7vbhUPgRYFE6WE0GjTHQ5dLa8rnFY6MRRaEFuZ6vQBFdeuVo+MHW2gm4/pmK0kATXQLzNRnRL\nVIJLf6igXT74Rx+Fz3/exSQ996h0tpYDZwNPA7uAS4QQ1+sPhe0Qi8mqMU0N4UXQ+BZdOZwtr/UH\nJbTilOohrkIL8ifPVqwcrjygnbNV5J9foQiuZQTrbBkJ6g4c1gLT7T6nwcF/CVTORryHdIB8tV3B\nSPETexXw7ERdkLiNq1I1JJhdj+N+dKig70lDqFbUD1UiK06iyow4Cy0INmYrbgIpbv0Jkgxnq4je\ntx3GgPq4YCcCzfo6EKjrBwNNVsKL23uLmleBrcAJ+o4TToAlS2DQoMDaVBkgf7uquuzxoalVB8U7\nFF+t86tyDiV6daSCxGn9LZu3sXH6HKqnnOirvWIRWRB/oQXBz0ZUiVgQ8UzFEcR2qCybttmI26Pu\nSYIVudw2s+Pv7oDlzTDKRGwFISbjNHPRC+8jXaEj9B1DhsAnn8DQoYG0pzJmq6sQ4iohxGVCiICW\naMoltPL30htdJKfxVnFBVJTTaYJ3EaxyMekwhdZivP1R5oPQgnjORgyCYnK1wOXaiAmh43VYs64M\nBtjYJ3GfFBDWECLAYcA1GIQWgKbBihWBtakyZut5pCm9BpiqsN4ULm/m2zdlbgc1/OcwditXNnhw\nPmwXJ6EFoDU2sXu6N6GrMi4rCkfLreCKk9Cyyx4PuWO2vGaRD0rceKm32IQWJLMRrQhbiJiJHz99\nqG+WzpaTdlURg+hp1xwInILMSZZB584wbFhg7aqM2aoGlgCdgRqF9RL7S6pwOFEXXEN7LzYVX3ET\nWuDf2VJBMnQoySWgGlLiMFc5yE9nSxdPuYYUAxFZeTKUWFsFY3YBHaPuSfFiFDyqxE9dGVQ5tE/i\nFqMWlqtVDZxm3PGvf0FdKg1sTQ1U5TZFvKJSbP0fcDUy7cN5CutVQ9BL7yiuP1+EFqSdLb8xW17J\nB6GlAicCSWUd+bw2YjE6Vk5ZuxPmbYOJHlc080SeCNEgCdo5q2+GbiXmMVtW/VEhuPIpditD8Lzw\nAhxzTDRt+0HTtKXAjarqy0TBwtOQd4JLJ64iSycqZ6tYRBaoEVpusXK2/AitghZBeSImaqtgTLtE\nQyFQJIIrqrgoN86WTlwE1xiCd7f6AG2L8AwZAqedZlNaPUozyAshjhJCjEq9niSEuEEI8TlHJ997\nL+zZ47MHDm748wk2R1aOup3EbuUbfmK2nDKUxe0e+UScYrWcki95tvKekAWo7mxFwoiI2g2BqAPQ\nncZsZROXoPkgF57eB7luYNtPx7FjA2zNHJULUf8EOA4oEUL8G5gIvAzcJoQ4SNO0e01P7NIFtmyB\nb39bjp2eYbWYsSJ3SydolysC7ILNvc6cc0LQzla+CSvVROFqgbmzFffhw8jw6thE4PT5drb09+pV\nOBnPi5nT5dXpiYNg8eJsqUTFcKIuuPy4XNkuWSVwqbHANdfA/ff7aMEbQtO03KWcVCTEf4EDgArk\njMR+mqZtE0J0AmZomjbWUFb7wx/+QFNTE32WLOFzt94KwLtXXslnxx5LU1MT5eXlbc9nnfVXpAnX\nH6kPmy2e+yG1a1P6uWO3zG3jc78mEOWgWTxbHd+3CUrLocXiuW8TlJVDs/WzGNQCTc1QXubouU/P\njWhNzYjyMsvnXk0rKSkvpbWpxfZ5TVNP23rcPrds2c6Ov/6TLud93tV5Tvq7T/mGnO8n6ueeTaso\nLS+hpanV9Ll30yrKygXNTZqn5x5Naygvh6YmQn1etaKFue/v5XOndWrb369xk696O6yFphYoLy2Q\nZ7/vZw00tUJ5SXjPCxbCp3vguB4ezl8NTRqUC2jqq7Bfxnpj/Lx5ffu7TrdeEfarX/rz+89u6FIC\nozt4q2/VOvu7q9PnBqAUaFHwvBJoTd39cz3va3J+F+B7gB7G9skpp/Dhl76E6Nq1nc6wez733HMR\nQqBpmuf1fFQGyO/VNK0F2CWEWKxp2jYATdN2CyFaswuPHTuWlpYWSseNY8vMmdS8+CIDBgygh76/\ntLTtWaYfKwGGkvtj35+Mj3tPKVRWgygFrSXzeVULDDPZrz/3sNjfz2K/8XlIKbS0QKn5s1Zaihix\n3fJ49nNF71VoLS2I0lLT5/6ln6G1DEKUlqC1tNo+d049f9rSz7I+N88tO3ah7W6k4qARjs9z0t/+\nLcsRpX3RWjREqYjlc//SFWgtPW3LDWjZRmmpoKVFc/08qPRTWlrKnX5NlD733qeUztWCUQfJ9vfd\nuNZXfa31UFoX/vtQ9twApSXQIgzP+0FLa2rby3MLtGhQKsJ7rlkLQxrhoC4ezt+Y+u86WHG/uqae\nl6q5SQf23C8m/cj+/LuCtg06l8Kgtd7qHd0PVn/mXNxYPQ9HGpZ+62kFhuQ43oC1KuiFnLWns/Xz\nn0e75x7GaFqGvnDyrAKlYksIUalp2i7gEH2nEKIr6WV82hg+fHh6o6vMeLHvvvuCcX8btannAQ66\nUdd+167Uc7XJ9JvFWA8ndrPY38dBN7ba1JtCa4KS4c4Wqf6UkZaB8nL40P0SpKPQkL9HYDEDs+rT\nB//Tz1ZDkS2bt7H96b9T8c1zHbXrtL/d8RvDZ2zPPU6GXmuxT8MtY7W8x+kNTkcZhE5JSRPv/bOV\nulGyD0M25TghB8JDPElkmA1v7aO4jQVAmDMCU21uLoP6nTDKy6JqukXQWWWnDByQ43jMhh0jwWL4\ndvZWKBEwKtdnqGPyWY5SFDBfRzgzFPez2N8NONa449xz6frss+1za4WISrE1UdO0RgBN04xOVjlw\ngcJ2vLN9k7ngssJvXJeD853k3rJDVVJQJ/VYlWmpaKR6wj70jVmCUr+fzRAaAo11izsq82wpm4Xo\nN17Iqr6wCTtWy9BebYXPmK0og9z1totVdNl89nVVUFXqsq4AP8eoUkJ0IEto3XAD3H13BD3JRFk4\nnS60TPZv0DQtxEz8Hi6v29mJbsrPJ+cMSKczFN0uUB0WrY1NbJ4enzn9Kpf/satLZfb7OBK72YgL\ns14bH27r8XKeHxZkPcIkq721jT5mI8ZlNmFc+hEmOd5z/U5Yvtt/M3EI9vdKJ2R2+DZuugluvx1K\nIpw5kELlbMQDgMeQ40OvAjdrmrY5dewDTdMOy1nJV78KlZVw5pkmBxXNdrNyt6xcKJWzFm3q8utw\nRUlJRTndJkS5CnCaoASQXq/udIUltBoYGovZiJHn1soljOLkdET1u8Nhu76drbhQJHm7AEfi0rWz\nZUNc8m+5oQcwybjjq1+FO+8E4TmmXSkq5d7DwO3ImZefAG8LIXQrxn4sYqThRv3kk+0Oa9pNanqo\nk71uoo5bx8oLORyuXC5XHN2tuDlbQaLSNYs7sXG28uWGGoVr5aFdX85W3ChGh8sCT86WzeeXbw5X\nP+PGpZfC00/HRmiBWrFVrWnaNE3TtqRyal0NTBNCHIFJgHwG3/kOPPigfG2RikLTjlfYVaTgMhNd\nZmLISiAFILjAXeLTOMQUxcXZKhYRFBYqYrYKOmO8TlQiS2/bJQXjbOkUuuBy+P7qqmBA+5W1fJEv\ngksg1z0E4Oqr4dFHI+yNOaozyLcF+2ua9i/gTOC35JpGKIRMn68MF8alU8FlhdeM9D6y2Ge7W1EL\nrmJytoqJWDhbcXa1ohRZevseKChnK6ENT86Wg78vv4IrjIXcJgK99Y2RI2MRo5WNyh7dBWTYG5qm\nzQU+B/xFYTsOmYNj0WU1rGgklzjyIroUBM3Hgbg4Wwlq8etsFbSrFbXI8tF+wTlb+cII3LtwLsoH\n4WzpRL0UkRVlwJHIeC0ARoyAk06KrkM2qJyNOFXTtBkm+z/VNO0yVe24Z07Ww4JsweVmODG7jKLY\nLzvBFSd3S7WzVSjL8+TjeohGIne2onC1smcNWj3ymMTZigAvQ50uz3HtbHn4+4qb4OqOIe1lnz4w\nd67iUTJ1hOK1CSEud1x48WIFC1LbYSO6VDhcxnJBLngdI1Q6W4UitAoBP85W3rlaUQa3B1nehMTZ\nipiAYswcO1thpz0JkLbw9z59YNEiuS5YTAlrYNP5lIBPPpFjrs1Bp5t2MMSoIjDeQZ4tVcOJUblb\nqpwtv0Ir6tg1I/nuakHa2XKT9kEsCCnVgyriENzupH2F/Sw4ZyvuwsFMXNkNKXoZbkRdnq28ZOxY\n6BLvXxAq82wdDiwwLD79bWRs3P+An+SsYPx4OPpoePttWLYMjjoK/vxn2M8qIb8K5uA5fE8XSG5y\ncNmdoyifV9h5oMC/s5XPblbQospPjq1skbS4ez+LkuZU15Rw4nDnd2XlWeKDJA7O20hkP3L96Sju\na+JsxQiFLlfOPFtxF6Uu6QkcFXUnXKByuZ4ngbGp1w8gVyS8Cxkg/xRwhu3Z3brB9Olw8MHw4Yfw\nwQfw6qtweXoEUtOOR4g3FHbZhDCW9HF5jpeEp4sZGprg0p2tvlOOtCyTz4JKJ2y3SnUy0yGbPmNx\n936OnarWZTDtI5h8Qu6yeSO04iCyjEQwr0R3tiaGvS5jMRJiWor6ndCt3GLNSwV/V16TnAaV1DQj\nxUFM47SMqBRbJZqm6WN/4zRN0y2jt4UQHzmu5e23YeJEmD0bVqyQebcMiclCEVxGnAijEASXF8IS\nXFbOVtwFllE8LWKYo3JhoEJkWQkqN0OCNV1h3IG+u5KgCjNhlq95tvT34lf8BinO7YSSk3ZDzv9l\n6WwVoNDK4Npr4d57w2jJFyrF1nwhxEWapj0FfCyEGKdp2iwhxDDA+ZSmykoYN06KrR//GLZtgwce\nUNhNDwQluIKowyW5BFEDuX8xZDtbcRdZ0F5AxSHGSpWT5WdpHSNbtsIsB86Wb1crzPisfMTO/dKH\nIl0QirPl1LHz0P/AcCOOci0VFEGiVVNnK8Khw9AWoT7wQChVtE5RgKgUW5cCDwghvgdsAN4TQqwA\nVqSOOefMM9MZYB98UA4pdu0KDz8MgweH725BMIIrAnFlxIkoclKmqWIvZRO6Ry6ynLh4cRBV2US1\n9mEunDhbnoVWgcWPRIpLwRK4s+V2aDRqweVVGOnnLTTZFwEq10Y04sXVshNadlHSuQSa8dwelqXi\niTKxpWnaVuBCIUQXYFCq7s80TVvrurITToClS+U4bGsrzEil7zrmGLj+etner6vhrLMQ1e1Se7nE\nRZB8GA6Xi/Mb1g1haO/oXaSWxmZWTV9K3ZQDIutDvgmtoASWKlcLnDtbrkmElnpcDMslMVsGVIij\nmCwX1M7Z8vl3pmIh6mxy3WmNx31MX4slKp0tADRN2wZ87LuigQOl4Fq5Em69Fd54Q8ZwXXdduswn\nn6CtulYG13fsCBC+42VGxI6Vjp0AUelClVaUsc+EQcrqc4PTmLS4CK0gXSyVQgtyO1uR59Iy3uSc\n3FjcOChGd8ZqxmDU798MB+8xMGcr3xaRiIlIUkWGs+VRaKkQWFbulFvhlKt8/AcOM1EutpTSv798\nPPMMPPQQ7EzNyNNjuO6+Wz66d4f6eujePfghRtVCyqy+mIg1p4TtbOXjgtNBDxWqFlpg72zFbvgw\nVwyNTi4xYiYYrERE1MNfVuRwuRw5W/kmnNxSYEILDM7WSm/nq3KyDiZTcAXhTvUBOgZQb5DEW2zp\n9O0Ld9yR3j77bDj/fNi+HdasgU2bYPhwePNNOOAANO14wI3LlWVY5kr/EFbAvAPiMJQYhrPlR2BF\n6WqFEY8VhNCCgGYjOhVFTupRhR9hoWpWXRBku3Mpcjpb+SS0vHyfClBogb+YLdVDhkEN/5UgY7Xa\nhNbw4TBpUkCtqSU/xFY2hx8uM80DnHEG/PWvsGEDHHkkzJolF6MkgjQReUQDQ5QNJfp1tvLRqbIi\nzGD3oESWjpWz5Xv40K/g8nuzDEJMxNXl0jG857WrYN7HFs5WPgktHSffp3wQWBbi2Cn1O6HbWhhV\n6e68IGKzgqAEmci07e317Qv/+x+UhLUQjj/yU2wZmToVLroIfv97Ocx47LEwb17bYa31c4iSNx1U\nFG93yy6xadTulhdnKxFY3glaZOmYOVvK4rTcCi4nN0tVrplX4i64UtRWwZgxgLsFBeJNPogpM+yG\nqI04+F7VVUGVyzt6vggtyBJa/fvL9FB5IrSgEMRWx47wy19CRQU8/bQcVuzVK338xBPRtH/kn8Nl\nIsbt1XYAACAASURBVNS8ZJIPA7fOViK0vBGWyNLJdraUB8QHcYM0m44fJh5ukmGzdifMWw8T4yK2\nYvgZAc5cPj99d+MiOhDy9TuhWzOM6uCsynwSWn2BCn1jv/3gH/+Anj0j7JF78l9sgQyQf/JJWL1a\nql2QKSM2b25LG6HHcek4El9huFtWxyz2uxFcuTLIqxpKjHI2YpQUstCCTGcr8pmHbona5dJxekMN\n8fOtrYIxvXKXK1rciqBsnFzLAIZr3Thb+SC0OgJdAYFBaO2/P7z2GuyzT2T98kr+eHC5KCmRanfD\nBvlYutS2eLb4koSW8zY09IWpg0R3tpwQhatltxSPVwpdaIF0tma/nodCSyeXczYi6xElI20eitGd\nrYSAsLt2fq5pjvPqd8LyZvsycaUC6Jz16AN0whAMP3gwzJ+fl0ILCsXZipKYpGnwGrelwt0qFmer\nUGOzrKjpCuOiFiF+cbsEC8TDETOieMZj4mzZoFrchjjhwI2zNXBwPNwtgcyX1deu0Pe/L2ccjh0b\nTqcCIhFbcUSxeAt6ONFpzFY+xWpFuYRO2CLLyrnaugJmLYTJ40PtTvS4TZYaFooC8GMVs+U3X1tc\nUoDEALcxW1HTHWiXgeSyyzK3990XbrkFyvJfquT/O8jFtm1w8cUyKWplrjmxJtlBcsVtFQh+BJcT\nZysRWs5Z3L1faILLboiwpnMBOFt+iUvsl44CweXL2bISJF76FKfEuPkgtHJ8Xl5mI4ZNGdANGb/U\nyXigSxe4/HK4555I+hUGhROzlU2nTlBTI18/9RS8/XaOE2KwCtNocrpadsHxDeuGWB5zErvVgPX5\nduSK2conoRUXFnfvx+Lu0VoPW3ZIZ6voiZvg9CkMHMdsBRU/toBEaAVA/U5Y3sd5+YGDg+uLFVWp\nR5vQKimBVatg69aCFlpQyM5Whw4wdy4MGACaBs3tIwdl0tNNuesKyt2KQaxXNl4cLjNnK18FVtSu\nVjZhulzZJM6WgQJyuNqcrShEhsqEuCq+mwUitMBfBvkwEBjcnfPPh3POkUHvfW0jtgqGwnW2QObj\nOPnkaPsQQ0GVC7cOl5mzFcYsSKfEZRFqr0TlcCXOVhZxE54ehcLanTAvxjflnPidPRrgTM8oqd8J\ny3fj6rMJw90qQebPHYBM5QBAXZ28Nw9TP1M8rhSus5XNmWfC9Okwblx4bSoWWmEmNDUKrlxOV5xn\nI7oRWnFztaImSmdLU3wjjEX6CrvP0quo9eBw1R4AYzZ7bC8htolrM5ytGDmxZamHBohOnWR81nHH\nRdyr8ClsZwvSFuWePTJIPi7kkePVwBBbt8sqZisId2s4n2Q8cpUtFKJwt8J2trSR6UcQdSvBrfh0\nmsfLT74vN07NSFi7DeZFm1UkP/GTO8suj5oil63N2dJx+H0KK3ZLHHoo7NolV3k56qhwGo0Rhe9s\nPfigFFpTp8Lu3TJ+S4i2w5rW3Vncllu8ZI23IQ7L9FjFc9k5W7rgUhHDZSaeVAmqfHC1jIJLVRyX\nUYRkuz9hOVtBiCurdpQ4XEEvfOzHlbBzulKfc20XGBPFyHRMHKDAyP7s3X6vfc40tYzZcvB9CjLv\nlshdpCgofGerqgpOOUW+/uMfYfLkaPuT55g5XG4yyCeoIYzZimE4W2EJLeWYiSmV2ej9xiTZ7FPu\nbBW6iALnwsmvU2V3npMM8rstDkbkcFWSI2FpEVH4YgvgsMOgd2/5+rXX2h3WtBwzDe1mIpq5VAXo\nahnJFlxOYrbiFDCfTT64WlbookuF+MoWPl6draCGAlWgtF9BL/ejKgg86z1H5mwl+MdGyNVVwYBO\n5seASARXhXHj1FPVVp5nFIfYGjZM5vKwIafgcopioeUGL8v1qCCfna18FlpmqBJe4N7ZyhZZuURX\nVIIsyNgw5QQg5JKYLZfE8XtiIrpsnS0dh4JLucv185/LZXeKmOIQW35w62p5xWdduYSWyrxX2XFb\nTmcj+nW3glhQupDxK7icOltORFX28bgInbwSXYooemcr7sOebr6PBtGV09nScRE471R06eX0c/RH\n13br8RQvxSe2WluhthYWB+ACReBqDe29OBRHayiL2x7Z5KuzVWiulhluBZdReORyttwKlbxylOKI\nIsGl3NlyE88UNn5n/kX1XfUQXO/I2TLi8PuULaDs9iVYUzxiq6QETjpJvl63DmbPzn2Om6zxAQkt\nq3itsEWWHXHOs5XgHaOzZRRKhSiY8ub9KBBckTpbYX3OhZC01GX/60Y7dLaMePg+ORZVO4Bt7usv\nVIpHbAkB06bBlCly+8UXYWemkHEVt+VUQDkp51KMhRWb5XTZnnx0torB1dLx4m5pI2FzLczcmEdC\nBLUTBoLGs3D1KbgCidnyMvQVlCBSVWcefe8B6jfDci8LjAcxuWMPsM6wXVsbQCP5ReHn2cqmvFw+\nP/ssdO4MjzxiXk6FqxWTxKVe4rXcrI+YOFvxx8saizVdYdyBAXXIBVaiyfh+4i6ssskVw5YzH5iP\nXFyBOVv6e3AbE+X1PLu6wsKpUAkhOXBdN6gqBwbh/rNUmXF+L2Ccj/a738FZZymqPH8pPrF17bXw\n5z/D3r0yk20WmtYd4SSobz5qRFZMBJkRtwtR685W3ZQDAuqRRGVG+AaGZrhbDQ6C97PdMKtz4uqa\nuRVcW7bCrI9g8gkBdioHdiJKpcAKczkfJ06WXiaIfunO1sSg5pt4Tc5p/Fz8nh8Gbhyh7LIBiK/6\nzdCtI4zqgbclhVQIrh1kOlo/+YlccDqhCMXWoYfC738PZ5wBL7wAjz0Gl18eda9MyZVfq2GdzHcV\nVcoHHafOlsoZkSpwIrC8lNfLBSG6svvgtg03gisuzlYh4XbI0DbrvcebY4azZSUY/N50fWZDNxVO\nCwzHFtiUU0Guev0OvTm9di4+xzZny6oenNflGWOA/o9+BN/5TsAN5g/FE7NlpJdhYPuqq6CxMeOw\n5jaob77/LrmhYd2QNqFltu0Ht64WWMdsDWlbVbHBt9DKx3UOGxjqWtC5rUvfr6odI7qzFRV+nStV\nSxqpwmvsm9J1HUfA2m4wrwl7wRBUolY/GGO8CiEAXvHnW78Zlue6dzkRkV771QzsSr1++GH43vc8\nVlSYFJ+zBXIRzNdfhxNOgJYWmQ4iC20bzoYTzbAbYoyAxQwN1FUyc7bi5mJFSS4hlMudUu2oOXW3\nnDpb2aIobiInDvgVTJYOVy6HxOTGWdsdxjj9baYylidfCNrVcotDV8rW2cquL4iYwFVAS+p1x44u\nTy58ilNsCQHHHy+/EHv2BNOGT8GleomeIAVXdsyW6nby0dVyg+phx+x4NK9kx2w5dZq8BOOrJur2\njQQ+m9PlzX/tJpi3GCY6HSLW6y8G0RVnt8yqbynhlBGz5aQuJ4LLCXuAGUhnC+DMM4t+aR4zinMY\nsUDJNZToJIO72ULTuQhyNmKhC61ceB0ezHWeE+FU0xX2ndDDUxoFv0OA+Ta70Io4ps1w5WwZcevo\nRPne3SYzdTosqdrVUlGfnkG+GwxwMxrj9/qsBD4GppMePjz0UPjjH6FnT5+VFx6J2FKFWdyWk1iu\nkOO9glgQ2hizlQwfeidbIAURh2Ukl6CZK2qZN6sp0D4UKkEkflVVn+5seSJucVxG3IgqL7m+4vze\ncRizpZJ5SMGl/4v4ylfg/fdlAvGEdhTnMGKYhBy/5WSGYq4hxQaGxCbPlpv1EAvJBQtaaOnogsss\nZ1V1SwtjxjkJAgmmT16Jaggxji6WGZ6dLS/4nZXopp0gibnQYiTUrXEYs6UKPdT5ySehrAwmT5Yh\nOgmmJGIrDHT3ykp0mQiy1vlVvuK2GtYN8ZUSwo3g0p2tk6dUem5PBbowcyq6VCxsrVrghSWysjET\nONu3tDJvVhPHTHa7Bki6TrfCJx+HD/NFZOm4jtnKxm3wdI5YI9/ku9BSNAnBVcyWH3YBHxi2L7oo\n4AYLg0RsecWLW2UnuiwEF3gPlrcTXCoD5uOWQV6FiHLbViG5ajrVNSWROFtRYJvPKsd5YeK1n0ZC\ndbbsCCv3kx/CcrR0weUj+anj2Yh+2Aa8T3ro8OijA26wcEgGVwE+/hg0zXl5M7HkRnzNx1WMly66\nvOAn/5bTYPmWxmZ2Tv/QczuFQJgCLyx0Z8sPbpyqfHO18s3R0vEVswXqZyXGMWdWFHnGzNpz0Y/6\nyhBithpIC63zzoP//CfgBguH4na2Skvl8/jx8NprMu9WmJjFc2ULrtRxp4LLzAWzcrhUuVulFWUM\nmdDXdz0JavGbAiJMZyufhFa+iiyd2Dhb2XiJ7wriWngQWXbfCSVLLjkYaqzrDVVBz2fR47S+9CV4\n4IEkGN4Fxf1J/fjH6dcnniiX7jFgmkledbB7rtmIAc9WVDE7sX9jPYunr1bQm/ym0NwtFc6WE/JF\naAUxw9BrP9yWNz7WdPHpbAVJDD5fNzj5TmR//p7J4XLVr4PlXX3U74YLL4Tu3UNqrDAobrF17bXw\nyCPp7SuugN/8JqNIm+AaTXCzCkNO/6CasorSxNlKUUiCS5WzFdZi0kESB5HlFqube21vGH2cx0rD\nSGzq9LOO0NXyI5x8f5cs+ljXGwaYLUKdEAuKW2wBXHklvPlmevuii+CddzJiuBytlehXMNmdr0CM\n2cVu+XW3mhtbEmerAAnS2fKSKDVIrIZ6AnGzNgDvZj02qW3Crs9r18G8/3moNMwM8k7yZanGhdDy\nS7s6NGARMkmok0VNTPpavw6Wb0xtRClYE0wp7pgtnWOPhRdegNNPl9tHHy23TzutrYj2LogjA+5H\nzNZUdEohOltWAtRrjFu245U9ezGO+cRUxmz5FVbGlBiq1n7UMQqtwB2sFmAiiLWZu7W+yCSRDtMU\nmc1KdNr32t4wZpSzspFjfE8LTPb5xWV8lsrvR8Y1fBm4M/X6MODnDirIiuOq6w1VFR46ElYutCIn\nEVsgE7Gddhr84hdwzTVy3+mny+2rr24rFqngypWrywF+c29ZoTtbB04Z3LZPtVhxQxBZ8o11O30P\ndgLKz3Cj8dwghZffPFuqMMusr2odydCE1rPIm+kuEFtT7Y1P9eE9EKuBmmYoLUXb5Exxee2v7mxN\nvNRF8HYc1kVUcX2CmmH4J+CHpBditqIEuBG4QG5qI0HcDPzaUOYD4DSgI/AdwGE+tPp10K0SRu3j\not86ZqLWiAZ8BKzzUHcCkIitTK6+GqqrZfAfwO9+lyG2IATBlUtMKRBdqvm0oo4hE1Y6Ejl6mSBE\nV5Aiyw2LGBaa+xRkWxtqhtBj3HYaSGdJVCVynGKV5FWV4ApCYC3u3o+KOXupfnYXXXftAEA8mtXu\n4SDeTYUqlJZCayvccQfceKP6DmWRV86WSnwILdvvyQsgrnRR2fWgLTJs/9qkjD4ceDXwIHCwRV0G\nd8uzs5WNmfBqAfRIkcpKGJmMP7olEVvZXHCBXETzC1+AGTNg7VqorY26V8oIwt1qaWxmzvTdTJri\n/Jy4CKOgyOdAeV3g7Nyyi/pZ2zlsco+MY2EJrqiy6XthSeW+dPhoL0KDjjSyz+c2ULLbJHff3/4G\nhx6K6N07va+mBjZtgttug1274Hq8/WdeCGwH9gdsFnNoc7aC+tFoJWri4I55wFRoNQFzgd0gLjHs\nf+45mDTJvKKPPpJL2tBefAOwaBEMGCC/C489BrffLvd/A3geyHEb8uVsWaG/9xmGfevWQZX33I/F\nSiK2zDCuWD50KKxeDZ07R9efmBO3DPJBozL7ftwwCpyqmjLqxlWblglacPkVWl6WCvLTVt8vbqDq\nxfaRzdv/rxN7Du9AL26Hfv3g1FPbrx83bRocdph8fdddiO1Xof3oYXed+DuI1Kop2uHAK9ZFPTlb\nTpeUsXOP9GNRiC6Prpalo/UtEM9m7fv972HKFOvcU336wPPPw6eftj82ahQMS/1A69sXbrpJrjf4\nve/JfVOAPwJ9rPuqzNnKZjnwTup1dXUitDySiC0zDjoIzj5b/krZsUP+kbz9NhwoB88thxJjEOCe\nnfzUz/qKTtHXRqybckDgbSW4QxctXsTRzi3N7ZytoMknN4uZ0HRdGQN2rKZ8hQzWaa0S7B1TTkcO\nhkGDqP7Nb6ju0MG+nkMPlZm4dUfk4YcRW85Be3Cq44B5DPdv8T5w4H5oHVbAXcCxmUV1Z2tSN4d1\n6+QSXE4FjaK1AB2xFfgFcj0/gBrgDiDHfB5LkaUBF4P4u2HfEUfIJJ9nnWVfqRBwxhm5+wzQqRN8\n97uwcqVMT9QKfBm4DzjU/JR2zpaqwPethte6+EtwTSK2zOjQAaZOhd275azEnTvhlVfaxBYEFLsV\ngFAzW9Ba9VBisTlb+YjdbD4rgWPlbOnnqHS3YimyPgOeBvaaHxYPQQea27ZbupdQumQTHbt6yCw5\ncSI0NMDo0bBnD0ydiuj/bbSv3Ql2pvrvgE+AOVn7V6yQOu3LoD0PHJM+5Ctmy8yd8uIaGQVXK/A/\nYC1QB5xo0oYX1iHjndZk7bsUmGxzngAuBg7K2r8NuDMttLRKEAs/hf3289lRq34IePhhGdP30ENy\n33XA/cC4VJlcsxFVzjS89FLpuCV4IhFbdjz/PHz1qzJQ3gRTwRWGu+WyfjPB5ZQGhjAUe2GWOFu5\nMYtRUzEU6SU43qmwyeVsqRJcGf1p1aietxPR1Nq2q6lnObsHup8RqaebcDycqN/09dRi3wYxy8F5\nN94IV19Nac+eMnjYK0OGyHiYLl3k9p13IkY9g3bcV82Fx0oQ38jad8stcPnl0pX/9rcBEGeCNhfY\nVxZpc7aO8t5Vz8HmrcASMGhUmV/qfsN2DdAlVcbJHWodaefKyJOkhdYhQP8vwV//Kp2a53LU+Udg\nWta+Z0A8I19qHUCs2SaH1YLmwQeloLv5Zrl9LfAXoHdmMcuYrVwzDRNCIRFbdpSUQP/+7s8LUnDF\naBaiTjE6W27itqwmA8Q99svO2VKBmegbfvMSBt27ot3+GdMPZMvRNZ7acRy/dQeI+9vv1oYB54Co\nvLv9wS5d4Nxz1cV0VlfDrFkwLmVd7NyJOHsCTJ9ue5p2O4hev4RzzpEB99deCxUVcN11AIixAu1t\nDUaknS2zXF2B81TqYcf1qedxQK5ZfvPJFGpm1AF/Xwnl5XDMMdDYaFPffHjmGUQzcLx1MfH+h+EI\nLZAO1ze+IWO4brhB7jsTmU7EgKOYrezh0UR8hUYitoIiZika/LhbuYirs9VA+6z5uVw61eSadWk8\nbhReQabIcIqTmC2vMWFmQmv/yxex3+PplQi2HtKZrrNl6oQjJnwkh/bPPptpHOu6PVPB9Rdk7qtU\nbiSxLH1IG5va1+ckxJNPwj4qp3jl4JBD5NJhjz4qY2Q2yjwAWi3QB0TZIemyQsDllyMuuyyzjooK\nKbiWLZMLBmsa4ijQnoO13dKzEQMRXKuBW8mM9dFZZXg9HOicei+lpTJ8Y/dumD1b7puFzDNlx3rD\n6wFAz0Myj9fWwjPPQI/Ud/gb2VZgFi0t0NQEn1g4xpWV8POfZ4SUhELHjnD99bB8uXS6NOBcoBcw\nFvg/j7MRs8XX75Gfu3EircUweoI7ErHllFtugZNPhoOtEp5YoFJ0RSTccg0lhu1smYmoIM7NJcxy\nOVNu01uYlc/VRpB5ttw4W25EV7bQKtndwsD7PmsTWq3lgnc/HMeO/as4+Z7J6TiRc86BuXM5mSPY\nzGwX7yTF7sxN8YBJmbIymDULMXas+/pVMmaMfE4JLfr0QSxdKm+6brj/fim87paunDgbRlwEvUqR\nN9EOPgXXYuANMm/OLwFbbM4pK4P33ku7d9ls2ACDBsnJSevNi7Tjl7+Eq65yWNiG0lIp6uPKAw9I\nUXrvvXJ7PfLzr4EJm6BTE+T8d7AfMku9zk7g38hlgt6wOU//TiZ4QmiaSS6YoBsVQouiXU/ceSd8\nJ/XzqmNHWLEiIzWEqyB5J2LJqowCoWV0trID5J04KFbiY8/mXbx/2+tMevA00+Mq8COwvOLUBcv+\n7ILIIWZ3fYISWyvrd/Hv59Zx7q0DPZ1vFF6WcWKtGkNvX8bQHy1v2/XGpqNo7lbOyfxL7vjDH+D/\n/s9THxzx1FMwYYJ83a0bdO8eXFtuWLlSBsuDTAfgNR5M02SAdbarc8cdaEfdAgOBapeCayUyTuqb\nyMBxM049Fe67r/3+mpq002TF9u0yfs0JHTvCvvs6K1sIaJpMH9HYCMOHe6vjOmRcXC1yOPLdrOMv\nvQQjDIF5xfYZmyCEQNM0p/OD25+fiK0cbNkiAxMfe0xuV1ZKwWX4h+xYcOW52LKiZVcj616eTd8p\nRwYyTBeF0NJxK7iCTNYatuDasn4vn8wMNvXDyK9/woCH02NLM945iC1Hdk0LLZDZ1X/7W1i1yqQG\nn+yzD5x/vnVupEJh7145nLZ+vUwpYEDbF/gQhNOv0D+Rw4RGJgCn/CS9XVEhY9kKKCF0LPn3v+Xa\nvkZ+8hPTokC7a59BWRn88IcweHDuNBZFiF+xlQwj5qKmRlrUW7bAH/8oMzz37QvvvNNmgztOAxGD\nPFxB0NrYxObpC+g75UjPwshM1EQpstxSiBnxA82zpWmMuWgh+z6dXpH5g3+NbS+0QAqhCy5Q34di\nokMHOXUfWNCxI90feIDamhr4+GPESuCkg+CWD22TZgIyk7nRrBoKjD5dJvSsCCKjZoItxxwj0xLd\neisbN21iyQUXcOh3bALdOnWC3/wGPv44c3+3blK4HRCvuNtCInG23HDWWVJw6XzwgUxImMKR4Mol\ntgJytrKD483ybHl1t4zOVqERdkC9HU6ujxuHy2pJoeF8wiKGsWP9blpmfqRcbJXubGHQnZ8y9Mdy\n6LD1/9u79/CoqnOP498XSGJIgCRAAEVEEFS8YpFiKyCgcqkCRTkIqFhorVaptRyrVtEerHipRavH\nai1YrYKAjwh4vCEqEAUU5CKgQKABuUi4JdyCAZJ1/tgzk5nJZDIzmT2z2fN+nifPXPaaPWvWMwkv\nv7322mlCwfquHG2XWb3QUnFXVFTEtm3b6NGjh/UfRu+E9LZt4bEt1pwefweAd7Dm9Lzi9/x4YMJJ\n+HfcpZYtW0ZWVhadOkWwiNr+/dalgQ4fts6o/e47iGV9uBRS12TL5dl5nL3xRuCFqceMCdhsgo97\nO4Tdq8h7ky03OpnSNYj8mozh2nm3HS09xpLltax+Hq1KQ/sJW3yFFsCnu36ihVYCFRcXs2bNGuvB\n4sXQt691f8sWeLijtQ6W/88zwIsEFlqffaaFlsMUFhaydevW2huCNQ1m+3ZYv96aFqOFlu30MGI0\n6tWDRx+1bp991prEGaTWQ4qxHEqMsn1txVVNq8fHuu5TvYw0crs75yrw0RzSS9bSCjUVcfFI0mo7\nQzHSgiwzJ502XZqzgTZxmxN2/i830PpfVUt6L1nSmeN5aVpoJVCLFi24wHtmWXq6dYLAqFHw0UfW\nkgc31/DCdOAm4Krp8NO6rIiq7NChQweyorluYZMmWmQlkBZb0Wrc2Fq/5tlnk92TahJxHcRQ/Ods\nJVI85knVtM6Vv0hW0Y9UbUlZvN4rVMEVaZHldbT0GN8t30OnATEs7BvMGC686VtOnVp1htnSzzpz\noFuIOVrKVt5kq0ePHtYTrVpZV8u4/nor7QilcWOYPBnOOy9xHVVRKSwsJDc3N7LDiCrhtNiK1sGD\n1lonJ6narokYS7qVyGTLzono4T57XYugZByOjLa4CuZNtuoie+1h8mfvJXNrua/QqkwXFhZ1o/zU\nDC20kiAg2fJq1Ag+/DA5HVJxEXWypRJK52xF65VXqoqtEJfoiPisxDiLJNWK9OLT0RY0iZqzlYgz\n/sK9xybaR100xfKaUJJxuNObbMUiY0c5DTeW0bXXajqO38Lpk6tWhv90x2X0OnWxFlpJEjBnS7lG\nVHO2VMJpshUt/3laL79s//slaamIaBKuRCRbiVxaobbP7l88nexLVoQTa7LValoxF40MLL6LBzXl\n0AXZ7Lm2KX2afR6vLqoYhEy21ElPky1n02IrVn/8Y8CyD24UaYFTUX6QfQXvUDa0evu6JjLJWr8q\n0msTJqqwqm0c7Ei+/OdsRXpZoDbP76DTnYW+x0c6ZHLk7IasevM8+qYtdOFqZCefanO2lCvonC1n\n02IrGVy2sKlkpJHZPfQ1I4MnoLtx8c9ECi7uvMlarGeShhOcbNVWcLWcuTug0Fo1vRO7huUD6CFD\nB9Fky5002XI2nbOVaNEWWnGc37Vptz0pjCk/ztGCFbW2OxkLrWT0uaa0LB4p2mbOCvkTSqg5Wxvo\nGHLifd6CEi4e9o3v8dKCi7XQciids+VOOmfL2TTZShSHpFmbdrePeKJ8pMIlW3apqXCM92dzumjO\nkoy2cAw3Z8u/4Or08nq6jqm6/Mfq186h9PIcQAstJ9Jky5002XI2LbZOBnG+pmK8Cy5vstVo6NVx\n22dNakvnIk3vnF6UeVOss9gct0Srtu3BhyEjWWfr4mfW0PPuJb7Hn7xwOWtu7MTZbNRCy6F0zpY7\n6ZwtZ9Ni62RRS8FVuTYrqkVN41lwJSrZiudhUO++IhkDbyESyQKoXmeu3sLF878O22Znh1Z8MTD8\nSRbRFFo1zds6tL4xvd5bBDVcj3TDVR3ZeWGras+HPRvRGDq8+Z+AQmvunKspGtgW0ETLyTTZcidN\ntpxNiy2niXOKFU4kBVdwgROqvZ3Jll3zzPz3H2nBFfzYW9hkHjpKwwNlAduf+ukDZB75ofYOFBRY\nFwAGbuL9gE1HchryQ3Zm7fsI0+e0o8cZf+WT5Ow4UHPD7IXwrbVUwxTu9T1dXnSIso93kH1hHsca\np2MEMg4cAyB/+V4GDPvY13b6l4MpvtSao3UX/4i5z8p+mmy5kyZbzqbFVqKEmuheU1G1tobtEaRb\nEN1le0IVG+EKnFDt45Vs2V1YhXvfWFO+Uwt38vyF48j44VjI7Z+O6E5Jyxzf4yF0sO5MmmTdCz75\n7QAAEzhJREFUdu/u2/Za0Gt/aJjBbeueYXfb/BrfP3i+ln9RmFlSxkPtnyCr5CgA6/qfTfG51r56\ncyl8/711cfXDh+H00wEIvLS6x6Twk6k/mNpbC62TiCZb7qTJlrNpsRWriROtROJXv7LvPWJMuWI5\npBiN4OKkLslWsgqsYLEUXE0XlDC511jf472n5QVsb3ZpD3q9PgtEqr/4tNPg6adrPLTHnj2cUlbO\nKxvOhLZ9ARjArKj6l7e11Fdorb+yA/+cewuVDerzLPdYDYyBsjJYvjzk64+fOMHRo0dpfPBgtb4f\nohRTX2j88N/oN2I0/aLqmUomTbbcSZMtZ9NiK1qeQz4A3HorHD1a9bh3b+J+DDC44ErgYcZw/IuT\naJKteBZXXb9aRtcVy2ptV5qTy8yBQziWkRG2nf9nunThcs5ZvSFs+wfvetJ3f+6d/XnxuV/6Hr/H\nkPCd+v3vrZ+a9O0L8+bBP/4BXbpA06a8x5CAgivUWYgXzFlH7tYSAHK2W4cOt1/Uir9/FOI/BSIw\ne3aNXSjds4dly5YxYNEieOIJ68mxY+HZZ2kU/tMpB9Nky5002XI2LbaiNWIE5OfD1Z4U5667qrY1\nbozZuBHS0yE3F4jwWom1iaHgijbdioW3OIkk2YpHkdXg+HHySvYDUL+ykiUDekX82lfLD8LIkQC0\n2lPzuDQ1+8g+eJjXrwh5QC20++9n4IQJDIznr1OmZ67W22/DKadYKRiQnXaIw3mNAgotqawke88R\nWq4r5leDX622q+OZaVVpVhRKS0tZvnw5Ax59FK67zkrCLknsEh8q/jTZcidNtpxNTE2HMex8UxGT\njPeNq8mT4WvP2WZ79sD06YHb//53uP12IEzBFU1CFdw2gtfaXWx5tctey5F3CwKKrXgfHqxXUcGa\nHl04Z1NhtW3Pjbkt4PHYhml+G5+r0/v+e+zwgMc30yywQX4+jBtXVRzFy5o10LMnlJRU2zT38f7M\nv7eq0Ly972TOnRe4svvCsT8FwAhcMfwp6NYt6i7s8SZbAwZE/VrlXEVFRWzbtk2LLZdZtmwZWVlZ\nWmzZREQwxoSYExIZTbZi9cuqQ0a+uS9Ll1qHFQ8dCpgHYxZbt3VKuUKlWxD3CfOx2Lz9NMyHmynu\nGccCyxj++tB9XLzWWiwzt7TUV2gVN6tajmBuv58xdvILNe/nmmuqH+6N1C23cLP38FmiXXCB9R26\n9lrYu9d6bvduAAbe9z4D3/c7+3GhVWidSKvPkaYNmfdgHwru+ElMaZY/X7KlxZaraLLlTppsOZsW\nW/EgAnPmWPenTAksxPyYxXEuuLzPEeJ5P96iyyvuxVd6BtIt9g+WWVbGde/OIfvIYd9zrXZ9z+9e\ner5a29WdzueST5dSkW99plpPT7j6atiyJea+JVW7drBuXdXjL7+EH//Yur9wYWDb3Fwa7NpFk/R0\nhgJD4/D2OTk5dOnSJQ57Uk6ic7bcSedsOZsWW3bZv99KvEKdiWaHKCbOx30+17FyzNLFyMDwk8LT\ny8vJKqv+vne99DzjJ4VJkD6tWiDzos6dqWiSon9QunaFb76B4uLq2845x5orGEeabLmTJlvupMmW\ns2mxZZfZs+Gqq2D+/NDb7TijMFkFVwTJVovdxazt3oW80upzkPy9OCpwYvptI4fBFVfUtYfuce65\n1k8CaLLlTppsuZMmW86mxVa8de9uraG0YwcsXlxtc50PJdYmGQVXULLVbdkXPPDMk6Qfq1ros+fi\nAtJOnABgf05uwMvzBGjUCGbM4LYYJnIre2iy5U6abLmTJlvOpsVWvHXsCBs3Qrj/YdQl1YqkmIqy\n4ILAeVzBc7yCt1eTnkG9rt249oN3yd+7h5fG3Vlz25EjyXv99cg6p5JKky130mTLnTTZcjYttux0\n9CgcPw5pabW3jbcoFz8NVWAFbw9VcEllJVn793HlzGnM+nhewLYXR43h7Z8NAuDDnFOgfn247LLI\nO6WSSpMtd9Jky5002XI2Lbbs1rw5fPUVtI/jsgiRFlL+12OMwxyx4IJLKitZ2q8nXVavDGg3ZcQo\ndjdrzsTf3UNZVpbvzEF1ctFky5002XInTbacrV6yO+BKmZnW+kgABw5YC1T6MS8loU9rCX0x7ChV\nrs2i16tLmHPjUD4e0t9XaB1KS2Nfbh43PT+FW59+ngcf+BOHzszXQusk5k22lLt4ky3lLoWFhWzd\nujXZ3VA10GTLDiIwdy4MHmytv/XGG9CrFzRp4mtiXgK5tQ7vEes1EiNYlyuczhtXMP8PVwU8V3hq\ne87+n4eRgUOoyM/itdh2rRxGky130mTLnTTZcjZNtuzkvfDxzJnWJV3ifYmiuiRVUb42/Vg5TQ/s\nZcXtP/I9N3H4/QyY+C6XT3wX894yTbFcRpMtd9Jky5002XI2LbbsdN99kJ1t3Z8yBXr3Dii44nI4\nsa4FVwSHFydOvp/y/qewd0jVZXL+PPIBHvrFBN7/8QB2Nz+dmcO716Ejyok02XInTbbcqUOHDpxx\nxhnJ7oaqgRZbdurc2bpYdZs21uMFC6qlW0kvuPz34dnPoM9m8/b4wcweP4jZ4wdx/xuP+5r9kJbB\ni9f8mvGj/0xF/QaY3rD/snIKCgri0AnlJJpsuZMmW+6kyZaz6Zwtu515JmzdCvXqWYXWRx9ZK8vX\n86tzoymWapprVcczD9NPlNPv2w/IWn6Eaa+NDNmm7dQitrZsi+kNt/k9n5GRQffummy5jSZb7qTJ\nljvpnC1n02QrUbzXrevXD+bNC982nEjOKlwb4qcmxlCvsoKxi55jzuTBAYXWfw/6C4MmzGbQhNmw\nahVbRliFVrDyck223EiTLXfSZMudNNlyNk22EuWFF2D0aOt+//4waRLcfTcQ4yV8oj0bMcRZiDll\nJax+4iLalG4LaDrtkuGsb3EOf+01DkQwvw2/a0223EmTLXfSZMudNNlyNk22EuUXv4BXXql6HHSB\nalP9Moq1i3Gu1ojlU3nz5etZ99h5vkKrQupRkpnD5b8tYOSoaTzS7yHMXbUXWqDJlltpsuVOmmy5\nkyZbzqbJViKNGgXNmsE114TcnIiEq9vHS5g698aA52Zd+HOuGzOrqh8RFFj+NNlyJ0223EmTLXfS\nZMvZNNlygwgTrgv3rWbJ3KpqbswNkxky+i3GDJ/iey7aQgs02XIrTbbcSZMtd9Jky9k02UqW996D\nnj2t5SBE6r6/WlaGH7FpKlM/rUq0xg16ipcvGxPQJpZCCzTZcitNttxJky130mTL2bTYSrSLLoKW\nLWHXLli0CG6+Gf72N8jLA2I8lOjR+MQBHnlnPM2z9lTbNnzzdN/9e7o+yaTe4wK2x1poQVWyNXTo\n0Nh3ohzHm2wNGDAg2V1RceRNtnr06JHsrqg4KiwsJDc3l06dOiW7KyoELbYSrXVr2LkT2reHoiJ4\n/XU4csSaPN+4MRBbwZVVcZjni+7gxr1Twzd85x3+cs01/CW23oekyZY7abLlTppsuZMmW86mc7aS\nQQQ++cSXZvH223Br4FWpoz078bmisb5Cq6x+JsN7TQv4Ydo0a30vG1IKnbPlTjpny510zpY76Zwt\nZ9NkK1natoWFC63V5HftghkzYNs269Bi/foAmIkL2HfVdWRXHK51dxnmGAAH6zei58CFrGrW2bct\nLpcECvfemmy5kiZb7qTJljtpsuVsmmwl0/nnW9dObNnSerx4MQwbBrt3wwcfQK9eND2xnwxzrNYf\nAJo3p/GWb1g5qzPmJXw/dtNky5002XInTbbcSZMtZ9NkK9maN4cdO6BTJ9iwAd56C/LzrRXnvSZN\nImPGbwJeVr4wxL4aNPClYomkyZY7abLlTppsuZMmW86WtGKrpKQEYwwiorfGUH/GDBr16UO9ffsC\nCq2yRx7hhxtuYNctZeRdbUCEfR8YSsqc0W8RoaSkhPnz59OnTx9H9Edv43O7ZcsWCgoK6NatmyP6\no7fxud24cSNff/01559/viP6o7fxuV25ciU5OTm0bNnSEf1x022ed351HYgxps47ifpNRRL/pkop\npZRSMTLGxLwoZlKKLaWUUkqpVKET5JVSSimlbKTFllJKKaWUjbTYUkoppZSykRZbSimllFI20mJL\nKaWUUspGWmwppZRSStlIiy2llFJKKRtpsaWUUkopZSMttpRSSimlbJSUayPmiJgDyXhjpZRSSqno\nbTXGtI31xUm7NuKfbNiv3dexv8TGfbdtZ+POz7Fx3+fauG+792/juBgb+705r7V9Owc2cZZt+95A\nR9v2vdnGfm+ivW37Bpv7vtu+vleuzbJt36y1b9e27/9k3feh/TbuHGDFSbpvgHvrdG1EPYyolFJK\nKWUjLbaUUkoppWykxZZSSimllI202FJKKaWUspEWW0oppZRSNtJiyyEWHE12D5xpwfpk98CZvljw\nQ7K74EjbF2xOdhccx3y+KNldcKadC5LdA4f6LNkdcCUtthxCi63QFmxIdg+c6YsF5cnugiPt0GKr\nGrO4INldcKbvFyS7Bw71ebI74EpabCmllFJK2UiLLaWUUkopGyVrBfldQIuEv7FSSimlVPSKjTEt\nY31xUootpZRSSqlUoYcRlVJKKaVspMWWUkoppZSN4l5siUhHEVkpIis8twdE5Lcicr2IrBWRChG5\nJOg194tIoYh8KyJXx7tPTlDTuPhtHycilSKS5/ecq8clzHdlut/zRSKywu81rh4TL8/nXCciX4vI\nVBFJF5FcEZknIhtE5EMRaRLUPhXHJUNEJojIahFZJSLzRaR1UHtXj0uo74rn+bGez71GRB4Pau/q\nMYEaf4cuEpHFnu/LHBHJDmqfCuNyl+c7scb7b5CIPOn53KtE5C0RaezXPpXH5WER2e75t2iFiPTz\nax/duBhjbPvBKuZ2AqcDZwMdgE+AS/zanAusBBoAbYFNeOaSufXHf1w8j1sDHwBFQF4qjkvwmPg9\n/xTwYCqNCXAG8B8g3fN4BjAKeAL4g+e5e4HHPfc7pfC43Axk+7UZC/wzVcYlzJhcAcwDGnieb+a5\nTfXfoS+Byz3P3QJMSJXviudzngd8DWQA9T3fkXbAlUA9T5vHgcd0XGgPPAz8PkT7qH+P7D6MeCWw\n2RizzRizwRhTCEhQm0HAdGPMCWPMFqAQ6Gpzv5LNNy6ex08D9wS1SbVxCR4Tr/8Cpnnup8qYHASO\nAVki0gDIBHZgff5XPW1eBQZ77g8kNcelIbDTGHPYr00WsM9zPxXGJeSYALdjFeMnAIwxez3tU/13\nqIMxxrtE+nzgOs/9VPiugFUkfGGMKTfGVACLgCHGmPnGmEpPm6VYAQCk+Lh4tgXXLBDD75HdxdYw\n4I1a2pwG+P8Du8PznJv5xkVEBgLbjDFrgtqk2rhU+66ISHdglzHmP56nUmJMjDElwF+B77A+4wFj\nzHyghTGm2NNmF5DveUmqjkupZ1wQkT+LyHdYacVjnpe4flzCjElHoIeILBWRT0XkR56XuH5MIOzv\n0DrP31yw/iPnLSpSYlyAtUB3z5SEhsAArCNP/kYD73nup/K4tAYMcKfn8Opkv6kbUY+LbcWWiKRh\nVcVv2vUeJyO/cZkpIpnAH7GiypQV5rsynNqLddcRkXbA3ViHQk7F+t/5SKxffH8ptW5LiHHJFpER\nAMaYB40xbYB/Ac8kr5eJFea70gDINcZ0A/5Aiv0dDvNdGQ3cISLLsFLQY8nrZeIZY9ZjTUf4CKug\nWglUeLeLyAPAcWNMSv3dDTMuLwDtjDEXA7uwCviY2Jls9Qe+MsbsqaXdDgIr69ae59zKOy57sY4J\ntwVWi0gR1mdfISL5WGPQxu91bh6Xat8VEamPFePO8GuXKt+VLsDnxpj9nkj7beAnQLGItAAQkZbA\nbk/7VB2XWVjj4m+apx2kxrjU9F3ZhjU+GGOWARUi0pTU+bsS8rtijNlojOlrjLkUmA54L6aZCt8V\nAIwx/zLGdDHGXAGUAhsBROQWrERnhF/zlB4XY8we45mkBfyTqkOFUY+LncVWuFTC/xjoXOAGz5ki\nZwJnYU1idCvfuBhj1hpjWhpj2hljzgS2A52NMbuxxmVYioxLqO/KVcC3xpidfs+lyndlA9BNRE4R\nEQH6AN9gff5bPG1GAXM891N5XL4VkbP82gwGVnnup8K41PRdmQ30BuusX6yJ4vtInb8rNX1XmgOI\nSD3gQeBFT/tU+K4A4DcGbYCfA9M8Z9ndAww0xvhf5T7Vx8V/xfghWIcbIYZxaRD/LoPnmOeVwK1+\nzw0GngOaAf8nIquMMf2NMd+IyEysPxDHgd/4VZKuEmpcghg8hWiqjEuYMak2hytVxsQYs1pE/g18\nhRVlrwReAhphHX4eDWzFmnOSyuOyAmtc3vAUFBVYZ6Dd7mnv+nEJ810BeFlE1gDlWGcopsSYQNhx\nuV1E7sD6WzvLGPOKp31KjIvHW2ItMeT9nAdF5DkgHfjIqk1Zaoz5jY6L/K+IXAxUAluAX0Ns3xe9\nXI9SSimllI10BXmllFJKKRtpsaWUUkopZSMttpRSSimlbKTFllJKKaWUjbTYUkoppZSykRZbSiml\nlFI20mJLKaWUUspGWmwppZRSStno/wFxQsYD/CDiYwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa805cb7250>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"Precip = 1650\n",
"cuCap.GetQ_Balance(Precip)\n",
"cuCap.Plot_basin(cuCap.CellETR, ruta=ruta_images+'Map_ETR_Turc.png', lines_spaces=0.01)\n",
"\n",
"cuCap.GetQ_Balance(Precip)\n",
"print 'Caudal Captacion:', cuCap.CellQmed[-1]\n",
"\n",
"cuCap.Plot_basin(Precip - cuCap.CellETR, ruta = ruta_images+'Map_RunOff_mm_ano.png',\n",
" lines_spaces=0.01,\n",
" colorTable = 'jet_r')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"___\n",
"### Caudales extremos por regionalización\n",
"\n",
"Se calculan los caudales extremos máximos y mínimos para los periodos de retorno de:\n",
"- 2.33, 5, 10, 25, 50, 75 y 100\n",
"\n",
"Se utilizan las siguientes metodologías:\n",
"\n",
"- Regionalización con gumbel y lognormal."
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#Periodos de retrorno para obtener maximos y minimos\n",
"Tr=[2.33, 5, 10, 25, 50, 100]"
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"QmaxRegGum = cuCap.GetQ_Max(cuCap.CellQmed, Dist='gumbel', Tr= Tr, Coef = [6.71, 3.29], Expo = [1.2, 0.9])\n",
"QmaxRegLog = cuCap.GetQ_Max(cuCap.CellQmed, Dist='lognorm', Tr= Tr, Coef = [6.71, 3.29], Expo = [1.2, 0.9])\n",
"QminRegLog = cuCap.GetQ_Min(cuCap.CellQmed, Dist='lognorm', Tr= Tr,)\n",
"QminRegGum = cuCap.GetQ_Min(cuCap.CellQmed, Dist='gumbel', Tr= Tr,)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Se guarda el mapa con el caudal medio, y los maximos y minimos para toda la red hídrica de la cuenca "
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"Dict = {'Qmed':cuCap.CellQmed}\n",
"for t,q in zip([2.33,5,10,25,50,100],QminRegGum): \n",
" Dict.update({'min_g'+str(t):q})\n",
"for t,q in zip([2.33,5,10,25,50,100],QminRegLog): \n",
" Dict.update({'min_l'+str(t):q})\n",
"for t,q in zip([2.33,5,10,25,50,100],QmaxRegGum): \n",
" Dict.update({'max_g'+str(t):q})\n",
"for t,q in zip([2.33,5,10,25,50,100],QmaxRegLog): \n",
" Dict.update({'max_l'+str(t):q})"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Caudales Máximos\n",
"\n",
"Adicional a los caudales máximos estimados por regionalización, se estiman los caudales máximos por el método de hidrógrafa unitaria sintética:\n",
"\n",
"- sneyder.\n",
"- scs.\n",
"- williams "
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cuCap.GetGeo_Parameters()"
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tiempo viaje medio Captacion: 0.571268382451\n",
"Número de curva: 80\n"
]
}
],
"source": [
"#Parametros pára maximos \n",
"TcCap = np.median(cuCap.Tc.values())\n",
"#CN = 50\n",
"CN=80\n",
"print 'tiempo viaje medio Captacion:', TcCap\n",
"print u'Número de curva:', CN"
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAEYCAYAAACgDKohAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl8TNf7xz+TEBFJxL6GaImEIKjWWlE/SpVWVe0Siq99\n3/fUUqGotUoRa6uKUrWUyFC09jX2SILWlkSQWLLM8/vj6SQzmXsnsyWzOO/Xa17MOefee87Jnfvc\nc55NQUQEgUAgEAgMwMnaHRAIBAKB/SCEhkAgEAgMRggNgUAgEBiMEBoCgUAgMBghNAQCgUBgMEJo\nCAQCgcBgrC40vvzyS5QqVQo1a9bUqZs/fz6cnJyQmJhohZ4JBAKBIDtWFxq9evXC/v37dcrv3buH\nAwcOoGLFilbolUAgEAiksLrQaNy4MYoUKaJTPmLECMybN88KPRIIBAKBHFYXGlLs2rUL3t7eqFGj\nhrW7IhAIBAIN8lm7A9l5+fIlZs+ejQMHDmSWiUgnAoFAYBvYnNCIjo5GbGwsatWqBSLCvXv3ULdu\nXZw8eRIlS5bUaqtQKKzUS4FAILBvTH0Zt4ntKSLKHEBAQAAePHiA27dvIyYmBuXLl8e5c+d0BEb2\nYx3xM23aNKv3QYxPjO9NHJ8jj43IvJ0bqwuNrl27omHDhrhx4wYqVKiAtWvXatUrFAqzB2mvxMbG\nWrsLuYoYn33jyONz5LGZi9W3pzZv3qy3/vbt23nUE4FAIBDkhNVXGgJ5QkJCrN2FXEWMz75x5PE5\n8tjMRUF2vPfzJm9dCQQCgamY8+wUKw0bRqlUWrsLucqbPD4fHx8oFArxEZ9c/fj4+Fj8vra6TkMg\neBOJi4sTq2RBrqNQWN4tQWxPCQRWQNy7grxA7j4z5/4T21MCgUAgMBghNGyYN3nP3xFw9PEJ3kyE\n0BAIBAKBwQihYcMEBQVZuwu5ihif7ZKamoo+ffrAx8cHhQsXRp06dbBv3z7Jtlu2bIGfnx8KFy6M\nEiVKoEOHDvj3338z63v06IEyZcqgcOHCePvttzFr1qy8GobN4FDzSXaMnXdf8AZj6/duSkoKhYaG\n0p07d4iIaPfu3eTh4UFxcXE6be/evUsPHz7MPK5bt27UuXPnzPqoqCh6+fIlERFdv36dSpUqRfv2\n7cuDUdgO1ppPufvMnPtPrDRsGEffExfjs13c3NwwdepUeHt7AwDatGmDSpUq4cyZMzpty5cvnxlQ\nVKVSwdnZGWXKlMmsr1atGlxdXQFwgNH8+fOjRIkSeTAK28GR5lMIDYFAkCMPHz7EzZs3Ub16dcn6\nY8eOwcvLC4ULF8bdu3cRFhamVT9o0CAUKlQIAQEBmDRpEurUqZMX3bZZ7Hk+hZ+GQGAF7OneTU9P\nR+vWrVGlShUsX75cb9v79+8jODgY/v7+WLRokVYdEeHIkSPo0KED9u7di3r16uVmt22WvJzP3PDT\nEEJDILAChty74eGAORG6fXwAc+PuERG6dOmC5ORk7Ny5E87Ozjkec+LECbRu3RqJiYmS9QMGDEDB\nggWxYMEC8zpnLOZOKGD2pOb1fOaG0BBhRGwYpVJp1xY4OSHGpx9bCLT65ZdfIj4+Hnv27DHoAQcA\naWlpcHNzk61PT0/XW59r2MCEOsJ8Cp2GQCCQpH///rh27Rp27doFFxcX2XabN2/G3bt3AXBMrcmT\nJ6NDhw4AgMePH2PLli1ISUmBSqXC/v37sXXrVnzyySd5MgZbwmHm02S7KxvAzrsveIOx9Xs3Li6O\nFAoFFSxYkNzd3cnd3Z08PDxo8+bNdOfOHXJ3d6e7d+8SEdGkSZOofPny5O7uTpUqVaLx48dnmoQ+\nfvyYmjZtSkWKFCEvLy+qV68e7dq1y5pDswrWmk+5+8yc+0/oNAQCKyDuXUFeIAIW2jAnTwLR0ZY9\npz3b+RuCGJ9AYH8IoWEBnjwBmjcHOnYExMujQCBwZMT2lAWYNQuYPJn/v38/0LKldfsjsH1s5d4V\nODbCTyMbtvDDe/kSqFgRqFULuHIF8PMDIiKs2iWBHWAL967A8RE6DRtk7Vrg8WNeaYwYARw6BJw6\nZZlzO/qeuBifQGB/WF1ofPnllyhVqhRq1qyZWTZ27Fj4+/sjMDAQHTp0wLNnz6zYQ3nS04FvvgHq\n1wfefx/o1w/w8gKyhYkRCAQCh8HqQqNXr17Yv3+/VlnLli0RFRWF8+fPo0qVKvj666+t1Dv9bN0K\nxMQA48cDCgXg6QkMGgRs3w5cv27++R3ZWxoQ4xMI7BGrC43GjRujSJEiWmX/93//Bycn7lr9+vVx\n7949a3RNL0S8ovD3B9q2zSofOhQoUIBXIAKBQOBoWF1o5MSaNWvQunVra3dDh/37gQsXgLFjASeN\nWSxZEujdG1i3DvjnH/Ou4eh74mJ8AoH9YdNCY9asWcifPz+6du1q7a7oMGcOUL48INW1UaOAjAzg\n22/zvl8CgaUICgpCwYIF4enpCQ8PD/j7+1u7S3aNo8ynzUa5DQ8Px549e3Do0CG97UJCQuDj4wMA\n8PLyQmBgYOZesvpNz9LfXV2DcPgwMHCgEsePS7fv1AlYulSJ998H2rY17Xrqstwej7W+v+njs3UU\nCgWWL1+OXr16WbsrDoE151OpVCI8PBwAMp+XJmNy1CoLEhMTQwEBAZnf9+7dS9WqVaP4+Hi9x1mr\n+59+SlSkCNHz5/Jtzp0jAohmzcq7fgnsBxv56eklKCiIVq9ebe1uOAzWmE+5+8yc+8/q21Ndu3ZF\nw4YNcePGDVSoUAFr167FkCFDkJycjBYtWqBOnToYOHCgtbuZydWrwK+/AoMHA+7u8u0CA4FWrYBF\ni9gB0BQcfU9cjM/2mTBhAkqWLIkmTZrg8OHD1u6O3eMQ82myuLEBrNH9Xr2IChYkevQo57ZKJa82\nli837VqRkZGmHWgnvMnjs4ef3smTJyk5OZlSU1Np3bp15OHhQbdv37Z2t+wWa8yn3H1mzv0nwogY\nwb17wFtvAf/7H7BkSc7tiYAGDdhj/Pp1IJ/NapAEeY0h926/fsC//5p+jbJlgZUrTT8+O61bt8bH\nH3+MQYMGWe6keYm5EwpYdFLzYj5Fulcrs3AhoFKxdZQhKBTs+Ne+PfDLL0DnzrnbP4FjYckHviWw\n+3hZNjah9jqfVtdp2AuJiXzPde7MueUNpV07DmIYFmZ82HRH2BPXhxif7fL06VP88ccfeP36NTIy\nMrBp0yb8+eefaNWqlbW7Zpc40nyKlYaBLF8OJCcD48YZd5yTEzsA9u4N/PEH8OGHudM/gcCSpKWl\nYfLkybh+/TqcnZ3h5+eHnTt3onLlytbuml3iSPMpdBoG8OIFhz9/913g99+NPz41lXUhVaoAkZGW\n75/A/rDXrQmBfSFCo1uJtWuB+HjWT5iCiwswciSgVAInTli0awKBQJCnCKGRA+rw5w0aAI0bm36e\nvn2BIkWMC5tuz3vihiDGJxDYH0Jo5MDPPwOxsVnhz03Fw4PDpv/6K3DtmsW6JxAIBHmK0GnogYg9\nu9PTgUuXtKPZZicqCihWDChdWr7N48esG+nSBVi92vL9FdgPQqchyAuETiOP2bcPuHhRN/x5dp4/\nB4KCgM8/129WW6IEW1Ft2GB+2HSBQCCwBkJo6GHOHMDbm1cG+li4kC2kjh0D9u7V33bUKHYQXLgw\n5+s7+p64GJ9AYH8IoSHDX38BR46w1ZOLi3y7hARWlE+dCnTqBEyaxEJBjkqVuN333wNPnli+3wKB\nQJCbCJ2GDJ9+Cvz5JxAXpz+a7dixwKZNwK1bwN27QLVqwObNwBdfyB9z8SJQqxYwcyYLGcGbh9Bp\nCPKC3NBpGCQ0Hj16hFevXhl1YldXV5QsWdKkThlKbv3wrl7lh//UqUBoqHy7f/4BKlfmDH3/+x+X\n9enDwiYqSn+AwjZtgFOnWCgVLGjZ/gtsHyE0BHmB1RThEydOhFKpRGRkpMGfiRMnmtQhW2DuXH6Q\nDxmiv93MmUC5cqzcVjNtGpvorlun/9hx49iaau1a+TaOvicuxme7LFu2DPXq1YOrqyt6a97gACIi\nIuDv7w93d3c0b94cd+7csVIv7QdHmk+DYk81bNgQPXv2NOrEGRkZJnXI2ty9C2zcCAwYABQvLt8u\nOhr44QcWDvnzZ5V7ewMDB/IKpVs3wNVV+vgmTdhhcN48jtgswqYLbIly5cphypQp2L9/P15qZBFL\nSEhAhw4dsGbNGnz88ceYPHkyOnXqhL/++suKvbV9HGo+Tc7EYQPkRvdHjCBydiaKjdXfrls3oho1\niDIydOsePiQqVIho4UL95/j1V07StHmz6f0V2Cf28tObPHky9erVK/P7ypUrqVGjRpnfU1JSqGDB\ngnT9+nVrdM/uyOv5lLvPzLn/zLaeSkpKwoIFC3Djxg1zT2V11OHPu3RhJzw5Ll1iZffMmdL+GyVL\nAiNGALNnsw+HHG3bAv7+poVNFwisQVRUFGrVqpX53c3NDZUrV0ZUVJQVe2W/2ON8miQ0FixYgICA\nAHzxxRc4dOgQhgwZgqNHj1q6b3nOsmVASgpbROljyhTgvff4oS/H6NHsSb5okXwbddj0CxeA/ft1\n6+15T9wQxPjsj+TkZBQuXFirzNPTE8/1vR0JZLHH+TRpJz0xMRG//PILTp06hVWrVqFPnz6oX7++\njoLHnnjxAli8GPj4Y6BGDfl2J04AO3cChw7pj0VVuDDHq5o1i3UcRYtKt+valYXQnDmAHeZjEeQi\nVarwS4ypFCoE3Lxpuf4AgLu7O549e6ZV9vTpU3h4eFj2QrmBuRMKWHxS7XE+TRIavr6+8PPzg5+f\nH3r06IGkpCS4yml87YQ1azj8eU5JliZOBP7v/4BmzXI+5+DBbI4bFiYf3dbFhb3ER4wA/v4bqF8/\nqy4oKMjg/tsjYnz6sfQD3xJUr14d6zRMA1NSUhAdHY3q1atbsVcGYoMTao/zadL2VPny5bW0+15e\nXnYtNNLS2Ku7USP94c8jIniFMWuWYed1c+NVxJIl+vPZ9+ljfNh0gSA3ycjIwKtXr5CRkYH09PTM\nNKXt27dHVFQUduzYgdevXyM0NBSBgYHw9fW1dpdtGoeaT1O058OHD6cCBQpQ48aNadq0aXTkyBFK\nS0szWRtvKiZ2X4eNG9mKadcu+TYqFdG77xK1b2/cuV+/JqpUiWjgQP3tpk7lPly5klUWGRlp3MXs\njDd5fJa6d3OL6dOnk0KhICcnp8xPaGgoERFFRESQn58fubm5UbNmzSguLs7KvbV9rDWfcveZOfef\nSUfOnz+fXr58SX/99RfNnDmTgoKCqHr16iZ1oHfv3lSyZEmqUaNGZlliYiK1aNGCfH19qWXLlpSU\nlCTdeQv88FQqooAAourVpc1n1ezYQaRQEF2+bPw11q8nypePKDpavs3jx0QFCxJpWOO90Q9VR8Ce\nhYbAMcgNoWFS7KmVK1eiX79+FlnpHD16FO7u7ujZsycuXrwIABg3bhyKFSuGsWPHIiwsDE+ePMGc\nOXN0jrVEKIbff2fl97p1gJz/YkYGx4qqUwdYv974axh6/NChwIoVwO3bQPnyxl9HYD+IMCKCvCA3\nwoiYJG7+/vtv2rBhg8mSKjuxsbFaK42qVavSgwcPiIjo/v37VLVqVcnjTOy+Fk2aEHl7E6WmyrfZ\nsIEof36i27dNv44hK5WYGHYsHDnS9OsI7ANL3LsCQU7I3Wfm3H8mKcK//vprzJo1C97e3ggODsb6\n9evx8OFD06SWBI8ePUKpUqUAAKVLl8ajR48sdm5Njh/n4IKjRmmHAtEkNZXjSfXty2HN5bh9m50D\n5fjkE+Cdd1gxLoePDzsWfv89n8sR7fw1EeMTCOwPk4RGkyZNcOnSJZw+fRotW7ZEZGQkPv/8c0v3\nLROFOcm59RAWxv4TffrIt1m9Grh/H5g8Wb7Ny5fABx/Ib28B7NMxezawYwdw8qR8u7Fj2ZR8+fKc\n+y8QCAR5jUl+Gr1798b69evRsWNHdOvWDd26dbNop0qVKoWHDx+iVKlSePDggd4Q6yEhIfDx8QHA\npr+BgYGZ9vHqNz2p71FRwK5dSgQHA4UKSbfft0+JyZOBIUOCUKaM/PmOHAlC8eLAn38qMWcOMH68\n9Pny5VOidm1g0qQgHDggf742bYKwaBGvTJRKpUHjscfv6jJb6U9ej08gyCuUSiXCw8MBIPN5aTIm\nb2z9x5MnT2j+/PlmBdiKiYmhgICAzO9jx46lOXPmEBHRnDlzaNy4cZLHmdP94GAiNzei+Hj5NnPn\nEnl6EiUkyLeJi+PghCdPEn33HZGvL5vZyvHXX2xaGxEh3+bPP7nNkiU5DkNgp1jgpycQ5IjcfWbO\n/WeyyW316tWpY8eOtG3bNkpNTaXVq1eb1IEuXbpQmTJlyMXFhby9vWnNmjWUmJhIzZs3J19fX2rR\nogU9efJEuvMmDjwujk1ghw2Tb5OURFS0KNGMGfrP1akTUe/e/P/0dKJatYjmzdN/TLt2RO+9x+a+\ncjRsSFSqVKReBb29I0xuBYLcxWaExqRJk+jq1au0fv16atWqFRUpUoRat25tcidMxdSBDx/OQkOf\nD82UKUQlShA9eybfRqnklch/hl5ERHTkCJGHB9H9+/LHXbzIllQ7d8q32bWLCIikjRvl29g7QmgI\nBLlLbggNk/w01q9fr5WUSR17Kq9DiZhia5yQAFSoAHz+uXx2vUePgLfe4tDnw4dLt0lPB+rWZeX3\nqFHadZ07c+Y/fVn5unfn6LYXLkiHV1epOHCiszO3ySVbAIGVEH4agrzAaules2PPsaeWLuWItvrC\nn8+Zw1ZV/fvLt1m1Cnj9Wjol7Lx5wNat+q2kpk8Hrl0DfvpJut7JiYMnXroE7N0rfx6BIDdITU1F\nnz594OPjg8KFC6NOnTrYt28fACAuLg5OTk7w9PSEh4cHPD09McvQgGxvKA41n6YsT+w19lRyMlGx\nYkRt28q3uXOHqEABoh9+kG+TkMD6jr175dt89RXHqtIXmuR//yN6+215x8IDByLJ25vo/fflz2HP\niO0p2yUlJYVCQ0Ppzp07RES0e/du8vDwoLi4OIqNjSUnJydS6VPKCbSw1nzK3Wfm3H8mrTS8vb2R\nlJSEefPmIX/+/Jg6dSoCAwMtKctyhdWreXtKX/jzr77irH3BwfJtpk0DGjbUn/9i9Gje5tqwQb7N\nlCnAP/9wWHYp8uXjra8jRwBbThkscDzc3NwwdepUeHt7AwDatGmDSpUq4cyZMwAAIoJKpbJmF+0K\nh5pPUyTN999/b7KUsiTGdD81lahCBaLGjeXbXL/OYTy2bJFvc/EiBxa8eTPna27bRlSqFNHTp/Jt\nRo8mKluW6MUL6frkZF7VfPJJztcT2A8m/vSsxoMHD8jV1ZVu3LiR+WZcvnx58vb2pl69elG8Ptt1\ngQ55NZ9y95k5959JivATJ07g5s2b6N69u6VlmFEYo8zZsIGV1r/9xgEKpejShfUMZ85IK6eJgObN\ngXffZb1HThBxwqa6dYG5c6XbxMez0n3aNF2Fuprp04HQUCAqCqhWLefrCmyfnO5dIiA52fzruLub\nb0SRnp6O1q1bo0qVKli+fDlSUlJw/fp1BAYGIiEhAQMHDsTz588z9+htEktNKGD2pOblfNpMwMJP\nPvmE/Pz8qHz58tSzZ09at25dZoDBvMTQ7mdkcOjzgAB5HcO5c+xQ9/vv8uf55ReiMmX0m+Fm59Il\nXpno830MDWVdS/YViXpP/PFjdkQMDjb8uvaA0GnI8+wZ34/mfoy5V6VQqVTUqVMnatOmDaWnp0u2\nefDgASkUCkpOTjbvYrmJpSbUzEnN6/mUu89MfPQTkYk6jbyOPWUue/bwW/q4cdIrCIBjSzVqBLRu\nLV3/8iWvBMLCAGPS9wYEcGyrESPk24wYwS8uCxZI1xcvzufYtAm4e9fwawvsF3d34Nkz8z/u7ub1\n48svv0R8fDy2b98OZ2dn2XYKhcK29+QtNaFmTqpDzKcpkiYxMZFWr15Nz8x9jTETQ7vfuDHrM+Ss\nlI4e5ReII0fkzxEaSlS/vvxKZdEieWuqxEReSehbxcyfT+TuzqsKKWJj2SFx+HD5cwjsBxN/ennK\n//73P2rQoAGlpKRolZ84cYKuX79OKpWK4uPjqVOnTtS8eXMr9dJ+sMZ8yt1n5tx/Bh2pVCqNPrEp\nxxiLIQNXx3FavFi6XqVik9ZWreTPoRlfSooLFzila6VKRDIRT2jFCqIqVeTjUr14QVSunP5cGj16\ncD+EztH+sXWhERcXRwqFggoWLEju7u7k7u5OHh4etHnzZvrxxx+pUqVK5O7uTmXLlqXg4GB6+PCh\ntbts01hrPnNDaBikCB85ciSGy7lGS69esHjxYsyfP9+k1Y+hGKLMaduWzVXj4oBChXTr9+9n09kz\nZziznhSdOvGKdPVq3bqMDDa/nTEDOHWKt49WrJBu9847QNeuwJgx0tdZtYqdBW/d4sx9mhFSAeDy\nZfYSDw0Fpk7VO2y7IPv4HA194xMe4YK8IDcU4QaFRlfrLYyhRYsWJnXIkly+DOzezQ9ZKYFBBEyc\nCHTsKC8wDh8G9u0DbtyQrl+6FPD1BVq2BIKCgHr1OLFTkyba7ZydgcWLgTZtgB49gNKldc8VEsJW\nVjNmcCKm7AQEsBBcvJj1K1JjEggEglzF5DWKDZBT93v00B/+/JdfiJyciK5ela5PSyOqWZPom2+k\n62NjiXx8iB49yir7+2+iatWIXr2SPqZzZ6KQEPk+b97MviJyfiBq/YvcdpvAPrDzn57ATpC7z8y5\n/0zy07AV9C2x4uKAypWBwYOBhQt169PTeaunQQN5j+zvvgMWLQIuXgRcXLTriNjfo3NnXjloMnQo\nUKQIr3Cyc/cu4O8PREQA772nW69SAbVrA9WrA5s3S/erSRM+z82b8mlqBbaN2J4S5AU246dhK+jr\n/tChbG30X6gXHdauJXJx4dWCFDnFl9q8mahFC+mcGM+ecUypy5elj80pLtVvv/FqYtWqSL31GzZI\nH28vCD8NgSB3kbvPzLn/TPLTsHXi44EffgC6dQP+C/WixevX7GXdvz/HmZJCX3yphATWhaxYIe0Y\n6uEBfPst0Lcvrxyyk1NcqjZt9K+APvqI9RthYbziEQgEgjzDZHFjA8h1f9o0fhOPipI+bvFi1nXI\nObHnFF8qJCTn7HxERF98QbR0qXRdTnGpIiN5DMeOSdevX8/1u3fn3A+B7WHnPz2BnSB3n5lz/zmc\nTiMlhZMsNW4M7Nype0xKCsd66tMHkApZn1N8qYgIzsVx4gRHodXHgwestzh2jE1os18np7hUH37I\nq6LISN0VTVoa62wqVGBrLYF9IXQagrzAJpIwbdmyBf369cOnn36Kdu3aaX1sgR9+ABITgfHjpesX\nLwZSU3mLSIrt2zlo4aRJunUvXwKDBrE/RU4CA2Cz2mnT+Jjsfx+FgpXsS5fKm/N+9pkShw8DBw/q\n1uXPz2M4epSFkj2iVCqt3YVcxdHHJ3gzMUpojBkzBt27d0dsbCy8vLxQrFgxrY+1SUsD5s9n66IG\nDXTrnzzht/px49i6KTs5xZcKDQXatZP36ZCiVy/g+XNg2zbdupziUlWtCnz2GetPpF4KevcGihXj\n/goEAkGeYMxeVsmSJWnr1q0m74VZmuzdX7dOf6TaCRNYjyAXPFJffKlz54h8fYmyhY0xiBs3OMRI\nYqJuXU5xqaKi2Jdk2zb5PgPylloC28TIn55VaNq0Kbm6upKHhwe5u7uTn59fZt3BgwfJz8+PChUq\nRB988AHFxcVZsaf2gTXmU+4+M+f+M+rI4sWL001Dsg/lEZoDz8hgp7oaNaTNYO/fZ+X3kiXS59IX\nXyo9neidd4j++MP0vs6eTdS3r3RdTnGpgoOJ/P25H9mJj+dx9expet8EeY89CI2goCBas2aNTnl8\nfDwVLlyYtm3bRq9fv6YxY8ZQ/fr1rdBD+8Ia85kbQsOo7al+/fph48aNll7sWITffweuXOGtJykz\n2NmzgZIlgX79pI8fM4ZjTNWrp1u3eDEnPzInMsro0cDJkxyWJDt9+nBIkEWLtMvVe+LTpnE8qk2b\ndI8tVozHtHkzcOeO6f2zBo6+5+8I4yOJfdHt27cjICAAn332GVxcXDB9+nRcuHABN+SUc4JMHGE+\njRIaSUlJWLRoERo1aoQBAwZg6NChWh9L8/XXX6N69eqoWbMmunXrhtTUVNm2c+awz0WnTrp1sbHs\nUzF9uq5nN5AVX2r2bOljFy9mXYk55M8PrFwJDBgAvHqlXaeOSzVjBltcZadSJRYM06axEj87I0fy\nv3L5OAQCU5kwYQJKliyJJk2a4PB/bzxRUVGoVatWZhs3NzdUrlwZUVFR1uqm3eAI82lQwEI1V65c\nQWBgIADg2rVrWnUKc3NKZiMuLg6rVq3CtWvX4OLigk6dOuGnn35Cz549ddoePQocPw4sWSJt1RQa\nyuapUtlp09M57MfUqUCpUtp1RPyQnzmTEyHpY+5cXo3IpZIF2Iy3ZUs29Z0xQ7uuSRN26pswAVi7\nlss0I6ROnszOfqtWsTWWJt7e7Mi4ahUwZQqvPuwBR45wC5g3vtRUfmExFx8f6RclQ5g7dy6qVasG\nFxcX/Pjjj2jXrh3Onz+P5ORklCxZUqutp6cnnj9/bn6HcwtLTShg8qQ6zHyavLGVyyQmJlLVqlUp\nMTGR0tLS6OOPP6YDBw5otVF3v00bouLFpZXUV66wIvmXX6Svs3w5UdWq0vqETZuIPvxQWkeiyeHD\nRN27EzVvTvTPP/rbPn9OVLkyp4HNzp07rFf5+2/pY8ePl1fkR0WxQnz6dP3XF9gGOf30rl+3TGZS\nfWmGjaV169a0ZMkSGjZsGA0aNEirLiAggLZv3265i1kaS02oBSc1L+ZT7j4z59Fv1EojLylSpAhG\njRqFChUqwM3NDS1btsT//d//6bS7dIn1GV99Bbi56Z5n6lQOAPjZZ7p1iYn8Br9pk+6LQ0IC+2pI\nOdZp8uQJbxvt3Ancu8ehSX79VT6trLs76y769uUVkmbGR29v9i8ZOpRzgBw5op2PYexYDqK4dCnr\nbjSpVo2YjD81AAAgAElEQVTNgRcvZv2JPYRNf5PzaeSEjw9w/br5ffDxMf8c2alevTrWrVuX+T0l\nJQXR0dGoXr265S9mKSw1oepzWRC7m09jpcyDBw9oypQp1KFDB/r8889p6tSp9EAuHocZREdHk7+/\nPyUkJFB6ejp9+umntGnTJq02AKh7d347T0jQPcfp0/xisH+/9DUGDSL6+GPpuuBgTsGqD5WKqGtX\nouPHs8qWLzcsxEjnztKWXC9ecLj18HDpgHezZhEVKSKdIfD4cR7vokU5X98WEAELbZekpCTav38/\nvXr1itLT02njxo3k7u5Ot27dosePH5OXlxdt376dXr16RWPGjKEGDRpYu8s2jbXmU+4+M+f+M+rI\no0ePkru7O7399tvUvXt36t69O7399tvk4eFBxzWfnBZgy5Yt1KdPn8zv69ev11nCASAgmOrXn0bT\npk2jhQsXav1Q69WLpFq1IjO3lyIjIzPrL14kcnGJpI0bs9qr6w8cYBPbgwcjtc6neTwR0bhxkRQS\nol1/6FAkdehAdPasbnvN7w8eEJUqFUlbtujWq+NS7d6te/yePZFUsiTRpEnS569RIzIzH7q+64vv\n1v1u60Lj8ePHVK9ePfL09KQiRYpQgwYNKCIiIrM+IiKC/Pz8yM3NjZo1ayb8NHLAWvOpvs8iIyMp\nODiYgoODadq0aXknNOrXr099+/aljIws77eMjAzq27evxd80zp8/TwEBAfTy5UtSqVQUHBxMS7NF\n/wNA+fMT3b2re7xSKR/wT6UiataMaNw43bqUFNZxnDunv383bxK1bs2JmrLz6BGfPydHwDVreKWT\nXWeiUrF+ZMwY6eMWLeLVldQC7/ffedzr1+u/tsC62LrQEDgGVl9puLq60rVr13TKr169Sq6uriZ3\nQo65c+dStWrVqEaNGtSzZ09KTU3VqgcgmQVPpSJq2FB+62nrVqIyZTjvRXbGjuWPPlJTiVq2JIqJ\nkW+zfz9R//76z6NSEX3wAdGWLbp1ly/zSkhK5/bqFVGFCpwzROqcNWoQVa8un6/DVtB8C3dE9I1P\nCA1BXmB1oVGqVCnaK5GVaM+ePVS6dGmTO2EqAOjKFd3y3bv5bfv8ed26Fy+IKlaUfhM/e5ZXGTmt\nECZN4iRMOTFiBNGOHfrb3LzJOgypECPt20fSRx9JH7dmjXwSqR9/5PGvW5dzH62JEBoCQe5idaEx\nbNgwKlu2LG3cuJFu375Nt2/fpg0bNlDZsmVpxIgRJnfCVKQGnpFBVKsWK5qlkIsvlZZGVLcuUTar\nXh0OH2YluSG8emWYGe6cOURffqlbro5LJZUzIy2NBVzv3rp1GRlE771HVLYsm/gKbA8hNAR5gdWF\nxuvXr2no0KHk4uJCTk5O5OTkRAUKFKDhw4fTa7nASbmI1MB/+onI2ZmDBGZHX3ypb74hya0uTZ48\nIQoKkk+cJEVUFFHbtvq3ilJTiQIDOfFSdvTFpfr5Z/ZBkdgxpL/+4tXG5MmG91WQdwihIcgLrC40\n1KSkpNDFixfp4sWLlGJK2FcLkX3gqan8gJULDPjFF9Jv5rdv8xZRfLz8tVQqom7dtM1rDWX5chZK\n+jh1isjPj7fP1ERGRlJ6OguUuXN1j8nIIKpTh6hjR+lzdu1K5Ooqnwfd2ojtKYEgd8kNoWFSjnA3\nNzfUqFEDNWrUgJuUR52VWLeOg/ZNmaJbJxdfiogd8mbP1h9+Y/16wNdXOk9HTvTvz856587Jt3nn\nHaB1aw5ZoolmXKr797XrnJw4JMnWrcDZs7rnnDOHHRPlElIJBAKBseSY7rVdu3bYuHEjPD09c8zO\nt2vXLot2Lic0Uxa+egVUqQJ07KgbuC89ndOq9uzJSZY02biRI8T+/ru85/etW+ylvWuXYRn7pHj8\nmIMp7t4t7bkOAMnJ7L2+bRtQs6Z2XZcuQIECQHi4djkR0LQpe5rv2aN7zmnT2Fv+2DGgYUPT+i6w\nPCLdqyAvsEq612LFimUGIyxatKhOtj5bydy3YgWQlMQB/7KzahXn2h4yRLs8Pp5XJd99Jy8w0tI4\nQODy5aYLDAAoUYLf+LMLLU3c3TnoYr9+QEaGdt3cucAvv3Buck0UCl4l7d0rnSt87FigXDlg+HBA\npTK9/wKBQADAvjdW1d1/9owDFk6dqtsmIYGoaFEiCUth6tGDaOFC/dcw1LzWUAwxw+3alR34su+J\nz5hB9O670kr1jz4iatxYOrjihg226fAndBoCQe4id5+Zc/8ZpdOYNGkSvv/+e53yFStWYIqUIiGP\n+PZbfotW55XQZOpU3pZp1Uq7/I8/gGvXdFcfmhw5wkEIu3SxXF+//poDDv77r3ybhQt5i+3hQ+3y\nUaOAR49Yv5KdmTM5AOK+fbp1XbtyWPbx44GUFPP6L3gz8PDwgKenJzw9PeHh4YF8+fJh2LBhADht\ngZOTU2adp6cnZs2aZeUe2zYONZ/GSBhvb286deqUTvmJEyeoQoUKJksuUwFA8fFEnp7SQQIvXiQq\nWJAd6DRJTuZ831LOf2pMMa81FEPMcMPDOeR79pWDOi6VVL+++IKodm3p86qDGU6ZYl7fBZbByJ+e\nVUlOTiYPDw86evQoERHFxsaSk5MTqXLKGSCQJC/nU+4+M+f+M2ql8ejRI0ndRfHixfEw+2txHhEW\nxrqA7ImJiFh5PXQoJ2DSZPp0DpWukSxL59jBg1lX4Olp+T5Xq8Yrn4UL5dv07Ml6mJ9/1i5v3x4I\nCNC1sgLYwuriRdZ9ZKdBA14xzZtnf2lhBdbll19+QcmSJdGoUaPMMiKCSijJTMLe59MooVGhQgUc\nOXJEp/zIkSMoX768xTplDEuWsDK7YEHt8m3bOHz+pEna5WfPsgXT1Kny5zTHvNZQBgzQb4arUAAh\nIUqMH895PzTLFy3iLa7sKYR9fYGQEJ6P9HTdc86Zw//aigmuI+TQ1oejjG/9+vU6GTMVCgV8fHxQ\noUIF9O7dGwkJCVbqnf1h7/OZo8mtJvPnz8esWbMQFhaGDz74AAAQERGBCRMmYNy4cRg7dmyudVQK\nhUKBt94iXL2qnUTpxQvA35/fxnv0yCpPTwfee4/ftv/rvg6WMK81lJzMcJVKJU6dCsK1a8Dq1dp1\nw4ZxX3//Xbv8zh02Pf7uO6B3b91zTp3KKxJbMMF9k5Mw5WTymJQEnD9vfh8CAwEvL9OPj4uLQ+XK\nlXHr1i1UrFgRACcJun79OgIDA5GQkICBAwfi+fPn2CelULMVLDWhgFmTmtfzmRsmt0ZvbI0fP55c\nXV0zw4i4urrSOKkY43kAANq4Ubd8+nTp+FLz5hH16iV/PkOi11qanKLhpqWx1/ehQ9rl+uJSDR9O\nVL68dNyp5885JpWcFZYgb8jppxcZaZnMpOYaqM2YMYOCgoL0tnnw4AEpFApKlspDbCtYakLNnNS8\nnk+5+8yER38mRq001KSkpODKlSsAAH9/f7i7u5smscxEoVAgPZ20UqbeucM6g8hIoF69rPLbt4Hm\nzYEzZ4CiRaXPN2UKr1C6ds3dfmdn5Ejg/feBTz+Vrj9zBujenbfWNLfhvv8emD8fuHxZe6WVkMDj\n6N5d19ER4O234GBgwwZuI8h77GWlUbVqVUycOBHBwcGybR4+fIiyZcsiKSkJHh4epl8sN7GRlUZe\nz6dNrDRsCanuS8WXUqmIWrTgkOFyHDliePRaKcwxfJCLhqtp5z9qFNH48dr1+uJSbd7MwQxPnNCt\ny8ggqlePqFw5tiSzFsJPw7Y5duwYubu767zxnjhxgq5fv04qlYri4+OpU6dO1Lx5cyv10n6wxnzK\n3Wfm3H9Gx55KT0/H8ePH8dNPP2H9+vVaH2ujVErHl9q4kd/EO3WSPi4piff6Fy827boqFftQLFli\n2vEFCvC1+/eX99oODWXl/oULWWX64lJ17swWWn36sFe7Jk5O7Nvyzz+s3xEIpFi/fj06dOiAQoUK\naZXfvn0brVq1gqenJ2rWrAlXV1ds3rzZSr20HxxmPo2RMFevXqXKlSuTs7MzOTk5Uf78+UmhUJCL\niwt5eHiYLLlMRbP7aWlENWvqRpN99Igj2Mql3DUneq2a2bM5gdOPPxL98ovp51m2TH803P37eYWQ\nnq5d3rmz9CpJHQp+1izp83XuzH4sd+6Y3GWBiRj50xMITELuPjPn/jNqpTF8+HDUrVsXT58+hZub\nG65evYrTp08jMDAQ27Ztyw2ZZjBy8aVGjOBPhQrSx5lrXhsezv4etWvz231sLPD336adKycz3JYt\ngapVdVc0cnGpKlRgD/SvvmLz4+zMmcOaPVsxwRUIBHaAMRKmaNGidOnSJSIi8vT0zMwXrlQqqUaN\nGiZLLlNRd18uvtS+fZzBLvubuZqbN4lateJViin88QfRypXaZSoV5xiPjjbtnI8eETVrxilnpfbE\nHz3idLXZc2TIxaVKT2dLsiZNpK2lJk9mgxBzVlqmInQaAkHuInefmXP/GbXSIKLM/BklSpTAP//8\nAwAoX748bt26ZVlpZgRS8aVSUnjVsWoVtKyr1Kij1373nWn+GJcu8Yqib1/tcoWCdQwLFmg75RlK\nTtFwS5Tg8w8YwKsENXJxqZydgR9+4L6uWqV7vnHjgDJleDVmJw6pAoHAmhgjYZo0aULbt28nIqIu\nXbpQy5YtSalUUrdu3ay20pCLLzVyJNHEifLHTp5MtGmTadf95x/2hdDn5/DkCdHAgWwZZQr6ouGq\nrcGyR9/dvl0+LtW0aRyj69493brwcF5tSPm8CHIHI396AoFJyN1n5tx/Rh25b98+2rZtGxERRUdH\nk5+fHykUCipRooRVthoAUFAQUXbfwlOniPz9iV6+lD7OHPPa589ZGBiS5TY2lmj0aNPMceXMcNVE\nR+umqFWp+JgxY6TP5+9P9Mknuv3JyCB65x3rm+C+SQihIcgLrC404uLiKCPb63VCQgKpVCqKkzNP\nykUAUJkynE9DTWoqR3qVk2HmRK9NTycaOpTowQPDjzl5kigszPhrERGtXRupNxruvHlEISHaZZcv\n88rr+nXd9seOESkU0hZeR4/yamP6dNP6agpCpyEQ5C65ITSM0mlUqlQJ8fHxWmVFixZFYmIiKlWq\nZPZWWXaePn2Kjh07wt/fH9WrV8eJ7OZB4Ci3mk6TCxcCdeoAUiF/zIleS8RWSP37A6VKGX5cvXqA\nnx97XxuLj4/+aLjDh7NuJSIiq6x6ddazDBumrfMAWO8zcCDPwZMn2nWNGrEfS1gYcPeu8X0VCARv\nCMZIGIVCQY8ePdIpj42NJTc3N5MllxzBwcG0Zs0aIiJKS0ujp9mWBwC03sJv3SKqVInjMkmxbp3p\nb9LLlpkXx2f5cqKICOOPU6mIOnRgPxApzp4lqlqV6MWLrLInT4i8vYlWrNBt//Qpx6Xq00e3LjaW\nqEAB9lsR5C4VK1YkAOIjPrn6qVixouT9B+Ry7KmhQ4cCAJYtW4ZevXplWlABQEZGBk6ePAkXFxcc\nO3Ysp1MZzLNnz1C7dm1ER0fLttGMn0IEtGjB+bW/+EK3bXQ0v2H/9pvx1lI7dwLJyUC3bsYdl51p\n0/htvlo1447LKRru2LHs5a0OfQ4Ahw8DH38MnDzJcag02b0baNsWOHQIaNZMu27yZGDWLPYXqV/f\nuH4KBAL7wJzYUwZtT126dAmXLl0CEeHq1auZ3y9duoRbt26hTp06CA8PN6kDcsTExKB48eLo1asX\n6tSpg379+uHly5ey7dev52B+HTvq1qWl8baMKea1p05x3gpzBQbApsHff6+bxlUOdT6GnMxwp08H\nduzQjsfWtCmbHHftyk6Pmnz8MQuhvn2B7FM6fjxQujRvfZkaz8xQHCXfhBxifPaLI4/NbIxZloSE\nhOhsEeUWp0+fpnz58mWmlx02bBhNnTpVq426+w8fssObXDgMU81rY2LYEsmSWRiTkw23vsquSNVn\nhvvHH2wBpenImJrKZaNH67Z/+JAdIqWi2q9dy0pxU02SDeVNVoQ7Ao48PkceG5EVQqPnBQ8fPkSD\nBg1w+/ZtAMDRo0cRFhaG3377LbONQqFAcHAwzpzxgbc30LKlFwIDAzMT3yiVSly8CJw9G4Tw8Ky3\nB816ue9JSUCvXkoMHAi0aJFze2O+V60ahLAwoG1bJZydDT/+jz84k9/u3UEoW1a3/sMPlahcGVi2\nLOv4e/eAgQODsH07kC+fdvvx45WYNw84fToItWtnne/994NQrx5w544SGzYArVpZdvziu/guvuft\nd6VSmbkb5OPjg9DQUJO3p3IUGu3atcPGjRvh6emJdu3a6T3Zrl27TOqEHE2bNsWqVavg6+uL0NBQ\nvHjxAmFhYZn1CoUCe/YQZswA/vxT1/M7KYlzVOzcCRQubPh1U1M5x8WMGUCRIhYaTDYuX+aotdOm\nGXfclSvAhAm8HeWUbXMxPp6ttSIj2fJKzZo1rKu4dAnQTPFOxPGsEhM5bpXm1t2ff3KOj9BQ/alx\nBQKB/ZGrOo1ixYpBoVBk/l/fx9IsXrwY3bp1Q2BgIC5cuICJEyfqtBk2DFi5UldgaJrXGiMwiPgh\nOWpU7gkMAAgIYDPXlSvl26jfFDSpVg348ENpM9zixTnFbf/+2vqIXr34Wn36aJcrFKxjuXqVQ6Vr\n0qQJGxSEhQH37hk3NkORGp8jIcZnvzjy2MzGIhtkVgIATZ4sXWeqee033xD9/bd5/TKG8HCi336T\nrpPbV9VnhqtSEX34oW5IkIQENrXNHmCRiMdcsCCbLGsSE8MmuN275zgMk3D0fWMxPvvFkcdGZCWd\nRnJyMgBYLdUrwEusly8Jrq7a5aaa1/74I+DqCrRvb9l+5sTXX/PqoU4dw4/RZ4YbG8umtIcOAZo+\nl5GRQLt2wOnTHGJdTXo6m9d6eQEHDvAKRM2kSbxa+/tv4L33TBqeQCCwMfI03evChQvJ29ubnJyc\nyMnJicqXL08LFiwglSVNjAxEqvupqUQtW/JbsjEolURLllimX8aSkcHpXI1NhrRvH1H//tJ1v/5K\nVKeOttMfEVtL1alD9Pq1dvm5c0TOzkT/+VJm8uwZUenSHF7dCn9igUCQC5jw6M861pjGY8aMocKF\nC9PMmTMpIiKCIiIiaObMmeTl5UVjpKLk5TJSAzfFvPbaNT7Omg/FV6/YFDcpKavMkCXy8OEsIKQY\nP56oVy/tcb1+TVS3Luf8kGpfpAjR/fva5WvWsAlu9qi65uLoWwBifPaLI4+NKA+FRpEiRWjr1q06\n5Vu3bqWiRYua3AlTyT7wI0eIevY07hyPHhENGWJ6IiZLEh9PNHgwr5aIDLtxX76Uj4ablkb0wQe6\neoxr14jc3XXDmrx4QVSlCtEXX2iXZ2RwEEhvb8P8SwzF0X+YYnz2iyOPjSiPhcZ1ifCp169fJy8v\nL5M7YSqaA1dHr9V8U8+JFy/47f7581zonIncvEk0YYJxq56oKKJ27aSj4T58SFS5MoeL12TVKg6F\nrhlanYi36QCinTu1yw8f5vKvvjK8XwKBwDYxR2gYpQgfPnw4iAiLFi3SKh8xYgQyMjKwePFi0xQr\nJqJW5hABPXtyNruGDQ07VqUCRo9m09py5XK3n8Zy7BiHLxk+3PBjli/nkCBSoUZOnAB69ACOH2ez\nXIBNbzt0YF+PrVu1ld/9+gF79rBPiGY04I4dufzGDdubM4FAYDi5HntKzevXrxEeHg4/Pz+EhIQg\nJCQE/v7+WLNmDdLT0zF06NDMT16yYQNQubLhAgNgi6CQENt8+DVqxP2aNk1p8DEDBnCQwXPndOve\ne48FULduQEYGlykUnP71r7/Y+U+TuXO53YQJhpWbiqPbwovx2S+OPDZzMUpoXLt2DXXq1EGZMmUQ\nFxeHuLg4lC5dGnXq1NEKZHj58uXc6q8O0dFsKjtpkuHHrF7NntM1a+Zev8ylY0cgIYFXHYagUHBA\nxlGjgBcvdOsHDOA8IKGhWWXFinGgx+HDefWgxssLWLaMVy+a169UiT3lN2zg6LkCgeDNw2ZjTxmC\nQqFAy5aEFSu0/RH0sXcvcP8+0Lt37vbNEhCxMOzdm1dShrB/P/DrryxAsvPiBa9iZszgSLdqxo5l\nn47jxwEXl6zyzz5jb/Hz54ECBbjs+XOgShXgrbdYoGhuawkEAvsgz7anbJGePQ0XGBcuAGfP2ofA\nAPiBHBoKLF7Mqw5D+PBDdlD89VfdOjc31l8MGQL8FwcSAIceUal042AtXQr8+y9v5anx8ODvf/0F\nbNli/JgEAoF9Y9MBC3PCGGl57x7Ha5o3TzfQn62iVCoRFBSEZ89YjzB/PnS836V4/Zo9v7/5BqhR\nQ7d+1y7OwXHsGOcgAYBr13jL7rfftFPlrlzJ3vVnz3K8LID1GvXqcYDE69ezzmHq+BwVMT77xZHH\nBjhwwEJL8fw5h+qYOdN+BIYmnp6cHGnSJF4R5ESBAqx3GDoU+Ocf3fp27YDWrTkxlfq+8fNjodSj\nB0e9VdOnDxsY9OmTpUR3dmYBfPcuHyMQCN4c7F6nkVP309NZeTtlCmfAs2fOnmWdhaHWSzdusGDY\nsYO3lTTJyABatWKFe79+XEbEcbfy5wd+/jlLX3HjBhsNzJ3LgkjN55+zjujmTaBsWfPHJxAI8oY3\nWqehDyLehhk82P4FBsABDWvWBNatM6y9ry+Pv0cPTnmribMzsHkzb9edOsVlCgXwww+8baWZvdfX\nl/UdEycCcXFZ5XPnslCWiFgvEAgcFKOExqRJk/D999/rlK9YsQJTpkyxWKcsxdKlrBj29bV2T0xD\nyla8TRvWWRw4YNg5Gjdm/4xBg3RzfpcoAWzaxHnE4+O5rHhxFkrDhgG3bmW1HT0aePttNt1Vn+et\nt4ARI7i9WvCYOz5HQozPfnHksZmLUUJjw4YNqFu3rk553bp1sX79eot1yhJs28YPxSZNrN0Ty9Ov\nH1svGeoO07EjC05NKyg1777Lvh1du2bpLFq04Gt07Zq1Qsmfn1ch+/ezX4yaiRPZ/2P4cF2hJBAI\nHBBjYo4UKFCAbt++rVMeHR1NBQoUMDmWianIdf+vvzixkCOTkcERbv/917D2KhXRoEFEGzZI1/Xs\nSTRpUlbZq1dEgYHaZUREI0cSFS9O9PhxVtkPP3Bcqp9+Mn4cAoEg7zHy0a+FUSuNChUq4MiRIzrl\nR44cQfny5S0kxszj9m32URg50to9yV2cnIBZs9gi7L98WHpRKDil66+/cjKm7HXffQf8/jub3AJs\ngbV5Mx+j+Sf/6ivA3V17fkNCgMBAdhJ8+dLsoQkEAlvGGAnzzTffUJEiRWjlypV069YtunXrFn3/\n/fdUtGhRCgsLM1lymUr27ickaIcWt3cMCc/84AHR0KFE6emGnTM5mahFC6LLl3Xrbt0i8vHhSLtq\nli/nkOhPnmSV7d/PK4u9ezX7ymUzZxrWDz4m0vDGdogYn/3iyGMjysPQ6ERE48ePJ1dX18zMfa6u\nrjRu3DiTO2AOmgN/9Yq3XzQfbvaOoTfulStEU6caft7794maNpXe2vrtN96WUufNUKmI2rYl6tRJ\nO1x7cDBRxYraYeU/+4yoUCHp3B5SOPoPU4zPfnHksRFZIUd4SkoKrly5AgDw9/e3Wp5wzdDoY8ey\naW3FilbpitWJjGSv7gEDDGt/9Sr7XOzYwdtNmkyZAty5w2a3CgXnI69ZE5gzBwgO5jYJCYC/P1tm\nLVzIZdHRQLVqrEBfu9ZiQxMIBBYmT/009u7di06dOiE4OBilS5eGu7s7fvjhB0RERJjUAUswbx7Q\nqdObKzAAoFkzduDbudOw9v7+LByCg9nXQpPp04EHDwC1dXWJEixAhgxhwQBwhNzFi4FFizhfB8Am\nucOHc9vTpy0wKIFAYHMYJTQ2bdqEL774AlWqVEFMTAzS/rPHzMjIwNy5c3OlgzmxYQOHwHjnHatc\nPlcx1la8e3eOBWWoz8T777NX99Ch2uayzs7svzF/fpZA+PBD4MsveWWhNsPt1An46COgb18gNZXL\nJk0CSpY0zATX0W3hxfjsF0cem7kYJTTmzp2LVatWYeHChciXL19mef369XH+/HmLdw4AVCoV6tSp\nIxssMTmZYykJmDFjOJJtbKxh7bt0Aby92btbk+LF2Xqqe3fengI4ftfLlxxaHeCtq+XLgZgYXu0B\nHCdr1iz2Kt+61SJDEggENoRROg03NzdcvXoVFStWhIeHBy5cuIC33noL0dHRCAgIwMtcsLdcuHAh\nzpw5g2fPnulE0TVnX86RSU1l4TFypGFbdkSsCwkKAjp31q5buZIf/vv28QokKoozAe7dm+U4uXQp\nOwheuMCrvowMoG5dICmJdSemRsEVCAS5Q57pNMqWLYsbmine/uPIkSN4++23TeqAPu7du4c9e/ag\nT58+Fj+3I+Piwm/+ixfzdlVOKBT84P/5Z+DPP7Xr+vYFypcHpk7l79WrA2FhvAJJSuKyAQNYSPTr\nx1F41VFw4+KylOQCgcBBMMbUKiwsjPz8/Ojo0aPk7u5OSqWSwsPDqXjx4rR06VKTTbjk+Pzzz+nc\nuXOkVCqpbdu2OvVGdt/uMNfsLy2NaNw4ovPnDWv/7BlR8+ZEV69ql794QVSnDtGvv/J3lYqoTRui\nLl2yzHAvXybKn5/ou++yjmvfnk1w5bzWHd2sUYzPfnHksRGZ9+zMl5NQ0WTs2LF4+vQpWrRogVev\nXqFZs2YoUKAARo8ejUGDBllUmP3+++8oVaoUAgMDoVQqZZdSISEh8PHxAQB4eXkhMDAwM3mKWpll\nr9/VeiJTjz96VImWLYHt24Pw8iXw6pX+9mfOKNG/P9C/fxC2bAGuXs2q37oVaNhQieRkoFu3IKxZ\nA/j5KTF5MjBrVhCqVwe6dlVi5EigbdsglCsHdOigxK5dwKRJ3N7S47P172J84rutfFcqlQj/L3S1\n+nlpMqZImpSUFDp16hSdOHGCnmt6d1mQCRMmkLe3N1WqVIlKly5NhQoVoh49emi1MbH7bxwqFdHs\n2WPP/UYAACAASURBVEQREYa1v3yZvcaTk7XLd+8mqlUry/Fv714iT0+i6Gj+/uoVUbVqRO3aZa1A\nxowhUiiIDh60zFgEAoH5mPPsNPjI1NRUevfdd+natWsmX8xUlG/o9pSl+fZbfvAbQkQE0eef64Yn\nmTKFqHv3LKEwdChRgwa8FUZEdPw4C4mtW/l7UhKHJgGIQkLYG10gEFgXc56dBivC8+fPj5iYmMzU\nr4LcR728tBTDhgH//muYKewHH7Ap84gR2v4W06axCe533/H3sDBOpztzJn9v0IBzdwweDDx5AhQu\nDFy8CIwbx74fvr6cuzw11fFt4cX47BdHHpu5GGU9FRwcjFWrVuVWX2Rp2rSpjrmtwDTUjniGZP/r\n0YO9wTUtoNSOf99+C/z9N+Dqyvk1vvkGOH6c28yezfk3xozh7x4eHIIkKoodCseMAWrUyHIcFAgE\n9oNRfhoDBw7Epk2bUKlSJdStWxeFChXSql+8eLHFO6gP4adhOjt2cKiQnGJVEbEp7Ycfsve4mtOn\n2afj+HH2AF+yBFiwADh/nlcXu3cDbdsCERG8atFkzx5ewdy4wZkIFy4EqlSx/BgFAoE05jw7jRIa\nzZo109uJQ4cOmdQJUxFCwzz27+fsfyNHsq+GHGlpnP1v7FigYcOs8h9+4FXG/v28AmnTBihaFNi4\nkeu7dOGQJpcu6Tr4paayH8lXXwGvXrEQmTyZVyUCgSB3MevZaQGditWw8+7nSF7Yih85QjRjhnbY\ncymePiX64AOiGze0y3v3Jho/nv//4AFRiRJEGzfy94cPiYoWJRo7VvqckZGRdP8+K8gBotKlidat\n46yEjoCj2/o78vgceWxEeaAIf/HiBQYPHozy5cujRIkS6Nq1K+Lj402TUgKbokkToFUrjnirUsm3\n8/RkPUi/flmxqAD2JP/jD84IWKoUh0QfNIjjUZUsyVtW8+cDW7ZIBzAsXZqP+ftvoEIFjrrbsKHh\nQRcFAkEeY4hkGT16NLm5uVG/fv1oyJAhVKxYMfr8889NllSWwsDuCwzg0iWi0aNzznp44QJRy5bs\nJa7m9m02q1WvQgYPJmrUiM1wVSqigQOJnJyI6tZl3w65VU1GBtHatUSlSvHKo3dvXr0IBALLYs6z\n06Aj33rrLfrxxx8zv584cYLy5ctH6YbmGM0lhNCwLDdvEg0fzk56+vjjD87kp/nn37OHqGZNdgh8\n8YKoenWi0NCs+qgoog4dWBg0acLbYnI8fcoCLH9+dh785hui16/NG5tAIMgi14VG/vz56d69e1pl\nrq6udOfOHZMvbAkcXWhYY1/1zh1eKWT3Bs/OmjVEI0Zol02bRtS1K68kLlzguFPHj2u3OXOGqHVr\nFh716kXSqVPy17h+Patt1araOcntAUffF3fk8Tny2IjyQKeRkZEBFxcXrbJ8+fIhPXvKN4Hd4+3N\nVkxjx2ZFsZWiVy+2dFq0KKts6lR26Fu2jNPDzprFSZuePctqU6cOm9z++Sfw+jVQrx7w2Wfsw5Ed\nX19uu3s3h1tv3ZodDm/dstx4BQKBcRhkcuvk5IQWLVqgQIECmWV79+5F06ZN4ebmllmW1w54wuQ2\n93jyhIXH9Ons4CcFEdC7Nz/I27fnssRE9goPD+e8Gx99xApyKWdCIuDAAb7O6dOcW3z6dKByZd22\nr1+zgJoxg811R47kLIFWSk8vENg1ue6n0atXL4NOtnbtWpM6YSpCaOQuz58DEybwp1w56TapqUCH\nDvwAr1+fy86eBb74grP3EfGqo1kzYPx4oHZt3XMQcW7zKVM4adOXX/L/y5fXbXv/Pp9n/XqgbFkO\nY9Ktm34/E4FAoI3w03BQbGFf9eVLDkqojmQrxZMnRM2aEd26lVX2ww9EQUFsQXX3LivYCxUi+vBD\nokOHWO+RfXzp6USbNhFVrkxUoAAf8/Ch9DX/+ovonXdY39GwIdHp0+aP1dLYwt8vN3Hk8Tny2Ijy\nKGCh4M3E1ZXjSi1bxqsAKby8eDuqTx9A7b7z5Ze8zTRpEq8Y1Jn8GjZk7/L69YEjR7R9Q5ydeYvq\nyhX2/9i2DXjrLT7Hkyfa16xfn2NXrV7NOo569Tiu1qNHuTINAoFAjQWFV55j5923K9LTiSZMIDp7\nVr7N2bNErVrx6oSI/33nHaJt27TbJScTLVpE5O3NVlGrV0ub1L58ye1KliTy8iKaOZNIKn1LUhLR\nyJFE+fIRFS5MtHBhzv4mAsGbjDnPTrt+6gqhkbeoVETTpxMdPSrfZs8eTgOrDgUSE8OOf6tWZSVv\nUpOaSrR+Pft0lCvH/hjPnumeMzmZk0h5eXGYkgULsgSTJlev8vYXQOTvT7R/v8lDFQgcGnOenWJ7\nyoaxtZj+CgWb1R47Bhw8KN2mdWtWeo8bx999fDig4enTgJ8fK7Hv3OG6Y8eU6NGD82189x2wfTuH\nEpk8WXubqVAhVsbHxAD/+x8ryStXBlau5GCKavz8gL17gV27WEH/4YfAp58Ct2/nynTkiK39/SyN\nI4/PkcdmLkJoCIxCoWAfjmvX+OEsRd++gIsL60EA9rdYsQK4cIHNd5s3Z4ur8+fZcsrJicOoHzsG\n/PYbl/v4cCKnmJis83p5scltTAzQqRMwdCjg789RdTMysvrXti37fXz9NQu3atVYL5KcnKtTIxC8\nGVhwxZPn2Hn37Z7Vq4k0ostooVIR9ehBtGuXbl16OtHOnUTNm3PoEamtq4sXOa1sgQLsZX7hgu55\n7t0j6t+fdRnVqrHuJHtcq3v3+DwAb4Ft2pRzRF+BwNbJKdRPTpjz7BQrDYHJ9O7N/65Zo1unUACr\nVvEK4/Rp7TpnZ3YIPHgQ2LwZOHOGt5bGjWMLK4Az+23YwCuaYsXYYbBNG7a4UpuXlyvH21rXrwN1\n63KSqHr1gH37tNts2MCrmNKl2aejRg2O1rtiBXDyJPDyZe7Mj0BgaVQqXkHXrct+VFbBPHllXey8\n+zliL7biv/5KtGSJdF1iIvtwrFrFgQg10RxfYiLR/Pnso9G+PVFkpPaK4NEjoilTiIoUIWrQgFcq\n2fNuZA+KePiwdn16OvuPNG/OeT5YtBA5OxMFBBD17En07bccTFFKIW8s9vL3MxVHHp8tju3JE6J2\n7fie7dxZ2pLQUMx5doqVhsBsPvkEqFoVmDtXN2dGkSIcO6pgQaB7dyAkBDh8WLrdyJG8sggJ4bhV\ntWrxauXFC9aFfPUVK9E7dgQGDuQVw7p1rPQGWHfxyy+8cnF3B5o2ZWW4eqXj7Mz+IwcPsj9JbCwr\n3ydOBCpW5JAmw4dzHnNPT9bFdO7M4zp4EEhIyOWJFAhkuHiRV9F79nA4nc2brRdCx6h0r7aGCCNi\nW6itqqZOlQ/rERPDjoBHj3Lu8OBg6XAhQJaT3+7d/PAeOJAV5AALis2bOYxISgoLnD59tH9IR4+y\nAvzIEY6NNWMGUL26/jHcvw+cO8ehUNT/xsZm1VeowEEXNT9lyhg4QQKBCWzcyNupXl7A1q1Ao0bm\nnzPPcoTbGkJo2B5nz/Lb/owZ/GYvh0oFHDrEAiQ5mT3BP/kE0IiJmUlSEutNVqzgh/7QoUBQEAsm\nlYqtuObMAW7eBIYMYaur4sX5WKmgiKNGAQEBQP78ho0pMTFLgKiFyY0bWaulUqV0BUnFiiIelsA8\n1IE5ly3j1e+WLayXe/2aLRHffdf0c4vYUw6KLe6rGkJUFHto5+SVrR5fYiLRsmWcEXDwYHmv8/R0\ntsZq0YKoRg2i77/PsrpSqYiUSvZId3PjeFmxsVnHqlREO3aw7gLgBE81arAj4uzZfN6YGMPzkz97\nRvTnn+yxHhzMVmDOzll6kiJFiGrXjqTRo4k2bya6ds1xcp+rsdf70xCsPba7d4nq1+d7adSorN/S\nxYt8r5Uvb54FlTnPTpt96t69e5eaNWtG1apVo4CAAFq0aJFOGyE0ZHj4kGjrVqL79y3aH2OIjuYH\nt5Tnthqp8V24wIEK/+//iBYvJoqPlz42KopowAAORTJ6ND/w1Zw7x8KgQAE2+710KasuI4PoyhWe\nnqlTiT77jMjXl9PRAkTu7kTvvUfUpw8rxQ8elA+amJ0XL4hOniRasYKoXz8iX99IKlAgS5C4u3Ma\n3CFDOK3thQv2He7E2g/W3MSaY4uI4MgH7u58nxLxC9O8eUQuLkQffMDJ0szBIYXG/fv36dy5c0RE\n9Pz5c/L19aWrV69qtXF0oWESJ06wQwJApFCwqdHcuZzLNY+5d49XDqZYebx+TfTLL/xQ79KFs/ZJ\nZRd+8oTDilSpQvTpp/yDU1tdRUezYClYkKhtW/3hT1684KyC69axEGrVKmsaAf4Rf/ABC8KVKznK\nriEWVqmpLBzWrmVh0agRR/tVn7dAAY7P1a8fC5uTJ/ULWoHjolIRhYXxC4y/P4fFIeIVc9OmfK8s\nXGiZFas5z0670Wl8+umnGDJkCJo3b55ZJnQa2QgPB/r3Z83s4sXsWr1jB2/CA7yR3749x9aoXTtP\nNt0fPwamTWO/jA8+YE9xY/n3X86fceAA+2uEhOgmasrI4BAiS5Zw+8GD2VqrUCHg4UOejmXL2OKq\nb1+eCl/fnC1Qnjxh7/JLl4DLl/lz6VJW1N2KFfmcAQH8qVGDLcmkdDOafb11i/UjZ85k6UvUmRKd\nnVl3U7t2lo6kVi3OlChwTJ4+5WyYO3ZwLprVq/neXbeOdXiVK7O/UfXqbKzx999Zic9MweF1GjEx\nMVSxYkV6nu2V1U66bzIGL5FTU/kVGODX4cePtetjYnivpWnTrH2YihWJhg1jRYDUK7wFSUvjy0yb\nxpFyf/6Z39KN3QJQqViP8OWXRB99RBQeLp3L/MoVooEDdbeunj7lRVfjxkTFi/M0eHvzVtjgwURL\nl/J21L17+r3GVSqif/7hgIjffEMUEsKrhYIFs/w+/P2JgoIi6auvWJdy86b+aVapiG7f5tXVpEmc\nG71kyawViULBEYG7dOExHDxIlJBg1PRZHLE9ZRkuXeKVsrMzr5pVKvZLat+ef64TJ/LKOyODaPly\njuTcu7d5kQ3MeXba/EojOTkZQUFBmDJlCj755BOtOoVCgeDgYPj8Z4fp5eWFwMBABAUFAcgKOmav\n37/99tucx5OUhKBvvwUOH4by88+B/v0R9N9qTLZ9YiKwYweU+/cDaWkIKl4caNcOysqVgbp1EdSy\nZa6Njwjw8grC3r3AoUPfonbtQIwdG4QSJYw7X3IyMGOGEocPAzVqBKFXL+D1ayUUiqz2u3crsW8f\ncOBAEPz9gfffV6J2baBZM67fuVOJu3cBN7cgXLsGHD2qxJ07wP37QXBzA8qWVaJCBT6fnx/w7JkS\n5coBLVtK9y8iQokHD4BChYJw6RKwbdu3ePIkEP/8E4SMDMDFRQkfH6BhwyAEBAAqlRKVKgEdOgRB\nodA9X2SkEgkJgKtrEM6dA/bvV+LmTeDRI64HlChVCmjUKAh16gDOzkr4+gKffWa5v5e+7wbdn3b6\nXTNgYW5e7+BBYOHCIHh6AhMmKFGzJpCcHIQ+ffjvOWECMHhwEC5eBDp3VuLpUyA8PAgtWhg/nvDw\ncACAj48PQkNDHdPkNj09HR9//DFat26NYcOG6dS/8dtTZ8/yGvXhQ/aC69HDuOOTkznmxo4d7Azx\n7BmviVu35vO2aQMULpw7ff+PW7c4SOHjx2y6+sknWb4YhnLjBu/MnTjBznw9emj7TqhUvHW1eDFv\nXXXpwltIVaoAb7/NQ9bk9WsgOpodDdWf69c5CVVKClCpEoc9yf5Rm/lm5/VrPj77Fpc6ZErRotrb\nW+r/e3lJny8+XteX5ObNrPoyZbTNf2vXZv8SYQJsO6SmAqNH83ZqkyZsTuvhwebgK1eyX8b8+fw3\nCw3lrdWRI9kR9fZt/psb+3PXxGH9NHr27InixYtjwYIFkvVvtNDYtIm92YoX54f+O//f3pdHRXWk\nb7/d0OwgO8gisigIKCruOn5gTDSaOMzEOcn3S5wxapzRyYIZo/E3ifHEfJlkJmYcszueJOMYjTFG\nTUxc4tKJMSAuMSigiLIIhkWgWRpo6O77/fFY3NsbXBoQlHrOqdN3qb636t669dS71Fvjune91lai\n48dxrX37iMrLMZFhxgwQyLx5vT6Lrbwccy6KijAje84cdKJyOzu9nujwYdg/2tpg05g719SOcukS\nZtUWFKCjvXoVeaOiQCIxMeJvTIwpoQgCyiglE5ZKShAjKzbWkkwiI4kcHS3LW18PewkjEkYmVVU4\nHxZmSSQjRmB2vbVrnT9vOpckN1dcGdHX13IuSXQ0Igxz3F6UlcFu8eOPRCtWYILq6dNEv/89xnFb\nthA98ADR118T/fnPIPwPPkBUhJdeIjp6FFEK5s2zvwx3JWmcPHmSpk+fTiNHjiSFQkEKhYJeffVV\nmj17dnueu5001Gp1u6jZDr0ei1Js2IAZP7t2EQUG9uyNjUYM2/fsQSooQM89aRII5De/sbRE2wGr\n9buFujp07hcuwKg8cyZu39GEQSlu3gSv7t9PNGoUjIyJidbz6nSYqX7likgmbFuvB6EwMrFFKFot\n/iMlkjNn1O2qqWHDRBJhxBIba12Qq6y0lEouXsQ9lErc29z4Hh1tSUxNTfgvI5Jz53AdFnbF05No\n9GhTIomLs05w1tDR+7vT0Vt1U6sR1l+rxYTVtDRIEq+9Bin7gw8wiHnmGUx+/cc/MCH1/feJNm4E\niTz9dMeOFnJwV5KGHAw40qiuRjyNI0fQev75T/nTmu2FIGA4vGcP0d696HmI0FulpYFA7PTEkvth\ntrRgdJWRgf2pUyEAyflwBAGj7g8/BAmkpeHjDA6WV2RrhFJQgMQkFKl0wlReHh6o3/TpKVRSYqrm\nYtvl5RDerKm6wsJMpQCjEeoscyK5dAnlcHaGFMLIhP2GhZnWs7UVEoiUSM6fFyP9uriAZKVEkpho\n/Vlz0pAPQcA47/nn0UZ278axBQvQlt56CxGY338foW/S0kAYWVlYv+ZXv0LstaAg/K+62rY6VA44\naQwEZGejJZWVIR44i0t+u1FcDPLYs4foxAn0ZhERIoFMmyZfHLADBgPE+mPH0KEnJcEE4+XV+X9b\nWlD0b7/FaN5oRFHDw2FHiYxEGjoU6pzOSIURipRM2G9bG64llU6khEIEF1tzIrl0Cf93coJLsDmZ\nDB9uqp5qa4NNR0okFy9C7y0IkGSs2Uv8/EyfaX6+qfvvTz9B2iOC5JGYKNpHmAuwuS2Iwzrq6/G5\n7t6N8P1btmAQs2YN0cSJcKutrcWqlHV1+LwDA2HD0OsxNkxKwvs8eBASx2OPcZuGXRgwpLFrFyYn\neHsjLOvEiR3nP3+e6NNPMfQcOxa/cnUOXUFVFazYe/agJ9bpMPyZNw8kcu+9GLr2EgQBMXgOHMDa\nApGRuHVQkPxr6PVEpaWwoxQWIhUViRFtnZygU5YSSmRk5yQll1DMbSgeHjh/7ZolmeTloVOJiLBU\ndcXFod6M6LRaSBTmaq7ycpwfPNiSTOLjRSIQBJRfKpGcOyfaWxQK3FNqbB8zxrbxfqAiJwerVBYU\nwA7x0ENQlZ48iUjOTzwBCeL99yFRLF5M9OqrGBS9/rpotzh6FJLKpEmIxNxd/xROGncp1EePUsqR\nI1B4Tp6MoUpHxmijEcOSNWvQu/3yCyxrrq4Yqowdi9VbkpPRQ/SkaqszT6ypUy1ceHpaBXD1Kjis\nshIjtXnzoD7qDnQ6ouvXTQmlsBDVI8KjZUTCfiMiUHVb9dPpcB2p7YT9trZ2bJSvqrL06rp0CWXy\n8rKu6oqOFl/1zZumkxXZb309Xk1UlKVUMnw4/i8IEHSZNHL4sJpKSlKotFSsW1SUKZGMHdvzJrfb\ngZ5omzt3ggQ8PDCGKy2FVjkyEhP1CgsxCTU6Gp59R44g7PmTTyLwprMzbCD/+Aee5bPPQgLuCXDS\nuBtRW0vqWbMo5fRp+N9t2tSxEr+sDHHGT5zAEOXpp3H8yhXoHdj043Pn0EM4O0N5zUiEKa+lrkb2\ngnli7d2LxIa3Hh4gq4QEooQEUhsMlPI//4Pl9XrYH7SiAp5YhYUw+M6Zg+r2tNtpUxM0dlJCKSrC\n8epqNQ0dmmKh+oqIsP0qpYRibkPR6azbUGJioGYrKLD06rp8GWq56GjrhOLjAzIoLbWUSvLycE+V\nCnnNyaSwUE0zZqRQZSWIRBoJ+OpVsU6hoZYuwOa2lv6G7pBGWxukho0bMVZ6/30Yu3fvxvElS4ie\new6f6oYNeAerV2P9l5dfBsmePInPeMQI5O2O/cIaOGncbcjJgXqnuBgWsj/+seP8e/agJQ4ejEUm\nRo2ynddohO7j7FkxsRgWTk7oFaQSyciR3XPVMBpFZTnzL83JQa/OMGgQyCQxsZ1QKCFBvrW6E9TX\nwxMrOxtVHDsWnVZoKNwYe9PttL4eJCBVfxUXg1cFASNHc9VXWJh1IbC11bbKS6ezbkOJikIZrLkJ\nl5Whg7Km6oqIQPkKCiyN7wUFeK0eHnhN5p5cgYFoTswFmJHJpUuiC7C/v6ULcFRU/yYSOfjlF7jT\n/vADPKDuuQefr7Mz0UcfQZ364otYSGzhQpAEUxCMGgWnxb/9Dc9i9WrrqlbNt6dJd/A4BW1YZXc5\nOWncTdizBw7b7u5YmGLaNNt5tVo4ev/735Bp//536078nYEpsKUSydmzWEiCWUGZNJKcjNZtz32k\nqK42JRG2LV0ez9fXlEQSElCWgAC7b6vTgTzKypCqqixXEXR3B6FIk5ub3be0CUGAAdTcnnL9Omwt\nROiApYQydChRSIilr4FcQpFKJ0FBmOzIVFx5edjOz0fnbcsQ7+CAvOZkwtRUAQGWUkliIsg5O9vU\nRpKTg5E5EdRr0nhbY8eCyHrRr6JH8f33IIyGBkzGO3UKUsbixfikV6yABPr667DDqdXYfvBBPItX\nX0Vbe/55vGMTtLRQ4eufkeMHb1P4L6fJ6OFJysJrdosgA5s0Pv0Ub+pOH6IYjZBhX34Z6zp+8QWp\nCwpsi8hnzsBHT6PBEGbOnJ4tjyBgSCwlkbNnoRR3cIBkwKSR5GTYTLrYs1qoAAQBBglGIlIyYdH8\niNArSUmEbfeQwrexUSQVlphLKoNSiU43NBQfeGgoOnip1NJdvbgggNTM7Sk3bqC5KBS4t7lNRWoQ\nJwKh2FJ5tbTgP1IyiYqCpFNaamk7qaqCJBQXR+ThoaaZM1PaCcXNTXxdUpuJNLijlExGjkSZWfBG\nln7+GeUiMjXHsZSQ0DNa1I7QlXcnCJAUVq2CGnDdOkzC02hgo8jMhMfUqlXwC3n3XWiPn3oK5Pvq\nq/BmW7MGnnxS6K6U0JW/vE9Dj/ybPJpvkhAbR4on/wwWkuMyaAMDmzSOHYPenIUuvRNRXw8fuq++\ngsz63ntELi7WG67BAMvYiy8S3XcffPe64i7UHTDlt7lEUlGB3nLECFOJZPToDsPIyv4wBQFyv5RE\n2HZDg5gvONhSxZWQ0CuhUAwG8JuUWKqqRPULEVFRkZoSElJ6TWoxGvFYpIRSWChq/hwc0MFLCSUy\n0tSdWEooUjKxRSgBAah7SQkM4U1NiNt17Ro6eKlUEhuL5OGBa0vJJCcHROzgAOnFfNZ7ayvUW1IX\nYPaqVSpRi8okk1GjelYalNs2GxogSezaBY3y8OGwU8ydi/0XX0R9HnoIBJKSgnFhZSW8pzw8EBrE\nJHSOIFDljqNU+8o7NOzSl6RQECnmzYM2YcaMHhkgD2zSEATI8ps3402kp99Zfn+XL6N1XbkiTvm0\n1SiuX8cIIzOT6I03sGi2tbyscw8M7P7U0c4gCBj6Sknk3DkcUyjQayQn42uKiBCTLcV9V+9dWmpJ\nJLm5UN0xhIWZkkh0NIjE0xOjNS+vXntOjY14FOZSi/SrUyrxqqTEYi612IPO3IlVKrwKc/UX41hG\nKNZUXs3NpiqvoUPxCHU6MpnMeOkSnoF5vK5hw0AyN26YksnlyyAlV1cIs1J3YE9PU++tc+fEurAx\ni1QiGT26W4PxTpGXR/Tb30Kdt2IFfD/y84nWroWqKisL3dGRI/gU/vlPSEivvIJn/9e/oikyCHX1\ndOXFrTTok3coqOYSGf38Sbn0CSx3MGSIJKOAhxwRYXfZOWkwVFai4x02DJ5E/T2wzv79UDE5OWGo\n0tHIZtcueFENGQJjd0KCZR5BgLSybp24hkZgIDrN8HDxV7odEtI7HWZ5uUggzJ2muFj0VVUq0Tsy\nEmFuRSwNGWK/3YRNnzZXceXliXoPc6hUIoFIyUTOtnTf07PLc2KkUgsjmMpKS1uLm5upOiw0tHsT\n7MzdiRmpmLsTS6UU5k4sl1Cio0UTlFaL18LUXcXFkHqsuQdrNOB+ZjcpKsI1fHxEIklIgJDd3Ix7\ns6Z244ZYx5gYS8+tnvBE2rULE/bc3KAd37IFY6Pp0+G7kpYGKerUKZga4+KghjIYQBaxseK1tKdz\nqXDlOxSTsZVc2hpJmDCBFE8+CWs5m+ckCPiedu4k+uwzvLyyMrsNPgObNC5etOxAs7LgCL1gQfdW\nX+8tGI1oQWvXYji0Z4/VUYNaraaU5GQoQD/+GMOZV1+1nDAnCHAPWrcOQ8s1a6Cua2jA/vXrlr9s\nu60NX545sUgJJiSk55TIGg16gOJiUh85QilOTu37VFwMmwlDUJApkZiTS1eHkQaD2DM2NCDV1yPZ\n2pbuNzXJu4+rK5GXF6kdHSklKKhz0vHxgVLb11dMVqQwrdbS1mJepJ6UWjpyJyYiam5W08SJKSZS\nSkQERtXFxZZkcuWKSCgxMcjr5obPob4e12eEIo3XFRuLvI6OeAZXr1oGdwwNFckkPBxlqKkRY28V\nFor1Cg+39NwaPNhUaLelnmprg6H6zTdBEq6uIIalS+Ex1daGsd/+/fCemjsX2uTmZpBFfPytC+n1\nVPrul9T6z7cpqug4GZ2cSfl/H4GmYfx45BEEeA4worh6FeLUww8jxcV1/aXewsAmjSVLYGlb6HOa\nywAAHbZJREFUsQJO0QxGI8Kd5udDRuwvM4waGmC3+OILSBmbN9tUxqrffZdS3nwTX8p//gMbhhQs\nrsC6dfhKn38e/n1yR+hGI766joilrAx6DjnE0kV1k9UPU6uF6C0lEpaKiqDEZ03W29tSQpESi59f\nzzpI6PXQtXRGLre21VeuUIqrq2W++nrRZcgWPD1BHuZkIt03P+frSwaliqqqTIlFKrWwXya1SFNX\npZavv1ZTeHiKifqrpASDYCLRnVhKKsHBaF4dEQqTTlQqPKbaWthMrMXrCg1FvqYmXJdJJtLgjomJ\nuKarK+5x/TrsJZcvi88jKMjURtLaqqZHHkkxaT7l5ZAqTpxACP7MTJGs9u/HHNasLLjZLl2K4IM1\nNSAL5gWvv1FJ+c/9m0K+ep+8G0rJGD6ElMuXwTDCRLLcXJEoLl1CJRhRJCZym0Z30F7xsjKopXJy\noOefM0ccWmk0OBcQgA61N8JpyAWLmJeXh+HHihXWG4DBAGftdeswVNmyxdTNVBAQA3zdOnxNq1dD\n79kbfqFGI3qdzojFYECPYItYgoNB3B4e3Wv0ra24p5RIpMQi9Vd1c7MuoQwejHNubuhJpNsq1e3x\nxNPpRAKprYVyvqYGSbptbV9qbTeHTLJpdvWlijZfKm3ypZJGXyqtUJFWa1p1hUKUWqQeYnI0Ih25\nExsMyBMYaKr6Cg3F6712zXK2fHOz+Ao9PVGG5mYIplevIo9KJRrfg4MhHLe0mIazlwZ3jI3F4zAa\n8Vjz89GFsObj7S1KIpGRsEXU1YnzKR54ACHNo6JQX3d3CPl79mBs87//i/+SIFDtwVP0ywvv0PCf\nPyNHQysJM2dCBfXAA6jMlSsgip07wXpDh4KhHn5YDAgqCBCdDh1Cu1m/3p6Wd+vdDmTSWLQILD15\nMgjivfcQqOUPf8BqO2z0e/EiRvW/+Q1RaurtL+yhQ4hQq1SiYcycaT1fURHUamfPwnK2dKn4JQsC\n6vbSS2jhq1aBJPs6cpzRCJedjoilogIdpYsLeougIPzaSkFBUD531VhuMECpbU1KYdu27BpE+ICt\nkQnb7uhcV/7j4mKfzojpcuQSjHRfDtn4+2OAEhhIQkAgNboGULVDIJUbA6hUF0ilugBqdAukNpU4\nQDGXWkJCOl97nXlXS9VehYXobK25E4eF4dXU1oreXYxUmppgAgsORlkEAQJhRQXyaDQgm+HDRd+Q\n1lbcv6BADO7o5QX10eDByKPVognn5qLpMlJzckJ5rl0DgZSWQpo4exbNa82aW1rx5mYq/NunpPr3\nOxRWfhZzKx5fiG82Lg6VZkTx00+4ASOKCRPwEKqqENft0CEMFLVaeFD9+tcIYmUnBjZpbN+OkXhF\nBSxTCxagxX78segHt3gxOlZBwLGsLCgczZ2iewOCAKlizRqIlnv34iuwhh07IDFERxNt307q8nKo\nbwQBrhkvvQQp5bnnoPs0/zKbmhA7Y9s2DIGUSuTpzJjb0XkPj56ZXSUIUNNUVrYn9YkTlOLtbXKs\nPVVXi1OmbZGK+bFBgzqXElg5mpvxvJqabG/be665mai5mdRElNJRWRiRdGRgt2ZsN09y3pE52dgi\nmJs30VGx92CLYN3cSO3pSSlDhpDeL5C07oFUpwqgKmUglesDqMYxkLRuAaR1D6Qm9wAyqFys2lps\nFdtoBPebz6avrMR5qTtxWBg4uLUVUoWUVLRa3MvPD3na2iAtlJWhg/fygu0kKEi8RnU1UV6emmpr\n8faCgkAk58/DjnHpElRSZWUY09XW4l6rV0NDrrtcRFeefY8ij20h95YaEkbEY27FggW4+WefgSiy\nsnDx3/0ORDFlCsScjAyQxKFDmLQydixU07NmIWKhQoFCdsPVfmCTxkMP4aGPGIGX8cknWMVuyRJY\npPbuBalMnQo/Z39/tKRNmzBk+POfey8Sq1YLwtq5EyOIDz+0LhXU1aFsn3wCQli/nsjJCTp/hQIG\n84sXsT7kk0+i82AwGDC1dNs2+Pbddx8a5/TpaFxarahTl2P4Nd9uaMAXrFTivl3xLJIeGzQInaTc\ngIV6PTowa4RSUWG539wMqaQjUmHJxwdDSWdntAH225NqKaOR1IcPU8q4cR0TT1NTx0Z46fG6Otu2\nEHf3rpONtXPOzqaSrVaLZ8yIRPKrzs6mFKXS9Bxb4ckMgqcnGXwDqMUrkBpdAqhWFUg3lZBkGLFo\n3QPJ4BtAPsMDaHCEUzu5WJNabLkT19TgPHMnDg/HozEY8KivXxcJpbERzcHbG1prnQ7/LymBkT8y\nMoWCgsDrzFtMocDncO+9eFxM4P8/vzJS5fYjpPl/b1PMpf2kcFCSIi0N/UtcHKI77NyJoFL+/pi4\n8fDDWCijqEgkiePHcWFGEjNnom1mZuK/J09Ch/boo3C7txMDmzRefhkvJD+faPZsOE47O8Mt9cIF\ndKALF+L8W29BAfnss2hRV69ivv+MGdAt9iQKC6EKy86GfWLVKuud0smTmNjX1gbD/YwZOH7iBCSL\n8+excPBTT5l6C124AA+xXbsw7HnsMcQj6G54D1swGPCV2UM8dXWm3keenvhSvb1BJmzbWpKed3e3\n3bGzzs2cUKyRjUZjvXNzchJJREoocvbtPefsLKqt3N3FbVtDcKktpDOS6ei4dFKk+TPw8UHy9ha3\npcnWcXd3XNcKwbS/A+mxqirRgGAGvfsgavIMpDrXYKpzDaZG9yBqdA+mRg8kpyHB5DU8mPzjAykk\nQkVBQaaPzFZ0YlZtFxcQyqBBGA/pdKINJj8f+fz8RBOcVguhKywM49OiIozhUsfWUcELH5P3jncp\nsDafjP4BpPzjUiyckZkJovjuO9zot78FUSQn4/tmRHHjBqIV3ncfkocHFo358Uf0DxoNJIypU5FG\njeq2bXZgk8Znn0GiqK0FeezaBRXOrFkYDlRXQ+0zdCikj5AQSBkuLnjriYkIBHP4MHSNw4Z1v2BH\nj0KyMBpBXvffb5lHr4dE8corUKFt3oxWevIkyOLMGZDbM8+Is63KynC9bdvQsTz2GO7TjVhMtx1M\n4azRgEw0GuvJ2rnGRlzD3b3rhOPtjY+R2REEAcTR2ooeQ6cz3Tbfl7Nt73+YxMHcjohEMmFEYuvX\n3jwqFXpCc3Kvq8O3xJJGY7ovPW5uI3FwsCSUjojH2xv/aWtDj2yuGmNEX16OxFaFMkOzux81uAVT\nwy1C0boHUaNHMOl8gsllaDB5Dgsmv/ggCk70J89BeP+duRO7u0Mz6uSE8VJDA5pMRQU+y6leF6hk\n9TsUc2obObdpSZg0iRQLFyLTF19gQQw3N3zb8+fj2z5+HCSRmQkr/H33QZLw8oJB5ORJWNj9/ESC\nmDrVVI2u00E/plB0HJi0Ewxs0mB+eUlJGKXfcw+I4dAhEMjFi3g5iOUM9v7d75B33z7Io+np8I1+\n9120mmee6dySZw2CgFgBK1eiUezda52Erl2DeHnhAgjs8cfRkF56CY1mxQqi9HRSnz+PeRpffAGp\noqQECwY/+mjPkFsfw67YTIKAd9RVwtFoxC/f0RGdJktsX3q8s20Z59WFhZSSkNB5XhcXJDZ6FAT0\nVAYD2nZzMzr4pibxV7pt69f8mFYr+pgqldaJham5mCpSmqTHPTzQPpOSMABqbRUHA7ZIRrpvrmZT\nKESSl5KLn5+YPD1RbqNRfC5MsmHEwpJ5sDAiMiodqNEtsF1aYQRDwSK5+IwIJv+EIDqY8ROFD0lt\nJ5TiYqIZv2qjpKJ9pP/X2xRZ/B3mVvxuPr7FrCwYrJ2cIPHfcw/e3/HjOE6EQey0aahnfj5IIi8P\nmgJGEBMnop7MKzQ7G+nCBfRVTk4Qde6/H9KJnRjYpFFWho72++8hBv70ExrWuHGQQGJjIad+9RUe\n/vTp0HdnZ4MY5s/H+cuXIWmMHg011tixECXl6rmbm2EV27YNo4utW01tD0RoCP/9L/ScI0bAhlFb\nC7I4eRLktWIFyvXtt6TesIFS8vPRCBcsEI1gHaG2FlLKpUv4mI1G3NdotEy387iTE1RnLLm5kfqX\nX9CpSo8z47D5Menx7rpNt7Xh2Uh/e2FbnZ9PKeHhnefX6TDStpZ0OtOp4Yxg5CbmqeXiAunFwQHf\nh3TiBntHjKTa2kACzN5intg8lJoaSmlpEVVMzs4dE42EcMjZGeVgRgL2PNizaGxEW2YGepY0Gsup\n8t7epuTi64v7ODmJdWXXZsR28yZReTkJFRWksKIiO6JUUbJnSDu5tLr70tD8QzSo8QYZwyNIOW0K\nrnPsGOowezZcr+rrQRSXL+N7nTABz+DGDRi4GxtNVU0jR6LvyMkRCYK5c4WGQpoYNQr5emoFJhro\npNEbF2aNWRCwzfalCQUQk16Pl//yy/C/M3enrK0lWrYMxvo1a0AE69eD7J5+GjLvtWsgnb170dgW\nLEBjtDUbW6sFSZ4+DaKoqcHobNw4NGBm3GV1kKbbeVyhQCd0y6uo3Rgs3e/KOeboz8CasPS9dERC\n0s5TqRS3zX9v1zmVCu+KSSC2BgZGI56jLYKxJzU3W24z6YQRFnue5moud3eRlBwcQObsvQuCSEh6\nvSiNMFJg79KMiNolBOb5N2iQafL0xP1UKtyTfafs+qz8TN3GyMbcC8zJCQTj44PrurnhGDOM6PXi\nterqSKipJQoNIYW7O6aYG43wdgoJgZ/wjz9im615W12NbzMgwFSKaG0VySEnB9d3dwcpjBwJgoiK\n6vUQSAObNDZsEBuoNBHht74eBm+W2GJDoaH41WigO/X3R2fEZjQ1NMCxW6FAQx43TozRZO1+goCJ\nePfea1nQ774TV4F/4QVIPWo1PKHmz4dNZft23Pexx3DMPOhiWxtE1NOnIQqXlaGxjRkD1dq4cfgI\nOPAeWcdkjYR0OnFkLR1ly/ntjbzS0X1nM8VtQaEQSYcRUFd/VSq0calkwn5ZGzcYRBLQ6US1ly01\nWUfnGEEIAu4hJSGp+pCRK8vLysCkB/ZeGxuR6urEyR6eniLZuLmJ12YEx67H7CpM5VVfL16Hga0t\n4+EBF6yGBoQw8vbGoPD6dajJp05FPhcXuGmxBVwcHEAITHpISOh8jpVeD3Ubm/dUWoo+KzW141h1\nnTaXu5Q0Dh48SOnp6WQ0Gmnx4sW0evVqk/N2VbywECLlsWMwWFdUoLMdMkRcZi00FA0iKgqNJjUV\nv4mJ8MSSO2+hrQ2ztv/2N5CJUgmvicWLYdxiNpXHHoOtgsWfMhqJLl8m9datlNLYiAbK4kGPH48U\nGtq1evdD9PQa4f0Nt7V+TAUjJR9bv7bOSR0DpOoxG9vqigpKkUb/k0p80u9SareRkhLbd3YWVY5S\nd19GvIykWDmZAwEjCZYaGvCr1YqdPbuPkxPuISUgdn2pmvDWIEPd2EgprA5Muqquxnfr44OOW6GA\nqikqCudra2GraG1FnyJVLYWEWEqQbW2QUqSTYevqTPM5OGCSCIuuEBYmbz5SJ7grScNoNNLw4cPp\n6NGjFBISQuPHj6dPP/2U4iRBurq9cp8gwBB19ChIRK1GY/DxQUOvqsILEgRIIvHx0Cv+6U9oLB3h\nyhUYrHNyYL/IzYVBvq0NxvmHHgJZjB6NBnP6NFJODu43fDhtvHmT0teuReyZ2xHaoifAZkfdvCn+\n1tSg3mYqvo1Hj1I6k8zM1X89nczvYQ5r7aibxzZ++SWlz5vXcT5WLqn6ylydZW1fTh57/sPUiTKw\nceNGSk9P7zgTUx11QkBWtzuSFpubO57hLnV4YGTB1FmM1BgxMcmFEahORxuvXqV0b28QUGMjyjJ4\nMLQP7u6iDy4zTDPVUmwsjrW2wo7BpIPr10XvPwZHR5CJNOROb8Zyl6A7fWcfBmLqGFlZWTRs2DCK\nuDX6fuSRR2jfvn0mpNFtKBQggvh4zIMwGKCHZFLI99+DRFxdxdDeLi4IZ/mrXxG99prlrExBwCS+\np57C/1hjZC6fbC7FuXOwf+h0kHLGjwfJxMe3j7o069b1rZdUS4slATAdsV5vvRNkumJ/f/yyAD8q\nlYU6T3P5MuKE2VL39VQisjxmrWPs4WMaR0fTdRBs/dfcgUCq3mIj4c7ydLbflf/IhIYNsnoSCgXa\nP0seHuIgTqpGk7OvUIiqJ3O1WkeE1NREmsZGqJrYeZ0OcUpGjcJkPT8/kAAjhfx8JAaVCtqAsDBc\nZ+5cS8eYOxT9ljTKysooXOKfHBYWRllZWb17UwcH2AbGjcNkPJ0OnlnHjsGF9/RpURS+ehXzP2bN\ngmuvkxNG1I88Ahc71vjj4sSlyKqrib7+GgQxezbiDvTWZDxzNDVZJ4CaGnxQ1gjAxcWUABISRO+U\nngiV7uV1V6jZbGLwYNic7lasW4fUk5CO/JnaSJqkKjbpfktLx+el+zYmFLaDqdAGDxaPscHGzZuw\nKYaGQjpITiaaN88+F/07FP2WNPoFnJ3hojt9Oj4OrRZSxldfwR5RWopYT87O6Ezr6tAgHR3RoIYN\nAwElJoI8nJ1NG29WlvXGfWu76OBBjLKkxztSj5jrkqVwczMlgKQkkQD6KPJvEVtZ5y4Fr58dYCoy\nler2DaisoGjhwp4nxLsE/damkZmZSevWraODBw8SEdFrr71GCoXCxBiuuFP0/BwcHBz9DHedIdxg\nMFBsbCwdPXqUBg8eTBMmTKAdO3bQiBEj+rpoHBwcHAMW/VY95eDgQG+//Tbdd9997S63nDA4ODg4\n+hb9VtLg4ODg4Oh/6N256j2EgwcPUlxcHA0fPpxef/11q3mefvppGjZsGI0ePZrOnz9/m0vYPXRW\nv8uXL9OUKVPIxcWF3nzzzT4oYffQWf22b99OSUlJlJSURNOmTaMLFy70QSntR2f1+/LLLykpKYnG\njBlD48aNo2PHjvVBKe2DnG+PiOj06dOkUqnoiy++uI2l6z46q993331H3t7eNHbsWBo7diy98sor\nfVBK+yHn/anVahozZgwlJiZSqpxVTYV+DoPBIERHRwtFRUVCa2urkJSUJOTl5Znk+eabb4Q5c+YI\ngiAImZmZwsSJE/uiqHZBTv2qqqqEM2fOCC+88IKwYcOGPiqpfZBTv4yMDEGj0QiCIAgHDhy4696f\nVqtt387Ozhaio6NvdzHtgpy6sXwzZswQ5s6dK+zevbsPSmof5NRPrVYLDz74YB+VsHuQUz+NRiPE\nx8cLpaWlgiCgr+kM/V7SkE7yU6lU7ZP8pNi3bx/9/ve/JyKiiRMnUl1dHVVUVPRFcbsMOfXz9/en\n5ORkcuwj19juQE79Jk2aRINurRkyadIkKisr64ui2gU59XNzE9fTbmxsJH9p6I1+DDl1IyJ66623\naP78+RQYGNgHpbQfcusn3KEafDn12759Oz300EMUemu+lJy22e9Jw9okP/NOxTxPaGjoHdPxyKnf\nnYyu1m/Lli10v7VFq/op5NZv7969NGLECJozZw5t2rTpdhbRbsip240bN2jv3r20bNmyO65zlfvu\nMjIyaPTo0TR37lzKzc29nUXsFuTULz8/n2pqaig1NZXGjx9P//3vfzu97p03dOW4a3H8+HH66KOP\n6IcffujrovQ40tLSKC0tjX744QdasGABXb58ua+L1CNIT0830ZXfacTRGZKTk6mkpITc3NzowIED\nlJaWRvnScCF3OPR6PZ07d46OHTtGWq2WJk+eTJMnT6aYmBib/+n3pBEaGkolJSXt+6Wlpe2ilDTP\n9evXO8zTXyGnfncy5NYvOzubli5dSgcPHiQfH5/bWcRuoavvb9q0aaTX66m6upr8+nkoezl1O3Pm\nDD3yyCMkCALdvHmTDhw4QCqViuZJAzX2U8ipn4ckPMj9999Py5cvp5qaGvLtwQWRegty6hcWFkb+\n/v7k4uJCLi4uNH36dPr55587JI1+bwjX6/XtxhydTickJSUJubm5Jnm+/vrrdkN4RkbGHWVIlVM/\nhnXr1glvvPHGbS5h9yCnfsXFxUJMTIyQkZHRR6W0H3LqV1BQ0L599uxZISoq6nYX0y50pW0KgiAs\nXLjwjjKEy6lfeXl5+/apU6eEiIiI21xK+yGnfnl5ecLMmTMFvV4vaLVaITExUcjJyenwuv1e0rA1\nye+DDz4ghUJBS5cupTlz5tA333xDMTEx5O7uTh999FFfF1s25NSvoqKCxo0bRw0NDaRUKulf//oX\n5ebmmoyC+ivk1G/9+vVUU1NDy5cvJ0EQSKVS9X5wyh6CnPrt3r2btm7dSk5OTuTu7k47d+7s62LL\ngpy6SXGnhfWRU7/PP/+c3nvvPVKpVOTq6nrHvDsiefWLi4ujWbNm0ahRo8jBwYGWLl1K8fHxHV6X\nT+7j4ODg4JCNfu89xcHBwcHRf8BJg4ODg4NDNjhpcHBwcHDIBicNDg4ODg7Z4KTBwcHBwSEbnDQ4\nODg4OGSDkwYHBwcHh2xw0uDg4ODgkA1OGhwDDo8//vgdERuJg6M/gpMGx10FpVJJDg4OpFQqLZKD\ngwMtWrSINm3aRNu2bevrotqNgwcP0rPPPkvfffddp3k//PBDWrJkCVVWVt6GknEMBPT72FMcHF1B\neXl5+/ZXX31FS5cupfLy8vaQ3a6uruTp6dlXxesRVFRUUHp6Og0ZMqR9/y9/+QtlZmZSQUGBSd5F\nixaRo6MjtbS09EVROe5CcEmD465CYGBge/L29iYiooCAgPZjnp6eVtVTf//73ykmJobc3NwoKSmJ\nPvnkE5PzqamptHz5clq5ciX5+flRYGAgvfXWW6TT6WjZsmXk7e1NERERtGPHDpP/LFu2jNLT08nX\n15d8fX1p1apVJtdtbW2l9PR0Cg4OJldXV5o8eTKdPHmyS3UOCgqi1NRUmjVrltXzPLwcR0+CkwbH\ngMdf//pX+uijj+i9996jvLw8WrNmDf3pT3+iAwcOmOTbvn07eXl5UVZWFq1Zs4aeeeYZmjdvHsXH\nx9O5c+foD3/4Ay1atMhEFbR9+3YSBIEyMzNp8+bNtHnzZtq4cWP7+eeee4527dpFH3/8MZ0/f55G\njhxJs2fP7vJyxYcPH7ZJGhwcPYreieTOwdH3+PzzzwWlUmlxfOHChcKDDz4oCIIgaLVawdXVVfjh\nhx9M8qSnp7ev0SIIgpCSkiJMmTLFJE9AQIDw61//un2/ra1NcHJyal9TIiUlRYiNjTX5zyuvvCKE\nh4e339vJyUnYtm1b+3mDwSBER0cLL774os16ffzxx0JxcXH7vtFoFAIDA4UPP/xQ2LVrl/D444+b\n1Mc8PwdHd8BtGhwDGrm5udTS0kKzZ882Oa7X62no0KEmx0aNGmWyHxgYSCNHjmzfd3R0JB8fHxNJ\nY9KkSSb/mTx5Mq1du5YaGxupsLCQ9Ho9TZkypf28UqmkyZMnd2kt6rNnz5KrqyulpaWRj48P3bx5\nk3bu3ElTp06VfQ0ODrngpMExoGE0GomIaP/+/RQeHm5yTqVSdbivUCisHmPX7A66sqDR4cOH6Ykn\nnmhfJvf06dOUnJzc7TJwcFgDt2lwDGjEx8eTs7MzFRUVUVRUlEkyJxF7cOrUKZP9jIwMCgkJIQ8P\nD4qOjiaVSmVi+DYajZSRkdHp6mlSfPvtt3TPPfcQEVFLSwvt27eP5s+fTxqNptvl5+AwB5c0OAY0\nPDw8aOXKlbRy5UoyGo00ffp0amxspMzMTHJwcKAlS5Z06/o3btygFStW0LJlyyg7O5veeOMNWrt2\nLRERubm50bJly2j16tXk5+dHkZGR9Oabb1JlZSUtX75c1vWbmpooNzeXJkyYQEREBw4coOTkZPLw\n8KAdO3bQ4sWLu1V+Dg5zcNLgGPBYv349BQcH04YNG2j58uXk5eVFo0ePNnGPtaYusnVMevzRRx8l\ng8FAEydOJKVSSU888QSlp6e3n3/99ddJoVDQokWLSKPR0JgxY+jQoUMUFBQkq+zZ2dk0a9YsUiqh\nNIiMjCRfX1/aunUrLVq0SPYz4OCQC75GOAdHLyE1NZVGjhxJmzZt6tHr/uc//6HU1NT2yX09nZ+D\noyNwmwYHBwcHh2xw0uDg6CV0xQOqq+AKAo6+AicNDo5ewrFjx3pcNUWEsCGbNm2SHbDwxIkT5OLi\n0uPl4BiY4DYNDg4ODg7Z4JIGBwcHB4dscNLg4ODg4JANThocHBwcHLLBSYODg4ODQzY4aXBwcHBw\nyAYnDQ4ODg4O2eCkwcHBwcEhG5w0ODg4ODhk4/8DVuBQ/Lt6sfAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa804b92c50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Obtención de la lluvia de diseño.\n",
"Intensidad = [40.9, 49.5, 55.5, 60.6, 67.4, 75.7]\n",
"# Lluvia efectiva \n",
"lluviaTr,lluvEfect,S = cuCap.GetHU_DesingStorm(np.array(Intensidad),\n",
"\tTcCap,\n",
"\tCN=CN,\n",
"\tplot='si',\n",
"\truta=ruta_images + 'Q_max_LLuvia_Efectiva_descarga.png',\n",
"\tTr=[2.33, 5, 10, 25, 50, 75, 100])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Se presenta en la figura como para diferentes periodos de retorno se da una pérdida de la cantidad de lluvia efectiva "
]
},
{
"cell_type": "code",
"execution_count": 92,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAEYCAYAAAB/QtA+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVOX+wPHPgMgiIKCCsggI4gY6oImVImZp6dXMLM1y\nrZulZlb6u/da1zZbTDMtq4u2mGWbtqi5lAvghhtuKCqyKLK4C24swjy/P46MIGjAnGEO8LxfL156\n5pw55zuPNV+eXSeEEEiSJEmSSqwsHYAkSZJUt8jEIkmSJKlKJhZJkiRJVTKxSJIkSaqSiUWSJElS\nlUwskiRJkqo0mVgMBgNhYWEMHDiw3LnY2FhcXFwICwsjLCyMGTNmWCBCSZIk6XYaWDqAisybN4/2\n7dtz6dKlCs9HRESwYsWKGo5KkiRJqgzN1VgyMjJYvXo1zzzzzG2vkXM6JUmStEtzieWll15i1qxZ\n6HS6214TFxeHXq+nf//+JCYm1mB0kiRJ0t/RVGJZtWoVHh4e6PV6hBAV1kw6d+5Meno6+/btY+LE\niQwaNMgCkUqSJEm3o9PSWmHTpk3ju+++o0GDBuTl5XH58mUGDx7M4sWLb/sef39/4uPjcXNzK3fu\nTrUeSZIk6fZMSg1Co2JiYsSAAQPKvX7q1Cnj33fs2CF8fX1vew8Nf7xa5/XXX7d0CHWKLE91yfJU\nl6nfnZocFXarqKgodDodzz77LMuWLePzzz/HxsYGe3t7fvrpJ0uHVy8cP37c0iHUKbI81SXLU1s0\nm1h69uxJz549ARg3bpzx9QkTJjBhwgRLhSVJkiT9DU113kvaNXr0aEuHUKfI8lSXLE9t0VTnvdp0\nOp2c8yJJklRFpn53yhqLVCkxMTGWDqFOkeVZnp+fHzqdTv7U4I+fn59Z/i0128ciSVL9cuLECdnC\nUMPMNSVDNoVJkqQJ8v/Xmne7MpdNYZIkSZKmyMRiIevXw44dlo6i8mSfgLpkeUp1mUwsFpCfD489\nBi+/bOlIJEnSijfffJMRI0ZYOgxVyMRiAb/9Bjk5sH8/FBdbOprKiYyMtHQIdYosT6kidWV9Q5lY\nLODLL6Ezu2l5NZFjxywdjSRJtZ3WBj3IxFLD0tJg+4YrRDfsy288wt54g6VDqhTZJ6AuWZ61z8yZ\nM/H29sbZ2Zl27doRHR3Nm2++ydChQxk1ahTOzs6EhISwZ88eAGbPns2QIUPK3GPSpEm89NJLgLK+\nWWRkJI0bN6Zv376cO3euzLXbt2/n3nvvxdXVldDQUGJjY43nevXqxWuvvUb37t1p1KgRaWlpZv70\nVWTSEpYap8WP99//CvESc4QAIUB8NXilpUOqlOjoaEuHUKfI8ixPi/+/ljh69Kjw8fExrq5+4sQJ\nkZqaKt544w1hb28v1q5dKwwGg/jPf/4junXrJoQQIjs7Wzg6Oorc3FwhhBBFRUXC3d1d7N27Vwgh\nxN133y2mTJkiCgsLxaZNm4STk5MYMWKEEEKIjIwM0aRJE7F27VohhBDr168XTZo0EefOnRNCCBEZ\nGSl8fX3F4cOHRXFxsSgqKqrW57pdmZv6byEnSNag4mL4/usC4mw/hLu6k70zHX30HOAflg7tb8k+\nAXXJ8qy6yZNh3z7T76PXw9y5VXuPtbU1hYWFHDx4kCZNmtCyZUvjue7du9O3b18ARowYwbx58wBo\n3rw5PXr0YOnSpTz99NOsWbOGZs2aodfrSU9PZ/fu3WzYsAEbGxt69OjBgAEDjPdcsmQJ/fv3N963\nd+/edOnShdWrVxs7+EePHk3btm1NKQqzkU1hNWj9euiZ8R3NCjLhtdfYEjqJ0IvRiD17LR2aJEl3\nEBAQwNy5c3njjTdwd3dn+PDhZGdnA0oCKeHg4EB+fj4Gg9LEPXLkSL777jtASRYlSSE7OxtXV1fs\n7e2N7/X19TX+/cSJE/z888+4ubnh5uaGq6srW7du5dSpU8ZrfHx8zPeBTSRrLDXoqy+KeddqJoaO\noVj16cOlQ924vOMNdO98hOMvt98lUwtiYmLkb9kqkuVZdVWtZaht2LBhDBs2jCtXrvDss8/yr3/9\ni4CAgDu+Z9CgQUyYMIFDhw7xxx9/MGvWLABatGjBxYsXycvLMyaX9PR0rKyU3/V9fHwYOXIkUVFR\nt723lkeQyRpLDTl3Dqx++5UAwzGspv0HdDqC723MlzyNw/IfIDPT0iFKknQbSUlJREdHU1hYSMOG\nDbG3t8fa2rrCa0WpEVp2dnYMHjyY4cOHEx4ejre3NwAtW7akS5cuvP7661y/fp0tW7awcuVK4/ue\neuopVq5cyV9//YXBYCA/P5/Y2FiysrLM+0FVosnEYjAYCAsLY+DAgRWenzRpEq1bt0av17NPjUbX\nGvDdt4Kpxe9R4BcEgwcDEBIC83WTwGCATz+1cIR3Jn+7Vpcsz9qloKCAf//73zRr1gxPT0/Onj3L\ne++9V+G1t9YkRo0aRUJCAiNHjizz+vfff8/27dtp0qQJb7/9NqNGjTKe8/b2Zvny5bz77rs0a9YM\nX19fZs+ebWxi03JtBTS6COVHH31EfHw8ly5dYsWKFWXOrVmzhvnz57Nq1Sp27NjBiy++yPbt2yu8\nj1YWtRMCnm/1J/87/qAyiWXsWOO5Dh1gwYUh3FuwEU6ehEaNLBipJFmOVv5/VVtGRgZt27bl1KlT\nODo6WjqcMurNIpQZGRmsXr2aZ555psLzy5cvN2b+8PBwcnNzOX36dE2GWGW7d8MTx9/liqs3PPVU\nmXNhYfBB0ctw8SJ8842FIvx7ct6FumR51g8Gg4HZs2czbNgwzSUVc9JcYnnppZeYNWvWbat6mZmZ\nZUZDeHl5kanx/onod7bRk01YT30FGjYscy40FFacu5vrYeHw0UdKs5gkSbXetWvXaNy4MRs3buTN\nN9+0dDg1SlOJZdWqVXh4eKDX6xFC1Ilq8bVrELLqPS7bNsF+0j/LnQ8LA9Bx6MGXITkZ/vijxmOs\nDNknoC5ZnnWfg4MDly9f5sCBA3h5eVk6nBqlqeHGW7duZcWKFaxevZq8vDwuX77MyJEjWbz45lBc\nLy8vTp48aTzOyMi44z/a6NGjjdtvuri4oNfrjf9TlzRHmPN423epTCv6g+Mj3yJ+165y569cAYhk\nrf1gctzdYfp0Im8MWqiJ+OSxPNbKsWQ5MTExLFq0CECd7YpNmrdvRjExMWLAgAHlXl+1apXo16+f\nEEKIuLg4ER4eftt7aOHjrQudIvKwFYbzF257TatWQjz2mBDiww+VpV527665ACtJLkGiLlme5Wnh\n/9f65nZlbuq/haaawm4nKiqKBQsWANCvXz/8/f0JDAxk3LhxfPbZZxaO7s5cTh/leMMgdG6ut70m\nNBT27gWefhqsrZV19SVJkmopTQ43VosWhi+eaNSO43bt6Hn+19te88478Npryh4tjSM6gacnrFlT\ng1FKkuVp4f/X+qbeDDeuU4qLaZGXynm31ne8TOnAVzb+onNniI9XJr9IkiTVQjKxmNPJkzQUhVxu\nfufEEhqq/LlnD0piOXsWMjLMH18VyHkX6pLlWTc5OTlx/PhxAMaMGcP06dMBiI2NLTNNIjg4mE2b\nNlkixBqhqVFhdY04lowOuObtR2JiIomJiRw6dIjExEQOHz7MoEGDeOutt2jeHFq0uNHPMr6L8ubd\nu0HDq5dKklTe5cuXb3uu9Ny8gwcP1kQ4FiMTixnlHTjGT8ALP/ej+MfrgPIfV6tWrbC2tub999/n\nueeew9PT82YHfseOSgd+fDw88ohF4y9NDglVlyxPqS6TTWFmVHAomUVY4dbEm2+//ZY9e/Zw5coV\nkpOTWbVqFUVFRXz88ceA0hyWmAh52CsLiMXHWzh6SZJKLFq0qMyiuK1bt2bo0KHG45YtW7J//36s\nrKxITU392/v5+/uzceNGAHbt2sU999yDq6srXl5evPDCCxQVFRmvtbKy4vPPP6d169Y0btyY6dOn\nk5qaanzPE088Ybz+/PnzDBgwAFdXV5o0aULPnj3VKoIqkYnFjK4dPsJ2BD16PMJTTz1FaGgoDg4O\nAAQGBvLoo4/yv//9j8uXLxMWpuwwefAgmuzAl30C6pLlWbv07NmTLVu2AMomXdevXycuLg6A1NRU\nrl69SqdOnap1b2tra+bOncuFCxeIi4tj48aN5aZR/PXXX+zbt4/t27fzwQcf8M9//pMffviB9PR0\nDhw4wA8//ADAhx9+iI+PD+fPn+fMmTO8++67Jnzq6pNNYWa0J/kghQgiIu6r8PzUqVNZtmwZCxcu\n5JFHXlbeswfu6tIFvv5aWe241BaoklSvWXBvYn9/f5ycnNi3bx9Hjx6lb9++7N+/n6SkJLZt20aP\nHj2qHU5YybBQlJrPs88+S2xsLJMmTTK+/q9//YtGjRrRrl07goODefDBB407Tj700EPs3buXESNG\nYGNjQ3Z2NmlpaQQEBHDvvfdWOy5TyBqLuRQXs+18BlboeOCBiAov6dq1KxEREcydOxcvr+u4uNzo\nZ+ncWblAQ81hsk9AXbI8a5+ePXsSHR3Npk2biIyMJDIykpiYGGJjY01qcjp27BgDBgygRYsWuLi4\n8Oqrr3Lu3Lky17i7uxv/bm9vj4eHR5njK8raUEydOpWAgAD69OlDYGAgM2fOrHZcppA1FnM5eZJo\nYaAprfD3d7rtZVOnTmXAgAH8/PNPhIY+pQw5/kibHfiSZFEW3ps4IiKClStXcvz4cV599VUaN27M\nkiVL2L59e5naRVU9//zzhIWF8dNPP+Hg4MC8efP45ZdfqnUvR0dHZs+ezezZs0lMTKRXr1507dqV\nXr16VTu+6pA1FjPJ3b+fXYCT9b3c2NK6Qv369aN9+/bMmjULvV6QkABFNjc68HfvrrF4/47sE1CX\nLM/ap6TGkpeXh6enJz169GDt2rWcP38evV5f7ftevnwZZ2dnHBwcOHLkCJ9//nm177Vq1SpSUlIA\nZU5NgwYNsLKq+a95mVjMZNPatRiAhq7/uON1VlZWTJkyhQMHDtCw4Try8+HIEaBLF8114EtSfda6\ndWucnJyIiFCatp2cnAgICKB79+7GOSqV3TK49HWzZ89myZIlODs7M27cOIYNG3bba//uGceOHeP+\n++/HycmJe++9lwkTJlhkZJhcK8xMJoeFEbV3L8FhV9kV73DHawsKCvD398fPrwNxcev45hsYeeUz\nmDABTpyQHfhSvSDXCqt5cq2wWmZjcjJhVo1o5nHnpAJga2vLiy++SFzceho02HtzyDFoqgNfkiSp\nMmRiMYMzZ86QcPkyQVa+NGtWufeMGzcOR0dHGjWazeHD3JyBr5F+FtknoC5ZnlJdJhOLGURv2ACA\nswitdGJxcXFh3LhxXLr0EwcOnAB7ewgOljUWSZJqHZlYzGDDypU4A1eKu1c6sQC8+OKLCGHg5Mlv\nyMtDUzPw5bwLdcnylOoyzSWWgoICwsPDCQ0NpUOHDkybNq3cNbGxsbi4uBAWFkZYWBgzZsywQKS3\ntzE2lp5ACm2rlFh8fHwICOiCEH+RlISSWM6dg/R0c4UqSZKkOs0lFltbW6Kjo9m7dy8HDhxg48aN\nbN26tdx1ERER7Nmzhz179vDaa69ZINKKnThxgpSsLHoDyQRWKbEA9Or1ALCd+PhLypBj0ERzmOwT\nUJcsT6ku01xiAYwLNRYUFGAwGHB1Lb9fvFaHJZasWNrTxpYsPKucWB577AGgmL/+ilY68Bs00ERi\nkSRJqixNJhaDwUBoaCjNmzcnMjKS9u3bl7smLi4OvV5P//79SUxMtECUFduwYQPNGjakpXsgAqsq\nJ5aePe9Gp2vE7t3rwM5OM0voyz4BdcnylOoyTSYWKysr9u7dS0ZGBps2bSI2NrbM+c6dO5Oens6+\nffuYOHEigwYNslCkZQkh2LhxI/fZ2XHeNQigyonF1taWZs16cvLkOuWFzp2VIccaraFJkiTdStOL\nUDo7O9O/f392795dZlkCR0dH498feughxo8fz4ULF3Bzcyt3j9GjR+Pn5wcoQ3r1er3xt8WSdm61\njhcvXkx2dja9ra3JcgjE2jqG+Hjo1atq9wsOfoCNG1ezZMmPeDk7E3n+PKSnE5OWpmq8VTku3Sdg\niefXtWNZnuWPJcuJiYlh0aJFAMbvS5MIjTl79qzIyckRQghx7do10aNHD7F+/foy15w6dcr49x07\ndghfX98K71XTH2/+/PkCEMkgFt27QHh6Vu8+77xzSABixoyFQuzYIQQI8csv6gZbRdHR0RZ9fl0j\ny7M8DX4d1Xm3K3NT/y001xSWnZ1Nr169CA0NpVu3bgwcOJDevXsTFRXFggULAFi2bBnBwcGEhoYy\nefJkfvrpJwtHrdiwYQO+Hh60ApIMVR8RVqJ373aAJ2vWrLvZgW/hGfjyt0p1yfKsfWbOnIm3tzfO\nzs60a9eO6OhoDAYD7777LoGBgTRu3Ji77rqLzMxMAF566SU8PDxo3LgxnTp10lRfsLnJRShVUlxc\nTLNmzRjUti1fxcUxMPQkeU28Wbeu6ve6dAkaNx6Dvf0KLl8+g3XnzuDhAX/+qX7gkqQRWl6EMikp\nifvvv59du3bh4eFBeno6xcXFLFu2jO+++45ffvmFwMBAEhIS8Pb2ZteuXUybNo3o6GicnJw4evQo\nLi4uZTbo0gJzLUKp6T6W2mT//v1cvHiR3q6uYGfH4VxP7mpbvXs5O4Or6wNcvLiIvXv30qVLF/j9\nd6UDv5LLcqstJiZG/patIlmeVTd58mT2qbA1sV6vZ24VNw2ztramsLCQgwcP0qRJE1reWHH8yy+/\nZPbs2QQGBgIQEhICgI2NDVeuXCExMZGuXbvSpk0bk+OuTTTXFFZbHTx4EIAu+fkQGMiZc1Ufalxa\nx473A7Bu3TplZNiNDnxJkmpeQEAAc+fO5Y033sDd3Z3hw4eTnZ3NyZMnadWqVbnre/XqxcSJE5kw\nYQIeHh4899xzxu2D6wWTemg0riY/3vTp04WVlZXIb9NGFA0cJECIt9+u/v0mTRLCykovIiMjhdi6\nVenAX7lSvYAlSWNqy9fR5cuXxRNPPCFGjBgh2rZtK1asWHHH68+ePSsiIyPF9OnTayjCyrtdmZv6\nbyFrLCpJTk7Gx8cH27Q0rnm2Bqo+h6W0du3AYHiArVu3ctXXV3mxHnX+SZKWJCUlER0dTWFhIQ0b\nNsTe3h5ra2ueeeYZXnvtNZKTkwFISEjgwoUL7N69m507d1JUVIS9vT12dnYW2SLYUqrUx3LmzBny\n8/Or9AA7Ozvc3d2r9J7aKCUlhUBvbzhxgpxm6iQWeIDr12cRu38//Tw94dAhVWKtDtknoC5ZnrVL\nQUEB//73vzly5Ag2Njbcc889LFiwAHd3dwoKCujTpw/nz5+nbdu2/Pbbb1y6dImXXnqJtLQ07Ozs\n6Nu3L1OnTrX0x6gxVUos06ZNIyIiokqjBTZv3swXX3xR5cBqm+TkZB7t1g2AM85KR17TptW/n7KK\nTXdsbOxYt24d/Tp0sGhikaT6LCQkhB07dlR4btq0aeVWYff09GT//v01EZomVSmx3HPPPYwcObJK\nDyguLq7S9bVRTk4O58+fJ7BhQwBO2pleY2nWDJo0scfOrofSgX///bBwIRgMYIEqtfztWl2yPKW6\nrErfUGPHjr3tuZycHObMmUNSUlKl31NXpKSkABBQXAx2dqQXeQKmJRZQmsNsbB7g0KFDZHp6wrVr\ncOKEqeFKkiSZlUm/+s6ZM4fg4GAef/xxNm7cyAsvvMCWLVvUiq3WKEksgbm5EBjI2fNWWFlBBUuX\nVUm7dnDxYh8A1l+6pLxooQ58uX+IumR5SnWZSYnlwoULLFu2jAEDBrBw4UI8PDxYtmyZWrHVGiUj\nQgJOn1YSy1lo0sT0Fqv27SE3N4SmTd1ZV1ITlP0skiRpnEkz74OCgmjbti1t27ZlxIgR5OTkYGdn\np1ZstUZKSgrNmzenUVoaDBjA2RTTm8GgZGSYFXr9/ayLXY+hRQusLJRYZJ+AumR5SnWZSb9Te3t7\nExcXZzx2cXGpl4klOTmZQB8fKCgw1ljUSyzg6fkAZ86c4ZCvr5zLIkmS5pmUWFauXEmvXr3o0aMH\nb7zxBps3b6aoqEit2GqNlJQUAkq2T1Yxsfj4QKNGAPcCsKNRIyWxGAym37yKZJ+AumR5SnWZSYnF\nx8eHnJwcZs2ahY2NDdOnT0ev16sVW62Ql5dHZmYmgU5Oygve3pw7p05i0emUWktWViCurq7sLChQ\nRobJNcOkOsjX1xedTid/avDHt2RVD5WZ1Mfi6OiInZ0d3bp1o1u3brz66qtqxVVrpKamAhBwYw5L\nsXsLzp83bXJkae3aQXS0jq5du7LjxiABDh0CNXZ5qwLZJ6AuWZ7lHT9+3NIhSCoxqcbSqVMnvvvu\nO7ViqZVKRoQFAjRqxIXrTgihTo0FlMSSkQF6fTgH09K4CrKfRZIkTTMpsbz33nu88847+Pj4MGrU\nKBYvXszp06dNCqigoIDw8HBCQ0Pp0KFDuaUSSkyaNInWrVuj1+tV2aOhuoyTI/PzoUULzp5VXlcz\nsQC4u3fFYDAQ7+ZmkSHHsk9AXbI81SXLU1tMSiw9evQgISGB3bt306dPH6KjoxkyZIhJAdna2hId\nHc3evXs5cOAAGzduZOvWrWWuWbNmDSkpKRw7doyoqCiee+45k55piuTkZFxdXXG7cMGsicXGpisA\nO5s0kXNZJEnSNJMSy9ixY1m8eDEODg48+eSTfP3112zevNnkoBwcHACl9mIwGHAtGXF1w/Lly41r\nloWHh5Obm2tyTam6UlJSCAgIgOxssySWgACwsYHMzGb4+/uzQwg4fLjGR4bJPgF1yfJUlyxPbTEp\nsbi6ujJ27FicSkZEqcRgMBAaGkrz5s2JjIykvbLUr1FmZiY+Pj7GYy8vLzIzM1WNobKSk5OVbUnN\nlFgaNICgIKVbpWvXruy8cAGuXpUjwyRJ0izV9rzPycnhq6++4h//+AdBQUEm3cvKyoq9e/dy6dIl\n+vTpQ2xsLD179qzWvUaPHo3fjRFULi4u6PV64283Je2y1T1ev349x48f54lHH4XLl4m5do2dO2OA\nSJo2Nf3+Jcft2kWybx/06dOE9AsXOAU0T0wk5sYoGrU+z52OS7dh18Tz6vqxLE9Znlo6jomJYdGi\nRQDG70uTmLL95Icffig6dOggHnvsMfHLL7+IwsJC8eWXX5q0peWt3nrrLTF79uwyr40bN078+OOP\nxuM2bdqIU6dOlXuviR/vbx07dkwA4uv331e2Dl60SEycKISLi7rP+e9/hbCyEmLDhi0CEMtBiA8+\nUPchfyM6OrpGn1fXyfJUlyxPdZn63am5RSjPnTtHbm4uoEw+XLduXblJlwMHDmTx4sUAbN++HRcX\nFzw8PEx6bnUYF59Upscbm8LUmsNSon17pUvF0TEMa2trZQZ+DXfgl/yWI6lDlqe6ZHlqi+YWoczO\nzmbUqFEIITAYDIwYMYLevXsTFRWFTqfj2WefpV+/fqxevZrAwEAaNWrE119/bdIzq8u4XL6NjfJC\nixaqzbovrWRkWFqaPR07dmTniRNyLoskSZplUmIpWYTy7rvvBpQ+DFOFhISwZ8+ecq+PGzeuzPH8\n+fNNfpapkpOTcXBwoHl+vvLCjRqL2pPig4KUJfgPH1ZGwX1/6BCGQ4ewqsHdJGPkHu2qkuWpLlme\n2iIXoTRByVBj3alTypjgJk1UW4CyNHt7aNXq5siwS4WFJF27BidPqvsgSZIkFchFKE2QnJx8cw5L\n8+YIdGZpCgOlOSwxUamxAOyAGu1nkb8NqkuWp7pkeWqLSYml9CKUr776KtHR0Rw8eFCt2DTNYDCQ\nmppaZg5Lbi5cv26exNK+PSQlQUBAG5wcHdkJcga+JEmaJBehrKbMzEwKCgrMOuu+tPbtlaR1/Lg1\nd3Xtyo4GDWq0A7/0PAHJdLI81SXLU1s0twhlbWEcEWbGWfellYwMK+ln2V9cTH5CgvoPkiRJMpHm\nFqGsLYxzWHx84Nw5aN7crImlbVvlz5KRYUVCsO/QIRBC/YdVQLZhq0uWp7pkeWqLJhehrA1SUlKw\nsbHBp6GywVfpGovaEyQBnJygZcubNRaAHfn5cs0wSZI0p9KJ5cyZM+Tl5ZV5zVyLUNYGycnJ+Pn5\n0aAkm9yYHAnmqbHAzZFhnp6eeDVrpnTg11A/i2zDVpcsT3XJ8tSWSieWS5cu8frrr/PKK6+wadMm\nc8ZUK6SkpNzsXwFjjcXBQfkxh/bt4cgRZXmX8PDwGh9yLEmSVBmVTiyBgYF88MEHvPvuu2RnZzN+\n/HhmzJhRL/epFkLcXC7/1CnlxRuJxVy1FVBqLHl5cOIEdO3enRTgfHy8+R5YimzDVpcsT3XJ8tSW\nKi/pYmtry9ChQxk6dChZWVksWbKE1NRUwsPDeeyxx2hUsiBjHXbu3DkuX758c6ixTgceHmZPLCXb\n0pR04APs3LOHh8z3SEmSpCozqfPe09OTqVOn8vnnn9OuXTtef/11Jk+eTHR0tFrxaVLJiDBjU1iz\nZtCgQY3UWEDpVuncuTM6YGdaGhQXm++hN8g2bHXJ8lSXLE9tUW2jr/DwcMLDwykoKOD3339n3Lhx\n+Pr6Mm3aNLUeoRklc1hKT44EOHsWOnQw33Pd3MDDQ0ksTk5OdPDyYkdmJiQnQ5s25nuwJElSFZiU\nWCZMmEBQUBA9e/Y0rhFWuqmsZF+VuiY5ORmdToe/v3+5xGLOGgsozWGHDyt/73rXXazIzETEx6Mz\nc2KRbdjqkuWpLlme2mJSU5i7uztHjhzhhRdewMPDg4cffpg5c+YQf6NDuXHjxqoEqTUpKSn4+Phg\na2trTCxXryod6zWRWBITlXmRnSIiOAec3rLFvA+VJEmqApMSS+vWrfn888/ZvHkzqampPPLII6xc\nuZKJEyei1+vJysqq8j0zMjK477776NChAyEhIXz88cflromNjcXFxYWwsDDCwsKYMWOGKR+jyowj\nwgwGOH26zKx7c0yOLK1dO7h0CbKyIORGLTEhLs68D0W2YatNlqe6ZHlqi0lNYfHx8QwaNAgHBwca\nNWrE6NHThGaIAAAgAElEQVSjsbOzY9iwYRw5coQ5c+Ywe/bsqgXUoAFz5sxBr9dz5coVOnfuTJ8+\nfWhbsqbJDREREaxYscKU8KstJSWFQYMGKUu5FBXVyOTIEqVHhun1IQAkHDnCA0Ioo9MkSZIszKQa\ny6hRowgPD2fmzJnEx8eTnp5Owo2FEdu2bUtoaGiV79m8eXNjf42joyPt2rUjMzOz3HWihtbIutXV\nq1c5e/YsrVq1KjM5siTE5s3N+/ySxJKYCE2bNqW5szMJ+flg5vlEsg1bXbI81SXLU1tMSiwdO3bk\nl19+YdeuXURGRtK7d2+6d+8OwM8//2zy5Mnjx4+zb98+45yN0uLi4tDr9fTv35/EGlw+/uSNXRt9\nfHzKJJaSbWhKhgSbi7s7uLreXMkluG1bEgAq2M5ZkiTJEkzeMD0oKIhly5Zx+fJljh07xkMPKdP1\n0tPTycnJqfZ9r1y5wpAhQ5g3bx6Ojo5lznXu3Jn09HT27dvHxIkTlWapGpKRkQGAt7d3mVn3Bw+C\nv7+yWKQ56XRlR4aFhIdzCCjevdusz5Vt2OqS5akuWZ7aoto8lltNmTKl2u8tKipiyJAhjBgxgocf\nfrjc+dKJ5qGHHmL8+PFcuHABNze3cteOHj0aPz8/AFxcXNDr9cZqc8l/jFU5Xr9+PaAklpgbm5xF\ntmhBQgI0bx5DTEzV7led43btIvn9d+XYxt6efCBl2zayzPQ8eSyP5XHdPo6JiWHRokUAxu9LkwgT\nzJkzR0ybNk3k5uYKIYT44osvRGZmpim3FEIIMWLECPHSSy/d9vypU6eMf9+xY4fw9fWt8DoTP16F\n3n77bQGIvLw8IV54QYjGjUVBgRANGggxbZrqj6vQnDlCgBBnzgixa9cuAYhlzs5CGAw1E4AkSXWa\nqd+dJjWFubm58eqrr7J06VIAnn76aVatWmVSotu6dStLlixh48aNhIaGEhYWxtq1a4mKimLBggUA\nLFu2jODgYEJDQ5k8eTI//fSTSc+sipMnT9KsWTPs7OyMc1iOHlUGh4WE1EwMpUeGtW/fHp1OR8Kl\nSzf7fCRJkizIpKaw3NxcHBwclC/ZGxxMXDP+3nvvpfhv1r6aMGECEyZMMOk51ZWRkaH0r4AxsZTs\nEBwcXDMxlF4zLCLCgUAvLxIyMpQOfE9PszwzJibGWIWWTCfLU12yPLXFpBpLUVERs2bNwmAwGF87\nf/68yUFpWUZGhjIiDJTE0rw5CQlgYwNBQTUTg48PODqW6sAPC5MjwyRJ0gyTEstLL71EUlIS48aN\no2vXrkRERFhsfklNMdZYhDDWWA4eVNaAbNiwZmLQ6W7uJgkQEhpKMnBt506zPVP+NqguWZ7qkuWp\nLSY1hel0OhYuXMiUKVPYv38/QUFBxsmNddG1a9e4cOGCklguXVIWB2vRgoRf4J57ajaWdu3gxgA1\nQkJCEMDh3bvpXLNhSJIklWNSjeWbb76hf//+uLm5sX//frZt26ZWXJpUZg7LjY7yay4tOHGi5jru\nS7Rvr6wXlpurJBaAhNOnMa4to7KSoYmSOmR5qkuWp7aYPEFy8eLFfPDBB+zYsQN3d3fmzZunRlya\nVJJYSs+6T8tTlsyvqY77EqVHhgUEBGBva6v0s+zdW7OBSJIk3cKkxHLlyhWaNGnCunXrmDRpEkOG\nDDF5VJiWlSznUnrW/aELSmKp6RpL6ZFh1tbWtG/Xzqwd+LINW12yPNUly1NbTEos/v7+6PV6Ll26\nRN++fSkqKqrTe96X1Fi8vLyMNZb4rBY4OkLLljUbi78/2NqWGhmm15NgbS1HhkmSZHEmJZZ+/fqx\nZcsWEhMTsbW1pXnz5sYv37ooIyODJk2aYG9vryQWOzt2Hm1McDBYmdyoWDXW1spINOPIsJAQThUX\nc27XLrM8T7Zhq0uWp7pkeWqLyWuFlV63Kz4+nqbm3unKgm6dwyJatCDhoI7Bgy0TT/v2sHmzst+Y\nsQM/LY1eublQR3fvlCRJ+yr9e/aZM2fIy8u74zW+vr51uins5MmTZWbdX2/agvPna77jvkT//pCZ\nCWvXlkosAPv2qf4s2YatLlme6pLlqS2VTiyXLl3i9ddf55VXXmHTpk3mjEmzbl3O5aKtsqtXTXfc\nlxg6FLy9YdYs8PDwoKmbm5yBL0mSxVU6sQQGBvLBBx/w7rvvkp2dzfjx45kxY4bJm3nVFnl5eZw/\nf75MU1i2sMxQ4xI2NjB5MsTEQHy8jpBOnUiwsTFLYpFt2OqS5akuWZ7aUuUuZ1tbW4YOHcpnn33G\n2LFjWbp0Kc8//zyLFi3i6tWr5ohRE8pMjszLg5wcUvNa4OFh/n3u7+Sf/wRnZ5g9G4KDgzloMGCQ\nNRZJkizIpM57T09Ppk6dCsCOHTt4/fXXKSoq4uGHH6ZXr16qBKgVFe0cefBCC4s1g5VwdoZx4+DD\nD2HGjBCuFhdz4vBh/K9dAxXnFMk2bHXJ8lSXLE9tUW2QbHh4OLNnz2bmzJmcOXOGcePG8e6776p1\ne4uraDmXPVktLNYMVtqLLyrDj/fuvdGBLwQcOGDhqCRJqq9Un31R0lQWFRVlsT1TzKGiGsvxQsvX\nWAC8vGD4cPjjjw4AZunAl23Y6pLlqS5Zntpi1ml9jasxlyIjI4P77ruPDh06EBISwscff1zhdZMm\nTaJ169bo9Xr2mWF47a1OnjyJm5ubsmTNjRpLNtqosQC88grk5Tnh6upPQsOGsHu3pUOSJKme+tvE\nYjAYSEhIoKCgAFA28vr999/N9mXeoEED5syZw6FDh4iLi+PTTz/lyJEjZa5Zs2YNKSkpHDt2jKio\nKJ577jmzxFLarUONDVbWnKMZHTqY/dGVEhICDz4I166FKIllyxZV7y/bsNUly1Ndsjy15W8Ty/PP\nP8+YMWPo0aMHGzduZNiwYSxdupQXXnjBLCsZN2/e3Lini6OjI+3atSMzM7PMNcuXL2fkyJGA0reT\nm5vL6dOnVY+ltFtn3ec09MA/wAotzQedOhUKCkI4evUaBceOKbMnJUmSatjfJpaIiAh2797Nli1b\n2L59O+vWrWPJkiVs3rxZWTPLjI4fP86+ffsIDw8v83pmZubNL3mURSFvTT5qu7XGkqWhZrASvXqB\nn18IxcLAEYDYWNXuLduw1SXLU12yPLXlbxNLQUEBU6ZM4fr164wZM8b4elRUFM7OzmYL7MqVKwwZ\nMoR58+aVWY/MEvLz8zl79qwxsRiysjmR31wTHfel6XQwfrwS1F5be2XmpCRJUg3723ksjz/+ODEx\nMTRq1KjMOmCpqamMGjXKLEEVFRUxZMgQRowYwcMPP1zuvJeXl3FvFFBqE15eXhXea/To0fj5+QHg\n4uKCXq83tseW/Jbzd8cltaMrV64QExPDvRnZZNEFnS6GmJi/f39NHnfsWAQ0ZJ3OE7/VqyEmRpX7\nR0ZGauLz1ZVjWZ6yPLV0HBMTw6JFiwCM35em0AkhhMl3UdnIkSNp2rQpc+bMqfD86tWr+fTTT1m1\nahXbt29n8uTJbN++vdx1Op0ONT5ebGwskZGRrF+/nt49e2JoaMsM8SpDDr1l3MlRS1q27AInc0kn\nGTIylPHIkiRJlWTqd6dqw41zcnKYM2cOSUlJJt1n69atLFmyhI0bNxIaGkpYWBhr164lKiqKBQsW\nAMo+MP7+/gQGBjJu3Dg+++wzNT7CbZXZOfLMGayEgTPWnrRubdbHVtvAgRFkcpICUK05LEal+0gK\nWZ7qkuWpLSYt6TJnzhy++uor2rdvz7Bhw3jhhRf49ttvCQoKqvY97733XoqLi//2uvnz51f7GVVV\nZufIG1s2Wvl4YWNTYyFUSZ8+kXz66UdswJHuK2JwfvJJS4ckSVI9YlKN5cKFCyxbtowBAwawcOFC\nPDw8WLZsmVqxaUZGRgYuLi7KIIKsLACc23paOKrb69GjBzqdjiV4kf9njCr3LGmXldQhy1Ndsjy1\nxaQaS1BQEG3btqVt27aMGDGCnJwc7Ozs1IpNM0rPYbl8NAsnoEVn7SYWV1dXOnXqxIHUq7jnJnPh\nQAZuHb0tHZYkSfWESTUWb29v4uLijMcuLi51MrGU3jkyY2cWxVgR9qC7haO6s8jISJLzlX6WmLdM\nn88i27DVJctTXbI8tcWkxLJy5Up69epFjx49eOONN9i8eTNFRUVqxaYZpSdH5hzO4rSuOV3CrS0c\n1Z317NmT/MJ8Yq0duboqhr/ZVVqSJEk1JiUWHx8fcnJymDVrFjY2NkyfPt24HEtdUVBQwJkzZ4xN\nYcUns7js5KnZjvsSERER6HQ6or286ZYfwzffmHY/2YatLlme6pLlqS0mJRZHR0fs7Ozo1q0br776\nKtHR0Rw8eFCt2DShZKkYb29vLl4Ep8tZ4Knd/pUSbm5udOzYkd22BlqTzJKZGVRisJ0kSZLJTEos\nnTp14rvvvlMrFk0qvQ/Lli3gSRZOQdpPLKA0h209mU4h0PJ4LCtWVP9esg1bXbI81SXLU1tMSizv\nvfce77zzDj4+PowaNYrFixebfZXhmlYmsWwooBnnaKavHYklMjKSvPx8djo6MsAxhlmzLB2RJEn1\ngUmJpUePHiQkJLB792769OlDdHQ0Q4YMUSs2TSidWA5HKztH2rSsHYklIiICgFhvbx60jyEuDrZu\nrd69ZBu2umR5qkuWp7aYlFjGjh3L4sWLcXBw4Mknn+Trr79m8+bNasWmCSdPnryxE6YTFw/eWJq/\nFvSxADRp0oSQkBBiDQZcziYT7JLB7NmWjkqSpLquSokl9pb9PVxdXRk7dixOTk6Vfk9tUzLUeNs2\n8DAos+5r06KOkZGRbE1X+lmm94xl+XKoznJusg1bXbI81SXLU1uqNPN++fLl+Pv7V/p6IQQrVqyg\nZ8+eVQ5MK0oSS2ws+FhlgYFaU2MBJbF88skn7HZy4h+NomnY8EnmzIH//c/SkUmSVFdVadn8tWvX\nVrlz3sPDgwcffLDKgalBjWXzW7RowT/+8Q8OH17Is2n/ZuTZOVBQoOyqVQucO3eOZs2a8U67dkwr\nLGRc72S++QbS08Fd24sHSJJkIaZ+d1apxmKpBGEphYWFnD59Gg8Pb775BuYFZYGNZ61JKgBNmzYl\nODiY2OvXmZaSwv99cZKFC32YPx/eesvS0UmSVBepth9LXZSVlYUQgoICb65fB98GtWNy5K0iIyPZ\ncuIE14GAExsZOBA+/RSuXav8PWQbtrpkeapLlqe2yMRyByVDjU+d8sHKClzza2di6dmzJ9fy89nd\ntCksX87UqXDhAnz9taUjkySpLtJcYnn66afx8PCgY8eOFZ6PjY3FxcWFsLAwwsLCmDFjhtliKdk5\nMinJG70erE/VzsRSMp8lJjAQ1q7lnk5X6dYN5syh0su8yHkC6pLlqS5ZntqiucQyZswY/vzzzzte\nExERwZ49e9izZw+vvfaa2WIpqbHs3+/N/XdfhdzcWplY3N3d6dChA7HFxZCXh+7PtUydCqmp8Ntv\nlo5OkqS6RnOJpXv37ri6ut7xGlNHelVWRkYGDg5OFBQ4c3+HbOXFWphYQGkO25KYyPUmTeDXX3n4\nYQgMhFmzoDLFKduw1SXLU12yPLVFc4mlMuLi4tDr9fTv35/ExESzPScjIwNHR2W5/Lu8bkyOrKWJ\nJTIykqtXrxJ/zz3wxx9YFxXw8suwcyfUscUSJEmysColFicnJ5ydncv9+Pj4cP/99/PXX3+ZK06j\nzp07k56ezr59+5g4cSKDBg0y27OOHz9OcXFLgoPB5WrtWs7lVpGRkVhZWbGqUSO4dAk2bGD0aGja\nlEot8yLbsNUly1Ndsjy1pUrzWObPn1/h6zk5OcTHxzNgwACWLVvGgAEDVAmuIo6Ojsa/P/TQQ4wf\nP54LFy7g5uZW4fWjR4/Gz88PULZO1uv1xv8IS6rPFR0LIUhMTKSw0I+hQ4GsLGIAUlOJbN/+b9+v\nteNmzZqh1+v5KjaWt5yc0P36KzscHOjfH775JpLDh+H0ae3EK4/lsTyuueOYmBgWLVoEYPy+NIlQ\n0Zw5c0S3bt1Mvk9aWpoIDg6u8NypU6eMf9+xY4fw9fW97X1M+XiZmZkCEDBf/PSTEOLll4VwcBDC\nYKj2PS3tyy+/FIDY0aePEE2bCnH9ujhzRgg7OyGefvrO742Ojq6RGOsLWZ7qkuWpLlNTg6p9LP37\n9+fIkSMm3WP48OHcc889JCUl0bJlS77++muioqJYsGABAMuWLSM4OJjQ0FAmT57MTz/9pEbo5SQZ\nV2oMIiICyLox1LgWzbq/1eDBg2nYsCHf29jAuXOweTPNmsGYMfDtt3DqlKUjlCSpLqjSWmF/58CB\nA/Tt25fs7Gy1bmkSU9a7WbBgAePGjcPP7wRpaS2hZCHNWr5a8+DBg4nbto2M3Fysn3kGPvmEY8eg\nTRv4z3/gnXcsHaEkSZZm6lphqtZYvvjiC/R6vZq3tJgjR5IAO3r39lZeKKmx1HLDhw/n1OnTxHTu\nrExiMRho3RoeeQQ+/xyuXLF0hJIk1XZV6ryfNGlSha/n5uayZ88eUlNT2bRpkyqBWVp8fBLQmshI\nK2WiRx1JLP3798fJyYnvra3pnZmpjDfu1o2pU+HXX+Grr6Cif+aYmBhjp59kOlme6pLlqS1VSiwJ\nCQkVvu7s7MxDDz3E888/X6X9WrTsyJGjQIjSAnbpkrJiYx1ILPb29gwePJhffvuNTxs0wO7XX6Fb\nN7p1g3vvhY8+gvHjoUGV/suQJEm6SdU+Fq2pbjvh9evXsbV1wNl5Kjk578Lhw9C+PXz/PTzxhBki\nrVl//vknDz74IL+GhvLIpUtw7BjodCxfDoMGwQ8/wLBhlo5SkiRLqdH9WNLT0yt1XcuWLasVjFak\npR1HiCKCg4OUF7Jq96z7W/Xu3ZtmzZrxvU7HIykpcOAAdOrEgAEQFKQs8zJ0aK0eACdJkgVVqfPe\nz88Pf3//2/6UnK/tNmxQhhpHRLRRXsis3bPub9WgQQOGDh3KH4mJXNLplM4VwMoKXnkF9uyBW5de\nirn1BckksjzVJctTW6qUWHbt2sXOnTvZuXMnO3bswM7Ojl9//dX4Wsn52q4ksQwefEuNpUULC0Wk\nvuHDh5Ofn8/vQUHGxAIwcqSyZfGsWRYMTpKkWs2kPhYnJyf2799Pq1at1IxJNdVtJ2zd+nlSUn6m\nuPi80hw0aRJ8842ybH4dIYSgVatWtLGzY+2RI5CQAMHBALz9NkyfXuYlSZLqEU3NY6kLhID09CTc\n3IJu9jFkZYGXl0XjUptOp2P48OGsP3aM0w0bwv/+Zzw3fjzY28OHH1owQEmSai2ZWG6RkgKFhUcJ\nDAy6+WIdmcNyq+HDh1NcXMzSTp1g8WLj7MgmTWDsWFiy5GYroGzDVpcsT3XJ8tQWkxOLro4NHfrz\nzytAJuHhdT+xdOjQgZCQEH7Iz4fLl5VMcsPLLyvbFn/8sQUDlCSpVqpSH8vAgQPLHK9Zs4aePXvi\n4OBQ5vUVK1aoE52JqtNOOGDAPv74I5Sff17KY48NUdrGbG2Vb9r33zdTpJbz/vvv85///IfEtm1p\n17Ah7NtnHGf8+OPw119w8iQ4OVk4UEmSakyN9rE0adKkzM9TTz2Fj49Puddrs+3blRFhbdrcqLGc\nPw/Xr9fJGgvA008/jYODAzOcnZX5LNu2Gc9NmaKMV1i40IIBSpJU+5i06L7GVfXjHT8uBLwtAHH1\n6lXlxf37hQAhli41Q4TaMHXqVGFlZSWONGokxJNPljkXESGEj48Q69ZFWya4OkruH6IuWZ7qMjU1\nyM77UpT1M5No3tznZvNeHZt1X5EpU6ZgZ2fHDG9vWLoUzpwxnps6VWkKi462YICSJNUqMrGUsmkT\nWFsfpUOHUh33dWzWfUXc3d0ZP3483x87RlJhobLE8Q39+kHbtrBqVSR1d1W5midX4lWXLE9t0Vxi\nefrpp/Hw8KBjx463vWbSpEm0bt0avV7Pvn37VHt2TIzAyiqJoKBbRoRBnZp1X5EpU6Zga2vLDA8P\nZU5LcTGgLPMyZQrs3w8bNlg4SEmSagXNJZYxY8bw559/3vb8mjVrSElJ4dixY0RFRfHcc8+p8tzs\nbEhOPsf16zm0adPm5omsLGVih62tKs/RKg8PD8aPH8+SM2dIOnEC1q41nnvqKXB1jZHLvKhIzrtQ\nlyxPbdFcYunevTuurq63Pb98+XJGjhwJQHh4OLm5uZw+fdrk55b0rwDlayx1uBmstKlTp2JrZ8c7\n9vbw2WfG121tYfBgZejx/v0WDFCSpFpBc4nl72RmZuLj42M89vLyIrOkH8QEsbFga3ubxFLHlnO5\nHQ8PD55//nm+y8/n2OrVkJZmPDdrViSNGsllXtQi+wTUJctTW2pdYjGXTZvA0zMJGxsbfH19b56o\nRzUWUGotDRs25B2dDqKijK+7usIzzyibgJ08acEAJUnSvFq3Aa2XlxcnS32zZWRk4HWHGsXo0aPx\n8/MDwMXFBb1eb/ztpqRdNjg4kkOHwM9vK82bN6fBjX15YzZsgOxsIm8klpLrb31/XTt+7vnn+WTe\nPB745BO8uncn8h//ICYmhm7d4JNPYN68SGbP1k68tfG4dJ+AFuKp7ceyPE0vv0WLFgEYvy9NotJ8\nGlWlpaWJ4ODgCs+tWrVK9OvXTwghRFxcnAgPD7/tfSr78X79VZkD6e/fQQwcOPDmiaws5cRnn1U+\n+DogKytL2NnailEgxLRpQoibE9CGDRPCyUmInBwLBlgHyAl96pLlqS5TU4PmmsKGDx/OPffcQ1JS\nEi1btuTrr78mKiqKBQsWANCvXz/8/f0JDAxk3LhxfFaqk7m6lP6VYrKyksuPCIN61RQG0KJFC8ZP\nmMBiIH7OHKXWduO3nKlTlfUqb/xzSNVUUp6SOmR5aotJG31pXWUXUgsLA1vb42zf7s/ChQt55pln\nlBMrV8LAgbBzJ9x1l3mD1ZicnBzaBAbif/48255/HqtSCbx3bzh6FFJToWFDCwYpSZJZyI2+TJST\noyzoGxhYwYiwejDr/nZcXFz44MMP2QEsiooiptSS+lOmKEXz44+Wi6+2K90nIJlOlqe21PvEsnWr\nsjK+m9tthhrrdODhYaHoLGvEiBHc06UL/zYYuFyq7evBB5Uti2fPRi7zIklSOfU+scTGKs05168n\n4eTkhEfpJJKVpSSVBrVu8JwqrKysmL9gAed1Ov7atMk4O1KnU2otCQlwh0USpDuQfQLqkuWpLfU+\nsWzaBF27QkrKUYKCgsruiFnP5rBUJDQ0lOfGjuUzYN/EicbXn3hCKZrZsy0XmyRJ2lSvE8uVK7B7\nN0REQFJSUtkRYaD0UAcEWCY4DZkxaxaOdnZM3LIFoax9Q8OG8OKLysKUe/ZYOMBaSPYJqEuWp7bU\n68SybZuyiO/dd+dz4sSJsv0rV64ow55CQiwXoEa4urry7HPPsRX49plnjB0r48YpWxbLWoskSaXV\n68Si7L8C7u4pCCHKJpZDh5Q/ZWIBYOaHH9LVz4//O3aM3J9+AqBxY/jnP+Hnn+HECQsHWMvIPgF1\nyfLUlnqdWGJjoXNnyMysYERYQoLyp0wsgNKR/+kPP3AGeO3ZZ5VZksDkyUpn/ty5lo1PkiTtqLeJ\nJS9PmfcYEQGHDx8GoHXr1jcvSEgABwfw97dQhNoSExNDl27dmPDoo8y/fJnNw4cD4OMDw4bBwoVw\n8aKFg6xFZJ+AumR5aku9TSw7dkBhIfTsCXFxcbRp0wZnZ+ebFyQkQIcOyhaKktF7ixbh37gxY//4\ng2u//gooQ4+vXlU2npQkSaq335qbNilNOPfcY2DLli306NHj5kkhlMQim8GMStqwHR0d+eLHH0kG\nXhs5Ei5coFMneOAB+PhjKCiwaJi1huwTUJcsT22pt4klNhY6dYKMjIPk5OSUTSxnzsC5czKx3MZ9\nDz7I80OGMPfqVbYOHQooi1OeOgWlVn6RJKmeqpeJpbAQ4uKUZrDNmzcDlE0ssuO+nFvbsGd+9RUt\nXVwYu349eUuWcP/9SqKePRsMBsvEWJvIPgF1yfLUlnqZWHbvVjrvIyKUxOLl5VV2cxuZWP6Wk5MT\nX/74I0nA9GeeQXf6FFOmwOHDsGaNpaOTJMmS6mViuTF5nO7dBZs3b6ZHjx5ll3JJSAB3d+VHAipu\nw+7dty/jHn+cOfn5bH/sMYY+LvD2lhMmK0P2CahLlqe21MvEEhsL7dvDlStpZGVllW0GA9lxXwUf\nLFyIt6srY7ZsofjjD5k8GWJilFqhJEn1k+YSy9q1a2nbti1BQUHMnDmz3PnY2FhcXFwICwsjLCyM\nGTNmVOn+RUXKUvml+1ciIiJuXlBcrMy6l4mljNu1YTs7O/PFDz9wBBg6dSpPN1uKszPMmlWj4dU6\nsk9AXbI8tUVTicVgMDBx4kT+/PNPDh06xA8//MCRI0fKXRcREcGePXvYs2cPr732WpWesW+fMmm8\npH/F1dWV9u3b37wgNVXpgJGJpdIe6NuXTz/6iBXA6DHDeKv/ZpYtg7Q0S0cmSZIlaCqx7Ny5k9at\nW+Pr64uNjQ3Dhg1j+fLl5a4zZcvM2Fjlz5LE0r17d6xKT4KUHfcV+rs27PGTJzP/vfdYbjAQvex+\nAnVH+OijmomtNpJ9AuqS5aktmkosmZmZ+Pj4GI+9vb3JLNkeuJS4uDj0ej39+/cnMTGxSs/YtAkC\nA8Ha+jRJSUkV96/odMqse6lKJvz733zy3/+y/HohAbou/LYwmwsXLB2VJEk1rdZtjdi5c2fS09Nx\ncHBgzZo1DBo0iKSkpNteP3r0aONQYmdnFzZu1DN0aCRbtmwBoFGjRsZrY2JiYONGIgMCwMHB2G5b\n8ttQfT4u3YZ9p+uD77uPeZcv8+LcuXQqasP/vfgDX3zb3+Lxa+24suUpj2V51lT5LVq0CKDs1Ivq\nEhoSFxcn+vbtazx+7733xPvvv3/H9/j5+Ynz589XeO7Wj7d/vxAgxDffCPHiiy8Ke3t7UVBQUPZN\nQeXAeBgAABatSURBVEFCPPJI9T5AHRYdHV2l6+eOGSMAcY+Vp8g5nWueoGqxqpandGeyPNVlamrQ\nVFPYXXfdRXJyMidOnKCwsJAff/yRgQMHlrnm9OnTxr/v3LkTIQRubm6Vun9J/0rJiLBu3brRsGHD\nmxfk5UFysuxfqUDJbzmV9eJXX/GfewexzZBFn5ZenI2PN09gtVRVy1O6M1me2qKpxGJtbc38+fPp\n06cPHTp0YNiwYbRr146oqCgWLFgAwLJlywgODiY0NJTJkyfz041Npypj0yZo2RJcXS+xb9++8v0r\niYnKeiTBwWp+rHrrnc2/0d99CgcKrtC1a1cOfvqppUOSJKkmqFNx0qbSH89gEMLdXYgRI4RYs2aN\nAMS6devKvmHRIqWt7PDhGo5U+6rb1PDDD0J48qtobt1AOIL449FHhbh+Xd3gaiHZdKMuWZ7qMjU1\naKrGYk5HjyqLFpc0g1lbW9OtW7eyFyUkgK2tMmxMUsWQIWDj+wgB+iMENW3KgF9+YU5QECI93dKh\nSZJkJvUmsdw6fyUsLAxHR8eyFyUkKGu9NKh1g+XMrrpt2A0awEsvwdb4AGb/fJxH7rqLV9LSGO3r\ny6VOnZT19teuhStX1A1Y42SfgLpkeWpLvUksmzZBixbg41PAzp07y/evgFwjzEyefhpcXODTTxux\ndPt2pk+cyHc6HcFHj7Ju7lx46CFwdYUePeC//4W//lKWR5AkqVaqF4lFCKXGEhEBu3fvoqCgoHxi\nOX8esrNlYrmN0vMEqsrREZ5/Hn79FVJTrXjzk0/Yum0bDn5+9Ckq4rn+/bk8cSLk58O770Lfvkqi\nuesueOUV+P13pR2zDjGlPKXyZHlqS71ILGlpkJlZduHJ7t27l71ILuViVi+8ADY2GJd56datG3v3\n7mXKlCksWL2akN9+Y+PMmZCTA3/+Cf/5Dzg4wKefwiOPgIcHtGoFTz4Jn3yiLJ9cWGjZDyVJUoV0\nN0YA1Ek6nQ4hBF9/DWPHwsGDMHVqP44fP15+KZhPPoFJk5QM5OlpmYDruGeege+/h/R0aNr05uvb\ntm1jzJgxJCUl8eSTTzJ9+nSCgoKUkwUFShLZvl35iYtT/o1AGWih10PnztCli/LTrp3sI5MkE5V8\nd1b7/fUhsYweDatWQXZ2MU2auDFs2DCioqLKXvzss/DLL8pe96U3/ZJUc/iwMjbijTfg9dfLnsvL\ny+Ptt99m3rx55Ofn8+STT/Lf//6X1q1bl79RRsbNRBMfr/yU9MnY2yt7JOv1N39CQpTajyRJlSIT\nyx2UFE6rVsr3y7/+tYNu3brx7bff8tRTT5W9+O67ld+AZVtthWJiYlQZeTNggJIP0tOVHHCrM2fO\n8MEHH/DZZ59RWFjIU089xWuvvUbgnYaAGwxw7JhSs9m1S9kbYd8+yM1VzltZQVCQkmCCg2/+BASA\ntbXJn6k61CpPSSHLU12mJpY6P0EyPV2Z8zh3rhDDhw8Xjo6O4uLFi2UvLC4WwtFRiIkTLRNoLaDW\nBLTYWOXf4/PP73zdqVOnxMsvvyzs7OyEtbW1GD16tEhOTq78gwwGIdLShPjtNyFef12Ihx8WIiBA\nCJ1OCQCEsLUVQq8X4oknhHjrLSF+/lmIhAQh8vNN+YiVIif0qUuWp7pMTQ11vsby3XeCp56CP/44\nwcMPB/Diiy/y4Ycflr0wLU3pGI6KUprEJLMRArp1g7Nn4cgRKL1UW0VOnTrFzJkz+d///sf169cZ\nNWoUr776Kq1atapeAFevKm1yhw4pnW4HDyqBHD9+8xorK/D3h9atb/4EBSl/tmwp+3CkOk82hd2B\nTqfjn/8U/PwzjBo1mc8++5TU1NQye74AsGIFPPwwbNumNIlJZrV2rTJ15ZNPYOLEyr0nOzvbmGCK\ni4uNCcbf31+doK5dU5ZnOHJESTxHjyrNa8eOlZ282aAB+Poqv4gEBCh/tmoFfn7Kj5ub7KOTaj2Z\nWO5Ap9PRpo3A1/ciW7f6MHjwYBYvXlz+wueeg4UL4eJFcHau+UBrATXbsIWA++5T1vxMSVHmuVRW\nVlYW77//PgsWLKCwsJDu3bvz2GOP8eijj+JpjtF8QsDp0zeTTEqK8pOaqvycP1/2+kaNlMTj56f8\n6eNT9sfLC2xtZZ+AymR5qksmljvQ6XSA4MEH32Xt2lfZv38/HTt2LHvRhg1w//3KRIuPP7ZInLWB\n2v/j7tihNIm9+SZMn17192dmZvLll1+ydOlSDh48iE6no3v37jz++OM8/PDD5Wul5pKbqySY48fh\nxInyf168WP497u7EODsT2batkmg8PW/+2by58uPubrGBBbWRTCzqkonlDpTEkoebmx933aVn7dq1\nZS/IyVFGCjVqBHv2yCGpNezRR5XVW1JToVmz6t8nMTGRpUuXsnTpUg4dOgRAQEAAkZGR9OrVi8jI\nSLy8vFSKuoquXFGGR588qfyU/D0r6//bu/egJs71D+DfEFAgCQew3MRrgQjBFLRDFW0d0fEy7Ygd\nh7ax3hGpMnMKpSjD6R+nl2nVjs4o1bFQD+DxAlNrW6wSpFqs6HBpq+hPgVpEqtw9QChIIZDs7481\nS1bCRVhNgOcz88zuvru8eX0n8cle3jfseJyaGvaG0+OsrNhO8fBgB4e6uvZeuriwA4JcXOi9SwRF\niaUfIpEI48YlQ6uNxIULF7Bo0SL+AevXsyP28vPZ6UPIM1VWBvj7s/dZ9u8Xps6SkhLk5OQgNzcX\nly5dgkajAQB4e3tj4cKFXJgt0ZjS2clOJ1RbC9TV8Ze1tex0NvX1bHR2mq7D3r4n0UyY0DucnXvC\nyYldOjrSgwjEpFGXWLKzsxETEwO9Xo/NmzcjPj6+1zHvvvsu1Go1JBIJ0tLSEBgYaLIukUgEe3s5\nfH2l+PXXXx+dwTxy6hQ7p/u//82O2CP9elqXGiIjgbQ09l65UPfhDXQ6HW7cuIHc3Fzk5uYiLy8P\nLY/Gtvj4+GDhwoWYN29e71muAdjb20OhUGDKlCmwshJ+5qMh9SfDsANBGxrYePCAjf/9j7/e2NgT\njxJrn2QyNsE4OrIJx7Du4AD84x/8cHDoCZmsZ2ljM+R+EApdChPWqEoser0ecrkcFy5cwMSJExEU\nFISMjAz4+vpyx6jVahw4cABnz55FYWEhoqOjUVBQYLI+QyJJT0+HSqXq2VFXxw6Qmz6dfRLMAj4Y\nlm7fvn2IiYkRvN7qavbnb8LCgKNHBa+eR6fT4fr167h48SIuXryIS5cucYmmLxKJBAqFAv7+/ryY\nPHky/4vKE3pa/dlLdzd7n6epqfeyqYlNPMbR3MwuW1qAv/5iB58OZPx4NsFIpb2XEknvpUTCnmEZ\nLyUSdsSsvX1P2NkN+ozqmfXnGDHcxGJR58FFRUXw8fHB1KlTAQAqlQqZmZm8xJKZmYn169cDAObM\nmYOWlhbU19fDzc3NZJ0eHtMQFhbWU8AwwJYt7HiG//6XksogaQb65jtEnp5AdDTw+edAXBw7G8vT\nIhaLMXv2bMyePRuxsbHQ6XQoLy9HV1dXr2NbWlpQUlKCmzdv4tatW8jOzkZaWhq3XyqVQqFQcCGT\nyZ6oLefPn4etrS2vzMHBARMnTuTC1JnUE7O2Zi+RDeUmFsOwn5OWlp5obWXjr796orWVvZdkvNRo\n2G8NDx+yZQ8fAn//PbT229n1JB3Duq0tG4/WNbdvs2OSbG3ZRGfYP378wDFuHBvG64+HjQ1734sM\nikUllurqat7TPJMmTUJRUVG/x3h6eqK6urrPxLJ9eyysjb/1/Oc/wJkzwL597ISFxOzi49mxqQkJ\nQFbWs3tdsViMGTNm9Ll//vz5vO3GxkbcunULJSUl3FKtVvMSzpM4e/Zsv/tlMhk8PDy4RGO8brwt\nkUiG9PoDEonYswyplP0GMFw6HZtg2ttNL//+m11vb2fXDWWmoqODjZYWdlldzV766+zs2afTDb/N\nxsRifqIxLG1s2ARoWDcO43LDurV1Tzy+bRxiMX9pWA8JAYy+bFsii0osT0Nk6f8B69b1nNoXFbGD\nKP75T3M3bUSpNB6ZLjAnJ+Bf/wJ27GCnarPUS+UTJkzAggULsGDBAl65RqNBR0fHE9UVHR2N/UZP\nLDAMg5aWFtTU1PSK2tpaFBQUoKamxuTrGJ/peHt7955g1VKIxT33aARWuXEje7POWHc3m2A6O02H\nVsuGYd1Q3tXVs0+rZbcN5YZ9xsu+orubTYLGZTodW27Yb1g3lBu2+5OSYvGJxaLmCsvPz2eWLVvG\nbe/cuZPZtWsX75h33nmHycjI4LZnzJjB1NXVmawPAAUFBQXFEGI4LOqMJSgoCOXl5fjzzz/h4eGB\njIwMpKen844JDQ3FwYMH8dZbb6GgoACOjo59XgZjLOe5BEIIGTMsKrGIxWIcOHAAS5cu5R439vPz\nQ1JSEkQiESIjI/Hqq68iKysL3t7ekEgkSE1NNXezCSGEGLGox40JIYSMfKPy+bns7Gz4+vpCLpdj\n9+7d5m7OiDRt2jQEBARg1qxZeOmllwAAzc3NWLp0KWbMmIFly5YNOAZkLNu8eTPc3Nx4c9P11387\nd+6Ej48P/Pz8kJOTY44mWyxTffnRRx9h0qRJ3OPjxtM1UV/2r6qqCosWLYK/vz+USiUSH82RKOj7\nc1h3aCyQTqdjvLy8mMrKSkar1TIBAQFMaWmpuZs14kyfPp1pamrile3YsYPZvXs3wzAMs2vXLiY+\nPt4cTRsR8vLymGvXrjFKpZIr66v/bt26xQQGBjJdXV3M3bt3GS8vL0av15ul3ZbIVF9++OGHzN69\ne3sdW1JSQn05gNraWubatWsMwzBMa2srI5fLmdLSUkHfn6PujMV4kKWNjQ03yJI8GYZhoH9s1HVm\nZiY2bNgAANiwYQO+//57czRtRHj55Zfh5OTEK+ur/06fPg2VSgVra2tMmzYNPj4+vcZvjWWm+hIw\n/XBOZmYm9eUA3N3duWmwpFIp/Pz8UFVVJej7c9QlFlODLKurq83YopFJJBJhyZIlCAoKwuHDhwGA\nN8OBu7s7GhoazNnEEaehocFk//U16Jf078CBAwgMDERERAR32Yb68slUVlaiuLgYc+fO7fPzPZQ+\nHXWJhQjjypUruHr1KrKysnDw4EHk5eX1mhtrOHNlEeq/4YiKikJFRQWKi4vh7u6O999/39xNGnHa\n2toQFhaG/fv3QyqVCvr5HnWJxdPTE/fu3eO2q6qqLGuK9BHCw8MDAODi4oLXX38dRUVFcHNzQ319\nPQD2t+hdXV3N2cQRp6/+8/T0xP3797nj6D07MBcXF+4/vi1btnCXZqgvB6e7uxthYWFYt24dVq5c\nCUDY9+eoSyzGgyy1Wi0yMjIQGhpq7maNKO3t7Wh79DvvDx8+RE5ODpRKJUJDQ7l5sY4cOcK9IYlp\nDMPw7gP01X+hoaHIyMiAVqvF3bt3UV5ezj2JR1iP92VdXR23/u2332LmzJkAqC8HKzw8HAqFAtHR\n0VyZoO/Pp/XkgTmp1WpGLpcz3t7ezM6dO83dnBGnoqKCCQgIYAIDA5mZM2dyfdjY2MgsXryYkcvl\nzJIlS5jm5mYzt9RyrV69mvHw8GDGjRvHTJ48mUlJSWGampr67L/PPvuM8fLyYnx9fZlz586ZseWW\nx1Rfrlu3jlEqlUxAQACzcuVK3rRO1Jf9u3z5MmNlZcV9xmfNmsWo1ep+P99P2qc0QJIQQoigRt2l\nMEIIIeZFiYUQQoigKLEQQggRFCUWQgghgqLEQgghRFCUWAghhAiKEgshhBBBUWIhhBAiKEosZMzY\ntGkTTe9DyDNAiYWMClZWVhCLxbCysuoVYrEY4eHhSExMxLFjx8zd1CHLzs5GbGwsfv7552fyeikp\nKYiIiKCfRyBPzNrcDSBECMaTEv7www+IjIxEXV0dN3GhnZ0dZDKZuZoniPr6esTExGDKlClDrqO4\nuBhr167FzZs3Bzw2PDwc1tbW6OjoGPLrkbGJzljIqODq6sqFo6MjAHZqdUOZTCYzeSns888/h7e3\nN+zt7REQEIDjx4/z9oeEhCAqKgpxcXGYMGECXF1d8cUXX6CzsxPbtm2Do6Mjpk6divT0dN7fbNu2\nDTExMXB2doazszN27NjBq1er1SImJgbu7u6ws7NDcHAwrly58pR6p4e/vz+ysrIGfTxNJUiGghIL\nGbM++OADpKam4tChQygtLUVCQgK2bt0KtVrNO+7EiRNwcHBAUVEREhISEB0djdDQUCgUCly9ehUb\nNmxAeHg475LRiRMnwDAMCgoKkJycjOTkZOzbt4/bv337dpw8eRJpaWkoLi6GUqnE8uXLud/DeFps\nbGyGdcZDyGDQ7MZk1Dl16hTefPNN6HQ6XvmmTZvQ2NiI06dPo729Hc899xx+/PFHzJ8/nzvmvffe\nw+3bt3H27FkA7NmHVqvlnU24urpi3rx53G+Cd3d3QyKRID09HatWrUJISAhqa2tRVlbG/c2nn36K\npKQk3Lt3D+3t7XByckJKSgrWrFkDANDr9ZDL5Xj77bfx8ccfm/x3HTlyBCEhIZgyZQqam5uRkpKC\nvLw8JCQk4Pr162hra8P9+/exYsUKVFVV4fbt23B2dkZsbCz0ej0OHjyIGzduYOvWrXjxxRe5Oi5f\nvoyEhATcuHEDra2tqK6uxp49e3q9JiGDRWcsZEwqKSlBR0cHli9fDplMxsWXX36JiooK3rEvvPAC\nb9vV1RVKpZLbtra2hpOTE++MZe7cuby/CQ4ORnV1Ndra2nDnzh10d3dj3rx53H4rKysEBwejpKRk\nUO3/7rvvEB0djd9//x1//PEHIiMjERUVhUOHDsHOzg7r16/H2rVrkZKSAgDIzMzE6tWr0dXVhcrK\nSl4dZWVlqKioQEREBCIiIpCUlDSoNhDSF7p5T8YkvV4PADhz5gwmT57M22djY9PvtkgkMllmqHM4\nBvs742+88QYaGxvR1taGtWvXAmBvzAcFBSE4OBgA8Msvv0ChUAAAlixZAoZhkJubyyUOQx3t7e1Q\nqVQAgN9++w1+fn7D/neQsY3OWMiYpFAoMH78eFRWVuL555/nxeOJZigKCwt52/n5+Zg4cSKkUim8\nvLxgY2PDu7ym1+uRn5/PJYKByGQynD9/HosWLeLKLly4gMWLF3PbJ06cgEqlgkajgVQqxfHjx7Fq\n1Sro9Xp0d3ebrOPkyZNQqVRobW0d6j+dEEosZGySSqWIi4tDXFwcUlNTcefOHVy/fh1JSUk4fPjw\nsOuvqanh7td888032LNnD2JjYwEA9vb22LZtG+Lj46FWq1FWVoatW7eioaEBUVFRg36N8+fP8xKJ\n8bZGo0FhYSFWrFiB1NRUAMCxY8ewceNGJCcnc2dGj9fx9ddfQ6VS4auvvhp2H5Cxiy6FkTHrk08+\ngbu7O/bu3YuoqCg4ODggMDCQ92iwqUtTfZUZl69ZswY6nQ5z5syBlZUVtmzZgpiYGG7/7t27IRKJ\nEB4eDo1Gg1mzZuHcuXNwc3MbdPvLy8uxa9cubvvBgwfcZTBbW1vMnTsXR48exWuvvQYACAwMRGFh\nIWbOnAmxWGyyjuDgYOTk5OCVV14ZdDsIeRw9FUaIwEJCQqBUKpGYmChoveZ4QoueCiNDQZfCCCGE\nCIoSCyECG+yTXUNBFxjISECJhRCB/fTTT4JfBgMANzc3JCYmPtNJKPPy8mBra/tMXo+MHnSPhRBC\niKDojIUQQoigKLEQQggRFCUWQgghgqLEQgghRFCUWAghhAiKEgshhBBBUWIhhBAiKEoshBBCBPX/\n6UsKFf2/IGkAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa7ff9af510>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Calcula los HU para la descarga\n",
"Tscs,Qscs,HU=cuCap.GetHU_SCS(cuCap.GeoParameters['Area[km2]'],\n",
" TcCap,)\n",
"Tsnyder,Qsnyder,HU,Diferencia=cuCap.GetHU_Snyder(cuCap.GeoParameters['Area[km2]'],\n",
"\tTcCap,\n",
"\tCp=0.8,\n",
"\tFc=2.9)\n",
"\t#Cp=1.65/(np.sqrt(PendCauce)**0.38))\n",
"Twilliam,Qwilliam,HU=cuCap.GetHU_Williams(cuCap.GeoParameters['Area[km2]'],\n",
"\tcuCap.GeoParameters['Long_Cuenca [km]'],\n",
"\t780,\n",
"\tTcCap)\n",
"#Agrupa los hidrogramas unitarios para luego plotearlos\n",
"D = {'snyder':{'time':Tsnyder,'HU':Qsnyder},\n",
" 'scs':{'time':Tscs,'HU':Qscs},\n",
" 'williams':{'time':Twilliam,'HU':Qwilliam}}\n",
"#Hace el plot de ellos \n",
"cuCap.PlotHU_Synthetic(D,ruta=ruta_images + 'Q_max_HU.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Hidrogramas unitarios calibrados para la cuenca, williams muestra un rezago en este caso con las demás metodologías"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#QmaxRegGum = cuCap.GetQ_Max(cuCap.CellQmed, Dist='gumbel', Tr= Tr, Coef = [6.71, 3.29], Expo = [1.2, 0.9])\n",
"#QmaxRegLog = cuCap.GetQ_Max(cuCap.CellQmed, Dist='lognorm', Tr= Tr, Coef = [6.71, 3.29], Expo = [1.2, 0.9])"
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAq0AAAGBCAYAAABM2oh7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVPX+P/DXgMiqsikqLqigpGIDdDXTAPd9udbN6paS\ndr3m7rXlXu3aw/SraWm/NDO1sk3LrRJTXDKHcsHtClpugCKCCggJoggOzO+PT8MAMyDMcs4sr+fj\n4cP5zJlz5s3pmG8/533eH4VGo9GAiIiIiMiKOckdABERERHRwzBpJSIiIiKrx6SViIiIiKwek1Yi\nIiIisnpMWomIiIjI6jFpJSIiIiKrZ5VJa3l5OSIiIjBy5Ei9bQkJCfD29kZERAQiIiKwaNEiGSIk\nIiIiIik1kDsAQz744AN07twZhYWFBrdHRUUhLi5O4qiIiIiISC5WN9OamZmJ3bt34+WXX67xM1wP\ngYiIiMixWF3SOnv2bLz77rtQKBQ1fubo0aNQKpUYNmwYzp07J2F0RERERCQHq0pad+3ahYCAACiV\nSmg0GoMzqpGRkcjIyEBSUhKmTZuG0aNHyxApEREREUlJobGie+1z587F119/jQYNGqC4uBh37tzB\nmDFj8OWXX9a4T7t27XDq1Cn4+vrqbatttpaIiIiIpGVK2mlVSWtlCQkJWL58ud4DV9nZ2QgICAAA\nHD9+HM888wzS09MNHkOhUBh1cmJjY/H555/Xez9z7W8KOb/bEfF8kxR4nRGRPTA2L9Oyyu4B1a1d\nuxYKhQKTJk3Ctm3bsGbNGri4uMDd3R2bN282+/cFBQXJur+tfrcj4vkmKfA6IyKy4qQ1Ojoa0dHR\nAIB//vOfFe9PnToVU6dOlSssIiIiIpKBVT2IZS28vb1l3d9Wv9sR8XyTFHidERExaTVIqVTKur+t\nfrcj4vkmKfA6IyKy4gexzMHUgl8iIiIiMg9T8zLOtBIRERGR1WPSaoBKpZJ1f1v9bkfE801S4HVG\nRGTF3QOIiIiIyAY9eABcuQKkpACXLonfU1JMPixrWomIiIiofsrKgIwM/cT00iUgPV1sr0YB01bE\n4kwrEREREekrLweuXzecmF6+DJSWGt5PoQDatAE6dgRCQnS/RowwKRwmrQaoVCrExMTItr8p5Pxu\nR8TzTVLgdUZEFqPRADk5hhPT1FSguLjmfVu0qJqYal936AC4uZk9VCatRERERPYuP99wYpqSAty5\nU/N+/v6GE9PgYMDLS7r4wZpWIiIiIvtw507NiWl+fs37NWliODENCQHMuCKfqXkZZ1qJiIiIbMW9\ne0BamuHENDu75v08PavWl1ZOTP39RR2qlWPSagBrWqmueL5JCrzOiBxMaal40MlQYpqZWfN+rq7i\ntr2hxLRFC5tITGvDpJWIiIhIamo1cPVq1cRUm5xevSqe3DekQQOgfXvDiWnr1oCT/a4bxZpWIiIi\nIksoLxczo4ZmTK9cEU34DXFyAtq2NZyYBgWJxNUGsaaViIiISC4aDXDzpuHENC0NuH+/5n1btTKc\nmLZvL271UxVMWg1gTSvVFc83SYHXGZHMNBogL8/wrfzUVKCoqOZ9AwIMJ6bBwYCHh3Q/gx1g0kpE\nREQEALdv6yel2te3b9e8n6+v4cQ0JARo3Fi6+O0ca1qJiIjIcdy9W3Nimptb836NGtWcmPr5SRe/\nDWNNKxEREVFl9++LelJDyen16zXv5+6uaxlVvdl+s2Y23zLK1jFpNYA1rVRXPN8kBV5nRAY8eCCe\nwDeUmGZkiDpUQ1xcgA4dDCemLVvadcsoW8eklYiIiKxTWZlIQA0lpleuiO2GODuL1lCGEtM2bcR2\nsjmsaSUiIiL5aDRAVpbhxDQtTawOZYhCIZrpG0pMg4KAhg0l/THo4VjTSkRERNZNowFycgwnpqmp\nwL17Ne/booXhxLR9e1GDSg6DSasBrGmluuL5JinwOiObkZ9f85P5hYU17+fvr/9EfseO4qEoLy/p\n4ierxqSViIiI6u7OnZoT07y8mvdr0sTwjGlICODtLV38ZLNY00pERERVFReL2/aGEtObN2vez8Oj\n5sTU358toxwca1qJiIio/kpLgcuXDSem167VvJ+rq66XafXEtEULJqZkMUxaDWBNK9UVzzdJgdcZ\nGU2tBq5eNZyYpqcD5eWG92vQQDzoZCgxbdWKLaNIFlaZtJaXl+Oxxx5Dq1atEBcXp7d9xowZiI+P\nh6enJz7//HMolUoZoiQiIrIC5eVAZqbhxPTyZdGE3xCFAmjXznBiGhQkElciK2KVNa3vv/8+Tp06\nhcLCQr2kNT4+Hh9++CF27dqFY8eOYebMmUhMTDR4HNa0EhGRXdBoRC2pocQ0NVUsW1qTVq0MJ6bt\n24tb/UQSsbua1szMTOzevRvz5s3DihUr9Lbv2LED48aNAwD06NEDBQUFyM7ORkBAgNShEhERmY9G\nI56+N5SYpqQARUU17xsQYDgxDQ4WD0cR2QGrS1pnz56Nd999FwUFBQa3Z2VloXXr1hXjwMBAZGVl\nmTVpZU0r1RXPN0mB15mdKSgwnJheugTcvl3zfj4+hp/KDwkBGjeWLn4imVhV0rpr1y4EBARAqVRC\npVKZ5dZ+bGwsgoKCAADe3t5QKpUV//NXqVQAoDfWqmm7pfc3ZZyUlCTp9zn6mOebY445NjiOjwey\nshDj7Q1cugTVL7+IcXY2kJsL8Wkg5s/fK8aNGgEhIVA1aQIEBiJm4EAxzs4GmjTR/77ISOv4eTnm\n2MBY+zo9PR3mYFU1rXPnzsXXX3+NBg0aoLi4GHfu3MGYMWPw5ZdfVnxm8uTJ6NOnD8aOHQsACA0N\nRUJCgsGZVta0EhGRxZSUAGlphmdMr1+veT9396otoyrPmAYEsGUU2S1T8zKrSlorS0hIwPLly/Ue\nxNq9ezdWr16NXbt2ITExEbNmzeKDWEREZBkPHojWUIYS04wMUYdqiIsL0KGD4cQ0MBBwcpL0xyCy\nBnb3IJYha9euhUKhwKRJkzB06FDs3r0bwcHB8PT0xIYNG8z+fSqVqmKKW479TSHndzsinm+SAq8z\nCysrE830DSWm6emi16khzs6iNVT1pDQkBGjThi2jiMzMav9ERUdHIzo6GgDwz3/+s8q2Dz/8UI6Q\niIjIVmk04pa9ocQ0LU2sDmWIQiESUEMzpu3aAQ0bSvtzEDkwqy0PMAeWBxARORCNBsjNNZyYpqYC\n9+7VvG+LFoYT0w4dRA0qEZnMIcoDiIiIKvzxh+HENCUFKCyseT9/f8O38oODgUaNpIufiIzCpNUA\n1rRSXfF8kxQc8jq7c0fMjlZvsH/pkmjAX5MmTQwnpiEhos8pEdksJq1ERCSP4mJRT2poxvTmzZr3\n8/AwnJh27ChmU9kyisgusaaViIgsp7QUuHLFcGJ67VrN+7m6inpSQ4lpixZMTIlsEGtaiYhIXmVl\nwNWrhm/lp6cD5eWG92vQQDyBbygxbdVKtJQiIvoTk1YDWNNKdcXzTVKwiuusvBzIyjI8Y3r5smjC\nb4hCIXqZGkpM27YVTfiJiOqASSsREQkaDZCdbTgxTU0F7t+ved/AQMOJafv24lY/EZGJWNNKRORo\n8vIM38pPSQGKimrer1kzw4lphw6Ap6d08RORTWJNKxER6SsoMJyUpqSIPqc18fExnJgGB4t2UkRE\nMmHSagBrWqmueL5JCjVeZ3fvitv2hhLTnJyaD+jlVTUxrfzaz89iPwcRkSnqlbTm5OTgfm01TQa4\nubmhWbNm9dqHiIj+VFIinsDfsUM/Oc3Kqnk/Nzf92VLt64AAtowiIptTr5rWl19+GVFRURX1CIo/\n/6dX2yF+/fVXfPLJJyaGaRzWtBKRzdFogN9/B/bsEb9+/VX0OjXExUXUkxpKTgMDAScnaWMnIqqF\npDWtTzzxBMaNG1cxnjJlCjp16oTo6GgolUqD+5SVlRkdHBGRQygoAH76SZeoZmbqtikUNSembdqI\nXqdERA7ApO4BCxYswM2bN/Hbb7/h0qVLePzxxxEdHY3o6GhERkaaM06jGJvRs6aV6ornm4xSXg4k\nJ4sENT4eOHJENOjXCggABg8WvwYMgOrsWV5nRGTzZO0eEBISgrfeegsAcPfuXWzduhVffPEFtm7d\niuLiYuzevRstW7Y05SuIiOxDXh6wf79uNjU7W7fN2Rl48klgyBCRqD76KG/tExFVY9JM65w5c7Bw\n4UJ4eHhUvPftt9/i2WefxYULF/DJJ5/gvffeM0ugxmBNKxHJpqwMOHVKzKTu2QMcP151OdNWrUSC\nOmQI0K8f20kRkd2TdaZ1/Pjx6NGjB1544QX0798fTZs2xdmzZ/Hss88iNDQU4eHhphyeiMi2ZGcD\n+/aJRHXfPjG7quXiAvTpo0tUO3fmE/xERPVg0v2nbt26Yfv27Thx4gRiYmLQr18/9O7dGwCwZcsW\npKenmyNGyalUKln3t9XvdkQ83w5OrQYOHQLefBOIjASaNwfGjQO++UYkrO3aAVOmAHFxQH6+eNjq\n1VeBLl3qlbDyOiMiMsPiAh07dsS2bdv03s/IyMDt27dNPTwRkXXJytLVpe7fL57813JzA2JidLWp\nISGcTSUiMhOTalqtHWtaichkpaXA4cO62tSzZ6tu79RJ96R/dDTg7i5PnEREVk7Wmtb3338ft27d\nwhtvvIHGjRvj008/xZAhQ9gxgIhsW3q6rh3Vzz8DRUW6bZ6e4sGpwYOBQYOA9u1lC5OIyJGYVNPq\n6+uLefPmYevWrQCAiRMnYteuXWYJTE6saaW64vm2E/fvA3v3ArNnA488ImpRX3lF1KIWFQFdu4pa\n1AMHRK3qjh1iu0QJK68zIiITZ1oLCgrg4eEBNze3ivcqt78iIrJKGg2Qmqq75a9SAcXFuu2NGwMD\nBuhu+7dqJVuoREQkmFTTumLFCpSVlaF58+Z48cUXAQArV67EjBkzzBagKVjTSkQV7t4FDh7UJaqX\nL1fdHh6ue4Dq8cdFiyoiIjIbU/Myk5JWjUaDSZMmYePGjejatSvc3Nzw1FNPYebMmUYHZE5MWokc\nmEYDnDune9L/l1/EQ1Vavr7AwIEiUR04ULSrIiIii5E1adW6ePEikpOT0bFjRyiVSlMPZzbGnhxT\n15OXcz16Ob/bEfF8W5nCQtELVZuoXrum26ZQAN2765r7P/aYWD7VBvA6IyJ7IGv3gC+++AJbtmzB\n559/juTkZNy6dcuqklYisnMaDZCcrHvS/8gR0fBfq1kzXV3qgAGAv798sRIRkUlMmmn94osvMHz4\ncLzzzjs4ffo0Jk+ejKysLJYHEJHl5OeLpv7a2dSbN3XbnJ2Bnj11talKJeBkUpMUIiIyE1lnWouK\niuDn54f9+/fj7bffxsiRI7F+/XpTDomSkhJERUWhtLQUpaWlGDVqFBYvXlzlMwkJCRg1ahTa/9lu\nZsyYMXjzzTdN+l4islLl5cDJk7ok9dgx8Z5WYKBuNrV/f8DbW75YiYjIYkxKWtu1awelUonCwkIM\nGjQIarUanp6eJgXk6uqKgwcPwsPDA2VlZejVqxcOHz6MXr16VflcVFQU4uLiTPqumrCmleqK59tC\ncnKAffvELf99+4Bbt3TbXFzEylPa2dSuXe1+qVReZ0REJiatQ4cORVRUFBo0aABXV1f4+/vj9ddf\nNzkoba/XkpISlJeXw8fHR+8zvO1PZEfUajGDqq1NPXWq6va2bUWSOmQI0KcP0KiRPHESEZFszNI9\nQOvq1avw9/c3eba1vLwckZGRSEtLw+TJk7Fs2bIq2xMSEvDUU0+hVatWCAwMxLvvvovOnTvrHYc1\nrURWLCtLrEK1Z4+oUb19W7fN1RWIidE96d+xo93PphIR2TvJalpzcnLQqFEjuLu71/iZtm3bGh1I\nZU5OTjh9+jQKCwsxcOBAJCQkIDo6umJ7ZGQkMjIy4OHhgfj4eIwePRqXLl0yeKzY2FgEBQUBALy9\nvaFUKitus2mXRuSYY44lGO/fD/z2G2Ju3gT27IHqzBmxHYIqMBDo0QMxL78MREdDdfy42N6pk3XE\nzzHHHHPMcb3G2tfp6ekwhzrPtKampmLdunUoKyvDqFGjEBUVZZYAHmbhwoXw8PDAnDlzavxMu3bt\ncOrUKfj6+lZ5n31aydJ4vh/i6lXdLf8DB4CiIt02Dw+gb18xkzpoENChg3xxWjleZ0RkDySbaQ0O\nDsayZctQUlKCH374AVOmTEHLli3xwgsvVMxkmsOtW7fg4uKCJk2aoLi4GPv378dbb71V5TPZ2dkI\nCAgAABw/fhwajUYvYSUiGdy/L1ae0iaqFy5U3d6li+6Wf+/eogyAiIioDkyqab1+/To2btyIy5cv\no0ePHvjb3/5mcj3r2bNnMX78eGg0GpSXl+PFF1/Eq6++irVr10KhUGDSpElYvXo11qxZAxcXF7i7\nu+P9999Hjx499H841rQSWV5qqkhQ9+wBDh4Eiot12xo1Ek39Bw8Ws6lt2sgXJxERycoqlnEFgGPH\njmHr1q1Qq9UYNWoU+vTpY47DmoRJK5EF3L0LqFS6RDUtrep2pVLXjqpnT9GiioiIHJ7VJK1a2vKB\nn3/+GW3btsXcuXPNefh6YU0rWZpDnG+NBjh/XnfL/5dfgNJS3XYfH2DgQN1saosW8sVqpxziOiMi\nuyfriliGuLq6YuzYsRg7diwKCgrMfXgikkJhoXhwSrsKVUaGbptCAXTvrluFqnt3sXwqERGRBZl9\nptWasDyAqI40GuDMGd0t/8OHRcN/raZNxSzqkCGiRrVpU/liJSIim2Txmdby8nL8/vvv6NixI1xd\nXZGXl4dff/0VQUFBUCqVRn8xEcnsjz9EU//4eNHk/8YN3TYnJ6BXL92T/uHh4j0iIiKZPDRpfeWV\nV3Dq1Ck4OTnhnXfewZIlS9CsWTNkZGTg6aefxsyZM6WIU1KsaaW6sqnzXV4ulkfV3vJPTBTvabVs\nqbvl37+/qFUlq2BT1xkRkYU8NGmNiorC2rVrUVpaivfeew/79++v2LZu3TqLBkdEJsrN1S2Vuncv\ncOuWbluDBkBUlO5J/7AwLpVKRERW66E1rZ999hnOnTuHBQsWoLCwEC3+fDJ47dq1aNKkCZ599llJ\nAjUGa1rJ4ajVwPHjutrUU6dEvapWmzYiSR0yRKxG1aiRfLESEZFDsXhN6zPPPAOVSgVPT88qCwdc\nvnwZ48ePN/qLichMrl/Xzabu3y9qVbVcXYHoaN1t/9BQzqYSEZFNYvcAA1jTSnUly/l+8EA83a+t\nTU1Orro9OFj3AFV0NGDiKnUkP/65JiJ7YDV9Wm/fvo3PPvsMw4cPR8eOHc11WCICRJ9UbXP/AweA\nO3d029zdxa1+7WxqcLB8cRIREVmISTOtK1aswGeffYbOnTvj2WefxYgRI/DVV19hwoQJ5ozRaKxp\nJZt1/z7w66+6RPX8+arbH3lE9wDVk08Cbm7yxElERFRHss605ufnY9u2bThx4gTWr1+Pl19+GY8/\n/rjVJK1ENiU1VXfL/+BB4N493TYvL9GGasgQ0eS/bVv54iQiIpKBSTOtX375JcaNG1cxvn37Ntzc\n3OBmJbM+rGklSzPpfN+7B6hUuif9U1Orbn/0UV1tas+eQMOGpoZLNop/ronIHsg609qqVSscPXoU\nPXv2BAB4e3ubcjgi+6bRABcu6G75//ILUFKi2+7tDQwcKBLVQYNEs38iIiICYOJM6+zZs7FmzRr8\n5S9/Qb9+/dCvXz/07NkTDRqY7fkuk7CmlWR35454cEp72//q1arbH3tMV5vavbto+E9ERGSHZJ1p\nbd26NW7fvo2kpCQcOHAA8+fPR25uLn777TdTDktkuzQa4OxZ3S3/Q4dEw38tf38xizp4sJhVbdZM\nvliJiIhsiEkzrevWrcOkSZPMGY9ZsaaVLE2lUiHm0UeBn37SJao3bug+4OQEPP64rh1VZKR4j6ge\n+OeaiOyBrDOtjz76KL7++mu88MILphyGyPaUlwNffw28+y5w7pwYa7VooUtS+/cHfH3li5OIiMhO\nmDTTOnr0aFy8eBFFRUXo27cv+vXrh0GDBiEgIMCcMRqNNa1kEWfPAlOmiFv/gKhD7dVL96R/t25c\nKpWIiKgaU/Myk+5TPvnkkzh79ixOnjyJgQMH4uDBg3j66adNOSSR9bpzB5gzBwgPFwlrs2bAp58C\neXmiddW//y3aVDFhJSIiMjuTktYJEybgyy+/hIeHB/7+979jw4YN+PXXX80Vm2xUKpWs+9vqd9st\njQbYuhUIDQVWrBClAFOnAhcvQtW+PdC4sdwRkp3jn2sionomrQkJCVXGPj4+mDBhAho1alTnfYhs\nSkqKuO3/zDPA9evAX/4CnDgBfPih6KtKREREkqhXTeu//vUvzJo1q84H12g0WLlyJZYvX25UcKZi\nTSsZrbgYWLIEWLoUKC0FfHzE+OWXAWdnuaMjIiKyOabmZfVKWvfs2YPs7Ox6fUFAQAAGDx5c78DM\ngUkrGWX3bmDaNODKFTGOjRXJK3uqEhERGU3SpNXWsE8r1UtGBjBzJvDDD2LctSuwZg3Qu3eNu/B8\nkxR4nRGRLdNogMJCwNtbxj6tRHahtBR4/33g7beBe/cALy9gwQJg+nTAxUXu6IiIiKxSaSmQnQ3c\nvCnW1bl5U/er+vj+fdO/z6wzrUVFRfDy8jLX4UzG8gB6KJVK9Fw9f16Mn3lGdAgIDJQ1LCIiIjlo\nNMAffzw8Cb1xA8jPr/txvbyAoiIrKg8YN24cVq9ejT/++APXr1/H448/bq5DG4VJK9Xo5k3g1VeB\njRvFODgYWL0aGDhQ3riIiIgs4P79hyeh2tcPHtTtmM7OQEAA0Ly5+NWihe515XFAgEhaZV3Gtbp+\n/frh4sWLeOyxx5CSkmLUMUpKShAVFYXS0lKUlpZi1KhRWLx4sd7nZsyYgfj4eHh6euLzzz+HUqk0\nNfwKrGm1Y2Vlok513jxRYOPmBsydC7z2mnhdTzzfJAVeZ0RkSHm5WN+mLrfnb9+u+3GbNKk9CdX+\n8vcHnEzq+F8/Zk1ac3NzsW/fPixYsAAdOnRAv3796n0MV1dXHDx4EB4eHigrK0OvXr1w+PBh9OrV\nq+Iz8fHxSEtLQ0pKCo4dO4bJkycjMTHRnD8K2aNjx0QpwP/+J8ZDhwKrVgHt28sbFxERUSX37tUt\nEc3OBtTquh3TxaVqwllTUhoQALi7W/bnM5ZZk9ZHHnkEw4YNQ1lZGb766iujj+Ph4QFAzLqWl5fD\nx8enyvYdO3Zg3LhxAIAePXqgoKAA2dnZCAgIMD74Skyd0ZBzRoSzMQbk5wP/+Q+wfr0o1mndGli5\nEhg1yuQlV3m+SQq8zohsX1kZkJtbt1v0d+7U/bi+vg+/Pd+8uWg3LuWsqCWYNWnt3bs3rl69Cl9f\nX6SlpRl9nPLyckRGRiItLQ2TJ09G586dq2zPyspC69atK8aBgYHIysoyW9JKdqK8HPjiC+D114Fb\nt4AGDYA5c4D//hfw9JQ7OiIisnEaDVBUVLc60Zwc8ddSXbi61u32fECA+KyjMGvSeuTIETzxxBPI\nz89Hz549jT6Ok5MTTp8+jcLCQgwcOBAJCQmIjo42Y6S1Y02rHThzRpQCHD4sxjEx4kGrav8AMhXP\nN0mB1xmRtNRqkWTW5Qn6e/fqftymTR9+e755c1FTauKNQLtk1qRVpVIhLi4Oubm5aNGiBYYOHWrS\n8Ro3boxhw4bh5MmTVZLWwMBAXLt2rWKcmZmJwBpaFMXGxiIoKAgA4O3tDaVSWfE/f5VKBQB648o/\nj6Htlt7flHFSUpKk32d143v3EPPTT8DKlVCVlQE+PohZtQp4/nmoEhKAnByeb4455phjBxxrNEB4\neAxu3gT27FEhPx/w8RHjpCQxLikR49xcsT8Q8+fvNY/d3QFvbxV8fYHQ0Bg0bw4UF4txTIwYX76s\ngo8P0L9/7fGGhlrP+TLHWPs6PT0d5mDWllfx8fEYMmQIACAuLg4jR46s9zFu3boFFxcXNGnSBMXF\nxRg0aBDeeuutKg917d69G6tXr8auXbuQmJiIWbNmGXwQiy2vHIhGA2zdCsyeDVy/Lgp3pk4VCwZ4\ne8sdHRERWYglGtwrFGLl7ofdnm/RQtvKybI/o72wqpZXmZmZWLJkCYYOHYrr168bdYwbN25g/Pjx\n0Gg0KC8vx4svvoh+/fph7dq1UCgUmDRpEoYOHYrdu3cjODgYnp6e2LBhgzl/DLI1ly4B06YB+/eL\ncffuoq1VRIS8cRERkVEs1eC+UaO63Z739xePQZB1MetMKyBmQX/88UeMGTMG/fv3N+eh683YjF6l\nUlVMcRvD1P1NIed3S664GFi8GFi2TPxT28cHeOcd4OWXJXtE0qHON8mG1xnZC0s3uK9tZlTb4J7k\nY1UzrTt37sQff/yB1157DSdPnjTnoYmq+vFHYMYM4MoVMZ4wQSSsTZvKGxcRkYOxZIP7h92el6PB\nPcnHrDOtX331FVq0aIG4uDj4+fnhrbfeMtehjcKaVjt09SowcyawY4cYh4WJUoBKi08QEZHp7t2r\n2+357GzRg7Quqje4r23ZT2ttcE/GMzUvM2vSun//fgwYMMBchzMZk1Y7UloKrFghHqwqLhb3eN5+\nG5g+nYVHRER1VL3BfW1JqTEN7h82M2oPDe7JeFaVtE6bNg2XL19G3759MXz4cISGhprr0EZhTaud\nOHhQ9Fy9cEGMx44Fli8HamhzJiW7PN9kdXidUW0qN7h/2MyoqQ3uDSWlzZo5VoN7Mp5V1bQ+//zz\n6NGjB44ePYq4uDjZk1aycTduAK++CmzaJMYhIWKBACuazScishS1WtfK6WEzo8Y2uK9tZpQN7sna\nmHWm9YcffkCfPn3QpEkTcx3SJCwPsFFqtahTffNNoLAQcHMD5s0DXnuN/5wnIpum0QAFBXW7PX/r\nlvh8Xbi76xLO2mZGmzUTdaVEcrCqmdYjR45g69atKCkpQUxMDKZNm2bOw5MjSEwUpQCnT4vxsGHA\nqlVAu3byxkVEVAttg/uH3Z6vT4N7JyddK6fanp5ng3tyFGZNWocPH4527dqhZcuWSE5ONuehJcWa\nVhnk5QH2dVx4AAAgAElEQVT/+Q+wfr0Yt2kDrFwJjBxp1f8nttnzTTaF15k8NBrRuL4ut+fN1eC+\n8ms2uCeqyug/DgkJCcjOzsYjjzyCsLAwAEBUVFTF9giuRkR1UV4ObNgAvPGGSFxdXIA5c0RpgKen\n3NERkR2qrcF99aS0vg3u69JXlP9rIzJOvWtab9++jREjRuDcuXNwcnJCXl4eevTogU8++QRdunRB\nSUkJXK2k7pA1rVYuORl45RXg6FEx7tNHPGj1yCPyxkVENkfb4N7Q7XhLNrjXvvbzYysnooeRvOXV\nv//9b0RHR2PIkCEAgOvXr+Obb77B+vXrsWXLFrRp0wY7d+5ERkYG5syZAzc3N6ODMxWTVitVWAi8\n9ZaoVS0rE//HX74ceO45qy4FICLpPazBvfa1sQ3ua6oRZYN7IvOTPGldunQp3njjDb338/LyMH36\ndGzYsAGurq5YsmQJDh48iH379hkdnKnYp9XKaDTA5s3Av/4l/qZxcgKmTROLBFhJx4n6surzTXbD\n3q4zORvct2ghGtzz38dE0pO8e0CzZs0Mvu/n54e1a9di3bp1aNWqFXbt2oX09HSjAyM7c/EiMHUq\ncOCAGPfoIdpahYfLGxcRmYUlG9zX1sKJDe6JHIfZZloBYPv27VCpVOjZsycAIDo6GoEyrlrE8gAr\ncO8esHgxsGyZeKLB1xd45x1g4kQWgBHZgAcPRJIpVYP76kkpG9wT2Q/JZ1obNWpU462qBw8eICIi\nAs8//7zRAZEd2bkTmDED0M64T5woElZ/f1nDInJ0lmpw7+FRe40oG9wTkSnqnbROmDABw4cPR8OG\nDfHEE09U2dazZ0/MnTsXL730ktkClANrWk2Ung7MnAnExYlxt26iFKDa9WIPrOJ8k92r63UmR4P7\nyq/Z4J6ILKneSaubmxs+/vhjDB48GGFhYZg6dSoef/xxODs74/DhwwgKCrJAmGQTSktFF4CFC4Hi\nYtFB++23xcNW7JBNZBTtrOjvv1umwf3DZkabNhU9SImI5FbvmlatvLw8vPbaa9i4cSPUajUAYMSI\nEdi0aRM8PDzMGqSxWNMqoZ9/Fg9aXbggxs8+KxLYli3ljYvIhhQXA2fOAElJYiXj06eBs2fF+3VR\nlwb3LVqIz7DBPRFJTfKWV9XduXMHly5dgp+fn9XNsjJplcCNG2IFq2++EeOOHcUCAf37yxsXkZXL\nz6+anJ4+Lf7NZ+ipem/v2mtE2eCeiGyB7EmrNWOfVgtSq4GPPhLLrd65A7i5Af/9r0hgHajvDGta\n6WE0GiAzs2pyevo0kJGh/1lnZ7EgXHg4oFTqfk9O5nVGRLZP8u4BREhMFMuvJiWJ8YgRwAcfAO3a\nyRsXkczKyoBLl3SJqXYmNS9P/7Pu7uIZxfBw3a+uXbkCExFRTTjTSnWXlwf8+9/AJ5+Icdu2wMqV\nwMiR8sZFJIP790W9aeVb/GfOGO5V6utbNTkNDxeVNHzAiYgcCWdayfLKy4HPPhMJa16eaLD42mvA\nvHmiMSORnbt9W7/+9Px5w2vdt2mjS0y1t/hbt2YrKCIiUzFpNYA1rZUkJYlSgMREMe7bVzxoFRpq\nvu+wYaxptS8aDXD9un79qaEVqZ2cgM6d9etP/fzMHxevMyIiE5LW7OxsrF69GufOnYNCoUDnzp0x\nZcoUBAQEmDM+kkthITB/PrBqlZhpbd4ceP99YOxYThmRXSgvB1JSqianSUlAbq7+Z93cgLCwqrf3\nw8J4o4GISEpG1bQePnwYgwcPRkBAAHr27AkAOHr0KHJycrB3796K9+TGmlYjaDTAt98C//qX6Fbu\n5ARMnw4sWCAWASeyQSUlwG+/Vb3Fn5wM3L2r/1lvb/36006duD4GEZGpZGl51bNnT4SFheHjjz+G\n059NAcvLyzF58mT89ttvOHLkiNEBmROT1nq6cEEsEPDzz2L8+ONi+VWlUt64iOqhoEAkpJVnUM+d\nE13aqmvVqmpyqlSK5wt5M4GIyPxkSVrd3d2RlJSETp06VXn/woULCA8PR3Fdl2+xMPZpraN794D/\n+z/g3XeBBw/Eo87LlgEvvcRO5Q/BWkN53bihX396+bL+5xQKMVuqrT3VJqhNm0ofszF4nRGRPZCl\ne0CTJk1w5coVvaT1ypUr8Pb2NjoYkkFcHDBjBnD1qhi//DKwZAng7y9vXESVlJcDaWn6/U+zs/U/\n27Chfv1pt25ctpSIyNYZNdM6a9YsbN26FcuWLcMTTzwBQNS5vvHGGxg7dixWrFhhdECZmZkYN24c\nsrOz4eTkhH/84x+YMWNGlc8kJCRg1KhRaN++PQBgzJgxePPNN/WOxfKAWly5AsycCezcKcaPPipK\nAaykHpkcV2kp8PvvVZPT5GSx8Fp1TZpUnT0NDxeNLVxcpI+biIhqJ8tM67Jly6DRaDBhwgSo/ywU\nc3FxwSuvvIJ33nnH6GAAoEGDBlixYgWUSiWKiooQGRmJgQMHIrRai6WoqCjExcWZ9F0OqaQEWL4c\nWLQIKC4GGjUSr6dM4ZMmJLk7d/TrT3//XVSpVNeypX7/03btWH9KROQojMpSGjZsiA8++ABLlixB\nWloaAKBDhw7wMEP/l+bNm6N58+YAAC8vLzzyyCPIysrSS1otOYNqtzWtP/0kHrS6dEmMn3tOJLAt\nWkgWn71hrWHdZWfr15+mpup/TqEQq0VVn0Ft1kz6mK0FrzMiIhMXF/Dw8EBYWJi5YtGTnp6OpKQk\n9OjRQ2/b0aNHoVQqERgYiHfffRedO3e2WBw27/p1YM4c0coKEE+kfPSRWCiAyMw0GvEwVPX+pzdu\n6H/WxQXo2lW//rRRI+njJiIi62Z00pqTk4NDhw4hJycH5eXlVbZNmTLF5MCKiorw9NNP44MPPoCX\nl1eVbZGRkcjIyICHhwfi4+MxevRoXNLOHlYTGxuLoKAgAIC3tzeUSmXFjIVKpQIAuxtrqQ4cAL7/\nHjFffgncuQNVw4bAuHGI+fBDwNXVauK19bGWtcQj5VitBpo2jcHp08CPP6qQkgKkp8egsBAAVH+e\nGfF5d3cVgoOBPn1iEB4OqNUqtG0LDBigO96DB0CjRtbz81nLOCYmxqri4Zhjjjmuy1j7Ot3QsoJG\nMOpBrG+++QYTJkxAeXk5fHx8oKhUVKZQKHD9+nWTglKr1Rg+fDiGDBmCmTNnPvTz7dq1w6lTp+Dr\n61vlfYd+EOvIEVGnmpwsxiNHAh98APyZwBPVV1ERcOZM1RnU334TD05V17y5fv1p+/bsoEZE5Mhk\n6dPatm1bjB8/HvPnz0cDCzy8M27cOPj7+9fYhSA7O7tiudjjx4/jmWeeMZjFO2Sf1h07ELNzJ/Dp\np+KNoCBg5UpgxAhZ4rF3cv63tqTcXP3605QUceu/uuBg/frTP8vSyUzs9TojIsciS/eAgoICxMbG\nWiRhPXz4MDZu3IiwsDCEh4dDoVBg8eLFuHr1KhQKBSZNmoRt27ZhzZo1cHFxgbu7OzZv3mz2OGzS\n9u1iQYA7d0Sx4OuvA3PncoF0qpFGA6Sn6/c/zcrS/2yDBkCXLlWT00cfBRo3ljxsIiJyQEbNtL7y\nyivo3Lkzpk+fbomYzMahygNOnxbLrpaWAv36AatXiweuiP6kVgPnz1dNTpOSgNu39T/r5SUS0sq3\n+Lt0AVxdpY+biIjsgyzlASUlJRg5ciTc3d0RFhYGl2qdvOfPn290QObkMEnr3btAZCRw8SLwz3+K\nRQLYvNKh3b0LnD1b9fb+2bOiTW91zZrp158GB7P+lIiIzEuW8oB169Zh//798Pf3R2pqqt6DWNaS\ntBrL5mpaZ80SCWuXLlD99a+IYcIqGWuoNczL068/vXRJLH1aXbt2VW/vh4eLNr28ZKybNVxnRERy\nMyppXbhwIZYvX47Zs2ebOx6qr61bgU8+AdzcRB/WW7fkjogsRKMBMjL0+59eu6b/WWdnICxMv/7U\n21v6uImIiMzBqPIAPz8/HD9+HB06dLBETGZj9+UBV6+KTKSgQNSwmqE/LlkHtVpMnlevP83P1/+s\nh4d+/WnXruLfMURERNZClprWV199FY0bN7b6MgC7TlrVaiA6WvRjHTUK+P573uO1UcXF+vWnZ84A\n9+/rf9bfv2rtaXg4EBIiZlaJiIismSw1rffu3cMnn3yCvXv3olu3bnoPYq1cudLogKyBTdS0Llwo\nEtbAQNGT9c+ElbVv0qrv+c7P182can9duGC4/rRtW/3608BA/tvEEfHPNRGRkUnr+fPnER4eDgC4\ncOFClW0K/o1qeb/8AixaJLKXr74C/Pzkjoiq0WiAzEz9+tOrV/U/6+xsuP9ptQXeiIiIHJpR5QG2\nwi7LA/LzRUaTmQnMmyeSV5JVWZl4Wr9y/enp0+Kp/urc3YFu3arWn4aFifeJiIjsmSw1rbbC7pJW\njQZ4+mngu+/EQgK//CJWviLJ5eYC69YBP/4o6k/v3dP/jI+P/u39jh3FylJERESORrKa1pEjR+Lr\nr79G48aNMXLkyFo/GxcXZ3RA1sBqa1rXrRMJa+PGwKZNBhNW1r5Z1v/+B6xcKbqLiUb9KgAxaN1a\nP0Ft3Zr1p2Qe/HNNRFSPpNXPz6+iXtWPNZTS+/13sYgAAHz8segST5J48EA0Z1i5Ejh8WLynUADD\nhwM9e4pFyPhHgoiIyLJYHmAL7t8HuncXfZFiY4ENG+SOyCFoSwDWrAGyssR7jRsDEycCU6cCVt6m\nmIiIyKqYmpcZtbr49u3ba9y2dOlSo4OhGrz2mkhYQ0KAVavkjsbu/e9/wEsvidv7b74pEtbQULF+\nQ1YWsGIFE1YiIiKpGZW0vvDCC3j55Zdxr9LTJ5mZmejTpw/ef/99swUnF5VKJev+VezcCXz4oahf\n/fZbwMtLuu92IA8eAFu2AL17A5GRwOefA6WlogRg3z7g3Dmx4Fj108/zTVLgdUZEZGTSeuzYMSQm\nJkKpVOLkyZPYvHkzunXrBjc3NyQnJ5s7RseVlSWm/ABgyRIgIkLeeOxQbi6weLEoER47VtSsNm4M\nzJ4NpKSIfzMMGMAHqoiIiORmdE3r/fv3MWXKFHz11VdQKBR47733MGPGDHPHZxKbrmktKxPZ0sGD\nwKBBwO7dgJNR/8YgA06fFg9WffONtguAKAGYPh0YN+6hE9pERERUT7Is4woAycnJSEhIQHBwMK5d\nu4bjx4/jzp07aNSokdHBUCXLlomEtVkz4IsvmLCagbYLwKpVwKFD4j1tF4Dp04H+/XmaiYiIrJVR\nf0W//fbbiIqKwqhRo5CcnIxTp07hwoULCAsLw6+//mruGCUne01rYiLw3/+K1198AQQESPfddqh6\nCcChQ6IEYNYssZLVzp3AwIHGJaw83yQFXmdEREbOtH788cfYuXMnBg4cCADo1KkTEhMT8eabb6J/\n//4o0d5vpforKACef16UB/zrX8DgwXJHZLNOnxazqps26UoAOnUCZswAXnwR4E0BIiIi22FUTeut\nW7fg7+9vcNsvv/yCqKgokwMzB5uradVogBdeEFlWeDhw9Cjg6ip3VDblwQPghx9EvWrlEoChQ0Wy\nyhIAIiIieZial3FxAWvy5ZfA+PGAp6doFtqxo9wR2YzcXGD9erEQQGameK9xY2DCBLEQQHCwvPER\nERE5OtkexFKr1Th+/DgyMjJQWlpaZdu4ceOMDsgamLrOt1H7p6SIRqCAuKdtZMLqaGuU11QCoO0C\nYOkSAEc73yQPXmdEREYmrRcuXMCIESNw5coVaDQaODs7Q61Ww8XFBa6urjaftEqutBR47jng7l3g\n2WfFUq1UI7Va1wWg8nN/w4axBICIiMheGVUeMHjwYHh7e+PTTz9F8+bNkZSUhIKCArzyyitYtGgR\nBgwYYIlY681mygNeew147z0gKAhISgKaNJE7Iqt065YoAfjoo6olAC+9JEoAQkLkjY+IiIhqJktN\nq5+fHxISEtC1a1c0adIEx48fR6dOnZCQkIDp06fjzJkzRgdkTjaRtO7bJxYPcHYW04Y9e8odkdVJ\nShIPVslVAkBERESmMzUvM+omqkajgYeHBwCgadOmyMrKAgC0atUKqampRgdjLSTr05qTI7IuAFiw\nwCwJq730c1SrgW3bgKgo0UhhwwaRsA4bBuzdC5w7J2ZX5U5Y7eV8k3XjdUZEZGRNa9euXZGcnIz2\n7duje/fuWLp0KZydnbF+/XoE8zHtuikvF7Wr2dlATAzw73/LHZFVYAkAERERGWJUecDevXtx9+5d\njBkzBpcvX8awYcNw8eJF+Pv7Y8uWLVbzlKtVlwf8v/8HzJ4N+PoCyclAq1ZyRySrpCTxYNXGjSwB\nICIiskdW06c1Pz8fPj4+UCgU5jicWVht0nr6NNCjh64T/qhRckckC7VatxBA5S4A2oUABgxgFwAi\nIiJ7IUtNKwDk5OTgu+++w8cff4yPPvoI3377LdasWYOPPvrI6GAAIDMzE3379kWXLl0QFhaGlStX\nGvzcjBkzEBISAqVSiaSkJJO+szqL1rQWFYm2Vg8eiL6sZk5YbaH27dYt4J13gPbtgb/9TSSsjRoB\nM2cCly4Bu3aJZ9NsIWG1hfNNto/XGRGRkTWt33zzDSZMmIDy8nK92VWFQoEp2ib5xgTUoAFWrFgB\npVKJoqIiREZGYuDAgQgNDa34THx8PNLS0pCSkoJjx45h8uTJSExMNPo7JaXNzLp2FW2uHIi2BGDT\nJuD+ffFex46iBGD8eJYAEBERUc2MKg9o27Ytxo8fj/nz56NBA6MX1aqT0aNHY/r06ejXr1/Fe5Mn\nT0afPn0wduxYAMAjjzwClUqFgICAKvtaXXnAli3A2LGAmxtw4oRIXO2cWg3s2CFKAH75Rfc+SwCI\niIgciyzLuBYUFCA2NtbiCWt6ejqSkpLQo0ePKu9nZWWhdevWFePAwEBkZWXpJa1WJT0dmDRJvF6x\nwu4T1lu3gE8+EV0Arl0T7zVqJLoATJvGLgBERERUP0Zlnc899xx27dqF6dOnmzueCkVFRXj66afx\nwQcfwMvLy+jjxMbGIigoCADg7e0NpVJZ0d1AWydWfax9r6bt9d6/d2/g+eehKigAevVCzOTJ9Tpe\nfcZJSUmYNWuWxY7/sHFqKpCYGIONG4H798X2jh1jMH060L69Ch4eQEiIdPFYeiz3+ebYMcba19YS\nD8ccc8xxXcba1+np6TAHo8oDSkpKMHLkSLi7uyMsLAwuLi5Vts+fP9+koNRqNYYPH44hQ4Zg5syZ\neturlweEhoYiISHBbOUBKpWq4sQbQ2//+fOBhQuBwEDR3srPz+hj1/u7JVBbCcD06cDAgfZbAiDH\n+SbHw+uMiOyBLC2vVq1ahZkzZ8Lf3x/NmjXTexDL1GVcx40bB39/f6xYscLg9t27d2P16tXYtWsX\nEhMTMWvWLIMPYllFTWtCAtCnj3j988+AHf3Fk5cnSgBWr9YvAZg6VTxkRURERATIlLQ2a9YM//nP\nfzB79myjv7gmhw8fRlRUFMLCwqBQKKBQKLB48WJcvXoVCoUCk/6sC502bRr27NkDT09PbNiwARER\nEXrHkj1pzc8HHn1ULO00bx6waJF8sZhRcrJuIYDKXQCmTRNdABo3ljc+IiIisj6yJK1+fn44fvw4\nOnToYPQXS0HW8oDoaOCpp4Dvvwd69hQzrtXKKCzBUrcRtSUAq1aJH0VryBDRBcCeSwBqw9u2JAVe\nZ0RkD2RZXOCll17Cxo0bjf5Sh7B2rUhYGzcWjUklSFgtIS8PWLpULATw9NMiYW3USCSqFy8Cu3cD\ngwc7ZsJKRERE0jFqpnXKlCnYtGkTunTpgm7duuk9iFXTKlZSk6084PffgcceE/fOv/1W9Ga1MWfO\niFnVr79mCQARERGZTpY+refPn0d4eDgA4MKFC3oBObTiYrFM6/374okkG0pY1WogLk50AWAJABER\nEVkTo2ZabYUsNa2LF0M1bx5iOnYETp0CTOgxawxjYtd2AfjoIyAjQ7zHLgB1w1pDkgKvMyKyB7LM\ntFItNm0Sv69YIXnCWl+GSgBCQkRvVZYAEBERkTXhTKs5nT8PdO4M+PgA2dlW+fCVtgRg1Sqg0oIV\nGDJEJKuDBrEEgIiIiMyPM63WZOtW8fvo0VaXsObn6xYC0JYAeHmJEoBp01gCQERERNaNc2oGVF4z\nt17+TFpVnTqZL5h6qh77mTPAP/4BtGoFvPGGSFhDQsTDVllZ4ncmrMYz+lohqgdeZ0REnGk1nwsX\ngN9+A7y9AQOrc0lJrQZ27hQJaeW/6wYPFl0AWAJAREREtoY1reaycCEwfz4QGwts2CDNd1Zz+zaw\nfr0oAbh6VbynLQGYOhWQcQKYiIiIHJxkNa0jR46s80Hj4uKMCsamaetZ//Y3Wb4+MxOIiQHS0sQ4\nOFg8WBUbyy4AREREZPvqfJPYz8+vzr9sXb3rxy5cAM6eFaUB/ftLXn92/TrQt69IWDt0UGH3brHE\n6owZTFgtjbWGJAVeZ0RE9Zhp3SDTLW+boJ1lHTUKaNhQ0q++eVMkrCkpQHg4sGCBaF9FREREZE+M\nrmlVq9U4fvw4MjIyUFpaqjugQoEXX3zRbAGaQrKa1m7dxEzrjz8Cw4ZZ/vv+lJMD9OkDnDsnQvj5\nZ8AOJrqJiIjIDpmalxmVtF64cAEjRozAlStXoNFo4OzsDLVaDRcXF7i6uqKwsNDogMxJkqT14kUg\nNBRo0kRkkRLNtN66JWZYz54FunQBDh4EmjaV5KuJiIiI6s3UvMyoxkezZs1CZGQkCgoK4OHhgfPn\nz+PkyZNQKpXYvn270cFYi3rVjxkoDbB0/Vl+PtC/v0hYQ0OBAwd0CStr36TF801S4HVGRGRkn9YT\nJ04gISEBnp6ecHJyglqtRkREBJYtW4bp06fjzJkz5o7TekncNeCPP4ABA4DkZLEowM8/AwEBknw1\nERERkWyMKg/w9fXFyZMn0b59ewQHB2PdunXo27cv0tLSEBYWhnv37lki1nqzeHnApUui+WnjxqI0\nwNXVct8FoKBAJKwnTgAdOgAJCUBgoEW/koiIiMgsJOvTWlnXrl2RnJyM9u3bo3v37li6dCmcnZ2x\nfv16BAcHGx2MzalcGmDhhLWwUKxodeIE0K6dqGFlwkpERESOwqia1nnz5lVkyosWLUJGRgb69OmD\nffv2YeXKlWYNUA51rh+roTTA3PVnRUXA0KFAYiLQtq1IWFu3NvxZ1r5Ji+ebpMDrjIjIyJnWQYMG\nVbxu3749zp8/j/z8fPj4+EChUJgtOKuWkiIKSxs3BgYOtNjX3L0rumgdPgy0aiVqWNu2tdjXERER\nEVklo/u02gKL1rQuXgzMmwe88ALw1VcW+Yp794ARI0Si2rKlqGF1pOoLIiIish+S1bROmDChzgf9\n7LPPjArGpli4a8D9+8Do0SJhbd5clAQwYSUiIiJHVeea1tzc3Cq/tm/fju+//x6pqalITU3FDz/8\ngO+++w63bt2yZLySeGj9WGoqkJQENGpksDTA1PqzkhLgr38F9u8HmjUTiWvHjnXbl7Vv0uL5Jinw\nOiMiqsdM686dOyteL1myBO7u7tiwYQM8PT0BAHfv3sXEiRMRFhZm/iitjXaWdeRIwM3NrIcuLQWe\nfhrYswfw9xcJ6yOPmPUriIiIiGyOUTWtLVq0wIEDB9C5c+cq7//+++/o168fbt68abYATWGxmtaI\nCOD0aeCHH0S7KzN58AB45hlxWF9fURLQrZvZDk9EREQkG1mWcS0qKsL169f13r9x44bVLCxgMWlp\nImFt1Aio1EXBVA8eAM89JxJWb2/gp5+YsBIRERFpGZW0PvXUU3jppZfw7bffIj09Henp6fj2228x\nceJEjBkzxtwxSq7W+jFtacCIETWWBtS3/kytBl58Edi+HWjSRNSyhofX6xBGfzeZhuebpMDrjIjI\nyKR1zZo1GDFiBGJjY9GhQwd06NAB48ePx7Bhw/DRRx+ZFNDEiRMREBCAbjVMMyYkJMDb2xsRERGI\niIjAokWLTPq+ejNz14CyMiA2Fti8WUze7t0LPPaYWQ5NREREZDdM6tN69+5dpKWlAQA6dOhQ8VCW\nKQ4dOgQvLy+MGzcOZ86c0duekJCA5cuXIy4u7qHHMntN6+XLQIcOgJcXkJMDuLubdLjycmDCBOCL\nL8Qh9+4FnnjCTLESERERWRHJ+rQa4unpWeOMqLF69+6Nq1ev1voZ2dZDqFwaYIaEddIkkbB6eAC7\ndzNhJSIiIqqJUUnryJEja91el1lQUxw9ehRKpRKBgYF499139boYmEqlUiEmJkZ/gzZpfeYZ4/b/\nk0YDTJkCfPqpyH137QKefNL4eOvz3WRePN8kBV5nRERGJq1+fn5Vxg8ePEBycjKuXbtm8QexIiMj\nkZGRAQ8PD8THx2P06NG4dOmSRb8TgCgNOHVK3Mc3oWuARgNMnw6sXSue44qLA/h3EREREVHtjEpa\nN2zYYPD9OXPmoHHjxiYF9DBeXl4Vr4cMGYIpU6YgPz8fvr6+Bj8fGxuLoKAgAIC3tzeUSmXFjIX2\nidw6jbdtgwoAundHzJ+lAfXaH8DBgyqsXg1s3x6Dhg2BBQtUaNAAAIyIp5axlrmOx3HtYy1riYdj\n+xvHxMRYVTwcc8wxx3UZa1+np6fDHEx6EKu6S5cuoXfv3sjJyTHpOOnp6RgxYgTOnj2rty07OxsB\nAQEAgOPHj+OZZ56p8WSY9UGsv/wFOHkS+O47scZqPWk0wOuvA++9B7i4iH6sQ4eaJzQiIiIiayfL\n4gI1uXjxosnHeP755/HEE0/g0qVLaNOmDTZs2IC1a9di3bp1AIBt27aha9euCA8Px6xZs7B582aT\nv7O6yv9CAABcuSISVi8vYPDgeu+v0QBz54qEtUEDYNs2yyWserGTRfF8kxR4nRERGVkeMGPGjCpj\njUaDGzduID4+HhMmTDApoE2bNtW6ferUqZg6dapJ31Fv27aJ34cPN6prwFtvAe+8Azg7i36sD3mO\njbO+JPQAACAASURBVIiIiIiqMao8oE+fPlXGTk5OaNq0Kfr27YsJEyagQQOTOmmZjdnKA7p3B06c\nEEtW1fNBs7ffFkmrszPwzTdmW5OAiIiIyKaYmpeZtabV2pglaU1PB9q1Azw9gdzces20LlkiygKc\nnICvvwaee860UIiIiIhslVXVtNqLKvVjRpQGqFQqvPeeSFgVCuDzz6VLWFn7Ji2eb5ICrzMiIhNW\nxFKr1Th+/DgyMjJQWlpaZdu4ceNMDsxqaBcUqMd9/W3bgNWrxetPPwVefNECcRERERE5EKPKAy5c\nuIARI0bgypUr0Gg0cHZ2hlqthouLC1xdXVFYWGiJWOvN5PKAq1eBoCCxzmpurvj9IbZu1S2YtW4d\n8I9/GP/1RERERPZClvKAWbNmITIyEgUFBfDw8MD58+dx8uRJKJVKbN++3ehgrE7l0oA6JKwaDbBw\noXi9bBkTViIiIiJzMSppPXHiBN588014enrCyckJarUaERERWLZsGebMmWPuGCVXUT9Wz9KAX34B\nzp4FvL1VqNYVTDKsfZMWzzdJgdcZEZGRSatGo4HHnzOPTZs2RVZWFgCgVatWSE1NNV90csrIAI4d\nEzOsdVwJYNUq8fvIkYCrqwVjIyIiInIwRj2I1bVrVyQnJ6N9+/bo3r07li5dCmdnZ6xfvx7BwcHm\njlFyMTExwIoVYjBsWJ1KAzIygO+/FyteLVkSY9H4aqNd95ekwfNNUuB1RkRkZNI6b9483L17FwCw\naNEiDBs2DH369IG/vz+2bNli1gBlo/056lgasGYNUF4uHsJq2dKCcRERERE5ILMtLpCfnw9fX19z\nHMpsjH1KTbV5M2KefVb0Zc3NFQsL1KK4GGjdGsjLA44cAUpKVLLNjKhU8n23I+L5JinwOiMieyBp\n94D4+HgEBQUZbGnl7OyMoKAg/PDDD0YHYzUSEsTvw4Y9NGEFxPKseXlAZCTw+OMWjo2IiIjIAdVr\npnXYsGEYOnQopk6danD7mjVrsGPHDuzZs8dsAZrC6Iy+Z08gMRHYvFnXdLUGGg0QEQEkJYmVr8aP\nNy5WIiIiIntm6kxrvZLW1q1b46effkKnTp0Mbr948SL69euHzMxMowMyJ6NOzrVrQJs2dS4NOHQI\nePJJoGlT8TCWm5sJARMRERHZKUnLA3Jzc+HkVPMuCoUCeXl5RgdjFbZtgwoQba7qUBqwcqX4fdIk\nXcIqZ09F9nOUFs83SYHXGRFRPZPWVq1a4cyZMzVuP3PmDAIDA00OSlb1WFAgMxP47jvA2RmYPNnC\ncRERERE5sHqVB8ycORP79+/HqVOn4O7uXmXbvXv38Nhjj2HAgAH44IMPzB6oMeo9DV1YCLRrB9y7\nJ0oDvLxq/fi8ecDixaLsdfNmE4MlIiIismOS1rTm5OQgPDwcTk5OmDZtGkJDQwEA58+fx4cffgiN\nRoP//e9/CAgIMDogczLq5JSWAr//DoSH1/qx+/dFm6tbt4BffwV69zYhUCIiIiI7J2lNa7NmzXDk\nyBGEhYVh7ty5+Otf/4q//vWvmDdvHrp164ZDhw5ZTcJqtIYNoSooeOjHNm8WCWt4ONCrV9VtrGl1\nHDzfJAVeZ0RERqyI1bZtW+zevRt//PEHUlNTodFoEBISAh8fH0vEZ5U0Gt0DWNOnAwqFvPEQERER\n2TuzrYhljUydhq7JkSNidtXPT3TIqlbeS0RERETVSFoeQMKqVeL3SZOYsBIRERFJgUmrAbXVj12/\nDmzbJtpcvfJK/fe3NNa+SYvnm6TA64yIiElrvX38MaBWA6NHi+4BRERERGR5rGmth5ISscJrTg6Q\nkABERZnt0ERERER2jTWtEtqyRSSs3boBTz4pdzREREREjoNJqwGG6scqt7maMaP2NlesaXUcPN8k\nBV5nRERMWuvs2DHg5EnA1xd4/nm5oyEiIiJyLKxpraO//x3YtAl4/XVg6VKzHJKIiIjIYdhdTevE\niRMREBCAbt261fiZGTNmICQkBEqlEklJSRaP6cYNYOtWwMkJmDLF4l9HRERERNVYXdL60ksvYe/e\nvTVuj4+PR1paGlJSUrB27VpMnjzZ7DFUrx9buxZ48AAYNQpo27b++0uJtW/S4vkmKfA6IyKywqS1\nd+/e8PHxqXH7jh07MG7cOABAjx49UFBQgOzsbIvFU1oqklYAmD7dYl9DRERERLWwuqT1YbKystC6\nUlf/wMBAZGVlmfU7YmJiKl5v2wbcvAl07QpUervO+0tNzu92RDzfJAVeZ0REQAO5A7C02NhYBAUF\nAQC8vb2hVCor/gLQ3nKrbbxoEQDEYPp0ICHh4Z/nmGOOOeaYY4455hgVr9PT02EOVtk94OrVqxgx\nYgTOnDmjt23y5Mno06cPxo4dCwAIDQ1FQkICAgIC9D5r7FNqKpUKMTExOHEC6N4d8PEBrl0DPD3r\nt78c5PxuR8TzTVLgdUZE9sDuugcAgEajqfGHGjlyJL788ksAQGJiIry9vQ0mrOawapX4feLEuies\nRERERGR+VjfT+vzzz0OlUiEvLw8BAQFYsGABSktLoVAoMGnSJADAtGnTsGfPHnh6emLDhg2IiIgw\neCxTMvrsbKB1a0CtBtLSgHbtjP6RiIiIiByeqTOtVpe0mpMpJ2fhQmD+fNHm6ocfzBwYERERkYOx\ny/IAue3fr8KaNeK1MW2uKhcgS03O73ZEPN8kBV5nRERMWg369VexClbnzkDfvnJHQ0REREQsDzCg\nVy/gyBFgzRrAAgtuERERETkc1rTWwpiTc+oU8NhjQJMmQGYm4OVloeCIiIiIHAhrWs1MtLlSYeJE\n4xNW1rQ6Dp5vkgKvMyIiJq1V5OcD334rXk+dKm8sRERERKTD8oBqjh0DDh0C5syxUFBEREREDog1\nrbUw9eQQERERkXmwptUCTK0fY02r4+D5JinwOiMiYtJKRERERDaA5QFEREREZHEsDyAiIiIiu8ek\n1QDWtFJd8XyTFHidERExaSUiIiIiG8CaViIiIiKyONa0EhEREZHdY9JqAGtaqa54vkkKvM6IiJi0\nEhEREZENYE0rEREREVkca1qJiIiIyO4xaTWANa1UVzzfJAVeZ0RETFqJiIiIyAawppWIiIiILI41\nrURERERk95i0GsCaVqornm+SAq8zIiImrURERERkA1jTSkREREQWx5pWIiIiIrJ7TFoNYE0r1RXP\nN0mB1xkRkRUmrXv27EFoaCg6duyIpUuX6m1PSEiAt7c3IiIiEBERgUWLFpk9hqSkJFn3t9XvdkQ8\n3yQFXmdEREADuQOorLy8HNOmTcOBAwfQsmVL/OUvf8GoUaMQGhpa5XNRUVGIi4uzWBy3b9+WdX9b\n/W5HxPNNUuB1RkT0/9u786CorrQN4M9taJBNRUB2AQ3JQEBwxATcxcioRIJOdDCJIrhUJOMWQTJa\nakUTFwqNITrEwigmRnGN6DgYEjUEFePKGEcdgwsI2qCImgYEmr7fH5b3S7PZrN3I86uiqu92zntu\n39v1cvr0PXrW03r69Gm4u7vDxcUFcrkcYWFhSE1NrbUff1xFRERE1LHoVdJaUFAAZ2dnadnJyQkF\nBQW19svKyoKvry+Cg4Nx+fLlFo/j1q1bOj2+vdbdEfF8U1vgdUZEpGfDA7TRt29f5OXlwdTUFGlp\naQgNDcW1a9fq3V8QhCbVs3Xr1qaG2CLHt9e6OyKeb2oLvM6IqKPTq6TV0dEReXl50nJ+fj4cHR01\n9jE3N5dejxo1ClFRUXjw4AG6detWqzwOIyAiIiJ6MejV8IB+/fohJycHubm5qKysREpKCkJCQjT2\nKSwslF6fPn0aoijWmbASERER0YtDr3paDQwMsH79egQFBUGtVmPq1Knw8PDAxo0bIQgCZsyYgT17\n9iAxMRFyuRwmJibYuXOnrsMmIiIiolb2Qk/jSkREREQvBr0aHtDa8vPzERgYiFdffRXe3t5ISEio\ntc+BAwfg4+ODPn36wM/PD0ePHgUAVFRU4PXXX0efPn3w6quvYuHChXXW4erqKh3/2muvtWp7pk6d\nCltbW/Tu3VtaV1JSgqCgILzyyiv4y1/+gkePHrVqDB1Jzevniy++AAB8/PHHcHJykia8OHz4sI4j\npfasrs8Q3tdEpO8am5OsXLkS7u7u8PDwQHp6ulZ1dKieVoVCAYVCAV9fXyiVSvTt2xepqakakxeU\nlZXB1NQUAPDrr79i7NixyMnJ0dhWXV2NAQMGYM2aNRgwYIBGHT179sS5c+dgaWnZ6u05fvw4zM3N\nMXnyZFy8eBEAEBsbCysrKyxYsACrV69GSUkJVq1a1eqxdAT1XT87d+6EhYUFPvzwQ12HSC+Auj5D\neF8Tkb5rTE5y+fJlvPvuuzhz5gzy8/Pxxhtv4LfffnvuE586VE+rnZ0dfH19ATx9CoGHh0et58A+\nS1gBQKlUwtrauta2iooKqNXqOhNTURShVqtbI/xaBg4cWCuG1NRUhIeHAwDCw8Oxf//+NomlI2jo\n+ulA//tRK6vrM4T3NRHpu8bkJAcOHEBYWBgMDQ3h6uoKd3d3nD59+rl1dKik9Y9u3bqF7OxsvP76\n67W27d+/Hx4eHhg9erTGEAK1Wo0+ffrAzs4OQ4cOhaenZ61jBUHAiBEj0K9fPyQlJbVqG+pSVFQE\nW1tbAE+TrKKiojaPoSOoef2sX78evr6+mDZtGr+6pWb542fIpk2bADx9agrvayJqb+rLSWpOJuXo\n6FjnZFI1dcikValU4u2338bnn3+u8dzXZ0JDQ3HlyhUcPHgQkyZNktbLZDJcuHAB+fn5+Pnnn5GR\nkVHr2BMnTuD8+fP497//jQ0bNuD48eOt2pbnaerkClS/mtdPVFQUbty4gezsbNjZ2XGYADVLzc+Q\nzMzMWvcx72siao+a+9nV4ZJWlUqFt99+G5MmTcJbb73V4L4DBw6ESqVCcXGxxvrOnTsjODgYZ8+e\nrXWMvb09AMDGxgZjx47Vqru7Jdna2krPslUoFOjevXub1v+iq+v6sbGxkW7E6dOn48yZM7oMkdq5\nP36GhIaG4vTp07yviahdqu+zy9HREbdv35b2q2syqbp0uKQ1MjISnp6emDNnTp3br1+/Lr0+f/48\nAMDKygr379+XvvYtLy/HDz/8II1vfKasrAxKpRIAUFpaivT0dHh5ebVGMySiKGqMpwwJCUFycjKA\np9M+Pi8xp8ap6/pRKBTS63379rX6e04vrro+Q7y9vXlfE1G7oG1OEhISgpSUFFRWVuLmzZvIycnR\n6olLejW5QGs7ceIEvv32W3h7e6NPnz4QBAErVqxAbm6uNHnB3r178fXXX8PIyAhmZmbS5AV3795F\neHi49COJSZMmYfjw4RrlFxYWYuzYsRAEASqVCu+++y6CgoJarT3vvPMOfvrpJxQXF6NHjx74+OOP\n8dFHH2H8+PHYvHkzXFxcsGvXrlarv6Op7/rZvn07srOzIZPJ4Orqio0bN+o6VGqn6vsM8fPzw4QJ\nE3hfE5HeakxO4unpiQkTJsDT0xNyuRz//Oc/tRo60KEeeUVERERE7VOHGx5ARERERO0Pk1YiIiIi\n0ntMWomIiIhI7zFpJSIiIiK9x6SViIiIiPQek1YiIiIi0ntMWomIiIhI7zFpJSKdiIiIQEhISLPL\nGTNmDCIjI1sgorYpl4iImoZJKxE1KCIiAjKZDAYGBjAyMkKvXr0QExODsrKyZpWbkJCAbdu2tVCU\n+umP504ul8PJyQnh4eG4e/duo8oZNmwYZs+e3UpRtoxn7ZTJZLX+DAwMGvUPwOHDh/Hhhx8iIyOj\nFSPW3ubNmzFt2jQUFRXpOhSiDq1DTeNKRE0zYsQIbNu2DZWVlcjMzMTUqVNRXl6O9evXN6m8qqoq\nWFhYtHCU+unZuauqqsLly5cRGRmJ8PBwpKent3ksVVVVkMvlrVK2QqGQXh88eBAzZsyAQqGQ5iE3\nMTHROp7CwkLMnTsXPXr0qLe+J0+ewM/PD2fPnkWnTp1aoAX1i4yMhKGhIZ48edKq9RBRw9jTSkTP\nZWxsDBsbGzg6OiIsLAzvvfce9u/fL22Pi4vDSy+9BFNTU/j4+ODbb7/VOH7YsGGIiopCTEwMunfv\njoEDByIiIgJjxoyR9qmsrMTcuXNhZ2cHExMTBAQE4MSJExrllJeXY8qUKbCwsIC9vT1WrlxZK1Zt\nyqlJm3K1aWdD587BwQFvvPEGJkyYgFOnTmldbkREBDIyMrBhwwap1zIvL0+rdtZ13p+t/+CDD7Bo\n0SLY2NjA1tYWMTExzTqP3bt3l/66du0KALCxsZHWWVhY1BtPUyQmJuLKlSvIz89vchmNwRnPiXSP\nSSsRNZqxsTEqKioAAIsWLcKWLVukJOIf//gH3n//faSlpWkc8ywRO378OL7++msAgCAI0vaYmBjs\n3r0bycnJyM7Ohre3N0aOHInCwkJpn/nz5+PIkSP47rvvcOTIEVy4cAE///yzRj3alFOTNuVq286G\n3LhxA4cPH0a/fv20Lvfzzz9HQEAAIiIiUFhYiLt378LJyUnrdtZ13gFg+/btkMvlyMrKwoYNG7Bu\n3Trs3LmzWedRG/XF0xjnz5/H4MGDYWRk1GZJKxHpAZGIqAFTpkwRx4wZIy3/8ssvopWVlThx4kSx\ntLRUNDExEY8fP65xzNy5c8XRo0dLy0OHDhV9fHzqLbe0tFQ0MjISt23bJm2vrq4We/XqJS5evFgU\nRVFUKpWisbGxuGPHDmkfpVIpdu3aVYyIiNC6nJq0Lbe+dgYHB9d36sQpU6aIhoaGorm5uWhiYiIK\ngiC++eabYnFx8XPLrXn+Zs2aJS1r2866zvuz9f3799dYN2LECHH69OmNKr8+e/bsEWUyWZ311hVP\nTcnJyWJubm6d2yoqKsQDBw6IoiiKbm5uGjE+ePBAjI+PF0NDQ8VffvlFTEpKEteuXSvOnz9fo4y1\na9eKa9asEb/66isxOjpaY9uhQ4fE9evXi8nJyWJycrJWMRFR2+CYViJ6rrS0NFhYWEClUkGlUiE0\nNBQJCQm4fPkynjx5gpEjR2rsr1Kp4OrqqrGub9++9ZZ//fp1qFQq9O/fX1onk8kQEBCAy5cvS/tU\nVVXB399f2sfMzAze3t6NKqeuup9XbkPtdHNzq7ddADBkyBAkJSWhrKwMSUlJ2LJlC4qKitCtW7dG\nnb+aMWvbzvrOe+/evTWWHRwcpB8aNeU8aquh60AbGRkZ0rASZ2dnjZ7W7777DnPmzMGmTZtw48YN\nTJs2Db///jscHBwQHx8PAIiKioKrqysWLFgAAJgyZQp2796N8ePHQ6lUYuHChcjOzkZxcTEmT56M\n8PDwZsVLRC2HSSsRPdezxMvQ0BAODg4wMDAA8PTrbgD417/+BWdnZ41jav7AxszMrEl1/3EIQXM0\npxy1Wg1Au3bWZGpqKiW269atw8WLFzFnzhx8//33zSq3PjXbWd95r1m+IAhSPI0pv7Gaeh0AwJUr\nV3Ds2DFcuHABoiji8ePHGknr+PHjUVxcjLKyMoSFhQEAzp07Bw8PD+n13r17NY4pKSlBXl4eAMDQ\n0BCPHz+Gr68vRowYgeTk5CbHSkQtj2Naiei5niVezs7OUsIKAJ6enjA2NsatW7fQs2dPjb+aSVhD\nevXqBblcrvFDH7VajaysLHh6ekr7GBoaavyIqbS0FJcuXWpUOXXV/bxyW6qdALB06VL88MMPOHfu\nnNblGhkZobq6ulntbIzWLr8pqqqqkJOTgxUrVmDBggWIjY1FYGCgRgJqYWGBH3/8EYGBgdK63bt3\nIywsDI8fP8axY8cwdOhQKWEvKytDZmYmhg8fDgDo1KkTrly5gmXLluHChQtYt25d2zaSiBrEnlYi\najJzc3NER0cjOjoaarUagwcPhlKpxKlTp2BgYIBp06ZpVY6pqSlmzpyJ2NhYWFlZwc3NDWvXrkVR\nURGioqIAPO2hmzp1KmJjY2FtbQ17e3ssX75co3dQm3Jq0qbclmon8LTX+s9//jPi4uKwc+dOrcp1\ndXXF6dOnkZubC3Nzc3Tr1q3R7WyMppzH1paYmIj3339fY52trW2tH8z9+OOPUhIKALt27cJ//vMf\nbNq0CY6OjhrDG+Lj4xEREQFfX1/k5uaib9++UCgUCAkJQWVlJZ/LSqRnmLQSUbMsX74cdnZ2WLNm\nDaKiotC5c2f4+vpKYwYB7b5SXr16NQRBQGRkJB4+fIg+ffrg+++/h62trbRPfHw8ysrKMG7cOJia\nmmLWrFm1JjnQppyatClXm3Zqa/78+Zg8eTJu3rypVbnR0dGYMmUKPD098eTJE9y8eVOrdtZ33lvq\n/WispgwtOH78OFatWoUzZ87Aw8MDI0aMAACkpKRg//79uHr1KpYsWYLFixdDLpcjJycHq1atko4P\nCAhAeno6Bg0aBD8/P/z6669ISkqCUqmEjY0NlixZAgCwtrbGggULsGvXLpSWlqKsrAxz5sxpcluJ\nqOUJosiHzxERkf7YunUrhg0b1uDkAm1NH2Mi6mg4ppWIiIiI9B6TViIi0jv8EpCIamLSSkREesXW\n1hYJCQnIyMjQdSgAgM2bNyMzMxOdOnXSdShEHRrHtBIRERGR3mNPKxERERHpPSatRERERKT3mLQS\nERERkd5j0kpEREREeo9JKxERERHpPU7jSkQAnk6LuWjRIty6dQtqtVrX4RDpNUNDQwwfPhypqakw\nNjbWdThEHQIfeUVESElJwbx587B37174+fnByMhI1yER6bXy8nL87W9/w8svv4z4+Hhdh0PUITBp\nJSL06tUL33zzDfr376/rUIjajevXr+O1117DTz/9BG9vb12HQ/TC45hWIsKtW7fg5+en6zCI2hUX\nFxc8fPgQR44cgUKh0HU4RC88Jq1EBLVazSEBRI1kaGgItVoNQRDw8OFDXYdD9MJj0kpE9AcZGRlw\ndnZu82Op/RJFkT9eJGoDTFqJqF1ISUmBv78/zM3NYWdnh4CAACQmJrZKXYIg6OTY9szNzQ1Hjx5t\n1TpkMhl8fHw01i1evBiRkZGtWi8R6QcmrUSk99asWYN58+YhNjYWhYWFUCgU+PLLL3Hy5ElUVVXp\nOjxqQ3fu3EFKSkqzy6murm6BaIioLTFpJSK99vjxYyxduhSJiYkYO3YszMzMAAA+Pj745ptvIJfL\nMWzYMGzevFk6ZuvWrRg0aJC0LJPJkJiYCHd3d3Tp0gVLlizBjRs30L9/f1haWmLixIlQqVTS/qIo\nYuXKlbCxsUHPnj2xfft2aVtlZSWio6Ph4uICe3t7REVFoaKiog3ORPuUlJQEd3d3WFtbIzQ0FHfv\n3pW2paen409/+hMsLS3xwQcfYOjQoRrvY10WLFiAJUuW1Pt1/IEDB+Dl5YVu3bohMDAQV69elba5\nubkhLi4OPj4+MDc3R3V1Ndzc3BAfH4/evXujc+fOmDZtGoqKijB69Gh06dIFQUFBePToUcucDCJq\nFiatRKTXsrKyUFlZiZCQkEYdV/Nr+vT0dGRnZ+PUqVOIi4vD9OnTsWPHDuTl5eHixYvYsWOHtK9C\nocCDBw9w584dJCcnY8aMGfjtt98AALGxscjJycHFixeRk5ODgoICLFu2rPkNfQEdPXoUCxcuxJ49\ne3D37l306NEDYWFhAID79+9j/PjxWL16NYqLi/HKK68gKyurwfIEQcC4cePQpUsXJCcn19p+7do1\nvPPOO0hISMC9e/cwatQojBkzRuMfkpSUFKSlpeHhw4cwMDAAAOzbtw9Hjx7F//73Pxw8eBCjRo3C\nqlWrcO/ePVRXVyMhIaHlTgoRNRmTViJ6LkFoub/Gun//PqytrSGT/f/H1YABA2BpaQkzMzNkZmZq\nVU5sbCzMzMzg4eEBLy8vjBw5Ei4uLrCwsMCoUaNw4cKFP7RXwPLlyyGXyzF48GAEBwdj165dAJ72\nHH722Wfo0qULzMzM8NFHH2kkvDqhyzeoAdu3b8fUqVPh4+MDuVyOlStX4tSpU8jLy0NaWhq8vLzw\n1ltvQSaTYfbs2bC1tW2wPFEUIQgCli1bhuXLl2skowCwa9cuvPnmmwgMDISBgQGio6NRXl6OkydP\nSvvMmTMHDg4OGrNYzZo1C9bW1rC3t8egQYPg7++P3r17w8jICGPHjtW4NohIdziNKxHpNSsrK9y/\nfx9qtVpKXE+cOAEA6NGjB7SdH6V79+7SaxMTE40EycTEBIWFhdKypaUlOnXqJC27uLjgzp07uHfv\nHsrKytC3b19pm1qt1jqGjubOnTsa58rMzAzdunVDQUEB7ty5U+tJC05OTtJrLy8v5ObmQhAEpKWl\nYcCAAdK2UaNGwcnJCV9++WWt+lxcXKRlQRDg7OyMgoKCOut4pua1UHNZqVQ2ptlE1ErY00pEzyWK\nLffXWAEBATA2NkZqamodcT0t0MzMDGVlZdL65j7ovaSkBOXl5dJyXl4eHBwcYG1tDVNTU/z3v//F\ngwcP8ODBAzx8+FD3Yx51+QY1wMHBAbm5udJyaWkpiouL4ejoCHt7e9y+fVtj//z8fOn1pUuX8Pvv\nv+Px48caCeszn3zyCVasWKHxvtesDwBu376tkah21Kc7EL0ImLQSkV579sOpqKgo7N27F0qlEqIo\nIjs7W0pYfH19sW/fPpSXlyMnJwdfffVVs+oURRFLly5FVVUVMjMzcejQIUyYMAGCIGD69OmYO3cu\n7t27BwAoKChAenp6s9v5IqisrERFRYX0N3HiRGzZsgUXL15ERUUFFi5cCH9/f/To0QPBwcG4dOkS\nDhw4gOrqaqxfv16jt/t5hgwZAi8vL2zdulVaN2HCBBw6dAjHjh2DSqVCfHw8OnXqhICAgNZoLhG1\nMSatRKT3YmJisHbtWsTFxcHOzg52dnaYOXMm4uLi0L9/f8ybNw9yuRx2dnaIiIjAe++9p3F8zd61\n5/W22dvbw9LSEg4ODpg0aRI2btwId3d3AMDq1avx0ksvwd/fH127dkVQUBCuXbvWsg1up4KDSFh4\nnwAAAelJREFUg2FqagoTExOYmpoiIyMDy5cvx7hx4+Do6IibN29Kj6uysrLC7t27ERMTA2tra1y9\nehV+fn4aY01rqvm+ffLJJygpKZHWv/zyy9i2bRv+/ve/w8bGBocOHcLBgwdhaGhY5/F1rWNPLJH+\nEkQOxiLq8ARB4LhM0ilRFOHk5ITt27djyJAhug5Ha4Ig4LPPPkNQUBA8PT11HQ7RC409rUREpBPp\n6el49OgRKioq8OmnnwIA/P39dRwVEekrJq1ERKQTWVlZ6NWrF7p3745Dhw4hNTW1weEBRNSxcXgA\nEXF4AFETcXgAUdthTysRERER6T0mrUQEmUyGyspKXYdB1K6oVCqNmdqIqHXxbiMiuLq64uzZs7oO\ng6hdyc3NhaWlpa7DIOowmLQSET799FP89a9/xcmTJ9njSqSF8vJyzJ49G4MGDYIgCOxxJWoDhroO\ngIh0LywsDKIoYvz48VAoFFCr1boOiUivGRoaonfv3pg5cyaUSiW6du2q65CIXnh8egARSUpKSrBv\n3z6UlpbqOhSidkEURQQGBsLb21vXoRC98Ji0EpGGiooKlJSUQKVS6ToUIr0mCAIsLCzQuXNnXYdC\n1CEwaSUiIiIivceR40RERESk95i0EhEREZHeY9JKRERERHrv/wDqf23ZybCtvQAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa805dc6b90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Realiza la convolucion de los hidrogramas sinteticos con la tormenta de diseno\n",
"HidroSnyder,QmaxSnyder,Tsnyder = cuCap.GetHU_Convolution(Tsnyder,Qsnyder,lluvEfect)\n",
"HidroWilliam,QmaxWilliam,Twilliam = cuCap.GetHU_Convolution(Twilliam,Qwilliam,lluvEfect)\n",
"HidroSCS,QmaxSCS,Tscs = cuCap.GetHU_Convolution(Tscs,Qscs,lluvEfect)\n",
"\n",
"DicQmax = {#'Snyder':QmaxSnyder,\n",
" #'Williams':QmaxWilliam,\n",
" #'SCS': QmaxSCS,\n",
" 'Gumbel': QmaxRegGum[:,-1],\n",
" 'Log-Norm': QmaxRegLog[:,-1]}\n",
"#Plot de maximos \n",
"pyt.PlotQmaxTr(DicQmax,Tr,ruta=ruta_images + 'Q_max_Metodos_Tr_descarga.png')\n",
"#Tablas de maximos \n",
"DataQmax = pd.DataFrame(DicQmax, index=Tr)\n",
"#Escritura en excel.\n",
"writer = pd.ExcelWriter(ruta_images + 'Qmax_captacion.xlsx')\n",
"DataQmax.to_excel(ruta_images + 'Qmax_captacion.xls')"
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"{'Area[km2]': 7.0903081048583987,\n",
" 'Centro_[X]': -75.638641,\n",
" 'Centro_[Y]': 6.2339039,\n",
" 'H Cauce_Max [m]': 2332.0,\n",
" 'Hmax_[m]': 2542.0,\n",
" 'Hmean_[m]': 1973.9344,\n",
" 'Hmin_[m]': 1609.0,\n",
" 'Long_Cau [km]': 6.2291962890625001,\n",
" 'Long_Cuenca [km]': 5.252536773681641,\n",
" 'Pend_Cauce [%]': 9.9195762388338498,\n",
" 'Pend_Cuenca [%]': 40.385818481445312,\n",
" 'Perimetro[km]': 17.13229974269867}"
]
},
"execution_count": 99,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cuCap.GeoParameters"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
PlanetExp/rcnn | rcnn_session.ipynb | 1 | 24022 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"- - - - - - - - - - - - - - - - - - - - \n",
"Loaded dataset data/grids_9x9_1000.hdf5\n",
"X.dtype = float64 X.shape = (1000, 9, 9)\n",
"y.dtype = float64 y.shape = (1000,)\n",
"- - - - - - - - - - - - - - - - - - - - \n"
]
}
],
"source": [
"import tensorflow as tf # version 0.12.0rc0\n",
"import rcnn\n",
"\n",
"# %config InlineBackend.figure_format = 'retina' # double res graphs\n",
"\n",
"# Load constrained dataset\n",
"from grid_dataset import load_grid_dataset\n",
"datasets = load_grid_dataset('data/grids_9x9_1000.hdf5')\n",
"\n",
"# Some magic to autoreload external imports\n",
"# from http://ipython.readthedocs.io/en/stable/config/extensions/autoreload.html\n",
"%load_ext autoreload\n",
"%autoreload 2"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Hyperparameters\n",
"learning_rate = 1e-3\n",
"training_iters = 2000000\n",
"batch_size = 128\n",
"display_step = 50 # Steps after to give some feedback during training\n",
"validation_step = 1000 # Steps after to run a round of validation to \n",
" # check against overfitting\n",
"\n",
"# Network Parameters\n",
"n_input = 1000 # Data input\n",
"n_classes = 2 # Connected or not connected\n",
"grid_size = 9\n",
"height = grid_size\n",
"width = grid_size\n",
"depth = 1\n",
"dropout = 0.5 # Dropout, probability to keep units\n",
"\n",
"# tf Graph input\n",
"with tf.name_scope('input'):\n",
" X = tf.placeholder(tf.float32, shape=[None, height, width, depth])\n",
" y = tf.placeholder(tf.int32, shape=[None])\n",
" keep_prob = tf.placeholder(tf.float32) #dropout (keep probability)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Construct model\n",
"rcnn = rcnn.Model(X, y, output_size=2, learning_rate=learning_rate, dropout=keep_prob)\n",
"\n",
"# Initializing the variables\n",
"# Note: tensorflow needs to have this initializer after\n",
"# the model constructor above in order to catch all variables \n",
"init = tf.initialize_all_variables()\n",
"\n",
"# Merge all summaries for tensorboard writer \n",
"merged = tf.merge_all_summaries()\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "ValueError",
"evalue": "Variable train/loss/inference/conv1/weights already exists, disallowed. Did you mean to set reuse=True in VarScope? Originally defined at:\n\n File \"/home/jovyan/work/rcnn.py\", line 112, in conv_relu\n initializer=tf.random_normal_initializer())\n File \"/home/jovyan/work/rcnn.py\", line 129, in inference\n conv1 = conv_relu(X, [1, 1, 1, 32], [32], 'conv1')\n File \"/home/jovyan/work/define_scope.py\", line 60, in decorator\n setattr(self, attribute, function(self))\n",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mValueError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-7-55f20c8c5070>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 22\u001b[0m \u001b[0mbatch_X\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mbatch_y\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdatasets\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtrain\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mnext_batch\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mbatch_size\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 23\u001b[0m \u001b[0;31m# Run optimization op (backprop)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 24\u001b[0;31m summary, _ = sess.run([merged, rcnn.train],\n\u001b[0m\u001b[1;32m 25\u001b[0m feed_dict={X: batch_X, y: batch_y,\n\u001b[1;32m 26\u001b[0m keep_prob: dropout})\n",
"\u001b[0;32m/home/jovyan/work/define_scope.py\u001b[0m in \u001b[0;36mdecorator\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 58\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mhasattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 59\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mvariable_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mname\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m \u001b[0;31m# pylint: disable=undefined-variable\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 60\u001b[0;31m \u001b[0msetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mfunction\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 61\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mgetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 62\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/rcnn.py\u001b[0m in \u001b[0;36mtrain\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 163\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mname_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'train'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 164\u001b[0m \u001b[0moptimizer\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtrain\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mAdamOptimizer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mlearning_rate\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlearning_rate\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 165\u001b[0;31m \u001b[0mminimize\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0moptimizer\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mminimize\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mloss\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 166\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mminimize\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 167\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/define_scope.py\u001b[0m in \u001b[0;36mdecorator\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 58\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mhasattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 59\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mvariable_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mname\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m \u001b[0;31m# pylint: disable=undefined-variable\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 60\u001b[0;31m \u001b[0msetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mfunction\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 61\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mgetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 62\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/rcnn.py\u001b[0m in \u001b[0;36mloss\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 173\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mname_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'cross_entopy'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 174\u001b[0m \t\t\tdiff = tf.nn.sparse_softmax_cross_entropy_with_logits(\n\u001b[0;32m--> 175\u001b[0;31m \t\t\t\tlogits=self.inference, labels=self.y)\n\u001b[0m\u001b[1;32m 176\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mname_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'total'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 177\u001b[0m \u001b[0mcross_entropy\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mreduce_mean\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdiff\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/define_scope.py\u001b[0m in \u001b[0;36mdecorator\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 58\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mhasattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 59\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mvariable_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mname\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m \u001b[0;31m# pylint: disable=undefined-variable\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 60\u001b[0;31m \u001b[0msetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mfunction\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 61\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mgetattr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattribute\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 62\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/rcnn.py\u001b[0m in \u001b[0;36minference\u001b[0;34m(self)\u001b[0m\n\u001b[1;32m 127\u001b[0m \u001b[0;31m# Convolution Layer\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 128\u001b[0m \u001b[0;32mwith\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mvariable_scope\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'conv1'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 129\u001b[0;31m \u001b[0mconv1\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mconv_relu\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m32\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;36m32\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m'conv1'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 130\u001b[0m \u001b[0;31m# conv1 = conv2d(X, params['Wc1'], params['bc1'])\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 131\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/home/jovyan/work/rcnn.py\u001b[0m in \u001b[0;36mconv_relu\u001b[0;34m(input_tensor, kernel_shape, bias_shape, layer_name, act)\u001b[0m\n\u001b[1;32m 110\u001b[0m \u001b[0;31m# Create variable named \"weights\".\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 111\u001b[0m \t\t\tweights = tf.get_variable(\"weights\", kernel_shape,\n\u001b[0;32m--> 112\u001b[0;31m \t\t\t\tinitializer=tf.random_normal_initializer())\n\u001b[0m\u001b[1;32m 113\u001b[0m \u001b[0;31m# Create variable named \"biases\".\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 114\u001b[0m \t\t\tbiases = tf.get_variable(\"biases\", bias_shape,\n",
"\u001b[0;32m/opt/conda/lib/python3.5/site-packages/tensorflow/python/ops/variable_scope.py\u001b[0m in \u001b[0;36mget_variable\u001b[0;34m(name, shape, dtype, initializer, regularizer, trainable, collections, caching_device, partitioner, validate_shape, custom_getter)\u001b[0m\n\u001b[1;32m 1020\u001b[0m \u001b[0mcollections\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcollections\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcaching_device\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcaching_device\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1021\u001b[0m \u001b[0mpartitioner\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mpartitioner\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mvalidate_shape\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mvalidate_shape\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1022\u001b[0;31m custom_getter=custom_getter)\n\u001b[0m\u001b[1;32m 1023\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1024\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/conda/lib/python3.5/site-packages/tensorflow/python/ops/variable_scope.py\u001b[0m in \u001b[0;36mget_variable\u001b[0;34m(self, var_store, name, shape, dtype, initializer, regularizer, trainable, collections, caching_device, partitioner, validate_shape, custom_getter)\u001b[0m\n\u001b[1;32m 847\u001b[0m \u001b[0mcollections\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcollections\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcaching_device\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcaching_device\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 848\u001b[0m \u001b[0mpartitioner\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mpartitioner\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mvalidate_shape\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mvalidate_shape\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 849\u001b[0;31m custom_getter=custom_getter)\n\u001b[0m\u001b[1;32m 850\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 851\u001b[0m def _get_partitioned_variable(self,\n",
"\u001b[0;32m/opt/conda/lib/python3.5/site-packages/tensorflow/python/ops/variable_scope.py\u001b[0m in \u001b[0;36mget_variable\u001b[0;34m(self, name, shape, dtype, initializer, regularizer, reuse, trainable, collections, caching_device, partitioner, validate_shape, custom_getter)\u001b[0m\n\u001b[1;32m 343\u001b[0m \u001b[0mreuse\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mreuse\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtrainable\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mtrainable\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcollections\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcollections\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 344\u001b[0m \u001b[0mcaching_device\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcaching_device\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpartitioner\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mpartitioner\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 345\u001b[0;31m validate_shape=validate_shape)\n\u001b[0m\u001b[1;32m 346\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 347\u001b[0m def _get_partitioned_variable(\n",
"\u001b[0;32m/opt/conda/lib/python3.5/site-packages/tensorflow/python/ops/variable_scope.py\u001b[0m in \u001b[0;36m_true_getter\u001b[0;34m(name, shape, dtype, initializer, regularizer, reuse, trainable, collections, caching_device, partitioner, validate_shape)\u001b[0m\n\u001b[1;32m 328\u001b[0m \u001b[0minitializer\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitializer\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mregularizer\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mregularizer\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mreuse\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mreuse\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 329\u001b[0m \u001b[0mtrainable\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mtrainable\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcollections\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcollections\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 330\u001b[0;31m caching_device=caching_device, validate_shape=validate_shape)\n\u001b[0m\u001b[1;32m 331\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 332\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mcustom_getter\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0;32mNone\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/opt/conda/lib/python3.5/site-packages/tensorflow/python/ops/variable_scope.py\u001b[0m in \u001b[0;36m_get_single_variable\u001b[0;34m(self, name, shape, dtype, initializer, regularizer, partition_info, reuse, trainable, collections, caching_device, validate_shape)\u001b[0m\n\u001b[1;32m 631\u001b[0m \u001b[0;34m\" Did you mean to set reuse=True in VarScope? \"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 632\u001b[0m \"Originally defined at:\\n\\n%s\" % (\n\u001b[0;32m--> 633\u001b[0;31m name, \"\".join(traceback.format_list(tb))))\n\u001b[0m\u001b[1;32m 634\u001b[0m \u001b[0mfound_var\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_vars\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mname\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 635\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0mshape\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mis_compatible_with\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mfound_var\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mget_shape\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mValueError\u001b[0m: Variable train/loss/inference/conv1/weights already exists, disallowed. Did you mean to set reuse=True in VarScope? Originally defined at:\n\n File \"/home/jovyan/work/rcnn.py\", line 112, in conv_relu\n initializer=tf.random_normal_initializer())\n File \"/home/jovyan/work/rcnn.py\", line 129, in inference\n conv1 = conv_relu(X, [1, 1, 1, 32], [32], 'conv1')\n File \"/home/jovyan/work/define_scope.py\", line 60, in decorator\n setattr(self, attribute, function(self))\n"
]
}
],
"source": [
"## Launch the graph\n",
"with tf.Session() as sess:\n",
" sess.run(init)\n",
" step = 1\n",
" \n",
" # Profiling tools (only on tensorflow >= 0.12.0rc0)\n",
" # Print trainable variable parameter statistics to stdout.\n",
" # param_stats = tf.contrib.tfprof.model_analyzer.print_model_analysis(\n",
" # tf.get_default_graph(),\n",
" # tfprof_options=tf.contrib.tfprof.model_analyzer.TRAINABLE_VARS_PARAMS_STAT_OPTIONS)\n",
" \n",
" # param_stats is tensorflow.tfprof.TFProfNode proto. It organize the statistics\n",
" # of each graph node in tree scructure. Let's print the root below.\n",
" # print('total_params: %d\\n' % param_stats.total_parameters)\n",
" \n",
" # Add a summary writer for train steps\n",
" train_writer = tf.train.SummaryWriter(\"./logs\", sess.graph)\n",
" \n",
" # Keep training until reach max iterations\n",
" while step * batch_size < training_iters:\n",
" \n",
" batch_X, batch_y = datasets.train.next_batch(batch_size)\n",
" # Run optimization op (backprop)\n",
" summary, _ = sess.run([merged, rcnn.train],\n",
" feed_dict={X: batch_X, y: batch_y,\n",
" keep_prob: dropout})\n",
"\n",
" train_writer.add_summary(summary, step)\n",
" \n",
" # Display training steps\n",
" if step % display_step == 0:\n",
" # Calculate batch loss and accuracy\n",
" summary, loss, acc = sess.run([merged, rcnn.loss, rcnn.predict], \n",
" feed_dict={X: batch_X,\n",
" y: batch_y,\n",
" keep_prob: dropout})\n",
" \n",
" train_writer.add_summary(summary, step)\n",
" \n",
" print(\"Iteration \" + str(step * batch_size) + \\\n",
" \", Minibatch Loss= \" + \"{:.6f}\".format(loss) + \\\n",
" \", Training Accuracy= \" + \"{:.5f}\".format(acc))\n",
" \n",
" # Run a round of validation once in a while\n",
" if step % validation_step == 0:\n",
" print(\"Validation Accuracy:\", \\\n",
" sess.run(rcnn.predict, feed_dict={X: datasets.validation.X[:batch_size],\n",
" y: datasets.validation.y[:batch_size],\n",
" keep_prob: 1.}))\n",
" \n",
" step += 1\n",
" print(\"Optimization Finished!\")\n",
" train_writer.close()\n",
"\n",
" # Calculate accuracy\n",
" print(\"Testing Accuracy:\", \\\n",
" sess.run(rcnn.predict, feed_dict={X: datasets.test.X[:batch_size],\n",
" y: datasets.test.y[:batch_size],\n",
" keep_prob: 1.}))\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
csunny/blog_project | source/libs/analysis/pandas/practise.ipynb | 1 | 31442 | {
"cells": [
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>0.685162</td>\n",
" <td>0.791786</td>\n",
" <td>-0.447688</td>\n",
" <td>-0.911904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>0.369106</td>\n",
" <td>1.140169</td>\n",
" <td>-0.170676</td>\n",
" <td>1.724625</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"datas = pd.date_range('20160301', periods=6)\n",
"df = pd.DataFrame(np.random.randn(6, 4), index=datas, columns=list('ABCD'))\n",
"df"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1 = df.reindex(index=datas[0: 4], columns=list(df.columns)+ ['E'])\n",
"df1"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1.loc[datas[1:3], 'E'] = 3\n",
"df1"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.01119</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>1</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>1</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1.loc[datas[2:4], 'A'] = '1'\n",
"df1"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.01119</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>1</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" <td>3</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1.dropna()"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.01119</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>1</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>1</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" <td>5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1.fillna(value=5)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 20,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"pd.isnull(df1).any().any()"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" <th>E</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td>4.000000</td>\n",
" <td>4.000000</td>\n",
" <td>4.000000</td>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td>-0.786717</td>\n",
" <td>-1.337661</td>\n",
" <td>0.163729</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td>0.760165</td>\n",
" <td>1.714374</td>\n",
" <td>1.499628</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
" <td>-1.668247</td>\n",
" <td>-2.796977</td>\n",
" <td>-1.139497</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td>-1.297893</td>\n",
" <td>-2.208064</td>\n",
" <td>-1.112467</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td>-0.672101</td>\n",
" <td>-1.844696</td>\n",
" <td>0.040937</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>-0.160925</td>\n",
" <td>-0.974292</td>\n",
" <td>1.317134</td>\n",
" <td>3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td>-0.134420</td>\n",
" <td>1.135726</td>\n",
" <td>1.712541</td>\n",
" <td>3</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df1.describe()"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2016-03-01 NaN\n",
"2016-03-02 NaN\n",
"2016-03-03 1\n",
"2016-03-04 3\n",
"2016-03-05 5\n",
"2016-03-06 NaN\n",
"Freq: D, dtype: float64"
]
},
"execution_count": 23,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"s = pd.Series([1, 3, 5, np.nan, 6, 8 ], index=datas).shift(2)\n",
"s"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>0.685162</td>\n",
" <td>0.791786</td>\n",
" <td>-0.447688</td>\n",
" <td>-0.911904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>0.369106</td>\n",
" <td>1.140169</td>\n",
" <td>-0.170676</td>\n",
" <td>1.724625</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-2.051040</td>\n",
" <td>-1.169761</td>\n",
" <td>-3.011760</td>\n",
" <td>-2.103457</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-3.851890</td>\n",
" <td>-4.174442</td>\n",
" <td>-5.796977</td>\n",
" <td>-1.287459</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>-4.314838</td>\n",
" <td>-4.208214</td>\n",
" <td>-5.447688</td>\n",
" <td>-5.911904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df.sub(s, axis='index')"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>0.146294</td>\n",
" <td>-1.802667</td>\n",
" <td>-0.541906</td>\n",
" <td>0.045834</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-0.904747</td>\n",
" <td>-1.972427</td>\n",
" <td>-2.553666</td>\n",
" <td>-1.057623</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-1.756636</td>\n",
" <td>-3.146869</td>\n",
" <td>-5.350643</td>\n",
" <td>0.654918</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>-1.071474</td>\n",
" <td>-2.355084</td>\n",
" <td>-5.798331</td>\n",
" <td>-0.256987</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>-0.702368</td>\n",
" <td>-1.214915</td>\n",
" <td>-5.969008</td>\n",
" <td>1.467638</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df.apply(np.cumsum)"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"A 2.062230\n",
"B 2.808416\n",
"C 3.932702\n",
"D 2.864122\n",
"dtype: float64"
]
},
"execution_count": 27,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df.apply(lambda x: x.max()-x.min())"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0 17\n",
"1 13\n",
"2 19\n",
"3 19\n",
"4 14\n",
"5 12\n",
"6 19\n",
"7 14\n",
"8 15\n",
"9 12\n",
"10 19\n",
"11 16\n",
"12 14\n",
"13 18\n",
"14 18\n",
"15 14\n",
"16 13\n",
"17 12\n",
"18 18\n",
"19 10\n",
"dtype: int32"
]
},
"execution_count": 30,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"s = pd.Series(np.random.randint(10, 20, size=20))\n",
"s"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"19 4\n",
"14 4\n",
"18 3\n",
"12 3\n",
"13 2\n",
"17 1\n",
"16 1\n",
"15 1\n",
"10 1\n",
"dtype: int64"
]
},
"execution_count": 31,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"s.value_counts()"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<bound method Series.mode of 0 17\n",
"1 13\n",
"2 19\n",
"3 19\n",
"4 14\n",
"5 12\n",
"6 19\n",
"7 14\n",
"8 15\n",
"9 12\n",
"10 19\n",
"11 16\n",
"12 14\n",
"13 18\n",
"14 18\n",
"15 14\n",
"16 13\n",
"17 12\n",
"18 18\n",
"19 10\n",
"dtype: int32>"
]
},
"execution_count": 32,
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"s.mode"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df.iloc[:3]"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>0.685162</td>\n",
" <td>0.791786</td>\n",
" <td>-0.447688</td>\n",
" <td>-0.911904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>0.369106</td>\n",
" <td>1.140169</td>\n",
" <td>-0.170676</td>\n",
" <td>1.724625</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df.iloc[3:6]"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [],
"source": [
"left = pd.DataFrame({'key': ['foo', 'foo'], 'lval': [1, 2]})\n",
"right = pd.DataFrame({'key': ['foo', 'foo'], 'rval': [4, 5]})"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>key</th>\n",
" <th>lval</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>foo</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>foo</td>\n",
" <td>2</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"left"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>key</th>\n",
" <th>rval</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>foo</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>foo</td>\n",
" <td>5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"right"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>key</th>\n",
" <th>lval</th>\n",
" <th>rval</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>foo</td>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>foo</td>\n",
" <td>1</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>foo</td>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>foo</td>\n",
" <td>2</td>\n",
" <td>5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"pd.merge(left, right, on='key')"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A</th>\n",
" <th>B</th>\n",
" <th>C</th>\n",
" <th>D</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2016-03-01</th>\n",
" <td>-0.864896</td>\n",
" <td>-1.668247</td>\n",
" <td>1.135726</td>\n",
" <td>-1.139497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-02</th>\n",
" <td>1.011190</td>\n",
" <td>-0.134420</td>\n",
" <td>-1.677632</td>\n",
" <td>1.185332</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-03</th>\n",
" <td>-1.051040</td>\n",
" <td>-0.169761</td>\n",
" <td>-2.011760</td>\n",
" <td>-1.103457</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-04</th>\n",
" <td>-0.851890</td>\n",
" <td>-1.174442</td>\n",
" <td>-2.796977</td>\n",
" <td>1.712541</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-05</th>\n",
" <td>0.685162</td>\n",
" <td>0.791786</td>\n",
" <td>-0.447688</td>\n",
" <td>-0.911904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2016-03-06</th>\n",
" <td>0.369106</td>\n",
" <td>1.140169</td>\n",
" <td>-0.170676</td>\n",
" <td>1.724625</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
]
},
"output_type": "execute_result",
"metadata": {}
}
],
"source": [
"df"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {},
"outputs": [],
"source": [
"df2 = pd.DataFrame({'A':['foo', 'bar', 'foo', 'bar', \n",
" 'foo', 'bar', 'foo', 'bar'], \n",
" 'B':['one', 'one', 'two', 'two', \n",
" 'three', 'one', 'two', 'one']\n",
" 'C': np.random.randn(8),\n",
" 'D': np.random.randn(8)})"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2.0
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | mit |
julienchastang/unidata-python-workshop | notebooks/Python_Ecosystem/Scientific_Python_Ecosystem_Overview.ipynb | 1 | 8695 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# The Scientific Python Ecosystem\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Python\n",
"\n",
"Python is a interpreted, high-level programming language that is meant to be easily understandable and usable for a multitude of purposes. It is composed of libraries that contain useful tools for you to do quick and efficient data analysis and visualization. These libraries are like Lego blocks - you can pick and choose which ones you want to build your end product. The Scientific Python Ecosystem is composed of key libraries (i.e. NumPy, SciPy, Pandas, Matplotlib) that serve as a basis for most other libraries (i.e. MetPy). In this notebook, we'll briefly touch on several of these foundational libraries of the SciPy Ecosystem."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Getting Python: Anaconda\n",
"\n",
"Anaconda provides distributions of Python and the main third-party packages either as a full distribution or as a lighter-weight verison, \"Miniconda\". We recommend using Anaconda to build and maintain your Python stack, as it provides command line tools to download and update Python libraries. You can check it out at https://www.anaconda.com/distribution/."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Jupyter\n",
"\n",
"The Jupyter library provides \"literate programming\" interfaces for Python and other programming languages. This file is displayed using the Jupyter library, either within Jupyter Notebook or Lab. It incorporates code, prose, and other text (equations, HTML) to make a seamless document for your analysis or presentation by working in small blocks. This also allows for quick prototyping and debugging of code as you write!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# The Building Blocks of the SciPy World"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"While Python is the basis for everything, this figure demonstrates how packages build on top of each other (causing dependencies). Additionally, packages are constantly under development, so this structure does have some transient nature to it, as the SciPy world continue to expand (see Dask as a recent addition to this framework)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data Analysis/Computation Libraries"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### NumPy\n",
"\n",
"NumPy is the primary numerical computation library in Python. It works with N-dimensional arrays and matrices and performs basic computations on them."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"x = np.arange(1,11)\n",
"y = np.arange(100,110)\n",
"mean_x_y = np.mean([x,y])\n",
"print(mean_x_y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Pandas\n",
"\n",
"Pandas is an excellent library for handling tabular data and quickly performing data analysis on it. It can handle many textfile types."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"df = pd.read_csv('../Pandas/Jan17_CO_ASOS.txt', sep='\\t')\n",
"df.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### xarray\n",
"\n",
"xarray is a Python library meant to handle N-dimensional arrays with metadata (think netCDF files). With the Dask library, it can work with Big Data efficiently in a Python framework."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import xarray as xr\n",
"ds = xr.open_dataset('../../data/NARR_19930313_0000.nc')\n",
"ds"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Dask\n",
"\n",
"Dask is a parallel-computing library in Python. You can use it on your laptop, cloud environment, or on a high-performance computer (NCAR's Cheyenne for example). It allows for lazy evaluations so that computations only occur after you've chained all of your operations together. Additionally, it has a built-in scheduler to scale with your computational demand to optimize your parellel resources."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### SciPy\n",
"\n",
"The SciPy library has a lot of advanced mathematical functions that are not contained in Numpy, including Fast Fourier Transforms, interpolation methods, and linear algebra operations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Scikit-learn\n",
"\n",
"Scikit-learn is the primary machine learning library for Python. It can do simple things like regressions and classifications, or more advanced techniques like random forests. It can perform some neural network operations, but for big data implementations, check out the `keras` library."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Scikit-image\n",
"\n",
"An image processing library built on NumPy"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Visualization Libraries\n",
"\n",
"### Matplotlib\n",
"\n",
"Matplotlib is one of the core visualization libraries in Python and produces publication-quality figures without much configuration. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"plt.plot(x,y)\n",
"plt.title('Demo of Matplotlib')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### CartoPy\n",
"\n",
"CartoPy is the primary geographical mapping and visualization library in Python, as support for Basemap has been discontinued. It can handle various projections and transformation to/from projections to map data accurately for your problem."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Atmospheric Science Libraries"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### MetPy\n",
"\n",
"MetPy is developed at Unidata with support from the user community as a replacement for GEMPAK. Its primary functions are to read in data, perform meteorological calculations on it, and visualize it in useful way for education and research. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Pint\n",
"\n",
"Pint is a unit-handling library, which MetPy relies upon for its calculations. Pint allow units to be attached to NumPy arrays, which allows for unit-aware calculations and easy conversions to reduce unit-based errors."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### netcdf4-python\n",
"\n",
"This is another Unidata package that serves as an interface from Python to the netCDF-C library. As a result, netCDF files can easily be read and written in Python."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Siphon\n",
"\n",
"The Siphon library, developed at Unidata, is a remote access library, built for accessing data on THREDDS servers, but also has hooks into the Wyoming, IGRA, and Iowa State upper air databases, the National Buoy Data Center, and the NHC and SPC storm reports as well. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For more information on the SciPy Ecosystem, check out these links: https://www.scipy.org/about.html and https://scipy-lectures.org/intro/intro.html"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "conda-env-unidata-python-workshop-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
MaxPowerWasTaken/MaxPowerWasTaken.github.io | jupyter_notebooks/superseded/Multiprocessing in Pandas minimal.ipynb | 2 | 1833 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Easy Multiprocessing on Pandas DataFrames"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Python's `Pandas` library is great for all sorts of data-wrangling tasks. What doesn't come out of the box with Pandas is parallel processing. Here is a simple approach for taking a Pandas DataFrame and a function, and applying the function to chunks of the DataFrame in parallel.\n",
"\n",
"First let's download a dataset"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(244, 7)\n",
" total_bill tip sex smoker day time size\n",
"0 16.99 1.01 Female No Sun Dinner 2\n",
"1 10.34 1.66 Male No Sun Dinner 3\n",
"2 21.01 3.50 Male No Sun Dinner 3\n"
]
}
],
"source": [
"import pandas as pd\n",
"import seaborn as sns\n",
"\n",
"df = pd.DataFrame(sns.load_dataset('tips'))\n",
"print(df.shape)\n",
"print(df.head(3))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Say we wanted to get tip percentage. We can "
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
alex-ip/geophys_utils | examples/10_gravity_point_discovery_and_access_demo.ipynb | 1 | 5378811 | null | apache-2.0 |
QuantStack/quantstack-talks | 2018-08-23-jupytercon-native/notebooks/xframe.ipynb | 1 | 6900 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<center> <h1>xframe is a dataframe for C++, based on xtensor and xtl</h1> </center>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#include <string>\n",
"#include <iostream>\n",
"\n",
"#include \"xtl/xbasic_fixed_string.hpp\"\n",
"\n",
"#include \"xtensor/xio.hpp\"\n",
"#include \"xtensor/xrandom.hpp\"\n",
"#include \"xtensor/xmath.hpp\"\n",
"\n",
"#include \"xframe/xio.hpp\"\n",
"#include \"xframe/xvariable.hpp\"\n",
"#include \"xframe/xvariable_view.hpp\"\n",
"#include \"xframe/xvariable_masked_view.hpp\"\n",
"#include \"xframe/xio.hpp\""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"using fstring = xtl::xfixed_string<55>;\n",
"\n",
"using data_type = xt::xoptional_assembly<xt::xarray<double>, xt::xarray<bool>>;\n",
"using coordinate_type = xf::xcoordinate<fstring, data_type::size_type>;\n",
"\n",
"using variable_type = xf::xvariable<coordinate_type, data_type>;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Variable with 2D Data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Dry temperature variable"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"data_type dry_temperature_data = xt::eval(xt::random::rand({6, 3}, 15., 25.));\n",
"dry_temperature_data(0, 0).has_value() = false;\n",
"dry_temperature_data(2, 1).has_value() = false;"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature_data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"auto time_axis = xf::axis({\"2018-01-01\", \"2018-01-02\", \"2018-01-03\", \"2018-01-04\", \"2018-01-05\", \"2018-01-06\"});"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"auto dry_temperature = variable_type(\n",
" dry_temperature_data,\n",
" {\n",
" {\"date\", time_axis},\n",
" {\"city\", xf::axis({\"London\", \"Paris\", \"Brussels\"})}\n",
" }\n",
");"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature.select({{\"city\", \"London\"}, {\"date\", \"2018-01-04\"}})"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature.locate(\"2018-01-03\", \"Brussels\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature.locate(\"2018-01-03\", \"Paris\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Relative humidity variable"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"data_type relative_humidity_data = xt::eval(xt::random::rand({3}, 50.0, 70.0));\n",
"\n",
"auto relative_humidity = variable_type(\n",
" relative_humidity_data,\n",
" {\n",
" {\"city\", xf::axis({\"Paris\", \"London\", \"Brussels\"})}\n",
" }\n",
");\n",
"\n",
"relative_humidity"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Compute water vapour pressure using Broadcasting"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dry_temperature"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"auto water_vapour_pressure = 0.01 * relative_humidity * 6.1 * xt::exp((17.27 * dry_temperature) / (237.7 + dry_temperature));"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"water_vapour_pressure"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Variable with 3D data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"data_type pressure_data = {{{ 1., 2., 3. },\n",
" { 4., 5., 6. },\n",
" { 7., 8., 9. }},\n",
" {{ 1.3, 1.5, 1.},\n",
" { 2., 2.3, 2.4},\n",
" { 3.1, 3.8, 3.}},\n",
" {{ 8.5, 8.2, 8.6},\n",
" { 7.5, 8.6, 9.7},\n",
" { 4.5, 4.4, 4.3}}};"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"auto pressure = variable_type(\n",
" pressure_data,\n",
" {\n",
" {\"x\", xf::axis(3)},\n",
" {\"y\", xf::axis(3, 6, 1)},\n",
" {\"z\", xf::axis(3)},\n",
" }\n",
");"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"pressure"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"pressure.select({{\"x\", 1}, {\"y\", 4}, {\"z\", 1}})"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"pressure.locate(0, 5, 2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Masking"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"auto masked_pressure = xf::where(\n",
" pressure,\n",
" not_equal(pressure.axis<int>(\"x\"), 2) && pressure.axis<int>(\"z\") < 2\n",
");"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"masked_pressure"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "C++14",
"language": "C++14",
"name": "xeus-cling-cpp14"
},
"language_info": {
"codemirror_mode": "text/x-c++src",
"file_extension": ".cpp",
"mimetype": "text/x-c++src",
"name": "c++",
"version": "-std=c++14"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
intel-analytics/analytics-zoo | docs/docs/colab-notebook/orca/examples/fashion_mnist_bigdl.ipynb | 1 | 14788611 | null | apache-2.0 |
EderSantana/blocks_contrib | tests/DelayLine.ipynb | 1 | 85859 | {
"metadata": {
"name": "",
"signature": "sha256:e1c45b0ff2c887a302d3c3841e0f9ac78f090f38f5e81b6c6ae1f689014d25b2"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"from fuel.datasets import Dataset\n",
"from librnn.pylearn2.datasets.music import MusicSequence\n",
"from blocks.bricks import Sigmoid, Tanh, MLP, Linear, Rectifier\n",
"from blocks.bricks.recurrent import SimpleRecurrent, GatedRecurrent, LSTM\n",
"from blocks.bricks import recurrent\n",
"from blocks.initialization import Orthogonal, IsotropicGaussian, Constant\n",
"from blocks.algorithms import GradientDescent, Scale, Adam\n",
"from fuel.streams import DataStream\n",
"from fuel.schemes import ConstantScheme\n",
"from theano import tensor\n",
"from blocks.bricks import WEIGHTS, BIASES\n",
"from blocks.graph import ComputationGraph\n",
"from blocks.filter import VariableFilter\n",
"from blocks.main_loop import MainLoop\n",
"from blocks.model import Model\n",
"from blocks.extensions import FinishAfter, Printing\n",
"#from blocks.extensions.saveload import SerializeMainLoop\n",
"from blocks.extensions.monitoring import TrainingDataMonitoring, DataStreamMonitoring\n",
"from blocks.bricks.cost import BinaryCrossEntropy\n",
"from blocks_contrib.bricks.recurrent import DelayLine"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"class MusicFuel(Dataset):\n",
" def __init__(self, which_set, which_dataset):\n",
" self.pylearn2_dataset = MusicSequence(which_set=which_set, which_dataset=which_dataset)\n",
" self.sources = self.pylearn2_dataset.get_data_specs()[-1]\n",
" \n",
" def open(self):\n",
" num_examples = self.pylearn2_dataset.get_num_examples()\n",
" return self.pylearn2_dataset.iterator(1, num_examples, mode='sequential',\n",
" data_specs=self.pylearn2_dataset.get_data_specs(), return_tuple=True)\n",
" \n",
" def get_data(self,state=None,request=None):\n",
" return next(state)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import theano \n",
"\n",
"x = tensor.tensor3('features')\n",
"mem_dim = 5\n",
"preRNN = SimpleRecurrent(dim=48, activation=Tanh())\n",
"RNN = DelayLine(96, mem_dim)\n",
"h = RNN.apply(x) # h is hidden states in the RNN\n",
"state_to_output = Linear(name='state_to_output', input_dim=96*mem_dim, output_dim=48)\n",
"pre_out = Rectifier().apply(state_to_output.apply(h))\n",
"out = Linear(name='out', input_dim=48, output_dim=96)\n",
"y_hat = Sigmoid(name='last_layer').apply(out.apply(pre_out))\n",
"y_hat.name = 'output_sequence'\n",
"\n",
"predict = theano.function(inputs = [x, ], outputs = y_hat)\n",
"\n",
"y = tensor.tensor3('targets')\n",
"#cost = BinaryCrossEntropy().apply(y, y_hat)\n",
"cost = tensor.nnet.binary_crossentropy(y_hat, y).sum(axis=2).mean()\n",
"cost.name = 'BCE'\n",
"\n",
"state_to_output.weights_init = out.weights_init = IsotropicGaussian(0.01)\n",
"#RNN.weights_init = Constant(1.)\n",
"RNN.weights_init = IsotropicGaussian(.01)\n",
"RNN.biases_init = state_to_output.biases_init = out.biases_init = Constant(0)\n",
"RNN.initialize()\n",
"state_to_output.initialize()\n",
"out.initialize()\n",
"\n",
"cg = ComputationGraph(cost)\n",
"params = VariableFilter(roles=[WEIGHTS, BIASES])(cg.variables)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/Users/eder/anaconda/lib/python2.7/site-packages/theano/scan_module/scan_perform_ext.py:133: RuntimeWarning: numpy.ndarray size changed, may indicate binary incompatibility\n",
" from scan_perform.scan_perform import *\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"trainset = DataStream(MusicFuel(which_set='train', which_dataset='jsb'))\n",
"testset = DataStream(MusicFuel(which_set='test', which_dataset='jsb'))\n",
"validset = DataStream(MusicFuel(which_set='valid', which_dataset='jsb'))\n",
"batch_size = 1\n",
"num_epochs = 100\n",
"cost.name = \"sequence_log_likelihood\"\n",
"algorithm = GradientDescent(\n",
" cost=cost, params=params,\n",
" step_rule=Adam(0.001))\n",
"main_loop = MainLoop(\n",
" algorithm=algorithm,\n",
" data_stream=trainset,\n",
" model=None,\n",
" extensions=[FinishAfter(after_n_epochs=num_epochs),\n",
" TrainingDataMonitoring([cost], prefix=\"train\",\n",
" after_every_epoch=True),\n",
" DataStreamMonitoring([cost], validset, prefix=\"valid\"),\n",
" DataStreamMonitoring([cost], testset, prefix=\"test\"),\n",
" Printing()])\n",
"main_loop.run()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/Users/eder/python/pylearn2/pylearn2/utils/iteration.py:783: UserWarning: dataset is using the old iterator interface which is deprecated and will become officially unsupported as of July 28, 2015. The dataset should implement a `get` method respecting the new interface.\n",
" warnings.warn(\"dataset is using the old iterator interface which \"\n",
"/Users/eder/python/blocks/blocks/log.py:147: FutureWarning: comparison to `None` will result in an elementwise object comparison in the future.\n",
" if value != default_value:\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"-------------------------------------------------------------------------------\n",
"BEFORE FIRST EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 0\n",
"\t iterations_done: 0\n",
"Log records from the iteration 0:\n",
"\t test_sequence_log_likelihood: 66.5426330566\n",
"\t valid_sequence_log_likelihood: 66.5427780151\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 1\n",
"\t iterations_done: 229\n",
"Log records from the iteration 229:\n",
"\t test_sequence_log_likelihood: 12.7564840317\n",
"\t train_sequence_log_likelihood: 18.843875885\n",
"\t valid_sequence_log_likelihood: 12.4118967056\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 2\n",
"\t iterations_done: 458\n",
"Log records from the iteration 458:\n",
"\t test_sequence_log_likelihood: 14.2806081772\n",
"\t train_sequence_log_likelihood: 11.4923467636\n",
"\t valid_sequence_log_likelihood: 11.9762706757\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 3\n",
"\t iterations_done: 687\n",
"Log records from the iteration 687:\n",
"\t test_sequence_log_likelihood: 11.2280302048\n",
"\t train_sequence_log_likelihood: 11.34171772\n",
"\t valid_sequence_log_likelihood: 11.288236618\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 4\n",
"\t iterations_done: 916\n",
"Log records from the iteration 916:\n",
"\t test_sequence_log_likelihood: 11.2489356995\n",
"\t train_sequence_log_likelihood: 10.9005889893\n",
"\t valid_sequence_log_likelihood: 10.9042282104\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 5\n",
"\t iterations_done: 1145\n",
"Log records from the iteration 1145:\n",
"\t test_sequence_log_likelihood: 10.6666545868\n",
"\t train_sequence_log_likelihood: 10.5895252228\n",
"\t valid_sequence_log_likelihood: 10.4539556503\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 6\n",
"\t iterations_done: 1374\n",
"Log records from the iteration 1374:\n",
"\t test_sequence_log_likelihood: 10.5364952087\n",
"\t train_sequence_log_likelihood: 10.2857971191\n",
"\t valid_sequence_log_likelihood: 10.1746063232\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 7\n",
"\t iterations_done: 1603\n",
"Log records from the iteration 1603:\n",
"\t test_sequence_log_likelihood: 10.9462614059\n",
"\t train_sequence_log_likelihood: 10.0910396576\n",
"\t valid_sequence_log_likelihood: 10.0758295059\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 8\n",
"\t iterations_done: 1832\n",
"Log records from the iteration 1832:\n",
"\t test_sequence_log_likelihood: 9.95141410828\n",
"\t train_sequence_log_likelihood: 9.95424938202\n",
"\t valid_sequence_log_likelihood: 9.91554927826\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 9\n",
"\t iterations_done: 2061\n",
"Log records from the iteration 2061:\n",
"\t test_sequence_log_likelihood: 10.0116691589\n",
"\t train_sequence_log_likelihood: 9.8499250412\n",
"\t valid_sequence_log_likelihood: 9.78990459442\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 10\n",
"\t iterations_done: 2290\n",
"Log records from the iteration 2290:\n",
"\t test_sequence_log_likelihood: 9.68646526337\n",
"\t train_sequence_log_likelihood: 9.67256832123\n",
"\t valid_sequence_log_likelihood: 9.5977191925\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 11\n",
"\t iterations_done: 2519\n",
"Log records from the iteration 2519:\n",
"\t test_sequence_log_likelihood: 9.92022037506\n",
"\t train_sequence_log_likelihood: 9.5371131897\n",
"\t valid_sequence_log_likelihood: 9.56313037872\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 12\n",
"\t iterations_done: 2748\n",
"Log records from the iteration 2748:\n",
"\t test_sequence_log_likelihood: 9.49722290039\n",
"\t train_sequence_log_likelihood: 9.41157722473\n",
"\t valid_sequence_log_likelihood: 9.52156352997\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 13\n",
"\t iterations_done: 2977\n",
"Log records from the iteration 2977:\n",
"\t test_sequence_log_likelihood: 9.53739356995\n",
"\t train_sequence_log_likelihood: 9.29652309418\n",
"\t valid_sequence_log_likelihood: 9.76044368744\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 14\n",
"\t iterations_done: 3206\n",
"Log records from the iteration 3206:\n",
"\t test_sequence_log_likelihood: 9.40819740295\n",
"\t train_sequence_log_likelihood: 9.19443893433\n",
"\t valid_sequence_log_likelihood: 9.27327346802\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 15\n",
"\t iterations_done: 3435\n",
"Log records from the iteration 3435:\n",
"\t test_sequence_log_likelihood: 9.90093994141\n",
"\t train_sequence_log_likelihood: 9.09687995911\n",
"\t valid_sequence_log_likelihood: 9.95949363708\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 16\n",
"\t iterations_done: 3664\n",
"Log records from the iteration 3664:\n",
"\t test_sequence_log_likelihood: 9.19744682312\n",
"\t train_sequence_log_likelihood: 9.01790714264\n",
"\t valid_sequence_log_likelihood: 10.4548749924\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 17\n",
"\t iterations_done: 3893\n",
"Log records from the iteration 3893:\n",
"\t test_sequence_log_likelihood: 9.18597698212\n",
"\t train_sequence_log_likelihood: 8.94530487061\n",
"\t valid_sequence_log_likelihood: 9.15009403229\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 18\n",
"\t iterations_done: 4122\n",
"Log records from the iteration 4122:\n",
"\t test_sequence_log_likelihood: 9.16871547699\n",
"\t train_sequence_log_likelihood: 8.88837337494\n",
"\t valid_sequence_log_likelihood: 8.98441791534\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 19\n",
"\t iterations_done: 4351\n",
"Log records from the iteration 4351:\n",
"\t test_sequence_log_likelihood: 9.47048282623\n",
"\t train_sequence_log_likelihood: 8.83262825012\n",
"\t valid_sequence_log_likelihood: 9.04933929443\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 20\n",
"\t iterations_done: 4580\n",
"Log records from the iteration 4580:\n",
"\t test_sequence_log_likelihood: 9.01980686188\n",
"\t train_sequence_log_likelihood: 8.79022502899\n",
"\t valid_sequence_log_likelihood: 9.14806842804\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 21\n",
"\t iterations_done: 4809\n",
"Log records from the iteration 4809:\n",
"\t test_sequence_log_likelihood: 9.14241313934\n",
"\t train_sequence_log_likelihood: 8.75098228455\n",
"\t valid_sequence_log_likelihood: 9.21454811096\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 22\n",
"\t iterations_done: 5038\n",
"Log records from the iteration 5038:\n",
"\t test_sequence_log_likelihood: 8.99683761597\n",
"\t train_sequence_log_likelihood: 8.71278858185\n",
"\t valid_sequence_log_likelihood: 9.42289447784\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 23\n",
"\t iterations_done: 5267\n",
"Log records from the iteration 5267:\n",
"\t test_sequence_log_likelihood: 9.48575210571\n",
"\t train_sequence_log_likelihood: 8.6813583374\n",
"\t valid_sequence_log_likelihood: 10.740486145\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 24\n",
"\t iterations_done: 5496\n",
"Log records from the iteration 5496:\n",
"\t test_sequence_log_likelihood: 8.97317314148\n",
"\t train_sequence_log_likelihood: 8.64957809448\n",
"\t valid_sequence_log_likelihood: 8.85156154633\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 25\n",
"\t iterations_done: 5725\n",
"Log records from the iteration 5725:\n",
"\t test_sequence_log_likelihood: 9.11082363129\n",
"\t train_sequence_log_likelihood: 8.62181854248\n",
"\t valid_sequence_log_likelihood: 8.91409111023\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 26\n",
"\t iterations_done: 5954\n",
"Log records from the iteration 5954:\n",
"\t test_sequence_log_likelihood: 9.5344209671\n",
"\t train_sequence_log_likelihood: 8.58941745758\n",
"\t valid_sequence_log_likelihood: 8.89215946198\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 27\n",
"\t iterations_done: 6183\n",
"Log records from the iteration 6183:\n",
"\t test_sequence_log_likelihood: 9.33521842957\n",
"\t train_sequence_log_likelihood: 8.55719566345\n",
"\t valid_sequence_log_likelihood: 9.03122711182\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 28\n",
"\t iterations_done: 6412\n",
"Log records from the iteration 6412:\n",
"\t test_sequence_log_likelihood: 9.54921340942\n",
"\t train_sequence_log_likelihood: 8.53171825409\n",
"\t valid_sequence_log_likelihood: 9.17234325409\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 29\n",
"\t iterations_done: 6641\n",
"Log records from the iteration 6641:\n",
"\t test_sequence_log_likelihood: 9.46071434021\n",
"\t train_sequence_log_likelihood: 8.51789665222\n",
"\t valid_sequence_log_likelihood: 9.11627960205\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 30\n",
"\t iterations_done: 6870\n",
"Log records from the iteration 6870:\n",
"\t test_sequence_log_likelihood: 12.947063446\n",
"\t train_sequence_log_likelihood: 8.48627948761\n",
"\t valid_sequence_log_likelihood: 9.67812824249\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 31\n",
"\t iterations_done: 7099\n",
"Log records from the iteration 7099:\n",
"\t test_sequence_log_likelihood: 8.87196445465\n",
"\t train_sequence_log_likelihood: 8.4728717804\n",
"\t valid_sequence_log_likelihood: 9.2174539566\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 32\n",
"\t iterations_done: 7328\n",
"Log records from the iteration 7328:\n",
"\t test_sequence_log_likelihood: 8.92094993591\n",
"\t train_sequence_log_likelihood: 8.45069789886\n",
"\t valid_sequence_log_likelihood: 9.37887191772\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 33\n",
"\t iterations_done: 7557\n",
"Log records from the iteration 7557:\n",
"\t test_sequence_log_likelihood: 8.84011745453\n",
"\t train_sequence_log_likelihood: 8.43128490448\n",
"\t valid_sequence_log_likelihood: 11.5261592865\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 34\n",
"\t iterations_done: 7786\n",
"Log records from the iteration 7786:\n",
"\t test_sequence_log_likelihood: 9.07308006287\n",
"\t train_sequence_log_likelihood: 8.41185760498\n",
"\t valid_sequence_log_likelihood: 8.9277715683\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 35\n",
"\t iterations_done: 8015\n",
"Log records from the iteration 8015:\n",
"\t test_sequence_log_likelihood: 8.84221076965\n",
"\t train_sequence_log_likelihood: 8.39264392853\n",
"\t valid_sequence_log_likelihood: 8.86141777039\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 36\n",
"\t iterations_done: 8244\n",
"Log records from the iteration 8244:\n",
"\t test_sequence_log_likelihood: 8.94195365906\n",
"\t train_sequence_log_likelihood: 8.37358188629\n",
"\t valid_sequence_log_likelihood: 9.08795452118\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 37\n",
"\t iterations_done: 8473\n",
"Log records from the iteration 8473:\n",
"\t test_sequence_log_likelihood: 8.92644119263\n",
"\t train_sequence_log_likelihood: 8.35467529297\n",
"\t valid_sequence_log_likelihood: 9.45892810822\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 38\n",
"\t iterations_done: 8702\n",
"Log records from the iteration 8702:\n",
"\t test_sequence_log_likelihood: 9.17625713348\n",
"\t train_sequence_log_likelihood: 8.34016990662\n",
"\t valid_sequence_log_likelihood: 9.08087921143\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 39\n",
"\t iterations_done: 8931\n",
"Log records from the iteration 8931:\n",
"\t test_sequence_log_likelihood: 9.15528297424\n",
"\t train_sequence_log_likelihood: 8.32591629028\n",
"\t valid_sequence_log_likelihood: 9.46311187744\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 40\n",
"\t iterations_done: 9160\n",
"Log records from the iteration 9160:\n",
"\t test_sequence_log_likelihood: 9.06723690033\n",
"\t train_sequence_log_likelihood: 8.3093957901\n",
"\t valid_sequence_log_likelihood: 9.52698516846\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 41\n",
"\t iterations_done: 9389\n",
"Log records from the iteration 9389:\n",
"\t test_sequence_log_likelihood: 9.43352603912\n",
"\t train_sequence_log_likelihood: 8.30132389069\n",
"\t valid_sequence_log_likelihood: 9.42552661896\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 42\n",
"\t iterations_done: 9618\n",
"Log records from the iteration 9618:\n",
"\t test_sequence_log_likelihood: 8.91323375702\n",
"\t train_sequence_log_likelihood: 8.29711437225\n",
"\t valid_sequence_log_likelihood: 12.0997753143\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 43\n",
"\t iterations_done: 9847\n",
"Log records from the iteration 9847:\n",
"\t test_sequence_log_likelihood: 9.33824157715\n",
"\t train_sequence_log_likelihood: 8.28573417664\n",
"\t valid_sequence_log_likelihood: 8.72438335419\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 44\n",
"\t iterations_done: 10076\n",
"Log records from the iteration 10076:\n",
"\t test_sequence_log_likelihood: 9.31497383118\n",
"\t train_sequence_log_likelihood: 8.26232814789\n",
"\t valid_sequence_log_likelihood: 8.99101638794\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 45\n",
"\t iterations_done: 10305\n",
"Log records from the iteration 10305:\n",
"\t test_sequence_log_likelihood: 9.23551845551\n",
"\t train_sequence_log_likelihood: 8.24557304382\n",
"\t valid_sequence_log_likelihood: 8.95511054993\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 46\n",
"\t iterations_done: 10534\n",
"Log records from the iteration 10534:\n",
"\t test_sequence_log_likelihood: 9.11524200439\n",
"\t train_sequence_log_likelihood: 8.23083782196\n",
"\t valid_sequence_log_likelihood: 9.11250686646\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 47\n",
"\t iterations_done: 10763\n",
"Log records from the iteration 10763:\n",
"\t test_sequence_log_likelihood: 10.3494768143\n",
"\t train_sequence_log_likelihood: 8.2225522995\n",
"\t valid_sequence_log_likelihood: 9.29803943634\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 48\n",
"\t iterations_done: 10992\n",
"Log records from the iteration 10992:\n",
"\t test_sequence_log_likelihood: 8.89259910583\n",
"\t train_sequence_log_likelihood: 8.21332836151\n",
"\t valid_sequence_log_likelihood: 9.59388828278\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 49\n",
"\t iterations_done: 11221\n",
"Log records from the iteration 11221:\n",
"\t test_sequence_log_likelihood: 8.92092990875\n",
"\t train_sequence_log_likelihood: 8.19742298126\n",
"\t valid_sequence_log_likelihood: 8.89411067963\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 50\n",
"\t iterations_done: 11450\n",
"Log records from the iteration 11450:\n",
"\t test_sequence_log_likelihood: 9.16327667236\n",
"\t train_sequence_log_likelihood: 8.18489265442\n",
"\t valid_sequence_log_likelihood: 9.30712604523\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 51\n",
"\t iterations_done: 11679\n",
"Log records from the iteration 11679:\n",
"\t test_sequence_log_likelihood: 8.95643424988\n",
"\t train_sequence_log_likelihood: 8.18184280396\n",
"\t valid_sequence_log_likelihood: 9.39746856689\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 52\n",
"\t iterations_done: 11908\n",
"Log records from the iteration 11908:\n",
"\t test_sequence_log_likelihood: 10.0577373505\n",
"\t train_sequence_log_likelihood: 8.17080116272\n",
"\t valid_sequence_log_likelihood: 9.22853946686\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 53\n",
"\t iterations_done: 12137\n",
"Log records from the iteration 12137:\n",
"\t test_sequence_log_likelihood: 9.63022327423\n",
"\t train_sequence_log_likelihood: 8.16060161591\n",
"\t valid_sequence_log_likelihood: 9.14624881744\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 54\n",
"\t iterations_done: 12366\n",
"Log records from the iteration 12366:\n",
"\t test_sequence_log_likelihood: 9.64744853973\n",
"\t train_sequence_log_likelihood: 8.1499376297\n",
"\t valid_sequence_log_likelihood: 10.3511371613\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 55\n",
"\t iterations_done: 12595\n",
"Log records from the iteration 12595:\n",
"\t test_sequence_log_likelihood: 9.10130596161\n",
"\t train_sequence_log_likelihood: 8.1413564682\n",
"\t valid_sequence_log_likelihood: 8.93024253845\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 56\n",
"\t iterations_done: 12824\n",
"Log records from the iteration 12824:\n",
"\t test_sequence_log_likelihood: 9.97962474823\n",
"\t train_sequence_log_likelihood: 8.13224506378\n",
"\t valid_sequence_log_likelihood: 8.99156284332\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 57\n",
"\t iterations_done: 13053\n",
"Log records from the iteration 13053:\n",
"\t test_sequence_log_likelihood: 10.9663763046\n",
"\t train_sequence_log_likelihood: 8.11718654633\n",
"\t valid_sequence_log_likelihood: 9.51932144165\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 58\n",
"\t iterations_done: 13282\n",
"Log records from the iteration 13282:\n",
"\t test_sequence_log_likelihood: 9.07116127014\n",
"\t train_sequence_log_likelihood: 8.1139755249\n",
"\t valid_sequence_log_likelihood: 9.56406974792\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 59\n",
"\t iterations_done: 13511\n",
"Log records from the iteration 13511:\n",
"\t test_sequence_log_likelihood: 9.45077133179\n",
"\t train_sequence_log_likelihood: 8.11029720306\n",
"\t valid_sequence_log_likelihood: 9.18837738037\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 60\n",
"\t iterations_done: 13740\n",
"Log records from the iteration 13740:\n",
"\t test_sequence_log_likelihood: 11.1868638992\n",
"\t train_sequence_log_likelihood: 8.10033226013\n",
"\t valid_sequence_log_likelihood: 9.99776268005\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 61\n",
"\t iterations_done: 13969\n",
"Log records from the iteration 13969:\n",
"\t test_sequence_log_likelihood: 13.9327459335\n",
"\t train_sequence_log_likelihood: 8.0854101181\n",
"\t valid_sequence_log_likelihood: 9.2832069397\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 62\n",
"\t iterations_done: 14198\n",
"Log records from the iteration 14198:\n",
"\t test_sequence_log_likelihood: 8.97519397736\n",
"\t train_sequence_log_likelihood: 8.0908164978\n",
"\t valid_sequence_log_likelihood: 10.228266716\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 63\n",
"\t iterations_done: 14427\n",
"Log records from the iteration 14427:\n",
"\t test_sequence_log_likelihood: 8.87990951538\n",
"\t train_sequence_log_likelihood: 8.07586765289\n",
"\t valid_sequence_log_likelihood: 9.43871688843\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 64\n",
"\t iterations_done: 14656\n",
"Log records from the iteration 14656:\n",
"\t test_sequence_log_likelihood: 8.89872264862\n",
"\t train_sequence_log_likelihood: 8.0668554306\n",
"\t valid_sequence_log_likelihood: 9.22456932068\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 65\n",
"\t iterations_done: 14885\n",
"Log records from the iteration 14885:\n",
"\t test_sequence_log_likelihood: 11.3140945435\n",
"\t train_sequence_log_likelihood: 8.06011867523\n",
"\t valid_sequence_log_likelihood: 9.21197795868\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 66\n",
"\t iterations_done: 15114\n",
"Log records from the iteration 15114:\n",
"\t test_sequence_log_likelihood: 8.87504577637\n",
"\t train_sequence_log_likelihood: 8.05079746246\n",
"\t valid_sequence_log_likelihood: 9.62853050232\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 67\n",
"\t iterations_done: 15343\n",
"Log records from the iteration 15343:\n",
"\t test_sequence_log_likelihood: 9.07861995697\n",
"\t train_sequence_log_likelihood: 8.05015563965\n",
"\t valid_sequence_log_likelihood: 11.7880830765\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 68\n",
"\t iterations_done: 15572\n",
"Log records from the iteration 15572:\n",
"\t test_sequence_log_likelihood: 8.9037733078\n",
"\t train_sequence_log_likelihood: 8.03646564484\n",
"\t valid_sequence_log_likelihood: 9.08445167542\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 69\n",
"\t iterations_done: 15801\n",
"Log records from the iteration 15801:\n",
"\t test_sequence_log_likelihood: 8.95507335663\n",
"\t train_sequence_log_likelihood: 8.03246593475\n",
"\t valid_sequence_log_likelihood: 8.9407377243\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 70\n",
"\t iterations_done: 16030\n",
"Log records from the iteration 16030:\n",
"\t test_sequence_log_likelihood: 9.16425514221\n",
"\t train_sequence_log_likelihood: 8.02136039734\n",
"\t valid_sequence_log_likelihood: 9.68922138214\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 71\n",
"\t iterations_done: 16259\n",
"Log records from the iteration 16259:\n",
"\t test_sequence_log_likelihood: 9.11354923248\n",
"\t train_sequence_log_likelihood: 8.01672458649\n",
"\t valid_sequence_log_likelihood: 9.00119304657\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 72\n",
"\t iterations_done: 16488\n",
"Log records from the iteration 16488:\n",
"\t test_sequence_log_likelihood: 9.03979969025\n",
"\t train_sequence_log_likelihood: 8.02077674866\n",
"\t valid_sequence_log_likelihood: 10.2955055237\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 73\n",
"\t iterations_done: 16717\n",
"Log records from the iteration 16717:\n",
"\t test_sequence_log_likelihood: 9.49771022797\n",
"\t train_sequence_log_likelihood: 8.0038766861\n",
"\t valid_sequence_log_likelihood: 9.02913188934\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 74\n",
"\t iterations_done: 16946\n",
"Log records from the iteration 16946:\n",
"\t test_sequence_log_likelihood: 9.17886352539\n",
"\t train_sequence_log_likelihood: 8.01253032684\n",
"\t valid_sequence_log_likelihood: 9.02485847473\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 75\n",
"\t iterations_done: 17175\n",
"Log records from the iteration 17175:\n",
"\t test_sequence_log_likelihood: 12.9398078918\n",
"\t train_sequence_log_likelihood: 7.9994893074\n",
"\t valid_sequence_log_likelihood: 9.12105751038\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 76\n",
"\t iterations_done: 17404\n",
"Log records from the iteration 17404:\n",
"\t test_sequence_log_likelihood: 9.4165391922\n",
"\t train_sequence_log_likelihood: 7.99137020111\n",
"\t valid_sequence_log_likelihood: 10.2705745697\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 77\n",
"\t iterations_done: 17633\n",
"Log records from the iteration 17633:\n",
"\t test_sequence_log_likelihood: 9.43873119354\n",
"\t train_sequence_log_likelihood: 7.98357629776\n",
"\t valid_sequence_log_likelihood: 9.06366252899\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 78\n",
"\t iterations_done: 17862\n",
"Log records from the iteration 17862:\n",
"\t test_sequence_log_likelihood: 9.20733356476\n",
"\t train_sequence_log_likelihood: 7.97897148132\n",
"\t valid_sequence_log_likelihood: 9.71095943451\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 79\n",
"\t iterations_done: 18091\n",
"Log records from the iteration 18091:\n",
"\t test_sequence_log_likelihood: 9.46918678284\n",
"\t train_sequence_log_likelihood: 7.96783924103\n",
"\t valid_sequence_log_likelihood: 9.52183628082\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 80\n",
"\t iterations_done: 18320\n",
"Log records from the iteration 18320:\n",
"\t test_sequence_log_likelihood: 9.787109375\n",
"\t train_sequence_log_likelihood: 7.97162342072\n",
"\t valid_sequence_log_likelihood: 10.3529748917\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 81\n",
"\t iterations_done: 18549\n",
"Log records from the iteration 18549:\n",
"\t test_sequence_log_likelihood: 9.34245681763\n",
"\t train_sequence_log_likelihood: 7.97804689407\n",
"\t valid_sequence_log_likelihood: 8.81162166595\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 82\n",
"\t iterations_done: 18778\n",
"Log records from the iteration 18778:\n",
"\t test_sequence_log_likelihood: 9.17775344849\n",
"\t train_sequence_log_likelihood: 7.96550559998\n",
"\t valid_sequence_log_likelihood: 9.21496391296\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 83\n",
"\t iterations_done: 19007\n",
"Log records from the iteration 19007:\n",
"\t test_sequence_log_likelihood: 9.27416801453\n",
"\t train_sequence_log_likelihood: 7.9493932724\n",
"\t valid_sequence_log_likelihood: 9.18375873566\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 84\n",
"\t iterations_done: 19236\n",
"Log records from the iteration 19236:\n",
"\t test_sequence_log_likelihood: 9.51619148254\n",
"\t train_sequence_log_likelihood: 7.947889328\n",
"\t valid_sequence_log_likelihood: 10.1315689087\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 85\n",
"\t iterations_done: 19465\n",
"Log records from the iteration 19465:\n",
"\t test_sequence_log_likelihood: 9.62265586853\n",
"\t train_sequence_log_likelihood: 7.93665075302\n",
"\t valid_sequence_log_likelihood: 9.02186775208\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 86\n",
"\t iterations_done: 19694\n",
"Log records from the iteration 19694:\n",
"\t test_sequence_log_likelihood: 9.807056427\n",
"\t train_sequence_log_likelihood: 7.92619895935\n",
"\t valid_sequence_log_likelihood: 9.94027900696\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 87\n",
"\t iterations_done: 19923\n",
"Log records from the iteration 19923:\n",
"\t test_sequence_log_likelihood: 9.264128685\n",
"\t train_sequence_log_likelihood: 7.92955446243\n",
"\t valid_sequence_log_likelihood: 9.5747461319\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 88\n",
"\t iterations_done: 20152\n",
"Log records from the iteration 20152:\n",
"\t test_sequence_log_likelihood: 9.4467754364\n",
"\t train_sequence_log_likelihood: 7.9255361557\n",
"\t valid_sequence_log_likelihood: 8.89367389679\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 89\n",
"\t iterations_done: 20381\n",
"Log records from the iteration 20381:\n",
"\t test_sequence_log_likelihood: 9.97718429565\n",
"\t train_sequence_log_likelihood: 7.9424738884\n",
"\t valid_sequence_log_likelihood: 9.17107772827\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 90\n",
"\t iterations_done: 20610\n",
"Log records from the iteration 20610:\n",
"\t test_sequence_log_likelihood: 9.58899974823\n",
"\t train_sequence_log_likelihood: 7.91354703903\n",
"\t valid_sequence_log_likelihood: 9.60063648224\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 91\n",
"\t iterations_done: 20839\n",
"Log records from the iteration 20839:\n",
"\t test_sequence_log_likelihood: 9.30982303619\n",
"\t train_sequence_log_likelihood: 7.91529560089\n",
"\t valid_sequence_log_likelihood: 9.02134990692\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 92\n",
"\t iterations_done: 21068\n",
"Log records from the iteration 21068:\n",
"\t test_sequence_log_likelihood: 9.3317565918\n",
"\t train_sequence_log_likelihood: 7.90058851242\n",
"\t valid_sequence_log_likelihood: 9.54315662384\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 93\n",
"\t iterations_done: 21297\n",
"Log records from the iteration 21297:\n",
"\t test_sequence_log_likelihood: 10.9732942581\n",
"\t train_sequence_log_likelihood: 7.89270210266\n",
"\t valid_sequence_log_likelihood: 10.7303514481\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 94\n",
"\t iterations_done: 21526\n",
"Log records from the iteration 21526:\n",
"\t test_sequence_log_likelihood: 9.38461971283\n",
"\t train_sequence_log_likelihood: 7.89978981018\n",
"\t valid_sequence_log_likelihood: 9.57057571411\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 95\n",
"\t iterations_done: 21755\n",
"Log records from the iteration 21755:\n",
"\t test_sequence_log_likelihood: 9.06534767151\n",
"\t train_sequence_log_likelihood: 7.89829206467\n",
"\t valid_sequence_log_likelihood: 9.21898555756\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 96\n",
"\t iterations_done: 21984\n",
"Log records from the iteration 21984:\n",
"\t test_sequence_log_likelihood: 9.2264995575\n",
"\t train_sequence_log_likelihood: 7.88807916641\n",
"\t valid_sequence_log_likelihood: 9.5773191452\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 97\n",
"\t iterations_done: 22213\n",
"Log records from the iteration 22213:\n",
"\t test_sequence_log_likelihood: 9.37216091156\n",
"\t train_sequence_log_likelihood: 7.87892103195\n",
"\t valid_sequence_log_likelihood: 9.45323467255\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 98\n",
"\t iterations_done: 22442\n",
"Log records from the iteration 22442:\n",
"\t test_sequence_log_likelihood: 9.15624904633\n",
"\t train_sequence_log_likelihood: 7.88360548019\n",
"\t valid_sequence_log_likelihood: 9.50130176544\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 99\n",
"\t iterations_done: 22671\n",
"Log records from the iteration 22671:\n",
"\t test_sequence_log_likelihood: 9.59429073334\n",
"\t train_sequence_log_likelihood: 7.87264347076\n",
"\t valid_sequence_log_likelihood: 10.0189352036\n",
"\n",
"\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-------------------------------------------------------------------------------\n",
"AFTER ANOTHER EPOCH\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 100\n",
"\t iterations_done: 22900\n",
"Log records from the iteration 22900:\n",
"\t test_sequence_log_likelihood: 11.3405399323\n",
"\t train_sequence_log_likelihood: 7.86959314346\n",
"\t training_finish_requested: True\n",
"\t valid_sequence_log_likelihood: 9.01933002472\n",
"\n",
"\n",
"-------------------------------------------------------------------------------\n",
"TRAINING HAS BEEN FINISHED:\n",
"-------------------------------------------------------------------------------\n",
"Training status:\n",
"\t epochs_done: 100\n",
"\t iterations_done: 22900\n",
"Log records from the iteration 22900:\n",
"\t test_sequence_log_likelihood: 11.3405399323\n",
"\t train_sequence_log_likelihood: 7.86959314346\n",
"\t training_finish_requested: True\n",
"\t training_finished: True\n",
"\t valid_sequence_log_likelihood: 9.01933002472\n",
"\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"RNN.W.get_value()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 5,
"text": [
"array([ 7.64556369e-03, -1.12429112e-02, -1.37316471e-03,\n",
" 5.28146978e-03, -8.37879535e-03, 1.60080451e-03,\n",
" -6.71908446e-03, 7.13120541e-03, 1.30790770e-02,\n",
" -7.64275203e-04, -3.80641402e-04, 3.97207402e-03,\n",
" 1.06865028e-03, -7.41479266e-03, -4.67641838e-03,\n",
" -3.77409905e-03, -1.04616666e-02, -1.46204149e-02,\n",
" -7.31603568e-03, -1.98591920e-03, 1.69958454e-02,\n",
" -1.71224829e-02, 2.80601555e-04, 8.22969247e-03,\n",
" 3.71123594e-03, 1.78842414e-02, 4.98409243e-03,\n",
" 1.08513338e-02, -1.66491896e-03, 8.32113530e-03,\n",
" -2.48410180e-03, 6.15986995e-03, 2.60509383e-02,\n",
" -1.08450800e-02, 7.91752338e-03, 4.22274740e-03,\n",
" 7.78383110e-03, -2.88396212e-03, 7.90130626e-03,\n",
" 2.34810496e-03, 2.27363203e-02, -2.91154976e-03,\n",
" -7.98106641e-02, 1.03723891e-02, -1.15065612e-02,\n",
" -9.10019651e-02, 1.53547553e-02, -2.90602427e-02,\n",
" -1.31002292e-01, 5.33228219e-01, 9.18755770e-01,\n",
" 7.53949344e-01, 9.21748817e-01, -4.24741320e-02,\n",
" 5.61629772e-01, 4.91839826e-01, 2.85587072e-01,\n",
" 6.48680925e-01, 7.04001367e-01, -1.93320699e-02,\n",
" 6.71472669e-01, 5.40538192e-01, 5.88816941e-01,\n",
" 7.73667574e-01, 7.74141371e-01, -3.77491564e-02,\n",
" 5.24023652e-01, -2.02730931e-02, -1.70849562e-02,\n",
" -1.99103765e-02, 6.62021756e-01, 4.65835184e-01,\n",
" -2.67463829e-02, -1.98366735e-02, -2.49054544e-02,\n",
" 5.10907829e-01, -1.62777994e-02, -2.87311804e-02,\n",
" -1.74178295e-02, -2.42642853e-02, -1.97981037e-02,\n",
" 6.01405799e-01, -2.01502051e-02, -1.47034423e-02,\n",
" 2.54132211e-01, -1.61650628e-02, -2.90785469e-02,\n",
" 4.13660645e-01, 3.91079813e-01, -4.20999900e-02,\n",
" -2.36372985e-02, -3.88454534e-02, -2.72426810e-02,\n",
" 6.95665598e-01, -1.07875787e-01, 1.00057483e+00,\n",
" 8.04865733e-03, 7.15281488e-03, -8.43766145e-03,\n",
" 7.26915244e-03, -3.00741824e-03, -7.52018858e-03,\n",
" 4.70733969e-03, -1.72955580e-02, -1.32153148e-03,\n",
" 3.52924550e-03, 2.08454337e-02, -3.32558091e-04,\n",
" 1.90786570e-02, -1.26844952e-02, 3.94622423e-03,\n",
" -3.85024259e-03, -1.21951485e-02, -2.03337930e-02,\n",
" 2.73376293e-02, 3.38070584e-03, 6.06906321e-03,\n",
" -7.40647447e-05, -4.47588600e-03, 9.70642269e-03,\n",
" -8.42945185e-03, -3.76700377e-03, -1.79678074e-03,\n",
" -9.17243026e-03, 1.37365730e-02, 1.91276129e-02,\n",
" -3.63241881e-03, -2.12389398e-02, -5.94921084e-03,\n",
" 8.55297688e-03, -6.09513884e-03, 7.43929995e-03,\n",
" 9.74905677e-04, -9.98190884e-03, 3.60867009e-03,\n",
" 7.50483712e-04, 1.67002697e-02, 7.27292430e-03,\n",
" 1.43754140e-01, -1.57753881e-02, 2.08743922e-02,\n",
" 2.12055981e-01, -2.29693903e-03, 1.40979841e-01,\n",
" 5.54649346e-02, 1.15098670e-01, 6.32365525e-01,\n",
" 5.89845836e-01, 2.75168687e-01, -1.27270604e-02,\n",
" 2.38147572e-01, -3.66017483e-02, 1.36750519e-01,\n",
" -4.08056304e-02, 7.58528054e-01, 9.96785909e-02,\n",
" -3.73136774e-02, -2.60773413e-02, 3.24263453e-01,\n",
" 2.89264381e-01, 2.07199886e-01, 1.97208971e-01,\n",
" 3.59971911e-01, -2.56323237e-02, 6.10688776e-02,\n",
" 2.68180549e-01, 1.75925449e-01, -1.39204990e-02,\n",
" 4.77483243e-01, 5.46779437e-03, -9.36682057e-03,\n",
" 3.00864756e-01, 6.41954616e-02, -2.86199711e-02,\n",
" 3.22578475e-02, 9.88152623e-02, 1.02196567e-01,\n",
" -1.89771522e-02, 1.77106038e-01, -9.21930932e-03,\n",
" -5.77150583e-02, 1.82270959e-01, -1.35957524e-02,\n",
" -2.89089605e-02, -2.21555084e-02, -2.75857411e-02,\n",
" 3.80470276e-01, 1.64506301e-01, -1.73525065e-02,\n",
" 3.20210755e-01, 1.80151835e-01, 9.26088512e-01,\n",
" 3.88752553e-03, 1.08688939e-02, 2.09790152e-02,\n",
" 9.59823374e-03, 4.59615979e-03, 1.55307231e-02,\n",
" 5.10337250e-03, -3.32438038e-03, -8.16993881e-03,\n",
" -4.80911788e-03, -2.10660350e-04, -4.58650570e-03,\n",
" 5.75106940e-04, 6.73060911e-03, 4.57308721e-03,\n",
" -1.10745826e-03, -5.65432757e-03, 4.45055682e-03,\n",
" -4.31114994e-03, -1.17157516e-03, 6.10321108e-03,\n",
" 7.25740148e-03, 1.19127212e-02, 1.54198613e-02,\n",
" 6.19333424e-03, 5.96601143e-03, -9.47645307e-03,\n",
" 5.21731330e-03, 9.20767430e-03, 1.57177262e-02,\n",
" -7.15131813e-04, -8.92477762e-03, 1.85395067e-03,\n",
" 5.59865788e-04, -1.97884697e-03, 1.10737775e-02,\n",
" -1.24300048e-02, 1.12278713e-02, 4.66238987e-03,\n",
" -8.32298247e-04, 1.16304941e-02, -1.44333700e-02,\n",
" -8.33915919e-02, -1.26889087e-02, 1.60314096e-03,\n",
" 1.49270520e-01, 2.41177641e-02, 7.40745068e-02,\n",
" 9.00958255e-02, -4.08675931e-02, 3.70410383e-01,\n",
" 3.34154934e-01, -1.56389605e-02, 4.04900312e-02,\n",
" 6.52545616e-02, 2.93422043e-01, -4.83367406e-02,\n",
" 6.72618598e-02, 3.20060462e-01, 1.42934581e-03,\n",
" 7.38926306e-02, -1.50324237e-02, 2.80234963e-01,\n",
" 1.74677521e-01, -2.14967243e-02, -2.15783417e-02,\n",
" 8.74030963e-02, 4.41225320e-02, -3.17117228e-04,\n",
" 1.68189541e-01, -1.42331747e-02, 8.81632674e-04,\n",
" 1.12026125e-01, 1.76139623e-02, -2.36386172e-02,\n",
" -1.64772384e-02, 8.66944715e-02, 4.13726689e-03,\n",
" -1.89168137e-02, -1.99361630e-02, 2.14368179e-02,\n",
" -1.85260158e-02, 9.38636661e-02, -6.30055554e-04,\n",
" 8.44348446e-02, 3.49570625e-02, 3.12848240e-02,\n",
" -1.88625734e-02, 2.30024114e-01, 1.45516083e-01,\n",
" 2.19341576e-01, 1.44238085e-01, 2.33308915e-02,\n",
" -3.32897529e-02, -1.32263631e-01, 6.75918102e-01,\n",
" -1.10246539e-02, 8.78811162e-03, 6.66244479e-04,\n",
" 7.24292535e-04, -1.23528391e-02, -1.58281829e-02,\n",
" -5.97855821e-03, -8.15707073e-03, -2.84049683e-03,\n",
" -1.99169274e-02, -7.69431982e-03, -7.65804108e-03,\n",
" 5.32840053e-03, 1.06757544e-02, 7.41842249e-03,\n",
" -4.79329703e-03, -1.63526665e-02, -7.55768456e-03,\n",
" -1.18959881e-02, 1.01712774e-02, 1.99312270e-02,\n",
" 7.49486382e-04, -1.58620335e-03, -1.65117644e-02,\n",
" 1.18378410e-03, -1.00742169e-02, 4.04528202e-03,\n",
" -1.33197503e-02, 4.59323142e-04, 7.19577260e-03,\n",
" 1.19888205e-02, 1.21541033e-02, -7.05899030e-04,\n",
" -1.23232296e-02, 3.78156151e-03, -1.61414649e-02,\n",
" -1.26285423e-02, -1.40715409e-02, -1.77215750e-03,\n",
" 1.24527486e-02, -6.40264305e-04, -7.56389927e-03,\n",
" -1.16366185e-01, -2.93462025e-03, -3.43317837e-02,\n",
" -1.26975223e-01, -1.85003225e-02, -4.90184426e-02,\n",
" 1.36234596e-01, 2.95423090e-01, 3.49737823e-01,\n",
" 1.77149341e-01, 1.57342315e-01, -6.06790259e-02,\n",
" -4.72597294e-02, 2.27283835e-01, -1.03017939e-02,\n",
" 1.02393277e-01, 8.99254382e-02, 7.57260062e-03,\n",
" -5.89912124e-02, 3.39736119e-02, 9.58469138e-02,\n",
" 1.06965221e-01, -3.50846052e-02, 2.97027566e-02,\n",
" 4.88856882e-02, -2.38727760e-02, -8.89885984e-03,\n",
" 1.16341978e-01, -1.43161239e-02, -1.49740395e-03,\n",
" 1.35219023e-01, 1.02456003e-01, 3.58139575e-02,\n",
" 2.59768873e-01, 9.49801952e-02, 4.20345739e-03,\n",
" 6.45914972e-02, -3.85954627e-03, 3.53821218e-02,\n",
" 4.37274650e-02, -3.80760841e-02, -1.90453744e-03,\n",
" 1.93699285e-01, 5.20268977e-02, 6.19367771e-02,\n",
" 3.50756943e-02, 7.97706619e-02, 2.05152676e-01,\n",
" 2.40176186e-01, 1.75884306e-01, -1.45378076e-02,\n",
" 1.86869681e-01, -1.63428336e-01, 4.52507257e-01], dtype=float32)"
]
}
],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
imprm/nummet_I | ComputerArithmeticExamples.ipynb | 1 | 14275 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"ESE - Numerical Methods I: Basics of Computer Arithmetic - Examples"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Integers"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. Express the number `140` as a binary (base 2) sequence (manually)! How many bits do you need?\n",
"2. Express the number `16` as a binary (base 2) sequence (use `'{0:b}'.format(16)`)! How many bits do you need?\n",
"3. Add `140` and `16` in binary (manually)!\n",
"4. Using 8 bits (no sign bit) to represent `140`, what would be the largest number you can add without causing overflow?\n",
"4. Subtract `16` from `120` in binary!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Express the number `140` as a binary (base 2) sequence! How many bits do you need?**\n",
"\n",
"as a <a href=\"http://nbviewer.ipython.org/github/imprm/nummet_I/blob/master/ComputerArithmetic.ipynb\">reminder</a> (8 bit):\n",
"\n",
"<table>\n",
"<tr>\n",
"<th>$2^7$</th>\n",
"<th>$2^6$</th>\n",
"<th>$2^5$</th>\n",
"<th>$2^4$</th>\n",
"<th>$2^3$</th>\n",
"<th>$2^2$</th>\n",
"<th>$2^1$</th>\n",
"<th>$2^0$</th>\n",
"</tr>\n",
"<tr>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"</table>\n",
"\n",
"Let's see if 8 bit (largest factor = $2^7$) is enough:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 140/2**8"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0\n"
]
}
],
"prompt_number": 17
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"so we know that an 8 bit representation suffices. Now let's split `140` in base two components:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 140/2**7\n",
"print 140%2**7"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"1\n",
"12\n"
]
}
],
"prompt_number": 18
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 12/2**6\n",
"print 12%2**6"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0\n",
"12\n"
]
}
],
"prompt_number": 19
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 12/2**5\n",
"print 12%2**5"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0\n",
"12\n"
]
}
],
"prompt_number": 20
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 12/2**4\n",
"print 12%2**4"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0\n",
"12\n"
]
}
],
"prompt_number": 21
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 12/2**3\n",
"print 12%2**3"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"1\n",
"4\n"
]
}
],
"prompt_number": 22
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 4/2**2\n",
"print 4%2**2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"1\n",
"0\n"
]
}
],
"prompt_number": 23
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"so that our result is:\n",
"\n",
"<table>\n",
"<tr>\n",
"<th>$2^7$</th>\n",
"<th>$2^6$</th>\n",
"<th>$2^5$</th>\n",
"<th>$2^4$</th>\n",
"<th>$2^3$</th>\n",
"<th>$2^2$</th>\n",
"<th>$2^1$</th>\n",
"<th>$2^0$</th>\n",
"</tr>\n",
"<tr>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Express the number `16` as a binary (base 2) sequence! How many bits do you need?**\n",
"\n",
"Python has a built-in formatter for this purpose:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# meaning: take the 0th value from within the parenthesis and format it as 'b', which stands for binary\n",
"'{0:b}'.format(16)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 24,
"text": [
"'10000'"
]
}
],
"prompt_number": 24
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Add `140` and `16` in binary!**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<table>\n",
"<tr>\n",
"<th>$1$</th>\n",
"<th>$0$</th>\n",
"<th>$0$</th>\n",
"<th>$0$</th>\n",
"<th>$1$</th>\n",
"<th>$1$</th>\n",
"<th>$0$</th>\n",
"<th>$0$</th>\n",
"</tr>\n",
"<tr>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"<tr>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"</table>\n",
"\n",
"so that"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 1*2**7 + 0*2**6 + 0*2**5 + 1*2**4 + 1*2**3 + 1*2**2 + 0*2**1 + 0*2**0\n",
"# and to check\n",
"\"{0:b}\".format(156)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"156\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 25,
"text": [
"'10011100'"
]
}
],
"prompt_number": 25
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Using 8 bits (no sign bit) to represent `140`, what would be the largest number you can add without causing overflow?**\n",
"\n",
"we can check that manually"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 1*2**7 + 1*2**6 + 1*2**5 + 1*2**4 + 1*2**3 + 1*2**2 + 1*2**1 + 1*2**0"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"255\n"
]
}
],
"prompt_number": 26
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"or <a href=\"http://docs.scipy.org/doc/numpy/user/basics.types.html\">here</a> under `uint8`, for unsigned integers. The largest number we can add is therefore `155` to yield:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"\"{0:b}\".format(255)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 27,
"text": [
"'11111111'"
]
}
],
"prompt_number": 27
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Subtract 16 from 120 in binary!**\n",
"\n",
"We know that"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'{0:b}'.format(120)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 28,
"text": [
"'1111000'"
]
}
],
"prompt_number": 28
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'{0:b}'.format(16)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 29,
"text": [
"'10000'"
]
}
],
"prompt_number": 29
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Subtraction is implemented as assition of the negative number; to get the negativ representation of an integer we invert all bits and add `1`:\n",
"\n",
"```\n",
"16 = 00010000\n",
"\n",
"-16 = 11101111 + 00000001 = 11110000\n",
"```\n",
"\n",
"<table>\n",
"<tr>\n",
"<th>$0$</th>\n",
"<th>$1$</th>\n",
"<th>$1$</th>\n",
"<th>$1$</th>\n",
"<th>$1$</th>\n",
"<th>$0$</th>\n",
"<th>$0$</th>\n",
"<th>$0$</th>\n",
"</tr>\n",
"<tr>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"<tr>\n",
"<td>$0$</td>\n",
"<td>$1$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$1$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"<td>$0$</td>\n",
"</tr>\n",
"</table>\n",
"\n",
"\n",
"which we can check (since we now have a sign bit the maximum power reduces from 7 to 6):"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 1*2**6 + 1*2**5 + 0*2**4 + 1*2**3 + 0*2**2 + 0*2**1 + 0*2**0"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"104\n"
]
}
],
"prompt_number": 30
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Floating Points"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src=\"files/img/float_to_binary.png\" width=\"700\">\n",
"\n",
"1. <a href=\"http://www.madirish.net/240\">Convert</a> the number `75.75` to binary (single-precision)!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The integer part is straightforward:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'{0:b}'.format(75)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 1,
"text": [
"'1001011'"
]
}
],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The fraction is a sum of $2^{-1} + 2^{-2} + 2^{-3} + 2^{-4} + 2^{-5} $ so for `0.75` we find `11` so that $2^{-1} + 2^{-2} = 0.75 = 0.5 + 0.25$\n",
"\n",
"so that our number in binary becomes\n",
"\n",
"`1001011.11`\n",
"\n",
"we move the floating point up **six** places.\n",
"\n",
"`1.00101111`\n",
"\n",
"So we find our exponent as"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'{0:b}'.format(6+127)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 2,
"text": [
"'10000101'"
]
}
],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and our fraction as (only the part after the leading `1`): \n",
"\n",
"`00101111`\n",
"\n",
"to yield, with `0` as sign bit for a positive number\n",
"\n",
"`0 10000101 00101111000000000000000`"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
atulsingh0/MachineLearning | python_DC/ST_Python_02a.ipynb | 1 | 355141 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Statistical Thinking in Python (Part 2)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# import\n",
"import pandas as pd\n",
"import numpy as np\n",
"import seaborn as sns\n",
"from sklearn.datasets import load_iris\n",
"import matplotlib.pyplot as plt\n",
"\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"nohitter_times = np.array([ 843, 1613, 1101, 215, 684, 814, 278, 324, 161, 219, 545,\n",
" 715, 966, 624, 29, 450, 107, 20, 91, 1325, 124, 1468,\n",
" 104, 1309, 429, 62, 1878, 1104, 123, 251, 93, 188, 983,\n",
" 166, 96, 702, 23, 524, 26, 299, 59, 39, 12, 2,\n",
" 308, 1114, 813, 887, 645, 2088, 42, 2090, 11, 886, 1665,\n",
" 1084, 2900, 2432, 750, 4021, 1070, 1765, 1322, 26, 548, 1525,\n",
" 77, 2181, 2752, 127, 2147, 211, 41, 1575, 151, 479, 697,\n",
" 557, 2267, 542, 392, 73, 603, 233, 255, 528, 397, 1529,\n",
" 1023, 1194, 462, 583, 37, 943, 996, 480, 1497, 717, 224,\n",
" 219, 1531, 498, 44, 288, 267, 600, 52, 269, 1086, 386,\n",
" 176, 2199, 216, 54, 675, 1243, 463, 650, 171, 327, 110,\n",
" 774, 509, 8, 197, 136, 12, 1124, 64, 380, 811, 232,\n",
" 192, 731, 715, 226, 605, 539, 1491, 323, 240, 179, 702,\n",
" 156, 82, 1397, 354, 778, 603, 1001, 385, 986, 203, 149,\n",
" 576, 445, 180, 1403, 252, 675, 1351, 2983, 1568, 45, 899,\n",
" 3260, 1025, 31, 100, 2055, 4043, 79, 238, 3931, 2351, 595,\n",
" 110, 215, 0, 563, 206, 660, 242, 577, 179, 157, 192,\n",
" 192, 1848, 792, 1693, 55, 388, 225, 1134, 1172, 1555, 31,\n",
" 1582, 1044, 378, 1687, 2915, 280, 765, 2819, 511, 1521, 745,\n",
" 2491, 580, 2072, 6450, 578, 745, 1075, 1103, 1549, 1520, 138,\n",
" 1202, 296, 277, 351, 391, 950, 459, 62, 1056, 1128, 139,\n",
" 420, 87, 71, 814, 603, 1349, 162, 1027, 783, 326, 101,\n",
" 876, 381, 905, 156, 419, 239, 119, 129, 467])"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAj0AAAF9CAYAAADvIdnwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3Xm4XWV99//3GcgIgQhKgkQUrd+qRQSVQQZxKopa+aEi\n6IMoFid4kII1j61Kq7Uoo0orVLFKLFYcSxEfqTODiTIIyiP9amUIQ4wEAonkhHCG3x/32rjZnJyB\nnGHvs96v68qVs9d9773u79472Z9zr3ut3TU0NIQkSdJM1z3dA5AkSZoKhh5JklQLhh5JklQLhh5J\nklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLvdM9AICImA18GjgM2ACcmZlnbabvHsC5\nwG7AjcC7MvO6pvYjgY8Ai4HLgGMz855hHucy4MLMXNa0LYBPAfsAa4DzM/PUCSlSkiRNq3aZ6TkD\n2BM4CHg3cEpEHNbaKSLmAZcCP676LwcujYi5VftewPnAKcDewELgCy2P0RUR5wAvbdk+F/g2cDvw\nPOA44MSIeNdEFSlJkqbPtIeeKsi8DTghM2/IzIuB04Djh+l+BLAhM5dmcSKwHnh91X4ccFFmXpiZ\nNwJHAYdExC7VvnYCvg+8Criv5bEPpISkd2bmbzLzO8DZwBsnsl5JkjQ9pj30ALtTDrMtb9p2JWWm\nptXeVVuzq4B9q5/3AS5vNGTmHcDKajuU2aGVwHOBdS2P83Pg0Mzsb9m+7ZiqkCRJba0d1vQsBta0\nhI3VwJyI2L5lPc5iyjoeWvo+q6n9rmHadwbIzG8B3wIoy3f+KDN/D/y+cTsi5gDHAhePvyRJktRu\n2mGmZx7wYMu2xu3ZY+w7e4ztYxIRXcAFwNbAx8ZzX0mS1J7aYaZnI48OJY3bG8bYd8MY20cVET3A\nMuAQ4KXVDNCYDA0NDXV1dY21uyRJ+qNJ/wBth9BzJ7BDRHRn5mC1bRHQl5mti43vrNqaLQJWjbF9\nRBHRC3yFcmbXKzLzp2Mroejq6mLduj4GBgZH79zmenq6WbBgrvW0oZlUC1hPO5tJtYD1tLNGLZOt\nHULP9cBDlMXGP6m2HQBcPUzfFcDSlm37Ua7L02jfnzJTQ0QsoaznWTHGsXwWeAlwcGYuH63zcAYG\nBunv7+w3XzPraV8zqRawnnY2k2oB66mzaQ89mdkXEcuA8yLiGEpIORk4GiAidgTuz8yNwNeAUyPi\nbOAzwDsp63i+Wj3cucAPI2IFcA3wCeCSzLxttHFExMuqfb4duLnaL8BAZq6ZmGolSdJ0aYeFzAAn\nAdcCPwDOAT5YXa8HyqGpwwEycz3lGjsHUkLNXpTDUH1V+wrgHZSLE14J3AMcs5l9DrXcPqza9i+U\nM8Aaf3625eVJkqTp1jU01PrZry0wtHbtAzNimrG3t5uFC+djPe1nJtUC1tPOZlItYD3trKpl0hcy\nt8tMjyRJ0qQy9EiSpFqY9oXMM8m1/72aNfc+wODA5g8Zbrv1LP5k5+2mcFSSJAkMPRPqlrvW8bw/\n2Z7+EULP8ht/Z+iRJGkaGHom0NxZPWy79ewRF5Rt1esRRUmSpoOfwJIkqRYMPZIkqRYMPZIkqRYM\nPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIk\nqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYM\nPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIk\nqRYMPZIkqRYMPZIkqRYMPZIkqRZ6p3sAABExG/g0cBiwATgzM8/aTN89gHOB3YAbgXdl5nVN7UcC\nHwEWA5cBx2bmPcM8zmXAhZm5rGnb44DPAi8D7gY+lJkXTkiRkiRpWrXLTM8ZwJ7AQcC7gVMi4rDW\nThExD7gU+HHVfzlwaUTMrdr3As4HTgH2BhYCX2h5jK6IOAd46TDjuADYprrvR4HzI+J5W16eJEma\nbtM+01MFmbcBB2fmDcANEXEacDzwjZbuRwAbMnNpdfvEiDgEeD2wDDgOuKgxOxMRRwG3RcQumXlb\nROwE/BvwFOC+lnHsCrwS2CUzbwduioh9KSHsmAkvXJIkTal2mOnZnRK+ljdtu5Iy29Jq76qt2VXA\nvtXP+wCXNxoy8w5gZbUdyuzQSuC5wLphHntlFXiax7EvkiSp47VD6FkMrMnM/qZtq4E5EbH9MH3v\natm2Gth5LO2Z+a3MfEtm3ruZcYz02JIkqYNN++EtYB7wYMu2xu3ZY+w7e4ztj2UcY7nvw3p6Rs6R\nPT1d9Pa2Q9YcWaOO0erpFDOpnplUC1hPO5tJtYD1tLOpqqEdQs9GHh0sGrc3jLHvhjG2P5ZxjOW+\nD1uwYO6I7fPmzmLhwvnjechpNVo9nWYm1TOTagHraWczqRawnjprh9BzJ7BDRHRn5mC1bRHQl5n3\nDdN3Ucu2RcCqMbaPNo7Het+HrVvXx8DA4GbbN/RtYu3aB8bzkNOip6ebBQvmjlpPp5hJ9cykWsB6\n2tlMqgWsp501apls7RB6rgceoiw2/km17QDg6mH6rgCWtmzbj3Jdnkb7/pQzuYiIJZQ1OSvGMI4V\nwC4RsVNmNtb27D/G+z5sYGCQ/v7Nv/kGBoZGbG83o9XTaWZSPTOpFrCedjaTagHrqbNpDz2Z2RcR\ny4DzIuIYSkg5GTgaICJ2BO7PzI3A14BTI+Js4DPAOylrcb5aPdy5wA8jYgVwDfAJ4JLMvG0M47il\numDhv0XEe4C9gCOBAyeuWkmSNF3aZfXTScC1wA+Ac4APZubFVdsq4HCAzFwPvIoSRK6hBJNXZGZf\n1b4CeAfl4oRXAvew+WvsDA2z7c2UU9lXAO8H3pqZ125pcZIkafpN+0wPlNke4K3Vn9a27pbb11Cu\ns7O5x1pGdXhrlH3uOsy2NcChYxiyJEnqMO0y0yNJkjSpDD2SJKkWDD2SJKkWDD2SJKkWDD2SJKkW\nDD2SJKkWDD2SJKkWDD2SJKkWDD2SJKkWDD2SJKkWDD2SJKkW2uK7t+pkU/8Aq+55YMQ+3d1d7Lhw\n3hSNSJKkejD0TLHnPG0H1q5/cMQ+N/zPPRz+4qfS0+1EnCRJE8XQM8UWbz+fxdvPH7HP79f2TdFo\nJEmqD6cSJElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElS\nLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6\nJElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLRh6JElSLfRO9wAAImI28GngMGADcGZm\nnrWZvnsA5wK7ATcC78rM65rajwQ+AiwGLgOOzcx7mto/BhxDCXyfy8ylTW3PAv4ZeC5wB/D3mfnl\nCSxVkiRNk3aZ6TkD2BM4CHg3cEpEHNbaKSLmAZcCP676LwcujYi5VftewPnAKcDewELgC033Pxk4\nAngN8FrgTRFxUtU2C7gEuAZ4NnAacEFE7Dnh1UqSpCk37aGnCjJvA07IzBsy82JK4Dh+mO5HABsy\nc2kWJwLrgddX7ccBF2XmhZl5I3AUcEhE7FK1nwB8MDOXZ+aPgaVN+3kmsAvwocy8JTM/D/ySEsQk\nSVKHm/bQA+xOOcy2vGnblZSZmlZ7V23NrgL2rX7eB7i80ZCZdwArgX0iYjGwBLiiZT+7RMSOwL3V\ntr+MiK6I2BcI4DokSVLHa4fQsxhYk5n9TdtWA3MiYvth+t7Vsm01sPMY2hcDQy3tq4EuYOfMXAn8\nLXA6sIkSiE7LzB89hpokSVKbaYfQMw94sGVb4/bsMfadPYb2eQCZuWm4/UREL/CnlEXSzwdOAv5P\nRBw45kokSVLbaoeztzby6HDTuL1hjH03jKF9I5QFy03Bp3k/bwaem5m7Vduur87mWkrTIbPR9PRs\neY7s7u6it7ebnu7py6SNOiainnYwk+qZSbWA9bSzmVQLWE87m6oa2iH03AnsEBHdmTlYbVsE9GXm\nfcP0XdSybRGwagztd1IOZS2irPNptA1V7c+lLFxu9nPgBeMpZsGCuePpPqx582ezcLv5bfFGnoh6\n2slMqmcm1QLW085mUi1gPXXWDqHneuAhyiLkn1TbDgCuHqbvCsrMS7P9KNflabTvDywDiIgllPU8\nyzNzVUSsrNq/1LSflZm5OiLuqh6r2TOAW8ZTzLp1fQwMDI7ecQQbHniQtfc9MO0zPQsWzJ2QetrB\nTKpnJtUC1tPOZlItYD3trFHLZJv20JOZfRGxDDgvIo6hhJSTgaMBqjOr7s/MjcDXgFMj4mzgM8A7\nKWt1vlo93LnADyNiBeV6O58ALqkWKTfaPx4RjVmfUykLlwEupKzhORX4LCUAvY1yTZ8xGxgYpL9/\ny958g4ND9PcPMjT9Ez0TUk87mUn1zKRawHra2UyqBaynztrgYxUoi4avBX4AnEO5ls7FVdsq4HCA\nzFwPvAo4kBJq9gJekZl9VfsK4B2UixNeCdxDufpyw+nARcA3qr8vyMxPVve9FXhZ9dg/B94HHJOZ\n35uUiiVJ0pTqGhoamu4xzBiXXnnz0AueteMWJ+4f/fxODth98bQe3urt7WbhwvmsXfvAjPgNYibV\nM5NqAetpZzOpFrCedlbV0jXZ+2mXmR5JkqRJZeiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1\nYOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm1YOiRJEm10DvdA9Cjbb/t\nHH543Z10dXVtts+m/gGe/dQdeOIO86dwZJIkdS5DTxvabdft2W3X7Ufss/reDdx9f5+hR5KkMfLw\nliRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJ\nqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqgVDjyRJqoUx\nh56I+EpELJjMwUiSJE2W8cz0vBaY07whIn4ZEUsmdkiSJEkTbzyhp2uYbU8GtpqYoUiSJE0e1/RI\nkqRaMPRIkqRa6B1H36Hqz3Dbt0hEzAY+DRwGbADOzMyzNtN3D+BcYDfgRuBdmXldU/uRwEeAxcBl\nwLGZeU9T+8eAYyiB73OZubSpbbtqHK8G1gKnZ+Y5W1qfJEmafuMJPV3ANyNiU9O2ucCXIqKvuWNm\nvnic4zgD2BM4iLJOaFlE3JqZ32juFBHzgEuBLwJHA+8CLo2IXTOzLyL2As4H3g7cAJwDfIESYoiI\nk4EjgNcAs4ALI2J1U8D6d2ABsBfwTOCLEfHfmfndcdYjSZLazHhCzwXDbPvilg6gCjJvAw7OzBuA\nGyLiNOB44Bst3Y8ANjTNzpwYEYcArweWAccBF2XmhdVjHwXcFhG7ZOZtwAnABzJzedW+lDIrdFZE\nPBt4CfAnVd+bIuKFwH6AoUeSpA435tCTmW+dpDHsXo1jedO2K4G/Gabv3lVbs6uAfSmhZx/g1EZD\nZt4RESuBfaoZqiXAFS372SUidgReCNxQBZ7G/U94rEVJkqT2Mp6ZnodFxFbAnwDbAvcBv87Mgcc4\nhsXAmszsb9q2GpgTEds3r8ep+t7Ycv/VwLOa2u8apn3nqm2opX015bDdzsCuwC3VIbDjgI3AJzLz\nM4+xLkmS1EbGFXoiYmfgHykLjuc2NT0QEV8BPpiZq8Y5hnnAgy3bGrdnj7Hv7DG0zwPIzE0tbY39\nbA28jPKcvA54NvDPEXF3Zn5zrMX09EzNCXE9vd30dHfT2zs5+2vUMVX1TLaZVM9MqgWsp53NpFrA\netrZVNUw5tATEbtQDkH1A2cCv6TM8mwLPA84Cnh5ROyVma2zLSPZyKPDTeP2hjH23TCG9o1VHbOa\ngk/zfvopZ3S9MTM3AtdFxO7AO4Axh54FC+aO3mkC9PUP0dc/xMKF8yd1P1NVz1SZSfXMpFrAetrZ\nTKoFrKfOxjPT8w/AbZQFx+ta2r4eEf9IObPqr4G/Gsfj3gnsEBHdmTlYbVsE9GXmfcP0XdSybRGw\nagztd1IOZS0CVja1DVXtq4A7qsDTkMCfj6MW1q3rY2BgcPSOW+j+dX38Yf1G1q59YFIev6enmwUL\n5k5ZPZNtJtUzk2oB62lnM6kWsJ521qhlso0n9LwEeNMwgQeAzFwfEf8AfIbxhZ7rgYcoi5B/Um07\nALh6mL4rgKUt2/ajnIHVaN+fsqiZ6nvBdgaWZ+aqalHz/sCXmvazMjNXR8QKYGlEbJOZ66v2ZwK3\njqMWBgYG6e+f/DffQP8gA4OTv6+pqmeqzKR6ZlItYD3tbCbVAtZTZ+MJPTsAvx2lz02UBcNjVl1f\nZxlwXkQcQwkpJ1Ouw0N1ZtX91QzM14BTI+JsSrh6J2WtzlerhzsX+GEVYK4BPgFckpkrm9o/HhGN\nWZ9TgdOrtu9RZnYuiIj3A8+hXMTwDeOpR5IktafxrBzqpVoXM4JNPLYzwk4CrgV+QLmg4Acz8+Kq\nbRVwOJTZJOBVwIGUULMX8IrM7KvaV1DW4JxCOR39HkpwaTgduIhy/Z+LgAsy85PVfQeBV1Kek2uB\njwN/lZmXPoZ6JElSmxlvQNnir5wYThVa3lr9aW3rbrl9DfDcER5rGdXhrWHaBoH3Vn+Ga18FHDrm\ngU+jri7IlfexYWP/iP12fvzW7LTD5C52liSpE4w39Hyq9SsnWriEfIo8fru5/Pnzl4zab8WvVht6\nJElifKHnch59ZtTm+mmSdXV1sc28WaP26+7qmoLRSJLU/sbzNRQHVWdDHUq5qN+3M/OOSRuZJEnS\nBBrPxQkPAP4v1ZWNgT9ExOsy878mZWSSJEkTaDxnb30E+D7wRMphru8AZ03GoCRJkibaeELPHsD7\nM3NVZv6ecgHCZ0TENpMzNEmSpIkzntCzNeW6NwBk5p2U6/I8bqIHJUmSNNHGE3q6ePR1evqBnokb\njiRJ0uTo/O+jlyRJGoPxXpzw5Iho/lrvrYATIuLe5k6Z+eEtHpkkSdIEGk/oWUn1HVhNVgGvadk2\nBBh6JElSWxnPxQmfPInjkCRJmlSu6ZEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg\n6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEkSbVg6JEk\nSbVg6JEkSbXQO90D0OTa1D/A+g2bRuzT29PN3Nm+FSRJM5ufdDPczo/fmptuWztin1t/t57DX/S0\nKRqRJEnTw9Azw+226/aj9lm/4aEpGIkkSdPLNT2SJKkWDD2SJKkWDD2SJKkWDD2SJKkWDD2SJKkW\nDD2SJKkWDD2SJKkWDD2SJKkW2uLihBExG/g0cBiwATgzM8/aTN89gHOB3YAbgXdl5nVN7UcCHwEW\nA5cBx2bmPU3tHwOOoQS+z2Xm0mH20QNcC3wjMz88IUVKkqRp1S4zPWcAewIHAe8GTomIw1o7RcQ8\n4FLgx1X/5cClETG3at8LOB84BdgbWAh8oen+JwNHAK8BXgu8KSJOGmY8f00JVZIkaYaY9tBTBZm3\nASdk5g2ZeTFwGnD8MN2PADZk5tIsTgTWA6+v2o8DLsrMCzPzRuAo4JCI2KVqPwH4YGYuz8wfA0tb\n9xMRTwP+N/Cria1UkiRNp2kPPcDulMNsy5u2XUmZqWm1d9XW7Cpg3+rnfYDLGw2ZeQewEtgnIhYD\nS4ArWvazS0Ts2LTtPMpM0ZpxVyJJktpWO4SexcCazOxv2rYamBMRrd+WuRi4q2XbamDnMbQvBoZa\n2lcDXY37R8RbgdmZef5jK0WSJLWrdljIPA94sGVb4/bsMfadPYb2eQCZuWm4/UTE44F/BF48nsG3\n6ulphxw5Pj09XfT2drds637E351uJtUzk2oB62lnM6kWsJ52NlU1tEPo2cijw03j9oYx9t0whvaN\nABExqyn4zKbM/mwAPgX8a2be9BhqeNiCBXO35O7TYt7cWSxcOH/Ytk6sZyQzqZ6ZVAtYTzubSbWA\n9dRZO4SeO4EdIqI7MwerbYuAvsy8b5i+i1q2LQJWjaH9TsqhrEWUdT409V0FvAHYEBEnVNvmAi+I\niNdn5pjP5Fq3ro+BgcHRO7aRDX2bWLv2gUds6+npZsGCuR1Zz3BmUj0zqRawnnY2k2oB62lnjVom\nWzuEnuuBhyiLkH9SbTsAuHqYvisoZ1w1249yXZ5G+/7AMoCIWEJZr7M8M1dFxMqq/UtN+1mZmaur\ns7aafal6vDPHU8zAwCD9/Z315hsYGNrsmDuxnpHMpHpmUi1gPe1sJtUC1lNn0x56MrMvIpYB50XE\nMZSQcjJwNEB1ZtX9mbkR+BpwakScDXwGeCdlrc5Xq4c7F/hhRKwArgE+AVySmSub2j8eEY1Zn1OB\n06tx3Nw8rojoA+7NzNsnp3JJkjSV2mX100mUKyD/ADiHci2di6u2VcDhAJm5HngVcCAl1OwFvCIz\n+6r2FcA7KKecXwncQ7n6csPpwEXAN6q/L8jMT25mTEMTVZwkSZp+0z7TA2W2B3hr9ae1rbvl9jXA\nc0d4rGVUh7eGaRsE3lv9GW1MW3QWlyRJai/tMtMjSZI0qQw9kiSpFgw9kiSpFtpiTY+m18ZN/dx0\n672P2NbT083Wazbwh/UbGRgYpLu7i6cv2Y6urq5pGqUkSVvG0CMO2H0n/rDhoUds6+ntZtsFc+hh\niIH+QX7+m7vZZdE2zJnlW0aS1Jn8BBML5s1iwbxZj9jW29vNwoXz2XpWN/39g9yyat00jU6SpInh\nmh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5J\nklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLhh5JklQLvdM9AHWGHR83jyt+\nsYrurq7N9tn00ABPf9J2PHWnbadwZJIkjY2hR2PytCduy9OeOHKYuXfdRm5bvX6KRiRJ0vh4eEuS\nJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWCoUeSJNWC\noUeSJNWCoUeSJNWCoUeSJNWC37KuCdPd3cUvb76Xe9c9OGK/Jy/ahqeO8o3tkiRNtLYIPRExG/g0\ncBiwATgzM8/aTN89gHOB3YAbgXdl5nVN7UcCHwEWA5cBx2bmPU3tHwOOocxyfS4zlza1BfApYB9g\nDXB+Zp46gaXOaNttPZs3Hxyj9vv+tXcYeiRJU65dDm+dAewJHAS8GzglIg5r7RQR84BLgR9X/ZcD\nl0bE3Kp9L+B84BRgb2Ah8IWm+58MHAG8Bngt8KaIOKlqmwt8G7gdeB5wHHBiRLxrwquVJElTbtpD\nTxVk3gackJk3ZObFwGnA8cN0PwLYkJlLszgRWA+8vmo/DrgoMy/MzBuBo4BDImKXqv0E4IOZuTwz\nfwwsbdrPgZSQ9M7M/E1mfgc4G3jjhBctSZKm3LSHHmB3ymG25U3brqTM1LTau2prdhWwb/XzPsDl\njYbMvANYCewTEYuBJcAVLfvZJSJ2BK4HDs3M/pbH9ziMJEkzQDuEnsXAmpawsRqYExHbD9P3rpZt\nq4Gdx9C+GBhqaV8NdAE7Z+bqzHw4MEXEHOBY4HvjrkiSJLWddgg984DW030at2ePse/sMbTPA8jM\nTaPtJyK6gAuArYGPjVqBJElqe+1w9tZGHh1uGrc3jLHvhjG0bwSIiFlNwedR+4mIHmAZcAjw0sz8\n/ZgrAXp62iFHbrlGHZNRT09PF729U/s8TWY9U20m1QLW085mUi1gPe1sqmpoh9BzJ7BDRHRn5mC1\nbRHQl5n3DdN3Ucu2RcCqMbTfSTmUtYiyzqfRNtS4f0T0Al8BXgq8IjN/Ot5iFiyYO967tLXJqGfe\n3FksXDh/wh93LGbS6zOTagHraWczqRawnjprh9BzPfAQZRHyT6ptBwBXD9N3BeWMq2b7Ua7L02jf\nnzJTQ0QsoaznWZ6ZqyJiZdX+pab9rMzM1dXtzwIvAQ7OzOaF1WO2bl0fAwODo3dscz093SxYMHdS\n6tnQt4m1ax+Y0McczWTWM9VmUi1gPe1sJtUC1tPOGrVMtmkPPZnZFxHLgPMi4hhKSDkZOBqgOrPq\n/szcCHwNODUizgY+A7yTslbnq9XDnQv8MCJWANcAnwAuycyVTe0fj4jGrM+pwOnVfl5W7fPtwM3V\nfgEGMnPNWOsZGBikv7+z33zNJqOegYGhaXuOZtLrM5NqAetpZzOpFrCeOmuXA4EnAdcCPwDOoVxL\n5+KqbRVwOEBmrgdeRbmmzjXAXpTDUH1V+wrgHZSLE14J3EO5+nLD6cBFwDeqvy/IzE9WbYdRDnX9\nC+UMr8afn018uZIkaap1DQ0NTfcYZoxLr7x56AXP2nFGJO7e3m4WLpzP2rUPTHg9/3HFzWwzb9aI\nfXp6ujjoOU+csH1OZj1TbSbVAtbTzmZSLWA97ayqpWvS9zPZO5BaHXrArqP2+f61d0zBSCRJddIu\nh7ckSZImlaFHkiTVgqFHkiTVgqFHkiTVgqFHkiTVgqFHkiTVgqFHkiTVgqFHkiTVghcnVFvq6e4a\n9QKFGzf187LnLWHWVj1TNCpJUicz9KgtHbTH6F9B8bObVvPgQwOGHknSmHh4S5Ik1YKhR5Ik1YKh\nR5Ik1YKhR5Ik1YKhR5Ik1YKhR5Ik1YKnrKujPbCxn66urhH7zJ3dQ6/5XpJqz9CjjvX0Jdvx69vv\nG7FP34P9zJ+zFfv82aIpGpUkqV0ZetSxttt6Nns9Y8cR+6zbsIn/vm3tFI1IktTOnPOXJEm1YOiR\nJEm1YOiRJEm14JoezWizeru5/fd/4HvX3M68ubPY0LeJgYGhR/XbZt5Wo64PkiR1NkOPZrQ5s3p5\n7QufSm/pH9ldAAAXW0lEQVRvNwsXzmft2gfo7x98VL/vX3vHNIxOkjSVPLwlSZJqwdAjSZJqwdAj\nSZJqwTU9ErBxU/+o63oGB4d42fOXTNGIJEkTzdAjAa/c98mj9nGxsyR1Ng9vSZKkWjD0SJKkWvDw\nljRGS56w9aiHuO665wH+Yr+nsO38WVM0KknSWBl6pDF6+pLtePqS7Ubs8/Nf383AwKMvfihJmn6G\nHmmCrbl/I/2jBJ+F28xmq96eKRqRJAkMPdKEevqTtuPmu9axem3fZvtsemiA39xxP/vttngKRyZJ\nMvRIE2j+nK3YbdftR+zT92A/1/367ikakSSpwdAjTbHu7i5uvmsdGzcNjNjvCQvnjhqgJEljZ+iR\nptjsrXo46uAYtZ8XQ5SkiWXokdrU/Q9sIleufdT2np5utr63jz+s30hvTxdPXrRgGkYnSZ2nLUJP\nRMwGPg0cBmwAzszMszbTdw/gXGA34EbgXZl5XVP7kcBHgMXAZcCxmXlPU/vHgGMoF2b8XGYubWp7\nHPBZ4GXA3cCHMvPCCSxVGrODnrMTfQ/2P2p7T283C+bPgoEBfvLLVczeavSzwBY9bh5dXV2TMUxJ\n6hhtEXqAM4A9gYOAJwPLIuLWzPxGc6eImAdcCnwROBp4F3BpROyamX0RsRdwPvB24AbgHOALwKur\n+58MHAG8BpgFXBgRq5sC1gXAbGBvYF/g/IjIzLxmkuqWNutxC+YMu723t5uFC+ezdnYPB+6+04hn\nigHc9rv1zN6qZ9QLJu6604LN7lOSZoJpDz1VkHkbcHBm3gDcEBGnAccD32jpfgSwoWl25sSIOAR4\nPbAMOA64qDE7ExFHAbdFxC6ZeRtwAvCBzFxetS+lzAqdFRFPBV4J7JKZtwM3RcS+wLspM0NS29lh\n27nssO3cEfs840kL+UPfQyP2GRwa4r+uvp3tRwk98+f0ss+zFo17nJLUDqY99AC7U8axvGnblcDf\nDNN376qt2VWUWZllwD7AqY2GzLwjIlYC+0TEJmAJcEXLfnaJiB2BvYCVVeBpbv8/j6UoqV10d3eV\nw2GjOPxFTxu1z39edcuoC6yHhoZ49lNHP+tsh+3m0u0hN0lTqB1Cz2JgTWY2L15YDcyJiO2b1+NU\nfW9suf9q4FlN7XcN075z1TbU0r4a6Gpq39x9JQF/sd9TRu2z5v4+fnfPhhH73H73H9hx4TyesHAu\nvT3drNs4wLp1fY+6kvX6BzaNur/ttpnN4u3nj9pPktoh9MwDHmzZ1rg9e4x9Z4+hfR5AZm5qaaOp\nfaTHHpOenpnxxfWNOqyn/bR7LYu2n8+iUULIM57yOG6prlXU3TNI14ZNbNjUz+DA0CP6bTN/FrNG\nWaj9mzvuI2+/b8Q+a9c/yMJtRv6nvOmhQbq6YKvekZ/Xh/oHR+zT1dUF3d10DQ0yODi02X5b9XSz\nZzx+xH0B9PZ0M9qE2EP9o3/fW3d3F1uN9p7pgllNX4+yuffaaF+z0thfu83ktfu/nfGaSfVMVQ3t\nEHo28uhg0bjd+uvi5vpuGEP7RoCImNUUfJr3M9pjj+qV++/aXv/CJ8CCBSOvF+k0M6meTq9l0RMm\n5lT7Z/3JEybkcbR5nf5ea2U99dUO8fBOYIeIaB7LIqAvM1t/fbuzaqOl76oxtN9JOZS1qKVtqKl9\npMeWJEkdrB1Cz/XAQ5RFyA0HAFcP03cF8IKWbfvxx0XQK4D9Gw0RsYSyJmd5Zq4CVja3V/tZmZmr\nq/vuEhE7NbXvX22XJEkdrmtoaPPHnKdKRJxLCS/HUELKF4CjM/Pi6syq+zNzY0RsA/wG+HfgM8A7\ngdcBT6uu07MP8EPKqevXAJ+o7vv/VftZSjkV/n9RZn3+DTg9Mz9ZtX8bmAO8h3I216eAAzPz2sl/\nFiRJ0mRqh5kegJOAa4EfUC4o+MHMvLhqWwUcDpCZ64FXAQdSQs1ewCsys69qXwG8AziFcrr5PTzy\nGjunAxdRrv9zEXBBI/BU3gyso8zuvB94q4FHkqSZoS1meiRJkiZbu8z0SJIkTSpDjyRJqgVDjyRJ\nqgVDjyRJqgVDjyRJqoV2+BqKjhcRs4FPA4dRvrbizMw8a3pH9WjVOK8BjsvMy6ttTwY+S/mm+luB\nv8rM7zbd56XA2cCulItAHpuZtzS1nwi8F9gG+CpwfGZunOQ6dqJcQ+lFlOf7K8D7M3NTp9UTEU8F\n/plynap7gH/KzDOqto6qpVVEXAqszsxjqttPpsPqiYhDKZe4GKJc22sI+HpmHt5p9UTErGo8R1K+\nV/BfM/Nvq7ZOq+Vo4PM88nXpAgYzszcinkK5lltH1FPtc2fgXMolWe4BPtl0Dbkn01mvz+OrWl4C\n3A18NDMvaIdanOmZGGcAewIHAe8GTomIw6Z1RC2qwPPvwDNbmv6D8u3yz6VcrPGb1T++xhWtvwl8\nDngesKbq33jM1wIfAo4FXky5qvZpk1pI8XXKRST3A44AXg18pGq7mA6pJyK6gEuB1cBzKBfb/EBE\nHNFptbSqanhFy+ZOfK89E/hPylfSLAIWA39ZtXXa6/MpyofQy4A3AsdGxLEdWsuX+ePrsQjYBfgf\nygVpoTPfa18F1lM+S04EPhoRr6naOu31+Q9gJ+CFVS1nVb9ATHstXqdnC0XEPMoLc3BmXlFt+1vg\nJZn54mkdXCUingF8qbr5bOBFmXl5RLyY8oZ6QiMpR8R3gSsy88MR8WFg/0YdETEX+B3w6ur+Pwa+\nl5kfqdr3A/4L2H6yfouIiAB+BeyYmWuqbUdQLjz5Zso/qI6oJyIWUX6j+cvMfKDa9nXKBTm/3km1\ntNS1ELiB8h/brzLzmE58r1X7+SJwW2Z+oGV7R9VTvSargRdn5pXVtvcBTwcupEPfa031vR94K/As\nytcLdcxrU+1jO+Be4M8y81fVtq9R/g19kw56fSLiucDPgF0z87Zq2/uAQ4G/ne5anOnZcrtTDhMu\nb9p2JbD39AxnWC8Evk+ZTmz+Jvi9geta3ixXVv0a7Zc3GqorX18H7BvlC2KfD1zRdN8VwCzKczJZ\nfge8vBF4mmxLSf0dU09m/i4zj2wKPPtR/sP+UafV0uIMYBlwU9O2TnyvQZnp+fUw2zutnv2B+xqB\npxrTaZn5l3T2e60R6N4HLM3Mh+i81wagD3gAeGtE9Fa/3O0H/JzOe312Be5uBJ7KLygzNwcwzbUY\nerbcYmBNZvY3bVsNzImI7adpTI+Qmedl5nuHScKLKb9JNFtN+f6z0dq3oxxierg9Mwcox6J3ZpJk\n5v0tx3+7KN+n9v1Rxsso7dNST0NE3Er5x76csoakI2upZkAO4I+HGxs6sh4ggJdHREbE/0TEqRGx\n1SjjZZT26ahnV+DWiDgqIm6KiN9GxAeqfz+dVkurdwN3ZuY3q9sdV09mPkj5f+ydlAB0E/DtzPz8\nKONllPbpqGc1sF1EzGna9iTK5MCOI4wVpqAWFzJvuXmURYHNGrdnT/FYxmtzY589hvZ5Tbc3d/+p\ncDqwB+U3gJNGGU8713MYZW3CuZRDXh332lTrxs4D3p2ZD5ZfVh/WifU8CZhL+RB6PfAUyrqYuaOM\nl1Hap6OerSmHst4OvIXy4fIvlBMBOq2WVm8DPtZ0u1PreQZl/dgZwG7AORHxfTqvnp9SDtH/U0Sc\nQFnb81eUxeZzRhnLpNdi6NlyG3n0E964vWGKxzJeG4HHtWybzR/Hvbna1lZtbKZ9SuqOiI8DJwCH\nZ+avIqJj68nM6wAi4iTKGovPAQtHGEs71vJ3wNWZ+b1h2jrutcnMlRGxfWbeV236RUT0UBZffp7O\nen36KWe7HJmZdwBExC6UWZL/Alpnpdu5lodFxPOBJ1K+QLqh495rEfESSnjbuZr1+Xm1uPcDlFns\njnl9ql94Xkc5q3YdZabmNMovc4OUXxo2N5ZJr8XDW1vuTmCH6nhjwyKgr+k/y3Z1J2WszRZRUvpo\n7fdQ3oQPt1cfCNs33X/SRMQ5lN8e3pSZjdX9HVVPRDyh6eyMhl9RjlGvGmGs0Ga1VN4AHBoR6yNi\nPfAm4H9FxDrgjhHGC+1ZD8P8G76J8tvq7+iselYBGxuBp5KUwwId9e+mxcHA5Zl5f9O2TqxnT+A3\nVeBp+DnlsFDH1ZOZ12bmUymzPEso6+LuBn47wlhhCmox9Gy564GHKIvNGg4Arp6e4YzLCmDP6rBE\nw/7V9kb7/o2G6ky1PYDlmTlEqXH/pvu+ANhEOXNn0kTEKZRp+jdk5lebmjqtnqcA34iIxU3bngf8\nnrK477kdVAuUBfO7URYV7k6Zqr+4+vmndNZrQ0T8eUSsaVmbsAflbM0r6KzXZwVlneHTmrY9k3Kd\nlBV0Vi3N9gauatnWaf8PQFmn8rSIaD768gzgFjrs9YmIhRFxRUQszMzfZ+Yg8CrKCRo/ne5aPGV9\nAkTEuZSV9sdQfnP6AnB0Zl48neMaTkQMAgdVp/91U94sN1IWnv4F8H7gWZl5RzX9/Svg74FvAacA\nT8/MParHegNlDcdbKP9o/5VyOuFfTeL4n0E5E+AfKReEbHZ3J9VTPf/LKaeqnkQJQZ8DPlrV9gvg\nl51Qy2bq+zwwVJ2y3onvta2rMV0OfBh4KuWiamdXfzrq9YmI/6Qc9nk3ZU3PsqquczutlqaabqGc\ntfWVpm2d+F5bQJlF/C7l3/+fVvt9f/V3R70+EXEdcC3l/+mXAJ+kTAZczzS/Ns70TIyTKC/wD4Bz\ngA+2Y+CpPJxyqwT+Gsp04TWUC5Yd2pgCr045PIwS5n5GWT1/aNP9LwJOpSyIvIzyAb50ksf/F5T3\n7Qcob/q7KFObd1X1HNop9TQ9/w8AP6FcQfYTmflPVdtfdEoto+nE91pm/oFy+OTxlN8wPwucl5ln\ndujr8ybKBfyuoPxi9qnM/OcOraXhCZT1Hg/r0PfaOko4WFyN6Uzgw5l5foe+Pm8AnkYJaycAr8vM\n69rhtXGmR5Ik1YIzPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIkqRYMPZIk\nqRYMPZIkqRYMPVKbiYi3RMQPI+L3EbExIn4TEWdHxI7TPbbxioi/q74faUsf580RscNEjKmTjeX5\njIjBiHhz9XNvRJzY0u5zqdoy9EhtIiK6IuI/gDMo307+Qsr31xwPPB+4pgM/rIZo+r63xyIiDqR8\nV9S8iRhQhxvL87kIuKj6+Y2U73ECfC6l3tG7SJoiJwGvAPbKzBuatt8RET+mfDPxe4H/Mx2Dm0bd\nbGFwqpPM/H3TzdZfbH0uVWuGHql9HA8sawk8AGTmxoh4EfC7xraIOAD4O+B5wGzgZuCjmXlh1f55\nyofcfcCbgUHgHODLlG90fx7wG+AvM/Pq6j4LKDNNhwKzKN+EvDQzr63a51aP8UrKNyDfBHwkM785\nUmER8QHgPdVj/idwQmau3cw+rwXel5nXRsQLgR9UD3NLRLwH+BSwZ2ZeX93/m8CLgIWZORQRXcBq\n4MTM/FJEvIDyzczPB+4GLgHen5nrq/tvBfwD5VvItwV+CZySmd+t2o8GPlD1+QCwhBJAT8jMn2ym\n3s9XP66pnvutqzqOzczfVX12Bj5G+XbtbYArgb/OzF+O9FxW930f8L+B7YEVwNsz83+qtkHgLUAX\n8K/VtgHgxS3P5Vszc9kYnp9bgK8Bh1C+cf61wCrK+2BfynvsJ8B7M/PG0cYuTScPb0ltICKeAuwC\nfH9zfTLz9sx8qOq/E/Ad4KfAc6o/PwXOj4jHN93tCGATsCflMMeHKKHj45QPuY3Ap5v6/99qHIcA\ne1E+UK+KiN2r9n8A/gx4OfCnVf8vR8STRijvyZQP3JcAr6r2+68j7HN50z6vonzIDlX3Ox+4FXhZ\n9Tx0AwdRQsWe1ePtTQkvl0bEs4HvAt+uxn1k1e+/mvZ/AfDSqu05wFeASyLiFU19ngS8g3K4aA/g\nAcphopEcCSwEDqA8X8+lPH9ExNaUoLBT9ZzsC2wALo+IJaM87pOBF1SPeQCwuHpeWn0ZOJHy3C3i\n0c/lRWN8fgCOo4Tyl1PeZxcBd1R99wIGgG+MMm5p2jnTI7WHxiLlu5s3RsR/UmYxGm7NzN2AOcCH\nMrN5vcbHgaOBpzc9zprM/Ouq/ROUD90vZ+al1bbPA2dXP7+EEhh2yMz7qvt/ICL2p8zSHAPsCqyv\nxnF/RHwQ+BGwdoTa+oDDM3NNtZ/jgcsiYlfgKSPtMzOPiYh7m2rZGBGXAH8OnE75wN1ECUovoswS\nHQJcUY3vr4HLMvPj1WPcHBFvAn5brW+5kxIMn5OZv6j6fCIingP8NSWQQfm/8h2NWZiIOBP4ZkTs\nmJmrN1P3fdV9BoBfR8SXKYcvAY4CHge8LjPvrR7zjcBvKQFjpEOYm4A3ZeYD1f3+hSpMNcvMByPi\n/urnu6u+zc/lgxHx3pGen8y8vNr+7cz8YeOxq9fuMmBlZvZHxFspIVhqa4YeqT2sqf5+XMv2t/PH\nRafvAV4NkJk3R8QXIuIEYDfKgufdKb/F9zTd/+bGD5m5ISIesY0SSGZVP+9Bmf29verXMKupz8cp\nM0V3R8RPKTMCX2ocCtmM3zQCT+WnlEMvf0YJaKPts9UlwLERMZsy4/N9yuzPiymHyV4JNA4v7QE8\nLSJaxzcEPAN4QnX7yuqwWEMvjw5y/9308/1N49yc31aBp/k+jf5/Bvy6EXjg4UOYPwN2q2Z7flWN\nswsYyswFVdfVjcBTWQvMHWEcI9mTkZ+fRuj5TUv73wCfBI6LiB9RZh3//TGOQZoyhh6pPdxMWSdx\nEPDVxsbG+g94xG/pRMQzgSsoa26+C3ydMrtzdcvjPjTMvgY3M4ZuygfznpQP2mYPVuNZUX0gv4xy\nSOjNwAcj4uDmmYAWAy23G6HswbHscxg/qtoOqsawDLgNOL46zPYcytlvjZoupMyEtD7+3ZSZlyFg\nf+API427cWixRetjjjb+rpa/W3VTXrM7KSF2OK3P55YY7flp6GtuyMxzI+KrlFm1lwAfprwPdm/M\nKkntyNAjtYHMHIyIT1E+OM7bzGLW5nUz7wR+l5kHNzZExKv548zAY3EjsACYnZkPz2pExGeBnwOf\njoi/A67MzG8B34qIk4D/R1krsrnQ8/SImN80O3EAJXj9ihKARtwnLWcbVYdTLgNeQzm89WbKwuWt\ngL8HfpGZtzfV9MzMvKXpsf8UOI1yCOlGyvO1U2Z+p6nPRynh4+9Gec4eq18Ab46IHZoO+82hLC7/\nQmYO8sgZuceq9Uyt1tujPT+/an3Aas3Yh4CPZeYyYFm1xuwOymUWvjYB45YmhaFHah+nUWYprqjW\n51xKmQV5NmUR6UuBz1V9VwJLIuLllA+m51EON0A5k+ux+A5wA2WB63uA2ynrS44G/q3qsyvwpoh4\nO2X9yT6UMHbVCI87F/hKRPwt5eyfc4ALMvP2iLhzhH1eWN3/D5RgskdE3FOFp0soi3fvyszbACLi\nJ5S1Ms3rW86kLA7+J+CfKAuL/5myJurXVYD6FnBetdbo/wGvB5ZSzoAayWMNlwBfAt5PeV7eR1mn\ncwown3Jm3UT5A0BE7El5nzziuWSU52czj3kv5RDirhHxN5Q1Xm+hzGxdO4FjlyacZ29JbSIzhzLz\nSOBtlMMtlwFJCQmrgQMz8+1V909RzqD5IuUU67+hfIjeSjkzZ3M2e42WanbhpZRDZhdRwsj+wKGZ\n+eOq27spa2i+WI3t7ymnl4+0nuNq4HrKTNCXgW9Rgs1o+/xRdf9fUs4u+jJljRPV7R4eebbb9ygf\n6I1DW2TmT4GDKYeKrgX+g3Ka/Uszs7/qdjjl8OB5lNBzFHBMZv4bI3vM17vJzHWUWZG11bgvp4TV\n/Rohbgs0j+sHwM8oofSVtDyXY3x+WmfaBiiHBQersf+ScojrkOYZI6kddQ0NeZ0qSZI08znTI0mS\nasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQI0mSasHQ\nI0mSauH/B++ESLAePjPtAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbce70668>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Seed random number generator\n",
"np.random.seed(42)\n",
"\n",
"# Compute mean no-hitter time: tau\n",
"tau = np.mean(nohitter_times)\n",
"\n",
"# Draw out of an exponential distribution with parameter tau: inter_nohitter_time\n",
"inter_nohitter_time = np.random.exponential(tau, 100000)\n",
"\n",
"# Plot the PDF and label axes\n",
"_ = plt.hist(inter_nohitter_time,\n",
" bins=50, normed=True, histtype='step')\n",
"_ = plt.xlabel('Games between no-hitters')\n",
"_ = plt.ylabel('PDF')\n",
"\n",
"# Show the plot\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"## ecdf\n",
"def ecdf(data):\n",
" n = len(data)\n",
" x = np.sort(data)\n",
" y = np.arange(1, n+1)/n\n",
" return x,y"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhcAAAF2CAYAAADdmboqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3XmcXFWd9/FPLenupJMOnQQSJAESCT/CYgRHcQEF0cFl\nxnFQUERZB2dkeFxg1McFcX1mRMBRZgS3ITJIFFQGFTfUUUAWESFACIcEwpbEkL2rt1TX8vxxbiXV\nVdX7rbq1fN+vV7+67rnnVp0+3Ul969xzz43l83lEREREwhKPugEiIiLSXBQuREREJFQKFyIiIhIq\nhQsREREJlcKFiIiIhErhQkREREKlcCEiIiKhUrgQERGRUCWjbkCtbdmSCnXVsHg8xpw5nWzf3kcu\npwXJakl9Hw31ezTU79FR3++1776zYuOpp5GLKYrHY8RiMeLxcfW3hEh9Hw31ezTU79FR30+cwoWI\niIiESuFCREREQqVwISIiIqFSuBAREZFQKVyIiIhIqBQuREREJFR1tc6FmbUDfwL+2Tl3+wh1jgau\nBo4CHgHe55z7c+1aKSIiIqOpm5GLIFisBA4fpc4M4Fbg98AxwN3ArWY2vSaNFBERkTHVRbgws2XA\nPcDiMaq+E+h3zn3UeR8EUsCp1W6jiIiIjE9dhAvgNcBvgFcAoy2BdixwZ0nZH4LjREREpA7UxZwL\n59w1hcdmNlrV/fHzLIptBo6oQrNERJpaKt3L9Wtu4tnUBhbNOoB3LzuVWW0zo26WNIG6CBcTMAPY\nXVK2G2gf7xPE4+GuD59IxId9l9pR30ejWv2ez+fJZPNksjky2RzZbJ5MLk8ulyOXh2wuTz6XJxt8\n5fP+ey74yuby5PKVH+fzefJ5yOXzkIdc3r8e+LJ8sJ0P2uG3/WN/n6q9x++pO+yY4cfngsJhx1By\nXIXX3NM+9rav2LRpCYaGsv7JfKtK+nA8/bz38bOdv6V32gYAdm3r4XP/+20W9Z1IydOWbo7wOlNr\ni3+GCgfVrC0lxxQ9jsViJBJxMpnssB3lbRn7hSrVKD9s6n0J8OKl8/j7Vy8Z++AqaLRwMUh5kGgH\n+sf7BHPmdBKLhX/zma4uzSmNivo+XLlcnsF0hv7BDAO7/Vf/4BDpoRzpTJb0UI6e3b3cvvVWtqU3\nMzuxL8vbT4JsO+mhLEOZHLuD74XtoUyOoWyOTCbHUCZLOijLZHJ7wkQm29p3m4xCx4u3DjsP3Zvf\nygOPb42sPRKuZzaneNcbl9HRVvu3+kYLFxuABSVlC4BN432C7dv7Qh+56OqaTk/PANlsLrTnlbGp\n70eXzmRJ9Q2R6k/T0++/p/rT9A1k6Bscon8wQ9+gDw79uzMMDGbo351hMJ0d/YmTaTqOvJNYWxqA\ngVwvG56/hfTal9Tgp6q+WAxixIjFIO439jwu3heLlXyn+HFs2DHEYsQLdQuvUXJ8PPjQEwvqFh4X\ntyuRiPu/9WEfqyv8DGU/U+X/8zbn5zLAxj3bM/JzWXJw94jPVOlpyooq1hn7ecqOqVgnmvbEYjGm\nTUuQyWSHjU6UPs94fheVXqzs91WxEaWbFZ6npOhFL5zLQN9uBvpKB/wnr7u7c1z1Gi1c3AN8tKTs\nVcDnx/sEhSHUsGWDT2VSe63S97lcnl19aXakdtM7kCbVP+S/gse9/UP0BAEi1T80dkgYr2SatsUP\nE+/sIdfXBfHcnmBRkJiZYk5XO9MScaYlE0xLxv1XIkYy4R8nk3H/OBHfWxbsTybiJAqP4zGSyTiJ\neIxE3H/3pzMhEYvtObUZj8eIx2J795c8LtRJxIe/ee8JCaVv8Iz8JlwPksk43d2d7NjRF9rfeyq9\nVHMuxqEafV8rUbW37sOFmc0HdjnnBoEfAP9qZl8GvgH8E34exo0RNlEkFJlsju09g2zbNcjW4Pu2\nXYM8n9rJps67ybTtJNfXRXr9UZBpm9RrxIAZHUn/1T6t6HGS6e3+e0d7kultiT3ff7Hlh6zv2wJA\nom0LyViSTEk+P3LBYt538qum2ANSa7PaZvK+5edE3QxpQvUYLkqHFTYBZwPXOedSZvY3wNeB9wIP\nAW90zg3UtokiE5fP59m4cwc3uB+weXATnfl5LOh9BTt35dm6a5Cdqd0VJ3u1Lb2fxMwtxPBv7m08\nvOcURCwGs6ZPY9aMNmbNGOH79GnM6vTbMzumTfi04A0bnx9eEGPYv9JZ02by7mVaakZE9qq7cOGc\nS5Rsx0u2/wQ0x8ldaVq9A0M89Zcenn2+l6e3buNxfs9gYjuQ3ztXgT42p/tJP1f5z7m9LcG82R3s\nmt1L8QmOrnkDXHTiy5k53Y88xKs8lL9o1gHs2tazZ3vpPouZ3tHBk9ueZuFMDaWLSLm6CxcijWb3\nUJZnNqdYv7GHJzf1sH5TD1t2DvqdRZMfK0WA5KwUhx8yj3n7dDCvq4O5s6czb3YHc2d30NmRJBaL\ncfWqR3lk25o9xyzeZxEL5syozQ8HvHvZqcPOy5991Ds4cP78hjz/LCK1oXAhMgH5fJ6NW/t4YqMP\nEes39vDclj6/PgHsmfzYcfDIkx+LHTF/Me/76xeN+pqlb+61PgVRel4+mdS6IiIyOoULkTE8v6Of\nh5/czmPP7ODxZ3eS6h+qWC8GzLJHGeocffLjrGkzicfi4w4KmnQnIo1G4UKkxGA6w5qnd/DI+u2s\nXr+d53dUni/cPaudJft38YL9p7EudjvbM8/TP9RfeQm+wKxpM/nEsRdpjoKINDWFCxFg684B/rx2\nKw89sZXHN20mfmCwrsO8Lkj5Sz/3nzuDww7sxg7ch6UL96F7ll8s9upV1/LUtnUVn/eQfRaTjCe1\njoCItBSFC2lZqf40f3rsee5+dDPr/rLFLxS1Tw/JffZe0ZFo28KS/dZzwfJzmNPVUfF5nk1tGLad\njCXpnDZDYUJEWpbChbSUoUyOB9Zu4Q9rnuZxfk9sRg+56V20vTBHYva2isf0x7aNGCyg/FLNw+Ys\n1RwJEWlpChfSEp54fgsrHv4+2zPPk+2dBfG9YSLRtoU4CUa6qHLRrANGfe6or+YQEak3ChfStHp2\np/j6Ayt5rncDQ5msP9UxDRLdg5AbfjllPBYjV7Lq5Hiv6NDVHCIiwylcSNNJD2W549GnuPn5FeQT\nuyEOsZJbcSQTcTL5vWMVmngpIhIehQtpGr0DQ/zsvsf5/fafk5+5lVhi5NUjFSZERKpH4UIa3u6h\nLL+69xl+evdTZA/8I4nuLRWX2i491aEwISJSHQoX0rBy+Ty33fs0//3zNewYSAWXkm6pWFeLV4mI\n1I7ChTSktc/tZOVv1vLUphQAbbaq4qWkyViSw+Ys1UiFiEgNKVxIQ9neM8hNv3uCex/dvKdswX5J\nds3eXlb3yLnLFCpERCKgcCENIZvL8as/Psstd64nHdzme0ZHkre//iB+sf07MDT8hh7JWFKXh4qI\nREThQupaKt3LNX/+Lk/3bCCTmkWao4jF2jjh6AN4+wkv5IYnV5Ia6i077pB9FkfQWhERAYULqVOp\ndC/Xrb6RNdsfJx/LQdIvfrVPxxo+9NLzWbTfTJLJOOt3PFN27KxpMzn7iNMjaLWIiIDChdSJVLp3\n2BLavYODPNW3ntJrSjtm97Fov71zKBZ3H8iOgYf3bOuqEBGR6ClcSGSKA0Uun9tzemPXth7yuTix\nePkxpff5uOCl7+Erf7iWZ3q0GJaISL1QuJDIrFi9ksd2rB1X3eJLSot1dcziwmPOI5MZeTVOERGp\nLYULicy6netH3Ne2ex4Hz9+H5wf/ohEJEZEGo3AhkUile8nms8PK8nlgqJ25bfO5+KQz2aejK5rG\niYjIlChcSM2UzrHIky+pMI/zDz+How/dN5oGiohIKBQupCZS6V6+cO+VFdekACAX54PHnsWh+ytY\niIg0ugrz8UXCNWawAA6bs5RD959fw1aJiEi1aORCqm7F6sqraObTbSQTCWzeQZx5xGkRtExERKpB\n4UKqbt3OJ8vK8uk2lufexnmvX04yoQE0EZFmonAhVZVK95KpcFXIq9rfwbtOOJJYLDbCkSIi0qgU\nLqRqCnMtSsVjcc448agIWiQiIrWg8WipmuvX3FRxroV1vzCC1oiISK0oXEjVPN3zbFmZ7lgqItL8\nFC6kKnK5PH27h4aVJWIJ3bFURKQFKFxI6PL5PNff9jhZdpfuULAQEWkBChcSupvveJLfPbABSi4E\nyaE7l4qItAKFCwnV7as28tO7noZkujRblN5JREREmpTChYRm7XM7uf5XDoCZ9nDZyEWCRAStEhGR\nWtM6FxKKrbsG+M8fPUwmtpsOe4Rs55ayOku7l0TQMhERqTWFC5myrX07+fwd15I+dDsd5Im1pcvq\nxIjpElQRkRahcCFTks/n+dKd32FoxqayORbFrPsQXSkiItIiFC5kSn7xx2dI5beMGCySsSSHzVnK\nu5edWtN2iYhIdBQuZNJWPbWBWzbcSHz28NMgiViCmdM6WTTrAN697FSNWIiItBiFC5mU/sEM33ro\nBhL7lE/cnJGczv877pMRtEpEROqBLkWVSVlx26qKV4QAHNS1qMatERGRelIXIxdm1g58DTgF6Aeu\ncM6V36vb1/174AvAIuAB4APOuQdq1VaBP67ZzEOZX5OoMNHiyLnLNL9CRKTF1cvIxeXAMcAJwAXA\npWZ2SmklMzsc+C4+XLwIWAXcamYdtWtqa9uR2s11v36IeNe2sn2HdS/lfcvP0RwLEZEWF/nIhZnN\nAM4DTnbOrQJWmdllwIXAj0qq/zXwiHPuu8GxHwP+GTgc+HPtWt16Uulerl9zE49teYrc0iyxklEL\nrWMhIiIFkYcLYDm+HXcXld0JfLxC3W3AEWb2yqD+ucAu4IlqN7JV7QkV29eSyWcgDrG28npax0JE\nRArq4bTI/sBW51ymqGwz0GFmc0vqfh/4GT58pIHLgLc753bVpKUt6Po1N/HItjU+WIxg1rSZGrUQ\nEZE96iFczAB2l5QVtttLyucCC/DzMl4GXAesMLN5VW1hC3sm9VzF8lnTZjK7rYsj5y7jE8depFEL\nERHZox5OiwxSHiIK2/0l5V8EHnLOXQNgZv8IrAHOAb40nheLx2PE46MtVD0xiUR82PdmkUr38p1H\nvk8q3Tt8Rx6O2ncZZx35jsgDRbP2fb1Tv0dD/R4d9f3E1UO42ADMM7O4cy4XlC0ABpxzO0vqvgT4\nSmHDOZc3s1XAQeN9sTlzOomVzkYMQVfX9NCfMyo9gyk++/sr6NmdKtvX1TGLS056fwStGlkz9X0j\nUb9HQ/0eHfX9+NVDuHgQGAJeDtwVlB0P3Feh7kb8lSHFDPjjeF9s+/a+0Ecuurqm09MzQDabG/uA\nOpdK9/KZP1xOaqi34v6DZi1kx46+Greqsmbr+0ahfo+G+j066vu9urs7x1Uv8nDhnBsws+uAa8zs\nXGAhcDFwFoCZzQd2OecGgW8C15rZn/BXi5wPHAh8Z7yvl8vlyeXyIf8UkM3myGQa/4/uW6u+WzlY\n5OMcOc8447BT6+7nbJa+bzTq92io36Ojvh+/yMNF4CL8Cp2/xV9aeolz7pZg3ybgbOA659yNZtaJ\nv0z1APyox4nOua21b3JzWrfzybKyfLqN/3PkhSxbuCCCFomISKOpi3DhnBvAT8o8p8K+eMn2tcC1\nNWpaS0mle8nks8PK8nk4Ov82BQsRERk3TX2VPVasXllWFsvHeMerj4igNSIi0qgULmSPdTvXl5Xt\nm1xIV2eFJTlFRERGoHAhRfJlmx889qxomiIiIg1L4UIAP98ilx8eLjri09lneldELRIRkUalcCGA\nn2+RY/glVtOSiYhaIyIijUzhQoDKl6Ae1LUogpaIiEijU7gQgLJLUAHevezUCFoiIiKNTuFC/M3J\nKixaGvWNyUREpDEpXLS4VLqXz91zBZTcbiWB5luIiMjkKFy0uBWrV9KXKb8R2dLuJRG0RkREmoHC\nRYtbW2Ei56xpMzn7iNMjaI2IiDQDhYsWly25Q2wM+MSxF2m+hYiITJrCRQtb/ewm8vnha1vMSHYq\nWIiIyJQoXLSoVLqXr7uriZX8BcRjscoHiIiIjJPCRYv6+oPXk40PlpVr4SwREZkqhYsW9VTqqbKy\nWdNmauEsERGZMoWLFrSrL112HxHQRE4REQmHwkULuu2BdRXLFSxERCQMChctZudAD//bfwOl8za1\nIqeIiIRF4aLFXP3nGyCZLivXipwiIhIWhYsWs7F/Y1mZVuQUEZEwJaNugNRGKt3LNx9cSTY+OOwe\nZYlYQhM5RUQkVBq5aBErVq/kid61ZXMtZiSnK1iIiEioFC5aQCrdi9tR+QoRLZolIiJhU7hoAStW\nryRPvqz8yLnLtGiWiIiETnMuWsC6CrdVP6x7Ke9bfk4ErRERkWancNHEUulerl9zE5l8tmyfrg4R\nEZFqUbhoUql0L1+490pSQ71l+xIkNIlTRESqRnMumtSK1SsrBgvQglkiIlJdGrloUut2ri8rS8aS\nHDZnqSZxiohIVSlcNK182ebnj/u4ToeIiEjV6bRIE0qle8nlh4eLjrgWyxIRkdpQuGhCK1avJEdu\nWNm0pO56KiIitaFw0WRGWo1TK3GKiEitKFw0mZFW49QkThERqRWFiyYz0mqcmm8hIiK1onDRRFLp\nXq3GKSIikVO4aCIrVq8sK0sQ16iFiIjUlMJFE6m0cNbS7hdG0BIREWllChdNIpXuJatTIiIiUgcU\nLppEpatEls4+RKdERESk5hQumkTZVSJ5OO+od0XTGBERaWkKF02g4lUiMTRqISIikVC4aAKVrxLR\nct8iIhINhYsmUGnhrKXdSyJoiYiISJ3cct3M2oGvAacA/cAVzrkrR6h7VFD3JcBa4APOud/VqKl1\nRwtniYhIvamXkYvLgWOAE4ALgEvN7JTSSmbWBfwKeAQ4ErgZuNnM5tWuqfVlpFMimm8hIiJRiXzk\nwsxmAOcBJzvnVgGrzOwy4ELgRyXVzwZSzrn3BdufNrM3An8F/KJGTa4rlRfO0ikRERGJTuThAliO\nb8fdRWV3Ah+vUPc1wC3FBc65Y6vXtEZQfgdUnRIREZEo1cNpkf2Brc65TFHZZqDDzOaW1F0CbDWz\nr5vZJjO7y8xeWbOW1plUupdcfni46EzO0CkRERGJVD2MXMwAdpeUFbbbS8pnAh8FvgK8ATgd+JWZ\nmXNuw3heLB6PEY/HptDc4RKJ+LDvtfSdVd8jR254e+Jxksl6yIzVF2XftzL1ezTU79FR309cPYSL\nQcpDRGG7v6Q8AzzgnPtMsL3KzP4aeA/wb+N5sTlzOonFwgsXBV1d00N/zrGs3VF+Ceoh8xbT3d1Z\n87ZEKYq+F/V7VNTv0VHfj189hIsNwDwzizvnCh/DFwADzrmdJXU3AY+VlD0OLBrvi23f3hf6yEVX\n13R6egbIZnNjHxCSVLqXTC5TVv6uQ9/Gjh19NWtHlKLq+1anfo+G+j066vu9xvvhtR7CxYPAEPBy\n4K6g7Hjgvgp17wFeXVJ2GPDd8b5YLpcnlyufBDlV2WyOTKZ2f3TfWlX+IydIMD0+o6btqAe17nvx\n1O/RUL9HR30/fpGHC+fcgJldB1xjZucCC4GLgbMAzGw+sMs5NwhcA1xoZp/CB4qzgMXA9ZE0PkJa\nlVNEROpVvcxOuQi4H/gtcBVwiXOucMnpJuA0AOfcM8DJwFuAh4E3A29yzm2qeYsjpFU5RUSknkU+\ncgF+9AI4J/gq3Rcv2b4bv2hWy7p+zU1lZVqVU0RE6kW9jFzIOKXSvTy2fW1ZuU6JiIhIvVC4aDAr\nVq8kkx9+lUhnslOnREREpG4oXDSYsomcebjk5RfrlIiIiNQNhYsGky2dyBlDwUJEROqKwkUDSaV7\nK9ymTEREpL4oXDSQFatXlpUlSETQEhERkZEpXDQQLZwlIiKNQOGigZTNt0ALZ4mISP1RuGggleZb\naDKniIjUG4WLBpFK95aVab6FiIjUo3GHCzO7zMzGd69VCV2lyZyabyEiIvVoIiMXFwPDwoWZ3Wpm\n+4fbJKmk0mROzbcQEZF6NJFwEatQ9mpgekhtkVFUmsyp+RYiIlKPNOeiAWjxLBERaSQKFw1Ai2eJ\niEgjmWi4qPQBWh+qq0yLZ4mISCNJTrD+V81soGi7HbjMzFLFlZxz5065ZbKHFs8SEZFGMpFwcTuw\noKTsD8C84EuqRItniYhIIxl3uHDOnVDFdsgo4sTJkduzndBUGRERqWMTPS2yh5nNAGYDu5xz/eE1\nSYr5K0WGj110JHX1r4iI1K8JhQszmwV8GDgdWFJUvha4HrhSQSNcK1avLAsX8VilJUdERETqw7jD\nhZnNxc+7WATcDHwd2IkfvXgJ8DHgNDM73jm3qwptbTmpdC9ux7qy8oO6FkXQGhERkfGZyMjF5/CX\nrh7hnHu2dKeZLQR+jl8m/FPhNK+1VRq1iBHj3ctOjahFIiIiY5vIzMA3Ax+uFCwAnHPPAZ8E3hlG\nw6Ty+hbWfYiuFBERkbo2kXAxH3h4jDqrgAMn3xwpSKV7yWh9CxERaUATCRdtwMAYdQaAaZNvjhSM\ntOS3Ri1ERKTeacGEOrVu5/qyMi35LSIijWCi61xcbGZ9o+zXx+oQpNK9WvJbREQa1kTCxTPAaeOs\nJ1NQ6SqRw7qX6pSIiIg0hIks/30wgJl1AgPOuT3rUZvZ4cB659xYczJkHMquEslr1EJERBrHhOZc\nmNk7gfXA0SW7vgw8Z2Z/H1bDWlnZKZGYblQmIiKNY9zhwsxOwC/x/RNgQ8nuDwA/Bm40s1eG1roW\n5O8lIiIi0rgmMufiY8BVzrkPle5wzj0GnGNmefxCWm8KqX0tZ6RLUEVERBrFRE6LHA18e4w6XwOO\nmXxzWttI9xLRJagiItJIJhIuOhh7Ea3twIzJN6e1VbpKBDSZU0REGstEwoUDXjFGnVcCT0++Oa2t\n0r1EFncu1mROERFpKBMJF9cDnzOzF1TaaWYH4O+cemMYDWtF2XxueEEezn/xu6NpjIiIyCRNZELn\nfwBvB1ab2X8BdwE7gLnAq4CzgceBy0NuY0vwV4mUnhKJMbt9ViTtERERmaxxj1w457LA64BvAmcB\nNwG/Br4PvAMfPl6jhbQmp9JVIvPiCyNoiYiIyNRM6N4izrndwEfM7OPAEmAOsAV40jmn5RmmoHS+\nRT4Ppyw5JaLWiIiITN5Eb1wGgHMugz8FIiFIpXvJVLhR2eEL94+gNSIiIlOjW67XgUqnRGLEmJbU\nr0dERBqP3r3qQKVLUPeJVbwoR0REpO4pXNSB0huV5fNw8n5viag1IiIiUzOpORdhM7N2/NLhpwD9\nwBXOuSvHOOZg4GHgzc6526veyCqqNBP28EULat4OERGRMNTLyMXl+HuSnABcAFxqZmNdKnE1TbrU\neAyY29URdTNEREQmJfJwYWYzgPOA9zvnVjnnbgEuAy4c5ZgzgKZZEztR9muIEYvFImmLiIjIVEUe\nLoDl+NMzdxeV3QkcW6mymc0F/g14L/5DfkPzK3MONy3WHklbREREwlAP4WJ/YGuwdkbBZqAjCBKl\nrgRWOOfW1KR1VbZi9UpyDL+nyLR4IqLWiIiITF09TOicAewuKStsD/sIb2avw9959fwatKvqUule\n3I51ZeUHzday3yIi0rjqIVwMUhIiirb7CwVm1gFcA7zPOZee7IvF4zHi8fDOpiQS8WHfJ+I7q75X\nfrOyPJy3/HSSWkBrTFPpe5k89Xs01O/RUd9PXD2Eiw3APDOLO+cK5wcWAAPOuZ1F9V4GLAZ+aGbF\n6eDnZvYd59wF43mxOXM6qzJZsqtr+oTq9wymeGzb2rLyfWIHcOD8+WE1qyVMtO8lHOr3aKjfo6O+\nH796CBcPAkPAy/G3cQc4HrivpN69wNKSsnX4K01+Pd4X2769L/SRi66u6fT0DJDN5sY+IPDv93+r\nbNQin4cT5/0NO3b0hda+ZjbZvpepUb9HQ/0eHfX9Xt3dneOqF3m4cM4NmNl1wDVmdi6wELgYf1t3\nzGw+sMs5NwgMWyfbzAA2Oue2jvf1crk8uVz4N3DNZnNkMuP/o1u7/YmystyuudhR8yf0PDLxvpdw\nqN+joX6Pjvp+/OrlBNJFwP3Ab4GrgEuC9S4ANgGnjXBcw97mPZsf/geaz0Ps2aM5YN74UqGIiEi9\ninzkAvzoBXBO8FW6b8QA5JxryGs2/doWpRM5Yyzed16op2xERESiUC8jFy2l0i3Wcz1zWPyCrgha\nIyIiEi6FiwiU3mI9n4f0k8s55IDZEbVIREQkPAoXNZZK95IpucU6AJk2XvgChQsREWl8Chc1VumU\nCPkY82Z30NXZVvsGiYiIhEzhosZKT4mAn29x8P6abyEiIs1B4aLGsiWnRArzLRYvmBVRi0RERMKl\ncFFjFRfmyLRx4HyFCxERaQ4KF3Xi4P0VLkREpDkoXNRQKt1bXhhM5uzsmFb7BomIiFSBwkUNjbR4\nlk6JiIhIM1G4qKGRFs86SJM5RUSkiShc1FDplSKAn8y538zaN0ZERKRKFC5qaKRbuGrkQkREmonC\nRY1UnMwJzJoxjdlamVNERJqIwkWNjLTs98J9ZxKL6TbrIiLSPBQuamSkZb8P2LczgtaIiIhUj8JF\njWTzuWHbhStFFu6ryZwiItJcFC5qJE7JqY88kGljka4UERGRJqNwUSPtyY7hBdkksRgcME+nRURE\npLkoXNTI7szg8IJEhgVzZtA2LRFNg0RERKpE4aJGcgyfc0EMnRIREZGmpHBRI5UW0FK4EBGRZqRw\nEaFF+2llThERaT4KFzUw0uqcB87XyIWIiDQfhYsaqLQ6Zywf07LfIiLSlBQuamDdzvVlZR1D+2nZ\nbxERaUoKFzUxfDpnPg/L214fUVtERESqS+GiBtoS7cMLMkleuN++0TRGRESkyhQuaqDSAlq6p4iI\niDQrhYsaqLSA1v5zZ0TTGBERkSpTuKiyVLq3bAGtGGjZbxERaVoKF1VW6TJUSu+QKiIi0kQULqps\n3c4ny8rmxQ+IoCUiIiK1oXBRZdl8dth2Pg9veMFbI2qNiIhI9SlcVFmlG5YdMl+XoYqISPNSuKiy\nRGkX52OTXCjmAAAW00lEQVTMnd0RTWNERERqQOGiytqTw4NELJ8krmW/RUSkiSlcVFnZAlrxTDQN\nERERqRGFiyorX0Cr0iwMERGR5qFwUUWVFtASERFpdgoXVVRpAa24ulxERJqc3umqqNICWod2vzCC\nloiIiNSOwkUVlS6gRR7OPuL0aBojIiJSIwoXVVRpvsWsNt1qXUREmpvCRS1peQsREWkByagbAGBm\n7cDXgFOAfuAK59yVI9R9M/B54BDgCeAS59xPatXWiUgQJ1t0KWpMWU5ERFpAvbzbXQ4cA5wAXABc\namanlFYysxcBPwS+BSwHvgH8wMyOql1Tx690dc72eHtELREREamdyEcuzGwGcB5wsnNuFbDKzC4D\nLgR+VFL9dOA3zrn/DLa/ZmZvAU4DHq5Vm8erdHXOodzuiFoiIiJSO5GHC/wIRBK4u6jsTuDjFequ\nANoqlM8Ov1lTk0r3DjslApDTkloiItIC6uG0yP7AVudc8U03NgMdZja3uKLz9oxQmNkRwEnAr2vS\n0gnQAloiItKq6mHkYgZQer6gsD3iJAUzm4eff3GHc+7H432xeDxGPB7eZRuJRHzY94KKC2jNWUIy\nqYARlpH6XqpL/R4N9Xt01PcTVw/hYpDyEFHY7q90gJnNB27DLyVx6kRebM6cTmJVuOV5V9f0YdvZ\nfK6szsXHn09XR2for93qSvteakP9Hg31e3TU9+NXD+FiAzDPzOLOucI78gJgwDm3s7SymR0A/BbI\nAic457ZN5MW2b+8LfeSiq2s6PT0DZLN7A0W+wvyK7ECcHQN9ob12qxup76W61O/RUL9HR32/V3f3\n+D4g10O4eBAYAl4O3BWUHQ/cV1oxuLLkF0H9E51zWyb6Yrlcnlwu/ImV2WyOTGb0P7qx9svkjKfv\nJXzq92io36Ojvh+/yMOFc27AzK4DrjGzc4GFwMXAWbDnFMgu59wg8AlgMX49jHiwD/woR0/NGz+C\nVLq3rCxBIoKWiIiI1F69zE65CLgff7rjKvyqm7cE+zbh17EAv4LndOBeYGPR17/XtLVjqHSlyNLu\nJRG0REREpPYiH7kAP3oBnBN8le6LFz1eVst2TVbZlSK6G6qIiLSQehm5aCplt1qP6W6oIiLSOhQu\nqkDrcIqISCtTuAhZpcmcIiIirUThImSVJnPqShEREWklChchq7Tst64UERGRVqJwEbKyZb91pYiI\niLQYhYuQxSlZWjwW05UiIiLSUhQuQtae7Bi23TbyjV1FRESaksJFyHZnBodtZ0hH1BIREZFoKFyE\nLEdu1G0REZFmp3ARMi2gJSIirU7hIkRaQEtEREThIlRaQEtEREThIlRaQEtEREThIlRlC2ihBbRE\nRKT1KFyEqHQBrThxLaAlIiItR+EiRKULaHWUbIuIiLQChYsQlS6gVbotIiLSChQuQqQFtERERBQu\nQpNK95YtoKUFtUREpBUpXITk2w/fUFamNS5ERKQVKVyEZO32J8rKtMaFiIi0IoWLkGTz2bIyrXEh\nIiKtSOEiJJXmV2iNCxERaUUKFyFJlHRl6baIiEir0DtgSEoXzCpdUEtERKRVKFyEZFALaImIiAAK\nF6HoGUyRLVtAS6tciIhIa1K4CMFX77m2rCyurhURkRald8AQPLplbVmZ1rgQEZFWpXARgmxOa1yI\niIgUKFyEIF9hfoXWuBARkValcCEiIiKhUrgIQSI2/AZlWkBLRERamd4FQ6AFtERERPZSuAjB4JAW\n0BIRESlQuAhBluFXi+RKFtQSERFpJQoXU5RK95aVaW1OERFpZQoXU/Tth28oK0uQqFBTRESkNShc\nTNHa7U+UlWl1ThERaWUKF1OUzWt1ThERkWIKF1NUaX6FVucUEZFWpnAxRaV3P9UCWiIi0ur0TjhF\nbfH2YdtaQEtERFpdMuoGAJhZO/A14BSgH7jCOXflCHWPBq4GjgIeAd7nnPtzrdpaandu9/BtLaAl\nIiItrl5GLi4HjgFOAC4ALjWzU0ormdkM4Fbg90H9u4FbzWx67Zo6XL5kwSwtoCUiIq0u8nARBIbz\ngPc751Y5524BLgMurFD9nUC/c+6jzvsgkAJOrV2L99ICWiIiIuUiDxfAcvzpmbuLyu4Ejq1Q99hg\nX7E/AK+oTtNGt2L1yrIyLaAlIiKtrh7Cxf7AVudcpqhsM9BhZnMr1N1YUrYZWFjF9o1o3c71ZWVa\nQEtERFpdPUzonAHsLikrbLePs25pvRHF4zHi8diEGjiiGMPOg8SI8Q/LzyCZrIfM1vwSifiw71Ib\n6vdoqN+jo76fuHoIF4OUh4PCdv8465bWG9GcOZ3EYuGEi2XzDuHh5x/bs33k/MM4cP78UJ5bxq+r\nK7L5vC1N/R4N9Xt01PfjVw/hYgMwz8zizrnCpRYLgAHn3M4KdReUlC0ANo33xbZv7wtt5OKsw9/J\nN3bfwIa+TbywexFnLjuNHTv6QnluGVsiEaerazo9PQNks7pKp1bU79FQv0dHfb9Xd3fnuOrVQ7h4\nEBgCXg7cFZQdD9xXoe49wEdLyl4FfH68L5bL5cnlwrmmY3p8Bhcf+166uzvZsaOPTCZHJtPaf3hR\nyGbV71FQv0dD/R4d9f34RR4unHMDZnYdcI2ZnYufnHkxcBaAmc0HdjnnBoEfAP9qZl8GvgH8E34e\nxo2RNF5ERETK1MvslIuA+4HfAlcBlwTrXYA/5XEagHMuBfwN8GrgT8DLgDc65wZq3mIRERGpKPKR\nC/CjF8A5wVfpvnjJ9p+Al9SoaSIiIjJB9TJyISIiIk1C4UJERERCpXAhIiIioVK4EBERkVApXIiI\niEioFC5EREQkVAoXIiIiEiqFCxEREQlVLJ8P5z4bIiIiIqCRCxEREQmZwoWIiIiESuFCREREQqVw\nISIiIqFSuBAREZFQKVyIiIhIqBQuREREJFQKFyIiIhIqhQsREREJlcKFiIiIhCoZdQMamZm1A18D\nTgH6gSucc1dG26rGY2YvAL4KnIjvxxuBjznn0mZ2MPBN4BXAU8CHnHO3FR37OuDLwBLgbuB859z6\nov0fBP4FmAXcBFzonBuswY/VcMzsVmCzc+7cYPtg1PdVYWZt+L47HdgN/Jdz7hPBvoNRv1eNmS0E\nrgZeDWwDvuKc+0qw72DU96HQyMXUXA4cA5wAXABcamanRNqixvRDoAN4FfBO4G+BzwX7bgE2Ai8B\nrgduDv5zwMwWATcD3wb+CtgK/E/hSc3sbcCngPOB1wIvBy6r/o/TeMzsncAbS4r/B/V9tXwVOAl4\nPfAu4HwzOz/Yp7/56roJSOH/7/4g8AUz+7tgn/o+JLpx2SSZ2Qz8H9fJzrk7grJPACc5514baeMa\niJkZ8Cgw3zm3NSh7J/Al4Ez8P/b9CunfzG4D7nDOfdbMPgscV+hvM5sO/AX4W+fc7Wb2e+DXzrnP\nBftfBfwKmNuqnyYqMbNuYBX+P9VHnXPnmtlr8f9xqu9DFvT3ZuC1zrk7g7KPAIcC30V/81VjZvsA\n24EjnXOPBmU/wP/t34z6PjQauZi85fjTSncXld0JHBtNcxrWX4A3FIJFkdn45P/nkn+Yd+KHLMH3\n9e2FHc65AeDPwCvMLA68FLij6Nh7gDb87072uhy4DlhTVHYs6vtqOQ7YWQgWAM65y5xz/4D+5qtt\nAOgDzjGzZPDh5lXAA6jvQ6VwMXn7A1udc5miss1Ah5nNjahNDcc5t6vknGYMuBD4Db6PN5YcshlY\nGDwebf8++FMte/Y757L4c6wLEQCCEYrj2XsaqkB9Xz1LgKfM7D1mtsbMnjCzTwZ/++r3KnLO7cb/\n//JP+KCxBviZc+5a1Peh0oTOyZuBn4hVrLDdXuO2NJMvAUfjPwVcROU+LvTvSL+D9mAfo+xvecGE\n5GuAC5xzu/2HuD1G69ux9qvvRzcTfwrkvcDZ+Detr+MnM6vfq28Z8GP8iN1RwFVm9hvU96FSuJi8\nQcr/aArb/TVuS1Mwsy8C7wdOc849amaDwJySau3s7d+Rfgc7gn2MsF+/H+/TwH3OuV9X2Ke+r54M\n/mqC051zzwGY2UH4SeG/AkpHPtXvITGzk4DzgIXBKMYDwYTNT+JHS9X3IdFpkcnbAMwLzrUVLAAG\nnHM7I2pTwzKzq4APAWc45wozsDfg+7TYAmDTOPZvw/+D37PfzBL4/zw2IQDvAN5qZikzSwFnAO82\nsx7gOdT31bIJGCwEi4DDD5/rb766jgHWBsGi4AHgQNT3oVK4mLwHgSH8JKCC44H7omlO4zKzS/FD\nxO9wzt1UtOse4Jhg+L7guKC8sP+4oueZgT+lcrdzLo//XRxXdOwrgTT+ygiB1+CHhZcHXz/Gz5Zf\nDtyL+r5a7sHPzTqkqOxw/LoK9wAvUb9XzUbgEDMrHrVfBqxHfR8qXYo6BWZ2NX6m8bn4Tx0rgLOc\nc7dE2a5GYmbLgIeA/4dfkKzYFvw/zEfwEw7fAnwMOMI591wwlPwo8Bngp8ClwKHOuaOD534Hfk7B\n2fj/VP4Lf6nYh6r8YzUkM7sWyAeXosZR31eNmf0Yf9rpAvyci+uAz+IXd3oIeBj1e+jMrAs/ifM2\n4AvAYfg++ljwXX0fEo1cTM1FwP3Ab4GrgEsULCbsLfi/w0/i/0FuxA8jbnTO5YC34oca/4RfbOit\nheFk59zT+NVRzwX+iJ+x/dbCEzvnvg/8K36y3C/xlw1/tCY/VYML+v7vUN9XyxnAOvyliyuArzrn\n/jPo97egfq8K51wPfvGy/fH9dwXwWefct9T34dLIhYiIiIRKIxciIiISKoULERERCZXChYiIiIRK\n4UJERERCpXAhIiIioVK4EBERkVApXIiIiEioFC5EREQkVAoXIiIiEiqFC5FJMLOzzex/zex5Mxs0\ns7Vm9mUzmx912ybKzD5tZutDeJ4zzWxeGG1qZOPpTzPLmdmZweOkmX2wZL/6UhqawoXIBJhZzMz+\nB7gcfwfR1wCHABcCLwX+1IBvCvnga9LM7NX4e2TMCKNBDW48/bkA+H7w+F34e1wA6ktpDsmxq4hI\nkYuANwIvc84V30r5OTP7Pf4uov8C/N8oGhehOFMMKK3EOfd80Wbphzz1pTQ8hQuRibkQuK4kWADg\nnBs0sxOBvxTKzOx44NPAXwHtwJPAF5xz3w32X4t/M9kJnAnk8HfY/R7wjeC4tcA/OOfuC47pwo+c\nvBVow9/B8aPOufuD/dOD53gz/s6Na4DPOeduHu0HM7NPAh8InvPHwPudcztGeM37gY845+43s9fg\n7wwMsN7MPgB8FTjGOfdgcPzNwIlAt3Mub2YxYDPwQefcDWb2SvwdJV8KbAF+AnzMOZcKjp8GfB5/\nN9HZ+NtiX+qcuy3Yfxb+zrqfD74vwge99zvn7hrh5702eLg16PuZwc9xvnPuL0GdhcC/4e+kOQu4\nE/iwc+7h0foyOPYjwP8B5gL3AO91zq0L9uXwt+aO4W/NjZllgdeW9OU5zrnrxtE/64EfAG8C9gXe\nhr+78FXAK/B/Y3cB/+Kce2SstotMlU6LiIyTmS0GDgJ+M1Id59yzzrmhoP4LgF8A9wIvDr7uBb5l\nZvsWHfZOIA0cgx8e/xT+zf2L+DeTQeBrRfV/HrTjTcDL8G9cfzCz5cH+zwNHAm8ADgvqf8/MDhzl\nxzsY/8Z2EvA3wev+1yiveXfRa/4B/2aWD477FvAU8PqgH+LACfg372OC5zsWHxJuNbMXAbcBPwva\nfXpQ71dFr/8d4HXBvhcDNwI/MbM3FtU5EPhH/GmGo4E+/OmF0ZwOdAPH4/vrJfj+w8xm4t+QXxD0\nySuAfuB2M1s0xvMeDLwyeM7j8bf4/laFet8DPojvuwWU9+X3x9k/AP+MD79vwP+dfR94Lqj7MiAL\n/GiMdouEQiMXIuNXmKy5pbjQzH6M/1Re8JRz7iigA/iUc674fPoXgbOAQ4ueZ6tz7sPB/n/Hv7l9\nzzl3a1B2LfDl4PFJ+Dfmec65ncHxnzSz4/CjDucCS4BU0I5dZnYJ8Dtgxyg/2wBwmnNua/A6FwK/\nNLMlwOLRXtM5d66ZbS/6WQbN7CfAXwNfwr+xpfGB5ET8qMebgDuC9n0Y+KVz7ovBczxpZmcATwTz\nDzbgA9iLnXMPBXX+3cxeDHwYH3zA/3/2j4VRBTO7ArjZzOY75zaP8HPvDI7JAo+b2ffwp70A3gPM\nAd7unNsePOe7gCfwb+SjnfpKA2c45/qC475OEFqKOed2m9mu4PGWoG5xX+42s38ZrX+cc7cH5T9z\nzv1v4bmD390vgWeccxkzOwcfNkWqTuFCZPy2Bt/nlJS/l72T7z4A/C2Ac+5JM1thZu8HjsJP/FyO\n/1SaKDr+ycID51y/mQ0rw7/xtwWPj8aPOD4b1CtoK6rzRfzIxxYzuxf/CfeGwhD6CNYWgkXgXvyQ\n/ZH4IDTWa5b6CXC+mbXjRzB+gx/NeC3+9MqbgcJpiaOBQ8ystH15YBmwX7B9Z3A6pSBJeWB6rOjx\nrqJ2juSJIFgUH1OofyTweCFYwJ5TX38EjgpGLx4N2hkD8s65rqDq5kKwCOwApo/SjtEcw+j9UwgX\na0v2fxz4CvDPZvY7/Cjaykm2QWRCFC5Exu9J/HnsE4CbCoWF8/Mw7FMnZnY4cAd+TsRtwA/xoxX3\nlTzvUIXXyo3Qhjj+DfAY/Btasd1Be+4J3vhejz+VcCZwiZmdXPzJtkS2ZLsQfnaP5zUr+F2w74Sg\nDdcBTwMXBqdnXoy/2qbwM30X/8m+9Pm34EcS8sBxQO9o7S6ckipR+pxjtT9W8r1UHP8724APi5WU\n9udUjNU/BQPFO5xzV5vZTfhRopOAz+L/DpYXRklEqkXhQmScnHM5M/sq/j/oa0aY1Fc8r+GfgL84\n504uFJjZ37L3k+5kPAJ0Ae3OuT2f0s3sm8ADwNfM7NPAnc65nwI/NbOLgNX4c/kjhYtDzayz6NP2\n8fiA8yg+aIz6mpRc3RAMw/8S+Dv8aZEz8RM4pwGfAR5yzj1b9DMd7pxbX/TchwGX4U89PILvrxc4\n535RVOcL+Df5T4/RZ5P1EHCmmc0rOl3UgZ9ku8I5l2P4CNNklV4ZUro9Vv88WvqEwZyeTwH/5py7\nDrgumAP0HP7y6R+E0G6RESlciEzMZfhP3XcE8yduxX+qfxF+Mt3rgG8HdZ8BFpnZG/BvAH+FH6YG\nf+XIZPwCWIWf6PcB4Fn8+f+zgOuDOkuAM8zsvfj5AS/Hh54/jPK804EbzewT+KsNrgK+45x71sw2\njPKa3w2O78UHgKPNbFsQUn6Cn8S40Tn3NICZ3YWfy1A8/+AK/CTJ/wD+Az/B8j/xc1YeD4LKT4Fr\ngrkgq4FTgY/ir7gYzWRDHMANwMfw/fIR/DyKS4FO/JU8YekFMLNj8H8nw/qSMfpnhOfcjj/1tMTM\nPo6fg3M2fqTm/hDbLlKRrhYRmQDnXN45dzpwHn6Y/peAw78ZbwZe7Zx7b1D9q/gZ+/+Nv3Ty4/g3\nq6fwVwKMZMQ1DoJPy6/Dn2r5Pv5N/zjgrc653wfVLsDPcfjvoG2fwV82Otr59vuAB/EjG98DfooP\nEGO95u+C4x/GX83wPfwcFILtBMOvrvk1/o2zcEoE59y9wMn4Uwz3A/+Dv3z2dc65TFDtNPxppWvw\n4eI9wLnOuesZ3aTXi3DO9eA/5e8I2n07PhS+qhCWpqC4Xb8F/ogPf2+mpC/H2T+lI0dZ/OmkXND2\nh/GnRt5UPAIiUi2xfF5rtYiIiEh4NHIhIiIioVK4EBERkVApXIiIiEioFC5EREQkVAoXIiIiEiqF\nCxEREQmVwoWIiIiESuFCREREQqVwISIiIqFSuBAREZFQKVyIiIhIqP4/6vjFra591RQAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbd0a1da0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Create an ECDF from real data: x, y\n",
"x, y = ecdf(nohitter_times)\n",
"\n",
"# Create a CDF from theoretical samples: x_theor, y_theor\n",
"x_theor, y_theor = ecdf(inter_nohitter_time)\n",
"\n",
"# Overlay the plots\n",
"plt.plot(x_theor, y_theor)\n",
"plt.plot(x, y, marker='.', linestyle='none')\n",
"\n",
"# Margins and axis labels\n",
"plt.margins(0.05)\n",
"plt.xlabel('Games between no-hitters')\n",
"plt.ylabel('CDF')\n",
"\n",
"# Show the plot\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhcAAAF3CAYAAAAWxWmPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl4JFl55/tvRK7aS0tJpdrXjqqu6h3obpo2Dcas3sDG\ngMEXMGOPwVzbFx7b1/u9dzx35jLAeBljbI+HNm7chjLYGLfBZofeF7qrt6ro2hdVSSWVtkwp94j7\nR2SmcpOUkjKVKen3eZ56lBkZGXHqSFX56pz3vMdwXRcRERGRWjEb3QARERFZXxRciIiISE0puBAR\nEZGaUnAhIiIiNaXgQkRERGpKwYWIiIjUlIILERERqSkFFyIiIlJTCi5ERESkpvyNbkAhy7JCwJPA\nL9u2/b15zrkF+HPgBuB54IO2bf+g2nuMjkYWLElqmgY9PW2Mj8/gOKpeCuqTStQnxdQf5dQn5dQn\n5dZan2ze3GFUc17TjFxkA4v7gesXOKcVeAD4LnAr8AjwgGVZLbVqh2kaGIaBaVbVfxuC+qSc+qSY\n+qOc+qSc+qTceu2TpgguLMs6BDwK7Fnk1HcCs7Zt/6bt+TUgAry93m0UERGR6jRFcAG8GvgmcCew\nUPh2O/BgybGHsu8TERGRJtAUORe2bX8699iyrIVOHcTLsyg0AhyuQ7NEZBVEklHuO36Ui5EhdnRs\n4z2H3k5HsL3RzRKRFWiK4GIJWoFEybEEEKr2Aqa58NyWz2cWfZXKfeLE46QjEZx4HCcRx4knvK+J\nBG4yiZvJ5P9Q8Lj4WBo3nX3uON7zTMY75jjgOOA6uK7rvZ79iuPiutmvjgOu652XfZw/VvAe1/HO\nMVtaGHzf+2m/fmXx6Gx6lr/4/t9w5tp5dnRs471H3lHVB6LruqQyDqmUQzLtkExl8l9TaYeM45Jx\nHDIZl7TjksnkHpd8zXjnua53zfxXABccXO9r9oDj4vWNd7jsPUXXIfeadwzAyb7RofA6c+cB+Pwm\nqVQmn5SWf0+2DcX3mLv3WPf3SLRcAWDq2jS///W/ouvqXfnrzl0nd93F/i5z/bBUy0mny/VRKQMw\nTAPXcZd13fL7LO99fZvC/Nrbb6K7I+T1jQOO4+I4Lq7rzj0uOZZ7XnrM+yflZvs9ez0391r2fbnv\nR/Z875iLAQRDAWKzSTIZp+jemey/U8dxcTKV2wQUfG/don5xKxwj+3M69zh/inc8/965zi3q54Kf\nJbfCsfyh7Alz5xRfv7B9bskxA+9zKffvufS98/99ixqQPaW4jwqeFf395+uTns1t/Ng7byQYXHlo\nsNaCizjlgUQImK32Aj09bRjG4okznZ01yxFdszLxOJETNtNnznL18hUSo6Mkxq6RHB8nM1t1lzeV\nTCRC5uQJuu96RVXnJ1MZIrNJorMpIrNJIrMpZuMpHrj8BS7FTwMwmZjmv3z3M+xNvo5YIk0imSGZ\nypBI5b463rG093y5HxLrVbhvvGguNOEb58JItGHtWYyBN5/syz7OPS99XHrMzB8zSp7PzQVXelzp\neTXn5J/Hovzdnz6snztZ1OULkzgpl+6BthVfa60FF0PAlpJjW4Ar1V5gfHxm0ZGLzs4WpqdjZDLO\n8lq5xjipFMnhYRJXLpO8coXk1RHiFy6QGBryRgpWwufDME0Mnw/D5wOfH8Pvyz83fD4wfZWPmSYY\nhvfVNMAwMfJfvdcwTS9YLDuv5PXsV19bOy133cXJc9eYiiaYjCaYiiaZjCaYjCaZmkkwPZNkKppk\nejZJMlXh7+9PEr75LEbB4NZYYphLzwytrK+qZBjg95n4TAPTMDAM72Dux9o0DDCyX7PnG3jnGdnz\nvbcUHMudl7texetUeG/2sWka+P0mmYz3q1fZe4raUHhPg3PmZqa5lP/7dfn6efmNg0X3zrWlUltz\n18F1cTMuhlvwK5+T/Y0yO8TiOmRHsbK/VWf/4BT85p1xcZIZnLQ3GuZmXNyMg5P9WpNhiFXWbIGF\nYXijOj7T+zdtmgamz/t5zj32jpt4/5S957mfTYP8g7kvRv6o97OSu1HBPb2vBf//Z38ui69T4foF\nFzYqHCu4RNk98g/naZ9hQDDoJ5XK4LpuhfcaJdcp6ANjrs2Fx0rfX/T7dOHfr6Rfeja3EWr1MzEx\nw3y6u6sLPNZacPEo8Jslx+4C/rDaC+SG4RaTyTik0+szuHDiceJnzxA7c9r7ap/AicXmf4NpEt6y\nBV9PD75NPfg3bcLf3Y2/sxMz3IIRCmOGQ5ihEGYojBEIZAMJX1WjRPWQSmcYnYxzdSLG1ckYVydm\nvccjMa49/QSZpa4n9ycJ7nkOs20acDFMp+TlbvYMdhAO+gkFfAT8JkG/STD3OGAS9PsI+k0CAV/R\na6HssYDPxOcz8JkGPp+JP/vVZ3rH/NnXzQb16UL8fpPu7jYmJmaW9O/GcRzGI9s4evwrXJm+ymB4\nC2/Y+8MECZGIp0kkUqQSGZKJNKmkN3WUTmZIJNIkE2nvnHiKRDxNulIg2GT8fhOf38x/9fnNog9Y\nw/QCqbnnRhXPmfuAzi5rNAoemyWP516j5Hnp6/Ocb+TuMRdYFgWqlc7NtjEQ8NHT08bk5Oy6/f91\nqZb7b6decr8grFTTBxeWZQ0AU7Ztx4F/AP6LZVn/HfhL4Jfw8jC+0MAmrglOPEbk8ceZfvRhYqdP\nQSZT8TwjECCweTPBrdsJ79pFeN9+2vfvo3egu2l++AslkhmGxma4NBrlzNVRnk99m5hvnEy0g+TZ\nGyAdrOo64aCPTe0hOtuCdLUF6WwN0tEWoKMlQFtLgO9M/RPnZ0crvtdv+PnDN/6ikhCzXNdlNpok\nMh1nJpIgMhVnNpokHk8Tm00Sm0kRm00Sj6UKAoIdDLIDgH97+MSqt9k0De+D3mfiD5iEWwK0tgcJ\nBHz4Az6CQR+hsJ9A0HseCPrw+334/NkA0Gdi+rKP/V4QGAz66e1tJxKNAdnfxpswMFxNuYBD1r9m\nDC5KQ6YrwPuAz9q2HbEs60eBvwB+EXgWeJNt2wv82r2xuZkMUw99n2tf+iKZaKT4RZ+P4OBWwrv3\n0HroEOG9+wj09nlTCgVMf+OTWyPJKJ957vNcjA7R5vbSM3U7V4ZTXJ2I5X9gggeewtftBQC+7jhB\nniN58jYMoKczTH93i/dnUwt9m1rY1B7MBxShgG/B+//Tg5UDC4CDPQc2VGDhui4zkQTTk3Emx2eZ\nHI8xPRnDybhMXJshOp2oeaXBYMhHIOgnEDC9D/uQn1DITyjsJ9TiJxQOeI/D/vwHvTekbnijPb7c\n47kP/8IRBNOs/c+432/S1hEimU43XVAuUm9NF1zYtu0reW6WPH8SuG1VG7UGuY5D5LFHuPbP/0Rq\ndO6DMbBlC52330mLdZDwrt2YoaoX2qwqx3V56fIIR09/ibHkCGknA/4kALNEGU7Pkpwo/jHwtRcH\nTx19MT5yz+30dbUQWGGAtKNjG1PXpueuHWjH7/exvW0r7z64/mq4ua7L7EySqYkY0xMxpkr+pJKV\nR74qMQxobQsSDPsJtwRoaw/R2hYk3BogGPIRDOZGBMzsaID3oR8M+Qm3+PEHGje9JiLL03TBhaxM\nemqSia//O5HHHyM9fi1/PLhlkM0/+x5aD13ftP9RT0QSPHfmGi+cHef4+QmS2x/1RiJyafUFAh0R\nXn5kCzsGOti+uY3tm9v53KnzPH/teP6cvZt2MNi78qxngPccentRLYb33fAOdg4MNOVUUbWSibQ3\nZTGTZGo8xrXRKONjs8xEEszOJMlU+fcKBH20tAZoaQ3SP9hBW0eI9s4Q7Z1hOjpDtLYH6zIyICLN\nS8HFOjL9yENc/bv7ipIzAwNb6P2Jn6Tjtpd7SZZNZmR8lseOj/D0yTHODxePPITbpuZ93/UDe/jA\nTcXb0JQGAO85VLsRhY5gOx+86f355/4mmCpailQyzYUz44xcnmby2izjY7NEpuJVvz8Y8tHV3UJX\ndytd3S1097Vmn7cQCgeaLilNRBpLwcU64KRSjB39PJPf+oZ3wDBoPXyErle+ivZbb8PwN9e3OZ5M\n8+SJUR589jIvXSoJIPxJ2q97EbNtmoyRpvBjymf4aA+0zRs4lAYAG00m4zATSRCdTjA+OsO1sRkm\nRmeYmowxG00u+v6OzhA9m9vo6GqhtS1AR1eYzmwAEW4JNO2Il4g0n+b61JElS45e5cpf/DmJc2cB\n8G3axOAv/BKt1sEGt6yY67qcHprm+89e5vETV0kUzNkbBuzbGSa99RnGnItk3AyVZvRb/S38v6/6\n3dVrdJOLzSa5eHaCS+cmGB2OMHltdtFEStNn0NIaZOfeHrp7W+nZ3EZrW5D2zjChsP47EJHa0P8m\na1jkqScZufev89MgrUduYMsHfgF/R2eDWzZnJp7iG8+c4VujD5AKTODEOkk6NwBBBnpaufvGQe48\nvIW/P/N3PH/t3ILX2tW5Y1Xa3Gwcx+XqlWmGL00TmYoxO5MkMhVndHjhKpbtnSF6+trY1NNKe1eI\n/sFO+gc7VNpeROpOwcUa5LouY188ysTX/tU7YBj0vfWn6H7jm8uWkTbKyMQsX3nM5qnYNzE6xjDa\nHAzAFxxlS+dJ3n/o59i/rSs/1H4xUrm6ZUegHdMwa55D0eyi03HOnx7n/OlrXL4wueDqjLaOIIPb\nu+jtb2dTTyut7UG6e9s0EiEiDaP/fdYY13UZufd/Mf3Q94HsNMgvfpDW6xbcTXbVTEUTfPG7Z3j4\n+WH8+5/M150o0jLFge2big6VLvX0G34O9hzYMDtkxmMpLp2b4MKZcS6dm2AmUro/n6ejK0xbe5CW\nNm9lxq59vfRsrm6/HBGR1aLgYo2Z/PY384FFcHAr23/9/8Tf2fhpkFgizVcfu8C/P30Stj9L8KZp\n8KcqnrujY1vZsUorPdZzUOG6LqPDES6cGefCmXGuXp6uuP9Dd28r23d3M7iji+27uwmFA6vfWBGR\nJVJwsYYkh68w9sWjAPh7e9nxG7+Fr6OjoW1yXZeHXjzP5099kUxoEtNyMYKVVyYUjkaU2ggrPeKx\nFCOXpzn54ggXz04Qny0PvlraAuzY08Pg9i627eqmq1u784rI2qPgYo2IPv0DRj73WdxEAkyTrR/6\n3xseWFwYu8b/ePI+ov4rGB0OlQbm/YaftkDrhhiNqCSZ8OpLnHxhhPOnr5WNThgGbNnexc69PezY\n00PfQLumOERkzVNwsQbETp3k8p/9Sf755ne8i/Cu3Q1rT8Zx+NcnTvLVyb/FCCYrBhU5B3sOrPsR\niULpVIapiRiXzk9w5sQoV69EypaH+gMmu/f3sdfqY/vuHiVeisi6o//Vmlxy9CpDf/JHgLdjad/b\n30H3a1/XsPZcuTbDXzzwNFf7vzbv9MdGW+GRSmU49eJVjj97hZGh6YrntLYHue7wAHutzfQNtGs5\nqIisawoumpjruoz8zWdwZmfAMBj8jx+i/eZbGtaebx87w/0v/QNsHcMwy0s8b6QVHq7rMnRhgu99\n/SVOnxitWLyqu6+VA4f62ba7m4GtnZruEJENQ8FFE4s8/hixE95GXD1v+bGGBRbpjMNf/tNz/Nvw\n0cpLS/FGK37n9o+s66DCdV2uXJrijD3K2ZfGiE4XLxft7m3luiMD9Pa309PXRntnSAGFiGxICi6a\nVCYWY/QL9wMQ2LyZnjf/aEPaEUuk+dQ/Pc8LZ8cJ31x5I7H1HljMRBKcsUd5/gdDTI7Hil4zfQbW\nkS3sua6PnXt7FEyIiKDgomld+8cvkpnyPsz73/2/YQaDq96Gq5Mx/uQfnuXy2Az4kxiBdNHrBgaH\new+u22mQyfFZnntyiBPPXina6dPvN9m1v5cbb9tO/9YOTOVPiIgUUXDRhGKnTuZ3OG278Sbajtyw\n6m04NTTFn/zDs0RjXi2GwVttJinOs2gPtK27lSCZjMP5U9ewnx/m/KnipaO9/W3c+LLt7DvYT0tr\nQFuMi4jMQ8FFk3Edh6v3fw4As6WFze9696reP5KM8mdP3MeFyBDO9k6MszfwznsO80D0G5TEFutq\nIzHHcTl1/CpPPniOqYm5qQ/DgP2H+rn59p30Day/0RkRkXpQcNFkph95mMT5cwD0/sRbCW7uX7V7\nR5JR/uCh/0bCjWEEvU3Gdg+e5013vJkHvlF8roGxLpaZZtIOJ567wtOPXiQyFc8fb2kLcODQADe8\nbBudm1QlU0RkKRRcNJF0ZJqxf/g8AMEtg2y657Wrev8/fuxvSbjFCYvTjrc65ODmAzw3cjx/3Ore\nv6bzLFLJDC8eu8yxxy4yE52r19HV3cLL7trF/usHME0lZ4qILIeCiyZy7Z+/TCYSAWDzO9+F4a//\ntyeSjHLf8aOcnrjAbDqGUZKbmNtk7FfveD9//NBnuDA9tKaLY8VjKV585jLHnrhUtLdHb38bt9yx\nk30HN2M2ybb1IiJrlYKLJpGJRvO7nba/7OW0HbmxbvfKBRQXI0M4rkMkFQUoCyw6Au35IKIz3MGH\nb/3Amk1edByXJx86x9OPXCgqeNW/tYPbXrmLXft6tYxURKRGFFw0iYmv/xtu0huer3dNi3tfuJ8T\nEycrvuYzfLQH2tbVRmNTEzG+9cBxhi/NlebeunMTt71yF9t2bVJQISJSYwoumkAmGs0vPW05eIjw\nzl11u1ckGcWeODXv64d6rls3y0vTqQzPPnmJpx46nx9x2bKtk7tet5/+wc4Gt05EZP1ScNEExh/4\nCk7MS6Tse+tP1eUeuamQE+MncSneB8N1od3fzp5NO9ZsLkUh13WxnxvmiQfP5Ut0m6bBTa/Ywcvv\n3q1Nw0RE6kzBRYNlolEmv/ttANpvuY2Wffvrcp/7jh/l+WvHK762JbiT37/7w3W572qLzSb53r+d\n5Iw9twfKlu2d/NDrr6O3f+1P8YiIrAUKLhps+uEH53ItfvTH6nKPSDLKifHKORZ+N8yvveK9dbnv\najt/+hrf/MpxEnGvTHkw5OPu11/Hgev7lVchIrKKFFw0kOu6TH3/ewCE9+4lvGt3Xe5z7wv3k3aL\n9wVxHZOW5BZ+/7UfoDPUUZf7rhbXdXnyofM8+eC5/LFd+3r44R+7nlBYP+IiIqtN//M2UPz0KZJX\nLgPQdfer63afU5Nnip67LoRPvZ7fffdddIVDdbvvakjEU3zzKyc4f/oaAOEWP6/90UPs2tfb4JaJ\niGxcCi4aaOpBb9TCCIXpePkr6nKPSDJK2s2UHf/Qj95Gd8faDizGRiJ87Usv5Mt29w928PqfPExH\nV7jBLRMR2dgUXDSIm8kwc+wYAO233IIZrs/+Ffe+cH/ZMdMw2b+9qy73Ww2ZtMPTj13gqYfO5wti\nXX/zIK963QF8fq0EERFpNAUXDRI7+RKZiFfUqeO2l9ftPqVTIgBW97663a/eopEEX7n/GSbHvaW7\nfr/Jna/dx5FbtzW4ZSIikqPgokGiT/8AACMUovXIkbrdJ+OWl+t+3+F31e1+9RSbTfKVvz+WDyw2\nb+ngdT9+iE09rQ1umYiIFFJw0QCu6+aDi7YjN2AGgvW7V8lzH+aaLOmdiKf4l88/y+S1WQBufeVO\nXv6qPdq5VESkCWmCugHiZ8+SHvdWN7Tfcmvd7nNudAzXKQ4vwv765HbUUyqV4YGjzzE24m2wdtMr\ndvCKuxVYiIg0K41cNEDk8UcBMPx+2m66pS73cF2XP3vqbzFKBkXMNVZMKjab5N//6UVGhrz8lEM3\nDXLna/aqKJaISBNTcLHK3EwmH1y03XQzvpb6jCQ8ZY8y4x+m9CN4V+eOutyvHsZHZ/jqF59jetJb\narr7QC+vfuN1CixERJqcgotVNmufIDOdXSVy+511uUcskea+bz0HVmnGBWtmY7LTJ67y7X+1SSW9\nGh37D23mNW85qMBCRGQNUHCxymaefQbwVom03XBjXe7xr4+eJz7wA3wln8M+fE2fzOm6Lo9/7yw/\neOQC4O1meudr93HDbdsUWIiIrBEKLlbZ7IsvAtB66HrMQKDm1x+bjPHvT1zEd2Sq7LUD3Xtrfr9a\nSiXTfOerL3Hq+FUAQmE/b/ypI2zdsanBLRMRkaVQcLGKUqOjJC8PAdB2/eG63OPz3z5Fijg+f6ro\nuM/wNXV9iyuXpvjWvxzP51f09bfzpp8+QnunSnmLiKw1Ci5WUfS5Y/nH9Vgl8vTZIZ5zvkb45msY\nZnG+Rau/pWmnRM7Yo3z9yy/mS3nvO7iZ17z5IIGgr8EtExGR5VBwsYqiTzwOQHDbdgK9td2103Fd\nPvvi3+PrHq34ejOuEnFdl+eeHOKRb5/GcVyCIR93v/46Dlzfr/wKEZE1TMHFKnHicWKnTwG1L5wV\nSUb5syfvIxEeKVt6CtARaG+6VSKu6/Kdr9qceHYY8PYIedNP3cDWncqvEBFZ6xRcrJL42TPgePt8\ntNY43+K+40e5GD9DpV/2j/Qe4j2H3t50UyJPfP9cPrDo7mvlDW89Qnev9ggREVkPFFysktipk94D\nn4/w7j01vfapifMVjx/sPsAHb3p/Te9VCyeeG+aph7029w2085PvvplAUD+KIiLrhf5HXyW54CK8\nazdmsHYblTmuSzyZLvpOGhgc7j3YdFMhAMcev8jD3zoNQHtniDf99A0KLERE1hn9r74KXMchns23\naNl/oKbXfvyli7i+ZFGuhYnZlCMWLz0/zCPf9gKLUNjPG956mPaOUINbJSIitdYUwYVlWSHgU8Db\ngFngE7Ztf3Kec98K/GdgB/A08Ku2bT+9Wm1djuTQJZy4V78hXMPgwnVdvnD6KEZJKYhmXGlx/vQ1\nvvkvJwAIhny89eduVY6FiMg61Sxbrn8cuBW4B/gQ8AeWZb2t9CTLsq4HPocXXNwIHAMesCyrqSst\n5fMtgJZ9+2tyzUgyyice/yvioZGy1/Zvqm1Ox0pNjM3w7X/1AotwS4CffPctCixERNaxho9cWJbV\nCnwAeINt28eAY5ZlfQz4MPClktNfDzxv2/bnsu/9LeCXgeuBH6xeq5cmF1wE+gfwd3Wt6FqRZJT7\njh/lxPhJ0m66bIWIgdFUlTij03H+8b6nScTTALz2Rw/S299cK1dERKS2Gh5cADfhteORgmMPAr9d\n4dxrwGHLsl6ZPf/ngSngdL0buRKxfL7Fykct7jt+lOevHZ/3dat7f9MsO3Ucl+9+7aV8YPGqH9nP\nrn21LR4mIiLNpxmCi0FgzLbtdMGxESBsWVavbdvXCo5/HvhxvOAjk/3zFtu2y3fpahLpyQnSY2NA\nbfItLkQuVTzuN/wc7DnQVCtEnnroHBfOjANw5NZt3HDb9ga3SEREVkMzBBetQKLkWO556VKCXmAL\nXl7GY8AHgXsty7rFtu2xam5mmgamOX/Co89nFn1dqdkzc4MqHZaF37/860aSUWZSs8UHXbhh8yHe\ne+QddRuxWE6fXL0SKaplcdfr9q3o795sav1zstapP8qpT8qpT8qt1z5phuAiTnkQkXte8knK/wc8\na9v2pwEsy/qPwHHg/cB/q+ZmPT1tVa2m6OxsqeZyi5q8dA4AX1sbA9fvxzCX9wM0HY/w/3z3E2Tc\nTNHx9mA7v/fDv7LSZlal2j5JxNN88yuP47peWe+f/Q+3s6lnfSZw1urnZL1Qf5RTn5RTn5Rbb33S\nDMHFENBnWZZp27aTPbYFiNm2PVly7m3AH+ee2LbtWpZ1DNhV7c3Gx2cWHbno7GxhejpGJuPMe161\nJo7bAIT37GVyKrbs6/zRU/+T6USk7Pierh1MTMws+7rVWEqfxGMp/vXoc4xdjQJwxz17cQ237m1c\nbbX+OVnr1B/l1Cfl1Cfl1lqfdHe3VXVeMwQXzwAp4A7g4eyxu4EnKpx7GW9lSCELeLzamzmOm9/a\neyGZjEM6vbJvtJvJED/vTQ2Edu9Z0fVOjpfnrIbNVt598O0rbme1FuuTTMbhy/c/w9XLXhC0/9Bm\njty2bdXa1wi1+DlZT9Qf5dQn5dQn5dZbnzQ8uLBtO2ZZ1meBT1uW9fPAduCjwHsBLMsaAKZs244D\nfwV8xrKsJ/FWi/wCsBP4m4Y0fhGJixdxk0nAG7lYiYxb8kPnwu/f8dGmWRkC8Oh3zuQDi4M3bOHV\nb7KasqCXiIjUV7NkkHwEeAr4FvCnwO/Ztv3l7GtXgJ8BsG37C3j1L34br67FncBrqk3mXG2Ji3Mb\niq1ks7JIMopL8WiLYRh0hTuWfc1aO3dyjGef8FaybN25iVe/6boFp59ERGT9avjIBXijF3hJmWUb\nYti2bZY8/wzwmVVq2ookhoYA8HV0rqh41r0v3F92bE9H81ThnBib4Zv/4tXeaGkN8CM/cT3mMhNX\nRURk7WuK4GK9SmaDi+C2bSu6zqnJM8UHXPjFm96zomvWyvjoDF/+u6dJJjIYBvzIT1xPa1vtdn0V\nEZG1R79e1lFy+DIAoa0rCy5Kl59i0BS5Fo7j8u2vniAe88qQ3/3669i2q7vRzRIRkQZTcFEn6elp\n0hMTwMpGLrx8i+b01MPn8wmcL797D4dv2drgFomISDNQcFEnyctD+cehHVWX4Shz3/GjZcd8+JZ9\nvVo5f/oaTz54DoDNW9q5+fYdjW2QiIg0DQUXdZK4eMF7YBgEBweXfZ1Ke4kc6F7ZstaVSqczPPh1\nb6fX1vYgb3zbkXVXulZERJZPnwh1ksiOXAQ29+NrWX5Z19L6Fj7D1/At1R//7lmmJ+MA3PmafbR3\nhhvaHhERaS4KLuokedlL5gxuXVkeQixVUjLcdRuazDl0foJj2XoWO/b2cOD6/oa1RUREmpOCizpw\nXZfklWxwsWX5UyKRZBSH4pELp4HpnYl4mm8/cAKAUNjPa96sCpwiIlJOwUUdZKancGa9DV1Xsgy1\nUvEss4Hfsu9//SSR6QQAr37jdbS1l25mKyIiouCiLnJTIrD8aZFIMoo9carseKOSOV96cYTjx64A\nsO/gZvYd1HSIiIhUpuCiDhJXCoKLZU6L3Hf8aPl+IhgNSeZ0HIdvPuCV925rD/LqN1636m0QEZG1\nQ8FFHeRGLvw9vZjh5a2kqLQE1ere35Bkzoe/dZrRYa9Y1svu3k0oHFj1NoiIyNqh4KIO8smcK1gp\nks4Ul/wUAWBMAAAgAElEQVRu1BLUq1emefrRiwAMbOvk4A3LT1AVEZGNQcFFHeRGLkKDy8+3mM3M\nFh90V38/EcdxeeTb3qZpfr/JG996WNuoi4jIohRc1FgmGiUTmQYguMzgotIqkUYs+Xz60QtcvjAJ\nwB337KNz0/KLgYmIyMah4KLGkldWvlLkZOkW68D+TXuW3abliMdSPPOYNx2yeUs7r/4RJXGKiEh1\nFFzUWKJwGeoyRy7KtliHVc+3eOy7Z0gm0oC3lbrPrx8VERGpjj4xaix5xdtTxNe1CV9b2/Iu4hZP\ngfgwVzXfYnhoKl/TYv+hzWzbuWnV7i0iImufgosay+8pssydUIcmJ3Dd4voWYf/q5Tq4rstj3zmD\n60Iw5OPO1+xbtXuLiMj6oOCixpJXvN/4Q8vMt/jrZz+HUfJdMVcxmfP86WtcvjgFwM2379SOpyIi\nsmQKLmooE4uRnhgHIDi49D1FIskoI6kLZcd3de5Ycduq4bouj37HSyZtaw9y48u3r8p9RURkfVFw\nUUNFK0WWOC0SSUb5w8c+ASWDFAYG7zn09lo0b1Ennh1mYsyrr3HzHTsJBHyrcl8REVlfFFzUUPGG\nZUsbubjv+FGiqZmy46tV8judzvDEg+cA6O5t5fAty68uKiIiG5uCixrKjVyY7e34OjqW9N5Ke4l0\nBNpXbQnqi09fYSbibad++z178fn0oyEiIsujT5AaygUXocGtS6qoGUlGmUkVl/v2GT5+5/aPrMqo\nRSqV4ZnHvFyP/sEOdu/vrfs9RURk/VJwUUP5DcuWWDzr3hfuLyuc1epvWbXaFi8+c5mZaBKA2+7a\n1ZBS4yIisn4ouKgR13FIXbsGQKC/f0nvPVWh3PdqrRDJpB2efcKbkunf2sGufRq1EBGRlVFwUSPp\nyQlwHAACvX1Vvy+SjJKuUO57tVaIvPDMZaLTXq7Fza/YqVELERFZMQUXNZLOjloA+Hur++0/kozy\nnx/7ZNlxH75VmRJJxFM8mV0h0jfQzl6r+qBIRERkPgouaiQ1PhdcBHqqCy7uO36USCpadvxA996a\ntWshJ54dJhH3Nie74569GrUQEZGaUHBRI7mRC8Pvx9fZWdV7Grn8NJXK8HR2hcjA1k627+6u+z1F\nRGRjUHBRI7lkTn93D4ZZXbdmXKfoueGaq7b89IUfXCY2kwLgZa/arVELERGpGQUXNZIPLqrMtwCI\np2LFBwxWp65FsmDUYlsnO/Zo1EJERGpHwUWNpMfHgOrzLSLJKBmckqNuxXNr7fmnh4jPeqMWL9eo\nhYiI1JiCixpwXZfUNW831GpHLu594f6yY+YqfDtSyQzPPHoRgC3blGshIiK1p+CiBpyZGdxEHKi+\nxsWpybNlx1ZjlcjzPxgiHsuOWtytUQsREak9BRc1ULQMteqci/IpkHqvEknEU/zgkfMAbNnexbZd\nGrUQEZHaU3BRA0UFtKrMuQj6QkXPW33130vkqYcvkEx41UDvVF0LERGpEwUXNZAqCi4WHw2IJKPM\npot3QU1kkjVvV6GpiRjPPeXV1dhzoI8t27vqej8REdm4FFzUQDo7LeLr6sIMBBc9v1IyZ71HEZ58\n8BxOxsUw4PZ79tT1XiIisrEpuKiB1LXsMtQq8y0q7YK6f1P9PvCjkQQnXxwB4OCNg3T3ttXtXiIi\nIgouaiA9nl2GWmW+RWllTqhvMueJZ6/gZvNHb7ljZ93uIyIiAgouamKpIxcmxVMgPsy6JXO6rsvx\nY1cA2L67m67ulrrcR0REJEfBxQo5qSSZ6WmgupGLSDJatgg17K/fB/7Q+Umi0wkADt64pW73ERER\nyVFwsUK5KRGoroDWvS/cj1NS9tusYzLn8We9UYtgyM+eA9UV+BIREVkJBRcrVLgMtZppkUrJnLs6\nd9S0TTmJeIqz9igA1x3uxx/w1eU+IiIihRRcrFB6fGkFtDJupuzYew69vaZtyjn5wlUyGW8S5uCN\ng3W5h4iISCl/oxsAYFlWCPgU8DZgFviEbdufnOfcG7Ln3gacBH7Vtu3vrFJTy+RGLsxwGLO1dcFz\nK+VbQP22WT/x3DAAff3tbN7SUZd7iIiIlGqWkYuPA7cC9wAfAv7Asqy3lZ5kWVYn8O/A88AR4B+B\nf7Qsq2HJBOnsShF/T++ihbDuO3607JiP+kxVjI1EGR2OAGDdoEROERFZPQ0fubAsqxX4APAG27aP\nAccsy/oY8GHgSyWnvw+I2Lb9wezz/8uyrDcBLwO+tkpNLpLKJnRWk29xIXKp7Fi9dkJ94vverqs+\nv8mBw/11uYeIiEglDQ8ugJvw2vFIwbEHgd+ucO6rgS8XHrBt+/b6NW1xhSMXiyktnuUzfHUpnhWd\njnP+tDddc/jmrbS0Ll6SXEREpFaaYVpkEBizbTtdcGwECFuWVfqJvRcYsyzrLyzLumJZ1sOWZb1y\n1Vpawk2n8zkXgc2bFz0/noqVXMCtS77FU49cyFfkPHLb1ppfX0REZCHNEFy0AomSY7nnoZLj7cBv\nApeBNwLfA/7dsqxtdW3hPNJTU+B4oxGLBReRZJRMSX0Lp2J658pEp+OcyFbk3H+on67uhZNMRURE\naq0ZpkXilAcRueezJcfTwNO2bf/f2efHLMt6PfBzwH+t5mamaWCa8yde+nxm0deFJCNTcw3u6cHv\nn/89f3Ps78vbYpgLvmc5XnjmMo7jBS2vuHt3Ta6/lD7ZKNQnxdQf5dQn5dQn5dZrnzRDcDEE9FmW\nZdq2nfvVfgsQs217suTcK8CJkmMvAVVXoerpaatqe/POzsVLcjvpuWmO3l1bCXfPv9voqYny4lnX\n919H9wLvWapkIs3xZ7xRC+vwAPutgZpdG6rrk41GfVJM/VFOfVJOfVJuvfVJMwQXzwAp4A7g4eyx\nu4EnKpz7KPBDJccOAp+r9mbj4zOLjlx0drYwPR0jkynfvbTQ5KXh/OMZI0hsYmbec123eArEAN57\n6B1MLPCepfrev71EbDYFwMGbBmt27aX0yUahPimm/iinPimnPim31vqk2l+IGx5c2LYdsyzrs8Cn\nLcv6eWA78FHgvQCWZQ0AU7Ztx4FPAx+2LOv38QKK9wJ7gPuqvZ/juPlpg4VkMg7p9MLf6OT4BABm\nezuO4cOZ5/xIMopTEly0+ttoMVsXvUe1pidjPPukt9R1z4E+Bnd01ezaOdX0yUajPimm/iinPimn\nPim33vqkWSZ5PgI8BXwL+FPg92zbzi05vQL8DIBt2xeANwA/DjwHvAV4s23bV1a9xUB60pu18Xdt\nWvC81dis7NTxq/kVIq/84X1VTf2IiIjUQ8NHLsAbvQDen/1T+ppZ8vwRvKJZDZeeygYXm+YPLiLJ\nKPbEqbLjtdyszHVdXnphBIAt2zrp3LS+5u5ERGRtaZaRizUpP3KxqXvec+594X5cSvMtjJpuVjZy\neZqJMW9hjUp9i4hIoym4WIH0pJdzsdDIxanJs2XHrO79NS2e9WJ2hYg/YLL/kEp9i4hIYym4WCYn\nlcSZ8VZj+Lu6FjjTLXtay5LfyUSa08evAnDg+gGCoaaY6RIRkQ1MwcUyZSbnCmj5FpgWCfqK64MF\njXBNRy1OnbiazzA+dNNgza4rIiKyXAoulimXbwELT4sk0vHi95GsaTtefNqbEunubaV/sKOm1xYR\nEVkOBRfLlFspAgsHF6VLUF1qt4555PI0o8MRAA7fslXLT0VEpCkouFimopGLzso5F5FktGxrslpu\nVfb8D4a8+wdMrjuiVSIiItIcFFwsU26liK+jE8NfOYny3hfuLzvmw1eT+8dmk/lEzuuObCEUViKn\niIg0BwUXy1RNAa1Ky1APdO+tyf1PPDtMJuONgxy5ZWtNrikiIlILCi6WKZOdFvEtWPq7fBKkFstQ\nXdflxWcuAzC4vYve/tqtPhEREVkpBRfLNFedc/7gonQZaqu/tSbLUC+dm2B60luFcuhmLT8VEZHm\nouBimaqpzlm6DLX0+XIde/wiAOHWAPsObq7JNUVERGql6uDCsqyPWZZV3Ubu65yTSODEYsDCO6KW\nLkMtfb4cVy5OcvGsF9gcuXUbfn9tEkRFRERqZSkjFx8FioILy7IesCxrw43LV1NAq17LUJ9+9IJ3\n34DJkVuVyCkiIs1nKcFFpQpNPwRsuP29iwpodVcu/X3f8aNlx1a6DDWVTHPpvHfvQzcO0tIaXNH1\nRERE6kE5F8uQqWLk4kLkUtmxlS5DPW2PkcnuI7L/eu1+KiIizUnBxTKkI9P5x772yvt5ZNzi/Aqf\n4VvxMtSXnh8GoKu7hYGtnSu6loiISL0sNbiolDZQy4rWa0JmytsR1dfeMW91zngqVnzAdVe0DHV6\nMsZQdkrEOjKgfURERKRpLbVm9J9YllX4qRkCPmZZVqTwJNu2f37FLWti6Vxw0VV5TxGo/UqRZ7LL\nTw0DDhweWNG1RERE6mkpwcX3gNLdsR4C+rJ/NoxccDHfhmVQPpyzkuGdTNrh5AsjgJdr0blpw+XQ\niojIGlJ1cGHb9j11bMeakpnOjVysTt7DSy+MkExkADh4g3Y/FRGR5rbsrTQty2oFuoAp27Zna9ek\n5pcfuZhnWiSSjJYdW+4yVMdxeOqhcwBs6m1l267KS19FRESaxZKCC8uyOoBfB94F7C04fhK4D/jk\neg80XMfJj1zMV52z0lbry12GOnR+ksh0AoCXv2q3EjlFRKTpVR1cWJbVi5d3sQP4R+AvgEm80Yvb\ngN8CfsayrLtt256qQ1ubQiYSAdfLoJgvofPU5Jmi5wbL3w319IlRAAJBH3uu21CpLSIiskYtZeTi\nP+EtXT1s2/bF0hcty9oOfBWvTPjv16Z5zSc3agGVEzojyShpN1Ny1FjWMtRUKsPpE1cB2HtdHz6f\nypKIiEjzW8qn1VuAX68UWADYtn0J+F3gnbVoWLPK5VtA5ZGLSlMi5jJrldnPDucTOa87okROERFZ\nG5byqTcAPLfIOceAnctvTvPLROZKevg7ileLRJJR7IlTZe9ZTr6F67o8//QQAH0D7WzbNf/uqyIi\nIs1kKcFFEIgtck4MCCy/Oc0vM5NdCWIYmG3FO9Dfd/wobklFCwNjWfkWYyNRJsa83NjDt2xVIqeI\niKwZmsRfokzUG7kwW1owzOLuq7RZmdW9f1n5FhfOjANeRc59Bzcvo6UiIiKNsdQ6Fx+1LGtmgdeX\nv3nGGpGbFvF1lG9YVrpZmYG57FUi509dA2Bgayeh8LoeDBIRkXVmKcHFBeBnqjxv3ZoLLsqrc5Zt\nVgbLGrWIzSYZueztvLpby09FRGSNWUr5790AlmW1ATHbtvO/pluWdT1w1rbtxXIy1ryFRi5KNydz\nl7lZ2eULk/nHO3arIqeIiKwtS8q5sCzrncBZ4JaSl/47cMmyrLfWqmHNKj09/6Zltdp7/uzJMQDC\nLX56+9f9TJOIiKwzVQcXlmXdg1fi+yvAUMnLvwr8M/AFy7JeWbPWNaHMtDdd4eusz6ZljuNw/pSX\nzLnX2qxVIiIisuYsJefit4A/tW37/yh9wbbtE8D7Lcty8QppvblG7WsqTiqJE/Nmfvyd5TUuSi1n\ns7KLZyZIJtIA7N6vfAsREVl7ljItcgvw14uc8yng1uU3p7llpucKaJUmdNZqszL7+WEAWloDbN+j\nfAsREVl7lhJchFm8iNY40Lr85jS3on1FSkp/l25WBkvfrCyTcbh0bgLwpkS0l4iIiKxFS/n0soE7\nFznnlcD55TenueWrcwK+9rlEy8qblS19Geq5k2Mk4t6UyK59vctspYiISGMtJbi4D/hPlmVtrfSi\nZVnb8HZO/UItGtaMMjNz9cPMtrnAodKUyHLyLc685K0SaesIsmNvzzJaKCIi0nhLSej8H8BPAy9Y\nlvW/gIeBCaAXuAt4H/AS8PEat7FpFAYXvta52Z9Tk2fLzl1qvkUm43DhtLdKZNf+PkxTq0RERGRt\nqnrkwrbtDPA64K+A9wJHgW8AnwfegRd8vHo9F9LKFdAyW1ow/IVxWUmFC3fp+RYjQ9Nzq0Q0JSIi\nImvYkvYWsW07AfyGZVm/DewFeoBR4Ixt27WqIdW08jUuClaKRJJRHLf4r+43QsvKtwDw+01try4i\nImvaUjcuA8C27TTeFMiGktsRtbD0970v3F9W9tu/xHwL13Xz+RY79vTgDyw9X0NERKRZaK3jElTa\nV6TSEtStbRVzXud19UqEyFQcgL2WCmeJiMjapuBiCSoFF5mSJaiuCz93fTWbx845fWLUu67PYPcB\nBRciIrK2KbhYglxw4S/IuShNNDGA/o6l5UxcOHMNgO17egiGljVTJSIi0jQUXFTJdZx8Ea1K260v\nV3Q6zsTYLAA7VdtCRETWAQUXVcpEo96cB8XBha+sC5dWnyJX7htgh/YSERGRdaApxuAtywrhbXr2\nNmAW+IRt259c5D27geeAt9i2/b16tzETmc4/LlyKGvKHmU3P5p/7jeCSrnvxrBdcdHSF6dzUssJW\nioiINF6zjFx8HG831XuADwF/YFnW2xZ5z5+zipuk5fItoHjkIpGOF59Hqupruq7LpXNeVc4de7ox\nDFXlFBGRta/hwYVlWa3AB4BfsW37mG3bXwY+Bnx4gfe8G1halaoVykTLNy2LJKNkSmpcuCXPFzI6\nHCEe86py7tijfAsREVkfGh5cADfhTc88UnDsQeD2SidbltUL/FfgF1lqgsMKFO0rkt20bKUbluWm\nRAwDVeUUEZF1oxmCi0FgLFv1M2cECGcDiVKfBO61bfv4qrQuy8muFDH8foygl1ex0g3LzthefYuB\nbV2EwoEatFJERKTxmiGhsxVIlBzLPQ8VHrQs63XAK4FfWO7NTNNYcMdRn88s+prjxrykTV97O4GA\nz5sSKSmghQv/4aZ34/cvHrNNTcQYG/EClgPX91f1nkaZr082MvVJMfVHOfVJOfVJufXaJ80QXMQp\nCSIKnueXYViWFQY+DXzQtu3kcm/W09NWVeJkZ2fxyo2xpJe4GezqpLu7jT/7zl/jlpTQ6ja2s3Ng\noKp2HH9mOP/41lfsoqu7+VeKlPaJqE9KqT/KqU/KqU/Krbc+aYbgYgjosyzLtG07lw25BYjZtj1Z\ncN4rgD3AFy3LKowOvmpZ1t/Ytv2ham42Pj6z6MhFZ2cL09MxMpm55MzZMW9VB61tTEzM8OLV4n3b\nXBde2fVGJiZmqMZzT18CYMu2Thycqt/XCPP1yUamPimm/iinPimnPim31vqku7utqvOaIbh4BkgB\ndwAPZ4/dDTxRct5jwIGSY6fwVpp8o9qbOY6L4yy+O3wm45BOz32j09k6F2ZbB+m0Uz4lAuzs6S16\nz3yi03FGhrzr7bmur6r3NIPSPhH1SSn1Rzn1STn1Sbn11icNDy5s245ZlvVZ4NOWZf08sB34KPBe\nAMuyBoAp27bjQNEWpJZlAVy2bXus3u3M7yvS6dW4qBSebOmpruzG+dPX8o/3XLd5xW0TERFpJs2S\nQfIR4CngW8CfAr+XrXcBcAWYb5vRxYcgaiS/I2r7/PuK9HSFq7rW+dPeFMum3tY1kWshIiKyFA0f\nuQBv9AJ4f/ZP6WvzBkC2bVdfVGIF3HQaJ+4ldJrt7USS0bJzDNfArCJRNJNxuHzBSyXRRmUiIrIe\nNcvIRVMrLqDVVrF4VlumulUiF8+Mk0p6+RqqyikiIuuRgosqFJf+7uDUZFHqB64Lt4ReX9W1zp3y\n8i1CYT/bd6sqp4iIrD8KLqqQmSkILtraK64U2dFTqZhoMcdxOH3Cq8q5c18PpqnuFxGR9UefblVw\nCoOL9rZlrxS5cnGKZMKrcr7/UH+tmiciItJUFFxUoTDnwmyrvBlrfxWrPs6+5K2Y9ftNtu3qrk3j\nREREmoyCiyrkcy58Psxw5eWmHa0Lbzzmui5nT3rBxY69PQQCq7LQRUREZNUpuKhCbuTC19pGNFVe\npttwjUX3KxkfnSE67e3HtudAX+0bKSIi0iQUXFQhl3Pha29f9jLU3CoRw4Bd+xdP/hQREVmrFFxU\nITdyYba1VVyGenNw8WWoucJZ/Vs7CbcsPIUiIiKylim4qEIu58LXXnkZ6rbuhZMzMxmH4aEpAAa3\nd9W+gSIiIk1EwUUVCnMuKi1D7etaeKXIyNA06ZS329323VolIiIi65uCiyoU5lxUsnmRZaiXzk0A\nYPoMtmjkQkRE1jkFF1XIjVykwxVyJVyDno7Qgu+/eM7bBXXLti4tQRURkXVPwcUinGQSN5kE4NGp\nF8teN2f78Pvm78bZmSRXL3vbtW/bpb1ERERk/VNwsYjC6pwXnWtFr7kubJu5a8H356ZEQPUtRERk\nY1BwsQinYEfU2QqzIv2dC49GXDrrTYm0dYTo2dxW07aJiIg0IwUXiyjcETUWKq/C2dtZuRx4zvDQ\nNABbd3YtWsVTRERkPVBwsYjC4CIeLO+uhZahzs4kmZqIAV4yp4iIyEag4GIRzsxs/nE6WLLSw4W+\nrvlHLoYvTeUfq3iWiIhsFAouFpGJZYMLnw8zXDJKkfHTu1Bwka3KGQz56O5TvoWIiGwMCi4W4eT2\nFWlpIZFJFL/oS9O9QI2L4UtevsXA1k5MU/kWIiKyMSi4WIQT93ImfC0tODhFrxkG89a4SKcyjA57\n9S2UbyEiIhuJgotFZGJecGG2tFbcV2Q+V4cjOI73DpX8FhGRjUTBxSKcfHCx8P4hpa5c9PItDAMG\ntnbUvF0iIiLNSsHFIhYMLhZIo7hwxqvmObCtk0DQX4+miYiINCUFF4vIBRdOsLw8pzFP9yXiKUay\nxbN27u2tX+NERESakIKLReSCCzt2oey1Ha27Kr7n0rlJ3GyCxs69PXVrm4iISDNScLGIXHBx1YkU\nHXdd+NkDP1PxPedOjgEQbvHTN9Be3waKiIg0GQUXi8gtRU1U2LRsW3f5qITruvmdUHcf6NN+IiIi\nsuEouFiAk0riptMAJALFXWVAxcJYkak4szNJAAZ3LLxjqoiIyHqk4GIBTiyef5wMVDcCMTYyt9HZ\nwKCWoIqIyMaj4GIBTmxu07JUoLSrKgcbuc3KgiEfXT2t9WqaiIhI01JwsYDCkQvCxRuU+Y1gxfdc\nyQYXW7Z1aT8RERHZkBRcLKBw5CJqpopey5AqPZ1UMp3fT2Rwh0p+i4jIxqTgYgG5lSIA8ZLVIm7J\nJmYAI5en8/UtBrWfiIiIbFAKLhaQmZ0LLhLBxac4Ll/wpkR8PoP+wc66tUtERKSZKbhYQOHIRdK/\neHCRy7foH+zE51fXiojIxqRPwAXkqnMaoSBuSXKmD1/R80zGYeSyt5+I8i1ERGQjU3CxgFxCZ8zn\nlr12oHtv0fOxkSiZtJeHsUX5FiIisoEpuFhAbinqrL8kedOF9x1+V9GhyxcmATAMbxmqiIjIRqXg\nYgG5kYuy6pwGdASLNyS7ctHLt+jtbycU9q9K+0RERJqRgosFZLIjF4uV/nZdl5ErXr6FRi1ERGSj\nU3CxADfhBRelm5aVmokkiM96RbU2az8RERHZ4BRcLCCTXS2SWmTkIleVE2DzQPsCZ4qIiKx/Ci4W\nkKtzkSqpWWGWdNvVbHDhD5h092mzMhER2dgUXCzAiXvTIk6ouPZ32F+8idlwNpmzr78d01SXiojI\nxqZPwgW42eAi5ssUHU+k53ZLTaczDGeLZ23b3b16jRMREWlSTbFm0rKsEPAp4G3ALPAJ27Y/Oc+5\nbwH+ENgPnAZ+z7btr9S6TW46jZtOA5Ao6SWHuaJao8NRnIz3fKsqc4qIiDTNyMXHgVuBe4APAX9g\nWdbbSk+yLOtG4IvA/wRuAv4S+AfLsm6odYMyC+wrUphzMTzkTYkYBtqsTEREhCYYubAsqxX4APAG\n27aPAccsy/oY8GHgSyWnvwv4pm3bf5Z9/inLsn4c+BnguVq2y5mZzT9OhIpjsMLS38PZzcp6N7cT\nDDW8O0VERBquGT4Nb8JrxyMFxx4EfrvCufcCwQrHaz4fkZmJ5h/HS7Zbz5X+dl2X4SEv32Jgu0Yt\nREREoDmmRQaBMdu20wXHRoCwZVm9hSfanvwIhWVZh4EfBr5R60blalwAJAuKaIWMcL709/RkLF88\nS5U5RUREPM0QXLQCiZJjueeh+d5kWVYfXv7F923b/udaNyq3DBWKy3+n3GT+8ZVL0/nHW7Zp5EJE\nRASaY1okTnkQkXs+SwWWZQ0AXwdc4O1LuZlpGpjm/BU3fb5svJWcCyIKEzodHPzZolpXs0tQ29qD\ndPe2YhgLV/Jcq3J9ku8bUZ+UUH+UU5+UU5+UW6990gzBxRDQZ1mWadt2bm/zLUDMtu3J0pMty9oG\nfAvIAPfYtn1tKTfr6WmrKggIMlfborT8d3d3GwCjV7zKnDv39tLTs/7Lfnd2tjS6CU1HfVJM/VFO\nfVJOfVJuvfVJMwQXzwAp4A7g4eyxu4EnSk/Mriz5Wvb819i2PbrUm42Pzyw6ctHZ2cLspDcqkTbB\nKTl/YmKGRDyVL/vdO9DGxMTMUpuyZuT6ZHo6RibjLP6GDUB9Ukz9UU59Uk59Um6t9Unul+vFNDy4\nsG07ZlnWZ4FPW5b188B24KPAeyE/BTJl23Yc+B1gD149DDP7GnijHNNlF6/AcVwcx130vPRs5U3L\nfJik0w5DF+YGVfoHO0mnm/+HYqUyGWdD/D2XQn1STP1RTn1STn1Sbr31SbNM8nwEeApvuuNP8apu\nfjn72hW8OhbgVfBsAR4DLhf8+aNaNyiX0Jks2bQs7PeGroazyZw+v0mfdkIVERHJa/jIBXijF8D7\ns39KXzMLHh9arTblgotU8Z5lmNl8jVxlzv4tHesuEUdERGQl9Kk4j7mRi+JpkV2dO3Ach5HsSpEt\n21XfQkREpJCCi3k4iezIRcm0yHsOvZ1rV2dIp7y5MdW3EBERKabgYh6Z3MhFSUJnR7A9PyUCMKDg\nQkREpIiCi3k4sVzORfmy1dxmZZt6WmhprbTViYiIyMal4GIelXIuTExc1+XSeW8Z6uCOTQ1pm4iI\nSKEWsqIAABcLSURBVDNTcDGPuZyLueAi7A8zE0nkNysbVDKniIhIGQUX83Aq5Fwk0nGujc5V4uzt\nr65SmYiIyEai4KICN5PBzW5clirZtGwsW/LbNA26exVciIiIlFJwUUFmnu3WXWB0JAp4oxY+v7pP\nRESklD4dK8jE5oKLwpELHz5GsyMXfQMdq94uERGRtUDBRQWZWCz/uHDk4kDbfqLTCQA2b1FwISIi\nUomCiwoKg4tchU4Tk9d3vzF/fPMWbVYmIiJSiYKLCubLuYiOpQEvmbN3s4ILERGRShRcVFA0LZLN\nuXBwGBvx8i16+pTMKSIiMh99QlZQPC0yN3IxOuytFOnTlIiIiMi8FFxUUBRcZKdFfKkAkSlvukTJ\nnCIiIvNTcFFBbilq2oSMzwsu2mbn9hFRcCEiIjI/BRcV5EYuCndEbYv1AGAY0LtZlTlFRETmo+Ci\nglxwUbgjaiDaCnjJnP6AryHtEhERWQsUXFQQj04DJTuizng7oGpKREREZGEKLio4MXQCmAsuzLSf\nYMIbuVBwISIisjAFFxXEZrIjF9mci5bZrvxrWoYqIiKyMAUXFfhTDjA3ctEy0wlkkzn7FVyIiIgs\nRMFFBcG0C8wldIazIxebelsJKJlTRERkQQouKgimvaAit2lZS9zLs+ju1RJUERGRxSi4qCCQygDZ\nTctcg8CsF1SovoWIiMjiFFxUEEhlp0UCBqF4G6brdVNvv4ILERGRxSi4KOE6Tj7nIuU3CGeTOUHJ\nnCIiItVQcFHCSSTyj5MBg3DMy7cIhnx0dIUb1SwREZE1Q8FFCbcguEj5DVqylTl7+9sxDGO+t4mI\niEiWgosShSMXKZ9BeNYbuegb0JSIiIhINRRclIhEx/OP00YYfzoEQJ/yLURERKqi4KLEV178l/xj\n151L5uzRMlQREZGqKLgoMTw+lH9spOf2FOnubW1Ec0RERNYcBRclfNkCWgC+pBdcdHSHCAT9jWqS\niIjImqLgokQoPfc4GPeCi4EtXfOcLSIiIqUUXJRocbyNyRxMggkviVP5FiIiItVTcFEqmQRgOrwJ\nI1v2W8tQRUREqqdEghL+tAPAVEtP/piWoYqISCWz8TRXxmeW/X6/z6RjOkEkEiedcap6z2BPG63h\n5v74bu7WNUBu07JIyAsu0v4Ere3BRjZJRESa0Gw8zW/8+cPMJtKLn1xDrSE/H/vgK5s6wNC0SIlA\ndtOymaAXXMRbIyr7LSIisgTNG/Y0SCDt4gIxfzcA8dbpxjZIRESaUmvYG0FY8bRIR1jTIutdMA0J\nfysZ0yv7nWiNNrhFIiLSrFrDfvZtXX65Ar/fpLu7jYmJGdLp6oKLtUDTIiWCaYgG55I53Y7EAmeL\niIhIKQUXJfxph5ngJgBcHCKB8UXeISIiIoUUXBSIJKNFwUUyFMMx188wlYiIyGpQcFHg3hfuJ5h2\nmQr3ARBrn8RUF4mIiCyJEjoLnJo8y10Zk9mAt9V6rHWaA917G9wqERGR5Umn00xPT837umn62LRp\nU83v2xTBhWVZIeBTwNuAWeATtm1/cp5zbwH+HLgBeB74oG3bP6hNS1xSdIHhjVYkWqd53+Ffrs2l\nRUREVpltn+CXfun989ZrGhgY5OjRL9f8vk0RXAAfB24F7gF2A5+1LOucbdtfKjzJsqxW4AHgb4H3\nAh8EHrAsa69t27GVNiJkBIkFCjYp60jTEVTpbxERWZsOHz7C97//xKrft+EJBdmA4QPAr9i2fcy2\n7S8DHwM+XOH0dwKztm3/pu35NSACvL0WbXHisXzZb9eIEzMjtbisiIjIhtLw4AK4CW8E5ZGCYw8C\nt1c49/bsa4UeAu6sRUN86QyRUC8ATmAKB60UERERWapmCC4GgTHbtgt3fhkBwpZl9VY493LJsRFg\ney0a4k+7zAa9SmuZ4DRuLS4qIiKywTRDzkUrUFoGM/c8VOW5pefNyzQNTLNyYks4ESLlCwOQCkXx\nGT78/maIvxrL9/+3d+fRVlRXHse/gBEQxTGKthricvkT4gA4CzgAtlNUlul2IqKSgC6lndqhnYlD\nEqc2QqLEOAWH4JDGKBoJmiiggko0ajBbI6ACSkBGlUF5r//Yp6C4b+CB9XjD3Z+1WNxbp4ZT+91b\nteucU7datVzt/xAxKRXxqCpiUlXEpKrmGpPGkFwspWpykL3/so7zls5Xoy22aFfzqNnNdmQFQGUl\nizZdSOetd2HzzdtVO285at++bUNXodGJmKwu4lFVxKSqiElVzS0mjSG5mAlsJamlmWWDHDoAS8xs\nQTXzdiiZ1gH4pK4bmzfvixpbLn7Ypz8jpz/AUr7g3zp1pH+nE5g/f92fdtdctGrVkvbt27Jo0RJW\n1PGpfc1dxGR1EY+qIiZVRUyqamoxqesFd2NILt4EvgL2B15O03oC1d07MxG4tGRad+D6um6soqKS\niorqR1Ns1Kodg845e7Un1DWnp9R9UytWRDxKRUxWF/GoKmJSVcSkquYWkwZPLsxsiaQRwHBJA/DB\nmf+N/44FkrYBFprZUuBx4GeSbgPuAs7Cx2E82iCVDyGEEEIVjWUEyYXAZODPwDDgqvR7F+BdHicA\nmNli4PvAQcDrwL7AkUX8gFYIIYQQitHgLRfgrRfAGelfaVnLkvevA3utp6qFEEIIYS21qKyMX3MI\nIYQQQnEaS7dICCGEEJqJSC5CCCGEUKhILkIIIYRQqEguQgghhFCoSC5CCCGEUKhILkIIIYRQqEgu\nQgghhFCoSC5CCCGEUKhILkIIIYRQqEguQgghhFCoRvFskcZCUmvgDuB44EvgVjP734atVbEkbQcM\nBQ7F9/FR4DIzWy6pI/Ab4ABgOnCBmY3NLdsHuA3YCXgFGGhm03Ll5wMXAZsAjwGD09NsmwRJTwOz\nzWxAet+RMoyHpA3x/ToZWAbca2ZXpLKOlGdMtgfuxB+a+Blwu5ndnso6UkYxScfJ14FzzGxcmtaR\neopBUzgu1xCT/YFbgT2AGcAtZnZPbplmHZNouVjdLUA34BDgbOAaScc3aI2K93ugDdAdOAk4Brgu\nlf0BmIU/GO5BYFQ6qCJpB2AUcA+wNzAXeCJbqaQfAFcDA4FewP7ATfW/O8WQdBJwZMnkJyjPeAwF\negOHAacAAyUNTGXl+hl5DFiMHx/OB26QdFwqK5uYpJPa74DOJUX1+V1p1Mfl6mIiaRvgGfxJ312A\nIcAwSUem8h1pxjGBeHDZSpI2wv/Ah5vZ+DTtCqC3mfVq0MoVRJKAKcA2ZjY3TTsJuBnojx8kt85l\nx2OB8WZ2raRrgR5ZLCS1BT4FjjGzcZJeBJ4zs+tSeXfgT8CWjfkqDEDS5sDf8IPjFDMbIKkX/mUv\nq3ikWMwGepnZhDTtEmAX4CHK8DMiaTNgHrCbmU1J0x7HPy+jKJOYSOoEPJze7gEcmvah3r4r+AVw\noz0u1xKTM4Fzzex7uXmHA+3M7NTmHJNMtFyssifeTfRKbtoEYL+GqU69+BQ4IksscjbFM+O/lhzQ\nJuDNnOBxGJcVmNkS4K/AAZJaAvsA43PLTgQ2xOPa2N0CjADezU3bj/KMRw9gQZZYAJjZTWb2Y8r3\nM7IE+AI4Q9IGKUnvDrxBecXkYOB5fN9a5KbX53elsR+Xa4rJH4Ezqpl/0/R/c44JEMlF3rbAXDP7\nOjdtNtBG0pYNVKdCmdnCkn7QFsBg/MuxLX4lljcb2D69rq18M7yrZWW5ma3A+6a3pxFLV109WdU1\nlCnLeOD9v9MlnSrpXUkfSLoyfVbKMiZmtgz/npyFJxrvAs+Y2X2UUUzMbLiZXVRNi0p9xqBRH5dr\niomZfWRmr2bvJW2Nd0M/lyY125hkYkDnKhvhg9fysvet13Nd1pebga54lnwh1e9/tu81xad1KqOW\n8kYp9ZUOB842s2V+QbpSbfu7pvImGY9kY7wLZBBwOn4g+zU+aKxcYwLQCXgSb+XaHe8/f57yjkmm\nPmPQsoYyaCIxktQGH+s2C7grTW72MYnkYpWlVP3DZO+/XM91qXeSbgTOBU4wsymSlgJblMzWmlX7\nXlN85qcyaihvzLEbArxmZs9VU1aO8QD4Gh+dfrKZzQCQ9B180FjW55vX7GMiqTfwI2D71IrxRhqs\neCXe6ld2MSlRn9+VDWoogyYQI0nt8KR0Z6B7roWj2cckukVWmQlslfq7Mh2AJWa2oIHqVC8kDQMu\nAPqZWTZCeSa+v3kdgE/qUP4Z/oVYWS6pFX7Q/YTG60Sgr6TFkhYD/YAfSlqE3zpWbvEAr9/SLLFI\nDG+OLcfPCPio/PdTYpF5A9iR8o1JXn3GoMkelyVtgifknfGBnlNzxc0+JpFcrPIm8BU+QCvTE3it\nYapTPyRdgzd5n2hmj+WKJgLdUldBpkeanpX3yK1nI7xL5RUzq8Tj1CO37IHAcvwujMbqYLyJOxsk\n9SQ+8n9PYBLlFw/w/WojaefctM74bxdMBPYqw5jMAnaWlG/p7QRMo3xjklefx44meVxOY5RGAR2B\ng8zsHyWzNPuYxK2oOZLuxEeBD8Cv1O4HTjOzPzRkvYqSbpt6C/gp/gMseXPwD+47+ODGY4HLgO+Z\n2YzUND4F+AkwGrgG2MXMuqZ1n4iPXzgdPxjfi99KdUE971ZhJN0HVKZbUVtSpvGQ9CTezH02PuZi\nBHAt/iNSbwFvU0YxkdQeH8Q5FrgB2BWv+2Xp/3KMSQVwSLptsl6/K03luFwSk4H49+UY/C6QzHIz\nm18OMYmWi9VdCEzGf/hkGHBVY/pjFeBY/G9+Jf6BnYU3s80yswqgL9689jr+40l9s+ZxM/sQ/zW4\nAcCr+IjmvtmKzewR4Gf44L8x+G1Sl66XvaoHKR7HUZ7x6Af8E78V7n5gqJn9KsXkWMosJma2CP9R\nsW3x/boVuNbM7i7XmAArr0rXw3elqRyXK1kVl+PxW1NHs+pYOwsf2FkWMYmWixBCCCEUKlouQggh\nhFCoSC5CCCGEUKhILkIIIYRQqEguQgghhFCoSC5CCCGEUKhILkIIIYRQqEguQgghhFCoSC5CCCGE\nUKhILkIIIYRQqEguQlgHkk6X9BdJ/5K0VNL7km6TtE1D121tSRoiaVoB6+kvaasi6tSU1SWekiok\n9U+vN5B0fkl5xDI0aZFchLAWJLWQ9ARwC/4E1YOBnYHBwD7A603wpJB/JsI6kXQQ/hySjYqoUBNX\nl3h2AB5Jr0/Bn1cCRCxD87DBmmcJIeRcCBwJ7Gtm+cdiz5D0Iv5kyIuA/2mIyjWglnzDBKWcmNm/\ncm9LL/IilqHJi+QihLUzGBhRklgAYGZLJR0KfJpNk9QTGALsDbQGpgI3mNlDqfw+/GSyAOgPVOBP\nORwJ3JWWex/4sZm9lpZpj7ec9AU2xJ9EeamZTU7lbdM6jsaftvgucJ2ZjaptxyRdCZyX1vkkcK6Z\nza9hm5OBS8xssqSD8aczAkyTdB4wFOhmZm+m5UcBhwKbm1mlpBbAbOB8M3tY0oH4UyD3AeYATwGX\nmdnitPy3gOvxJ7Zuij/i/BozG5vKT8Of9nt9+n8HPNE718xermF/70sv56bYb5z2Y6CZfZrm2R74\nOf5U1E2ACcDFZvZ2bbFMy14C/BewJTARGGRm/0xlFfjjtFvgj9NG0gqgV0kszzCzEXWIzzTgceAo\n4NvAD/AnHg8DDsA/Yy8DF5nZO2uqewjfVHSLhFBHkr4LfAd4vqZ5zOxjM/sqzb8d8CwwCeiS/k0C\n7pb07dxiJwHLgW548/jV+Mn9RvxkshS4Izf/H1M9jgL2xU9cL0naM5VfD+wGHAHsmuYfKWnHWnav\nI35i6w18P2333lq2+Upumy/hJ7PKtNzdwHTgsBSHlsAh+Mm7W1rffniS8LSkPYCxwDOp3ien+f6U\n2/5vgT6prAvwKPCUpCNz8+wInIl3M3QFvsC7F2pzMrA50BOP1154/JC0MX5C3i7F5ADgS2CcpB3W\nsN6OwIFpnT3xx7XfXc18I4Hz8dh1oGosH6ljfADOwZPfI/DP2SPAjDTvvsAK4P/WUO8QChEtFyHU\nXTZYc05+oqQn8avyzHQz2x1oA1xtZvn+9BuB04BdcuuZa2YXp/Jf4Ce3kWb2dJp2H3Bbet0bPzFv\nZWYL0vJXSuqBtzoMAHYCFqd6LJR0FfACML+WfVsCnGBmc9N2BgNjJO0EfLe2bZrZAEnzcvuyVNJT\nwL8DN+MntuV4QnIo3upxFDA+1e9iYIyZ3ZjWMVVSP+CDNP5gJp6AdTGzt9I8v5DUBbgYT3zAj2dn\nZq0Kkm4FRknaxsxm17DfC9IyK4D3JI3Eu70ATgW2AP7DzOaldZ4CfICfyGvr+loO9DOzL9JyvyYl\nLXlmtkzSwvR6Tpo3H8tlki6qLT5mNi5Nf8bM/pKtO/3txgAfmdnXks7Ak80Q6l0kFyHU3dz0/xYl\n0wexavDdecAxAGY2VdL9ks4FdscHfu6JX5W2yi0/NXthZl9KWm0afuLfML3uirc4fpzmy2yYm+dG\nvOVjjqRJ+BXuw1kTeg3ezxKLZBLeZL8bngitaZulngIGSmqNt2A8j7dm9MK7V44Gsm6JrsDOkkrr\nVwl0ArZO7yek7pTMBlRNmP6Re70wV8+afJASi/wy2fy7Ae9liQWs7Pp6Fdg9tV5MSfVsAVSaWfs0\n6+wssUjmA21rqUdtulF7fLLk4v2S8suB24FzJL2At6L9bh3rEMJaieQihLqbivdjHwI8lk3M+udh\ntatOJHUGxuNjIsYCv8dbK14rWe9X1WyrooY6tMRPgN3wE1reslSfienEdxjeldAfuErS4fkr2xIr\nSt5nyc+yumyzGi+kskNSHUYAHwKDU/dMF/xum2yfHsKv7EvXPwdvSagEegCf11bvrEuqROk611T/\nFiX/l2qJ/81m4slidUrj+U2sKT6ZJfkCM7tT0mN4K1Fv4Fr8c7Bn1koSQn2J5CKEOjKzCklD8QP0\n8BoG9eXHNZwFfGpmh2cTJB3DqivddfEO0B5obWYrr9Il/QZ4A7hD0hBggpmNBkZLuhD4O96XX1Ny\nsYukdrmr7Z54gjMFTzRq3SYldzekZvgxwHF4t0h/fADnt4CfAG+Z2ce5fepsZtNy694VuAnvengH\nj9d2ZvZsbp4b8JP8kDXEbF29BfSXtFWuu6gNPsj2fjOrYPUWpnVVemdI6fs1xWdK6QrTmJ6rgZ+b\n2QhgRBoDNAO/ffrxAuodQo0iuQhh7dyEX3WPT+Mnnsav6vfAB9P1Ae5J834E7CDpCPwEsDfeTA1+\n58i6eBb4Gz7Q7zzgY7z//zTgwTTPTkA/SYPw8QH740nPS7Wsty3wqKQr8LsNhgG/NbOPJc2sZZsP\npeU/xxOArpI+S0nKU/ggxllm9iGApJfxsQz58Qe34oMkfwn8Eh9g+St8zMp7KVEZDQxPY0H+Dvwn\ncCl+x0Vt1jWJA3gYuAyPyyX4OIprgHb4nTxF+RxAUjf8c7JaLFlDfGpY5zy862knSZfjY3BOx1tq\nJhdY9xCqFXeLhLAWzKzSzE4GfoQ3048BDD8ZzwYOMrNBafah+Ij9B/BbJy/HT1bT8TsBalLjbxyk\nq+U+eFfLI/hJvwfQ18xeTLOdjY9xeCDV7Sf4baO19be/BryJt2yMBEbjCcSatvlCWv5t/G6GkfgY\nFNL7Vqx+d81z+Ikz6xLBzCYBh+NdDJOBJ/DbZ/uY2ddpthPwbqXheHJxKjDAzB6kduv8exFmtgi/\nyp+f6j0OTwq7Z8nSN5Cv15+BV/Hk72hKYlnH+JS2HK3Au5MqUt3fxrtGjsq3gIRQX1pUVsZvtYQQ\nQgihONFyEUIIIYRCRXIRQgghhEJFchFCCCGEQkVyEUIIIYRCRXIRQgghhEJFchFCCCGEQkVyEUII\nIYRCRXIRQgghhEJFchFCCCGEQkVyEUIIIYRCRXIRQgghhEL9P4/vQx2hOabcAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbda014a8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the theoretical CDFs\n",
"_=plt.plot(x_theor, y_theor)\n",
"\n",
"_=plt.plot(x, y, marker='.', linestyle='none')\n",
"\n",
"plt.margins(0.02)\n",
"plt.xlabel('Games between no-hitters')\n",
"plt.ylabel('CDF')\n",
"\n",
"\n",
"# Take samples with half tau: samples_half\n",
"samples_half = np.random.exponential(tau/2, 10000)\n",
"\n",
"# Take samples with double tau: samples_double\n",
"samples_double = np.random.exponential(2*tau, 10000)\n",
"\n",
"# Generate CDFs from these samples\n",
"x_half, y_half = ecdf(samples_half)\n",
"x_double, y_double = ecdf(samples_double)\n",
"\n",
"# Plot these CDFs as lines\n",
"_ = plt.plot(x_half, y_half)\n",
"_ = plt.plot(x_double, y_double)\n",
"plt.legend(('_'),loc='lower right')\n",
"\n",
"# Show the plot\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"illiteracy = np.array([ 9.5, 49.2, 1. , 11.2, 9.8, 60. , 50.2, 51.2, 0.6,\n",
" 1. , 8.5, 6.1, 9.8, 1. , 42.2, 77.2, 18.7, 22.8,\n",
" 8.5, 43.9, 1. , 1. , 1.5, 10.8, 11.9, 3.4, 0.4,\n",
" 3.1, 6.6, 33.7, 40.4, 2.3, 17.2, 0.7, 36.1, 1. ,\n",
" 33.2, 55.9, 30.8, 87.4, 15.4, 54.6, 5.1, 1.1, 10.2,\n",
" 19.8, 0. , 40.7, 57.2, 59.9, 3.1, 55.7, 22.8, 10.9,\n",
" 34.7, 32.2, 43. , 1.3, 1. , 0.5, 78.4, 34.2, 84.9,\n",
" 29.1, 31.3, 18.3, 81.8, 39. , 11.2, 67. , 4.1, 0.2,\n",
" 78.1, 1. , 7.1, 1. , 29. , 1.1, 11.7, 73.6, 33.9,\n",
" 14. , 0.3, 1. , 0.8, 71.9, 40.1, 1. , 2.1, 3.8,\n",
" 16.5, 4.1, 0.5, 44.4, 46.3, 18.7, 6.5, 36.8, 18.6,\n",
" 11.1, 22.1, 71.1, 1. , 0. , 0.9, 0.7, 45.5, 8.4,\n",
" 0. , 3.8, 8.5, 2. , 1. , 58.9, 0.3, 1. , 14. ,\n",
" 47. , 4.1, 2.2, 7.2, 0.3, 1.5, 50.5, 1.3, 0.6,\n",
" 19.1, 6.9, 9.2, 2.2, 0.2, 12.3, 4.9, 4.6, 0.3,\n",
" 16.5, 65.7, 63.5, 16.8, 0.2, 1.8, 9.6, 15.2, 14.4,\n",
" 3.3, 10.6, 61.3, 10.9, 32.2, 9.3, 11.6, 20.7, 6.5,\n",
" 6.7, 3.5, 1. , 1.6, 20.5, 1.5, 16.7, 2. , 0.9])\n",
"\n",
"fertility = np.array([ 1.769, 2.682, 2.077, 2.132, 1.827, 3.872, 2.288, 5.173,\n",
" 1.393, 1.262, 2.156, 3.026, 2.033, 1.324, 2.816, 5.211,\n",
" 2.1 , 1.781, 1.822, 5.908, 1.881, 1.852, 1.39 , 2.281,\n",
" 2.505, 1.224, 1.361, 1.468, 2.404, 5.52 , 4.058, 2.223,\n",
" 4.859, 1.267, 2.342, 1.579, 6.254, 2.334, 3.961, 6.505,\n",
" 2.53 , 2.823, 2.498, 2.248, 2.508, 3.04 , 1.854, 4.22 ,\n",
" 5.1 , 4.967, 1.325, 4.514, 3.173, 2.308, 4.62 , 4.541,\n",
" 5.637, 1.926, 1.747, 2.294, 5.841, 5.455, 7.069, 2.859,\n",
" 4.018, 2.513, 5.405, 5.737, 3.363, 4.89 , 1.385, 1.505,\n",
" 6.081, 1.784, 1.378, 1.45 , 1.841, 1.37 , 2.612, 5.329,\n",
" 5.33 , 3.371, 1.281, 1.871, 2.153, 5.378, 4.45 , 1.46 ,\n",
" 1.436, 1.612, 3.19 , 2.752, 3.35 , 4.01 , 4.166, 2.642,\n",
" 2.977, 3.415, 2.295, 3.019, 2.683, 5.165, 1.849, 1.836,\n",
" 2.518, 2.43 , 4.528, 1.263, 1.885, 1.943, 1.899, 1.442,\n",
" 1.953, 4.697, 1.582, 2.025, 1.841, 5.011, 1.212, 1.502,\n",
" 2.516, 1.367, 2.089, 4.388, 1.854, 1.748, 2.978, 2.152,\n",
" 2.362, 1.988, 1.426, 3.29 , 3.264, 1.436, 1.393, 2.822,\n",
" 4.969, 5.659, 3.24 , 1.693, 1.647, 2.36 , 1.792, 3.45 ,\n",
" 1.516, 2.233, 2.563, 5.283, 3.885, 0.966, 2.373, 2.663,\n",
" 1.251, 2.052, 3.371, 2.093, 2. , 3.883, 3.852, 3.718,\n",
" 1.732, 3.928])\n"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAgsAAAF2CAYAAADgC9tMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3X+cXGV96PHP7G4S8mthg5BogUAjfUiwDbFytUWtP25L\nEa61Wi9YqxLE39Yo3qvXimK5tr0q2gZoSy/WoLWtNFVbrrnU1uqtoqVVC7GS8AiU8ENIyI8Nm90N\n2ezu3D/OzGZ3szs7uzsz58w5n/frBdkzM2fmmXl29nzP9/k+zymVy2UkSZKm05F2AyRJUrYZLEiS\npJoMFiRJUk0GC5IkqSaDBUmSVJPBgiRJqslgQZIk1WSwIEmSaupKuwHztXfvoZqrSnV0lFixYikH\nDgwwOuoCVFli32ST/ZJN9kt2tXPfnHLK8lI9j8t9ZqGjo0SpVKKjo67PQy1k32ST/ZJN9kt2FaFv\nch8sSJKk+Ul9GCKE8AZgC1AGSuP+HY0xpt4+SZKKLgsH4y8At4/bXgh8HbgtneZIkpQdfYNDbNm2\nk4f2HGL1yuVsvHgt3UsWtrQNqQcLMcYjwBPV7RDCByo/fmDqPSRJKo4t23ay/YH9ABzs38+WbTvZ\n9Or1LW1D6sHCeCGEHuB9wBUxxqNpt0eSpLQ9tOdQze1WyFqB49uBH8cYv5x2QyRJyoLVK5fX3G6F\nrAULbwSuT7sRkiRlxcaL17J+zcmctGwh69eczMaL17a8DZkZhgghnA/8BHDrbPbr6Kg9t7Wzs2PC\nv8oO+yab7Jdssl+yq9l9s6L7BN77mg1Nee56ZSZYAC4EvhljfHI2O61YsZRSaeaFMLq7F8+1XWoy\n+yab7Jdssl+yK899k6Vg4bnAt2e704EDAzNmFrq7F9PXd5iRkdH5tE8NZt9kk/2STfZLdrVz3/T0\nLK3rcVkKFp4F/NlsdxodLde1FvfIyCjDw+3ViUVh32ST/ZJN9kt25blvsjT4dSrQm3YjJEnSRJnJ\nLMQY68uFSJKklspSZkGSJGWQwYIkSarJYEGSJNVksCBJkmoyWJAkSTUZLEiSpJoMFiRJUk0GC5Ik\nqSaDBUmSVJPBgiRJqslgQZIk1WSwIEmSajJYkCRJNRksSJKkmgwWJElSTQYLkiSpJoMFSZJUU1fa\nDZAkSY3TNzjElm07eWjPIVavXM7Gi9fSvWThvJ7TzIIkSTmyZdtOtj+wn4P9Q2x/YD9btu2c93Ma\nLEiSlCMP7TlUc3suDBYkScqR1SuX19yeC4MFSZJyZOPFa1m/5mROWraQ9WtOZuPFa+f9nBY4SpKU\nI91LFrLp1esb+pxmFiRJUk0GC5IkqSaDBUmSVJPBgiRJqslgQZIk1WSwIEmSanLqpJSyZqzjLkmN\nZGZBSlkz1nGXpEYyWJBS1ox13CWpkQwWpJQ1Yx13SWokgwUpZc1Yx12SGskCRyllzVjHXZIaycyC\nJEmqyWBBkiTVlPowRAhhIfD7wGuAI8BnYowfTLdVkiSpKvVgAbgeeBHwi0A3cGsIYVeM8eZUWyVJ\nKiwXS5so1WGIEEIPcAVwZYzx+zHGbwDXAc9Ns12SpGJzsbSJ0s4sPB84GGO8o3pDjPHjKbZHkiQX\nS5sk7WDhJ4FdIYTXAb8FLAS2AL8TYyyn2jJJUmGtXrmcg/37J2wXWdqzIZYBPwW8GbgceC/wLuDd\nKbZJklRwLpY2UdqZhWFgOfCaGOOjACGE1cDbSGZIzKijo0RHR2na+zs7Oyb8q+ywb7LJfskm+6W1\nVnSfwHtfs6Guxxahb9IOFh4HnqoGChUROL3eJ1ixYiml0vTBQlV39+LZt04tYd9kk/2STfZLduW5\nb9IOFu4ETgghPDPGeH/ltnXArnqf4MCBgRkzC93di+nrO8zIyOi8GqvGsm+yyX7JJvslu9q5b3p6\nltb1uFSDhRjjj0II24BbQghvB54OvB+4tt7nGB0tMzo6cy3kyMgow8Pt1YlFYd9kUyP6xbnqjef3\nJbvy3DdZGGB5LXA/8C3gFuD6GOMfptoiSQ3hXHUpH9IehiDGeIhkJsTl6bZEUqM5V13Kh9SDBUn5\n5Vx1tTOH0Y7JwjCEpJxyrrramcNox5hZkNQ03UsWsunV69NuhjQnDqMdY2ZBkqQpTB42K/IwmsGC\nJElTcBjtGIchpIKyeEuqzWG0Y8wsSAVl8ZakehksSAVl8ZakehksSAVl8ZakelmzIBXUxovXHlez\noHyzTkVzZbAgFVSji7c8EGVftU4F4GB/UqdiAZ/q4TCEpIawYDL7rFPRXBksSGoID0TZZ52K5spg\nQVJDeCDKPhcZ0lxZsyCpISyYzD4XGdJcGSxIaggPRFJ+GSxIGeKMAklZZM2ClCHOKJCURQYLUoY4\no0BSFhksSBkyeQZB/+GjbN66nb7BoZRaJEkGC1KmVKe2dXWWABgeKTscISl1BgtShlRnFCxbvGDC\n7Q5HSEqTsyGkDFq9cjkH+/dP2JbUnvIwy8nMgpRBrrSnousbHGLz1u1cdeMdbV+3k4dZTmYWpAxy\ngSMVXZ6ukJmHWU4GC1LG5CFlKc1XPQfYdvmu5GFY0WEIKWPykLKU5queC5O1y3clD8OKZhakjMlD\nylKar3ouTNYu35U8DCsaLLSxdknBaXbykLKU5queA6zfldZxGKKNtUsKTrOTh5Sl1Ap+V1rHzEIb\na5cUnGYnDylLqRX8rrSOwUIbMwUnSfPnkO7MHIZoY6bgJGn+HNKdmZmFNmYKTpo9zyKzKc1+cUh3\nZmYWJBWKZ5HZlGa/1LOmQ9EZLEgqFM8isynNfnFId2YOQ0gqlDQLgx0CmV6a/eKQ7swykVkIIbwi\nhDAaQhgZ9+9fpd0uSfmT5lmkQyDT8+w+27KSWVgH3Aa8CShVbnsqveZIyqs0zyIdApmeZ/fZlpVg\nYS3wwxjj3rQbIknN4tooaleZGIYgySz8KO1GSFIzmWpXu8pKZiEAvxxC+CDQCWwFPhxjPJpusySl\nKW8Fgaba1a5SDxZCCGcAi4HDwKuBs4AbgBOA98y0f0dHiY6O0rT3d3Z2TPhX2WHfZFOW+uWW2+9l\n+wNJ2v5g/35uuf1errr0vJRblY4s9YsmKkLflMrlctptIIRwUozx4LjtVwJ/BiyLMdZsYLlcLpdK\n0wcLktrXG377qxzoO1brvKL7BD57zYUptigdT/YfYfOtd/HAo0+y5rQT2XTpBk5ctih3r6lU1HUA\nTT2zADA+UKjYSZJZWAHsP36PYw4cGJgxs9DdvZi+vsOMjIzOu61qHPsmm7LUL2esXDYhWDhj5TJ6\newdSbFE6PnXr3dx93z4ADux4ius+/72mZ1jSeM12laXvzGz19Cyt63GpBwshhF8C/gI4LcZY/auw\nAdgfY6wZKACMjpYZHZ05OzIyMsrwcHt1YlHYN9mUhX65/KJz2DJ6rGbh8ovOSb1Nadj1eN9x283+\nHNJ4zXaXhe9Ms6QeLADfAQaBT4cQrgXWAB8HPpZqqySlzoLARBpTLp3mqfFSr8aIMfYDFwKnAN8F\nbgZuijF+MtWGSVJGbLx4Leed/TRWdJ/AeWc/rSVTLmtN8+wbHGLz1u1cdeMdbN66nb7Boaa3R+nK\nRIHjfOzde6jmG+jq6qCnZym9vQO5TQ+lZb7T2uybbLJfsilL/bJ56/axWSoA69ecXOgMUJb6ZrZO\nOWV5XQWOqWcW1L5c514qJpetLh6DBc2ZfzCkYppcv2A9Q/4ZLGjO/IMhFZPLVhdPFmZDqE1tvHjt\ncTULkvLPWSrFY7CgOfMPhiQVg8MQkiSpJoMFSZJUk8MQkpQhebsst/LBzIIkZYjrlyiLDBYkKUNc\nv0RZZLAgSRni+iXKImsWpIxzDLtYXL9EWWSwIGVcdQwb4GB/Mobt+hb55folyiKHIaSMcwxbUtoM\nFqSMcwxbUtochpBaaC71B3kew7YeQ2oPBgtSC82l/iDPY9h5q8cw+FFeOQwhtZD1BxPl7fNwQSXl\nlcGC1ELWH0yUt88jb8GPVGWwILXQxovXsn7NyZy0bCHr15ycyfqDvoEhrv3TO9m0+Vts3rqdvsGh\npr1WO3wes5G34EeqKpXL5bTbMC979x6q+Qa6ujro6VlKb+8Aw8OjrWqW6mDfZNP1X/wBd9+3b2x7\n/ZqT27qOoJWaWbPg9yW72rlvTjlleamex1ngKGmCh3abSp+rPBejqtgMFiRNsHrVcnoPHTm2nYNU\nurMUpPmZdc1CCOHWEMKFIYS6UheS2suVl6zj/HUr6Vm+KBd1BOAsBWm+5pJZGAW+DBwIIXwOuCXG\n+KPGNktSWrqXLuTDb3xeW46/TsdZCtL8zDqzEGN8DbAK+G3gBcDOEMJ3QghvCiF0N7qBkjRfzlKQ\n5mdOUydjjH0xxptjjC8A1gBfBX4feDyE8LkQws82spGSNB95m6IptdqcCxxDCAuBXwF+A/glYA/w\nZ8BpwLdCCNfEGD/RkFZK0jw4S0Gan1kHCyGE5wOvB34NWAz8DfBy4GsxxnLlMXeTDFMYLEiS1Obm\nkln4JnAX8CHgz2OMB6d4zD3A/51PwyRJUjbMJVg4D/hhjHFCmXQIoQvYEGP8bozxa8DXGtFASelx\nfQJJMLcCx7uAk6e4/Szgn+bXHElZ4voEkqDOzEII4e3Af6tsloDvhRBGJj2sB3iogW2TlDLXJ5AE\n9Q9D3AI8jSQT8WHgr4D+cfeXK9tfbGTjJKVr9crlHOzfP2G7mRz2kLKprmAhxjgIXAsQQigDn6jc\nJinHNl689riDdzNVhz0ADvYnwx5OeZTSV+8wxAuB78QYh4FvAM8JIUz52BjjNxvXPElpavX6BA57\nSNlU7zDE/yNZ4vmJys9lktqFycpAZyMaJql4Wj3sIak+9QYLZwH7xv3cFCGEbcCeGOMVzXoNSdnV\n6mEPSfWpt2bhoal+bqQQwmXARSTFlJJS9GT/ET51693seryvpYWGLsssZVO9NQtfr/cJY4wvmW0j\nQgg9wMeBf53tvpIab/Otd3H3fUky0UJDSfUOQzxMUo/QLNcBnwN+oomvIbVUO08DfODRJydsW2go\nFVu9wxCXN6sBIYSXAC8Afhq4qVmvI7VaO08DXHPaiRzY8dTY9nwLDds5cJJU/zDE64FbY4xHKj9P\npxxj/LN6XzyEsIgkQHh75bnr3XVMR0eJjo6pJmYkOjs7Jvyr7Mh73zz8RP9x211d2X+vnZ0dbLp0\nA5/88++x6/FDrF61nCsvWTevtt9y+70TAqdbbr+Xqy49r1FNLoS8f1/aWRH6ZjYrOP4dydTJW2o8\nrgzUHSwAHwGqF56akxUrllIqTR8sVHV3L57rS6jJ8tY3T/YfYfOtd9F/+OiE2595+kn09CxNqVWz\nd+1bLmjYcz28p/+47Xb6LLIkb9+XPMlz39Q7DNEx1c8NcCmwMoRQHRBdBBBC+LUYY3c9T3DgwMCM\nmYXu7sX09R1mZGR02sep9fLaN5+69e6x4kCABZ0dnPuTK3jDhYHe3oEUW1afZvTLGSuXcaDvqQnb\n7fBZZElevy950M59U2/QPutLVFdmRvxqjPHJSbefCnw1xrhhFk/3C8CCcdsfJ8lOvK/eJxgdLTM6\nOnPt5cjIKMPDo46dZlC1b/Ji1+N9E7aXLu7iXa/6GYC2ep+N7JfLLzqHLaPHvneXX3ROW30WWZK3\n70ue5Llv6q1ZeBnwnMrmi4APhhD6Jz3sbODM2bx4jPGRSa9ziKTu4cHZPM9stHPRmdqDqxAez/UT\npPZWb2ZhF3Ajx5Z4vgwYf4nq6lUn/3vDWtYkrj2fLWkt/tNMtVYhNLOluegbHOKW2+/l4T39nLFy\nGZdfdI6/N2qpUrk8u+UTQggPAc+OMe6f8cEtsHfvoZpvoKurg56epfT2DjA8PMrmrdvHMgsA3UsW\n0NFR8g93Crq6OrjhS//Od3fsGbtt/ZqTc30GOvn3L4vvd/J3Rulrh9+bImvn78wppyyfeYYAMJdi\nxSdo48WTNl68lvVrTuakZQvpXrKAvsGjHOwfYvsDyZCEWqtoi/+Y2dJc+HujtM0lWDgLaNsy5urY\n6afe+fzjZlH4BWy9NaedOGE77+P7k99f3t+vGsPfG6Vt1rMhSGYs/GkI4RPA/cDh8XfGGB9uRMNa\nwUK09G26dAPXff57E2oW8syrKmouNl689riaBamV5lKzcBTorGyO37lEMpOh8/i9mme2NQvjWWyW\nrnYe58sz+yWb7Jfsaue+qbdmYS6Zhf88h30yyelckiTNbNbBQozxn6o/hxAWxRiPNLZJkiQpS+aS\nWSCE8Fbg/cDpIYSfIllf4ccxxo82snHKJodvJKlYZj0bIoTw68D/Aj4LDFVu3kmyquN7G9g2ZVR1\nFUynnEpSMcxl6uR/AzbFGD9CZRXHGOP1wDuAtzSuacoq53xLUrHMJVgIwDenuP0bwOnza47agXO+\nJalY5hIs7CYJGCb7eeCx+TVH7WD8Kpjr15zsWgGSlHNzKXD8E+APQwjvIVlbIYQQfgn4KPAHjWyc\nsskpp5JULPVeovrjwO/FGHuBW4Ee4AvACcA2YBi4Cfi9JrVTkiSlpN7Mwm8CfwT0Av8BPB34n8A6\nkqGMe2OMfU1poSRJSlW9wcIu4MshhLtJhh42M+maECEkZQwxxisa2D5JkpSyeoOF3wB+C1hNcj2I\nMzi2xoIkScqxuoKFGOP3gVcBhBAeBF4eY9xfey9JkpQHc7k2xFnNaIgkScqmuayzIEmSCmROF5JS\nvnhhKElSLWYW5IWhJEk1mVmQF4bKEbNEkprBzIK8MFSOmCWS1AxmFuqQ9bO1ubavut+Du/voXrKA\nUqnEmauWe2GoNmaWSFIzFCaz0DcwxOat27nqxjvYvHU7fYP1rymV9bO1ubavul/fwFH6Bo9y5qrl\nbHr1+kwFQpods0SSmqEwwcKnv7Jjzgf8rJ+tzbV9WX9fmj0vHy6pGQozDPHQ7rkfGFevXM7B/v0T\ntrNkru3L+vvS7Hn5cEnNUJjMwupVc0/PZv1sbar29Q3OPOyS9fclScqGUrlcTrsN87J376Gab6Cr\nq4OenqU89GgvN992T8OLFLNa/Lh563a2P3Asa7B+zcmZO+Os9k1v7wDDw6NpN0cV9ks22S/Z1c59\nc8opy0v1PK4wwxDdS5uTnq0WCQIc7E9qIbJwUG5mPUJWAyRJUnMUZhiiWbJaJNjMqviszw6RJDWW\nwcI8ZXWqWjPrEbIaIEmSmqMwwxDNsvHitcel5LOgWVXxfYNDjI5OLBPJSoAkSWoOg4V5KtpUtS3b\ndtI3eHRsu3vJgpYGSNZLSFLrOQyhWZk85NDRUWrpwdp6CUlqPYMFzUraNRrWS0hS6xksaFbSXsgp\n7WBFkoooEzULIYQ1wB8CFwD7gRtjjNel2ypNJe0ajawWlEpSnqUeLIQQSsA24F+A84CzgS+EEB6N\nMX4h1cYpc9IOViSpiFIPFoCVwF3A22OMA8ADIYR/BJ4PGCzkUHVGw8NP9PPM00/iDRcGlizKwq+i\nJGkqqf+FjjHuBl5T3Q4hXAC8EHhrao1qkFZM82vHqYTjl8j+7o49HD06wrte9TMpt0qSNJ1MFTiG\nEHYB3wS+A3wp1cY0QCum+bXjVMLjZjTsdkaDJGVZ6pmFSV4JrAJuAv4A2DTTDh0dJTo6pr9oVmdn\nx4R/W+nhJ/onbP/gP/Zz/Rd/wJWXrKN7aWPO/ie/xsNP9NPVlakYkL6BIT79lR08tPsQq1ct57RT\nlnGw/8DY/Wc+fXnm2lxkaX5nND37JbuK0DeZvER1COFVwOeB5THG4VqPLZfL5VKpritstty1f3on\n392x57jbz1+3kg+/8XlNeY1GPnejTG7jhp86ha6uDh549EnWnHYimy7dwInLFqXYQkkqrPa4RHUI\n4VTg52KMfzvu5h3AQqAbODDljhUHDgzMmFno7l5MX99hRkZae53xN1wYOHp0hO3372N8THb/Iwfp\n7R1o6GtUz9rfcGFo2HM3yv2PHJywvevxPjZvesGEvslam4ssze+Mpme/ZFc7901Pz9K6Hpd6sACc\nBXwphHBajPHxym3PAfbGGGsGCgCjo+XjLmw0lZGRUYaHW9uJSxZ18a5X/Qybt24fK+gDOOPUZQ1r\nS/U1xmv1+5zJGacuo/fQkQnb49uYRt9oZvZLNtkv2ZXnvsnCAMt3ge8BnwkhrA0hvAz4OPDRdJvV\nOGmvepi2or9/SWp3mahZCCGsAm4EXgoMADfEGD9Wz7579x6q+Qa6ujro6VlKb+9AbiO+dmXfZJP9\nkk32S3a1c9+ccsry9qhZgLG1Fn4t7XZIM2nHdS0kab6yMAwhtY12XNdCkuYrE5kFtY+in1l7iexj\niv67UPT3r2Ixs6BZKfqZtZfIPqbovwtFf/8qFoMFzUrRz6yd2XFM0X8Xiv7+VSwOQ8xS0VOPq1cu\n52D//gnbReIlso8p+u9C0d+/isXMwiwVPfXombWqiv67UPT3r2IxszBLRU89ematqqL/LhT9/atY\nzCzMkgVukqSiMbMwSxsvXntczYLmp29giJtvu2fKOpCi14iofv6uSM2TieWe58PlnttXtW8+dNO3\nufu+fWO3r19z8lh6d/JFuMbfp+Zo1+9M3n9X2rVfiqCd+6atlntWPtV7pvfQ7unrQIpeI6L6+bsi\nNY81CznSNzjE5q3buerGO9i8dTt9g0OptqfemSOrV01fB2KNiOrl74rUPAYLOZK1aZ31nuldecm6\naaegOT1N9fJ3RWoehyFyJGtp2HoXreleOv0UNKenqV5F/V2xsFOtYGYhR7KWhvVMT2q+rGUUlU9m\nFnKkkdM6G3G2UtQzPamVspZRVD4VLlhIO2U339evtX/3koUTAoYt23bO+f1Vz1YADvYnZyv1HvjT\n/oylIvEaFWqFwg1DNCNlN5tZCPN9/Zn2b9T7m8/ZimlRqXUc7lMrFC6z0IyU3WzOwuf7+jPt36j3\nN5+zFdOiUus43KdWKFxmoRlFgLM5OM739Wfav1Hvbz5nK1krtJQkzU+hMgt9g0MMj4zS1ZmsbhlO\nP6khKbvZnIXPtwhxpv0bVeQ4n7MVr58hSflSqGBhy7ad3LOrd2y7q7OjIYV3Mx0cG1nwN9NBPAsp\nySy0QZLUOIUKFpo1lj7TwXE+MwskSUpboYKFtKYYzSVIqWYjHtzdB2UolUqcuap2VsIpi5KkZihU\ngWNaU4zmUvBXzUb0DRylb/AoTw7MPA3RKYvFk7WLh0nKp0JlFtIaS59Lwd902YdaWQmnLBaPQ1zZ\nY4ZPeVSoYCEtcwlSJg+ZjL+9avIfpZ942lIO9g9N+dg0+Eez+QwQs8cATnlUmGChb2CIm2+7p20O\nXNVsxFQ1C1U333bP2OyOg/37CaefyPo1J2dmyqJ/NJvPpX5rSyNgNYBTHhUmWPj0V3a01YGrnmxE\nfOTghO0HHuvjf//3FzezWbPiH83mc02L2tIIWA3glEeFCRYe2j3xQHXPrgNcdeMdbZFlmErf4BAj\nI+W0m1GTfzSbzzUtaksjYDWAUx4VJlhYvWo5vYeOjG0Pj5Q52D804WyjncbYt2zbyeRQIZx+Uipt\nmY5/NJW2NAJWAzjlUWGChSsvWTdWs9B/+CjD487Kq2cb7TTGPvkMqauzxJtefm5KrZmafzSVNgNW\nqTEKEyx0Lz124Nq8dftYUADHzjbaaYx98hnTuWeuyGwWREqLAavUGIUJFuBYZfSu3YfoXrIASnDW\nqu6xs41mpyxnGuaYzTCIZ0ySpFYpVLAwfpgBYP2akyecdTT7ADzTMMdshkHGnzG1U62FJKn9FCpY\nmGmYodkpy5lef67DIO1UayFJaj+FChYmDzOMjpbpGxxq2Vn4TMMccx0GyWqthRkPScqH1C8kFUJ4\nRgjhr0MI+0MIj4QQPhlCaMoRZePFa1m2eMHYdt/gUa6++V9adhGemS5kNdcLXc3lQlWt4IWtJCkf\nspBZ+CKwH7gAOBnYAgwD72/0C3UvWchTQ8MTbus/fBRofvq+nrPsuQ6DZLXYMasZD0nS7KQaLIQQ\nAvCfgJUxxn2V2z4MfIImBAszaebBbD51BTMFGlmdHuYKjpKUD2kPQ+wGfrkaKFSUgBOb9YJrntE9\n7X3NPJjN5yy7XdP5cx1WkSRlS6qZhRjjk8A/VLdDCCXgncDXmvWaXZ0T46OlJ3Rx5OgIAE8NjfDJ\nL9zFj/cNNLwgbz5n2e2azs9qxkOSNDtZqFkY7xPAecBz6t2ho6NER0dp2vs7K8FB9d/H9g9OuH/o\n6OjY0s/jr+J4sH8/t9x+L1ddel69TanpTS8/l09/ZQcP7T7E6lXLufKSdXR11ZfYOfPp3dx9374J\n2/Xum2WT+0bZYL9kk/2SXUXom1K5nI0rF4YQPga8B/ivMca/qXe/crlcLpWmDxYm+/CffIe7frR3\nbHtBZwdHR0anfOyK7hP47DUX1v3czfJk/xE233oXDzz6JGtOO5FNl27gxGWL0m6WJKn91XUAzURm\nIYRwA/AW4LWzCRQADhwYmDGz0N29mL6+w4yMjHK0MuRQNTxNoABwxspl9PYOjG33DQwdlx3oXtqa\ndQN+85U/Pfbz6NFhenuHazy6PUzuG2WD/ZJN9kt2tXPf9PQsretxqQcLIYRrgDcDl8YYvzzb/UdH\ny4yOzpwdGRkZZXh4lEf39k+4vbpnV2dp7BLP1ZqFyy86h+HhYx1/8233jM1o6D10hJtvu8cx+Qao\n9o2yxX7JJvslu/LcN2lPnVwLXA38LvCdEMLK6n0xxj3zff6+wSFuuf1eHt7Tzxkrl3H5ReccV2hY\ntWzxAt572Yaaz9fsQkNXPJQkZVHa1Rgvr7ThauCxyn+PV/6dty3bdnL3ffs40PcUd9+3jy3bdvKy\n562ma4phi3pmJzR7pcR2nSIpScq3tKdOfgz4WLOef9fuQ8dtX//FHzA8adiie8kCXv3iZ874fM1e\nKbFdp0hKkvIt9ZqFZhqZFBSMjJYZeOr4wsC+waNs/cb9M9YfNHvdgOnWYmjW8ITDHrPnZyapiNIe\nhmiqw0eO1tweLwtn8a9+8TPpXrKAUmlitqNZwxMOe8yen5mkIsp1sDB5/YVSqcSSRZ1TPjYL1y3Y\n+o376RvRusCfAAARLUlEQVQ8Srl8LNsBzRuemO55+waH2Lx1e8uuxtlOHCqSVES5DhaqUyHHb59+\n6rIJt3V1ljJz3YKpDkR9g0PHTQ1tVGAzXcFmls+e0w5ksno5cElqplwHC296+bmcd/bTWNF9As86\nawUAP3r0yQmPWXrCAja9en0mxp2nOhBt2baTvsFjwyfdSxY0LLCZ7kJPWT57TjuQ8eJYkooo1wWO\n3UsWctWl59HTs5QP3fTtCddXqKoud52FwrWpZlt85DP/OuExHR2lhrVruoLNLF9aOu1AxotjSSqi\nXAcL4z20e5qDSqWsoXrGCslFpLZs29nyg8JUB6I0DtzNniI6H1kOZCQpr3IfLPQNDHHDl/6d/sGp\nZ0KctaobSP+MdTppHLizfPac5UBGkvIq98HCp7+yY8LwQ1dniSWLuqCUBArVg01Wz1izfOBOg5+H\nJLVe7oOFycMPyxYv4FPvfP6E2/oGhxgeGaWrMxmTCKef5BmrJEkVuZ4NAbB61cxT3bZs28k9u3oZ\nHikzPFKmq7MjE7MjJEnKgtxnFq68ZB2f/Wrk/kcOcsapy6bMGNRbr5CFGROSJLVa7oOF7qUL2XTp\nBq77/PfY9XgfN992DwA/3jcwdsCvt14hCzMmJElqtdwHCwCbb71rrMjxYP+xFf+qB/x6K+yzOmNC\nkqRmKkSw8MCkVRvHe2jPobor7LM6Y0KSpGbKfYEjwJrTTpz2vtkc8F3qV5JURLnPLPQNDHF0eJQF\nnR2UKbPmGSfS1VmaULMw9tgpChgBixolSYWW+2Bh8qJMJyzsnHbIYaoCRsCiRklSoeU+WJi8KNOD\nu/vYvHX7lJmCyQWLu3YfYuCpictEW9QoSSqa3AcLq1ctp/fQkbHt0dGJmYKbb7uH9162gcf2DRx3\n/YhyOVmkacLzjatxcN0FSVIR5L7A8dKXPJMTly2kVILuJQs4fGRiQBAfOQjAx//i3xgePRYYdHWU\nxq5IOXZbZ2lCjUN12OJg/xDbHzg2bCFJUp7kPli49ev382T/EOUy9A0eZXR06scdOjwxiBgpl8eu\nSFl17pkrJmQOXHdBklQEuR+GmFyzUJ50/wkLO7nqxjvoLJUYLh+7d/niBVMu1jR+6GF0dPohiuk4\ndCFJaje5DxYm1yxUlSr/6z88PHZbV0eJkXKZ5YsX8L5ff/aUizVt3rp9rOYBkqGNjo5SzZUfx3PJ\naElSu8l9sHDlJet45+9/87jby2P/O2bZkuMvXz3Z5KGGjo7SjPvU2t+hC0lS1uU+WOheWn+Kf/Iw\nwlRDBvNd8tkloyVJ7Sb3BY4Ay5cuqHl/V2dpyuWbp5rtMN8ln10yWpLUbnKfWQC4euNz+eAff/u4\nNRMgCRSue8cFUxYZTjVkUO9Fp6Yz3/0lSWq1QgQLf/31+6YMFADC6SdNOxuhUUMG9cyAcJaEJCmr\nCjEMUesS1bU0asignsWbXOBJkpRVhcgsrDntRA7seGrK+368b2Da/apDBtWz/o985l/5iactHduv\n3gxAPTMgnCUhScqqQmQWNl26gfPOfhpdnaXj7qtnaGH8Wf89u3q5Z1fvrDIAk19jqtes5zGSJKWh\nEMHCicsWcdWl53HdOy7g3DN76Oos0dVZ4twze+oaWqh1ll9PBqCe4QxnSUiSsqoQwxBV3UsW8t7L\nNsx6v8mFjpPvq+d1Z5oB4SwJSVJWFSKzMF/jz/rPPbOHc8/sMQMgSSqMQmUW5sqzfklSkWUqWAgh\nLAK+B7wjxnj8BR0kSVLLZWYYohIo/CWwLu22SJKkYzIRLIQQ1gJ3Amel3RZJkjRRJoIF4BeAfwR+\nDjh+MQRJkpSaTNQsxBhvqv4cQkizKZIkaZKsZBYkSVJGZSKzMB8dHSU6OqYfuejs7JjwbzvpGxji\n01/ZwUO7D7F61XKuvGQd3UvzcyXKdu6bPLNfssl+ya4i9E3bBwsrViylVJq5zKG7e3ELWtNYN3zp\n37n7vn0A9B46wme/GvnwG5+Xcqsarx37pgjsl2yyX7Irz33T9sHCgQMDM2YWursX09d3mJGR0Ra2\nbP7uf+Tgcdu9vdNfJbPdtHPf5Jn9kk32S3a1c9/09Cyt63FtHyyMjpYZHS3P+LiRkVGGh9urE884\ndRm9h45M2G6391CPduybIrBfssl+ya48900WB1hmPvIXhFeilCRlQeYyCzHGzrTbkBVek0KSlAVZ\nzCxIkqQMMViQJEk1lcplSwQkSdL0zCxIkqSaDBYkSVJNBguSJKkmgwVJklSTwYIkSarJYEGSJNVk\nsCBJkmoyWJAkSTUZLEiSpJoMFiRJUk2Zu+pkI4UQFgF/BLwSGAQ+GWP8VLqtKp4QwjOA64EXk/TD\nXwEfiDEOhRDOBG4Gfg7YBbwnxvgPKTW1sEII24A9McYrKttnYr+kJoSwEPh94DXAEeAzMcYPVu47\nE/smFSGE04A/Bl4I7Ac2xxg3V+47kxz3S94zC9cBzwZeBLwduCaE8MpUW1RMXwROAC4ALgP+C/A/\nK/f9LfAY8LPA54EvV76QapEQwmXARZNu/hvslzRdD7wU+EXg14E3hRDeVLnP70x6tgKHSI4r7wZ+\nJ4TwK5X7ct0vub2QVAhhCbAPuDDG+K3KbR8EXhpjfEmqjSuQEEIAdgArY4z7KrddBnwCeD3JF+zU\nGONTlfv+AfhWjPHalJpcKCGEHmA7yR+5HTHGK0IILyEJFuyXFFT6ZA/wkhjjHZXb3gf8FPDn+J1J\nRQjhJOAA8KwY447KbX9N8t35MjnvlzxnFtaTDLP887jb7gCem05zCms38MvVQGGcE4HnAf9W/XJV\n3EGSxlNrXAd8Dtg57rbnYr+k6fnAwWqgABBj/HiM8Ur8zqTpMDAAbAwhdFVOhC4A7qIA/ZLnYOHp\nwL4Y4/C42/YAJ4QQTk6pTYUTY3xy/LhdCKEEvBP4R5I+emzSLnuA3KTusqySQXgBx4aEquyXdP0k\nsCuE8LoQws4QwgMhhKsr3x37JiUxxiMkf7veShI47AT+b4xxCwXolzwXOC4hKQwar7q9qMVt0TGf\nADYA5wNXMXUf2T9NVin+vQl4e4zxSHKSNGa674790hrLSIYc3gxcTnIg+hOS4mD7Jl1rgdtIMnI/\nDdwQQvhHCtAveQ4WnuL4jqpuD7a4LQJCCB8D3gX81xjjjhDCU8CKSQ9bhP3TCh8Bvhtj/NoU99kv\n6RoGlgOviTE+ChBCWE1SpP33wOTMqH3TAiGElwJvBE6rZBnuqhQwXk2SKc11v+R5GOLHwNNCCOPf\n4yrgcIzxYEptKqwQwg3Ae4DXxhj/pnLzj0n6ZLxVwOOtbFtBXQq8IoRwKIRwCHgt8BshhD7gUeyX\nND0OPFUNFCoiSUrb70x6ng3cVwkUqu4CzqAA/ZLnYOFu4ChJ4UnVC4DvptOc4gohXEOSUr00xrh1\n3F13As+upMSrnl+5Xc31CyRp1PWV/24jqeZeD/wL9kua7iSprXrmuNvWkczdvxP4WfsmFY8Bzwwh\njM/IrwUepAD9ktupkwAhhD8mqVa9giQqvwV4Q4zxb9NsV5GEENYCPwB+l2SBrPH2kkzb+yFJkd3L\ngQ8A5046q1KThRC2AOXK1MkO7JdUhRBuIxkKejtJzcLngGtJFgT6AfDv2DctFULoJilq/Afgd4Bz\ngM+QfP6fIef9kufMAiQFdN8Hvg7cAHzIQKHlXk7ye3Y1SWT+GElq7rEY4yjwCpJ03fdIFp95RV6+\nXO2q0i+/gv2SptcC9wPfIjnJuT7G+IeVvnk59k3LxRj7SBbKejrwr8AngWtjjJ8uQr/kOrMgSZLm\nL++ZBUmSNE8GC5IkqSaDBUmSVJPBgiRJqslgQZIk1WSwIEmSajJYkCRJNRksSJKkmgwWJElSTQYL\nkhoihPDzIYQLatz/YAjhw5WfPxJCeHDcfaMhhNdXfr4mhPAf4+5bF0J4WTPbXnmdFSGEK5r9OlI7\nMliQ1Ch3AGtq3P8c4LrKz+XKf1P5BHD+uO2vVPZttuuA32jB60htp2vmh0jS/MUY99f5uEFgcNxN\npea06Diteh2p7RgsSBkSQhgF3gm8DjgPuA/4YIzx/4x7zCXAR4B1wI+BvwQ+GmMcGvcc1wKXAwuA\nFwIPAR8GXg+cAtwD/FaM8WuVfdaSnFm/EDhEcqXW98YY91Tu/wZwZ2XfV5FkJf8P8JYY40DlNcvA\nlhDCi2KMx6XzK8MOW2KM187wGXyE5FLyZ1X2OQO4pvK8L6lcKvg6kiuWLiS5yt/7Y4zfr+x/DfBi\nkqubvgy4Jca4KYRwJfCbwNnAKPBvwLtjjP9WuUT3Gyr7j8QYOys/vw94C8nVBCNwXYzxL2q1X8oj\nhyGk7Pk94LPAzwDbgC+HEJ4HEEL4ZeBW4CaSYOFtwKuBz016jrcBvwr8aozxAeB64M3Ae4BnAX8P\n3BZCODuE8HTgmyQHw2cDFwPdwD+HEBaPe853kxyAn0NyCeVXVJ4Pksv2loBNlf/mY/wQxfkkAdEn\ngVdWbrsdWE0SCPwnkiDm2yGE9eOe44Ukl0NfD1wfQnhF5TP4X0AAXgKcAHy68vhNwF8B3yEJDAgh\n/C5JoPAOks9sM/BHIYS3zvP9SW3HzIKUPVtijDdVfv5ACOFFJGfEdwK/BfxJjLF6kNsVQngb8PUQ\nwvtijA9Xbv9cjPEugBDCMuAK4B0xxi9X7r86hABJUPA64JEY41XVBoQQLgP2MjEQ2RFj/FDl5wdC\nCH8PXAAQY9xTeb6+GOOhRn0QMcZ9IYQRoD/GeDCE8FLgucDTYowHx72X55Mc8KsZjTLwkWpbKgHR\nG2OMf1m5/5EQwmeAGyqv0xdCOAwMxRj3hhCWkARHl8UY/66yz4MhhLOA95MEa1JhGCxI2fP/Jm1/\nB/jFys/PBs4PIbxp3P0lkrT6WqAaLNw/7v5AMhzxL+OfNMZ4NUAI4beBZ4UQJh/kFwHnjNu+d9L9\nTwInzvBeGm0DSUb0kUpwUrWw8l/VE+ODlhjjHSGEc0IIV5O8p7NJMjfTZVfXkWQe/iKEML4QsxNY\nGEJYFGM8Mu93I7UJgwUpe45O2u4ERio/dwAfJxmmmOzxcT8fnvR8tYr3OkhqFN42xeMOjvt5qoNj\nq4sCO0iClGdP8drj2zf+/RNC+HXgFuDzwLdJMgM/DdxY43UgyazEyXcaKKhoDBak7DmfpFah6ueB\n71d+/iEQYozj1yF4EfAu4K1MOkhW3EcSMJxf2b+63z8DX6jcdinwaIzxaOW+HpLhh+uAf2rEm5qH\n8Wf2PyQZOlkUYxzLdIQQbgbuAv5omud4P3BzjPEd4/b51Rqvcy8wDKyOMd4+bp93kWRw3jaH9yG1\nLYMFKXveHUKIJFX+byFJl2+s3Pcx4NYQwodIDvRnkBTp3R9jfGKqJ4sxHg4h3AB8NISwj2QmxJUk\nRXvbSA6Kbwb+PITwUZIz9usq9/9wquecRj+wNoSwIsZ4YDZvuI7nPTuEcCrwd8B2ks9gE/AISQHi\nG0iyBtN5BLgghLCBJDPxK5X9CCEsrMwk6QeeEUI4M8a4K4RwE8lndohkKOjFJJ//7zTwvUltwdkQ\nUvbcRDLLYDtJAeEvxhjvAYgxfpEkC/AK4AckZ/+3k0xnrJpqsaP/UXnsH1f2+wXgohjj/THGXZXt\n5SQLK32DJEPx4nrXRqj4JEkh5memub/WQky17rseuAT4aoxxFPjPJIHUrSSf0fOBV8QYa2VA3gns\nIakHuZNkJsXrKvdVF4D6LLAU+GEIYRVJgeMfkExD3UHyGV4dY/xojdeRcqlULk/3/ZTUapX1Ci6P\nMU6eCilJqTGzIEmSajJYkLLFVJ+kzHEYQpIk1WRmQZIk1WSwIEmSajJYkCRJNRksSJKkmgwWJElS\nTQYLkiSpJoMFSZJUk8GCJEmq6f8DhVrAK9FMinwAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbb96c0b8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.804132402682\n"
]
}
],
"source": [
"# Plot the illiteracy rate versus fertility\n",
"_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')\n",
"\n",
"# Set the margins and label axes\n",
"plt.margins(0.02)\n",
"_ = plt.xlabel('percent illiterate')\n",
"_ = plt.ylabel('fertility')\n",
"\n",
"# Show the plot\n",
"plt.show()\n",
"\n",
"# Show the Pearson correlation coefficient\n",
"# print(pearson_r(illiteracy,fertility))\n",
"print(np.corrcoef(illiteracy,fertility)[0,1])"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"slope = 0.0497985480906 children per woman / percent illiterate\n",
"intercept = 1.88805061064 children per woman\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAg4AAAF2CAYAAAAGIhAIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XeYW+d55/0vgOm9sJPTKR2RlERRlqxGUiQldoqi7CSy\nN8WWY2f39Sbxa+9u8qas43izxTWR7Wy8K6/l9ChaSyRFDqsaRVGFkihKIqlDTWcblul9BsB5/8AM\nhjOcAmAAHJTf57p8UXgAnHPjGRjnPk91WJaFiIiISCCcdgcgIiIi8UOJg4iIiARMiYOIiIgETImD\niIiIBEyJg4iIiARMiYOIiIgETImDiIiIBEyJg4iIiAQsxe4AZurq1a4pV7ByOh0UFWXT2tqD16vF\nriJF9Rx5quPoUD1Hnuo48gKt49mzcx1BH3tGkcUBp9OBw+HA6Qy6biQIqufIUx1Hh+o58lTHkRfJ\nOk74xEFERETCx/auCsMwvgA8DViA47p/vaZp2h6fiIiIjIqFC/O/APuue5wGvATsticcERGJN529\ngzy99wyNl7som5vLE1uXkJeVZndYCcn2xME0zQHgyshjwzD+aPg//2jid4iIiIz19N4znKxtAaC9\nu4Wn957ha7+63OaoEpPticP1DMMoBP4A+JJpmkN2xyMiIvGh8XLXlI8lfGJtcORXgQumaT5vdyAi\nIhI/yubmTvlYwifWEoffBn5kdxAiIhJfnti6hOVVxRTkpLG8qpgnti6xO6SEFTNdFYZh3A0sBJ4J\n5n1O59TzVF0u55h/JTJUz5GnOo4O1XPkRaKOi/Iy+A+fXxG248W7SH6PHZYVG6t2GYbxp8CDpmmu\nD+Z9lmVZDocWEREREQlB0BfQmGlxAO4BXg/2Ta2tPdO2OOTlZdLZ2YfH451JfDIF1XPkqY6jQ/Uc\nearjyAu0jgsLs4M+diwlDrcCfx/sm7xeK6C1zj0eL263vqCRpnqOPNVxdKieI091HHmRqONY6sSb\nA7TZHYSIiIhMLmZaHEzTDL69RERERCbk8XoictyYSRxERERk5po6z7Orbh9mWw2/seRXuHfe3WE9\nvhIHERGRBHCtr4Xdtft598pJf1lLf/hHAChxEBERiWPdgz3sb3iRIxfewGP5uicyXOk8umQDq+Y9\nAGEef6rEQUREJA4NegZ56dxRDjW+Qr+nHwCnw8mqhffxyOL1lM6dS1tbD25veDMHJQ4iIiJxxOP1\n8Fbzu+ypO0jHYKe//M45t/NI5SbmZM0iJSVykyaVOIiIiMQBy7L4qOUMO2v30dxz2V9+U0Eljy3e\nSlleSVTiUOIgIiIS4+o7mthZu5ea9np/2fzsueyo2sKy4luI5tYLShxERERi1JXeq+yu3c+Jqx/6\nywrS89lWsYF75n8KpyP66zgqcRAREYkxXYPdVNcf5ujFN/FavsGNGa4MNpatZU3JStJcqbbFpsRB\nREQkRvS7B3jp3BEON73KgGcQgBSHi9WL7mdj+TpyUu1fZFmJg4iIiM08Xg/HLh1nb/1Buga7/eV3\nzb2DRyo3MSuzyMboxlLiICIiYhPLsjh57RS7a/dxufeqv9woXMyOxVsozV1kY3QTU+IgIiJig9r2\nBnbW7qWuo9FftjBnPjuqtrCk6OaozpQIhhIHERGRKGruucLu2n2cvHbKX1aYXsAjlRu5e94KW2ZK\nBEOJg4iISBR0DHSyt/4Qb1w67p8pkZWSycbydTy48H5SbZwpEQwlDiIiIhHU7+7ncNOrvNh0hEHv\nEAApzhTWLHqAjWVryUrNsjnC4ChxEBERiQCP18PRi29RXX+I7qEeABw4+PS8O9lWuYGijEKbIwyN\nEgcREUkqnb2DPL33DI2Xuyibm8sTW5eQl5UWtuNblsWJqx+yu3YfV/ta/OVLiwwerdrMotwFYTuX\nHZQ4iIhIUnl67xlO1vou6O3dLTy99wxf+9XlYTn2J221PF9bTWPnOX9ZSe5CdlRt4Zaim8JyDrsp\ncRARkaTSeLlrysehuNjdzK7afXzUcsZfVpxRxPbKjdw5d3nMz5QIhhIHERFJKmVzc2nvbhnzOFTt\nAx3sqTvIm5fewcICIDs1i83lD7Ny4b2kOhPvMpt4n0hERGQKT2xdcsMYh2D1ufs42PgKL587ytDw\nTIlUZwprS1axoWwNmSmZ4Q47ZihxEBGRpJKXlRbymIYhr5vXLrzB/oYX6RnqBXwzJe6bfxdbKzdQ\nkJ4fzlBjkhIHERGRaXgtL+9dPsnuugO09Lf6y28tXsKjVZtZkDPPxuiiS4mDiIjIFD5u/YRdtdU0\ndV3wl5XllfBY1RZuKqyyMTJ7KHEQERGZwPmui+ysreZM61l/2ezMYrZXbWbF7NtidhOqSFPiICIi\ncp3W/jb21B3k7eb3/DMlclKz2VKxnpUL7sHldNkcob2UOIiIiAC9Q70caHyZV86/jtvrBiDNmcpD\npat5qPRBMlMybI4wNihxEBGRpDbkGeLVC8c40PASve4+AJwOJ/fPv5stFevJT8+zOcLYosRBJAiR\nXuNeRKLHa3k53nyCF+oO0DbQ7i9fPmsZ26s2My97jo3RxS4lDiJBiOQa9yISHZZlcab1LDtrq7nQ\nfclfXplfxo6qrVQVlNsXXBxQ4iAShEiscS8i0dPUdZ6dNdWYbTX+srlZs3m0ajO3z1qWtDMlgqHE\nQSQI4VzjXkSi51pfKy/U7eedy+/7y/LSctlSsZ7759+d9DMlgqHEQSQI4VjjXkSip3uohwMNL3Hk\n/DHclgeAdFcaD5c+yLqS1WSkpNscYfxR4iAShJmscS8i0TPoGeKVc0c52PQyfe5+wDdTYuWCe9lc\n8RB5aWotDJUSBxERSRhey8ubl95lb/1B2gc6/OUrZt/G9qpNzMmabWN0iUGJg4iIxD3LsjjV8jG7\navdxsafZX764oIIdVVupyC+1MbrEYnviYBhGGvCXwOeBAeDnpmn+ib1RiYhIvGjobGJnTTWftNf5\ny+Zlz2VH1WZuLV6imRJhZnviAPwIWAOsB/KAZwzDaDBN8ylboxIRkaBFc5G0K73XeKFuP+9d+cBf\nlp+Wx7bKDdwz71OaKREhtiYOhmEUAl8C1pmm+e5w2feBewAlDiIicSYai6R1DXazr+Ewr114E6/l\nBSDDlcH6sjWsK1lJmkuruUaS3S0OK4F20zSPjhSYpvldG+MREZEZiOQiaQOeQV5qeo3DTa/Q7xkA\nwOVwsXrhfWwqf4ictOywnUsmZ3fiUAk0GIbxm8AfA2nA08B/NU3TsjUyEREJWiQWSfN4Pbxx6TjV\n9YfoGBxNRO6aewePVG5kVmbxjM8hgbM7ccgBbgZ+B/giMB/430APvgGTIiISR8K5SJplWXxw7TS7\navdxufeKv/zmwsXsqNpMWV5JOEKWINmdOLiBXODzpmmeBzAMowz4fwgwcXA6HTidk4+YdbmcY/6V\nyFA9R57qODpUzzNTlJfBf/j8iilfE0gd17Y38Muze6htb/CXLcyZz2du3sqyYkMzJaYRye+x3YnD\nJaB/JGkYZgIBp5FFRdkBfYHy8jKDj06CpnqOPNVxdKieI2+iOr7Y2cw/fbiLt8+P7ilRnFXI47c+\nwuqye3A6ldAFIxLfY7sThzeBDMMwFpumObJV2VKgIdADtLb2TNvikJeXSWdnHx6Pd0bByuRUz5Gn\nOo4O1XPkTVTHHQOd7Kk9xNELb/lnSmSlZLKpYh1rS1eS5kqlo6PPzrDjSqDf48LC4AeU2po4mKZ5\n1jCMvcAvDMP4Kr4xDn8IfDvQY3i9Fl7v9OMoPR4vbrd+BCJN9Rx5M6njaM6xj3f6Lkeex+Olu7+X\nF5uOcPjcEQY9gwCkOFw8uOgBNpavIzs1Cyz0twhRJL7Hdrc4APw68GPgNaAX+JFpmn9tb0giiSka\nc+xFAuH2enil6XX21B6ia6gbAAcO7p63gm0VGynOLLQ5QpmM7YmDaZpd+GZUfNHeSEQSXyTn2IsE\nwrIs3m0+yQvHDnCpe3SmxJKim3m0agsluQtsjE4CYXviICLRE4k59iLjTdYlVtNez86avdR3Nvlf\nW5KzgEcXb2FJ0c02RizBUOIgkkTCOcdeZDLju8R+uv9N8hbX8uG1M/7XzM4u5pHKjayYdTtOh2ZK\nxBMlDiJJJC8rTWMaJOL8XWCp/aQurKEx/zxc8xVlp2Sxpephdtz2MN2dgxr0GIeUOIiISFgtmpdB\nd99HpMxrwOHyJQapzhTWLFrJhrK15GVmk+pKBQbtDVRCosRBRETCwu1189qFN2mec5hUd6+v0IJP\nzbmTx27aRGFGgb0BSlgocRCJQRMNLivKy7A7LJEJeS0vJ658wO7a/Vzrb/WXLyu+hUerNrMwZ76N\n0Um4KXEQiUETrbcw3fr/InY421bD8zXVNHWN7hxQllvCjsVbuLmwysbIJFKUOIjEIK23ILHuQvcl\ndtZWc7rF9JfNyihie9Vm7pxzuzahSmBKHERikNZbkFjV1t/OnrqDvNX8Lha+5f5zUrPZXP4wKxfe\nQ4pTl5VEp7+wSAzSegvxJ9H3Aekd6uNg48u8cv4oQ143AKnOVB4qWcXDZWvITNEYnGShxEEkBoVr\nvYVEv5jFkkTdB2TI6+bI+WPsb3iRXrdvd0oHDu5fcDdbKtZTkJ5vc4QSbUocRBJYol7MYlGijUvx\nWl7eufw+L9QdoLW/zV9+26ylPFq1mfnZc22MTuykxEEkgSXaxSyWJdK4lDOtZ9lZU8357ov+soq8\nUnYs3sriggobI5NYoMRBJIEl0sUs1iXCuJRzXRfYWVPNx22f+MvmZM5ie9Vm7ph9q2ZKCKDEQSSh\nJcLFLF7E8z4gLX2tvFB3kOOX3/OX5abmsKViPQ8s+DQup8vG6CTWKHEQSWDxfDGTyOsZ6mV/w4sc\nOX8Mt+UBIM2VxsMlq3modDUZmikhE1DiIBICzVaQeDboGeLV869zoPFl+oZnSjgdTh5YcA+byx8m\nP11dWjI5JQ4iIdBsBYlHXsvLW83vsafuAO0DHf7yO2bfxvaqTczNmm1jdBIvlDiIhECzFSSeWJbF\n6VaTnTXVXOxp9pdX5ZezY/FWKvPLbIxO4o0SB5EQjJ+t0N03xJPPnlSXhcScxs5z7Kyp5mx7rb9s\nbtYcdlRt5rZZSzVTQoKmxEEkBCOzFU41tOL2WLg9Fidr1WUhseNqbwsv1O3n3Ssn/WX5ablsrdjA\nvfPv0kwJCZkSB5EQjMxW+MZPjtLePegvV5eF2K1rsJv9DS/y2oU38QzPlMhwpbO+bA1rS1aR7lKL\nmMyMEgeRGdACSxIrBj2DvHTuNQ41vkK/ZwDwzZRYtfA+Npc/RG5ajs0RBkYzlmKfEgeRGdACS2I3\nj9fDm83vsLfuEB2Dnf7yT81ZziOVm0gnl5/vip8LsWYsxT4lDiIzoAWWxC6WZfHhtdPsqttPc89l\nf/lNBZU8tngrZXklADz57Mm4uhBrxlLsU+IgEiI1qYpd6jsaeb6mmtqOen/Zgux5PFq1mWXFt4yZ\nKTHVhTgWv8Pq/ot9ShxEQqQmVYm2y71X2V27n/evfugvK0jPZ1vFBu6Z/ymcDucN75nqQhyL32F1\n/8U+JQ4iIVKTqkRL52AX++oPc/TiW3gtLwCZKRlsKFvLmkUrSXOlTvreqS7EsfgdVvdf7FPiEONi\nsSlRfNSkKpHW7x7gxXNHeLHpVQY8vmm/KQ4Xqxfdz8bydeSkZk97jKkuxPoOSyiUOMS4WGxKFB81\nqUqkeLwejl16m731h+ga7PaX3z13BY9UbqQ4sygs59F3WEKhxCHGxWJTovioSVXCzbIsTl79iF11\n+7jSe81ffkvhTTy6eDOluYvCej59hyUUShxinJoSRZJDbXsDz9fspb6z0V+2MGc+j1VtZUnxzTZG\nNjV1pyYfJQ4xTk2JIomtuecyu2r388G1U/6ywvQCtldt4q65d0w4UyKWqDs1+ShxiHFqSpREorvT\nUe0DHVTXH+LYxeNYWABkpWSysXwdDy68n9QpZkpMJdp1rO7U5KPEQUSiRnen0Ofu53DTq7zUdIRB\n7xAAKc4U1ix6gI1la8lKzZrR8aNdx+pOTT5KHEQkapL57tTtdXP0wlvsazhM91APAA4cfHrenWyr\n3EBRRmFYzhPtOlZ3avJR4iAiURPNu9NY6RaxLIv3rnzA7rr9XOsb/exLiwx2LN7Cwpz5YT1ftFsA\n1J2afGIicTAMYwfwHGABjuF/f2ma5q/ZGpiIhFU0705joVvkbFstO2uqaew65y8rzV3IjqqtGEWL\nI3JOtQBIpMVE4gAsBXYDX8GXOAD02xeOiERCNO9O7ewWudjdzK7aaj5q+dhfVpxRxPbKjdw5d3lE\nZ0qoBUAiLVYShyXAR6ZpXrU7EBFJDHYM2mvrb2dP/UHeuvSuf6ZEdmoWm8sfZuXCe0l1xspPrkjo\nYuVbvBQ4ZHcQIpI4otlk3zvUx6GmV3j53GsMed0ApDpTWVuykg1la8hMyYzYuUWiLVYSBwPYZBjG\nnwAu4Fngm6ZpDtkblohA7Aw0DEY0muyHvG5eu/AG++tfpMfdC/hmStw3/y62Vm6gID0/oucXsYPt\niYNhGKVAJtAH/CpQAfwYyAC+Pt37nU4HTqdj0uddLueYfyUyVM+RZ2cd/2Lfx2MGGv5i38d84/E7\noh5HNARSz17LyzvN77Pzk3209Lf5y2+fvZTHbtrCgpx5EY8znun3IvIiWccOy7LCftBgGYZRYJpm\n+3WPPwP8PZBjmuaUAVqWZTkckycOIjJzX/jzA7R2jo5XLsrL4G//bKONEYVfR/cATz5zgtrzHVQt\nyudrj68gPyf9htd90HyGf/zgeerbRmdKLC4q5zeWf4alc24K23lEoiToC6jtLQ4A1ycNw87ga3Eo\nAlpufMeo1taeaVsc8vIy6ezsw+PxzjhWmZjqOfLsrOPSuTljEofSuTm0tfVENYZI++Ez7/P+J74d\nKVtP9/ODf3yHr//aaKvKua6LPHd2L6dbTH/ZnKxZ7Fi8mTvn3o7D4QioTsaf5/v/8E7Ctt5MRr8X\nkRdoHRcWZgd9bNsTB8MwNgD/BCwyTXPkl2kF0GKa5pRJA4DXa+H1Tt9q4vF4cbv1BY001XPk2VHH\nX9x8C097R8c4fHHzLQn3d2641DnucRdut5eWvjb21B/gePMJ/0yJnNRstlSsZ+WCe3A5XXg8FhBY\n6+2N5+lMuLoMlH4vIi8SdWx74gAcA3qBnxmG8W2gCvgu8B1boxIRv2RYG2D89M1F89N4rmYPr54/\nhnt4pkSaM5WHSh/k4dLVZKRkhOU82ttB4o3tiYNpmt2GYWwE/go4DnQBPzVN8wf2RiYiycQ/ffNq\nBwUVl7iQ9Qo1Tb5GUKfDyf3z72ZLxXry0/PCc55x00TjceaKJCfbEwcA0zTPAIk10ipO6cdLklVO\nZgr3rnRztf4ol/vbweMrXz77VrZXbmJe9pywnGey1ptYWCJbJBAxkThI7NCPlyQby7I43XqWXbXV\nXOi+5C+vKijn0cotVBWURyWOZN45VOKLEgcZQz9ekkyaOs+zs7Yas63GXzY3aza/ueIzLM5aPDzo\nMTo09kHihRIHGUM/XpIMrvW18kLdft65/L6/LC8tly0V61ldcg+zivOGp1ZGL3HQrpYSL5Q4yBj6\n8ZJE1j3Yw/7GFzly/g08lm8QQ7orjfWla1hXupp0Vxoupz2rGSbDzBVJDEocZAz9eEkiGvQM8vK5\noxxsfIV+z+hMiZUL7mVLxcPkpuXYHKFI/FDiICIJy2t5efPSu+ytP0j7QIe/fMWc29leuZE5WbNt\njE4kPilxEJGEY1kWH7WcYVftPi71XPaXLy6oYEfVViryS22MTiS+KXEQkYRS39HEztq91LTX+8vm\nZ8/l0arN3Fq8hJFN8bRmiUholDiISEK40nuN3XX7OXHlA39Zfloe2yo3cu/8T+F0jB30qDVLREKj\nxEFE4lrXYDfV9Yc5evFNvJZvM58MVwYbytawtmQlaa6JWxG0ZolIaJQ4iEhcGvAM8lLTEQ41vcKA\nZxAAl8PF6oX3san8IXLSpt4uWGuWiIRGiYNImKjPPDo8Xg/HLh2nuv4QnYOjrQR3zb2DRyo3Miuz\nOKDjaM0SkdAocRAJE/WZR5ZlWXxw7RS7avdzufeKv/zmwsU8VrWF0rxFQR1Pa5aIhEaJg0iYqM88\ncuo6Gni+Zi91HY3+soU583m0agtLi272z5QQkchT4iASJuozD7/LPVfYVbefk1c/8pcVphewrXID\nn5535w0zJUQk8pQ4iEwi2DEL8d5nHktjNDoGOqmuP8SxS8f9MyUyUzLZWLaWNYseINWVaktcIqLE\nQWRSwY5ZiPc+81gYo9Hv7udw0xFebHqVQe8QACkOFw8ueoCN5evITs0a8/pYSnZEkoUSB5FJJNuY\nBTs/r8fr4ejFt9hXf5iuoW4AHDi4e94KtlVspDizcML3xUKyI5JslDiITCLZxizY8Xkty+LE1Q/Z\nXbuPq32j515SdDM7qrawKHfBlO9PtuROJBYocRCZRKyNWejsGeTHz31Izbl2SufkhL1ZPtqf95O2\nOnbWVtPQ2eQvK8lZwI7FW7ml6KaAjpFsyZ1ILHBYlmV3DDNy9WrXlB8gJcVJYWE2bW09uN3eaIWV\ndFTPkfejX37A+59c8z9eXlUcl83yF7ub2VW7j49azvjLijMKeaRyE5+auzyomRKRGOOg73LkqY4j\nL9A6nj07N+i5zGpxEIkTjc3x3SzfPtDB3rqDvHHpHSx8+X52ShabytexatH9pDqD/zmK9wGpIvFI\niYNInCibl0tb18Do4zhplr/S2cmPjzxPa8bH4PQAkOpMYW3JKtaXriErNdPmCEUkGEEnDoZhPAP8\nHDhommZ893OIxJEvb1vK3x4wx4xxiGVur5vXLrzJc+YBvFm+hMeyIH+gkj9Y9zkKMwpsjlBEQhFK\ni4MXeB5oNQzj74BfmKZ5Nrxhich4edlpfPO37435fmGv5eW9Kx+wu3Y/Lf2tMDxkwdM+m6FzNzPg\nKqZwi5IGkXgVdOJgmubnDcPIAx4Hfgv4Q8Mw3gKeBp4xTbMzzDGKSJwwW2vYWbuXpq4L/rJ0dzGd\nn1Ti7fLtWllWFR9dLCIysZDGOAwnB08BTxmGUQ58AfhL4K8Mw/gl8KRpmu+GLUoRiWkXui+xs6aa\n062mv2xWZjHbKzexOOcWftHxMY1WbExrFZGZCXlwpGEYacCjwG8AG4DLwN8Di4DXDMP4M9M0vxeW\nKEUkJrX2t7Gn7iBvN7/nnymRk5rN5vKHWbnwHlKGZ0po5oNI4ghlcORKfF0UvwJkAjuB7cDhkcGS\nhmG8D/w5oMRBJAH1DvVyoPFlXjn/Om6vG4A0ZyrrSlfzcOmDZKZk2ByhiERKKC0OR4ATwH8G/tE0\nzfYJXnMKqJ5JYCISe4Y8Q7x64RgHGl6i190H+PaUuH/B3WypWE9Ber7NEYpIpIWSONwBfGSa5phh\n3YZhpAArTNM8bprmYeBwOAIUkbE6ewZ5avepqO4I6bW8HG8+wQt1B2gbGL1XuH3WMh6t2sS87LkR\nPb+IxI5QEocTwDzg6rjyCuBVIOuGd4hI2Pxsz+mo7gh5puUsO2urOd990V9WkVfKjsVbWVxQEbHz\nikhsCihxMAzjq8B/HH7oAN4xDMMz7mWFQGMYYxORCURr6elzXRfYWVPNx22f+MvmZM3i0crNLJ99\nKw5H0Evci0gCCLTF4RfALHxLuXwT+Feg+7rnreHHvwxncCJyo0gvPX2tr5XnzlZzsuUDf1lOag7b\nKtdz//xP43K6wno+EYkvASUOpmn2At8GMAzDAr43XCYiUfblbUtvGOMQDt1DPRxoeIkj54/htnwN\nipbHhftSBfMy72TVqrvCch4RiW+BdlWsBo6ZpukGXgbuMgxjwteapnkkfOGJyHh52eHdEXLQM8Qr\n549ysPFl+tz9vkLLgftKCUMXqsCdzrmc/rCdT0TiW6BdFa/gGxB5Zfi/LXxjHcazALVjisQBr+Xl\nrUvvsqf+IO0DHf7yO2bfRvvZcs40DvnL4mUnThGJvEAThwrg2nX/HRGGYewFLpum+aVInUMk2VmW\nxamWj9lVu4+LPc3+8qr8cnYs3kplfhmdVYM87T0T9u4QEYl/gY5xaJzov8PJMIzPAZvxDcQUkQl0\ndA/ww2fep+FSZ0hrODR2nuP5mr180l7nL5uXNYdHqzZz26yl/pkSeVnh7Q4RkcQR6BiHlwI9oGma\n64INwjCMQuC7wNvBvlckmTz5zAne/8TX+BfMGg5Xe1vYXbeP966MzpTIT8tla+UG7p13l2ZKiEjA\nAu2qaILhHWwi4/vA3wELI3gOkSl19g7y9N4zUV2RMVi15zvGPJ5uDYeuwW72NbzI0Qtv4hmeKZHh\nSmd92RrWlqwi3RVbn09EYl+gXRVfjFQAhmGsA1YBtwE/jdR5RKbz9N4zUV2RMRRVi/JpPT06w2Gy\nQYsDnkFePvcahxpfod/jW/PB5XCxauG9bCp/CMudxk+fi+0kSURiU6BdFb8FPGOa5sDwf0/GMk3z\n7wM9uWEY6fiSha8OHzvQt/o5nQ6czslXsHO5nGP+lchIhHpuutJ9w+OUlNj5PC6Xk689voIf/OM7\nNFzqomxeLl/etnRMjB6vh2MXj/NC7UE6Bjr95XfNu4MdizcxO2sWAD985v0xSdIv9n3MNx6/I7of\nKEYlwnc51qmOIy+SdRzMypH78U3H/MUUr7OAgBMH4FvAyKZYISkqyg5o6du8vMxQTyFBiMd67uge\n4MlnTtDdNzSmfHFJAYWF2TZFNblv/9sHbiizLIt3Ln7AP32wkwudozMlls25mV+//TEWF5ePeX3T\n5e4bHsfiZ7VTPH6X443qOPIiUccOy4rk0IWpGYZRB8wFRnbaTB/+t980zbxAjtHS0m1N1+KQl5dJ\nZ2cfHo930tfJzMRzPf/wmff9Aw4BUl1OllUW8eVtS8nLjp3m+8nquK69kV+e3UNNe72/bEHOPD5z\n01ZunXXLhIn1+M98x02z1OIwLJ6/y/FCdRx5gdZxYWF20JvOBL075vAMi8dM0+wYVz4HOGCa5oog\nDvcgkHrj5ZkfAAAgAElEQVTd4+/ia7X4g0AP4PVaeL3TJz8ej5fWzv6YH/wW7zweL253fP0QNFzq\nHPM4OzOF3//s7QAx+VlG6vhy71V21+7j/asf+Z8rSM9nW+VG7pl3J06HE4/HYqJxzV/cfMuYdRq+\nuPmWmPysdorH73K8UR1HXiTqONAxDluAkYXq1wB/YhhG97iX3QSUB3Ny0zTPjTtPF75xEvWTvGVG\n4mHwm0Rf2dxc2rtbxjyOZZ0DXeyuOcjrF9/Ca/l+EDJTMthQtpY1i1aS5kqd5ghap0FEQhdoi0MD\n8BNGl5n+HHD9ttoju2P+p7BFFgHjp65FajviZDXTxYns8sTWJTe0REHsTc/sdw/wrx+9zAsfH2LA\nMwhAisPF6kX3s7F8HTmpGqMwU529g/xi38c0Xe6mdG4OX9x8S1x8h0WiKegxDoZhNAJ3mqbZMu2L\no+Dq1a4pP0BKipPCwmza2nr4wT+f8Lc4AORlpeJ0OmLiohDvUlKc/Pi5Dzl++rK/bHlVcVzf1T75\n7Mkx3xe7Po/H6+H1i2+zr+EwnYOjye7dc1fwSOVGijOLoh5TooqVv3miu/53WV0VkRFoHc+enRv5\nMQ74ZlYsBGIicQjG9XeWXq9FZ69vFL26LcIj2MWJYp3dLVSWZXHy6kfsqtvHld7RgYxLim/m0crN\nlORqvbRws/tvLhIPQkkcKoCecAcSDdf3637jJ0fHPKcfiJkLdHGieGHn2Iea9np21lRT3zm6NUxJ\n7gJ+687PUppepru0CIm38S4idgglcfgu8H8Mw/geUAP0Xf+kaZpN4Qgs0vQDEX5fe3wF3/+Hd8aM\ncYhnk419iKTmnsvsrN3Hh9dO+8uKMgp5pHIj9y68k+KiXNra4jJvjwtPbF1ywxgHERkrlDEOQ8DI\njjjXv9mBb0ZEVHfLCWaMw/V3abE28C3eqc9yZtoHOqiuP8Sxi8exhv9vlZWSycbydTy48H5SXamq\n4yhRPUee6jjyYm2Mw8MhvCfmaDqaxII+dz+HG1/hxXOvMeT1jblJcaawdtFKNpStISs1y+YIRUTG\nCjpxME3z1ZH/Ngwj3TTNgfCGJJL43F43Ry+8xb6Gw3QP+boeHDj49Lw72Va5gaKMQpsjFBGZWCgt\nDhiG8e+APwRKDMO4Gd/6DRdM0/yLcAYn0aOum+iwLIv3rpxkd90BrvWNjrFZWmywo2oLC3Pm2xid\niMj0Qlly+t8A/wP4K0aXhj4DfMcwjD7TNH8QxvgkSrSqZuSdbavh+ZpqmrrO+8tKcxeyo2orRtFi\nGyMTEQlcKC0O/xH4mmmaf2sYxn8AME3zR8NLUP9/gBKHOKT565FzofsSu2r3carlY39ZcUYR26s2\nceec23E6tLWwiMSPUBIHAzgyQfnLwF/PLByxi6anhl9bfzt76g7yVvO7/pkS2alZbC5/mFUL7yXF\nGVJPoYiIrUL55WrGlzyM34jqfuDijCMSW9ixZkGi6h3q42Djy7xy/ihDXjcAqc5U1pWsYn3Zg2Sm\nZNocoYhI6EJJHP4X8NeGYXwd39oNhmEYG4C/wDfuQeKQpqfO3JDXzZHzxzjQ8BI97l7AN1Pivvl3\ns7VyPQXp+TZHKCIyc4Fuq/1d4L+bptkGPAMUAv8CZAB7ATfwU+C/RyhOkZjltby8c/l99tQdoKW/\nzV9+26wlPFq1hfnZc22MTkQkvAJtcfg94H8CbUAdMB/4L8BSwAl8bJpmZ0QiFIlhH7d+ws6avZzr\nHu2lK88rZUfVFm4qrLQxMhGRyAg0cWgAnjcM43183RNPMm6PCsMwADBN80thjE8kJp3rusiu2mrO\ntJ71l83OLGZ71WZWzL4NhyPoVVxFROJCoInDbwB/DJTh25+iFBiMVFAisaqlr40X6g7wzuUT/pkS\nOanZbK1YzwML7sHljOpWLSIiURdQ4mCa5rvAZwEMw6gHtpum2TL1u0QSR89QLwcaXuLV86/jtjwA\npLnSeKhkNQ+XriYjJcPmCEVEoiOUvSoqIhGISCwa9Azx6vnXOdD4Mn1uX++c0+Hk/gWfZkv5evLT\ntd6FiCQXrUAjMgGv5eXt5vfYU3eQtoF2f/ny2bfyaOUm5mbPsTE6ERH7KHFIcNq8KjiWZXG61WRn\nTTUXe5r95ZX55Ty2eAuV+eX2BSciEgOUOCQ4bV4VuMbOc+ysqeZse62/bG7WbB6t2szts5ZppoSI\nCEocEp42r5retb4Wdtfu590rJ/1leWm5bK1Yz33z7w7rTAm1AIlIvFPikOC0edXkugd72N/wIkcu\nvIFneKZEuiuN9aVrWFe6mnRX+C/oagESkXinxGEKsXJ3GEocI++pb+4kLysVh8NB+TxtXgUw6Bnk\npXNHOdT4Cv2efsA3U2LVwnvZXP4wuWk5ETu3WoBEJN4lTeLQ2TPIU7tPBXXxjZW7w1DiuP49AMur\nipP+ztbj9fBW87vsqTtIx+DoCukr5tzO9spNzMmaFfEY1AIkIvEuaRKHn+05HfTFN1buDkOJI1Zi\njwWWZfFRyxl21u6jueeyv/ymgkp2LN5CeV5p1GLR9uUiEu+SJnFobA7+Qhord4ehxBErsdutvqOJ\n52v2UttR7y+bnz2XHVVbWFZ8S9RnSmj7chGJd0mTOJTNy6Wta2D0cQAX0li5O5wojunGPcRK7Ha5\n0nuV3bX7OXH1Q39ZQXo+Wys2cO/8T+F0OG2MTkQkfjksy7I7hhm5erVryg+QkuKksDCbxvNtQY9x\nmEwsDJp88tmTMTWGYaSe29p6cLu9tsXROdjFvvrDHL34Fl7LF0eGK4MNZWtYW7KStAjMlIiWWKnj\nRKd6jjzVceQFWsezZ+cG3eyaNC0OednhayKOhUGT4R7DEAvJ0Ez0uwd46dwRDje9yoDHt3Gry+Fi\n9aL72FT2EDlp2TZHKCKSGJImcQinWBh4GO4xDLGQDIXC4/Vw7NLb7K0/RNdgt7/8rrl38EjlRmZl\nFtsYnYhI4lHiEIJYGHgY7jEMsZAMBcOyLE5eO8Xu2n1c7r3qLzcKF7OjaguleYtsjE5EJHEpcQhB\nLAw8DOfo/M7eQbzesUNFYnkWRm17Aztr91LX0egvW5gznx1VW1hSdLP2lBARiSAlDiFItCl1T+89\nQ2fvkP9xXlZqRJOhUMdTNPdcYXftPk5eO+UvK0wv4JHKjdw9b4VmSoiIRIESB7mhW8LpdER0YGSw\n4yk6BjrZW3+INy4d98+UyEzJZFP5Oh5ceD+prtSIxSoiImMpcZCoj9kIdDxFv7ufw02v8mLTEQa9\nvhaRFGcKDy66n41l68hOzYponCIiciMlDhL1MRvTJSpur5ujF99iX/1huod6AHDg4NPz7mRrxQaK\nMwsjGp+IiEwuJhIHwzCqgL8GHgBagJ+Ypvl9e6NKHtEeszFZomJZFieufsju2n1c7RtNLJYU3cyO\nqi0syl0QtRhFRGRiticOhmE4gL3AW8AdwE3AvxiGcd40zX+xNTiJiIkSlU/aanm+tprGznP+spLc\nheyo2sItRTdFO0QREZmE7YkDMBc4AXzVNM0eoNYwjBeBlYAShxg3MkOi6Uo3i0sK+MJGg6z0wL9W\nF7ub2VW7j49azvjLijMKeaRyE5+au1wzJUREYoztiYNpms3A50ceG4bxALAa+He2BRWiSC3bHMvL\nQV8/Q+L46csMDXn4/c/ePu372vrb2Vt/iDcvvYOFbw2J7JQsNlU8xKqF95HqtP2rKSIiE4ipX2fD\nMBqAEmAP8JytwYQgUss2x/Jy0DfMkGieesXJPncfBxtf4eVzrzHkdQOQ6kxhbckq1peuISs1M2Kx\niojIzMVU4gB8BpgH/BT4K+Br073B6XTgdE6+UqDL5RzzbyQ1Xeke8/h0Qxu9A27ysmfWOjD+uE1X\nuklJsa8Jv7NnkJ/tOU1jcxfecburls/PnTC2Ia+bV88do7ruMD1DvYBvpsT9C+/mkaoNFGYURCX2\neBbN73IyUz1Hnuo48iJZxzG5rbZhGJ8F/gHINU3TPdVrLcuyYmWJ4W//nzc5fvrymLK7l87lm799\nb1iPG45jhjOe/Jw0XE4nVYvy+drjK8jPSfc/57W8HGt6h3/5cDdXekZnStw5/1b+ze07KC1YGNXY\nRURkjPjbVtswjDnAfaZp7rqu+DSQBuQBrVO9v7W1Z9oWh7y8TDo7+/B4Irvv+xc2GrxvXmXouvPU\nnGunra1nxscdGvLQ2NxF2bxcvrDRmPExZ6LmXPuYx06Hgx9/fbW/nkdiO9PyCc+d3UNT1wX/a8vz\nSvjszdu4uagKLGz9HPEmmt/lZKZ6jjzVceQFWseFhdlBH9v2xAGoAJ4zDGORaZqXhsvuAq6apjll\n0gDg9Vo3bNA0EY/Hi9sd2S9oVnoKS8sL/eMRAErn5Mz4vFnpKTcMOIz0Z5lK6Zwc2roGxjwe+WJ6\nPF4a2s6zs7aaM61n/a+ZlVnM9spN3DnndhwOh63xx7tofJdF9RwNquPIi0Qdx0LicBx4B/i5YRjf\nwJdIfBf4C1ujClEs7JwZaZN9xms9rfzdh8/x1qX3/DMlclKz2VzxMCsX3EOKZkqIiMS9mBjjYBjG\nPOAnwENAD/Bj0zS/E8h7r17tmvIDpKQ4KSzMpq2tR5lthPQO9XKw6WVeOfe6f6ZEmjOVdaWrebj0\nQTJTMmyOMDHouxwdqufIUx1HXqB1PHt2bvyNcQD/Wg6/YnccEpwhzxCvXjjGgYaX6HX3AeB0OLlv\n/t1srVhPfnqezRH6xPI6GCIi8SYmEgeJL17Ly/HmE7xQd4C2gdGBknctXM62sg3MzphtY3Q3iuV1\nMERE4o0SBwn4jtyyLM60nmVnbTUXui/5yyvyyvgVYxt3V94ak02PgW7jnQgSuXUlkT+bSDxR4iAB\n3ZE3dZ1nZ001ZluNv2xO1iwerdrC8lnLSE11RTXmYEy3jXciSeTWlUT+bCLxRImDTHlHfq2vlRfq\n9vPO5ff9ZblpOWytWM/98z+Nyxm7CcOIZJjpMiKRW1cS+bOJxBMlDgFK5GbSie7Iu4d62N/wIq+d\nfwO35QEgzZXGw6UP8lDJajJS0ic7XMyZaBvvRJXIrSuJ/NlE4okWCg/QSDNpe/cgJ2t9zaSJ4omt\nS1heVUxBThq3VeVTcccV/uzYd3j53FHclgenw8nqhffx5/f9IVsr1sdV0pBsrv9bLq8qTqjWlUT+\nbCLxRC0OAUrkZtK8rDR+71du481L77K3fj815zr8z90x+za2V21iblZszZSQiSVy60oifzaReKLE\nIUCJ2kxqWRanWj5mZ201l3pGN66qyq/gscVbqMgvszE6ERGJNUocApSIA+waOpvYWVPNJ+11/rJ5\nWXPYsXgLtxYvIZRdRzt7Bnlq96kbxoIk8hgR8dHfWCQ5KHEIUCI1k17pvcYLdft578oH/rL8tDy2\nVq7n3nl3zWimxM/2nJ5wypym0iU+/Y1FkoMShyTSNdjNvobDvHbhTbyWb5GmDFc668vWsq5kJWmu\nqe8OA7mjbGyeeCxIIo8RER/9jUWSgxKHOBNKc/CAZ5CXml7jUNPLDHgGAXA5XKxaeC+byh8iNy0n\noHMHckdZNi93zJbbI2NBEnWMiIzS31gkOShxiDPBNAd7vB7euHSc6vpDdAyO3v19as5yHqncxOys\n4qDOHcgd5Ze3Lb1hjAMk5hgRGUt/Y5HkoMQhzgRy8bYsiw+unWZX7T4u917xl99cUMWOxVsoyysJ\n6dyB3FHmZU88FiSRxojIxBL1b6xBnyJjKXGIM9NdvOs6Gnm+Zi91HQ3+sgXZ89ixeAtLi4yQZkqM\n0B2lJCMN+hQZS4lDnJns4n255wq76vZz8upH/tcWpOezrXIj98y7E6fDt0joTO6eEvWOUmQqGvQp\nMlZSJQ52NDmGcs6p3pOXlTYmeXiq+j1m33Ke41ff8c+UyEzJYGPZOh5c9ABprtQxxw7l7klNtZLM\nNOhTZKyk2qsinPtNdPYO8uSzJ/nGT47y5LMn6ewdDNs5p3vP03vPcLL+Mt35p6jN38VbV97Ga3lJ\ncbhYV7KKb933h6wvW3ND0gCh3T0l8j4dItPRHhkiYyVVi0M4mxwDvXMP5ZxTvcfj9VA3+AEZy00c\nqaPJyt1z7+SRyg0UZxZNeexQ7p7UVCvJTF10ImMlVYvD+IvkTJocA72YhnLOid5jWRbvXfmAv3jr\nB7jnf+hPGjwdxZS2b+aLyz43bdIAod09hbPeREQkviVNi0NnzyBuj5cUl29WgVFSMKMmx0Dv3EOZ\niTD+PWtWZfKDd/+a+s4m/2vS3YV4LxjcnFMV1OcI5e5JsylERGRE0iQOP9tzmlMNbf7HKS7njAb4\nTXUxnelgwpGL+6Wey+yqreZ/nx4dU1CUUcgjlRu5a+4d/pkSkaamWhERGZE0icNkeyiEaqqL6Uzn\nfbcPdLC37hBvXDqOhQVAVkomm8ofYvXC+0idYNCjiIhINCRN4jDZHgqREMxgwpHWifrmTizHEN7Z\ntViz6rAcHgBSnCmsXbSSDWVrcQ+5+J/Pnda0SBERsU3SJA6T7aEQCcHMXHh67xlO1l3FNaeJ1AW1\nOFKHfE9YcO/8u9hWuYHCjAIAntx5UivYxSGtgyEiiSRpEofJ9lCIhEAHE3otL3V9H5N+22mcGX3+\nck/7LDJalvGbD20d83pNi4xPWrI4spSYiURX0iQO0RTIYMKzbTU8X1ONe9F5/5xYb3ceQ+cMvF3F\nLKny7Vx5/Y+i12uNOUa0p0XqBzo0SvgiS4mZSHQlTeLQ2TN4Q1eFHRe9C92X2FlbzekW01+W6snB\ne/FmUjoWkOFwUl412krx1O5TY2aD5GSmkuJy2DItUj/QoUnmJYujkWwqMROJrqRJHH6257StF722\n/nZeqDvA283v+WdK5KRms6n8IVYtvJcU58R/CvNc+5jH/YNu/vd/WhvxeCeiH+jQJPM6GNFINpM5\nMROxQ9IkDuOnY35Q18KTz56MeMtD71AfBxtf5uXzR3F73QCkOlNZV7KK9WUPkpmSOel7O3sH8Xis\nSZ+PNv1AhyaZ18GIRrKZzImZiB2SJnEYPx3TsvBv2PS1X10e9ibVIc8Qr144xoGGl+h1+wY+OnBw\n3/y72Vq5noL0/GmP8fTeM4xPG4ySgpBjmin9QEuwopFsJnNiJmKHpEkcRqZjflDXgnXd1XjkDihc\nTapey8s7l9/nhboDtPaPjk24bdYSHq3awvzsuQEfa/zdWYrLwVe2Lws6pnDRD7QES8mmSOJJmsRh\nZDrmk8+OroUAo3dA4WhSPdN6lp011ZzvvugvK88r5bHFW1lcUBH08cbfrS0rL9IsBokrSjZFEk/S\nJA7gGzMw2UZXM2lSPdd1gZ011Xzc9om/rDijmLSrS7l4uoC99Z08sXXQf9EPtFtEd2siIhJrkmpb\n7af3nuFUQxtuj4XbY43Z6CqU7aZb+lr5xal/5n8cf9KfNOSm5vD4zTsourCBujPZdHQP+cdSXB/H\nydoW2rsHb3jueiN3a9/60qcB+NbP3+bJZ0/S2Ts406oQEREJSVK1OEzVHRFMk2r3UA8HGl7iyPlj\nuC3fnhJprjQeLlnNQ6WryUjJYOflo5OeK9huEa2fICIisSKpEofx3RFer0Vn72DA4wYGPUO8cv4o\nBxtfps/dD4DT4eT+BZ9mS/l68tNHuzem6voItlskVtZP0MqRIiJie+JgGMYC4EfAWqAX+Ffgj0zT\nDHt7/BNbl/CnT71Fd59vI6nO3iH+41+/zrLyoikvgl7Ly1vN77Gn7gDtAx3+8jtm38r2yk3MzZ4z\n4bkmG58Q7NiFWFk/QS0fIiJie+IA/BJoAR4AioGnATfwh+E+UV5WGv2D7jFlbo81Zj2H61mWxamW\nj9lVu4+LPc3+8sr8ch5bvIXK/PIJzzPdnXmwI81jZZBkrLR8iIiIfWxNHAzDMIBPA3NN07w2XPZN\n4HtEIHGYyg0Xxc5z7Kyp5mx7rb9sbtYcHq3azO2zluJwOCY9Vqh35pMlHLEypS1WWj5ERMQ+drc4\nNAObRpKGYQ5g+mUVQ1S1IA/zXMcN5SMXwau9LbxQt593r5z0P5eXlsvWivXcN/9uXE7XtOcI9c48\n1rsCYqXlQ0RE7GNr4mCaZgdwaOSxYRgO4HeBw5E6Z4pr7AxUB+ByOai5fJXfe/Zv8BY1gsMLQIYr\nnYdL17CudBXprsAHAYZ6Zx7rXQGx0vIhIiL2sbvFYbzvAXcAdwX6BqfTgdM5ebeBazhRGPn3Ykvv\nmOctpwfmNOBZUIfD5RkudLCm9H62Vj5MXnrwzfFf2b6Mn+05TWNzF2XzcvnytqWkpEy/ZEb5/Dze\n/+TamMeBvC8WjK9nCT/VcXSoniNPdRx5kaxjh2XFxu6LhmF8B/g68Gumae4M9H2WZVlTjTcY75v/\n6xgnzl4FvLhmXyB1YQ2OtNHNr9wt88huv5W//+PPBhF9eHR0D/DkMyeoPd9B1aJ8vvb4CvJz0qMe\nh4iIJI3AL6DDYqLFwTCMHwP/Fvj1YJIGgNbWnmlbHPLyMuns7MPj8TI45MZZcIXUEhNnZo//dZ7O\nQobOGVg9BZTfNIu2Nt9znT2DN7Qe5GVHbu2C3/vMbf7/9g65aWtzT/Hq2DG+niX8VMfRoXqOPNVx\n5AVax4WF2UEf2/bEwTCMPwN+B3jcNM3ng32/12vh9U7fauLxePmkpZ76rAOkz24dfX9vDt4LBhkD\n88lwOKioyuOLm2/B7fZV9FO7T/kHLLZ1DfDU7lPq55+Cx+P1151Ehuo4OlTPkac6jrxI1LHd0zGX\nAH8K/DfgmGEY/j2nTdO8PNPjd/YO8ot9H9PQ2kxqyVm605pgOLmyBtMZOn8TnmsLKchJ54e/v3LC\nY0RiwKJWYBQRkXhl98iU7cMx/Clwcfh/l4b/nbGn957hw/YT9Fe+6EsagDRnOkPnbqb/g9V4ri0C\nHFPOehj/XDjWLgh0kysREZFYY/d0zO8A34nU8Ruau3CVXMThsLC8DlytFQxdXoy7Z2y+9KtrF096\njEisXRDr0y5FREQmY/sYh0jyeC2GGpbhLbiKp3Uu2a58eob3qbjesy/XTDpuIRJrF0y2zkM4uzDU\nHTJKdSEiEj52d1VEVN/AEFZ/Du7mCqzBLPoGbkwaIPp3/L+6djF5Wak4HJCXlepv8QhnF4a6Q0ap\nLkREwiehE4fx6zs4HA6y0m9cMjraey48+3INnb1DWJZvh85nX64BwtuFMdGxOnsHefLZk3zjJ0d5\n8tmTdPaGfQPSmKSuIRGR8EnoxMEoKbjhccmcnDFl2RkpUd9zYbKL+vhppTNJaCYa1Bkrd97RTmAi\nMcBVRCRZJXTi8JXty7jjplkU5WVwa0URAGfPj93gKsXljHp/92QX9c7e0a6UvKzUGSU0T2xdwvKq\nYgpy0lheVcwTW5fEzJ13tBOYiepCRERCk9CDI/Oy0vjG43dQWJjNf/7p62P2gRjh8Xp58tmTUR04\nN9FMjW/9/O0xr3E6HTOKY6JBnbGyLXa0ExhtziUiEj4JnThcr7F54otT/6An6ltZ23VRj5VtsWMl\ngRERkeAlfOLQ2TPIj5/7kO7eiWdUjGdX8300LuqxcucdKwmMiIgEL+ETh5/tOT2miyLF5SArPQUc\nUDEvD7fHy6mGNv/zdt39xspFPRqS6bOKiCSahE8cxndR5GSm8sPf9e1L0dk7yFO7T5Hi8k3bNEoK\ndPcrIiIyhYSeVQFQNm/yqXhP7z3DqYY23B4Lt8eyZYaFiIhIPEn4Focvb1vK3x4wqTnXTumcnDEt\nCoGM7tdyxSIiIqMSPnHIy07ja4+v4Pv/8A4Nlzp5avcpAC5c6wlowaWRNQcgerMuREREYlXCJw4A\nTz5zwj9Asr177CqFeVmpOJ2OSUf3x8qiSSIiIrEgKRKH2nGrRV7P6XT4B0tORGsOiIiIjEr4wZEA\nVYvyJ31uukRAyxWLiIiMSvgWh86eQYbcXlJdTiwsqhbkk+JycOFaj797YqIBkMCYsm996dMaFCki\nIkkv4ROH8QtAZaS5bhjc+OSzJ28YAAloUKSIiMg4CZ84jF8Aqr6584ZNrcYPeGxo7qKnf+wS1RoU\nKSIikgSJQ9m8XNq6BvyPvd6xLQl/8/yHuD1jp2V6vNYNZSNjIbSug4iIJLOEHxz5+LrF5Oek4XD4\npl72DYxtSTh7roPuvrFl41+T4nKMGfdwsraF9u5BTtaOdmuIiIgkg4RvcXjmpRo6htdu6OwdwjHu\neevGt+BwOMY8s6y8yN+qoHUdREQkmSV84jB+jMNEicJ4RkkBKS7nmO6IkS6K8a0TU03nVLeGiIgk\nmoRPHMaPcZiMwwEupwOjpICvbF92wwX++pkX4Ou+WFZeNOW6DlquWkREEk3CJw5f3raU3/3LI9O+\nLj87bcoVJMd3SeRkpk6bBKhbQ0REEk3CJw552YF1DVzf5TBRF0MoS09ruWoREUk0CT+rAiA3O3XS\n5xxww1LSE82cCGXpaS1XLSIiiSbhWxwA/vSJe/iTv3n9hrUZwJdUjO9ymKiLIS8rLejxCaG8R0RE\nJJYlReLwf1/6ZMKkAaBkds4NZTPpYghkJoVmW4iISLxKiq6KqbbVnshMuhgCWSBKi0iJiEi8SooW\nh6pF+bSe7p/wuQvXem4oG+liGGkZ+NbP32bhrGz/66dqJQhkJoVmW4iISLxKihaHrz2+grxJBkhO\n1Q1xfcvAqYY2TjW0TdtKMP54Ex0/kNeIiIjEoqRIHPJz0vlvv3Mfy6uKyc9OIy8rlbzs1Gm7IaZq\nCZjsuUC6OTTbQkRE4lVSdFWAbz2HYGc4jB8kOf65Cc8TwEwKzbYQEZF4lRQtDqG6vmVgWXkhy8oL\n1UogIiJJLWlaHEKhlgEREZGxYipxMAwjHXgH+PemaU6/wYSIiIhEVcx0VQwnDf8MLLU7FhEREZlY\nTCQOhmEsAd4EKuyORURERCYXE4kD8CDwInAfvn2nREREJAbFxBgH0zR/OvLfhmHYGYqIiIhMIVZa\nHKtPmqIAAAzpSURBVERERCQOxESLw0w4nQ6czsl7N1wu55h/Y1FnzyA/23OaxuYuyubl8uVtS8nL\njq/dMuOhnuOd6jg6VM+RpzqOvEjWcdwnDkVF2Tgc0w+LyMvLjEI0ofnxcx/y/ifXAGjrGuBvD5h8\n87fvtTmq0MRyPScK1XF0qJ4jT3UceZGo47hPHFpbe6ZtccjLy6Szsw+PxxvFyAJXc679hsdtbTfu\n2hnL4qGe453qODpUz5GnOo68QOu4sDA76GPHfeLg9Vp4vda0r/N4vLjdsfkFLZ2TQ1vXwJjHsRrr\ndGK5nhOF6jg6VM+RpzqOvEjUcSx2ME2fBSQY7ZYpIiLxIuZaHEzTdNkdQ7RpTwwREYkXsdjiICIi\nIjFKiYOIiIgEzGFZSTekQEREREKkFgcREREJmBIHERERCZgSBxEREQmYEgcREREJmBIHERERCZgS\nBxEREQmYEgcREREJmBIHERERCZgSBxEREQmYEgcREREJWMztjhlOhmGkA/8T+AzQC/zANM0f2htV\nfDMMYwHwI2Atvjr9V+CPTNMcNAyjHHgKuA9oAL5umuYhm0JNGIZh7AUum6b5peHH5aieZ8wwjDTg\nL4HPAwPAz03T/JPh58pRHYeFYRiLgL8BVgMtwJOmaT45/Fw5queQDV/j3gH+vWmaR4bLypmiTg3D\neBjf974SeAP4imma9cGcN9FbHL4P3AmsAb4K/JlhGJ+xNaL490sgA3gA+BzwCPBfhp/bBVwEPgX8\nA/D88I+GhMgwjM8Bm8cV70T1HA4/Ah4C1gP/BviKYRhfGX5O3+XweRbowvdb/P8C/9UwjEeHn1M9\nh2g4afhnYOm4pyb9fTAMowR4Hvg/wF3AteHXByVhN7kyDCMLX6VsNE3zteGyPwEeMk1zna3BxSnD\nMAzgNDDXNM1rw2WfA74H/Ba+H4E5pmn2Dz93CHjNNM1v2xRyXDMMoxA4ie9H4LRpml8yDGMdvv+j\nq55nYLhuLwPrTNM8Olz2B8DNwD+i73JYGIZRALQCt5qmeXq47P/i+04/j+o5JIZhLAH+afjh7cBa\n0zSPTPf7YBjGt4GVI9dAwzAygWbgkZEWi0AkcovDcnxdMW9cV3YUuMeecBJCM7BpJGm4Tj5wL/De\nyJd12FF8zWUSmu8Dfwecua7sHlTP4bASaB9JGgBM0/yuaZpfRt/lcOoDeoAnDMNIGb75eAA4gep5\nJh4EXsRXV47ryqf7fbgH8CcIpmn2Ae8RZJ0n8hiH+cA10zTd15VdBjIMwyg2TbPFprjilmmaHcD1\nfWUO4HfxfYHn47uLuN5lQM2OIRi+c1gF3Ab89LqnVM/hUQk0GIbxm8AfA2nA08B/RXUcNqZpDhiG\n8bvAT/B1U7iAp03TfNowjB+heg6JaZr+3wRfLuY33Xc3LN/tRE4csvANeLreyOP0KMeSqL4HrADu\nBr7BxPWtug7ScN/lT4GvDv/wXv/0ZN9r1XNwcvB1S/wO8EV8P6j/C9+AX9VxeC0BduNrQbsN+LFh\nGC+ieo6E6eo0LHWeyIlDPzdWxsjj3ijHknAMw/gO8PvAr5mmedowjH6gaNzL0lFdh+JbwHHTNA9P\n8JzqOTzcQC7wedM0zwMYhlGGbxD1QaB43OtVxyEwDOMh4LeBRaZpDgAnhgfq/Sm+lkrVc3hN9/sw\n2XWxLZiTJPIYhwvALMMwrv+M84A+0zTbbYopIRiG8WPg68Cvm6Y5MiL3Ar76vd484FI0Y0sQjwM7\nDMPoMgyjC/h14DcMw+gEzqN6DodLQP9I0jDMxNdkq+9y+NwJfDKcNIw4AZSieo6E6eo0LHWeyInD\n+8AQvgE4I1YBx+0JJzEYhvFn+Jp3HzdN89nrnnoTuHO4mX3EyuFyCc6D+Jp0lw//bze+0efLgbdQ\nPYfDm/jGOy2+rmwpvnnvbwKfUh2HxUVgsWEY17duLwHqUT1HwnS/w28OPwb8sw9XEGSdJ+x0TADD\nMP4G3wjeL+G7k/gF8AXTNHfZGVe8Gp4C9AHw3/AtrHW9q/imDn6Eb12H7cAfAcv+//buPsaOqozj\n+Lettr6iEDXiHyAxm1/bgEjDqqGktiiJIoFtjJEopViRshZp1YQqbmlp6vs20VaxBtJCo2BNDAkv\nKaABX3ipxkLA0vCEYourmAKa2lYawe76x3MuGS+7t1P3trm7/D7JJnP3zDkzc9q988wzZ+Y0XdXZ\nYZK0ARgqj2NOxP3cFpJuJdO6nyPHOGwEVpIvK3oU+CPu41GRdAz5VNAvyIGnU4H1ZH+ux/08apIG\ngdnlccyW3w/ldtx24BrgdmA50BURMw5nm+M54wA5YG8rcA+wFljmoGFUziP/z/SRVxJPkymupyNi\nEOgh015/IF+o0+MvgPYq/Xw+7ud2+BSwA/gteVGxJiJ+UPr4PNzHoxYRe8mXbB0P/B5YDayMiOvd\nz23z0tX/ob4fIuIp8k3KC8h/jzcDcw93g+M642BmZmbtNd4zDmZmZtZGDhzMzMysNgcOZmZmVpsD\nBzMzM6vNgYOZmZnV5sDBzMzManPgYGZmZrU5cDAzM7PaHDiYmZlZbQ4czKwtJJ0haWaL8p2Sri7L\nKyTtrJQNSrqoLC+X9KdK2XRJ5xzJfS/bOU7SgiO9HbOxzoGDmbXLfcC7WpSfDvSX5SEq79hv8h2g\nu/L59lL3SOsHLjwK2zEb01516FXMzEYvIv5ec73ngecrv5pwZPboZY7WdszGNAcOZh2kTJF7OTAP\neA/wBPDViLitss65wApgOvBX4GZgVUS8UGljJXAx8GpgFvAUcDVwEfBW4DHgqoj4ZakzjbzingXs\nI2eU/VJE7C7l9wJbSt2PkdnK24CFEfGvss0hYIOk2RHxspR/uTWxISJWHqIPVgDzI+KkUucEYHlp\n96wyVXM/ORvrZHIWwKURsbXUXw7MIWduPQe4ISIWS7oE+DzQBQwCDwFLIuKhMnX5/FL/YERMKstX\nAgvJ2QYD6I+Im1rtv9l451sVZp3nG8CNwLuBO4BbJL0fQNKHgU3AOjJw6AU+DmxsaqOXnC53bkQ8\nCawBLgW+AJwM3A3cKqlL0vHAb8gT4wzgo8AxwIOSXltpcwl5Mj6dnJK6p7QHOW3yBGBx+RmN6m2M\nbjI4Wk1OBwywGTiRDAreSwY090s6tdLGLHLa91OBNZJ6Sh98ExBwFvAa4Pqy/mLgZ8ADZJCApK+T\nQcMiss++B1wr6bJRHp/ZmOaMg1nn2RAR68ryVyTNJq+UtwBXAT+KiMYJb5ekXuAeSVdGxJ/L7zdG\nxMMAkt4ALAAWRcQtpbxPEmSAMA8YiIgvNnZA0gXAs/xvULI9IpaV5Scl3Q3MBIiI3aW9vRGxr10d\nERHPSToI7I+IPZI+CLwPeEtE7Kkcy5nkyb+R6RgCVjT2pQRHn4mIm0v5gKT1wNqynb2SDgAvRMSz\nkl5HBkoXRMSdpc5OSScBS8nAzewVyYGDWef5VdPnB4Czy/IMoFvSZyvlE8jU+zSgETjsqJSLvGXx\nu2qjEdEHIOka4GRJzSf8KcDUyufHm8r/CbzpEMfSbqeRmdKBEqg0TC4/Dc9UA5iIuE/SVEl95DF1\nkRmdkbKu08mMxE2SqoM4JwGTJU2JiH+P+mjMxiAHDmad58Wmz5OAg2V5IvBt8lZGs79Vlg80tddq\n4N9EckxD7zDr7aksD3eiPNoDCieSAcuMYbZd3b/q8SPpk8ANwI+B+8mMwSnA91tsBzLjEs2FDhrs\nlcyBg1nn6SbHNjScAWwty9sARUT1PQezgSuAy2g6YRZPkMFDd6nfqPcg8NPyu08Af4mIF0vZseQt\nin7g1+04qFGoXvFvI2+vTImIlzIgkq4DHgauHaGNpcB1EbGoUmdui+08DvwHODEiNlfqXEFmdnr/\nj+MwGxccOJh1niWSgnxaYCGZUv90KfsWsEnSMvKkfwI5wG9HRDwzXGMRcUDSWmCVpOfIJyouIQf8\n3UGeIC8FfiJpFXkl31/Ktw3X5gj2A9MkHRcR/zicA67RbpektwF3Ao+QfbAYGCAHL84nswkjGQBm\nSjqNzFicX+ohaXJ5ImU/8A5J74yIXZLWkX22j7xdNIfs/6+18djMxhw/VWHWedaRTys8Qg4+PDsi\nHgOIiJ+T2YEe4FEyK7CZfESyYbgXK325rPvDUu8DwEciYkdE7Cqf30i+xOleMnMxp+67F4rV5CDO\n9SOUt3rpU6uyNcC5wF0RMQh8iAyqNpF9dCbQExGtMiOXA7vJ8SNbyCcy5pWyxsumbgReD2yT9HZy\ncOR3yUdbt5N92BcRq1psx2zcmzA0NNLfqpkdbeV9CBdHRPPjlWZmHcEZBzMzM6vNgYNZZ3EK0Mw6\nmm9VmJmZWW3OOJiZmVltDhzMzMysNgcOZmZmVpsDBzMzM6vNgYOZmZnV5sDBzMzManPgYGZmZrU5\ncDAzM7Pa/gulzb7wceYjEgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbb8f8390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the illiteracy rate versus fertility\n",
"_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')\n",
"plt.margins(0.02)\n",
"_ = plt.xlabel('percent illiterate')\n",
"_ = plt.ylabel('fertility')\n",
"\n",
"# Perform a linear regression using np.polyfit(): a, b\n",
"a, b = np.polyfit(illiteracy,fertility, 1)\n",
"\n",
"# Print the results to the screen\n",
"print('slope =', a, 'children per woman / percent illiterate')\n",
"print('intercept =', b, 'children per woman')\n",
"\n",
"# Make theoretical line to plot\n",
"x = np.array([0,100])\n",
"y = a*x+b\n",
"\n",
"# Add regression line to your plot\n",
"_ = plt.plot(x, y)\n",
"\n",
"# Draw the plot\n",
"plt.show()\n"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAigAAAF9CAYAAAAuppNcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xd0XNd17/HvoBAESIJgB9iLyM3ei1glUVS1VSMXucVy\nrPjZiVP8/OwkdmzHSRxbcWy5xnGRbDkusWJREiVLshrF3ns7bAALSIIEARIkGlHm/XEvSAhiwVwO\ncGcGv89aWJq5d2awcTiA9py7zz6RaDSKiIiISCJJCzsAERERkZaUoIiIiEjCUYIiIiIiCUcJioiI\niCQcJSgiIiKScJSgiIiISMJRgiIiIiIJRwmKiIiIJBwlKCIiIpJwMsIOAMDM7geeAaJAxP/v751z\n7zWzocBPgNlAEfC3zrlXmz13EfBtYDiwGnjUOVfYrj+AiIiIxFWizKCMBZ4H8v2vAuDj/rnngGPA\nNOC/gcVmNhDAzAYBi4GfAdOBUuDZdo1cRERE4i4hZlCAMcAO59yp5gfNbCEwDJjlnKsBvm5mtwIf\nA74KPAqsd8497j/+EeCEmS1wzi1r159ARERE4iaRZlD2Xub4LGCTn5w0WYF3uafp/MVExDlXDWxq\ndl5ERESSUKLMoBhwp5l9AUgHnga+hHep51iLx5YAA/3b1zovIiIiSSj0BMXMBgPZQDXwHrxLOt/1\nj+UAtS2eUgtk+bevdV5ERESSUOgJinPusJn1cs6d8Q9tM7N0vILYJ4EeLZ6SBVT5t2t4ZzKSBZS3\n9vtHo9FoJBKJPXARERFps/+Bhp6gADRLTprsBjoDJ/AKaJvLB477t4v9+y3Pb27t945EIlRUVNPQ\n0Nj6gDuw9PQ0cnOzNWYx0rjFTmMWjMYtdhqzYJrGra2EnqCY2e3Ar4GBzYphp+AtGV4OfNbMspxz\nTZdy5vnHAdb495teK8d/7pdjiaGhoZH6er0pY6ExC0bjFjuNWTAat9hpzBJL6AkKsArvks1Pzeyr\nwAjgMeAbeCt0jgA/N7N/Bu4FZgAf9Z/7BF4C8zngBbzE5IBz7q12/QlEREQkrkJfZuycOw/cAfQB\n1uN1jf2Rc+4/nHONeElJPrAB+ABwv3PuqP/cQ8CDeH1R1gF5wAPt/kOIiEjSKimr4pk391FZUxd2\nKNJMIsyg4JzbjZekXO7cQeCWqzz3FWB0G4UmIiIp7oeLd1B4vIJTZUN5cMHwsMMRX+gzKCIiImE5\nfrqSwuMVAPTMVYeKRKIERUREOqwNe04CkBaB6aP7hhyNNKcERUREOqx1foIyfkRv8rpqBiWRdPgE\n5ftPb6ExGg07DBERaWfFpZUUn6oEYN6k/iFHIy11+ATllTWH2FPU6sazIiKSIpou70QiMHuCEpRE\n0+ETFIC1u0rCDkFERNrZej9BGTOkJ3nddHkn0ShBwXuT1qu9sYhIh1F86jzHSr3LO7PGqjg2ESlB\nAc5X17HnkC7ziIh0FOsvrt6JMM2UoCSiDp+gdM3OBGDd7pMhRyIiIu0hGo02u7yTR26XTiFHJJfT\n4ROU2RMKANi49xR12iRKRCTlFZ+q5PjpKgBmjOkXcjRyJR0+QZk/eQAA1bX17CwsCzkaERFpa029\nT9LTIkwd1SfkaORKOnyCMvGG3nTL8S/z7NFqHhGRVBaNRlm32/tbP2ZIj4uX+SXxdPgEJT09jRl+\ne+PN+0q5UNcQckQiItJWDpWc42R5NQCzxuryTiLr8AkKwI3j8gGovdDA9oOnQ45GRETayrpd3uWd\njPQIU0bq8k4iU4ICjBqUR/euXhX3Wq3mERFJSY3R6MVL+ROG9yKnc0bIEcnVKEEB0tIizPDXwW/b\nX0rNhfqQIxIRkXg7UHyWsopaQJd3koESFN9Mf6nZhfpGtu7XZR4RkVTTtK1JVmY6k0b0DjkauRYl\nKL7hA3LpmevtxdBU4S0iIqmhobHx4uaAk0f2JqtTesgRybUoQfGlRSLMHO3Nomw/WEZVjS7ziIik\nij2Hz1BRVQfAzDFqbZ8MlKA0M8N/09Y3NLJ536mQoxERkXhZ51/eycnKYPywXiFHI62hBKWZofnd\n6JPXGbi0kZSIiCS3uvpGNjrvQ+dU60Nmhv7Xlwz0r9RMJBK5WCy7s7CM89V1IUckIiLXa2dhGVW1\n3mX7Wdp7J2koQWmh6c3b0Bi9WFAlIiLJq2nhQ7ecTEYPyQs5GmktJSgtDOzblQF9ugCwZpdW84iI\nJLPaugY27ysFYProvqSn6X97yUL/Updxo9/AZ++RM5RV1IQcjYiIBLV1fym1/h5ruryTXJSgXMbM\nZm/iteqJIiKStNb525f06JbFDQO7hxyNxEIJymX0ycvmhgHeG3ntTiUoIiLJqKqmnm0HvM7gM8f0\nJS0SCTkiiUVC7ZRkZi8CJc65j/n3vwN8GogCEf+/n3bO/dA/vwj4NjAcWA086pwrjEcss8b2Y3/x\nWQ6fPE9xaSUDeneJx8uKiEg72bzvFPUNjcDbZ8YlOSTMDIqZvR+4q8XhMcDngQIg3//vE/7jBwGL\ngZ8B04FS4Nl4xTNj9KVse62KZUVEkk7TQoe+edkMze8WcjQSq4RIUMysB/AYsK7FqTHAZufcyWZf\nTVWrHwfWO+ced87tBh4BhprZgnjElNulE2OH9QBg7a4TRKPReLysiIi0g7Pna9lVVAbAjeP6EdHl\nnaSTEAkK8E3gKWB30wEz6wYMAPZe4Tk3Asua7jjnqoFNwOx4BdW0mufUmRoOHq+I18uKiEgbW7f7\nJE2fK28clx9uMBJI6AmKmS0E5gP/3OLUWLyaky+a2REz22JmH2l2vgA41uI5JcDAeMU2ZeSllsgq\nlhURSR6rd54AvC1M8nvmhByNBBFqkayZZQE/Aj7lnKs1s7edBhqBXcB3gZuBH5vZWefcc0AOUNvi\nJWuBrFjjSE+/fJ7WLaMTU0b1Yd2uEtbvOckH7xjV4Zv8NI3VlcZMLk/jFjuNWTAaNzh+upKiE+cA\nmDOhgIxr7L2jMQumrccr7FU8X8GrI3mt5Qnn3FNm9rxz7ox/aIeZjQI+CTwH1PDOZCQLKI81iNzc\n7Cueu23WENbtKuFs5QWOlFYzxbRNN1x9zOTKNG6x05gF05HH7Q9rjwCQFoE75wyjR27nVj2vI49Z\nIgo7QXkf0M/Mzvn3swDM7CHnXG6z5KTJbuAW/3Yx3sqe5vKBzbEGUVFRTYO/FK2l4f26ktM5g6qa\nel5dU8TQvh17uXF6ehq5udlXHTN5J41b7DRmwXT0cYtGo7yx4TAAY4f1hIYGyssrr/qcjj5mQTWN\nW1sJO0G5Cchsdv8xvLqTz5vZPwFznHO3NTs/Bdjj314DzGs6YWY5/vkvxxpEQ0Mj9fWXf1NGgOnW\nh2Vbj3uXeW4bRafM9Fi/Rcq52pjJlWncYqcxC6ajjtuBY2c5WV4NeK3tYxmDjjpmiSrUBMU5d6T5\nfX8mJeqcO2hmS4C/M7PP4PU3uQP4EF4tCnj9UD5rZp8DXsBLTA44596Kd5yzxuazbOtxai40sO3A\naaaP1mUeEZFEtMZf0NApI42po/qEHI1cj4StCHLObQAeAj4CbAf+EnjYObfOP38IeBD4GF7/lDzg\ngbaIxQblkde1E6AdjkVEElV9QyPr/P3TJo/sTXZW2BcJ5Hok1L+ec+6RFveXAEuu8vhXgNFtHVda\nWoSZY/rxx/VH2HaglMqaOrp0zrz2E0VEpN3sKirnXFUdADeOVe+TZJewMyiJZrbf6Ke+Icr6PSdD\njkZERFpas8vrfdKlcwbjh/cMORq5XkpQWmlwv64XNwxcveNEyNGIiEhztRca2Ly3FPA2BsxQT5Ok\np3/BVopEIswe782i7Dt6llNnqkOOSEREmmzed4raugbA23tHkp8SlBjcOLYfTdtNNbVRFhGR8DUt\nYOjdvTM3DOgecjQSD0pQYtAztzOjh3g7HK/eoR2ORUQSQUXVBXYc9HYunjVWOxenCiUoMWoqli0p\nr9YOxyIiCWD97pM0+h8YtXNx6lCCEqNp1odO/sZTa3aoJ4qISNhW7TgOvH0xgyQ/JSgxys7KYIrf\nnXDt7hLqtW+DiEhojpVWUnjc285t7viCkKOReFKCEsBsv0L8fHXdxeueIiLS/poWLKRFIswaq9U7\nqUQJSgDjhvUkN8frJLtKq3lERELRGI2yyu9LNWF4T3K7dAo5IoknJSgBpKelMdPP1LfsK6Wqpi7k\niEREOp49h8opP1cLwJwJuryTapSgBDRnfFPr+0Y2uFMhRyMi0vE0zZ7kZGUw+YZeIUcj8aYEJaAh\n/bpR0CsHuPRLIiIi7aPmQj0b/Q+HM8f0JTMjPeSIJN6UoAQUiUQuzqLsPXKGUrW+FxFpN5v2Xmpt\nP0erd1KSEpTr0Hw779W71BNFRKS9NM1c983LZsSA3JCjkbagBOU69OremdGD8wDvl0Wt70VE2l5Z\nRQ27i8oBrx5Qre1TkxKU6zTXrxwvKaviwDG1vhcRaWtrdpXQ9HHwxvFqbZ+qlKBcp2nWh6xMrzhr\n5fbjIUcjIpLaos16n4wa2J2+edkhRyRtRQnKdercKYPpo73W9+t2l3DBL9oSEZH4O1RyjmOllYB6\nn6Q6JShxMM//JamubWDTPvVEERFpKyu3e7MnGelpTLe+IUcjbUkJShyMHJRH7+6dgUu/PCIiEl/1\nDY2s9VdMTh3Vm5zOGSFHJG1JCUocpEUiF4tldxWWUVZRE3JEIiKpZ/uB05yv9rYWmaPi2JQXlwTF\nzHrH43WSWdMvS5RLu2uKiEj8LN/mLUTo3rUT44b1DDkaaWsxJyhmlmdmPzazCWaWbmavAiVmttvM\nhrVBjEmhT172xZ4oK7arJ4qISDydPV/LtgOnAe8DYXqaLgCkuiD/wt8GFgL1wAPAfODDwF7gm/EL\nLfmoJ4qISNtYvbOERv+D3zyt3ukQgiQodwMfds7tBt4NvOqc+zXwBbzEpcNSTxQRkfiLRqOs8P+m\njhiQS0GvLiFHJO0hSILSFTji374NeNW/XQ1c13aSZvaimT3R7P5QM3vVzM6b2Q4zu63F4xeZ2XYz\nqzSz18K+xKSeKCIi8Vd4/FLvk/kT+4ccjbSXIAnKLuBdZnY3UAC85B9/FNgdNBAzez9wV4vDzwLH\ngGnAfwOLzWyg//hBwGLgZ8B0oNR/fKjUE0VEJL5WbDsGQKeMNGaMVu+TjiJIgvIl4HFgCfBr59w+\nM/sW8LfAPwUJwsx6AI8B65odWwgMBz7hPF8HVgMf8x/yKLDeOfe4f7npEWComS0IEkO8qCeKiEj8\nXKhrYO3ukwBMH92X7Cz1PukoYk5QnHMvAQOBqc65D/mHfwtMcs79IWAc3wSe4u0zMLOATc655k1F\nVgCzm51f1iyuamBTs/OhUE8UEZH42bT3FNW19YCKYzuaQOu0nHOnnXNbm91f55zbE+S1/JmS+cA/\ntzhVgHd5p7kSvOSoNedDM7dZT5SVOzSLIiISVFPvk97dOzPKb+UgHUOr5srMrBBoVWMP59zw1n5z\nM8sCfgR8yjlXa2bNT+cAtS2eUgtktfJ8aHr7PVH2HD7Dim3HeNfsIaRFImGHJSKSVErPVrPnUDkA\n8yYW6O9oB9Pai3m/oJUJSoy+gldH8tplztUALVsFZgFVzc63TEaygPJYg0hPj3/Dn5unDmTP4TOc\nOlPD/uKzjB2aGl0Pm8aqLcYslWncYqcxCyaVxm3NzhKiQARYMHkAGRlt8zOl0pi1p7Yer1YlKM65\nr7TR938f0M/Mzvn3swDM7CHga8DYFo/PB5oajBT791ue3xxrELm52bE+5ZoW3TiUX77iqKyuY/XO\nk8ydMiju3yNMbTFmHYHGLXYas2CSfdwaG6Os8C+RTxrVh5FDe7X590z2MUs1gcqhzWwiMIFLfU8i\neMnFDOfcozG81E1AZrP7j+HN1HwOGAr8nZllOeeaLuXMA5b7t9f495tiygGmAF+O6YcBKiqqaWho\njPVp1zR7XD9e23CUVduOcfTYCLpkZ177SQkuPT2N3NzsNhuzVKVxi53GLJhUGbddRWWcLPMmzGeP\n7Ud5eWWbfa9UGbP21jRubSXmBMXMPsOllvZNs29Nt5dd9klX4Jw70vy+P5MSdc4VmtkhvIZwPzez\nfwbuBWYAH/Uf/gTwWTP7HPACXmJywDn3Vqw/U0NDI/X18X9TzptQwGsbjlLX0MiKbce5dVro9btx\n01Zjluo0brHTmAWT7OP21uZiALKzMpg0ole7/CzJPmapJsgFpL8AvoFXpFqKt2pmEt4S4efiFZhz\nrhG4D++yzQbgA8D9zrmj/vlDwIN4fVHWAXl4ewMljMH9ujGkXzcAlm9tueBIREQup6qmno3Oa3R5\n49h+dMq8riblkqSCXOIZCPzUOVdjZlvxLus858+sfAuviVsgzrlHWtw/CNxylce/AowO+v3aw4JJ\nBfzyj+c4fPI8h06cY0h+t7BDEhFJaGt3neCCP5Mxb6J6n3RUQWZQKrlUe7IfGOff3o1XNyLNzBrb\nj0y/8nyZZlFERK7pLf9v5eC+XRmqD3UdVpAEZSVe8WoO3oqZe80sDa9gtSKewaWCnM6ZTDdv74g1\nu0qo1QaCIiJXVHSigsMl5wGYP6k/EfU+6bCCJCh/D9yJV4vyG7wakTK8VvU/j1tkKWTBpKYNBOvZ\n6E6GHI2ISOJatuXSxoCzx/ULORoJU5C9eHYAI4AnnXPn8fbE+SrwsHPuH+IcX0oYNSiPvj28pVjL\ntx6/xqNFRDqm2gsNrNlVAngbA+Z0Tv7WDBJcoD4o/sZ81f7tErziWLmCSCTC/IkF/P6tg7gjZygp\nq6Jfz5ywwxIRSSjr9pRQc8G7DL5gUv+Qo5GwBemDctV9eWLZi6cjmTuhgMXLCmmMRlm+7TgP3Twi\n7JBERBJK00KCgl45jBzYPeRoJGxBZlBa7suTAYzCq0v5UjyCSkV5XbOYOKIXW/aXsnL7cR5YMIz0\nNO37ICICUHzqPAeKvXUWC1QcKwRIUK60L4+ZfQJYBHznOmNKWfMnFbBlfylnKy+wbf9ppozqE3ZI\nIiIJoWlpcXpahNnjW26zJh1RPD/CvwzcFcfXSzkTR/Sie9dOwKVfRhGRjq6uvoHV/saAU0f1ITen\nU8gRSSKIZ4LyEOqDclXpaWnMn+gVfm0/cJrSs9UhRyQiEr6Ne09RWVMPwILJKo4VT7yKZLsBPQmw\nk3BHs2BSAS+uKvJ2Vtx6nAcXqKZYRDq2pt4nvbt3ZsyQHiFHI4kiHkWyABeA1c65pdcdUYrr3T2b\nCSN6se3AaZZvO8a9c4eSka5iWRHpmErKq9hz+AzgFcemqThWfHErkpXWu2lyf7YdOM3Z8xfYuv80\n00zFsiLSMTUtLU6LRJg7QRsDyiWtSlDM7COtfUHn3FPBw+kYJo7oRY9uWZSfq+WtLcVKUESkQ6pv\naGTldq84tunvokiT1s6g/LzF/SgQwesmWwfkAg3AKbw9eeQqvGLZAp5fWcSOwjJOnqmmb1522GGJ\niLSrTXtPUVF5AfBmlkWaa1Xxg3MurekL+CCwFZjinOvinMsDDNgA/FvbhZpavEZE3u2mAjERkY5k\n6eZiAHrldmbC8F4hRyOJJkh15jeATzrntjYdcM7tAz4NaLPAVuqZ25lJI3oDsGLbMeobGkOOSESk\n/Rw/XXmxOPbmKf1JS1NxrLxdkAQlD6i5zPF0QNcpYtA0pVlRVcfmfaUhRyMi0n7e9GdP0tMizJuo\nyzvyTkESlDeB75vZ0KYDZjYG+AHwQpzi6hAmDO9Fr1yvKKxpqlNEJNXV1jWwyi+OnWZ96N5FnWPl\nnYIkKJ8CegAHzKzUzMqAHXjFsp+OZ3CpLi0twnx/S/Hdh8opKa8KOSIRkba3bncJVbVe59ibJw8I\nORpJVDEnKM65YmAScDdeUey/ALcBc5xz5fENL/XNn3ipMdFbKpYVkQ5g6Wbvb11BrxxscF7I0Uii\nCtJJFudcA/CK/yXXoUe3LCbd0IvN+0pZse04D8wfTmaGOsuKSGo6dOIchce9bdtunjyAiDrHyhW0\ntlFbA1DgnDtpZo28s9X9Rc659HgF11HcMmUAm/eVcr66jo3uJDeO01bjIpKamopjO2WkMWeC/tbJ\nlbV2BuVjwNlmt6+YoEjsxg7rSd+8bE6eqeaNTcVKUEQkJVXV1LNml1ccO3NMP7p0zgw5IklkrUpQ\nnHO/aHb7520WTQeVFolw85QB/O7N/ewvPsvhknMM7tct7LBEROJq9c4TXKjzej7dMlXFsXJ1MRc7\nmFknM/sHM7vBv/9TMztvZq+YmVoBBjRvYsHF2pM3Nh0NORoRkfiKRqMX2ykMye/GsILckCOSRBe0\nk+xngFwzuxP4KPA1oBvwzfiF1rF0zc5k1th+AKzZWUJlTV3IEYmIxM++o2cpLq0EvLo7kWsJsorn\nPcDDzrlNZvafwFLn3NfM7BXgpSBBmNkIvEZvc4HTwPedc9/0z30Hr79K0waFUeDTzrkf+ucXAd8G\nhgOrgUedc4VB4gjbrVMHsmLbcS7UN7Jy23Funzk47JBEROKiqTg2OyudWWP6hRyNJIMgMyi9gN3+\n7duBP/q3TwM5sb6YmUWAF4ESYDLwf4Avmtn7/YeMAT4PFAD5/n+f8J87CFgM/AyYDpQCz8b8EyWI\nIfndGNHfm/Z8Y3MxjVHVIotI8jt7vpYNe04CMGdcAVmdtNhTri3IDMoBYIaZ9QWGcakXyv3AwQCv\n1w/YDHzKOVeJ16H2dWAe8Fu8BOUx59zJyzz348B659zjAGb2CHDCzBY455YFiCV0C6cO5MCxXZws\nr2ZXURnjh6msR0SS21tbjtHQ6H3gWjhNl3ekdYLMoDwG/AZYAbzhnNtqZv+IV38Scw2Kc+6Ec+5h\nPznBzOYCC4A3zawbMADYe4Wn3whcTEScc9XAJmB2rHEkiumj+9Itx1t698ZG7c8jIsmtvqGRN7d4\nf8vGDe1BQa8uIUckySJIq/ungJnAw8C7/MPrgTv8c4GZWRFewrEKeAYYi1dz8kUzO2JmW8zsI82e\nUgC07A9fAgy8njjClJmRxgJ/f56tB0opPVsdckQiIsFt2nuKs+cvAHDrtEEhRyPJJFBPdefcNryC\n2KFmlgG87px7PQ7xPAjcA0wBHgcMaAR2AXcBPwV+bGb3+Y/PAWpbvEYtkBWHWELjtX+GaPTSnhUi\nIsnotY1e24Te3TszcYQuWUvrxVyD4he1/hvwV0AnYBTwr2ZWCXzSORd4faxzbpP/Pf4W+G8gF3je\nOXfGf8gOMxsFfBJ4DqjhnclIFhDTpoXp6Ym1902/XjlMGdmHTXtPsXzbMR68eTidMhKjqKxprBJt\nzBKdxi12GrNgEmncik5UsP+o14R80fRBdErQ4thEGrNk0tbjFaRI9tPAh4FP4S0NBm/lzA/xLq98\nIZYX84ttZzvnnmt2eBde8tPNOVfW4im7gVv828V4K3uay8crum213NzsWB7eLu67+QY27T3Fuao6\ndh46y8LpiTU1mohjlgw0brHTmAWTCOP2yz965YOdMtO59+Yb6JbTKeSIri4RxkwuCZKgfAL4S+fc\nYjP7HoBz7n/M7AJeP5KYEhS8lUDPmNlA59xx/9h04BTw12Y2xzl3W7PHTwH2+LfX4K32AcDMcvzz\nX44lgIqKahoaGmMMu20N6ZNDv545lJRV8fyy/UwZ0TPskAAvY87NzU7IMUtkGrfYacyCSZRxO1d1\ngaV+V+zZ4/pRX1tHeW1iNqBMlDFLNk3j1laCJCjDuPwMxVbeOZvRGuuBDcATZvYZ//UfA/4FLwH5\nO//4s8AdwIeAm/3nPgF81sw+B7yAl5gccM69FUsADQ2N1Ncn3pvylikD+O3r+zhQXMHew2cY3j9x\nWkMn6pglOo1b7DRmwYQ9bks3FVPnf/9bpgxIin/DsMdM3i7IBaQiYMZljt9FgD4ozrlG4D6gEm/1\nzo+Bx51z33fObQAeAj4CbAf+Eq+L7Tr/uYfwCms/BqwD8oAHYo0hUc2bcKmh0WsbjoQcjYhI6zQ2\nRnljk7e0eNTA7tr8VAIJMoPy78APzawAL8G51cz+HK9o9jNBgnDOncBLRC53bgmw5CrPfQUYHeT7\nJrqczhnMG1/A65uOsn7PSd5zyw306JbUC5REpAPYur+U0xU1ANyaYPVzkjyC9EF5Eq/O5LNANvBf\nwCPAF51zP4pveHLrdK+lS0Nj9OJeFiIiiex1v/akR7cspozsHXI0kqxiTlDM7GHgaefcYKAvkO+c\n6+ec+1bcoxPye+Zc7B3w1pZi6uobQo5IROTKjpVWsqvI6/Rw8+T+ZGjprgQU5J3zA7wOrjjnSq+w\nR47E0SJ/FuVcVR1rdpWEHI2IyJW97jdmy0iPsGCy9t2R4IIkKHuBCfEORK5s3NCeFPTyNop+bcNR\notrlWEQS0PnqOlbu8LpFzBjdj+5dErvviSS2IEWyW4Ffmdn/A/YBb9ssxjn3sXgEJpdEIhEWTR/E\nL19xHDl5nr1HzmCDe4QdlojI2yzbeowLdd4y3dtnqDhWrk+QGZRRwHLgHF7fk2EtvqQNzBmXT06W\nl0++uuFoyNGIiLxdfUPjxcs7owblMSRfS4vl+sQ8g+Kcu+Xaj5J4y+qUzk2T+/PS2sNs3neKU2eq\n6ZOntswikhg2uJOUn/P2btXsicSDyquTyMKpA0mLRIhGLxWiiYiELRqN8up6r5lkn7zOTL5BS4vl\n+ilBSSK9undm6ijvF3/5tuPUXKgPOSIREdhffJbC4+cAb9fitLRIyBFJKlCCkmQW+V0Zq2vrWbn9\nRMjRiIjAH/3Zk+ysdOZNKAg5GkkVrUpQzOw+M+vc1sHItY0c2J0h/r4Wr204QqOWHItIiE6dqWbT\n3lMALJjUn+ysIItDRd6ptTMovwZ6A5jZQTPr1XYhydVEIhFum+E1bispr2br/tKQIxKRjuz1jUeJ\nRiESgVunDQw7HEkhrU11zwJfMbPlwFDgYTOruNwDnXNPxSk2uYKZY/rx+7cOUn6ullfWHmbKyD5h\nhyQiHVB1bT3Lth4DYNqoPvTurpWFEj+tTVC+AHwT+BgQBb57hcdFASUobSwjPY1F0wby9NID7D16\nloPHKhi0lACyAAAgAElEQVTePzfssESkg1mx7Tg1F7z9wW6fMTjkaCTVtCpB8XcwfhLAzBqBAuec\nNoUJ0U2T+/P8qiJqLzTwyrrDfPL+8WGHJCIdSGNjlFc3eMWxwwpyGTFAH5IkvoKs4hkGnAQwsz5m\nlhffkKQ1cjpnsmBif8BrkHTqTPU1niEiEj+b95VSerYG8BqzRSJaWizxFXOC4pw7BHzazI4DJ4DT\nZlZsZn8T9+jkqm6bfqlxW9MnGRGRthaNRnl57SEAenTLYpqpDk7iL+YExcw+ATwG/AZ4EHgI+B3w\nb2amjQLbUe+8bKaP9v4wLN96nMqaupAjEpGOYN/Rsxw45q2TuH3GIDLS1VJL4i/IgvW/BT7rnPt+\ns2OLzWw/8DfAE3GJTFrljpmDWbf7JLV1DSzdXMy7Zg8NOyQRSXEvrz0MQHZWBgsm9Q85GklVQdLe\nIcBLlzn+MjDy+sKRWA0ryMUGeWVAr208Sn1DY8gRiUgqO1ZayRa//9LCqQPUmE3aTJAE5RAw/TLH\nZwBa2ROCO2Z6y/vOnr/A2l36JxCRtvPyOm/2JCM9osZs0qaCpL7/BfzAzHoCK/1j84CvAt+JV2DS\nehNv6EV+zxxOlFXxyrrDzBmfr4p6EYm78nO1rNnp7QE2Z3w+eV2zQo5IUlmQGZTvAP8NPA5sBrYA\n38Zrh/+v8QtNWistEuGOmd4mgkdPVbKzqCzkiEQkFb228Qj1Dd7+X00ztyJtJcgy40bn3N/g7c1z\no//V2zn3V845FUCEZM74fLrlZALw0prDIUcjIqmmuraepZu9tvZTRvamoFeXkCOSVBe4usk5dw5Y\nH8dY5DpkZqRz67SBPLu8kN2Hyik8XsGwAnV2FJH4eGvLMapr6wG4c5ZmT6TtafF6Crl12kCyOqUD\n8Ic1h0KORkRSRX1D48VmkDcM6M7IgWogLm1PCUoK6dI5k5snez0JNrlTHD9dGXJEIpIK1u4qofxc\nLQB3afZE2klCLGA3sxHAD4C5wGng+865b/rnhgI/AWYDRcDfOudebfbcRXhFusOB1cCjzrnC9ow/\nkdw+YzCvbzxKfUOUl9Ye5mN3jwk7JBFJYtFo9OLS4vyeOUwa2TvkiKSjCDyDYmaDzewOM8s2s77X\n8ToR4EW8HiqTgf8DfNHM3u8/5DngGDANb/XQYjMb6D93ELAY+Bleb5ZS4NmgsaSCHt2ymDM+H4DV\nO05QVlETckQiksy2HzxN8SlvNvbOWYNJUwsDaSdB9uLpZGa/xZvNeBEoAH5kZq+aWZCqzH54y5U/\n5Zw74Jx7GXgdmGdmt+DtnvwJ5/k63ixJ054/jwLrnXOPO+d2A48AQ81sQYA4UsZds4YQiUBDY5RX\n1mkTQREJJhqN8sIqr56te9dOzB7XL+SIpCMJMoPyRWASsBBo+nj+XeAG4Ouxvphz7oRz7mHnXCWA\nmc0F5gNL8ZYwb3LONZ8GWIF3uQdgFrCs2WtVA5uane+Q+vXMYbo/qfXW1mLOV2sTQRGJnTt8hv3F\nZwG4Y8ZgMjPSQ45IOpIgCcrDwKedc0uBKIB/++PAfdcTjJkV4SUcq4Fn8GZnjrV4WAnQ1F/5Wuc7\nrLtvHALAhbpGXtugWRQRid2Lq4sA6NI5g5unaFNAaV9BimQHAPsvc/ww0PP6wuFBIB/4T7zC1xyg\ntsVjaoGm/srXOt8q6Sm4VfiIgd2ZMLwX2w+e5vVNxbx77lA6d7r+muimsUrFMWtLGrfYacyCide4\nHTx2lp1F5YDXNbZrTqfrji1R6b0WTFuPV5D/Y+0CFgE/bXH8/f65wJxzmwDM7DPAr/CKX3u0eFgW\nUOXfruGdyUgWUB7L983NzY451mTw8B2j2f6fK6msrmPtnlLuv2lE3F47VcesrWncYqcxC+Z6x+2l\nxTsAyM7K4D23WUonKE30XkssQRKUrwD/Y2Zj/ef/qZkZ8BDwvlhfzF8BNNs591yzw7uATsBxoOU6\n2Xz/OECxf7/l+c2xxFBRUU1DQ+p16R/QszMjBnTnQPFZnnlzH3PH9SXjOjPe9PQ0cnOzU3bM2orG\nLXYas2DiMW5HT55nrb8p4MJpA6irraO8NnVr2fReC6Zp3NpKzAmKc+4FM/sT4B+ABuD/ATuA9znn\nfh8ghmHAM2Y20DnXlHhMB07iFcT+PzPLcs41XcqZByz3b6/x7wNgZjnAFODLsQTQ0NBIfX1qvinv\nnjWY7z2znfJztSzbcowFk+JzHTmVx6wtadxipzEL5nrG7fkVXiupzIw0Fk0b1GHGX++1xBJzgmJm\nnwV+45yL11Le9cAG4An/0s4w4DHgX/AKZo8APzezfwbuBWYAH/Wf+wTwWTP7HPACXmJywDn3Vpxi\nS3qTRvZmQO8uFJdW8ofVh5g7IZ/0NF1nFZHLKymvYu3uEgAWTOxP9y6pf2lHElPQZcZxm9Pxd0C+\nD6gEVgE/Bh53zn3fP3cv3mWbDcAHgPudc0f95x7CK6z9GLAOyAMeiFdsqSAtEuFdc7wVPSfPVLN2\nV0nIEYlIIntpzWGiUUhPi2hTQAlVkBqUtXhJw7fiFYRz7gReDcvlzh0EbrnKc18BRscrllQ0c3Q/\nnltRRElZFUtWHeLGsfmkpakbpIi8XVlFDSu3e1faZ4/Lp1f3ziFHJB1ZkATlLPDvZvYPwD6guvlJ\n59zCeAQm8ZOWFuGeOUP46Qu7KSmrYt2eEm4c27K2WEQ6upfXHaahMUoEuHv2kLDDkQ4uyCWeSuAp\nYAmwBzjU4ksS0Kyx/eib512ZW7KyiMZoNOSIRCSRVFReYNkWr+/l9NF9ye+ZE3JE0tEFWcXzSFsE\nIm0rPS2Nd80ZwpN/2MPx01VsdKeYMTrwHo8ikmJeXnuYC/4Klndp9kQSQKDWombWBxgFNG3MEMFr\nkDbDOfevcYpN4mz2uHyWrCyi9GwNS1YWMs36aGdSEaGi8gJvbDoKwLRRfRjcr1vIEYkE2834g3ht\n7ZcDb+Jt6vcG8BKXdhmWBJSRnnbxk9HRU5Vs2VcackQikgiaz57cM3douMGI+ILUoHwB+C0wFq9g\ndgZwP96mfTE1SJP2N3dCAT1zvd0Bnl9ZSFS1KCIdmmZPJFEFSVCGA99wzu0BtgJ9nHNLgL8G/iae\nwUn8ZaSnXdzp+HDJebYeOB1yRCISJs2eSKIKkqDUcmkH4f3AeP/2BmBkPIKStjV/YgF5Xb3ukEs0\niyLSYWn2RBJZkARlA/Cof3s7cJt/eyxwIR5BSdvKzEjnLn8WpfD4ObYf1CyKSEfUfPbk3nnDQo5G\n5O2CJChfAf7azP4v8CtgupntBH4HPBvH2KQN3TTp0h4bi5drFkWko3nb7In1YVDfriFHJPJ2MSco\nzrnleJdyFjvnTgPzgdeArwJ/Ed/wpK10yky/uKLn0IlzbNaKHpEO5W2zJ3M1eyKJJ1AfFOfcsWa3\nd+EVyEqSuWnyAF5ed5iyiloWLz/I5JG91RdFpAPQ7Ikkg5gTFDN742rntRdP8sjMSOOeOUP5xcuO\n4lOVbNhzkplj+oUdloi0Mc2eSDIIUoPScu+dYiAHmAWsil9o0h7mTiigT563Y+mzywtpaGwMOSIR\naUtnztdq9kSSQtz24jGzfwQGXXdE0q4y0tO4d+4wfvbibk6UVbFmZwlzJxSEHZaItJElq4q4UN9I\nBLhPK3ckgQWZQbmSXwLvjePrSTuZPS6fgl7ezqXPrSikvkGzKCKp6OSZ6os7Ft84rh8D+2j2RBJX\nPBOUOUB9HF9P2klaWuTiJ6nSszWs2H485IhEpC08v6KQhsYo6c1+50USVbyKZHOBScAPrjsiCcX0\n0X0ZuOoQR0+dZ8nKIuaOzyczI/3aTxSRpFB86jyrd5wAYP6k/vTtkRNyRCJXF2QG5TDvLJTdiNdd\n9rPxC03aU1okwgPzvU9U5edqWbrl2DWeISLJZPHyQqJcWr0nkuiCFMl+tA3ikAQweWRvhuZ3o+jE\nOV5cfYgFE/uT1UmzKCLJrvB4BZv2ngLg1qkD6dEtK+SIRK4tyCWeBa19rHNuWayvL+GJRCI8uGA4\n3/rdVioqL/DqhiO8W5+0RJLeM28dAKBzp3Tu9jtIiyS6IJ1klwJNG7c0bzva8lgU0MfvJDNuWE9s\nUB7uyBleWnuImyb3p1tOp7DDEpGAdh8qZ2dROQB3zhxM1+zMkCMSaZ0gNSj3AEV4S4r74BXI3go4\n4O+BYf7X8PiEKO0pEonw0C0jAKiubeDF1YdCjkhEgopGoxdnT7pmZ3LbDLWqkuQRZAblW8BfOOde\nbnbsTTP7BPCUc+6x+IQmYRnRvzvTrQ8b3Cne2HSURdMG0jsvO+ywRCRGW/ef5sCxCgDeNXsI2VmB\ntl8TCUWQGZQBeCt3WqrAm1GRFPDgTSNIi0Sob4iyeHlh2OGISIwaG6P8fpk3e9KjWxa3TBkQckQi\nsQmSoKwGvmZm3ZoOmFlP4DHgtXgFJuHK75nDgsn9AViz8wSHS86FHJGIxGL51mMUn6oE4N65Q+mU\nqZJASS5BEpS/AmYDxWa2wcw24fVGGQ78ZTyDk3B5f9TSiAK/f+tg2OGISCvV1NbzzDLvd7Z/7y7M\nm6j9tST5BOmDstvMxgAPA2P9w98Hfuucq4r19cysP/Bd4BagCvgd8PfOuQtm9h3g03grgiL+fz/t\nnPuh/9xFwLfxkqPVwKPOOV2PiJO8rlncPmMwL6wqYvvB0+w+VM6EEb3CDktEruG5ZQcoP1cLwHtu\nHkF6Wjx3NRFpH4Eqppxz5UBTkpCJ1+Y+6G/A74HTwFygF/Ak3p4+nwfG+P/9RbPHV/jfdxCwGPhH\n4BXgy8CzfiwSJ3fNGszSzcWcr67jf5fuZ/zwnmGHJCJXcfZ8Lb9/cx8AowfnMVEfKiRJxZxUmNkg\nM/ujmc00s2xgM7AWKDKzyTG+lgEzgY865/Y451YCXwI+4D9kDLDZOXey2VeNf+7jwHrn3OPOud3A\nI8DQWBrJybVlZ2Vwz9yhABQeP8f63SfDDUhErmrx8kKqaxsAeO/CG4hEItd4hkhiCjLr8W2gO3AS\nrxfKEGA+3mxGrEuMTwB3OudKmx2LAN39ItwBwN4rPPdG4GKnWudcNbAJrz5G4ujmyQPo3b0zAE+/\nuZ+6+saQIxKRyzl+upKlm4oBmDM+n6H5uSFHJBJckARlIfAJ51wRcDfwknNuFfDvxJgcOOfOOude\nbbpvZhG8QtvX8GZPosAXzeyImW0xs480e3oB0HJHuxJgYIw/j1xDZkYaDy7w+u6VlFfz0iqV+Ygk\nov9deoDGaJTMjDQeunlE2OGIXJcgNSiZQJmfTNwK/IN/PA2vduR6/DswGZgBTAcagV14RbQ3Az82\ns7POueeAHKC2xfNrgZh3wUpPVwHZtcyZWMBrG49y8FgFv/6jY9qo3uSo6VOrNb3H9F5rPY1ZbNzh\ncjbv8yaj75k3nH69utDQoNnO1tB7LZi2Hq8g/4fZDPwZcBzoAfzBzDoBfwdsCRqImX0Dbwnze51z\nu4BdZva8c+6M/5AdZjYK+CTwHFDDO5ORLKA81u+dm6suqa3xiQcn8vnvr6Cyuo4XVh/iEw9MDDuk\npKP3Wuw0ZtcWjUb536c2AtAtJ5P3LBqlPXcC0HstsQRJUP4v8ALQG/iGc+6omf0QuA+4M0gQZvY9\n4BPAB51zzzYdb5acNNmNtxwZoBjIb3E+Hy+BiklFRbU+abRCQV5nbhyXz5qdJ/jDyiLmjc+nf+8u\nYYeVFNLT08jNzdZ7LQYas9Zbu6sEd9j7bHbf/OF0zc7UuMVA77VgmsatrQTpg7LezAqA3GYJxOPA\nF51zZbG+npl9Gfhz4H3OucXNjv8TMMc5d1uzh08B9vi31wDzmj0+xz//5VhjaGhopF6Fn63y3ltG\nsNGdpK6+kV+/upe/eY9WdcdC77XYacyu7kJdA799zVtW3CevMwunei3tNW6x05gllqB9UBqBM83u\nX2mlzVX5Dd++CHwNWGVm/ZqdXgL8nZl9Bq+/yR3Ah/BqUQCeAD5rZp/Dm9H5MnDAOfdWkFikdXrn\nZXP/TSN4+vV9bDtwmh2Fpxk/TH0WRMLyyrrDnK7wui+895YbyFAdhaSIsN/J9/oxfBFvRc4xvNqW\nY865DcBDwEeA7Xirex52zq0DcM4dAh4EPgasA/KAB9r7B+iIHlo4ku5dOgHwP6/vp6FRnzhEwlBW\nUcOLa7y9W0cPzmPqKO3XKqkj1GUYzrlvAN+4yvkleDMpVzr/CjC6DUKTq8jpnMlDN4/gZy/upri0\nkmVbj2unVJEQ/O/SA1yoayQSgYcXjVJTNkkprZpBMbOpZqatMOWi+ZP6M7hvVwAWLztIVc31rjAX\nkVjsO3qGNbtKALh5ygAG+b+PIqmitZd4luI1RsPM3jCzvDaLSJJCWlqE9906EoDz1XW8sKoo3IBE\nOpDGaJRf+4WxXTpn8MD84SFHJBJ/rb3EUwd83MzexCtSvcnMLttvxDm37HLHJfWMGdKDKSN7s3lf\nKa9uOML8SQUU9NKyY5G2tnLbcQ6dOAfAffOGqeeJpKTWzqB8C2/X4Dfx2s8vxptVafn1ZnzDk0T3\nvoXeqoGGxii/fnUv0Wg07JBEUlp1bT2/f+sAAAN6d+GWqar/ktTUqgTFOfeveF1jh+Ft5jfTv93y\nS/OMHUzfHjncNWswADuLytnoToUckUhqW7KqiIqqOgDev2gk6WlhL8YUaRutXsXjnKsAKszsFmCL\nc05VkQLA3bOHsGrHCU5X1PDbN/YxYXgvsjqpplok3krKqnh1/REApozszbihPUOOSKTtxJx6+43Q\n7jazNWZWaWZnzGyVmakHSQeVlZnOw4u8gtmyilpeWF0UajwiqSgajfKrV/fS0BglIz3C+xbeEHZI\nIm0q5gTFzB7Eq0E5hreT8T8BJcDTZnZvfMOTZDFlZG/GD/c+zb2y7jAlZVUhRySSWja4U+wo9HYT\nuWPmYPr2yAk5IpG2FeTi5T8CX3XOPeic+45z7tvOuQeArwJfiG94kiwikQgfXDSKjPQI9Q1RfvWa\nCmZF4qW6tp7fvObtKNK7e2fePWdouAGJtIMgCcpo4FeXOf4bYML1hSPJrF/PHO6Y6RXM7jhYxuZ9\npSFHJJIanltRyJnzFwD4wG2jyMpUjZekviAJyjHgchc/R9JsA0HpmN49eyg9c7MA+M1re6mtawg5\nIpHkdrjkHK9tOAp4l1In39A75IhE2keQBOXXwI/M7C4zy/W/7gZ+CPxPfMOTZJPVKZ33L/QKZk9X\n1PLi6qJQ4xFJZo3RKL/8o6MxGqVTZhofWDQq7JBE2k2QBOVfgS3Ai0C5//UCsA2vaFY6uGnWh3FD\newDw0prDFJdWhhyRSHJase04B4orALhv7jB6de8cckQi7SfIMuMa59z9wFjg/cDDwFjn3L3Ouep4\nByjJJxKJ8KE7jMwMr8PsL17eQ6MKZkVicq7qAk+/uR+A/r27cNuMQSFHJNK+Wt2orSXn3B5gTxxj\nkRTSr0cO98wZyjPLDrL/6FmWbTnGzVPUkluktf536QEq/V3CP3z7KDLS1TFWOha946XN3DlrMAP6\neJsHPr30AGfO14YckUhy2HvkDMu3HQdgzvh8bHCPkCMSaX9KUKTNZKSn8ad3jiaC18ehaXt4Ebmy\nuvoGnnzJm5zOycrgvbeoY6x0TEpQpE3dMKD7xd1WN+w5yZb96o0icjXPryy62In5/beOJLdLp5Aj\nEgmHEhRpc39y0wh6dPN6o/z3Hx01F7TPpMjlHC45x0trDgMwbmgP5k7IDzkikfDEXCRrZiOArwPj\ngayW551zw+MQl6SQ7KwMPnjbKL7/zHbKKmpZvKzw4uaCIuJpaGzkyT/sudjz5CN3jiYSiYQdlkho\ngqzieQooAH4HaFmxtMrUUX2YMrI3m/eV8trGI9w4rh/DCnLDDkskYfxx3REOlZwD4MEFI+iTlx1y\nRCLhCpKgTAbmO+c2xTsYSW0fvG0Uuw+VU3OhgSf+sJsv/ekMMjN0lVGkpKyKZ1cUAjC8fy6Lpg0M\nOSKR8AX5v8NeoEu8A5HU1zO3M+/xVyQUn6rk+ZWFIUckEr7GaJSfv7SHuvpG0tMiPHLXaNLSdGlH\nJMgMyl8APzSz7wIHgcbmJ51zy+IRmKSmmyf3Z6M7ya6icv6w5hBTR/XRpR7p0JZtOYY74u2z+u45\nQxnQp2vIEYkkhiAzKBPw2tz/FHgDWNrs6804xSUpKhKJ8NG7RtO5UzrRKPzsxd3U1WvHY+mYyipq\neHqp185+QO8uvGv2kJAjEkkcQRKUL+MlJ+OBYS2+tIJHrql392zet9C71HOstPLitXeRjqQxGuVn\nL+6muraBSAQ+etdotbMXaSbIJZ5uwGPOuaI4xyIdyIJJ/dngTrGzsIyX1x5m6qg+jOjfPeywRNrN\nGxuPsvtQOQB33ziEEQP0/hdpLki6/izwQLwCMLP+Zva/ZnbazI6Y2X+YWSf/3FAze9XMzpvZDjO7\nrcVzF5nZdjOrNLPXzGxYvOKSthWJeMWA2VnepZ4nXtzNhTpd6pGO4fjpSp5eegCAQX27ct88/ekS\naSnIDMpx4N/M7L3AfqCu+Unn3MdifL3fA6eBuUAv4EmgHvg88BywBZiGlxQtNrPRzrmjZjYIWAz8\nI/AK3qWnZ4FJAX4mCUHP3M68b+FIfv7SHo6fruLZ5YW8d6H2HZHU1tDYyE9f2HVx1c7H3z1Wl3ZE\nLiPIb8UMYDVQAwzknXUorWZmBswEPuqc2+OcWwl8CfiAmd3iv94nnOfr/vdtSoAeBdY75x53zu0G\nHgGGmtmCAD+ThGT+xALGD+8JwCvrDrPv6JmQIxJpWy+uPkThca8h2wMLhjOor1btiFxOzDMozrlb\n4vj9TwB3Ouda7iDXHbgR2OScq2l2fAUw2789C7i4pNk5V21mm/zzWuqcJCKRCB+9czT/+LN1VNfW\n85Mlu/jKIzPJ6Rxkck8ksR06cY4lK4sAbyPNO2cODjcgkQQWZC+eq/5GOecOt/a1nHNngVebvXYE\n+Evgdbx2+sdaPKUEb9aGVpyXJNEztzMfvn0UP16yi9KzNfzqVcej94wLOyyRuKqrb+AnL+yioTFK\nVmY6H3/3GDVkE7mKIB9Ti4DoVc6nBwsFgH8HpuBdRvoMUNvifC2XNijMucb5VkvX9d9WaxqreI/Z\nvEn92VFYxqodJ1i9s4RJI/swZ3zq7OTaVuOWylJtzJ5eup9jpZUAPLxoJP3bqCFbqo1be9CYBdPW\n4xUkQWl5iScDGIWXUHwmaCBm9g3gr4D3Oud2mVkN0LPFw7KAKv92De9MRrKA8li/d26uNuWKVVuM\n2V8/PJUD/7GUkrIqnnp5D9PG5pPfK7V2VdB7LXapMGab3EleWuNNLk8d3ZcHbx3V5jsVp8K4tTeN\nWWIJUoPy1mUOv25mB4F/ApbE+ppm9j3gE8AHnXPP+oeL8TrWNpePt4qo6XzLj9j5wOZYv39FRTUN\nDY3XfqCQnp5Gbm52m43Zn98zln99aiNVNfU89tR6/uEj00hPS/5PNW09bqkoVcbs7PlavvWrjQB0\ny8nkT+8wzpypusazgkuVcWtPGrNgmsatrcSzEnEfAZb4mtmXgT8H3uecW9zs1Brg82aW5ZxrupQz\nD1je7Py8Zq+Tg3d56MuxxtDQ0Eh9vd6UsWirMRtWkMs9c4fy3IpC9h09y3PLCrk3hXpE6L0Wu2Qe\ns8ZolB89t5OzlRcA+LN3jaFbdma7/DzJPG5h0ZgllngVyeYCfw/E1LPczMYAXwS+Bqwys37NTr8F\nHAF+bmb/DNyLV5vyUf/8E8BnzexzwAt4icmBK8zwSBJ595wh7CwsY3/xWZ5fWcTYYT25QV02JQm9\nsvYwOwvLALh9xiAmjugdckQiySPI3HkRXiLS/GsbcA/wdzG+1r1+DF/EW5FzDO8SzjHnXCNwP95l\nmw3AB4D7nXNHAZxzh4AH8fqirAPyiGOHWwlPeloaj94zluysdBqjUX78/E6qaurDDkskJgeOneWZ\nZQcBGJLfjT+5aUTIEYkkl0g0erUFOe9kZjdd5vAFYLtz7nxcompf0fLySk3rtVJGRho9enShPcZs\n9c4T/GTJLgCmWR8+df/4Ni8sbCvtOW6pIpnHrKqmnq88uY7SszVkdUrnK4/MoF+PnHb53sk8bmHR\nmAXjj1ub/VGOS5GsmfVO0uREEtjscfnsKixj5Y4TbHSneG3DUW6bMSjssESuKhqN8ouX91B61usx\n+ZHbrd2SE5FUEqQGJQ94DPgesAt4GVhoZnuBu51zMdWhiFzNh+4wikrOUXyqkt+9uZ9h/XNVjyIJ\nbfm246zfcxKAuePzmZ1C/XxE2lOQGpRvAwvxNvR7AJgPfBjYC3wzfqGJQFZmOp+6fzxZndJpaIzy\nn8/u4FzVhbDDErmsQyfO8d9/3AtAv545fPD2USFHJJK8giQodwMf9jfoezfwqnPu18AX8BIXkbgq\n6NWFR+4aDUD5uVp+smQXjTHWTom0tfPVdfxg8XbqGxrJzEjjk/eNo3Mn7SklElSQBKUr3vJfgNu4\ntJdONdfX5l7kimaO6cetU71tlnYUlvHiqqJwAxJpprHRW212se7kDmNwv24hRyWS3IIkKLuAd5nZ\n3Xgb9r3kH38U2B2vwERaeu/CGxhW4P3Rf3ZFIbuLykKOSMTz3IpCdvj9Tm6ZOoC5EwpCjkgk+QVJ\nUL4EPI7X0v7Xzrl9ZvYt4G/xWt2LtInMjDQ+ef94unTOIBqF/3p+J2UVNWGHJR3cln2lLPFn9Eb0\nz+XhW0eGG5BIiog5QXHOvQQMBKY65z7kH/4tMMk594d4BifSUu/u2Xz83d4WTRVVdXzv99uprWsI\nOSrpqErKq/jJC16vntycTD71wAQytCOuSFwE+k1yzp12zm1tdn+dc25P/MISubJJN/Tmgfne/jyH\nSs7x5B92E2vDQZHrVXuhgR88s53q2nrSIhE+ef94enRrucG6iASlVF+S0rvnDGX66L4ArNt9khdX\nHxrdFFEAACAASURBVAo5IulIotEoT760m6OnKgF4zy0jsME9Qo5KJLUoQZGkFIlE+LO7xzC4b1cA\nFi87yOZ9p0KOSjqKJSuLWLfba8Y2Y3RfbleHY5G4U4IiSSurUzr/v737jo+juhY4/ltJtiQXuRt3\nXDDHcrfpGEwzxRCawaEkYEpoMRBC8kLeCwkJIUDoECAkAQKEXmIIvYUABhswGDtuh+Juy122XFSs\nld4f964YFlnSSiPtanW+n48/Xs3Mztw5O+XMvXdmLjtlJO3btKIS+OuLC1i13t64YBrXJ4vW8fx0\n98Ds3Xdrz3nH5jfbd0QZk8osQTHNWpcOOUw9eQSZGRFKy6Lc9dxcthXvTHaxTJpauqaIB3yn2A7t\nWnPZKSPIbm2PfzKmMViCYpq9Pft25KyjBYD1m0u41z/N05gwFW4t5a5n51JW7p4Ue9mkkXTOy0l2\nsYxJW5agmLQwflQvjtjLPWl20fLNPPTqIruzx4SmuLScO5+dw+Zt7j1Q5x2bz8BeeUkulTHpzRIU\nkzZOP2IPRgzsAsCH89bwwnR7sbZpuPJoBX9+YR7L17r+TSeM689+Q3dLcqmMSX+WoJi0kZmRwcUn\nDqPfbu7Onn99sJT3565OcqlMc1ZZWcmjbyjzFrvH2I8b3oMTDxqQ5FIZ0zJYgmLSSm52Fj85dRSd\n89wDsx55TZm/xN7ZY+rnpRnLeG9OAQBD+3diysQhdseOMU3EEhSTdjq1z+aKyaPIzc4kWlHJ3dP+\ny5KComQXyzQz0+cWMO29xQD06daOqfYYe2OalO1tJi316daOS08eQVamu/349qfnULBxe7KLZZqJ\nz75Yz99fdS9ndwnvSHKzs5JcKmNaFktQTNrK79+ZC48fRgTYVryTW5/63N5+bGq1cOkm7nthHpWV\n0DYniytPG223ExuTBJagmLS295DunHWMe0bKpqJSbn3qc7buKEtyqUyqWlJQxF3//C/l0UqyW2Xy\n0++PpnfXtskuljEtkiUoJu0dOro3k8YPBKBg4w5ue3oOO0rsabPm21at38btT8+htCxKVmaES08Z\nYc86MSaJLEExLcJxB+xe9UK3ZWu2ctvTcyguLU9yqUyqKNi4nZuf/JxtxTuJRODC44cxrH/nZBfL\nmBbNEhTTIkQiEU47fA8OG9MbgMWri7jjmTmUlFmS0tKt3bSDm56YTdH2MiLAuRPz2XtI92QXy5gW\nzxIU02JEIhF+cNSeHDyyJwBfrtzCXc/OpXRnNMklM8myrtAlJ1v8I+ynTBzCQX77MMYkV0rdNyci\n2cAsYKqqvueH3QlcBlQCEf//Zap6rx8/AbgdGAjMAC5QVXvGualWRiTClGOGUB6tZMb8NSxavpk7\nn5nD5aeOJKd1Su0OppGtK9zBzU/MpnBrKQBnHbUn40f1SnKpjDExKVOD4pOTJ4ChcaPygauAnkAP\n//+D/jt9gWnAA8DewAbg+SYqsmmmMjIinH9cftX7VBYt3+w7zlpzT0tRsHE7Nz72GRuLXHJyxoTB\nHDa2T5JLZYwJSokERUTygZlAdS+5yAdmq+q6wL/Ywyx+BHyiqneo6kLgXKC/iIxvmpKb5iojI8KP\nvpfPAcN6APDVyi3c+tRsthXb3T3pbvnardz42GdVbyY+Y8Jgjty7b5JLZYyJlxIJCnAI8DZwAK4Z\nBwARaQ/0Br7Yxff2B96L/aGqxcBnfj7G1CgzI4Pzv5dfVa2/pGArN/vOkiY9LSko4uYnZrN1x04i\nwDkTh1hyYkyKSolGd1W9L/ZZRIKj8nF9Tq4WkYnARuA2VX3Ej+8JxL+udi1gdbWmTlyfFKF1VgZv\nfbqSFeu2cf2jn/Kz00bTrWNusotnQrRg6Sbu/ud/KSmLkhGJcH6gBs0Yk3pSpQZlV4YAFcACYCJw\nP/BXETnRj28DlMZ9pxTIbrISmmYvEolwxoTBHHfA7gCsKyzm+n98yvK1W5NcMhOWjxas5fan51BS\nFiUzI8IlJw2z5MSYFJcSNSi7oqqPiMi/VHWzHzRPRPYELgFeAEr4bjKSDRQmspxMe0NpncVilY4x\nO+2IwXRo15rH3/ySLdvL+OPjn3HF5FHkh/DArnSOW2MJK2avf7ycx95wrcQ5rTO5/NSRDB/YpcHl\nS1W2rSXOYlY/jR2vlE5QAALJScxC4DD/eRXuzp6gHsDsRJaRl2dV+YlK15idccxQenZrzx1Pzqa4\nNMrNT3zOFaeP4ZCQ7vBI17g1pvrGrKKikodfXsA///MVAB3bZ/PbH+3PoD4dwyxeyrJtLXEWs9SS\n0gmKiPwOOFBVjwwMHgMs8p9nAgcFpm/jx1+TyHKKioqJRisaWNqWITMzg7y83LSO2aiBnbnytNFV\nD3G75bFP+XpFIScdPIBIJFL7DKrREuIWtobErLQsyn0vzONTXQ/Abp1y+Z8zx9C5bSsKC7c3RnFT\nhm1ribOY1U8sbo0lpRMU4EXglyJyJe75JkcDPwQO9eMfBH4uIr8AXsIlJl+r6ruJLCQaraC83DbK\nRKR7zPJ378QvfzCWO5+dw+ZtZUx7bzGrN2znvGOH0Cors97zTfe4NYZEY7apqIS7np3L8nXbABjY\nK4/LTxlJXtvWLSr2tq0lzmKWWlKxwa0y9kFVZwGnAmcD/wUuBc5Q1Y/9+GXAJOA84GOgI3ByUxfY\npKfde7Tn11P2od9u7QDX0fKmx7958qhJPUsKivj9I7OqkpP9hu7GVWeOIa9t6ySXzBiTqEhlZWXt\nU6W3ysLC7ZY111FWVgadOrWlJcWstCzKX1+cz+wvNwDQoW1rLjlpOHv2rXtfhpYYt4ZKNGbvzVnN\no28o5VF3TDvp4AEcf2D/ejfLNVe2rSXOYlY/Pm6NtoOlYg2KMSklu3UmUyeNqLoNecv2Mm5+YjZv\nzlqBJfjJV7YzyoOvLOShVxdRHq2kdVYGF584jBPG1b/PkDEm+VK9D4oxKSEjEuGUQwbRv0ceD7y8\ngJKyKE+89SVLVhdx1tFCbrbtSsmwfnMx906bxzL/zJrunXKZevII+nZvl+SSGWMayo6qxiRgL+lG\nr657c8+0eazesJ2ZC9ayuKCIi04YxoCeeckuXovy0YK1PPL6IopLowCMGdyV84/Lp01OqySXzBgT\nBmviMSZBPbu05eqz96p6G3LsybOvfbScCmvyaXTFpeU88PIC/vKv+RSXRolEYNL4gUydNMKSE2PS\niNWgGFMPOa2zuPD4oQzr35nH3vyC0p1Rnn7nK+Yv2cg5E/Pp0iEn2UVMS1+v3sLfXlzAusJiALrk\n5XDhCUMZ3EIevmZMS2IJijH1FIlEOGhkT/bo04H7XpjH8rXbmL+0kF8/8BGnHzGYg0f2tE6aISnb\nGWXa+4t545MVxCqp9s3vztlHi9WaGJOmLEExpoF6dG7Dr87am+ffX8xrHy+npCzKQ68u4pOFa5ky\ncQhdO9jjsxtCl2/m/hfns9bXmuS0zuTMCXsybkQPSwCNSWP2HBR7DkpC7HkBNft69RYefHkhBRt3\nAJDdKpMTxvVn4gG7061re4tbAorLynlxxnJen7G06umNIwZ2YcoxQuc8a0LbFdtHE2cxq5/Gfg6K\nJSiWoCTEduTa7SyP8sL0pbz60bKq5oheXdsydfIo+nZpY3GrRUVlJe/PWc1z7y5mW/FOANpkZ3HG\nhMEcONxqTWpj+2jiLGb1YwlK47MEJQG2I9fdsjVbefQN5evVRVXD9s3vzqTxA+neqU0SS5a6vlix\nmaf+/SVLCrZWDTtgWA8mHzaIju2yk1iy5sP20cRZzOrHEpTGZwlKAmxHTkxFZSUfzC3g2Xe/ZusO\nVxuQmRHh0DG9OX5cf/La2DtiAFat38Zz7y7m8682VA3r060tP548mj6dc21bS4Dto4mzmNWPJSiN\nzxKUBNiOXD8lO6O8+vEKXvlgCdEKt8/ltM7kqH36MmHvvrTLbZl3oqwr3MFLHy7jg3kFVc1hbXOy\nOP7A/hy1Xz/rt1MPto8mzmJWP5agND5LUBJgO3L9xOK26Ov1PPPOV3y8cF3VuOzWmRw+pjdH7duP\nDi3krbsr12/jlRnL+Gjh2qrEpFVWBkfu3Zdj9+9Hm5xWtq3Vk8UtcRaz+mnsBMVuMzamCe3WuQ0X\nnzico/ctYtr7i5m3eBOlZVFe/Wg5b326kgOH9+CIsX3ok4bvkqmsrGTBskLenrXyW005mRkRxo3o\nwQnjBtjdOcaYKpagGJMEA3rmceX3R7OkoIiXPlzK7C83sLO8gnc/X827n69mSL+OHD62D6MHdyUr\ns3m/kWJHSTkfzCvgnc9WsWbTjqrhrbIyGD+qF8fs28+evGuM+Q5LUIxJogE987jslJGsXLeN1z9Z\nzkcL1lEerWDR8s0sWr6Zdrmt2De/OwcO78mAnu2bzS225dEK5i3exMwFa6qSr5h2ua0YP6oXR+7T\nt8U0aRljEmd9UKwPSkKsrbZ+6hq3oh1lvD9nNe/MXsWmotJvjdutUy5j9+zG6MFdGdSrAxkZqZWs\nlO6MsnBpIZ9/tYHPvlhf9QyTmAE923P42D7sm9+dVlmZtc7PtrX6sbglzmJWP9ZJtvFZgpIA25Hr\nJ9G4RSsqmL+kkBnz1zD7i/WUxX2nXW4rRgzswpB+HZF+HenWMbfJa1cqKipZsW4bX6zYzPylm1i4\nrPBbNSUA7du0Yr/83ThgeA8G9MxLaP62rdWPxS1xFrP6sU6yxrRAmRkZjBzUhZGDulBcWs4sXcen\nup4FSwspj1awrXgnM+avYcb8NQB0ap/NoN4d6Nu9HX27t6Nf93Z0ap8dWtISrahg7aZiVq7fxsr1\n21laUMRXq7ZQUhb9zrRtc7IYMagL+w/twdD+nZp9HxpjTHJYgmJMisvNzuLgkb04eGQvSsuiLFi6\nidlfbWDh0k1s9M1AhVtLmbVoHbMWffv25a55OXTpkEPXDjnktW1Nm+ws2ua0Ijc7i6xMn7z4/0rL\nouwoLaekNMr2kp1s2lrKpqISNhaVsnFLCeXRXV9Z9uralpGDujB6j64M6p1HZoYlJcaYhrEExZhm\nJLt1JmP27MaYPbsBsGFLMbp8M7piM8vWbGX1hu1VD4IrLYuyasN2Vm3YHm4ZWmXSp1tb9ujTgT37\ndGSPPh1ob0/ENcaEzBIUY5qxrh1y6Toil3EjegLu7pmCjTtYsW4r6wqL2bilhA1bSthYVMLW4p2U\nVtMkU53c7Ew6tsumS14OnX0tTO+ubenTrS1dO+aS0UzuJjLGNF+WoBiTRrIyM6r6oVQnWlFBcWmU\nHSU7q2paYv3ks1tlkpudRU52piUgxpikswTFmBYkMyODdrkZLfbdP8aY5sN6shljjDEm5ViCYowx\nxpiUYwmKMcYYY1JOSvVBEZFsYBYwVVXf88P6A38DDgCWAj9V1TcD35kA3A4MBGYAF6jqkqYtuTHG\nGGPClDI1KD45eQIYGjfqeWA1sBfwKDBNRPr47/QFpgEPAHsDG/z0xhhjjGnGUiJBEZF8YCYwIG74\n4biakYvUuRFXS3Ken+QC4BNVvUNVFwLnAv1FZHzTld4YY4wxYUuJBAU4BHgb14wTfADDfsBnqloS\nGDbdTxcb/15shKoWA58FxhtjjDGmGUqJPiiqel/ss4gER/XENe8ErQX61HG8McYYY5qhlEhQatAG\nKI0bVgpk13F8nWTa21brLBYri1liLG6Js5jVj8UtcRaz+mnseKV6glICdI4blg3sCIyPT0aygcIE\nlhHJy8utX+laMItZ/VjcEmcxqx+LW+IsZqkl1dPFVUCPuGE9gII6jjfGGGNMM5TqCcpMYKy/BTnm\nID88Nv6g2AgRaQOMCYw3xhhjTDOU6k087wIrgIdE5PfACcA+wDl+/IPAz0XkF8BLwDXA16r6bhLK\naowxxpiQpGINSmXsg6pWACfimm1mAWcCJ6nqSj9+GTAJ91yUj4GOwMlNXWBjjDHGhCtSWVlZ+1TG\nGGOMMU0oFWtQjDHGGNPCWYJijDHGmJRjCYoxxhhjUo4lKMYYY4xJOZagGGOMMSblpPpzUBLmH+p2\nL+724x3Arap62y6mHQP8GRgBzAMuUdXPAuPPAH6Peynh68AFqrqxcdeg6YUcs6uAi4AuuFu/L1fV\nhY27BskRZtwC000GnlLVtLx4CHlbOxX4A9Ab95bzC1V1eeOuQXKEHLffAucDbYE3gEtVdUOjrkAS\nJBKzwHcOAh5W1UFxw1vEuQBCj1uDzgfpeBC8BRgLHAr8GLhGRCbFT+SfOvsy7mFwY4EZwMsikuvH\n7wvcj3v4235AJ+Chxi9+UoQVs4uBK4GpwF7AUuBVEclp/FVIilDiFpiuA3AXgWcBpaGwtrUDgceB\nm3FPjy4DnmyC8idLWHG7CDgXOAP3FO5ewN+aoPzJUKeYxYjICOAZIBI3vCWdCyC8uDX4fJBWCYrf\nOc/HZWlzVPUF4Cbg0momPx3YoapXqXMFsBWY7MdPxV3JPqaq84CzgGNFZPfGX5OmE3LMpgA3q+qr\nqvoVcAkucx7X6CvSxEKOW8zNwJeNWe5kCjlmPwMeUdX7VfVL4HKgh4jEv1y02Qs5bhNxx7XpqrrA\nz+eIxl+LppVgzGKJ2wfAmmpGt4hzAYQetwafD9IqQQFG4ZqtZgSGTcdlvfH28+OCPgAO8J/3B96L\njfBPr13uh6eTMGP2M9xVbUwlLqvuEEpJU0uYcUNEDgEOwTVZpKswY3YoMC02QlWXqupAVd0UWmlT\nR5hx2wgcJyK9fK3KmcB3mhrTQCIxAzgal3jcUc24lnIugHDj1uDzQbolKD2BDapaHhi2FsgRkS7V\nTLs6bthaoE8dx6eL0GKmqh+qanD8BUAm3z1gpoPQ4iYirYG/4KpTSxqnuCkhlJj5prBOQCsReU1E\nCkTkeRHp1WglT64wj2vXAlFgJVCEu5o9M/QSJ18iMUNVJ/nagl3NqyWcCyDEuIVxPki3BKUNUBo3\nLPZ3dh2nza7j+HQRZsyqiMh+uLbMm1R1XQjlTDVhxu03wCxVfTvUEqaesGLWzv99J/AI8D0//KXQ\nSppawtzWBgDbgeOA8bhE5e+hlTR1JBKz+s4r3c4FEG7cqtT3fJBuCUoJ3w1i7O8ddZx2Rx3Hp4sw\nYwaAiBwAvAa8rKrXhFTOVBNK3ERkGO7K4qd+eIT0Fda2Fru6+5uqPq6qnwI/AEaISDpWu4e5jz6M\nuyvjVVWdAZwGTBCRfUIsbypIJGb1nVe6nQsg3LgBDTsfpFuCsgroKiLB9eoBFKvq5mqm7RE3rAdQ\nUMfx6SLMmCEih+JuXXyL9Kw6jgkrbqfgmisWi8hW4BUgIiJF/tbGdBJWzDYAOwGNjfB9TzYCfcMu\ndAoIJW4i0g0Xn7mxEb4/xQYg3Tp8JhKzusyrJZwLINy4Nfh8kG4Jyue4A1fwKupg4JNqpp0JHBg3\nbBzfdA6aibsNDwAR6Ytrc5wZVmFTRBgxmwkgIsOBF3C3OZ6mqtHQS5s6worbXcAQXOe0UcCPcJ3J\nRgH/CrfISRfK/um3q09xMQJARLoCXXG3MqabsI5rm3DV9UNjI3zcugBLQixvKkgkZrVpKecCCDFu\nYZwPIpWV6fXIBRH5M26HPA+3ET0ETFHVF0RkN2CLqpaISHvcLZ1PAH8FLgZOBfZQ1WJfVfwO7haz\nWbheyltU9eSmXqfGFmLMPgDygGP4phqe2PebbIWaSFhxi5vnIcC/VTWz6dak6YS4rZ2C6ztxHjAf\ndyvkbqq6b1OvU1MIMW73AkfhnoVSiLu1va2qjm/qdWpsdY1Z3HemANeo6sDAsBZzLoBQ49bg80G6\n1aCAezDMp8C/gT8Bvw70Mi4Avg+gqltxnevG4za6fYGJsROGqs7EPQHvGlyv4424HywdNThmfsPd\nH3d1thzX6z327/tNtypNKpRtrYUJa/98Dtdv52a+ubo7qYnWIRnC2tauAP4JPIY76W4C0vJESx1j\nVpsWdi6AEOIW1vkg7WpQjDHGGNP8pWMNijHGGGOaOUtQjDHGGJNyLEExxhhjTMqxBMUYY4wxKccS\nFGOMMcakHEtQjDHGGJNyLEExxhhjTMqxBMUYY4wxKccSFGOMMcakHEtQTKMSkUNEpEJE+qVAWTJF\n5CMRGVOHac8RkYpaplkiIr/xn38rIjW+cM3H4ezESm1SgYicLiKvJLscYRORoSJybA3j3xGRB/3n\nb+0Tcdv/FBGJBsb1FZHTGrPsfjltROTHCUyfKyLzRaRPY5bLhMMSFNMUUuV9Cr8A5qvq7DpMW0nt\n5d4buCWB6U3zdSzurazp5iXcdrwrJwM/8Z9r2safBHoG/n4YOLrBpavdz/2/OvHvJPoj8ECjlciE\nJivZBTCmKYhIHnAV336NeIOo6saw5mVSl4hEcCfb3ya5KI0hUtNIVd1cl5moaimwrq7zDVF9LrIf\nBf4oIoeq6n9CLo8JkSUopsFEZCJwLe7NlduAV4CfVndwE5EM3BXZRcDuwDLgdlX9ix9/CO4tq6fg\n3lTbA5gBXKaqiwLz+YWfRw9AgVtU9fEainkRsCJuHm2BG/2y2uPe4Hmlqn4WmGYK8GugNzAPmKqq\nH/txS4C/q+q11axnb+Be4DBgMy45Co6/xo8rwF2dP6SqPxGRA4EbgH2A9cCLwP/6t9TGlnk3cADu\npFmKezPtT1X1O01SIrI7sAQ425dhEDAH+JmqfhiY7lzgf4D+fvq/AH9S1crAPP4P99ttB0ar6rbA\n928BjlTVUf7vjri3vt6jqpf7YccDjwNdcK9fr207eAuY7H+jfsCHwDm4mrCzgDLgTlW93n+nNfAH\n3O/ZG7ctvgX8WFU3BtbjVD+P0T7+16vq3+JjF7APUKiqi6sb6X+T+4GDcW8RXgXcoKoPBqapy+/6\nLG5b6Aacoqrvi8hPgEv8+n8N/EFVn/Tf6QXchtsOosAHuN/1Kz/+737xG3C/fzvcG2ovUNU1fpn9\ngGv8yfrwatbtHWCJqtb49l4ROQd4UFUz/HcOAQ7x8x0oIq2A64AfAB2A/wLXqOqb/vtTgKtxtVTn\nAP9W1UkichLwS2A4kAnMB/5PVd/w+1CsiSkKDFDV5TVtywCqWiEizwI/A/5T03qZ5LImHtMgItIF\n9/r2+wHBvfL+YOCmXXzlNuBXuFeXD8edbO8UkcvjprsFmArsB+wE3hGR9n6Z1+NObFP9PO4E7hWR\ni2so6ol8t4r+GdzB/WxgFLAYeENEOvjxEeAC4DRgL1wy8FQNy8CXLxN4HeiMi8Vk3AEzvnp8PO71\n46OAu0RkBPAmLsEbDpwBjAXeiPvetbgkbgTuIHspcGYtxboV+D0wBlgEvOlP2IjIhbjf6xpcknk1\nLpm5IW4eZwOHAt8PJifei8BwEenu/z7C/39YYJpjgddUtYy6bQeZuKToDD+fMbjkqhh3or8PuE5E\nhvnpb8I1SZwN7OH/P8IvJ+g2H4shuCaOe2Ox2IVjgVdrGA8uZtNxv+U9wF9FZDKAiIykbr/rVNxv\neQww0yfh1+EStGG4E+0jvl9XG9zJNco3idF64CMRCTa1nAF08tMcg9uOr/Pj9sElU7cCk2pZv9oE\nm38m4S4qnuKb5qOHgQm+PKOBp4EX/cVNzCBcM9Fo4FciMhaXtD3m138/XC3NIyKShbuAuRVYgbtQ\nWZnAtvwSMEFEchq43qYRWQ2Kaag+QGtc7cRK3EHieKrZtnyCcQlwharGTvR3i8hA4H+BuwKT/0xV\nX/ff+wHuIHS6iDwGXAGcrqqv+WmXiMgA3IHovmqWGwH2Bf4cGLYn7oB9pKq+7YddAmwCuvrJKoHz\nVPULP/4W4DkR6aqqG2qIyQQgHxikqkv9d88F4vu+VAK/DVxFPwK8rqp/9OMX+3X/WkTGq+p7fvjr\nqnqP/7zUX2WPw1Vd78oNqvq0X84FwOHAhbiT99XA71X1mcA8O+BO3L8JzOMeVdVdzH86rqboSNwJ\n5UjgeeAkEemmqutxJ/r/S3A7uDrWZ0hE3gb2U9Wr/N834Gq3huOurD8GnlHVD/x3V4jIm7hELuhW\nVX3Zz+NXuMRgf1wtTnUm+hjV5HVVjZ347xCR/XDb6TO45LQuv+srqvpObIb+d71DVR/yg+72J9RW\nwOm4moizYjVngd/1AlwSC+43uUhVo8AXIvKkXx9UdYOvedhW16aculDVQhEpA4pVdZOI7OHLO1pV\n5wZiNNrHJpb8VQLXBvaZUbgay78EYnIX7kJjN1VdJSLbgKjfvhCRGrdlnxyDqw3NxiVsse3FpBhL\nUEyDqOocEXkCeElECnBXii8B06qZfAhum4s/ILwL/EREuvm/KwlUvfoDnuJONEOBHOBxEQnWSGQC\nrUUk27eHB3Xxyw22kY/wy/kosJxSfIc7ETnID/4y8J1C/39uNesWNBzXJLA0MO85IlIcN926WHLi\njQX2EJGtcdNV4hKe2IlsYdz4LbgksSb/CZSlXERmASNEpCsuybxBRP4QmD7Dz3MAUOKHfbWrmatq\nVERe5dsJyo9xJ/7DRGQh7ur4FRLbDr4OjN+Oq7KPLbNERMCdaFDVx0XkCJ+47OmXI3wTt5hFgXkU\n+XlUGz8fnyG+bDX5T9zfHwLH+c9jqNvvWrWt+ZrJngS2T1/eW/z4u3Hb9RZf/phsX96Yr31yElOX\nbSVso/3/0/3FQkwW3+xTMVXbmN9nNvmapHxcrVhsXpnxC6njthxLsNf7/3skvjqmqViCYhpMVX8o\nIr/DXZkdibuSf99/DopQfee5WFPjzsCwnXHTZOKqs2PTTuabg02wLPHJCUCsb0bwoBY//2rF2q3j\n1NYBsJLqm0/jlxmfsGTgTu7XVbOM9YHP1a1jbWWqLZ5XAG9X873luP4c1ZU33r+A231NSG/cifcd\n3FX9QGC6TzYbsh3s8tZvEbkP1//kYeAF4He4K/TecZMmEr+JwLuBK+9d2VV8oe6/azC+tW2fGbhE\n6/hq5hlsfqvPthK2DNw+cRDfLht8EyPg2/uv74f0Gu6CZzruuNKW6i9+YsuBmrflmNixoMZHFoaI\n8QAABJVJREFUCZjksj4opkFEZF8RuU1Vv1TVu1T1eOA84HB/RRO0EHfgPShu+HhgTVw18z6BZXQF\nBuM6sS7CdbDcXVUXx/4B38OdjL5DVTfhOlR2CwyO1UIEl5Ml7tkODW2P/xzoICL5gXkPBvJq+d48\nYKiqLgmsV2vgDqBvA8sUXM9WuKrtT1V1He4kOSgunvvgOpwmcjJ7Ddc8djkw09/S+RYuQfkeLmmA\nxLaDOhGRzrgmq0tU9eeq+ohvTshPcB3i1aX/CQTi640DYp2tE/5dVbUI1z/pW/MVkWd8U+M8XOfi\nLYF5LsfdQju+TmvmNNat8cH5zsP9Br3itrHzgXNrmMeVuM6yk1X1Tt8UG+srFPtNq5aT4LYc6yu1\nup7rZ5qA1aCYhioCpvo257/hmj9OA77wbdzgDwyqulVE/gJcKyKbgE9w/UAuxvU9iIng2owv8vO/\nBdeZ71lfrR/rHLkVV5V+GO7AHKzWjfcxrgnlH74sX4rINOAecQ96Wu3LkI2rrj9+F/Opy8nuHb+8\nf4jIVNxV4p+Iu1qsxq3Ae776/m5c58Z7cE1aX9RhuTX5g4isA5biOp62wf1e4GJ3nYiswJ2MR+Hu\nQJqmqjvjmhB2yTeXvIfrwHy9H/w28CCuev2HfrpEtoO6KsI1X5wkIrP9+l2G+81nJjCfKuLuODsK\ndxdJbc4QkY9xHV9PxnUWjzXx1Pd3vRH3u32B63T6PeAEXMffub5cz4nIVbj1/w0ujrX1lwnaBgwW\nke7+BB+WbUB/EemtqgtE5CXgPhG5FNdfaDKuz9g5NcxjBXCiiIwDVuIS3VjfmuzAcjr5C4Al1LIt\nB+Y9FldjNReTsqwGxTSIutt2T8YlCbNxTTvluCvPmODV1BW4u25uxF1ZXYTrCHdH3PR/xSUT7wNb\ngcNVtSQwjztwB6sFuAP11YFOitV5HneACzoX1wzxNO4k2RvXaXZTDfOpjPv8nStQ3yx0LK6253Xc\nHS6P8+3q/O9Q1Y9wdxWNwtUWPY+rbZigquXVLD8R9+ISvY9x7e7jVXWtX+5tuKvVqbh43o7rbHxJ\n4Pt1Xe6LuNqBf/t5r8CdhOcH++RQ9+2gNpVApY/Pqbj+P3NxfV1ycAnP0MDdGtXNc1fL2R9Yq6q7\n6jwb9BAuKZmLS8Qmq+obUP/fVVXvxt1tdC0uRufh7qCa7mtYDsbdQvwarq9KTz/PXXVkrs5duMTn\n9Rqm2VV8anpw2324fl5zfJPeacBzfvh83G3i56lqTR27f4NLLl/EHVtiNS6xu7jw81yDu7trTB23\nZXDHq7d8LZ9JUZHKSnv4pUkdvt353/hnGoQ43064K6zDNfCck3Qn3zz749DA3SImRFLD83BM6hH3\nvJxVuGTvndqmN8ljNSgmFYXeiU9VC3FV7VeGPW9jTLMyBZhryUnqswTFpKLGqta7ERAR2auR5p+q\nrJq0cVl8mwlxD7i7kpo755oUYU08xhhjjEk5VoNijDHGmJRjCYoxxhhjUo4lKMYYY4xJOZagGGOM\nMSblWIJijDHGmJRjCYoxxhhjUo4lKMYYY4xJOZagGGOMMSbl/D9XOsoCKIElowAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbb8fd080>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Specify slopes to consider: a_vals\n",
"a_vals = np.linspace(0, 0.1, 200)\n",
"\n",
"# Initialize sum of square of residuals: rss\n",
"rss = np.empty_like(a_vals)\n",
"\n",
"# Compute sum of square of residuals for each value of a_vals\n",
"for i, a in enumerate(a_vals):\n",
" rss[i] = np.sum((fertility - a*illiteracy - b)**2)\n",
"\n",
"# Plot the RSS\n",
"plt.plot(a_vals, rss, '-')\n",
"plt.xlabel('slope (children per woman / percent illiterate)')\n",
"plt.ylabel('sum of square of residuals')\n",
"\n",
"plt.show()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Bootstrapping** \n",
"● The use of resampled data to perform statistical inference \n",
"**Bootstrap sample** \n",
"● A resampled array of the data \n",
"**Bootstrap replicate** \n",
"● A statistic computed from a resampled array "
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"rainfall = np.array([ 875.5, 648.2, 788.1, 940.3, 491.1, 743.5, 730.1,\n",
" 686.5, 878.8, 865.6, 654.9, 831.5, 798.1, 681.8,\n",
" 743.8, 689.1, 752.1, 837.2, 710.6, 749.2, 967.1,\n",
" 701.2, 619. , 747.6, 803.4, 645.6, 804.1, 787.4,\n",
" 646.8, 997.1, 774. , 734.5, 835. , 840.7, 659.6,\n",
" 828.3, 909.7, 856.9, 578.3, 904.2, 883.9, 740.1,\n",
" 773.9, 741.4, 866.8, 871.1, 712.5, 919.2, 927.9,\n",
" 809.4, 633.8, 626.8, 871.3, 774.3, 898.8, 789.6,\n",
" 936.3, 765.4, 882.1, 681.1, 661.3, 847.9, 683.9,\n",
" 985.7, 771.1, 736.6, 713.2, 774.5, 937.7, 694.5,\n",
" 598.2, 983.8, 700.2, 901.3, 733.5, 964.4, 609.3,\n",
" 1035.2, 718. , 688.6, 736.8, 643.3, 1038.5, 969. ,\n",
" 802.7, 876.6, 944.7, 786.6, 770.4, 808.6, 761.3,\n",
" 774.2, 559.3, 674.2, 883.6, 823.9, 960.4, 877.8,\n",
" 940.6, 831.8, 906.2, 866.5, 674.1, 998.1, 789.3,\n",
" 915. , 737.1, 763. , 666.7, 824.5, 913.8, 905.1,\n",
" 667.8, 747.4, 784.7, 925.4, 880.2, 1086.9, 764.4,\n",
" 1050.1, 595.2, 855.2, 726.9, 785.2, 948.8, 970.6,\n",
" 896. , 618.4, 572.4, 1146.4, 728.2, 864.2, 793. ])"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAgIAAAF3CAYAAADXQiMjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsvXmYpFdZ9/8556l97b17prtnz1QyCdljFAKEJQiiKAjK\nK4iCoKLghiuvij8VRF7FDVkUBSOiIgLKKhjCJmsIZkJmUrPP9PT0XtW17+f8/rhr6e7pJLP0kFnO\n57rqqn6qnuX0yaTPfe7leytrLQ6Hw+FwOK5M9OM9AIfD4XA4HI8fzhBwOBwOh+MKxhkCDofD4XBc\nwThDwOFwOByOKxhnCDgcDofDcQXjDAGHw+FwOK5gnCHgcDgcDscVjDMEHA6Hw+G4gnGGgMPhcDgc\nVzC+c70wlUoFgfuAn0+n0194hHNuAt4BPAH4NvDqdDp9/5k+Y2GhcE6yh1orBgaiZDIljHHKiW4+\nTsfNyWrcfKzGzcdq3Hys5lKZj+HhuDqT887JI9A2Av4Z2PMo50SAjwOfB24GvgJ8PJVKhc/lmWeD\n1gqlFFqf0Rxc9rj5OB03J6tx87EaNx+rcfOxmsttPs7aEEilUtcAXwW2P8apLwbK6XT6N9LCLwEF\n4EVnP0yHw+FwOBwXgnPxCDwVuAf4HuDRzKHbgS+t+ex/2tc5HA6Hw+G4CDjrHIF0Ov3Ozs+pVOrR\nTt2E5AWsZA649myf6XA4HI7Ln2YTpqagUtGEw4bJSfC1V6lyGe69F5aXNX19hqc9DSKRjR9DPg8f\n/CBkMpqBAcMLXwiJxMY/51z51Kfg1a+GalUTChne8Q549rPP757nnCx4BkSA2prPakDwTG+g9bnF\nYDxPr3q/0nHzcTpuTlbj5mM1bj5W852aj6kpKJflGeWyZmbGsL0dhP7iF2F+Xr6bn9d88YuG5z53\n48fwkY/AqVPynFOnNB/5iOEVr1h9znnPhzFQLKIKBVQhj8rnez8XCvLK53o/rzjn1m/m2W8LTDHB\n95f+nVe/uo+pqfP5jS+sIVDl9EU/CJTP9AYDA1GUOvdkjETiguclXlK4+TgdNyercfOxGjcfq7nQ\n8zE9vXr3HQhAf7/8XK9DNNr7rl7vfbeRlEoQCq0+7j6nvYCTz8LJPIl8HnI5cSN0XmuP1/usUAB7\nbtUG17TfJ5nmBg7wpdrTznseLqQhMA2MrflsDJg50xtkMqVz9ggkEmHy+Qqtljnr6y833HycjpuT\n1bj5WI2bD1nzslnIZEBrzbZtYXy+CtZu7Hz0wgFw4gQcOKAplSAeh6c9zZDNynnVKnz4w/JdNAov\neEHvu3OiUkEvzKPm5uR9fh69MM/TPzHPUnqJaDNHn8ozkchj3iU7c4oF1Dku4GeDVQobT2ATCYjH\n5ed4HJtI8I//ESdrkuzlOr7Abfi90iPOQ39/dP0v1nAhDYGvAr+x5rMnAX94pjcwxp5XjWarZWg2\nr8z/idfDzcfpuDlZjZuP1VzJ85HNwtycol5XeB7MzUE4bIjHN3Y+jh6FQkFc7Pv3w6lTstAbAwcP\nGjqpaOm05A40m2I0pNOGZnPNzYpF9MI8emGh/b7yJZ+pzs/FwrrjuWPtB0tn/rt0F/D2om1jcWw8\njul81n2Xn82aY5tIYGJxmYBH8Ia//Tjcf39v6b722ubp83CWbKghkEqlRoFcOp2uAh8E/iiVSv0Z\n8DfAzyJ5Ax/YyGc6HA6H4+wwRrzVjYbC77ckk6DXhLurVcXBg4qHHlK0WpBKwROfKDv1jWR5WbN3\nL5RKim98Aw4flvHFYhCJaEAMj9kZxcCJB7iu8DU261mumZ0jcWDFIr84jyqfceR5XWwkwlR9hDkz\nTJY+CjpBIxTneS+NycLeXrBVMkFsfJQ8fpqRWHexJxI5fSI3GJ9PMzEBrRZ4nhx35uic73meY1q7\nXZ8BfhK4O51OF1Kp1PcD7wJ+GtgLPCedTlfO85kOh8PhOA9yOajVZMdZqylyOXtanHluzrJvnyaT\nUWgtO/d4HDZv3tixHDhgWFqSpejBB6U6IB4Xj8RXP5XhdVvvJXDPZ3jbh/+b4eZs78IscOSx72+i\nMezwMGZ4RF4jI72fuy/5nliM77kRMpne0jiQaPKM3199T59PQ3+UVrZE6zvsMarXDY2GGBvGyPH5\ncl6GQDqd9tYc6zXH9wG3nM8zHA6Hw3HmnMluv9EQI6Beh4MHxeU+MWHYs0cS9ATN9LTi8GE52rlT\nXhtNqaT59Kclh252Fq4zD/ID+U/xbPtpbj/xVXzfaAGwMk1xmST58AhjNwxjVyzkaxd2Mzxy1jWG\nN9+s+dznZG4CATk+3x33RvLkJ2s++lEJj4TDcvx4ewQcDofDcRFxJrt9v99SqykOHoRs1iMQsGQy\nHvv2tbjxRjlnetqQy2mUknB1JgPz8xs/3s98xlAsajxl+OvWL/Az/D20Vp9jhob4WPOZfKz1bD7n\nfwZZPcjYWJPP/ufGjyccNuzZo1cdX0z09xvuvFOvOj5fnCHgcDgclzArPQCeZ5mdVUxPK5pNxcCA\nYetWxdoobjgMDz5oue8+TTZrGR5WJJMWpVbuLjUzM5ajRxVKwZYtF0ZYp9HQLGcMf5r/OV7K3QC0\n0HxD38a3J+7ih9/9TJrX38g7X+7jvvs0tRoEgzA5eWF26rfcojl8WDwUiYQcX0wegdtv19Rqhnxe\nkUhYbr/deQQcDofjimalByCTURw6RDeG3GppQqEWmzatvubhh6HZ9KhUoFhUGANKKebne1vxb37T\nkM368PvFI1AoSFb/WVOroRd7WfxqcXFVNv9b7l9gqDLNztYhAL7M7bxq+AMs6WE2DTT5wbaHIhAw\njI/3dsKBwIVZnJeWDLt26VXHFxNDQ4a77tJ0jLuNqOJwhoDD4XBcwnTi/QDNpsJaCAQszaYs4Otl\nlReLstAlk4pSSTLQ43HL2Fjv3EBAEwpJrNxaEdmJxdo3KJV6i/mahV0vLEiJ3uKCZPPnlh91/Lev\n+Pmr6naeH/wP/IEE8TBcdVVvPE95iua//ksMn2RSji/ETn1wUJPJ9GLwg4MXl0dgchKmpswqGebz\nxRkCDofDcYmxMhxQKFjqdUWrpVhasnz72yLBGwhYbrzREgyevoj5/YZvftPj0CGp2x8agqWl1bvs\neNxQLil+YuEveKL5MpszS2z/+1n63zGPKpfOa/w2EMAMSULfofwwB/OjHPRS/LV5FYFQnIkJSdSb\nmOiNZ2LCcMcdupvEt/K7jWR42LC4qInFwO+X44sJn4+27PLGjcsZAg6Hw3GJsTYhsFSS5PiHH4Z8\n3qPZlM+PHLHcfvvp14sXQFEoQK0mqn3VqmJhoXeOtfDE8mf5o+br5YN6+/UI2EgEM7Q2g3+4e2xX\nfGYTya5gznv+H9x7r49yGUwJAp4swLEYXLuiRd2mTXD8uKHVUoRC9rRwx0axcyecPCmJkvG4uSCV\nEhcbzhBwOByOi4QzKf0DqNcVy8sSCshmZWEvlSCd1hw7JveJRkWxr1qFtbvHbFbc3zMz4hGYmhKP\nwNBQzw2+nIHvL30QgDJh7gk+l+DWAZ70/OHubn5VmV70zORs15LPawYG5HKfTzQEnvtc+Xll8mK1\nKhUM1ooNUa1eKJe95klPgpVJkxdTaOBC4AwBh8PhuEg4k9I/gHLZUq+LhTA3J4YBwMKCGAZ+f69J\nTzZ7+iJ25IhheVkzPS0GRCAg5YHf+O8sga33EvjvT/OGD32GgdocAB/X38crg//Gk68qcdPrNnZR\nLJUk3g0y5lqtI5QDWveelU73hIeWlhTpdLNb6riRhMOmK3ncOb7ccYaAw+FwPI6s9ALkcr2NdT4P\nxshudK1nIBRSLCxYqlVFpSJd+2ZmFKdOweKiNPKJxWDXLkssdvqO1u8XWd9sFq5qPcwP1j7J8yr/\nxXcd/TK+L4twfUfAp0KId5hX4nl0df83kptvFu9EPg+jo1IXn81CX5/lmmt6pY+BgKZc7iXxBQIX\nZqd+IZLxLnacIeBwOByPIyu9AMbIggiyyw8G7bqegWrVEgpJVv/Xvw7lsmJpSXb3nbBAKCShg5mZ\n1mnP/NrXDMZofpM/4Q/5XVlPV8T/zdAwnwvfxfuXn8On7dPJ6X5iYaku2Gj6+yUJEMSgCYcVt9wC\noMjnew+s1w2RiO4KBW6EtO56XIhkvIsdZwg4HA7H40DHEzA9rZmbs3ieJhQy9PWJEXD0qMVaRTxu\nufpqRX9/TxTI71csLlpKJUWxKPdZXIRiUQyJYlHCAwMDsF6MWynNcPYgb2j1RPT/N3AL87d+L7e9\n4S6aN9zEB97g4z8/pCm0m/TFYrB798bPw7XXKnK5FrmcIhiEWExx8qQiHDarchZ27dJkMoZCQeZE\nav2vnMX6QuIMAYfD4Xgc6HgC5uZsV+bXGBEAyuctjYb8ec5m4fDhJuPjvWsXFy3gEY1Kxn+rJaED\npeRda+lMVy6LMNBzn9u+sNnE98C3eP6BL/H05Q/gp0mNAE+KfJXILVezdWuTm26SU0slQ1+fJhyW\n+yYSF6axnrWW666TG3/rW+LdkF2/Znm511/X8wypVKe9jcLzLoB74grFGQIOh8PxONARAvI8qfm3\n1hIIiACQUhAMWppNhc+3VvpXYvwiGqQYH1fMzloGByXHoFwW93Y4DP3xJjuX7if8V1/A/+Uv4v/q\nV9ClIj+3Yhxv87+WU8mruTG2WjwnldIcPy79BbSGHTsujEcgElHUavK79Pcr/H6D3y8JjH19vfGM\njirqdUO1KuWDo6OnSyc7zg1nCDgcDscF4tHKAT3PkskoymXL/LwiFFK0WpaHHxZBG4Drr7eEQqfL\nyPp8hkOHNMWiYnHREA5L6CAcFuPimeWP8arCu/me2a8QM4XTx6U0BxM38Z/q+3lz61fwtWBhAW67\nrfec8XHDdddpFhakZG/79hXKghtIIGDp65NFvVi0BAKKcFgMoGjUrDovkRBvgc8nx46NwRkCDofD\ncYF4rHLAtqYO1spr3z7wPB8DA1Ljv3+/4RnPkPbAK5meltbBrZb0FahUJJ+gXoctTPG+2ksI0Oie\nb7Wmef0NNJ74ZBpPuoMPnPoePvbFQb71LWgsg19JeCGT6T3jppvgwIEW2axHMAhXXXVh5iiZhFzO\n0mgoBgdlca/XpUPi2iZHnU6ISq1zI8c54wwBh8PhuECsFP7x+Sz9/T13dr0urvyFBUUmIyWBs7N0\nSwgjEen4t16t/MKCdMgrlWB5WdzrzabkC/x65c8I0KCF5p+GX4N6+lN4zhtvFzW/NvN/06vb9/nE\nSxEKwfJyzxXv9ytuvlkxNiZue8+T0r2Nxhj5HSoVRbkMExPg88kcWdubr1ZLkUyy6tiFBjYGZwg4\nHA7HBWKl8E+9riiXe67uuTlLsegxMyNdAyMRmJ2VxTAQEIPg5Mn1s+LTaUM2K/ednZUKgUgEErmT\n/GTzvQB80HsRvxd7M8+IN3n2mp31ww/L9Y0GbeVBWeQLhZV5CLadc6DxPBH6WX70/kHnxNQUXQGf\nalVx6pRly5beGFaOp+NdWfud4/y4ADmgDofD4QDZ5VerluXlTu1/Ty+gXNbMz8PiouLBB+HLX4b5\neekauLTUWXQ1R4+KQNBKolFNNiuLaKUiO/vlZXh97rcJU6WF5g/Mr2Mtq1r3dhgc1AQCYjx4nozH\n8+D66/WKZ4jxMjdnmZmBYJDTXPUbQUdVECQHwRiF1pIsmew5MUgm5bP1vnOcH84j4HA4HBeIlcI/\noKhWZcedy0GlYvH5NCdOyG47HIZiUZQCd+6Uxb1el93y1JRpi9wIS0uGcFi3r5H4/neX7uVHzQcA\n+Bv1Sg4FrmFcy7lrSSYNk5O6HVYQff8nPAGU6p07PS3vo6MSFrAXaAO+UtJXaxgdNYyMnH6e1rTz\nK5wnYKNxHgGHw+HYYJpNOHoUjh/XHD1qyWSgVrMEg+IRqNcV1ir27bOcPCkZ+5lMb+e/tCRle/m8\n5v77IZdb/ad6ZEQzNQX794uA0GTzGG899TIAMvTzO/a3aTYlZLBp0+l/5u+6SxEOtwiHLbGYlAYO\nDlquvrp3bqGgyWZVW76489yNn6vJSamKkIZDV4ak78WG8wg4HA7HBtOJe1er0Gh4VCqGgQFFrSY7\n7nLZkk6LMdARAVJK3PPhMAwNdSoOIJPRpzXYeegh0/U02Nk53nbiRQyYJVpofoz3sOwN4fN13Pmn\newQqFctTn+oxMQGFAsTjlp07YWCgd+7UlKFW8xGPy7hAxrbRXImSvhcbziPgcDgcG0wn7h0MSjy7\n0VAEApZIRDwC4bDC8xSBAGza1GvBOzIiYYFQyBKPiys8EoFQaPWf6khEwgJXVx/gE4tPJtV4CIA3\nBP6Az/qfhc8nVQATE5bv/u7Ta+38fk0waNm2TRb/UMgyMNBaVaYYjWoGBizhsCUclhi9i8tfnjiP\ngMPhcJwna4WDPM9w/LhmcVFRrcL4uMS1O2VxnmcxxnD0qEc+L0aAdN6DYNDQbIpLvlCQ+P/27at3\ny7v8x7jh2Cd57ewbiNgyAO+ffB3vrv0SgZLcL5GAVMoQi50eUw8EDPm8plpVRKOWrVstW7fKdR36\n+gzGeGzaJB6BrVvFc2Hcxv2ywxkCDofDcZ6sFQ4qFm1X9GbtO0hcv3O+1pKIp5QkB0YiuhsWKJfl\ns8xMDf8XvkLgns8Q+Oxn+P30w9171Qjw5p1v54Hrfwy+LJ91Qgy12qOPu1IxgKLZPL3L4Z49sG9f\ni2JR09dnecITRLfAcfnhDAGHw+E4T6pVxdQUXR38UkljrSzEJ09KiWC9brnlFlHPK5U08/O6mxvQ\nakn3QL9fqgCyWWgtZnlu44N834FPc8sHP0ewcfoqfDh6Hb87+jYeCH0XozkxAGIx6OsTj0CzqWm1\nDGsz7SsVTbEo+gXBoIwbbLv/gZwbCHTEjAw+n5QbOkPg8sQZAg6Hw3GedMSBQEoAjx1rkUj4OHZM\n6vtjMVhc9Ni7t8nkZCcRTwR95uZ6Cn+5nFQPXF/9Bu+cfzGb7cyq59hIhPodT+Gfs3fxSZ7DTGgb\nR4+C30oYodOJsNGQRbvRMOsK70xNGXI5H7Z93eysyBg7kZ4rE2cIOBwOx1lijOzaMxlx72eziv37\nLYWCJpk09PeLVG+xqJifFylhn4/u55GIZmjIcuyYolCQhdtaKR/8cfM+/jj3WkKIX/+QP8XR1F3c\n9rvPpPHdT4RQiOz7NNlPamo5SQrseBSMkVetJh6Bq69WxOOnL+6RiAakP4HPJ82KgkHjkgGvUJwh\n4HA4HGdJp0dAvS6GwAMPWEolj3C443Zvcsst4iHotNSt12FmRjLtPM9QqfjYvBkOHhQjIOQ1+L/5\n3+Jnam8HoEyYX4y/i69seSFbJpv8w5295/v9hltukUqCz3xG1AV9PvEIeB5cc414IYJBS6HAqkZH\nnef39fno6wNQDA62TjvHceXgDAGHw+E4S+p1xalTivvuU5RKioUFy/i4LMLBIBij2bvXMDMjUsAj\nI7JTHxkRj8D4uGJ2VioLqlWIlBf5h8KP8zT7eQCO66280PtXDurrmVQwNtZrBgSwfbvmwAFDLqfw\n+cDnUzQakm9gjAgSBQIQCEhHwrU5Ajt3KhqNFqWSVA3s3Oka+FzJOEPA4XA4zpJy2XL//YrFRfEI\nVKuKbBZSKfl+3z5DLOYjEqGr8Ld5M1gri/nDD1vAIx6HgcYcn23eyTaOA/B535388qa7maoMkQjT\nLt9bXbO3sGDYtMnHpk2SjOh5okXQaWc8Pi4hg/l5GetaIhHLtdf2Fv9g0BkBVzLOEHA4HI6zJBxW\n7fi67MK3bYNWyxAKiZJfoSBZ+UNDskNXyjI0ZNm9W3b2rZZmaEhi+T9p/7FrBLwz9Bre1P8mNm3y\nEV8QA2JkxHLHHas9ArGYJhq11OuKnTulA6HkIIgBEInAwID0EAiHT9/tJ5OQy9mu7oHLDbiycYaA\nw+FwPAorxYI8TxbU5WWo1w3ZrIdSna58hpMndVsN0LCwoGk2ZYc+MCCLczQqi3mn0U65DBOcBOCI\n3sFvBt9CTMsOf3gYrroKnv50GBtb7REIBAzHj3sUi1AsikJgX5/qygEPDoqOQCJh160EcA18HCtx\nEsMOh8PxKHTEgoyRBMHFRcXyMvT1aTxPPALHjxus9VEua6anfUxPi2fAGEswCP39kliYz8s9tZYY\nfsQUeXLtcwDMqjGsFcMjHBZvQDhsiEQM4+Orx7SwIGOSjoAiYOTzWcbGLAMDBp/PEo8bduz4Ts6U\n41LFeQQcDofjUSiXFQ8/DKWSplYT3f2FBcWhQ1L6FwzKOYcPS5e+cFjKBG+9VTL3OzX95TLtdruG\nclkz0G/5mc++mqvMAQD+Wb+YRkOMhK1bV6oVWprN1e79XE56Dfh8El4IBhVjY5ZKRdFsKnbsEHf/\n8DC0Wi4R0PHoOEPA4XA4HoXDhy3ZrPypPHFCYurlMhw/LiWBySTMzCiiUTEKikXI5w27dvlYXpYF\nvdWCoSHF/HwLAK0NO7/2Qe449e8AvJ8f4V32p6DZExUql8HvV2SzHocPN1d5BRoN021s1CkZrFQU\n5bLC5zPU66otH+xEghyPjTMEHA6H41GoVDT33WfJ5RTNprTMbTZFwGduTnbwIIl5xogXIJHQTE1Z\nFhcVxSLt3bvtlg/u2gmj+/4CgEPs4FX8NY2mwvMkJFAoyD37+6HRsFi7Olnwuus009OGXE4TChlG\nRhSZjFQXbNkC8bghEnEiQY4zwxkCDofD8Sjs3WsoFn14njQLOnlSFv1cTr73+cT932rBbbfJZ4cP\nGxIJH4mEfB8Ow+bNCk838f3vt+h/w99zVfEBAP7K9xqqJkooIOcGg/CEJ8j9AwHxCijVWjWmatVw\nzTUdL4XG55PugbWaxvNaTE5KF0MnEuQ4E5wh4HA4HGswRtzzMzMwM6PZu1fCAMGgLPqFghgFrZZ4\nB6JRqNct+/fDwIBhxw7N8eMiQ1ypwHBgmas/+y/cvve9RA7spbM+L3nD/CMvwRi5r7QjljyEfJ62\nh8CwffvqOH88rjl61FAqKSoVaTIkMsUGn895AhxnhzMEHA6HYw25tob/yZOKgwd7i3QuB56n6OsT\no6DZlN1+swmDg4prrgHw2L+/SX+/Jhk3vPbY6/mB+/+WYKvSvX/DH+aegR/mnf2/SnM6TqghJYix\nmDxnbAwSCUUyKUZAs7m6fLBQMESjPqJRyRFoNm1XLjiZdHLBjrPDGQIOh8OxhkZDDIFKBZJJifMb\nI676eFw8AKOjUsYXDoMxlhtuUGjdUfnTJJNw19fewgtP/GX3voVd18Mrf4JD3/Uj/N3b+5mf1iQK\nkvnv84newO7dlmgUAgHL4KAiEJB4/0qPwMCAplQy1GqK0VHQ2uL3QyhkGRlxVQKOs8MZAg6H44qn\nIxpUqykqFUuzKXr9+bwk62WzIiVsrRgH1oqx0N8vhoFShmrVY35ePAWDg4YbTn2GFz/8hwBMDd/I\n3p//S/qfeQNX7VZ4M9DXZzlxopcXMDkpZYObN1uGhqQ0MRCwKCWJhisJhw2JhAgWBQIiGtTfr9r3\nckaA4+xwgkIOh+OKp2ME5HJS65/LKWo1KeHrtAg2RkIAHQOgVuuV7vX1eczOWjwPJkppXn3vy3j5\nvz0fbQ1Ffz//9IL3k9lxs6gPAQcOQKXiYa14GVot8DxLMmnYtavXMwB67ytJJKQsUCkxAmIxuXX7\n9g7HWeE8Ag6H44qnWlVMTcH0tKj/KSVx+uXlTrthKRNsNkUnoFIRw0BrWcQXFmAzM/zwgTfy9ON3\n41nJ8q8F47z/+9/LQnQrm62lVpMywPl5zeHDch8Q4Z+JCdi1S1byVkvG0GisLyhkjCKRENnifF4R\ni8HgoG1f60IDjrPDGQIOh+OKZ27OUix6LC5CoaBotSRHIJ0WOeFarSPaIwt0xxiwVnbnN0x9gncU\nf4qEkZrChg5w5Nk/zb+nfo1T9WFifiiVFJlME4D9+0UQqF4Xr0OzCdB5liUQgGJRY62IA5XLq5MF\ny2VLvS4OXQlX9BZ+JyDkOFucIeBwOK54jNGk05Z0WhoBJZNSPnjihKXVkjAByILtefJdtQq2ZXjZ\nkTfx65U3yX1QfHL4JfzPs/4vT/uJcXzf0njTBr9fUSpZ4nHxCMRimmBQyguNEREhnw/yecvoqEgG\nFwqGeh2qVcvw8OpdfiikWFiwVKuKQMCSSIh3wnUSdJwLzhBwOBxXPAcPGioVH9aKW/7ECUneazbF\nOxAIyKvjEfA8eb298bO8tPY+ABb1CL9/7d38b99T2Kqa3HijSA3H450/s4pCQTwCxaKhr08qC+bm\npPJAJIQV1aohGhU1wUDAEgrJZyupVi2hkCYUkmuCQcPIyHdqthyXG84QcDgclyXrtQ9utVR316xX\npEp7niaTkZ1+sSju+kpFhIPKZQkNNBpyrrVSTbC5epSXNsQI+KbvVl6/+/2UkxPEorB7tyabNdRq\nmn37DPW6pq/PsG2beASuukozNSUyxSAeiFYLwmGLUqr9bEMiodb1CITDinpdcgd8Pks47PICHOeO\nMwQcDsdlSa97H2QyCqVkwZXqALtKdCefN/j9ssM2RhZon0/UBJUSb0A0KgaBtbKDfzl3AxIO+Nmh\n9zO6fYI7niD3CwSkxv/IEYu1HuEwaK05fLjJrbdK06Ft2zQTEyJZHAiIhgAoIhFDOAyt1iN7BIJB\nSzLZW/xdyaDjfDhrQyCVSgWBtwMvAMrAn6bT6bc+wrnPB94ITALfAn4xnU5/69yH63A4HGeGZNwL\nzaZql9bZFd/1Fs9t2zTFougF+P0wOCi1/fW6LPr1usTxWy3oSxh+rfxGfrrxxwB8LfJUYldPMD5u\nCIVEH+DqqzVgCQbFuOgoEAaD4hFIpTTz84ZSSTMxYYlGFUoZIhHYskWaD9XrFmNkkV+7408mIZez\nNBrK5QU4zptz8Qj8CXAzcCewDbg7lUodS6fTH1p5UiqV2gP8E/Aq4MvArwAfT6VSO9LpdPV8Bu1w\nOByPhedZMhlFo6E4ccJy/LjC8xSjo5bbb1+9g45EDJWKR7MpCXydevx4vFciWKtBQhX4m8VX8LT8\nxwFY8EbIL7VJAAAgAElEQVT4uz1vZutWy513Wq67Tq5bXjZ89auKI0ckvDA5KR6F/n7Z2YfDpp04\nKNUJo6OGrVtFIbBWkxBGoSDPt/b0SgCtaXs0nCfAcf6claBQKpWKAD8F/EI6nX4gnU7/B/AW4DXr\nnP4s4NvpdPqf0un0UeC3gDFgz3mO2eFwOM4IpWQhPnZMkc9rqlXNzIzHgQOrz5udFS2BfF6qAfx+\neRWLveTAZCvDR4rf1zUCHgzfwktTX+JY8noGBgyTkxatZQc/MwO5nEd/v3gisllDMtli9255XrEo\nXQV9PtoNh2xbobBnhHR+diJBjgvN2XoEbmhf85UVn30JeP065y4B16ZSqSe2z38FkAMOn8M4HQ6H\n44zoJAnOzWmUsrRaIhR06JDE/fv6YHhYXPQdFhc1y8uSG9Dp+nfVVbJbtxZGzCwfrf0A15qHAPjs\n5v/Dm7b/NbGhELt2wdCQYmZGxIdiMUsmI2WIpVInv0CxaZMFxMVfKmnicYhELMvLkMlojh6VhMQd\nO8R7EI+3DZCkEwlyXFjOVmJ4E7CYTqebKz6bA0KpVGpwzbn/CnwCMRTqiOfghel0Oneug3U4HI7H\nopMk6HmWpSXF3Jx4BEQ+WHoI7Nu3Ovnu1ClDPi/XFovy3mlDXK1Y/qX6I10j4D3xn+NNqb8lUw51\n9QROnLDk85p6XZHJeBw5YqhUeverVEQgaG6us5iLUFCrpZieVhSLinpdUSppTpyw3d4CnXcnEuS4\nkJytRyAC1NZ81jkOrvl8EAkF/BzwNeDVwHtTqdRN6XR68UweprVC67P3i3meXvV+pePm43TcnKzm\ncpqPVguKRUWz2Sv9M0YW9VZLsvNvuknjW/HXb2wMHnywVzro93fCBXB149t8l70PgLfqX+Td429i\nDHH5ay0eg2hUFvPlZUky7OvT3Xu1WtDXp9oNguS5V10F2azl+HExFsbG5H79/RAIKIaGxHgIhxXB\noHRA1I/jf5rL6d/HRnC5zcfZGgJVTl/wO8flNZ//MbA3nU6/EyCVSv0MsB94OfD/zuRhAwNR1HkE\nyBKJ8Dlfezni5uN03Jys5nKYj0xGFuNgkK4XIJeTxT0YlJj7kSOsKh8sFETvf25Owge1mrj0g8Ew\nP8J/AtDAx5+Hf5dAI8LkpLjuBwbgSU+C/fvFaIjF5H7NJlx3nfQCKBREhnhoSL7v75cxDg/L98Gg\nhASCQdi8Wc675prHYeLOgMvh38dGcrnMx9kaAtPAUCqV0ul0uuNbGwMq6XR6ec25twB/0TlIp9M2\nlUo9AGw904dlMqVz9ggkEmHy+QqtlnnsCy5z3HycjpuT1VxO8yGyvLID11ri/JGIIhCQ70MhiMUM\n2WzvmsFBOHVKE42K90ApiMXCxGIVnj39UQC+5L+TVlI+CwblPh1jYvNm23bvy+I+Omqwtlc6GAjY\n9rMt2ayMMZ9X1GqKkRGpVCgWDYGANB9aObaLgcvp38dGcKnMR39/9IzOO1tD4H+BBvDdSEkgwJOB\nb6xz7ilOrxBIAV8/04cZYzHm3GNjrZah2bx4/yN9p3HzcTpuTlZzqc+HMbIDr1Y1hYLlwAFFNquw\nVpr8NNvZTYmE6f4MkkDo92tisV6CXy4HI3aO61t7Afhi7FmEwzA8bBkfl+5/ShlmZjTFoqG/XxGJ\nKIJBSzBoGBwUL8Thw4pazZLNWsbHbbdfQX+/Ym5OXMubNll27zbs3CnjWTm2i4lL/d/HRnO5zMdZ\nGQLpdLqSSqXuBt6ZSqVeAUwArwN+AiCVSo0CubZOwN8C70mlUvchVQOvArYA/7CB43c4HI4uuZw0\n7FlYsOzfr6jVNH6/7L7rdVmAjaHbRKhDJCKLdseLAGAaLX537rXdc74YfgaBAIyMWKJRWFoS1T+l\nLEpplpYs4bDkDGzaBMGg4dAhjbWSM1AuW6anW4yOSiXAwIBledm28xakcZDD8XhwLoJCv4IoC34W\nKQf8nbaeAMAM8JPA3el0+gOpVCqKlBaOI96Ep51poqDD4XCcCSt7CuRyouBXqylOnNDMzsr3c3O9\nuH+rJeWCK8sHSyXpBthqiTGQz1neUvlFnln6GAAfib6Y6o5r6DcQiyk2b4YDB3T7vtI2eGhIs2OH\n3LPZ1ASDhlJJEgaVkjyAYlGeq7UkAN5wQ8/jaa0rEXQ8Ppy1IZBOpytIwt/L1/lOrzl+D/Cecx6d\nw+FwPAYrewoYA6dOScb/4iIsL/eaB7VaPYGh48dXu3Onpw35vG7H6uFF+ffyE7W/BuDLvjt4beQd\nbK7LYr60BMeOyXsn1t9oSN5Bh0zGYIymUIDlZUW1CtJ9sNU9x++33XF3jh2Ox4PLo/bB4XBcURgj\nCXXz84rFRYVpr8HRqDQYOnZMsbAgJYPT070ywnxeDAMRFOoxMKDJ5eS7HYW9/EntVwA4rHfxUwP/\nQkMHKRYlQXBgQIyMjoExM9MLOTz4IExNGSIRTT4vvQV8PrDW0tdnmJjoPTeZFBXCjhqh6xfgeLxw\n3QcdDsclx1ovQD4vCX/Forjq63Xdjfe3Wr16f79fygMXFlZ7BDIZQzKpGQtkuLv8EkLUqKoQvzzx\nPvzJAUYVXH21LP5KWfx+8DxFJCJlhKWSJRhUbNoE4HH4cIvhYY9w2DI6qkgmLbt3Qzzee67rF+C4\nWHCGgMPhuOSoVhVTU1Id4POZ9o5cUSxKGZ+45MVrkMvR9RjU62IYDA2tzhHYtEmzeKrO22Z/jO0t\nUUF/Q/9fcXLwesJ+8SicPCkeB62hXFaUSqIdYIzoBNRqcOKEarcO1sTjBq0VuZwhmVTE44bJycdh\nshyOx8AZAg6H45Jjbs5SLHoA5HKaSMSwdas0+ymXxRBQiq52wEo8DxYX20aAMfi+vZfb7vksz/vq\nR9lc/CYA/zz0ar55wysZD1doNiUkMDYmxkWhoEgm5bNoVASAlpelf4DoBig8r8XkZC/5Lxg0qwSM\nHI6LCWcIOByOSw6fTxMI2HYCoLQXBovPJwI90ailr09Rq4liX7mte6oUbPGmebm6h/jP/jeBz9+L\nXlrilhX3vm/4WXzwe/6YkSjEYpZGQ1GpiAERjYoiYDRKVxgoFhMJ4cFBQzCoCIctO3dK1UCjofD7\nXfzfcXHjDAGHw3FJYQzU64blZfEINJuWkydtO+vfUCzC8rJeVS4I8Mv8JT9l7+bayj74FvJqY7Vm\nfvut3Df6HD53w2v4nh0+tJacg5MnDdPTHW15SfxrNkX7f3i4IxVsGBlRhMOSg5BIGBf/d1wyOEPA\n4XBcUnREg3w+Kb+bn7eEw5pWC5aWNCdO9HoKdMoGd3CEt/Kbq+7T2rKV+p3PoH7n0/mcfgqHFoeo\nVKCxCCdOGPbsgXhc8dBD4lEIhXqJif39HREiSzBo2bRJdv31ulQAOHEgx6WEMwQcDsdFy0qxoI6L\nvdFQNJsKa6USIJtVzM8rfD7RD8i1G52Xy53qAtjKie493z762/T93Iu462e3ibUAzH1Ys7go8sK1\nmnwcj4tHoFiUxMBGQ67XWjE21nmGVA40GprJSYvW4gFw4kCOSwlnCDgcjouWlWWCtZoil7P4/ba9\naEtoYGZGFulO856FBXHhZ7OS1d9swk6OdO/5bv0KfqA1xF0r+plls4ZCQWr/azVpKrO8LPean+/l\nGDSbMDNj2+EHMT6KRYUxplvCCE4cyHFp4QwBh8NxwVlvZ6/PQM5sZZlgKGSYnFSMjloCAUU+L8l4\nPl9v9x8IyCK8sKBYXu70FLD8LO8G4BA7mGOUZNKysnxw61bN/LylUBAVwEQCHn4YqlV5VqMhFQOJ\nBIyPS4Jgo2GxVlEqWbZsUXieiAO55EDHpYZTFnQ4HBeczs5eGv6orvv+sZAyQREHKhY1c3O2LQ5k\nSCQ0g4MKpRShkLTvle9Ut4kQwDP5LLfwvwD8pe+1RKKK/ftXCwr5/YZduxSjoz1NAEkylKTARAIm\nJ0VVMBg0DA0Ztm+X86NRRaViGRqyjIxY+vvPzMhxOC4W3D9Xh8NxwanXZYe+uCjv9bp61PObTTh6\nFI4f15w4YclmRTHQ8+RPVl+fxlpDuWxJJCyzs5avfAVmZ6UzYL3ebvZjW/wJrwdgnmH+vvXj+HwQ\nCKz+07d1q6JWa1EsWkol+ayTaOj3i2FQKEjZ4Pi4xhgpDwyFDLGYZWhIOS+A45LFhQYcDscFp1wW\n2V8QI6BcfvQe7lNTUCho6nXp5FerWfr7Fa12LaAxhsFByRH4yldE7ndwEGZnpccAyAL+stp7uYEH\nAfgdfgciEfz+0yWGs1nLpk0eY2NyXbksyYJLS3S9DQMD8l04bNt6AqJlkEjYtorgRs6Yw/GdwxkC\nDofjghMOK+p1qb/3+Szh8KNn1Vcqsqr29yuaTUurZYnHLSMjct3oqKJeN1SrCr9fkUiIO35wUGL3\nfr8iFDD8Bm8FYC/X8R79cpJhKf3btWu1xHBHoGh4WPIBAgHRB2i1LAMDqpt/EA5bUinJUwBDreak\ngx2XPs4QcDgcFxRjoFKxNBoan88Sj0ut/aPh8xkeekiztCRJeHv2WCYne9f5fBZQgCIcNhw96nWF\ng/x+Q6PhcWf10+zkKABvUa/DC3j4fOLuTyZXewTCYcPysiYcFjd/Jy+gkysgY6YdDhDRIBmPkw52\nXPo4Z5bD4bigdASA/H5Lq6Wo1R47qz6flwqDYNCilHT9W9mqN5+XEIO1ck+RGpa6/0pFjIIfr70X\ngFlG+IB9frf7IEhp4UoSCQgELLGYIhIxXT2A7dsVWhuqVUs0arjqKhm/ax3suJxwHgGHw7HhrCwX\nzOUkyU4WTYvWqrvQgiQGTk1JOCAcFjd7uayJxSAcFk2AQEDR32+79z5+XPPFLypKJcX+/RLT9/tF\nN6BUgmC9wLNa/wXAv3j/B0MAvye7e2tFgXBlaKDZ7LU0DofFqBgbk3drFUtLMDgoRkAgoBkZefQc\nB4fjUsIZAg6HY8NZKQTUkeV9JLGdTmIgyPvUlAEM9br8eRKXf2vVvb/+dcvCglwzPS3GxPCweASq\nVfhR+0lC1AD4gH0+LSOiQ/W6jGVtsmCnm2GpJEZIq9VTEiwWLa2WlDA2m4pMprmBM+VwPP44Q8Dh\ncGwYHU/AzIxGa9Hcj8el9K5QkHM8T7LxWy0JFxSLoujXasl3Wmt27rQ0Gi0KBY1Shr4+aSiUTIqB\nsbys2bdPQgadayUXQd6fV/8QAMeZ5Cvmtu7YajV5X5ssCFKmODOjUcqyfXunesAQiUAgYCiXpbNg\nX9/aax2OSxtnCDgcjg2j4wnwPGkIlM9b+vok/i6VArC0pFCK7qKezRqaTSkFbLWg2WwRicC11ypy\nOcnMDwRsV2K4UrEcOmSp1xWeJ94Az5Pyvrk5CDcL3NX6NAAfUs8nGJC+BOGwnDM0BFqvXsinpw3N\npq+tGKgoFi1PfKKM7/hxQ6kkoQpQGNPC4biccIaAw+E4b9Z6AiIRyOct+bzC7zfU6xLP9/ksjYZq\n19xLiCCZ1CwuymIbjRqGhxXRqOX4ccuJExprRcJXKUsyqdpZ+4q5OXHfV6uye89mxSh4rv0kYaoA\n/Kt9wap2xPW6jHXPntW7+khEdxMP63VLrWapVsWbMTCgWF6W/gLRqJQYuoZCjssJZwg4HI7zZj1P\nQCikiMdte4ct5Xf1uqJaXZ1tb61heFgzPCwlgfW6YXpaQgSBABSLHrOzhvFxRaUii/f0tCQdBoO9\nboHj4zB/qsmPZf4RgCkmuN93G2G/eAwGB+U1MgLF4mqPgOcZ+vt9BALiEYjFREioWBRdgtFR1W4t\nLONzOC4nXPmgw+E4bxoNcft3NALqddVW3ZMEu1BISgE9T0ICQ0O9ErzR0d53waCEEDqCQlK7L8ZE\nIGCJRBThsCKREM+AXCOL9gjzfKj0Azy9eQ8AHw68EH9AEQhIeWBfn4xvdNQyPLz6T9+OHYqBgRae\nZ+jrM1x9tdzXGDFaBgdXj8/huJxwHgGHw3HeeJ4lk1HdHb/fb7u1/uWyaAFoLaGBoSHL4CB03OvZ\nrEWpnrtdjALLQw9pFhYUhYLs9vN5WZB9PhgYMBw86HVd/Tf69/G+h3+Q4eo0AF/2P5m3+H+dgF8M\nj3hcwgNSDgjR6OpdfTRq2bNHMT4uHo1IRBQIg0HIZCyl0pmLITkclxrOI+BwODYEpaSGv9FQ7Xi8\nolTqLb6d11qSSVlcV4r0FIviSSiVFNWqtPqt1xX5fCfJ0GJM796/WXhD1wh47+Av8NLRj1Hw+rBW\nzvH7ew2E5L7rj0GMBkNfnyUUku/OVgzJ4bjUcB4Bh8NxXhgjXQWXlqSzYDwujYI8z5LLgVKKvj4Y\nGJDFvtVanWzXbMLx41AsKmIxy5490nLYWon/VyqQyUgmf7msqdcNJ09KrX9HIGiyeRyAT/a9iN+N\nvBmtIRKR/gM+nwgOxWJiCHheR7eg5xXQWjwAxsiYOwZLoyHfPZIYksNxOeAMAYfDcV7kcuK2r1YV\nzaZk7xtj0Cva8eVytisqtFZQaN8+yGSkfDCT8di3r0WxaCiXfZRK4h3w+RTFoiKbbfL1r0M2q7uC\nP0+p38N2jgBwsjlGPi/GSK0mRobWdMsMw2EZb7W6fsJfL+lRUa2KEdKRJYbTx+5wXA44Q8DhcKzL\nSplgv19c4uu12q3XFbWaolyW42DQEggoTp4Ud3owKLH1xUVFMGiIxeALX4B8XpNIGGo1zcIC3QRD\nz9NMTEClYohGxdNQLIoa4I4dmqNHZZffqBt+mzfze7wRjcWg+DDPIxSSHX293vs9rJX3el0SFXfv\nXl8UqF4Xr0YnjBEMyuK/cg4cjssNZwg4HI51WSkT3BHzWa/TXrksZX+RiBzHYrZdIuh19QMqFcOu\nXZJx//nPWyoV+dNTrWqOHm3S3y/HzaaiWGyxZQvs3q1ZWBBjIhwGv18zM9NkZgbqdc0fe2/g11p/\nCsASA/zG+N/zjdqTsE3YuVOSAzsaAp4n/Q62boXhYUtf3/oegXLZUq9rPE9RE4ViRkbA6QY4Lmec\nIeBwONalWlVMTcliHQoZJifXF9LpJNMVCrLgxuMQCmlyOUsmA8vLlmCwV0J49Ki43et12iWAGr/f\nUCiI7sD4uGZ83LBvn6Fa1UxNSVXBwIBlclIzNCTu+he1/g2AB3gCP8AHKVUm2+5/SzarqFR6OQax\nmFQeDA6KuuDk5OrfoeP9KJV0u9OgJRhc3wPicFxuOEPA4XCsS6cRD0jy3txci02bTj+vVrOEw5rx\ncTkOhUSZz1qPgQFFoSAlgNksRCKKqalWt/6/0QClDDfe6LXvpoAWpRKMjUkpYiik0Vq6AB48KPK+\nPk8xyjwA/8oPMx+cZLyPtjGiGBuTvIVAQF7RqBgAt95q2bLF4Fvzl6/j/fD7bdtgkeTBavUCTKzD\ncZHhDAGHw7EuPp8mELDdZkA+3/px9UhEyuqaTdEJiERkIZ2ft1groQK/X6oAAgHLpk2yWwep39+8\nWROPG6pVRShkGRlR3UTAWEwTiYjBEI1CPK5JJOCGgZOEZ2SVXgpsIhKRvIFoVHb98Tjd65JJ8Tz0\n9RkmJgx79pz+u64URAIpTQyFOqJCGz+3DsfFhDMEHA7Huvj9hpkZTaUiXfeGh9dfEQMBS1+fhA2M\n6cTZpTeA1qqtLyBCPdIXwBKJSEJhIADJpCGfl1yCaNSyZYul2YR771U8/DAsLnbi9LKYx2JwR+We\n7vO/6n8Sw8Owfbt4BHw+eVan06DfD7t3w1OeYrj55vV/144gUseYGRsTD4JUQGzwxDocFxkuAuZw\nONalI+pjrWon8a1/3kpBoFpN8gGMkV12qSQufanLl6TCUEiMAc+zBALSzKdUEl2AUkkzPQ333w9L\nSx7BoKJeh0ymI0csC/Mdix8F4JjexkxkB0qJ4mAkYhkaEmGjTpJgswlKtbjppkf/fZXqvRyOKwnn\nEXA4HF2aTTh6FCoVzZEj4h4PhURnv1RaPzTQEeMBy8yMJBhOTSkOH4ZQSGGMhAukV4All9Pteyqs\ntSwsaDKZnqBQNCrlhDMzMD0tC3Mn479W06hjx7gj/ykAPux/IfW6iBZNTEiLY8+T2H6zKa798XHY\nskUSEh8p+18Mnl7ZYCc04XBcCThDwOFwdJma6qjuiRpfuawYHhYFP2g95vWdBMOTJyGbVW2ZXkkW\n3LpV3PUzM4ZEQjM4KGWADzzQJBqVP0WZjGL//haVioyjXpfdfTAIrcVltn/hb0h9+p1oLC0079Kv\noloVj0GtJgmCCwtSKdBoyKI+Pw+lknlUMaBO2SCIlkAnh8HhuBJwhoDD4QDE5T4zA/Pz4huPRCzF\noqVSgUTCsH37+uWDnWtzOchkNOm05cgRTbEoyXf9/eJRWF6WXgE+n8j0ViqSHBgKaQ4fllBELAbb\nt0sFwkMPycI+XDrOz2fexnO/+F4C9V6TgHfw06QrUgcYDEqy4NCQGCOFgoQlYjFJGpyYECMkm11f\nGCkcVtTrvYRH12HQcSXhDAGHwwHA8jJUKtLkp3M8MmJJpQAUzeYjZ811yu9mZy2VikezKZ9rLYts\no2HYtEnuOzUlJX5Siqg4daoFaGIxuebgQcOOHTAyornt1H/y20degm+FN2Lm6ifzqzO/xIer30tI\nibeiVoMdO+DIEelymExKOEGSES2bN4sB80jCSNJwaGUHxPObS4fjUsIZAg6HAxB3urjZe+2ArYVj\nxxTRqGFwcH2PgDHiRVhaUiwtSZZ/oyGCQeUyXaPgyBFZtINBxdycIZ8Xb8HwsObQIXl+OAzJpCaZ\nhIWpKn/07dfho0VLeZy4/fksvuwXOLX5Zj75ck2lrfwnGgOGvXvlHmNjmpMn5dlaQzxu2bmzN14p\nFVz9eyST0g+hJyXsPAKOKwdnCDgcDgBmZ2WRHBiQ42zW0N/f2alrFhZaXdGglaxsOtRp7xuLyaKe\nSEgi4cKCyARHInDypOgBXHWVnLuw0KS/X3d36bWaYXZ/llcffhNjTWkt/OdPvJsb/78fJB433P9x\nA+jurl1KBDXXXw+HDsH+/fLMvj4Zw+iopVql21Z4vVyBlQmPnWOH40rBGQIOhwOQevv+flheNlir\niEQUfX3iFXg0QaFGQ+SD63XL8LBqiwiJu35gQGLyw8PiIQgG5RUO91oEb9sm+QTFImxTJ3jl4b/i\nmi+9l2BDrIoDyZs5sOd5PDlu2tLAms2b4cQJ8TBoLRUFIDkCw8MWa0WUaHLScsMNCs+T8kbXOMjh\nOB1nCDgcVzCdJD9rZeGW8jkRA4rHDYWCptFQ7Rr+9XMEPM9SLksyYKslWv/BoHgYJCZvmJuDuTlp\nTBQMWsplxeysGAWJhGFoai/P/vZf8OSZD+LZXj7AoYkn89c3vIOWUUxNWTZtgoEBQzCoiUZl/FpL\n+OHb35bxj44aNm3yqNVgcFARCBgGBiyDg9+pWXU4Li2cIeBwXMF0kvw8T1T+lpdtt/5eKWkt7Pc/\ntshOx4CwVs7NZACkOuDIEcXCgkJrKQWsVGBiwqIVXH3iv/muz/85e07d272XUZry9/0Qn7jmtXxi\n4Tas1dywB+bnNV//epNt20SaWCnRDBCBIjEI6nUYGFCEw9KwCAxjYxdwAh2OywBnCDgcVwCdnX8v\nGU4Wzo7GPsiuWnb2ABpjJNs+mZTyv1pt/dBAq6Xw+xWLi5bjxzWZjMUYRV+fLNL5vHgHfD55+bXh\ntvS/8kOH/4LxhQe796l6Ee7Z8jK+defP8/I/2Er/Phj8lCQfHjsm+QWeJ4mEnqcYHJTfodUS4yMc\n7vyeon2webNl82bpPdBqPXLpo8NxpeMMAYfjCqCz84fVJXR+v+1+vrAg2f/1ulyTz8uCG4vJYtts\nri8o5PdbHn4YMhmPmRkoFFTbcBC1wOVl8QRoDYlAlT86/lKeWf5E9/qMf5j/3PJqPjrxKgqBQbZ6\nTfbtk/tls6L3X61KnkE2a8hmReVw5Th9PqlUWFwUEaRdu8SoyeVMd4wOh2N9nCHgcFwB1OuyIHcE\nc/r7ZYfcKZuzVrT65+fh1ClxtW/eLKI/09MQjxuuumr9XXU8DqWSYn5eDI5cTur3q1VZjFstCQe0\nckX+rvEjPLX5OQBOxXbxX0/4RT4/+WJy9agICkXh+us12ayUG5bLikxG7jc0ZJmcFDliv1+eA/Jz\nOCyGjLVSLmitLP6JhCIYNC5B0OF4FJwh4HBcAayV0C2XZafcKZvz+eDrX5ddfKfM7tQpEf2RkkHN\n0lKrnbW/mkIBlLKEw7LoWysLM4jL3low9SYfaTyfJzb/B4B7+n+Ij/7oe2h6QVq5Jt91Y+9+8bhh\nfh7yeR/1uoQEkklRB6zXWywsgFK6LUjUUyTctk2MAb+f9jgV/f2t08SDHA7Hapwh4HBcAYRCioUF\nS7Uqsr7Dw722wZ2qgWJRfu7E8wcHpUTv+HHo67M89anr5whUq4pAQOSDOy17tRYDAcQr8NP5P+sa\nAf8aeglvHn8HEyd9JJOW66/XBIMtlpelXPG66xSHDimOHbO0WtK6OBazNBqWsTFNuUzXewGS2BiJ\nSI6DqAhKK+JQyDI66nIDHI7H4qwNgVQqFQTeDrwAKAN/mk6n3/oI5z6hfe4twEHgF9Pp9OfOebQO\nh+OcqFZF07/TBKhalRV7ZdXAqVOymHbK7ObmpBNgMimx/r17m9x66+n3npuzNBrSHyCblVCBhAsk\nbr+j+CC/3XwjAN/w385rwu9kwue1a/8Vi4stvvd7Owo+CmMM1aplcNDH8rJ4KPr6FMPDilKpiTHQ\navUEiBoN8UTccIOEKJLJFrt3y3fBoDMCHI7H4lz0s/4EuBm4E/g54A2pVOoFa09KpVIJ4NPAt4Hr\ngA8DH06lUkPnPFqHw3FOhMOiBeB5sjh2muqsrBrYtEkW8GBQXO3JpCQK+nzi6vf71/9z4fNphoYs\n0ahlbEwMiVgMBgbgptgh/mHueQSpUyHEbwy/i2jCY/NmifvH4zA0pAkERPBHWhUrxsc1yaQhHjf0\n91cApJcAACAASURBVItQUDRqGBjQpFKidhgKybjGxyGRsAQCls2bxQjQutM/4DsyvQ7HJc1ZeQRS\nqVQE+Cnge9Pp9APAA6lU6i3Aa4APrTn9J4FCOp1+dfv491Kp1HOAW4FPndeoHQ7HGWMMVCqya/f5\nbHuxl52y51kyGdXWAegl9hkDsZjhyBGPVksa+Gzfvr6gUDhs2qqDEnbw+8UQCJw6wRvvew7DzTkA\nfqv/r5hN7makbSREoxLPHxoy9PX1XPiBgCUYtO3KAGkJ7PdblIJg0BAOw/btkM9rGg3xYkxMGHbs\nUPh8oizoxIMcjjPnbEMDN7Sv+cqKz74EvH6dc58K/MfKD9Lp9O1n+TyHw3Ge5HLS6KfTZrdWWy2y\n00noq1TEzQ5iCBQKssha2yvNW49EAhoN25X7ldCD5cX7/4DRuvQKeF30L/m38Evo1xLvj8ctnqcJ\nhw07d4phslLj4IEHoFrVWCsiQZ08hs7zIhGpcjBGvAKhkPwejyV85HA4TudsDYFNwGI6nW6u+GwO\nCKVSqcF0Or204vMdwNdTqdS7gOcBR4FfTafTXz6vETscjjPGGFhcVNRqUjaYTEpJ4OKi7LLLZcXJ\nk1ItcPy4LKSNhrxmZzUDAz1DIZtdP1lQjIueRkGjIQmEm3MPA/DJ8PO4O/xKQlqy/4NBRTwO4+Mi\nRVytao4fNxSLiljMsmcP5HK6a4B0VA4TCal8qNct2axuhzloVytoBgdlbE48yOH4/9l78zjJ0qrO\n+/s898a+5L7UkrV0VXX0TgOyiaI4is4wiICMu6A48yry0ddltEcHFB1ecR0dEVBx3GeQVxT3ldZR\naWy2phe6O7qrupasrNwjMyIz9ojnmT9O3IjMqmzoKrqrM6vO9/OJT1TcuFveyqpznrP8zuVxuY5A\nGmhetC36fPEE7yzww8AvAV8FfAPwt4VCoVAsFueeysWsNVh7+S5+ENht79c7+jwu5Xp5JmtrAAZj\nZA7A0pInnxfj3unAww97ajWLtbC6OlDwA6hUJGUwOiqV/2tr0eCh7ayuisBPuy3te90uZDYW2F8/\nDcBZDlGvy+Ciel1W+K2WnLvRMDz0kOPwYfmvqFy2PPaYo9OR/bpdcVIkBWDx3nH2rEgW12py/eVl\niRhEf5fJpCcMP7/QwPXy+/FU0eexnWvteVyuI9DgUoMffa5dtL0D3FcsFt/e+3x/oVB4BfAtwDuf\nysVGRzOYzyPWl8+nrvjYaxF9HpdyrT+TRkNy8SsrIh3svRj6ZlOK9eJxMbLNpoztrVRS/V78oSEx\nxBsbEo6/7TZ27MkfGpL9z56V64x0V3jH/a9i2K0B8A/uy2l1Uj2lQTh+HG6+Wa6XSIhDMj8vTkIq\nJed73vMiZUCZW9BoiNDRc58rQkNDQ7C4KMeOjsq9jY3JfQwPP31jhK/134/LRZ/Hdq6V53G5jsAc\nMF4oFGyxWIxihNNAvVgsrl+07zzw6EXbHgN2kCTZmVKpesURgXw+RaVSp9vducDpekKfx6VcL89k\nfh7On7esrorBr1YlXTA6Ksa0VHJYawlDWFxMYUydXE6OLZWkk+DYMfm8uup6EYbtzM7C3JwlHofJ\n7jw/9emv4Uj1MwD88tAP8+HwFSSa9X4nQVR8ODkpxz/wgOvNMRC54FjMUSjAoUOWhQUx8Om0OAMf\n/Wj0dzUQFBoaksLGeFw+R4qDnw/Xy+/HU0Wfx3b2yvMYGck8pf0u1xH4NNAGXgxEuf4vBj6+w77/\nCrzsom03Ab//VC/mnMe5K8/1dbuOTmf3/iVdbfR5XMq1/kysNVy44Jibk1B6IiGRgXYbwtAxM2M4\nebLLxoal0xEnYWFBIgfxuKQQVlakzW/fPnZ8VsmkZXHR4x58hF965DXs78wC8Ov57+Xtwdv6zken\nI9edmHBY61lbM2SzjpkZy8c/7qlUpA7glltgdNRTr3dptQwrK7YfFcjnJaJw7Jjj4YdtT/fAc9NN\nnk7n6a8LuNZ/Py4XfR7buVaex2U5AsVisV4oFH4HeG+hUPh24CDwA8AbAAqFwhRQLhaLDeC9wFsK\nhcLbEOP/BuAo8HtP4/0rivJZWF72xGKWdtv0Q/NTU2LQk0nD7KxjejrgwAHDJz4hxjaqEeh0pBq/\nUJDP9frO/+HNzzumz9/Pjz/878l1ZTn+69N38Y74W0l0DDaQfH8iIT3/QSAG/dAhDxg+9SlHPh+S\nzwMYSqUuqRTMzBiCwJNMyjGtllzrec+DG26wTE3J9TOZz2/BoCjXO1eSSft+4JPA3cAvA28tFotR\nm+A88B8AisXiOeArkY6BB4FXAv+uWCzOf743rSjKUyMWs4yMeFIpTzodCf144nFDPO7JZi2JhIj5\nHD48EBRKpWTa38iIRAaGhz1Hj+7830U2a/mWJ95BrlumTciPHXwPf3jH20hnDLGYnCOfl3OOj0t9\nQCRoBDA8bMnlRBAol/NMTtped4FnctIwMiKphHwe9u2zzMxIFCCV8uRyjkOH/LbzKYpyeVy2xHCx\nWKwD39Z7XfydvejzRxEBIUVRrjLOQbPpKJcDjJHVvvee2Vk4dEjy8amUY3VVQuxBINGAen0wayAI\npMXQGNn3ErxntPwER5Y/CcD7c9/OB7Jv4HhcztVuy3mHhuCGG+A5z/G9sL+0NYahJ593rK4GeC9t\nf9msdA2cPSv3nEhIPUEyKeJD1opokGgJSBeESgkrypWjQ4cU5RolEhIKQzHmzSbEYlGKwNFqGZpN\n3xfhaTTE2LbbUhvQanXJ5YJeC59hcRFotQgf+DSxj3+M2Mf+lfDj9/JlS4v9az6SuAOAjQ1PJmP6\nHQlBIGOErRX9glzO4NxAACgSA4o+P/wwlEoBExPStri66rj1Vs+NN35ugSRFUS4PdQQU5RokEhJa\nWjJsbEi3wPnzYuxHRyXEns87ikXpKNjYkBV4IiHOgLXS098o1Sgs381tG/dy51/cw/hbPoVpXiwl\nIjwRu5G/iL2Kel1qEcJQQvrDw1HdgaHVgnPnLJOTvt/it7lpSadl/3gc6nWZMLi4KD/D6ChMT8ML\nXyjFj62WRDM6HXFy0mmDtRoRUJQrRR0BRbkGKZcjZ0AM+qOPirEXAw/FouPFL4YzZxy1WkgQyMq7\nVBq09a2ueH73oZdzovrgJef3xtC96RbaL3gRf1l5Ee/7zEt5uHGUjU2D6UUe4nHpPhgelvvIZqXg\nr1o1PPqoFCF2u4ZSyeGc/FfU6Rg2NroAVKuyrV6XWQkg0YT1dWi1xItotQy12t6v2laUZxN1BBRl\nj+KcGPWtGv3RKrteN6yvw9KStAOWy7KKNkb6+MfHwTnH0JDlwgUJ3yeTIuJz5oyszm/i8b4TULMZ\n5g+/gOnXvJD2C19M5/lfgB8aBuDC+y3nHrNUlsVoJ5NyfDIp18rnpWVxZcXzyU8apqdhZERW8WHo\nOXTIMjfnqFYNmYxn/36LMbC87DDGkEp5pqcNiYRjaEjUCJeXPY2GDDmamFBJYUX5fFBHQFH2KOUy\n2zT+y2XfV/5bWvJUqwGdzqB/PwwlV59Migzv9LShXHbEYpZEQoSBrO2pB3rPl5/8g/61vuUL7iN9\n4zS/cNel97GyItMHR0cHzkYsJm2K2ax0I9x/P4ShIQhgackwNNRlfDy6V8fMTNA7m8EYiQgcOjTY\nNjra7f9sjYYnmbQkk/Jdo6ERAUX5fFBHQFH2KO222eFzFEK3xOOefN5QLku4f3NTQvPDw3D8uAwQ\nOnLE4pynWjWMjUlkYCSocNeZ7+EV1Q8A8ETmVmqjBzk84dhp6NC+fbanTSARgDCE/fs9hw8PRg1P\nTZn+fINkEsbGJCIQi3mOHTPMzbn+Cn9qSn6uVuvibfKzpVKDQsEwjFoHNSKgKFeKOgKKskcxxnPu\nnOkby6NHB8YwmXSASAc3GlEroRjpZlPqBc6dg3zekUrJyjuXg/2ts7zn5Cs51HoCgDOx4/zQgd+k\nXBYZ350YHnakUnKtRCISC4ITJyCddjQalpMnHe22RB7GxmBkxAGmd6+eQ4cGxjxqBdxpG0idgPcy\ntMh7+awoypVzbYxOUpTrkEpFogDeG9ptQ6Uy+C7qrW82pTrf+8Ekv1ZLiu9aLdMb3GP63795+R19\nJ+DPR76eb7rpI5xM3Yb3cuxOOCfn3zofLJGAzU3J4zcanuFhi+v5Ee12l5kZ03NOTG9/uc9EQmod\nIkGhrdu2cnG7oaIoV45GBBRlj1KtSqFfNLUvl5NwP4D3hgMH4NFHxYDPz0shoHNipJeXLRsbjlJJ\nWvWaTXEsbtu4F4B/nnoN/3n4fdiupd2Q6y0vD85/8X0kEmwz1o2GAQwLC471dWlhnJqSeQXWGqpV\n6SQIQ8/IiGFqynNxeH9kROaNlMvSRhgVRHa7pnct2b/b1dSAonw+qCOgKHuU2VlHuSz/hFstw+xs\nhztEz4dYTIb6LC6KE1AuSyTA+8EQoWrVcu5chzC0WAvtpTUONx4H4JOZL2JlVVoAk0lJJZw6tXNq\noNl0VCqWRkPSEO221CNcuACdjsX7qLBR0gJRt4O0E3729r+dCiJjMd/fFv2siqJcOZoaUJQ9hnPS\n87+5aXn8cc/DD8P58zJcKCJanYeh7But+Dc3xahLzt0xOWlZXxexoZs2BkNEP7zxfGIxQ7c7iCRM\nTe3838WxY5ZsViIT7bYUB3oP1aqn05FOBOegVvOUy57RUXECgkDuY6c5AdHPOD8v9zdIK5jPmTZQ\nFOXy0IiAouwxolXywoLHe2mjM8Zw/ny3v4+1EI97NjcNqdRgrLC1kkao12F01FCpdBketuzPbfC6\ne94FQIsYJzN3UFsTvYGxseisO6/cazXHxIQUCy4syLZEQtoFjaGfNsjlDDMzYK0nkfD98+40JyD6\nGYNAVv+Vimd4WFb//RZHTQcoytOCOgKKssdotUQsqN02zM9LS97EBNx88yCH3+lIv/7amqFUkkhA\n1NrXbkt04ORJiQh0PvIxvvdj38b++mkA/ib4KubXksTjsn+tJob8BS/YuUYgm7V0u56VFUOtJoWK\nUVtfo7H92uvrIhecz7Nl7oCs/rcKI0WtkbkcgKfbHQgKKYry9KKOgKLsMWo1T6tlWVuTVX4mI3n8\npaWBkZ6dhVLJsLkpQ4YSCYkKgBjgXM4Qui53fuidvPaRnyXwEk34QPh13JX/RWJWjPfUFNx+uxzn\n3M4Rgfl5RyIRcuiQ1B/EYqJVYIwYcu9heVnSAcPDci8yYliOl9TFznUA1kYdBK4vKKQoytOLOgKK\nsseIBHUmJw31uuTPh4ZE2CdasdfrlkRCRILCUIxwuy2RglQKXjH8cd70K9/F+OLDADRiWX72yLt5\n98bXysjh3sCg0VFPIiHHHD785BGByUnP4qIMCEok6AkMeeJxjzHRGGNPNisSw1tFgHYSRhofl3qC\nrVECRVGeGdQRUJQ9RiSok0xKlT5Izj+Xc1v2cSwsWJaWZFpfoyErfN/p8r0X3sZ3Pv5LBD2jPnvD\nF/PXr38PxfO3MvFAvX/OVEociExGBIvy+Z0jArmcI58PcE6mDGYyjqkpmXiYSIjB39iQOoYg8AwP\n+0sEgi7uAtA6AEW5emjXgKLsQYyRToBudyAWVKtt32dtTd5jMWkdpNPh15rfwXdX/zsBjlqY40//\n3S/yNz/859T2HWX/fgnlR0I9iYSkET6XcM+BA6IgKHMMHKOjsj2TkYLFUgmCwJBOQ6NhKZW2r/C1\nC0BRnl00IqAou5yLpwx2OqY3hU+K76pVKcg7enQQum82Lc2mqPnV6+CabX6r+0Ze5/4YgHvjX8i7\nv+i3GDmxnze9xBME8OEPi0NhraQTul0RBoqkfKvVnVMDYJiYkHsrlw25HKTTHmNgcRFWV8UJ2LcP\ngsATBBZrB+fR1b+iPLuoI6Aou5yLRXXqdanILxY9a2uyWl9bg/vvHxjXUklmDZw5I7oB39j+PV6H\nOAF3m5fzrekPcEM7Q/1Ch0jz/9FHpZug1ZJXuSwGut0WJ2RxsctO1GqejQ2ZedDtQqXi6XY91aql\n3Zb6gEoFlpc909NPPrNAUZRnB3UEFGWXE7ULRtP2hoYMiYQnDC1LS5IiSCbhxInBin1kxHL4sKNe\nt9Tr8BweAGCeKV7FH5JLpEil4NAhy2OPOapVT70ukYDV1UiHQHr+5+YM2azn9tt3jggkEmLsWy1P\nEHjCEJwzlEoeMMTjEvbvdj2jo45bbrl6z05RlM+NOgKKssuJ2gVBnIJGw7FvHywsOMJQhHwAnnhi\nYKSzWcfmpogNxeMwXV8E4AyH8ckU6bRMB2w2HZ1OQDptaLclHTAxIedoNiW3f+AAgKFU2jki0GxK\nN0A8DpubYvjjcc/qqu3NQTBkMp6bb3bceecz9ZQURblS1BFQlF1OMmlYXvb9ccMjI4bTpyXXXi5L\nDUE8DsPDgxX7vn0wNyfGvF5u8XL+CYAiN/ZC/R7nHCdOWDY3pQZgYiKaTNhzHqYhl5Mphem0Z2Ji\n54hAMimRinJZJg0GAb2JiLKt3fbk856JCR0OpCi7EXUEFGWX02h4kklZ3YPh9GnH8LA4AclkpNAH\n6+sDIx1NG2w04FXh3zDWKQHwv3k98TiMjBhuvz1gYaFDMhkSBFLYNzwsTgRIdGBy0nD8uFw3DHeO\nCDQannTakk575uZkW6sFYBkbg4kJiQi0WuoEKMpuRB0BRdnlRAJCUY2AMZImOHLEUq2K0c1moVDY\nLig0Pm7IZuHf+b8GYJFJ/tG+nHwaDh+WVr19+ywjI13qdTHahw9LcSHAyIjj+HGIxw2ZjOPYsZ1X\n9FvvL2o/7HRgeNjR7RpSKZER3ioipCjK7kEdAUXZ5RjjOX/eUK1Kb3467ZibszjnsVZa87JZmJzc\n2pLnuHDBUi4bXti9F4D/wxdhYmG/y+Azn4HnPc9xyy2GIBh0CiQSkhqYmfFMTEi0QWoNdjbi0vs/\nMPILC1CribTxyIhEGUShUJ0ARdmNqKCQouxy5uagVrN0u5ZazbK8LKvuKC1gDD0xn8Ex8/MypnjI\nr3MbIiN8Dy8GBmOBGw0ZEpRISLX//v0ybTAy/LmcJx43vXy/oVLZ+f62CgI1m3IMGGIxqQ8wRpwI\nFQpSlN2JRgQUZZdTLlueeIJeBT5kMpahIVhZEfngKBRfKg1SA+WyFAHeuvGx/nk+yosAWe3X61I/\nsLZmGRlxhCGcOyczAmSIkaQgIqcBRBVwp2LBaDBQueypVMRRqdXkOmNjhhtucFhrsFYjAoqyG9GI\ngKLsck6fdqyvS6h9fd3w8MOOctly4YIoCjYaEtJ/5JGBkW42HRcuwIsb0i1QJ8l9PIdWazAWeHMT\nVlYGxywsiPBPuw0bG4alJUezKSJBzaah3X5yIaBI9KhS8ZTLlnrdUK0aymU5JhZTJ0BRdisaEVCU\nXYysxi3nz8sqe2RExIJWVmRQz8aGtP41GnDzzYMV+/79ltZGk2/p/h4AH+ZLaRMHL+dMpSSdcPCg\nZW3N4X0UbZBzyZAhy8aGo1Kx5POOEyd2LvZzTqITzabBOXBOpgYmk46REUMi4TQtoCi7GHUEFGUX\nUy7D0pKMAk4kxHgvLDhuvjmk2RzMBYjH4ezZwYr9X//V8YqNDzHFEgDv4jsB+pr/ExPSIVCvy6o/\nCKTDYHpa5gQALC87crmAXA7AsrraZWZm53sUB0CiCcmkYXpaRIaGhrq9OQKKouxW1BFQlF1INGho\nbs7S6cCFCzJcaHQUjh2zhKGMIq7XZf9GA44f3z506AXNewCYYx9/y5cD4jAMDfUGETnHgQOW9XWP\n9+IEVCquHxGYnLQsLXmaTUsq5Rgf37lGoN02ZDIyYyAMDcY48nlxKKamtGVQUXY76ggoyi4kyrnX\n6565OSnaGx+XiMDamuPOO0PqdflsjEQGTp3qGel6nRsf/jAvrd8NwEPciseSSEhE4PBhSTEcOWJZ\nX++wb58lCCSsPzEB4+NiuO+919NsBqTTALLvTsRinrU1QyJhmJgYnGN4GG0ZVJQ9gDoCirILabdl\nImAyaRgflzY/ayGfh8OHRQQokbC0WrLfcLjJ6/1fkfuOD5H4+7/lu2vV/rke5DaMkRqAsTHP2Bgc\nPAjZrCeRsCQSHuck/RBu+R8hl7PU645Y7FIJ461IB4Pc3+iotAs6p7UBirJXUEdAUZ4FotB/u22I\nxaTH3m7p4QkCWWWvr0Or5Wg0LLGYfDcy4gBR7Nu38hA/wU/ylc2/J1VtwJ8OzlFOTPAh+2reZb6P\nbCCFgBMTkl4YH6en9ucYGhJBoeFhSRlEkw47HYcxoiMAnlTqybsGwlCKFyNnJZVyWhugKHsEdQQU\n5VkgCv2DvJfL/hLD6b3UBUgPvmgFiBCQCAw1GoZ38f28jI/0j+nu20/zla/i5B2v5hc/8VL+4Z9i\nlFbluzCEsTHodg2lkuPAAc+BAyL2470nmRQj3mhIusF7eY9en+1nSSQGMsPNpmN6+ul+YoqiPFOo\nI6AoV5mt7XbW+p7RlbB7FBnodMTy1mqG1VVDoyGKf8bA6qpleFichIPIlJ9/4qW8c+Qn+e37ngfW\nsvKgJfGwjAbO5WQKYRjSy+WLQ3DoEBhjGBnxhKHUDczPi2FvNAylkumnDODJBYXabdMXFQKv4kGK\nssdQR0BRrjJb2+3W18Xgj4/7bZGBWs3TalkWFz1LS6IXkEqJ6E+365ieDqnVYJgyIHMEPlz9gr5E\n2NqaY3Y27E8gFJGgQeh/ZEQM9cVCP0tLIk0Mkvdvt6XIsN02rK09ebFgFN3Y6ZyKouxuVFlQUa4y\nrZah3ZbV9+ysrOyzWfkuKhIMQ8Pp057ZWSkUrFRgeVmM+r59loUFWZln2QRggxx2S5FBMiljims1\neXW7EmnI5WQgUTIpHQmiESB0OuJoLCzA8rInk5GBR7Wax3vXKxa8lK2zBmQA0TPw0BRFecbQiICi\nXGVqNc/6uiUWk/575zybm1KsF62mT5/2tNshQSAGOpkUg5tMinDQzTeHhLSJ05ZzksK5Qdj+oYcc\nnY4lmx0UIY6PS0pgYsIwM+NIpQwbG4PahLNnwTlLPA4guf6pKdPL9xuc6+7481hL7xwaCVCUvYg6\nAopylYnHTT8aYK0I+XQ629vtnBOhn0ZDxg9vbEjk4MQJSKctDz4IKer9c1bJkEgMcvjGDJyAdnug\nPui9OCJBYFhf9+Ry8t5uS8pCiglFbXB0FA4dcj25YBUHUpRrFXUEFOUqs7wsEQFZZcvwn05nuxRv\nteqAkPV1MebZrEQMul04c8aRzVoyDLQCaqS3DQXy3pHJWCYnxQGwFmZm5DyplKFWExXAU6ck5B8E\nlnZb7uXAAQCPc47p6YHxV3EgRbk2UUdAUa4ysZglmYRWSz4nkxCG2yvyDx601Goyvnd4WCYPJhJi\nyGMxifWnt0QEaqTI5wfnuPNOy+KiDAyCgYbA8LBnclIkhRMJGTUcsW+fOBlhKDoABw5Ateq3aR0o\ninLtoY6AolxljHGcPWtZXTWkUiLGs7AgxnpmJgrjO6pVSxBsH+hjrWdkxDE7axkOq9Ar5G/YDOPj\nA0diaMhxxx2WeNxz9qyh1ZK0gLWwuirXSCYhnXZENcNhCMePw8zM4DxSL6CRAEW5ltGuAUW5ypw8\nCUFgCUMxygsLkpvf2LDMzso+i4vStz8yIh0GzabMFchmxahbC6/yf9E/Z8VnCYLBNfJ5EQqK5hBE\nqoT1uqfbNTgnOgbZLORyjlhM6hN2mi6oKMq1jUYEFOUqsFVSeG7OsLoqPfuVCmxuGj75ScPQkKNQ\nkPB+pWJJp0U7IJ2W/v9uV1oIu13LC859iB/v/gQAD3Abn0k8l7GyIUoNOGfIZGQQUCIhjoQoFRo2\nN00vLeHpdCyFgusLCq2tSZeCoijXD+oIKMpVYKuk8MKC58wZMcylkjgC588DWGZnO9xxBwSBo9Wy\nbG5K1KDZlFepBNW5Em9b/k9yLiZ5FX9IqxtQqw0seK3mKZdlVkGjISJCqRTEYhIFKJV8L9qwc0ug\noijXD+oIKMpVoNUy/WE+yaRhdlaEfjodmJoScaGREU8yKRGBW24xXLjQpdUSvYFKRdIFuRy8pP0J\nsl6EhL6V93GOQ9guHDo0KBZMJg3eS10BSERCxhZLvj8MPbmcZ3JSWwIV5XpHHQFFuQpEksEAjz7q\nMUbEhDY2JFqQTkMmY2g0ZIVeLnuOHQvIZODTn5bVfDIJGVPjtZXfBaBJnH/kZYCIDdVqgyK/RkOu\nMT0tBX+djnQd5POGXA5GRx0zM9oSqCjKFTgChUIhAbwbeC1QA36+WCz+wuc45gjwIPDKYrH4T1dw\nn4qyxzF89KOectmysiLh+ijvn0jA6KhneNhz8GC0qrfMznqWly1LS+IsfJH/CL/W/U5u6J4C4O/4\nMtrEATH0WyMCqZQY/MlJR6lkMEYckTAE8AwNbRcwUhTl+uVKIgI/BzwP+FLgCPA7hULhTLFY/KPP\ncsx7gPQVXEtRrgk+9jFPtRoShpISaLclzN9uSzRgbMxz441SwQ8wN+dot0OeeEJqA+7q/jRv6/wE\nthfG/9v4v+U/tt8NfiDxu7ExiAgkEp7xcQCZXOic7QsTjY3B8LC7ZOyxoijXJ5flCBQKhTTwJuAr\ni8Xi/cD9hULhZ4C3ADs6AoVC4ZuA7Od7o4qyl4lW492uKPdVKtLSl07DwYMy4CeXc/32vUzGkk6L\nxPDh2AV+vPN2ANbMCG8f/Vn+YvgbKM0abG8OQTYLN900iAgMDckMg3LZkM/D4cOeatVgjDgAWhug\nKErE5UYEntM75qNbtv0L8CM77VwoFMaAdwKvAD5zJTeoKHuZqG2wXvfcc4+s7jc2RMUvmZSIQL0u\ncwceflgKB8MQMhlHtRrgHHxZ7a/653vt+N9RPXIj0wnDZlUkgbNZesbdXXL9MPTE4/J9Pg9BYBgb\nc1oboChKn8sVFNoHrBSLxa2dxotAsmf0L+YXgN8qFouPXOkNKspeJmobXFiQuoBWS4r3Wi1HNA5V\nzgAAIABJREFUEIght9bQblvm50P+4R8GxxojUYNXt/8YgEdNgcdit5DJyPYwFJGhIJBzDg9vv+7y\nsiEIDMmkOCCdjtQhbB09rCiKcrkRgTTQvGhb9DmxdWOhUPhy4AuB/3hltyb/QVprLvu4ILDb3q93\n9HlcyjP9TKJIwPKyiPucPj0Q65GCPcvQkGgELC/DJz8pf47FJIUgrX6GseUiX9q+G4APxl9PLAab\nm5YbbxRFQmOko2BkBKrVqBhQNAqcM9TrBmMgnfYMD0ejjg3e+/6+V+N57DX0eWxHn8d2rrXncbmO\nQIOLDP6Wz7VoQ6FQSALvBb6rWCy2rvTmRkczGHP5jkBEPp+64mOvRfR5XMoz9UxKJQn9Dw+LpPDS\nkkQEjJHUQDQeeH1d3lMpGTM8OytGPSoo/KrirwLQIsb7zHdTqaRIJCSy0GzKexjKnysV+gWA3otj\nkUjIq1aTbdletU6ULrhaz2Ovos9jO/o8tnOtPI/LdQTmgPFCoWCLxWKUkJwG6sVicX3Lfi8EjgIf\nLBQKWy35XxUKhd8uFotvfioXK5WqVxwRyOdTVCp1ut1L86bXG/o8LuWZfiYXLsAjj4iI0AMPiHpg\npSKOQDT85777JEoQi0kEoFaT2oBoW+vx87x69TcAeD+v50xjiLStc+iQo9GwdDriCEiUQGoE1tbk\n+t7LtZpNQ7VKf8RwpSJOQCrl+/tejeex19DnsR19HtvZK89jZCTzlPa7XEfg00AbeDFwT2/bFwMf\nv2i/e4ETF207iXQc/P1TvZhzHueuvKip23V0Orv3L+lqo8/jUp6pZ1IswspKyPIyzM3Jin1oSBwA\nURiU9sF4XAx2NitjgjsdR3dplakPfYgvufs3iNOmQ8A7zF0k4rL6X193vOhFloWFnshQRooMy2W3\nbU7A2Bh0uzJzoFKRbUEgNQJB4HecKaC/I9vR57EdfR7buVaex2U5AsVisV4oFH4HeG+hUPh24CDw\nA8AbAAqFwhRQLhaLDeCJrccWCgWAC8ViceXpuHFF2Y1EtQErK5a5Oc/CgqFUkpV7tUp/rHCrJQ5C\nu90b9dto8IXzf8lrTr6fsV/8G14eaQMDv8EbeMwfx7QkhbB/v2Vx0bO5aajXxYkwZrugEIijceoU\n1GqGeNyRy0ndgAoJKYqylSsRFPp+RFnwbqAMvLVYLP5J77t54I3A7+xwnPYrKdc8UZdAo+Hpdi2N\nhtQLOCc5+VhM6gWck9W98Y63d3+CNz/6q2Q75W3nmp+4nf/Z/UZ+avPNxJFj43GJCNxwQ8j4uEQE\n8nk4ehS2OgEgtQgSdfCAIQg8U1MqJKQoynYu2xEoFot14Nt6r4u/e9ISymKxGDzZd4pyrdBuS03L\n9LShVvOk0yLo45zk7ZNJMc7WSnrg7a0f5wfaP9c/vjG+H/f1/4F/Ofz1fLJ9Ox/8/w3xM+CbkRQx\nHD9uSSblz0EgHQGiTLg9ItBum16roKfTMQQBGglQFOUSdOiQojyNBIGnVDJsbsLKCrRanlrN0GoN\nZgsY4/De8sbm+/pOwMn8nXzka/4bR97wUm65PaDzcfCfhqEhTyZjegV+MDnpGR93OCfth8ZIfcDk\nJGSz2yMCsZjHOdMz/p5EwmOvjW4nRVGeRvS/BUV5mjFGWveaTcPKiulX9Uctf2Fo2d86y880fgCA\nM/YIb3/xh3ho8ss4dWZ74Gx83PSNdxjC6KhhZESMfhh6UimYnpZrXszQEH3jn0h4jQYoirIjGhFQ\nlKcJ52BlxbC6KkqCa2swPy9OQbks6YCuTBnmhxq/0O8IeH3ygzQuTHJTHsbHJbxfrdr+OYeHJY0w\nNiafazXLc58rEwZLJTmf99Bsbk8NRMOItDxHUZTPhjoCivI0US5Ln36jYVhclNTA6uogGhA5AsN+\njTd0fhuA/22+jvvbN3NgU44/eVIM+eKiY2MjpNWSoj+QaEK1CmtrjlYroFKRzgEwVKuGUmmHfkBF\nUZTPgaYGFOVpolYznD1reOwxMf5nzogjUKvRF/+p12GmfZoEIrj5m/6b6XTk+3YbJibkn+TkpCUI\nPNmsdAo0m9J9YC3ccIMll3Pk855k0ve6AhxDQ/rPWVGUy0cjAoryNHHqlKdaDQhDOHtWVv/ZrDgF\nIO1/QQCH2rP9Y9bDcUIj44gnJ+mLkwSB48CBkI0NSQ1kMpIaSKelfXBmxlCpeHI5SyIhBYXed5+N\nH1tRlD2OLiEUZQeckxz/0pJhbU0+f65919Ys9bpnfZ2+fkC1Kn8GWfE/v3EPv979TgBqpHiicxDv\nJSLgnOe22+Sf5NGjhlisS5Tf73blGtbC1JQY/4kJ2UdaEx0TE1c+l0NRlOsXjQgoyg5EwkAg7+Wy\nf1IhnsG+nlbLkkhIKN8YqfQPQzH0Lw/+mb/ovpoUDdqEfE/yV2j4YZIxqfw/ftxQqciqvtPxHD1q\nWV/3nDolCoKZjGgJOCeiQOvrjqNHLeIsGFqtvS91qijK1UcjAoqyA5Ew0JN93um7Q4cMmYzDGM/k\npCj+BYEYcIC3up8iRYMaKV4XfIA/Tn89sdggLZDPeyYn5Z9kKmVIJDz5PBw6JK2A6TRMTbmecNBg\nnyCQ9sBUSiMCiqJcPhoRUJQdiISBOh1DGHomJi5twYtSArOzEhGw1nP4sOHxx8U4ey9CQNHAn4Ne\nagN+P/wmPhz/KrKhtP0NDcHBg+I8DA3Jqj4Wk1V+IiGTAqenDdksHDwI+fxgH+8N3st55BhFUZTL\nQyMCivIkGDN47YQMFzIEgcE5mfR35oyj3bYMD4sQ0MaGpAWmWGCG8wAs2SliMTlvEMjLWhlBfODA\n4PyRgU8kxMhHwkD5/FO/R0VRlM+FRgQUZQvR9MDFRYu1npERWWWXSoZuVwxyNE643Ta0WoZqVZwA\n7z1PPGG5cAEee0xaBZtNKfT7Jf4zSZoA/GPqK2m3pXbAWgn5HzwIt94KxkitQbNp2NiQiEMqJWqC\n+Twkk6ZXuCjzAyJnQQoO5VhFUZTLQR0BRdlCVPgXBGKMKxWPMWJondteOBiLeRqNSNEPHn0Uzpyx\nNJuiH9Bqyevl/CNfxwcB+FX7H/lI6wvodqNOAVhcpF/oF4X3l5Y8GxsB1so9VauDccO1muxTq0lx\nIkCrZajVtFhQUZTLRx0B5bojyu23WmJgMxn6ev5R4V8mA5WKp1IxJJOe6enB8bKPRAayWTHaZ87A\nww8b5udFQKhWk/MDvIX3ArDMOD/kfgLnxKC3WvKezcKJE4ZEwvXnAVhrWV311OvSkphMikNy8KAn\nkTCsrXmqVUujIUWC8XhULKgRAUVRLg91BJTrjnJZwujJpMgBdzr0WwNjMYkEVKuQSBhyOTHAm5si\n7BPtA+I8JJMyXTCRsH3dAGvpG/vD/gyv4i8B+F37zXRTQ8R6Of3omvm848gRt609cX3dYUxILAZj\nY3IfJ06IKFGz6bHWEIt5kknTT1ckEuoEKIpy+agjoFx3tNtmW3FdtMIHqeAvlz3driUeHxTmRQY+\nMroRqZSh3ZbCwFxOnIVaTWSB860V/rrzNcTo4DD8buKN5HJyHin8k9cdd8DMzPZ7HBmx1GqOWs0w\nOjpoRQwCSKelNiCXA/B0u9ujCYqiKJeDOgLKdUcQeNbWROmvVqNfEAiDiX3OOZaXDaWStAXKavvS\n0nzvPXNzjvvuC1hclG25HKTDFh+qvY4CjwFwFz/Jo/5GEnUYHYWjR+UVBDAx4XjsMUsq5ZiZkSLC\nbNaxf78lm5UIhTFy/TD0hCF950MiAe5JxY4URVE+F9o+qFyXeL/9fSeitrxqVYrxBsWCg30eewwu\nXAhoNqWuoFyWlsEvd3/Pi/g4AD/P9/CzfF//eqmUtAqGoQwLOnjQ0unAxoZltjeGYGYGcjnXK0rs\nMjoqBYyJhDgjicSgnVAjAYqifD5oREC57uh0BqkBYy5tu3NO2gXbbVmBx+Myb6DbhTD0jIzI/s7B\n7Kzl5EmYm5Pj2m1Zpe9zc/3z/Vd+DJBrRvoBIyOGm26ChQVLtepxTgx7vW4BRxhKxMA5x6lThmZz\ncP/drmFszKOFgYqiPB1oREC57qjVJNze7coKP2rHiyiXxag7J5GAlRW/7XO0f7kMs7OexUUZLFSv\nS6phbQ3yzVUAqqRpkALEkajVBkJE9brpDxOKJhSmUu6z3kulogqCiqI8vagjoFx3xONi3J94AlZW\nZMUf4dzASC8vSy1BpyNheZkqKJX6ALWaoV631GpiyOt1Cf3X6zDULQGwwlj/3O22nD8eh+FhT70u\n8wUi+eJczl1SNNhqibOwuSmvqC5AURTl6UJTA8p1x/KyFN7lcrCxIQY/kvaNVuCbm2CMJQg8Yehx\nzvTaBw2NhqzaT53yrK0ZYjHJ+0cCQckkzCCpgVVG+9fN58UJiMclPbBvn5xvZMRx6607Tzes1Tyd\njiWblc+R1LCiKMrThToCynWI5dw5MdrWwu23S14epBo/k4HTp0UdMBYzjI3B/DyUSpDJeEZHpUag\n07E4Jw7A5qacLwjglvqneA1/AsD93N6/arstTkI+D5OTnkxGhhPt33/pKj+SOlbRIEVRnml0baFc\nd8zNOTqdwSp+bm6Ql4/FPNVqNOzHkErB+fMSos9kDGBZWRFDvLzsqNdldZ9OyyseOn6+8t0EODbI\n8jbe1j/39LToDGQyMD7uee5zPXfc4ZmevnSVH0kdq2iQoijPNBoRUK47slnLxoas3lMp+RxFBIaG\nYGVFhIKMcSQSMkY4m5XoQRh6YjHZf3LSMj4uq/xuV1bxL/Kf4Pba/YB0C5znIBCpEErXwNGjnhtv\nFH2CiwWKIiKpYxUNUhTlmUYdAeWap9OB2VlpzUulHOm0I5u1pFJS2JfLDSIC1sLoqGdx0TE3Z2m1\nwHuHteC9IZGAqSnZP5t1xOMG7w21mkQR/k33zwFoEuc3zRvAi0BQIiFCQkeOQKHge9d88tnBkdSx\nigYpivJMo6kB5ZpndlbEeiLRHoBcThT6crlBoeBWlpdlDoFzhkZD5ghE43630mzScxbgFZ2/5s3N\nXwbgX2Ivo2alwi9KHYA4Ffv2iTDQTgJFEVEaQEWDFEV5ptGIgHLNERXatduSW9/YsMzNidFNJDzp\ntOWWWyRfv74uK/2oAM85uHDB8KlPWdbXJZ+fToP3kc/se2OHHaWS5eRJERt6ZefP+F+dbyZOmypp\nfpz/ijG9mQN5OcfBg9EoYRl0FF1z66yDiEjqWAsDFUV5plFHQLnmiArtQN5nZx31uvyqdzoG5zpA\n0N9/q0BPuQwPPgiVioT7Gw1YWDAcPy4phk7HUip1ALj3Xsf585Yj3Sf4vc63EqfNBlm+JvbHfNS9\nkG5XDHqzOZAqTqVEJXBlxTE1den1FUVRrjbqCCjXHK2WYX1djH4YepJJy8qKY2NDxvkeOSIteaUS\ntFq+188/OHZlxbCyIimFIJAK/7Nn4fRpw/Cw43Wvi4oLLY0G/Pf2fyFJkzYhr+DP+JR5Ed2unM+5\nwXwB5yQyUK9LC+JnKxZUFEW5WmiNgHLNUav5/pAgMeyOTMYyPW3IZCyLi45kUsb7JpOGjY3txy4u\nSqdAMikGfGHBsLYmrYTNpuUjH5FiwfV1x4s7H+E1/BkA7zJv5hPhi0gkpDvAWkkFTE5CKuU5cgSy\nWUMQWJxzTE6KiJAKBCmK8myiEQHlmmBrXUCtBktLnlrNkMl4xsYsnY7r1wgYY/nwh6XILx6Hl7zE\n9EcRx+MyHGhpSZyBREKiAtHY4kwGpqYkInDihOULPvReAEqM8HZ/F85JOqHdlvuK2grHxsA5T7MJ\nm5ue48cHLYuKoijPJuoIKNcEW+sCFhehVotkeQ2NRpeZGUtUePdP/+TodkNSKVhbM/zrv3oOH5bz\nLC97SiXbq9aX1r9aTSID09OyT73uMCsrfOHHP8CXVP8UgPfHvpG6GSZE9m23JSUwPi4RAWsdMzMB\n8Tik04ZKpXNVn4+iKMqToY6Ack0QCfAABIH03weBCACNj1tyOdfXEchmLdVqJBAErdZgdR6LWUZH\nZeUfSQan09LOlwpavGzzr3jNvb/P2B1/zZdL6T9dLP8r820ke1MCo9RAtyvHjo3B9LTUFwSBIZXy\njIxoREBRlN2BOgLKniZKCUhaQKrz63UpyBNJYBntK9K+vjcgyHHPPVLol0zCV3zFwCCHoTgM5bKM\n/E2l4NjoGnetv5MveeB/kamvbrv+uann8TPxH+aMu4V4k36nQBhK2uHIETh6FKanpU6h2ZRIQTKp\nToCiKLsDdQSUPU2UEshkYG5OIgP5vEwLFGdA0gFb2wnn5nzfIEsr3+B8m5vSOhhNEvzC2t28a/k/\nMdW+0N+nOb6P7td/HcUXfyO//pFbuOcei1mV81k7mC4YyQonk56xMdkWvRRFUXYL6ggoe5qoVbDR\nMJw5I45AZGyTSRHqqVYta2ueRsOSTDqWlraX6ZdKgzB9qWQ5e9bQ2WzwU7Uf5bva7+nv98hNX81D\nL/12hr/25dz5fMPq/Za1tYHT0O2KM5BOS2ogn5eIwKFDsLJi2b+f/oChdltTA4qi7A7UEVD2NNIq\naJmfh9VVi/dQr4txnpnxbG5alpe7TEyIgNDmpmV+vku1aonFJJ2wujowyJ/+tGNtzfK91Z/huzri\nBKyacd51xy/T+LevBuDAyQ53Ph/On3eUyyFra5KOaDTEAalUZFhQtSrbajVDELieIqEnl5P0hKIo\nym5AHQFlTxOGhtOnPcWiodXyDA0ZqlURAyqXYX1d2gebTd9vF9y/3/LRj0o3QDoNX/RFg9W5tZZu\nV+YGAHyK5/DNIx/iyP4pDq5KzUA8Lvtba6lUPKWS6dcGJJPynstJTYJznnYbnvtcg7WOVsuQyzlm\nZp69Z6YoirIVdQSUPc3p0552OySflxqBSkUcAGvBWkO9bjh7tsPznx+QSMgxZ850yeWkO6Ddhscf\nH6zO5+YcOb/JHTwEwJ/EXstafIqxDan+B2i1ZP+HHpKIQCpFPz2QzcLNN8P+/ZBIGG65RbQJqtUu\nt96qUwQVRdl9qCOg7BkuHiY0NATOWdbXPY2GoVbzVCqy0u92TV8dcHjY8vjjjnLZMjQk7YOnTkk4\nP5WCG24YRAT27bN8d+XniCGtgX/bfhkAlYrnM5+BkRHPS14i+8diEj0wRhyBIJA2w1tu8RjjSSYN\njYY4DhMThkTCqZywoii7DnUElD3DxcOEymVPteqAsB8ByOcl/L++Lu+plKzyb7ghZHQUIKBY7BAE\nlnxenIu5uV5aYPYcL/2XD/JVG/8DgL80X8l98ReRrMvEwEOHAAyPPNLhJS+BdlucgXRaHI5EAp7z\nHM9XfIVjfh7KZdsbP2wwpqORAEVRdiXqCCh7hq2iQdHnmRlDrSbywbmcYWjI0+1Kzj6RgNFRRxBY\n4nFZtYehRAiqVfk8zgrfWvsjhl/1B8Tu/Sivjs5NyF2xnyaREGdi3z45NhaDMJSIwHOeY3noIU+z\nKXMN9u2DQgEyGcP4OMRijnZbZI1VQEhRlN2KOgLKnsEYz7lzhkbDkEx6jh71pFK+rxR47pzoB4Sh\nJ58XPYFMBrpdx+OPyz6ZDOTzjvzJ+/nByv/Hl7b+pp8GiLgv8xJ+wt3FE/ZGsimRCc5kBt+PjopB\nHx933HlnQC4n6YjhYRgbczSbnnrdYgwcOuQJAshm1QlQFGV3oo6AsmeoVCQK4L2h3Za8PUiOvlQS\n3YAgkGFD3a5nZkbaCKOBQc7J+9wcfHDtOyh0H+mfu3PzrTRe93o+YF7Hr/7NMZ54AkxDvjtwwDE5\nKR0K2azn6NFoO4yMOMIwIBaT+oFaDapVKURcWoLVVTh2TLsEFEXZvagjoOwZqlXLhQuDIr9cTlbd\nkUJgsykV+t0uPP44nD8voj6JhEQDNjakrW94+Ym+E/AH8W/gj459L+/6P7cAcPp/WOr1wcChoSGp\nD5iaijoBwHsJ8xtjOHzY0Gh41tcNYWio1SxrayIulM3KmOHIcVAURdmNqCOg7BlmZ6VdD0RRcHa2\n0xPuCalWRR4Y4IEHoFo1TEyI4uDcXJcDB0RNcN+Ze/nx5f+3f84fsT9Ja2Oy//nMGUe7bWm1pIag\nWpUoxIULMkWw0zGUSpJKiMU8GxtSFNhsSsShXvcMDxuyWbnHdrt7lZ6OoijKlaGOgLJrubhdMAwt\ns7OezU0J0R8+bMnl4PRph/cGY6Q+oN02zM/D/Hyk9W8xy0u85fxbef3m7/bP/36+jnOd/dwx6YgK\n+fbvl7D+4qI4AiA1At2uZ2lJRIJyOYkI5HIQi5lex4KkBlIpudfNTdl3YkJkjhVFUXYrl+0IFAqF\nBPBu4LVADfj5YrH4C0+y7yuB/wYcB04Bby0Wi3925berXE9c3C74+OMOa0U8CAyzs10SCchkQmZm\npE4gk4G1NekcCEPoNjt87dp7+bHuO8h1ywCsM8R/S76N34x/D2narK8PCvmSScfoqGVmRuSBs1l5\nHxoyTE7KdTc2xEPY2IDxcU+h4Gm1DPE4eO8YGzP9e4zEhxRFUXYr9nPvcgk/BzwP+FLgzcCPFQqF\n1168U6FQuAP4IPA+4DnArwF/WCgUbr/iu1WuWZyTor6lJcPaWlTYt71dMBaTGoFHH4ULFyCdtuTz\nlmrV9aYIeh58UESFNjfh1vV7+HD5pfxc64f6TsAfDX8LLx65j/fY76LaDOl0YHJy8M/g+c+XGoFK\nRdICMinQs2+fJww9mYw4CiCh/1RKUgTOORIJ33MW5PqxmEQIFEVRdjOXFREoFApp4E3AVxaLxfuB\n+wuFws8AbwH+6KLdvwH4cLFY/JXe53cXCoWvBv4D8ODnd9vKtcZOYkGxmO9vA1hcFAGfSOp3dtax\nf79EBIyBhx6S1sJWC36Z7+ctvLcflS9m7+QXj/13PpN/EcufEXEfa8Xh6HQGq/ZSSQy9dCjQizjA\n5KTnhhtkn0xG9q/VPM5ZDhyQ7c45UilDsymfjYFEQtMCiqLsbi43NfCc3jEf3bLtX4Af2WHf3wLi\nO2xXkVXlEnYSCxof95TLvl8jcOCArNajroHxccvICNRqjlpNagRSKTgan+Mt9fcCsGZG+Knsj1F8\n2ZvYrAcMpeHoUUutJl0GiQS84AUDsZ9sVhyNcllW9bkcnDjhOXTIE4aGVGrQCphKyaCjTieqTbDk\nch6QbZHksKIoym7mch2BfcBKsVjcqsCyCCQLhcJYsVhcjTYWi8Xi1gMLhcKtwL9B6gsUZRtBIFP8\nIqM6MSHTAh98ECoVEQcaGnIMD1syGVH4m5hwxGKwuGiZmzOcOuVZWTHctvFY/7zfOvbHnJ56HjfG\nA+JdOW7/fkejYWm35fP09CAikMtJjr9alTx/Pg/793uOH/eMjflL7rlcHggcjYw4rDU94+9JJDz2\nSpJviqIoV5HLdQTSQPOibdHnxJMdVCgUxpF6gX8uFot/epnXVK4TjBm8AD72MVhakl/RRsNSr3fI\n5x0bG4ZcToR95uehXrfMzsLamqFeh1fyV/1znkzczPSEaAJYO5AJbrflFQTSWRBx4IAICC0tGby3\nTE0N8v4XU6lInYD3UiwYGf+tQ5EURVF2O5frCDS41OBHn2s7HVAoFKaAv0Oyta+/nItZa7D28out\ngsBue7/e2QvPw3sIAtHsDwJRBjx/Hk6fhlZL5HuDwDIzIy2DmYz8XqyswKc/DZ/5jPz5Tncfb3ES\ndPoz+0paiRzlsuPECfpzA2ZnLdmsOABhCJublrD3LyEWg1tuMaRShnJZxISMsayteYyR74eGxKno\ndunNEBj8DBMT0ae9VSS4F35Hrib6PLajz2M719rzuFxHYA4YLxQKtlgsRvHUaaBeLBbXL965UCgc\nAO4GusCXbk0dPBVGRzMYc+X/oebzqSs+9lpkNz+PUkkMdaLnVjYaot/fasnnzU3J6U9Py1TBdlsm\nDN5/v+TzNzYg3q7ya93/hwDHBlm+L3g31WqKzU24/XYx3s2myP4GgZy33U5RLtOfDOi9fO/9IHqw\nsSEGPpeTfYyR/aen5doRQ0Ps+QmDu/l35NlAn8d29Hls51p5HpfrCHwaaAMvBu7pbfti4OMX79jr\nMPjr3v4vLxaLy5d7c6VS9YojAvl8ikqlTrerfdy7/Xk4B8vLsLJiMEZW/82m5N/PnJEugAMHYHLS\n8eijUtGfz8vwn3odikXL0qLnt7pv4nYeAuC/8HZOtSfIbNaZnJQJhJubogtw5IijVLI0mykSiTpT\nU461NbkX78XQW2uo1UwvjeBZXhaBoVgMhoclOpDPiyMQFS/m8/TPs9fY7b8jVxt9HtvR57GdvfI8\nRkYyn3snLtMRKBaL9UKh8DvAewuFwrcDB4EfAN4A/TRAuVgsNoAfBY4iegO29x1I9KDyVK7nnMe5\nK2+/6nbdttaw653d+jzW1kS6N9Vzrp3znDvnWV8P+6vwWAwWFhxDQ5Ia8B7OnXM88gg4Z/lP/n18\nE38AwB/wOn6F7ySRkOhBs+k4cWIQwrvvPsfhw5ZEIppR4PoqggBjYzA+bkgm5ZjVVU+5LE6E1BU4\nxsdl34uHCXW2DzLcc+zW35FnC30e29HnsZ1r5XlcicTw9yOV/3cDZUQt8E96380DbwR+B1EeTAH3\nXnT8bwPffiU3q1ybNBqGUglmZ+Xz4cMQhpbVVcn/t9swM+N57nMtS0v0V/Y332xJpSC9ep53uh8F\n4GFu4k28hyhHby3ccIPF+y5ra5aREccLXmA5d06cgHQabrxx0D4ougKwvm5YX/fkcjJjIAjkFYaR\nSJDqAyiKcm1w2Y5AsVisA9/We138nd3y55s/v1tTrhcWFz3Ly0E/DVStdnn8cceZMxZrpW6gWjXc\nf3+XG26w/cjB0pLj9Gl4T/v7yLFJF8u38D6aYZYQMeBjY2Ct49ixXlEAljNnutx+uxQMbm6KrHBE\nuQyrq4ZMRsYOx+OeeNyTz0vKAlQkSFGUawsdOqQ868RiYvCDwPdW3oZMxpBISEoAZOVqBfgKAAAg\nAElEQVSeyVjy+UFO/sABy4nMPP/e/QUAv8R38ymeRy4lkYBsVgYG3XmnJZEYCP8cOWIJAjHmo6Oe\nY8cGK/x2W7QMMhkAj3NSBDg+LvMLtC1QUZRrDXUElGeFrZMFNzcdp05ZTp8WdcDbb3fkcp4gsDQa\nA12BbNZx//2WjQ2p4L/9dseXhPf0z/mbfCvpdJRakPepKRgfd1y4YPsOxOHDjtHRgHRaOhOSycEK\nX6YcgnOGXI7e/ADf6wbQSICiKNce6ggozwpbZwvMzRlmZ8VQWytKga1Wl9FRWFoSpyGV8qyvSytf\nqwUjy49z40//LG889X4ANsnwWHATudSg9S+dlnx/qSRywN4bOh05x9Z2wa0MDUmxYqkkn0dHNQKg\nKMq1jToCyrNCo2GYnZX3YhFOnhRBIGMkb3/ihGVoCI4fl/3HxgwPPGAZOv8w31N+J1/d+iOCXoFf\nF8vPx3+QeDzoiwTV6+JAAKytWQoFcQrCEGo1y/Cw5PxjMeh2B6kBa6Wu4GI5YUVRlGsVdQSUZ4XF\nRc/mphTwnTwpY4Ujwz03Z0gmuwSB7U/yq1bBnj/LXy2/lGRP1bpFjD8d+UZ+hh/k4dYxWk0RGUqn\npdNgYUFSA947mk35Ve92DalUFwj69xKLqdFXFOX6RR0B5Rlnaz1AVGzXaFjuvttTKlkuXBDDvbkp\n+1sLExOWatXz2GOGbldSA7cnnug7Af/TvpE/vv0uNkcO8sgnLK3WYHZAtyvnWV+HffvgppssIyNd\nqlVDJuO58UYZEiRzBnyvMFBRFOX6RB0B5Rlnaz1As2kolz3//M+O9fUQayXnX6/TN8hhCHNzjnw+\nZN8+2RZ3TZ6/+nf9c/6P9A9Sq+0nYxyZjO21GEqoP5eTc46OwpEj0h54662D8H8i4RkZMYyMRGJG\nV/FhKIqi7DLUEVCeUZyDs2cNd99t2NyEqSnPK15hqNelRqBelxV8t0s/DTA+DkNDlkce8SzOdfm6\n5u9zV/MdTLfOA9AkzqIb5/iUZWJC0grNphT+Sc6fvv5AMum44w5LIuF0KqCiKMoOqCOgPKOUy/CP\n/wgLC6I1Va/DP/xDh8VFT7dricclJZBIwP79ckwqBSdPOkZLZ/nA2tdyY7fYP999sefz9vxPYxN5\nGo0OzsH+/ZZqVVb38bgMAwI4etRz002GMOxq+5+iKMqToI6A8ozSbhtaLdvrzZccfrNpOXZMnIRa\nTVr28vlBu9/4OLRalh8u3tV3Ah6P38yvH3orf2pfTb1hyKXgttssR49KO2C7LamA4eHBmOBDhzy5\nnGdyUiWBFUVRngx1BJRnDCkS9Cwvez7xCSn6Gx2Fo0cd2awoBVobjQf2bGwY2m3I5Tz/t707j5Oj\nKhs9/qvqnunZ12Qyk30hnBiSsAkBg2ETUPGFqIDickERxeUiiBdUBN8LgoqvG3oFURb3BUR4lQuI\niBoCEUNCQkg4MQswJJmQTGbr6enp6a56/3iqp5eZyTpZZvr5fj759FSdqq7qk545zzl1lsnVbbwl\n+hcAfhG5hFun/IAZR/qM73aIx6GkBMaN82hogLo6l74+aW1oaoIZM6CqymfOHJ9Jk3RKYKWU2hV3\n94cotW/S8/a3t0sB39cH8bj05i8tlU6BMrUwdHZKWjIJb9r8FDc9fjoRXzoN/KL8MsqrQhQVySOE\nUEheJ0yQDoKplPQNCIcBpBWgvt6jqkqCAO0ToJRSQ9MWAbXPBhsW6GaFlvG4w5o1Di++6ASL+8jI\ngM5Ol85OKcxTKWna37HDoSG1lZu7v8C7e+/vf48/Rt7Ncvd4ajuhtdVl0iQJIsrKoKfHJRqVRwG+\nL2sLjB3rcPLJHq7rUF/v988gqJRSanAaCKh9NtiwwOyCd9s2n2XLZL2Avj4JHLZuhaOP9nj9dejo\nkKhh82bwo938//jpTPZfA6A1NIabq77GfakPQJ9DWxv09npUV8s5nZ3Q3OxRWiozBfq+tCj09sqs\nROGwrxMFKaXUHtBHA2qfJRIO7e1Sm29vl+00z4Pt211eekkeBUSj8gw/FIIzznCprXVpboY1ayT9\n47139AcBPyv5KB9fuIJfhj5ItNuhu1uGB6b7ArS1SWDR0OAyb55LeblMDlRf7zNnjkw+NHasPhJQ\nSqk9oS0Cap/FYj6JhMSSiYRDLOb1p3V0wNNP+/T0uP19ASIR6czneR4vvwzFxS719TB52zKu8b4D\nwJLwKdww9vvUtaXwPBkOCHJ+T49HY2Mmdk0mpUXghBPSX2OHhoYUM2celI+vlFKjgrYIqD3meVIb\nf+MNaaovKXGIRPyg855PaWmmRSAadVi/3mX7dmnGj0alLwBAaalLJOKyvSXFotVf58/R06mjDYCv\nuF/BDTnU17ukUlLzTyYlIJg1y8V1fbq6wHV9Zs50mT7doa4uRSTiUVeXYvp0Z7BbV0opNQRtEVB7\nLL9PQDzuU12dO3Vv2qpVPs3NDr4vKwqC9OyPx+HFFz3KV/+L+7ddz/G9SwHoooIb677DvysWUFkO\nmzZ5lJS4/Z0Py8thzBiP6dMztf9kMkV5OcyePfg9KKWU2j0NBNQe6+vLrW2XlkqLwGBT96ZSLrW1\n8MYbUvg7jjwaWOAs5aJ7bmHauif7j11WPJ9PlN5NV/10ykIweTJs2+ZSXg7bt8u5Y8d6vOtdLlu2\nePT0OJSW+kyc6FJd7dHRMfg9KKWU2j0NBNQAQw0L9H2fl15y+lfxmzXLp72d/oK5sjIzfLCkxKO3\nV1YF9DyYy4t8t+0LnPHsU/3X6XKr+En9NdxZeTVJQpQG/QFSKZksCFyamqSD4VFHeYwbB57nkkzK\nnAEVFR6ui04frJRS+0EDATXAUMMCN2+WoXqplEMs5rNiRYrJk6Xk7+pyaW72mDZN3iMWk0cBvg/l\nRHmScxnr7wCgJ1LDs/M/yVc7P8MbfbV4vdJZJb18cCIBJ5wA27Z5tLc71NT4nHmmTEO8c6eP78sj\ngKqqg50zSik1+mggoAaIxRxefpmsmr9Dba1PV5dLSwv9U/w6jktra+a4efNcQEYObNvmsmOHdPb7\nCL9mLBIEfLvsWtYv+iyljdWMaXap7pO5BVpaMhMDFRVBMuly3nnS0RBk7QHPkymD07V/39c1BJRS\nan/pqAE1wIYNPm1tIRIJl7a2EBs2SGHb0uL1rwfQ1eWwZo1Ha6tLPO7Q2uqybl1m+OCqVR47d0Jf\nwufT3AXACuZxI1/hhU2VJBIe8bi0AkSjMk+ATAgkhX9Xl7QGxOMO8bhLLOYTi+UW+jphkFJK7T9t\nEVAD9Pa6rF7t09npUFXls2CB1PRra13WrvWJRh0qKnyKilwWL5ZHCdXVcP75mRaB4mKZUfAYXmAu\nLwFwB5cTLnKCiYDgpZd8OjocXNenqUkCDN+H+nqYO9eluFiGCobDUFzsUFLCkJ0TlVJK7RsNBNQA\n1nrEYmHCYXlMYG2Ks86CtjaPqqpw8Gze4ZlnUoBMGNTdDUuWeFx6qbxHS4uH57l8hJ8DECfC/byX\nykooLpYphqdMka/fli0ye2B6IiBZltijvt6huFj6KjgOxOM+TU2gjwOUUmr4aCCgBqiokKF7vb0y\n5K+iQmr648a5dHb6xOMOJSU+5eXSgz/diz8UyrQITJ7scnJ4GZ/s/TEAD/MueiI1TB0D73iH9C1I\nX6OxERIJj5oamXdgxgyfefMcYjHo65NCv7Y2PWGRBgFKKTWcNBAoYEMNE4xEPF5+WVYIrKqCI4+U\nwt11PV56KdS/v6LC49VX3f7Og3PnBn0Ekknmd/yd63v+D2FSdFHBDaGbmDABTjrJp6nJw/PglVdc\nHEeuOXasz+zZMi/B5Mk+FRU+ZWXyqCCZdHAc7ROglFIHggYCBWyoYYIbN8rwv1RKXjdulOOXL4fO\nTodEQl67umSMfygEYdfj6OhSKr5wP5H/fohP7Njef52ruI1X3GnMrZGavSwXnHne7zg+Y8Y4hMMS\nnPT2SlDS1iaPBNL/lFJKDT8NBApYZ6fDkiXQ3u5SU+OxYIEME9y2zWXnTgkCyspkKCB4tLS4bN0q\nqwiWlkJnp8u01AYW7biP82L3M2HNaznv3+7WckfRp/gVl1BSLI8CyspkKGAyCbNny2OFzZud/sAj\nEoGiIhfX9UilnKBDoLQEpFL6aEAppYabBgIFbOlSn5YW+Qq0tIRYujTJlCmwfr1HV1d6oiDZBnj1\n1cz+CdtX8sUt32RR8iFCZIYN+mVl9L79nXxr84XcuekcWruKSSXBSUoLxPbtLm1tSQASCbl2Z6fM\nCdDXJ48p0ulFRX5/i0V6Wyml1PDSQGAUSj/7j8cdtm3zKSmB8eMZMBNfR4fLypVS2FdWZjoF1te7\nbNiQ6SxYXx8MH6xxCD/zNFfHv8k5/hP979NHmL9Gzub5mRdw+R/fAeXl9HzPxb9Pav6eR39fAPCp\nqnKpq/Npb08FQxShqkoeDUQiPrW1cr3qanQdAaWUOsA0EBiF0s/+m5shGg1RWupQXi77ZWY+8fLL\nHtGodNiLRmUboLXVo7TUpbRUjuvaHiPym99z45/uYm7viv7zuynjgZqPcE/tZ2kpmsikcUkuL5e0\nRMKjoUFWD+zultkCKytloaLOzhTV1TB1qrQubNki6xhMmCDnVlSkOyfqOgJKKXWgaSAwCiUSDu3t\n0Nzs8u9/S2185kz5lx0IlJS4vPZapi+AMVITHzPGZdUqaOx7nU85d3HF9nupurKVucF5O6nljtAV\n3FP+CYobG4hGoSICJ56YGT44ZYoMQXzjDTknHQhUVnpUVbmUlfn09vokkw6TJvnEYhAOO5SWejn3\nqJRS6sDSQGAUisV8EgmXTZt8du6Umv2OHTIUb+7czHHr1nmEQi6VlZltgNWrPb7sfZ0v+bcS8r10\n2c6Gopnc4V7Br4o+RNSpxCHJ2+dl3i+ZzOor4EuLQCgkLRFFRTBxIjQ2OkCK4mKoqcl0/hs/3qe2\nVmv+Sil1sGkgMAqVljokEj4lJVIrLy6WXv6RSO5x9fUyOiC/L0BZxOdzyW8TwsPD4amyd3D8fR/n\nut+cyZJnQsTjUF4CTU0utbXS9F9eDtOmZVoEjjxS1h5IpSQYqK6GpiafhgaPceMcqqt9ff6vlFKH\nAQ0ERqFk0udvf3NYtQq2bYNx46Q1YPz43ONqaz26u116e2UYX22tB77PO3iMcmIAfDT0E16cdSGP\nnQbjF8sUv+kJhCZO9JgwwSWRkGBjzJhMi0BNjcexx7qMGSOjAkpLfY491mPqVOkQqM//lVLq8KCr\nD45CixfDjh0hYjGZw7+lRQr6WGzgsa4rfQimpjZy3vJbqZt/DN/d8L7+9KWcSF+f/FxVlZ5KWF6b\nmqCkxCMU8ikp8Rg3LvO+kyZBebmH60J1tU9Dg08oJEGA1v6VUurwoS0CI0Q0Co88Am1tLrW1Huee\nCxUVgx+7davL2rWwdq2cV1oqte+GhtzjUs3buKj1ERZFf8OJyaWQNR9QN2X8KPwJNpfMYGzUAzxi\nMZfx4zMtAtGoS2Nj5tFCMpl5NOC6UFbmMmuWTzjsB48oHO0HoJRShxkNBEaIRx6BzZvlvysWc3nk\nkSTve9/gx27Y4NHeLmsF9PbKY4EdO+CF5R7hlSso/vNjFP/5Me5buSLnPA+H5MLT+Pyq9/OrnnfT\n7VRAEnp7pXDv6pJgQO5BhghGo3JP2RMBgXQQdByfVMrpnxGwutpDKaXU4UUDgcNUIgFr1kitu6LC\n47XXZPKf9FA/38/UvvOVl7usWyeFcQk9nJp4kg+se4KzVv+R2odaBhz/ojOH34Qv5sW5F3L3A41s\nuNSl+6+ZZ//HHCPXOuoomWI4vejQ7Nku5eUevb1OzkRAIIHB+PGwZYvXv1qhDgtUSqnDjwYCh6k1\na2DnzhAgr8uXp/qn900kYOPGoWvXS5Z4+L7LJF7nKc5hhrcJOjLpfjhM30lv4faNb+fB3nPZGJ4J\nQJMnNfpo1GP8+Ez3kWhUrhUOe8ydm9lfXCydBdMd/tITAYFMB+x5DpMnA/hEIj5h/bYppdRhR/80\nHwLJJDQ3Q0+P2z+BTn4h2dzs8vDD0NEhQ+2SSZfXX88s+DNnztAtAuBSGmvlcf6DGWwCoD1Ux4Yj\nz2bm595O4rQz8KtreP5Kl3VPuMSj8sx/1ix5z6lTXbZsyVxLZgD0MMYlHpf1BiorpYWgstLL+Rxp\nOj2wUkqNDBoIHALNzWQt6uPS3OwxbVruMY895vUvCNTT47B+fYqKiszkP2vX5gUB8Tjhl9cQXrWS\nG15/gQV9f2N6EATc4NzIynNuZPykODefnzmvo8OjsdHN2Qap6cucAPRvA1RXy5DAdABSWZm+74EB\niQ4PVEqpkUEDgUOgp8cdZDu/MHUpLpbWg3AYiotdSkrksUBVOMZ8byUld68gvOoFilatJGTX4iSl\naf/DWe/yPT7N98qv4/y60IBgY8YMl46OTL+DGTPkPhYudHn0UZ+uLofKSp+FC2X/pEnQ3Dx4C4BS\nSqmRSQOBQ8JjyRK3v9n/1FMH1qiLiz1Wr8502Ds1spQPbr6PefHnOSJlCa334J+Dv/uO0oks84/h\nUe8s7glfxvjxDtOnkzPOH6ChQeb9Ly6WRwMNDXIfjY0e558fIl2br6tL9xFgyBYApZRSI5MGAofA\n+vXySCCVgq4uh/XrPWbPzj1m7Vro64NJyVf4au+NXND+wKDvlZoyleS8Y+g7+hiSc48mOfdoPv+N\nMfzlL2G6u8FJyRj/6mo44ojcc+vrJS2RSE8xLPtnz4Y1a1L9Ixby700ppdToMWIDgXgcnnsOOjtd\nqqo8TjxRarUjwaZNLo89Bl1dsiJfJJL3aMD3qWrZyH/Gf87/Tv2ACAkAOt1qnoycw9rSY4nNmsdV\n983Br6kd8P4dHbIGgOvKLIBVVXDssTKfQLZEwmX+/Nxt8IIhg6A1f6WUGv1GbCDw3HPwxhty+/G4\ny3PPJVm48BDf1B56/HGPnTuln8DOnfD4YymuPm8TxUsWUxT8e6pla//xfYS5g8u4s/56drpjAGiK\nJflszeDvv3OnTPyTSkltv6NDXvPV1Hg5/RVqarTgV0qpQrPXgYAxJgL8EHgPEAO+Za399hDHHgvc\nAcwFVgOftNYu3/fbzVi3zuXXv85MbnPxxS4LF46AgszzcKMxana0clLyGU7nH5y5/e/Uz3990MMf\n5lyu5RbWcQQNjktvXJrxpbf/4J939myXlhZIpaRFYOpUn8pKBgzhO/10eOqpJO3tLjU1HqefPsyf\nVSml1GFvX1oE/gs4DjgNmAr8zBjzirX2weyDjDFlwCPAz4FLgE8Cjxhjpltre/bnpgEefNCjtVVq\ns62tsv2xj+3vu+bxfYjHcbq7caJdwWsUpzsqP3cHP0ejucd0d+MOdXwsNrCPX1Z5npo8hcSCt3Ld\no2/l0Z7Ted2ZCEBRKsnYsZnau+MMHfSEwzLmPz298LhxMHWqPE7JVlYG556bdwNKKaUKyl4FAkHh\nfhlwjrV2JbDSGHMb8BngwbzD3w/ErLXXBdtXGWPeCVwI/Gz/bhu2bJFJbzJcSCakMI73wNYUoS3b\ncTq7MoVxNKtA7v95kAI7+7hUan9vdZdeYyIv1CzktJveSt9bTsGbPAWAZ//t0vKyixeMGqiqkjkE\nolFZbOjEE4duEZg/3yUW8+nokKl9jzvOp6REWhI8LfOVUkpl2dsWgaODc57N2vc08KVBjp0fpGVb\nApzMsAQCKe7kSs7mSSqJUrElSsn43pxjqvb3InvILynBr6jAL6vALy+Xn8vL8Ssqs7Yzad/4YQWb\nO2tYFT6GV92pNDal+Ov7c9+zujp3ml/X9TjttMz2mDFDl+jjxnmcfXZm+F9DA9TVQVubBgJKKaVy\n7W0g0ATssNYms/ZtA0qMMfXW2ta8Y1fnnb8NOGrvb3Ogetq4nHtx93LmOj8Uyiugy6WQrqjALxu6\n8O4/JruAD87d20n0t73i8o+/uvT0QHUpnHzywNr9RRe5/OIXfv9cA297m0t1dar/ef5JJ8mKfoMZ\nOPzPHfQ4pZRSam8DgTKgN29fejuyh8fmH7dPukvquDj+U97CUrqooDdcxrU3S0HtVlVS0TSWTi9E\nsrQ8p/AmEgHHGY5b2GczZngUF2cK50mTBlbTp03z+PSnM7X6cNjjyCMd0gFDJDJ0AJQ//E8X+1FK\nKTWUvS0i4gwsyNPbsT08Nv+4Ibmug+sOXmjfeSdcccV7+F38PZSUyHbyvCAx5EJVKXT24KQ8Dm2x\nP9D73w8PPOCxYweMGQMXXOAOKKznzYM1a/z+PgGzZkkLQl8fFBVBdbWDu4cV/VDIzXlVmif5ND9y\naX7k0vzINdryY28Dgc3AGGOMa61NV2MbgR5rbfsgxzbm7WsEtrKH6urKcYaovV9yifzblaqq0j29\n1EFVWwvXXLP74/KnBN5fh2t+HEqaJ7k0P3JpfuTS/Mg1WvJjbwOBF4A+4CTgmWDfW4F/DXLsUuC6\nvH0LgK/u6cV27uweskVgV0Ihl6qqUjo7e0iltHec5sdAmie5ND9yaX7k0vzINVLyo7a2fI+O26tA\nwFrbY4z5GXCnMeajwETgGmSeAIwx44AOa20ceAD4mjHmO8BdwBVIv4Hf7en1PM/H8/Z9GdtUyiOZ\nPHz/kw42zY+BNE9yaX7k0vzIpfmRa7Tkh+PnT0C/G8aYUmRmwfcCHcBt1trvB2kecKm19mfB9puB\nHwGzgFXAJ6y1q4bv9pVSSim1P/Y6EFBKKaXU6DE6ujwqpZRSap9oIKCUUkoVMA0ElFJKqQKmgYBS\nSilVwDQQUEoppQqYBgJKKaVUAdNAQCmllCpgGggopZRSBUwDAaWUUqqAjbiV6o0xi4AHAR9wgtff\nW2svMsZMBX4MnAy8AlxtrX0i69y3Ad8BpgPPApdbazcd1A8wzIwxxchnuhjoBe6x1l4fpE2l8PLj\nEuBecr8fDuBZa8PGmGnI2heFlCcTgTuAhUAr8D1r7feCtKkU3ndkLJIfZwLbgVustT8N0qZSIPlh\njIkAy4BPW2v/Eeybyn58fmPMVcDngUrgfuAzwdozI8JgeZKVZoBl1trKvP1nA98GpgFLkDx5NSv9\nGuBzQDnwW+BKa23vAf0ge2kktgjMBv4bWdK4EWgCPhakPQxsAY4HfgH8IfgjiDFmEvAH4G7gzcAO\n4KGDeucHxu3IH7SzgA8AlxtjLg/SCjE/fkPme9EITAHWA98N0h+i8PLkfqALOA64CrjFGHN+kFaI\n35GHgPHAqUh+fDuoYECB5EdQ4P0a+XuabZ9/P4wx7wVuBC4HzkBWqb3tgH6QYbSLPMEYMwX4IxDJ\n2z8VqZj+CMmTjmA7nf4+4EvAR4G3Iav1fu2AfID9MOLWGjDG/Bx41Vr75bz9ZyBfyoZ0BGqMeQJY\nbK29yRhzE3CKtfaMIK0UaAH+Iz/yGymMMbXANuAMa+3Twb5rgSOBXyJ/1AomPwZjjPki8BHgKOSX\nsNC+IzXATmCOtXZNsO8B5I/9Hyiw74gx5njgOWB6utYW/M4sAq6nAPLDGPMm4FfB5jzgdGvtP/b3\nb6gx5u/AX6y1NwfpC4A/A/WHe6vAUHkSpL0XaUHaDBxlrS3OOu8W4ARr7dnBdjmSJ+dYa58xxiwB\n/mSt/VqQfirwJyRPEgfn0+3eSG0RWDfI/vnA8rwv3NNIE1c6vf+X1VrbAyzPSh+JTgHa00EAgLX2\nNmvtx5BovNDyI0cQKF0LXGet7aMwvyM9QDfwEWNMOGjeXACsoDC/I9OB7dlNt8jKqG9GAsVCyI9T\ngSeR+3ay9u/z74cxxgVOABZnnbsUKAaOHu4PcAAMlScA7wS+gDzyyHcSuXnSDbyA5EkYaVnJzpNn\ngDJg7rDd+TAYcX0EAAO83RhzPRBCmj1vRJqCt+Qduw2YGPy8u/SRaDrwijHmw0jzUzHyfPwWCjM/\n8n0K2Gyt/UOwXXB5Yq3tNcZ8BvgB0gweAu611t5rjLmdAssP5P5rjDElWQXeZORv4TgKID+stXem\nf5a4sN/+/H7UACXZ6dbalDGmNUj/53Dc+4GyizzBWntZsP/MQU7dVZ7UIX+Ts/OkzxjTFqQ/Pxz3\nPhxGVCBgjJkMlCK1nAuRzhm3B/vKkM5y2XrJPNPZXfpIVIE8Bvg4cCnypfwREKMw8yPfZcDXs7YL\nNU/ehPSr+S+kJvJ9Y8yTFGZ+/BPYCvzAGHMl0lfgaqRTaQmFlx/Z9uf7UJa1PdT5o9GoyJMRFQhY\na18zxtRba9uDXauMMSGkU8u9QG3eKRGkUASIMzDzI0DbgbrfgyCJ9M692Fr7OvR3avkUwbO5vONH\ne370M8acAExAeummxZEoPduozpOgFnMZMDHoqbwi6Pz1ZaQptKC+I0ELyQXA74BOpPZ2G9IT3kMq\nFdlGdX7k2Z/fj3jW9lDnj0ZD5UmMEZQnI66PQFYQkLYWieRbkF7i2RqR6B+ko8eu0keirUA8HQQE\nLNLstLvPOxrzI9s5wD+stR1Z+woxT44D/p03XGkF0hxeiPmBtfZ5a+0MpDVgEtLnaDuwgQLMjyz7\n831oRQq+/vSgklbP6MmfwewqT7YDCXLzpAipsB5WeTKiAgFjzNnGmB3GmJKs3cciw1gWA8cHQ0DS\nTkE6rBC8npL1XmXBuUsZuZYCJcaYI7L2zUbG/y6l8PIj23xkTG+2pcBxBZYnW4Ajgo5LaW8CNlGA\n3xFjTK0xZrExptZa+4a11gPeBfwNeWxQUPmRZ19/P5611vrAv7LTgbcgBeHKA3nTh1h+nlQAxyB5\nkkL6AWTnySlIa8Cqg3mTuzOiHg0gPS5jwE+CoSwzkGa9byA9N5uB+4wxNwPnIb1YLw3OvQf4fDBU\n6E/AV4AN1tq/H9RPMIysteuMMY8gn/lTSB+B64CbKMD8yDMH+Hnevr9TeHnyR+R35CfBUKdZwBeD\nfwX3HbHWtgVDvG4zxtyKzMFxKTJi4AXgNQooP/Lsy+/Hxqyhkz8E7jTGvIQEoGMsHFYAAAOoSURB\nVD8E7jrchw7up7uB1cGkQY8C/xdYY619Jkj/IdInZw3wBtJp985gFNNhY0S1CFhro0iT71gk+vwx\nkqnfCiL785BmmGXI5DqL0s3mwXCh9yATOzyH9HJ990H/EMPvg8iEOYuB+4DbrbX/r4DzI62BvGe3\nQZ6cTwHlibW2EynsmpDP9C3gJmvtTwr4O/I+4AikVnYlcIG1dnkhfj+QTpLAPv9+LMo6/7fIZDk/\nAh5HZh687qB8iuG1x5PrWGs3AhcgHbafQzpwvzcr/ZfAN5GA4VEk+P7ScN7scBhxEwoppZRSaviM\nqBYBpZRSSg0vDQSUUkqpAqaBgFJKKVXANBBQSimlCpgGAkoppVQB00BAKaWUKmAaCCillFIFTAMB\npZRSqoBpIKCUUkoVsJG21oBSaj8YY/4GLBwi2QfGWmt3BsdegixhPDdIXw18x1r74C7eL4ksAvYk\n8OVgWtr0sfcClwTXcfKu+3tr7UX7/MGUUvtMWwSUKiw+8FtgHDKnfPa/pqwg4HfIHOm/Bk4GTkLm\nSv9tsOjMUO93BLL+xRHAs8aYiXnXf2aw6wIfG+4PqpTaM9oioFTh6bHWbh8qMVjJchFwgrU2ewnZ\nW4M15m8yxvwqvRjNIO/3mjHmHKQF4Vbgf2WlJXZ1baXUwactAkqpfFcAf8oLAtK+i6xm2LKrNwhW\nPbwXeI8xpmj4b1EpNVy0RUAp1c8YEwHmAD8dLN1a2wUs2cO3exEoBWYCa4blBpVSw04DAaUKz4eM\nMRcOsv9BMuvHtw3DddqD1+qsfQuNMV15x71irZ2LUuqQ0EBAqcLzMHAtuT33AaJIAOAD9cNwnXQA\n0J6171/AB/Ku3TcM11JK7SMNBJQqPF3W2k1DJRpjlgELkFED+WnVSMvBf1prF+/mOm8GuoF1Wft6\ndnVtpdTBp50FlVL5fgy80xhzzCBpVwFvBXZZmBtjKoEPA7+z1qaG/xaVUsNFWwSUKjylxphxQ6S1\nAXcD5wN/McbcADwBlAEfAq4GrskaOpj/fsXAm4AvB9s3DPfNK6WGl7YIKFV4LgK25P3bGry+y1rr\nI4HAzchEP8uAvwInAoustbfv4v3WA3cBzwMnWmu3HvBPo5TaL47v+4f6HpRSSil1iGiLgFJKKVXA\nNBBQSimlCpgGAkoppVQB00BAKaWUKmAaCCillFIFTAMBpZRSqoBpIKCUUkoVMA0ElFJKqQKmgYBS\nSilVwDQQUEoppQqYBgJKKaVUAfsfm4tM1C7p1r8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbddfb400>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"for i in range(50):\n",
" # Generate bootstrap sample: bs_sample\n",
" bs_sample = np.random.choice(rainfall, size=len(rainfall))\n",
"\n",
" # Compute and plot ECDF from bootstrap sample\n",
" x, y = ecdf(bs_sample)\n",
" _ = plt.plot(x, y, marker='.', linestyle='none',\n",
" c='blue', alpha=0.1)\n",
"\n",
"# Compute and plot ECDF from original data\n",
"x, y = ecdf(rainfall)\n",
"_ = plt.plot(x, y, c='red')\n",
"\n",
"# Make margins and label axes\n",
"plt.margins(0.02)\n",
"_ = plt.xlabel('yearly rainfall (mm)')\n",
"_ = plt.xlabel('ECDF')\n",
"\n",
"# Show the plot\n",
"plt.show()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** bootstrap confidence intervals ** \n",
"● If we repeated measurements over and over again, p% of the observed values would lie within the p% \n",
"confidence interval."
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"## creating a bootstraping statistics func\n",
"def bootstrap_replicate_1d(data, func):\n",
" \"\"\" resampling the data and calculate the stats \"\"\"\n",
" sample = np.random.choice(data, size=len(data))\n",
" return func(sample)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def draw_bs_reps(data, func, size=1):\n",
" \"\"\"Draw bootstrap replicates.\"\"\"\n",
"\n",
" # Initialize array of replicates: bs_replicates\n",
" bs_replicates = np.empty(size)\n",
"\n",
" # Generate replicates\n",
" for i in range(size):\n",
" bs_replicates[i] = bootstrap_replicate_1d(data, func)\n",
"\n",
" return bs_replicates"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"10.5105491505\n",
"10.5060359239\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAF9CAYAAAAeKoJ9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3XuYXWV58P9vMjGQaEZpqBl+QvCHh1sIEQPl9CJIte9F\nsVYUhQv1ZxHwAB4oBiX1VHw9oeHggSqIUjVWLUpDqY3YUvEFxUQTDgEC3KAoQRKjRGBCMmHIJL8/\n1tqy2ZnJ7Elm9uy18/1c11wz+3nutddzz+zZc8+znrXWhC1btiBJklRFE8d7AJIkSdvLQkaSJFWW\nhYwkSaosCxlJklRZFjKSJKmyLGQkSVJlWchIkqTKspCRJEmVZSEjSZIqa9J4DwAgInYBvgQcD2wA\nLszMi4aInQNcAswG7gDOyMybB4k7AbgiMyc2tH8aOJWiiLs8M+eNZi6SJKl12mVG5gLgQOBo4J3A\nuRFxfGNQREwFFgHXl/GLgUURMaUh7pnAF4AtDe1nAycBxwGvA94UEXNHOxlJktQa417IlMXJacCZ\nmbk8M68G5gPvHiT8JGBDZs7LwlnAOuCEhrjzgXsH2f5M4COZuTgzrwfmDbEfSZJUAeNeyAAHUBzi\nWlzX9lPg0EFiDy376t0IHF57EBEvA14GfLI+KCL2APYCftKwn70jYsb2Dl6SJI2fdihk9gAeysxN\ndW1rgF0jYvogsasa2tYAewJExGTgyxSHpzYOsu2Whu3XABNq20uSpGpph0JmKvB4Q1vt8S5Nxtbi\n/hFYlpk/GmI/ZGZ/E/uRJEkV0A5nLW1k60Ki9nhDk7EbImIW8DZg/7J9wiDbEhGT64qZofYzpC1b\ntmyZMKHxqSWNpv7+fpYvXz5s3AEHHMDkyZNbMCJJo2TU/4C2QyHzILB7REzMzM1lWw/Ql5mPDBLb\n09DWA6ymOAtpN+C+iADoAiZERC/wDuD/UnwDe4CVddtuKbdvyoQJE+jt7WNgYPPwwRXV1TWR7u4p\n5tkhqpjnzTffxNnnX8m06TOHjFm3diUXvr+PAw88CKhmntvDPDvLzpInPJnraGuHQuZW4AngMOBn\nZduRwNJBYpdQnGlU7wjgE8DVwL/UtR8GfJNiMfHvM3N9RKwEXgp8u24/KzNzzUgGPDCwmU2bOvsF\nB+bZaaqU58DAZqZNn8mzel4wbFxjTlXKc0eYZ2fZWfIcC+NeyGRmX0QsAC6NiFMpFt6eDZwMUJ5R\n9GhmbgSuBM6LiM8ClwGnU6x9+W5m9gF/msGJiL3K5/913e4uAT4TEQ9SzM6cR3GqtiRJqqB2WOwL\nMBe4CbgOuJjiWi9Xl32rgRMBMnMd8CrgKGAZcAhwbFnENON84ApgYfn5G5n5+dFKQpIktda4z8hA\nMSsDnFJ+NPZNbHi8DDioiee8nmKdTH3bZuB95YckSaq4dpmRkSRJGjELGUmSVFltcWhJkkZq88Am\nMu/+0+OhTmOdNWu215qROpiFjKRKWv/Iai5ftIppSx4bMmbd2pXMnwtz5gy7rE5SRVnISKqsZq41\nI6mzuUZGkiRVloWMJEmqLAsZSZJUWRYykiSpslzsK6ml+vv7WbHi9m3G1J9WLUnbYiEjqaVWrLid\ncy5ayLTpM4eMWXPfUmbsc3ALRyWpqixkJLXccKdNr1v7QAtHI6nKXCMjSZIqy0JGkiRVloWMJEmq\nLAsZSZJUWRYykiSpsjxrSVLH2jywqalr0syaNZvJkye3YESSRpuFjKSOtf6R1Vy+aBXTljw2ZMy6\ntSuZPxfmzDmohSOTNFosZCR1tOGuWSOp2lwjI0mSKstCRpIkVZaFjCRJqiwLGUmSVFkWMpIkqbI8\na0nSTs1rzUjVZiEjaafmtWakamuLQiYidgG+BBwPbAAuzMyLhoidA1wCzAbuAM7IzJvLvonAp4CT\nganAD4H3ZObvy/6XADcDW4AJ5VMuy8xDxig1SRXgtWak6mqXNTIXAAcCRwPvBM6NiOMbgyJiKrAI\nuL6MXwwsiogpZcgHgBOB1wOHAn8GfLPuKfYDbgF66j6OGf10JElSK4z7jExZnJwGHJOZy4HlETEf\neDewsCH8JGBDZs4rH58VEa8ETgAWUBRm783MG8vn/gLwnbrt9wXuysw/jFlCkiSpZca9kAEOoBjH\n4rq2nwIfHCT20LKv3o3A4cCCzPx4rTEing28FfhxXex+wPJRGLMkSWoD7VDI7AE8lJmb6trWALtG\nxPTMXNsQe0fD9muAWfUNEfFR4B+BPwJH1HXtC0yMiNuAZwLXAO/PzHWjkYgkSWqtdihkpgKPN7TV\nHu/SZGxj3ALgP4BzgGsjYj9gI/A84FfAW4DdgM+Vsa8dyYC7utpladHYqOVnnp2h3fJsl3GMVFfX\nRCZNGv+xt9vPc6yYZ+cZqxzboZDZyNaFSO3xhiZjnxKXmfcBRMTJwG+B4zNzQURMB/oyc6Cuf1lE\n9GTm75odcHf3lOGDOoB5dpZ2ybNdxjFS3d1T2G23p4/3MP6kqt/HkTJPDacdCpkHgd0jYmJmbi7b\neigKjkcGie1paOsBVgNExN8AN2fmaoDMfDwi7gN2Lx83XijirvLzc4CmC5ne3j4GBjYPH1hRXV0T\n6e6eYp4dot3y7O3tG+8hbJfe3j4efnj9eA+j7X6eY8U8O08t19HWDoXMrcATwGHAz8q2I4Glg8Qu\nAeY1tB0B1Bb5XgB8HfgMQERMA14I3BkR+wI/B2Zn5v1l/Jxy378cyYAHBjazaVNnv+DAPDtNu+RZ\n1Tfrdvn+1bTbeMaKeWo4417IZGZfRCwALo2IU4E9gbMpLmpHRMwAHs3MjcCVwHkR8VngMuB0inUz\n3yuf7ovAR8vFvCspLo53T2b+MCImAPcCX4mI91KskbkUuCwzH21RupIkaRS1y+qiucBNwHXAxcBH\nMvPqsm81xUXuKM8uehVwFLAMOAQ4NjNrc9VfBOZTXPn358Am4Lhy2y3Aq4Fe4AbgKuDact+SJKmC\nxn1GBopZGeCU8qOxb2LD42XAoDc8KYuV+eXHYP0PUlz1V5IkdYB2mZGRJEkaMQsZSZJUWW1xaElS\nZ+jv72fFitu3GZN5d4tGI2lnYCEjqSnNFimXL7qTadNnDhmz5r6lzNjn4NEenqSdlIWMpKasWHE7\n51y0sKki5Vk9LxgyZt3aB8ZieJJ2UhYykpo2bfpMixRJbcXFvpIkqbIsZCRJUmV5aEmShrF5YFNT\nZ1vNmjWbyZMnt2BEkmosZCRpGOsfWc3li1YxbcljQ8asW7uS+XNhzpxBLzwuaYxYyEhSE4Zb6Cxp\nfLhGRpIkVZaFjCRJqiwLGUmSVFkWMpIkqbIsZCRJUmVZyEiSpMqykJEkSZVlISNJkirLQkaSJFWW\nhYwkSaosCxlJklRZ3mtJkkaBd8iWxoeFjCSNAu+QLY0PCxlJGiXeIVtqPdfISJKkymqLGZmI2AX4\nEnA8sAG4MDMvGiJ2DnAJMBu4AzgjM28u+yYCnwJOBqYCPwTek5m/r9v+08CpFEXc5Zk5b6zykiRJ\nY6tdZmQuAA4EjgbeCZwbEcc3BkXEVGARcH0ZvxhYFBFTypAPACcCrwcOBf4M+Gbd9mcDJwHHAa8D\n3hQRc8cmJUmSNNbGvZApi5PTgDMzc3lmXg3MB949SPhJwIbMnJeFs4B1wAll/0TgvZl5YxanD3wB\nOKJu+zOBj2Tm4sy8Hpg3xH4kSVIFjHshAxxAcYhrcV3bTylmVBodWvbVuxE4HCAzP14WQkTEs4G3\nAj8uH+8B7AX8pGE/e0fEjB1PQ5IktVo7FDJ7AA9l5qa6tjXArhExfZDYVQ1ta4A96xsi4qPA7yhm\nY95Xt+2Whu3XABMat5ckSdXQDoXMVODxhrba412ajG2MWwD8BfA/wLUR8YxyWzKzv4n9SJKkCmiH\ns5Y2snUhUXu8ocnYp8Rl5n0AEXEy8FuKs6HuLNsm1xUzQ+1nm7q62qH+Gzu1/MyzM4xWnp3+fWqV\nrq6JTJq0/d9LX7edZWfJE8Yux3YoZB4Edo+IiZm5uWzrAfoy85FBYnsa2nqA1QAR8TfAzZm5GiAz\nH4+I+4Ddy20nlPEr67bdUtu+Wd3dU4YP6gDm2Vl2NM+d5fs01rq7p7Dbbk8flefZGZinhtMOhcyt\nwBPAYcDPyrYjgaWDxC6hONOo3hHAx8uvLwC+DnwGICKmAS8E7szM1RGxEngp8O26/azMzDUjGXBv\nbx8DA5uHD6yorq6JdHdPMc8OMVp59vb2jeKodl69vX08/PD67d7e121n2VnyhCdzHW3jXshkZl9E\nLAAujYhTKRbenk1xUTvKM4oezcyNwJXAeRHxWeAy4HSKtS/fK5/ui8BHI+I2ilmXTwH3ZOYPy/5L\ngM9ERG125jzg/JGOeWBgM5s2dfYLDsyz0+xonp3+Jtsqo/V683XbWXaWPMdCuxyUmwvcBFwHXExx\nrZery77VFBe5IzPXAa8CjgKWAYcAx2Zm7V/FL1Jcg+YS4OfAJoqL39WcD1wBLCw/fyMzPz92aUmS\npLE07jMyUMzKAKeUH419ExseLwMGvXVsZm6hKGTmD9G/meJ07PcN1i9JkqqlXWZkJEmSRsxCRpIk\nVZaFjCRJqiwLGUmSVFkWMpIkqbLa4qwlSeOnv7+fFStuHzYu8+4WjEaSRsZCRtrJrVhxO+dctJBp\n02duM27NfUuZsc/BLRpVZ9o8sKnpgnDWrNlMnjx5jEckVZ+FjCSmTZ/Js3pesM2YdWsfaNFoOtf6\nR1Zz+aJVTFvy2Dbj1q1dyfy5MGfOoJfMklTHQkaSWqiZolFS81zsK0mSKstCRpIkVZaFjCRJqiwL\nGUmSVFkWMpIkqbIsZCRJUmVZyEiSpMqykJEkSZVlISNJkirLQkaSJFWWhYwkSaosCxlJklRZFjKS\nJKmyLGQkSVJlTRrvAUgaO/39/dx22wq6u6fQ29vHwMDmrWIy7x6HkUnS6LCQkTrYihW3c85FC5k2\nfeaQMWvuW8qMfQ5u4agkafRYyEgdbtr0mTyr5wVD9q9b+0ALRyNJo8s1MpIkqbLaYkYmInYBvgQc\nD2wALszMi4aInQNcAswG7gDOyMyb6/rnAe8ApgO/AM7MzLvKvpcANwNbgAnlJssy85CxyEuSJI2t\ndpmRuQA4EDgaeCdwbkQc3xgUEVOBRcD1ZfxiYFFETCn7TwfmAu8CDgJ+A1wTEbuWT7EfcAvQU/dx\nzFglJUmSxta4z8iUxclpwDGZuRxYHhHzgXcDCxvCTwI2ZOa88vFZEfFK4ARgAXAycH5mXlM+9xnA\nw8ARwI+AfYG7MvMPY5yWJElqgXaYkTmAoqBaXNf2U+DQQWIPLfvq3QgcXn59NvDtur7aIaRnlo/3\nA+7ZwfFKkqQ2Me4zMsAewEOZuamubQ2wa0RMz8y1DbF3NGy/BpgFkJk/a+h7G9AF/KR8vC8wMSJu\noyhurgHen5nrRiUTSZLUUu0wIzMVeLyhrfZ4lyZjG+OIiEMp1t7Mz8w/RMQk4HkUxdtbgFMpDjkt\n2JHBS5Kk8dMOMzIb2boQqT3e0GTsU+Ii4nDgB8CizDwXIDM3RcR0oC8zB8q4k4FlEdGTmb9rdsBd\nXe1Q/42dWn7mWX2dnFun6+qayKRJW//8dobXLZhnJxqrHNuhkHkQ2D0iJmZm7frpPRQFxyODxPY0\ntPUAq2sPIuJo4PvAD4E31gdm5mMN295Vfn4O0HQh0909pdnQSjPP6uvk3Dpdd/cUdtvt6dvs3xmY\np4bTDoXMrcATwGFAbY3LkcDSQWKXAPMa2o4APgEQEfsDV1Ocov3GusKIiNgX+DkwOzPvL5vnlPv+\n5UgGPNQ9azpFV9fEbd6bp1PsDHn29vaN9xC0nXp7+3j44fVbte8Mr1swz05Uy3W0jXshk5l9EbEA\nuDQiTgX2pDj76GSAiJgBPJqZG4ErgfMi4rPAZcDpFOtmvls+3ZeBleX2fx4Rtd08CtwN3At8JSLe\nC+wGXApclpmPjmTMAwOb2bSps19wYJ6doNPfGDvZcK/LTn7d1jNPDaddDsrNBW4CrgMuBj6SmVeX\nfauBEwHKs4teBRwFLAMOAY4ti6EZFLM6+1EUM6vqPk7MzC3Aq4Fe4AbgKuDact+SJKmCxn1GBopZ\nGeCU8qOxb2LD42UUV+1tjFtDcar1tvbzIPD6HRqsJElqG+0yIyNJkjRiFjKSJKmyLGQkSVJlWchI\nkqTKspCRJEmVZSEjSZIqy0JGkiRVloWMJEmqLAsZSZJUWRYykiSpsixkJElSZVnISJKkyrKQkSRJ\nlWUhI0mSKstCRpIkVZaFjCRJqiwLGUmSVFkWMpIkqbImjfcAJG2f/v5+Vqy4fZsxmXe3aDSSND4s\nZKSKWrHids65aCHTps8cMmbNfUuZsc/BLRyVRsPmgU1DFqFdXRPp7p5Cb28fL3rRLCZPntzi0Unt\nxUJGqrBp02fyrJ4XDNm/bu0DLRyNRsv6R1Zz+aJVTFvy2JAx69auZP7czcyZc1ALRya1HwsZSWpD\nwxWpkgpNL/aNiO9GRPdYDkaSJGkkRjIj8zrg3UBvrSEibgdemZnOX0tSC21rHU29WbNmu45GHW0k\nhcyEQdqeCzxtdIYiSWpW8+tocB2NOpprZCSpolxHI3lBPEmSVGEjmZHZUn4M1r5DImIX4EvA8cAG\n4MLMvGiI2DnAJcBs4A7gjMy8ua5/HvAOYDrwC+DMzLyrrv/TwKkURdzlmTlvR8cvSZLGx0jXyFwV\nEf11bVOAb0dEX31gZr58hOO4ADgQOJpi3c2CiPhNZi6sD4qIqcAi4JvAycAZwKKI2Ccz+yLidGAu\n8BbgXmAecE1EvCgzN0bE2cBJwHHAZOBbEbFmqKJJkiS1t5EUMt8YpO2bOzqAsjg5DTgmM5cDyyNi\nPsUZUgsbwk8CNtTNopwVEa8ETgAWUBQ352fmNeVznwE8DBwB/Ag4E/hwZi4u++cBHwcsZCRJqqCm\nC5nMPGWMxnBAOY7FdW0/BT44SOyhZV+9G4HDKQqZs4Hf1PVtoZhJemZE7AHsBfykYT97R8SMzFyz\nAzlIkqRxsF1nLUXE04AXAM8EHgHuycyB7RzDHsBDmbmprm0NsGtETM/MtQ2xdzRsvwaYBZCZP2vo\nexvQRVGw7ElR2Kxq2HZC2WchI0lSxYyokImIPYFPUSzKnVLXtT4ivgt8JDNXj3AMU4HHG9pqj3dp\nMrYxjog4lGLtzfzM/H1EvBAgM/sbth1sP9vU1dXZJ3vV8jPP9lbVcau1uromMmlS9V4rVf/9bNbO\nkieMXY5NFzIRsTfF4Z9NwIXA7RSzMc8E/gJ4M/DXEXFIZq4a8om2tpGtC4na4w1Nxj4lLiIOB34A\nLMrMc+u2JSIm1xUzQ+1nm7q7pwwf1AHMs71Vddxqre7uKey229PHexjbbWd5ne8seY6FkczIfAK4\nn2JRbm9D379FxKcozih6P/DeETzvg8DuETExMzeXbT1AX2Y+MkhsT0NbD/CnWaCIOBr4PvBD4I0N\n29biV9Z9vaV++2b09vYxMLB5+MCK6uqaSHf3FPNsc729fcMHaafX29vHww+vH+9hjFjVfz+btbPk\nCU/mOtpGUsi8AnjTIEUMAJm5LiI+AVzGyAqZW4EngMOA2hqXI4Glg8QuoTilut4RFEUWEbE/cDVF\nQfXGusKIzFwdEQ8ALwW+XbeflSNd6DswsJlNmzr7BQfm2e46/U1Po6Oqr++aqo+/WTtLnmNhJIXM\n7sCvhom5i2JBbtPK678sAC6NiFMpFt6eTXEqNRExA3g0MzcCVwLnRcRnKQqm0ynWzXy3fLovU8y2\nnA38eUTUdlPb/hLgMxHxIMUi3/OA80cyXkmS1D5GsvJmEuU6k23oZ/vOhJoL3ARcB1xMsWj46rJv\nNXAiFLM+wKuAo4BlwCHAsWUxNINiVmc/imJmVd3HieVznQ9cQXF9miuAb2Tm57djvJIkqQ2MtOjY\n4dsRDCYz+4BTyo/GvokNj5cBW93KtTw81DXMfjYD7ys/JElSxY20kPlC4+0IGrjsWpIktcxICpkb\n2PqMoaHiJEnjbPPAJjLvHjZu1qzZTJ48uQUjkkbfSG5RcHRE7AW8huJCcj/IzN+O2cgkSTtk/SOr\nuXzRKqYteWzImHVrVzJ/LsyZs9URe6kSRnJBvCOBayjOEgJ4LCJen5n/PSYjkyTtsGnTZ/KsnheM\n9zCkMTOSs5Y+TnEH6edQHGL6Id41WpIkjaORFDJzgA9k5urM/D3FRe/2jYhpYzM0SZKkbRtJIfMM\n4E93os7MBymuG/Nnoz0oSZKkZoykkJnA1teR2cQw126RJEkaK51/33BJktSxRnpBvLMjov42qk8D\nzoyIP9YHZebHdnhkkiRJwxhJIbOSJ+9ZVLMaOK6hbQtgISNJksbcSC6I99wxHIckSdKIuUZGkiRV\nloWMJEmqrJEu9pXUAv39/axYcfs2Y5q5GaAkdToLGakNrVhxO+dctJBp02cOGbPmvqXM2OfgFo5K\nktqPhYzUpoa72d+6tQ+0cDSS1J5cIyNJkirLQkaSJFWWhYwkSaosCxlJklRZFjKSJKmyPGtJajGv\nEaN2snlgU1Ovt1mzZjN58uQWjEgaGQsZqcW8RozayfpHVnP5olVMW/LYkDHr1q5k/lyYM+egFo5M\nao6FjDQOvEaM2slwr0epnblGRpIkVZaFjCRJqqy2OLQUEbsAXwKOBzYAF2bmRUPEzgEuAWYDdwBn\nZObNg8R9CHh+Zp5S1/YS4GZgCzChbF6WmYeMYjqSJKlF2mVG5gLgQOBo4J3AuRFxfGNQREwFFgHX\nl/GLgUURMaUh7g3ARykKlnr7AbcAPXUfx4xiHpIkqYXGfUamLE5OA47JzOXA8oiYD7wbWNgQfhKw\nITPnlY/PiohXAicACyKiC/gn4O+AXw6yu32BuzLzD2OQiiRJarF2mJE5gKKgWlzX9lPg0EFiDy37\n6t0IHF5+/Qxg/zJuySDb7wfcsyODlSRJ7WPcZ2SAPYCHMnNTXdsaYNeImJ6Zaxti72jYfg0wCyAz\nHwWOBIiIwfa1LzAxIm4DnglcA7w/M9eNRiKSJKm12qGQmQo83tBWe7xLk7GNcVuJiEnA84BfAW8B\ndgM+BywAXjuSAXd1tcNE1tip5WeeY7tfqUq6uiYyaVLrXru+D3WescqxHQqZjWxdiNQeb2gytjFu\nK5m5KSKmA32ZOQAQEScDyyKiJzN/1+yAu7unDB/UAcyzM/YnjYbu7insttvTx2W/O4OdJc+x0A6F\nzIPA7hExMTM3l209FAXHI4PE9jS09QCrm9lRZjZeg/uu8vNzgKYLmd7ePgYGNg8fWFFdXRPp7p5i\nnmOkt7evZfuSRktvbx8PP7y+Zfvzfajz1HIdbe1QyNwKPAEcBvysbDsSWDpI7BJgXkPbEcAnhttJ\nROwL/ByYnZn3l81zyn0PdobTkAYGNrNpU2e/4MA8x3J/UtWM1/uB70MazrgXMpnZFxELgEsj4lRg\nT+Bs4GSAiJgBPJqZG4ErgfMi4rPAZcDpFOtmvtvEru4G7gW+EhHvpVgjcylwWblIWJIkVUy7rC6a\nC9wEXAdcDHwkM68u+1YDJwKUZxe9CjgKWAYcAhybmcPO1WfmFuDVQC9wA3AVcG25b0mSVEHjPiMD\nxawMcEr50dg3seHxMmDYe8nX35qgru1B4PXbP1JJktRO2mVGRpIkacQsZCRJUmVZyEiSpMqykJEk\nSZVlISNJkirLQkaSJFWWhYwkSaosCxlJklRZFjKSJKmyLGQkSVJlWchIkqTKspCRJEmV1RY3jZQ6\nRX9/PytW3L7NmMy7WzQaSep8FjLSKFqx4nbOuWgh06bPHDJmzX1LmbHPwS0clSR1LgsZaZRNmz6T\nZ/W8YMj+dWsfaOFoJKmzuUZGkiRVljMykqRt2jywqam1XbNmzWby5MktGJH0JAsZSdI2rX9kNZcv\nWsW0JY8NGbNu7Urmz4U5cw5q4cgkCxlJUhOGW/sljRfXyEiSpMqykJEkSZVlISNJkirLQkaSJFWW\nhYwkSaosCxlJklRZFjKSJKmyLGQkSVJltcUF8SJiF+BLwPHABuDCzLxoiNg5wCXAbOAO4IzMvHmQ\nuA8Bz8/MUxraPw2cSlHEXZ6Z80YzF0mS1DrtMiNzAXAgcDTwTuDciDi+MSgipgKLgOvL+MXAooiY\n0hD3BuCjwJaG9rOBk4DjgNcBb4qIuaOciyRJapFxn5Epi5PTgGMyczmwPCLmA+8GFjaEnwRsqJtF\nOSsiXgmcACyIiC7gn4C/A345yO7OBD6cmYvLfc8DPg4MOvsjSZLaWzvMyBxAUVAtrmv7KXDoILGH\nln31bgQOL79+BrB/GbekPigi9gD2An7SsJ+9I2LG9g5ekiSNn3YoZPYAHsrMTXVta4BdI2L6ILGr\nGtrWAHsCZOajmXlkZt4xxH62NGy/BphQ216SJFXLuB9aAqYCjze01R7v0mRsY9xQ+yEz+5vYzzZ1\ndbVD/Td2avmZ51P19/dzxx23bzPm3ntzh8clVdHmgU3ce28O+/u0//6zmTx58rDP5/tQ5xmrHNuh\nkNnI1oVE7fGGJmMb44baDxExua6YGWo/29TdPWX4oA5gnk+1dOmdnH3+lUybPnPImDX3LWXGPgeP\n1tCkylj/yGq+8v1VTPvZuiFj1q1dyVc+PoWDD27+d8T3IQ2nHQqZB4HdI2JiZm4u23qAvsx8ZJDY\nnoa2HmB1k/upxa+s+3pLk9v/SW9vHwMDm4cPrKiurol0d08xzwa9vX1Mmz6TZ/W8YMiYdWsfGM0h\nSpUy3O8HFL9HDz+8ftjn8n2o89RyHW3tUMjcCjwBHAb8rGw7Elg6SOwSoPG6L0cAnxhuJ5m5OiIe\nAF4KfLtuPyszc81IBjwwsJlNmzr7BQfmOVicpB0z0vcV34c0nHEvZDKzLyIWAJdGxKkUC2/PBk4G\nKM8oejQzNwJXAudFxGeBy4DTKda+fLfJ3V0CfCYiHqRY5HsecP5o5iNJklqnXVYXzQVuAq4DLgY+\nkplXl32rgRMBMnMd8CrgKGAZcAhwbGb2Nbmf84ErKK5PcwXwjcz8/GglIUmSWmvcZ2SgmJUBTik/\nGvsmNjyD1ZbmAAAYiUlEQVReBhzUxHMO9lybgfeVH5IkqeLaZUZGkiRpxCxkJElSZVnISJKkyrKQ\nkSRJlWUhI0mSKqstzlqSxlt/fz8rVmz7PkqZd7doNJKkZlnISMCKFbdzzkULvY+SJFWMhYxU8j5K\nklQ9rpGRJEmVZSEjSZIqy0JGkiRVloWMJEmqLAsZSZJUWRYykiSpsixkJElSZVnISJKkyvKCeJKk\nltg8sKmpW33MmjWbSZN2bcGI1AksZCRJLbH+kdVcvmgV05Y8NmTMurUrmT8XDj7Y24GoORYykqSW\nGe5WINJIuUZGkiRVloWMJEmqLAsZSZJUWRYykiSpslzsq47X39/PihW3b9Xe1TWR7u4p9Pb2NXVK\nqCSp/VjIqOOtWHE751y0kGnTZw4Zs+a+pczYx9M9JalqLGS0UxjulM91ax9o4WgkSaOlLQqZiNgF\n+BJwPLABuDAzLxoidg5wCTAbuAM4IzNvrut/A/BxYA/gv4C3Zebasu8lwM3AFmBCucmyzDxkLPKS\nJEljq10W+14AHAgcDbwTODcijm8MioipwCLg+jJ+MbAoIqaU/YcAXwXOBQ4FdgO+XvcU+wG3AD11\nH8eMRUKSJGnsjfuMTFmcnAYck5nLgeURMR94N7CwIfwkYENmzisfnxURrwROABYA7wKuyMxvlc/9\nZuD+iNg7M+8H9gXuysw/jHlikiRpzLXDjMwBFAXV4rq2n1LMqDQ6tOyrdyNwePn1YcANtY7M/C2w\nsmyHYkbmnh0fsiRJagfjPiNDsZbloczcVNe2Btg1IqbX1rfUxd7RsP0aYFZd/6pB+vcsv94XmBgR\ntwHPBK4B3p+Z63Y8DUnSjqrdIbv+8ggDA5u3ips1azaTJ08ehxGq3bRDITMVeLyhrfZ4lyZjdxmu\nPyImAc8DfgW8hWL9zOcoDkm9djvHLkkaRSO5Q/acOQe1cGRqV+1QyGxk64Kl9nhDk7EbhuvPzE0R\nMR3oy8wBgIg4GVgWET2Z+btmB9zV1Q5H5MZOLb8q5Nnf388dd2x9sbt6996bLRqNpNHQzB2yu7om\nMmlS+79HDadK77c7aqxybIdC5kFg94iYmJm1+cMeioLjkUFiexraeoDVzfRnZmOJf1f5+TlA04VM\nd/eUZkMrrQp5Ll16J2eff6UXu5N2Mt3dU9htt6eP9zBGTRXeb9tVOxQytwJPUCzI/VnZdiSwdJDY\nJcC8hrYjKK4bU+t/KcXhIiJiL4r1MUsiYl/g58Ds8gwmgDnlvn85kgEPdcy2Uwx3bLqd9Pb2ebE7\naSfU29vHww+vH+9h7LAqvd/uqFquo23cC5nM7IuIBcClEXEqReFxNnAyQETMAB7NzI3AlcB5EfFZ\n4DLgdIp1Md8rn+4S4McRsQRYRrEG5vuZeX9ETADuBb4SEe+lWCNzKXBZZj46kjEPDGxm06bOfsFB\nNfLs9F98SYOrwvvTSHRaPq3ULgfl5gI3AdcBFwMfycyry77VwIkA5dlFrwKOoihUDgGOzcy+sn8J\n8A6KC+L9FFgLnFr2bQFeDfRSnKJ9FXBtuW9JklRB4z4jA8WsDHBK+dHYN7Hh8TJgyKXqmbmA8tDS\nIH0PAq/focFKkqS20RaFjCRJzapda2Y4Xmtm52AhI0mqFK81o3oWMpKkymnmWjPaObTLYl9JkqQR\nc0ZGktRxXEez87CQkSR1HNfR7DwsZCRJHcl1NDsH18hIkqTKspCRJEmV5aElta3+/n5WrLh9mzHN\nLOaTJHUuCxm1rRUrbuecixYybfrMIWPW3LeUGfsc3MJRSZLaiYWMWq6ZmRYoZluGW6y3bu0Dozk0\nSVLFWMio5ZqZaQFnWyRJw7OQ0bho5rRIZ1skScPxrCVJklRZFjKSJKmyLGQkSVJluUZGkqRtaPZM\nS29AOT4sZCRJO6Vm75CdeTeXL7pzm2daegPK8WMhI0naKTVzh2x48lIQ3oCyPVnIaFR5WwFJVeKl\nIKrPQkajytsKSJJayUJGo87bCkiSWsXTryVJUmU5I6Omuf5FktRuLGTUNNe/SNL2G+yfwa6uiXR3\nT6G3t4+Bgc2A16MZKQsZjYjrXyRp+zTzz6DXoxm5tihkImIX4EvA8cAG4MLMvGiI2DnAJcBs4A7g\njMy8ua7/DcDHgT2A/wLelplr6/o/DZxKsT7o8sycNyZJSZLUoJnTvTUybVHIABcABwJHA88FFkTE\nbzJzYX1QREwFFgHfBE4GzgAWRcQ+mdkXEYcAXwXeDiwHLga+Dvxtuf3ZwEnAccBk4FsRsWaooqlT\neHltSRpbzVwluJk1hM1ebdj36yeNeyFTFienAcdk5nJgeUTMB94NLGwIPwnYUDeLclZEvBI4AVgA\nvAu4IjO/VT73m4H7I2LvzLwfOBP4cGYuLvvnUczedHQh08x05qN/+DVv+9u7iXjRoMdswYW8kjSU\nZq4S3Mwawmaex8NPTzXuhQxwAMU4Fte1/RT44CCxh5Z99W4EDqcoZA4Dzqt1ZOZvI2IlcFhE9AN7\nAT9p2M/eETEjM9fsaCLtrJm1LZcvunOHfwklaWc1WmsIR+Pw0840E98OhcwewEOZuamubQ2wa0RM\nr1/fUsbe0bD9GmBWXf+qQfr3LPu2NPSvASaU/S0tZJp5kT3xxBMAPO1pT9uhmGZnUlzIK0ntr9nD\nWMPd6LJ+Jn4ozfyNgfEtiNqhkJkKPN7QVnu8S5OxuzTRPxUgM/ub2M82dXVt+zqCN91yKz9fevM2\nY9b+4Xdcff2dTO1+9pAxf1yd7Pr03UYl5s9nvnib49nw6O8o6rz2iGnHMe3MMe04pk6Naccx7cwx\n7TimP9x/C5/7VT9Tu28ZMqaZ9/2N6x7icwv+a9jnGe5vzIbe3zP3LX/Ni1607zb3d/DBYzOj3w6F\nzEa2LiRqjzc0Gbuhif6NABExua6YGWo/2zKhu3vKNgP+6uVH8FcvP2LYJ+rohTmSJLVAO9yi4EFg\n94ioH0sP0JeZjwwS29PQ1gOsbqL/QYrDSD0NfVvqtpckSRXSDoXMrcATFAt1a44Elg4SuwT4Xw1t\nR/DkQuElwEtrHRGxF8X6l8WZuRpYWd9f7mdlpy/0lSSpU437oaXy+i8LgEsj4lSKwuNsiuvEEBEz\ngEczcyNwJXBeRHwWuAw4nWLty/fKp7sE+HFELAGWAZ8Dvp+ZK+v6PxMRtdmZ84DzW5CmJEkaA+0w\nIwMwF7gJuI7iInYfycyry77VwIkAmbkOeBVwFEWhcghwbGb2lf1LgHcA51KcWr2W4iq+NecDV1Bc\nn+YK4BuZ+fkxzUySJI2ZCVu2DL9iW5IkqR21y4yMJEnSiFnISJKkyrKQkSRJlWUhI0mSKstCRpIk\nVda4X0emHUTEycDXKK7yO6Hu8+bMnBQRM4FLgZdRXCH4Q5n5vbrt/wr4LLAPxcX53paZv25tFsPb\nRp5bKO4efnJdW811mflX5fZVz7P28zySIo8XAfcA78/MH9Vt3yl5HkRxOYPZwO3AezPz53XbVyJP\ngIjYk+I6UEdRXFbh87VLJ0TEc4GvAIcDv6HI89q6bTsiz7qY5wO3ZebUhvaOyDMiDgMuBF4M/Ba4\nIDMvr9u2U/I8BvgM8EIggQ9k5g/rtu2IPOtiuoE7gQ9m5oK69h3O0xmZwr9S3K5gj/Lz3sAvgc9F\nRBewiOJeTS8BLgD+JSL2gz9dPfgq4HLgL4CHgH9vdQJNGirPzwJnNvQdTpFz7ZduJtXP83MR8efA\nfwDfBvanuJji1RHx/0DH/Dxref4PsBw4CPgucG35hlO1PKH4Oa0DDgTOAj4ZEceVfVdT3NX+IOBf\ngKs6NM9aPv9Jwz3lOiXP8gKoP6C4pthLgI8CF0fEsVC59yEYOs/nUVzP7J+B/Sj+kfz3Mr+O+Xk2\nxMyneK/6k9HK0+vIDCIiPgCcAswCjgW+DuyVmevL/oXADzLzqxHxf4AjM/PlZd8U4HfA32bmDeMx\n/mbV55mZTzT0/RewOjPfUj7uiDyBvwEuy8xn1/U/BLw9Mxd2UJ5/T3FxyBdm5pay/wfALZn5oYj4\nGPDSKuQZEc8C/gjsn5l3lm1XUhQvV1EUMs8ur/5NRFwL/CQzP9YpeWbmmRHxGuDLFHm/ODO76rat\nzOt2mJ/nCuDMzJxVF38p8PTMfHOn/DwprlL/msycWxe/FnhHZl7ZKT/PzDyzfPxSiqLt6RQzTwvK\n9lHJ0xmZBhGxG3AOMK/84/4y4Ee1IgYgM4/PzK+WDw8Dbqjr6wNuppjRaFuD5Fnf9wqKe1J9sK65\nU/JcC0yPiNeW/a8BngHcVm7SKXn+v8BNtSKmdBtP5nEo1cmzD1gPnBIRkyIiKO6xdgvFz+vmWhFT\n+imdlefNZf8rgQ9R/MfbqEqv223leQ1FMd7omeXnjvh5ZuYNtSKm7DsNmAzUDv12ys+TiJhMcUuh\ndwL9DduOSp4WMlt7J/BgZl5VPt4HeCAizouI30bELQ1TZntQVNj11lDcM6qdNeZZbx7wtcysz6sj\n8szMnwBfAq6MiCeAf6OYjfllGd8ReVKM+TkNMTOB3cuvK5NnZj4OvJvi3mp9wF0UM6JfY/g8OiHP\nr5f9b6/7B6pRR+SZmSsz8xe12Ih4NnASxWFS6JA8azHlIaY+ij/0H8vMB8quTsrzQxT/VP3PIJuP\nSp4WMls7DfhC3eNnUPyH8CyK+zx9k+KP4IFl/1Tg8YbneJyGY9htqDFPACJiH+DlFItE63VEnhHx\nDIri9B+Bg4FPUhyDf2EZ0hF5UhRoh0bEWyOiq1xY+GqK//qgennuS7G26RDgLcDrI+KNDJ9HJ+T5\nhia267g8I2JXitfxKoo/9NB5ef6eYm3Iu4CP1WaK6ZA8I2Jf4O3Ae4fYblTy9KylOhFxMMV/sVfU\nNW8CHsrMM8rHt0Zx1svbKSrQjWz9Td8FeHiMh7vdhsiz5niKdRTZ0N4peZ4DkJmfLB/fWp4l8fcU\nbyYdkWdmroiIt1EUpJcAtwJfBP6yDKlMnuWhztOAPcv//m4pF/N+GPgRML1hk12ADeXXnZLnd4bZ\nvKPyjIinU/xhfD5wRN2hw47Ks7wR8nJgeUTMAt5Dse6rE/L8CMXamX/MzIeG2HxU8nRG5qmOAW7I\nzEfr2lZTnKJbL4G9yq8fpDhjpF5PuV27GizPmr9m8FXjnZLnQRRvHPVuoTjjBzonTzLzGxRrC/bM\nzIPL5t+Un6uU54HAveWbZM0tFIfKhsujE/Lce4j4eh2TZ0RMA/6b4myev8zM++riOiLPiNi3XABb\n706ePPTbCXm+iGKty4URsS4i1lH8zn45IhaVcaOSp4XMUx0K3NjQtgTYPyLqr62yL0/+QVhCsTAW\ngIiYCswp29vVYHnWHDxEX6fkuYriDbLei4DadQs6Is+IODoivpOZWzJzTfn6PZbitFaoVp6rgOdH\nRP0M8r4UP7MlwEERUf9f3Ut5Mo9OyXM4HZFn+Tq9CngucFRm3t2wbUfkSXGY9ysN8X9Bsb4EOiPP\nFRQzai8BDig/VlHM1Ly1jBuVPD209FT7U6yBqfcdim/8lyLiAor/fv+a4lggFKeUvS8izqG4vsO5\nwK8y8/rWDHm7DJYnEbE3MI3iP4NGnZLnV4GfRMTfU0xdH0fxM31J2d8ped4DvCoi3kHx3+37KdZ5\n1S5EVaU8v09xDYqvRsQnKQrPD5QfNwAPAF+PiI9T/IE4mOI4PXROnsPplDzfChwN/C3QG8V1ZQD6\nM/NhOifPa4B/iIjzKK6hcgzwRoqzeKBD8my8sF1EbAJ+n5m1GZdRydMZmad6Ng3H5spjmP+bosK8\nneIY5omZubzsv59iXcmpwC8o/li8lva2VZ6lGRRXh92qr1PyzOLKtsdT/KFbDrwJOLb2n18H5bkK\nOJFi7c9twAuAv8rMDWV/ZfLMzF7gFRRnOPyC4qqvH8vMr2bmZoripQdYRvHH4DWZ+dty247Is4lt\nOyXP4ymuTv2fFP+91z7+rdy2I/LMzAcpipejKdavnQG8vop/V0b4ut3SsO2o5OkF8SRJUmU5IyNJ\nkirLQkaSJFWWhYwkSaosCxlJklRZFjKSJKmyLGQkSVJlWchIkqTKspCRJEmVZSEjSZIqy0JGUmVF\nxN4RsTkijhrl5/1xRPzzCOKfGxFLI2JjRPxrE/FPGXdEfD0irmtiu6si4rhmx7WjIuLMiPhcq/Yn\nbQ9vGimp6sbiPiuvBQZGEP8e4DnAi4E/NrnNliG+HlREvAF4ZmZePYJx7agvAisi4n9l5s9auF+p\naRYykqpuwmg/YWY+MsJNdis2y3tGsE3T446IicDHgXePcFw7JDMHIuJi4DzgZa3ct9QsCxmphSJi\nM/AO4M3AwcCvgdOA2cCHKO7+eg1wcmY+Xm7zvyj+kBwM/AH4PvCB8s7sRMRewPnAX1L8QV0DfCsz\n/6HsPxn4MPCJ8vNewB3AmUP9lx0Rk4FPAq+jmGl4DPgf4J2ZuTYi9i7H/nrgHOAlwGrgU5n5lfI5\nvlY+3UPA3wHPAK4D3paZv6t7jqMz84Zym6e0DTeOJr7ftdwXUdzx/LrMPD4iXgP8A7A/0AWsAD6Y\nmf9dbvdj4NeZeeo2vn/vyczFZezLyu0Gyp/Dkh0Z9yBeR/Gz/Z+63H4NXAIcVe7z98BZFLM784E9\ngZ8Ab87MhyLiZeX2JwCfBmYCPyu/L+dQvCb7gc9n5qfq9v094HMRcVBm3rQdY5fGlGtkpNb7BMUf\nkhcDjwL/SXEr+2Mp/qi8BngrQES8GLgW+AHFH903AAcC/133fP8BTANeAbyQoqg5JyJeXRczk6KA\neiMwB1gPfH0bY5xPcXjl74Dnl59fQVFs1buIYqbgRWUel5TFSM0bKP4AHwn8NXBQmX/NYIdU6tua\nHce2PA/Yg6LY+lBEHAhcCXwLmAUcSlEELIiIof65G+z7942y77XAdymKgh5g8SiNu95xwLWZuamh\n/SPAdyheG7cCC4APluP8G+AQYF5dfFfZ/waK4mcOsBzooyiULwU+ERGzahtk5u+BZeUYpLbjjIzU\nepdn5g8AIuKbwMUU/6nfB9wZEbdS/GECeB/wX5n5mfLxfRHxJuBX5ULRX1D88fpuZj5YxnwhIj5A\nMcvzH2XbJOAdmXl7ud8LgasiYkZmrhlkjL8AvpeZN5aPH4iIa8vnrHdhZi4qn/NDwLuAw4D7y/5H\nyv0OAPeUC2GPrdt+sMMr9W3NjmNbtgAfy8zflOM8AHhXZn65FhARX6CYtZkBPDjIc2zz+xcRfUB/\nZv6h7B+Ncdc7DPjaIO3/mZnfKvf5FeDVFDNLN5dt1/Lka6nmw5l5S9n/I+DQzJxXPj6Pojjan2KW\nquYO4PDtHLs0pixkpNb7Vd3X6wHKIqamD9il/PpA4PkRsa7hObYA+5aHX74IvD4iDqX47//FwLMp\n/vuud3fd14+WnycPNsDM/HZEvKL8w/ZCihmXAG4Y6jkzszciGp/zV2URU7/fQfe5g+MYzi/rnnN5\nRPwxIs4B9qX4nr2k7G78ntUbi+9fs3ooZo0a/bLu6/Xl58bX0rPrHm9h69ffr+vGvbH8Ge7CU/2B\nopiS2o6HlqTWe2IEsRMpDoG8GDig7uMFwLcjYirFoYwPUpwt8zXgCAaZVcjMwfY76ILTiLgU+Ffg\nacDVFIcivjNI6OPDPOdw/Y2e8s/VCMaxTbX1RuVzvgy4h+JQyq3AR4E3NfEcY/H9a9ZmBi+yBhvT\n5mGeq3Gb4eIp991MnNRyzshI7e0OYL/M/NN/zRHxIoo1GP9A8V/+S4AZmflQ2f9nFIdItutsnnL7\ntwMnZuaVde37Ao0zQzuiv/zcXdf2Qso1MmM4jrkUi35PqHvO95Rf7vAZUGM07tXAn+/o2HbAs4FV\n47h/aUgWMlJ7uxC4ISL+CfgnioWzX6SY+r8HeHoZ93cRcSXFotRPUfxuNx4eaDTUH+1eirUtr4mI\nW4CpFNdJOZDibJxRkZmrI+I3wFkRcS+wO8XC4dpi316KQzijPY4HgOMi4gjgt8DLgY+VfcN9z+q1\n8vv383L77R1Ts/1DORC4aju3lcaUh5ak1hrRxdsy8+fAMRSHk24C/h24C/jfmbkpM5dSzDCcWbb/\nM/B/KQ5jHLw9YynPjDmBYsHnbRRnTO0KfADYLyJ23cb2W4Z63iH8f8AzKQ7xXEoxy7S5bhyv385x\nbMs/UhQU3wduoTj9/RSePHOnPpdtGYvv31D+HTgyIuoPLw13xlfTY95WTETsTnF21783sa3UchO2\nbBmLi2JKkkZLeVp4Au/PzIUt3vf7gL/NTC+Ip7bkjIwktblyluf/UMy+tUx5QcLTKS4EKLUlCxlJ\nqoDMXAD8MSKOb+Fu3wn8IDN/0sJ9SiPioSVJklRZzshIkqTKspCRJEmVZSEjSZIqy0JGkiRVloWM\nJEmqLAsZSZJUWRYykiSpsixkJElSZf3/+ZO4JInlD6kAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbbc82fd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Take 10,000 bootstrap replicates of the mean: bs_replicates\n",
"bs_replicates = draw_bs_reps(rainfall, np.mean, 10000)\n",
"\n",
"# Compute and print SEM\n",
"print(np.std(rainfall) / np.sqrt(len(rainfall)))\n",
"\n",
"# Compute and print standard deviation of bootstrap replicates\n",
"print(np.std(bs_replicates))\n",
"\n",
"# Make a histogram of the results\n",
"_ = plt.hist(bs_replicates, bins=50, normed=True)\n",
"_ = plt.xlabel('mean annual rainfall (mm)')\n",
"_ = plt.ylabel('PDF')\n",
"\n",
"# Show the plot\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 779.33772556, 820.76646617])"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Confidence intervals of rainfall data\n",
"np.percentile(bs_replicates, [2.5, 97.5])"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAF9CAYAAAAeKoJ9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3Xu8XGV97/FPsmO4aAIYbEKFaFPxB4SICeVWhKK2B7Ve\naeUgHouAFxBqERSOF8R6Q7kE71AUL7HqQWk81EasVj2KSjSIYtiQnyhoAokRUkICCWxyOX+sNWQY\nZt+SPZc1+/N+vfYre9bzzFrPejJ75jvPetZaE7Zu3YokSVIVTex0AyRJkraXQUaSJFWWQUaSJFWW\nQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFXWpE43ACAidgI+BRwHbAAuzcz5g9Sd\nC1wOzAFuAU7PzJvqys8D3ghMA34GvDkzbyvLng3cBGwFJpRPuTEzD23FfkmSpNbqlhGZS4B5wDHA\nm4ALIuK4xkoRsSuwCPhBWf8GYFFE7FKWnwacDZwBHAz8DrguInYuV3EA8AtgRt3Psa3aKUmS1Fod\nH5Epw8mpwLGZeTNwc0RcBJwJLGyofgKwITPPKx+fFREvAl4JLABOAi7OzOvKdZ8O3AccCXwX2B+4\nLTPvafFuSZKkNuiGEZmDKALVDXXLfgQc1qTuYWVZvR8DR5S/nwN8ua6sdghpt/LxAcCvd7C9kiSp\nS3R8RAbYC7g3MzfVLVsN7BwR0zJzTUPdWxqevxqYDZCZP2koez3QB1xfPt4fmBgRv6IIN9cBb8vM\n9WOyJ5Ikqa26YURmV+DhhmW1xzuNsG5jPSLiMIq5Nxdl5j0RMQn4c4rw9lrgFIpDTgt2pPGSJKlz\numFE5iEeH0RqjzeMsO5j6kXEEcA3gUWZeQFAZm6KiGnAxszcXNY7CbgxImZk5h9G0titW7dunTBh\nwvAVJUlSozH/AO2GIHM3sGdETMzMLeWyGRSBY22TujMals0AVtUeRMQxwDeAbwEn1lfMzAcanntb\n+e9TgREFmQkTJrBu3UY2b94yfOUe1dc3kalTd7Ef7IdH2RcF+2Eb+6JgP2xT64ux1g1B5pfAI8Dh\nQG2Oy1HAkiZ1FwPnNSw7Eng/QEQcCFxLcYr2iXXBiIjYH/gpMCczf18unltu+zejafDmzVvYtGl8\nvyDBfqixH7axLwr2wzb2RcF+aJ2OB5nM3BgRC4ArIuIUYG+Ks49OAoiI6cD9mfkQcA1wYURcBlwJ\nnEYxb+ar5er+BVhePv8pEVHbzP3AMuB24NMR8RZgD+AK4MrMvL/lOypJksZcN0z2heIidj8Hvgd8\nHDg/M68ty1YBxwOUZxe9GDgauBE4FHhhGYamU4zqHEARZlbW/RyfmVuBlwLrgB8CXwe+U25bkiRV\n0IStW7d2ug1Vs/W++x4c10OEkyZNZI89noj9YD/U2BcF+2Eb+6JgP2xT9sWYT/btlhEZSZKkUTPI\nSJKkyjLISJKkyjLISJKkyur46deSNDAwQH//0iHrzJ49h8mTJ7epRZKqwiAjqeP6+5dy7vyFTJk2\ns2n5+jXLuehsmDv34Da3TFK3M8hI6gpTps1k9xn7droZkirGICNphw0MDLBkya1D3k/GQ0OSWsEg\nI2mH3XLLUs65+BoPDUlqO4OMpDHRykNDWzZvInPZkHUc8ZHGJ4OMpK734NpVXLVoJVMWP9C03BEf\nafwyyEga1nCnR99+e7a8DU4GltSMQUbSsIY7PXr1HUuYPuuQNrdKkgwykkZoqBGR9WtWtLk1klTw\nFgWSJKmyHJGR1HLDnXU03BlJkjQYg4yklhvurCPn2EjaXgYZSW3hHBtJreAcGUmSVFkGGUmSVFkG\nGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmS\nVFkGGUmSVFkGGUmSVFmTOt0ASdpRWzZvInPZoOWPPPIIAE94whMGrTN79hwmT5485m2T1FoGGUmV\n9+DaVVy1aCVTFj/QtHz1HUvYdbfpTJk2s2n5+jXLuehsmDv34FY2U1ILGGQk9YQp02ay+4x9m5at\nX7OCKdP2GbRcUnUZZCQxMDBAf//SQcuHOmwjSZ1kkJFEf/9Szp2/cNBDL6vvWML0WYe0uVWSNDyD\njCRg+EMzktSNPP1akiRVlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRV\nlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVVlfcNDIidgI+BRwHbAAuzcz5g9SdC1wOzAFuAU7PzJvq\nys8D3ghMA34GvDkzb6sr/xBwCkWIuyozz2vJTkldZGBggP7+pYOWZy5rY2skaex0RZABLgHmAccA\nTwcWRMTvMnNhfaWI2BVYBHwROAk4HVgUEbMyc2NEnAacDbwWuB04D7guIvbLzIci4hzgBOBlwGTg\nSxGxerDQJPWK/v6lnDt/IVOmzWxavvqOJUyfdUibWyVJO67jQaYMJ6cCx2bmzcDNEXERcCawsKH6\nCcCGulGUsyLiRcArgQUU4ebizLyuXPfpwH3AkcB3gTcD78rMG8ry84D3AQYZ9bwp02ay+4x9m5at\nX7Oiza2RpLHRDXNkDqIIVDfULfsRcFiTuoeVZfV+DBxR/n4O8OW6sq3ABGC3iNgL2Ae4vmE7T4uI\n6dvdekmS1DHdEGT2Au7NzE11y1YDO0fEtCZ1VzYsWw3sDZCZP8nM+vLXA30UgWUvimCzsuG5E2rP\nlyRJ1dLxQ0vArsDDDctqj3caYd3GekTEYRRzby7KzD9GxDMBMnNgBNsZUl9fN+S/zqntv/1QnX6o\nQhs7ra9vIpMm7Vg/Vek10Wr2RcF+2KZVfdANQeYhHh8kao83jLDuY+pFxBHAN4FFmXlB3XOJiMl1\nYWaw7Qxp6tRdRlO9Z9kPhSr0QxXa2ElbNm/irrvuHLKfDjroICZPnjyi9dnf29gXBfuhdbohyNwN\n7BkREzNzS7lsBrAxM9c2qTujYdkMYFXtQUQcA3wD+BZwYsNza/WX1/2+tf75I7Fu3UY2b94yfMUe\n1dc3kalTd7EfKtQP69Zt7HQTutqDa1dx2VdWMmXaPU3L169ZzqVv28i8eQcPuZ4qvSZazb4o2A/b\n1PpirHVDkPkl8AhwOPCTctlRwJImdRdTnFJd70jg/QARcSBwLcUp2ifWBSMyc1VErACew7YJwUcB\nyzNz9WgavHnzFjZtGt8vSLAfaqrQD+P9DXQkhjqrC0b3/1yF10S72BcF+6F1Oh5kyuu/LACuiIhT\nKCbenkNxKjXlGUX3Z+ZDwDXAhRFxGXAlcBrFvJmvlqv7F4rRlnOAp0REbTO1518OfDgi7qaY5Hsh\ncHHr91KSJLVCt8w+Ohv4OfA94OPA+Zl5bVm2CjgeIDPXAy8GjgZuBA4FXliGoekUozoHUISZlXU/\nx5fruhi4muL6NFcDX8jMj7Z87yRJUkt0fEQGilEZ4OTyp7FsYsPjG4HHHaguDw/1DbOdLcBbyx9J\nklRx3TIiI0mSNGoGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmS\nVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFkGGUmSVFmTOt0ASep2WzZvInPZ\nkHVmz57DpEk7t6lFkmoMMpI0jAfXruKqRSuZsviBpuXr1yznorPhkEMOaXPLJBlkJGkEpkybye4z\n9u10MyQ1cI6MJEmqLEdkpB4wMDBAf//SQcuHm98hSVVlkJF6QH//Us6dv5Ap02Y2LV99xxKmz3L+\nhqTeY5CResRQczjWr1nR5tZIUns4R0aSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWW\nQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaS\nJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFXWpE43QNLwBgYG6O9fOmh55rI2tkaSuodBRqqA/v6l\nnDt/IVOmzWxavvqOJUyfdUibWyVJnWeQkSpiyrSZ7D5j36Zl69esaHNrJKk7OEdGkiRVlkFGkiRV\nlkFGkiRVlkFGkiRVVldM9o2InYBPAccBG4BLM3P+IHXnApcDc4BbgNMz86Ym9d4JPCMzT65b9mzg\nJmArMKFcfGNmHjqGuyNJktqkW0ZkLgHmAccAbwIuiIjjGitFxK7AIuAHZf0bgEURsUtDvVcB76EI\nLPUOAH4BzKj7OXYM90OSJLVRx0dkynByKnBsZt4M3BwRFwFnAgsbqp8AbMjM88rHZ0XEi4BXAgsi\nog/4BPAPwG+abG5/4LbMvKcFuyJJktqsG0ZkDqIIVDfULfsRcFiTuoeVZfV+DBxR/v4k4MCy3uIm\nzz8A+PWONFaSJHWPjo/IAHsB92bmprplq4GdI2JaZq5pqHtLw/NXA7MBMvN+4CiAiGi2rf2BiRHx\nK2A34DrgbZm5fix2RNL4tGXzJjKX0dc3kalTd2Hduo1s3rzlMXVmz57D5MmTO9RCqXd1Q5DZFXi4\nYVnt8U4jrNtY73EiYhLw58BvgdcCewAfARYArxhNg/v6umEgq3Nq+28/tK8fxntfd7sH167iqkUr\nmbL4gabl69cs59K3TWTevIPb3LLO8X2iYD9s06o+6IYg8xCPDyK1xxtGWLex3uNk5qaImAZszMzN\nABFxEnBjRMzIzD+MtMFTp+4yfKVxwH4otKMf7OvuN9QtJKD4P9xjjye2sUXdwdduwX5onW4IMncD\ne0bExMysjcXOoAgca5vUndGwbAawaiQbyszGr0u3lf8+FRhxkGk2bDyeDDV8Pp60sx/WrdvY0vWr\n9dat28h99z3Y6Wa0je8TBfthm1pfjLVuCDK/BB4BDgd+Ui47CljSpO5i4LyGZUcC7x9uIxGxP/BT\nYE5m/r5cPLfcdrMznAa1efMWNm0a3y9IsB9q2tEP4/0NsBeM17+X8brfjeyH1ul4kMnMjRGxALgi\nIk4B9gbOAU4CiIjpwP2Z+RBwDXBhRFwGXAmcRjFv5qsj2NQy4Hbg0xHxFoo5MlcAV5aThCVJUsV0\ny+yjs4GfA98DPg6cn5nXlmWrgOMByrOLXgwcDdwIHAq8MDOHHXfPzK3AS4F1wA+BrwPfKbctSZIq\nqOMjMlCMygAnlz+NZRMbHt8IDDv1v/7WBHXL7gb+fvtbKkmSukm3jMhIkiSNmkFGkiRVlkFGkiRV\nlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVlkFGkiRVVldcEE8a7wYGBujvXzpoeeayNrZGkqrDICN1\ngf7+pZw7fyFTps1sWr76jiVMn3VIm1slSd3PICN1iSnTZrL7jH2blq1fs6LNrZGkanCOjCRJqiyD\njCRJqiyDjCRJqqwRB5mI+GpETG1lYyRJkkZjNCMyfwfsXL8gIpZGxD5j2yRJkqSRGU2QmdBk2dOB\nJ4xNUyRJkkbHOTKSJKmyDDKSJKmyRhNktpY/zZZLkiS13Wiu7DsB+HpEDNQt2wX4ckRsrK+Ymc8b\ni8ZJkiQNZTRB5gtNln1xrBoiSZI0WiMOMpl5cisbIkmSNFrbddPIiHgCsC+wG7AW+HVmbh7LhkmS\nJA1nVEEmIvYGPggcRzE/pubBiPgqcH5mrhrD9kmSJA1qxEEmIp4G3ABsAi4FllKMxuwG/AXwGuAF\nEXFoZq5sQVslSZIeYzQjMu8Hfg8cm5nrGsr+LSI+CCwC3ga8ZYzaJ0mSNKjRXEfm+cA7moQYADJz\nPUXYecVYNEySJGk4owkyewK/HabObcBe298cSZKkkRtNkJkEPDRMnQG280woSZKk0RrtvZa8HYEk\nSeoaox09+Vjj7Qga7DJEmSRJ0pgaTZD5ITBjhPUkSaUtmzeRuWzIOrNnz2Hy5MltapHUO0Zzi4Jj\nImIf4OXAw8A3M/OulrVMknrEg2tXcdWilUxZ/EDT8vVrlnPR2TB37sFtbplUfaO5IN5RwHXAruWi\nByLi7zPz2y1pmST1kCnTZrL7jH073Qyp54xmsu/7gO8CT6U4xPQtYH4rGiVJkjQSowkyc4G3Z+aq\nzPwjxdV794+IKa1pmiRJ0tBGE2SeBKypPcjMuymuG/PksW6UJEnSSIwmyEzg8deR2QT0jV1zJEmS\nRm60F8STJEnqGqO9IN45EfFg3eMnAG+OiP+ur5SZ793hlkmSJA1jNEFmOXB8w7JVwMsalm0FDDKS\nJKnlRnNBvKe3sB2SNG555V9p+3mnaknqMK/8K20/g4wkdQGv/CttH89akiRJleWIjNQGAwMD9Pcv\nHbR8uPkRkqTmDDJSG/T3L+Xc+QuZMm1m0/LVdyxh+qxD2twqSao+g4zUJkPNgVi/ZkWbWyNJvcE5\nMpIkqbK6YkQmInYCPgUcB2wALs3M+YPUnQtcDswBbgFOz8ybmtR7J/CMzDy5YfmHgFMoQtxVmXne\nWO6LJElqn24ZkbkEmAccA7wJuCAijmusFBG7AouAH5T1bwAWRcQuDfVeBbyHhptcRsQ5wAkUVyP+\nO+DVEXH2GO+LJElqk46PyJTh5FTg2My8Gbg5Ii4CzgQWNlQ/AdhQN4pyVkS8CHglsCAi+oBPAP8A\n/KbJ5t4MvCszbyi3fR7wPqDp6I8kSepu3TAicxBFoLqhbtmPgMOa1D2sLKv3Y+CI8vcnAQeW9RbX\nV4qIvYB9gOsbtvO0iJi+vY2XJEmd0w1BZi/g3szcVLdsNbBzRExrUndlw7LVwN4AmXl/Zh6VmbcM\nsp2tDc9fDUyoPV+SJFVLxw8tAbsCDzcsqz3eaYR1G+sNth0yc2AE2xlSX1835L/Oqe2//TDyfhjv\nfaUd19c3kUmTqvM68n2iYD9s06o+6IYg8xCPDxK1xxtGWLex3mDbISIm14WZwbYzpKlTdxm+0jhg\nPxRG0g/2lXbU1Km7sMceT+x0M0bN137BfmidbggydwN7RsTEzNxSLpsBbMzMtU3qzmhYNgNYNcLt\n1Oovr/t96wif/6h16zayefOW4Sv2qL6+iUyduov9MIp+WLduY5tapV61bt1G7rvvwU43Y8R8nyjY\nD9vU+mKsdUOQ+SXwCHA48JNy2VHAkiZ1FwON1305Enj/cBvJzFURsQJ4DvDluu0sz8zVo2nw5s1b\n2LRpfL8gwX6oGUk/jPc3MO24qv69VbXdY81+aJ2OB5nM3BgRC4ArIuIUiom35wAnAZRnFN2fmQ8B\n1wAXRsRlwJXAaRRzX746ws1dDnw4Iu6mmOR7IXDxWO6PJElqn26ZfXQ28HPge8DHgfMz89qybBVw\nPEBmrgdeDBwN3AgcCrwwM0c6bn8xcDXF9WmuBr6QmR8dq52QJEnt1fERGShGZYCTy5/GsokNj28E\nDh7BOputawvw1vJHkiRVXLeMyEiSJI2aQUaSJFVWVxxakqpuYGCA/v6lg5ZnLmtjayRp/DDISGOg\nv38p585fyJRpM5uWr75jCdNnHdLmVklS7zPISGNkyrSZ7D5j36Zl69esaHNrJGl8MMhIUpfbsnnT\nsIcnZ8+ew+TJk9vUIql7GGQkqcs9uHYVVy1ayZTFDzQtX79mORedDXPnDntlCqnnGGQkqQKGOnQp\njWeefi1JkirLICNJkirLICNJkirLICNJkirLICNJkirLICNJkirL068lqeK8YJ7GM4OMJFWcF8zT\neGaQkaQe4AXzNF45R0aSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaS\nJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFWWQUaSJFXWpE43QKqCgYEB+vuX\nPmZZX99Epk7dhXXrNpK5rEMtk6TxzSAjjUB//1LOnb+QKdNmNi1ffccSps86pM2tkiQZZKQRmjJt\nJrvP2Ldp2fo1K9rcGkkSGGQkqedt2bxpyMOfs2fPYfLkyW1skTR2DDKS1OMeXLuKqxatZMriBx5X\ntn7Nci46G+bOPbgDLZN2nEFGksaBoQ6NSlXm6deSJKmyDDKSJKmyDDKSJKmyDDKSJKmyDDKSJKmy\nDDKSJKmyDDKSJKmyDDKSJKmyDDKSJKmyDDKSJKmyDDKSJKmyDDKSJKmyuuKmkRGxE/Ap4DhgA3Bp\nZs4fpO5c4HJgDnALcHpm3lRX/irgfcBewH8Cr8/MNWXZs4GbgK3AhPIpN2bmoa3YL1XHwMAA/f1L\nBy3PXNbG1kiSRqorggxwCTAPOAZ4OrAgIn6XmQvrK0XErsAi4IvAScDpwKKImJWZGyPiUOAzwBuA\nm4GPA58HXlKu4gDgF8AL2BZkHmnZXqky+vuXcu78hUyZNrNp+eo7ljB91iFtbpUkaTgdDzJlODkV\nODYzbwZujoiLgDOBhQ3VTwA2ZOZ55eOzIuJFwCuBBcAZwNWZ+aVy3a8Bfh8RT8vM3wP7A7dl5j0t\n3zFVzpRpM9l9xr5Ny9avWdHm1kiSRqIb5sgcRBGobqhb9iPgsCZ1DyvL6v0YOKL8/XDgh7WCzLwL\nWF4uh2JE5tc73mRJktQNOj4iQzGX5d7M3FS3bDWwc0RMq81vqat7S8PzVwOz68pXNinfu/x9f2Bi\nRPwK2A24DnhbZq7f8d2QJEnt1g1BZlfg4YZltcc7jbDuTsOVR8Qk4M+B3wKvBfYAPkJxSOoVo2lw\nX183DGR1Tm3/e6kfemlfpNHq65vIpElj+zfQi+8T28N+2KZVfdANQeYhHh9Yao83jLDuhuHKM3NT\nREwDNmbmZoCIOAm4MSJmZOYfRtrgqVN3GWnVntZL/dBL+yKNxpbNm7jrrjuH/Bs46KCDmDx58nat\n37+tgv3QOt0QZO4G9oyIiZm5pVw2gyJwrG1Sd0bDshnAqpGUZ+YDDWW3lf8+FRhxkFm3biObN28Z\nvmKP6uubyNSpu/RUP6xbt7HTTZA64sG1q7jsKyuZMq35ORDr1yzn0rdtZN68g0e13l58n9ge9sM2\ntb4Ya90QZH5JcQr04cBPymVHAUua1F0MnNew7EiK68bUyp9DcbiIiNiHYn7M4ojYH/gpMKc8gwlg\nbrnt34ymwZs3b2HTpvH9goTe6ofx/gaj8W2oM/Zgx/7We+l9YkfYD63T8SBTXv9lAXBFRJxCETzO\nobhODBExHbg/Mx8CrgEujIjLgCuB0yjmxXytXN3lwPcjYjFwI8UcmG9k5u8jYgJwO/DpiHgLxRyZ\nK4ArM/P+Nu2uJEkaQ90y++hs4OfA9yguYnd+Zl5blq0Cjgcozy56MXA0RVA5FHhhZm4syxcDbwQu\noDhNew1wSlm2FXgpsI7iFO2vA98pty1Jkiqo4yMyUIzKACeXP41lExse3wgMerA2MxdQHlpqUnY3\n8Pc71FhJktQ1umVERpIkadQMMpIkqbIMMpIkqbIMMpIkqbIMMpIkqbIMMpIkqbIMMpIkqbK64joy\nUqsNDAzQ37900PLMZW1sjSRprBhkNC709y/l3PkLmTJtZtPy1XcsYfqsQ9rcKknSjjLIaNwY6sZ4\n69esaHNrJEljwTkykiSpshyRkSQNasvmTcPOIZs9ew6TJ09uU4ukxzLISJIG9eDaVVy1aCVTFj/Q\ntHz9muVcdDbMnTvovXylljLISJKGNNT8MqnTnCMjSZIqyyAjSZIqyyAjSZIqyyAjSZIqy8m+kqTt\nNtjp2X19E5k6dRfWrdvIfvvN9vRstYxBRpK03UZ2evYWT89WyxhkJEk7xNOz1UnOkZEkSZXliIwk\nqWW8xYFazSCjnjAwMEB//9JBy4d7I5XUGt7iQK1mkFFP6O9fyrnzFzJl2sym5avvWML0WYe0uVWS\nwDk0ai2DjHrGUG+W69esaHNrJEnt4GRfSZJUWQYZSZJUWQYZSZJUWQYZSZJUWQYZSZJUWQYZSZJU\nWQYZSZJUWQYZSZJUWV4QT5XgLQgkSc0YZFQJ3oJAktSMQUaV4S0IJEmNDDKSpI7ZsnnTsIeGZ8+e\nw+TJk9vUIlWNQUaS1DEPrl3FVYtWMmXxA03L77/nTl7/kmVE7DfoOgw645tBRl3BybzS+DXcYeOr\nFt06aNBZv2Y5F50Nc+ce3MomqosZZNQVnMwraTBDBR3JIKOu4WReSdJoGWTUFh46ktQKThaWQUZt\n4aEjSa0w3GRh59D0PoOM2sZDR5JawTk045v3WpIkSZVlkJEkSZXloSVJUs9yMnDvM8hIknrWjk4G\nHu6MSzAIdZpBRmNmqD94T6+W1Ck7Mhl4uDMuPSuq87oiyETETsCngOOADcClmTl/kLpzgcuBOcAt\nwOmZeVNd+auA9wF7Af8JvD4z19SVfwg4hWJ+0FWZeV5LdmocGuoP3tOrJXWj4Q49ZS7zrKgu1xVB\nBrgEmAccAzwdWBARv8vMhfWVImJXYBHwReAk4HRgUUTMysyNEXEo8BngDcDNwMeBzwMvKZ9/DnAC\n8DJgMvCliFg9WGjS6A32B+/p1ZK60XCHnvwS1v06HmTKcHIqcGxm3gzcHBEXAWcCCxuqnwBsqBtF\nOSsiXgS8ElgAnAFcnZlfKtf9GuD3EfG0zPw98GbgXZl5Q1l+HsXojUFmBGqHjvr6JjJ16i6sW7eR\nzZu3PFru4SNJVeQ1rqqt40EGOIiiHTfULfsR8I4mdQ8ry+r9GDiCIsgcDlxYK8jMuyJiOXB4RAwA\n+wDXN2znaRExPTNX7+iO9DqvzitJjzXcoam+vokcddThbWzRY42HycrdEGT2Au7NzE11y1YDO0fE\ntPr5LWXdWxqevxqYXVe+skn53mXZ1oby1cCEstwgMwJ+c5GkbYY7NHX/PXdyzl13svfef/aYEeya\nRx55BIAnPOEJg25jqKAxkvvYXbXo1p6erNwNQWZX4OGGZbXHO42w7k4jKN8VIDMHRrCdIfX1ded1\nBC+89GMs/c09g5ZP2ryWs0577Xav//bbk/Vrlg9avuH+P1BkxdGVWW655Z0r7+a2VaV8192mD1r+\n0Pp7ee8n/i+7Tv2TpuX/vSrZ+Yl7DFq+Yd0fOfu1L2C//fZvWr5s2W3M//y3hlz/U2Y+a9D2QfGZ\nNmlS6z/pYraeAAAR+ElEQVTXWvXZ2Q1B5iEeHyRqjzeMsO6GEZQ/BBARk+vCzGDbGcqEqVN3GUX1\n9rno/W9v6fqf//yjOeOMlm5CkjQKxfvyGzvdjI7qhqGFu4E9I6K+LTOAjZm5tkndGQ3LZgCrRlB+\nN8VhpBkNZVvrni9JkiqkG4LML4FHKCbq1hwFLGlSdzHwlw3LjmTbROHFwHNqBRGxD8X8lxsycxWw\nvL683M5yJ/pKklRNHT+0VF7/ZQFwRUScQhE8zqG4TgwRMR24PzMfAq4BLoyIy4ArgdMo5r58rVzd\n5cD3I2IxcCPwEeAbmbm8rvzDEVEbnbkQuLgNuylJklqgG0ZkAM4Gfg58j+Iidudn5rVl2SrgeIDM\nXA+8GDiaIqgcCrwwMzeW5YuBNwIXUJxavYbiKr41FwNXU1yf5mrgC5n50ZbumSRJapkJW7cOPhtb\nkiSpm3XLiIwkSdKoGWQkSVJlGWQkSVJlGWQkSVJlGWQkSVJldfw6Mt0oIvamuObM0RSncH+0dpp2\nRDwd+DTFHbd/B7wlM7/TmZa2TkTsRHGK+xmZ+cNy2dMZYt8j4q+By4BZFBcpfH1m3tnelo+tQfrh\ncOBS4FnAXcAlmXlV3XN6rh+geV/UlU0FbgXekZkL6pb3XF8M8prYB/gX4K8oriL+zsz8Wt1zeq4f\nYNC+OIpiX/cDfg28LTO/W/ecnumLiPhT4GPAcyludfNV4O2ZOTCe3i+H6YeWv186ItPc14D1wDzg\nLOADEfGysuxaijtoHwz8K/D1Mvj0jPLN6SvAAQ1F/5dB9r18I/86cBXwF8C9Zf3KatYP5QUav0lx\nzaNnA+8BPh4RLyzLZ9Jj/QBDviZqLqK4w3z9c8bLa6KP4jXxEMVr4hLgXyPigLK85/oBBu2LpwD/\nDnwZOJDivfTa8oOuF/vi34CdKa4wfwLwEuB9ZdmgnxXjpR/a9X5pkGkQEbsDhwHvz8zfZua/A98C\nnh8RzwX+DHhjFj5EkSBPGXyN1RIR+1Pc6uHPGpY/jyIxD7bvrweWZOZHMvM24GTg6RFxdPtaP3YG\n6wfg5cCqzDy/fH1cDSwATizLX0cP9QMM2Re18ucAzwP+0FDUU30xRD/8LfBU4DWZeXtmXgksYtvt\nVHqqH2DIvjgSeCQz52fm7zLzQoqAV7sFTc/0RUQExUVZX5uZyzLzx8C7gRNH8FnRM++XQ/TDq2nT\n+6VB5vE2Ag8CJ0fEpPI/6UjgFxR/jDeVt0uo+RHF0GGv+CvguxT7NKFu+WEMve+HAY8ebiivtnwT\n1e2bwfrhOoo/tka7lf/2Wj/A4H1BREymuF3Im4CBhucdTm/1xWD98FfAdzPzwdqCzDwuMz9TPuy1\nfoDB+2INMC0iXgEQES8HngT8qizvpb74A/CCzLy3YfluDP9Z0UvvE836YQIwlTa9XzpHpkFmPhwR\nZwKfoDis1Ad8LjM/FxEfoxgqrLea4v5QPSEzr6j9XmS4R+3F0Ps+XHmlDNYP5X27lteV/QnFUOq7\ny0U91Q8w5GsC4J3AzzPzv5qU9VRfDNEPs4A7I+JC4DXAPcB76m6z0lP9AEP+fVwfEZ8CromILRRf\nlk/OzN+UVXqmLzLzfqB+zssE4EyKgDdu3i+H6If/atf7pSMyze1PcZz3UOC1wN9HxIkUN6h8uKHu\nw8BObW1dZwy37+OubyJiZ4pjwyspRiVgHPVDOQfkDcBbBqkyXvriSRTfOnenuBfcFyk+yOeV5eOl\nH4iIJ1EEu3cDhwAfoJgT8cyySi/3xcXAXIpwP57fLy+mmA/zzvqFrXy/dESmQUQ8HzgV2DszHwZ+\nUU7QehdF0p7W8JSdKGZp97qHgCc3LKvf94d4/ItvJ+C+FrerIyLiiRRh9xnAkXVDyOOpH64E3t1k\naL1mvPTFJuDezDy9fPzL8sydNwCnMX76AeA8gMz8QPn4l+VZK/8EnEGP9kVEfBh4M3B8Zt4aEePy\n/bKhH26rW97S90tHZB5vHnB7GWJqfgHMpDitckZD/RkUd+judcPt+7jpm4iYAnyb4myN52bmHXXF\n46IfyrMN/hK4NCLWR8R6ir+Rf4mIRWW1cdEXFPvz64ZlCexT/j5e+gGK98+bG5b9Anha+XvP9UVE\nfJxiVPLVmVk742bcvV8O0g9teb80yDzeSuAZEVE/WrU/cCfFLP2Dy9MOa55TLu91i4F5Q+z74vIx\nABGxK8Uwa0/1TXn89+vA04GjM3NZQ5Vx0Q8U14N4BsUQ8kHlz0rgfIozEWD89MVi4MDytVGzP8W1\nQ2rl46EfoHgNNJ6ivx/F+yf0WF9ExAUUI2//s/66QYyz98vB+qFd75ceWnq8b1BcE+MzEfEBij/C\nt5c/PwRWAJ+PiPcBL6U4DvzazjS1rX7A0Pv+WeCtEXEu8B/ABcBvM/MHHWhrK70OOIbiOgnryusk\nAAxk5n2Mk37IzC1A/TcrImIT8MfMrH2bGhd9QXEtlfOBT0XEJcCxwAso5tjB+OkHgM8A10fEP1Ec\nSngZRX88uyzvmb4oT0F/F/BB4Cd17wUwjt4vh+mHl9KG90tHZBpk5jrg+RSzqX9GcUXC92bmZ8o3\n75dSDH3dSHEu/Msz865OtbfFttZ+Kff9ZQyy75n5e+A4iusk/Ixi4uMr2t3gFtnKtr44juLUwv+g\n+PZZ+/k36Pl+gLrXxHBlPd4X9X8b64G/oRiFWQr8I8UcgZvL8l7uB3hsX/yUYl9fS3GI6dXAC2vf\nxHusL15K8Rn6Lra9D6wCVpbvly9nfLxfNuuH2s8raMP75YStW4d6X5IkSepejshIkqTKMshIkqTK\nMshIkqTKMshIkqTKMshIkqTKMshIkqTKMshIkqTKMshIkqTKMshIkqTKMshIYywivh8Rn+10O3ZU\nRHwyItZFxH0R8ZROt2d7RcR7IuLO4WuOap1Pi4gtEXH0KJ5zckSsjIgHI+JlI6j/mHaX2/uHYZ4z\nMyJuLW++VzkRsVfZ/id1ui2qDoOMNPZeAfxTpxuxIyJiDnA6cDZwUGbe0+Em7Yj6e2WNleUU99H5\nySiecwnwTSCA/xxB/e1p95XAhZm5YZTP6wrlDUf/D8U97qQR8e7X0hjLzLWdbsMYeDLFh+h3MnN5\npxvTbTJzK/DHUT5tD+D6Vt1kNiKeCzwLeGEr1t9GHwfujogPZ+Ydw9bWuGeQ0bgVEZ8D9s/Mw+uW\nzQTuBP4mM78XEa+juJvxvsAW4CbgLZn587L+ncA1wIuApwB/B7wXuDMzTynrjGQdnwCOAI4FHga+\nVNbZUtY5BPggcDjwAPB14JzM3FiWnwu8kWKUIIFLMvPLQ+z7HsD7gZcAe5Ztemdm/iAiTgI+RxFk\n7oiIL9T2pWEdBwIXAkcCTwTuAj6ZmfPL8guA5wDfKfd/T+CnwGm1uyFHxBbgVIq7Ax8JrAUuz8z3\nleXvAU7KzD+r2+5jlg3XjuFExPeBXwMHAc8EzqC4O+8HKP4/n0rR5/8FvCkz10TE0yheJ8dk5g/L\ndSxm22tgIvANiv+TPcu6W4HPRcQFmTlrR9vdxDnAv5Uhq7ZvbwVOA/amuOvwZzPz/XXlrwPOBf4U\n+D5wPXB6fX8PJyKOBS6g6L81wBeAd2fm1vK1fTlwNPBcivB3FkVfXFS263rgNZl5L0Bm3hcR3wXe\nQvG6kYbkoSWNZ58DDomI+jft/wWsKEPMK4CPAR+iOBzwPGBn4NMN6zkDOBN4AcUH9aMi4uUjXMd7\nKT5I5lB8IJ1J8eFORDwd+B7FB92hFLe9/x/AJ8vyD1J8YJ4BHAh8FPhURJzWbKcjYiJFuDiy3MY8\nYCnw7Yg4mGJo/+/K6ofQ5DBZROwCfBu4hyJcHQB8FbgkIp5VV/UoijDzwnJ7f0IR2updAnwW2J/i\n2/g/R8RzyrJmh1ceXTaKdgznVOCysq3foviQfQXwD8Azyn+fD7yzoR31zgJWAX8BvBp4OcWH8XJg\nL2AC8GaK19xYtRuAck7MXwOL6pa9BHg78IZyH84D3hkRtdfVqylCxkeAZwNLgH9usl9DbfeIcps/\nAOYCr6MITufXVTsf+ArFa/OXwALgHRSvvb+leE2f17Dq/wBeOtJ2aHxzREbjVvlN+k6KD53at9QT\nKb5RAtwLnJqZXykfrygn8X68YVXfzMzv1x5ERH3ZmhGu4z8z85Pl77+LiH+i+OD/V4qQUmtLbYTm\nVOAvyw+ws4ATMvNb5fPvLMPZecAVTXb9WIoPnQMz87Zy2ekRcSjwtsw8ISL+u9YHmbm+yTqeSPHB\n/8nafIyI+Odym3OAX5X1JgH/KzPXlXWuAD7csK7P1/XPhRHxtnLff9Rku9vbjuH8MjOvrj2IiJ8B\nX8vMH5eLVkTEd8p11kxoWMetmVn7AP9tRHwbOLIcIVldvi7WlSM6e45Ru2vmAU+gCKQ1s4CHgOXl\n4ayvRcTdFMEKilD15cz8VPn4veXI3+xRbPcfgcWZ+fby8a8j4g0UgbXmPzLzSwAR8WmKgPKOzLyp\nXPYdipBT7xZg74h4ambePYr2aBwyyGi8+wJlkImIuRSjAl8AyMzrI2K/iHgXsB/FoaFn8fiRzNsH\nW/ko1nFbw+P7gcnl7wcCP6+FmHK9PwB+EBF/QTHC8+WIqP8m3QdMjoidMvPhhnUfCNxfF2Jqfkgx\n0jOszLw3Ii4HXl322zMoDi1sLbdds7oWYprsV82yhsfN6uxoO4bzmP/DzPxyRDw/Ii6kONy0H8WI\n2g+HWEez/ditxe2umVH+Wz9v51+BkynCxa0Uo3DX1M3RmQ18sWE9/4/RBZk5NExczsyvN9T5Td3v\nD5b/1s992chjgw8UI1UTKPbLIKMheWhJ490XgH0jYh7FaMyPaxMMyyH4X1F8s/0xxSGfs5usY+Ng\nKx/FOhrDBmz7xv/IEO2v/Q2/kuKDsPZzIPDMJiGmfr3N1jXUth4VEdMpvjWfSjm3g2KUp3Hdzbbf\naDRthLovYKNox3Ae839Yjhz9H4pRjmuBV1EcHhnKiPdjDNtdUwu5j4agzFyTmc+mGN36GnAYcH0Z\nqmsaPwNG8v9VbySvl2Z1tjRZVq+2H8PVkxyR0fiWmcvLiZqvBI6nmCNQcx7w6cw8o7agnDczGmOx\njluBEyNiQm0iZ7mO+RSjO5uAp2XmdXXbeDPF6NLpTdb3K2C3iDggM2+tW/6cclsjcSKwOzCr7nBX\n7bDL9n4YNzMATGlY9sy631891u2IiCdTzCs5PjOvqVu+P9DsMNv2GOv+W1X++xRgRbm+E4Hdy0NH\nN1DMPboSOIHiUOpNFCHnY3XrOWSU27218TnlYdETMvOI0e5EnT+hGJ1auQPr0DhhkJGKUZlPUnw7\n/Wrd8hXAkeXQ//3Ayygm1BIRkzNzYATrHot1fJJiLsIVEXEZxZv8RRSnRq8vRw/eHxHrKa5r8lyK\neSgfGGR93wZupjgc9WaKwxH/SDGKUz9BeKgP1BUU81P+Z0T8iCI0zaf48NlpBPs0UjcAT46IcyjO\nDntB+bOmLF/egnasozh76uUR8QtgV4r+mUdxZtJYGOv+u5liNGVeuW4oDjleEhHrKM4M2gf4K4rD\nR1CcMfXv5Zykr1McVnwVxQgRABExFZhcO6OoiYuBJeX8ni9ShMx3Ucz/GcxIgto8irk9q0dQV+Oc\nh5ak4lTbrcDCzHygbvmZwGqKN/7FFKdYv6Ysq30LHe4Mjx1eR3mRsP9BMU/jJuDLFIc7aqemnkVx\n5sl7Kb4h/2/gXfWn2TasbwvwN8AvgIUUZ6scADwvM5fUVR20XeVIxcUUFy67jeJD+DMUc0hG862+\n2TYeXZaZ/4/i1N5zgH6KM3Pe3YJ2PCozN1GM0B1IMXr1TYpQ8HbggIjYua6do7lgXf1+bU+7h/r/\n2EBxevjz6pZ9lqKvzi+3cTVwHeVZaOUI3vEU82iWUpwN1zhn5qPAz4bY7s0UZ2f9bbmOTwCXZeYH\nh2jzSPrsucC/j6CexIStW8f6gpeSpHaLiL+mCLlPzcwRzXVqso4LKK7RM2tMGze6NsyguO7OnMz8\nzXD1JUdkJKkHZOZ/UYyKnNTptuygf6Q4LdwQoxExyEhS73gd8Nao7k0j/5TiENdbOt0WVYeHliRJ\nUmU5IiNJkirLICNJkirLICNJkirLICNJkirLICNJkirLICNJkirLICNJkirLICNJkirr/wPgyr3N\nUj/qEgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbbc82d68>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Generate 10,000 bootstrap replicates of the variance: bs_replicates\n",
"bs_replicates = draw_bs_reps(rainfall, np.var, 10000)\n",
"\n",
"# Put the variance in units of square centimeters\n",
"bs_replicates = bs_replicates /100\n",
"\n",
"# Make a histogram of the results\n",
"_ = plt.hist(bs_replicates, bins=50, normed=True)\n",
"_ = plt.xlabel('variance of annual rainfall (sq. cm)')\n",
"_ = plt.ylabel('PDF')\n",
"\n",
"# Show the plot\n",
"plt.show()\n"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 115.35526634, 179.50653195])"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Confidence intervals of rainfall data 95% = 97.5 - 2.5 \n",
"np.percentile(bs_replicates, [2.5, 97.5])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Nonparametric inference ** \n",
"● Make no assumptions about the model or probability distribution underlying the data\n",
"\n",
"** Pairs bootstrap for linear regression ** \n",
"● Resample data in pairs \n",
"● Compute slope and intercept from resampled data \n",
"● Each slope and intercept is a bootstrap replicate \n",
"● Compute confidence intervals from percentiles of bootstrap replicates"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def draw_bs_pairs_linreg(x, y, size=1):\n",
" \"\"\"Perform pairs bootstrap for linear regression.\"\"\"\n",
"\n",
" # Set up array of indices to sample from: inds\n",
" inds = np.arange(len(x))\n",
"\n",
" # Initialize replicates: bs_slope reps, bs_intercept_reps\n",
" bs_slope_reps = np.empty(size)\n",
" bs_intercept_reps = np.empty(size)\n",
"\n",
" # Generate replicates\n",
" for i in range(size):\n",
" bs_inds = np.random.choice(inds, len(inds))\n",
" bs_x, bs_y = x[bs_inds], y[bs_inds]\n",
" bs_slope_reps[i], bs_intercept_reps[i] = np.polyfit(bs_x, bs_y, 1)\n",
"\n",
" return bs_slope_reps, bs_intercept_reps"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0.04418571 0.05512004]\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiwAAAF9CAYAAAAnTTMmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3X+UXWV97/F3MiEhwRmJcZWgEDGVfoHItRERqPi7XfaX\nimit1WtVWq1V6y3Y4rVq7YLWawGx0B+iiFJr9bZXQXvFai26RHrJNYjlhlG+RQIESExLDJ0QkgyZ\nyf1jn4GTMz+Sk5yzz3NO3q+1spLZz/7xnO/s2fPJ3s95zrw9e/YgSZJUsvm97oAkSdK+GFgkSVLx\nDCySJKl4BhZJklQ8A4skSSqegUWSJBXPwCJJkopnYJEkScUzsEiSpOIt6HUHmkXEIuBm4O2ZeUNj\n2bHAx4DnA/cD783M/9W0zc8CHwFWAjcBb87Mu+ruuyRJ6p5i7rA0wsrngJOalg0BXwF2Aj8NXAJ8\nJiJOarQfC1wLXAU8C3gA+GK9PZckSd1WRGCJiBOBNcBTW5p+CXgy8PrMvCMzPw5cB/xMo/03gbWZ\n+WeZ+QPgTcBxEfG8mrouSZJqUERgoXrccz1wBjCvdXlmbp9akJlnZ+YnGl+eDtzQ1LYDuKWxH0mS\nNCCKGMOSmVdM/TsimptWAndFxP8AXg/8B/BHmfmlRvvRwMaW3W0GjulebyVJUt1KucMym8dRPeY5\nEvhl4G+Az0fEMxvtS4BdLdvsAhbV1kNJktR1RdxhmcNu4IHM/O3G1/8aEc8F3gK8lWowbms4WQRs\n3d8D7NmzZ8+8efP2vaIkSWpV2y/Q0gPLJmCyZVkCJzf+fT+wvKV9OfC9/T3AvHnzGBvbwcRE62HU\nDUND8xkZWWzNa2TN62fN62fN6zdV87qUHljWAO+NiHmZuaex7ETg7qb2M6dWjoglwGrgA+0cZGJi\nkt27PcHrZM3rZ83rZ83rZ80HV+ljWD5H1ce/ioifjIi3AT8PfLzR/kngORFxfmNulk8Bd2bmt3rT\nXUmS1A0lBpapOylk5jbg56juqqwDfgd4dWbe2mi/BzgbOAf4DtXg3FfU3WFJktRd8/bs2bPvtQbb\nnq1bt3sLsSYLFsxn6dIjsOb1seb1s+b1s+b1a9S8tkG3Jd5hkSRJ2ouBRZIkFc/AIkmSimdgkSRJ\nxTOwSJKk4hlYJElS8QwskiSpeAYWSZJUPAOLJEkqnoFFkiQVz8AiSZKKZ2CRJEnFM7BIkqTiLeh1\nByTpUDc+Ps7o6LpZ21etOpmFCxfW2COpPAYWSeqx0dF1nH/pNQwvWzGtbduWDVx0HqxefUoPeiaV\nw8AiSQUYXraCI5cf3+tuSMVyDIskSSqegUWSJBXPwCJJkornGBZJKtjkxG4yb5+13XcQ6VBhYJGk\ngm1/cBNXXbeR4TUPTWvzHUQ6lBhYJKlwvoNIcgyLJEnqAwYWSZJUPB8JSVIb9mca/QULDq+xR9Kh\nwcAiSW3Yn2n0Tz311B70TBpsBhZJapODYKX6FRVYImIRcDPw9sy8oaVtBPg+8AeZ+emm5T8LfARY\nCdwEvDkz76qv15IkqduKGXTbCCufA06aZZWLgKNbtjkWuBa4CngW8ADwxS52U5Ik9UARd1gi4kTg\ns3O0nwm8CPhRS9NvAmsz888a670J+FFEPK/1Do0k9dJcg3XnmslWUqWIwAI8H7geeB/wcHNDRCwE\nPg68DbiyZbvTgUeDSWbuiIhbgDOal0tSr801WHfz+rUctdKButJciggsmXnF1L8jorX5vcB3M/Of\nZ2g7GtjYsmwzcEyn+yhJB2u2wbrbttzbg95I/aWIwDKbiDgJeAtw8iyrLAF2tSzbBSxq5zhDQ8UM\n5Rl4U7W25vWx5p21rzoODc2fsebdqv/Q0HwWLPB763lev7prXXRgoXoU9IeZ+cAs7TuZHk4WAVvb\nOcjIyOID6JoOhjWvnzXvjH3VcWRk8aPrNK/brfqPjCxm6dIjurLvfuR5PriKDSwRsQL4GeC/RMSl\njcVLgI9FxK9m5i8B9wPLWzZdDnyvnWONje1gYmLyYLus/TA0NJ+RkcXWvEbWvLPGxnbss31sbMe0\nmu9ru4Ppz9at27uy737ieV6/qZrXpdjAAtwHPK1l2beAy4C/bXy9BjhzqjEilgCrgQ+0c6CJiUl2\n7/YEr5M1r58174x9/TKcmJh8dJ3mmnfrl6jf171Zj8FVbGDJzElgffOyiNgN/Htmbmos+iTwexFx\nPvBlqqByZ2Z+q9bOSpKkripxdNKe/W3LzHuAs4FzgO8ARwKv6F7XJElSLxR3hyUzh+ZoWznDsq8B\nJ3S1U5IkqadKvMMiSZK0FwOLJEkqnoFFkiQVz8AiSZKKZ2CRJEnFK+5dQpLUKePj44yOrpu1fdWq\nk1m4cGGNPZJ0oAwskgbW6Og6zr/0GoaXrZjWtm3LBi46D1avPqUHPZPULgOLpIE2vGwFRy4/vtfd\nkHSQHMMiSZKKZ2CRJEnFM7BIkqTiOYZFUl+b651AmbfX3BtJ3WJgkdTX5non0Ob1azlq5ak96JWk\nTjOwSOp7s70TaNuWe3vQG0nd4BgWSZJUPAOLJEkqno+EJKmFA3ml8hhYJKmFA3ml8hhYJGkGDuSV\nyuIYFkmSVDwDiyRJKp6BRZIkFc/AIkmSimdgkSRJxTOwSJKk4hlYJElS8YqahyUiFgE3A2/PzBsa\ny04HPgz8F+A+4JLMvKppm58FPgKsBG4C3pyZd9Xdd0n9ZXJi96yz1jqbrVSeYgJLI6x8DjipadlR\nwFeAvwR+HXgW8KmI2JiZ/xgRK4BrgfcDXwM+AHwReEbN3ZfUZ7Y/uImrrtvI8JqHprU5m61UniIC\nS0ScCHx2hqazgE2Z+f7G13dGxAuB1wL/CPwmsDYz/6yxnzcBP4qI503doZGk2TibrdQ/ShnD8nzg\neuAMYF7T8n8E3jTD+o9v/H0a8GgwycwdwC2N/UiSpAFRxB2WzLxi6t8R0bx8A7Chqe0ngNcAf9hY\ndDSwsWV3m4FjutVXSZJUv1LusOxTRBwOfIEqoHy8sXgJsKtl1V3Aohq7JkmSuqyIOyz7EhFHAP8A\nPA14TmbubDTtZHo4WQRsbWf/Q0N9k9v63lStrXl9Br3mpb2uoaH5M9a8W/0cGprPggVl1aAXBv08\nL1HdtS4+sETEMPBVqrctvzAz1zc13w8sb9lkOfC9do4xMrL4oPqo9lnz+g1qzUt7XSMjix/tU3Pf\nutXPkZHFLF16RFf23Y9KOx/UOUUHloiYR/W25eOA52XmHS2rrAHObFp/CbCa6u3N+21sbAcTE5MH\n11ntl6Gh+YyMLLbmNRr0mo+N7eh1F/YyNraDsbEd02rerX6Oje1g69btXdl3Pxn087xEUzWvS9GB\nheptyy8AXgqMNeZlARjPzK3AJ4Hfi4jzgS9TBZU7M/Nb7RxkYmKS3bs9wetkzes3qDUv7ZfTxMTk\no31qrnm3+jmo39cDZT0GV4kP+/Y0/gCcTfU25y9TDbad+vMFgMy8p7HOOcB3gCOBV9TcX0mS1GXF\n3WHJzKGmf//Cfqz/NeCErnZKUteNj48zOrpu1vZVq05m4cKFNfaofVPT/c/0eMLp/qWDU1xgkXRo\nGh1dx/mXXsPwshXT2rZt2cBF58Hq1af0oGf7z+n+pe4xsEgqxmxT5fcTp/uXuqPEMSySJEl7MbBI\nkqTi+UhIkg4xgzDAWYceA4skHWIGYYCzDj0GFkk6BA3CAGcdWhzDIkmSimdgkSRJxTOwSJKk4hlY\nJElS8QwskiSpeAYWSZJUPAOLJEkqnoFFkiQVz8AiSZKKZ2CRJEnFM7BIkqTiGVgkSVLx/PBDSRpA\n4+PjjI6um7Et8/aaeyMdPAOLJA2g0dF1nH/pNQwvWzGtbfP6tRy18tQe9Eo6cAYWSRpQw8tWcOTy\n46ct37bl3h70Rjo4jmGRJEnFM7BIkqTiGVgkSVLxDCySJKl4BhZJklS8ot4lFBGLgJuBt2fmDY1l\nxwFXAmcAdwPnZubXm7b5WeAjwErgJuDNmXlXvT2XJEndVMwdlkZY+RxwUkvTF4GNwCnAZ4BrI+KY\nxjbHAtcCVwHPAh5orC9JkgZIEYElIk4E1gBPbVn+Iqo7J7+VlQ9R3UU5p7HKm4G1mflnmfkD4E3A\ncRHxvPp6L0mSuq2IwAI8H7ie6rHPvKblpwG3ZObOpmU3Ntabar9hqiEzdwC3NLVLkqQBUMQYlsy8\nYurfEdHcdDTV46Bmm4Fj9rNdkiQNgFLusMxmCbCrZdkuYNF+tkuSpAFQxB2WOewEntCybBHwcFN7\nazhZBGxt5yBDQ6XntsExVWtrXp9+qfm++jc0NJ8FC6avU/rr6rZu1GW2fZasX87zQVJ3rUsPLPcz\n/V1Dy4FNTe3LZ2j/XjsHGRlZfECd04Gz5vUrveb76t/IyGKWLj2i7e0GXTfqMts++8Ghfj4MstID\nyxrg3RGxKDOnHv2cCXy7qf3MqZUjYgmwGvhAOwcZG9vBxMRkB7qrfRkams/IyGJrXqN+qfnY2I59\ntm/dur3t7QZdN+oy2z5L1i/n+SCZqnldSg8s3wLuBa6OiAuBlwGnAm9stH8S+L2IOB/4MlVQuTMz\nv9XOQSYmJtm92xO8Tta8fqXXfF+/ZGbr/6H+y6kbdSn9XJlLP/ddcyvxYd+eqX9k5iTwcqrHPDcD\nrwXOysz7Gu33AGdTzcvyHeBI4BV1d1iSJHVXcXdYMnOo5ev1wAvnWP9rwAnd7pckSeqdEu+wSJIk\n7cXAIkmSimdgkSRJxTOwSJKk4hlYJElS8QwskiSpeAYWSZJUPAOLJEkqnoFFkiQVz8AiSZKKZ2CR\nJEnFK+6zhCRJvTM5sZvM22dtX7XqZBYuXFhjj6SKgUWS9KjtD27iqus2MrzmoWlt27Zs4KLzYPXq\nU3rQMx3qDCySpL0ML1vBkcuP73U3pL04hkWSJBXPwCJJkornIyFJ6lNzDZCda+Cs1I8MLJLUp+Ya\nILt5/VqOWnlqD3oldYeBRZL62GwDZLdtubcHvZG6xzEskiSpeAYWSZJUPAOLJEkq3n4Hloj4+4gY\n6WZnJEmSZtLOHZZXAoc3L4iIdRFxbGe7JEmStLd2Asu8GZYdBxzWma5IkiTNzDEskiSpeAYWSZJU\nvHYmjtvT+DPT8q6JiGOAjwLPA7YAl2XmZY2244ArgTOAu4FzM/Pr3eyPpAM3Pj7O6Oi6GducSl7S\nXNoJLPOAayNivGnZYuCzEbGjecXMfFEnOtfwv4C7gGcCqxrHuzszvwR8CfhX4BTgFY3+nZCZ93Xw\n+JI6ZHR0Hedfeg3Dy1ZMa3MqeUlzaSew/PUMy/6mUx2ZSUQcCZwG/EZm3gncGRFfBV4cEWPAU4HT\nMnMn8KGIeDFwDnBBN/sl6cA5lbykA7HfgSUz39TNjsxiB7AdeFNEvAf4SeA5wB8ApwO3NMLKlBup\nHg9JkqQBckCDbiPisIg4KSLOiIgTI2Ko0x0DyMxdwDuAt1KFlx8AX8nMTwFHAxtbNtkMHNONvkiS\npN5p69OaGwNgPwicTTV+Zcr2iPh74P2ZuamD/QM4EfgH4BLgZODPI+J6YAmwq2XdXcCidg8wNOSb\npeoyVWtrXp9u1Hx8fJzbbpt58CzA059+MgsXLpy1LwdiaGg+CxZM395zqV6zfR96zWtL/equ9X4H\nloh4CnATsBv4MLAOeBB4PPAs4PXAz0fEszOz9c7HAWmMSfkN4JjG3ZbvNULT+4DrgWUtmywCHm73\nOCMji/e9kjrKmtevkzVfu/b7vOviz884eHbblg1ceeFiTj11+gDag+nDyMhili49oqP7VPtm+z6U\nwvNhcLVzh+WPgXuAl2TmWEvbFyLig8B1wO8D53aof88E7miElSnfoxrDcj/Vu4aaLQfavsMzNraD\niYnJA+6k9t/Q0HxGRhZb8xp1o+ZjYztmHTw71b516/YZlx/MMTu9T7Vvtu9Dr3ltqd9UzevSTmB5\nMfC6GcIKAJm5LSL+GPg4nQssG4GnRcSCzNzdWHYi1duc1wDviYhFTYHmTODb7R5kYmKS3bs9wetk\nzevXyZrv6xfCbMc6mF8k3din2lf6z27p/dOBayewPBG4cx/r/IBqMGyn/G/gIuATEfEnwAnAexp/\nbgDuBa6OiAuBlwGnAm/s4PElSVIB2hkxswDYuY91xmlzIO9cGndzXkwVgr5DNXbmgsz8RGZOUoWU\n5cDNwGuBs5w0TpKkwdNuuOjqNPwzyWq+7pfM0rYeeGG9PZIkSXVrN7Bc3joNfwuHZ0uSpI5rJ7Dc\nQPX4ZX/WkyRJ6ph2puZ/QUQcC5xFNUHbVxwvIkmS6tDOxHHPBf6RaoZZgIci4lWZ+U9d6ZkkNUxO\n7KYazjbdbMslDZZ2HgldSDW77FuBCeAvgEuBp3ehX5L0qO0PbuKq6zYyvOahaW2b16/lqJXTZ9WV\nNFjaCSyrgTOmPisoIs4FNkTEcGZu60rvJKlhtpl1t225twe9kVS3duZheRywZeqLzLyfat6VJ3S6\nU5IkSc3aCSzzmD4Py25gqHPdkSRJms7P4ZYkScVrd+K4d0VE88d0Hga8MyJ+3LxSZl5w0D2TJPWF\n8fFxRkfXzdq+atXJLFy4sMYeaRC1E1g2AK9uWbYJeHnLsj2AgUWSDhGjo+s4/9JrGF62Ylrbti0b\nuOg8WL36lB70TIOknYnjjutiPyRJfWy2d3FJneIYFkmSVDwDiyRJKl67g24laU5Ooz+4ZvvezvV9\nnet8AAfkav8ZWCR1lNPoD67ZvrdzfV/nOh8ckKt2GFgkdZzT6A+umb63+/q+OiBXneAYFkmSVDwD\niyRJKp6BRZIkFc/AIkmSimdgkSRJxTOwSJKk4hlYJElS8QwskiSpeAYWSZJUPAOLJEkqXvFT80fE\nQuAjwK8Bu4BPZuZ7G23HAVcCZwB3A+dm5td701NJktQt/XCH5XLgxcDPAa8F3hwRb260fQnYCJwC\nfAa4NiKO6UkvJUlS1xR9hyUilgLnAC/KzO82ll0CnBYRPwSeCpyWmTuBD0XEixvrX9CrPkuSpM4r\nOrAAZwIPZuaNUwsy8yKAiHgPcEsjrEy5kerxkCRJGiClB5aVwN0R8XrgD4CFwKeAPwGOpnoc1Gwz\n4CMhSZIGTOmB5XHATwFvAd5IFVI+BjwMLKEahNtsF7Co3YMMDfXDUJ7BMFVra16fbtTc7586ZWho\nPgsWHPz55LWlfnXXuvTAshsYBn4tM+8DiIinAG8D/glY1rL+Iqow05aRkcUH2U21y5rXr5M19/un\nThkZWczSpUd0dH8aTKUHlk3Azqmw0pBUj33uB1a1rL+8sU1bxsZ2MDExecCd1P4bGprPyMhia16j\nbtR8bGxHR/YjjY3tYOvW7Qe9H68t9ZuqeV1KDyxrgMMj4mmZ+cPGspOo5lxZA7wnIhZl5tSjoTOB\nb7d7kImJSXbv9gSvkzWvXydr7i8EdUqnrwVeWwZX0YElM/8tIq4Dro6It1GNYXk31duWbwDubbRd\nCLwMOJVqrIskSRog/TA66XXAD6nunFwNXJ6Zf5mZk1QhZTlwM9Wkcme1PD6SJEkDoOg7LACZuY3q\nrskbZ2hbD7yw5i5JkqSa9cMdFkmSdIgzsEiSpOIZWCRJUvEMLJIkqXgGFkmSVDwDiyRJKp6BRZIk\nFc/AIkmSimdgkSRJxTOwSJKk4hlYJElS8Yr/LCFJB2d8fJy1a7/P2NgOJiYmp7WvWnUyCxcu7EHP\nJGn/GVikAXfbbet418WfZ3jZimlt27Zs4KLzYPXqU3rQM0nafwYW6RAwvGwFRy4/vtfdkKQD5hgW\nSZJUPAOLJEkqnoFFkiQVz8AiSZKKZ2CRJEnFM7BIkqTiGVgkSVLxnIdFktQTkxO7ybx91nZnYVYz\nA4skqSe2P7iJq67byPCah6a1OQuzWhlYJEk94yzM2l+OYZEkScUzsEiSpOIZWCRJUvH6agxLRFwH\nbM7McxpfHwdcCZwB3A2cm5lf71kHpR4ZHx9ndHTdjG133JE190aSOq9vAktEvAb4BeDqpsVfBG4F\nTgFeAVwbESdk5n3191DqndHRdZx/6TUML1sxrW3z+rUctfLUHvRKkjqnLwJLRCwFLgK+07TsRcBK\n4PTM3Al8KCJeDJwDXNCTjko9NNu7LbZtubcHvZGkzuqLwAJcAnwaeHLTstOAWxphZcqNVI+HJEnS\nACl+0G3jTspzgQtbmo4GNrYs2wwcU0e/JElSfYq+wxIRi4ArgLdl5q6IaG5eAuxq2WQXsKjd4wwN\nFZ/bBsZUra15Zx1MPYeG5rNgwfTtx8fHue02B/Kqd2Y7N2dbt/lvdV/dtS46sAB/BKzNzH+eoW0n\n8ISWZYuAh9s9yMjI4vZ7poNizTvrYOo5MrKYpUuPmLZ87drv866LP+9AXvXMbOfmvrbRYCo9sPwq\ncFREbGt8vQggIl4FfBA4qWX95cCmdg8yNraDiYnJg+mn9tPQ0HxGRhZb8w4bG9txUNtu3bp9xuUO\n5FUvzXZuzsRrS/2mal6X0gPL84HDmr6+CNgDnA8cB/z3iFiUmVOPhs4Evt3uQSYmJtm92xO8Tta8\nsw7mAj3b98KLvnrtQK4TXlsGV9GBJTP3+m9c407Lnsy8KyLuAe4Fro6IC4GXAacCb6y9o5Ikqav6\ndnRSZk4CL6d6DHQz8FrgLCeNkyRp8BR9h6VVZr6p5ev1wAt71B1JklSTvr3DIkmSDh0GFkmSVDwD\niyRJKp6BRZIkFc/AIkmSimdgkSRJxTOwSJKk4hlYJElS8fpq4jhJnTU5sZvM22dsm225JPWCgUU6\nhG1/cBNXXbeR4TUPTWvbvH4tR608tQe9kqTpDCzSIW542QqOXH78tOXbttw7w9qS1BuOYZEkScUz\nsEiSpOIZWCRJUvEMLJIkqXgGFkmSVDwDiyRJKp6BRZIkFc/AIkmSiufEcZKk4sz1sRGPPPIIAIcd\ndtijy4aG5jMyspixsR2ccMIqFi5cWEs/VR8DiySpOPv62Igljz+K4WUrprVt27KBi86bZPXqU+ro\npmpkYJEkFWmuj40YXnbsjG0aXI5hkSRJxTOwSJKk4hlYJElS8QwskiSpeMUPuo2IJwGXAy8EHgb+\nHnhPZo5HxHHAlcAZwN3AuZn59R51VZIkdUk/3GH5AnA48BzgNcBLgQsbbV8CNgKnAJ8Bro2IY3rR\nSUmS1D1F32GJiACeDRyVmQ80lv0hcHFEfBV4KnBaZu4EPhQRLwbOAS7oVZ8lSVLnlX6H5UfAz0+F\nlSaPB04HbmmElSk3Uj0ekiRJA6ToOyyZ+Z/Ao2NSImIe8A7geuBoqsdBzTYDPhKSJGnAlH6HpdXF\nwGrgvcASYFdL+y5gUd2dkiRJ3VX0HZZmEfGnwDuBV2fm9yNiJ/CEltUWUb2TqC1DQ/2W2/rXVK2t\neWdZT+kxQ0PzWbDAn4luq/u60xeBJSL+HPgt4HWZ+cXG4vuBk1pWXQ5sanf/IyOLD66Daps17yzr\nKT1mZGQxS5ce0etuqMOKDywR8QHgLcCvZua1TU1rgHdHxKLMnHo0dCbw7XaPMTa2g4mJyYPvrPap\n+SPgrfl04+Pj3Hbbulnbn/70k1m4cOG05WNjO7rZLamvjI3tYOvW7b3uxsCbup7XpejAEhEnAu8D\nPgj8n4g4qqn5W8C9wNURcSHwMuBU4I3tHmdiYpLdu/3lWSdrPrNbb72V8y+9huFlK6a1bduygYvO\nm2T16lOmtRn+pMd4fRlMRQcWqhAynyq0vK+xbB6wJzOHIuIs4BPAzcAPgbMy876e9FTqkOFlKzhy\n+fG97oYkFaXowJKZfwr86Rztd1JN2S9JkgaYw6glSVLxir7DItVlfHyc0dHZB7uuWjXzYFdJZZmc\n2E3m7bO2d/pn2WtHfQwsEjA6um4fg12ZcbCrpLJsf3ATV123keE1D01r68bPsteO+hhYpAYHu0qD\noe6fZa8d9XAMiyRJKp6BRZIkFc9HQlKfmGsw4VyDDCVV5voZeuSRRwA47LDDZmx38GzvGVikPjHX\nYMLN69dy1MpTe9ArqX/s62doyeOPcvBswQwsUh+ZbXDfti339qA3Uv+Z62doeNmxDp4tmGNYJElS\n8QwskiSpeAYWSZJUPMewSDWbaypv3+0jSTMzsEg1m2sqb9/tI0kzM7BIPeC7fSSpPY5hkSRJxTOw\nSJKk4vlISNoHp/OWpN4zsEj74HTektR7BhZpPzidtyT1lmNYJElS8QwskiSpeD4SkrpktsG6zmYr\nSe0zsEhdMttgXWezlaT2GVikLpppsK6z2UpS+xzDIkmSimdgkSRJxev7R0IRsQj4K+Bs4GHgw5l5\naW97NXgmJyd5+OHts7Y/7nHDMy4fHx9ndHTdo18PDc1nZGQxY2M7mJiYnHUm2Nbtmjm7rKQ6zTXb\n9YEOop/rGgdex2bS94EFuAR4JvAC4Djg0xFxd2Ze08tODZobvv1tLr7yiywZXjatbeyB9Xzqsgt5\n0pOePK1tdHQd5196Tdszwc61nbPLSqrTvma7PpBB9Ad6bTyU9XVgiYglwG8AL8nMW4FbI+Ii4B2A\ngaWDHtm9myOetJrHPeGYaW17hg5ncnJy1m1nmyV2X5xdVlIp5roedXqfmlm/j2F5BlXouqlp2Y3A\nab3pjiRJ6oZ+DyxHAw9k5u6mZZuBwyNi+rMLSZLUl/r6kRCwBNjVsmzq60X7u5OhoX7Pbd03Z43m\nzeP220f58Y8fmNZ0xx3Jti0bZtxs25YN3HHH8Iz7nmu7h//zR8Cetvc5lwM93oG0dXp/ttnW67ZS\n+lFa24Fe47Zt2cDQ0LNZsKDs3011/+6ct2fPzIXuBxHxKuDyzHxS07ITgFFgWWY+2LPOSZKkjik7\nvu3b/cATI6L5dSwHdhhWJEkaHP0eWP4VeAQ4vWnZc4G1vemOJEnqhr5+JAQQER8FngOcAxwDXA28\nITO/1Mt+SZKkzun3QbcA51HNdPsN4D+B9xtWJEkaLH1/h0WSJA2+fh/DIkmSDgEGFkmSVDwDiyRJ\nKp6BRZIkFc/AIkmSitf3b2uOiEVUb2s+G3gY+HBmXjrLuquBjwInA7cBv52ZtzTa5gMfBN5A9RlF\nXwV+JzPlPltsAAAJGklEQVT/vdH+08AtVB8aMa+xy5sz89ldemnF6lTNW9b7FeDvMnN+y/IPUc2x\nMx+4KjPf3cnX0i/qqrnn+WM6WfOIeBAY5rGa7gGGM/PhRrvnOfXV3PP8MR2u+auAPwGeDNwIvCUz\nNzS1H9R5Pgh3WC4Bngm8AHgb8IGIOLt1pYhYAlwHfKux/k3AdRGxuLHKe4BXA68CTgOeAPxN0y5O\nAr5HNfX/1J+XdP7l9IVO1XxqvccDl9PyCWIR8S7gNcDLgVcCr4uI8zr9YvpELTXH87xZR2oeEU+i\n+sW5ksdqenRTWPE8f0wtNcfzvFmnav4zwGeBi4HVwDjwP5u2P+jzvK/vsDQK+BvASzLzVuDWiLgI\neAdwTcvqrwEebkp0vxsRvwj8CvBpqvB2bmb+S2PflwOfa9r+ROAHmfkfXXtBfaDDNZ9yMXAH8BMt\n278TeF9m3tQ49ruBC4EZ0/+gqrnmnud0vOYnApsy855ZDud5Tu019zyn4zV/F/DpzPxEY9/vBL4R\nEU/IzB/TgfO83++wPIMqdN3UtOxGqjskrU5rtDX7F+AMgMy8cGqG3Ij4CeA3gW82rXsS8G+d6XZf\n61jNASLi+cDzqW4j0rT8aOBY4Nstx3lKRBx1oJ3vU7XUvMHzvNLJms9aU8/zvdRS8/1sP1R0suYv\nAK6dasjMuzNzZWb+uFPneb8HlqOBBzJzd9OyzcDhEbFshnU3tizbTPX5Q4+KiD8CfkT1+US/19R0\nIrA6Iv5fRNwTEVdExHAHXkO/6VjNI2Ih8DGq25A7Z9h2T8v2m6meNx/DoaWumoPn+ZROXltOBI6I\niG9GxMaIuC4ijm/a1vO8UlfNp9o9zztU88Yj5qXAYRHx1YjYFBFfbDyam9r2oM/zfg8sS4BdLcum\nvl60n+u2rvdp4FnAPwNfj4jHRcQC4CepkugbqQYNPYe9b7EfKjpZ8z+kGuh2/SzHITPH9+M4g66W\nmnue76WTNT+B6mJ+AfAyYAdwfUQcged5s1pq7nm+l07V/HGNry+jquMvN5Z/uWnbgz7P+z2w7GT6\ni536+uH9XHev9TJzfWPU8xuAxcDZjfS5DDgrM29pXOzfALw8IpYf/MvoKx2peUSsAt4MnNtYPq9l\nvZ3w6B2BfR1n0NVSc8/zvXTy2vIS4Kcz85uZeTPwOuBw4KV4njerpeae53vpVM2n7tBcmZmfzczv\nUtX85Ig4nQ6d5/0eWO4HnhjVW5KnLAd2ZOaDM6zbejIuBzYBRMQvNZ6zAZCZu4D1wBMbXz+UmRNN\n2/6g8feTD/pV9JdO1fyVVP8DWh8R24CvAPMiYiwifq2x7byW7ZdT3Vbc1KkX0yfqqrnn+WM6dm3J\nzEea3p0ydW25i6qmnuePqavmnueP6VTNHwAeAXKqoTHQdgvV2JWOnOf9Hlj+lapIpzctey6wdoZ1\n1wA/07LsOTw22OgS4NenGhrPM38K+H5EnNi4qD+ladvVjWP/8KBeQf/pRM3XUL2l9gSqQV/PoBrk\nvKfx73/IzE3ABuDMluNsyMzNB/8y+kotNfc830vHri0R8cOIaL62HAEcT/UuFc/zx9RSc8/zvXSk\n5o3w912qawkAEfFEqv/w39Wp83zenj2t0zD0l4j4KFXRzqEavHM18IbM/FJj9PF/ZubORgC5g+qt\nyh8H3ko158rTMnNHRLwD+CPg9VSF/SCwPDNPi4h5wM1UafFcqv+lXgF8MzN/p7YXW4hO1bxln88H\nvpGZQ03L3k319rr/SpXOPwNcnJmXdfklFqeOmnue762D15bLqMZRvJHqf6IXUs0Psjoz93ieP6bL\nNf9J4Kcbh/I8b+hgzV8JfKqxn1HgIuCoqcn4OnGe9/sdFoDzqJLdN4A/B94/9fZkqltNrwbIzG1U\nA4GeR3WyPhv4haaL+F9SFfijwP+leib38sa2e6hO/jHgBqq3bn29cexDUadqvi8XA39HNR/A3wF/\nfShexBu6XnPP82k6VfPfBz4P/C3V/1LnA7/UqDd4njfrZs1/MTP3eJ5P05GaZ+YXqALgxTx2h+as\npuMc9Hne93dYJEnS4BuEOyySJGnAGVgkSVLxDCySJKl4BhZJklQ8A4skSSqegUWSJBXPwCJJkopn\nYJEkScUzsEiSpOIt6HUHJB16Gp9j9E3guMzc0Ov+SCqfd1gk9YqfCyJpvxlYJElS8XwkJKlrIuIX\ngAuAk4CHgK9QfaJr63rzgf8G/BbwFOAe4COZ+bFG+9QjpFdSferrcuAm4Hcy8/am/Zzf2MdyIIFL\nMvOz3Xp9kurjHRZJXRERy6g+Sv4TQFB91PxzgYtmWP1S4L3AB4CnA38BXBYR72xZ7xLg7cBpwCPA\nNyNiuHG8D1KFlbc39nEZ8FcR8dbOvjJJveAdFkndcgywELg3M+8D7ouIl1Jdd54wtVIjcPw28LuZ\n+XeNxX8RESuB9wCXN+3zXZn5tcZ2rwPuBV4TEX8L/C7wmsz8amPduyLiqcC7gSu69SIl1WPenj2O\ne5PUHRHxGeC1wCbg68CXgWuBM4FvAE8FjgLWAKsz8/81bftyqjs0y6keKX0DWJaZDzat813gX4BP\nA98BHmbvwbxDVKHpiMzc1Z1XKakOPhKS1DWZ+V+pHgf9KbAM+Azw1ZbV5jX+tJq6Pj3StOyRlnWG\ngImmdX8FeEbTn6cDP2VYkfqfgUVSV0TEsyPi0sy8IzMvz8yXAucALwJ+omnVH1AFkTNbdvE84EfN\nd1SAU5v2/0TgeOC7wO3AbuApmbl+6g/wy8Dvd/q1SaqfY1gkdcsY8PaIGAeuBBYDvwr8G/AAjbsq\nmbktIj4GXBARPwbWAj8PvJVqDMuUeVSDaH+rse9LgPuBz2fmzoi4AvjjiNgG/B/ghVR3dv6k669U\nUtcZWCR1RWbeHhGvoHrnz9uoHt18A/hFYAV7jzX5XeA/gA9RjWm5A3h7Zn6yaZ09wMeBv6EatPvP\nwIsyc2fTPv6d6m3UT6IakPu+zPxwV16gpFo56FZS8RrzsHwDeKpT+UuHJsewSOoXMw3MlXSIMLBI\n6hfeDpYOYT4SkiRJxfMOiyRJKp6BRZIkFc/AIkmSimdgkSRJxTOwSJKk4hlYJElS8QwskiSpeAYW\nSZJUvP8PxOSVcNRjuB8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbbcf3eb8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Generate replicates of slope and intercept using pairs bootstrap\n",
"bs_slope_reps, bs_intercept_reps = draw_bs_pairs_linreg(illiteracy,fertility, size=1000)\n",
"\n",
"# Compute and print 95% CI for slope\n",
"print(np.percentile(bs_slope_reps, [2.5, 97.5]))\n",
"\n",
"# Plot the histogram\n",
"_ = plt.hist(bs_slope_reps, bins=50, normed=True)\n",
"_ = plt.xlabel('slope')\n",
"_ = plt.ylabel('PDF')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAg4AAAF2CAYAAAAGIhAIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XmQXEd+4Pdv5nt1V3V1VVdX3ycaaAAEQBA8QM6tGZ07\nu1LIa4WsXXtXsrTr8P6jiA3vRqz9nyMc4fAfVqwcjg1rtUtb6/VKq2s0Gs6M5tLMcA4Ob5DE0QAa\n6EbfR9131ctM/5ENgBwSGICDJgAyPxEIoJuvql9ldfD9Kt/vEMYYHMdxHMdx7oS83yfgOI7jOM7D\nwwUOjuM4juPcMRc4OI7jOI5zx1zg4DiO4zjOHXOBg+M4juM4d8wFDo7jOI7j3DEXODiO4ziOc8dc\n4OA4juM4zh3z7/cJ/LR2dmq37WAlpSCbTVAsNtDaNbvaL26d959b4w+GW+f959Z4/93pGg8OpsRd\nP/dPdWYPASkFQgikvOu1ce6CW+f959b4g+HWef+5Nd5/+7nGH/rAwXEcx3Gce8cFDo7jOI7j3DEX\nODiO4ziOc8dc4OA4juM4zh176KsqHMdxHMd5G6UQm+vQTEK8/54/vdtxcBzHcZwPA2MQOzt4y1cx\n6TSMje3Lj3E7Do7jOI7zkBPVCnJnG53Jombn8P392xdwgYPjOI7jPKxaLeTGOsTjqJkDIPf/RoIL\nHBzHcRznYdPrITc3wBj0xCSEQu8+Jgj25Ue7wMFxHMdxHhZaI3e2odFAD49APP7uYzod5OomjOQg\nkrrnp+ACB8dxHMd5CIhSEVksoHODmKHhdx+gNXJ7C1ot9MQ49Cegpe75ebjAwXEcx3EeZPU63vYm\nOtmHmp0D8e75EzeCisE8JpnCX1uF0Bh4sXt+Oi5wcBzHcZwHUbdrEx99HzU5Df57XLKbTeTmBiaR\nRI1NILc2Eb6P7s9AoQD58Xt+Wi5wcBzHcZwHiVL2lkO7jR4ZhWj03ccEgU2O1Bo9OoYsFhCbG+j+\nDP7iJbxuGx5/dF9OzwUOjuM4jvMgMAZRKCArJXR+CDMy+t7H7O4iaxVUfhjRbuOtr6IHcohSidDS\nFdTwCJ5WUK26zpGO4ziO82EkalW8K5dBCNTsHCbV9+5j6jV7jCfRuUG8rQ0QAmPAf/VlhNHoZB+y\nVkMdPQpHjuzLubodB8dxHMe5X9ptm8cQjaKmZ8Hz3n3M9VyHUAg1NGLLMWMxTCSK/+YZVH8GnR1A\n1Os26BgcJNSowvo6xNL3/JRd4OA4juM4H7TrOQpKocfGIRx+9zFvL68czCPLJVs5EYvjX74I4TAq\nl0NWKqipGczoKDSbeFcXIZ2GqWmotO75qbvAwXEcx3E+KHuDqGS9ihoagUTiPQ8T5RKysIvODYKQ\neNubqL40/pVFZK+HzmSR5TLEEwSHj9qEypVrNyowRDS8b+2nXeDgOI7jOB+AG8FAdsD2Y3gve7Mn\nTCJpg4PdHXQqDfU6/rVrqMFBvEoFpCR44knwPOTWJgSB7SQZidjnqdehW4dw8p6/Dhc4OI7jOM5+\nenuvhVsNonp7eWV2AFksYOJxTC/AP/sGKpeHWBzZCwgefQxiMbtz0aih8sOQ3AsQWi3byyEWhelR\n6N37l+MCB8dxHMfZD92uDQaEuPUgquslmNUyKpNF1mrIWhUD+BfOofv70ak0st1Czc9j+jOIYgG5\nuY4eyKGG5m7+rK1NMAaTTCGKO7CqYWjinr8sFzg4juM4zr309qTG4RGIvXfbZ1GvIbe30Kk0JhZH\nlssY38dfuoKOxtHpDKLdRs0cwOTziEYd78pldCp9s/V0ENif1e2ikylkYRdvdwcGczA6Cvd+VMX9\nDxzm5+f/MfAsYADxtr/1wsLCfT8/x3Ecx7lTolhAlop2ZsTwyHsfdL280vPQqT5ktYyORPH2dgxU\nXxrZaKCHh1GjY3aE9tJViERQUzO2ZFNrxPY2slFD9/UhWi38lWV0qg81PoF37g24eBZ+4e/d89f4\nIFyY/xj4ytu+DgPfAr54f07HcRzHedhUm12efe48y1s1poZS/Nbnj9AXf48Sx33y9t2DWw2iujES\nu9nE9KWQlQpGCKhU8BrrmL40olG3lRJHjwEg19fAmJslm9dvbZSL6FQfRnrI1VWIxuysiksXCX/x\nL5DtDnz89L681vseOCwsLHSA7etfz8/P/6u9f/6r936E4ziO47zTs8+d58xiAYByvcCzz53nd39t\nf2Y1vEOnY3cPwuGbuwHv4UZFRSqNEALRaEKrhXftGjqbRfg+xvdRjz0OkYgNMBoNe6sjHrfPUSnb\nKotEChOOINdtUyg9Oo5cuUb4a19FlkqooSHM40/A4VtUbvyU7nvg8Hbz8/MZ4F8C/+3CwsI+5II6\njuM4H0bLW7Xbfn3PKWWTEbtdO4jqehnkj9srryQaxUSidkdhL2lS9/VBLIbUGnX8BCaRRBSLyPVV\ne6tjaBh4225GNG5zIbY3QUj0yAiisEvoL/4zcnMTk8vRe+YZ8EP4hQK0xvblpT9QgQPwz4C1hYWF\nv7zfJ+I4juM8PKaGUpTrhXd8vS/eNmRK54cwyVv8HKVsRUWvh4lEka0WRmu8rQ10NIaJJ5BBgDp4\nCJMdQFQrNvExnbl5q6PVss8RCqFjcWSxAFpjBvPQbBL+8l8jlpcgnSF44imIJ/AKBYL+fkw2C83m\nvizBgxY4/Dbwv97NA6QUSPke95L2eJ58x9/O/nDrvP/cGn8w3Drvv/1Y43/yy4/wh186x/Jmjanh\nFL/zd4/i+/f4PaxWkNvbmGwWM3wQ773yGIxBFHYRlQo6Hkf2OhB0EIUd+5+TSfxeFz09gxkewWu1\nkCtLmGgMMzeH53l7yZMbe8cnEMUCQgXogQFQCu/5v0VeuADJJOrU45j+fvxCAUME8gOECgWkUpCM\n7svvsTDG3PMnfT/m5+efBL4H5BcWFip3+jhjjBHv9eY5juM4zr3Qau0NjIrB8PCtWznX67CxYW9b\ndLugNRQK0G7b1tLtNkxOwsQEKGWfUwhbNhkKQRDApr39QTQKpZL9dzptEyO/+1144w177OHDkM/b\n54/F7PGFgj2+17PfS6XgV37lJ726u76APkg7Dr8AfPduggaAYrHxE3cc+vpiVKstlNI/7Tk6t+DW\nef+5Nf5guHXefw/NGvd69laBMTZJMRx+76FRezkLRmuEMVCqQ62GqNVs3kK3i4mn0fPHwfMQF64g\nOu2bPR6qbcT2NUSjjk4kkdXKjWBDJ1J4P3wR7+WXQYOem0UPjyFrZcxWERIJ5PYOpt1BKIWOhJGl\nMl5vi9hnP/0T1ziTee9ZGbfzIAUOp4Hv3+2DtDZo/ZN3TZTSBMED/Av6IeHWef+5Nf5guHXefw/s\nGmuN2NlBNOoEb6tq4MfP9Xp5Zb2O8kOITttWWZSKmFgCIT20H0IfOmxbRBcKyEoJlR/C5IftbY3N\nbfu9eAIRaMTmJioSRQ/kkefOEvrRD6DdIpieRU9MIGp1TKuFTmcRuzuwu4tRAYQjiHYHWdild+AQ\naihPzJh9WeMHKXA4BvyH+30SjuM4zkeXKBXt6OqBHHrowK2P2yuNNJ6PUArRbiHKZUwohAmFECEP\ndfg4JtVnj91YQ2eyNxIfb5RnxhK2F0OhAL6PzuWRy1cJf+HPkfUKemwSNT2L6Hag1cZks4hCAYoF\nRLcLkSgiUMjiBsHcHEH+BGJhgdC3vgZH5uH44/d8jR6kwCEPlO73STiO4zgfQY2GrXhI9t26gRNA\nu23LKwG0gXYTUatgjMF4HkII1KF5THbADre6sgiJxI3hVjdKK8MRjB9Clou2tDKXQ+5sE/7j/4jc\n3UYPj9I7dgKhNKLTQWf6kcUiXLuGDDrocAQhJWJnk2ByhuD4o4jFS0S/+f9ipI8aGbvlyO6f1gMT\nOCwsLOzPK3Qcx3GcW3lb+2c1OQ3+LS6L18srWzbHQXTatidDL8D4PgJQk9OY4WGbG3Ft2baUvj7c\n6npppe9jQmFEtQqA6c9ApUL4L/8MubqCzuXoPf0JECC7XVR/Fq9WxlteRnQ76HAY44XxtrcJJibR\njxzDW1km/Cf/Ebo9grFRO6+iXIbH96cB1gMTODiO4zjOB0YpOxyq3bYNnKLR9z7OGNuUqbCLkQLR\n6UC7CZ3gxg6DHhpCjU8C2OCg27WJj9GozXm4tgzG2KCkXrfPm0phuj1CX/sy3sWLmGyG4InTEAkj\nlUKl+qFWwVtZQnS6mGgUE47g7e6gRsbofeJTyI11on/y/0GzjRodRVbLyFoNdfAwambKVmnsAxc4\nOI7jOB8d1wOBctE2cBoZvfWx9Tre1iZGa+h2Ee22zTWQ0lZa9PejpmcgHEbs7CDr1ZtNoYIAubYK\n3S4mFEI2amDAxOMYIQg9/x28c29h4nHUyVPoVMo2hEokkY0G3rVlRK+L8X10zAYMOj9E7xOfRuxs\nE/7Pf4yoVVCjY0jfR7baqIOHCEYnCL/8I0Kvvwr/1a/tyxK6wMFxHMf5SBC1KnJnG93Xf/s8hl4P\nubGOaDWh10N0Orak8nrAkEiiZw9AImGTKVevobMD9jm1tq2o63VMJILs2YDDRCPocITQj17Af+0V\nkB5q/ig6N4AMFMTj6FYLb3UV0WnbuRXRGF5hG7I5es98Akolwn/2x4jdXfToGAiJ7PZQs3MEo2OE\nX3mJ2Ksv0zn9DBw9SrS3P5MbXODgOI7jfLhdT2iMRm87iApjENvbiFIBtLEX8G4XjMEohYhEUIeP\nYNL9djfiymWbTDlzwFZK7O4iKyVMNIrA2NsSoRA6lcA78xqRF36A6QWo2RnUyBjSaEQkivYD5Ooq\notPBSImKJ/B2tpH9aYKnPw6NBuEv/DliawM1PIzM5UBp1IFZgrEJwq/uBQxPnUYdPoJXraAnJ+CU\ny3FwHMdxnDsXBPbTfxDYT+i3GkQFiGrFtnlWAbQ7iF4How3CaAiFUQcOYnI5m7OwdBVCoRvJlDdK\nK8MRjBCIRgOExPRnEJcWiHzn29CooaamUZPTSGOQkQgag7+xjm53QApUPIZXLCKFIHj6GWi2CD33\nRbylqwRDI8jBQYQXRk2MosbGCb3+KrHXXqXzxNOo+aN45RLBxDhq6Cl8o2wHyVukbvw0XODgOI7j\nfLgYcyPnQOWHIZm89bHtNnJjzY657rQh6NlcBK0RUqKnZm2io9Y2Z0GpG9Mwb5RW+mGMkMi9igvd\nl0aurhL+iz/FKxYIxsYxJ0/arpGhMFoI/I0N2zBKSEjEEKUyntEEjz0OBkJf/Qre4gLBQN7+/EgE\nNTaBHhnDf+NVQq+/SufJp1EHD+GXy/Qmx1FPPmlbTtdqiM012FmHT3z2ni+vCxwcx3GcD43rjZlu\n5Bzcyt5YbFG0sySECjBIRKAA0KOjtlLC8250kdRDw7Y3QrOJvHoFpMRID9Fu2mAjmYRCgchzX0Ru\nrKPyQ/Q+9nGIxDAhDyM8vM0NaNoAwyTiUKsh65rg2KMQ9gl9+5t4Z98k6B9AD40hYhH00AhqfAL/\nzdcIvfYKnSefQs0dwi+X6E0cRj112gYM1RpydQVv5RqeDuDjT+/LGrvAwXEcx3n4NZu2FPJtzZZu\nRRQLyPV1TLsFvQDhSQgUwgTo3CB6esbuKJSKyFLRfm9o6GZpZRDY59/LfyAWh1aL0F9/AXn5Eiab\npXf6GUgmMULYMsqtTbsTYAw6lYJaFVmrEcwfgUQc/9vfJHTmDEFfGj0ygUhE0fkR1NgY/ptvEHnj\nNTqnnkDNzuFXKvTGJ1BPnoaeDRi8lWXkyordERkbB0/aoVf7wAUOjuM4zsPr+iAquNls6VYaDbzV\nFXsB73XtboJWmG4HslkbcCSTtvpifRWdSttdC6XsbYp22yZWBj1AQCSC0YrQN/7GllYmUgRPnEZn\ns0ij0dEY3tYGVGugDSZpAwxZLtuAoa8P//nvEHrlBVSiDzU6Bok4Oj+EGhnBP/cWkddfpXPqSYID\nc/ilEr3xSdRTYzZgqNfwlpZswIBBj49jlMJfvIyMReCTH9uXJXeBg+M4jvPwuT5gqtGwOQDXB1G9\nl14PubaK3N2BTgcTCgMC0WxCXx969oDt4Nhq2VsQ16svwDaJqtUwvo/UCozG+CF0KEzo+9/Bf+1V\nmzx57CR6dBihQUTCsL21twMQQKoPOm1ktUpw8BAMDOJ9/3nCP/w+KhpBDY9jkknM0DBqaBjvwjki\nr79O57FTBDMH8SsleqNjdJ88bRMe6zW8K1eQaysYIdBjY6AN3uVL6FCIYO4gfjIOQ0P7svQucHAc\nx3EeKqJYsLcQBvOYoeFbH3g9SXJvl4Fo2A6lajYgnkAdPYYZHLTVFyvXbI+GsXEIhW6WVvohW1qp\nAttCOhzBe+VlIi/8AHSAmj+CHp9CaAXhKOxsI6+V7PGJlN2tqFYIZucw+Tzeyy8Qfvbfo30PNTyM\nSacx+SFUfhjv4nm7w/DYKdTMAfxKkWB8jO5TewFDrWoDhvUVQKInJhG9Ht7li5hojGD2ICRimEwW\nNTx0+6TQn4ILHBzHcZyHQ72Ot7158xbCrRo4sVdeuXQVUSpCKISJx6DZRITD6LmDtjICbLlms3lj\n1+L6dEwjPUCA0oDARGLIc28R/e63odVCzx5AHzxo/1s4jCzsIleXMcpAPAE6QNZrBDMzqOFR5JlX\nifyH/wcjQOXz6EwGkRskGBpGXlwgcuY1OsceRX3mczZgGL0eMHShWsFfvIxYtzM19PgUotfBW7iA\niURRBw/bjpSZDCabQ5SKeOfOwtFDkB6852+DCxwcx3GcB1unc2NA1G0HUV0/dumq7fwoBDqRRDQa\nCGXQE5Po8Qm7o1AoICslu2sxPGLzGq5cxiDAYJMeARONIK9eIfrNr0OxiJ6aQh07DlKAH0aUS/hL\nVwFj50lIiVetEUxNosYnkG++TuQ/2QFUengIPTCAyOVRuUHk5YtE3nidziPH6Hzqs/iV0jsDhkoZ\nf/ESYn0D/JDdYei08BbO21bVh+Yx8QQmk0Vns3i7O8jzZ9EDA6gnnoKDU1Bt3/O3wwUOjuM4zoNp\nr2TyHUOjbnfsxjpy8TIEASadtjkL9TpqaNhWSsRididiZRndn7W7FtfzGrTGGAOexAgB4TBme4vo\nn/4nxMY6anQc9Yt/xyZfej6iVkFuLoIWmFgUI328epVgbMyOwz5/nsi//t8RzSY6P4jJD8FgHpXN\nIa9cJvLm63SPPELn0z+DXy4RjI7eDBjKZfzLFxEb6xAOoSemoN2yOwzJBGp+HpPow/T324Bhewt/\n4Tw6l0c99TRmYAAhjK2qCN37wdMucHAcx3EeLMbYHYFq+ebQqNsQhQLy4nlEtYbJZhHdLqJawQzm\nUdMzmFSfLde8sgjxuK2euD76Ogjs7oLngdZ2N6NaJfRXf4l39TI6P0TwC5/HxGIgQDTqyLV1G2RE\no+hQCK9WJRgepXfsGOLyRSK//3u270NuCH1gFgbyBAMDeFevEDlzhu7ho3Q//qkbj7uRw1As4l++\nhNjeAD+MnpyBVgPv4gVMMok6euTmDkO6H29jHX/hgp3O+dQzmGwWul28M68TOvsGjA3Bz33+nr89\nLnBwHMdxHhiiWrGDqPqzN2ZA3FLDXlTlxgY6m8X0p5GVCiaTQR19BJOxF1J5bRmEsOWaQP3KMv/u\n+xssl3pMZcL89lM5+kISel1CX/oK8uxZTH+a7ud+AdJpMBo6TbxrazZgiEQwkRCyVsMkkvSeegaW\nrhD5N79/I2kzODALg0OodD/e0jKRt96ge/AQ3U9+Eq9aIRgbpzsxsRcwlPAvLSA3N+0wrImpG6/N\npFKoo0cxiQRmIIdOJPBWV/F3dtAjI6hjx+3sjGYT76Uf4b35BkJr9JEj8NlPgt6H98js3cd5WO3s\n1G77AnxfkskkKJUaBME+rKADuHX+ILg1/mC4dd5/77nGrZbNY4jF0Pmh2zZwotdDXlnEv3wJnUyi\nEwlkuWybP83O2UoJY2wpZbttb3OEw7Z8s1rl935Q4MzmzXv/j47G+Bf6HN6rL0MsRvDEaUw+b7tJ\ndrr4q9fQgR1ypaNRvFoN1Z9Fz83B6iqRr3wJb3cLNTCIGpuAoTw6lUauLeNfW6F3YA6TH8KrVQjm\nj6DHJ23VRa2Gv7CA3NnCRKLokWFErWZ3NNJp1MQExBOYgQFMNIZcW0UEPfToOHpyEtOXhmoV740z\nhM69hfYk+tgJgrlDhDdWSHuG0vHHb/t7PDiYuk1kdov3724f4DiO4zj3TK9n8xi0tqWQ4fCtjzUG\nsbGO//pr4Huo4RE7YKrdQs8ftpUSnmdLKWsVe5tjeMR+XS7a3AXPY7nyznHT11aK+Duv0Tv9DHp8\nAtkLoNXEW11FdzuYcAST7kPUKpBI0HviKdhYI/Lv/gC5vY7pz9F99DHMkL2tItdWCZ99k2B6js7H\nPoZfqxOMjNJ96ml7a6RYwL+4gNzetkmOk5OIegNvYQHd109w/ATEYpiBAdvBcnUViUGNT2LGxzHJ\nFKJUxP/G1/AvLWCicbqnn0FPTOJdvkj4G19DxCPwsdP78pa5wMFxHMf54GmN2NpCVqo3Z0DchqhW\n8F55ybZpHpvAq1XsEKupaXsLIhK5OaUyYxMfRamIt3jJ3l6QHoRDiG6XqUyEcqt547mnY5rO3/8v\nkZ2uHXq1soLpttCRKKY/i2jWERiCU48jdraI/NEfIlfW0Jl+eicewwyNYBJx5MYm/ltvoWZm6Dxj\nAwaGxug+OWkDhsKu3WEo7NiAYXoaUa/hXbqITmcIHn0MolG7w+D5dofB8+xrHB2z5aLbW4Se/w7y\nyhVMOk33Z34WMziId+4s/lefQ6fTBI+exEunoK9vX946d6vCuSfcOu8/t8YfDLfO+y9Ur9Dfa1IO\nxekl07c/uNPBe/1V5NoqenQcEfQQ7TZqdBQ9NWMDjuv9HRIpzOCgTWDc3rJjsYXARCKIXhfth/Au\nXaT1jW/xf4WOcjWRZ6o/zD+ZCkj6Gv/aNWi3MNEoRGPQaNhkyrmDiMIu4a//DfLaku0jMTONGR7D\nxGPIjXW81TXU5CRqdBS/0SCYnUNPTYNSNunx4gVkqYiJxVC5QbxKFbG9ic5m0JPTEIlicjmMFHhr\naxAOoyanb07iXF0l9OpLyJUVdD5P8NRpTDyB/8YZxNYmOpdDHTqM8DxQAV40TH9fnFJ/3t2qcBzH\ncR5SjYad3ZBOw6E5TKUFt7qoaY1cOG8/wY8Mo0dGkdUKOp9HnXjU3t/vdJDLSzf7O+z1cBBBAICJ\nxSHo2mqJjU2iX/0ycnMD/+gRfveJSWS3i9Zd/NUVaNQx0Rj09WPaLaTRBMeOI4pFIn/2J3iLi6hY\nnN6xE5ixCUwsirexYfsmjI7RffIp/E4HhkboTk7Zn7m9jb9wAVkpomMJgslpZKlkczOyA6jHTkE4\nYnMyVIBcX8PE4rYb5fAIeB7y2jL+yy8itzfR45N0fvXvgwH/zKvIchk1Nk7wiU8jBAitMUrj7e7g\nNetw5BD03/u30QUOjuM4zv7qdm3io5SoyWlENHz76ZVrq4RefAGdSKCmp5CFAiabJXj8SVtyeH3o\nVK9nL7BC3BhCJQAdjyOUQqgAUSwR+sqX8JYXUdMHaf/X/wihFHTaiJVV/FoFE49DNotpd5Bao44e\nRVdrRL7w58jLlzGRCL1HjqHHJzDRKN7mBvL8BnpklO6pJ/C7PRgZoTs5bUs7t7f2AoayfQ0TU4hS\nCf/SBUxukOCxxyAcRWcHEEEPubaCjqdQjxy3t22MscmfL79oB2IdmKP3qc8gGg38l15ENmoEBw6h\nTj5mp3tioBfs9bzoYPr6bYJprbYvb6cLHBzHcZz9odQ7KxtisdsfX60Q+v7z0OkSTE4hd3eh00Od\nPGUvhIDY3kY2aqj8MEQi9mLZqNtuj4kERmtErwetJuEvP4dcOIcZm6DzG/8YpLTBxPoafqGAjsfR\n2Qx0A2SvhzpwEN2qE3ruOfyL5zG+R3D4MGZyCh2O4u1uIy9cQI8M0j15Cr/Xg9HRdwYMFy8gyxV0\nMomamECUyviXFtD5YYKTj9veD9kBRKeDv7GGSqVRx0/a19frIc+9RejVl6HZIjh6lO7P/xJyd4fQ\nd74FSqMOHyEYHkG293ZrOh27xtqgB7LQ7RG6sogUGj7+9L68rS5wcBzHce4tYxDFIrJctJUNe3Mh\nbqnXw3/hh8iNVdTMAWSljKxW0YeP2EoL378xQ0IP5FC5GVtauXLN9nmIx+0ORqeDUYrw176K/9or\n6FyO7q//AwhH7EV5Yx25u4OOJVDZHAQ9pNKo2QME7Rahr/8N/sULGGFQs3Po2Vl0KIK3s0Vocws9\nNEj3xKP4RsPYKN2JaftatzbxFi4gazV0Io6aGEcUS/gXL6GH8/ROPWl7P2Qy0O7gbayhU2l6J09h\ncoO2FPWVlwm98TomCAhOnkQdOoy3tET4a1/BhEMEj5zAZDLIdgvR7WIaTWSxAFKiB3LISpnQm2+g\nY3GCQ/PImSmYnYBy8/Zr/z64wMFxHMe5Z0S9htzaRKczP3EQFcbgvfE6/tk3CcYnMPlhZKmEmpm1\nlRLRqH2+7S10sg81cwBRKOAtXgQDJhbDhELIdguDxPvudwh//3lMMk7nV/4L6O+3n8jXV5Fbm6h4\nAj0wCL0OMuihpqYIuj1Cf/tNvIVzCK1Rk7PoQ3MYL4Qs7BDa3MbksvQefRTPaBjfCxgAsb2Fd/4s\nstFAxxOo0VF7S2LxMnp4hN5Tp8H30f1ZRNv2qdCZLMHJxzG5HKJawf/h8/hvnkWHQwRPPIGemMa7\neIHIl/4K3Zem9/QziGgM0elAp4OoVhGVMoQj6PwQcmMd/5WXMAOD9E49gRkdxfSlEb68/dr/NO+x\nq6pw7gW3zvvPrfEHw63z+9Ru2zyGcNjep/e8Wx7q+5JMeZv6l79OLzMA8RiiVkWPT6CmZ+046B97\nPlGt2C15YzCRKCYaRTYbGCHxXnqR0N9+HTyf7s/+POQGodNF7m4j19fQ8aR9TtVFGFCjE6AC/Bd/\nhHfxAqLTQU1Oog/PY7wwcncXub2JyQ4QjI4jhUGNjtnGTVIiNzeQF84jW010IolJpxGFHbxqFTU8\nih4ft0NTeAn3AAAgAElEQVSpMhlEo4ls1tGZLHp6FpPJIIpF/Fdf3uvbkLS5G4NDeG+ewVu5hh4a\nJnjkuL3u77XElsUC1G2nShNLIFeWbenp2Bh65oBd83j8nWt8B7/HrqrCcfZZtdnl2efOs7xVY2oo\nxW99/gh98ds0rHGcD7tgLykvCG6UDt5WoYD/g+9CKmYbHxWK6EzmZuvkXg+5ugJKoUdGEZ023tVF\nTDeASBiTSCCaDUy7jXjrLSJf+zKiF9D5mc9hJqfsJ/u1tRsVCnpwCKEVtNu2E6PReC/+0LaqbjRR\nExPo+XmMH0aWinjb25hMht6xE0ghMKMj9MYnQXr2VseFc4hWC5NIoobHELs7+FcXUWOTdA8eRvg+\nOpNBNhp4OzvoXI7g6FHbtGl7m9CX/xrv6lXMYI7uL/0dm2x55nW8F19ATc3S/blfQAQBQgWgFGJn\nG9HtYPrSmOwA/uIiot2iNzWNfvQkejB/+6ZZ+8AFDo5zF5597jxnFgsAlOsFnn3uPL/7a4/e57Ny\nnPvAGMTOjm3ClB+2n+hvp9XC/8H37KfkyUlQbYQU9E4/YzskGrOX6Niwn54Bubpit+h9HzOQhWYT\nWi24coXol76ALNfoffpTqENHbICxtmoDhmgUnR+EwCC6HdToKCDwXnkR79Ilu7sxNETv6Y9hQmFk\nqYC3s4NJ9xMcPoIIhTAjI/TGJmxJ5NoKcuECot2BRBw9MoYo7OItX0FPTtE9cgTh+5Duh2YDWSzY\nAVvHT2BiceTaKqFvfcP2ohgZo/N3fwWhNd6bryFLZdTBQ3RPPY5sNRHdrr29UizYKZ+ZDKbj419c\nwPgeanoWPTGFyeVuu6uzn1zg4Dh3YXmrdtuvHeejQFTKNskwO2DzGG5HKfzXXkFeuogaG8X0pfB6\nXXjqCVS0D6O5mUiZG8Sk+5Fbm4h6DTwfnc0iOh1Eo4HYWCP0V1/A21qnd/rjdE+cRHTbeJvryJVr\n6EgElc0hjEZ0ujagweC99ire4mVkpYjK5QlOfQ4iIWSphCzuQjJFMH8YEQqjh0cwY2Pg+8jVFeSl\nBRu8xBLo0SxiZxe5fBU9PU1w+Iidppnqg3YLUS5h8nn01LQNSK4t47/yEt7Otu0m+au/hqhV8X/0\nQ2S3Q/DIcYLTo8hmA9FqYuoNZKUMCHR/P6Jcxj/zOirdT/DIcfTYmB3ctU+5C3fKBQ6OcxemhlKU\n64V3fO04HxnNps07SCTs5MrbDaLSGnH5EuHXXkFlsjYZsN1FzR/FTE9Bvh+WN/A2Nmwi5cQUcnvL\n3qbwPHQ2Z7tE1utQKhH+q7/EW75C77HH6f3yryK7HcTWJv7KMiYUQg0MIoxGttuooTx4Hv5bryOX\nlpG726jsAN1Pfw4RjiDLJcRqAVIp1IF5RDSKHspjRscgFEKsrCAvXUC0u3aHIT+Et7uDXC6ip2fR\nA0fBk3aQVbu1t4MxjJ6csj0lFi8Rev11RLWCPnSIzic/jdzeIvTtb4IUBCceQ2WzNhhqNBH1KlRq\niJCPzg4gN1YJvXYZnR+m9/QzmKFh2/DqbhgD7fZPPu59cMmRzj3xUVnn+5nj8FFZ4/vNrfN76PVs\nwAC2H0ModNvDxfoaoRd/iJESk0ghOx2CmVn09AzEYvjdNpl2lXLH0EtnkIVdKBbtJ+n+vVaHjQY0\nm4S/9EW88+cIDh+m95mfQfYCTKWMv7QE0sNksxhjkJ02ejCHET7+uTfsxX9rC5PuIzh+EhGLQrli\nbwGkEqjcMCIRR+Xztlw0HEYsL+NdvgidLiSTmEQCubtj8yMOzN34tK/7+pDtts3DGB5BT04hVIA8\ndw7/3Ju2D8XhI5gDc4iVZVvimeij9+hj9jxaLYQQiEoJajVMPIGJxfGWlxClInpiwgYo+aF3JDze\nEaUQhQKhZo30gUlKInLPkyNd4ODcE26d959b4w+GW+e30dr2S2g0bMDwEy5iolzCf+kFqNQwmX5E\ns4Uen0AfPIhJpm50kPRDHulDM5SX19Gbe5US6X5bWlmrYjo9/K99hdDLL6Fnpul+9ucQCKhV8ZaX\nwGjMwCDGaGSng84OYHyJf/YsYmMNubGJSSYIjp1AJFOIYhFRrUA8hhocRiQTqNwgZsSO2xZXr9iA\nQWk7xjqRsDkPQY9g9gD0ZxBCovtStjulUuixcfT4BKLVxDv7Jt7CBUAQHD2GGRtFLF7Gv3oVnR8i\nOHYMISR0u6AVolK5kWBphMRfWkT0uvSmZmBy6v0lPHa7N4IcMzCAl82QySZdVYXjOI7zwRDFArK0\nl3ewl6x4S80m3uuv4a2toNNpZDSCjidRp56wn9KVQm6s2w6SQ8OYoAOXLyOLVVQqjYnGkJUSNOp4\n3/oGoR9+D50fpf2bv4kIRxGVMt7SMqgeJpfHAKLVRPT3o5Ip/EvnEesbyI0NCIXonX4akUwhy0XE\n8hImFkVNTUEyZV/P8IidlHn1Ct7iJVvymExhonG8wjamVqU3OwepFMLz0Kk+W8XRsoGQGh1DVCqE\nvv9dxOIiIhql99jjmP4M3sI5/PNn0RNTdH/+FxHdLqLbs7s21Qr0epi+Pow2eBcvYKJR1MwMemzy\n/SU8Nho2YAB0bhBG96aM7mMexH0PHObn58PA7wG/AXSAf7+wsPA/3d+zchzH+Yi6Pmkylf7JDZw6\nHeSlBfyLC+hozE6VjETpnXzcDm4CxO4uslKy2+6JBN7Kki01HB9GDScRpZLtnPiD7xH59rcwfSk6\nv/4PoM8mB3oXL9rKiNwgQghoNRHpDCYZx7u4gLe1jdhcR2DonTqF6EsjS2VYvgqRCGp8Avr60AO5\ntwUMV/EWL4MKIJFEp2N4xR1EvU5vZhYSCVtW2Ze2SY/dDnpyCjU8jNjZIfTNryFXrmH60gSnn4Fo\nFHnuLN4bZ1BzB+keP4lst21w02rZPA2l7S2OUhH/zTdQ/RnUo4+hR0buPuHRGES1gigUbAvrvVst\nH5T7HjgAvw98Bvg5oA/4k/n5+aWFhYV/e1/PynEc56Ok07F5DNcnTfq3uTwEAXJlGe+tNzFao6UH\noRDq2HHKmTzPfvUiy5sLTPd5/NbnDpAaGkFurCPaLdtbYWgYCBDFArzyMtGvfwVkiPbf+xUYGoZy\nCe/N1xHNNmpoCCEFotmEvjQmEsO7chlRKCDW15BK0XvkGGQHkOUyrKzYfg8TE5i+DDqXw+SHIBxC\nXlnEW7yM0QYSCXS4D69YwGu3UDOzmGgcQiFMOm1vSXQ6qOlZTG4Qub6G/5Xn8Lc3UQN5ep/6NKIb\n4F84j+h26B0+inrqNLLZtOfarCOqdYQn0YkEcmuL0PIV1NAwvY99HJMfwqT67u490hpRKCCrZXQq\nbcd232qHQimbJ7IP7muOw/z8fAbYAj67sLDwvb3v/Uvg0MLCwu/cyXO4HIcHg1vn/efW+IPxkVtn\npfamKnZtHkM0eutjtUZsbuKfexNTrSGkgHAEdfCQvYiFw/zrP36VM0vlGw95dCTGP38sBtEYemDA\nTnjsdUivXqX1J3+K6XTpfu5z6MkZu8Owcg3ZrKMGh8D37MUvkcSEI8jLF5HVCmJ9DdFqERw5BvlB\nZLmMaTXtRT+bw2Qy9pZEdsAOwlpaxFtcxGiDSfVhfA+vVMR4Pnp2FhMKISIRdLofmk2E76FmDtjS\n0KtX8M+fRZRK6KE8am4eUa/ZvgpSEhx7FDJ7jzPGlpE2GhAOYyJR5LUlRKOBHh9HT83Y/IW7TXjs\n9ZC7O4hW0+ZzpPtvvUPRaiELu/j1GunxPKX+/Icux+ETQPl60ACwsLDwv93H83Ecx/loMObmp9f8\nkE1e/AnHehfPIzY3EVKCJ1GzB9AHDtoLYaeDXF56d6+TUgc9Omfv9e/uwrVlQl/6K2g3CJ7+BL25\neUS9in/2DWSlihoeRvWn7cXXT2BSfcirV5GNmu3cWK3TO3wYBvPIeg2zvo4J+Zj8EDqbw+Rydus/\nErE7DEuLdlck0YcJ+XilEiYSJjg4D76HiMTsqO5GDdHroeaP2GqKixcI/e03Ee0WemSE4PBRRKlA\n6OUfoRNJeqeegETCNqSq1RCNOqLRwMTimEgEf3UFtCKYmITJaZt/cLe3E5pNm7+gtX38rYaFaY2o\nlG0SaKsFUtimWqOj0Azu7mfegfsdOMwCS/Pz8/8N8D8CYeBZ4H9ZWFh4uMs9HMdxHlCiWkHubKP7\ns7Yfw23ur4tqBbl4Cbm6huh2QEo7t+HwEdtbQCnk+prdsRjMMzWwRXn15hb51GAcWdjFbG0T+eJf\n4m1tEpw+DZ/6OGzt4p97C1kpEwzmMVMZRK2OEQITTyCXl5HNhp0NUS4THDiAOvEYolbD7GxjfA8G\n87ZCIpeDTMZ+yr98Ee/aEgQGk0qiPQ+vUsbE4qj5QyAkIpFA92ehUUf0uqgjxyDkI8++hXflsq30\nGB4hGBpBbm3gv/wSJpej98zHwfNtG+hqBdloQLdrB255Pt7iJUwkaoOq0fH3lfAoqhUbZF2f+3Gr\nNt6dDrKwiyiXQSlMLGabRKX7EWHfPu5DGDgkgUPAPwV+ExgB/gBoYBMmHcdxnHulZSc0EovZYVK3\nu6A1GsjlJbz1VTuNUWnU8Aj6keP2EzogtreR9ar9NNzu4F25zO/Mh/hDkiwX20z3efz2RI/QH/3f\n+MtX6R1/jO7nf5lQ0IWzZ5GrmwSDOYKpaWS1iml30dEo3so16LQRW9t4hR2CySnUseM2yXB3B0I+\nIjeAyuVtEma6397KWLyEv3INAoVJXg8YKohkEnX4KBhtkyEHcohaGVSAeuQYGIP/5uuIlVWM79lS\ny/4McmUF//VX0SOjBJ/4FAKD6HVtH4ZGA9ELMLEIotfBX7mGSvejTpx8fwmPWiNKJdtBM9lnm0m9\nV57J2xIjRb0OnsT0Z9DZAYjF7vIX4v2534FDAKSA31hYWFgFmJ+fnwL+e+4wcJBSIOWt3xzPk+/4\n29kfbp33n1vjD8aHcp2DALG5gdAaPTUJ4TC3fHWdju3euL6G3NpCdDrowTz6+AnE0BCelIhyCbG7\nawOI6ADe2gpCK/TQEP3RCP9iYBcqFfwvP4f/zfP05g/S/Z3/DqkDwkuX8Yq7MD6GOTiHVyxAp4VJ\nxPBXVzHdNmzv4G9uEExMoA5/EtFsIIu7CD+EHhzA5IdhcBDZ148O+fhXFmF5CWHApFIYDF61iuxP\no48dRSqD6UtiBgYR5RIShTp5CtlqEnrlRcT2tq1OmJ2FaAR/bRU219FT0+hHTyCDAKm60O4gmnY3\nxYQjyEoJsXYNnc9jTp+GkVFEXx93tb8QBIidHTu4K5PBHDqE914BR69ng4XCri0fjUYx05OY/gxC\nyne9n/v5e3y/kyP/EfBvFhYWEm/73i8Cf/72792OMcaI+9y323Ec54GkNWxvQ61m73cnbvO/1SCA\n9XVYXbV/qlUYGIDjx2F62n76rddhYwP6+uz9+tVV6HRgcNB+b2cHKhX46lfh5ZdhYgJ+8RftY69c\ngc1N+5yDgzc7Rfr+zecpFGxVxPAwHDxo8we6XbszkkrZ1zA0ZH9WKAQLC7C8bM8/lbKvt9GATMY+\nh9aQzdo/5TKk03DoEOzuwpkzUCrZT+kjI7ZF8+qq/XtuDvJ5e05a29bN9bptsR0KwdqaPbexMZiZ\nsT/rbhMe223Y2rLrns/b838vtdrNdQW7frnc3f+8W3u4OkfOz88fAs4D8wsLC5f3vvfPgd9eWFh4\n5E6eo1Com5+049DXF6NabaHURyBD+j5x67z/3Bp/MD4s63xjVyCXw/Rnbn2g1ojtbcTGGmJzC7Gz\nBfEE+vAR9MFD9j55u43c3MD4IUwyaasw6g0YyNot/VIRqhW857+L98IPMdkBgp/9OUgmEUtLyI0N\nTKbfjriulJBAIhGltXQN3e1hSgVCqysEA3mYmcYECtFu2h2GRAozOgxDI5h4HC09/KuXYWUVofVe\nSaOGRtPmOAzmQWvMwID9NF4uQSaDmp5FrK3hXThnL/qJhE0g7HURG5t2x2FmBpNK21wOre1wq2YD\npMQIiVxbA2HQ4xOYiSl7m+RuEx6rVdti2/dthcV7VbEohSgWbJ5DtwvRCGZgL+nzDvMl7vT3OJNJ\nPFyBA8D8/PwXgSzwz7A5Dn8E/M8LCwv/55083pVjPhjcOu+/e7HG93PWxsPiof9dbjSQW5u2nfHg\n4K0HUV2vqthaRxSKyGvXQArU/GGbD5BI2H4NW5sQBDZA2NlGVivovjQ6N4isVRGlIt5LLxH6wXcx\nsTjdT38WBvOI5St4a2uYdBo9NIKsVWzVgicJFwrEQ5L6VgHvyiKqP4uemUYojel2EJ5v+ywMj6BH\nbImo8Xy8K5eR66s2MIinAIPotlGZARgYQCiFGhzCpFJ4lRI6N4gaHcdbuop3+SLGGDsXoq8P0Wza\n8dd9faiJKYjHbcKj0ohO2/ac8Hzodmz76XAYPT6JHnsfCY/GIEpFZLmE2cuxeM/8hb0qClEu2Yel\n+23+yO12im7hTn+PH8ZyTIB/CPwfwPNAE/j9Ow0aHMe5O88+d54zi3a6Z7le4NnnzvO7v/bofT4r\n557YmwOBlOiJydsOohKVMnJzHUoVvOWriFaTYHYOfeJRuzuhNWJrC9moofqzyFrVVgvEEwSzc7bS\n4doS8o03CD//HRCGzmc+B2MTiNUVvBe+h0mmCA4dxqvbT9haenjFAlJpdLMBK0t40TjBiRNggFYT\nvDCiL20DhtFRCEdAGOTSVcT6KkIZTCIJwiYpqkwW0qMIDWpvIJQsFdGRCL3jJ/EWzhM++1WMF0In\nkva2RL2GXFvF5PKoEycxvo8IetBsINot2x7a96DdxisU0ek06vAR9Oj7GGkdBLbqoV6zFSzTs+8O\n5K4nRe5sI9ptTCSMHhmz+SN32376A3LfA4eFhYUatqLiN+/vmTjOh9+7aux/7GvnIaQ1cnsLWi3b\nwOl2mfX1ug0u6nXk0hXk7g5qYgL1mc9h8nkQ4uaMiv4MJhrDu3oFIhH07AHodPFWlhHnzxP67t8i\nOi2C0x9Dz80jVpfxfvQCJh4lmJtHNut4O9sYDLJcRhqDaTUJXb6ESSTg2DF0J8B0u4hQGJHsQ4+O\nosfGbdCjtT3H9TXQBpNK2QFRQReVG4R4DCEkanTC/rtQwAwMEIwcwzv7FuE3X0dH4+i+NEJ6iFoV\nUa+hhkYwswdASIzWiHbLVkn0ehjPHidrdcxAluCxU5iRkbvv8Njp2OFgvR5mYGCvU+aPabft7kKx\nYHdQ0v22PXYyeXc/6z6474GD4zgfnKmhFOV64R1fOw8pYxDFoi3fG8zbOQy3spejIBp15NoqcnkZ\nPZCj9/O/ZC/U1y+YO9voRAqdSOFdW7KdFWdmQBvk6gpicZHQd76FrFQIHjtFcPQYcnsT/4fft3Mh\nDs0hmk0aWzv8QWuMpd4I0zT4p+0i2cW3MKEwwaFDyHDIJgVKbgYM4+Pg+WA08spl5OYmKI1JJGwZ\npOqhB3LocATp+aiJSVuWWS6j84PogRz+W2/iVV6z3SHTadAga1XwPNTwCKa/H2EMaAO9FrLVtBMx\npYRKGa/TsdMsjzzy/kZa1+u2YZOUNn/hx4M4Y2yjpu1tZLOBCfnooRGba3G7Ft8PmIfnTB3H+an9\n1uePvCvHwXn4iHoNub2F7uu//SCqXm8vkbGO2Nm2bZJjMXqf+BR67qD9ZH+9t0Mkgk724W2sYrRB\njU/Zhkgba4jFK4S+/x3k5ibqyFHan/9lZLGA//ILCC+EmpuzeQGbW6A1f1Af5zXRBwJKRPi3wST/\nw1QDEYmCDsAISKcwmTzB2Lg9f62QVxbthEuj7S0JY+/N64EcxvMRkTBmagYlQFSrqKlpSGcInX0T\n0+1ikklIpTBBYBszJZP2mHgCY4wdrqU0ol7DKI2RAq9UBG17VAQTk3c/0toYW+JZKto5HNd3TN6u\n20UWC4jtLduoqS+NOjB39zsZDwgXODjOR0hfPOxyGh5mezsHhMOoqZnbDjiSO9u2BLFZJ3T2LKbb\nJTh5EvXICZvJ3+shV67ZDonJFHJzHdHtocfG7FCm9XW8pSW8HzyPf22ZYGaW9q//Q2S9RuiVlxAC\netNziKCH3FjHKINsN0EIlnhnMt/V5BC0LmEEEEtixkbh2GFMrYXo9BCrKzahUxtMLAoI2zY5M4gR\nEhGLoQ7MInoKUavaCol4nNCZVzFCopMpOwirXkOoANOfQY2OQcgHA0YphOohGg1720MFeJUqxvNs\nF8zJafup/25yCtT/z957BluWned5z1p7n5xvzrG7b+cwOYIASQCEJYZiFClZwSBAm6oyFGirXGXR\nZZarXBZdFlmWi5AIkBQpskqCSckECUoEQICDwcxgBjOdw+3um3M44Z58zt5rLf9YHaZnegbdg+7p\ntJ8/U7fPud1rr3Pn7m+v7/3eV1lxaWUHncndVL8gKmU7sbKzAyEX09tnjZreR3/yIBAUDgEBAQH3\nO2+fbugfeG8LYmNsjHWpAO02zvlzyPw23tQ+9ONP2CdcrW3xUa+jU2nk1gbO5oYVJGZzyI113DNn\ncF97FWfuMrqvn+ZP/yy0WoTOnAAt8McmEMbgrK2CUYhmE4HAGIMzfYHxgQGK6bFryxoztWtTEmps\nnJDEFi5zs7C6hgHM1WuKRDGpJAaJSCRtwdBq2xyL0TFkyMV94zVIJtGZLKJaRm5ugiPRPb2odBrh\nOICwHgyej6zX7elFq42oVSAet5bQQ0O3L3hstWw7otXCdHaiut9x4uP7V6ZV1q3GIZNG77pyuvCQ\neA4FhUNAQEDA/crVQqCyg+rpe1/hnCgVkdtbGHXlyH9uDj0yTOun/5Z9mr46flkqoFMphO/jzs3Y\nnv7ImE1UfOM7OG++gXPxPKSztH/0x0C4OOfPIjwff3wS4Uic1RXwNcJr2ZMBZXBmLiFaDVRPD7/k\nLvB5P8G8k2ZM1PhMXxVv9wvWgbHeQG6uQKmAafm2YDBALI5JJjGAyOZQE5PIagVZrqCGh5Fra4Re\nfw2VzWK6u5H5AiK/jYknbDsiGgUpuGYI2GxYl0chodVC1KqQzqD2HcAMDt5+m6BWswUD3HxE8oq+\nQRQKCEege/rs2OXt+jw8AASFQ0DAfcjN/BY60u8Tdxzw0CF2SsjtLXSuw+oY3ut9V/QOxoBYWcad\nnkanUrR/9McxQ8N2UuJqqFUsgRECZ34e3dGJf+AQcqeE+9YbyJMncM+egWgY72OfhEQceekCtH30\n2BhEwrhLi5imhzAKHMeaMV2ahlod092J6e8HR5IKG34lNIPp7UFN7kZ6OSiXEWsryK1NjBCQSyPw\nbWviigaBzk7U+ISdwigV8fv7cZaWCL3+OqrbCiCvjS12dKJHRq63BxyJQSAbNag37NN9s4loNTGZ\nDtSeqdsXPF4VMxYK1iCqf+DGQkApO0q5voZoNdGpNHpy0oZ/PSSnCzcjKBwCAu5Dbua38E9//tg9\nXlXAh0K9blsJiYRNrnwvA6erokaAfAH3zCmE1lb4OLXX9uuv/l3hsDVQWlpApzP4+w4g6nXcE28i\nT5/GOXMaYQzeM89BdxfOxWlMrYEZHcMkEzjzc9BsAQbhhjDGxbl8EVmrYbIZa5lsBCYWg3AI09OL\nv3sK2WohSyXE+ipycwswmGgUEXIhm0V7GpTBdPfiD4/gFAvIchnV1YU7O0v45Al0dy86k0EuLSGU\nQvcPoHu67GSEMSAdWxxVq8h6He1IZKN1bWxTjx65fcGj1tcjx9NZ9OjYjfqHRgO5uYHY3kZIge7t\nQ3V2vXcL6SEjKBwCAu5DAr+FRxDPu1YIvK+BU7t9Te9AvY578jiyvIN35Bjq8SftDbLdRq7Y3AUT\nCuGsrWCiMdS+/eD7uKdPIi+cxzl9EtFooI4cQw8P4lyewayuYIaGUZNZnLmZK2OZjhX3GXBmZ6Ba\ntr4Kw8PgOLZgCIUx3d34e/Yh2y3k9jZifQ25vWmLimgE4TiYdAYTdiEUwvR24/cNIre2cGpVVK6D\n0NxlxMYGqq8PqTXy0nlwQ+jhUVQ2h2y3wFfX9keUy9aWWQhoNZFgQ7nGJm5f8NhuW8OmRh3d0Xnj\nxIrW9vRhbQ1Zr6HjCfTEhDXMeohPF25GUDgEBNyHBH4LDx4f2M5bazsBUatZA6f3OkpX6prRk1EK\n99wZ5OoKamIX7R/9CRuSpBRybdW+JxzG2VjDOC5q9xRIabUK09O4585YjcGefXiTu3HmZ3FOnMAM\njqAmd+PMXia0MI8JhTDhiE2bnJ9F7JTR8Rj0DdqThWgUYlFMRxf+1F5ks4nc2kCsriFL26CwdtHh\nECadxhiBcCRmbBx2jyNmF5GVCjqdxZ2bQUSjqP5BxPISoRNvYpJp1N4DmGgM2Wwg2m1MJAS+QZaK\n4PkYhG1HXI3DHh27/Zv5FatntLb6hf6B669dMXMSmxsIDLq7F39i8uYZE48IQeEQEHAfcqf8FoJs\nig+PD2LnLYoFZCGP7urG3MxdEOyT7vY2slrGSIlz+RJy9jK6q4f2T/+cDXUyBrG1hazsYCIR5E4J\nozRqbAITjeJMX8C5cBbn/Hnk1hZqdBTvuRdxF+YInT6O7h/Cn5zEmZ0hvDSPCocwiQRGaeTCHE55\nBxONWgfEUAgTj9uioaMTf+8+ZLOBXFu1a8hv2zZCLIpJRTDJDEL5CMfFn9wNuSyhwrad6ojFkHPz\nkM3aiYnL04Tm59AdnXhPPou84uwolI+Jx6Hdtu0BY9BG2mmOSBQ1PoEZHr5twaMo79ggqUjEXtvV\nVoMx9rW1NWSlbMO1xsZtQfJeraNHiKBwCAi4D7lTfgtBNsWHx221l6pVnM11dDL9vgZO1+yfwxFY\n3yB0/izGdWl/4lOY8Qnb278qogxHrNHTdh41OopJpXEuXcC5cAHnwnnk6gq6r4/Wpz6FXF0jfPxN\ndP8A/tEnkHOXCb2xgI5GUVeMl8TiArJYhFAI3dVpWxGpjNVL5HL4Bw4iGw3kyrLVA2xtAMKeMMQT\n6BoZtzUAACAASURBVEQcqTU4Dv6+fZBKIre2UfUG2nFhZgaRzOGNjxM6exbOn0ePjNJ+8RCyUbcm\nTdEYJnUlkCqfx0gJUkCjiUgm0fsPWMHi+9lsvxOtrePmThGdTN+oX/A826pYXbGuld3d+COjdzLC\n+qEgKBwCAh5iAq3Eh8cttZdaLatjcF3UyNh72gxfs38OR2FnB/fcWWS9jv/U06jDR+1T79UUTMfF\ntNo4W1vooWGbWjlzGfdbL+FcnsaZX0DncrQ+/knk1hahU6fQ3d14jz2OMz+H+/qr6Fgck83ascrF\nBcROAZwQOpNBRKKYdBqiMUw2i3fgILJRt2LFLZu1ILSGeBKTiGHiSYTXRoQi+FNTmEgUJ7+FchyM\n0biL8zA2Bj0TyJdeIVSto6am0E8+hdwpIfPb1gEym0WUy3bENBTCSAfZaqAyGfTuKXtCcDuCx6tF\nQb12fVLlSsEmqhV7ulAsYGJRawiVy923IVP3mqBwCAh4iAm0Eh8e79teuqpPaLWsjuG9+uP1uhU+\nhsPQauG++V2cQh5/ah+t51649udyfQ20glYLp7iGHhjEn5hELi0Q+sqfIWdncOZnIBqj/ZGPIGp1\nQmfPoLu6aB99HHdxjtB3XsMkEuhcB+ZKFoVbyIN00MkMIhqFVNq2LNKpKwVDE2dhHrG9hSwUrDV0\nPIZJpmzB0GxALIp/5LCd4ijk0coGWbmrK/hj4+holMgb34FYGL13L15nLzK/jdzYsHbRsYQtRmo1\n2w5xJKLdQmdzeIcO336kdaNh9QtKYbq67P5f+UxEPo9cWbJGTV3d+AcOfaAI60cNYYy512v4vtja\nqrzvBdxqJnnA90ewz3efD7LHgcbh9rmjP8tXTZd2iuie3vfuwbdatmAQAuP7uGdOI9ZWoa+f9kc+\nCtnsdffIRsMKKvPbNvRpeASxvk7o9EnE3Cxy9jJCCNpHHkNqhVxegmwOb2ICd2kRubJijZZiMYzv\nWzOnYtGOFUaiiFgMk8lCPG6jsQ8fsa2C9TVEPm9v6mh0PAXZLCbsIpptTGcX/u49YAzOThETjiAL\neRACf3I3cnMD98RbmGgM/fTTZId6KU/PopTBpFMY4eDkN6HVxsRjdlJCa0zPlQmJ2xQ8ikrZ6hdC\nISt4vFqsXbkWmbevqYGh25++eAC41Z/j7u7UbY+EBIVDwB3hUdvne3FDftT2+F5xp/ZZVMo2iCrb\ngel4D1vjq8WA52FCYdwL5xCLC3AliMoMDV8XR5ZLaAPu9iYqk0OPjSOKBULH34LFeevc2PTxDx+C\ncBi5tADJNP7kLpzVFeTigp1siMVtVsPaGhTz1io6FEJEo+hcJyQTmHgS/8hhRK2OXF1BlK6YIGkf\nkmnb1nBchN/GdPfh796FaHvI8g7Gca07ZTSGmpjEmbmMe+YUJtdB+7nnkdoQym+SyqXYcaKoZtvq\nI4xBx+OIZgsBqKHh2xc8GmMFp6UiJpG0zo2ue13XsLqMqDfQV08eHoAI6w/K3SwcglZFQMAHIBAd\nBrwnzaYdiYxGbfDRzZ5ktbYTCLUKKp7EnZ9Dzs6CVvhPP4fet88KH4sF2/PXxgol43G8Q0cR9Sqh\nl75hBYyXL+FUa3h792ISKdyVJXQygX/kKHJ9g9B3XkYnM9Y1UXs4ywuYUgmBBDdsxyq7ejBXC4bD\nhxD1Bs6li9Y+uVREXAnC0h2dAEivje4dwJ+cQNbrOJubaGGnFEwmh3foKO7J40T+5Evo4RFaP/FT\n9n0ry5hYzK7F0cjZBYxwMPGEFXb6Cj0xaRMmb0fw6PtWv1CtoLMd1wOnmk3k8jJycx1cBzUwbFsd\nD1CE9f1IsHsBAR+AQHQY8C5832oPlLI3vpsJ94yxT76lAjqdgZ0y4ddfg0YTvW8//uNPQih03Uba\nU4idEjgOat9+69/w2ivI+TnE3BxOaRs1Mk57aj/u6hK63cY7eBixvU341VdR6TS6d9CubXkFygV7\nQxXSHuH39l/RFcRswdBo4kxPI4pFRLGAMGDSaVRHhzV/8jz84VH8kRFkvYazuoIxGlGvI/r68cYm\nCH3nVdzXXkXt20/r5/9r5PYm7uxldCqN6R+EUhE5MwP9XZhkGlGuYIxBHzhoTwFuR/DYbFr9gudZ\n/UJv3zWbaLm0iKhW0R0dqP0HMMlA33OnCAqHgIAPwDtFh9WGx29+6WSgIXgUueqhUC2jevvfU1x3\nLS8ilcF4Pu5L30RUyujBEfxnnrUGTs2mdXxst23BoA1q126M6+KeeAs5O4tYnMPZWEf3DuA99hTu\n6irkN/H2HUQUi4RffxWVzuD3DyC8NnJ5CVEqgpQYrUG6mMF+TCaDicbwDx5CNhs4F84jijYjAgNk\nsqjODivsVD7+2ATtoSFkuYxcXQHfQ3g+emSEdipN5KW/xv3mX+E//iTeRz6Gs7yEe+4MpiOHGhxG\nbm0iZy6hs1lMJg3NJoSieI89junqvi2NgahWrH7Bcax+IWY1EXJ5CbG6ihCgBocxe/c/8BHW9yOB\nxiHgjvCo7fNVjcPZ+QK+uv4jeGSy8661LB61Pb5X3M4+i1LRihQ7Om088824MjZJIgHNJs6pk4hi\nHjJZvKefxfT121HBjXWo1RCVCsJroSZ2YeIJ3NMnkDOXEUvLOCtL6JzVNzhraxjXmiqJ8g6hSxdR\n6RSkMuC1EVubyO0CJiSh5Vnx49DwFUFjBP/QYevGuDCPLBRtcYGBjg5UrtOuSQj8XbvQvX3IYhFR\nLmPabaTj4E9MYtCEv/lNZL1G+/kX0KMTOHMzyFoV1d2NCUdxVleh3cJ05MDzEc0Gsq+P9GOHKIrI\nDf//vC/G2P0uFqxPRGeXPZ2plO3pQqmEzuYwQ0MPVYT1ByXQOAQE3GdcNWj6J//qZUrV9rU/D1oW\njwhXPRQSyfcOoro6Nuk46Fgc99RJ+3U0iv/M8+hduwFswVAqQb2GrNdRo2OYXIe1lL54EbG6jLO4\nhIlH8Q8dwclvITc28fdMQbVK+K03UKkUanAY2i3E2ipyO48JuxjjI9oCPTKCyWUwoeiVE4amTcIs\nFXHKJYwQ9qg/m4NmC6k1/r59+B1dyEIeZ24W02pBLG5bCjslwv/lKwgpaH3sE5hcDvfyReTZU6je\nPkwqhVxeBkB1dSGrVUS1hh4cRI2N42QzkEtAsYY93ngflLrmnKkzOatf0NoWRsvLCKPQ/YOoXXse\nygjr+5GgcAgI+D4IfBIeMdpte/OX8r2DqK6eHiiFTiZxL1zAXZrHGPAPHEIfOAjhsBU+bm1Co2F7\n8YND+FP7cC5O47zyMmJlCWdhAeM4eFN7cHZ2cLY3UGO7MO0WoRNvoRIJ1MAQwmvB6rL1TQiHQXvI\nags1Ooru6IBwBO/AIZzWlYKhWLQ20lKguvuswVOziTAG/+AhVDqNyOdxLk0jfB+TzaEPH0MszhH5\nk/+ATqZp/fhPIqSDc+EcZnPNrqNWw52fw8Ti6O5uxM6OzaIYHbP7dQuCx2sTS+sVRrMhPv14jtRQ\nL6q3F6pV5KWLVjCaSqF377ajo4/46cKHTVA4BAR8H9ypTImA+xytrwVM6b7+m98A3x5Wlc3hLMwR\n/s6r4Pvo4WHU0cesfXKljFycx9TqiGoZ3d2LmtqHMzdD+CtfRqysIJcWwW/hj00im02cQsFmJShF\n6OwpdCKOGhhAtJr2hKGwhYnEMVojS0XUxCSmoxMRjpDffYDfuaRZeK3FmKry35WXSUmF6uvHpFKI\nRsNOHBw9BtEYorCNvLhuL6mrG3/PHpwzp4j82y+ih4Zo/sLfQzTquOfPQjyGGh9HbOdxL15A5TpQ\nvX3InR2bMDm1Dz0wcFs6g9/90zOcnC8BUKq1+WI0wj/qbOJcvIjwPfTAgBWRPiIR1vcjQeEQEPB9\ncKcyJQLuX67lRXT3WD3CO3m7yVNHJ7JUIvzNr1uXyK5u1OEjmJ5eK3ycnUFUKsidHXRHDv/o4zir\ny4T/y1dgdQ05N4PTaqCGx8DzcEo7qJEREOBcOA+xGKp/8MrI55rNqIjF0Z5GVrdsqFVPD8IN4+8/\ngGi3+d0TZU6oNCApyg5+q+NpfiV3JWUzHEEdOABuCLGxgSwvWDvswUH0yCihN14n9MV/jdqzl8Yv\n/UOcjTXc49+FTAY1sRtnbRX3wnl0Ty+qrx9Z3kGHwvhHj9nwrVsVPF6dhCjkWdio3vDS4lIBuarR\nk5OPZIT1/UhQOAQEfEACV8aHnEoFZ20Nncq8ZxDVtYCpTA7thnG//S0oVyCXwz/6mD2eB6v2L2xb\ncWEyjXf0GHJ7i9A3/wqxvIxcmMWpVVH9AyjRhaiWbZYFBufSRUwyju7vt22NtVVkcRsTS6ARyI0N\n1Og43sAAMhTCn9qH8D3c06cQhTzz4WfgbRKMeRNHp5Low0coe4YvvlFhoSEZjbp8+oldJAd7Cb/0\nEvLrf4l/9Akav/w53LlZwq98C93Tg9q1G2dhAefiBfTAIESj1vipsxv/qWesSPRWb+5KIbaumFul\ns6iRMUa7S5QWy9feMjKYQx079n18kAF3mmCqIuCO8Cju829+6eQ1Eyi4uxMV8Gju8b3AVR65eolS\n3cfreo+n5qvplomUtVg+fdKGMaVS6NFx1MSkvaFubcLmpo25jsbQu3bZE4cL55FLC8h5O9Ggu7tt\nHHajjhoaAcfgzC9gwlFMOoXw2lAo2CIlmUbUq8h8HjUxie4fRIZDeHtsweBMX0AW8tZcKhzh13PP\nc1xdd1882in5xwdc5Ooq/9dSnOOt68mPx0JV/sf6m7SfewF15KgN18pv4w8OQTiCuzCHcVx7ulCt\nIJpNdH8/enLXbfkkuNon59XY2SjgpbOYaAy5topcW2VHhvnCjGCh2AoK8u+DYKriESZ4qr1/CUyg\nHjKUshkGRsH+3Zi6D+/8hdtsWnFkKITK5nDPn0MuLaGjEdTuPeiJSUyuw7Yu5i4jikVwQ6h9B6DV\nxDn+FnJxETk/B4U8IpVEDQ4gmw10phe/sxN3eQEdjqA7OxGeB+vrOIU8KpVEh0K4i/P4o2N4+w8h\nQw5qcgqtfUJnT9mn92YVFYnjjU0gpOSzapl/zS7m/QhjcfhMbA3nQg3T08WcSALXr3FOpGh+9pdx\nz5xEfvtbqJFRTDiCu7iIyWas8VOxZFs3I6PokdHbc3is162fgyth1yimbZCzc4hKFd3bg3/scRKx\nGJ975s58pAF3h6BwuM8JrI3vX4KJiocEY+y4X2UH3dOLzmas8K7uX3/P1UkJra3wcW6W0KVpcF30\n2Ch6dBzd04uoVnAunEPkbXKk2rUHAOfcGcTivD1h2NqESBTd24to1DGpNKqrE2fV+jKYXAe0PdjY\nwilso9JpVCiMOzuLPzpG+yMfQ4Zc6/OgFaHzpxHrG8hmE52I443vAgxCSPTQMPH+Af5JrYaztIBu\ntaFrEH/3k5j8FuNnVjlO7tpljkU8Qq+/ij86igyFcS9fQvX24o9P4OS3kcUiemKXdca8DcGj2Ckh\n8nmIRNCdXZidArz1FrLh4w+OYA5133ykNeC+JCgc7nOCp9r7l2Ci4sHnmptjrsPqGN6JUtdGJnVH\nJ876GqE337Dq/sEh9MAgun/ATlTMXEZub4Lno8YnIBJFzlzCWVywJksbayAcWyS0PTuR0NmFs76G\nDoetk2O7DdtbuNvbqFQaPxIldOkS/sioLRgiYdT4pLWePn8WubaGaLUw6TTe0BAojXBce1LQ1YXc\nKeOeOW0vZXQUPbELMTdD+D/8EaRz/P0f+zj6jQKLW3XG4oZ/8EQ3priBe3EaNTSCGp9Abm9jEPgH\nD2F6+25d8Hg1WGqnaN0yOzqQS4u4szOIvl544glUy2CCttsDR1A43OcET7X3L8FExQNMo2GDqOLx\nmxs4GYPY2sQpltAdnYhmi9DLL0G1jOkbQPf2ogcGbW9+dQWxumL7/aNjmGQKuTiPXFiwiZWbm6B9\nVDqL4ytkPIHuStiCpdXEZLKIVhOzsYlbyKMyGfxEnNDli6iBQdof/UFEOGQnJrSyxlDrq4hWG5PN\n4Q8NI7VChMKoPRPWfKlQwDlxHMIh/Mnd6OER3HOnif7h7+MPDtL8238fp1Km8/wpfmUggzrag7Ow\nACtl235Ip+3pQq4D/4mnbOz0ewge39VO/cQuso0yol5Dp7PoSBRn5hJIiRoZw+w/iBsJQTwOrdqH\n8GEH3GkCceR9zoOicXjQ9/lBINjjO4DnWY2CMfak4CbH7aFKiazfoCQj+M02zulTyK0tdE83um8A\n091jn5431m06ZbWKHhq2o5hrK7ZgmL2EWFlFeC10Ko0ATDqDjsdwijuYSNg+ubfamGoFd3sLncmg\nhCFyYRrVP4i/fx8iHMEfGUVogzt9AbG+imi3MZ2dqI4upO+hszn06CgmFkNubiFXVzDJBGrPXkxX\nN85b3yU0PY23Zw/eiz+As7KMMz9vLaETCUKL8zYCe2jY5lBUK6jePvSu3bcUaf0ukfBAjM/9yCTO\n9iYin8d0dNgJkdT1h57gZ/nuE4gjH2GCp9qAh4l7VghfibEWtao1cIrH3/WWq4mUZDPQ1Yl89buE\n5ucx6Qz+wUOQzaJ7+xA7O7hvfRdRKqL7+vHHJ5BbWzhvfRfn4gV7AtFoYOIJTCQCiRQqFkPWq8iG\nwMRj0GpgSg3c7U10NkO7s5PoubOInl5aP/hDiGgUNTiK0B6hC+cQyyvWwbGnC5XOIrSCTAZ/dBQj\nHeTGmg2+ynZQOPYUXzjvsfjXFcbVCp/enyD26c/izl4m/PJLqMFhVF8/zuoyprMLb/de5PYWcm0N\nMzpK+/Enb0vwuLBevuHrxe0m7sxF1PAoZs/eIML6IST4RAMCAj407oXYVxQLyEIe3dWN7u199xsa\njWsZEqqrG3d+Bt54BdFWeAcOIuJxdG8/wmvjnLly+tDVjTp4GFkq4Zw9g3P+nC0YqmVMJIZJptCx\nGMSTiFYT6fkQjiKaDUy9jrO9hU5naHd3Ez1zCtHRReujP4SIRtADw2AUoQvnkEsLYDS6t8+OYSof\n092LGhkCTyGXbPKl6e7Fe/FjGGP4na8tctJLAi5F0YFeNfzKKy/hD41CZxfO0gL+8DD+3v04m+vI\njXX0xOR7W2jfDK0RxSKyVGA0E6JU8669NNKfxn/28Tvz4QXclwSFQ0BAwIfGhyr2veq1kEzf3MCp\n3baTEoDu7EKuLBN6/TWk9uHxo2hfYLId6HDEth5WVyGdwT94EFmt4Vy+jHP2FGJpCVkrY9wIOh6H\nRAITT9gTAoCQi2jUoVlHbm/bgqG3j8ipk4hMltZHfgCRSKP7+hFK4V48j1xcsO2UgX5MNI4wBj0w\ngBkctCONMzOIcgUzNIT32BNQLRP61l8j2i3mxI037fmGwMTiuEsLqJExVC6H3LQiTn/fAeuGeauC\nR99H5rcR1aqN6C4W+exwi39DnIWyH4iEHxGCwiEgIOBD40MR+7bbyLVV64r4VpWFzXVGe9eut0WU\nsgVDq2ULhkKe0CsvI0pF1MQuVHcX9HahRQQxN38ltCmG3rsP0faQqyu4J08iFhcQ5R0QBiJxTDSC\nSaQRQoMTwhiQtYo90cjbgqHVP0D05ElEIkH7+RcQqRS6bwChfNyL08iFOQwCPTQEbhghBf7ELujt\ngVIJ5+xZaLfQYxP4Tz+H3Fwn/NX/jIlE8J99DpNIMv7VBY63r58cjIc91NAQotFEFvKYTAb12BOY\nrq5bd3hsNpHbW1CvI5p1xE4ZEgn0nj3Esjk+d+c/xYD7mPuicJiamvoJ4E+w+ariyn//eHp6+mfv\n6cICAgLuKHd1hFUpq1FoNtH9A3zxy9OcnC0A19si/+gH+m08c1c3AnDf+i5yfQ01MIiZ2guA7u+D\ndg339e/gG1CTu+39NV/EPX0cMTeLKJfB8yEStu6OqRS4LiYawzTqOOWSPRkoFTGJFK3+QaKnTuDE\nonjPPAfZtPV9UAr34gVbMDgh1NAwOC4yFMLbswdyHYj8FvL4WwgMatce1MgYcmGW8F/8OTqbpf2x\nj4MxuHOX0dEY/2B/As7UmffCjHRE+G/GQ7grq6ieXvznnsekM7e8paJauaYNoVxBKg81OITaeyCI\nsH6EuS8KB2A/8KfAZ7CFA0Dz3i0nICDgbnBXxL5vD5nq6cX0DwA3aYuslCA0jE5nkefOIhcXEdkM\n/jPPWe1ALgf1Bs6r34aoa30PpIOo13DOnEFeOI+oVKDZgnAIk0hAKgmRKCqeQNaqOIVtaDaQhQIm\nmcIbGCR88iRR18V78knIdaK6uxFK40xfwFmYw4RCqJFRBAIRjeHv3Y9Kp2wmxXffQIRd/L370b39\nOBfPE/qLP8f099H6kU8hqzXcS9PobBqVTONsb5Ltj/K5j48itzYQjTK6e5j2+OM3FYS+534WC8jt\nbSiVELWqtdLeswfVeRunFAEPLfdL4bAPODM9Pb11rxcSEBDw4CAqZeTmBjrb8S4dw7vbIgnkwjzO\n7GVwXbwnnkRgMLE4xpE4J48jKhX0xAT0d8HWDs7Jt3DPn8PslJD1OsZxIR5Fp1OIeAKVSCKrVdyN\nDWi2kDt5WzAMDhE+dYKQlHhHjkJPD6qrG6F8nOlpWzBEI+ixCXujjifwDxyGSBixuIBz/gwmkcA/\nZqO4nQvnCJ89jRoexvvkpxD5PKHzZ1HZTjuGuV1AjYzg9x/BWV9DLi1iJibwR8dvXfColHXQXF9F\n7OwgjEb3D+IfPgLR6J3+6AIeYO6XwmE/8NV7vYiAgICbc9/5iTSb1sApGkWNTbxb3Fev8+mDcb7Y\natmwpKTkM7FV5MUa/qHDkEjanmgqZS2iN7esF8PgMI4Ezp4l9PJr6ELBHtNLiYlGMYkk5HLoWAJZ\n28FdW7Vr2SlhEkm8wWFCZ04RVhrvwCHo7Ud1dyE9D+fClROGeBQ9MQlKWbvpg4fAaGtHnc+js1m8\nZ57DhEKEzp9DVCv4Y2O0Dx1Bbq7jXrqATqUxjoNTzONPTMLQkHWRbDTw90xhBgZvXfDYallPiuUl\nRLUK6Qxq7z4bix2cLgTchPvCAGpqaqqKbVU8DjjAl4BfnZ6e9t73G3n4DaAeFIJ9vvvcyz3+sJNA\n3xPft6OTSlkDp3f22a/cBJESnckiNzdw5mYQ23nUnj3ogUFkvYbKZHHm53CWFlG9fZjOLnAcxNws\nkTdfJ9GoUs8XMdqA42DSaUxHFyqdQu6UkcWCFWFWSphkEj/XaUOmmh7e3v0wOITu6kT4HmJmBndh\nzk5c9A9gPIXp7bUFQ7uNvHwRuVNGd/fgT03ZSOxLl0D5+GPjmJ5enLVVaxYVjyGLRYjG8McnEM0G\nYnsbkknU7ilMz23c7KtV5NIizvKSHfkcHrFF2O2EVn1Agt8Xd5+H2gBqampqBIgBDeBngHHg/wai\nwD/+Xt8vpUDK975ux5E3/Dfg7hDs893nXu7x4mb1XV+77oe4jisW0KJSQff2QTLJDf+67yPW122G\nRHcXolQkdOYEcnkFPTSIeuxxnPIO0nUQ7RbhV15C5zowBw4go1HEyjL1b73K55tDzMlj7KLIL8nX\nSaVj6J4eTCqNqJQJLy5gWk1EpQyJJGp4FPfcOcJz8+jJ3eixMURXF6LVxrlwAbk4j06lbJy272P6\n+yntOchvn6wx/3KdcWp8dihD4rHHkeUdItNnQbroXZOYZJLQ1hasLWMcF9mso5Nx9LGjyFKR0OoS\ndHWjXnwBMllu6XzBGESpiLxwAbG1icnm0EePYHr7EFJ+aDeE4PfF3edu7vH9cuKQnZ6eLr3t658E\n/gBITk9Pv+8CjTFGBMdpAQF3lV/74mu8cW7j2tdP7u/lVz/9IWUfl0qwuQldXdDRceNrWtvXKhXo\n7YVaDebmYHYWMhl44gloNm0WRbMJJ09CIgFDQ5BO2+/92tdgbY1fE4d4I9x3/RpDFX51pAw7O7Cx\nAY2G/fsTCbuWM2fs15OTsGsXdHdDuw3T0zA/b9fa0wOeB+PjcOQIbGzwa6/XeaOdvP7v5Ay/2mFz\nMxgdtS2G7W3ruNhuQ7UKw8PQ32/XUa3a9U9N3brgUSlYWrJrbjTsmqem7LUEPOrc9g30vigc3snU\n1NQ+4AzQMz09nX+/9+bzVfO9ThzS6RjlcgOlgiOxu0Wwz3efe7nH5VqbL/zZORbWK4z2pfjFv7mf\ndOIuaxzqdeT6GiaRxHS/I3bZGEQhjygWrR+B7yOWl5Hzc4BBPfYEhMI2tloInNOnQArrjpjNYSoV\nQl//KmJlFdOoI2s1fmnkpyi612/EOeHxW7VvWO+CWg1SSXQ2i3PpMqJaRQ0OYnbtxnT3IloN5Mwl\nxNIKOtcBHVnQoHbtxuzdi1xaQl6+iBHwy+pxiv71a8m5mn/1QtReQ6WCcRxEo47wffyxCUQqZU9T\nvDZ6bAw9sevWBY+tFvLCeeTMZetFceAgZmj4nkdYB78v7j63use5XOKBbFV8AvgjYGh6evrqCOYx\nIP+9igYArQ1af+/iRykd9NI+BIJ9vvvciz2OR1z++586fMOf3bU1tNtWxyAEfv+QvUlq7OkC16Ow\nVSYH2Q7k0gpyYQ4qFdpHjmE6u5ClAqbt41w4D9Uq3tg4prsb02oR/vKf4szPWyOlchmpNSqTYSzs\nUXzbJY03t2FjG5IJvMEh3JkZ5Nw8uq8Pdegopq8P0agjT55Erq6gcznMyChCStSuvaiJCeT8PM5f\n/iWEQ3gTu9GdnYyeaFD0rxddownQhSLGGGS5DJEI3sQuhJSIrQ1MaQc1uRszMnL9hv+99r5UxD3x\nFnJzEzU8QvujP2xPWOCGvbzXBL8v7j53Y4/veeEAvALUgS9MTU39GjAJ/Avg/7inqwoICPhw0doa\nONXrVvj4TpFerWaFj4kEqqcXubmJWF7E2djA37UH/ewL1g55p4SYn8fJb6NHRtF792GkIPxXX0Ve\nvIhpXtEotFuQSONNTUFHB58prfCFUos5mWKXV+QzjdP4g4O4c3OEFhfRXZ2oQ4cwfQOISgXnBUSy\nZgAAIABJREFU5Enk5joqk0EPD9kJj30H0SMjOBcvEPr6VzGxGGrffhu1vbWJXFniF8dyfGEFFmqG\n0ZjmF3vrUNyhksrxb5pjLKx7jG3k+cU9DokDhzG9vbcmeDQGOT+Pe+oEGIV/4DD+ix+99emKgIBb\n5L5oVVxpTfwG8AxQAT4/PT39v93K9wZTFXeWDzp2F+zz3edh3mNRyCOLBXR3z7udDZtNWzC4Ljqd\nQea3kevryKUFdE8f/tFjyGrFvm9lGbmyjB4YQo+MoKMxwt/4Os6ZE9D2rEV0rQHJBP7+A9DZBZUy\nzuIiVCtIz4NMinhXJ/WLM5jyDmQy6D170P2DiEoVOTdjn+QzOUQyDrEY3qGj6L5e3HNnkSurmHQK\nPT6JjoRwCkWM42AyGZAOtFoIIaDZQFSr6MFh9OAgv/GtdU5sX/9cb3lypd3GOX0S5+I0ursb/9gT\n0Nl5hz+hO8vD/LN8v/BQT1UATE9Pnwc+ea/XEXBv0gsDHl2uRlnrVObdQVSeZwsGpWymRKmIc/mi\n1THE43g/+MNgwNncgPw2zsxldFcP/lPPoFNpQq+9TOS11xCtJtSqiJ0dTCKO/9ST0NUNtRruudOY\nnTJSKXQ6jd/RSWhtBdbXEJEo6thR9OAooryDc+I4sphHJTOowUFEPI539HFMLodz5hShUyfRuSz+\n0WMgsWObfhTd2YVQPkIpjFbIagXhtfFHJzAHDiG3NnHmZ5iv3Ch0/J4BYNtbhN76LrKQx9+zj/ZP\n/WxgAx3woXBfFA4B9w8fanphwKNLq2UNnMJh1MiYnSC4itbIrU2o1dDdPch6DTk7g7O0gFA+3hNP\nY3JZnI0NzPa2tVzOpPEffxLd04P73deJvPRNqDehXkMU8ph4HP+Z56CrB2oV3HNnoVAAoyGZxk8m\ncFZWcVZWIBaFI0fwewYwhQLO8beQ5SI6mUJ19UI2i3f0MYjHcc+cQhwvYjo78Y4eRShlfSLiCXTH\nFR8Hz8MIbBvFDaMmJzDJtC145mfRI6P4Tz7NaPk8pZnvEQCmFPLSRdwzpyAcxjv6GGZk9K5/XAEB\nbycoHAJu4ENJLwx4dLmaTNluWx1DJHL9tbdnTnR1g+PiLC8hVleQpSL+wUPokTHk5gbywjncy5cw\njmtvnkNDiNNniP3RH0C9Ds0GzvoaJhrFe/Y5RG8fpl7BPXcaCkUwGpNKo2NxnI1VnM01cMPo3Xus\n5XSjgjz+JuyUMYkEuqMb09mN99hjEArjnjqO3CmjerpRR44iPA/ZbltHx0gU2W7Z9oQBubUOqTT+\noWMIRyI21hGlHdTkLvTo2DXB4/sGgFUquKdP4izOowaGaH/yv4JU8P9mwL3hvtA4fD8EGoc7S6Bx\nuH95oPfYGJuDUNmxQVTJG296YqeE3N5CZzvAkVb4uLWJXFtFjU+g9h9ElndgaQln5hLS9/D3H0JP\nTCBmLhP+8y9DoYBQHs7KCiYUwnvqWet9UKvhzs/D9qZdSjqDiccQq2uIdtumTg4OoSd3IYp5nKUl\nEn6LejiKDoUxPX14R48htMI5cxpZr+N39VjfCOVj3BAimcTUGzYsK55AXD3p6OtDjU4g2i1kfgvj\nhlBTezF9/d9b8GgMcnkR5/QpRL2Ov/8Aes/eG09nHlAe6J/lB4S7qXEICoeAO0Kwz3efB3WPr45P\n6lwHJtdx4w2zWsXZXEcnUph4HLm1AYUCzuIipqsT/9gTCK2QC/PI6QvIShV//370/gOI5RVCf/on\nyPV10D5yeQWkwHv2eRgYwtQqOEuLOGtrGGEw2RwmHENurmPabaQ2qP5+9K7d9qRjdRFRbyLjMWKZ\nFLWuHlqHjiGaTZxzZxDNhi16uroR2lgL6UgYUa5cOcFIIUolZKWKGh3BDA5DpYws5DHpjLWEvhXR\nYr2Oc2kaZ+YyJpnCP3T41gqNB4gH9Wf5QeKhF0cGBAQ8hDQa1o8hFkONT95oOtRs2tdCIVRP35VJ\niVXk4gKEQ/gvfgSTSts0y7OnkFvbqL37aH/iRxDFIuEvfh45v4gB5MoSQmm8Z59HDwwimg3khbM4\nq6sYIdAdGUwobkc9/TzCV5ieLrw9+xBbGzjH37J20K6LyWRQE+Pw9JOojTzud7+DaLfRPX3osVGE\nE4JUCi0FolBANF10Ko3YXMcpl/End6MOdSMLeeTCLKa7F++5FyGZfM9tuopYW8OZPo8sFlGDg3gf\n/yQmlb57n09AwAckKBwCAgLuLJ5niwJj0INDNyr93/5aVzeyVETOz9kxylYT78hjmIEB5Noq7svf\nwlldRu3aRfsHP45pNIj8u3+LnL6AcRzkyjLC8/CffhY1MY6oVnEvXUAsL4N00LlOTCRshZaqZP/t\nbBpv70E7yXD8LYRRGCkxqSR6fBx//wHccgVeeQWnalsSOp2GWByTyaI9H2drExGPo5IZ3PUVnHoN\nf+8+VDKJ3NxCLsyhh0bwH3viRg3HzWi1kLOzOLOXwHVRYxNWxBnEWAfcxwSFQ0BAwJ1Ba8TWFqJW\ntUFUb89BUMo+8TebdlKiZpMZxeYGTqGAP7UXf/ceRLlM6Kv/GefyJdTIGK2/9XcwQPiP/1/ck2+h\nHRe5topsNmk/+TR6z15EtYJ78SJiYQ6ExHR2QziE2NoEBLRbyFQC7+gxnK1N3FMnEcKwI0J8vu+j\nzEU6GU27/GJHno5XXkU6AkaH0L1RTCKFzmahWsZZXsKkM+hMFmdtFSeZxDvyOCIcQmxuIosF1PgE\n+mYx3+9kcxN39rLVQWQyqMeeQHf3PBT6hYCHn+CnNCAg4PtGFAvIQh7d2YXunbz+wttFkV3dEI7Y\nSYmdkhU+DgzR/pFnQCmcl18ifPI4qref1s/+PCaeIPznX8Z97RW0ADbWCVV28J54hva+A7ZguDSN\nmJ0FITA9vZhwCGd9He2G7AlDNIx35CjOdh73zGmQwvpCpNL8Vt/HOO6nwEBxB75YEvzTri5ERw6G\n+zFuDLO+gTN7Gd3ZbQuG9TVUdw/e088ilI+zvYUR0hpEDQy9vw7B85DzcziLCwDorm7U01OYXO6e\nZ0cEBNwOt104TE1N/Xvgd4C//F7JlQEBAQ85tRrOxho6mX6XgdO1YqKj0xo4bWxArYpcXMRk0ng/\n+MOYWBx5/C3Cr7yESWdo/uTPYLp7cL/6F4S/9nWM0NboKF+kfexxvMOHEbUqzuxF5OVZMAbT2wch\nF7m5iQ67GKPt1MXe/cidIu70eYzrgtaYZAa9azdqfIL5kzeeCsy7WfTuHKRTUCkgV+ZQnd2YZBJn\nbRk1NIz/wotWvLi6jIkn8A4fs0mZ70exgHv5kk3ZTCRQV3Mz3umQGRDwgPBBThw08B+BwtTU1O8D\nvzc9PX3xzi4rIODB44OOsj6QtNvWwMlx3mXgdM0NMpm2wsetDag3kMuLCMB76mlMTy/i8kWif/EX\nGEfS+hs/jhkdw/nrbxL5l/8npt1ClEo4hS3aBw/j/9hPQmUHOTeLc/kSaIPu7UOEXOTmBiYasSZL\nzRb++CROeQdnbgbjhDBKQyKKf/AwamISZ2OT0KvfZjx0mKK8PuUwkgkh8+s4q8uwZwITjeOsreFP\n7rLjoDslxMICdHbiPf3c9dCom6GuTIIsLYKU6EwG9kzZdsQ7MzgCAh4wPtA45tTUVBr4OeDvAs8B\n3wF+F/j309PT5Tu6wu9BMI55fxDsM/zml05es+uG28gauEXuiz1+u1ahr//Gm+DVKYpoFJ3JIrc2\nrZ/B+jqiWkEdOIQeG0dsrBP+T3+CqFdpffJTmH0Hcb7zGpH/+CWolqFaw93apjU1hXnmOUSlAltb\nuDOX0FphevsRjovcXsdE4xjPx2k38EbGcCoVqNUwkRCi1kRnsqg9ezBjY4itTUIXpzGOi+7uodQ9\nyG8Xc8xXNOOyyWdzeeJ9HYRKJVIhwc7QGH46Zx0fa1V0/yBq9573Fy7u7FjtQqlki4VkCpNK2TbN\nrUZhPwLcFz/LDzn33TjmleLgt4HfnpqaGgP+HvAvgd+Ympr6Y+A3p6en3/wgf3dAwIPKQ23XbQyi\nUECWCtbLoH/g+mtvi8HWvX12FHFpwQZXbW6iJ3bhv/ARqNcJ/7vfw1leov2xH0Y99Qzy9Cmiv/o/\nweYmtFq4m5t4E+M0Pvk3rIBybg7n8kW0r6zTpGvNoYhFMOEoolJBDQwiGnXrFBmK2HHLRAL/ySOY\n0WHk+jruyy9hXBe/bwAzOoruHyC5s8P/UJvF9IfxczlC2wqdz6P3HYCBLsTMAs7SAmp0HP3Mc+8t\neNQaubSAXFiw46W5DmQ6jc7kMB0dgX4h4KHjA4sjp6amwsCPA38H+ASwAfwBMAR8a2pq6n+Znp7+\n9TuyyoCAB4CH1a5bVMq29ZDJ3ahjuGof3Wqhe3qR1Yr1YajVcNdWUF1deD/8SXBd3D/7/widPkn7\nmRdo/8LfRc7OEPu1f45YWgHl4W5t4g8OUfuFv02o2UQuLeJeuoT2W+iBITt+ublhxyJjCeROAb+n\nDxlycYrb6FAY2fYxiQTq4JOokTHk2hqhl76FCbmo4RH06Bi6fxC5voz71puYZArV3YOzuY5TreEd\nOoKQDm4hD7QxY2N4/cPvLXisVnFmLyMLeVRnN3p4BIyBzk5UOvNQGTYFBLydDyKOfAHbovhpIAb8\nJ+DHgK9dFUtOTU2dAP5XICgcAh5Yblez8L5ZAw8A77reH5ogW96GSAT19hFDre2kRLVse/aRKM7y\nErSb1r0xGsF7/kVMJovzjb8i/K1v4B86RuOf/c+IjQ2iv/6/Iy9eAK1xCgV0Vzf1n/oZXM8ntLqK\nc/kipt1G9/djnBByawMRT6KTKZz8FrqjG51KI2tVe8LQbEM8hf/0YdTIKHJ5ifA3v4GJhFHj4+jJ\n3ejOLpyleUKvfRvT0YHq6cXZ3kTEYviPPwW+h5PfxoQjqIMHYe8EuliDdx7xGoNcXbEJnUKg+gYw\nmazdlq7uG0dQAwIeUj7IicNLwHHgnwN/OD09XbrJe84CX/l+FhYQcK+53YjxdDz8QEeQv+t6Gw0+\n93PHrpsYGWMnJYoFO3bZ2YVcX8f4PmJ1BeF7+IePYvr7EcffJPaVL6NGRmn8k38GzTqR/+c3cU+e\nxGiNUy6hMzmaf/PHcYTB3dzCmb2MqTfQA/2YUAS5uY6IxdHpDM72FqTS6FQK2W6iwxFkZYdyNMPn\nD3yCeRKMlav8t994iVTMQe2dQk/twyQSyJlLhC6eR/f0oXr7cfNb6L4U3jPPI2pVxPoaZDJ4jz0J\n2Syue5PWQqOBMzuD3FxHd/eidu2x3xuNXBkzfUhFsAEBN+GDFA5HgTPT09M3lOJTU1MucGx6evqN\n6enprwFfuxMLDAi4VzzUmoWb8K7rLfvXigZRKdu8iVQG1dtv2watFiK/jdzZQe+Zwp/chbg0TfTX\nfw+TSND47D+EcJjwH/4+oVe/jUEjqjWIJ2j+0CdxIiGcQh5ndgYadXTvIKarx4oq4zF0LmddGsNR\ndCSKNKDDEUSljIhE8J95nt/yJjlRtichRVJ8vv9FPvd8F4RCuNPTiJ0iqrcP09OHLBdRw6O0d+9B\nlndwlhbRvb34z78I8fi7N+T/Z+/No+S67vvOz73v1d5Vve87tsIOriJFiaJEW7ZlOY4djSeenEwc\nWd5PJhorXjIz5/gkHs/JRLF9rESOZUsaOU5Oxhrbiq1ItmUtlGXtXACS2IrE0t3otfZ9e+/eO39c\ngABIgARANNAA3ucf9quuen3rslDv9+79/r5fYxAb63Z8WqNm56x5Va1i9Ryzc29s9BQQcBdyI4XD\nYWAMyL3q8Xngb4Er/AsMCLjzuFs1C1dCVMrMJSVH6hcfmx1NQrNpdQyxGGpsApnLIot5qFat8HFq\nCv/hRxC5LNGPfgTR7dJ+349hxiYIfeb/I/ylL4DSiK4HIZf22x7HTSSQ5SLyxQVEq4EeHbUFQ3YD\nEYuhBwdwshuIqrT+C6EQOhzGqVYQoRD+o4+hpmYInTjOYrMLzsXOjrM6TujEcei0bYHjOMhqBT07\nj0nvhlIRZ+UcamoG/cBDV+506HTg6FnczGlM7wB+eg+y00a2muientf4VQQE3GtcU+GQTqd/Afil\n84cCeCadTqtXPa0fWLyJYwsIuK1sNc1CtdHlP3zmRU6dKzMz0nNzfCKaTdsRkUjwT9/3AJ/6q4x9\nv8MJPnAoaQ2cxsbPd0os2SX79TV0Mon3jndCu0Xkv/4Rcn2dzrvfg963D/dznyXyuX8F3Q4CMAi6\n99+P7B/EKZUQL2dw6nXU6BgMDVkNQ6SDHhrE2dhAVooYJwQ9cVQohCyXcVwH/7HH0VMTuEdfwD16\nFD04wGyfQ6lx8e3MU0P1DyAaDWS9hpqbh1QvslhArK+htm3Hm5m9YqeDyGdxTp/BVV04tA//LY9i\nsjlbeAwNw6WdJAEB9zDX5OOQTqfj2MJBAr8G/BZwyb0J5vzxn2UymVtaPAQ+DluDYJ43n3//Zy9w\n5OX8K8dvyifiQtgUWD+GC3fevm9XGDzPdkrUqlAug+/jrK2ClDbm2XEJfelvcE6/hPfWx1CPvA3n\nqS8T/ZNPQ61ivQ6Uwk/vQYyOYEol5LlzyEoVPTKMiSfsdkckik6lbCtlu40Iuei+XrQbQZbykOrD\nf/AhzPAo7pHDOBsrqKEx1P0PoLbvoL5wjk8ea7Ogoswm4Gd686QiDmp+HkJhG2ntOKhdaRtNfaV5\nWFjAWTmH6e3F377Dfpa9JuWWwusffOOgqoDrJvi+2Hxuu49DJpNpAr8OkE6nDfDvzj8WEBBwi1hc\nvwmaC61tWmSjYQuGC3v75wOqZKOGGh5FdLu2U0JrRC6LaDXx03sxfX2EvvE1nKMvoNK7af/CB5HP\nP0fin/0slIqYnh5EJIyemUdPTkK5iDh6DKdSRA+OoKan7d2/56FGRnDW13FyWXDDMDSE74ZxSnlk\nr8R/8vsw/f2EnnsG8czT6LEJuu/9EdTUFPLMaUJf/TJ9PT38YnoAp7aOiSXwZ3ejtEaUS9DTg3fo\nfhgYeO08FIs4Z04hGg30zAzeY29HVKtWU9HXBzvnMdX2a7sqAgICrnmr4h3ANzOZjA88BTyUTqev\n+NxMJvO1mze8gICAC8yOJSnVOhePr1NzIYoF2xExNGzzHeByY6ehYXQsirOxjlEKUakg8jkbNz05\nTeiZ7+I8fwQ1Okrnf/5JxPI54r/yIcT6KmZwANGTwIyM4U9NWzHl8aOISpnK8CQfS7+TBZFk3ivx\nM8Mn6N1Yxl1fB9fFjI3jh1zcfBbZ24f37h/ARGOEXjiMKJbRczN4TzyJHh7GPXmC8Fe/gu7rR01O\n49QqCAze3oNWh5DPYYaGbTT1q1sjlUIuLeIsL2FicfztO6AniSzkcZaX0P0DqG07ECEnED0GBLwO\n1yqO/CpWEJk9/7PBah1ejQGCf3EBAZvAT/3QXv7TFzKXaRyuiXodJ7tuOyIuEfaJShmZz1ljpwud\nEr5nQ5w2NtBDQ/iPvR3n+ItEnnoKk4jR/ZEfhUaT2G/8a5yls/hDI9DXj0n14U/NIBo1nJdesmmY\nff2YySl+P3yIw6FRAEpunD9ot/mV6gnM5BTKcXELWZzefrwfeC/GcQg9/zzUa5htO+j+4N/DRGK4\nx1/EOXEMPTCEPzmDU68gwi7+/kNQr+Hks+iJKdR9D7y2NbJicytEpYKemLA5E0oh8zmoVDBDQ3b1\nJSAg4Jq41sJhHshf8nNAQMAtJpUI82sfePTa94U7HRtEFQpdHkTVaFgdQyKBmpiy3QyFPMLrIjY2\nIBzBu/9BnKUFIn/2aXAc/MceQ8fjxP7D7yAzJ1Gjo6jRUYjG8GfmkPUazsIZZLWG7k2hJiaQ5RL4\nXc5OD182rLOpCfTUFE5uA2doiO4P/j3wfUJHDkOni79jF+qxxzBaEzr2IrTaqNFRRCyOaDbQgwP4\nc3OIagWZz6Jmt+HNzV2+SqAUYnkZ99wiJhRCbduBOXS/DeBaWbadGsMjr587ERAQcEWuVeOweKWf\nAwICtiAXrKC7XXsnfeHi2G7bx10XPTGJLORtp4RSyEIO0eng70wjSyXCX/hLhNb46T3okTFin/x9\nnBeexx8bR09NIaSLmppEtNs4S4vIeg0dT6DGRpDVKqLsY3r7oVJivrxMaWDHK8Obb2wgMHR/6IcR\nzSbuc0+Dp/D37EW95RH72LNPgwA9NAI9CtnpoMfGUfPbcKoVKBfxt+/ETExe3hpZswWMKBQwY2N4\nD70FIhFEqWjTMhM91hravWG3/YCAe55r1Th85VpPmMlknrzx4QQEBNwwxiAKBWS1bIOoes5rIDzP\nFgxK2U6JasVmSmAQpRKyWkFNzyG0IvTtb1q754lJ1OQU0f/3PxN6+jv4w2P48/NIrVETE3Y1Y3UN\n2WygY1H00BCiXkNUa5ieFNQrOCeOgRPiZ+Mn+Fg7zoKTYl7X+MCeGKqRxn36uzZyev8BvPsfQuY2\ncL/9DZuuOT6F6DQQXQ81NQnROKJcQraa+Pv2YQYvWcXQGrG+hrtwBiMkan4bZv/B8wXR+WTL3n5r\nmx0ETgUEvGmutexewuoXAgICtiCiWrHOjn0DqPnt9i5ca6tbaDbRI6OITsd2SgCmXkcWrJBQTc3g\nHD8KnTa6fxA9MU7os39O7FtfRw+O4O1II7pt9MAARitELotsNNHhkC0YqlWoVjGplNVTvHQChIua\n347Rir61c/yK0Pj33YcoFnCOLNlMiAcfxtt3AHdpidA3voZJpVBTs8hWA9ot1NQsOBJRrWIiUfyH\nH4HkJYLQVgvn7Gn7vgeH8A49YAWR7bbdjvA8q1+4IAQNCAi4KVyTj8NWJvBx2BoE87z5XHGOWy3r\nxxCL2T17x7m48lAp2ccAmc1itEZ0OshcDhONovv6cE6fgmYT+npRA4OEnvoS4b/9Cqp/ED08alcU\nevvAgGw1Ea0m2nWhpwfRrGM0kEwgqg3k6jmQDmpuO6guslhET8/i792LzBeQayuYeBx96H78+e02\n+yG3gRocRsZj0GxhomHMxBTGaEStjhkdQ+3YeXG7xRhEdh3n7AJohZqZtdsVUtoVj3weHMcaNsVi\nV5zHG5rngJtKMMebz233cUin0/8E+HQmk+mc//lqmEwm85+vdxABAQHXTrXR5eN/cZTFtQqz/RHe\n/8MHSPXZ1kNRLiELebvycKFTQvngn1+297r4w8O4qys4ays2OGpwEOeb3yDx1FdQvb14u/chWw2E\nAJNMIhtN6LTtBbk3hWg2MbUGJh5HNGrIky+B5HzB4CHzWfT0DJ37HsTN53CPHcUkEvhvfwI1OYWb\nOUHo6W+jRsbQk1OIVhMjJHr7DoTXQdSq6Ok51AMPX9QitNs4C2dtyFRvP/6+fZBM2UKiXEKWiph4\nAj05dWUb6YCAgJvGtW5V/CHw19h2zD98necZICgcAgI2C635xJ8d5vkla/5UbjX51BdP8cH3bLct\nl4nkZZ0SGI2oVJCVMrpvADodQqdeRvemMKPjOE9/m/hTX0bF4nj79iHrNYTvYcIxRLcNXQ+Eg0nE\nEZ0OtJqYcNQmQ54+h0Dgz84iOx1kuYCenqO77wBuuUzo1MuYZA/+E+9C9/XhnjyJKBTQoyOIeALR\n7UBvH2piEtluI5t1/LntmOlpu9VijN0WWTiL6HRQUzOoxx63xYRSiGzWtn0G+oWAgFvKtXZVyCv9\nHBAQcOsQ5RLkVlgstC97fHG1bAWOE1N2VeHckn1+o47I5zDxBMYNIVdXMMkkenAI5+lnCP3dVzCR\nKN7e/ch6HdGoYxzHBlJpazRlonHwu4h2G+O6iFYLsbyCFOBNzSDbLZxqFTU1jRkeRNQauKtrmFQP\n6vEnMLEY7ssZZL6AGhtHtFrIdhvd14fp7bPHnodKpzEj57UI3S7y3CLO2io63oPeuQvT129/1+lY\noWengxkaQo3svGXzHxAQYLnunqTzHRY/mslkKq96fAT4QiaTuf9mDS4gIABoNHA21qC3F3btYHYi\nR+mSzIrZsRTGcW1rJcZeXHNZhNHoUBhZKmHiMfTQEO53vkPo61/FSMfmSHTbiEoZAGEMRmkwmkq4\nh98feJizoX7mvRI/d+4pUmtLOAK8iXFMt4vTqKPGpzB9KWSnjahUMckU3sOPgNG4iwuowSH8yWmr\nj2i3MYOD6Hgc0W6DEPiH7oe+Pru6UCoiz5yxXg0Tk9ao6cK2Q6NhDZuEsPqFK8VgBwQE3BKuVePw\ng8BD5w/fCfwf6XS6/qqn7QTmbtrIAgLudbpdK3yUEjUzh4iGwRh++qEB/qDRYLHiMzsY46f2RRHV\nKsL3EYUcolZDR2KIroeMSPTAIM4z3yb0ta+CEfjbtyO0dY4U2gchMY6L0BpCDsY3/H7/QzwXmwSs\n2+PHhh7ll/g76HZxWl3U2ChEEwhpMJ6P6RvA37kLmi1CZ0/jT0ziz8wi6zXb3TA6hgqFke0WxOP4\nB++zF3/PQy6cxVk+h47G0PPbMAMDF7cqyiUbVBWNoccnXusKGRAQcMu51hWHBeCjXLSZ/nHg0ljt\nC+mYv3zTRhYQcK+ilBU1ttvWwCkWe2W/n7xPcriP//VHkrZTAoPQBooFq3GIxmwRYIzVFRx+hshX\nv4LRBj03DziIRhXRaoN0MNEYQmsEBiMkotsFpTkb6r9sSGeT48iCtuMJhyESw4QkJHpQ89uR1SrO\nuXOoqUn8yWlEqwHSQY9PghuyKxuDg/jz2yActnbXR04iarWLRk0XOieUsvkZ1TI61YeanQ+yIwIC\nthDXqnE4DmwDSKfTi8ADmUymcLMHk06nPw9sZDKZn7zZ5w4I2PJcGjg1MooZnwCwS/jFAowMw+gI\n8uRpTNezz282cRbPYtwQOp4AR0I0hnz+COGvfBl8D39mBiIRZLUC9bp1jkzEkdogtLJlv1IIT0Gr\njvA95uvrlPq3vzK0OV3FDI9hkr0YN4yMR1ETkziVMk5uHX9yBhmPIetNTE8PamoGYQyrLAraAAAg\nAElEQVQCgz85iZmeseNdXcVdXsS4IdTsPObg8EVRY7eLzOcQ7RZ6YPCyXI2AgICtw434rmaBSeCm\nFg7pdPrHgffw+l0bAQF3JaJeQ2Y37B32+QvmK4/1pFATUzjFHJVqld96ao2zpS5zbpefHquTHEgC\nEhOL4pw4TvjLX4BmGzUzg4n3IKoVxEYWwi6qpxcpFNJXgAClodtBNJugFQgwToSfW3mKj4VDnI0O\nM68q/HRkGZ0cQ7gh1MgIolJCtpvnY7KLOJUKOtmDGRoGDNKR+Nt3YEbGEPUazvFjiHIJM3SJUdMF\nmk2rXzDG6hcmJm/T/4WAgIBr4UYKh3mgcTMHkU6n+4EPA9+9mecNCNjytNtWxxAOX1ySv2DqFI2i\nJqftXfjyOXAlH/lmgcNrtqviCC4fz/fyi+MRxMsvEXnqi8hKGX9iBmb7EPUa7tnTGMdBDfQj0EjP\nQwgB2kCjiWg3MEJgHBfk+bv7RIxUKMwv159B909jpIN0I/jJFG6zgQi5+Nt34OayiGrFGkQlEqCU\nNZbauQuT6kWsr+N+51sgBGp6BrN332VbDqJSRhQKEIlYd8dI5Hb8HwgICLhObqRw+DDwyXQ6/e+A\nU0Dr0l9mMpmlGzjnbwJ/hF3JCAi4LVSbXT71+RMsbtSYHU3y/vfuIRXfJDGe79u2Qt+3or9IxC7V\nryzbzoHxCUSlgrO0iLlwQV9e4fRal0uT6xerisgffQInu4E/OoE/PYNotnBOncRIBzU4BAKE5yHO\nS5REtQqNBiYSgnAI4fsYjL34CxeTSqC378AgkFqjY3FQCgaH8EdGcYp5jJTowWF0JIowGpNMonbs\nAiFwFhcQx45i+vrw9x+AnktsorW22zGVEjrZi56dC/QLAQF3GDdSOPxf2G+ud3B5foU4f3xd3wLp\ndPpJ4HHgAPCxGxhPQMBN4VOfP8Hzp+0OXLle4FOfP8EHf+zQzf0jxiDyeWStghoZg54eK4ZcXYFO\nBz06hmi1cJbPYRDWSjmXw305A0NDbB9IUsxe1CXPFxbRCszeQ+huh1DmBAaJumA/3e0iMWgkolyE\nZgMTi1MbGOb3Rt7O2cQo890iP7/+NXqSMdTufeB7yG4HE45gonH03Bx0PZxyEZVIoodHIRyy4xsd\nwZ+eRdRquCeOge9bT4eduy53cPQ86zHRbKD7BwL9QkDAHcyNFA7fe7P+eDqdjmCLhV84b2d93eeQ\nUiDl1b+AHEde9t+AzeFumOelbP01x657896PqJQRuRxmcBAzvgtXa0T+fPvkyKj1Psiu2Sc7AlOr\n4h4/jknEMdu3I4Thg401fntZcZYee8EPLSCHh3BOnQTlo0cnMa5EdtqgfIyUyFwe2Wmhe3oRg8PI\nWoXfG32c5/q2AVAK9/Af9/0DfjW2gFOrYmIRxNAwZnYeWS0TyucwyRRMTOA4DjguemoaMzyMs7aC\n++Jh6OlB7d0DqV6cSwuCVsvqF5RCDw7B1OT13VncBu6Gz/JWJ5jjzWcz5/i6C4dMJvO3F35Op9OR\nTCbTeRN//18BT2cymS/d6AkGBhJ2z/YNSKVuLPAm4Pq4E+e5Uu/wkU8fpt7yLnt8x3Qf/f2Jq7zq\nOmg2YXXVbgU8eNDeaReLUDjfKTE9Zn+vNSSj0GrB0aP2tenznQ2Li3DkCJw9y792XZiagmgIjh0H\nzzt/HLV/S3kQciGXs+fq74eRIfv3Wh709bLQM3rZEBc7LokeA3t3wfQ0rK1BJWdfOzpobZ7DYdi2\nza4kLC3B4sswOQn3H3itPqFatX8/FIJd8xdbLe8g7sTP8p1GMMebz2bM8Q2lY6bT6Z8DfhWYBnZh\n/RtWMpnMb1znec4Ao8CF6K4L3z7tTCaTupZzFAp180YrDqlUjGq1Rana5hOfO87ieo3ZsSQ/9UN7\nSSUCQ5mbwaXzrNSdlXb3258+wpFLnBhDjmTftoE3//nwPCtyBOt/EApBtYrMZTGpFCaZQm6sYzzP\nujZ6XZyTJ+1y/ti43aY4t4TMZJBnzyKNJjI7TUOGcV7OQL2BnprARG2OhPAVWhicjSyi20YNDmHi\nCWQhD8pHRCIQCqHmtvFvR57gcPPixfz+Ho9/cSiMs76GNgJSvbb4CLmQSKAnJ6Hdsf4S0Rh6dhYz\nMHj5doPWiFIRUS5jEj2YoaGLIVV3EHfyZ/lOIZjjzeda57i/P7E56ZiXkk6n/xHwfwO/A/zK+YdP\nAP82nU63MpnMb13H6Z4ALo2y+zBWJ/ErV376a9HaoPUbFz9KaT7+2WOv7GGXah0+/tljN38P+x5H\nKX3HxeQurFUvO07EXP75+w4C3Nh70RqZy0KjgT82bh0Sm03k2QXrmjg2aZfvCyVbMXseztICIruB\nNzKKSKaQS+eQZ15GnluGRgM1OII/0Etk8QxOsYg/PIYZG0e2WlCvo7VG5rM4rTZ6ZASVGkdms4hy\nEe2GEfEe1M5ddPcfwF09x8/nvs3v9dzHgptiNiH4mUQes+7gJ1IY1wXHwfT2YYaHEMUS4swCemQU\n78D9F+OqlQGMFXoW8ohGHdXXj5mZv1hQ3GGfhUu5Ez/LdxrBHG8+mzHHN3I78EvABzOZzH9Kp9P/\nAiCTyfz78xbU/xK45sIhk8mcu/Q4nU7XsNHcZ29gXG/I4kbtdY8D3hyVeoff/vQRFtaqm9+VcBOZ\nHU1SrhcuO4Yb67IQxQKyVEQPDWNGx2xuxOKCjaSenEKUy7ZTwpHnLaXXkcuLNsNhfBJndQXn7FnE\n+gqUytDXh96+A2fhDPJsBiYn0Tt3I1ptRK2OMQq5voHb7aLGx/Cm+5Ebq7inT2EiMegdQO/Zh787\njbOwQOS5Z1FTU0SffIIP+T5yYwUdjUG8144pHMH09WNiMWS5BPkCemYWMzj42vTJdtsWQJ6HGRqy\nLZUBAQF3PTdSOKSBr13h8aeA331zw9lcrnaBCLg5fOTTh19Z8t+0roRN4P3v3fOaAgGus8uiXreW\nz8le2zGglG2t9LzznRJNnHNLGCHB6yI3SjiLZ1HxBHpkDCefRSw9j1hfQxYKmGgUMz+PWFkmdOYU\nangYnU7bO/l6DdPxkdk1nG4XPTaONzyEWF3DPXkUIlHM6ATqwEH8bdtxMxlCT38XvXMX7UcexanX\nkcvLkEygBocQUtgOit5e0AbRamLicfwDhy43ajqPqNcQ+bwthoaGL65A3AVUm13+8K9OsrRRZ2a0\nh3/6nt13RPEbEHAruZHCYR1bPLx6VeAxYPXNDCaTybz/zbz+jbj0AjE5lMBXmg999Ot31N3xVub0\n8mWBqXfMik4qHr5iQXBNK1SdjtUxuC5qZg6ktDqARgM9MorQCmd12RYM3Q6iWsVZPgdao1K9yFIJ\neeolWF9F5vMIIdATE5DL4T77DKq/H2/3XqTyEfUGGI1cXkF2ujYXYmgcsbqEe+R5TCSMnppG3/cA\n/tQ07oljhL/7bbwDB1Hb34mTy+MuLKBTKRgcsBHakQg6GrcBV0qjp6et++OrtQkXAqdKRUw8gZ6c\nurzd8i7h0mKxWG3zKX1nFL8BAbeSGykcfh/43XQ6/YtY74Z0Op3+PuA3sLqHLculF4iP/Mnzm9+z\nf4+xfaqX4vH2K8d3+orO665QKWUNnM7f8ROJXMyZGBq2wsf1NTAG0+ki6nXkxrptvYxGkY06zsoy\ncn0Nkc3ajoqBQXS1gnv4CCrVg7d7N8JXyEYD02kjshugFWZiCjU+gVhawH36m5hIFLVjB/6h+9FD\nI7jHXiSU3cB74CHMxCRyfR1n4Swm1QsDgyAdCLmYcBhcF5NK2YIheQU9slLWd6JeRff2o+a2vXbL\n4i4i2M4MCHhjrjVW+8PAv8lkMiXg00A/8MdAFPg84GP9GP7NJo3zphN8Qdx8PvgP7+c3/8szl2kc\n7mSuuIVhDKJQsM6HI6OYZMomPa6csxfWyWlkdgPh++B1kJUaVEp2FcJxoNPGKWaRy6uIQgHTbUNP\nCnwP59iL6FgCP50GAbJeh1YHmV1Fego1Pwu7dmGOnSD0ta+iz28nqIOH0PEewieOYtbX8B55DFK9\ntmNjadEWBNGo7dxwHQiF0D0pzMQEanTsyisHnY7VL3Q6mKEh1Ojoa59zFxJsZwYEvDHXuuLwvwD/\nESgBZ4Bx4P8E9gISOJnJZKpXf/nWI/iCuPn09kT40D+8765RSb96C0PUqsgzi+i+886HzSbyzGlI\nJFDTs8hcFlEpg/KRpTKm3UKsryLabYSvML6Pc24BkSuA17XbAdEY8lQG3DD+jp0YN4SsN6BeRWZz\nSO3jzc3jz23DOf0yfO5zyFgc7+G3oPYdQIdcwieOYeJJOu94EhENITeymHYLnUggwBYxjsT0JDEj\nI9a8KdV7ZefGet0WDFJa/UI8fusmfAvw/vfueY3GISAg4HKuycchnU6fANrAEeAnsKsOrSs991ZH\nYudytdd9A64r6e9PUCo1Lrug3dJcgnuAq83zXcGF0KlYDD08Yv0ZNtZtPPXwCKJUQtaqGKORhQIa\ng7OygsgXrN2z6+KcW0Ssr6OVjzTnvdmXbVORmp3FRGOIWg1RreDksgit8ea2Y3buRJ48jpvJQDJF\n5G2PUp/fid/tEjr1MnpoGO+RR5G+QhTydvshGreFiefZMY6MYKZnbNfDlYyYjLGrJsUCJha3Do/h\ne/ffwl39Wd4iBHO8+VzrHA8PJzfNx+EfA/87MIv9zpsButf7x7YSVxPEBQS8gu/bgkFrKwYUArm2\nau2TR8cQzYZtrdQGUciB40KhQHjhDBjQiR5YW8ZdXsYoBX4XgbTn8H3U1AykklCt4GSz1qgJg79t\nO2zbiTh+jPBffAbd04P3Pd8Du9JEjI9z4hh6fJLOe96L7HRx8nl0KAypXkSzAeUCJplCb9+BnpvH\n9PdfWZeglN12qVVsnPddrl8ICAi4OVxT4ZDJZJ4F3geQTqfPAj+cyWQKr/+qgDuJYAXmErRG5HLI\nRg01Og7RqDV0ajZtwaB82ymhDSKfAyGh3SL04osY5aGHRhBrq7gnj2I0mE4Hcf6cTruFGp/EDA0i\nSmU4exankEMIib9jB3p+O/LEMUL/7U/xU7103/0DqLk5qFQIZU7CnjTdH3wvptbEKZXQ4bDd7ji/\nRWJGx1A7H7SFztW2Gbpdux3RbmMGB1HDQeBUQEDAtXMjWRXzmzGQgNvLLUmGvAMQ5RKykEcPDqFG\ntts78vVV9PAIJtX7SqcEuSwSMMrgPvMtRKuJnppCFAq43/omoBAdH+F1oVKxXQmj4/i7diJKZeTL\nLyELRXAlalcaPTOPPPYikc/8KX5/H50f/CH02DiyXsU5fQq1Yyf+A/eD8XEqVTw3hMHg5LLghlDb\ntqF277M2z1eLqW40bMEAVr8wcRNyOAICAu457jwj+YBN4Z7vMmk0cDbW0Ikkan671RqcOWUjoC90\nSngeolhAdLvoWAL3W3+HLBZQ23diKhXc73wL4yubC9FsQLWGqNcwg4N4B++zng0nTuKUS5iQi793\nN2ZyBnn8KOE//1N0Xy+d9/4QjIwialWclRXUjp3o/fch2i2cRhN6E9Aq4ZTWINWL//Aj6B07MT1X\nEfcag6hWEIUCRKPo8Yl7Wr8QEBDw5gkKhwDgHu4y6XbtKoKUqOlZ6HRwFs7YAmJ6FpnPIQoFRLWK\nqNdQg4OEDj9D6NwKaucOvGiM8He+BZ0uYHBqdUy9hqiVMal+1P6DUK/iHHvRRlaHw/h792FGR20R\n8ex/wwwM0HnPexHDI4haDfJ5/Plt1nOh20Uo324lZHNQzGIGRui+7R2Y1zNh0tr6SlRK6GQvenbu\n6isRAQEBAddBUDgEAFe3Xb5r0dp6K7Ra1sBJCGsRHQ6jpmYQpRLO4gKmXsOplFGj4zhHnyf0hb9G\nbd+Gn95F6PBhRKOBEga3UcNUa1CtIHqS+PvvQ1YrOMdfRDQaEI3i792PGRxGvvwy7pHnMMkknXf/\nAAwPI9ttTKOOPzODSKZAgDEGx/dg9RzCCaH37oMn347vxjHqKs1EnmeLnVbTrpZsC/QLAQEBN5eg\ncAgA7qEuE2MuOjwOj2AGh17RLejxCUSjjrO0YP0MSkXUyBhks0S/8Ff4M/N4Bw8SOvwcslpBC4No\n1XEqdShXELEI/t4DyFqV0NHnEY0WJhFH7d2HSfUizp4m9MILkEjQefxdiFFrSY3v409MInp7EdLB\nGIMolXFKBUim8N/+BP6efbi9SehPQKmBbW66hFbLCji1tvqF8YnbMbsBAQH3AEHhEHDPIOo1ZHbD\nth7OzlvDpkLhYqfE8hLU6shSATU8gqlWiXzpC6jRcTr3P0j4xRcIHXnWRmG328h6HVHMI5ww/t7d\niFqN0NEXEZ0WOtGD2rcXE44i1ldwjx6FWITOo29FTEwhAByB7h+2LZmxOKbVRBSzOM06enyc7o+8\nD71t++tuMbyiXwiFrE9DJHKLZjMgIOBeJSgcAu5+2m27qhAOo2bm7DbE0oJdcejts3kRtZo1UBoY\nxHS7RD79X9G9/Xj3PYh78gSh48fQ2kCng2jWIZ9DIlE7d0GrRejoi5hOF5NMomZ3gyMRhSJOLgch\nB+/+B2HbPEJIm1+RiGP6B21uRa2Gs3EalEbt2Enn0cdsJPfVthi0tt0e5SK6J4WennltKFVAQEDA\nJhF82wTcvfi+dXj0fbsN0WzgLJ5FDwyipmaQ62vIUglRKmISCdCK8H//c0wojLf3AO7iWSJf/iLa\nVxi/i+h0ELkNHF/hz8/jd7qEjh3DaB+d7MVMzdjEyVoNkcsiJXT37sXs3gOOBF9DJIweGIJIGFHI\n46wuQySGd+hB9EMPWSvo13k/rK0hV7KoC/HdgX4hICDgFhMUDgF3H8bYRMdaBTUyhsDgrJxD96RQ\nM3PIXBa5tISolDGhMKAJPfUV8D38uXmcXJbw333VriB4XYS2DpKy08WfnUeprrWANgbV2wupXoyQ\niG4HWSggPQ9v5y68g4fACUGrDk4YPTGBEAKnkMO029A7gPfO70Xv2w+x2NXfT7ttx4yGnXPo7SlM\nYNMbEBBwmwgKh4C7ClEpI/M521EwPmm3KKJR1PQsolTCPX4UU6kiXAG+j/vC88hqFX9kBNlsEvrO\ntzHNBigPtEFkszi1Gv7UNFpp5KmXwXHQfX0QjWOkRBiDzGeR7Rb+jl14j7zVaherJUQogh6fxKCt\neNHz0RMT+A8+bPULr+OpIOo1RC73SiaG7olD8oI4MiAgIOD2EBQOAXcHzaYtEhKJi4ZNjQZ6YtJ2\nSpw4iqhU7WpEt4Nz8gyUSphkDzqZJHTsKJRK1rzJGCjkCVXKqJFRVCyOc24B44YwA/1WrOiGwQ0h\ninmcZh1/+066b38CoQ3kNpBhFz02gVY+opBHSImem8N/4C2YycmrCx6NQZSKyHIJE08E+oWAgIAt\nR/CNdJdz12dQeJ4tGAA9PoEsFZHra7ZTwvdwXs5AqYxQCjot5PoGophDSIlJJHBOn0EUNsA/395Y\nLRPKbaAGBtGDg8iNNUw4gu4bRKAhHMZE44hSAadWR23fTvtd34PodHGWl8F1UZMTVkhZrUA0ht67\nF/++hzAjI1fXJPi+FTzWqza2OwicCggI2KIEhcNdzl2bQaHPL/03GuiRUUSzibO2gh4ZxUgHefYM\nslgEr4NoNq3zY6lojZFCYeTaKnJtBdP1QQD1Fm5+HROL4/f2Igs2Ylr19SM9BeEQKtGDzOdwNzZQ\nu9I0//H341SqOJmTEImgJqYQUiI6bYj34D/wMHr/fszA4NXfR6dzfgvDs4FTo6O3bAoDAgICboSg\ncLjLuRszKESpiCwW0INDEArZjInBIdspsXAGZ2PD3sHXatDtQqWMLBYwbgjKZULnljCdLhgQXhs3\nm8M4Dn40ituoI+JxdCqFbPuIcBg1mMLJbRDKZlHp3TTf/X5kLk/ouWcx8ShqfgdCCoTWmEQCtfN+\n1J69kEq9ZuyvrACtV5ntdfnAo6P0TI1dPckyICAgYIsRFA53OXdVBkW9jpNdt94FQ8M2xTLZazsl\nlhZxjr4Inocol8Eo8Dyc5RUMCppNQgsL6E4TtED4Nlpa+AolBE6njUz0oBJJZLtl7/5Hksj1dUL5\nIn46TfeffB+sLBP5u6+h+gZQ+/aBdBFKo3tT6F1pVHr31TskjOFTf/4Czy9VASg3PD75fI0P7tp2\nCycxICAg4M0RFA6vw1bRB9zIOC685ux6lVQ8hBCCubE7NIOi07E6BtdFDY3YaGgdt50Sa2uETh7H\ndLuIStlqCISDs7gAzQbG83CXlzC1OgYQXhdRKiHbTbQxCOFAIo5SLk6jiRodQY2O2lWLcgl/1246\n7/penFMvEfrSF1Dj43QfeSvCdUErSKXw9+xDbd959cAppax+oVZhMd+87Fd3wwpQQEDAvcU9UzhU\nG10+/tlj13Xx3Sr6gBsZx6WvATi0ffDO0zYoZYOoOh10/wCyXLIZEdMziHyO0He+iel2oVRCOBLT\nk8Q9lYFcHi0E7uoKolgEYVcYRLWKrNdsS2Q0gokn0d0Obr2OPzaGNxYjtLaGqVXxd6bxH30M9+QJ\nIn/5WdT8Nrrf+/0Iads46evF33fw9VMnu3ZVg3bbrmAM72B2vEn59F2yAhQQEHBPcs8UDp/43PHr\nvvhuFX3AjYxjq4z9hjDG3qFXSuiBQYTWyFIRPTaOqNcIfedbmGYTKmWE46CHhnFeyuAuP2edG7Mb\nhPIFMD74CtGoIas1RLuDiscxQ32IZhO3WsIfn8ILh3FyWUSribd3P/7+g4ROHifyhb/E37Ofzo/+\nGMb3kcrH9PfjHziEmZi8eodEo2ELBrCBUxOJV351z6WQBgQE3HXcM4XD4vr1X0i3ij7gSuN4o+2L\nrTL260XUqq8EUZlED6JUQo+MWrOm555BVKtQqSDDIdTEJHLhDOGnvohWQLWEm91Aewrhe9bboVpF\ntJqonh7M6BiyWkYWy6jJCZQjkKUqJh7HP3gINT2DmzlO+GtP4R+4D+/73oNpt3HaLdTYON7Bg5jh\nq3Q9GHMxcCoaRY9PXNHc6Z5JIQ0ICLhruWcKh9mxJKVa5+LxNVxIr3Z3eKu1D1caxxttX9xxd7bt\nNnJtFSIRdLIXWS2jh4YxyRTu0RcQ+Tyi2QDHQc3N4pw7R/iLfw3tLnRauGtroHzr61CvI5p1RLOJ\nCUdRk5PIUsWmXo5OgABZq6F7+1AHD6L7+nFPn0bmNvAeehS9/wCiXLaW1NOzdPYfgP7+K4/7QuBU\ntYxO9r7+1kVAQEDAXYAwxtzuMbwpcrna674B15X09ydYXC5dt8bhanzkT56/7fqBD33065Tr3VeO\n+3rC/PY/e/sNn+/NFkMX5rlUauBfT46Cb3MgUAoTj1sNQ98AJh7HPX4UsboC7TZCOqjpKWQ2h/Pc\ns8h6BeNrZHYdGi3wu9avodVENBrWtGmwH1mugAY1OoowBqfTwh8ewYyOYlwXZ2UF47j4b38CtXu3\ndZz0ffSOnfh79kFPz5XH7Xm2K6PVRA8MYnr7Nj1w6obnOOC6COZ58wnmePO51jkeHk5e9xfXPbPi\nkErcvCXiraAfuNlbEbdcCGoMIpdD1quoZC+yVkVojZqcxsmcxFk4i+m2EW4IPTePrlQIPfUUcn0V\nwG4JNOrQ6SIbdUynjWw2MSEXNTiMbDeQxRJ6ZAS0wfE6qJFx/MEBTLeLs7KM6UnRec97YXYeubaC\nu76Gv2cvatduiEavPO5m83xXh7b6hfGJzZujgICAgC3IPVM43Ey2gn7gZm9F3MpiSJRL1oMh0YNx\nXGS3g56YxDlzivA3vw6ej4lG0XPboFHH/cbXcRbPYIy1cRaVGrSauI06RvnIZhMtJLq/3zpI1qv4\n/QPWlMkY9PgYfrIP6jXk0hIMDtL6H/8RDI/grK1Cbh3/4APoHTuu2lIpqhVEPm+3UkbHIBLZtPkJ\nCAgI2MoEhcMNsBX0AzdTZFdtdm22wiVsSjHUaCA31jGRCCYURnQ66OERnOUlwt/+FsbzMD1xzMSk\nXRV45ru4L70EvodpNXGKRUyjgVOrWw8Grw3aoJO90G7j1Bv4fb0gQwhXYiYn0bE4lMrI5UXM+ASd\nv/8Buw2S3cCUS/hveQQ9O39lXYLW1vOhXLSmU4F+ISAgICAoHG6Eu00Z/6nPn6Da9F45TsVDN7cY\n6natjsEYCIWoVZp88vkai9k6c/IkP9OXJznYh56atm6PR4/hHnsB0W6iuz5OIYep1ZHVKjrkgtdB\nKoWORW27ZbOBTqbwwyGEdNHTs5hYGLGxgSyV0LNzdJ78cXDDNnJbCLzH34GenL6yLsHzkAUrxtT9\nA6htOzZdvxAQEBBwpxAUDgGv2ZaQUtycLhGtrYFTq4kJRZCdFnpwiE8+tcrzq9ZB8Qhh/iA2zS/2\nOshTL+G+cBhZLKOlQOQLOKU8sl5HhyMgNLJew8TiIB1Eu4vuSaAjMWTIRc3PY8IRnOVzyLxBpXfS\nefxdSGNsATEyjPfkuzFjY1ceb6tl9QtKYYaG0GPjb34OAgICAu4ygsIhYFM0G6JYQJaKmHDYhj9F\nI2gM7lNfYWk9yaUfvcVSl9Bf/g3O+oYtEColnGwWp1ZDJeIYIWy7YywJUYnsdNCJBLq3FxF2UTvT\naMdFLiyAlKj0Hvy3vg2BwSkX0eOT+I++9aoplaJWtfqFUAg9PHJ1YWRAQEBAwNYoHNLp9Hbgd4G3\nAQXgo5lM5jdv76juHW6qZqNWw1lbQ0v70TKhCEY6ON/8Ok6phD89w+xAiFJevfKS+coKFEpQr+Gs\nZnAaNfxkChUO4RQKqGQKYnFkp4mOxVEDA8hoHH/PboSQOKdPY8Iuav9+vIcesSsM1QpqZg71+BOQ\nfG1KJcbYlM1yCZPoQU/PgLsl/jkEBAQEbGlu+zdlOp0WwOeB7wD3ATuBP06n08uZTOaPb+vg7hFu\nimaj04EzG4hiHW1AhFy06+I8812cfBZ/Zg5/dh5RrfDT/SU+kfNZUBHmOyV+/u79fkYAACAASURB\nVOwXcRZfwm3U8fv6UJEYbiGPSvaj4wlks4FJxNGDw5CIoffsRwmBPP0SwgmhDh7Ee+hhpDa4zTr+\nth2ovfuvHFXt+1a/UK+h+wZQc9tAyjf33gMCAgLuIW574QCMAoeBX8hkMg3gdDqd/jLwdiAoHLY6\nSiHX15DdNvQlEK6DcRzc548gs+v4s/N4c48giwXE0iLi5ZcYOnGUX0UgGlXk2QVko4Xq70NFo7jZ\nLCrZj4nFkPUyRKLooSFEqhdv734QEvelE9ZB8sAhvPsfRCofp91B7dyFt3vPlVsl222rX/A8q18Y\nvYrOISAgICDgdbnthUMmk1kH/qcLx+l0+m3AO4Cfu22DukE2y4p6q8R7X4YxiHye+kaeTzxbYqns\nsWM0zk+m8qSyq6jZObxH34bMbSDPnoFzC4SOHAZtMM0mzumXkc0WanAAZUDms+fzKZLIagkTjcLg\nMKZ/AO/gIYQB9+RxENIWDAcOIY3G8X38PfvQ26/swSDqNatfOB+GRSx2GyYrICAg4O7hthcOl5JO\npxeAaeBzwGdu62BugM1yX9wq8d4XENUKMpvFGMMnny3x/FobgKcXavj9ET745DuQays4mZOItTXc\nFw4j2m1Mq4U8cwqn3kANDKGkg5PdQCdTdkuiXMTE4ujRUeTAMN1D94H2CGUyoA3+/v34+w8htUK6\nLmrffvTM7Gu1CcZYk6lSERNPoCenrmrsFBAQEBBwfWypwgH4B8AY8DHgd4APvtELpBRIefUee8eR\nl/13M1nK1i87Pr5QotnxSSXe3OrAq8+7lK3jurdhX77VQq6tUq01+fgzFRbKXeptBVyc/4UGhI+/\nCKUCzuHDiEbdGj+dPoVoNtH9A5iUxClsYFIpu8JQLmPicWvfPDSMeeBBfBShoyeQSuHt2Y0+eAih\nDW4ijjp4EDMxiXQcLpsFpRCFPKJaxfT1YXbsQEjJ3aJguJWf5XuZYJ43n2CON5/NnOMtGXKVTqff\nB/wXIJnJZPzXe64xxogtYs7z65/8Nk8f37jssYf3jvJrH3j0pp73ZpzzuvA8WF2FahWk5Nf/ZpWn\nl5tXfOrDiTa/tvEVKBahUoFTp6DVgr4+0BrKZdvu6Lr297GYTZ6cmoK3vMWKLE+cgG4X9uyB++6z\n5kt9ffDAAzA29loxY6cD2az979CQfW5AQEBAwLVw54VcpdPpEeCtmUzmLy55+DgQBlJA8fVeXyw2\n3nDFIZWKUa22UGpzU9h+4vvTHMnk8C75O6fOlSmVGm/6vJ6nWFyvMTuW5Ce+P/2mz3lNaI3I5RD5\nHAiB8X3kyjKn1lzgovVySBh6pGKHV+Jnj32ZZiGLu3AG025DIgGJHkSxhAm5iGgU02yC48LIKHp6\nGnX/g9D1cJ61Wxpq23b0fQ9Y2+h4L+rQIevBIARUWhfH12hYwaMQVr8wOAAGuBVzcxu4lZ/le5lg\nnjefYI43n2ud4/7+xHWf+7YXDsA88Jl0Oj2VyWTWzj/2EJDLZDKvWzQAaG1ek7NwJZTSmx7fGo+4\n7J3rvyxye2ak503/3XjE5Z+/7+Blj232exGlos2V8H2M5yPXVxGNBmpwiJnRBKXViysO+708/9vi\nXxGrluiesgWDTsQxsThOvYGRAhMKYTzPdjUMDqPm5lGHDiF8H3HiOLLZRM1uQx04gIlEMWOjqH0H\nMH399o8oAxirX6iUEcUiRKP4w2MQPr8VdI/E896Kz3JAMM+3gmCON5/NmOOtUDg8DTwD/D/pdPpD\n2ELiw8Bv3NZR3SBbIQDrTVGv46yuQKeN6XRw1tag28EMj6B274VGg5/dOMbHwwkWOi7zrSw/d+K/\n45zKgOpgQmF0qgenWsdg0JEIeF2EpyDVj79rJ2rfAYTSyJdfQtTrMDFF951PQk8SPTGF3rsX0/Mq\n90qlEMWidZBM9QWBUwEBAQG3idteOGQyGZ1Op/8+8FHgm0AD+J1MJvPR2zuyG+OODcDqdpEry4hK\nBVpNnI11DGCGhtETkxjPI/TM01Ct0Lexzr9cWsCsbeAuLWC6HUwkbLclag1kq4WORAGD6HbRvX3o\nbdvx9x9ASAe5cBpRrsDYGN6jb0P096Nn51G70vYcrx5XIQ+tFmYgCJwKCAgIuN3c9sIBXvFy+B9u\n9zjuSZRCbqwjshvWLjqXtZ4HE1Po/n6MlISeexZRKmIKeUILC7C2grN0DtNtW5FjJAbtJrTbmEgU\nhIv0fFRPEr1vO/7+gwjXQS4vIQpFzNAQ/pPfAyOjVs+wbcdr/RWaTatfMMbqF8YnbvgtbkkfjICA\ngIA7lC1ROATcBoxBFArIlXPUskU+eaLLQjfEbN8oH3h0mGRPFOfIYeTqKjRrOGfPIJaXcZaXMK0W\nwglhwmHodJDtDqYnASEX2Wqj4gn8nXP4DzyAcF3k6ioin4W+fvzHH8dMzqB27ETPzb/G5VFUK9aw\nKRKx7o5XcoG8TraaD0bAjREUgAEBW4OgcLgHEbUqcmEBsb6Kk8vxyeIIh5v2Al3K+3zyb8/xyxyH\nRhNneRGWlnGXFqDVRDgOOhTGeF2k8lGxOEIKhFLgupj0HroPPoQIhZEba4hsFuJx1COPoefnUbt2\nW9OmSw2ZtLb6hUoJ3ZO66fqFV8eGv/r4buJuvrgGBWBAwNYgKBzuJdpt5MJZnMWzyI0NTKoX79D9\nnP1iHrioul2saZzVk8jlZeTiAjQaCEeiHQeURhoP3ZNECnA6HVQoBtMz8K4n8HBxVlcRhSy4IfwH\nHsCk96B270VPTF7u8uh5NnCq2UD3b55+YTNiw7cqd/PF9V4qAAMCtjJB4XAv4PvIc+dwTh5Drq5i\n+gfoPvIYIuSCdJiLbHCkffGCPV9exv3G16HWQEiBdlxQPsJ10D1JhCPPFwwRmJ3He8ujyP4+qJaQ\n51Ywno/avR914CBq7z7M2Pj/3959R8dx3Yce/87M7qIvKkmwAizSJSkWUbJ6s4qtRlNusuznSkm0\nY9mJYjnPeUocW3HKsZ8T58mKJcViRMkniZ+tOIp15JMX2ZZsdVKFpCiWK5IASAIkQJQFFouyZWbe\nH7MgUYkFuAAWu7/POTjEzszu3v1hOfObW4fWIPT1ef0XbNtbcKp6/pR+/Fk/0mUCsvnimksJoBCZ\nTBKHFM3KKmDXxWhpxvf2m5jHGr2E4eprMQJ+DMfBaDyG/80d/EFPjB8naqk3S1jWfoR7fvswRqIP\n1zJxcTENsCsqMACrpxcnEMBeXEPikktxS4KYHW0Y+gDYcZzl5xDf8D7sVatx584bMsuj0R32+i/4\n/Thz5nozSE6DWTvSZRKy+eKaSwmgEJksI6ecnojW1u4zfgCfz6S8vIhQqOesJsF48KndQyZ2Wr+8\nMqMvRkZHO9aO7fgOH8SZM4f4RZdhBPzQ349x8iSB116C7ghuKITVeBTr2BFob8cwfbiWCa4LgTyc\nYBAj4WD0deP6fLiLFpG48GIoq8DoDuO2tmL1hHFXKIpu/gCdi5cTL6s43eTguqf6L7hFxTiVVSMX\npRIpSeW7PCsT3AyTrnOGGJvEeOqlGuM5c0pm35TTs8WsqQKORPDteBXfnj04c+YSvWUTFBZihrug\ntYXAyy9CqAO3pwdfUyNGQz1GWxuGAa4vAI6NW1CAW1KCEUtghrtwTQt72Qrs8y+AYNBbE+JoPUZ7\nJyxfRv/Hbsdcvw6WL8EN9XgzOCYSXv+FnghOWTn20uUy/8I0yKXaFSHEzJDEIUUZXwXc34+1Yzv+\nt3bgVlQS3fRRKA1itrfjHjuG/+XfYTSfwI3bWEfrMY82JBMGA9fvA8fBLSnCCZZBbwSzowPXsnBW\neE0PZn7AWwfiZDNmy0ncmhqiH7kdZ+063GApxsBqnf39mM0t3tTSVVXekErkTjgXyN9YiNwgiUOK\nMrZ9NR7HevMN/K+9glNaSuzDH8OtqvJGTdTX43vpBaymJhwMrPpDGEePektPu976ERjgllfgFBdj\n9ESwWk7gmCb2uYrEhRdhWCZYFm5XJ2ZTE87CJUTv+iL2+g1QXHy6HN3dEGoh0tbDP+0IcaS1h5p5\n3acuHtnc21945G8sRG6QxCFFGVcFbNtY7+zG//vncfPyiG36CM6CBZgtJzC1xvfKi1hHj2C7YNUf\nwtfYBJ0hjEQcNxDANS1vCufiYoxwF1ZjI67fR+K8NcQvuhSzvx8Cfoh042tqwpk7j9bPfpGtLcUc\n2dlLzfHDbL5lJaWxHsxQB0ZJCZxTw4+f28Hu+hAw9OIxa5p6xKTJ31iI3CCJwywTDvfyxC/e5sjJ\nHmqNXjbfeBPFK8/BbGnG2vsuvu0vY713CAcD8/AhrLaTGKF2b82IQD4UFOBWVmEXlWCF2vE1NOAG\n/CTWrSd+xRWYkR4MF1xcrPfeg4oK+j9/F/ZFl7D1mQPsbjh9R/nEv7/Fvbeei127DCPgA7+fI82j\nXzwyvqlHnDX5GwuRGyRxmC3iccz6Op585gC7EiWAn5BbirOnh/v63sL3xnbMgwcx7Dhm3WHMzhBm\newdG1FuAyi0qgcoK7JISzPY2/HWHvRqG8zcQv+oazEgEo7cf13Gw6g5BSTHRz34e+9IrTs3yODwp\naOh2cKuqhmyrqS4h1B09/Th58cjYph6RNvI3FiI3SOKQ6eJxzMZj+H/3PGZHK/XWpZA4PQL1aFOI\nwPZnMHp7MI83QmcnVnu7tyx2IA+3NIhbVu71Yehox3eoGUyLxIYNxK++FiMewwqHcUwT69hRyM8n\n+qnPYF9+5elhk5EIZlsrNaU+Ontip957tDvKuzeu5rFn9o64eGRcU49Iu2z9G0unTyGGksQhU8Vi\nmMeb8L36MlZTI/FLLyd6+WZqfraTzqPhU4ctDZ/AOrgfwmGstnaI9uHmFUBpGU5ZGZQEoe0kvuYT\nYPlJrD+f+DU3YBhgdoZwHRdONmNZFtGP34F9zbXepE2ui9EZwuxoxy0oxFmwkM0fXzjuHWWwKDsv\nHiJ3SadPIYbKqcRhJu4cJvye0aiXMLz9FmbDYRLrLyD28Tswov34XnyBP2jazWO9c6n3l7E0fJx7\n3vg3zOYjGH193pLWlZU4JUEoLsVoP4mp94PfT2Lt+cRv+CBhK5/H2stooIjaeAdf7txB/m0fIfH+\n671poW0bo7UVM9yJEyzDrl1GuD/Btl+e/gwP3Hmx3HGJnCGdPoUYKqcSh3TeOaSaEKT8nv39mMeb\nsPbuoefwER71r6IhcAU1bUVsef73VLz9KtbRYwS6O/lyVx+PrriZ+uB8Hlm5kXs6nqS0oBCnqAS3\nrATzZCtmYyMEAl6nx+tuwC0txWpu4bH4XHaaFQCE8ubzo8vv5N7r13s1HC3N0N+PW1k5ZMEpueMS\nuUw6fQoxVE4lDum8c0j1Yjrue/b1eQnDoYNYhw9iz6vmkblXsPtoGIjT2dPJ473NfEPvhlAIK9LN\noxd8hreqVwPQUXshPyoo5Bv7/wOrvR1rfyNYFvF160lc/wFvToeTLVj19bjdYRrK1g4tT3PYWwET\ncKrmwIKiiX8GIbKYdPoUYqicShzSeeeQ6sV0zPfs7fUShiMNGEcboLCQ6Ec+jhss5egjrwGnF4eq\nN0swjzdidnVidHdTX754yHvUB+fjP6jBtIivXkPigzfjVs/HbG/FfE9jhMOQsElcez1LogsI1YVO\nl6csgDN/AQTGbnqQOy6Ry7K106cQk5UziUO4J0bCdvBZXvW7Wlx2VncOqV5MR9ytXFuDefA9rONN\nGI2NYBokrrkOp6IC/wvP43tzB7W+tYQKFpx6jWXtDVjHjnnDKudWs7SnmY6i8tP7WxtIqJXEb74V\nd9FizFC7lzB0tIID8auuJnHzRsjL486mk2zr66OhK0HN/CCbb119xqRh1M8gd1xCCJGzcmZ1zL94\n9BV2HWw7tf1sV7c8Ux+HUfc53igJ68QJaDuJEY+TWLMeSkuwXn0Va+8eaG/Fd6KZcMzl4XNvob64\nmmWtddzzyhOUFflx8vLBcelyDB5Zdzv1lTXU9rdx18J+SmoXY0QimE1HMU82Y7gWiUsuJnbLJsjP\nx2xrxejrxSmvwC0rT/uCU7La3dSTGE8PifPUkxhPPVkdMw3GmtFwss5UfTmi/8PP3uDry+PQ1eXN\nr7BwEXZRMdbedzD1fqzjxzFPnMCNRXFjUUrb2vnzd/8KNy8Po2oOdkUQJx6DSASju5tyx+Ubh39J\n7NzbcJfWYvT1Yh0+BMebMA2XxIaLiG3cBHn5mK0nwXG8/gvzF4xaXiGEECJVOZM4jDWj4VQYnpQc\n7ejHqAzjBvw4pfMwjjcR2L8Pq+4Q4e4+Hll6I4er53lzJ7gOy9sbuGffLyl2Y1j9fRixGGYkTJev\ngH/c+KfUz1lKTbHJlqoQZQ0NGMcbsWyb+Nr1RG++FQryMdvbwe/HmTsP8vOn7LMKIYTILTmTOIw1\no2G6GeEuaosMdkVOb6vxx8DyQdzG//sX8OkDuP19uLbNo8s28nbFiiGv8Vbh+Tzs83H/q1sxIhGM\neBx7UQ0P3fw1drpe34ZQBP455PKN7kYS5yiiN94ERcWYnR04gLN4yemZH8WMkpkHp5bEV4jplTNX\nlqme0dBILjtNqIO7lyTY2mdzJOJSW+Bw51IX643t+PR+HNfFcWxvWuhQB/Vr5o76evWlCzE6OrAX\nLiL+oQ/jrF5Nw/5CSAw6JlBO35YvYZQEMXt7cAyGzL8gMoPMgzG1JL5CTK+cSRzCPbERNQ5nfVcy\nMC3z8eMQ7sJIJKC3l/JjR/iTqlLsZaX4X3kJ65UDOP48bMB3ohmjs8Ob6dHnZ2lk6AiJAbXhE/Tf\n9QeE1qxn67E8jrzrYjsJME6Xecn8UgyfH7eoCKd6/tl9lhTInd3kyDwYU0viK8T0ypnEYeuz+9J3\nV+K6GKEOL2GIdGP09mL09WE1H8fJLyQxfyH+V14kUHcIu6gEx5eHr6EeozuM0duLE/DjzpmL4/dx\nz+s/4eGLPs3hskW4hoFhGCwNxLnzhuUkTJt/ejfBHif5ZzKgxAeWz6KmMo/Nt6zGqQymKULjkzu7\nycnleTCmI9nM5fgKMRNyJnEYPqrinbp2Hnxq98ROZK6L0dGBebwJenowuzohHodQB4ZtkygJ4n/7\nTfxHG3CDZdh5BfgP7MeNdGNGYzg+H87cubg+H2Z3BDPqUhqLc/+z38WpriZxw80krrwK18nHv38P\nrmFxwFk3pAh9jsGPv3L5qaWup5Pc2U1OLs+DMR3JZi7HV4iZkDOJw/BRFa4Luw+neCJzXYz2dswT\nx6GrE6uzE8eyIBzGDIdxAn6sA/vwNx7Dqagk4c8jb9cunP4ejFgM1+fDKS/H9ltYvf0Ydh/YMYye\nHtyKKuIbN5G44UZcO0HgnXdwCgpwCguJnGgjkTesv4LBjCQNIHd2k5XLMw9OR7KZy/EVYibkTOIw\nMKrinbp2Bs95NXAiG7VKNd+XTBiaMNpaMSIR3IICnHgUq/EkLgZm3SGslmaoqsL25xF4YztObw9G\n3Mbw+3CC5Th+Cysaw4rFMWJR6OvFLSsnduNG4rduhIRN4K03cIKlxOfNw3foECxcyCNLrsdtiQ35\nHGpx2XSGbQi5sxMTJcmmENknZxKHgVEVDz61+1TVKZw+kY2oUn16N/cpF7O1FeIx3OIScFws/R6u\nncA8Wo8Z6sSeMwdMA/8rL+H293vLUlsmTkkxruXDdF3M3l5v9ctoFLeslNgHbiP+4Y9BNEpgx+s4\n5eXEzllJYM9OjOISYh+7HWf5Co48/vaQz+CzDLZsOm/6gjaM3NmJiZJkU4jskzOJw4CxTmQjJm06\n0YVZGcXJy8Ps78U6dBDCYazGo9Dfj1M1D7ejncDvXvASBsf2mhD8fvD7wDAx4nGIRDDjcdySYmLX\n3kDsE5+Evl4Cr7+GXTmH2NoNBHbtINDWRvRDt+Gct+5UU8Twu7XzaitkFIOYVSTZFCL75FTiMGYP\nb9umJuijM3K6WaCmEOjpwTrZjNF0AqupEdcycMorMOvqCTz3K5x4HMN1cS0LfH7wWzh5edDfT3fM\n5uHLPkd91VJq6WHzNYsIxvvxv/YqnXPm84PgJRxtjbO0Jczmqz5I0RWXgGkOKa/crQkhhMg0OZU4\njGiOeHYf963Px6w/zJZy2NpbwJGIQ01egrvLQ/je3YvR3IxTXIw9dw6+g+/h2/4aTjSOgQuGgYsL\nfh9OUZHXHHHyJCQSPHzT13lr4VoAOiiDN9r52oIIscsv47FXQ+x2DSBAyKzCbi7k3mFJA5y+WxtI\neB54fIfMnyCEEGJGzXjioJRaAPwQuBboBX4O3K+1jp3xiZMwvDliX3074aBLaSCPsnAr9y12cBNx\nAttfw9zTij23GnfhQqy97+KrP4wdjYFp4poGbjyBkV+AU1oK/X1YJ47jJmzckmLsCy+krnYNxE+/\nV12gArO9Ad+RBuoLrxqyb7ye5pkyf4JMACWEEGLGEwfgF0A7cAVQCWzDm1j5T9P9RjUV+UOaI+Ku\nwdd2wZoyg7vmFTHnhV9jhLtJLFqEu2gx5v59+OrqcONRXNMCnwWxGOTn48ydC719WI1HceMJ3GCQ\nxPrziX/0E2DbLD3QSYjTM0Iui3Vgr1PErriKmueO0DlKB82xZMr8CZmSwAghhJg5M5o4KKUUcDEw\nT2vdltz2LeD7pDNxOHYMa+cetlTF+MOjBoNGY5LAYFcnbGvq5OsVVRilFVjv7sZ39BhutB8sCwwL\nIxrFKCwisagao7cPq74eN5FMGC5eR3zjbWBZ+PbvJbRwKdGyavydtvc5ixw+f+vFJJYuBsNg862F\nE+q7kClD2jIlgRFCCDFzZrrGoRm4aSBpSDKA0rS+y/HjkLApDbdjUUmCkYtA1RfOwbfraazGY7ix\nKK7pA5+J0ROB4mISi5Zh9vbiq6uDaD9OaSnOmnXEbroJ/AGshnrsJUuJXXk1j73Wwd64C3j9Fqx5\nVZQsW3LqvcbqaT5WU0CmdJLMlARGCCHEzJnRxEFr3QX8euCxUsoAvgr8Jq1vdOIERjiCfc655B9u\nJeJaIw5Z1nIYs64Ox7IwXDAjYdziYhLnrMTs78c6dBCjtw+nrALngguIXXM9FBZitTRjL1pM/NLL\n8dUdxti9kwZ36IX9yMnIiPcbzVhNAZkypC1TEhghhBAzZ6ZrHIb7PnA+8L60vurSpRjP/ZaC3/4a\nX9UtYA5KHFwXn5PgvfIl3H3LA6xoa+Ce3T+naEktZjSGdVBj9PXilJWTOP8CEhddAuUVmB3tOMEg\n8Qsvxmw5ju/APpxFi3AWXsiSd+OEjoZPvUWqd+aZ3hSQKQmMEEKImZMxiYNS6nvAHwGf0FrvT/V5\npmlgmiObHgZYlgk//SlmZxi3opJlbjdvk3/6AMMgYfnptrxJl95avJ4fFRfzZ7/6HkZvL25FBc6G\nC7HXrceprMTX24NbWIC94hKsUAf++oM41dU4562FqiqM6mq2KJutz+7jSHM3NdUl3L1xNT7fyOGW\nw9XOD7LrYNuQx6k8LxNYljnkX5F+EuPpIXGeehLjqTeVMTbcwQs3zBCl1EPAl4BPa62fmshzXdd1\nDWPsxAGA73wHWlqgvp5jbb3cf/HdhANF3vONkUGt6Ongyef+ClavpmvlWh4MrOFwPI/lRS73XlJO\nqROFxkaoqoLly6GkBBYuhPz8Ea81EV2RKA/+bCeHG7tYvqiUe+/YQGlx3lm9phBCCHEG41xAR3nC\nTCcOSqlvA38GfFJr/fREn9/eHnHHq3EIfulOYrv34CQSfPeiz/NW9eozvuaFXQ38T3M/7pxqvp9Y\nztuJ4Kl9Gwr6+MbyGPa5K8Hvx5k3D4Lp7cs5G1mWSTBYQDjch207M12crCQxnh4S56knMZ56qca4\nvLxowonDTA/HXAV8E/hb4FWl1LyBfVrrllRew3FcHGec5KehATcRw+iPUR+cP2K3LxGnMNGHYZos\nc7u5u/QkdtFC3PJy6k4Ghxxb7xYRXaVwS4K4c+aAYUBiYl/8bJ5IybYdEhOMh5gYifH0kDhPPYnx\n1JuKGM90H4dNeGMWv5n8Aa/axAVGDn2YoHBvjCf+6wBHL7iHpW0N3PPmvzHP7qFj0MRMACVOlB+1\n/QrmVkNFFU75fOIrV4PfR+3vm9kVO91cUFORj7Ok5tRCVJMhEykJIYSYrWZ6OOb3gO9N1es/9sxe\n9jaEID9Ix6J1/J/SMo74y0Yct8jswz1nNW5VBYm168Hnx9IHMGJR7rpyDVv39XOkvc+rHdi05qyS\nBsj80RNCCCHEWGa6xmFK6WOdQx7vL5xPwhz5kd3iIPEb1kBeAGv/XoxIBHvlapzaWoId7fzxLQtx\nKyrTVq6xJlJKZxNGNjeHTJTEQggh0ierx8LY9tC+D7Y5eutHo1GI1diAb8frOHPnEbt1E255OUZf\nH3btsrQmDQC3X7uCYKEfw4BgoZ/br10BnG7C6IzE2H3Ya8KYrHS+1mwnsRBCiPTJ6hoH04TBnUkt\n1yVgOvQO+9i19OAUBbEvuwqztwezvQ1n/oKzHl45lqdeOES411seM9wb56kXDnHv7evT2oQx2mtl\nyp33dJdDmoaEECJ9srrGYeWSoZ0gVwZdFs8pGrKtyHL5wicvxlmzBqu1BbewEGfpsilLGmDsi/rw\n0SFnsxbE8OfWzCvJmDvv6S7HaLEQQggxOVmdOGzZdB7nn1NFRb7BmnkFuMUlvNcaHXKMLy9AWU8X\nRGPYS5fjTsOcDGNd1AdqIcBrwjibtSA237qK9csrKSsOsH55JZtvXZUxd97TXY7RYiGEEGJysrqp\nIlgY4L47zqc8FuFbj+9gZ9vIsax2IsE/vNnNkZMnqJnXPC3V96MtFvXA4zuGHGOaxlmVY7R1JTJl\ndcvpLoessSGEEOmT1YkDQLgnxkNPvs6uDpfRZtbst2F3XQcwfXMqzNRFPVNWt8yUcgghhJi4rE8c\ntj67j10dkOp03DNVfT8dF9NMufPOlHIIIYSYuKxPHI40D00EDANKCvxg4KUnQwAADndJREFUwNLq\nIAnb8SaJSpqp6nu5mAohhJgNsj5xqKkuIdR9ukPkumWVpy7Q4d4Yjz2zF5/l1UaoxWVSbS6EEEKc\nQdYnDndvXM2T/605dKyTJXOLhyQG2361f0htg88yR3RIzJS5D4QQQohMkPWJQ7AowLfuupRQqGfE\nCmGpDAuUBamEEEKI07I+cQDoikT5wc920XAizMIqbwKopraelCZcypS5D4QQQohMkBOJw4M/28mu\ng20AdEZiQ/YFC/2YpjHmSIZMmftACCGEyAQ5kTgcbuwac59pGvzgq1eO2D7Qt6GhuZtg4elRGNJ5\nUgghRC7L+sQh3BPDdkbOGDmgZl7JqB0gB/dtAFi/vFL6NgghhMh5WZ84bH12H12DmieKC/zUzCum\nqa1n1CRhoAOk9G0QQgghRsr6xGH4BFAYLsdORujui1N/IkykNz4iKWho7sZ107dSpRBCCJEtsj5x\nGD4BVH+/TSI5miLcG+e7//oWw6ejth2XSN/oK1XKvA5CCCFyWVYvqw1wx3UrKC0OYBheApAYNgQz\n0pcYkiQA9EWHPh68UuVAs0ZnJMbuw16zhhBCCJErsr7G4WfPHzrVxyHcGx/naI9hGMDpBGNwB8p3\n6tqHHCt9H4QQQuSSrE8cRvRxSIFaXIbPMs84ymLAmfo+SLOGEEKIbJP1icPwPg5n4rMM1OIytmw6\nb8QFfnjNgmF4C2adaV4Hma5aCCFEtsn6xOHujav56j+8OO5xg+dpCPfGePCp3UNqCobPIDl4lc2x\nyJBOIYQQ2SbrO0cGiwKnls0ejYGXNAxfNXN4B8jNt65i/fJKyooDI44fy/BmDBnSKYQQYrbL+hoH\ngJU1FbxbN7J/AkBJkX9EzcFoNQXBwsCEmxkG+kYMrrkQQgghZrOcSBz8vrErVhbPKR6x7WwWtkql\nQ6R0mhRCCDFbZX1TBUx8ZMVkmiUGpDLPg8wFIYQQYrbKiRqH5YtK6djXP+q+praeEdsGmiUGagYe\neHwHC6uKTh1/plqCVDpESqdJIYQQs1VO1Djce8cGgkX+UfedqRlicM3A3oYQextC49YSpNIhUjpN\nCiGEmK1yInEoLc7jb794GeuXV1JaFCBY6CdY5B+3GeJMNQFj7UulmeNsmkKEEEKImZQTTRXgDcuc\n6KiI4Z0kh+8b9X1SGH0xmREaQgghRCbIiRqHyRpcM3BebTnn1ZZLLYEQQoicljM1DpMhNQNCCCHE\nUBmVOCil8oA3ga9orcefJ1oIIYQQ0ypjmiqSScNPgdUzXRYhhBBCjC4jEgel1CrgdWDpTJdFCCGE\nEGPLiMQBuAb4LXAZ3rpTQgghhMhAGdHHQWv96MDvSqmZLIoQQgghziAjEoezYZoGpjl2JYVlmUP+\nzUThnhhbn93HkeZuaqpLuHvjaoJFs2vRq9kQ59lOYjw9JM5TT2I89aYyxrM+caioKMIwxm/dCAYL\npqE0k/PQf+xh18E2AELdUZ78b8237rp0hks1OZkc52whMZ4eEuepJzGeelMR41mfOHR09Ixb4xAM\nFhAO92HbzjSWLHWHjnWOeBwKjVx8K5PNhjjPdhLj6SFxnnoS46mXaozLy4sm/NqzPnFwHBfHccc9\nzrYdEonM/IIumVtMqDs65HGmlnU8mRznbCExnh4S56knMZ56UxFjaWDKALLolRBCiNkiE2scxq8+\nyDIytbUQQojZIuMSB621NdNlEEIIIcTopKlCCCGEECkzXDfnWgaEEEIIMUlS4yCEEEKIlEniIIQQ\nQoiUSeIghBBCiJRJ4iCEEEKIlEniIIQQQoiUSeIghBBCiJRJ4iCEEEKIlEniIIQQQoiUSeIghBBC\niJRJ4iCEEEKIlGXcIlfppJTKAx4GPgr0An+vtf7BzJZqdlNKLQB+CFyLF9OfA/drrWNKqVrgMeAy\noAH4mtb61zNU1KyhlPoV0KK1vjP5uBaJ81lTSgWAfwA+BUSBx7XWf57cV4vEOC2UUouAR4CrgXbg\nQa31g8l9tUicJy15jXsT+IrW+sXktlrOEFOl1A143/tlwGvAFq11/UTeN9trHP4OuAB4P3AP8G2l\n1EdntESz3y+AfOAK4JPAh4C/Su77JXAcuBD4F+Dp5ElDTJJS6pPAzcM2/ycS53T4IXA98AHgfwBb\nlFJbkvvku5w+TwHdeOfiPwb+Ril1W3KfxHmSkknDT4HVw3aNeX5QSi0Gngb+GXgf0JY8fkKydpEr\npVQhXlBu1Fq/lNz258D1WuvrZrRws5RSSgH7gHla67bktk8C3wc+h3cSmKu17k/u+zXwktb6OzNU\n5FlNKVUO7MY7CezTWt+plLoO7z+6xPksJGPbAlyntX45ue0bwLnAvyLf5bRQSpUBHcAarfW+5LZ/\nx/tOP43EeVKUUquAf0s+XAdcq7V+cbzzg1LqO8CVA9dApVQB0Ax8aKDGIhXZXOOwHq8p5rVB214G\nLpmZ4mSFZuCmgaRhkFLgUuDtgS9r0st41WVicv4O+Amwf9C2S5A4p8OVQOdA0gCgtf7fWuu7ke9y\nOvUBPcBmpZQvefNxBbATifPZuAb4LV6sjEHbxzs/XAKcShC01n3A20ww5tncx2E+0Ka1Tgza1gLk\nK6UqtdbtM1SuWUtr3QUMbiszgK/ifYHn491FDNYCSLXjJCTvHK4C1gKPDtolcU6PZUCDUuqzwJ8B\nAWAb8DdIjNNGax1VSn0V+Ee8ZgoL2Ka13qaU+iES50nRWp86J3i52CnjfXfT8t3O5sShEK/D02AD\nj/OmuSzZ6vvABuAi4D5Gj7fEeoKSbZePAvckT7yDd4/1vZY4T0wxXrPEF4Ev4J1Q/wmvw6/EOL1W\nAc/g1aCtBR5SSv0WifNUGC+maYl5NicO/YwMxsDj3mkuS9ZRSn0P+CPgE1rrfUqpfqBi2GF5SKwn\n4wHgDa31b0bZJ3FOjwRQAnxKa90IoJSqwetE/RxQOex4ifEkKKWuB+4CFmmto8DOZEe9b+LVVEqc\n02u888NY18XQRN4km/s4NAFVSqnBn7Ea6NNad85QmbKCUuoh4GvAp7XWAz1ym/DiO1g1cGI6y5Yl\n7gA+rJTqVkp1A58GPqOUCgONSJzT4QTQP5A0JGm8Klv5LqfPBcDBZNIwYCewBInzVBgvpmmJeTYn\nDruAOF4HnAFXAW/MTHGyg1Lq23jVu3dorZ8atOt14IJkNfuAK5PbxcRcg1eluz758wxe7/P1wHYk\nzunwOl5/pxWDtq3GG/f+OnChxDgtjgMrlFKDa7dXAfVInKfCeOfh15OPgVOjDzcwwZhn7XBMAKXU\nI3g9eO/Eu5N4Avi81vqXM1mu2So5BOgd4G/xJtYarBVv6OC7ePM6bALuB84bdlcnJkgptQ1wk8Mx\nTSTOaaGUegavWvcevD4OPwG+gzdZ0TvAHiTGZ0UpFcQbFfRrvI6nK4HH8eL5OBLns6aUcoD3J4dj\nnvH8kGyO2wf8JfAs8G3gHK31BRN5z2yucQCvw95bwPPAQ8BfSNJwVjbhfWe+iXcncRyviuu41toB\nPoxX7fUm3oQ6H5YTQHol43wbEud0+DRwCHgJ76bih1rrHyVjvAmJ8VnTWofxJtmaD+wA/h74jtZ6\nq8Q5bU7d/Y93ftBaH8GbSflOvL9HGfCRib5hVtc4CCGEECK9sr3GQQghhBBpJImDEEIIIVImiYMQ\nQgghUiaJgxBCCCFSJomDEEIIIVImiYMQQgghUiaJgxBCCCFSJomDEEIIIVImiYMQQgghUiaJgxA5\nSCnlKKU+l/z9CaXU88nfa5L7rk4+3jawL/n4cqXUFTNTaiFEJvCNf4gQIgtVA13J34fPOz/48R8B\n1qDHLwNfAF6ZspIJITKaJA5C5CCt9ckz7DYGHdc9DcURQswikjgIkYOSS/F+QWv9k3GOewJYorW+\nLvkcF9imlHp/cpnvBcAPgBsBG68m4uta60PJ528DioBS4BLgr/FWSPxfwOeBWiCafN5XtNb1yecV\nAd8FPgaU4K1yex/eMsxNwENa678eVM4v4S0RvCi5QqAQYopIHwchxJkMbraYj1cbcS9wr1KqEPgd\nXsJwFXA10ApsV0rNH/S8jwH/DbwP+Gny+V8Hvgacg7cM8Ll4CcWAp/CSkc8B64E64Dm8JORfgM8O\nK+fngCclaRBi6kniIIRIida6JflrONmE8Sm8moTPaq3f1VrvA7bg9Z3YMuipIa31D7TWh7TWTcBB\n4HNa6//SWh/TWv8OL1FYC6CUUsBNwJe11r/RWtcBXwaeAKqAx4FzlFKXJI8/F7gsuV8IMcWkqUII\nMVkbgEqgy7vWn5IHrBz0+ODgnVrrXymlLlZK/SWgkj/nAY3JQ9bg1XRsH/ScKPAnA4+VUm/g1TJs\nH/hXa63T87GEEGciNQ5CiMkygQPAOrzmhIGflcAfDzqub/CTlFL/C3gBL+n4DfAl4O8GHRJP4b0f\nB+5QSvmBTwPbJvcRhBATJYmDEGKy3gVqgC6tdV2ySeEo8D28/g5juR94QGv9Va31Vq31Drxah4HR\nHPuT/1408ASllKWUqldKfTS56adAPl5fibnA/03XhxJCnJkkDkKIiYgAq5RSFXidFDuAXySbHlYC\nP8Hrn7DnDK9xDPigUmqVUupcpdRfAx/Ba+JAa30QeBr4kVLq/ck+DFuT+3+XPCacPOYvgP9MPhZC\nTANJHITITS4jJ34avG8sfw/8IfB48mJ9NdAG/D+8/gbzgRvG6W/wGaAQeAP4PV7/hi8Bc5VSi5LH\nbAZeBH6ePG4h8EGtdceg13kCr9ZBmimEmEaG657pHCGEEJlJKfUF4Nta66UzXRYhcomMqhBCzCpK\nqQ3AKuAvgQdnuDhC5BxpqhBCzDaXAj8GXkUSByGmnTRVCCGEECJlUuMghBBCiJRJ4iCEEEKIlEni\nIIQQQoiUSeIghBBCiJRJ4iCEEEKIlEniIIQQQoiUSeIghBBCiJRJ4iCEEEKIlP1/jrTtlJ3AiYcA\nAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x15fbba412b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Generate array of x-values for bootstrap lines: x\n",
"x = np.array([0,100])\n",
"\n",
"# Plot the bootstrap lines\n",
"for i in range(100):\n",
" _ = plt.plot(x, bs_slope_reps[i]*x + bs_intercept_reps[i],\n",
" linewidth=0.5, alpha=0.2, color='red')\n",
"\n",
"# Plot the data\n",
"_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')\n",
"\n",
"# Label axes, set the margins, and show the plot\n",
"_ = plt.xlabel('illiteracy')\n",
"_ = plt.ylabel('fertility')\n",
"plt.margins(0.02)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
ibmkendrick/streamsx.health | samples/HealthcareJupyterDemo/notebooks/experimental/Create VCAP Service Credential.ipynb | 3 | 1845 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Create `vcap_services.json` to capture Bluemix VCAP service credential\n",
"\n",
"Usage:\n",
"* In [Bluemix](http://bluemix.net), create `Streaming Analytics` service\n",
"* Open the `Streaming Analytics` service\n",
"* Click `Service Credentials` tab\n",
"* Click `New Credential` button (if one is not already available)\n",
"* Copy the `Key Name` and `Credentials` into the cells below\n",
"* Run all cells to create `vcap_services.json`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"key_name='Streaming-Analytics'\n",
"credentials={}"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import json\n",
"\n",
"vs = {\n",
" 'streaming-analytics': [\n",
" {\n",
" 'name': key_name,\n",
" 'credentials': credentials\n",
" }\n",
" ]\n",
"}\n",
"with open ('vcap_services.json', 'w') as outfile:\n",
" json.dump(vs, outfile)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| apache-2.0 |
nehal96/Deep-Learning-ND-Exercises | Sentiment Analysis/Handwritten Digit Recognition with TFLearn and MNIST/handwritten-digit-recognition-with-tflearn.ipynb | 1 | 29680 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Handwritten Number Recognition with TFLearn and MNIST\n",
"\n",
"In this notebook, we'll be building a neural network that recognizes handwritten numbers 0-9. \n",
"\n",
"This kind of neural network is used in a variety of real-world applications including: recognizing phone numbers and sorting postal mail by address. To build the network, we'll be using the **MNIST** data set, which consists of images of handwritten numbers and their correct labels 0-9.\n",
"\n",
"We'll be using [TFLearn](http://tflearn.org/), a high-level library built on top of TensorFlow to build the neural network. We'll start off by importing all the modules we'll need, then load the data, and finally build the network."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Import Numpy, TensorFlow, TFLearn, and MNIST data\n",
"import numpy as np\n",
"import tensorflow as tf\n",
"import tflearn\n",
"import tflearn.datasets.mnist as mnist"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Retrieving training and test data\n",
"\n",
"The MNIST data set already contains both training and test data. There are 55,000 data points of training data, and 10,000 points of test data.\n",
"\n",
"Each MNIST data point has:\n",
"1. an image of a handwritten digit and \n",
"2. a corresponding label (a number 0-9 that identifies the image)\n",
"\n",
"We'll call the images, which will be the input to our neural network, **X** and their corresponding labels **Y**.\n",
"\n",
"We're going to want our labels as *one-hot vectors*, which are vectors that holds mostly 0's and one 1. It's easiest to see this in a example. As a one-hot vector, the number 0 is represented as [1, 0, 0, 0, 0, 0, 0, 0, 0, 0], and 4 is represented as [0, 0, 0, 0, 1, 0, 0, 0, 0, 0].\n",
"\n",
"### Flattened data\n",
"\n",
"For this example, we'll be using *flattened* data or a representation of MNIST images in one dimension rather than two. So, each handwritten number image, which is 28x28 pixels, will be represented as a one dimensional array of 784 pixel values. \n",
"\n",
"Flattening the data throws away information about the 2D structure of the image, but it simplifies our data so that all of the training data can be contained in one array whose shape is [55000, 784]; the first dimension is the number of training images and the second dimension is the number of pixels in each image. This is the kind of data that is easy to analyze using a simple neural network."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting mnist/train-images-idx3-ubyte.gz\n",
"Downloading MNIST...\n",
"Succesfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.\n",
"Extracting mnist/train-labels-idx1-ubyte.gz\n",
"Downloading MNIST...\n",
"Succesfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.\n",
"Extracting mnist/t10k-images-idx3-ubyte.gz\n",
"Downloading MNIST...\n",
"Succesfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.\n",
"Extracting mnist/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"# Retrieve the training and test data\n",
"trainX, trainY, testX, testY = mnist.load_data(one_hot=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Visualize the training data\n",
"\n",
"Provided below is a function that will help you visualize the MNIST data. By passing in the index of a training example, the function `show_digit` will display that training image along with it's corresponding label in the title."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAEICAYAAACQ6CLfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFIVJREFUeJzt3X2QHHWdx/H35wghQGIgZC+GpwSEUrgDo+xxRh4KIXA8\ngyWEBx9CIUYUVCBHHXKo1GGVHiIcyiFEiCQikQfloCw8JTwUaqGyQITEAMGwQbiQbMRAeLoQ+N4f\n3csNy07P7Dzv/j6vqq2d6W8/fKd3PtMz3T3bigjMLD1/0+4GzKw9HH6zRDn8Zoly+M0S5fCbJcrh\nN0tUEuGXtImklyTt2MhxG9DXDEm9zV5OmWV/RdJVNU7btr5brZ7H2unrqSPDn4ev/+dNSa+W3P/4\nUOcXEW9ExNiIeLqR47aSpNMk3duo+UXERRFxeqPm1yySzpX0nKQXJF0jaXSN82no+ms0STsPeN6/\nJCkkfalZy+zI8OfhGxsRY4GngaNKhv1o4PiSRrW+S2s2SUcAc4CPADsB7wW+2tammiQiVgx43n8A\neBP4SbOW2ZHhr0TS1yXdKGmhpPXAJyRNl/RbSeskrZL0HUmb5uOPyl9Fp+b3r8/rP5e0XtL9knYa\n6rh5/TBJT+Rbpu9K+o2kU8r0vYWkH0r6q6SlwF4D6hdIWpEvZ6mko/PhewBXAPvlW4S1+fCjJS2W\n9KKkpyV9ZYjr8Lr89i75Y/6UpGck9Uk6bwh9by/p1ny6pySdkQ+XpF9I+veScW+RNLfKNmcBcyNi\nWUQ8D1wEnFLtY6xW/q5gWb7e/yTptEHG+aqkv+SP78SS4WMkXSrpz5JWS7pS0pgGtPUp4O6IeKYB\n8xpcRHT0D9ALzBgw7OvABuAoshewzYF/AP4RGAXsDDwBnJmPPwoIYGp+/3pgLdANbArcCFxfw7h/\nC6wHjslr5wCvA6eUeSyXAPcCWwNTgD8CvSX1mcDk/DGdDLwETMprpwH3DpjfgcDf5eO/P+/zyCrX\n69eB6/Lbu+SP+SpgDPBB4H+BXSv1nS97MXA+MDqfVy9wUF7fFugD9icL85PAlnltJ2AdsG2ZHpcC\nHyu5Pynvc3wNz6N3rL+S2lH5c0b5On0V2DOvzQA2At8CNsvrrwC75PXvArfm6+ZdwB3ARSXTlv59\nrwa+U0WvytfhJ5qarXaHu4oV0cvg4b+7wnT/DNyc3x4s0FeVjHs0sKSGcU8FfjXgj7aK8uF/uvSx\nAJ8vfXIMMv4S4IhKT96S8a8AvlXleh0s/O8uqT8EHFepb2AfYMWAeX8F+H7J/RPyefwFmD6Ev/3K\nAcvdPO9z+xqeRxXXX8m4PwPOyG/PINvQbFFS/ynwZbIXvteAKSW1/YDlJdOW/fsWLP8jwIuly2zG\nz3D+rPzn0juS3gd8m+wt6RZkIf5dwfTPldx+BRhbw7jblvYRESGp6G3a5AF9rywt5h8XzibbupIv\nZ2K5mUmaDnyDbOs/mmzLtLBg+YUiotzjLOp7CrCjpHUlwzYhe6fQ7zbgO2QvmvcPoaWXyLam/cbn\nv9cPYR4VSTqS7AVrV7JAbwE8UDLKXyLilZL7K8n+9u8mW+d/kPTW7BrQ0iyyDdcrFcesw7D8zJ8b\n+HXEq8m2lLtExLvIdgw14g9RZBWwff8dZc+A7QrGfw7YoeT+W4cTJe0MfA/4HLBNRGwFPMb/P4bB\nvn75Y7IdQjtExHjgGprzmMv2TfaisDwitir5GRcRR5WM8w3gD8BUSccPYblLyT7O9Hs/8GxEvDDE\n/suStDlwS97jpHy9/5K3r8dt8vH67Qj8D7Ca7F3Be0se+/j8b1FrP1sCHwPm1zqPag3n8A80DngB\neFnSbsBnW7DMnwEflHRUfsThS0BXwfg3AedL2krZeQRnltTGkgW8j+x15DPA+0rqq4Ht+3di5sYB\nz0fEa5I+BJxYUiPfefeJWh9clX3fD2yQNCff+bWJpD0k7ZX3cCDwcbIdWLOAKyVNrnK5C4DPSHqf\npAnABcB1/cV8Z+w1Q3gcf5P3+NYP2ZZ7NNl6fyN/F3DQwOmACyWNlnQAcBhwS0S8QfaC+x+SuvId\nnNtLOmQIPQ30MWAN8Ks65lGVkRT+OWRPrvVk7wJubPYCI2I12efZS8k+z74HeJhsZ9lgvkb2bqEX\n+DnZk7t/Xo+Q7Tz6fT7Oe3n7x5Y7geXAakn9b88/B3xD2RGP88lCCmR7ocl2QhV99KlWUd8bgcOB\nvfP6WrL1/y5JW5GF9fMR8VxE3JtPe23eY/+x7W0HW2hE/Ay4DLgvn/cTwL+VjLID8JshPI79yHbm\nvfUTEevIPmrdCjwPHEf2ol7qGeDlfB3MB06LiOV5bQ7Zx4Dfk218fkn28eEdlJ2ncEWFHmcBCyL/\n8N9MasEykiFpE7K3g8dFRNNfuSv0cgDw6Yj4ZDv7aJb8xe0hsr3yG9vdz3Dk8NdJ0qHAb8m2JF8m\n26v8nogot/U36wgj6W1/u+wLrCD7zPhPwEcdfBsOvOU3S5S3/GaJaulJPhMnToypU6e2cpFmSent\n7WXt2rVVnetRV/jznV2Xk53RdU1EfLNo/KlTp9LT01PPIs2sQHd3d9Xj1vy2Pz+s9Z9kJzzsDpwk\nafda52dmrVXPZ/69gScj+x7yBrJTTY9pTFtm1mz1hH873v5lj2cY5Lx2SbMl9Ujq6evrq2NxZtZI\nTd/bHxFzI6I7Irq7uopOezezVqon/M/y9m96bZ8PM7NhoJ7wPwDsKmknZf9U8UTg9sa0ZWbNVvOh\nvojYKOlM4Bdkh/rmRcTShnVmZk1V13H+iLiD7H+Wmdkw49N7zRLl8JslyuE3S5TDb5Yoh98sUQ6/\nWaIcfrNEOfxmiXL4zRLl8JslyuE3S5TDb5Yoh98sUQ6/WaIcfrNEOfxmiXL4zRLl8JslyuE3S5TD\nb5Yoh98sUQ6/WaIcfrNEOfxmiXL4zRLl8JslyuE3S5TDb5Yoh98sUQ6/WaLqukS3pF5gPfAGsDEi\nuhvRlJk1X13hz30kItY2YD5m1kJ+22+WqHrDH8AiSQ9Kmj3YCJJmS+qR1NPX11fn4sysUeoN/74R\nMQ04DDhD0v4DR4iIuRHRHRHdXV1ddS7OzBqlrvBHxLP57zXArcDejWjKzJqv5vBL2lLSuP7bwCHA\nkkY1ZmbNVc/e/knArZL653NDRPx3Q7oys6arOfwRsQJ4fwN7MbMW8qE+s0Q5/GaJcvjNEuXwmyXK\n4TdLVCO+2GNt9oMf/KBsLT8UW9Y222xTWF+2bFlhffr06YX1/fbbr7Bu7eMtv1miHH6zRDn8Zoly\n+M0S5fCbJcrhN0uUw2+WqBFznP+GG24orD/88MOF9Xnz5jWynZZat25dzdOOGlX8FNiwYUNhfcyY\nMYX1LbbYomxtzz33LJz2pptuKqz7P0PVx1t+s0Q5/GaJcvjNEuXwmyXK4TdLlMNvliiH3yxRw+o4\n/znnnFO2dvnllxdO++abbza6nRGh0nH8Sl577bWa6/fee2/htCeccEJhfeHChYX1SZMmFdZT5y2/\nWaIcfrNEOfxmiXL4zRLl8JslyuE3S5TDb5aoYXWc/+abby5bq3Qcv9J3xzfffPOaemqEffbZp7B+\n7LHHtqiToVu0aFFhfcGCBWVrvb29hdPec889hfWTTjqpsH7jjTeWrfl/AVSx5Zc0T9IaSUtKhk2Q\ndKek5fnvrZvbppk1WjVv+68DDh0w7DzgrojYFbgrv29mw0jF8EfEfcDzAwYfA8zPb88HOvd9qZkN\nqtYdfpMiYlV++zmg7EnUkmZL6pHU09fXV+PizKzR6t7bHxEBREF9bkR0R0S3d7KYdY5aw79a0mSA\n/PeaxrVkZq1Qa/hvB2blt2cBtzWmHTNrFWXv2gtGkBYCBwATgdXA14D/Am4CdgRWAjMjYuBOwXfo\n7u6Onp6empt94oknytaWLFlStgZw8MEHF9bHjRtXU09WbMWKFWVrRxxxROG0jz32WF3LvuSSS8rW\n5syZU9e8O1V3dzc9PT2qZtyKJ/lERLkzKQ4aUldm1lF8eq9Zohx+s0Q5/GaJcvjNEuXwmyWq4qG+\nRqr3UJ+NLLfcckth/fjjj69r/hMnTixbG6mnmg/lUJ+3/GaJcvjNEuXwmyXK4TdLlMNvliiH3yxR\nDr9Zohx+s0Q5/GaJcvjNEuXwmyXK4TdLlMNvliiH3yxRDr9ZoobVJbpt+LnyyivL1pr9vx1effXV\nsrUHH3ywcNq99tqr0e10HG/5zRLl8JslyuE3S5TDb5Yoh98sUQ6/WaIcfrNE+Tj/CLBq1aqyteuv\nv75w2ssuu6zR7bxNUW/N9vLLL5etHXjggYXTvvDCC41up+NU3PJLmidpjaQlJcMulPSspMX5z+HN\nbdPMGq2at/3XAYcOMvyyiJiW/9zR2LbMrNkqhj8i7gOeb0EvZtZC9ezw+4KkR/KPBVuXG0nSbEk9\nknpG6vXRzIajWsP/PWBnYBqwCvh2uREjYm5EdEdEd1dXV42LM7NGqyn8EbE6It6IiDeB7wN7N7Yt\nM2u2msIvaXLJ3Y8CS8qNa2adqeJxfkkLgQOAiZKeAb4GHCBpGhBAL/DZJvY44i1atKiwXum751df\nfXXZ2lNPPVVTTyPdqaee2u4W2q5i+CPipEEGX9uEXsyshXx6r1miHH6zRDn8Zoly+M0S5fCbJcpf\n6W2A5cuXF9ZPP/30wvrdd9/dyHaGZMqUKYX1rbcue+Z2VS666KKytTFjxhROe+aZZxbWH3/88Zp6\nAth2221rnnak8JbfLFEOv1miHH6zRDn8Zoly+M0S5fCbJcrhN0uUj/NXqehfXF9xxRWF065YsaKw\nPnbs2ML6+PHjC+tnn3122Vql49kf/vCHC+uVzgNopkqPu5Jx48aVrR155JF1zXsk8JbfLFEOv1mi\nHH6zRDn8Zoly+M0S5fCbJcrhN0uUj/NX6f777y9bq3Qc/+ijjy6sz5kzp7C+//77F9aHq8WLFxfW\nV65cWdf8N9tss7K13Xbbra55jwTe8pslyuE3S5TDb5Yoh98sUQ6/WaIcfrNEOfxmiarmEt07AAuA\nSWSX5J4bEZdLmgDcCEwlu0z3zIj4a/Naba+rrrqqbG3PPfcsnPaCCy5odDsjwpNPPllYX716dV3z\nnzFjRl3Tj3TVbPk3AnMiYnfgQ8AZknYHzgPuiohdgbvy+2Y2TFQMf0SsioiH8tvrgWXAdsAxwPx8\ntPnAsc1q0swab0if+SVNBT4A/A6YFBGr8tJzZB8LzGyYqDr8ksYCPwHOiogXS2sREWT7Awabbrak\nHkk9fX19dTVrZo1TVfglbUoW/B9FxE/zwaslTc7rk4E1g00bEXMjojsiuru6uhrRs5k1QMXwSxJw\nLbAsIi4tKd0OzMpvzwJua3x7ZtYs1Xyldx/gk8Cjkvq/g3k+8E3gJkmfBlYCM5vTYmeYMGFC2ZoP\n5dWm6GvS1dhqq60K61/84hfrmv9IVzH8EfFrQGXKBzW2HTNrFZ/hZ5Yoh98sUQ6/WaIcfrNEOfxm\niXL4zRLlf91tTbXHHnuUrT322GN1zfuQQw4prE+fPr2u+Y903vKbJcrhN0uUw2+WKIffLFEOv1mi\nHH6zRDn8ZonycX5rqt7e3rK1jRs3Fk47fvz4wvpZZ51VS0uW85bfLFEOv1miHH6zRDn8Zoly+M0S\n5fCbJcrhN0uUj/NbXRYuXFhYf+WVV8rWxo0bVzjt3LlzC+v+vn59vOU3S5TDb5Yoh98sUQ6/WaIc\nfrNEOfxmiXL4zRJV8Ti/pB2ABcAkIIC5EXG5pAuBzwB9+ajnR8QdzWrU2uP1118vrF988cWF9dGj\nR5etHXfccYXTzpw5s7Bu9anmJJ+NwJyIeEjSOOBBSXfmtcsi4pLmtWdmzVIx/BGxCliV314vaRmw\nXbMbM7PmGtJnfklTgQ8Av8sHfUHSI5LmSdq6zDSzJfVI6unr6xtsFDNrg6rDL2ks8BPgrIh4Efge\nsDMwjeydwbcHmy4i5kZEd0R0d3V1NaBlM2uEqsIvaVOy4P8oIn4KEBGrI+KNiHgT+D6wd/PaNLNG\nqxh+SQKuBZZFxKUlwyeXjPZRYEnj2zOzZqlmb/8+wCeBRyUtzoedD5wkaRrZ4b9e4LNN6dDaKnvt\nL+/kk08urE+bNq1s7eCDD66pJ2uMavb2/xoY7BngY/pmw5jP8DNLlMNvliiH3yxRDr9Zohx+s0Q5\n/GaJ8r/utkKjRhU/Rc4999wWdWKN5i2/WaIcfrNEOfxmiXL4zRLl8JslyuE3S5TDb5YoRUTrFib1\nAStLBk0E1rasgaHp1N46tS9wb7VqZG9TIqKq/5fX0vC/Y+FST0R0t62BAp3aW6f2Be6tVu3qzW/7\nzRLl8Jslqt3hn9vm5Rfp1N46tS9wb7VqS29t/cxvZu3T7i2/mbWJw2+WqLaEX9Khkh6X9KSk89rR\nQzmSeiU9KmmxpJ429zJP0hpJS0qGTZB0p6Tl+e9Br5HYpt4ulPRsvu4WSzq8Tb3tIOkeSX+UtFTS\nl/LhbV13BX21Zb21/DO/pE2AJ4CDgWeAB4CTIuKPLW2kDEm9QHdEtP2EEEn7Ay8BCyLi7/NhFwPP\nR8Q38xfOrSPiXzqktwuBl9p92fb8alKTSy8rDxwLnEIb111BXzNpw3prx5Z/b+DJiFgRERuAHwPH\ntKGPjhcR9wHPDxh8DDA/vz2f7MnTcmV66wgRsSoiHspvrwf6Lyvf1nVX0FdbtCP82wF/Lrn/DG1c\nAYMIYJGkByXNbnczg5gUEavy288Bk9rZzCAqXra9lQZcVr5j1l0tl7tvNO/we6d9I2IacBhwRv72\ntiNF9pmtk47VVnXZ9lYZ5LLyb2nnuqv1cveN1o7wPwvsUHJ/+3xYR4iIZ/Pfa4Bb6bxLj6/uv0Jy\n/ntNm/t5Syddtn2wy8rTAeuuky53347wPwDsKmknSaOBE4Hb29DHO0jaMt8Rg6QtgUPovEuP3w7M\nym/PAm5rYy9v0ymXbS93WXnavO467nL3EdHyH+Bwsj3+fwL+tR09lOlrZ+AP+c/SdvcGLCR7G/g6\n2b6RTwPbAHcBy4FFwIQO6u2HwKPAI2RBm9ym3vYle0v/CLA4/zm83euuoK+2rDef3muWKO/wM0uU\nw2+WKIffLFEOv1miHH6zRDn8Zoly+M0S9X9n3/JewkbQBgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x12599ccc0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAEICAYAAACQ6CLfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFVRJREFUeJzt3XmYXXV9x/H3JwGkJiSAGdOYhRiW0IAYcZ48IptVVKDG\nwFOCosHIrixiRVtKsQG0IDwIjxXUhKUEw1qURYsFkkoFqpSBsoQ9hBDBLBOjJGyGwLd/nDN4Geae\nO3P34fd5Pc88uXO+Z/nek/u559xzzp2jiMDM0jOk1Q2YWWs4/GaJcvjNEuXwmyXK4TdLlMNvlqi3\nbfglDZX0gqQJ9Ry3Dn3tI2lZo5dTZtnflPSjKqdtWd/tRtICSac1e9p6a5vw5+Hr+Xld0sslv39+\noPOLiNciYnhELK/nuM0k6UhJt9drfhHxrYj4Ur3m1wiS3i/pVkm/l7Sxj/q7JN0o6UVJyyR9poZl\n3SnpizU13GCSZkl6Js/BTyVtWa95t0348/ANj4jhwHJgesmwK3qPL2mT5ndpTbABuBo4qkz9R8CL\nwLuB2cBFknZsUm9NJWkX4AfA54G/BF4FLqjX/Nsm/JVI+rakayRdJWk9MEvSbpJ+I+mPklZI+ldJ\nm+bjbyIpJE3Mf1+Q138hab2kX0t670DHzev7SXpC0vOSvi/prnJbEEnvlPRjSX+Q9DDwwV71UyUt\nzZfzsKRP58PfR/YfvWf+rr8mH/5pSfdLWidpuaRvDnAdXpY/3i5/zl+Q9KykbkknD6DvcZKuz6d7\nWtJx+XBJukXS2SXjXidpXn96jIhHI+JS4JE++h8BHACcGhEvRsR/Az8HZvV3HfSHpCF5zyvz19bt\nkv6q12gdkhbl/2+/lDS+ZPopkhZKWivpMUl/W2Urs4AbIuLOiHgB+CYwU9I7q5zfmwya8OcOBK4E\nRgLXABuBE4FRwO7AvsAxBdN/jmwFbk22d/GtgY4r6d3AtcA38uU+DUwrmM8ZwHhgErA/2daq1BN5\n7yOBfwGulDQ6Ih4CjgfuyPd+RuXjv0C2JdgSmA6cKOlTBcuv5MPAdsAngdMlbV+pb0lDyEJ3DzAW\n+DjwDUkfi+x68cOAwyXtJWk2MBX4u3za9+aBek8VvU4GXomIpSXDHgB2qmJelfwc2J5si7sY+HGv\n+izgn8leA4/01CUNB24DLifbO/k8ME/S5N4LUHas6Y+SPlSmh53Inh8AEfEE8HreV80GW/jvjIif\nRcTrEfFyRNwTEXdHxMb8BTEP2Ltg+usioisiXgWuIHtRDnTcTwH3R8SNee18YE3BfA4Gvh0Rf4iI\nZ+i12xYR10bEivw5XQksAzrLzSwi/isiHs7Hf4BsF7noOVdyWkS8EhH3AQ8D7+9H37sBIyLizIjY\nEBFLgEuAz+Y9/o7sjWsBcB5waES8mNeejogt83EGajjwfK9h64AtqphXWfm6vSwi1kfEK8BpwAcl\nDSsZ7WcRcVdE/Ak4BdhL0hhgBvBERFyevy7vBW4ADupjOa/l6+I3ZVpp6PMdbOH/bekvknaU9B/5\n7tk6sq3VqL4nBWBlyeOXyFbuQMd9T2kf+Zbu2YL5jOnV9zOlRUlflPRAvgX4I7AjBc8h/6hze767\n/TxwZNH4lUREuedZ1Pc2wISenvO+/55sK9njRuAdwOKI+HW1/fXyAjCi17CRwPo6zR94Y4t8Tv5x\nbB2wJC+VrufS18DzZCF9D9m62b3XuvkM2focqL6e7wjq9HwHW/h7fwVxLtku2XYRMYJsN0wN7mEF\nMK7nF0ki2/UtZyXZ7nOPN04nSpoE/BD4MvCuiNgSeIw/P4e+vnJ5NfATYHxEjAQupjHPuWzfZC/8\nJ/OtVs/PFhExvWScs8h2WSdKmlmnnh4H/qL0+AvZnsrDdZp/jy+QfdT5KNmby3b58NL1XPoZf2Q+\n3u/I1s2iXutmeEQcX0UfpXti5B8dhgBPVjGvtxhs4e9tC7J33BfzAzJFn/fr5efArpKmKzvjcCLQ\nUTD+tcApkrZUdh1B6YtgOFnAu8neR44i2/L3WAWMU34QM7cFsDYiXsk/K362dGH5wbt6HAAr6vvX\nwAZJJ0naPN9Svk/SB/MePkr2WfcLZMcKfpDvEleUHzDcHNgs/31zSZsBRMQ6sj2Kb+UHJPcC/obs\n40Xpgds9BvA8N82X0fOzKdk6/hPwe+CdZMdiepue74W9A/g22bGZFcBNwE6SPidp0/xnWl+f+fth\nAXCApA/nxxLOAP49Il6qYl5vMdjDfxLZi2s92V7ANY1eYESsItuNO4/sxbEt8H9kL5a+zCHbW1gG\n/ILsQFDPvB4Evg/8bz7OZODukmlvI3uXXyWpZ/f8y8BZys54nEIWUiALCrBVr3lUq6jvjWRbxml5\nfQ3Z+h+h7Dz0ZcCxEbEyIm7Pp70k73GSsrMX5Q74bQu8TLbXMDR/XHrk/0tku77dZAfZjoqIx/La\neLKNweIBPM95+TJ6fi4C/o1sK/47sq3v//Qx3QKy0K8BdiF7o+v5CPBJsgOCK8j2oM4i+wj0Jvrz\nxWW79dVY/vo4nmxvbxXZG+IJA3huheQ/5lEbSUPJXiQHRcQdLe7lI8AREXFoK/toFWWnW7eNiH6f\n/kyZw18FSfsCvyHbUvwj2UG3bfMjv2aDwmDf7W+VPYClZLuenwQOdPBtsPGW3yxR3vKbJaqpX44Z\nNWpUTJw4sZmLNEvKsmXLWLNmTb+u+6gp/PmBr++RnZK5OCK+UzT+xIkT6erqqmWRZlags7PsleFv\nUfVuf36K60JgP2AKcIikKdXOz8yaq5bP/NOAJRGxNCJ6voM9oz5tmVmj1RL+sbz5ix/P0sc17pKO\nltQlqau7u7uGxZlZPTX8aH9EzIuIzojo7OgougTezJqplvA/x5u/9TUuH2Zmg0At4b8H2D7/yyyb\nkX277Kb6tGVmjVb1qb6I2CjpeOAWslN9l0ZEvb9XbWYNUtN5/oi4Gbi5Tr2YWRP58l6zRDn8Zoly\n+M0S5fCbJcrhN0uUw2+WKIffLFEOv1miHH6zRDn8Zoly+M0S5fCbJcrhN0uUw2+WKIffLFEOv1mi\nHH6zRDn8Zoly+M0S5fCbJcrhN0uUw2+WKIffLFEOv1miHH6zRDn8Zoly+M0S5fCbJcrhN0tUTXfp\nteaIiML61VdfXbZ2+umnF077+OOPV9VTPUyePLmwvmjRosL66NGjC+ubbOKXd5Ga1o6kZcB64DVg\nY0R01qMpM2u8erw1/nVErKnDfMysifyZ3yxRtYY/gIWS7pV0dF8jSDpaUpekru7u7hoXZ2b1Umv4\n94iIqcB+wHGS9uo9QkTMi4jOiOjs6OiocXFmVi81hT8insv/XQ1cD0yrR1Nm1nhVh1/SMElb9DwG\nPgEsrldjZtZYtRztHw1cL6lnPldGxH/WpavEvP7664X1Cy+8sLD+la98peplDxlS/P4/bNiwwvrG\njRsL6y+//HLZWqVrDMaNG1dY33nnnQvrCxcuLFurdI1ACqoOf0QsBd5fx17MrIl8qs8sUQ6/WaIc\nfrNEOfxmiXL4zRLl7zy2gYsvvriwXsupvEpfa50zZ05h/dRTTy2sL1++vLB+zjnnlK3NnTu3cNpK\npxEXLy6+rGSfffYpW7vrrrsKpx0xYkRh/e3AW36zRDn8Zoly+M0S5fCbJcrhN0uUw2+WKIffLFE+\nz98Er732WmH99ttvb9iyTz755MJ6pfP4lUyYMKGwfsEFF5St7b333oXTnnjiiYX1FStWFNaLrgN4\n6aWXCqf1eX4ze9ty+M0S5fCbJcrhN0uUw2+WKIffLFEOv1mifJ6/CVavXl1Yv+qqq2qa/0477VS2\nduSRR9Y070aaOXNmYf38888vrFc6z2/FvOU3S5TDb5Yoh98sUQ6/WaIcfrNEOfxmiXL4zRLl8/xN\ncMMNN9Q0/WabbVZYL/rb+Ntss01Ny26lK6+8srC+2267FdZXrlxZtjZ//vzCab/+9a8X1ocOHVpY\nHwwqbvklXSpptaTFJcO2lnSbpCfzf7dqbJtmVm/92e2/DNi317CTgUURsT2wKP/dzAaRiuGPiF8B\na3sNngH07DfNBw6oc19m1mDVHvAbHRE9F1avBEaXG1HS0ZK6JHV1d3dXuTgzq7eaj/ZHRABRUJ8X\nEZ0R0dnR0VHr4sysTqoN/ypJYwDyf4u/tmZmbafa8N8EzM4fzwZurE87ZtYsyvbaC0aQrgI+AowC\nVgFzgBuAa4EJwDPAwRHR+6DgW3R2dkZXV1eNLbef9evXF9Z33XXXwvqSJUsK6zvssENh/fHHHy+s\nv11VuifB2WefXfW8H3vsscL65MmTq553I3V2dtLV1aX+jFvxIp+IOKRM6WMD6srM2oov7zVLlMNv\nliiH3yxRDr9Zohx+s0T5K711sGHDhsJ6pVN5Vp0pU6Y0bN5z584trJ933nkNW3azeMtvliiH3yxR\nDr9Zohx+s0Q5/GaJcvjNEuXwmyXK5/kHgbFjx7a6BXsb8pbfLFEOv1miHH6zRDn8Zoly+M0S5fCb\nJcrhN0uUz/PXwYIFCxo6/8MOO6yh87c0ectvliiH3yxRDr9Zohx+s0Q5/GaJcvjNEuXwmyXK5/nr\n4Omnn251C2YDVnHLL+lSSaslLS4Zdpqk5yTdn//s39g2zaze+rPbfxmwbx/Dz4+IqfnPzfVty8wa\nrWL4I+JXwNom9GJmTVTLAb8TJD2YfyzYqtxIko6W1CWpq7u7u4bFmVk9VRv+HwKTgKnACuC75UaM\niHkR0RkRnR0dHVUuzszqrarwR8SqiHgtIl4HLgKm1bctM2u0qsIvaUzJrwcCi8uNa2btqeJ5fklX\nAR8BRkl6FpgDfETSVCCAZcAxDezRzBqgYvgj4pA+Bl/SgF7MrIl8ea9Zohx+s0Q5/GaJcvjNEuXw\nmyXKX+ltA8OGDSusT5gwoUmdWI/Jkye3uoWG85bfLFEOv1miHH6zRDn8Zoly+M0S5fCbJcrhN0uU\nz/O3gVdffbWwvm7duiZ10l6WL19eWD/33HMbtuyZM2c2bN7twlt+s0Q5/GaJcvjNEuXwmyXK4TdL\nlMNvliiH3yxRPs9fB7vssktN02/YsKGwfuaZZxbWp0+fXtPy29WsWbMK6w899FDV8z777LML6yNH\njqx63oOFt/xmiXL4zRLl8JslyuE3S5TDb5Yoh98sUQ6/WaL6c4vu8cDlwGiyW3LPi4jvSdoauAaY\nSHab7oMj4g+Na7V9zZgxo7B+xBFH1DT/tWvX1jR9uzrrrLMK63fffXdN899xxx3L1o45pviu8kOH\nDq1p2YNBf7b8G4GTImIK8CHgOElTgJOBRRGxPbAo/93MBomK4Y+IFRFxX/54PfAoMBaYAczPR5sP\nHNCoJs2s/gb0mV/SROADwN3A6IhYkZdWkn0sMLNBot/hlzQc+Anw1Yh40x+Vi4ggOx7Q13RHS+qS\n1NXd3V1Ts2ZWP/0Kv6RNyYJ/RUT8NB+8StKYvD4GWN3XtBExLyI6I6Kzo6OjHj2bWR1UDL8kAZcA\nj0bEeSWlm4DZ+ePZwI31b8/MGqU/X+ndHTgUeEjS/fmwU4DvANdKOgJ4Bji4MS22v80337ywvvPO\nOxfWFy9eXFhfunRpYf34448vW/va175WOO2kSZMK67VauHBh2dqcOXMKp630J82LTuUB3HLLLWVr\nKXxlt5KK4Y+IOwGVKX+svu2YWbP4Cj+zRDn8Zoly+M0S5fCbJcrhN0uUw2+WKP/p7joYNmxYYb3o\nXDfAPvvsU1ivdB3AhRdeWLZ26623Fk577LHHFtYrmT9/fmH9qaeeKlurdB6/khNOOKGwPmHChJrm\n/3bnLb9Zohx+s0Q5/GaJcvjNEuXwmyXK4TdLlMNvlihlf4GrOTo7O6Orq6tpyxssrrvuusL66aef\nXlivdB1Au9phhx0K60Xfx4fK5/GHDElv29bZ2UlXV1e5r+C/SXprx8wAh98sWQ6/WaIcfrNEOfxm\niXL4zRLl8Jslyt/nbwMHHXRQYf2AA4rvgbpq1aqytblz5xZOe8cddxTW99xzz8J6JYcffnjZ2rhx\n4wqn3WQTvzwbyVt+s0Q5/GaJcvjNEuXwmyXK4TdLlMNvliiH3yxRFU+kShoPXA6MBgKYFxHfk3Qa\ncBTQnY96SkTc3KhGU1bpfPfYsWPL1s4444x6t2NvE/25imIjcFJE3CdpC+BeSbfltfMj4tzGtWdm\njVIx/BGxAliRP14v6VGg/KbGzAaFAX3mlzQR+ABwdz7oBEkPSrpU0lZlpjlaUpekru7u7r5GMbMW\n6Hf4JQ0HfgJ8NSLWAT8EJgFTyfYMvtvXdBExLyI6I6Kzo6OjDi2bWT30K/ySNiUL/hUR8VOAiFgV\nEa9FxOvARcC0xrVpZvVWMfySBFwCPBoR55UMH1My2oHA4PwTsmaJ6s/R/t2BQ4GHJN2fDzsFOETS\nVLLTf8uAYxrSoZk1RH+O9t8J9PV3wH1O32wQ8xV+Zoly+M0S5fCbJcrhN0uUw2+WKIffLFEOv1mi\nHH6zRDn8Zoly+M0S5fCbJcrhN0uUw2+WKIffLFGKiOYtTOoGnikZNApY07QGBqZde2vXvsC9Vaue\nvW0TEf36e3lNDf9bFi51RURnyxoo0K69tWtf4N6q1arevNtvliiH3yxRrQ7/vBYvv0i79taufYF7\nq1ZLemvpZ34za51Wb/nNrEUcfrNEtST8kvaV9LikJZJObkUP5UhaJukhSfdL6mpxL5dKWi1pccmw\nrSXdJunJ/N8+75HYot5Ok/Rcvu7ul7R/i3obL+mXkh6R9LCkE/PhLV13BX21ZL01/TO/pKHAE8DH\ngWeBe4BDIuKRpjZShqRlQGdEtPyCEEl7AS8Al0fEzvmwc4C1EfGd/I1zq4j4hzbp7TTghVbftj2/\nm9SY0tvKAwcAX6SF666gr4NpwXprxZZ/GrAkIpZGxAbgamBGC/poexHxK2Btr8EzgPn54/lkL56m\nK9NbW4iIFRFxX/54PdBzW/mWrruCvlqiFeEfC/y25PdnaeEK6EMACyXdK+noVjfTh9ERsSJ/vBIY\n3cpm+lDxtu3N1Ou28m2z7qq53X29+YDfW+0REVOB/YDj8t3bthTZZ7Z2Olfbr9u2N0sft5V/QyvX\nXbW3u6+3VoT/OWB8ye/j8mFtISKey/9dDVxP+916fFXPHZLzf1e3uJ83tNNt2/u6rTxtsO7a6Xb3\nrQj/PcD2kt4raTPgs8BNLejjLSQNyw/EIGkY8Ana79bjNwGz88ezgRtb2MubtMtt28vdVp4Wr7u2\nu919RDT9B9if7Ij/U8A/taKHMn1NAh7Ifx5udW/AVWS7ga+SHRs5AngXsAh4ElgIbN1Gvf0YeAh4\nkCxoY1rU2x5ku/QPAvfnP/u3et0V9NWS9ebLe80S5QN+Zoly+M0S5fCbJcrhN0uUw2+WKIffLFEO\nv1mi/h8lFSWK9jI8twAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1280ddc88>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Visualizing the data\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"\n",
"# Function for displaying a training image by it's index in the MNIST set\n",
"def show_digit(index):\n",
" label = trainY[index].argmax(axis=0)\n",
" # Reshape 784 array into 28x28 image\n",
" image = trainX[index].reshape([28,28])\n",
" plt.title('Training data, index: %d, Label: %d' % (index, label))\n",
" plt.imshow(image, cmap='gray_r')\n",
" plt.show()\n",
" \n",
"# Display the first (index 0) training image\n",
"show_digit(0)\n",
"show_digit(10)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"## Building the network\n",
"\n",
"TFLearn lets you build the network by defining the layers in that network. \n",
"\n",
"For this example, you'll define:\n",
"\n",
"1. The input layer, which tells the network the number of inputs it should expect for each piece of MNIST data. \n",
"2. Hidden layers, which recognize patterns in data and connect the input to the output layer, and\n",
"3. The output layer, which defines how the network learns and outputs a label for a given image.\n",
"\n",
"Let's start with the input layer; to define the input layer, you'll define the type of data that the network expects. For example,\n",
"\n",
"```\n",
"net = tflearn.input_data([None, 100])\n",
"```\n",
"\n",
"would create a network with 100 inputs. The number of inputs to your network needs to match the size of your data. For this example, we're using 784 element long vectors to encode our input data, so we need **784 input units**.\n",
"\n",
"\n",
"### Adding layers\n",
"\n",
"To add new hidden layers, you use \n",
"\n",
"```\n",
"net = tflearn.fully_connected(net, n_units, activation='ReLU')\n",
"```\n",
"\n",
"This adds a fully connected layer where every unit (or node) in the previous layer is connected to every unit in this layer. The first argument `net` is the network you created in the `tflearn.input_data` call, it designates the input to the hidden layer. You can set the number of units in the layer with `n_units`, and set the activation function with the `activation` keyword. You can keep adding layers to your network by repeated calling `tflearn.fully_connected(net, n_units)`. \n",
"\n",
"Then, to set how you train the network, use:\n",
"\n",
"```\n",
"net = tflearn.regression(net, optimizer='sgd', learning_rate=0.1, loss='categorical_crossentropy')\n",
"```\n",
"\n",
"Again, this is passing in the network you've been building. The keywords: \n",
"\n",
"* `optimizer` sets the training method, here stochastic gradient descent\n",
"* `learning_rate` is the learning rate\n",
"* `loss` determines how the network error is calculated. In this example, with categorical cross-entropy.\n",
"\n",
"Finally, you put all this together to create the model with `tflearn.DNN(net)`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise:** Below in the `build_model()` function, you'll put together the network using TFLearn. You get to choose how many layers to use, how many hidden units, etc.\n",
"\n",
"**Hint:** The final output layer must have 10 output nodes (one for each digit 0-9). It's also recommended to use a `softmax` activation layer as your final output layer. "
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Define the neural network\n",
"def build_model(learning_rate):\n",
" # This resets all parameters and variables, leave this here\n",
" tf.reset_default_graph()\n",
" \n",
" #### Your code ####\n",
" # Include the input layer, hidden layer(s), and set how you want to train the model\n",
" \n",
" # Input layer\n",
" net = tflearn.input_data([None, 784])\n",
" \n",
" # Hidden layers\n",
" net = tflearn.fully_connected(net, 200, activation='ReLU')\n",
" net = tflearn.fully_connected(net, 40, activation='ReLU')\n",
" \n",
" # Output layers\n",
" net = tflearn.fully_connected(net, 10, activation='softmax')\n",
" net = tflearn.regression(net, optimizer='sgd', learning_rate=learning_rate, loss='categorical_crossentropy')\n",
" \n",
" # This model assumes that your network is named \"net\" \n",
" model = tflearn.DNN(net)\n",
" return model"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"WARNING:tensorflow:From //anaconda/envs/tflearn/lib/python3.5/site-packages/tflearn/summaries.py:46 in get_summary.: scalar_summary (from tensorflow.python.ops.logging_ops) is deprecated and will be removed after 2016-11-30.\n",
"Instructions for updating:\n",
"Please switch to tf.summary.scalar. Note that tf.summary.scalar uses the node name instead of the tag. This means that TensorFlow will automatically de-duplicate summary names based on the scope they are created in. Also, passing a tensor or list of tags to a scalar summary op is no longer supported.\n",
"WARNING:tensorflow:From //anaconda/envs/tflearn/lib/python3.5/site-packages/tflearn/summaries.py:46 in get_summary.: scalar_summary (from tensorflow.python.ops.logging_ops) is deprecated and will be removed after 2016-11-30.\n",
"Instructions for updating:\n",
"Please switch to tf.summary.scalar. Note that tf.summary.scalar uses the node name instead of the tag. This means that TensorFlow will automatically de-duplicate summary names based on the scope they are created in. Also, passing a tensor or list of tags to a scalar summary op is no longer supported.\n",
"WARNING:tensorflow:From //anaconda/envs/tflearn/lib/python3.5/site-packages/tflearn/helpers/trainer.py:766 in create_summaries.: merge_summary (from tensorflow.python.ops.logging_ops) is deprecated and will be removed after 2016-11-30.\n",
"Instructions for updating:\n",
"Please switch to tf.summary.merge.\n",
"WARNING:tensorflow:VARIABLES collection name is deprecated, please use GLOBAL_VARIABLES instead; VARIABLES will be removed after 2017-03-02.\n",
"WARNING:tensorflow:From //anaconda/envs/tflearn/lib/python3.5/site-packages/tflearn/helpers/trainer.py:130 in __init__.: initialize_all_variables (from tensorflow.python.ops.variables) is deprecated and will be removed after 2017-03-02.\n",
"Instructions for updating:\n",
"Use `tf.global_variables_initializer` instead.\n"
]
}
],
"source": [
"# Build the model\n",
"model = build_model(learning_rate=0.1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training the network\n",
"\n",
"Now that we've constructed the network, saved as the variable `model`, we can fit it to the data. Here we use the `model.fit` method. You pass in the training features `trainX` and the training targets `trainY`. Below I set `validation_set=0.1` which reserves 10% of the data set as the validation set. You can also set the batch size and number of epochs with the `batch_size` and `n_epoch` keywords, respectively. \n",
"\n",
"Too few epochs don't effectively train your network, and too many take a long time to execute. Choose wisely!"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Training Step: 8910 | total loss: \u001b[1m\u001b[32m0.16469\u001b[0m\u001b[0m\n",
"| SGD | epoch: 010 | loss: 0.16469 - acc: 0.9856 | val_loss: 0.07542 - val_acc: 0.9782 -- iter: 49500/49500\n",
"Training Step: 8910 | total loss: \u001b[1m\u001b[32m0.16469\u001b[0m\u001b[0m\n",
"| SGD | epoch: 010 | loss: 0.16469 - acc: 0.9856 | val_loss: 0.07542 - val_acc: 0.9782 -- iter: 49500/49500\n",
"--\n"
]
}
],
"source": [
"# Training\n",
"model.fit(trainX, trainY, validation_set=0.1, show_metric=True, batch_size=100, n_epoch=10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Testing\n",
"After you're satisified with the training output and accuracy, you can then run the network on the **test data set** to measure it's performance! Remember, only do this after you've done the training and are satisfied with the results.\n",
"\n",
"A good result will be **higher than 98% accuracy**! Some simple models have been known to get up to 99.7% accuracy."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Test accuracy: 0.9972\n"
]
}
],
"source": [
"# Compare the labels that our model predicts with the actual labels\n",
"predictions = (np.array(model.predict(testX))[:,0] >= 0.5).astype(np.int_)\n",
"\n",
"# Calculate the accuracy, which is the percentage of times the predicated labels matched the actual labels\n",
"test_accuracy = np.mean(predictions == testY[:,0], axis=0)\n",
"\n",
"# Print out the result\n",
"print(\"Test accuracy: \", test_accuracy)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
gregorjerse/rt2 | 2015_2016/lab13/Extending values on vertices.ipynb | 1 | 6863 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Extending values on vertices to a discrete gradient vector field\n",
"During extension algorithm one has to compute lover_link for every vertex in the complex. So let us implement search for the lower link first. It requires quite a lot of code: first we find a star, then link and finally lower link for the given simplex."
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from itertools import combinations, chain\n",
"\n",
"def simplex_closure(a): \n",
" \"\"\"Returns the generator that iterating over all subsimplices (of all dimensions) in the closure\n",
" of the simplex a. The simplex a is also included.\n",
" \"\"\"\n",
" return chain.from_iterable([combinations(a, l) for l in range(1, len(a) + 1)])\n",
" \n",
"def closure(K):\n",
" \"\"\"Add all missing subsimplices to K in order to make it a simplicial complex.\"\"\"\n",
" return list({s for a in K for s in simplex_closure(a)})\n",
"\n",
"def contained(a, b):\n",
" \"\"\"Returns True is a is a subsimplex of b, False otherwise.\"\"\"\n",
" return all((v in b for v in a))\n",
"\n",
"def star(s, cx):\n",
" \"\"\"Return the set of all simplices in the cx that contais simplex s.\n",
" \"\"\"\n",
" return {p for p in cx if contained(s, p)}\n",
"\n",
"def intersection(s1, s2):\n",
" \"\"\"Return the intersection of s1 and s2.\"\"\"\n",
" return list(set(s1).intersection(s2))\n",
"\n",
"def link(s, cx):\n",
" \"\"\"Returns link of the simplex s in the complex cx.\n",
" \"\"\"\n",
" # Link consists of all simplices from the closed star that have \n",
" # empty intersection with s.\n",
" return [c for c in closure(star(s, cx)) if not intersection(s, c)]\n",
"\n",
"def simplex_value(s, f, aggregate):\n",
" \"\"\"Return the value of f on vertices of s\n",
" aggregated by the aggregate function.\n",
" \"\"\"\n",
" return aggregate([f[v] for v in s])\n",
"\n",
"def lower_link(s, cx, f):\n",
" \"\"\"Return the lower link of the simplex s in the complex cx.\n",
" The dictionary f is the mapping from vertices (integers)\n",
" to the values on vertices.\n",
" \"\"\"\n",
" sval = simplex_value(s, f, min)\n",
" return [s for s in link(s, cx) \n",
" if simplex_value(s, f, max) < sval]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us test the above function on the simple example: full triangle with values `0`, `1` and `2` on the vertices labeled with `1`, `2` and `3`."
]
},
{
"cell_type": "code",
"execution_count": 87,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(1,): []\n",
"(2,): [(1,)]\n",
"(3,): [(1, 2), (1,), (2,)]\n"
]
}
],
"source": [
"K = closure([(1, 2, 3)])\n",
"f = {1: 0, 2: 1, 3: 2}\n",
"for v in (1, 2, 3):\n",
" print\"{0}: {1}\".format((v,), lower_link((v,), K, f))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let us implement an extension algorithm. We are leaving out the cancelling step for clarity."
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def join(a, b):\n",
" \"\"\"Return the join of 2 simplices a and b.\"\"\"\n",
" return tuple(sorted(set(a).union(b)))\n",
"\n",
"def extend(K, f):\n",
" \"\"\"Extend the field to the complex K.\n",
" Function on vertices is given in f.\n",
" Returns the pair V, C, where V is the dictionary containing discrete gradient vector field\n",
" and C is the list of all critical cells.\n",
" \"\"\"\n",
" V = dict()\n",
" C = []\n",
" for v in (s for s in K if len(s)==1):\n",
" ll = lower_link(v, K, f)\n",
" if len(ll) b== 0:\n",
" C.append(v)\n",
" else:\n",
" V1, C1 = extend(ll, f)\n",
" mv, mc = min([(f[c[0]], c) for c in C1 if len(c)==1])\n",
" V[v] = join(v, mc)\n",
" for c in (c for c in C1 if c != mc):\n",
" C.append(join(v, c))\n",
" for a, b in V1.items():\n",
" V[join(a, v)] = join(b, v)\n",
" return V, C"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us test the algorithm on the example from the previous step (full triangle)."
]
},
{
"cell_type": "code",
"execution_count": 92,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"({(2,): (1, 2), (2, 3): (1, 2, 3), (3,): (1, 3)}, [(1,)])"
]
},
"execution_count": 92,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"K = closure([(1, 2, 3)])\n",
"f = {1: 0, 2: 1, 3: 2}\n",
"extend(K, f)"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"({(2,): (1, 2), (2, 3): (1, 2, 3), (3,): (1, 3)},\n",
" [(1,), (2, 4), (2, 3, 4), (3, 4), (4,)])"
]
},
"execution_count": 100,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"K = closure([(1, 2, 3), (2, 3, 4)])\n",
"f = {1: 0, 2: 1, 3: 2, 4: 0}\n",
"extend(K, f)"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"({(2,): (1, 2),\n",
" (2, 3): (1, 2, 3),\n",
" (3,): (1, 3),\n",
" (3, 4): (2, 3, 4),\n",
" (4,): (2, 4)},\n",
" [(1,)])"
]
},
"execution_count": 101,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"K = closure([(1, 2, 3), (2, 3, 4)])\n",
"f = {1: 0, 2: 1, 3: 2, 4: 3}\n",
"extend(K, f)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
WNoxchi/Kaukasos | FADL1/importfastaitest.ipynb | 1 | 1000 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"from fastai.imports import *"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"yay it works!\n"
]
}
],
"source": [
"print(\"yay it works!\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (FastAI)",
"language": "python",
"name": "fastai"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
pioneers/topgear | coroutine_spin_test.ipynb | 1 | 16679 | {
"metadata": {
"name": "",
"signature": "sha256:246de87d1823dcfd28158f479ebeba5932bd42b37de3a5679728fa970c2fcc5c"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src=\"http://mirageforum.com/forum/attachment.php?attachmentid=159&d=1370617142\">"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"back to [Index](index.ipynb)"
]
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"coroutine_spin_test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"2014-07-19"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"testing performance of coroutines"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Cross-notebook include shim\n",
"with open(\"nbinclude.ipynb\") as nbinclude_f: # don't rename nbinclude_f\n",
" import IPython.nbformat.current\n",
" get_ipython().run_cell(IPython.nbformat.current.read(nbinclude_f, 'json').worksheets[0].cells[0].input)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 38
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"class CoroutineSpinner:\n",
" def __init__(self, coroutine):\n",
" self.coroutine=coroutine\n",
" self.running=False\n",
" def run(self):\n",
" self.running=True\n",
" while(self.running):\n",
" delay=next(self.coroutine)\n",
" if delay < 0:\n",
" return\n",
" time.sleep(delay)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 39
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import time\n",
"import numpy as np\n",
"times=np.zeros(shape=[100], dtype=np.float32)\n",
"def time_test():\n",
" i=0\n",
" last_time=time.time()\n",
" while True:\n",
" now=time.time()\n",
" times[i]=now-last_time\n",
"# print i, times[i]\n",
" last_time=now\n",
" i+=1\n",
" if i == 100:\n",
" yield -1\n",
" yield .01"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 40
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"cs=CoroutineSpinner(time_test())"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 41
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"cs.run()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 42
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 43
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 44
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot(times)\n",
"plt.xlabel"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 45,
"text": [
"<function matplotlib.pyplot.xlabel>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAD9CAYAAABTJWtQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X94U+XdP/DPaZtSLGL51RZyMgNJSotIqCsEfXTmEbpC\np0HASWGDCmzro2DnVKi6Z9fguS5qq3Obrl+hbvwomwOG22w2QgXkqegjaflRmKMgraSSpLSwQhCQ\nkh/c3z/unTRim5QCp6fk/bqu+7Ip9znnzunJ/T6fc5IoMMYIAACAiCimtwcAAADKgVAAAIAghAIA\nAAQhFAAAIAihAAAAQQgFAAAI6lYoVFVVTU1PTz9qMBgaSktLizrrU1hY+IbBYGgwGo2H6urqMqXf\nL1y4cG1KSkrr3Xff/Ulo/6VLl76akZFxxGg0Hpo5c+Zfzp07d8f1PRUAALhujLGwze/3x+p0ukaH\nw6H1er0qo9F4sL6+PiO0z9atW3OnTZtmY4yR3W43mUwmu/Rvu3fvfuDAgQOZY8eO/SR0me3bt2cH\nAoEYxhgVFRWVFBUVlUQaCxoaGhrazW0RK4Xa2tqJer2+UavVNqlUKl9eXt6mysrK6aF9rFarJT8/\nv4KIyGQy1Xg8nqSWlpZUIqIHHnjgw0GDBp29er3Z2dk7YmJirkjLuFwu8cbEHAAA9FTEUHC73WqN\nRuOUHoui6HK73epr7RPO2rVrF+bm5tq62x8AAG6OuEgdBEHo1vdgMMaEniy3cuXKn8bHx3vnzp37\nx55uGwAAvurqObm7IlYKarXa7XQ6NdJjp9OpEUXRFa6Py+US1Wq1O9K6169f/4TNZst9++23v9dV\nn96+vqaU9vOf/7zXx6CUhn2BfYF9Eb5dj4ihkJWVta+hocHQ1NSk9Xq98Zs3b55tsVisoX0sFot1\nw4YN84mI7Hb7pKSkJE9KSkpruPVWVVVNffXVV5dWVlZOT0hIaL+uZwEAADdExFCIi4vzl5WVLcnJ\nyXlvzJgx9bNnz96ckZFxpLy8vKC8vLyAiCg3N9c2atSo43q9vrGgoKD8zTfffEpafs6cORvvu+++\nj48dO5am0Wic69atW0BE9PTTT//mwoULA7Kzs3dkZmbWPfXUU2/evKcJAADdIVxvqXEzCYLAlDw+\nOVVXV5PZbO7tYSgC9kUH7IsO2BcdBEEg1sN7CggFAIBbzPWEAr7mAgAAghAKAAAQhFAAAIAghAIA\nAAQhFAAAIAihAAAAQQgFAAAIQigAAEAQQgEAAIIQCgAAEIRQAACAIIQCAAAEIRQAACAIoQAAAEEI\nBVCE3/2OyOvt7VEAAEIBet2xY0Q//CHRzp29PRIAQChAr3vnHaLBg/l/AaB3IRSg123ZQvT660RW\nK5HP19ujAYhuCAXoVY2NRCdPEs2ZQzRqFFF1dW+PCCC6IRSgV23ZQjRzJlFsLNFjjxH9+c+9PSKA\n6IZQgF71zjtE3/0u/3nWLKK//pUoEOjdMQFEM4QC9Jrjx4lcLqJvfYs/1umIRowg+uij3h0XQDRD\nKECv2bKFaMYMfulIMmuWvJeQGJNvWwB9AUIBbjrGiA4cIFq2jOjll4k+/5z/PvTSkUQKhStXer69\npiaiX/2Kb7MrV64QrV1LNHw4f+cTAHBxvT2A7jh/nmj3bn654fhxojNniCZOJHrwQaIxY4hiEG29\nzufj7yJyuYhOnSK6cIHo4kX+uy1biL78kmjuXB4I99xDlJ7Of37wwa+uJyODKCmJB8YjjxD1789/\n7/XySX7fPqLERCK1ml9qSkggunSJr7+hgWj9eqKDB4m+8x2i117j61u2jGjKFCJB4AF18CDR4sU8\nGH73O6LCQl6tLFki+24DUByBKbh+FgSBMcbol78kWrWKKDubX3ceOJDIbif64AOic+eIvv99omee\nIbrzTvnHGAgQ7dpFdOQIvzY+blzfCimPh8jvJxo6tGfLf/AB0dKlfKJNTiYSRaKUFKIBA3gbNIjo\n4YeJ7ruvY79cvkxUVcUn5Rkzvr7OzZt5RfHpp0RaLf9g26FDRAYDPxlobydyu3m7fJnottt4Gz6c\n6HvfI7JYeFh4vUQbNxK9+ir/+zDG29ChfP0LF/IxNTURmc1ERUVETz7Zwx0JN4THw5taTaRS9fZo\n+i5BEIgxJvRo2b4QCsXF/MyzuPjrfRwOojff5JcCcnL45YhBg3hwJCbyM9j2dj55hD7VhAQ+iSUn\n85+7Egjw987/8Y9E27fz99JPmMDPdg8fJtqwgU+CmZm8mjlzhug//oNv6+xZfoCrVETDhnW0wYOJ\nhgzh/x06lP88dCgfc//+PXsx+P1EbW38bDghgahfP/6z9NwvXeIV1xdf8HHt2cO/VuKf/+Rnyffd\nRzRvHj87b28namkham3lE3f//nydiYkdk31bG9ELLxDt3Uv0yiv8sk/cDa47vV4+mbe1EWVl8f3T\nE4zx/RMby/eJ0MlL5fhxHgz5+UQ/+Qn/20ST/fuJVq7kx016Om9qNf/b33Yb/298PG8qFa/MPB5+\nUhYby08GkpO/en8okrY2otpa3urq+InFv/7FX7+nTvHXlVZLpNfzEwKDgT+WtnU9J19XrvDXgc/H\nn098PD9+Q48Nlarj+Vy+TPTZZ7wabWnh+2TAAKLbb+ev3ZQU/tq+Ea+BL77gJ1vvv8+P//PneWtv\n58dlcjLfVkJCx/GclUX0xBMd67ipoVBVVTX1mWee+XUgEIj9wQ9+8LuioqLSq/sUFha+sW3btmm3\n3Xbbl+vXr38iMzOzjoho4cKFa7du3fqd5OTkU5988sndUv8zZ84Mnj179ubPP//8Tq1W2/SnP/3p\n8aSkJM/XBvfvUFixgk/O//M/XY/z3Dmi3/6WT8xffMHbhQv8j92vH2+hB9GlS/zAO3WK90lM5DtZ\nOvjj4vhB8fnn/MUxZw4/4z1xgk+E+/cTjRzJJ5G77+5Yr9PJJ1yVih/cgwbxA+/UKaLTp3k7c4a3\ntraOdvo0/8NfusTXI03sUouL4wdobCx/HtKfzefjy37xBd8WET+A29t5H2k9CQlEd9zBJ9aBA3mo\nTZnCAywQIKqsJPrDH4h27OD/npra8cJrb+ft4kW+T8+f5wfi888TPfdcxyWevq6piWj5cr4vvvc9\noqee4hORHGesXi8/dj7/nF9yGz6cV8WieG0T7bVyOol++lP+d//v/+Z/+6NHeWtt7bg09+WX/Fjz\nenm77TZ+mS8pif/e7ebH9LBhXx2vNGkJAj+WpGO4vb0j7E0mfjyOH8+fc0xMxzodDj4RS+3ECX6J\n8tw5fjIV+jq5coUfy4EAX0dcHG8xMfx3fj8f+5kzPBAGDuSvda+Xby/00/SM8cexsXwbPh/RN75B\nlJbGL1tKJ1nnz/PXX2srX68UoNJcolJ1tPZ23v/CBb4+aXxSU6n4fnK5+D6ZPJmfbA4cyMOnXz8+\nbmnekk50GePH6dSpofv9JoVCIBCIHT169Kc7d+6colar3RMmTNi7cePGORkZGUekPjabLbesrGyJ\nzWbLrampMf34xz9+3W63TyIi+vDDDx8YMGDAhfnz528IDYVly5a9MnTo0H8tW7bsldLS0qKzZ88O\nKikpeeFrg/t3KPzsZ/yP97Of9eQphscYn1AvXepoPh8/gHw+fpDrdDd+u+GEVjdS8/s7DvgrVzpe\naHFx/Exl0KAbM3kw1vmZdDRpbiYqKyN6+20+QQ8ZwifnO+/kZ6ojR/LHoZWfNPmETkB+P/9bSRMh\nEf+7fvklD9hPPuFvv/2//+NfCjhiBN9Gairf7vHjfMKRKsjQCjAm5usTrjRBSC/p0H+X/qZS1XTp\nEh+Lx8PvrxQV8Ynnely+zMcrvUkgdDyMdUza0j7R6Xp+zLa386oi9DUSGjrS8/T5+PZCJ1+pUo90\nVi8FQ3t79yr4QKDjjD50LpHmk4SEjkpbpeo4TkLnG7+f75frPdG6nlAIu1tqa2sn6vX6Rq1W20RE\nlJeXt6mysnJ6aChYrVZLfn5+BRGRyWSq8Xg8SS0tLampqaktDzzwwIdNTU3aq9drtVotH3zwwYNE\nRPn5+RVms7m6s1CQ+Hw8gW8GQeBn0HfccXPW3xPSmcX1vkh7ItoDgYhPzsXFvPn9/CzQ5eJn8U1N\n/JJbVdVXK79AgE8igQCflFSqjssR0mTI2Fcvx6SnE91/P9EPfkBkNHY+6bS387NiaaIJPTu8cuWr\nP18dAqF9QqlUfIJKSOCT44069vv142Eph4SEm78tQei4ZNYdsbG8currwoaC2+1WazQap/RYFEVX\nTU2NKVIft9utTk1Nbelqva2trSkpKSmtREQpKSmtra2tKeHG4ffjphP0jrg4fvlQreYlvdykyRtA\nLmFDQRCEbt2FvrpM6e5yUt9w/ZcvX04ffcQTOCvLTGazuburBgCICtXV1VR9g75NMmwoqNVqt9Pp\n1EiPnU6nRhRFV7g+LpdLVKvV7nDrTUlJaZUuMZ08eXJ4cnLyqa76Ll++nE6f5p9HQB4AAHyd2fzV\nE+YVK1b0eF1h39SVlZW1r6GhwdDU1KT1er3xmzdvnm2xWKyhfSwWi3XDhg3ziYjsdvukpKQkj3Rp\nqCsWi8VaUVGRT0RUUVGR/+ijj74brr90px4AAG4yxljYZrPZpqWlpX2q0+kai4uLX2SM0erVqwtW\nr15dIPVZvHhxmU6naxw3btyh/fv33yP9Pi8vb+Pw4cOb4+PjL4ui6Fy7du0Cxhi1tbUNnjx58k6D\nwXAsOzt7+9mzZ5M62zYfHmMLFjC2Zg0DAIBu+PfcGXF+76z1iQ+vzZvHP808f35vjwgAQPmu5y2p\nfeILGfDuIwAAefSJUMA9BQAAefSJUEClAAAgjz4TCqgUAABuvj4RCtI3GQIAwM3VJ0IBlQIAgDz6\nRCjgRjMAgDz6RCjgRjMAgDz6RCigUgAAkEefCAVUCgAA8ugToYBKAQBAHn0iFFApAADIo0+EAioF\nAAB59IlQQKUAACCPPhEKqBQAAOTRJ0IBlQIAgDz6RCigUgAAkEefCAVUCgAA8ugToYBKAQBAHn0i\nFFApAADIQ/GhwBhRIEAUG9vbIwEAuPUpPhSk/5eCIPT2SAAAbn2KDwXcTwAAkI/iQwH3EwAA5NMn\nQgGVAgCAPBQfCj4fKgUAALkoPhRQKQAAyEfxoYBKAQBAPooPBVQKAADyiRgKVVVVU9PT048aDIaG\n0tLSos76FBYWvmEwGBqMRuOhurq6zEjL1tbWTpw4cWJtZmZm3YQJE/bu3bt3QlfbR6UAACAjxliX\nze/3x+p0ukaHw6H1er0qo9F4sL6+PiO0z9atW3OnTZtmY4yR3W43mUwme6RlH3zwweqqqqocxhjZ\nbLZpZrP5fzvbPhGxf/yDsbFjGQAAdBOf2rue28O1sJVCbW3tRL1e36jVaptUKpUvLy9vU2Vl5fTQ\nPlar1ZKfn19BRGQymWo8Hk9SS0tLarhlhw8ffvLcuXN3EBF5PJ4ktVrt7moM+PAaAIB8wk63brdb\nrdFonNJjURRdNTU1pkh93G63urm5eURXy5aUlLxw//33f/T888//4sqVKzF79uy5t6sxrFq1nE6d\nIlq+nMhsNpPZbL72ZwkAcAurrq6m6urqG7KusKEgCALrzkoYY9f0zUSLFi1a88YbbxTOmDHjr1u2\nbPnuwoUL1+7YsSO7s75PPLGcDh/moQAAAF939QnzihUreryusJeP1Gq12+l0aqTHTqdTI4qiK1wf\nl8sliqLoCrdsbW3txBkzZvyViOixxx57p7a2dmJXY8DXXAAAyCdsKGRlZe1raGgwNDU1ab1eb/zm\nzZtnWywWa2gfi8Vi3bBhw3wiIrvdPikpKcmTkpLSGm5ZvV7f+MEHHzxIRLRr166H0tLSjnU1BtxT\nAACQT9jpNi4uzl9WVrYkJyfnvUAgELto0aI1GRkZR8rLywuIiAoKCspzc3NtNpstV6/XNyYmJl5c\nt27dgnDLEhG99dZbP1q8ePH/u3z5cr/+/ftfeuutt37U1RhQKQAAyEfg715SJkEQmNXKqLyc6O9/\n7+3RAAD0DYIgXPO9Xkmf+EQzKgUAAHkoPhRwTwEAQD6KDwVUCgAA8lF8KKBSAACQj+JDAZUCAIB8\nFB8KqBQAAOSj+FBApQAAIB/FhwIqBQAA+Sg+FFApAADIp0+EAioFAAB5KD4U8L/jBACQj+JDAZUC\nAIB8FB8KqBQAAOSj+FBApQAAIB/FhwIqBQAA+Sg+FFApAADIR/GhgEoBAEA+ig8FVAoAAPJRfCjg\nay4AAOSj+FDA11wAAMhH8aGASgEAQD6KDwVUCgAA8lF8KKBSAACQj+JDAZUCAIB8FB8KqBQAAOSj\n+FBApQAAIB/FhwIqBQAA+Sg+FFApAADIJ2IoVFVVTU1PTz9qMBgaSktLizrrU1hY+IbBYGgwGo2H\n6urqMruz7G9+85unMzIyjowdO/afRUVFpV1tH5UCAICMGGNdNr/fH6vT6RodDofW6/WqjEbjwfr6\n+ozQPlu3bs2dNm2ajTFGdrvdZDKZ7JGW3bVr139OmTJlh9frVTHG6NSpU8M62z4RsbFjGfvHPxgA\nAHQTn9q7ntvDtbCVQm1t7US9Xt+o1WqbVCqVLy8vb1NlZeX00D5Wq9WSn59fQURkMplqPB5PUktL\nS2q4ZVetWvXkiy+++LJKpfIREQ0bNux0V2PAF+IBAMgn7HTrdrvVGo3GKT0WRdFVU1NjitTH7Xar\nm5ubR3S1bENDg2H37t3feumll4oTEhLaf/GLXzyflZW1r7MxtLYup1WriAYPJjKbzWQ2m3v4VAEA\nbk3V1dVUXV19Q9YVNhQEQWDdWQljTLiWjfr9/rizZ88Ostvtk/bu3Tvh8ccf/9Px48dHddZ34MDl\n9OyzRFrttWwBACB6XH3CvGLFih6vK2woqNVqt9Pp1EiPnU6nRhRFV7g+LpdLFEXR5fP5VF0tK4qi\na+bMmX8hIpowYcLemJiYK21tbUOGDBnSdvUY8D/ZAQCQT9h7CllZWfsaGhoMTU1NWq/XG7958+bZ\nFovFGtrHYrFYN2zYMJ+IyG63T0pKSvKkpKS0hlv20UcffXfXrl0PEREdO3Yszev1xncWCES4pwAA\nIKew021cXJy/rKxsSU5OznuBQCB20aJFazIyMo6Ul5cXEBEVFBSU5+bm2mw2W65er29MTEy8uG7d\nugXhliUiWrhw4dqFCxeuvfvuuz+Jj4/3SqHSGVQKAADyEfi7l5RJEAR2++2MXC6igQN7ezQAAH2D\nIAjXfK9XovhPNKNSAACQj+JDAfcUAADkg1AAAIAgxYdCbCyR0KMrYwAAcK0UHwq4nwAAIB/FhwIu\nHQEAyAehAAAAQYoPBVw+AgCQj+JDAZUCAIB8FB8KqBQAAOSj+FBApQAAIB/FhwIqBQAA+Sg+FFAp\nAADIR/GhgEoBAEA+ig8FVAoAAPJRfCigUgAAkI/iQwGVAgCAfBQfCqgUAADko/hQQKUAACAfxYcC\nKgUAAPkoPhRQKQAAyEfxoYBKAQBAPooPBVQKAADyUXwooFIAAJCP4kMBlQIAgHwUHwqoFAAA5KP4\nUEClAAAgH8WHAioFAAD5RAyFqqqqqenp6UcNBkNDaWlpUWd9CgsL3zAYDA1Go/FQXV1dZneXfe21\n156LiYm5cubMmcFdbR+VAgCAjBhjXTa/3x+r0+kaHQ6H1uv1qoxG48H6+vqM0D5bt27NnTZtmo0x\nRna73WQymezdWfbEiROanJycKq1W62hraxvc2faJiL3wAgMAgGvAp/au5/ZwLWylUFtbO1Gv1zdq\ntdomlUrly8vL21RZWTk9tI/VarXk5+dXEBGZTKYaj8eT1NLSkhpp2WefffaXr7zyyrJIoYVKAQBA\nPmGnXLfbrdZoNE7psSiKrpqaGlOkPm63W93c3Dyiq2UrKyuni6LoGjdu3D8iDfCjj5bT8uX8Z7PZ\nTGazuVtPDAAgWlRXV1N1dfUNWVfYUBAEgXVnJYwxobsbvHTpUv/i4uKXduzYkd2d5bOzl9NLL3V3\n7QAA0efqE+YVK1b0eF1hQ0GtVrudTqdGeux0OjWiKLrC9XG5XKIoii6fz6fqbNnPPvtM19TUpDUa\njYek/t/85jf319bWTkxOTj71tQHi8hEAgHzC3XDw+Xxxo0aN+szhcGgvX74cH+lG8549eyZJN5q7\nsyxjjCLdaP7lL2/m7RgAgFsPXceN5rDn4XFxcf6ysrIlOTk57wUCgdhFixatycjIOFJeXl5ARFRQ\nUFCem5trs9lsuXq9vjExMfHiunXrFoRb9uptRLpEhUoBAEA+Ag8VZRIEga1axei//qu3RwIA0HcI\ngnBN93pDKf4TzagUAADko/hQwNdcAADIR/GhgEoBAEA+ig8FVAoAAPJRfCigUgAAkI/iQwGVAgCA\nfBQfCqgUAADko/hQQKUAACAfxYcCKgUAAPkoPhRQKQAAyEfxoYBKAQBAPooPBVQKAADyUXwooFIA\nAJCP4kMBlQIAgHwUHwqoFAAA5KP4UEClAAAgH8WHAioFAAD5KD4UUCkAAMhH8aGASgEAQD4IBQAA\nCFJ8KODyEQCAfBQfCqgUAADkg1AAAIAgxYdCjOJHCABw68CUCwAAQQgFAAAIQigAAEAQQgEAAIK6\nFQpVVVVT09PTjxoMhobS0tKizvoUFha+YTAYGoxG46G6urrMSMsuXbr01YyMjCNGo/HQzJkz/3Lu\n3Lk7rv/pAADAdWGMhW1+vz9Wp9M1OhwOrdfrVRmNxoP19fUZoX22bt2aO23aNBtjjOx2u8lkMtkj\nLbt9+/bsQCAQwxijoqKikqKiopKrt82HBwAA1+Lfc2fE+b2zFrFSqK2tnajX6xu1Wm2TSqXy5eXl\nbaqsrJwe2sdqtVry8/MriIhMJlONx+NJamlpSQ23bHZ29o6YmJgr0jIul0u84YkHAADXJGIouN1u\ntUajcUqPRVF0ud1udXf6NDc3j4i0LBHR2rVrF+bm5tp6/jQAAOBGiPh5YUEQWHdWxBgTejKAlStX\n/jQ+Pt47d+7cP3b278uXLw/+bDabyWw292QzAAC3rOrqaqqurr4h64oYCmq12u10OjXSY6fTqRFF\n0RWuj8vlEkVRdPl8PlW4ZdevX/+EzWbLff/99yd3tf3QUAAAgK+7+oR5xYoVPV9ZpJsOPp8vbtSo\nUZ85HA7t5cuX4yPdaN6zZ88k6UZzuGW3bds2dcyYMYdPnz49tKttE240AwBcM7qOG80RK4W4uDh/\nWVnZkpycnPcCgUDsokWL1mRkZBwpLy8vICIqKCgoz83Ntdlstly9Xt+YmJh4cd26dQvCLUtE9PTT\nT//G6/XGZ2dn7yAiuvfee/e8+eabT/U83gAA4HoJPFSUSRAEpuTxAQAokSAIPb7Pi080AwBAEEIB\nAACCEAoAABCEUAAAgCCEAgAABCEUAAAgCKEAAABBCAUAAAhCKAAAQBBCAQAAghAKAAAQhFAAAIAg\nhAIAAAQhFAAAIAihAAAAQQgFAAAIQigAAEAQQgEAAIIQCgAAEIRQAACAIIQCAAAEIRQAACAIoQAA\nAEEIBQAACEIoAABAEEIBAACCEAoAABCEUAAAgKCIoVBVVTU1PT39qMFgaCgtLS3qrE9hYeEbBoOh\nwWg0Hqqrq8uMtOyZM2cGZ2dn70hLSzv27W9/e7vH40m6MU/n1lVdXd3bQ1AM7IsO2BcdsC9ujLCh\nEAgEYpcsWVJWVVU1tb6+fszGjRvnHDlyJCO0j81my21sbNQ3NDQY3nrrrR89+eSTqyItW1JS8kJ2\ndvaOY8eOpU2ePPn9kpKSF27eU7w14IDvgH3RAfuiA/bFjRE2FGprayfq9fpGrVbbpFKpfHl5eZsq\nKyunh/axWq2W/Pz8CiIik8lU4/F4klpaWlLDLRu6TH5+fsW777776M16ggAA0H1hQ8Htdqs1Go1T\neiyKosvtdqu706e5uXlEV8u2trampKSktBIRpaSktLa2tqbcqCcEAAA9FxfuHwVBYN1ZCWNM6E6f\nztYnCAILtx1BiLjqqLFixYreHoJiYF90wL7ogH1x/cKGglqtdjudTo302Ol0akRRdIXr43K5RFEU\nXT6fT3X179VqtZuIVwctLS2pqampLSdPnhyenJx8qrPtdydsAADgxgl7+SgrK2tfQ0ODoampSev1\neuM3b94822KxWEP7WCwW64YNG+YTEdnt9klJSUmelJSU1nDLWiwWa0VFRT4RUUVFRf6jjz767s16\nggAAcA0YY2GbzWablpaW9qlOp2ssLi5+kTFGq1evLli9enWB1Gfx4sVlOp2ucdy4cYf2799/T7hl\nGWPU1tY2ePLkyTsNBsOx7Ozs7WfPnk2KNA40NDQ0tJvfen0AnbVt27ZNHT169FG9Xt9QUlJS1Nvj\nkbOdOHFCYzab/3fMmDGH77rrrn++/vrrhYzxIJ0yZcqOaAxSv98fO378+LqHH374b9G8L86ePZs0\na9asd9LT049kZGTU2+12U7Tui+Li4hfHjBlzeOzYsZ/MmTPnj+3t7f2iZV8sWLBgbXJycuvYsWM/\nkX4X7rkXFxe/qNfrG0aPHn30vffe+3ak9ff6E7y6+f3+WJ1O1+hwOLRer1dlNBoP1tfXZ/T2uORq\nJ0+eTK2rqxvPGKPz588PSEtL+7S+vj5j6dKlr5SWli5jjFFJSUlRUVFRSW+PVa722muvPTt37ty3\nH3nkEStjjKJ1X8yfP79izZo1Cxlj5PP54jwezx3RuC8cDod25MiRx9vb2/sxxujxxx/fvH79+vxo\n2Re7d+9+4MCBA5mhodDVcz98+PAYo9F40Ov1qhwOh1an0zUGAoGYcOvv9Sd4dfv444/vzcnJqZIe\nv/zyyy+8/PLLL/T2uHqrTZ8+/d0dO3ZMGT169NGWlpYUxnhwjB49+mhvj02O5nQ6xcmTJ+/ctWvX\nf0qVQjTuC4/Hc8fIkSOPX/37aNwXbW1tg9PS0j49c+bMIJ/PF/fwww//bfv27dnRtC8cDoc2NBS6\neu7FxcUvhl5tycnJqdqzZ8+kcOtW3HcfdeezEdGiqalJW1dXl2kymWqi9bMdP/nJT3716quvLo2J\nibki/S45Hvj6AAACo0lEQVQa94XD4Rg5bNiw0wsWLFh3zz33HPjhD3/424sXLyZG474YPHjwmeee\ne+61b3zjGydGjBjRnJSU5MnOzt4RjftC0tVzb25uHhH6jtHuzKeKC4XufjbiVnfhwoUBs2bN+vPr\nr7/+49tvv/186L9F+mzHreLvf//7w8nJyacyMzPrWBdvT46WfeH3++MOHDhwz1NPPfXmgQMH7klM\nTLx49dfDRMu++Oyzz3S//vWvn2lqatI2NzePuHDhwoA//OEP3w/tEy37ojPd+OxX2P2iuFDozmcj\nbnU+n081a9asP8+bN+/30tt1pc92EBGF+2zHreTjjz++z2q1WkaOHOmYM2fOxl27dj00b96830fj\nvhBF0SWKomvChAl7iYgee+yxdw4cOHBPampqS7Tti3379mXdd999Hw8ZMqQtLi7OP3PmzL/s2bPn\n3mjcF5KuXhOdfY5M+rxYVxQXCt35bMStjDEmLFq0aM2YMWPqn3nmmV9Lv4/Gz3YUFxe/5HQ6NQ6H\nY+SmTZvyHnrooV2///3v50XjvkhNTW3RaDTOY8eOpRER7dy5c8pdd911+JFHHvlbtO2L9PT0o3a7\nfdKlS5f6M8aEnTt3ThkzZkx9NO4LSVevCYvFYt20aVOe1+uNdzgcIxsaGgwTJ06sDbuy3r5h0lnr\n6vMN0dA+/PDD+wVBuGI0Gg+OHz++bvz48XXbtm2bGu2f7aiurn5QevdRtO6LgwcPGrOysvaOGzfu\n0IwZM/7i8XjuiNZ9UVpaukx6S+r8+fMrvF6vKlr2RV5e3sbhw4c3q1QqryiKzrVr1y4I99xXrlz5\nkk6naxw9evTRqqqqnEjrFxiLystuAADQCcVdPgIAgN6DUAAAgCCEAgAABCEUAAAgCKEAAABBCAUA\nAAj6/zD7RJx/7WdrAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x181e7b0>"
]
}
],
"prompt_number": 45
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 37
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | apache-2.0 |
DJCordhose/ai | notebooks/workshops/tss/cnn-standard-architectures.ipynb | 2 | 108858 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Training on an Advanced Standard CNN Architecture\n",
"* https://keras.io/applications/\n",
"* The 9 Deep Learning Papers You Need To Know About: https://adeshpande3.github.io/adeshpande3.github.io/The-9-Deep-Learning-Papers-You-Need-To-Know-About.html\n",
"\n",
"[Neural Network Architectures](https://medium.com/towards-data-science/neural-network-architectures-156e5bad51ba)\n",
"\n",
"\n",
"top-1 rating on ImageNet: https://stats.stackexchange.com/questions/156471/imagenet-what-is-top-1-and-top-5-error-rate"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import warnings\n",
"warnings.filterwarnings('ignore')"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
}
],
"source": [
"%matplotlib inline\n",
"%pylab inline"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pylab as plt\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from distutils.version import StrictVersion"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.18.1\n"
]
}
],
"source": [
"import sklearn\n",
"print(sklearn.__version__)\n",
"\n",
"assert StrictVersion(sklearn.__version__ ) >= StrictVersion('0.18.1')"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.2.1\n"
]
}
],
"source": [
"import tensorflow as tf\n",
"tf.logging.set_verbosity(tf.logging.ERROR)\n",
"print(tf.__version__)\n",
"\n",
"assert StrictVersion(tf.__version__) >= StrictVersion('1.1.0')"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using TensorFlow backend.\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"2.0.8\n"
]
}
],
"source": [
"import keras\n",
"print(keras.__version__)\n",
"\n",
"assert StrictVersion(keras.__version__) >= StrictVersion('2.0.0')"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.20.1\n"
]
}
],
"source": [
"import pandas as pd\n",
"print(pd.__version__)\n",
"\n",
"assert StrictVersion(pd.__version__) >= StrictVersion('0.20.0')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Preparation"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# for VGG, ResNet, and MobileNet\n",
"INPUT_SHAPE = (224, 224)\n",
"\n",
"# for InceptionV3, InceptionResNetV2, Xception\n",
"# INPUT_SHAPE = (299, 299)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import os\n",
"import skimage.data\n",
"import skimage.transform\n",
"from keras.utils.np_utils import to_categorical\n",
"import numpy as np\n",
"\n",
"def load_data(data_dir, type=\".ppm\"):\n",
" num_categories = 6\n",
"\n",
" # Get all subdirectories of data_dir. Each represents a label.\n",
" directories = [d for d in os.listdir(data_dir) \n",
" if os.path.isdir(os.path.join(data_dir, d))]\n",
" # Loop through the label directories and collect the data in\n",
" # two lists, labels and images.\n",
" labels = []\n",
" images = []\n",
" for d in directories:\n",
" label_dir = os.path.join(data_dir, d)\n",
" file_names = [os.path.join(label_dir, f) for f in os.listdir(label_dir) if f.endswith(type)]\n",
" # For each label, load it's images and add them to the images list.\n",
" # And add the label number (i.e. directory name) to the labels list.\n",
" for f in file_names:\n",
" images.append(skimage.data.imread(f))\n",
" labels.append(int(d))\n",
" images64 = [skimage.transform.resize(image, INPUT_SHAPE) for image in images]\n",
" y = np.array(labels)\n",
" y = to_categorical(y, num_categories)\n",
" X = np.array(images64)\n",
" return X, y"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load datasets.\n",
"ROOT_PATH = \"./\"\n",
"original_dir = os.path.join(ROOT_PATH, \"speed-limit-signs\")\n",
"original_images, original_labels = load_data(original_dir, type=\".ppm\")"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"X, y = original_images, original_labels"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Uncomment next three cells if you want to train on augmented image set\n",
"#### Otherwise Overfitting can not be avoided because image set is simply too small"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# !curl -O https://raw.githubusercontent.com/DJCordhose/speed-limit-signs/master/data/augmented-signs.zip\n",
"# from zipfile import ZipFile\n",
"# zip = ZipFile('augmented-signs.zip')\n",
"# zip.extractall('.')"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"data_dir = os.path.join(ROOT_PATH, \"augmented-signs\")\n",
"augmented_images, augmented_labels = load_data(data_dir, type=\".png\")"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# merge both data sets\n",
"\n",
"all_images = np.vstack((X, augmented_images))\n",
"all_labels = np.vstack((y, augmented_labels))\n",
"\n",
"# shuffle\n",
"# https://stackoverflow.com/a/4602224\n",
"\n",
"p = numpy.random.permutation(len(all_labels))\n",
"shuffled_images = all_images[p]\n",
"shuffled_labels = all_labels[p]\n",
"X, y = shuffled_images, shuffled_labels"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Split test and train data 80% to 20%"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"((3335, 224, 224, 3), (3335, 6))"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from sklearn.model_selection import train_test_split\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)\n",
"X_train.shape, y_train.shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Training Xception\n",
"* Slighly optimized version of Inception: https://keras.io/applications/#xception\n",
"* Inception V3 no longer using non-sequential tower architecture, rahter short cuts: https://keras.io/applications/#inceptionv3\n",
"* Uses Batch Normalization:\n",
" * https://keras.io/layers/normalization/#batchnormalization\n",
" * http://cs231n.github.io/neural-networks-2/#batchnorm\n",
" * Batch Normalization still exist even in prediction model\n",
" * normalizes activations for each batch around 0 and standard deviation close to 1\n",
" * replaces Dropout except for final fc layers\n",
" * as a next step might make sense to alter classifier to again have Dropout for training\n",
"* All that makes it ideal for our use case\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from keras.applications.xception import Xception\n",
"\n",
"model = Xception(classes=6, weights=None)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"____________________________________________________________________________________________________\n",
"Layer (type) Output Shape Param # Connected to \n",
"====================================================================================================\n",
"input_1 (InputLayer) (None, None, None, 3) 0 \n",
"____________________________________________________________________________________________________\n",
"block1_conv1 (Conv2D) (None, None, None, 32 864 input_1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block1_conv1_bn (BatchNormalizat (None, None, None, 32 128 block1_conv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block1_conv1_act (Activation) (None, None, None, 32 0 block1_conv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block1_conv2 (Conv2D) (None, None, None, 64 18432 block1_conv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block1_conv2_bn (BatchNormalizat (None, None, None, 64 256 block1_conv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block1_conv2_act (Activation) (None, None, None, 64 0 block1_conv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_sepconv1 (SeparableConv2D (None, None, None, 12 8768 block1_conv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_sepconv1_bn (BatchNormali (None, None, None, 12 512 block2_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_sepconv2_act (Activation) (None, None, None, 12 0 block2_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_sepconv2 (SeparableConv2D (None, None, None, 12 17536 block2_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_sepconv2_bn (BatchNormali (None, None, None, 12 512 block2_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"conv2d_1 (Conv2D) (None, None, None, 12 8192 block1_conv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block2_pool (MaxPooling2D) (None, None, None, 12 0 block2_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"batch_normalization_1 (BatchNorm (None, None, None, 12 512 conv2d_1[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_1 (Add) (None, None, None, 12 0 block2_pool[0][0] \n",
" batch_normalization_1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv1_act (Activation) (None, None, None, 12 0 add_1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv1 (SeparableConv2D (None, None, None, 25 33920 block3_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv1_bn (BatchNormali (None, None, None, 25 1024 block3_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv2_act (Activation) (None, None, None, 25 0 block3_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv2 (SeparableConv2D (None, None, None, 25 67840 block3_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_sepconv2_bn (BatchNormali (None, None, None, 25 1024 block3_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"conv2d_2 (Conv2D) (None, None, None, 25 32768 add_1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block3_pool (MaxPooling2D) (None, None, None, 25 0 block3_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"batch_normalization_2 (BatchNorm (None, None, None, 25 1024 conv2d_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_2 (Add) (None, None, None, 25 0 block3_pool[0][0] \n",
" batch_normalization_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv1_act (Activation) (None, None, None, 25 0 add_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv1 (SeparableConv2D (None, None, None, 72 188672 block4_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block4_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv2_act (Activation) (None, None, None, 72 0 block4_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block4_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block4_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"conv2d_3 (Conv2D) (None, None, None, 72 186368 add_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block4_pool (MaxPooling2D) (None, None, None, 72 0 block4_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"batch_normalization_3 (BatchNorm (None, None, None, 72 2912 conv2d_3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_3 (Add) (None, None, None, 72 0 block4_pool[0][0] \n",
" batch_normalization_3[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv1_act (Activation) (None, None, None, 72 0 add_3[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv1 (SeparableConv2D (None, None, None, 72 536536 block5_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block5_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv2_act (Activation) (None, None, None, 72 0 block5_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block5_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block5_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv3_act (Activation) (None, None, None, 72 0 block5_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv3 (SeparableConv2D (None, None, None, 72 536536 block5_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block5_sepconv3_bn (BatchNormali (None, None, None, 72 2912 block5_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_4 (Add) (None, None, None, 72 0 block5_sepconv3_bn[0][0] \n",
" add_3[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv1_act (Activation) (None, None, None, 72 0 add_4[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv1 (SeparableConv2D (None, None, None, 72 536536 block6_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block6_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv2_act (Activation) (None, None, None, 72 0 block6_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block6_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block6_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv3_act (Activation) (None, None, None, 72 0 block6_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv3 (SeparableConv2D (None, None, None, 72 536536 block6_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block6_sepconv3_bn (BatchNormali (None, None, None, 72 2912 block6_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_5 (Add) (None, None, None, 72 0 block6_sepconv3_bn[0][0] \n",
" add_4[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv1_act (Activation) (None, None, None, 72 0 add_5[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv1 (SeparableConv2D (None, None, None, 72 536536 block7_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block7_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv2_act (Activation) (None, None, None, 72 0 block7_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block7_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block7_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv3_act (Activation) (None, None, None, 72 0 block7_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv3 (SeparableConv2D (None, None, None, 72 536536 block7_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block7_sepconv3_bn (BatchNormali (None, None, None, 72 2912 block7_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_6 (Add) (None, None, None, 72 0 block7_sepconv3_bn[0][0] \n",
" add_5[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv1_act (Activation) (None, None, None, 72 0 add_6[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv1 (SeparableConv2D (None, None, None, 72 536536 block8_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block8_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv2_act (Activation) (None, None, None, 72 0 block8_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block8_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block8_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv3_act (Activation) (None, None, None, 72 0 block8_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv3 (SeparableConv2D (None, None, None, 72 536536 block8_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block8_sepconv3_bn (BatchNormali (None, None, None, 72 2912 block8_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_7 (Add) (None, None, None, 72 0 block8_sepconv3_bn[0][0] \n",
" add_6[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv1_act (Activation) (None, None, None, 72 0 add_7[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv1 (SeparableConv2D (None, None, None, 72 536536 block9_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv1_bn (BatchNormali (None, None, None, 72 2912 block9_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv2_act (Activation) (None, None, None, 72 0 block9_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv2 (SeparableConv2D (None, None, None, 72 536536 block9_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv2_bn (BatchNormali (None, None, None, 72 2912 block9_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv3_act (Activation) (None, None, None, 72 0 block9_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv3 (SeparableConv2D (None, None, None, 72 536536 block9_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block9_sepconv3_bn (BatchNormali (None, None, None, 72 2912 block9_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_8 (Add) (None, None, None, 72 0 block9_sepconv3_bn[0][0] \n",
" add_7[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv1_act (Activation (None, None, None, 72 0 add_8[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv1 (SeparableConv2 (None, None, None, 72 536536 block10_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv1_bn (BatchNormal (None, None, None, 72 2912 block10_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv2_act (Activation (None, None, None, 72 0 block10_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv2 (SeparableConv2 (None, None, None, 72 536536 block10_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv2_bn (BatchNormal (None, None, None, 72 2912 block10_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv3_act (Activation (None, None, None, 72 0 block10_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv3 (SeparableConv2 (None, None, None, 72 536536 block10_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block10_sepconv3_bn (BatchNormal (None, None, None, 72 2912 block10_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_9 (Add) (None, None, None, 72 0 block10_sepconv3_bn[0][0] \n",
" add_8[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv1_act (Activation (None, None, None, 72 0 add_9[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv1 (SeparableConv2 (None, None, None, 72 536536 block11_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv1_bn (BatchNormal (None, None, None, 72 2912 block11_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv2_act (Activation (None, None, None, 72 0 block11_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv2 (SeparableConv2 (None, None, None, 72 536536 block11_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv2_bn (BatchNormal (None, None, None, 72 2912 block11_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv3_act (Activation (None, None, None, 72 0 block11_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv3 (SeparableConv2 (None, None, None, 72 536536 block11_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block11_sepconv3_bn (BatchNormal (None, None, None, 72 2912 block11_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_10 (Add) (None, None, None, 72 0 block11_sepconv3_bn[0][0] \n",
" add_9[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv1_act (Activation (None, None, None, 72 0 add_10[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv1 (SeparableConv2 (None, None, None, 72 536536 block12_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv1_bn (BatchNormal (None, None, None, 72 2912 block12_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv2_act (Activation (None, None, None, 72 0 block12_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv2 (SeparableConv2 (None, None, None, 72 536536 block12_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv2_bn (BatchNormal (None, None, None, 72 2912 block12_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv3_act (Activation (None, None, None, 72 0 block12_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv3 (SeparableConv2 (None, None, None, 72 536536 block12_sepconv3_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block12_sepconv3_bn (BatchNormal (None, None, None, 72 2912 block12_sepconv3[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_11 (Add) (None, None, None, 72 0 block12_sepconv3_bn[0][0] \n",
" add_10[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv1_act (Activation (None, None, None, 72 0 add_11[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv1 (SeparableConv2 (None, None, None, 72 536536 block13_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv1_bn (BatchNormal (None, None, None, 72 2912 block13_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv2_act (Activation (None, None, None, 72 0 block13_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv2 (SeparableConv2 (None, None, None, 10 752024 block13_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_sepconv2_bn (BatchNormal (None, None, None, 10 4096 block13_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"conv2d_4 (Conv2D) (None, None, None, 10 745472 add_11[0][0] \n",
"____________________________________________________________________________________________________\n",
"block13_pool (MaxPooling2D) (None, None, None, 10 0 block13_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"batch_normalization_4 (BatchNorm (None, None, None, 10 4096 conv2d_4[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_12 (Add) (None, None, None, 10 0 block13_pool[0][0] \n",
" batch_normalization_4[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv1 (SeparableConv2 (None, None, None, 15 1582080 add_12[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv1_bn (BatchNormal (None, None, None, 15 6144 block14_sepconv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv1_act (Activation (None, None, None, 15 0 block14_sepconv1_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv2 (SeparableConv2 (None, None, None, 20 3159552 block14_sepconv1_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv2_bn (BatchNormal (None, None, None, 20 8192 block14_sepconv2[0][0] \n",
"____________________________________________________________________________________________________\n",
"block14_sepconv2_act (Activation (None, None, None, 20 0 block14_sepconv2_bn[0][0] \n",
"____________________________________________________________________________________________________\n",
"avg_pool (GlobalAveragePooling2D (None, 2048) 0 block14_sepconv2_act[0][0] \n",
"____________________________________________________________________________________________________\n",
"predictions (Dense) (None, 6) 12294 avg_pool[0][0] \n",
"====================================================================================================\n",
"Total params: 20,873,774\n",
"Trainable params: 20,819,246\n",
"Non-trainable params: 54,528\n",
"____________________________________________________________________________________________________\n"
]
}
],
"source": [
"model.summary()"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model.compile(optimizer='adam',\n",
" loss='categorical_crossentropy',\n",
" metrics=['accuracy'])"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# !rm -rf ./tf_log\n",
"# https://keras.io/callbacks/#tensorboard\n",
"tb_callback = keras.callbacks.TensorBoard(log_dir='./tf_log')\n",
"# To start tensorboard\n",
"# tensorboard --logdir=./tf_log\n",
"# open http://localhost:6006"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## This is a truly complex model\n",
"### Batch size needs to be small overthise model does not fit in memory\n",
"### Will take long to train, even on GPU\n",
"### on augmented dataset 4 minutes on K80 per Epoch: 400 Minutes for 100 Epochs = 6-7 hours"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Depends on harware GPU architecture, model is really complex, batch needs to be small (this works well on K80)\n",
"BATCH_SIZE = 25"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"early_stopping_callback = keras.callbacks.EarlyStopping(monitor='val_loss', patience=5, verbose=1)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Train on 2668 samples, validate on 667 samples\n",
"Epoch 1/50\n",
"2668/2668 [==============================] - 228s - loss: 1.5403 - acc: 0.3827 - val_loss: 1.7899 - val_acc: 0.2864\n",
"Epoch 2/50\n",
"2668/2668 [==============================] - 227s - loss: 0.7724 - acc: 0.7043 - val_loss: 1.8531 - val_acc: 0.1634\n",
"Epoch 3/50\n",
"2668/2668 [==============================] - 227s - loss: 0.3242 - acc: 0.8849 - val_loss: 2.0106 - val_acc: 0.1634\n",
"Epoch 4/50\n",
"2668/2668 [==============================] - 227s - loss: 0.1614 - acc: 0.9442 - val_loss: 1.0445 - val_acc: 0.6732\n",
"Epoch 5/50\n",
"2668/2668 [==============================] - 227s - loss: 0.1077 - acc: 0.9636 - val_loss: 1.8615 - val_acc: 0.6672\n",
"Epoch 6/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0941 - acc: 0.9696 - val_loss: 0.5575 - val_acc: 0.8471\n",
"Epoch 7/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0389 - acc: 0.9903 - val_loss: 0.2147 - val_acc: 0.9370\n",
"Epoch 8/50\n",
"2668/2668 [==============================] - 227s - loss: 0.1639 - acc: 0.9423 - val_loss: 5.5276 - val_acc: 0.6027\n",
"Epoch 19/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0440 - acc: 0.9858 - val_loss: 0.1080 - val_acc: 0.9730\n",
"Epoch 20/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0102 - acc: 0.9970 - val_loss: 0.0629 - val_acc: 0.9820\n",
"Epoch 21/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0016 - acc: 1.0000 - val_loss: 0.0224 - val_acc: 0.9925\n",
"Epoch 22/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0012 - acc: 0.9996 - val_loss: 0.0323 - val_acc: 0.9925\n",
"Epoch 23/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0088 - acc: 0.9981 - val_loss: 0.0366 - val_acc: 0.9895\n",
"Epoch 24/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0022 - acc: 1.0000 - val_loss: 0.0206 - val_acc: 0.9925\n",
"Epoch 25/50\n",
"2668/2668 [==============================] - 228s - loss: 4.3747e-04 - acc: 1.0000 - val_loss: 0.0205 - val_acc: 0.9955\n",
"Epoch 26/50\n",
"2668/2668 [==============================] - 228s - loss: 2.4045e-04 - acc: 1.0000 - val_loss: 0.0214 - val_acc: 0.9955\n",
"Epoch 27/50\n",
"2668/2668 [==============================] - 227s - loss: 1.2870e-04 - acc: 1.0000 - val_loss: 0.0215 - val_acc: 0.9955\n",
"Epoch 28/50\n",
"2668/2668 [==============================] - 228s - loss: 1.2512e-04 - acc: 1.0000 - val_loss: 0.0207 - val_acc: 0.9955\n",
"Epoch 29/50\n",
"2668/2668 [==============================] - 227s - loss: 1.2204e-04 - acc: 1.0000 - val_loss: 0.0207 - val_acc: 0.9940\n",
"Epoch 30/50\n",
"2668/2668 [==============================] - 227s - loss: 1.4413e-04 - acc: 1.0000 - val_loss: 0.0180 - val_acc: 0.9940\n",
"Epoch 31/50\n",
"2668/2668 [==============================] - 228s - loss: 1.0454e-04 - acc: 1.0000 - val_loss: 0.0177 - val_acc: 0.9940\n",
"Epoch 32/50\n",
"2668/2668 [==============================] - 227s - loss: 9.5120e-05 - acc: 1.0000 - val_loss: 0.0190 - val_acc: 0.9940\n",
"Epoch 33/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0520 - acc: 0.9865 - val_loss: 10.2590 - val_acc: 0.3298\n",
"Epoch 34/50\n",
"2668/2668 [==============================] - 227s - loss: 0.1653 - acc: 0.9509 - val_loss: 8.3792 - val_acc: 0.3463\n",
"Epoch 35/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0503 - acc: 0.9839 - val_loss: 0.5858 - val_acc: 0.9040\n",
"Epoch 36/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0241 - acc: 0.9936 - val_loss: 0.0859 - val_acc: 0.9835\n",
"Epoch 37/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0083 - acc: 0.9966 - val_loss: 0.0759 - val_acc: 0.9835\n",
"Epoch 38/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0028 - acc: 0.9993 - val_loss: 0.0173 - val_acc: 0.9940\n",
"Epoch 39/50\n",
"2668/2668 [==============================] - 228s - loss: 6.1125e-04 - acc: 1.0000 - val_loss: 0.0132 - val_acc: 0.9940\n",
"Epoch 40/50\n",
"2668/2668 [==============================] - 228s - loss: 3.5885e-04 - acc: 1.0000 - val_loss: 0.0094 - val_acc: 0.9940\n",
"Epoch 41/50\n",
"2668/2668 [==============================] - 228s - loss: 1.7750e-04 - acc: 1.0000 - val_loss: 0.0134 - val_acc: 0.9940\n",
"Epoch 42/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0012 - acc: 0.9996 - val_loss: 0.0355 - val_acc: 0.9880\n",
"Epoch 43/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0073 - acc: 0.9985 - val_loss: 0.0206 - val_acc: 0.9940\n",
"Epoch 44/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0089 - acc: 0.9970 - val_loss: 0.8736 - val_acc: 0.8156\n",
"Epoch 45/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0340 - acc: 0.9884 - val_loss: 1.0533 - val_acc: 0.7391\n",
"Epoch 46/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0578 - acc: 0.9824 - val_loss: 0.6811 - val_acc: 0.9235\n",
"Epoch 47/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0150 - acc: 0.9948 - val_loss: 0.0795 - val_acc: 0.9835\n",
"Epoch 48/50\n",
"2668/2668 [==============================] - 228s - loss: 0.0030 - acc: 0.9989 - val_loss: 0.0187 - val_acc: 0.9925\n",
"Epoch 49/50\n",
"2668/2668 [==============================] - 227s - loss: 5.4766e-04 - acc: 1.0000 - val_loss: 0.0252 - val_acc: 0.9925\n",
"Epoch 50/50\n",
"2668/2668 [==============================] - 227s - loss: 0.0021 - acc: 0.9996 - val_loss: 0.0254 - val_acc: 0.9925\n",
"CPU times: user 2h 48min 12s, sys: 16min 5s, total: 3h 4min 17s\n",
"Wall time: 3h 10min 1s\n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f03c8646b70>"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%time model.fit(X_train, y_train, epochs=50, validation_split=0.2, callbacks=[tb_callback, early_stopping_callback], batch_size=BATCH_SIZE)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Each Epoch takes very long\n",
"## Extremely impressing how fast it converges: Almost 100% for validation starting from epoch 25\n",
"\n",
"## TODO: Metrics for Augmented Data\n",
"\n",
"### Accuracy\n",
"\n",
"### Validation Accuracy\n",
""
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3335/3335 [==============================] - 81s \n"
]
},
{
"data": {
"text/plain": [
"(0.0052181122955644744, 0.99850074882092688)"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_loss, train_accuracy = model.evaluate(X_train, y_train, batch_size=BATCH_SIZE)\n",
"train_loss, train_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"834/834 [==============================] - 20s \n"
]
},
{
"data": {
"text/plain": [
"(0.01086848787854011, 0.99640287576819497)"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"test_loss, test_accuracy = model.evaluate(X_test, y_test, batch_size=BATCH_SIZE)\n",
"test_loss, test_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"379/379 [==============================] - 9s \n"
]
},
{
"data": {
"text/plain": [
"(0.00010616126536950952, 1.0)"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"original_loss, original_accuracy = model.evaluate(original_images, original_labels, batch_size=BATCH_SIZE)\n",
"original_loss, original_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model.save('xception-augmented.hdf5')"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-rw-rw-r-- 1 ubuntu ubuntu 239M Oct 1 14:32 xception-augmented.hdf5\r\n"
]
}
],
"source": [
"!ls -lh xception-augmented.hdf5"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Alternative: ResNet\n",
"* basic ideas\n",
" * depth does matter\n",
" * 8x deeper than VGG\n",
" * possible by using shortcuts and skipping final fc layer\n",
"* https://keras.io/applications/#resnet50\n",
"* https://medium.com/towards-data-science/neural-network-architectures-156e5bad51ba\n",
"\n",
"http://arxiv.org/abs/1512.03385\n",
"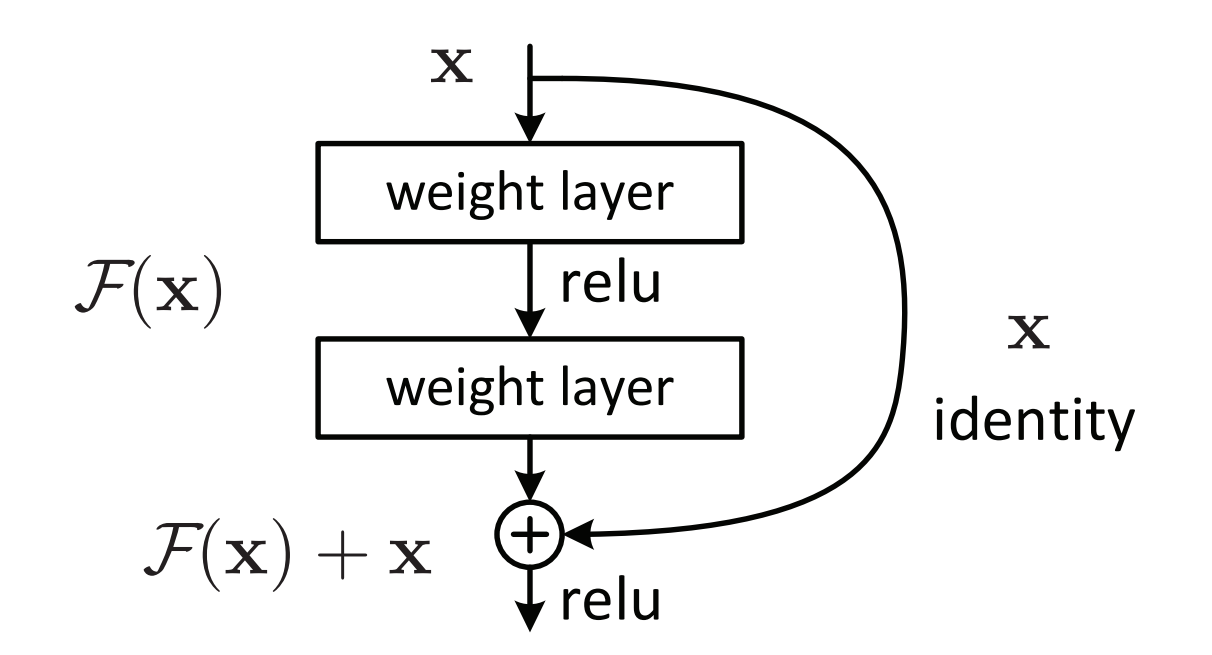"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from keras.applications.resnet50 import ResNet50\n",
"\n",
"model = ResNet50(classes=6, weights=None)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"____________________________________________________________________________________________________\n",
"Layer (type) Output Shape Param # Connected to \n",
"====================================================================================================\n",
"input_2 (InputLayer) (None, 224, 224, 3) 0 \n",
"____________________________________________________________________________________________________\n",
"conv1 (Conv2D) (None, 112, 112, 64) 9472 input_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn_conv1 (BatchNormalization) (None, 112, 112, 64) 256 conv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_50 (Activation) (None, 112, 112, 64) 0 bn_conv1[0][0] \n",
"____________________________________________________________________________________________________\n",
"max_pooling2d_2 (MaxPooling2D) (None, 55, 55, 64) 0 activation_50[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2a_branch2a (Conv2D) (None, 55, 55, 64) 4160 max_pooling2d_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2a_branch2a (BatchNormalizatio (None, 55, 55, 64) 256 res2a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_51 (Activation) (None, 55, 55, 64) 0 bn2a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2a_branch2b (Conv2D) (None, 55, 55, 64) 36928 activation_51[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2a_branch2b (BatchNormalizatio (None, 55, 55, 64) 256 res2a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_52 (Activation) (None, 55, 55, 64) 0 bn2a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2a_branch2c (Conv2D) (None, 55, 55, 256) 16640 activation_52[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2a_branch1 (Conv2D) (None, 55, 55, 256) 16640 max_pooling2d_2[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2a_branch2c (BatchNormalizatio (None, 55, 55, 256) 1024 res2a_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2a_branch1 (BatchNormalization (None, 55, 55, 256) 1024 res2a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_17 (Add) (None, 55, 55, 256) 0 bn2a_branch2c[0][0] \n",
" bn2a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_53 (Activation) (None, 55, 55, 256) 0 add_17[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2b_branch2a (Conv2D) (None, 55, 55, 64) 16448 activation_53[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2b_branch2a (BatchNormalizatio (None, 55, 55, 64) 256 res2b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_54 (Activation) (None, 55, 55, 64) 0 bn2b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2b_branch2b (Conv2D) (None, 55, 55, 64) 36928 activation_54[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2b_branch2b (BatchNormalizatio (None, 55, 55, 64) 256 res2b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_55 (Activation) (None, 55, 55, 64) 0 bn2b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2b_branch2c (Conv2D) (None, 55, 55, 256) 16640 activation_55[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2b_branch2c (BatchNormalizatio (None, 55, 55, 256) 1024 res2b_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_18 (Add) (None, 55, 55, 256) 0 bn2b_branch2c[0][0] \n",
" activation_53[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_56 (Activation) (None, 55, 55, 256) 0 add_18[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2c_branch2a (Conv2D) (None, 55, 55, 64) 16448 activation_56[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2c_branch2a (BatchNormalizatio (None, 55, 55, 64) 256 res2c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_57 (Activation) (None, 55, 55, 64) 0 bn2c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2c_branch2b (Conv2D) (None, 55, 55, 64) 36928 activation_57[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2c_branch2b (BatchNormalizatio (None, 55, 55, 64) 256 res2c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_58 (Activation) (None, 55, 55, 64) 0 bn2c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res2c_branch2c (Conv2D) (None, 55, 55, 256) 16640 activation_58[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn2c_branch2c (BatchNormalizatio (None, 55, 55, 256) 1024 res2c_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_19 (Add) (None, 55, 55, 256) 0 bn2c_branch2c[0][0] \n",
" activation_56[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_59 (Activation) (None, 55, 55, 256) 0 add_19[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3a_branch2a (Conv2D) (None, 28, 28, 128) 32896 activation_59[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3a_branch2a (BatchNormalizatio (None, 28, 28, 128) 512 res3a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_60 (Activation) (None, 28, 28, 128) 0 bn3a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3a_branch2b (Conv2D) (None, 28, 28, 128) 147584 activation_60[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3a_branch2b (BatchNormalizatio (None, 28, 28, 128) 512 res3a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_61 (Activation) (None, 28, 28, 128) 0 bn3a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3a_branch2c (Conv2D) (None, 28, 28, 512) 66048 activation_61[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3a_branch1 (Conv2D) (None, 28, 28, 512) 131584 activation_59[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3a_branch2c (BatchNormalizatio (None, 28, 28, 512) 2048 res3a_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3a_branch1 (BatchNormalization (None, 28, 28, 512) 2048 res3a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_20 (Add) (None, 28, 28, 512) 0 bn3a_branch2c[0][0] \n",
" bn3a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_62 (Activation) (None, 28, 28, 512) 0 add_20[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3b_branch2a (Conv2D) (None, 28, 28, 128) 65664 activation_62[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3b_branch2a (BatchNormalizatio (None, 28, 28, 128) 512 res3b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_63 (Activation) (None, 28, 28, 128) 0 bn3b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3b_branch2b (Conv2D) (None, 28, 28, 128) 147584 activation_63[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3b_branch2b (BatchNormalizatio (None, 28, 28, 128) 512 res3b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_64 (Activation) (None, 28, 28, 128) 0 bn3b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3b_branch2c (Conv2D) (None, 28, 28, 512) 66048 activation_64[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3b_branch2c (BatchNormalizatio (None, 28, 28, 512) 2048 res3b_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_21 (Add) (None, 28, 28, 512) 0 bn3b_branch2c[0][0] \n",
" activation_62[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_65 (Activation) (None, 28, 28, 512) 0 add_21[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3c_branch2a (Conv2D) (None, 28, 28, 128) 65664 activation_65[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3c_branch2a (BatchNormalizatio (None, 28, 28, 128) 512 res3c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_66 (Activation) (None, 28, 28, 128) 0 bn3c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3c_branch2b (Conv2D) (None, 28, 28, 128) 147584 activation_66[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3c_branch2b (BatchNormalizatio (None, 28, 28, 128) 512 res3c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_67 (Activation) (None, 28, 28, 128) 0 bn3c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3c_branch2c (Conv2D) (None, 28, 28, 512) 66048 activation_67[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3c_branch2c (BatchNormalizatio (None, 28, 28, 512) 2048 res3c_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_22 (Add) (None, 28, 28, 512) 0 bn3c_branch2c[0][0] \n",
" activation_65[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_68 (Activation) (None, 28, 28, 512) 0 add_22[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3d_branch2a (Conv2D) (None, 28, 28, 128) 65664 activation_68[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3d_branch2a (BatchNormalizatio (None, 28, 28, 128) 512 res3d_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_69 (Activation) (None, 28, 28, 128) 0 bn3d_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3d_branch2b (Conv2D) (None, 28, 28, 128) 147584 activation_69[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3d_branch2b (BatchNormalizatio (None, 28, 28, 128) 512 res3d_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_70 (Activation) (None, 28, 28, 128) 0 bn3d_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res3d_branch2c (Conv2D) (None, 28, 28, 512) 66048 activation_70[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn3d_branch2c (BatchNormalizatio (None, 28, 28, 512) 2048 res3d_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_23 (Add) (None, 28, 28, 512) 0 bn3d_branch2c[0][0] \n",
" activation_68[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_71 (Activation) (None, 28, 28, 512) 0 add_23[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4a_branch2a (Conv2D) (None, 14, 14, 256) 131328 activation_71[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4a_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_72 (Activation) (None, 14, 14, 256) 0 bn4a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4a_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_72[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4a_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_73 (Activation) (None, 14, 14, 256) 0 bn4a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4a_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_73[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4a_branch1 (Conv2D) (None, 14, 14, 1024) 525312 activation_71[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4a_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4a_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4a_branch1 (BatchNormalization (None, 14, 14, 1024) 4096 res4a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_24 (Add) (None, 14, 14, 1024) 0 bn4a_branch2c[0][0] \n",
" bn4a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_74 (Activation) (None, 14, 14, 1024) 0 add_24[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4b_branch2a (Conv2D) (None, 14, 14, 256) 262400 activation_74[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4b_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_75 (Activation) (None, 14, 14, 256) 0 bn4b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4b_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_75[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4b_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_76 (Activation) (None, 14, 14, 256) 0 bn4b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4b_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_76[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4b_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4b_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_25 (Add) (None, 14, 14, 1024) 0 bn4b_branch2c[0][0] \n",
" activation_74[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_77 (Activation) (None, 14, 14, 1024) 0 add_25[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4c_branch2a (Conv2D) (None, 14, 14, 256) 262400 activation_77[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4c_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_78 (Activation) (None, 14, 14, 256) 0 bn4c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4c_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_78[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4c_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_79 (Activation) (None, 14, 14, 256) 0 bn4c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4c_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_79[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4c_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4c_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_26 (Add) (None, 14, 14, 1024) 0 bn4c_branch2c[0][0] \n",
" activation_77[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_80 (Activation) (None, 14, 14, 1024) 0 add_26[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4d_branch2a (Conv2D) (None, 14, 14, 256) 262400 activation_80[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4d_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4d_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_81 (Activation) (None, 14, 14, 256) 0 bn4d_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4d_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_81[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4d_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4d_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_82 (Activation) (None, 14, 14, 256) 0 bn4d_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4d_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_82[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4d_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4d_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_27 (Add) (None, 14, 14, 1024) 0 bn4d_branch2c[0][0] \n",
" activation_80[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_83 (Activation) (None, 14, 14, 1024) 0 add_27[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4e_branch2a (Conv2D) (None, 14, 14, 256) 262400 activation_83[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4e_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4e_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_84 (Activation) (None, 14, 14, 256) 0 bn4e_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4e_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_84[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4e_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4e_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_85 (Activation) (None, 14, 14, 256) 0 bn4e_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4e_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_85[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4e_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4e_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_28 (Add) (None, 14, 14, 1024) 0 bn4e_branch2c[0][0] \n",
" activation_83[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_86 (Activation) (None, 14, 14, 1024) 0 add_28[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4f_branch2a (Conv2D) (None, 14, 14, 256) 262400 activation_86[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4f_branch2a (BatchNormalizatio (None, 14, 14, 256) 1024 res4f_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_87 (Activation) (None, 14, 14, 256) 0 bn4f_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4f_branch2b (Conv2D) (None, 14, 14, 256) 590080 activation_87[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4f_branch2b (BatchNormalizatio (None, 14, 14, 256) 1024 res4f_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_88 (Activation) (None, 14, 14, 256) 0 bn4f_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res4f_branch2c (Conv2D) (None, 14, 14, 1024) 263168 activation_88[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn4f_branch2c (BatchNormalizatio (None, 14, 14, 1024) 4096 res4f_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_29 (Add) (None, 14, 14, 1024) 0 bn4f_branch2c[0][0] \n",
" activation_86[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_89 (Activation) (None, 14, 14, 1024) 0 add_29[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5a_branch2a (Conv2D) (None, 7, 7, 512) 524800 activation_89[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5a_branch2a (BatchNormalizatio (None, 7, 7, 512) 2048 res5a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_90 (Activation) (None, 7, 7, 512) 0 bn5a_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5a_branch2b (Conv2D) (None, 7, 7, 512) 2359808 activation_90[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5a_branch2b (BatchNormalizatio (None, 7, 7, 512) 2048 res5a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_91 (Activation) (None, 7, 7, 512) 0 bn5a_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5a_branch2c (Conv2D) (None, 7, 7, 2048) 1050624 activation_91[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5a_branch1 (Conv2D) (None, 7, 7, 2048) 2099200 activation_89[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5a_branch2c (BatchNormalizatio (None, 7, 7, 2048) 8192 res5a_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5a_branch1 (BatchNormalization (None, 7, 7, 2048) 8192 res5a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_30 (Add) (None, 7, 7, 2048) 0 bn5a_branch2c[0][0] \n",
" bn5a_branch1[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_92 (Activation) (None, 7, 7, 2048) 0 add_30[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5b_branch2a (Conv2D) (None, 7, 7, 512) 1049088 activation_92[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5b_branch2a (BatchNormalizatio (None, 7, 7, 512) 2048 res5b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_93 (Activation) (None, 7, 7, 512) 0 bn5b_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5b_branch2b (Conv2D) (None, 7, 7, 512) 2359808 activation_93[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5b_branch2b (BatchNormalizatio (None, 7, 7, 512) 2048 res5b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_94 (Activation) (None, 7, 7, 512) 0 bn5b_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5b_branch2c (Conv2D) (None, 7, 7, 2048) 1050624 activation_94[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5b_branch2c (BatchNormalizatio (None, 7, 7, 2048) 8192 res5b_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_31 (Add) (None, 7, 7, 2048) 0 bn5b_branch2c[0][0] \n",
" activation_92[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_95 (Activation) (None, 7, 7, 2048) 0 add_31[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5c_branch2a (Conv2D) (None, 7, 7, 512) 1049088 activation_95[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5c_branch2a (BatchNormalizatio (None, 7, 7, 512) 2048 res5c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_96 (Activation) (None, 7, 7, 512) 0 bn5c_branch2a[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5c_branch2b (Conv2D) (None, 7, 7, 512) 2359808 activation_96[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5c_branch2b (BatchNormalizatio (None, 7, 7, 512) 2048 res5c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_97 (Activation) (None, 7, 7, 512) 0 bn5c_branch2b[0][0] \n",
"____________________________________________________________________________________________________\n",
"res5c_branch2c (Conv2D) (None, 7, 7, 2048) 1050624 activation_97[0][0] \n",
"____________________________________________________________________________________________________\n",
"bn5c_branch2c (BatchNormalizatio (None, 7, 7, 2048) 8192 res5c_branch2c[0][0] \n",
"____________________________________________________________________________________________________\n",
"add_32 (Add) (None, 7, 7, 2048) 0 bn5c_branch2c[0][0] \n",
" activation_95[0][0] \n",
"____________________________________________________________________________________________________\n",
"activation_98 (Activation) (None, 7, 7, 2048) 0 add_32[0][0] \n",
"____________________________________________________________________________________________________\n",
"avg_pool (AveragePooling2D) (None, 1, 1, 2048) 0 activation_98[0][0] \n",
"____________________________________________________________________________________________________\n",
"flatten_2 (Flatten) (None, 2048) 0 avg_pool[0][0] \n",
"____________________________________________________________________________________________________\n",
"fc1000 (Dense) (None, 6) 12294 flatten_2[0][0] \n",
"====================================================================================================\n",
"Total params: 23,600,006\n",
"Trainable params: 23,546,886\n",
"Non-trainable params: 53,120\n",
"____________________________________________________________________________________________________\n"
]
}
],
"source": [
"model.summary()"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model.compile(optimizer='adam',\n",
" loss='categorical_crossentropy',\n",
" metrics=['accuracy'])"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"early_stopping_callback = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10, verbose=1)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"!rm -rf ./tf_log\n",
"# https://keras.io/callbacks/#tensorboard\n",
"tb_callback = keras.callbacks.TensorBoard(log_dir='./tf_log')\n",
"# To start tensorboard\n",
"# tensorboard --logdir=./tf_log\n",
"# open http://localhost:6006"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Depends on harware GPU architecture, model is really complex, batch needs to be small (this works well on K80)\n",
"BATCH_SIZE = 50"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Train on 2668 samples, validate on 667 samples\n",
"Epoch 1/50\n",
"2668/2668 [==============================] - 100s - loss: 2.1220 - acc: 0.3006 - val_loss: 4.5823 - val_acc: 0.1784\n",
"Epoch 2/50\n",
"2668/2668 [==============================] - 98s - loss: 1.5765 - acc: 0.3632 - val_loss: 2.5742 - val_acc: 0.2129\n",
"Epoch 3/50\n",
"2668/2668 [==============================] - 98s - loss: 1.5738 - acc: 0.3977 - val_loss: 9.8474 - val_acc: 0.1229\n",
"Epoch 4/50\n",
"2668/2668 [==============================] - 98s - loss: 1.6634 - acc: 0.3718 - val_loss: 2.2513 - val_acc: 0.2129\n",
"Epoch 5/50\n",
"2668/2668 [==============================] - 99s - loss: 1.4943 - acc: 0.4142 - val_loss: 1.8982 - val_acc: 0.3103\n",
"Epoch 6/50\n",
"2668/2668 [==============================] - 99s - loss: 1.3737 - acc: 0.4738 - val_loss: 1.6681 - val_acc: 0.3448\n",
"Epoch 7/50\n",
"2668/2668 [==============================] - 99s - loss: 1.2788 - acc: 0.5172 - val_loss: 1.5733 - val_acc: 0.3403\n",
"Epoch 8/50\n",
"2668/2668 [==============================] - 99s - loss: 1.2163 - acc: 0.5607 - val_loss: 2.1635 - val_acc: 0.2969\n",
"Epoch 9/50\n",
"2668/2668 [==============================] - 98s - loss: 1.1085 - acc: 0.5806 - val_loss: 2.3244 - val_acc: 0.3463\n",
"Epoch 10/50\n",
"2668/2668 [==============================] - 98s - loss: 1.1379 - acc: 0.5952 - val_loss: 3.7634 - val_acc: 0.2759\n",
"Epoch 11/50\n",
"2668/2668 [==============================] - 98s - loss: 0.9957 - acc: 0.6244 - val_loss: 1.8038 - val_acc: 0.4423\n",
"Epoch 12/50\n",
"2668/2668 [==============================] - 99s - loss: 0.8906 - acc: 0.6788 - val_loss: 0.9986 - val_acc: 0.6312\n",
"Epoch 13/50\n",
"2668/2668 [==============================] - 99s - loss: 0.8452 - acc: 0.7009 - val_loss: 1.9867 - val_acc: 0.3943\n",
"Epoch 14/50\n",
"2668/2668 [==============================] - 99s - loss: 0.7398 - acc: 0.7395 - val_loss: 2.1141 - val_acc: 0.4783\n",
"Epoch 15/50\n",
"2668/2668 [==============================] - 99s - loss: 0.6464 - acc: 0.7804 - val_loss: 2.3086 - val_acc: 0.4738\n",
"Epoch 16/50\n",
"2668/2668 [==============================] - 97s - loss: 0.5739 - acc: 0.7984 - val_loss: 1.3224 - val_acc: 0.6762\n",
"Epoch 17/50\n",
"2668/2668 [==============================] - 98s - loss: 0.3891 - acc: 0.8666 - val_loss: 4.0835 - val_acc: 0.4003\n",
"Epoch 18/50\n",
"2668/2668 [==============================] - 99s - loss: 0.4333 - acc: 0.8490 - val_loss: 3.6039 - val_acc: 0.3298\n",
"Epoch 19/50\n",
"2668/2668 [==============================] - 98s - loss: 0.4827 - acc: 0.8407 - val_loss: 7.1415 - val_acc: 0.2819\n",
"Epoch 20/50\n",
"2668/2668 [==============================] - 99s - loss: 0.6920 - acc: 0.7954 - val_loss: 7.4663 - val_acc: 0.1229\n",
"Epoch 21/50\n",
"2668/2668 [==============================] - 99s - loss: 0.6403 - acc: 0.8193 - val_loss: 6.1310 - val_acc: 0.1679\n",
"Epoch 22/50\n",
"2668/2668 [==============================] - 99s - loss: 0.3194 - acc: 0.8969 - val_loss: 4.3824 - val_acc: 0.1364\n",
"Epoch 23/50\n",
"2668/2668 [==============================] - 99s - loss: 0.1450 - acc: 0.9524 - val_loss: 2.8166 - val_acc: 0.5367\n",
"Epoch 24/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0871 - acc: 0.9719 - val_loss: 3.4144 - val_acc: 0.4423\n",
"Epoch 25/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0619 - acc: 0.9831 - val_loss: 0.1683 - val_acc: 0.9505\n",
"Epoch 26/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0260 - acc: 0.9914 - val_loss: 0.1448 - val_acc: 0.9505\n",
"Epoch 27/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0365 - acc: 0.9891 - val_loss: 0.3352 - val_acc: 0.9025\n",
"Epoch 28/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0230 - acc: 0.9936 - val_loss: 1.3329 - val_acc: 0.8231\n",
"Epoch 29/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0260 - acc: 0.9918 - val_loss: 0.3287 - val_acc: 0.9505\n",
"Epoch 30/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0157 - acc: 0.9959 - val_loss: 0.3259 - val_acc: 0.9100\n",
"Epoch 31/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0422 - acc: 0.9865 - val_loss: 0.2643 - val_acc: 0.9355\n",
"Epoch 32/50\n",
"2668/2668 [==============================] - 97s - loss: 0.0408 - acc: 0.9869 - val_loss: 0.4775 - val_acc: 0.8771\n",
"Epoch 33/50\n",
"2668/2668 [==============================] - 97s - loss: 0.0243 - acc: 0.9936 - val_loss: 0.2358 - val_acc: 0.9400\n",
"Epoch 34/50\n",
"2668/2668 [==============================] - 97s - loss: 0.0278 - acc: 0.9921 - val_loss: 0.4836 - val_acc: 0.8681\n",
"Epoch 35/50\n",
"2668/2668 [==============================] - 97s - loss: 0.0139 - acc: 0.9963 - val_loss: 0.0390 - val_acc: 0.9865\n",
"Epoch 36/50\n",
"2668/2668 [==============================] - 98s - loss: 0.0465 - acc: 0.9846 - val_loss: 0.4080 - val_acc: 0.9040\n",
"Epoch 37/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0664 - acc: 0.9809 - val_loss: 0.5346 - val_acc: 0.8996\n",
"Epoch 38/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0240 - acc: 0.9921 - val_loss: 0.7532 - val_acc: 0.8306\n",
"Epoch 39/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0395 - acc: 0.9884 - val_loss: 2.1401 - val_acc: 0.7301\n",
"Epoch 40/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0526 - acc: 0.9854 - val_loss: 1.2753 - val_acc: 0.8066\n",
"Epoch 41/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0234 - acc: 0.9918 - val_loss: 0.5262 - val_acc: 0.8801\n",
"Epoch 42/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0043 - acc: 0.9985 - val_loss: 0.0439 - val_acc: 0.9925\n",
"Epoch 43/50\n",
"2668/2668 [==============================] - 99s - loss: 8.5488e-04 - acc: 1.0000 - val_loss: 0.0094 - val_acc: 0.9970\n",
"Epoch 44/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0014 - acc: 0.9993 - val_loss: 0.0620 - val_acc: 0.9760\n",
"Epoch 45/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0050 - acc: 0.9981 - val_loss: 0.0402 - val_acc: 0.9820\n",
"Epoch 46/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0049 - acc: 0.9989 - val_loss: 0.0728 - val_acc: 0.9775\n",
"Epoch 47/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0148 - acc: 0.9955 - val_loss: 0.2296 - val_acc: 0.9610\n",
"Epoch 48/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0152 - acc: 0.9940 - val_loss: 0.3280 - val_acc: 0.9070\n",
"Epoch 49/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0074 - acc: 0.9989 - val_loss: 0.0928 - val_acc: 0.9685\n",
"Epoch 50/50\n",
"2668/2668 [==============================] - 99s - loss: 0.0133 - acc: 0.9974 - val_loss: 0.3310 - val_acc: 0.9250\n",
"CPU times: user 1h 18min 22s, sys: 4min 42s, total: 1h 23min 4s\n",
"Wall time: 1h 22min 49s\n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7fd731bf6eb8>"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# https://github.com/fchollet/keras/issues/6014\n",
"# batch normalization seems to mess with accuracy when test data set is small, accuracy here is different from below\n",
"%time model.fit(X_train, y_train, epochs=50, validation_split=0.2, batch_size=BATCH_SIZE, callbacks=[tb_callback, early_stopping_callback])\n",
"# %time model.fit(X_train, y_train, epochs=50, validation_split=0.2, batch_size=BATCH_SIZE, callbacks=[tb_callback])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Results are a bit less good\n",
"### Maybe need to train longer?\n",
"### Batches can be larger, training is faster even though more epochs\n",
"\n",
"## Metrics for Augmented Data\n",
"\n",
"### Accuracy\n",
"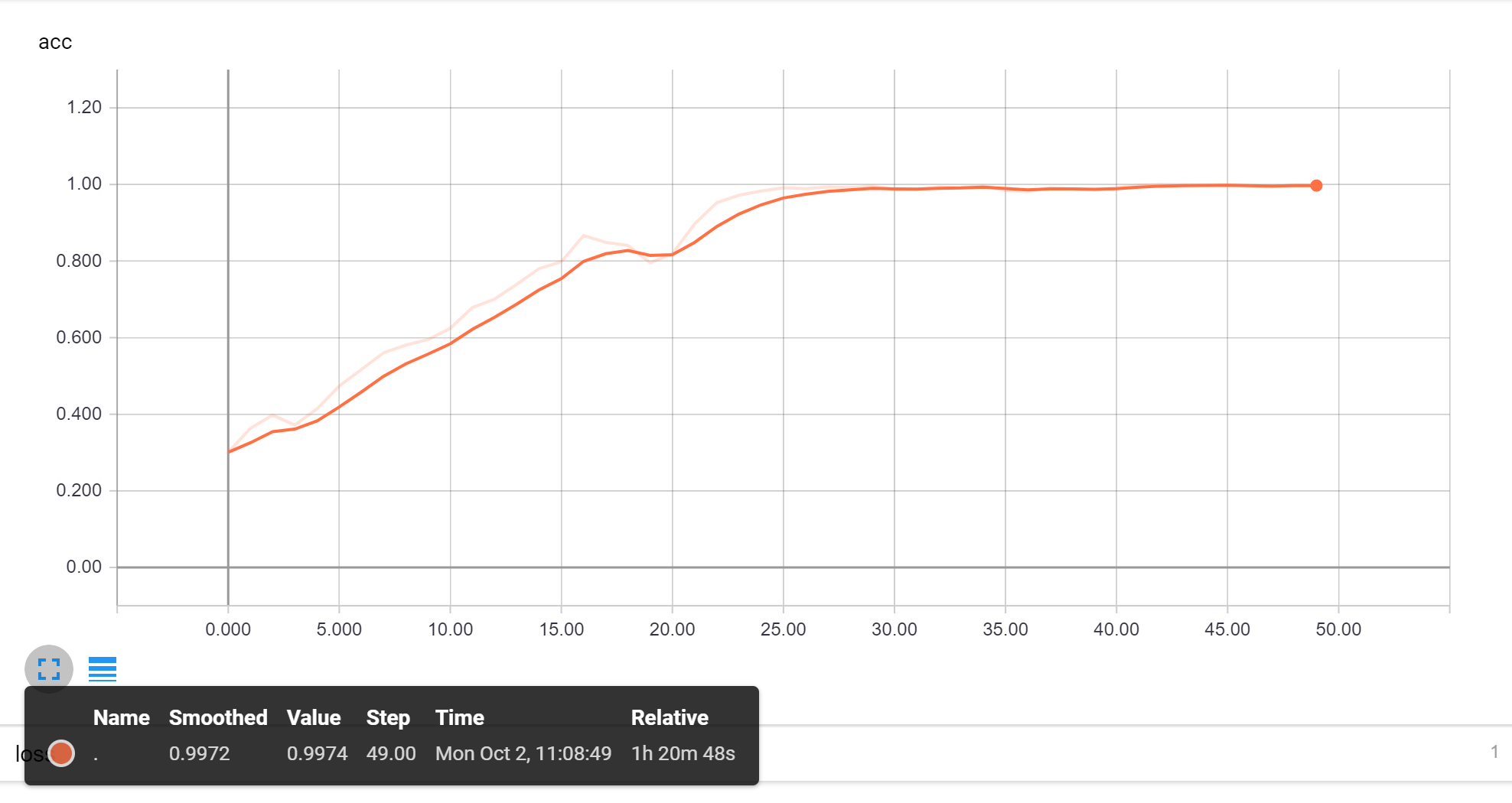\n",
"### Validation Accuracy\n",
"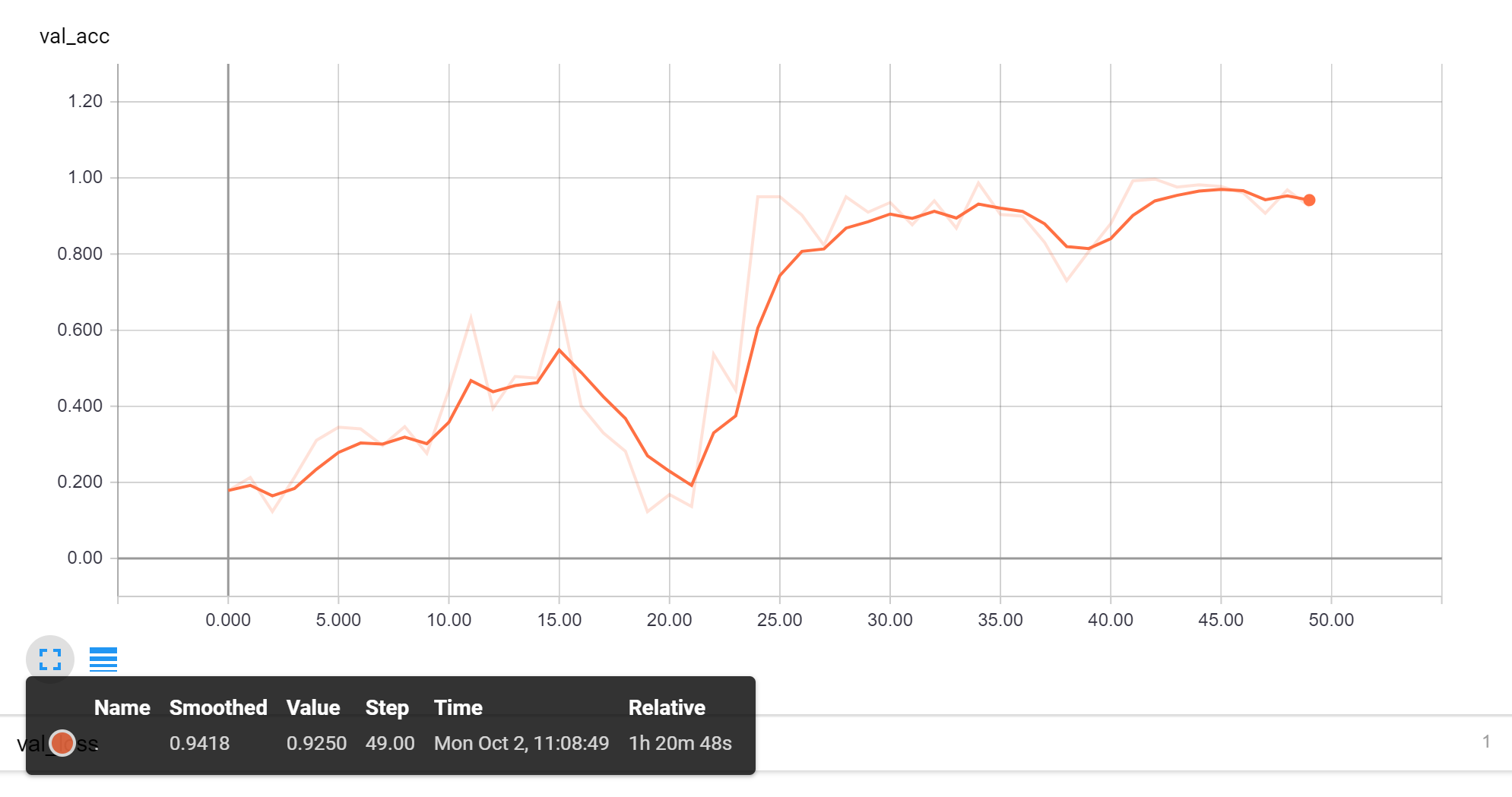"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3335/3335 [==============================] - 38s \n"
]
},
{
"data": {
"text/plain": [
"(0.22209251228569152, 0.9361319339972386)"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_loss, train_accuracy = model.evaluate(X_train, y_train, batch_size=BATCH_SIZE)\n",
"train_loss, train_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"834/834 [==============================] - 9s \n"
]
},
{
"data": {
"text/plain": [
"(0.29912034460573461, 0.91726617318549031)"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"test_loss, test_accuracy = model.evaluate(X_test, y_test, batch_size=BATCH_SIZE)\n",
"test_loss, test_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"379/379 [==============================] - 4s \n"
]
},
{
"data": {
"text/plain": [
"(0.1593474517459674, 0.95778363487022222)"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"original_loss, original_accuracy = model.evaluate(original_images, original_labels, batch_size=BATCH_SIZE)\n",
"original_loss, original_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"model.save('resnet-augmented.hdf5')"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-rw-rw-r-- 1 ubuntu ubuntu 271M Oct 2 09:22 resnet-augmented.hdf5\r\n"
]
}
],
"source": [
"!ls -lh resnet-augmented.hdf5"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"# No Hands-On Possible\n",
"## All experiments take ours of compute time even on GPU\n",
"## We can experiment with the results in the final notebook: [How well do the different models generalize to real life?](cnn-comparing-all-models.ipynb)\n",
" \n",
"---"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
santanche/java2learn | notebooks/pt/c05exercicios/s02resolucoes/small-challenges-03.ipynb | 1 | 4703 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Small Challenges 3\n",
"\n",
"Dadas as seguintes classes:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"public class CA {\n",
" public String toString() {\n",
" return \"primeiro\";\n",
" }\n",
"}\n",
"\n",
"public class CB {\n",
" private CA referencia;\n",
" public CB(CA referencia) {\n",
" this.referencia = referencia;\n",
" }\n",
" \n",
" public String toString() {\n",
" return referencia + \" segundo\";\n",
" }\n",
"}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Exercício\n",
"\n",
"Como você escreveria em uma única linha um código para imprimir `primeiro segundo` usando as strings produzidas pelas classes."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"primeiro segundo\n"
]
}
],
"source": [
"System.out.println(new CB(new CA()));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Outro desafio\n",
"\n",
"Estude o código a seguir:"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"maior: 30\n",
"menor: 9\n"
]
}
],
"source": [
"public class C {\n",
" protected int valor;\n",
" public C(int valor) {\n",
" this.valor = valor;\n",
" }\n",
" public void operacao(int novoValor) {\n",
" valor = novoValor;\n",
" }\n",
" public String toString() {\n",
" return Integer.toString(valor);\n",
" }\n",
"}\n",
"\n",
"public class CMaior extends C {\n",
" public CMaior(int valor) {\n",
" super(valor);\n",
" }\n",
" public void operacao(int novoValor) {\n",
" if (novoValor > valor)\n",
" valor = novoValor;\n",
" }\n",
"}\n",
"\n",
"public class CMenor extends C {\n",
" public CMenor(int valor) {\n",
" super(valor);\n",
" }\n",
" public void operacao(int novoValor) {\n",
" if (novoValor < valor)\n",
" valor = novoValor;\n",
" }\n",
"}\n",
"\n",
"\n",
"C maior = new CMaior(12);\n",
"maior.operacao(30);\n",
"maior.operacao(15);\n",
"maior.operacao(9);\n",
"System.out.println(\"maior: \" + maior);\n",
"\n",
"C menor = new CMenor(12);\n",
"menor.operacao(30);\n",
"maior.operacao(15);\n",
"menor.operacao(9);\n",
"System.out.println(\"menor: \" + menor);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Exercício\n",
"\n",
"Como você escreveria o método `operacao` para que mostrasse o maior e menor valor "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"public class CVetor {\n",
" C referencia;\n",
" public CVetor(C referencia) {\n",
" this.referencia = referencia;\n",
" }\n",
" \n",
" public void operacao(int valores[]) {\n",
" for (int s = 0; s < valores.length; s++)\n",
" referencia.operacao(valores[s]);\n",
" }\n",
" \n",
" public String toString() {\n",
" return referencia.toString();\n",
" }\n",
"}"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"maior: 30\n",
"maior: 9\n"
]
}
],
"source": [
"int valores[] = {30, 15, 9};\n",
"\n",
"CVetor vetorMaior = new CVetor(new CMaior(12));\n",
"vetorMaior.operacao(valores);\n",
"System.out.println(\"maior: \" + vetorMaior);\n",
"\n",
"CVetor vetorMenor = new CVetor(new CMenor(12));\n",
"vetorMenor.operacao(valores);\n",
"System.out.println(\"maior: \" + vetorMenor);"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Java",
"language": "java",
"name": "java"
},
"language_info": {
"codemirror_mode": "java",
"file_extension": ".java",
"mimetype": "text/x-java-source",
"name": "Java",
"pygments_lexer": "java",
"version": "10.0.1+10-Debian-4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-2.0 |
srcole/qwm | misc/Sawtooth PAC.ipynb | 1 | 159245 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# A sawtooth wave has statistical phase-amplitude coupling\n",
"\n",
"This notebook is to show that a sawtooth wave will generate spurious phase-amplitude coupling, particularly at high frequencies (i.e. above 20-60Hz)\n",
"\n",
"Library dependencies:\n",
"* [pacpy](https://github.com/voytekresearch/pacpy)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%config InlineBackend.figure_format = 'retina'\n",
"%matplotlib inline\n",
"\n",
"import numpy as np\n",
"import scipy as sp\n",
"import matplotlib.pyplot as plt\n",
"\n",
"import seaborn as sns\n",
"sns.set_style('white')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1. Simulate a 20Hz sawtooth wave"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0xaad0320>"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6YAAAG2CAYAAABsy5tZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAewgAAHsIBbtB1PgAAIABJREFUeJzs3Xl8VPW9//H3mcm+AxKSACFREQQEQVqlslmVxaogvy4C\nVkQrVatel4JLhVoVwau3UrG01laxWK4sFosbspWooHXBhcsiKATMCoTsZJuZ8/sjTmBmTpL5fDNz\nzpnk/Xw8eNzrZDI5SV8z8/h+5/s9R9N1XQcRERERERGRRRxWHwARERERERF1bRyYEhERERERkaU4\nMCUiIiIiIiJLcWBKREREREREluLAlIiIiIiIiCzFgSkRERERERFZigNTIiIiIiIishQHpkRERERE\nRGQpDkyJiIiIiIjIUhyYEhERERERkaU4MCUiIiIiIiJLcWBKREREREREluLAlIiIiIiIiCzFgSkR\nERERERFZigNTIiIiIiIishQHpkRERERERGQpDkyJiIiIiIjIUlFWHwCFT3FxMbZu3dry33379kVC\nQoKFR0RERERERFY4efIkvv3225b//uEPf4jMzEwLj8gXB6ad2NatW/HII49YfRhERERERGRDM2fO\ntPoQWnApLxEREREREVmKA1MiIiIiIiKyFJfydmLZ2dk+/71gwQIMGDDAoqMhIiIiIiKrfPXVVz7b\n/PzHClbjwLQTi4+P9/nvAQMGYOTIkRYdDRERERER2YX/WMFqXMpLREREREREluLAlIiIiIiIiCzF\ngSkRERERERFZigNTIiIiIiIishQHpkRERERERGQpDkyJiIiIiIjIUhyYEhERERERkaU4MCUiIiIi\nIiJLcWBKREREREREluLAtA2PPfYYBg4ciNdee63Dj7V//37MnTsX48aNw5AhQzB69GjccssteO+9\n90JwpERERERERJEryuoDsKvNmzdj5cqV0DStw4+1ZcsW/Nd//RdcLlfL45WVlWHbtm3Ytm0brr/+\nejz44IMd/jlERERERESRiJ+YGti6dSvuvvtu6Lre4cfau3cv7r33XrjdbgwbNgwrVqzAhx9+iLVr\n1+Lyyy8HAKxYsQIrV67s8M8iIiIiIiKKRByYnkbXdTzzzDO4/fbb4XK5QjIwXbJkCerr65GdnY3l\ny5dj5MiRSE1NxeDBg7F06VJMmjQJuq5j6dKlOHnyZAh+CyIiIiIiosjCgel33nvvPVx99dVYtmwZ\ndF3H4MGDO/yYBw8eRF5eHjRNw6233or4+PiA+9x///1wOByoqKjAxo0bO/wziYiIiIiIIg0Hpt+5\n+eab8fXXXyM6Ohp33HEHnn766Q4/5rvvvgsA0DQN48ePN7xPRkYGzj33XADNe1GJiIiIiIi6Gg5M\nv+NwODBhwgSsX78et912GxyOjv9p9u3bBwDIyspCWlpaq/cbNGgQdF3H7t27O/wziYiIiIiIIg3P\nyvudt99+G/369QvpYxYWFgIA+vTp0+b9srKyAAAlJSXweDwhGRQTERERERFFCo6AvhPqQSkAlJeX\nQ9M0pKSktHm/5ORkAM0nX6qqqgr5cRAREREREdkZB6Zh1NDQAACIi4tr836xsbEB30NERERERNRV\ncGAaRlySS0RERERE1D6OnMIoISEBQPufgp7+9fY+XSUiIiIiIupsODANo+TkZOi6jpqamjbv591X\n6nQ6kZqaasahERERERER2QYHpmGUk5MD4NTZeVtTXFwMAEhPTw/3IREREREREdkOB6ZhNGDAAABA\nQUEBamtrW73f7t27oWkaBg0aZNahERERERER2QYHpmE0duxYAIDb7UZeXp7hfUpKSrBv3z4AwJgx\nY0w7tlDRdR0NTW64PbrVhxJR3G4PGpvcVh9GRGFratiaHFtTw9bk2JoatibH1tSwNXNFWX0AnVnf\nvn1xwQUX4NNPP8UzzzyDsWPHIikpyec+ixYtgsfjQffu3TFlyhSLjlRNwdFqPPH3T5BfXIXcrBTM\nvW4k+vZKtvqwbG/Vpq+wcuNXcGjATy49BzMmDrT6kGyPralha3JsTQ1bk2NratiaHFtTw9bMx09M\nO6i0tBSTJk3C5MmT8fTTTwd8/YEHHoDD4UB+fj5mzJiB7du3o7y8HHv27MHtt9+Od955B5qm4Y47\n7oi4M/Iuf2MP8oubT9x0qKgKf13/fxYfkf19U1CBlzfsg8ejw+XW8b8bv8JXh09YfVi2x9bk2Joa\ntibH1tSwNTm2poatybE1a3Bg2kEulwv5+fnIz8/H0aNHA74+ZMgQLFy4EFFRUThw4ABuuukmjBo1\nCtOmTcPmzZuhaRpmz56N6dOnW3D06nRdx392l/jctnPfUS53aMe/Py0IuG315gMWHEnkYGtq2Joc\nW1PD1uTYmhq2JsfW1LA1a3Bg2gZN06BpWlD3O/3/+rvmmmuwbt06TJkyBZmZmYiOjkZqaipGjx6N\nZcuWYd68eSE9bjOcrHcZ3n6kpNrkI4ksu745HnDbR3tKDO5JXmxNDVuTY2tq2JocW1PD1uTYmhq2\nZg3uMW1F7969sXfv3pDdr3///li8eHEoDs0WTlTVG95+qKgSZ/dNM/loIkdKYozVhxBx2JoatibH\n1tSwNTm2poatybE1NWzNGvzElJScqDR+oTtYVGnykUSW1pbOVJ9sNPlIIgdbU8PW5NiaGrYmx9bU\nsDU5tqaGrVmDA1NSUtbqDFyVyUcSWdqauSRjbE0NW5Nja2rYmhxbU8PW5NiaGrZmDQ5MSUlrT9j8\nokroOq+RZUTX9VZnLvkG0Tq2JsfW1LA1Obamhq3JsTU1bE2OrVmHA1NS0toLXW29C8fK60w+mshQ\nW9eERpfH8GucgWsdW5Nja2rYmhxbU8PW5NiaGrYmx9asw4EpKWltJgngk7Y1rS2nATgD1xa2JsfW\n1LA1Obamhq3JsTU1bE2OrVmHA1NS0toMHAAcKuaT1khbbw5HSqrhchvPznV1bE2Oralha3JsTQ1b\nk2NratiaHFuzDgempKTt2STOwBlp683B5fag8GiNiUcTOdiaHFtTw9bk2JoatibH1tSwNTm2Zh0O\nTElM13WUt/VCV8gZOCNtvdABPHW7Ebamhq3JsTU1bE2Oralha3JsTQ1bsw4HpiRWU9eEplY2hQNA\ncVktTtY3mXhEkaG9FzruWwjE1tSwNTm2poatybE1NWxNjq2pYWvW4cCUxNpae+91uLjahCOJLO2/\n0HEGzh9bU8PW5NiaGrYmx9bUsDU5tqaGrVmHA1MSa2u/gtehYj5p/bX3BpHPGbgAbE0NW5Nja2rY\nmhxbU8PW5NiaGrZmHQ5MSSyYGTgucwjU3gxcRU1Dm3tBuiK2poatybE1NWxNjq2pYWtybE0NW7MO\nB6YkVlHT0O59uMwhUEV1MH83vkGcjq2pYWtybE0NW5Nja2rYmhxbU8PWrMOBKYk1NbnbvU9+cRXc\nHt2Eo4kMuq6jsY0TEHjxTG++2JocW1PD1uTYmhq2JsfW1LA1ObZmLQ5MSawpiAsLNzS6UVJWa8LR\nRIZgX/Q5c+mLrcmxNTVsTY6tqWFrcmxNDVuTY2vW4sCUxFzuwCdtYnx0wG180p7iMph9M/6bcWnI\n6diaHFtTw9bk2JoatibH1tSwNTm2Zi0OTEnMbTAD179vWsBtfNKe4jKYgcvokYAkvxe7wmM1aAxi\n6U1Xwdbk2JoatibH1tSwNTm2poatybE1a3FgSmJGS0OMX+g4A+dlNAMX5XQgNyvV5zaPR8eREl5T\nzIutybE1NWxNjq2pYWtybE0NW5Nja9biwJTEjJ60Z/fhDFxbXAZvDs0vdCkBt/MN4hS2JsfW1LA1\nObamhq3JsTU1bE2OrVmLA1MSM3rSpiXHome3eJ/bjlfUofpko1mHZWtGf7Po1l7oivkG4cXW5Nia\nGrYmx9bUsDU5tqaGrcmxNWtxYEpiRpvpo5wO5GamBtzO2aRmTUZLQ6IcyMkK/JsdLOTfzIutybE1\nNWxNjq2pYWtybE0NW5Nja9biwJTEDGeTolpb5sDZJKC1pSEasnslw+HQfG7PL6qErvOaYgBbU8HW\n1LA1Obamhq3JsTU1bE2OrVmLA1MSM5xNcjqQ25szcK1pbc9CTLQTfdOTfG6vrXfhWHmdWYdma2xN\njq2pYWtybE0NW5Nja2rYmhxbsxYHpiQm2xjOGTgAcLkMltNENT/9/M/0BvANwoutybE1NWxNjq2p\nYWtybE0NW5Nja9biwJTE3K3sWcjonoj4WKfP7UdKqg1fGLsal8d4Mz0AbqhvA1uTY2tq2JocW1PD\n1uTYmhq2JsfWrMWBKYm1tv7e4dDQLyMl4L6FR2vMOjTbMjplu/O7FzqjDfWcgWvG1uTYmhq2JsfW\n1LA1Obamhq3JsTVrcWBKYkYXbOYyh7a19uYAtDIDxyU1ANiaCramhq3JsTU1bE2Oralha3JszVoc\nmJKY0WxSVBvLHA7ySdvqPg8A6JYch7TkWJ+vFR+vxcn6JlOOzc7YmhxbU8PW5NiaGrYmx9bUsDU5\ntmYtDkxJrK0nLc/0ZsxoM3101Kmn35kGM5eHi6vDekyRgK3JsTU1bE2Oralha3JsTQ1bk2Nr1uLA\nlMTaWuaQk5ECzfcyT8jnDJzxchrnqaef8YZ6vkGwNTm2poatybE1NWxNjq2pYWtybM1aHJiSmP/S\nkCinBu27V7e42Chk9kj0+XpFTQPKq+pNOz47amvWEmhtQz3fINiaHFtTw9bk2JoatibH1tSwNTm2\nZq0oq36w2+1GSUkJqqur0djYiNjYWKSkpCAjI6PlSWO2/fv34/nnn8dHH32EsrIypKWlYciQIZg5\ncybGjBmj/LgffPAB/vGPf+Dzzz9HRUUFEhMTce6552Lq1KmYMmWKZb+vKpff6cdPf8ICzRvqi47X\n+tx2qKgK3VLiwn5sdtXeC53xhnrOwLE1Obamhq3JsTU1bE2Oralha3JszVqmDUyrq6uRl5eH999/\nH1988QWOHDkCj8G1gqKiopCTk4MLLrgAo0aNwiWXXIKYmJiwH9+WLVvwX//1X3C5XC0DxbKyMmzb\ntg3btm3D9ddfjwcffFD8uE888QRefPFFAGh53KqqKvznP//Bhx9+iNdffx1/+tOfTPkdQ8V/mUPg\nC10Ktn9Z5HPboaJKjBiYHvZjsyvDExBEnZqQ6NMzCdFRDjSddr/DxVVwe3Q4HZE1cRFKbE2Oralh\na3JsTQ1bk2NratiaHFuzVtiX8n755ZeYO3cuRo8ejblz5+Jf//oXDh06BLfbDV3XA/41NTXhwIED\nWLVqFe666y6MGjUKCxYswOHDh8N2jHv37sW9994Lt9uNYcOGYcWKFfjwww+xdu1aXH755QCAFStW\nYOXKlaLHXbNmDV588UVomobhw4dj+fLl2L59O1599VVceeWV0DQNO3bswCOPPBKOXyts3P4vdFGB\nM3D+Dnbx2ST/WUvg1AWbgeZrZGVnJPt8vb7RjZKyWv9v61LYmhxbU8PW5NiaGrYmx9bUsDU5tmat\nsH1iumvXLixZsgQ7duwAAOj6qf+hs7KycPbZZ6N79+5ISkpCQkICGhsbUVNTg+LiYhw+fBgFBQUA\ngNraWqxZswavvvoqJk6ciDlz5mDgwIEhPdYlS5agvr4e/fr1w/LlyxEfHw8ASE1NxdKlS3HXXXdh\nw4YNWLp0KaZOnYqEhISgHvf555+Hpmno378/XnrppZZPRbt3744nn3wSuq7jjTfewD//+U/ceeed\nSE+PjBkq/2UOUX4zRDm8zlMAo6UhTv+Zy8xUfFPg+4ZwqKgSvXsmhfXY7IytybE1NWxNjq2pYWty\nbE0NW5Nja9YK+cC0srISTz31FF599dWWpbr9+/fH+PHjcfHFF+O8885DYmJiO4/SvPT3008/xY4d\nO7Bp0yYUFxfjrbfewttvv42f/vSnmDdvXlCP056DBw8iLy8Pmqbh1ltvbRmUnu7+++/Hxo0bUVFR\ngY0bN2Lq1KntPm5lZSWOHDkCTdMwZcoUw6W606dPxxtvvAFd1/Hll1/isssu6/DvE266rgfuWfCb\ngeuZFo+k+GjU1J26rlPhsRo0NrkRE+005Tjtpr09CwCQ2zsF+Nj3PoeKqjB6WO9wHpptsTU1bE2O\nralha3JsTQ1bk2NratiatUK6lDcvLw9XXnkl1qxZg5iYGEyfPh3//Oc/8frrr+Pee+/FRRddFPRg\nMjk5GePHj8eDDz6If//733j55ZcxefJkOJ1OrFq1CldddRW2b9/e4WN+9913ATTv/xw/frzhfTIy\nMnDuuecCaN6LGgyH49Sf1uVyGd4nOjq65f93OiPjBcBoiYP/E1bTtIDlIR6PjiMlXfc6T0YvdNEG\nJyHw15U31LM1NWxNjq2pYWtybE0NW5Nja2rYmrVCOjD95S9/ifLycsyYMQObNm3Cb3/7WwwaNCgk\njz1y5Eg8/fTT2LJlC6699locO3YMv/jFLzr8uPv27QPQvLw4LS2t1fsNGjQIuq5j9+7dQT1ucnIy\n+vXr17Jct6mpKeA+a9euBdA8QD3vvPMUjt58wcwkATxrmb+mdjbTA0BuJpfUnI6tqWFrcmxNDVuT\nY2tq2JocW1PD1qwV0oHppZdeijfeeAMLFixAz549Q/nQLXr16oWHH34Yb775Ji699NIOP15hYSEA\noE+fPm3eLysrCwBQUlJieDZhI7/+9a/hdDrx9ddfY/bs2fjPf/6DEydOYN++fZg/fz5Wr14NTdNw\n22234YwzzujYL2ISwxe6qCBf6Iq77pM2mDeIpIQY9Ozmu5T8eEUdqk82hvXY7IqtqWFrcmxNDVuT\nY2tq2JocW1PD1qwV0oHpH//4R+Tk5ITyIVuVnZ2NZ599tsOPU15eDk3TkJIS+MQ8XXJy8xm4dF1H\nVVVwT9jLL78cS5cuRXZ2Nj755BPMmjULP/jBDzB16lSsWbMGWVlZeOKJJ3DLLbd0+Pcwi9FptP2X\nOACtXYC4687ABbOkBmjeUO8vv4vOwrE1NWxNjq2pYWtybE0NW5Nja2rYmrXCfrkYu2toaAAAxMW1\nfTHh2NjYgO8JRk1NDRITE6FpWsC/48ePY+fOnThx4oTawVvA/5pYgPETNrtXMhx+Z387VFjpc3bm\nrsT4uljBzVx21VO3szU1bE2Oralha3JsTQ1bk2Nratiatbr8wPT0kxSF2mOPPYZ58+Zh7969mDFj\nBt566y3s2rUL7777Lh566CHExsbilVdewfXXXx8xg1O34UxS4AWFY6Kd6JPue9rs2noXjpXXhe3Y\n7MxlsPzbaOaSG+pPYWtq2JocW1PD1uTYmhq2JsfW1LA1a3X5gan3mqTtfQp6+tfb+3QVAHbs2IGX\nX34Zmqbh17/+NebPn4/c3FxERUWhZ8+emDlzJlasWIH4+Hh88803+P3vf9+xX8QkwVzfyetMPmlb\nGM3AOQ3eIHJ7c0O9F1tTw9bk2JoatibH1tSwNTm2poatWcvWA9P58+dj/vz5WLBgQdh+RnJyMnRd\nR01NTZv38+4rdTqdSE0NfAL7W7NmDQAgMzMTN954o+F9Bg4ciGuvvRa6ruO1114TLRG2iuFptA2W\nOADcUH+6YM+Ol9E9EfGxvpcOOlJSbfj9nR1bU8PW5NiaGrYmx9bUsDU5tqaGrVnL1gPTNWvWYO3a\ntS2DvHDwnqzJe3be1hQXFwMA0tPTg3rc/Px8aJqGYcOGQdMCZ1q8LrzwQgCA2+3GkSNHgnpsKxme\nRruVGThuqD8l2M30DoeGfhm+bxAutweFR9ueOOmM2JoatibH1tSwNTm2poatybE1NWzNWrYemAII\n++brAQMGAAAKCgpQW1vb6v12794NTdOCvi6r97qljY3Bnzpacl+rGM8kGQ+8ja+N1UVn4IzOjtfq\nzCXfIAC2poqtybE1NWxNjq2pYWtybE0NW7OWrQemjz76KB599FE88sgjYfsZY8eOBdD8iWVeXp7h\nfUpKSrBv3z4AwJgxY4J63NzcXOi6jk8//bRlkGrkk08+AdC8RLhfv36SQ7dEsEscAKBbchzSkmN9\nbispq8XJ+tb/Hp1VsGfHA/gG4cXW1LA1Obamhq3JsTU1bE2Oralha9ay9cD0Jz/5Scu/cOnbty8u\nuOAC6LqOZ555xnCv6aJFi+DxeNCtWzdMmTIlqMe94oorAACVlZV4+umnDe/z9ddfY+XKldA0DePH\nj0dSUpLh/ezE5TJY4tDKTBIA5Gb6Pml1HThcXB3y47I7yRuE0QxcVzwFOVtTw9bk2JoatibH1tSw\nNTm2poatWcvWA1OzPPDAA3A4HMjPz8eMGTOwfft2lJeXY8+ePbj99tvxzjvvQNM03HHHHT5n5C0t\nLcWkSZMwefLkgMHn5MmTcdFFF0HXdbzwwgu488478cknn6C8vByFhYVYsWIFZs6ciZMnTyI5ORlz\n5841+9dWYriZvpUnLACc2dtgmUNx13vSGr7QtfIG0S8zBf7bkrviRZvZmhq2JsfW1LA1Obamhq3J\nsTU1bM1aUVYfgB0MGTIECxcuxPz583HgwAHcdNNNPl/XNA2zZ8/G9OnTfW53uVwtJzk6evRowOMu\nXboUd911F3bs2IGNGzdi48aNAY/bs2dPLF26NCKW8QKymSSgtQ31Xe9JG+z1xAAgPjYKmT0SUXT8\n1J7nipoGlFfVo1tK+5cq6izYmhq2JsfW1LA1Obamhq3JsTU1bM1a/MT0O9dccw3WrVuHKVOmIDMz\nE9HR0UhNTcXo0aOxbNkyzJs3z/D7vGfcNTrzbnJyMv72t7/hD3/4A374wx+iZ8+eiI6ORkpKCoYO\nHYq77roLb731Fs4///yw/m6hZHxdrNbPOmy8/r7rzcBJzo4HtLahvmu9QbA1NWxNjq2pYWtybE0N\nW5Nja2rYmrVM+cR0/vz5Hfp+TdPCegIkr/79+2Px4sVB3793797Yu3dvu/ebMGECJkyY0JFDsw3p\n0pA+PZMQHeXweaIfLq6Cx6PD4Wj9BbKzMXyDaOP3z81KwfYvi3xuO1RUiREDg7tcUWfA1tSwNTm2\npoatybE1NWxNjq2pYWvWMmVgumbNmjav5dkWXddNG5hS+5qEm+mdTgeyM5LxTcGpWbf6RjdKymqR\n1dP+J3sKFf8Xuiino83nBGfg2JoqtibH1tSwNTm2poatybE1NWzNWqYt5dV1XfQPALp3747s7Gz0\n7dvXrMOkdkj3LABAbiaftP5/t+iotidqcoyW1HSxkxCwNTVsTY6tqWFrcmxNDVuTY2tq2Jq1TPnE\n1P+kP0YaGhpQXV2NAwcOYMOGDfjggw8QFxeHP/3pTzjrrLNMOEoKhtILncGT9mBRJS4elhWy47I7\n/ws2t/c365kWj8T4aNTWnbqGWMHRGjQ2uRET7QzLMdoNW1PD1uTYmhq2JsfW1LA1Obamhq1Zy5RP\nTLOzs9v9179/f4wYMQI/+9nP8OKLL+Kee+5BYWEhfvnLXxpeW5Ss4f+EBdpeGgIAuUanIO9iG+qb\n/M7y1t4LnaZpONNveYjHo+NISde5phhbU8PW5NiaGrYmx9bUsDU5tqaGrVnLtmflnTNnDoYPH47C\nwkK89NJLVh8Ofcd4M33byxz8L9oMcGlIe28OAM+Qx9bUsDU5tqaGrcmxNTVsTY6tqWFr1rLtwBQA\nfvSjH0HXdWzYsMHqQ6HvuAyv79R2RkkJMejZLd7ntuMVdag+2RjSY7Mrj0eHxyObgQNaeaEr7jpv\nEGxNjq2pYWtybE0NW5Nja2rYmhxbs56tB6ZpaWkAgIKCAouPhLyMr4sVxJPWYEN9fheZhXN7jPZ5\ntH+WauOLXXedGTi2JsfW1LA1Obamhq3JsTU1bE2OrVnP1gPTXbt2AQBiYmIsPhLyUtlMD3TtZQ7S\nizV7ZfdKDrh22KGiqpazVnd2bE2Oralha3JsTQ1bk2NratiaHFuznm0Hph9//DFWrVoFTdNwzjnn\nWH049B2jzfTRQa2/D5xNOthFXuhUltMAQEy0E33Sfa8dVlvXhGPldSE7Njtja3JsTQ1bk2Nratia\nHFtTw9bk2Jr1TLlczJ///Oeg7udyuVBbW4s9e/bg448/hsfjgaZpuPrqq8N8hBSsJsMZuPaXORjP\nwHWNpSGqs5ZA85Ia/zO7HSqqRHr3hJAcm52xNTm2poatybE1NWxNjq2pYWtybM16pgxMlyxZAk1r\n/8lwOu/H3yNGjMCPf/zjcBwWKVB90mb0SERcjBP1je6W246UVMPl9gT9pI9UqrOWAHBm7xTkfeZ7\n26HiKlw4JDMUh2ZrbE2Oralha3JsTQ1bk2NratiaHFuznmmF6bou+peamoobbrgBzz//vHhQS+Hj\nchkscwjiSetwaMjxOw25y+1B4dHOf43ajszAdeUN9WxNjq2pYWtybE0NW5Nja2rYmhxbs54pn5i+\n+OKLQd1P0zTExMSgR48eyM7O5oDUhjq0zCErFfsOl/vcdqioEv0MrpvVmRgvpwn2b8YlNadja21j\na2rYmhxbU8PW5NiaGrYmx9asZ8rAdNSoUWb8GDKB8QWbO/akHX9Bhw/L1oyWhkRFBTfp0i05DmnJ\nsaiobmi5raSsFnUNLsTHmvL0tQxbk2NratiaHFtTw9bk2JoatibH1qzXuReLU8gZzsAFuf7e6Exv\nXWGZg9ujdpY3r1y/GUpdBw53gQs3szU5tqaGrcmxNTVsTY6tqWFrcmzNehyYkojhBZsdwc0m9ctM\ngf/q7K6wzEH1ulheXfXU7WxNjq2pYWtybE0NW5Nja2rYmhxbs56tB6alpaUt/8gejK7xFOwZy+Jj\no5DZI9HntoqaBpRX1Yfk2OyqI/s8ACC3t9HMZed/g2BrcmxNDVuTY2tq2JocW1PD1uTYmvVsPTAd\nN24cxo8fj0suucTqQ6HvGK6/7+BsUmd/0hq/0AV/Yi/jvR6dfwaOrcmxNTVsTY6tqWFrcmxNDVuT\nY2vWs/XAFDh1mRmyh46csQzomk9a4830wf/N+vRMCpjlPFxcBY/BXojOhK3JsTU1bE2Oralha3Js\nTQ1bk2Nr1rP1wDQ9PR29evVCenq61YdC3+nIZnqgq87AGSynEbw5OJ0OZGck+9xW3+hGSVlth4/N\nztiaHFubMqYxAAAgAElEQVRTw9bk2JoatibH1tSwNTm2Zj1bD0zfffdd5OXlIS8vz+pDoe90dGlI\njtEMXHHnnoHr6KwlAORmdsE3CLYmxtbUsDU5tqaGrcmxNTVsTY6tWc/WA1OyH/8ZOIcW/FneAKBn\nWjwS46N9bis4WoPGJndIjs+OOro0BOiiS2rYmhhbU8PW5NiaGrYmx9bUsDU5tmY9DkxJxH+Zg3Qm\nSdO0gCetx6PjSEl1h4/NrtyeEMzAdcFTkLM1Obamhq3JsTU1bE2Oralha3JszXocmJKI/wycU/iE\nBYAzu9iFm42X0wQ/awm0NgPXuZeGsDU5tqaGrcmxNTVsTY6tqWFrcmzNelFm/8CTJ0+ioKAA9fX1\ncLvdAWfc1XUdLpcLDQ0NqKmpwVdffYV33nkHGzZsMPtQyYD/C510Jglo5Ulb3HmftE0Gm+mlf7ek\nhBj07BaPY+V1Lbcdr6hD9clGJCfEdPgY7YitybE1NWxNjq2pYWtybE0NW5Nja9YzbWBaWlqKhQsX\n4t///jdcLpdZP5ZCzH82KTpKNpMEADldbQYuBJvpgeYN9ae/0AFAflEVzjv7DOVjszO2JsfW1LA1\nObamhq3JsTU1bE2OrVnPlKW8jY2NmDVrFjZt2oSmpqaWa5MG+6979+5mHCYFIRQzcNm9kuHw24B/\nqKiq016vNmQvdF1sQz1bk2NratiaHFtTw9bk2JoatibH1qxnysB0zZo1yM/PBwDExMRg0qRJ+MUv\nfoH+/ftD0zR873vfw5w5c3Dttdfi/PPPh8PRfFiapuH3v/893n33XTMOk9rh9ujwv0awyhM2JtqJ\nPulJPrfV1jXhWEVdK98R2UJxljega11TjK2pYWtybE0NW5Nja2rYmhxbU8PWrGfKUt6tW7c2/7Co\nKKxZswYDBgwAAPTq1QsLFy5EVFQU7rnnnpb779y5E/fccw9KS0vx/PPPY8KECWYcJrWjoxdrPl1u\nZmrAmd0OFVYivVuC0uPZmdHfTXLBZi+jGbjOeqY3tqaGrcmxNTVsTY6tqWFrcmxNDVuznimfmH71\n1VfQNA1Tp05tGZQCwPnnnw+geSDa1NTUcvuIESPw7LPPwul0Yt++fXj77bfNOExqR0cv1ny6rrSh\n3viCzfK9Hhk9EhEX4/S57UhJteELaaRja2rYmhxbU8PW5NiaGrYmx9bUsDXrmTIwrapqDvjcc8/1\nuf2cc86Bw+FAY2Mj9u/f7/O1IUOGYPz48dB1HW+99ZYZh4n9+/dj7ty5GDduHIYMGYLRo0fjlltu\nwXvvvdehx62trcWyZcswbdo0fO9738PQoUMxadIkLFq0CEePHg3R0YdfqGaSACC3d9fZUO82Osub\nwsylw6EhJ9P3DcLl9qDwaI3ysdkVW1PD1uTYmhq2JsfW1LA1Obamhq1Zz5SBqdPZPGuQlpbmc3ts\nbCwyMjIAAAcOHAj4vosuughA8yeu4bZlyxZMmzYNr7/+Oo4ePQq3242ysjJs27YNN998Mx5//HGl\nx923bx8mTZqEZ555Bnv37kVNTQ2amppw+PBhvPTSS7jqqquwa9euEP824WH0QudUmEkCutZ1ngyX\n1DhUZy67xhsEW1PD1uTYmhq2JsfW1LA1Obamhq1Zz5SBabdu3QAAZWVlAV/LyckBYDz49J6N98SJ\nE+E7OAB79+7FvffeC7fbjWHDhmHFihX48MMPsXbtWlx++eUAgBUrVmDlypWixz1+/DhmzZqF48eP\nIyUlBQsWLMDWrVuxceNG3H///YiPj0dVVRVuv/12nDx5Mhy/Wki5QnB9J69uyXFIS471ua2krBZ1\nDZ3vUkJNIdpMD3SdNwi2poatybE1NWxNjq2pYWtybE0NW7OeKQPTwYMHQ9d1w7Pr5uTkQNd1w08N\nS0tLAQAeT3jXZC9ZsgT19fXIzs7G8uXLMXLkSKSmpmLw4MFYunQpJk2aBF3XsXTpUtEActGiRais\nrERCQgKWL1+O6dOnIzMzE3379sWsWbOwZMkS6LqOo0eP4rXXXgvjbxgaodxMDwC5fsscdB043An3\nLRifflx15rJrzMCxNTVsTY6tqWFrcmxNDVuTY2tq2Jr1TBmYjh07FgDw/vvv4x//+IfP1wYPHgwA\n+Oyzz3z2mTY1NWHt2rUAgPT09LAd28GDB5GXlwdN03DrrbciPj4+4D73338/HA4HKioqsHHjxqAe\nt6ysDBs2bGh53EGDBgXcZ9y4ccjJyUFUVBT27NnT4d8l3Iw206vuWQC6zpM2VNfFAoB+mSnQ/F4j\nO+NJCNiaGrYmx9bUsDU5tqaGrcmxNTVszXqmDEynTJnSspf0sccew8SJE7F7924AwGWXXYa4uDh4\nPB7ccMMNeO6557BixQpce+21+Oabb6BpGi688MKwHZv3U1xN0zB+/HjD+2RkZLScuGnLli1BPe6G\nDRvgdrsRFxeH6667rtX7rV+/Hrt27cJjjz0mO3ALGJ+trCMvdEan0+58T1qXKzSb6QEgPjYKGT0S\nfW6rqG5AeVW90uPZFVtTw9bk2JoatibH1tSwNTm2poatWc+UgWlMTAyeffZZJCUlQdd1HDlypGV5\nbmpqKm655Rbouo7y8nIsWbIEjz/+eMsniLGxsbjxxhvDdmz79u0DAGRlZQWcnOl0gwYNgq7rLQPq\n9niXJg8dOhRxcXE+X3O5Tq3Lj4mJkR6yZUI5kwR0nTO9hfLseABwZhe4cDNbU8PW5NiaGrYmx9bU\nsDU5tqaGrVnPlIEp0Hz5l7fffhvXXXcd0tPTkZ2d3fK1W265Bb/4xS+gaRp0XW/5l5qaiiVLluCs\ns84K23EVFhYCAPr06dPm/bKysgAAJSUlQe153b9/PzRNQ79+/QA0f9I6e/ZsDB8+HEOGDMGYMWPw\nu9/9LrIuF2O4KVxt7T0A9OmZhGi/majDxVXweAJnrCJZyN8gDDfUd643CLamhq3JsTU1bE2Oralh\na3JsTQ1bs55pA1MAOOOMM/DQQw8hLy8Pqam+swi//vWvsXHjRixYsAB33nknnnjiCWzevLnV5bWh\nUl5eDk3TkJISGM/pkpOTAQC6rrdcl7Utx44dA9B8iZwFCxbgV7/6FT788EPU19dD0zQcP34c//u/\n/4urr74an3/+ecd/ERMYXt+pA09Yp9OB7Ixkn9vqG90oKatVfkw7CvlJCLrADBxbU8PW5NiaGrYm\nx9bUsDU5tqaGrVnP1IFpe/r06YMZM2bgtttuw5QpU1oGg+HU0NAAAAHLbf3Fxp46Vbb3e9pSW9v8\nZF23bh1Wr16N733ve1i5ciW++OIL7NixA/Pnz0diYiIqKirwq1/9CsePH+/Ab2EOoz0LHVniAAC5\nmZ3/SRvqGbgcoxm44s41A8fW1LA1Obamhq3JsTU1bE2Oralha9YL6cA03Ncb9VdeXt7hx3AoXji3\nPfX1zZubjx8/jlGjRmH58uUYPnw4YmJi0K1bN8yYMQPPPfccHA4HTpw4gb/85S9hOY5QMr5gcwdf\n6LrAMgfDzfSKpx8HgJ5p8UiMj/a5reBoDRqb3MqPaTdsTQ1bk2NratiaHFtTw9bk2Joatma9kI7K\nJk6ciL/97W9obGwM5cMGaGpqwvLlyzFx4sQOP1ZCQgKA9j8FPf3r7X266r2PrjcHft9998HpdAbc\nZ+TIkRg3bhx0XQ/6MjRWCuX1nby6wjKHUJ8dT9O0gDcIj0fHkdJq5ce0G7amhq3JsTU1bE2Oralh\na3JsTQ1bs15IB6YJCQl46qmnMGnSJKxevRpNTU2hfHjU1dXh5ZdfxuWXX44nnngCiYmJ7X9TO5KT\nk6HrOmpqatq8n3dfqdPpDNgfa8R7bMnJyRg4cGCr9/v+978PACgtLW1Z/mtXxpvpQz8Dd7CzzcCF\nZebS4A2isPP83diaGrYmx9bUsDU5tqaGrcmxNTVszXohHZi+8cYb+NGPfoSioiL89re/xSWXXIIn\nn3wSX3/9dYce97PPPsOjjz6KsWPHYuHChSgpKcH/+3//D6+//nqHjzknJwfAqbPztqa4uBgAkJ6e\nHtTjes/y297lYJKSklr+/2D2rlop1KfRBoCkhBj07Bbvc9vxijpUnwzvp+5m8v+7ORwanI6OzVye\nabhvofPMXLI1NWxNjq2pYWtybE0NW5Nja2rYmvWiQvlgycnJeOqpp3DNNdfgsccew6FDh/DCCy/g\nhRdeQJ8+fTB69Gicd955OPvss3H22We3LKM9XU1NDfLz87F3717s3LkT27dvbznDra7ryM3NxUMP\nPYSLL744JMc8YMAAAEBBQQFqa2tb/RR29+7d0DQNgwYNCupxzz33XHz22WcoLy/HyZMnDX9XAC0n\nPYqKikL37t0VfgPzNIX4LG9euZmpOFZe53NbflEVzjv7jA4/th34z1yG4m+WY7ikpvPMwLE1NWxN\njq2pYWtybE0NW5Nja2rYmvVCOjD1uvjii/H6669j3bp1eO6551BQUIBvv/0Wr7zyCl555ZWW+8XE\nxCApKQkJCQlobGxETU0NTp486fNY3n2a5557LubMmYNJkyZB0zo2e3G6sWPHAgDcbjfy8vJwxRVX\nBNynpKQE+/btAwCMGTMmqMcdN24cVq5cCY/Hg02bNmHKlCmG99u+fTsAYNiwYSqHb6pwLA0BmpeH\nfLSnxOe2Q0WVneeFzm8GLrqD+zwAILtXMhwOzecaYoeKqqDrekifH1Zha2rYmhxbU8PW5NiaGrYm\nx9bUsDXrhe1yMVFRUfjJT36CjRs34o9//CMuueQSREdHQ9f1ln8NDQ0oKyvDt99+27LH8vSvx8bG\nYtKkSXj++eexbt06TJ48OeT/I/bt2xcXXHABdF3HM888Y7jXdNGiRfB4POjWrVurA0x/o0ePRlZW\nFnRdx5IlSwzPWLxhwwZ88skn0DQN06ZN6/DvEm6hPo22V2ffUO//dwvFm0NMtBN90pN8bquta8Kx\nirpWviOysDU1bE2Oralha3JsTQ1bk2Nratia9cLyienpHA4HLr30Ulx66aWoq6vDRx99hC+//BIH\nDhxAcXExqqqq0NTUhNjYWCQnJ6Nv374488wzMWLECAwfPjyoM+B21AMPPICf/vSnyM/Px4wZM3Df\nffdh0KBBKC4uxrJly7B582ZomoY77rjD53hKS0sxa9YsaJqGCRMm4O677275mtPpxKOPPoqbb74Z\nxcXF+PGPf4y77roLF110EVwuF9avX48//vGP0DQN559/Pq655pqw/54dFb4Xus59nSeX35KaUPzN\ngOYlNUdKfM/sll9UhfRuxsvGIwlbU8PW5NiaGrYmx9bUsDU5tqaGrVkv7APT08XHx2PcuHEYN26c\nmT+2XUOGDMHChQsxf/58HDhwADfddJPP1zVNw+zZszF9+nSf210uF/Lz86FpGo4ePRrwuBdffDGe\neuop/OY3v0FxcTHmzZsX8LiDBw/GkiVLIuLjfP8nLNDx048DQEaPRMTFOFHfeOq6ToeLq+Fye0L2\nomAVXdcD3iA6eoY3r9ysFOR95nvbwaJKfH9wRkge30psTY6tqWFrcmxNDVuTY2tq2JocW7OHyK4o\nhK655hqsW7cOU6ZMQWZmJqKjo5GamorRo0dj2bJlAYNKL++AsrWB5RVXXIG3334b119/PXJzcxEf\nH4/U1FScf/75WLBgAVauXIlevXqF7fcKpXDNwDkcGvpl+s7CudweFB5t+xI+kcDj0aH7vT+EYs8C\n0NqSms4xc8nW5NiaGrYmx9bUsDU5tqaGrcmxNXsw9RNTu+vfvz8WL14c9P179+6NvXv3tnu/jIwM\nPPDAA3jggQc6cniWC9dmegA4MysVXx0u97ntUFFlwAtgpAn1xZpPl9vbYElNJ9nrwdbk2JoatibH\n1tSwNTm2poatybE1e+AnphS0cFwXy8tw30IneNIaLqcJ0ZtDt+Q4pCXH+txWUlaLugZXSB7fSmxN\njq2pYWtybE0NW5Nja2rYmhxbswcOTCloYZ1N6qTLHAxnLUO4DyPXb4ZS14HDneDCzWxNjq2pYWty\nbE0NW5Nja2rYmhxbswcOTCloxktDQrP+vl9mCvy36R7qBE/YcO3z8OpSbxBsrU1sTQ1bk2Nratia\nHFtTw9bk2Jo9cGBKQQvnkzY+NgoZPRJ9bquobkB5VX1IHt8q4VxOA3TmJTVsTYqtqWFrcmxNDVuT\nY2tq2JocW7MHDkwpaG7D04/zSdsWwzeHEO1ZAIxn4A52ghk4tibH1tSwNTm2poatybE1NWxNjq3Z\nAwemFLRw7lkAms/05i/SlzkYbaZ3OkJ3zdre6UmI9nvhPFxcBY8n8OdGErYmx9bUsDU5tqaGrcmx\nNTVsTY6t2QMHphQ046UhoXvSGq+/j/AZuDCesh1ofqPJzkj2ua2+0Y2SstqQ/QwrsDU5tqaGrcmx\nNTVsTY6tqWFrcmzNHjgwpaCF+0mbY7Q0pDjSZ+DCu2cBAHIz+QYhxdbUsDU5tqaGrcmxNTVsTY6t\nqemMrYWaZQPT8vJyvP/++/jXv/6FlStXttxeWlqKqir+j2RHhtd4CuGTtmdaPBLjo31uKzhag8Ym\nd8h+htnCvZwGaG2vR6S/QbA1Kbamhq3JsTU1bE2Oralha3JszR5MH5hu2rQJP/vZz/CDH/wAN998\nM+6//348+uijLV9fs2YNLr74Yjz88MMcoNpMuGeTNE0LeNJ6PDqOlFaH7GeYLdyzlkAnXVLD1sTY\nmhq2JsfW1LA1Obamhq3JsTV7MG1g6na7MW/ePNx555348ssvoet6y7/TFRYWoqmpCatWrcLUqVNR\nUFBg1iFSOwxnk0x40uZH8GxSuPd5AK3MwEX4khq2JsfW1LA1Obamhq3JsTU1bE2OrdmDaQPT3/72\nt1i/fj10XUdycjKmTp2KqVOnBtxvwIABSEhIgK7rKCoqwq233oqmpiazDpPaYDibFPL194FP2oMR\nPJsU7gs2A0BSQgzOSIv3ue1YeR2qTzaG9OeYia3JsTU1bE2Oralha3JsTQ1bk2Nr9mDKwPSTTz7B\n2rVroWkaxo8fj40bN2Lx4sW47LLLAu57ww03YOvWrbjwwgsBAF9//TXWrVtnxmFSO9weE17oeneu\nU5Ab7fPwP114KBiduj0/gt8g2JocW1PD1uTYmhq2JsfW1LA1ObZmD6YMTFevXg0AyMrKwjPPPIO0\ntLQ275+Wlobnn38eWVlZAIC333477MdI7XO5jDbTh3aZQ3avZDj8rht1qKgqYMl3pDCagXM6Qv+0\n62wb6tmaHFtTw9bk2JoatibH1tSwNTm2Zg+mfWKqaRqmTZuGmJiYoL4nJiYGP/7xj6HrOr766qsw\nHyEFw3/PgtOhQdNC+0IXE+1En/Qkn9tq65pwrKIupD/HLMab6UP7NwM634Z6tibH1tSwNTm2poat\nybE1NWxNjq3ZgykD0+PHjwMAzjzzTNH35eTkAADPzmsT/rNJod5I72V0nadIXeZgxnWxgM63oZ6t\nybE1NWxNjq2pYWtybE0NW5Nja/ZgysA0Pr55o29tba3o+yoqKgAASUlJ7dyTzOA/mxTq/QpenWmZ\ngxnXxQKAjB6JiItx+tx2pKQaboOfHwnYmhxbU8PW5NiaGrYmx9bUsDU5tmYPpgxMs7OzAQA7duwQ\nfd+mTZsAAP369Qv5MZGc/2xSOGaSgM61zMFwn0cYZi4dDg39/M6Q1+TyoOBYTch/lhnYmhxbU8PW\n5NiaGrYmx9bUsDU5tmYPpgxMx40bB13X8c477+CTTz4J6nteffVVfPDBB9A0DWPGjAnzEVIwApaG\nhHgjvZfRDNzBCJ2BM+P0416GbxCFnePvxtbax9bUsDU5tqaGrcmxNTVsTY6t2YMpA9Of//znSE1N\nhcfjwZw5c7Bq1SrU19cb3re0tBSPP/445s+fDwBITEzEzJkzzThMaoOu6wGn0g7XnoVuKXFIS471\nua2krBZ1Da6w/LxwMvOF7kzDJTWRN3PJ1tSwNTm2poatybE1NWxNjq2pYWv2YMrANDU1FU8++SSc\nTifq6urw8MMPY+TIkfjNb37Tcp+ZM2diwoQJGD9+PFasWAGPxwOHw4HHHnsM3bp1M+MwqQ1G13cK\n1xMWCLxws64Dh4sj70lr1mZ6oLUlNZE3A8fW1LA1Obamhq3JsTU1bE2Oralha/ZgysAUAMaOHYu/\n/OUvOOOMM5pnc1wuVFVVtZy+eufOnfj222+h6zp0XUdycjKWLFmCSZMmmXWI1AajTdlhfaHrJE9a\nwzeIMJx+HAD6ZabA/2zwhyLwzYGtqWFrcmxNDVuTY2tq2JocW1PD1uzBtIEpAPzgBz/AO++8g/nz\n5+P73/8+4uLiWgaiuq7D6XRi6NChuPvuu7Fp0yZMmDDBzMOjNhgvcQjPExZo7UxvkfekNbxgc5je\nIOJjo5DRI9HntorqBpRXGy+btyu2poatybE1NWxNjq2pYWtybE0NW7OHKLN/YEJCAmbOnImZM2dC\n13VUV1ejpqYGcXFxSE1NhdPpbP9ByHRmnUbbq9PMwBldsDmsf7cUFB/3vSzToaIqdBsQF7afGWps\nTQ1bk2NratiaHFtTw9bk2JoatmYPpn5i6k/TNKSkpCArKwvdu3fnoNTGzDqNtlfv9KSAF4T84ip4\nPIHHYWdm7lkAOseZ3tiaGrYmx9bUsDU5tqaGrcmxNTVszR4sHZhS5DDzbGXex+6XmexzW32jGyVl\nta18hz2ZPXN5Zie4phhbU8PW5NiaGrYmx9bUsDU5tqaGrdmDKUt5b7zxRqXvczgciImJQWpqKjIy\nMjB48GCMHj0acXFd+2NuK5j9QgcAuZmp+KbAd/boUFEVsnomhfXnhpLh0pAwbaYHgByjvR7FkTUD\nx9bUsDU5tqaGrcmxNTVsTY6tqWFr9mDKwHTHjh3QNA26rrechVdVamoqHn74YZ6t12SGSxzCuDQE\naG1DfSUuHpYV1p8bSma/QfRMi0difDRq65pabis4WoPGJjdioiNjqTxbU8PW5NiaGrYmx9bUsDU5\ntqaGrdmDKUt5L7roIlx00UVITm7+qN97Ft74+Hj0798fQ4cORf/+/ZGUlNTyNe/9Tr+/ruuoqKjA\n3XffjXXr1plx6PSdJpM3hQOtbaiPrGUOZl9PTNO0gDcIj0fHkdLqsP3MUGNratiaHFtTw9bk2Joa\ntibH1tSwNXswZWC6fPlyXHLJJaiuroau65g0aRJWr16NnTt3Yv369Vi1ahXWr1+Pjz/+GOvXr8dP\nfvITAIDT6cSiRYuwa9cu5OXlYf78+ejevTt0Xcfvfvc7lJSUmHH4BMBt+IQN3xIHoJUZuAhb5mDN\nzGXgG0R+BJ0hj62pYWtybE0NW5Nja2rYmhxbU8PW7MGUgemuXbvwxBNPQNM03HfffViyZAmGDh1q\neN9zzjkHjz76KBYtWgS3240FCxbg8OHD6NWrF2bOnInly5cjNjYWDQ0N/NTURFbsWUhKiMEZafE+\ntx0rr0PNycaw/txQMrwuliPcez0i+5pibE0NW5Nja2rYmhxbU8PW5NiaGrZmD6YMTF988UW43W6M\nGjUKs2fPDup7pk6diksuuQSNjY147rnnWm4/55xzcMUVV0DXdfz73/8O6XHu378fc+fOxbhx4zBk\nyBCMHj0at9xyC957772Q/py6ujpMnDgRAwcOxLPPPhvSxw4Xs89W5hXpF242ezM9YDwDdzCCZuDY\nmhq2JsfW1LA1Obamhq3JsTU1bM0eTBmYfvTRR9A0DZMnTxZ932WXXQYA+PDDD31u937aWlxcHJoD\nBLBlyxZMmzYNr7/+Oo4ePQq3242ysjJs27YNN998Mx5//PGQ/axFixbh8OHDHT4RlJkMZ+DCvMQB\naO102pHzpDX7ulgAkJ2RDIfDt61DRVUte7btjq2pYWtybE0NW5Nja2rYmhxbU8PW7MGUgWlFRQUA\nICEhQfR93svCVFb6hp2WlgYAKC8vD8HRAXv37sW9994Lt9uNYcOGYcWKFfjwww+xdu1aXH755QCA\nFStWYOXKlR3+Wdu2bcPq1asjalAKtDKTZMoMXGRvqDd7Mz0AxEQ70Sfd9xTttXVNOFZRF9afGyps\nTQ1bk2NratiaHFtTw9bk2JoatmYPpgxMu3fvDgD44osvRN/3+eef+3y/14kTJwDIB7qtWbJkCerr\n65GdnY3ly5dj5MiRSE1NxeDBg7F06VJMmjQJuq5j6dKlOHnypPLPOXHiBB566KGWS+dEEuM9C+Ef\nXEf6hnrDs+OZMHOZm2m0oT4y3iDYmhq2JsfW1LA1Obamhq3JsTU1bM0eTBmYjhw5ErquY/Xq1Thw\n4EBQ33Pw4EGsXbsWmqbhggsu8PnaRx99BADIycnp8LEdPHgQeXl50DQNt956K+Lj4wPuc//998Ph\ncKCiogIbN25U/lkPPfQQysrKcM0113TkkC1hxRIHAMjokYi4GN/rOR0pqYbb4HjsyHgzvUVvEBGy\npIatqWFrcmxNDVuTY2tq2JocW1PD1uzBlIHpz3/+cwBAQ0MDZs2ahXfeeafN+2/ZsgWzZs1CXV3z\nR9nTp09v+drmzZuxZcsWaJqGUaNGdfjY3n33XQDN1xMaP3684X0yMjJw7rnnthybijVr1mDr1q3o\n3bs3fvOb3yg9hpWaXAZLHEyYSXI4NPTzO2tZk8uDgmM1Yf/ZoeD/QhfldJiyjDuSl9SwNTVsTY6t\nqWFrcmxNDVuTY2tq2Jo9RJnxQ4YPH4577rkHv//971FeXo677roLGRkZGDFiBHr37o3Y2FjU1dWh\nsLAQn3/+OUpKSlqWut54440YOXIkgOYlt8899xx0XUdcXJzPgFXVvn37AABZWVkte1eNDBo0CLt3\n78bu3bvFP+PIkSNYtGgRHA4HFi9ejMTEROXjtYrbY82eBaD5SfvVYd/9xIeKqtAvI3CWyW78rycW\nHeYzvHlF8gwcW1PD1uTYmhq2JsfW1LA1Obamhq3ZgykDUwCYM2cO4uLi8Ic//AG1tbUoLi7GW2+9\nFUkLsPkAACAASURBVHA/74A0Li4Od955J2688caWrx08eBC6riMqKgqPPPIIMjIyOnxchYWFAIA+\nffq0eb+srCwAQElJCTweDxxBXtvI4/Fg3rx5qKurww033NAyyI40RpvpnSbsWQBaedIWVmL8iLb/\nN7MD/9O2h/uaWF7dUuKQlhSLipqGltuKy2pR1+BCfKxpT3slbE0NW5Nja2rYmhxbU8PW5NiaGrZm\nD+b81b9z/fXXY+PGjfjlL3+Jc845B7quB/zLysrC7Nmz8eabb/oMSgEgMzMT119/Pf75z3/i6quv\nDskxlZeXQ9M0pKS0PZuTnJwMoHngXFUV/Efsf/7zn/H555/j7LPPxt13392hY7WSVXsWgMg+BXnA\n0hATltN4+b9B6DpwuNj+y0PYmhq2JsfW1LA1Obamhq3JsTU1bM0eTB+K9+jRA3fffTfuvvtuVFVV\n4ejRo6ioqEBsbCwyMjLQs2fPVr/3gQceCPnxNDQ0z1B4L03TmtjY2IDvac///d//YdmyZYiKisJ/\n//d/IyYmRv1ALWbVBZsBoF9mCjSt+YnqdShCnrD+M5dm/c2A5iU1n+0/5nPboaJKDMzp3sp32ANb\nU8PW5NiaGrYmx9bUsDU5tqaGrdmDqZ+Y+ktJScHZZ5+NkSNH4rzzzmtzUBouwS7JlWpoaMDcuXPh\ndrtx2223tZw8KVK5LNpMDwDxsVHI6OG7L7eiugHl1fWm/HxVHo8Ot8dvz4KpL3RG+xbs/wbB1uTY\nmhq2JsfW1LA1Obamhq3JsTX7sHRgGqxPP/00bI/tvRZqe5+Cnv719j5dBYAnnngChw4dwtChQ3HL\nLbd07CBtwPi6WHzStsXwBAQmbaYHWjvTm/2X1LA1Obamhq3JsTU1bE2Oralha3JszT5MXcpbVlaG\nzZs3Iz8/H3V1dfB4PC0nO/LSdR0ulwsNDQ2orq7G/v37cfz4cezZsycsx5ScnAxd11FT0/bprL37\nSp1OJ1JTAwM63fvvv4+VK1ciLi4OixcvDtunsmay/oUuFTu+LPa5Lb+oEiMGpJt2DFKGF2s28W/W\nOz0JUU6Hz/92+cVV8Hh0OEy4NpcqtibH1tSwNTm2poatybE1NWxNjq3Zh2kD0zfffBMPPfQQ6utl\nH+fruh7W6wjl5OTgo48+ajk7b2uKi5ufZOnp7T+x3nzzTQBAfX09Jk+e3Or9dF3Hs88+i2effRYA\nsHXr1paz/9qN0Vneokw6yxsA5GYGzsAdLLT3DJzLHbicxmniC12U04HsjGQcLDw161bf6EZJWS2y\neiaZdhxSbE2Oralha3JsTQ1bk2NratiaHFuzD1P+6t9++y3uu+8+1NXVGZ6Jt7V/ADBw4EDMmjUr\nbMc2YMAAAEBBQQFqa2tbvd/u3buhaRoGDRoU1ONqmtbmP//72f1TVaPN9DFRTtN+fm5vg2UOxfZe\n5tDkcgfcFmPiWd6A1s6QZ+83CLYmx9bUsDU5tqaGrcmxNTVsTY6t2Ycpf/WXX34ZLpcLmqbhwgsv\nxHPPPYc333wTV155JTRNw7Rp0/D2229j9erV+N3vfodzzjmn5Xuvu+463H///WE7trFjxwIA3G43\n8vLyDO9TUlKCffv2AQDGjBnT7mM+8sgj2LlzZ5v/gOZB6Zw5c7Bz5058+umntv20FAAamwKftGae\nSrtnWjwS46N9bis4WmN4XHZhtDQk2uQXuki8cDNbk2NratiaHFtTw9bk2JoatibH1uzDlL/6f/7z\nHwDN1yH961//inHjxuGss87CD3/4Q+i6ji+++AK5ubkYOnQofvazn+HVV1/FxIkToes6Fi5ciNLS\n0rAdW9++fXHBBRdA13U888wzhntNFy1aBI/Hg27dumHKlCntPmZ0dDTi4+Pb/Gd0XzszetLGRJv3\npNU0LeBJ6/HoOFJabdoxSBm/0Jk3awm0tqHe3jNwbE2Oralha3JsTQ1bk2NratiaHFuzD1NKLS4u\nbvlkNDr61CzKeeedBwA4ePAgysvLW26Pjo7G4sWL0aNHD9TX1+OVV14J6/E98MADcDgcyM/Px4wZ\nM7B9+3aUl5djz549uP322/HOO+9A0zTccccdPmfkLS0txaRJkzB58mQ8/fTTYT1Gq9n1SZtv49kk\no9lBW8zA2X5JDVuTYmtq2JocW1PD1uTYmhq2JsfW7MOUv7p372afPn18bu/bt2/LJ4XepbJe8fHx\nuOqqq6DrOj744IOwHt+QIUOwcOFCREVF4cCBA7jpppswatQoTJs2DZs3b4amaZg9ezamT5/u830u\nlwv5+fnIz8/H0aNHw3qMVjOcgTP7SWuwod7Os0lW7/MAgKSEGJyR5vtp/LHyOtScbDT1OCTYmhxb\nU8PW5NiaGrYmx9bUsDU5tmYfppSalNT6GaX69u0LADhw4EDA17x7TQ8fPhyeAzvNNddcg3Xr1mHK\nlCnIzMxEdHQ0UlNTMXr0aCxbtgzz5s0z/D7viYzCeeZgO2g02Bhuhxk4W7/QNVm7nMbLeBbOvn83\ntibH1tSwNTm2poatybE1NWxNjq3ZhymXi0lPT0dlZSUKCgoCvtavXz8cOHAAX331VcDXnM7mJ1J1\ntTnr0vv374/FixcHff/evXtj7969Sj/L/xNiuzN60pq9zCE7IxkOhwaP59RpvQ8WVYb9kkKqjN4c\nzDwBgVduVio+3uO7T/tQYSXOO+sM048lGGxNjq2pYWtybE0NW5Nja2rYmhxbsw9T/uojR46Erut4\n7bXX0Njo+5H0mWeeCV3XW06QdDrvoC82NtaMw6Q2WL2ZvvnnOdEn3ffT99q6JhyrqDP1OIJlvJzG\n3FlLIPJOQc7W5NiaGrYmx9bUsDU5tqaGrcmxNfswpdQrr7wSAFBYWIgbbrgBn376acvXvv/977d8\n7a9//WvL7V9++SVWrVrVfHav3FwzDpPaYLw0xILZpEyjDfX2fNLaYdYSiLwN9WxNjq2pYWtybE0N\nW5Nja2rYmhxbsw9T/uojRozAhAkToOs6PvvsM1x33XUt1wwdNWoUcnJyAAD/8z//g4kTJ2LatGmY\nMWMG6uqaZ1YmTpxoxmFSG4xmk6KcNnnS2vRMb01u6y/YDAAZPRIRF+M783ekpBpug83+dsDW5Nia\nGrYmx9bUsDU5tqaGrcmxNfsw7a/+5JNPYvLkydD15vXm3pMeORwOLFq0CLGxsdB1HUeOHMHevXvh\ncrkANJ8A6frrrzfrMKkVTX4zcNFRDkv2CUTShvpGgxk4K/YsOBwa+vmdIa/J5UHBscBr9toBW5Nj\na2rYmhxbU8PW5NiaGrYmx9bsw7S/emxsLJ5++mm8+uqrmDNnjs+lY4YPH46VK1e2LOvVdR1xcXGY\nNm0a/v73v3OPqQ34z8BZMZMERNgMnOE+D/P3LACR9QbB1uTYmhq2JsfW1LA1Obamhq3JsTX7MOWs\nvKcbPHgwBg8eHHD7oEGD8Pe//x11dXWorKxEjx49EB0dbfbhUSsa/Z60Zp963KtbShzSkmJRUdPQ\ncltxWS3qGlyIjzU95zb5z1oC1uxZAIzfIPKLKoERfQzubS22JsfW1LA1Obamhq3JsTU1bE2OrdmH\nKX/10tJSlJaWBpyR10h8fDwyMjIQHR2NmpoafPDBB3jzzTdNOEpqi/9sUrQF13fy8n/S6jpw2IbX\nebLDRa69jM70drAwMmYu2Vr72JoatibH1tSwNTm2poatybE1+zDlrz5u3DhccskleO+990Tft23b\nNsyePRuPPfZYmI6MguF2e3yuRQUA0RZspPcyXuZgvyet/6wlAERZNHPZLzMF/ltM7HjRZramhq3J\nsTU1bE2Oralha3JsTQ1bsw/TavWe9EjCewKk6urqUB8OCdhp7T3Q2r4F+z1p7TQDFx8bhYweiT63\nVVQ3oLy63pLjaQ1bU8PW5NiaGrYmx9bUsDU5tqaGrdlHSBd5f/zxxygpKWnz6ydPnmz3cTweD6qq\nqvDiiy8CANLS0kJ2jCRnPJPEGbj2NDXZZ88C0PwGUXy81ue2Q0VV6DYgzqIjCsTW1LA1Obamhq3J\nsTU1bE2Oralha/YR0oGpy+XC3LlzDU9Lres6XnrpJfFjapqGMWPGhOLwSJHRpnCrZpIAoHd6EqKc\nDrhOu65TfnEVPB4dDof5p0RvTZPBdadiLFoaAjS/Qez4stjntvyiSowYkG7REQVia2rYmhxbU8PW\n5NiaGrYmx9bUsDX7CGmto0aNwrRp06Drus8/L//bg/k3fPhw3HfffaE8TBIyWuJg5UxSlNOB7Ixk\nn9vqG90oOVHbyndYo9FgBs7SmctM+y+pYWtq2JocW1PD1uTYmhq2JsfW1LA1+wj5+ZoffPBBXHXV\nVS3/res6brzxRmiahjvuuAPDhw9v9zE0TWs5O2+vXr1CfYgkZPSEter04165WSkBZyk7VFiFrDOS\nLDqiQEZLamIsPTuewZnebLakhq2pYWtybE0NW5Nja2rYmhxbU8PW7CPkA9OkpCSMGjXK8GsDBgxo\n9WtkX3abgQOaT6e9Bd/63HaoqBIXD8uy6IgCuQz/bta9QfTsFo/E+GjU1jW13FZwtAaNTW5LT45w\nOramhq3JsTU1bE2Oralha3JsTQ1bsw9Tan3xxRfxwgsvBPVpKdmP8dnKrJ6BM9pQb69lDkYzl1bu\n9dA0LeAMeR6PjiOl9jnrNVtTw9bk2JoatibH1tSwNTm2poat2Ycpf/VRo0Zh1KhR6N69uxk/jkLM\n+PTj1s7AGZ6CvNheyxyMNtNbv6Qm8A0i30bLQ9iaGrYmx9bUsDU5tqaGrcmxNTVszT5CupS3tLQ0\nlA/ng3tNrdNocJY3KzeFA0BSQgzOSIvH8Yq6ltuOldeh5mQjkhJiLDyyU5qa7Lekxu4b6tmaGrYm\nx9bUsDU5tqaGrcmxNTVszT5COjAdN26c4aViOkrTNOzZsyfkj0vBsePSEKB5Fu70FzoAOFRchfPO\nOsOiI/Jlz5lLey+pYWtq2JocW1PD1uTYmhq2JsfW1LA1+wj5X13lkjDB/CPr2HEmCbD/hZuNZi6t\n/rtlZyQHXDvsUFGlbZ5jbE0NW5Nja2rYmhxbU8PW5NiaGrZmHyH9xPT0y8RQ59HkttemcC/DfQuF\n9plNMpqBi3Ja+3eLiXaid88kfHvaBvqauiYcq6hDercEC4+sGVtTw9bk2JoatibH1tSwNTm2poat\n2UdIB6ZPPvlkKB+ObKLRYAbO6j0LQPMpyP3ZaUN9k98MXHSUIyxL3aXOzEr1eaEDgPyiKlu80LE1\nNWxNjq2pYWtybE0NW5Nja2r+f3t3HldVmf8B/HPYQRZxC3HNZRTEpdGyUnE3sVywckrNckpzHzNt\n2pyyMm2ZFrV1XjZuWWpOi6OmuYBLP7Vc0hQVXEFAEBBE9sv5/cFAXO4BeR7uuedc+LxfL1/Z4dzn\nPPf6uefyPfd5nsOsmYfxaSXT0x57b/ychaCG9eDlYd2Py8k3YNFYXc0IFV83M1y1BCq5cmmSITXM\nmhxmTRyzJodZE8esyWHWxDFrcpg18zD0lU9PT0dsbCyOHz+Os2fPIjOzdr/YzqrilSTA+LH3AODi\noqBVhVXLCouKkZCabVCPrBVUONEZvfR4KTNPqGfW5DBr4pg1OcyaOGZNDrMmjlmTw6yZh12H8lZH\nUlISVqxYgR07diAxMdHm502aNEH//v3x17/+FS1btnR090iD9ipvxp/ogJI37ZlLGVbbLiRmoVWQ\n7VUmR6v4urkbvMJbKTNfgWPW5DBr4pg1OcyaOGZNDrMmjlmTw6yZh0Nf+e+++w7Dhg3DqlWrkJiY\nqLn6bkpKCtatW4eRI0fim2++cWT3qBIVryQBgJtpribZvmnNcANii6UYxcXWK6e5GzyRvlSgvxfq\n+3pabUtKu4m8/CKDevQHZk0csyaHWRPHrMlh1sQxa3KYNXHMmrk47JX//vvv8fzzzyMvLw+qqsLP\nzw/9+vXD+PHjMWnSJIwbNw69evVCvXr1oKoqcnNzMX/+fGzZssVRXaRKFBSac5U3ALi9qTmHOWh9\nOJhhnkep1hU+IFQVuJhsgteNWRPGrMlh1sQxa3KYNXHMmhxmTRyzZi4OGcqbmpqKV199FQDg6emJ\nOXPm4JFHHoGHh4fNvvn5+fjqq6/wwQcfIC8vDy+//DJ69uyJhg0bOqKrpKFI401rhjkLANCqqR8U\npeSNWuq8Ca7AaS49bpLXDChZ6e3Y2VSrbReuZKJjqwYG9agEsyaOWZPDrIlj1uQwa+KYNTnMmjhm\nzVwc8sqvWbMGubm5cHFxwdKlSzFhwgTNohQoKVyfeOIJLFmyBIqiIDc3Fxs3bnREN6kSmleTTDI0\nxMfLHUEN61ltu34jHxk38gzqUQmtBQjMctUSqGzegvFX4Jg1ccyaHGZNHLMmh1kTx6zJYdbEMWvm\n4pBXfu/evVAUBYMHD0afPn2q9Zjw8HAMGTIEqqpi586dOveQqqL1pjXT1SQzvmm1rsCZ5aolUNlK\nb2a4csmsiWLW5DBr4pg1OcyaOGZNDrMmjlkzF4e88gkJCQBKik0RpfvHx8fbvU9Ufdrj7839pjV6\nQr3WPA+zLD8OAM2a+MKtwuT+i0lZNgsAOBqzJo5Zk8OsiWPW5DBr4pg1OcyaOGbNXByS1ry8kq/p\nvb29hR5Xuv/Nmzft3ieqPu05C+Z5097elFfgRLm5uqBlkJ/VtrwCC5LTjX2vMWvimDU5zJo4Zk0O\nsyaOWZPDrIlj1szFIa98o0aNAABnzpwRelzp/o5a+Ojs2bOYN28e+vbti7CwMPTu3RtTpkzB3r17\na9RudHQ0Zs2ahb59+6Jz587o3r07Ro8ejQ8//BDp6el26r1+zLzKG2DOYQ7a9xIzz4cDYM4hNcya\nOGZNDrMmjlmTw6yJY9bkMGvimDVzcUha77jjDqiqio0bN+LGjRvVesyNGzewceNGKIqCO+64Q+ce\nAjt37sTo0aOxadMmpKSkwGKxIC0tDVFRUZg0aRLefPNN4TYtFgvmzp2Lp59+Gj/99BNSUlJQVFSE\nnJwcxMTE4JNPPsHw4cNx7NgxHZ6R/RRazH0FrnGgN+p5u1tti0/J1jxBO4rmic5Ew2mASj4grhj8\nAcGsCWPW5DBr4pg1OcyaOGZNDrMmjlkzF4e88qNHjwYApKWlYdq0abf8ljA9PR1Tp07FtWvXAAAj\nRozQtX8xMTF49tlnYbFY0LVrV6xevRoHDhzAN998g8GDBwMAVq9ejbVr1wq1++677+K///0vFEXB\noEGD8NVXX+HAgQPYtGkT5s6dCx8fH6SlpWHKlClISUnR46nZRWGhuYc5KIpiczWpuFjF5avVuwii\nhwKTL0AAlCxBXpHRV+CYNXHMmhxmTRyzJodZE8esyWHWxDFr5uKQV75Xr17o168fVFXFr7/+ioiI\nCLz11luIjo7GuXPnkJSUhHPnziE6OhpvvfUWIiIicPjwYSiKgj59+qBv37669q/0nqktW7bEihUr\n0KNHDwQEBKBTp05YunQphg4dClVVsXTpUuTk5FSrzZSUFKxevRqKomDEiBFYunQpunXrhoCAALRr\n1w5PPvkkVq1aBTc3N2RmZuLzzz/X9TnWhLNeTTJyQr3TDg1JMuGQGmatSsyaHGZNHLMmh1kTx6zJ\nYdbEMWvm4rC0vv322+jWrRtUVUVWVhZWrFiBKVOm4IEHHsCAAQPwwAMPYMqUKVixYgUyMzOhqirC\nwsLw3nvv6dqv8+fPIzo6GoqiYOrUqZoLND3//PNwcXHB9evXsX379mq1u2PHDhQVFQEAZs+erblP\nWFgYBg0aBFVVERUVJf0c9KZ1NclMV+AA802oN/tVSwDw9fFAo/rWeU/NyEV2ToFBPWLWZDBrcpg1\nccyaHGZNHLMmh1kTx6yZi8NeeX9/f6xatQozZsyAn58fVFWt9E9AQACmTZuGtWvXwtfXV9d+7dmz\nB0DJ8IJ+/fpp7hMUFISQkBAAqPY9VVNSUuDt7Y1GjRqhadOmle7XqlWrsv3NSmv58YpLVxtNe0K9\ncSc6rQ8HMy1AUEr7KpyRrxuzJopZk8OsiWPW5DBr4pg1OcyaOGbNXNwceTAPDw/MmDEDkyZNwpEj\nR3Ds2DGkpaXh5s2b8PHxQaNGjdC5c2f06NEDXl5eDunT6dOnAQDBwcGoX79+pfuFhobi5MmTOHny\nZLXanT17NmbPnn3LW91cunQJQEnhblZFFd607m4uUBTFoN5oaxnkBxcXxeq+ThcSS755N6KvWkND\nzDZnASj5gPjl1FWrbRcSM9G5bSND+sOsiWPW5DBr4pg1OcyaOGZNDrMmjlkzF7sWpsXFxXBxufU/\npqenJ+655x7cc8899jy8lCtXrgAAmjdvXuV+wcHBAIDk5ORqP08AqFevXqU/S0lJwe7du6EoCrp3\n717NHjteQYVhDma8kuTh7opmjX0RX24CfXZuIa5dz0PjQLH759qD5hU4d3PNWQC0r8BdNPLKJbMm\njFmTw6yJY9bkMGvimDU5zJo4Zs1c7JrYvn374p133kFsbKw9m9VVRkYGFEW55TeWfn4lN7ctnSNr\nD/Pnz0d+fj4AYPz48XZpUw8Vlx8309Lj5Wnf58mYyeHaN7k23weE1pCa80YuQsCsCWPW5DBr4pg1\nOcyaOGZNDrMmjlkzF7u+8qmpqfjiiy8wYsQIjB49GmvWrEFGRoY9D2F3pYXhrYYOe3p62jymJt58\n882yRZeGDx+OO++8s8Zt6qWwwv2l3E22wlsp7eW0jXnTas3zMOOVy6CG9eDlYf3BdTn5Biwa90Jz\nBGZNHLMmh1kTx6zJYdbEMWtymDVxzJq52PWV9/DwKFvAKCYmBgsXLkR4eDimT59utUqtmVR3SK49\nLVq0CKtWrYKiKOjQoQMWLFjg8D5Ul8VSjHLTAAAA7iabSF/KTBPqtecsmO/KpauLglYVVsgrLCpG\nQmq2w/vCrMlh1sQxa3KYNXHMmhxmTRyzJodZMxe7Jvbnn3/GokWL0KtXL7i4uEBVVRQWFmLXrl2Y\nOXMm+vTpg4ULF1Z7ASFH8PHxAXDrb0HL/1x2YabCwkLMmzcPK1euhKIoaNeuHZYvX655ixqz0LyS\nZMKx94C5hoYUFDrHKm+AeT4gmDU5zJo4Zk0OsyaOWZPDrIlj1uQwa+Zi11fe19cXkZGRWL58Ofbs\n2YMXX3wRXbp0KfsWNSMjA2vWrMFDDz2E4cOH44svvkBqaqo9uyCs9NY12dlVX3EonVfq6uqKgADb\nYNxKZmYmJk6ciE2bNkFRFISFhWHVqlVo2LChVL8dxVlWKwOAQH8v1Pf1tNqWlHYTefmO/6beWeYs\nAJVNqHf8BwSzJodZE8esyWHWxDFrcpg1ccyaHGbNXHR75Rs2bIgJEyZg/fr1+OmnnzBr1iy0adOm\nrEiNi4vDO++8g379+mHSpEnYsmULCgocf6PY1q1bA/hjdd7KJCUlAQCaNGkifIzLly9jzJgx+PXX\nX6EoCsLDw7Fq1SoEBgYKt+VohU5yf6dSrSu8aVUVuJhskiuXJhwaAgC3NzXHFThmTQ6zJo5Zk8Os\niWPW5DBr4pg1OcyauTgksS1atMC0adOwZcsW/Oc//8HEiRPRpEkTqKoKi8WCffv24dlnn0Xv3r3x\nyiuv4OjRo47oFgCgQ4cOAICEhIQq7zl68uRJKIqC0NBQofZjY2PxyCOP4NKlS1AUBWPGjMEnn3xi\n6uG75aVl5tls8/J06O1vhZhlmENaZq7NNi9Pc57oWjX1s9lmxJAaZk0OsyaOWZPDrIlj1uQwa+KY\nNTnMmrk4/FJKaGgo/v73vyMqKgorV67Eww8/DH9//7LbsKxfvx5jx47Ffffdh08//RSJiYm69ic8\nPBwAYLFYEB0drblPcnIyTp8+DQDo06dPtduOj4/HxIkTkZ6eDkVRMHv2bCxYsMCQBZdkaQW+RRPb\nN4ZZtNGat3DF8W9arZNrc5O+bj5e7mjayPp+uxk38pFxw/ZDTk/MmhxmTRyzJodZE8esyWHWxDFr\ncpg1czGsQlIUBT179sTrr7+Offv2YdmyZYiIiIC3tzdUVcWlS5fw4YcfYtCgQXjiiSd060eLFi3Q\nvXt3qKqKJUuWaM41XbRoEYqLixEYGIiRI0dWq92ioiLMnj0b165dg6IoePHFF/H000/bu/u603rD\nao1xNwvtK3COPdFlZucjPcv6JNGkgQ/qebs7tB8itBcicOyVS2ZNHLMmh1kTx6zJYdbEMWtymDVx\nzJr5mOKrO3d3dwwaNAjvv/8+Dhw4gE8++QSjR4+Gr68viouLcfDgQV2P/8ILL8DFxQUXL17E2LFj\nsX//fmRkZODUqVOYMWMGtm3bBkVRMHPmTKsVea9evYqhQ4ciIiIC77//vlWbX3/9ddnw34iICDz4\n4IPIycmp8o8ZaZ0ktE4mZtGsiS/cKiyPfjEpC8UV11DX0UWtD4em5v1wALT/TR09oZ5ZE8esyWHW\nxDFrcpg1ccyaHGZNHLNmPqYbfH7p0iWcPXsW58+fr3LOpz2FhYVh4cKFmD9/PmJjY/Hkk09a/VxR\nFEycOBGPPvqo1faioiJcvHgRiqIgJSXF6mcrV64EAKiqii1btmDLli237EfpcGGzUFUVF5Os37Su\nLgpa3OZrUI9uzc3VBS2D/HC+3HCQvAILktNvIriRY/p9Icm5PhwA7ROxI6/AMWtymDVxzJocZk0c\nsyaHWRPHrMlh1szHFIXp6dOnsXXrVmzduhXx8fFl21VVRUBAACIiInTvQ2RkJMLCwrB8+XIcPHgQ\n165dg4+PDzp37oxx48ahf//+mo9TFMXqvwCQkZGBhIQEq223IrKvo1xNz0FOnvXS3S1u84O7SVcr\nK3V7sL/ViQ4oedM67ETnZMNpAOOH1DBrcpg1ccyaHGZNHLMmh1kTx6zJYdbMx7DC9Ny5c2XfJF68\neBFASSEKAG5ubujTpw9GjRqF/v37w8PDwyF9at++PRYvXlzt/Zs1a4aYmBib7YGBgZrbnY3WrCty\nEQAAIABJREFUG7bi8t5mVPKmjbfadiExE726BDvk+M42nAYAGgd6o563O27mFpZtS0jJRmGRxSEf\nbMyaHGZNHLMmh1kTx6zJYdbEMWtymDXzcWhheunSpbJiNC4uDsAfxSgAdOrUCaNGjcL999+PBg0a\nOLJrpEFrzLrWPZTMRvsGxI4Z5lBYVIz4qzestnl7uuK2Bj4OOb4sRVHQuqk/Tp5PK9tmKVZxOfkG\n2javr/vxmTVxzJocZk0csyaHWRPHrMlh1sQxa+ake2F65coVbNmyBVu3brX6FrG0IA0KCsLw4cMx\natQotG3bVu/ukIALSc43xAHQvtp13kHDHBJSbqDIYj1xv3XTALi4mG+odkVtmgVYneiAkquJjjjR\nMWvimDU5zJo4Zk0OsyaOWZPDrIlj1sxJl8L06tWr2Lp1K7Zs2YITJ06UbS8tRr29vTFkyBCMGjUK\nd999tynnV5JzDnEAAD8fDzSq741r1/+4aXJqRi6ycwrg66PvsHBnnK9QysgJ9cyaOGZNDrMmjlmT\nw6yJY9bkMGvimDVzsmthunr1amzduhXHjh0rK0JL/+vi4oKePXti1KhRGDJkCHx8zP1VeV2Xk1eI\n5DTrW9g08PdEfT9Pg3ok5vZgf6sTHVByRbFz20a6HtdZPxyAyibU63+iY9bkMGvimDU5zJo4Zk0O\nsyaOWZPDrJmTXe9junDhQhw9ehTFxcVQVRWqqqJt27aYM2cOdu3ahRUrVmDUqFEsSp1AxWXHAaC1\nk7xhAeNWLdO8J5aTXIFrGeRnM4TlQmKm1TxwPTBrcpg1ccyaHGZNHLMmh1kTx6zJYdbMya6FKVDy\nDWlgYCDGjx+PDRs2YPPmzZg8eTKCgoLsfSjSkeYQB5PfdLg8IybUq6pqc08sRQFaBTnH6+bh7opm\nja2XaM/OLcS163m6HpdZE8esyWHWxDFrcpg1ccyaHGZNHLNmXnYdyjtkyBCMHDkSffv2hZubKW6R\nSpKceYgDYMwVuIwb+cjMLrDaFtyoHrw8nee9cHuwv80qdReSMtE40Fu3YzJr4pg1OcyaOGZNDrMm\njlmTw6yJY9bMy67fmC5ZsgQDBw5kUVoLOPMQBwAIalgPnh7W93O6lHwDFkuxbsfUOpE603AaoJIP\niCv6fkAwa+KYNTnMmjhmTQ6zJo5Zk8OsiWPWzMvuQ3nJ+VmKVVxMtj7Rubu52AwbMDNXl5L7PJVX\nWFSMhNRs3Y7pzCu8lWrj4An1zJocZk0csyaHWRPHrMlh1sQxa3KYNfNiYUo2ktNuIr/AYrWtVZAf\nXF2dKy6OXrXM2YfTANonZj2H1DBrcpg1ccyaHGZNHLMmh1kTx6zJYdbMy7mSSw4RF3/dZpuzvWGB\nyibU6/emPZeg8bo1da7XLdDfC/V9rZeYT0q7ibz8Il2Ox6zJYdbEMWtymDVxzJocZk0csyaHWTMv\nFqZkI07jDduuRX0DelIzWicZva7A3cwtxJXUm1bb6vt6olF9L12Op6fWFT4gVBU2Q4XshVkTx6zJ\nYdbEMWtymDVxzJocZk0cs2ZuLEzJRqzGFbh2zZ3vRNeqqZ/NNr2GOZy7ov3hoCiKxt7m5sghNcya\nOGZNDrMmjlmTw6yJY9bkMGvimDVzY2FKVizFKs5XeNO6uSpONykcAHy83NG0YT2rbRk38pFxw/73\nedIaTuOMHw6A4+YtMGtymDVxzJocZk0csyaHWRPHrMlh1syNhSlZSUzNRm5+hYn0Tf3h7uZaySPM\n7fZmWm9a+19N0rpq2d4Jh9MAlaz0psMS5MyaHGZNHLMmh1kTx6zJYdbEMWtymDVzY2FKVjTnKzjp\nlSRAe5iDHhPqzyXYttm2uXNNpC/VrIkv3Cqs6HcxKQvFxapdj8OsyWHWxDFrcpg1ccyaHGZNHLMm\nh1kzNxamZKU2DXEAgNub2l6BO3/FvlfgsnMKkJRmPZG+gb8nGgZ42/U4juLm6oKWQdbzPfIKLEiu\n8BxrilkTx6zJYdbEMWtymDVxzJocZk0cs2Z+LEypjKqqOHo21Wa7M67wVkrrCtzRsykoLCq22zGO\nxWq8Zs0D7da+EbTmLfwSc9Vu7TNrcpg1ccyaHGZNHLMmh1kTx6zJYdbMj4UplYlLuI74qzestnl7\nuqJVkPNNpC/VONAbtzXwsdqWdbMAh0/b702785d4m20dWzv3ia5z20Y223ZpPE9ZzJocZk0csyaH\nWRPHrMlh1sQxa3KYNfNjYUpltILcq0szuLs5b0wURUG/7s1ttu/61T5v2owbeThyJsVme/gdtsd0\nJvd0bgpPD+sFFM4nZtpttTdmTRyzJodZE8esyWHWxDFrcpg1ccyac3DeBJNdFRYVI/roFZvtA+5s\nYUBv7GtAD9vn8MupZGTdLKhx29FHrthMMu/ctpHNVT9n4+Pljns6N7XZbo8PCGZNDrMmjlmTw6yJ\nY9bkMGvimDU5zJpzYGFKAIBfY67iRo71G79JAx90ur2hQT2yn+BGvghp3cBqW5FFxd5jtid2Ubt+\nvWyzTevE6owGdLd9HtFHEmCx1Gy+B7Mmh1kTx6zJYdbEMWtymDVxzJocZs05sDAlAJW8Ybu3gIuL\nYkBv7E/r5KP1nEVcSMy0uceWp4cr7u1ie+XKGXVp3xgNA7ystmXcyNdccEEEsyaOWZPDrIlj1uQw\na+KYNTnMmjhmzXmwMCVkZufjV40VvGrLlSQA6N3Ndu7F2cu2iweI0JpEf2/npvDxcpdu00xcXRT0\n+7Pt3IvdNRgewqzJYdbEMWtymDVxzJocZk0csyaHWXMeLEwJe45eQZHFetx96O0N0LRRPYN6ZH++\n3u7o2SnIZvvuw3Jv2iJLMaKPJNhsH9ijpVR7ZqX1YXfg9yTczC2Uao9ZE8esMWuVYdbkMGvimDU5\nzJo4Zk2OvbNmFBamhF0ab/badPWtlNZz2v1rvM1k+Oo4eiYF17PzrbY1CvBCWDvbZbudWcsgf5v7\nohUUFWPfb4lS7TFrzFplmDU5zJo4Zk0OsyaOWZPDrImzd9aMwsK0jrucnIW4+OtW2zzcXNC7azOD\neqSfP3dogvq+nlbbrmXm4UTcNeG2dmoMj+jfowVca8kcj/IG2mm+B7PGrN0KsyaOWZPDrIlj1uQw\na+KYNTn2ypqRWJjWcVrLSd8d1hT1vGvHuPvyXF1d0FdjDL7WFciqZOcU4ODvyTbba+NVSwDo060Z\n3FytT+CnLqQj6dpNoXaYNWbtVpg1ccyaHGZNHLMmh1kTx6zJsVfWjMTCtA6zFKvYfdh23H1tuBdW\nZQZqPLefjyciN7+o2m3sPXYFRRWW4O7QMhDNm/jVuH9mFODriR4ht9lsF5nvwayVYNaqxqzJYdbE\nMWtymDVxzJocZk2cPbJmNBamddiR01eRnpVnta2Bvye6/amJQT3S3+3BAWjd1N9qW16BRXNivBZV\nVbH9kMZS7bX4wwHQvrr406HLNif8yjBrJZi1W2PWxDFrcpg1ccyaHGZNHLMmp6ZZMxoL03LOnj2L\nefPmoW/fvggLC0Pv3r0xZcoU7N2715Tt1tR30edstvX7c+0cd1+e1pv2u+i4ak2qP3k+zWaOh5ur\nC/p0q31zPMrrEXIb/Hyshwtdu56LfdW86TWz9gdmrWrMmhxmTRyzJodZE8esyWHWxNU0a0ZjYfo/\nO3fuxOjRo7Fp0yakpKTAYrEgLS0NUVFRmDRpEt58801TtVtTZy9n4LjGJPLBPWvX8tlaBvRoAQ93\nV6ttV1Jv4uBJ23kIFW3cHWezrVeXYPj5eNitf2bk7uaKwXe1stn+n6g4qGrVHxDMGrMmglmTw6yJ\nY9bkMGvimDU5zJq4mmTNDFiYAoiJicGzzz4Li8WCrl27YvXq1Thw4AC++eYbDB48GACwevVqrF27\n1hTt2sN/omzfsD07BdXacfflBfh6YvBdtif0jbtjq3zTXkrO0ryxdWS/tnbtn1mNCG9jM6n+QmIW\njp5NrfJxzBqzJopZE8esyWHWxDFrcpg1ccyaHNmsmQELUwAffPAB8vLy0LJlS6xYsQI9evRAQEAA\nOnXqhKVLl2Lo0KFQVRVLly5FTk6O4e3WVGJqNv7vuO19jUb3b+ewPhhtVN+2qDgC5sylDJy6kF7p\nYzbuirXZ1q19Y7RtXl9j79qnYYC35ip5/9lt+7qUYtaYNRnMmhxmTRyzJodZE8esyWHWxFWWtW81\nvkU2mzpfmJ4/fx7R0dFQFAVTp06Ft7e3zT7PP/88XFxccP36dWzfvt3Qdu3hP1FxqDg8v2OrQITe\n3tBhfTBaUMN6uLdLsM32bzWuTAJASnoOoo/ajs+PrEMfDgAQ2c/2+f4Wew1xCdc19mbWAGZNFrMm\njlmTw6yJY9bkMGvimDU5Wlk7FpuKK6nZBvSm+up8Ybpnzx4AgKIo6Nevn+Y+QUFBCAkJAVAyZ9TI\ndmsqLTMXO3+xXTb6oQHtHXJ8M9G64njwZDLir96w2f5tlO1k+zbNAnDHnxrr1j8zahXkr7kUudZV\nOGbtD8yaOGZNDrMmjlmTw6yJY9bkMGviKsvaHo2i3UzqfGF6+vRpAEBwcDDq16/8K/7Q0FCoqoqT\nJ08a2m5Nfb/nvM2S0S2D/HBnaJBDjm8m7VsEoku7RjbbK16Fu34jH9sPXrLZ7+GB7aEotXtFPC0P\nanxA7DueiOQ06xs4M2t/YNbkMGvimDU5zJo4Zk0OsyaOWZOjlTWthbTMpM4XpleulFw5aN7cdix2\necHBJcMIkpOTUVx863sB6dVuTeTmF+HH/7tgs/3B/u3hUsuXHK+M1lW43YcTkJaZW/b/m/adR0GR\n9b9NcKN6uKez7dCSuqBTm4bo0DLQaltxsYrv9/yxnH12TgGzVgGzJo5Zk8OsiWPW5DBr4pg1Ocya\nOK2smX1l3jpfmGZkZEBRFPj7+1e5n59fyepnqqoiKyvLsHZr4sf/u4TcfIvVtiaB3gi/o3bf06kq\nf+7QxOYGzkWWYmzaex4AcC7hOjbvt/1wGN2/fa2/f1hlFEXRnKvx06HLyLpZgIJCC1ZuiWHWKmDW\nxDFrcpg1ccyaHGZNHLMmh1kTV1nWzMzN6A4YLT8/HwDg5eVV5X6enp42jzGi3Zo4eDIJ3g1ut9oW\n2a8d3Fzr7vUJRVEQ2a8d3v/qiNX2jbvjEBt/XXPIQwN/LwzoUfU34bXd3WFN0bRRPSRd+2PoUX6B\nBdPe3gl3N1dcu55r8xhmjVmTwayJY9bkMGvimDU5zJo4Zk2OVtbMrO4m/H9cXPR5CfRq154CfD0w\nSOP+UHVN+B3N0CjA9gJCZePwR/VtC3c3V82f1RWuLgoi+9reDywzu0DzA5VZK8GsiWPW5DBr4pg1\nOcyaOGZNDrMmrrKsmZX5qyed+fj4ALj1t5Xlf36rb0H1bNeexgz8E7w86vyX5nBzdan2KneNArxw\n392tdO6RcxhwZ0vNDwgtzFoJZk0OsyaOWZPDrIlj1uQwa+KYNTkiWTNanS9M/fz8oKoqsrOrvq9P\n6fxPV1dXBAQEGNauPfh6u+PpyM4Y3qeNQ47nDIbe09pm7kJFf+7QBIum94aPl7uDemVunu6ueGpk\n5yr3YdZsMWvimDU5zJo4Zk0OsyaOWZPDrImrTtbMos5ffmndujUOHTpUtopuZZKSkgAATZo0MbTd\nmnB1dcGD/dvhoQHt4evjofvxnImrqwumjO6C5z/aZ/OzNs0CMPGBUHT7k/7/Rs7m3i5N0e1PjXHs\nbKrVdnc3F4zo04ZZ08CsyWHWxDFrcpg1ccyaHGZNHLMmpzRr/3fAdoEoM6nzhWmHDh0AAAkJCbh5\n8ybq1aunud/JkyehKApCQ0MNbbcm5o3rjkH9O+l+HGfVqU1DTHygE/7935J7yjZp4IPHIkIQ3q1Z\nnV2e/VYURcHsR+7AS5/8jCup2VAUoH/3Fhg3tCOaBPoY3T3TYtbEMWtymDVxzJocZk0csyaHWRNX\nmrXY0ycQb3RnqlDnC9Pw8HAAgMViQXR0NIYNG2azT3JyMk6fPg0A6NOnj6Ht1kR9P89b71THje7f\nDgN6tEDGjTy0CvLnCa4aGgZ446PnBuBiYiaaNPCBH6/uVguzJo5Zk8OsiWPW5DBr4pg1OcyauIYB\n3pgztjse22J0TypX5+eYtmjRAt27d4eqqliyZInmnNBFixahuLgYgYGBGDlypKHtkv7q+3ni9uAA\nnuQEuLooaNu8Pj9QBTFr4pg1OcyaOGZNDrMmjlmTw6yJM/tLVecLUwB44YUX4OLigosXL2Ls2LHY\nv38/MjIycOrUKcyYMQPbtm2DoiiYOXOm1cq5V69exdChQxEREYH333/fbu0SERERERHVJXV+KC8A\nhIWFYeHChZg/fz5iY2Px5JNPWv1cURRMnDgRjz76qNX2oqIiXLx4EYqiICUlxW7tEhERERER1SUs\nTP8nMjISYWFhWL58OQ4ePIhr167Bx8cHnTt3xrhx49C/f3/NxymKYvVfe7VLRERERERUV7AwLad9\n+/ZYvHhxtfdv1qwZYmJi7N4uERERERFRXcI5pkRERERERGQoFqZERERERERkKBamREREREREZCgW\npkRERERERGQoFqZERERERERkKBamREREREREZCgWpkRERERERGQoFqZERERERERkKBamRERERERE\nZCgWpkRERERERGQoFqZERERERERkKBamREREREREZCgWpkRERERERGQoFqZERERERERkKBamRERE\nREREZCgWpkRERERERGQoN6M7QPrJzc21+v8zZ84Y1BMiIiIiIjJSxVogJyfHoJ5oY2Fai12+fNnq\n/1977TWDekJERERERGYSHx9vdBescCgvERERERERGYqFKRERERERERmKQ3lrsQEDBlj9f4sWLeDj\n42NQb4iIiIiIyCi5ublWU/0q1gpGU1RVVY3uBBEREREREdVdHMpLREREREREhmJhSkRERERERIZi\nYUpERERERESGYmFKREREREREhmJhSkRERERERIZiYUpERERERESGYmFKREREREREhmJhSkRERERE\nRIZiYUpERERERESGYmFKREREREREhmJhSkRERERERIZiYUpERERERESGYmFKREREREREhmJhSkRE\nRERERIZiYUpERERERESGcjO6A1Q9Z8+exb/+9S8cOnQIaWlpqF+/PsLCwjBu3Dj06dPHdO2S83JU\nJt544w2sWbMGixcvxqhRo+zWLjkPvbIWHR2NjRs34rfffkN6ejo8PDzQqlUr9O3bF4899hgaNGhg\nx2dBzkCvrG3fvh0bNmzAiRMncPPmTTRq1Ah33HEHxowZg7vvvtuOz4CchaM+Q3NzczFq1ChcunQJ\nM2bMwIwZM+zWNjkHPbJW+rvZrcyfPx/jxo2TOkZVFFVVVbu3Sna1c+dO/O1vf0NRUREURSnbXvpP\nN2HCBLz44oumaZecl6MysWPHDsyaNQuqqmLRokUsTOsgPbJmsVjw97//Hf/973+t2izfdsOGDfHR\nRx+hW7duNXsC5DT0yFpRURHmzp2LH3/80SZrpe3+5S9/wYIFC2rYe3Imjvy96h//+AfWr18PRVEw\nffp0FqZ1jF5ZGzt2LI4ePVrlPoqi4KWXXtKlMOVQXpOLiYnBs88+C4vFgq5du2L16tU4cOAAvvnm\nGwwePBgAsHr1aqxdu9YU7ZLzclQmdu3ahWeeeQa8JlZ36ZW1d999t6woHTRoEL766iscOHAAmzZt\nwty5c+Hj44O0tDRMmTIFKSkpejw1Mhk9s1ZalEZERGDdunXYv38/1q9fj4iICCiKgvXr1+Ozzz7T\n42mRCTny96qoqKiyopTqHr2ypqoqTp8+DQB49dVXceTIEc0/hw8fxiOPPGL351XaCTKxyZMnqx06\ndFCHDBmi5uTk2Pz8b3/7m9qhQwf17rvvVm/evGl4u+S89M5EcXGx+uGHH6ohISFqx44d1Q4dOqgd\nO3ZUv/32W3t0n5yIHlm7evWq2qlTJ7Vjx47qc889p7nPiRMnyvZ5/fXXa/QcyDnonbVnn31Wc5+p\nU6eqHTp0UO+66y41Pz+/Rs+BnIOjfq9KS0tTe/XqZfU5unTp0pp0nZyMXlmLi4sry9TZs2ft2eVq\n4zemJnb+/HlER0dDURRMnToV3t7eNvs8//zzcHFxwfXr17F9+3ZD2yXnpXcm9u7dixEjRuDjjz+G\nqqro1KmTvbpOTkavrO3YsQNFRUUAgNmzZ2vuExYWhkGDBkFVVURFRUk/B3IOemVt9+7dsFgsUBQF\n06ZN09xnxIgRAICsrCxcuHBB/kmQU3Dk71Uvv/wy0tLSEBkZWZMuk5PSM2unTp0CAHh7e6Ndu3Z2\n67MIFqYmtmfPHgAlY7n79eunuU9QUBBCQkIAlIw3N7Jdcl56Z2LSpEmIi4uDu7s7Zs6ciffff79G\n/SXnpVfWUlJS4O3tjUaNGqFp06aV7teqVauy/al20ytrf/nLXxAVFYV///vfaNOmzS33d3PjOpO1\nnaN+r9qwYQN27dqFZs2a4aWXXpJqg5ybnlkrLUw7depk2DBxFqYmVjrOOzg4GPXr1690v9DQUKiq\nipMnTxraLjkvvTPh4uKCIUOG4IcffsC0adPg4sJTT12lV9Zmz56No0eP4scff6xyv0uXLgEA/P39\nq9ljclZ6ntduu+029OzZU/NnRUVF+PLLLwEAzZo1w+233y7Qa3JGjvi96vLly1i0aBFcXFywePFi\n1KtXT7q/5Lz0zNrvv/8ORVEQEhKCDRs2YPz48ejRowe6du2KYcOG4Z///CeuX79e4+dQFV7GM7Er\nV64AAJo3b17lfsHBwQCA5ORkFBcX3/KXfr3aJeeldya2bt1a9k0V1W16Z62qX9ZSUlKwe/duKIqC\n7t27V7PH5Kwc+VmXm5uLlJQUHDlyBCtWrMCZM2fg4eGBBQsW8LOzDtA7a8XFxXjuueeQm5uLJ554\nAj169KhZh8lp6Zm1mJgYAMBXX32FwsJCq29NL1y4gH/961/YuHEjPvnkE3Tt2lX2KVSJZ0sTy8jI\ngKIot7yy7+fnB6BkNa2srCzD2iXnpXcmWJRSKSPPP/Pnz0d+fj4AYPz48XZpk8zLkVl76qmncN99\n9+GFF17AmTNnEBwcjDVr1qBXr15S7ZFz0Ttrn376KY4dO4Z27drhmWeeqVFfybnplbVLly4hOzsb\nqqrCYrHg0UcfxcaNG8tWtp88eTLc3NyQnp6OyZMnlxXI9sbC1MRKf4Hy8vKqcj9PT0+bxxjRLjkv\nZoIcxaisvfnmm2ULRgwfPhx33nlnjdskc3Nk1pKSkqAoStmfxMREvPLKKzh8+LBUe+Rc9Mza77//\njo8//hhubm54++234eHhId9Rcnp6Ze3q1ato2rQpXF1dsXjxYrzyyisIDQ1FQEBA2QWR0vVBsrKy\n8Pbbb9fgWVSOhamJ6TX8h8OKqCJmghzFiKwtWrQIq1atgqIo6NChAxYsWODwPpDjOTJrX3zxBY4f\nP46ff/4Zb7zxBgIDAxETE4OnnnoKx44dc1g/yBh6ZS0/Px/z5s2DxWLBtGnTyha0obpLr6zddddd\n2L17N3777beyVcUrGjx4MPr16wdVVbFjxw7cuHHD7v3gb6Mm5uPjA+DWVzrK//xWV1D0bJecFzNB\njuLIrBUWFmLevHlYuXIlFEVBu3btsHz5cs3l9an2cWTWWrduDXd3dwQGBuLBBx/EqlWr4Onpiby8\nPN2+WSDz0Ctrb731Fi5cuIAuXbpgypQpNesk1Qp6n9dutYr4wIEDAZTMe/7999+r3W51sTA1MT8/\nP6iqiuzs7Cr3Kx077urqioCAAMPaJefFTJCjOCprmZmZmDhxIjZt2gRFURAWFoZVq1ahYcOGUv0m\n52Pkea19+/YYMWIEVFXF0aNHdV/JkoylR9b27duHtWvXwsvLC4sXL+bIJgJg/O9rpYsqAUB6errd\n2i3FlJtY69atAeCWE4yTkpIAAE2aNDG0XXJezAQ5iiOydvnyZYwZMwa//vorFEVBeHg4Vq1ahcDA\nQOG2yHkZfV7r1KlT2d8TEhLs2jaZix5Z27x5MwAgLy8PERER6Nixo80foGRxm2XLlpVtS0xMrMEz\nIbMz+rxWWFhY9nc9Rh+xMDWxDh06ACj5QLt582al+508eRKKoiA0NNTQdsl5MRPkKHpnLTY2Fo88\n8gguXboERVEwZswYfPLJJxy+WwfplbXPP/8c48aNw8yZM6vcLy8vr+zvnPpQu+mVtfILamn9qbgf\nv1Wt/fTK2ty5c3H33Xdj8ODBVe4XFxdX9vfSItmemGATCw8PBwBYLBZER0dr7pOcnFx2s90+ffoY\n2i45L2aCHEXPrMXHx2PixIlIT0+HoiiYPXs27yNZh+mVtdTUVBw+fBi7d+9Gampqpfvt3bsXQMm9\ndfX4BY7MQ4+svfbaazhy5EiVf4CSonTy5Mk4cuQIDh8+bDXUkmofvc5r/v7+uH79OhISEnDu3LlK\n9yv9Jr9Zs2Zo06aNSNerhZ/WJtaiRQt0794dqqpiyZIlmuPJFy1ahOLiYgQGBmLkyJGGtkvOi5kg\nR9Era0VFRZg9ezauXbsGRVHw4osv4umnn7Z398mJ6JW14cOHAyj5xfCf//yn5j6bN2/G/v37oSgK\nIiMjb7mgCDk3PbLm7u4Ob2/vKv9o7Uu1m97nNaDk9mpaPv/8c8TExEBRFDz55JNyT+AWWJia3Asv\nvAAXFxdcvHgRY8eOxf79+5GRkYFTp05hxowZ2LZtGxRFwcyZM62GCl29ehVDhw5FRERE2X2H7NEu\n1V56ZY2oIj2y9vXXX5cNXYqIiMCDDz6InJycKv9Q7adH1rp06YJRo0ZBVVV89913mDp1Ko4cOYKM\njAzExcXh7bffxnPPPQdFUdCqVatbDvml2oGfoeQoemTtjjvuwP333w9VVbF//348/vjj+OWXX5Ce\nno7Tp09j/vz5eO+996AoCnr27IlHH31Ul+fGS3gmFxYWhoULF2L+/PmIjY21uUKhKAqRIV0WAAAN\n6UlEQVQmTpxoE5CioiJcvHgRiqIgJSXFbu1S7aVX1ogq0iNrK1euBFCyEMiWLVuwZcuWW/ajdKgT\n1V56nddee+015OTk4KeffkJUVBR2795t025ISAiWLVsGf39/+z8xMh1+hpKj6JW1N998E7m5udi9\nezcOHTqExx57zKbde++9F0uXLrX/k/ofFqZOIDIyEmFhYVi+fDkOHjyIa9euwcfHB507d8a4cePQ\nv39/zceVTowvP0HeHu1S7aVX1ip7jMj+VLvYM2sZGRlISEgQzh/VDXqc1zw8PLBkyRLs3LkTGzZs\nwIkTJ5CZmQk/Pz+EhITg/vvvx6hRo+Dq6qrrcyNzceRnKNVtemTN09MTH3/8MX766Sds3LgRJ06c\nQFZWFgICAhASEoLIyEgMGzZM1+elqKqq6noEIiIiIiIioipwjikREREREREZioUpERERERERGYqF\nKRERERERERmKhSkREREREREZioUpERERERERGYqFKRERERERERmKhSkREREREREZioUpERERERER\nGYqFKRERERERERmKhSkREREREREZioUpERERERERGYqFKRERERERERmKhSkREREREREZioUpERER\nERERGYqFKRERERERERmKhSkREREREREZioUpERERERERGYqFKRERERERERmKhSkREREREREZys3o\nDhAREZnBoUOHMGHChBq3c/r0aQDAhg0bMH/+fADAO++8g+HDh9e4bWdQVFSEhx9+GLGxsfj+++/R\ntm3bGre5Y8cOzJgxA0OHDsUHH3xgh14SEZHZ8BtTIiKi/1EUpUZ/XFxsP1YVRTHgmRhn6dKliImJ\nwZgxY+xSlALAoEGDcOedd2Lbtm3YvHmzXdokIiJz4TemREREANq3b49ly5ZV+vPp06dDURQ0aNAA\nr732WrXaLC1Y64q4uDgsX74cPj4+mD59ul3bnjdvHsaMGYOFCxciPDwcfn5+dm2fiIiMpaiqqhrd\nCSIiIrPr2LEjFEVBcHAwdu7caXR3TOnxxx/HoUOHMHnyZDzzzDN2b3/69OnYtWsXxo0bh5dfftnu\n7RMRkXE4lJeIiIhq7Oeff8bBgwfh7u6Oxx9/XJdjPP3001BVFevWrUNSUpIuxyAiImOwMCUiIqIa\n++ijj6AoCgYMGIAGDRrocowuXbrgT3/6E4qKivDZZ5/pcgwiIjIGC1MiIiIdbNiwAR07dkTHjh2x\nadMmq5998MEH6NixI/785z8DAK5fv473338fw4YNQ7du3dCrVy889dRT+Pnnn60e98MPP2D8+PG4\n66670K1bN0RGRmLlypUoLi6usi95eXlYsWIFxo8fj3vuuQedO3dGeHg4Zs2ahd27d9f4uZ45cwaH\nDx8GAERGRla579atWzF16lT07t0bYWFh6NmzJ0aNGoW33noL8fHxtzxWZGQkVFXF999/j+zs7Br3\nnYiIzIGLHxEREenoVosfnT59GpMnT0ZKSkrZvvn5+di3bx/279+P119/HZGRkZgzZw62bdtm1V5M\nTAxiYmLw22+/4b333tNs//fff8eMGTOQnJxs9djU1FRs374d27dvR79+/fDee+/Bx8dH6jlu2LAB\nAODl5YV77rlHc5+CggLMnDkT0dHRAP54XbKyspCVlYXTp09j9erVeOmll/Doo49Weqy+ffvirbfe\nQl5eHjZt2lTlvkRE5DxYmBIRERmkqKgIU6ZMQWpqKnr37o377rsPiqJgx44dZQXcokWLcOjQIWzb\ntg3t2rXDQw89hNtuuw0xMTFYvXo1cnNzsXXrVowcORJ9+/a1av/s2bOYMGECcnNzoSgKwsPD0b9/\nf9SvXx8JCQn4/vvvERcXh6ioKEyZMgUrV66UWkV4x44dUBQFd955Jzw8PDT3WbJkCaKjo6EoCkJD\nQzF8+HAEBwcjMzMTv/76KzZv3oyioiK8/vrr6NatG0JCQjTbadOmDZo2bYrk5GTs2LGDhSkRUS3B\nwpSIiMggBQUFuHr1KubMmYNJkyaVbX/ooYfw1FNPYd++fcjJycEPP/yA8PBwfPTRR3B3dwcARERE\noGvXrmW3Zdm2bZtNYTpv3jzk5OTAzc0N77zzDiIiIqx+/uSTT+LVV1/FunXr8Msvv2DlypV44okn\nhJ5DXFxc2bexnTt31tzHYrFg3bp1UBQFnTp1wtdffw03tz9+BXn44YfRp08fzJ07F6qq4ssvv8Qb\nb7xR6TE7d+6MpKQk/PLLLygoKKi0GCYiIufBOaZEREQGURQFISEhVkVpqYcffhgAoKoq3Nzc8MYb\nb5QVpaUGDhyIgIAAACUFYnnR0dE4c+YMFEXBX//6V5uitPT4L7/8Mlq0aAFVVbFixYpbzlet6Pjx\n42V/b9euneY+165dw40bNwAA9957r1VRWuqBBx5Aly5d0KVLF9SvX7/KY7Zv3x4AUFhYiJiYGKH+\nEhGRObEwJSIiMtDQoUM1tzdv3hwAyr5lbNKkieZ+wcHBUFW1rPAr9eOPP5b9ffTo0ZUe393dHSNG\njAAAXL16FadOnRLqf2xsbNnfKytMAwIC4OJS8ivHli1bKr3Vy/r167Fu3TrMnTu3ymOWP865c+eE\n+ktERObEobxEREQGatOmjeZ2Pz+/sr+3aNGi0sd7eXkBgM03neW/yTxz5ozNN6rl5ebmlv395MmT\nCAsLq7rT5ZQvMiu7TYyXlxfCw8MRFRWFhIQEDB06FH379kX//v3Ru3dvNG7cuNrHq3icxMREoccS\nEZE5sTAlIiIyUOlQ3Kp4e3tX+rPKFiu6evUqFEWBqqr429/+Vu3+pKWlVXtfAFbf1Pr6+la636uv\nvoqxY8ciKSkJBQUFZSsCA0BISAgGDBiAYcOGoW3btrc8ZvnjZGVlCfWXiIjMiUN5iYiIDOTq6qpL\nuzdv3gRQUrhW90/5x1VXQUFB2XE8PT0r3S8oKAg//PADJk2ahMaNG1sdNyYmBh999BHuv/9+zJo1\nC9evX6/ymOVva1N6fCIicm78xpSIiKgW8vLyQl5eHm677TZERUXpdpzSYlRVVVgslioLbV9fX8yZ\nMwdz5szB8ePHsWfPHuzfvx8nTpyAxWIBAGzfvh3p6elYs2ZNpe2UL0ZLhzITEZFz4zemREREtVCD\nBg2gqioyMjLKij49lJ8Lm52dXe3HdenSBTNmzMBXX32F/fv34+WXXy4bsnz48GEcOnSo0seWP075\n4xMRkfNiYUpERFQLdenSBUDJt4vHjh2rct9NmzZh3rx5+PDDD4VXuS2/MFNlq+2eP38ea9euxRtv\nvKG5WFFAQADGjRuHZ555pmzbmTNnKj1m+eNUtTAUERE5DxamREREtdDAgQPL/v7FF19Uul9hYSE+\n+OADbNq0CZ9++ilUVRU6TvlVhS9duqS5z7Fjx/Daa6/hyy+/xI4dOyptq/xCUOXnkVZU/jiVrWpM\nRETOhYUpERFRLTR06FA0b94cqqpi165dWLZsmc0+qqrixRdfxJUrV6AoCnr37l3pvUgr071797K/\nx8TEaO7Tv39/eHh4AAA++ugjzQK2oKAAq1evBlCykFL5disqPY6Pjw9CQ0OF+ktERObExY+IiIhq\nITc3N7z77rt47LHHUFRUhGXLliEqKgoPPPAAmjRpgsTERHz33Xdl9zf19fXFP/7xD+HjtGjRAsHB\nwUhKSsLhw4c19wkMDMTEiRPx2WefITMzEyNHjsTo0aMREhICLy8vxMfH45tvvkFiYiIURcHIkSPR\nunXrSo955MgRKIqCO++8Ey4uvMZORFQbsDAlIiKqJtFhrkbr1q0b/v3vf2P27NlIS0vDyZMn8fvv\nv5f9vPR2LUFBQVi6dKn0fM2IiAgsX74cx44dQ05OjuYw3FmzZiEpKQmbNm1Cfn4+1q5da/Xz0r4M\nHjwYCxYsqPRYp0+fRnp6OhRFwbBhw6T6S0RE5sPClIiIqBpK7/NZ+t/qPqay/av6megxq/p5jx49\nsH37dqxbtw67du3CuXPnkJWVhXr16qFdu3YYNGgQxowZg3r16t3i2VRu9OjR+OKLL1BUVIRdu3bh\ngQcesNnH1dUVb7/9NkaMGIFvv/0Wx48fx7Vr16CqKho2bIhu3bph5MiRCA8Pr/JYP/74I4CS1XgH\nDx4s3WciIjIXRXW2y79ERERkOtOnT8fOnTvRr18/fPrpp7odZ/DgwUhISMDUqVMxa9Ys3Y5DRESO\nxYkZREREVGNPP/00AGDv3r2at4Sxhz179iA+Ph5eXl6YMGGCLscgIiJjsDAlIiKiGuvSpQvuvfde\nFBcXl62ua2+rVq2Coih45JFHUL9+fV2OQURExuBQXiIiIrKL2NhYjB49Gm5ubti5cycaNGhgt7aP\nHz+OMWPGoHHjxti8eTP8/f3t1jYRERmP35gSERGRXbRv3x7Tpk1Dbm4uPv74Y7u2/d5770FRFLz6\n6qssSomIaiEWpkRERGQ3kydPRmhoKL7++mucO3fOLm3u3LkTBw8exLBhwzBw4EC7tElERObCobxE\nRERERERkKH5jSkRERERERIZiYUpERERERESGYmFKREREREREhmJhSkRERERERIZiYUpERERERESG\nYmFKREREREREhmJhSkRERERERIZiYUpERERERESGYmFKREREREREhmJhSkRERERERIZiYUpERERE\nRESGYmFKREREREREhmJhSkRERERERIZiYUpERERERESGYmFKREREREREhmJhSkRERERERIZiYUpE\nRERERESGYmFKREREREREhmJhSkRERERERIb6f09CJojf5jzOAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0xaa3f438>"
]
},
"metadata": {
"image/png": {
"height": 219,
"width": 467
}
},
"output_type": "display_data"
}
],
"source": [
"# Define sawtooth shape in some number of samples\n",
"x1 = np.array([0,.01,.05,.1,.2,1,.9,.8,.7,.6,.5,.4,.3,.2,.1,.05,.01])\n",
"t1 = np.arange(len(x1))\n",
"\n",
"# Interpolate sawtooth so it has 50 samples (50ms = 20Hz wave)\n",
"from scipy import interpolate\n",
"f = interpolate.interp1d(t1, x1)\n",
"t2 = np.linspace(0,len(t1)-1,50)\n",
"x2 = f(t2)\n",
"\n",
"# Tile the new sawtooth to last 5 seconds\n",
"x = np.tile(x2,100)\n",
"Fs = 1000.\n",
"t = np.arange(0,5,.001)\n",
"\n",
"# Plot sawtooth\n",
"plt.figure(figsize=(5,2))\n",
"plt.plot(t, x)\n",
"plt.ylim((-.1,1.1))\n",
"plt.xlim((0,.5))\n",
"plt.xlabel('Time (s)')\n",
"plt.ylabel('Voltage (a.u.)')"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Calculate comodulogram for that sawtooth\n",
"from pacpy.pac import comodulogram\n",
"from matplotlib import cm\n",
"\n",
"# Comod parameters\n",
"fp = (6,40)\n",
"fa = (20,200)\n",
"dp = 2\n",
"da = 4\n",
"pac_method = 'mi_tort'\n",
"\n",
"f_phases = np.arange(fp[0], fp[1]+dp, dp)\n",
"f_amps = np.arange(fa[0], fa[1]+da, da)\n",
"\n",
"comod = comodulogram(x, x, fp, fa, dp, da,fs=Fs, pac_method=pac_method, w_lo=3, w_hi=3)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABJMAAAPFCAYAAADRA6ngAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAewgAAHsIBbtB1PgAAIABJREFUeJzs3XmcjfX///HnmdU+mJB9yy67j6VCQtkZUVHRQmSLlJI+\nRUIfWn5JH4QWSyofIcs0SYqMRMm+L4mxzFjGmH1cvz98zzHHObhm5py5zozH/XabW83lXO/364y5\nhvfTe7EZhmEIAAAAAAAAMMHP6gIAAAAAAACQcxAmAQAAAAAAwDTCJAAAAAAAAJhGmAQAAAAAAADT\nCJMAAAAAAABgGmESAAAAAAAATCNMAgAAAAAAgGmESQAAAAAAADCNMAkAAAAAAACmESYBAAAAAADA\nNMIkAAAAAAAAmEaYBAAAAAAAANMIkwAAAAAAAGAaYRIAAAAAAABMI0wCAAAAAACAaYRJAAAAAAAA\nMI0wCQAAAAAAAKYRJgEAAAAAAMA0wiQAAAAAAACYRpgEAAAAAAAA0wKsLgCSYRjauHGjfv/9d/35\n5586efKkYmNjdfnyZRUoUECFCxdWmTJl1LhxYzVr1kx16tTxWN+HDh3SqlWr9Mcff+jIkSO6ePGi\nUlNTVbBgQZUvX17169fXQw895NE+7bZv366IiAj9+eefOn78uC5evCjDMBQSEqKKFSuqcePGat++\nve666y6P9w0AAAAAuV1UVJS+++47bd26VQcOHNCFCxeUnJys/Pnzq1y5cqpTp47atGmjZs2aWV2q\nw6ZNm7R+/Xr98ccfioqK0oULF5SWlqZChQqpfPnyqlOnjlq1aqWmTZtaXeptzWYYhmF1EbertLQ0\nLViwQF988YX++ecfx3Wbzeby2vS/TXfffbcGDhyoBx54INN9Hz9+XOPHj9f69etv2G/6PuvXr6+x\nY8eqVq1ame7Tbvfu3Ro3bpz++usvU323atVKY8aMUbly5bLcNwAAAADkdufOndPbb7+t8PBwpaWl\nSbr5mKtKlSoaM2aMpaFSRESEpk2bpgMHDjiu3azm8uXLa9CgQerWrVu21YhrCJMscuzYMb300kva\nvn270wNys98O++vsr+nevbveeOMN5cmTJ0N9R0REaPTo0UpISHBp82Z9+vv76+WXX1bfvn0z1F96\n8+fP1+TJkx0/0Mz2nTdvXr399tvq0KFDpvsGAAAAgNxuy5YtGjp0qM6fP5+h8Z4kPf3003rppZfc\nTnDwlqSkJL322mtasWKFqbHx9TU3adJE7777ru644w7vFwsHwiQLHD16VI899pguXLjguGb/bbjZ\nQ3v9awzDUL169fT5558rODjYVN+rV6/WqFGjdOXKFVP9uutz5MiRGjBggKn+0vv000/1zjvvuDz8\nN+s7/WttNpumTJmiTp06ZbhvAAAAAMjttmzZov79+ysxMdFxLf246nruxnuPPPKIxo0b5/1idTVI\neu6557Rp06YMjRPT/7phGCpfvrzmzZun4sWLZ0PVkAiTst2FCxcUFhamqKgoxzX7wx0aGqru3bur\nSZMmKlmypAoUKKALFy5o3759Wrt2rX744QdduXLF5YdB69atNX369Fv2vX//fj3yyCMuP1iCg4PV\ntWtXtWvXTmXKlJF0debUypUrFR4eruTkZKcH1c/PTzNmzFCLFi1Mv++NGzfq2WefdTz49vdQsGBB\nhYWF6f7771epUqWUlJSkI0eOaNmyZfrpp5+Ulpbm1HdwcLC++uorVa9e3XTfAAAAAJDbnT17Vt27\nd1dMTIzjmn2FyUMPPaQOHTqoQoUKCgoK0j///KOIiAgtX75c8fHxjvGZ/b9vvPGGHn30Ua/X/PLL\nL2v58uUukwhCQkLUs2dPNW/eXKVLl1ZAQICio6O1detWffXVVzp27JjLuLhOnTpauHCh/P39vV43\nCJOy3RtvvKGvvvrK5WHp16+fXnjhhZvOMDp06JBeeOEFHThwwOX+yZMnq2vXrje81zAMhYWFae/e\nvU7XKleurA8//FCVK1d2e9/evXs1fPhwHTt2zKnPEiVKKDw8XHnz5r3le05MTFS7du109uxZp5rr\n16+v999/XyVKlHB736ZNmzRq1ChFR0c7/WCrUaOGlixZcst+AQAAAOB28fzzz2vt2rVO47ZixYrp\n//2//6cGDRq4vefEiRMaMWKE0/Yr9m1GwsPDbzhW84Q1a9ZoyJAhLmPbBx98UBMmTFCBAgXc3mcY\nhqZNm6aPP/7Y5d7Ro0erX79+XqsZ1/hZXcDt5PDhw1q8eLHLN/zLL7+s0aNH33KpWuXKlbVo0SJV\nq1bNaWqfYRh6//33lZKScsN7ly1bpj179jg+twdCc+fOvWGQJEnVq1fXvHnzVLJkSac1q2fOnNGc\nOXNMve/Zs2frzJkzjn6lqxu8zZo166Y/nJo2bapPP/1UBQsWdHqve/bs0dKlS031DQAAAAC53ebN\nm12CpPz582v27Nk3DJIkqXTp0vr0009VvXp1p/FeYmKiPvjgA6/WPG3aNJexcdu2bfXBBx/cMEiS\nro4Lhw0bpkGDBrmMi2fPnu20Py+8hzApG3377beOb2z7w9KyZUs99dRTptvInz+/pk2bpsDAQKfr\np0+f1qZNm2543yeffOLyoI4fP95U0ly8eHF99NFH8vO7+u1if1Dnz5+vpKSkm96bnJysefPmOU0/\n9Pf315QpU276A8KuSpUqmjRpktMPNsMw9Mknn9zyXgAAAAC4HcyaNcvx//bx3siRI1WtWrVb3ps/\nf37NmDFD+fLlk3RtvLdixQqdPn3aK/X+9ttv2rdvn9O1QoUKZWivpsGDB6t06dJO12JiYhQZGemR\nGnFzhEnZKDw83GUTseeffz7D7ZQrV05dunRx2d1+3bp1bl+/ZcsWHTp0SNK1mUE1atRQy5YtTfdZ\nq1YtderUyanPixcv6vvvv7/pfatXr9bFixcdfdtsNj3wwAOmfqjZtWnTRg0bNnRaE3v48GFt3brV\ndBsAAAAAkBudOHFCGzdudBprhoaG6pFHHjHdxp133qm+ffs6jfdSU1O9tr3ImjVrJF0dI9rHeT16\n9FCRIkVMtxEQEKB27dq5jIu3bdvm0VrhHmFSNjl79qyOHz/udC00NFR16tTJVHv333+/y7UjR464\nfW14eLjT5/YHNaN69erlcm3lypU3vWf16tUu18LCwrKlbwAAAADI7SIiIpxO67bZbOrcubMCAgIy\n1M71Yy7DMLw25tq6datsNpvjQ5IeeuihDLdTrlw5l2v2LVbgXRn77kKmHTx40PH/9uS0du3amW7P\nfupa+jbtG1xfb8OGDS4zotyFUbfSoEEDhYSEKDY21jH18bffflNSUpLb/Z5SU1O1efNmp76Dg4PV\nvHnzDPfdqlUrRzv2vtetW6d///vfGW4LAAAAAHKLDRs2uFxr3bp1htspWbKkqlWrpn379jnGXIcO\nHdKJEydclpNl1eLFi3X06FEdPnxYBw8e1JEjR1SrVq0Mt+Nu2xX79izwLsKkbBISEqI+ffrozJkz\nOnPmjE6fPq1ixYpluj178pyeuyMQo6OjdfToUadAp0SJEipVqlSG+/Tz81PdunX1yy+/ONpLSkrS\njh071KhRI5fX79q1S/Hx8U4nsdWqVUtBQUEZ7jskJESVKlXS4cOHHdeioqJ06tQp3XnnnRluDwAA\nAAByOsMw9McffziN9wICAlS3bt1MtdegQQOXvYy2bNni8TDJz89PlSpVUqVKldSmTZtMt3PgwAGX\na56uFe4RJmWTmjVrqmbNmh5r7++//3b63Gazud1Me//+/Y7/twc6WamjRo0a+uWXX5yu7dy5022Y\nlL5vu6z0Xb16dR06dMjpB+XOnTsJkwAAAADclv7++28lJCQ4/gFfkipVqpSpf8CXro73rrdz5051\n7do1S3V6w6VLlxQREeGyCqdZs2YWVXR7Yf5XDrV+/XqXaxUrVnS55i6prVSpUqb7LV++vMu1G+3V\n5Om+K1So4HIt/UwlAAAAALidXD/mstls2Tbes1JqaqpGjx6tS5cuOV2vW7dulraTgXmESTnQhQsX\ntGrVKpcE9oEHHnB57T///ONyrWTJkpnu290sIHd93Oh6ZpbXZaZvAAAAAMjtvDnes8928rUx1969\ne/X4449r7dq1jjGxYRgKDAzU2LFjLa7u9sEytxxo5syZjqmMdqGhoW6XmsXExLhcc7cczqzr93m6\n2cbf7vouXry4x/qWdMO+AQAAACC3y81jLsMwZBiG4uPjdeLECW3fvl3h4eHauHGjYwsX+9I+f39/\nTZgwgVlJ2YgwKYfZsWOHvvjiC6cE1maz6amnnnKZqSRd3YD7eoUKFcp0/+nvtT+8sbGxbl8bHR3t\nUlNW+i5YsKDLtRv1DQAAAAC5nbvxXkhISKbby5cvn/z9/Z0OfIqPj9eVK1ey/ZS0iIgIDR8+3OW6\nzWZzOuk7NDRUEydOVIsWLbK1vtsdy9xykNjYWI0cOdLlJLdy5crpiSeecHtPXFycy7UCBQpkuob8\n+fO7XLt+nWp29W0Yxg37BgAAAIDc7vLlyy7XsjLmkjI25vOmqKgoSdfCo/Qhkn1GUosWLbR69WqC\nJAsQJuUQycnJGjx4sI4fP+64ZhiGAgICNHny5Bvu1p+SkuIyOyg4ODjTdbjrJzk5+YY1X89Tfdvf\n0436BgAAAIDczt14KLMnud3sfivGXadOnZJ0bblb+g/7ePDnn39Wly5d9NlnnzE2zGaESTlAamqq\nhg0bpt9//91leduoUaNUv379G97r7oHy9/fPdC3u7k1NTXX72pSUFI/2HRDguirzRn0DAAAAQG7n\nbrznbtyUERkZ83lTVFSUy6wk+0f6UOnUqVOaPHmywsLCOO07G7Fnko9LTk7WsGHDtG7dOpcg6ZFH\nHlG/fv1uen9aWprLNU+HSdnVt7s1utcv+QMAAACA24W7MVdW9zZyN2azYtzVpEkTtWnTRnfddZeK\nFCmiy5cv6/jx41q/fr2WLl2q+Ph4x9jYZrPp4MGDevzxx7Vo0SKVK1cu2+u93RAm+bD4+Hg9//zz\n2rRpk0uQ1LlzZ7355pu3bMPTs3kyMtsoICDApa/U1NRMT7t0V3dgYGCm2gIAAACAnM7deM9dwJQR\n7sZ8Voy7evfu7XKtcuXKatWqlYYMGaI33nhDP/zwg+PXbDabzp8/r+eff15Lly7N8gwt3BxfXR8V\nHR2tAQMGaPfu3S5BUrdu3TRx4kRT7QQGBjqtKZWyFia5+8F0o3AoMDDQo2FS+r7tG65ldT2wO1FR\nUVq7dq3j87Jlyypfvnwe7wcAAADwVfHx8U77tbZu3VolS5a0sKKbu3Tpkvbt22d1GaZUq1bN7UnV\nmeEu5MnqkrSMjPmsUqRIEX344Yd644039NVXXzmNmQ8dOqQvvvhCTz/9tMVV5m6EST7o4MGDGjBg\ngE6ePOkSJPXp00djx4413Za7nfgTEhIyXVt8fLzLtRttqp0vXz6XvhISEjIdzLg7qSArG3rfyNq1\nazV+/HiPtwsAAADkZH369LG6hBvat2+fT9eX3oIFC9SoUSOPtOVuvOduzJYRGRnzWe3f//639u3b\np23btjntp7RgwQLCJC9jA24fs379ej322GOOzcaka0HS8OHDMxQkSVLhwoVdrrkLZcxKf699dlDR\nokXdvrZIkSJe61u6Oo3xRn0DAAAAQG7n6fHelStXlJiY6HQtODhYefPmzXSb3uTv769Ro0a5XD95\n8qR27NhhQUW3D8IkHzJ//nwNHDhQcXFxjmuGYSgwMFCTJk3SwIEDM9ymu0Dn3Llzma4xJibG6XOb\nzabQ0NAb9m0PnDzRt7t7b9Q3AAAAAOR27sZ758+fz3R714/3JN8fczVq1EilS5d2ub59+3YLqrl9\nsMzNB1y5ckVvv/22FixY4DQbSZJCQkI0bdo0/etf/8pU2+4eqrNnz2a6Vnf3FitWzHTf0dHRHu27\nePHimW7vRq7f+f/06UZKSnJN/JH7hPzS2eoSbqlHi+5WlwAAkqTyVhdgUuucsepFRwe6/r3J1/yq\ne6wuwZS/lTNOcbri4/+uH7/vrI6O/9HxeU47HavR6dMqnJRkdRmSpAvBwdpSooRX2i5TpozLNU+N\n9+wrZG403vMlDRs21IkTJ5z2Co6KirKwotyPMMliycnJGj58uH766SeXIKl8+fKaMWOGKlasmOn2\ny5Yt63Lt77//znR77u6tVKmS6b6PHTvm0b6z8rW5keuncCYlFVZioudDK/ie/A3vtrqEWyp+3bRj\nALBKTgmTGt1hdQXm5PXM9iledVA5Y3uBC/L9YE6S0uT+RGRf5avLnG4kNClJJXzk703e/J12FyZl\n13jPl7gLvGJjYy2o5PZBmGShuLg4Pffcc9q6davL/kiNGzfWtGnTFBISkqU+qlev7nLt0KFDmW7P\n3b1VqlTxub4BAAAAILerXr26Yyxp33w6J4y5UlJSdOLECR0/flzHjx9XhQoV1Lx580y3d+XKFZdr\n7jYnh+cQJlkkLi5OzzzzjP766y+XIKlbt2566623FBCQ9d+eKlWqKG/evEpMTHT8cNm9e3em29ux\nY4fT1EFJql27ttvX3n238ywPwzC0c+fOTPVrGIZ27drl1HdwcDBhEgAAAIDbVoECBVS+fHmnFSAn\nTpzQhQsX3G7OfSvuNq2+0Xgvs9asWaNhw4Y5BUAtWrTIUpiUke1Y4Bm+vVA3l0pOTtZzzz3nNkga\nMmSIJk2a5JEgSZL8/PzUsGFDp42w4+LiMrUZ2ZkzZ3Tw4EGna+XKlVOpUqXcvr5YsWKOZWj293nw\n4EG3m7rdyl9//eXYmNz+tWrYsKGCgoIy3BYAAACA3C1AUqCPfHh7BkeTJk1cDj6KjIzMcDspKSn6\n/fffnf4BP0+ePKpfv36Wa0yvXLlyunLlimw2m6OvrVu3Kjk5OdNtpl/tk74feA9hkgVGjRrlsrTN\n399f48eP1+DBgz3eX8uWLV2urVq1KsPtrFq1yvFDyh7otGjR4pZ9p//BZhhGpvpesWKFy7X77rsv\nw+0AAAAAQG7iqfHeunXrdPnyZUnXxnvNmjXz2EQHu0qVKrnswRUfH6/w8PBMtbd161aXzbYDAwOz\nNNMJt0aYlM0++eQTRUREuMxIeuutt9SzZ0+v9Nm+fXvHDwD7UrclS5bowoULpttITk7WvHnzXNLe\nHj163PS+zp2vnY5l7/uLL75QSkqK6b7PnTunpUuXOvUdEBCgLl26mG4DAAAAAHKje++917GkzT7m\n+umnn3T48OEMtTNnzhyXaw8//LBHakwvICBA7dq1c5l0MHfuXJcZVmZ88MEHTu3YbDY1b95c+fLl\n80i9cI8wKRvt27dPH374oUuQ9NxzzyksLMxr/d5xxx164IEHnB7MS5cu6fXXXzfdxuTJk3XixAlJ\n106bq1+/vttNttOrVauWateu7dT3P//8o//85z+m+jUMQ2PGjHFZ4vbQQw+paNGccaIIAAAAgOzl\nr6vLy3zhw9vn9gUFBSksLMxpzJWWlqYxY8aYXjo2Z84cbdu2zekf8EuWLKlWrVp5ulxJzpMS7H3u\n27dPn3/+eYbamTZtmsvSPEleWfEDZ4RJ2WjChAmOGTn2UKRevXoaPny41/sePHiw/Pyu/nbb0+o1\na9ZowoQJt0x/Z82apYULFzo9oDabTS+++KKpvocOHep0n2EYmj9/vmbPnn3T+wzD0FtvvaV169a5\nzEoaNmyYqb4BAAAAILd79tlnHUvH7GOuv/76S6NGjbploPTdd9/p3XffdZn08MILLzjGkDdy4sQJ\nVa9e3eVj6dKlN73vX//6l9OWKPaap06danqJ3rRp0zR9+nSXujt06OByGBQ8j9PcssnGjRsdiWn6\nfYf+/PNP1ahRwyN9lC5dWj/++KPbX6tatap69+6t+fPnO210Nn/+fO3fv19jxoxxmWV0/PhxTZ06\nVd9//73LA9qlSxc1bNjQVF0tW7ZU69attXbtWqe+p06dqh07dujFF1902Rxt7969mjhxojZv3uzS\nd//+/VW2bFnzXxgAAAAAyMWKFi2q4cOHa/LkyU5jroiICPXs2VOvv/66GjVq5HTP2bNn9d///tdp\n4oB9rNqoUaMMbSty/cwgM8aOHastW7bo8uXLjprT0tI0cuRIRUZGatCgQW4Pe/r999/1wQcfuOxD\nLF3dj+nNN9/McC3IOMKkbDJv3jy31zPz0GXWSy+9pD/++EO7d+929G2z2bR582Z169ZN1apVU8WK\nFRUQEKDjx49r+/btjgBHuvaAVq5cOcMP6IQJE/Twww/r5MmTTn1///33ioiIUO3atR27+h85ckR7\n9+51vM7et81mU+PGjZ1mOgEAAADA9eynufmC7Bp09+vXT5GRkfr5558lXRtz7du3T48//rjKly+v\nqlWrKl++fDpx4oS2bdum1NRUl/HeHXfcoffeey9TNaQfP95K2bJl9dFHH2nAgAGOFTz2mr/55hst\nXrxYNWrUUMWKFRUcHKxz585p586dio6Odrz2+rpnzJihggULZqp2ZAxhUjZISkrSxo0bHd/s3giQ\nzGxUFhwcrFmzZunpp5/WgQMHnKYUStL+/fu1b98+x+vtD3L611WsWFFz5sxx2X3/VooWLarZs2fr\nmWee0alTp1z63rFjh3bs2OHUb/r3ZbPZVL9+fX388cfZGsABAAAAQE7x/vvva9CgQdq8ebPLmOvv\nv//WsWPHHK+9frwnScWKFdNnn32mYsWKZUu9zZo100cffaSXXnpJly5dcql5z549jskQ6WuWnMeK\nNWvW1PTp03XnnXdmS91gz6RssWvXLiUlJckwDK99mHXHHXdo4cKF6tixo9MPD3ft2K/ZX9e2bVst\nWLBAJUqUyNTXoVKlSvr666/VvHlzl77d9Zu+70ceeURz585VgQIFMtU3AAAAAOR2+fLl0+zZs/XE\nE0/Iz8/P1HhPkmMVyKJFi1S5cuUM95vRcWl6LVu21JIlS9SgQQPTY1T7WDFPnjzq16+fvvzyS4Kk\nbMbMpGxw9uzZbJlNY7aPAgUKaOrUqXrsscc0d+5c/fLLL0pNTXX7Wj8/PzVv3lxPPvmk7rvvvizX\nWKxYMc2ZM0fr1q3TF198od9++01Xrlxx+9qAgAA98MAD6tevn+rVq5flvgEAAADcHuynufkCb5/m\ndr3AwECNGTNGDz/8sObMmaOIiAglJia6fa3NZlPdunX1xBNPqEOHDpnqzxNj3TJlymjBggWKjIzU\n559/rt9+++2GNUtSuXLlHGPF4sWLZ7l/ZJyvPF+52oMPPqg9e/ZYXYaLhg0bqmHDhkpISND27dt1\n9OhRXbx4UTabTSEhISpTpozq1q2r/Pnze7zvVq1aqVWrVrp06ZL++usv/f3337p06ZL8/f0VEhKi\nihUrqk6dOgoKCvJ43wAAAACQ21WtWlXvvPOOJkyYoB07dujw4cM6f/68DMNQoUKFVLJkSdWrV08h\nISGZ7qN06dIeHes2a9ZMzZo1U0pKiv766y+dOHFC58+fV3JysooUKaLQ0FBVq1ZNpUuX9lifyBzC\nJChv3rxq0qSJmjRpku19FyxYUPfee2+29wsAAAAAt4PAwEA1aNBADRo0sLoU0wIDA9WoUSOXE+jg\nOwiTAOD/pKZm9yRkAMi53C+Q90E5plB4ir/SrC7BlLRsX/x0e7kdT3MDshMbcAMAAAAAAMA0wiQA\nAAAAAACYxow7AAAAAECucjuf5gZkB2YmAQAAAAAAwDTCJAAAAAAAAJjmKzP/AAAAAADwCE5zA7yL\nmUkAAAAAAAAwjTAJAAAAAAAApjHjDgAAAACQq3CaG+BdzEwCAAAAAACAaYRJAAAAAAAAMM1XZv4B\nAAAAAOARnOYGeBczkwAAAAAAAGAaYRIAAAAAAABMY8YdAAAAACBXYZkb4F3MTAIAAAAAAIBphKQA\n8H8uHr3T6hJu6V9WF2BSqtUF5CL8QX17Kmp1ASY0CbW6ApO6WF2AORvV3OoSbukX3Wd1CabsVzWr\nSzAlVf5Wl3BTNu1WkBZZXQYAH8XfUQEAAAAAuYq/fGew69uxIZA5LHMDAAAAAACAaYRJAAAAAAAA\nMM1XZv4BAAAAAOAR/vKd09xY5obciJlJAAAAAAAAMI0wCQAAAAAAAKaxzA0AAAAAkKsEyHcGu75S\nB+BJzEwCAAAAAACAaYRJAAAAAAAAMI0ZdwAAAACAXIXT3ADvYmYSAAAAAAAATCNMAgAAAAAAgGks\ncwMAAAAA5Cr+8p3BLsvckBsxMwkAAAAAAACmESYBAAAAAADANF+Z+QcAAAAAgEcEyHdOc2PQjdyI\n72sAyEFSrS7ApBSrC8hF+FrennLCs56SE4qUFJhodQXm+CvN6hJuKSAH1ChJQUq2ugSTgqwu4Bau\nWF0AAB/GMjcAAAAAAACYxswkAAAAAECuwmlugHcxMwkAAAAAAACmESYBAAAAAADANF+Z+QcAAAAA\ngEdwmhvgXcxMAgAAAAAAgGmESQAAAAAAADCNGXcAAAAAgFyF09wA72JmEgAAAAAAAEwjTAIAAAAA\nAIBpvjLzDwAAAAAAj+A0N8C7mJkEAAAAAAAA0wiTAAAAAAAAYBoz7gAAAAAAuQrL3ADvYmYSAAAA\nAAAATCNMAgAAAAAAgGnMuAMAAAAA5Cr+8p3Brr/VBQBe4CvPFwBY76DVBdxa53JWVwAgW4RYXYAJ\nta0uwJxT7XLCF1Nar/usLuGWfkn2/Rol6eLOO60uwZwUqwu4uTz7EsRfOwDcSI4Ik5KSknTmzBnF\nx8crMTFRycnJCg4OVv78+ZU/f34VKVJEwcHBVpcJAAAAAACQ6/lUmHTlyhXt2bNH27dv1/bt23Xg\nwAGdPHlS58+fv+l9NptNxYsXV/ny5VW+fHnVq1dPjRs3VtmyZbOpcgAAAACArwjwlwJ9ZLQbwDo3\n5EKWP16XL1/WunXrtHbtWm3YsEGxsbGOXzMMw1QbhmHo1KlTOn36tDZv3qxvvvlGklSiRAk1a9ZM\nHTt2VPPmzeXnx37jAAAAAAAAWWFZmLR9+3Z99dVXWrVqlRITEyW5D49sNpvpNq+//9SpU1q6dKmW\nLl2q0NCZYPUiAAAgAElEQVRQtW/fXo888ojuuuuurBUPAAAAAABwm8r2MCk8PFwzZ87U3r17JTkH\nQLcKjq4Pi65/vbv77fdER0dr/vz5mj9/vpo3b66+ffuqRYsWmXoPAAAAAADf5R8gBaRZXcVV/pav\nBwI8L9u+rVeuXKkZM2bo4MGDNw2Q3M1OKlCggIoWLar8+fMrKChIgYGBSkpKUmJiohISEhQTE6OE\nhASX+2w2m1P79rY3btyojRs3qmrVqho+fLhat27tqbcJAAAAAACQq3k9TNq2bZvGjx+vPXv2OMIc\ndwGPJFWoUEG1atVSrVq1VLFiRZUrV05ly5ZVUFDQLfu5cOGCTp06pWPHjmn37t3as2ePdu3apZiY\nGMdrru933759Gjx4sO6++269+OKLatKkiSfeMgAAAAAAQK7ltTApJiZGU6ZM0fLly2UYhgzDcIQ5\n9gApNDRUzZo10z333KN77rlHxYsXz3R/hQsXVuHChVW9enU9+OCDjuv79+/Xxo0bFRkZqY0bNyol\nJUWSnGrZvn27+vXrpw4dOuiVV15RsWLFMl0HAAAAAMBaAX5SoI+cohbAOVDIhbwSJq1YsUJvvfWW\nYmNjHSGSzWaTYRjKkyeP2rZtq7CwMDVr1swb3TupWrWqqlatqn79+ikuLk4RERFauXKlNm3apLS0\nNKdQadWqVfr55581atQoPfroo16vDQAAAAAAIKfxaJh08eJFvfnmmwoPD3cJkSpXrqy+ffuqQ4cO\nKlCggCe7Na1AgQIKCwtTWFiYTp8+rYULF2rx4sWKiYlxhEpxcXEaN26cfv75Z7399tsqWrSoJbUC\nAAAAAAD4Io+GSR07dlRMTIwjSDIMQ1WrVtXQoUPVtm1bT3aVZSVKlNCIESM0ZMgQrVixQjNmzNCx\nY8ccdf/000/q2rWr1q9fb3WpAAAAAIAM8PeXAnzkFDV/H1luB3iSRx+v6OhoxwyfUqVKacSIEerU\nqZMnu/C4wMBAde/eXV27dtV3332nGTNm6MiRI5Kuvh8AAAAAAABc4/GtwAoVKqRXXnlF4eHhPh8k\npefn56euXbtq5cqVev311xUSEmJ1SQAAAAAAAD7HozOTnnzySQ0ePDhHBzF+fn7q06ePOnfurOnT\np1tdDgAAAAAgg/z9pUDD6iquYpkbciOPhkljxozxZHOWKlSokF599VWrywAAAAAAAPApHl/mBgAA\nAAAAgNzLR/a3BwCYkmh1ASalWV0AkMPlhL+hXba6AHPypSVYXYIpQf5JVpdwS8FByVaXYE4eqwsw\nydef82CrC8giP0m+sryMKRzIhfi2BgAAAAAAgGm+nodnSXx8vObOnet0bciQIRZVAwAAAAAAkPNZ\nGial3+C6UqVK6t+/v0fbj4+P10cffSSbzea4RpgEAAAAALmcvyTbLV+VPVgPhFzI0jDp22+/dQp6\ntm/frilTpihPHs8vdDYMw6kvAAAAAAAAZJxPZKSGYcgwDK1Zs0Z9+vTR2bNnrS4JAAAAAAAAbvhE\nmGSz2WSz2WQYhnbt2qWePXtqz549VpcFAAAAAMiJ/HV1HY4vfPjKqXKAB/lEmGSfmWQPlU6dOqXe\nvXvrxx9/tLo0AAAAAAAApOMTYdL1bDabEhISNHToUM2ZM8fqcgAAAAAAAPB/fCZMstlsKlSokAzD\ncHx+5coVTZ06VWPHjlVaWprFFQIAAAAAcgSWuQFe5TNhkiTNnj1bVapUcQqUDMPQ//73Pz399NOK\njY21uEIAAAAAAIDbm0+FSaVKldKXX36ppk2bugRKmzdvVq9evfT3339bXCUAAAAAAMDty6fCJEkq\nUKCAZs+ere7du7sESkePHlXPnj21efNmi6sEAAAAAPgsfx/7AHIZnwuTJCkgIECTJk3SkCFDnAIl\nm82mixcv6plnntGSJUssrhIAAAAAAOD245Nhkt2QIUM0efJk+ftfi3JtNptSUlL02muvaerUqRZW\nBwAAAAAAcPvx6TBJkrp166ZPPvlEBQoUcFyzL3ubM2eOhg4dqsTERLf32my27CoTAAAAAOArOM0N\n8CqfD5MkqVmzZlqwYIFKlCjhso/SmjVr1KdPH509e9blvvQzmgAAAAAAAJB1AVYXYFbVqlX19ddf\n67nnntOePXsceygZhqFdu3apZ8+e+u9//6saNWo47gkIyDFvD4AvyAE/MlKSrK7AnNRUqysAcra8\nwVZXYEIO+XmU73Ky1SWYkq9QgtUl3FJexVtdgjkFcsgfQqk+/g/fea0uAIAvyxEzk+yKFy+uBQsW\n6L777nPZmPvUqVPq3bu3fvzxR8frAwMDrSoVAAAAAGAVlrkBXpWjwiRJypcvn2bOnKlevXo5AiXp\naqiUkJCgYcOGacGCBZKk4OBg+fnluLcIAAAAAADgs3Jk0uLn56fx48dr5MiRTtdtNpvS0tI0YcIE\nffDBB5Kk/PnzW1EiAAAAAABArpQDdgi5sQEDBqh06dJ69dVXlZKSIunaxtwzZ87UmTNnlCdPHsXF\nxVlcKQAAAAAg2/iJ5WWAF+XImUnpdezYUXPnzlWhQoUc1+yB0rfffqvo6GgLqwMAAAAAAMhdcnyY\nJEmNGjXSwoULVapUKaeNuQ3DcNpXCQAAAAAAAFmTK8IkSapcubK++eYb1a5d2+WkNwAAAADAbYTT\n3ACvyjVhkiQVLVpU8+fPV+vWrZmRBAAAAAAA4AWWhkmlSpVSyZIlHf/188t6OXny5NH06dP1+OOP\nEygBAAAAAAB4mKWnua1du9Yr7dpsNo0dO1ZlypTRf/7zH125csUr/QAAAAAAfJB9mZsvYI4DciFf\neby8ol+/furXr5/VZQAAAAAAAOQauWrPJAAAAAAAAHhXrp6ZBAAAAAC4DfnLd05RY9cV5ELMTAIA\nAAAAAIBphEkAAAAAAAAwzePL3JYuXerpJj2qW7duVpcAAAAAAPAmXzrNjWVuyIU8/ni98sorstls\nnm7WYwiTAAAAAAAAMs9rWa1hGN5qOtN8OeQC4AOOWl3ArQU+YHUF5gSmWl0BkMOFWF2ACbWtLsCc\njYX+ZXUJpvymJlaXcEvHfqtudQnm7LO6AJN8/c/Kf6wuAIAv81qY5GvBjS+GWwAAAAAAL/ClZW5p\nVhcAeJ6vPF4O7kIfXwumAAAAAAAAblceD5NKlSqVpftPnjzpCI8Mw5DNZlPJkiU9URoAAAAAAACy\nyONh0tq1a7N0f/Xqrmuxs9omAAAAAOA24kvL3Hx9fywgE/ysLgAAAAAAAAA5B2ESAAAAAAAATPOV\niX8AAAAAAHiGn64udfMFTOFALsS3NQAAAAAAAEwjTAIAAAAAAIBpLHMDAAAAAOQuvnSam68stwM8\niJlJAAAAAAAAMI0wCQAAAAAAAKb5ysQ/AAAAAAA8g2VugFcxMwkAAAAAAACm+UpWCwAAAACAZ/jJ\nd2YEMYUDuRDf1gAAAAAAADCNmUkAYJfH6gJMuGh1ASalWl0AAK/LIT+PCuqS1SWYkiPqLGJ1ASYV\nsLoAk1KsLuAWcsLfiwBYhjAJAAAAAJC7BMh3Rru+UgfgQSxzAwAAAAAAgGmESQAAAAAAADCNCXcA\nAAAAgNzFX74z2vWVU+UAD2JmEgAAAAAAAEwjTAIAAAAAAIBpHp/499FHH3m6SY+2OWTIEI+1BQAA\nAADwQX7yneVlTOFALuSVMMlms2WpDcMwnP5/+vTpWS3LgTAJAAAAAAAg87y2JVn6QMhX2spqyAUA\nAAAAAHC781qY5GvBjSfDLQAAAACAD+M0N8CrcsTMJAAAAAAAAPgGj4dJjRs39nSTAAAAAAAA8BEe\nD5PmzZvn6SYBAAAAADCPZW6AV3FIIQAAAAAAAEwjTAIAAAAAAIBpvjLxDwAAAAAAz2CZG+BVvvJ4\nAYD1oqwuwIQmVhdgUprVBQA5XIjVBZhQ2+oCzNmiRlaXYMoO3W11Cbe2yeoCTNprdQEmpVhdwC3E\nWF0AAF/GMjcAAAAAAACY5tEwafbs2UpJ8fWI3ZzU1FTNmTPH6jIAAAAAABnlp6vLy3zhgykcyIU8\n+m09depUdezYUREREZ5sNtutXbtWHTt21NSpU60uBQAAAAAAwKd4PCM9fvy4hg8frkcffVRbt271\ndPNetXnzZj3xxBMaPHiwjh07ZnU5AAAAAAAAPsejG3DnzZtXiYmJMgxD27Zt0+OPP64WLVpo+PDh\nqlmzpie78qjIyEh9/PHH2rJliyTJMAxJV98PAAAAACCH4TQ3wKs8OjNp2bJlqlu3riTJZrPJMAz9\n8ssv6tGjh/r3768NGzY4ghqrJSQk6KuvvlKXLl309NNPa8uWLU611axZU//73/8srBAAAAAAAMD3\neDSrLVeunBYuXKhPPvlEH330kVJTUyVdnemzYcMGbdiwQSVKlFC3bt3UvXt3lS9f3pPd35JhGNq0\naZNWrVql8PBwxcXFOQIkm80mSfLz81O/fv30wgsvKDAwMFvrAwAAAAAA8HUen/jn5+en5557Tq1b\nt9Zbb72lzZs3O4IawzB06tQpzZw5UzNnzlSNGjV0zz336N5771XDhg0VEOD5eYixsbHatGmTNmzY\noLVr1yomJsZRiySn2urUqaNx48apRo0aHq8DAAAAAJBNWOYGeJXXHq8qVaroiy++0KpVqzRlyhRF\nRUU5BTeStHv3bu3Zs0ezZ89W3rx5Va9ePdWqVUs1a9ZUpUqVVL58eeXJk8d0n7GxsTp69Kj27t2r\n3bt3a+fOndqzZ4+uXLni1K/kHCIVK1ZMw4YN08MPP+y4DgAAAAAAAFdez2o7dOig1q1b64svvtBn\nn32mc+fOOQU29oAnPj5ekZGRioyMdLq/aNGiKlq0qEJDQ5U/f34FBQUpICBASUlJSkxMVEJCgs6d\nO6eoqCglJCQ43Xv9/kzX91ukSBH1799fffr0UXBwsKffOgAAAAAAQK6TLRP/8uTJowEDBujJJ5/U\nggUL9Omnnyo6OlqSa8BzvZiYGMXExOjgwYM3bP9mm3q7a79s2bJ6/PHH1bNnT+XLly/D7wcAAAAA\n4MP85TvLy3ylDsCDsnUVaZ48efTMM8+ob9+++uGHH/TNN98oMjLSZf+i6xmGcctT4G52ryQFBASo\nadOmevTRR/XAAw+wnA0AAAAAACATLNmSLCAgQO3bt1f79u31zz//aPXq1frpp5+0bds2x/5G0rWA\nKCPBT/rQKSAgQPXr11f79u310EMPqWjRop57EwAAAAAAALchy/e3L1OmjPr376/+/fvr/Pnz2rJl\ni3bs2KHt27fr4MGDjuVwt+Lv76+SJUuqQoUKqlOnjho3bqx69eopb968Xn4HAAAAAACfwmlugFf5\nyuMlSSpSpIjatm2rtm3bOq4lJSXpxIkTOnv2rBISEhQfH6+UlBTlyZNH+fLlU758+VS0aFGVKVNG\ngYGBFlYPAAAAAACQ+/lUmOROcHCwKlWqpEqVKlldCgAAAAAAgIvY2FgVKlQoW/o6ffq0Xn31Vc2d\nOzdb+nPHz7KeAQAAAADwBvsyN1/4YJnbbaFr167asmWL1/tZtWqVunTposjISK/3dTM+PzMJALJN\nQasLMOGo1QWYlGp1AUAOlxOeoRirCzCnsC5YXYIpOaHOqDusrsCkEKsLMCnN6gJuIdnqAoCcJSoq\nSn379tWgQYM0ePBgj58gHxcXpzfffFMrV66UYRiWn1DPzCQAAAAAAIAsSktL0/Tp0/Xkk0/q9OnT\nHmv3t99+U+fOnR1Bki8gTAIAAAAA5C4sc4MFbDabDMPQ77//ri5dumjNmjVZai8lJUXvvPOOnnrq\nKUVFRfnEjCQ7wiQAAAAAAAAPsIc9Fy9e1NChQzVu3DglJ2d83ei+ffsUFhamzz77TFeuXJHNZnMK\nkvz8rI1zCJMAAAAAAACyoFq1ao4laPbgxzAMLVq0SA8//LAOHTpkuq3Zs2erZ8+eOnjwoMtsJMMw\nVLFiRc2fP9/j7yEjCJMAAAAAALmLn64uL/OFD0bdt4XFixfrqaeecrpmD5T279+vHj16aNGiRTdt\nIyoqSk888YTeffddJScnOwVJhmHIz89P/fv317Jly1S/fn2vvRcz+LYGAAAAAADIgsDAQI0ePVpz\n585V8eLFXWYpJSYmaty4cRo2bJhiY2Nd7l+6dKm6dOmiLVu2OEKk9EFS1apV9dVXX+nFF19UUFBQ\ntr43dwiTAAAAAAAAPKBZs2Zavny52rVr53Tymn2W0g8//KBu3bpp69atkq7urTR8+HC9+uqrunTp\nkstsJH9/fw0ZMkRLlixR7dq1LXlP7gRYXQAAAAAAAB5lP83NF3Ca220nJCREH374oRYvXqyJEycq\nISFB0rVA6eTJk+rbt6969eqlNWvW6OzZs273RqpVq5YmTZqkqlWrWvVWboiZSQAAAAAAAB728MMP\na+nSpapTp47LsrfU1FR9+eWXOnPmjMtspKCgII0cOVLffPONTwZJEmESAAAAAACAV5QrV05ffvml\nhg4dKn//a9PU7LOU0p/8ZhiGGjZsqKVLl2rAgAHy8/PdyMZXJv4BAAAAAOAZLHODD/Hz89PgwYNV\nsWJFjRw50jELKf2yNkkqU6aMpk2bpqJFi1pRZob4bswFAAAAAACQwyUnJ+v999/XK6+84rScLT2b\nzaYTJ06oc+fOCg8Pt6LMDCFMAgAAAAAA8ILffvtNnTt31qxZs5ScnOy0d5J9aZudYRiKiYnRiBEj\nNGzYMJ07d86qsm+JMAkAAAAAkLv4+9gHbjtxcXF6/fXX1a9fPx07dszt/kjdunXTPffc47I5t2EY\n+uGHH9ShQwetXLnS4nfiHmESAAAAAACAh6xdu1YdO3bU4sWLnUIk6erso8KFC+vDDz/U5MmTNWfO\nHI0ZM0ZBQUGO++2B0oULFzRq1CgNHjxYZ8+etertuGVpmLRr1y4ruwcAAAAAAPCIc+fOacSIERo8\neLBOnz7tCJLsDMPQvffeq++++07t2rVzXH/yySe1ZMkS1ahRw+0spbVr16pTp05aunRptr+nG7F0\nf/sePXqoWrVq6t69uzp37qzQ0FArywFwu4u2ugAT6lldgEmpVhcA5HD5rS7AhLutLsCcfapqdQmm\nHDpX2eoSbm2b1QWYtNfqAkzy9T8r46wuIIs4zQ3ZbNmyZZo0aZIuXrzoNkTKkyePXnrpJfXp08ft\n/ZUrV9bXX3+tDz/8UHPmzNGVK1ckXZuldPHiRb366qsKDw/XuHHjVKJEiWx5Xzdi+eO1f/9+vfPO\nO5o6daruvfdehYWF6f7771dgYKDVpVnOMAz16NFDu3fvliR1795dkyZNylKbBw4cUOfOnT1RniSp\nY8eOevfddzN17/bt2xUREaE///xTx48fdzx0ISEhqlixoho3bqz27dvrrrvu8li9AAAAAAB42ujR\nox3Bz/VBUs2aNTVlyhRVrnzzfzgICAjQyJEj1bJlS40ePVr//POPyxK5n3/+WZ06ddIrr7yiHj16\nePU93bRWy3pOxzAMpaam6ueff9bPP/+sQoUKqVOnTurWrZvuvjuH/LOXFyxYsEC7d+92+kbMKnsw\n5ck2M1PDuHHj9Ndffzmupa8nOjpaZ8+e1ebNmzV9+nS1atVKY8aMUbly5awoFwAAAAAAU9IHP/7+\n/nr22Wc1dOhQBQSYj18aNmyo5cuXa8KECVqyZImjTft/L126pLFjx1oaJvnEBtzX72h+8eJFLVy4\nUL169VLnzp01d+5cn9tsytt27dqlKVOmOL4unrJ377V5v1lpN7P3zp8/X7169dL27dtdEtb0H9K1\n74t169apa9euWrVqVabrBQAAAHAbsS9z84UPlrnddgzDUJkyZTRv3jyNGDEiQ0GSXb58+TRx4kR9\n9NFHKlKkiEdzAU+wNExq166dAgMDHQGCPTxIHywdOHBAU6ZM0f33368BAwYoPDxcycnJVpbtdSdO\nnNDAgQO98j737Nnj9Pn1IY7ZD/u9GfHpp59qwoQJSktLc+o7/e/79d8D0tVQKSEhQS+++KJWrFjh\nga8CAAAAAACeZxiGwsLCtGzZMjVo0CDL7bVp00bfffedWrZs6VOBkqXL3D788EPFxsZqxYoVWr58\nubZtu7qrX/oZK9K1ZXDr16/X+vXrVahQIXXo0EHdu3dXnTp1rCrfK44fP65+/fopOto7OwHv3bvX\n6WubXcvdNm7c6JhpJckRIhUsWNCxT1apUqWUlJSkI0eOaNmyZfrpp5+UlpbmFC699tpruuuuu1S9\nevVsqRsAAAAAADMKFy6st956S23atPFou6GhoZo5c6YWLVqkd955RwkJCR5tPzMs3zOpUKFC6t27\nt3r37q2jR4/q22+/1XfffaeTJ09KkstSKEm6ePGiFi1apEWLFqlixYrq3r27unbtquLFi1v2Pjxh\n7969GjhwoE6fPi3pWuDiKadOndKFCxecNgW75557NHv2bI/14U5iYqJeeeUVpxlNNptN9evX1/vv\nv++yC/1dd92ltm3batOmTRo1apSio6MdX4fk5GSNGTNGS5Ys8WrNAAAAAHIwP/nO8jKf2FwG3tai\nRQtNnDhRd9xxh9f6ePTRR9W0aVO9/PLL2rFjh9f6McOnvq0rVKigESNGaO3atfr888/VrVs35c2b\n96bL4A4fPqz33ntP999/v5599lmtWrUqRy6DCw8P12OPPeYIkrzh+iVukrJlg/PZs2frzJkzkq4F\nglWqVNGsWbNuepxh06ZN9emnn6pgwYKSrh2JuGfPHi1dutTrdQMAAAAAYMasWbO8GiTZVahQQV9+\n+aUGDx7s9b5uxqfCpPSaNGmiyZMn69dff9XkyZPVvHlzl3100gdLaWlp+vXXX/Xiiy/q3nvv1Rtv\nvOFYNufL4uPjNXbsWL3wwgtKTEyUJKd9iTzJijApOTlZ8+bNc5ph5e/vrylTpqhAgQK3vL9KlSqa\nNGmS09fDMAx98sknXqkXAAAAAABf5u/vryFDhlhag8+GSXZ58+ZVt27dNHfuXP30008aOXKkKlWq\n5PbUL/u12NhYff3113rsscf00EMPadasWV6d8ZNZ4eHh6tChgxYvXuyylC8zu73fSvqT3Oy8HSat\nXr1aFy9elHRtedsDDzygatWqmW6jTZs2atiwodOyv8OHD2vr1q1eqRkAAABADsdpboBX+XyYlF6J\nEiU0YMAArVy5Ut9884369Omj0NDQmy6DO3r0qN5//321bt1aTz/9tFauXGn5MrhNmzbpscce0wsv\nvKDTp0+7bEpduXJljR8/3uP97tmzx2mGUPHixVWsWDGP95Pe6tWrXa6FhYVluJ1evXq5XFu5cmWm\nagIAAAAAwArR0dHatWuXfv31V61atUpLly51ySiSk5MdK5d8leUbcGfW3XffrbvvvluvvfaaNm/e\nrFWrVmndunWOvXmuPw0uLS1NkZGRioyMVMGCBdWpUyf16tXLklPB+vXr53ZjcZvNpg4dOuitt97S\nzp07PdpnXFyc/vnnH0d/NptNtWvX9mgf10tNTdXmzZudfi+Cg4PVvHnzDLfVqlUrRzv2sHDdunX6\n97//7bF6AQAAAADwtDVr1ujHH3/U77//rhMnTrj8+n333afQ0FDH53/88YcGDRqkFi1aqE+fPvrX\nv/6VneWakmPDJDs/Pz81bdpUTZs2lSQdOHBAn3/+uZYsWeIU0kjXQpvY2Fh9+eWX+vLLL1W3bl09\n9dRTateunUdPTjMjfX2hoaEaO3asHnroIa/0tXfvXpfT4by9xG3Xrl2Kj493Oj2uVq1aCgoKynBb\nISEhqlSpkg4fPuy4FhUVpVOnTunOO+/0ZNkAAAAAcjr7MjdfwDK329bSpUs1c+ZMHT16VJLc7o3s\nLoc4ceKEEhISFBERoYiICDVt2lTjxo1TuXLlvF2yab7yeGWJYRjatGmTfvzxR/3yyy86fvy447ok\npxkt6e+RpG3btumFF15QxYoVNXr0aLVs2TLbarbZbAoKCtLjjz+uQYMGmdqQOrOs2Hx7//79Ltdq\n1qyZ6faqV6+uQ4cOOf0+7ty5kzAJAAAAAOAz4uPj9dprryk8PNwpQLo+OLrRwVsnT550ek1kZKTC\nwsI0ceJEtWvXzjtFZ1CODpO2bt2qlStX6vvvv9e5c+ckyWVTbrvrf5PSz1YyDEOHDx/WwIEDFRYW\npjfffFOBgYFerT0wMFCdO3fW0KFDVbJkSa/2JbkPk+zL3GJiYrRq1Sr9/vvv2r17t86fP6/U1FSF\nhoaqRIkSatKkiVq3bq06depkqM8DBw64XKtUqVLm3oCuHoF4vfQzlQAAAAAAsNKlS5fUu3dvHTx4\n0GV1kOQ66cWd9Evh7Ct94uLiNHLkSL333ns+ESjluDDpyJEjWr58ub777jvHF/hGSZ/9eqlSpdS9\ne3e1b99eO3fu1PLly7Vp0yZduXLF5fVLlizR2bNnNXPmTK8texs0aJB69+7t9c2v07v+JLeyZcsq\nLi5O48eP1/fff6/U1FRJzl+/qKgonTx5Un/++admzJihevXq6eWXX1aDBg1M9Wnfoym9UqVKZfo9\nuJuB5K4PAAAAALc5lrnBAmlpaRo2bJhjYsX1W+4EBwerYsWKbk9aTy86Otrpc3s7qampevHFF/W/\n//1PVatW9XT5GeIrj9dNnTt3TitXrtTy5csdG1PfKkAKDg5WmzZt9PDDD6tp06aO19x1113q1q2b\noqKitGjRIi1cuFCXLl1yOgVu/fr1mjlzpgYOHOiV9zN8+HCvtHsjqampOnjwoNPeRbGxserQoYOS\nkpJMzeCSri4J7N27t5555hm99NJLt+w3JibG5Vrx4sUz/T7chW9nz57NdHsAAAAAAHjKxx9/rMjI\nSJcxdtu2bdW7d281btxYAQEBtzwI7OOPP9aKFSv03//+V8ePH3fauiclJUWvvfaavv7662zf9zk9\nnw2TkpOTtWbNGi1btky//vqr0tLSTK01rF27tnr06KFOnTqpYMGCN2y/ZMmSGjFihB599FENGDBA\nB1+qx7kAACAASURBVA8edLRrGIZmz56tp556SsHBwV54d9nr0KFDSk5OdkpFL1y44PQ1vNE3obtl\ng3PmzNHx48f1/vvvy9//xjF7dHS0S7uFChXK9Ptw9/sZGxub6fYAF97btsxzzlldgEmpVhcA5HBp\nVhdgguu/GfmkIrpgdQmmFC7q+3WeuSPzf4/LVoWtLsAk/qwEcpWYmBjNnTvXadwdHBysd999V23a\ntMlQW0FBQQoLC1Pnzp313nvv6dNPP3XZO/jHH3/McLue5HNhUmRkpJYvX64ffvhBly9flnTrWUhF\nixZVly5d1KNHD1WpUiVD/ZUsWVLTpk1Tp06dlJZ27W9uly9f1qZNm7JtQ25vSr9f0vVfP5vNprp1\n66pTp06qW7euihUrpqSkJJ09e1ZbtmzR6tWrtX//fqe1njabTT/88IMmTZqksWPH3rDfuLg4l2tZ\n2WQ8f/78Tp8bhqFLly5luj0AAAAAuZS/fGd5ma/UAa+aO3euEhISnFYETZ48OUuBT2BgoEaPHq0S\nJUpo8uTJTuP5RYsWESbt379fy5Yt08qVK3X69GlJNw6Q7L8WEBCg++67Tz169FCrVq0UEJD5t1Kh\nQgU1bdpUGzZscOrryJEjuSJMcrce0zAMFS5cWBMnTlTr1q1dfr18+fJq1KiRBg4cqOXLl2v8+PGK\ni4tzSlkXLFigevXqqVOnTm77TU5OdrmWlZleQUFBjv+3P6Du+gAAAAAAIDv9+OOPTkHSgw8+qPbt\n23uk7X79+mnLli1as2aNo4/ffvtNycnJTuPk7GRpmDRnzhwtX77ccYS8mWVslSpVUlhYmLp166Y7\n7rjDY7VUrlxZGzZscLqWkpLisfattHv3bpeNvypWrKjPPvtMJUqUuOX9Xbp0UbVq1dS3b19dvHhR\n0rUw591339WDDz7o9vQ7d1+/my2LuxV3gaF943AAAAAAAKxw/PhxHT161CnHeP755z3ax7Bhw7Rm\nzRrH56mpqdq1a5fq16/v0X7MsjRMmjJliiOUkG4cIBUoUEAd/j979x0fVZ3vf/x9UklIaAFDkQ4a\nOiiCuCJgl6UILBYQFQXLAquuFSy7WNAVlMULuhYQBBRQFxBF1gLIXgvlZ8CEppRA6KSQQhKSmTm/\nP7gzZpJAJslMzknyej4e53HnnMx8v58zmax33nzLwIEaPny4unfvHpBaShoxU5HFou1kwIABio2N\nVXJysg4dOqT8/Hy9+eabPgVJbhdffLH+8Y9/FFuU/NixY/r44481atSoYq8pPG3QrSJhUlBQULFr\nLper3O0BAAAAqKbYzQ2VyD1Axq1Zs2Z+323toosuUuvWrZWUlOS5duDAgZoZJrmVFCIZhqFevXpp\nxIgRuuGGG1SrVq2A1uDeFazw6KhLLrkkoH1WlrFjx3qdu1yuEoOZ0vTr108DBgzQ2rVrvX5nq1at\nKjFMCgkJKTZyyOFwlHsYXkmjkEoaEQUAAAAAQGVJS/t9lxzDMMq8lrOvLr74Yu3fv99z7p45ZAVb\nhEnS7yFO06ZNdfPNN2vYsGFq3rx5pfV/6NAhxcXFqXHjxmrcuLFatmxZqf1XpvIESW5333231q5d\nK+n3qW4JCQk6ffp0sQWyQ0ND/RomFR7p5P68WDU/FAAAAAAASUpPT/c6b9CgQUD6KfqdOy8vLyD9\n+MLyMMm9Xd61116rESNGqE+fPufcpj6QFi5cWOl9VkWXXHKJIiIivD60TqdTv/zyi/r06eP13MjI\nSOXm5npdy83NVWRkZLn6du/uV1hFFvQGAAAAUE0xzQ2VqOh33KLfg/3l1KlTXud16tQJSD++sPTP\nq3Pnzho+fLgGDx6s6OhoK0uBj0JCQhQXF6f4+Hiv0M89TbCw+vXrKzU11eva6dOnFRMTU66+i4ZJ\nhmEELPEFAAAAAMAXRb+XHjlyJCD97Nu3z2vdaSu/D1saJn3yySdWdo9yql+/frFrheeIFn6ee/2r\nws9r0aJFufotqY/yBlMAAAAAAPhD48aNPY9N09T27duVm5uriIgIv/Wxb98+7d+/3+v7dZMmTfzW\nflmVf/GcSlDSbmAlycrK0uLFi7Vr1y6vBbQRGCVNUytpcexmzZoVu5aSklLufksa/VRddtwDAAAA\n4EdBOju9zA6Hrb91wx+6du3qtZ6Rw+HQv//9b7/28dZbb3mdR0VFqXPnzn7toyxs97FOTU3V7Nmz\nNWLECE2YMMGn1+zbt08vvPCChg0bpquuukr/8z//oxMnTgS40porKyur2LV69eoVu1bSAuYHDhwo\nd78HDx4sdq1169blbg8AAAAAgIoKCQnRH/7wB8/MHNM09fbbbxdb46i8vv32W33++eeetg3DUO/e\nvSu0uVZF2SZMKigo0PTp03X11Vdrzpw52r59u3777TefXpucnCzp7HCykydP6s0339RNN92kxYsX\nB7LkKsPhcOjEiRPatWuXfvjhBx09erRC7RVdB0kqeepbXFxcsWt79+4td78lvTZQWy4CAAAAAOCr\nkSNHep2fPHlSjz76qPLz8yvU7g8//KBHH3202PXhw4dXqN2KskWYlJKSopEjR2revHk6c+aMZ6ra\n0aNHfXrj3WGSYRiepO706dN68cUX9fDDD5c4Baum+Mtf/qIuXbroqquu0s0336x77rlHn376abnb\ny8/P1+7du4vtuNexY8diz+3SpYvXuWmaSkxMLFe/7nmnhfsNDw8nTAIAAABQnHs3Nzsc7OZWI/Tt\n21eXX3651+ikH374QXfddVe5BlVkZmZqxowZGj9+vGc3dXfbXbp00dVXX+3vWygTyzdLzMzM1Nix\nYz2jkNxhgWmaMk1T+/fv18UXX3zeNtxhklvhNv7zn/+ooKBAc+bMCUD19tesWbNii2DHx8eXu73N\nmzeroKCg2KJfJS381ahRI7Vu3VpJSUmeP6Y9e/YoNTW1zAtnb9u2TdnZ2V7D+i699FKFhYWV+14A\nAAAAAPCXKVOm6NZbb1VeXp7nu2t8fLyGDh2q3r1764orrlBsbGyx1zkcDqWlpSk1NVUJCQnavHmz\n1qxZo7y8vGLf54ODg/XUU09V5m2VyPIwadq0afrtt9+83hz3yKRGjRrpzJkzpbZx2223qUWLFtqw\nYYPi4+M9b7b7l7d27VrNnz9fd999d6Buw7aKjhgyTVMbN24sV6AjSQsXLvRqyzAM9e/f/5zP79ev\nn9eK86ZpavXq1RozZkyZ+v3888+LXevbt2+Z2gAAAAAAIFAuuugizZw5UxMmTJDL5fJkEg6HQz/8\n8IN++OEHz3PduYdpmiV+p3b/vPB3acMw9Nxzz+mSSy4J/M2UwtJpbvHx8VqxYkWxIKlz58567733\ntGHDBnXt2rXUdrp27aoHHnhAH374oT7//HP17dvX6403TVOvv/56jVyUe8CAAQoPD/e65nQ6NX/+\n/DK3tXnzZn333XfFpriNHj36nK8ZPHiw57H7d/HBBx+ooKDA537T0tKKfU5CQkI0ZMiQMlQPAAAA\noMZgmhss0r9/f73yyiue7+GFB7q4j6IK/8x9uF/n/rlhGJo0aZJuueWWSr2fc7E0TFq0aJHnsfsN\nvf3227Vs2TJdeeWV5Wqzbdu2evfdd3XPPfd4/ZIKCgq0YMGCihVcBUVFRem6664rFq598MEH2r17\nt8/tpKam6oknnvCcFx6V1LZt23O+rlOnTurcubPX7+LQoUN69dVXferXNE1NmTJF2dnZXv3eeOON\natCggc/1AwAAAABQGQYPHqxly5apTZs2Xt/Fix5u5/uZaZqqV6+e3n77bf35z3+u9Hs5F8umuTkc\nDn3zzTdea+D07dtXf/vb3/zS/hNPPKHdu3fr+++/9/SxcuVKPf74435pvyr5y1/+oq+++sozGsgw\nDJ05c0YPPPCA3nvvvfOGQZJ0+PBh3XPPPTp27JjX9cjISD333HOl9j9p0iTdf//9nr5N09SiRYsU\nGxurcePGnfN1pmnqhRde0Pr164uNSvrLX/5Sar9Amfln587A6mF1AQAqRS2rC/BBB6sL8M1unX/t\nTbs48UsLq0soXfn2Ual8O60uwEdOqwsoRemrjQA4j4suukjLly/XZ599pgULFnjtVu/+flt01o8k\nr4EY9evX1+jRozV69OgSd1C3kmUjk3bu3Om1HpJhGH5fROqxxx7zOk9NTa3Q1vRVVYsWLXTfffd5\nfSgNw9DRo0c1cuRIzZ07Vzk5OcVel5WVpXnz5mnIkCE6ePCg57o7/HvqqadKXHi7qH79+unqq68u\nNudzxowZeuihh7zadtu1a5fuuusuffjhh8WG9o0fP17Nmzcv25sAAAAAoOYI0tnpZXY4bLGHOqwQ\nFhamP/3pT1q1apU++ugj/fWvf1X//v3VsGFDhYSEFJv6Fh0dra5du2rs2LGaM2eO1q9fr4kTJ9ou\nSJIsHJlUNNS56KKL1KZNG7/20aFDB7Vs2dIrrNi1a1epI3GqowkTJmjPnj1as2aNpN+H0eXm5mr6\n9OmaNWuWunfvriZNmsjpdOrYsWPaunWrHA5HsSF2hmHorrvu0siRI33u/8UXX9Sf/vQnHTlyxKv/\n//znP/rqq6/UuXNntWjRQi6XS/v379euXbs8zyvc72WXXaZJkyb5620BAAAAACDgevTooR49vKcZ\n5ObmKjMzU+Hh4apbt26JI5XsyrIwKSMjw/PYMAy1a9cuIP3ExcXpwIEDnvO0tLSA9GN3hmFoxowZ\nCg4O1urVq4vN2ywoKNCmTZuKvcY9La3wtfvuu0+PPPJImfpv0KCB3nvvPd177706duxYsVFKCQkJ\nSkhI8OpX8l7BvkePHnrzzTer1B8YAAAAAAAliYiIUEREhNVllItlA+5yc3O9zkNDQwPST1RUlNd5\nSdO57KzwdoEVFRISotdee01Tp05VnTp1fF5RXjob5jRt2lT/+te/yhwkubVp00bLli3TFVdcUWxF\n+5L6LbyC/a233qp58+YV+30CAAAAQDHs5gYElGUjk2rXru11npqaGpB+Tp3yXlG3bt26AeknEIqO\nwPHXiJxbbrlFf/zjH/XRRx9p5cqV2rNnz3lr6Nixo0aOHKlhw4YpLCysQn03atRIc+fO1fr16/XB\nBx9o48aNcrlcJT43JCRE11xzje6++2517969Qv0CAAAAAAD/sCxMuuCCCzyPTdNUYmKiZySKP/32\n229eU7ViYmL82n6g9OrVSzt3Bm4ritq1a2vcuHEaN26c0tLS9MsvvyglJUWnTp2Sy+VSVFSUWrRo\noU6dOgVksa/+/furf//+ysrK0rZt23Tw4EFlZWUpODhYdevWVevWrdW1a9cKh1cAAAAAAMC/LAuT\n4uLivM7T09P1008/qU+fPn7rY9euXTp48KBXQNWqVSu/tV9dNGjQQP3797ek7+joaF155ZWW9A0A\nAACgmnJPc7MDprmhGrLsz6tly5Zq2rSpjh496hk59Nprr+mTTz7xWx8zZ870Oo+NjVX79u391j4A\nAAAAAKierrnmGqtLOCfDMPTNN99Y1r+lWe0NN9yg999/3zNyaPv27XrxxRf1zDPPVLjtefPm6bvv\nvvMEVYZhqF+/fhVuFwAAAAAAVH+HDx8utsO5XVi9y7llu7lJ0pgxYxQScjbPcv+CFi9erMmTJys7\nO7tcbebn5+u1117T9OnTvd7c4OBg3XvvvX6pGwAAAABgY1bv4Fb0QJXm3mXcLocdWBomNW3aVLfe\neqvX9vOmaWrFihUaOHCgZs+ereTkZJ/aOn78uObOnavBgwfrvffe87TpHpU0cuRItWjRImD3AgAA\nAAAA4AvTNEs8fHmNHViekT766KP67rvvdPjwYUm/B0onTpzQnDlzNGfOHMXExCguLk6xsbGqXbu2\nIiIilJeXp+zsbJ08eVK7d+/WiRMnJMkrmHL/34suukiPPfaYNTcIAAAAAACqpIqGN+5sonBWceGF\nF6pFixaqXbu2oqKi5HK5lJ2drfT0dO3evdszU6vwaw3DUJcuXdSkSZMK1eMvlodJkZGRmjt3rkaP\nHq3U1FRJxd/slJQUff/99+dso/Avt/CQL9M01bhxY73zzjuqXbt2IMoHAAAAANhNkOyzi5ql84FQ\nEbt27Srza/bv3697771XR48elXQ2lwgNDdV1112noUOHqmfPnqXmE3v37tVnn32mTz/9VCkpKZ5B\nN0lJSfrzn/+sAQMGlOt+/MkWH+uWLVtqyZIl6tSpU7FgyH2cawiYO6ErOnfQNE1ddtllWrZsmWJj\nY624LQAAAAAAUEPs27dPo0aN8gqSLr30Uq1cuVKvv/66+vXr59NAl7Zt2+qRRx7RmjVrNHz4cE/u\nkZWVpUmTJmndunWBvpVS2SJMkqQLL7xQS5Ys0ZQpU9SgQYNicwF9WXzK/ZqYmBg9/vjjWrBggS64\n4AIrbgcAAAAAANQQDodDjz32mNLT0z1ZxrXXXqsFCxaoTZs25WozKipK06ZN03333ecJlBwOhx5/\n/HEdP37cn+WXmW3CJEkKCQnRnXfeqXXr1mnmzJm6/vrrVbdu3fOOSnIfderUUb9+/fTKK69o3bp1\nuvfeexUUZKvbAwAAAABUhmBZv4Ob+7DLdDsE1Pz587Vjxw7PgJe2bdtq5syZnh3sK+Kvf/2rLr/8\nck+gdPr0ac2ePbvC7VaE5WsmlSQsLEw33XSTbrrpJknSwYMHtX//fh09elQ5OTnKy8tTZGSk6tat\nq+joaLVu3Vpt27a1uGoAVd4pqwvwQRerCwBQKarAUo8Hm1SN0d+7dbHVJfgm0eoCfLDT6gJ8tNfq\nAnzksLqAUgRJCre6CKBqME1TH3zwgWeJHsMwNGXKFIWGhvqtj6eeeko333yzp79Vq1bpmWeeUXi4\nNX+otgyTimrRooVatGhhdRkAAAAAAABeEhMTdeLECc+opNjYWF1xxRV+7SMuLk5t2rTR/v37JUln\nzpzRzz//rD59+vi1H18xDwwAAAAAUL0wzQ2VaPfu3Z7HhmGoQ4cOAemnXbt2XmtL79u3LyD9+IIw\nCQAAAAAAoJzS0tK8zuvXrx+QforuBJeVlRWQfnxBmAQAAAAAAFBORTf/Sk9PD0g/RXdwq1WrVkD6\n8UWVWDMJAAAAAACfBck+08sYwlHt1atXz/PYNE0lJvp/V4WcnBzFx8d7FvmWpEaNGvm9H1/ZMkxK\nTExUUlKS0tPTlZeXJ4fDIZfL5TU3sLwmTpzohwoBAAAAAACkiy/23jk0JSVF3333nfr16+e3PpYt\nW6bc3FzPIt+S1KWLdVs92yZMSktL05tvvqk1a9YoNTU1YP0QJgEAAAAAAH+Ji4tTdHS0srOzPSOH\nXnrpJfXq1UsREREVbn///v164403vIKkVq1aWbrrvS0G3K1YsULXX3+9Fi9erJSUFJmmGZADAAAA\nAFADsJsbKlFoaKhuuukmr9whOTlZ999/v/Ly8irU9sGDB3XPPfcoJydH0tlpdIZh6JZbbqlQuxVl\neZi0evVqTZ48WdnZ2Z43JRAHAAAAAABAIIwbN04hIWcnf7lHJ23evFlDhw7Vjz/+WOb2nE6nPvzw\nQ9188806evSoV67RuHFjjR492m+1l4el09zS0tL097//3RMiFcZIIgAAAAAAUBW0aNFCY8eO1bvv\nvusZ1GKapg4cOKB77rlHbdu21R//+Ed169ZNF198sWJiYoq1cezYMW3fvl2bN2/W559/rtTUVK+8\nxDRNBQUF6YUXXlBYWFhl36IXS8OkhQsXKjMz0ytIcr853bt3V5cuXdS4cWNFRUUpNDTUwkoBAAAA\nAFWGe5qbHTDNrcZ4+OGHtXXrVm3evNlrlpRpmtqzZ4/eeOMNz3ODgoJUu3ZthYeHKzc3Vzk5OV6D\natyPiw68efjhh3XllVdWwt2cn6V/Xl9++aXXm2sYhrp166apU6cqLi7OytIAAAAAAAB8FhwcrHfe\neUcPPvigfvrpJ0/e4R6lVDgscjqdyszMPGdbJQ26efTRRzVu3LjA3UAZWLZm0r59+5SUlCTp98St\nffv2mjdvHkESAAAAAACociIiIjRv3jxNmjRJISEhXiOMyrPus2maatq0qebOnWubIEmycGTSnj17\nvM4Nw9DTTz+t2rVrW1QRAAAAAKBaYJobLBQUFKQJEyZoxIgRevfdd7Vq1SqvUUjn2ySs8Oil5s2b\na/To0Ro1apTlayQVZdmf18mTJ73OW7Rood69e1tUDQAAAAAAgP80btxYzz77rJ566il9//332rhx\no7Zt26akpCSlpaUVe37Dhg3VunVrXXrppbryyivVs2dPC6r2jWVhUlZWluexYRhq06aNVaUAAAAA\nAAAERGhoqPr376/+/ft7ruXn5ys7O1v5+fkKCwtTVFSU7UYfnY9lYVJkZKTXeYMGDSyqBAD+j8Pq\nAnzAMOmax2l1AdUMf0N+4+TNBGBnwZJpl/+ZsksdsJWwsLAqnYNYtgB3s2bNvM4zMjIsqgQAAAAA\nAAC+sixM6ty5s+exaZravn27VaUAAAAAAADAR5aFSbGxserYsaPn/NixY0pISLCqHAAAAABANeEM\nlpwhNjmY5oZqyNLNEkePHq2nn37asy3e7Nmz9fbbb1tZEgAAAAAAgF9lZ2frzJkzcjgccrlcMk2z\nwm02bdrUD5WVj6Vh0vDhw7V48WLt3LlTpmlqw4YNWrhwocaMGWNlWQAAAAAAAOW2fft2rV69Whs2\nbFBSUpIcDv/u9mMYhnbs2OHXNsvC0jDJMAzNnDlTt9xyizIzM2WapqZNm6aUlBQ9+OCDqlWrlpXl\nAQAAAACqINf/TXOzAxfT3GqUkydPatq0aVqzZo0k+WUEkh1ZtmaSW8uWLTV//nzFxMTIMAyZpql3\n3nlH/fr10/PPP69Vq1Zp7969SktLU35+vtXlAgAAAAAAFHPkyBGNHDlSa9askWmaniDJMAy/HnZg\naVY7a9Ysz+OrrrpKy5cv9wRKGRkZ+uijj/TRRx/5rT+rh4EBAAAAAIDqxzRNPfLIIzp27JgknTP0\nqS4jlSwNk956661ib7Bpmp5r1eVNBgAAAABUHmdQkBzBlk/EkXS2FlR/X375pbZt21ZixiFJ0dHR\naty4sWrXrq3Q0FArSvQrW8wiLTr0y82fw7cIpgAAAAAAQCB88sknxa4FBwdrzJgxuu2229SyZUsL\nqgocW4RJdpnzBwAAAAAAUBZZWVnatGmT1yyr8PBwzZs3T5deeqnF1QWGpWFS06ZNreweAAAAAFAN\nuYKD5QyxxdgJuYLZzq26i4+Pl8Ph8KwBbRiG/vrXv1bbIEmyOExau3atld0DAAAAAABUyMmTJ73O\no6KidMstt1hUTeVgJTAAAAAAAIBySk1N9Tw2DEMdO3ZURESEhRUFnj3G/QEAAAAA4CfOoCA5bTK9\njN3cqr/gIp+1mrCkD59qAAAAAACAcoqJifE6z8/Pt6iSykOYBAAAAAAAUE4XXXSR57Fpmjp48KCF\n1VSOKjXNraCgQBkZGcrPz1eTJk082+4BgF8cs7qA0h1sfYHVJQCoBPkKs7qEUu1RO6tL8MluXVT6\nk+wg3uoCfLDb6gJ8dMjqAnxkWl1AKWpJamF1EeXnUrCcssc0N5dN6kDgdOjQQfXr19epU6ckSTt2\n7FB6errq169vcWWBY9uRSSkpKVq+fLmmTJmim266SZdccom6du2qvn376tprr1VaWprX87du3aox\nY8Zo8eLFysrKsqhqAAAAAABQkxiGoaFDh8o0z6bELpdLixYtsriqwLLdyKQDBw7ovffe08qVK1VQ\nUCBJnl/I+Rw6dEibN2/Wli1bNGvWLI0dO1b33nuvwsLs/y97AAAAAACg6ho3bpw+/vhj5eTkyDRN\nzZ07VzfddJPatasaI3nLylYjkz788EMNHjxYn3zyifLz82WapkzTlGEYnuNcDh8+LOls8JSZmak3\n3nhDt912W42YqwgAAAAA+J1TQXIo2BaH015fuxEgDRs21DPPPOPJMPLy8nTfffdp165dVpcWELb4\nVJumqcmTJ+uFF17whEi+BEiFucMk92tM09SOHTt02223ad++fYEsHwAAAAAA1HDDhg3TxIkTPZnG\nkSNHdNttt+lvf/ubEhIS5HK5rC7Rb2wxzW3GjBlavny5JHmFR0Wnt/kyMqnoc9PS0nTPPfdo+fLl\n1XrxKwAAAADAWWcX4LbHKucswF0zJCcnS5KGDh2q/Px8vfvuu54RSsuWLdOyZcsUHh6u9u3bq379\n+oqKilJ4eHi5+zMMQ9OmTfNX+WVmeZi0evVqzZ07t1iI1KhRI/3pT3/SH/7wB1100UXq1avXedt5\n5JFH1KhRI33++edyOBxe7R0/flwvvfSSZsyYEbD7AAAAAAAANdN1111X4gAY98wpScrLy1NCQkKF\nd6Z3j3yyMkyydJpbfn6+V8DjXiPpzjvv1LfffquHHnpIPXv2VJ06dUptq3PnznrllVe0cuVKde/e\n3fPLcv/ivvjiCyUkJATsXgAAAAAAQM3lzjQKH5KKLeNT0vPKctiBpWHS0qVLdeTIEU/gYxiGxo4d\nqylTppR7F7a2bdtq0aJFuuGGG4q9yR999JE/ygYAAAAA2JhLQXIq2BaHyx5LFaMSFA6NzrUGdEnP\nKethB5Z+qr/44gvPY8Mw1KlTJz355JMVbjckJEQzZsxQ+/btPW2bpqmvv/66wm0DAAAAAAAUVdER\nR1VpZJJlayZlZGTol19+8RqV9Mgjj/it/dDQUD3xxBMaP368J7nLzs7Wb7/95gmZAAAAAAAAKuqD\nDz6wuoRKZVmY9Msvv8jlcnmCnjp16qhPnz5+7aNv375q2LChUlNTPdd+/fVXwiQAAAAAqMbOTjGz\nBye7udUIpW0aVt1YNs2tcMBjGIa6dOmioCD/l9OlSxevYWCnTp3yex8AAAAAAAA1hS3CJElq2LBh\nQPpp0KCB13l2dnZA+gEAAAAAAKgJLJvmVnQUksvlCkg/p0+f9jqPjIwMSD8AAAAAAHs4u5uby201\n1gAAIABJREFUPbCbG6ojyz7VMTExXucpKSkB6efIkSNe50VHKgEAAAAAAMB3loVJhae1maapX375\nxe9b3KWlpSkxMdGzyHfRfgEAAAAAAFA2lk1z69q1q0JCQuR0nh18ePr0aa1fv14DBgzwWx8ffvih\n145xISEh6tKli9/aB1DNHLO6gNLt1kVWl4BKFmKbQfrVg6OK7KiTr3CrSyjVHrW1ugSfHDjYzuoS\nfLPb6gJ8kGx1Ab7KtLoAHzmsLqAUWVYXUCFOBckho/QnVgKnTeoA/MmyMCkqKkqXXHKJNm3aJMMw\nZJqm5syZo379+vllV7ekpCTNnTvX07ZhGOrevTtrJgEAAAAAgFIVXTbHbpo2bWpZ35aFSZI0cOBA\nbdq0yXO+fft2vf7663rssccq1O7Jkyc1btw45ebmek1xu/HGGyvULgAAAAAAqBmuvvpqr0zBTgzD\n0I4dOyzr39Jl5UeOHKmWLVtKkmcE0dy5c/Xyyy8rPz+/XG1u2LBBw4YN06FDh7x+6Y0bN9bIkSP9\nUjcAAAAAwL5cCpZTIbY4XFVkijVKZpqmbQ8rWToyKTg4WE888YQmTJggwzA8gdIHH3ygb775Rrfe\neqv69Omj2NjYYq8tHBQdOnRImzdv1pIlSzwLebt/7n48adIkhYWFVdq9AQAAAACAqs2OI5OsDpIk\ni8MkSbrmmms0ceJEzZ492ytQOnz4sGbOnKmZM2eW+Lr77rtPubm5Sk1NVUZGhud64SBJOvuLHzFi\nhIYPHx7wewEAAAAAAKjuLA+TJGnixIk6efKkli5d6gmUpOJpm/vcNE1t3769xDSucJBkmqauvPJK\nTZ06NYDVAwAAAADsxKlg2+yHapc6UD52GAVkR7YIkyRp6tSp6ty5s6ZNm+ZZOLtoMFSY+7ykIWfu\n0Un33XefHn74Yb/sDgcAAAAAAGqOb7/91uoSbMs2YZJ0dkHunj176q233tLq1avlcDgkqViwVJLC\nYVOvXr00YcIE9e7dO6D1AgAAAACA6qlZs2ZWl2BbtgqTJKl169Z69dVX9dhjj2n58uXatGmTtm3b\npuzs7HO+Jjg4WHFxcerZs6cGDx6szp07V2LFAAAAAAA7cSlITtlj4WSXTEkuq8sA/Mp2YZLbBRdc\noPvvv1/333+/TNPUgQMHlJ6erszMTGVmZio8PFx169ZV3bp11bx5c9WuXdvqkgEAAAAAAKo924ZJ\nhRmGoVatWqlVq1ZWlwIAAAAAAFCjVYkwCQAAAAAAXzkVJIfssRGTUy4xzQ3VjT3+ugAAAAAAAFAl\nECYBAAAAAADAZ0xzAwAAAABUKy4Fy6lgq8uQJLnklOSwugzArywNkyZPnlyp/RmGoWnTplVqnwAA\nAAAAANWJpWHS8uXLZRhGpfRlmiZhEoDzO2Z1AaVLUmurS0AlC5bT6hKqFbv8K3Vp8hVmdQmlSlZz\nq0vwzZ4qMhA/yeoCfJFpdQE+Omx1AT4qsLqAUpywugAANmaL/7qaphnQ9isrsAIAAAAAWM+pINv8\nA4JTgf2+C1jBFmFSoMIed0gV6LAKAAAAAACgprA8TPJn0FM4lDJNU7Vq1VKPHj381j4AAAAAAEBN\nZ2mY9MEHH1To9fn5+crJydHJkyf122+/acuWLdqzZ48nVDpz5owaNmyol19+WSEhludmAAAAAIBK\nYK/d3Jgpg+rH0oSlV69efm9z69atevHFF5WYmChJ+vzzz3X69GnNmTOHtZMAAAAAAAAqKMjqAvyt\ne/fuWrJkifr37y/TNGWaptatW6eZM2daXRoAAAAAAECVV+3CJEkKCQnR66+/rmbNmskwDJmmqXnz\n5unXX3+1ujQAAAAAQIC5/m83Nzscrur5tRs1XLX9VEdGRmrSpEkyTVOGYcjpdOqdd96xuiwAAAAA\nAIAqrdqGSZI0cOBA1a5dW9LZ3d2++eYbnTlzxuKqAAAAAAAAqq5qHSaFhYWpW7duMs2zq+efOXNG\nW7dutbgqAAAAAEAgORUkh4JtcTir99du1FDV/lPduHFjr/P9+/dbVAkAAAAAAEDVV+3DJJfL5XWe\nmZlpUSUAAAAAAABVX4jVBQTagQMHvM7Dw8MtqgQAAAAAUBnO7qRmj6+7TjmtLgHwO3v8dQXIyZMn\nlZCQIMMwPOsmNWrUyOKqAAAAAABATZCYmKikpCSlp6crLy9PDodDLpfLk1FUxMSJE/1QYflU6zDp\ntddek8PhkGEYnmutW7e2sCIAAAAAAFCdpaWl6c0339SaNWuUmpoasH4Ik/zM6XTqtdde04oVK7yC\npNjYWHXo0MHCygAAAAAAgeZSsJwKtroMSWdrQc2xYsUKvfjiizp9+rRfRh+dS+GswwqWhklHjhyp\ncBtOp1P5+fk6ffq0UlNTtX37dn322WdKTk72PMc0TRmGoeuuu67C/QEAAAAAABS1evVqTZ482RMi\nBSrwCWRI5StLw6Srr746IG9uSb+40NBQ3X333X7vCwAqU5jOWF0CKlkIi3b6lYN/HfabcOVbXYJv\nquU4fFQPoVYXUAr+eICySEtL09///nfPYJbC7BD++Jvl/wsRiDe16C/OMAxNmjRJzZo183tfAAAA\nAAB7cSnIRtPcgqwuAZVg4cKFyszM9MojTNNUUFCQunfvri5duqhx48aKiopSaKjdw+TSWR4mBXKe\nnzuouuOOOzR+/PiA9QMAAAAAAGquL7/80pNvuEcndevWTVOnTlVcXJzF1fmf5WGSFLghX506ddKj\njz6qK664IiDtAwAAAACAmm3fvn1KSkqSYRiefKN9+/aaN2+eateubXF1gWFpmHTZZZf5pZ2goCCF\nhISodu3aatCggdq3b6+rrrpKzZs390v7AAAAAICqw6kg26yT52SaW7W3Z88er3PDMPT0009X2yBJ\nsjhMWrhwoZXdAwAAAAAAVMjJkye9zlu0aKHevXtbVE3lICIFAAAAAAAop6ysLM9jwzDUpk0bC6up\nHLZYMwkAAAAAAH9xKlhOm3zdtcuucgicyMhIr/MGDRpYVEnlYWQSAAAAAABAOTVr1szrPCMjw6JK\nKg9hEgAAAAAAQDl17tzZ89g0TW3fvt3CaioHYRIAAAAAoFpxKfj/prpZf7iY5lbtxcbGqmPHjp7z\nY8eOKSEhwcKKAo8wCQAAAAAAoAJGjx4t0zRlGIYkafbs2RZXFFiWrkh25513Wtn9eRmGoQULFlhd\nBgAAAAAAsLnhw4dr8eLF2rlzp0zT1IYNG7Rw4UKNGTPG6tICwtIwadOmTZ7Uzk4Kp4kAAAAAgKrF\npSDb7KLmYkJQjWAYhmbOnKlbbrlFmZmZMk1T06ZNU0pKih588EHVqlXL6hL9ylafatM0z3uU93Vl\nOQAAAAAAAMqqZcuWmj9/vmJiYmQYhkzT1DvvvKN+/frp+eef16pVq7R3716lpaUpPz/f6nIrxNKR\nSZKKBTjnGxF0rrCHUUQAAAAAAMAqs2bN8jy+6qqrtHz5ck+glJGRoY8++kgfffSR3/ozDEM7duzw\nW3tlZWmYNGjQIE8QVFBQoG+++UZOp9Pz88LhUXR0tNq0aaOoqChFR0fL5XIpOztbaWlp2rt3rwoK\nCiT9HiwxyggAAAAAaianguSwyTQ3p70mBCFA3nrrrWIDXQovoVPdMgpLw6QZM2ZIko4fP64///nP\ncjgcXm90p06dNHz4cF111VVq3rz5OdspKCjQzp07tWLFCq1atUpZWVmeBDAiIkKvvvqq1zZ9AFCi\nU1YXULoktba6BACVIF9hVpdQqiS1sroE3yRZXYCPDlldgC+OW12Aj9KsLsBHBVYXUIp0qwsAqiR3\naGQYhle45M8ZVXYIpiyf5nbixAndfvvtOnr0qCcAatiwoZ577jldf/31PrURGhqqrl27qmvXrpo4\ncaKeffZZffvttzIMQ7m5uZoyZYrmz5+vTp06BfhuAAAAAABATVVTluGxNExyOp2aMGGCjhw54rnW\npk0bzZ8/XxdccEG52mzQoIHmzJmjv/3tb1q6dKkMw1BWVpaeeOIJLV++XGFh9v+XPgAAAABA+bkU\nLKf1Yyckna0F1V/Tpk2tLqFSWfrXtWTJEiUkJHhGJNWrV69CQVJhU6dO1a+//qr4+HhJ0r59+/Te\ne+/pz3/+c4XbBgAAAAAAcFu7dq3VJVQqS1cCe//99z1BkmEYevLJJ/0SJLk9/fTTkuTpY9GiRXK5\nXH5rHwAAAAAAoKaxLEzatWuXDh36faXBOnXqaNCgQX7to3PnzmrTpo3nPD09XVu3bvVrHwAAAAAA\ne3Eq2FYHUN1YFibt2LHD89gwDHXr1k2hoaF+76d9+/ZeK53v3r3b730AAAAAAADUFJaFSSkpKV7n\nDRs2DEg/kZGRXucZGRkB6QcAAAAAAKAmsGwB7qLb5aWnpwekn2PHjnmds5sbAAAAAFRvLgXZZnqZ\ny9qlimEze/fu1cGDB3Xq1CmdOnVK+fn5qlWrliIjI9W4cWM1b95cLVq0UFCQvT83loVJ9erV8zw2\nTVOJiYmehbj9JScnR/Hx8Z4FuCWpcePGfmsfAAAAAADgfL755ht99tln2rJli08DaWrXrq2ePXvq\nxhtv1MCBA205KMayqOviiy/2Ok9JSdG6dev82seyZcuUl5fnda1Lly5+7QMAAAAAAKCor776SoMG\nDdKkSZP09ddfKy0tTaZplnpkZ2fru+++0+TJk9W/f399/PHHVt9KMZaFSXFxcYqKipIkz8ihF198\nUdnZ2X5pPykpSW+88YbXSKd27dqpefPmfmkfAAAAAGBP7mludjiY5lbzOBwOTZ06VQ899JD27t3r\nCYkMw/D5cL8mLS1Nzz33nMaNG+e3vMQfLPtUh4WF6frrr/faae3o0aN+eYOSk5M1duxY5eTkSJLn\nlzZq1KgKtQsAAAAAAHAu+fn5Gjt2rJYsWVIsRHI736gkt6LB0vfff6877rjDNoGSZWsmSdK4ceO0\ncuVKuVwuzxu0detWDRkyRH/729/Ur1+/MrXndDq1ZMkSvf766zp9+rTnl2UYhlq2bKmRI0cG4jYA\nAAAAAAD09NNPa/PmzZJULECSzq6H1LlzZzVp0kTR0dGqVauWTp8+raysLCUnJ2vXrl2e5XoKZxqm\naWr37t16+OGH9d5771XyXRVnaZjUpk0bjRo1SgsXLvRK3I4cOaIHHnhALVu21KBBg9SjRw/FxcUp\nJiamWBtHjx7V9u3btWXLFq1atcozB9H9ppumqbCwML366qsKCbH0dgEAAAAAlcCpIDlsspubk2lu\nNcaSJUu0atWqYiFSWFiYBg0apNtuu01dunQ578ZjTqdT8fHxWrZsmdasWaOCggJJ8hqhtHTpUt16\n660Bv5/zsTxdefzxx7V161YlJCR4Df0yTVNJSUmaM2eO57lBQUGKjIxUrVq1lJubq5ycHK9hYO7H\nhdsICgrSSy+9pK5du1biXQEAAAAAgJoiNzdXs2fP9sojJKlDhw6aMWOG2rZt61M7wcHB6tmzp3r2\n7Knx48frySef1I4dO7wG4Pzzn//U0KFDVatWrYDdT2ksj0jDwsL0/vvvq3v37iXODyw8d9DpdCor\nK0snT55Udna2XC6X18+LhlERERGaPn26Bg8ebNXtAQAAAACAam7x4sVKSUmR9Pu6zT169NCHH37o\nc5BUVPv27fXRRx/pkksu8cpLTp06pU8//dQvdZeX5SOTJCkqKkqLFi3SzJkztWDBAjkcDq+5gWXh\nfoM7duyo1157Ta1bt/Z7vQCqqSyrCyjdXpXvP0QoWbCcVpcAlChfYVaXUKr9qiL/P9YhqwvwUbrV\nBfgizeoCfJRpdQE+clhdQClyrC6gQpwKkdMeX3dtUwcC66uvvvI6j4mJ0dtvv62IiIgKtRseHq5/\n/etfGjhwoFJTUz3XP/vsM40ePbpCbVeE5SOT3EJCQvT444/riy++0LBhw1SrVq0SVzQvSeHndezY\nUa+++qqWLVtGkAQAAAAAAAIqPT1diYmJntlVhmHooYceUp06dfzSfp06dfTwww972jZNUwkJCUpP\nt+5fImwXkbZs2VIvv/yynn32Wa1fv14bN25UQkKCDh48WGwLvLCwMDVo0ECdOnXSJZdcot69e6tz\n584WVQ4AAAAAAGqaxMREzy710tnRRP5ebmfQoEF66aWXPDu9maapnTt36oorrvBrP76yXZjkFhkZ\nqYEDB2rgwIGeazk5OcrJyZHL5VKdOnUsXWwKAAAAAGBPLgXJaZPd3Fz2mRCEACk8/cwwDHXt2tXv\neUWtWrXUtWtXbdy40XPt4MGDhEm+iIyMVGRkpNVlAAAAAAAASPIOkySpcePGAeknNjbW6zwz07o1\n4ohIAQAAAAAA/KS0dZ/91W5IiHXjg6rUyCQAAAAAAErDNDdUpvr163udHz9+PCD9nDhxwuu8QYMG\nAenHF7YPkwoKCrRjxw4dP35cp06d0qlTp5Sfn697773Xa4u97OxsnTp1ShdeeKGF1QIAAAAAgJqk\nYcOGnsfundbOnDmj8PBwv/WRl5enbdu2eXZzkwiTisnJydGyZcv07bffen4JRd1+++1eYdK2bds0\nbtw4derUSXfccYeGDh3qWUkdAAAAAAAgELp3766goCBPyJOXl6cvv/xSN998s9/6WL16tfLy8jw5\nh2EYlu5mb6vxdk6nU3PmzNGAAQP0j3/8Q1u2bFFeXp5M0/Q6SnL48GGZpqnt27dr8uTJGjhwoOLj\n4yv5DgAAAAAAVnMqSA4F2+Jw2utrNwKgTp06iouLk2manpFDr7/+urKzs/3SfnZ2tmbOnOk1YCYu\nLs7SkUm2+VSfOHFCY8aM0ezZs5WRkeEJjgzD8DrO5fDhw57Hpmlq//79GjNmjBYsWFAZ5QMAAAAA\ngBpq6NChXucnT57UxIkTVVBQUKF2CwoKNGHCBJ08eVKSPDnJ9ddfX6F2K8oWYdKxY8f0pz/9SfHx\n8cUCJEnnHZHkVjhMcr/W4XDolVde0cKFCwNaPwAAAAAAqLlGjhypunXrSpJndNLGjRt15513Kjk5\nuVxtHjx4UGPGjNHGjRu9BtfUrVtXd9xxh1/qLi/Lw6Tc3Fw9+OCDnlXJiwZIF154oa655ppS23Gn\nfYVDJ/cv8OWXX9bmzZsDUD0AAAAAwG6cCpZTITY57LGrHAIrMjJSDz30kCeTcOcR8fHxGjJkiP7+\n978rMTHRp7Z++eUXPffccxo6dKi2bdvmue4efHP//fcrKioqIPfhK8sX4J4xY4Z27tzplbIFBwfr\njjvu0KhRo9SiRQtJZ+cDns+sWbO0ceNGzZo1Sz///LPXolQul0vPPvusVq1apdDQ0MDdDAAAAAAA\nqJFGjRqlDRs2aP369Z4ZU6ZpKjc3V0uXLtXSpUtVu3ZtdezYUc2aNVNUVJQiIyOVk5Oj7OxsHTp0\nSDt37tTp06clySuYcv/fAQMGaOzYsZbdo5ulYVJycrKWLl3qNRqpbt26evfdd9W1a9cyt9e7d299\n+OGHWrRokV555RU5nU7Pzw4cOKDVq1cXm8cIAAAAAADgD9OnT9ddd92lHTt2FFu+Rzq7mPbmzZvP\nOXuq6Gyrwtc7deqk1157LYDV+87SaW7z5s2Tw+GQdPaNCQkJ0ezZs8sVJBV2xx136NVXXy12fdmy\nZRVqFwAAAABgfy4F/99UN+sPF9PcapTo6GgtWLBA/fr1KxYMFR6tdK7jXGtIDxkyRIsWLVJERIRV\nt+bF0jDJPfTL/YaNGDFCl112mV/aHjhwoEaMGOG1Nd+2bduUm5vrl/YBAAAAAACKio6O1ttvv61p\n06apUaNGxTYVK7prfUk72Ltf06pVK/3jH//Qq6++apsgSbIwTNq7d6+OHj3qdW38+PF+7eOBBx5Q\nUNDvt+h0OpWQkODXPgAAAAAAAIoaPny41q5dq+nTp+vqq69WRETEeUcluY+GDRvqxhtv1Jw5c7Rm\nzRpbLtdj2ZpJ+/fv9zpv06aNLrzwQr/2ceGFF6p9+/b69ddfPdcOHTqkXr16+bUfANWEw+oCSndE\nTa0uAUAlOKMwq0so1RE1sboE3xyzugBfVYXR81lWF+CjTKsLqCbyrC6gQlwKss0uai7rN1GHhUJC\nQjR48GANHjxYpmlq3759SkpK0rFjx5STk6OCggJFRUWpTp06qlevntq2bavmzZtbXXapLAuTUlNT\nPY8Nw1Dr1q0D0k+7du20e/duz3lmJv9xAQAAAAAAlcswDLVt21Zt27a1upQKsywiPXXqlNd5vXr1\nAtJPrVq1vM7z8/MD0g8AAAAAAEBNYNnIpOjoaK/z7OzsgPRTeASUFLjQCgAAAABgD04bTXNzMs0N\n1ZBln+qYmBjPY9M0dfDgwYD08+uvv3qtiN6gQYOA9AMAAAAAAFATWBYmNW3qvYjs7t27lZGR4dc+\nEhMTdeTIEa9r/l7kGwAAAAAAoCaxbJpb586dVa9ePU+A5HK5tGTJEt1///1+6+ONN97wOq9fv77i\n4uL81j4AAAAAwH6cCpbDNtPc7FEHyu6aa64pds0wDH3zzTc+PTeQzlVHZbEsTDIMQ3379tWqVatk\nGIZM09TcuXM1ZMgQNWlS8a1mlyxZog0bNnjaNgxDffr08UPlAAAAAACgujt8+LAnU3ArvIxOac8N\npHPVUVksXQlszJgxXueZmZmaMGFCsZ3eyurjjz/W888/X+zNvf322yvULgAAAAAAqFkMw/A5vHE/\nN5CHHVgaJnXt2lU33HCDZ+SQJO3cuVO33nqrvv/++zK3t2/fPj3yyCN67rnn5HK5JMnT9hVXXKGe\nPXv6tX4AAAAAgP24FCynQmxxuJjmhmrIsmlubk899ZS2bNmitLQ0z5CwAwcOaNy4cWrZsqWuuOIK\nxcbGFntdcnKyDh8+rLS0NCUkJGjTpk3asmWLJHmFU5IUERGhyZMnV9o9AQAAAACAqq8s09Yqa4qb\nHVgeJjVp0kRvvfWW7rrrLuXl5XlCINM0lZSUpAMHDnie6/7FmKZZ4pQ1988LtxEcHKwZM2aoXbt2\ngb4VAAAAAABQTezatSsgz60OLJ3m5ta1a1e99dZbatCggVcg5B6pVFK6575e+Cg8f9A0TYWHh+ul\nl17S1VdfXan3AwAAAACwjktBcirYFofLHl+7Ab+yzaf68ssv14oVK3T55Zd7BUhlXYTK/dqWLVtq\n6dKluvnmm628LQAAAAAAgGrF8mluhTVq1Ejz58/Xjz/+qPfff1///e9/S92Cr+iopfbt2+vee+/V\noEGDFBJiq9sDAAAAAACo8myZtvTp00d9+vTR8ePHtWXLFv3888/avn270tPTlZmZqaysLIWFhale\nvXqqW7euWrVqpZ49e+rSSy9VXFyc1eUDAAAAACzknuZmB0xzqxk2b97sdd6jRw+/D3DZvHmzfv75\nZ+3evVu7d+/WG2+8obZt2/q1D1/ZMkxyi42N1R//+Ef98Y9/tLoUAAAAAACAEo0ZM8ZrNtX//u//\nKiYmxq99zJ07V999953nfO/evTUzTNq5c6dWrlypm2++mRFFAGwg1+oCSrUxp7fVJQCoBPl5YVaX\nUKr8Q3WsLsE3iVYX4KskqwvwwXGrC/CR/f97flaB1QWUItPqAoAqyb05WCDExMR4rS994sSJgPTj\nC0vDpLfeektff/21FixYoHbt2mnYsGEaMmSIGjZsaGVZAAAAAIAqzKFgOWwyzc0udaDqy831Dsuz\ns7MtqsTC3dwyMzO1bt06SWeTu99++03Tp0/Xnj17rCoJAAAAAADAdjIyMvTjjz96jXoKDrYuqLRs\nZNLPP/+sgoICGYYhwzBkmqZatWqlyy+/3KqSAAAAAAAAJEk5OTn66quvyvXa1atXKzo6usI15Ofn\n68SJE1q1apXS09O9wqRGjRpVuP3ysixMSkpK8jx2zym87LLLrCoHAAAAAFBNuBQsp032m3Ixza3K\nioyM1OrVq/Xf//7Xp+e71zMyTVPTpk3zay3utgvr3LmzX/soC8umublcrmLX6tevb0ElAAAAAAAA\nxT377LMKCzu7MYZpmuc8ijrfc8tzuGd1SWcX3+7QoYPatWtXqe9FYZaFSS1atCh2LTk52YJKAAAA\nAAAAimvevLnuu+8+r0CnpKOo8z23PIebaZqqVauWXn755cp8G4qxLEz6wx/+4BmJ5F4z6fvvv1dW\nVpZVJQEAAAAAqgGXguRUsC0Ol3Vfu+En48ePV8uWLS0dmeQ+2rZtq/nz5+viiy+24J34nWWTSCMi\nIjRp0iQ9//zznpQtMzNT06ZNszxhAwAAAAAAkKSwsDDNmDFD33333TmfM3v2bM9AGcMwdPfdd6t2\n7doV6jcoKEihoaGKiopSw4YN1aZNG7Vt27ZCbfqLpSuSjRo1SpmZmZo1a5bnTV+xYoVOnz6tJ554\nQhdeeKGV5QEAAAAAAKhLly7q0qXLOX8+e/Zsr/Nx48YpJiYm0GVZxvLl7R944AF169ZNTz/9tI4c\nOSLTNPX1119r7dq16tWrl3r06KFu3brpwgsvVL169VSnTh2FhFhedqUwTVMjRozQjh07JEnDhg3z\n+6itvXv3avXq1fr555+1f/9+ZWRkyOFwKDo6Wi1btlSPHj104403qmvXrn7tV5J++eUXffXVV4qP\nj1dycrIyMjJkmqbq1q2r1q1b67LLLtNNN91k6aJiAAAAAKoe9zQ3O2CaG6ojS1OZWbNmeR7fcMMN\n+vTTT5WVlSXTNOVwOPTjjz/qxx9/9Ft/hmF4gpmqYPHixdqxY0eJi3lVVHJysp5//nmvLQ4L95Oe\nnq60tDTFx8dr3rx56tGjh5555hl16tSpwn3v2LFDU6dO1bZt20rsOyUlRSdPntSmTZs0Z84c9e/f\nX1OmTClx0XYAAAAAAOygpLWTqitLw6S33nqrWFDinl/oflxTbd++XdOnT/eac+kvX331lZ588knl\n5uZ6vdclvd/un8fHx+uWW27RE088obvuuqvcfS9atEivvPKKnE6nz32vX79eGzdu1EskI7crAAAg\nAElEQVQvvaSBAweWu28AAAAAAALh22+/9Tpv0KCBRZVUDlvMF3MHCUW3vPNngFKVgqnDhw/rgQce\nUH5+vt/b/vLLL/XYY4/J5XJ5girp3O914Z+7XC69/PLLOnPmjO67774y9/3+++/rH//4R7Gw8Hx9\nuz8Tubm5evTRR+VyuTRo0KAy9w0AAACg5nDvpGYHdqkDgdWsWTOrS6hUtgiTAjGNq6pKTk7W3Xff\nrZSUFL+3/euvv2rKlClyuVxe18PDwzV06FBdf/31nkXPDxw4oC+++EJr1qwpFmr985//VFxcnK66\n6iqf+/7hhx88I62k34Oi6OhoDR8+XAMGDFDTpk115swZ7d+/XytXrtS6des8I5jcwdfTTz+tdu3a\nKS4uroLvBgAAAAAAKA9Lw6SmTZta2b3t7Nq1Sw888ICOHz8uSX6d3maapp588knl5eV5XWvbtq3e\neOONYtsLtmrVSv369dM999yjhx56SAcOHPCEOi6XS88++6zWrFmjiIiIUvvOy8vTU0895RmJ5L6v\nHj16aObMmYqNjfV6frt27XTdddfpp59+0mOPPaaUlBTP+5Cfn68pU6bo3//+d0XfEgAAAAAAqqRv\nvvlG1157rWX9WxomrV271srubWXNmjWaPHmyV9jjTytXrtTOnTu9RgbFxsZq3rx5xcKcwuLi4rRw\n4ULdeuutOnr0qOf1J06c0Ny5czVx4sRS+37vvfd04sQJr2l17du31zvvvKOoqKhzvu7yyy/X+++/\nr1GjRik7O9vz+p07d2rFihW6+eaby/IWAAAAAKghnAqSwybTy5zs5oYyMk1TTqdTBQUFOnPmjHJz\nc5WRkaFDhw5p8+bNWrdunZKTk7Vz507LavRrmJSfn69169apQ4cO7Lzlo5ycHE2bNk2ffPJJQBce\nf/fdd4tNMXv++efPGyS5XXDBBZo9e7ZGjhzpea1pmlq0aJHGjx+v8PDwc742Pz9fCxcu9BphFRwc\nrOnTp583SHJr3769Xn75ZU2cONGr/nfffZcwCTVSTlbpowEBVH2uM+f+b6ttZFtdgI8C8+90AZBr\ndQE+KLC6AB9VlTodVhdQCqfVBQBVlsvl0vr16/X1118rMTFRKSkpysnJkcPhKLbsTHn4e5Ou8vBr\nRJqUlKSHHnpIN9xwgy699FI9/vjj/my+2lmzZo0GDhxYYpAUEuK/nG/Lli3au3evV/sdOnRQv379\nfG6jU6dOGjRokFfQlZGRof/85z/nfd2XX36pjIwMT9+GYeiaa67RxRdf7HPf1157rS699FKvP5h9\n+/bp//2//+dzGwAAAAAABFpiYqKGDx+uCRMmaMWKFfrtt9+Unp6uM2fOyOl0enYzr8hhB34dmXTg\nwAFJZ0OD06dPKysr67zPX7Fihdf5wIEDFRYW5s+SbOmnn37SrFmzFB8f77WDnTssadOmje69915N\nmTLFL/2tWbPG69wwDI0YMaLM7dxyyy367LPPvK598cUXGjJkyDlf8+WXXxa7Nnz48HL1XTQ8+uKL\nL3TppZeWuS0AAAAA1ZtLwXLaY78puWwy3Q6Bt337dt15553Kzc31Cn38PYrIDoGSX/+63DuQud+o\n+vXrn/f5Tz31lNeb2rdvX8XExPizJFu6++67i4VI0tn3beDAgXrhhReUmJjot/7+93//t9iHd8CA\nAWVu55JLLlHdunWVmZnpmeq2ceNGnTlzpsSpbg6HQ5s2bfLqOzw8XFdccUWZ++7fv7+nHXff69ev\n13PPPVfmtgAAAAAA8Cen06knnnhCOTk5Xt/3S1I0DPLluYXXIA4JCVHfvn39UHX5+TVMys72njwf\nHOxbAmuH+X5WKPyhiImJ0TPPPKMbb7zRr32kpKQoKSnJ6/2NjY0t1056QUFB6tatmzZs2OBp78yZ\nM0pISFDPnj2LPX/79u2ePyT377hTp07lGn1Wt25dtWnTRvv27fNcO3r0qI4dO6bGjRuXuT0AAAAA\nAPzlyy+/1N69e4tlG+7vwnXq1FHt2rWVk5OjU6dOSTqbBdSrV08RERFyuVyehbbd3KGUOzvo1auX\nxo8fry5duqhevXqVd3Ml8GuY5HR6L9Lm3uIexbk/UGFhYbrjjjv04IMP+rQgdVn9+uuvxfrs2LFj\nudvr0KGDNmzY4HUtMTGxxDCpcN9uFek7Li6u2B9nYmIiYRIAAAAALy4FyWmT6WUudnOrET755BPP\nY/d374YNG+qRRx7R1Vdf7Ql/tm7dqttuu83zvXbIkCGaPHmy57X5+fnavXu3vv32W3344YdeM4O2\nbt2qunXrWh4kSX5egDs6Otrz2DRNbdmyRZmZmf7sotoIDQ3VsGHDtGbNGj3++OMBCZIk6bfffit2\nrU2bNuVur2XLlsWu7d+/v1L6btWqVbFrhUcqAQAAAABQ2XJzc7VlyxavgQ/R0dFaunSphg8f7hX+\ndOvWTXXr1pV0Njf5+uuvvdoKCwtTly5d9PDDD2vNmjXq06ePJ5zKz8/Xo48+qpycnMq5sfPwa5jU\nvHlzr/O8vDxNmDBBSUlJ/uymynvwwQe1du1aTZs2TU2aNAloX4cOHSp2rSJ9ljQKqKQ+znW9PNPr\nytM3AAAAAACVYffu3XI4HJJ+H5U0ceLEEr//Goah7t27e6auHT169JyZSYMGDfTuu++qd+/enucf\nOnRIs2bNCsyNlIFfp7n16NFDISEhcjqdnkRuy5YtuummmxQbG6vGjRufd72ciRMnKjQ01J8l/X/2\n7jw+ivr+4/h7ckEg4Qo34b6CXCKgqAhBRE45BLRVUURQfyCgUlqKpV4oeFSrRVtQEEQRsVLaSkAE\nhaogDYfhPuWSQyFcOUl2d35/pLtmsgE2yW5mk7yej8c8mpnMfL+fSQKYd7+HhWEYWrBgQcDa99XE\niROLra/k5GSva7Vq1Sp0ezVq1LCcm6ap06dP+9x3zZo1/da3pMv2DQAAAKDscgbRNDcn09xKvWPH\njlnOw8LCrriLedu2bbVu3TrP+aZNm/KdieNu65VXXtGAAQOUkpIi0zS1aNEi3X///apXr55f6i8M\nv4ZJ0dHR6t27t5YvX+61U9mpU6fyXUPJ/Xn3/L9AKauLfLt32MutUqVKhW4v97PueZuXm8p45swZ\nr695UfrOPY3SjWmUAAAAAAA75R1I0bx58ysuZdOyZUtJv+zitn37dg0bNuyy99esWVP333+/Zs2a\nJcMw5HA49PHHH+vJJ5/0Q/WF4/eIdPLkyZb5gO7Vx93BQ+4jr7yf99dRluXdYU9SkdZnqlixote1\nlJQUW/o2TfOyfQMAAAAou5wKlSNIjmAZIYXAyczM9HxsGIYaNGhwxfubNWtmOd+zZ89V+8gdNpmm\nqa+++qqAVfqX38Ok2rVr65133lFMTIxXkJM7WMpvlFDez/vrKMuys7O9vgblypUrdHv5TVPMysrK\n9978rvurb/c7Xa5vAAAAAADskN+smtzq16+v0NCckNE0TR08ePCqbdauXVuNGzf2nB84cEBnz54t\nWqFFEJDJm23bttXy5cs1duxYNW/eXKGhoT6NGArUyKSyPDopv7DF/UNbGPk9615oLK/s7Gy/9h0W\n5j0r83J9AwAAAABQHMqXL285v9rvqWFhYZa1jNPS0vJdFiivZs2aWfKNHTt2FLBS//Hrmkm5Va5c\nWRMmTNCECRNkmqbOnz+vS5cuyel0SsoJjm677TbP9DfDMLRkyRJVq1YtUCWVSe6vd27+DpOKq++Q\nEO/s0+VyFbo9AAAAAKWTS6FyBu7X3QJxMc2t1Ktatarl/MKFC1d9pkGDBjpx4oTn/IcffrjqZlmV\nK1e2nOe36VVxKZY/XYZheH1x81O3bl3FxMQUQ0Vlh79H8xRktFFYWJhXXw6H44o7+l1JfnUHcvc/\nAAAAAACuJveuar5OW6tfv76+++47z/n+/ft14403XvGZvL8Tnzt3roCV+g97FJZy4eHhXtP8ihIm\n5Tfa6HLhUH5Bj7/6dr9TYYMpAAAAAAD8IS4uzrJW8dGjR3Xs2LErPtOoUSNJ1h3dribvVLj8fj8v\nLraHSWV5PaPikN/uaxkZGYVuLz093eva5RbVrlChgl/7TktL87lvAAAAAGWXSyFy/m8nNbsPl/2/\ndiPAoqKi1KJFC8u1d95554rP5N7RzTRNbdiw4Yr5yKVLl7Rt2zZLaFWpUqVCVlx0tk4inTFjhuX8\naiueo+CqVKnidS2/UMZXuZ91/6Bfbp2rqlWres3hTEtLK/RUxrx1G4bBGlsAAAAAANv17NlTe/fu\n9awL/cknn6hx48Z68MEH872/bdu2lvPk5GT985//1ODBg/O9/5NPPlFaWpolTLraGkuBZGuYNGTI\nEDu7LxPyW6uqKNsH5g2HDMO4bDhUtWpVz+Lquftu0KBBofrOr27W2IJ/BccijVcSFl740X0ASo4s\nG4et+yw0+P/OlCR5L/cYpErC3+8lZRfdklIngNJk+PDhmj17tlwulydQevnll7Vu3To98sgj6tKl\ni+V342rVqunaa6/V999/77l/xowZatiwoTp06GBpe/369frTn/5keV6S2rVrVyzvlp8S8l8BKKzc\nC4G5nT59utDt5fdsjRo1fO77zJkzfu27Zs2ahW4PAAAAQOnk/N80t2DgZJpbmVCnTh0NHTpUS5Ys\nkWEYnoBo48aN2rhxoxo1aqQVK1ZYnrnjjjv0/fffS8oZqHHhwgWNGDFCvXr10nXXXSfDMLRx40at\nWbPGElIZhqFWrVrZOlOHMKmUq1+/vte1o0ePFrq9/J5t0qSJz30fOXLEr303bty40O0BAAAAAOAv\nkydP1oYNG/Tjjz9Kkif8kfJfU3j48OGaO3euTp486bnf4XBo5cqVWrlypee+vDN+JOm+++4L1Gv4\nhIi0lIuLi/O65ss2hZeT37PNmzcPur4BAAAAAChO0dHRevfdd1W3bl1PiOQepZTfYIuIiAg99dRT\nlmvuACr3kTtIMgxD7du3v+zaSsWFMKmUa968uSIjIyX98kO5a9euQre3fft2r0S0TZs2+d6bd0Ex\n0zS1Y8eOQvVrmqZ27txp6btcuXKESQAAAAC8OBUqR5AcwTLdDsWjYcOGWrZsmYYNG6aQkBBPqJRf\nmCTlLNw9ZcoUy05u7gDKfbiZpql69erp9ddfV0iIvXEOYVIpFxISoo4dO1p+MFNTU7Vt27YCt/Xz\nzz/rwIEDlmsNGjRQ3bp1872/Ro0anmlo7j8ABw4c8FrE2xdJSUlKTU2V9MsQv44dOyoiIqLAbQEA\nAAAAECjR0dGaPn26Vq5cqUcffVQtWrS44kZUDzzwgGbPnq2YmBjLiCRJlvPu3btr8eLFqlOnTnG9\nymWxZlIZ0L17d33zzTeWawkJCQVe+T0hIcET5Lj/t1u3blft+9ChQ54wyTRNJSQkaMSIEQXq+7PP\nPvO6dssttxSoDQAAAAAAikv9+vX1+OOP6/HHH7/qvd27d9eXX36pL774QmvWrNGPP/6olJQUVatW\nTddcc4369u2r6667rhiq9g1hUhnQt29fvfTSS3I6nZ4gaOnSpXr00UdVpUoVn9rIysrSwoULvaa4\nDR069IrP3XHHHZo/f76kX6bZvf/++/rVr36l8PBwn/o+e/asli1bZuk7LCxMAwcO9Ol5AAAAAGWL\nS6FyBsmvuy6mucFHERER6t+/v/r37293KVfFNLcyoHr16urZs6dlqltKSoqmTZvmcxszZ87U8ePH\nJcnTTocOHfJdZDu31q1bq02bNpa+f/zxR7388ss+9WuapqZOneo1xa1Pnz62boMIAAAAAEBZRZhU\nRowbN86zQJd7hNDq1as1ffp0S9CTnzlz5mjRokVeK8hPmjTJp77Hjx9vec40TX3wwQd69913r/ic\naZp6/vnntXbtWq9RSRMmTPCpbwAAAAAA4F+ESWVEixYtdM8991i2J5SkDz74QA888ID27Nnj9cyx\nY8c0ceJEvfbaa5Y1jwzD0MCBA9WxY0ef+u7evbtuvfVWr75fffVVTZw4UUePHvV6Zs+ePXrggQcs\nIZa77zFjxlx2JXwAAAAAcClEzv/tpGb34eLXbpRCwTGJFMVi8uTJ2rJli3bt2iXpl+0G//vf/2rw\n4MFq2bKlGjdurLCwMB07dkzbtm3zBDjSL9PbmjZtqmeeeaZAfU+fPl3Dhg3TiRMnLH1//vnnWrVq\nldq0aaMGDRrI5XLp0KFDnnArb5DUuXNny0gnAAAAAABQvAiTypBy5cppzpw5GjVqlPbv3+81Umjf\nvn3au3ev53534JP7vsaNG2vu3LmKjIwsUN/VqlXTu+++q4ceekinTp3y6nv79u3avn27pV9Jlvs6\ndOigt99+22sRcAAAAAAA/C0xMdHuEq6oc+fOtvVNmBTk3GHK1dY18lX16tW1aNEiPfPMM1q+fPkV\n284b+PTq1UvPPvusqlatWqi+mzRpoiVLlmjKlClav379ZfvOfc3d9913360pU6aofPnyheobAAAA\nQNnhVIiMINlFzck0txJrxIgRQTuYwTAMz6wjOxAmBbG8P7T++iGOiorSq6++ql//+teaN2+e/vOf\n/8jhcOR7b0hIiG666Sbdf//9uuWWW4rcd40aNTR37lytXbtW77//vjZu3CiXy5XvvWFhYerZs6dG\njhypa6+9tsh9AwAAAABQUP4a3FGaECYFqeuvv167d+8OaB8dO3ZUx44dlZGRoW3btunw4cO6cOGC\nDMNQ5cqVFRsbq/bt26tixYp+7zs+Pl7x8fFKSUlRUlKSjh49qpSUFIWGhqpy5cpq3Lix2rVrp4iI\nCL/3DQAAAACAr4JtdFIwhFuESVBkZKRuuOEG3XDDDcXed3R0tLp27Vrs/QIAAAAovVz/20ktGLiC\npA4UTjAEN8GoRIRJZ86c0U8//aTz58/rwoULysrKUr9+/SyjVrKysuRyuVhTB0ARZNhdwFVlnapk\ndwkAikOm3QX44Ce7C/BRSalTF+0uwAfB/+9kjmy7C/BR/stMBI9LdhcA2G7IkCF2lxC0gjZMWr16\ntdasWaPExEQdP37c6/O33HKLYmJiPOdbtmzR//3f/6lbt2669957df311xdnuQAAAAAAoBSZMWOG\n3SUEraALk5YtW6bZs2fr8OHDkvIfUpbffMXjx48rIyNDq1at0qpVq9SlSxc9++yzatCgQaBLBgAA\nAAAEEadCZAbJ9DIXu7mhFAqan+r09HQ98cQT+v3vf69Dhw7JNE2ZpinDMCzH5Zw4ccLzsWma2rBh\ng+68806tWrWqOMoHAAAAAAAoE4IiTEpJSdHdd9+tlStXegVIkjzB0pXkngrnfi41NVVPPvkkgRIA\nAAAAAICf2B4mOZ1OTZgwQfv37/cESdIvAVJERITi4uKu2s6ZM2cs5+4wyuFwaNKkSdq3b19A6gcA\nAAAABJec3dzCguJgNzeURraHSW+//bY2bNjgNRKpV69eeu+997R582YtW7bMp3ZefPFFxcbGWkYx\nGYah7OxsPfXUU2zpBwAAAAAAUES2hknJycmaN2+eJUSKiIjQrFmz9Je//EU33nijwsJ8WyM8IiJC\nd955pxISEvTggw96BUc7duzQmjVr/P4OAAAAAAAAZYmtu7nNmzdPGRkZMgzDM8Vt5syZuu222wrd\nZnh4uH73u9+pVq1amjlzpmXR7sWLFxepbQAAAABA8MvZQS1YppfZPiEIxaBnz57F2p9hGFq9enWx\n9pmbrWHSmjVrLEFS79691bdvX7+0PXLkSG3atEmrV6/29LFx40ZlZWUpIiLCL30AAAAAAAAcP37c\nkz0Uhyvtdl8cbItIjx07psOHD1uujR071q99TJgwwXLucDi0c+dOv/YBAAAAAAAgybI7faCOYGBb\nmJR3d7V69eqpRYsWfu2jRYsWaty4seXakSNH/NoHAAAAACC4OBUaVAdQVO4d74NlYzHbprmdPXvW\n87FhGGrevHlA+mnZsqUOHTrkOb9w4UJA+gEAAAAAAGWXv4Oe3JuVlS9fXvfdd58qVqzo1z4Ky7Yw\n6dy5c5bzatWqBaSfvF/ozMzMgPQDAAAAAADKpj179hTp+aysLKWnp+v06dPav3+/Nm3apBUrVujc\nuXMyDEOXLl3SV199pXnz5qlWrVp+qrrwbJvmVqFCBct5RkZGQPo5f/685bxSpUoB6QcAAAAAEByc\nCpFDoUFxONnNDT6IiIhQlSpV1Lx5c/Xr109//OMftWbNGo0YMcIz4ungwYO6//77g2LGlW0/1XlH\nIp04cSIg/fzwww+WBaoCNQIKAAAAAADAXypUqKCnnnpK48ePl2maMgxDR48e1e9+9zu7S7MvTKpd\nu7bnY9M0tXPnTr+PTvrhhx8s6yVJUp06dfzaBwAAAAAAQKCMGzdO1113nWcB7nXr1mnt2rW21mTb\nmknt2rVTxYoVlZ6eLklyOBxaunSp7r33Xr/18de//tVyHhUVpTZt2vitfQClTWCm2/rVj0zVLXNs\n+5e6lHLYXYCPSkKdp+wuwEcl4K/2HCXhmw6UHC6FyhUk/4iGsJsb/GDChAkaOXKkDMOQaZqaO3eu\n4uPjbavHtpFJYWFhuvnmmz1DtUzT1OzZs73WOCqsNWvW6LPPPvO0bRiGbrjhBoWEMF8VAAAAAACU\nHF26dFHNmjU955s3b9bZs2dtq8fWZGX48OGW89OnT2vSpEnKysoqUrvr16/XpEmTvK7feeedRWoX\nAAAAAADADm3atPEsxm2appKSkmyrxdYw6ZZbblGXLl0so5PWr1+vBx54QAcPHixwexcvXtSrr76q\nMWPGKDMzU5I8bbdt21a33nqrv18BAAAAABBkXAqRU6FBcbjYzQ1+kndDsWPHjtlUSRCsxDB16lTd\nfffdyszM9ARKW7du1aBBg3TDDTfopptuUq1atbyeczgcOnv2rJKTk7V9+3YlJiZq5cqVyszM9ARI\nbqGhoZoyZUpxvhYAAAAAAIDf5N20zN+bmBWE7WFSixYt9Prrr2vcuHFyuVyeQMnhcGj9+vVav369\n597cw7nyW2jK/Xl3kOQOlf74xz/quuuuC/zLAAAAAAAABMC+ffs8mYkkVapk3+Y8QTHeLj4+XjNn\nzlS5cuUk5YRB7i+Q+8gr9+fch/s59+cNw9D48eN11113Fev7AAAAAADsY/fUtrwHUFS7d+/W/v37\nLddq1KhhUzVBEiZJ0h133KElS5aoSZMmlhFGeQ+3K33ONE1VqVJFs2fP1tixY4v9XQAAAAAAAPwh\nKytLzzzzjNf1uLi44i/mf4ImTJJyprz94x//0PTp09WsWbN8RyblDY4k6yilKlWq6LHHHtOKFSvU\nrVu34n4FAAAAAAAAvzhy5IhGjRqlpKQkyxS3li1bKjY21ra6bF8zKa+IiAgNGzZMw4YN09atW5WY\nmKgtW7Zo586dOn/+vLKzsz33Goah6OhoNWrUSB07dlSnTp3UtWtXz3Q5AAAAAEDZ4zJD5HQFx/Qy\nwwyqMRwIkGXLlhW5DafTqaysLKWlpSk5OVk7d+7Uli1b5HQ6LfcZhqH+/fsXub+iCLowKbcOHTqo\nQ4cOlmsZGRm6ePGiypUrp8qVK3uNUgIAAAAAAChOU6ZMCUg+kXejMUmKiYnRPffc4/e+CiKow6T8\nREZGKjIy0u4yAAAAAAAALPLbQKwo8q4PHRoaqhdffFEVK1b0az8FVeLCJAAAAAAArsTpDJHDESTT\n3JxMcytLAjV7yjRNRUVF6bnnnguK9aEJkwAAAAAAAIrI36OS3OrUqaM+ffro4YcfVtWqVQPSR0ER\nJgEAAAAAABTBY4895pd2DMNQeHi4KlSooGrVqql58+Zq3ry5X9r2J8IkAAAAAECp4nKGyukIjl93\nQ53BMd0OgeWvMKmk8Pufrp49e/q7Sb8xDEOrV6+2uwwAAAAAAIASy+9h0vHjx2UYRsDmChZFoBbC\nAgAAAAAAKCsCNu4v2IKbYAy3AASbs3YXcHXf1LK7AgDFwWF3AT44bXcBPjpjdwG+umh3AT7ItrsA\nH5WEP0AINKczRM4g2c3NyW5uKIWCYxKpjy4XCF0puCJEAgAAAAAA8J+AhElFDXDc4ZC7HcMwFBsb\nqwYNGqhixYqKioqSy+VSamqqzp07p7179yo1NdXrWcMw1LZtW9WpU6dI9QAAAAAAACCH38OkPXv2\nFPiZQ4cO6aGHHtLJkycl5QRB4eHh6tWrlwYNGqROnTqpYsWKV2zj4MGD+te//qVPP/1UZ86c8azb\ndPjwYY0dO1Y9evQo1PsAAAAAAEqWnN3cgmOam4vd3FAK2T7N7YcfftC9996r8+fPS8oJkjp27Kjn\nn39eTZo08bmdpk2b6oknntCYMWP04osvaunSpTIMQykpKRo/frz+8pe/ECgBAAAAAACftGrVyu4S\nLsswDO3atcu2/m1dCczhcOg3v/mNzp0755nSdtttt2nBggUFCpJyi4qK0osvvqiHH37YM9XN4XBo\n8uTJ+umnn/xZPgAAAAAAKKVM0wzqw062hknz58/Xrl27POscNW3aVK+//rrCwoo+YOrJJ59Uly5d\nPIFSWlqaZs2aVeR2AQAAAADBzekIkSM7NCgOp4Pd3EoywzCC7ggGtv1Um6ap999/37O2kWEYmjp1\nqsLDw/3Wx5QpUyz9/fvf/9alS5f81j4AAAAAAEBuVxtBVJARR8E2IsnNtjWTduzYoZ9//tmTqtWq\nVUs33XSTX/uIi4tTkyZNdOjQIUnSpUuXtGXLFt14441+7QcAAAAAAJQudevWLdRzFy9eVGpqqmUU\nkTsEqlq1qlq2bHnZ3ep3796tQ4cOyeFwSJJlAE6nTp3Upk2bor+YH9gWJu3du9fzsWEYAVvYqlmz\nZvrhhx885z/88ANhEgAAAACUYi5XqFxO2/ebkpRTC0qmL7/8ssDPbNq0SWPHjvUESaZpqkqVKho+\nfLgGDRqkZs2aXbWNtLQ0LV++XB9++KH27t3rCZS2bt2qvn376p577ilwXf5m210CwwkAACAASURB\nVDS3s2fPWs6rVq0akH4qVqxoOU9JSQlIPwAAAAAAoOxKSkrS6NGjlZKS4pmS1q9fPyUkJGjSpEk+\nBUlSTo5x1113aenSpRo/frwkeTYXe/7557VkyZJAvoZPbAuTQkKsXZ87dy4g/eTdwa18+fIB6QcA\nAAAAAJRN6enpmjx5sjIzMz3T0u6991699tprqlatWqHaDA0N1bhx4zRt2jRPm6Zpavr06ZYZWHaw\nLUyqUqWK52PTNLVjxw6/95Genq6tW7da5inWqFHD7/0AAAAAAIKIM0RyhAbH4WQ3t7Lgb3/7m44e\nPerZca19+/aaNm2aX9q+55571LdvX0+glJ2drTfffNMvbReWbT/VLVu2tJyfOXNG69at82sfS5Ys\nUUZGhuVa27Zt/doHAAAAAAAou5xOpz7++GPPyCFJmjp1ql/7ePLJJz0fm6ap1atXKzU11a99FIRt\nYVJcXJyio6Ml/bI6+QsvvOAV/hTWoUOH9Oabb1pGJTVq1EgNGjTwS/sAAAAAAADff/+9Lly44Dlv\n0KCB2rVr59c+6tevr2uuucZz7nQ6tXnzZr/2URC2hUnh4eGeYVpux44d0yOPPKLMzMwitX306FGN\nGjVK6enpkuQZCnbXXXcVqV0AAAAAQAlg99S2vAdKtf3793s+NgxDzZs3D0g/jRo1smQoR48eDUg/\nvrB18ubo0aMVFpazXaN7dFJiYqIGDRqkDRs2FLg9p9OpRYsWafDgwTp58qRlVFLt2rV17733+q12\nAAAAAACA3KOSJKlSpUoB6Sc8PNxynpaWFpB+fBFmW8/KGfr14IMP6p133vEsUmWapo4cOaJRo0ap\nadOm6t+/v9q3b6+WLVsqJibGq41Tp05p586dSkxM1Geffabk5GTPSCQpZ1RSSEiInn/+eUVERBT3\nKwIoUS7aXcDVHba7ABQ7W/+lLoUcdhfgo5JQ53m7C/CVf5ZQCLySUGdJ+MGUpGy7CyglSsr3G7Bf\n3pDnzJkzAennxIkTlvPIyMiA9OML2/8T9fHHH9f333+vxMRET6Ak5YRABw4csKxQHhISoooVK6pc\nuXLKyMhQenq6ZYiX++PcI5LcfXTt2rUY3gYAAAAAYDunJIdx1duKhdPuAhBo1apV83xsmqaSkpLk\ncDg8M7H84fz5857d6t3ZR+3atf3WfkHZvkdhaGio5syZoy5duliCodyhkvtwOp26ePGiTp8+rdTU\nVLlcLsvn84ZRhmHoN7/5jR5++GFb3g0AAAAAAJRucXFxlvOLFy9qxYoVfu3jvffek8NhHTHYvn17\nv/ZRELaHSVLO0Kx58+Zp/PjxCgsLs4wwKsjhZpqm6tatq7lz52r06NF2vRYAAAAAACjlWrRooerV\nq0v6ZT3ol156SWfPnvVL+1u3btXcuXM9bRuGoVatWpXtkUluISEhGjdunL744gvde++9io6Otow6\nupLc98XGxmrKlClauXKlbrzxxmKqHgAAAAAQNJzKWfYpGA6muZV6ISEhuuOOOyzZxZkzZ/TAAw8o\nOTm5SG1v2bJFjzzyiJxO6w/Sr3/96yK1W1S2r5mUV+3atTVt2jRNmTJF3377rTZu3KikpCQdPnw4\n31SvevXqaty4sTp27KiuXbuqU6dONlQNAAAAAADKqlGjRmnx4sXKzMz0zJzav3+/+vXrp8mTJ2vQ\noEFeC3Vfyblz5/Tuu+9q/vz5cjqdllFJTZs21dChQwP1Kj4JujDJLTw8XPHx8YqPj/dcy8rKUmpq\nqrKyshQREaGoqCh2aAMAAAAAALaqUaOGJk6cqJkzZ1qW4blw4YKmTZumV155Rb169fLsVl+zZk1F\nRUV5NhhLTU3ViRMntGvXLiUmJmrt2rVyOByW3eqlnKxk5syZCgmxd6JZ0IZJ+YmIiLCskg4AAAAA\ngBf3NLdgwDS3MmPkyJHatm2bEhISvDYIu3Dhgj799FN9+umnPrWVd7d60zQVEhKi559/Xm3atAnM\nCxRAiQqTAAAAAAAAgtWrr76qiIgILVu2zBME5Q6EfJV3k7HIyEhNnz5d/fv392/BhRQ0C3ADAAAA\nAACUZCEhIZo5c6ZmzpypKlWqWAKkgu5W795o7Nprr9Xf//73oAmSJEYmAQAAAABKG6a5wWaDBw9W\n79699dFHH+nTTz/VwYMHLZ/PPfLILe/Ipeuvv14jRoxQr169AlprYRAmAQAAAAAA+FlkZKRGjRql\nUaNGaf/+/Zbd6k+ePKm0tDRdunRJ5cqVU8WKFVWvXj01adJE1113nW6++WbVrVvX7le4LFvDpFat\nWhVrf4ZhaNeuXcXaJwAAAAAAKNuaN2+u5s2b67777rO7FL+wNUwqyOJTAAAAAAD4xCEp2+4i/idY\nptsBfmT7NLf85gkGAsEVAAAAAABA0dkeJgUCwREAAAAAAAhWpmnqwoULysrKUmRkpCIjIxUWVnIi\nGlsrLepiUllZWUpPT1d6errnmnsbPdM0Vb58eY0bN061atUqaqkAAAAAgJLCpeDZRc1ldwGwW1ZW\nltavX6///ve/SkxM1NGjR5WSkuI1ECYmJkaxsbG65ppr1KVLF3Xt2lUVKlSwqeorszVM+vLLL/3S\nTnp6ug4cOKDExET94x//0IEDB2QYhjIzM7VgwQLNmzdPLVq08EtfAGCrkvN/VgDBiT9DZVCG3QX4\nKFgWdwEA+EtaWpoWLVqkBQsWKDk5WdKVZ1KdOXNGycnJSkpK0kcffaQKFSpoyJAhGjt2rKpVq1Zc\nZfskxO4C/KFChQpq166dHnroIf373//WlClTFBISIsMwdObMGT344IM6efKk3WUCAAAAAIAyYMuW\nLerbt69ee+01nTlzRqZpeoIk94yq/A73faZpKi0tTR9++KH69u2rzz77zOY3sioVYVJuhmFo5MiR\neuaZZ2SapgzDUHJysp544gm7SwMAAAAAFAencnZRC4YjWKbbodh89NFHuv/++/Xzzz97concx5Xk\nFy5duHBBkydP1qxZs4rpDa6u1IVJbsOHD1ePHj08yV9SUpL+9a9/2VwVAAAAAAAorVauXKnnnntO\nDofDKzzKPepIkipWrKiYmBiVL1/e8rncU+Fyh0pvvfWWPvzww2J/p/yU6pUDxo4dq6+++srzhZ8/\nf74GDhxod1kAAAAAAKCU2b17t6ZMmeIZjeRmmqaioqJ0xx13qEuXLmrXrp1q165tucfpdOro0aPa\nsWOHvvvuOyUkJCgjI8NzjzvXmDFjhjp37mz7utClOkxq27atYmNjdfz4cUk539hTp06pdu3aNlcG\nAAAAAAgY9zS3YMA0tzLjxRdfVGZmpicAMk1ToaGheuSRRzR69Ogr7swWGhqqxo0bq3Hjxrrjjjs0\ndepUvfPOO3rnnXfkcuVsCWgYhhwOh55++ml99NFHxfJOl1Nqp7m5XXPNNZYhYtu3b7exGgAAAAAA\nUNp8/fXXSkxMtARJFSpU0IIFCzRhwoQrBkn5qVixoh5//HG9//77Xs9+//332rBhg99qL4xSHyZV\nqlTJcu4epQQAAAAAAOAPS5Ys8XzsHpH01ltvqVOnTkVqt2PHjnrrrbe8Fu7+5JNPitRuUZX6MCk1\nNdVyfunSJZsqAQAAAAAUC3ZzQzFyOBxav369Z10jwzA0dOhQ3XjjjX5pv0uXLho+fLinbdM0tW7d\nOmVnZ/ul/cIo9WHSzp07LQle1apVbawGAAAAAACUJtu3b1daWprl2sMPP+zXPvK2l56ern379vm1\nj4Io1WHSxo0bdezYMcu1GjVq2FQNAAAAAAAobU6ePGk5b9GihWJjY/3aR7169RQXF2e5tn//fr/2\nURCldje3Cxcu6Omnn7ZcMwxDbdu2takiAAAAAECxYDc3FKOzZ896PjYMQw0bNgxIPw0aNNCePXs8\n5+fPnw9IP74olSOTvvvuO9199906fPiwZc5iu3btVL16dbvLAwAAAAAApUTeKW5RUVEB6Sdvu1lZ\nWQHpxxe2jkyaNWtWkdtwuVzKyspSWlqakpOTtXPnTp04cUKmaXrdO2jQoCL3BwAAAAAA4JZ3F/nc\nI5X8KW+7lStXDkg/vrA9TMq7vV1R5Q6R3G0bhqEGDRpo2LBhfu0LAAAAABCEmOaGYpR7oy/TNAO2\nMPa+ffs8s68kqVq1agHpxxdBMc3NNE2/HYZheA532+XKldOrr76q8PBwm98UAAAAAACUJi1btrSc\nnzx5Utu3b/drH9u2bdOJEycs1xo0aODXPgoiKMKk3AFQUQ83d7gUGxurd999l4W3AQAAAACA3zVu\n3Nhr5/g///nPfu3jjTfesJxXr17dK8QqTraHSf4cleQ+QkJC1LFjR02bNk0rVqxQp06d7H5NAAAA\nAEBxcU9zC4aDaW5lQo8ePTyzpUzT1Pr167Vw4UK/tP3+++/r22+/tWwwdsstt/il7cKydc2kGTNm\n+KUdwzAUHh6uChUqKCYmRk2aNAnY6ukASrOf7S7g6lbaXQCKna3/UpdCwbJ+RmmQancBvvrR7gJ8\nlGF3AT7ItrsAAAhaI0eO1CeffCJJntBnxowZMgxD9913X6HbXbhwoacdN8MwdP/99xe55qKw9T9R\nhwwZYmf3AAAAAAAARdakSRP17dtXCQkJnmV4XC6XXnjhBa1du1YTJkxQu3btfG5v69atmjVrltav\nX28Z8WQYhnr37q24uLgAvs3V8f93AgAAAABKF4eCZzAdo2LLjKefflqbN2/Wzz/nzHhwB0Dffvut\nvv32WzVr1kw33HCD2rRpo7p16yo6OlqRkZHKyMhQSkqKjh8/rh07dmjjxo06ePCgJHkCJLeYmBhN\nmTLFlvfLjTAJAAAAAACgiCpXrqxXX31Vo0ePVlZWlqRfAiVJ2r9/vw4cOHDVdtz3u593Xytfvrze\nfvtt1apVKwDVF4ztC3AHWlpamrZu3arFixfr2Wef1U8//WR3SQAAAAAAoBTq3Lmz3nrrLUVFRXlC\nody7z/uyqVh+z8TExGj27NkFmioXSLaOTGrVqpXnY8Mw9PXXXysmJsavfYwfP14bNmzwnPfo0SMo\nUjwAAAAAQIC4FDy7qLnsLgDFrWvXrvr73/+uP/zhD0pMTJRkDYd85Q6WunTpopdfflk1a9b0e62F\nZWuYlHvoVqDUqlXLkuwdP3484H0CAAAAAICyq2HDhlq4cKHWrl2r999/Xxs3bpTTaU04c488yis0\nNFQ9evTQqFGjdN111xVLzQVh+5pJuecPBkLetlNSUgLWFwAAAAAAgFt8fLzi4+N17tw5fffdd9qx\nY4eOHDmiU6dOKT09XdnZ2YqKilKlSpVUuXJlNW3aVB07dlSHDh1UsWJFu8u/LNvDpEAyTVNJSUmW\nwKo4RkMBAAAAAGzkVPDsohYs0+1gq6pVq6pv377q27ev3aX4hd/DpOzsbJ0+fbpQz546dUqXLl0q\ncg1ZWVk6ffq0PvzwQx06dMgyL7FKlSpFbh8AAAAAAKCsCsjIpNGjR+vQoUM+3Zt7xNCwYcMCUY5F\n8+bNA94HAAAAAABAaRXi7wbDw8P1xz/+0eft7nLz5ZmCHrlHJVWvXl3t27f39ysDAAAAAIKJe5pb\nMBxMc0Mp5PcwScrZtm7AgAGSftn+Lr8jryvdW9hDkidUmjp1qkJDQwPxygAAAAAAAGVCwBbg/v3v\nf69169YpNTXV50WvA7U4drly5TRp0qRSs9AVAAAAAAAILJfLZXcJVxQSEpDxQT4JWJgUExOjp556\nSp9++ull70lMTPTstGYYhtq3b6/w8PBC92kYhkJCQhQeHq6oqCjFxMSoSZMm6tGjh+rUqVPodgEA\nAAAAJYh7ilkwCJY6UGCtW7e2u4TLMgxDu3btsq3/gIVJkjR48GANHjz4sp+Pi4uznL/11luKiYkJ\nZEkAAAAAAABXFajZU6VBQMMkAAAAAACAkiq/9Z7tFgwhl+1hUjB8EQAgR7LdBVzdyR/trgBAsSgJ\ncyKy7S7AR0fsLsBHJeF7XlLwtfSPEr4FmXs3t2BQwr+U8M4tgjFgKm62hkkzZsywnEdHR9tUCQAA\nAAAAwNUxKMbmMGnIkCF2dg8AAAAAAHBFuUcimaapyMhI3XrrrerXr5+6detWpI3ESirbp7kBAAAA\nAOBXTHODn7h3n3czDEOZmZlKSEhQQkKCoqOj1atXLw0YMEBdunQpM1PgQuwuAAAAAAAAINgsW7ZM\no0ePVr169WSapmV6m/v84sWLWrp0qUaNGqWuXbvq+eef15YtW2ysungwMgkAAAAAACCPuLg4xcXF\n6Te/+Y22bdum5cuXa+XKlfrpp58keU9/S05O1qJFi7Ro0SLVqVNH/fr1U79+/XTNNdfY9QoB4/cw\nqWfPnl7XDMPQ6tWrfbo3kC5XBwAAAACgFGGaG/ysXbt2ateunX7/+99r06ZNWr58uVatWqXk5Jwd\nod3Bknv00okTJzR37lzNnTtXDRs21IABA9SvXz81adLEtnfwJ7+HScePH5dhGJbhX5ebM5jfvYFU\nVuYuAgAAAACAwOjUqZM6deqkadOm6bvvvlNCQoK++OILXbhwQZJ3sHT48GG99dZbeuutt9SyZUtP\nsFS3bl3b3qGoAjbNLe8Xz5d7A4mt+wAAAAAAgL+EhITopptu0k033aRnnnlG33zzjRISErRmzRql\npaVJ8s5G9uzZo7179+pPf/qT2rdvrwEDBqhPnz6qXr26be9RGKyZBAAAAAAoXRySsu0u4n+CZbod\nAiosLEzx8fGKj49XVlaW1q5dq4SEBK1bt04ZGRmSvIOlpKQkJSUlacaMGercubP69++v3r17q1Kl\nSra9h68CEiYVZBQQI4YAAAAAAEBpERERodtvv1233367MjIytGbNGiUkJOjrr79WdnZOypk7WHI6\nndq4caM2btyo5557TjfffLP69++vnj17qkKFCna+ymX5PUzas2dPQO4FAAAAAAAoSSIjIzVgwAAN\nGDBAqamp+uKLL7R8+XJ99913cjhyhq3lDpays7O1bt06rVu3TuXLl1f37t01YMAAdevWTREREXa+\nigXT3AAAAAAApYtLwbOLmsvuAhAsoqKiNGTIEA0ZMkTnzp3TqlWrtHz5cm3atEkuV84PSu5gKSMj\nQ59//rk+//xzRUVF6bbbblO/fv108803KyQkxM5XIUwCAAAAAAAoTlWrVtXdd9+tu+++W6dPn9bK\nlSuVkJCg77//3rMcUO5gKSUlRcuWLdOyZctUtWpV9e7dW08//bRt9dsbZQEAAAAAAJRhNWrU0IgR\nI/TRRx/pq6++0pQpU3TttddKygmSDMOQYRgyTVOmaers2bNavHixrTUTJgEAAAAAShencnZRC4Yj\nWKbboUSoXbu2Ro4cqcWLF2vt2rUaM2aMQkNDJckTKgUDprkBAAAAAAAEiR9//FGrVq3SqlWrtG3b\nNs+0N/copWBAmAQAHmftLsAH/7W7AAAoYUrC3+2SlG13AT5w2F0A4Dv3yKRgwMgk+ODo0aNauXKl\nVq5cqd27d0uSJ0SSgmtUkhSAMGnWrFn+btKvHnvsMbtLAAAAAAAAZdzVAiRJlgDJ/bmmTZuqb9++\nxVdoPgISJgVTWpYXYRIAAAAAALDDkSNHPAHSnj17JHmPQMrN/bmGDRuqb9++6tevn1q0aFF8BV9G\nwKa55U3TgkEwh1wAAAAAAD9hmhuCiDtAWrFihfbu3SvJtwApNjbWEyC1atWq+Ar2QcDCpGALboIx\n3AIAAAAAAKXP4cOHPSOQChIg1a1bV71791a/fv3Utm3b4iu4gAISJhHcAAAAAACAsuTw4cNasWKF\nVq5cqX379knyLUCqWbOm+vTpo379+unaa68tvoKLwO9h0owZM/zdJAAAAAAAvnMoeDZJDJbpdgiI\nQ4cOeUYgFSRAql69unr37q2+ffuqU6dOxVewn/g9TBoyZIi/mwQAAAAAAAgKP/zwgydA2r9/vyTf\nAqSqVavq9ttvV79+/XT99dcH3fJABRGwNZMAAAAAAABKg8IGSJUrV1avXr3Ut29fdenSRaGhocVX\ndAARJgEAAAAASheXgmcXNZfdBaCwDh486AmQDhw4IMm3ACk6Olq33Xab+vTpo5tvvllhYaUveil9\nbwQAAAAAAFBE/fv3l2EYXpuM5Q6R3J+rWLGievTooX79+qlr166KiIgo1lqLG2ESAAAAAADAFeQX\nIEVGRio+Pl79+vVT9+7dS32AlFtQh0kpKSlKTExUUlKSDh06pFOnTik9PV3Z2dmKjIxUpUqV1KBB\nAzVt2lSdO3dW69atS/QCVgAAAAAAP3AqeHZRC5bpdig0d85gmqYMw1BcXJz69eun+Ph4RUZGSpJ+\n+umnYq+rfv36xd6nW1CGSWvWrNEnn3yib775Rk7nL3/y8htalpiY6DmvVq2aBg4cqF//+tdq0KBB\nsdULAAAAAABKp9xZhGma2rt3r/bu3avXX3/dtpoMw9CuXbts6z+owqSkpCQ9/fTT2rt3ryTv8MjN\nPWcx7+eTk5M1f/58LVy4UMOGDdOkSZMUHR0d8LoBAAAAAEDZcLmsoiwJmjBpzpw5euONN+RyuTzf\nmCtNWbvc50zTlMPh0Mcff6yvv/5ab7zxhtq0aROQmgEAAAAAQYhpbvCjYFtOJxjCrBC7C5Ck119/\nXa+//rqcTqdnDmLuOYm+HpI8z5qmqePHj2vkyJFKSkqy8/UAAAAAAABKDdtHJi1fvlyzZ8+2BEjS\nL0lbhw4d1KFDB7Vu3Vo1a9ZUVFSUypcvr7S0NKWmpurEiRPatWuXNm/erN27d0uSpa3U1FSNHTtW\n//znP1W9evXif0EAAAAAAFDi1K1b1+4SgpatYVJKSoqef/55r+umaWro0KEaM2aMGjVqdNV27rzz\nTknSnj17NGfOHCUkJFiCqbNnz2ratGn661//6rfaAZRG4XYX4IOSUCOAsiHb7gIA4PIcCp6/poJl\nuh0K7Msvv7S7hKBl6zS3+fPn6/z585YpbZGRkXrnnXf0wgsv+BQk5RYXF6fXXntNb7zxhiIiIiT9\nslj32rVrtWnTJn+/AgAAAAAAQJlia5j0j3/8wxIkhYeHa86cObrllluK1G7v3r31xhtveC2StWDB\ngiK1CwAAAAAAUNbZFiYdPHhQJ06ckCTPottjxoxRp06d/NJ+fHy8fvWrX3nado9OSktL80v7AAAA\nAIAg5VLOLmrBcLgC/K6ADWwLk9yLZbuFh4frwQcf9Gsfjz76qEJCfnlFh8Ohbdu2+bUPAAAAAACA\nssS2MOnMmTOejw3DUIcOHRQdHe3XPmrWrKl27dp5doaTpMOHD/u1DwAAAAAAgLLEtjApMzPTch6o\nLfdiY2Mt5xcvXgxIPwAAAACAIOFUzi5qwXA4A/yugA1sC5OioqIs54FayyjvItzuXd4AAAAAAABQ\ncLaFSQ0bNvR8bJqm9u3bF5B+fvzxR8t5vXr1AtIPAAAAAABAWWBbmNShQweFh4d7zo8cOaKkpCS/\n9pGcnKxt27Z5RicZhuG33eIAAAAAAEGKaW5AQNk6za1Pnz4yTVOGYcg0TU2fPl0ul//2Tfzb3/4m\npzPnT65hGLrllltUrVo1v7UPAAAAAABQ1tgWJknSxIkTVaFCBc/5jh07NG3aNL+0vW7dOn344Yee\noCo8PFyTJk3yS9sAAAAAAABlla1hUmxsrF544QVJ8oQ+S5cu1YQJE3Tu3LlCt7tixQpNnDhRpmnK\nNE1J0mOPPaYWLVr4pW4AAAAAQBBzSMoOksMR4HcFbBBmdwF9+/bVpUuX9Ic//EFOp1OmaeqLL77Q\n5s2b9dBDD2nw4ME+T03bvHmz5s+fr9WrV3tCJMMwNGLECD388MOBfA0AAAAAAIAywdYwac2aNZKk\n6OhoPfjgg5o7d66knN3dkpOT9corr+i1115TmzZt1Lp1azVu3FjR0dGKiopSdna20tLSlJycrN27\ndyspKUknT570PO8e6RQWFqY9e/bo/vvvL1BthmFowYIF/n1hAAAAAACAEs7WMGncuHGendbc3EGQ\n+2OHw6GkpKSr7vTmHokkydKmw+FQYmJigerKXQMAAAAAoIRxKnh2UQuWOgA/sn2am2QNgtznhmFY\nQqWryR3+5L7fl2cv1w4AAAAAAACsgiJMulqAU9CAh0AIQOHUtLsAH3S3uwAAxaIkrNaabncBPtpq\ndwE++snuAnwQFL86+KAk/PkBgJLN9n8RCjpyCAAAAACAK3IqeHJFprmhFAqKBbgBAAAAAABQMtga\nJtWrV8/O7gEAAAAAAFBAtk9zAwAAAADAr5jmBgRUiN0FAAAAAAAAoOQgTAIAAAAAAIDPmOYGAAAA\nAChdHJKy7S7if4Jluh3gR4xMAgAAAAAAgM+CbmTS/v37lZSUpOPHjyslJUXp6ekyTdMvbRuGoRdf\nfNEvbQEAAAAAAJRFQREmuVwuffDBB1q4cKF+/PHHgPRhmiZhEgAAAACUBS4Fzy5qLrsLAPzP9jAp\nOTlZ48eP19atW/02AgkAAAAAAACBYWuYlJ2drccee0xbt26VlDMNLVAIqgAAAAAAAIrO1jBp8eLF\n2rp1q1eIRPADAAAAACg0p4JnF7VgmW4H+JGtYdK8efPyDZI6d+6srl27qn79+oqOjlZERERARy0B\nAAAAAADAN7aFSQcPHtTJkyc9IZFpmipXrpxef/113XrrrXaVBQAAAAAAgCuwLUzasWOH52P3TmtP\nPfUUQRIAAAAAoGiY5gYElG1h0rlz5yzn1atX19ChQ22qBgAAIJjYvuGuD8LtLgAAANgkxK6OL126\n5PnYMAy1bt1aoaGhdpUDAAAAAAAAH9j2f3tFR0dbzmNiYmyqpGxJS0tTx44d/dbetddeq8WLFxf4\nuYMHDyohIUFbtmzRoUOHdOHCBTkcDkVHR6thw4bq0KGD+vTpo3bt2vmtVgAAAABlRLBMcZOCqxbA\nT2wLk5o1a2Y5P3v2rE2VlC27d++WJNt2xzt27Jiee+45ff31155ruWs5NGT3oAAAIABJREFUd+6c\nzp49q61bt2revHnq0KGD/vCHP6h169Z2lAsAAAAAAPKwbZrbtddeq8jISEk5C3Bv27bNrlLKlD17\n9ng+Nk2zWPtetWqVBg4cqK+//lqGYVh28st9SPJ8fuvWrbrrrru0YMGCYq0VAAAAAADkz7YwKSIi\nQgMGDPCEB2fPntVXX31lVzllhntkklveIKegh69WrFihJ554QpmZmTIMw/O8OzTKe+T+vMvl0owZ\nMzRnzhx/fzkAAAAAlEYu5eyiFgyHK8DvCtjA1q1C/u///k+fffaZMjMzZZqmZs6cqc6dOysqKsrO\nskq1vGFScUx327dvn6ZOnSqXy/q3aLly5TRo0CDdfvvtio2NlSQdOXJEy5cv18qVK5WVlWW5/89/\n/rPi4uLUrVu3gNcMAAAAAADyZ2uYVLduXU2dOlXTpk2TYRg6evSoxo4dqzfeeENVq1a1s7RSyel0\n6sCBA5YAqVGjRlqxYkXA+jRNU7/73e+UmZlpuda0aVO9+eabatq0qeX+Ro0aqXv37ho1apQmTpyo\nI0eOeEYruVwuTZs2TStXrvRMkQQAAAAAAMXLtmlubsOHD9ejjz7qmTKVmJiogQMHav78+SzK7WcH\nDx70jPZxTyFr27ZtQPv85z//aRkNZZqmatWqpXnz5nkFSbnFxcVp4cKFqlOnjmU63c8//6y5c+cG\ntGYAAAAAJZxTObuoBcPhDPC7AjawdWSS2+OPP67q1atr5syZcjqdOn36tF566SW99NJLio2NVcOG\nDVWpUiWVK1euSP0YhqEXX3zRT1WXPHmnuEkKeJj0zjvvWBbaNgxDzz33nGrVqnXVZ2vWrKlZs2Zp\n+PDhnmdN09QHH3ygMWPGFPnnAQAAAAAAFFxQhEkul0sOh0PR0dE6f/68JzSQcraS//HHH4vchzuM\nKMthUu6d3NwCGSZt2rRJBw8etHw/W7Vqpe7du/vcRuvWrTVgwAD961//8oRSFy5c0Oeff66BAwcG\npG4AAAAAAHB5tk9zO3funH71q1/ppZde0vnz5722hs+9s1dx7DpWmuUdmRQaGqprrrkmYP2tXLnS\ncm4YhoYOHVrgdu666y6va8uXLy90XQAAAABKOaa5AQFla5jkcDj06KOPatu2bVcMfS63fXxBDuSE\nSbm/Fs2aNVNERETA+vvmm2+8vvY9evQocDvXXXedKleuLEmecHHjxo26dOmSX+oEAAAAAAC+szVM\n+uCDD5SUlOQV/PhjJBIjk6xOnjypCxcuSCqexbfPnDmjw4cPW67VqlVLdevWLXBbISEhat++veX7\neOnSJW3fvr2oZQIAAAAAgAKydc2kBQsWeI1cMU1TLVu2VHx8vJo1a6YqVaqw0LIfFPfi2/v27fN8\n7A6vijKlrlWrVvrPf/5jubZjxw516tSp0G0CAAAAKKUcdheQh+0LzAD+ZVuYtGfPHp08edKy01dU\nVJRmzpyp2267za6ySq0rhUmpqalasWKFvvvuO+3cuVPJycnKzMxUTEyMatSooU6dOik+Pl6dO3dW\nSIhvfwvu37/f61qTJk0KXX/Dhg29rh06dKjQ7QEAAAAAgMKxNUxyc49cIUgKnLw7uUVERCgmJkbP\nPvusli1bpoyMDEmyjBT76aefdOrUKW3fvl3vvfeemjVrpt/85jeKj4+/an/57cBXp06dQtdfu3Zt\nn/oAAAAAAACBZVuYlJycbDmPjY0lSAqg3ItvG4ah0NBQ9e/fXykpKZYAKe/6Urk/d+DAAT366KO6\n44479MILL1xx8e68318pZ82kwqpRo4bl3DRNnT59utDtAQAAACjFXJKCZelcQ0xzQ6ljW5iUnZ3t\n+dgwDLVp08auUkq91NRUHT9+3HNumqbS09MtUwyvtOOd+/Pue/7973/rxIkTmj17tqKiovJ95syZ\nM17XKlWqVOh3yP2se5H2ixcvFro9IH8H7C7AB3+zuwAAKGGyr35LUAi2BV4AALg828Kk6Ohoy3nF\nihVtqqT027NnjyUwyhsiNWvWTIMGDVLHjh1Vq1YtuVwuJScna+vWrVq1apW2bt3qGbHkDpW2bNmi\n3/72t3r77bfz7TM1NdXr2uWCJ1/k9/ORkpJS6PYAAAAAAEDh2BYmNWrUyHKe37Qo+Ed+i2+bpqnI\nyEhNnTpVw4cP9/p8bGys2rdvr5EjR+o///mPnnrqKcu0MtM09dVXX2n27Nl65JFHvJ7Pzs72Gu1U\nlF358ptSl5WVVej2AAAAAJRiTuVMdQsGIbJ5H3XA/2ybudm+fXuFh4dLygkmkpKS5HIFy5/20mXX\nrl2ej03TlGmaqlatmpYsWZJvkJRXt27dtGTJEtWvX98yQsk0Tf3tb3/T2bNnvZ7JL+gJDQ0t9Dvk\n96zDwXBwAAAAAACKm21hUlRUlHr06OEJJ86dO6cvvvjCrnJKtc6dO2vIkCGeaWzlypXTm2++qebN\nm/vcRp06dfTmm296jRDKzMzU3Llzve53Op1e1/wdJgEAAAAAgOJn62C7sWPH6ssvv5TT6ZRpmnrl\nlVd08803F2ltHXi78847deedd3rOXS6XQkIKniO2atVKd999txYuXOhZO8k0TX322WeaPHmy5d6w\nMO8fraKMJMq9YLsbARMAAACAfDn/dwQDfm1BKWTrBoVxcXGaMGGCZyHo48eP6+GHH8532hT8pzBB\nktvIkSO9rv388886ePCg5Vp4eLhn1JlbUcKk/EY65beOEgAAAAAACCxbwyRJGjNmjG6//XZP8LB1\n61YNGDBA8+bNsyz4jOBQr149NWzY0Ov6li1bLOf57b6WkZFR6H7T09O9rhVlQW8AAAAAAFA4tq8p\nbxiG3nzzTb3yyiuaO3euDMPQ2bNn9corr+iVV15RgwYN1LRpU9WoUUOVKlVSRESE1y5hBfHYY4/5\nsfqyqW3btjpy5Ijl+3DmzBnLPVWqVPF6Li0trdB95n7WHTxWq1at0O0BAAAAKMUc/zuCgXn1W4CS\nxtYwqU2bNvled6/FI0lHjhzR0aNH/dYnYVLRVa1a1eta3qmJvtxTEMnJyZZzwzAUExNT6PYAAAAA\nAEDh2Bom5beGjnv9pNyjXvKuvVNYRRnRhF9UqFDB61re72W9evW87inKtMX8nq1Ro0ah2wMAAAAA\nAIUTFNPc/HHP1fgrkIKUkpLidS3vtLb69et73VOUEWb5PdukSZNCtwcAAACgFAum3dwY04BSyPYw\niZAn8Fwul86dO6fk5GQlJyerVq1aRQpi8k45k7yntcXFxXndk3fHt4LI79nmzZsXuj0AAAAAAFA4\ntoZJM2bMsLP7MmHmzJl6//335XK5PNeGDBlSpK/9tm3bvEaLXXPNNZbz5s2bKzIyUpmZmZ41sHbt\n2lXoPrdv3+7V5+XW3AIAAAAAAIFja5g0ZMgQO7svE2JjY+VyuSxBzJYtWwrd3uHDh3Xy5ElLe+Hh\n4WrXrp3lvpCQEHXs2FHffPON597U1FRt27bN696r+fnnn3XgwAHLtQYNGqhu3bqFfAsAAAAApZpT\nwbObG9PcUAqF2F0AAivviCHTNHX06FHt3LmzUO0tXLjQ0pZhGLrxxhsVERHhdW/37t29riUkJBS4\nz4SEBM90SHef3bp1K3A7AAAAAACg6MpEmJScnKy//vWvuvXWW+0updh16NBBtWvX9ro+d+7cArd1\n6NAhLV261Gu62YgRI/K9v2/fvgoLyxn85p7qtnTpUp0/f97nPrOysrRw4UKvPocOHVrA6gEAAAAA\ngD/YvgB3IG3YsEGLFy/WmjVr5HQGy1L+xcswDA0aNEizZ8+WYRieUGfFihW688471bVrV5/aycjI\n0KRJk5SRkWEJdlq2bHnZNqpXr66ePXvq888/9zyTkpKiadOm6S9/+YtP/c6cOVPHjx/31C3lBGT5\nLfANFF2wjIW+kpJQIwAAgM2CaZpbmRjCgbKm1P1YX7hwQe+995769OmjUaNGadWqVXI4HGV617iH\nHnpIVatW9XwN3MHME088oc2bN1/1+fPnz+vBBx/Url27PKGQaZoKCwvT9OnTr/jsuHHjFBISYul3\n9erVmj59+lW/J3PmzNGiRYss4ZVhGJo0adJVawYAAAAAAIFRasKkLVu26Le//a26deuml19+WYcP\nH5Zpmp41dsqySpUq6be//a3lmmEYSklJ0QMPPKDXXnst36lnmZmZ+uSTT9S/f399//33liDJMAyN\nHj36qjuqtWjRQvfcc48lyJKkDz74QA888ID27Nnj9cyxY8c0ceJEvfbaa159Dhw4UB07diz4FwEA\nAAAAAPhFiZ7mlpaWpmXLlunjjz/W/v37JckrtECOIUOGaN++fXrvvfckyTPlzel0as6cOZo3b57a\ntGmj2NhYhYaG6qefflJSUpJnWlveUKdXr156/PHHfep78uTJ2rJli3bt2mXp+7///a8GDx6slv/P\n3p3HRVn1/x9/X4AQgriHuKZmbqWZZlmZdy5l5q65lJaat2Z2p1n92ixLu7O6874rrWzRNLXMJXLN\nTNMs09RcU1PcERWBREVAtuv3h98ZGa4BZ4ZhG1/Px4OHcriuc84M1xnm+sw5n1O/vmrXrq2AgABF\nR0dr586dDkFA2++0bt26eu2117z8zAAAAADwORmS0ou6E//HZ6ZwAJeVyGDS7t27NXfuXC1btkwp\nKSkOy6XyCiL5+/sXRveKreeff16SNGPGDMtzlpmZqe3bt2v79u0O5TkDOoZhqHv37ldc3pZdUFCQ\nPv30Uw0ZMkRRUVGWgN/+/fu1b98+S7vZj6tdu7amTZum4OBgTx46AAAAAADwkhITI01NTdWCBQvU\nu3dv9e7dWwsWLFBycrJDwCFnIMm2zK1mzZoaM2aM1qxZUxRdL1aef/55ffjhh6pcubJD0MZZ/iJb\nuW2WUPny5fXvf/9bEydOdDswV6lSJX311Vd64IEHLO3mbDt7m7ZZUHPmzFF4eHi+HjsAAAAAAMi/\nYj8z6cCBA5o7d64WL16s8+fPX3EWku3nwcHB6tixo3r16qUWLVoUWn9LgrZt2+quu+5SZGSk5s+f\nr7179yorKyvX4+vWrauePXuqT58+Cg0N9bjd0NBQvfvuu+rfv7+mT5+udevWKSPD+RYLfn5+uuOO\nO/TII4+odevWHrcJAAAA4CqUpUs7uhUHud9qASVWsQwmpaena8WKFZo7d662bt0qSS4HkZo2bare\nvXurU6dOCgkJKZwOl0CBgYHq27ev+vbtq6SkJG3fvl2nT59WYmKi0tPTFRISourVq6thw4ZenxHU\nvHlzNW/eXCkpKdq5c6eOHDmis2fPyjAMlS1bVtWrV1fTpk35/QEAAAAAUAwVq2DSsWPHNHfuXEVG\nRtp3F3OWUNu2BMr2swoVKqhbt27q1auXrr/++sLveAkXGhqqu+66q9DbDQ4O1m233abbbrut0NsG\nAAAAAACeKfJgUlZWllatWqW5c+dq48aNlhw6zvIg2QJJhmHo/fffV9u2bRUQUOQPBQAAAABQHJj/\n91UcFJd+AF5UZBGYU6dO6ZtvvtHChQsVFxcnyfksJBtnCaIl6d577y24TgIAAAAAAMBBoQeTfv75\nZ3399df65ZdflJWVdcVZSJJUqlQp3XPPPbr77rs1duzYQu0vAAAAAAAALiuUYFJCQoLmz5+vefPm\n6eTJk5Jcm4XUtGlTdevWTQ888IDKli2r+Pj4wuguAAAAAAAAclGgwaQNGzZo7ty5Wr16tTIzM12a\nhVS1alV16dJFPXr00HXXXVeQ3QMAAAAAAICbvB5MOnv2rL799lt98803Onr0qKTcZyHZykuXLq37\n7rtP3bt3Z2cvAAAAAACAYszrwaTWrVsrPT0911lItnJ/f3/dfvvt6tatmzp06KDg4GBvdwUAAAAA\nAABe5vVgUlpamgzDcBpAMgxDN998szp16qT7779flStX9nbzAAAAAAAAKEAFmjPJNE0FBATolltu\nUfv27XXvvfeqSpUqBdkkAAAAAAAACpBfQVVsmqYMw1B4eLhq166t8uXLOyx9AwAAAAAAQMlTYDOT\nDMOQaZo6ceKE5s2bp3nz5kmSatasqfbt26tDhw66+eabC6p5AAAAAAAAFACvz0wKCgqSaZr2mUmS\n7N+bpqmjR49q+vTp6t+/v1q3bq0333xTu3fv9nY3AAAAAAAAUAC8PjNp/fr1Wrp0qSIjI7Vjxw5J\njru5SZcTcsfFxWnWrFmaNWuWrr/+enXr1k1dunRReHi4t7sFAAAAALhqZEpKL+pO/J/Mou4A4HVe\nn5kUGhqqfv366ZtvvtGyZcs0ePBgVaxY0T4zSZJ9tzfbUjjTNBUVFaVJkyapbdu2Gjx4sBYtWqSU\nlBRvdw8AAAAAAAD5UGAJuCWpbt26ev755/Xzzz/rww8/VLt27eTv7++QiNsWVJIuzVjKzMzUxo0b\n9cILL+jOO+/UCy+8oA0bNhRkNwEAAAAAAOCiAkvAnZ2/v7/atWundu3a6e+//9Z3332nyMhIRUVF\nSXIMKEmXl8ElJydr0aJFWrRokcLDw9WmTZvC6C4AAAAAoETLlJRR1J34Pyxzg+8p0JlJzlSoUEFD\nhgzRkiVLNG/ePPXp00ehoaFXXAZ36tQp+45wAAAAAAAAKBqFHkzKrkmTJho/frx+/fVXvfPOO7r9\n9tslyekyOFtgKadRo0Zp9erVysgoLlFnAAAAAAAA31Uoy9yuJCgoSF27dlXXrl0VExOjb7/9VpGR\nkTpx4oSky7vBZZ+pZLNy5UqtXLlSZcuW1QMPPKCuXbuqadOmRfI4AAAAAADFQYaKz25uTHyA7ynS\nmUnOVKtWTf/617/0008/6YsvvtADDzygoKAgexDJ2RI40zSVmJior776Sv369dN9992njz76SNHR\n0UX9cAAAAAAAAHxKsZiZlJtWrVqpVatWSkpK0pIlS/Ttt99q165dkqxJu6XLy+OOHj2qyZMna/Lk\nyWrWrJm6d++ujh07KiwsrNAfAwAAAAAAgC8pdjOTnAkNDVX//v01f/58LV26VIMGDVKFChUsS96c\nzVratm2bxo0bp7vuuktPPfVUET4KAAAAAEDhsO3mVhy+2M0NvqdEBJOyu/766/XCCy/o559/1pQp\nU3TPPffI39/fkpw7Z1ApLS1NP/74YxH1GgAAAAAAwDcU62VueQkICFD79u3Vvn17JSQkKDIyUpGR\nkTp48KAkx6TdkpzuBAcAAAAAAAD3lLiZSc5UrFhRQ4cO1bJly/TNN9/owQcfVEhIiGUZHAAAAADg\namDbza04fLGbG3yPTwSTsmvatKkmTJig9evX66233lLLli2LuksAAAAAAAA+o8Quc7uSoKAgde/e\nXd27d9fx48e1cOFCLVq0qKi7BaBYKwkviexKCQDuSSnqDriopPQTAICSceeUb9WrV9eoUaPYzQ0A\nAAAArgq2ZW7FAcvc4Ht8bplbXmzJuAEAAAAAAOCZqyqYBAAAAAAAgPy5Kpa5AQAAAACuJpkqPsvL\nMou6A4DXMTMJAAAAAAAALiOYBAAAAAAAAJexzA0AAAAA4GPYzQ0oSMxMAgAAAAAAgMsIJgEAAAAA\nAMBlLHMDAAAAAPgYdnMDChIzkwAAAAAAAOAygkkAAAAAAABwGcvcAAAAAAA+ht3cgILEzCQAAAAA\nAAC4jGASAAAAAAAAXMYyNwAAAACAj2E3N6AgEUwCALtSRd0BFwQXdQd8DH8GUVwVlxsgX1BccqYA\nAOA7WOYGAAAAAAAAl/GRLAAAAADAx7CbG1CQmJkEAAAAAAAAlzEzCQAAAADgY0jADRQkZiYBAAAA\nAADAZQSTAAAAAAAA4DKWuQEAAAAAfEymik8Cbpa5wfcwMwkAAAAAAAAuI5gEAAAAAAAAl7HMDQAA\nAADgYzJUfHZzKy79ALyHmUkAAAAAAABwGcEkAAAAAAAAuIxlbgAAAAAAH8NubkBBYmYSAAAAAAAA\nXEYwCQAAAAAAAC5jmRsAAAAAwMdkqvjsosYyN/gegkkAYJdS1B1wQUxRdwAAAADAVY5lbgAAAAAA\nAHAZM5MAAAAAAD4mQ8VnN7fistwO8B5mJgEAAAAAAMBlBJMAAAAAAADgMpa5AQAAAAB8DMvcgILE\nzCQAAAAAAAC4jGASAAAAAAAAXMYyNwAAAACAj8lU8VlellnUHQC8jplJAAAAAAAAcBkzkwAAAAAA\n8EEnT57UkiVL9McffygqKkqJiYlKS0tTSEiIatasqSZNmqh9+/Zq1apVUXcVJQzBJAAAAACAj7m6\nd3P7+++/9e9//1srVqxQZualZXaGYdh/fu7cOe3atUu7du3SnDlzVK9ePb300ksEleAylrkBAAAA\nAOAjtmzZogceeEDLli1TVlaWPYhkmqbDl3QpwGQYhqKiojR48GC988479p8BeWFmEgAAAAAAPmDL\nli365z//qdTUVIcgUvZZSdllDypJ0vTp03XhwgW9/vrrhdNhlFgEkwAAAAAAPubq280tLi5Oo0eP\nVmpqqr3MNE35+/urY8eO6tSpk6677joFBgbq+PHjWrlypRYvXqzk5GSHgNO8efPUsGFD9evXr1D6\njZKJYBIAAAAAACXcuHHjFB8f7zAjqXLlynr//fd1yy23OBxbo0YNtWrVSkOHDtXTTz+tnTt3Sro0\nQ8k0Tb399tu65557FB4eXuiPAyUDOZMAAAAAACjBNm3apJ9++skhkBQSEqLPP//cEkjKrlq1avri\niy/UoEEDh1xJqampeu+99wq83yi5CCYBAAAAAHyMbTe34vBV8MvtPv30U/v/bUvWxowZo/r161/x\n3JCQEE2dOlWlS5eWdHl20tKlSxUbG1tgfUbJRjAJAAAAAIASKiYmRr/99ptDku2KFSuqb9++LtdR\npUoVPfroow6zkzIyMvTtt996ta/wHQSTAAAAAAAooVauXKmsrCxJl2cldenSRQEB7qVI7tOnj8P3\npmlq2bJlXusnfAvBJAAAAACAj7Ht5lYcvgp2N7dff/3VUta2bVu364mIiFD9+vUddnY7ePCgYmJi\n8t1H+B6CSQAAAAAAlECmaWrr1q0OS9wCAgLUtGlTj+pzlqx7y5YtHvcPvotgEgAAAAAAJdCxY8eU\nkpIiSfZ8R3Xq1FFgYKBH9TVs2NBS9ueff3reQfgs9xZRAgAAAABQ7Nl2cysOCm43t6ioKIfvDcNQ\nnTp1PK6vVq1alrLDhw97XB98FzOTAAAAAAAogY4fP24pi4iI8Li+KlWq2P9vGIZM03TaBkAwCQAA\nAACAEighIcFSdu2113pcX+XKlS1lcXFxHtcH38UyNwAAAACAj7Ht5lYcFNxubvHx8ZaysmXLelxf\n6dKl5e/vr6ysLHtZcnKysrKy5OfHXBRcxtUAAAAAAEAJdOHCBUtZaGhovuoMCQmxlJ0/fz5fdcL3\nEEwCAAAAAKAESktLs5R5upNbXuc7awdXN5a5AQAAAAB8zNWxm5uzIE9AQP5u8/39/S1lGRnFZckg\nigtmJgEAAAAAUAJlZlrzMeU3t5GzYFL2HEqARDAJAAAAAIASydksJGcBJnekp1tndJUqVSpfdcL3\nsMwNAAAAAOBjro7d3JwFefK7JM1ZMCq/eZjgewgmATmkpKQ4fB8UlFhEPQEAAACKRs73wMnJyUXU\nE88Up/fwBdkXZzuv5fd35ez8oKCgfNUJ30MwCcjh2LFjDt+Hh28pop4AAAAAxUN0dHRRd8EtV8t7\n+HLlylnKLly44HF9WVlZSk1NlWEY9rKgoCAFBwd7XCd8EzmTAAAAAAAogcqXL28pO3PmjMf1JSQk\nWMoqVqzocX3wXQSTAAAAAAAogapXr24pi4uL87i+7OeapinDMFS5cmWP64PvYpkbkEPbtm0dvq9R\no4ZKly5dRL0BAAAACl9KSopD+oec75GLm/r162vOnDlF3Q2X1K9f32t1OQsm5Uzb4Q5n59apU8fj\n+uC7CCYBOUREROjhhx8u6m4AAAAAcFGZMmXUokWLou5GoWvQoIE9v5FhGDJNUwcPHvS4Pmfn1qtX\nz+P64LtY5gYAAAAAQAkUGhqqWrVqOZTFxMQoMdGzHeR27dplKbvxxhs9qgu+jWASAAAAAAAl1G23\n3SbTNB3KNmzY4HY96enp2rx5s8NObtdcc42aNWuW7z7C9xBMAgAAAACghGrTpo2lbPny5W7Xs3bt\nWl24cEHS5eTbrVq1UkAA2XFgRTAJAAAAAIAS6q677lK5cuUkXc6btGbNGh06dMiteqZNm2Yp6927\nt1f6CN9DMAkAAAAAgBIqMDBQPXv2dFjqlpmZqZdeeklpaWku1TFt2jRt377dYYlbRESE/vGPf3i7\nu/ARBJMAAAAAACjBhg4dquDgYEmXZyft2LFDzz777BUDSkuWLNGkSZPsgSTbErfRo0fLz4+QAZzj\nygAAAAAAoASrUKGCRo0aZZ+dZAsMrVy5Ug8++KC2bNliOScuLk7jx4/Xc889Zz/P9m+LFi3UtWvX\nQuo9SiLDzJn2HQAAAAAAlDjDhw/Xzz//LEkOM40kqVatWrrhhhtUunRpxcTEaPv27crIyLAcV6lS\nJUVGRqpy5cpF8AhQUhBMAgAAAADAByQnJ2vEiBHatGmTZZaSJIe8SjmDSJJUuXJlzZgxQ3Xr1i2k\nHqOkYpkbAAAAAAA+oHTp0vr88881cOBA+fn52fMn2b6yy15mGIZuvfVWzZ07l0ASXMLMJAAAAAAA\nfMz+/fs1bdo0rVy5UqmpqU6PMQxDTZs21cCBA9WpU6dC7iFKMoJJAAAAAAD4qPT0dO3atUuHDh3S\nmTNnZJqmwsLCFBERoZtvvllly5Yt6i6iBCKYBAAAAAAAAJeRMwkAAAAAAAAuI5gEAAAAAAAAlxFM\nAgAAAAAAgMsCiroDAEoO0zTVq1cv7dmzR5LUo0cPTZw40attHDx4UMuXL9fWrVt1+PBhnT17VhkZ\nGSpTpoxq1aqlZs2aqWPHjmrSpIlX2wW8xTRN/fbbb9q8ebO2bdsH4YqWAAAgAElEQVSmEydO6Ny5\nc7pw4YJCQ0NVrlw5Va9eXbfeeqtatWrl1WuZ8YOSLi0tTatWrdLGjRu1c+dOxcfH6+zZswoICFC5\ncuVUp04dtWjRQh06dND111/v1bYZPwAAuI4E3ABcNnv2bL3xxhsyDEOS1L17d68Fk6KjozV+/Hj9\n8ssv9jJbOzbZX66aNWumsWPHqnHjxl5pH8ivzMxMzZkzR19++aWOHz9uL895HUuO1/JNN92kxx9/\nXO3atfO4bcYPSrrMzExNmzZNM2fOVEJCgqQrj51bb71VY8aMUbNmzfLVNuMHAAD3+b/22muvFXUn\nABR/u3fv1jPPPKOsrCyZpinDMNSgQQO1b98+33WvXLlSjz32mA4ePCjDMJzeQNjYfn7y5EktXLhQ\noaGhuvnmm/PdByA/jh49quHDh2vBggU6f/78Fa9j6fK1HBsbq+XLlysmJkZ33XWXAgLcmzTM+EFJ\nFx0drSFDhmjx4sVKTU21X6e5fd5p+3lMTIwWLlyos2fP6o477pCfn/vZGxg/AAB4hmASgCuKiYnR\noEGDdP78eXuZt4JJ33//vZ555hmlp6c73DzY3rTn/Mr+c9M09csvvygwMFDNmzfPVz8ATx05ckT9\n+/fXsWPH7DeiV7qOnV3re/fu1caNG9WlSxeXA0qMH5R0x44d0yOPPKIjR464PH5y/nzHjh3666+/\n1LFjR7cCSowfAAA8xzI3AHmKjo7WoEGDdOLECXuZbWZSfpe57d+/X3379lVqaqpD3UFBQerWrZvu\nvfdeVa9eXdKlmR/Lli3TihUrlJaW5nDT4efnp6lTp+ruu+/2uC+AJxITE9WzZ0+dPHnSXmYbHxUr\nVlSPHj102223KSIiQqGhoUpMTNS+ffv0008/6ccff3SY6WfTtm1bffjhh1dsm/GDku7ixYvq1q2b\njh49ai+zjYdatWqpT58+at68uSpXrqyMjAzFxMTot99+07x583Tu3Dn7sbZ/H330Ub3wwgsutc34\nAQAgfwgmAcjVX3/9pccff1yxsbGSZHnjnp9gkmma6tmzp/766y+Hsrp16+qDDz5Q3bp1c+3TqFGj\ndPToUYc39OHh4VqxYoWCg4M96g/giXHjxumbb75xuBYNw9CgQYM0evRoBQUF5XruwYMHNXr0aEVF\nRVnOf+utt9StW7dcz2X8wBe8+eab+vLLLy3BmVGjRmn48OG5nnfu3Dk9//zzWrNmjeXcBQsWqFGj\nRnm2y/gBACD/3F9cDuCqsGLFCvXv398eSPK2RYsWae/evfbvbW/Ip0+fnusbeUlq0KCBZs2apYiI\nCId8GqdPn9a0adMKpK+AM4cOHdKCBQssgaD/9//+n55//vk8A0mSVLduXc2dO1f169e3LJ/53//+\np/T09FzPZfygpIuPj9fXX39tGT/PP/98noEkSQoLC9PkyZN12223OVzHpmlq6tSpV2yb8QMAQP4R\nTALgIDk5WWPHjtXo0aPt0/9N08w1EaqnPvvsM8tNxPjx4xUeHn7Fc6+99lpNmTLFnhvDdgM+e/Zs\nXbx40av9BHITGRmpzMxMSZev4TZt2mjw4MEu1xESEqLJkyerVKlSDuWxsbHauHFjrucxflDSff31\n1/aAqe0abtGihR599FGXzg8ICNDrr79uHwe263jNmjVKTk7O81zGDwAA+UcwCYDdihUr1KlTJ8ts\nC0lu7zCVly1btujgwYMO9Tds2FBt2rRxuY7GjRurc+fODkGus2fP6ocffvBaP4G8rFixwrLz0xNP\nPOF2PTVr1lTXrl0tAdu1a9c6PZ7xA1+watUqSXK4BocOHepWHdddd50aNmzoUEdGRoZ2796d6zmM\nHwAAvINgEgBt3LhR/fv31+jRoxUbG2v5xLZu3boaP36819pbsWKFw/eGYahXr15u19OnTx9L2bJl\nyzzuF+CquLg4RUdHO5RVrFhRTZo08ai+e+65x1J2+PBhp8cyflDSnTt3TgcOHHDYKa106dJq3bq1\n23XVqlXLUpbX8mzGDwAA3uG9qQYASqxBgwbZ39BLjtsyd+rUSRMmTNCff/7ptfZ+/fVXy4wOZzfT\nV3LLLbeobNmyOnfunH2pwe+//66LFy9eMV8NkB8HDhyw/982Xm688UaP67PtGpW9zri4OKfHMn5Q\n0oWFhWnr1q06ePCgDhw4oIMHD8rf39++dMwd2Xdjs8mrHsYPAADeQTAJgF32IFLFihU1duxYdezY\n0attxMfH68iRIw5v5sPDw1W1alW36/Lz81PTpk21bt06e30XL17Url271KJFC6/1GcipbNmyevjh\nh3X69GmdPn1asbGxqly5ssf1ZWVlWcr8/f0tZYwf+IqgoCA1atToijuvXcnBgwctwaGcwVkbxg8A\nAN5DMAmApMtL2gIDAzVgwACNGDFCoaGhXm9n//79ljbzczPRsGFDrVu3zqHszz//5M08CpQ3boKz\nO3bsmMP3hmE4TQbM+AEu27hxo44dO+YQHAoLC8t1TDB+AADwHoJJACRJpUqVUpcuXfSvf/1LERER\nBdZOVFSUpaxOnToe1+csX0ZuuWaA4uqXX36xlNWuXdtSxvgBLomLi9PYsWMtOf769u2b64YRjB8A\nALyHYBIAjRgxQg899FC+lum46vjx45ay/ASvqlSp4lIbQHGVmJio5cuXW5bqtGvXznIs4we4tBPc\n+PHj7XnFbEu0q1atqmHDhuV6HuMHAADvIZgEQKNGjSq0thISEixlzpbzuCpnACyvxMVAcfTJJ58o\nJSXFIZhUsWJFp0tlGD+4mmRmZkqSzp8/r0OHDmnLli1aunSp9u/fb9kwonz58vroo4/yXJ7N+AEA\nwHsIJgEoVPHx8ZaysLAwj+vLfq5tR51z5855XB9QmHbt2qUvv/zSslRn8ODBlplKEuMHV5d///vf\n+uqrryzlOcdL48aNNWnSJKfLzrJj/AAA4D0EkwAUqqSkJEtZfhJ9h4SEWMrOnz/vcX1AYTl37pzG\njBlj2cmtZs2aGjhwoNNzGD+4mpw6dcppUFW6HEgaPny4nnrqKfn5+V2xPsYPAADec+W/vADgRenp\n6Zabg6CgII/rCwwMtJSlpaV5XB9QGNLS0jRy5EhFR0fby0zTVEBAgN566y2n17XE+MHV5dSpUzJN\n0+mXbSbQ1KlT1adPH61ateqK9TF+AADwHoJJAAqVszfa/v7+Htfn7NyMjAyP6wMKWkZGhp566ilt\n3rzZslzn2WefVbNmzXI9l/GDq8nJkydlGIbTL1uuJMMw9Oeff+rJJ5/Uk08+6XT2kQ3jBwAA72GZ\nG4BCZUuomp2338wDxVVaWpqeeuoprV271umW5oMGDcrzfMYPrhamaapv375q2rSpqlevrjJlyigx\nMVH79+/X6tWrtWrVKmVlZdnHj3Rpl7ehQ4dq5syZTmccMX4AAPAegkkAClVAgPVlJz+f5Kanp1vK\neIOP4ig5OVlPPPGENm7caAkkdenSRa+99toV62D84GphGIZGjx7tUFalShU1aNBAXbt2VVRUlMaM\nGaOoqCiHY3bs2KE33nhDEyZMsNTJ+AEAwHtY5gagUJUqVcq+PMEmP2/mnX3SnFu+GaCoxMfHa8CA\nAU4DSd27d9fbb7/tUj2MH+CSevXqae7cubrxxhsdlryZpqmFCxdq165dlnMYPwAAeA/BJACFytnu\nNykpKR7Xl5ycbCnLT0JVwNsOHDigPn36aM+ePZZA0sMPP6yJEyfmumNVTowf4LKQkBB9+OGHKlOm\njEO5aZqaPXu20+NzYvwAAOAZgkkAClW5cuUsZRcuXPC4vuzn2j5xrlChgsf1Ad70yy+/qH///vZE\nwtLlQNKoUaM0duxYt+pj/ACOwsPDNXjwYMvsJGe7uzF+AADwHoJJAApV+fLlLWV///23x/UlJCQ4\nfG8YhipWrOhxfYC3zJ49W48//rjD7lKmaapUqVKaOHGiHn/8cbfrZPwAVt26dbOUJScn68CBAw5l\njB8AALyHYBKAQlWtWjVLWVxcnMf1OTu3cuXKHtcH5FdWVpYmTJigN954Q1lZWZIuBZFM01TZsmU1\nbdo0de/e3aO6GT+AVbVq1VSlShVL+YkTJyzH5cT4AQDAM+zmBqBQ1ahRw1J27Ngxj+tzdm6dOnU8\nrg/Ij7S0NI0aNUpr1qxxWNYmSbVq1dLUqVNVu3Ztj+tn/ADOVa5cWadOnXLIP3b+/HmHYxg/AAB4\nD8EkAIWqQYMGlrKDBw96XJ+zc+vVq+dxfYCnkpKSNHz4cP3xxx+W/Ei33nqrJk+erLJly+arDcYP\nfEVycrKio6PtX+3atVPNmjU9rs82CzC7nAm3GT8AAHgPwSQAhapevXoKDg5WamqqPVHqnj17PK5v\n165dlp2wbrzxxvx2E3BLUlKSHnvsMe3YscMSSOrevbsmTJiggID8/8ll/MAXTJw4UTNnznQoy8zM\n1NChQz2uMy4uznItV6pUyeF7xg8AAN5DziQAhcrPz0/Nmze3L/2RLt2I79y50+26Tp8+bUmwWrNm\nTVWtWjXf/QRclZaWpuHDhzsNJD355JOaOHGiVwJJEuMHvsG23MwwDPvX+vXrPa4vOjpap0+fdijz\n8/OzLGtj/AAA4D0EkwAUujZt2ljKli9f7nY9y5cvt98U2G7e77777nz3D3DHs88+a1na5u/vr/Hj\nx2vkyJFeb4/xg5KucePGDt+bpqlNmzbp5MmTHtW3dOlSh7oMw1CTJk2cLitl/AAA4B0EkwAUuvvv\nv98+U8O21ODbb79VYmKiy3WkpaVp1qxZliUGvXr18mpfgbx89tlnWrlypWVG0oQJE/Tggw8WSJuM\nH5R0zZo1s8zgycrK0rRp09yu68yZM5oxY4blWr733nudHs/4AQDAOwgmASh0lSpVUrt27RyWGpw/\nf16vvPKKy3W89dZbiomJkXR5t6xmzZo5TbAKFIR9+/bpgw8+sASShg8frp49exZYu4wf+IKePXva\nrz1bUGfu3LnatWuXy3VkZWXp6aef1tmzZx3KK1asqL59+zo9h/EDAIB3EEwCUCRGjhwpP79LL0G2\nG4lVq1bpjTfecHiT78ynn36qr776yuFTYcMw9MwzzxRon4Hs3njjDaWnp0u6HEi6+eabNWrUqAJv\nm/GDkm7QoEGqXLmyQ0ApIyNDI0aMUFRU1BXPT05O1hNPPKGNGzdaArpPPfWUSpcuneu5jB8AAPKP\n3dwAFIkbbrhBDz30kGbPnm1PwCpJs2fP1v79+/XSSy9ZPuWNjo7Wu+++qx9++MFy89C1a1c1b968\n0B8Hrk6//fabNm/ebL8RlS5di9u2bVPDhg290ka1atW0evVqpz9j/KCkCw0N1csvv6zRo0fbywzD\nUHx8vPr06aMnnnhCDz30kEJCQhzOS0tL0/fff68PPvhAMTExlmu5U6dO6tOnT55tM34AAMg/w7zS\nRzAAIGnTpk165JFH7DfPti3PJ06c6HGdFy9eVP/+/e1bM2d/gy5J9evXV+3atRUQEKDo6Gjt3LnT\n3nb2466//nrNnz9fwcHB+XmIgMtGjBihNWvWOASTJDnMVsivqlWr5hpMkhg/8A0fffSRPvjgA0mO\n48c0TQUGBqpp06b2/EqnT5/W9u3blZKSYjnWMAzdcsst+uKLLxQYGHjFdhk/AADkD8EkAC4piGCS\nJMXHx2vIkCGKiopyWO5g4+xGPftxtWvX1hdffKHw8PB89QNw1cWLF9WyZUulpaUVWBumaeY5M8mG\n8QNf8NFHH+nDDz9UZmamvSzn9ZqzPPvPDMNQly5d9MYbb7gUSLJh/AAA4DlyJgFwS/YlPd5QqVIl\nffXVV3rggQfsyw1M07R/5WzbFsgyDEMdOnTQnDlzeCOPQrV7925dvHjR4Tr19perGD/wBU888YQ+\n//xzVa1a1XId55S93DAMVapUSa+//rreeecdtwJJEuMHAID8YGYSAJds2rRJjz76qENZjx499Oab\nb3qtjT/++EPTp0/XunXrlJGR4fQYPz8/3XHHHXrkkUfUunVrr7UNuOqHH35wyPNSUKpVq6ZVq1a5\nfDzjByVdZmamvvvuO33zzTfavXu3srKynB7n5+enG2+8UZ06dVK/fv0UFBSU77YZPwAAuIdgEoBi\nJyUlRTt37tSRI0d09uxZGYahsmXLqnr16mratKklISuAyxg/8AVJSUnaunWr4uLilJiYKMMwVKFC\nBVWqVElNmjRRWFhYgbTL+AEAwDUEkwAAAAAAAOAyciYBAAAAAADAZQSTAAAAAAAA4DKCSQAAAAAA\nAHAZwSQAAAAAAAC4jGASAAAAAAAAXEYwCQAAAAAAAC4jmAQAAAAAAACXEUwCAAAAAACAywgmAQAA\nAAAAwGUEkwAAAAAAAOAygkkAAAAAAABwGcEkAAAAAAAAuIxgEgAAAAAAAFxGMAkAAAAAAAAuI5gE\nAAAAAAAAlxFMAgAAAAAAgMsIJgEAAAAAAMBlBJMAAAAAAADgMoJJAAAAAAAAcBnBJAAAAAAAALiM\nYBIAAAAAAABcRjAJAAAAAAAALiOYBAAAAAAAAJcFFHUHAAAoyUzT1K5duxQVFaUzZ84oIyNDISEh\nCgsLU40aNXTdddepQoUKRd1NAIVs6NCh+vXXXyVJ9erV0+LFi2UYRhH3qnjbs2ePevXqJdM0JUnv\nvvuuOnfuXMS9AgA4QzAJQJEaOHCgNm/e7NG5hmHI399fgYGBKl26tMqXL6+IiAjVr19frVq1UvPm\nzRUUFORWnVOmTNGUKVMcyt566y11797doz7Cd2VlZWnGjBmaPn264uPjcz3uH//4h6ZOnVqIPQNQ\n1L766iv9+uuv9uDRSy+9lGsgKTIyUi+++KJDWbVq1bR69Wqv9snZ37eWLVvqyy+/9Go7+dGoUSN1\n795dkZGRMgxDEyZMUMuWLXXttdcWddcAADmwzA1AkTMMw6MvScrMzFRKSooSEhIUFRWldevW6bPP\nPtOQIUPUsmVLjR8/Ps8bfVf6BOSUlpamf/7zn3rnnXeUkJCQ6/VpGIYaNGhQxL0FUJiOHj2q//zn\nP/bXgTZt2qhVq1ZXPK+w/u4U979vo0ePVnBwsCTp3Llzeumll4q4RwAAZwgmAShytunspmna/++J\nnDfzaWlp+uqrr9ShQwfNnTvX434BOb3xxhtav369w81Ybtdvw4YNC7NrAIrYCy+8oNTUVJmmKT8/\nPz333HNunV8Yf3uK89+38PBwPfLII/bX1PXr12vevHlF3S0AQA4scwNQ7HjjTW72mSGpqal67bXX\ndPbsWQ0fPjzfdePqduzYMS1YsMASSDIMQw0bNlS9evUUGBiopKQkHT9+XI0aNSrC3gIoTJGRkdq2\nbZv9Q40ePXqobt26Rd2tEuef//yn5s2bp8TERJmmqf/+97+67777VLZs2aLuGgDg/xBMAlDseGPq\nve3m3vavJL333ntq2LCh7r777nzXj6vXTz/9pKysLPt1ZZqmgoOD9dlnn6lFixZF3DsARSUpKUmT\nJk2y/+0JDAzUk08+WdTdKpFCQ0PtS4kNw9DZs2f13//+V6+//npRdw0A8H8IJgEoVgzD0MiRI11+\nA26aptLT03XhwgUlJCRo3759Wrx4sdatW+cQSLK9uX/ttde0YsUKBQYGFuTDgA+Lioqy/992jT3y\nyCMEkoCr3JQpUxQfH2+fldSnTx9VqVKlqLtVYj300EOaPn26EhISZJqmFixYoL59+zLbEwCKCXIm\nASjRDMNQYGCgypcvr+uvv14PPPCAPvnkE3300UcKCQmxHH/y5EktWLCgCHoKX5GQkGApu/3224ug\nJwCKi1OnTmnOnDn2Dy78/f01dOjQou5WiXbNNdfo0UcftQfts7KyNGnSpKLuFgDg/xBMAuCT7rnn\nHv33v/+15F8yTVPz588vol7BF6SmplrKmH0AXN0++eQTpaenS7r0Icd9993H64IX9O/fX9dcc42k\nS3+/f/vtN+3cubOIewUAkAgmAfBhbdq00QMPPGAPKNmWvP3111+KjY0tyq6hBMvMzLSUBQUFFUFP\nABQHsbGxWrhwoX1WkiT16NGjiHvlG0JDQ9WhQweHZesffvhhEfcKACARTALg4/r37++0fM+ePYXc\nEwCAL/riiy+UlpZm/75KlSq66667irBHvqVnz572/5umqXXr1umvv/4qwh4BACQScAPwcU2bNlVA\nQIBlNklMTEy+6s3KytKOHTsUExOj+Ph4paWlqUyZMrruuut00003KTQ0NF/1OxMdHa1Dhw7p1KlT\nSkpK0sWLFxUQEKCQkBCFh4erTp06ql27tld2w7M5dOiQ/vrrL505c0bnz59XSEiIypcvrwoVKqhx\n48YFtk3zkSNHdOjQISUkJOjMmTMqXbq0KlSooGrVqunGG2+Uv79/gbRb1Hbs2KG9e/fq3Llzuvba\na9W0aVPVrl3b7XpOnjyp/fv3Kz4+XgkJCQoKClLFihVVpUoVNWnSpMAS0EdHR2vXrl2Ki4tTSkqK\nypQpozp16qhZs2b2pSq+yDRN/fnnnzpx4oQSEhJ0/vx5lStXThUrVlTt2rULZWv4ixcvaufOnTp8\n+LASExPl7++vypUrq2rVqmratKlKlSrl9TbPnj2rPXv26OjRozp37pwMw1C5cuUUHh6uJk2aqFy5\ncl5vs7hJS0tTZGSkw+6h3bt3L+pu+ZTbb79dVatW1cmTJ+1lc+fO1WuvvVZ0nQIAEEwC4NtKlSql\ncuXKWZImX7hwwaP6YmJi9PHHH2v16tU6c+aM02MCAgJ0xx13aMiQIflOzLxhwwYtWrRI69at099/\n/33F48uXL6/27dvr4YcfVoMGDTxqc8+ePZo7d65++OEHnT17Ntfj/Pz81LBhQ919993q27dvvvOD\nxMbGavr06Vq7dq2OHj2a63FlypTRHXfcoYEDBxbKDmq5PY+25Symaapt27aWn7ds2VJffvml/fsp\nU6ZoypQp9u+rVKmitWvXSpL27dunV199VTt27LDUc8MNN2jw4MHq3r17noHCs2fPasaMGVq9erX2\n79+f63HBwcFq2bKl+vTpo3bt2uV6nKtSU1M1e/ZsLVy4UIcPH861zc6dO2vkyJH262TDhg0aPHiw\nw3E//fSTqlat6rSOyMhIvfjiiw5lTz75pEdbr7dt21YnTpywf28Yhvbu3et2PTt37tSsWbP0yy+/\nKDExMdfjIiIi9I9//ENDhgxRjRo13Gojr+tGujReP//8c61evVoXL150WkdoaKjatGmjgQMH6uab\nb3ar/ZzS0tL03XffadGiRdq2bZuysrJyPbZx48bq16+funXrlmsAc86cOZowYYJDWb169bRkyRKP\n+/jzzz9r+PDhDmUDBgzQ2LFjPa4zNytWrNDZs2cdxmbHjh293k5RyHnteZM7Y84wDHXs2FHTp0+3\nB+2WLl2qF154waeD1ABQ3LHMDYDPsyVFzc7ZTm95MU1TkydPVqdOnbRgwQIlJibat3/O+ZWZmal1\n69Zp0KBBeuaZZ5wmbL6S7du3q2fPnho8eLC+++47nTlzJtf2sn8lJiZq/vz56tGjh1588UUlJye7\n3ObFixf1wgsvqFevXpo3b559pkFuX6Zpavfu3fr444/Vvn17vfPOO06f6ytJTU3VpEmTdN9992nm\nzJk6duxYnu0mJSXphx9+0IABAzRs2DBFR0e73aa7cvbhSj/PK+iT8+cHDhzQwIEDtXPnTqf17N+/\nX++++64lmbxNVlaWPv/8c3Xo0EEff/yxoqKi8nz+UlNT9fPPP2vkyJHq16+fdu/e7fHzsmbNGrVv\n317vvvuujhw5kmeb8+fPV+fOnfXDDz9Yno/s/16JK8+xO/V44uTJkxo1apT69OmjJUuW2IMJuX2d\nOnVKX3/9te6//35NmDBBKSkp+e5vRkaGJk6cqN69e2v58uVKS0vLtf0LFy5o2bJl6tevn1588UWH\nJVnu+P7779W+fXu9+uqr+uOPP+wzcXL72r17t1555RV169ZN27Ztc1pnly5dFBgY6PD4Dhw44FFw\nz8Y2Uyj7tZV9qZQ35dzQoVKlSqpfv36BtFVUXPnb486XJ3IuG7Rd0wCAokMwCYBPS05O1rlz5yzl\nFSpUcLmOtLQ0jRo1Sh9++KH9JszZjb1pmg7Jvg3D0LJly/TYY4+5FWSZN2+eBgwYoL179zoEbrLX\n76zdnInGIyMjNXTo0DxnDtgkJSXpkUce0XfffWevw5U2swfQpk+frscee8ytG9W///5bAwcO1Gef\nfaaLFy+63e66devUu3dvbdq0yeU2PZG9T1f6HeR2TM7jpUsBvCeffFLnz5/PtR7DMNS5c2f5+Vn/\nZKekpOiJJ57Qu+++q/Pnz7v9/G3fvl0PP/ywvv/+e7efk6lTp2rEiBFKSEiwX3PO2s3eZlJSkkaP\nHm2/zjx1pee3IO3cuVO9e/fWDz/8cMXxmfP3mJmZqTlz5uihhx7SqVOn3G7bVn9aWpoef/xxzZw5\n02GGnLPjc74mRUZGasSIEW49h1lZWXrppZf09NNPKy4uzvK4c2vXdtzhw4c1cOBA/fjjj5Zjw8LC\n1L59e0s9ixcvdrl/2Z0/f14//fSTvR/SpZlOjRo18qi+vMTHx2vLli3258IwDN15551eb6eoOXtd\n8vTLUy1atLBsdLB8+fL8PjQAQD6wzA2AT9uwYYPDLjA2NWvWdLmOSZMm2Wce2OoKCgrSTTfdpGrV\nqtlnHmzfvl2pqamW9rZu3ar3339fzz777BXbWrVqlcaNG+dQlr3NevXqqUaNGgoJCVF6eroSExO1\nb98++41pzra3bdumGTNmaMiQIXm2+/rrr2vHjh0OQQHDMOTv768bbrhBNWvWVGhoqDIzM/X3339r\n9+7dSkhIsNyobt68WW+99ZZeffXVKz7W06dP66GHHtLx48ct7UpSjRo1dMMNN6hs2bK6cOGCTp48\nqd27dyszM9Oh3bNnz2rIkCH65JNPCuxGLuf1k/OmKLfZSnIO0AgAACAASURBVFcyefJk+4weZ9ep\nrZ2uXbtazk1JSdGAAQO0e/dup8/ftddeq0aNGql8+fK6ePGiYmNjtXPnTqWnpzs8f6mpqRozZoyS\nk5PVq1evK/ZZkmbPnq333nvPob+2tgMCAtSsWTNVrVpVycnJOnjwoA4dOuRw/tixYz1anlbUNm7c\nqBEjRig1NdX+O5MuPY9+fn6qX7++fawkJibq8OHD9seePbiyd+9e9enTRwsWLNC1117rcvu25/uV\nV17Rr7/+6nDdXHPNNWratKnCw8OVkZGhmJgY/fnnn/bxkv139dtvv2nu3Lm5blCQ07PPPqvly5c7\nXGe2/vj7+6tJkyaqUqWKrrnmGsXGxmrbtm1KSUlxeMwZGRl6+umnNXPmTDVv3tyh/p49e9oDA7bH\ntHTpUv2///f/3J7JsmzZMvssLVt9BTUrac2aNZbn1tcSb+d3BqDkeL3YuJsLLjAwUC1atND69evt\n18jmzZuVnJys0qVL57uPAAD3EUwC4NO++OILS1lYWJgaN27s0vmmadqXe5mmqXLlyumJJ55Qr169\nLEvlUlNTNWPGDE2ZMsWe8Nt23pdffqmhQ4fmmZD2/PnzeuWVVyztly9fXmPGjFHnzp0VHBzs9NwD\nBw7os88+c/g039b2559/rsGDB+d6U7B161YtWbLE4UbR399fQ4cO1eDBg3Pt85o1a/Tmm286LDMz\nTVPffPONBg8enGduGNM09cwzz1gCSf7+/urVq5eGDBmi6667znLeuXPnNH/+fH3yySf22Ty2G9Vn\nn31WkZGR+c7dlNP69esdvh85cqS2b9/ucCO/YMECS7t5JTy2BcFmzJhhr8fPz08tW7ZUgwYNZBiG\n9u3bp02bNql27dpOr9dx48Y5DSTdd999GjZsmNOZGCkpKVq6dKkmT56suLg4+zmmaWr8+PFq2LDh\nFWdw7N27V2+//bYlkBQQEKChQ4dqyJAhCgsLczhnz549evPNN+1LozIzMwssF0tBiYuLc1i2artB\nDgsL02OPPaZ+/fo5TUh//PhxffbZZ1q4cKEyMjLswZW4uDiNHj1as2bNciuhfGxsrBYtWmR//iMi\nIjRy5Eh169bNcs3Fxsbqo48+0rx58+xltt/3lClT1KtXrysmY58xY4ZDIMmmTJkyGjlypHr37m3Z\ncCAlJUVffvmlfTZn9hmMzz//vJYsWeLwWnbnnXeqSpUqio2NtZfFx8frt99+cztAnHPWm7+/v7p0\n6eJWHa5as2aNpezWW28tkLaKwmOPPeZywDE3L7/8stauXevwOlWuXDl98sknbtd12223Obwep6en\n69dff9W9996brz4CADxDMAmAz5o2bZp9CYJ0+Wa7devWLn/amj1gcNNNN2nq1KmqWLGi02OvueYa\nPf7446pdu7ZGjRrl0EZ6erp+/PFHPfjgg7m2NXPmTHtuJFt/y5Ytq7lz56pWrVp59vP666/X22+/\nrebNm+vVV191aPvMmTPasmVLrjc52XN+2B7rq6++qr59++bZ5j333KMmTZqoX79+On78uL08KytL\nCxcu1OjRo3M996OPPtLmzZstNxgffPCBWrZsmet5thv3zp07a9iwYdq3b5+9jsTERD3//POaOXNm\nnv12V87ft7MgUfny5XO9LpwxTVMpKSn266tGjRp6//33LYGc06dPO01q/d1332nx4sUOz19QUJDe\nfvvtPJP/BgcH68EHH9T999+vkSNH6vfff5d06TpPS0vT008/re+//97pkjqbN998U+np6Q5tBwcH\n65NPPsn1d9eoUSPNnj1bb775pj0pec4dFou75557zr6kzzZOGjZsqA8//FARERG5nle9enW9/vrr\n6ty5s5588kn7slvTNLVt2zZNnTpVI0eOdKkP2Wf6SFKrVq303nvvWYJ3NuHh4Xr99ddVo0YNvfvu\nuw6vC3///bc2bNigNm3a5NpeXFyc3n//fUvgsG7dupo+fbrCw8OdnhccHKzhw4erWbNmGjZsmD0x\nuGmaiomJ0bx58/Too4/ajzeMSzugTZ061aGtRYsWuRVMOnr0qCXQe9ddd7k1Nt2R/TVMuvRakdtz\n4ipbkDImJsbjTRS8JTg4ONcPMFzx/vvvWwJJpUqV0pQpU9xORC/JaaB706ZNBJMAoIiQMwmAz0lN\nTdXEiRMtN082Q4cOdame7OdGRERo2rRpLt2U3Hfffbr33nstS6G2bNmS53nffvut/f+2G6EXX3zx\nioGk7Pr06aNbb73V0vauXbtyPWfr1q0Oj7VKlSpXDCTZVKxYUa+88opDPgzTNLVu3bpcz0lKSrLv\nymM7PigoSJ9++mmegaTswsPDNWvWLFWrVk3S5aDfpk2btHXrVpfqKErZc86ULVtWM2bMcHqjdO21\n1+q2225zKMvKytLkyZMtQdL//ve/Lu8iFRoaqs8//1w33XSTw+/t2LFjeSa13bx5syUIaBiG/vOf\n/7j0u3vppZfUo0ePIs155IkNGzZo48aNDuOkZs2amj59ep6BpOxuvfVWffbZZ/ZZSNlnLbqaKD97\nnqLrrrtOH3zwQa6BpOyGDh2qG2+80fK85zVOJemTTz5xSBZumqYqVqyoWbNmuRQ0admypcaMGeOw\nzMn2mHPKvsTSdtyqVavc2sAgMjLSUlZQS9wOHz7skOvMMAyv5mWyvUZ4+6uwLFy4UB9//LHltWL8\n+PEe78KZ8/k1TVM7d+7Md18BAJ4hmASgREtLS9Pff/+tv/76S4sXL9bYsWPVunVr++yU7DfKhmGo\nQ4cObn3aazvvueeec+mmzaZ3796Weg4ePJjr8Xv37tWJEycsAaxu3bq53KaNs+3e4+Pjcz0+e74l\nyToT50ruvvtuVapUSYZhKCQkRA0aNHC6RM1m7ty5unDhgr1NwzA0aNAgNWnSxK12w8LC9PLLL1tu\nkD///HO36ikqtsf+6KOP2oNirvjhhx8UExPjUEenTp2c/t7zUqpUKcuW7LZlkblxNovt3nvvVfv2\n7V1u9+WXX7YHIgrz5jY/si+XzT57L69lq840adJEAwYMcLhmz50757AMzRWGYehf//qXZXlZXpwF\niI8cOZLr8WlpaZblr4ZhaNy4cW5tYPDwww8rIiLCIeB84sQJRUVFORxXo0YNSyA8JSVFK1eudLmt\n7P2VLr1G3HPPPS6f7w5nQYw6deoUSFslzfr16zVu3DjLtTNs2DD16NHD43orVKhgX0pqq/uvv/5S\nRkZG/jsNAHAby9wAFCu2XB75yaeS/RPY7DcWtiUf7goLC3N7Gn2zZs0c+mOapkM+kJzKlCmjF154\nQdHR0YqOjtaxY8d03333eXSz7Sy5eF4zHwICAux5TUzTVFRUlGJjY91arjF79myFhYW5dJM5f/58\nh8dlGIYefvhhl9vKrm3btoqIiNCpU6fs/f/111+VlpZ2xVwwxYWrSa9tFixYYCkbOHCgR203aNBA\nzZs31x9//GF//vbv36+YmBhLgCszM1OrV6+2XJODBg1yq83Q0FANGzZMEyZMKBHBpNjYWP3yyy8O\nfa1Vq5bHyd4feughzZgxw6Fs9erVbj2PZcqUcfs16aabbnL43jRNnTlzJtfj169fb994wKZatWpu\nt+vv76+uXbvq008/lXTp9bROnTqKj49XvXr1HI7t1auXNm/e7FC2ePFipwnoc9q0aZNiYmIclrh1\n7tw5z9xl+XHgwAFLmTsbO1xJSZu9Z7Nv3z6NGjXKvow1+wc5Tz/9dL7rr1Wrlnbu3Gm/LtPT03Xk\nyBFdf/31+a4bAOAeZiYBKHa8OY3f9ml4SEiI3nvvPZUvX97lftjeBN9yyy1uJciVLt3s5Zw1kJSU\nlOvx1atX16BBg/TKK6/o008/1YoVKzx+450zMbikPD+5rVevnsONS1pamkaMGGGf/eKK6667zqVA\nUlxcnI4ePSrp8s1SnTp13NrRKqc77rjDof/p6eklZulDRESEW0G7zMxMy7LE0qVL6+abb/a4D86C\nIjlv6CXpzz//tM8os6lWrZpD4NRVnTt3LjHBvi1btlhmON5xxx0e11ezZk17vhhb4GPXrl1KT0+/\n4rm29m+88UYFBLj3eWD268x2/eS1hGzTpk2Wdl0J6jjz0EMPadasWVq/fr1+//13ff3112rVqpXl\nuI4dO9pfv2zPzcaNG/OcWWnjbIlb9+7dPeqvK7LnibOpXr261+ovicvcYmNjNWzYMMvrROPGjfWf\n//zHK204y7Xkzt8qAID3MDMJgM9w9kmuYRiqXbu2Jk2apIYNG3pUr6efeIaGhjq8qU5LS/OoHnck\nJSVpx44dlvKsrKxcz+nQoYO2b98u6fJN5p49e9SxY0d17NhR7du315133unWkprc5MxnZBhGvhPW\n3nDDDU7b8TQvR2Gw3Zw3bdrUrfP27t1rT9xtU6lSpXz1xdnzt23bNsuNePa8W57236Zs2bJq0qSJ\nQ4L84spZDi5vXLPR0dH2x37x4kXt2bPH5efTk9cyZ+M3ryCzs9cRTwKH0qXny5Xn7JprrtH999+v\nBQsW2J+bzMxMLV26NM+ZW6mpqVq5cqXDtVS3bl3LbCxvOnHihKXMG4m+bUG0qlWravXq1fmuL7v8\nzvrNy4ULFzRs2DCdPn3aXmaapiIiIvTxxx8rKCjIK+04+9DC2e8CAFDwCCYBKHY8nd6f86a0Tp06\nevjhh/Xggw/ma6mDp7Nmcu6IlVdAxxNJSUk6dOiQoqKitHfvXu3YsUN79+61bz+eXV7Pad++ffXl\nl18qNjbWYXlgRkaGlixZoiVLliggIEBNmjTRnXfeqdatW+umm27yKAiwZ88eS7/Wr1/v9V2Lst/Q\nFGfuzmTI/vzZfqdHjx71+vPnbEmms/w6+Wm3YcOGV0xKXxzs3r3b4XvTNPW///1P//vf/7zaTl7L\nYHNyZ4aljbPXwLxek44cOWIZ454G5N3Rq1cvh6Wcpmlq8eLFeQaTVq5cqQsXLjgscctPbh5XxMXF\nWZ6fgto1rrjLzMzUU0895bC7pmmaKl26tD7++GNVrlzZa205CyaVlNd7APA1BJMAFDvuBCkCAgIU\nFBSkcuXKqXLlyqpdu7YaN26s2267zWs5FK655hqv1OOpAwcOaM+ePTp06JCOHTtmz6l09uxZh+Oy\nB4JsN1SuCA0N1ccff6wBAwYoJSXFYeel7LMDtm7dqq1bt2ry5MkqW7as7rzzTt1zzz36xz/+oTJl\nyrjUlrMcLQUxMyWvXDDFiS2ZrKsK+vmz1ZWYmGj5mbMbtvwsT6xbt67H5xamM2fOWJ7jgrhmnT3n\nufHGLEEp9yCzbWOD7I/Tz88v37PgXNGsWTPVrl3bHswyTVN79+7VwYMHc71mFi1a5PC9LU9TQXKW\nh87ZEuOrwbhx47R+/XqHQJK/v78mTZrk9UC3s+c4+46DAIDCQzAJQLFiGIZGjhypJ598sqi7YldQ\nCVzzcuzYMc2ZM0fLli1zmi8kZ/4LW24oT29yGzVqpFmzZunll1/Wvn377HXm1t65c+e0fPlyLV++\nXAEBAbrrrrvUq1cvdejQIc92cgbAcrbjDaZpOm2nOHI3mFQYz19u7Xj75tnVAGRRO3funKWsIJ5z\nd4JJBR3gzpnzRrqUm6uw9OzZU5MmTXJ4zVm0aJHGjBljOTY2NlYbNmxwCKLfcccdXp0N44yzAEZJ\nyQPmTR9//LHDskTb7+DZZ58tkJ30nD3HBJMAoGiQgBsAipH09HRNnDhRnTp10syZM5WQkOA0eWr2\nbbalS8Eef39/NWvWTA8++KBHbTdu3FgLFy7Ua6+9pgYNGji0a2vPWYApMzNTa9eu1b/+9S/17dvX\nsiwou/Pnz1vKCiLJrCvJjIsDdwOVRfn8OQugBAcHu9X/7Lw1u6agFcZzLhVOTjVXXbx40VJWmDM0\nu3fvbt/0wPb6s3TpUqfHLlq0yLJcr6CXuElyOkbcTYpe0i1evFgffPCBJZD04IMPavDgwQXSprPX\nzOI0dgDganJ1/dUDgGIsKSlJI0aM0ObNmx2CODY5A0rh4eGqV6+eGjdurCZNmqhly5YKDQ3Vpk2b\nNG/ePI/64O/vr759+6pv3746fPiwfvzxR61du1Y7duyw37DlDCpk79eOHTs0YMAATZ8+3Wmy3pyf\nKhuGoeeee07dunXzqL+5KYrZZIUhZxJbwzA0YMAAPf74415tJ2e+L8n5TKL8zAjwdg6xghIYGOjw\nOA3D0Ndff+10V6n8KMyZP1firC/OAkwFpXLlymrdurXWrl1rf205efKkNm3apJYtWzocu3jxYofX\nxbCwMLVr167A+xgUFGTZDe/ixYvF6vdYkH7//Xe9/PLL9u9tgaTbb79d48aNK7B2izrQCQC4jGAS\nABQTr7zyij2QJMkhd1HDhg116623qlGjRqpbt67q1KmT601LZmamV/pTu3ZtDRs2TMOGDdP58+f1\n+++/a+PGjVq/fr1DMubsy+sMw1BKSoqGDx+uZcuWWZaalCtXztJOVlbWVZu41l3OlsVlZGQUyvMX\nFhZmKUv6/+3de1BU1x0H8O9FHhpwUcAqDwWtEJSioNKpWtPqYGOYgAQTX401VoWR+EqCsdZHND5i\nVHRi7dhgCKJp1KDFoCISiR3SoMaqEBTIaBg0PEddkZertHv7h73XvdxFdlfYRf1+ZnaGve7e87vn\n3l28P875nYYGi/f3OO99XOaMZOjRo4cqaWZnZ/dUX7Pdu3dXTZk1NvWtI02aNAn//Oc/FdsyMjIU\nyaTLly/j6tWriiluERERVplu5uzsrEom6XS6ZyKZ9OOPP2LBggWq1QD79++P7du3y6PKOkLLPgc6\nVyKWiOhZwmQSEVEnkJOTg+PHj6umC4SGhmLNmjXw9/c3eV/G/rP9uLp3747w8HCEh4cDeFCn5NSp\nUzh+/DjOnTsHvV6vuPmsr69HUlKS4i/XgPFkyK1bt9o93qeVLfvPWPKkoqLC4v1ptdrHCQeA5aOb\njNV/ao2rqysqKysV13d7xN6ZCYIAFxcXRcJPr9dDq9UaXU2rI4wdOxY9e/ZEbW2tnCz66quvsHr1\nank6mbGpb9aY4gY8SGC0/Ow9C7V7bt68iblz5yqmf4qiiB49euDjjz/u8Fpoxvr4WS18TkRka6yZ\nRETUCXz++efyz9KIpMGDByMlJcWsRBJgnWWSe/fujalTpyI1NRUHDx6El5eX/G/Sjd/JkydV7/Pz\n81Ntu3TpUkeG+lQx7D+pn63Vf0FBQaptRUVFFu+vpKTErNcbKy5vSa2UpqYms5JJxq7ZwsJCs9t9\n0vj5+ammtErF+S3x5z//GVu2bMGBAweQl5eH8vLyR77e3t4eUVFRihjq6urwzTffyM9PnDihuC76\n9++PIUOGWByjOdzc3FT987QnxnU6HeLi4lBZWSlvE0URDg4O2LFjR7tP/TTGWB9bK8FJRERKHJlE\nRGRjOp1OXo1IIggCFi9erKqRYwpjN3xtjeCoqalBaWkpfvzxR8TExJg1bWDw4MFITEzEtGnTFMdQ\nXV2NxsZGxV+NR4wYIf9smAzR6XQW173461//ih9++AHe3t7w8vKCt7c3AgMDFQmup8WwYcNgZ2en\nuImtqqpCRUUFvL29LdpnWloaTp06BW9vb/kxcOBA9O/fX9W2RDp3+fn50Ov1RmsstaWgoMCs1QeN\n1cGyZOrV1atXzXr9iBEjcPz4ccW27777zux2DS1atAgODg6KPh86dGinKkoeGhqqSpoVFBRg5MiR\nZu+rpqYG//jHPxTbpIL/jxITE4PU1FTFtszMTIwdOxYFBQXyiDFpJKe1RiUBQL9+/ZCfn6/YVlVV\nZbVklrXp9XosXrwYly9fVo2gXbt2reK7vSMZJrIkvr6+VmmbiIiUmEwiIrKxiooK1TQxAEYLWLdF\nFEVF0VpJa3WUNmzYgEOHDsk35YIg4Oc//7nZN4yhoaHQaDSqla9aJpP8/f3h6uqqWG5dp9Ph8OHD\nmDp1qlltAg/q7nz66aeqpMKGDRsQExNj9v46OxcXFzz//PMoLi5WnOP9+/fjnXfeMXt/er0eSUlJ\n+OmnnxTb33zzTSxYsECxzc3NDf7+/opkjFarxalTp8wueHzp0iWUlpaalUwyluC0ZCTIuXPnzHr9\n8OHD5Z+lxMW///1vlJaWYsCAAWa3f/bsWZw4cUKxTRAEfPXVV50qmTRs2DDs2bNHfi6KIo4dO2ZR\nsffc3FwAytFlhv3amueffx5BQUFyAkMUReTm5kKv1yMnJ0fxWjs7O0RFRZkdm6WMJTCqqqqs1r61\nrV27VvG7RUokxcbGIjo62mpxVFdXq7YZGz1IREQdj9PciIhsrLVCxObcaEsOHjxo9C+3xpaxBgAP\nDw80NjYqVmRrOQrDFKIoqqYcCYJgtMbPyy+/rCguLooikpOTLao3smvXLlX89vb2cm2np1FkZKT8\ns9R/X3zxhUXTGw8dOoSffvpJ0X+CIGDChAlGXz9lyhTV1J6kpCTVtrakpKSYHathzSbpuC9fvmzW\nPkRRRHp6ulmfrcDAQPj7+6uO8S9/+YtZbUs++ugjAA9XQRQEAUFBQfDx8bFofx1lzJgxcnJL6q+r\nV6/i9OnTZu/LcASS1I+//vWvTXpvy6RwXV0dLly4gG+//VbeJq0i1rt3b7Njs1TLkXsAcO3aNau1\nb03JycnYt2+fKpE0fvx4vPXWW1aNRfq+kjg5OcHT09OqMRAR0QNMJhER2Vhr9R7Onj1r1n5KSkqw\nceNGozfKrS3r/cILLyiei6KIL7/8UrFamym+/vprufC3dLM4YMAAo9P03njjDdVqP+Xl5Vi9erVZ\nbV66dAkpKSmqG5zIyEijK489LSZPnqwawVJXV4clS5aYtZJfZWUltmzZolo9MCwsrNU6XTExMXKB\nXSmh8/333+OTTz4xud2TJ0/i2LFj8vtNNWDAANV1U1lZiTNnzpi8j9TUVHlklTltz549W/5Zijsr\nKwtpaWkm7wMAPvvsM1y4cEHV56+//rpZ+7EGZ2dnTJo0SZX4Xb16tVmJ38zMTOTn5yu+l7y8vFTf\nPa2JjIxUfY+kp6ejqKhIcQ1NmjTJ5JjaQ3BwsGpbcXGxVWOwhqysLKPfE8OHD8eWLVusGsu1a9fk\nUajS972x80BERNbBZBIRkY15e3urRvCIooitW7eaXBMmNzcXM2fOlAsLt7xRbu3mLzAwEKGhoYrX\n379/H/Pnzzd5ClF1dTXWr1+vqvkUERFh9PV9+/ZVFNaVbgi//PJLLFu2TLXctDFXrlxBfHy8asRV\nly5dEB8fb1LcTyoXFxe88cYbqv47e/Ys4uLiTCouXVNTg7lz5yqmG0r7WrRoUavve+655xAfH69q\ne9u2bYoi8q3Jy8vDkiVLLBp15+LigpCQEMW1KiU37ty50+b709LSsHnzZrOTWMCD0XS+vr6q437v\nvfewf/9+k/aRmZlpNNnr5+eHiRMnmhWPtfzhD39At27dFNuuX7+OOXPmtDqi0lB+fj5WrFihSvj+\n8Y9/NDkGjUaD8PBw+b3Ag2SSIWm1SWvq27cv+vTpA+Dh9fA4Bco7owsXLmDp0qXyc+kc+Pv7429/\n+xscHR2tGo+xgv9hYWFWjYGIiB5iMomIyMbs7Ozwu9/9TnGjCjyYUjJ9+nRcvHjR6PtEUcT58+ex\nYMECxMbGoq6uDqIoKm66pNc96mZ7/vz58s+GbUdFRSEtLU0ecdTS/fv3kZGRgddee01VK0Sj0Txy\ntMWKFSsUq0VJ033S09MxceJE5OTkGE0qNTQ0YNeuXZg8eTJu3LihOEapaLk1VhSytXnz5mH48OGq\n/vvXv/6FiIgIHD582OhotHv37uHAgQOIjo5GaWmpvF3qv6lTp7ZZy2bWrFkYPXq0KrHy/vvvY+HC\nhUZHtdXW1mLz5s2IjY2FTqeTr1NzGSYopWu1rKwMU6ZMaXUkX2FhIebNm4eVK1dCr9dDFEWzi73b\n29vjo48+gpOTk9GROrGxsa2uqldeXo4VK1bgnXfeUYwcE0UR9vb22LBhg0XJNWvw9vbG8uXLVd9N\n58+fR2RkJI4ePWp0Rb36+nrs2LEDM2bMkBPZ0j6GDBmC6dOnmxWH4VQ3w2tHum5feuklqyc2ACg+\ng8CD+m/mFnjvrK5du4b4+HjV+e3Tpw8++eQTuLi4oLm5GY2Njbhz5w5u3bqFmzdvmvXQarVmxWTs\nM8ZkEhGR7bAANxFRJxAfH4+MjAzcu3dPUb/mhx9+wLRp0+Dj44NBgwbB1dUVzc3NuHHjBoqKilBb\nWwvg4Y2tIAgYMGAA7t69q1jp6FGFYUePHo3XXntNnrIjta/VarFy5UqsX78egwYNgpeXF5577jnc\nvXsXNTU1KCoqkusVSaQY3n///UdONXN2dsb27dsxY8YMOQkmtVtaWoo333wTGo0GwcHB6NWrF0RR\nREVFBQoLC+U+atlmeHg45syZ81jn4UnRpUsXbNu2DVOnTkVVVZWi/2pqavCnP/0Ja9aswdChQ9Gr\nVy/Y29ujuroaBQUFaGpqMtp/Q4cOxbJly0xqf9OmTZgyZYq8vLvUdnZ2NrKzszFo0CD4+fnB0dER\nlZWVuHjxIv7zn/8ortOuXbuaXSdr8uTJSElJQXl5ueJzUlZWhpkzZ6Jv374ICgqCi4sL6urqUFRU\npIhRFEV4eHhg5syZSExMNKvtwMBArFmzBsuXL5eTQlIMubm5yM3NhZeXFwICAuDu7i4nFq5cuaIq\nsC/1wZIlSywqtG9Nr776Ki5cuID09HTFdVZdXY2EhAQ4OzsjJCQEvXr1gl6vR0VFBb7//ns0Nzer\npkZ5eHgopkyZatSoUfD09ER1dbXR91qzALSh0aNH49ixY4ptp0+fxsCBA20ST3tKSkpCbW2talRZ\nY2MjoqOj0dDQ0GotPlN5e3urCqk/Sst6XV27dlWsMklERNbFZBIRUSfg6emJDz74AAkJCdDr9QCg\nuFmuqKiQb4ol0r8bjkaaMGEC1q1bh5UrVyoKcdfV1+LhdwAACddJREFU1aGkpASBgYFG21+1ahW0\nWi2+/vpr1WiXe/fu4eLFi6oRUobtS+zs7LB8+XK8+OKLbR5zQEAADhw4gLi4OFy/fl3Vbn19vaLI\nbss+MXx9REQENm3a1GabT5Of/exnSEtLw7x581BYWKjqP51Op6on1Fr/hYWFYefOnSaP7nB3d8fe\nvXsxZ84clJaWqkaulJSUKOrHGF4rgiAgLi4O58+fN3tlNQcHB2zcuBFz5szBvXv3VO2Wl5crVqZr\n+Rlxd3fHp59+ipKSErPalURHR0Oj0SAhIQF3795VtV9VVaX43BkWNW/5OVm2bBlmzJhhURzWtmHD\nBri6umL37t2q66ypqanVz6nhMXt4eCAlJcWikYOCICA6Oho7d+5UJZN8fX1tlpALDw/He++9pxhF\n+e233z4R57WthJ70e6jl6+vq6hTXtbXU1taipKRE8T0ybtw4o3X5iIjIOjjNjYg6BUumvHSk9orH\nnOk8ERER2Lp1KzQajeIGuLV9GN7UeXl5YevWrdi2bRucnZ3lmyvD9z3qL8AODg7Yvn074uPj4ejo\nqGr/Uccm3Tj6+vpi9+7d+P3vf2/S8QIP6sWkpaVh8uTJsLe3b7Ndw38TBAHdu3fH6tWrkZiYqCrO\n3NEsvUba81p3d3fHZ599hrlz56Jbt25m95+joyMWLlyIlJQUODs7m9W2p6cnDhw4gKioKFXSpmXb\n0vOuXbvi3XffxeLFiy0+5hEjRmDv3r3o16+fSe1KxxoSEoKDBw8iICBAFZc5xo0bhy+++AKjRo0y\nuX3Dz4mfnx9SU1PNTjjY4jvJ0NKlS7Fp0yb06dNHkZB81HUmHfNvfvMbZGRktFrY3RQxMTFGR3e1\nXO3NmjQaDcaMGSPHIooizp07Z1LdN2MsPTeWtmNKW8Z+D7XcZunDHGfOnFEluF5++WWz9kFERO2L\nySQisjnphqOz1A1pz3gM92XK/iZMmIAjR45g1qxZ6NGjh+r9ho9u3bph5MiRWL9+PbKysvDSSy/J\n+4mIiJCTM1K7+/btM1rfRNKlSxcsWLAAmZmZiI2NhY+PzyPbFwQBDg4O+NWvfoVNmzbh+PHj+OUv\nf2l2H2k0GqxZswZZWVl4/fXX4evr22a7fn5+ePvtt5GdnY0pU6aY3ebjMve8Gntfe3F0dMTbb7+N\nnJwcxMbGIiAgoM3+8/T0RFxcHE6cOIF58+ZZnIhzcXHBhx9+iH379mHcuHGKa87wYW9vj/HjxyM9\nPR2zZs167GMODg7G0aNHsWrVKgwdOhR2dnatHuvgwYPx4YcfYv/+/YolxC09hwAwcOBAJCcnY+/e\nvYiIiICbm9sj+9ve3h7Dhg3Dxo0bceTIEbPrvLTXdWMsNnNERkYiOzsbS5cuxZAhQ9ClS5dWj9nJ\nyQm//e1vkZqaio8//rjVVStNJU1hbDnCKyoq6rH2+7haJjSMjdQyxeOem45op63vkfZ4mOrEiROK\n566urhgzZozF/UBERI9PEDvbcAAiIpJdvXoVxcXFqK2tRVNTE5ydneHm5gZPT08EBwfD3r5jZyvf\nunULxcXFqK6uRkNDA3Q6HRwdHdGjRw/4+voiKCjI7GLGpqioqMCVK1eg1Wpx+/ZtiKIIV1dX9OrV\nC0OGDHnsG9On3c2bN1FUVCT3X3NzM1xdXeHu7o6goCBFUqU9NTY2Ij8/H2VlZaivr4eTkxP69u2L\nsLAw1YqFM2bMwLlz5+QRHYIgICcnB15eXma3e/PmTRQWFuLGjRu4ffs2nJyc4O3tjeDgYHnFrY5W\nUlKC8vJyaLVa1NbWwtHRERqNBj4+PggODlativY0uH37NgoLC6HVaqHVaiGKInr27AkfHx+EhIS0\na1FsnU6HkSNHygXcBUHAqFGjkJyc3G5tWOL+/fsYO3asfPyCICAyMvKZm3bbke7evYtRo0Ypzv3s\n2bORkJBg69CIiJ5pTCYRERGR1bVnMomefhkZGXj33XcV10tiYqJihT9b2bFjB3bs2CHH5uLigry8\nPJusMPc0Onr0KBISEuT+tbe3x8mTJ62WKCYiIuM4zY2IiIiIOrXDhw8rnms0GoSHh9soGqVp06Yp\nEkeNjY3IysqyYURPl/T0dAAP62SNHz+eiSQiok6AySQiIiIi6rTKyspw+vRpxaikV155pdOM/HF3\nd8crr7wixwYAn3/+uY2jejqUlZUhLy9PUV9p9uzZNoyIiIgkTCYRERERUae1detWReFtQRBsUnj/\nUaSVMIEHI2gKCgpQVFRk46iefH//+98VK5eGh4fjF7/4hY2jIiIigMkkIiIiIuqEmpubsW7dOmRn\nZytGJb3wwgvo37+/rcNT6N27N6ZNm6YYnbR7927bBvWEa2howOHDhxXnfuHChbYOi4iI/q9jlwEi\nIiIiImpDUlISLl68CF9fXzg6OqKmpgbffPMNtFqtagn5uLg4G0X5aHFxcUhPT0d9fT1EUURmZibm\nz5+Pfv362Tq0J1Jqairq6+shCAIEQcDEiRPh7+9v67CIiOj/mEwiIiIiIptycnLCqVOnFNukJALw\nsPjyiy++iNDQUFuE2CY3NzcsWrQIa9euhSAI+O9//4udO3figw8+sHVoT5yGhgbs2bNHHpWk0WiQ\nkJBg67CIiMgAp7kRERERkU15enoCeJhAMhyNJNXM8fDwwKpVq2wSn6mmT5+OoKAgiKIIURRx5MgR\nXL9+3dZhPXH27NmDO3fuyEnERYsWwd3d3dZhERGRASaTiIiIyGYMCyvTs0ta6l1Kwhg+AKBnz57Y\ntWsX3NzcbBlmmwRBwLp16+Dg4CCPTtq8ebOtw3qi3Lp1C8nJyXJCMSQkBNOnT7dxVERE1BKTSURE\nRGQThqNQWtbFoWeLp6ennIBp+Rg7diwOHTqEwMBAW4dpkkGDBuGtt96Sk2EnT57EmTNnbB3WEyMx\nMRGNjY0QRREuLi7YsmULvx+IiDohQeSfBImIiIjIxpqamvDdd9/h+vXr0Ol06N27N8LCwuDl5WXr\n0Cwye/Zs5OXlAQACAgLklcmodcXFxXj11Veh1+sBABs3bsTEiRNtHBURERnDZBIREREREREREZmM\n09yIiIiIiIiIiMhkTCYREREREREREZHJmEwiIiIiIiIiIiKTMZlEREREREREREQmYzKJiIiIiIiI\niIhMxmQSERERERERERGZjMkkIiIiIiIiIiIyGZNJRERERERERERkMiaTiIiIiIiIiIjIZEwmERER\nERERERGRyZhMIiIiIiIiIiIikzGZREREREREREREJmMyiYiIiIiIiIiITMZkEhERERERERERmYzJ\nJCIiIiIiIiIiMhmTSUREREREREREZDImk4iIiIiIiIiIyGRMJhERERERERERkcn+BysJcz//OSvt\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0xc4c6eb8>"
]
},
"metadata": {
"image/png": {
"height": 482,
"width": 585
}
},
"output_type": "display_data"
}
],
"source": [
"# Plot the comodulogram\n",
"plt.figure(figsize=(6,5))\n",
"clim = [0,.3]\n",
"cax = plt.pcolor(f_phases, f_amps+da, comod.T, cmap=cm.jet, vmin=clim[0], vmax=clim[1])\n",
"cbar = plt.colorbar(cax, ticks=clim)\n",
"cbar.ax.set_yticklabels(clim,size=20)\n",
"cbar.ax.set_ylabel('Modulation Index', size=20)\n",
"plt.axis([f_phases[0], f_phases[-1], f_amps[0]+da, f_amps[-1]])\n",
"plt.xlabel('Phase frequency (Hz)', size=20)\n",
"plt.ylabel('Amplitude frequency (Hz)', size=20)\n",
"plt.yticks(np.arange(50,250,50),size=20)\n",
"plt.xticks(np.arange(10,40,10),size=20)\n",
"\n",
"plt.tight_layout()\n",
"figname = 'ReviewerResponse_SawtoothComod'\n",
"plt.savefig('C:/gh/fig/PD/'+figname + '.png')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
philipwangdk/HPC | uwhpsc/labs/lab17/Tridiagonal.ipynb | 2 | 16008 | {
"metadata": {
"name": "",
"signature": "sha256:03891f69e60e29f26299bb857e71dcb46c7d215cad80ca995116987e2a0eeb44"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Solving tridiagonal systems using scipy.sparse\n",
"\n",
"This notebook illustrates how to use the scipy.sparse module to define a tridiagonal matrix and solve a linear system with such a matrix.\n",
"\n",
"See <http://docs.scipy.org/doc/scipy/reference/sparse.html> for more documentation on sparse matrix routines.\n",
"\n",
"Note that it would be inefficient to set up a full matrix that only has three nonzero diagonals and then call the general numpy.linalg.solve routine to solve the system. This would perform Gauss Elimination on the full matrix without taking advantage of the fact that most of the lower triangular part is already full of 0's. So it would take $O(n^3)$ flops to solve an $n\\times n$ system. By using the sparse routines, the same system can be solved in $O(n)$ flops."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
}
],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from scipy import sparse # to define sparse matrices"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First a simple example to illustrate how data is specified in a banded matrix. For a tridiagonal matrix only the diagonals numbered:\n",
"\n",
"* $-1$ (the subdiagonal) \n",
"* 0 (the main diagonal) and \n",
"* $+1$ (the superdiagonal) \n",
"\n",
"are nonzero, and the data is specified by providing three 1-dimensional arrays of data giving values along these three diagonals."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"d_main = linspace(1,5,5) # values that will go on main diagonal\n",
"d_sub = 10*d_main # values that will go on subdiagonal\n",
"d_super = 100*d_main # values that will go on superdiagonal\n",
"data = [d_sub, d_main, d_super] # list of all the data\n",
"diags = [-1,0,1] # which diagonal each vector goes into\n",
"A = sparse.spdiags(data,diags,5,5,format='csc') # create the matrix\n",
"print A.shape"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"(5, 5)\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that although $A$ is a $5 \\times 5$ matrix, the full matrix is not stored. Only the non-zero elements are stored along with information about which elements these are. The format 'csc' means it is stored in compressed sparse column format,and so if you print out $A$ you will see this information by columns:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print A"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
" (0, 0)\t1.0\n",
" (1, 0)\t10.0\n",
" (0, 1)\t200.0\n",
" (1, 1)\t2.0\n",
" (2, 1)\t20.0\n",
" (1, 2)\t300.0\n",
" (2, 2)\t3.0\n",
" (3, 2)\t30.0\n",
" (2, 3)\t400.0\n",
" (3, 3)\t4.0\n",
" (4, 3)\t40.0\n",
" (3, 4)\t500.0\n",
" (4, 4)\t5.0\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you want to see the full matrix, you can use the function `todense` associated with any sparse matrix, which fills in all the 0's and returns a numpy `ndarray`:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print A.todense()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[[ 1. 200. 0. 0. 0.]\n",
" [ 10. 2. 300. 0. 0.]\n",
" [ 0. 20. 3. 400. 0.]\n",
" [ 0. 0. 30. 4. 500.]\n",
" [ 0. 0. 0. 40. 5.]]\n"
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that only the first 4 elements of the \"d_sub\" vector were used since only these columns needed to be filled. Also only the second through 5th elements of the \"d_super\" vector were used since only these columns needed to be filled. More generally, the elements of a vector that are used in filling the matrix correspond to the column being filled.\n",
"\n",
"Here's another example with the same data, but filling different diagonals:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"data = [d_sub, d_main, d_super] # list of all the data\n",
"diags = [-2,0,3] # which diagonal each vector goes into\n",
"B = sparse.spdiags(data,diags,5,5,format='csc') # create the matrix\n",
"print B.todense()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[[ 1. 0. 0. 400. 0.]\n",
" [ 0. 2. 0. 0. 500.]\n",
" [ 10. 0. 3. 0. 0.]\n",
" [ 0. 20. 0. 4. 0.]\n",
" [ 0. 0. 30. 0. 5.]]\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sparse matrices are a special matrix class for which the `*` operation is overloaded with matrix or matrx-vector multiplication, so you can compute `A*x` or `A*B`:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"x = ones((5,1))\n",
"print \"A*x = \\n\",A*x\n",
"print \"B*x = \\n\",B*x\n",
"C = A*B\n",
"print \"A*B = \\n\",C.todense()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"A*x = \n",
"[[ 201.]\n",
" [ 312.]\n",
" [ 423.]\n",
" [ 534.]\n",
" [ 45.]]\n",
"B*x = \n",
"[[ 401.]\n",
" [ 502.]\n",
" [ 13.]\n",
" [ 24.]\n",
" [ 35.]]\n",
"A*B = \n",
"[[ 1.00000000e+00 4.00000000e+02 0.00000000e+00 4.00000000e+02\n",
" 1.00000000e+05]\n",
" [ 3.01000000e+03 4.00000000e+00 9.00000000e+02 4.00000000e+03\n",
" 1.00000000e+03]\n",
" [ 3.00000000e+01 8.04000000e+03 9.00000000e+00 1.60000000e+03\n",
" 1.00000000e+04]\n",
" [ 3.00000000e+02 8.00000000e+01 1.50900000e+04 1.60000000e+01\n",
" 2.50000000e+03]\n",
" [ 0.00000000e+00 8.00000000e+02 1.50000000e+02 1.60000000e+02\n",
" 2.50000000e+01]]\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Solving sparse linear systems\n",
"\n",
"If `A` is a sparse matrix then you need to use `scipy.sparse.linalg.spsolve` rather than `numpy.linalg.solve` to solve a linear system with this matrix, e.g."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from scipy.sparse.linalg import spsolve # to solve sparse systems\n",
"\n",
"b = A*ones(5) # create right hand side\n",
"print \"b = \\n\",b\n",
"\n",
"x = spsolve(A,b) # solve for x, should be all 1's\n",
"print \"x = \\n\",x"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"b = \n",
"[ 201. 312. 423. 534. 45.]\n",
"x = \n",
"[ 1. 1. 1. 1. 1.]\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Steady-state diffusion"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Recall that for the steady-state diffusion equation in one space dimension, $u''(x) = -f(x)$ for $a < x < b$, we need to solve a system involving a tridiagonal matrix with $-2$ on the diagonal and 1 on the subdiagonal and superdiagonal. We can easily set up such a system:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"n = 10\n",
"d1 = ones(n)\n",
"d0 = -2 * ones(n)\n",
"A = sparse.spdiags([d1,d0,d1], [-1,0,1],n,n,format='csc')\n",
"print A.todense()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[[-2. 1. 0. 0. 0. 0. 0. 0. 0. 0.]\n",
" [ 1. -2. 1. 0. 0. 0. 0. 0. 0. 0.]\n",
" [ 0. 1. -2. 1. 0. 0. 0. 0. 0. 0.]\n",
" [ 0. 0. 1. -2. 1. 0. 0. 0. 0. 0.]\n",
" [ 0. 0. 0. 1. -2. 1. 0. 0. 0. 0.]\n",
" [ 0. 0. 0. 0. 1. -2. 1. 0. 0. 0.]\n",
" [ 0. 0. 0. 0. 0. 1. -2. 1. 0. 0.]\n",
" [ 0. 0. 0. 0. 0. 0. 1. -2. 1. 0.]\n",
" [ 0. 0. 0. 0. 0. 0. 0. 1. -2. 1.]\n",
" [ 0. 0. 0. 0. 0. 0. 0. 0. 1. -2.]]\n"
]
}
],
"prompt_number": 9
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The final project will involve working with this matrix!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Warning on singular matrices\n",
"\n",
"The SciPy sparse solver seems to have a bug --- if you try to solve a singular system with `x = spsolve(A,b)` it returns `x = b` rather than warning that it's singular. "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"A = sparse.csc_matrix(ones((3,3)))\n",
"print \"A =\\n\", A.todense()\n",
"\n",
"b = A*ones(3)\n",
"print \"b =\\n\", b\n",
"x = spsolve(A,b) # should be all 1's\n",
"print \"x = \\n\",x "
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"A =\n",
"[[ 1. 1. 1.]\n",
" [ 1. 1. 1.]\n",
" [ 1. 1. 1.]]\n",
"b =\n",
"[ 3. 3. 3.]\n",
"x = \n",
"[ 3. 3. 3.]\n"
]
}
],
"prompt_number": 10
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It should instead give a warning like the dense solver does:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from numpy.linalg import solve\n",
"A = A.todense()\n",
"x = solve(A,b)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "LinAlgError",
"evalue": "Singular matrix",
"output_type": "pyerr",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[0;31mLinAlgError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-11-3c984f375b08>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0mnumpy\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlinalg\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0msolve\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0mA\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mA\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtodense\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0mx\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msolve\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mA\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mb\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/Users/rjl/anaconda/lib/python2.7/site-packages/numpy/linalg/linalg.pyc\u001b[0m in \u001b[0;36msolve\u001b[0;34m(a, b)\u001b[0m\n\u001b[1;32m 379\u001b[0m \u001b[0msignature\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m'DD->D'\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0misComplexType\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mt\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;32melse\u001b[0m \u001b[0;34m'dd->d'\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 380\u001b[0m \u001b[0mextobj\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mget_linalg_error_extobj\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0m_raise_linalgerror_singular\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 381\u001b[0;31m \u001b[0mr\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mgufunc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0ma\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mb\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0msignature\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0msignature\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mextobj\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mextobj\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 382\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 383\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mwrap\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mastype\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mresult_t\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/Users/rjl/anaconda/lib/python2.7/site-packages/numpy/linalg/linalg.pyc\u001b[0m in \u001b[0;36m_raise_linalgerror_singular\u001b[0;34m(err, flag)\u001b[0m\n\u001b[1;32m 88\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 89\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0m_raise_linalgerror_singular\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0merr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mflag\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 90\u001b[0;31m \u001b[0;32mraise\u001b[0m \u001b[0mLinAlgError\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"Singular matrix\"\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 91\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 92\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0m_raise_linalgerror_nonposdef\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0merr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mflag\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mLinAlgError\u001b[0m: Singular matrix"
]
}
],
"prompt_number": 11
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Also remember that a matrix can be very close to singular (ill-conditioned) and you may get answers with few digits of accuracy numerically even if it the matrix is not singular. "
]
}
],
"metadata": {}
}
]
} | mit |
bajorekp/ForexPredictor | Mnist.ipynb | 1 | 3657 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.\n",
"Extracting /tmp/data/train-images-idx3-ubyte.gz\n",
"Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.\n",
"Extracting /tmp/data/train-labels-idx1-ubyte.gz\n",
"Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.\n",
"Extracting /tmp/data/t10k-images-idx3-ubyte.gz\n",
"Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.\n",
"Extracting /tmp/data/t10k-labels-idx1-ubyte.gz\n",
"0.918\n"
]
},
{
"ename": "SystemExit",
"evalue": "",
"output_type": "error",
"traceback": [
"An exception has occurred, use %tb to see the full traceback.\n",
"\u001b[0;31mSystemExit\u001b[0m\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/bajorekp/Developer/Python/virtualenvs/scipy/lib/python3.5/site-packages/IPython/core/interactiveshell.py:2889: UserWarning: To exit: use 'exit', 'quit', or Ctrl-D.\n",
" warn(\"To exit: use 'exit', 'quit', or Ctrl-D.\", stacklevel=1)\n"
]
}
],
"source": [
"from __future__ import absolute_import\n",
"from __future__ import division\n",
"from __future__ import print_function\n",
"\n",
"import argparse\n",
"\n",
"# Import data\n",
"from tensorflow.examples.tutorials.mnist import input_data\n",
"\n",
"import tensorflow as tf\n",
"\n",
"FLAGS = None\n",
"\n",
"\n",
"def main(_):\n",
" mnist = input_data.read_data_sets('/tmp/data', one_hot=True)\n",
"\n",
" # Create the model\n",
" x = tf.placeholder(tf.float32, [None, 784])\n",
" W = tf.Variable(tf.zeros([784, 10]))\n",
" b = tf.Variable(tf.zeros([10]))\n",
" y = tf.matmul(x, W) + b\n",
"\n",
" # Define loss and optimizer\n",
" y_ = tf.placeholder(tf.float32, [None, 10])\n",
"\n",
" cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y, y_))\n",
" train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)\n",
"\n",
" sess = tf.InteractiveSession()\n",
" summary_writer = tf.train.SummaryWriter('./mnist.log', sess.graph)\n",
" # Train\n",
" tf.initialize_all_variables().run()\n",
" for _ in range(1000):\n",
" batch_xs, batch_ys = mnist.train.next_batch(100)\n",
" sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})\n",
"\n",
" # Test trained model\n",
" correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\n",
" print(sess.run(accuracy, feed_dict={x: mnist.test.images,\n",
" y_: mnist.test.labels}))\n",
"\n",
"\n",
"tf.app.run()\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
surchs/Logbooks | rescue_comp.ipynb | 1 | 1629484 | null | gpl-3.0 |
jakevdp/data-CDCbirths | BirthsByDay.ipynb | 1 | 61837 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# USA Births Data\n",
"\n",
"*By Jake VanderPlas. See http://github.com/jakevdp/data-CDCbirths/*\n",
"\n",
"This dataset records birth rates in the USA by year. It was compiled from data on the [CDC website](http://www.cdc.gov/nchs/data_access/Vitalstatsonline.htm) and is aggregated so as to comply with their terms of use.\n",
"\n",
"*(This was inspired by Andrew Gelman's recent [NYC R Meetup](https://www.youtube.com/watch?v=ObS1hkOxyPA&feature=youtu.be) talk. Some of his writeup on the topic can be seen [on his blog](http://andrewgelman.com/2012/06/12/simple-graph-win-the-example-of-birthday-frequencies/))*"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"import seaborn; seaborn.set()\n",
"\n",
"import pandas as pd\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>month</th>\n",
" <th>day</th>\n",
" <th>gender</th>\n",
" <th>births</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1969</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>F</td>\n",
" <td>4046</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1969</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>M</td>\n",
" <td>4440</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1969</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>F</td>\n",
" <td>4454</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1969</td>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>M</td>\n",
" <td>4548</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1969</td>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>F</td>\n",
" <td>4548</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year month day gender births\n",
"0 1969 1 1 F 4046\n",
"1 1969 1 1 M 4440\n",
"2 1969 1 2 F 4454\n",
"3 1969 1 2 M 4548\n",
"4 1969 1 3 F 4548"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"births = pd.read_csv('births.csv')\n",
"births.head()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Some data is mis-reported; e.g. June 31st, etc.\n",
"# remove these outliers via robust sigma-clipping\n",
"quartiles = np.percentile(births['births'], [25, 50, 75])\n",
"mu = quartiles[1]\n",
"sig = 0.7413 * (quartiles[2] - quartiles[0])\n",
"births = births.query('(births > @mu - 5 * @sig) & (births < @mu + 5 * @sig)')\n",
"\n",
"# set 'day' column to integer; it originally was a string due to nulls\n",
"births['day'] = births['day'].astype(int)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Choose a leap year to display births by date\n",
"dates = [pd.datetime(2012, month, day)\n",
" for (month, day) in zip(births['month'], births['day'])]"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfgAAAF3CAYAAABJzllyAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXecI2d9/9+jLu1K229vr9jns8+Pe6MZG2xMCAQTQyCU\n0HuLgVBCSCi/AKHEgcT0apqNQzfVxhTHDePez757rre9u929bZJWWtX5/fHMMxq1vd1jdVvueb9e\nfnlvRjPzSBrN5/nWx7JtG4PBYDAYDMsL30IPwGAwGAwGw/xjBN5gMBgMhmWIEXiDwWAwGJYhRuAN\nBoPBYFiGGIE3GAwGg2EZYgTeYDAYDIZlSGChB2AwHAlCiDLQK6Uc82x7MXC5lPIS59+vA96Bus8D\nwJ3A+6SUSc8xZwIPA/8mpbyiybVuAb4qpfxRzfZVwE+klBc2OOYE4DNSyhcLIdYBj0op40f4XtcB\nm6SU0SM5vsH5noga9wnzcb4ZrvNs4JvAQeBiKeV0K693mLFcA/ynlPIx599h4DfA16SUP3O2rQO+\nBqwBpoErpJQ/cfYdB3wFWIW6l/5ZSvl75zxfAJ7hHPML4KNSyqb1x87ncoWU8lzPtncC/wjkgceB\nf5RSjgshgsCXAX2P3SClfL9zzJnOeGOADfyrM6Y1zpj+fqZxGJY/xoI3LEuEEE8CPgI8S0p5DnAW\nUAS+WvPStwPXApcLIfxNTtfwISml3N9I3B2OB8ScB768+AfgG1LKpyywuL8UGPeI+1OBu1Ci6f1u\nvwfcLqU8A/hr4BNCiLOcfb8Gfi2lPA94DfAjR9w/CKwGzgDOA05DCXWjcUSFEJ8AfgT4PdsvAd4P\nPENKebYztm84u18LnOic/2zgYmciC+pe/qYzUXgD8GMhhE9KuQ94sNk4DMcOxoI3LFcGUBPYNmBC\nSlkWQvw/1AMYACFEHHgl8BTgHOAlwA+bnO8FQoh/RllL10opP+W1zIUQHwWeCqwEHgOeBKwWQvwW\neBvgF0J8FXgy0Am8X0p5nRDiFOBbQBiwgKuklLWTEABLCPF157wF4F3APcBm4B1Syj847+mbzpi+\n4D1YCPF24N3ApDM+vb0f+Dqwwhn7buClwMnAD4DjpZS2ECIG7AROl1Ie8hwfBP4HeCZQAu4G3oOa\nOL0AyAohOqSU/+I55kPAaVLKVzr/vhD4opTyPCHEBcB/or63Msoavl4I0YYStA1AN5ACXiGl3OJ4\nWEaBU4CvSCm/XPPZfRR4seff70QJ8784n7nmPOBVAI71fAfwQiGED+iSUn7d2feQM86yc8yPpJQF\n5738Bngdyuqu5dlAFCXGH6+57h+llEPOv38BXCGECABJ57OIoJ7XISDrvC7pfBYACc92UPfUPUKI\nr0spiw3GYjgGMBa8YblyA3AHsEsIcb8Q4ovAk6SUt3pe8ypASik3o6y3dzc5l4V6yD4FOB94lRDi\nbxq8bi1wrpTyFcCbgO1Syuc6x0eA30spnwC8D/gv55j3A7+SUj4RuBS4SAhh1Z+aEEoEzkN5Jn6M\neuB/xbkWQogE8Hzgu94DhRDnAP8OPF1K+WRgiorl+jLgDinlBVLK9UAGeLWU8g6UaOr3+Q/O9Q9R\nzYdRE4OzUBamDxWa+AzwK+B/vOLu8A3geUKITuffbwW+KoToAr4DvMr5nF7gbF/rjGNMSvlUKaUA\n7kWFX3Dey5iU8vRacRdCnAFEpZSP621SyldIKX/rOVZzD0qcEUKsRk1aBlCTil1CiP8WQtwlhPgT\nsMoR9XuAlznWeQQ1kVhJA6SUv5RSvg8Yr9l1L/BM530CvBr1ffcAPwcmgEHnv61Syuud130Q+Dch\nxF7gD8DbpZRl51r7gf3A0xqNxXBsYATesFRp5Db3oaxIpJRFKeWrUKL736gH5veEEF4L/e3A1c7f\n1wJPcNy3ja51lZSyLKVMAT9FuXBrx3CXfsBSbRkC5KWUP3f+fhhlMQNcB/yLEOJnwIuAdzWJm07o\neLCU8vfO+QVqYvLXQohelDfi194cA4e/An4npRx2/v11PT7H0r9LCPFex8NwBmoyA8oKfbPz91up\nD2+AEt6vSSlLzri/CDzXs79usiKlHEHFv1/jiPqzUZ+/9oD8UgjxIHA9yko+04mTXy2EeKcQ4vOo\nmHeb57S3NxgbKKt+W5N9tbwWOEsI8QhwpXP9PBBEufNvkVKej/JQ/EgIsRK4AtiCEvobgFtRHpZZ\nI6W8Dfgk8CshxF0oYS455/k8MIS6X9YAPc53FQd+C7xWSrkWuAj4hhN/12zHhImOaYzAG5Yqh4De\nmm39znaEEG8UQlwmpTwopfxfKeVbUa7QlwghuoUQTwNOR4nrTuDPqId5Myu+7Pnb57y2lqkZxut9\n6NtUBPZ6lIX4Y+Bc4FEhxPoGx5dq/m0BBSnlBPATlNX3elTSVaOxe3/r7rmEEFcAH0OJyNeB33te\n+7/A05wYcZuU8k8Nzu2jWsT9KEE8HF9GuapfDvxUSplxjt0kpTxX/4cS1t87IYargDRqMvCDmuum\nm1ynjCfefRgiKME8S0r5UpT7eytKcCeklL8GkFLeC+xAeSw6UQlzZ0opn4kKHWwVQjxBCPGg898D\nM13UCX/c5Lzn81Gep6STQHoR8G1nwppETUgvQQl3Tkp5gzOmu1Ghlyd7Tu1H5Z0YjlGMwBuWKr8F\n3qXd2Y4l+BqUFQXqwfZfTvaz5hRUHHkClYB0tZTyOCnlCU5G+d8CL/K4SjWWc259nZc612/kStcU\nmYXQCSH+F3iZk6F/OSquuqbBS3uEEM9zjrkMFW/d6uz7Miomb0kp72tw7B+AZztuZ3Dc0A7PBj4n\npbwWGEF5JvwAjuh+HxXPbWS9A/wOeJsQIuDEqi9HTRJghs9HSnknSnz/2XPuu4ANQoiLnPd5FirH\nYJUzzu9KKb+DspifT7VwN7vWFqDRhKnRcR9HeXUQQpyN+iyuQ1VfTAsh/tbZdwoq8e0R4IU4CXFO\nyOFyVI7G/Z6JynkzXB/gOOBWIUTcuZ8/hJrEgPpMXuacP+i87zsBCbRrj5MQ4kTgVFRynWY96vMz\nHKMYgTcsVf4JZXFtFEI8jHKN/lBKeTWAlPJ7qFKh3wghpBBiM+rh+zeo2OYLgc94TyilvBn18HwH\n1djAhBDifpR19QXHrar36f97XesbgZLjcoV6d77+98eBVwohHkI9zK/znNvLMPD3juv6A6gSKB1v\nfQQYo7H1jpRyIyqh7CYhxL0o17b3+p91xvlVVPjhRM/h30W5h6+mMZ9AlcE9hCrv8qO+G/0eZyrT\n+i4wqLPbHdf936MmZg+hJhevllLuAT4LvFUIcR8qC/0XwEmeczWrdNiISvQ7pckYvMe9H7jUcdF/\nF3i5lHJQSpkDngO8TwjxKMpj8nop5QGUV2FECLERlWD4HSnldTO857rrOjkg/4n6/iWQc8YCagKU\nEEJsQon3HpTHIIW6hz/njPfHwFuklDvBTZ5c4eRSGI5RLLNcrMGwtHGst5uBk+U8lqM51uQHgLVS\nysvn67zOuQOoBLKrdW5BqxBCvBx42ny/h8WMU9UxJBtXZBiOEVpeJufEnyadf+6QUr7R2f4KVHnP\nBc6/3wy8BeXa/IRTGhNFzeL7ULGt1zbI4jUYjlmEEB9HJcK9az7F3WEHKjb//Pk8qRDiNOBPwPWt\nFncAKeUPhBAvEEKc4Vj0yxonxHQu8HcLPRbDwtJSC94pG/lzbQxKCHEuyj0ak1Je4GSj/h54AqpO\n9E/AE1Gu0nYp5ceFEC8DniqlbJYEZTAYDAaDwaHVFvzZQEwI8TvnWh9Elax8EpWt/E3ndU9G1eIW\ngIIQYhuqrvZCVBkKwI2o+l+DwWAwGAyHodVJdlOophfPQXXz+iEqeeW9VJe1JKi48UG54zuc7cma\nbQaDwWAwGA5Dqy34LThNJqSUW4UQx1PpBx4BThNC/A8qQci7EEccVcqU9GzX25pSLJbsQGC2Ja8G\ng8FgMCx5mpajtlrgX49ytV8u1Mpbm4EzpOoLfjyqrOm9Tgz+k0It3hBB1XNuRJUkXYpq5fhcoFH5\nkMv4eOaIB9rXF2dkJHXEx883Cz2ehb5+LYtlPItlHJrFNJ7FNBZYXOMxY2nOYhnPYhmHZrbj6etr\nvkhlq13030LVcN6Gcs+/oaaVpw0gpTyIqlm+HbgJ+KBTe/pV4HQhxO2oftsfa/F4DQaDwWBYFrTU\ngpdqFaNXN9m3C7jA8++rUE0jvK/JorqGGQwGg8FgmAOmk53BYDAYDMsQI/AGg8FgMCxDjMAbDAaD\nwbAMMQJvMBgMBsMyxAi8wWAwGAzLECPwBoPBYDAsQ4zAGwwGg8GwDDECbzAYDAbDMsQIvMFgMBgM\nyxAj8AaDwWAwLEOMwBsMBsMip1As88ObtjI8w4JayUyeUrncdL/h2MMIvMFgMCxyNu8Z5/f37uXm\nBwfr9hVLZb7x68d49xf+xI1371mA0RkWK0bgDQaDYZGTnMoDMDSWrdv3wJYR7npsCIBNu8eP6rgM\nixsj8AaDwbDI0QI/PFEv8AfHKm77obHmLnzDsYcReIPBYFjkJDOOwI9nKdt21b5DE9MAdCfCjCZz\nTOeLR318hsWJEXiDwWBY5CSnCoCKt48nc1X7RiayWMAZJ/QAcGDUWPEGhRF4g8FgWOSkHAseqMuk\nPzSZpTMe5rj+dgAOjE4d1bEZFi9G4A0Gg2GRk/QI/JAnDl8slRlL5ejriDDQ0wYYC95QwQi8wWAw\nLHJ0kh3AsCeTfiw5jW1Db2eUVT0xAPYfMha8QWEE3mAwGBYxtm2TyhRY0RUFqrPmR5wEu77OKIm2\nEJGQn5EGmfaGY5PAQg/AYDAYDM3J5IqUyjaretrI5opVFvrIpBLz3o4IlmXR1xlleDyLbdtYlrVQ\nQzYsEowFbzAYDIsY7Z5PtAVZ3dvGyESWXKEEwL7hNAArHfd8X2eUXKFEKlNYmMEaFhVG4A0Gg2GB\nGR7P8P6v/Jmt+ybq9mmxjsdCDPS2YQN/vG8vdzx6ALlnglDQx/H9cQD6OiMAxk1vAIzAGwwGw4Lz\nqzt2MZqc5mu/fKxuX8WCD7G6V2XK/+zWHXzr+k0MHppiw+oOAn71KO/rVHF6I/AGMAJvMBgMC04s\nrNKhsrn6LnSTWuBjFYH3cvJxXe7fWuA37hxj487RVgzVsIQwAm8wGAwLTCTsB2A6X6rbN5ZSmfJd\n8TCrPALfHg0CcMpxne42LfB/3niQ//nRw+QanM9w7GCy6A0Gg2GBKRSbr+OuW9P2JCLEYyFOGEjQ\n2R7i4nNW8dDWQ6xflXBf25OIVB07MZWjPxRrzaANix4j8AaDwbDAeF3zZdvG5ylxG01OY1nQGQ8B\n8JHXPtEtgzvrxN6q8wQDPgJ+H8WSmjBMpvP0dxmBP1YxLnqDwWBYYDK5iit9Mp2v2jeWzNHZHsbv\nqzyuZ6px/9gbnsQl560GYCKda/o6w/LHCLzBYDAsMNnpSt36aHLa/btctplI5+hOhGd9roGeNk51\nEu8mPS1ut+6bqOppb1j+GIE3GAyGBcZrwY95BH5yKk+pbNMdjzQ6rCkd7cqdr70Bv/7zLj79/Qf4\n6c3b52G0hqVCy2PwQogHgEnnnzuBLwBfBIpADniNlHJYCPFm4C3O9k9IKa8XQkSB7wN9QAp4rZTy\nUKvHbDAYDEeTjCcGPzpZEXgt9rXJc4ejo11Z/JPpHHuGUvz8th0AbNlb30jHsHxpqQUvhIgASCkv\ncf57A/A54HIp5SXAdcAHhBD9wDuBC4DnAJ8WQoSAtwMPSykvAq4GPtzK8RoMBsNC4E2y87rox1Iq\nht41Bxc9QEebsuAnpvIMjnhWlzPt6Y8pWm3Bnw3EhBC/c671QeBlUsohZ38QyAJPBu6QUhaAghBi\nG3AWcCFwhfPaG4GPtHi8BoPBcNTJ5or0JMKMJnNVcXNtwc/VRR8O+omG/Uymc1UThol0Dtu252fQ\nhkVPq2PwU8BnpJTPAd4GXAuMAAghLgAuB64EElTc+KDc8R3O9mTNNoPBYFg2FIplCsUyfZ1RLKs6\nMW7cseDnkmSn6WgLM5HOV7n584Uymen6bnmG5UmrLfgtwDYAKeVWIcQosEoIcSHKmr9USjkqhEgC\ncc9xcWACJe7xmm1N6eqKEQj4j3iwfX3xw7/oKLLQ41no69eyWMazWMahWUzjWUxjgcU1nmZjmdAi\n3hmlczzLVLZYea1TGrd6oIO+vva5Xa8rxsGxQ0w4i9Wctr6H2x8aZCw5zdr+xfO5wOL5nhbLODR/\n6XhaLfCvR7naLxdCrEJZ5M9AJdM9Q0o57rzuHuCTQogwEAFOBTYCdwCXAvcCzwVum+li4+OZIx5o\nX1+ckZHUER8/3yz0eBb6+rUslvEslnFoFtN4FtNYYHGNZ6axDI2p55YPiEeDDI1n3ddOOm1qp1LT\njDA313o0pCYHW3aPEw0H6GpTrW3HJqeJLKL6qcXyPS2WcWhmO56ZJgGt/pq/BSSEELcBPwDeCHwe\naAeuE0LcLIT4dycm/wXgduAm4INSyhzwVeB0IcTtwJuAj7V4vAaDwXBU0Rn0sXCARHuIXKHEdF5t\n073kw8G5eyZ7O6Lu+bsTYbriys3vjckbljctteCllEXg1TWbe5q89irgqpptWeClrRmdwWAwLDxe\ngdfZ75NTeSKhALmCI/Chudti4rhObrhrN6Di751O6dyYEfhjhkXkqDEYDIaF4ca79/C+L9/hWs5H\nk6yT9BYNB+hoUyKs14CfzpcI+H1VbWpny8lrK6vMdRuBPyYxAm8wGI55tu6bYDyVq2oyc7RwLfiI\nx4J3OtDlCyUioSNLHPa69UMBH52Oi35sAd6j4fCkswXe/F8381vH6zIfGIE3GAzHPKmsyjTP5o5s\n/fQHtozwts/e4ibMzQXd5CYaDlRazHos+HDwyB/T55/WDygLPh4L4vdZjE5mj/h8htbx2M4xSmWb\nn9wyf+2EzXKxBoOhpdi2ze2PHGCgJ8aGNZ2HP2ABSDulZN6WsXNhy94J8sUyW/ZN0N89t+VZp51E\nukjIj9+nHsnX/mELhWKZXKFEwrHqj4TXX3oKp5/Qzfmn9+OzLOKxoFtbb1hcePsfzBfGgjcYDC3l\n13fs4ru/3cy3rt+00ENx2XkgSb5QsdZTGW0xNxb4fKHE4Ei66fn0w3lkYu7Wcb6oxhEK+KvE/Mc3\nbyNX+Mss+GDAz4VnDrgxfNX8xnSzW4xMTqmJl983f/2EjcAbDIaWMZ7K8Ys/7QQqItoKrv6d5Ipr\nH5jVa/cMpfiP793HzQ8OAlAqV7q7NbLgJ6fyfOqa+/nIt+5h066xhuecdNZdHx6fu8AXCmUAggGf\nm2Tn7iuWj6hErhmJthC5fMn1GhgWD0kn7+Iv8djUYgTeYDC0DK+oB/2tedxkc0VueXAQuXdiVm1Y\ntQiPJZUoT00X3RYy2QYC/+P/28aeYWW9/+bOxglQE+kjt+ALJSXwoaCPWCTAZResq9o/nwKvk/jM\nuvCLD+0FMgJvMBiWBIVi2f17arrY1DV8y0OD3LNpqOG+w/HojlH377HU4TPEdUKdrjFPOfF3aCzw\nw+MZ/D6L09d1sWn3ODsPJOteo92rR2LB5z0WPMALL1rP+af3u/vDR5hF34hETZa+YfGgBb49Mn+p\ncUbgDQZDy8h7BL5Utl1R9VIslbn291v4yc3Ns4dvvHsPv3Rc/bXcL0fcv2dT4629CnosaY81m52u\nH18qU6A9FuSCMwYA2FUj8Ll8yc2+n5oukpku1J1jJgqeGLymLRx0/26JBd+ChC7DX4YW+PI8pkcY\ngTcYDC1Di5dmKltvIQ+NZymVbcZTOUrlct1+gBvv3s0Nd+2m3MADsGn3uPu3drvPhLbYdRvYKgu+\nQZJdKlsgHg25rV4naqzfianqaw7P0U2vJ0HaggdVE6+ZV4GvKcMzLA5K5bI78SyVGv8GjgQj8AaD\noWVo97NmqoF1q7PTy7bNeAOBzhdKJDMFCsVynWu5UCyRzhbczOPZ9FmvzZhPZ5u76IulMtlckXgs\n6IrjRLp6jHpM0bAS4rm66QsNBL7NK/Dz6aKPGYFfjEyk8ui5a2keTXgj8AaDoWVo8ep0xHGqQRLc\n4MiU+/ehBl3WvKJdm8SWnFLifMJAApijBa9j8DMIvBb/eCzotnqtFUct+Cc7Nf57h5uX0zWiUCzj\nsywCniTEtmiLXPTtxkW/GPHmjhiBNxgMSwJd463d21PZBhb8odkLfK11rMX2+JVxLOYWg592XfQV\nsastk9OTgfZokEjITzjod9dvd8fgWPDnndyHBWzbN3nYMXjJF0sEa2rdY62y4E0MflHi9UzNp8Cb\nTnYGg6Fl5F0LPgykZnTRAxxq0EbV2x++Nr6ts9e7E2ES7aGmWfTjqRw/vWUbg4emODCq2sm6SXbO\npMOyYNpJliuXbXw+y03Ai8dCWJZFR3uIiVoL3hnDyp4Ya1e0s+NAkkKxXOVyn4lCsUyo5rVtkdZY\n8LFwgIDfZ1z0iwxvmMhY8AaDYUlQrBJ46urUC8USwxPZylrlh7HgD9W56JVQdbSF6ElEGEvmGibi\nfeeGTdz52BB7htLuA7Q2ya4nESGTKzI4kuadn7+dP9y313Xftzsu8872MKmpfFUyoG5Q0tEeZsOa\nTgrFMruHUof/cBzyhfrJgNeCP9LFZhphWRad8TDJKdOudjFRJfAmyc5gMCwFXAveEfB0jQWvauNh\n/UACCxhpJPAzWvBa4MN0x8OUynad+zmbK1Zl2mum8yVs2+bA6BTt0SAdbSGyuSJf+cVGsrkiN923\nzxX/eEwLfAibSuwfIOm8JhELsmFtBwBb907M/MF4KJTKBAPVIu614EPzaMGDmshMpPNNKxYMRx9j\nwRsMhiWHG4Nv1zH4Ys1+JTKRsJ+uRLjhSmejk9NYlhKm2iS7SY8F3xWPANQtpvL4LrVK17OftLZq\ne6lss3c4zVgyx2nruoiGA5TKtuvC72gPufH5uGPB61ay3kz6dDZPwO8jHPSz3kn2m4sFXyiWGrjo\nPRb8PAv86hXtlMo2IxNm2djFgp5IWhiBNxgMSwTdZ91Nsqux4HWWfSjgpzcRYSyVo1jjohxNTtPZ\nHmagJ0YqU6jKdE962nu6deo1Av/wdtXp7kmnrqgb331yGIAzTughEq5OSZpM5z1Z9Co5rTNeXyqX\nyhSIx4JYlkV3R4Rw0M/+Q7NfNjZfqI/Bh4J+N6t+PpPsANb2xwE44EluNCws+j7raA8ZgTcYDEsD\nbaHr8qxGMXhQNeA9HVFsu9oCLxTLjKfy9HZEPI1mKvsnp/L4LIv2aNAV33HPftu22bhjlPZokBMG\nElWWMVS64J2xvptYuCKka/ramJjKVbLotYveseC9Wc9a4AF8lsXKnhgHxzKUZ/GgLpdtSmW7YUKe\nHut8JtkBrF3RDsD+USPwi4V0tkDA76MtEjQxeIPBsDTQAh4NBYiE/HVlct4+7L0dysXuLZUbPJSm\nbNusWdHe0EJPpvPE24L4fJYbBvBOEA6OZZhI5zltXRc+y+Lic1ZXXf/AaIaBnhid7WE3rt6TiNCd\niJAvlN2Yv5tk54xBjzFfKJErlFwXPsCqnjaKpTIjDcINteTdCU69iMdaJfCOBT8XL4OhtaSzedqj\nAfw+y5TJGQyGpYHbhjWorJPaJDt3JbWAz820V6VyXQDsOqhi2cf3x93seK+FPpnJ098ZBSri650A\nbHaS6045Xp3vRRev57R1XTyyfZTf37sXgD7neN0N79yTe92Jx77hNFGntEyPw7Jg6z6VRFfrwgdY\n1RsDYP+hKfq7YjN+PpUQRQML3pk0zLeLvr87RsDv44Cx4BcN6WyBnkQUv39+Bd5Y8AaDoWV4Bawn\nEWY8lavqT19ZC91fseA9yV97HIFftzLuTgB0L/hcvkQuXyLhuP+1BT+WyvGnRw5UZc+f6gi8z7I4\nbV03UU+8XZ/3FX99Ms+/cB0vecaJbue9Utl2xwXKqj6+P86O/UlyhVKdCx9gVW8boAR+tp9PbaMb\ngBNXJVjRFXVb4M4Xfr+Pld1RDoxmGpYUGo4uqh1yiXhMeaJmE9qZLcaCNxgMLcPbZ311Xztb9k1y\nYDTDcY6bOO+Jwfc6lrTXRb97KEXAb7Gqt83t1a1d8HpNc91fPRT00xYJsGn3OJt2j3NwIsvmPRN0\nJ8KscM6t8bq9teu/Kx7m756+HqiIPiih9XLKcV3sOphi2+Cku/xtlQXfowReZ+PPRH4GC/5lz9zA\ny5654bDnOBJW9rSxb2SKyXTeff+GhUGHrdqiQUpTKiej2bLKc8VY8AaDoWXkiyX8Pgu/z8fqPiV8\n3t7zXgu/Kx7GsnBL5YqlMnuHp1jd107A76uLwdfWqEPFTQ+wZc846WyB41bEsSyralze5jGNBM4r\n8CfUCLw4TvWc37x7vDIGTwy+tzNCwO+blQWfLzSPwbeS7gYJi4aFQTdTikeDbphovtz0RuANBkPL\nKHi6tK12XNf7DlVa03ot/IDfR3c8zCGnc93IRJZiqexmfbfH1ANQi1LK00ZW4xXmXE2JnpfwYQRe\nZ/0DnLiqo2rfiavVv/cOpxtOMvw+Hyu7Y7Nygc8Ug28lel1407J24Ul71jvw+43AGwyGJULe02d9\ndZ8Saq8FX1kLXQluT0eUcacWXiewaRe8z7LobA+5SXaNrGdtEQMMDqv4fadHrDXe5jFd7TNb8Ct7\nqhPl2iIBwiE/Y8kc6Wz9JANUol2uUOKORw5w49176s6vabRU7NHAu+hM2bb5w31765oIGY4OaU87\n5IBP3QelkhF4g8GwyCkUS654t0fVmurVLnolyCEnyay3I4Jtq1Xh9NKy3tr1zniYybQSpVQDcdUu\nTgBtBHUexoJvtD/RpiYN/V1RfDXufcuy6I6HGU9NV60250XH4b/z2838+OZtZBossgPeCc5RtuCd\nSc9kOsfm3eP84I9b+fntO47qGAwKV+CdJDtg3pIfTZKdwWBoGfliuUr8Vve28fiucabzRSKhQMWC\n9VcEHlSinRZF78Irne1hSuUkqUyhoXv8tX9zCjfctZvHd427i9Q0stC9Al/b/AaUm/1z73paU9d5\ndzzMgdGJX2H4AAAgAElEQVSMmxDoHQNUMuk1emnaWtwJzlGOwbstd6fybqWB3DOBbdt1+QqG1pLN\nq4lsNBSoxODnqdmNseANBkPLyNcsm9qTqO4XX1sm1ttRyaSvWPDBuuMf2X7IE4Ov7O/vjvH6S09l\noLfiVm9owXtc9M0ELRELEQk1toG6nHHsGUphWdVjBBioE/jqDn6a/Axlcq1Ex+CT6Tyb9yiBH0/l\nqioYDEcH72/AxOANBsOSoVgsV1mnHe3VrV7znl70UGvBK1H0WvAXn7OKaNjPNb+TbhOb2vg3VFrK\nQnU8XaM9BkeKzkJPZQqs6Iy6rlVNrWs/19SCX5gku/ZYEJ9lMTSeZdeBysI4W+awCp5hfvB6sbQF\nXzQCbzAYFgsbd45y0717qpZ2LZXLdX3WdcLbxJS24Ct18FAR+NHJrLswjdc6Huhp4xXPOpliyWY0\nmSPgtxqul65jzMGAr6ELXieZnbG++4jeb3ei0vymtowOIOD3cdKaSvb94QT+aJfJ+SyLRFuQfSNp\nSmWbM9f3AMpNbzi66MWVggEffjfJbn5c9CYGbzAY/iKSmTxX/vhhta77qgQffs0TgUqf+VCVwOta\ndmXB11qwXYkwPstyXMXKmqkVaF2HDsp6b+Ri19fpbG+8PxoO8JX3XuS2oJ0r3QlPnfzKeoEHeN/L\nzuaXf9rFDXftVi76tmDda/I1E5yjSUdb2O0K+Ownr0XuHZ/TMreG+aGRBT9f3exaLvBCiAeASeef\nO4BPA98FysBG4HIppS2EeDPwFqAIfEJKeb0QIgp8H+gDUsBrpZSHWj1mg8Ewew6OZtwuc0lPXXUl\ntuh10ev6a2XB12aR+32qoc2hyWliTjvZWE18uycRoS0SYGq6WFUi56Wzpn1tI5rF12dDd9xjwQ80\nFvhgwO8mGOoku2KpzA9v2so5G3o544Qet1Xv0XbRQ8WLYQFibSeretoci77sWpKG1uMtlVxSjW6E\nEBEAKeUlzn9vBP4H+KCU8iLUvfUCIcRK4J3ABcBzgE8LIULA24GHnddeDXy4leM1GAxzZ2is0pJV\nC7b627FOPVayjo1ry7FRHXhfZ4SJVI5kJo9lQaSmF7tlWQw4ZWiBJsKoY/2NEuzmA23B+yyLtf3t\nTV+ns/W1i/5Xd+zk/x4Y5NvXbwLqcxCOJpmcCoGsWaE6Ba7ua6NYshkeN/XwR5OC10U/z0l2rbbg\nzwZiQojfOdf6EHCelPI2Z/9vgWcDJeAOKWUBKAghtgFnARcCVzivvRH4SIvHazAY5siQRxC8jWZc\n97snQ9xbf+19TVWmfUcEG9UpLhYO1NWhgyOwg81bra7ubePENR2cfVLvEb6rmYmEAqzojNIZD8+4\nnKu2zKfzJcaS0/zunr3OdnXMQjW6AdwFd846UcXfV/dWGhHpCZSh9RSdeyBQFYNfGgI/BXxGSvkt\nIcQGlEh7SQEdQIKKG792e7Jmm8FgWEQMjSsLvr87xsh41q2l9q71rgn4fbRHg64F7+1Vr9GlcsWS\nTXe8sQteJ7lN5xonr0XDAT73nmcwMtK6mPIHX/0E1+Jqhhb/XL7IQ9sOuYKuvRu1SYZHk9c+5xRu\nf2Q/z3vq8QCscdYK2DeS5omnrDjq4zlWaRSDL5WXRpLdFmAbgJRyqxBiFDjXsz8BTKBEPO7ZHm+w\nXW9rSldXjMBf4Orq64sf/kVHkYUez0Jfv5bFMp7FMg7NQo9nNJkjEvIz0NPG0FiGru52ggEfo1PK\nBdyZiFaNsbczytBYhr6+ODYWoaC/av+p63v55Z92ApCIhxu+v1ddehq7h9K88jmnzPj+W/nZ9PUd\n/jUrnBXlcoUS251ytO5EmIlUju6ednDCFwP9Cfq6Z147fj7p64vT1xfnlJMqb+IsJydhNJU/6vfU\nQt/DmoUYh+VMbgdWdhB3cjvi8ei8jKfVAv96lKv9ciHEKpRI/14IcbGU8lbgucBNwD3AJ4UQYSAC\nnIpKwLsDuBS413ntbfWXqDA+fvjlGZvR1xdv6Wx/riz0eBb6+rUslvEslnFoFno8tm2z/1Ca/q6Y\nG2/ef2CCWCTIsDOuYr5YNcb2SIBduSJ7B8fJThcI+q2q/Z3RyiQ9XLPPy/v/4RyApvsX+rMByDrJ\nhJnpIg9tGaG3I8K6lXHuS46wc/co+5xGOaV84aiNtdnnYts2sXCAHYMTR/VzWwzf00KOI5PNYwHj\nY2ly08qzNTo+BfTNajwzTQJaLfDfAr4jhNDC/HpgFPimk0T3OPBTJ4v+C8DtqMS/D0opc0KIrwLf\nE0LcDuSAV7R4vAaDYQ5MpPPkC2X6u6KVhLJCmVikeZe2ShxeHVvrnu71rN1em0G/1NCfycbth8jm\nijz51BVu0uFEOs/wWIbejsgRl+vNJ5Zl0d8dZe9wmrJtN8x9MMw/hZL6DViWtbRi8FLKIvDqBrue\n0eC1VwFX1WzLAi9tyeAMBsNfzCFn7fa+zihF55mk48q6gUeteOnlWcdSOQqlslsOp/FZFvFYkFSm\nsCiE7y9Bx+Cl0w725DWdjKVUM6ADY1MkMwXO6F8c7mlQ3+POAykOjmbI5IqctNqkPbWaQrHs3ufz\nHYNf2r8eg8GwoOh2sm3RoCtmOrlOl/oEatq4VvrNZykUSw1rwHVHu/HU0u6NrrPldZ+AzvaQ24Rn\ny16VV9x/FGPvh6PP8Z58+Kq7+dQ197NvOL3AI1r+FDzrNZhe9AaDYdGQzTkrYYUDFRe9Y8FrN6O/\nxgp3+81PTDd00QOcvFZ1q9PNWJYq4Zo2uvGYV+BVznB/V7TuuIVCfzeaVLbxMreGelKZPJ/7ycPs\nPji3OH6xVPkN+Oa50Y1pVWswGI6YisD70WFDbcEXHTejv9aCd6zEkYlsXa96zYsuOpH2aJCLzl7V\nqqEfFcI1+QftsSA6tL3/0BSwOC14zXz1RD8WeGzXGI9sH8Xvs3jn35/FH+/bSzZX5LILT5jxuEKx\nTJvT8bCyXKwReIPBsMBkHIGPhQM4uu42u3Et+BqB746HsSzYP6oELtSgUUww4ON5T13XolEfPQJ+\nH5ZVcdG3R4N1eQWLyYKvFfhm69gb6tELLT2yfZTkVJ7//eNWgMMLfKkSgw/oJDsTgzcYDAtN1mk0\nEw0HKjH4Yk0MvkbQAn4f3fEI+w+psta/dOnWxYxlWe4EJhr2E/Cr1e103kHA76Onxi2+kHQ7i/1o\njMDPHi3wpbLt9nGASiObZhSKdsti8MaCNxgMR4w3Bp9xTPiKBd/YRQ+q3/xoUj0Qa8volhvhoJ9c\nvkQ86izuYlm87tJT2HUgxclrOxfVwi5+n4/uRNhZzU816DHMDv2ZWRbc8tCguz0zXXDXRqjFtm0V\ng6/NojcueoPBsNBkPS76lGPNuwJf1kl29QKvMulVktlCrKR2NNFx+PZYpab//NNWcv5pKxdqSDOy\nurfNFavpfHGBR7N0ODQ5TXs0yPpVCR7ZPupuT08Xmwq8dy14mP8ku+X9yzIYDC0l482ir3HRF10L\nvkEZXGfFLR30H/2V1I4m2kXf3mRp28XGq58j+Ie/2gBUu+jLtj1vseHlhm3bjCan6emIcMEZ1RO3\nzHTzSgTtvq/UwZsYvMFgWCRkc0UsVDmYLgmrteADDSx4bwMVXwMX/nJCT3zisaUh8N2JCKccp8oU\ncx6B/+i37+U/r31goYa1qElmChSKZXo7Ipy7oddt5gQwNd3cC1JwXPGmDt5gMCw6srkiEWdJ13BQ\nRfxqk+waWfCnrevmbS84nd6OCMIRk+WKK/DRpVPTH3Ema9OFSlfCfSNptg8mGXTK+wwVdEfH3o4I\nwYCfT7zpKbzyr08GYGqGXgK1qwkGTAzeYDAsFrK5IrGwEoNKL/raRjeNLfQnn9rPk0/tPwqjXFh0\njkH7ErHgAcLOynLaRZ/KVETqtof28/JnbViQcS1WdAZ9j7OMcTQcoNNZcyEzkwVfrI7BV1z0xoI3\nGAwLTCZXIur0kq+46Gtj8MvbBX849OcSXyIxeICIu469EvjkVN7dd/emoQUZ02JmIqVWDeyKV3JL\n9EJJUzPE4Iul6lJSHa4qG4E3GAwLSdm2mc4VKwLvJtnVZtEf248ZN8luCVnwoaAPC8g5WfSpTEXg\nk1P5eROg5YL2dGhvFkBbRP0uZozB11nwSuCLJsnOYDAsJLl8CRtcgQ/VLTbjZAgf6xb8EozBW5ZF\nOOR3hWvSY8FDpXrCoNBhqVDIK/CHt+DdGLzfNLoxGAyLCG8NPFCfRd+kVe2xxsVnryLeHuaEVYtn\nWdjZEA753SQ7HYNviwSYmi6SmS4smbK/o4H+nCKetssxx4KfMQZfamzBz1eSnbHgDQbDjOQKJf7j\ne/dx4917qrZ7a+ChkkymBb5oXPQArFnRzhuff8ai6lg3GyJBZcGXymWSjot+ZY9aGMdY8NXoXAXv\n6oGRkB+/z5oxi75YrI7B69/KfNXBGwveYDDMyL7hNDsPJNl5IEk8FuTCMweA6ja1oPuu+yplcjrJ\nrkkWvWFxEwkFGBrP8rbP3upuW9kVY/tgcsa48rGIdtGHPRa8ZVnEHI9HM+oseMsk2RkMhqOIblsK\n8Id797p/a9dj1JNYFAr46xebOcZd9EsVbY2Wyrb7XWoLPmsEvgptwUdC1V0ZY5Hg7GLwptGNwWBY\nCHQTD4CDYxnKztqntTF4UH3X63rRLzHXtEFRK1ahgM/t0GZc9NVMF0pYVv3Kie2RAJnpIrbdWLCL\ntZ3sTKMbg8FwNNFNPNb0tbFvZIqxyWl6O6PsOpgCqtcQDwX9bsyxuMRd9A88cB+//OV1fOxjn5rV\na2+99f94z3v+5S+65otffBkrVw5gWRb5fB4hTuEd73gPodDRz8CvFXib2dV2H4vk8yUiIT+WVX2v\nxyJBSmWb6XylX4QXt0yurhe9seANLWbngSRX/vhh82M+xtEu+jPX9wBwYCyDbds8sGWESMiPOK7L\nfW0w4CPnxuCXdhZ97cN6vl57uPNceeWX+eIXv87Xv/4denv7+MY3vjIv554r3ngyKDHS3pqZMsOP\nRaYLpbrPCyrrD6SaJNq5i83UuOjnqw7eWPDLiHLZnteFO77ws0eYTOe5/s7dvPSSk+btvIbFx/BE\nlp5EuKE7XS+DuW4gAcCBQ1N0tqs1w5986grXvQhODN7jovf7rHkTv6NNM7fqzTf/kZ///KcUi0Us\ny+JTn/oMtm2zZYvk3e/+R6am0rzwhS/h0ksvY8uWzXzuc58lEgkBfj7wgQ9RLpf5wAfeQ0dHJ099\n6oW84hWvaTqGl73slbzqVS/hHe94d8Pr/vCH19LXt4IXveglJJNJ3vOey/nWt66Zl/cfCtQLVtss\nSr8WiqHxDBt3jPHM81Yf9Xsu51jwtXS0Kc/LZDrHCo+nS1MXgzed7AyNGJnIcvmVt3H34/PXRtLn\n/EhSNU0uDMsH27b50f9t5V+/die/u2dvw/2jyWl6OyIMdKsEqwNjGe567CAA527oq3q9z2dh2+q4\nYqm8ZK33mdi3by+f+czn+MpXrmLduhO4++67sCwLn8/HlVd+mS996Rtcc813mJiY4IorPsl73/sB\nrrnmGl70ohfzxS9eiWVZjI2NceWVX55R3AHC4TD5fK7pdS+77O+48cbrAfjDH27kOc957ry9T+25\ni4T8hII+Xvj0E1wXfaMY/Od/8jBfuu7Rebv+XLnu1h1c+4ctbN49ftSvnSuUqkrkNHod+Ml042eo\nu5qc38TgDTMwNJ4hVyixbyTNU5jdAh73bR7mhrt28/6Xn9swPhSLBBhP5UxJzDLm0R1jrrDv2J+s\n25+cyrvLYPZ3R7EskHsmGEtO09ke4pwNvVWv13pu244Fv0Tj7zPR2dnFJz7xUaLRKHv27OaMM84C\n4KyzzlEd4MIR1q07gYMH9zM6eoiTTtrg7D+Xr33tSwAMDKwiEDj843dqKk002tb0uqtWrSYWi7Fr\n107++McbueKKK+ftfY47/dVX97XxoVc/Eahki9eG7XL5Eo9sHyUU9GPb9lG3oMu2zeY9Stg37hzj\n1HXdR+3atm0rC76Bi14vOFPbCVBTrGlVa1kW0XCAYHB+bG8j8MsEnY2p24TOhq/8YiMAm3ePc+7J\nfXX7Z9Nq0bC0GZmoZMgnM/UPIR1/7+2IEgz46e+KcXAsA8Arnr6+Lu6oH+xl23Zc9MvLSZhOp/n2\nt7/BddddT7lc5r3vfYfryt+06TFs2yabzbJ79y5Wr15Lb28f27dvo6/vXB566AHWrj0eAN8Mn4s3\nNHDttVfzrGc9m6mp5te97LIX8p3vfJMVK/pJJDrm7b2efkI3cu8E55+20t0WCvrw+6y6Mrm9w2ls\nlCWbzZXcLm5zYXgiy0Qqx8lr57588P6RKbfb3qM7xnjJJXM+xRGTL5axqW5Tq3Fd9FO5hsfWJtkB\nvP/l58xbl0Aj8MsEPRPUC30cDu9DpFnGZsiZRRoLfvmS9bhaRz317u62pNrWnVCuxrc+/3Ruf2Q/\nAE9zGt540Tkgtm1TKpWXtAVvWRb33ns3b3rTa5x/w0c+8h+ceebZvPWtr6erq4u1a49ndPQQAwOr\nsCyLd7/7cjKZNG9+89uJx+N84AMf4sor/4tAwIdtW/zrv37ksBbue9/7Dnw+H+VymQ0bBJdf/k8E\nAoGG1wW4+OJLuPLK/+Lf//0/5vX9X3r+8Zy2rpsTBiotdnXzlloX/a6DFe/PeGqaWKR9ztf77g2b\n2DY4yRf/6aKG7u5t+ybZum+C555/fN2+TY717vdZ7BtJM57KuSV9rSbXoE2tRrvoJ5q46HUynfd3\nsm5lYt7GZgR+maBLkmZrwesHNzR3H+Udd1y6gWVnWB7oxUQCfouJVI5iqVxVyzteswzm8SvjHL9S\nND2fz+3EpbxKS7nJzbnnPoEbbripbvvHP/7ppq+vZcMGwZe+9A36+uKMjKTc7V/72rcbnuMnP/lV\n0/E0u26pVGRgYIAnPen8psceCT6fxfpV9WKjmrdUC/zuocp7G0/lWN03N4Evlsrs2J+kWLIZnsiy\ndkX18clMnk99/34AnnTqCno7qhPWtuyZAOAZ567mpvv3sWn3GBecUT8BbQWN2tRqtAWfbPKMrfSK\naM3vZHn5z45hdMvD2VrwOw9UfpCpJgKuF1BIZgquK8mwvMg6y4Gu6WvHBsaS1VZ8ReBnZw3p55Ry\n0ZeXnYt+sfHoow/zlre8jle96nVH7ZqxcKAui373wbT791iqsTt6JvYfmnI7IA6PZ+r2//SW7e7f\n4w3Ofyg5TSjo44IzVDhh277JOV3/vs3D/PMXbmOowbUPhyvwDSx4naA4kW78mdiOwPtalLNgfn3L\nhNIcY/A7D1Rcas1ml9q6A+V2myu2bbN9cNLtfGZYGCbSOT51zf1V37lmOlcReFAx95vu38f3btzs\nHgtzEHivi36ZJtktJs4882y+970fcvHFzzxq12yLBCiWypVFhUpl9h+acq3QRgJ8OLwJnsPj2br9\nm3ZVMuMbubtTmTyJWIjj+tsJB/1snaPA3/bwfuTucT70jbtJz7A4TCPcPvQNLHjLsuhsCzf1kupn\n43yWN3sxAr/EyeaKbNo97lrwhVla8PuGKzPuZKbxDZ3zCPxocu4/2tsfOcAnr7mfn9+2Y87HGuaP\nx3eNsW1wkge3Hqrbl82p73jNiorA3/bwfm59aD+FYomxVA7LgkTb7JJ+Kkl2atJpLPjlh27eojsZ\njqVylG2b4/pVrL6RMZAvlLj6d5KrnYljLTs8k8+hGoEv23aVBVw7gbBtm+RUnngshN/nY/2qBIOH\npuYs1Ppaj+8am9MxjZaK9ZJoD5GcyjesbdcueiPwhjpK5TLv+vztfOYHDzI4MgVAzmPB37d5mK/9\ncmPDpQeTU3lCQR8+y2puwRcqAl/rup0N0omL3enUTBsWBp0J38hNOO246Ff3qVKs0clp19pIZ4tM\npHJ0tjdugNMI10VftimWl3aSnaExzzh3NQDX/mELpXKZMef+OnG1itc3ctF/4WePcMuDg9zy0H43\nX8jLrgNJQgEfFvUu+uRUnlLZdr1IEzXnz+ZKFEs2CWfisWGNqiTYNjh7Kz7lMXKaPQ+bMZOLHqCz\nLYRtNw6Fas1vlYu+5Ul2QogVwP3AX6EmFFeh2hpvAd4kpbSFEG8G3gIUgU9IKa8XQkSB7wN9QAp4\nrZSy3gRZIGzb5pu/eZz1Awme9cS1CzKG6/+8250B6oe3Nwavy+D+9qnrXAtNk8oWSMRCFIrlhjd0\nuWxXWfCN3GaHQ7e1zJqFKRaUmQQ+m1MtNnU/+ZGJrPsgSmcLTKRzrF0RrzuuGdoSKds2pSWeZGdo\nzIY1nTz19H7ufGyIrXsn3YTd1b1tRMOBOgs7nS3weJWLPVeXJDeeytHXGSWbL9ZZ8GOO9/DEVQnu\nkyN197G+X+NOQpsus3t85xjnnFTdp6EZqWzlGZhq4tFsxkwueqjOpNd/a+ylbMELIYLA14EpwAI+\nihLwpwNh4HlCiJXAO4ELgOcAnxZChIC3Aw9LKS8CrgY+3MqxzpXpfIm7Hhua185xc6FQLPGH+yqd\nx7SIFhwL3usOqi1psW2bVCZPPBYk0RZqWP+sb1pt2R1J8kk04nfGNruwgaE16PK3iVT995zNF4mE\n/XTHw1iWys3QKRMHxzIUS/acyo0qWfQ6Bm+chMuRk1YrK3kinXO9ez2JCN3xMOM14bzBkXTVv8eS\n9S72TK5INBJgRWeU8VTOje9DxeV/gtMquXYCoZ9fiVhF4KPhAA9uHWnabrj2+qlMgZBjgc85Bj9D\nFj1U2vs2MnTcGHyL5sGt/vV9BvgqcMD5dxboEUJYQBzIA08G7pBSFqSUSWAbcBZwIXCjc9yNwLNa\nPNY5obNI0wtUI/7AlkNVpSr65sk5Fvz+0Sl3X62FPp1XLq14LEQiFmQ6X6r6QUEl+WqgO0Yw4GNo\nbO4W/Dytl7DsufvxId5x5W1HlJx0cHSKX92xs6HbU6OXe23oos8ViYYCBPxqKVCv9bTXydPoap+9\nwOsYfLHF5T+GhSWhy78yBTc/pzsRoSseJpMruqEfgH1O+FBPCmrDfdlcEdtWHr8VXaodsrcBk54Q\n9HVGScSCjNfcx8kpJcjaRR/w+zj7xB5Gk7mq8r1m5AolCsUyx/UrL2cjV3o6W+DezcMN4+jTh3HR\n64lDowonfb5Wdf5rmcALIV4HjEgpf+/Z/EXg88DjwArgViABeIMlKaDD2Z6s2bZo0N3dpo4gkWM+\n+JPTbOSS81Q8rNaC92ZM165k5Lq0okHPD7X6ptbni4YDrOiKcnA8M6vZsBevi9/QnG2Dk2RyRVdQ\n58Jnr72fX9y+kz/et6/h/nLZdh+Q6Wx9uWM2XyIaVg+gnkSkap+2vLoSc7DgnSeKvo6JwS9P4o61\nnMrkXcHuToRdb493srrPuY/OOlGtRjhaI/BTWfWsiUUC9HZEnNdUjh9zLPiuRJjOeJiJdK7qWVTr\nogc4z+nM+cCWw0d1tUt+jROKauSi//Udu/jqLzby01u31+3LHybJLuS0oW1U4VSyWzsRbmUM/vWA\nLYR4FnAOys3eCzxdSrlJCPGPwH8Dv0NZ85o4MIES93jNthnp6ooRaLAC0mzp65t9rPGA4/bMTBfo\n6WlvSQxlpvEMjmZY2RPj1PW93PzAoDuLzBfL9PXFOThR+RGVsKrONercwCt6250fyhD+ULDqNdv3\nqY+7qyPKcTYMjkwRjIToqhGBGfE83NviEXehiiNlLt9PK5nvceh1JfxB/5zPrR+uu4bSDY8dGc9W\ndSoMhIP0OYvGFEtlCsUyifYwfX1xVvfHq8qLBkdVWOa4VR2zHlcsqh6y7U5jnFgktKDf22K5Z2B5\njSWP+m3nSzaTTrhv7eou1qxMwCMHsH2Ve3loPIvPZ/G089Zw3W07yBbKVdff5RgjPZ0x1q1R8fO8\nXRljJq+EccO6Hvp72tgzlCYWj7rtXEuO9bt2oHKfPjEQgF9sJJUtHva9jjnPw854mHgsSCZfqjsm\n44j4jXfv4VWXnlYVS/c5mrOyP9HwWj3dKswZjtb/FrRerViRqFqVUfOXfk8tE3gp5cX6byHEzcDb\nUGKufSYHUHH3e4BPCiHCQAQ4FdgI3AFcCtwLPBe47XDXHD+COLGmttPU4Rh0bsqyDXsHxxuK1y9u\n30FHW4hLzlszr+OxbZt0Jk9Xe5yckxyiQwbFUpmhoSRbdldKPYZG0lXn2utklwawcX6n7N43QVe0\ncjvoCUO5VKbTKZF6bOtw1drfh2PSM1PftmuUgZ62WR9by1y/n1bRinGMOS70/cOpOZ+7sz3MyHiW\nbfvGGR5O1rn6tuytnhdv3zOGVXI6FDqeHb9lMTKSor1mwaFhp+d8EHtW4+rri5NzPD8jjtVWKpUW\n7HtbLPcMLL+xFJ3nzdDoFMNjWfq7ooyMpAg7k/qd+8ZZ1RXBtm12HUiysjtGCDXRHByqvs+1F9Sy\nywSd1+wenHBfc2Akjd9nUZwuEHPi3Nt2jbK6Vz1PDjqer3Kh6B6jPZLpTO6w73XPfvU87GgP0xYJ\nMpGarjum5HGvf/4HD/C2F5zO53/6CG2RoLtMbCZdfxxAblqNZXRsqm6//r2MjabrjMTZfk8zTQJm\n5aJ3xBchxAYhxPOEEEfq2n8T8FMhxC0owf+glHII+AJwO3CTsy2Hit2fLoS43TnuY0d4zZbgTVxr\nFIdPZfL86o5dXPP7LfN+7XyxTLFk0xYJuLM+u2p/ifFUzm05Wut+1y6t9ljQnQXXLiijXfSRkJ+V\nTlysNrt130iaj37nHj7wtT/z2M762tHpqkSZuceXjxX0A+5Iwj3jziRqLJlzF4HxouPvAz3qO/SW\nGOk8i6jzgNLu0Vr6Gqxj3Qz9kNLxRhODX55Ew34CfouDY2oVy27Hs6dd9LpUbiyZYzpfcjPsIyF/\nXU8N/eyJhgP0aBf95DSP7hglXygxllIrF/p8lpsPMpHKkcqo2nI3yc7joteLt8ymA6d+Hna2h4jH\ngn9EW7gAACAASURBVKSzhbrmXHpxndV9bdy7eZj75QiPbB/lzscOuvkGkVBjeznkWOm1eU7gjcEf\ndphHxGEteCHE/wM2CCE+jIqZPw78HfDm2V5ESqnX9pHAHxvsvwpVPufdlgVeOttrHG28gjiVLUDN\nQ3DznorlNN8tO7W1HosEqlYh0uQKZSbTedasaGf3wVRd0oiOycdjIXeRmtrWk1rgw0E//Y5Ld6hG\nQDbuGGPPkJo93/HoAU4/oXqJxlzeCPxs0MmSOhY5W0rlclXN8Za9E3VeEt31a93KBAdGM1WJdlnn\n+4k4lntPA4EP+C0655RFr/7vxuBNo5tliWVZxGMht3y2p0bg9URy2EmWU0sNW/QkInVJdnpiGwsH\n6GxX1Rx3PT7EXY8PcdkF6xhP5djgJOjpe3H74CSf/+nDvPDp6ysGi2cFNm34zJR8qkk7LvpEe5h4\nTNWsT2ULbp4BqOehBbzh0lP5j+/dx583Vnp7TLu/o2ZJdmosuQaTjZJtY1kLm2T3ApQF/XLgWinl\ns4DzWjKaJYT3YdxoOdVNuz11nw3Kk0CVus3mBqy7tnO9tkiwYdxmIpWjVLbpjodpiwTqkkbcpJRY\n0F3WsbaEw2vB65XEarNXvV6MTXvG65LwZivw92wach8ExyJuwuYcl+VNThUol2334XrAiZkXiiVX\nYPX3uKrXseA9bT4riZTVFrxFxaLo6YjOqQmHfq2+r02S3fLFazGvXqEmlt01SXY6G157gboSKsve\n+7xxBT4SJOD30emJb//p0QPYNm4vBr3vkR2jFEuq61wyU6AtEqhaJMnvs7CYrQWvrt/RFnK79NU+\nMzO5EpGw3w0LbN1XMeBcgW9SJqct+EZdRu2y3VIv12wE3u+4zP8WuEEI4QdiLRvREiFTZcHXW15e\ngddu0lre/9U7+dA375rztSs/iEBDgddi2enMSGtd9O6MNRYi6lhvtbXy0x6B72hr0kHKsTwHemJM\npvN1Lnyvi75Zo5xDE1m+9svH+MUx2s7Wtm33/plr/a3OLj51ncqL0C76K/73Qb503aNA5XvVvea9\nE6la12K3kxjXHgvS5uSU9HXOIamSiiWiH6wBUwe/bEl4LNzjHAGOhgOEg3733tQCv8IR+H4n3Oct\n4/Va8FBdzaEnCmudEjbtIdjttMnddTDF8Hi2zvtkWRbBgG9WBpQ2eDrawx6Br68qioYDhIJ+Em2h\nqhLlVCZPMOBr6q3S5XONsujLtt2yLnYwO4H/oxBiI6oxza3ALcCvWzaiJYL3C659ME9O5avc2Yca\nrLOdyuRJTuUZmWjcAjadLTCWnG5Ymqbd6cqCr5816h9VR7uqc09nC1X1mxUXfcWCrxX4rOfhHwz4\naI8G6xZMyOTUeXRJymbPpAaUBb+iM0ok5G/aNlKPdeQYteCn8yU33jdXC143FFnb1057NMjB0Qxl\n22b3wRR7h9UDUE/UVve10R4NstOzqIduQKRj8MGAjxMGEpwwkHCbc8wl/g6VMrm866I3FvxyRded\nQ6UhlmVZdMXDTS14XWuuQ3tQeX7qZ1E8Vp+wfFyNwOvKkKnpIsVSGbG2Pvk34PfNzoJ3rp9oCxGP\n6vK/Wgu+6BpDtbkqE+l80xp4qIQLGsfgwVpIC15K+c+obPbzpZRl4HIp5b+0bERLhKoYfM2Deb+T\nQXz8SjWrra37hOrlDGvrxctlm3/675v556/82V0DufraWuCbWPDj1Ra8bUPaM0Y94wwH/e5NW+ei\nd66huzN1tIfqVnHSEw3dDnL7/moRny6UiIYDnLgqwcGxTMMGEod0ktgxGqP33jtzt+ArK70N9MQY\nmcy6fbv1hE2LeCwcYP2qBKPJSq95dxLnyZ7/t1edxztedKYbz+zrmKPA11jwRuCXL94YtVfguuJh\nUpkCP7t1O3uH01V5HMc7C9Ls8TSgcXOKnPuw1pDwWZbrGq91xWtOPb5e4IMBH4XS4Xt3pLMF/D6L\naDhAu7bgPb/Fsm2rhlBNBD6dLTR1z4MnBr8YLXghxInAO4BvCiG+A7xHCPHtlo1oieC14Gtd9Pud\nWOhZ61Vjh0YW/BZPDKdW+LYNTroivX0wWW85T1diVo0EXs+aE20ht/nDoFNKsmXvBPtGpuhqD2NZ\nlvujqk2yc+NKzg+3sy1ENlesmoVmckUsC1Y6Gdrez6Fs2+TzJcIhPyc5ta2NrPhKG9XcEeUjLHWq\ncjnmmGQ37mkAsrI7hm1XJo75QpliqewKfSQUYL3T6nOHMxGbdi34isAH/D4Cfh9t0SNz0essehOD\nX/7orpm11mtnu3rmXH/nbg6MZuj15HGs6m3D77OqBF676LWAXnT2KgCeclo/oEKA2lNpWZZ7fo1l\nVfrPewn4fRRnsbrm1HSRtkgAy7LocJ6X3nBkLl/CxhNCaJCM2iyDHiqd7BrF4MuLIAb/M1TezW0o\nF73+75hmKlvQJeT1FrwTXzrTEfjRBgLvbShSu1zrA1tGgIoHYF9Nh7MqC77BbHbEjcGH3Bv2Mz98\niAe3jPCl6x6lXLZ52V+dBKgfQSjgq7PgdaZrxYJ34vCeyUYmVyQWDrgC4W1PWSiUsVExfHd1pwZr\nNGvvhk3jVqrLHW8uRyZXbNgKsxnaDdrVHnYnWdJT956ZLjKdKxIO+fH5LNavUgKvuxx6Eylr0W7S\nubrodQxeu+gDJot+2aJj8Ketq7aeLzp7Fad7tnkFMeD3sbqvjX0jU+4ql7UC//SzBvjsP17AS55x\nIn6f5a5Sp9Fuen3frlsZd937XmZrwWemC24fkxVd6n735qro30nMteDrfxPNMujB08muQbhAWfCH\nHeIRM6tGN1LK97duCEuTzHSR7kSE0eR0Xf3ygUNTWKjEkERbqE7gC8WSmyQC1Ra8bds8uHWEaNjP\ns5+4lm/+5nH2DqerStDcGHy0sQWvPQYdbWGeftYA98lhBkem2LxngnS2wBNO7uPcDX3u66ORQFUM\n/vFdY9z56AFWdsfchJcOZ9Y8mc65CTOZaeW28vkswkG/W3YFlQS7cNDP+lUJLGC7J/6r8X42Y8n6\nVaY0dzy8n1RqmieIvob7lypTNZ6Tqenq8pyZ0F6WWCTAgNMty9vYZmq64E7CAE5wBV7de4OH1ES0\nkYj/9RPX0t8VY23NKoSHo65Mzljwy5ZLzz+OUNDHM85ZXbVdHNeFOK6LT1x9Hzv2J+uej8f3x9kz\nlObAaIY1fe2kpwuEAj73WWZZlltX/5HXPrHOJd7lcfdfeOaAG/+vZTYxeNu2yUwX3WdadyJCwO+r\n6imRcatNGrvooXkGPRy+Dn5BY/DAnUKIF/0FzW2WHeWyTTZXpCcRxmdZdQ/p/aMZejoihIN+ehJh\nxlLVyXJq9mq7Mztvlvukk3h31kl9rBtwLPiRWgtel8k1jsGDcrkk2oJ0JyK84dJTgcqKcO01SSyx\ncKDKgv/Vn3bis+DNl53mulw7nUz6yXSNBe/MnCMhv5vQBZDLV2L4kVCA/u4Ye4fTdUmD3vyEmdac\n/+YvH+WHN21tun+por9LfS/U3kugLIibHxx0LR6NfmCEAn7Xgvd6ezLTRTf7F1RSZiwccHt5bxuc\npCsebuhyPK4/zt9esG7O9blumZyJwS97ggE/z33K8e79Vcsbn3cqPYkIL3jaCVXbtZWsf+9T2QLR\nBhY4qPuwtkuoLpXrTkR42lkD7ipz9eM7vMDnCiVKZdu9hs+y6O+OMjRWWXsjOyuBb24r+3wWAb9v\nBgv+/7N33mFSlWfjvqfsznZ2l11YehNfUYqooEhRYwtq7P2LPYhENCZREyEoKNiT2MtnSURN8stn\nYk00asSaxAoqljcWOktZWLa3Kb8/zrxnzszOLgvLmRnW574uLmbOnDnvM7NnznOengYFr5QKK6XC\nwEzgKSBotimlvtNTRBpbgkSwLOj8XH9cclR9Uxu1Da30jyaFFOZlEwxFbGsLYlO6jFXuzNg0JWxl\nxbn0LbEmuXXkou+oTM5aN8su2zAZ0Saz39kQAqwTt7E5aJ/QtY1tFOUH4n44xoI3bvRQOExLa8i2\nDnMC/ngLPiGGP6hPAU0twTiFHo5E4kZHJktGNDQ2t8UlCvYUzN+yPHrRS5Zo99YnlTz+D80n32yJ\n294aDJPl9+L1eijrlYPP64nraNjQHKS5NWRnyYN1c1ff2EZVTTO1Da2MGLBrZzgZa0Qa3Qj9eudz\n248PZlzCTHa7e2aTafDUZl9HuoJR8MluTJ1k+TwEQ+FOh2Q5m4YZ+pbk0dwa4p6/fsorH6xJ2i+i\nuCDbvq5C5xY8QCDL22EWfVoUvNba29E/vuN18A3NsbKOgtysuIuymcBlWoOak9m5j0kwiSn4mFVs\n9ivIy8LrtbJH129piEtAa2y2sj4DWT6roUOS88PZLMLIYEry8nPaW/ChcMS+KDe3BtvdlZvjmUx6\nOzs7eqycbF9cDN7MkzcxfOPqdU5Mq6m3Mr7Nd9VRJn04EqGpJURLa6idFbu7Y9yXxkWYrF1tTfSm\nKrEPQWtbyE7g8fu87VztNfVWwyPn37Iwer6afIg9drGCt1300X734qIXEjHXny21zdz2x6XUNrTa\n53FXMNeSwdsJH8W62e2ggi+1fkdLv6rij69+ZbvozU1Ilt/HLZdM4vzpe9nv2Z6Cz/J7O6yDT2uS\nnVLq3wnPfcAHrkm0G2A6hpX3yqUwL5uGpjZb8ZjkuRH9rQtnUgW/qR6vx8Ne0cEtZp4xxG4eTALL\ngLJ8gqFIXCZ+Q7PlGvd4PHZDh0QGV8QGEOQG/Hg9HrveOpkFD7FYU3NrKImCt+T5+39W8dXabY5M\nfmu/3GwfrW1h+3toSejuZOpY3/q4kve/3ATELHaThLc1IVchEonw8vtrWL851hQjMdt/d8dY8KYd\n8NbaZhqb2+Ju6Mw5kVhN0doWjstgNjdKBvP9Ov+WBblZhMIRlq+wvAG7XMEnWPDS6EZIxFRofL5y\nq90QbEeSOfcZVsqiGQduNx/HnHudVec4w50GM3vDYPeLcPyOsvy+OK9DZy56sDLpWzrIok9LDF4p\ntSTqoj/Q4ZoPA81YPeW/s5gEuSEVhRTlWfOP6qPuJpPkNDJatpHY+jAcibBmUz39escS2OqaYhdu\nc8EviCp4e/iCw33d2NwWZ4WbTHqnJT/SceH2eDzkOybFOR8Dce1qI5EILa2hdlmhvQoC9p3mTU98\nxBPRITrmJDcn/z8/XMff/r3SdtEHbBe9dcOx7Osq7n9mOS2tITv0MLx/LwLZvnYu+hWVdfzpn1/x\nwr9Xxj57S89S8ObGb39Vjtfj4cV3V/OTu97miZe1Yx/rMydWW7QGQ7aHBKCiNEHB1xgFH++iB/jv\nGutGdFCfnZ/wlwwPUgcvdI5RpsZQmjSmH2cdPnKHjtGvd/5280OM4dNZHD5Wgx+7npocAUPsdxR/\n3XT2j8jdjgWf7ffR1mEdfKdv7RaduegPi7rj709w0WdprU91T6TMxyj4oRWFdsZzXWMroXCYr9bV\nUFGaZ5enxeJN1sV5w5ZGWlpDDOpbQCDbR3aWl7qG+Bg+xG4MzE2AsW4jkYhdt2kwJ7LzjnKPgfGW\nmfOGoEMLvjlIa7S8LfFkDmT5+PkZ+3L+9L0o65XD8uj0OGeSHcBf3/yGv775ra2IjQJKrF2trm9h\nZfR7HNaviD7FuWza1hQXLzN13s5M+2QW/NrN9R22A850ttQ24/dZHeQm7t2HqppmQuEIb35cae9j\nzp267VjwiQq+KsmFyXTq2lLbTGFe8k6I3SHRghcFLyRirj/GIzV13AA7M35X4u/CwBlnybFhcN9C\ne/4GxMKu7RS8Q6lvz0WfneW1Jyw6CYcj7cbE7kq64j873LXVM5yVG2qpbWjffW3lhlpKCgPxvYsb\nWlm9sZ6W1lBc0wVzMpvOSEu/smrc9x5ixd8Lc7PjLXij4KM3CKVRC97Epxuag4TCkbhSKqPgnUo8\n8WLvVOqJCt7cGDS1BO04erLM2L2GlDBtXH8O2bd/u/eau9nWtjCRSKwvunFdeTwerjprvF2LXV3X\nwsoNtWT5vfQvy6NPSS6tbeE4N7SJ9ztj84kKvrUtxLWPvMc1D+54T/9MYEtNs12NcdykoXbXKw+x\nvgImubAmoSFSazAUr+CjLnrzN0nqondUUJje87uSWAxeyuSE5OQnXH96FXatLHRH6crIWGfTMENu\nwM/tP57MydOGA7Fy0sRae6dbfrsuer+XYCjSLoco7Z3sgGVKqXOVxWDzzzWJMoSttc1c//sPWPR4\nfLrBtvoWttW32i0XzUSl2sY2VkYbiDjjmrEYvHVx/kBvxuf1sO/Isuj7s6htaLMt15gFH3XRF8W7\n6E0TG2ephrHCnD+cRPeVU6knJtk5Y/Cmfr2j0pfEzxeLwcfvvz76o3AqoFFDSpg8pp/9OdZtbmBw\nnwJ8Xm+swYRjKE1Ng6XYnaV5iU2FTHe8UCcNYpZ9XcWn327p8PV00dIaor6pzf5b9i/L596fTuOI\nAwYSwSqnhNg5UV3bwkPPf8byb7cQDkcIhiJxLvr+Zfn4fd5Yi2RjwTv+Ns7zwA2rqV0MXrLohQSy\n/d643IxeBbv+PISYBd+2gxa8wVjxxhOWmOm/YxZ88oEz4TBpt+APAhYAL/Ed6mRXGbVAE4fBrKyM\nuechlgxX29hqW5rOGI6Jpdc3tlG1rYlVG+oYNaTEvtBaZXRhO5HDnHBGwZvxi6Zm1JxsZY6kFHOn\n2rsowOWnjOXWWZPafZ6uxODrGtti7Us7UfBDK2LlcyZ2lXiCfxttapM4OKIk+mP+9JsthMIR+1gm\ni9yp4I0FH3a47RNj8J+vjA24SVYOEwyFueupT/jtnz/u8PO4yZsfr+fxl3VS2Uwf/t6O5j4+rzeu\n4sA5bW5LbTP//mwjv/nzx7a7z5l9nJ+Txdxz9ueiY62+B2bFxCx6Q0mRCwo+sRe9WPBCAok5QcUu\nKfiuWfDts+gNzql22VneuPG4QNzNdVcVfKIsblvw2y0+1FoPdW31DKaj6WZmoMrwaPtE53hBo4Sd\nllGhI4veZNg760LNyV3T0EJejt920efnZtHS2EJ2lo+C3Cy2ROvFq+zpTE4L3jqR/X6v7RlIxNxQ\n5Ab87WqTjQJ48pX/2kMbcjpR8M4TOyvqUk68IaiPtvI1/QAM5rsxMXzTzKdPNHP1iZc1S5au5Rdn\n7xdnuRsSXfRfrNpqP25oDrYLP5i2rGD9uDrqG+AWr324ltWb6jlh8rB2F4gt0byBxHpeM3pzzaZ6\nu6d8IsYSSOwDbqz37KxYWU7HLvpdf2H1JLroJQYvJKEgN4ua+la8Hg+FedlsaWr/W+8uWV2IwZuJ\nmMkUfIlDwe81uKRdRYjX4yGQ7YsmJW/fRQ/tu9lZMfhO39otOpRKKbVAa31ddMBMBHD+UiNa6wvd\nEyv9bNjSmHT7V2tr8BArg7Nd9A1tsd7gjgunuVOtb2qzbxpMnSXEks+21bXQr3c+9c1W0wfnhbF3\nUQ7rtzQQiUTYHLXgnVO+bAXfSUmSccsX5Lb/kw+NVgPUNrahV1tVAJ1Z8ACjh5ey/NuttpJIdgdb\nXpLbfhBFdH9TJ288IX2jXo/WYJgVlXWs3FBn1387cbroG5uDdqIeWEk7iQr+C8cI2621zXY5mpNN\n1Y20BsP2zPQd4et1NTQ2Bxk7onfS143HpXJLQxIFH/XGJCj4/mV5eD0e1myqS9r4Jjfgsy8UgQ4s\nh7yAn9a2Vnt/g/P7cScGn9jJTlz0QnvM9agw2u/DDbpiwcdc9O1H1JY4PAvOVuFOcoyC76IF35Ji\nC76zX58JPr+BNWjm9ei/74SL3tmL2LhXg6EwKyprGVBeYCtAZxb91toWivKz4xStz+slL+CnzqHg\nnTWfiQ1kGpra2imp0qIAbcFw3DHKklnwnSh4c8xkJ3JxQYDfXjYFvy9WK789BX/ZyWNY+KMD6dfb\nstCTJZkMKGtfgmV12LNO6Owsr/3+4gRrctXGurjBNoYmhwW/sboRp+c72Q2Bc0b95g4y7e97ejm3\n/3Fppx2vOuLXf1rGHf/3cVwPeENjtBc8xEI+Tozyd7oCwcqp6F+Wx5qN9XFtjA3FBQH7QtHRHOrE\npCGDMznTzRi8sZrcjC8Kuy8m5t3VuQs7Q5cs+OYgXo8nqYJ2evtGd6jg/XH/d0QyCz4SiRCJpK+T\n3fPR/38PvABsBTYBz2mtH3NNogxho+OCbKzN1RvraQuG7cYsYLl2fF6PHYNP5vYsyLO6h22uacZD\n/AXdVvANsSz5xBi5XSpX20zVtiYKcrPiTqiYgu/4RDEKPvHmweCJusoMuZ1MR7LW9MW535Ptn8wi\n9jrGPQ7uW2grgMSTfEVlbbuyMIDXl61n3sPvWm1vowrSNHhJbAQTDIXjRtQmG9vb0hpizaZ6ahvb\n4mZAdxVzbjz8wuftLAXnehu2NLJ5WxN3PfWJXWZpEieT9bYe3r+I1mDY9qg4LzZtwbA9erIjC76X\nw1vgjHHmBfy2G93VGHy0e5i46IVkmITgovzk16Ndgb9LFnyb3TQsGQfu3Zf+ZfntqpIM5sZgZ2Lw\nxphKa5KdUupkYBlwPjAD+FgpNd01iTKAYCgcl1xn3KRmjrZzfKHX46EgL4vKqkaCoXBSq6gg1+r/\nvXlbE6VFgThLu7jQuOhbaWkL0RYMtysjMX3K121uYEttc7uuT+bin2x0rCF/Owoe4hOwtmfBJ+K8\n4TAX+Y6mPBlrfaij2x5Yk6N+dvo4Alk+ln+7lY7s6XVVDXxbWWsrUBMuSYzZN7YECYYidp5EsrG9\nazbX2+tsrt7xWnqTWVtV08x/18Zb8c71Vm+s476nl7Ps6ypefHeV/R6f15M0yWh49DOZ7H/n37ap\nJWjH1ztq8Xn2kXtyztGKa88/IO6c9Ho9thfHlRh8VEwZNiN0RkGOUfDuW/CdZdE3NgeTxt8NM4/f\nhxsumtjhDUBJQYCcbF+HN9qGZBa8qZhLdxb9fGCi1voUrfXJwBTgZtckygA2b2uKy9w2Ct640fsU\nx9/NFeVl267Y0qL21phpD1pd134casxF32In2BUkuNGHRTPNl31VRTAUiUuwg9jFvzMXfe9eOXiI\nz75PxJnxvj2XUyJOC35gVLF3FNM2sa1hFfFToIb1K2L08N4M6luQNPbsJBKO2M1tTMJjYs8C003P\nyJHMgneO7d3UQWJlhzJEIjQ5+u9/8nV8KZ5zvS9Xb2NVdAbBsq+raGkNUVXTTGlRIOkPfHh00I/J\nIRjjiPE3t4ZiMfgOFPyAsnwOGz8gruLBUF6cS1mvnF3e5AYcMXhx0QudYLyURS666LdnwVtNw9qH\nRBPprGPeedP3Yu45+2/XzW7H4NuSWPBproNvA+y2WlrrVUCPniZnLC9zghhl09CcPOOyaDuZyU4L\nqixBORflZePxWArerJMYJx/UtwCvx8PSr6qA9oqzKy76PsW5XHv+BI45qOMWBnEu+k7uapPhvCE4\n+8g9OeN7e7TrjW4Y2q+ILL+XkYOS90Ef2jdm2XdkATa2BG0FapShqZs3mH74FaV5+LweuwLBiVG6\n0HHlREeYpj6jhpQQyPLxyTdVca8n3lAUF2Rz9MRBtLaFef/LTdQ2tLa74TP0L8uPswomj67g2vMP\nYJ+hJYTCEftc2Z7lkIwfnzian5+57w6/ryvEFLy46IWOyc+NJdm5xfaGzVgVKpGkeUldpVd+NgO6\nkJxrGlg5u9mFw0bB7/Ty26WzLPpTog//C/wlmk0fAs4GlronUvoxsdwBZfms2lhnj3B1lrA52U/1\n4bNoPXayuOakfSp4Y9l6oP1QBa/XQ1F+dpwFnxiDD2RZ8W4zF358Qimcs0yuM4YkuMQTcZZQ7biL\n3lI0gWwfew4qjuvml8jREwcxbVz/Du+cD99/IFtqm1lf1cDAPgV8qDe326ex2YrB5wX8HcbgnV35\nSosCSS341U4Fn8RFv3JDLV6Ph8F923935vgFuVnsPbSEpV9VsbG6kb7Rkj/jYZg8uoJ3lm/g3KOt\nNr//eG8NS5auA9on2Bm8Xg+jBpew7GvrpiE/N4uhFUV28pz5rDsyhcuwvTGb3cFYO6mILwq7LyP6\n9yIneq1wi+1Z8PagmSSVRbuapC76NMfgfwAchzVcphY4GTgNCG7nfbs9JnPZJJHFLPjkXY+mjetn\nPy5JEk91JuUVJlFqxQUBttW32hftXkniUsNMvXhxbrva8q5k0XeFOAt+B130gWwfHuK9GR3h83o7\ndYv1Lc3jslPGctPMSfbEvUQamq2Z5sbVnBfwt1PwxoIPZPso65VLTUOrnZwGlotufVUDA8sL8HiS\nu+iv//0HzP/d+4B1ofjP8kr7h9nUapoC+VBROU0jJLA8QYEsHz88WrFoxoHsO7KM/uX5ZPu9dn1+\nsgQ7w/nH7MXYEb0pyM2ymyeZGy+Tb9CRiz5dJFbFiQUvJGNQnwLu+9khjBzonoI318Wttc1U1Vhz\nLpzKviOPqTuyWL9TpzfBtuBd/I10eBXXWp/v2qoZjrl4miQxW8E3tRHI9rVTpD6vl/kXTOA/n21s\nN+QFLKvmp6eP44+vfhXX5MZQUhBg1YY6uzSvKL/9TcLQfkW89Ukl4/csaxcTMidPZ0l2XcHpLsvN\n8dPc0PVIjNfjYWi/og6zTXcWEw7x+zwcc9AQnntnJWC501vaQrY12qsgu9289GbHyFq7I2Bdi21h\nNzQH7ZyG5tZgOwXvLJsLhsK8sWwdf3j1Ky47eQzj9yynKZp3kZPtt0sCTYvecDjCxuomyoutXgCm\nHNDr8dCvd74dGujMmi7Ky+aK08bF1cqapD4TjtgZF72bJMYTxYIX0kVWNGT58vtrePn9NZQWBaht\naGXhjIPoU5wb85juYDhy52Rp700w3bXT2snuu4htwfdOtODbKOjgZBjctzCpG9cwZnhvxlycvBmK\nKRszTVt6FbS34A/auy+bqhv5/sT2MXRz8nS3LaiZNAaW0mpuaF9X3hnzzjugW+snw1isuQE/NdAK\nJwAAIABJREFUJ04dzoRRfZn38Lus2miFK0wMu7w4l8otjTQ4RunaCj7LZ3el2lobU/AmKa8oP5vy\n4ly+WFVNS1tsgIuzb/SWmmZWR9dctbGO8XuWx91A9E9Q8JVbG2lpCzGkon18rn9ZTMF3ZsEbnBcA\nM8bXeCsyzYJPvPn0uXjxEoTOSEwi3RrtBrpmY72l4I1HdjtJdrsCv9+UjzoUfAos+B7tat9ZzIW/\nf4IFX98cdMWdY5SPcdsmc9HnBvyc8b2RSQczmASO7rZhNRa83+dJeUvXjkicVmeeG0VqBkIYpb1x\na8wKNzXqOQF/u57+4FDwedl2LHybo1mOs2vepm1NVG6x1lwXHQLT3BKL8RcXZJMb8LM+uo8ZPJQs\ni91ZPrij8fDdzUUvFryQLoxSBatRzQXT9wKgNmq4mCmN28ui3xUkteBTkGTXlTr405VS7n8DGURt\nQyu5AT8lUUu6oamNYChMS2vIlbu98uhFvi6azLejtaHjR5ZzxP4DGT0suYegqxgFv6Mlcm7itOAh\n5k4zPxRToVARbf/rbFBkkuACWT77RmDpV1XMf/Q9qrY12Z6aovxs22sSP7kuVgK3qbrJVt5mfKQp\nkcvJ9uHxeBhQls/GrU20BcO2N8b02ndi3Plej2eHu8mZ3Ajbgs9wF72vm2EjQdhZnCHLsuJcu0TY\n/HYa0hKDz7BGN8B04Gul1L1KqQmuSZJB1DS0UpSfTZbfRyDLR11TW6djBbuLszY9J9u3w1ZZSWGA\ns4/cs9t3oibJLpOsQlNfbxR8lt8bVw5o+giYHvOVcQreGYO3bqI++u9mVm+q5/NV1XFJjbGZAg4F\n76jF/2rtNnvi38bqRtqCIfv4Rrb+ZXmEIxE2VjeyckMtPq+HQUlKaIyCLykM7HCvdrOWXSaXQX8r\nSKLgxYJPCR999AHXXTcnbtv999/Niy++kHT/RYvm8+67/+bvf3+eBx64JxUiphxnVVHvooD9G7cV\nvO2id9+gMdespJ3s0lkHr7W+ANgb+A+wQCn1oVLqSqVUH9ekSiOhcJj6xjZ6Ra3ZvBw/jc3BDkvk\ndgXOOGwy93yqyMvxW32Zt9OmNpWYcbTGcvV4PHFzmWMWvHHRO1oMOxV8Qvni1trmuBh8r4QfP8Rb\n8B9/E2tiE4lA5ZbGuCQ7gP5lljJfWVnHmo319C/LT1rGVtorhz7FuXEdEbtKYkvgnSmTc5NEa8TN\ni5cQI1kzls4atJjXOttnd8dpwfcuyon9xuvjLfjExmKuyOLvxEWfjix6J1rrBqXUKmANsCcwFnhN\nKfWg1vruzt4bvRH4EDgc2AY8BBRjTac7V2u9Uik1A7gYqwRvodb6b0qpXOAJoByoA87TWlclW2NX\nUt/YRgQoilqG+Tl+tta2xGomXTgZeuVnk+X30hYMu9q6cXt4PR6OmTSYEhemjO0seTl+vj9xMPvt\nXWFvy82xJt9BzIIvLgyQneVNcNHHyuRyA357tCNYfeCN8inKz7Yz5p3NcpwxePO+vYaU8OWqatZX\nNcR5CAB71O6fl3xNazBsP0/E6/Gw4KKJO2XdJvYnCGT7CLV03Ioz1STqC7HgU0NHg5JCoRC33LKQ\njRs3smVLFVOmTGPOnKuT7vvHPz7Ba6+9jM/nZ9y48Vx88Y/5n/85lT/84S9s3bqVk08+hhdeeJWc\nnBwuueRCHn30CR544B4++WQZ4XCYM844m8MOO4JvvvmaO++8nUgkQq9evbjmmmvR+kuefHIx2dlZ\nrF+/jsMPP4pzz3V3IGmcBd8rh/zo3JD2FnzqFHwwWZJdOrPolVKLgLOAlcCjwE+01s1KqSJgBdCh\ngo/G7h8EGrAU+q3A41rrp5RShwKjlVLNwGXA/kAu8LZS6hVgFvCx1vp6pdQZwK+AK3b2g3YV220b\ndVfnBfysa2mwm9244c7xeDz0Lsphw9bGtFrwACdPG5HW9ZNx+vf2oLy8kM2brbi2seALcrPsH47X\n46FvSR4bqhv5au02Rg4sptkk2WVbwyRKCwNURscAb61tsZtPONtlxsfg27fLnbLvAL5cVU3llkaa\nW+Jd9IP6FDCsXyErorXwh+zbv8PPtLOu9XYKPstnz7TOBKRMLn189NEHXHbZTPv5+vXr+NGPLmGf\nfUbzi1/8ipaWFk455dikCv6bb75myZJXeeCB3+Hz+Zg79yreffffjBs3nk8//YS1a1czYsQefPDB\ne+Tm5nDggZP4z3/+RWXleu6772FaWlq45JILmDDhIG65ZSFz585nyJChvPDCszz55GImTDiQjRs3\nsHjxn2htbeXEE7/vuoJPtOA9Hg+9CrJjSXZNbXggziPotiyZWCYXAg7XWq9wbtRa13Zh6MxtwP3A\nNdHnB2MNq3kF64bhJ8ARwDta6zagTSn1NZaHYDJwS/R9LwHzuiBrt4klXhkXfRYRoCqafe1WQkZZ\nsVHwu34ASE/D1MYnDmkZWF7Amk313PTER/zi7PF2kl1OVJnGK/hm8nL8+H1ecgM+PJ4kLvom6/1T\nx/ZjW30r++1ZxsS9K3j42eVU1TTb1qpzktS0cf1ZUanZa3CxXfu+K0lU8NlZPtoPok0fiQpdLPjU\nsd9+B7BgwY328wceuIeGhnpWrPiWjz76kLy8fFpbk98Mrl69kn32GYPPZ53L48aNZ8WKbzjkkO/x\n73+/TWXlei6++Me8+ebr+Hw+jjvuBD766AO0/tK+qQiFQlRWrmf16pXcfvtNAASDQQYNskp7R4wY\ngdfrJScnh0DA/eucsxLIXCt65WezZlO93Yc+L8efkpvQjHPRK6XOAyLAN8BUpdTU6EseIKK1Xqy1\nfq+T958PbNZav6yUuib6vqHAVq31kUqpecAvsFrh1jjeWgf0AoqwOug5t7mOseCMq9woE9PG1DUF\nH63ndnN8Yk/BJDomZqCfdcRIKkpzefqtFXyoN9PSGsJDrIywd69coJosv5etdS20hcL0ys/CE50H\nne33smpDHfc+/SmnHjqCxqgFf/TEwXade0lJLh4PbKlpoiBq+TuV7qR9KlhX1cDk0f1wgzxHDN7r\n8XQ6fyAdJFojPTjEu9tQUFDIVVfNYe3aNTz//NNJ9xkyZCh/+tOThEIhvF4vy5YtZfr0Y5kw4UAW\nL36U3NxcDjpoMg89dD/Z2QH22mtvqqqq2G+//bn66rkEg0Eef/x3DBgwkEGDhjBv3vX06dOXZcs+\noqbGXN5TezI4by6NEu2VH2BFqI7GFiuvKhUZ9NCBi97Oondv3c4s+MMg6cROT3T74u0c+wIgopQ6\nAtgXeAwrxv5c9PXngUXAB4CzlqgQK1Zf69hutrmOsfBMXbVx35hBJAUuZVyaUrl0xuB3F8zfpKQw\n/rsqyM1i+kFDeOm91Sz7usqOu5tEomMmDWFov0I+/WYLS7+qYmtti90C2OOxZgJU1TTzod5Mtt9r\nzzR3xuj8Pi+lhQGqapvtEjCnBZ+d5ePsI/Z07bP7fV56FwXYUttCOBLJuCQppzg+ryfj5OupeDzJ\nv2uv18e77/4brb+goqIfSo1i48aN7d47fPgefO97RzBr1kVEImHGjh3P1KmHAtC3b18qKvrj8XgY\nPHgopaWlAEyZMo2lSz/k0ktn0NTUyLRph5GXl8eVV17DDTdca98s/PKX89i8eVOCfO6fFx6Ph4rS\nvLjumkWORLuG5iAl5anxmPqSuujTGIPvbqtarfUh5rFSagkwE0uhH4uVPHcIsBx4D1iklAoAOcCo\n6PZ3gGOA97FK9d7c3polJXn4uzECs7y8kE3RgST77l1BYV42ZaWW5bY1atkP7F9MeXnnQ1t2hulT\nRrBhWzNHHDTMnpfuxjo7QrrXT8TI0zt68zWgb1FSGQ8YVcFby6xhLqVFAXuf8vJC9hnZh+qGT+3J\nfGUlefbrZcW59kCa97/cZE+JGjKwJM7dV1FWwBcrtlBckEOW30u/ipQ4l2wWzprMHX9cat94ZNLf\nqax3rCzQ5/WkXbZ0r+/ETVmOOupQjjrq0Lht8+ZZkdGZM9vHun/729vbbZs9+xJmz76k3fb77ouV\n0d17711xr11//bXt9i8vn8CUKX9I2Lp3nHz/+tc7Ce9x57t5aO6Rcc/79bHOzzY8tAXDlBTlxq3t\n5t/I7/OCJ/ab2BzVKQUFgQ7X7a48nbno/6a1PlYptSLJyxGt9fCdWO/nwMNKqVlYFvnZWusapdRd\nwFtYZXtztNYtSqn7gceUUm8BLVhT7Dqlunrno5EmieubtdsoKQzQ3NBitWoNW3dcldHmJm3NrXay\n167mgu8r6/jNrXFJZekg3esnEidP9G+S5SWpjHsN7GUr+Cy/r90+uQ5lXVqQHXs9rvd8hFUb6ghk\n+9hW3RAnR6+8LMIRWLWhlrwcf8q/p4AHfnH2eDtzOlP+TuXlhVRvi/0GvV6PnMNRRJaOSaU8WVFj\n+fNvrAmVWb7YOeq2HFl+D03NbfYaW7dGG2Y1tSVdt6vydHYT0Jm/eUb0/8OSvJa8JqMDtNbOYxyV\n5PWHgYcTtjUBp+/IOt2lvqmN6roWxo6IdYQz7uBgKIzP64nLuBbSw56DiinKz0Z1MGrS2T0uJ0m2\nerGj1/+xk4baj9dGW9COGd6bL1dX0xYMJ21sZPoWhMKROPd8qslE97c3wUUvCJmEuX5viIZiUzFo\nxuD3eeN70Ue1qJu/kw7D+1rr9dGHG4D9gKnANCyFf5FrEqWRNZusYSIDHd3H8hwnQHFBtpT9ZAAj\nBxZzx2VTOsxS71uSZ7vUkyngvYeVMmpICVefNT6u+9/J0yyn1IlTh7FvdOqfGVDhxCREwo6P1e3p\neJMkNglCpmB+76ZfRir60BtMrxNDLAbv3ppduTr9Fas+fSRWHHwa8Kx7IqUPo+AH9YkpeOcdXvEO\n9g0X0oPX66G8OJf1VQ1Js8yL8rK56qzx7bYfsm9/Dh5dQXaWjwl79eH9LzclPb6z8+DQfjveja4n\n40wYEgUvZBoF0Q6lG1yuikpGls9r9+aAzJkmp4DvAU9j1bVPBNrPLO0BbIrG8Pv1jmVd5sa1Rc2c\nDm9C5/SJ9vffksQC7wiPx2O3ft13ZBl7DS7mjO/t0W4/c34U5GZx1uEjd4G0PQenghcXvZBpFEYt\ndtOmOhV96A1+v5dg0mly6W10s1FrHVFKfQmM1Vo/ppSq2O67dkOSTXNz3uGVigW/29CnxFLwprxx\nR/H7vFx99n5JX+tVEOCGiyZSVpybccNe0o3zWiV96IVMI7Etbaot+KQu+jRb8J8ppe4GXgeuiDat\n6ZGari7axc4Zl3HG4Hd0tKeQPvYZZtXq7j201JXjDygvEOWeBOfFSix4IdOwOlfGrump6ENvyPJb\nSXam+iVaDJTeaXLAJcCftdafAdcBFXShZG13pK6xjbyA1b7UYDVKsR6Lgt99GDO8N1eduS8zj987\n3aJ8p5AYvJDpOJuVpTqLPhKxqm8gNiAoXa1qD8FRDqeUmobVUvavgDtmUZqpa2ylMC/+js4bHU/a\n0By0Z4oLuwejXLLehY6Jt+Bd7MEpCDtJQW42m7c1Rx+n1oIHq5ud3+e1FX26suivwlLw/bBGxL6G\n1Wr2UOATrMS7HkM4HKG+KUgfR1tDQ16OpeCLC6UGXhA6Q+rghUzHacTlpdCCT+xHb2LwnnRY8Frr\n4wCUUv/ASq5bGX3eD6vVbI+ivqmNcCRiZ1k6ycvJwkNzu+llgiDE4xEXvZDhGKs9N+BPqZcpcWSs\nyaL3pTmLfrBR7lE2AAPcESd91NRb5VSFSTrVnThlGFvrWuJi84IgtEfK5IRMxyj4VMbfwSqTA+xu\ndqnIou/KJ3xPKfUE8CespLxzgCWuSZQmjIJPNq51XLSrmSAIneM0iMSCFzIRW8GnMP4ODhd9ggWf\n7jr4i4HZWNPgIsArwP2uSZQmaqKNDwpzJc4uCDuLRyx4IcMx3ewKUmzB2y5624K3tnvSNA8eAK11\nC/Dr6L8eS63tok/tXZ0g9CSkF72Q6RSm2YJPjMGnuw7+O4Ftwcu0OEHYaZyXKrHghUwkbS56X4KL\nPhqDT8s0ue8aNXViwQtCd/F4PHZjKFHwQiYytF8R++5RxsS9+qR03cQku0iGxOBRSg0D9gZeBgZq\nrVe4JlGaEAteEHYNXo+HUCQiLnohIwlk+bj81LEpXzexTC6Ugjr47VrwSqkzgeeAu4DewL+UUue4\nJlGaaGoJApAXkPnegtAdjGIXC14QYmQllsllSAz+F8BkoFZrvQHYD7jGNYnSRFvQmtPr98tFSRC6\ng7lgiQUvCDH8iY1uoln0bvba6cqhQ1rrWvNEa10JhDrZf7ckGIrgQUZcCkJ3sWPw8lsSBJvEOvhI\nhnSy+0wpdRmQrZTaF/gxsMw1idJEMBjG5/PG1fEKgrDjiAUvdIV77rkDrb+gpqaahoZG+vcfwIoV\n37L//hNYsODGnT7uI488SO/eZZx44ik79f677vo1Z5zxP/TtW9HutRdffIHCwiKmTJm2w8eNuegt\nxW4Pm0lzJ7tLgV8BTcCjWENnfu6aRGmiLRTG75MLkiB0F4nBC11h9uwrAHj77Vf57DPNzJmXsnTp\nhzzzzF+6ddzuGmmXX96xeps+/bidPm7MRW85wO1hM+m04LXW9cAvXZMgQwiGwtJrXhB2AUaviwUv\ndBUzGz0SibB27RquvPJyqqurmTx5KhdeeDFLl37I73//MOFwmKamJq67biF+v5/58+fSt28F69at\nZdSofbjyypiqWrt2DQsW/IprrplHfX0999xzB1lZWQQCOSxceAs+n5cbbriOLVuq6NOnL59+uoy/\n/vXvzJ59MVdfPYfrr7+WhQtvoaKiH0uWvMonn3xMYWEhpaW9GTJkKE888RjZ2VmsX7+Oww8/inPP\nvZC1a9ewaNF8srKyqKjoR2Xleu6++0EgSaObTOhFr5RagzVcZlt0U3H08TfADK11j3DXWy56uSAJ\nQnfx2Ba83DALO05raws33/wbQqEgp5xyHBdeeDErV65g3rwbKCsr4/HHf8eSJa9y1FHTWbt2NXfc\ncR+BQIDTTz+BrVu3ALB69Ur+9rfnmD9/EQMGDOS+++7kiCOO4rTTzuLtt9+grq6WN95YwoABA1m4\n8BZWr17JOeecAcQs6uOOO56XXvob55//I1588QVmzbqcJUteteXcuHEDixf/idbWVk488fuce+6F\n3HvvnZx33kUcdNDBPP/8M1RWrrf3T8yij1j/pb3RzRvAyVrrUq11KXAs8CxWb/r7XJMsxQRDYfxy\nQRKEbmNi8OKiF3aG4cNH4Pf7CQRy8Pl8AJSVlXHHHbdx440L+OijDwiFLDf3gAGDyM3Nxev10rt3\nGa2tVj+Td9/9N62tLbayPuecC9m8eTM/+cksXn/9n/j9flavXsno0WMAGDx4KKWlpQ4pPBx55PdZ\nsuSfVFVV0dDQwLBhw+PkHDFiBF6vl5ycHAIBa5T46tUrGTPGqrEfO3bfuP3N7yEUjcHbFnyay+TG\naK2fMU+01i8C47TWHwE5rkmWYoKhsN1pSBCEnUdc9EL3aH/e3HrrjcydO585c66jrKyccNgyfzuK\nX59++tnMnv1TFi2aTzgc5uWX/8706cdx110PMHToCJ577mmGDRvB8uWfArBu3Vqqq6vjjpGfX4BS\ne3HXXb/m2GOP75Kcw4aN4NNPPwHgs88+jXvNKHhT/26S7NzM6+5Kkt02pdQlwOOADzgb2KKUGkUP\nanXbFoyQG5ALkiB0F49k0Qs7iDlnrFbHzvPGenzUUdO59NIfUVZWzuDBQ9mypSrufYmPASZMOJDX\nX/8nTz75GPvvP4FbbllITk4uPp+Xq6+eS0lJKTfeOJ/Zsy+mb98K2wp3cvzxJ3HllZczd+51SWVN\nlHPWrMu46abr+eMfn6CgIB+/P6ZibQs+nGDBpzmL/n+AO4FbsOrfXwHOBU6lByXfiYteEHYNkkUv\n7AgnnXQSU6bUATB+/P6MH7+//dqzz74EwGWX/TTpex944NF2jy+88GJ721VXzbEfP/jg7+Leu3z5\nJxx33AlMmHAQa9as5ssvPwOwk+IARo8ey0svvW4/dx47mZyffbaca665lgEDBvL888/EWfHeBAWf\nEb3otdZrgbiCQqVUrtb6btekSgNtQSmTE4RdgdTBC7sD/fsPYP78uTz66EMEg0Guvfbabh+zb9++\nXHfdHHJyrPyBX/5ynv2aL1qlFQqnbppcV7LoTwWuBfKxXPI+IAD0dU2qFBOJRAiGwvYfQBCEnUem\nyQm7A6Wlvbnrrgfs5+XlhWzeXNetY44bN56HH16c9DXTsa5dDD7NLvpbgR8BPwMWAUcD9a5JlAbM\nFy0WvCB0H2O5S9tnQYhhyrDtGHy0TM7N++CumKzVWuvXgP8AvbTW84GT3BMp9ZiyBWl0IwjdR8rk\nBKE97WLwGVIm16iU2hP4EjhUKdWj3PMAweitlFyQBKH72ApePGKCYONPKJPLlCz6X2G55n+INTr2\nEuDhri6glOoDfAgcrrX+b3Tb2cBsrfXB0eczgIuBILBQa/03pVQu8ARQDtQB52mtq7q67o4QFAte\nEHYZphhFkuwEIUaiBR/OkGEze2utT4s+nqCUKtVab+3KwZVSWcCDQINj23jgQsfzCuAyYH8gF3hb\nKfUKMAv4WGt9vVLqDKwbjSu6su6OEoq2DpQYvCB0H1MfLONiBSFGYh18KAVlcl0xWWc7n3RVuUe5\nDbgfqARQSvXG8gZcQawN0ETgHa11W3Tu/NfAWGAy8FJ0n5eAI3Zg3R0iGFXwkkUvCN1HyuQEoT1m\nNkPYjsFb29NaBw+sUUq9BrwLNEe3RbTW13f2JqXU+cBmrfXLSqlrgCzgEaxs/GbHrkVAjeN5HdAr\nur02YZsrGBd9lih4Qeg2XimTE4R2GD1uPMaxGLx7a3ZFwf8n+n/0fiNJA97kXABElFJHAPsCnwDf\nYln0OcDeSqnfAEuAQsf7CrGm1dU6tpttnVJSkoff7+uieDHq26wvvLAgQHl54Xb2Th3pliXd6yeS\nKfJkihyGTJKnvLyQQCALgOLivLTLlu71nYgsHZMp8rgth9/nwevzUl5eaOuqPn2KCGQl11vdlacr\nnezmK6UKgBHAp0BedEb89t53iHmslFoCzHQk2Q0B/qS1/lk0Br8omp2fA4wClgPvAMcA7wPTgTe3\nt2Z1deP2dknKps3Wx2ltDXa70cGuYlc0Xdid108kU+TJFDkMmSSPkSUYtCZ9NdQ3yzkcRWTpmEyR\nJxVyeD0emlssPdPc0gbA1i31SRO8uypPZzcB23UOKKUOB5ZhjYjtB6xUSh293VU7x0PUI6C13gDc\nBbwF/BOYo7VuwbL091FKvYXVaGdBN9fskKAk2QnCLsNudCMuekGIw+v1xMrkMiSL/iZgKvB3rfU6\npdQhwB+Bf3R1Ea31YQnPVwIHO54/TELpnda6CTi9q2t0BzuLXobNCEK3ibWqld+TIDjxeT2EIgkK\nPs1Z9F6tdaV5orX+jFg8vkcQjH7R0phDELqPdLIThOT4vB67c2o44n47565Y8GuVUj8AUEoVA5cC\nq12VKsXEXPRicQhCd5EyOUFIjs/ndZTJRVzNoIeuWfAzsWbCD8LKgh+P1XWuxyC96AVh1yHz4AUh\nOV6PJ25crCcDLPhJwLla61ZXJUkjsUY3ckEShO5i9LpY8IIQj8/noTValh0Ou++i74rJ+kNghVLq\nAaXUFFelSRN2L3pJChKEbuORGLwgJMXn9cR60WeCi15rfSqwF/Av4JdKqS+VUgvdFSu1mGlyfr9c\nkAShu8g8eEFIjrNMLhKJZIQFj9a6DqvxzL+BViy3fY8hGJQyOUHYVUirWkFITrwFT/pj8EqpnwNn\nYnWZewI4Rmu91lWpUoyMixWEXYfMgxeE5MQp+HAEt++Bu5JkNwCYobVe5q4o6cNkNUonO0HoPll+\n60ZZhjcJQjw+b6xMLhyJ4HFZw3dFwc8BjlFKjcFqMesHhmqtr3VVshRiLHgZFysI3efICYMYUF5A\n71456RZFEDIKb9SCj0QiKYnBd0XB/xXIBUZiDXyZhtWXvscgvegFYdfRr3c+/Xrnp1sMQcg4TF5K\nOBLJmDI5BXwPeBq4DZgIDHZTqFQjjW4EQRAEt7EVfDgSbXTj7npd0WgbtdYR4EtgrNZ6PVDhrlip\nxW50I1m/giAIgkuYEtJgKBKtg0+/i/4zpdTdWONbn1RK9QcCrkqVYsywGbHgBUEQBLdwuugj4cyo\ng58F/Flr/TlwHZb1frarUqUYicELgiAIbmMUfCgUsabJpduC11oHgbeij58DnnNVojQQkmlygiAI\ngsuYSi2TSZ8JMfgeT5sk2QmCIAguY1zyoXDYisFngIu+xxMSF70gCILgMnFZ9BlSJtfjkUY3giAI\ngtuY9s3GRZ/2aXLfBSTJTthdqKxcz8yZF3R5/6uv/ikbNlS6KFE85557RkrW+eijDzjuuCO57LKZ\nzJ59MbNmXchrr72akrUFYWcxSXWhaB18JnSy6/GEQmE8HhlvKfRUet557fF42H//CSxYcCMATU1N\nzJ59MYMGDWbkyD3TLJ0gJCfRRZ/2aXLfBYLhCH6f1/UvWxB2JbNnX8y4cWP47LMvaGho4IYbbqGi\nooJHHnmQf/3rbXr3LmPTpo0A1NfXc/PN11NbWwvAFVdcyfDhe3DeeWcxaNAgNm7cwB577MnVV8+l\noaEh6b5nnnkSY8fuy+rVqygpKWXRoltpbW3l+uvnUVOzjREjhhGODm765puvufPO24lEIvTq1Ytr\nrrkWrb/kyScXk52dxfr16zj88KM499wLWbNmNbfcspBgMEggkMOCBTfS0tLMbbfdSEtLC4FAgKuv\nnkufPn3tzx6JROK+i9zcXE444WRef/2fjBixB7feuoht27ZQWbmRKVOm8aMfXcJZZ53MQw8tprCw\nkKeffoqmpkbOPvvcVPypBAFwlMnZFry764mLHstFLxn0wu6Gx+Nh3Lhx3HHHfUyYcCBzixkHAAAd\n6UlEQVSvvvoSWn/JRx99wCOPPM4NN9xMU1MjEGHx4kc54ICJ3HXXA1x11Rxuv/1mADZsWM9Pf3o1\nDz20mLq6Ot588/UO962sXM+MGbN44IFH2batmi+++JxnnnmKYcOGc++9DzFjxgza2toAuOWWhfz8\n57/k7rsf5KCDJvPkk4vxeDxs3LiBRYtu48EHf88f/rAYgHvvvYNzz72QBx54lNNOO5OvvvqS++67\nk1NPPZO7736QM8/8IQ88cM92v4/S0lJqaraxadNGRo8ewyOPPML//u/vefbZv+DxeDjyyO/z6qv/\nAODll19k+vQfuPBXEYSOiXWyC8c9dwux4LGaDoiCF3ZHRo0aBUCfPn3ZunULq1evRKm9AAgEAuy1\n194AfPvt1yxd+gH//OcrANTVWdb50KHD6d27DICxY8exZs0qVqz4Jum+vXoVU17ex16vtbWF1atX\nMWnSZACGDx9OcXEJAKtWreD2228CIBgMMmiQNb5ixIgReL1ecnJyCASshphr1qxm9OgxAEyZMg2A\nO+/8DY8//juefPIxIpEIWVlZ2/0uKisr6dOnL0VFRXzxxedceeWV+HwBWlutm45jjz2B+fPnMG7c\neEpLSykpKdnRr1sQuoUvmlVnErvFRZ8CgqEwWX5xzwu7H4kXiKFDh/OXv/yZcDhMKBTiq680AEOG\nDGOvvUZx5JHfZ/PmTbzyimXJrl27mvr6egoKCvj000+YPv04qqurOeqo6e32TXYtGjp0OJ9++jFT\npx7K6tWrqanZBsDgwUOZN+96+vTpy7JlH1FTU2MkbneMIUOG8fnnn3HAARN55ZWXqK2tZejQoZx5\n5g8ZPXos3377NZ9/vrzT76GhoZ4XXniGhQtv5W9/e56CgkKuvXYOS5d+zvPPPw1ARUUFBQUFLF78\nKMcdd2KXv2NB2FX4Ei14l9WOKHisuymx4IXdhY7u+j0eDyNH7smUKdOYMeM8SkpK6NWrGPBw3nkX\nctNNN/Dcc0/T0NDARRfNBCA7O8DChdeydetWxo7dl4MPnsLo0WOS7puonD0eDyeeeAo33XQ9s2Zd\nxNChgyksLALgyiuv4YYbriUUCuH1evnlL+exefOmBNmtx5de+hNuvfVGHnvsEXJzc5k37wYmTZrM\n7bffTGtrCy0tLVxxxVXt1v7oow+47LKZeL0+QqEgF110CYMGDSYYDLJgwa+44IILKC0tR6lRVFVV\nUVZWxg9+cBJ33nk71123sNt/B0HYUYyCbwtaCt7jsob3JCar7M5s3ly3Ux/mp3e/TUFeFjdcdOCu\nFmmnKS8vZPPmuu/s+olkijyZIoehu/Kce+4ZLF78/zJCll1NMnmWLHmVb7/9xnHTkj5Z0kUmyQKZ\nI08q5HjxP6v4v9e/4ZIT9uGBZz9j7IjeXHHauG7JU15e2OFdgljwSJKd8N3lu1Q58uCD97Js2Yfc\ncssd6RZF+I6SaMFLHXwKCIYj+P2i4IXvHo899qd0i5AyZs68NN0iCN9xUp1FL1oNq9GNWPCCIAiC\nm7SLwUsdvLtEIhFJshMEQRBcx8w7MWVyu72LXinVB/gQOBzIA+4CQkALcK7WepNSagZwMRAEFmqt\n/6aUygWeAMqBOuA8rXXVrpYvFLa+6CxR8IIgCIKLGIXe1hNc9EqpLOBBoAGrJuYOYLbW+jDgr8Av\nlFJ9gcuAg4GjgZuUUtnALOBjrfU0YDHwKzdkDJlZ8BKDFwRBEFzETJMLBlNTB++2VrsNuB+oBCLA\nGVrrT6KvZQFNwETgHa11m9a6FvgaGAtMBl6K7vsScIQbAgbDMklOEARBcJ/ERjduV7G4puCVUucD\nm7XWL0c3ebTWG6OvHQxcCvwWKAJqHG+tA3pFt9cmbNvlmFiIxOAFQRAEN7Fd9D2gTO4CIKKUOgLY\nF3hMKXUCcCgwBzhGa71FKVULFDreVwhsw1LuhQnbOqWkJA+/37djUvqbrP/8XsrLC7ezc2pJtzzp\nXj+RTJEnU+QwZJI8mSQLZJY8IkvHZIo8bstRurEeAH+2pXrz8rI7XbO78rim4LXWh5jHSqklwEzg\nSKxkukO11tXRl98DFimlAkAOMApYDrwDHAO8D0wH3tzemtXVjTss58boe7J83ozopmRId3endK+f\nSKbIkylyGDJJnkySBTJLHpGlYzJFnlTIUV/fDEBd9P/WlrYO19yBTnYdvpaqRjeR6Fp3AquAvyql\nAF7XWi9QSt0FvIUVMpijtW5RSt2PZfW/hZVxf7YbggUlyU4QBEFIAe2myfWEcbFa6+9FH/bu4PWH\ngYcTtjUBp7ssGqFosoOUyQmCIAhuYneyMzH4JNMVd+l6rh59N0CS7ARBEIRUYHeyM1n0Lqud77xW\nM+UK4qIXBEEQ3KT9PHix4F3FuOjFghcEQRDcpJ2LfnfuZLc7EAwbF700uhEEQRDco52LfjfvZJfx\nGFdJlrjoBUEQBBeJTZNLzbCZ77xWC0mSnSAIgpACzDS5NonBp4agxOAFQRCEFCAx+BTTJgpeEARB\nSAE+T2IWvbvrfee1mnHRSwxeEARBcBN7XOzuPk1ud0Hq4AVBEIRU4E3IohcXvcuYTnbSqlYQBEFw\nE783teNiv/NaLRSWGLwgCILgPmbYTMSyKyUG7zaxaXLS6EYQBEFwD19CQzWJwbuMlMkJgiAIqcCX\nYLJLDN5lpNGNIAiCkAo8Hk9c3F1c9C4jrWoFQRCEVOGce+IRC95dxEUvCIIgpApnHF6y6F0mKC56\nQRAEIUWYTHqQaXKuE5QyOUEQBCFFiAWfQoLSqlYQBEFIEX5H3F2y6F0mJK1qBUEQhBThdNGLBe8y\nsRi8NLoRBEEQ3MXpopcYvMvYZXISgxcEQRBcRiz4FBIKhfHgfixEEARBEOKS7CQG7y7BcASfz+t6\nT2BBEARB8EsWfeoIhsISfxcEQRBSQpyL3mUNLAo+FJEaeEEQBCElOAfOyDQ5lwmGwu1G+AmCIAiC\nGzgNSnHRu0woFMbvtp9EEARBEIi34GWanMsEQxFpciMIgiCkBMmiTyGSZCcIgiCkilTG4P2uHh1Q\nSvUBPgQOB8LA76P/Lwcu1VpHlFIzgIuBILBQa/03pVQu8ARQDtQB52mtq3a1fMFwRFz0giAIQkro\nMTF4pVQW8CDQAHiA3wBztNbTos9PUEpVAJcBBwNHAzcppbKBWcDH0X0XA79yQ8aQWPCCIAhCioiz\n4HfzMrnbgPuByujz/bTWb0YfvwgcAUwA3tFat2mta4GvgbHAZOCl6L4vRffdpUQiEUIhq9GNIAiC\nILiNrydY8Eqp84HNWuuXo5s80X+GOqAXUATUdLC9NmHbLsXj8XDkhEEcMq7/rj60IAiCILQjblzs\nbhyDvwCIKKWOAPYFHsOKpxuKgG1YSrzQsb0wyXazbZdz5uEj3TisIAiCILQjldPkXFPwWutDzGOl\n1BLgEuA2pdQhWus3gOnAP4H3gEVKqQCQA4zCSsB7BzgGeD+675tsh5KSPPx+307LXF5euP2dUki6\n5Un3+olkijyZIochk+TJJFkgs+QRWTomU+RJhRyFBTn247LeBZ2u2V15XM+idxABfg48FE2i+xx4\nKppFfxfwFlbIYI7WukUpdT/wmFLqLaAFOHt7C1RXN+60cOXlhWzeXLfT79/VpFuedK+fSKbIkyly\nGDJJnkySBTJLHpGlYzJFnlTJ0drSZj/etq2RPH9yM76r8nR2E5ASBa+1Pszx9NAkrz8MPJywrQk4\n3V3JBEEQBCF1xHWyk0Y37vPRRx9wwAEHsGnTRnvb/fffzYsvvtCt427atJGTTjqGdevW2tvefvtN\nZs26iEgkslPHXLRofpfkeuSRBznrrJO57LKZXHrpDH72s9l89ZXeqTUFQRCEXYMzi97tGLwo+CjZ\n2dnceOMC+/mu6DDUp09fLrlkNjfddD0AtbW13H//XVx33cKdPn7v3mWUlZVvdz+Px8OZZ/6Qu+9+\nkHvvfYgrrriS+fPn0traulPrCoIgCN2np2TR7zZ4PB4OOuggmptb+ctf/swpp8RHBp566k+8+urL\neDxw+OFHceSR3+eKK37M7373B5Yv/5SrrvoJL774Gps2beTmmxfym9/cbb/36KOP4a23XueZZ/7C\nl19+znnnXURFRT9ee+1V/vznP+D1ehk7dl8uuWQ2mzZt5Ne/vpnW1lZqaqq54IKLmTr1UM4553QG\nDx6C35/F1VfPIRDI4ZNPlnHPPXeQlZVFIJDDwoW3kJeXFye300swePBQ9txzLz75ZBmDBw+x19my\npYoZM2YxZMgwbrjhWh566DEArrjiCk4++UxGjdrHxW9eEAThu0Uq6+BFwRNThD//+S+ZMeM8Djro\nYPu1FSu+5bXXXuX++x8hHA7zs5/NZuLESRQVFbNp00beffdfVFRU8MUXn/HFF59zyCGHtTv+lVfO\nYebM89l779EcddR0amtrePTR/+WRRx4nEAhwww3X8v7779pW9/jx+7N27df8+te/ZerUQ2lubub8\n82cwcuSe9jHffvsNjjjiKE477SzefvsN6upq2yn4REpLS6mp2cbq1djrLF/+CY888iC//e29BAIB\nVq5cQWlpKevWrRPlLgiCsItJZQxeFLyDoqJeXH75z1m48DrGjBkHWAp+w4ZKLr/8EgDq6+tYu3YN\n06Ydyr/+9TbLl3/CD394Pu+99x8+++xTrrnmunbHLS4uZty48RxxxNEArF27hm3bqrnyyssBaGxs\nZP36dYwZM47Fix/lhReeJTc3m1AoZB9j8OAhccc855wLWbz4UX7yk1mUl5ez996jt/v5Nmyo5NBD\nDyc/v8Bex+Px2Oscf/xJ/P3vz9O3bwUnnHDCTnyDgiAIQmfETZOTGHxqmTx5KoMHD7ET2QYPHsKw\nYSO4++4HufvuBzn66GPYY4+RTJt2KK+++g/y8wuYOHESb731Bm1tbZSUlHR4bOMp6NdvAH369OWO\nO+7j7rsf5KSTTmWffcbwyCMP8P3vH8u8edczceJEwuGw/V5vwkCcl1/+O9OnH8dddz3A0KHDee65\npzv9XN9++w2rVq1k771Hx60zfvz+9jqHHno47733H95883WOP/74nfr+BEEQhI5xDjfb7afJ7Q54\nPJ64L/onP/k5H374PgB77DGS/fefwKxZF9Ha2so++4ymvLwPHo+H1tZWDjhgAoWFhfj9fiZNmrLd\ndQBKSko488z/YfbsGYRCYfr168+RRx7NYYcdwb333sH//d+fmDhxf+rqajs81qhR+3DLLQvJycnF\n5/Ny9dVz2+3z//7fk/zzny/j9frw+/3ccMMt+Hy+uHX22We0vU52djb77rsfNTXbKCoqyojaVEEQ\nhJ5EKufBe3a2XCsT2by5bqc/TKY0WzCkS57f/vZWDjnkexx99GHyfWSwHIZMkieTZIHMkkdk6ZhM\nkSdVcnyoN3Pv058CcM8VU8nLyeqWPOXlhR3eJYiLXrD52c9mU1dXx377HZBuUQRBEHok8b3oxUUv\npIjf/OaedIsgCILQo0llHbxY8IIgCIKQIuLL5NxdSxS8IAiCIKSI+Fa1YsELgiAIQo8glVn0ouAF\nQRAEIUU46+AlBi8IgiAIPQRjwbs9SQ5EwQuCIAhCyjBJdm5b7yAKXhAEQRBShkmyczv+DqLgBUEQ\nBCFl+MWCFwRBEISeh7HgJQYvCIIgCD0IicELgiAIQg/EH82ilxi8IAiCIPQgfNE6+BTod1HwgiAI\ngpAq7Dp4seAFQRAEoefg9Xjsf66v5foKgiAIgiDY+HwecdELgiAIQk/D5/W4PkkORMELgiAIQkrx\n+7wpyaL3u76CIAiCIAg2xQXZ5ATcV7+i4AVBEAQhhVx99n4pSbITBS8IgiD0CL799hseeOBumpub\naWpq5KCDJjN+/P48++xfWbDgxg7f9+67/6axcRuHHTY96etvvLGEffYZQ1lZ2S6RsyA3a5ccZ3uI\nghcEQRB2e+rq6liwYC433ng7AwYMJBwOM2/eL+jde/tK+cADJ1FeXsjmzXVJX3/qqT8xbNgwYNco\n+FQhCl4QBEHY7Xn77TfYf/8JDBgwEACv18uvfnU9y5d/zPPPP8OVV15OdXU1kydP5cILL2b27Isp\nLe1NbW0NRxxxNFu3buTMM89n3rxf0NDQQEtLMxdf/GOCwSBfffVfFi6cz7x513P99fPo27eCDRsq\nOfzwo1ix4hv++1/NpEmTmTnzUpYu/ZDf//5hwuEwTU1NXHfdQvr06cu11/4y7rgTJhzk+nfiqoJX\nSvmAh4A9gQhwCRACHo4+/y/wI611RCk1A7gYCAILtdZ/U0rlAk8A5UAdcJ7WuspNmQVBEITdj6qq\nKvr1GxC3LTc3F5/PT2trCzff/BtCoSCnnHIcF154MR6PhyOPPJqpUw/lxRdfAGDdurXU1tbw61/f\nTXV1NatXr2LSpCmMHLknV101B7/fT2Xleu688z6am5s57bTjeeaZlwgEApx66g+YOfNSVq5cwbx5\nN1BWVsbjj/+OJUteZerUQ9sdNxW4bcEfB4S11lOUUocANwKNWAr8JaXUE8CxSqkPgMuA/YFc4G2l\n1CvALOBjrfX1SqkzgF8BV7gssyAIgrCbUVFRwX//q+O2rV+/jo8/Xsrw4SPw+/34/X58Pp/9+uDB\nQ+P2HzZsOMcffzLz588lGAxy6qlntlunf/8B5OXl4/P5KS3tTWFhIRAb/1pWVsYdd9xGXl4emzdv\nYuzYfbt0XDdwtQ5ea/0sMDP6dChQDTQBvZVSHqAQaAUmAu9ordu01rXA18BYYDLwUvT9LwFHuCmv\nIAiCsHsyefJU3n33X6xbtxaAYDDIPffcQXFxCZA8Yz2x2cy3335NY2Mjt956B3PmzOe3v70NsNz9\n4XA46XsSufXWG5k7dz5z5lxHWVk54XC4w+O6jesxeK11SCn1e+Ak4FRgC/AyljW+DXgDOA2ocbyt\nDugFFAG1CdsEQRAEIY68vHzmzl3ArbcuIhwO09jYyJQp0xgyZCgff7zUsWfHyn7gwME8+uhDLFny\nKuFwmBkzLgFg9OixLFp0HVddNSdBwbd/fNRR07n00h9RVlbO4MFD2bKlqsPjuo0nEomkZCGlVF/g\nPawY/LFa6y+UUj8G9gb+AXxfa31pdN+/AouAOcDNWuv3lVK9gLe11mM6WiMYDEX8fl9HLwuCIAhC\nT6NDl4LbSXbnAAO11jdhueZDWDF2U4tQCRyMpfgXKaUCQA4wClgOvAMcA7wPTAfe7Gy96urGnZa1\nsxKJdJBuedK9fiKZIk+myGHIJHkySRbILHlElo7JFHkyRQ5DV+UpLy/s8DW3XfRPAb9XSr0BZAE/\nwVL0TymlmoEWYIbWeqNS6i7gLay8gDla6xal1P3AY0qpt6L7nu2yvIIgCILQI3BVwWutm4Azkrz0\napJ9H8Yqn0t8/+nuSCcIgiAIPReZJicIgiAIPRBR8IIgCML/b+fug62qyjiOf6/akJo4lcRQZjCp\nP6WSFPEdAwzNzDSjBCFUMCzJhooM86Ucx1FHLMoxRMAQNSK1ItN0NLm8GYHooCD9oNSm7I80HRxU\nUOT2x1qne8EDci9734O75zNz5nD22bCeu/ba61kv+xIqKBJ8CCGEUEGR4EMIIYQKigQfQgghVFAk\n+BBCCKGCIsGHEEIIFRQJPoQQQqigSPAhhBBCBUWCDyGEECooEnwIIYRQQZHgQwghhAqKBB9CCCFU\nUCT4EEIIoYIiwYcQQggVFAk+hBBCqKCmlpaWRscQQgghhILFDD6EEEKooEjwIYQQQgVFgg8hhBAq\naLdGB/BOJakZON+2G1R+T+AJYFmbww/bvrLOuXOBL9p+scDyBwAPA8Nsz25z/Algme1ziyqrA7Fd\nBIwDetne0MllD2AnrZccRzMwxvbqRsZRs614JD0LHGj79ZJjaFh72SKOCcAJwLuATcB42481MJ5e\nwETgfTmm5cD3bK+rc+6HgT62f19wDAOA3wIft/3PfOwaYJXtW4ssaztj+RWwEmgi1ckk23d2Zhzt\nEQm+41ryq5FW2h64nec2lVD+X4ChwGwASZ8A9qDx9TICmEWKrVM7gWxnrRdIMZTRFjpqW/F0Vn01\nur0gqTdwqu1j8+c+OZZPNiie3YE5wGjbS/OxkaR6OrXOXzkBEFBogs82AD8HBufPjbqPWoA/2h4G\nIGlPYJ6k1baXNyimbYoEv2O6SZoIvBvoAVxqe06erTUDh5AaxWm2X+6MgCRdDRwH7Ar8yPZd+atJ\nkj4EvAqcY/uFHSyqhTSiP1BS1/zzjQDuAPaTNBY4A9gTeAH4AjAcGEXq0H9g++EdjOEt8ih7DTAF\nuB24Nc8SHwcOJc2MhgK9gWtJncfNtm8vKISO1MsM4A7b90k6GLjO9ucKiqeeH0pqtj1F0kHAZNsD\nG9hu68bTCeVuq72Msb1a0teA7ravkHQZcDrwPGnAdpnteQWFspbUPkYBD9heLumIPDj8Ceme+Q/p\n/jkM+Dap3+lOqq+bCoqj5hSguZbcAWzPlPR1SfsD00kz2FeBs4AJwO6SFhU8i28hrYg1SRpr+8ba\nF5K+A5wJbATm254gaSkwxPbfJQ0BjrM9rqBYNhuI2n5F0hRgiKQzgf606XclHQn8mLQV/hww3Pb6\ngmLZLrEHv2P6ANfbPhEYA4zNx/cCfmF7AOnCnlxS+b0lzW3zOgvoabs/MAi4RNLe+dyZtgcB9wIX\nFxjD3aSEBdAPeITUrt4PfNr2UaSBZD/Szfqi7f5lJPfsPGB6XvLdIOmIXO5D+Xr8GrgkH+ti+/gC\nk3tb7amXqcDZ+dxRwLQS4tkendVudyZbay81LfC/GfVngMNJSb4HBc4kbT8HfB44FnhE0irSTPlm\n4II84LkPuCiXuw/p+hwNjJfUrahYsl7A03WOPws8Clxl+xjS4KMPcDVpkFr0DL6WVC8AviXpo/nz\nXsCXgKNzHAdIOoU08BiZzzmHVH9l+neOo1edfncKcG6+1+8FDi45lreIGXw7SHoPsN72xnxoITBB\n0mjSTde2Ph/P7/8gjbTL8FTbmU7eS+yb99zJ8fTMf27O74tJo/MdVbvxZgGTJT0NLMjHNgGvA7Mk\nrQP2JY32AUp7ZkHSe0mdXjdJFwJdgQvz1w/m90W0/vxlxNLeetnNdrOkGyTtQ1qGnFBkQFu02yY2\nT0xbLo+X3m7bGU9pttJevrHFabV4DgKW2G4B1kt6tMhYc+Jaa3t0/twXuB/oQmpHkO6h2rMK82y/\nCbwqaQUpIT9fVDykAd4RdY7vT2oXfwKwfU+O92xKvHa2X5Q0jrRtsSjHsDjXAaR77GPATcACSdOA\nrrafKium7COk1bmv1Ol3u9ee0bJ9S8lx1BUz+PaZARwnaRfgA6Tll5m2R5ISaNv6bMQ+0Spgbk76\ng4E7gb/l747O78eTlpALYfsZ0nLzN4Hb8uG9gdNtD83Hd6H15t9UVNl1jACm2T7J9snAUcCJQDfg\nyHzOMcCTZcfSgXq5DbiBtDz7JsWaQWu77UZ6OLNH/u6wLc7tjHbbnnjKtLX2shH4YD6nb35fCfST\n1CSpC2m7p8i6OgS4UVJtILwGeCm/j8z39PeBe/L3hwNI2oM0M1xTYCyQ9t8HS+pXOyDpPNIg4l5y\n8pc0LG87baLkfJJXB0yama8HjpS0q6QmUr/mvKW0DJgElJpUJXUlrQCtpX6/+6+8nYGk70o6vcx4\n6okE3z7XA9cBfyZdxKnAREl/APYjPW1aT1md5mb/bh5Nr5M0H1gCbGrzxOvwPML8FHBNQWXXyp8N\n7Gv7r/nzG23iuB14jNYOs8wEMprWZIrt14C7gAOAsXlv9STgqhJj6Wi9zCAt6U8vIaYt2+0vgc/m\n9rCtRFXWtepoPEWr117uJu35/kzS/aQ+ssX2CtIS+WLSNs8b+VUI278hzUKXSlpImr2PB74KzJS0\nALiS1sFpV0kPAvOBK2y/VFQsOZ5XSFsEl0paKGkxaTtpKGmb4OJ8vYaTZrBPAqdJ+nKRcfDWh5nH\nAa8BL5OeaF9EakfP2J6Tz5lKus9nU6wWYFDeDn0I+B1wue2fUr/fPR+4Jfc7h5IGRp0q/qvaUHkq\n4dcEiyapB2k1aPDbnhw6Xd7jHmJ7cp7BrwAG1n51q5NjGUBqzxe+3bnh/1vM4ENoMElnAA8Alzc6\nlrBVL5CW6JeQZs1TG5Hcs53hV3TDO0DM4EMIIYQKihl8CCGEUEGR4EMIIYQKigQfQgghVFAk+BBC\nCKGCIsGHEEIIFRQJPoQQQqig/wJoaoqXpX/yYgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10a22f190>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the results\n",
"fig, ax = plt.subplots(figsize=(8, 6))\n",
"births.groupby(dates)['births'].mean().plot(ax=ax)\n",
"\n",
"# Label the plot\n",
"ax.text('2012-1-1', 3950, \"New Year's Day\")\n",
"ax.text('2012-7-4', 4250, \"Independence Day\", ha='center')\n",
"ax.text('2012-9-4', 4850, \"Labor Day\", ha='center')\n",
"ax.text('2012-10-31', 4600, \"Halloween\", ha='right')\n",
"ax.text('2012-11-25', 4450, \"Thanksgiving\", ha='center')\n",
"ax.text('2012-12-25', 3800, \"Christmas\", ha='right')\n",
"ax.set(title='USA births by day of year (1969-1988)',\n",
" ylabel='average daily births',\n",
" xlim=('2011-12-20','2013-1-10'),\n",
" ylim=(3700, 5400));\n",
"\n",
"# Format the x axis with centered month labels\n",
"ax.xaxis.set_major_locator(mpl.dates.MonthLocator())\n",
"ax.xaxis.set_minor_locator(mpl.dates.MonthLocator(bymonthday=15))\n",
"ax.xaxis.set_major_formatter(plt.NullFormatter())\n",
"ax.xaxis.set_minor_formatter(mpl.dates.DateFormatter('%h'));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Apparently American women *really* love their holidays!"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.3.5"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
darioizzo/d-CGP | doc/sphinx/notebooks/symbolic_regression_3.ipynb | 1 | 76709 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Multi-objective memetic approach\n",
"\n",
"In this third tutorial we consider an example with two dimensional input data and we approach its solution using a multi-objective approach where, aside the loss, we consider the formula complexity as a second objective.\n",
"\n",
"We will use a memetic approach to learn the model parameters while evolution will shape the model itself.\n",
"\n",
"Eventually you will learn:\n",
"\n",
" * How to instantiate a multi-objective symbolic regression problem.\n",
" \n",
" * How to use a memetic multi-objective approach to find suitable models for your data"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"# Some necessary imports.\n",
"import dcgpy\n",
"import pygmo as pg\n",
"# Sympy is nice to have for basic symbolic manipulation.\n",
"from sympy import init_printing\n",
"from sympy.parsing.sympy_parser import *\n",
"init_printing()\n",
"# Fundamental for plotting.\n",
"from matplotlib import pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1 - The data"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# We load our data from some available ones shipped with dcgpy.\n",
"# In this particular case we use the problem sinecosine from the paper:\n",
"# Vladislavleva, Ekaterina J., Guido F. Smits, and Dick Den Hertog.\n",
"# \"Order of nonlinearity as a complexity measure for models generated by symbolic regression via pareto genetic\n",
"# programming.\" IEEE Transactions on Evolutionary Computation 13.2 (2008): 333-349. \n",
"X, Y = dcgpy.generate_sinecosine()\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAV0AAADnCAYAAAC9roUQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9eZAj93kl+BKZOKtQ933f1dV3d/VJcyyOJMoaSZR2JXtkr7SyJWs8G2F7aTlGa4U1ntgdWqJIHWEFNSE7YkOUz5Vt2h7Lkk1KoiVKpkg1m81ukn1UoYAqFIAqFAr3DeS1fxR/2YlE4k6gG935IjqarK48kMh8+f2+733vo0RRhA4dOnToaA0Md/oEdOjQoeN+gk66OnTo0NFC6KSrQ4cOHS2ETro6dOjQ0ULopKtDhw4dLQRT4d91aYMOHTp01A6q1D/oka4OHTp0tBA66erQoUNHC6GTrg4dOnS0EDrp6tChQ0cLoZOuDh06dLQQOunq0KFDRwuhk64OHTp0tBA66erQoUNHC6GTrg4dOnS0EDrp6tChQ0cLoZOuDh06dLQQOunq0KFDRwuhk64OHTp0tBCVXMZ06CgJURQhCAJyuRw4jgPDMDAYDKBpGgaDAQaDARRV0mxJh477ElSFwZS6taOOIoiiCJ7nwXFcwX+Tf5MTLc/zEEURnZ2dOhnruJ9Q8gbXI10dVYMQrNfrRW9vL8xmMwwGAwRBAEVRMBgMRb8fCoWQSCQwPT1dQLQkIiZ/dDLWcb9AJ10dFSGKIjiOk6LWQCAAu90Oi8VSdjtCxBRFgWFu32pkdcVxHFiWLdhGJ2Md9zp00tVREoRsSepATqIV0lIS1H6XEKiSSJVkLE9VUBQFmqalvDEhZ52MdbQbdNLVUQRBEArytBRFFaUGBEGQ/r8c8dVK0Gr7I9vL88hkv/KXgNVqLYiMdULWcTdCJ10dEgRBkNIIQDHZEiiJVBTFssRaLemWQiUyTqVS2NzcxOHDhwu2MRgMYBimKE2hk7GOOwmddO9zEMJkWVaKXisREyFdUlTzeDwADiJgm82Gjo4O6U8zQc6RkClN09JnAiDJ2ZTbkNSEPFWhk7GOVkEn3fsURGPLcVzVZCvf1ufz4fr16xgdHcWZM2ekn6fTaaRSKcRiMezs7CCVSoHnebAsW0DGFoulaSRXKjIm50jSJ/l8vuDf5AU8Eh3rZKxDa+ike5+BFMcSiQSsVqtEKtUQSz6fh9vtxt7eHoaHh3Hx4kXQNC2RKk3TsNvtsNvt0jaxWAy7u7uYmJhAMplEPB7H7u4uMpkMKIoqiozJOTULpT6rnIyVWmM1NYWuqNBRL3TSvU8gb2LI5XK4ceMGzpw5UxVxZLNZbG1tIRQKYWpqCuPj4+jr65OW8+VA9t/Z2YnOzs6CfxMEQYqME4kE/H4/stksANyVZOxwODA6Oip9Dl3epqMe6KR7j0PZPUY0s8poTg3pdBqbm5uIxWKYmZnB0tISDAYDHA5HQ5IxAoPBUJaM0+k0EokE9vb2kMlkAABWq7WIjJsJORkLgiARrDwXns/n9cYPHVVDJ917FMqGBnnHGEVRBZIvJZLJJFwuF9LpNObm5nD48OGykrFqzqUWyMl4aGhI+rkgCMhkMkilUkilUggEAshkMlJuenNzs4CMlR1yjUKpGy4VGQN644eO0tBJ9x5DqYYGOUqRZjweh9PpBMdxmJubQ19fX1WSsUpKB61gMBhUVRGpVAoOhwMdHR0FZAwcRMY2mw2dnZ2w2Wyw2Wx1k3E1L49qGz+Un4vI2/TGj3sfOuneI6jU0CCH8ueRSAQulwsAMDc3h97e3rLHarQjTWuQlIk8KgYOrkk2m5Ui4/39faTTaamRQp6mqJaM6yXCWho/tra2MDExAZPJVDIy1gm5faGTbpuj2oYGJURRRDAYhMvlgslkwuLiIrq6uqo65t1GuqVAdMM2mw2Dg4PSz0VRLEhTBIPBIjIm0bHVai3Q/2pNdmpkHI/HpUhX/iKVb6M3frQvdNJtQ9TT0CDfNhAIIJ1OY3d3F0eOHKm5iaHZOd1mg0jV1MhYHhmHw2Gk02kIggCLxSIRdE9PD2w2W1XqjXpACnZq36ne+NH+0Em3jSBvaLhx4wYOHTpU9QMlCAL8fj+2trbQ09MDq9WKY8eO1XUe9fgptAMoioLVaoXVasXAwID0c0LGb775JvL5PDweTwEZK9MUjZJxuYhab/xof+ik2wZQdo9RFIVoNFpVDlIQBPh8Pmxvb2NgYACrq6swm8346U9/Wvf5VFI/KH/3bot0awUhY5PJhImJCZjNZgC3yZhojSORCFKpFARBgNlsLiDjjo6Omsi4HjKspfFDFEWkUimYTKYig3ldUdFc6KR7F0NNY1ttdMJxHLxeL3w+H4aHh3Hu3DkYjUZNzstgMBTlGUvhXiBdAmUEKo+M+/v7C34vl8tJaQqfz1eSjG02W4HXcDNQ6p4Jh8Ow2WwwmUxFn02XtzUPOunehVAj22plTizLYnt7G7u7uxgfH8f58+c1f6jVIt1yy+F7lXRLgaIoWCwWWCyWkmScTqfh8/mQTqfB87xExjabTZL8NZuMBUGQinFy6I0fzYVOuncRyjU0KEGIj/x7LpfD1tYWgsEgJicnJV+ESserdxnbDuoFrdGoeqEcGefzeSkyZlkW165dA8/zMJlMRWkKrciY53nV+0tv/GgudNK9C1BNQ4MSREFAyDYSiWB6ehqLi4tV6021Il2SMyxF8vcS6TYDFEXBbDbDbDajr68Pfr8fq6urRWS8u7srubYRMpY3ftSaPir3nZU6T/nfBNU0flAUBZPJpJMxdNK9o6iloUEJURRx/fp1pNNpzM7OSkqGakFIu57uLIPBIC1BQ6EQnE4nWJaVcpwdHR3o7OxER0eHZnnkuwWtJAslGROQpT8hY7/fj1QqBY7jYDQaiyLjUt9BqUi3nvOU/y0/T3Kcy5cv4/Tp09ILW03adr8oKnTSvQMgVojkpqzlRkskEnA6nUilUpicnMTY2FhdN2mtWlslkskkLl26BJvNhiNHjsBoNBY0HSSTSezt7SGdTiOTyeD69esSETfDT7cV0XQzmiPqAYkaTSZTUfegPDLe29srS8a1Rrr1nKf8b5IWUXbhKbe51xs/dNJtEeTFiWQyCYfDgZMnT1Z9I0WjUbhcLgiCgLm5OQBAT09P3TciiVZrAWmsWF9fB0VROH36NGw2m7QMVvNGEAQBr776KqanpwvMzbPZbMHvk+jYZDLV/Jla9TDeLaRbDpXIOJ1OIxAIIJVKIR6P48aNGwUvw46ODphMJs3PS6n6UP4MuH8aP3TSbTLUJjQwDCPpbSttGw6H4XK5wDAM5ufn0d3dDQDwer0NRaq1RLqiKGJvbw+bm5vo6urCwsICotEobDZbxW3JZySuYcPDw9K/8TyPdDqNZDKJSCQCr9eLXC4HmqZVyfh+QLMidjUyvnLlClZWViRFxf7+Pra2tsCyLBiGUU1T1ENwjQ4mJfuopvGDdGlW29J+J6CTbpOg1tBA/jAMU1bnKooi9vf3sbm5CavVipWVlSLPWTKxoV5U0+AgiiL8fj82NzfR09ODU6dOwWKxIBqNIhKJ1H1sArVJE8BBQYYskUOhENxut0QEyqis1TnjZkdV9ebZ6z2W2WyG1WpFT09Pwb+xLCu9EIPBINxuN/L5vETGcpP5SqsTLT5TNY0fAPDcc8/h2rVr+PznP9/Q8ZoJnXQ1RjUNDaWiTEJyW1tb6OrqwrFjx0pGk43mZMttL28Z7uvrw+nTp2GxWKR/r7UjrVYwDIPu7m4pqieQF48CgQCSySQ4jgNN08jn89jZ2dFcVtVqVLMCasWxjEaj6negfCFub28jn88XrU7kZMzzfNNyx8pnKxaLFZ3z3Yb2vDPvQtTS0KDMpwqCgJ2dHWxvb6Ovr0+KKMuhGaQrCAJ2d3fhdrvR398vtQwrcae0t0ajET09PUVRWTweh8PhAM/zBbIqefcXkVU1s3CkBUhlv1WoleBLvRCVZOzxeKRUkdlsRi6XQygUQkdHB8xmc9NeLLFYrOj+uNugk26DqKWhQQkywtzr9WJoaAhnzpypOnfZaHpBTvyE9N1uNwYHByuex93W8GA0GmEymTA5OSn9jBT3kskkUqkUvF6v1IpLTGpIqqIRY3Ot0cr0gpbEV46M9/f3kcvlivL2yjl4WpBxLBbD9PR0Q/toNnTSrRP1NDQQkOGQL7/8MkZHR+tq1W000qUoChzHYXt7Gx6PB0NDQzh79mxVpN/osVsBucZV2f0lt28MBoPIZDKqxubNGPlTCa1USLTixckwDKxWK+x2OxYWFqSf8zwvfQdyMlYqWmw2W03yQj3SvQchCAKSySQYhqnJgAa4PcI8EAiAoihcuHCh7uVuI8TH8zySySQCgQDGx8drNsO52yLdWlDOvlGuMZaP/CERGcdxSKfTTZ1M3MpIt1VQy+nSNI2urq4ilQFRtKRSKUSjUfh8PkleqIyM1cg4Ho/rpHuvQD6h4cqVKzh79mzVhElGmIfDYUxNTeHixYt4+eWXG3q46kkv8DwPj8cDn88Ho9GI8Zl5dPQMQKRqI/52Jt1SoCh1Y3P5mHie5+F0OpHJZApIgKQptFgetyrSbWVETYqd1aCUokVOxkqtt81mg9lsxuXLlxGNRou2vdugk24ZlJrQQHS2lUBGmMfjcczMzGB5eVm60Umk2kikq+xzLwWO4+DxeLCzs4OxsTGcP38ef/HCdfzPV9wwmXbQbTXiD96zjKm+yrpb4N4k3VKQTybe3t6WjN9LRWQkVymXttXS8NGqSLeVETXP8w2rScqRcSaTQSAQwKVLl3Djxg18+MMfhtVqxUMPPYQnnniioeNGo1F88pOfxJtvvgmKovCNb3wDFy9ebGifOumqQK2hQZ5GIDrbUvlPMsI8k8lgdna2aIQ5cDtSrZd0aZou6tpRguRsd3Z2MDExIaUz3KE0/u5GHN0WIzo7TIimWTzxnAP/41dOVHXsdsjpao10nkc8L4LlBRhpQ1mNMdG3yiVVymaDzs5O1ZROq9QL7Ua6pUDTtPRS/PKXv4yHHnoIL730ktTQ0ygeffRRvPvd78YzzzyDfD6PdDrd8D510pWByL54ni9qaJCj1NI+FovB5XJVHGFebh/VwmAwlNyeeOr6/X5MTEwU2TzuxLKgADBvPXPdVga7sSzynAATU71D2f2C1zwxfP9WEP49Fg7Bg186PYr+DvUXLsMwqrlKebOBvPNL7onQ2dkpGQc1G83UzqodS0162Kxjkc65qamphvYVj8fx4x//GN/85jcB3O7qaxQ66aL2CQ3KjjLSqmswGDA3N1dVIr9a0hUEEbvxLEQRGOu2wGAoTE/IwbIstra2EAgE0D00hh9E+nD9xh4GOiL4P98+j0MjB1HZkN0MEQD/1vbJHI/+ThOMdHUP+/1EuvuJHL53M4hBuxFszIAcx+Pbr+/h4xcnK28sQ6lmA7lBjd/vRzQalX4mzxfXOu6nEloZ6daS020EWt+TLpcLg4OD+PjHP45r165hdXUVX/3qV2se5KrEfU269U5ooGla0h+6XC5YLBYsLy/XlMCnabriEj3L8vjcv6zhDV8cAIUjY3b8wXuWYTHSBdvn83lsbW1hf39fKtT912/fxI3dJPo6jAinWfzf37mFr/3ycQx0mjE/2IFHVnrxnZsR5MHCzBjwf71rseoIS0n42TyHn63twGyx4PBYN6ym4ttqO5zBeiAFu4XG6lQPGEN7mJREMxwoSoSRPrgv+jpM2IlmwQsiaA0+g9ITIRgMIhaLYWJiomDcD5kwodUgzHslvSCH3LVPC3AchytXruCpp57C+fPn8eijj+ILX/gCHnvssYb2e1+SbiMaWyItunnzJvr6+nD06NG63nzl0gMEz1zZwVVPHIOdB7m/N3xx/M2rPnzswhQMBgPy+TzW1tYQCoUksjUYDMiyPG7sJjDQeVDAsVsYhFN5bOynMNB5sMx73+E+nB41o3twFKPdFnSai28FbySDr/94E7uxLI6Pd+GTD86g08xIka4gCHC6vfhv391AMHfwsx4T8H+ctGK4t1OK1G4EOXz+tesQRBEAhZPjdvzBe5bagni7LAwEAeD4g5dMJM1ioNOkCeGqgRRXS/no5nI5qeFDPiJerjHu7OysqDFudXqhFcfKZrNVmTBVi4mJCUxMTOD8+fMAgF/8xV/EF77whYb3e1+RLrlp6/GxlbfI0jSNyclJzM7O1n0u1aQXnPspWIy3z9HCGODcTyGXy8HtdiMYDGJlZaVoWoSJNsBEG8DyIkzMWwQpooBYDQYD+qw05oY6i44LAIksh9/7h+tIZjnYzDR+cGsfoVQej73/sNTt9fLLL+MnASOiogVDPQdkHE6xuJbpwf9+qF/ydP07Rx4CWFiMB/6ol7fC+Ldbu/j5QyN3vSZ1uMuMdx4awL+uhxDOCug1UHj/seHKG9aJchGofNxPKY0xafggBR+lqTzRGLc60m0F6UajUU3dxUZGRjA5OYm1tTUsLy/j+eefx+HDhxve731BuvIJDS+99BIeeOCBqsmW53n4fD54PB4MDg5idXUV+/v7DRXBgOpId36wA5e3I7C/9ZLI5Dl08Am8+uqrGBsbA8/zGBsbK9rOYKDwn//dDP7HC5sHsjcA52f7cHjELvud8gqEtb0kUjkOvW8VjEwdBlz1xOB0e7Hn24YgCDhz5gye/4ELJjoiXU8TQ2E3wUoeCaIoIvsvAQz3doLCwfUEm8fWzh46Uj6Iolikd21m80E9ODPdg+XhTrx8OYS3XZiqqthYL+rRz5bTGBMyTiQS8Pv9yGQyoCgKNE2DoigEg8GmmMrL0aqcbjO60Z566il85CMfQT6fx9zcHJ5++umG93lPk668oQGoLbKVa1tHRkYKuraIq1UjqIZ0f/H0GG76E3jTF0Mul8NEh4j/uDqD6YlRyUCkFN6xMoTJPhtcwRR6bEacne6VinBAZacwE0NBEN8iAQCZbA7pdAbpZAKrq6t49dVXYTKZcHS0Cy85wxAEEaCAHCfgyKi94Djz3Qb4Mhy6rQxY8WDqwdtPH8JUnxWiKEp6VzkxyNtBCRnXY3CuFewWBj1mqqmEC2iba5Vfw6GhoYJjeL1exOPxppjKK9GqnG4zHMZOnjyJy5cva7rPe450SzU0KDW2pdpeWZaF2+2W5FZqvgiV/HDVsBfP4vFnHXAEkhjrtuBXT9gxzZQnXYHN4cNzPM53CpicmsfxuXHQbxV0qtHKLg13YmlYPX1QafvDI3YcHrXjNXcIHMvCQNP42M/N4diRwpTKI8dHsBVO43s39kCBws/N9eGXTo0W/M6Hl43413AXrvkS6LLQ+C/vmMFUnxXAwXejRgzy3nyl3pWQMPm7FWiVWqMVOl2DwQCj0Yiurq4CWVUpPwS5baP8BVgtWpXKiEajd30LMHAPkW6lhgaCUqQrH2E+NTWFBx54oOSNUqvGlhdEfOYfbmA3loXdwsAXy+LJH6fw+LtGVX8/nU5Lc9Dm5uZw7OhRVa1ws/x0RVFEcD+A9wzFMG/rAKw9ODrRiwuzvUW/y9AG/M7b5/Fr58YgiiI6LcUvsw4jhf/nvUsAqq8sl+rNJ+OO5NNxWZYFx3FwOp0FNo5aPuitIl1BEFoSFap1Q5a65nLbxmAwWDBd4k6bysvRDmY3wD1AutU2NBAoo9RMJoPNzU1Eo1HMzMxUNcK81kg3mMxjL55Fj+3ghuyyMIgkOWxHcjgi+71UKiX19s/NzWFgYKDk56hG/VAOajPSyAw0l8uF7u5unFs9jZ+v4OsLvBWtmpmSxETUDlqQoNFoRG9vb8HYmXQ6jfX1dXR3d0uRsbyQJI+MG8ldtiK10SoT81rIvZKpPBlCKh+CKSfjVr2w2sHsBmhj0q21oYGAEGYymcTm5iZSqRRmZ2exsrKiOijv26/v4p9e98NipPGJB6Zxeqqn5ki3w0RDAMAJIhgDBeGt4paZPrgZk8kknE4ncrkc5ufny3ayETT6YMpzumQ8kNPpRHd3d1Um6rUeq5kPHikMDQwMFFT1SSEpmUwikUhgd3e3IHcpJ+NKy+VWGtG0YimuRZeYmqm8fPgqWY1kMhlcunSp6abysVgMo6Pqq8e7CW1HuvU2NBDwPC9Ns52bm0N/f3/Jh+kfru7gj553gaIAQQR+95k38PVfOYm5PlNNkW6nhcGvXpjCn760fUA+FIW3zfegj2Fx9epVsCwrnUurQCJlEtna7XacPHkSVqu1Kce7Ex1satOJgdu5S+KPQGawySM0QgryseH3WqTbDHKnqINCaV9fH/r6+iQr1NXVVWkAZiqVgsfjkTTGWpnK6+mFJoHneak/vZYvJhKJwOVyIZ1OY2RkBIuLixW3+bsruzAYADNz8DZOZDk8d2MPv/W2mZqX9r9ydgJHRu3YDKXRxfCwJX2IRNI4efJk0bjsZkMURUSjUYRCITAMgxMnTjSNbIHWjUivFqVyl/JJEz6fr2DShNVqldpzm2lu3spIt1XHIfI0ojEuZSpPhmCm0+kCKWG1pvI66TYJZN59NRBFEaFQCC6XC0ajEYuLi4hGo1Ufi6EpKAM04jBVTz512g5wgV2InIjRyUkEg8GWEq4oiggGg3C5XDCbzejq6sLRo0ebftx28WqQR2gEhBRisZg0oVlpbk5crrTw022ltWMrtLOVNLqlTOUFQUA2m5Vegmqm8so8vU66dxCkILS5uQmbzYbDhw9LI8xTqZT05VXCJx6Ywh/80y0kcxwgirCZGLz/+EjND1Y0GoXT6TzQrM7Po7u7G+l0WhPruWpAXj5OpxM2mw3Hjh0DwzB4/fXXW3L8diFdNRBSoGkafr9fekkRc/NkMolYLAafz1cgr5KnKWqp6LcyjdGqSLceNQYxJ1e29cpN5YmuOxAI4Pd///dhMBjwrW99CxcuXMDx48cxPj7e8LmfOXMG4+Pj+M53vtPQvuS4p0iXjA53u93o7u7G8ePHi760WpQHb1saxJc/xOCf39yD1UjjP54Zx2SVRt/AQUpjY2MDDMNgcXGxYDnbqLUjQbmHVBRFhMNhbGxswGq1FvhEyHXMzTi2HO1MugTKzyo3N5eDyKuIhePm5qbkvVyNa1grybAVka7Wxyl13Z9//nk88sgjmJmZwQsvvIAXX3wRf/iHf9jQsb761a9iZWUF8Xi8of0o0Xakq/aQC4IAn8+H7e1tDAwMlK2+1yr3OjvTi7MztaUA5CmNQ4cOqbqPaUG6hMzUrgkhW7PZjCNHjhTdpFoMtryfSBeoLjetJq8iXhWEjOX5YqU3QrsX0pRoFbl3dnaC4zj82q/9mibXz+v14rvf/S4++9nP4itf+YoGZ3gbbUe6cshnflU7zbaebrJSkJOOPH9sNpuxsrJSRHRyaEG6pEFC/vCEw2E4nU6YTKaCtIoSjZKuUudbiVjbnXQbOX/5ZGJlvlg5DDMcDiOZTMJutxfki7VugW7XSLcUtL6/fud3fgdPPvkkEomEpvsF2pB0KYqSJiPs7u5ifHy8phHmWpGufNwOKU5ZrdayRCeHFg8QkX0xDCOlMspF11oen+h8aZpGNBqVTNzlZEFegHebeqEeNCPXqmZU8/rrr2N+fh6CIBS148pH/pDIuN4OsFZFuhzHtaTDjkCL7+g73/kOhoaGsLq6ih/96EeNn5QCbUe6oiji6tWrGB4eLhpDUw20JF2/3w+v14uOjo66fXUbgcFgQDQahcfjAU3TVZGtVqAoCvF4HFtbW6AoCtPT0xBFUeoII9pXk8kkDQ7s6+tDR0fHXW/nqAZBEHA9yOHGqzsY7bbgwfleGJrwMhFFEQzDwGw2F32XpAOMWGaSDrB6mg7utfRCNpvVbCTQiy++iG9/+9v453/+Z2SzWcTjcXz0ox/FX/zFX2iy/7YjXYqicO7cubqXE42SLlFGxGIxMAyjWqxrBaLRKKLRKHiex/LysqY+opWQTCalLrqlpSX09PRIhTk17eubb74JlmXh8XiQSqUA3G7P1VJu1Uw8/bNd/M1rSVCGLBiawtuX+vH7v7AAThARSuUBUBjUwNy8HBmW6gCT64vlTQeVLDNbNYutFX4MWjqMPf7443j88ccBAD/60Y/wpS99STPCBdqQdBtFvTcamS66ubmJ7u5u9Pf3Y3Z2tuWEG4vFsLGxAYqi0N3dXaSKaCbS6TQ2NjaQzWZhtVpx/Pjxiu3CJpMJFosFIyMjUtpF3p6rlFvJibijo6OlS9NSiKRZ/N3r+zAaAKvlwGPih+shfPDkCK56EwgkDqYyT/RY8Mix4YbsH2tNY8jzxcqmg3KWmfl8HuFwuOmWme3spdss3Pk7ug60shouiiL8fj82NzfR29srKSNu3rzZdMmXHLFYDE6nE6IoYmFhAd3d3bh+/XpLRqFns1k4nU4kEgksLCygv78fV69erfvY8vbc4eHbUxjkBirEQYzMBZOTcatNzlN5DgYKoHFwTIqiQBsoXHbHEEmzGO0+WNZuRzJ4fSeOM1P1P/xaLfsrWWZGIpGKlplavPBalV6Ix+Oae+kCwEMPPYSHHnpI0322Jem2AkTzu7W1hb6+PqyurhbkjBiG0Ux9UO6mjMfj2NjYKCBbgkadxiohl8vB5XIhGo1ibm4Ohw8flsiulhdftb9bavlMOpNIhT+dTheY1hiNxqa+fEa6LOi3GbEb40AbReQ4AXYzAzNjgM10+7uzGg2IptmGjtXs5gjSAk06NAnULDOJKY7Sj6JWr5NWrFai0WhTSLcZaEvS1aryrnbzCIKAnZ0duN1uDAwMFJEtAZkI3AgIaaqRbiKRwMbGBniex8LCgurSqVFP3VIg04WDwSBmZ2dx6NChomuuZg1ZCo2sTORtovJRNHLTmkgkgng8jkuXLsFkMhVFbI1GjoyBwufeM4PHnt1AICNipt+KP/gPiwin8njBEYbdQkMUgXRewGh34+5sdyK3rWaZqRyEWY9lZqsiXT29cJfDaDSCZdkCMpU3WAwODlbU/Gqhs1WLluVkOz8/X9aboVGtLVAYWXEch62tLezt7WF6ehoXLlwoOyRRqdMthWakg+SmNb29vWBZFseOHSsqKpHCXaM+CcN2E37/59aqyHEAACAASURBVHpw6NAh6WeTvVZE0yze3E0CAM5MdWNlpLJcsBxakTartgGj1CDMWiwzWzmUUifdJqLRSIAoGMxmszQvyuPxYGhoqGAWWqV9sGxjS0l5eiCZTGJjYwMsy2JhYaEqI5xGiV8+Sn17exs7OzuYnJyURrlX2rZawm+Fny75W62oJO/Xlxfuasljqi37GQOFdxwaxIML/aCAps9P0wqN5o1rscyMxWK4fv16QU5ebpmpFeLxOBYWFjTdZ7PQlqTbKBiGQS6XQzAYhMfjwejoaNVkS0DTNLLZbEPnQdN0gYH5wsJCQcdSJWjRyut2u7Gzs4OxsTFcuHCh6qikGTndZkHer19N4U7emksKd+VyreY2IVuCZjmMqVlmvvLKKzhy5IhkDqS0zFRe53pfBnp64S4GeRu/8cYbmJycxIULF+p66zaq9yUV5FgshkOHDtVlYF4v6ZK8dSKRQF9fX00dffJjq437uZu1tkpUU7jb29tDJpORluQej0ciiWboT1ulna2H3DhBBE3Vdo6iKEqrD2W+WO6ju7+/35BlZruM6gHalHTruTHJSHWfzwez2YzFxUWMjY3VfQ71Lu3lc9C6urowOjpa98QImqaRy+Wq/n1RFLG7u4utrS0MDAygp6cH09PTdb107qb0gpYoVbgLBoPw+/2gabrIPUy5dL7bO+5qTS9kWB5/8hM3LrljMNIUPnJ2HO9aGay8YRmU89GVW2aS8fCVLDObMX69WWhL0q0FHMfB7XZjd3cXExMTuHjxIjweT8MkUGukSyb8ptNpzM/Po7+/Hy6Xq2kTfeUgXXROpxO9vb2SIuPKlSt1H7+d0gtawGAwwGKxFLyo5d1gyWQS4XC4oHAnJ+NmNiDUilqLW395yYefbUUxZDeB5UV882UPxrotODpWueW81s9cq2WmIAj4sz/7M+zt7cHj8WBubq6hhiWPx4OPfexj8Pv9MBgM+I3f+A08+uijde9PDW1JutV8kSzLwu12Y29vTyJbcqNp4b9QbaSbTqfhcrmQTCYxPz9fMOG30UJYJdIlkyKcTifsdjtOnz5d0EHWSE74fiNdtdRJpcJdMplENBotMKxRdtzJya+VY95riXSv+eLosRkP5p8xB9dgPZCsSLpafp5SlpnJZBLvfve78cUvfhHf+ta38N//+3/H8ePH8Sd/8id1H+fLX/4yTp8+jUQigdXVVTz88MM4fPiwVh+lPUm3HPL5PNxuNwKBQMlKPCmkNYJKxJ3JZOB0OiWyPXLkSNFD2yjplts+HA7D4XBI7bpqb/9GSLcWnS5wb1g7Vhu1lYrW5A0IOzs7BYU7kpoQRbHpufFaI93+DhM2Q2mYGcNb5wf02spbqNZznFpBURTsdjve//7344tf/CK++c1vNnzdRkdHpYnCdrsdKysr8Pl8OumqgQj69/f3MT09XVb2pEWkW6ojLZPJwOVyIR6PlyRbglpzskqokWY0GoXD4YDRaFQ1L1du30jTgnyEezAYRDabRVdXV1Fe825ZVjcCLV4apRoQiKduPB5HNpvFK6+8UqB51bpwV2uk+/GLk3jsXxwIJvMQARwa6cTPzVWWNLarly7B1tYWXnvtNZw/f17T/bYl6cof4lwuh62tLYRCIUxPT2NhYaHiDUWaIxo9BznhZbNZuFwuxGKxopbZUmi0o0xOuqRdGEDVrmNapBdCoRA2NjZgs9lgNpvhdrulriVCGplMRjPbvTuJZrw85J66PT09iMfjOHXqVIHmVZ7DJDaOjRTualUvTPdZ8cX/dQWOQApmowGHRzphpCtv3yqzGwItv59kMokPfehD+KM/+iPNDaXaknSB274AkUgEMzMzWFxcrPpG0qKFl3zBcrKdnZ3FyspKTcvQRtMLuVwOV69eBcuyWFxcrEk2U4sCQYlcLoednR10dnbi6NGjsFgsYFlW+g6ICXcymUQmk0EikYDX623Laj/QGjmc/Bhqmldl4U7elltL4a4enW6vzYhzM7VJslrlu8CyrKbyPZZl8aEPfQgf+chH8MEPflCz/RK0Lemur69jYGBA1RegEoxGY8Okm8vlkM1mceXKFczNzdVEtgSN5HTT6TQcDgei0ShOnTpVU1MFQT2RLumcSyQSGBkZkUxTlJ+DTJGw2+2Smfnw8LAqaRBHrGYspbVCK0i30rK/msKdctKEWuHuXjMwj8VimkWjoiji13/917GysoLf/d3f1WSfSrQt6Z44caLuKK2RnG4ul8Pm5ibC4TBomsbFixfrfhjrIV25zeLk5CR4nq+LcIHaSDebzWJjYwOpVAoLCwtIpVJVf275EEs10ii3lFZGxXcqP3w3kG4pVCrcKTvBRFGEzWaD0WhUNTcvh/VACq9747CaDHhwvg/d1tIvx3Y0u3nxxRfx53/+5zh27BhOnjwJAPj85z+P97znPZrsH2hj0m0E9UR4+XweLpcL4XAYMzMzWF5exssvv9zQw1gL6crTKfPz8zh8+DA4joPP56vr2EB1hTT555YXBtPptGYFjFJLaeJwRchYbulot9tViaZZaIX6QmtiL1W4czgcMBgMBebmlZoPAOCqJ4avvbAFg4ECL4h4wRHGZ9+9UJJ4WzUfTcvGiAcffLDp33Xbkm4jN2ct2+bzeWxubiIUCklkq9TZ1rtUq4Z0WZbF5uYmgsEgZmZmCtIpWkz0LbU9aSrx+/1FnxtofkdaKYcrEhUnEgns7e3B6XSCZVlwHAeXy9VUo/O7NdKtBRRFgaZp9PT0FKw2SPNBKpVSXW10dHTgry+H0GGmYbcckOxONIsrnhj+/dKA6rF0hzF1tC3pNhtyT9np6WnVQh1JU9SbfyxHunLSK2WzqIXhjXJ7QRDg8Xjg8XjKOo4ZDIaqFSBaNkeoRcWZTAa3bt2C3W4v8EuQR29kSnG9kVerC2nNhBoZlmo+kOfgI/EEciyHXJJ6S+tOIRyNI5ezqxbueJ4va4+qFWKxWFWufHcL7mvSVbvJWZbF1tYWAoFARU/ZZjQ38Dwv2SySTrpynraNQE7aoihiZ2cHW1tbGBkZqWgEVKufbjMnO5DobXBwsMAvQd466vf7kUwmC5oRyJ9SBtxy3M053WYdR5mD/8AZK/72tV1YzDSyeQ4WI4dRcx43b95EPp+XcsTkurIsC6vV2vTPE4/HWzqYtVG0Lek2+gAQwiPEoiTbajxlG22ykJOe3Ne3VpvFRo7PcVyBL0Ml83aCdmgDLhW9qRlwK4didnZ2FrXotoJ071SkWw1+4fAgGAOFlzYjsPXa8MGTI5gbuN3pqCzchUIhBAIB+P3+ml9ytSAWi2Fqakqz/TUbbUu6jYIQpiiKkkfD1NRUVWRLoJWJuNfrhdvtxvDwcF02i/UinU5jd3cX/f39OHnyZE1RSSPdbHcS8mYE+cBGjuMkwtjd3UUymZTGmHd2dkoTkJtJvqIo1hXpJrIcUnkeXRamYGZbKdStkqAoPLwyiIdLOIwpC3e3bt3C6OgojEaj9JJTK9yRnHG9abpoNIrjx4/Xte2dQNuSrhZLa6IGqHZaghKNRLpkynAqlUI6na46wtQC8Xgc6+vrYFkWw8PDBSNoqsW9Zu3IMIyqt65c/xqPx7G3t1fRuKZe1BPp3vAn8a9rQQAATVF479FBTPWVd9lqlom5EmQlWeolR1I/gUAAyWRSVSZYjbF5O3npAm1MuvWCFKjC4TDGx8frIluCeiJdYrPocrnQ09MDm82GpaWluo5fK1KpFBwOBziOw+LiIrLZLBKJRF37aof0QqOQjzHP5XIwmUwYGRlR1b+KoijliomcrVY7x1oj3WSOw7+u7aO/wwQjbUCG5fEv1/fxiQcmy7bpNqK4qQXl0hilUj9ymWAwGCxqKScvOfm1baepEcB9RLocx2F7e1vy1R0bG0N/f39DN18tka7SZvHUqVOwWCz46U9/Wvfx5fsu93DLGyoWFxclqVA+n9etHauE/PzV9K9kWGMikUAkEoHH45GKS8qouNQ9V+uyP5XjAVASwVqNNKJpDllWKEu6rSrY1arTLTcIk0TF4XAY29vbyOfzEEURTz/9NPx+PzweDxYXFxsu3D377LN49NFHwfM8PvnJT+Izn/lMQ/tTQ9uSbrURhHxixMTEhFSgcrlcmnjqVuMSFg6HsbGxAYvFomqz2EiekBTj1CIKucaYNFTIj9Mqa8d7hXTLfUelhjXKJVfK6cSEiO32A8lVrfeB3cKANlBI53nYTDTiWQ6dZhrWCnndenPHtUKriFreUi5HKpXCI488gieffBJ//dd/jcceewynTp3C17/+9brP9zd/8zfx/e9/HxMTEzh79ize//73a2rrCLQx6VaCXHo1NjZWYGIOaGfvSB4iNcRiMTgcDjAMg8OHD6t2TylVFLVCjXSVGt+lpSXVh1kra0fgoCgXiURgt9tVGxPanXSB+uoIJpMJfX19Ba3aSq+E7e1tsCwLQRBgNpul6LiSGZDNRON9R4fwL9f3Ecuw6DQzeN/RITCGu8NKs9nk3tHRgfe+9734whe+gKeffrrhPPWlS5ewsLCAubk5AMAv//Iv4x//8R910iUo9QDwPC9FtmNjYyXVAFoYmZfK6SYSCTgcDoiiiKWlpbIawkZJV24PKQgCXnrThR+86cXIYB/+twfPwm4tXZxrRD9Lotd8Pg+n04loNIre3l4EAgGpOk0iOZ7nm6rTbQW0VC2U8krY2toCy7LI5XIFDmJKMyB5wXWy14pPPDCJLMvDaqRB3yWE2yqQl7kW5O7z+TA5OSn9/8TEBH72s581vF8l2pZ0gcJlK8/z8Hq98Hq9GB0drSi9qhSlVgNltEwcuFiWxcLCQlVdMlqM7OE4DqFQCM9d2cBT11gIIgV6K4S/v3kZf/ufzqKrRG98I+kFURQRj8fxyiuvYHZ2FktLSwXWjnIJVjgclqI6sqyWF5vaAa3Q6ZJl9MjIiPQzeT4zFArB7XaDZdliMyCrFYb7jHDl0OK7UVuNNeM7b2vSBQqbCkZGRqrWuWo5J00+dHJhYaGm6b6NkC6JNF977TX09/fjH7eNYAUOjIGCIAKBRBZ/+6oPv/7gjOr29ZCuIAjw+XzY3NwEwzCS+kMpd5JLsGw2G8LhMObm5qRldTgcViWQUumJO41WpEfUClxq+Ux5e24ikZDGl99NFpmtSidpaZQ+MTEBj8cj/b/X621oYngptDXper1eqW211qYCLUiX53lEIhFcu3YNCwsLBUMnq0W9pBuJRLC+vo5cLoeVlRUMDg4i/uy/QR7ssLyIUKq0P0ItpCufKDwwMIATJ05gc3NTIolKbcAkv6dcVhMCSSQSkmZTmZ4gvgmtnEKghrvFe6Fei0xyHVv1AmnF96VlC/DZs2fhcDiwubmJ8fFxfOtb38Jf/dVfabJvOdqadC0WC86dO1fX27wR0iV2h6FQCAzD4MKFCy3z1I3H45I135EjR7C9vS29bH5+oR/fft0P4a3hgWbGgAcXSnvtVltIIwTf0dEhTRTWytpRTiBymRARzycSCezs7CCZTEo+sMqqfyvQDt4LlSwyiTNbOp3G5cuXi9qeteyEbEcvXYZh8LWvfQ2/8Au/AJ7n8YlPfAJHjhzRZN8Fx9F8jy3E4OBgS43Mic3i/v4+Zmdnsbi4iJ/97GcNPYy1jHJ3OBzI5/MFY3nk0epn3r2EDMvjB7f2YWFo/M475vHAfOlUR6VCWjKZxPr6OgAUDblstmRMTTyv1MKSqj8piu7t7TXN7LxdXcaU2leWZfHmm2/i+PHjUs6dWGTyPA+LxVLUEVbPObVqPpqWXroA8J73vEdTw3I1tDXpNnKD1kK6cglWrf4MlVBpOKW8sYGkMEptbzHSeOKDR6s+dqn0gnxKxNLSkmpB8E40R6hpYUVRRCKRwPr6OjKZjGR2XsnAplbcqZyu1iARKE3Tqh1h2Wy2gIyVqR7S4FEpKm7VfDStSbcVaGvSbQTVRGpy+Vklm8VGzkMt0mVZVkphlJsu3MhwSyXpEiPwYDBYcXz83eK9QNITJpMJMzMz0s/l6Qk1AxuinqhlSnErIt1mk245YqcoClarFVarVdUik1zLVCpV0SKzHdMLrUJbk26zHgKiiNje3m66zaIyvcDzPNxuN3Z3d0uap8vRaFeZIAgQBAHb29vw+XyYmpoq6yFMcLe3AZdLTxD5GmnVJROKCRGrpSfuFWvHesiwFotMYgYEHJB1s8lXJ902hyAI2NnZKbBZrKZI1+ictFwuV0D08nblarZvpPGAZVm89NJLNStA7oY24Dwn4IY/gVAig2ycw7EaWnWHh4eln8sLTfJZbPKCHc/zd30hrZXHKGWRybIsUqmUFBG/9tprBSsM8sdsNmtyPaPRKMbHxxveTytxX5MuWSJTFAW/34/NzU309/fXZLNYzvug2u2j0Sh2d3cxODhYcWKD2vb1pBdCoRAcDgd4nsfFixdrVgE0expEJbC8gO++GcBOLAuGEuHZZTGyHcPqdO1RTyn5ldxfNxQKIR6PFxBxPU5i5dCKaLrZkafRaERPTw/S6TTsdjsmJiYKLDJjsRh8Pl/RiHi73Q6bzVbzucXj8aYoDJqJtiZdLaZH7O7uYnt7Gz09PVhdXa0pxwfcLsjVerMQ1zGHwwGapus6NlDbrDLgtpeu0WjE8ePHcfXq1bpkV3c6vbCfzGMnnsVYjwUcyyFjpXB5O4aTk92atMIqC02iKGJ8fBw0TSOZTCIajRalJ+TNHfVEk1pHup5IBokshyG7GQOdpqYcoxTkhTS5RaZ8hSG3yPR6vZJFpjIqLvdii8fjeiGtHSCKIkKhkLScrHVqghz1NDdEIhE4HA5YrVYsLi4iHA7XRbjk+NVEnOl0GhsbG8jlclhaWmr4Rq3lhdcM0hVFQH4GFAUIFY7BCWLdZjCkyFUuPUE8YEl3mLK5o9IKRstI99kbAfxkIwwDRYGigA+vjuHIqL2lpFvpni5lkSk3A6pkkanndFuMem5QQngWiwV9fX2Ym5tryIOTYZiqSZdImwwGg+Q6Fo/Hsb+/X/fxK6UXSCNHJBKpu2uuUTSDdAc7Tei1GhFI5GCkRAQzIt610qUa5UbSLH7sCCGe49FrZfDvFvrQXcKPohTKEWK57jAyooYMxVRr7iD71YoQ/fEs/s0ZxmiXBbSBQpbl8Xev+XFouLNlqoJ6dbqlzICUFpnRaBSf+tSnQNM0nnnmGQSDQZw8ebJAdVEvPv3pT+Of/umfYDKZMD8/j6efflpTYm9r0q0FxGaRpmmJ8G7evKmJ/0KlfcijTHljA9m+UcMbtUhXroKYnZ3F8vJyU8k2lUrB5/NJvf9KUb3WpGtiDHj/8WG8uh1DKJlB1yCDB+aK9cQsL+D5tSAMFDDSZUIsw+KH6yG879hwTVFvrVFoqe4w0twhz20ajUbY7XZks1lJF9sI+abzAgwUJb2ALEYaoTSLHCfckfSCFlCzyHzhhRfwgQ98AFNTU3juuefw4x//GI899ljDx3r44Yfx+OOPg2EY/N7v/R4ef/xxPPHEEw3vl+CeJ91EIoGNjQ0IgoDFxcWCZbVWpjel9pHL5eB0OhGPxyUjHOWDq8UYdznpiqIIn88Ht9vdkqnCxNoxFothdHQUqVRKEtWTQonVagXHcZo/8B1mBj+/2I9cLodbt0KqUW4qxyPHCRiyH+Q0u61G7CXyyOR52C2tvf3lFX95eoJEcXt7e9je3i4wryEFu1radAc6TTDSFBI5Dp0mGoFkHuM9ZthMNEKC0JKmhVZE1KQd/ZOf/KSmx3rXu94l/feFCxfwzDPPaLZvoM1Jt1zkkUqlsLGxgXw+X9JmUSsjcyVpknbhYDCIubk5rKyslDzXRiVfJL0giiL29/exsbGB/v7+mjwp6skl8jyPXC4nWTsuLy8jl8sV3PykUBKJRJBOp/Hqq68WkAkhlGY+nCbGAIgAxwtgaAPyvAAKB74UtaCZygISxZlMJqkhRZ6ekLfpKuewqUmvuiwMPnZ+En9zZQc78Sym+2z4pVOjAKrLtWqBVpCull66pfCNb3wDH/7whzXdZ1uTLlCcL8xkMtjY2KjKZlHrSFc+raLaJgMt0gvZbBavvPIKrFarZEhTLcj1q5ZQyBRjl8sFANJnFAQBoigWKCkMBgO6u7vR0dGBeDyOkydPFpAJ6RSTV6wJGWtlSWgz0Tgz041Lm1FQFAAReGC+74CMa4DaNfJEMnjDl4Agilga7sTiYGOeD/JjlEtPKKVXpMgkb+6Y7rPi0++cBy+IBSuAVs5Ha5UrXD3X/J3vfCf8fn/Rzz/3uc/hAx/4gPTfDMPgIx/5SMPnKEfbky5BNpuFy+VCLBbD/Pw8BgcHK34ZRqNRMyNzj8dTVwdbI3rXVCqFW7duIZFI4OzZs0UzpKoBIcxqHsRwOIz19XV0dXXh7NmzuHz5MgBILx2j0QhRFCUCJv8djUYlC0d5Hz8Rtcsr1qFQCFtbW+A4TjJfIWQibzOtBctDnRixm5HK8+gw0TUX0YBi0g0kcnjRGUa31QijwYDL7igYA4W5gfLjzxtBqYYEeZHJ7XYjnU4XeOuS60dWZa0cv95MNNLB94Mf/KDsv//pn/4pvvOd7+D555/XfIXT9qTLsiw2NjYkk+xyS3klqimClQMxW/H7/ZiYmKjLZrKeLzSXy2FjYwPJZBIzMzPweDx1ES5QXWdZKpXC2toaKIrCsWPHYLPZpBv+jTfeQFdXV0GESh7qTCaD9fV1CIKApaUl0DQtETEAKcInPf82m02amiA3XyH2jsqojgjqq0G31VgX2coh/652Y1mYGAOsxoPP2m1hsB1ON5V0S0GtyCT31iU+yDzPS625PM9r2hmmRCtamhOJRN33fTk8++yzeOKJJ/DCCy9UfX/VgrYnXZfLBbvdXld13mg01kW6pLFhY2MDJpMJw8PDWFxcrHk/tYLjOMlakpjgEAe0elEu0s7n89jY2EA8Hsfy8rKkuiA55NXVVaTTaSQSiYIH22KxgGVZKZ8uLxoRkGhY/jfZNzkvk8mE/v7+AhmQ3PA8GAxKUV0+n4fP52ua4bnyxWRmDOD42z/L8yIGKkzhbSVKpSfeeOMN2Gw2xOPxovSEvDOs0RQERVFNJ91oNNoUje5v/dZvIZfL4eGHHwZwkEL74z/+Y8323/aku7KyUndOtJ6cbjQaxfr6OiwWC06cOIFcLofd3d26jl8tBEGAx+OBx+MpyhU3Q3Iml5uR1QM5DxLBUBRVMEpmbGysYHRSb28vuru74fV64XK5YLFYYLfbpajYYrHAYDAUkKOcgMkfcj7AwYNM0zR6e3sLcvXpdBo3btyQlBuks0m5vG4kT6xML8z02+AKZeCPZwGKgoUx4NBw8bTnuwnkOxsYGCiI4NTSEwAKmhHsdntLVA+1oFmNERsbG5rvU4676yq2GLWQLpnwCxwQPVnWkOVaM0CKVpubmxgaGlL1ZWi08UBOuqIoYnd3F5ubm9LYehIJk99Ri2BI5O90OjE4OFhknEOmF8TjcSlVkMlkYDKZJNImEWo5IpZHxBzHFZyH0WjE2NiY9DKSD3SUj66RV/+VzQnloCRdi5HGO5YHEEjkIIgHzRq2BiPdVjStqPmElEpPkFWM2vUj17BZ6Ylq0I5euoBOulU3NmSzWSwuLhZJz2rpSCsFQmzyJR0xpOnq6irry9DoDU9Ilxyvu7sbZ8+ehdFohCAIBVGm2rFIl53FYsHJkydVlRPy6QXKAlAikShy9yKE2NXVJUnKlEQMHBADKaBaLBYpV6ls2R0dPZBLKav/2x4PHMEsQnkaPZ02rE73YnKoV3VagtqLzcwYMNlbfzfjnQDP81WlDmiaVh2Imc1mpe9Mbuco1xO3arBoO7YAA/cA6TZrVA5pbIjFYmXbZxstxsnPw2AwSCRG0zSOHTtWMCWhGeA4Djdu3IDZbMbx48dhtVolsiXRndrnJhMtyMuonuGAJGcrTxVwHCc91B6PB8lkEgAKolO73Q6KouD1erG3t4f5+Xn09fUVROWiKBZ8BuC24Tkh/2u+OHgujkmTAfFkGj90hHEqHALFZSXSIcdttgNYq/yGG5GMyU3OlXaOpOBJvrNMJoMbN24UkLHWk4nb0ewGuAdItxGoPUQsy2Jra0uag1ZJDdFoTpXsI5VKYXt7WzNDmkogCgjyUpmYmACAAqJSezh5npeuz9zcXFXSvFrAMIyqCUoymUQ8Hoff78eNGzeQzWYltQNpEDGZTEXnXK5g5/DH0WdlYGQM6LB0g07YMDbbi8leq0T+pNc/mUziypUrRdaOWuU5W2HrCDRHp6s0riGqlcnJyaL0hFYyQOCgvqKF10Kr0fakq9WNWk9jA9A46RLT5+vXr2NpaanphjSENP1+P+bn5yXtp7JIpra83t3dhdvtxvj4OM6dO9cSkT1wkALp6uoCRVHY29tDb28v5ufnwbIsEomEpO3N5/OwWq0F6Qmz2VwyT2wxMWB5EYxBhAgRLM9B4DkpX9zd3S0RSSqVwqlTp6Q8p7xLTNnYUY9VZjmJVSzDIsMK6LUZa+6kU0MrPHuJn4RaeqLUtAlCxCS3Xwmkvb7d0Pak2yhEUay7sQGo/waWk7zJZMLhw4frWqJXC1EUsbOzg62tLYyPj0tFslgsBo/Hg0wmg66uLtVRNeFwGBsbG+jp6cGZM2c0XyZWApGupdNpLC0tSdfJbDajs7OzIGebzWYRj8clSVQ2m4XJZCrQEhNJ1NmZPvzIEUKGF8ELAsZ7bBjtsR3YRMoiYpKqAG5X9AkpEINu5YRis9lckJ6oFNGVmo/2ojOMH66HQFFAh4nGr5wZx3BX89t4G0GpBoxSM9jkvroej0dqWKqkPonFYqrt/Xc77lvSFUURe3t7SKfTSKfTdTU21HtcQn6E5NfW1hqewlBueRoKhbC+vo7e3l6cO3cODMNIedvp6WlEo1FJRE+MakhlOhgMgmEYHD16tClC8XIgs9vk0rVyQ/NqegAAIABJREFUxCV/qJV+tyRPLJ9wa7fbcarfhrzBjO7OToz3WmGkbxOfIAiS6TvJOxPylRfsyDHljR3kmMlkEn6/v6jgpNTDqi37d2JZPL8WxHCXBYyBQiTN4n++7sd/fnBamwvcJNTa9VbKV5eoT4LBYFF64vLlywiFQk1Lw33pS1/Cpz/9aezv7xdN4G4UbU+6tUaaxMB8Y2MDXV1d6OnpwfT0dNMJV95Q0dfXV0DyjUz0JdurSYHkRbkTJ06oFsmMRiMGBwcLIo9UKgWHw4FAIACbzYZsNovr168XLNurXQLWA7kEbXh4GOfOnWuo2YH43cofHpKaSCQS4BP78Ps3EXjLy5VMf/D7/cjlcpIVKHA7ApbniOVEDEC6rsrGDnJMZbsuyW0qBznGMhwMFCVZUPZYGezGc0Uv2JdcYTx3MwiL0YAPnRzF4lBzi6+VoEWrsVzFQiBfybz66qu4evUqfvVXfxX9/f145JFH8OlPf7rRUwcAeDwefP/738fU1JQm+1Oi7Um3FkSjUTgcDqlSb7PZcO3atYbVB0D5SDMWi2F9fR1ms1l1SoUW9o7yGz2Xy8HhcCCVSkmdZMpqvhphyiPLmZkZnDhxQvpMpLAUj8fhdruRTCYlw2mydNfCMSyZTGJ9fR0mk6mkBE0LGI1GVW1qPB6Hx+ORug1pmsbm5mZBY4fRaKypYEciYoPBgJ6enqJjEs+JXC4nDXLs6OhAzmBFJptFzkbDbDQinGYx1l2YpvjxRghf/L4LtIECL4q4tBXFlz90GLP9xauSVikkOI5rSiOFfCXzxBNP4H3vex/+/u//HjRNY29vT7PjfOpTn8KTTz4pGd9ojbYn3Woi3WQyCYfDAUEQcOjQoYK3p1ZOY2oGHyRi5Hm+6Lhq29cLEulyHIetrS0EAgHMz89LA/t4nq/Y3BAIBLC5uVkyslRTFfA8L0WLXq+3SN5FSKoaImZZFk6nE4lEoiXqDTXE43E4HA709fXhyJEjku0mcUXb39+Hy+UCy7Kw2WxFBTsANXXYAbcjOoZhkMlkcOTIEckAKJFI4NxwGj90+iEIInpsDB6e6Mf+/r6U/vn7q36YGIPUmBFO5fGDW0H8p58rjtJapZBolalOIpFAd3c3GIbRTK/77W9/G+Pj4zhx4oQm+1ND25MuULori9g8ZjIZ1cYGQDtPXfnbXW5evri4WNZeEmicdCmKws7ODnZ3d6Xx7dV0kgG3o/DOzk6cPn26pso7TdPo6ekpuOHl8q7d3V3J8EapsyWpFdI67PP5MDMz0/QJF2rIZrPSy1GZuy61zCUTIMiAylwuB7PZXFCwIwMqy3XYkf+ORCKShwRN05Kb2AdGR/GuszwyeR5GcMikDq4tMQCKRTnksiIYHBgNlbtyrZwa0Yr6SL1TuMvZOn7+85/H9773PS1OryTuCdJVIpfLweVyIRqNVpwLpmWkK480q9H4KrevB8FgEJFIBEajsahIBpQmW/JC4jgOKysrRTOp6gWRd8mVGPJoUW6MwzAM0uk0ent7cerUqaalEkqBpFP8fr90n1QDtQkQ8uIZcZ5Lp9MF0imiDpF32GWzWaytrQEA5ufnVZ3YaFFEl9kAg8GCDmthV1+yaw9fen4TySwHVsjDABGj3B7W1jIFjQmkbtAqW8dWGZjXg1K2jm+88QY2NzelKNfr9eL06dO4dOmSVCTVAvcE6ZJIl7hwEdI7dOhQRdLTinS9Xi+CwaAUadYSUdA0jXw+X9MxE4kE1tbWpILN5ORkwRSJUmRLrlE4HK5o8q4VlMY4qVQK6+vrEEUR09PTyGazePPNNwuW7SRibNaUA1LUJOkULVy1SKuzsnhGPCc2NzeRSqWkXDiRSi0tLamK/OXddaUKdm9bHIDVyOD7ayFYGBofPDWCmV6zpIX1+XxS2sdisSCbzSISiTTVwKYVBuaEdLVcFR07dgyBQED6/5mZGVy+fFlXL6iBuGJ5vV5MTU3h4sWLVT9EDMMUTDuoBUR2RmQlSqOXalFLpJvNZiXN6vLyMrq7u3Hjxg0kk0lYrdaSQw0FQcDOzg48Hg8mJydx7ty5li/jyRijaDSqmu6RL9sjkQjcbjfy+TwsFotEwiR/Wu+5p9NpaSJzMwt1BOSlKH+5BYNBrK2twWazoaenBy6XC06ns6AoSUixmoLdmakunJnqkgp2FEVJyhz5dvv7+/B4PFJumoz/kY9O0uIl1woD82Qy2RQv3VbgniBdh8MBhmFw8eLFmt+wpIBRK8LhMBwOhyTO7+/vr/tGq4Z05V66CwsLUmTE8zyGhobg8Xjgdrul5b1c2hUOh+F0OtHf34+zZ8+23KKPWC4Sa8rFxcXbqghBwC1/EjlOwGy/DX0dxct2YrIib3ggzQfks1YyWeF5HpubmwiFQlhcXCxQELQK+Xwe6+vrYFkWp0+fLlCxkBRMPB7H3t4eNjY2pG43eXqC5NyrcWJTFuxIM8nS0hKA4pecPDctJ+JaDWxakV6IxWJNbSYCgK2trabs954g3VZ66hLtq8FgwNGjR9HR0SFFDfWi3HBKURTh9Xqxvb2NyclJ1SJZT0+PFDXKpV0bGxuIRCKSh6rVakUmk2mqxlaJSCQCh8OB3t7eIsJneQFP/XATN/0JGCgKRsaA//LOeczI5E6lTFbkVpG7u7tFVpEkfwoAgUAALpcL4+PjOHv2bMs+OwH5Dn0+X0m/ilIFO6JiCIfDBZF/Ld7ERC7o9/tB0zRYloUoiqBpWkqJyF9ycvc35WTnalp1W0W67Wh2A9wjpNsIqiVdUuHOZDJYWloqWLo1mhdWi3TlzRRkum81RTKGYWCz2bC7uwue57G6uoqOjg5VjS15cJvR7EBMT0RRLNnN9ponhuu7CYx1H6QLomkWf3HJi//6H5Yq7t9sNhc1dRCyiMfj2N/fRyKRQD6fh9lsxsTExB2JbmOxGNbW1qSXTiUyiqZZXPPGkOcFHBqxY7L3wJ5SOcaIkKK81Vn5wiFETGbbjYyMSMZG5SZ2EA2zspmE5Im3t7cL5rApJzs3S6dbcJ2aNDWiFbgnSLeR3GQlwmRZFi6XC6FQSFrWK49Hood6oSTdeDyOtbU1qZnCYrFUZbdIcttq6gmlxlZuoagkYrmXba1ETBQc5HqVK9Qlshwo6vb3ZzPRiKTqv47EKrK7uxtOpxO5XE4qpioLWfJIsZ7PWQlkdp8vnETUNIzvbeQwEvDifceGMdKlnkeOZVh882UPMnkejAG4tBXFh1fHsDB0W1lSKvJXvnAIKXIcB4PBIKVUSuX75RI2tYIdmeys1GkrJzsLgoBsNguPxyPdQ/UYAFVCu3rpAvcI6TYCo9GoSpiCIMDtdmNnZwfT09NYWloqKzurJy9MQFQHJJrOZrNSg0A1nWRkwgTxc6imGl+u2SEej2N7exupVEpqUyURcSmCkruQTUxMVLWMn+k/MJfJsjxMjAHBVB4PztcfjcrPYWpqquA7k0e5HMdJWmK5Z6+aeXoj52AdmMBzfgHfv7UJXhAhAvjjn7jx/31iVbVV99ZeAqkch/GeA1KOZ1j81BUpIN1SkHsTE38Pt9uN0dFRMAwDv98Pp9MJoLB5hdhT1tNhJ7835NtdunQJFosFoVAIbrcbLMtqaukI6KTb1lBGunJDmtHR0apcxxptbiBTha9cuVJUJKvU3EBypt3d3Q07gKk1O8iJWElQJFLkeR5OpxNdXV01ncP8YAd+/eIU/vIVHyIZDqtTPfjwmfG6zp2sDqo5B9LBpPychIiJzIrMWVMqCkqByPjsdjvOnDmDZ64GcMOfAMsfEC4ApPM8nvieA//vR08WbS8IgPwrNhgocEJtetRUKoVbt26hs7NTSknJQT4niU4TiQQEQYDNZiv4nI0U7AwGA0ZGRkpOdiaWjvLJzp2dnTUNxNRJ9w6jkTcmGUEuz6GS/Fu1y6J6c7qkG2t7exsAauokS6fTcDgcEEURR44cadqEiXJEHA6H8cYbb0g+tqRYU0ukeGGuD+dneyGIAG2o/Xskto+ZTKahJg+aptHd3V1QnCHddaTZgbSSkzwmISmKoqQORHm7d47jkeMEKGkzlFLXZC8OdeInGyEEk3kYaQrxLI+3LVanESU+yaFQSJIS1vI5ScGOOHqxLCvJyeSa6UrDRLe3twtkmKRgR0yHlDl4cn3JZGeiYZbPzVO7j+LxOGZmZqq6Nncb7gnSbRQ8z+Py5cswm804ceJEzRaGtUa6oihif38fGxsbGBwcxIULF3Dp0qWCfFopsiU5ZjLx4U4Uh4ADyVwgEMDy8jIGBwcLIkWlD4M8NVHKZ5WukW+JIsDr9WJ2dhbDw8Oa647l3XXj4wcROCGoeDyOQCCAW7duSYqQoaEh5PN55PN5mEwmnJ7qxrPXA9hL5MG/FbGaGQP+/ZI6kQ50mvCxC5N4yRVBnhPw8EoXDo9W1qKSQtno6CjOnDlTc36aEF0pb+JYLAav11sg1VN6E6fTady8eRP9/f04deqU5AdSrmBHXujK1A/JE8snO8ulc8QHul0jXapCO11rbIkaBJG51AoilN/f38f58+fr1v1lMhncvHkTp0+frvi7xOvAYrFgcXERZrMZgiDgxRdfxODgoPSQK7WRZAw7yTGPjo62vLmBNIOQacGkC64U5EQcj8drIuJyICmVvr4+zM7OtqS1VYlUKoW1tTVYLBbMz88XSPWIasJiscCbMeIv30zhRuAg5/+/nBjBf3vvEhgNCndE98txHJaXl4vc65oBuVQvkUggnU5LErTJyUkMDg6WVMKUSk8QyKeWyLeXe+smEgk8+uij2NrawuLiIt7+9rfjgQcewDve8Q5NPt9TTz2Fr33ta2AYBu9973vx5JNP1rurkg/nfUm6+XweTqcT0WgUS0tLWFtbkyYp1IN8Po9r167h7NmzJX8nk8nA4XAgl8theXkZXV1dBUUy4rVKCIroTsnvBYNBDA8PY2Zm5o6QDDHzttlsWFhYqLsiLc8pEiIWRbGoG0vtMxLLSpZlsby83HJTdXL+pI1aKR2UQx4pks+ay+VUNbb1eEKTYt38/Lzmc+qqRSQSwdraGoaGhtDd3S19r3Lbz0qFSWV6QslHpYj4ox/9KH77t38bkUgEyWQSH//4xxv+PD/84Q/xuc99Dt/97ndhNpsRCAQKFCI1ouQXck+kF6q94TiOg9vtht/vL/BmIDnZeotQ5XK6HMcVSM6I9lFZJFMz2g4Gg3A4HNK/BwIBqROH/GmkJbYakAGW2WwWy8vLDbdelsudEvcsIj0iRNzZ2YloNCpZVt6pYYT7+/twOp0YGxuruIxXm2JBTHEIEauNE1Jb5chBCmUdHR13pLsQOLiniWadmOMDKJAHqhUmy7nN1VqwCwQCOHHihKb3wte//nV85jOfkVqhGyDcsrgnSLcSBEGAz+fD9va2NB9M/sA0SrqkGKc8ptfrlVpfz58/X3WRjPgr5PN5HD16tIDo5DPAvF6vFD0pibhRyB24ZmdnMTQ01DRyL+VMlkwmsbu7C5fLBYPBAJPJJHVI1eLV2ygymQzW1tZA0zROnTpV9/WVm+Iou+tINExGSBF3MnmbczWFsmaD1CKmp6fLGkqVerkq3eY4jqvamxg4uP+/8pWvwOPxaG6GtL6+jp/85Cf47Gc/C4vFgi996UtlV6/14p4hXTVPXWLO7XQ6yxrSaOE0pnbMwcFBnD9/XmrzrVQkI40FwWAQ8/PzqpaUyodWHj2RIZO5XA5Wq7WAiKtNB5Ain8vlwvDwcFVdVM0Asec0GAy4cOGC1CBSyqu3WllXLSBa7b29PSwtLTWtaFlqnJA8Io7FYjCZTBgYGJCW761s587n87h16xYA4PTp03URntJtDv9/e2ce3NR99vuvbHmXLbANAm8YY8kLYMCyWVKWlIxJoSQtTBKSlEJDGUheIOY1JGFpKDQMiweSENJhe2l4J5kk09vpZbjQS94QlzXgBXCIE1ve8Y68arN2nfuH7+9wJEu2JEs6Xs5nhpkmKT4/WdL3POdZvg+sR50deRP7+fkhKioKjx49Qm5uLl588UXU1dW5FSQN5KVrMpnQ3d2Ne/fuobi4GK+88gpqa2s9HmyMGtG1pbu7G5WVlQgLC0NmZuaAblKeEl0y8hkaGkp/MG2HG+y9gUxDmLi4OJesBu1FT8x8ItOti/Rikg+zrRCTVTlBQUFDiuiGAml96ujo6GdMM5BXr1KptGrrst1e4aoQk44AT1k/ugqJdIlfwjPPPIOAgACfrExiYps/9vQjNxklth11Zkb/Z8+exaVLl6BUKrFy5UokJibCaDS6JbqOvHSBvvTC6tWrwePx6Pe8o6PD4+msUSO6JNIlwgEA06dPd6pvMyAgYEiiq9Vq6b7ZtLQ0hIeHOzVJBoBekhkZGemx9eaO8olarRZKpRKdnZ10L2ZoaCjtzWAwGJCamsrKoyuJsGtqalwypmFGT8y2LntCTAYdBhJivV5PR9DMfKUvYQpdUlKSVWrHlZVJgxUmB4N05YSEhHjss+kMzECiqakJd+/exebNm7FhwwaUlZXh4cOHXrnub3/7WxQUFODZZ59FZWUlDAaDx710gVHSvQA8df/SaDSQSCR2V/M4oq6uDkFBQfQjj7OQntmuri4YjUYsXLjQ6bwt2dvm7+8PsVjMypebVOJbWlogEAjo7RdMcYqIiPB6sYa0XwUFBSE5OdkrETZTiOktwGYz/VoFAgGdU2WzWMcslCUnJ7v1u2emYUiHiCvRP0VRdHtiSkqKS98lT6HX63HkyBHcvn0bZ86cwYwZM7x+TYPBgA0bNqC0tBSBgYE4duwYli5d6u6PG90tYwDo3ld3Cj6NjY2gKMrplcukZ7apqQlTpkxBbGwsiouLkZGRQUcUjsSWtKup1WqIxWLWGrzJ9N2ECROs2tAoiqLFiQgUU5zcfVy3B+ns6OnpYaU4RAYd2tra0NzcDD8/P/D5/H6v1Vf7vojfrzd+F8wiFvN9ZY7/RkREQK/Xo7y8HOPHj2etB/r+/fvYvn07Xn75ZezcuZOVDg0PMPpF12Qyue1/QPxYk5KSBvz/MYtkEydOpMXKYrGgsrISXV1dVnaJpAgA9EWVpBvA9pHRl5BVOXw+H2Kx2KnNCcwpLPKHWcBytZOAadATHx+P2NhYVn4XZISYtMOFhYU5vOnY5sM9KcRM68WEhASf5Y/JayVCLJfLYTAYaH9mb69MskWn0+Hw4cO4e/cuzpw5Q2+zHqFwojsQ7e3t6O7uph317dHT0wOZTIawsDCIxWIEBgZa9RKSnDJzwEGlUtGz6hqNBiKRCMnJyaxED8zx4YGa+p2F+bhOXqvFYrG66dgr6pAhC4FAgGnTpvksT8iEWbh05gbIFGLy/tqLEl19LQaDAVVVVXQunY0UE/D0sy0SiRAfH2/VS6xUKj2+MskexcXFyMvLw5o1a5CXlzdSo1smo190ST7SHbq7u9Ha2or09PR+/42MCpvNZkgkErtFMkcfvp6eHrobIDw8HBqNBhqNBv7+/lY509DQUK9FekyB8fb4sG0uUaVSAQC9aUChUNACw9Z+K5VKhYqKCgiFQiQlJbn95baNEpVKJZ0PZ9547AnxQIUyX2IymVBdXQ2NRoO0tDSHE362K5NUKlW/lUkRERFuTddptVocOnQIxcXFOHPmDNLS0jzx0oYDnOgOBDG4zsjIoP+d0WhETU0NHQETn1JnHcDIjiuJRNLPAYz0YJI/vb299FTSUD7AtpA9bsSjgK3ppdraWrS1tSEkJIT+3dlGxN5+pCbvp1qt9shknT1IzynzpkM6RMhr9ff3R01NDcLCwliL9IGn044JCQmIiYlx67NmGxE7Wpnk6GcXFhZi586deP3115Gbmzsaolsmo190LRaL29sbmIY1ZBKrubkZiYmJdEeDM2LL3HbrqgMY+QCTPzqdzmrSTCgUOj3gQNrXAEAsFrPiUQA8jfRJUYZ8qZgevaS67q31Qcz8MRtGQUSIiVOXWq2mF0QO1DPtLYhJjtlsRmpqqsfztcwNFsQQhzzZhYeH090hR48exYMHD3D27FmkpKR49AzDBE50B8JoNOLBgweYMmUKPYmVmJhoZU8HOBZbMvLb3Nw8pMiBCXPAgfyxHXCwfXwlG4O7urpY23gLWBvT2Iv07eFIiJmvNSwszKXfq1qtpodVkpOTWYsqiTEMKZTxeDx6Cou8XhIRM288nhRi5s0nKSmJ7t/2BcTMqaurC2+//TYqKioQEhKC5cuXIycnB6tWrfLZWXzI6Bddd+0dgb4vRUlJCWJiYmgHLdsimaNJso6ODnrk19sOYLaPr8yCDtBXpEpISEB8fDwrOUKmX4OjMWZXMJlMVo+vzubDzWYzamtr0d3dzapPgSuFMubwCtMe0t1xbiY6nQ7l5eUICgqCWCxm5ebT29uLv/zlL3j06BHOnj2LmJgY/PDDD9BoNFi2bJnPz+MDONG1R29vL2QyGV0UWbRokdNFMjKMQfxUnWm98gbd3d2oqKhAYGAggoODodFo+nURMFvXvEVnZyeqqqowceJETJkyxWs3H1sLTI1GY2UOYzKZ0NjYiPj4eMTFxbFy8/FUoYwpxMxOAiLEtgYx9v4+eQLzpnfEQFAUhbt37+Kdd97BG2+8gS1btrDSvcMCnOgyIQMKCoUCYrEYUVFR+P777zFv3jynHMBqamqg0+kgFovdNj4fKmSJpclk6vcIb7FY+j2q83g8r+RMyap1AJBIJHajucZuLX5qUSEowA/SBCEigj0baRmNRrS3t6Ourg4WiwX+/v79CpMD2SV6EjJR5q2UBhFi5vtLhJj5/ppMJpSXlyMiIgLTpk1jzej9wIED+Pnnn3H27FkkJyf77No9PT3YuHEjysrKwOPx8Le//Q0LFizw2fUxFkQX6MslDgRzw+/UqVPp1SQWiwWPHj2CVqtFeHg4bUnHzCESI5b29naPPDq7C/McTH9eZ/6eSqWCQqFw6VF9sHN0dHQMuGpd9kSNT/5dCwvVJxjRgkC8uyzZY8JrsVjo3wdz/NtgMFilYZim8MwOEa3RggJZO54o9RBPDMPC5Cj4ufG+Ms+RkpLi00lD29U6crkcer0eERERiIyM9Kjlp7PnuX37Nt577z1s3LgRb731ls9Ff/369Vi0aBE2btwIg8GA3t5eX09/jg3RNRgM/ewdgadFhNraWkyePBlTpkyxWyQjEaKtMPn7+0OtViMmJoa10UjmqpzY2FjExcUNOVJ1p3WNaUzjzMqe/P+phlylhzCkT2Sbe7R4RRqDpSlD9zYgKQ1nJ7lsO0TUvVr8s5ZCh44HQXAgDJQflqVPxJqsOJfOQRztRCKRTyfKbFEoFKioqMDEiRORkJBgdeNRqVRW3sveGnJQq9X485//jMrKSpw9exbTpk3z2M92FqVSiVmzZnnFltEFxq7okhHLiIgI+nHPmSIZ8++GhIQgNDQUarV6SK1c7kLWi5MpLm9ez2Aw0Dcd0roWFBREv84nT55Y7XcbjA/+JUOvwYLQwL4bVatChxcyRFg+3f3quU6ns0ppuJtPr5Krcex/qjA+CDCaTNDr9ejoNeM/54Yjerxw0AjRaDTSblRsTpSZzWZUV1dDpVIhLS3NYbeI7ZCDvRVC7goxRVG4desWdu3ahU2bNuHNN99k7eZTWlqKTZs2IT09HT/88AOkUilOnDjhtY3ZDhgboms0GunIlXgMAKBzns4WyTQaDaqqquDn54fk5GSrPlfi9UmESaFQwGg00iYpQqHQY4YwzFU5ZBrO15AiY3V1NZRKJb1Ic6DWNSbXytvx9wctiAoLhNFsgdZoxrvLkjEl0vXeYWI01NraSufih0LlEzU+LqjFJGGfqFooCm0KPY68kAyDtm/st6WjB9/UatGl52FadBhezpwMUdQ4dHd30+1XbE2UAU+jffL0445Y2j4BME3EnRFilUqFffv2oba2FufOnWN9NXpJSQnmz5+PO3fuYN68ecjNzUVERAQ++OADXx5j7IguWXWjVCrpiq2zk2QGgwG1tbVQqVQuOYDZmqQQQxgSPQiFQpemrpgbC5KSklhbPOjImIYUc5gRMWldEwqFVk5kForCdxXt+L62G8EBfvhNxmSkThrc49gW8gg/YcIEj3VH6E1mHP2mGq1KPUID/aDSmfGLaZFYPz8eAGAwW3DgsgzNPTqEBvDQrdEjJozCrydr4cfj0bl/b/TVDgaJso1GI1JTUz3aPWMrxMyxX/JaKYpCdHQ0bt26hd27d+Ott97Cpk2bWItumbS1tWH+/Pmor68HANy6dQtHjhzBlStXfHmM0b2YktDY2EhHH2SG23YBpKPhhoaGBrS2tiIxMREpKSkuiRyPx4NAIIBAILCaYCOPcQ0NDVbN/uSLalu4Yq7KmTRpEisbCwgqlYo2+LE1sObxeAgNDUVoaChdjGTeeJjG4eHh4UiNiMDchZPcal1j9rrOnDnTo9N1QXx/bH8uCf+3TI4nKj0kojA8x8g1t/To0KrQQRTRtwEEJj3qu/SYsmQGkmKi6Xaurq4u1NfX9xv5dccEZzCI011tbS2mTp0KkUjk8Ruyo20kzLHfgwcP4u7du+jt7cWaNWswYcIEWCyWYSG6kyZNQnx8PGQyGVJSUvDdd9/Z9VVhi1EV6XZ3dyMoKMjpSTLyAa6rq6OLIN4skpFmf5KWYBauAgMDIZfL6VYjNlblAH0RFDFBGapHAdMAR6FQ0FsNSIfIQK1rpMe0qamJtTXjTd1avP9/KiAM7LsJBQYHodcSgBMvz8S4UPtGNo6GVzxhC6nT6VBRUQE+nw+JROLTyJpAURSuX7+OPXv2YOvWrVixYgUePnyI0tJS7NmzZ1iILtCX1yWdC0lJSfjss898bcY+dtILJpPJqSKZQqGwshhk4wMMPN1LptFoEBQUBLPZjJCQEKvHVl9MEDHdyBITEzFp0iSviJy9cV9/f38rISaPzuPHj0dSUhK2XSt2AAATyklEQVRrzfQGgwEfXHyIMrkewvAwWCgefimJxh8WOD/x58gW0hVTePLeNDU1eSSX7S5KpRJ/+tOf0NzcjDNnzjht+j9GGRui+84770AgECArKwtSqRTh4eH9vhxarRbV1dUwmUwQi8VO7VDzBqQoRHqGyWMicwqJ5EzJl5SZL/WkEBFjmnHjxg3J7tBdyJQZsdg0GAwICwuz6jH1hOuaszBz2QlTEiFT8tGi1GFKZCieSYqEv9/QzuGKKTwZtiDBARtOXBRFoaCgAHv37kVubi7eeOMNn0a0iYmJ9O+Dz+ejpKTEZ9ceAmNDdGUyGe7du4fCwkI8ePAABoMBM2bMgFQqRWpqKi5evIgXXngBM2fOZC1aAJ6uynF2ZJYYhhMRJj61zOhQIBC4LErEmMZgMNCbE9iAOTZLomzSQ0xeM7OQQ16zN1Iwvb29tCGLL01ybE3hSReBxWJBTEwMJk6c6PGbrTMoFArs2bMHcrkcp0+fRnx8vE+vD/SJbklJiVeWRHqRsSG6tuh0OpSUlOCTTz7BtWvXkJ6eDovFAqlUiqysLGRlZdGDEr7AnVU5jrA3Ycbn8636hx1Fh8wom618KUGtVltFco5EzlFrE/EhIELsrkiSjhG5XO7ziTJblEolKioqEBkZiejoaDovzjSF97avBkVR+Pbbb7Fv3z7k5eVh3bp1rOVrOdEdYdTX1+P8+fN49913IRAI0NXVheLiYty7dw/FxcV4/Pgx4uLikJ2dTYvx+PHjPSpCZFWOUqn06jJK2+hQq9XSgw1EmFQqFaqqqnziijYQxNxcoVAgJSXFLQ8LW2cuYpHo6jZj0o5GnjzYEhfijtbT04O0tDS7qS+z2dxv0y/gWVP4np4e7N69G11dXTh9+jS92p4tpk6dSn8nN2/ejE2bNrF6HicZu6I7GGRmvrCwEIWFhSgpKaEne4gIz5o1y62o1GKx0AUQtgy0ySBHV1cXnjx5Aoqi6MWDnhzkcOVMpOXJG0spHfVMk+iQ9Ez7+/vDaDSiqqoKOp0OqamprJm9A0+nH8lotSu/E0+ZwlMUhW+++Qb79+/Hzp07sXbt2mHRjdDS0oKYmBjI5XLk5OTg5MmTWLx4MdvHGgxOdF3BaDTixx9/pIX40aNH4PP5yMzMRGZmJrKysiAWiweMEjs7O1FdXY2oqCgkJiaytorEbDbTj83E2JxsMvDEIIcraDQayGQyBAcH077FvsDe7jaj0Qij0QiRSIS4uDifrAyyBxF+vV7v0VFiV03hu7u7sWvXLiiVSpw6dYruNx9u7N+/HwKBADt37mT7KIPBie5QIFt+S0pKUFhYiKKiIroQxswPi0QilJeXQ6VSITg42KHVoa/OzBy0GMiIxdYKkmwxHmiQwxWII1lnZ6dHNhEPBVIoCwoKgkgkorsImK1r7m6qcBW5XI6amhqvtugxMZlM/byIjx8/Dh6Ph9LSUmzbtg15eXmsbdiwB9MfWqPRICcnB/v27cOvfvUrto82GJzoehqKotDS0kJHw99//z2qqqoQEhKC3//+9/jFL36BzMxMr276dQQp2AUEBDhtTGPLQIMcRIidSbkwHck84YzmLs4UypivmWmQ7kxx0hX0ej0qKirg5+eHlJQU1nrEu7q68O6770KhUEAqlaKyshINDQ24ffv2sEgrAEBtbS29zsdkMuH111/H3r17WT6VU3Ci6020Wi0WLlyITZs2Yf78+SgpKUFxcTEePHgAs9mMjIwMOhpOS0vzWqqB7EgjG4w9HVEyuwcUCgXdPWBvkIOYm/v5+UEikbA2YQf0FYZkMplbhTJ7vry2ZjDO5vvJjbqhoQHJycmYMGHo9pbuQFEUrly5gg8++AB79uzBq6++yqYF4miFE11vYzQa+z2Wker6/fv3UVRUhMLCQlRUVEAoFEIqlSI7OxtZWVmIjY0dUmTBbOaPi4vz2ZoaR4McFEXBaDQiMTERsbGxrHVIeKtQZrswlNm65sj8hqQ1yJg3Wzn+zs5OvPPOOzCZTPjrX//q0wWVQF+qiXzmL1++7NNr+xhOdIcLZJklSUsUFRXR695JNJyZmQmhUOiUcDKNadgcZwb6HldlMhnGjx8PgUDg0UEOV2AavvsiXzpY65pWq6XbwNjKZ1MUhUuXLuHQoUPYu3cv1qxZw0p0++GHH6KkpARKpZITXQdwousDLBYLqquraRG+f/8+ent7MX36dFqIZ8yYYfWIbjQaUVNTA5VK5Xafq6fQ6/WorKyE2WxGSkpKv+Ihs5KuUCjojRzM/mFPjfmSiJIYrbNVFCKFzKqqKvD5fHozib1RX2/T0dGBHTt2gMfj4dNPP6Wdw3xNU1MT1q9fj7179+LDDz/kRNcBnOiyhMFgQGlpKS3EZWVlCA4OxuzZs2E0GiGXy3H8+HHExMSwlo+zWCxoamqymmxzFmcGOVyJ2ofTRJnZbKZz66mpqbRT20Dj3J4abGBCURQuXryII0eO4P3338fLL7/Mau72pZdewu7du6FSqXDs2LExK7qjyk93NBEYGIi5c+di7ty5APq+QDdu3MCWLVsQHR0NoVCIVatWITY2FpmZmfREna8WZhKTnMjISGRnZ7scsQUEBCAqKor2wGCO+fb09KChoYE2vhlsuoxZKMvOznZbtJp7tDh0tQr1nVrEjw/G7l+JXd5w0d3dDZlMhsmTJyMrK8vqvSADC0y7TOZTgK3v8lBa1+RyOXbs2IGAgAAUFBSwVrQjXL58mW6xvH79OqtnYRsu0h1BFBUVITw8nDZoJx4K9+7dQ1FREYqLi9HT04OUlBS6UDdr1iyPrh83GAz0CiFvm+QQf1pHgxxhYWFoa2vzSKHMYLbgjf9+iE6NAaGBfPQazYgI5uO/189BSMDgNxSTyYSqqipotVqkpaUNqT97sNa1gVbKUxSFf/7zn8jPz8f+/fuxevXqYdGZsHv3bnz++efg8/l0IXL16tX44osv2D6at+DSC2MFk8mEn376ifaWKC0tBY/Hw+zZs+lBjpSUFJcjU2a7k7c2FjgDGeRoamqCXC4Hn8+3auESCoVu9UbXd/biP756hLCgp5G0xmDCxy/NgEQ0sP1ne3s7qqurvTrqPVDrmp+fH73NY8eOHQgJCcGJEyeGrUHM9evXufTCaODq1avIzc2F2WzGxo0bsWvXLraPxAp8Ph+zZs3CrFmzsHnzZlAUBbVajfv376OwsBBHjhxBZWUloqKiIJVKIZVKMXfu3AEr/CqVChUVFYiIiEB2djZr7U5AX9GupqYGwcHBWLhwIQICAqwiw+rqarcGOcKD+TBTFMwWCv5+PFgoChYLIAh2/FoNBgNkMhkoikJmZqZXe5EDAwMRHR1tJaQkYiwpKcHBgwfx+PFjiMVivPDCC2hoaBi2ojvWGRWRrtlshkQiwbfffks7hn311VfDai/ScIL09RYVFdERcVtbG5KTk+m0xJw5c2AwGHDnzh3ExMQMeXXPUCF77J48eQKJRDLo6hXmKvnBBjkI/3XnMf7Xg1Z668iLM0XY8uzUfj+b2Rc9bdo01roBgL4ljHl5eQgPD8dHH30EtVqN4uJiREVFYenSpaydi2OUpxfu3r2L/fv345tvvgEAHD58GEBfHonDOcxmMyorK2kT+GvXrkGhUGDJkiVYvHgxsrOzkZ6ezkoL1lAmygjObOQQCAQobVajqUeLGGEwsqeMs7t5hHg3sNmSZrFY8Pe//x0fffQRDh48iBdffHFY5G45aEZ3eqG5udnK0T4uLg6FhYUsnmjk4e/vj7S0NKSlpaGlpQU5OTl4//338fjxY9y7dw8nT57ETz/9BIFAYGXyM5CRzlAhSzK1Wu2QNwEzNxhPmjQJgPW2hpaWFrqFSxIeDmGAEGo1nx7koCiKNn6XSCSIjIz0yGt0h7a2NuTm5iIyMhI3btzw6Vl0Oh0WL14MvV4Pk8mEl156CQcOHPDZ9UcDo0J07UXr3F3ffXbt2kUX2mJiYrBgwQIAfb/nzs5O2gT+66+/RkNDAxISEui9dFKpdMgm8LYTZampqV55P5ktXMSom9nCVV9fD41GA6AvXREREYEZM2awttbIYrHg66+/xieffIJDhw7h17/+tc8/50FBQSgoKIBAIIDRaMTChQuxfPlyzJ8/36fnGMmMCtGNi4tDY2Mj/c9NTU0e9wPdsGED3WtYVlbm0Z893HDU2cDj8RAdHY3ly5dj+fLlAPqEoK6uDoWFhSgoKEB+fj7UajXS09PpiDgjI8NpUxjm43tWVpbPH9/9/f0xbtw4jBs3jn5tHR0dmDp1qlXkPZRBDndobW1Fbm4uJkyYgBs3bvh6nTgNj8ejN1oQT2IuwHGNUZHTNZlMkEgk+O677xAbG4vs7Gx8+eWXmD59useucfPmTQgEAqxbt27Ui+5QMRgMVibwP/74IwICAjBnzhy6UJecnGyVlnC1UOZtSB5ZJBLZTaGQzgGSH3Z2kMNVLBYLvvzyS3z66ac4fPgwVqxYwbrImc1mSKVSVFdXY8uWLTh69Cir5xmmjO5CGgD861//wvbt22E2m7FhwwaveG7W19dj5cqVnOi6CEVRdGsTGWuuqamBSCSCVCqFUCjEzZs3kZ+fj6SkJFa9XE0mE2pqaqBWq5GWluZ0HnmwQQ53NnK0tLTg7bffxuTJk3H8+HFWR5vt0dPTg1WrVuHkyZOYMWMG28cZbox+0fUFnOh6DoqiUF5ejry8PFRWViIpKYmOckl+eM6cOT41ge/s7ERVVRXi4uI8sruNrAliei0wR3wdDXJYLBZ88cUXOHXqFI4ePYrnn3+e9ejWEQcOHEBYWNhIWJ/ja0Z39wLHyIPH48HPzw+/+93vsHbtWvB4PJjNZvz8888oLCzEP/7xD+zduxcURVmZwKempnp8OMNgMNAuabNnz3ZrCak9mAJLYA5y1NTUQKPRIDAwEMHBwXjw4AGSk5ORn5+PhIQE3Lx5E0Kh0CNn8RTt7e0ICAjAuHHjoNVqce3aNbz33ntsH2tEwUW6LsBFur6FPLIzTeCJXy/plMjOznY7KmV2SSQlJfnc0JtgMBjQ2NiIffv24f79++Dz+Zg5cyZWrFiBzZs3s3ImRzx69Ajr16+H2WyGxWLBK6+8gn379rF9rOEIl17wBN4W3cbGRqxbtw5tbW3w8/PDpk2bkJub65VrjVSITy3TBL6lpQVTp061MoGPiIgYUIh1Oh3Ky8sRGBgIiUTC6jLGxsZGbNu2DUlJScjPz0d4eDjq6+vR2tqKZ555hrVzcQwJTnSHymuvvYbr16+jo6MDIpEIBw4cwB//+EePXqO1tRWtra3IzMyESqWCVCrFxYsXuXHmQSAm8MRt7f79+9DpdP1M4AMDA+nJO4VCAbFYTFtLsnXuCxcu4Ny5czh+/Diee+45n+VuuRu81+FEdyTym9/8Blu3bkVOTg7bRxlx6PV62gS+uLgYZWVldLriueeew5tvvolp06ax1inR0NCArVu3QiKRID8/n+599RXcDd7rcKI70qivr8fixYtRVlbG6iqe0cK5c+dw+vRprFu3DgqFAsXFxairq0NsbCwdDUulUkRFRXk12rRYLDh//jw+++wzHD9+HEuXLh0WnQncDd7jcKI7klCr1ViyZAn27t2L1atXs32cUUFdXR3i4uKscrdkIINpAq9QKJCamtrPBN4T1NfXY+vWrUhPT8eRI0d8Ht06grvBewVOdEcKRqMRK1euxPPPP4+8vDy2jzPmMBqN/Uzg/fz86Gm6rKwsSCQSl0zgzWYzzp8/jwsXLuDjjz/GkiVLhkV0C3A3eC/Cie5IgKIorF+/HpGRkfj444+9dh3OKcp5mCbwRIgrKysxYcIEWoSzs7MdbtKoq6vDtm3bMHPmTBw6dIg1sxx7cDd4r8KJ7kjg9u3bWLRoEWbOnEkXeA4dOoQVK1Z49DoURUGj0Vg5RZ04cYJzinISiqLQ2tpqZQIvl8tpE/isrCzMmjULX331FT7//HOcOHECixYtGjbRLeC7G/wYhhNdDvv09vZi4cKFOHXqFObNm8f2cUYsZrMZMpmM7h++evUq5s6diwsXLgzJB9hb+OoGP4bhRJfDGs4pyruQlT8cYxaHbz57dk4crOLv74/S0lI0NTWhqKiIG232MJzgcjiCE90xzrhx4/Dss8/i6tWrXruG2WzGnDlzsHLlSq9dY6yyYcMGTJw4kbNWHEFwojsGaW9vR09PDwDQTlGpqaleu96JEyeQlpbmtZ8/lvnDH/7g1Rsmh+fhRHcM0trail/+8pfIyMhAdnY2cnJyvBaFNjU14cqVK9i4caNXfv5YZ/HixawuyeRwHc5PdwySkZGBhw8f+uRa27dvR35+Pr1pl4NjrMNFuhxegyzylEqlbB+Fg2PYwIkuh9e4c+cOLl26hMTERLz66qsoKCjA2rVr2T4WBwercH26HD7h+vXrOHbsGC5fvuy1ayQmJiI8PBz+/v7g8/koKSnx2rWGE9xGk2EJ16fLMTb497//jdLS0jEjuK+99hoWLFgAmUyGuLg4nD9/nu0jcQwCF+lyjBoSExNRUlKC6Ohoto/CwcFFuhyjHx6Ph2XLlkEqleLs2bNsH4eDwy5cyxjHqOHOnTuIiYmBXC5HTk4OUlNTsXjxYraPxcFhxWDpBQ6OEQmPx9sPQE1R1DG2z8LBwYRLL3CMCng8XhiPxwsn/xvAMgBcOZ9j2MGlFzhGCyIA//v/u3vxAXxJURRnSsAx7ODSCxwcHBw+hEsvcHBwcPgQTnQ5ODg4fAgnuhwcHBw+5P8B6I1garh1veQAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"from mpl_toolkits.mplot3d import Axes3D \n",
"# And we plot them as to visualize the problem.\n",
"fig = plt.figure()\n",
"ax = fig.add_subplot(111, projection='3d')\n",
"_ = ax.scatter(X[:,0], X[:,1], Y[:,0])\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2 - The symbolic regression problem"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"# We define our kernel set, that is the mathematical operators we will\n",
"# want our final model to possibly contain. What to choose in here is left\n",
"# to the competence and knowledge of the user. A list of kernels shipped with dcgpy \n",
"# can be found on the online docs. The user can also define its own kernels (see the corresponding tutorial).\n",
"ss = dcgpy.kernel_set_double([\"sum\", \"diff\", \"mul\", \"sin\", \"cos\"])"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\tData dimension (points): 2\n",
"\tData dimension (labels): 1\n",
"\tData size: 30\n",
"\tKernels: [sum, diff, mul, sin, cos]\n",
"\n"
]
}
],
"source": [
"# We instantiate the symbolic regression optimization problem\n",
"# Note how we specify to consider one ephemeral constant via\n",
"# the kwarg n_eph. We also request 100 kernels with a linear \n",
"# layout (this allows for the construction of longer expressions) and\n",
"# we set the level back to 101 (in an attempt to skew the search towards\n",
"# simple expressions)\n",
"udp = dcgpy.symbolic_regression(\n",
" points = X, labels = Y, kernels=ss(), \n",
" rows = 1, \n",
" cols = 100, \n",
" n_eph = 1, \n",
" levels_back = 101,\n",
" multi_objective=True)\n",
"prob = pg.problem(udp)\n",
"print(udp)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 3 - The search algorithm"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"# We instantiate here the evolutionary strategy we want to use to\n",
"# search for models. Note we specify we want the evolutionary operators\n",
"# to be applied also to the constants via the kwarg *learn_constants*\n",
"uda = dcgpy.momes4cgp(gen = 250, max_mut = 4)\n",
"algo = pg.algorithm(uda)\n",
"algo.set_verbosity(10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4 - The search"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"# We use a population of 100 individuals\n",
"pop = pg.population(prob, 100)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"# Here is where we run the actual evolution. Note that the screen output\n",
"# will show in the terminal (not on your Jupyter notebook in case \n",
"# you are using it). Note you will have to run this a few times before \n",
"# solving the problem entirely.\n",
"pop = algo.evolve(pop)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 5 - Inspecting the non dominated front"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"# Compute here the non dominated front.\n",
"ndf = pg.non_dominated_front_2d(pop.get_f())"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" Loss: Model: \n",
"\n",
"1.6049416203226965e-36 | c1*(x1*cos(x1) + cos(x1)) + 2*c1 + 6*cos(x0*sin(x1)) |\n",
"1.4444474582904268e-35 | c1*x0 - 2*c1 + 6*cos(x0*sin(x1)) |\n",
"1.3000027124613843e-34 | c1*x0 + 2*c1 + 6*cos(x0*sin(x1)) |\n",
" 0.8559137162832793 | sin(x1) + 5*cos(x0*sin(x1)) |\n",
" 3.04427756327168 | 2*c1*x1*cos(x0*sin(x1)) |\n",
" 4.714418293710785 | 3*cos(x0*sin(x1)) |\n",
" 8.875932935300025 | 4*cos(c1 + x0) + 1 |\n",
" 9.493068363220251 | 5*cos(c1 + x0) |\n",
" 13.422370193371659 | 2*c1 - 2*x0 |\n",
" 13.42237019337166 | c1 - 2*x0 |\n",
" 13.486758301564212 | c1 - x0 |\n",
" 15.41066772551229 | 2 - x0 |\n",
" 18.679277437831498 | c1 |\n",
" 18.85767317484314 | 0 |\n",
" 18.85767317484314 | 0 |\n"
]
}
],
"source": [
"# Inspect the front and print the proposed expressions.\n",
"print(\"{: >20} {: >30}\".format(\"Loss:\", \"Model:\"), \"\\n\")\n",
"for idx in ndf:\n",
" x = pop.get_x()[idx]\n",
" f = pop.get_f()[idx]\n",
" a = parse_expr(udp.prettier(x))[0]\n",
" print(\"{: >20} | {: >30}\".format(str(f[0]), str(a)), \"|\")"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO3de3zU5Zn38c+VyYEQfDhJEBCQCLq1grRSStVqLepLa602i+3WQ9XWB599tm5b3Q1ou9vWrhbZ7a67bvusrOeu2qqNRWpr01LFomKBXQqIB5CDkVOAcNAISWZyPX/Mb8YcZpJJmMlMZr7v1yuvzNy/05Ufes09933/7tvcHRERKRxF2Q5ARET6lxK/iEiBUeIXESkwSvwiIgVGiV9EpMAo8YuIFBglfskbZuZmNjkD5/0PM/u7dJ+3L8zs82ZWb2bvmdlHsh2PDEymcfySLma2FSgHqty9KSi7HrjK3T/VD9d3YIq7b8r0tfrCzE4AtgAl7h7u4zneAm5y98VpDK39+XP6Hkp6qMYv6VYMfD3bQeSxicCriTaYWXE/xyIDlBK/pNs/An9jZsMSbTSzM8xspZkdDH6f0W7b82b2fTN70czeNbM6Mzs22YXM7G/NbKeZ7TCzr3TaNtTMHjazPWa2zcy+bWZFwbZrg2v8i5kdMLPNQVzXBs0oDWZ2TbtzPWhm/xC8/pSZvWNmNwf77TSz69rte7GZ/Y+ZHQrO9d12Yb0Q/D4QNNV8IjjmK2b2mpntN7PfmNnEBH9rmZm9B4SAPwU1f8xsq5nNM7O1QJOZFZvZh4J7ecDMXjWzz3X6W35kZs8E9/gVMzsx2BaL709BfF80s2PN7JfBuRrN7A+x+ygDl/4BJd1WAc8Df9N5g5mNAJ4B/g0YCfwz8IyZjWy32xXAdUAlUJroPMG5Lgy2nQ9MAc7rtMvdwFCgCjgH+HJw3piPA2uDOB4Ffgp8DJgMXAX8u5kNSfI3HhecexzwVeBHZjY82NYUXGsYcDHwl2Z2WbDt7OD3MHcf4u4vB9tuBaqBUcAfgMc6X9Ddm909Fs9p7n5iu81fCq41DDBgCVBH9B7eCDxiZid32v97wHBgE3B7cI1YfKcF8f0MuBl4J4htdBCr2ocHOCV+yYS/B240s1Gdyi8GNrr7T9w97O6PAa8Dl7Tb5wF3f9PdDwOPA9OTXOMLwb7rg/6E78Y2mFkI+CJwi7u/6+5bgR8CV7c7fou7P+DuEeBnwHjgtiDB1gEtRD8EEmkN9m11918B7wEnA7j78+6+zt3b3H0t0SR+TtI7BTcAP3D314J2/zuA6Ylq/d34N3evD+7ZLGAIsMDdW9z998AviSb7mFp3/2NwvUdIfo9jf+sYYGLw9/7B1TE44CnxS9q5+3qiyWZ+p01jgW2dyrYRrTnH7Gr3+n2iSSyRsUB9p/PEHEv028K2TtvbX2d3u9eHg7g7lyW79r5OnbPxOM3s42b2XNDEdBD4P0E8yUwE/jVoSjkANBKttY/r5pjO2t+HsUC9u7e1K+vrPYZo090moC5oEuv8byoDkBK/ZMp3gP9Nx4Szg2iia28CsL0P599JtJbe/jwxe4nWVCd22t6X6/TWo8DTwHh3Hwr8B9FEDombSOqBG9x9WLufcnd/qRfXbH/eHcD4Tu3wff7bg29MN7t7FdFvZjeZ2ey+nEtyhxK/ZEQwHPBnwF+3K/4VcJKZXRF0Qn4ROIXot4Peehy41sxOMbPBRD9oYteOBNtvN7NjgmaTm4D/6uOf0xvHAI3ufsTMZhLts4jZA7QR7XeI+Q/gFjP7MMQ7pS8/iuu/QrSfocbMSszsU0QT9k9TPH53+/jM7LNmNtnMDDgERIIfGcCU+CWTbgMqYm/cfR/wWaIdhvuAGuCz7r63tyd2918DdwG/J9oU8ftOu9xINAFuBpYTrYnf3/s/odf+L3Cbmb1LtK/j8XYxv0+0I/XFoGlnlrs/BdwJ/NTMDgHrgYv6enF3bwE+F5xjL/Bj4Mvu/nqKp/gu8FAQ3xeIdpz/jmg/xsvAj939+b7GJ7lBD3CJiBQY1fhFRAqMEr+ISIFR4hcRKTBK/CIiBWZATOp07LHH+gknnJDtMEREBpTVq1fvdffOT9APjMR/wgknsGrVqmyHISIyoJhZ5yflATX1iIgUHCV+EZECo8QvIlJglPhFRAqMEr+ISIEZEKN6+uKRRx5hw4YNlJSU0NrayimnnMKVV16Z7bBERLIuL2v8jzzyCG+88QalpaWYGaWlpbzxxhs88sgj2Q5NRCTr8jLxb9iwgVAo1KEsFAqxYcOGLEUkIpI78jLxl5SU9KpcRKSQZLSN38y2Au8SXbEn7O4zzGwE0ZWZTgC2Al9w9/3pvG5rayulpaUJy0VECl1/1PjPdffp7j4jeD8fWOruU4CldF2Q+6idcsopRCIdV4eLRCKccsop6b6UiMiAk42mnkuBh4LXDwGXpfsCV155JSeffDJtbW24Oy0tLZx88ska1SMiQuYTvwN1ZrbazOYGZaPdfSdA8Lsy0YFmNtfMVpnZqj179vT6wldeeSWRSIRwOMztt9+upC8iEsj0OP4z3X2HmVUCvzWzVBd8xt0XAYsAZsyYoYWBRUTSJKM1fnffEfxuAJ4CZgK7zWwMQPC7IZMxiIhIRxlL/GZWYWbHxF4DFwDrgaeBa4LdrgEWZyoGERHpKpNNPaOBp8wsdp1H3f1ZM1sJPG5mXwXeBi7PYAwiItJJxhK/u28GTktQvg+YnanriohI9/LyyV0REUlOiV9EpMAo8YuIFBglfhGRAqPELyJSYJT4RUQKjBK/iEiByds1d5955hk++clPMnjwYJ5++mlCoRAXX3xxtsMSEcm6vKzxP/PMMwwaNIiKigrMjBEjRjBo0CCeeeaZbIcmIpJ1eZn4I5EIZWVlHcrKysq6LM4iIlKI8jLxDxs2rFflIiKFJC8T/4EDB3pVLiJSSPIy8YdCIZqbmzuUNTc3EwqFshSRiEjuyMvEf/HFF3PkyBEikQjuTmNjI0eOHNGoHhER8ng458UXX8xTTz0FwOc///ksRyMikjvyssYvIiLJKfGLiBQYJX4RkQKjxC8iUmCU+EVECowSv4hIgVHiFxEpMEr8IiIFRolfRKTAKPGLiBQYJX4RkQKjxC8iUmCU+EVECowSv4hIgVHiFxEpMEr8IiIFJuOJ38xCZvY/ZvbL4P0IM/utmW0Mfg/PdAwiIvKB/qjxfx14rd37+cBSd58CLA3ei4hIP8lo4jez44GLgXvbFV8KPBS8fgi4LJMxiIhIR5mu8d8F1ABt7cpGu/tOgOB3ZaIDzWyuma0ys1V79uzJcJgiIoUjY4nfzD4LNLj76r4c7+6L3H2Gu88YNWpUmqMTESlcxRk895nA58zsM8Ag4H+Z2X8Bu81sjLvvNLMxQEMGYxARkU4yVuN391vc/Xh3PwH4C+D37n4V8DRwTbDbNcDiTMUgIiJdZWMc/wLgfDPbCJwfvBcRkX6SyaaeOHd/Hng+eL0PmN0f1xURka705K6ISIFR4hcRKTBK/CIiBUaJX0SkwCjxi4gUGCV+EZECo8QvIlJglPhFRAqMEr+ISIFR4hcRKTBK/CIiBUaJX0SkwCjxi4gUGCV+EZECo8QvIlJglPhFRAqMEr+ISIFR4hcRKTB5m/g3b95MRUUFQ4YMoba2ls2bN2c7JBGRnJCXiX/z5s2sWLECMwOgqamJFStWKPmLiJCniX/NmjVEIpEOZZFIhDVr1mQpIhGR3JGXib+pqalX5SIihSQvE39FRUWvykVECkleJv7p06cTCoU6lIVCIaZPn56liEREckdKid/MvmZmwzMdTLpUVVUxa9as+PuKigpmzZpFVVVVFqMSEckNqdb4jwNWmtnjZnahxYbL5LCqqioikQiRSITq6molfRGRQEqJ392/DUwB7gOuBTaa2R1mdmIGYzsq69atw8wwM+666y7WrVuX7ZBERHJCym387u7AruAnDAwHnjSzhRmKrc/WrVvHkiVL4u8PHjzIkiVLlPxFREi9jf+vzWw1sBB4EZjq7n8JnA78eQbj65OlS5fS2traoay1tZWlS5dmKSIRkdxRnOJ+xwLV7r6tfaG7t5nZZ9Mf1tE5ePBgr8pFRApJqk09kzonfTP7CYC7v5boADMbZGZ/NLM/mdmrZva9oHyEmf3WzDYGv9M+Wmjo0KG9KhcRKSSpJv4Pt39jZiGizTzdaQY+7e6nAdOBC81sFjAfWOruU4Clwfu0mj17NiUlJR3KSkpKmD17drovJSIy4HTb1GNmtwC3AuVmdihWDLQAi7o7NugMfi94WxL8OHAp8Kmg/CHgeWBe70NPburUqQDs2LEDiNb0Z8+eHS8XESlkFs3PPexk9gN3v6XXJ49+M1gNTAZ+5O7zzOyAuw9rt89+d+/S3GNmc4G5ABMmTDh927ZtnXfp0bPPPgvAhRde2OtjRUQGOjNb7e4zOpd329RjZn8WvHzCzD7a+aeni7p7xN2nA8cDM83s1FQDdvdF7j7D3WeMGjUq1cPi5s2bFx/Hf8UVVzBvXlq/VIiIDFg9jeq5iWit+4cJtjnw6VQu4u4HzOx54EJgt5mNcfedZjYGaOhFvCmZN29evJkHou37O3bsYN68edx5553pvpyIyIDSbeJ397nB73N7e2IzGwW0Bkm/HDgPuBN4GrgGWBD8Xtzbc/ekvr6+S+duUVER9fX16b6UiMiAk+oDXN8P2utj7/+XmT3Qw2FjgOfMbC2wEvitu/+SaMI/38w2AucH79OquDjx51mychGRQpJqJiwG/mhm1xGdsO3u4Ccpd18LfCRB+T4go+Mqw+EwZ555JuXl5ZgZ1157LRs2bODFF1/M5GVFRAaElBK/u99iZkuBV4D9wNnuvimjkR2FM844g6lTp1JUFP1CU1JSwtSpU0llBJOISL5LKfGb2dnAvwK3AVOBfzezr7j7ju6PzI4Pf/jD8aQfU1RUxLRp0+JDPGP6OsN0UVERpaWl8feDBg2ivLy8T+dKl8rKSo477risxiAiuS/Vpp5/Ai539w0AZlYN/B74s26PypJkbfmJkry79yn5t7W1xV+Hw2GOHDmS1cTf1NREQ0ODEr+I9CjVxP8Jd4/E3rh7rZkty1BMRy0cDncZ1RMrb/8w15w5cwB48sknuz3fjTfeCMDdd0e7NW677TYA/v7v/x6Auro6IpEI06ZNO/rg+2jt2rVZu7aIDCypztVzrJndZ2bPApjZKcBlmQvr6Lz11lsdauQQraG/9dZbWYpIRCR3pJr4HwR+Q3SIJsCbwDcyEVA6XH/99bz55pu0trbi7rS2tvLmm29y/fXXZzs0EZGsS3k+fnd/PJi0DXcPm1mkp4OyqXOSP/fcXj+DJiKSl1Kt8TeZ2Uii0zQQTK9cEKua1NXV8eqrr7JmzRrmzJlDXV1dh+2bN29mz5497N69m9raWjZv3pylSEVEUpNq4r+J6FQLJ5rZi8DDwI0ZiypH1NXVsXDhwvgyjrt372bhwoWEw2EgmvRXrFgR709oampixYoVSv4iktNSfYDrv83sHOBkovPxv+HurT0cNuAtWrSI5ubmDmXNzc00NzdTXFzMmjVriEQ6tnhFIhFWrlxJVVVVf4YqIpKynhZiqU6y6SQzw91rMxBTzmhoSDxxaOwJ4KampoTbW1paMhaTiMjR6qmp55JufnJukfXeqK2tZfXq1bz88svMnDmT2tqun2GVlZVdyiZMmEB5eTltbW3xJqBk5++vJp+GhgbeffddDh06xMqVK5N+YImIQM/TMl/XX4H0p9raWmpqauI18+3bt1NTUwNAdfUHX3Lmzp3LHXfcEW/OmTBhApMnT45PB9HY2MioUaO6TA8BH7T3Axlt9mloaGDTpk3xbyHNzc1s2hSdRinRB5eISKpLL44EvgOcRXRkz3LgtmCmzYybMWOGr1q1Km3nmzlzJtu3b+9SXlpayumnd1xDvqGhIZ5UzznnnC5PBFdUVDBixAiKi4sTTv3Q1tbG4cOH0xJ3KBSirKwMgLFjx3LeeeexcuXKLv0QEJ2e4phjjun2fJrbRyS/9WnpxXZ+CuwB/hyYE7z+WfrC61/tV+dqL1HbfPsPxkRzADU1NfH2228nvVZfJ4FLJPbNw93jf0OipB/bpzuxuX1EpPCk+gDXCHf/frv3/2BmOTtlQ0/Gjh2bsMY/bty4LvP2zJkzh927dwPdzwF0+PBhBg8e3GXbkCFD+PKXv3zUMX/lK18B4P777+fhhx+Ol5eVlSVM/mVlZd3OHaS5fUQKV6o1/ufM7C/MrCj4+QLwTCYDy6T58+d3mUmzvLyc+fPnd9l37ty58eaVLVu2JJwDaPfu3WzYsIFQKNRhWygUYvr06WmOvqOJEycmnIJ64sSJGb2uiAxcqSb+G4BHgZbg56fATWb2rpkdylRwmVJdXc3ChQsZN24cZsa4ceNYuHBhh47dmAsuuICamhpGjx5NfX09O3bsIBwO4+60tbUxbdo09u/fz/bt25k1axYVFRVAtO1/1qxZGR/PX1lZyeTJk+MfTmVlZUyePFkduyKSVKoPcHXfSzgAVVdXJ0z0iVxwwQVccMEFSbc/9thjQHT0TjYe3KqsrFSiF5GUpVrjx8ymmdnnzKw69pPJwAaKVJ4HSKdlyz5YBuHBBx/s8F5EJBWpLr14PzANeBWINXI7kNdP7vYk1ecB0mX8+PFs3bo13qYfCoXYunUrEB1qKiKSilRH9cxy91MyGskAtGDBgi5j9A8fPszNN9/Mo48+mvJ5LrvsMq666qoe90vWkbtt27YOI30SiY37FxFJtann5WDVLWmnN88DJPPqq6/yi1/8IqV9k60l3JP24/5FRFLNJA8RTf67gGaiM3S6u2dvkdkc0JvnAZKJrfubimTPEbS1tXHttdcmPGbZsmVs27YNiPYJTJo0Sc1CIgUu1Rr//cDVwIV8MEHbJZkKaqDozfMA6bBt27aEzxFMmjQp4f7Lli1j69atmBlmFu8TUIewSGFLtcb/trs/ndFIBqBYB+6CBQvYsWMHY8eOZf78+Rnp2AWor6/n05/+NFu2bKGoqCie9JPV4Lds2dLlobJYn0BLS0t87L+IFJZUE//rZvYosIRoUw9A3s/Hn4rePA+QDuecc07KTTWJZg1tL9k8PyKS31Jt6iknmvAvIE/m4x9I7rnnHsLhMOFwmKuvvpp77rknpeM6Nwv1VC4ihSHVJ3fzcl7+geCee+5h+fLl8dq7mbF8+XIAbrjhhm6PnTRpUodx//BBn4BWCRMpXKk+wHU8cDdwJh/Mx/91d38ng7EJdEj6MUVFRbz44os0Njb2eHxZWRnDhg2juLiYcDjMgQMH2LFjBx/96EfTOmW0iAwcqbbxP0B0krbLg/dXBWXnZyIo+cDRJufm5ub4tNKdpbIIj4jkn1QT/yh3f6Dd+wfN7BvdHWBm44GHgeOITvOwyN3/1cxGEF3E5QRgK/AFd9/f28ALhbsnTP7hcJjVq1czd+7cbieQS2Tx4sWUl5djZjz33HMcOnSISy+9NF0hi0iOS7Vzd6+ZXWVmoeDnKqCnZRfDwM3u/iFgFvBXwdO/84Gl7j4FWBq8lyTOOuushGP3Gxsb2b17NwsXLqSuri7l8y1evJjhw4dTVFSEmVFSUsLw4cNZvHhxukMXkRyVao3/K8C/A/9CtI3/JaDbDl933wnsDF6/a2avAeOAS4FPBbs9BDwPzOtl3AUj1oG7fPlyzIxwOExjYyNNTU1AtClnwYIFLFmyJKXzVVdXJ+wzGD58OL/5zW8oKiqisrKS0047Lb1/iIjkjFRr/N8HrnH3Ue5eSfSD4LupXsTMTgA+ArwCjA4+FGIfDgknkjezuWa2ysxW7dmzJ9VL5aUbbriBn/zkJ2zdupX6+vp40o9pbW1N+VzJ5vuJNSeVlpZy4MCBvgcrIjkv1Rr/tPbt8O7eaGYfSeVAMxsC/Bz4hrsfSrWz0t0XAYsAZsyYoV5IoguuJOqoHT16NHfffXdK53juueeSrhv8yiuv8PGPf5xBgwYddawikrtSrfEXmdnw2Jugg7bHDw0zKyGa9B9p95TvbjMbE2wfAzT0LuTC1X7935iysjLmzp2b8jkOHTqUsM/g0KEBt4KmiPRRqon/h8BLZvZ9M7uNaBv/wu4OsGjV/j7gNXf/53abngauCV5fA6hXMUXt1/81M0aPHk1NTU2vRvVceuml7N+/n9bWVtyd1tZW9u/fr1E9IgUk1Sd3HzazVcCniU7JXO3uG3o47EyiM3quM7M1QdmtwALgcTP7KvA2HzwbICnoaf3fVMSS/I033giQcjORiOSHlFf2CBJ9T8m+/f7LiX5IJDI71fNIZtTV1fHqq6/S2trKnDlzmDt3LhMmTIiP71+2bBkjR47k1FNPzXaoIpJmKS+2Lvmjrq6OhQsXxkcD7d69m1WrVlFVVRUf3x8KhWhsbGT9+vVZjlZE0k2JvwAtWrSoy5TMs2bNSji+f//+/axdu5Zdu3b1Z4gikkFK/AWooaHrQKpEQzxjmpqaEh4jIgOTEn8W1dbWsnr1al5++WVmzpxJbW3/rGtTWdn1mblkD4G1tbVRUVGR6ZBEpB8p8WdJbW0tNTU18Xnxt2/fTk1NTb8k/0984hNdypYvX55wfP/IkSMzHo+I9C8bCFPzzpgxw1etWpXtMNJq5syZbN++vUt5aWkpp59+ekavvWfPnoSrcF199dVMmTKF4uJiIpEIhw8f5qKLLmLt2rUATJs2LaNxiUh6mdlqd5/RuVw1/izZsWNHwvL+WBkr2dKLmzZt4te//jWf/OQnaWlp6bJQu4jkh5TH8Ut6jR07NmGNf9y4cTz55JMZvfacOXOSLs4CsHnz5vi3gtraWo4//njN3yOSR1Tjz5L58+dTXl7eoay8vJz58zO/PEGyOX8Ahg4dyooVK+LfCpqamjh06BBHjhzJeFwi0j+U+LOkurqahQsXMm7cOMyMcePGsXDhQqqrqzN+7WRz/gAcd9xxRCKRDvu7O++++27G4xKR/qGmniyqrq7ul0SfSKI5f373u98lHc+frF9ARAYe1filg2Tj+Y920XcRyR1K/NLBrl27Eo7m0QgfkfyhxC8dHDx4kFmzZsWf1q2oqKC4uLjLPD4iMnCpjV+6qKqqoqqqKv5+2bJlWYxGRNJNiV8AuPXWW+Nz8X/729+mra2NO+64I9thiUgG6Pu7cOutt1JSUhKfi7+kpISSkhJuvfXWbIcmIhmgxC8UFRUlnIu/pKSEmpoaDh8+zOHDh7MUnYikmxK/UFycuMUvNoRTQzlF8osSvxAOh5OWL1y4kIEwg6uIpE6JX2hra0s4F7+e1hXJT0r8wh133EFrayutra24e/y1RvWI5CctxCLduvfeeznppJMwM8LhMG+99RbXX399tsMSkRRoIRbptVjSbz/M86STTuLee+/NdmgichT0AJckdeKJJyYc5nnSSSfx7LPP9ns8O3fu5Lrrruv364rkG9X4Jamehnn2p/LycsaMGdPv1xXJR6rxS1LhcDjh/PzhcJgLL7yw3+J44oknGDx4MBUVFTz33HPs3buXyy+/vN+uL5JvVOOXpN56662EwzzfeuutfovhiSeeYPTo0R36GUaPHs0TTzzRbzGI5Bslfknq+uuv58033+wwzPPNN9/s11E9xx57bMJ+hmOPPbbfYhDJN2rqkW51TvLnnntuv14/WT9DsnIR6VnGavxmdr+ZNZjZ+nZlI8zst2a2Mfg9PFPXl/zQ3XQSItI3mWzqeRDo3AM4H1jq7lOApcF7kaR27tyZsJ9h586dWYpIZODLWOJ39xeAxk7FlwIPBa8fAi7L1PUlPxw5coS9e/fG+xna2trYu3cvR44cyXZoIgNWfzeUjnb3nQDuvtPMKpPtaGZzgbkAEyZM6KfwJNcUFxfT1NREU1MTxx13HABNTU1q4xc5Cjk7qsfdF7n7DHefMWrUqGyHI1kSa8uvqKigrKyMQYMGcfzxx1NeXp7lyEQGrv5O/LvNbAxA8Luhn68vA0xjYyODBw+OD+uMjeWvrKykoUH/+Yj0RX9/X34auAZYEPxe3M/XlwHmwIEDDBs2rMtY/lAoxMaNG9m1a1eP56isrIw3E4lIZodzPga8DJxsZu+Y2VeJJvzzzWwjcH7wXiSp4uJiSktLE25LZUrxpqYmfTMQ6SRjNX53/1KSTbMzdU3JP+FwmCNHjiRs0y8rK2PatGlJj21oaGDjxo0cOnSIlStXMnHiRCork44nECkYOdu5KwIwcuRI6uvrE47l766Dt6GhgU2bNsW/FTQ3N7Np0ybV/kXQlA2S4775zW/y4IMPsnfvXoYPH05xcTHhcJj9+/ezd+9eTj311ITHbdu2LeGHRSr9AuoTkHynxC85LxQKxcfyp6q5uTlheU/9ArE+ASV+yWdK/JLzWlpaEnbwVlRUJD2mrKwsYfLvrl9AfQJSKNTGLzlt3rx57Nu3r0tN3d0pKytLetzEiRMTTuc8ceLEhPurT0AKiWr8ktPq6+s5+eSTuyz3aGbs27ePhx9+OOmxFRUVjBgxIt4v0NjYyKZNmxLuO378+C6rjbW1tfH666+zfv16QqFQyjEPGzaM0047LeX9RfqbEr/ktOLi4j7Py9ObfoHu1heORCIpJ34z48CBAynHKJINSvyS08LhcNK1f9va2rj22mvTcp2VK1cm7BNobm7mpZdeYujQocyePZupU6cmPcf69evZv38/ZsayZcsYOXJk0lFHItmkNn7JaePHj2fLli0Jh2b2pvmlJ4n6BCKRSLxp6ODBgyxZsoR169YlPH79+vU0NjZiZpgZoVCIxsZG1q9fn3B/kWyyVB57z7YZM2b4qlWrsh2GZMkll1zCtGnTOPHEEykuLqa1tZW1a9eyfft2nnzyybRdp6GhgW3bttHc3ExzczMbN25k9+7dHfYJhUIcf/zxXY6dOHFi0m8lZ599dtpiFOkNM1vt7jM6l6upR3LewYMHeeGFF9i4cSNAfPWtzh2+R6uysjI+fPN73/tewn0ikUjC8u76CERyjRK/5LzKykree+89ysrKMDPGjx9PY2MjQ4YMydg1hw4dysGDBxOWJ+pXWLZsWdKmJz0TIJg6iSEAAAu8SURBVLlGbfyS80aMGMGoUaM6zMc/atQoRowYkbFrzp49u0vTTUlJCbNnJ55jsLm5uUs/BERr/HomQHKN2vgl511xxRVJ289bWlp6da6SkpKk0zx3NnjwYIYPH04oFCISibB//37ef//9hPueddZZDBs2LD6fUKImntiawYMGDdIKYglojqT0Uxu/DFjpaj9va2ujtbU15cT//vvvJ030nbVfG/iEE05Iul9300wXMs2R1L+U+CXnJRvHHw6H+dnPfpbSOWpra7n55ptpaWlh3LhxzJ8/n+rq6rTF+OCDD8bb+JPFW1xczNtvv01bWxv79u1j+vTpVFVVpS2GgUpzJPU/tfFLzhs/fnzCcfzjx49P6fja2lpqamrizULbt2+npqaG2tratMU4adKkeIz79+/vEm8kEmHnzp3x8qamJlasWMHmzZvTFsNApDmSskNt/DIgzJs3j/r6+vi8O+PHj+fOO+9M6diZM2eyffv2LuWlpaWcfvrpaYtxypQpTJkyheLiYsrLyxkxYgSlpaUcOXKEAwcOcOTIkS7HDIT//xKpqKjgmGOOOerzDBo0qMuDc/BBf0g2ZaIvpr/7MdTGLwNaqkk+kR07diQs723HcE82btzIxo0bOfXUU7v0P0yaNClvxvTH7ls6En+u3pNM9MXkUj+GEr/kvbFjxyas8Y8bNy6tT/7GfOc73+mS0JK1+w8ZMiStfQ2Ztm7dOhYvXkwkEqGxsbHH+Yt6kmyOpEGDBvGxj33saEI9KnV1dUQikW7XdO6NXOvHUBu/5L358+d3qbmVl5czf/78jFwvFAp1aabYt29fl7JQKMT06dMzEkMmrFu3jiVLlsSfXu5p/qJU9HbdhIEoF/sxVOOXvBerUS9YsIAdO3YwduzYtI/qaW/jxo0cc8wxHdYC2LJlC3v27OFDH/pQ/LmAffv2pTwqadasWZx77rkZiTdVS5cupbW1tUNZa2srixcvpqWlpU/9JbFab2yOpLKysqzXhtPtaNZ/hsz0CyjxS0Gorq7utyYVM0u4FsB7773H8OHDe32+t99+GyDriT/RFBYQHbG0bt26PneUt58jKR/1df1nyFy/gBK/SJq5e9Ind2+55ZZeneull17ivvvu4/XXX+emm25izpw5nHHGGekKtVeSzV+Uzumxc8HmzZvZs2cPbW1t1NbWHvXzFn1Z/xlg165dtLS0UFxcTH19PSUlJWn7AFAbv0ialZeXJ/xq39sRIi+99BIPPPAA4XAYiPYTPPDAA7z00ktpi7U3ks1f1JdvMblq8+bNrFixIq3PW/SlH2PXrl1EIhFKSkowM4qLi4lEIik1DaVCiV8kzTZs2MCePXtobW3F3WltbWXPnj1s2LChV+d58sknuww5bWlp4b777uO5555LZ8gpmTp1KpdccglDhw4Fot8ALrnkEioqKvo9lkxZs2ZNl6m3I5EIa9as6fM5KysrmTx5MmVlZUC0pj958uRum7daW1sTflh07mPpKzX1iGRAb9b7TWbfvn0Jy8PhMCtWrMhKm//UqVO7DN9cvXp1v8eRKcn+zY7237K3/RjJms/S1aymGr9IPzrvvPOoq6tLad+RI0cm3RZr889Ws0/MunXreOedd9i2bRt33XXXUQ3tzAXJvr3097eaZAv+JCvvLSV+kTS76KKLup2b//bbb08p+c+ZM6fbmUSz3eafiXH92TZ9+vQutepsPG9RUlKSsJ8o0UOAfaHEL5Jm3/rWt/jMZz4Tb+PvrK2tjUWLFvV4njPOOIPrrrsuXvNPNKdNS0tLRp4+TkWycf1Lly7NSjzpUFVVxaxZs+I1/IqKCmbNmtXvs6ged9xxhEIhwuEw7k44HCYUCqVtVI/a+EUy4Fvf+hY//vGPmTRpUsLtqT61ecYZZ8SHb15zzTUJ90nWF5Bpycb1JysfKKqqqnJiuuxMzumTlRq/mV1oZm+Y2SYzy8xz8yJZFquxJdKXB5aStfl31xeQSbHRPamWS+7o98RvZiHgR8BFwCnAl8zslP6OQyTTrrzyShobG7u01RYVFTF37txeny9Rm39paSlz5sw5qjj7qrfrEkvuyEZTz0xgk7tvBjCznwKXAr0b5CyS437wgx8A8NRTTzFs2DCKi4sZNGgQNTU1XHDBBb0+X6zJ58knn2Tfvn2MHDkyq0/yxoZ1Ll26lIMHDzJ06NCjnq1T+ke/L8RiZnOAC939+uD91cDH3f1rnfabC8wFmDBhwunbtm3r1zhFRAa6ZAuxZKONP9HKC10+fdx9kbvPcPcZo0aN6oewREQKQzYS/ztA+8VSjwcSL5EkIiJpl43EvxKYYmaTzKwU+Avg6SzEISJSkPq9c9fdw2b2NeA3QAi4391f7e84REQKVVYe4HL3XwG/ysa1RUQKXb+P6ukLM9sD9HVYz7HA3jSGk0mKNTMUa2Yo1sxIZ6wT3b3L6JgBkfiPhpmtSjScKRcp1sxQrJmhWDOjP2LVJG0iIgVGiV9EpMAUQuLvef7b3KFYM0OxZoZizYyMx5r3bfwiItJRIdT4RUSkHSV+EZECk9eJfyAt+GJmW81snZmtMbNV2Y6nPTO738wazGx9u7IRZvZbM9sY/B6ezRhjksT6XTPbHtzbNWb2mWzGGMQ03syeM7PXzOxVM/t6UJ5z97WbWHPxvg4ysz+a2Z+CWL8XlOfifU0Wa8bva9628QcLvrwJnE90YriVwJfcPSfn/TezrcAMd8+5h0zM7GzgPeBhdz81KFsINLr7guBDdbi7z8tmnEFciWL9LvCeu/9TNmNrz8zGAGPc/b/N7BhgNXAZcC05dl+7ifUL5N59NaDC3d8zsxJgOfB1oJrcu6/JYr2QDN/XfK7xxxd8cfcWILbgi/SSu78ANHYqvhR4KHj9ENFEkHVJYs057r7T3f87eP0u8Bowjhy8r93EmnM86r3gbUnw4+TmfU0Wa8blc+IfB9S3e/8OOfofa8CBOjNbHSxCk+tGu/tOiCYGoPeLyPavr5nZ2qApKOtf89szsxOAjwCvkOP3tVOskIP31cxCZrYGaAB+6+45e1+TxAoZvq/5nPhTWvAlh5zp7h8luhbxXwVNFpIe/w84EZgO7AR+mN1wPmBmQ4CfA99w90PZjqc7CWLNyfvq7hF3n050rY+ZZnZqtmNKJkmsGb+v+Zz4B9SCL+6+I/jdADxFtKkql+0O2n5jbcANWY4nKXffHfwP1gb8Jzlyb4N23Z8Dj7h7bVCck/c1Uay5el9j3P0A8DzRNvOcvK8x7WPtj/uaz4l/wCz4YmYVQacZZlYBXACs7/6orHsauCZ4fQ2wOIuxdCv2P3zg8+TAvQ069u4DXnP3f263Kefua7JYc/S+jjKzYcHrcuA84HVy874mjLU/7mvejuoBCIZB3cUHC77cnuWQEjKzKqK1fIiukfBoLsVqZo8BnyI6Xexu4DvAL4DHgQnA28Dl7p71TtUksX6K6NdmB7YCN8Tae7PFzM4C/gCsA9qC4luJtp3n1H3tJtYvkXv3dRrRztsQ0Yrt4+5+m5mNJPfua7JYf0KG72teJ34REekqn5t6REQkASV+EZECo8QvIlJglPhFRAqMEr+ISIFR4hfphpm91/NeIgOLEr+ISIFR4hdJgUX9o5mtt+i6CV8MyseY2QvBvOnrzeyTwcRbD7bb95vZjl+kveJsByAyQFQTfZryNKJPBa80sxeAK4DfuPvtwRoQg4P9xrVbD2BYlmIWSUg1fpHUnAU8FkyetRtYBnyM6JxQ1wWLvUwN5qvfDFSZ2d1mdiGQ07NuSuFR4hdJTaJpvmMLv5wNbAd+YmZfdvf9RL8ZPA/8FXBvfwUpkgolfpHUvAB8MWi/H0U02f/RzCYCDe7+n0RnsPyomR0LFLn7z4G/Az6atahFElAbv0hqngI+AfyJ6KyJNe6+y8yuAf7WzFqJrvX7ZaIrvT1gZrGK1S3ZCFgkGc3OKSJSYNTUIyJSYJT4RUQKjBK/iEiBUeIXESkwSvwiIgVGiV9EpMAo8YuIFJj/D7Dvuppt6KPpAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Lets have a look to the non dominated fronts in the final population.\n",
"ax = pg.plot_non_dominated_fronts(pop.get_f())\n",
"_ = plt.xlabel(\"loss\")\n",
"_ = plt.ylabel(\"complexity\")\n",
"_ = plt.title(\"Non dominate fronts\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 6 - Lets have a look to the log content\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"# Here we get the log of the latest call to the evolve\n",
"log = algo.extract(dcgpy.momes4cgp).get_log()\n",
"gen = [it[0] for it in log]\n",
"loss = [it[2] for it in log]\n",
"compl = [it[4] for it in log]"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAEWCAYAAABsY4yMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO3deXxU533v8c9PG0IgIZDGILEvAhtDwFjgGDA0ufG+xXHiJUmTOE2dNk3rJUudm/SV3Nzmtrc3S5MmtUMS12lim7g1jnfH+4qNWQzGBpvNgNl3EBJCSPrdP86RIxMJJNCZM3Pm+3695qXRmTPn/B4NfOeZ55x5jrk7IiKSPHlxFyAiItFQwIuIJJQCXkQkoRTwIiIJpYAXEUkoBbyISEIp4CUSZrbezD4Sdx2dMTM3szHh/TvM7B/jrqk7zOxZM/tC3HVIZlPAS8bKhOA1s8+Z2Ytx1iByohTwIiIJpYCXyJnZNDN72cz2mdlWM/upmRWFj5mZ/cjMdpjZfjN73cwmmNn1wKeAr5vZQTN7sJNtn25mT5jZHjPbbmb/83j77EbdpwG3AWeHNewLl/czs/80s51mtsHMvmVmHf5fMrM8M7vFzNaa2W4zu8fMBoSPPWZmXz5q/WVm9rHw/nQzWxj+XRaa2fQOtt8rbOOEdstSZnbIzE4Jf7/EzJaG6803sw905+8g2UsBL+nQAtwEVAJnA/8D+FL42HnALGAsUA5cDex29znAncC/uHtfd7/06I2aWSnwJPAYUA2MAZ7qwj67xN1XAn8FvBzWUB4+9G9AP2AUMBv4DHBdJ5v5O+Cj4XrVwF7gZ+FjdwHXtmvPeGA48HD4JvAw8BOgAvhhuLziqBoPA/Pabwe4CnjO3XeY2RTgduCL4XZ+DjxgZr2687eQ7KSAl8i5+2J3f8Xdm919PUHIzA4fPgKUAqcC5u4r3X1rFzd9CbDN3X/g7o3uXufuC7qwzxNmZvkEb0LfCPe3HvgB8OedPOWLwDfdfVMYxt8BPm5mBcB9wGQzGx6u+ylgXrjexcBqd/9N2Ia7gbeAP3mj46g3CuCT4TKAvwR+7u4L3L3F3X8NHAY+eCLtl+yigJfImdlYM3vIzLaZ2QHg/xD0rHH3p4GfEvRqt5vZHDMr6+KmhwJru7vPk1QJFAEb2i3bAAzuZP3hwH3h8Mg+YCXBp4uB7l5H0Eu/Jlz3GoJPLRD09jccta3O9vM00NvMzgrfLCYTvHm07f8rbfsPaxgabl8STgEv6XArQe+zxt3LgP8JWNuD7v4Tdz8TOJ1gqOZrbQ8dZ7vvAqNPZJ/dcHQNuwg+dQxvt2wYsPkYNV7o7uXtbsXu3rb+3cC1ZnY20Bt4Jly+5ah9dLofd28F7iHoxX8SeCh882jb//eO2n9J+IlAEk4BL+lQChwADprZqcBftz1gZlPDnmchUA80EvRwAbYTjHN35iFgkJndGB5sLDWzs463z27aDgxpO0Dr7i0EYfq9cH/DgZuB33by/NvCdYeH7U2Z2eXtHn+EIMi/C/wuDOu25WPN7JNmVmBmVwPjwzZ35C6CoaNP8cfhGYBfAH8V/o3NzPqY2cXh8QtJOAW8pMNXCXqWdQSB87t2j5WFy/YSDEHsBr4fPvYrYHw4tPD7ozca9lLPJRiX3gasBj7UhX12x9PAm8A2M9sVLvtbgjejdcCLBIF6eyfP/zHwAPC4mdUBrwBtb0LtD5J+hHbB7O67CY4xfIXgb/J14BJ330UHwmMP9QRDL4+2W76IYBz+pwR/4zXA57raeMlupgt+iIgkk3rwIiIJpYAXEUkoBbyISEIVRLlxM1tPcJCrBWh299oo9yciIn8UacCHPtTZkf+jVVZW+ogRIyIuR0QkORYvXrzL3VMdPZaOgO+yESNGsGjRorjLEBHJGmZ29Dee3xP1GLwTnP+7OJwdUERE0iTqHvwMd98STlv6hJm95e7Pt18hDP7rAYYNGxZxOSIiuSPSHry7bwl/7iCY/GhaB+vMcfdad69NpTocRhIRkRMQWcCHc16Utt0nmPf7jaj2JyIi7xflEM1AgmlS2/Zzl7s/FuH+RESkncgC3t3XAZOi2r6IiBybvskqIpJQGXUe/In6yVOraW518gzyzcjLM/LMyM+DPLPwBvl5hpmRnxf83h1D+pcwfXQF4ZCTiEjGS0TA3/bcWhqaWo6/4kmaMqycr51/KmePrjj+yiIiMcuo+eBra2v9RL/J6u64Q4s7re60tkKrOy3ueGv75eGybjTbgedX7eTHT65m24FGzqmp5KvnjWPS0PITqlVEpKeY2eLO5vlKTMCnQ+ORFn77ygZ+9swa9jYc4YLTB/GV88ZSM1BXPxOReCjge1hd4xFuf3E9v3hhHfVNzVxxxmBu+shYhg4oibs0EckxCviI7K1v4rbn1nLH/PW0unPN1GH87YfHcEpZcdyliUiOUMBHbPuBRv7t6dXMffVdCvKNz04fwRdnjaZf78Iub8OAvO6e2iMiOU8BnyYbdzfwr0+u4r6lm7t1EBegtFcBv/xsLWeN0hk6ItJ1Cvg0W7W9jidWbKeltet/23uXbKK5xXn0xnMoK+56z19EctuxAj4R58FnmrEDSxnbzTNrzqmp5OO3vcx37n+TH149OaLKRCSXaKqCDHHGsP58+UNjmPfaZh5+fWvc5YhIAijgM8iXPzyGSUPL+ebvl7P9QGPc5YhIllPAZ5DC/Dx+dNUkGo+08NX/WkYmHR8RkeyjgM8wo1J9+ebF43lh9S5+80qn19IVETkuBXwG+vRZw/izcSm+9/BK1uw4GHc5IpKlFPAZyMz4lys/QElRPjf9bilHWlrjLklEspACPkOdUlbMP31sIss37+cnT62OuxwRyUIK+Ax2wYQqPn7mEH72zBoWb9gbdzkikmUU8Bnu25eOp7q8Nzffs5T6w81xlyMiWUQBn+FKiwv54VWT2bingX98eEXc5YhIFlHAZ4FpIwfwxVmjufvVd3lyxfa4yxGRLKGAzxI3nVvDaVVl3DLvdXYdPBx3OSKSBRTwWaJXQT7/evVkDjQ2c8u9y/UtVxE5LgV8Fhk3qJSvnz+OJ1du53cL3427HBHJcAr4LPP5GSOZPrqC7z60go27G+IuR0QymAI+y+TlGd//xCSamlu5e+HGuMsRkQymgM9C1eW9mTK8P8+v2hl3KSKSwRTwWWr22BRvbjnAzjqdUSMiHVPAZ6nZY1MAvLBavXgR6ZgCPkuNryqjok+RhmlEpFMK+CyVl2fMGpvi+dW7aG3VOfEi8qciD3gzyzez18zsoaj3lWtmja1kT30Tb245EHcpIpKB0tGDvwFYmYb95JxzaoJx+OdW7Yi5EhHJRJEGvJkNAS4GfhnlfnJVZd9eTBhcxvOrdsVdiohkoKh78P8KfB3QNeciMntsisUb93Kg8UjcpYhIhoks4M3sEmCHuy8+znrXm9kiM1u0c6fOCOmuWTUpWlqd+WvUixeR94uyBz8DuMzM1gNzgQ+b2W+PXsnd57h7rbvXplKpCMtJpinD+9O3VwHPaZhGRI4SWcC7+zfcfYi7jwCuAZ52909Htb9cVZifx/TRFTy/aqemEBaR99F58Akwe1yKzfsOsXZnfdyliEgGSUvAu/uz7n5JOvaVi2a9d7qkjmGIyB+pB58AQweUMCrVR9MWiMj7KOATYlZNilfW7abxSEvcpYhIhlDAJ8TscSkON7fy6jt74i5FRDKEAj4hPjiygqKCPI3Di8h7FPAJ0bson7NGDtA4vIi8RwGfILNqUqzecZAt+w7FXYqIZAAFfILMHhecLqlevIiAAj5Rak7py6CyYo3DiwiggE8UM2P22BQvrtlFc4sm8BTJdQr4hJk1NkVdYzNL390XdykiEjMFfMLMHFNJnmkcXkQU8InTr6SQM4b11zi8iCjgk2hWTYrXN+9nT31T3KWISIwU8Ak0e1wKd3hhtXrxIrlMAZ9AEwf3o7ykUMM0IjlOAZ9A+XnGOTUpnl+1i9ZWXeVJJFcp4BNqVk0luw4eZuW2A3GXIiIxUcAn1OyxbdMW6GLcIrlKAZ9Qp5QVc+qgUp5btSPuUkQkJgr4BJs9LsXiDXs5eLg57lJEJAYK+ASbXZPiSIvz8trdcZciIjFQwCfYmSP6U1KUr2kLRHKUAj7BehXkc/aoCp0PL5KjFPAJN3tcio17Gli/qz7uUkQkzRTwCTerJjhdUr14kdyjgE+4EZV9GF5RonF4kRykgM8Bs2pSzF+7m8PNLXGXIiJppIDPAbPHpjh0pIXF6/fGXYqIpFFB3AVI9M4eXUFhvvGZ218lP8+6/Ly+vQqoKi+mql9vqvoFP6vb/T6oXzGF+eojiGQqBXwO6NOrgO9/YhIrtnZv4rG6xma27jvEu3saWLBuNwca3/+NWDNI9e1FVXlvqvsVU3NKXy6dVE3NwNKeLF9ETpC5Z850srW1tb5o0aK4y5BO1B9uZuv+Q2zZ1/i+n1v3N7Jl3yHW726gpdWZOLgfV5wxmMsmV1PZt1fcZYskmpktdvfaDh9TwEtP2Vl3mAeWbWHekk28ueUA+XnG7LEprjhjMOeOH0hxYX7cJYokjgJe0m7V9jrmLdnM/Us3s3V/I6W9Crhw4iCuOGMIZ40cQF43jgWISOdiCXgzKwaeB3oRjPX/t7t/+1jPUcAnT0ur88q63cxbspnH3thKfVMLg8t789EzqrlyyhBGpfrGXaJIVosr4A3o4+4HzawQeBG4wd1f6ew5Cvhka2hq5okV25m3ZDMvrN6JmfGjqydz2aTquEsTyVrHCvjIzqLx4J3jYPhrYXjLnPEgSbuSogIunzyYyycPZseBRr5892vcOPc1AIW8SAQiPYnZzPLNbCmwA3jC3Rd0sM71ZrbIzBbt3Kmv0+eKU8qKueO6qdSOGMCNc1/j/qWb4y5JJHEiDXh3b3H3ycAQYJqZTehgnTnuXuvutalUKspyJMOUFBVwx3VTmTpiADf9bqlCXqSHpeVriO6+D3gWuCAd+5PsUVJUwH8o5EUiEVnAm1nKzMrD+72BjwBvRbU/yV4KeZFoRNmDrwKeMbPXgYUEY/APRbg/yWJtIT9tpEJepKdEeRbN68AZUW1fkqekqIDbPzeVz9+xkJt+txR3+OgZg+MuSyRraSpAyShtIX/WyApuvmcpv39NPXmRE6WAl4xTUlTArz5X+17I3/faprhLEslKCnjJSO178l+5Z5lCXuQEKOAlY/UuylfIi5wEzSYpGe9QUwufv2MhL6/bHfm+LpwwiB9cNYmSIl0LR7JDLHPRiPSUtp78nQs2UHfUVaWOpbtdl/0NTfzmlQ1smXOIX352KqlSXaxEspsCXrJC76J8vnDOqMj3M7Mmxd/evYSP3foSv75umqYzlqymMXiRds4dP5C5159Nw+EWrrx1Pos37Im7JJETpoAXOcrkoeXM+9J0ykuK+OQvFvDo8q1xlyRyQhTwIh0YXtGHe/96OqdXl/Glu5bwqxffibskkW5TwIt0YkCfIu76yw9y/vhB/O+HVvDdB1fQ2po5Z52JHI8CXuQYigvz+dmnpnDdjBHc/tI7/M1dS2g80hJ3WSJd0qWAN7MbzKzMAr8ysyVmdl7UxYlkgvw849uXns63Lj6Nx97cxqd+uYA99U1xlyVyXF3twX/e3Q8A5wEp4DrgnyOrSiQDfeGcUfzsk1NYvnk/V946n427G+IuSeSYuhrwFv68CPgPd1/WbplIzrhoYhV3feEs9jY0ccW/v8Syd/fFXZJIp7oa8IvN7HGCgP+DmZUCrdGVJZK5akcM4N6/nk7vony+dOcSWnTgVTJUVwP+L4BbgKnu3gAUEgzTiOSk0am+fOPC09i87xDPr94ZdzkiHepqwJ8NvO3u+8zs08C3gP3RlSWS+c4dP5CKPkXMfXVj3KWIdKirAX8r0GBmk4CvAxuA/4ysKpEsUFSQx5VnDuGplTvYUdcYdzkif6KrAd/swbzClwM/dvcfA6XRlSWSHa6eOpTmVue/F2uuesk8XQ34OjP7BvDnwMNmlk8wDi+S00an+jJt5ADmvvquvuUqGaerAX81cJjgfPhtwGDg/0VWlUgWuXbaUDbuaUjLBUlEuqNLAR+G+p1APzO7BGh0d43BiwAXTqiirLiAu3WwVTJMV6cquAp4FfgEcBWwwMw+HmVhItmiuDCfj00ZwuNvbtcUBpJRujpE802Cc+A/6+6fAaYB/xBdWSLZ5dppw2hqaWXeEh1slczR1YDPc/cd7X7f3Y3niiTeuEGlnDGsnLtf3UgmXchecltXQ/oxM/uDmX3OzD4HPAw8El1ZItnn2qnDWLuznkUb9sZdigjQ9YOsXwPmAB8AJgFz3P3voyxMJNtcMqmKvr10sFUyR5eHWdz9Xne/2d1vcvf7oixKJBuVFBVw2eRqHlm+lf2HjsRdjsixA97M6szsQAe3OjM7kK4iRbLFtVOH0XiklfuXbo67FJFjB7y7l7p7WQe3UncvS1eRItli4pB+nF5dxl0LdLBV4qczYUR62DXThvHWtjqWbdKEqxKvyALezIaa2TNmttLM3jSzG6Lal0gmuXxyNb0L8zWNsMQuyh58M/AVdz8N+CDwN2Y2PsL9iWSEsuJCLvlAFQ8s28LBw81xlyM5LLKAd/et7r4kvF8HrCSYpEwk8a6ZNoyGphYeXLYl7lIkh6VlDN7MRgBnAAs6eOx6M1tkZot27tSlzyQZpgwrZ+zAvhqmkVhFHvBm1he4F7jR3f/k1Ep3n+Pute5em0qloi5HJC3MjGumDmPZpv2s2KIziiUekQa8mRUShPud7j4vyn2JZJqPTRlMUUEecxeqFy/xiPIsGgN+Bax09x9GtR+RTFVeUsSFEwZx32ubOdTUEnc5koOi7MHPILjE34fNbGl4uyjC/YlknGumDqOusZlHlm+NuxTJQQVRbdjdXwQsqu2LZIMPjhrAyMo+zF24kSvPHBJ3OZJj9E1WkQgFB1uHsnD9XtbsqIu7HMkxCniRiF155hAK8427X3037lIkxyjgRSJW2bcX544fyLwlmzjcrIOtkj4KeJE0uGbqMPY2HOEPb26PuxTJIQp4kTSYOaaSIf1765utklYKeJE0yMszrpwyhPlrd7P74OG4y5EcoYAXSZM/GxdMxTF/7e6YK5FcoYAXSZMPDCmntLiAl9bsirsUyREKeJE0yc8zpo+u4IXVu3Q5P0kLBbxIGs0cU8nmfYfYsLsh7lIkByjgRdJoZk0wDv+ihmkkDRTwImk0oqKEweW9eXG1Al6ip4AXSSMzY8aYCuav3UVLq8bhJVoKeJE0m1mT4kBjM8s374+7FEk4BbxImk0fXQGg0yUlcgp4kTSr7NuL8VVlGoeXyCngRWIws6aSxRv26lJ+EikFvEgMZoyppKmllVfX74m7FEkwBbxIDKaNGEBRfp7G4SVSCniRGPQuyufM4f15QePwEiEFvEhMZtZUsnLrAXZp+mCJiAJeJCYzx1QCOl1SoqOAF4nJhMH96Ne7UAEvkVHAi8SkbfrgFzV9sEREAS8SoxljKtmyv5F3dtXHXYokkAJeJEbn1GgcXqKjgBeJ0bABJQzp31vzw0skFPAiMTIzZo6pZP7a3TS3tMZdjiSMAl4kZjNrKqnT9MESAQW8SMymjw7G4TW7pPQ0BbxIzAb0KeL06jKNw0uPU8CLZICZNZUs2biXhqbmuEuRBIks4M3sdjPbYWZvRLUPkaSYOaaSIy3Ognc0fbD0nCh78HcAF0S4fZHEmDpiAEUFebykcXjpQZEFvLs/D6g7ItIFxYX5TB3RX+Pw0qNiH4M3s+vNbJGZLdq5c2fc5YjEZsaYSt7aVsfOOk0fLD0j9oB39znuXuvutalUKu5yRGJzzpjg3//8terFS8+IPeBFJDC+uozykkJd5Ul6jAJeJEPk5xkzRlfy0hpNHyw9I8rTJO8GXgbGmdkmM/uLqPYlkhQzxlSydX8j6zR9sPSAgqg27O7XRrVtkaRqu4zfi6t3MTrVN+ZqJNtpiEYkgwyrKGHYgBKdLik9QgEvkmFmjKnkFU0fLD1AAS+SYWaOqaTucDPLNmn6YDk5CniRDDN9dAVmuoyfnDwFvEiG6d+niAnV/TQ/vJw0BbxIBmqbPrj+sKYPlhOngBfJQDPHVNLc6ryq6YPlJCjgRTLQmcP706sgT9MWyElRwItkoOLCfKaNHKADrXJSFPAiGWrGmEre3l7Ht+9/g8Ub9mh+Gum2yKYqEJGTc+3UYSzfvJ+5C9/l1y9vYHB5by6dVM2lk6oYX1WGmcVdomQ4y6ReQW1trS9atCjuMkQySl3jEZ5YsZ0Hl23hhdW7aG51Rqf6cOmkai6bVM0ozVmT08xssbvXdviYAl4ke+ypb+LRN7by4LItLHhnD+5wenUZl02q5pJJ1Qwu7x13iZJmCniRBNq2v5GHl2/lgWVbWPbuPgBqh/fnxo+MZWZNZczVSboo4EUSbuPuBh58fQtzF27k3T2HuHRSNd+6+DQGlhXHXZpETAEvkiMaj7Tw8+fW8bNn11CUn8fN547lM2cPpyBfJ8wl1bECXq+6SIIUF+Zzw0dqeOKmWZw5vD/ffWgFl/70JRZv0Ddic5ECXiSBhlf04Y7rpnLbp6ewr6GJK299mb//79fZU98Ud2mSRgp4kYQyMy6YUMWTN8/mi7NGce+STXz4B88y99WNtLZmztCsREcBL5JwfXoV8I2LTuORG85h7MBSbpm3nCtvm88bm3VBkaTTQVaRHOLu3PfaZr738Er2NjTxmbNHcOmkair6FDGgbxGlvQr0Ddkso7NoROR99jcc4fuPv81vF2ygfQQU5efRv08hA/r0CkI/vLW9AVT06cWEwWUM6V8SX/HyPgp4EenQht31rNtVz56DTeypb2J3fRN76g+zp76JXeGyPfVNHDzqwiPTRg7gyimDuXBiFWXFhTFVL6CAF5GT1Hikhb0NTeyqa+K5VTuYt2Qz63bV06sgj3PHD+TKKUM4p6ZS59vHQAEvIj3K3Vm2aT/zlmzigWVb2NdwhMq+RVw2aTAfmzKY06s122W6KOBFJDJNza08+3bQq3/qre0caXHGDSzliimD+ejkwQzqp+kSoqSAF5G02FvfxEPLt3Lfkk0s2bgPMxiT6kt+Xtd786XFBXzo1FO4cEIVIyv7RFhtMijgRSTt3tlVz31LNvH29rpuPW/r/kZe3xScoz9uYCkXTBjEBRMGceqgUg37dEABLyJZZcu+Q/zhzW08+sY2Fq4P5r0fUVHC+RMGccHpg5g0pJy8bnwqSDIFvIhkrZ11h3ly5XYefWMb89cEV7Sq6lfM+acP4vzTBzFt5IBuDQEljQJeRBJhf8MRnnprO4+9sY3nVu3kcHMrFX2KOH/CIC6eWMVZIwfk3KmaCngRSZz6w808t2onjyzfytNv7aChqeW9sL9kYhXTciTsYwt4M7sA+DGQD/zS3f/5WOsr4EXkRBxqauG5VTt46PX3h/0FbT37URWJHcaJJeDNLB9YBZwLbAIWAte6+4rOnqOAF5GTdaiphWff3sHDy7fy1ModHDrSQmXfIOwvmljFWSOTFfbHCviCCPc7DVjj7uvCIuYClwOdBryIyMnqXZTPhROruHBiFYeaWngmDPt7F2/mt69sfG/ytEzSv6SIe/7q7B7fbpQBPxh4t93vm4Czjl7JzK4HrgcYNmxYhOWISK7pXZTPRROruGhiFQ1NzTz79s6wV998/CenUVQTtkUZ8B19BvqT8SB3nwPMgWCIJsJ6RCSHlRQVvBf2uSLKQ8ybgKHtfh8CbIlwfyIi0k6UAb8QqDGzkWZWBFwDPBDh/kREpJ3IhmjcvdnMvgz8geA0ydvd/c2o9iciIu8X5Rg87v4I8EiU+xARkY4l/2teIiI5SgEvIpJQCngRkYRSwIuIJFRGzSZpZjuBDSf49EpgVw+Wkw3U5uTLtfaC2txdw9091dEDGRXwJ8PMFnU24U5Sqc3Jl2vtBbW5J2mIRkQkoRTwIiIJlaSAnxN3ATFQm5Mv19oLanOPScwYvIiIvF+SevAiItKOAl5EJKGyPuDN7AIze9vM1pjZLXHXExUzW29my81sqZktCpcNMLMnzGx1+LN/3HWeDDO73cx2mNkb7ZZ12kYz+0b4ur9tZufHU/XJ6aTN3zGzzeFrvdTMLmr3WFa32cyGmtkzZrbSzN40sxvC5Yl9nY/R5uhfZ3fP2hvBNMRrgVFAEbAMGB93XRG1dT1QedSyfwFuCe/fAvzfuOs8yTbOAqYAbxyvjcD48PXuBYwM/x3kx92GHmrzd4CvdrBu1rcZqAKmhPdLgVVhuxL7Oh+jzZG/ztneg3/vwt7u3gS0Xdg7V1wO/Dq8/2vgozHWctLc/Xlgz1GLO2vj5cBcdz/s7u8Aawj+PWSVTtrcmaxvs7tvdfcl4f06YCXB9ZsT+zofo82d6bE2Z3vAd3Rh72P94bKZA4+b2eLwQuUAA919KwT/iIBTYqsuOp21Memv/ZfN7PVwCKdtuCJRbTazEcAZwAJy5HU+qs0Q8euc7QHfpQt7J8QMd58CXAj8jZnNirugmCX5tb8VGA1MBrYCPwiXJ6bNZtYXuBe40d0PHGvVDpYlpc2Rv87ZHvA5c2Fvd98S/twB3EfwkW27mVUBhD93xFdhZDprY2Jfe3ff7u4t7t4K/II/fjxPRJvNrJAg6O5093nh4kS/zh21OR2vc7YHfE5c2NvM+phZadt94DzgDYK2fjZc7bPA/fFUGKnO2vgAcI2Z9TKzkUAN8GoM9fW4tqALXUHwWkMC2mxmBvwKWOnuP2z3UGJf587anJbXOe4jzD1whPoigqPSa4Fvxl1PRG0cRXBUfRnwZls7gQrgKWB1+HNA3LWeZDvvJvioeoSgF/MXx2oj8M3wdX8buDDu+nuwzb8BlgOvh//Zq5LSZmAmwXDD68DS8HZRkl/nY7Q58tdZUxWIiCRUtg/RiIhIJxTwIiIJpYAXEUkoBbyISEIp4EVEEkoBL3ISzOxGMytp9/sjZlYeZ00ibXSapMgxhF9SMQ++bdjR4+uBWnffldbCRLpAPXjJSmb2D2b2Vjh3+N1m9lUzG21mj4UTsr1gZqeG695hZj8xs/lmts7MPt5uO18zs4XhhLsVyUUAAAKQSURBVE//K1w2Ipy7+9+BJcBQM7vVzBaF83m3rfd3QDXwjJk9Ey5bb2aV4f2bzeyN8HbjUdv+Rbitx82sd9v2zGxFWMvc9P01JbHi/paXbrp19wbUEnwbsDfB/Nqrga8SfAOyJlznLODp8P4dwH8RdGjGE0wxDcGUD3MIJnfKAx4imJ99BNAKfLDdPgeEP/OBZ4EPhL+vp908/W2/A2cSfEuxD9CX4BvIZ4TbbgYmh+vfA3w6vL8F6BXeL4/776xb9t8KeuA9QiTdZgL3u/shADN7ECgGpgP/FYyqAMEFE9r83oNhlhVmNjBcdl54ey38vS/BvB8bgQ3u/kq7518VTtNcQHABh/EEXzE/Vo33uXt9WOM84ByCr6S/4+5Lw/UWE4Q+4fbuNLPfA7/vwt9B5JgU8JKNOppONQ/Y5+6TO3nO4Q6eb8A/ufvP37fxYM7u+na/jyT4hDDV3fea2R0EbyjdrbGjWloIPokAXEzwCeIy4B/M7HR3bz7OfkQ6pTF4yUYvApeaWXE4x/bFQAPwjpl9AoKDo2Y26Tjb+QPw+XAbmNlgM+vooillBIG/P+z9X9jusTqCYaKjPQ981MxKwhlArwBe6KwQM8sDhrr7M8DXgXKCTxQiJ0w9eMk67r7QzB4gmF1zA7AI2A98CrjVzL4FFBJcwnHZMbbzuJmdBrwcDuscBD5N0Ktuv94yM3uNYBx9HfBSu4fnAI+a2VZ3/1C75ywJe/pt07z+0t1fCz8ddCQf+K2Z9SPo/f/I3fcd728hciw6TVKykpn1dfeD4TnozwPXe3jdSxEJqAcv2WqOmY0nGAv/tcJd5E+pBy8iklA6yCoiklAKeBGRhFLAi4gklAJeRCShFPAiIgn1/wFneMOEZp3DUAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# And here we plot, for example, the generations against the best loss\n",
"_ = plt.plot(gen, loss)\n",
"_ = plt.title('last call to evolve')\n",
"_ = plt.xlabel('generations')\n",
"_ = plt.ylabel('loss')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
patrick-kidger/equinox | examples/init_apply.ipynb | 1 | 3057 | {
"cells": [
{
"cell_type": "markdown",
"id": "14148da3-23fb-480b-ae31-93878cda86fa",
"metadata": {},
"source": [
"# Compatibility with init-apply libraries\n",
"\n",
"Existing JAX neural network libraries have sometimes followed the \"init/apply\" approach, in which the parameters of a network are initialised with a function `init()`, and then the forward pass through a model is specified with `apply()`. For example [Stax](https://jax.readthedocs.io/en/latest/jax.example_libraries.stax.html) follows this approach.\n",
"\n",
"As a result, some third-party libraries assume that your model is specified by an `init()` and an `apply()` function, and that the parameters returned from `init()` are all JIT-trace-able and grad-able.\n",
"\n",
"Equinox can be made to fit with this style very easily, like so."
]
},
{
"cell_type": "code",
"execution_count": 1,
"id": "05bcc516-c80a-492b-af63-0e5dec66f438",
"metadata": {},
"outputs": [],
"source": [
"import equinox as eqx\n",
"\n",
"\n",
"def make_mlp(in_size, out_size, width_size, depth, *, key):\n",
" mlp = eqx.nn.MLP(\n",
" in_size, out_size, width_size, depth, key=key\n",
" ) # insert your model here\n",
" params, static = eqx.partition(mlp, eqx.is_inexact_array)\n",
"\n",
" def init_fn():\n",
" return params\n",
"\n",
" def apply_fn(_params, x):\n",
" model = eqx.combine(_params, static)\n",
" return model(x)\n",
"\n",
" return init_fn, apply_fn"
]
},
{
"cell_type": "markdown",
"id": "5965f2e9-483a-475e-b316-a595daf6eb0f",
"metadata": {},
"source": [
"And that's all there is to it.\n",
"\n",
"Example usage:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "e25e63c7-3cb6-4727-9c28-0016b03acb87",
"metadata": {},
"outputs": [],
"source": [
"import jax\n",
"import jax.numpy as jnp\n",
"import jax.random as jrandom\n",
"\n",
"\n",
"def main(in_size=2, seed=5678):\n",
" key = jrandom.PRNGKey(seed)\n",
"\n",
" init_fn, apply_fn = make_mlp(\n",
" in_size=in_size, out_size=1, width_size=8, depth=1, key=key\n",
" )\n",
"\n",
" x = jnp.arange(in_size) # sample data\n",
" params = init_fn()\n",
" y1 = apply_fn(params, x)\n",
" params = jax.tree_map(lambda p: p + 1, params) # \"stochastic gradient descent\"\n",
" y2 = apply_fn(params, x)\n",
" assert y1 != y2\n",
"\n",
"\n",
"main()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "jax0226",
"language": "python",
"name": "jax0226"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.12"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
| apache-2.0 |
aitatanit/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers | Chapter3_MCMC/Ch3_IntroMCMC_PyMC3.ipynb | 1 | 1153635 | null | mit |
mercybenzaquen/foundations-homework | foundations_hw/08/Homework8_benzaquen_congress_data.ipynb | 2 | 271784 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied (use --upgrade to upgrade): pandas in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages\r\n",
"Requirement already satisfied (use --upgrade to upgrade): pytz>=2011k in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from pandas)\r\n",
"Requirement already satisfied (use --upgrade to upgrade): numpy>=1.7.0 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from pandas)\r\n",
"Requirement already satisfied (use --upgrade to upgrade): python-dateutil>=2 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from pandas)\r\n",
"Requirement already satisfied (use --upgrade to upgrade): six>=1.5 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from python-dateutil>=2->pandas)\r\n"
]
}
],
"source": [
"!pip install pandas"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied (use --upgrade to upgrade): matplotlib in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages\n",
"Requirement already satisfied (use --upgrade to upgrade): numpy>=1.6 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from matplotlib)\n",
"Requirement already satisfied (use --upgrade to upgrade): python-dateutil in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from matplotlib)\n",
"Requirement already satisfied (use --upgrade to upgrade): cycler in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from matplotlib)\n",
"Requirement already satisfied (use --upgrade to upgrade): pyparsing!=2.0.0,!=2.0.4,>=1.5.6 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from matplotlib)\n",
"Requirement already satisfied (use --upgrade to upgrade): pytz in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from matplotlib)\n",
"Requirement already satisfied (use --upgrade to upgrade): six>=1.5 in /Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages (from python-dateutil->matplotlib)\n"
]
}
],
"source": [
"!pip install matplotlib"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/mercybenzaquen/.virtualenvs/Homework8/lib/python3.5/site-packages/matplotlib/__init__.py:1035: UserWarning: Duplicate key in file \"/Users/mercybenzaquen/.matplotlib/matplotlibrc\", line #2\n",
" (fname, cnt))\n"
]
}
],
"source": [
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Open your dataset up using pandas in a Jupyter notebook"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"b'Skipping line 7054: expected 13 fields, saw 14\\nSkipping line 7581: expected 13 fields, saw 14\\nSkipping line 8088: expected 13 fields, saw 14\\nSkipping line 9719: expected 13 fields, saw 15\\nSkipping line 10019: expected 13 fields, saw 15\\nSkipping line 10235: expected 13 fields, saw 15\\nSkipping line 10550: expected 13 fields, saw 15\\nSkipping line 10641: expected 13 fields, saw 14\\nSkipping line 10764: expected 13 fields, saw 15\\nSkipping line 11075: expected 13 fields, saw 15\\nSkipping line 11168: expected 13 fields, saw 14\\nSkipping line 11290: expected 13 fields, saw 15\\nSkipping line 11606: expected 13 fields, saw 15\\nSkipping line 11697: expected 13 fields, saw 14\\nSkipping line 12141: expected 13 fields, saw 15\\nSkipping line 12230: expected 13 fields, saw 14\\nSkipping line 12664: expected 13 fields, saw 15\\nSkipping line 12738: expected 13 fields, saw 14\\n'\n"
]
}
],
"source": [
"df = pd.read_csv(\"congress.csv\", error_bad_lines=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Do a .head() to get a feel for your data"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>M000112</td>\n",
" <td>Joseph</td>\n",
" <td>Jefferson</td>\n",
" <td>Mansfield</td>\n",
" <td>NaN</td>\n",
" <td>1861-02-09</td>\n",
" <td>TX</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>85.9</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>D000448</td>\n",
" <td>Robert</td>\n",
" <td>Lee</td>\n",
" <td>Doughton</td>\n",
" <td>NaN</td>\n",
" <td>1863-11-07</td>\n",
" <td>NC</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>83.2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>S000001</td>\n",
" <td>Adolph</td>\n",
" <td>Joachim</td>\n",
" <td>Sabath</td>\n",
" <td>NaN</td>\n",
" <td>1866-04-04</td>\n",
" <td>IL</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>80.7</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>E000023</td>\n",
" <td>Charles</td>\n",
" <td>Aubrey</td>\n",
" <td>Eaton</td>\n",
" <td>NaN</td>\n",
" <td>1868-03-29</td>\n",
" <td>NJ</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>78.8</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>L000296</td>\n",
" <td>William</td>\n",
" <td>NaN</td>\n",
" <td>Lewis</td>\n",
" <td>NaN</td>\n",
" <td>1868-09-22</td>\n",
" <td>KY</td>\n",
" <td>R</td>\n",
" <td>No</td>\n",
" <td>1947-01-03</td>\n",
" <td>78.3</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"0 80 house M000112 Joseph Jefferson Mansfield NaN \n",
"1 80 house D000448 Robert Lee Doughton NaN \n",
"2 80 house S000001 Adolph Joachim Sabath NaN \n",
"3 80 house E000023 Charles Aubrey Eaton NaN \n",
"4 80 house L000296 William NaN Lewis NaN \n",
"\n",
" birthday state party incumbent termstart age \n",
"0 1861-02-09 TX D Yes 1947-01-03 85.9 \n",
"1 1863-11-07 NC D Yes 1947-01-03 83.2 \n",
"2 1866-04-04 IL D Yes 1947-01-03 80.7 \n",
"3 1868-03-29 NJ R Yes 1947-01-03 78.8 \n",
"4 1868-09-22 KY R No 1947-01-03 78.3 "
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.head()\n",
"\n",
"#bioguide: The alphanumeric ID for legislators in http://bioguide.congress.gov."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Write down 12 questions to ask your data, or 12 things to hunt for in the data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1)How many senators and how many representatives in total since 1947?"
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"house 15065\n",
"senate 3552\n",
"Name: chamber, dtype: int64"
]
},
"execution_count": 70,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['chamber'].value_counts() #sounds like a lot. We might have repetitions."
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"count 18617\n",
"unique 3188\n",
"top D000355\n",
"freq 30\n",
"Name: bioguide, dtype: object"
]
},
"execution_count": 71,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['bioguide'].describe() #we count the bioguide, which is unique to each legislator.\n",
"#There are only 3188 unique values, hence only 3188 senators and representatives in total."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 2) How many from each party in total ?"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"True 10284\n",
"False 8333\n",
"Name: party, dtype: int64"
]
},
"execution_count": 79,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"total_democrats = (df['party'] == 'D').value_counts()\n",
"total_democrats"
]
},
{
"cell_type": "code",
"execution_count": 271,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"False 10355\n",
"True 8262\n",
"Name: party, dtype: int64"
]
},
"execution_count": 271,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"total_republicans =(df['party'] == 'R').value_counts()\n",
"total_republicans"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 3) What is the average age for people that have worked in congress (both Senators and Representatives)"
]
},
{
"cell_type": "code",
"execution_count": 218,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"count 18617.000000\n",
"mean 53.314841\n",
"std 10.679143\n",
"min 25.000000\n",
"25% 45.400000\n",
"50% 53.000000\n",
"75% 60.500000\n",
"max 98.100000\n",
"Name: age, dtype: float64"
]
},
"execution_count": 218,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['age'].describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4) What is the average age of Senators that have worked in the Senate? And for Representatives in the house?"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"chamber \n",
"house count 15065.000000\n",
" mean 52.366850\n",
" std 10.507940\n",
" min 25.000000\n",
" 25% 44.600000\n",
" 50% 52.000000\n",
" 75% 59.600000\n",
" max 89.700000\n",
"senate count 3552.000000\n",
" mean 57.335529\n",
" std 10.463303\n",
" min 28.200000\n",
" 25% 49.875000\n",
" 50% 56.800000\n",
" 75% 64.400000\n",
" max 98.100000\n",
"Name: age, dtype: float64"
]
},
"execution_count": 219,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.groupby(\"chamber\")['age'].describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 5) How many in total from each state?"
]
},
{
"cell_type": "code",
"execution_count": 246,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"CA 1534\n",
"NY 1347\n",
"TX 985\n",
"PA 939\n",
"IL 849\n",
"OH 809\n",
"MI 670\n",
"FL 629\n",
"NJ 556\n",
"MA 478\n",
"NC 470\n",
"GA 441\n",
"VA 428\n",
"IN 424\n",
"MO 414\n",
"WI 386\n",
"TN 381\n",
"MN 356\n",
"LA 343\n",
"WA 338\n",
"MD 334\n",
"AL 334\n",
"KY 323\n",
"SC 283\n",
"IA 282\n",
"OK 277\n",
"CT 272\n",
"MS 251\n",
"CO 248\n",
"KS 243\n",
"AR 227\n",
"OR 227\n",
"AZ 226\n",
"WV 222\n",
"NE 184\n",
"NM 155\n",
"UT 154\n",
"ME 146\n",
"NH 142\n",
"RI 141\n",
"ID 138\n",
"MT 130\n",
"NV 130\n",
"HI 123\n",
"SD 123\n",
"ND 119\n",
"WY 108\n",
"VT 104\n",
"DE 102\n",
"AK 92\n",
"Name: state, dtype: int64"
]
},
"execution_count": 246,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['state'].value_counts()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 5) How many Senators in total from each state? How many Representatives?"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"state chamber\n",
"AK senate 58\n",
" house 34\n",
"AL house 263\n",
" senate 71\n",
"AR house 158\n",
" senate 69\n",
"AZ house 158\n",
" senate 68\n",
"CA house 1458\n",
" senate 76\n",
"CO house 179\n",
" senate 69\n",
"CT house 201\n",
" senate 71\n",
"DE senate 71\n",
" house 31\n",
"FL house 558\n",
" senate 71\n",
"GA house 370\n",
" senate 71\n",
"HI house 65\n",
" senate 58\n",
"IA house 214\n",
" senate 68\n",
"ID senate 70\n",
" house 68\n",
"IL house 778\n",
" senate 71\n",
"IN house 356\n",
" senate 68\n",
" ... \n",
"OK house 207\n",
" senate 70\n",
"OR house 155\n",
" senate 72\n",
"PA house 870\n",
" senate 69\n",
"RI senate 72\n",
" house 69\n",
"SC house 209\n",
" senate 74\n",
"SD senate 71\n",
" house 52\n",
"TN house 310\n",
" senate 71\n",
"TX house 910\n",
" senate 75\n",
"UT house 85\n",
" senate 69\n",
"VA house 357\n",
" senate 71\n",
"VT senate 69\n",
" house 35\n",
"WA house 267\n",
" senate 71\n",
"WI house 317\n",
" senate 69\n",
"WV house 148\n",
" senate 74\n",
"WY senate 73\n",
" house 35\n",
"Name: chamber, dtype: int64"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.groupby(\"state\")['chamber'].value_counts()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 6) How many terms are recorded in this dataset?"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"count 18617\n",
"unique 34\n",
"top 1961-01-03\n",
"freq 559\n",
"Name: termstart, dtype: object"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['termstart'].describe() #here we would look at unique."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 7) Who has been the oldest serving in the US, a senator or a representative? How old was he/she?"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>15237</th>\n",
" <td>107</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>2001-01-03</td>\n",
" <td>98.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"15237 107 senate T000254 J. Strom Thurmond NaN \n",
"\n",
" birthday state party incumbent termstart age complete_name \n",
"15237 1902-12-05 SC R Yes 2001-01-03 98.1 J. Strom Thurmond "
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.sort_values(by='age').tail(1) #A senator!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 8) Who have been the oldest and youngest serving Representative in the US?"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>18073</th>\n",
" <td>113</td>\n",
" <td>house</td>\n",
" <td>H000067</td>\n",
" <td>Ralph</td>\n",
" <td>M.</td>\n",
" <td>Hall</td>\n",
" <td>NaN</td>\n",
" <td>1923-05-03</td>\n",
" <td>TX</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>2013-01-03</td>\n",
" <td>89.7</td>\n",
" <td>Ralph M. Hall</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"18073 113 house H000067 Ralph M. Hall NaN \n",
"\n",
" birthday state party incumbent termstart age complete_name \n",
"18073 1923-05-03 TX R Yes 2013-01-03 89.7 Ralph M. Hall "
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"representative = df[df['chamber'] == 'house']\n",
"representative.sort_values(by='age').tail(1)"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>5422</th>\n",
" <td>89</td>\n",
" <td>house</td>\n",
" <td>J000151</td>\n",
" <td>Jed</td>\n",
" <td>Joseph</td>\n",
" <td>Johnson</td>\n",
" <td>Jr.</td>\n",
" <td>1939-12-27</td>\n",
" <td>OK</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1965-01-04</td>\n",
" <td>25.0</td>\n",
" <td>Jed Joseph Johnson</td>\n",
" </tr>\n",
" <tr>\n",
" <th>452</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>B000401</td>\n",
" <td>Lloyd</td>\n",
" <td>Millard</td>\n",
" <td>Bentsen</td>\n",
" <td>Jr.</td>\n",
" <td>1921-02-11</td>\n",
" <td>TX</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1947-01-03</td>\n",
" <td>25.9</td>\n",
" <td>Lloyd Millard Bentsen</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"5422 89 house J000151 Jed Joseph Johnson Jr. \n",
"452 80 house B000401 Lloyd Millard Bentsen Jr. \n",
"\n",
" birthday state party incumbent termstart age \\\n",
"5422 1939-12-27 OK D No 1965-01-04 25.0 \n",
"452 1921-02-11 TX D No 1947-01-03 25.9 \n",
"\n",
" complete_name \n",
"5422 Jed Joseph Johnson \n",
"452 Lloyd Millard Bentsen "
]
},
"execution_count": 57,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"representative.sort_values(by='age').head(2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 9) Who have been the oldest and youngest serving Senator in the US?\n"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>554</th>\n",
" <td>80</td>\n",
" <td>senate</td>\n",
" <td>L000428</td>\n",
" <td>Russell</td>\n",
" <td>Billiu</td>\n",
" <td>Long</td>\n",
" <td>NaN</td>\n",
" <td>1918-11-03</td>\n",
" <td>LA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>28.2</td>\n",
" <td>Russell Billiu Long</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4427</th>\n",
" <td>87</td>\n",
" <td>senate</td>\n",
" <td>K000105</td>\n",
" <td>Edward</td>\n",
" <td>M.</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1932-02-22</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1961-01-03</td>\n",
" <td>28.9</td>\n",
" <td>Edward M. Kennedy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7721</th>\n",
" <td>93</td>\n",
" <td>senate</td>\n",
" <td>B000444</td>\n",
" <td>Joseph</td>\n",
" <td>R.</td>\n",
" <td>Biden</td>\n",
" <td>Jr.</td>\n",
" <td>1942-11-20</td>\n",
" <td>DE</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1973-01-03</td>\n",
" <td>30.1</td>\n",
" <td>Joseph R. Biden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1111</th>\n",
" <td>81</td>\n",
" <td>senate</td>\n",
" <td>L000428</td>\n",
" <td>Russell</td>\n",
" <td>Billiu</td>\n",
" <td>Long</td>\n",
" <td>NaN</td>\n",
" <td>1918-11-03</td>\n",
" <td>LA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1949-01-03</td>\n",
" <td>30.2</td>\n",
" <td>Russell Billiu Long</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4979</th>\n",
" <td>88</td>\n",
" <td>senate</td>\n",
" <td>K000105</td>\n",
" <td>Edward</td>\n",
" <td>M.</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1932-02-22</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1963-01-09</td>\n",
" <td>30.9</td>\n",
" <td>Edward M. Kennedy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9910</th>\n",
" <td>97</td>\n",
" <td>senate</td>\n",
" <td>N000102</td>\n",
" <td>Don</td>\n",
" <td>NaN</td>\n",
" <td>Nickles</td>\n",
" <td>NaN</td>\n",
" <td>1948-12-06</td>\n",
" <td>OK</td>\n",
" <td>R</td>\n",
" <td>No</td>\n",
" <td>1981-01-05</td>\n",
" <td>32.1</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4978</th>\n",
" <td>88</td>\n",
" <td>senate</td>\n",
" <td>H000237</td>\n",
" <td>Fred</td>\n",
" <td>Roy</td>\n",
" <td>Harris</td>\n",
" <td>NaN</td>\n",
" <td>1930-11-13</td>\n",
" <td>OK</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1963-01-09</td>\n",
" <td>32.2</td>\n",
" <td>Fred Roy Harris</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8271</th>\n",
" <td>94</td>\n",
" <td>senate</td>\n",
" <td>B000444</td>\n",
" <td>Joseph</td>\n",
" <td>R.</td>\n",
" <td>Biden</td>\n",
" <td>Jr.</td>\n",
" <td>1942-11-20</td>\n",
" <td>DE</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1975-01-14</td>\n",
" <td>32.2</td>\n",
" <td>Joseph R. Biden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1666</th>\n",
" <td>82</td>\n",
" <td>senate</td>\n",
" <td>L000428</td>\n",
" <td>Russell</td>\n",
" <td>Billiu</td>\n",
" <td>Long</td>\n",
" <td>NaN</td>\n",
" <td>1918-11-03</td>\n",
" <td>LA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1951-01-03</td>\n",
" <td>32.2</td>\n",
" <td>Russell Billiu Long</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3314</th>\n",
" <td>85</td>\n",
" <td>senate</td>\n",
" <td>C000388</td>\n",
" <td>Frank</td>\n",
" <td>Forrester</td>\n",
" <td>Church</td>\n",
" <td>NaN</td>\n",
" <td>1924-07-25</td>\n",
" <td>ID</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1957-01-03</td>\n",
" <td>32.4</td>\n",
" <td>Frank Forrester Church</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7171</th>\n",
" <td>92</td>\n",
" <td>senate</td>\n",
" <td>N000171</td>\n",
" <td>Samuel</td>\n",
" <td>Augustus</td>\n",
" <td>Nunn</td>\n",
" <td>NaN</td>\n",
" <td>1938-09-08</td>\n",
" <td>GA</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1971-01-21</td>\n",
" <td>32.4</td>\n",
" <td>Samuel Augustus Nunn</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5527</th>\n",
" <td>89</td>\n",
" <td>senate</td>\n",
" <td>K000105</td>\n",
" <td>Edward</td>\n",
" <td>M.</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1932-02-22</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1965-01-04</td>\n",
" <td>32.9</td>\n",
" <td>Edward M. Kennedy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4426</th>\n",
" <td>87</td>\n",
" <td>senate</td>\n",
" <td>M001100</td>\n",
" <td>Maurice</td>\n",
" <td>J.</td>\n",
" <td>Murphy</td>\n",
" <td>Jr.</td>\n",
" <td>1927-10-03</td>\n",
" <td>NH</td>\n",
" <td>R</td>\n",
" <td>No</td>\n",
" <td>1961-01-03</td>\n",
" <td>33.3</td>\n",
" <td>Maurice J. Murphy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9909</th>\n",
" <td>97</td>\n",
" <td>senate</td>\n",
" <td>Q000007</td>\n",
" <td>James</td>\n",
" <td>Danforth</td>\n",
" <td>Quayle</td>\n",
" <td>NaN</td>\n",
" <td>1947-02-04</td>\n",
" <td>IN</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1981-01-05</td>\n",
" <td>33.9</td>\n",
" <td>James Danforth Quayle</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5526</th>\n",
" <td>89</td>\n",
" <td>senate</td>\n",
" <td>H000237</td>\n",
" <td>Fred</td>\n",
" <td>Roy</td>\n",
" <td>Harris</td>\n",
" <td>NaN</td>\n",
" <td>1930-11-13</td>\n",
" <td>OK</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1965-01-04</td>\n",
" <td>34.1</td>\n",
" <td>Fred Roy Harris</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10452</th>\n",
" <td>98</td>\n",
" <td>senate</td>\n",
" <td>N000102</td>\n",
" <td>Don</td>\n",
" <td>NaN</td>\n",
" <td>Nickles</td>\n",
" <td>NaN</td>\n",
" <td>1948-12-06</td>\n",
" <td>OK</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1983-01-03</td>\n",
" <td>34.1</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8824</th>\n",
" <td>95</td>\n",
" <td>senate</td>\n",
" <td>B000444</td>\n",
" <td>Joseph</td>\n",
" <td>R.</td>\n",
" <td>Biden</td>\n",
" <td>Jr.</td>\n",
" <td>1942-11-20</td>\n",
" <td>DE</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1977-01-04</td>\n",
" <td>34.1</td>\n",
" <td>Joseph R. Biden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2223</th>\n",
" <td>83</td>\n",
" <td>senate</td>\n",
" <td>L000428</td>\n",
" <td>Russell</td>\n",
" <td>Billiu</td>\n",
" <td>Long</td>\n",
" <td>NaN</td>\n",
" <td>1918-11-03</td>\n",
" <td>LA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1953-01-03</td>\n",
" <td>34.2</td>\n",
" <td>Russell Billiu Long</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1665</th>\n",
" <td>82</td>\n",
" <td>senate</td>\n",
" <td>P000460</td>\n",
" <td>Charles</td>\n",
" <td>Edward</td>\n",
" <td>Potter</td>\n",
" <td>NaN</td>\n",
" <td>1916-10-30</td>\n",
" <td>MI</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1951-01-03</td>\n",
" <td>34.2</td>\n",
" <td>Charles Edward Potter</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7720</th>\n",
" <td>93</td>\n",
" <td>senate</td>\n",
" <td>N000171</td>\n",
" <td>Samuel</td>\n",
" <td>Augustus</td>\n",
" <td>Nunn</td>\n",
" <td>NaN</td>\n",
" <td>1938-09-08</td>\n",
" <td>GA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1973-01-03</td>\n",
" <td>34.3</td>\n",
" <td>Samuel Augustus Nunn</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6623</th>\n",
" <td>91</td>\n",
" <td>senate</td>\n",
" <td>T000410</td>\n",
" <td>John</td>\n",
" <td>Varick</td>\n",
" <td>Tunney</td>\n",
" <td>NaN</td>\n",
" <td>1934-06-26</td>\n",
" <td>CA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1969-01-03</td>\n",
" <td>34.5</td>\n",
" <td>John Varick Tunney</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3868</th>\n",
" <td>86</td>\n",
" <td>senate</td>\n",
" <td>C000388</td>\n",
" <td>Frank</td>\n",
" <td>Forrester</td>\n",
" <td>Church</td>\n",
" <td>NaN</td>\n",
" <td>1924-07-25</td>\n",
" <td>ID</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1959-01-07</td>\n",
" <td>34.5</td>\n",
" <td>Frank Forrester Church</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8270</th>\n",
" <td>94</td>\n",
" <td>senate</td>\n",
" <td>L000174</td>\n",
" <td>Patrick</td>\n",
" <td>J.</td>\n",
" <td>Leahy</td>\n",
" <td>NaN</td>\n",
" <td>1940-03-31</td>\n",
" <td>VT</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1975-01-14</td>\n",
" <td>34.8</td>\n",
" <td>Patrick J. Leahy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6070</th>\n",
" <td>90</td>\n",
" <td>senate</td>\n",
" <td>K000105</td>\n",
" <td>Edward</td>\n",
" <td>M.</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1932-02-22</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1967-01-10</td>\n",
" <td>34.9</td>\n",
" <td>Edward M. Kennedy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4977</th>\n",
" <td>88</td>\n",
" <td>senate</td>\n",
" <td>B000254</td>\n",
" <td>Birch</td>\n",
" <td>Evans</td>\n",
" <td>Bayh</td>\n",
" <td>NaN</td>\n",
" <td>1928-01-22</td>\n",
" <td>IN</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1963-01-09</td>\n",
" <td>35.0</td>\n",
" <td>Birch Evans Bayh</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4976</th>\n",
" <td>88</td>\n",
" <td>senate</td>\n",
" <td>M000851</td>\n",
" <td>Walter</td>\n",
" <td>Frederick</td>\n",
" <td>Mondale</td>\n",
" <td>NaN</td>\n",
" <td>1928-01-05</td>\n",
" <td>MN</td>\n",
" <td>I</td>\n",
" <td>No</td>\n",
" <td>1963-01-09</td>\n",
" <td>35.0</td>\n",
" <td>Walter Frederick Mondale</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8823</th>\n",
" <td>95</td>\n",
" <td>senate</td>\n",
" <td>B000243</td>\n",
" <td>Max</td>\n",
" <td>S.</td>\n",
" <td>Baucus</td>\n",
" <td>NaN</td>\n",
" <td>1941-12-11</td>\n",
" <td>MT</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1977-01-04</td>\n",
" <td>35.1</td>\n",
" <td>Max S. Baucus</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4425</th>\n",
" <td>87</td>\n",
" <td>senate</td>\n",
" <td>T000322</td>\n",
" <td>John</td>\n",
" <td>Goodwin</td>\n",
" <td>Tower</td>\n",
" <td>NaN</td>\n",
" <td>1925-09-29</td>\n",
" <td>TX</td>\n",
" <td>R</td>\n",
" <td>No</td>\n",
" <td>1961-01-03</td>\n",
" <td>35.3</td>\n",
" <td>John Goodwin Tower</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9367</th>\n",
" <td>96</td>\n",
" <td>senate</td>\n",
" <td>B001225</td>\n",
" <td>William</td>\n",
" <td>Warren</td>\n",
" <td>Bradley</td>\n",
" <td>NaN</td>\n",
" <td>1943-07-28</td>\n",
" <td>NJ</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1979-01-15</td>\n",
" <td>35.5</td>\n",
" <td>William Warren Bradley</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2222</th>\n",
" <td>83</td>\n",
" <td>senate</td>\n",
" <td>K000107</td>\n",
" <td>John</td>\n",
" <td>Fitzgerald</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1917-05-29</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1953-01-03</td>\n",
" <td>35.6</td>\n",
" <td>John Fitzgerald Kennedy</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1562</th>\n",
" <td>82</td>\n",
" <td>senate</td>\n",
" <td>G000418</td>\n",
" <td>Theodore</td>\n",
" <td>Francis</td>\n",
" <td>Green</td>\n",
" <td>NaN</td>\n",
" <td>1867-10-02</td>\n",
" <td>RI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1951-01-03</td>\n",
" <td>83.3</td>\n",
" <td>Theodore Francis Green</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4318</th>\n",
" <td>87</td>\n",
" <td>senate</td>\n",
" <td>H000385</td>\n",
" <td>Carl</td>\n",
" <td>Trumbull</td>\n",
" <td>Hayden</td>\n",
" <td>NaN</td>\n",
" <td>1877-10-02</td>\n",
" <td>AZ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1961-01-03</td>\n",
" <td>83.3</td>\n",
" <td>Carl Trumbull Hayden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10890</th>\n",
" <td>99</td>\n",
" <td>senate</td>\n",
" <td>S000852</td>\n",
" <td>John</td>\n",
" <td>Cornelius</td>\n",
" <td>Stennis</td>\n",
" <td>NaN</td>\n",
" <td>1901-08-03</td>\n",
" <td>MS</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1985-01-03</td>\n",
" <td>83.4</td>\n",
" <td>John Cornelius Stennis</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11433</th>\n",
" <td>100</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1987-01-06</td>\n",
" <td>84.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17417</th>\n",
" <td>111</td>\n",
" <td>senate</td>\n",
" <td>I000025</td>\n",
" <td>Daniel</td>\n",
" <td>K.</td>\n",
" <td>Inouye</td>\n",
" <td>NaN</td>\n",
" <td>1924-09-07</td>\n",
" <td>HI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2009-01-06</td>\n",
" <td>84.3</td>\n",
" <td>Daniel K. Inouye</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17418</th>\n",
" <td>111</td>\n",
" <td>senate</td>\n",
" <td>A000069</td>\n",
" <td>Daniel</td>\n",
" <td>Kahikina</td>\n",
" <td>Akaka</td>\n",
" <td>NaN</td>\n",
" <td>1924-09-11</td>\n",
" <td>HI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2009-01-06</td>\n",
" <td>84.3</td>\n",
" <td>Daniel Kahikina Akaka</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17416</th>\n",
" <td>111</td>\n",
" <td>senate</td>\n",
" <td>L000123</td>\n",
" <td>Frank</td>\n",
" <td>R.</td>\n",
" <td>Lautenberg</td>\n",
" <td>NaN</td>\n",
" <td>1924-01-23</td>\n",
" <td>NJ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2009-01-06</td>\n",
" <td>85.0</td>\n",
" <td>Frank R. Lautenberg</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15780</th>\n",
" <td>108</td>\n",
" <td>senate</td>\n",
" <td>B001210</td>\n",
" <td>Robert</td>\n",
" <td>C.</td>\n",
" <td>Byrd</td>\n",
" <td>NaN</td>\n",
" <td>1917-11-20</td>\n",
" <td>WV</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2003-01-07</td>\n",
" <td>85.1</td>\n",
" <td>Robert C. Byrd</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2110</th>\n",
" <td>83</td>\n",
" <td>senate</td>\n",
" <td>G000418</td>\n",
" <td>Theodore</td>\n",
" <td>Francis</td>\n",
" <td>Green</td>\n",
" <td>NaN</td>\n",
" <td>1867-10-02</td>\n",
" <td>RI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1953-01-03</td>\n",
" <td>85.3</td>\n",
" <td>Theodore Francis Green</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4872</th>\n",
" <td>88</td>\n",
" <td>senate</td>\n",
" <td>H000385</td>\n",
" <td>Carl</td>\n",
" <td>Trumbull</td>\n",
" <td>Hayden</td>\n",
" <td>NaN</td>\n",
" <td>1877-10-02</td>\n",
" <td>AZ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1963-01-09</td>\n",
" <td>85.3</td>\n",
" <td>Carl Trumbull Hayden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11432</th>\n",
" <td>100</td>\n",
" <td>senate</td>\n",
" <td>S000852</td>\n",
" <td>John</td>\n",
" <td>Cornelius</td>\n",
" <td>Stennis</td>\n",
" <td>NaN</td>\n",
" <td>1901-08-03</td>\n",
" <td>MS</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1987-01-06</td>\n",
" <td>85.4</td>\n",
" <td>John Cornelius Stennis</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11976</th>\n",
" <td>101</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1989-01-03</td>\n",
" <td>86.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17972</th>\n",
" <td>112</td>\n",
" <td>senate</td>\n",
" <td>A000069</td>\n",
" <td>Daniel</td>\n",
" <td>Kahikina</td>\n",
" <td>Akaka</td>\n",
" <td>NaN</td>\n",
" <td>1924-09-11</td>\n",
" <td>HI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2011-01-05</td>\n",
" <td>86.3</td>\n",
" <td>Daniel Kahikina Akaka</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17971</th>\n",
" <td>112</td>\n",
" <td>senate</td>\n",
" <td>L000123</td>\n",
" <td>Frank</td>\n",
" <td>R.</td>\n",
" <td>Lautenberg</td>\n",
" <td>NaN</td>\n",
" <td>1924-01-23</td>\n",
" <td>NJ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2011-01-05</td>\n",
" <td>87.0</td>\n",
" <td>Frank R. Lautenberg</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16320</th>\n",
" <td>109</td>\n",
" <td>senate</td>\n",
" <td>B001210</td>\n",
" <td>Robert</td>\n",
" <td>C.</td>\n",
" <td>Byrd</td>\n",
" <td>NaN</td>\n",
" <td>1917-11-20</td>\n",
" <td>WV</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2005-01-04</td>\n",
" <td>87.1</td>\n",
" <td>Robert C. Byrd</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5423</th>\n",
" <td>89</td>\n",
" <td>senate</td>\n",
" <td>H000385</td>\n",
" <td>Carl</td>\n",
" <td>Trumbull</td>\n",
" <td>Hayden</td>\n",
" <td>NaN</td>\n",
" <td>1877-10-02</td>\n",
" <td>AZ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1965-01-04</td>\n",
" <td>87.3</td>\n",
" <td>Carl Trumbull Hayden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2665</th>\n",
" <td>84</td>\n",
" <td>senate</td>\n",
" <td>G000418</td>\n",
" <td>Theodore</td>\n",
" <td>Francis</td>\n",
" <td>Green</td>\n",
" <td>NaN</td>\n",
" <td>1867-10-02</td>\n",
" <td>RI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1955-01-05</td>\n",
" <td>87.3</td>\n",
" <td>Theodore Francis Green</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12518</th>\n",
" <td>102</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1991-01-03</td>\n",
" <td>88.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16869</th>\n",
" <td>110</td>\n",
" <td>senate</td>\n",
" <td>B001210</td>\n",
" <td>Robert</td>\n",
" <td>C.</td>\n",
" <td>Byrd</td>\n",
" <td>NaN</td>\n",
" <td>1917-11-20</td>\n",
" <td>WV</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2007-01-04</td>\n",
" <td>89.1</td>\n",
" <td>Robert C. Byrd</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5967</th>\n",
" <td>90</td>\n",
" <td>senate</td>\n",
" <td>H000385</td>\n",
" <td>Carl</td>\n",
" <td>Trumbull</td>\n",
" <td>Hayden</td>\n",
" <td>NaN</td>\n",
" <td>1877-10-02</td>\n",
" <td>AZ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1967-01-10</td>\n",
" <td>89.3</td>\n",
" <td>Carl Trumbull Hayden</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3213</th>\n",
" <td>85</td>\n",
" <td>senate</td>\n",
" <td>G000418</td>\n",
" <td>Theodore</td>\n",
" <td>Francis</td>\n",
" <td>Green</td>\n",
" <td>NaN</td>\n",
" <td>1867-10-02</td>\n",
" <td>RI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1957-01-03</td>\n",
" <td>89.3</td>\n",
" <td>Theodore Francis Green</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13063</th>\n",
" <td>103</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1993-01-05</td>\n",
" <td>90.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18072</th>\n",
" <td>112</td>\n",
" <td>senate</td>\n",
" <td>I000025</td>\n",
" <td>Daniel</td>\n",
" <td>K.</td>\n",
" <td>Inouye</td>\n",
" <td>NaN</td>\n",
" <td>1920-09-06</td>\n",
" <td>HI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2011-01-05</td>\n",
" <td>90.3</td>\n",
" <td>Daniel K. Inouye</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3763</th>\n",
" <td>86</td>\n",
" <td>senate</td>\n",
" <td>G000418</td>\n",
" <td>Theodore</td>\n",
" <td>Francis</td>\n",
" <td>Green</td>\n",
" <td>NaN</td>\n",
" <td>1867-10-02</td>\n",
" <td>RI</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1959-01-07</td>\n",
" <td>91.3</td>\n",
" <td>Theodore Francis Green</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13609</th>\n",
" <td>104</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1995-01-04</td>\n",
" <td>92.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18616</th>\n",
" <td>113</td>\n",
" <td>senate</td>\n",
" <td>L000123</td>\n",
" <td>Frank</td>\n",
" <td>R.</td>\n",
" <td>Lautenberg</td>\n",
" <td>NaN</td>\n",
" <td>1920-01-22</td>\n",
" <td>NJ</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2013-01-03</td>\n",
" <td>93.0</td>\n",
" <td>Frank R. Lautenberg</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14156</th>\n",
" <td>105</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1997-01-07</td>\n",
" <td>94.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17517</th>\n",
" <td>111</td>\n",
" <td>senate</td>\n",
" <td>B001210</td>\n",
" <td>Robert</td>\n",
" <td>C.</td>\n",
" <td>Byrd</td>\n",
" <td>NaN</td>\n",
" <td>1913-11-19</td>\n",
" <td>WV</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>2009-01-06</td>\n",
" <td>95.1</td>\n",
" <td>Robert C. Byrd</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14693</th>\n",
" <td>106</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1999-01-06</td>\n",
" <td>96.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15237</th>\n",
" <td>107</td>\n",
" <td>senate</td>\n",
" <td>T000254</td>\n",
" <td>J.</td>\n",
" <td>Strom</td>\n",
" <td>Thurmond</td>\n",
" <td>NaN</td>\n",
" <td>1902-12-05</td>\n",
" <td>SC</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>2001-01-03</td>\n",
" <td>98.1</td>\n",
" <td>J. Strom Thurmond</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>3552 rows × 14 columns</p>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"554 80 senate L000428 Russell Billiu Long NaN \n",
"4427 87 senate K000105 Edward M. Kennedy NaN \n",
"7721 93 senate B000444 Joseph R. Biden Jr. \n",
"1111 81 senate L000428 Russell Billiu Long NaN \n",
"4979 88 senate K000105 Edward M. Kennedy NaN \n",
"9910 97 senate N000102 Don NaN Nickles NaN \n",
"4978 88 senate H000237 Fred Roy Harris NaN \n",
"8271 94 senate B000444 Joseph R. Biden Jr. \n",
"1666 82 senate L000428 Russell Billiu Long NaN \n",
"3314 85 senate C000388 Frank Forrester Church NaN \n",
"7171 92 senate N000171 Samuel Augustus Nunn NaN \n",
"5527 89 senate K000105 Edward M. Kennedy NaN \n",
"4426 87 senate M001100 Maurice J. Murphy Jr. \n",
"9909 97 senate Q000007 James Danforth Quayle NaN \n",
"5526 89 senate H000237 Fred Roy Harris NaN \n",
"10452 98 senate N000102 Don NaN Nickles NaN \n",
"8824 95 senate B000444 Joseph R. Biden Jr. \n",
"2223 83 senate L000428 Russell Billiu Long NaN \n",
"1665 82 senate P000460 Charles Edward Potter NaN \n",
"7720 93 senate N000171 Samuel Augustus Nunn NaN \n",
"6623 91 senate T000410 John Varick Tunney NaN \n",
"3868 86 senate C000388 Frank Forrester Church NaN \n",
"8270 94 senate L000174 Patrick J. Leahy NaN \n",
"6070 90 senate K000105 Edward M. Kennedy NaN \n",
"4977 88 senate B000254 Birch Evans Bayh NaN \n",
"4976 88 senate M000851 Walter Frederick Mondale NaN \n",
"8823 95 senate B000243 Max S. Baucus NaN \n",
"4425 87 senate T000322 John Goodwin Tower NaN \n",
"9367 96 senate B001225 William Warren Bradley NaN \n",
"2222 83 senate K000107 John Fitzgerald Kennedy NaN \n",
"... ... ... ... ... ... ... ... \n",
"1562 82 senate G000418 Theodore Francis Green NaN \n",
"4318 87 senate H000385 Carl Trumbull Hayden NaN \n",
"10890 99 senate S000852 John Cornelius Stennis NaN \n",
"11433 100 senate T000254 J. Strom Thurmond NaN \n",
"17417 111 senate I000025 Daniel K. Inouye NaN \n",
"17418 111 senate A000069 Daniel Kahikina Akaka NaN \n",
"17416 111 senate L000123 Frank R. Lautenberg NaN \n",
"15780 108 senate B001210 Robert C. Byrd NaN \n",
"2110 83 senate G000418 Theodore Francis Green NaN \n",
"4872 88 senate H000385 Carl Trumbull Hayden NaN \n",
"11432 100 senate S000852 John Cornelius Stennis NaN \n",
"11976 101 senate T000254 J. Strom Thurmond NaN \n",
"17972 112 senate A000069 Daniel Kahikina Akaka NaN \n",
"17971 112 senate L000123 Frank R. Lautenberg NaN \n",
"16320 109 senate B001210 Robert C. Byrd NaN \n",
"5423 89 senate H000385 Carl Trumbull Hayden NaN \n",
"2665 84 senate G000418 Theodore Francis Green NaN \n",
"12518 102 senate T000254 J. Strom Thurmond NaN \n",
"16869 110 senate B001210 Robert C. Byrd NaN \n",
"5967 90 senate H000385 Carl Trumbull Hayden NaN \n",
"3213 85 senate G000418 Theodore Francis Green NaN \n",
"13063 103 senate T000254 J. Strom Thurmond NaN \n",
"18072 112 senate I000025 Daniel K. Inouye NaN \n",
"3763 86 senate G000418 Theodore Francis Green NaN \n",
"13609 104 senate T000254 J. Strom Thurmond NaN \n",
"18616 113 senate L000123 Frank R. Lautenberg NaN \n",
"14156 105 senate T000254 J. Strom Thurmond NaN \n",
"17517 111 senate B001210 Robert C. Byrd NaN \n",
"14693 106 senate T000254 J. Strom Thurmond NaN \n",
"15237 107 senate T000254 J. Strom Thurmond NaN \n",
"\n",
" birthday state party incumbent termstart age \\\n",
"554 1918-11-03 LA D Yes 1947-01-03 28.2 \n",
"4427 1932-02-22 MA D No 1961-01-03 28.9 \n",
"7721 1942-11-20 DE D No 1973-01-03 30.1 \n",
"1111 1918-11-03 LA D Yes 1949-01-03 30.2 \n",
"4979 1932-02-22 MA D Yes 1963-01-09 30.9 \n",
"9910 1948-12-06 OK R No 1981-01-05 32.1 \n",
"4978 1930-11-13 OK D No 1963-01-09 32.2 \n",
"8271 1942-11-20 DE D Yes 1975-01-14 32.2 \n",
"1666 1918-11-03 LA D Yes 1951-01-03 32.2 \n",
"3314 1924-07-25 ID D No 1957-01-03 32.4 \n",
"7171 1938-09-08 GA D No 1971-01-21 32.4 \n",
"5527 1932-02-22 MA D Yes 1965-01-04 32.9 \n",
"4426 1927-10-03 NH R No 1961-01-03 33.3 \n",
"9909 1947-02-04 IN R Yes 1981-01-05 33.9 \n",
"5526 1930-11-13 OK D Yes 1965-01-04 34.1 \n",
"10452 1948-12-06 OK R Yes 1983-01-03 34.1 \n",
"8824 1942-11-20 DE D Yes 1977-01-04 34.1 \n",
"2223 1918-11-03 LA D Yes 1953-01-03 34.2 \n",
"1665 1916-10-30 MI R Yes 1951-01-03 34.2 \n",
"7720 1938-09-08 GA D Yes 1973-01-03 34.3 \n",
"6623 1934-06-26 CA D Yes 1969-01-03 34.5 \n",
"3868 1924-07-25 ID D Yes 1959-01-07 34.5 \n",
"8270 1940-03-31 VT D No 1975-01-14 34.8 \n",
"6070 1932-02-22 MA D Yes 1967-01-10 34.9 \n",
"4977 1928-01-22 IN D No 1963-01-09 35.0 \n",
"4976 1928-01-05 MN I No 1963-01-09 35.0 \n",
"8823 1941-12-11 MT D Yes 1977-01-04 35.1 \n",
"4425 1925-09-29 TX R No 1961-01-03 35.3 \n",
"9367 1943-07-28 NJ D No 1979-01-15 35.5 \n",
"2222 1917-05-29 MA D Yes 1953-01-03 35.6 \n",
"... ... ... ... ... ... ... \n",
"1562 1867-10-02 RI D Yes 1951-01-03 83.3 \n",
"4318 1877-10-02 AZ D Yes 1961-01-03 83.3 \n",
"10890 1901-08-03 MS D Yes 1985-01-03 83.4 \n",
"11433 1902-12-05 SC R Yes 1987-01-06 84.1 \n",
"17417 1924-09-07 HI D Yes 2009-01-06 84.3 \n",
"17418 1924-09-11 HI D Yes 2009-01-06 84.3 \n",
"17416 1924-01-23 NJ D Yes 2009-01-06 85.0 \n",
"15780 1917-11-20 WV D Yes 2003-01-07 85.1 \n",
"2110 1867-10-02 RI D Yes 1953-01-03 85.3 \n",
"4872 1877-10-02 AZ D Yes 1963-01-09 85.3 \n",
"11432 1901-08-03 MS D Yes 1987-01-06 85.4 \n",
"11976 1902-12-05 SC R Yes 1989-01-03 86.1 \n",
"17972 1924-09-11 HI D Yes 2011-01-05 86.3 \n",
"17971 1924-01-23 NJ D Yes 2011-01-05 87.0 \n",
"16320 1917-11-20 WV D Yes 2005-01-04 87.1 \n",
"5423 1877-10-02 AZ D Yes 1965-01-04 87.3 \n",
"2665 1867-10-02 RI D Yes 1955-01-05 87.3 \n",
"12518 1902-12-05 SC R Yes 1991-01-03 88.1 \n",
"16869 1917-11-20 WV D Yes 2007-01-04 89.1 \n",
"5967 1877-10-02 AZ D Yes 1967-01-10 89.3 \n",
"3213 1867-10-02 RI D Yes 1957-01-03 89.3 \n",
"13063 1902-12-05 SC R Yes 1993-01-05 90.1 \n",
"18072 1920-09-06 HI D Yes 2011-01-05 90.3 \n",
"3763 1867-10-02 RI D Yes 1959-01-07 91.3 \n",
"13609 1902-12-05 SC R Yes 1995-01-04 92.1 \n",
"18616 1920-01-22 NJ D Yes 2013-01-03 93.0 \n",
"14156 1902-12-05 SC R Yes 1997-01-07 94.1 \n",
"17517 1913-11-19 WV D Yes 2009-01-06 95.1 \n",
"14693 1902-12-05 SC R Yes 1999-01-06 96.1 \n",
"15237 1902-12-05 SC R Yes 2001-01-03 98.1 \n",
"\n",
" complete_name \n",
"554 Russell Billiu Long \n",
"4427 Edward M. Kennedy \n",
"7721 Joseph R. Biden \n",
"1111 Russell Billiu Long \n",
"4979 Edward M. Kennedy \n",
"9910 NaN \n",
"4978 Fred Roy Harris \n",
"8271 Joseph R. Biden \n",
"1666 Russell Billiu Long \n",
"3314 Frank Forrester Church \n",
"7171 Samuel Augustus Nunn \n",
"5527 Edward M. Kennedy \n",
"4426 Maurice J. Murphy \n",
"9909 James Danforth Quayle \n",
"5526 Fred Roy Harris \n",
"10452 NaN \n",
"8824 Joseph R. Biden \n",
"2223 Russell Billiu Long \n",
"1665 Charles Edward Potter \n",
"7720 Samuel Augustus Nunn \n",
"6623 John Varick Tunney \n",
"3868 Frank Forrester Church \n",
"8270 Patrick J. Leahy \n",
"6070 Edward M. Kennedy \n",
"4977 Birch Evans Bayh \n",
"4976 Walter Frederick Mondale \n",
"8823 Max S. Baucus \n",
"4425 John Goodwin Tower \n",
"9367 William Warren Bradley \n",
"2222 John Fitzgerald Kennedy \n",
"... ... \n",
"1562 Theodore Francis Green \n",
"4318 Carl Trumbull Hayden \n",
"10890 John Cornelius Stennis \n",
"11433 J. Strom Thurmond \n",
"17417 Daniel K. Inouye \n",
"17418 Daniel Kahikina Akaka \n",
"17416 Frank R. Lautenberg \n",
"15780 Robert C. Byrd \n",
"2110 Theodore Francis Green \n",
"4872 Carl Trumbull Hayden \n",
"11432 John Cornelius Stennis \n",
"11976 J. Strom Thurmond \n",
"17972 Daniel Kahikina Akaka \n",
"17971 Frank R. Lautenberg \n",
"16320 Robert C. Byrd \n",
"5423 Carl Trumbull Hayden \n",
"2665 Theodore Francis Green \n",
"12518 J. Strom Thurmond \n",
"16869 Robert C. Byrd \n",
"5967 Carl Trumbull Hayden \n",
"3213 Theodore Francis Green \n",
"13063 J. Strom Thurmond \n",
"18072 Daniel K. Inouye \n",
"3763 Theodore Francis Green \n",
"13609 J. Strom Thurmond \n",
"18616 Frank R. Lautenberg \n",
"14156 J. Strom Thurmond \n",
"17517 Robert C. Byrd \n",
"14693 J. Strom Thurmond \n",
"15237 J. Strom Thurmond \n",
"\n",
"[3552 rows x 14 columns]"
]
},
"execution_count": 58,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"senator = df[df['chamber'] == 'senate']\n",
"senator.sort_values(by='age')"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>554</th>\n",
" <td>80</td>\n",
" <td>senate</td>\n",
" <td>L000428</td>\n",
" <td>Russell</td>\n",
" <td>Billiu</td>\n",
" <td>Long</td>\n",
" <td>NaN</td>\n",
" <td>1918-11-03</td>\n",
" <td>LA</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>28.2</td>\n",
" <td>Russell Billiu Long</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4427</th>\n",
" <td>87</td>\n",
" <td>senate</td>\n",
" <td>K000105</td>\n",
" <td>Edward</td>\n",
" <td>M.</td>\n",
" <td>Kennedy</td>\n",
" <td>NaN</td>\n",
" <td>1932-02-22</td>\n",
" <td>MA</td>\n",
" <td>D</td>\n",
" <td>No</td>\n",
" <td>1961-01-03</td>\n",
" <td>28.9</td>\n",
" <td>Edward M. Kennedy</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"554 80 senate L000428 Russell Billiu Long NaN \n",
"4427 87 senate K000105 Edward M. Kennedy NaN \n",
"\n",
" birthday state party incumbent termstart age complete_name \n",
"554 1918-11-03 LA D Yes 1947-01-03 28.2 Russell Billiu Long \n",
"4427 1932-02-22 MA D No 1961-01-03 28.9 Edward M. Kennedy "
]
},
"execution_count": 59,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"senator.sort_values(by='age').head(2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 10) Who has served for more periods (in this question I am not paying attention to the period length)?"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>congress</th>\n",
" <th>chamber</th>\n",
" <th>bioguide</th>\n",
" <th>firstname</th>\n",
" <th>middlename</th>\n",
" <th>lastname</th>\n",
" <th>suffix</th>\n",
" <th>birthday</th>\n",
" <th>state</th>\n",
" <th>party</th>\n",
" <th>incumbent</th>\n",
" <th>termstart</th>\n",
" <th>age</th>\n",
" <th>complete_name</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>M000112</td>\n",
" <td>Joseph</td>\n",
" <td>Jefferson</td>\n",
" <td>Mansfield</td>\n",
" <td>NaN</td>\n",
" <td>1861-02-09</td>\n",
" <td>TX</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>85.9</td>\n",
" <td>Joseph Jefferson Mansfield</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>D000448</td>\n",
" <td>Robert</td>\n",
" <td>Lee</td>\n",
" <td>Doughton</td>\n",
" <td>NaN</td>\n",
" <td>1863-11-07</td>\n",
" <td>NC</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>83.2</td>\n",
" <td>Robert Lee Doughton</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>S000001</td>\n",
" <td>Adolph</td>\n",
" <td>Joachim</td>\n",
" <td>Sabath</td>\n",
" <td>NaN</td>\n",
" <td>1866-04-04</td>\n",
" <td>IL</td>\n",
" <td>D</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>80.7</td>\n",
" <td>Adolph Joachim Sabath</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>E000023</td>\n",
" <td>Charles</td>\n",
" <td>Aubrey</td>\n",
" <td>Eaton</td>\n",
" <td>NaN</td>\n",
" <td>1868-03-29</td>\n",
" <td>NJ</td>\n",
" <td>R</td>\n",
" <td>Yes</td>\n",
" <td>1947-01-03</td>\n",
" <td>78.8</td>\n",
" <td>Charles Aubrey Eaton</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>80</td>\n",
" <td>house</td>\n",
" <td>L000296</td>\n",
" <td>William</td>\n",
" <td>NaN</td>\n",
" <td>Lewis</td>\n",
" <td>NaN</td>\n",
" <td>1868-09-22</td>\n",
" <td>KY</td>\n",
" <td>R</td>\n",
" <td>No</td>\n",
" <td>1947-01-03</td>\n",
" <td>78.3</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" congress chamber bioguide firstname middlename lastname suffix \\\n",
"0 80 house M000112 Joseph Jefferson Mansfield NaN \n",
"1 80 house D000448 Robert Lee Doughton NaN \n",
"2 80 house S000001 Adolph Joachim Sabath NaN \n",
"3 80 house E000023 Charles Aubrey Eaton NaN \n",
"4 80 house L000296 William NaN Lewis NaN \n",
"\n",
" birthday state party incumbent termstart age \\\n",
"0 1861-02-09 TX D Yes 1947-01-03 85.9 \n",
"1 1863-11-07 NC D Yes 1947-01-03 83.2 \n",
"2 1866-04-04 IL D Yes 1947-01-03 80.7 \n",
"3 1868-03-29 NJ R Yes 1947-01-03 78.8 \n",
"4 1868-09-22 KY R No 1947-01-03 78.3 \n",
"\n",
" complete_name \n",
"0 Joseph Jefferson Mansfield \n",
"1 Robert Lee Doughton \n",
"2 Adolph Joachim Sabath \n",
"3 Charles Aubrey Eaton \n",
"4 NaN "
]
},
"execution_count": 60,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Store a new column\n",
"df['complete_name'] = df['firstname']+ \" \"+ df['middlename'] + \" \"+df['lastname']\n",
"df.head()"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th></th>\n",
" <th>termstart</th>\n",
" </tr>\n",
" <tr>\n",
" <th>complete_name</th>\n",
" <th>termstart</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Barry Morris Goldwater</th>\n",
" <th>1981-01-05</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Daniel Kahikina Akaka</th>\n",
" <th>1989-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Max S. Baucus</th>\n",
" <th>1977-01-04</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Carl Thomas Curtis</th>\n",
" <th>1953-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Samuel D. Brownback</th>\n",
" <th>1995-01-04</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James Thomas Broyhill</th>\n",
" <th>1985-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Donald M. Payne</th>\n",
" <th>2011-01-05</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>J. Strom Thurmond</th>\n",
" <th>1963-01-09</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">Eugene A. Chappie</th>\n",
" <th>1985-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1983-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James M. Inhofe</th>\n",
" <th>1993-01-05</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Barry Morris Goldwater</th>\n",
" <th>1977-01-04</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Richard Milhous Nixon</th>\n",
" <th>1949-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">Barry Morris Goldwater</th>\n",
" <th>1975-01-14</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1973-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Wayne Lyman Morse</th>\n",
" <th>1955-01-05</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Roger F. Wicker</th>\n",
" <th>2007-01-04</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Kirsten E. Gillibrand</th>\n",
" <th>2009-01-06</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">Barry Morris Goldwater</th>\n",
" <th>1971-01-21</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1969-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Harry Flood Byrd</th>\n",
" <th>1965-01-04</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward J. Markey</th>\n",
" <th>2013-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Barry Morris Goldwater</th>\n",
" <th>1979-01-15</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Richard C. Shelby</th>\n",
" <th>1993-01-05</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edwin Washington Edwards</th>\n",
" <th>1971-01-21</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Mark Steven Kirk</th>\n",
" <th>2009-01-06</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Roman Lee Hruska</th>\n",
" <th>1953-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>William V. Roth</th>\n",
" <th>1969-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Varick Tunney</th>\n",
" <th>1969-01-03</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Robert Theodore Stafford</th>\n",
" <th>1971-01-21</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Milton Horace West</th>\n",
" <th>1947-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Milton Robert Carr</th>\n",
" <th>1977-01-04</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Milton Willits Glenn</th>\n",
" <th>1961-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Milton Robert Carr</th>\n",
" <th>1979-01-15</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"2\" valign=\"top\">Milton Willits Glenn</th>\n",
" <th>1959-01-07</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1957-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"17\" valign=\"top\">Milton Ruben Young</th>\n",
" <th>1979-01-15</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1977-01-04</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1975-01-14</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1973-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1971-01-21</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1969-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1967-01-10</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1965-01-04</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1963-01-09</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1961-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1959-01-07</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1957-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1955-01-05</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1953-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1951-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1949-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1947-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th rowspan=\"6\" valign=\"top\">Milton Robert Carr</th>\n",
" <th>1993-01-05</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1991-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1989-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1987-01-06</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1985-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1983-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Abe McGregor Goff</th>\n",
" <th>1947-01-03</th>\n",
" <td>1</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>15045 rows × 1 columns</p>\n",
"</div>"
],
"text/plain": [
" termstart\n",
"complete_name termstart \n",
"Barry Morris Goldwater 1981-01-05 2\n",
"Daniel Kahikina Akaka 1989-01-03 2\n",
"Max S. Baucus 1977-01-04 2\n",
"Carl Thomas Curtis 1953-01-03 2\n",
"Samuel D. Brownback 1995-01-04 2\n",
"James Thomas Broyhill 1985-01-03 2\n",
"Donald M. Payne 2011-01-05 2\n",
"J. Strom Thurmond 1963-01-09 2\n",
"Eugene A. Chappie 1985-01-03 2\n",
" 1983-01-03 2\n",
"James M. Inhofe 1993-01-05 2\n",
"Barry Morris Goldwater 1977-01-04 2\n",
"Richard Milhous Nixon 1949-01-03 2\n",
"Barry Morris Goldwater 1975-01-14 2\n",
" 1973-01-03 2\n",
"Wayne Lyman Morse 1955-01-05 2\n",
"Roger F. Wicker 2007-01-04 2\n",
"Kirsten E. Gillibrand 2009-01-06 2\n",
"Barry Morris Goldwater 1971-01-21 2\n",
" 1969-01-03 2\n",
"Harry Flood Byrd 1965-01-04 2\n",
"Edward J. Markey 2013-01-03 2\n",
"Barry Morris Goldwater 1979-01-15 2\n",
"Richard C. Shelby 1993-01-05 2\n",
"Edwin Washington Edwards 1971-01-21 2\n",
"Mark Steven Kirk 2009-01-06 2\n",
"Roman Lee Hruska 1953-01-03 2\n",
"William V. Roth 1969-01-03 2\n",
"John Varick Tunney 1969-01-03 2\n",
"Robert Theodore Stafford 1971-01-21 2\n",
"... ...\n",
"Milton Horace West 1947-01-03 1\n",
"Milton Robert Carr 1977-01-04 1\n",
"Milton Willits Glenn 1961-01-03 1\n",
"Milton Robert Carr 1979-01-15 1\n",
"Milton Willits Glenn 1959-01-07 1\n",
" 1957-01-03 1\n",
"Milton Ruben Young 1979-01-15 1\n",
" 1977-01-04 1\n",
" 1975-01-14 1\n",
" 1973-01-03 1\n",
" 1971-01-21 1\n",
" 1969-01-03 1\n",
" 1967-01-10 1\n",
" 1965-01-04 1\n",
" 1963-01-09 1\n",
" 1961-01-03 1\n",
" 1959-01-07 1\n",
" 1957-01-03 1\n",
" 1955-01-05 1\n",
" 1953-01-03 1\n",
" 1951-01-03 1\n",
" 1949-01-03 1\n",
" 1947-01-03 1\n",
"Milton Robert Carr 1993-01-05 1\n",
" 1991-01-03 1\n",
" 1989-01-03 1\n",
" 1987-01-06 1\n",
" 1985-01-03 1\n",
" 1983-01-03 1\n",
"Abe McGregor Goff 1947-01-03 1\n",
"\n",
"[15045 rows x 1 columns]"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"period_count = df.groupby('complete_name')['termstart'].value_counts().sort_values(ascending=False)\n",
"pd.DataFrame(period_count)\n",
"\n",
"\n",
"#With the help of Stephan we figured out that term-start is every 2 years \n",
"#(so this is not giving us info about how many terms has each legislator served)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"#We double-checked it by printing info from Thurmond, whom was part of the senate but appeared as if he had\n",
"#served 26 periods of 6 years each (26*6 IMPOSIBLE!)\n",
"Thurmond = df[df['lastname'] == 'Thurmond']\n",
"Thurmond\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 11) Who has served for more years?\n",
"\n",
"Senators = 6-year terms BUT the data we have is for 2-year terms\n",
"Representatives = 2-year terms \n"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th></th>\n",
" <th>bioguide</th>\n",
" </tr>\n",
" <tr>\n",
" <th>complete_name</th>\n",
" <th>bioguide</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Robert C. Byrd</th>\n",
" <th>B001210</th>\n",
" <td>52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>J. Strom Thurmond</th>\n",
" <th>T000254</th>\n",
" <td>52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward M. Kennedy</th>\n",
" <th>K000105</th>\n",
" <td>50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Daniel K. Inouye</th>\n",
" <th>I000025</th>\n",
" <td>50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Cornelius Stennis</th>\n",
" <th>S000852</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Ted F. Stevens</th>\n",
" <th>S000888</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Ernest F. Hollings</th>\n",
" <th>H000725</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Russell Billiu Long</th>\n",
" <th>L000428</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Patrick J. Leahy</th>\n",
" <th>L000174</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Max S. Baucus</th>\n",
" <th>B000243</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Orrin G. Hatch</th>\n",
" <th>H000338</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph R. Biden</th>\n",
" <th>B000444</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Richard G. Lugar</th>\n",
" <th>L000504</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Claiborne de Borda Pell</th>\n",
" <th>P000193</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Pete V. Domenici</th>\n",
" <th>D000407</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles E. Grassley</th>\n",
" <th>G000386</th>\n",
" <td>34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Quentin Northrup Burdick</th>\n",
" <th>B001077</th>\n",
" <td>34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Milton Ruben Young</th>\n",
" <th>Y000047</th>\n",
" <td>34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Warren Grant Magnuson</th>\n",
" <th>M000053</th>\n",
" <td>34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John W. Warner</th>\n",
" <th>W000154</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Little McClellan</th>\n",
" <th>M000332</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>William V. Roth</th>\n",
" <th>R000460</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Jackson Sparkman</th>\n",
" <th>S000701</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James Oliver Eastland</th>\n",
" <th>E000018</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Henry Martin Jackson</th>\n",
" <th>J000013</th>\n",
" <td>32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Frank R. Lautenberg</th>\n",
" <th>L000123</th>\n",
" <td>30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John D. Rockefeller</th>\n",
" <th>R000361</th>\n",
" <td>30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Forbes Kerry</th>\n",
" <th>K000148</th>\n",
" <td>30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Richard C. Shelby</th>\n",
" <th>S000320</th>\n",
" <td>30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Paul S. Sarbanes</th>\n",
" <th>S000064</th>\n",
" <td>30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Jocelyn Birch Burdick</th>\n",
" <th>B001076</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John E. Walsh</th>\n",
" <th>W000818</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward J. Markey</th>\n",
" <th>M000133</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward Hall Moore</th>\n",
" <th>M000895</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Robert Charles Krueger</th>\n",
" <th>K000333</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Wallace Humphrey White</th>\n",
" <th>W000396</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>David Henry Gambrell</th>\n",
" <th>G000034</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>David Kemp Karnes</th>\n",
" <th>K000011</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward E. Kaufman</th>\n",
" <th>K000373</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward David Crippa</th>\n",
" <th>C000906</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Donald Stuart Russell</th>\n",
" <th>R000525</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Holmes Overton</th>\n",
" <th>O000146</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward Vivian Robertson</th>\n",
" <th>R000320</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Clayton Douglass Buck</th>\n",
" <th>B001013</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James Howard Edmondson</th>\n",
" <th>E000055</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Carte P. Goodwin</th>\n",
" <th>G000561</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Vera Cahalan Bushfield</th>\n",
" <th>B001169</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Hurst Ball</th>\n",
" <th>B000099</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph H. Bottum</th>\n",
" <th>B000656</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Eva Kelly Bowring</th>\n",
" <th>B000709</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles Ezra Daniel</th>\n",
" <th>D000031</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Ernest S. Brown</th>\n",
" <th>B000913</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James Thomas Broyhill</th>\n",
" <th>B000966</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles Wayland Brooks</th>\n",
" <th>B000874</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edwin Washington Edwards</th>\n",
" <th>E000067</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Joseph Hickey</th>\n",
" <th>H000561</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Christopher S. Murphy</th>\n",
" <th>M001169</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Wilbert Lee O'Daniel</th>\n",
" <th>O000034</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Clarence Norman Brunsdale</th>\n",
" <th>B000982</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Dempsey Hoblitzell</th>\n",
" <th>H000665</th>\n",
" <td>2</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>448 rows × 1 columns</p>\n",
"</div>"
],
"text/plain": [
" bioguide\n",
"complete_name bioguide \n",
"Robert C. Byrd B001210 52\n",
"J. Strom Thurmond T000254 52\n",
"Edward M. Kennedy K000105 50\n",
"Daniel K. Inouye I000025 50\n",
"John Cornelius Stennis S000852 42\n",
"Ted F. Stevens S000888 42\n",
"Ernest F. Hollings H000725 40\n",
"Russell Billiu Long L000428 40\n",
"Patrick J. Leahy L000174 40\n",
"Max S. Baucus B000243 38\n",
"Orrin G. Hatch H000338 38\n",
"Joseph R. Biden B000444 38\n",
"Richard G. Lugar L000504 36\n",
"Claiborne de Borda Pell P000193 36\n",
"Pete V. Domenici D000407 36\n",
"Charles E. Grassley G000386 34\n",
"Quentin Northrup Burdick B001077 34\n",
"Milton Ruben Young Y000047 34\n",
"Warren Grant Magnuson M000053 34\n",
"John W. Warner W000154 32\n",
"John Little McClellan M000332 32\n",
"William V. Roth R000460 32\n",
"John Jackson Sparkman S000701 32\n",
"James Oliver Eastland E000018 32\n",
"Henry Martin Jackson J000013 32\n",
"Frank R. Lautenberg L000123 30\n",
"John D. Rockefeller R000361 30\n",
"John Forbes Kerry K000148 30\n",
"Richard C. Shelby S000320 30\n",
"Paul S. Sarbanes S000064 30\n",
"... ...\n",
"Jocelyn Birch Burdick B001076 2\n",
"John E. Walsh W000818 2\n",
"Edward J. Markey M000133 2\n",
"Edward Hall Moore M000895 2\n",
"Robert Charles Krueger K000333 2\n",
"Wallace Humphrey White W000396 2\n",
"David Henry Gambrell G000034 2\n",
"David Kemp Karnes K000011 2\n",
"Edward E. Kaufman K000373 2\n",
"Edward David Crippa C000906 2\n",
"Donald Stuart Russell R000525 2\n",
"John Holmes Overton O000146 2\n",
"Edward Vivian Robertson R000320 2\n",
"Clayton Douglass Buck B001013 2\n",
"James Howard Edmondson E000055 2\n",
"Carte P. Goodwin G000561 2\n",
"Vera Cahalan Bushfield B001169 2\n",
"Joseph Hurst Ball B000099 2\n",
"Joseph H. Bottum B000656 2\n",
"Eva Kelly Bowring B000709 2\n",
"Charles Ezra Daniel D000031 2\n",
"Ernest S. Brown B000913 2\n",
"James Thomas Broyhill B000966 2\n",
"Charles Wayland Brooks B000874 2\n",
"Edwin Washington Edwards E000067 2\n",
"John Joseph Hickey H000561 2\n",
"Christopher S. Murphy M001169 2\n",
"Wilbert Lee O'Daniel O000034 2\n",
"Clarence Norman Brunsdale B000982 2\n",
"John Dempsey Hoblitzell H000665 2\n",
"\n",
"[448 rows x 1 columns]"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"terms_served_by_senators= senator.groupby('complete_name')['bioguide'].value_counts()\n",
"years= terms_served_by_senators * 2\n",
"total_years_served = years.sort_values(ascending=False)\n",
"\n",
"pd.DataFrame(total_years_served)\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th></th>\n",
" <th>bioguide</th>\n",
" </tr>\n",
" <tr>\n",
" <th>complete_name</th>\n",
" <th>bioguide</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>John D. Dingell</th>\n",
" <th>D000355</th>\n",
" <td>60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Jamie Lloyd Whitten</th>\n",
" <th>W000428</th>\n",
" <td>48</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Sidney Richard Yates</th>\n",
" <th>Y000013</th>\n",
" <td>48</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles Edward Bennett</th>\n",
" <th>B000371</th>\n",
" <td>44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C. W. Bill Young</th>\n",
" <th>Y000031</th>\n",
" <td>44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles B. Rangel</th>\n",
" <th>R000053</th>\n",
" <td>44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>David Ross Obey</th>\n",
" <th>O000007</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Don E. Young</th>\n",
" <th>Y000033</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Charles Melvin Price</th>\n",
" <th>P000522</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Jack Bascom Brooks</th>\n",
" <th>B000880</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>William Huston Natcher</th>\n",
" <th>N000009</th>\n",
" <td>42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Henry A. Waxman</th>\n",
" <th>W000215</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Fortney H. Stark</th>\n",
" <th>S000810</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Peter Wallace Rodino</th>\n",
" <th>R000374</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward J. Markey</th>\n",
" <th>M000133</th>\n",
" <td>40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John P. Murtha</th>\n",
" <th>M001120</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Henry Barbosa González</th>\n",
" <th>G000272</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Dante Bruno Fascell</th>\n",
" <th>F000041</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Robert Henry Michel</th>\n",
" <th>M000692</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Nick J. Rahall</th>\n",
" <th>R000011</th>\n",
" <td>38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>William S. Broomfield</th>\n",
" <th>B000890</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Carl Dewey Perkins</th>\n",
" <th>P000230</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Edward Patrick Boland</th>\n",
" <th>B000600</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Thomas E. Petri</th>\n",
" <th>P000265</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James L. Oberstar</th>\n",
" <th>O000006</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>George E. Brown</th>\n",
" <th>B000918</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Michael McDade</th>\n",
" <th>M000399</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Norman D. Dicks</th>\n",
" <th>D000327</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Philip M. Crane</th>\n",
" <th>C000873</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>James Claude Wright</th>\n",
" <th>W000763</th>\n",
" <td>36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Richard Schmidhauser</th>\n",
" <th>S000131</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Richard Walsh</th>\n",
" <th>W000100</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Robert Foley</th>\n",
" <th>F000237</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Robert Hansen</th>\n",
" <th>H000173</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Keith J. Rothfus</th>\n",
" <th>R000598</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Kathleen C. Hochul</th>\n",
" <th>H001062</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Kathleen A. Dahlkemper</th>\n",
" <th>D000608</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>D. Bailey Merrill</th>\n",
" <th>M000656</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Katherine M. Clark</th>\n",
" <th>C001101</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>K. William Stinson</th>\n",
" <th>S000928</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Walker Barr</th>\n",
" <th>B000170</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Scofield Ammerman</th>\n",
" <th>A000177</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Peyton Wyatt</th>\n",
" <th>W000777</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph P. Kennedy</th>\n",
" <th>K000379</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Oliva Huot</th>\n",
" <th>H001001</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Jefferson Mansfield</th>\n",
" <th>M000112</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph James Maraziti</th>\n",
" <th>M000121</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Francis Smith</th>\n",
" <th>S000579</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Edward Hendricks</th>\n",
" <th>H000492</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Joseph Anthony LeFante</th>\n",
" <th>L000561</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Daniel T. Kildee</th>\n",
" <th>K000380</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Williams Gwynne</th>\n",
" <th>G000543</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John William Flannagan</th>\n",
" <th>F000191</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John W. Cox</th>\n",
" <th>C000836</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Darwin Gale Schisler</th>\n",
" <th>S000128</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Travers Wood</th>\n",
" <th>W000700</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>David A. Levy</th>\n",
" <th>L000267</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>David Alan Curson</th>\n",
" <th>C001089</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>John Schiller Wold</th>\n",
" <th>W000671</th>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Abe McGregor Goff</th>\n",
" <th>G000253</th>\n",
" <td>2</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>2171 rows × 1 columns</p>\n",
"</div>"
],
"text/plain": [
" bioguide\n",
"complete_name bioguide \n",
"John D. Dingell D000355 60\n",
"Jamie Lloyd Whitten W000428 48\n",
"Sidney Richard Yates Y000013 48\n",
"Charles Edward Bennett B000371 44\n",
"C. W. Bill Young Y000031 44\n",
"Charles B. Rangel R000053 44\n",
"David Ross Obey O000007 42\n",
"Don E. Young Y000033 42\n",
"Charles Melvin Price P000522 42\n",
"Jack Bascom Brooks B000880 42\n",
"William Huston Natcher N000009 42\n",
"Henry A. Waxman W000215 40\n",
"Fortney H. Stark S000810 40\n",
"Peter Wallace Rodino R000374 40\n",
"Edward J. Markey M000133 40\n",
"John P. Murtha M001120 38\n",
"Henry Barbosa González G000272 38\n",
"Dante Bruno Fascell F000041 38\n",
"Robert Henry Michel M000692 38\n",
"Nick J. Rahall R000011 38\n",
"William S. Broomfield B000890 36\n",
"Carl Dewey Perkins P000230 36\n",
"Edward Patrick Boland B000600 36\n",
"Thomas E. Petri P000265 36\n",
"James L. Oberstar O000006 36\n",
"George E. Brown B000918 36\n",
"Joseph Michael McDade M000399 36\n",
"Norman D. Dicks D000327 36\n",
"Philip M. Crane C000873 36\n",
"James Claude Wright W000763 36\n",
"... ...\n",
"John Richard Schmidhauser S000131 2\n",
"John Richard Walsh W000100 2\n",
"John Robert Foley F000237 2\n",
"John Robert Hansen H000173 2\n",
"Keith J. Rothfus R000598 2\n",
"Kathleen C. Hochul H001062 2\n",
"Kathleen A. Dahlkemper D000608 2\n",
"D. Bailey Merrill M000656 2\n",
"Katherine M. Clark C001101 2\n",
"K. William Stinson S000928 2\n",
"Joseph Walker Barr B000170 2\n",
"Joseph Scofield Ammerman A000177 2\n",
"Joseph Peyton Wyatt W000777 2\n",
"Joseph P. Kennedy K000379 2\n",
"Joseph Oliva Huot H001001 2\n",
"Joseph Jefferson Mansfield M000112 2\n",
"Joseph James Maraziti M000121 2\n",
"Joseph Francis Smith S000579 2\n",
"Joseph Edward Hendricks H000492 2\n",
"Joseph Anthony LeFante L000561 2\n",
"Daniel T. Kildee K000380 2\n",
"John Williams Gwynne G000543 2\n",
"John William Flannagan F000191 2\n",
"John W. Cox C000836 2\n",
"Darwin Gale Schisler S000128 2\n",
"John Travers Wood W000700 2\n",
"David A. Levy L000267 2\n",
"David Alan Curson C001089 2\n",
"John Schiller Wold W000671 2\n",
"Abe McGregor Goff G000253 2\n",
"\n",
"[2171 rows x 1 columns]"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\n",
"terms_served_by_representative= representative.groupby(\"complete_name\")['bioguide'].value_counts()\n",
"years= terms_served_by_representative * 2\n",
"total_years_served = years.sort_values(ascending=False)\n",
"\n",
"pd.DataFrame(total_years_served)\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 12)The most popular name in congress is...."
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"John 1448\n",
"William 935\n",
"James 855\n",
"Robert 753\n",
"Thomas 512\n",
"Charles 488\n",
"George 355\n",
"Richard 333\n",
"Joseph 314\n",
"Frank 308\n",
"Edward 266\n",
"David 251\n",
"Michael 239\n",
"Paul 219\n",
"Henry 192\n",
"Daniel 171\n",
"Donald 152\n",
"Harold 146\n",
"Peter 137\n",
"Albert 132\n",
"Walter 124\n",
"Howard 123\n",
"Carl 118\n",
"Mark 94\n",
"Jim 92\n",
"Ralph 91\n",
"Tom 90\n",
"Samuel 85\n",
"J. 85\n",
"Jack 81\n",
" ... \n",
"Angelo 1\n",
"D. 1\n",
"Harmar 1\n",
"Muriel 1\n",
"Sandy 1\n",
"Beto 1\n",
"Jocelyn 1\n",
"Orland 1\n",
"Heidi 1\n",
"Irwin 1\n",
"Abe 1\n",
"Betsy 1\n",
"Larkin 1\n",
"Clayton 1\n",
"Chip 1\n",
"Darwin 1\n",
"Lera 1\n",
"Thurman 1\n",
"Markwayne 1\n",
"Carter 1\n",
"Ward 1\n",
"Jed 1\n",
"Andrea 1\n",
"Nan 1\n",
"Billie 1\n",
"Garland 1\n",
"Cliffard 1\n",
"Harve 1\n",
"Filemon 1\n",
"Rolland 1\n",
"Name: firstname, dtype: int64"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df['firstname'].value_counts()\n",
"\n",
"#this might be counting the same person many times but still we can get an idea of what names are more popular"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Make three charts with your dataset"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1) Distribution of age"
]
},
{
"cell_type": "code",
"execution_count": 115,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x134b5d048>"
]
},
"execution_count": 115,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY8AAAEJCAYAAABsc6siAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X9M1Heex/HnwAAD69DgjgUsIwQxNYs2btdKu1arotlc\nT9OtFdYeW/dkdZuiMVxwm6vpVTfexvOKGmWxl1at22PjlrKXzS7NNrU9ldZGbLC2LPY25ZRh6DQI\nywl4OPya7/3R8F1RuvItX+TL+XokTfh+P/N9z/v7dfTVz/c73y8uwzAMRERELIia6AZERGTyUXiI\niIhlCg8REbFM4SEiIpYpPERExDKFh4iIWKbwEBERy9yjeVFZWRn19fX09vaSmJjI0qVLWb16NW1t\nbWzevBmPx4NhGLhcLh577DFWr15tbltRUcGJEycAWLZsGQUFBeZYW1sbBw8epLGxEZ/PR2FhIXPn\nzrV5F0VExG6jCo/HH3+cp59+mtjYWEKhENu3byczM5N77rkHgKNHj+JyuW7a7vjx49TV1VFaWgrA\nzp07SU5OZvny5QDs37+fe++9l23btnHu3Dn27t3LgQMH8Hq9du2fiIiMg1GdtkpLSyM2NtZcdrvd\nJCYmmstfdZN6TU0NK1euJCkpiaSkJFatWsXJkycBCIVCXLp0iby8PGJiYsjJyWHGjBnU1taOqvGG\nhoZRvW6iTYY+J0OPoD7tpj7tdaf1OeprHocOHeKpp56ipKSExx9/nMzMTHNs06ZNPPPMMxw8eJDu\n7m5zfTAYJD093VxOT08nGAwC0NLSQnJyMh6PZ8TxW7nT/qDG02ToEdSn3dSnve60PkcdHhs2bOC1\n117jn/7pn3j99ddpbGzE6/Wya9cuysvL2b17N+FwmAMHDpjbhMNhEhISzOWEhATC4fCIY0Pj165d\nG+s+iYjIOLP0bSuXy8W3vvUtHnzwQU6fPo3H4yEzM5OoqCgSExMpLCzkk08+MQPC4/EMC4Oenh5z\npnHj2NB4fHz8WPdJRETG2agumN9ocHCQuLi4rxwfugbi9/sJBALMnDkTgKamJvx+vznW2tpKOBw2\nAyUQCLBo0aIRazY0NAybbuXn53+d1m+7ydDnZOgR1Kfd1Ke9JlOflZWV5nJ2djbZ2dmW69wyPLq6\nuvjjH//I/fffT2xsLJ988glnzpzh+eefp7GxkYSEBFJTU7l69SpHjx5lzpw55uxh8eLFVFdXM2/e\nPACqq6t59NFHAUhNTSUjI4Oqqip+8IMfcO7cOZqbm8nJyRmxj5F2MBQKWd7h283r9Q67DuREk6FH\nUJ92U5/2mix9Tp8+3ZagG9XM4+233+aVV14BICUlhc2bN5OVlcXp06c5duwYXV1dxMfHc99997Fl\nyxZzuxUrVnD58mW2bt2Ky+UiNzfX/JouQHFxMeXl5axfv55p06ZRUlKir+mKiEwCrsn8y6A087DH\nZOgR1Kfd1Ke9Jkuf06dPt6WOHk8iIiKWKTxERMQyhYeIiFim8BAREcsUHiIiYpnCQ0RELFN4iIiI\nZQoPERGxTOEhIiKWKTxERMQyhYeIiFim8BAREcsUHiIiYpnCQ0RELFN4iIiIZQoPERGxTOEhIiKW\nKTxERMSyUf0Oc5GJFIl8zsBAiM7OaAYGBsdcz+2eTlTUPTZ0JnLnUniI4w0MhGhq+r5t9TIyfkts\nrMJDZCx02kpERCxTeIiIiGWjOm1VVlZGfX09vb29JCYmsnTpUlavXg1AfX09R44cob29nVmzZlFU\nVITP5zO3raio4MSJEwAsW7aMgoICc6ytrY2DBw/S2NiIz+ejsLCQuXPn2rl/IiIyDkY183j88cf5\nxS9+wS9/+Uuee+45/vCHP3D+/Hm6u7vZs2cPa9eu5dVXXyUzM5N9+/aZ2x0/fpy6ujpKS0spLS2l\nrq6Od955xxzfv38/mZmZHDlyhLVr17J37166u7vt30sREbHVqMIjLS2N2NhYc9ntdpOYmEhtbS1+\nv5+cnBzcbjd5eXkEAgFCoRAANTU1rFy5kqSkJJKSkli1ahUnT54EIBQKcenSJfLy8oiJiSEnJ4cZ\nM2ZQW1tr/16KiIitRv1tq0OHDnHq1CkGBgZYv349mZmZ1NTUkJ6ebr4mLi6OlJQUWlpamD59OsFg\ncNh4eno6wWAQgJaWFpKTk/F4PCOOi4iIc406PDZs2MCPf/xjLly4wN69e8nMzCQcDpOYmDjsdfHx\n8Vy7dg2AcDhMQkKCOZaQkEA4HB5xbGi8o6Pja++MyGhERcXQ1/ehbfV034jciSzd5+FyucjOzubB\nBx/k/fffx+PxmEExpKenh/j4eICbxnt6esyZxq22vVFDQwMNDQ3mcn5+Pl6v10r7EyI2NtbxfTq9\nx87OaFvrRSIdNDU9ZVu9rKzf4/XONpedfjyHqE97TZY+ASorK82fs7Ozyc7Otlzja90kODg4iNfr\nxefzcerUKXN9OBymtbUVv98PgN/vJxAIMHPmTACampqGjbW2thIOh81ACQQCLFq0aMT3HGkHJ8PF\nda/X6/g+nd6jHXeVX88wDFvrDQwMDjt+Tj+eQ9SnvSZTn/n5+WOuc8sL5l1dXXzwwQeEw2EikQjn\nz5/nzJkzPPDAAyxYsICWlhbOnj1Lf38/VVVVZGRkkJqaCsDixYuprq6mo6ODjo4OqqurWbJkCQCp\nqalkZGRQVVVFf38/tbW1NDc3k5OTM+adEhGR8TWqmcfbb7/NK6+8AkBKSgqbN282ZxMlJSUcPnyY\nsrIysrKyKC4uNrdbsWIFly9fZuvWrbhcLnJzc1m+fLk5XlxcTHl5OevXr2fatGmUlJRMmmmfiMid\nzGXYPYe/jYa+Euxkk2Eq6/Qe+/o+tPXZVunprxEIrLOt3pfPynrAXHb68RyiPu01WfqcPn26LXX0\neBIREbFMT9UVWw09Pt1evTbXE5GxUniIrex+fDp8eZpJRJxFp61ERMQyhYeIiFim8BAREcsUHiIi\nYpnCQ0RELFN4iIiIZQoPERGxTOEhIiKWKTxERMQyhYeIiFim8BAREcsUHiIiYpnCQ0RELFN4iIiI\nZQoPERGxTOEhIiKWKTxERMQyhYeIiFim8BAREctu+TvMBwYGOHToEPX19Vy9epWUlBSefPJJ5s2b\nR1tbG5s3b8bj8WAYBi6Xi8cee4zVq1eb21dUVHDixAkAli1bRkFBgTnW1tbGwYMHaWxsxOfzUVhY\nyNy5c8dhN0VExE63DI/BwUF8Ph8/+9nP8Pl8nDt3jn379rFnzx7zNUePHsXlct207fHjx6mrq6O0\ntBSAnTt3kpyczPLlywHYv38/9957L9u2bePcuXPs3buXAwcO4PV67do/EREZB7c8bRUXF8eaNWvw\n+XwA3H///dx9991cvHjRfI1hGCNuW1NTw8qVK0lKSiIpKYlVq1Zx8uRJAEKhEJcuXSIvL4+YmBhy\ncnKYMWMGtbW1NuyWiIiMp1vOPG505coVQqEQfr/fXLdp0yYA5s6dy1NPPWXOHILBIOnp6ebr0tPT\nCQaDALS0tJCcnIzH4xlxXEREnMvSBfPBwUHKyspYunQpqampeL1edu3aRXl5Obt37yYcDnPgwAHz\n9eFwmISEBHM5ISGBcDg84tjQ+LVr18ayPyIichuMeuZhGAZlZWXExMRQWFgIgMfjITMzE4DExEQK\nCwt5+umnCYfDeDwePB7PsDDo6ekxZxo3jg2Nx8fHj/j+DQ0NNDQ0mMv5+fmT4tpIbGys4/u0s8fO\nzmhb6lxvpOtpTqrndkcPO36T4c8c1KfdJkufAJWVlebP2dnZZGdnW64x6vB46aWX6O7u5rnnniMq\n6q9PWIaugfj9fgKBADNnzgSgqanJPN3l9/tpbW01gwYgEAiwaNGiEWuOtIPd3d2jbX/CeL1ex/dp\nZ48DA4O21LneV11Tc0q9gYHBYcdvMvyZg/q022TqMz8/f8x1RnXa6uWXXyYUCvHss8/idv8lbxob\nGwmFQhiGQXd3N0ePHmXOnDnm7GHx4sVUV1fT0dFBR0cH1dXVLFmyBIDU1FQyMjKoqqqiv7+f2tpa\nmpubycnJGfNOiYjI+LrlzKO9vZ13332XmJgYNm7cCHw57d+4cSMul4tjx47R1dVFfHw89913H1u2\nbDG3XbFiBZcvX2br1q24XC5yc3PNr+kCFBcXU15ezvr165k2bRolJSWTZtonInInu2V4+Hw+Xn/9\n9a8cX7hw4V/dvqCgYNiNgTfW3r59+61aEBERh9HjSURExDKFh4iIWKbwEBERyxQeIiJimcJDREQs\ns/xsKxEZLioqhr6+D83lzs7oMd8s6XZPJyrqnrG2JjJuFB4iYzQ4+GcCgXW21szI+C2xsQoPcS6d\nthIREcsUHiIiYpnCQ0RELFN4iIiIZQoPERGxTOEhIiKWKTxERMQyhYeIiFimmwTvcJHI53R2ttr4\n62N7baojIk6m8LjDDQyEaGr6vm310tNfs62WiDiXTluJiIhlCg8REbFM4SEiIpYpPERExDKFh4iI\nWHbLb1sNDAxw6NAh6uvruXr1KikpKTz55JPMmzcPgPr6eo4cOUJ7ezuzZs2iqKgIn89nbl9RUcGJ\nEycAWLZsGQUFBeZYW1sbBw8epLGxEZ/PR2FhIXPnzrV7H0VExGa3nHkMDg7i8/n42c9+xi9/+Ut+\n8IMfsG/fPtrb2+nu7mbPnj2sXbuWV199lczMTPbt22due/z4cerq6igtLaW0tJS6ujreeecdc3z/\n/v1kZmZy5MgR1q5dy969e+nu7h6fPRUREdvcMjzi4uJYs2aNOZu4//77ufvuu7l48SK1tbX4/X5y\ncnJwu93k5eURCAQIhUIA1NTUsHLlSpKSkkhKSmLVqlWcPHkSgFAoxKVLl8jLyyMmJoacnBxmzJhB\nbW3t+O2tiIjYwvI1jytXrvDFF1+QlpZGS0sL6enp5lhcXBwpKSm0tLQAEAwGh42np6cTDAYBaGlp\nITk5GY/HM+K4iIg4l6XwGBwcpKysjCVLljB9+nTC4TAJCQnDXhMfH8+1a9cAbhpPSEggHA6PODY0\nPrStiIg416gfT2IYBmVlZcTExFBYWAiAx+O56R/7np4e4uPjRxzv6ekxZxq32vZGDQ0NNDQ0mMv5\n+fl4vd7Rtj9hYmNjHd1nZ2e0rfVcLpet9cajptPrAbjd0eP+uXH6Z3OI+rRfZWWl+XN2djbZ2dmW\na4w6PF566SW6u7t57rnniIr6csKSlpbGqVOnzNeEw2FaW1vx+/0A+P1+AoEAM2fOBKCpqWnYWGtr\nK+Fw2AyUQCDAokWLRnz/kXZwMlxc93q9ju7TvgcifskwDFvrjUdNp9eDL/9cxvtz4/TP5hD1aS+v\n10t+fv6Y64zqtNXLL79MKBTi2Wefxe3+S94sWLCAlpYWzp49S39/P1VVVWRkZJCamgrA4sWLqa6u\npqOjg46ODqqrq1myZAkAqampZGRkUFVVRX9/P7W1tTQ3N5OTkzPmnRIRkfF1y5lHe3s77777LjEx\nMWzcuBH4cpq+ceNGHn74YUpKSjh8+DBlZWVkZWVRXFxsbrtixQouX77M1q1bcblc5Obmsnz5cnO8\nuLiY8vJy1q9fz7Rp0ygpKZk00z4RkTvZLcPD5/Px+uuvf+X4nDlzht3bcaOCgoJhNwbeWHv79u2j\naFNERJxEjycRERHLFB4iImKZwkNERCxTeIiIiGUKDxERsUzhISIilik8RETEMoWHiIhYpvAQERHL\nFB4iImKZwkNERCxTeIiIiGUKDxERsUzhISIilik8RETEMoWHiIhYpvAQERHLFB4iImKZwkNERCxT\neIiIiGXuiW5ARG4WFRVDX9+HttVzu6cTFXWPbfVEFB4iDjQ4+GcCgXW21cvI+C2xsQoPsc+owuOt\nt97i1KlTNDc3s3DhQoqKigBoa2tj8+bNeDweDMPA5XLx2GOPsXr1anPbiooKTpw4AcCyZcsoKCgw\nx9ra2jh48CCNjY34fD4KCwuZO3eunfsnIiLjYFThMXXqVJ544gnOnz9PX1/fTeNHjx7F5XLdtP74\n8ePU1dVRWloKwM6dO0lOTmb58uUA7N+/n3vvvZdt27Zx7tw59u7dy4EDB/B6vWPZJxERGWejumC+\nYMEC5s+fz5QpU0YcNwxjxPU1NTWsXLmSpKQkkpKSWLVqFSdPngQgFApx6dIl8vLyiImJIScnhxkz\nZlBbW/v19kRERG4bW655bNq0CYC5c+fy1FNPmTOHYDBIenq6+br09HSCwSAALS0tJCcn4/F4RhwX\nERHnGtNXdb1eL7t27aK8vJzdu3cTDoc5cOCAOR4Oh0lISDCXExISCIfDI44NjV+7dm0sLYmIyG0w\nppmHx+MhMzMTgMTERAoLC3n66acJh8N4PB48Hs+wMOjp6TFnGjeODY3Hx8eP+F4NDQ00NDSYy/n5\n+ZPi2khsbKyj++zsjLa13kjXvpxW0+n1xqOm2x190+fQ6Z/NIerTfpWVlebP2dnZZGdnW64xLl/V\nHboG4vf7CQQCzJw5E4Cmpib8fr851traagYNQCAQYNGiRSPWHGkHu7u7x6N9W3m9Xkf3OTAwaGu9\nr7r+5aSaTq83HjUHBgZv+hw6/bM5RH3ay+v1kp+fP+Y6ozptFYlE6OvrIxKJEIlE6O/vJxKJ0NjY\nSCgUwjAMuru7OXr0KHPmzDFnD4sXL6a6upqOjg46Ojqorq5myZIlAKSmppKRkUFVVRX9/f3U1tbS\n3NxMTk7OmHdKRETG16hmHr/5zW+oqqoyl9977z3y8vJITU3l2LFjdHV1ER8fz3333ceWLVvM161Y\nsYLLly+zdetWXC4Xubm55td0AYqLiykvL2f9+vVMmzaNkpKSSTPtExG5k40qPPLy8sjLyxtxbOHC\nhX9124KCgmE3Bl7P5/Oxffv20bQgIiIOogcjioiIZQoPERGxTOEhIiKWKTxERMQyhYeIiFim8BAR\nEcv0y6AmkUjkcwYGQjZX7bW5nojcCRQek8jAQIimpu/bWjM9/TVb64nInUGnrURExDKFh4iIWKbw\nEBERyxQeIiJimcJDREQsU3iIiIhlCg8REbFM4SEiIpYpPERExDKFh4iIWKbwEBERyxQeIiJimcJD\nREQsU3iIiIhlo3ok+1tvvcWpU6dobm5m4cKFFBUVmWP19fUcOXKE9vZ2Zs2aRVFRET6fzxyvqKjg\nxIkTACxbtoyCggJzrK2tjYMHD9LY2IjP56OwsJC5c+fatW8iIjJORjXzmDp1Kk888QRLly4dtr67\nu5s9e/awdu1aXn31VTIzM9m3b585fvz4cerq6igtLaW0tJS6ujreeecdc3z//v1kZmZy5MgR1q5d\ny969e+nu7rZp10REZLyMKjwWLFjA/PnzmTJlyrD1tbW1+P1+cnJycLvd5OXlEQgECIW+/G13NTU1\nrFy5kqSkJJKSkli1ahUnT54EIBQKcenSJfLy8oiJiSEnJ4cZM2ZQW1tr7x6KiIjtxnTNo6WlhfT0\ndHM5Li6OlJQUWlpaAAgGg8PG09PTCQaD5rbJycl4PJ4Rx0VExLnGFB7hcJiEhIRh6+Lj47l27dqI\n4wkJCYTD4a/cNiEhwdxWRESca0y/w9zj8dz0j31PTw/x8fEjjvf09JgzjVtte6OGhgYaGhrM5fz8\nfLxe71javy1iY2Nt67OzM9qWOtdzuVyOrjceNZ1ebzxqut3RN30O7fxsjif1ab/Kykrz5+zsbLKz\nsy3XGFN4pKWlcerUKXM5HA7T2tqK3+8HwO/3EwgEmDlzJgBNTU3DxlpbWwmHw2agBAIBFi1aNOJ7\njbSDk+Hiutfrta3PgYFBW+pczzAMR9cbj5pOrzceNQcGBm/6HNr52RxP6tNeXq+X/Pz8MdcZ1Wmr\nSCRCX18fkUiESCRCf38/kUiEBQsW0NLSwtmzZ+nv76eqqoqMjAxSU1MBWLx4MdXV1XR0dNDR0UF1\ndTVLliwBIDU1lYyMDKqqqujv76e2tpbm5mZycnLGvFMiIjK+RjXz+M1vfkNVVZW5/N5775GXl8ea\nNWsoKSnh8OHDlJWVkZWVRXFxsfm6FStWcPnyZbZu3YrL5SI3N5fly5eb48XFxZSXl7N+/XqmTZtG\nSUnJpJn2iYjcyUYVHnl5eeTl5Y04NmfOnGH3dtyooKBg2I2B1/P5fGzfvn00LYiIiIPo8SQiImKZ\nwkNERCxTeIiIiGVj+qquiEwOUVEx9PV9OGxdZ2f0mL7+7XZPJyrqnrG2JpOUwkPkDjA4+GcCgXW2\n1szI+C2xsQqPO5VOW4mIiGUKDxERsUzhISIilik8RETEMoWHiIhYpvAQERHLFB4iImKZwkNERCxT\neIiIiGUKDxERsUzhISIilik8RETEMoWHiIhYpvAQERHLFB4iImKZwkNERCxTeIiIiGW2/CbBHTt2\n8Nlnn+F2uzEMg29+85vs27cPgPr6eo4cOUJ7ezuzZs2iqKgIn89nbltRUcGJEycAWLZsGQUFBXa0\nJCIi48iW8HC5XGzYsIGlS5cOW9/d3c2ePXt45pln+M53vsOvf/1r9u3bx89//nMAjh8/Tl1dHaWl\npQDs3LmT5ORkli9fbkdbIiIyTmw7bWUYxk3ramtr8fv95OTk4Ha7ycvLIxAIEAqFAKipqWHlypUk\nJSWRlJTEqlWrOHnypF0tiYjIOLEtPI4dO8aGDRt44YUXuHDhAgAtLS2kp6ebr4mLiyMlJYWWlhYA\ngsHgsPH09HSCwaBdLYmIyDix5bRVQUEBaWlpuN1uTp8+ze7du3nxxRcJh8MkJiYOe218fDzXrl0D\nIBwOk5CQYI4lJCQQDoftaElERMaRLeGRlZVl/vzII4/wwQcfcO7cOTwejxkUQ3p6eoiPjwe4abyn\npwePxzPiezQ0NNDQ0GAu5+fn4/V67Wh/XMXGxtrWZ2dntC11rudyuRxdbzxqOr3eeNQcjx7d7ujb\n8nfQzr9D42my9AlQWVlp/pydnU12drblGraEx1dJS0vj1KlT5nI4HKa1tRW/3w+A3+8nEAgwc+ZM\nAJqamsyxG420g93d3ePUuT0ikc+BVgYGBm2q2GtTnb8Y6VqVk+qNR02n1xuPmuPR48DA4G35O+j1\neh3/dx0mV5/5+fljrjPm8Ojp6eGzzz7jW9/6FtHR0Zw+fZpPP/2U9evXk5CQwK9+9SvOnj3Lt7/9\nbaqqqsjIyCA1NRWAxYsXU11dzbx58wCorq7m0UcfHWtLjjEwEKKp6fu21UtPf822WiIiYzHm8BgY\nGODXv/41oVCIqKgo7rnnHp599llSUlIAKCkp4fDhw5SVlZGVlUVxcbG57YoVK7h8+TJbt27F5XKR\nm5urr+mKiEwCYw6PxMREdu3a9ZXjc+bMMW8YHElBQYFuDBQRmWT0eBIREbFsXC+Yi8j/X1FRMfT1\nfWhbPbd7OlFR99hWT8aXwkNEvpbBwT8TCKyzrV5Gxm+JjVV4TBY6bSUiIpYpPERExDKFh4iIWKbw\nEBERyxQeIiJimcJDREQsU3iIiIhlCg8REbFM4SEiIpYpPERExDKFh4iIWKbwEBERyxQeIiJimZ6q\nKyKO8FWPeO/sjGZgYNByPT3ifXwpPETEEfSI98lFp61ERMQyhYeIiFim8BAREcsm/JrH1atXeeml\nl/jkk09ITEzkySef5OGHH57otkRE5K+Y8PA4dOgQMTExHD58mIsXL/Iv//IvZGRkkJaWdlv7MIwQ\n167d/E2Pr8vt9uFyxdhWT0TESSY0PHp7ezl79ix79+4lNjaW2bNnM3/+fGpqavi7v/u729pLJNJN\nS0uRbfUSEnJITv5H2+qJiDjJhIbHF198QXR0NCkpKea6jIwMLly4MIFdicj/B19138hY6N6Rv5jQ\n8AiHwyQkJAxbFx8fz7Vr1yaoIxH5/8Lu+0ZA945cb0LDw+Px0NPTM2xdT08P8fHxt72XqKgppKbu\ntK1eTEyqbbVExBn+2mzm69wJP5lnMi7DMIyJevPe3l4KCwvZs2ePeerqF7/4BVOnTr3pmkdDQwMN\nDQ3mcn5+/m3tVUTk/4vKykrz5+zsbLKzsy3XmND7POLi4liwYAGVlZX09vbyX//1X9TV1bF48eKb\nXpudnU1+fr753/U772SToc/J0COoT7upT3tNpj6v/7f06wQHOOAmwR//+Mf09vayYcMGysrK2Lhx\n423/mq6IiFgz4fd5TJkyhZ/+9KcT3YaIiFgQvWPHjh0T3cTXdffdd090C6MyGfqcDD2C+rSb+rTX\nndTnhF4wFxGRyWnCr3mIiMjko/AQERHLFB4iImLZhH/b6q8ZGBjg0KFD1NfXc/XqVVJSUnjyySeZ\nN28eAPX19Rw5coT29nZmzZpFUVERPp9vQnotKyujvr6e3t5eEhMTWbp0KatXr3Zcn/DlM8W2bt3K\nQw89xObNmx3Z444dO/jss89wu90YhsE3v/lN9u3b57heT58+TVVVFe3t7SQlJVFUVMTs2bMd0+O6\ndetwuVwAGIZBX18f3/ve91i/fj3grGPZ0dHBK6+8wp/+9CdiYmLIycnh7//+74mKinJUn59//rn5\nFPC77rqLgoICFixYAEzc8Xzrrbc4deoUzc3NLFy4kKKivzzk9VY9VVRUcOLECQCWLVtGQUHB6N7U\ncLBwOGy88cYbRltbm2EYhlFXV2esW7fOaGtrM7q6uowf/ehHxpkzZ4z+/n7j3//9341t27ZNWK/B\nYNDo7e01DMMwPv/8c2PDhg3GRx995Lg+DcMw/vmf/9l44YUXjLKyMsMwDKOzs9NxPe7YscP4z//8\nz5vWO+l4fvzxx0ZRUZHx2WefGYZhGB0dHUZHR4ejerzetWvXjHXr1hmffvqpYRjOOpaGYRgvvvii\nUV5ebvT39xtXrlwxSkpKjD/84Q+O6nNwcNDYsmWL8eabbxqRSMSor683fvjDHxpffPHFhPZZW1tr\nfPjhh8Yrr7xilJeXm+tv1dPbb79tFBcXm5/df/iHfzCOHz8+qvd09GmruLg41qxZY6bk/fffz913\n383Fixepra3F7/eTk5OD2+0mLy+PQCBAKBSakF7T0tKIjY01l91uN4mJiY7r8/Tp03zjG99g7ty5\n5rqzZ8+o4zQEAAAFtUlEQVQ6qschxghfBHTS8XzjjTdYs2YNWVlZACQlJZGUlOSoHq935swZEhMT\nmT17NuCsYwkQDAb57ne/i9vt5q677mLevHkEg0FH9fn5559z5coVHn30UVwuF3PmzGH27NnU1NRM\naJ8LFixg/vz5TJkyZdj6W/VUU1PDypUrzc/uqlWrOHny5Kje09HhcaMrV67wxRdfkJaWRktLC+np\n6eZYXFwcKSkptLS0TFh/hw4d4qmnnqKkpITHH3+czMxMR/XZ09NDZWUl69atG/YPs5N6vN6xY8fY\nsGEDL7zwgvmYfqf0GolE+O///m86OzvZsmULzzzzDEeOHKGvr88xPd6opqaGRx55xFx2Wp/z5s3j\n/fffp6+vj46ODj766CPmzZvnuD5vZBgGzc3NjuzzVj0Fg8Fh4+np6QSDwVHVnjThMTg4SFlZGUuW\nLGH69OmOfJz7hg0beO2113j++ed5/fXXaWxsdFSflZWV5ObmMnXq1GHrndTjkIKCAsrKyvi3f/s3\ncnNz2b17N5cvX3ZMr52dnQwODlJbW8vOnTt58cUXuXTpEv/xH//hmB6v19bWxqeffjosPJzWZ15e\nHsFgkB/96Ec888wzzJw5kwceeMBRfU6fPp3ExER+97vfMTg4yMcff8yFCxfo6+tzVJ9DbtXTjeMJ\nCQmEw+FR1Z4U4WEYBmVlZcTExFBYWAh8+Tj3G/9QJupx7tdzuVxkZ2fz4IMP8v777zumz6amJurr\n6/nbv/3bm8ac0uP1srKy8Hg8uN1uHnnkEWbPns25c+cc0+vQKcq/+Zu/4a677mLKlCmsXLmSjz76\nyDE9Xq+mpobZs2czbdo0c53T+vz5z3/OQw89REVFBYcPH+bq1atUVFQ4qs/o6Gh++tOfcu7cOX7y\nk5/w5ptv8t3vfpepU6c6qs8ht+rpxvGenh48Hs+oak+K8HjppZfo7u5m69atREV92XJaWhpNTU3m\na8LhMK2trY55qOLg4CAej8cxfV64cIG2tjaKior4yU9+wu9//3tqa2v5x3/8R/x+vyN6HA2nHM9v\nfOMbN83ghr7V5MTjeeMpK3DOsQTo6uri4sWLfO973yM6OpopU6awdOlSzp8/77jjOWPGDHbs2MHh\nw4fZtm0bra2tZGVlOep4Dvmqnvx+P/DlZzUQCJjjTU1N5titOD48Xn75ZUKhEM8++yxu91++Wbxg\nwQJaWlo4e/Ys/f39VFVVkZGRwfTp0297j11dXXzwwQeEw2EikQjnz5/nzJkzPPDAA47pc/ny5ZSV\nlfGv//qvvPjii6xYsYJvf/vbPP/88zzwwAOO6HFIT08PH3/8Mf39/UQiEd577z0+/fRT5s2b55jj\nCbB06VLeeusturq6uHr1Km+++Sbf+c53HHc8//SnP/E///M/PPjgg8PWO+lYJiYmkpSUxPHjx4lE\nIvzv//4vp06dIj093XHHs7m5mf7+fnp7e/nd737HlStXWLJkyYQez0gkQl9fH5FIhEgkYv7d+aqe\nUlO//GV1ixcvprq6mo6ODjo6OqiurmbJkiWjek9HP9uqvb2dTZs2ERMTY844XC4XGzdu5OGHH+aP\nf/wjhw8fpr29naysLDZt2jQh3/3u6upi7969ZoKnpKTwxBNPMH/+fADH9Hm9N954g9bWVvM+Dyf1\n2NXVxa5duwiFQkRFRXHPPfewdu1a5syZ46heBwcHefXVVzl9+jSxsbE89NBD/PCHP8TtdjumR/jy\nf8D6+/vZtGnTTWNO6rOxsZHXXnuNYDBIdHQ0c+bMobCwkMTEREf1WVFRwbvvvkskEmH27NkUFhaS\nnJwMTNzxfOONN6iqqhq2Li8vjzVr1tyyp1/96le8++67uFwucnNzb/pFfF/F0eEhIiLO5PjTViIi\n4jwKDxERsUzhISIilik8RETEMoWHiIhYpvAQERHLFB4iImKZwkNERCxTeIiIiGX/B60YTyXGZiY0\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x110082748>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.style.use(\"ggplot\")\n",
"df['age'].hist(bins=15, xlabelsize=12, ylabelsize=12, color=['y'])"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x10fcb2b70>"
]
},
"execution_count": 104,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAD7CAYAAACCPlZYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXm4nePZvs8rQc1DUZSIKlpTRAiKSlLl19Yc89SYVfsV\npVQ/fKE64fsMRWlpg2oVNasYWokpSARJjDWEUENaDYkQIrl+fzzPyn6zstbaa+3sed/ncbzHfodn\nuN9nhft9puuWbYIgCIIg6J706mgDgiAIgiBoO8LRB0EQBEE3Jhx9EARBEHRjwtEHQRAEQTcmHH0Q\nBEEQdGPC0QdBEARBN2aRjjYg6LlIir2dQRAEDWJbjaRvlx69pBntUMcISUNbwxZJx0p6VtIfJC0m\n6W+SnpC0d+tY2zIkjZb0atm9W1q7ffM731t6Z0m/lfTlZvKMkjSgwv1hki6qls92pzqGDx/e4TaE\nTd3Hps5qV9jUdW1qEe1k2PR2qGMEMLQ1bAGeAz6fz7cC7mnQlt5t9I6jgKeArfP1csCjrd2+LXzn\nUcCACveHAb+qksdxxBFHHD3t6NNnFbcUwI3+P71dh+4lnQt8A5gL/Mz29ZJWBa4DliFNJRxj+2FJ\nOwBnAosBLwOH2v5Q0mTgeuCbwIfAAbZfyVUMknQisApwsu2bmrHnh8A+uY6bbZ8p6VJgbWCkpD8C\nRwIrS3oC2BNYATgPWAr4N3CI7XckjSI54W2AayW9DgwHPgXetz1Y0meAS4HNgdnAibZHSxoG7Aos\nmeu+xfaPqpj9Z2B/YAwwFLgJ2CC/z1LArcDywKLA6bZvk9QXGAk8BGwNvAHsZvtjSccCR2d7ngWO\nA/4ArJTfeS/gd9nWJ6r9LmXteihwCjANmAjMqvYbjBpV7UnHcOWVcMghHW3F/IRN9dEZbYLOaVfY\nVB9tZdOQIe+0fqE1aK/FeMrD6v1sbwzsAJwraRXgAOAu2wOATYCnJK0InAZsb3tzYDxwQqG8abb7\nAZcAFxbur2p7G2AX4OxmDNoBWNf2FsCmwOaStrV9DPBPYLDtc4AjgAeyfa8DFwF72h5IGkX4eaHY\nRW1vYft84H+AHW1vSnLiAN8D5mbbDwCukrRYfrYJsDfQD9hX0uoVzDZwH/BVSb2A/UiOv8QsYPfc\nZl8D/q/wbB3gItsbAe+TPloAfgT0t90f+I7tf+V3ftD2gMJHFHX8LuQPtzOArwDbkj9Cugr9+3e0\nBQsSNtVHZ7QJOqddYVN9dEabWkJ79ui3Aa4FsD1V0mhgIDAO+L2kRYFbbU+QNJjkIB6WJFLvdEyh\nrJJzu5bUuy5xSy7/OUmfa8aeHYEdcq9VpB76uqRer/JRzpeAjYB7s129gDcLz68rnD9EcuTXk3rd\nkBzfr7KNL+T59vXys7/b/gBA0rNAX9IHRxGRRggeIjn5xW1PybaUnv9C0nakUZPPF9phsu1J+Xw8\nsFY+nwD8SdIt5ParwVbU/l0AtgRG2f5PfpfrSO1akSuvbDrv37/j/8Pq6PorETbVR2e0CTqnXWFT\nfXQGm0aPHs3o0aMXqoyOXHUvANsPSvoqsBMwQtJ5wHukOeIDq+R1lfOPy8tvpv5f2L68QZufzqMG\nlZg5zyj7u5IGAjsD4yVtVqW8EkXb51D7t7kOuJk0agBNbXAgsBKwqe25eZpj8Srll+7vBGxHGnU4\nVdJGNeoVtX+XYrq66GxDdUEQBJ2JwYMHM3jw4HnXZ555ZsNltOc++geB/ST1krQy8FVgrKQ1gam2\nf0eaCx5AWmC2jaQvAkhaUlKxV7hv/rsf8EiV+ppzNncDh+V5bSR9XtJKzeR5gTRfv1XOs4ikikPT\nkta2Pc72cGAqsAapDQ7Kz9cD+uQyG8L2g6Qpg9LIRuldlyO15VxJQ0ijApSlKWdN2/eT5tSXBZau\nUXVzvwvAY8B2klbIozQdulMhCIKgp9PmPXpJvYFZtm+RtDVpqHgucFIewv82cJKk2cAM4Nu2/y3p\nENKits+QeqynAS/mYleQNIE0J71fvlfs2Ve6LtnyMYDte/OWsUfyyPcMkhP+d6W8Oc9sSXsBF0la\nDugNXEBaxFae59yCE/y77YmSXgAulTSRtPhtWC5zgaoq1V+8b/u8Cvf/CNye2+Zx0u6BqmVKWgS4\nRtKypA+BC21Pr2ZPM79LKc3bks4gfRRMIy1QrMqQIbWeBkEQdD/69FmlXetTWq3fhhVImwC/sb1V\nK5U3GdisNAfckbYEC4ckt/W/vyAIgu6EJNyZBHMkHU3qZZ7aisW2yDO0kS1BEARB0Klp8x59EFQj\nevRBEASN0el69O2FpDlZrnWipBtLC+xqpB8k6faFrHNY3jNe6VldcrwN1jdK0vOSnlKS5/1VXifQ\nqqiGZK2kH7d2fUEQBEHb0i0cPTAzi7v0Iy2qO7qOPC3uSmaxmkOASqI2bcn+WdimH/AJSQWvLajW\nNv/dRvUFQRAEbUR3cfRFHgG+WLqQdK6kSZImSNqnkG45SXfkXvKvC+l3kDRG0uOSrpO0ZL4/WdIv\nJT1OkqDdnLRi/Ym8Ar1ZJP1Q0tjcKx9euH+gpMdyWZcWBHAWKALA9qfAyUAfSRvnMk7I7zlR0nH5\nXl9Jk+Zllk6U9D/5fGBukycknVNMB6wuaaSkFyT9Mqf/BbBETv+HZup8VikQztOS7qrVPpLiiCOO\nOLrFseaaFQd5O5zuEqZWMG/73A4kmVhUkN1VUogbJ+n+nGcgsD4wBbg7p72fJonXjySdTJJ4/WnO\n8+8s/Yqkw0n670/WZWBBcleSgNskbUvazrcvKVDNHEmXkIRvrqlVXt4rPxH4stJ+9WH5nXoDjykp\nD75H9d7574HDbY9VcuLFdJsA/UlbAF+QdJHtH0v6XpYCRilSXbU61wH2tX2UkjLensCfKhnR2bTu\ngyAIWkp7a9jXS3dx9EsoSdmuAUwGLsv3t6Wy7O4MYKzt1wAkXZvTfkxtideixG01mdxqVJPc3QTY\njPQRIpJiXb3/Wkr1b0sKyjMrv89NJEGiiusQlOb2l7Y9Nt/6E0khr0Q1Od7i+9aqs5rc7gJ0Ngnc\nIAiCzkRXl8BtTT60PUDS4iTFu12prNteyzGb5iVeZ1a5Xw8VJXcl/Rdwpe2Gtv3l0YuNSaI4q1VJ\n9impt11i8cJ5rbZoRI63nvyLV0sYErhBEATV6WoSuG1Jae56FinMaimi3IOkSHDzye7mZ1sozSf3\nIg2dP0R9Eq8lppMkY2vaVKCS5O7KwN+BvfI5StKxa9YqU0nR7hfAFNtP5/fcXdLiufw9gAdIIwMr\n5zI/Q9Ldx/b7wHQlLX5oUhdsjk/yBwZV6nywyrsHQRAEHUR36dEXpWGfkvSipH1tXyfpKywou7s+\nyeFfTJpPvs/2zQBqRuK1wFXAZZI+BL5i++Oy55dJOp/k9KbY3ibXO5/kbo60dxpwT/7o+IQUznZK\nhfe8RtLHwGeAvwG75Xd+UtKVpEiABn5re2J+n5/k+28wvyTuEcAVkuaQ1ia831zbAr8FJkkab/tg\nSVeV1TlBUt8KbVWVkMANgqC70N7StvUSgjk9FElL2Z6Zz38ErGr7B+1sQwjmBEEQNIDUuGBOd+nR\nB42zk5IAziLAqyRdgCAIgqCbET36oMOIHn0QBEFjtKRH3yUW40naXdJcpRju1dI0KzurJCM7oBXS\nzCdE0xpUq1fSZpIuWIhyt5T0qKQnJT2jLJhTI31VCdwaeX5cOG/1tgmCIAhaTpdw9KRV4XeQFOk6\nC+3SFbU93vbxC1HEVcARtjcFNgKur6faBusol8aNbnoQBEEnodM7+rx1a0vSSvT9yp5dLOk5SfcA\nnyvc315JqnWCpCuyclx5uTMknack03qvpBULj/dRkqR9XtI2zdj3GUm/V5KBHS9pcL7fV9IDSlK6\nj0vaqpDnRzn9k5J+XihugXpVCMAjabikK3O5kyUNVZL4nSjpzsLWtyIrkwV4nHg+lzVQSep3vKSH\nyrYRrplHGF4ojgBIulnSOCXZ2yPyvQWkcYFFFBK4ccQRRzc6Oqu8bT10hcV4uwF3235d0lRJm+bt\nZHuQJGXXl7Qa8CzwOyWnMgIYYvtlpS1gxwC/Kit3KZI63gmSTgeGA8fmZ71tbynpm8AZJFndanwP\nmGu7n6QvkbbJrUtyrl+3/YmkdUgKfQNzmbsAA21/LGn5QlnV6i32kNcGBpN6548Cu9s+SUmZbifg\ntjL7LiDJ2I4i7eW/Km8FfA7YNkvpbk/al79XzjMQ2BCYRVLsu8P2E8Chtt9TEiYaJ+nGCtK4fUmK\nfyGBGwRBt6GzytvWQ6fv0ZOG60vDzTfQNHy/HU3ytm+RhGcAvgS8YvvlfH1VTlvOnEK515AkXUvc\nlP+OJ8m/1mLbnB/bL5BWsK8HLEbapz4x271+Tr89MKK07972ew3WO9L2XGASaTHlPfn+JCpIzdo+\niySxew+p7e7Kj5YH/qI0n34+Sfq3xL2238sCRDfR1DbHS3qK9IGxBsmhV+KVeiVwgyAIgralU/fo\nJa0AfA3YSJJJcq4mRW5bIHmV86rFl10Xe80l8ZuWyL+Wyv0B8Hbu6fcGPqojbz31lj4QLGl24f7c\nanlsTwZ+I+kK4F+5Xc8iCQUNzb3wYt+6fI7dkgaRfost80jEKJqkbcvbsm4J3NC6D4IgqE5P0Lrf\nG7ja9jGlG0pzx18lSbweLelqYBVgCPBH4AWgr6S1bb8CHAyMrlB2L9JQ9fWkaHEPVbGhuY+GB3P+\n0Uq7AvpkG5YDXs9pvk2T5vy9wOmS/pQj5K1ge1oL6q0rjaRv2b4zX65H0r9/L9v3z3z/0LJsO+Qp\nhY+B3fPzNYBp2cl/GdiqkP4TSb1tz2nAdiC07oMgCGrRGlr3nd3R7wucXXbvJmA/29+T9DXgGZJc\n7BiA7IgOJQ1L9yZJtP4m5y32VGeS9O5PJ82n71shTaVrSO1W6rX+Grg0D9HPBobZnq0U4/5GSd8m\nDZfPzPbdLWkT4HElOds7STK79dRbTj1pDpZ0HvAhyckfkEcDzgGuUpLf/WtZnrGkdl4d+IPtJyQ9\nDXxH0jOkD5lHCunnSeNWeZeqhARuEARdgc4qb1sPPVYwR9IM28u0MO9uwP626w0GE1RAIZgTBEHQ\nEFJI4DZCizyMpDNJYXAPaVVrgiAIgqAN6LE9+qDjiR59EARBY7SkR98VttdVRdIqkq5VCks7TtId\nktZRQWRmIcoeLumEVrLzeEkfSaprqkDSjNaot5k6hmVdgieUhHueyIvsqqVfTtIx1Z4HQRAEnZMu\n7eiBm0lbxNa1PRD4MWkFPiyEDKsqK8wtDPuRVtvX1OIv0KztrWTjn20PsL1p/vt8jbQrAN9thTqD\nIAiCdqTLOnpJQ4BPbF9eumd7ku2H8+Uykm5Qksj9QyHf6UoysxMlXVa4P0rS+ZLG0qSQV3q2tqSR\nedTg/ryNDkl7K8nBPilpdBU71wYWBX4GHFC4P1/wGEm3S9qu6XJBed6CjeOAYyWtJOkv+X0ek/QV\nJf5RyKM84lGU+J1XbQV7l5L0NyXZ3gmSdsmPfgGsnXv+Z+e05+b3nyBpn3xvULZzgbav0j5xxBFH\nHJ3i6Moyt7XoyovxNiKprlWjP0nt7W3gYUlb2x4DXJTV4pB0taSdbJe2ly1qe4v8bHihrN8CR2dJ\n3S2AS0kKd6cDO9p+S9KyVezYD7je9mOSvihpZdv/ys+q9dxryfMumkcvkPRH4DzbYyT1IUkFb6Dk\nXA8CLgS+Djxl+90K9eyrpKmvbMtXSLK3u9v+QOnj4FHgduAUYMOC1O1QoJ/tjSV9jiSJe38zbb8A\nIYEbBEFnoSvL3Naiy/bo62Cs7bfyaq+naJJh3V4pbOtEksjOhoU815UXohRUZ2vgBklPkvbkl6YH\nHibtRT+C6h9N+5MkcAFuIYkANcdcqsvzFm38OnBxtus2YGlJS5K0/g/OaQ7L15UoH7r/mOT0fyFp\nAvA34PPZkZezLU0SxFNJokQD87NqbR8EQRC0M125R/8MTUFYKlEuw7qIUsCbS4ABtt/MvfaiPOvM\nCuX0IinCLRAr3vYxkgYCOwPjJQ0oqtxJ2oikB/83SZD07yeTRHY+Zf4PraoysSwo9DOvCpIk7eyy\n9B9KekdpemMghSmDOjgQWAnYNAe8mdyMbUVbSizQ9tUyhQRuEARBdXqCBG5VbN8n6WeSjrB9BYCk\njUnSrtVYnOQ035W0NOlD4YYa6bE9Qykk7F62/5Lr6Wd7opLM7jjSsPU3SPK3RTnb/YHhtuep+0l6\nOQ+zvwoco/QFsAawRSFfvfK89wDHAf+by97E9oT87Hek0YCrauxhq7RFYzlganbyQ2gKrjMDKO4a\neBA4SkmCeEXgq8APaQreUxchgRsEQVCdniCB2xx7ABdKOoUUNOZV4HiS4yxiANvvKwV2eQZ4iyT1\nOl+aKhxEkrk9jdRmfwYmAueqKY7732xPLMu3L/Ctsns3kyR8z5X0arblOeZfb/AB9cnzHgdckofZ\ne5P0/0sr428Dfg9cWeO99imbo/8uKV7A7bnMx7Nt2P6PpIfzlMdI2z+S9BVgAmmq4STbUyWVO/qa\nOwhCAjcIgs5CV5a5rUUI5nRTJG0O/J/tQR1tSzUUgjlBEAQNIYUEbgBI+hHwHRqbmw+CIAi6IdGj\nDzqM6NEHQRA0Rkt69N15e10QBEEQ9HjC0QdBEARBNybm6INmkdQXGEna5rc18AawG0mU5yiSxO9L\nwMG2Z0kaAUwHNieJC51s+6YqZbf9CwRBENSgT59VmDLl7Y42o82IOfqgWbKjfxHYzPYkSdcBt5K2\n2U3Lac4C3rZ9SXb0S9reN2+3u832uhXKdUjgBkHQ0QwZAl3FF8aq+6AtmWx7Uj4fT5K13VjST4Hl\nSfr8dxfS3wJg+7kqErpBEARBOxCOPqiXclnbJUhiPLvaflrSMGBQlfRVvz5DAjcIgqA6PVoCN2h3\nKjnrpYG3JS1Kkup9o4G8QEjgBkEQ1CIkcIP2pHwCy6QwvWOBqcBjNGnhV0obBEEQdACxGC/oMCTF\nP74gCDqcrrTqPhbjBV2O+NAMgiBoW0IwJwiCIAi6MeHogyAIgqAb0yMdvaQZncCG/pLmStqxgTwn\nSHpO0gRJT0r6X0m9m8kzStKAfD5Z0mdbaO8ISUNbkjcIgiDoOHrqHH1nmBjeD7gD2B+4p7nEkr4D\nfB3YwvYMSYsAJ5D2s39QZ50d9t6qEqouJHCDIOhIutJCvJbSUx09kpYEbiOpui0KnG77tiz3ehfw\nKEnX/XGSMMwZwErAgbYfz/kvAjbM+c+wfbukDYAR+V4vYE/bL1cwYU9gO+AxSYvZ/qQZk/8b2Nb2\nDADbnwLnFN7n1yRt+SWAv9iutNlShfQ3A2sAiwMX2r4i3z8cOBmYBkwEZtk+NmcbJOlEyvTrJf0Q\n2AdYDLjZ9pm5He8mbbsbAHwLeL3coJDADYKgIxky5J2ONqHN6bGOHpgF7G77A0krkhz7bfnZF0kO\n+llJjwP72d5G0q4khzsUOBX4u+3DJS0HjJX0N+A7wAW2r8297gWG1iVtDbxs+y1Jo4CdgJurGSpp\nGWAp21NqvM9/235PUi/g75JutP10jfSH5vSLA+Mk3Uhy+qcB/UmjBKOApwp5Vs3tsH5uq5sk7QCs\na3sLpe75bZK2JTn1dUiBbsbVsCMIgiBoQ3qyoxfwS0lfBeYCny9osk+2/Ww+fwb4Wz6fRNJ4B9gR\n2EXSSfl6MWBN4BHgVElrkHq3L1Woe3/g+nx+AzCMGo5+AcPTvP7ZpNGI/W0/Cuwn6UjSb7oqsAFQ\ny9EfL2n3fL4GsC6wGjDa9vu5nhvy/RKV9Ot3BHaQ9ASpTZfKeV4HXmvOyYcEbhAEQXVCArflCDgI\nWBHY1PZcSZNJPVqYX6d9buF6Lk1tJlKv/8Wysl+Q9CiwM3CnpKNsj55Xcepx7wnsKuk00vD+ZyUt\nZXtmJWPznPwHkvrafs32PcA9km4HFpO0FnAiKbrc9Bw9bvFKZWUbBgFfA7a0/XEeVSilrzVpXkm/\nXsAvbF9eVkdfoOL7FAkJ3CAIguq0hgRuj1x1n1kWmJqd/BCgb+FZPSvE7gZKc9dI6p//fsH2ZNsX\nkUK59ivL93Vggu2+tte2vRZwI2k6oBa/BC7N0wTkYfKSc16WNNQ+Q9IqwDebKWs5YFp28l8Gtsr3\nxwHbSVouTzvsWaOMUhvdDRwmaals1+clrVyWJgiCIOggelyPPm9HmwX8EbhD0gTSgrvnCslc5bzI\nWcAFkiaSPpheAXYF9pF0MDAbeAv4WVm+/VhwmP4m0tz+HyT9FTjc9nzLQG1fmp3pY5JmkRz7w8CT\nucf/VH6H14GHmnmXu4DvSHoGeIE03YDtNyX9nKRf/x/geeD9Ku3gnOfe/LHwSF5BP4M0WjK3Qp4F\nGDKkuRRBEARtR58+q3S0CW1Oj9O6l7QJ8BvbWzWbuAdSmkLIH0Q3A7+zfWsb1VVpx10QBEFQhZZo\n3feooXtJR5N68qd2tC2dmDMkPUlaePhKWzn5IAiCoH3ocT36oPMQPfogCILG6HE9eklzJD0haaKk\nGwsLwlaTdH0zeVssB1ulvIoSse0lHStpUF6FXytNv9xbL13vL+nDkoyupI3ymoVaZdR8H0nDJF3U\nqP1BEARB29DVF+PNtF3Scb8SOBo4z/ZbJKW2WrS4Kympt+05Lc3fhjT3TpOAPoWtfF8BngU2JS1I\n3Jq0wK+t7ZhHSOAGQdBR9AT5W+j6jr7II+StbHkP9x22N8771s8GvgHMAS63fQlp69exknYhtcPe\ntv8haSBwIfAZ4COSgtyLkoaRtsAtTRoJGSLpYmB70kr32c0ZKGl74FySWt444BjbsyX9krTv/lPg\nHtsnS1oJuAzok7Mfb/sRScNJyn3rkHQAzi3J1wLLZJGbjYDHbR9crN+2s9LflsB9wGbAJTRJ/W4N\n3JttHQCcRxLA+TdwiO35tCJzW12Q08zKbQGwuqSRwNrALbZ/VK1NQgI3CIKOoifI30IXH7on79PO\nQ887kFTsSpR6lUeT9sj3s92ftBivxFTbm5Ecaknh7jmSpvxmwHDgF4X0mwJDbQ+RtAdJ+nV9krLd\n1jUNlT5D0sDf2/YmJC38Y/L0we62N8r2/TRnuZA0OrElsBfwu0JxGwODc53/I2nVfL8/aW//BsAX\ns9RuOWOArZW0+ucAo4Ft8rOtgTF5D/1FJEGggdnun5e9z6LAn4HvZ7u/TnL2AJsAe5M+vPaVtHqt\ntgmCIAjajq7eo18iS6+uAUwmOexytgcuLa36sv1e4VlpP/t4YI98vjxwtaR1SR8LxTa6tyQPSwpI\nc20u8y1J9zVj65dIq9hLAW6uAr5L6lF/JOkK4K+kiHaQHOf6ahrbXjo7Z4BbcxCcd3O9W5D2u4/N\n0xbkffVrkRx7kTEkFb2HgHG2J0v6Yh5BWCpfb0gaFbg3198LeLPC+7xp+4ncBh/keiHFAChdP0v6\n0PpnpUYJCdwgCILqhAQufGh7gFJglruB3WhAM54mSdc5NLXFWcB9tofmKYDi4HKzkq7NsMCEtO05\nkrYgfZDsDfxXPhdJona+KYHsSItz4CpcFyVqi+9U5FFgIKn3/ki+90+SkE/pWsDTtrdZMHvt92nA\nDiAkcIMgCGrRIRK4hV5lZyB5PXsWcBwLqtBBmnM+urCyfIVmylyOpt7noTXSPUAalu4laTWgOY23\nF4C+ktbO1wcD9+f2XN72XaT48iXJ3HvyO5Ht3qRQ1m6SFlOKujeINN9fF7mn/Trp3UqO/RHgeJoW\n4r0ArCxpq1z3Ikrhd8vfZ1VJm+U0S5faOAiCIOg81N2jz/O9V5AWo62ZHc/Rtr/bVsbVwbyere2n\nJL0oaV9Sr7XEFcB6wERJnwCXA7+m+srwc4CrlALO/LVqxfbNkr5GWhcwhQWHyEssAnycdeUPBf6S\nHeI40lTDisCteVQC4Af573HAJXm7W2/Sh0WprSeS5tZXBH5i+21JXyo3sZrtJIe+i+3SB80jpI+k\nMfndZkvaC7hISVu/N2nR3bM0Sd/Ozm19saQlgA9J0w0LNFUNO0ICNwiCDqMnyN9CA4I5kh4jLQq7\nzfam+d7TtjdqQ/u6NHnF/1jgINvPt1KZw4EZts9rjfI6khDMCYIgaIw2F8yx/XrZrc64l7xTkIfz\nJwFjWsvJB0EQBEGjNLIY7/U8fO+8teo45o/4FhTIq983bINyG1+JEQRBEPRYGunRfwf4HrA6abFa\n/3wdBEEQBEEnJYLaBB1GzNEHQRA0Rkvm6BtZdf8F4PskEZZ5+Wzv2kiFQdcj6wmMJInsbA28QdIs\nOBg4iqTy9xJwsO1ZkkYA04HNgVWAk23fVKXstn+BIAgCeo62fTmNrLqfQJJhnQTMLd23fX/bmBZ0\nFrKjfxHYzPYkSdcBtwIjbU/Lac4C3rZ9SXb0S9reV9L6pJ0a61Yo16F1HwRBezFkCHT1UcQ27dGT\n9oL/qkGbgu7DZNuT8vl40sjOxpJ+SpINXoqkTljiFgDbz0n6XLVCQwI3CIKgOq0hgdtIj/4gUsS0\nuylInJa0zoPuS+7R3267FB3wRJJw0jBgV9tP5+h+g2wflnv0t5eG6yVNt71shXKjRx8EQbsRPfrm\n2Yg0JzuEpqF7A19rpMKgy1LpH9bSwNt5u+WBpLn7evMGQRAE7UAjjn4v4As5alrQ8yj/DDZwOkn5\nbyrwGLBMjbQVCQncIAjai54ieVtOI0P3twBH2Z7atiYFPYXYXhcEQdAYbT10vzzwvKRxzD9HH9vr\ngiAIgqCT0oijH95mVgRBEARB0CaEMl7QYcTQfRAEQWO0afQ6SVtJGifpA0mfSJojaXrjZgZBEARB\n0F40MnR/MbAfcANJ2vTbwHptYVTQuQgJ3CAIuio9Vfa2SCOr7h+3vbmkiQXhlCdtb9qmFgYdTkjg\nBkHQVekOIjlF2nrV/YeSFgOeknQO8BaNhbkNujYhgRsEQdDOtLcEbl/gHWAx4AfAcsCvbb+0UBYE\nnZ6QwA2CoKsSPfoGevS2X8uns4AzG6kk6BaEBG4QBEEXpJF49NsAZwB9mT8e/dqtb1bQCQkJ3CAI\nuhw9VfZ98klqAAAgAElEQVS2SCND98+ThuzHA3NK922/2zamBd2d2EcfBEHQGG29GO992yMbtCkI\ngiAIgg6kkR79L4HewE1EPPqgFYgefRAElVhrrbV47bXXmk/Yjenbty+vvvrqAvdb0qNvxNFXWh9t\n220Wj17SKsAFJOGV90ir/o8HVgd+aHuXhSh7ODDD9nkLUUZf4A7bG7e0jGbKvwM4wPZ0STNsL9OS\nOvP2tvOBLYFpwCfAObZvlbQZSejm+Lx98q/AisAvSFsoL8vpv2L744oV1K67ajuHow+CoBLZmXW0\nGR1KtTZo61X3NZdNSRpm+6pGKq+Dm4ERtvfPdWxMUlqDGgu8mkNS71awrUSb/Wu0vXOVehqt8xZS\nOx4IIKkPsGuuYzxp3QXAgHTLA3K6S4Gf2/5TPZVI6m17TvMpgyAIgnbDdqscwBOtVVYubwgwusqz\nQcAokhzvc8AfCs9OJ60AnwhcVrg/itSrHUtaVDgcOCE/W5sk8ToOuB9YL9/fG5gEPFnJFtIOhIkV\n7h+R63ky27h4vv850tTHU/nZVvn+gdnmJ4BLaRppmQx8Np9PL6+TJFh0Ts77FHBkBVu+Boyq0c6D\ngNuBlUnqd9OyHUcB7wIvl9oXODe3xwRgn0L+B0hKec/ne6cCL+T7fyq1c4W6HUccccRR6ejpVGuD\nfL8hf9rIYrzmaO290hvR1NOsRH9gA+Bt4GFJW9seA1xk+ywASVdL2sn2X3OeRW1vkZ8NL5T1W+Bo\n2y9L2oLkbLcnfTTsaPstSQsIvtTgRttX5HrOAg4HLgF+RfpgGKok8r60pC8D+wJb254j6RKS47+m\njnoOB96zvWUedn9Y0j1u0jwA2JDkuGth2/+SdARwou1ds+1fIQvfSBoK9LO9cZ4KGCfp/px/U2BD\n21MkDQD2AfqRxJWeAB6vVnEI5gRBUE5su21dWtPRuxXLqoextt8CkPQUSZJ1DLC9pJOAJYEVgKdJ\n884A15UXImkpUqCWG9QUYWXR/Pdh4CpJ15N64vVSTRr2a6RAMOQvsxmSticNmY/L9S9O+niphx1z\nXXvn62WBdYGqq1gkXQxsC3xse8sG3mlb4Nps+1RJo4GBwAzSbzElp/sqcLPTfP7Hkm5roI4gCIKg\nlenMPfpngL1qPC8uDJsDLCLpM6Se8wDbb+Ze++KFdDMrlNMLmOY8L13E9jGSBgI7A+MlDXAO4tIM\nV1ImDVsqskJaAVfZPrWOcivl/b7te2ukeQbYs3Rh+78krUiaplgYir93pXati9C6D4KgHtZcc1Ve\nf/2dNiu/s0a5aw2t+9Z09A+3YlnYvk/SzyQdURgG35iksV+NxUnO9F1JS5M+FG5opp4ZkiZL2sv2\nX3I9/WxPlLS27XGk3vY3gD6kOewijUjD/h34LnChpF453d+BWyRdkIfPVwCWKfSQa9VzN/BdSaNs\nfyppXeAN2x8V3q/Ujkfb/k2+vVStNqnCg8BRkq4mrcr/KvBDYP2ydA8AIyT9gjR0vwtp5X5FDjmk\nBZYEQdDjeP31d9p0qm/IkLb7iFgYBg8ezODBg+ddn3lm4wr0jUjgrgL8HPi87W9K2oC05ep3kHqK\nDdfePHuQnOIpwEfAq6TtdWuUpXO24X1JV5B6sW+RFsTNl6YKBwGXSjqN1CZ/Ji3mOzc7T4C/2Z5Y\nIe96kqaQHLFJC/2qScMeD/xW0uHAp8Axth/L9d6Tnf8nwPeAKWU2V7L/CtKUxRN52H8qsHuFdLsD\nF0g6GfgXqQd+co32WKBO2zdL2oq0EG8ucFIewp/P0dt+MoexnUjaDln8DRYg5uKCIOhqnH322Vx+\n+eVMnTqVNddck5/+9KfsvvvuzJ07l5NOOomrr76aZZddlhNOOIHvf//7fPrpp/Tq1Yvp06dzwgkn\ncOedd9K7d28OOeQQfvKTn9A0a9w2NLKPfiQwAjjV9iaSFgGedBvtIQ+6P7GPPgiCSlTaQy6pjXv0\n1L13/8Ybb2TbbbdllVVW4YYbbuCwww7jpZde4uabb+biiy/m3nvvZckll2SvvfbivvvuY/bs2fTq\n1Ys99tiD1VZbjfPOO48PPviAnXfemcMPP5wjjzxygTpacx99I/HkV7J9Pak3h+1PKWjeB0EQBEFP\nYM8992SVVZKky957780666zDY489xg033MBxxx3HaqutxnLLLccpp5wyL88777zDyJEjOf/881l8\n8cVZaaWVOP7447n22mvb3N5G5uhn5kVcBsjDuO+3iVVBEARB0Em5+uqrOf/88+dJ1M6cOZN///vf\nvPnmm/Tp02deuuL5lClTmD17NqutthrAvD3ua665Zpvb20iP/gTgNuCLkh4GrgaObROrWhlJp0p6\nWtIESU/klfTV0g6TdFEr1Tsi7z9fmDJ2z3Y/k//uVng2TNKqhevf5n359ZQ7XNIbuT2ezfv3W83u\nQlmj8t76IAiCLs+UKVM46qij+PWvf820adOYNm0aG264IQCf//zneeONN+ZLW6JPnz4svvjivPvu\nu/znP/9h2rRpvPfee0ycWGnpV+vSiKN/hrRNbGvgaJIQy/NtYVRrkkcevgX0t70J8HXg9WaydcjE\ncbk0r6RNSMp3u9jeENgN+F9JG+Ukh5B0/wGwfZTtRn6T82wPsL0B0E/SoGZzBEEQ9GBmzpxJr169\nWGmllZg7dy4jRozg6aefBtIw/oUXXsibb77Je++9xznnnDMv36qrrsqOO+7ID37wA2bMmIFtXnnl\nFR544IE2t7kRR/+I7U9tP2P7aduzgUfayrBWZDXg33lNAbb/Y/ttAEkDJT0s6SlJj2bxHIDVJY2U\n9IKks0sFSZpRON9T0u8lLS3plZKTlrRM8bqQfoCk0ZLG5bJXyfdHSTpf0lgWHCE5kaQ1PyXb/ipp\n58PJkvYkBfu5JvfKFy/1niX1yr3yiXkU4LgqbaNsw+KkrYkLaARIOl3SY7msywr3R0n6ZX72vKRt\nSmVJujaPQNzE/DoGCxogxRFHHHHMd3Rm1l9/fU488US22morVl11VZ555hm23XZbAI466ih23HFH\n+vXrx2abbcZOO+3EIossQq9eydVeffXVfPLJJ2ywwQZ89rOfZe+99+btt9t+736zq+6VhoZXJ0my\nHkDTfu5lSVrydQ0VdxRKzvshYAnSnvXrbD+gtMf9eWBv208o7bv/iLTV7nSSxO5skmb7Nrb/KWm6\n7WVzuXsCO9k+TNLvgFtt3ybpSJJW/kmSRpB05G8jaejvavtdSfsA/8/24UpRAZ+ptD1R0njgENuT\nCvf6Ab+3vXnOe4LtJ/OzUaSPA4Bf2t4x31/W9vSysocDR5K25PUFRto+KD8bQZP07fK238v3r87t\n99dc1+P5Pb+Z7dhB0g9IcrhHKOkePAFs6QrhjCU5JHCDICin0gr4riiYc9ddd3HMMccwefLkhvNK\n7Ru97v+RhojXAIqhRqcD/91IZR2B7ZlKc8RfJUnQ/llpX/4TwJslB2T7A6D0Nfn3wvWzJEf4T6qr\n//0OOInk0A8lBbUp8iWSdv+9ShX0At4sPF9AmrcBKtn0CvAFSRcCdwL3VMl7nu3zlEYfbpS0T95Z\nUaSWpHBJFng8qY0AtgMuBLA9SdKElrxUEARBkc6oWlfOrFmzGDVqFDvuuCNvv/02Z555JkOHtspy\np4WiWUfvFHr2Kkl72r6xHWxqdfJm7QeAByRNAr5NcvTVHPcC8rqlogr35w1J2x4jaS2lOe5etp8t\nK0/A07a3qVJfNQnZZ0jD85MK9zbP96ti+z2l+f3/R1pPsQ8pAE619HMk3UVy0vMcvZqXFC61U7GN\nyqn55RkSuEEQdBdsM3z4cPbbbz+WWGIJdt555xYp2RVpbwnch/MQdUVlvM6KpPWAubZfyrf6k4K+\nvACsKmkz2+MLQ/e1eFvSl0jhXPcgjWqU+AMpJGulX/UFYGVJW9l+VElsaL0KHwTl/B9wvaT7bL8m\naS3gx0DpE3E6aQql/J1XBD7Janb/yLZVojRHL2AbFoxy17CkMOmD6kBgtNKiwX61EocEbhAE3YUl\nlliCsWNrioE2TLtK4JJU8UaQYo0D/IM05NypHT1JT/4iScuRZGdfAo6yPVvSvsDFkpYAPiStyC+n\n2Iv/MWnYeiop9OrShWd/BM4iyefOlzfXtVfBjt7ABcCz1Fjhb3uCpB8Bt+ePg9nADwtz9lcBl0n6\nkLQbolTW6iS9+V753ilU5nhJB5Ki9U0Efl1md0skhS/NdT8DPEeNELVBEARB29OIBO442wMlPWl7\n03zvKdsx2ApkR76L7WEdbUtXQVLo3wZBUJGeLo/d3ovxSoQyXhUk/Qr4Bmm/ftAAPf0/5iAIFqSz\nb7HrajTSox8AXERaPf40sDKwV5WIbkHQLIqgNkEQVKBab7Yn0SE9+rzXfBBpq5iAF7JoThAEQRC0\nGn379u3xvfq+ffs2n6hOmlXGkzS0dAC7khz9esAuaiU99JaggkpdhWeDJN2+EGUPkjRX0mGFe5vk\neye0tNyFsU8F/XlV0Y/P959XUvobo7JY8VXKrdqOFdLuohTTPgiCoM149dVX5wV96alHKWBOa1BP\nj36XGs9Mk2hKe9PcuM7Cjvs8Tdp//vt8vT/wVCMFSOptu1oo37Yal9rf9pOSDiHr5DeTvm47bN9O\nUvprNXr6V3sQBAtPW6jadSfqEcw5tD0MaSmSziUthJsL/Kyg7LaMpBtIawoet31wTj+ZtC1tF9L7\n7237HxWKfi2XsbLtf+U6SopwSDoCOIq0Ne0l4GDbs7J87CxgU+AhSbeRlOKcj+2ase90YGeSZO8Y\n299ptEny30dIan0le/cnbQ8EuNP2KU2PdB6wI2kL3X5OMr3HksR2ZgPP2j5A0jBgc9vfl9SX9BG0\nIvAv4FDbb+T3n04S9lkFONl21Y/BkMANgmBhGTKk7aRxuwN1B7WRtKKkXykFUBkv6cK8Cr+jUB7K\n7md7Y2AH4FzlYDEkYZxjgQ1IoXW3LuSdansz4DIKzrACfwH2yXnHM79i3o22t8hbDZ9nfuW51W1v\nZfuHwA+B79ouyfCWRHmq2XeR7S1t9wOWlLRT/U0yH98kK+hJWg34JTA41ztQ0q453VLAWNsbkcRu\nhuf7PyJF/OsPFD82SiMAFwEj8vM/5esSqzqpAO4CnE0QBEHQYTSyve7PJEewZ74+kCSYU0lkpr3Y\nBrgWwPZUSaOBgcAMkvN6C9J+f2AtYEzOd3P+O56kcFcJk+Rgrwe+nOspStj2k3QWsDzJWd5deFZU\nj3sYOF/SH4GbnILjUMO+Wtry9fDHLF27PE2qdAOBUbb/k+v7I2lk4TbSSEhpFOQaoCRzPAH4k6Rb\ngFsq1PMVmtruD8zv0G8BsP2cpM/VMjYkcIMgCKrT3hK4q9k+q3D906ws15koTvhW06svPqul0V76\neJhN+pg5lvkd/QhSNLqn85B2MZb7zEIZZ0u6A9iJJCO8YzX76tCWr4cD8hz9OaTRilKI2nonw0s9\n9p1IHwO7AqdmOdtK6SpRfLea9YYEbhAEQXVaQwK3kXj090jaTynWeS+lUKt3N5urbXkQKNm0Mmlo\nvHWFhlPI2h9V2PC9NEn7flHS6EZFJK1t+xnb5wDjSKMD1aikLd8oJcf6P8BukvqQ2mQ7SZ9VilS3\nPzA6p+tVqOdAUkhfgDVt30+Sz12W+eV+IY0+7J/PDyL9FrXsCYIgCDqARnr0RwLHk4Z3ITmImZKO\nJgWIWyC4SluRndUs27fkue0JpCHok3IvvHxbmaucN4vtR6s8+h+SA50KPAYsU6X84yUNyfY9DYwk\n6dIvYJ/r15av9g7z7ueFgRcC/237GEk/psm5/9X2Hfn8A2CLvAjwHWDfrKt/jaRlSY76QtvTy1bI\nH0vStP8heTFeFdtqtveQIbWeBkEQNE+fPqs0n6gHU7cyXmdCKQTrb2xv1dG2BC0nlPGCIAgao621\n7pHUj7RobF6+Wlun2oI8gvB9muaegyAIgiCoQiNa978nreJ+hjQMDWnI/rDquYKgOtGjD4IgaIy2\n7tFvZXuDBm3q9EiaYXuZ5lPWLGM10jz2PnWmnwxsVtru1pZIGgWcaPuJFuQdRrLz2LwDYIbt81rd\nyCAIgqDNaMTRj5W0ge1n28yajmGhu5R5P3xdTr616uwuhARuEAQtJaRv66MRR38l8Kikt0j7pEUa\nuu9XM1cXpBl519tL6xJKowE5/R22N5a0AWmP/aKknQl72n65vIoKdS5JUpfbMOc90/ZteW/9pSRJ\n2dmk3vno3NvelSSsszZwi+0f1fl+86Rs8/XtwLm2H5B0KGlL3TRgIknOtzx//2zTEsDLwGHAYsBI\n25vnxZJPkrbovSHpJWAj2wuUFRK4QRC0lJC+rY9G9tFfQdov/Q2StOnONB8wpatSS961SKUtb98B\nLsiSt5sDb9RZ56nA3/NOgq+R5HyXAL4HzM0fVAcAV0laLOfZBNibtHZiX0mr11lXue0ASFoVOIOk\nerctSZ63EleRtjL2J20ZHJ7jAXwm7//flqQZ8FVJawLvVHLyQRAEQdvTSI/+X7ZvazNLOhe15F2b\n4xGSktwawM22X6oz346k0L8l7f3FgDVJTvNXALZfkPQqKUwwpA+DDwAkPQv0Bf7ZgK3lbMn8UrnX\nAesWE+S99cvZLgnrXEWThO6YbO92wM9Jevu9qC6mExK4QRAENWhvCdwnJf2JFKZ0nsRpe2+vayeq\nzaF/Sh4FUZpcXqw8ge1rJT1KGvG4U9JRtkfXWe+etl8s3qgwh12vzG8t5r1HpiizW8+kebU0D5LU\nCde0faukU0g7NKpq9YcEbhAEQXXaWwJ3CZJj2ZE0ZF8avu/qVHJa1eRdXyUNxwPsRppLn78w6Qu2\nJ9u+CLiVpsAyzdV7N0ltrlROqW/7IFliV9J6QB/gheqvU1ddrwL9legDbJHvP0aSyl0hS/vuXV6Q\n7enAfySVdP8PBu4v2HoQUPpY+Q/wLZpkdYMgCIJ2pu4efWePS78QLCFpCnlxIXAeSZDnygryrpcD\nt0p6kuSYZ1Yobx9JB5MWzr0F/KxCGgMTJJVi1F9PmqO/UNLEbMtk0mK7XwOX5vuzgWG2Z1fo6dda\nyX9HDs4D8IjtffMUwDPAc6Qofth+W9IZwKOkxXhPVSnvEOCyvIbgFXL72H4t21Vy/A+RQva+X82w\nkMANgqClhPRtfTQimLMGaVFaqSf3IHCc7XoXmwXBfIRgThAEQWO0RDCnkaH7EaT45Z/Px+35XhAE\nQRAEnZRGevRP5e1UNe8FQb1Ejz4IgqAx2rpH/66kgyT1zsdBwLuNmdj1kTSjxrNBWXympWUvkF/S\nCElDW1pmC+3oK2lS4fpISeMkLdeedgRBEAQLTyPb6w4jzdGfT1r4NYa0KKun0VwXdGG7qJ2li2uA\nvLDwe8CQWovqikjqbXtOteuytK1haxAEPYiQvm2MRhz9T0grvqcBSPos8L+kD4Aeh6RzSSqBc4Gf\n2S6Jxiwj6QZgI+Bx2wfn9JNJ4jK7kNp9b9v/aLDO7YFzgd4k5blj8gr8X5K2On4K3GP7ZEkrAZeR\ntuMBHG/7EUkDgQuBzwAfkeR9XyyvK1WnvYGTga8Vfve1gUuAlYAPgSNt/yPLA88C+gMP55GPL5Lk\neV8jbxEsJyRwgyBolJC+bYxGHH2/0v/sAWz/R9KmbWBTZ0d5KL1f1rb/HDBOUmlLWX+SdOzbJIe3\nte0x+dlU25tJOgY4CTiyQvnbSSpFmhPJUd+eNe9HkHrWL0u6CjhG0jXA7ra/nI1bNue9EDjP9pi8\nV/7ubNdzwLa25+YPh18Ae1Wwoy9pBGfTLG9b4rfA0dmGLUia99vnZ6vb/kq2YziwPrCN7U+aadMg\nCIKgjWjE0feStEJZj76R/N2JbYBrAWxPlTQaGAjMAMbmaHZIegpYizTNAXBz/jueJondch6wvWvp\nIveUAb4EvFIIkHMV8F1S7/ojSVeQFOjuyM+/DqyvprHxpXPgnOWBqyWtSxqer/Yb/ou0BmNf4IJs\ny1LA1sANhXKLokE3lJVxW3NOPiRwgyAIqtPeErj/BzySh6UhqaZVEoPpidQrS/txlfstqQcA23Ny\nz3p70m/yX/lcwJa2Z89XgHQJcJ/toTnqXrXB85lkVTtJU23/ibR4c1oO2FMtT63rBQgJ3CAIguq0\nqwSu7auBocA7+Rhq+w8N19g9eBDYT1IvSSuT9N3HtnGdLwB98xw5ZOnZUi/d9l3ACTRJ7t4DHFfK\nnEPHAixLU+CbWmqHsv1v0jqEn0nawfYMYLKkeUP9krpdmOIgCILuREO9StvPAs+2kS2dHkm9gVm2\nb5G0NTCBtBjvpDyEv35ZlkphbBvFALY/VooV/5dsxzjSYrsVSbK8pcA0P8h/jwMukTSBtHjvAdJQ\n/7mkULenUSPYTKHeVyXtBvxV0h6kRXWX5fyLAH8mxa1v0fuFBG4QBI0S0reNUbdgTjCvV/ybHDM+\nWEhCMCcIgqAx2lowp0cj6Wjgj6TgM0EQBEHQJYgefdBhRI8+CIKgMaJHHwRBEATBfISjD4IgCIJu\nTE8VvAkaIO+3Hwk8RBLMeQPYjbTF7yiSaM5LwMG2Z2WRn+nA5sAqwMm2b6pSdtu/QBAE3YbQuW+c\nmKMPmiU7+heBzWxPknQdcCswsqCUeBbwtu1LsqNf0va+ecvhbbbXrVCuQ+s+CIJGGDIEerLfaskc\nffTog3qZbLsUunY8Sdp3Y0k/JcnqLkXS0y9xC4Dt53I8gIqEBG4QBEF1WkMCN3r0QbPkHv3ttvvl\n6xOBpYFhwK62n5Y0DBhk+7Dco7+9NFwvabrtZSuUGz36IAgaInr0seo+aDsq/cNaGnhb0qJUCUNb\nI28QBEHQDsTQfVAv5Z/QBk4nafxPBR4DlqmRtiIhgRsEQSOE/G3jxNB90GGEYE4QBEFjxNB9EARB\nEATzEY4+CIIgCLoxXcLRS1pF0rWSXpQ0TtIdktaR1FfSpOZL6DgkjZL0vKQnJT0haehClDVI0u0N\n5llN0vXNpJks6bMLmyYIgiDofHSVxXg3AyNs7w8gaWOS4tobNBAHXVJv23PaxsSa7G/7yWoP1dhk\ndaPv+xawTyuUGZPpQRAEXZBO7+glDQE+sX156V5JuCXv76Zw/gdgyXzrv2w/KmkQcBYwDfgS8GVJ\nBwLHkqRbHwO+a9uSZgAXAjsDHwK72f5XFny5DFib5PCOyWVXLKfCa8w3cpJtvTvnGQB8S9KXgTOB\nxYCXgUNtfyjpG8D5wEzg4UIZSwIXARvm+s+wfXvezz6UtPWtl6RDgDtsbyypF3A28A1gDnC57UvI\n298kLQHcCNxo+3flP0X5S9WwoeJvUaFdQgI3CIK6CfnbltHpHT2wEUmJrTmmAl+3/YmkdYBrgYH5\n2abAhranZIe6L7C17TmSLiHtAb+GpO42xvZpks4GjgR+DvwKGG17qJJnWrqZcsq5RtIs0kfC9vne\nOiRt+HGSVgROA7a3/ZGkk4ETJJ0L/BYYbPuVLD1b4lTg77YPl7QcMFbS3wrvu7Ht97PTLX18HA30\nBfrlD5vl832TtsZdB1xp+491tHctG96p8VvMRwjmBEFQL0OGvNPRJnRJuoKjr5dFgd9I6k/qrRa1\n1cfanpLPtyf1osdlp704UPpE/MT2nfl8PPD1fP41UgAXco99hqRK5VT7V3hAcehe0rLAa7bH5Vtb\nARsAD+eyFgUeAb4MvGL7lZzuGtLHB8COwC6STsrXiwFr5vN7bb9fwY7tgUtLow623yuZRJKsPcf2\ntVXeoRLVbHgLuLjKbxEEQRC0I13B0T8D7FVHuh+Qgqr0k9Qb+KjwbGbhXMBVtk+tUMYnhfM5NLVP\npeH4WuVUSltOuU332J5PXU7SJlXylvLsafvFsjxblZVdLw+ThvQbcfRUsWE41X+L+Qit+yAIguq0\nhtZ9p191b/s+YDFJR5TuSdpY0jZlSZcj9SQBvg30rlLk34G9JK2cy1pBUp9S0TXyfDen75V75JXK\nWbNK/koU63oU2EbSF3NZS0paF3ge6CvpCznd/oU8d5PWB5Dz1OMi7wWOzs4XSSsUnv0P8F6egqjH\n5lo21PtbcMghTUc4+SAIgvkZPHgwZ5xxxryjJXSFHj3AHsCFkk4h9Q5fBY4vS/Nr4EZJ3wbuokqv\nNkdTOw24Jy9O+wT4HvA61VeWHw/8VtLhwKekxXiPVSlnSlneamXOu2/733nR3LWSPpOfnWb7RUlH\nA3dKmgk8SFpkB2mB4QWSJpI+2F4Bdq1SV4krgPWAiZI+AS4ntVtpKP84Sb+T9Evbp1Swd4Ik5/Pr\nSXP0F2YbBEzONtT1W0BI4AZBUD8hf9syQgI36DBCAjcIgqAxQgI3CIIgCIL5CEcfBEEQBN2YcPRB\nEARB0I0JRx8EQRAE3Ziusuo+6ECyut5I4CFga1KMgd1IIkJHkQR+XiIp/c2SNAKYDmxOiklwsu2b\nqpTd9i8QBEG3ICRwW0asug+aJTv6F4HNbE/KUry3AiNtT8tpziKJ5FySHf2StveVtD5wm+0F1PEk\nOSRwgyColyFDoKf7rJasuo8efVAvk0vBhEjywGsBG0v6KbA8KU7A3YX0t8A83YLPtaehQRAEQRPh\n6IN6+bhwPgdYArgS2NX20zlq3qAq6at+fYYEbhAEQXVaQwI3HH1QL5Wc9dLA25IWJUXue6OBvECS\nvg2CIAgqM3jwYAYPHjzv+swzz2y4jHD0Qb2UT4wZOB0YSwoR/Bgp1G21tEEQBEEHEIvxgg4j6+YH\nQRDURay6j8V4QRckPjSDIAjalhDMCYIgCIJuTLdz9JJmlF0Pk3RRB9ozXNIbkp6Q9IKkv+S95S0t\nbzNJFzSTZpCk22s8v0BStYVzC01+5xPy+QhJQ9uqriAIgqA23c7RU3nhV7uND+fY9OWcZ3uA7S+R\n4rjfJ2nFlpRve7zt4+tJWsU+AbsAz0oaVClNEARB0H3oUXP0WeHt98CKwL+AQ22/kZXcPgI2BVYG\njmjWKA0AAA38SURBVAAOAbYAHrV9WM6/A3AmsBjwcs7/oaTJwHXA14FzSM68Iravl/Qt4ADgIkmn\nAzuT9qWPsf2dXNco0kr2IcBywOG2H87O+Ye2d5G0JHARsCFJhvYM21V78pnBwIRs7wHA/bm+4fD/\n2zv3YCur84z/HgiiByLaWGWqQDVWEi8ISBGhjudIvaAJHS+ThkZHkSSdTqZibIyXmFoqSWptmjHR\ntDUqCdoYo5GICuOlDtHRMYoc5I4mmpZ4QdEUUqROgKd/rLV79jnssy9yON/mnPc3s+fs77bWs9f+\nzn6/9a613peRwBHACOAm29/Jx75KWj73FmkJ3VLb/yzpCOAW4CDgPeBztl+qUX8nIgRuEAS1iEl4\nu0dfNPQtkpbl9wIOBBbm7e8A82zfJWlm3j4nHzvA9kmSpufzJ9leI2mppDHAa8C1wFTb2yR9Gbgc\nmJuv32R7Qp0a24GPlTTZvh5A0nxJZ9t+OB8baPtESdOAvwNOy/tLvfWvAP9he5akYcBzkh6vUfcM\nkpF/CLhR0kDbO/Kx0aQHgWHAeknfBcbnNjoOGAwsA5bm828F/tL2LyVNBP4FmFpnGwAQIXCDIKhF\nW9vGoiXs1fRFQ/+e7fGljRyx7YS8eRIdhv1O4Iay60o94ZXAG7bX5O3VpHCvI4Cjgaez+3sQ8EzZ\n9fc0oLG8GztV0hVAC+mhZBVQMvSlRDAvAKMqlHM68Ml8PSRPw8huK02Bbc4CLsueiOeAM4BF+ZSH\nbW8H3pG0kZSQZjLwgO3fAb8rjf1LGpKP3auObvmguj59EARB0Gv0RUNfjWpj9aWQrTvpHL51J6md\ndgKP2v5MN9dvbUDHOOB5SYNJru/xtl/P7vN9K2jaQeXvSsB5tl/utFMa3k29Z5B666uycd6PNGRR\nMvRdw9xWuz8GAL8pf6j6IEQI3CAIgu6JELiVqTbo+wzJdX0XcAHwVANlPAvcLOmj2VXdAhza1cjW\nKk/SeSQX/BdJRt2kHvRQ4Hzg3gY0PQJcCvx1Lnus7eVVdMwgjfX/OJ/fArwiad8K55bqexr4V0n/\nQOqxfwL4N9u/lfSqpPNt35fLG2N7RZX6dyFC4AZBEHRPT4TA7S+z7ktcCsyUtJw0uWx2N9e463vb\nm0gT9O6W9CLpoWF0HXUCXFZaXkeaAHeq7Xdtbwa+RxoeWEwKJ9vd56hUx/XAIEkrJK0E/r47AZL2\no7ObHtvvkXLMf7K7+mwvJc1ZeJE0pLAC2JzPuQCYJWm5pFXA9ApVR0ScIAiCAokQuEFNJA2xvTU/\nLDxJml1fzXNQb7lx8wVBUJOYdd9BhMAN9hS3SjqaNOv++z1h5EvEg2YQBMGeJXr0QWFIctx/QRAE\n9fNBevR9cYw+CIIgCIJMGPogCIIg6MPEGH1QKBECNwiCWsRkvN0jxuiDmuQcAYtJS/Emk+Ld/xlw\nIfB50vr6XwAX2v7fnDtgCzCBFF3vy7bvr1CuIwRuEAS1aGuLibslYow+2JMcSYrLfyxpHf15wE9s\nT7Q9DlgHzCo7f7jtKaQ1+jfsUloQBEHQK4TrPqiXV22vzO9fIMX/P07SXOAAYAgpUl+JnwLYXivp\n4O4KjRC4QRAE3dMTIXDDdR/UJLvuH7Q9Jm//DTAUuAiYbntVTh50iu1Lsuv+wZK7XtIW2/tXKDdc\n90EQ1CRc9x2E6z7Yk1S6sYYCb+aseN0l++nu2iAIgqAXCNd9UC+VYuF/lRSf/y3g58CHq5xbkba2\nnpIXBEFfZcSIQ4qWsFcTrvugMCIyXhAEQWOE6z4IgiAIgk6EoQ+CIAiCPky/MPSSdkqaX7Y9UNLb\nkhb2cD3HSmrPueffkfRK3n60J+v5ALqm5jY4o2zfYkmTGyxnZrWlckEQBEHz0V8m420FjpU02Pb7\nwGnAhkYKkDTQ9o5q59heBYzL598BPFQpIlyNevbUwPUG4Ct0XuteN5IGApcAy0iT73qECIEbBEEt\nIgTu7tFfDD3AIuBs4H5gBnA3cDKApD8GbiLlW98GzLT9cl4bfi5pGdkASf8JLLD9QL7uLuAe2w9W\nqG8XCybpylzeYOA+23MlfRRYCLQDY4HTJB0P/C2wD/AycIntbZJuBKYB24HFtq+WNB24hhSG9m3g\nAtubKuhZBgyVdIrtn3XRdTopet0A4FngC7a3S9oA3AWUjo8FfiRpGzAROLXKdbeRwuQOAM63/YsK\nmoh19EEQ1KKtbWPREvZq+oXrnrS860fADEmDgTGk5WAl1gJ/YvsE4DrgG2XHxgHn2m4D7gAuBpC0\nP3AS8HA9AiRNA0baPjGXOUXSpHx4NPDNHF52O3AVcKrtCcBKYHZ2mU+zfaztsWUaf2Z7Uta+APhS\nlTb4GmlJXLmu/YDbgXNsH0+KcPf5slM22j7B9o9JDyOfsj2e9GBR7bo38nm3A5fX00ZBEARBz9Nv\nevQ5etsfknrzD9O5x30AMF/SH5EMYnm7PGZ7cy7jSUm3SPoIcD4p1vvOOiWcDpwpaVmuewhwFKkX\n/kvb7fm8ycDRwDNKfu1BwFPAu8AOSbeSvBMP5fNHSfonYDjJA/BSlTZYImmupBPLdn8cWG/7V3l7\nPslF/928fU/ZuaKj3WpdtyD/fYHkhahIhMANgiDonp4IgdtvDH1mIXAj0AocVLb/euAJ2+fmcK/l\nDuWtXcqYT8ra9mly775OBMy1Pa/TzuS639rlvMW2L9qlAGkCaX7Bp4C/As4AbsnlPiJpKnBlDR1f\nA66lcxCbagPlXT9/J0lVjr2f/+6gyn128cVVSgiCIOjntLa20tra+v/bc+bMabiM/uK6LxmkO4A5\ntld3OT4MeC2/n1mjrB8AlwG2va4BDY8AsyS1AEg6NHsGyvUBPAOcIunwfF6LpCMlDQWG2V5EcoWX\n+r77A6/n3v8uDwddsb2Y1Ps/Ju9aCxyZvR0AFwBLurl8S66v0ev2GpYvL1rBroSm+mhGTdCcukJT\nfexuT7pZ6C89egPYfg24ucLxfwR+IOlaaoy5235L0lo6XNNV6yy7brGk0cCzeab5FuAvup6by58F\n3CNpn3zsGtIkwfvzHAMBX8yXzCFlinuHZGiH19AF8HXgvlzftlzfAkkDSHMXbqv0GYDvA7dJeo80\nGe+zdV7XLRECNwiCWhQVAnfJkiWdetN7Lbbj1cALaCHNhP9w0Vr29le6/ZqL6667rmgJuxCa6qMZ\nNdnNqSs01Uczasq/mw391vYX132PkMfA1wDftv3bovUEQRAEQS0iqU1QGJLi5guCIGgQN5jUJgx9\nEARBEPRhwnUfBEEQBH2YMPRBEARB0IcJQx/0OpLOlLRO0ks5/n9ROm6XtFHSirJ9B0p6VNJ6SY9I\nGtaLeg6T9ISk1ZJWSrq0aE25/sGSfp4zMa6W9PUm0TUgZ4pc2Ax6soZfSXoxt9VzzaBL0jBJ90pa\nm7+/Ewu+z49SR5bPdkmbJV3aBO10dW6fFZL+XdI+RWvKumbn34MP/JsQhj7oVfKa+5tJUf2OIeUf\n+FhBcuZlHeVcBTxuezTwBHB1L+rZDlxu+xhSHoUv5LYpUhNOGR/bbI8j5Yk4VdKUonUBs0mrYEoU\nrQdgJ9Bqe5ztiU2i6yZgke2PA8cD64rUZPul3D7jgRNI0TcXFKkpR0T9HDDO9hhSjJkZRWrKuo4B\nZgETSEHSPpGjqTamq9H1ePGK1+68gEmkEL+l7auAKwvUMwpYUba9Djgkvx8OrCtQ20+BP20yTS3A\nc6R8DIXpAg4DHiOFs17YLN8d8CrwkS77imyn/Um5NLruL7ytct2nA08VrQk4MNd/IMnIL2yG/z1S\nTpXvlW1fC1xBikxat67o0Qe9zaHAhrLtX+d9zcLBtjcC2H4TOLgIETm08FhS+t9DitaU3eTtwJvA\nEttrCtb1LdIPXvmyocLbKet5TNLzkj7bBLoOBzZJmpdd5bcqheFuhrYC+HPgh/l9YZps/wb4JvBf\npHDom20/XqSmzCrg5OyqbwHOAkY0qisMfRBUp9fXn+a8BvcBs23/TwUNva7J9k4n1/1hpB+e1qJ0\nSTqblD55OdUTKxWxdniKk0v6LNLQy8kVdPSmrg8B44Fbsq6tJC9a4feUpEHAdODebjT0miZJR5DC\nio8C/gAYIukzRWoCcMqncgPJe7WIlCp8R6VTq5UThj7obV4DRpZtH0ZHQqFmYKOkQwAkDQfe6s3K\nJX2IZOTvtP1AM2gqx/YW0g/OhAJ1TQGmS3oFuJs0Z+BO4M2i28n2G/nv26Shl4kU+/39Gthge2ne\n/gnJ8DfDPTUNeMH2prxdpKYJwNO237W9gzRnYHLBmgCwPc/2BNutwH8D6xvVFYY+6G2eJ2W9G6WU\ntOfTpPGwohCde4UL6Ug/fBHwQNcL9jB3AGts39QsmiQdVJrVK2k/Uqrk9qJ02b7G9kjbR5Dunyds\nXwg8WISeEkqZJofm90NI488rKfD7y+7dDZKOyrumAquL1FTGDNKDWokiNa0HJknaV5JI7bSmYE0A\nSPr9/HckcA5pqKMxXb05sSBe8bINcCbpH+tl4KoCdfwQeB14nzQ2N5M0GefxrO9R4IBe1DOF5JZb\nTjKky3Jb/V5RmrKu47KWduBF4Et5f6G6soZT6JiMV3Q7HV723a0s3dtNoOt40gP2cuB+UlruojW1\nAG9TlhysCTRdQXoIWkFKRz6oaE1Z15Oksfp20oqOhtsqQuAGQRAEQR8mXPdBEARB0IcJQx8EQRAE\nfZgw9EEQBEHQhwlDHwRBEAR9mDD0QRAEQdCHCUMfBEEQBH2YMPRBEARB0IcJQx8EQRAEfZj/AwsF\nco06WWUYAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10fcaf5c0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df.head(20).sort_values(by='age',ascending=True).plot(kind='barh', x=['complete_name'], y='age', color=\"y\")"
]
},
{
"cell_type": "code",
"execution_count": 136,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEWCAYAAACjYXoKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXuQHFd9P/rpmel57czO7OxLu1oJPQwYb9lcsOJgILGM\nHdshBKtSqU0FJ8RUfJMYkpvaPIrXz0GOZRuwiURIIPULKSCVqgRRiVRJoHJvxdFyIZALCiRxrYtQ\nEGxL1msf2tmZnZ333D9G2u3z7aP+nNWMemel/lS5rNnp6T59+vT5Pj7fh9VqtVoIECBAgAABOkBo\nswcQIECAAAG2PgJhEiBAgAABOkYgTAIECBAgQMcIhEmAAAECBOgYgTAJECBAgAAdIxAmAQIECBCg\nY0T8utBnPvMZfOc730Emk8Gzzz4LAPi3f/s3fOlLX8Lp06fx9NNPY8+ePWvHHzt2DCdOnEA4HMbD\nDz+M17/+9X4NNUCAAAECbBC+WSZ33303PvzhDyt/27lzJ37v934Pt9xyi/L306dP45vf/CYOHz6M\nD37wg/jsZz8L03SY2dnZro35WiIYZ3cRjLO72Arj3ApjBG6ccfomTG6++Wb09fUpfxsfH8fY2Jjr\n2JMnT+LNb34zwuEwRkZGMDY2hh/84AdG17lRHpxfCMbZXQTj7B62whiBG2ecPcmZLC4uYmhoaO1z\nLpfD4uLiJo4oQIAAAQJ4oSeFSYAAAQIE2FrwjYDfCHK5HObn59c+LywsIJfLaY+dnZ1VzLOpqalr\nPr5uIBhndxGMs7vYCuPcCmMEttY4jx49uvZ5cnISk5OTxr/3VZi0Wi0jIn3fvn344z/+Y7zjHe/A\n4uIizp07h5tuukl7rO6Gz5w505XxXkuk02kUCoXNHgZFMM7uIhhn97AVxghsnXGOj493JPh8Eyaf\n/OQn8cILL6BQKODRRx/F1NQU+vr68LnPfQ7Ly8v46Ec/il27duFDH/oQJiYmcOedd2J6ehqRSASP\nPPIILMvya6gBAgQIEGCDsK7HEvSBZdI9BOPsLoJxdg9bYYzA1hnn+Ph4R78PCPgAAQIECNAxAmES\nIECAAAE6RiBMAgQIECBAxwiESYAAAQIE6BiBMAkQIECAAB0jECYBAgQIEKBjBMIkQIAAAQJ0jECY\nBAgQIECAjhEIkwABAgQI0DECYRIgQIAAATpGIEwCBAgQIEDHCIRJgAABAgToGIEwCRAgQIAAHSMQ\nJgECBAgQoGMEwiRAgAABAnSMQJgECBAgQICO4Vunxc985jP4zne+g0wmg2effRYAUCwWceTIEczN\nzWFkZATT09NIJpMAgGPHjuHEiRMIh8N4+OGH8frXv96voQYIECBAgA3CN8vk7rvvxoc//GHlb8eP\nH8ett96KT37yk5icnMSxY8cAAKdPn8Y3v/lNHD58GB/84Afx2c9+1qh3fIAAAQIE2Bz4Jkxuvvlm\n9PX1KX87efIk7rrrLgDA/v378e1vf3vt729+85sRDocxMjKCsbEx/OAHP/BrqAECBAgQYIPYVM4k\nn88jm80CALLZLPL5PABgcXERQ0NDa8flcjksLi5uyhgDBAgQIACHb5yJCSzL2vBvZmdnMTs7u/Z5\namoK6XS6m8O6JohGo8E4u4hgnN3FVhjnVhgjsHXGCQBHjx5d+/fk5CQmJyeNf7upwiSbzWJpaWnt\n/5lMBkDbEpmfn187bmFhAblcTnsO3Q0XCoVrN+guIZ1OB+PsIoJxdhdbYZxbYYzA1hrn1NTUVf/e\nVzdXq9VSiPTbb78dMzMzAICZmRns27cPALBv3z584xvfQL1ex4ULF3Du3DncdNNNfg41QIAAAQJs\nAL5ZJp/85CfxwgsvoFAo4NFHH8XU1BQOHDiAw4cP48SJExgeHsb09DQAYGJiAnfeeSemp6cRiUTw\nyCOPXJULLECAAAF0aLaAlwt1nC1UMZaO4lX9EQQ7TGewWtdhzO2ZM2c2ewgUW8n0DcbZPQTj7B46\nGeOLy3X87pd/iHqzhUjIwrNv34vdmWujW2+FuQSA8fHxjn4fZMAHCBDghsPZQhX1ZluPrjdbOFes\nbvKItj4CYRIgQIAbDmPpKCKhtmMrErIwlo5u8oi2PnoqNDhAgAAB/MCr+iN49u17ca64zpkE6AzB\nDAYIEOC6AyPYLQC7M5FrxpPciAhmMkCAANcdXi74R7AHaCPgTAIECHDdISDY/UcgqgMECHDd4TLB\nftky6VWC/XrKdwmESYAAAa47bBWC/Xpyx23NUQcIEOCGxWVt/vzZOYz2RbTa/FYh2HXuuF4f85Ww\nNUcdIECAGxbXkza/VdxxJtiaTyBAgAA3LK4nbX6ruONMsHVHHiBAgBsS15M236k7rpcI/ECYBAgQ\nYEvhsjZ/oVRf40xuVPSSy+/GfQoBAgToSZhmr982MbAlqvFeS/SSyy8QJgECBOgp9JK23evoJZdf\n8IQCXBV6yVcb4PpCL2nbvY5eIvB74gl95StfwXPPPQcAuOeee/D2t78dxWIRR44cwdzcHEZGRjA9\nPY1kMrnJIw1wGYH2GOBaoZe07V5HL+XTbPoITp06hX/5l3/BRz/6UYTDYTz11FN44xvfiH/+53/G\nrbfeigcffBDHjx/HsWPH8NBDD232cANcQqA9BrhW6CVte7OxlTwAm17o8ZVXXsFNN90E27YRCoXw\nute9Dt/61rfw7//+77jrrrsAAPv378e3v/3tTR5pACeC5kIBrhbNVrtt7jdfKeHF5Tpk3/DL2vad\n25PY1cObpx+47AH46MzL+N0v/xAv5uubPaQrYtNF/o4dO/A3f/M3KBaLsG0b3/3ud7Fnzx4sLS0h\nm80CALLZLPL5/CaPNIATgfYY4GoRuEjNwTwAvWS5bPoT3L59Ox588EEcOnQI8Xgcu3btQijkNpgs\nSz9Fs7OzmJ2dXfs8NTWFdDp9zcbbLUSj0Z4eZ73RxPfnijh7dh5j/VG8diSFsHgut6WB2zZpfJdh\nMs5eQq8/98u4luM8f3ZO2SAvlOq4bWJgw+fp9bnsxtqcyLYU/mgim1Du+YVzy4pgPvKzr8EtY/1X\nPeajR4+u/XtychKTk5PGv910YQIAd999N+6++24AwF//9V9jcHAQ2Wx2zTpZWlpCJpPR/lZ3w1sh\n9jydTvf0OF9c3hra41YZ52X0+nO/jGs5ztG+iLJBjvZFrupavT6X3VibE32W4gGY6LOUez69tKoI\n5tP5VexIXZ1tkk6nMTU1dVW/BXqAMwGA5eVlAMD8/Dy+9a1v4a1vfStuv/12zMzMAABmZmawb9++\nTRzhjYet0lxoq4zzegHjO0xw2UX6gf078Ymf2Xvduki7sTYZf9RL3GVPPMVPfOITKBaLCIfDeOSR\nR5BMJnHgwAEcPnwYJ06cwPDwMKanpzd7mDcUtkp45lYZ5/UCxneY+PB7KZz1WsKPtdlL3KXVarWu\nRrnoaZw5c2azh0DR6yZ6C8CL+bpS/6gXo2q2yjgvo9ef+2VcaZzffKWEj868vPb5A/t34s7t6/lf\nfrode30uu7E2/STYx8fHO/r99a0aXKfoxgLbKvWPtso4bxQwbduP/COT5lh+wI+1uZUi33pzVAE8\n0Y0FtlUW6VYZ540C5lbxw7XTK2vCj3EslGr4P+8Yx0q1gb5oGBdXaz27/ntzVAE80Q3tb6tksG+V\ncV4vYFo/4zv88OH3yprwYxyZRATzpXaiomUB/XH1/EGeyQ2Mbpjo3dD+/NAgu7HQA4LdX3RKsPtB\nrvfKmvBjHKu1Fv73/3dm7RofuXe38n2vWGlAIEx8Rzcefje0Pz80yF651wDmYNp2L2xevdIcqxtr\nkwnni6s15XkslWsA1oVWr1hpQCBMfIfJw+9U++uV8Ezm7+2VcQZYx0R/FO+9czuKlQZSsTAm+jeP\nYN/soAs/rDAmnHdkYor1syMTU37fK1YaEAgT32Hy8Dt1NfSC9ggAfbEInjrx8to4nrx/j/L9S4U6\nfq/DcfZKZM/1gnoLilvl2bfvVb4PCHZ/CfZdxPrpJcs9ECY+w8RE79TV0Cum78WSaqJfXK0BsNe+\nP5WvKN+fyleu26i0XoCJJXiOrJ2AYO/uOHJ9EYRDIcwVaxhO2cjE1aIkjSZQabawWm+i3GihBfjO\nUZli80dwg8HERO80lr9XyHU2joGErXw/kLSxUfTKxrMVYCJ4mZsrINi7i1IVeOK5F9eu8Yf3qdb7\nD/I1fPif/kex7m/Obfw98QPBW9eD6DSWv1fIdTaOXDyE/3XPLsxf0spy8Y2XiuuVjWcrwETwMjeX\nH+gV102n4zBxwZ4vqNb5+UIFk4PrwuLMsvr9mUJFESZBaPANDJMFxrS/HekInrx/D84UKhjvj2Gn\nWOR+aI/LlfqaIBhK2Vip1iGXU6vVjo2/EqpN4JBDK7uajatXInu2ApjVAXA3VzdQb7Y17jPL7fX7\nmgFbqTjrx/r1I/jjlWId/z2/imKlgaXVMEJWAjvT6rnGBcE+Lgj28X7xfb/6vfMay5WG9hp+IXjz\nfIaJRm9CsH/4//4fz3NcayTsMP5nsYxipYEmWtg9EHcdwwh2k42r08gek02jU+2ul7RDL5hYHX5Y\nei8WanjpYnvt1BotRCzgpqy/rhs/uLZiral+rjZdx7xmwFYUw9cM2Bv6fqnSdOWh7NykFi+BMPEZ\nJq4GttC7QVx3ilJNXcSP3bPLdQwbZzci2xhMfu/HNfwAE2omwrtTS89EsK5U+dq51vCDawtbwGgq\nihDabtyIxovbbAJemkcIwM05+4o8yUq1rkSDrdbqcOah+IlAmPgMkw2ULfThPltxVwyn1IXWDU25\n2gB+mK/hzItn2xpRzkbY8f3Sal0ZY75cB6Ca4IxgN/FJd1qbyOT3nW4svRIEwISaiZuLuSY7HQNg\ntnauNfywwGpNC08896MrkutA5wT7aNpGPBK+YjSYnwiEic+4zHecLVQx1h918R0AX+ghy1I0u6dE\n/kY3NOUf5mv4Xw5X2hP37cEtDmJwZ1b15e7MujcDRrCb+KRZrgrjoNjvgc43ll4JAmBCzcTN1ena\nMRGsJmvnWsOP7HVGrgOdE+zVOnC+WF1zNydst7vZLwTCxGecMuA7GMG+KPI3FkX+Rjc05fPiHBeK\nVVWYiDHqXsZuEOwsV4Vtfuz3QOcbC3teJuiGNcksDxM3F1s7bJzbUqpg3aYRrCwRrxsw5do6sSAZ\n+b0tHRNz4RaajGA/u1LHUrmBYqWJJbuBSAiYSK1fo9FQ21HVxWc/0RPC5NixY/ja176GUCiEnTt3\n4r3vfS/K5TKOHDmCubk5jIyMYHp6Gslkkp+sx3F22Ywz8RI4TBPuhqa8PaNuTONiYzIJAljsQjkV\ndi/MjdUN1w4bp4mCwCyobliTchuRn03WBTuGjjPUUqxR9yg638hNIiK7MZ/sua8Igr0kPmdiljIX\nmZh7kd2UtXHo/j1rkW2vdhHsLVceykRq/Xtpbf7BPbuxWdh0YTI3N4fnnnsOR44cQSQSweHDh/H1\nr38dp0+fxq233ooHH3wQx48fx7Fjx/DQQw9t9nA7xkCf4BESbv8oI66ZJt0NE55VKzUJAmAupm7k\nqrBrmLh2mIbJvu9GUEWnFgEA5Elkj8m6YAQ8E97L5aZijT52zy6g33WZjmCybrphnbPrhATBLtmK\nkWQEy9UWQiEgFglhW8p9/dOFuuJOltdYWq0q851frcJpWS+VVcs7X1ELQfqJTRcmiUQCkUgE5XIZ\niUQC1WoVuVwOx48fx8GDBwEA+/fvx8GDB68LYVKq1PHIHeMoXVocpWod0u0yIgj2UUGwM03aRPNb\nI9gvx/oLgl1WK227h9YXqUn2OnMxmZDjrJxEtd5Q8l3qjYZyDRPXjtyEH/+p3YBjE2bhl90IqujY\nIgCP7DEh11moNRPepWpDGUO51vC+4FXARFCYWKSdXocR7C8Vanh5qR0CXW+2YIfcIdDsGhOZKIpV\n4Fyhgm3pGPrEbbBCkH5i04VJKpXCO97xDrz3ve9FLBbDbbfdhttuuw35fB7ZbBYAkM1mkc/nN3mk\n3UEuaeNJx8v4iZ/R8QgqwX6oBwl2k+x1tkGakOMs2sUOh/G4uA8nTDaVBSH0Fkqq4FwSgjUvyoCb\naPydVi0wEbzZhI1nvnqqI0uQuZAWV7wVhIGkjWf/3yuPoRswEd7dyOTflvbmfxjBbhICzTimlSrw\nB/+Px/pORRQ32dXwdd3CpguT8+fP48tf/jI+/elPI5lM4o/+6I/wta99zXWcdQWVanZ2FrOzs2uf\np6amkE5vUtaOAV6bqOOpB/auPfybR9OwI8JEf+mcqq0UqrjjVbm178+fnVPJ8VIdt00MbGgc58Q1\nLhSr+PFd69e4WYzzdWKcjeIyDj23vjEd/tlXu+ad3evq+XmhSTdd55BzcbZQxY855kLex3lxH63i\nsvJC68aZS1aVFzqXtJVjRlJ15fuRVMx1jtvSwG0e823y3L3OkbpYVwTvUw/sdY0hf2ZOCL0G0umN\nrZsXzi0rAufIz74Gt4yt+6lyyZrLTescBxsDANQbTXx/rrg2F68dSSEcChl/bzKXF8i9Vmp1PH+2\nsHaO14+7z5EsL+MP79uzZhUk7bByr9vSNSEI1HWx9PKKmIs60ukh5RpW4aKilFkWlHMUz55XLO9S\ntabM53+cvqhYP9Gwhf9jg3uBE0ePHl379+TkJCYnJ41/u+nC5Ic//CFe+9rXIpVqs0p33HEH/vu/\n/xvZbBZLS0tr/89kMtrf6274WvY46BQ/Wq7jQ//krR2O96vaynh/VLmn0b6I8v1oX0T53sS/PqEh\n2J3nYONcWq0oi3x5teqa91OFOl682OYaqo0mEhEoXEMiGsKff2t9o3/y/j2uc+zIquPckVXHyebq\nlaVV5YV+JV/GzpRqRemsLOc5Vio1xTW5Uqkp37PyIADwosFz90KxolomcgwAMJoS6yIV2dC6AYDT\nYr5O51exI7W+ekKWSrBbaKnXIGO4PBeeSbmFOl6Yu1yGpIZWs6GsG5O5HBH3OiLu9XsXeX7Hwkpd\nsQr+8L49GHWcYyBu4fH79uD8JWEzELeUa+isezkX1XpTeTcrtaZyzEDCdlWacH7faDYV3qbeaF71\n/pdOpzE1NXVVvwV6QJiMj4/jb//2b1GtVmHbNp5//nns3bsX8XgcMzMzOHDgAGZmZrBv377NHmpX\ncFoQ16eX3cR1ImKtbRypWBiJiCoKmEvExJ1R7pBgZ+4lgJeTWKmoPn4dfxQWOTXSXcHmajgtEjz7\n3NxOowVccMTq5xIJ5XvmmvyhQeIZi+JjCoCJS7AbgRnMLViuq+HeMnrI5BqMJ2AclQlnErGgrIuw\n0KZYfgcArFRrisJUrqouvVoTeCW/bhWko+q6YWNoX1vlXeR7xCpNtGDhfLGytnZ3acoa+YVNFya7\ndu3CXXfdhQ984AMIhULYtWsX7r33XpTLZRw+fBgnTpzA8PAwpqenN3uoXcFYWn1ZdXH4cyu1tX+3\nWsD8Sk3RzBjBXm008cR9e3C2UMFYOoZG010TaJEQ7DlBsA8Kgn2xpEaZLIkok8tj98JwKoK4HVlz\nI+gimAukoOQry1V85t9eWfv8gf07lbmq1FWh+Yf3uUMnO42Ccm1uhaprY2JRfEwBMBG83QjMYFxD\nqaaOo1zfOMnPBBZrVWvCmZwm64LldwBAX9TGYx58hQwNlsrSBfIeA8Dcirp25laqgIN3YdUCgjwT\ngXe+85145zvfqfwtlUrhscce26QRXTvUmurLekij0ZtooV5otCzPlwDgBHt/3FL8xfJ9zSWj+KOv\neV+jLu71D4T1U6x4k4sAkIqFsVxuv6QWgEQ0rHzPNqZ5QRjPr9SAQfUYRrCzTVgK3pwmso1F8TGC\n3WRNdCMwg1lQQ3028uV2hJZlwaVkmFSxZQKLRSiZ1A9j6yITVV1U/VG3BDwnCPZzhYoSpFJreK/v\ntHhmTz3gfmbDfapgHBbhWrsHYsp97B5Q5yLIM7mBoTOvXydKLDAtlLlEWPY6wKNAVmvAaYcJL83n\nkghDLdfcmrJLixWhqmfFy3pWvKyXx+HVPIhtTINJdaMf0mz0wynvF5rNdy4hOJeEO7JtNGUj5Oio\nN5xUhSITFiaZ/N3IVcmJ+com5PPwdo+WG6oPv1zXWMVEcLLqCiYN5iyRAyKtpaVKE6/kK2vr20IM\n433qMaMig31UZLC7cjyEEiLD0s8XqnjtgHTjql4E21Lnq9ZseX4O8kxuYGwX5vV2jXmdkhqN2FiY\n9sey1wHg9EoNlXoTzSZQqTfx8nINu/vXF3pL+Kjk50wigvlSHUD7xe2Pu5cS02J3ZlWtS1ejiYVf\nniOadJ/IQk5qNFBmNbCSFjWDsjGFmprJLIUFUyB8yV4HEIJKsIdEBjtzQVUbvLghWzusosBloeiV\nAZ9nmePCaj54r1ujzwmCPRdXr8IsKJeSknI/s3AohBcX15W2PUJpazRbilCUbq3twgLbfhX5NN1C\nIEx8RtJWCeOk7d7czheFRlOs4rUOHzwjtmvSj9p0+1FZu1D5E0m7yGtUNb5aSfI//lPqCxsJeZPr\nADAmhO+YEL6MYK83WspGI8cNcIK9UFU3pkP37QEcGxMTaNpjBK/CLJONZK93kqtSbngT7LuEArBL\nKAAsYxvg1g2zsEyEIlNC9MmuKhqtdphyswnUGk00Wqo1yQj2sAEBXxJzIeebE+yqsNGVr/ELgTDx\nGUvlOkbT0fWQ2nIdED5lll0eDQMTmfganxGLSOHB/ajsZWPnYOQ6wLPoGbkOAI2G+tI3RIY7I9hN\nNGW2CUvhfmGlqrgmc32cM5EJcKMyOY1YJhvJXr8ST2JiTTKCvcHcin0ql6bjdlimPuM7TKK5WAfD\nhB2hvGJFKB7yMyP5zxbU73/nJ3a4mlvJoq3yHbFaQliIF69c5+vbLwTCxGeYhNRmYyFFo8nGVB98\npW55EtcmflSm8TN3BiPXAWAwqW6gg0l1DOlYGHkHuZ6MhV3nyMQjazkHTbRwy7AafskIdpMy4GwT\nzsbVnIWs2ISbrZbyvBoaS1DmZ0j3UTfqmDGsVr0tAoC7Jllou+Trzhc1kW0kU58VrNyZieLxn9p9\nRf4J4AQ7I9eBdhi0l/XOxsHIdQDYlVPPkRV8W63lLSxMLEG/EAgTn1GsqLHrq1U3kTqeimClFl8j\nILenpaYsNsii+iLsGYgpC3RI87IlbCjRWrLepCSu5aZSb6oWQ7PpdhNcXK0qXMRFsdBLhFwHOifY\nmdBs34t30mG/INj7xQu/Wmso1mal7p4Llp9xkZQpMdHGGcHOwsEB7r6UG+SQ2CClVZ3TFDK9UHSH\nwzoFTr7sHapdFdp5VSO8i7Um6o3WmouqWLUAB8HOyHWAKyKrjZbSSyQVVV1QjFxvnxee52BjGOuP\noq/cXHvX00Lx9BOBMPEZqZjtqoklcaZYx0tL6z2ykxFLMZ93CL+1JP6aaMEOhxAKAXY4hKbGJ1Wu\ntXDaEc3yKuH7TkZV4johuJ10LEJ7wI+koihWywDaWu6IICB12qG0Gjol2JmbDGgX5HP2JLdDwN6M\n45iW5Umwm8wFcx+NCO5nRBT37EaL4xFBCMvnAXD3pSV4gJBwvWVESLlGGUdOWKw5YbEyocf4PoC7\nN4cSlrLRDybcPsTtwlW2Xb5nkhwXQi1uh1Cstv/dAmDb7o2+VPXmTOS7PiHGwKId/UQgTHzG2WVu\nXjOCnXFsJvkbjGCv1FtKVng0rC5iF8mvIbYTEUt52WR2ukniWKcEeyoWUTZYXWHNSl34xmvqZybQ\nTOaCFWGsipwF+cxMGnAxgr0l3HEtjUbP3JfzK1XH+YCFlSrg4AGKojChbnMrivI0xYpqhY0SoWfi\n2imR7PVSo4XqJXK92miiVHdv9Ky6QkO4oGTOGCvSCHB3cjikhjiHxTBNFDK/EAgTn2HSfS1hAzsy\n8TWtKRlVX3oWAbIoXjbpXgI6J9hNSP56S7WQ6uKkJlYDI9ibLe9oF5MoKHYvzGowmQtGsF8seW+Q\nJg24soJgzwhuZ7lSX/t3qwUUqqp1BPDcIEawm2z0Y+kolsqra+N0t6VW+aWwpa4bk4RZlr1uAcra\n1AU3sOoKcxp3nTMwwySPapQEZjDLw0Qh8wuBMPEZqRgUYlDjacBqTc1gd2s83tEwg8koDpOXjWlE\nDCa/b7ba/urLfutmU1WrGLkOAAuCS1gQBHuZ1C4yKSHCImpkprN8HrUG548YwT6QjOITHs/MhDNZ\nkS4TYVUwch0ARtM24pHwmg8+I1oLMILdxIfPIsISNlBvtjf6aDiEhK0Kk3lRgmShpJYgATjBXq6r\nVoMu6owR7EOEP9qR8XZHA0AIwm0ovmfCORpuKftJNBSEBt8wWKm2lMxb3QKTBKUMRR1J2UjY4Su+\nsPmy6u4oVNwkPyPYI8K8johV7gpf1hCtnWavA+7EL/nCLpW9axexJmAAsCcXxVMP7L1i6ZiLq+p8\ntjOd1+/XJMyUEew6Utq5QbLeGpfHqQh4l1DkuUEV8cyk4GQEe72hEsoJ280fMbdhtWEpLqhqQ118\n4/3qJq8TWIxgN4k665Rgj0bUdyiq2W1P5SuK9fN/vWVCCR+WvKNc/9EwcNngtC593iwEwsRnmORn\nsKzWcEg10aUfNZdQNVBZEgPgBHs4ZMFJzoQF0yqJVp2FdXHVuxikSbJfNNxSriNzahipLLvdRSy4\n+myv1Lx924NJG8uV9fmUeSTsPgFgLGN7hoAy4RwNQXleGi6XzoVpbpCX4MwJ4lp6aVeJpQgAgyQv\nh4XkVsj3ACfYTYIRGMGesEMoOAj2qHgoDcFDys8Ar4ghEzylC3Wl6u3F8BOBMPEZTOMHOOlWosSe\n+hJYGsaeEezNlqph9gkNU/qYdfl0zN3GuIj2XOiE3DryqyqZmxcaf63OtfGFkjfHVK57v9ADCe7D\nl1aaPIbV91quNt3PK6UcQgl2k9ygTFztlCjHuVyB2wpzjINZikB7fTvvVb4DjDyvNuqKgtFsaOrC\nEYI9RKLSgDYf5yTYpStMBhvIuZJhvzorrS/aUoRen+BHmTuZJdT6iUCY+IxoxEKtaa1ZFTrTl+Vf\nMIKd9aaU0AzWAAAgAElEQVQG2qUevISaSyMSG0+1rhaC3JtzvyhLQstdFlou4yJ015Fht+P9UeQr\n62SurENmUlWVCT3GiZTraiZ/pe7e3Aoiv6ik6Y3B6ns5oRPejGA3yQ1yuVhFkVC29ralVAVhm0ZB\nqNRURcYOqcKGhc9Hw9ytGLHafMtl3kWu71eEe+m33zLhKsKomwunK6xY9X6mLHsdAAoVTYVvh3B2\nEfTCgjJJjPQLgTDxGY2mSko3BCkNcM2MbX4mWd+sKQ/zvzfFi9Jsul+UoT5v95CJVsXcJozMdeUs\naAIFlgXHJENVB5IRpQx+OqG+NvEI39x0HfOcYKXfWblzgBPs2YS4D005Fbl5SffPjkwUxSqunEci\nmpnpiO10HNhhrUcrpoU2zsLnTaIVi1VvC2r3oJrYm9FUemYEO3umLHvd5F5CLXdnSxWqNWrky7xG\n2HRhcubMGRw5cgSWZaHVauH8+fP4hV/4BfzkT/4kjhw5grm5OYyMjGB6ehrJZHKzh9sxGN8BtAn2\nYhVrWlWfWOiMYDcJP5YRMfOC8GUhiybWD/P3ykZhukQ85jZZrTYUl0c7+3x9We8Z8CbXgfamsOTB\nMbFAApPSHKWqt1CU9b1kPTYm3AFOsEuuQW8Jqi6khnAhVRvelqKMvtOVyncR7EKhmsh4J+rlEjxa\nkTVvC1viPXSdgRPsLcGpyMraJkrdaCqKFQfBLi2LqA3UW+sWluQM2+/DpfG0LlunN2gJ+vHxcXz8\n4x8HADSbTTz66KO44447cPz4cdx666148MEHcfz4cRw7dgwPPfTQJo+2c9Qb3D3EdAtJsEuyti+q\nhh8nNWtrTJD8Y8I9FI9A2VSkEmuST8D8vdJPrfNbM6FmR0Jr2qFuc2Pkehve7gh2r7tyqpbbH3dr\nCEwo2oRgZ/MAcNclixIEgLgdwYf+6cohs0woMnId4AS7fANa4vNCiYcGs1wUaUhruHH0RUNYrqx/\nTkTVCY3aFmqtdZd1TNyqq1KFpsUCcyfXGhZO5a9cop5Z/35i04WJE88//zxGR0cxNDSEkydP4uDB\ngwCA/fv34+DBg9eFMDFxD22UYJcvX6nGw4/lvk0K0rpgkjjGotIsq6VUP9YFCtghNZrLFglsTDuU\nzch0iWOszDcj2BuCaE1qiFbZY0bORbHSVDgTXb6M052he17MdbnNoGW0bFy1JCwLJhQjhFwHuBs3\nHFKrYkfEMzfpEyLb4c4LgWOSZ8KCDRifl4ioyccJzW5Lw7lJAIlJ9QW/0FPC5Bvf+Abe+ta3AgDy\n+Tyy2SwAIJvNIp/Pb+bQugYT91CnBDvTUAFNFr3QiJgFxch1wE1+yxe20bQ8X0agvUF6dXxkfmmT\nBlysjzYj2ENQhaLM2AbcNZhkxd7VWkOZz0pNJcdZGZPLx3i5LutN72oCAI/mYgR72Goh5iC+dXPB\nCHZWFTsdhRqerLG8GTGts9Jkngkj2MOW93NnwggAdg6oOTMySVRqDVKJMKm+4Bd6RpjU63WcPHny\nitaHxZo5bBHUDMIaOyXYmYYKdE6wm5jXLDHMJCeBZbizuTBxpcVsVROOh0XBPkKwVxremx/Ae7tk\nEjaecWziks8wySxnrktWrh8AVmtCcMp2zIRgj4gJlp8BzmcwZUq3SW8XLXdZVWyTKKihPlsJWJA8\nFnvuJoECZRIyzmBSfcEv9Iww+Y//+A/s2bMH/f39ANrWyNLS0tr/M5mM9nezs7OYnZ1d+zw1NYV0\nOq09thcwVKyt+WEtANlkxDXe1XMXXC90Op1b+35buuYi2J3nWH7lvErQl2vK7wFgVJxjNB1VzlFb\nWHRp/M7vV+cWXBqRvI/hvprrhXUes/Tyistlkk4PKeew5srKptBqNpRz7B2sKQR7Kgrl+8rCgnK+\nSq3lGmdlYdG1KTiPOffiWRfB/uO71ufzrPj+rPgeAMbSdWUuxsQzmzt1TjnHXKmKOxznqF1cdOUs\nyPtoLC66NnrnMSN9VTWvp892naN/qeaKUHIec/HMBcGDqWuzkl9UyPVKI+S6xrZ0DX1RVTA6j8kl\nai5lyvl98ex5VxsHub5RWISE8xypwoJi3aRs97po5b3PwZ77eH8Ny+Ur3ycAnH9Jfe4XilXlHJGL\nCy4vg/McA8s1V6RhJ/vf0aNH1/49OTmJyclJ49/2jDD5+te/jre85S1rn2+//XbMzMzgwIEDmJmZ\nwb59+7S/091woVC4pmPtBJUGXKUi5HjTcXdJc+cxOoLd+f1I2kZclFuR19AR7M5jdKSz83sduS6v\nkRQJWUm7pRwzIXiEiUzUdY6EHXYR7M5jShqC3fm9LklUXkOnQTqP0RHszu91xfbkNaIRlfuJRlri\nHOpcjPercxELtxT/eyzccl1D1+7ZeUwopFoVTz2wx3UOHcHuPGYgoTYKG0hElO91iXryGjoC3nmM\njmB3fq9zk5m8885jpKfDsizXOXSRl85jdC5U5/e6KEB5DV0HTucxrrw0Wx2DLhL4ave/dDqNqamp\nq/ot0CPCpFKp4Pnnn8ev//qvr/3twIEDOHz4ME6cOIHh4WFMT09v4gi7Bx7JwknlaqOlNP6p1tUX\no2ZQH4mBEewuQjnjdhOEHJR6C0BIvMCuiHnNi8HmgmWvm3BUzK3ICPaBuOrDz2qmuyLIWsn91Bve\n/NJqXZPcJsAIdkmuXyzVXLxLpwS7SaIec/Uygt2kjUNFEOxPPbCxTH6AE+xJWd1buNJMQoNlgIks\n1MjGYLKf+IWeECaxWAx/8Rd/ofwtlUrhscce26QRXTuYhNQyUrm9KV+5bhbjGQBOsLPKrJL400XD\nlMmLUJWRKnX3xtOyvCOtmCBgkUPt+VJ5gqog2JlAW6mp1map5uYzZF0n+VlnVTj5JZMNlBHsjFwH\nDOrCEYLdJFEvFol4EvCZmCqcZTCiSfdMXfa6M8O9IgRaXcNdMoI9X/bmbkzKw5cF7yLni/GKJuvb\nLxgLk1arheeeew7/+q//ikKhgGeffRYvvPAClpaW8OY3v/lajvG6AqsCCnCNRiafuXvA8/pILoJd\nbJCMoFwSWq6siQXwF8EkEoUJRpa9zhJAgXZuhdfmFg5b7dC0S4iEhfA20A5ZXSzZEEqWzTDJWWAE\nu0x21UXgsSZdjGA3UZaYNbkkNulD9+3BmCNfOWtgCTLrZigZQcHBXQ4k3VthpwS7HVbDuW1NZiQT\nBglbLVgpLReTzq1+wViYfPGLX8Tzzz+Pt7/97fjzP/9zAMDg4CC+8IUvBMJkAzCJC2cZ7GxTMGnx\nytw/fSL8Uso8Fn0EmLhMVE4lpEkds8PwPCaX9M5eN+l2x7R+JixM3Bksei4uoo/iQrlsijBr6bYB\ngG2icOa2tHoSkwg8mZ8hS+FLzq8iysObRJ2xDPYiqWNWaUBxn1Y0AUyDCXXdDIpWOas1KMmAurB0\n1tyKZa/nV+sYTUfX7mN5tQ5k1Dlnyk4sYqHmqEwcEd0eWWScnzAWJl/96lfxsY99DP39/fjsZz8L\nABgZGcGFCxeu2eCuR5ho41Lzyoh1Ppr27meSsNXfayrQG2mQXihVVddQWYaQQk+wO2GHvbPXAcCy\nQp6aV4v46FmuAMAz2JmwMLEa2Fww3/hFmUyo4TsAN8HuBCtvA+gJYSdYJVyTnuTFinovK8Ka5Hko\n3nwIABSqqtBbroQw7BhqVAQ0RMNupe6mwZgrUtBrPmXuUJbUdLs8n161+pgyZOLp8AvGwqTZbCIe\nF+RPuez6WwBvmMSFF6uq1hQJxYE+5zm8X2iT3ApGsEti1dUcy+BFscNq/oYsEcK4CIC7RFx9V4QL\nihXj00IMgwkLE6tBKhHyGFeZe7Ex9cdVS1Cby0IEjlx7Dc3ai5EyOizB0ySPKh238bGvXvlepGWy\nKhQAxocAXKhVRZkSk3UhVyfLHepGIAxzpbFyLH7CWJi84Q1vwF/+5V/iV37lVwC0NcIvfvGLuP32\n26/Z4K5HJKPe/nmAE3+MR1ghwghw96+W2dLSb/2E8FubFCct17y1bROylhHsTFOW5SikmxFoC1tn\nCGhICtKwd0UBkygpdgxzg5nwHdL1KOfKZO0xsJL+jFwHgEZTLc7ZajWwEcuE8UsAgFZDsc4tcQ20\nuCLDrAJmbZoEwjD+k7nSTFzFfsFYmLz73e/Gn/7pn+Lhhx9GvV7Hu9/9btx22234zd/8zWs5vusO\nJj7OaMRa8wNblz47wQl2Hp6ZS3oX5OuURwB0WuvGq6oygj0iBK+s48TKUQC8Flqp6n2v2QSPkmJ8\nxatEWQ3ZidHkGnlR4qYgBI5JRFjEWp8j69JnJ1aqdeUaqzW1Si2zJAEgHAp7Cgs2TsbnAUAqFkbR\nwTUkYyr73Y3y8MzarDebioXVaro3elYCh7nSTFzFfsFYmCSTSfz+7/8+lpaWMD8/j6GhobXaWQHM\nYdKVr1JXLQsZtssIdla4EACyce/2qyz80kQQJGMyDl/d6F8zFMPTD+xd+14TOUkJdliW4nOOC7PB\nhKNiRCu7V1ZUENBwO8JpIt0yMqDBpBbaYJ+NvENgyfIfJq0JGME+kvLm65glCfBGYSyk1sSNy6yK\nbpSHX6movGGporr0hvoiNJKQtnqQrsmG6po0sbz9woY4EwDo7+9fK3nSbDYRkj6BAJ5YFNm9i5qN\nJyLIwYgIB2SamUnimCx1Jl9IFn5pQjpX695+6QJpYARwgp2j6SrHIsE2L3avLDcD4AKeRTBJy0QX\nPccI9tGU+kxHUq5TULchs0gLklzXBDykiRuLhdSu1lWBt6rJ62kKNxeEm2svIde187lBgp2R64Cm\nfbD4nrkmpQtW8pJ+wliY/OIv/qL27+FwGAMDA/jxH/9xTE1NBYQ8wajIUtb1pWg01eZBMaFtM83M\nxIRnBHtVhF9WxR4cj4jiiJqVxCJmzFwi3gQ72/xSsTCWy+svdDrmDvYfYZus4AmeFu6MBnF3AJy4\nzsRt/OjilQMFpLtPNkQDOME+V1KF95P378GQ0AE6JdjTMRsfm/EWeszVe2a5qrTU/b2f3IG9Gafr\nh7tYYxF3GR7lPlvqRl/XbPS0PHwXCHZ5r7/zEzvw6gFz16RJhQe/YCxM3vOe9+Db3/42Dhw4gMHB\nQczPz+Pv//7v8cY3vhHj4+P40pe+hM9//vP4jd/4jWs53i0P2Wb2Spnj3tqfm2B3kuMmYb/LmnOM\nOmLxpVYlX7ZVQq4DQKnmXQKEuREuj8PrhWWbnyTXdZ0t82VV011aDSnFdOcFeb4oyHNXDxBd2C7h\nbliCZ3/cxsc9IqAArsVKV1neoG2AtG76ohHvTVqQ601JfINHElKCnZHr4G0BTARSpwS7Ca/IkoNv\nHlZdwdJD0GmIfzdhLEy+/OUv42Mf+9ha69zx8XHs3bsXH/jAB/CpT30KO3fuxPvf//5rNtDrBSaZ\n49yf6+36Ge7jseesYx7bxBm5DvAcD0YuAp0T7LzRGN9YGPmtK6zpuo+Qd0QYC6ow4UyYxj/Rb6M/\nZl+RJwM4wc589MwiANq9WLxcvWlRTkWOsy8WxooHuQ7w7HWTTVhanNIiLYkeNGXRg8as1Il3D/eV\nmndk5pbMMymVSqhUKkof9kqlglKpBKBdMr5arV7p5wEugZGkAPfRM9cPy1kA+ObFtC5GrgPAeNrG\ncqVNQMbCIaSTMiFL3bhKVXf/6kbLu4EWI9gZuQ5w4S3DcqWLycTdwdwRjHcxyV5nGr+uYrUEI9iZ\n5WJCCDNX76oIQImL+TRRENhzN9mEi4JgXxEE+46MjUzcvmIAyfZ+G0vl9fWf6XPPN+vhzpQ+Ftjh\nJ4yFyV133YVDhw7hp3/6pzE0NISFhQV85StfwV133QUA+M///E+Mj49fs4FeL7AljxDRFDckSXDM\nanBpl5pNmoWiMq2LkesAr8w63m+jP26vWR06pYrl3LA4e5Nie6wb42DSRt4RUZYTEWXM1QZwLVXy\nXjJAwiR7nZHfbN0A3DWjaz3gXFtM2AB8fbda6jNvNdX5ZOQ6AExk1Oc+IapFusoaNd3PjBHsLPKN\nJR8D7aRaJbBCuL0tq+UZQOIqUb+JpXuNL/1Lv/RL2LZtG77xjW/g4sWLGBgYwP333497770XQLuv\nyOOPP37NBnq9wEWua4i/FVGqpC0MHDkexGqQm7QuUiUElUuQ7iF2DpNyFKwyq0m0C7NM4nZojWCv\nNpouTZqS63Bv3HQjF5aeSUQNS8QrC42+4tLwefa6JL9dkT/MZQhOsLOwdOYmA9wVkmUGO2vnbOJK\nk/16YmKnMwkZ75RgN3EFz2t6t8BRLdoOe+fk9BKMhUkoFMIdd9yBXC6H5eXltb/PzMzgbW97G6LR\nzfPVbSWYkHJ90YhnZA+zGmTvDN3LJtOn5DJn52DkOtBud+v1IphoyuyFZAR7saJGpRUqrk61ro27\nUhN+a2LpmeT1sBIhbHMzyV5nCZ5MMAOcYM8lVeGcS6q/Z5o2AGwTBPs2oakwRcWkDE9RuMLke7Yk\nLKy8sLCALhDsBgmzrx6MKgT7oJhPFvHIarr5CWNh8q1vfQt/8id/gm3btuHUqVPYsWMHTp06hZtv\nvhlve9vbruUYryuYJEuxUg/Sfz4o/OcmvdUpyBhMCiiyF8FEU+6UYDcRrGwjZ4U1TfJ6WOgv0+hN\nKids77eR9iDYTTRlxnlcXHW7bpzhxS6BpgkUGBACaUBsoLDUpmrSVDQJfWduRVaiHugWwe4NFlXJ\nkkCZG9hPbKgE/aOPPoo777wT73nPe/Dxj38cJ06cwKlTpzoeRKlUwp/92Z/h1KlTsCwLjz76KMbG\nxnDkyBHMzc1hZGQE09PTCvm/VWHiw4/aFmqtdT9oTKxP5nZhLwHAN+G+mIX6pTFEwyGkxDBHDfqE\n0NBfkr0OdE6wm2ygNIKJuDtMNreNKgiSYDchjBnBbpTgRoQ3Ezb9ooijzjKZJ/kubG2aKGRZUuCz\n0Wwora/bBVfVczCCfYwEmJiAEeyscZuJtekXjIXJ/Pw87rzzTuVvd911F37t134N7373uzsaxOc+\n9zm84Q1vwO/8zu+g0WigUqng7/7u73DrrbfiwQcfxPHjx3Hs2DE89NBDHV2nF2BSV4iZrq7Kw6LE\ngglnwuoO1Zqqe6gm/GImfUJCUmsKbVxr6phgN3A1MEuPEewmGirrGMkIdpMwauY2NHHHMeHNCHZZ\n0XeuWMXrcupcXCi4ORNnV0lGsLOWAQDfpJNRnszKCPYS6Yliwsswgj2XFCVZoiK6zkBZ8gvGwqS/\nvx9LS0vIZrMYHh7G97//faTT6bUyK1eLUqmE733ve3jf+94HoJ1Rn0wmcfLkSRw8eBAAsH//fhw8\nePC6ECbRsPdngC8QVv5dLifd8tqRiaJYxRUjqcKi4J+IPjZycwHc8mBgBLssETIqCHaTF7pTgp1p\nwYBJZrl3awJW7hzgbkMTtyKL1mJW3KBIwhvUaEsjwsU0IrQd50Zf1Wz0OoVAgoe+e1frNQF7T+sG\n7SYYwc5EQ8wWlSg0gTB+wViY3HPPPfje976HN73pTfiZn/kZPP7447AsC+94xzs6GsCFCxeQTqfx\n6U9/Gi+99BL27NmDhx9+GPl8fq2QZDabRT6f7+g6vQLpI7WFjxQAdzUQt0vDIEqKcQmsEx2rrwQY\nJD4aEPCMYC+J1KaVKpCLOj/z6CJm6TGN3oQQZho9I9hZNjbAXR4mLpE9uahSs0oaeoxgL5ZreOSO\ncZQ8OBOWlMjKr5UMstd3iPnaIeaLdZQEOifYt6UjNM+E8YqcE/ROzvQTxsLkwIEDa/++6667MDk5\niXK5jImJiY4G0Gw28aMf/Qi/+qu/ir179+Lzn/88jh8/7jrOkvGaWxQyyah1FUlGLMrEZJOm/RzI\n9yblzGMiKicmtCYT4pqWhydCb5i4sACgPx7xtCzYOFmPeKBzgj0WgZhL1yUMNGXuEikTJYOFso6k\nbSw55nsk7Z5vmdIhP7NN3KQBF7POWRkToHOCXdcTaLvIM2EEO3P5mXkI/MFVp7gMDQ11ZQC5XA6D\ng4PYu3cvAOBNb3oTjh8/jmw2u+ZWW1paQiaT0f5+dnYWs7Oza5+npqaQTqe7MrZrgdbFRZeWK8db\nn1twabHOY5ZeXnGZ8On0+vNozC+o52u0XNdIFBcVgj0ZhXJMtLDoCgJwfr8jW3Nl6ctrVC8uujZ6\n5zG1hUUXcS3PsXj6nEtzS6dz6/cm7rUm7rW6IL5vuueiRs5Bn1l+ERLyGkN9NRfB7jxmJFVzEezO\n7yv5RZf/Xl4jcnHB5Y5TjhFzYWnGWbow71JUnMeMpdXnPpZWx4lldS5ammsUFhZdm2x6bP2Y8y+e\ndRHsb9q1/sz7lmqu8GV5jYaYi4Z47unigmodRd3rYvtKzWVZOI9h7ylbuwBQOHvelWjqPCZG7nXA\n8f1lRaiT/e/o0aNr/56cnMTk5KTxbzcxX7KNbDaLwcFBnDlzBuPj43j++ecxMTGBiYkJzMzM4MCB\nA5iZmcG+ffu0v9fdcKFQ8GPoVwWd71yO19KUTXcec5OITc/ExT1rzG95jUZLJdgbLfUYnUXg/F5X\nNdg17xrrRjlGU7BPnkOnuTmP0fEZns+/pfmezJfOMnF+r7ME5TV0vIzzGB3Bztax/F7njtvoOXRc\nw0bO0dRkr8vfh6ym8twjVlM5RldOSF2bbst8o3NRbajJw9VmyHUOXQa78xhdrorz+/H+KJbLTSWk\nXF5jW8pGX1QNlnEeo4ue28j3G0E6ncbU1NRV/RboAWECtCsSf+pTn0K9Xsfo6Cje+973otls4vDh\nwzhx4gSGh4cxPT292cPsDgyii/pI2XQZZVKuixBQUlQQAOyQSrBLUpllr1cbKi+jq/PEIpgShGgF\ngHJdDY2siXGwmlcmBHxMCEbpjmOhvybtWRkvY0KwMzCC3WQu9grORFQhcSd4is9hURdG1o0DgIQd\nUrogRsXiiwkFQQap8E6j3DUZDbct8suW+dUEwuwSJYlyIjzepDJxjVTnpgS7wX7iF3pCmOzatQtP\nP/206++PPfbYJoxm88EIdkZQmoSAsj7x3che70Z5+OFkRI3lF9FcrPqrCQHPSEzmozfJ62G8DCPY\njeabEuy8UVhBx1E5IuRMBBIDK6NTIG2Sd5NNHOCKTIHUjQMMgiZsoFhdF0iSjjOpTMyeay8R7Aw9\nIUxuJJhYDZ0S7CaFBxnBfmbZOxmQkesA16pMqr+yRDxWKdek2i4jMQcSkTVNGnCHYrM8FYAn+yVs\nlWAXl+jKMzVpFMaee0kI57JGODN0SrBXhLLVpytYSd4hE+Ka3euFFbdAGnIMxSTRtNFU3ZtP3KcK\nLDZOk/3ELwTCxGeYWA1M02UbSzoO7LDiCrkowbLsWSXdRsu7GyTAtSqT8vBMcLJ6VCbVYQdIngjT\npOU1apprsFyV1ZpoRStclybuDBZVZlK4kD33IdFCIdenPi+TWlEsg53VB5Oh2E2NqW6H4ZnsalLB\nIZuw8YxHGDRN/DVYe3MrqntzbqWmFI9ja7MvaqHeXA+k6dP0qPELgTDxGcmIqtEnNSXoWRkHZn43\nWmpto4Zm62FWAfNbm7hdWFijSWkZ5vvOJW0sOcrDZxMkLFKn0BvkiXjBxPXDlAgTH36nMOF2ouS5\nW4KXCcG9YXpp2gAXWLSHB3FhAUB/LITlyvrnPtmXxSAXi4VB6wh2T2iWFQtRZmszbxB+7BcCYeIz\nqk13FIkEK+Ogi/ZygpHrgEEXxHrnrjSWyWxSHp6R30z7M3EDsM2Ju2V4pjPbyFmSKAsSMBknK91x\n+Rxez50R7PMlVdOeF5o20OYa1MZq6hiYZW6Sn1TXRCsq3xsoQ6xhGSPYTdZeMqqWC5JN5upi/Uul\n77rIMwlwdTBKKCRg0V6MXAd4BjsTFiZFAxnBviqy10tVd3l4oyrLTsjcSwO3ItucWPIaI9cBvkGy\nSs+sxwfAuQaT3hgm1osXRvq8S6UAbUXFy6W3TVRplrW3TCwTZnmb3Ge/6CYqDWdGsLNIQ4A3mWOZ\n+swN5icCYeIzOn1ZAQPfN8tuB89gZ215XR3eNPt7p9nrAHeJMJhYUIxrYLW3TNxkrPgmjQgzeKaM\na2ClOwCg3mwqgrO1wdp7lgWlp7mucEWtoWr0TwouokrWt8k7xELbTSLwzhfdLqRBx/JjBLtJpj57\nrswNZtIm2S8EwsRnmLoavMxnFknFyHXAZJP27inRjT7cJuU9QpJ43mAgvYkFxaxF9sKalFORPnqZ\nT+Aq+yKIbRNtnI3TxMfPiogygv2VfAWf+bdX1j7/9lsmlC6KgLuysKwazNY3I9eB9ZDyy/cxkFTv\nw6SJFxNIzMXKhDvAn2s61nJl6isI8kxuXJiEZzLXDoukMomoseUmK4bBhIUui1mCEexmG33LVRZj\nIzBxc9FkPxLwYOK6ZAR7RGyg9lXUMWPjNInmYq5J1gXRxJIcEtq21OirDW/XTy4RwuLq+ueMJhKL\nhZQzch3guVYuiEcSAm9cxbk077noRt5PtxAIE59hEij0mqGYUi5F+mrjEaBSX9+Y4uIpmnRfqze9\nP7Owx3AohJeI1rVNEOzbBMFustEzvzMjOU3cXJWGdwgzKyVu4nZhBDvznZs04GKBGSYCiVWcZhs9\nI9eBtvvH2ZiqId0/xPWj6044JvrmMQF/U04tSZSTlbth0CmUEewGzd+Yu41Z7yZJuX4hECY+w6QH\nfLXpHc1VrnuXUzHtYOj1srF+JyZa18WyOs7F1RAGHOcx2eg7JTlNrB8mOLPE9WPif2cEO/vexP8e\nIQS7iTsuHCJVCWg7Zx78kSTuHzZOo+rHBom/yjk01BDrFMqUIROLlbnbTHrpOH+/JUrQB+gOTMpa\nm7gjvGAisEzqOHlpqEybN7kP5pYBOMnJ5tMkUIBuGsSaZHlBACe2GQ9g4n9nmnQ3IgmZhWRiFTNu\npyLWrysHyqAhFO3fbhD8IdtFSD8WU4ZMlKVV2Za3trHacwWRtLtSCUKDbxikDJpKdVqkzqQmEKvj\nxLxyo3gAACAASURBVASSSfZ6p90F28d4k5y81zdPTmOdFtkmbLIxMWLbDoc8hYVJ1A4j2E3cXIxv\no6HaBlYxixSUfMZ8SQ2HjYYtVOqXLoe2wiAhNfZD8j0ziI5jG3k3ijCytrxsvtNxGx/7qsd9+ohA\nmPgMk6ZSLBqL+d/H+qPoI1E7zK0SEQS7LQh2E6KVvWwm+RkuiPeVZUtTtw00rWpFxV4mFBkpDXAr\njQkLEyuOXcMkyo/di648vDJOA+uH8UPbRFvfbSlJ0HuT60DbSlMIdukeNeCgmFLGcn9MyHHW8ZQF\nsTSaDZUnE1Um/EQgTHzG3sGYUuJbk9NF+68zrcrETcbcAKFQCC96aMoJTT8TCfayMUFgAurOMAhh\nlqXEB0R0ENvIGSkNGBTGJFqsST9xZnmYWGmlmuWupusAI9hNrB+2fsMhrN3rcMp2KQAmAmvPgEqw\nZ8UhJtY7U8oYd+NSUsqatgJkLkZFEMuoCGJxVpm4UnSoXwiEic9otLzzDQBuebDYdBNfLcsyZgR7\nxaCfCW0ja5Agx7Q7dh8m7jgpfPui6nyyiBkTQpht0iwyKEF6xAOcuDax0th8seAPk3wYdkyl1s49\nufy9HVK1cZPouXLDO8vepKIvU8oYOb4jK/rQZ93XYHNxXlQmfvL+PRhwNGvslF/tJgJh4jNMHj7b\nnNjLZEJQynQNqUDScFkD7ZBp9IxHAPhGbom8CJnkaFJMsilyWZpichjBbjLfNAGO+OdZj3igOwQ7\nmy8mkIzCj4mywzgVs+g5Vk/Nm4sD+HtGIwktVdhogud4nklVJegrgqA3ak3gE3pCmLzvfe9DMpmE\nZVkIh8N4+umnUSwWceTIEczNzWFkZATT09NIJpP8ZD0Ok5eNbU5Mozep49QpwW6yiFk/CBPB6rI8\nhKuBEcZDSdVNMKRZQlRTJoU3TeY7E48Id4T66jG3iwkPxp6JSTLrcJ86X8MirJe5yhJRC/XWekn0\npMaNy4RFo+mdlEvJdRiWMnFCswezahXsmTWhCl7dNs8EY9z2tkhblqqw/aGmSrNf6AlhYlkWPvKR\njyCVWncIHj9+HLfeeisefPBBHD9+HMeOHcNDDz20iaPsDkxIULY5MeKakesAtP3XN1Ie3kQbHxS9\nLwaEg91EsJZY61Pic54vqW6CQ/ftwbDYQznBTsrDG0QGsfBi1uTLJNmVbdJGEUwN78/M+jHpYMhK\n9TAwch0AYhvNXtcgYYc9I+zYMzMR3q48E3GOSl0VijLBc36FV2n2Cz0hTFqtlmthnzx5EgcPHgQA\n7N+/HwcPHrwuhIkJCcrcXCzyx8QNEI14vyhcQ+XaOAu5NfGv06RF2p9dxPHXNRoqIb/ZBmmSDMgs\nQRmVI3u/mIBp9CbzXW2opdsrYukwBYC58wC+ybK5YuQ6wHNuTEr6s/dsfkVTkmWDtedYczeWXzTU\nZ4vSNJsTyQX0iDCxLAuHDh1CKBTCvffei3vuuQf5fB7ZbBYAkM1mkc/nN3mUPoJF9hAugrmGAE6w\nL5bcmcxDDuPExPpx5ZE0Nl6GhLl3WBx+KnYV4ccCLEPeJEmUJVeGQ7w8PAPjM0zmmxlATCAxdx7A\nN1n2TBm5DvBEVBNliFnf2zOi30lGWAQGeSYsT4QJtGjYUqo025I09BE9IUyeeOIJDAwMYHl5GYcO\nHcL4+LjrGOsKpvDs7CxmZ2fXPk9NTSGdTl+zsXaK+sVFl5tAjrc+t+ASFs5jaucuuMJEnd9bhUWV\nlA7BdY3KwqKLYHceU19YUMfUbCnfL728orzw+XId6fSQ8puhQs3VGlW5xrlVF/cjx9nKL7rm0HnM\nWH9N0czG+mPK963FBZdrR14jcnHBFUnlPGa8v+ZKBlTOMT/nchmm0znlGqnFmktYOM+xcPqcS2A5\nz2GyblDwniuTZ1a9uOjaZJW1JeYTYj5rBuNMFhZc7jjnMTuzNVcO00avUSPrtz6vfl9ruNcFe0cg\n1marJd4zMQbA/R6WL6jvcrVRV5872QvOnz6nXH9upYrbd6prbyM4evTo2r8nJycxOTlp/NueECYD\nAwMAgP7+fvzYj/0YfvCDHyCbzWJpaWnt/5lMRvtb3Q0XCoVrPuarhc5NIMeryylwHqOLgnJ+r8ut\nkNfQEeye89ZS53WnCHvcmY26fq9LyHIeo+N+TJ6d85hcQnXH5RLq9zpNWl6j3T1wXeMLhy31HBp1\n3fm9zmUor6GLxnIeo9Oknd+brBud+8h5zHhaTQYcT7ufmY5XUe5Vw/k5v9fl08hr6NxxzmMawvJ+\n6gF1/epKAdF1I9avzurY6DvSEtY90PK8j4P37nZdQ1eZ2HkM2wsGk1Ec/pr3u26KdDqNqampq/ot\n0APCpFKpoNVqIR6Po1wu47/+67/w8z//87j99tsxMzODAwcOYGZmBvv27dvsoXYFJpm3aUKwsygo\nE781JdiJT7khUkLkZwCU8O1G0uLiqptgH3VUgDVqjkXcQ532OwF4XgOrA2USuMHmOxVTBW9KU0OM\nubEY38HaI5hgTvQ7mStWlZ4oJnXhWH6SiZuLvSOVuvc4FkUL48VVd9JisaK6P1eF+5PlFy0I3mZR\n8DZ+YtOFST6fxzPPPAPLstBoNPATP/ETeP3rX4+9e/fi8OHDOHHiBIaHhzE9Pb3ZQ+0KTDJvWec+\n5vtOGRQF5P3XvWsslQi5DvCNaalcd7ldAJGgRvgISrAb+K1Zlnyn/U4AICQLIIZk1rewjoTv2yRw\ng823dKfr3OuMYGeFHE1yXdgzHRe918dF73XGYQG8YoAJOZ6Nq++IJPpZ//VcUiXHBzX1+Af7bMXL\nkBXHMGGzLa3O1bb05kRyAT0gTEZGRvDMM8+4/p5KpfDYY49twoiuLYwyb4n1QkuhGJSH1xHszohC\n9sK7kgmr7j4KTOjtFmVMcpomR50S7Cb1kdjmxDRhlk8DcC2WbcIm2etsvldqKnFdrIYUKw4wqK5A\nCoSaWILsmbJqAIxcB7h1bxLaLhvGyc+s/3o8opLjMU2UH/MysMKwUiHYaCfSbmLThcmNBhYuC3Dr\nhfUTN3EDMBcTe+FZGRPALESZJXWNCVfDmHA1MCvOpKYV691C+50kbDxDWsCyc9By5gaWCbP0THJV\n2DiYRm+ySbMioat17w2WuQQBkzL3/B1ZrWk+O4bK36Gq0sL4939yB14tWhgzBYBVPlgR+8lBzX7i\nFwJh4jNcWqxGo2fWywpxy5jUo2IbPXvhq1eTvS4ETtkgqYtlsDNNmjW2Avh8Mk14tc5zWdg5WJ0n\nE/fR9n6VYN/ev3GXBxMGNDGSuEcBt1vwSdkQirgVWRmTS8Pw+mj0jtRbqiUn6+ixd2hUVD8e1VR1\nZedgiZEmvIxfCISJz5BZ4TmNH5XVDWJarkl5+O3EupHmsvxsVE6lw+x1wJ3B/oTIYGfjCJGe5gD3\nfTO+w6RXOHumCdtCvblehiQhngfbYAGgL6oKXmlhmQgkRkyzxEgTuAj2lSpuzpm7FWlPFXBXmUnN\ntlLVe/0O99lYdrzLgyJh0CTggZWGYYmRAwmVlxlI3OBJizcSpIne0pjozM/PtFy5Yeo2UBl8JUdR\nqUu3gPrZpB0ue+lNItsYAck0UJMS9Gnil2YuEVbyAtBsbmKgrEeHieuSoRvl4ZlAMkngZBp7N5Ql\n1lKXkesATzStEpffqqiwvFpzvyQyA74gMuBZMEIqZinl+lOxGzxp8UaCiYnOKuUyn3G5Jj5XNVaD\nwSarQJzC5D5252IKwZ4Rbi4TDZN1UmSC18SdwRqWsXOY1IHS5bJsBCb3ITevkti8TIR3p+0NTJ4p\nK9VjQrA7n/lHf9p9H8ySM4ls63TtmRQy7Y/b+LhHBnxTXOPpB6QiAxxyCO+g0+INBJMe8KOCa5Al\nRNhGbhLBxDYndg6TEGfZy1sS04xcb8+XN0G5JBoQ5UUDIinQdIECu8gxTBNmdaAuz6fXxsK+N9HG\n2eZlstF32t7AZJwXy2okYdyOY8AhL2SQykcEqVwQZdlLVbclaNJCweszwNcea35lUr6GWSbnhEvw\nfLGK1zhI/Avi+wsrVbzuRs0zudHAtB2AbwpsI2eWDcBfevaimJRELwv3T10Q07l4S81ej+t4F2+C\nclzURxoX9ZGaYpOWja+AdiKel9CLCZeebGZnoknTLohE47fAtXF2DWYptsfvXXadEeyMXL98b85x\nynuVa++iIJWdeVRXeodMLDkGuvZEwIN0QZnkUTHLZFi4BIeFS3BUVDUYvZHzTG40mGRLs02BRXgw\nch3gZv6E2KQnxCbNmg8BvOLpYtndfXBURGsxkjMquIio2B+rYr7lZwAoCF6mJLTDAiFiTRotsT4f\nTOM/W1A10HOFKl6dFcmuxEUlrZ8+jdslFfNuA8ssKEauA9yy3iY2SJmIx8LBAU6wL1fclRO2C3cb\nW3tJW3XXyVgadh9Xmi+nZZEWQRXyFOx7PxEIE59hki3NNgVWtromchJ0rYEpwU6iYUxcJsxNQMl1\ncJKTbfQmGfAsMYy5Jhm53r4PQrATkn9nNoqnHtjrqSAwJUQqMnJuAW4VM9cN06QBblnr6q05YVJK\nn2avSwXiKtaefCfkZyZsAE6wszbJJkLRLwTCxGcwHz9gYpnYWCqva0xZEQ5oElHjgthXimSTNvGN\nMzPfxOXHuBsm1Iwy4EliGBM2JuQ6y2CnnS1bXEGgBLuBYGXCgj3TEUGuj2g2NmZZL4l6a08/sLFw\ncBN0Y+0tV9xVJJwVBUo19T6eesD9HjZbnGB3vodyrhjn4icCYeIzJkS13YnsxsupMILSxGrolGCX\nm2FIExo8Jsz8MWGDmxR6ZNzNDiHUdgihZsIfsSRRJmzM+pl4R88x4WwSGdQNwcpaQrPESOnh03j8\nXJ0SF8V8XhQbZFvhctyHgXXPCPZurD3msnaR46JgJeAm2M8Jgl3mmcyvqHkm6ZjKuVxNyHi3EAgT\nnyG1QZ12yDZyRlCyDVZ3DvmisA22RkhUAMgIV0NG7H8m5VYYdyPJcdlSl0XGATzUerjPey5MIttY\n7oR0kUhhbZIjwgSShSYh1/XtDZRzWFDyGlzJrAbVpIf7hCtMzGcuYePiqsPyjqtzydYuwDlBk7XH\nBCcTauw+AWAoqR4zJMi0EaGQjQiFzNXC+EauGnyjQW7COgKeuQH25lT/eUbICpMYek6we9cQM8kz\nyZfdZr7TDTAkCU6NU5ndS41ooCb1qHiotbdbZfdAFEtlXFFoAjziiwlnk9bArGpBHyHX2+PwtoDi\n4RYql9x10XDIFSggWwI8IVoCAG3B6RRIUpC6uAox/yZlY0o1twsKDpebydpLCM5DJpczocaUKQBI\nRVuCQJfVFaAoAHGxY0uBpSsc6xcCYeIzWGYuwEsorIqaVrY4ByPXAb7xuF4UYf2YuNKKJB+AuesA\noFDxFmq0RL2BC4rdC+vtUqx6b1wm98rWhVkpFFUgNZrSDWNQHp5wJlKIyc8mOTdMIDF3XCyibtKa\nzsDUjSWVOJ1SV66rzzUWUedrW9oW5d/V+8wLcvzJ+/dgTEQr1kX/l6rgwso11T0qQ63TQhj1Rw20\np2uEQJj4DBN3BYvw2HBTKc36Kla8NzddVz4nTAj4NCkPz9x1umM2KtRMhB5LnmT1qlYNktMkd1MS\nBT7ZujDr3+4tkEzOwQh2VqpH1/lPolizPIlpxnOxKCqT+zDhj1aqLc9jLFiujpBOmIRJyxwnKSwu\nrLiTEp3nKDdUYVRuaCbDJwTCxGeYhDXKCA+ZoMb8vWYvivfm1i9M9H4xTGbZAJygZAQ9ALxK9DzJ\nip4newdjniGzJgX9+kVBPnkIExYmyWmsoF83GonRxEeakMifiaQW5GdGrgNAXhDsy4JgH5BzJTbY\nSmNdP2pd+izBXGEmvAs75pzI/TlfUAl2E85ER9I7hQU7h4nF6hd6Rpg0m0188IMfRC6Xw/vf/34U\ni0UcOXIEc3NzGBkZwfT0NJLJJD9Rj8MkrFEuUpmgxl42kxeFbW4yfv2jP636vqXWpnNRsVBU5pMG\n2ma+V3Z6teFdxn5YdJQcdnWU5LH8nUY4ATyEk62LHYLj2pHR+MbJfNvhsEENMZXPkJZHReTLVIQm\nPGTgw0/HbHxs5sprb04XweTYYE3qyrEKyiaKDLPOWU6NZUFpjqVTuNg5sjHVjZWNbdxi9Qs9I0y+\n8pWvYPv27VhdXQUAHD9+HLfeeisefPBBHD9+HMeOHcNDDz20yaPsHCZhjbsHvAn2pVWh2a2qG9N2\n4SbTbW4s81ZmXJ8VAs3ERcUspL4oUKionyVYdjoPz3QTwoOD6jWYdscinEx8+MMpG7GIo7eLjCoj\ngkCqHFfjGTfhM5KRFir1dT4jGVGvtELyj2whjHTVpF0RSGIcrKqwSfScVIaeekDlK5iwAdpz7BQG\ncs4TEXWjT0SkQtDAzux675dmo+EaZzSkWotR0d6gVFfdWCWh6JhYrH6hJ4TJwsICvvvd7+Lnfu7n\n8I//+I8AgJMnT+LgwYMAgP379+PgwYPXhTAxsRoYwZ4Rnf2kZtaSbjJNshQLOWS8DYsGM7nX+RV3\nclpOnIYlDDLhfGaZ12iimeOEuF6tue9DwoT89gIj101gwmfYIn1ffqb5R1YLMQe5rmsZzVw3zDoa\nSEbxia+pWd8SOuve6YJi5DoArNTq2JFdD7xot2N2BsJYruxzJ6KRsGc5IaBNwDvfdenejIbb83h5\nPmXou3wPt+ssVp/QE8LkC1/4An75l38ZpVJp7W/5fB7ZbBYAkM1mkc/nN2t4XYVJvR5GsLNyKrpE\nKNkulNX0YfkwJpwJK4Sn8xe/RoyTlYdnAsuEM2F8BXMlsMQzwKAdLrHiTKIA2TlM+Iy5FXd5jiHH\nlLGw9UaLN88aFN0zB4X3OhpSBZLU1l2JfJrcihFh3YwI64aR6wCQtCP40D9dOZKKjaMbdfhYGZ5a\ngxfW9AubLky+853vIJPJYNeuXZidnb3icZZutwIwOzur/G5qagrpdLrr4+wW+kuLLrJXjnfp5RWX\n6ZpOD62fI15zVRp1nmMsXVO0lbF01HWNlYuLrnDW9Lb1Y1bmFlwvm/Mc5YUF5XzlWst1jZS411RU\nvddt/eo4t/W7x7krV3OVh3ces72/5uIrnN+nit5jAIDyhXmXsHAew57HaEodw2jKfR8Q82UB4hrn\nxDVqSKfX/XGNefX39YZ7vmvnLrj63TuPGUqq4xxKuse5ePqcyxWWTufWb+OUOs7FUhXpXevfJ0uL\nqpvMds/39y8uulxQu4fWj1kVa3P3QFxdN2K+t2nmO5pfVKybaFgdx0Ux30tivgHgvDjmQrGKH3vV\n+r0O9Yn57FPHEbm44GogJ8dZX1hUcpyeEO9yZWHRVU7F+X3+zHlXMIPzeW0UR48eXfv35OQkJicn\njX+76cLke9/7Hk6ePInvfve7qFarWF1dxac+9Slks1ksLS2t/T+TyWh/r7vhQqHgx9CvCrpIFDle\nHaHrPEYSlHOlqvK9dHM9/cAe1zUysZbSyzsTaynH6DR+5/c6LVheg91rQ5zjKc04dbWJnMdkRVHA\nbALiPlp4/J/XX9aP3Osepy46znmMzpp0fq+LBjNZg85jdoiotUwipJ5Dw6nIaySj7iZdzmPssOAz\nwu5z6FoLOI8ZEhr/UCrqWhdO1Jvua5zXWKTKMZpujxt55pfPEXXUQoM4h46Al+fQkePKe9ZsKZxK\ns6leQ2dNymu4AjPEe3au4LbMlbUXd5dTudr9L51OY2pq6qp+C/SAMHnXu96Fd73rXQCAF154Af/w\nD/+A3/qt38Jf/dVfYWZmBgcOHMDMzAz27du3ySPtDvrsdjQK0N4Q+jQRTKxkBTPhz2jIc+l2WW1Y\nyka/2lAvwqJdTLgfdq/FikhqrLibHDE3l3TLPCHcMqWayFmoumtzyZIrkhxn1V9XRNJiNBwHhOuG\nVWGW7G5LU4aEgRastFVyPWW73S6stUAIKiktbyMeUYMqZMY2wNdv1LZQu1Su3w6HEBPzLbPsnxKF\nIAEgGrHWQoatS5+dYLwMYECwt5oKpyJDrU0irRj/yXKgXJFvQTkVNw4cOIDDhw/jxIkTGB4exvT0\n9GYPqStYEl3m7FDc9SI0Gi1FEZX+9QGRAyLd5yYNcxpNleS/aVA9CYt2MeF+ynXvzzpNWoK9TIxg\nH0nZiHtFUYFvoMWqm0eAI8RYlv/Q9UxhnEe1Q4Ie4HyGCdHF+56rEUp1EaG0UlOt0ZUaXOvbggiZ\nFWOo1dXQXxnQwMj19jjV90yub/aOAZxgZ6HWJvW/WLWLlHgPZR6VSS6LX+gpYXLLLbfglltuAQCk\nUik89thjmzyi7sMke51pZkuk5pVJwxxWckVuoE89sEcpEcIS/QCeqcw0aQAYEmTtkND4GcFu0sSL\nZcmz1qgmSaJMS+2UoAf4xmRSN4tFz8VIhFLYWvfIWZc+S7AoKdaqllk2ACfYWbMy3XxKrZ+FWg+n\n1PpfQxo3xKAo9DgoBlKouJ+ZU5FhocV+oqeEyY0Ak7jwitDMZJmGxZLqZ71YqgEi7NErCa99bdYn\nxDu7t1RTr1Gq6a/h9dmk9a8sbS8/M82tG+VUWN6DicuPPneSZ2JSSp9pqcxlaHJMPKxybdL1w6KP\nALXtrk4gMWGRsKFsoLpkV/ZMTMbJEjDH+6NY9li/JrXnqo06Hr9vD85fbm3dUAUrrQpsebdR9hOB\nMPEZJu4hZsaz7PVUFKpvXKN1mZSg93qhTco4sBfWxGqo1jWfHUPREew7HJqbSTl+JpCYy2+7Qaw/\nKwvDwJ45oCfYnTCZC1qnDCrX1tA2UfAGa7vLOi2agL1nJutXR7A7wdaviQLAWlszy6WXEAgTnyFf\neJ0iwTZylr1eFa5Z+RngLxsrBRETGqqspAvw7oImVoN06T1xn5rJzDLxQwbl+E2EngxVVeZKnE+3\nvcqNRwoDZim66llpOupRgl0T5ScRFetTJsmZBJAwsOZvjGBviLbUDU3XSVbmPmK1lErQEU1yZb6y\nrsm0WkChogoDtn5H0ypfl4m7x8mqF69UvdsLs3fMTwTCxGfU65z4Y/2rTfpsMzBtfLlcw2g6uraI\ni6IYnx22gBrUzwKsfDbTggFOsLNMfJPkNFamXj4j9wvvXSYfcLuPzhYqigLAtNhM3MYzX/W2TBjB\nvijK8Cytqu7R9r01lYTBhuhudXHVXW7fudGblPyvNeqKm6opXDvMMo9HVMtbFzFWrDRxyDEOF0fV\n8q4EDQADSdUalOt354ConD2grl9Rwk3bdZIpEay9cLXuXZvOTwTCxGeYVA2WpJusK8R8xhVRKmJv\njl/jyftVgn0sbWO50uYoYuEQ0klV5THhZVhF1IQNxV+s830zgr3W9M4ANuEz5DjniqpfOpMAYKk5\nOZ7X0NQpY4JzWDZrEiq/SdY3I9h1OQkS4VAIL3kS7KpGL8ulmFibQ8kIli+FD1sAskl1G+LZ67x/\nDCvOmYh4cz8AUK03lHPIyLWoMHPlZxNXmgxdL9dVJaIuJJD8rMvJ2SwEwsRnmJjXssii1MwqQhuR\nAqkkuyRqtHHWJ0EWynNFkZCaQUCbYFcy8UU5lXZ4pqV8lmAC50LBW2CZRP7InBoZSr1StdTNS8w3\nKxsDALm4mrOQi4uCfqSzpYnvnOfkcIGUFJtsn3CVhcMW0BCfnXOREcJfVimFuwuiFFjM1cYsRQDo\nj3v30ilULff6FkjYYc9z5CtNF8G+05HgbpJnMpGx0R+zrxgVyWSDiXLqFwJh4jcMoi9YnggTSCba\n+IiIVBkRrDLrWc54hPa1VatBumbitppYFrfdrrL/Wajgk/96eu3zb79lArscHe1YQcqELRLPNIl6\nzZY30cq0cTusWoqS+AaAxbI7Z2HUg/uR1g3znQPc+jERrKzZEnOrvGbAxpP378GZQgXj/TFXsizA\nrYJKra0UXN4g7ZB6HyaVt0tkIz9b4AVA2TlqDdVyaYikRZM8k2UNJwhNm4QrwaSlhV8IhInPMCHM\naBlvIpBYKOulU3gS7LuyUSxX1vuap4XGZOImYK4ZnfWzXbgrdg/GXGVGnGi03CVZxJ0q0Uc6ejxf\n9iZak1ELldXLZ2t/dqJc9+aGAB40wRQI5nYEeBQUy14HDCxO4lYJAbg5Z7s6CjrBrIKYrbZJlm19\nmWsIAOoNbzeXSQHQpVXvcG7WSZRxLgBQJEoCrZxAQsr9RCBMfIZJJArTzJhAskUik61JZJpfqa79\nu9UCFlaqChkrhYuMgpKtV3WEMHPNmJSHd0HcCiNrTRopsZc+X/bu5a1LapSbKQsf7hMlW2SUlHzG\nuihAltfTbDWV7HVdzRaWJMcisZot4OVCHWcLVYylo3hVf8S1wbENlLVJHuqzkS87+CVZ3wa8usJN\nOXttvsf7Y7hJI/x2C4J9tyDYWSTWxZIu0lDwR3220itnQNxLOGTBuejDunBEJzZRmgTCxGcYhfIR\nbYNFSVWblvK9bqOfyERRrGJN4MjcCUawu5Iai6qmDfCErG1pVTvcJs0faDotinthiXq6QnlSYLGX\nXhYmPC94mSEhNIc0fEaz6R2Wy0KY85qAiTFRDYAFVUQjISyXHeXhNUmiFRFpJZ8ZI9hfKdbx3/Or\nKFYaWK40ELIS2JlWt5kBEqHEOJGWsI6aGmKh2WwowtlqqeS51WxbeZbV/k/jmXRZvc++fa/mqHXI\n93RCuGAnNFwa63NDIw1lNJiu46lPCISJz7iqUD6xStnmxlwqQDsixktjZ0JvqM8Wm7hbs+uPR9Y2\nr1qjibRoQTgQtxRhMxB3q1XsXiKhlppPIPgMySPoBBYrasm4hpDVVDauiOXW+FmJEGn9SJefTnhL\n64etCzvEgyYy5Jkxgr1YU++9WHXPBdPoGSfSbHHSORTyrpv1g3wNHxa9SuR8uqzeYhW7M+vzwTZy\nOwzFFazj0hjnwYT3UllVhPIaftQvBMLEZzAyF+B+0oGEupHnEtJ05n24GQHJ3EPJqKVs4jry2FvK\n8gAAGRFJREFUXJaP1yXqveIQrOmoO9WZRYSV61DyCeQLvVqt45E7xlFaI0HdlYm3pyI4dP8enFlu\nuzx29KuvRUjwS9JqMNH4mQXFAh5MCvpJAS9rQZkETbCsbkawhy3i49dArhzXBllRN0iTKCnmQpXf\nnylUXMJkZ0atWjCcVKUB28gXV1suBWGbsCaZ4GS5LLtEVYNdmqoGfiEQJn7DIJqLVZhN2JayucU0\nrVWdG6iugOLuXMzVdMoJpm2HDNqzsgKJKwZarOx5Il169WbD1RDKieE+G3OlNsFuWdBaUHPl2loI\nZqsFnF+pYdxxHEvgDFncdRkXuUFxMYw9A1EsldcDHjJin09G1ai0pCYqLRpW14UtpJ6JIsOqBjOC\nvdb05lQAjbIky74I62eHsH5MoqQYwW5CwK82WooLKhVVHwobJ1MQ2vfiHUwQtqwNudo2E4Ew8Rkm\niUysledqraFsbtW66g8ey0SRXG1eMQIKaPfoKNccHfFcKyHkSbBX6xbVcpmFZKLFMtdNwvYmWqXm\np3sZZXjmk/fvwbjDxcSykE3AcoNkRGdTfA6LiAgdEVupe5eHrzQsGozAqgYzmCQtMmVpe5+3pWgS\nJfVqQbC/Wgg/kxBm2UpAVtbe1R/Bs2/fi3PF9WADJ0ZTUaxUywAuKzJ6a9IrmMBV1HW1prjaKo2m\n8g6VZdSFjwiEic9gggK4lAjmWLgRkRhmh8N43OOFbwiBJTUqAFgsuX30ThNc+oslwW6SOFYo1xQL\nqSA0ehMtlrn0WBl75vcGuMBi+QasyjPAa5mxKKqVqoZcF0hGw4q7LR1TVX4WRQW43Z/niqp7iEVr\nmSQtMjfVS4UaXl5aF7xhC8pmH0JLWM3utRdqAUnbQtIOIRGxXAS7SQgzK3XSamlbwqzfZ51XDWaV\nhftiETx14uUrPveQtcFor2uIQJj4DBZaCfAIDvbCrxj0TGEmeC4pNnGhMZkkjo33R5G/lKBhWXAl\nFF4oqvdxoejWYlMxlZuROR6sIRQj1wEgG48ox2RFsSeWs8DK9QPtWlDO6LiYMMPY82ACD+AEO4ui\nAoCdwge/U/jgWbSWicbPyvGznj+NFs9ef7lQx+9++YeKRSqVCAbG3ZxdqWOp3ECx0sSS3UAkBEyk\n1q9hUjWYJRizSEOTWmh+YdOFSa1Ww0c+8hHU63XU63Xs27cP73rXu1AsFnHkyBHMzc1hZGQE09PT\nSCaT/IQ9DuaTBrirgPl7WbIV0M4BOeyxCWfjIcX/nhWcikniGAutnMjERJHG/7+9cw+Kqn7/+Hsv\nsFx2YVluchXw/mVAM7USNB2/2Ug1mhFmNqZNY4lMyTil+RsH5melVoqWt9FJM5tGcSboYrcZhQQt\nDcsZh5RJykQQWJZ2AXFZlj2/P/ixcvbC5+iue87i85pxZPecPed9nvM55/l8nudzca7F3rRwvAS7\nY83NeMtVEvS2rZI0St7LLTnMuciHqvjXGuqQQGdNzSFoZDnjoWeFRFjJdYA9+zGrhQWwY/Ss3lpC\navzJWn75dXRYLGcjZHyS05RELnpiXTH12kNpYyMCnAZxsnIixh7O6Z4mDmpNaoP5k3O6ak2yzsHq\nXiwkrOgrRHcmAQEBKCoqgkqlgs1mw4YNG3D58mXU1NQgIyMD8+fPR3l5OcrKyrBkyRKx5XqMkJg0\nqwcHq/Y3yiG5HhXi3CfRda3p9nES1Ep09wb1hzPCApHoMFZAyIPCCjFZ+vhN/P+d69y6YU1ZwWp5\ntN2ywsb1hyRsNqC124oRDgmitPAAWPtgt2da+J1Nq8FKrvdfx9Az5Q7Yyd1nVnIdYHfnZrWwAPY9\n6+0bujssKwwGsHMNLGcjJHnOKhdXO3vxz7/9FYTePg5KGTBay79xLJ1Gh9akyaE1KWTQIuscrJyf\nkLCirxDdmQCAStVvgN7eXthsNqjVatTU1KC4uBgAMGvWLBQXFw8LZyJkqVp1gIwXX1c7drvlgCCl\nDMFKOYIUMqeH1QaO91JxNahLG6yEYVAvp3CH0E5DpxX/M8jpOYYJhDwozBf9Tf4x2m72ApGOc2sN\nnWAf+f8PY2u3FbGhSqeH0dTDOc0w69g9k2VP1kvYccyO69yPEl23Jx2AJpivkzWhX5dl6KVuAfYY\nJtaocIB9z1jdYYWEl1i5hmSH1qTjPWUl14Hb5cLdS1pIKFgGIDVc6TY85o0QK+scLOc+WhvA66ww\nxkVY0VdIwpnYbDasW7cOLS0teOyxx5CYmAiTyQStVgsA0Gq1MJlMIqv0DjHqQHQNCme4GgPC6p/O\nemC7ethTiLASf6wwgZAHhfVARzrkZaJcTIvByg8NPIyZiRHo7Ox0cZ3slwbLnqyXsJDQJWuQKAvW\nYEKA3SmCZUvgdlhwoEXqGBZkhWVY5QZg25tVkRlIrqtVSpfJdYD9khYSCma1slghVlZFRwisMNf1\nTiuvbN5NbshbSMKZyOVyvPfee+ju7sY777yD2tpap31kbqoytbW1vP3z8vKg0Whc7isFzG0G3sut\n+L+pTnpvXL3hFBN+KEVn395yQ89PXHdbkZkYYd/efr3ZKZmr0eh45zA2tDg9TBpNpH17opbjvTQS\ntcE8nf8JtWH7U2PttcdxMWooHBdoB5CpATLd2ELd+S8vuR6qkjvZIiHMytOREBbk8v4GBga6/N54\n7aaL64zi7cOyZ/M/zU7J78H3Q2vsdcqp3Ok9teoNTuGjwce4ZWh3is87nsPpGHP4xxiptfJeTCO1\nzjr/aO7gvci3PzUW/4kLs29PZ9x3VrkRYu9/W9v4rfeePmg0t7f/0dzBc0aOGoWQqrPxdKbqnHVe\nbungdTYIUKgxfsTt8yRHcA7haOdjZGr6y6bFYsHdwHV18O5pyVNjeOdg2fJOKS0ttf+dnp6O9PR0\nwb+VhDMZICQkBA888ADq6+uh1WphNBrt/4eHh7v8jasLdlVDlQpOy8yae530JjjU/hLCVbx9YkP5\nvY9iQ5W87a6S647nSAzntywSwwN5+ySGyni1qsRQmdMxktQyJKn7QyndN286XSurZtfpsBpe0X9T\nnc4xJoIf8hgTwb/WgUTqjY7+mrRjItVV/N3xHCx7ulqvZPB2VzkVx3O46iU1eB9X4SPeOVy0fhzP\n4ar30eB95DLn+LvjMa4bb/GOcd10C0lqfkVuqPs+UG4GWqOuyg3L3sEBcuw/xx+oOni7EI2sBHuS\nWs7TmaSWO+ls7+51ar0P3sdi7WPaEwA0Gs1dv5MaTfxrbTSZkay+fSUsW94JGo0GeXl5d/VbQALO\npKOjA0qlEiEhIbBYLLh48SJyc3PR0dGByspKLFiwAJWVlZgyZYrYUr2CkOkPlHL+9B0OA9yZ4aNu\nh+S6q/g6Ky7NCh8JgRXOELLuCqt30OBEqqXP5pRIZSU4AXaPr2AlP/kd7HBDhCS2VQ5jhRw/p0UM\n3Wki0mF2Wa2LkCDrGELG3AgJXw4FK7wEsMsvKx8nRCNr7i0hOllde4XY01NY18qypS8R3ZkYjUbs\n2rULHMeB4zjMmDEDGRkZSE1NRUlJCSoqKhAdHY3CwkKxpXoFITORtnTyp4dv7bLwXpCsBCZroBPA\njkt7A1b8nBV/FwIrkSrkpcGyRWOHBXt+abR/XjcrmTe2QkhimzV1TFcvv5up4z1jzS4r5Bh3kufy\nJM7PgnVPhL5Ah9IoZO4tFqwei546XiGwnIWQ8u0rRFeQnJyMLVu2OH2vVquxYcMGERTdWxpM/ELe\nYOpxKgisXiLMGr+AnlZCEqWewnrYhLQaWAhJpLLwtLOBkMQ2q7cW6+UnZOYE1jGEjLnxRovUU1g6\nhWgU0n2YBes58kargBUKlpKzYCF9hcMMncP0IK4W9mGFqbzR02q41KpYYxKE4GkoQciLizVdOesY\nQmZOYB3DF61Rb+ANnUJG4rNglQtvlF9vjNSXCv6p2o8JYsz4C7DDVKxCLqQG6otYqy9qVSleCMsI\nrQm7uw5hU4gMPT6DNV5AyEhnlg5ftEa9AUvnQG2+5Ybefs8dnyIhI/FZ+OIZ8Zd7IgT/VO3H6Lt6\nneLvjiNvPW1eC6nZ+UvzWWgYwJOwjMc1YcagR4CdH2KNFxAy0pn1AvVFa9QbsHR6ozbPKleAb54R\nf7knQpD2m2QYImQpT0+b18OptuOLMICn9hKyVC2rBcXS4I2wjZR6/gwFS6c3yrdUwkv+ck+E4L/K\n/RQh62t4WsCGU21HCh0FWBh7bE7jEZIdxk+yWlAsDd4I2/hLa9TT3l5CkEqFy1/uiRD8/wr8DCF9\n0z0tYMOptiOkJecpntpLyHiZe63hfsIb3ZeHU4VLKlCJ9TG+KMTDqbYjpCXnKZ7ayxvjZYbTPbvX\neCNPRs7b+5AFfYwvBoUNJ3wxythTvDFehvAt5Ly9D1nSx0hhUJg/4Q/hCHoxEQQ5E0LiUDiCIPwD\nejIJSUO1foLwD5wXoCAIgiCIO4ScCUEQBOEx5EwIgiAIjyFnQhAEQXiM6FlNg8GAnTt3wmQyQSaT\nYc6cOcjJyUFXVxe2b98OvV6PmJgYFBYWIiQkRGy5BEEQhAtEdyYKhQIvvvgiUlJSYDabsXbtWkyc\nOBEVFRXIyMjA/PnzUV5ejrKyMixZskRsuQRBEIQLRA9zabVapKSkAACCgoKQkJAAg8GAmpoaPPro\nowCAWbNm4ddffxVRJUEQBDEUojuTwbS2tuKff/7B2LFjYTKZoNVqAfQ7HJPJJLI6giAIwh2ScSZm\nsxnbtm3DsmXLEBQU5LRdJnO15BBBEAQhBUTPmQBAX18ftm7dipkzZ2Lq1KkA+lsjRqPR/n94eLjL\n39bW1qK2ttb+OS8vD/Hx8T7R7SkajYa9kwQgnd6FdHoPf9AI+I/O0tJS+9/p6elIT08X/FtJtEz2\n7NmDxMRE5OTk2L978MEHUVlZCQCorKzElClTXP42PT0deXl59n+DjSFlSKd3IZ3exR90+oNGwL90\nDn6X3okjASTQMrl8+TKqqqqQnJyMN998EzKZDIsXL8aCBQtQUlKCiooKREdHo7CwUGypBEEQhBtE\ndybjx4/H0aNHXW7bsGGDj9UQBEEQd4OiuLi4WGwR3iYmJkZsCYIgnd6FdHoXf9DpDxqB+0OnjOM4\nzotaCIIgiPsQSSTgCYIgCP+GnAlBEAThMaIn4D2hqakJ27dvh0wmA8dxaGlpwaJFi3Dz5k2cOHHC\nPjZl8eLFmDRpkmg6y8rKUFVVBblcjuTkZOTn58NsNktuIktHnStXrkR5ebmkbAkA3377LU6cOAEA\nkp4Y1JXOY8eOiW7PPXv24LfffkN4eDg++OADABjSfmVlZaioqIBCocCyZcswceJEyenU6/UoLCxE\nQkICAGDMmDF4+eWXRdP5yy+/4NixY7h+/To2bdqEtLQ0+/5Ssqc7nXdlT26Y0NfXx61YsYLT6/Vc\naWkp9/XXX4stieM4jmttbeVWrVrF9fb2chzHcdu2beMqKiq4w4cPc+Xl5RzHcVxZWRn32WefiSnT\nrU4p2ZLjOO7atWvcmjVrOIvFwvX19XEbN27kbty4ITl7utMpBXteunSJ+/vvv7k1a9bYv3Nnv4aG\nBu6NN97grFYr19LSwhUUFHA2m01yOltbW3n7+RJXOhsbG7mmpiauuLiYq6+vt38vNXu603k39hw2\nYa6LFy8iNjYWUVFRAABOIv0KgoODoVQqYTab0dfXB4vFAp1OJ7mJLB119vT0QKfTAZCOLQGgsbER\no0ePRkBAAORyOSZMmIBz587h/PnzkrKnO52A+PYcP348QkNDed+5K481NTWYPn06FAoFYmJiEBcX\nhytXrkhOJyCeXV3pjI+PR1xcnNO+UrOnO53AndvTr8Ncgzlz5gyysrLsn7///nucOnUKo0aNwtKl\nS0ULeajVajz55JPIz8+HSqVCZmYmMjMzJTeRpTuddXV1krElACQlJeHIkSPo6upCQEAAfv/9d6Sl\npdmn3gGkYU9XOkeNGgWNRiMpew7grjy2t7dj7Nix9v10Oh3a29tF0Qi41wn0h2bWrl2LkJAQLFq0\nCOPHjxdLplukZs+huFN7DgtnYrVaUVNTY1/v5PHHH0dubi5kMhmOHDmCQ4cOYeXKlaJoa2lpwfHj\nx7F7926EhIRg27ZtqKqqctpP7IksHXVu3boV1dXVkrIlACQkJGD+/Pl4++23ERQUhJSUFMjlzg1s\nse3pTufcuXPxzDPPSMae7hDbfkIZ0BkREYHdu3dDrVbjr7/+wvvvv4+SkhKXk8YSbO7GnsMizHXh\nwgWkpaUhLCwMABAWFmYvZHPmzEF9fb1o2urr6zFu3Dio1WrI5XJMmzYNdXV19gksAQw5kaVYOh96\n6CHU1dVJypYDzJ49G5s3b0ZxcTFCQ0MRHx8vOXsCzjrj4uIkaU8Abu2n0+nQ1tZm389gMNjDn2Lg\nTqdSqYRarQYApKWlYcSIEWhqahJNpzukZk933I09h4Uzqa6u5oW4BgobAJw9exZJSUliyALQH5P8\n888/YbFYwHEcLl68iMTERMETWYqpMyEhQVK2HKCjowMA0NbWhnPnziE7O1ty9gRc65SKPTmO48XE\n3dlvypQpOHPmDKxWK1pbW9Hc3IzRo0dLTmdHRwdsNhuA/lZ2c3MzYmNjRdPpDqnZ0x13Y0+/HwHf\n09OD/Px87Ny5E8HBwQCAnTt34urVq5DJZIiOjsaKFSvscVYx+Oqrr1BZWQm5XI6UlBS8+uqrMJvN\nKCkpQVtbm30iS8fkmJg6U1NT8corr2Dv3r2SsiUAFBUVoaury77kc3p6Orq6uiRnT1c6pVA2d+zY\ngT/++AOdnZ0IDw9HXl4epk6d6tZ+ZWVlOHnyJJRKpU+7st6JzrNnz6K0tBRKpRIymQx5eXmYPHmy\naDpDQ0Nx8OBBdHR0IDQ0FCkpKVi/fj0AadnTnc67saffOxOCIAhCfIZFmIsgCIIQF3ImBEEQhMeQ\nMyEIgiA8hpwJQRAE4THkTAiCIAiPIWdCEARBeAw5E4IgCMJjyJkQBEEQHkPOhCBEZmDaCoLwZ4bF\nrMEE4SkGgwEHDx7E5cuXwXEcsrKysHz5cnzxxRc4efIkLBYLJk2ahOXLl9tX9isoKEB+fj6OHj0K\ni8WCnJwcLFy4EABgsViwb98+nD9/HhEREZg1axa+++477NmzBwCwatUqzJ07F9XV1WhqasLhw4dh\nMplw4MABXLp0CcHBwcjJycG8efMAAFeuXMHHH3+MpqYmqFQqZGdnY+nSpejt7cXevXtx4cIF2Gw2\nxMXFYd26dfZJTwnCV5AzIe57bDYbNm/ejIyMDLz22muQy+Wor69HZWUlTp06heLiYoSFheGjjz7C\ngQMHUFBQYP9tXV0dPvzwQzQ2NmL9+vV4+OGHER8fj2PHjsFgMGDXrl0wm83YtGmT03nPnDmDt956\nCxqNBjKZDFu2bMG0adNQWFiItrY2bNy4EQkJCcjMzMQnn3yCnJwczJgxAz09PWhoaAAA/PTTT7h1\n6xb27t0LpVKJq1evIjAw0Ge2I4gBKMxF3PdcuXIFRqMRL7zwAgIDA6FUKjFu3DhUV1fjiSeeQHR0\nNFQqFZ5//nmcPn2aF5Z69tlnoVQqMXLkSIwcORJXr14F0L+29tNPP42QkBDodDp7C2Mw8+bNg06n\nQ0BAAOrr69HZ2YmFCxdCLpcjJiYGc+bMwenTpwEACoUCzc3N6OzshEqlss80q1Ao0NnZiRs3bkAm\nkyE1NZXW8CBEgVomxH2PwWBAVFSU0yJb7e3tiI6Otn+Ojo6GzWbjre43eN0UlUoFs9ls/21kZKR9\n2+C/XX2n1+vR3t6O5cuX27+z2WyYMGECAGDlypU4evQoVq9ejdjYWOTm5mLy5MmYOXMmDAYDtm/f\nju7ubsyYMQOLFy92uWAYQdxLyJkQ9z2RkZFoa2uDzWbjvYR1Oh30er39s16vh0KhQHh4OAwGw5DH\njIiIgMFgQEJCAgDwFkQaYPBqhpGRkYiJicGOHTtcHm/EiBF4/fXXAfS3erZu3YqDBw8iMDAQubm5\nyM3NRVtbG959913Ex8dj9uzZwg1AEF6Aqi/Efc/o0aMRERGBzz//HD09Pejt7UVdXR2ysrJw/Phx\ntLa2wmw248iRI5g+fbqgWv8jjzyC8vJy3Lx5E+3t7fjhhx+YGoKDg/Hll1/CYrHAZrOhoaHBvhJj\nVVWVfbGtkJAQyGQyyGQy1NbW4tq1a7DZbAgKCoJCofCbJXeJ4QW1TIj7HrlcjrVr1+LAgQPIz8+H\nTCZDdnY2li1bhvb2dhQVFcFqtWLixIl46aWXBB0zNzcX+/fvR0FBASIiIpCdnW1fIRBwXmNdLpdj\n3bp1OHToEAoKCmC1WhEfH4/nnnsOQP/S1J9++iksFguioqKwevVqBAQEwGg0Yv/+/Whvb0dQUBCm\nT5+OmTNnes02BCEUWhyLIHzAjz/+iJ9//hlFRUViSyGIewKFuQjiHmA0GlFXVweO49DU1IRvvvkG\n06ZNE1sWQdwzKMxFEPcAq9WKffv2Qa/XIzQ0FFlZWZg7d67YsgjinkFhLoIgCMJjKMxFEARBeAw5\nE4IgCMJjyJkQBEEQHkPOhCAIgvAYciYEQRCEx5AzIQiCIDzm/wAAm3gSTCRqaQAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x136d74828>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df.plot.scatter(x='congress', y='age');"
]
},
{
"cell_type": "code",
"execution_count": 151,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x1389b4fd0>"
]
},
"execution_count": 151,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAADzCAYAAACBg31OAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXusZFd59vlba1/qdu6n7zebdtsYdxybD48dYCZgEU1E\nxjM2UmQm41FkFBPGM8mHOoqCkgjJUUCBQNI24YOMlIgoQkPGiWJr5psIjYbYBD4IwRgItG2M8bXd\n7u5zP6eue++11vyxL7WralfVru7T9un2fqQj9ym/Z61Vu9Z63lV7P++zhDHGUKBAgQIF3jSQb/QA\nChQoUKDA64uC+AsUKFDgTYaC+AsUKFDgTYaC+Efg1KlTb/QQerDTxgPFmPJgp40Hdt6Ydtp4rnQU\nxD8CO20y7rTxQDGmPNhp44GdN6adNp4rHQXxj8D58+ff6CH0YKeNB4ox5cFOGw/svDHttPFc6bDf\n6AHsZCwtLb3RQ+jBThsPFGPKg502Hth5Y9pp43kj8cUvfpEnn3yS2dlZPvvZzwJQr9d58MEHWVpa\nYs+ePZw4cYJqtcrS0hInTpzg4MGDAFx77bXcd999Y/sQhY6/QIECBS4cL559hav3Hd629p555hnK\n5TKf//znE+L/8pe/zPT0NHfeeSePPvoojUaDe+65h6WlJT796U8ncXlxRe7420r3/K61Rsp8d7U8\npUDkizVaI3K02/YVQa4WoR10MCJf7IZXJ0/WthCU7VKuNn+y/horXjNX7PNrZ6irztg4KSS7SlOo\nHG0uN5Y521rJ1f+cO5PruhpjEEbjmfHRFavEbHk2V//HZvZSdSu5Yt82sxfXdsbGSSGZs6u55pVl\nDLZl5erfAiwr37zOvV6MxsnZ/yRrcJJYkzN2WJvlnNdkFK7edxjx3+YjfvP/vjI25vrrrx/4BvTE\nE0/wwAMPAPDe976XBx54gHvuuSds8wL27lck8aehtUbE/xUCIbJZ1RgTTg7CyWRGTSZjkBgQoI0e\nmiiMMQTaIITBNqAMmBH9Kx0ghUAbPTQufE8KbQxl6RJohT+CUi0ErnQgnhxD2lVGc7q+ypbfwYKR\nJB1oxVanQcl2kFKy6beGxpalw3x5CktYKK3wTHbLxhiafhtlBHOlOepenWAIUWut6LQ3WN88Q9Wt\nMVPbh21lk6otJPOlaRDQCtqsdjaHjtUVNgJB02viWi6WtDLni0BwuLZAzSljCUlgdEZrISwhmHer\nbAVtSjqg6pSRQz4DYcAWgpb2cLSFbdlD5ytaowQopbCFwBoxX4XRIARKKaSUI9dAOLfHb2pMtK4C\npRBCIIesLWMMRofXRyuFGNF/+La663UUoRujiXc9WinkiASk4/7HcMBF4RI/Ld3Y2GBubg6Aubk5\nNjY2kv+3tLTExz72MarVKh/84Ae5/vrrx7Z3xRJ//GHHH3Q8mYwxPR9+TPgGwkWR+nsDmDSpx4Qf\nxQIIYzBGoyFJADHhG6MxCISQCAFCawymJwHEhK+NASkAgRQWaI3G9CQArXWYFDAgBFJIXCFwjIXf\nlwBCwreRQnbJPlrY0YUBuoS/2mnQ0l2ilQgEpicB+Cqg7jXpqCAhcCktFktTeEqxFXQTQEz4trTQ\nhGvUsixqhGP1tEref9Nv0wratJQfXV3BjDuDQbOVSgBKK7z2Op2gRTNoA9AMmrS8OhV3qicBxIRv\nCQsVtVpxqhyyKzT9FqteNwG40sYWNhoIMATaJ9AKx7JwZDcBSASHaovMlWtYMiQaAzginBXpBGAJ\nwbxTwZU2SIEGWjrA6zRwpdWTAIQBR1rhnBICA3gmwA8UjuhLANG8DidU+FqgNYExAwlAmJDo0qQY\nr4t0AjCpeZGQrTEQrYF0AogJP030RmsUBiG7CSBeVyIaaxwbki/Rmkj1H/03WVdRuyY9pui1GPHr\ncV/0xfZzQPxaPwdsCy5FMhnZXdjf/Pw8X/jCF5iamuL555/nM5/5DCdPnqRcLo/8+yuS+Idl9nhS\nxB++MWaA8IfFxm3170KSxBIlAE8btDFdwk/HRv2IiMA70c4dKQYnjpThJkJrAqNRRoMgug2Uio36\njxNAYBSWkL2En4oFkgTwUn2V1U69h/CTaxgnOMLd1WqrTkcHmTt2RUjqi9YUSmsqTikh/PRe2MSx\n0qIqLVZbm9T9VorwuwhCymHGnUEZxWvrL+AFzYTw02gELRpBi6ZXZ6Y8zzW73poQvupr2QhBxa1y\nyKmw6TVQWqEwUX/p/jWB0vgqTADXzBxgV3U2IfzeaxXCiRL/rFNOCH/wWpkkAVQsh1m3mhB+D/oS\nQElaYd8ie65ANwGUIgLO2gWLFFmaaJ2ETQzOa4RIJQCDIHtn321To7QJhwhj16BIzeWsbyLxejE5\n12A6AaRfH9a/MQa24VZP2HB+4n/44YeTfx8/fpzjx4+P/Zu5uTnW19eT/87OhrcjbdtmamoKgKNH\nj7Jv3z7OnDnD0aNHR7Z3RRL/uHt+Usou6Y/J1FLKXPcc40mmo2cEo1oVUiKNQetg/ISREpQaf98/\n6t8xGcSQEQsMJf00NNDRirrqjH2eoICaUwYpGX7zI0wABmgFHZrKH9lmgEEZTcdv0BrzPKEZtNht\n7QMhBwh/YAxCYAlJm3H9hwlgoTKdSfppaMCREtdyGDkBCBNAyXKQY9qMEwBCjn/2FM1RKcT4+95R\nu6NuEYVh0XzKtQZkvFUf+4wi3da4nbeQMmf/0RrMEZv3GUJuTNDc3XffPTYm3pjGeMc73sHjjz/O\nXXfdxeOPP84tt9wCwObmJlNTU0gpOXfuHGfPnmXv3r1j278iiX/bMdHDk3CnWiAPJrhOOb9KT3Ll\nL1VsgTchtvFWz0MPPcRTTz3F1tYW999/P3fffTd33XUXJ0+e5LHHHmP37t2cOHECgKeffpqHH34Y\n2w5vB374wx+mVquN7aMg/gIFChS4WGzjzuCjH/1o5usf//jHB1677bbbuO222ybuoyD+AgUKFLhY\nTHCPfyegIP4CBQoUuFhcXrx/ZXr1pJ/sZyFWCZDSGI9sK3pgNK5QQulQWzy2/0TqJsY/PzChmkLk\neMygtaKjApRWo9s1Bi/wkUJijZuxxuAHHoEKxk4WoTVr7TW8Ebr+GL7fot5cQ6jRD5cFEHRatNst\nHEY/CLWRnFl9la2tVcS466oCGp1NxJiH2xAWPy0111A5xuoHirbyx36uEmgHPnrcZ0U4Xz3lo9To\nErhYqaP71C1DgiGWMo/pP44ZF9uj2c+zBmN1XY41aFLjyBs7sv8812gSxA/Bx/3sEFyRlg1tpTN1\nvbEuGHolaEabntegKwmFruogSxcMIeEH2tBJXUkR/X1P/9GTemUMOmlTRfJP0zsxtI52EeGECfX+\nCpXS8XdDQ8Jf91uElQMwY5ep2C5Wn47fUwGrnSavtTdSiymsQ+hRwhhD02/x07VXkkraabvGvtou\nXNvtUe0IrdnsbPLU0ilaQQuB4K2L13J49jCu01vZ6nstTq+9xHee/ya+8rEth2sP3MRsbTfG6n4B\nlUC7tcXzp0/x7Ol/B6BSqnLowFtwS5WemgUbSavZ4Kcv/ISNrbCw5eZrbuHW69/N7PRCbzGcClht\nLvPjM9/HCzpIITmyeC1ztV09/UNI+G2/yYYXtlm1y9y270YWK/NYqVgRzYG636YdJZJpu8S+6gxl\ny+n5rCRhjYQj7aSStiQcSpbd+1kRztdAK9rGj/oRzNgVXOlgpaSaaR1+/PcSgyvlgMLHpOZw0ldK\n/ix65lVEtGkFTkZs3L8gkmCKXlXKqP6FEOFrkXR0YA0yqMOHwTWYrsVJXouLyzLWIMYgLWtbKncB\nxN3X5IozD/9sW/q7WFyxxB+jP6sPk5kN7DxGFHjEbRrA1wZvxBUUqQSSJvzBNlMJIFYGZcSmE4Ay\nmo7yE8If6JswAZQtB20MK50GZ9ubmULHcAek8I2m4bd4bu0lzrbWMsc6ZVfZX9uNJS0anS1+vHSK\ndjC4yxcIrls4xuHZsJz91dWX+M4L/4UgQ8JpWQ7X7b+J6doint/h+dM/5qenf5TZf9mtcPjgW7Cc\nEp12i2df+AmbWxuZsTe95R3cdsO7qVVn2Giu8OMzP8DLkIUKIblq8RiztV1Ylk3bbyWE34+qXebW\nfT/HrsoCQki2/BYdnb0bn7JLHKjOUrIcbNFL+P2IE4BAoFKEPzDWKAGULKf7rXHIvI4TgBXPpVGF\nSzGpQ1RfMqIaOEkAsWZfDt3QJoVc9BJ+P4zRGENP7Lg1CAwQ/kBslACiTnrqG7aN+D+Yk/j/z4L4\nLxmyvHryeJ9At6x8bJwx1P1gvLaasOI0r/+Pr/xcXwmNMbxcXxooPMpCx/fZCNq5fH1+cO5pXqrn\ns8htNVfY9Otj43QQ4NXXaPqDxVf9UB2f5Y3lXP0bX7DayCbnftx20610cnj11MozzM3uy9XmLXtu\nZLqSz9fn7QuHKDturlh7SNLvx5QsU8vpFVSWIrevT16vHGE0trRy3cFIV+WOjc3Zf/yNNa9XT1bN\nwrYR//94LFec+bvntqW/i0XxcPcyhYgLe3Ig/g6RB3qCfYAe4VHT23/4LSVXmznjwtj892hVcuts\nNEzuKzVZ7CXxh9kBuELf1uQoVD3ZyPKY/td//Vf+/u//ntOnT/Mnf/InPWXGjzzyCI899hiWZXHv\nvfdy0003vV5DLVCgQIHJcHnx/uun6rn99tv5wz/8w57Xjhw5wu/+7u9yww039Lx++vRpvv3tb3Py\n5El+//d/n7/6q7+6IOvRAgUKFHhdcJmpel434r/++usHSokPHDjA/v37B2KfeOIJ3vWud2FZFnv2\n7GH//v0899zOuDcW43LKQ/2+H+NiL5f+3+jYS9V/gcsQIufPDsGOvMe/urrKddddl/y+sLDA6urq\nBbUVmqZ1JWOjvMjTGuRhD4wSOaYJ1RJKG9SoTG40dvRgVxkz0mffBhzLQRmNp9XQWD/waaoOU7aL\np9VQozVtDK9urfBqYxVtYKEyxVxpKvMaeMrnmeWfcb61ghW9x2GqDqM1rrSYqixQUdMst5ZCf/T+\nOGPoNDbZWl8mCDxctwR2tse8MRqv0abZauJgo1CZSiUA1QnQp5u0N1uUyzbNBYEsZU/lqUqFA7v2\n0Glv4Tgl9JD+AWYq81QqNTABAgvNsPkimHWneblxnqnOFnumdlNzsh+yCgQ12+XFrVWmnBL7ajPY\nQ4zZLASOCCsrFHqo0Z0AZu0KVbuEFIJADz+/QQBu5NaZbw1E50wonUgzsyCNCR+WRkl9lCAilkbn\nORMj3lHl9dgPPeHynR2QyEO326ANwNpBrJ4DO5L4twMx4fd7kRtjeiZ/TPhpSVjWJEkTfmy5HLop\nm5Ao+xOA0UgEpHzHRdRPfwKwoz7j/iUSS8iBBOAFPi3VCbX8IhxbSQhcafUkgJjwzzTWqAfthEDa\ndY/VVr0nAXjK5+nl5zjfXGXT75685QoL0ZcAYsLXQtKJk43lsH/6EH7QZrm1HEnyDJ36JvWNZZrt\nJr4OZYltr03FreA4Ljh2ZKWr8Zod2u0W9XYjoXrXcnCkjUYRRL7yMeH7m23qjUYY2IBqs4qomp4E\nMF2tsn9xN7Zj45uAjurQUR2qTgVh2WjbST6Xmeo8lXINLUTix2+hcKSNQKYSQEj4tuXiR5/Nqlen\nsdam6pTZW9udqGwEgqrlhgfrAJ7RrHot6r7HlOP2JICE8FO3AywjwgNxjEo+vzThpw+JcSA6D6D7\nuDkmfKtPx661DvXyqb662vbUfCc6T0LTkwBCwhcDfv4mIwHERG9lrMH+OgAR/iPTT3+cx35609Z/\ndkB/rI4Kx7Y9Aeyg2zh5sCOJf2FhgeXlrqRvZWWFhYWFzNhTp05x6tSp5Pe77747lINl7BbSBzck\nlbuQ+H5nx2p0dHoWQL/lcjyppDBYhJ7oIiL8/skQ9yONCXeziRX/4ASUUiKR2FLSDnzW/CaBiUqs\negeAEIKSlJSMzc82l3hu4xxbfmtgv6wwNFSHdt1jrV1nrb3KanudzYyjFj2jwKjwVCqjEcICaXUJ\nPwXfaLBc9k8fYmXtDK+efZZmq5EQfgyNoeE1kV6LaqlKECh8P2CrPXiEpKd8POVTslxc6dB4boWg\n7lGvD8pHm60mtKDWqmIv2Bz4+atDwtc+fp+Es+m3wIeaU6EytcDs7G4Usf9/dxQKjdIelpC40qHm\nzFK2y3hGh+83hY4J6Hh1mkGbGbfG9QtvwY7OA+jftXtGseq1aAQeu8pTHKrNZZNGnACEjWUMVcul\n5pTDb49D5pUbbUwsIZAiW9uePmglJvuwO9kzr+JEB1FxlgBHiMwTtNJ++BBuPAT0EH5//0miIK4D\nGO6dn9TXZBSZDfQftzskdoADuDB//ME3NvmfvJF4XYk/773eW265hc997nPccccdrK6ucvbsWY4d\ny9bJZn1Q4zK5iKoEdfzvkbEylBiO0+ELgYTkxKHxsSL0LR/TrhASzyj8IUcW9rd7trE28ihECBNA\nPeiw1FiloUZr6z0TgAFbDJJYP3yjWV8/x0ZjfWScxlDvNJBKstUZfb5vR3notsLfbNNsjo5tNJvs\nP7SIscxA0hmI9VvsqswweARML5TRtFSHecvFGyNf7eiAtg4QjD8PoKMVVdsZP1cAhKBqu0NvEaXj\npBBIcmjmo1s/4+ZfkoBytJl8sx1z6ycdm3z7GBUbn4kxdq2mvkHkjIV8/vhjUez4s5HlMV2r1fjS\nl77E5uYmn/rUp7j66qv5gz/4Aw4dOsQ73/lOTpw4gW3b3HfffW+sDrqw2CfZ/Y0Ny3+hxAQXNXfk\nJJ/TpfpM3/Rz5U2Iy+wzf92If5jH9K233pr5+gc+8AE+8IEPXMohFShQoMD2oNjxFyhQoMCbDMU9\n/gJXJnLq0CeQq18SZfukp2QWKLAduMwsGy6zPJUP4zxcYklZHk/u0OAtfBCbx4tchMLi3L7lebzI\nZeTHP25qaa1ZLE9Ts0ebgQmgIh1mSzNM2eWRsY6wqFglXMvFFeP88AXTMwtMl6dHPogUwJRbxXEd\npsujzwd1pcN0pYYzU6JWHR07VashtKDqVHGlMzJ2rjyHK12mndrI62ohWSjNUnOqVK3SyDZL0mbW\nKVMW1thzDkrSwlMKaRh7doKFCGXEOTzmMfn88GMb5dgXf3RsPj/8xLM/R/+xrDLvGkz+Jkf/6b8Z\nGpvnfU8CKfL97BBcse6ciY4/QwNs6FUAZPmG9xebDOr4u6/HstC0VExFCyArFnrrA0Tfa2H/Ck8r\nNvxWohDRWqOjRZjmFa01rcBjxWthCMd4vrnOanuLRuAlG1sJlKRDzSlRcSqJjv/FtZdY62xQD7oK\nH1dY2JaDY1WxrJBElfJRukOgglDtE8FG4Pktzm6eRmuFMQa/1aBV36TtNfEj4zWBoOZWcNwSwnWT\nop5Oo0m73WKr3UjaLFkOjm0jLIER4WfhNz28l+p0NlpdHT8wVZtianGWxRuPUJ6dCl9UAQQ+fuDj\npRQ+c+U59swd5Niht+PYJbTRrDWWWO+sUvebSdGYhWSuNM3hmUMcmT0S9q8CXt06y4bXoJmydi5L\nh8XyNG/fdYx9U/MAtH2flU6Djgp6HFTL0mLWrXLNzB5Klh3NlYDA6LDvlNrFEpKKdJh2K4kpX7+0\nsWcOpSSMxhgk4/3w49dM4gSe2gsajRTgWt2agaE6+sw5nK3D75dvxn/b7+CZ+ffRuh7W/1jNf+pM\nDinl9rlz/vaNueLMX2Rbjb/euGKJP0Y8UaCX8PuR1hWP8vfuSQAmR2ycAGK99IhYEen7/T7C70fs\n3R+YkPBXI8IfiDOGpeY6y60tNIaaXabilIdW7r64/jIrrTUQEseqJITfD6V8lOrgqTae304IP+s9\nBa0mzfoGSitKKcIffE8ar9Gk0QwJXdpdwu9HnAC8rQ61hRkWb7yK8kz2twGhFCbwsKXDvrkjXHPo\nZpyMb0TGaFabS6y3V7GlzVUzhzk8ezi7fx3w6uZZtvwmc26Vt+8+xt7afGb/bd9n1WsSaM2sU+Ga\n2ZDws66V0orAhN7xFcthOkrOA7GkCByG6tvjdmV0OA+p2CwkBVtRHYBrDWr2Y+Q95wJ6/fDHVe6m\n6Wikx75WpHc/o2N7x5qO3Tbi/485if9zBfFfMvT78aucHvswvvw7htYGP2esr/L78S+3NvHHKuZD\nvLiZz4+/5Xuse61cktiX119jxW+MjQN45dyP2Ohsjo1TKgCvg5fjmEPVbrPRXM811v27jhDkLJW/\n/br3Yzmjb9UAVKTLrupsrv6PVGeZLlVz9b/bnca1R99+AhAGpmw3s/ipH/FczTNWYfL51kP44M/O\nQYhG65GHtfTH5u0/r8f+JLHD4raL+OVHfz5XnH7o37elv4tF8XD3AjGJeiunAv6SYdQuKyv2UvSf\n94JNMtZwIee7snmJZKL+cybzMHb7338cv924zJSJOwLb/Tn80z/9E1/72tcAeN/73sev/MqvUK/X\nefDBB1laWmLPnj2cOHGCajXfxqMfV+TD3QIFChR4PWFJkesnD1555RX++Z//mU996lN85jOf4ckn\nn+Ts2bM8+uij3HjjjTz00EMcP36cRx555ILHWxB/gQIFClwk0t5Ao37y4NVXX+XYsWM4joOUkre9\n7W3827/9G9/73vd4z3veA8B73/tevvvd717weAvifx1wKW7zJI6Gufqf5DjBSXApbjNcmimZ1x7i\nUt3lKMoL3nhcyuu6ncR/+PBhnnnmGer1Op1Oh+9///ssLy+zvr7O3NwcAHNzc2xs5DtvOgtX9D3+\nWE+cdg7Mo+oZ98AoVgk4UqCNRg8hq1jVAyLTNjaNQAV0VIAjbaTReDrAZAw1eRZvDAdr8zQDn+VO\nPdO7Pu5fANNOCV8FtIecaau0Ystr4kibXaVpNr1Wj2Szp12lMATsmb+KOb/J6bWXUENM0cp2Gcd2\nMVWN77VZ31olawlKaXFk97XUKnMEvsfLZ3/CmeXnM9t0nBKH9h/DKVepacNmYw015MHxNQvX8PZD\nb2e6PEtHBSy3NzOvlURwbGYP+6pzSCnZ6LRYyXAtBbCEZH9lGteyk3OHh93vt5FMO2UMBl8H2MIa\nOgctBI60Q9WYUtgjHtxKDNIKn3EoY4aLB4zBEvmMCUXk7CkIBRHSGl6NkChlxsxr6PPDz6HqmWQN\nMiY25ACFiNbgMDfei8V23uM/ePAgd955J5/4xCcol8tcffXVme/vYvq8Iok/lrtleezHWvq0jr5f\nA5yepNC9wFm6YGFMaLNsTJIA0jLOeEHGyac/AcSEH4Q6OhACS1hUEChMkgDShB81iCUspl2LquXQ\nUj5LXj2SmYbSQGVMV/UjBI7t4BoHT/lJAgi0YqvToKP80Io5ip0r1dBGs+W16EQJwCiFMQEq5RZq\nOVWu2fM2Ol6TVzdeIlBhAijbFRzHQRmDR9SuW2LP4kE8r8361gpgIsK/junqAjq6JrblcOzq/8CR\n/W/llbPP8urSz8I/d8oc3H8Mt1zFR4fvTcLczC6MVmzUuwng2OK13HzwZmYqXdvjsrQ4bO+iHXgs\ndTbRxiARXDu7l73VWUpW1y1zV2WauVKFjU6L5SgB2EKyrzJNxXaTuaIJlTjxsSlxArCxmHJcHGF1\nzzMglIIKIbCQSRs2EltaCNHrce9HhJlOABITOnCmCuRE/JmnE0BC+H0PtiM/fhN9zvHfW9FhLaJv\nDWBMTwK4ED/8rDUoUjUDWTr+pH9yaPNThVsyda1jGWn6WqXP39hOP/5JODiPDfTtt9/O7bffDsBX\nvvIVFhcXmZubS3b96+vrzM7OXvh4r0Q5Z8MPcu0Wsoo+hsVCPg1yR+twEzRqBxRNvpbyu4Q/fAB4\nWoW+8mNml1KKs61NNvzWWJmnMHB6a5lm0OkSfgYsBL7yWW6tocfYQ9sINlorNL1NlNEjrYldJBVn\nmplKl/Cz+4d2u8FS/QyOWxopdXWFRc2uctvBW5guz468XsIYKpbDnup0D+EPwITJMdAK17JHzhVh\nQvXOvFvtIfzsdg22sKjapR7Cz4oDgysFtuwlscHQVCEVo+d1HGvJyE583BoY4XGf1T9j+h+lrR8V\nm7f/UfU1cSzGUHW2Z+9b+9gtueIan34iV9zm5iYzMzMsLy/zyU9+kk9+8pP84z/+I1NTU9x11108\n+uijNBoN7rnnngsa7xW54x8n3ZNSjr31k44ddwxc3I4QAq3Ga5uFEBgpUcEY0g8HAFrl2lJYloVv\nVC5tvxH07vKHQGHwjcbX/tCjEGME0alN49oE8NDsqy6gxtzTV4DllimXa7S1N7pNo7h25gDTlbmx\n/Rsh2F2ZpjTG3gIBtmXhSCvz1ltvm+F8caQ9/vMSIkok4z32QWAJxsYmVbs5tO0iuqVj5dj1Sinz\ntylELm19uso91xrc5v4nkRjnwXbLOf/sz/6Mer2OZVncd999VKtV7rrrLk6ePMljjz3G7t27OXHi\nxAW3f0USf4ECBQq8npikpiMP/uiP/mjgtampKT7+8Y9vS/sF8RcoUKDAReJyK3oriL9AgQIFLhJ5\nK7N3Cgriz4OJPtTLawK8kbjiVAUF3rR4Q4+GvQBckQVceTzu46f6eb3Ax/l3x5IyKRjvxx+1JYUc\n7cUeDgBJ6iD34QMgUApHWthjypUEoYxUCoEz5t5kqC23Ij/+0fsES2t0oLBNKH0cBomgZldRSo33\n+BcCW0gsaVOxRj+Inbar+DrAIlQDjYIrJK3ADz/TUR9BKKrBGI0Y81FJQmVT+HfjVFWhVFdphRl1\niHs0T5XJ4UefmqPj/fh1Mv9Hxablj/n98POtq7i9XGswisuzBvOMdVxbk2I7C7heD1yRO34RqQDS\nlrUwKAsjLmoZohcO9dKyWwCWoVeOJWRB6PkcyuOMQUXk3+PHH03KQGuMEDiWg23Cwh7dL+vUoTJc\nCwOWwMFBaY02Cp0+/N0YAq2pBx1WvQYGcC0bpXUiqYynvwB8FbDWbrAZtCBSipSMjNQ43etjIVBG\ns+LVUUYjLRcjFBVjoXTQo9yxtGKruc7LS88mOvqyW2OqNguWDCWrUZtlu0LFncJ1phBC4BmFI0Kd\nuG+6AlBkTffcAAAgAElEQVQ7uuZbnS184yMsB2EsasJCGUVbdRU+03aVxeoix/fcQNWpxlUDCfmn\nNUaukJQsm6pTQgjBZtChJC1K0g515cl1jT4Go7sCUqOxTaScSX1UEnClzaxTTRw4w3MJoqrp1Ocq\nIhWLJW2EEHS0j4wKt6QQ3crliLSsaE4JIcL3oXVYZCV65xUMSh2z5nVcTCWlTEn+M3TwpvfsCJlq\nM1bidHX0OslzY/30R/j59/vxxwe1pBV1MWELBtdgPNZ0zUH/WGNekNtMxDuI03PhyiR+QplaVubv\n/7ATCVw0+WMnzZjwe/4uShTpZBETfnqLLYTAFlbKuz9cGDHh09euazlRwU6YAMJisMHdiiUlFhKl\nFBqNp1QP4ff0b1lYRqKMxtcKTwWsthtsBa2B9x++L0HJSAKtegi/t/9wLy2ERcUo2n6TRmudl84/\ni+6rnG17Ddpeg7JbZWpqDtcuUy3NJISfRlwbYAsr/LZEl/DTkEKC5SKNpiZCotxVWeD4nuNUnMrA\n9eomgLA4qWw5VJ3B8wA6WtHRipKQlCwnJFmTbXQRhNt/bBPOkX7CT8YaSS+1Vsl5DFKQEH4aGtOT\nACwhewi/B0KiAKENUpiBQ016xxAVmcVESTiHBprsK4SK/3dWhWvSplLhXO57fVj/6b6y1mByLeI1\n2Fc41t+m6fumklWHkO4/rgjebsJP+r/MmP+KJP4Y8UTP48efTgCjtM0xUUpj6ASj2w0TgKDtBwTh\nCyNjXcuhGbTQY+aQZVlYWLy4tTKyoClOQA2/zUv1lZFtxu+r5TXZSp3Eldl/lABefeV7rLXWRsa2\nvSZ6S3P9kVtHFnQBBEahVYd6kG2VECNMAJL/5uCt1EpTI2MhrEXYXZoae/Rdx2gC5VMecgBNz1iB\nve4U1TEe/3ECkPEGYQQ0Bt8ElK3SWB26EQJjdC7ffillLj/+hLz6dt6ZbVpW7rMrLkiHP65uJkXq\neWoGJvH4vxBcyrYvBa5o4i9QoECB1wPFjr9AgQIF3mS4zHi/IP4CBQoUuFgUO/4h+OIXv8iTTz7J\n7Owsn/3sZwGGHiW2tLTEiRMnOHjwIADXXnst99133+s11Fww0cO/PB/3JHp1ZTR5POkTJUOOAQRa\noY3OVVY+iWdfXp//0C00gHG+NKSseXMspLxjNcag0FhjRZ6TwZBvrN25ko8cJvLuz3mtdgLyrpfL\nEZfLZxDjdSP+22+/nfe///18/vOfT16LjxK78847efTRR3nkkUcSt7l9+/bx6U9/+qL67JKjyJSL\n9cTqrpxylG+4MQZPaVSkdjNKRwqg7P47KpT1hWohM/Q7YdPvcL69QVv52FIy61SpOIO6dWMMq50G\nK+16KL/sk6ul4euAp5af50xjBaU1U26NucpcZgIIlKIThAbKZekQGJXIMPv7b7XWWamfAdtmtjbP\nVnMTPcSYrWS7SCF46bUfM12ZY3b2IJY1OO200SjVwlMejhCh7HUIqU3bNa6aPUzHKHSnTsUu4WQ8\nkDWRokoZxZnGOmXLZr48hT0kAZWFHape4r/PjAqVITN2CaMVraCNI23sDLVOSPihmkRpgxChHbEc\nUrvgIHGkFVprKxUpcIYQitYYQXjeghBD1SrGGGT0Tsb54aetyHX04HYYnaXrW2D4w81EqhmPmWy1\nUNxWfM1HrsFUvwLGmiimzwMYNdaLQVG5OwTXX389S0tLPa898cQTPPDAA0B4lNgDDzyQEP/FuEWn\nJ5tML+RYW59KADHhCyF6FAr9ErQewqdXlhYedhJ6y4eKz5DwE3vmWB4e1wKkEkDDb7PU3qSt/ET1\norRiqbOF61nMumECSBN+W/f6b0oTngkQvw9fBTy18jyvNVbY8LsKmUarTd1r9CQAXwV0Ah+/T5sv\nhUVFRG6f0XVrttdY3XqNllfHS8k3Z2pzGKN7EkDZdhHSoqN8jFGgfRp+g3p7nVp5jrnZA1iWgzYK\npdoEyqeVct+UCFxp9ySAabvGVXNHKDsVDKFcU+kA3wsL1+IEEMsSFdHYoza9QNFuBAMJICb8+DNJ\n1z2kf48J3xEycWDVQEcF+DpIEkD4N10dvAnZPpJ1GoxRPQnAQeJYfX78hMlYiFBFlRCg1uHfWim9\nuzEDCSAm/Fizn57Xgzr8rj15lrSyXxtPX5vD6gCGrsG+BJBOOKPGmib8dH1OQup9mv+spJQ11u3A\nZcb7b+w9/o2NjaFHiS0tLfGxj32MarXKBz/4Qa6//vrc7eqI2Ps/i3Bh9RV89BF+jLQGOFChNXFc\njDXQbhSrtCYwBq1NQvi9/fcWjb3UWKKlvExBpgE6RrHc2YI2tJQ/QPjJ+41+pDE8t/oyL2ye6SH8\nNBqqnUoAMwghM22UNeFpTVJYWFrzwvlTtPwGfsZJV/FBLdO1OfygjVGajvYwarDduteg7jVotNeZ\nm9mP7biZdssaQzvStrvS4brFa6m6U3EhbQ8UJkkArrQp2U4P4afhGRUlAJ+9lVnmS7WhqzadAKad\nEqVhHvuiNwGUpUsksM+I7SYAC0PFdhnqxx/VogRKhV78QvQQfrdJkXyrVVrjSDHUjz9NzOlddZ46\ngPRr/f2na2GAAcLvxoa7oJ4DUVLvYVj/yUYwx1gJV2q+sWZczwvBdrtzXmrsqIe78Qc6Pz/PF77w\nBaampnj++ef5zGc+w8mTJymXy7nayasXzusF7ukAxPjj2oSU6EDl8+MXoR/+uKJxDXg6oDXkaMH+\n2KXW+lDST6Oh2tSYHnmwStimoRk0qXe20GNG65kAiejZuQ9D3WswLxnrsa8xBGiqTnXsvW+FibTw\n40vxPaNDvX6eZwkw/mAViL4iiOGk3xMrcPL48QNEtxLze8yP1+Fn7bCHd7/9fvzpTVCeNRjfetru\nsW4Xinv8E2DYUWK2bTM1FRbmHD16lH379nHmzBmOHj060MapU6c4depU8vvdd9+97eMUE1gaCTHB\nw7lo4m8nJpt/IUlsZ2jeB5iTIv6qPz5ukjYn63+C6Ali87aYv81L8QlM9P4vAQlO0v+kJJznKMTt\n7vONxutK/P1Hs73jHe/g8ccf56677uLxxx/nllvC48s2NzeZmppCSsm5c+c4e/Yse/fuzWzzQj+o\nicYd3vTIFzuJdGGbSX/yJicIzhmaV+kzKeKH9OPjJmlzsv7zL+7t16/k15BdGvXMRO8/52d1qfqf\nVOm0HZvFy4z3Xz/if+ihh3jqqafY2tri/vvv5+677x56lNjTTz/Nww8/jG2HSokPf/jD1Gq112uo\nBQoUKDARih3/EHz0ox/NfD3rKLHbbruN22677VIPKTcu1e2LvBvOiXamE+y4L8XefBI1VuhImvM2\n2iXYxl6qbycF3nzIU3uzk3B5jTYnjNYjCSivF3iPW6HJ5wUex45ia60VXuBhifFPD5RWtJSHH/hj\n/fgbnQZKeVgYrBEt2wgIPJY2XgU1+uGqUAHt+gaq08YZUwAlFWxsbmK80Gp5aP9C4iBZWTmD8EPl\nzjC4wsYVNhudzfC6joBFWA8RqGDsddVa8dP1M2x2GqMzq9HUvRYvbJ6n6bdHxorIhlkbDaO83iNZ\nr6f80I8/hx9+oHSvuiVzqGG/eTzuTSR/7He5zOo/XC/j/fCTdUU+P/xJ1qBhgrMD4r/J0f92Ia2O\nGvWzU7CjVD3bBRE92Y/vC6eLUpKYtF5ZqdBxs1+DbEALgZACh7AIJ7ZY7vcC1+GLSCm6vxtNqPKI\n+1e0lc9SezNUwEiJY0Tosx89SYihtKLudzjdXEvskW0h2VWapmTZXUtcY2h4DZ5dfYEnz59KdrFV\nu0qtNI3AIohathEEQYcz66fZaofS2eeXJG9ZvJaF6f0IO1UwpgJWN87ynaf/mVa7DoBl2RzaexXl\nSrXHFVQqWFtf4bmXn0uu8UxtiiMHDuOWSinbZYkw0KhvUm9tAnDm/PPs23U1i4th/7EIsyRsLGlj\nhIWUNq/UzyIb5zk8tY+p0lTPNwWLUEp5vtMI339nC0da7KvMUbKdnuuqVcBaZ4tzkavo0+uvcGRq\nNz83f4SZUrXbbnTGwXMbZ1nuhO9frghumj/MkanF0JUz1pGb7scspRVaN2OwdbSzihUmsV5eCKQI\ntfltHSYp10R+/Gk/fMKiERHJOj0DUmtsOejHL0QYZ6XqAJRSoba/TxsfSz3TOv5YWtm/BrSJ1ooU\n4XU0GqF1eDBQv+2yiCTTqb6y/PBhUE00UF+Tllz31AFc3NkBWecBbAdkRlHiToYwF1MptUPRVl0t\ncboacGxpfVTMpY3BjPjqFicAbUgIP7O9KAEoo+mkCH9YrNKajg6o+21ON9cH/PBjxAmgo9r8dPV5\nvn/+6aG3LSp2lapTQ+mApfXT1NubmXFCCK5evI6ZyiJbjTX+7enHaEWE1484AUjbZnNzg+deei7c\n5WZgujbFkf2HcByHZqtOo5XdP8DexcPs2n2EslsDYWHJ7MUkheTQ1D6m3BpKm+g8guz3b0uLfZVZ\npJBstLc41x5uI32ktovjC1chheS5jbOseI3s/hHcuHCIYzN7KdkOcpgOPx4DMiL7LuFntxt+w5FS\nJIQ/DNKYSNsPiC7hZyJODAwWaaWRLrpKCH8YjO5Wq44h0fSGa6zd9BiP/f6xilTssBGkz9noJ/zy\nNun43/a5/yFX3NP/8f/alv4uFlc08cfI48cfw1f59MLahH78ee5Rn2+usZpDWw/w7NprrI/xw4/x\nrZe+Sb3vYJUsBF6HrcZqrjYbq6us1vPFBm3FRjubHNOwLMmRPXvwtD829rojNzO3eDhX/3uqe9B5\nfY20PzTpplGSLtM5PP4B3nfgBg5MLeSKrUg3l2ZeIKhIO9ccdADXzuc/JBl9zkQMYwxBzjVAzvMA\nIJ9v/oXE5tHsj2pzu4j/hr+4K1fcU7/96Lb0d7G4vL6fFChQoMAOxHbeNjpz5gwPPvhgUmR67tw5\nPvjBD9JoNPja176W1Dv92q/9GjfffPMF9VEQf4ECBQpcJLZT1XPgwAH+9E//FAi/qdx///3ceuut\nPPbYY9xxxx3ccccdF91HQfwFChQocJG4VIqdH/3oR+zdu5ddu3YBF2demUZB/BeISa6/iCoBtvNh\nSvhgK2818UQO77nbVN74e+aQbcA1DJr8lZetTh23ND3+ob3R+KqT7zyACfq3cvo9xfbQcpvV05OM\nNW/sRJXnBRLk8ly6AHzrW9/i3e9+d/L7V7/6Vf7lX/6Fa665hl//9V+nWq1eULtX9MPdfouI+Kl+\nFtLWsMaEBJRFVl1dcSTHBtSQlaIiSac2oIxiy2+x6tUzqbXl+2wFLTytCLRiy2vTyngYaoxhpbnG\nRmeTVtAhUB4rrWVUxoNLYwyW1mijQt2yCthqb2WO1QQKoXwC5WO0ptlus9kcjDXGoFc7+Oeb+G0P\nq+zQmZPoyuDEF0Jw9b6DTE9NIy2JDgJW6yuZici2XQ7uO0qpXMOxXVyrgu1UMz+v+uYyy0sv0Oo0\nqFVmOLL/OIsLRwZijdFsNM6x0VzB1x5lp8p0dQ8lJ9vsryxLofwRgS1tbGvQYx9g3q1xy+6rmS/V\nsEVoxZ3lsBkTPoTSYEtISpaTeXYAgCtk2B4i9PEf4XEvumaVWELgWtlqnbRKJpSWCqwMFU6sKgsT\nb9cxc2iiSKl60jLQrLH2f97DYrVWvcWSI/pPO4aOanNc/9v1cPfm//3XcsX94CNfye0NFAQBH/nI\nRzh58iQzMzNsbm4yPR1udP7u7/6OtbU17r///gsa7xW5409/2P1e3MlpSCldb6x1Tk8yEdm7qjC4\nh/CJ7ZlFNzadAGLCj1YEUoBEMi9tpp0KW36bVW8LbQytwKcetPG0SvTmUlrMlWtM67B4qKl9tDGs\nNtdYb2/QCNrd5CFt9k7tJ1A+q61lAhNgjMbSBm0UzXSBloS52jwqlQBiwtfKp52KLZVd9pV302y3\n2GzWw+u20sE736TVaOEHUVJqt6m0ysiKjTdnoyuhdPGqfYeYnp4iQId1BDoUte+e24dSPqtbqxij\nsW2XQ/uO4pZr+OjwJ2jTCtpUVAvHLuPYoV1HY2uZpaUXabQ36AThWJt+k83GKjO1BQ7tv4HdC1dh\nMGw0zrHZWqbhNZLagLbq0PGblJwqM9XduE4F6BK+nyq86yhFSQfY0sKyHKQQLESEP1eqYUU7vGQn\nbXSSAICo3iMSmYrwJ0Cjgg6W8nsSgCussMYhlTwEKdKWXb29iEk5Na8DY1CB6kkA6YNKRM8a0OGh\nMNG8BBLC75/XWmtEnw4+Jvz+g0/iIqt45ztqDfbr8LVSSCkHZLFJEVafDl/AwMEzw84DyNP/tkAO\nSZAZyOsN9IMf/ICjR48yMzMDkPwX4H3ve99FHVR1xRL/OC/unkMiMnYVyd9rTaBNpKkf7QUutMYz\nJhRBSznwlVkIgWM5zEubmu3y5MpLtHW2NXM8ttlyjaC5wanVF2imCT+FwBiQNnum9rNWP0crqPcS\nfgodE4QJYGqetdWz6MDrIfwYymgUmlKpxCIWrzzxM7xGBy8Y/BbS6rShA+VWiYWr9nDgbUe6hN/f\nv/ZBwO65vZSq01Qq0wnh97//ZtCGoE1ZNjn32vO023U6GWPtKI+lzbNsNFaYm3mG+cUDNPxmpra/\npTq0VIe232T39GHmqos9hN97rVSYAIzmlw/fxL7qbEL4PRBdj32iYrWE8PtgUgmgZmDGrQ69TZAU\nc6V964fMaxBJAihbsqfAqje264cfaIMR4UDHedxbxiDlIOFnxZq+1/rHmvbDH1VbkOXHP0yS2uvH\nn7//7fLjvxSWDd/85jd7bvPETsYA3/nOdzh8OJ/sOQtXJPFvtxe40UGuD1ZKicnpxy+lRWDUGIf7\nkEAafpNGDm1/YAzG6Ewi70dHBwhjxsYqNK1Wi9ZWC6VHe/e3Ox2OLMxmEv5g/z7z5Smyj6HpRcNv\n4nutTNJPw1M+gVHU/fG1BW3VoWyXcnn3d3TAvFvNJv00hOievDXuXroA13Jy3RsWUoZFWLk89sXQ\nBDEwVmNyz2sxZDOVFZvHOz/5FpFzDebV9ueN3el+/J1Ohx/96Ed85CMfSV778pe/zIsvvogQgt27\nd/Obv/mbF9z+FUn8BQoUKPB6Yrt3/KVSib/+67/uee23fuu3tq39gvgLFChQ4CJxublzFsRfoECB\nAheJSyXnvFQoiD8HQnnd9uPStDmhH/529z+BOniyswO2/2pN1OJEt3CvQCH8FfiWthM7yXI5Dy6v\n7yc5kceL26R+hqHHK3ysH78Go3FklCZG9q9QSrHg1igPcaCMYSM4MrOXq6b2MGUPP2zeQjDtVDi6\ncIy9td2ULHdorCttqnaF2swi0+VprBFfU6tOlb37DnL4+muZn5sfGieFZO+eAyzUDrJnej/VEWMt\nWy6HZw9x/a7r2FtdxBlxDcrSZdqdZm52HzOV2ZH8s6u2iyOzhzkyc4gpZ3hhiyMs9td2c2R6kd2l\nadwRZwdUpM1VtUWkicqvRnyuEnCxcKU18owBTOjYGXvx55lXQopwDo5KrFqHFQBm9BroceHM4XGP\nyeeHfyF+/Hn6j///2NjU/3/9/fhlrp+dgiu2gCvLdztLv2sIdcSizws99uNPqzOy/fijQpLIdjeW\nigUqlHam29Ba4WtFQ7UTbbk2hvPNDTb8Nm3dLcKyEdhS4shuEVHTb/PjpZ+x3N6gHnQAsJDUnBLz\nlXnmyjNJ7EpjieeWf8JGeyNR7pSkgyUttLQTWZ4xhk59nVZjjWankVhB19wqTqmKMzWHFXmN+x2P\nM997irXTZ1lfD+2NLWmxe/dejt5wE2+99Z1JbKu9ydmlZ6m31mn6oYNo2XbZPbWHd1x1G1fvvibp\n/+X1l3lm+VlW2+v40TUoSzf045d20qbWis2VV9naWmYzZe+8q7aLq/Yc4+3H/muc6EyBlt/i2fOn\nWGmuUI+cUR1hsau6yM37jnPD7rd2r1Vrk+c2XmOj08SL5JgVy2FPeZZ37buOfbX5ZKxKKzQ6suMO\n/14CtrCoOmVkouM3NP0WvlHJZ40JLbWrVolpt1uc1u8nn55XUoTzIOk/svo2aQmmDhODIwR2Sp5o\n+tZATx1Lvx9+hg5eYKICsT7v/j59fNePP1tbP7AGjRmQhWb1P6oWJ6v/fjVTt/9UfUXfmLargOud\nX/5fcsV9+3/+y23p72JxxRJ/jMSLO2OypRHuUhQgxnqRxwkAACGGaovjBNDRmo4Kegi/H3ECWPNa\nSEEP4fejFXT40dLPWG1vsVCZYzZF+P1YbSzzzPmnaPgNkDZiyDUwxtBpbNDYWsF1yjjTc0MPl/A7\nHq89+TTN5U2uueEm3nrLLwy9ts32FueWnqUkJf/VW36BI4tHh/b/8sYr/PvZH+Mpv4fw+xEmgDN4\nrTpX7TrKzcfenRB+P8IE8BR+0OHmfTfwthTh92OltcXzG69RsVzetf+t7K3ODR1rmABMSOQpwh8Y\nqzG0gjaBVlTtEtNDqpHjdmN5oyWGa9bTCUCIQcIfiNfd8ynGySyN1khBNIbhkseeitgx0si8axCi\nYq6oLmKUJLPnoBYx+uFq/wFMl8KP/13/x/+aK+5b/9MXtqW/i8UVT/wwmb+3r1Sur2Tx19k8vuUr\n7TpbwXhtPcDZxjotnc8D58XNpWSHOgpLjfP88PyPc7VpmbDIKQ+uW7wBPeI2SYyy5fD23dfk8ut5\neulZnll7IVf/t+67mbKbz6vk2uk9uT6rKdtlf3X4La00SsIampyyYvM+AHRG2DWkISb0w897JoVN\nPs2+0XpszUq6/+322J+k3Uvtx//ur/xvueL+y6/9p23p72JRPNwtUKBAgYvETrp/nwcF8RcoUKDA\nRaKQcxYoUKDAmwyXm5yzIP4UJnKtj9URuWLztxlEkr08Hu+h18n4dj3l5fZtnwSWsHI47YSHkyuj\nsXI8D1DGJLbE4xBolet9CURuHbogn8c+TLbYJ/XOzzWvJmjzUsBALq+dNwOKWz07COkn/6OsWA0p\nOZkIj0wJ7WAzYo0h0Dohc2N0pOwZnPxeENAIPLSBinAIjMZn8GGsMYZNr8VapxmapyFCK+chHu/t\nwMfXimm3Qk0rNv02QUYxVstv8dzKs6y11rAiQg3IXqi2sClZLgYoO1V85Q01O7t65mr2Te3DtUto\nDBvtBi09+PBaCsmB6jw1u0Tda+FIC9d2sTO+Fje8Nq/Wl+howYHpw3T8JivtlcwEMOvOMl+eZ8Nr\n01aKqlOi4pQH3pdAsK8yw6xTwZYWBjPUlM0Sgnm3gittOsrDEgJbOtnXCknVdhMlj9IKNYT7hDFh\ngjShBFQKkfm5AqAVCIEikhhLiZURpyP1TyIwAOwhDpexSscKfZ7DxDrMDTSyXE7aHaLWib37wzVg\nQtnpsPMAInvytM300HMG9KAab1isViolkx491jwccNEoiD8bX/ziF3nyySeZnZ3ls5/9LAD1ep0H\nH3yQpaUl9uzZw4kTJ5ITZR555BEee+wxLMvi3nvv5aabbsrdlzFdYh7lxR0TfuzPL0T3GAgT+YvH\nCSCWZsaSuPQcM1qjjEgSgBcENHwv3L1HTqBCCBwktpYoo/AId/YbnRbrXpO2DlIUF54DYBmdJACA\njvLxlOqxMBbSYq5UQ2vNpt8iMJqm1+S5lWdZb69TD1o916YsnZ4EEBM+0EOKQtrMl+eTBCAQXD17\nFXtr+7DtEkDi4T5fnmLWaDa9Jk3lIYXkYHWeql3GyJBIAgyBDvB9jS0sSraDLS0aXotX68vU/Tad\ndB2DU+WAU6UTtFhpLWMwzJZmmS/NI6WNBhSGpgptpct+m6pdpuKG0sr9lRlm3Er4LSP5YiRw6U0A\nMeGXpN3V0EfjVX0JICZ8S8geQhJCYBmDMipJ68IYJFHRTuSaCSFpa6N6E0BE+Jke99HcsYToIXwh\nuyViBvD7EkBM+FL2EqKIHFwNIpybdAlfyEE//LQfv9ImWVv9ayBQGkk3AfQcANOvw+9LACZF3On+\n0wVZae/+odcqNdZhdQBxbNbrF4PL7VvP60b8t99+O+9///v5/Oc/n7z26KOPcuONN3LnnXfy6KOP\n8sgjj3DPPfdw+vRpvv3tb3Py5ElWVlb44z/+Yz73uc/lvrjG5PPijglfZrQbLyyjNb7uHl6RNYL0\nBF73PLxoIWfJF4WU2EiEUvxk62wf4fdCRQnAKB9PBwyLjIlgrlTj+2f/nefXXhxq49yOTvUqSwfX\nriCFzNwFG6JEIG32VPfwlrmjOBHh9yM8rUwyV5piUVhUbTch/H4ERoc/vuJcY4261wrPCMh8/2Db\nFQ5MH8aJ5JA67q+v/6byaSufvdLixl1HEsIfeF+R/7yLRc12qdrO8B2o6CaAxdI0bio5pJGQlhHI\n2Gc+IfyB4HDMxgAaGzG0tiLuK0kAMHQOImSSAEpSDBB+/1hNlABEBuHH6PHD19mE3x8bKI0dffsd\neyZGRoFX//uP12BC1nnOAxhC+FmxO9mP/1LidRvt9ddfT61W63ntiSee4D3veQ8A733ve/nud7+b\nvP6ud70Ly7LYs2cP+/fv57nnnsvdVy4v7miyj70/LOXIY/D6Y1V062ccjAhJMM/tf2X0UNLvaRPY\nbG/m8u5vax9bWJm3iAYgrKGkn4YGyraDyXEaUWA0nvKHkn4aCnAsZ+zzBA3UbDf0zR8zhNAP38r1\nuRoRVtzm8ZhPToYaNwdEeDsv77zK5bEfBidjGTfWrJPnshB/O87Tf7z28qxBOcEazNPmJP3njckL\nGX324352Ct7QNLWxsZGcKDM3N8fGxgYAq6uryanyAAsLC6yurr4hYyxQoECBcZDCyvWzU5D7Vs/m\n5iau61Iul9Fa8/Wvfx0hBL/4i7+4bZnzcrtPVqBAgQJw+XFXbuL/1Kc+xYc//GHe8pa38JWvfIXv\nfe97WJbFiy++yL333ntBnc/NzSXnSK6vrzM7OwuEO/zl5eUkbmVlhYWFhcw2Tp06xalTp5Lf8x5k\nPHKYTQ4AACAASURBVAkEcgKpZ6gK2tb+c8o2k9i87U4yBvINYaI2L8VamWATIiYZ7SUZ7Bvd/wTd\nTzDWS0GCE83rCft/+OGHk38fP36c48ePT/T3EHLE5YTcxP/aa69x9dVXA/CNb3yDT3ziE5TLZX7n\nd34nN/H3GDsB73jHO3j88ce56667ePzxx7nlllsAuOWWW/jc5z7HHXfcwerqKmfPnuXYsWOZbV7o\nBzUZ8iqr49jtjZzETikYcy5uGirP/f14DDnjNCb3ElAT2OLqnNdglMXxQJtv8HkAEyHHOb6XtPvQ\nDzRf7KXQ9k/w/iftfzs2i1fsjl9KSRAEvPbaa1SrVXbt2oXWmnZ7/INEgIceeoinnnqKra0t7r//\nfu6++27uuusuTp48yWOPPcbu3bs5ceIEAIcOHeKd73wnJ06cwLZt7rvvvoku7Chdb/z/YzKN5XKj\nNMAGEXmhj9AVa42KH9amXAuzoJSiGXRwpARlRj64tRG4toOlJYHWw03ZjGGzs4nWmpJ0MMbgDXlw\nWpYurl3CkWUcofGVP/SA9BmnymJlgZrlEmhFZ0j/ktC+1wsCKo6FFAI15H0JwItqERwhMYah/TuR\nlNbTHiXpoBiehKbsEkaE19eWVqTgye5fAJt+h1lCu2aGPJAWJnpfvo+wRz8MTaSOpJJ1Vmw6iWk9\n8sFpTyIbo4MnknASyylHzOt4HIk8ckT/pu/fo2KFCNdUnjWYHk8eHX6/dfOoNsdJNpPYbVL1DHNn\n3anI7c75F3/xF7RaLba2trjpppv41V/9VV5++WX+/M//nAcffPBSj3MijPLjN2ZQoZNeJIncM9JL\nm9QuJ5GBphJATPhN1VualfZYjxe/Uoqm8jjf2Up222FBmCLQvcodm9Du2ZFWd/xG0/A7eFp1JZhG\ns9nZ4ofnTvHi5ume99WfAGLCLznTOJF2P1xYCqU9POWjIgKOCf8t81djRwelhMVjbbwgSBJATPgC\nQVjK0L1eFcvtSQAh4XucaazQUt2CL4nAkXZ4LaJYR4RqqnafU2jVKuGmEoAgJPxdlVn2Ty30LMCq\ntHsSQEz4/SnGEpJZp9STAGLCL0unx4HTQuBKuycBJEVKGTUjyScqRDIfwtqAXo/7tD4//FizpY6h\nT37UZNxfRPiuNajDT7fR7/vfE9uXAGKS7y9kTI81HRsKmWRPIWPeMzHS/Q3o8PusnEf68WfUAcTX\nvz82/n273Dnv+M9/nCvuP9/x8W3p72KRm/h93+frX/86lmXxi7/4i1iWxalTp1hfX+fd7373pR7n\nROj34wcyCb8fcQJQQ6p2kzhjUErjG01LZdXi9sYGStHqI/zMuCgB9BN+P7QxNPyw0vWH55/i5T7C\n70dJOrhWibI7kxB+Vv+YADDsrixw9fxVCeFnxbaDDq0gLNYyQ6qBY5SlTUf7nG2s0FL+0DiJiJII\ntDMqgdOoWiWmnRp7qnPsn1ocKZWrSjuXxNMSkjmnTNlyBgh/IBZByXLGyizjTQTGYIkwmQ/9xgDh\nNwAR3lMfdU2NMVFxH7hjJJlxFSwMEv5AbJQAhlWup/uPt0X9hJ/Vf4xxQpCJvPt19xCk0dcqTMxZ\n31a2i/j/+//nk7ni/u//7g+3pb+LRe5bPY7j8Eu/9EvJ757ncd111+E4ziUZ2HZBSomKyt/HQUiJ\nr8b7lod1AIJ6xxt731EIwbrXYDU6BWpUnGPZlKzBHWk/pBBMuxW+8fK3WPfqY6JBSpfpyq6RMaH2\n3OHnFq9hqjQ1NrbilMEYOkaNvfe75bc531zFH3N2gMYgzfDbSWk0VYf/sPsYU6Xa+FgdMCOtsXfp\nldF0tGKxPDO2TUV4GI89xo8/rrq1cmw8BIQPp6MTtca2i8HN4ccvZXi7LI/6TkiJyrkGMAY7Z/95\nffOT2EnaHbsGJdrk9/i/EGz3rZ5ms8lf/uVf8sorryCE4P7772f//v1DnQ4mHm/ewL/9279Niqie\nfPJJPvShD/GhD32IJ5544oI6LlCgQIErBdt95u6XvvQl3v72t3Py5Ek+85nPcPDgwcTp4KGHHuL4\n8eM88sgjFzze3CP55je/yeHDhwH4h3/4B377t3+b3/u93+MrX/nKBXdeoECBAlcCJCLXTx40m02e\neeYZbr/9dgAsy6JarQ51OrgQ5L7V0+l0KJVKbG1tce7cOX7hF34BoEdvX6BAgQJvRmynV8/58+eZ\nnp7mC1/4Ai+99BJHjx7l3nvvHep0cCHIPdoDBw7wjW98g69+9av8/M//PNCt5r1SEB5inU83r4zu\neWg1Cq3A6x7OPqb/tU4jl2a95bdotkc/N0jaRRGofOf4eirI1b/SiuXmSq5r5SmPTg7/IIBO0Ebl\nrEXY8tu5xhoeeJ7vzGOBQKnx/Rtie+4cHkrGhCqkXLHjn/HEyKtwjtvM2/9EVXgFgJRR35ifPNBa\n88ILL/DLv/zLfPrTn6ZUKvHoo49m9nmhyL3j/43f+A3+5m/+BsuyuP/++wH44Q9/mCSBnYhEupWS\nh2U9tDLG4ClNEGn2lQp90+0Mh0OlNWvtJp5RaGMQSmMhMw+9Xu80eGlrma2ggxQCV1rUnNLAgyBj\nDGcba5xtbtAIOtRsl92VGQ5kqFVafov/75mv8dzyz9hob+E4LlaphlUaNFETCGpOBRC0/Q1s5WBb\nFWxr8IH8lF1lpjxNU3kEzTUqdomaWxkYa6ADfrr0zP/P3rsHWXZUZ76/zP06r3pXdau71a2WWiDk\nBhksLgaDxzCyIcAEaDxYvh78GHNnIDxjhvD4D5iI4er6GmzAZrBn5LAdjgvG4QjLKBgrwhphz1gM\nBuSHwJJBNEhCj5Za/az3qfPar8z7x9771Hnsc3ae7mrUks6naHVX1arM3PvkXit35re+xen6aep+\ng7nSDIdmj7B/9tDQvfIjn2e3n6bu14l0hGuVqLhzOHZpqP8gbNMK6wRRB0taeFYJz51N2DgDKFsu\nnnR5qn6BC61tlsuzucwepTXt0CdUEbHWeIHNnFum4gzfq15KZyv2sZTEk/YQsyeR6k7+FRARhjG2\nkJRsd+j6E0aPIvOkccbsyXECWid03Yx9EqcMszw9foHGSUW/xtaZSNtMnLkg0gnt0hpR50HFimy0\nSu9SNIfbTRhFoqf/UY6t+3NGUzmHbAuuq9c2+7exHr8BW+hiMEnmblGm8OLiIktLSxw7dgyA1772\ntdx9990jlQ4uarymdM7nE1phsrodnLjdhKw0AAw6/EG+tBR0Nc5jrdnKHP5gh2kCShYANv0GT++s\n04j8oSQmR0hcaVFxPCSCs80NzrcSRc3Bdmu2x0p5lkO1JTphm/se/SLfXXuCtVa/YJ0rbRzHwypV\nkU5SICRz+INJXCXpYEu3GwBmnAoz3gxSyKH+S9KmZHvU3DJKKx678B3O1E+z4fe/YtrCYtab4dDc\nEa6avZogDroOvxn3r/Q9afcFgMThbxNE/tBYy5aHa5UopQFgkMOfIeHyl7oBAKAd+gQqGpKcTmiY\nSQAop0Vh5hwPV1hDcg8Zl9+TNtKyug4/+WGPk9FJVmsWAICeNzwxZAt0AwCIrsMf7D/jx2cBYNfh\nj9eYH3T4g/MasoIwKbc+dfgjufXQfV6yZ2JU/5kDHsmtH8HDz2zybXW3pu2ogDCcs5Bfk2Owjb2i\nc/7U//qvRnZ/9mP/wcju9ttv533vex8HDx7krrvuwveTfJZarcatt97K3XffTbPZ5N3vfvdFjXci\nx//Nb36T+++/n+3tbT70oQ/xxBNP0G63efnLX35RnV8utKO48DUo4dbrbtLIKGitaUc+7TgsfgXX\nmsfrF9gMWiOzVjNI4FR9lVYcFNIMm411vnXqa2x2tsbaudJmZn4fldLsyKzdDCXpcO3CS/DsUrHc\ncRzyyPl/ol5AHbWFRcWr4dolWvH4rR1POiRrV0Wgxo+1YpW4eu5ahBhPyRTAglfjQHVxZKWtDBaC\n62aW2VeqFer7CA1l20scZcG8klpQsp203OMY2zQRy0IU9q+VomxLrByHP4huZayirYVsATRiVT/Y\nfyI3bcbDh9FvALvd7waASWxN+zex1UpRdvamJMn/+b/+m5HdnT/2fiO7kydP8gd/8AdEUcT+/fv5\nd//u36GU4lOf+hRra2tdpYNBqXtTGF/1F77wBe69915uueUW/v7v/x4A13X5zGc+w0c+8pGL6vxy\nwWTvK5nsxQFCCEGklNm+qxD4cVjo9CEpmBEqE0vYam8WOn2AQEV4llfo9CHR4zfRuAdoRi0aQfF5\nQqRjNLrQ6QP4KqQsHdoFTj8bqyWssYlykC6aEYVOHxIefslyjETddLrKNdpUF+n/imyFQOSs8nNN\nUz1+Ix68kES6mNueZRKbHEoKKZMtkgl4+Kb1AIxqJqd2E+UBGN7XvcJea+0fPXqU3/iN3xj6/oc/\nvDeZv8ZXfu+99/LhD3+YW2+9tXtTDx06xJkzZ/ZkIFNMMcUUz1eYkTmvHD0f4xV/u93uK44CEEUR\ntv2Crtc+xRRTTFGI55s6p3EIuvHGG4coRV/4whe+B5LIU0wxxRRXNvY6c/dyw3gk73nPe3jggQf4\n9//+39PpdPjABz7A3/3d3/HzP//zl3N8lw0T6atPEMzN1eDN9eAn0Y2PDXRuuu2qycrLGPU/gR5+\nOEHtAFM9/smw97UTJrG8XLgsa88JGjU1nYRQOMk1PRdrb2H435UC432aubk5fuM3foMnnniC1dVV\nlpaWuP766y+r8NHFIlPtG8XZV1oTxarLbBjJgEhtPeGg0Elx9FGfnVIoNAcrc5xrb9OOwpE6+2EU\ncL65xvnGeRZKC9gjDlkFEIYdFDG10gwqjmiF7dw2PcvBthxafotZx0UKa6R2vytstI45ufldDs8d\nxXPKIwNW0Gly7vyT7GytMTO7gJIi96psJFrFrK2eZH52H+XyLKHIv34HQafd5Mzas1y1chi3VBl5\nr7Kxnms8y0plP7bl5o5VAiXLRUqJJLl3o8KKhaBk2dSjgJLt4owrpK4SFdaNKGDWqeBYVv7KLZ1L\nYUrNdC0HmcOXz2xBozSgEirouP4TgoFAoMYyazLZcY1ItPvHcNtTluiu/HOBxj4TcOszzv64Z7DX\n6Y/V4x+oB2DUv+lYtd4zPf68fJMrGUZ0TqUUP/uzP8sf/dEfXfFqnJDIMg9qcWcOP1SKqMd7d6Vw\nofugZBzgSPe/Fyit8SO/PwCkDj9QUV9QaIU+59t1Wj0BIEod/j+tPUrUw2ZZKi2yXF7qBoDE4bc5\nU3+Wp7ee2h2r1sgoQkUhrTBhzmQOH7eEtHcnnxCCmdJsXwDInGjC0Nm9ssXSIkfmr+0LAEGnwcnz\nj/GPj9+P6lmZX7V8iNnZJZSVBABbWOgoZLu+RrO1y++X0ubQ/mOUK7sBIHP4T5/+DkGwy/wpl2Y4\nfPAlfQHAEzaxjmkNZPyulPexUt0NAJnDn3HLVN1Kn/NwUonnbPSZw18o1ajYuxnnUghmbK8vAGil\niJSiqfrptiVpM9cbAFInprQaYnOVpI1ruVhCdlk0STEHhiSPpR4IAKnDt4TAsvrzAKwBLn1WI2KQ\nITQoW5zp2wtBGpS6Te7SIDPbERr74/TwTfIARtEyh/T4c7T0e68rr3/TnIHevIC94vG/50ufMbL7\n9Bt/YU/6u1QYrfillBw8eJCdnZ2RtW+vNGQUOK0VsVI9Dr9/VdGVwoXEiet0ZZ/zWiZFIkesdFqQ\nREW7Dn/AvOJ4XOus0A59Hts+z7M75/jG2mN9Dj/DemeD9c4Gi6UFZpwaqztneGb76eFrEgLtOGDb\n1GyHKIqw3BIyh4ustabe3kYIQdWdQQjBTlDPvVcbnQ02zm2wUFpkpbSPc+tP8+Djf4vKeWM4t3aa\nc2un2b98iGp1lu3mFo3WsGaIUhGnzj6KlDYH9h0FIXny7Hf7HH6GdmeHx558kJJX48jVN+B4ZXbC\nZu5YV9sXWG1fYLm8wpG5oyyUZoYcfoaM1ukISdlyhhx+d6xasx12kAhmHA+0pqXC3HeQjoro+HU8\nYbPgVREa1Ig3m46K6KgITzrJ20jirXNtVZbApGJsKbGk7Hf4GYRIApnWWKon8SvHdNDZZcFi8FYJ\nAZaVJH71rqrzNPb7ihUVrKq7z6BS3cVUkW22Es/Tzs+/rtF5AH1FXQqqh10qnm+Hu8ZbPW94wxv4\n+Mc/zlvf+laWlpb6LvRKS+DqhRASP4pQeU9Grx2AlIRRVJykIwSu5dKIOqO3flKUHY/15gX+8cK3\nC8e60dnk7OZT7BQkSmUBoFau4Rfw4LXWtIMGGLyKbnY2ePKpb7C6fb7Q9vzaaVb8Fu2BClmDSALA\nY0glCOLxejkdv0GzuYWX5/AGsNZe5ZX7vo+qgR5/qBXXVeaLk3/Q1MMOloFz8HWEHwW4dvEbsK9C\nPMsBYbAdIAS2AFmgx48QxErlSoUMQkqJMNCjFwKElXH2i7n1GNQYgMSpT6zHv8c5A8owD+BicSXt\n35vA2PH/z//5PwG46667+r4vhOCOO+7Y21FNMcUUUzyPcCUxdkxg7Ph/93d/93KOY4opppjieYsX\n7FbPFFNMMcUU+ZBXUFauCYwdfybFPAjHcVhaWuI1r3kNb37zm432HL+XyKhrppBCGHHxIzWKgDjc\nvyVdSpZHp2A/HMC2ygiahXkGnu2xXN3H6Z1iyQxbeiDJPVgehFOqYDVsYgP9fj8KCgutQ5rObvoh\npOyPojalkCMLxw9Ca009bDM34hC4F0EcYSmJa5CRblpnVZAIvRlBa5RBcr/Oiocb3KuLgYksv04H\n8lytdq8kYWGTc6ErCcaO/61vfStf+cpXuoe7a2tr/NVf/RWvfe1rqdVq3HPPPayvr/MzP/Mzl3O8\nxkiKqiR0LltKrPTreMR0zqhvTup4YqWI85gicUgjaqeFw/UuK3LAVmvNZqfFufY2FW+Wf3b1a9jq\n1Pnm+iN0ouEAULOrONIhcjWL1RWa/jbnd84MBQDPLnHzwZtZri4jpc33BU0eX/suT22fHGrTs0os\nVlewpJMeBoZsttYIVZhj62FLG2+lxMrSQRqNLU6efjQ3AFSdEkII2r5P2fEQEiKGD9kEgmqpllAq\ntaZClWaniR8OX/9cbZnl5QNI28USFgJBR0dDbUohedXKK7hm/mpKTgUJRCqmnXNNWmtE6hyebW6w\n3mmwVKoy51aH2g3iiHYUEOkYEDiRRc32cgNAzfKYcUrY0gKtiXOonMn1Q1l6uJaT9JclzOWxZVKt\n/oTKqIl0PESlTK6pR7dfQBAntEtHjsgZ6NIyi7ntvWqZXXqlHC4Y2EuT7Mqcj2DWDHHrx+jhJ7Rh\nUTjWwTwApUbXDpikHsClwLSs4pUCY1nm//gf/yP/+T//5z4658bGBh/5yEf4L//lv3DmzBl+7dd+\njd/7vd+7bIM1RSOM0Co/MUsp1RcARiWaZLclimNiIfoc/tAN601GATY6Tc636zSjcCjrVquYbb/O\nN9YepRN1ug4/jzxoaU3Tr3N+5wye7fLqQ69msbKEHCikIoCW3+Dx9cd5auspPLvMYmUZSzpDiVG2\nkH0BwLM8HGkT6XjIedkKGs0tTj6bBICuwx8IXJaQeLaHTAOAFBbVUiVx3gMO2ZU2aN0NAPOzyywu\nHsCyXaKBdy1P2mkbEbZl86p9r+DI3GFKTnnoXvUGgMzha/TQ9UuSQi5LXpU5r0qoYtpRQJhTZ8FC\n4MjdAFCzPGpOCUdaw8wvpboBYNfh212+eIaMS58MRuw6fHK47Tqdm0Ik9RJSemrCd8/X7reyYNHj\n8If0+DMHn+UsjOLWD9qO4eGb6vF3bXsCgIrjJMDkLJ56+xuXB7DbX3Jveh3+4LN9OfT4/8Pffq7Y\nCPivP3TbnvR3qTBe8W9ublIq9VdO8jyPzc1NAA4cOECzmc+9/l5D69GZiFlmp4wVwRiKWzYJbcui\nGbSoR+3Rmy89mTDf3b7AdtAeuV0kpMV8eYHXH7yZhy48khQLGdFyLASl0hw3zRzkmrmDSCv/49JA\n2atx08FXUvZmqfs7RDlODyDSCoTFcu0A2+11Yh3jj5BxjiSUZua5/rqbOPX0d3LfVCApQ9kK20gk\nlXKZslfBz1mBA13t/Wq5xv6rrsPzKkSoIacPdKmqFavEW67/MSruaOpmUkjEwtOajvJH3lMFNOOA\ndiugFYe4lj3ys4rRxCoiDGKOVw9RtpzRVF8psZDYWlO2vCGHn0EknilJxtNJQZbRczDlq2uFTlP7\nhMgnDmbzPVIKWwhETvW4wf4zKuTYZ6CHB59cpgG3fswbwJAtjHwDmCRnoL//0W8AQ7Z75Pj3Wpb5\ncsPY8d9888385m/+Jv/iX/wLlpaWWF9f5+677+bmm28G4LHHHmNlZeWiBnHvvfdy3333AXDLLbfw\ntre9jbvuuov77ruvW17sp3/6p3nlK19p1J6RHr8UEBvYCZG/ys83JlI5FbpyoEVSscsEFac00un3\ntUmqx24w2kgrbGkRGuzlh3FEFOc78l4oFI7ljHT6vQhURMktYVDehghFyXQ/H2V0/akbNfqsYpJV\nuclBhRAjJB2G7AQSM255liEsirj9ZAHATOMezLY9LkoP3+BeZav4y9O/me1e4UqSXDaBseN/73vf\ny1133cUf/uEfsrGxwcLCAq973et417veBcD+/fv5T//pP008gFOnTvHFL36Rj33sY1iWxa//+q/z\nAz/wAwC8/e1v5+1vf/vEbU4xxRRTfC/xgl3xu67Lu9/97pE1Hufn5y9qAKdPn+b666/vagDdeOON\nPPDAA8CVdWo/xRRTTDEKL1jHD3DmzBlOnjxJp9Ovt/LP//k/v+gBHD58mDvvvJNGo4HjODz00EMc\nO3aMmZkZ/vIv/5Ivf/nLHDt2jJ/7uZ+jUqlcdD9TTDHFFJcL1gs1c/e///f/zuc//3muueYaPM/r\n+9mlOP5Dhw7xzne+k4985COUSiWOHj2KlJI3v/nN/Mt/+S8RQnDnnXfy2c9+NjeX4MSJE5w4caL7\n9W23mZ2aT8Lvn4SqZfqOIgBtTO42xyR1Bkx1/pNC2xIMatlOIPGf2Jrc2lQ62wQTZW1MZGpqPFne\niPkADFs1PAvYNTfj4U/C1Te1vWx6/BP2/7nP7TJyjh8/flHFpV6wmbv33nsvv/7rv84111yz54N4\n05vexJve9CYA/vRP/5SlpSVmZ2e7P7/lllv4+Mc/nvu7eR/UOI3xLiUsZVTEqRLgKN30WGsqVolY\nawI1upC60AlV8hXzh3h8Z5XtoD1SD98TFoulMj941ffxyMZJNv0GQU5REkdIlkqzvGLpCBWnwprf\noBHlC51ZaVXPo3NHcOVZ6v4OzREJY1W7xIxbozx3Nae3n6Ee7NDJEVCTCGwE2nZZWjpAq7FN228S\n5Yy1ZHvUKnMsLV+Djjo021vs+Du5/dfcGnPVZVbmj9EOt2gHjZFibyulea5fvJYFr4IfxwQjDs8F\nEKuYVuijibGkNfLg1hGSqu2y4FYTVpOKE7ZTDjxhMeOUEuljkWnT5+vxQxL4/TjEkckhb/68yiSQ\n5VjdethlvsSAPeZANlnIJEEnUmAJPVYPv/ffpjx8Iz38VLhtEh6+eR5AwvO/VD3+wf5NF4vjYJrM\nd6Vgoj3+Q4cOXZZB1Ot1ZmdnWVtb44EHHuCjH/0oW1tb3XODf/iHf+Dw4cPG7VmWRPVQ0EZpgVuA\nrTVRyu3PAoBWCkVCjdMi0UifdasorWmErSQApLrqQieveWXH6374r/KuoRl0+G79PNtBGz8NAJ6w\nqDouc14VKQQLpRpHZvZxurHKifWTbPo7BCrGEZLl0hzfv3IdL1k41H0grtaLnG5scqG9QzN11HZa\n2UclF0ZJely3eJQgDjldP822v0MzpWFW7RKzbo19tX3YMvnoF8uL1DvbPL11knpQpxMHXYcfRD5b\nYSsZe20Gt1qj2mzQamzTSgNA2SlRLc+xsv86ZmZ2czxm1EGqm2dotnYDQObwrz7wcjw32babZQE/\n7LDdOkurJwCslBZ46dJRXnPoB3DSsVa1xo8jmqHfDQCZw68Hrf5AF4eUpY3dQ9fMHP6BygJlZ5cl\nFGtFI+gQqLgr5ewJi1mnxMHqQpKoRcLuQaV6+BnLJ+O5Z1RLIVBofB0hFTjSTuaFEGlxlB6uffqb\nMJxPkjmurlwzifPXWmP3OLXM4UuS7NFsrqikEeSAbfb2NOhosyIuY3n4YnesWZuQyS73J2bl0TDH\n6vFrhVLj+xepuukoPf7eNift/1Lxgk3g+pu/+RseffRRfvInf7JLscxwqTfx9ttvp9FoYFkWP//z\nP8/x48e54447OHnyJEIIVlZWeO9732t8gNyKdlekSuu0/sV4OpjWmkglhVrC1OGPQhIAmkRapTrr\no9ttBR2+vX0W0F2HPwqnG6t8d/NZji9dw/XzB0e+PiqtOd3Y5FRjo1BjPIhDTm0/Cwj29zj8PNQ7\n23zrwsO0/Z2Rlb4guVdBq0HY8Tlw1fVUawsjbWMVUd88i0RypMfh58EPO/j+OkfnDvCaQ6/qOvy8\n/v04YrW9M+zwc1CSNoulGgcHHP7QWLWiGfqUpcPB6iL2uHmtNba0+hz+KEgknrSToioF2zAqzZgd\nN/+S7jWOEEjR7/BHNNrtt2isg8Vbxo7BMBO2N8u3UBo7TebKxjrWdpL+db7G/14lcP3f/3ivkd3/\ne/PbjNtUSvGhD32IpaUlPvjBD14SxX0Qxo7/p37qp0b+7M/+7M8uqvPLhV7HDxDHykg3HGDbDwof\nOkicbxAHRnuv650dtsY40l7MOu7I5J9BPHjh6e7bxDgoFeduJeXhG89+jWfqp4xsr164luIsALCE\nxb7qgZHbZL24afEI18ya5YM8tnnG+L6+bt8xbINciJJIKnSZwBHS+LOqWY5Reb5MLmRUwZZe2IBr\nm/Uv0cZ6MqZ6+NrQbpI2L5ftKLu9cvz/z4NfMLP7gbcat3nPPffw5JNP0m63u46/XC7vCcXdGPFW\nBgAAIABJREFUeKtnqrk/xRRTTJGPvS7Esr6+zkMPPcRP/MRPcM8993S/v1cUd2PHn2XlKqXY3t5m\nbm7uiiy0PsUUU0zxvcbYbcGLwGc/+1l+9md/llar1ff9vaK4Gzv+VqvFpz/9ae6//35UWvLth37o\nh3jPe94z5ddPMcUUL2rspWTDgw8+yNzcHEePHu2jqr/lLW/hXe96VyHF3QTGjv8zn/kMnU6HT37y\nk6ysrLC6usqdd97Jpz/9aX7pl37pojr/XsGY10sibxsYvE5JwBZWrrhYf5saR1o40iIs2GcXCMrS\nIyAu5OO3Ah8/Tgq9j7s+rTVRHKN0XLgfrbTCVxFCSLQBZ78VNnHsYo17S9jEOtGtLLLdCposBTVq\n7rACZy8iFbMTdox46K60iLTCMrCNUQRRaFRLV5GogJrML6XNtPNjneoIGaQuCHRSS3YC3nrhge0E\nWwnasM3LhUm3PS7nWCfJ3C3KG3jkkUf4+te/zkMPPUQQBLTbbe64444+PzuO4m4C48Pdf/tv/y13\n3HFHX/JWp9Ph/e9/P3/4h3940QO4HMgOdxNZ212FP63z2RKaAQ6w1oSxws+5NULrrva5EBArRSeO\nujTA3TZ1Kg2dfJ0cBoesBc2hACARrHg1ak4p4Z8rRaAiduLOUABoBT5P1leph20CFWMLmVzjALMj\nOSSMCVXU5d1n2YWDAUBpxdn6GVZbq9TDBo6wiOOQrfZmbgCouhWEkPgqomKXcCwPyy4PPVSOsJnx\nZpHCQpPkOSAkKicAeNLCFhKFxpU2s26ZY3MHmBkIAJGKebq+ykZnh0Yc4AoLS8hcWV9X2hypLlKx\nXZASG4EjbRzLGrIVaV5HooAJNpKK7eUGgEFnL4RIagjkzC0HiZWyf0AnLJwcfn+sEl3/lFNMlgqY\n5AL0tym1xpIicTYZrVjIXOcjeuSZe5kteRLI2c+z5wVG8ODV8JwwygMooFKa2vbSMnfvVL5tXpu9\nY92rw92Pf/OLRnYfvGmyZNdvf/vb/MVf/AUf/OAH+yju99xzD0888QQf+MAHJh4rTMjjr9frfQqc\n9Xod26BS0fcaOpOb7XnAuvxmpboBoNfh904aSyQPlas1QRzj6x6HL2WfrW1JqlJ2A0Cg412HL+gu\n26QQlKTHQcshiCPWggaxUqx4M9Qcr49xYlkWZcvCtWyCOAkAjaDDUzur1IM2fk/gCFPNdltpJBIt\nEkceqjDJT+gJHLGOsRCgssxhwZn6adbaa9SDRtcy0DFIyVJtH1Ecsp0GgF6HnyUhtaIORB3KkY9r\nJwHAlU7X4UfoboZwrGMsrbCFBQgUgpK0sWXi8DNVzY6K6HR22A7azLllrps7QMV2OVm/wEan0c1h\n6I5Vx7jaQgqRSDNbTp/DzxChiVRIqKLkLcyykYhd5c3Ub2kgRFGP2tiR3w0AXYef/WHXPoojhNwN\nAA4SKawBZ5QsKlT2mUmJ0uw6fCl7UlRTR61VSr2XWGhsORDk07+1UsQ9ASBz+LLXsQnRLUgie6+h\nNyB0TYd58N1cA4YTw0zyAHqfwazN7GtB/zM4CQ9fpNc/ONZx/e/16v97odXzJ3/yJ0MU94uF8Yr/\n85//PF/+8pf58R//8e5Wz//4H/+DH/7hH+4qdF4paEdx8Su1UsS6eBtIdxO8TPjCiu2gkzzIBhxk\nR1pGFL9ndlb5+urJkZnAGZKszRg1oiJULywED1/4Fo2wUWAJUmmCbtWx8dhXO8BCeaVQGtlCUHHK\nRqUuXWnjCKvw+gH2lWY5NrffiGY7YyXFUooIGQJY8mrJG1NBu1JDxS4XEx+6yVTkZwIP2LqW6Fbo\nGmuqFI4cnd06aIsots3eBkZlAvdiXAGW3P4N2pwk8arXnZnkAVScvVm4fvLhLxnZ/cor3rgn/V0q\njK/6J37iJ1hcXOSrX/0qGxsbLC4u8s53vvOSdHouF4y1Rwy1wDFw+oltooVu4nSSgjBmq4ROFBo5\nPU1y9jCqCEkvYjRoM7WeiKS6lAk8q2Skhx+jsQ1rBwQqwjJ8JXfzqmONgNWzyh+HrqSQybwqSqbq\nGmbbNAbXJUSy5z+BHr8RDJx+Ypasvk1yYbpvBob3aq/1+LO3DVPt/r2CyQLuSsJEh7uvf/3r+fCH\nP9z93qOPPsof/dEf8a//9b++HGObYooppnheYK95/JcbxiHv/vvv59ixY33fu+666/jqV7+654Oa\nYooppng+QabngkV/rhQYr/h7D2wyZIckU0wxxRQvZlxJTt0Exiv+l73sZdx55527qoFKcdddd/Gy\nl73ssg3usiIhIZvZSjFBgDOcABOwCoQw1/6LJwjEpvv20oB/nyFPsnmkrWH/goSpZIJJliGm9QjQ\n5u0m88TMOuPBG8F4WumJth3M+58gV2CSvifJG9jjReZeticM/7tSYLzi/4Vf+AU+9rGP8b73vY/l\n5WXW1tZYWFjggx/84OUc30XBRItbaZ2cr6VSubkFslNbK3E9ye+OcIJJn5pZt0Qz9FOFz5zBpQk3\nrrS7CWBK5x8IKxXTigL8OGTerdKO06StnGYl4EchFzrbzDplPNsZyZYRWtMOfWqlJexgmyD26eQU\nSLeQeJaL45aSsQTbdKIOUc5Bc8lyqThVKu4MZekmyWA6X8LNERKlY9bbGyx6c9iWk8tCEj3X1VIt\nZr0alrBybRPJZY9Zt9KlHI66/uyTbkQ+NcAZdSCcdqO1Yq3TYN4tJzLLeYeC6VzxdfJ5ViwvVc3M\n58FrEt6+1KIr25wbXJVCSNBYhfM6W0zE0CfHnNc/ab4KGqQw08OP44QtV8itF5Pp4Wf0a5M8gELt\n/lQeepL+9wLPtxW/MZ0Tkhv7+OOPs76+ztLSEtdff/0VqdfTidUQBSz7epCdoHWymtQpdUP0FscY\n5Gun1M5kTdfLV9a5SVF9ASBz+MKmZDt9EzeKY0IddwOAUopW5PNUY61PfVJrTTsMaEU+gYq6LB4/\nCjnf2e5bwQtgwa32BQChNa2ww7pf73OdYRzgBzsEcYeOCrGFxJUurlPGkl53rFprwrBJ09/Gj31C\nFVG2PMpOhaXqQUputW+sQidsoCwAOOm9bUb9+iNSSBa8WRzLJU6LiSTXFdCM+8t8usLuCwCZwz9Y\nW2TOq/bZDgaAXub3oOOoWs5uAMhujlZEA8+zjewPAOmcivRwoHeFRcUqJXr+QvQ5/MFAIzX9ASB1\n+ElBl4GGM45+j8Z+kkTWf12ZVj/0c9vzFi9aJ8llgzz8/KSoGJEWRBmvsZ//DI6zzSij42ihgz/r\ndfjDYx2fB7BXCVx/8OgDRnbvu+E1e9LfpWIix/98QSfedYCjHP4g+gPA+K2NLAAobcBrTgOARA45\n/EFEccya3+DkgMPP678dBpxrbbLaqY/dshHArFMi1opNf2fsJkQYBzT9bTzLQ1ruyLEmAaCFH7VZ\nqR2k5IzWakqScCKC2B9ZZas7ViGYd2fRQGvA4Q/CFTZXz6xwdW15yOEPtdv9u3jLqmo5WEKiChZw\nFpKltN/cN7uBsVbtUrJdZZAHYFtWNzt8HIROErGK+P1ZADCRzNA6LTRjmgeAGbfelIc/SR6AqR7/\nONu9cvz/32NfM7L7v176f+xJf5eKKy/tdo+RrQiKJrIQSSp9FBdzkIUQ2FISxMX7zlJIqlZ/Buko\n2JbFMwVOP+u/4npsbzYL9+k1sOk3iUZsu/TCsVwWy0u52z6D/btulYMzhwr1+JO3JkmkivvXWtOJ\nOsQGb82BjjhSW2amwOlDqsEkZGGiGICvYkp28WcVo/BjM02fQEd4KjLS7tcCHAOnB3SzfwvthEAp\njTTJAxBZiDDDJHkAptx60zyA3rcYE1zO3YnnSq/oYvGCd/xTTDHFFJcbz7fSi1PHP8UUU0xxiZiu\n+KeYYoopXmR4vrF6rjxKzmVAryTrOMRKozDj945gYObYadpxSBCN3zcHCFVMlCo3FuH89jlOnv82\nqoA3r7VmbfMZNrfPFF5XHEecPHOCVrte2H8Qdnhm/QmiuPi6Tp96gscffbhwP1ZrzUbrAp2gWdim\nJSQ7Qccob2Cz0+CRjWeSWrYF/a916qy1dwrvldaazaCFHwVj7TLbThya6dKkevymnItYGczVgb/H\n2uoJngEyaqoZzJ6rCXj9yuxZuZi2J4VEGP25UvCCXvH3MgQyNcRMb7wXmRa6Tlk6cY9M7DDtTXVz\nTuyUIqZSmed+O00r8vHjsJtUZccBZcsdOhAMVMRT9QtsB21iNFUr4cG31TBn/+z2Ge5/7Eucq5+l\nGbQ4v3GSpbmrObDvpX2Hh1pr1jae5uza4+y0NxEIauV5rlo+xtzcgQE6aciZM99mfes0W61Nqhee\nYKa6yIGDN1Ipz/b174cd6tunafk7tKIOm41zzFWWuGrxGLbVf12nTn6Xhx76Mmtr5wjikCce+SZH\nX/J9HL3h5X0HbVor2p0tWn6dVtjCsWxKTpW5yj5KXn/hc0tIDlaWqTolGnFIsLNB2XZYKs8ktMke\nbHbqfGf9JJt+g04ccrJ+jqtrK9yweKRPVEtrzabfYL3doBUnDKzTjsuhygJL5ZkhimQ7DAhUTISm\nHnQo2w4rXg3PcYfmQKbZF+iIMIxwhEXZLg3NKwHYQiCkIO7mmYxg7KTzUwtBnLLLpJBYA4e3vbLj\nGUUyo0sOuqB+brvoLkCsnGcgWWzs1rkgdf557Zry8AeZP6No0rAbbDLhvPHUU/M8gEvB822r5wVJ\n52yFCYNkHAdYQ1cLPXP4Q0iDRZevnX570HY3KSxZrbUin04c5idm6USVsmy5IAVP1i8kGvs5SVEi\npZi2VcTprdP87Xf/hrPbZ2iGrSHb+fI8S3NXs3/lJWxsPcu5tcfZaW8RDrBpXOlQK8+zf/k6arUV\nzpz5Nhvbp9lqbQ21WXUr1CqLHDx0I5btsr19mrbfSDT4BzDj1pirLnPVwnWcPXWSf3roK6ytn6UV\n9Nvals3SwgrXvuT7uOalx+kE27T9Os2wNVR0xpMOJafCXHU/1dIshyrLVJxybjEdV1iUbYfF8gw7\nQZPvrJ1ky9+hk8MmmnerHKot89KFI9TDNuvtHTpxwOAnYCGo2h6Hqgsslmq0ozB5K8tZ49oIypbD\ncqmGZzvp8jr/tVAAjrAo2SUsIRKHL8RQsleX154FgCwrNs9xZtx+IZFS9Dn8QfQlTPUmXuXMa9JE\nR0vKbuJXruPueZsSmS3FPPy+6xzluFOOfq/DH/UMwmg9/rz+y/beqGr+2VMPG9n91LWv2JP+LhUv\nSMffMaBZxrEi0IayCWMmZr+ZZq2TVtgq5CDHPLmzZiS3/PDpb3LPw39Bq4DmCYljj1RYuAXiSIc4\nDGkbtFnxaszOrxAU0DwBVp88zeqps7SD8Tx827J41T97PW6tXFhmsmx7vPHYm4feKPLQ8BucaZxP\nisUU4JrZg5Rsr5DmaSE4NneVkfRuWdocqS0azauaXaJiu/lZ4z3QWuOIROTLROPeSou1FEH3vAEU\n9W+JfCc6bKtSCWkzbr3p6ltNMNZsH/Z7qcd/18lvGdn95NGX70l/l4oX9FbPOAgpkgKnBtAjsgKH\n2sxefQ0mskYY68+0/KaR04fk0MZk3ztUIaZrHT8OjHj4AJEfFDp9SJLVHGkVOn2AKH1LMkGoQiOn\nD8m+rMknEE/Aa9fCXJHFYniVnweRtmmscT/BeE0c9C4P3yQPIKnXbNJ/N/PYEKZjNa1DvJe8/itp\n/94EL1rHP8UUU0yxV3iebfFfGY7/3nvv5b777gOS6vFve9vbaDQa/PZv/zarq6vs27ePX/7lX6ZS\nGS0NMMUUU0zxXGFK55wQp06d4otf/CIf+9jH+M3f/E0efPBBzp07x913380rXvEKfud3fofjx4/z\n53/+58/1UKeYYoopcvF8k2V+zh3/6dOnuf7663EcByklN954Iw888AD/+I//yI/8yI8A8MY3vpGv\nfc1MBMkUWplrgZvmASTGhv2jjfaXAaxUwtkEoaEevkQYa+fbwrCOLKCEef1Rk+LtkExS09oBWmvj\n/dZJageYstWF1qbTaiK+vikm0cPP7I0gzHn4xnNlwkJOV7Ie//OtAtdz7vgPHz7MI488QqPRwPd9\nHnroIdbW1tja2mJ+fh6A+fl5tre3jdtUSo1MFtr9mU4ErrTqo6L1QesuhU2n/86bLFprYhXTDkMs\nYSeHdiPmlNaaVuhzcmedDb9FHKuRtkpFnKuf47Gtp6nU5ql6VRyZvztXtkvUSjXcyiwz5XkqTjnX\nTiKoelXm5/axdPA6FmdXqLr5W2iudKjYHqiYZn0dB4EzIgA5WATNDhvxDu5MmWq5MjIALM0v8/KX\nv5qDV72UxfISFTt/rFbKeXfsEl8/9yANv44YFQC0Yqe9xSPnv8Vm8xxCRWkdhZzrEhausHi2cZ4d\nfwfGJHa5wqJme2z6LaI4GvlZSRJGz5JXAXSXCpwHoRN5Z60VYRyhVDxyXqEVKEUMxHE8cl5n81Np\nTaRJ+P2jbFOKZDavxzlgrZL+ZYFt389Sbv24/rs/E+MDQNaOMOw/K7SuCu5V0o65wFsRLCGN/lwp\neM73+A8dOsQ73/lOPvKRj1AqlTh69GjuafuoVcSJEyc4ceJE9+vbbrute/rf5SH36JZnCVxCCCzA\nwkoSuLIyS1myV9IpVjaWrH+tuimQSS6AJlQxrTjujtOxnFS6OUJlvJU0g/d0c4uzPZmxW2EHKQRz\nTlK4I0m6ibjQXOeLT36Fs80LAEjXQzgudhQS+W2CMCBUIRWnjGU5xJaFljKJ5JaFdBxmHY84CmgF\nbQSCilfBK9ewyrXu/XSWD1CKQkpb63T8Jk2/iWe5WFIS65iAGATEkc/65llcx2O2toiQFr6KcIVF\ns9nkWye/SxAkWayhC9rRlL0y0tf4QYcojlleWOHg4Ws5dtOrcLJkJ69MScWUOlv4YYtm2MIWFq7l\nIm0XLRON+lbU5mvnHqRqV/i+5Zcx480kMsNaUfe3efjsN9n0d3MRtjubzJUWmK8sI4VDjMJLg2Yv\n6+dcc43zrLO/ssSMV0togIArbVxp41hOqlgJG0ELiWDereBYFpqEmeNZNotelZrjDc9bdueKJHEQ\nnuVgWclYFBBohaWThUjvdoAUJPmeKZtGp+PQqSPu8vDT9ulJoFLpnEMlPHzRM6+zOhNZTkD6sOzy\n+YUAnThby9p92+vy7vOydQfUN0c+g+l19D3PYrj/3n9fTP8ZC6+XBtobMHptP/e5z3X/ffz4cY4f\nPz7YeiGupNW8Ca44Hv+f/umfsrS0xBe+8AVuv/125ufn2dra4ld/9Vf51Kc+ZdRGe4DHrzKnXEDf\nyjJ4EbLwg4yVIohj2gaSCRv+Dqeb25zv7Iy1lUKw3Vrlq0//Pedba2PbJAwJ/DbCcQvqDGiIQmzb\nxa3Ojq8HEIVsnn+aOI5QBRtRruMRxRYnn32aIBwtW6C1pkqJoweu54bvfzW2M5qLr1RMvXkhCZWW\nPXasZbvM0dnDPL72GNv++LfBWXeOxZkDhVtrAsHVtf0sVRbwrPG1EySCQ9V5VrwaNbdU0DLYwqIk\n7a7DHwVLg2NZSIPtNTEi8WoQWmtsUx6+UkhZrPEPk+vhJ/HGjIf/fNPj/6vTjxvZveXQ9YU2YRhy\n++23E0URURTx6le/mn/1r/7VnhJeroh3j3o9WQGvra3xwAMP8IY3vIGbb76ZL33pSwB86Utf4tWv\nfvUl9WHCAbZkcgBjFL0FtONivrgQgo1Oq9DpQ/L28MCzD451+lmbwnUpV2YM6gwI3FIVrzZX+CDZ\ntkOtPFPo9AGC0Gf1/LmxTj/rX9Y8XnHz68Y6fQApLWbKC4iCgjUA7ajNI+e/Vej0AerBttFE12ha\nUZuSPboITQaFZt4pGTl9gHLPKn9su8K8xnFRcaEMgyvmsbbpW6NpPYBJuPCmOQu9f4/DpDz8y6nH\nv5d7/I7jcPvtt/OJT3yC3/qt3+LEiRM88sgje0p4uSIc/yc/+Ul+5Vd+hU984hP8m3/zb6hUKtx6\n6608/PDDfOADH+Bb3/oWt95663M9zCmmmGKKXOz14a7nJduGYRiilKJWq/H1r399zwgvz/keP8Cv\n/uqvDn2vVqvx4Q9/+DkYzRRTTDHFZNhrqqZSig996EOcP3+eH/uxH+Pqq69me3v7ogkvg7giHP8U\nU0wxxfMZBmoWXZgcJksp+cQnPkGr1eKjH/1oH4Elw6Uogr44HL8w4xcrQw50QgfTONIiLKp5qzWz\njseCW2YzGK+340iLW46+lnse/9+stTfH2i6Wl5jzFnhi7RHiMQfMAsFLlm8AW3Jy6+nCsUqvjOuX\nCMLxejtlb4aXveQlPPidv8cv0OZ55dFXcqh2Fc82zxdq89jSpWSV6cTj75UUknJpgU4rIi4Qj5sr\nLVB2qjRyFEB7IYDl0gIWImF5jYElJJa0iFVcmLcg0vaEwRx00jMmE8aFTNk3GOyd61TquXC7QWuj\n5yXT7aeXYTQGArNncBKuyST1diEVpbtM+/yTUDVvu+02Y9tKpcKrXvUqnnjiiS7RJft7bm7uYoYK\nXIGsnr1AxupRcaKSOViUeUimVWu0SlxCZpvpi/cie3iU3pXBUloRxopw4EBUa00QB0RadSVj23HI\ns81N1gcCgCMtjlbnqdoelmXhhz5Pb5/mzu/cy+pAAFgqL3Pd8kspu7WE+hkHrO2c5zvnv0XcQ1MU\nCI4feDnXLh6jlBYk7wQtntp6iic3nxoaq4NAa0UnDnCFRRyFbG6exx8Qh6t4c7zk8PdTLs8lRdGj\niPNrZ/jbb/5vOn6/7Q/d8Hpu+f4fZXluH0hJFAVcaG/wVP3MkAMuCQcpJIGOsZEoYur+9lAAkEKy\n6C1hWy6RVtgIgqjNuZ3TRAMBYL60yJGFa/GcCgqwAD/y2fJ3+voXCI7OHuBAdRnX9rrBP1LRUGC3\nheRobYFZt4xt2YkSpQALORQAhAbXspFCdmnCEoElraE56ACeZaea+mJknQcAqQdklUmZmnk0aL3L\nZulKJcsc1prWSHrpnLvPw2A9gux52RWo0SPrV6g4Tg74e5/BnEDRVdWkX1a5SGO/+7smthmdm91n\ne69YPfdfeMbI7vX7jhTa1Ot1bNumUqkQBAEf/ehHede73sU3vvENarUat956K3fffTfNZpN3v/vd\nFzXeF6TjbwZh1+EPojcAJJzo0ZS4rOiKFqLP4edNWqUVoVIEKu5z+IPqTVor2lESAHaigGuqC1Qd\nN3fV6Ic+z9TPcOd37kUhuW75BspONZdzo+OwGwBu3HcjR5evo+RWc++PH7Q4uXWS72480efwB5EF\ngI3N8ziWx/VX30S5MjekWw9AFHFh/Qx/+42/4dXX3cwbb3oTy7P7cp1RFIestjZ4sn4aT9hdhz+I\nLADsBHX82GfRW+w6/GFbQRh1OLvzLDPeLIfnj3Yd/iAsIIgCtvwdjs5exVXVFVzbHbIT6Z8kHwOO\n1haZdUvYOeyc3gCQ5CHYSQbxiDoPWQBwhUgdfl7RH73raIXsc/h5evhZANBCdJ143jOQ6fGT2mUW\no2yT9BaJJitCNMJxk6zopRDdPsY+gz05BKPom70BYJzG/iR6/L15AHsly/y3F04Z2f3QvsOFNs88\n8wy/+7u/272mH/7hH+Yd73gHjUaDT33qU6ytrbGyssIv//IvU63mP+NFeEE6/kEefx5ilRZgMdgn\nC5UiNrDVWrPe2THW4w9UbEQxe3zrLP+0/oyRxEPNdvEcM4rhXz/2BRoGZQ5LdoUD80dzV5+DuKZ2\nFQdmVoy2H06sPsaOgdy0ZHe7pAgVq8RMacboXh2prTAzIjgO4ob5FTyDegAWkhmnbKbHbzmUDair\nk2jM6zTB0IjmqRXWCOc8iOQt2KT/RLvfnNs/gR6/0fVPcK+UorxHjv/vV581snvtytV70t+l4oqg\ncz4XmIRapZWZ/sgkevxighRuDca6Pp41vHIdhVHyC4NQIypJ5aHilIycPmCsP6Qw30O1pWV8r9wR\n8hd5sEwfFWEs12S0Nw4T8vCFNDofgGSDxpTbbrpImuTAcVJevfEzaGq7h/v9vW9i4/5cKXhxHO5O\nMcUUU1xGTAuxTDHFFFO8yGBdQat5E0wd/xRTTDHFJeP55fhftHv8aoIzbSHN9Pi7PGWTtrVJtdkE\ntrCwDVcUxrrxJLVszfqXxq+ygYqNH4E8dk4eLITxdSmtR8oxD8K0doEA488qE3k1QVISwmxeaUxt\nzerdAgj0aEnyQVthPlZTTMzDN30GTW0n7H8cpnv8VwB6+ftDP8voYUKkhTDGsCBSOqeT0t4inc9s\nyGhXsdZUnQrtqEOooiS45PClAbRIom4i2Zx8nTfWThyipOTIzApr7TqtKMh1mGXpMOuW2VdZoB0H\ntCMfX0VDTkgAcRyx0amzf+EYpcY5WkGdZtgaarNkuVTcGiszh/GcCnHsE6qYQA+L01Uslxm3Ss2r\npswOMfJQOo5DVtub7IQtHJFIEefSOYXElja2dFEIXBUS6yi3mLonbTzLpezWsIWNjSLWmihnBE56\nUPx04wL7S/MseLVcATVBIq62XKrgWVbXqed9VkInr/uetBPnq1MyaE5Kp9Bgy4T3HynVVcIcNa8i\npYkQ2EJhF9A5M2lxPYYHnylwSpHMwF7p4jzbjM6Z1K7IZ8zsqmqCRhL38PcHMcjDH8fYGaRzZosr\nEzrnSNvsmoZ6u3hcOS7dDC9IOmcnVmly03ACV95EiJXuCwDZg5AkpOzadR/CngSupAiLIs6ZiH0B\nIEUeQybLA8gCgFKKThRy1t8ZWpU2gjZrrW3acUCoFRXpMOtW2Fdd2K0dkLbZDDu00gAAEKUOf93v\nVwqNVcR24yxNPwkAmcPfN3uEijfbZxvFIVEcEKmIQEdUbY+aU+XAzD6cAbqjhegLAFEcstba5Omd\nc0MJXL0BYNfhe4iBZCelFSryuwEgc/gVtzbUv04L7kRaEaNxUsZLXuDc782zUEoCgADJnUgBAAAg\nAElEQVQqlsNSqcpSqTqUwNRdgYteh+8M8/tTvj4pZz5z+BXby0mgUn1SyL0OfxC20N0A0H1zHLF4\n0QMJXEJkWcf5jlNAN9ksS+AauKRufks/D18jhDW8zunh818MD//5ksD1jY0LRnbfv7hvT/q7VLxg\nHX8GjTkHOFaapACFHJrAvdBaEyiFHyuKNja01tSDJpEu5vZrrdnyW1zwG4XbEI2gTTPssL/S7/Dz\n2rzQ2uJU4wIbfmNsm7GKqDdXWagsDzn8QURxRNmyODCzH6dAblipmNXWBqd2iiUbXOngWB5Sjtfj\nV1ohVETVrQ45/CHbOCapMFA81Y/N7Oelc1ex1FOsJg+Jk0xW+HkJXYPwpJ3v8IcaTpxqnsMfhJu+\nUBjJHaNyHf5Q96kDLqJaZgEAKHxesl8w5eGb9A8XUQ+A4eC4V47/m5tmjv+mhSvD8b8gt3p6kWVf\nmuyvWVJgkHuFEAJbSlpRsXFim7zSF45VCLaDltHec80tM+9VC12ZEIluYJHTh6S27+GF64x48LZl\nc2T2qvzM1AEEKuJcY7XQ6UOyvYRBopQUkoXyvNFYhZTYmtztpEFEKmK5MlPcphCURHFhlQwl6Rjl\njmhE8kZiktSktXF9YwtR6PShJxel0A7jRLHetveqf+h/MzDq/zLq8T/fNnte8I5/iimmmOJyY8rj\nn2KKKaZ4keFKYuyY4EVL55xiiimmeLHiReP4TTi7Gf2raI9Ra00YKyO+eMbYEQbblnEcM+eVcQv2\nbZN6ADF+HBaOVWlFI+xQtYuF26SQlCwX10BDRyvF6eY6fjReC19rTScMKLtmRaFjBKKH4TEKAkGs\nVfeAcRwSvlDxZyWF4GBlgSiOjPaZYzRxXHxuYKVsolgVz6tIKWN+vyXM57UWEBfOa5L+MUtFydo2\nhclnlbVn0u6keQCT2k8CYfjflYIXNKun99S/V4o1T2c/Twt8UOwpcfiaMOXzp99EaT2CzukT6VRT\nMpWtjdOHsBdxHBOjUvnd5GEOVMSFTpOg56A3YTwkdoqkEIZNwse2c2iP55tbbPkNmnGQ0FOBThSw\nEw1r3K94s7iWQ0yaMKU1rbCDP8DZ10qBgFgrIq0oS4eS7bJUnsPrkTbWWtMM2jSjNn4c9unhb/p1\nBlGzK1iWQ6hVSgNNNDlj+gXyBIIZx0MiiNDYaV5FnLKx+q4LkMj0XiW2Ck1rQIJaCsFNC4e5urZI\n2XYBgRSM1M63dPoQS9Flq1hILKs/YFoIPOliS5kI16X3Tg6wa7qU4JxHMWHM9PfvkORJSEt2567O\nOWjNlDJhUI9f9EkMaJ18nqSSziLNAxCQykX3jymZA/3UU9D57KI8qWTyx5rRZGUPpTqPCTQRnbOH\n0j1IGYW9Y/V8Z3t84aQMN84t7El/l4oXpONvhYmzKtLjz/jKo2yzYKG0JlJ0Hf6o5BWlNSHQiXxi\nFaPyAnxPAIhUv8PP6z9QMefbO8nqHtIksmHYqbMUQnC+tcW236SZo7EPiQPuRAHN2GfFm8O17FyN\nfZkWBGmFnUSvv8fhDyKjKy6WZolU3Ofw8/rPCqJU7XLX4Q/bpQEgzQWYcUpdh593/VkASDKNJXHq\n8IdshURpha8iblq4mkOZwx/ycPQFADt9d8its9cTABxpU7Lc5PPIY5KkAUCkOcFdhz8i2S9jz7gi\nYZ7lztWeAIAQfQ5/yDalN2uR9tHj8HNtSQIAetfhj+bhpwHA4LlKcgbojnlUAlcWADJXZZQHMCaJ\ns2urNRW3mEFmgkcMHf/Lpo7/8qFjoMefTT4TDnA7igkNpZk3O41cx5TXf1P5Run9m50mZ9t1I9vT\nO2vUDTTuAcqWa9RmrCI2/EayKixAxXKT1ZVBu/6ILORBSATzXn4BmkFYqbyECWf/B/ddx77ybDF1\nUkPFdtNM1/Gwkcy5tQl46DnZ3TkoS4llsDrNVvkm3H6t1EiHPwiJNpKRzpLATNrsBgCDe5UFK1Pt\nfpP7r7WmbJvRYYvw6PaWkd0Nc/N70t+l4kXL6hFyd1VSBJNaoV1b4wEITPPG9QTtTrKLaI1YPQ8i\n7knWKexfmNWLhSRb18Txa7SxMxeY6xU5wjKrMyAmuK+GzimBmdPv2hp1L9L5atai8Vh1skVk1H9W\n4asIEzyDWdt7ib1s7/nG6nnROv4ppphiir3ClXRwa4Kp459iiimmuEQ8v9z+FeL4//zP/5yvfOUr\nSCk5cuQIv/iLv8jdd9/Nfffdx9zcHAA//dM/zStf+crneKRTTDHFFDmYbvVMhtXVVe677z5++7d/\nG9u2+dSnPsX9998PwNvf/nbe/va3X5Z+lek+JAndL1aKolqy3XNybbB3q7XxMkGmf4x22YUwspWY\nFS+HRH0yY6AUIVYxjuUU7rML6KOqjoNEpCJ3JgemMZZh3d12HLJg9FmZfaSQKVdOcCaUQ0PNMUIj\njdo13l/vtS8UZNMp+8ag/wnqAaAVk6yVTccqMBurUgr2iM75/HL7V0ACV7lcxrZtOp0OcRzj+z6L\ni4vAZMkhvVBKdfW4R/2sVwt8VGKH1poojrGlTDTctU4n67BdGEfshG1CHe/mBeSNP+Xix6hEyhcx\nMrlLKUUr9NkKfSxh4Qg5MmlMkjwYC94My6VZKpaTaysReMLCkwmNzRESZ8Q0kEAYdTi1c5otfwup\nFc6Ih8kGdBxwtnGGteYFUBF5fAkBoCK2Wuuc3nkaP9jBGhEkLASokLM7pzix+i2a/jZixGGwUIpm\nZ4sHz36Nh8/+E52gMXJy20gk8MDqk3xz7RkaQWfEZ5UGXSHwdZQka435XNFJUtdW2MCPAtSIwKaU\nIoxDOipMZLtVnH94nvYlhCDSEMV65LzWShHHikBBR0EYxSPndTbnFYJYJ1/nJYJleSMZo0ePea50\n1kZClTN6BrNcmFH9Z+2qOO46/HFj7Wrwp5x9Ux+wF5gmcF0E/vqv/5o//uM/xvM8brrpJt7//vdz\n11138aUvfYlKpcKxY8f4uZ/7OSoVs+zPwQSuiTnA6YTROSuxKFaEKV9ZI4hVTCsOaMfDGaxCDySA\noRNKZE7/Uarbr8SuHv8FvzlEoYyVAp1IDMckjilWCn/AyWitaYcddsI2nThEkPDXLSFB9icFaZ1W\nrdIQopCAH3V4tnmBUPVfl0Ay684kRUR0khQVxD7b/taQ+mbFrrBUXsCSyRuAVhFbnS3WOxtD92re\nW6Di1tCIZIUf+6y2ztOJ+6mplrA5OncNNWcGLSVCKXb8bR7feGxorDVnhuuXXkLFraIQ3QSuvJyB\na2vLHJvbR9UpIdIELsjnrDtaDkhhJ7SfQTuJoGqVcKTdnVexjglzVEKFBidNFsschBC7uRl97WqN\nJXfntdYQpVz4QThopBRYBfNaa91NTxCp9KYkS+AaTKCKu/emNwgKOSxVlvcM5jGfBp/BhOqpkXJ4\n+dKfByD6fm8QWR4AI3zAXiVwPbXTNLK7dqZaaPN7v/d7PPjgg8zNzfFbv/VbANx11117uvX9nDv+\n8+fP87GPfYxf+7Vfo1Kp8MlPfpLXve513HTTTczMzCCE4M4772Rzc5Nf/MVfNGpzkMdvqsefrBI0\n2mAl4Mcxm36bjhovWZA0DIpiqV2tNWudHdb8ZmF6fawUnTggLEhD11pT9xu0oyB5MMeMQWvNjt/g\nQnt9yIkOQiDxpEMjbFC0BVSWJaSUbPrFSS5Vp0Y7bA45/EFYwmKltMTpndNEBWOtOlWO73+l0ef6\nisWrecnc/tyM2UF4wjKykwhqVim3GtiQrRaUbAdp0K5IM11N9qAcMSKzdgBaaxxL9BWFGQWlkkUC\nOQ4/z9aE6tqt5GXQ5m4msqEef07/e+X4TzaGK9jl4WitePH6yCOPUCqVuOOOO/ocf7lc3rOt7+d8\nj/+JJ57ghhtuoFarAfCDP/iDPProo7zhDW/o2txyyy18/OMfz/39EydOcOLEie7Xt91225CNaeJH\nwkE3i4NSgG/i9AEtzAj7QghaUVDo9CFZieVUQMxts2x7+AZa9EIIOlG70OkDaBSx8jHZ92/FLURk\nlgfQCRt04k6hXaxj1prnC50+QDNsYpo0sdlpIhdMk3oME4rQhDoyc7yCbrZyoW1CrjcaqTbcaBDp\nGZHp82K6XSKEMLqmrD2jsaZbOkb9M/qaPve5z3X/ffz4cY4fP27U5mD7e4WXvexlrK6uDn1/L9fo\nz7njP3jwIJ///OcJggDHcXj44Yc5duwYW1tbzM8nWW7/8A//wOHDh3N/3+SDmiwBy/QRwTgBC6Xz\n0/zzmpzkwzVNQDNvcULRrQlszRudoM0J79Web7FO0j/G/ZvOV9MD58mN977NyQ6899523O3PWyxO\niu9FAtdf/uVf8uUvf3nire88POeO/+jRo/zIj/wIH/rQh5BScu211/KjP/qj/P7v/z4nT55ECMHK\nygrvfe97n+uhTjHFFFPk4nIf3L7lLW/hXe96V3fr+7Of/azx1ncennPHD/COd7yDd7zjHX3f+6Vf\n+qXnaDRTTDHFFJNhErd/MVtLs7O7NbDHbX2b4opw/JcT2XaESjnAoz6gTGM/0BobhT3m0EdrTRAr\nyrZHOy4WWhNCIlLGzjg0gg710AfGi8dprWkEbepBm5LjpRLG+QhVxGMbjxNrxf7agbE1Wpt+g1Ob\nT2LbJVy3OvL1VWtNq7HO5s55FucP4XqjXzm1VrSaGwRxQLkyjxzTvx90eObkI1QqVZavOjR2Tzzy\n22zWV/HKNSx3fK2BGXeGC62kiLwtR095KQRVp8R6u8FCqTq2Rm4UxzRjn4rtULa9sa/6AohQWEqP\nvX5IDiw7IqQk3PEH8ems00qBLKAKTsDDlxPsSWmKn6uk+91nsEg8LWPhGPPwJ4CpeNvFwdz1m2wt\n9bKcAOOtb1M856yey4FOrIb0vXs193snatfhqx6GRMoAsIXoCwBaazpRTNjDplAqJlQR7Tgc2nOW\n2ZddMSrdpWz2Yidoc6a1nRzspjQ6SaKz3ztRM4e/E7TxVSJ57AiJLSxc28XucSphHPL4xhNcaK1R\nDxOq2YxTYb60MBQAGv4OJ9cepd7Zphm1sYVFyS5RKc3huLXuA5g4/A02t56l1dkhUCEVp0zJrTK7\ncIhSqdYzVkW7uUnb36EZNNFAxSnjOmW8ylyfA/SDDs+efJTt+jr19g6WsJirzbG0fBVL+w/13YOw\n06K9s4EftPFjH89ycRwPtzIzFABm3JkuRTRGU5IuJbvETGkep6eguyUkh6tLzHmV7rhcIanaHvOl\nSl8AiOKYdhQS6Zgs/cgRFlXHpTIQAIROi8Bk49fJ+ZElxHAAUD2sL5HkdlhCUBpoU6NB6eQsKp3X\nQqfOejAApEqdkvQgNHOUOYeyEp1IPqc/661lMYiMztn7XGXPWW+ro55BndNul82TjrWXBjpOj787\nVq2R1nBQ7avJMUAZhb1j9Zxu+UZ2hypeoc3v/M7v8O1vf5udnR3m5ua47bbbOHHixNDWdxYILgYv\nSMffCqORksu7uuWaWNPv8IeNEy1yINK6z+EPojcAiOyW5q0ustWPVmyH/Q5/EFkAAGhFAc2wnQaY\nYThCdtUmn9p6itXWetfhD2LGqTDvzVN1Zzi18TjbnS1a0TCTxhaSkl2m5M0SBT5b22dodeoEaphO\nVLZLlLwac/MHUCqi3al3Hf4gKk4ZzymjLZczp57oOvxBWEIyV51jafkAswsL+I3N1OEP1xlwLRfX\nTgLAwsw+/v/2riVGjmLLnvhkZn27qrvdbWP7YfN5GDDywBODHsMIw3vMDhlWbFiys5DAiAUssITE\n3kZCSOyQYMXG1kgIaTYsvISReNJ4Rn7YILDBuNv976rKysyImEVkVmdlZVVFQXV3uR1HsuyC2xG3\nqzLPjYo890Qx1u7ndRDrAuChVpjBg7WDmPKKfVfiLqEocQ9Vx0NbRB3CzyJdAMrM04evoI+SJV0A\n0jE5sUkB8LgHovrbGKcLgF60oEOiPbGJH398oEua8LPo0uEnkshB9xX0NyfVh+Czscl7108hZNqL\n04mNC8CgwpUuACVnPJsevzbzz77I4mDJHR60A9iTxN8y8OOPpIQfDdfWJ7HSUMGwETSNbIEjIfCP\nlRu5zTxZNEMfq+18Es3in7ev4HZOg1Qe2q11tMXwlYoSEZrrywhzCD+LUmEKynAVdfPGdaw3ek/j\nyoJThnsPHdK2DUMwVz+MuX1HjCwbnj30F8yVZw0igbpTMPr8PcpxoFgzUnmkD5oZhiJzBm7TJVBK\nwaPESDpKoeCw4f0CybimcYkO32hMw1jTXpwkdqf9+G8aEv89E0L8e36Pvx8IiPFuplLDfXpS0aYJ\nwNi5XpkLFwftS2dhcmYwgPhYQLP9VEYpDNoLAMR++AaQUPoQFAPiN/XpAQBuOP+oMP0Eko5SI5he\nVoSMpNwct2yyq0N3THP/3vidHG8H1Jxjxa579VhYWFhY7Czu2hW/hYWFxbgwSQZsJrArfgsLC4u7\nDHuS+I32GA19w7VrIUWeHXNeLEG3Y+GgWON9e0rBR/BkMdm7dgiD6BjjDgan/e2gswijAK7B/JxQ\ntEXYJUHtB487EIbe/WEUGL1XFAS+CMw8YQDtn2TygSlDKwmlpb0w0aIrLd80ua772Rv3g4kWPpnX\nZOxkPONcDe+V9NjDYk2fM4zaBzAIiRXRsD+Tgj2p6mmG8ePFARpgSimkUmhHAkKqHullcmA1BeBS\nikhKtKXUBEDyNcgilvpFIkKE2As8Z35fhPjNX0dbhAhEhFCK3EPPKQAhBJoyQiQFRPx31laYABAy\nwnJrFTebt6FkBCEDhDLqUcI4hIFTDgIHhFIE7XX4YQPNsNVDWA4omo1N/HD9ewghcHB2Hq7nIcgx\nRitQB1EUYcPfgMs91GtzoIwjyDjJcUIhwggLt29hcWURBeaBM6ZzzZB7ySnAcTgch4A5DNVCFZRy\n+LJXQVF2SvAKZbjVaXDmoObVQAnrea8oCKpOCfOlfdhf3Y8ic1BxCtr0LjNm0kgUSAEJhSnuoshc\nrZjJ3MQMBAXGMe1VdDGTsco/69GUkvNKons9HMp1Yc0qUZJbM76GHELBKct37kz6AEjsrCmllmjm\nqVukBKUEPJNbnrZeKQWp4gehKlbWoFcmmqutT73OxiZjkMzrvPmT3PJ0+FuxsvN20RH6AMal6ln0\nzQwb5wrO8KAdwJ4kfl9oQWW6YWWgZ3eqACii9T6UELg5NsahEJ0CoOLVvVCix/JXKQURFwAZr+58\nEeA3f6NHB6+U0hrxuABQxI1COfLJSApEIoRQEqGSkCLCkr+KW62lnjEhI0QyQBSPkxB+ttFFKZUq\nAE0wULQam7j28/eIou4LmlKqC4DrIVAhCsxFFIbY8Ht1+OkCICERhRFuLd7E0upST2yBe+BUFwCX\nOXA5B3c14WdRKVTB4gJQdkvwPE34WS0+IRT1uABIpVBxy5rwK/M9n6tHGapOseOznyb8LNIFgBMC\nL034WcSdrSpD+FkQBbiUgxGCTlVJnCozuTIFOIzrApAsLmLC7xk3LgCIr2tCACfnuk7TQLJi7hB+\nFqkCoFI/Y6LDTxP+sFhguA4/nUM/P/7smNvhx3/bkPj3WeLfPqT9+JMCYKorbkcSnA7XC7ejCJtR\nBDXk65v22F/HLX996FGDSimstJu5h7pkIaTAtdWfsdAartmXUQCpFCgb/CxfKYUffvoHfvrlWg/h\nZ0EpxYGZfWjnNH5lQShH0BZYWusl/Cxq5Qo8j4Hz4bqD/XNHUcgh/J75CcUT+/8FByr7h36uJebA\nYY7Rds19pRnMFqtG21VSSsh+R62lQBVBgTm531azKBAGxngu4WfhEMAxuK5l0uFusrWotF7eSN9v\nYO3QyWEEHb5Syih2u/347zTi3/OqnvSKYGgsIeDUTN/LGYWKhncCEEIQyMjofNnsiUaDwCjDZmB2\n6g+lDkxO7CWEIGy1h5I+EN9IhnukYdhGszG8QABAwXHBuNlmaKVUgzRqapKYL80afa6hFOBDCmQC\njztGpA+YW0irZC/YhEzjzlsTGHvsg0AoZeoiPpIWftxb3KP0DCTx24VJ2r83wZ4nfgsLC4vtx53F\n/Jb4LSwsLP4g7izat8RvYWFh8YdxpxH/ntTxpyFjvbyUcuB+oFIKYSQQSWh55wAopRAJiQLlBodM\nC0y7ZdxTqA3t7isxF8fqBzDvVYeMqh1DH6wfQYkPtnklIJjyaqh79aHzc8Jx/KG/4rH7nxy6H/rA\n4Ydx//1Pol6dGzwmc/D0w3/Hf/zrSygXBv9epWIFDz3wJO479NhQk7E/738YTx95BkemDg2Mo4Tg\nL/sfQ80b7K+fxE67JZSZM/RzrXAPU05xy3p70LggcCk3inUJN+oCZQCKjIMZPDsg0H78QsqBj5D0\nc90tP/yh46Zkm4OQaOtNYqUQY9fhJ2qicer2s7A6/gmAL7SEMpFzduR0sfQt/XRfk7iCUFKfttux\nnwUooWCpp1xKKYRSQsa9PMnFLJREoLqFf1IK6PoRy+2UQiAjrAUt/Oavdz3sKzMXM14ZLuOdi74Z\ntfHz5goWMjJJ/SiRbNk4K4lG0MSV1Z+6rJUJCKa9Gjh1Oz0CHEAgAqz4K13zc8Ix5U2BEoYobupq\ntzZw7cb/4n9++LbrJnzwT4/gyOFj8AplSAAcBL6/gR9vXMbqxsLWmMzBkw8+i4OzR8HdIgBAhAFu\nLl3Hf/33f2IzZcNcLlbx5PF/R722DzJRaEQhVlZ/xY+/XtYmeTGO7X8U//bQc5iu7AMoA5RCI2jg\nyvL3+Gn9RieOEoon5h/F/fUjKDql2BRPq6HWQ7/rQHtKCPa5ZRQY72jpidKH2DQyNthV7uGB6hwq\n3NNqoo7Fd69MkwJgiFUvsQ5extdBNrZAODjlWwoVKSGBHtUYA1DhDhzKdO9BPH+kFESmYBClwCnZ\n8uNPnDPjazshIqW06iaxHE+ua5J63YVYzpnkquJFVZ5MOKk0pjp80z6A9Bj9LJhN+gDGpepZDcys\nCevuZGyy7EnibwShgRc4gVToIvycYCA+fF3Gh6j0k7klBcAXIUSa8HPGDOMCsB76mPFKcBnPjVVK\noRUF+HljCYvtTVCQ3EYvHSzRCFu4svKTbopKEX4WSQHYaG+g6lU7hJ+FLgCb+OGX/0Mr2MSRQw/B\nLZRy9UEMQNvfxM+/XsFDBx7FwX1HwZz8k7FkXAAuXf4ajzzwOOq12S3Cz+YQhVhZuwlHKDz952cx\nXd7X95yDZtDAP5evYbZUx321P3UIP+/3ElJgM2pj2ilp+WQfGYsuAAKMUNxfnUOZe/nywVQBAPRZ\nAqTfMi9VAFyaIfyeN0sXAEq6Cb93+q0CIBW6CD8vNl72pIX4fXX4nQIA1UX4ebEdS2ZDHX4Csz4A\n3RQ3cP5OrNn84/LjXzMk/pol/u1DMxounRRSIZRmVrNCCjNdM4D1oGVkC6ykREsGRt//ftlcxtWN\n20bzX99YwEZoJp1En47hLISM0Ao3jc4ZmC/OouxWhsYBwM2NX+HndAFnwQnDXw+cADOQWbqEwnPM\nPM+Lgwg3g4enDsBlBhrsTLftIBAFsJxTo/JQ4w4cg9jECsRYW2/QLwDo7SLT90qNoMMHzHId5djE\nUfp2xtW5e6cR/57f4++HkfbbtqM0kiHnpHYHGw/LRvhIqbH/jzkcYn5hOwPOv+0CwcBzhbtCR/hg\nRzm7wPizGmXM7dj03S5t+zbcA9ulqx+lb2dcSArosD+TgruW+C0sLCzuVkzG9w4LCwuLOxiTs5Y3\ngyV+CwsLiz+IO4349+RWj9Eep1RGZ94m1somXuQqUUAYzS+TCYYlAIcyOAZ73AR6394klhMCoaTR\nBeASZuTxTwD4IjDy7qfQHvfcIAOXcESGZ/4CZmcJa2WP2ZkMDFr9ZeYdL439+IFR/PjRJWvtG2rq\nh5+4hRrq8JVh7Ch+/IkKyGT+9NjDxtR9COa5jgNWx/87cOHCBVy6dAmUUtx77704ffo0fN/H+fPn\nsbi4iPn5eZw5cwalUslovEYYdWn200gauQhlWn7X0S/n+PFDN4BRSuODOFT8s5lYGcvzlLZrlrFc\nL1fSGcvzZKyREUpoHXU2Ns6tGQVYChoIpcRG0IIvwlw/fiUlGmEbDdFGJCK0RYhI9Xr387inoBm1\nIKHgxPpxoWSPGik5UCVQAkpJSBFAqKhHiaPPLHDAqQtCHTDKMO2WwOLDXtJgACIZYbm1hkbUAgMB\nIZpYo0wGBeqi5BQwXZiGy11M8SIK3M29g1xCUeAOyrGENBRhrG3PyAahG6pILOGlhOhCSXofCjJo\nRVGZu3A4R4lqO2ZOWU8O+hqQCOPfgYNqSWcfj31KCGinmMZ695xYSgg8yrTkV8n459DT4Cbj61gi\nfmiZUuyk74GOlh8AUn74+mXOOROJhDPV95IXm9Xdq8zrntiU7l8KoZ07s++pgQ6/d3793shUUe93\ndgCldGw6/oaBkhAAyoYqou+++w6ffvoplFJ4/vnn8fLLL/+R9Hqw68S/uLiI999/H+fPnwfnHOfO\nncMTTzyBGzduoFqt4qWXXsLFixfRaDTw6quvGo3ZEnLrIklW7B3S7n3j0wUg8djv1weQLgDJ6zCH\nNFW2ACilCT/Hmlfrv7cKgJASjaiN5aDZQ0ZCSqzHBSBSEkpKbIY+mqL3cJJIRGjLEJEU8apNoRUT\nfha6ADC9CicMCqqnaCS5KhEgUiECGcJjLhhxQKjTc+NSQjsFQP9eEZZaq2iJds+YFJoMhZLglKPk\nFDBTnIGTI6Gc4gUUuAcQEhO+i7Lj9ah0pFIIRQShJARUF+FncyVApwAQ6GKQEH4WReqiFBeA5HMO\n+4h4OWiXg2dC+Pl++FvXaxfhZ5EUAP0T+k+/5WRaspnIJw388NOEP4iQE/RTraQLQHI/Zhu9tuYX\nQNJEOe4+AGwV9vSY4yJ+Ewk5AJQMiF9KiTfeeANnz57F9PQ03n33Xbz55ps4dIzP1rgAAAQ1SURB\nVGhwl/oo2PWtnmKxCM45fN+HEAJBEGBmZgbffvstTp48CQB47rnn8M0334w0btJo0ulYJDSX9JNY\nzhg41QdbEEr7aoYZIWDx6sSXAu0c0k/GZJR1bvqIqL5+7NoOWhPvSruB680VLOWQPgAwSjFdKGO+\nOIWNoIUFfz2X9AGAM46yUwQHRTNqohE1+2rxQxV1CDnI+aaQzpVyDw4vo8yr4KwEytz8m05JLLU3\nseCvYbGxhBubt3pIPxlTEYJIKdS9Gg5PHcT+yv5c0geA9cjHgr+GKnMxW6yi6hZypZmUEHjcgccc\ncFBQQvv6xysAQWxXUHeKqBdKuaQPAC0ZYCncRCtqo62ivqQPABEkfBl2PmNGee78mrgoCKEoUo6q\n4+WTPgAQCgn9fsn4vesLSvX/T13X/aJp8v+Jvs5Yn/cq3cTVuc/65EBS9yCltC/p6/lZZ2VPB9yD\n2TkHzZ+Mo1L/3h4Qwz/DcfXqVdxzzz2Ym5sD5xzPPPPMyPw3DLv+cLdSqeDFF1/E6dOn4XkeTpw4\ngRMnTmBtbQ31eh0AUK/Xsba29rvGH8kvnBDjpzSEkLiTd/APjDp/ILKbE/lglMYrpOGglBo1XwF6\nf9wklhACl3sI1PAcpJIQBo1ahBCUuNeX8LPwODfS4lNC9LcZg9+LEgrH8Ou4UNLoGQUQby8Z52rY\nX6FGe6g4SteIWVPX9mnxTTCqH/92Ypxvw/LyMmZnZzuvZ2ZmcPXq1fFNgAlY8d+6dQtffvklPv74\nY3zyySdot9u4dOlST9wkNT9YWFhYpDG+9f7OYNdX/NeuXcOxY8dQqeg2/6eeegpXrlxBvV7H6upq\n5+9arZb785cvX8bly5c7r1955RUUs/t2o+zj5Zzx2g+z23CM2sO1aePYl+59ZOzzW1gYY5T7ardj\nB8R98cUXnX8fP34cx48fN58/humzgiAIcPHixYHzzczM4PbtLYuW5eVlzMzMjJzTQKhdxo8//qje\neust1W63lZRSffTRR+qrr75Sn332mbpw4YJSSqkLFy6ozz//fMdzO3v27I7POQiTlo9SNicTTFo+\nSk1eTpOWz25CCKFef/11tbCwoMIwVG+//ba6fv36WOfY9RX/0aNHcfLkSbzzzjuglOLo0aN44YUX\n4Ps+zp07h6+//hpzc3M4c+bMjuc2NzfYa36nMWn5ADYnE0xaPsDk5TRp+ewmKKV47bXX8MEHH0Ap\nhb/97W84fPjwWOfYdeIHgFOnTuHUqVNd/61SqeC9997bpYw05ufnd3X+LCYtH8DmZIJJyweYvJwm\nLZ/dxuOPP44PP/xw28bf9Ye7k4zfs9e3nZi0fACbkwkmLR9g8nKatHz2Ona9gcvCwsLCYmdhV/wW\nFhYWdxks8VtYWFjcZbDEb2FhYXGXwRK/hYWFxV0GS/wWFhYWdxks8VtYWFjcZfh/R7Rqq0QKT3oA\nAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x13809b7b8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df.plot.hexbin(x='age', y='congress', gridsize=25, legend=True)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
keiikegami/theano | MLE.ipynb | 2 | 2615 | {
"cells": [
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"theta : [ 4.05360992 1.95336957]\n",
"True theta: [4, 2]\n",
"sigma: 1.3160388223\n",
"True sigma: 1\n"
]
}
],
"source": [
"# 線形回帰の最尤法\n",
"# 勾配降下法\n",
"# 従属変数を転置する必要がある。\n",
"\n",
"import numpy as np\n",
"import theano as th\n",
"import theano.tensor as T\n",
"from math import pi\n",
"\n",
"a = np.ones((500, 1))\n",
"x = np.random.randn(500,1)\n",
"b = 2\n",
"c = 4\n",
"u = np.random.randn(500,1)\n",
"y = c * a + b * x + u\n",
"\n",
"X = np.hstack((a,x))\n",
"\n",
"n = len(y)\n",
"\n",
"tX = th.shared(np.asarray(X, dtype = th.config.floatX), borrow = True)\n",
"ty = th.shared(np.asarray(y.T, dtype = th.config.floatX), borrow = True) \n",
"sh_theta = th.shared(np.ones(2, dtype = th.config.floatX), borrow = True, name = 'theta')\n",
"sigma = th.shared(1.)\n",
"\n",
"liklihood = - (n / 2.) * T.log(2 * pi * sigma ** 2) - (1/sigma**2) * T.sum((ty - T.dot(tX, sh_theta))**2)\n",
"\n",
"g_theta = T.grad(liklihood, sh_theta)\n",
"g_sigma = T.grad(liklihood, sigma)\n",
"\n",
"\n",
"learning_rate = 0.0001\n",
"updates1 = [(sh_theta, sh_theta + learning_rate * g_theta)]\n",
"updates2 = [(sigma, sigma + learning_rate * g_sigma)]\n",
"\n",
"train1 = th.function([], liklihood, updates = updates1)\n",
"train2 = th.function([], liklihood, updates = updates2)\n",
"\n",
"iteration = 100000\n",
"for iter in range(iteration):\n",
" train1()\n",
" train2()\n",
"\n",
"t = sh_theta.get_value() \n",
"s = sigma.get_value()\n",
"print 'theta : ' , t\n",
"print 'True theta: ', [4,2]\n",
"print 'sigma:', s\n",
"print 'True sigma:', 1"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
phoebe-project/phoebe2-docs | development/tutorials/datasets_advanced.ipynb | 2 | 17640 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Advanced: Datasets\n",
"============================\n",
"\n",
"Datasets tell PHOEBE how and at what times to compute the model. In some cases these will include the actual observational data, and in other cases may only include the times at which you want to compute a synthetic model.\n",
"\n",
"If you're not already familiar with the basic functionality of adding datasets, make sure to read the [datasets tutorial](datasets.ipynb) first.\n",
"\n",
"Setup\n",
"-----------------------------"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's first make sure we have the latest version of PHOEBE 2.4 installed (uncomment this line if running in an online notebook session such as colab)."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"#!pip install -I \"phoebe>=2.4,<2.5\""
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"As always, let's do imports and initialize a logger and a new Bundle."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"import phoebe\n",
"from phoebe import u # units\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"logger = phoebe.logger()\n",
"\n",
"b = phoebe.default_binary()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Passband Options\n",
"\n",
"Passband options follow the exact same rules as dataset columns.\n",
"\n",
"Sending a single value to the argument will apply it to *each* component in which the time array is attached (either based on the list of components sent or the defaults from the dataset method).\n",
"\n",
"Note that for light curves, in particular, this rule gets slightly bent. The dataset arrays for light curves are attached at the system level, *always*. The passband-dependent options, however, exist for each star in the system. So, that value will get passed to each star if the component is not explicitly provided."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 78 parameters | contexts: constraint, figure, dataset, compute>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_dataset('lc', \n",
" times=[0,1],\n",
" dataset='lc01', \n",
" overwrite=True)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Parameter: times@lc01@dataset\n",
" Qualifier: times\n",
" Description: Observed times\n",
" Value: [0. 1.] d\n",
" Constrained by: \n",
" Constrains: None\n",
" Related to: None\n",
"\n"
]
}
],
"source": [
"print(b.get_parameter(qualifier='times', dataset='lc01'))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ParameterSet: 2 parameters\n",
" ld_mode@primary@lc01@dataset: interp\n",
" ld_mode@secondary@lc01@dataset: interp\n"
]
}
],
"source": [
"print(b.filter(qualifier='ld_mode', dataset='lc01'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As you might expect, if you want to pass different values to different components, simply provide them in a dictionary."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 45 parameters | contexts: constraint, figure, dataset, compute>"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_dataset('lc', \n",
" times=[0,1], \n",
" ld_mode='manual',\n",
" ld_func={'primary': 'logarithmic', 'secondary': 'quadratic'}, \n",
" dataset='lc01',\n",
" overwrite=True)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ParameterSet: 2 parameters\n",
" ld_func@primary@lc01@dataset: logarithmic\n",
" ld_func@secondary@lc01@dataset: quadratic\n"
]
}
],
"source": [
"print(b.filter(qualifier='ld_func', dataset='lc01'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note here that we didn't explicitly override the defaults for '\\_default', so they used the phoebe-wide defaults. If you wanted to set a value for the ld_coeffs of any star added in the future, you would have to provide a value for '\\_default' in the dictionary as well."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ParameterSet: 3 parameters\n",
" ld_func@_default@lc01@dataset: logarithmic\n",
" ld_func@primary@lc01@dataset: logarithmic\n",
" ld_func@secondary@lc01@dataset: quadratic\n"
]
}
],
"source": [
"print(b.filter(qualifier'ld_func@lc01', check_default=False))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This syntax may seem a bit bulky - but alternatively you can add the dataset without providing values and then change the values individually using dictionary access or set_value."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Adding a Dataset from a File"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Manually from Arrays\n",
"\n",
"For now, the only way to load data from a file is to do the parsing externally and pass the arrays on (as in the previous section).\n",
"\n",
"Here we'll load times, fluxes, and errors of a light curve from an external file and then pass them on to a newly created dataset. Since this is a light curve, it will automatically know that you want the summed light from all copmonents in the hierarchy."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 43 parameters | contexts: constraint, dataset, compute, figure>"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"times, fluxes, sigmas = np.loadtxt('test.lc.in', unpack=True)\n",
"b.add_dataset('lc', \n",
" times=times, \n",
" fluxes=fluxes, \n",
" sigmas=sigmas, \n",
" dataset='lc01',\n",
" overwrite=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Enabling and Disabling Datasets\n",
"\n",
"See the [Compute Tutorial](compute.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Dealing with Phases\n",
"\n",
"\n",
"Datasets will no longer accept phases. It is the user's responsibility to convert\n",
"phased data into times given an ephemeris. But it's still useful to be able to\n",
"convert times to phases (and vice versa) and be able to plot in phase.\n",
"\n",
"Those conversions can be handled via [b.get_ephemeris](../api/phoebe.frontend.bundle.Bundle.get_ephemeris.md), [b.to_phase](../api/phoebe.frontend.bundle.Bundle.to_phase.md), and [b.to_time](../api/phoebe.frontend.bundle.Bundle.to_time.md)."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{'period': 1.0, 't0': 0.0, 'dpdt': 0.0}\n"
]
}
],
"source": [
"print(b.get_ephemeris())"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.0\n"
]
}
],
"source": [
"print(b.to_phase(0.0))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-0.25\n"
]
}
],
"source": [
"print(b.to_time(-0.25))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"All of these by default use the period in the top-level of the current hierarchy,\n",
"but accept a component keyword argument if you'd like the ephemeris of an\n",
"inner-orbit or the rotational ephemeris of a star in the system.\n",
"\n",
"We'll see how plotting works later, but if you manually wanted to plot the dataset\n",
"with phases, all you'd need to do is:"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11\n",
" 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23\n",
" 0.24 0.25 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35\n",
" 0.36 0.37 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47\n",
" 0.48 0.49 0.5 -0.49 -0.48 -0.47 -0.46 -0.45 -0.44 -0.43 -0.42 -0.41\n",
" -0.4 -0.39 -0.38 -0.37 -0.36 -0.35 -0.34 -0.33 -0.32 -0.31 -0.3 -0.29\n",
" -0.28 -0.27 -0.26 -0.25 -0.24 -0.23 -0.22 -0.21 -0.2 -0.19 -0.18 -0.17\n",
" -0.16 -0.15 -0.14 -0.13 -0.12 -0.11 -0.1 -0.09 -0.08 -0.07 -0.06 -0.05\n",
" -0.04 -0.03 -0.02 -0.01 0. ]\n"
]
}
],
"source": [
"print(b.to_phase(b.get_value(qualifier='times')))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"or"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11\n",
" 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23\n",
" 0.24 0.25 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35\n",
" 0.36 0.37 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47\n",
" 0.48 0.49 0.5 -0.49 -0.48 -0.47 -0.46 -0.45 -0.44 -0.43 -0.42 -0.41\n",
" -0.4 -0.39 -0.38 -0.37 -0.36 -0.35 -0.34 -0.33 -0.32 -0.31 -0.3 -0.29\n",
" -0.28 -0.27 -0.26 -0.25 -0.24 -0.23 -0.22 -0.21 -0.2 -0.19 -0.18 -0.17\n",
" -0.16 -0.15 -0.14 -0.13 -0.12 -0.11 -0.1 -0.09 -0.08 -0.07 -0.06 -0.05\n",
" -0.04 -0.03 -0.02 -0.01 0. ]\n"
]
}
],
"source": [
"print(b.to_phase('times@lc01'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Although it isn't possible to attach *data* in phase-space, it is possible to tell PHOEBE at which phases to compute the model by setting `compute_phases`. Note that this overrides the value of `times` when the model is computed."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 43 parameters | contexts: constraint, dataset, compute, figure>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_dataset('lc',\n",
" compute_phases=np.linspace(0,1,11),\n",
" dataset='lc01',\n",
" overwrite=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The usage of `compute_phases` (as well as `compute_times`) will be discussed in further detail in the [compute tutorial](./compute.ipynb) and the [advanced: compute times & phases tutorial](./compute_times_phases.ipynb). \n",
"\n",
"Note also that although you can pass `compute_phases` directly to add_dataset, if you do not, it will be constrained by `compute_times` by default. In this case, you would need to flip the constraint before setting `compute_phases`. See the [constraints tutorial](./constraints.ipynb) and the [flip_constraint API docs](../api/phoebe.frontend.bundle.Bundle.flip_constraint.md) for more details on flipping constraints."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 43 parameters | contexts: constraint, dataset, compute, figure>"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_dataset('lc',\n",
" times=[0],\n",
" dataset='lc01', \n",
" overwrite=True)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ParameterSet: 2 parameters\n",
"C compute_phases@lc01@dataset: []\n",
" compute_phases@constraint: times_to_phases({compute_times@lc01@dataset}, {period@binary@component}, {dpdt@binary@component}, {phases_t0@lc01@dataset}, {t0_supconj@binary@component}, {t0_perpass@binary@component}, {t0_ref@binary@component})\n"
]
}
],
"source": [
"print(b['compute_phases@lc01'])"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ConstraintParameter: {compute_times@lc01@dataset} = phases_to_times({compute_phases@lc01@dataset}, {period@binary@component}, {dpdt@binary@component}, {phases_t0@lc01@dataset}, {t0_supconj@binary@component}, {t0_perpass@binary@component}, {t0_ref@binary@component}) (solar units) => [] d>"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.flip_constraint('compute_phases', dataset='lc01', solve_for='compute_times')"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [],
"source": [
"b.set_value('compute_phases', dataset='lc01', value=np.linspace(0,1,101))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Removing Datasets\n",
"\n",
"\n",
"Removing a dataset will remove matching parameters in either the dataset, model, or constraint contexts. This action is permanent and not undo-able via [Undo/Redo](undo_redo.ipynb)."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['lc01']\n"
]
}
],
"source": [
"print(b.datasets)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The simplest way to remove a dataset is by its dataset tag:"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 43 parameters | contexts: constraint, dataset, compute, figure>"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.remove_dataset('lc01')"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[]\n"
]
}
],
"source": [
"print(b.datasets)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But [remove_dataset](../api/phoebe.frontend.bundle.Bundle.remove_dataset.md) also takes any other tag(s) that could be sent to filter."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: EMPTY>"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.remove_dataset(kind='rv')"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[]\n"
]
}
],
"source": [
"print(b.datasets)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.5"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
opalbert/mltutorial | notebooks/data-mining/1. Web Scraping.ipynb | 4 | 192214 | {
"metadata": {
"name": "",
"signature": "sha256:bda576f544c5c3c928cf09474fc234c8a15aebe832608fcd49802d53914e2869"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Tutorial Brief"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Web scrpping a one of the most common method of collecting data. This tutorial covers the basics of web scraping.\n",
"\n",
"**Video Tutorial**:\n",
"\n",
"http://youtu.be/wT66i7jeyL8\n",
"\n",
"More About LXML:\n",
"\n",
"http://lxml.de/"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from datetime import datetime\n",
"\n",
"from lxml import html\n",
"import requests\n",
"\n",
"import numpy as np\n",
"import pandas as pd\n",
"import matplotlib.pylab as plt\n",
"\n",
"pd.options.display.max_columns=50"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Data and Data Source"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We will be working with the Nobel Prize data. We will get that from Wikipedia\n",
"\n",
"\n",
"Webpage URL:\n",
"\n",
"http://en.wikipedia.org/wiki/List_of_Nobel_laureates"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Before you Web Scrape - Read the ToS"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Please make sure that you read the ToS (Terms of Service) of the website before you web scrape any data. Most websites don't allows web scraping of their content. Some allow moderate use.\n",
"\n",
"For Wikipedia:\n",
"\n",
"> ## 4. Refraining from Certain Activities\n",
"> ### Engaging in Disruptive and Illegal Misuse of Facilities\n",
"> Engaging in automated uses of the site that are abusive or disruptive of the services and have not been approved by the Wikimedia community;\n",
"> ##### [Wikimedia Foundation Terms of Use](wikimediafoundation.org/wiki/Terms_of_Use#4._Refraining_from_Certain_Activities)\n",
"\n",
"**From my basic technical understanding**:\n",
"\n",
"This means \"automated uses\" like web scraping are not allowed if they are \"abusive or disruptive of the services\" but I would argue web scraping a single page is not \"abusive or disruptive of the services\". Web scraping will actually consume less servers time and bandwidth than reading the page in a browser. This is due to the fact that we will only request the page and none of the static files linked to it like CSS, images, javascript ... etc.\n",
"\n",
"**DISCLAIMERL**: I'm not a lawyer\n",
"\n",
"##Basic Rules:\n",
"\n",
"- Check if there is an API use it. It will make your life easier.\n",
"- Don't use scrape too much in a short time. It slows down the servers and might gets you banned from the website.\n",
"- Never scrape anything that is not public.\n",
"- Check /robots.txt for allowed paths"
]
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Fetch page & build HTML tree"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def print_element(element):\n",
" print \"<%s %s>%s ...\" % (element.tag, element.attrib, element.text_content()[:200].replace(\"\\n\", \" \"))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"page = requests.get('http://en.wikipedia.org/wiki/List_of_Nobel_laureates')\n",
"tree = html.fromstring(page.text)\n",
"print_element(tree)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"<html {'lang': 'en', 'class': 'client-nojs', 'dir': 'ltr'}> List of Nobel laureates - Wikipedia, the free encyclopedia a:lang(ar),a:lang(kk-arab),a:lang(mzn),a:lang(ps),a:lang(ur){text-decoration:none} /* cache key: enwiki:resourceloader:filter ...\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Locate The table"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"First we find all tables"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"tables = tree.xpath('//table')\n",
"for table in tables:\n",
" print_element(table)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"<table {'class': 'wikitable sortable'}> Year Physics Chemistry Physiology or Medicine Literature Peace Economics 1901 R\u00f6ntgen, WilhelmWilhelm R\u00f6ntgen Hoff, Jacobus Henricus van 'tJacobus Henricus van 't Hoff von Behring, Emil AdolfEmil ...\n",
"<table {'style': 'border:1px solid #aaa;background-color:#f9f9f9', 'class': 'mbox-small plainlinks'}> Wikimedia Commons has media related to Nobel laureates. ...\n",
"<table {'style': 'border-spacing:0;', 'cellspacing': '0', 'class': 'navbox'}> v t e Nobel Prizes Prizes Chemistry Economics1 Literature Peace Physics Physiology or Medicine Laureates by subject Chemistry Economics Literature Peace Physics Physi ...\n",
"<table {'style': 'border-spacing:0;background:transparent;color:inherit;', 'cellspacing': '0', 'class': 'nowraplinks hlist collapsible collapsed navbox-inner'}> v t e Nobel Prizes Prizes Chemistry Economics1 Literature Peace Physics Physiology or Medicine Laureates by subject Chemistry Economics Literature Peace Physics Physiolo ...\n",
"<table {'style': 'border-spacing:0;', 'cellspacing': '0', 'class': 'nowraplinks navbox-subgroup'}> by subject Chemistry Economics Literature Peace Physics Physiology or Medicine by criterion Country University affiliation Female Black Christians Chinese Indian Muslim Japanese Jewish ...\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**When locating the table watchout for client side javascript alteration to the HTML code**"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"table = tree.xpath('//table[@class=\"wikitable sortable\"]')[0]\n",
"print_element(table)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"<table {'class': 'wikitable sortable'}> Year Physics Chemistry Physiology or Medicine Literature Peace Economics 1901 R\u00f6ntgen, WilhelmWilhelm R\u00f6ntgen Hoff, Jacobus Henricus van 'tJacobus Henricus van 't Hoff von Behring, Emil AdolfEmil ...\n"
]
}
],
"prompt_number": 5
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Extract the Subjects & Years"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"subjects = [subject[0].text_content().replace(\"\\n\",\" \") for subject in table.xpath('tr')[0][1:]]\n",
"subjects"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
"['Physics',\n",
" 'Chemistry',\n",
" 'Physiology or Medicine',\n",
" 'Literature',\n",
" 'Peace',\n",
" 'Economics']"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"years = [item[0].text for item in table.xpath('tr')[1:-1]]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 7
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Extract Winners Data"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Testing for a sigle years"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"for index, item in enumerate(table.xpath('tr')[1][1:]):\n",
" subject = subjects[index]\n",
" print \"%s:\" % subject\n",
" for winner in item.xpath('span[@class=\"vcard\"]/span/a'):\n",
" winner_name = winner.attrib[\"title\"]\n",
" winner_url = winner.attrib[\"href\"]\n",
" print \" - %s\" % winner_name\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Physics:\n",
" - Wilhelm R\u00f6ntgen\n",
"Chemistry:\n",
" - Jacobus Henricus van 't Hoff\n",
"Physiology or Medicine:\n",
" - Emil Adolf von Behring\n",
"Literature:\n",
" - Sully Prudhomme\n",
"Peace:\n",
" - Henry Dunant\n",
" - Fr\u00e9d\u00e9ric Passy\n",
"Economics:\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Extract The complete table"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"year_list = []\n",
"subject_list = []\n",
"name_list = []\n",
"url_list = []\n",
"for y_index, year in enumerate(years):\n",
" #print year\n",
" for index, item in enumerate(table.xpath('tr')[y_index + 1][1:]):\n",
" subject = subjects[index]\n",
" #print \"%s:\" % subject\n",
" for winner in item.xpath('span[@class=\"vcard\"]/span/a'):\n",
" winner_name = winner.attrib[\"title\"]\n",
" winner_url = winner.attrib[\"href\"]\n",
" #print \" - %s\" % winner_name\n",
" year_list.append(year)\n",
" subject_list.append(subject)\n",
" name_list.append(winner_name)\n",
" url_list.append(winner_url)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 9
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Post Processing in Pandas"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"data_set = pd.DataFrame(name_list, columns=[\"winner_name\"])\n",
"data_set[\"subject\"] = subject_list\n",
"data_set[\"year\"] = year_list\n",
"data_set[\"year\"] = data_set[\"year\"].astype(np.int32)\n",
"data_set[\"url\"] = url_list\n",
"data_set.head(5)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>winner_name</th>\n",
" <th>subject</th>\n",
" <th>year</th>\n",
" <th>url</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td> Wilhelm R\u00f6ntgen</td>\n",
" <td> Physics</td>\n",
" <td> 1901</td>\n",
" <td> /wiki/Wilhelm_R%C3%B6ntgen</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td> Jacobus Henricus van 't Hoff</td>\n",
" <td> Chemistry</td>\n",
" <td> 1901</td>\n",
" <td> /wiki/Jacobus_Henricus_van_%27t_Hoff</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td> Emil Adolf von Behring</td>\n",
" <td> Physiology or Medicine</td>\n",
" <td> 1901</td>\n",
" <td> /wiki/Emil_Adolf_von_Behring</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td> Sully Prudhomme</td>\n",
" <td> Literature</td>\n",
" <td> 1901</td>\n",
" <td> /wiki/Sully_Prudhomme</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td> Henry Dunant</td>\n",
" <td> Peace</td>\n",
" <td> 1901</td>\n",
" <td> /wiki/Henry_Dunant</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 10,
"text": [
" winner_name subject year url\n",
"0 Wilhelm R\u00f6ntgen Physics 1901 /wiki/Wilhelm_R%C3%B6ntgen\n",
"1 Jacobus Henricus van 't Hoff Chemistry 1901 /wiki/Jacobus_Henricus_van_%27t_Hoff\n",
"2 Emil Adolf von Behring Physiology or Medicine 1901 /wiki/Emil_Adolf_von_Behring\n",
"3 Sully Prudhomme Literature 1901 /wiki/Sully_Prudhomme\n",
"4 Henry Dunant Peace 1901 /wiki/Henry_Dunant"
]
}
],
"prompt_number": 10
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Looking at the data"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"years_df = data_set[\"year\"].value_counts().sort_index()\n",
"years_df"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 11,
"text": [
"1901 6\n",
"1902 7\n",
"1903 7\n",
"1904 5\n",
"1905 5\n",
"1906 6\n",
"1907 6\n",
"1908 7\n",
"1909 7\n",
"1910 4\n",
"1911 6\n",
"1912 6\n",
"1913 5\n",
"1914 3\n",
"1915 4\n",
"...\n",
"1999 6\n",
"2000 13\n",
"2001 14\n",
"2002 13\n",
"2003 11\n",
"2004 12\n",
"2005 12\n",
"2006 8\n",
"2007 11\n",
"2008 12\n",
"2009 13\n",
"2010 11\n",
"2011 13\n",
"2012 10\n",
"2013 13\n",
"Length: 110, dtype: int64"
]
}
],
"prompt_number": 11
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Number of Prizes per Year"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.figure(figsize=(15,5))\n",
"plt.plot(years_df.index, years_df.values, linewidth=2, alpha=.6)\n",
"plt.grid()\n",
"plt.xlabel(\"Year\")\n",
"plt.ylabel(\"Number of Prizes\")\n",
"plt.show();\n",
"print \"Total Prizes: %s\" % len(data_set)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA30AAAFHCAYAAAAV9CVbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXuYXFWd7/1dfUnSuXQ6nXtaSCAQwiUhN+INpAVxUEFH\nxtF3dEajM3Pm8Zxh1FdH4aCIOiPoyMyg47xnHEfHGTlwYF5RQcULWggiQhKaJIQQgrnRnTRpOp1O\nJ51OX9b549fLvat6X9betXfV3tXfz/PUU7Wr9mVV7V9Vre/+3ZTWGoQQQgghhBBCapO6ag+AEEII\nIYQQQkh6UPQRQgghhBBCSA1D0UcIIYQQQgghNQxFHyGEEEIIIYTUMBR9hBBCCCGEEFLDUPQRQggh\nhBBCSA2TmuhTSn1DKdWtlNru8dpHlVJjSqnWtI5PCCGEEEIIISRdT983AVxd+qRS6gwAVwHYn+Kx\nCSGEEEIIIYQgRdGntX4EwFGPl/4ewMfTOi4hhBBCCCGEEIeK5vQppd4G4EWt9bZKHpcQQgghhBBC\nJisNlTqQUmo6gP8JCe383dOVOj4hhBBCCCGETEYqJvoALAewDMDTSikAeAWALUqpjVrrl9wrKqV0\nBcdFCCGEEEIIIZlDa52Ik6xiok9rvR3AQrOslNoLYL3Wutdn/UoNjeScW265Bbfccku1h0FyAG2F\nRIH2QmyhrZAolNrL0BDwsY8Bp0/L8gc/CKxZU52xkWwx7ihLhDRbNtwF4DEAK5RSB5VS7y9ZhaqO\nJMK+ffuqPQSSE2grJAq0F2ILbYVEodRetm0TwWfm9088UfkxkdonNU+f1vqPQl4/O61jE0IIIYQQ\nkgeefFLu3/hG4Mc/FhF46hQwbVp1x0Vqi4pW7yQkDTZt2lTtIZCcQFshUaC9EFtoKyQKbns5cQLY\nsQOoqwPe8Abg3HOB4WGgo6N64yO1icpi7pxSSmdxXIQQQgghhCTFo48C//mfwAUXAB/6EPDLXwJ3\n3glcdBFw/fXVHh2pNkqpxAq50NNHck+hUKj2EEhOoK2QKNBeiC20FRIFt72Y/L2NG+V+3Tqgvh7Y\nuRM4frzyYyO1C0UfIYQQQgghFaavD9i9G2hsdKp1zpwpXr+xMWDr1uqOj9QWDO8khBBCCCGkwvzs\nZ8C994p37y/+wnn+iSeAf/s34JxzgL/+6+qNj1QfhncSQgghhBCSY0xo5yWXFD9/8cXAlCnAnj1A\nr2c3a0KiQ9FHcg9zKYgttBUSBdoLsYW2QqJQKBTQ3Q3s3w80NQGrVhW/PnUqsHq1PDbtHAgpF4o+\nQgghhBBCKogRc2vXSk5fKaawC0UfSQrm9BFCCCGEEFIhtAY+/Wmgu1vaNFxwwcR1RkYkn+/kSeCW\nW4DFiys+TJIBmNNHCCGEEEJIDjl4UARfczOwcqX3Og0NUuAFoLePJANFH8k9zKUgttBWSBRoL8QW\n2gqJwje/WQAArF8P1AXMxE2BlyeeEO8gIeVA0UcIIYQQQkgF0Bp47jl5bPL2/FixApg9GzhyRIq+\nEFIOzOkjhBBCCCGkAuzeDdx+OzBvHvA3fwOokGyte+4BHnoIuPJK4J3vrMwYSXZgTh8hhBBCCCE5\nw92bL0zwAY43cPNmYGwsvXGR2oeij+Qe5lIQW2grJAq0F2ILbSW/vPwycOpUZY41MgJs3Qp0dRVC\nQzsNS5cCCxYAx46JlzCvaA10dUXPTRwbk6I3UTl4ENi1Czh+PPq2tQpFHyGEEEIImXQcOQLcfDPw\nrW9V5nh79gAnTkho55Ildtso5RR02bo1vbGlzY9/DHzmM9Erkf74x3KOduyItt1DDwH/8A/A009H\n266Woegjuae9vb3aQyA5gbZCokB7IbbQVvLJCy+I923XrspUx+zvl/tLL22PtJ1p63DgQLLjqRRa\nA488Io9NERtbnn1W7vfujbZdb6/ct7ZG266WoegjhBBCCCGTjs5OuT95EujrS/94Jox06tRo27W1\nyX2c8MgssHcv0NMjj81nboPWzvpGxNlC0TcRij6Se5hLQWyhrZAo0F6ILbSVfOIWIFHESFyM6Hvh\nhUKk7WbMkNYNQ0OOeMoTpngNEE24Hj8ODAzI4yiiT2tHxM+ZY79drUPRRwghhBBCJh3VEn1TpkTf\n1nj7KjHOJBkbA7Zskcf19dGEq/u9RhF9x48Dw8MilqN6VWsZij6Se5hLQWyhrZAo0F6ILbSV/HHi\nRHFIZ1dX+sc0ou+SS9ojb+sO8cwTu3ZJLuPChcB558lztu/BLfqOHrX3EDK00xuKPkIIIYQQMqkw\nwqOxUe4r4UEbGpL7adOib5tXT5+p1nnJJdHfg3u94WEn1DMMij5vKPpI7mEuBbGFtkKiQHshttBW\n8ocRFKtXy/3hw+k3Pzeevh07CpG3NS0e8iT6hoedNhMbN0YXfUaY142rFdsQT4o+byj6CCGEEELI\npMIIj7PPBubOFYESpwl4FIynz3gXo7BkiYif7m5pM5EHtm8Xobt0qYR3RhGuY2OO6Fu+XO4p+sqD\noo/kHuZSEFtoKyQKtBdiC20lfxjh0dZWuXw54+m77LL2yNs2NgLz54sYOnQo2XGlhTu0E4gmXHt6\ngNOnpfqmOT+2ou/oUbmn6CuGoo8QQgghhEwatHYEnlv0pR06aURfnJw+IF/FXAYHxdOnFLBhgzzn\nFq6HDwdv7xblRrxF9fSxXUMxFH0k9zCXgthCWyFRoL0QW2gr+eLoUREls2YBzc2VE30mvHPLlkKs\n7fOU19fRISGz555bLL5sP2sjbJcsiS/66OkrhqKPEEIIIYRMGtxeJKByYsp4+uLk9AH5quBpGrJv\n3Fj8vO1nHdfTNzwsLSLq6qShPXGg6CO5h7kUxBbaCokC7YXYQlvJF0ZQGAGycKE0Du/pcbxxaWBE\n31VXtcfaPi+ir79f+vPV1wPr1hW/ZvsevESfydULwqwzZ45T9ZMI/DgIIYQQQsikodTT19AALFok\nuX5pFUkZG5PCJEoBU6bE28f8+bLt0aPAyZPJji9JtmyR93vhhcCMGcWv2eQlDg8DL70kom3RIvHY\n1dUBx46FF4BhaKc/FH0k9zCXgthCWyFRoL0QW2gr+aJU9Lkfp+VFMx7EqVOBhx8uxNpHXR2weLE8\nznIxF1O1szS0E3CEa2+vv3A9dEhE44IFEgpbV+fkBYZ5+1i5059URZ9S6htKqW6l1HbXc3+nlHpW\nKfW0Uuo7SilG3BJCCCGEkNQZHXUqR5rwTqByoi9u5U5D1ou59PQAL7wgws40vndjI1zdlVUNRvSF\n5fXR0+dP2p6+bwK4uuS5nwC4UGt9MYDdAG5MeQykxmEuBbGFtkKiQHshttBW8kN3twi/+fPF62Yw\nYiotD5rJ55s6tTx7yXpe3+bNcr9mTfHn6yZMuHp5Ym2LubBdgz+pij6t9SMAjpY891Ot9dj44m8A\nvCLNMRBCCCGEEAJ4Cwr3clpiqtwefYasiz5TtdM0ZPci7D0kIfro6ZtIQ5WP/wEAd1V5DCTnFAoF\nXmUlVtBWSBRoL+lz6hSwc6d4XqLS3AysWCGFMaoNbaX6vPii2ERzc/B6pZU7Da2tIsj6+4Hjx6WH\nXxAHDwJz5wLTp9uNzy36yrEXdyEUrYPtf2wMeOYZ59ilTJkCXHBB/BYSpXR2ym3GDNmvH2HFXCj6\n0qFqok8pdROA01rr/12tMRBCCCGketx9N/DrX8ff/mMfk+bPZHJz6BDw+c+LkLvppmAh5JUvBsg2\nbW2Sj9bZCaxc6b+P3buB228HXvlK4AMfsBtjUjl9zc3AzJnAwADQ1xccxvjoo8Cddwbv721vA978\n5vLGZDAFXNatk4qofrg9faXC9cQJeV9TpgDz5jnP27Rt0JqiL4iqiD6l1CYAbwZwpd86mzZtwrJl\nywAALS0tWLNmze+uipgqWVzmssF91aza4+Fydpfb29szNR4uZ3uZ9pLu8tAQ8L3vFTAyAlx7bTuU\nAp57Tl4/7zxZ3295+vR2dHcDP/hBAWvWZOP9cLl6y3197RgdBX7zmwLuvRd45zv913/sMWDGjHa0\ntU18/dixArq6gK6udqxc6X+8fftk+fHHCzj7bHt77+oqoLkZ+O//vbz3u2RJO3bvBr773QLOOst/\n/TvvlPdzxRXtmDmz+PvU2ws8+mgBhQLw5jeXN5729nZoDfzXfxVw7BiwcWPw+pdfLuPZvbuABx6Q\n7795/eBBAGjHkiVOldP29na0tsrnJ+LZe/8PPljAvn3A8uXtaGrKjn1GWe7o6EBfXx8AYN++fUgS\npbVOdIcTDqDUMgD3a61XjS9fDeB2AJdrrXt8ttFpj4sQQggh1ePJJ4Gvfx1Yvhz4+MejbfvDHwLf\n+x5w9dXA29+ezvhIPtAa+OQnpWokAPze7wHXXee97qlTwIc+JF6oL39Zmoe7+cUvxPt86aXAn/yJ\n9z6Gh8XDfOqU9JD7zGfsxvnLX4rX7bLLgD/+Y7tt/Lj7bhnrddfJ+/Wip0e8nlOmAF/60sSiKjt2\nAF/5ioRhfuhD5Y0HAH77W+ALXxDP4+c/H94Y/fbbxWN6/fXARRc5zxcKwF13Aa99LfDe9zrPDw4C\nH/6wvI877vD25h48CPzN34gn8eaby39PWUApBa11IkHsIaekPJRSdwF4DMB5SqmDSqkPAPgKgJkA\nfqqUekop9c9pjoHUPuZKCSFh0FZIFGgv6WJT8MEP2/yeSkFbqR5794rAMXlpTz4pQtALE9q5ePFE\nwQfYFUnZvt3JkRsctB9naU5fOdiMM6yKpsl9PH68rKH8DvN93rAhXPAB/nl9foV2mprkNjTk39+P\noZ3BpBreqbX+I4+nv5HmMQkhhBCSbU6ckAITdXXA+vXRt7ft2UVqHyM2Lr8c2LpVbGLPHu9cTyMw\nSou4GGyKpJi8NSC+6CuXsEIoQPhFFVOopr+//PGMjQFbtgQfrxQ/4eon+gD53g8OyjmeMWPi6xR9\nwaTq6SOkEphYaELCoK2QKNBe0mPrVqnYuXJleLVFL7Lm6aOtVAe32Ni4UW5AsTBzEyQoABESs2eL\nN+nllye+Pjgonj6l5Hb6tH3lWbfoK9dejGg9fFg+g1Jsqmga0Tcw4O8ZtWXXLhGPCxcCZ55pt42X\n6NM6WJiHfe/Zoy8Yij5CCCGEVBTjhTCT9KiYSV1fn/ekl0wOSsWG8TJt2eItxsJEn/s1r9DJjg7J\n6VuxwmnVYOvtS6p6p9nH3Lkylu7uia/bVNFsaJD3MDrqHy5pi9uraNtCxUu49vbK5zlrlvfFIFvR\nR0+fNxR9JPcwl4LYQlshUaC9pMPRo8Dzz0sO1po18fbR0CAembEx4NixZMcXB9pKdSgVG21tIiYG\nBoBnny1eV+vyRZ/7eE1N8thW9BlP39SpydiLX4in1o7oC7uokkSI5/Aw8NRTdsdz4yVc/dppGMLa\nNpjnKfq8oegjhBBCSMXYvFkmpqtWORPnOGQtxJNUFi+xoZTj7TMCzXD8uIjBpiagpcV/v36ir79f\nPIv19eJBiyr6jKfPq6hKHPzGaQrbzJkT3sMyiWIuprDN0qXicY1CqXANE+X09JUHRR/JPcylILbQ\nVkgUaC/pYLwQcap2usmS6KOtVB4/sWHsqqNDcu4MbkERFIJowg5LPWhbtohn+cILJVcurqcviZw+\nwF/0uatohoVaGk9fOaKvnO9z6XsoR/SNjkq4t1LBon4yQ9FHCCGEkIrQ3Q3s3y8T5lWryttXlkQf\nqTx+YmP+fOCss8Sztn2787xNaCcgok8pyTUbGZl4PONVLEf0JYGX6ItaRbPc8E53YZsNG6Jv7yf6\n/KqrBn3n+/okgqClxbsdB6HoIzUAcymILbQVEgXaS/IYL8TatU5ftbhkSfTRVipLmNgwwswd4mkr\n+hobgQULREAdPizP9fQAL7wgjc5Xr5bnjHiLI/qSsJcFC0Tc9PQ4oaNRq2iWG97pLmwTp2KmEXed\nneKpM5+3n+hraZFzfuzYxEI9DO0Mh6KPEEIIIanjLjBRbmgn4Ewy/Yo6kNolTGyYBuE7djiVKcO8\nSG5KPVBejc6rndPX0AAsWiTfq0OH5Dn398umima5nr6wXoBhLFzoCNcDB0TIzZ/v/xnV1zsFnPr6\nil9ju4ZwKPpI7mEuBbGFtkKiQHtJlgMHJLyzuVn685VLljx9tJXKEiY2mpuB886T8MynnhKRYIRR\nmKcPKPZA+R2v2jl9QLE4HR6W/peAfRXNcjx9pYVt4uAWriYsNez8+H3vWbkzHIo+QgghhKSO8UIY\nL0y5ZEn0kcphKzbcVTx7eqSoy5w5Tn+9INxVJf0anUcRfWNjcnylJEQ0KdyiL04VzXIKuZQWtomL\neQ/m98FW9JV6+BneGQ5FH8k9zKUgttBWSBRoL8mhtRMil0RoJwDMnCn5VydOOKFz1YK2UjmM2Ljo\nomCxsXateJKeew7YuVOes/Hyudfr7PRvdG5En/HgBeEO7VQqOXtxVxqNEzpdTninbS/AMMxnbcI1\n43r6KPrCoegjhBBCSKo8/7xcmZ83TyorJoFS9PZNRmzFzfTpIgy1Bn74Q3nOJp8PkLyyxkaxq8ce\nk+dKxU0UT1/SlTsNRiAdOBCvimbc8E6vwjZxKT0nYeeIoi8+FH0k9zCXgthCWyFRoL0khzsnyqbA\nhC1ZEX20lcoQVWwYoXbsmNzbevrq6oDFi51tvRqdRxF9pUVckrKX1lYRkidOSE7fuedGK2QybZp4\nL0+dKu5pGIZXYZu4uM9JQ4NUJQ2Coi8+FH2EEEIISY2RkegFJmxhBc/JRVSxsXp1sXfNVvSVruvV\n6DwLnj6liscZ9fulVDxvX7lVO90Y4QqI0A7rsecl+gYH5TZlil3O5mSlIXwVQrJNoVDgVVZiBW2F\nRIH2kgw7d4onoq3NPrzOliQ9fS+/DDzzjIQDRuW3vy3g/e9vL38QKXLwoAjwqOG1L744UVzYsH+/\nCLNFi6JtF0RUsdHYKALx8ceLvXc2uN+v1/HKEX1J/rYsWSLez7hVNGfNku/P8ePA3Lnh6/sVtomL\nsa0XXrD7fTAXetzfebeXL8lIglqDoo8QQgghqbFjh9xHyTWyJUnR96//CuzdG2/bri7g9a8Hli0r\nfxxpoDVwxx0SZvilL9mH5A0Py/paA1/4gr2nqq8P+OIXpZn23/5t/HG7efllERvTp0cTGxs3iuhb\nvLi4EEsYZ5wh936NzuOEdybt6QOcscWtohm1mMv27XJfWtimHM44Q0SfTUP5GTPEo2e8e01NDO20\nhaKP5B5eiSe20FZIFGgvyWDyqaJ4WWxJSvR1d4vgmzYNeOUro2374osA0I4nnsiu6BsacsL3Dh2y\nH+ehQ46o6egAXvUqu+02bxavYk+P3CchDkx1x4ULo+3vgguA97zHEXG2nHce8K53SZ6cl/cojqcv\n6Zw+AHj1q8WTbntuSoka3nnkiNzbCDRb3vxm8eC97nXh65oCTocPS1h3UxN79NlC0UcIIYSQ1Dh5\nUu7L6eXlR1Kiz4QNrl0LvPvd0bbdtw+49VapKvmOdyTTgzBp3BP6zk570dfV5Tx+8kl7YWE+TwAY\nGBCPX7mY92BEii1K2YkJr+2uuML/ddN+YWhIWkgEnffSQi5J0tgIvOlN8beP2qsvDa/a7NnA1Vfb\nr29EX2+vhITS02dHBn+aCIkG+yMRW2grJAq0l2Q4cULu0yiw4C7kEicXD5Dtyuk5tnQpcPJkAf39\n0hMui7hD9zo77bdzr7tzp50w6O6WfD5DnMbfXpj3YERKtVHKCdcM8/Z55fRlBSOibcM7syCwSi/2\nZGFMeYCijxBCCCGpYURfGp6+KVOkSfvISHxxceCACJXmZmDlyujbK+VsZ8Rj1nB/Nm7vXRhG9E2b\nJt4sU4U1iNLPIE7jby/Me8iK6APsQzzTqt6ZBFE8fVpnQ2D5ib4o7SomIxR9JPcw74bYQlshUaC9\nJEOaog8oP8TTiJT16+OHZn7gA+0ARBSNjMTbR5qU6+m76iq5d4dteqG1s44J6Uza0xc1vDNN4oq+\nLP22RBF9J09KP7+mpuoKWHr64kHRRwghhJBUGB6WW2Oj3NKgHNE3NlZeaKdh8WIpFDI46FQrzRLu\nCX1/v90E/8QJKZ4yZQpw5ZVyv2ePVNH04+BBx2tq2gckJfry7OlLs3pnuUQJ78yKuHKHdY+NOYVc\n6OkLhqKP5J4sxcaTbENbIVGgvZSPO58vrf5Z5Yi+PXtE2MybF71/nZtCofA70RjmDasGpcLLxttn\nwkCXLBFxs3q1LJsG6V6Y975+vePpY3jnxOqdWfptieLpy4roc3/njx0T4dfcnN6FpVqBoo8QQggh\nqZB2aCdQnuhzN/suV5SaPoTbtjmT/KxghJcppmOT12eEoWlSbkStX96i1o4g3LgxelXIMPIc3plm\n9c5yMedpYEDEUxBZEX1uT5/xPFd7THmAoo/knizFxpNsQ1shUaC9lE+WRd/IiFOYpJzQTkBspbVV\neroND0tPuyxhhNd558m9jafPrLNkidxfeKGIxoMHvUXj88/LJNx4TZMWfVn29IWJ/Czn9NXVSTGk\nsTHn++pHVkRfY6OI/9FRaZkCVH9MeYCijxBCCCGpYHr0pdGuweC+6h+FnTtlktvW5gibcgnzhlUL\n4yUzVUajiD7j6WtocPL0vN5fqdc0aiuAIEZH5VwZgZIVaqF6J2Av0LMi+txjeOEFuWc+XzgUfST3\nZCk2nmQb2gqJAu2lfLLs6UuigIvB2Mq6dUB9vX1Pu0pR6unr6grua6i1480zog8QQQfIZ+fe3str\nmqSnz+xj5sz0ckPjEFf0Ze23xVagZ6lgivne79lTvEz8oegjhBBCSCoYT1+aom/2bBFa/f0SWmnD\n0JATgmly8ZJg5kzgggvse9pVAreXbNEi+byGhoKrcPb2ipCZNas4h27FCtn+yBEnrA7w9poa0dff\nHywwbchiaCdQGzl9QD49fUZ4GqGahTFlHYo+knuyFBtPsg1thUSB9lI+7uqdaaFU9BDPbduk39jy\n5ZKDVi5uWzHesKxU8Sz1khnPXVCIp7typ5u6Okcku0M8vbymjY0iikZHw0VRGFks4gLURp8+wPlc\ng0Tf6KhUulXKqcxaTUpFHkVfOBR9hBBCCEmFSoR3AtFDPN35Z0lz8cV2Pe0qhZnIm4m9jegrzedz\n485bHBsL9pomFeKZVU+fEXFBom9sTC4wKCV2kUXcXlk/+vrEY9vSIp71akPRFx2KPpJ7shYbT7IL\nbYVEgfZSPlkUfSdOAM88I16r9euTOb7bVqZNs+tpVynMRN5M7MsVfUuXAvPny36fey7Ya5pUMZdS\n4ZoVbDx97tBOk4+Ytd8WG3GepdBOoHgcDQ3ZuyCQRVITfUqpbyilupVS213PtSqlfqqU2q2U+olS\nKgMOYkIIIYSkQSVy+oBoom/rVglVW7kyPRGRpSqepV4yE7IZ1KsvSPQpVfz+zHv08pom5ekrFa5Z\nwUb0Zb1yJ2AnzrNUxAUoFn1z5mSrwE9WSdPT900AV5c8dwOAn2qtVwB4aHyZkLLIWmw8yS60FRIF\n2kv5VCKnD4iW05dk1U5Dqa24e9odOpTcceJQ6iVbvFgmyIcPS9XNUkZH5TXAv5WFEXhbtwI7dvh7\nTW1yxWzIanhnVE+fIWu/LXn09M2aJR4+IDtjyjqpiT6t9SMASn9+3wrgW+OPvwXg99M6PiGEEEKq\nS9bCO/v6gN27pcjI2rXpjSesp10lKfWSTZkCLFgguWZG3Lnp7hbhN2+ef7XJxYuBM84QsRPkNbXJ\nFbMhz+GdefL05Un0uQs4ZWVMWafSOX0Ltdbd44+7ASys8PFJDZK12HiSXWgrJAq0l/LJmujbvFmK\nUaxalewk3MtW3FU8y21ZUA5egikory8otNON21Pq5zWt9fBOY0OnTomI9sJL9GXtt8WmvUbWRB/g\njCVLY8oyVSvkorXWAKr4M0gIIYSQtBgdlQlvXV36Xg636AsSWGlW7SzF3dNu//70j+eHV2ikCdss\nR/Rdcomc2ylTgDVrvNep9UIubts24q4UE96ZZU/flClyO31abl5kUfQtWFB8T4JpqPDxupVSi7TW\nh5VSiwG85Lfipk2bsGzZMgBAS0sL1qxZ87sYaHOFhMtcNhQKhcyMh8vZXW5vb8/UeLic7WXaS3nL\nJ08CXV0FNDUBSqV/vOnTgT17CnjwQeBNb5r4enc38OtfFzB1KrBqVfrjqasDmpoKePZZ4Ikn2rFs\nWXXOR0cH0NDQjlmznNfb2uT1hx8uoLW1eH1ZpR1tbcH7nzMH2LixMN6Pz/v4O3cW0NUFnHNO/PFr\nDfT3y/LWrQU0NGTDvs3ykSPArFntGBwEnnhi4us7dwJAO6ZOzcZ4/Zabm4Ft2wr40Y+A3//9ia/3\n9sr3eccO4Iwzqj9eAJg9u4DzzwfWr8/GeJL5vnagr68PALBv3z4kidIpxhwopZYBuF9rvWp8+YsA\nXtZaf0EpdQOAFq31hGIuSimd5rgIIYQQki6HDwOf/jSwcCHw2c+mf7zPfQ548UXgppuAM8+c+PoD\nDwD33w+85jXA+96X/ngAYN8+4NZbxeN3223iGao0N9wgBW5uvdXx0nR3AzffLMu33lq8/k03AT09\nwC23SO5eOZjjlGMDJ08CH/mIeMruuKO88aTBZz4jlVA/9SngFa+Y+PovfwnceSdw2WXAH/9x5cdn\ny223AXv3Ap/4BHD22cWvDQ4CH/6weAO//GVWyqwkSilorRP5xFP7+VFK3QXgMQDnKaUOKqXeD+A2\nAFcppXYDuGJ8mZCyMFdKCAmDtkKiQHspD9OuIe3KnYagvD6t0w3t9LMV09Pu2DEpIFNptPYO75w/\nX4rZ9PY65wmQEMWeHmm+nUTIXBKFXLIa2mkwxVz8wjvzkNMHBBdzMVVxW1sp+PJMaqJPa/1HWusl\nWuspWusztNbf1Fr3aq3foLVeobV+o9a6L63jE0IIIaR6VKqIiyFI9B04IF6n5mapNFkp3D3tjOis\nJIOD0pahqUlEnqGuzvHiufv1mceLF4vwK5emJtnP4CAwPBxvH1kt4mIIq+CZh+qdQLBAz2I+H4lO\nFQINCEldj4z/AAAgAElEQVQWEwtNSBi0FRIF2kt5VFr0BfXqM20TNmxIJ8QyyFbcPe28+uKlSVB/\nO1OoxUv0hRVxsUWp8nv1Zd3TZ8RcFNGXxd+WoEqrFH21AUUfIYQQQhLHhA1W29OntbRqACpTtbMU\nd0+7HTsqe+wgL5lX2wbbyp1RKLdtQ1YbsxvCPH15qN4JBFdapeirDSj6SO7JYmw8ySa0FRIF2kt5\nGE9ftXP6nn9evH/z5gFnnZXOscNspVohnkFeMq+2DWmIvnI9fUaEZNXTZxve6W50n8XfFnr6ah+K\nPkIIIYQkTlZy+twFXKpVhGLDBrnfts2/4Eca2IR3dnaKN1RrR/QZQZgE5RZzqRVPn1v0ZREb0WdC\nqEk+oegjuSeLsfEkm9BWSBRoL+VRadHX0iL5eseOOblzIyOSSwc43rY0CLOV1lbg3HOlmElHR3rj\nKCXISzZ7tpybkyeBvj5Zd2BAREySk/vJHt6Zl5w+hnfWPhR9hBBCCEmcSuf01dWJ8NNaRAwA7Nwp\n4rOtLVnvVRxMPqEpKlMJggSTUsXFXNxFXJL0iAaJCRtqJbwz6zl9fuJ8bMwpjkRPX76h6CO5J4ux\n8SSb0FZIFGgv5VHpnD5gYoinEVhpevkAO1tZv17aF+zcGd/rFZUwL5k7xDONfD73senpc57L4m/L\njBly4WRgABgddZ7v7xfh19xc3PaD5A+KPkIIIYQkTqXDO4Fi0Tc05IRSmpy6ajJzJnDBBTKBNiGn\naRPmJXMXc8mq6Mu7py8vOX11dWKjgAg/A0M7aweKPpJ7shgbT7IJbYVEgfZSHtUUfUePStGU06eB\n5culcmea2NqKCfGsVBXPOJ6+pMNgywnvHB4WMVVf74irrFErOX2At0Cn6KsdKPoIIYQQkihaOzl9\nlQzvNDlHvb3FVTuzwsUXA1OmAHv2TKwymgZhXjIj+g4fBg4dKn4uKcrx9BmP06xZ1au8GkaQ6Bsb\nkwsPSsl5zzpeAp2VO2sHij6Se7IYG0+yCW2FRIH2Ep/BQRF+TU0SNlYpjDfi4EHgmWfk2OvXp39c\nW1uZNg1YvVoep13QxcZLNm0aMHeurHv6tEzskxbpJmTw+HGxiShkPbQTCBZ97tBOt2jN6m8LPX21\nDUUfIYQQQhKl0pU7DWZiunevFKNYuTJ7gsEUlUlb9Nl6ydyevaS9fADQ0CB2MDbmhPzakvUiLoAj\n+k6dmihq81K50+DVU5Gir3ag6CO5J6ux8SR70FZIFGgv8alG5U5g4sQ07aqdhii2cuGF8rkcPOiE\nVKaBrZfMncOXVluLuCGeZv2sCXc3dXUSuqm149kz+BVxyepvi/mc6emrTSj6CCGEEJIo1SjiAojX\nxXhVGhuBtWsre3wbGhqAdevkcZrePlsvWdqePiB+MRezfpY9fYB/iGdePX1u0Wd69FH05Z9Q0aeU\neqdSqnn88aeUUvcppdalPzRC7MhqbDzJHrSVfKI18ItfAPv3R9/u0UelSEUckrSX4WHgpz91JlBZ\n5dgx4LvfBe65x/t2//3+VQrdVEv0KeVMTletqtxkO6qtuKt4Rs1ze/554Kmnwtez9ZJVQvSV6+mr\nNdGX1f+i0vDOoSEJE25szP45IOE0WKzzKa31PUqpSwFcCeBLAP4/AK9MdWSEEEIIgAMHgLvvBs4+\nG/jEJ+y3e/554D//U/K6PvKR9MZnw0MPAffdJ1UbP/jB6o4liJ/8BPjZz4LXmTkTeP3rg9epVk4f\nACxeDHR1Aa96VeWPbcuKFSLGjhwBuruBRYvsttMa+F//S0T1bbcBLS3+69p6yRYuFNGitf04ouKV\nK2ZDHgq5AP6iz4R35sXTVxreaS5SzZmT3eqpxB4b0Tc6fn8NgH/VWj+glPpcimMiJBJZjY0n2YO2\nkk/MxOPIkWjbdXfL/YEDMqGNOmlJ0l5M+4Dt20UQVTrXzZaDB+W+vR2YP7/4tT17xMNkcx6qldMH\nAO98J/DqV4unr1JEtZW6OmDZMukl2NlpL7Z6e50CLS++GCz6bL1kDQ3ARz8qhVYaG+3GERWvXDEb\nasXTl5ecvlJxznYNtYWN6OtUSn0NwFUAblNKTQNzAQkhhFQIMwE5flzCJG0npkYsnjwJ9PVVb+Li\nbnw9Ogps3Qpceml1xhKE1s44r7564uc1Z46IPpsQ1WqFdwIihILEUFZoa3NEn21bCXN+zOOLLvJf\nN4qX7Iwz7I4fl1ou5AJEF31ZxX2etGYRl1rDRry9E8CDAN6ote4DMAfAX6c6KkIikNXYeJI9aCv5\nxKuogA3u5tfuybItSdmLKdYxe3bxctbo7xcvUlOTt2hyNz4Po5qirxrEsRWTPxfFNru6nMdh22XJ\nS1ZueGcW3kMQUcM7s/pfNGWKjHVkRAQrRV9tESr6tNYnABwBYK5LjgDYk+agCCGEEINXzygb3Ou6\nJ8uVRGtH5L3nPRJK99xz4nnMGuYzamvzDoU1Ez+bc1DNnL68EEf0udcNs+ksecnihHdq7axvGrxn\nlVqp3gkUC3SKvtrCpnrnLQA+DuDG8aemAPjPFMdESCSyGhtPsgdtJZ949YyyoVxPXxL2sncv0NMj\nXrLVqyUcT2tgy5ayd5045jPyq+A4ezZQXy+TweHh4H1VM6evGsSxlQUL5PPs6ZnY380Ptx0fPix5\neH5kyUsWx9N34oS8vxkz5GJJlokq+rL8X+QW6BR9tYVNeOfbAbwNwAkA0Fp3AsjATwghhJDJQBzR\n585HAeKJviQwBVw2bBDvmWkWbp7PEmGiTyknxDMszHayhXfGoaFBCrhobdekfXTUaT/S3CzC2xQr\nKiVrXrI4nr4shaeGUSvVO4Figc4efbWFjegb0lr/7lqSUoo/4SRTZDU2nmQP2ko+iRPe2d8vk2Qz\n2QrzinhRrr2MjTkePdOXbfVqGdO+fcBLL5W1+8Qxom/JEv91bEM8J5unL66tRAnx7O4Wm543Typ/\nAv4hnidPZstLNnWqFGAaGrL3amYpPDWMqIVcsvxf5CX6WL2zNrARffcqpf4FQItS6r8BeAjA19Md\nFiGEECLE8fSZ9RYsAObODfaKpMWuXTJxWrgQOPNMea6xEVizRh5nqaDL2FhxTp8fNsVctGZOny1R\nRJ/bExu2XZZCOwHxEket4Jm19xCEEX1G5BmMwM1L9U7AEdldXfK7OWNGvsZP/LEp5PJ3AP7/8dsK\nSLP2L6c9MEJsyXJsPMkWtJX8MTrqeI0A++qd7lwUM0GOWsylXHsxom7jxuLCKO4QT63LOkRi9PTI\nBG/OnGDvnI2n7/Rpqf43ZUp6fd+yRlxbMV5VG9uMIvqy6CWLGuJZC+GdeczpM5/3/v1yz9DO2sGm\nkMunADyrtf7Y+O2n4x4/QgghJFXMxM9Mmnp77YSSl+irZF7f8LD04wOc0E7DypWSZ3X4sDTYzgJh\n+XwGMwEMEt/08tkTxTbdnti8efqA6MVcovQZrDa1VL3TfN7mt4mir3awCe+8HsCDSqkrXM99MKXx\nEBKZLMfGk2xBW8kfRvTNnSseqNOniz1/frgLEMQVfeXYy/btMuFbulTCO93U10thFyA7BV1s8vkA\nO0/fZMvnA+LbSmurCIL+/nAPmFuYh1X+zKKXLGp4Zxbfgx9RRV+W/4vM5z0yIvcUfbWDjejrBPBm\nALcppT6e8ngIIYSQ3+G+2h+lOXi1PX0mtLPUy2cwz2/enI0Qz6iePhvRR09fOErZ2eepUyLwGhpE\n8IVV/mR4Z2Uxos6vemeecuJKP2+KvtrBRvRBa70fwOsAXKCU+i8ATamOipAIZDk2nmQL2kr+cE/8\nojQHN+vMmROvHxoQ314GB8XTp5Tj0Stl+XJ5P729wJ49sQ6TKHFEn59YnYyir5zfFpu8PvPaokVi\ny0CwWGR4Z2Vxe/rc34s85vSVft4UfbWDjejbAgBa61Na600AfgFp0E4IIYSkittjEUf0tbZG74dW\nLh0dktO3YoV/qXN3z75qV/EcHgaOHAHq6uRzCmLatPAwW+b0RcPG0+dVWTVouyx6yWrZ09fQIEWL\nxsbkuwE4j5WSokZ5Yfp058ICQNFXS9hU7/yzkuWvaq3PTm9IhEQjy7HxJFvQVvKH22NhK/qGh2XC\nWF8PzJ4tz8UJ8YxrLyZPzy+002Be37JFqpRWi0OHZIK6YIFdtc2w88CcvmjY2KaXJzbIQ5hFL1kt\ne/qAiXl97tBOd/VeINv/RUpJoSkDe/TVDr6iTyl17/j9do/btnIOqpS6USn1zPi+/rdSKkfRzoQQ\nQiqFV3hnWNsGd2inmWxVKq+vv1/689XXA+vWBa/b1iYT94EB4Nln0x1XELahnYaw3MrJGN5ZDu6W\nIn4hs17nKG+eviiFXEwT98bG/OTDlYq+PFbuNBihXVfnXDgj+SfI0/eh8ftrAFxbcntr3AMqpZYB\n+HMA67TWqwDUA/h/4u6PkCzHxpNsQVvJH3HCO92hnYYo/dAMcexlyxbxml14YbjoUcrx9lWzimdU\n0Wfr6ZtMoq+c35YZM2RiPTQkeaelaO19joIqf+a9kMvAgNzPmjXRS5ZV/ESfl2jN+n+REehz5ojw\nI7WB76nUWncppRoA/LvWel/prYxj9gMYBjB9fP/TIRVCCSGEkCLihHd6ib5KefrcDdltMKKvo8PJ\nBao0RgiHtWswhHlcmdMXHbe3r5Tjx0UENTUBLS3O836VP0+fFsGRNS/ZzJky5oEBuTASRN5COwH/\n8M48evqM6GM+X20RqN+11iMAxpRSLUHrRUFr3QvgdgAHAHQB6NNa/yyp/ZPJR5Zj40m2yIOtbNkC\nPP545Y73q18BTz1VueNFxe2xaGmRq87Hjjk9pLxw9+gzROmHZohqLz09wAsvSNGG1avttpk/Hzjr\nLJkg/su/AP/+7xNvd97p7QEK4vhx4L777PKn0vL0MafPnqCLEu7zU+r1MkLdvZ07tDNLXrK6OrkQ\noLXjyfMji+GpYRjRZzx8QeGdWf8vMmKboq+2aLBY5wSA7UqpnwAYv34HrbX+qzgHVEotB/BhAMsA\nHANwr1LqPVrrO93rbdq0CcuWLQMAtLS0YM2aNb9zh5svC5e5DAAdHR2ZGg+XuRx3ub8f+MxnZPmu\nu9oxY0a6x+vrA267rYC6Ojne9OnZ+jy0BnbtKmB0FJg1q31c8BVw/DjQ19eOefO8t//VrwCgHXPm\nFL/e1gY88kgB990HvPe9yY93506gq6uA884Dpk61314mhe3YsUO2B4AlS+R1s6xUO979bvvx9PW1\n48EHgSeeKOD3fs9//R/9qICdO4Fly9oxf77d/kVgtKO31/v1Z54BGhrSt98sLRvibt/WJss//3kB\n06cXv75lCwCI/ZZuf+RIAV1dQFeXs/7hw7J+c3N2Ph+z/PLLBbz8MtDfHzy+hgZZfvHFAgqF7Iw/\naLmpSb6vjz0GrF/fjqEhWRYxWLy+IUvjdy8vWCDLPT35+fxrZbmjowN9fX0AgH379iFJlA7pCquU\neh8Ac61Ijz/WWutvxTqgUu8CcJWpCqqU+hMAr9Ja/w/XOjpsXIQQUmv84hfA3XfL449+VEr+p8kz\nzwBf/rI8fu97gde+Nt3jReXkSeAjH5Er5XfcIc998YviTQv6fP7xH6UwyvXXAxdd5Dz/7W8DjzwC\nvOtdwBVXJD/eu+4CCgXgHe8ArrrKfruxMeDppx3PgJuXXgJ++EPp6/fxj9vv85/+SXoFNjUBX/qS\nlJT3Yvdu4PbbgWXLgBtvtNt3b6+s29ICfOELE1+/8UZZ5/OfB+bOtR/zZGb/fvm8Fi8Gbrml+LVv\nfQt47DHg3e8GLr+8+DVz/s46C7jhBnlu2zbgq18FVq0C/vIvKzJ8a/7+74HnngM+/GHg/PP91/vR\nj4Dvfhe4+mrg7W+v3PjK4d57gZ/9zPn+/+Y3wDe+IaHef/qn1R5dNEZG5Dyde26+2k3UIkopaK0T\n8dn7evqUUgrA7wNYAGCb1vrHSRwQwC4An1JKNQE4BeANAKqYwk4IIdnA3a+tszN90ecOCXviieyJ\nPq9iFK2tIvqC8vq8cvqA9PP6zH5tc+MMdXXA2rXerx0/LqLPVHa0DdczYxkcBHbsANasCV7PNrQT\nmBhmWyooJ2Mhl3JZskQ+0+7uiZ9pUM5laeVPpbIdGmlbzCXL78GPKIVcsk5DgxSjIrVFXcBr/wwJ\nw2wF8Dml1M1JHFBr/TSA/wCwGYBp/fC1JPZNJiel4RKE+JFlWzH5YIa0C46UHuO552QSnyXcRVwM\nYflkWicn+qLYi1+FxXKZNUtug4N2TekB8ZC61w1q/u7V9DuMujoRfloD41FIv2NkRPIT6+vzOdmN\nS7m/LY2Nkt85Nobx8ExhbCz4HHlV/sxyERTbXn1Zfg9+RCnkkuX/IlK7BIm+1wG4Qmt9IyQY+feT\nOqjW+ota6wu11qu01u/TWg8ntW9CCMkjmzfLvREqUVoLxMWIlNZWmcCbMWQFP08f4F85cmBAmrNP\nnz5xsmXTDy0ufX0itswkPEmiilVjO6afnl/oqHufUb2Tfr363JU7s1REJA94neeeHqnGOWeOf2Gc\n0u2y7CWz7dWX5ffgRy316SO1SZDoO621HgUArfVJOHl9hGQKkwBLSBhZthXTp+2aa+S+szN5YeLG\n7VEwx6xmrzgvvCZ+YZ4+Py8fUOwVefnl8ONHsRe3NyZpsRNUzj9oLCtXSk7O8LC0hChF63iePsD/\nPEzGyp1AMr8tXpU4bbzHpfaRxR59BjMmW09frYq+LP8XkdolSPStVEptNzcA57mWtwVsRwghJAKd\nnXKbMQN45StlYnTqlH04XxxeeknEwNy5Umhg2jRg3z55PivECe8MEn1Aenl9cT1mNkQds1somD6A\nXiGevb0yQZ01K7pA8PO4Mp8vPl7n2cauSrfLsmCK6unLonD1o5b69JHaJEj0nQ/gWtftAtfjt6Y/\nNELsYGw8sSWrtmIm5OvWSQK91xX/pHFPJhsbnUIfQflflcZr4ucOK/TyhBoRYtYrJYqAimIvaeTz\nGeKKviVLgPXrJb9u586JE+1yxhzm6Ztsoi+J3xYvj66NJ7b09yLLoZE2hVzGxiRMWylp6J4XjLiz\nKeSS1f8iUtv4ij6t9b6gWwXHSAghNYvWjtDauFHuo4bzxaF0wm88Qk88kW5YaRS8Jq/Tp8sk6tQp\nZ3LlptqevjRE3+LFcn/4MDA6GrxuaUGZmTOlNP7YGLB1a/G6cUM7AX/R587pI9GYP1/K4/f2Op+j\njV2VVv7MchEUm0IuAwNixzNmyPvKC36evslU0Ihkmxx9nQjxhrHxxJYs2srevVKsYc4c4Jxz5Lm0\nWwu4922Odf75IhAOHwZefDG940bBa/KqVHCIZ5joM14RG0Ftay/u/Mg0RN/UqSIIRkdlYh/EsWMT\nC8qYiwmlOZvlhKQyp6+YJH5b6uocgd/VJeHXL70kzy9a5L+du/JnZ2e2vWTu8E6/i0t5DO0EmNNH\nsg9FHyGEVBHj5duwwbmqXQ3RV18vY3CPqdr4hamVK/qUEpE2MpLMOE1+ZGtrevk7tjbhPq+moMzF\nF4sHac+e4s8sqfBO9+R9soZ3JoU7VPPQIRFyCxaIsAvCnMPnn8+2l2zqVLkNDzuesFKynJMYhFv0\nac3qnSR7+P4kKKUeGr//YuWGQ0h0GBtPbMmarYyNOW0STHglUBzOl5QwcWN6etXXAwsXOs+7i35k\nIcTTb/IX1LYhTPQ1NsokurQfmhe29pJmaKchjugzTJsGrF4tj42gHx113n8cT19Tk+y3NMx2snr6\nkvptcZ/nKHZlzuGuXXKfZS9ZWIhnlnMSg2hslJzs0VH53Q4SfVn7LyKTg6DrQIuVUq8B8Fal1Dql\n1Prx+3VKqXWVGiAhhNQqu3bJxGfhQuDMM53n3eF8aVTTPHRIRN3ChTJJMSxfLmKpt1e8QtVkeFjE\nRH39RAHh5+kbGZHwRtM83I+kPamVFH1hYal+IZsmxNOIvu5usa/58+PlHCnl3auPnr7ycJ/nKDmX\nZp3du+U+y4IprJhLXsM7gWJvH3P6SNYIEn2fBnAzgDYAtwP40vi9uRGSCRgbT2zJmq2YCfgll0zs\n7ZZmiKefSFFqojioFgMDcj9r1sTPxk/09fXJfUtLcGibbXVUW3uphOizHbPfWC68UMTzwYMi+pMY\ns9d5mKyFXJL6bYnr6TPrGKGRZdEX5unLa3gnUCz6mNNHskZQ9c57tdZXA/g7rfXrS28VHCMhhNQc\nw8PAU0/JYyO03FRD9AFOiOeWLeGVItMkqAKhn+gLC+00JF0dtZwqmLYsWCBe2Z4eZzJZSlBBmYYG\naQkCiKBPoq+gV5jtZBV9SdHcLAVYTp6U/DzA7hzNn1+c95dlL1lYr75a8PSdOAGcPi0XrKZMqe6Y\nCDGEpvlqrT+rlHqbUup2pdSXlFLXVmJghNjC2HhiS5ZsZccOuRp85pnFeXWGNEVfkEhpa5NJ5sAA\n8OyzyR/blqC8Hq+wQveyX48+g+1na2MvQ0PAkSMT8yOTpr6+uLKjF6agzNy53t4Fd1uOJISql/hm\nTl95KOWIvNOnRTDMnx++nbvyJ5BtL1lYeGctePpM1MHUqRMjFYBs/ReRyUOo6FNK3QbgrwA8A+BZ\nAH+llLo17YERQkgtY8rne3n5gGitBaIS5OVRqlgcVAsb0dfXJ94tg62nz3hF3P3Q4uKXH5kGYTYR\n5r1bsULaOBw5Is3agfREHz198XGfE1NtNup2WfaS1WohF2Ci6GPlTpIlbAr6vgXAG7XW39Ba/xuA\nqwFck+6wCLGHsfHElqzYyuAgsH27TOZMm4RSbML54nD8uEy2pk0Tj5AXRvQ9/bR4G6pBUHhnQ4OI\nl7ExKdxisBV9pf3Q/LCxl0rk8xnCPJRhY6mrc+xteFg+xwUL4o+nVPSNjYmIVsqZ/E4WkvxtcZ+/\nKHblXjfLgmkyFHIxIc9+oi8r/0VkcmEj+jQAdx20lvHnCCGExKCjQybd557rH4poE84XB7c3yM+D\nMH8+cNZZIja3b0/u2FEIu9rv5WUyE60w0QckFz5biXw+Q7miDyj2LC9eLHYWl9JzYFo3TJ+ezR5x\neaHWRV9QTp/WtRHeaX6LWLmTZAmbYJRbAWxVSv0CgAJwOYAbUh1VDB5/XAoP+PGKVwBvfat9mERa\n/PjHwaXQV60CXve6yo2nFigUCrm9anb0KPDDHwJvepPdRNXQ0wP85CfAtdfm848RAJ57Dvj5z4vD\n89y0tADveleyIXNZsZWw0E7DkiVSbbGzEzj77GSObStSNm4E9u4FvvMd+X31Yt064NWvtj/22Bjw\nwAPA0qXSMDyIIE8fIN+XvXtFcCxfLs/ZevoAu2IuNvZSLU+f1hP/z2zO7dKlIuqPHCmviAsg31Gl\nnDDbyZrPByT72+I+L3FFX5a9ZOY/68AB4KtfLX5Na7kgNmVKPgWTbXhnVv6LyOQidDqltb5LKfUw\ngEsgHr4btNaHUh9ZBIaGgDvvDA5D2rYNeOUrgUWLKjeuUrq7ZQIVxDPPAJdeyqukk4Xvfx947DH5\no7juOvvtHnoIePhhqfL21remN740+f73w3vBXXwxcNFFlRlPpRgdFcELONUU/UijmIutSNmwAbjv\nPrnA0NPjvc6zzwJr19rnrezYAfzgByLKwkRfVE+f1tFE3xlnyP2uXd4CypYkqmDa0tIivxUDAyKK\nZ892XrMtKKMUcNll8l+0YkV542loEHFx7JjcmM+XDNOmiTh/6SXHTm1obhZBPzBQbBtZo7VVBN2p\nUzI386IS36c0sA3vJKQaWF1D11p3AfheymOJzbZtIvjOOMN7Avzgg8ALL8ifczVFn7m67+fN+/d/\nlz/N/v7gxsKkmLxeLRseBrZulccvvxxtW7N+GpUdK4HWztj/7M8mXtF9+GERCKXVGcslC7ZimmLP\nmxc+OU66tQBgL1Kam4GbbvJvDv+DHwD79kmo6qteZXds0/vPFFAJ8ghFFX2mL9a0aXb5ZOeeKxdN\nDh8GXnzRe3IdZi82+ZFJopTYxJ49ch7dE/soBWXe+EZg5UqpHFsura0i+Hp7nfDOySj6kv5tuf56\nmddE+SyVAj72MflvcbdvyBrTpgGf/KTTXsSLs86q3HiSxKt6pxdZ+C8ik4+Ua41VBjOReO1rgdWr\nJ77+2986om/9+sqOzaC1M84rrgAuuGDiOvPni+jr7aXomwxs3+4U6HD3ubLBTHTzKvqOHpUJ4qxZ\nTtEQNwcPpiP6skCchst+4XxR0TpaDtqiRf4Xyvr6RPQ9+aSd6BsaEoFo6OoCzjnHf/2w8E6TC2m+\nO+52DTafU329eDMLBbkgF8WjYrDJj0waI/q6uor/R6LYlVLiSUoCd5itHs/2n4yiL2nihu3nZe6w\nYEF5RYSyivHsjYwULxOSBXIfRHjihEwO6+r8BV2a/a5sOXBArvA3N8sVVi/8Gg6TYPLa78ZcBACi\nn3Ozfk+PTKbzRtgENa3vQhZsJcrkvDScr1xeflnsZfZs8XKVw7p1Ipx27vSvwufGRGQYgn6PtXb2\n6TfOUhuJEtppMDmVmzc7gsVNmL1UsoiLwe//rJK5hW7c52Gy5/QRUhpl4Ofpo72QahAo+pRSDUqp\n5yo1mDhs3SqhUitX+l8RNmFM1RR9ZoK/fr1/vl7plWtSu7hL9isl4VGjo3bbDg05kyutJawrb4SF\nGNbydyGKUDDhfEAyv19JCoOZM8XTNDbmhCkHYcLbzdX9oPdz8qTsd8YM/1DFUtEXpXKn4eyzZf3e\n3vD8Ui+qIbT87KEaAhTwFn309JHJSqnoo6ePZIlA0ae1HgGwSymVUCBI8hgxFVQFb+FCuSJdLa/I\n2JjdOOnpi0ceY+NNyf4VK8SbMzbm5ACEUSqE8hjiWS1PXxZsJapQyKroA+ybuJ84IUWq6uqAa64p\nHosXNiXbZ86UvKUTJ+R3PY6nTynnN9nteTfYVu6sZNEJd4N2d+Xbann63BdoTKP7yejpy8JvC6k+\ntqpTTg0AACAASURBVKKP9kKqgU14ZyuAZ5RSP1dK3T9++37aA7Ohrw/YvVv++Neu9V+voUHyUqrl\nFdmzR8Y6b15wcjJF3+TBTJIvucSZNNme99L18ij6wrwS7omkX0uHPHLqlFx8qq+3z2dJsphL0iLl\n4oultPqePcH2647IMOHtXV3eIZVAeBEXQASb+zczjugDHOG6ZYu9tx2Inh+ZFNOny/djeFiqdQLF\nBWWivv9yoaePEAd6+kiWsRF9nwJwDYDPArjddas6Jg9j1arwL1Y18/rcE/ygZH+KvnjkLTa+v1/K\nxNfXS16UOe+2oYzGPkyuU5KVHSvB6Khz8cVPfDQ2Srj26GgyuWyGatuKOVdRmmInGZ6etEiZNs0p\nnuXlKTO4Ix2am8V2T570926HFXExJCH62trkMx4YkBYUboLsJcn8yKiU/p9Vo6CMgaJPqPZvC8kG\nzOkjWSZU9GmtCwD2AWgYf/wEgKdSHZUlbjEVRrVE38iIk+8S1oiZom9ysGWLeK8uukgmR1HPu1nP\n9K/Lm6fPtCyYPz+4+W4tfh/iiC63p68cr+fIiJRIV0pEZ1IEhUcCcjHDRGSsWSPHDxOyNp4+oNgj\nHFf0KWUfpuqmWuGU7mMae6pWPh9QHGZrzsFkFH2EAPJdcF/Qy2ODeVK7hIo+pdR/A3AvgH8Zf+oV\nAO5Lc1A2dHcD+/fLVZVVq8LXd+dBVJKdO+XP0FxNDmLWLAlFHRjIZ0XGapG32HgzOTYTzbii79xz\nxdPS329XPTEr2E6W0xB91baVOELBK5wvDocPi2hcsEBCMpPiwgtljAcPeofPuyMyzFXwsItwxp5t\nPX1HjojXUKl4JevNd7Gjo7jCaJC9ZEH0lXr6qjEWd5it6bvGnD4yWVGq2NvHnD6SJWzCO/8HgEsB\n9AOA1no3gKp3VzET5zVr7JqQVsvTZ1PAxaBUbVctJJLP9cILMuk2YXFxRV9razYq00bFNq8saq5j\nHog7OU/i9ystYdDQIGHKgLe3r/Qih3sMfu/HppAL4Hx39u4VQdvcHN6Y3Iv58yXfemhIquraUI0i\nLobS7301RR/gnAeTE0lPH5nM2Ig+QqqBjegb0lr/zu+klGoA4JN+Xxm0dsJwbMQUIH9KlfaKuJsR\nb9hgt00thrSlTZ5i4zdvlvs1a5ywj6jn3F2aPskiH5XCNhQtaq6jDdW0Fa3jC4UkxH2aIsUdHuku\nzuIXkRFmt7bhnW7R516Og/kvcYd4BtlLNUMqFy+WSqhHjsj/jBlLNQQo4FygMUxGT1+e/odIutiI\nPtoLqQY2ou9hpdRNAKYrpa6ChHren+6wgjl4MLzReSlJ97uywTQjXr5cKnfakMZEl2QHrzzUKKJP\na8c25sypboGiuFQzvLOaHD8uodtNTRMnyWEkIe7TFCkrVkhBkyNHROQZ/CIyjDgxIaelRC3kYkIy\nyxF9GzaIkNq+3Wk94MfIiPwHJZ0faUtDg7QiGhuTVhjVKihjcH/u06bF87YSUivQ00eyio3ouwHA\nEQDbAfwFgB8C+GSagwrDTJyDGp17Uem8viiFZgy1NtGtBHmJje/slNuMGdLU2jB9uoR7Dg7KLYjj\nxyW3a+ZM8RTmTfSZlgUNDeEtC2otp88tdqNWWMxyeCcgv8MmmsH87gVFZEybBsydK7bc3T1xf1EL\nuRjKEX3NzcB550mI4lPjpcr87OXwYVkv6fzIKJjzaIR1tUI7geLPfTJ6+YD8/A+R9HGLPr9CLrQX\nUg1sqneOAvgWgM9B2jZ8S2u/7krpo7UTImcb2mmo5ATZ3Yx4/Xr77Sj6ahczOVu3rvhKuLsQQpiH\n19iFmey6L2RU71tpT5SWBbX2XShHdLnD+YaHo29/8qR8jo2Nkr+WBub3ePNm8UAdOBAckRHkvbQt\n5DJlSrF3q9wedbZVPKsZ2mkwxzY5iFkRfcznI5MdI/qUqt5FIUK8sKne+RYAewB8GcBXALyglHpz\n2gPz4/nnZWIc1ujci0qKPncz4rCJi5taLF6RNnmIjdc6uKiPrcApLUs/c6aEdQ0NSd+wrBMl9yiN\narbVtJVyRJ87nC9OpIJbbEeJjojC0qUiKI8dkxYNxt79IjL8fo9PnxaPcGOjXblzt+CIGjZbytq1\n8lk/95y8Dz97qWYRF4M5trkIQNFXXfLwP0QqgxF9U6f6R3XQXkg1sPn7/3sAr9daX661vhxAO4B/\nKOegSqkWpdR/KaWeVUrtVEq9ynZb20bnXrivLKftFYlStdNNrXk3iLB3r4Q1zpkjrRZKiSv6gHyF\neEYRPrVWzbbcYhvlhKdXorqjUs7v3W9+Ex6R4We37tBOm99493ehXE/f9OlScMYdUeJFtatleh27\nmgKU4Z2EOBjRx3w+kjVsRF+/1nqPa/m3GG/fUAZ3APih1vp8AKsBPGuzUZRG517MmFEZr0hfn9OM\neO3aaNu6w/zyEK6XBfIQG28uVmzY4D2RpejzJumLINWyFbeHLq5QKOc8Vyoc0YRHPv54eESG3/ux\nLeJiSFL0AcUhnn72kgXRN2+e4wmtVkEZQ2OjE2Y7WT19efgfIpXBiL0g0Ud7IdXAV/Qppf5AKfUH\nADYrpX6olNqklNoE4AEAAddAg1FKzQZwmdb6GwCgtR7RWh+z2TZKo3M/KjFBdjcjjnqlZ+pU+dMc\nHs5Xw23iz9gYsGWLPPa7WGErbtztGgx5EX3ulgVRRV/ePX09PRK2OGdOfE9IOee5UuGIixcDZ5zh\nVOQMishYsEDyOnt6isN3bYu4GIyNuIVHOaxeLb/b+/YBL7008fXBwfTzI21Qyjmf1SwoYzDnYbKK\nPkIM7vBOQrJEUGHla+H043sJwOXjj48AKMdpfRaAI0qpbwK4GMAWAB/SWocUyY4fMummrU3EY2cn\ncPHF8ffzwAOyHy9MNbooVTvdtLaKuD16NPxqt9bA//k/UjTBjw0bgCuuiDeWPFAoFCJdNTt+HLj7\nbqC93TvUMg49PcBdd3lX3xweFu/FwoUyIfbCNozRy9MXpYfb3r3AT34CvOtdQEtL+Po2PPss8Ktf\nAX/0R8ETPnfLAttjJ+3pi2orSZGEZyiu6IsjtsvhkkukrY557EdDA7BokYzt0CFg2TJ5Pq7oa22N\nHvLvRWOjtJh4/HHgYx8r4KKL2oteN+0h0syPtKWtTb7T1fQ4Glpb5X9osoZ3Vuu3hWQPm/BO2gup\nBr6iT2u9KcVjrgPwl1rrJ5VS/whpC3Gze6VNmzZh2fgsoKWlBatWrcH27e0AgKGhAgoFxz1uEmJt\nltvagK6uAn7+c+DNb46+PQB873sFfP3rwJIlstzVJa+7lyU3JN7+e3oK6OoCenvbsXRp8Prd3cCd\nd048vnv5V78q4PRp4Oqr440n68sdHR2R1r/jjgJ+8xugp6cdN96YzHgefxzYu1eWvewBAK67rh1K\neW8vYq8dvb3Bx+vtlf3t3Amcfba8/vzzBRw6BNTVtWNkBHj0Uf/tv/MdWe7qAj7zmfjv1738xS8W\n0NMDLF7cjre8xX/9hQtl+dSpAh5+2G7/ra3yfn/1K+Daa5MZbzWWf/1rAGjHkiXx93f55e2YMgV4\n9tkCfvQj4E1vstv+gQcK2LMHOPfcdsyenf77PX1a7OGVr5Tf26D129qAJ58s4P77geuvl9cffVTs\ns7nZ7ngHDoj9b9yY3PuR6rrtOHoUeOQReb30+3zllckdL+7yBRcA99xTGG8BU93xLFvWjo4OoLMz\n/v9znpcNWRkPl6u3fOQIALRj0SLaC5ejL3d0dKCvrw8AsG/fPiSJCuu+oJQ6G8D1AJbBEYlaa/3W\nWAdUahGAX2utzxpfvhTADVrra1zreHaFGBiQqmpRWiCUsn8/8PnPy1XaW26Jt48HHwTuu0/CgK6+\n2nudBQvsr1SXcvfdwC9+AbzzncCVVwavu2UL8LWvicfq7W+f+Pp3vgPs2QO8973Aa18bbzy1hNbA\nJz8pnjkA+NznwvvF2fDtbwOPPAK88Y3iJSilsVG8fH6eiOFh4C//UsLd/umfvD0IQevcfLN4mD/1\nKeAVr/A+xtGjwI03ymcwezZw223leyo6O4HPflYeL1ok3ym/9/iznwH33gtcfjnw7nfb7X/nTuCO\nO6QK7kc+Ut5Yq8nXvibf1fe/H3iVddmqidx6q4QdfvSj0hDdhh07gK98Rdb/6EfjHzsK/f0S2hQW\n3mR+S6+8Un7vAOCee4CHHgL+8A+BN7zB7ni9vRIVkWRT8MOHJeLCi/p64Mwzq+/p01q+13PmJOPl\nLHcsL78suYaETHZ6e+V/Nqw1ESFhKKWgtU7kF97mL/K7AL4O4H4A45kaiF1iRGt9WCl1UCm1Qmu9\nG8AbADxjs+3MmeUJPkBC4ZSSCfLISLxJginKcdllwPLl5Y3HiyghbaZAw/Ll3mN5zWtE9D3xBEUf\n4FTRNDz5JPCWt5S/XxOWee658WyisVEmrf39cvMKfzTHaGmZONlsaxOb7uz0F30m1xRwyup79U+L\nggm5BmSS/OKL/iGscUIMa6WabVLhlW1tIvo6O+1FX7lVQ+NgW4TFqyJp1EIuQDIFXEpZtCj5fSaN\nu8dntVGKgo8QQ1a+l4S4sblOeUpr/WWt9c+11oXx28NlHvd6AHcqpZ6GVO/8fJn7s6axUTw7Y2My\nSY1KZ6fcZszAeEhN8kTp1Rc2mSztO1WLlIZLBGFEihEmTzyRTJVUr1y7qIQJnKBj2OT1lb53t2CL\ng7v3oM0+44gPd65jEucpiq0kxfCwFASpqytfSMTJ68tCpUk/vN5P1Jy+NKmGvZB8QlshUaC9kGpg\nI/q+opS6RSn1aqXUOnMr56Ba66e11pdorS/WWl9nW70zKcqpgmcmtevWJRtK5CaKdyNsQjd9OnDR\nReF9pyYDY2POZ/Ce94jn2HinykHryog+r8qdhjCb7u6W0OamJuB975PntmwRb3dc3L0H3/Uuee7J\nJ73FWdyWBe5qtgMD8cdaTQ4dkve/YIFcdCoHd69RW7Is+lpbpdhBf78j9rIk+gghhJBawUb0XQjg\nzwHcBuB21y23RKl26Mbt2SingmgYtqJvaAg4ckRixhcu9F/PjNWEpdYaJgE2jF27ZHK5aJFUCtyw\nQZ4v93MZHAROnZLJq6naFYcwD2+QsAwTA+Y9rl0rXrkzz5Rx79gRf7zu3oPnnAPMnStj3LNn4rrl\ntCxIMsTT1laSJEnR5Rb3Np5Pd0RDFkWfUhMvWMQJ70yLatgLySe0FRIF2gupBjai7w8BnKW1vlxr\n/XpzS3tgaRLX0+f2bCRV6t+L2bMlFKy/P9gTc+iQTPwWLgz2Oob1nZosGMFueoeZcvLuXLc4uMVY\nOcUUwnrSBYm++fPFi9TbC5wsaX7ivlhh3rO5jxvi6e49WPp5eu2zHOGT97y+JBujz5olt1On7D6P\n7m7xkhqPWhZxX4QbGxOPrlLJ9NwjhBBCiGAj+rYDmJP2QCpJXNHn9mykWSmtrs6ub5vtRNr0nQLK\nz+PKIjax8cPDwNat8tiIk+XLZTLs552yJYnQTvf2cTx9dXVSkRaY6O07cEAm/83NTuEW8xk8/bQI\niKgYr+nCheI1dO9zyxZgdLR4/XKagycp+qqRR5F0Y/Qov19JCs60cHupBwbkIsWMGdWvjAkw74bY\nQ1shUaC9kGpg87c6B8AupdRPlFL3j9++n/bA0sR4RY4enegV8aPUs5E2NhPdKBM6M+akCpfkje3b\nRdwsXeqEwoZ5p2wxwnxOmZdGyhF9gL8YMO9t/XpnIm281cPDwHibw0iYCyDGy2eOv2SJTNyffbZ4\n/XLER949fUnn1EXJ68tyPp/Bbbcmny8LoZ2EEEJILWEj+j4N4O2QCpsmn+/v0xxU2gR5Rfzw8myk\nic1EN8qE7vzzkytckjVsYuP9cjHNspd3ypZKePrcxWL8xKWXGHAX8PF771EF7/Aw8NRTE/fpFtGl\neZJZCe+sdB7FiRNAXx8wZYpcbEqCKJ6+PIm+ri4nny8rRVyYd0Nsoa2QKNBeSDUIFX2uNg1FtwqM\nLVWihni6RUMlmuDatG2IMqGrr0+ucEneGBwUT59SzmdgaGuTCwBe3ilbkhJ9s2ZJbubAgBTpcXPy\npBRCaWryLxbjZdPPPy+eyHnzgLPOKl5/3Tqxi507HQ+LDcZreuaZEwsIucNGT5+Wx+W2LIjSwiRr\nuEM7k/rdqDXRN2OG5DEPDUneNJAd0UcIIYTUCqGiTyk1oJQ6Pn4bUkqNKaX6KzG4NIkycXJ7NioR\n2gmEezeOH5er4tOm2YuNpAqXZI2w2PiODjmHK1ZMbHquVPnVTZMSfUr553LaHMNdEMOcX68wTMPM\nmdJrcmzMyXe0IaiC7fz5Ii5PnRJxCJTfsiCswE0UKp1HkUZOnYlSOHw4uNDT0JAUngqr7psFzOdj\nLrxkJbyTeTfEFtoKiQLthVQDG0/fTK31LK31LABNAK4D8M+pjyxlorRt2LFDvEXufLC0CRN9cTwI\nSRUuyRtG+Pi12TBiuKPD8U5FISnR595H6Xm3Ocbs2eI1OXlSQgpHRhwx5/feowreIK+p3z7L9TaZ\narbHjpXXV7AaJF3EBZDehfPnSzhyUDVe2+q+WcDYxm9/K/f09BFCCCHJEqk+mtZ6TGv9XQBXpzSe\niuHOIwnzerm9JZUiTPTF8SAkVbgkawTFxvf3Sz5mfb30qPPCeKeGhoBt26Ide2xMBJZSE72IcfDz\natmIvtKeZzt3Sk6ZKbDixcUXS77Znj124ZPGa3ruuf65hRs2iEjbsUMEaLmiz7aarQ2VzqNIK7zS\nJlIhD6GdBjNGI+qz4ulj3g2xhbZCokB7IdXAJrzzD1y3P1RK3QZgsAJjS5VSr4gfNp6NNHBP/r1E\nadwJXRKFS/LEli0izC66SM63H3GLmhw7Jvtvbk7Gm1KOpw8ovpgRFIZpmDpV+jgCdu89zGsKyGdx\n3nkygX/qqWRCHPNYwVPr9Fom1JroK70oQU8fIYQQkiw2nr5rAVwzfnsjgOMA3pbmoCpBqVfEDxvP\nRhqYgh1DQ95tJeJO6JIoXJI1gmLjS5uS+2HaGWzfbt/GA0g2tNO9n3JF3969TiuGsIsVtoLX7TVd\nty54XbdHOQnxkZToq2QeRW+vXDSaNSt5z5XNb1ceevQZliwp7suXFdHHvBtiC22FRIH2QqqBTU7f\nJq31+8dvf661/lutdUAmSX6wmTjZeDbSwm+i6/YgRM0VSqJwSV7o6QFeeEHCF403y4/Zs8U7NTrq\nFO2xIWnR51ep0rYXoLHpp56S/MTly6VyZxAXXghMnw4cPCh5YH4Yr+mFFwZ7TQEJpW1oEJFoWhaE\njSOIPHr60hRd5nsf1HImjXzCtGhsLG5pkZXwTkIIIaRW8BV9SqlP+9xuVkrdXMlBpkVYMZcono00\n8BMAL78sHsDZs6UCY1TKLVySNfxi401/ujVrJIwxDL8ec0FkzdNnbNqEBNvkoTY0OPYd5O2zCRc1\nTJ8OrFrljKPclgVJtW2oZB5FmqJrwQI5bz09Uim1FHd137lzkz9+GrjFcVY8fcy7IbbQVkgUaC+k\nGgR5+k4AGCi5aQB/CuAT6Q8tfbyaWbuJ4tlIAz8BUG64XDmFS/JE1AI8xjv13HPBeZ5u0hJ97lzO\n0VH7YjHuSX5dnYSt2uAWvF45pFG8pqX7BMr3diXZtqFSpJlTV1/vtG7w+v1Koz9g2hhxPGWK3UUa\nQgghhNjjW3pCa/0l81gp1QzgrwC8H8DdAG5Pf2jp4w7v/PSnJ75+7JjcVyO0E0hP9AHynvbuFe9N\nJQvUJMmxY8DXvgbs2FHAsmXtRa9pDXR3i1i/4AK7/U2fLgVfOjpE8F95Zfg25twkle85daqM+cQJ\n8dY0N4vg01qOUV8fvo+2NvEGr1xpHya3YoV4jo8cAW6+uTi/CnC8SbZeU0DE4bRpsm1Soi/M0/fo\no3Ih461vBV7xiomvFwqFil1hTbuQypIlEpLb2QmcfXbxa3nK5zOYsWYptLOS9kLyDW2FRIH2QqpB\nYE6fUmquUupvADwNoBHAOq31J2olp2/aNJksjY1Jo+PS2+CgTIRtPRtJk6boM+0Ldu/Ob6P2Rx5x\nWg2UnrvublnnNa+JVlXT/bnYYDxPSXn63Psy+47qTVy1Srw7r3+9/THr6oDLLpPHL7008fM0ns9L\nL7XfZ2Oj7LO+Hjj/fPvtvHB/F/zsdXgYuPde4OmngVtvBR56qHq2ffSoCK/GxvRy6oJykvNUudNw\nzjni5Vu2rNojIYQQQmoP3+mwUupLAN4O4GsAVmutj1dsVBXkox+V0DU/WlqqF2rkF9IWt4iLm5YW\nx6PU11fZyqRJoLUTvnnTTe2eE8W6uuLiEDaccYbcBxX3cZN0eKfZ18GDsu+lS+2LuBguu0w8udOm\nRTvuNdcAr361fwP0pia5CBKF664Drr22/O+QqWY7OCjVVb3CrbdvF6+i8S7ecw/wzDPApk2O96hS\nV1Y3bxYbXbUqvd+PoPD0PIq+5mbgi1/MVmgnr8QTW2grJAq0F1INgnwg/y+A0wA+CeCTqjgxRGut\nMxSEE5+GBmDRomqPwhsvT9/IiHhelHJyeuJgWlbs3i0TxLyJvoMHxZvX3CwCpzQcMS4LF4pnqqdH\nch6DJqCnTolobmyMV1DHj9LzHlVYKhVd8Jntyqmw6UVdXXKT+NZWsdXeXm/RZwrNXHutvI//+A8R\nfZ/9LPDe91bWY2/bKqQc3J4+rZ3cvXKq+1abpqZqj4AQQgipTXynylrrOq31NK31LI9bTQi+rNPS\nIhO5Y8ecRuqHD0s46oIFEgpVDmGFbLKM8fKtXw/88peFxPZrLgJoHdy+ACgO7UyyWEa5oq9WCcrr\nGxwUT59SkqO6Zo3kJp5/vuRGfvWrwF13AT/7WSH1cXZ3A/v3i4BZtSq947S0yDEGBqRSp6Hc6r7E\ngb20iC20FRIF2gupBgn5R0ga1NfLxG1szMmpSrJAQ1jLiqyitdOOIY0iO7afS1pirLQ9AUWfENS2\noaNDcvpWrHAqnLa0AB/6EPCOd8h3qVAAvv1t4MUX0x2nuSCxdq14gdPCeOuBYlvNY2gnIYQQQtKF\noi/jlHo3kuz9ZdOcPos8/7x42ebNk9YTScfG234uSVfuNNDT501Q2wa/9hxKAVddBdxwg3hwp05t\nT7XIi9aVCe00eHnrKfqSg3k3xBbaCokC7YVUA4q+jFM60U1yQmf2YUJG84J7gp9GDzLbsNe0xBhF\nnzd+4Z39/cCuXeLNM03mSznzTOB//k/gda+TvNh77gG+8pXisMgkOHDAyTVduTLZfXtBTx8hhBBC\nbKDoyzh+nr4kJnSmkffwsNPiIOuMjABbt8pjE9qZdGx8VE9f0mJs9mwpgNLfL/log4OSvzl9erLH\nyRt+om/LFrlocdFF3gVeDFOnAm1tBXzwg7KeKfKybVtyYzRevvXrkysuFIRXKHJei7hkEebdEFto\nKyQKtBdSDSj6Mo57ojs4KPeNjdFbEfiRt2IuO3dKxcy2tvQmta2tIoiN6PIjjR59gIgFEzL62986\nx0jDq5kn/ERf1HBKvyIvw8PljW9szBlLGrmmXri/v2NjyVX3JYQQQkhtQdGXcdwTXSPMFi9OzouQ\nt2IuXpPqpGPjlbL7XNIMuzT73LMnvWPkDa9qtj09wAsviCfUpiWDsRWvIi+f/3x5RV727JGCSybX\ntBJMny4XCIaHgSNHkq3uS5h3Q+yhrZAo0F5INaDoyzhu0ZdGrk6eirkMDUmVRkDK8qdJmAdUa4q+\nSlNfL2LNXc3WVHFdsyZ6P8DSIi9dXSiryEvauaZ+uG01yeq+hBBCCKkdKPoyDkWfw7ZtwOnTwPLl\nxU3E04iND/tc+vvF2zRzZjpl+U145/79ck/RJ5QWNvKr2umHl60kUeTFK9e0UrhtNcnqvoR5N8Qe\n2gqJAu2FVAOKvowzfbqEaQ0OShgbkOyEbuFC8aD09IgnLctUoxS+n+hLu6Km2a8JY6ToE9y9+ozI\nmTEDuOCC8vY7dSrwnvcgdpGXSuSa+uEORWblTkIIIYR4QdGXcZRyJvwHD8p9khO6hgYJbdMaOHQo\nuf0mzYkTwI4dksu4fn3xa2nExpuJdFeXd6hfpUSfIelegHnF7fk2FwHWrRM7tiHMVuIWeal0ARc3\nXp4+ir5kYN4NseX/tnf3QXbV9R3HP9/NbsgTyQImkCB0M4FIQHC3IYEBlWgHRVqV1qFTO4IpztjR\nKg6DT4ydKbTTGbWOIoO2zviA1lawWhlAkVplU60PSSBbAgmBjG4xbDaUhM2jIZvst3/8zsme3dzd\nnN/uuffch/dr5s6ec+7Zvb8sH27uN78nsoIY5AVloOhrANkCYO7csKR/kRphMZfHHw+9XhdcEPZA\nq7Z588Lv+eWXpd27T3y+1kUfPX1BtuhLh3YWXWjFLvJSy7mmlaQLO73wQvGr+wIAgOZQWtFnZjPM\nbJOZPVhWGxpF9gP/2WcXv0hEI8zrm6wnpVpj4yf7vVRru4YUPX2Vpb+Xvr5QjJ92mnTeefm/P29W\nYhZ5mWiuaa20t4dh2mm7ilzdt9Ux7wZ5kRXEIC8oQ5kfDT4kaYukKayT11rGF31Fq/e9+l56SXrm\nmdCD0dNTu9edrOirdk/f7NnhIYWezWosFtOI0t/33r3h66WXVrfAOfdc6ROfmHyRl9jFZKoh+77A\n0E4AADBeKUWfmb1S0rWSviypxbecPrlaFX312tO3cWPoxbj44rBp+njVGhtfZtGX/dkM7Rw1/ncR\nW2hNJSszZ44u8jJvXljk5Y47Qg/fwYPhvNJc01qi6KsO5t0gL7KCGOQFZci5/EHhPifpI5JqMDur\n8WWH9lVjZcDTTw/F1L59YfGKU08t/jWmo5ardmZNNtcxLfqqOezy9NPDa1P0jUpXsz1yJAxpPPfc\n2r12d7fU1SXdc4+0dWtY5KWrK8w1vfDC2sw1nUj2fYHtGgAAwHg17+kzsz+S9IK7bxK9fLlUv6cS\nggAAE7VJREFUu6fPLP9iLocPS3feKf3oR8W3o5Jdu8JedbNnh56+Sqo1Nn7x4vC72bUrDO1LDQ+H\n4njGjOIX1clKC0rm843KrmY7lU3Qp5uV8Yu89PeH62Ws2plFT191MO8GeZEVxCAvKEMZPX1XSHqb\nmV0raZak+Wb2DXe/MXvT2rVr1dXVJUnq7OxUd3f38e7w9H+WVjnfvLlXw8NST88azZpVndcLc5TW\naGBAGhyc+P4NG6Qf/7hXjz0mXX119f/827dLAwO9Wr5c6uiofH9fsnRiNV5/0SJp06Zefe970vXX\nh+cffLBXAwPSJZeskVn1/vwrVqzRz38u7d/fq97e+slj2edtbb0aGpKuuKKc11+3rlcdHdJtt63R\nPfdIzz7bq/37Jamc9vT29spd6upao/b2kFez+vnvxTnnrXCeqpf2cF7f56l6aQ/n9XPe19enoaEh\nSVJ/+i/LBTGvtAlZjZjZVZI+7O5vHXfdy2xXK3r0Uenee6XXvla64YaJ7/vsZ6Vt28KKgXffXfxK\nouN9+9thxcTrrpPe8pbqvlYlX/pS2C7ippukyy4L17ZuDb2dy5dLt95a3dc/diz0KGEs9+pnL696\nagsAAGgeZiZ3L+RTRlsRP2SaqO7qQJ7FXIaGwiqaUhjuGHo3qitdUbSsIWuVhr3WYhGXFAVfZfVU\nZNVTWwAAACoptehz93Xu/rYy24AgLW4GBk7chyyVrqKZSoufakqLrcmKvvHDJYpUqRiu9h59qJ5q\nZgXNh7wgL7KCGOQFZaiHnj7UgXnzwqIkL78cNr2uJN2PLN02odpF3/79YUXRWbPKK7Aq7WFYy54+\nAAAAYLoo+nDcZEM8s6toplsnVLvoS9uxZMnkQ+jSCbDVsHBh2Bh9zx7p0KFwjaKvcVUzK2g+5AV5\nkRXEIC8oA0Ufjpus6Ev3yuvpCfujSdUv+sqezyeFTbcXLx7bnlrs0QcAAAAUhaIPx01U9LmPDu1c\ntWq0h6tWPX0nK/qqPTY++3txp6evkTGPAjHIC/IiK4hBXlAGij4cl13MJeu558LwzvnzpQsuGC12\n0gVNqiVv0Vdt2aLvwIGwOfucOaNzGwEAAIB6RtGH4xYvDnPnBgfDlgypdGjnypVhuGM6rLGaPX3u\no8VnWoxOpNpj47PFML18jY15FIhBXpAXWUEM8oIyUPThuJkzpUWLpJGRUPhJ4Tgt+lavDl8XLAj7\nx+3bF3q9qmH37rCS6IIFYWXRMmV7+ij6AAAA0Ggo+jDG+Hl927eHTdlf8Qpp6dJwzWy0t69aQzxj\nhnZWe2z8ggXS3Llh9c5f/zpco+hrTMyjQAzygrzICmKQF5SBog9jjJ/Xl13AJbttQrUXc6mX+XxS\n+HOn7XjyyfCVog8AAACNgqIPY2R7+o4elR5/PJynQztT9VT01WJs/PhN2tmuoTExjwIxyAvyIiuI\nQV5QBoo+jJEt+rZskQ4eDNfGL6ZS7aIv7yIutTLRnx8AAACodxR9GGPhQqmjIxRz69aFa+N7+aTq\nbttw9GhYSMZsdGP0ydRibPz4HkeKvsbEPArEIC/Ii6wgBnlBGSj6MEZb22ihlc5fu/TSE++rZk/f\n4GBYNXTRorCiaD3IFn1tbVJnZ3ltAQAAAGJQ9OEE2QJn2bKwcud41dyrL3YRl1qMjZ81SzrjjHDc\n2RkKPzQe5lEgBnlBXmQFMcgLysBHV5wgW2ytWlX5nmxPn3uxr19v8/lS6e+FoZ0AAABoJBR9OEFa\nbLW1SStXVr5n1ixpzhzpyJGw2MvJHDgg3XGH9P3vn/ze2J6+Wo2NT38vFH2Ni3kUiEFekBdZQQzy\ngjJQ9OEEy5aFguv1r5fmz5/4vph5fVu3hh68Rx4JheJk6mmPvqxLLw1DO3t6ym4JAAAAkJ950WPz\nCmBmXo/twlhf+IL0xBPS+94ndXdPfu/990sPPxyO3/veiXsQDx2SbrklrCB6113MnQMAAEBrMjO5\nuxXxs/hIjSmL6elL5+lJ0vr1J79v8WIKPgAAAKAIfKzGlMXs1ZcO2ZSkzZtDj14ladEXM7STsfHI\ni6wgBnlBXmQFMcgLykDRhynLu23D4cPSiy9K7e3S8uXSsWPSpk2V763X+XwAAABAo6Low5TlHd6Z\nHbJ5+eXheKIhnmnRF7NdA/vdIC+yghjkBXmRFcQgLygDRR+mLLboW7IkrHzZ3i5t2ybt3Tv2Pnd6\n+gAAAICiUfRhyjo7w2Ire/dKR49OfF+2kJszR3r1q0OBt3Hj2PuGhsJcv7lzpQUL8reDsfHIi6wg\nBnlBXmQFMcgLykDRhylrawuFn3so2CYyvvdu9erwdfwQz+wiLlbI4rQAAAAAKPowLScb4llpyOYl\nl0izZkn9/dILL4zeO5X5fBJj45EfWUEM8oK8yApikBeUgaIP03KybRv275cOHJBmzw69glLYeD3d\nzH3DhtF7mc8HAAAAFI+iD9Nysp6+bCGXHbK5alX4un596A0cf28MxsYjL7KCGOQFeZEVxCAvKANF\nH6blZHv1TVTIrVghzZsnDQ5KO3ZIIyPhuNK9AAAAAKaOog/TEtPTlzVjhrRyZTjesCHM7Rsels44\nI8z3i8HYeORFVhCDvCAvsoIY5AVloOjDtOQt+iotzpKu4rlhw9QXcQEAAAAwuVKKPjM7x8weNbOn\nzOxJM7u5jHZg+rJFXzo3LzUyIu3cGY4rDdlctix8/5490rp1E993MoyNR15kBTHIC/IiK4hBXlCG\nsnr6hiXd4u4XSbpc0l+Z2YqS2oJpmD07DMc8fFj63e/GPvfii9KRI2He35w5J36v2eiCLtu2ha/M\n5wMAAACKVUrR5+6D7t6XHB+QtFUSA/sakNnEQzzzrMaZDvFMTaXoY2w88iIriEFekBdZQQzygjKU\nPqfPzLok9Uj6VbktwVRNtFdfnnl6Z58tLV4cjmfMkM48s/j2AQAAAK2s1KLPzOZJ+o6kDyU9fmhA\nE23bkKenz2y0t+/MM6X29vjXZ2w88iIriEFekBdZQQzygjJM4SN2McysQ9J3JX3T3e8f//zatWvV\n1dUlSers7FR3d/fx7vD0fxbO6+N8x45eDQxIe/aMff7558P5c8/16vDhib/fvVcjI9JVV03t9fv6\n+urq98E555xzznlrnafqpT2c1/d5ql7aw3n9nPf19WloaEiS1N/fryKZj19ysQbMzCR9XdJud7+l\nwvNeRrswNb/8pfS1r4Ueu/e8J1wbHpZuTtZkvesuqaOjvPYBAAAAjcbM5O5WxM9qK+KHTMGVkt4l\n6Q1mtil5XFNSWzBNlRZy2bkzbNmwaBEFHwAAAFCmUoo+d/+Zu7e5e7e79ySPH5bRFkxfpaIvz3y+\noowfLgFMhKwgBnlBXmQFMcgLylBWTx+aSGdnWJBlaCj07km1LfoAAAAATIyiD9PW3i7Nnx8Kvr17\nw7VaFn3pBFjgZMgKYpAX5EVWEIO8oAwUfSjE+CGeAwPh62R79AEAAACoPoo+FCJb9B08GIZ6zpwp\nLVxY/ddmbDzyIiuIQV6QF1lBDPKCMlD0oRDZoi8d2rlkSZjrBwAAAKA8pezTdzLs09d4fvIT6b77\npDVrpLPOku69V7rySunGG8tuGQAAANB4itynr72IHwKcdlr4+tJL0rFj4ZiVOwEAAIDyMbwThcgO\n76z1Ii6MjUdeZAUxyAvyIiuIQV5QBnr6UIi06Nu9W0pH5tLTBwAAAJSPOX0ohLv0wQ9Kw8Ph/NRT\npc98ptw2AQAAAI2qyDl9DO9EIcxGe/skevkAAACAekHRh8KUVfQxNh55kRXEIC/Ii6wgBnlBGSj6\nUJh0BU+pdou4AAAAAJgcc/pQmAcflB56KBx//OPS0qXltgcAAABoVMzpQ13KDu+kpw8AAACoDxR9\nKExa9C1cKJ1ySu1el7HxyIusIAZ5QV5kBTHIC8rAPn0ozHnnSd3d0sUXl90SAAAAACnm9AEAAABA\nnWFOHwAAAAAgF4o+NDzGxiMvsoIY5AV5kRXEIC8oA0UfAAAAADQx5vQBAAAAQJ1hTh8AAAAAIBeK\nPjQ8xsYjL7KCGOQFeZEVxCAvKANFHwAAAAA0Meb0AQAAAECdYU4fAAAAACAXij40PMbGIy+yghjk\nBXmRFcQgLygDRR8AAAAANDHm9AEAAABAnWFOHwAAAAAgl1KKPjO7xsyeNrNnzexjZbQBzYOx8ciL\nrCAGeUFeZAUxyAvKUPOiz8xmSLpb0jWSLpT0TjNbUet2oHn09fWV3QQ0CLKCGOQFeZEVxCAvKEMZ\nPX2rJW139353H5Z0r6S3l9AONImhoaGym4AGQVYQg7wgL7KCGOQFZSij6Dtb0m8z5zuSawAAAACA\ngpVR9LEsJwrV399fdhPQIMgKYpAX5EVWEIO8oAw137LBzC6XdLu7X5Oc3yZpxN0/lbmHwhAAAABA\nSytqy4Yyir52Sdsk/YGkAUnrJb3T3bfWtCEAAAAA0ALaa/2C7n7UzD4g6RFJMyR9hYIPAAAAAKqj\n5j19AAAAAIDaqclCLmb2VTPbZWabM9deY2a/MLMnzOwBMzs189xtycbtT5vZmzLXV5rZ5uS5z9ei\n7ai9mLyY2dVmtjG5vtHM3pD5HvLS5GLfW5LnzzWzA2Z2a+YaWWkBU/i76JLkuSeT52cm18lLk4v8\ne2iWmX0rub7FzD6e+R6y0gLM7Bwze9TMnkreL25Orp9uZj8ys2fM7D/MrDPzPXzWbUGxWSn0c667\nV/0h6XWSeiRtzlzbIOl1yfFfSPrb5PhCSX2SOiR1Sdqu0R7J9ZJWJ8c/kHRNLdrPo7aPyLx0Szor\nOb5I0o7M95CXJn/EZCXz/Hck3SfpVrLSWo/I95Z2Sf8j6eLk/DRJbeSlNR6RWVkr6VvJ8WxJv5F0\nLllpnYeksyR1J8fzFNauWCHp05I+mlz/mKRPJsd81m3RxxSyUtjn3Jr09Ln7TyW9NO7y+cl1SfpP\nSe9Ijt+u8OY57O79Cv8jXGZmiyWd6u7rk/u+Iem66rYcZYjJi7v3uftgcn2LpNlm1kFeWkPke4vM\n7DpJv1bISnqNrLSIyLy8SdIT7r45+d6X3H2EvLSGyKzslDTXzGZImivpiKR9ZKV1uPugu/clxwck\nbVXYg/ptkr6e3PZ1jf7357Nui4rNSpGfc8vYpy/1lJm9PTm+XtI5yfEShQ3bU+nm7eOvPy82dW8l\nE+Ul6x2SHnP3YYVskJfWVDErZjZP0kcl3T7ufrLS2iZ6b1kuyc3sh2b2mJl9JLlOXlpXxay4+yOS\n9ikUf/2S/sHdh0RWWpKZdSn0Ev9K0pnuvit5apekM5NjPusib1aypvU5t8yi7yZJ7zezjQrdm0dK\nbAvq36R5MbOLJH1S0l+W0DbUl4mycrukz7n7IUmF7HmDpjBRXtolvVbSnydf/9jM3iiJ1c9aV8Ws\nmNm7FIZ1Lpa0VNKHzWxpaa1EaZJ/XPyupA+5+/7scx7G4PH+AUnxWSnic27Nt2xIufs2SW+WJDNb\nLukPk6ee19henFcqVLLPJ8fZ689Xv6WoB5PkRWb2Skn/LukGd/9Ncpm8tKgKWbk2eWq1pHeY2acl\ndUoaMbPfKWSHrLSoSd5bfivpv9x9T/LcDyT9vqRviry0pEneW66Q9D13Pybp/8zsvyWtlPQzkZWW\nYWYdCh/i/9nd708u7zKzs9x9MBmO90Jync+6LSwyK4V9zi2tp8/MFiZf2yT9taR/TJ56QNKfmdnM\n5F/Kzpe0PhnPus/MLjMzk3SDpPsr/Gg0oYnykqxu9H1JH3P3X6T3u/tOkZeWVCEr/yRJ7v56d1/q\n7ksl3Snp7939i7y3tLZJ/i56RNLFZjbbzNolXSXpKfLSuiZ6b5H0tKQ3Js/NlXS5pKfJSutI/vt+\nRdIWd78z89QDkt6dHL9bo//9+azbomKzUuTn3Fpt2fAtST+X9Coz+62Z3STpnWa2TWEC4w53v0eS\n3H2LpG8rTFZ8WNL7k25OSXq/pC9LelbSdnf/YS3aj9qKyYukD0haJulvzGxT8nhF8hx5aXKRWZkM\nWWkBkX8XDUn6rMKKjZsU5lE8nPwo8tLkIt9bviRppoXtHdZL+qq7P5k8R1Zaw5WS3iXpDZnPItco\nDMe72syeUfiHgU9KfNZtcVFZUYGfc9mcHQAAAACaWJkLuQAAAAAAqoyiDwAAAACaGEUfAAAAADQx\nij4AAAAAaGIUfQAAAADQxCj6AAAAAKCJUfQBAFqGBT9N9kVKr11vZg9P9n0AADQy9ukDALQUM7tI\n0r9J6pHUIelxSW92999M4We1u/vRgpsIAEChKPoAAC3HzD4l6ZCkuZIOSPo9Sa9WKAJvd/cHzKxL\n0jeSeyTpA+7+CzNbI+nvJO2RdIG7v6q2rQcAIA5FHwCg5ZjZHIUeviOSHpL0lLv/i5l1SvqVQi+g\nSxpx95fN7HxJ/+ruq5Ki7yFJF7n7/5bzJwAAIL/2shsAAECtufshM7tPoZfvTyW91cw+nDx9iqRz\nJA1KutvMXiPpmKTzMz9iPQUfAKBRUPQBAFrVSPIwSX/i7s9mnzSz2yXtdPcbzGyGpMOZpw/WrJUA\nAEwTq3cCAFrdI5JuTk/MrCc5nK/Q2ydJN0qaUeN2AQBQCIo+AEArc4VFWTrM7Akze1LSHclzX5T0\nbjPrk/QqhaGg2e8DAKAhsJALAAAAADQxevoAAAAAoIlR9AEAAABAE6PoAwAAAIAmRtEHAAAAAE2M\nog8AAAAAmhhFHwAAAAA0MYo+AAAAAGhiFH0AAAAA0MT+H0WnYtLIW9amAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7fc3daf60dd0>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Total Prizes: 853\n"
]
}
],
"prompt_number": 12
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"years_df.value_counts()\n",
"plt.bar(years_df.value_counts().index, years_df.value_counts())\n",
"plt.box(on=\"off\")\n",
"plt.grid()\n",
"plt.xlabel(\"Number of Nober Prizes/Year\")\n",
"plt.xlabel(\"\")\n",
"plt.show();"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAXEAAAEACAYAAABF+UbAAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEetJREFUeJzt3X+MZfVdxvHnkW2NiBEwutCyyWBTsFbqFpuGSNABwRBj\nFkyISmxkoekfRiltjAL1D4gmSlHaGpuaqGx3qRZtaEPANJGtMgmGiLayy/LL1YRVVmXoD9YWEyOV\nj3/cM907s3fm3jnne+45n3ver2SS+2u++8x37j3zmWfuveuIEAAgp2/rOgAAoD4O4gCQGAdxAEiM\ngzgAJMZBHAAS4yAOAIlteRC3vcv2o7afsf207fdXl59t+6Dto7YfsX3mfOICAMZ5q+eJ2z5H0jkR\nccj2GZK+JOlaSTdK+kpE3G37VklnRcRtc0kMAPiWLSfxiHgpIg5Vp1+V9JykN0vaI+lAdbMDGh3Y\nAQBzNnMnbntJ0jslPSFpZ0SsVletStpZPBkAYKqZDuJVlfJZSbdExDfGr4tRH8Nr9wGgAzum3cD2\nGzQ6gH8qIh6sLl61fU5EvGT7XEkvT/i8j0s6Q9Kx6qITkg5FxEp1/bIkdX1+7bK+5Nni/Af6uH/s\nJ/uZaD93R8THepRn/Hu7VyPHJJ1YyzmTiNj0Q5Il3Sfpoxsuv1vSrdXp2yTdNeFz79xq7b58kJOc\nff4g57Ay1sk5bRK/VNJ7JD1l+8nqstsl3SXpM7bfW/3k+NkJn7s080+Sbi11HWBGS10HmNFS1wFm\ntNR1gBktdR1gRktdB5jBUtcB2rDlQTwi/lab9+ZXlo8DANiONl+xub/FtUva33WAGe3vOsCM9ncd\nYEb7uw4wo/1dB5jR/q4DzGB/1wFmtLKdG2/5Yh8AQL+1NomP/3W9z8hZFjnLImc5GTLWwRtgAUBi\n1CkAkBiTOAAkRidOzqLIWRY5y8mQsY6pL7sHtulR240XiYjmiwADQCeOomxH8/dDMwdxYEZ04gCQ\nGJ04OQcpy36Ss5wMGetgEgeAxOjEURSdODBfTOIAkBidODkHKct+krOcDBnrYBIHgMToxFEUnTgw\nX0ziAJAYnTg5e892lPjYsOZyR1/OtpCznAwZ6+C9U5BE84oGWER04iiqjU6cnh3YHJ04ACRGJ07O\nQcqyn+QsJ0PGOpjEASAxOnEURScOzBeTOAAkRidOzkHKsp/kLCdDxjqYxAEgMTpxFEUnDswXkzgA\nJEYnTs5ByrKf5CwnQ8Y6mMQBIDE6cRRFJw7MF5M4ACRGJ07OQcqyn+QsJ0PGOpjEASAxOnEURScO\nzBeTOAAkRidOzkHKsp/kLCdDxjqYxAEgMTpxFEUnDswXkzgAJEYnTs5ByrKf5CwnQ8Y6mMQBIDE6\ncRRFJw7MF5M4ACRGJ07OQcqyn+QsJ0PGOqYexG3vs71q+8jYZXfaPm77yerj6nZjAgAmmdqJ275M\n0quS7ouIi6rL7pD0jYj4SPsRkQmdODBfUyfxiHhM0isTruIBAQAda9KJ32z7sO17bZ+58cos/RM5\nhynLfpKznAwZ69hR8/P+UNJvVqd/S9I9kt674TbX2d4r6Vh1/oSkQxGxIp3c0K7Pr+lLns3OS9pt\nuzd5pu2ntBZ7udb5U7/+ZuutrZl1P/uSJ/n9c7eqO0ZP8igiVqrTe6t9PCZpZWxfp5rpeeK2lyQ9\nvNaJz3odhodOHJivWnWK7XPHzv6MpCOb3RYA0J5ZnmJ4v6THJV1o+0XbN0n6sO2nbB+W9OOSPjjh\n85ZLh20DOYcpy36Ss5wMGeuY2olHxPUTLt7XQhYAwDbx3ikoik4cmC/eOwUAEuO9U8g5SFn2k5zl\nZMhYB5M4ACRGJ46i6MSB+WISB4DE6MTJOUhZ9pOc5WTIWAeTOAAkRieOoujEgfliEgeAxOjEyTlI\nWfaTnOVkyFgHkzgAJEYnjqLoxIH5YhIHgMToxMk5SFn2k5zlZMhYB5M4ACRGJ46i6MSB+WISB4DE\n6MQHnNN2lPgonWse+L6X/Z5n2M8MGeuY+n9sYtE1rymQUZPvO9/zPqETH7As/TWdeFnN95O97BM6\ncQBIjE6cnIOUZT/JWU6GjHUwiQNAYnTiA5alv6YTL4tOfLEwiQNAYnTi5BykLPtJznIyZKyDSRwA\nEqMTH7As/TWdeFl04ouFSRwAEqMTJ+cgZdlPcpaTIWMdTOIAkBid+IBl6a/pxMuiE18sTOIAkBid\nODkHKct+krOcDBnrYBIHgMToxAcsS39NJ14WnfhiYRIHgMToxMk5SFn2k5zlZMhYB5M4ACRGJz5g\nWfprOvGy6MQXC5M4ACRGJ07OQcqyn+QsJ0PGOpjEASAxOvEBy9Jf04mXRSe+WJjEASAxOnFyDlKW\n/SRnORky1jH1IG57n+1V20fGLjvb9kHbR20/YvvMdmMCACaZ2onbvkzSq5Lui4iLqsvulvSViLjb\n9q2SzoqI21pPi6Ky9Nd04mXRiS+WqZN4RDwm6ZUNF++RdKA6fUDStYVzAQBmULcT3xkRq9XpVUk7\nN94gS/9EzmHKsp/kLCdDxjp2NF0gImL069kprrO9V9Kx6vwJSYciYkU6uaFdn1/TlzybnZe023Zr\nX7+09s8sb/P8SLn1ltetd/Lrb7be2ppt72eW+2f570+K/dy99oX0JI8iYqU6vbfax2OSVsb2daqZ\nnidue0nSw2Od+POSliPiJdvnSno0In5g1n8U/ZClv6YTL4tOfLHUrVMeknRDdfoGSQ+WiQMA2I5Z\nnmJ4v6THJV1o+0XbN0q6S9JVto9KuqI6v/HzlgtnbQU5hynLfpKznAwZ65jaiUfE9ZtcdWXhLACA\nbeK9UwYsS39NJ14Wnfhi4b1TACAx3juFnIOUZT/JWU6GjHUwiQNAYnTiA5alv6YTL4tOfLEwiQNA\nYnTi5BykNvbTdpT4aDtnGzLkzJCxjsbvnQJgXPPaB9gOOvEBy9JfZ+nEh5OTTrxP6MQBIDE6cXIO\nUpb9JGc5GTLWwSQOAInRiQ9Ylv56OF2zlCMnnXifMIkDQGJ04uQcpCz7Sc5yMmSsg0kcABKjEx+w\nLP31cLpmKUdOOvE+YRIHgMToxMk5SFn2M1HOou8Z01LG5bb/jS7w3ikACmlW0aAeOvEBy9JfD6dr\nlnLkPDUjPXt36MQBIDE6cXIOUpb9zJIzg0XdSyZxAEiMTnzAsvTXw+mapRw56cT7hEkcABKjEyfn\nIGXZzyw5M1jUvWQSB4DE6MQHLEt/PZyuWcqRk068T3jFZhKlXpbMA2WE/cSioBNPknMkGn5gvf7v\nZ677Z78t6l7SiQNAYnTiSWTpmlmTTrzUmpgNkzgAJEYnniQnhon7ZzmLupdM4gCQGJ14Elk6XNak\nEy+1JmbDJA4AidGJJ8mJYeL+Wc6i7iWTOAAkRieeRJYOlzXpxEusydsizI73TgHQU81/IA4BnXiS\nnBgm7p/lLOpe0okDQGJ04klk6XBZk068xJpZ9rIPmMQBIDE68SQ5MUzcP8tZ1L1s9OwU28ckfV3S\n/0l6LSLeXSIUAGA2jTpx2y9I+pGI+Fq5SJgkS4fLmv3vcenEF0uJOmXhNwkA+qrpQTwkfcH2F22/\nb/yKLP1TlpwYJu6f5SzqXjZ9xealEfGftr9X0kHbz0fEY9V119neK+lYdf6EpEMRsSKd3NCuz6/p\nS57Nzo+sSFoeO60a59d/vevX7sN6y+vWO/n1N1tvbc2s+1n+/lQ33/LEPCdvU2+9tTVb/v7sXrui\n68fz+Pnq9N4q6jFJK+v3YWvFnidu+w5Jr0bEPUUWxDpZOlzW7H+PSye+WGrXKbZPt/1d1envlPST\nko6UCgYAmK5JJ75T0mO2D0l6QtJfRsQja1dm6Z+y5MQwcf8sZ1H3snYnHhEvaNQxAQA6wnunJJGl\nw2XN/ve4dOKLhfdOAYDEeO+UJDkxTNw/y1nUvWQSB4DE6MSTyNLhsmb/e1w68cXCJA4AidGJJ8mJ\nYbIdTT+6/hr6YlEf6/xv90DvNaspsNjoxJPI0uGyZt/WbL+/bmNNOvHZ0YkDQGJ04klyAmhmUR/r\nTOIAkBideBL97FtZs/9r0ok3XKT3mMQBIDE68SQ5ATSzqI91JnEASIxOPIl+9q2s2f816cQbLtJ7\nvGKzBaVe6jyEOyCAZujEW8sZDT8AlJTlmLRddOIAkBideAv62Y2y5jDXpBNvuEjvMYkDQGJ04kly\nAmhmUR/rTOIAkBideAv62Y2y5jDXpBNvuEjvMYkDQGJ04klyAmhmUR/rTOIAkBideAv62Y2y5jDX\npBNvuEjvMYkDQGJ04klyAmhmUR/rTOIAkBideAv62Y2y5jDXpBNvuEjvMYkDQGJ04klyAmhmUR/r\nTOIAkBideAv62Y2y5jDXpBNvuEjvMYkDQGJ04klyAmhmUR/rTOIAkFiqTnzUkzV3avfWxpp960ZZ\nc5hr0omvX7O5vvXsO7oOsH3Nv7HzWRNA/yzeY33wnTgAZEYnDgCJtXYQj4iVttYGAIwwiQNAYrUP\n4ravtv287X+2feuE65cbJQMATFXrIG77NEkfl3S1pB+UdL3tt2242e6G2QBgcLY7ANedxN8t6V8i\n4lhEvCbpzyVds+E2Z9ZcGwCGbHk7N657EH+zpBfHzh+vLgMAzFHdg/gsz5hfqrk2AGBGdV+x+e+S\ndo2d36XRND7ukO07x86vNH3aYZmXu57y8+fyCK2UXJOc5Cy1phrnPHXeap5z4gxXNGc/93Limo1V\nHfjy2EUntvX5dd47xfYOSf8k6Sck/Yekv5d0fUQ8t+3FAAC11ZrEI+Kbtn9F0l9JOk3SvRzAAWD+\nUr2LIQBgvVZesTnthUB9YHuX7UdtP2P7advv7zrTVmyfZvtJ2w93nWUzts+0/YDt52w/a/uSrjNt\nZPv26nt+xPanbX9715kkyfY+26u2j4xddrbtg7aP2n7EdudP290k5+9W3/PDtj9n+7u7zFhlOiXn\n2HW/avt122d3kW1Dlok5bd9c7enTtj+81RrFD+IzvhCoD16T9MGIeLukSyT9ck9zrrlF0rNq4y8r\n5fy+pM9HxNskvUNSryo220uS3ifp4oi4SKMq8Oe7zDTmkxo9ZsbdJulgRFwg6a+r812blPMRSW+P\niB+WdFTS7XNPdapJOWV7l6SrJP3r3BNNdkpO25dL2iPpHRHxQ5J+b6sF2pjEZ3khUOci4qWIOFSd\nflWjA86buk01me3zJP2UpD9RH9/QWFI1fV0WEfuk0d9NIuK/Oo610dc1+uF9evXH+dM1eqZV5yLi\nMUmvbLh4j6QD1ekDkq6da6gJJuWMiIMR8Xp19glJ58092Aab7KckfUTSr885zqY2yflLkn6nOn4q\nIr681RptHMTTvRComtDeqdEdsI8+KunXJL0+7YYdOl/Sl21/0vY/2v5j26d3HWpcRHxN0j2S/k2j\nZ1WdiIgvdJtqSzsjYrU6vSppZ5dhZnSTpM93HWIS29dIOh4RT3WdZYq3Svox239ne8X2u7a6cRsH\n8T7/un8K22dIekDSLdVE3iu2f1rSyxHxpHo6hVd2SLpY0ici4mJJ/61+/Pr/LbbfIukDGr0Q7U2S\nzrD9C52GmlGMnoHQ68eW7d+Q9L8R8emus2xUDRQfknTH+MUdxZlmh6SzIuISjYa3z2x14zYO4rO8\nEKgXbL9B0mcl/WlEPNh1nk38qKQ9tl+QdL+kK2zf13GmSY5rNOX8Q3X+AY0O6n3yLkmPR8RXI+Kb\nkj6n0f721artcyTJ9rmSXu44z6Zs79Wo8uvrD8W3aPTD+3D1WDpP0pdsf1+nqSY7rtF9U9Xj6XXb\n37PZjds4iH9R0lttL9l+o6Sfk/RQC/9OI7Yt6V5Jz0bEx7rOs5mI+FBE7IqI8zX6I9zfRMQvdp1r\no4h4SdKLti+oLrpS0jMdRprkeUmX2P6O6vt/pUZ/LO6rhyTdUJ2+QVIvBw3bV2s0MV4TEf/TdZ5J\nIuJIROyMiPOrx9Jxjf7A3ccfjA9KukKSqsfTGyPiq5vduPhBvJpw1l4I9Kykv+jpC4EulfQeSZdX\nT917sroz9l2ff6W+WdKf2T6s0bNTfrvjPOtExGFJ92k0aKz1on/UXaKTbN8v6XFJF9p+0faNku6S\ndJXtoxo9qO/qMqM0MedNkv5A0hmSDlaPo090GlLrcl4wtp/jevE42iTnPknfXz3t8H5JWw5tvNgH\nABLjv2cDgMQ4iANAYhzEASAxDuIAkBgHcQBIjIM4ACTGQRwAEuMgDgCJ/T+NyTw/6ucHdQAAAABJ\nRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fc3da7bb910>"
]
}
],
"prompt_number": 13
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"By Subject"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.figure(figsize=(13,5))\n",
"\n",
"for subject in subjects:\n",
" df = data_set[data_set[\"subject\"]==subject][\"year\"].value_counts().sort_index().cumsum()\n",
" plt.plot(df.index, df, label=subject, linewidth=2, alpha=.6)\n",
"\n",
"\n",
"plt.grid()\n",
"plt.legend(loc=\"best\")\n",
"plt.xlabel(\"Year\")\n",
"plt.ylabel(\"Cumulative Sum of Given Nobel Prizes\")\n",
"plt.xticks(np.arange(1900, 2020, 10))\n",
"\n",
"plt.show();"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAwgAAAFHCAYAAAAFlGuHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd8FVX6+PHPSYMQEkoCgZCEUIMgAaQ3ifTQm50mqHwt\n6Iq7q7iyILKyIrq7rqs/dREXWBEBMbQAIsagBJC6SK8hhRpKEloS7vn9ccJNgCSEkJty53m/Xvfl\nnbl3Zs6TO+zOM3Oec5TWGiGEEEIIIYQAcCnpBgghhBBCCCFKD0kQhBBCCCGEEHaSIAghhBBCCCHs\nJEEQQgghhBBC2EmCIIQQQgghhLCTBEEIIYQQQghh57AEQSkVpJT6USm1Wyn1m1Lqpaz1U5RSCUqp\n7VmviBzbTFRKHVRK7VNK9XRU24QQQgghhBC5U46aB0EpVQOoobXeoZSqCGwFBgGPAKla6w9u+X5j\n4CugNVALWAs01FrbHNJAIYQQQgghxG0c9gRBa31Sa70j630asBdz4Q+gctlkIDBfa52htT4GHALa\nOKp9QgghhBBCiNsVSw2CUioEaAFszFo1Xim1Uyk1SylVOWtdAJCQY7MEshMKIYQQQgghRDFweIKQ\n1b1oEfBy1pOET4A6QHPgBPB+Pps7pv+TEEIIIYQQIldujty5UsodWAzM01p/B6C1Pp3j838Dy7IW\nE4GgHJsHZq27dZ+SNAghhBBCCHGPtNa5dft36ChGCpgF7NFa/z3H+po5vjYY2JX1finwmFLKQylV\nB2gAbM5t31pry7wmT55c4m2QmCVeiVnilZglXivHa8WYrRavFWPOjyOfIHQEhgP/U0ptz1r3BvC4\nUqo5pvvQUWAcgNZ6j1LqG2APkAk8r+/Uegs4duxYSTeh2FktZqvFC9aL2WrxgvVilnidn9Vitlq8\nYM2Y8+KwBEFr/TO5P6GIymebd4B3HNUmIYQQQgghRP5kJuVSbvTo0SXdhGJntZitFi9YL2arxQvW\ni1nidX5Wi9lq8YI1Y86LwyZKcxSllPQ8EkIIIYQQ4h4opdDFXaRc3JRS8pKXU72cWXR0dEk3oVhZ\nLV6wXswSr/OzWsxWixesGXNeHDrMaXGTJwvCWTh7giCEEEKI0stpuhgppSRBEE5DzmchhBBCOFLW\ntYZzdzESQgghhBBC3DtJEIQQxc5q/TytFi9YL2aJ1/lZLWarxQvWjDkvkiCUkPDwcGbNmlWk+3zu\nueeYNm1ake5TCCGEEEJYi9QgOFhISAinT5/G1dUVLy8vIiIi+Oijj+jXrx8jRoxgzJgxJd1EUQqV\n1vNZCCGEEM5BahBKkFKK5cuXk5qayrZt29iyZYv9Lr9cAAohhBBCiNJGEoRiFBAQQEREBL/99hsA\ncXFxdOrUCR8fH3r16kVycjIAffv25aOPPrpp27CwMCIjIwF45ZVX8Pf3p1KlSoSFhbFnzx7AzAA4\nadIk+zaRkZE0b96cSpUqUb9+fVavXg3Al19+Sb169fDx8aFu3bp89dVXDo9diJys1s/TavGC9WKW\neJ2f1WK2WrxgzZjz4lTzIORl3Lii29enn979NjeeFMTHx7Ny5UqGDh1KTEwMX331FatWrSIwMJCI\niAhmzpzJ9OnTGT16NO+//z4vvvgiADt37iQpKYm+ffuyevVq1q9fz8GDB/Hx8WH//v1UqlQJ4KYJ\ntjZv3syoUaNYvHgx3bp1IykpidTUVC5dusTLL7/Mli1baNCgAadOnbInJkIIIYQQQsgTBAfTWjNo\n0CCqVKlC586dCQ8PZ+LEiQCMGTOG+vXrU758eR555BF27NgBQP/+/Tlw4ACHDx8GYO7cuTz22GO4\nubnh7u5Oamoqe/fuxWazERoaSo0aNW477qxZsxg7dizdunUDzNOL0NBQAFxcXNi1axdXrlzB39+f\nxo0bF8efQgi78PDwkm5CsbJavGC9mCVe52e1mK0WL1gz5rxY4glCYe76FxWlFJGRkXTt2vW2z3Je\n2Ht6epKWlgZgTxjmzp3L5MmT+frrr1m8eDEAXbt25cUXX+SFF14gLi6OIUOGMHPmTLy9vW/ad0JC\nAn379r3tmF5eXixYsICZM2cyduxYOnbsyPvvv29PHoQQQgghhLXJE4RSatSoUfz3v/9l7dq1VKhQ\ngbZt29o/Gz9+PFu2bGHPnj0cOHCA995777btg4KCOHToUK777tmzJ2vWrOHkyZM0atSIZ555xmFx\nCJEbq/XztFq8YL2YJV7nZ7WYrRYvWDPmvEiCUILyG8Woffv2KKX4/e9/z8iRI+3rt2zZwqZNm8jI\nyKBChQqUL18eV1dX+/5u7HPs2LHMnj2bdevWYbPZSExMZP/+/Zw+fZrIyEguXbqEu7s7Xl5e9u2F\nEEIIIYSQBKEE3SgovvE+5zLAyJEj2bVrF8OHD7evS0lJ4dlnn6Vq1aqEhITg5+fHH/7wh9v20bp1\na2bPns0rr7xC5cqVCQ8P5/jx49hsNv72t79Rq1YtfH19Wb9+PZ988kkxRCtENqv187RavGC9mCVe\n52e1mK0WL1gz5rzIRGml2Ny5c/n888+JiYkp6aaIYuaM57MQQgghSg+ZKK0Munz5Mv/617949tln\nS7opQhQ5q/XztFq8YL2YJV7nZ7WYrRYvWDPmvEiCUAqtXr2a6tWrU7NmTZ544omSbo4QQgghhLAQ\n6WIkRCkk57MQQgghHEm6GAkhhBBCCCEKRBIEIUSxs1o/T6vFC9aLWeJ1flaL2WrxgjVjzoskCEII\nIYQQQgg7qUEQohSS81kIIYQQjiQ1CEIIIYQQQogCkQShhE2ZMoURI0YUy7H69OnD3Llzi+VYQuTH\nav08rRYvWC9midf5WS1mq8UL1ow5L5IgFJOvvvqKVq1a4e3tTUBAAH369OGXX35BqVyf7DjEypUr\nC5SMuLi4cOTIkWJokRBCCCGEKG2kBqEYfPDBB7z77rt8+umn9OrVCw8PD1atWkVMTAwVKlTg0KFD\nperOvouLCwcPHqRevXq5fp6ZmYmbm1sxt8paSvP5LIQQQoiyT2oQStDFixeZPHkyH3/8MYMGDcLT\n0xNXV1f69u3Lu+++C0B6ejqjRo3Cx8eH+++/n61bt9q3T0pKYujQoVSvXp26devyz3/+0/7ZlClT\nePjhhxkxYgQ+Pj6EhYVx8OBBpk+fjr+/P7Vr1+b777+3fz88PJxZs2YBcOjQIbp06ULlypWpVq0a\njz/+OAAPPvggAM2aNcPb25uFCxcSHR1NYGAgM2bMoGbNmowZM4amTZuyfPly+74zMjLw8/Nj586d\njvtjCiGEEEIIh7PEbeBxy8YV2b4+7f/pXX0/NjaWq1evMnjw4Fw/11qzdOlSlixZwpdffsmf/vQn\nXnzxRWJjY7HZbPTv35/BgwezYMEC4uPj6d69O6GhofTs2ROA5cuXs3TpUr788kvGjBlDjx49GDdu\nHElJScyePZtx48bZuwsppexdmiZNmkTv3r356aefSE9PZ8uWLQDExMTg4uLC//73P+rWrQuYPnmn\nTp3i/PnzHD9+nOvXr/PPf/6TefPm0a9fP8B0X6pVqxbNmjW7+z+qsJzo6GjCw8NLuhnFxmrxgvVi\nlnidn9Vitlq8YM2Y8yJPEBwsOTkZPz8/XFzy/lN37tyZ3r17o5Ri+PDh9rvwv/76K2fPnuXNN9/E\nzc2NOnXq8PTTT/P111/bt33wwQfp0aMHrq6uDBs2jOTkZF5//XVcXV159NFHOXbsGCkpKbcd08PD\ng2PHjpGYmIiHhwcdOnTINw4XFxfeeust3N3dKV++PE8++SQrVqwgLS0NgLlz5xZbsbUQQgghhHAc\nSzxBuNu7/kXJ19eXs2fPYrPZ8kwS/P397e8rVKjA1atXsdlsxMXFkZSURJUqVeyfX79+3d4NCKB6\n9er2956envj5+dmfEnh6egKQlpaGj4/PTcecMWMGkyZNok2bNlSpUoVXX32Vp556Ks84qlWrhoeH\nh305ICCAjh07smjRIgYNGsSqVatu6v4kRH6sdofGavGC9WKWeJ2f1WK2WrxgzZjzYokEoSS1b9+e\ncuXKsWTJEoYOHXrb5/mNYhQUFESdOnU4cOBArp/fywhI/v7+fPbZZwD88ssvdO/enS5duti7FRXk\nWKNGjWLWrFlkZGTQoUMHatasWej2CCGEEEKI0kG6GDlYpUqVmDp1Ki+88AKRkZFcvnyZjIwMoqKi\neO211/Ldtk2bNnh7ezNjxgyuXLnC9evX+e233+z1Avcyys3ChQtJSEgAoHLlyiil7E84/P39OXz4\n8B33MXjwYLZt28aHH37IyJEjC90WYT1WG2vaavGC9WKWeJ2f1WK2WrxgzZjzIglCMZgwYQIffPAB\n06ZNo3r16gQHB/Pxxx/bC5dvvTt/Y9nV1ZXly5ezY8cO6tatS7Vq1Xj22WftNQU5i45v3Tav5Ru2\nbNlCu3bt8Pb2ZuDAgXz44YeEhIQAZnSkUaNGUaVKFRYtWpTrcQDKly/PkCFDOHbsGEOGDLn7P4wQ\nQgghhCh1ZB4EcU/efvttDh48yJw5c0q6KU5FzmchhBBCOFJ+8yBIDYIotHPnzvHFF1+UqknehBBC\nCCHEvZEuRqJQPv/8c4KDg4mIiKBTp04l3RxRxlitn6fV4gXrxSzxOj+rxWy1eMGaMedFniCIQnnm\nmWd45plnSroZQgghhBCiiN1VDYJSyhXw0lrfPvNWMZEaBGEFcj4LIYQQwpHyq0G4YxcjpdR8pZSP\nUsoL2AXsVUr9sagbKYQQQgghhCh5BalBaJz1xGAQEAWEACMc2SghhHOzWj9Pq8UL1otZ4nV+VovZ\navGCNWPOS0ESBDellDsmQVimtc4ApO+DEEIIIYQQTuiONQhKqZeA14D/AX2BYGCu1rqz45uXa3uk\nBkE4PTmfhRBCCOFI91SDoLX+UGtdS2sdobW2AXHAQ0XdSKsKDw9n1qxZRbrP5557jmnTphXouy4u\nLhw5cqRIj19W5fwt/vvf/9KrV687bjN9+nQZzUkIIYQQhtZw5UpJt+KeFaRIuYZSapZSalXWqvuA\nUY5tlnMJCQmhQoUKeHt7U6NGDZ566ikuXboEmOxNqVyTt0L75JNPePPNN4t0n6XJ6NGjcXFxYenS\npTetf+WVV3BxceE///lPofab87d48sknWb169R23mThxIp9//nmhjmdlVuvnabV4wXoxS7zOz2ox\nWy1eKIKYDx+GGTPgiy+KpD0lqSA1CF8Ca4CArOWDwCt32kgpFaSU+lEptVsp9VtWVyWUUlWVUt8r\npQ4opdYopSrn2GaiUuqgUmqfUqrn3YdTOimlWL58OampqWzbto0tW7YU+A6/1V2/fv22dUopGjZs\nyJw5c+zrMjMz+eabb6hfv36RJ1xCCCGEEHk6fRo+/dQkB0eOwLFjkJpa0q26JwVJEPy01guA6wBZ\nRcqZBdguA3hFa90EaAe8oJS6D3gd+F5r3RD4IWsZpVRj4FGgMdAb+Fgp5XQzPQcEBNC7d292795t\nX3fs2DE6deqEj48PvXr1Ijk5GYC+ffvy0Ucf3bR9WFgYkZGRgLlj7u/vT6VKlQgLC2PPnj2AucM+\nadIk+zaff/45DRo0wNfXl4EDB3LixIlc23bx4kVGjhxJ9erVCQkJ4S9/+Yu9H7zNZuPVV1+lWrVq\n1K1bl48++ggXFxdsNhsLFy6kVatWN+3rgw8+YNCgQbkeJykpiQEDBuDr60uDBg3497//bf9sypQp\nDBs2jBEjRlCpUqU8nwb079+fn3/+mQsXLgCwatUqmjVrhr+//01997/44gsaN25M1apV6d27N8eP\nH7d/9v3339OoUSMqV67M+PHjb9ruyy+/pHPn7DKb3bt306NHD3x9falRowbTp0+3t3fECDOo17Fj\nx3BxcWHOnDnUrl2batWq8c4779j3obXmr3/9K/Xr18fPz49HH32U8+fP5xqfswsPDy/pJhQrq8UL\n1otZ4nV+VovZavFCIWJOS4MFC2DKFNi2DTw8oF8/ePtt8PZ2RBOLTUEuwNOUUr43FpRS7YCLd9pI\na31Sa70j630asBeoBQwAblz1/QczOhLAQGC+1jpDa30MOAS0KWAc+Rs3ruhehXTj4jM+Pp6oqCha\ntGhhX//VV1/x5Zdfcvr0adLT05k5cyZgLvTnzZtn38fOnTtJSkqib9++rF69mvXr13Pw4EEuXrzI\nwoULqVq1KnBzV5l169bxxhtvsHDhQk6cOEHt2rV57LHHcm3j+PHjSU1N5ejRo/z000/MmTOH2bNn\nA/DZZ5+xatUqdu7cybZt2/juu+/sxxgwYABHjx5l37599n3NnTuXUaNy74n22GOPERwczIkTJ1i0\naBFvvPEGP/74o/3zpUuX8vDDD3Px4kWeeOKJXPdRvnx5Bg4cyNdffw3AnDlzGDlypD1+gMjISKZP\nn86SJUs4e/YsnTt35vHHHwfg7NmzDB06lHfeeYfk5GTq1avHL7/8kuuxUlNT6d69O3369OHEiRMc\nOnSIbt263XSsnH755RcOHDjADz/8wNSpU9m/fz8AH374IUuXLiUmJoYTJ05QpUoVXnjhhVyPKYQQ\nQohS6uJFiIqCN9+EdevAZoOOHU1i0L8/lC9f0i28ZwVJEF4FlgF1lVIbgLnAS3dzEKVUCNAC2AT4\na61PZX10CvDPeh8AJOTYLAGTUJR5WmsGDRpElSpV6Ny5M+Hh4bzxxhuAucAcM2YM9evXp3z58jzy\nyCPs2LEDMHfJDxw4wOHDhwFz0f3YY4/h5uaGu7s7qamp7N27F5vNRmhoKDVq1Ljt2P/9738ZO3Ys\nzZs3x8PDg+nTpxMbG3vTnXQwXXkWLFjA9OnT8fLyonbt2rz66qvMnTsXgG+++Ybf/e53BAQEULly\nZSZOnGhPesqVK8cjjzxiT2Z2795NXFwc/fr1u6098fHxbNiwgXfffRcPDw+aNWvG008/fVN3oQ4d\nOjBgwADAJAJ5GTlyJHPmzOHixYvExMTc9sTi//2//8fEiRMJDQ3FxcWFiRMnsmPHDo4fP87KlSu5\n//77GTJkCK6urvzud7/L9e8HsHz5cgICAnjllVfw8PCgYsWKtGnTxv7b3mry5MmUK1eOsLAwmjVr\nxs6dO+3tmTZtGgEBAbi7uzN58mQWLVqEzWbLM0ZnZbW+rVaLF6wXs8Tr/KwWs9XihTvEnJEBv/4K\n//wnvP46fPedKUZu0sQkCiNHQuXKeW9fxrjd6Qta661KqQeBRoAC9mut0wt6AKVURWAx8LLWOjXn\nHVettVZK5TeWY9GM8/jpp0Wym8JSShEZGUnXrl1z/TznhamnpydpaWkA9oRh7ty5TJ48ma+//prF\nixcD0LVrV1588UVeeOEF4uLiGDJkCDNnzsT7lkdaJ06cuKn7j5eXF76+viQmJhIcHGxff/bsWTIy\nMqhdu7Z9XXBwMImJifb9BAUF2T8LDAy86TijRo3iiSeeYNq0acydO5dHH30Ud3f322JNSkqiatWq\neHl53XScLVu25Lnv3Cil6NixI2fOnGHatGn079//tmQiLi6Ol19+mVdfffWm9YmJiZw4ceK24+SM\nL6f4+Hjq1q17xzbdkPP3rFChgv33jIuLY/Dgwbi4ZOflbm5unDp1ipo1axZ4/0IIIYQoJkeOwC+/\nwNat2aMTubpC8+YQHg733VeizXOUOyYISqkjwHta609yrFuutb799vDt27pjkoO5WuvvslafUkrV\n0FqfVErVBE5nrU8Ecl6hBWatu83o0aMJCQkBoHLlyjRv3vxOTSmzRo0axciRI+nYsSMVKlSgbdu2\n9s/Gjx/P+PHjOXPmDI888gjvvfceU6dOvWn7gIAAjh07Zl++dOkSycnJ1Kp188MZPz8/3N3dOXbs\nGPdlnezHjx+3X0TXrFmT+Ph4+/dzvgdo164dHh4exMTEMH/+fObPn59rPAEBAZw7d460tDQqVqx4\n23Eg9247eRk+fDhTp07NNesPDg5m0qRJ9m5FOR08ePCmGLTWt8WUcz8LFizI9bO7aWtwcDCzZ8+m\nffv2Bd7mRlw3+kXKsiyXleXw8PBS1R6JV+K91+Ub60pLeyRexyzbY1+8GGJiCL961SwnJUGNGoQ/\n8QS0bk30li1w6hThWddMpaX9+S3v2LHDXruZ89owV1rrfF/AfmABMBsol7VuewG2U8Ac4G+3rJ8B\nvJb1/nXgr1nvGwM7AA+gDnCYrIncbtle5yav9aVBSEiI/uGHH3L9LDw8XP/73/+2L8+ePVt36tTp\npu80aNBAh4WF6bffftu+7tdff9UbN27U6enpOi0tTffu3VtPmTJFa631qFGj9Jtvvqm11nrt2rW6\nWrVqeseOHfrq1av6pZde0p07d7bvRymlDx8+rLXWevjw4Xrw4ME6NTVVHzt2TDdq1EjPmjVLa631\nJ598ops0aaITExP1+fPndffu3bWLi4u+fv26fV/Tpk3TTZs21fXr18/379G5c2f94osv6qtXr+qd\nO3dqf39/+99n8uTJevjw4flunzO+c+fO6XXr1tk/69Spk/7Pf/6jtdZ6yZIl+v7779e7d+/WWmt9\n4cIF/c0332ittT5z5oz29vbW3377rc7IyNB///vftZubmz3enL9DSkqKrlmzpv773/+ur169qlNS\nUvSmTZtua+/Ro0e1Uuqmv0l4eLh9n3/72990eHi4jouL01prffr0aR0ZGZlrjKX5fBZCCCGc1sWL\nWs+bp/X//Z/Wzz6r9Usvab1okdZJSSXdsiKXda2R63W8S/7pAwCXtdaPYoqMY5RSte+0QZaOwHDg\nIaXU9qxXb+CvQA+l1AGga9YyWus9wDfAHiAKeD6r8U4v513o3OZFGDlyJLt27WL48OH2dSkpKTz7\n7LNUrVqVkJAQ/Pz8+MMf/nDbPrp168bbb7/N0KFDCQgI4OjRo/bC3luP/c9//hMvLy/q1q1L586d\nefLJJ3nqqacAeOaZZ+jZsydhYWG0bNmSvn374urqelN3mREjRrB79+6b2pmb+fPnc+zYMQICAhgy\nZAhTp061d78qyLwQOb9TpUoVHnoo93n7Bg0axGuvvcZjjz1GpUqVaNq0qX1uAz8/PxYuXMjrr7+O\nn58fhw4dolOnTrkew9vbm++//55ly5ZRs2ZNGjZsaM/Mb21vfm1/+eWXGTBgAD179sTHx4f27duz\nefPmfGN1VrfeqXF2VosXrBezxOv8rBaz1eIlPZ3ov/4VJk2CmBizrksXU3g8dCgUsCuw1pA11VWZ\npu50Da6U2q61bpH1vjvwL6Cq1rpaMbQvt/bkmjdkTRddAi1yvLlz5/L5558Tc+OELQWioqJ47rnn\nbnpEdeXKFfz9/dm+fTv16tUrucY5AWc+n+Hmx9ZWYLV4wXoxS7zOz2oxO3W8NhucPAkJCRAfb/4b\nF0f0wYOEBwRAs2YweHCBkwKA5GTYtAk2bjQjnGbdsy3Vsq41cr2zWZAEob/WelmO5drAKK311KJt\nZsFYLUG4fPmyvSD5TnfmHenq1ausW7eOnj17curUKYYOHUqHDh344IMP7N/54IMPWLlyJWvXri2x\ndjoLZz2fhRBCiBKhNezebYYnjYszoxLdqnZtGDYMGjYs0C6vXoXt2yE2FrJGNAegUiV46y3w9Cyi\ntjtIoRIEpdR9Wuu9SqmW3D6akNJaby3idhaIlRKE1atXM3ToUHr06MHixYtv6s5T3K5cuUKXLl3Y\nt28fnp6e9OvXj3/84x/2QuOQkBCUUnz33Xc0a9asxNrpLJzxfBZCCCFKRHw8LF4Me/dmr/Pzg8DA\n7FdQEPj6wh26OdtsJhmIjTXJQXrWuJ7u7tCiBbRrZwY2KsFLtgIrbILwudb6GaVUNLkMN6q1zr3j\nt4NZKUEQ1uXs57NTP7rOhdXiBevFLPE6P6vF7BTxnj8PkZGm34/WUKEC9O1rJjXL5fZ+fjGfOGF2\ns2mT2e0NDRpA+/bwwAOl/4nBrfJLEPIc5jQrOXAB/qS1zn2KWSGEEEIIIUqTq1dh9Wr4/nvTlcjV\nFR56CPr0gRzzMN1JZiZs2GCmQcg5Kmi1auZJQbt25kGEMypIDcIOrXWpmWhAniAIK5DzWQghhLhL\nNhusXw/LlkFqqlnXqhUMGmSu6gtIa9i2DZYsgTNnzDpPT2jZ0jwtqFfvjj2RyoRCPUHIYa1Sahiw\n2CrDjgohhBBCiDJCa9i1y9QZnDxp1tWrZwqO69a9q10dPgyLFpkJlMEMZNSnj6kvcHcv4naXYgUp\nofg/zPwE6Uqp1KxXioPbJYRwYlYbX9tq8YL1YpZ4nZ/VYi4z8cbFwd/+Bv/6l0kOqlWDcePMOKN3\nkRycPg0TJkQzY4ZJDnx84Mkn4c9/hjZtrJUcQAGeIGitKxZHQ4QQQgghhCiQ5GRTgLxpk1n28oJ+\n/eDBB8GtIB1kzAhEO3aYEYn27TPTIYSEQI8e0LMnlC/vuOaXdvmNYtQQeA+oD/wP+L3WOrEY25Yr\nZ6hBWL9+Pc888wz79u0r6aaIUqosnc9CCCFEsblyBVatgh9+MAXIbm7QtStERJhRiu5Aazh40CQF\n27aZemYwu2nbFgYMgMqVHRxDKVHYYU5/Bv4DrAf6A+211kMc1soCKmsJQkhICLNmzaJbt275fueL\nL76ga9euDmlDdHQ0I0aMID4+3iH7F0WvtJ7PQgghRIm4fh1iYmD5ckhLM+vatDEFyL6+d9xca/j1\nV1i6NLvwGKBOHVN43KrVXQ1w5BTySxDyq0GoqLX+XGu9T2v9HlDHMc1zbkop1B1K3e/lYlBr7fAL\nyczMTIfuX1hPmenbWkSsFi9YL2aJ1/lZLeZSE29KCqxdC1OmwNdfm+SgYUOYOBHGji1QcnDgALzz\nDsyaZZKDqlXNA4epU+H116FLF5MclJqYS4H8EoTySqkHsl4tAc8b75VSDxRXA51RdHQ0QUFBAIwY\nMYLjx4/Tv39/vL29mTlzJgAbN26kQ4cOVKlShebNm/PTTz/Ztw8PD+fNN9+kY8eOeHl5ceTIEWbP\nnk3jxo3x8fGhXr16fPbZZwBcunSJiIgIkpKS8Pb2xsfHhxMnTjB69GgmTZqUa5vAPNWYMWMGYWFh\neHt7Y7O8QVHpAAAgAElEQVTZ8m2TEEIIIUSRyMiArVvho4/gtddg4UJTRezvD88/DxMmmGKBOzhx\nAj7+GN5/H44fN12HRo2Cv/zFPHjw93d8KGVVflUcJ4H381kukZmUC2Pc/v1Ftq9PQ0OLbF8Ac+fO\n5eeff2bWrFn2LkaJiYn069ePefPm0bt3b9auXcvQoUPZv38/vlmZ8rx584iKiiI0NBSbzYa/vz8r\nVqygTp06xMTEEBERQevWrWnRogWrVq1i+PDhN3UxKsiTja+//pqoqCj8/Pw4ceJErm3at28ffs46\nS4hwmDI/O+ddslq8YL2YJV7nZ7WYiz1ereHoUVMcsGULXL5s1ru6QrNmZlayZs3M8h2kpJieSOvX\nm6kRypeHXr2ge3fw8Mh7O6v9xvnJbybl8GJsh8hh3rx59OnTh969ewPQvXt3WrVqxYoVKxg5ciRK\nKUaPHs19990HgIuLC3369LFv/+CDD9KzZ0/Wr19PixYt8uyClF/XJKUUL730ErVq1cq3TStXrmTk\nyJFFErcQQgghLCY5GTZuNK/Tp7PXBweb4oDWrcHbu0C7Sk83vZFWrzbFxy4upvtQv35m2FJRcAUb\nB6qMK+q7/o4WFxfHwoULWbZsmX1dZmbmTUXMObsDAURFRfHWW29x8OBBbDYbly9fJiws7J7akfMY\nBWmTEAUVHR1tqTs1VosXrBezxOv8rBazQ+O9etUMIbRxI+Ts5VGpkhlKqH17CAgo8O5sNjPaaWQk\nnD9v1oWFwZAhZqKzgrLab5wfSyQIpd2tXX2Cg4MZMWKEvY7gTttcu3aNoUOHMm/ePAYOHIirqyuD\nBw+2PyHIrSuRl5cXl288vgNO3ph5MI9jFKRNQgghhBC5stnMZAMbN8L27eZ2P5g+P82bmy5E991n\nbvsXkNZml4sXw41e1MHBMHQoNGrkgBgsRBKEYpCens7VGwPtcvuoQP7+/hw+fNh+N3748OG0bt2a\nNWvW0K1bNzIyMti4cSMNGjSwd/nJ2T0oPT2d9PR0/Pz8cHFxISoqijVr1tC0aVP7/pOTk0lJScEn\n6xlb8+bNef/993nzzTe5du0af//73/ONoSBtEqKgrHaHxmrxgvVilnidn9ViLrJ4T5wwdQWbNsGF\nC9nrGzY0SUHLlnc9I9n589m9km7c36xSxRQet20LdyixzJPVfuP85JkgZI1clGcnda31Noe0yAnl\nrA8A6Nix40135ydOnMj48eP54x//yKRJk5gwYQKRkZH88Y9/5PHHH8fV1ZW2bdvyySef2LfJub23\ntzcffvghjzzyCNeuXaN///4MHDjQ/nmjRo14/PHHqVu3LjabjT179jBixAjWrl1LSEgIderUYfTo\n0XzwwQd5xhAYGJhrmz7++OOi+BMJIYQQwlmkpZlJB2JjIS4ue321aqb7UNu2cJcDnFy7Zh48xMaa\nXkk37pP6+EC3bubl7l6EMVhcfhOlRZN/glAioxiVtYnShCgMZz+frdbP02rxgvVilnidn9Vivut4\nMzNh1y5zW3/XLjOxGYCnp5mFrH17qFv3rm7va22SgY0bTcnCtWtmvbu7GdCofXto3PiueiXly2q/\ncX4TpckoRkIIIYQQonCuXTNDB61blz3DsYsLNG2aPTTpXd7aP3nSJAWbNsG5c9nr69fP7pVUoUIR\nxiBuk+cTBPsXlPICJgDBWutnlFINgFCt9fLiaGAu7ZEnCMLpyfkshBCiVLPZzFV8ZGR2bUFgoLmt\n36bNXY8rqjX89husWGGmQ7jBz88kBW3bQvXqRdh+UbgnCDnMBrYCHbKWk4BFQIkkCEIIIYQQogTt\n2QOLFkFiolkOCTFDBzVsWKjdHT9udndjxNPy5c1TgvbtzVODwhYdi8IrSK+telrrd4F0AK31Jcc2\nSQjh7KKjo0u6CcXKavGC9WKWeJ2f1WLONd7ERPjwQ/jHP8z7qlVh7Fh4/fVCJQfnzsHs2fCXv5jk\nwMsLHn4Y3nsPRo6EBg2KNzmw2m+cn4I8QbimlPK8saCUqgdcc1yThBBCCCFEqXHhAixbBhs2mK5F\nnp4QEQFduxZq6KArV2DVKvjhB8jIADc3s6uICKktKC0KUoPQE/gT0Bj4HugIjNZa/+j45uXaHqlB\nEE5PzmchhBAl7to1WLPGvNLTwdUVunSBvn2hYsW73t316xATA8uXZ9czt25t5i+4y1FPRRHIrwbh\njglC1g78gLaAAjZqrc8WbRMLThIEYQVyPgshhCgxNpt5WhAZCSkpZt0DD8DgwYWqFNYadu6Eb7+F\nU6fMuvr1YdgwqFOnCNst7kp+CcIdaxCUmZGrC9Ad6Ap0LtrmCSGsxmr9PK0WL1gvZonX+Vki5htD\nCb39NtHvvmuSgzp14A9/gHHjCpUcHDsG778Pn3xikgN/f3juOfj970tfcmCJ37iAClKD8DFQD5iP\neYIwTinVQ2v9vENbJoQQQgghikd8PCxeDHv3muVKleCZZ8xwQoWoFE5Ohu++g82bzXLFitCvHzz4\noOmpJEq3gtQg7AMaa61tWcsuwB6tdaNiaF9u7SlTXYxCQkI4ffo0rq6ueHl5ERERwUcffYSXl1dJ\nN02UYqX1fBZCCOFkzp83XYk2bjRPECpUMDUG4eGmevguXb4MUVFm3rTMTFPD3K0b9O5taptF6XGv\n8yAcAoKBY1nLwVnrRAEopVi+fDldu3YlKSmJXr16MW3aNKZPn17STRNCCCGElWhtxhaNj4eEBPP6\n7TczlJCra/ZQQoW4iZmZmV2AfClrQPy2bWHgQPD1LeI4hMPlWYOglFqmlFoGeAN7lVI/KaWigT1Z\n68RdCggIoHfv3vz2229s3LiRDh06UKVKFZo3b85PP/1k/97s2bNp3LgxPj4+1KtXj88+++ym/URG\nRtK8eXMqVapE/fr1Wb16NQAXL15k7NixBAQEEBgYyKRJk7DZbMUaoxAFYbV+nlaLF6wXs8Tr/Mps\nzJmZ8OOPMHMmvPIKvPGGKQhYtgy2bzfJQatW8NZbpmo4KzkoaLxaw7ZtMGUKLFhgkoPQUHOYMWPK\nVnJQZn9jB8jvCcL7tyzf6O+gcrwvE/aP219k+wr9NPSut7nRVSQ+Pp6oqCg6dOhAv379mDdvHr17\n92bt2rUMHTqU/fv34+vri7+/PytWrKBOnTrExMQQERFB69atadGiBZs3b2bUqFEsXryYbt26kZSU\nRGpqKgCjR4+mRo0aHD58mLS0NPr160dQUBDPPvtskcUvhBBCiDJAa9ixwwwddPp09nofHwgMNK+g\nIDMLciGKjwGOHDEzIB8+bJZr1DATKjdtKrMfl3UFHea0BtAakxhs1lqfvsMmDlOYGoSSTBBCQkJI\nTk7Gzc2NSpUq0a9fP6pXr86hQ4eYM2eO/Xu9e/fmiSeeYOTIkbftY/DgwTz00EO89NJLjBs3jooV\nK/L++zfnb6dOnaJ27dpcuHCB8uXLAzB//nw+//xz1q1bV4hIRUmSGgQhhBCFdvSouXI/lNUjvEYN\nUyEcGmoShHt05gwsWQJbt5plHx+z+86dweWO42M6L5u2sSlhExm2DB6s/WBJN+eO7qkGQSn1CPAe\ncKMPzEdKqT9orRcWYRsdqjB3/YuKUorIyEi6du1qX/f888+zcOFCli1bZl+XmZlp/05UVBRvvfUW\nBw8exGazcfnyZcLCwgBISEigb9++tx0nLi6OjIwMatasaV9ns9kIDg52VGhCCCGEKC2uXjW1BdHR\nsGWLWVexIgwYAJ06FcnQQZcuwYoV5hDXr4OHB/ToAT17Qta9Scvae2Yvi/YsIiElgfJu5WlRowXe\n5cpuj/yCFCm/CbS+8dRAKVUN+AEoMwlCaRMcHMyIESNuqy0AuHbtGkOHDmXevHkMHDgQV1dXBg8e\nbL+bHBQUxKFDt9eIBwUFUa5cOZKTk3GxcvouyoTo6GjCw8NLuhnFxmrxgvVilnidX6mK+dIl83Qg\nISG74PjMmezP3d2he3fo1avQQwfljPdGGcPKlWaUIqWgQweTe1SpUgTxlBKF+Y2TUpNYvGcxv53+\nDYCqnlUZ1GgQFT3ufqbp0qQgCYICcpx1JGetE4U0fPhwWrduzZo1a+jWrRsZGRls3LiRBg0a4OPj\nQ3p6On5+fri4uBAVFcWaNWto2rQpAGPHjqVnz57069eP8PBwTpw4QVpaGqGhofTs2ZMJEybw9ttv\n4+XlxdGjR0lMTOTBB0v/Yy4hhBBC5CMzE3btMsOR7tplbuHn5OYGAQFQt64ZU7QIrty1Ng8jvvsO\nzp416+67z9QZBAXd8+7LtItXL7J0/1I2xG/Apm14unsSUT+CrnW64u7qXtLNu2cFmQfhPaAZ8BUm\nMXgU+J/W+o+Ob16u7SlT8yDUqVOHWbNm3dTFCGDz5s388Y9/ZNeuXbi6utK2bVs++eQTAgMD+fjj\nj5k6dSrXrl2jf//+ZGZmUr9+faZOnQrAd999x+TJkzl69Cj+/v58/PHH9OjRg5SUFF5//XWWLVtG\namoqdevW5fXXX+eRRx4pidDFPSit57MQQohipDXExUFsLPz6a/b4oS4u0KAB1K5trtQDA80UxUU4\nA9nBg2betKNHzXJAgEkMmjSxbgHyddt1fjv9GxsTNvK/U/8j05aJq4srXWp3oU+DPmWuS1F+NQgF\nSRAUMATohClSXq+1XlLkrSygspYgCFEYcj4LIYTF7d9vRiA6dix7XWAgtG8PbdoUSbFxbk6dMgXI\n27eb5UqVTFeiDh2sWYCstSY+JZ7Y+Fg2J24mLT0NMP8/3aJGCwY1GoR/Rf8SbmXh3FOCUNpIgiCs\nwNnP51LVl7cYWC1esF7MEq/zK7aYT5wwV+g7d5plb28z41j79iZBcJDUVFOAHBNjei+dPh3NmDHh\n9OwJ5co57LClyo8//sgD7R8gISWB+JR4ElISiLsQx+lL2YN3BngH0C6wHW0D21K5fOUSbO29K9Qo\nRkqpo3l8pAG01nWLoG1CCCGEECIlxUxDvH492GxmWKBevUyxsYeHww6bkQHr1kFUFFy5Yp4SdOpk\nShj69XPYYUuVYxeOsfLgSn7a8hOV026/6K/oUZE2tdrQLrAdwZWCURboY5XnEwSllF+ORY2ZdflR\n4PfAVq31UMc3L9d2yRME4fTkfBZCCIs4fRo2bDDDBF29aq7QO3c2V+cO6kYEkJZmyhrWrIFz58y6\n++83dQYBAQ47bKmSfDmZ7/Z9x+bEzfZ1nu6eBPkEEegTeNPL1aXo6jtKi0I9QdBan83a2AUYCfwB\n2AH00VrvcURDhRBCCCGc3uXLZnigjRuzpyEGaNYMBg+GHHMaFaW8BkIKDIRhw8wIRVZwOeMyUQej\nWHd0HZm2TNxd3elapytdanehqmdVSzwhuJP8uhh5AGOAV4CfgYFa69sH4BdCiLtktf7LVosXrBez\nxOv87jnm69dhzx4zItH//mf69oDp4P/AA6ZfT/36RdLWW504YSY3u3UgpKZNTWlDixa3FyA742+c\nacskJi6G5QeWcynd/CHaBrZlYOhAfCv4OmXMhZXfPAhHgEzgH8BxIEwpFYYZ6lRrrb8thvYJIYQQ\nQpRd8fHmlv3mzabOAMw4offdB+3amatzB1UBp6TAsmXw88+mrAGKZSCkUkdrzfaT21myd4m94Lih\nb0OGNR5G7cq1S7h1pVN+NQhfZr3N9Qta66cc1KZ8SQ2CsAI5n4UQogxLSTEJQWysmeX4hho1zNV5\n27YOnYL42jVYuxZWrzbvXVygY0fo0sV6E5wdOX+ERXsWcfic6cpVo2INhtw3hDD/MMt3JZJhToUo\nY+R8FkKIMiYjwwxNunEj7N6dfcveywtatzaJQe3aDp1lzGYzOcnSpXDhglnXrBkMGWJyEys5e/ks\nS/YuYUvSFgC8y3nTv2F/OgV3csqC48IoVJGyEN7e3uzatYuQkJCSbopwMlbr52m1eMF6MUu8zi/X\nmLWGI0fMVfmWLWacUDAzGjdvbroQNW0Kbo6/3Nqzx8x8fOOBRe3apvC4YcPC7a+s/saX0i+x8uBK\nfjz2I9dt13F3dad73e70rt+b8m7l8922rMbsCA49Y5VSXwB9gdNa66ZZ66YATwNnsr72htY6Kuuz\niZjC6OvAS1rrNY5sX3EICQnh9OnTuOaY/vypp57iww8/LMFWFUxqampJN0EIIYQofc6ehU2bTGJw\n5kz2+pAQkxS0bg0VKxZLUxITTWKwe7dZrlrVDITUurVDH1aUOpm2TKKPRbPiwAouZ1xGKUX7oPYM\nDB1IFU/HdedyVg7tYqSU6gykAXNyJAiTgVSt9Qe3fLcx8BXQGqgFrAUaaq1tt3yvTHUxqlOnDrNm\nzaJr164l3RRRhpTW81kIISzr6lXYutV0ITpwIHt95comKWjXzmHDk+bmwgXTlSg21nQt8vSEiAjo\n2hXc3YutGSVOa822E9v4du+3nL18FoBGfo0Y1ngYQZUsVnBxl/LrYuSS28pcdtBRKfWkUmpU1mtk\nQbbTWq8Hzue2y1zWDQTma60ztNbHgENAm4Icp6z6/PPPady4MT4+PjRp0oTt27cDsHfvXsLDw6lS\npQr3338/y5Yts28zevRoXnjhBfr164ePjw/t2rXjyJEj9s83bNhA69atqVy5Mm3atCE2Ntb+WXh4\nOJMmTaJjx454e3szYMAAzp49y5NPPkmlSpVo06YNcXFx9u+7uLjY933lyhVeffVVQkJCqFy5Mp07\nd+batWtcvXqV4cOH4+fnR5UqVWjTpg2nT2dPSS6EEEKUWTabuTU/axb84Q8wZ45JDjw8TKHx734H\n06c7dO6CW127ZkYmmjQJfvnFPCXo2hWmTTMTLzt7cmDTNk6mnWRL0ha+2/cd03+ezmdbP+Ps5bME\neAcwvu14ftfud5Ic3KM7djFSSs0D6mImSbue46M593Dc8VlJxhbgVa31BSAA2JjjOwmYJwn3bP/+\ncUWxGwBCQz+9621yuxO8cOFC3nrrLSIjI2nZsiWHDx/G3d2djIwM+vfvz9NPP83atWtZv349AwcO\nZMuWLTTM6ki4YMECVq1aRYsWLRg1ahR/+tOfmD9/PufOnaNv37589NFHPP7443zzzTf07duXw4cP\nUyVrtIQFCxawevVqfH19ad++Pe3bt+fTTz9lzpw5jBkzhrfeeosvvvjitvb+/ve/Z+/evcTGxuLv\n78/mzZtRSvHll1+SkpJCQkIC5cqVY8eOHXh6et7130hYi9X6eVotXrBezBKvk0lKMrfmN22CixcB\niE5KMjG3b2/mLSiff3/2omazmYRg6dLs0VIfeMDkJtWrF/3xSsNvfDXzKgkpCTe9ElMSSb+eftP3\nfMr5MCB0AB2DO+KiCnTvO1elIebSoiA1CC2Bxrn26ymcT4CpWe/fBt4Hxubx3VyPOXr0aHvhbOXK\nlWnevHkRNa3oaa0ZNGgQbjkKlN577z0WLVrEa6+9RsuWLQGoV68eAOvXr+fSpUu8/vrrADz00EP0\n69eP+fPnM3nyZACGDBlCq1atAHjyySeZMGECACtWrCA0NJQnn3wSgMcee4wPP/yQpUuXMmrUKJRS\nPPXUU9SpUweAiIgI9u7da+/+9PDDDzNp0qTbYrDZbMyePZtNmzZRM+sOSbt27QDw8PAgOTmZgwcP\n0rRpU1q0aFGEfz0RHR0NYP8fLGdZdvb4rB6vLMtymVxeuRL27SP8yhU4fpzopCTzeVax8Y7t26Fl\nS8I7dCjW9nXpEs7u3TBzZjTJyRAQEE6dOhAUFE2tWlC9umOOv2PHjmKJL+dyWnoaLnVcOH7xOD//\n9DMXr10koGkAAEm7zO8R0DSAqp5VuXLoCtUqVCOiRwRNqjUh9udYYo7G3NPxd+zYUXrORwcs79ix\ngwtZw1sdO3aM/NyxBkEptRB4WWudlO8X894+BFh2owYhr8+UUq8DaK3/mvXZKmCy1nrTLds4RQ1C\nkyZNeO+99+jTp89N6xcsWMD777/P5s2b7esmTpzIuXPn+PTTT3nqqacIDAzk7bffBswPPmLECOLj\n43n33XfZunUr33zzjX3bxx9/nLCwMCZOnMhDDz3EiBEjGDNmDABvvvkmiYmJzJ49G4C1a9fy3HPP\ncfDgQcB0MTp06BAVK1akRo0apKWlUaFChZvam5mZyTvvvMOCBQu4cOECw4cP5y9/+ctNCZG4e6X1\nfBZCCKeSmWlmNd64EX77zcx2DFChArRqZeoK6tYtkWrfGwMkLVsGe/eadX5+ZsjSBx5wrgLka5nX\n+P7I96w5vIZrmdfs691c3AjwDiDQJ5CgSkEE+gQS6BNIBfcK+exNFNS9DnNaDdijlNoM3PjVtNZ6\nQCEbU1NrfSJrcTCwK+v9UuArpdQHmK5FDYDNuezCKQQFBXHo0KHb1gcEBBAfH4/W2j6BR1xcHI0a\nNbrjPmvVqsW33948wXVcXBwRERG5fr+gE4T4+flRvnx5Dh06RFhY2E2fubm58ec//5k///nPxMXF\n0adPH0JDQ+1JiBBCCFHqxMWZ/jpbtsClS2adi4sZkrR9ewgLK7HO/OfOmZ5NGzfCyZNmXYUK0Lcv\nhIcXy4ipxcambWyI38DS/Uu5eNV05WpeozktA1oS6BOIv5e/zFlQQgpymk3J+q8mu7i4QLc2lVLz\ngS6An1IqHpgMhCulmmft4ygwDkBrvUcp9Q2wB8gEni/Cbk0lKrcwnn76aSZMmECnTp1o0aIFhw8f\nxsPDg3bt2lGhQgVmzJjBhAkT+OWXX1i+fDlTpkzJc183REREMH78eObPn8/DDz/M4sWL2bdvH/36\n9cu1LQX987q4uDBmzBgmTJjA3LlzqV69Ops3b6Zly5Zs2LABX19fGjdujLe3N+7u7jcN6SpEbqKj\nrdXP02rxgvVilnjLiFOn4NtvIav7DGCmFm7XDtq0AR+fPDd1ZMzXrsG2babs4cAB8/QATHM6dICe\nPc18a8XJkfFqrdlzZg+L9y4mMSURgJDKIQxrPIwGvg0ccsyCKLPntQPcMUHQWkdndQWqr7Veq5Sq\nUJDtsrZ9PJfVt1fAZn//HeCdguy7LOnfv/9NF809e/Zk8eLFJCcn88QTT5CYmEidOnWYO3cuwcHB\nLFu2jOeff57p06cTGBjI3Llz7QXKSqnb7vzfWPb19WX58uW8/PLLPPfcczRo0IDly5dTtWrV2757\np33d+n7mzJlMnDiR1q1bk5aWRvPmzVm1ahUnT57k//7v/0hISKBixYo89thjjBgxogj+akIIIUQR\nSU2F5cshJsZU+5YrB507m6cFgYEl0iSbzSQDsbEmOUjPqrt1dzezH7dvD40bmwcbziQhJYHFexaz\n58weAHwr+DK40WBaBbQqcM8G4XgFqUF4FngGqKq1rqeUagh8orXuVhwNzKU9ZaoGQYjCkPNZCCGK\nQEYG/PADREWZeQxcXKBjR+jfHypVKpEmnTyZPUDS+RwDwdevnz1AUgUn7GJ/4eoFIvdFEpsQi9Ya\nT3dP+jboS3hIOO6uTj42ayl1rzUIL2DmI9gIoLU+oJRywIBaQgghhBCFpLWZ1TghIft15Ih5egCm\nvmDIEAgIKPamXboEv/5q6gqOHs1e7+eXPcdatWrF3qxicTXzKmsOr+H7w9+Tfj0dVxdXwuuE07dB\nX7w8irnflCiwgiQI17TW12489lFKuVHAGgQhhMiN1fp5Wi1esF7MEm8JuXHlvXUrHD9unhLcKigI\nhg6F++67p0PdbcyZmWaOtdhYM1DSjQGSypfPHiCpfv3SOxrRvf7GZy6dYWPCRmLiYki5ZiZuaBnQ\nkkGNBlHdq3TeZy4153UpUJAE4Sel1J+ACkqpHsDzwLI7bCOEEEIIUfTyuvIGqFzZ1BQEBZn/BgaC\nv3+xXIVfuZL94CI+HnbuhLQ085mLCzRpYroQNWtmJmJ2RlcyrrD1xFZi42M5dC57pMa6VeoyrPEw\n6lWtV4KtE3ejIDUILsDTQM+sVauBf5fUCENSgyCsQM5nIYTIQWvzhGDjRti8+eYr78aNoW1b84TA\n27tYmpKcnJ0I3EgKzp69/bsBASYpaNPG5C7OKu5CHGsOr2HnqZ1kXM8AoJxbOR6o+QDtAtsR6hsq\nBcilUH41CAVJEIYAK7TW1/L9YjGRBEFYgZzPQggBXLiQPSlAUo75Wovxyttmg+3b4eDB7GTgypXb\nv+fuDjVrZj/AaNDAvHfm6+Lky8lE7o9kU4KZ01YpRahvKO2D2tOiRgvKuZUr4RaK/NxrkfIA4O9K\nqZ+ABcAqrXVmUTZQCGEtVuvnabV4wXoxS7xF6Pp1U1MQGwv79pkrdDBPB1q3NolBUFCxXHnv2QOL\nFkFiIiQlRRMQEA6Y+Qlu7clUo4ZzDUma3298JeMKqw6t4oejP5BxPQM3Fze61unKQ3Ueoqpn1Vy3\nKQus9u84PwWZB2G0UsoDiAAeBz5WSn2vtR7r8NbdJXl8JYQQQpRRWpuagm+/zZ5C2M0Nmjc3SUGT\nJlBME3EmJsLixabUAaBqVahXz8xmHBSU73xqTu267ToxcTEsP7CctHTTzatNrTYMajQI3wq+Jdw6\nUZTu2MXI/kWTJPQCxgAPaq1L5EzIq4uREEIIIcqouDhzq/7AAbNcvTp0726G+ynGKYQvXIBly2DD\nBvPgwtMTIiKga1fThciqtNbsOLmDJfuWcCrtFAANfRsytPFQQiqHlGzjRKHdaw1CH+AR4CEgGtPN\naE1JdTOSBEEIIYRwEsnJ8N13pvAYoGJF6NfPzHLsVpBe0EXj2jVYs8a80tPNg4ouXaBPn2Kpey7V\njp4/yqI9i+yjEvlX9GfofUMJ8w+Tnhtl3L0mCF8DX2NqD3IZYLh4WS1BsGJ/OKvFbLV4wXoxWy1e\nsF7MEm8BXL588zigCQmmL8/16+b2fNeu0Lt3sU4jbLOZpwVLl8LFi2ZdixYweLAZHTUnq/3Gkasi\nOV3tNFuStgBQ0aMi/UP70zm4M64uxdPVq7hZ7Te+pyJlrfVjRd8kIYQQQji9zEyIjoYff8x9HFCl\nzC/nI7UAACAASURBVEhEgwaBb/H1XNba1BcsXpw9OFKdOjBsmJm8zMoupV8i6lAU87bPw/9+f9xd\n3eletzu96vXC092zpJsnikmeTxCUUr9orTsqpdK4feZkrbUukRIdqz1BEEIIIcocrWHbNlNwfCMx\ncHeHWrWyh/258fIs3ovO+HiTGOzda5b9/MwTg5YtnXtI0jvJtGUSfSyalQdXcin9EgDtg9ozMHQg\nVTyrlHDrhCPcUxej0kYSBCGEEKIUO3zYFBwfOWKWAwLMFfj995foOKDnz0NkpJlSQWvTk6lvXwgP\nL9Zyh1JHa822E9tYsm8JZy6dASDUL5RhjYcRXCm4hFsnHCm/BKHA/1KVUrWUUsFZLwv/Uype0dHR\nJd2EYme1mK0WL1gvZqvFC9aLWeIFTp+GTz+FGTNMcuDjA8OHw6RJEBZWYsnB1aumDnrSJDO1gouL\nGSBp2jTz34ImB870G2dczyDuQhy/HP+FGb/M4LOtn3Hm0hkCvAN4sc2LvNLuFY5sP1LSzSx2zvQb\n36s8/1kopd4A3LXWb2WtigUuAh7Al8B0h7dOCCGEEKVbWhqsWAE//WQKjj08oGdP6NEDypcvsWZd\nvWoSghUrIDXVrGvVypQ7VKtWYs0qdlpr4lPi2XtmLwkpCSSkJHAy7SQ2bbN/x6ecDwNCB9AxuCMu\nyolmexOFll8Nwnags9Y67cay1rqFUsoViNFadyzGduZsl3QxEkIIIUpaRoYpPl65Eq5cMR34O3SA\nAQOgcuUSaZLNBvv3m8Rg+3YzZCmYSc6GDYO6dUukWSXiwtULbE7cTGx8LEmpSTd95qJcqFGxBoE+\ngYRUDqFjcEfKu5VcMidKRqFHMbqRHGT5R9a660opKWMXQgghrEhr+PVX028nOdmsa9IEhgwxRccl\n4MQJU1uwaZOpNbihQQMzemqLFtYoQM64nsGOkzuITYhl75m99qcEFT0q8kDNBwipHEKgTyAB3gG4\nu1p45jdxR/klCF5KKQ+tdTqA1vpLAKVUOcDi04YUH6uNyQvWi9lq8YL1YrZavGC9mC0T74EDsHgx\n0Rs2EB4QYEYlGjrUJAgl4NZ51sB0H2rXzrz8/IruWKX5N7ZpG5sSNhG5P5LzV0yG5OriygM1HqBd\nYDuaVG+Cm8vdlY+W5ngdxYox5yW/s2UR8P+UUuO11pcAlFIVgY+yPhNCCCGEFZw8aYYs3bnTLHt5\nwciR0L59iRQfX74MUVGwbp2ZasHdHdq2Nc2pV88aTwtu2HtmL4v3Lib+YjwAgT6BdK7dmdYBrfn/\n7L17cFxXft/5Ofd23268ugGCAPFo8CE+RFHimyKBkUaCHjPSjDRDjSh7k3hrPck6u1XeWjvZ7FYm\nldrEqc16bSe1cWWdbBLv2o7Xdjy2KM3oMdZrJIykEQCSoihSQ4oURZHsBkgQAAE0gEbfftyzf5x+\nohskSDSABvp8qm417rm3+54futE4v/v7fX+/GqtmmWenWancSoPgAv4l8GvA1dTweuD/Bf6plDKx\nJDMsnJfWIGg0Go1GsxRMTsJrr8H776sEf48HnnpKlf/xeJZ8OomEmsprr8G0KtXPoUNw+PCS9lkr\nCwYnBzl69iif3fgMgDVVa3hu+3McbD+IqCQPSXPXLKgPghCiGkj3FbwopYyUeH53hHYQNBqNRqNZ\nRKSEUEgpfX/+c1UOyDDgoYeUANm3dH1Sp6fVVEIh1eDswoWs7OHee1V204YNSzadsmAiOsEr51/h\no+BHONKhyl3Ft7Z8i8c3Pa51BZo7QjdKW8FUYj5cpdlcafZC5dlcafZC5dm8KuydmFDJ/L29MDCQ\nHd+5UwmQ29oyQ4tlr23DqVOqCfOVK/mC4zQtLcox2LlzaVOJlvs9thM2b196mzcvvkksGcM0TB7Z\n8AjPbH2GOk/ppaHLbe9yUGk233UVI41Go9FoNKucc+fgnXfg7FmVRgRQWwsPPqiS+hf5Fr2UKjLQ\n16ccg2g0e8yylA46EICODvW4adOyNmRechzp8FHwI145/woT0QkA9rbu5Xvbv8e62nXLPDvNauVW\nGoSHpJQ/F0J4pZTRoictA5UWQdBoNBqNZlEYHISjR+EzlcOOaarb8l1d8MAD828xfJcMDSmnoK8P\nbt7Mjm/erHQF27erikSV5AzkIqXk7PBZjp47ykBYRXQ21m/khR0vsLVx6zLPTrMauKsUIyHEx1LK\n/ekGaYs6wztAOwgajUaj0SyAiQl45RX46CMVMaiqUsLjr39dRQ4WkUgETpxQWUyXLmXHGxuzpUmb\nmxd1CiuC4ESQo+eOcm74HABrq9fy3PbnONB2QAuQNSXjblOMEkKIPwTahRD/Fsh9ASml/I1STlJT\nnErLh4PKs7nS7IXKs7nS7IXKs3lF2Gvb8Pbb8OabqsWwacJjj8Ezz0DdneWw34m909Nw8aJqYvbp\np6oSEYDXC/v2qYDF1q3lX5p0Kd7jsZkxXjn/Cr2hXqSUVLur+fbWb9O9sXvJBcgr4jNdYirR5rm4\nlYPwLPAE8E3gY2Y5CIs5KY1Go9FoNCXCcVS04JVXVPQAYM8eJTxeV7ocdilhZERVG0pXHQqF8tOH\nhIAdO5RTsHv3slRKLUsi8QjvXHqHt798OyNA7t7UzTNbn9G9DDTLwnzKnO6RUp5aovncFp1ipNFo\nNBrNPJASfvEL1eAsXZVo40Z44QV1y76EBINKznDuXOExy1Li4t27lbagoaGkl15RSCkZi44RCocy\nW3AiyHBkmPTaZn/bfp7b/hzNNTrXSrO4LLSK0agQ4mXg4dT++8BvSilDpZqgRqPRaDSaEjJ7xb52\nLTz3HBw4UNJcnrExFZjo7VX+SFUVbNmSX3WokoXGaYamhugL9dE/0M9oZLTguGmYbGncwuF7D7N5\nzeZlmKFGk898IgjvAH8O/Flq6FeAX5FSfmOR5zbXfCoqglCJ+XCVZnOl2QuVZ3Ol2QuVZ3NZ2JtI\nqIpEvb0q2V9KqK6Gb39baQ1KWJXorbd6iEa7efvtrJyhu1vJGWpWaUbMnb7HkXiEE4Mn6A32cmks\nq8iusWro8HUQ8AXo8KvHltoWXEZ5VZ4vi8/0ElNpNi80gtAkpfzjnP0/EUL8w9JMTaPRaDQazV0j\npeoo1tcHx4/D1JQaX6QV+8iI8j/+7M+gvl6N7d8P3/ueihRUKo50GJ4eVilD4SDBiSCfj3xOwlGK\nbK/Ly77WfXR1dLF1zVZdiUhT9swngvAu8MfAX6CEyn8L+LtSyicWf3pF51NREQSNRqPRaApIJuHD\nD+G99+Datex4e7tSAB88CH5/SS41MwMff6wcg4sXs+ObN6uOxpsrLCMmmogyEB7IOAOhcIiB8ACx\nZCzvPCEE9629j85AJ3ta9uBxaUW2pry4qz4IOU/eCPxfQGdq6CPgf5RSXi3hHOeNdhA0Go1GU7FI\nCadPK33B0JAaq6tTDkFXl0r6L9Hd6StXVFXUU6cgHldjlqVKk3Z2qkZmq/lGuJSSmzM38wXF4SDD\n08NFz19TtYaAL5DZNq/ZTL23folnrdHMnwU5COVGpTkIlZYPB5Vnc6XZC5Vnc6XZC5Vn85LYe/my\ncgwuXFD7zc1KeLxnj0opKhGjo/CjH8GxY9mxe+9V/sfevap/wWp8f+2EzadDn/LV2FcZhyASj2SO\nD54ZpG1nG6Zh0lbXpjQEKS1BwBdYdeVIV+N7fDsqzeaFahA0Go1Go9EsF7NX7LW18OyzqvNxCYXH\nkQi88Qa8+66KGLjdStvc3a06Ha9GHOlwfuQ8faE+Tl47WZAmVOepyzgAN6I3OPzoYVpqWzCN0jlk\nGk05oiMIGo1Go9GUI5EI/M3fKJ1BesX+xBPw1FOqOlGJSCTg/ffh9dezGudDh+Dw4dXrGAxNDdEb\n6qUv1MfYzFhmfMuaLexctzPjFPg9fi0o1qxadARBo9FoNJqVQnrF/tprMD2txg4eVOlEJVyxSwmf\nfAIvvww3bqixbdtUH7UNG0p2mbJibGaMH5//MX2hvkxjsrXVa+kMdNIZ6KSppoJLMWk0OdzWQRBC\nNAD/DbAx53wppfyNRZyXJkWl5cNB5dlcafZC5dlcafZC5dlcEnuXcMV+6RK8+CJ8+aXab2mB55+H\nXbvmJzxeae9vNBHljYtv8M6ld4gn45iGSWdHJ12BLras2TKvKMFKs3mhVJq9UDqbbcfBs8K7A84n\ngvAToBc4DTioUqc6x0ej0Wg0mlKx0BX7PBkZUf7HiRNqv64OvvMdePjhkuqcy4akk+TDqx/y6oVX\nmbQnATjQdoDntj+nowWaBeNIyfVYjJBtE7JtgqnHOtPkn23cuNzTWxDzKXN6Ukq5b4nmc1u0BkGj\n0Wg0q4YlWrFPTys5w7vvqhYKbjc8+SQ8/bSqSrTakFJyeug0L517ietT1wGlLziy4wj3NNyzzLPT\nrEQiyWTGEUhvg7ZNvMiatMY0+debN2OUuX5loX0Q/mcgDLwK2OlxKeXNUk5yvmgHQaPRaDQrniVa\nsScS0NMDP/mJuqQQqofB4cPQ0FCyy5QVV8av8OLZF7kwqsrBNtc08/x9z7OnZY8WHGtui5SSkXg8\nLyIQsm1G081AZrHW7Sbg8WS2Do+HRrd7RXzWFipSjgL/CvinqBQjUClG2gVfAnQO4Oqn0uyFyrO5\n0uyFyrN53vaOjamWxO+8k12xd3WVfMUuJZw8CS+9pIIUoBqbvfACdHQs/PXL8f0djYzyo89/xLEB\nVQ62xqrh2W3P8siGR3AZC6/JUo42LyaVYG/McRjIcQJ6enrw7ttH1HEKznULQXuOIxDweGj3eKhe\njbl5zM9B+EfAZinlyGJPRqPRaDSaVYdtK/FxXx98/rlavQPcdx8cOVKaFXsKx4GzZ1XJ0kuX1Fhb\nm7rM/fevzs7HkXiENy6+wbtfvUs8GcdluHh80+N8a+u3qHaXrhysZuUipWQikSiICgzFYnmi2kHb\nps1x8LtcdMxyBtZZVtmnDJWS+aQYvQV8T0o5vTRTujU6xUij0Wg0ZY2UcPMmhELKMTh5UjkJoFKJ\ndu9WGoPt20u2Yg+FlP/R3w/hsBrz+eC734WHHoIVXlClKAknwQdXPuC1C68xFVMNHA62H+S57c/R\nWL1KGzhobkvCcfKEw2mnYCqZLDjXEIJWy8qkBqWdgboSNiAsZxaaYhQBTgkh3iOrQdBlTjUajUaj\nAZXDc+ECBINqpR4KqSZnuWzerFKJ9u8vWZOzqSnlFPT1qUunaWmBr30NHn109QqQT10/xcufv8zQ\n1BAA2xq3cWTHETbWb1zeyWmWlOlkkmA0mi8cjsVIziEcDsyKCrRaFu7V6D2XgPk4CD9KbbnoW/hL\nRCXkAM6m0myuNHuh8myuNHuhQmwOh+HVV+HDD+kJhehua8seq61VqUObN6u2xM3NJbtsPA4//anS\nOEejaqymBh58UPkgGzYsfirRcr2/l8YucfTsUS7evAhAS20Lz9/3PLvW7Vp0UWhFfKZzKCd7HSkZ\nTguHcxyCsUSi4FwBrEtFBXK3Bpfrtp+RUticCCdITCTwdqxs7/y2DoKU8k/u9sWFEH8EPAPckFLu\nTI2tAX4IbAAuA78spRxPHfsnwN8DksBvSCnfuttrazQajUazKMRiSmT85ptqhW4YsHUrfPObEAio\nze8v+SpdSpVC9OMfqwwmgB074JFHYOdOWK1ZEVOxKY4PHKcv1Mfl8csA1Hnq+M627/Dw+ocxjdUp\nEq1UoskkA6kUobQzMBCLESsiHLYMI696UFo4vBRNyqQjiV2PYYds7KCtHkM2iXACd5Obe/7lyq7l\nMx8NwldFhqWU8raWCyG+DkwBf5rjIPweMCKl/D0hxD8GGqSUPxBC7AD+AngQaAfeAbZJKZ1Zr6k1\nCBqNRqNZehxHrdB/9CMYH1dju3fD974Hra2Leunz51UftatX1X5HhxIe33ffol522Ug4Cc4MnaEv\n1MeZG2dIOip/vMpdRffGbp7e8jRe18q+Q1vpSCm5mRIOZ7QC0SjDc5QTbXC5lCPg9Wacgia3e0mE\nw8lIMuMAZJyBazYyXrgeNaoMvB1eAv8wgDDKW9S8UA3Cgzk/e4EXgHmpf6SUHwghNs4a/i7waOrn\n/wz0AD8ADgP/RUoZBy4LIS4CB4G++VxLo9FoNJpF49w5OHo0m+y/YYOqGbpt26JdMhpVGuePPlIS\nB1CVUA8fVllLqyV1OuEkuD51nVA4lNmujF8hElc6DkMYPND8AF0dXexetxu36V7mGWvulLjjMDhL\nOByybSJFhMOmELTlpAilHYKaJS4nKqVk6uQUo6+NYg/aRc9xr3XjCXjU1qEe3Y0rowfC7ZhPitHs\n8qa/L4Q4Cfyvd3nNdVLKodTPQ8C61M9t5DsDIVQkoaIppxzApaLSbK40e6HybK40e2EV2Tw4qByD\nzz5T+2vWqIjBgw/mpRCVyl7HUdGC3l7lHMRiatzrhaeeUr3ULGvBl1kwd2vvdGyaYDiY5wwMTg5m\nIgS5tPva6Qp0cbD9IH6vvwSzXhir5jM9T+7W3nAikVdKNGTbXI/FcIpkf9SaZkE50RbLwrVM3m/a\n5pkvZxg+OszMlzMACLfA0+7JOgOpzaxaveltt3UQhBD7yYqSDeAAUJLfiJRSCiFulS9U9Nj3v/99\nNm7cCEB9fT179uzJfIh7enoAVs3+qVOnymo+S7F/6tSpspqPtrf0+2nKZT7aXr1fsD8xQc/v/i58\n9hndra1QVUVPWxvs20f3wYMlv55tw7/5Nz2cPg11der44GAPgQD8yq90s38/9Pf38NFHZfL7uc2+\nlJKX33iZ4elhWh5oIRgO8tEHHzFpT9K2U4m5B88MAtC2s42mmiYiX0Roqm7i29/4Nh3+Dj7t+xQR\nFPg3+5fdHqi8/8e3s/fd997jZjzO+s5OQrbNez093IjFqD9wAIDB/n4A2g4dwhCC6MmTNLndPPnY\nYwQ8Hi739VFjmjz22GOZ178IBJbR/hMfnGDb+W1Mnpykf7Afs9rkmf/hGfwP+fnZBz9b8vmUev/U\nqVOMp9IjL1++zK2Yjwahh+xCPYESFv9rKeX5Wz4x+/yNwKs5GoTPgW4p5XUhRCvwnpRyuxDiBwBS\nyt9JnfcG8M+llP2zXk9rEDQajUazONg2vPWW2mIxME1VL/SZZ1RlohLjOCpa8OMfw8SEGmtqgs5O\nlUbU1FTySy4KjnQ4N3yOT4c+JTgRZGByADtRmJZhmRbtvnYCvgAdvg4CvgDtvnatJyhzIslkpuNw\nOjowaNvEi6zHvEahcLjN48EyjGWY+a3JFRpHLkQIfxRGJiWGZdDwjQYavtmA6V29UYIFaRCklN0l\nns8rwK8Cv5t6/FHO+F8IIf5PVGrRVuBYia+t0Wg0Gk0hjqOS/V95JbtS37tXpROtW3fr594lv/iF\nyl4aGFD7Gzeqy91778rpeDw4OUhvsJf+gX4mohN5xxqqGgj4AnnOQFNNE4Yov4WiRiGlZDQeL0gR\nGplDOLzW7c5LD+rweGh0l2cOfp7QOL0NzhIaC/B/zU/j4Ubc9ZWtdZnTQRBCfBc4LaW8nNr/58AR\nVAThN6WUxaobzX6N/4ISJK8VQgSBfwb8DvBXQoj/NvVavwwgpTwrhPgr4CwqUvHrOlSgQkLp8FCl\nUGk2V5q9UHk2V5q9sIJsllKt1F96KX+l/sILqnTpPLkTe0Mh5RicPav2GxuVY3DgwMpwDKKJKP/+\nr/89M+0zXJ24mhlfV7uOQ+2H2LxmMx2+DmqsmmWcZelZMZ/peRJznExUIHeLpsqJDvb303boEABu\nIWifpRUIeDxULbFweD5IKYmPxPNKj9ohm/hocScnV2h8MnqSb/7SN5d4xuXJrSII/ztwCEAI8Szw\nXwN/C9gL/Afgqdu9uJTyb89x6Mk5zv9t4Ldv97oajUaj0SyYYFCt1M+dU/tr18Jzzy3aSn18XAUo\nPvpI+SVVVSpzqbsb3CvgZmXSSfLh1Q959cKrnP/qPG21bVS7q3mw/UE6A51sqt9UlneOKx0pJRM5\n5UTT0YEb8XhR4bA/VU603efjW62tBDwe1lnWkpQTvVOcmIM9YOeXIB2wcaKFPRPmIzS2eqwlnH15\nM6cGQQjxqZRyd+rnPwIu5OgDPpFS7l26aebNSwcWNBqNRnP3jI2ppP++PrVSr66Gb38bHntsUbqN\nRaNK0vD220siayg5UkpOD53m6LmjDE2pIoRb1mzh8U2Ps2vdLl12tIxIOA7XZ5UTDdo2U0XKiRpC\n0GpZBXqBujLsuCelJDGRKGhKFhuKFS1n4/K7MmVH05u1zir7vgRLzd1qEIQQog6YBp4A/u+cY1pN\npNFoNJqVRTSquh+/8052pd7drVbqNaVPh3Ec+PnPVdQgHFZj+/apdKLm5pJfblG4PH6Zo2ePcmFU\nNWJormnm+fueZ0/LHh0tWGamk8lMp+H0NhiLkSxyE7XGNAu0Aq3W8pUTvRVOwinaoTg5VejkCFNg\ntVh5fQg8AQ+uuvJzclYat/oN/j7wCTAJnJNSHgcQQuwDBpdgbhpWX87jfKg0myvNXqg8myvNXigz\nmx0HPvgAXn0VJifV2P79aqVeojJBP/1pD9u3dxMKkdmuXoWpKXV80yb4pV+CzZtLcrlFxU7YfHL9\nE/pCfZwbVulXtVYtz257lq9v+Douw1Ve7+8SsVw2O1IyHI9nOg2nnYGxRKLo+c2WlddboMPjod7l\numOHbinsTUwl8kXDQZvYtRgyWejkmDVmQVMyq9XCcJXOyanEz/VczOkgSCn/SAjxFtAMnMo5dA34\nu4s9MY1Go9FoFsT4OPT3q9v4Q6n+nJs3w5EjJVmpRyJw8qS6xAcfFC921NSk/JB9+8pbgCyl5MLo\nBXpDvZy8djJTotRtunli0xM8veVpqtxVyzzL1U80mWQglSKUdgYGYjFiTmFOvZVTTjTtCLR7PHjK\nMCogHUl8OI4dsokGoxmHIDFWxMkRYK2z8rUCHR5c9Xfu5Gjuntv2QSg3tAZBo9FoNHNi2/Dpp6q5\nwLlzSmMAaqX+/POqdOkCFhmOo6oP9faqy+RWf2xqgkBAbR0d6nHNmvJ0DKZj03ndjD8f+ZybMzcz\nxzev2UxnoJMDbQeodlcv40xXJ1JKbuYIh9PbjXTr7Fk0pITDHV5vxiFocrvLUjicjCaJDcTynIHY\nQAwnVujkGJZREBXwtHswPOXn5KxGFtQHQaPRaDSasmd0FH7yEzhxQmkNQAmOd+2Cri64/36lObhD\nYjFV/TSdMnTqVFZPIARs366amu3erbTO5YaUkuHIMMGJYJ5DkOsMpGmsbqQz0ElnoJPmmhUiklgB\nxB2HwVnC4ZBtEykiHDaFoC1HOJx2CmrKtJxo4mZ+ilA0GCU+PEc50TXuggpC7ia3Fg6XKdpBKHMq\nMR+u0myuNHuh8myuNHthCW2OROBv/gbefRfSOdmbNimn4MCBeYuPpVT90dL6gWBQPd64oaIGuaxb\np17+0CEVIYDyeI/thM3A5AChcCjjEMy3o/F6/3o21m+cdwpHOdi71MzH5nCRcqLXY7Gi5URrTTNP\nKxDweGj1eDDLJCqQa68Td4gNxgqcAWemSDlRl8DTVqScaE35OTmzqcTP9VzMy0EQQnwd2CKl/GMh\nRBNQO59GaRqNRqPRLAqJBLz/Prz2GkxPq7FDh1S50paW2z71+nXyBMXBYFZQnIthQHt7NnVo2zbY\nsGH504aklHw1/hWfj3yeiQrcmL5BsRRc3dG49DhSMhSL5XUcDto24SLCYUMIWlJRgVyHwH8XwuHF\nQkqJM+OQnEySmEiQCCcIHwtz7ctrKkXoegzpFBEO15l5ToC3w4vVYiHM8rBLc/fcVoMghPgtYD9w\nr5RymxCiHfgrKeVDSzC/YvPRGgSNRqOpVBxH5fm8/LK6vQ9q1f7CC2rlPovp6Ww0IL0NDkKR7A6q\nq7OOQFpH0NpaXk3MRiOj9A/00xfqy/QkSGMaJq21rVlnwK+cgVprBTRbKGMiyWRex+GgbTNo28SL\nrEW8OcLhtDPQ5vFgLbNwOD4eJ3opSiKcIBlO5j9OJElMJpDxuddWwhC4m90FvQVc/vJxcjR3zkI1\nCN9DdU/+GEBKOZDqj6DRaDQazdIQCqnGZseOqVwgUJGCI0dg504QgtFRuHw53yEYGyv+cs3N+WLi\nQAAaGpY/MlCMqdgUZ4bO0Bvq5fzI+cy43+tnX+s+NtZvJOAL0FLbgsvQmcN3i5SSkVQ50VxnYDRe\nPKd+rdtdUEWo0e0umwWzE3OYOjVFuDdM5PNI0QhALobXwOVzYfpMXH4XLr8Lqz1VTajNg2HpiFMl\nMZ9vEltK6aQ/8EKI0neT0cxJJebDVZrNlWYvVJ7NlWYvlMjmcFg5BH19atWfZt06eOIJePhhMM2C\nxsi5WJZKEUo7Ah0dat/jWdjUZlMKe6WU3Ji+oTQE4ayoeGwm6+W4TTd7WvbQFejivqb7li1NaKV/\npmOOw2COTiC9RYuUE3ULQbvHw+THH/ONxx7LOARVZSocnrk4Q7g3zOTHkzhRZY8wBTX31+BudCsH\nIMcRMH0mrjpXQeWgnp4euh/uXgYrlo+V/rkuJfNxEP5aCPEfgXohxH8H/D3g/1ncaWk0Go2mYpme\nhtdfh56ebC5QTY0SHXd1wcaNIATRKLzxqmqMHI+rIkU7duRHBZqalI6gnBmcHKQv1Ed/qJ/x6HjB\ncY/Lw8b6jRxsP8j+1v26H8EdIKVkoohw+EY8XlQ47E+XE82JDKyzLAwh6PnqK7obGpbBiuI4MQd7\nwM5vNBayM04BgHeTF3+Xn7oDdStCJKwpH+bVB0EI8U3gm6ndN6WUby/qrG49F61B0Gg0mtVIPA7v\nvafKlc7MqHyfXbtUHdFdu1TZUpTP8OGH+Y2RDxxQDcnWrl3G+d8Bk/YkxweP0xfq48r4lcx4vbee\n9f71eRqCpuqmsklbKWcSjsP1WeVEg7bNVBHBiSEErUWEw3Wu8k7RSkaSTJ6YJNwXJvpVtGjar1hm\n9gAAIABJREFUkHutm7oH6/B1+vC0lDhUpllV3EqDMB+R8j8C/lJKObAYk7tTtIOg0Wg0qwwpVf+C\nl19W/QxAhQKOHFFhgJzTTp+Gl15SVYgAtmxRp91zzzLM+y4YiYzw489/zMfXPibpqIVrlbuKA20H\n6Ap0cU/DPdoZmAdTRZqMDcZiJIusD2pMs0A43GpZuMo9tJRCJiXTv5gm3Bdm6tMpZELZKEyB1WLl\nNxkLeHDVlbeToykfFipSrgPeEkKMAX8J/LWUcug2z9GUiErMh6s0myvNXqg8myvNXrgDm7/4Al58\nUamLQQkEjhxRjc1yuHwZjh6FCxfUfnOzaoy8Z095CItvZ+90bJqffPET3rv8HkkniSEMdq7bSVeg\ni13rduE2y6hU0jxYqs+0IyXDKeFwMBrNOANjRcqJAjQXiQo0lKic6FLZnIwkVbpQUPUaiPwiQiKc\nsldAzY4afJ0+avfULmrHYf29Vdnc1kGQUv4W8FtCiN3ALwPvCyFCUsonFntyGo1Go1mlDA2pUMCp\nU2rf74fDh5XGIOfO7ugo/OhHSqsMUFsLzzwDjzySyTgqaxJOgp7LPbx+4XUi8QhCCLo6ujh872Ea\nqsonn70ciCaTDKRShNLOwEAsRqyIcNjKKSeadgjaLAtvGQqHb4eTcJj4cILI2Qh20CZ+s7BqktVq\nKS3BwTrcDSvLmdSsTOalQQAQQrQCLwB/G9UobddiTuwW89ApRhqNRrNSmZxUzc3ef1/1NPB44Kmn\n4Mkn80oLzW6Q7HbD44/D00+rfgXlTLqj8ZXxK7xz6R1GIiMA3Nd0H0fuO0KHv2OZZ7i8SCm5OStF\nKBiNMjxHOdEGl4sOrzfPIWhyuzHKIXS0AKSUTH0yxfBLw8SHs7YblpEpL+rt8OLd5MXT4dGpZ5qS\ns1ANwq+jIgfNwF8DP5RSni35LOeJdhA0Go1mhZFIwLVrcOYMvPkmRKMqSvDQQ/Cd76joQc6pxRok\nHz4MjY3LNP85kFIyHh3PK0larKNxW10bR3Yc4f6m+ytukRd3HAZnCYdDtk2kiHDYFIK2VIpQwOPJ\nOAU1KzAqcDtmLs0w/OIwM1/OAGC1WKx5eg1V91ThbnIjjMr6nGiWh4VqENYD/0BKeaq009LMh0rM\nh6s0myvNXqg8myvK3kQCLl6k57XX6G5sVN3Krl3Lb128c6cSELS1ZYakhE8+mXeD5GVhaGqIS2OX\n8hyC6ZjyYgbPDNK2U9ljGiatdaqj8fa12zkUOLRs/QoWi2Kf6XCRcqLXY7Gi5URrTTNPJxDweGgp\nc+FwKf6OY0MxRn48wuTHqvyWy+ei8TuN+B/2l51TUFHfWykq0ea5mNNBEEL4pJRh4F8BUgixJve4\nlPLmYk9Oo9FoNCsAKeHq1Wyn46kpGBzMOgBCqOZmgQB8/etw3315T710SQmQv/xSjbW0KP9h167l\nFyBPxaY4PqDKkV4ev1xwvMaqIeAL0NraylN7nlI/17Wu6o7GjpSMxGIcC4fznIFwEeGwIQQtRYTD\n/hIJh1cCyZkkkx9PEu4NM3NRRQwMy6DhGw00fLMB07v6IiSalc+cKUZCiNellM8IIS4DBSdJKTct\n8tyKolOMNBqNpkwYH4f+fuUYDA5mx9vaYOvWbLeyVOvieBwGBlRQIRhUjwMDquUBQF2dyjhKNUhe\nNhJOgjNDZ+gL9XHmxpm8cqQ7mnbQ4VP9CQK+APXe+lW90I0kkwzM6jg8aNvEi/wf9uYIh9POQJvH\ng1XGUYHFQjqS6bOp0qSnppBx9fsyLIO6g3U0PtuoxcaaZWdBGoRyQzsIGo1Gs4zEYqryUG8vfP65\nEhqDWt0fPKiamnV0ZG79JxJKetDXpx6LpJ7j98PXvqYEyF7vEtoCRBNRBsIDhMKhTOrQQHiAWDIG\ngCEMdjTtoDPQyZ6WPSuuHOl8kVIykionmhsVGJ1DOLzW7S6oItTodq9qZ2kunJiDPajKks7V0bj6\n3mp8XT5q99bqiIGmbFiQBkEI8dPZJU2LjWkWh0rMh6s0myvNXqg8m1e8vVKqfgW9vXDypBIZg6oz\numePcgoeeCBz219K+OFf9iBlN8ePZ8XGhqGCC+nAQkeHevT5ltocyemh07x24TWuTlwtek67r52u\nQBcH2w/i9/qLnpPLSnqPY47D4CxHIGTbRIuUE3ULQfssrUDA46H/gw9WjL2l4r333uPhvQ9nnYCU\nQxC/ES/a0dhaZ+Hr9OE75MPduPIcy5X0mS4VpbLZcRIYKzzN8FYahCqgGmiapT/wAe2LPTGNRqPR\nLDPJJHz4Ibz1FoyMZMc3bVL9Cg4cgJoaIhEIfalShkIhuHhRCY7TEoSODuVDHDy49M7AbK6MX+HF\nsy9yYVR1XDMNk7a6tkzKUMAXoMPXQY1Vs7wTLQFSSiaKCIdvxONFhcN+l6tAOLzOslZ8OdG7wUk4\nxK7H8iICgx8NcqnhUsG5whB42rOdjDMdjX0re4GouXNs+xrDw0cxDA9tbX9/uaezIG6lQfgHwG8C\nbUBOcimTwH+SUv7B4k+v6Lx0ipFGo9EsJlLC6dNKOTw0pMbWrFH1Rru6iPrX8cknKtPo6lW4WaRk\nhc+nTu/sVFGC5WY0MsqPz/+Y/lA/oMTFz257lq+v//qqSBtKOA7XZ5UTDdo2U0VyugwhaC0iHK5b\nCZ3nSoB0JMmpJIlwguREksRk/qN9zSY2GEMmC9caZo2Z7wh0eLBaLAx35eksNFkSiTAjI68QDv8c\nKR0Mo4pNm/43XK665Z7aLVloH4TfkFL+20WZ2V2gHQSNRqNZRC5fVo7BBXWHneZm+N73cHbv5fwF\nQW+vig7EYtmnuN1Kh5ybOnTPPXkNkZccKSU3pm8QCoe4ePMiH1z9gHgyjstw8fimx/nW1m9R7S7z\njmtzMJ1MZjoNZ4TDsRjJIv8bq02zwBFoK/NyogtFOpLYjZhKARqwSYznOwDJqWTRlKDZWM1WxgnI\nRAUaKqf6kub2OI7N2Ng73Lz5Jo5jI4SB3/8IjY3Plr1zACUQKQshHgB2ABn5mJTyT0s2wzug0hwE\nnQO4+qk0e6HybC5re6VU1YhCIVWi9NgxNV5bC888w/iuR3jvAxf9/TA2ln3a1q0qQrBli6pgOnu9\nuZQ2pzsXByfyG5alhcZpDrYf5Lntz9FYXfqOa4tlryMlFyIRPo9EMs7AWJFyogJoKhIVaFikcqLL\n+ZmWUuLYjlr0hxMkw0kSE4mMUDg2GMOJFeopcjFrTVw+F6bfxFWXevS5MH0mVpOF1W4ViInL+u94\nEag0e2H+NjuOTTh8jNHR10gkxgGord3N2rXP4/G0LPIsS8dCRcq/BTwK3A+8DnwL+BBYFgdBo9Fo\nNAsgElHpQ+k6o8FgVkUMKhzw+ONEu5/mrQ+reftfZKMFTU0qZejQIfXzUiOl5ObMzTwnIBQOMRwZ\nptiNo4aqhoyuYG/LXjbUl0nHtXlw3bbpDYfpD4cLHAKPYeQJhzs8Hto9HjyrICogpSQ+Eic2GCMx\nnsg6ALMeb+cAuNe4M3f+3Y3ufEegzoUwdRRAc2dI6RCJnCcc7mNq6iSOo74Yvd6NNDUdobp62zLP\nsLTMJ8XoM2A3cFJKuVsIsQ74cynlk0sxwSLzqagIgkaj0ZSERAJ6euD115WTkEtNjcoN2rAB55Fu\nPjzXyKuvQjisDu/bB088AZs3L13jMiklA5MDXJ24mhcZiMQjBeeuBqGxlJLxRIJPp6boDYe5nK4U\nhSopur+ujg1eLx0eD02rpJyoE3OwB+z8qkAD+eVB58KwjMxdf5ffhVlnYrVYmVQgs1qXEtWUBtu+\nTjjcSzjcTyKRDaNWVW2hvr6buroDK/bvcUERBGBGSpkUQiSEEH7gBtBR0hlqNBqNZnGQUpUmfeml\nbCWirVthx46sYKC+HongzBl46d/BtWvqtHvugRdeUI7BUjE2M0ZfqI++UB/Xp64XHK+1aunwd+Q5\nAy21LSuqc3HCcbiWEhTnlhmdzhEUew2DA3V1dPp8bKmqWrELEFDOT2IiMe/yoC6/C0+7B1ejK88B\ncPlVCpDL58LwrPxoiaZ8SSanCYePEw73EY1+lRl3u9fi83Xi8x3CspqXcYaLz3y+UY8LIRqAPwRO\nANPAR4s6K00GnQO4+qk0e6HybF42ey9ehBdfhK9S/+Da2uDIEbj//kwoYHwc+t/Kb4bc1ATPPw97\n9959xOBObLYTNp9c/4TeYC/nR89n0oV8Hh/bGrflOQR+j78sF8tz2TtZpMzo9TkExTWmyT1eL4d8\nPnbX1pZ1B+K57C1WHtQO2iSnCqspFZQHTaUEuerK09nT31urG8dJ8Oabf8KuXQmmp08jpfrMGoaX\nurr9+HxdVFVtKcvvn8Xgtn+FUspfT/34H4QQbwI+KeWnizstjUaj0cwbKWFiIqsrSG/XU3fgfT74\n7nfhoYfAMDLNkPv64Ny5/GbI3/oWPPqo6oG2uFOWnB89T1+oj5PXTmInbADcppvd63bT1dHFjqYd\nGKJ8F8m5OFJyLScakHYIJuYQFK9LCYpzRcX1iyQoXiwSU4l8RyB0h+VBWy0M18p4fzWrFymTTEx8\nyOjoawwPf87UVBtCGNTU3I/P10Vt7W4Mw1ruaS45t+qDsB+YM9lfSnlysSZ1K7QGQaPRaFJMTsJr\nr8GJEzA1VXjc44FvfENtXi+RCLzxBvzsZ9lmyKYJu3cr8fH99y++YzA0NURvqJf+UD83Z7INFLas\n2UJXRxf7WveVffnRaDJZEBUYjMWIFelE7DGMgi7EK01QLB1JfDiOHbKJBqMZZyAxVuj8IMBqsvJK\ng3o6PLjqV5bzo1n9SCmZnj7N8PBLxGLqZorH04bP10Vd3UHc7vplnuHic1dlToUQPdzaQXisJLO7\nQ7SDoNFoKp5YDH76U7XaT6/000LjtK4gEIDWVnC5SCTggw+UL5H2I2Y1Q14UEk6Ca5PXCIaVyPjL\nm19yefxy5vja6rV0BjrpDHTSVLMMZZFug5SSm4lEXs+BoG0zEo8XPX+N213QiXilCYqT0SSxgVie\nMxAbKF421LCMgvQgT7tH6wM0ZU80eoXh4ReJRFS/F8tqZu3a56mt3bOi/l4XyoL7IJQTleYgVFoO\nIFSezZVmL1SezSWzV0ro74cf/SjblGDnTnjuOdWpbNY/NilVKtHLL2cbIm/bpmQIGzcufDq5TNqT\nmUpDwXCQD372AVVbq0g6+bnnXpeX/W376Qp0sWVN+eTzxh2HwZxOxGmnYKZIVMAtBK2z0oO+7O3l\nW088sQwzvzuklCRu5qcIRYNR4sPFnR/3GndeilDflT6efO5JhFEe799SoL+3VjZSSmZmLjI+/jMm\nJ48DYJo1NDY+i9//CIbhWnU2346F9kH4VYpEEparUZpGo9FUHIkEnDmjSpQGg2ps/Xq10t++veB0\nx1Hagp/8ROmUAVpalPB4166FlSp1pMPQ1FCeMxAKh5iITuSdNxIZoV2201LbosqOpoTG2xq3YZnL\nl88rpSScmyKUcgSG4nGcIjeffC5XgVZgnWVhzvolDprlW1bTiTvEBmMFeoFkpIhw2CWwWi28Hd48\nh8CsybfPPemuKOdAs3KJxYYJh/sIh/uIx1UlNyHcNDQ8zpo1T2Oa5Z3SuFzMpw/CH5B1EKqAx1E9\nEV5Y5LnNNZ+KiiBoNJoKRUq4ckUpiY8fz+YGNTSoiMGhQwUr/YEBdXp/v9Isg2qI/N3vwsMPK73B\nnTATnyloSjYwOUA8WXiX2evy5vch8HfQVte2rM4AQMxxODM9zeWUIxCMRplMFi6MDSFoyREOpx0C\n32KLMkqMlBI7ZBM5F8mUE41djxUtJ2rW5QuHvR1erBZLNxHTrGgcJ0Esdo1o9BLh8DFmZi5mjrlc\nDfh8ndTXfx23u/Qd1VcaJU0xEkLUAz+UUj5VisndKdpB0Gg0q5ZkUuUCnT6tVvrphgSgUogeegge\neUR1O04xOQnHjqnTr17Nnr5undIYdHdDVdWtLyulZHRmNK8hWSgcYiQyUvT8xurGTDOytEOwtnpt\n2aQLSSn5YmaG3nCYk5OTRGelCVUZBh1eb54z0GZZuFeQcHg2iYkE4WNhwr1h7AE775gwBO51+SlC\nnoAHl18LhzUrG5U29AXR6BVsO4hth4jFrmdKlAIYhkVt7T58vi6qq7chVkhltKVgoY3SZhMBNi1s\nSpr5Umn5cFB5NleavVB5Nhe1NxJRpUhzS5MODqp0ojQ+Hxw8qEoMdWT7U8bjKuOotxc++yxbprS6\nGh58UJ2+aVPxVCJHOlyduKrSg1IOwcDkADPxmYJz3aY706E47Qy0+9rnVWVoqd9jKSXXYzGOT07S\nHw7nCYk3eb08UFOTcQrWLEI50eX4TCejSaY/mybcGyZyNpKJEpg1JrX7avFuTKUJtXkwrNIuiirt\nbxgqz+ZytzcS+YLh4ReJRi/POiKwrBY8ngA1NQ9QW7sX0/TO6zXL3ealZD4ahFdzdg1gB/BXizYj\njUajWU1IqQTFJ0/mOwQ3bxY/v6lJre4PHlTdjlN5QVKqfmfpjKNIRJ1uGEpX0NWlHufKiBkID9Ab\n6uXYwLECvQCopmS5Dck6fB2sq11Xln0IYo7D4KwuxCHbzosUrHG7OVRXR5ffzzprZdcwl1ISH40X\ndiIeyTpBwhTU7qnF1+mjZmeN7i+gWbXEYkMMD7/E1NQpAFwuP7W1e/F4Ang8HXg8bRXZt6DUzEeD\n0J2zmwCuSCmDizmpW6FTjDQazYqgWAmhXCxLdTZOlyRNb14viYQKJqQDC8Gg0hdMT2efvn69cgoe\nfFA1OCtG2A5zfOA4vaFeghPZr+2mmiY21W/Kcwh8Hl+JfwELR0rJRJFOxDfmEBT7XS52VFfT6fNx\nb3X1ik+fiQ3HCPeFCfeF85yBNMIl8K73UnewjroH63DVriy9hEZzJyQSk4yOvs7ExPtImcQwLBoa\nnmLNmm9gGJ7lnt6KpCQaBCGEj5yIg5Ryjttfi4t2EDQaTdnz1Vfw4ovZEkI+n1rR5zoDzc3q9n+K\naBQ+/lhFCL78UskRZlNfn804am/PPxaJR7KVhXK0BI5Ud9VrrBoOtB2gM9DJpvpNZbd4TjgO13PK\njKYdgqk5BMWtRToR160wQXExkpEkkycnCfeGmbmYTfsya0286715PQesdVpQrFmdKKHxILYdymzR\n6GUcx0YIA5/va6xd+11cLv9yT3VFsyAHQQjx3wP/ArCBdPxWSinvKeks50mlOQiVmA9XaTZXmr2w\nim0eGVERgxMn1H5tLXznO/Qkk3QXqZHvOPD550pLcOqU6n8Gym9obs7veRYIgN8PIBmODOeJiYMT\nwbyuxGlMw+SB5gfoDHSya90uXMbSLaBv9R5PJ5N5zcfSnYiTRb7ba0yzoLJQq2XhKjNB8d18pqUj\niV2P5aUORb6IIOPq92B4DGr3qbSh6nvLKyKyav+Gb0Gl2bzU9sZiI0xO9jM5eZJY7Fqe0DhNTc0D\nNDUdweNpW5Q5VNp7vFCR8v8CPCClLF7OQqPRaCoZKVX5oJ//XG2JhKoy9OST8NRTqoRQT0/eUwYH\ns+VIx8ez49u2qbShffvA6wU7YTM4OUgwHOR0METoFyEGwgNEE9GCabhNN+117XllRgO+AF7X/MR5\ni4EjJcPxeF6/gZBtM5YrxM6huUhUoGERBMXLQTKSxB7I6gfskI09aGecgQwCqrdX4+vyUbe3Tncl\n1qxqkskoU1MfMzHRy8zMF5lxIYyM0DirLQjgdtcv42wri/lEEN4CvielnL7liUtEpUUQNBpNmTI+\nrlb4fX1qxZ+msxMOH4Y1a/JOn5xU4uK+PtXeIE1zs3pKZydU+SKcGDzB+ZHzBMNBbkzfoNj3nd/r\nzysxGvAFll1QHE0mGUilCKWdgYFYjFiRTsSWYdBuWXmlRtstC28ZNxubL1JK4iPx/KZkQZv46Bwd\nitfmlx/1bvLirncXPVejWQ1I6RCJnCMc7mNy8hOkVH8bqhzpXny+TqqqNmtdwRKw0BSjfcCfAL1A\nKgCOlFL+RiknOV+0g6DRaJaFWEw5AlevwiefqFbF6e+iujolDnjooYw4IB5XbQyCQfj0U1WONJ1O\nX1UFBw6oaMGGjUnOjvyCvlAfp4dO5zUhMw0z24k4xyGo88yhSl4CpJSMpYTDuVWEbqTzo2bRkNuJ\nOOUQNLndGCs0KiClxIk6JMNJEuGEepxIEBvKpgo50UKnSLgFnnZPQS8Cs2rlO0UazXyw7UHC4V7C\n4X4SiWwlterqe/H5Oqmt3TfvcqSa0rBQB+EE8D5wBqVBECgH4T8vcFKXgTCQBOJSyoNCiDXAD4EN\nwGXgl6WU47OeV1EOQqXlw0Hl2Vxp9sIKsfmrr+D8+WxZ0hs3sg0HQNUTTdUXnVx/P8FBM1N1KBRS\nzkH69MHBHgKBbu6/P1uO9HokSG+ol+MDxwnbYUB9Wd+39j72t+1ng38DrXWtS6obmE3ccbiWjgqk\nHIEB22a6iHDYFIK2nBShwf5+jnzzm9SUaVRAOhLHdnBsB2lnf07vJ6eUA5CYSOQ7A+FEYVoQ0D/Y\nz6G2QwC4/K6MkDi9WesshLEynaJirIi/4RJTaTaXwt5EYpLJyeOEw71Eo9lOjpbVjM/Xhc93qKw6\nGlfae7xQDYIppfyfSjwnAAl0z6qG9APgbSnl7wkh/nFq/weLcG2NRqMpzrVrSmj86af544aB09pG\n2NfBtZotfOHbz+XhGkJ/BhOFbQUQAlpalLh4chJ+7ddAWhMcGzjG73zURygcypzbWtdKV6CLg+0H\naahqWGQDixPOKSeadgiux2JFy4nWmmZGI5DeWmYJh3uqqkruHDgxJ7NQd6LOnAt8J+ogYzJ/f7YT\nUGSRP18Mr4FZZ+Lyu3D5XJg+k/pQPYFnA6pDcd3Kr6ak0dwtjpNgevo04XAf09OfZcTGpllNXd0B\nfL4uvN7yq6SmyWc+EYTfBq4Ar6AqGQELL3MqhPgKOCClHM0Z+xx4VEo5JIRoAXqklNtnPa+iIgga\njWaJCIfhtdfggw/AcUi4vAxv6WTQtYHLiQAXp1sJXncTL5JK7vXmtzIIBFSLA48H4sk4p66foi/U\nx9nhs5myo7VWLQfaDtDV0cUG/4Yl+2fpSMnQrKhAyLaZKCIcNoSg2e3OEw0HPB78JRQOSylJTCRI\njBfeqZ+dxlMsdeeuEapKkOExMLzqUVhC/WwZGDVGngOQ+6iFwxpNPlJKotHLhMO9TE6eIJlUslUh\nDKqr78fv76KmZheGofU15cRCU4wuo+725yGl3LTASV0CJlApRv9RSvmHQogxKWVD6rgAbqb3c56n\nHQSNRlMypB0j/NI72K++yczNKFMRg8/WfJ2PGp4lahU2D1u7Nt8R6OiAxkYVMci8ppR8OfYlvcFe\nPr72MTNxVc/eNEx2Nu+kq6OLB5ofWPT0oUgyycCsbsMDtk28yHeo1zAKKgi1eTxYJSwn6iQcYoOx\nfAFvyCY5XaTpQxGES2QW6kaVkV3gewyER+Qt9vMW/LPP8RgIt9B3MDWaBRKP3yQc7icc7iMWu54Z\n93g68Pu7qKt7EJer/JowahQLSjGSUm4s+YwUD0kprwkhmoC3U9GD3OtKIUTFewKVlg8HlWdzpdkL\ny2dzbDrOjU8GuHk6xNS5ILFLIcRACGGrsqEDjbs4uel5wtWtuN2woS3fEWhvh+rquV9/JDJCX6iP\nvlAfw9PDmXHnK4e/852/w4PtD1Jr1ZbcLiklI6lyorkpQqPFwh3A2lRUINchaHS7S7pg/ulPfkrn\nps5MFR87ZBO7HkMmC7/WzRoTd6M7/06935VJ40k/GlVG2S7qK+3vuNLshcqzeS57HcdmcvIk4XAf\nkch50veQXS4fdXWH8Pk68XoDSzvZElFp7/GtuK2DIIT4VYpHEP50IReWUl5LPQ4LIV4GDgJDQogW\nKeV1IUQrcKPYc7///e+zceNGAOrr69mzZ0/mDe1J1RtfLfunTp0qq/ksxf6pU6fKaj7a3tLvp1ms\n13/00W4mJuDll3sYviG5J9qM//1XOfvlR+BI9taoJjufTqvypFs3fo3hh5/nsuca9zSf5/DhVlpa\n4P33577edGyao39zlOHpYdbuWEswHKT/w34A2na20VDVQM1ADTuadtC4q5HuTd0lsS/uOGzt6iJk\n27z57rsMx+N49u0j6jgM9qeuf0iJZW8cO0aj280j3d10eDwM9Pez1u3m6VTTtp6eHiaAvQuYj3Qk\nX7vva9ghm3ffeJf4cJx93n0MnBvgKEcBMuLd/mv9uBvcPPrwo3g6PBy7dgx3k5snnnkCIUTx600v\n/+dV7+t9qLz/x7Pt/elP3yAc7ueBB0ZxHJv+/kGEcPHEE8/g83Vy/PgNhDDo7g6UxfzvZn+1/z8+\ndeoU46nmO5cvX+ZWzCfF6A/IOghVwOPASSnlC7d84q1fsxolfp4UQtQAb6G6NT8JjEopf1cI8QOg\nXkr5g1nP1SlGGo0mQzKpdMW5FYRCISUMbpgKsu+ro7SMnVMnGwZOcwvmxgDVWwP4H+igeV8AX2Du\nELiU+Z2LgxNBQuFQ0c7Flmmxt3UvXYEu7l1774L6EkgpmcgRDqf1Ajfi8aLCYX+qnGiuVmCdZZW0\nnGhyJlmQHmQPFGn2hRLy5pX07PDgafNgWHf/O9FoNEuP4yQYH+/h5s2fZLQFVVVb8Pm6qKvbh2ne\nIqyqKWsWpEEo8mL1wA+llE8tYEKbgJdTuy7gz6WU/0eqzOlfAevRZU41mopAStViwLZvvUWj2fOi\nUbVdv66cg9n62mp7jAevvcL94V5qayRVjdW4vvttGp57FHeNNedc7ITNwORAniMwMDmAnbALzrVM\ni3Zfe0GPAo/rzpv7JByH6ynhcK5DMFWknKghBC2WlXEE0o91rtLpGaSUxEfj+V1/QzbxkTmafTW6\ns05AyiFwry1typJGo1lapJRMTZ1kePhl4nGVMlldfS9NTS/g9a5f5tlpSkGpHQQL+ExKGzMgAAAg\nAElEQVRKua0Uk7tTKs1B6OnpyYSHKoVKs3k12ZtMwtCQuoM/OAgzM8UX++fP99DS0o1tq0X/Qv+k\nm5qURmBT3Qhbhz6g5ey7eEUM4TKhuxueeQZqagqeF0/G+fDqh3xx8wtC4dCcnYvrvfV0+DvynIGm\nmqZ5Rwhy3+PpZDLTaTi9DcZiJItct9o0C6ICrZaF25jfdaWUyITMlAQtVu8/dz85mcxEBZyZOZp9\ntXoKavyb1YXlTFfT53o+aHtXP5Vis5RJpqc/4/XX/x179qi1o2W10tR0hJqaB1a1418p73GaBYmU\nhRCv5uwawA7UXX6NRlPBRCLZdJ50L7HBwcK7+cUYH88X+1qWKgk61+b1qkfLyv+5qQnaG6N4f/Ex\n9PbCyS/UCxrA/v3w3HPQ3FxwfSklxweP8/K5l/NShUzDpLWuNeMMpLe7ERY7UjKcEg5/OD7OZ6EQ\nIdtmbI5fULNlFVQRakhFBRI3E9iXbeKjM4Sj07ds8JWu++/YqheAdO7O+3L5XPnpQQEPVsvqaval\n0WgUUkpsO0g43Ec4fIxkchLbvobLtZ3Gxu/g9z+MWEDKpGblMR8NQnfObgK4LKUMzXH6olNpEQSN\nphyIRuHcuawjEAzCzTk6oTQ1qao/7e1QW5u/oM9d7Kc3y4J53hBXIYrJSdWzYHQUTp6ETz4h05zA\nsmDvXhU1uOeeoi9xYfQCL559kSvjVwAI+AI8cc8TrPevp6W25a5Kj0aTSQbSvQVS0YGBWIyYU3gX\n3jKMggpC7R4PHsPAieeXAY0Go9ih4nfz54twi+LlQHP307X/q41MhMDl082+NJrVjOMkiMWuE4mc\nJRzuw7YHMscsqxW/vwu//1FM07uMs9QsJncVQRBCbAXWSSl7Zo0/LITwSCm/LO00NRpNOeE4cP68\nujH/yScqFSgXy1LNwDo68vsCeO/0f4njwOS0akccDhff0sempoq/xrZt0NUF+/YVnYCUklA4xKsX\nXuXT66pDcr23nsPbD9MZ6Jx3qpCUkpuzOw5HowzPUU60IS0c9nozDkGT240hBIlwIpXjP8PN0DjR\nYJT4ULzoHX+zzsTb4cW9zq0W8945egAUq/ev7/hrNBVPMjlNNBrEtkOZLRYbzHQ5BjDNWny+g/h8\nnXg861d1KpHm9tzqFtHvA/+kyHg4dew7izIjTR6Vlg8HlWdzudl77Rr09UF/P4yNZce3bFFb2iFo\nbr7Nnf9IJH/RPzGh7v5PTNDz8cd0r1unxicnlZMwH4SAujrw+dS2ZQt0dqpOZSlyhca5W1po7HF5\neHrL0zyx6YlbCorjjsO1Ih2HI0WEw6YQtOWkCKWdghrTRCYlb7/8NlvXd2IHJxhMRQcS4cJUI2EI\nrFYLT8CDt8ObzfH3mSvun3W5fa4XG23v6mcl2CylJB6/gW2H8hyCRGKs6PmW1YzHswGf70Gqq+/H\nyImgrgR7S00l2jwXt3IQ1kkpT88elFKeTlUh0mg0q4SpKTh+XDkGuaWRm5rU+ruzU3UQLorjwPBw\nNv8ovY0V/4cEKLFCbkiitja76M/d/H7lEPj9ar+2NuOVSCkZj44TDAcJfdGfcQRuJTTe3bKbZ7c9\ni8+TX9Z0MhUVyHUErsViRcuJ1ppmnmg44PHQYlm4DINkJFsGdDI4yUjIxh60uX71OtfaruW9jlE1\nqwxowIOn3YPh1nm+Go3mzojFhpiY6GVysp94vDD/0zAsLKsdjyeA19uBxxPAstp1+pBmTubUIAgh\nLkopt9zpscVGaxA0mtKQSMCZM8opOHNGpfcDVFUpfW9XF2zerG7aZ4hGYWAgX5k8MFCYfwQqB2nN\nmsxiP1lbQ7ymilitF7vaQ7TaYqbGIup1YZPETtpEE1HshI2dtG/7OBOfIZYsvK5pmLTWFhcaO1Iy\nlFNONO0QTKSFw47EtMGMStw2NCdMWpMuWhwXTQkXjQkTrw0yKknOJHEiDs6MQzKSVI/ThdEFAHeT\nu8AZcDfqMqAajebuSSanmZw8wcREL9HoV5lxl8uPx7M+zxlwu5u0yFhTwF2VORVC/CXwrpTyP80a\n//vAk1LK/6rkM50H2kHQaG5PIjF3Gn96u3YNplXPGwwDduxQkYI9e8DtkkqFPLtM0fBw8QuuWZPJ\nPbrZWM0xMciJ+BWm4tOZBX3SKb54Xgi1Vm3GAUg7BGmh8UwyWeAIDNo28dT3hzkjaTgbp/F0jJox\nSX3coDZhUGuY1JgmNaZxx03GhFvgaS9SBtRbWAZUo9Fo7pR0CdJwuI+pqdNIqW5uGIaXurp9+Hxd\nVFVt1TcfNPPibh2EFlQzsxjwcWp4P+ABvielvFb0iYtMpTkIlZgPV2k2L9TekRGlFzh/PusERCLz\ne257u4oUHDwIfhGGY8fg00+VQzAzU/gElwtaW7NChI4OaG8nYglODJ6gL9THlzeL1y8wDROP6cHj\n8nDtzDW2H9iOZVp4XB7chgeXy4vL9GKYHkzTQhipR+HGMC0QbjDcCOECwwXCBYabuJTEHIe4lMSl\nJOo43IjFGCkmHHYkGy7DpjMOjecT1EqDGsPEaxiQ+oo0qgzMajPv0ag2MKvm8XO1WVQUXGmfaag8\nm7W9q5/lsrlYCVKFoKbmPny+Lmpr92AYczeBvBv0e7z6uasqRlLK60KIrwGPAQ8AEnhNSvnu4kxT\no9HMl2gUPv5YpQdduFB43DRVZk9u+v7sbc0aWOuPw+nT8P/1wi9+kS8WrqsrLFHU0gKmyXRsOpXz\nH+TLz3s4PXSaeDJOApOYu5HWxl001W/DY/mQwsQRJg6CmOMQk5LkjY8Yazuk9h0HJyERSRAJiYiB\nkQCRVGNGMvuzSMYRyVhqLGfcASP9GkmwkpL1jmCt4aJRuGg0XDQkTbwXYogpBzDBbVJ9bzW+Th/V\n26rVIt+rq/5oNJrlZbbQeHr6dNESpHV1h3C765dxpprVzB13Ul5uKi2CoKlcpFSOwKwCQHz1VfHS\n/wcOKCGx36+akBWNMDtOttXx+fNw4kQ2UmCasHMnHDqkxAc+HxKI3Yhx9fOrfHH+C0YmRrg5dZOp\n6BSJpEVMeok5HhKOB497DV7TT61ZgyspEA6IxKxFfDK7iDcSUp2TVHM1AAOBIQSGAJPUoxBzHjMQ\nmCJ7zEy9jscwqDLMor8Da52Fr8uH75AP9xr3orx3Go1GM1+klExNfUok8gui0SCx2ACOk6+v0iVI\nNYvBXaUYlSvaQdCsFiYnVSbP8HBxjUA4nHUCinHvvSo9aO/eW/QeCIdVqCGtJRgYKHzRDRugqwtn\n5z7ssJWpwjN+aZzQFyGu37zBRNwmIVzEhYsELhLCjct04zLcuA03HpcHU5gYAmpycvjdwsgs5Ist\n6NViHwzTQLgFwiUQpnrERO2nx8z843nnFDkmzMLjnoAH70av/ueq0WjKgpmZLxkePsrMTH5qpsvV\ngMcTwOMJUFV1D9XVO/JKkGo0pUA7CCuYSsuHg9Vnc+5N+1y978SEOj442ENbW3fR53o82Wqf6dSg\ntWtVP7Cc0v+F2Da88w68+ab6OQe5ppFE43psz3rs+i3YM7VEg1EiQzZTcZvR6CTXZ8YYi0WJYxKu\nE4SbgdZqrLpqvFYVLo9FjeWiyWvx/7d358Fx3vd9x9+/ffZ49gZxg1iIpMRDh0VKoiRSrm/Hjqdp\n4ziJ07SJ6x5/dKbNuDNJmjSdHm477STpH3GajJs/mrRJW9uZpq3tOk7suLVdW6aoy5QoSjQliwfu\nc4G9n/PXP54HywUBUAQFElg835dmB4vneRZ6PnwWwPPF7xowkwymkwylk/Slkxjx2OY38OHzbz/9\nbd7/gfcH+w2152/Y99p7+lZELbPk3fu2M7Ntz7Gw8EWq1WCIZzxeoKfng5jmQUxzDMPIbsv/5+2Q\na7z33dYYBCHE1jUa12cBXS0GpqY2bgkwzaBbf19fMHvQRmMFUpuv47Ux3w+WPv7Sl2BlBUfHmD74\nBMv5e6lbRRo1E2fGx55wqTsWdXeahmfT8lwsXMq9NuVRl+V+l5UBDzWWp29wmAeLQ9xjptfM/5+P\n3/6PDyNtEEvJlHtCiGjxvDqLi3/K8vK30NojFkuyb9+H2Lfvw7ImgdhVpAVBiNugNSwurl0bbHw8\n2LaR/v61Y31LpWDbdv3hXGvNytnzjP/Jt5md8Si3CtR1H67qA+P6zBaudmk6TZbjDRb6WpQHgmKg\n3O/S7LVIJ2AoleNEb4n3Dj/AkWyRkXARMCGEEFuntU+9/mo4Nek5tHYARbH4FH19H5WBxmLHSBcj\nIbbJ9HQwc9DZsxsvFJxIwP79ayf/GR0NBg3fDt/2cSsuXsVrf3SWbJbGF1gcX2J5rk5t2aZR9Vld\n6wvDCGYgMtPB1J39MZb7akzlZpjOTdPsq6OzTfpTaQ4X93NfYZgjxVEOFu+hx+zZ8919hBDibmi1\nJqhUnqFafRbXDfuUoshmH6K//2OYZmlHz08IKRC6WNT6w8Huy1yrwXPPBYXBlSvXtxcKawuBsTEY\nGgoWHduKzry+41M7V6PyTIXmD5s4DY+a51F3XOqVCvValbrj4BO0YoAO/tManfBxSjFaR5K4g3Xc\nvmWs/Axldw7XD6qHVDzFyZGTnC6d5mjf0R0rBnbbNb7TopYXopdZ8u59m2XWWuO6y1jWRMfjGrY9\n1z4mmRyiUHiKQuEUiUTvXTzr2yfXeO+TMQhC3CLPuz6geHw8eFy6FGwHSKfh5Mlg9qD77tueLkJa\na+qX6kw9XWb+uQq1ukPd86h7Pg23haWrWH6VlmnRKjg0UzY60UClqpCp4/dYOP0Wdq+/fg5/O/gB\n8MDAA5wunebR4UdJxbc6sEEIIQSA77vY9nRHITCOZU3gefV1xxpGlnz+cQqF05jmIWmdFV1FWhBE\npGkNV68GXYbeeCMYUNzuqhOKxeDBB4OBxI88EnQjejssy+Xa5Rozl2ssXGvQPN/AWrDxfA2uy0pf\ni6ulRWaKU3hehd5amYFqGTPWojmYYGUshZcxUEqRT+YppAoUUgWKZpF8Mk/RLLa3FVIFesweMonb\n7OMkhBAR5zjLLC39Oc3m69j2NFp7644xjGx7WtJUaoxUqkQyOSJTk4pdTboYCXGDcjkoCs6cgZmZ\ntfv6+9d2Hbr33qA70a3QWuNbfjBmYMVlpWwzs9BkfqnF8kyLxngLd84B1w+mNnIdcByspE15aBa7\n+CYJ9wqDlSUGqsuk/RazD43hPHGSfYffQalQYn9+Pz1mD7lkjpiSwcNCCHEneF6LcvnrlMt/0bFw\nmSKZHOwoBoKCIB6X8Vui+0iB0MWi1h8O7kxmxwmmH712DV58ES5eXO3DH9z8nzoFJ04EhcGmi46F\nfNen/koda9zCqwaFgFNxWVmyqSzb1Jsudd+j5no4WgMaLBtsK2iecB2MVJ1UukI6vsDFuad5rDCH\n6dSp9qSpDBToPXqCgyfex/DJ91BM79tzv3ii9r6OWl6IXmbJu3do7bOy8l0WF/83rlsBIJ9/jPPn\nc3zoQz9NLBaNbpp7+RpvJmqZZQyCiAytgwXIblyUbG4uWCJgVSIRFARPPRV0H3qrgcVaa1pXW1TO\nVFg6W6FatYPBw55PzXNp+H674PAT4OQUTsoFr0qhMU8uvkA6NUfOHydjvUEj1mCpaLLQn+VKT4vq\nk0foP3KcU4fezQdHHiOdSN+5fyQhhBBrBAONV2g232Bx8SvY9jQA6fS9DAz8NOn0fVy69K3IFAdC\nSAuC6FqeF0w7uloMrBYEtdr6Y2MxGB4OugwdOxasRPxWU49qrZmZazL+9BJLZ1ZoTFvUPR/L92kM\nx1g+mggKgXwMJ6co9CQZSfuMzk5QOv8yg69fwlseZ742x2TG49p9/SwO5ij356jnU/Rm+hgrjnGw\n5yBPjj5Jf6b/zvxDCSGEaAsGGs+sGWQcDDS+/ssjkRhgYOBj5HKP7bkWXCFWSRcj0fXq9fWtAtPT\n6wcUQzDTUOcYglIpWJvgZoOLLd9n0rKYsCwmKk3KL1Zxn6uT+aGDCt9uTk6xeDxB5TGT3lKKUqPB\n2NISpZkZRq9dwxwfx2vUKTeXmK3PMuNXuXy4n8vHBqmXBjkx/AgHeg5QKpQoFUoycFgIIe4wz6vT\nao2vmYLUtqduOtA4l3uEYvE9MsBY7HlSIHSxqPWH83344he/xYED71tTDGy0KBnAwMD6YqC3d/Pp\nR7XWlF03KAQ6HnOWRe6yR/85m32vOhjheLREMkb8WJz8EYf9hSXGZqYYuHqV2OwsttOibtep2TXq\nTp26XWcp4TI3lOfysUGmD/XzwMjDPFV6iuNDx0kYG1coUbvGEL3MUcsL0csseXeW1j6OM49lTawp\nCFx3o18etzfQeLdlvtOilheil1nGIIhdybLWdw+anAwWI9u/f+2xyWSwIvHqgmSrKxTfbECx6/tM\n2zYTlsV4q8VUucX8bBNv0SW57JFasEkuuvSXXUpLHvmmR851yToOhXyV0d4ZBtPjxK7VaLzZoG4H\nRcAFu0bNbbBQiFPuy1Luz1LuH6Tcn8POmpQKJU6XTvHk6JMUUrc4/ZEQQohb4nktbHtyTTFg25Md\nMw1dF4ulbigESqRSozKWQIi3IC0I4o7TOmgBuLGL0Pz89ZmEOu3bt3Z14lIpaCm42UDiiuMwvtBk\narrO7FyL8myL+oJFfMklNdciuehgNIIpRROuS9a2ybpuUBC4LhnPI5myyAzMEe+5ihVfpG7XqNt1\nlmMWC70Zlvuz7YJguTdL0sy0uwuNFcfaU5AmjeSd+8cUQoiICAYOL63pHtRqjeM48xsen0j0rlmH\nIJUqkUgMyBgCITYhXYzEXeO6wWJjnS0DExPBGIIbGUbQUtDZPahUglxu86/veT5T43UmL9dYuNqg\nMt6kPmejl1xiLgRTilrQbIJtk3Ycso5L1nXI0iIXq5KOVSDVwM3bWAWXZtGm2tNi3qwxG2/RyiRo\nZpK0MkmamSRO0qA/O9AuBlYLgr50n/ziEUKIbeD7DrY9taYYCAYON9Ydq1ScVGr/DQuTjWIY2R04\ncyG6lxQIXWw39YfTOpghqFJZ/1heDroHTU+vnU50VS63fqzA8DDEN+jktpq56XmMt1pMvlZl6bkK\ntctNnCkLnPWvMRyHlFslac2Qdhcw9Tx5dxY/WWG532VmyGZhOEG5L0e1aGKlExsOVEgYCUbzo2uK\ngdHC6B0dULybrvHdErXMUcsL0csseW+d61bWzB4UdBGaQev1vzwMI98uBExzdYXiYZQy3maCrZNr\nvPdFLbOMQRC3TGu4fBnOnw9u+lcLgJUVqFY3vvnvpNT16UQ7C4Ji8eYDhxcdJxgrYFn83/l5vvX8\n66jnG/S95GAurf2fxvYZGAMesdQCSfcyfVefJT97EcuvgtKUR3K8fGyQyQO9VHv62//jdCJNMVXk\nQKpAYYNHf6afodyQrE4shBDbQGt/w+lEVxcf66RUjGRyZM1YAdMcwzAK0lIrxA6QFgQBwNISPPNM\n8Jid3fy4bDZYefjGR7EIIyNBl6HkBl3wXd+n4nlUXJeK57Hsukx1zCLUsjzScx7ZSY++8w75qx4x\nBWmliKWa+KNzxI1L5Jdewpx6g1hjbbNzK5Pk6rFh6o89TPHwQ5QKJQazg2sKgM1mERJCCPH2eF5j\nXfcgy5pC6/VNvrGYeUP3oBKp1H5iMRm/JcTdJF2MxDpaw+IivP46nDkDP/jB9X3FIjz+eHCz31kA\n5PMbdwlyfZ/Xm03KrhsUAI7LSsulZrnUwo8tyyPmgXI1MQcMR2PO+WRmPdIzHrkFD9N1Ma0GiXqF\nRGOJZPw1jNhLYE6j1Npr7mcyqFKJ5IF7yRw/Se/j72akOEpc5q0WQog7RmuN4yx0FAFBy4DjLG54\nfCLRv2460URCxm8JsRtIgdDFtqM/XKvmM3HBYfqaz/S4ZnZKMz+tsZuamO+jtCapNIfv1TxwRFMa\n1uD5aEejXR18DJ/7jt/+fKlpM1FvMVO38Wwf5elgoLAH4ONrHT48tPaI+R4x30X5LjHPJtFqYtZr\nZGpVss0mRmwZZS7zff88j442UIYLSuEP9BMbu4f0oaMUDz/E4NHHKA4fQN1sWqMuErU+jxC9zFHL\nC9HLvBfzau3Tal3r6B40jmVN4vstzp6d4tSp6/NRK5UglRpdN6WoYaR3MMH22ovX+Gailheil1nG\nIESE72uWxl0mXrSYu2BRvmTRuGrhLTjgXy+q0sA9QCIJhYxH3z6P/n0+xpwPMx5l38dzHTzXxvMc\nPNfBd118z6HpeywSYzEWp6VioH201piOhelYGK6D4TnEfYuEb5PwLFJui7h2UMoD5RE0JXiQrIFZ\nhv4yiXQDI5vCHh7AcEbo+ZEP0nv0BINHHiGVlbUEhBDibrGsSVZWzlCtPovrrqzbH48XSadT9Pa+\nv10IJJNDKBm/JcSeIS0IXcq1NRMv2Uy91GLhNYvqmxatcQtdX798PDFFoi/OvlyD3uQKxdgKOV0m\n1ViCVh1XW9h+k5bfwPIbWH4d229RS5ssZ9OUczkW81mW8lkqGRM/pvENTcprcXj+CkfnrtBfXwpu\n+pUPyseIGcRjBvFYnISRJBFPETfTJMwscTNDMpMnMTRC8sC9pA8ewbjnQLDYgTQ7CyHEXee6FarV\n51hZOYNljbe3JxIDpNP3rllbIB7P7+CZCiG2i3Qx6nKVOY/xFyxmzrcoX7KoX7FwZmzw1v87qLRB\neiRGb3+Vod4lhgrTDMSukZifwLVarLgNZnCZw2Eu5jOfUCyn01TSaepmmpqZoZ4yqaez+IkUyjBQ\nRpyYEUcZBsmYwVHP4hHf4f5EDDOdI2lmMdMFUpk8qXQeM5MnbmaC0cqJRPDRuPtT0gkhhFjP8+ob\nDCieaE8zahgZ8vknKBROY5qHZLyAEHuUFAhdwvc10686TJ6zmH/VYuX1FucufJuj+vENjzd6ExRG\nXAb6VxgqzjGcnSDfvAaL80wb8EZS8WYqzhUzxZSZYiFjUslnsMw4ViqBZcZxkgZm3CSbzJJL5sgm\nsmSTWcx4mt54nFIqRSmVYsw0KaVSDCQSxO7wL4uo9QGMWl6IXuao5YXoZd7NebXWtFpvsrJyhkbj\nAo6ztO4YpWJksw9TKJwmmz1O7C0mfNjNee+UqGWOWl6IXmYZg7CLTV2wOfeFCgvPN7AnLXDWzvmv\n6x70xEgNx+kdqDPYV2a4MM1g4hqp8gROq8VUOs2bsQTfsF3eTBtcu3+USiaFZSawUnGsdPCRuEEu\nkaE/lWHIzDOa6WEs28dgKkMhHqdgGO2PxXictPzVXwghupZtL1CtnmVl5QyOM9/eHoslSSZHb1h8\nbBTDMHfwbIUQu4m0IOyA6oLHi5+vcvXPKtiXm2v2xYpxcsM+fX0VhnsXGM5Oss+7Smxhjkosxngm\nw0T4uJY2uZJOUk64LBsuLTMetgrEyRgxxkyTezN5Hiz083DPCMeKoxTiCWkuFkKIPUZrjeuutLsL\nNRoXaDQutffH4z0UCqfJ558gldovA4qFENLFaKe5LkxNasa/U2fiaxWqL9XA0YAmpZoMHq5z37F5\n9ufHyaxcxa/VmEmnmUinrxcE2SwrhQK2maCZirFsOMxQw4lp0rpFnhYPF4d59/D9nOq/l7HMPmJ7\nZBpQIYQQa2ntU6+/SqPxWrso8LzammNisSS53KMUCk+RyRyTokAIsYYUCHdRtQoTE9cfcxdaeOcr\n7Jupkm1UyNhlUk6dnuI8peHL9N5XZrbHZCKTCYqBdJrpfB4rl6WVMrh68QLmyYdYMRxabo20VyOr\nm+R0nazf5MHiEO8eO83j+x8nm8zudPxtEbU+gFHLC9HLHLW8EL3MdytvqzVBpfIM1epZXLeyZp9h\nZNszDZnmQbLZ43es21DUri9EL3PU8kL0MssYhDvA92Fu7nohMD4efFxehrjt0j9XoW+uwmClRr41\nR68zi5FZpnW0Tv2EzfmhBF/NjrBYOIabTtFMxagnoBL3WFEWOAvkdANLX2bAajCiG6S0TX+mj1Kh\nxIHiCU7uP8lwbnin/ymEEELcQa5boVJ5lkrlmTVTkCaTQ+Tzj2OaB0mlxojHe6QLqRBiW0gLwi1o\ntda2CkxMwOQk2HbHefk++xZrDC1WGGlVSKslDG8Jx6gxf9jmzQc8FkditPblaJgxanHNStyl4TVI\neVWyfoOcbpD1G2R1g7RhMJIboVQoMVYco1QoUSqUyCQydzW7EEKIu8/3Her1l9szD12fgjRLPv84\nhcJTmOZBKQiEELdNuhjdIq1haWlti8DEBMzPb3z8vh6PA8Y0vTOTpMareI5NC5cGPuVRi5mDNeZG\nalSLSZbycWppl4yuk9XNdkGQ1i2KqUK7AFgtBoZzw8Skv6gQQkRG53Sk1erz+H4wiYVSBtnsO255\nClIhhLgVUiBswHFgamptq8D4ODSb64+Nx2FoyKO3p4ap6iRWluDqDO54A7+h0fj42qeyr8XUgQrT\no8vEklX8vI/VHyOZdMj6DUzlM5wbbhcDqwVBIVXY9Dyj1h8Oopc5ankhepmjlheil3mreX3fxbZn\nblisbHzNQGPTvIdC4Sny+Sd23erFUbu+EL3MUcsL0cssYxA6vPEGfOlLwUffD7oGxR2PpO2Ssj0G\n4i59RZt0roURt1C+jWvZOK/Z+LUGbqOGY9n4+GjtY6VarIwtsHJoBmewBlmPniKkzQxjhbE1xcD+\n/H4SRmKn/wmEEELsAM9rUq2+QLV6lmbzh2jtrTsmmI70SQqFp0il9u/AWQohRERaELSvmXzF5huf\nsxh/0SJdtzAth2LCo5D0yGTByzjUEw51XCzfx3NsPLuFb1toxwbbxk9WiSWXSCTnaQ7XWbzfZuE+\ng4HC4LpioDfdK31DhRAi4rT2aTReY2XlDLXaObR2wj2KZHIgnHVorD37UDy+T353CCHuish1MdJa\n07raonq2yvJrTV4/YzEzodE+xAwolYJHC49pq8lVXWXFaNCK1WmpBr6uknHLZFlTYcIAAAwESURB\nVL0yRXeBfa15eu0ZKmNZ6o89jPH4E4wO3EepUGK0MIoZl9UnhRBCgO9bWNZku8tQrfYSrrvS3p/J\nHKNQeIpc7hEMI72DZyqEiLquKhCUUh8BPgMYwH/UWv/GDfs3LRCcskPlbIXKmQrVqzazs8HYAs8F\ny4zTc6xK5ugEs6lpXkk2mEq4uLoBQG+9wkOTb3Jkdpx9jSp+T5HY2BjmgcPkDz9I34OPMzB27K4P\nHI5afziIXuao5YXoZY5aXtj7mYOVi5exrHEsa4JvfvP/cPJkFtueA9b+jkomhygUTlMonCKR6NuZ\nE95me/36biRqmaOWF6KXuWvGICilDOB3gR8BJoHnlFJf1lq/ttlrfMun+v0qlWcq1C40WFyA6RmP\n2eYis8MzzJ6cprF/hWavj2Osvbk3bYt3zI7zoFNltL+X7DtP0XP47zJ47DFyvbtjfYFz585F6s0K\n0csctbwQvcxRywt7L7PnNanVzrULgmDl4np7/wsvvMzDDx9HKYNkcqTdZSidvg/TPLTnug3ttet7\nK6KWOWp5IZqZN7OrCgTgSeANrfUVAKXUF4CPApsWCAsX5zn7z19moVyj5rWYHqlw5WSVueEm8UQw\nA1EsBhDDxGfAgP35LMcGBjl17/2MHD5OPLl7uwgtLy/v9CncdVHLHLW8EL3MUcsLey+z71vMzPzn\nNduClYuD8QNauxw48M9IJocjMQ3pXru+tyJqmaOWF6KZeTO77afYKDDe8fkEcOpmL/je5A/5bvYy\niweaTO+v4ad9EgaMGB5DpkGp2MN9o2McP3KcseEDxAzjjgYQQgix98TjRYrFd5JIDLSLgs6Vi03z\nAqZZ2uGzFEKI7bHbCoQtD4j48Psf5XNnv85AKs1fOTjCo8fu4+GjJyjke+7E+d11V65c2elTuOui\nljlqeSF6maOWF/ZeZqUUw8Of3HT/Xsv7VqKWF6KXOWp5IZqZN7OrBikrpU4Dn9ZafyT8/NcAv3Og\nslJq95ywEEIIIYQQXaorZjFSSsWBHwAfBKaAZ4G/frNBykIIIYQQQojts6u6GGmtXaXULwBfI5jm\n9PelOBBCCCGEEOLu2VUtCEIIIYQQQoiddXdX/dqAUuoPlFKzSqnzHdtOKKXOKKVeVkp9WSmV79j3\na0qp15VSF5VSH+7YflIpdT7c99t3O8et2kpepVSvUuqbSqmqUup3bvg6XZEXtpz5Q0qp58Ptzyul\n3t/xmq7IvMW8Tyqlvh8+XlZK/bWO13RFXtj693G4/x6lVE0p9Usd27oi8xav8UGlVLPjOn+24zVd\nkRdu62f18XDfK+H+ZLi9KzJv8Rr/XMf1/b5SylNKHQ/3dUVe2HJmUyn1+XD7q0qpf9zxmq7IvMW8\nSaXUfwq3n1NKvbfjNd2Sd0wF9xQXwu/LT4Xbe5VSf6GUuqSU+rpSqqfjNd1+z7WlzGqP3HdtC631\njj6AdwOPAuc7tj0HvDt8/reBfxU+fxA4BySAg8AbXG8FeRZ4Mnz+VeAjO51tG/JmgL8E/D3gd274\nOl2R9zYyPwIMh88fAia6LfMW86aBWPh8GFgAjG7Ku9XMHfv/BPhj4Jf2+DU+2HncDV+nK/LeRuY4\n8BLwcPj5vo73eVdkvp33dLj9HQTr+ez1a/y3gM+Hz9PAZeCebsq8xbz/gKDbM8AA8Hy3XWOC3zGP\nhM9zBGM+HwB+E/iVcPuvAr8ePt8L91xbzbwn7ru247HjLQha6+8A5Rs2Hwm3A3wD+Knw+UcJfiA5\nOlhM7Q3glFJqBMhrrZ8Nj/sj4Cfu7Jnfnq3k1Vo3tNZPA1bnwd2UF7ac+ZzWeibc/iqQVkoluinz\nFvM2tdZ+uD0NrGitvW7KC1v+PkYp9RPAmwTXeHVb12Teat6NdFNe2HLmDwMva63Ph68ta639bsr8\nNq7x3wA+D3v+Gk8DWaWUAWQBG6h0U+Yt5n0A+Gb4unlgWSn1RJflndFanwuf1wgWoR0Ffhz4w/Cw\nP+T6+e+Fe64tZd4r913bYccLhE1cUEp9NHz+cWAsfL6fYPG0VRMEF/rG7ZPh9m6xWd5VNw4UGaW7\n88JbZ4bgB/MLWmuH7s+8aV4VdDO6AFwAfjHc3O15YZPMSqkc8CvAp284vtsz3+w9fSjsevItpdS7\nwm3dnhc2z3wU0EqpP1dKvaCU+kfh9m7PfCs/t36GsECg+/PCJpm11l8DKgSFwhXg32mtl+n+zJtd\n45eAH1dKGUqpQ8BJoESX5lVKHSRoPTkLDGmtZ8Nds8BQ+HxP3XPdYuZVe/G+a0t2a4Hwd4C/r5R6\nnqBJyN7h87nTopYX3iKzUuoh4NcJmvn2gk3zaq2f1Vo/BDwG/LZSqrhD57jdNsv8aeC3tNYNYMP5\nl7vUZnmngDGt9aMEBeDn1A3jMbrYZpnjwLsI/pr+LuBjSqkPcBuLYe4yb/Vz6xTQ0Fq/utGLu9SG\nmZVSP0/Q6jkCHAJ+Obxx7nabXeM/ILhBfB74LeB7gEcXvqfDP9L8D+Afaq2rnft00H+m6zK9lShm\nfrt21TSnq7TWPwB+FEApdRT4sXDXJGv/YlMi+IadDJ93bp+882e6PW6SdzNdnRdunlkpVQL+J/AJ\nrfXlcHNXZ76Va6y1vqiU+iFwmOB93bV5YcPMfznc9STwU0qp3wR6AF8p1SS45l2bebNrrLW2CW8y\ntNYvhtf4CF3+noabvq/Hgf+ntV4K932VoAD+r3Rx5lv4Pv5Z4HMdn+/Fa7z6ffxO4H9prT1gXin1\nNMFf1b9LF2e+yfexx/UWXsK8l4AVuiivUipBcKP8X7TWXww3zyqlhrXWM2FXmrlw+56459pi5s10\nVebtsCtbEJRSA+HHGPBPgf8Q7voy8LMqmE3gEMEv2WfDPusVpdQppZQCPgF8cYMvvSvdJG/7kM5P\ntNbTdHFe2DxzOJPAnwK/qrU+s3p8t2e+Sd6DKlggEKXUAYL39Ovd/p6GDTP/HoDW+j1a60Na60PA\nZ4B/o7X+bLdnvsk17g/7aaOUupfgGr/Z7e9puOnPrq8BDyul0uH7+73Ahb16jTu2fRz4wuq2PXqN\nfy/cdRH4QLgvC5wGLu7Vaxy+l7Ph8w8Bjtb6Yjdd4/D8fh94VWv9mY5dXwY+GT7/JNfPv+vvuW4j\nc/ulnZ9003XeNm93lPPbfRD01Zwi+AvbOEHz3qcIRpr/APi3Nxz/TwgGylwEfrRj+0ngfLjv3+90\nrm3MewVYBKrh8fd3U96tZib4gVwDvt/x6O+mzFvM+/PAK2HOZ+mYFaFb8t7O+7rjdf8C+MVuy7zF\na/yTHdf4BeDHui3v7Vxj4OfC3OcJZwjppsy3kfd9wPc2+DpdkXermYEUQYvQeYLxU52zkXVF5i3m\nPUhw3/Eq8HWCboPdlvddgE8wM9Hq79ePAL0EA7Ivhdl6Ol7T7fdct5P5Cl1+37UdD1koTQghhBBC\nCNG2K7sYCSGEEEIIIXaGFAhCCCGEEEKINikQhBBCCCGEEG1SIAghhBBCCCHapEAQQgghhBBCtEmB\nIIQQQgghhGiTAkEIIcQtUYHvKKU+0rHt40qpP9vJ8xJCCLG9ZB0EIYQQt0wp9RDw34FHgQTwIsEC\nSpdv42vFtdbuNp+iEEKIt0kKBCGEEFuilPoNoAFkCVY+PwC8g6Bg+LTW+stKqYPAH4XHAPyC1vqM\nUup9wL8GlghWKD12d89eCCHEW5ECQQghxJYopTIELQc28BXggtb6vymleoCzBK0LGvC11pZS6gjw\nOa31E2GB8BXgIa311Z1JIIQQ4mbiO30CQgghuovWuqGU+mOC1oOfAf6qUuqXw90pYAyYAX5XKXUC\n8IAjHV/iWSkOhBBi95ICQQghxO3ww4cCflJr/XrnTqXUp4FprfUnlFIG0OrYXb9rZymEEGLLZBYj\nIYQQb8fXgE+tfqKUejR8WiBoRQD4m4Bxl89LCCHEbZICQQghxO3SBAOOE0qpl5VSrwD/Mtz3WeCT\nSqlzwDGC7kidrxNCCLFLySBlIYQQQgghRJu0IAghhBBCCCHapEAQQgghhBBCtEmBIIQQQgghhGiT\nAkEIIYQQQgjRJgWCEEIIIYQQok0KBCGEEEIIIUSbFAhCCCGEEEKINikQhBBCCCGEEG3/HwKudZY5\nzlIzAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7fc3daf01710>"
]
}
],
"prompt_number": 14
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"The effects of WW I and WW II"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.figure(figsize=(13,5))\n",
"\n",
"for subject in subjects:\n",
" df = data_set[(data_set[\"subject\"]==subject) &\n",
" (data_set[\"year\"].astype(np.int32)<1950)][\"year\"].value_counts().sort_index().cumsum()\n",
" plt.plot(df.index, df, label=subject, linewidth=2, alpha=.6)\n",
"\n",
"plt.grid()\n",
"plt.legend(loc=\"best\")\n",
"plt.xlabel(\"Year\")\n",
"plt.ylabel(\"Cumulative Sum of Given Nobel Prizes\")\n",
"plt.xticks(np.arange(1900, 1950, 5))\n",
"\n",
"gca = plt.gca()\n",
"\n",
"gca.add_patch(plt.Rectangle((1914,0), 4, 60, alpha=.3, color=\"orange\"))\n",
"gca.add_patch(plt.Rectangle((1939,0), (45-39), 60, alpha=.3, color=\"orange\"))\n",
"\n",
"plt.annotate(s=\"WW I\", xy=(1915,55))\n",
"plt.annotate(s=\"WW II\", xy=(1941,55))\n",
"plt.show();"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAwIAAAFHCAYAAAAStvtOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX++PH3mUnvIQmB0EINIIQEKQKCWZAmIM1FQJqy\nKn4VXdF1bayo7I9VsbdVF3EJFkRXUZS6GmAFVCT03gISEiCBkN7m/P64ySSBJJPATCbl83qePMy9\nd+69Z07CnVM+5xyltUYIIYQQQgjRsJicnQAhhBBCCCFEzZOKgBBCCCGEEA2QVASEEEIIIYRogKQi\nIIQQQgghRAMkFQEhhBBCCCEaIKkICCGEEEII0QA5vCKglApQSn2hlNqvlNqnlOqtlGqklFqnlDqk\nlFqrlApwdDqEEEIIIYQQJWqiR+B14HutdScgEjgAPA6s01p3AP5btC2EEEIIIYSoIcqRC4oppfyB\neK11m8v2HwBu0lonK6WaAHFa644OS4gQQgghhBCiDEf3CLQGzimlFiultiulPlBKeQOhWuvkovck\nA6EOTocQQgghhBCiFEdXBFyA7sA7WuvuQCaXhQFpo0vCcd0SQgghhBBCiCu4OPj6vwO/a61/Ldr+\nAngCSFJKNdFaJymlmgJnLz9RKSWVAyGEEEIIIa6R1lqVt9+hFYGigv4ppVQHrfUh4GZgb9HPdOCF\non+/ruB8RyavTps3bx7z5s1zdjJqtQaTR4f/CZ7Nqn3avFc+Yd6cyQ5IkINkn4b2s2r0lg3mb+gq\nSf7YJnlkW4PJo4byrHaCeS+8x7w3Vzo7GbWWUuXWAQDH9wgAzAY+Vkq5AUeBOwEz8LlSaiZwAphQ\nA+moV06cOOHsJNR6kkeVO3Hqio44cRn5G6qc5I9tkke2SR5VTp7Vtp04neLsJNRZDq8IaK13Aj3L\nOXSzo+8thBBCCCGEKJ+sLFxHzZgxw9lJqPUkjyo3Y8IgZyeh1pO/ocpJ/tgmeWSb5FHl5Flt24xx\nfZydhDrLoesIXAullK6taROiVrnKuNM6xwljBIQQwm4ayrPaGeT7oVJKqQoHC9e5HgGllPzIT736\ncZa4Lbuddu+6Ii4uztlJqNUkf2yTPLJN8qhy8qy2Le7nQ85OQp1VE4OF7U56CkR94cyKgBBCCCEa\ntjoXGqSUkoqAqDfs8vfcULqbpetXCFGXNZRntTPI90Olisoa9SM0SAghhBBCCHHtpCIgRAMlcae2\nSexy5SR/bJM8sk3yqHLyrLZNxghcPakIOFhMTAyLFi2y6zXvu+8+5s+fb9drCiGEEEKIhkXGCNhJ\neHg4Z8+exWw24+3tzfDhw3nrrbcYOXIkU6dO5a677nJ2EkUtJGMEqkFiQIUQdVlDeVY7g3w/VErG\nCNQApRQrV64kPT2d7du3s23bNmurfW2suAghhBBCiIZNKgIOEBYWxvDhw9mzZw8ACQkJ3Hjjjfj5\n+TF06FBSUlIAGDFiBG+99VaZcyMjI1mxYgUADz/8MKGhofj7+xMZGcm+ffsAYxXGuXPnWs9ZsWIF\nUVFR+Pv7065dO9asWQPARx99RNu2bfHz86NNmzZ88sknDv/sou6QuFPbJHa5cpI/tkke2SZ5VDl5\nVtsmYwSuXp1cR6Ai995rv2u99171zylu+T916hTff/8948ePZ+PGjXzyySesXr2a5s2bM3z4cBYu\nXMiCBQuYMWMGL7/8Mg888AAAO3fuJDExkREjRrBmzRo2bdrE4cOH8fPz4+DBg/j7+wOUWYjql19+\nYfr06Xz55ZcMGjSIxMRE0tPTyczM5KGHHmLbtm20b9+e5ORkawVECIC3P/qOnfuO89DMWwEYescz\ntGwWwgcvGn+Pjzy3iOZNg9n0y16m3zaQ0UNvACDipvuYNv4PPPXgBADG37OAKWNjGDu8ZIn3E6eS\nGXXnfHavf7OGP5UQQohiD8/7F+EtGjv8OR+3ZTcvv/813y6ei6hbpEfATrTWjBkzhsDAQPr3709M\nTAxPPPEEAHfddRft2rXDw8ODCRMmsGPHDgBGjRrFoUOHOHr0KACxsbFMnDgRFxcXXF1dSU9PZ//+\n/VgsFiIiImjSpMkV9120aBEzZ85k0KBBgNEbERERAYDJZGL37t1kZ2cTGhpK586dayIrRB0xcfQA\nNm87AIDFYiHlQjr7Dp+0Ht+y/SD9enSiX49ObP7NeF/KhUv4eHuwZfsB6/u2bj9Iv56dajbxNSQm\nJsbZSajVJH9skzyyTfKocjF9ul71uTf26twgnvMxvTs4Owl1Vr3qEbiaVnx7UUqxYsUKBg4ceMWx\n0gV4T09PMjIyAKwVg9jYWJ555hk+++wzvvzySwAGDhzIAw88wP33309CQgLjxo1j4cKF+Pr6lrn2\n77//zogRI664p7e3N8uWLWPhwoXMnDmTfv368fLLL1srCUL06R7Bw8/+C4C9B0/SJaIlSecucDEt\nA08Pd/YfOUX3rm0ptFh47O8fAbB52wFG3dyTVT9uB+D4ySQ8PdxoHBzgpE8hhBCiIvKcrycuXIDP\nPoOYGOhk3wqZ9Ag42fTp0/n4449Zv349Xl5e9O7d23ps9uzZbNu2jX379nHo0CFeeumlK85v0aIF\nR44cKffaQ4YMYe3atSQlJdGxY0fuvvtuh30OUfccOp6Ii4uZU4nn2LL9AH2u70ivqA5s2X6QbbsO\n0zWiFS4uZrp3acueQwnk5xew5bcD9OnekYi2zdh/+BSbfztQq1uJrpXELldO8sc2ySPbJI8qdy1j\nBMKaBDWI53y9HSOgNWzYAPPmwY4d8OWXxj47kopADahs1qA+ffqglOLRRx9l2rRp1v3btm3j559/\nJj8/Hy8vLzw8PDCbzdbrFV9z5syZLF68mB9++AGLxcLp06c5ePAgZ8+eZcWKFWRmZuLq6oq3t7f1\nfCGK9b2+I5u3HWDztgP0uT6CPtd3ZPO2/Wz5raQb2N3dles6tGT7nqNsjT9I7+gO9Okewebf9rPl\ntwP061G7vyCEEKIhk+d8HZWUBAsXwiefQE4OREXBAw+AKncW0KsmFYEaoEr90koP9C02bdo0du/e\nzZQpU6z7Ll26xD333EOjRo0IDw8nODiYv/zlL1dco2fPnixevJiHH36YgIAAYmJiOHnyJBaLhVdf\nfZVmzZoRFBTEpk2bePfdd2vg04q6IqZPV/r16MRP2/az+2ACXTuGc0N0BJt/O8Dm3/bTr0fJmJJ+\nPTqxYese0jOyCfD34YbuEfz06342/3aAvtfX3y8IiV2unOSPbZJHtkkeVe5axggADeI5X6/GCBQU\nwPffw/PPw5Ej4O9vzIYzaxYE2D88q16NEXCm48ePl7v/xx9/LLM9ffp0pk+fXmZfq1atuPHGGwkP\nD7fuGzhwIDt37iz3mosXLy6zPWbMGMaMGXPF+6S7VdjSt0cnXnrvK9q1aopSisAAHy5eymTf4VP8\n68XZJe+7viNznvuQgf0iAYjsFM7W+EOcS0mjS8dWzkq+EEIIG+Q5X4ccPw6xsXD6tLF9440wfjx4\neTnsltIj4GRZWVm8/fbb3HPPPc5Oimhg4rbspktES1IupHND95JB5JEdwwnw86ZRYMnA9D7Xd+T4\nqWT6FL3PbDYTGhxAj8h2FV7fzr2XTiGV6cpJ/tgmeWSb5FHlrnUdgZp6ziuc99Cv82MEcnPh88/h\nhReMSkBICDz8MEyd6tBKAEiPgFOtWbOG8ePHM3jwYCZPnuzs5IgGyGw2k7bvszL7Fr/y0BXvaxwc\ngOXkijL7fvz87xVeN7xFKLvWyRoCQgjhbDXxnI/p0/WaQ5garL17YelSSE0FkwmGDoWRI8HVtUZu\nryobyOpMSildXtqUUpUOvhWiLrHL3/Phf4JnM/skqDbLPg3tZzk7FUIIcXUayrPaGeri90NGhtEL\n8PPPxnbLljBtGrRoYfdbFZU1yu2ykR4BIYQQQgghaoLW8OuvsGyZURlwc4Nbb4VBg4wegRomYwSE\naKCuNe60IZDY5cpJ/tgmeWSb5FHl5FltW50ZI5CUBG+9BYsWGZWAjh3hb3+DwYOdUgkA6REQQggh\nhBDC/rQ2Bv/Gxxs/xbMBeXvDbbdBnz5On1lDxggI4UQyRqAa6mIMqBBCFGsoz2pnqE3fD1ob04AW\nF/7PnSs55ukJ118Po0eDn1+NJUnGCAghhBBCCOEIFgscOlRS+E9LKznm5wfdukF0NEREgEvtKnrL\nGIEaMm/ePKZOnVoj97rllluIjY2tkXuJukviTm2T2OXKSf7YJnlkm+RR5eRZbZtTxgjk58OuXfDv\nf8Ojj8Krr0JcnFEJaNTIGPz76KPG2gBTpsB119W6SgBIj4DdffLJJ7zyyiscPHgQX19foqKieOqp\np1A1GAP2/fffV+l9JpOJI0eO0KZNGwenSAghhBCiHrh0CZYvNyoBOTkl+5s0MVr9o6ONqUDtVO7L\nzYU9e4yOho4djcWG7UkqAnb0yiuv8MILL/Dee+8xdOhQ3NzcWL16Nd988w1eDl4Z7mpVFp9eUFCA\nSy2svQr7kMVfbIuJiXF2Emo1yR/bJI9skzyqnDyrbYvp3aFmbnThgtHyn5xsbLdsWVL4b9rUbrfJ\nzDTqGfHxsG+f0fkARmeDvSsCEhpkJ2lpaTzzzDO88847jBkzBk9PT8xmMyNGjOCFF14AIC8vj+nT\np+Pn50eXLl347bffrOcnJiYyfvx4GjduTJs2bXjzzZJVWefNm8cf//hHpk6dip+fH5GRkRw+fJgF\nCxYQGhpKq1atWLdunfX9MTExLFq0CIAjR45w0003ERAQQEhICJMmTQJgwIABAHTr1g1fX1+WL19O\nXFwczZs358UXX6Rp06bcdddddO3alZUrV1qvnZ+fT3BwMDt37nRcZgohhBBC1Cbnz8NLLxmVgBYt\nYP58eOopuOUWu1QC0tJgwwZ47TUjouijj2DnTigogHbt4I9/hOnTr/1jXK5eNffe++29drvWe6Pe\nq9b7t2zZQk5ODmPHji33uNaab775hq+++oqPPvqIp556igceeIAtW7ZgsVgYNWoUY8eOZdmyZZw6\ndYqbb76ZiIgIhgwZAsDKlSv55ptv+Oijj7jrrrsYPHgw9957L4mJiSxevJh7772XY8eOAcbo8OJQ\npLlz5zJs2DA2bNhAXl4e27ZtA2Djxo2YTCZ27dplDQ2Ki4sjOTmZCxcucPLkSQoLC3nzzTdZunQp\nI0eOBIywo2bNmtGtW7fqZ6qoVeK27JaWJhvi4uKktbISkj+2SR7ZJnlUOXlW2xb38yFi2jvwBklJ\nRk/AxYvQujU8+CDYIdLj/PmS8cXHjhkTDoGxpECnTtC9uzHO2N//mm9VoXpVEXCmlJQUgoODMVWy\nIET//v0ZNmwYAFOmTOG1114D4Ndff+X8+fM8/fTTALRu3Zo//elPfPbZZ9aKwIABAxg8eDAAt912\nG//5z394/PHHUUpx++23c88993Dp0iX8LpuOys3NjRMnTnD69GmaNWtG3759K/0cJpOJZ599FldX\nV1xdXbnjjjt47rnnyMjIwMfHh9jY2Bob9CyEEEII4VSnTxvN9JcuQYcOcP/94OFxVZfS2qhTbN9u\nFP5PnSo55uoKnTsbUUaRkcZSAzWhXlUEqtuKb09BQUGcP38ei8VSYWUgNDTU+trLy4ucnBwsFgsJ\nCQkkJiYSGBhoPV5YWGgN3wFo3Lix9bWnpyfBwcHWVn9PT08AMjIyrqgIvPjii8ydO5devXoRGBjI\nI488wp133lnh5wgJCcHNzc26HRYWRr9+/fjiiy8YM2YMq1evLhO2JOouaWGyTVopKyf5Y5vkkW2S\nR5WTZ7VtDhsjkJAAr79uBO137gz33QelykhVoTWcPFnS8p+UVHLMwwO6djUK/126gLu7ndNfBfWq\nIuBMffr0wd3dna+++orx48dfcbyyWYNatGhB69atOXSo/OmvrmXGodDQUN5//30AfvrpJ26++WZu\nuummCmcKKu9e06dPZ9GiReTn59O3b1+a2nFAjBBCCCFErXP0KLz5JmRnG/E5d99tNNtXgcVinF5c\n+E9NLTnm41OyrEDHjlW+pMPIYGE78ff357nnnuP+++9nxYoVZGVlkZ+fz6pVq/jrX/9a6bm9evXC\n19eXF198kezsbAoLC9mzZ481nv9aVp5dvnw5v//+OwABAQEopaw9FqGhoRw9etTmNcaOHcv27dt5\n4403mDZt2lWnRdQuMje1bTK/eeUkf2yTPLJN8qhy8qy2ze7rCBw8aPQEZGcbKwHfc4/NEntBAezd\nC0uXwmOPwcKF8N//GpWAgAD4wx9gzhxjvPG0aUZPgLMrASA9AnY1Z84cmjRpwvz587njjjvw9fWl\nR48ePPXUU6xZs+aK1vbibbPZzMqVK3nkkUdo06YNubm5dOzYkfnz51vfV9G5FW0X27ZtGw8//DBp\naWmEhobyxhtvEB4eDhizEU2fPp3s7Gw++OADQkJCyr2Oh4cH48aNY9myZYwbN+6q8kYIIYQQotbb\nuxfefdeYs/OGG4ypeioI+c7NNab3jI83pvvMzi45FhJSMrNo69Z2W1bA7tS1tDY7klJKl5c2pdQ1\ntZCLq/P8889z+PBhlixZ4uyk1Ct2+Xs+/E/wbGafBNVm2aeh/Sxnp0IIIa5OQ3lWO4O9vh927ID3\n34fCQhgwACZPvqIEn5UFu3cbhf+9eyEvr+RYs2Ylhf9mzWpP4b+orFFuaqRHQNiUmprKhx9+SGxs\nrLOTIoQQQghhf7/+Ch9+aAT4DxpkTNxfVJK/dMmY0z8+Hg4cMOoJxVq3Lin8l5rXpc5w+BgBpdQJ\npdQupVS8UuqXon2NlFLrlFKHlFJrlVIBjk6HuDoffPABLVu2ZPjw4dxo7+XshFNJ3KltErtcOckf\n2ySPbJM8qpw8q2275jECmzfDokVGJWD4cPjjH0lJVfz3v0as/2OPGbH/e/caswBFRMDEifCPf8Dj\nj8PQoXWzEgA10yOggRitdakx0zwOrNNav6iU+mvR9uM1kBZRTXfffTd33323s5MhhBBCCGF/GzbA\nJ58AkDpgND+730L8AmPm0GIuLsYCX8Vz/Pv6OimtDlCtMQJKKTPgrbW+VI1zjgM9tNYppfYdAG7S\nWicrpZoAcVrrjpedJ2MERL0nYwSqQcYICCHqsobyrHaGq/x+0OvWk/HRclLOw8bQP/KT583WY+7u\nxtz+0dHGDD9XuYZYrXBNYwSUUp8C9wKFwK+Av1Lqda31i1W8vwbWK6UKgfe01h8AoVrr5KLjyUBo\nhWcLIYQQQghhB9qiORl3jOSvt8CmTeTkwC/tJnPY8ya8vY0W/+hoY/2w2jC9p6NVJTSos9b6klLq\nDmAVRgjPdqCqFYF+WuszSqkQYF1Rb4CV1lorpcptEp0xY4Z1qsuAgACioqKqeEsh6pbiGNniFTar\nvV0UQ1q8AmVVtnfsPcaf/zT6qs+v8e3c88S0t1N+VXG7eF9N3a+ubRfvqy3pqY3bl+eVs9NTG7df\ne+01oqKiak16HLZd1BlQ3effa/9aQdR1bWrX87iWbe/YEc+f/270CJSX/4X5hYTnhpG0Kp5f//sN\nKiuTaO8wtDLxn2Zd8O2m+fMd0KEDbNoUx4UL4OoaU+H1avv2jh07uHjxIgAnTpygMjZDg5RSe4Eo\n4BPgba11nFJql9Y6stITy7/WM0AGcDfGuIEkpVRT4EcJDRINkTNDg+K27K5bS9c7ITQoLi7O+nAV\nV5L8sU3yyLYGk0cN5VntBHFxPxIz5ZUy+/Kz8jm2ch/n1sZTuH0nKjvLeszSKBj3G6JpOroXrfq3\nrDXTfDpKZaFBVakIPAj8FdgFjABaArFa6/5VuLEXYNZapyulvIG1wLPAzUCK1voFpdTjQIDW+vHL\nzpWKgKj3ZIxANcgYASFEXdZQntXOUPT9kHMxh2MrdnN+XTx6125Ufskk/5YmYXj2jabFrdE07dkc\nZarnpf9SrmmMgNb6DeCNUhdLAP5QxXuHAl8VrVbrAnystV6rlNoGfK6UmgmcACZU8Xp1VkxMDFOn\nTmXmzJl2u+Z9991Hs2bNePrpp22+12QyceTIEdq0aWO3+9dVpX8XH3/8MUuWLGHNmjWVnrNgwQKO\nHTvGBx98UEOpFEIIIYQt6cm5HF95gQt73oID+1EFBQAowNIyHJ/+0bS8NYrGkU2cm9BrlJmXSYGl\nAH8Pf7te1+Y6AkqpJkqpRUqp1UW7OgHTq3JxrfVxrXVU0U8XrfWCov2pWuubtdYdtNZDtNYXr/4j\n1B7h4eF4eXnh6+tLkyZNuPPOO8nMzASM2piyc9/Tu+++W6VKQF01Y8YMTCYT33zzTZn9Dz/8MCaT\niX//+99Xdd3Sv4s77rjDZiUA4Iknnqh3lQCZm9q20vHd4kqSP7ZJHtkmeVQ5eVZf6cJFV37cHMSn\nf0tn++QV/PjeGtSe3ajCQiztOuD7p9vp8s3/I2bNE/R4elidrQRczLnIhhMbeG3razy69lHWHLVd\nXqmuqgwW/ghYDDxVtH0Y+BxYZPfU1HFKKVauXMnAgQNJTExk6NChzJ8/nwULFjg7abVeYWEhZrO5\nzD6lFB06dGDJkiXceuutABQUFPD555/Trl07u1eshBBCCFE7nT3vRvwef+L3+nP8lBftk3+m14mV\nKAU6LAj/GVNoPaYbfs39nJ3Ua3I+6zzxZ+KJT4rnaOpR636zyUx2frbd71eVlYWDtdbLMKYPRWud\nDxTYPSX1TFhYGMOGDWPv3r3WfSdOnODGG2/Ez8+PoUOHkpJiLK0wYsQI3nrrrTLnR0ZGsmLFCsBo\nAQ8NDcXf35/IyEj27dsHGC3mc+fOtZ7zwQcf0L59e4KCghg9ejRnzpwpN21paWlMmzaNxo0bEx4e\nzt///ndrnLrFYuGRRx4hJCSENm3a8NZbb2EymbBYLCxfvpwePXqUudYrr7zCmDFjyr1PYmIit956\nK0FBQbRv355//etf1mPz5s3jtttuY+rUqfj7+1fYuj9q1Cj+97//WUe/r169mm7duhEaGlomtv7D\nDz+kc+fONGrUiGHDhnHy5EnrsXXr1tGxY0cCAgKYPXt2mfM++ugj+vcvGe6yd+9eBg8eTFBQEE2a\nNLFW4ubNm8fUqVMB4/doMplYsmQJrVq1IiQkhP/3//6f9Rpaa/7xj3/Qrl07goODuf3227lw4UK5\nn8+ZZPCZbQ1iAOM1kPyxTfLINsmjyjXUZ7XW8PsZD75dF8pzr7Vn7sKO/Gd1U46f8qLLuU3ckvY5\nEW0z6PlEZ/786WC6PdC/TlYCtNYkpify3aHvmL9xPk/99ym+2PcFR1OP4mp2JapJFHdG38lLg19i\nelSVAnKqpSo9AhlKqaDiDaXUDUCa3VNiD/fea79rvffeVZ1WXMg8deoUq1atYvz48db9n3zyCatX\nr6Z58+YMHz6chQsXsmDBAmbMmMHLL7/MAw88AMDOnTtJTExkxIgRrFmzhk2bNnH48GH8/Pw4ePAg\n/v5GfFjpEJcffviBJ598knXr1tG5c2ceffRRJk6cyIYNG65I4+zZs0lPT+f48eOcP3+eIUOG0LRp\nU+666y7ef/99Vq9ezc6dO/Hy8uK2226z3uPWW29l1qxZHDhwgI4djUmeYmNj+dvf/lZuXkycOJHI\nyEi++OIL9u/fz+DBg2nbti1/+IMxxOSbb77hiy++IDY2lpycnHKv4eHhwejRo/nss8+YNWsWS5Ys\nYdq0abz99tvWdK1YsYIFCxawcuVK2rdvz4IFC5g0aRI//fQT58+fZ/z48Xz00UeMHj2aN998k3/+\n859Mmzbtinulp6dz880389hjj/Hdd9+Rl5dnrXSV1/vw008/cejQIQ4ePEivXr0YP348ERERvPHG\nG3zzzTds3LiRkJAQZs+ezf33388nRSsXCiGEEOJKWsPxk17E7/Unfo8f51Ldrcc8PQqJ7HiJm7LX\nEl74I+YQDaMHQJ+uxmDhOkRrTUJagrXlPzkj2XrMw8WDyNBIoptGc13Idbi7uFdypWtXlR6BR4Bv\ngTZKqc1ALPCgQ1NVR2mtGTNmDIGBgfTv35+YmBiefPJJwChI3nXXXbRr1w4PDw8mTJjAjh07AKPV\n+9ChQxw9anQBxcbGMnHiRFxcXHB1dSU9PZ39+/djsViIiIigSZMrY90+/vhjZs6cSVRUFG5ubixY\nsIAtW7aUaRkHIwRn2bJlLFiwAG9vb1q1asUjjzxCbGwsAJ9//jl//vOfCQsLIyAggCeeeMJauXF3\nd2fChAksXboUMFrPExISGDly5BXpOXXqFJs3b+aFF17Azc2Nbt268ac//YklS5ZY39O3b19ryI9H\nJUv2TZs2jSVLlpCWlsbGjRuv6IH45z//yRNPPEFERAQmk4knnniCHTt2cPLkSb7//nu6dOnCuHHj\nMJvN/PnPfy43/wBWrlxJWFgYDz/8MG5ubvj4+NCrVy/r7/ZyzzzzDO7u7kRGRtKtWzd27txpTc/8\n+fMJCwvD1dWVZ555hi+++AKLxVLhZ3QGiTu1TWKXKyf5Y5vkkW2SR5Wr789qiwUOHvXmsxVhPPGP\njrzwbjvWbgzhXKo7vt4F9O+VwoN3HmPhU3u5K3A5bQ/+gNkFGP8HoxIAxP18yLkfogos2sKhlEMs\n27OMJ//7JAs2LWD1kdUkZyTj4+bDjS1vZHbv2bw89GVmdp9J96bdHV4JgKrNGvSbUmoA0BFjEPZB\nrXWejdOc4ypb8e1FKcWKFSsYOHBgucdLF0A9PT3JyMgAsFYMYmNjeeaZZ/jss8/48ssvARg4cCAP\nPPAA999/PwkJCYwbN46FCxfi6+tb5tpnzpwpE7bj7e1NUFAQp0+fpmXLltb958+fJz8/n1atWln3\ntWzZktOnT1uv06JFC+ux5s2bl7nP9OnTmTx5MvPnzyc2Npbbb78d13KW3ktMTKRRo0Z4e3uXuc+2\nbdsqvHZ5lFL069ePc+fOMX/+fEaNGnVFpSEhIYGHHnqIRx55pMz+06dPc+bMmSvuU/rzlXbq1Klq\nzapU+vfp5eVl/X0mJCQwduxYTKaSeraLiwvJyck0bdq0ytcXQggh6qOCAsX+wz7E7/Vn5z4/MrJK\niqONAvLEXCRqAAAgAElEQVSIvi6N6C6XaNsqE5MJo6vgu5/gfztBKbh9MES1d94HqKICSwEHzh8g\n/kw8O5N3kp6bbj0W6BlIdJNooptG065RO0yqKm3z9mezIqCUOga8pLV+t9S+lVrrK5uBxVWbPn06\n06ZNo1+/fnh5edG7d2/rsdmzZzN79mzOnTvHhAkTeOmll3juuefKnB8WFlZm9bjMzExSUlJo1qzs\nnMXBwcG4urpy4sQJOnXqBMDJkyetheWmTZty6tQp6/tLvwa44YYbcHNzY+PGjXz66ad8+umn5X6e\nsLAwUlNTycjIwMfH54r7QPnhNhWZMmUKzz33XLktRy1btmTu3LlMmjTpimOHDx8u8xm01ld8ptLX\nWbZsWbnHqpPWli1bsnjxYvr06VPlc5yhocadVofELldO8sc2ySPbJI8qV1+e1bm5JvYc9CV+rz+7\nD/iSk1syQUhocC7R16XRvWsaLZtll13gS2v4eiP8vAdMJpg8BLq0LXPtmN4dauhT2JZbkMvec3uJ\nPxPP7rO7ywzwbezdmKgmUXRv2p3wgPBaMelJVcYI5AMxSqlewCytdS4gK2JchcoWjurTpw9KKR59\n9NEy8evbtm2jsLCQ7t274+XlhYeHh3V2Ha219ZqTJk1i0qRJTJ48mY4dO/Lkk09yww03lOkNADCb\nzUyYMIGnnnqKJUuWkJKSwquvvspf/vIXACZMmMDrr7/OiBEj8PLy4oUXXrjiD3Xq1Kk88MADuLm5\n0bdv33I/T4sWLejbty9PPPEECxcu5ODBg3z44YfVipMv/fkefPBBBgwYUGZgb7FZs2Yxd+5cunXr\nRufOnUlLS2Pt2rX88Y9/5JZbbuGBBx7gq6++YtSoUbz99tskJSWVe78RI0YwZ84cXn/9dWbNmkVe\nXh779++nV69e1Vr0a9asWTz55JP8+9//pmXLlpw7d44tW7ZYw6CEEEKIhiAzy8yu/X7E7/Fj32Ff\n8gtKWr1bhmUT3SWN6OvSaNI4t/zVfS0W+OJH2H4AXMwwZTh0bFXOG50rKz+L3cm7iU+KZ+/ZveQV\nlgTONPdrTnTTaKKbRBPmG1YrCv+lVaUfIktrfTuwH9iolKp9v4E6ovQvv7x1BaZNm8bu3buZMmWK\ndd+lS5e45557aNSoEeHh4QQHB1sL7aWvMWjQIJ5//nnGjx9PWFgYx48f57PPPiv33m+++Sbe3t60\nadOG/v37c8cdd3DnnXcCcPfddzNkyBAiIyO5/vrrGTFiBGazuUyYy9SpU9m7d2+ZdJbn008/5cSJ\nE4SFhTFu3Diee+45a9hUVdZVKP2ewMBA6yDjy40ZM4a//vWvTJw4EX9/f7p27WpdGyA4OJjly5fz\n+OOPExwczJEjR7jxxhvLvYevry/r1q3j22+/pWnTpnTo0MHaA3F5eitL+0MPPcStt97KkCFD8PPz\no0+fPvzyyy+VflZnqO9xp/YgscuVk/yxTfLINsmjytW1Z3XaJRc2bAnitX+15tHnO/PR8hbs3O9P\nfoGJtq0y+eOIRP7+2AGeevAwtww8S9PQCioBhYXw2TqjEuDqAjNGVlgJcMYYgUu5l9iUsIk3fn6D\nR9c+yofxHxJ/Jp68wjzaBLZhfOfxPD/weebeNJeRHUbSzK9ZrasEAChbLZ1KqXitdXTR65uBt4FG\nWusQhyZMKV1e2oqWSXbkrZ0mNjaWDz74gI0bNzo7KVarVq3ivvvuKxN2lJ2dTWhoKPHx8bRt27bi\nk4VNdvl7vspl6+O27K5bXc5FS8jXpLi4OAlbqITkj22SR7Y1mDyq48/qggJFeoYLGVlmMjJdyMg0\nk57pUvTa2J9ywY2E055obRR4TUoT0TaD6OsuEXVdGv5+VZx9vqAQPl4D+4+DuxvcORLCKx5jFxf3\nIzFTXrHHx6xUSlYKO5J2EJ8Uz5HUI9bvb5My0SGoA9FNo4lqEkWAR4DD01IdRWWNcmshVQkNss4N\nqbVer5QaQhVXFhZVl5WVxdtvv22dQtRZcnJy+OGHHxgyZAjJyck8++yzjBs3rsx73n33XXr16iWV\ngDquNnyx1HYNonByDSR/bJM8sk3yqHKOeFZrDdk5ZqMwn+FCRpZRsM/IdCkq3JuL9rlYC/+lY/or\n4+pioXP7S0R3uURkp0t4exVWL3F5+RC7Cg6fAk8PuGsktAit9BRHjhFIykiyTvOZcDHBut/F5EKn\nxp2IbhJNtybd8HHzcVgaHKnCioBSqpPWej+QqJTqftnh7xybrIZlzZo1jB8/nsGDBzN58mSnpkVr\nzbx585g4cSKenp6MHDmyzMDk8HBjcMvXX3/txFQKIYQQolhBgbIW3tMzyi/IF7fap2e4kJnlQqGl\nemEqZpPGx7vA+PEqxNenAB+vAny8C/HxLsDX23jdukUW7u5XOV12Th78+zs4ngjenvCnW6Fp8NVd\n6ypprTl16ZS18H8mvWRxVncXd7o07kJ0k2i6hnbFw6Xiqc/risp6BOYAdwMvA+XFLpQfsC2qbejQ\nodapJ53N09Oz0nj20iFCom6rLd3NtVmDCVm4SpI/tkke2SZ5VFbp1vqMTBd+2LybTu16FBXkXUjP\nKCnkF4fnVLW1vjRPj8JyC/LGvoKign5hUeG/EE+PwvJj+e0lOxcWr4STSeDnDTNvhdBGVTo17udD\nxFzDbKJaa45dOEZ8UjzxZ+I5n3XeeszbzdtY4KtJNJ1DOuNqvnLK9LqswoqA1vpupZQJeEpr/VMN\npkkIIYQQot5IT4e0JG8yCn0ui60v1Ypvjb0v21qfmHyOX3eWv/5Nsctb68sU7L2Nlntfn5LXPt6F\nuLjUovGWmdmw6FtIPAcBPnD3GAjyd+gtCy2FHEo5RHxSPDuSdpCWk2Y95u/hT1STKKKbRNMhqANm\nU/UrWnVFVQYL79BaR9VQekrft8ENFhYNjzMHC9c5ThgsLIQQV0NrSEqC7dshPh5OnQLS9oGLt81z\nATzcC0vCb0oV3n2LC/tFLffG8RporXekI7/Df+IgNQ0a+cPdoyHQ1+ZpZVTz+yE9N503fn6Dk2kn\nrfuCvYKt03y2CWxTK2f4uVrXOlh4vVLqNuDLckvmQgghhBANnNZw8qRR8I+PNyoCxdzdIahxJr4B\numyrfTlx9t5ehbi6NoDiVlaOsVrwbweM7abBMGME+Dt20O3FnIu8uuVVkjKSaOTZiD4t+hDdJJrm\nfs3rVeG/qqpSEZiFMV6gUCmVU7RPa639HJcsIYSjyRgB2yR2uXKSP7ZJHtlWl/PIYoGjR0sK/6mp\nJcd8fKBbN4iOho4dwfXEb3V6+lC70Rp2H4VvNkFGlrFQ2KCeMCAKzFcXglPVMQIpWSm8uvVVzmWe\no5lfM/58w5/xc2/YxVmbFQGtdd2cD0kIIYQQws4KCuDgQaPgv2OHEf9fLDAQoqKMwn/79mCqyrKt\nDcnFDFix0VgfACA8DMbHQEigw299NvMsr255ldTsVFoFtOKh3g/h7Va1UK36rMIxAkqpDsBLQDtg\nF/Co1vp0jSWsHowR2LRpE3fffTcHDhxwdlJELSVjBKpBxggIIZwkNxf27TMK/7t2QXZ2ybGQEOje\n3Sj8h4dTcax+Q3lWl0dr2LoXVm+B3DzwcINhfaD3dZVkWDXY+H44k36GV7e+SlpOGm0btWV2r9l4\nunpe+33riKsdI/Ah8G9gEzAKeBMYV8n7G7Tw8HAWLVrEoEGDrPv69+9fphIQHh7Ohx9+yMCBAx2S\nhri4OKZOncqpU6cccn0hhBCiocjKgt27jcL/3r2Ql1dyrFkzo+DfvTuEhdmnLFtvnb0A//kRThTN\nx9+5NYwe4PCxAMVOpZ3ita2vkZGXQURwBPf3vB93F/cauXddUFlFwEdr/UHR6wNKqfiaSFBdpZSy\nOcjkWlp/i89z5ECWgoICXFyqMmxE1Af1Lu7UAepy7HJNkPyxTfLIttqUR5cuwc6dRuH/wAEoLLUo\nbuvWRuE/OhoaN665NNXZZ3VBIWzYDj/8ZmSkrxfcOgC6tLF7zamiMQInLp7g9a2vk5WfRZfGXZjV\nY1a9WwfgWlUWveahlOpe9HM94Fn8upyVhkU54uLiaNHCmPt36tSpnDx5klGjRuHr68vChQsB2Lp1\nK3379iUwMJCoqCg2bNhgPT8mJoann36afv364e3tzbFjx1i8eDGdO3fGz8+Ptm3b8v777wOQmZnJ\n8OHDSUxMxNfXFz8/P86cOcOMGTOYO3duuWkCo5fixRdfJDIyEl9fXywWS6VpEkIIIeqTlBT4739h\n4UJ47DFYutToAdAaIiJg4kT4xz/g8cdh6NCarQTUWQlJ8ObnsO4XoxLQszPMmQxd29ZY98mR1CO8\nuuVVsvKziGoSxX0975NKQDkqa/5NwlhVuKLtWrey8L0HD9rtWu9FRNjtWgCxsbH873//Y9GiRdbQ\noNOnTzNy5EiWLl3KsGHDWL9+PePHj+fgwYMEBQUBsHTpUlatWkVERAQWi4XQ0FC+++47WrduzcaN\nGxk+fDg9e/YkOjqa1atXM2XKlDKhQVXpqfjss89YtWoVwcHBnDlzptw0HThwgODgml3mWzhWnWxh\nqmG1pZWytpL8sU3yyDZn5FFSUslMPwkJJftdXKBTJ6PVv1s3Y+YfZ6tTz+rcfFj7M2zeZdSkgvxh\nXAy0be7Q28b07lBme/+5/bzz6zvkFebRs1lP7oy6s14sCqa1tntkSGUrC8fY9U7iCkuXLuWWW25h\n2LBhANx888306NGD7777jmnTpqGUYsaMGXTq1AkAk8nELbfcYj1/wIABDBkyhE2bNhEdHV1h2FFl\n4UhKKR588EGaNWtWaZq+//57pk2bZpfPLYQQQjjDzp3w9deQmFiyz90dunQxCv9du4KHh/PSV6cU\nFsL5NDh3wRgHcPYCHE+EtAyj1f+m7nBzT3Ct2ZDj3cm7ee+398gvzKdvi75M7TYVk6qb0zdprUnK\nyyM+I4P4jAy6+/gwvKih2F7qVUC4vVvxHS0hIYHly5fz7bffWvcVFBSUGUxcOowHYNWqVTz77LMc\nPnwYi8VCVlYWkZGR15SO0veoSppE/VBn405rUG2KXa6NJH9skzyyrSbyKC0Nli2D334ztr29ITLS\nKPx37gyutThixOnP6tx8OH8RzqZC8oWSgn9KmrGQwuXCQuC2Pxj/1pDiMQLbz2znX9v/RaGlkJjw\nGCZ2mVjnFgnTWnMyN5f49HTiMzJIKjVK3U0pqQjUZZf/MbZs2ZKpU6da4/xtnZObm8v48eNZunQp\no0ePxmw2M3bs2EoHEnt7e5OVlWXdTiq91GE596hKmoQQQoi6QGvYvBm++MKYBcjDA8aMgQEDrnrt\nqvorKweSU+FcUaH/3EVj+2J6xecE+kHjQOMnpOjflqFOWUDhl9O/sDh+MRZtYXDbwYzvNL7OVAIs\nWnM0O9va8p+an2895m02083Hh2gfHzp5edn93lIRsKO8vDxycnKs2wUFBWWOh4aGcvToUWvr+pQp\nU+jZsydr165l0KBB5Ofns3XrVtq3b28N1Skd1pOXl0deXh7BwcGYTCZWrVrF2rVr6dq1q/X6KSkp\nXLp0CT8/Y6W8qKgoXn75ZZ5++mlyc3N57bXXKv0MVUmTqB+kN8A2acmtnOSPbZJHtjkqj86eNQb+\nFg8f7NoVJk+GRo0ccjuHseuzWmtIyywq6JcK6Tl7ATKzyz/HZIKQgJKCfkgghAZCcAC41Y6uFJfW\nJj6M/xCtNSM6jGBUh1G1vhJQYLFwMDub+PR0dmZmcqlUmTHAxYWoosJ/By8vTA78LBVWBIpmCqow\nuFxrvd0hKarDSsfvA/Tr16/MH+ITTzzB7Nmzeeyxx5g7dy5z5sxhxYoVPPbYY0yaNAmz2Uzv3r15\n9913reeUPt/X15c33niDCRMmkJuby6hRoxg9erT1eMeOHZk0aRJt2rTBYrGwb98+pk6dyvr16wkP\nD6d169bMmDGDV155pcLP0Lx583LT9M4779gji4QQQgiHKiyE9evh228hP98Y8DtxIvTo0YDm+7dY\njNCd0gX9cxeMVv7cvPLPcXMt27Jf/NPIr1Z3n/yYuIvPTvwMfp0Z22ksw9oNc3aSKpRnsbA3M5P4\njAx2ZWSQXSq0KsTVlWhfX6J9fGjt4VFjFZnKVhaOo/KKgENnDaoPKwsLYYszVxZ2etxpdTlhZWGJ\n766c5I9tkke22TOPEhIgNhaKJ8/r0wduu612zP7jkGd1XlH8funY/eICf3nx+wBeHhDa6LKQnkbg\n710nakpaa05mnCM+5RjxqcdIyrpA4u7TPPyn1xnYuvaNZ8wqLGRPUeF/T2YmeaV+L83c3Ykuavlv\n5u7usML/Va0sLLMGCSGEEKIuyMszegDWrzfKv8HBcMcdxkDgeiErp2zLfvHri+lGuE95AnyMAv7l\nLfzenjWbdjuwaAtHLyUZhf+Uo6TmZliP+bh6MLRp51pVCUgvKGBnUbz//qwsCkv9jsI9POhe1PLf\n2M3Niak0VNgjYH2DUt7AHKCl1vpupVR7IEJrvdKhCZMeAdEAOLNHoM5xQo+AEKL2278fPv4Yzp0z\nwtkHDYJRo4xpQWsVW8/q4vj9cxeMGP6zpQbtZmSVf47JZMzVXzp2P6Tox712xO9frQJLIQfTThOf\ncpQdKcdJzy8ZwxDg5k10UBuig9rQ3j8MU84Zp38/pObns6Oo8H8kOxtL0Xe7SSnae3oS7eNDlI8P\ngU6YouqqegRKWQz8BvQt2k4EvgAcWhEQQgghhKhIZqYxG9DmzcZ28+YwdSqEhzs1WbYVx+8Xz8pT\nepaeiuL3XV2ubNkPCYRg/1odv19duYX57LtwkvjUY+xKPUF2QUl+hHj4Wwv/rX1Da8Vg4OS8POs0\nnydKTRZjVoqu3t5E+/oS6e2Nr0vtnZunKilrq7WeoJSaCKC1zqwNmS+EuDZ1boyAE0h8d+Ukf2yT\nPLKtunmktbEewLJlcOmSsQbAiBEwZEgtLBNrbQxc2LsXtm+CNIwCf2Fh+e/38rgidj8uIZGYwb3r\nRPz+1cgqyGXPhQTiU46x50ICeYUls+c08w6yFv6beQVVWPgvXkfA0bTW/J6ba53mMzE313rMzWSi\ni7c33X186OLtjWet+2MsX1UqArlKKWtAmVKqLZBbyfuFEEIIIezuwgX45BPYtcvY7tABpkyB0FDn\npqsMiwWOHIH4eOPnwgVjf9pJcPE2Xgf4lAzSDQkwBu+GBIBPOfPEp6bVu0pAel4WO1NPEJ9yjP0X\nT1GoSwbQtvYNtRb+G3sGODGVBq01x3JyrC3/50vN8e9lNhPp7U20jw+dvb1xc8L6CdeqKmMEhgBP\nAZ2BdUA/YIbW+keHJkzGCIgGQMYIVIOMERCiwdIaNm6E//wHcnLA0xPGjYP+/WtJGbmgAA4cMAr+\nO3dCeqlFuAIDoVs3cImH5h2MCoCH8weJ1rTU3HR2pBwjPuUYRy6dKRtD7xdGVFBrooPaEuh+FVM8\n2fn7oVBrDmVlEZ+RwY6MDNJKzfHvVzTHf5SPDxGenrjUgcL/NY0R0FqvVUptB3oDCnhQa33ezmkU\nQgghhLjCmTPGlKBHjxrbUVEwaRIEOLuxODfXCPmJj4fduyG71IJcjRtDdLTxEx5u1FYOp4Fnbeq6\ncLzk7AtFM/0c40T6Wet+szLRtVFLooPaEBkYjq+b/VfMra58i4V9WVnEp6ezKzOTzFLhW0GurtZp\nPtt4ejp0ga+aZrMioIyArJuAGzHWFXAFvnJwuoQQDiZjBGyT+O7KSf7YJnlkW0V5VFAAa9bA998b\nr/39jQpAdHTNp9EqK8so9MfHG5WAvFKDe5s3Lyn8h4XZrauiLj2rtdb8nnneWvhPzEq1HnMzu9A1\nsBXRQW3pEtgSTxf7Tet0tWMEckrN8b87M5PcUnP8N3Vzsy7w1cKBc/w7W1XGCLwDtAU+xegRuFcp\nNVhr/X8OTZkQQgghGqRjx4xegMREY7t/fyMUyMsZDceXLhnhPvHxRvhP6YG+bdoYBf+oKKMXoB7S\nWpNnKSAjP5v0/Gwy8nPIKDD+vXw7JTedC6Xm+Pdycadbo9ZEB7Whc2ALXE3Onz0ns7DQOsf/vsxM\nCkqF57by8LBO89m0huef1VpTmF5IwYUCCi4aP/kX8q2vCy4U4N3Vm8a32ffvrCpjBA4AnbU2RnIo\npUzAPq11xyrdQCkzsA34XWs9SinVCFgGtAJOABO01hfLOa9OjREIDw/n7NmzmM1mvL29GT58OG+9\n9Rbe3t7OTpqoxWSMQDXIGAEh6r2cHFixAn780RgXEBpqDAbu0KGGE5KSAjt2GIX/I0dKFu0ymYzE\nFBf+qxOfVEue1RZtITM/h4yCnFKF+exS21lFhfsca+E/31LBLEfl8HPzsg727eAXhtlUA7Pn2Ph+\nuFhqjv9Dpeb4V0A7T0+ifX2J8vEhyEFz/FvyLRSkFZQp5F/xOq0AXVh5ecCnmw/N/q/6f0PXuo7A\nEaAlRqGdotdHqnH/h4B9gG/R9uPAOq31i0qpvxZtP16N69VKSilWrlzJwIEDSUxMZOjQocyfP58F\nCxY4O2lCCCFErbdnj7EwWGqqUd4eNsyYFrTG1l9KSiqZ6SchoWS/i4uxRHF0NERGgs9VDGZ1oNzC\nfKMgX1R4txbki1rq00sdy8jPJrMgt9oNUK4mM76unvi4euLj4oGPqwe+rl74uHoUbXsWHfcg1DMA\nk3L+ANpzeXnWaT6PlRq/YVaK64pm+unm44PfNczxr7XGkm25omB/eUt+YUbVKlJmHzMugS64BBg/\nroGu1tfF++2twisqpb4teukL7FdK/YIxRqAX8GtVLq6Uag7cAvwdY3VigFsxxhwA/BuIox5UBEoL\nCwtj2LBh7Nmzh61btzJnzhz2799Pq1ateP3117npJuPjL168mJdeeonff/+dkJAQ/vrXv3LPPfdY\nr7NixQqeeeYZjh8/TkhICG+//TZDhw4lLS2NOXPmsGrVKkwmE3feeSfPPvsspjowcl3UHnUp7tRZ\nJL67cpI/tkke2fb993GcORPDL78Y261aGQuDtWjh4BtrDadOlRT+z5wpOebuDl27GoX/Ll3Aw8PB\niTFc3lqfkZ/Nxq17ad8trKRgn5dtLdRnFOSUmXe/qrxdPPB1KynU+7iUFOSv3PbEzeRSq2Pk434+\nxE3tNImlFvj6/bI5/q/z8iLa15eu3t54VWGOf23RFFyqoPW+1GtLnsXmtZRZ4eLvUqaQf8VrfxdM\nrjVfjqusavHyZdvF1UdV6rUtrwJ/AfxK7QvVWicXvU4G7DaE/uC9B+11KSLei6j2OcU17FOnTrFq\n1Sr69u3LyJEjWbp0KcOGDWP9+vWMHz+egwcPEhQURGhoKN999x2tW7dm48aNDB8+nJ49exIdHc0v\nv/zC9OnT+fLLLxk0aBCJiYmkF01HNmPGDJo0acLRo0fJyMhg5MiRtGjRokwlQgghhKjNcnKM8vfi\nxdCoEbi5wejRMHCg0SPgEBaLMQChuPCfklJyzNvbmOYzOho6dbJbV4TWmjMZZ7hwMZGM9Ayj1T4v\n2xpXb7TiZ1fYWp+YmMq+gFMVXt/VZC5pkS8u2JfZ9ixqwTe2vV09akWLvT1oDScKFBtzPfnviROc\nLTV429NkoquPD92L5vh3v+yPqjCnkNyTuRW25hemFaIttou7Jg/TFQX7y1vyzb7mWluRsjlGAEAp\n1QToiVEB+EVrfdbGKSilRgLDtdb3K6VigEeKxghc0FoHlnpfqta6UTnnV3uMgDMrAuHh4aSkpODi\n4oK/vz8jR46kcePGHDlyhCVLlljfN2zYMCZPnsy0adOuuMbYsWP5wx/+wIMPPsi9996Lj48PL79c\ntj6WnJxMq1atuHjxIh5FLRSffvopH3zwAT/88MNVfFLhTDJGoBpkjIAQdY7WxpT6SUlGg3vpf4vX\n2QIj8uaOOyA42AGJKCyEgweNgv+OHcbg32L+/kasf3S0Eftv59VgU7NT+WT3J+xO3g2X9oHZ9rhB\nb2vojae1db7i7drfWm9vFg2H8xXxuWZ25Jq4YFFQkAn+nfExm4kqmuazo5dXuXP8a61J35bO2WVn\nKUyvPGTHxa+SFvziQr5H7V9B+JrGCCilJgAvARuKdr2llPqL1nq5jVP7ArcqpW4BPAA/pVQskKyU\naqK1TlJKNQUqrFTMmDGD8PBwAAICAoiKiqr0hlfTim8vSilWrFjBwIEDrfv+7//+j+XLl/Ptt99a\n9xUUFFjfs2rVKp599lkOHz6MxWIhKyuLyMhIAH7//XdGjBhxxX0SEhLIz8+nadOm1n0Wi4WWLVs6\n6qOJGhAXFwdgDSGo9vaW3cZ2UahPvdzOPW+dHu6a80u2ZVu27bqtNXTtGkNSEqxeHUdqKgQEGNuH\nDxvvDwsz3p+YaGy3ahVDkyYQGBhH584QHGzH9OXnExMSAvHxxH33HeTmEhMWZhzPzIT27YmZMgXa\ntCFuwwZITiamUyc75oeGcPj6wNcciz+Gu4s7/Ts1xccrlIQ95/A0u9Gvdyd8XD3ZG38ST7MbQ2+M\nxtvVg41b90IexFxf8fPwPJdq1/PZwduFGkKv70Z8rolvN+8h2wJhPboBkL59B+1IY8rkobTz9GTj\nhg2cB1zK+f3kp+bz9bNfk30sm95hvXFv5s62S9sw+5q5qd9NuAS4sOXgFsw+ZgaOGIjJxVT+7zsZ\nYjpdef3asr1jxw4uXjTm4Tlx4gSVqcqsQbuAm4t7AZRSIcB/tdaRlZ5Y9ho3AY8W9Qi8CKRorV9Q\nSj0OBGitrxgjUNdmDWrdujWLFi0qUxH4xz/+wbFjx3j//feveH9ubi6BgYEsXbqU0aNHYzabGTt2\nLF27duW5555j1qxZeHl58corr5Q578yZM7Rt25aMjAwZE1APOLNHoM6NEXBCj0CcxHdXSvLHtvqW\nRwUFcPbslS38ycllp9QvzdMTmjSBpk3L/hscbIQA2S2PsrNL5vjfs6dsgsLCSub4b97cocsRJ6Yn\nsrwunFIAACAASURBVHTXUo6mGiugdW/anYldJuJ/6tOG8ay2k1wNe3NNxOeZ2ZVrIqfUV2WoWRPt\nbiHavZBWLpoNG34kZsorFV5LWzQXN1zk/NfnseRYMHmaCLktBP9+/g2iN+VaZw1SwLlS2ylF+6qr\n+Ff4D+BzpdRMiqYPvYpr1QlTpkyhZ8+erF27lkGDBpGfn8/WrVtp3749fn5+5OXlERwcjMlkYtWq\nVaxdu5auXY3/7DNnzmTIkCGMHDmSmJgYzpw5Q0ZGBhEREQwZMoQ5c+bw/PPP4+3tzfHjxzl9+jQD\nBgxw8icWQghRH+TkGIX8ywv8584ZYfbl8fcvv8Dv7+/Acnd6eskc//v3l53jPzy8pPAf6vgVfQss\nBaw6vIpVR1ZRaCnE38OfSV0mEd3UmSug1S1ZFtiVZyI+18zePBP5pQr/LVw00e6FRLtbaGrWVf6b\nyk3MJXlpMtlHjZmDfLv70nhiY1z8nb+mQW1QlVxYDaxRSn2CUQG4HVhVnZtorTdQFFqktU4Fbq5m\nOuuk5s2bs2LFCh577DEmTZqE2Wymd+/evPvuu/j6+vLGG28wYcIEcnNzGTVqFKNHj7ae27NnTxYv\nXszDDz/M8ePHCQ0N5Z133iEiIoIlS5bw+OOP07lzZ9LT02nTpg2PP16vJl4SNaAhtjBVV31qyXUE\nyR/b6koepaQYc/efPm0U+EvH75emlNGSf3lhv2nTq1/sq9p5pDX8/DNs3gyHD5fUTEyXzfHf6Irh\nhw5z7MIxYnfGkphurIDWv1V/xnUah5frta+AVh+e1RYNORqytCLLUvJvtlZkaciyKE4UKA7mmSgd\ntd/WtaTwH2yuuPc8pveVC01YCiykrkoldVUqulDj4u9C40mN8Y32LecKDVdVQoMUMA64EaNVf5PW\n+iuHJ6yOhQYJcTVksHA1yGBhIezOYoEffjAW8SodSWM2G43olxf4mzSpwXn9y3P2LCxdagz+LU5o\np05G4b9bN/Ct2UJeTkEOXx/4mrgTxriAUJ9QpkROoUNQOSug1eFntdaQD2UK8VlakV1UiM/SlxXu\ni99XdDxHV226SRMQ4WYh2t1CN7dCAqo6Dvey74fso9kkxSaRd8b4ow4YEEDw2GDMXrV/YK8jXFNo\nUFFp/MuiHyFEPdFQ406ro77Fd9ub5I9ttTmPfv8dYmOheCxhjx7Qq5dR2A8JceAUnpepUh4VFsL6\n9fDtt5CfbyzqNXYsdO9+9V0R12h38m4+3v0xF7IvYDaZGdJuCCPaj8DVbN+akr2e1YWaKwru2ZcV\n7IsL7tnltN5XfW3h8nkq8DJpvBR4KY2nyfjXq+jfILOmq5sF76v4u4v7+RAx7Y0pQc9/dZ6LGy6C\nBrdQN0KnhOLVwTl/I3VBZQuKHa/gkAbQWrdxSIqEEEII4TD5+fD997BmjVG+DgyEyZONRXNrpYQE\no8Zyqmgu/T594LbbnLbCb3puOsv2LuPX08baquEB4UztNpXmfs0del+tjQG0tlrfyyvEZ2lF7jV2\nPrsqrIX44sK7tTBfqpDvWep48b8eCkwOHpObsTuD5I+TKbhQgDIrAocEEjQiyCmLdNUlFYYGKaVK\nz+arMXpsbgceBX7TWo93aMIkNEg0ABIaVA0SGiTENTt82ChTJycb8f433WQ0rNfQwrnVk5dn9ACs\nX2/EMAUFGYsNXHedU5KjtWbr71tZvm85mXmZuJndGN1xNANbD6zaAl2H/0mBRzNrgf3/s/fe0W1d\nd77vZ6ODANirKklZjWqE5KbEjuzYVuLuOHZGLkocX2dekrcyTnxnrcm83MxM3n2z8iYz68bJzH0z\nmZJiucYtju3EdmyHtuMiF4HqjeoSAZJgRW9nvz8OCJASBYCdFPdnLa7D0zd+BPf57X2+v98vl+M+\nVDs/9Lj8NWzPj4GzZuUNUl8/y3G3n+XYDx5nnqHJdZJB6Hw2SODkegBs9TZqttZgWzATv9TTw5ik\nQVJKf/pkA/Bl9ArBrcANUsp9k9FQhUKhUCgUE08kAs89B2+/ra/X1cHWrbBkyfS267zs3w+PPaan\nKTIY4Npr4ZZbwGqd8qb4w348Xg8ft3/M8b7jADRVNXHP2nuoLDp/BbSkpnEgHMYTDLIvHCbQV0PC\nOL72Wwtx3EeQ3RQJ/dzpzJQpNdDiIOOgJUR6CVpcIBMgE0PW0/tkQqDFBvfpx2nx9Pa4vj0ZEGjh\nJIYqAxW3VlD22TLEZL9+uIDIJQ2yAPcD3wH+BNwqpWybqoYpFIrJRcUI5Gcm67tnAso++ZkJNmpt\nhSeegL4+Pbb2+uv1H9MMyZ44zEahEDzzjJ4RCGD+fPjyl/VUoFOElBJv0IvH68Hj83Cq/1Rmn8Pi\n4EurvsRl8y8bMf98TNPYGwrhCQbZFQwSHZprVYIR8jrxZ8tuPNt3c92nVmMXYJwk/zbjpJ/jiGcd\ndS0BMq474Bknfahjf9YxZzv2cjyvM/Kwy+zh1r+9EUulZfJucoGSqxs4CiSBnwAngbVCiLXoKUSl\nlPK5KWifQqFQKBSKMdDfD08+CTt26OuNjfpbgHSB3ZmFlPDJJ/DUUzAwoKcmuvFG2LxZH71M+u0l\nJ/pPZJz/jmBHZp/NZGNtzVrcdW5WVa3Caho+qx9OpdgVDOIJBtkbCpEYIvdcaLXidrlY53BQdbIF\ni33eqGfljwmJPe1YxxMCGcvhpI8wYz7smGHOe/YcOd5I4AIQAoQFDBYQZplegsEs9e3m7PbMMWbO\n2aevZ88xWCXeT4JqEDBGcsUI/DL964gHSCm/OkltGry/ihFQXPCoGIFRoGIEFIqCkFKfUH/mGQiH\ndf3/bbfp8QAzsiB9b6/+ymLnTn192TK4995JLwKmSY22njY8Xg+tvlZ6Ij2ZfU6Lk+baZtx1blZU\nrsBkGD5vOpBM0hoM4hkIcLg/jIxrGBJgjEvqjVZWmeysMNsplSa0uIaMS7Rjv0WKSrRhM+ZnyWCm\n20kfdLit53HSBx1zy3mcdLO+b6TtwjiJ0iT1fMjJWGME7pu0FikUCoVCoZhQEgm9INhzz2XT7K9Z\no2cEmsLaWoWTTMKf/gTPP6+XMrbb4YtfhCuumDSPUUto7PHsYd/JfRzuOEwkHMGQNGBJWFhmXEaj\ns5GGogZqLDXIUxIZl3jjXmRcEook8QajdIRiDISTiITEkQS3gBKjiUqzmQqzCYshCQQIEyA89Ob9\nrjHpsc5x0keYFR8+ez70mPPMvlum0ElXzGhmiEJQMZ24XC52795N/RRqMBXTj4oRyM9M0HfPZJR9\n8jMZNgqHwefTKwAPXfr9+tsA0DNrbtmi1waYUQ5eLAZ794LHA7t2QTRKS3s7V91wA9x1F5SWTvgt\ntZhGaG+I9vfbaX2rlcBAAIA66rCZbFQWVVJZVInL4tLFz8AAA4Au+/EnknQnEgRT2al5k4Ayk4lK\nh5lKhwWrzYSwCAwWQ3ZpPWu9O4zBYU3PmhcgkUnPyr/14W6u/pTqq3MxWEdAMXrUQGCCqK+vp7Oz\nE+MQLeNXv/pVfvrTn05jqwojEAhMdxMUCoVCMQQpdan82c6+16tr/0fCYIDqalixQk+wM01p9s8l\nHNadfo9HHwQkEtl9CxfChg3wta9N6IglFU4R2h0i4AkQ3BPkpP8kJ/tPIqVEq9ZYtGgRiyoXUVZS\nhsE6xFk3C7pEksOJCAdTUbqEhmY2oJltmKwGlpU4WFvqpKnMib3IhDCKEYOGR+RwAOzFo/4sM2og\np7jgOG+MwHQz22IEGhoa+K//+i8++9nPTndTFLMIFSMwCpQGVHEBomnQ3T2ywx+JjHyOxaLL5+vq\n9CrAg8vq6pmTCYiBAT1dkcej65SGzKazZAm43dDcrJcwniCSA0mCO4MEPUHCB8LIlCQQC3C45zAd\n5R30Nvay9MqlfOHTX8BhcWTO06TkaCSCJx3w2z1koOIwGlnndOJ2OllZVIR5PEEWc6Wvng7U8yEn\nY4oROOsCnwbqhxwvpZSPTEzzLnz+4z/+gx//+MecPn2ahQsX8uijj+J2u9m/fz/f+MY32LlzJ/Pn\nz+eHP/whN998MwD33XcfDoeDEydO8Pbbb9PU1MTjjz9OY6Ne0Pm9997jwQcf5PDhwyxbtoyf/OQn\nbNy4EYCrrrqKK6+8kjfffJNdu3Zx9dVX8/Of/5wHH3yQl156ieXLl/P000+zePFiAAwGA21tbTQ2\nNhKJRPgf/+N/8Oyzz9LX18eaNWt4/fXXkVLywAMP8Morr5BKpVi6dCkvvfQS1dXV02NUhUKhmEUk\nk3oRr0Enf9Dh7+gYPkE+FIdjuKM/uKyomKGzxN3duuPv8cCRI1mdksEAK1fqzv+6dRMq/0l0Jwi2\nBgl4AkTaIpn0JhoabaVtfFT6ET31PZTWlHLv2ntZUbkC0HP8H0o7/63BIAPJZOaaJSYT7rTzv7So\nCOOMNLZCMTHkHQgIIR4FGtGLiQ2NXZ9xA4GDB/+PCbvW8uU/G/U5I83sPv300/zgBz/ghRdeYMOG\nDRw5cgSz2UwikeDmm2/mgQce4PXXX+edd97h1ltv5eOPP2bZsmUAPPXUU7zyyiu43W6+8pWv8L3v\nfY8nnniCnp4ebrzxRv7lX/6Fu+66i1//+tfceOONHDlyhLKyssy5r776KhUVFWzcuJGNGzfys5/9\njEceeYT777+fH/zgB/z85z8/p71/+Zd/yf79+3n//fepqanhww8/RAjBL3/5SwYGBjh9+jRWq5XW\n1lbsdvuobaSYOagYgfwoDXxulH1GRkrd0W9thddea8Hlugq/X5/9H4myspEdfpdrhjr8Z/Puu9DS\nAidPZreZzdDUpDv/a9fqo5rzMNrvUcwXI9gaJLgjSPRENLNdmASOJgdd9V08K5+lU3ZiEAaubbyW\nm5ffDMJEayCg5/gPhQgPeUtRZTbjdrlwO5002GyFy32mANVX50fFCIydQt4IbACaRtTpKDJIKbnt\nttswDXkv+4//+I8888wz/NVf/RUbNmwAYEm6jOM777xDKBTiu9/9LgBXX301N910E0888QR/+7d/\nC8Dtt9/OxRdfDMA999zDQw89BMDLL7/M8uXLueeeewDYsmULP/3pT/ntb3/LV77yFYQQfPWrX6Wh\noQGA66+/nv3792dkS3feeSff//73z/kMmqbxi1/8gu3bt1NXVwfA5ZdfDoDFYqG7u5vDhw+zZs0a\n3G73BFpPoVAoZjdSwokT2QnxjnQa+vZ2PW+/waDLeUZy+G226W37mJESXngBfv97fd1mg9WrYf16\nWLVqwj6YlJLYqRhBjz7zH/fGM/sMVgOONQ6cbicsg2eOPMP209sBWFSyiDvX3EOfsZxfdPjZEwoR\nHzIam2+1Zmb+51utM8r5VyimikIGAnuAOqB9ktsybsYyiz9RCCF44YUXzokR+PGPf5xx/ofS3t7O\nwoULh21bvHgx7e3tmevVDMmhbLfbCQaDmXMXLVp03nOBYefabLZhEh6bzZa51lD8fj/RaHTE9m7d\nupVTp06xZcsW+vr6uPfee/n7v//7YQMfxexCzTDlR81252au20fToK0t6/z39mb3OZ26BL6p6Srq\n6maYfn8ikFIvVPD66/oo5667YONG/U3AKBnpeySlJHo0qgf7eoIk/Fn9lNFhxLHWgcvtoqipCGES\nfNT+EU+9/xTBeBBptLN88Q2YS1bycFeElPRmzm2w2Wh2OnG7XNRYZkcBKtVX5+eqy5ZNdxNmLYV0\nS1XAPiHEh0AsvU1KKW+ZvGZdOCxcuJC2trZzts+bN49Tp04hpczMQpw4cYIVK1bkveb8+fN57rnh\nhZ1PnDjB9ddfP+Lxhc5yVFZWYrPZaGtrY+3atcP2mUwm/uZv/oa/+Zu/4cSJE9xwww0sX76c+++/\nv6BrKxQKxYVAMgkHDuiO/86dMDTpWlmZroRxu+Gii2Zo8a6JQEq9ANhbb+lVf7/2Nf1Dj/eyKUn4\nUJigJ0iwNUiyP6vbN5WYcDY7cbqdFC0rQhj151p3uJvHdzzOJ50H8RvLMZS6KS9fwyGTDUJhDEKw\nrKgoM/NfNoaBikJxIVPIQODv0ktJJsPuyNWG5zojqaceeOABHnroIa644grcbjdHjhzBYrFw+eWX\nU1RUxI9+9CMeeugh3n33XV566SX+7u/+7rzXGuT666/nW9/6Fk888QR33nknzz77LAcOHOCmm24a\nsS2FqroMBgP3338/Dz30ENu2baO6upoPP/yQDRs28N5771FRUUFTUxMulwuz2TwsVapi9qF0p/lR\nGvjczBX7DE19v3v38Gw+1dW6EsbthsWLz9X0X3A20jR45BF4/3199v/rX9flQGO9XELj1V+9SrOp\nmdDOEKlwVrdvrjTjdDtxuV3YGofr9jWp8dyRFrYdeR8vTiL2i2ksa6TGWYNJCFamnf91TieuWf4q\nRvXV+VExAmMn73+HlLJFCFEPXCSlfF0IUVTIeXORm2++eZhzvHnzZp599lm6u7u5++67OXPmDA0N\nDWzbto1Fixbx4osv8s1vfpMf/vCHLFiwgG3btmUChYU4Nzfx4HpFRQUvvfQSDz74IN/4xjcyGXzK\nh5SOHHpurmud/fs//dM/8dd//ddccsklBINBmpubeeWVV/D5fHz961/n9OnTOJ1OtmzZwtatWyfA\nagqFQjHzyJf6fnDmv65ulgT0TgSpFPz85/Dxx2C1wje/qRctGO1lonqO/6AnSGh3iK7jXQzM0wt4\nWedZcbr1mX/rAl23H0wmaYtE8MZi7On34ek5wf7+Dj3Np6ihylGJu2Ip64vLcDudrHE4sKuJKoWi\nIPLWERBC/DnwNaBcSrlECLEM+Fcp5TWT2rBZVkdAoRgLqo7AKFB5ohWTTK7U942N2dT3czJrcjIJ\n//7vuh7KbodvfUuvB1Do6YEkoV16ga/w/jAyme33bPU2nM1Okmts+MvAF4/jjcXwxeO0x+N4w734\nw3784W6iyWyWIIfJxM3zmrh1/kqaHA4sM12LNVf66ulAPR9yMt46Av8ncCnwAYCU8pAQYi52gwqF\nQqG4wMiV+n7FiqzzP4Gp72cf8Tj867/Cvn16GtAHH9R1UHlI9Oo5/oOeIJHDEaQmkRKiUiPaYKZ/\npRnvciPtjhS+eA+xkAYhXc7aH+vPOP9aKoJdRinRIiwxGXBXLOaK2iY21qzAYlSaf4ViPBQyEIhJ\nKWOD8hEhhAkVI6BQzHqU7jQ/F5y+e4KZrfbxerPO/9DU9ybT8NT3Tuf47zVbbZQhGoX//b/h0CG9\nsMG3vw0LFpz38HhnnKAnSN+OAXqPhImkNEJaijAa/gYDp5YZ6F5uIulMMViaqP2t7dReegnxeD+x\ncDv9gWMYE/1UyAgLtQi1dhfr69y4a90sKV+CQczwmf8JRvXV+VExAmOnkIHAW0KI7wFFQojrgG8C\nL05usxQKhUKhmBikhFOndMd/xw69ou8gViusWaM7/6tXz+Kc/pNBOAz//M9w9Kj+SuQ739ELHwxB\n0zROHg1w8qM+Aq1BomdihFMaMU1DM0PfUhO9TWb6l1pJ2dNxbmYzdRYL1RYzwcBx3gvvw3TMgyEZ\nxgaUALXOWtx1n8Zd62ZRySKV41+hmCQKiREwAA8Am9ObXgX+c7ILjKkYAcVcQMUIjAKlAVWMAk3T\n/dfBmf/u7uw+hwPWrdOd/5Urx5T6/sInGISf/ER/ZVJRoQ8CqqoA3flvO9DPwQ968H/ST8qfTfOZ\nskHfcjP9TRasK+3UumzUWizUWSzUWizUWCxYDQZO9p9k285tnOzPvpJZVLIId3rmv85VN+UfedKZ\nK331dKCeDzkZb4zAbcCvpJT/PrHNUigUCoVi4kgmdQWLx6MH/Q4MZPeVlOha//XrYelSPf294jwM\nDMDDD8OZM3pk9He+Q6qklP07/Bz+sIdeTwCtLxtJLYqNONc5KHG7qG5yMa/ISpXFgnGEWfx4Ks6z\n+17k9aOvo0mNiqIKPtvwWdy1biqKKqbyUyoUCgobCNwCPCyEeAt4CnhFSpnMc45CoZjhKN1pfma9\nvnuSmQn2icf1GFaPR0/3GQ5n91VWZnP8NzRMT5rPmWCjUdHbCz/+MXR0EKtdwN5NWzn6aBf9rUeR\nIS1zmKHcRMV6F8suq2DZqlKMxvy6/QP+Azy661G6Ql0YhIFrG6/lluW38P6f3qeiUQ0Czofqq/Oj\nYgTGTiF1BO4TQliA64G7gP9PCPEHKeV/m/TWnQelFVQoFIq5SySiF/byeGDPHn0wMMj8+dkc//Pn\nz6Ec/xOB30/kn37Kbp+NY9pnCRythwOdmd3GGjPVG4pZfnkljUtdGApM1xmKh3hm3zO8d+o9AOYX\nz+fL675MfWn9JHwIhUIxGvLGCGQO1AcDnwPuBz4jpZzU4fv5YgQUCsVZzBXdqdKAznmOHoXf/Q72\n79dlQIM0NGTTfNbUTF/7ZhtaQiPeEWegrZdD29s49clpQl12MFqgvByEAfMiKzUbill1eSUL612j\nur6Ukh3eHTy550kGYgOYjWZuXHojm5dsxmiYg9qsudJXTwfq+ZCTccUICCFuAL4EXA20AP8B3DmR\nDVQoFAqF4nxEo/Cb30BLi54ByGCAZcuyM/9lZdPdwplNKpIi7o0T98Uzy4GjfXS0deEPhOhPJdM5\nwYvAYsG6oY55l5ax6vJKauc5xnTP3kgvT+x5gp2+nQAsrVjK1rVbqXGqkZpCMZMoJEbgy8CTwNel\nlNF8ByumhlmnO50GlI1yo3Sn+VHfodxMhX1274bHH4eeHj3Ad/NmuOYaPaX9bGCqvkNSSlIDKWLe\n2DCHP+6Nk+zXX59EwxH8vT10h0IMpDSkAWKuFLGSJOWVRhqWVbD29g2U147duFJK3j7xNs/tf45o\nMordbOf2lbdz5aIrzyvrVf9nuVF9dX5UjMDYKSRGYMtUNEShUCgUikECAXjqKfjoI329vh62bs1Z\ny2pOIDVJojtxzgx/zBtDi2hnHSwJh0L4A720m4P4nDGijSkiJSmSJUmW1Nq4uHExa1avxlFcPO62\n+YI+tu3cRltPGwDNtc3cteYuSm1zuSyzQjGzOW+MgBDiXSnlp4UQQc6tJCyllOPvNXI1TMUIKBSF\nMVd0p0oDOieQErZvh1//GkIhsFjg1lvhs5/VJUFzBS2pkehIZJz8jOPfEUcmRn42Gh1GzDVmAoY+\njkXb2Uc3p51x4k4NBNiAtcXFuBsaWLV6NVa7fULamtSSvNr2Kr87/DuSWpISWwlbVm/BXetWyT2G\nMlf66ulAPR9yMqYYASnlp9PLCSiyrlAoFApFbvx+eOwxPR0oQFMT3HOPngZ0rqDFNbpf7Kb3zV5k\ncmSH31RmwlJrwVpnxVJrwVRr5nSJxiedx2htbaVnSBolpxBcUlrG+sZGVqxahcliGXPbpJR0R7rx\nBX14A159GfTiDXgJJ/S8rVcsuoIvNn2RInPRmO+jUCimjkJiBAAQQswHBsP821UtgelFaSrzo2yU\nG6U7zY/6DuVmouyjafDmm/DCC3oqUIcDvvQluOyy2Z/+czQ2Cu0P0fFYB4muBAiw1Fiw1Fqw1A1f\nGm1GkprGgXAYTzDIzv4OAp+0gdcLQKkQuCsqcC9dytIVKzCMsnpaUkvSGeo8x+HvCHYQT8VHPKfW\nWcvda+5meeXyUd0L1P9ZPlRfnR8VIzB2zjsQEEL8X4BZSvmD9Kb3gX7AAvwS+OGkt06hUCgUFzSn\nT8O2bXD8uL5+6aX6IGC2BANPBKlQiq5nuuh/rx8A6wIrNVtrsNcPl+7ENI1doRCe3iC7gkEimqZH\nUbe1UdXfz/r+ftxr1lD/+c8jCpj5jyaj+IK+cxz+rlAXmtRGPKfEVkKds45aZy11rvTSWUextVjJ\ngBSKWUiuGAEPcKWUMji4LqV0CyGMwNuD0qFJa5iKEVAoCmOu6E6VBvSCIpGAl1+G116DVEpPW3/3\n3bBmDk18SikJfBKg66kukgNJhFlQcVMF5deVI4y6Ux1OpdgdCuEJBNgbDhPX0g56IsGCgwdx79mD\nu7eXeTU1iPNEUwdiAbxB7zkOf2+kd8R2CSGoLKo8x+GvddYqyc94mCt99XSgng85GXMdgcFBQJqf\npLelhBATE2GkUCgUijmFpukxAL/+NXR06NKfq6+G224Dm226Wzd1JHoTdD7RSXCn/pgtWlZEzb01\nWGosDCST7OwL4gkGORAOkxoyKdZos+E+fZrmF1+kurd3WDS1JuBYzxGO9R0b5vQH48ER22AymKhx\n1pzj8Nc4ajAbzVNiB4VCMb3kGgg4hBAWKWUcQEr5SwAhhBWYQy9tZyZKU5kfZaPcKN1pftR3KDeF\n2ieZhAMHwOOB1lYIpv3Sujo9JeiSJZPbzunkbBtJKel/u5+u57rQohoGu4GqO6pIXlrEO6EQnpM+\n2iKRTKo+gxCsKCrC7XTSHI9T+sQTemllgKYmknf9GYdED549T9Dqa2UgNnBOG2wm2zAZz6DTX1lU\niUFMfyom9X+WG9VX50fFCIydXAOBZ4B/E0J8S0oZAhBCOIF/Se/LiRDCBrwFWNHjCl6QUv61EKIc\neApYDBwHviSl7BvXp1AoFArFjCIWg717ded/1y69OvAgNTXwqU/BtdeCqeCUFbOfmDdGx7YOIkci\nAGhrbBy9wc7Txn5OHOvIHGcSgpVFRax3uVjrcOA0GOCNN+C3v4V4nJTdxpHrNvBuXZJdO/4hk7EH\noMpRRVNV0zCHv8RaovT7CoViRHLFCJiA/wd4ADiZ3rwI+C/ge4VkDRJCFEkpw+lr/Qn4S+AWwC+l\n/JEQ4q+AMinld0c4V8UIKBSFMFd0p0oDOuMJh3Wn3+PRBwGJRHbfwoXgdus/dXWzPxvQaNCSGr2v\n9tL9cjeBeBK/XWP358wcHjKDaTUYWO1wsN7pZLXDgW0w08+pU7BtG8ljR+iJ9LCvwcVL6+wErNlz\n5xfPx13rxl3nZr5rvnL6Zypzpa+eDtTzISdjrSOQBL4rhPi/gYvSm9uklOHznTPCNQaPtaCnZ8eP\nvQAAIABJREFUHu1FHwhsSm//FdACnDMQUCgUCsXMZ2BAl/t4PHDwoB74O8iSJVnnfy7VAhhK+EiY\nA784Q8fJEN2JJKfWGzl1nZ2UHRxGI2sdDtwuF01FRZiHVkxLJIg8/zR9L/6a7mAXZ0wRPti0hPbF\neoheQ1kD7lo3zbXN1DhrpunTKRSK2U7el7JpZ37XWC4uhDAAO4AlwL9KKfcKIWqklIPvQDsA1YON\nAaWpzI+yUW6U7jQ/6jt0fvbuhX/+5xbgKgZf3hoMsHKl7vivWwelpdPZwukjmdTYv7OHtne7+fCF\nP7Kkcj3RSgPHb7ZjWGrjCqcTt9PJsqIijGfP3vf2cqrlt5x58TES7afRBBxaM49dlzfRULeSLWnn\nv8xeNj0fbhJQ/2e5UX11flSMwNiZVHWmlFIDmoUQJcCrQoirz9ovhRDn1f/cd9991NfXA1BaWkpz\nc3Oms2hpaQGYs+utra0zqj0zcb21tXVGtWdS19/fra+nHxaFrLfuPTqq46d9PebPdPRTZd9Bpv3v\nO4PWg0H4n/+zJVP9d/FiMJlaWLoU7rvvKhyOwf+/mdHeqVqPx1NUuNZwbHsP2195C2Iay6s3kJCS\n1vl7qdpYwjc2XU+jzcZbb71FB7By8PznnoO2Nj4Vj3Ci9S1+d7INgCVLa+i540ai8Qqudy7hho03\nzJjPO5Hrc+Z5llYFjbb/a917dFTHz8X11v2nuAqdGfP3nmb/p69PD789Plik5TzkihH4tJTyXSGE\nTUoZHfGgUSCE+D4QQY85uEpK6RNC1AF/lFKuGOF4FSOgUBTCXNGdKg3otCIlfPQRPPWUnvXHbIab\nb4ZNm+ZW2s+hhEMJdn3o58RHvQR2hyCefWaZ5lmo3lDMyisqqV/sGq7bl1KvpObx6D/t7fjDftp6\n2oiIFL76ShZedQsbbvwadrtK0nfBMFf66ulAPR9yMtY6Aj8FNqBXFHaP4aaVQFJK2ZeuO3Ad8APg\nt8BXgH9IL38z2msrFAqFYuro7obHH4c9e/T1FSvgnnugunp62zUd9PVG2f1hN6c+6iW8PwxD0maY\nF1upu7iEVZdXMn+Rc/iJUsKxY1nnv6sLgFgqxsHQSTzVGicvvgj7ug3cs+Gr1LnqpvBTKRSKuUqu\ngUBSCPEfwHwhxE+BoSMJKaX8izzXrgN+lY4TMADbpJRvpCsW/1oI8d9Ipw8de/PnLi0tLZnXQIqR\nUTbKjdKd5meuf4c0DVpa4De/0dOBFhXBHXfoqT+FmDv26eqMsOcDP2c+7iN6OALp4r4IsC6zM//i\nElZfXkl1zVlVd1MpWh57jKvMZt357+/P7JIuFwcX2nnedpyTNUuwWIu4feXtfGbxZ+Zc1p+58j0a\nK6qvzo+KERg7uQYCNwHXAJuBTzhrIJDvwlLK3cD6Ebb3ANeOrpkKhUKhmEra2+GRR/RJbIANG2DL\nFigunt52TRZSSpJ9SeK+OHFvHP/pMCdOBOk8HSbcNyQPqhGKVhex8OJS1lxWSWn5WbqoREIv+OXx\nwM6dcPgwzJun76uoALcb/7KF/CrwDod624Ai1tas5e41d19QAcAKhWJ2cN4YgcwBQjRLKVunqD1D\n76tiBBSKQpgrulOlAZ0Skkn43e/glVf0VKClpXD33XoWoAsBqUkS/gRxb5y4L07MG9Od//Y4gXAC\nfyJBdyJBKKVlT7IKnKscLL60jNUXV+ByWYZfNBrVdVMej74cWj2ttlZPo7R+Pan58/jDsdd56dBL\nJFIJiq3FbFm9hfV16+fcW4A5yVzpq6cD9XzIyVhjBAbpFkI8D1yRXn8beFBKeXqiGqhQKBSK6efI\nEf0tgM+nr2/aBF/4Atjt09uusaAlNOId8YzDn1l2xJHJ9CSThEAqhT+hDwCCNkmkxkC0yohWZWVR\nvYum+hJWLyzGOljga5BQSJ/x93j0NwBDq6ctWjS8ehpwvO842/70Q04P6I/OTy38FHc03YHD4pgK\ncygUCsWIFDIQ+AXwGFkt/z3pbddNVqMU+VGayvwoG+VG6U7zM1e+Q9EoPP+8Hg8A+iT2vffC0jya\n25lgn1Q4NczRH5zhT/gTI4pYpYRAsaS9VHK0OEl3uSRSZSJaaaGo1MK6dIGv5XY7JoNh+Ml9fdnq\naYcO6UEUoAdMXHRR1vmvqMic8tobrzFQN8AbR99AkxqVRZXcu/ZeVlatnESrzC5mwvdoJqP66vyo\nGIGxU8hAoEpK+Ysh678UQnxnshqkUCgUiqkhkdD92mefhd5eMBrh85+H66/X04PONFLhFIGPA8TO\nxDLOf7I/OeKxwiAwV5ux1FkwVptpL9PY54rTWhQjYNLQw94slJvNXJYu8LXEbsdwtkQnEoE//Ul3\n/o8cyW43GqGpSXf8m5vPCZ5Iakl2d+zmkdZHcIQdGISBzUs2c/Pym7EYz5IWKRQKxTRRSIzAm+hv\nAB5H7zm3AF+VUl4zqQ1TMQIKRWHMFd2p0oBOCNEo7N6dlbPHYvr2hgbYuhXmz9CvUmBHgM4nO89x\n/A0WA+YaM9Y6K5ZaC5Y6C5ZaC1qFkX3xCDsCAfaEQkS1rOa/1mLB7XTidrlYZLWeX5/f2qrnTR3M\n9mM2w6pVuvO/dq2eRmkIsWSMvV178Xg97OrYRTSpxwosLFnI1rVbWVy6eOIMoph9zJW+ejpQz4ec\njDdG4H7gn4H/lV5/D/jqBLVNoVAoFJNMIAC7dmXl7MkhvnR9vZ4O9Mor4WwlzEwg0Zeg84lOgq1B\nAOyNdpzrnRmH31xhzjjyoVSKXcEgnqCffSdCJIZMJi2y2XTn3+mkzmrNfdP+fnjySdixQ19vbITr\nrtMHAWedG4qH2N25G4/Xw96uvSRS2ViBhSUL2bhgI1fVX4XRcFaMgUKhUMwA8g4EpJTHgZsnvymK\n0aA0lflRNsqN0p3mZzZ/h3p7s3L2w4eHy9mXLcsqWsrLx36PybSPlJL+d/rpeq4LLaJhsBmour2K\nks+UDJvB70sk2BkK4QkEOBiJoKWdfwFcZLfjdjppdjqptBQgx5ES3n0XnnlGlwTZbHDbbXrU9JBR\nUn+0n50dO/F4PRzsPkhKS2X2LSlfgrvWjbvOTWVRJS0tLRgb1SAgF7P5/2wqUH11flSMwNgp5I2A\nQqFQKGYBnZ3ZwrWD+f9Bl7OvXp1VtMz0WgDxjjgdj3YQPhQGwLnWSfXd1ZjL9MAFfzyOJxjEEwxy\nJBLJnGcUgiaHA7fTyTqnkxLTKB5xnZ3w6KNw8KC+vmaNnjc1PVLyh/20+lrxeD0c6T3CoHTVIAys\nrFqJu9bNutp1lNpKJ8ACCoVCMTXkjRGYLlSMgEJRIHNFd6o0oOcgJZw5k3X+z5zJ7rNYss7/6tXn\nyNlnJDIl6Xmth+6Xu5EJianYRPWWahxuB75EQnf+AwFODQY2AGYhWJV2/tc4nTjOTvOZj1QKXn8d\nXnxRj552OvXKaRdfDEKw07eTlw69xMn+k9l7Gs00VTXhrnWztmatSgGqKIy50ldPB+r5kJPxxggo\nFAqFYoYgpT7bP+j8d3Vl99nt+oy/260ntMknhZ9JRI5H6NjWQey07uQXbywmcpOL12UEzwk/HfF4\n5libwcCadJrP1Q4H1rEGN5w4Adu2walT+vrGjXDHHeB0MhAb4Mk9T/JJ+yf6PU02VlevZn3delZV\nr8JmsuW4sEKhUMwO8g4EhBBlwJeB+iHHSynlX0xiuxR5UJrK/Cgb5UbpTvMzU75Dmqbr/D0eXfff\n25vd53LpWv/mZlixAkajhhkvE2EfLabhf9FP3xt9aClJsExw/GY7n8yL0NM9kDnOaTSyLq33X1lU\nhHk8kc3xuP4G4PXXdeNWVsI990BTE1JK3jv5Ls/se4ZwIozFaOG2FbfxmcWfwWwcfU7VmfIdmsko\nG+VG9dX5UTECY6eQR8bvgPeBXcBg8mWl2VEoFIpJJJnUM/x4PHoB22Awu6+8PFu7asmSmZntpxBC\n+0J4H/Xh90Xwp5IcuMTAkU0WNEsYElBmMtGcTvO5dKQc/2Nh/3547DH9VYrBoGcDuvlmsFrpDHXy\n2K7HOOA/AMCq6lXcs+YeKooq8lxUoVAoZieF1BHYIaVcP0XtGXpfFSOgUBTCXNGdzgENaCym5/b3\nePRc/9Fodl9NDaxfrzv/ixbp2X9mK+FAgt2Pnabj3T66EwkCtQaO3WInPN9EldnMepcLt9NJvc12\n/hz/oyUU0rMBvfeevr5ggV44ob4eTWq8fvR1fnvwtyRSCZwWJ3+2+s+4ZN4lE3d/hWKu9NXTwRx4\nPoyH8cYIPC6E+HPgRSAToSWl7Jmg9ikUCsWcJRTK5vjft0+PVx1k0aLszH9t7Sx3/tM5/g/8yU/8\nuV4MQQ3NBGeutWG62sU1JS7cLhfzLJaJc77D4ezIas8eXRJkNsONN8LmzWA0crL/JNt2bssEA1+2\n4DLubLoTl9U1MW1QKBSKGUwhA4Eo8I/A99ClQaBLgxonq1GK/ChNZX6UjXKjdKf5mazvUH9/Nsf/\nwYPDc/wvWaLP/Dc369L1mUw++wwkk+xMp/k82h5kwYthSg8lMQCmZTbm3VvLbQ2lVBeS479QAgFd\nSzVYPS2VzfHPypVw111QU0M8Feel/S/whyN/QJMa5fZy7l17L6uqV01cW1D9UCEoG+VG9dX5UTEC\nY6eQgcB/B5ZIKf2T3RiFQqG4UPH7ded/xw44elTP/gO6TH3lSt35X7cOSkqmt53jpTuRoDWd5rMt\nEkFqkuoP4zS9EaM8ZaSyvIiLttQx/zPlEzfz39ubTaPU1pYdWRkMsHx5tnpaWRkAB/wHeHTXo3SF\nuhBCcE3jNdy6/FasplmUZkmhUCgmgEJiBF4DviClDE1NkzL3VTECCkUhzBXd6SzTgEoJPl/WPz2Z\nTUOP2ayn9xws8OWY5WnofbFYpsDXiSGBDc5OjUteSTKvHcpNZsovKab6z6oxlUxAaqOOjqxxjx/P\nbjcahxvXlZX4hBNhntn3DO+efBeA+cXz2bp2Kw1lDeNvj0KRj7nSV08Hs+z5MNWMN0YgDLQKIf5I\nNkZApQ9VKBSKs5BSd/gH/VOfL7vPZtOL1Q4W+JpNOf7PRkrJqViM1mCQHYEA3iE5/q0GA6utRax5\nP0VpSwSDZsFUbaL6rmpczePQ3UsJp09njdvent1nsQw3rt0+7NRoMsoO7w6e3/88A7EBTAYTNy67\nkc1LNmMyqHI6CoVi7lJID/ib9M9Q1FT9NKM0lflRNsqN0p3mp5DvkKbBkSNZ/7RnSBoFp1OX+7jd\neo5/8+jT0M8YpJQcjUbxBAJ4gkH8iQTt27cz77LLcBiNrE0X+GrwCrp/3kncqw8OSj9TSuXtlRjt\no6z4q99U11ENGtc/RKFaVJQ1blPTOcYNxALs6tiFx+dhf9d+kloSgIvKL2Lruq3UOmvHbIvRoPqh\n/Cgb5Ub11flRMQJjJ+9AQEr5yyloh0KhUMwakkk9yHewwFcgkN1XWqrL0d1uWLZs9ub4B0hJyaFw\nGE8wSGswSH8ymdlXYjJR5XRyz4IFLCsqgpiG/3k/3rf6QIKlxkLN1hqKlhaN8qYpOHQoa9z+/uy+\n4mLduOvX68Y1Dh9c9EZ6afW14vF5ONx9GE3qsQJCCJZVLGPjwo1sXLBRpQRVKBSKNIXECBwbYbOU\nUk5q1iAVI6BQFMhc0Z1OswY0FtPTe3o8errPSCS7r6oqm+azoWF2p/lMaBr7wmE8gQA7QyHCQ7Lu\nVJrNuNMFvhqH5PgP7grS8XgHyd4kwigo/1w55TeUYzAXOApKJIYbNzQkJK2iIltAoaHhnJFVZ6gT\nj9eDx+fhWG/2cWU0GFlZuRJ3nZu1NWspthaP3SgKxUQwV/rq6UDFCORkvDEClwz53QbcAagyiwqF\n4oInHNYLe3k8sHevnoZ+kPnzs87//Pmz2/mPplLsDoXwBIPsDoWID2bdAeZZrbrz73SywGodNpue\nHEjS+VQngY/1VyK2ehs1W2uwLbAVcNNo1rh79ugjrUHq6nTDrl+vF/4ack8pJWcCZzLO/5mBM5l9\nFqOF1dWrcde5WV29miLzKN9GKBQKxRyjEGnQ2WlDHxZC7AC+PzlNUhSC0lTmR9koN0p3OjIDA9k0\n9G+80UJt7VWZfQ0NWee/unr62jgRBJJJdoVCeAIB9ofDJIe8ga232XA7nTQ7ndQOiWqWKUm0PUr0\nmP7zxktvcHH5xRgsBipuraDss2UIw1kjIil1eY/PB15vdnnkiK6xGmTx4myaz7q6sy4hOdZ3LOP8\nd4W6MvvsZjtra9birnWzqnoVFuME1iSYAFQ/lB9lo9yovjo/KkZg7OQdCAghNpANDjYAFwNjiPpS\nKBSKmUl3d7bAV1tbNse/lHoa+sECX6Wl09vO8dI7mOM/GORwJIKW/qACWFZUhNvpZJ3TSYXZjJSS\nZE+SwJ4AkWMRoseixE7G0OLZtwWpaApHk4Pqe6qxlJvA33Wuw+/zDddRDSIELF2adf4rhr9o1qTG\noe5DeLweWn2t9EX7MvuKrcWsq12Hu9bN8srlKvOPQqFQjJFCYgRayA4EksBx4J+klAcntWEqRkCh\nKIy5ojudYA3o0Bz/J05kt5tMeoEvt1tPSuN0Ttgtp4XOeFzP8R8IcGxIjn+jEKxMO/9rnU4ccUH0\nRHq2/7i+TA4kz7mepcKIrTyOzTGAzezHpnkRPi90dupa/5FwOKC2Vp/pH1wuWqQH/w4hkUqw378f\nj9fDro5dBOPBzL5yeznuOjfuWjdLypdgELM4ClsxN5krffV0oGIEcjKuGAEp5VUT3iKFQqGYYqSE\nU6eyzr/Xm91nterp591uPR29rQCJ+0xFSsmZIQW+zgzR3lsMBlY7HDTbHCzrMyGOJIgci9B9rBev\nLz78QqkURiLYiiPYbL3YDJ3YEycx9nZCt8aIlJWd6/DX1upFvc4TRBFNRtnbuZcd3h3s6dxDNJkd\nrNQ4a1hftx53rZtFJYtUth+FQqGYYM47EBBC3ALsklIeT6//LfBF9DcCD0opR8ompJgilKYyP8pG\nuZkLutNcaegdDr3w7HnS0AOz5zskpeRYNJqZ+e8aMjNvF4LmuJ1VfjPzfYLkyRjRkx10JtJvXJNJ\nCIYQ8TA2ewCbuRubbMeGD7MthggBQ+vKGwxQUwO1tbR0d3PVtddmHf4CR1CheCiT439f1z4SqWx7\nF5Usysz81zprZ73zP1u+Q9OJslFu5kJfPV5UjMDYyfVG4O+BywCEEDcB9wJbADfwb8DnJr11CoVC\nMUrypaEfDPYdIQ39rEI7K8d/Xzrw1hiRzPPCqm4T9R0GSto1tGAYgEy5g1gci9aNLXECW+goNmcA\na2UYg2GIHNNshtqF587wV1fr+imAlhbYuLGg9vZH+zM5/g/6Dw7L8X9R+UW469w01zZTWVQ5AdZR\nKBQKRSGcN0ZACLFTSrku/fvPgUNSyv83ve6RUrontWEqRkChKIy5ojvNoQEdmoZ+50497ecgedLQ\nzyoSmsb+tPO/KxgkFEtS5EvhOJ2ixgcNnQaq+gTFRtMwJY7RacRWlcSePI2tZx+2/gMYTen6AEaj\nnrGnrm64w19ePm5j+cP+TKafo71HGezTDcLA8srluGt157/EVjKu+ygUs4K50ldPBypGICdjjREQ\nQggX+kvha4B/HbJvFitoFQrFhUCuNPTz5mVn/s9KQz/riKZS7A2H2TEwwKFTAUynEjhPp1h4OkVl\np6RKmKm0mHEajCBA2AW2RTZsi63YXCFsffsxH/Egjp3KXtRuhlVrdAOtXQtFE5NvX0qJN+jNOP+n\n+rP3NBvNNFU14a7VC3w5LI4JuadCoVAoxk6ugcDDgAf9bfJ+KeVHAEKI9UD7FLRNkQOlqcyPslFu\nZqPuNBjM5vjfv394Gvr6+mwmytraibnfdH2HQqkUOzv62b+/D9/hINbTSZxnUiwPS5xGIxVmM5Vm\nC0VFRiy1FmwNNuwNdmyLrVhTPsSuT3QjdXRkL2qzZYMiVq3SI6THSUtLC5s2beJE/4mM898RzN7T\nZrKxpmYN7lq9wJfVNP57zjZUP5QfZaPczMa+eqpRMQJj57wDASnlz4UQrwHVQOuQXV7gq5PdMIVC\noQDo7TPTuq8Yj6eCw30wWPRWCF3nP5jms2KW1zvv9kfZvd3PyX39BI5GsPboH7QGKDYZqTRbqZ5v\no+wiB7Z6G7YGG7Z6G0a7UY+CfuNV+L0HenuzF3U69ZGR2w0rVmS1/eMglozhC/rwBr28eexNXk2+\nSk+kJ3tLizOT439F5QrMxhGisBUKhUIxI8hbR2C6UDECCkWBXIC6006/Bc+eEjx7Szh2Ki1bSYYw\nljdlcvyvXXtOGvpZh689xJ73/bR/0k/8SDZtphBQYjdT1eBg8fJiKtLOv6ncNDyLjqbBm2/CCy9A\nPJ3+s6wsq4u66KIx6/wDsUDG4fcFfXgD+nKo0z9Iqa00k+lnacVSleNfoRiJC7CvnjGoGIGcjKuO\ngEKhUEw2UsIZny3t/BdzxmfP7LOYNVYtC9B8URtrb2yaKDn7tKBpGqdPhNj3gZ+Oj/tJnB6Su98M\nziYHC5tLWdlURtlCO8KYI7jh9GnYtg2OH9fXL74YrrtOD/wtMChCSklvtDfj5HuD3szvQ4t5DcVo\nMFLjqKHOVUeds45V1atoKG2Y9Wk+FQqFYi6iBgKzFKWpzI+yUW6mW3cqJRw/ZWfHnlI8e4rp6snq\nx+22FGtXDOBe3U/T0iBWqwaRTpjiQcBEfIc0TePIoQEOftBN144BUh1Dqu/aBMVrnTRcWs7qiyuw\n2wvokhMJePlleO01PVdqWRncfbf+iuQ8pLQUXeGuYQ6/L+jDF/QRS8ZGPMdmslHrrKXOVacvnfqy\nylGVmfFvaWmhcXnjqOwx11D9UH6UjXIz3X31bEDFCIydggYCQogrgYuklL8QQlQBTlVQTKFQjBZN\ng8PHHHj2lNC6r5jefktmn8uRpHlVP+5V/SxfEsJkmr3SwFRK49DePg5+0E2PJ4DWk41qFk4Dpetc\nLLm8nFXN5ZgtoyhmcOgQPPqoHgQsBFx9Ndx2W6aQVywZoyPUMUzK4w166Qx1ktJSI16y2Fo8osNf\naitVs/wKhUJxgZM3RkAI8XfABmC5lHKZEGI+8Gsp5acntWEqRkChKIwZqjsNBI34umx4O6z4uqx4\nO22cPGMnGM7OP5SXxnGv6se9eoAli0O55ewzXAOa1DQOhMLs/30HA6/1IgNaZp+h1Ej5ehdLL6tg\nxZoyjMZRaujDYXjuOXjnHX29rg62biXZsJiD/oN4fB72d+3HH/af9xKVRZUjOvwqjadCMUXM0L76\ngmCGPx+mm/HGCHwBvZrwJwBSyjPp+gKF3Hgh8Ah65iEJ/LuU8qdCiHLgKWAxcBz4kpSyr5BrKhSK\nmYOU0NNnxtepO/qDDr+v0zrM4R9KTWWM9av7ca/uZ9H8yKzO8R/TNPaFQniCQQ619VP3fAjHGX3m\n3VhtpnJ9McsvL+ei5SUYxlqcy+OBJ57QSyQbjSQ+dx171i/A43+LXa/tIpKIZA4d1O+f7fDXOGuw\nGC05bqJQKBSKuUghA4GYlFIbfEUshBjN9FEC+I6UslUI4QQ+EUL8AT396B+klD8SQvwV8N30j6JA\nlKYyP8pGuRmN7jSVgk6/dZij7+200eG3EIuPLG2xWVPUVceorYrqy+oY82qiVJbHZ43zP9J3KJxK\nsTsUwhMIsDccJhFLMe+tGEvejeHEQEVtEUvuraNhQ9nYnX+Avj546inYsYOElsRbXcRbVy7kQ+1N\n4q3ZIOP5xfMzFXrnueZhNIxCajRO1P9YfpSN8qNslBsVI5AfFSMwdgoZCDwthPgZUCqE+HPgfuA/\nC7m4lNIH+NK/B4UQ+4H5wC3ApvRhvwJaUAMBhWLaicUMdPiteDuteDsGZ/itdHVbSWkje+/FzgS1\nVTHqqmPU1UTTv0cpKU7OGoc/HwPJJDuDQTzBIAfCYVJp2aLrWJLLfp+grt9ApcNF7TXlVN5WidE2\nDmdcSnj3XeJPPU53zxk6kv38sbmEA6tqIHEEgIayBty1btx1bqod1RPxERUKhUIxBymojoAQYjOw\nOb36qpTyD6O+kRD1wFvAauCklLIsvV0APYPrQ45XMQIKRSGMQXeqaXDsZBHeThvezvRMf4eN7r6R\n5SNCSCpKE9RWp2f3085+bXUMR9HIQagTzhRrQLsTCVqDQTyBAG2RCIO9kUEIlmOl+Y8pKj6OYTEY\nsM6zUrO1BnujPec189F37ABd//kTwntbGYj2c3pxGR9etZSoy87SiqWZmf8ye1n+iykUipmFihGY\nPFSMQE7GFSMghPjvwJNSytfG0QAn8CzwoJQyMDQThZRSCiGUx69QTBEnTtvZ9uwCTnnPdVqNBklN\n1RBHv0qf5a+pjGGxXPj/pr5YDE965v9ENFvgyyQEK4uKWO9ycdEhSeDpbpL9SYTZSPkN5ZR/vhyD\naWwyoK6jezjR8huC29/BcOIkAFG7hR2fb8K5cRN31K1nbc1aXNaCQrMUCoVCoSiYQqRBLuA1IUQv\n8CTwtJSyo9AbCCHM6IOAbVLK36Q3dwghaqWUPiFEHdA50rn33Xcf9fX1AJSWltLc3JzREba0tADM\n2fWHH35Y2SPPemtrK9/+9rdnTHsmdf393fp6Wkc60noiIRgIXsfr71Ry2vcB4chu7v3CndRVRznt\n/YDysji3bl6J0Zg9/1L3+a835esxf0YDOlH227RpE6diMR559VXawmGs69cD0L59O2aDgQabjS2b\nN9P70UcYIpL6M0307giwvX071nlWbvv+bVjrrKO6v9Q0nv3Vv9G56z2a+s5g8Prw9IQAaK4pJXXJ\nxRxrXIe7dgWfu+xzE/p5J3p9cNtMac9MXD/bVtPdnpm4PmeeZ+mXAaPt/x7+zxdoXtU4vf3vDF9v\nbfXw7b/X3wjMmL/3NPs/fX16Dp7jg0Unz0NB0iAAIcQ64EvAHcBpKeU1BZwj0GMAuqVGpEkZAAAg\nAElEQVSU3xmy/Ufpbf8ghPguUCql/O5Z5yppUA5aWloyf3TFyMwZGxXwunn/YSePPT+frh4rBiG5\n5go/xc4/sHnT6ilq5AQwQa9+NSk5GolkZv67E9kCXw6jkbUOB26Xi6aiIt59+202bdpE/7v9dD3T\nhRbRMNgMVH6hktJNhefZl5rGSU8L7W+/TOzjDzB092T32e0Y3eup+vRmGj99E2bb7CmdPGf+x8aB\nslF+5oyNxigNUsHC+Wlp+SNX3fu/prsZM5Zc0qDRDATq0AcBd6EXFDt/GcvsOVcAbwO7ICOx/Wvg\nQ+DXwCLOkz5UDQQUigLJ8XAJhY0883Id731SDsCC2ghbv3ia+oWREY+f0YxjIJDUNA6lnf/WYJCB\nZLbAV4nJRLPTidvpZFlREcYhzn28M07Hox2ED4YBcKxxUHNPDeYyc957phJxjn/4Gr53fk9ix0cY\nBgKZfZrLiXnDpdReeT31l27GaLaM6XMpFIpZhIoRmDxUjEBOxhsj8E30NwHVwNPAA1LKfYXcWEr5\nJ8Bwnt3XFnINhUIxeqSET3aV8NSL8xgImjGbNG66poPrPtOFceqyS04LUkr6k0l88TjeeJxj0Si7\nQyHCqWxQc6XZjNvpxO1y0WiznTOzH++IM7B9gJ7XepAJidFlpPrPqnFd7Mr5FiARDXP03Zfoevc1\nkq0eDGF9AGEAtPIyLJdsZN5nbmBR8yYMxoIKuysUCoVCMWkU8iRaBHxbStk62Y1RFM6ceZU6Duaq\njXr7zDzxwjx27i8BYFlDkHtvP01NVXzYcbP9dbMmJf5EIuPw++JxvLEYvniciKadc/w8q1V3/p1O\nFlitnJW0gNiZGEFPkKAnSOxMDIDt7du57ovXUX1nNUbHyCOoaLCPo2+9gP+9PyD37EbEdDsbAK22\nBvsln2LBVbcwb+WlCMP55kVmJ3P1f2w0KBvlR9koN7O9r54KVB2BsXPegYAQolhKOQD8IyDT1YAz\nSCl7Rj5ToVBMB1LC2x9U8NwrtURjRuy2FHfc4OXTl/TM6nz+SQkdKYEvbqXd7884/p3xOInzyAcd\nRiO1Fgt16Z81Tic1luHyGykl0WNRgp4gAU+ARFc2VsBgN+Bc56TaVE3d1rpzrh/s8XH0j8/T+8Gb\nsP8AIi01EoC2aCGOS69g0aZbqFnaPHGGUCgUCoVigjlvjIAQ4mUp5Y1CiONk9f0ZpJQNk9owFSOg\nUBTG4X/DO9DItucWcOSEXvjbvaqfLbecobQkmefkmUNUA29K4EsKvCkDvpTAmxT4UwINIBmCkqZh\n55SZTLrDb7VmHP9aiwWX0TiihEemJOHD4czMf7I/ax9TsQlnsxOn24l9mf2cdKD9vhMcffNZ+j94\nC0Nbm16MAUAItCWNFF+2ifqrbqN8oZqWUigUI6BiBCYPFSOQkzHFCEgpb0wv6yepXQqFYpwkk/Dq\nHxfxu3eXkkwZKHEluOvWM7hXD0x300ZESghI8CYFvpQhvdQd/r7zVC42ADVGSa2IUVdePszhtxUQ\n8KAlNML7087/ziCpUDZWwFxhxulOO/+NdoRheBu6ju/jZMsLBLa/jeHY8Ux7MBqRTU2Ubryahqtu\no7hqwRgtolAoFArF9FFIsPAbZ6cKHWmbYmpRmsr8XKg2khJOnwaPBz78ELra6sFk4MpLu7n9eh9F\n9sIq/U6l7jQh4fdhI29FTATPle8DYBZQa5TUGiV1Ji3ze1VSIuKg9QXQgk60qIYWTRKLxolENbSI\nlt521k96e7IviRbP3tRSZ8HlduF0O7Eu1GMFoskoJwZO4At46T2yF7ljB9bd+9iz9yjucgcGQJrN\niNWrKf/UNTR+5laKSiqnxHYzmQv1f2wiUTbKj7JRblSMQH5UjMDYyRUjYAeKgKqz4gOKAfVuS6GY\nQqSEo0d159/jAb8/u6+mMsy9X/KxrDE0fQ0cgpQgE6DFQIsJjgQEL/SY6Y0IrDEoTUBVUlKekJQn\noSQBJQmJLQ4yLtCiAi1mRIsJgjEIDl44WQklJ8fUJttiG45mB4YmA36Xn33BfXgHvPi2+/AG2jEc\nP8mio90sPOrH1Z9NrSotFsRll1P16c00fPpGrI7i8RtIoVAoFIoZQq4YgW8DDwLzgPYhuwLAv0sp\n/2VSG6ZiBBRznFQKDh3SHf/WVujvz+4rKYHmZnC7YZn4GUbnvHHfT0tmnXctBlqUtFM+ZFtspG3n\nHi8lpCQcSxjwpnS5TZGAi8waJQapR9UWiMEKBqvEYAhgmH8JBrsBg9WgL23ZH6PdiLAKDDYDAQJ0\npbroSnXh03x4U168QS+huD5YEpqkur2fhUf9LDzWjTOUwG62U2QqwlJagXC7KbrkU1SuvwKTxTZu\n2yoUCoWKEZhEVIxATsYaI/Aw8LAQ4i+klD+dtNYpFIoMiQTs26c7/7t2QWjIJH9lpe74u93Q2AhC\ngNQk2h5I9A51yEdw3mOCVPQsp/2s42VhiqKC6BaCA0ZB2C6QVsn/396dh8d53Ye9/57ZN+w7uII7\nAZDg0LZ2iZQsUbJlSV6UxI6iKOmN28T1beOmrZ3btLHvfRonfdqmdZwmddLUdmRLsl1bli3ZkiwJ\nFmVR1MIBF5AEV3ABsa8zmMFs77l/vIOZAUnNgCCAATi/z/PwAeZ9ZwYHPx68c87M73fORp9Bc4mB\n3ZUa1DvB4sr66gBL9jmnNm87QE3X7EaGYOOa9M9IGAkGJwfpCfXQF+qjN9hLX6iPvpE+YsnYFW2y\nJA2a+iK0XIyx7twEpXELHkcFntIVuDY0onbuNIO7fj3cYMt8CiGEEFeTt0ZAa/01pVQr0Ay4so5/\neyEbJnKTnMr8lkuMwmNJDr88xfGDBme7DJJTBtaEQUXSYEOpQVOjwao6g1KXgT5hYBwyODOdAx8z\nYLwWbM5r/rn7+w9yc11b+raycOUA3cllA/PUV2dm0G51aVTqa8gO34/ZeS9hATTr7JrHS+I02ub2\n6Z6hDcaiYUajIQbGz9CXfDY94B8MD5I0rpy9KENTbfGywlbBCmsFjVMOVp4ZpPLkRRxxD0p5wVMB\ndXXmwH/nTli9mqutsbpc+lChSHzykxjlJzHKTWoE8pMagbmbTbHwl4FdQAvwPPAR4A1AJgJCzNF4\nX4JDP5rkwqtBwsfD5mL5wEqgpASqqqG6DtweIAqch8jVnkilBuzezKDd6tIzBuozBvJZX88dSdB0\nWyw94Fe2q46FZ0VreHPKyg9CNsIanAo+4U2wy53E8j7PGU3GGYuFGItOMhoLMRabNL+PBgmGg0wG\nJ4iGQtiiCRxRA8dUCLvtGI5ogsZogqZYggrDSZXyUG44KTPslCSseA0rdhUGwkDPzB+6enXmY5WG\nhrn/wkIIIcQN4H1rBNJ3UOoI0AYc0Fq3KaXqgO9ore9d0IZJjYC4wQyejXPkRyF6fhli6lQEjFT/\nVuBa66Jxo41V6y2U1szMfU//u1pOvEOhTv3PguadDiQUTwZtdMXNdJoWR5KPOyawBIeZmBgjFBwn\nNDFGeDLIVCjIVDBEbHISHZnCEU1ijxs4okkcsaQ54I8msWT97TssNhwWG24LuEvW47F78NjduO1u\nrOp9lg91u8HrNb+WlEBzszn4r5aVfoQQBSI1AgtHagRymlONQJaI1jqplEoopcqAAWDVvLZQiBvU\npc4YR54N0bc3SOzcVOaEVeFp8bLqHh+tD/uoWDmbP8VFpDVE4xCJwlTU/BqJkgxHmAxNEJ6YIBSa\n4FVHJa+UryKWTOKMhLm78y02nTtOd3xmyo4Nc7mx7DV3LCgcVjtOiw2H1WF+tdtxumw4nC4cHi+O\nkhKsbie4nWCNwNqPZAb4Ho/5L3vQ7/GAyyU5/kIIIcQszGb08Y5SqgL4O+BdYBJ4c0FbJfKSnMr8\nChEjw9BcOBDj6HNBBt4IEe+NZk7aLfi2eVlzr4/Wh7yUVOffDOu6JJLpAfyMf1MxmIrS3nGC3avr\n04P9RDjCVDBIbHKSeDhMNBEjZiSIJuPEknGiRoKYYe7E219axUvbbqffXgqj47RcPMWuY2/jiZu/\nr9VixeJ2YfW4sXk9OLxeHF4vbl8Jbp8Pj68Ud0kpyu0yB/kuh/l1+p/tKrGJ9MDGzyxszC4jf2e5\nSXzykxjlJzHKTWoE8pMagbmbTbHw51Lf/q1S6kWgVGt9cGGbJcTyYRiaU29M0fXTEEP7QiSHMivW\nKJeF0h0+mvb4aHnQi7t0nt6p1hrOnYODB6HzV2B4rhzwJ66+DFDcSDISDXL+Uj+Hj7mIGuZAP6Fn\n7vQVt1uIO6zEPBZiTitRh5veihq6Gzdzom4TFoedCovBR+O9bGtaSclHWykpK6estBKnxyP590II\nIcQSl2sfgQ8A75ukr7U+sFCNSv18qREQS1YyoTn+coSTPwsy8nYIYzyRPqe8Vio+5GP9AyU03+/G\n7pqnwb9hwKlTmV3FRkfN4+NHwea98v4WS/od9imHhYtGkO74GOeNIFGHIuawEnNaiTnMgb522nH7\nSvGWluLzlVLuKaXU7iVoq+KipZwzRgmTyo5CYQHu8SR52JvAuVjjfckBFUIsZ1IjsHDk9SGnudYI\n/BdyTASAu6+rVUIsM/EpgyPPhznzYoixAyH0ZOYdd0u5napbfGx8wMfmD7ux2uZpdJxIwPHjmV3F\nQqHMuYoKswDWUgblK8HlnJFeM5QM0zFylsDwGU4H+zAn1l4sysfmshVsr1xLrauccqeXCocPj82J\nUoqEhuMxC4GohTdjVoIG5pVAQaVFs8OZ5HZXklV2magLIYQQy1muDcV2L2I7xDWSnMr85iNGkQmD\nw89N0v1ykImDkxDNpM9YaxzU3u5j88dKWHerE8v7rZN5raJR6OzM7Co2lVVkPL32vd8Pa9aY6Tcn\nR8G9Aq01fZFRAsPHCZw9w/nQYPphdouV5orV+KvWsb1yLV67i/Z9h2m91dygK6ohELUQiFk5HLUQ\nyRrj11g1O50GfmeStTZdVBk/8neWm8QnP4lRfhKj3KRGID+pEZi72ewj8ARX+WRANhQTN6qJgSSH\nnw1x/tUQk0cnIZ7p/vaVLuru8NHyiI8V2x3zN/gPh81BfyBgTgLi8cy5Vaved+17rTXnJ4cJ9F8g\nMHKGvvBo+pzL6mBb5Rr8VetorViD02qf8SOnDNg/ZSEQtdIZsxDL+itfadP4nUn8ToNGa3EN/oUQ\nQohiMZt9BL5OZiLgBu7B3FPg0QVtmNQIiEU0cj7B4WdDXHwtSORE1hr/gKPJTeNdPlo/4aN+s2P+\nfujEhJnuEwhAVxcks4p716/PDP4vW/ve0AanR04T6AsQ6A0w0v8GWM0aAZ/dRVtlE/6qdWwpX4nd\nYiOuoT+p6E0o+pKK3oSFvqSiL6HILideZzcH/zscBrVz3Al4QUkOqBBiOZMagYUjrw85Xdc+Alrr\nz1/2ZOXAM/PUNiEKpq8rRuezIS69HiJ6NpKZ7loU7i0eVuwuYdvHvVStsed8nmsyNJQZ/J8+ba7+\nA2Zh79at5sC/rQ3Ky2c8LGEk6BrqItAX4GDfQSaiE+lz5XYPO+pa2VK5gRJvI/1JGyeSil9OmAP/\noaS6arGPBdhsN/A7DXY4k1Qs8GqmQgghhFha5rKLURhomu+GiGsjOZX5XR4jw9D0HDIH//1vBIn3\nZK/xr/A2e1l9j49tH/dRWjuPo+Le3sxKP+fPZ/1Me2bH2+3bzU2xssSSMToHOgn0BTjUf4hIPIIG\nYthxedfQUNlCWek6kmNHCVgqaI8DY1f+eAtQa9U02DT1Vk2DzaDeqjnx9iH23C55p7nI31luEp/8\nJEb5SYxykxqB/KRGYO5mUyPwk6ybFqAZ+N6CtUiIeWQYmjP7onT9NMjAmyGSA5k1/nFaKG3zsva+\nErY95MFdNk+Df63NAf/04L+vL3PO5YLWVti5E1pazNtZwvEwRwaO8N6lAO8OnmRcWwkrFxFVj62k\nDrdnBaWeagy7l0vApTiQcIANHArq0gN+gwarpt6mqbVqrraIUbdsviuEEEIUtdnUCOzOupkAzmmt\nLyxko1I/V2oExJwkE5oTr0U48UKI4bdCGGOZwlvltVK+08e6+300f8SD0zOPa/yfPp0Z/I+MZM55\nvWa6j99vpv/YZ6YaXQqP8bOew+wfPM2J4BAhHESUCwMLpc4SqjzVVHuqcNvc5tNZrdQ7HDQ4HObX\nvmep99ZSZbnBi3olB1QIsZxJjcDCkdeHnK63RqA99SSl0/dXSlVqrUdyPU6IxRSfMjj6YoTTPw8y\n+s5la/yX2qi4ycfGj/jYusczv2v8d3WZA/+DB83i32llZZli302bzBqALKeDAzx74Qjtwz2cmYqm\na5OVpYIyZykNnmrWl9Sy1lNKg9M5Y+BfYrWiskf8wzGwyqRZCCGEENdmNqlB/wz4ChAFphdR18C6\nBWyXyENyKs01/jufn+TsSyEmOkLoqaw1/qvs9K44xKN/cD8b7nLN3zKfsdjMNf4jkcy5mhrYscNM\n+2lq4vK354+M9vBsTyd7h3s5H818SmFV0OL1sLNyFTfVbGCDt5x6hwOXdWGrdyXvND/5O8tN4pOf\nxCg/iVFucq3OT2oE5m42xcL/BmjVWg8tdGOEyCc4lOTIjyc590qQ0JEwxDODf1uDk9rbfTQ/7GP1\nB5y8/vp5Nu12X/8PDYfhyBFz8H/kiDkZmLZiRead/xUrZgz+DcPgneFzPHfpGG+ODtAXS6TP2RVs\n95VwX+0aHl65jQrnzEJhIYQQQoiFNpsagZeAT2itJxenSemfKzUCAoCxSwkO/yjEhddChI+HIZm1\nxv8aF/V3ltD6cR+NLfO4xn8waKb7BAJw7NjMNf6bmsyB/44d5k6/WQzDoL3/JM/3dvHW2BAjicxE\nxW1R7CwpY09dEx9b0YrH7pyfthZL3qnkgAohlrNiuVYXgrw+5HRdNQLAl4B9Sql9wPRboVpr/S/m\nq4FCXM173wtx9B9HiZ4Oz1jj37XJw4pd5gZfNU3zuMb/6Gim2PfUKbMAGMz8/s2bM4P/iooZD0tq\nzcGJEb516lfsGxskmDVR8VkVN5VV8pH6Dexp2IrDOpcVe4UQQggh5t9sRiXfAH4BHMasEVBw1f2J\nxCK6kXMqRy8meOlLAwTfC5oHbArPFg+r7jE3+CpvmN1gelYx6u/PDP67uzPHrVbYti2zxn9JyYyH\nxQ2Do+EwB4JBXhk4y+Ghk8SSZt5/pc3CLeXVPNiwmbvqNmCzLM2duiTvNL8b+e9sPkh88pMY5Scx\nyk2u1flJjcDczWZEZdVa/6sFb4koeoah+dX/nODE3w2iI0lwWGh6rIpb/2kZnvJ5XOP/4sXM4P/S\npcw5h8Nc49/vNycB7pn1BVPJJIcnJwmEQhyZnGQiPsXpkVMMhYfx6gh+j4vPbr6bW6vXYbHIIv1C\nCCGEWNpmUyPwZ8A54DnMlYMAWOjlQ6VGoLhc6ozx6v/Tz9SJMACeFi8f/moddRvnIfVHazhzJjP4\nH8qqe3e7M2v8Nzebk4EsoUSCg5OTBIJBjoXDJLRGA32hXoZHOimLD9Kowvx288e4c/WdM5f1XCzF\nkncqOaBCiOWsWK7VhSCvDzldb43Ab2KmAn3psuNN19swIZIJzSt/Mcr5Z4YgrlFeK83/vJabnyi5\nviU/k0k4eTIz+B8fz5wrLTVz/afX+LfN/DMYjcfpCIUIhEKcjEQwUhNSBdRbk/T17aVi9AgNxGir\nb+M3t/0m5a7yubdVCCGEEKIAZrOh2NpFaIe4RjdCTuWZfVPs/Q/9xC9OAVB2Syl7vlpDWf0cC2rj\ncXOFn9QGX+0nT7K7sdE8V1WVWeZz3borNvgaiMUIhEIEgkHOTk2lj1uVosXrZbvXzdDAfl7reh6M\nBLXOUj6z7Xfx1/sL8ynAPJC80/xuhL+zhSTxyU9ilJ/EKDe5VucnNQJzN5sNxZ7gKsXBWutvL0iL\nxA1vKmTw8leG6X9hFAyNpcLOB75YR9sjc1hLf2pq5hr/WYN4Kivhox81B/+rVs1Y419rzaVYjAPB\nIIFQiJ5oOusNh8VCi8eDv6SEbV4vA8ELfPvgX9Mz0QPAHavv4FPNn8Jj98w5BkIIIYQQhTabGoGv\nk5kIuIF7gANa60cXtGFSI3BDOvLCJO/8WT/J4TgoqLm/gj1fqcZdeg3FtZOTM9f4j2d26WXNmswy\nnw0NMx6mtaZ7asp85z8UYiBrYzC3xcJ2nw+/z0ez14vTYiGaiPLjrh/z6tlX0VpT463ht7b/Fluq\nt1xvGOZXseSdSg6oEGI5K5ZrdSHI60NO11UjoLX+/GVPVg48M09tE0UiOJjkpX83yOheM1ff1uDk\nti/XsemuWe78OzZmDv4PHIATJzJr/CsFGzdmBv9VVTMeZmjNyUiEQDBIRyjEaCKzu2+J1coOnw9/\nSQmb3W5sWelCnQOdfOfwdxgOD2NRFvZs2MPHNn0Mh3UeNy0TQgghhCiguSRjh5FC4YJbLjmVsZjm\nwFMhOr8+gA4lwKZY+WgVH/5iBXZXnk8BBgeho8N85//06cxxqxVaWszBf1ubWfybJWEYHA+H+c5L\nLxHbvp1Q1q7AlXY7/tQ7/+vdbiyX5fcPhYd4rus59l/cD8DqstU83vY4q8tWX18gliDJO81vufyd\nFYrEJz+JUX4So9zkWp2f1AjM3WxqBH6SddMCNAPfW7AWiWVvago6O6Fjb5zgjwfw9YUAcK53c/ef\n1bFyu/PqD9QaenszK/1cuJA553BkBv/btoFnZn5+1DDoTK3xfygUYsowuBQK0ZhMUudwsDP1zv9q\np3NGca/Wmt5QL4HeAIG+ABfGzZ9pt9p5ePPD3LvuXixK9gQQQgghxI1nNjUCu7NuJoBurfXFWT25\nUv8APAgMaK23pY5VYqYWrQG6gV/XWo9d5bFSI7CMTE7CoUPm+P1op6b8/DirugexJgw8FRZW/WYN\nt3+u7MolQbWGc+cyg//+/sw5tzuzu29LCzhnTiAmk0kOp/L9OycniWf1l1VOJ/6SEvw+Hw0OxxWD\n/3Pj59KD//5Q5me6bC62123noc0PUeutnd8gLZRiyTuVHFAhxHJWLNfqQpDXh5zmVCOglNoI1Gmt\n2y87fodSyqm1Pn31R87wv4G/ArJXGPoS8LLW+j8ppb6Yun35HgViGZhO2w8EoKvLTNt3haNsONlP\nIxGq18DKXT6aPluLvTxrYzDDgFOnMoP/0dHMOZ8vs8b/li1XrPE/nkhwMDX47wqHSWYN/te73em0\nn+rLNgYztMGpkVMEegN09HUwEsnsh+dz+NhRvwN/g58t1VuwWea4fKkQQgghxDKSa8Tz34A/vsrx\nidS5h/I9udZ6r1Jq7WWHHwZ2pb7/FtCOTASuWaFyKoeGMuP37LR9mzL4EKOsCw1TtVXjqbZR+5la\nfH6f+W58IgHHj5sP7OiAUCjz4IqKzBr/GzZcscb/UCyW3uDrdCSSXsLKohRbU8t8tnm9lNtn7kL8\nyquvUNdaR6A3wMH+gwSjwcyPdFeYg/96PxurNhZl+o/kneYnucu5SXzykxjlJzHKTa7V+UmNwNzl\nmgjUaa0PXX5Qa31IKXU9xcJ1WuvpXIx+oO46nksssFxp+3a7mbHTVheh+kA/ejAKtVB2Rxk1n6rB\n6rGaHxv8+Mfmaj/Za/zX1WUG/2vWXLHGf9/0Bl+hEOezHmdXimavF7/Px3afD6/VOqO90USUo4NH\nCfQFeOHdF6iazKwiVOOtYWfDTvz1ftaWr122G4EJIYQQQsyHXBOB8hznXPPxw7XWWin1voUAv/M7\nv8PatWvNxpSXs2PHjvS7Bu3t7QBFe3v62EI8v9bwzDPtnDwJ8fhu+vvh0iXz/Lp1u9m+HZLJdtas\nMPBPtjL60ihv9ezHVm7jkX/3CN4tXtpfew0OHWL32bMQidB+6RLU1rL7k58Ev5/2ri5Qit2p/9/X\nXnuN/ngcl99PIBTiwN69ADTefDMuiwX7wYNs9Hh44v77cVmttLe3806qveF4mG8++01OjZwivipO\nLBnj0uFLAKwsXYm/wU/kZIRqVc3dW+9eEv9/835732Hzdupdo9nenjbXxy/q7ehQ+h2fgsdbbsvt\nWd7evXv3kmrPUrw9fWyptGfBbqfKA671+jd9bEldj5fg7XSslsr/dwFvd3R0MDZmlt92d3eTy/sW\nCyulngZe1Vp/47LjnwXu1Vr/Rs5nztx/LfCTrGLh48BurXWfUqoBeE1rfcUOTVIsvLjype23tZlv\n3m/daqbtT3ZO0v9kP/GROMqiqNhTQdXHqrDYLWbB75NPmuv9g/ngT33K/BQg+2dqzelIJP3O/0jW\nxmBeq5W2VL7/Vo8Hu8Uy47ET0QkO9h0k0Bfg+NBxkkZmidCmiib89X78Df7lU/B7PYqlAE2KwYQQ\ny1mxXKsLQV4fcprrhmJ/CPxIKfUY8F7q2AcAJ/CJ62jPc8ATwF+kvj57Hc9VtLLfPZmr7LT9gwch\nmEmhp6IiU7O7cWMmbT8RTND7/UEm9k8A4Frtou7xOlyrXZBMwgsvmP/icXN9/09/GnbuTKf+JAyD\nrqwNvoJZa/yX22zmBl8+H5s8nivW+B8OD9PR10GgL8CpkVNMTxQtysLm6s3sbNjJjvodlLvK0zGq\n3V0EE4E5krzT/Obj7+xGJvHJT2KUn8QoN7lW5yc1AnP3vhOB1Dv2twF3A62ABn6qtX51tk+ulHoK\nszC4Wil1AfgPwJ8D31NK/V+klg+de/PFtYpGzTX+AwE4fBgikcy52tpM2v7atTPS9tFaE3w7yMD3\nBkiGkii7ovrhairurUBZFHR3w7e/DT095gNuuw0efRS8XmKGQWfqXf9DoRCR6V2BgRq7Pb3MZ5PL\ndUXefl+oL73M57mxc+njNouNrbVb8df7aatvw+fwLUC0hBBCCCFuXHn3ESgUSQ2aP+FwZo3/zk7z\nzfppK1dmBv+NjTMH/9Piw3H6v9vP5JFJADxbPNQ9Voej1mHOLJ57Dl591cwvqqtqnyIAABhrSURB\nVKmBxx4jvGkThycnCQSDdIbDxLIG/yuczvQynyuussHXhYkL6cF/b7A3fc5pc9Ja24q/3s+2um24\nbPNSqrL8FcvHzfLRrxBiOSuWa3UhyOtDTnNNDRLL2MSEuUrn9Br/WRk4NDWZ2To7dpifArwfbWjG\n2scYenYII2pg9Vip+bUaSm8tNQfvnZ3w3e+aa4paLAT37OHgrl0EpqY4dvr0jDX+m1yu9Dv/tQ7H\nzJ+jNadHT6cH/8Ph4fQ5r8PL9rrt+Ov9NNc0Y7fOXCJUCCGEEELMjUwElqmr5VQOD89c4396HG6x\nmHtz+f3m4L8813pQKdGeKH3/2MfUWXPpzpIPlFD76VpspTZzG+HvfQ/eeosRh4OO1lYCu3ZxyuXC\nGDYH8Ral2Ozx4Pf52OHzUXHZGv9JI8mJ4RME+swNvsanxtPnylxl6TX+N1VtwmqZuUTo9cRIZEje\naX7Sh3KT+OQnMcpPYpSbXKvzkxqBuZOJwDLX15cZ/J/LpNBjs0Fzszn4377dXPlnNoy4wcjPRhj5\n+Qg6qbFV2Kj7TB2+Np85s3jnHfp/9CMCDgeB1la6m5thxQpQChvQ4vXiLylhu9dLyWW7AseT8fQa\n/wf7DhKOh9Pnqj3V+Bv8+Ov9rKtYJ2v8CyGEEEIsMKkRWGa0Njf1mh7892ZS6HE6obXVTPtpbQXX\nNabQh0+G6X+yn1hfDIDyXeVUf6Iai1Nx8dw5Aq+/TmBigktuN5SVwcaNOLxetqU2+Gr1enFftsHX\nVGKKw/2HCfQFONx/mFgylj7XWNKYHvyvLF0pg/+5Kpa8U8kBFUIsZ8VyrS4EeX3ISWoEljnDgDNn\nMoP/4UwKPV6v+Y6/329+AmCfQwp9MpJk6EdDjP3S3HzCUe+g7rFaevVF9r68n8DQEEPTxb4+H571\n62nbuBF/SQnNV1njPxgNcqj/EIG+AMcGj5EwEulza8vXpgf/dT7ZVFoIIYQQolBkIrBEJZNmkW8g\nYBb9TkxkzpWVgcPRzmOP7WbTJrDOLYUegNDBEP3f7ScxlgClCTdP8l7DeTr2jjCe9YlMqVLsqKxk\n5223sam2Futl796PRkbTa/yfHD6Joc2Jg1KKTVWbzJz/Bj+V7sq5N/YaSd5pbpJ3mp/0odwkPvlJ\njPKTGOUm1+r8pEZg7mQisITEYnD0qDn4P3TIXPZzWnV1ZpnPdevgl780d/mdq8REgoGnBxh/e4zR\nkVH63WO84x9k2JOAVN1uldXKzqoq/Js307RhA5bLZhwDkwPplX7Ojp5NH7darLTWtOJv8LO9bjul\nztK5N1QIIYQQQiwIqREosEjE3NgrEIAjR8zJwLTGxszgf+XKq6/xf6201gy9OkDX351gaCjIkI5x\nfsck/ZsjYIEGmw1/bS07t25l5Zo1qKy0H601PcGe9OC/Z6Infc5hdZhr/Df4aa1txWP3XH9jxewU\nS96p5IAKIZazYrlWF4K8PuQkNQJLTDBovuN/4AAcOzZzjf+1azOD/7p5TKEfH4ty6Bdn6fnRCSYv\najQw1hjj3M1BGiqsfLxhNTuam2lYuXLG47TWnB07mx78D04Ops+57e70Gv8ttS04rA6EEEIIIcTy\nIBOBRTI6mtng6+RJswAYzHf5N23KrPFfOcsU+tnkVA4ORDjy1hA974wy1TEEwRBoTcJpoG+L4b+j\nmt/ddhdVl804DG2Ya/z3mmv8j02Npc+VOktpq2/DX+9nc/VmbJal24Uk7zQ3yTvNT/pQbhKf/CRG\n+UmMcpNrdX5SIzB3S3cUdwMYGMis9HM2k0KP1Wou7zm9xn/pPKbQX7oY4shbw/S9M0asOwrxOEyM\nQyKGu3yCVds9bPu9XVSsrpnxuHgyzvGh4xzoPcCh/kOEYqH0uUp3ZXqln/WV67Eoy+U/VgghhBBC\nLDNSIzCPtIaenszgvyeTQo/DkRn8t7aCZ55S6A3D4EJ3iM59Qwy8N0GiJ5ZpzFQQn72HNb4+Wusn\nKfnt34CWlvRjo4koRwaOpNf4n0pMpc/V++rTg//VZatljf+lrFjyTiUHVAixnBXLtboQ5PUhJ6kR\nWEBam+/2Tw/+BzMp9LjdmTX+W1rMycB8MJIGp06M0/XWCEMHJkgOxNPnlFtRuiZJ0+g7tEwdx21J\nwj33wCOPgNPJZGwyvcb/0cGjxJOZx64uW50e/DeUNMxPY4UQQgghxJIkE4HrEI/DN75hFv5OKy2F\ntjZz8L95M9iuI8JG3CDWFyPWFyN6KcrFC5NcPBdipHeKIz3vsLn2AwCoEgsVO0pYv8NL84lXsO9/\n03yClSvg8ccZb6iko/ctAn0Buoa6Zqzxv6FyA/4GPzvqd1DtqZ57Y5cgyTvNTfJO85M+lJvEJz+J\nUX4So9zkWp2f1AjMnUwE5igahb/+a3PTL68XbrnFHPyvXw+Wa0yhT4aTxHpTA/7eqDn4740RG4oz\nGo8zFE8wEo8Tz06VKrNSc28Fm26uYlNzGdaDHfD035s7j9lsjH/4Dt5pqeDApe9zpvMM02lWVouV\nrdVb2dmwk7a6NspcZfMYFSGEEEIIsVxIjcAcRCLw9a/DqVPmLr9f+AI05Mmk0VqTGE9kBvnTX3tj\nJCYS6fsltWY0kWAoFmfYSDBZoZiqsRCpseJpdLJxTQlt6ytYU+o28/ZHR+Gpp9AdHYQTYc7XOPn5\nLdUct2VW+rFb7bTUtOBv8LOtdhteh3ehQiMKoVjyTiUHVAixnBXLtboQ5PUhJ6kRmEeTk/C1r0F3\nt7nU5xe+ALW1mfPa0MSH4jMG/NPv8hsR46rPmbTDcAVcKEtypixBqMpCpMZJtNLNKp8bv8+H3+ej\n3uHIFO1qjW5vJ/j0txge6aEvOc6vPljHyZZ6UGO4bC5zjf8GPy01LThtzoUPjhBCCCGEWDZkInAN\ngkH4y780VwOqqYE//Jcaz2iEof3hzMB/IIaOX/2TDKvXiqPBgaPegb3ewTFfjIB3iqPOKOYUwQpY\nWe/ODP6rL6swNpIJzr37Cq/8l//MtvAQ0cQUF5qqeeeurVgrq7i9vo2dDTvZUr1lSa/xvxgk7zQ3\nyTvNT/pQbhKf/CRG+UmMcpNrdX5SIzB3xT1SvAZjY+YkoP+SwXpbmEdXhhj78xDDoeQV97VV2HA2\nOHHUO9IDf0eDA6vPilKKC1NT/K/+fs5Pmct1WpRiq9uNv6SEHT4fZZdVGCdiU5zd9zP633iRROBd\nLKFJJkcmGV9ZwfEHb6b2jvv5g4adbKzaKGv8CyGEEEKIWZEagVkYvGTwD/9+Ek6FWBkL0bbVwG43\nzzlqHXi3e3GudKYH/VaX9arPEzcMfjo8zEujoxhaU2m387GqKnb4fHitMx8TnZzg7Bs/ZfDNlzEO\ndqCmMmv8G9VVOG++nYZPPsGaxq2yxn+xK5a8U8kBFUIsZ8VyrS4EeX3ISWoE5iAZThI6FKL39RBv\nPzNJVVhTUmJuBuZd56TEX4LP78PR4JjVQLwrHObJ/n4GYjEU8OGKCh6prsaZtcRQeHyIM6//mJE3\nX0EfOYKKm2v8K8BY0YjnpttZteth6jftRF3r0kRCCCGEEEJkkYlAlsREglBHiFAgRLgrzGRQc/gQ\nxGLgaHKz63M+Km/24aiZ/c5g4WSS/zM4yBvj4wCscDp5vK6OJrcbgInBi5xtf5axfa+hurogaaYa\nKcBoWkvJzXexetfD1DS1zHheyanMT2KUm+Sd5id9KDeJT34So/wkRrnJtTo/qRGYO5kIAFMXphj8\n/iDhE2FIZSNNhhVvXvTQt7qE2lu9PP5HdpzXsPCO1ppAKMTTAwOMJxLYlOLBqir2VFQw0XOaA+3P\nMrH/l1hOnwGtUQAWC8amTZTfdjdNuz9BWf2ahfh1hRBCCCGEKO4aASNuMPzTYUZfGkUbGmVXeJu9\nBOt9/P2rPoJxK62t8Pu/T7omYDbG4nGeGhigIxQCYIPbzUemRoi8/hyTb7+B5fyF9H21zQZbt1Bx\nyz2su/sT+Crr5/vXFDe6Ysk7lRxQIcRyVizX6kKQ14ecpEbgKsJdYfqf7Cc2EAMFFR+uoOqhKs5c\ntPI3X4epuLlT8O/9HthmGSWtNXvHx/nh4CDhZJLk2CAfPPYWW375PCN9/QBYAO10oFq3UX3bfazb\n9QguX/nC/aJCCCGEEEJcRdFVnCbDSfr+sY8L//UCsYEYzhVOVn9xNbW/XsuJbitf+xpMTcFNN8Fn\nPzv7SUB/LMZ/Pn+ev+0M0H3wTTw/+Aaf/Oof0vLMP2Dt68fweLDcdjt1/+Yr3PbMPu76j0/S/OAT\nc54EtLe3z+lxxURilFv7vsOFbsKSJ30oN4lPfhKj/CRGucm1Or/2/ScK3YRlq6g+EQgeCDLw9ACJ\n8QTKpqj6aBUV91dgsVk4dAi+8Q2Ix+G22+Dxx2E2C/NEY1Ge3P8qL/T0EBsewhcK8uDRd9nUfx5d\nWoL11nuov/MjrL1pD1b77IuMhRBCCCGEWEhFUSMQH4sz8NQAoQ4zZ9+9wU3db9XhbHASj8Pzz8OL\nL4JhwO7d8OlPQ64VQcPhEC/ve4n9p45zMhwnmvpgpbXnNHcOdlO+4wM03vUgq/27ZZlPsfCKJe9U\nckCFEMtZsVyrC0FeH3Iq2hoBrTXje8cZ/OEgRsTA4rJQ88kayu4qQynFiRPw5JPQ328O/D/6UXj4\n4atPAsYmRnjxVy/yztlTnIkaJNJZVRaqSXB/qYM79/wBDVs/JIN/IYQQQgix5N2wE4FYf4z+J/vN\nJUEBX5uP2s/UYq+wEw7DD38Ie/ea921sNFOB1q2b+RyX+i/y8lu/4MCF85yPQ5LpGYKFOkuSbbXV\nfPiDd9Gycfvi/WIpsu5yfhKj3GRt6vykD+Um8clPYpSfxCg3uVbnJ/sIzN0NNxHQSc3ISyMMPz+M\njmtspTZqP12Lb6cPpRSBADz1FIyPg9VqfgrwwAOZouDuC6d4af+rdFzqpSdpSW0roFDASmuStoZG\n7rt5N+tWbyrcLymEEEIIIcR1uqFqBCLdEfq/3U+0JwpA2W1l1Dxag9VrZXwcnn4aDhww77t+vfkp\nQEMDHD11mFfefZ3D/YP0Gdb081nQrLGBf/Uq9txyH411K+ft9xNi3hRL3qnkgAohlrNiuVYXgrw+\n5FQUNQLa0PT+fS/xwTj2Gjt1v1WHd4sXreGNN+AHP4BIBFwueOSRJKU17/LdX7zFkeFRhvX04N+K\nDYN1TgsfXLuOe2+9j+qK2oL+XkIIIYQQQiyEG2YioCyKus/UET4epuqhKiwOCwMDZjFwVxcYOkn9\nmr3Yat7jfx8MMk5m8O/AYIPLxk0bNrHntvvxeUsL+rvMhuRU5icxyk3yTvOTPpSbxCc/iVF+EqPc\n5Fqdn9QIzN0NMxEA8LZ48bZ4SSbh5z+Hn/wkTsj4BfHSQ8RqIvTbrTAJYMVDkk1eF7dubuHuW+7F\n5XQXuvlCCCGEEEIsmhuqRgDgWFeIv/nWy/RGjxEsjYPLgt0BCighyZYyL3c07+DOD+7GZrPPf8OF\nWGzFkncqOaBCiOWsWK7VhSCvDzkVRY2AYcAf/NlX6TZiJL0WVAk4HBaqLUlaKsu4a/uHuGn7rVis\n1vxPJoQQQgghxA2uYDtfKaUeUEodV0qdVEp98fqfD8LxBEmbhWqd5IGV5Xz1wQf51he+zL994gvc\n4r/jhpoEtLe3F7oJS57EKLf2fYcL3YQlT/pQbhKf/CRG+UmMcpNrdX7t+08UugnLVkEmAkopK/B1\n4AGgGfiMUmrr9T0n/P7HHuTf3/0oT//Jl/mjx/9vtm/ZOR/NXZI6OjoK3YQlT2KUW0fnmUI3YcmT\nPpSbxCc/iVF+EqPc5FqdX8exC4VuwrJVqNSgm4BTWutuAKXU08AjwLHredLbP3TjDvwvNzY2Vugm\nLHkSo9zGJiYL3YQlT/pQbhKf/CRG+UmMcpNrdX5jE5FCN2HZKlRq0Aoge/p2MXVMCCGEEEIIsQgK\nNRFYmksVLSPd3d2FbsKSJzHKrfvCQKGbsORJH8pN4pOfxCg/iVFucq3Or7tnuNBNWLYKsnyoUuoW\n4Mta6wdSt/8YMLTWf5F1H5ksCCGEEEIIcZ3eb/nQQk0EbEAX8GHgEvA28Bmt9XXVCAghhBBCCCFm\npyDFwlrrhFLq88CLgBX4XzIJEEIIIYQQYvEs2Z2FhRBCCCGEEAtn0YqFlVL/oJTqV0odzjrWppTa\np5Q6pJR6TilVknXuj1ObjR1XSu3JOv4BpdTh1Ln/vljtXwzzGKP21LFA6l/1Yv8uC+Fa4qOUqlRK\nvaaUCiql/uqy55E+RN4YSR9S6j6l1Lup4+8qpe7Oeoz0IfLGSPqQUjdl/f6HlFK/kfUY6UPkjVHR\n96Gs86uVUiGl1B9lHZM+NPMxV4vRDdmH5pXWelH+AXcCfuBw1rF3gDtT3/8u8P+mvm8GOgA7sBY4\nRebTi7eBm1LfvwA8sFi/wzKK0WvAzkL/PgWOjwe4HfhnwF9d9jzSh/LHSPoQ7ADqU9+3ABelD11T\njKQPgRuwpL6vB4YAq/ShWceo6PtQ1vkfAM8Af5R1TPpQ/hjdkH1oPv8t2icCWuu9wOhlhzemjgP8\nAvhU6vtHgKe01nFtbjp2CrhZKdUAlGit307d79vAxxe25YtnPmKU9birVocvZ9cSH611WGv9KyCa\nfWfpQ/ljlKXY+1CH1rovdfwo4FZK2aUP5Y9R1uOKvQ9FtNZG6rgbGNdaJ6UP5Y9R1uOKug8BKKU+\nDpzB/BubPiZ9KE+MstxwfWg+FWofgWmdSqlHUt//GrAq9X0j5iZj06Y3HLv8eA83/kZk1xKjxqzb\n30p9DPYni9DGQnq/+Ey7vAhmBdKH8sVomvShjE8B72mt40gfmk2MphV9H0qlvnQCncC/Sh2WPpQ/\nRtOKug8ppXzAvwW+fNn9pQ/lj9G0YulDc1LoicA/AT6nlHoX8AGxArdnKZpLjB7TWrdifrR2p1Lq\n8YVsYIFJH8pP+lBuOeOjlGoB/hwzhapYzSVG0ocArfXbWusWYCfw35VSZQVqY6HNJUbSh8zB7V9q\nrcPIO9tziVEx9aE5KcjyodO01l3A/QBKqU3Ag6lTPcx8x2kl5sy3J/V99vGehW9p4VxjjHpSj7mU\n+hpSSn0XuAn4x8Vq82LKEZ/3I30of4ykD6UopVYCPwQe11qfTR2WPpQ/RtKHrrzPcaXUaWAD5uuZ\n9KEr75Mdo/eKvA99NHXqJuBTSqn/BJQDhlIqgvk3V+x9KGeMtNb/o5j60FwV9BMBpVRN6qsF+BPg\nb1KnngM+rZRyKKWagI3A26lc1Aml1M1KKQU8DjxbgKYvmmuNkVLKOl0Vn8rVfQg4fOUz3xhyxCd9\nl+wbWutepA/ljJH0ITM+Sqly4Hngi1rrfdP3lz6UP0bSh9LxWavMDTRRSq3BvE6flNey/DGSPsTf\nAmit79JaN2mtm4D/BvzH1ABX+lCeGBVbH5qrRftEQCn1FLALqFZKXQD+FPAppf556i7/R2v9TQCt\n9VGl1Pcwiz4SwOe01tN5zJ8DvolZVPSC1vrni/U7LLT5iJFSygX8PNXprcDLwN8t8q+yIK4lPqn7\ndwMlgEOZhUT3aa2PI33om1n37+ayGAHnkT4E8HlgPfCnSqk/TR27T2s9hPShb6a+v2qMgAjShwDu\nAL6klIoDceCfaq0nUuekD5muGiOllBfpQ/lIH8rthh0PzSfZUEwIIYQQQogiVOhiYSGEEEIIIUQB\nyERACCGEEEKIIiQTASGEEEIIIYqQTASEEEIIIYQoQjIREEIIIYQQogjJREAIIYQQQogiJBMBIYQQ\nMyjTXqXUA1nHfk0p9bNCtksIIcT8kn0EhBBCXEEp1QJ8H/ADduAAcL/W+uwcnsumtU7McxOFEEJc\nJ5kICCGEuCql1F8AYcALhIA1QCvmxODLWuvnlFJrgW+n7gPwea31PqXUbuD/A0aALVrrzYvbeiGE\nEPnIREAIIcRVKaU8mJ8ExICfAp1a6+8opcqB/ZifFmjA0FpHlVIbge9qrT+Umgj8FGjRWp8rzG8g\nhBAiF1uhGyCEEGJp0lqHlVLPYH4a8OvAQ0qpf5067QRWAX3A15VSbUAS2Jj1FG/LJEAIIZYumQgI\nIYTIxUj9U8AntdYns08qpb4M9GqtH1dKWYGprNOTi9ZKIYQQ10xWDRJCCDEbLwL/YvqGUsqf+rYU\n81MBgN8GrIvcLiGEEHMkEwEhhBD5aMzCX7tS6pBS6gjwldS5/wE8oZTqADZjphFlP04IIcQSJcXC\nQgghhBBCFCH5REAIIYQQQogiJBMBIYQQQgghipBMBIQQQgghhChCMhEQQgghhBCiCMlEQAghhBBC\niCIkEwEhhBBCCCGKkEwEhBBCCCGEKEIyERBCCCGEEKII/f8i8+88NlFLDwAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fc3d2e79390>"
]
}
],
"prompt_number": 15
}
],
"metadata": {}
}
]
}
| gpl-2.0 |
neurotechuoft/MindType | Code/V1/EEG_Channel_Exploration.ipynb | 1 | 5526460 | null | agpl-3.0 |
qinwf-nuan/keras-js | notebooks/layers/wrappers/TimeDistributed.ipynb | 1 | 16195 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using TensorFlow backend.\n"
]
}
],
"source": [
"import numpy as np\n",
"from keras.models import Model\n",
"from keras.layers import Input\n",
"from keras.layers.core import Dense\n",
"from keras.layers.convolutional import Conv2D\n",
"from keras.layers.wrappers import TimeDistributed\n",
"from keras import backend as K\n",
"import json\n",
"from collections import OrderedDict"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def format_decimal(arr, places=6):\n",
" return [round(x * 10**places) / 10**places for x in arr]"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"DATA = OrderedDict()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### TimeDistributed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**[wrappers.TimeDistributed.0] wrap a Dense layer with units 4 (input: 3 x 6)**"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"W shape: (6, 4)\n",
"W: [0.317596, 0.688515, -0.688309, -0.48247, 0.387223, -0.718263, 0.281673, -0.106311, 0.576861, -0.083926, 0.631691, 0.92647, 0.579655, -0.024215, -0.805793, -0.842947, -0.955415, 0.656415, 0.44667, 0.633739, 0.701525, 0.917507, -0.185671, -0.105247]\n",
"b shape: (4,)\n",
"b: [-0.332867, 0.650317, 0.995501, -0.458367]\n",
"\n",
"in shape: (3, 6)\n",
"in: [-0.30351, 0.37881, -0.248093, 0.372204, -0.698964, -0.408058, -0.103801, 0.376217, -0.724015, 0.708616, -0.513219, -0.46074, -0.125163, -0.76111, -0.153798, 0.729255, 0.556458, -0.671966]\n",
"out shape: (3, 4)\n",
"out: [0.171595, -0.652137, 0.618031, -1.295817, -0.05994, -0.407387, 0.000875, -1.993142, -1.33639, 0.854801, 0.555804, -0.650907]\n"
]
}
],
"source": [
"data_in_shape = (3, 6)\n",
"\n",
"layer_0 = Input(shape=data_in_shape)\n",
"layer_1 = TimeDistributed(Dense(4))(layer_0)\n",
"model = Model(inputs=layer_0, outputs=layer_1)\n",
"\n",
"# set weights to random (use seed for reproducibility)\n",
"weights = []\n",
"for i, w in enumerate(model.get_weights()):\n",
" np.random.seed(4000 + i)\n",
" weights.append(2 * np.random.random(w.shape) - 1)\n",
"model.set_weights(weights)\n",
"weight_names = ['W', 'b']\n",
"for w_i, w_name in enumerate(weight_names):\n",
" print('{} shape:'.format(w_name), weights[w_i].shape)\n",
" print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))\n",
"\n",
"data_in = 2 * np.random.random(data_in_shape) - 1\n",
"result = model.predict(np.array([data_in]))\n",
"data_out_shape = result[0].shape\n",
"data_in_formatted = format_decimal(data_in.ravel().tolist())\n",
"data_out_formatted = format_decimal(result[0].ravel().tolist())\n",
"print('')\n",
"print('in shape:', data_in_shape)\n",
"print('in:', data_in_formatted)\n",
"print('out shape:', data_out_shape)\n",
"print('out:', data_out_formatted)\n",
"\n",
"DATA['wrappers.TimeDistributed.0'] = {\n",
" 'input': {'data': data_in_formatted, 'shape': data_in_shape},\n",
" 'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],\n",
" 'expected': {'data': data_out_formatted, 'shape': data_out_shape}\n",
"}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**[wrappers.TimeDistributed.1] wrap a Conv2D layer with 6 3x3 filters (input: 5x4x4x2)**"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"W shape: (3, 3, 2, 6)\n",
"W: [0.971827, -0.898904, -0.987921, 0.529589, 0.043586, -0.541366, 0.316759, 0.351387, -0.292323, 0.445466, -0.922655, 0.437413, -0.483267, -0.478014, 0.7408, -0.595028, -0.718381, 0.349594, -0.091293, 0.14291, 0.633818, -0.686841, -0.925272, -0.740397, 0.070594, 0.67408, 0.455314, -0.402251, 0.288807, 0.001378, 0.42892, -0.251869, 0.06113, -0.703784, 0.002676, 0.965023, 0.758788, 0.1193, 0.749321, -0.017408, -0.004115, 0.18981, -0.91507, 0.132792, -0.219057, 0.19682, -0.512841, 0.954544, 0.794403, -0.663179, -0.05377, -0.855038, -0.486641, 0.625844, -0.945869, -0.474979, 0.922345, -0.334843, -0.469456, -0.394364, 0.543681, -0.817676, 0.6093, -0.77635, -0.508683, 0.22456, 0.696262, 0.079806, -0.182646, -0.718939, 0.962504, -0.386231, 0.860488, -0.918945, -0.800484, -0.590285, 0.409804, -0.822098, 0.3489, -0.4508, 0.913208, -0.414455, 0.97663, 0.956314, -0.55547, 0.594094, -0.552044, -0.137467, 0.539049, -0.320055, -0.335577, 0.974746, -0.634747, 0.085161, -0.127183, -0.061717, -0.411844, 0.774181, 0.223395, 0.163937, -0.606967, 0.178549, -0.005153, 0.452476, 0.373127, -0.726827, -0.395458, -0.769671]\n",
"b shape: (6,)\n",
"b: [0.180389, 0.629217, -0.656262, -0.476575, -0.36398, 0.987756]\n",
"\n",
"in shape: (5, 4, 4, 2)\n",
"in: [-0.579677, 0.883193, 0.651172, -0.820251, -0.64795, 0.857328, -0.4689, 0.356044, -0.641528, -0.531973, -0.33586, -0.438823, 0.682186, 0.215781, -0.401735, 0.169171, 0.869358, -0.204078, -0.661876, -0.616139, -0.453943, -0.569439, -0.25218, 0.156473, 0.194797, -0.923921, 0.652204, -0.11765, 0.86293, 0.314218, -0.878496, -0.364761, -0.647821, 0.296841, 0.280105, 0.2753, -0.959741, -0.148037, -0.489424, -0.88939, 0.704443, 0.08354, 0.930112, -0.87023, -0.212285, 0.750133, 0.343506, -0.82568, 0.391491, 0.149626, 0.003594, -0.181464, -0.499632, 0.20694, 0.1007, 0.39826, 0.609736, -0.765775, -0.728474, -0.011711, 0.543543, 0.174309, 0.105794, -0.009876, -0.694421, -0.157031, 0.670853, -0.581331, 0.739486, -0.886014, -0.637039, 0.725753, 0.61919, 0.447635, 0.167298, 0.164242, -0.615436, -0.503061, 0.981698, -0.392795, 0.532215, 0.761817, 0.735562, -0.236234, -0.856381, 0.22419, -0.221125, 0.133757, -0.011162, -0.88018, -0.433047, -0.825617, 0.693626, -0.185243, -0.824829, 0.07932, 0.336478, 0.370138, -0.685905, -0.462037, 0.563862, 0.490274, 0.934239, -0.129323, 0.717792, -0.73658, -0.939587, 0.796637, -0.131382, -0.79957, -0.271279, 0.816961, -0.082096, 0.64553, -0.106661, 0.651369, -0.843208, -0.221077, 0.758074, 0.156006, -0.429501, 0.191698, 0.988067, -0.277344, 0.757645, -0.877824, 0.053841, 0.394075, 0.786359, 0.735302, 0.247852, -0.310899, 0.703408, -0.848404, 0.455067, 0.295289, -0.629316, 0.626332, -0.075289, -0.442735, -0.219408, -0.766048, 0.303257, 0.142211, 0.910002, -0.780858, 0.333242, -0.533434, 0.572575, 0.355883, -0.671924, 0.22028, -0.505951, -0.317892, 0.609641, -0.360548, 0.490007, 0.441024, 0.660294, 0.850007]\n",
"out shape: (5, 2, 2, 6)\n",
"out: [2.089554, -2.186939, -1.436176, -0.951733, -0.212962, 2.449681, 1.053569, -0.592297, -0.875753, -0.803289, -0.834779, -0.568349, -0.842922, 3.976765, -1.054281, 0.581773, 0.235047, 0.103039, -0.079684, 0.225164, -2.408352, -1.116154, 1.561833, -0.491674, 2.43274, -0.158393, -0.874487, -1.96851, -0.106465, 1.602375, 0.941225, 0.480547, 0.002478, 1.246195, -1.388929, -1.133004, 1.476556, -0.459852, -2.130519, -0.126113, -1.162246, 1.398016, -0.61384, 1.539333, -0.466156, 0.0395, 0.506595, -1.590958, -1.044266, 0.736233, 0.61792, -0.923799, 1.275832, 1.491487, 1.903216, -2.385963, -1.553725, -0.554848, -0.456638, 1.645426, 0.690056, 0.190637, -2.015925, 1.143469, -2.530136, 1.025159, -0.150503, 2.627801, -1.352068, 1.245647, 1.235627, -0.915363, 0.682646, 0.854592, -0.030856, 0.949627, 1.204568, 1.052329, -0.942961, 2.039314, 0.892454, -1.925232, 0.046332, 2.315713, -2.358422, 1.724373, -1.528506, 1.794933, 0.342617, -0.191888, -0.026605, 0.475714, -1.332559, -1.158213, 0.028725, 1.890396, -0.305622, 0.890336, -3.426138, 1.245994, -2.027975, -0.505022, 1.32001, 0.477823, -2.460816, -0.984189, 1.221664, 0.339475, 1.26535, 2.228118, 0.207158, -0.455112, -0.64988, 0.688864, 0.574933, 1.911587, -1.642423, -1.385077, 0.744757, -0.567276]\n"
]
}
],
"source": [
"data_in_shape = (5, 4, 4, 2)\n",
"\n",
"layer_0 = Input(shape=data_in_shape)\n",
"layer_1 = TimeDistributed(Conv2D(6, (3,3), data_format='channels_last'))(layer_0)\n",
"model = Model(inputs=layer_0, outputs=layer_1)\n",
"\n",
"# set weights to random (use seed for reproducibility)\n",
"weights = []\n",
"for i, w in enumerate(model.get_weights()):\n",
" np.random.seed(4010 + i)\n",
" weights.append(2 * np.random.random(w.shape) - 1)\n",
"model.set_weights(weights)\n",
"weight_names = ['W', 'b']\n",
"for w_i, w_name in enumerate(weight_names):\n",
" print('{} shape:'.format(w_name), weights[w_i].shape)\n",
" print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))\n",
"\n",
"data_in = 2 * np.random.random(data_in_shape) - 1\n",
"result = model.predict(np.array([data_in]))\n",
"data_out_shape = result[0].shape\n",
"data_in_formatted = format_decimal(data_in.ravel().tolist())\n",
"data_out_formatted = format_decimal(result[0].ravel().tolist())\n",
"print('')\n",
"print('in shape:', data_in_shape)\n",
"print('in:', data_in_formatted)\n",
"print('out shape:', data_out_shape)\n",
"print('out:', data_out_formatted)\n",
"\n",
"DATA['wrappers.TimeDistributed.1'] = {\n",
" 'input': {'data': data_in_formatted, 'shape': data_in_shape},\n",
" 'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],\n",
" 'expected': {'data': data_out_formatted, 'shape': data_out_shape}\n",
"}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### export for Keras.js tests"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{\"wrappers.TimeDistributed.0\": {\"expected\": {\"data\": [0.171595, -0.652137, 0.618031, -1.295817, -0.05994, -0.407387, 0.000875, -1.993142, -1.33639, 0.854801, 0.555804, -0.650907], \"shape\": [3, 4]}, \"input\": {\"data\": [-0.30351, 0.37881, -0.248093, 0.372204, -0.698964, -0.408058, -0.103801, 0.376217, -0.724015, 0.708616, -0.513219, -0.46074, -0.125163, -0.76111, -0.153798, 0.729255, 0.556458, -0.671966], \"shape\": [3, 6]}, \"weights\": [{\"data\": [0.317596, 0.688515, -0.688309, -0.48247, 0.387223, -0.718263, 0.281673, -0.106311, 0.576861, -0.083926, 0.631691, 0.92647, 0.579655, -0.024215, -0.805793, -0.842947, -0.955415, 0.656415, 0.44667, 0.633739, 0.701525, 0.917507, -0.185671, -0.105247], \"shape\": [6, 4]}, {\"data\": [-0.332867, 0.650317, 0.995501, -0.458367], \"shape\": [4]}]}, \"wrappers.TimeDistributed.1\": {\"expected\": {\"data\": [2.089554, -2.186939, -1.436176, -0.951733, -0.212962, 2.449681, 1.053569, -0.592297, -0.875753, -0.803289, -0.834779, -0.568349, -0.842922, 3.976765, -1.054281, 0.581773, 0.235047, 0.103039, -0.079684, 0.225164, -2.408352, -1.116154, 1.561833, -0.491674, 2.43274, -0.158393, -0.874487, -1.96851, -0.106465, 1.602375, 0.941225, 0.480547, 0.002478, 1.246195, -1.388929, -1.133004, 1.476556, -0.459852, -2.130519, -0.126113, -1.162246, 1.398016, -0.61384, 1.539333, -0.466156, 0.0395, 0.506595, -1.590958, -1.044266, 0.736233, 0.61792, -0.923799, 1.275832, 1.491487, 1.903216, -2.385963, -1.553725, -0.554848, -0.456638, 1.645426, 0.690056, 0.190637, -2.015925, 1.143469, -2.530136, 1.025159, -0.150503, 2.627801, -1.352068, 1.245647, 1.235627, -0.915363, 0.682646, 0.854592, -0.030856, 0.949627, 1.204568, 1.052329, -0.942961, 2.039314, 0.892454, -1.925232, 0.046332, 2.315713, -2.358422, 1.724373, -1.528506, 1.794933, 0.342617, -0.191888, -0.026605, 0.475714, -1.332559, -1.158213, 0.028725, 1.890396, -0.305622, 0.890336, -3.426138, 1.245994, -2.027975, -0.505022, 1.32001, 0.477823, -2.460816, -0.984189, 1.221664, 0.339475, 1.26535, 2.228118, 0.207158, -0.455112, -0.64988, 0.688864, 0.574933, 1.911587, -1.642423, -1.385077, 0.744757, -0.567276], \"shape\": [5, 2, 2, 6]}, \"input\": {\"data\": [-0.579677, 0.883193, 0.651172, -0.820251, -0.64795, 0.857328, -0.4689, 0.356044, -0.641528, -0.531973, -0.33586, -0.438823, 0.682186, 0.215781, -0.401735, 0.169171, 0.869358, -0.204078, -0.661876, -0.616139, -0.453943, -0.569439, -0.25218, 0.156473, 0.194797, -0.923921, 0.652204, -0.11765, 0.86293, 0.314218, -0.878496, -0.364761, -0.647821, 0.296841, 0.280105, 0.2753, -0.959741, -0.148037, -0.489424, -0.88939, 0.704443, 0.08354, 0.930112, -0.87023, -0.212285, 0.750133, 0.343506, -0.82568, 0.391491, 0.149626, 0.003594, -0.181464, -0.499632, 0.20694, 0.1007, 0.39826, 0.609736, -0.765775, -0.728474, -0.011711, 0.543543, 0.174309, 0.105794, -0.009876, -0.694421, -0.157031, 0.670853, -0.581331, 0.739486, -0.886014, -0.637039, 0.725753, 0.61919, 0.447635, 0.167298, 0.164242, -0.615436, -0.503061, 0.981698, -0.392795, 0.532215, 0.761817, 0.735562, -0.236234, -0.856381, 0.22419, -0.221125, 0.133757, -0.011162, -0.88018, -0.433047, -0.825617, 0.693626, -0.185243, -0.824829, 0.07932, 0.336478, 0.370138, -0.685905, -0.462037, 0.563862, 0.490274, 0.934239, -0.129323, 0.717792, -0.73658, -0.939587, 0.796637, -0.131382, -0.79957, -0.271279, 0.816961, -0.082096, 0.64553, -0.106661, 0.651369, -0.843208, -0.221077, 0.758074, 0.156006, -0.429501, 0.191698, 0.988067, -0.277344, 0.757645, -0.877824, 0.053841, 0.394075, 0.786359, 0.735302, 0.247852, -0.310899, 0.703408, -0.848404, 0.455067, 0.295289, -0.629316, 0.626332, -0.075289, -0.442735, -0.219408, -0.766048, 0.303257, 0.142211, 0.910002, -0.780858, 0.333242, -0.533434, 0.572575, 0.355883, -0.671924, 0.22028, -0.505951, -0.317892, 0.609641, -0.360548, 0.490007, 0.441024, 0.660294, 0.850007], \"shape\": [5, 4, 4, 2]}, \"weights\": [{\"data\": [0.971827, -0.898904, -0.987921, 0.529589, 0.043586, -0.541366, 0.316759, 0.351387, -0.292323, 0.445466, -0.922655, 0.437413, -0.483267, -0.478014, 0.7408, -0.595028, -0.718381, 0.349594, -0.091293, 0.14291, 0.633818, -0.686841, -0.925272, -0.740397, 0.070594, 0.67408, 0.455314, -0.402251, 0.288807, 0.001378, 0.42892, -0.251869, 0.06113, -0.703784, 0.002676, 0.965023, 0.758788, 0.1193, 0.749321, -0.017408, -0.004115, 0.18981, -0.91507, 0.132792, -0.219057, 0.19682, -0.512841, 0.954544, 0.794403, -0.663179, -0.05377, -0.855038, -0.486641, 0.625844, -0.945869, -0.474979, 0.922345, -0.334843, -0.469456, -0.394364, 0.543681, -0.817676, 0.6093, -0.77635, -0.508683, 0.22456, 0.696262, 0.079806, -0.182646, -0.718939, 0.962504, -0.386231, 0.860488, -0.918945, -0.800484, -0.590285, 0.409804, -0.822098, 0.3489, -0.4508, 0.913208, -0.414455, 0.97663, 0.956314, -0.55547, 0.594094, -0.552044, -0.137467, 0.539049, -0.320055, -0.335577, 0.974746, -0.634747, 0.085161, -0.127183, -0.061717, -0.411844, 0.774181, 0.223395, 0.163937, -0.606967, 0.178549, -0.005153, 0.452476, 0.373127, -0.726827, -0.395458, -0.769671], \"shape\": [3, 3, 2, 6]}, {\"data\": [0.180389, 0.629217, -0.656262, -0.476575, -0.36398, 0.987756], \"shape\": [6]}]}}\n"
]
}
],
"source": [
"print(json.dumps(DATA))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
catalystcomputing/DSIoT-Python-sessions | Session201811/code/02 Python Assignment.ipynb | 1 | 1845 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Assignment"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Strings\n",
"data = 'Hello World'\n",
"print data[0]\n",
"print len(data)\n",
"print data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Numbers\n",
"value = 50.4\n",
"print value\n",
"value = 5.6\n",
"print value"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Boolean\n",
"p = True\n",
"q = False\n",
"print p,q"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Multiple Assignment\n",
"p,q,r = 5,6,7\n",
"print p,q,r"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# No value\n",
"p = None\n",
"print p"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| apache-2.0 |
tuanavu/coursera-university-of-washington | machine_learning/3_classification/assigment/week7/module-10-online-learning-assignment-graphlab.ipynb | 2 | 443945 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Training Logistic Regression via Stochastic Gradient Ascent\n",
"\n",
"The goal of this notebook is to implement a logistic regression classifier using stochastic gradient ascent. You will:\n",
"\n",
" * Extract features from Amazon product reviews.\n",
" * Convert an SFrame into a NumPy array.\n",
" * Write a function to compute the derivative of log likelihood function with respect to a single coefficient.\n",
" * Implement stochastic gradient ascent.\n",
" * Compare convergence of stochastic gradient ascent with that of batch gradient ascent."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fire up GraphLab Create\n",
" \n",
"Make sure you have the latest version of GraphLab Create. Upgrade by\n",
"\n",
"```\n",
" pip install graphlab-create --upgrade\n",
"```\n",
"See [this page](https://dato.com/download/) for detailed instructions on upgrading."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from __future__ import division\n",
"import graphlab"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load and process review dataset"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For this assignment, we will use the same subset of the Amazon product review dataset that we used in Module 3 assignment. The subset was chosen to contain similar numbers of positive and negative reviews, as the original dataset consisted of mostly positive reviews."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"products = graphlab.SFrame('amazon_baby_subset.gl/')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Just like we did previously, we will work with a hand-curated list of important words extracted from the review data. We will also perform 2 simple data transformations:\n",
"\n",
"1. Remove punctuation using [Python's built-in](https://docs.python.org/2/library/string.html) string manipulation functionality.\n",
"2. Compute word counts (only for the important_words)\n",
"\n",
"Refer to Module 3 assignment for more details."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import json\n",
"with open('important_words.json', 'r') as f: \n",
" important_words = json.load(f)\n",
"important_words = [str(s) for s in important_words]\n",
"\n",
"# Remote punctuation\n",
"def remove_punctuation(text):\n",
" import string\n",
" return text.translate(None, string.punctuation) \n",
"\n",
"products['review_clean'] = products['review'].apply(remove_punctuation)\n",
"\n",
"# Split out the words into individual columns\n",
"for word in important_words:\n",
" products[word] = products['review_clean'].apply(lambda s : s.split().count(word))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"The SFrame **products** now contains one column for each of the 193 **important_words**. "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\"><table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">name</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">review</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">rating</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sentiment</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">review_clean</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">baby</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Stop Pacifier Sucking<br>without tears with ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">All of my kids have cried<br>non-stop when I tried to ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">All of my kids have cried<br>nonstop when I tried to ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Nature's Lullabies Second<br>Year Sticker Calendar ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">We wanted to get<br>something to keep track ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">We wanted to get<br>something to keep track ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Nature's Lullabies Second<br>Year Sticker Calendar ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">My daughter had her 1st<br>baby over a year ago. ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">My daughter had her 1st<br>baby over a year ago She ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Lamaze Peekaboo, I Love<br>You ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">One of baby's first and<br>favorite books, and i ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">One of babys first and<br>favorite books and it is ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">SoftPlay Peek-A-Boo<br>Where's Elmo A Childr ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Very cute interactive<br>book! My son loves this ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Very cute interactive<br>book My son loves this ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Our Baby Girl Memory Book</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Beautiful book, I love it<br>to record cherished t ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Beautiful book I love it<br>to record cherished t ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Hunnt&reg; Falling<br>Flowers and Birds Kids ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Try this out for a spring<br>project !Easy ,fun and ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Try this out for a spring<br>project Easy fun and ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Blessed By Pope Benedict<br>XVI Divine Mercy Full ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">very nice Divine Mercy<br>Pendant of Jesus now on ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">very nice Divine Mercy<br>Pendant of Jesus now on ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Cloth Diaper Pins<br>Stainless Steel ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">We bought the pins as my<br>6 year old Autistic son ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">We bought the pins as my<br>6 year old Autistic son ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">Cloth Diaper Pins<br>Stainless Steel ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">It has been many years<br>since we needed diaper ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">It has been many years<br>since we needed diaper ...</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
"</table>\n",
"<table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">one</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">great</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">love</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">use</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">would</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">like</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">easy</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">little</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">seat</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">old</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">well</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">get</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">also</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">really</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">son</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">time</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">bought</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
"</table>\n",
"<table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">product</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">good</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">daughter</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">much</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">loves</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">stroller</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">put</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">months</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">car</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">still</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">back</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">used</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">recommend</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">first</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">even</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
"</table>\n",
"<table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">perfect</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">nice</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">...</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">...</td>\n",
" </tr>\n",
"</table>\n",
"[53072 rows x 198 columns]<br/>Note: Only the head of the SFrame is printed.<br/>You can use print_rows(num_rows=m, num_columns=n) to print more rows and columns.\n",
"</div>"
],
"text/plain": [
"Columns:\n",
"\tname\tstr\n",
"\treview\tstr\n",
"\trating\tfloat\n",
"\tsentiment\tint\n",
"\treview_clean\tstr\n",
"\tbaby\tint\n",
"\tone\tint\n",
"\tgreat\tint\n",
"\tlove\tint\n",
"\tuse\tint\n",
"\twould\tint\n",
"\tlike\tint\n",
"\teasy\tint\n",
"\tlittle\tint\n",
"\tseat\tint\n",
"\told\tint\n",
"\twell\tint\n",
"\tget\tint\n",
"\talso\tint\n",
"\treally\tint\n",
"\tson\tint\n",
"\ttime\tint\n",
"\tbought\tint\n",
"\tproduct\tint\n",
"\tgood\tint\n",
"\tdaughter\tint\n",
"\tmuch\tint\n",
"\tloves\tint\n",
"\tstroller\tint\n",
"\tput\tint\n",
"\tmonths\tint\n",
"\tcar\tint\n",
"\tstill\tint\n",
"\tback\tint\n",
"\tused\tint\n",
"\trecommend\tint\n",
"\tfirst\tint\n",
"\teven\tint\n",
"\tperfect\tint\n",
"\tnice\tint\n",
"\tbag\tint\n",
"\ttwo\tint\n",
"\tusing\tint\n",
"\tgot\tint\n",
"\tfit\tint\n",
"\taround\tint\n",
"\tdiaper\tint\n",
"\tenough\tint\n",
"\tmonth\tint\n",
"\tprice\tint\n",
"\tgo\tint\n",
"\tcould\tint\n",
"\tsoft\tint\n",
"\tsince\tint\n",
"\tbuy\tint\n",
"\troom\tint\n",
"\tworks\tint\n",
"\tmade\tint\n",
"\tchild\tint\n",
"\tkeep\tint\n",
"\tsize\tint\n",
"\tsmall\tint\n",
"\tneed\tint\n",
"\tyear\tint\n",
"\tbig\tint\n",
"\tmake\tint\n",
"\ttake\tint\n",
"\teasily\tint\n",
"\tthink\tint\n",
"\tcrib\tint\n",
"\tclean\tint\n",
"\tway\tint\n",
"\tquality\tint\n",
"\tthing\tint\n",
"\tbetter\tint\n",
"\twithout\tint\n",
"\tset\tint\n",
"\tnew\tint\n",
"\tevery\tint\n",
"\tcute\tint\n",
"\tbest\tint\n",
"\tbottles\tint\n",
"\twork\tint\n",
"\tpurchased\tint\n",
"\tright\tint\n",
"\tlot\tint\n",
"\tside\tint\n",
"\thappy\tint\n",
"\tcomfortable\tint\n",
"\ttoy\tint\n",
"\table\tint\n",
"\tkids\tint\n",
"\tbit\tint\n",
"\tnight\tint\n",
"\tlong\tint\n",
"\tfits\tint\n",
"\tsee\tint\n",
"\tus\tint\n",
"\tanother\tint\n",
"\tplay\tint\n",
"\tday\tint\n",
"\tmoney\tint\n",
"\tmonitor\tint\n",
"\ttried\tint\n",
"\tthought\tint\n",
"\tnever\tint\n",
"\titem\tint\n",
"\thard\tint\n",
"\tplastic\tint\n",
"\thowever\tint\n",
"\tdisappointed\tint\n",
"\treviews\tint\n",
"\tsomething\tint\n",
"\tgoing\tint\n",
"\tpump\tint\n",
"\tbottle\tint\n",
"\tcup\tint\n",
"\twaste\tint\n",
"\treturn\tint\n",
"\tamazon\tint\n",
"\tdifferent\tint\n",
"\ttop\tint\n",
"\twant\tint\n",
"\tproblem\tint\n",
"\tknow\tint\n",
"\twater\tint\n",
"\ttry\tint\n",
"\treceived\tint\n",
"\tsure\tint\n",
"\ttimes\tint\n",
"\tchair\tint\n",
"\tfind\tint\n",
"\thold\tint\n",
"\tgate\tint\n",
"\topen\tint\n",
"\tbottom\tint\n",
"\taway\tint\n",
"\tactually\tint\n",
"\tcheap\tint\n",
"\tworked\tint\n",
"\tgetting\tint\n",
"\tordered\tint\n",
"\tcame\tint\n",
"\tmilk\tint\n",
"\tbad\tint\n",
"\tpart\tint\n",
"\tworth\tint\n",
"\tfound\tint\n",
"\tcover\tint\n",
"\tmany\tint\n",
"\tdesign\tint\n",
"\tlooking\tint\n",
"\tweeks\tint\n",
"\tsay\tint\n",
"\twanted\tint\n",
"\tlook\tint\n",
"\tplace\tint\n",
"\tpurchase\tint\n",
"\tlooks\tint\n",
"\tsecond\tint\n",
"\tpiece\tint\n",
"\tbox\tint\n",
"\tpretty\tint\n",
"\ttrying\tint\n",
"\tdifficult\tint\n",
"\ttogether\tint\n",
"\tthough\tint\n",
"\tgive\tint\n",
"\tstarted\tint\n",
"\tanything\tint\n",
"\tlast\tint\n",
"\tcompany\tint\n",
"\tcome\tint\n",
"\treturned\tint\n",
"\tmaybe\tint\n",
"\ttook\tint\n",
"\tbroke\tint\n",
"\tmakes\tint\n",
"\tstay\tint\n",
"\tinstead\tint\n",
"\tidea\tint\n",
"\thead\tint\n",
"\tsaid\tint\n",
"\tless\tint\n",
"\twent\tint\n",
"\tworking\tint\n",
"\thigh\tint\n",
"\tunit\tint\n",
"\tseems\tint\n",
"\tpicture\tint\n",
"\tcompletely\tint\n",
"\twish\tint\n",
"\tbuying\tint\n",
"\tbabies\tint\n",
"\twon\tint\n",
"\ttub\tint\n",
"\talmost\tint\n",
"\teither\tint\n",
"\n",
"Rows: 53072\n",
"\n",
"Data:\n",
"+-------------------------------+-------------------------------+--------+-----------+\n",
"| name | review | rating | sentiment |\n",
"+-------------------------------+-------------------------------+--------+-----------+\n",
"| Stop Pacifier Sucking with... | All of my kids have cried ... | 5.0 | 1 |\n",
"| Nature's Lullabies Second ... | We wanted to get something... | 5.0 | 1 |\n",
"| Nature's Lullabies Second ... | My daughter had her 1st ba... | 5.0 | 1 |\n",
"| Lamaze Peekaboo, I Love You | One of baby's first and fa... | 4.0 | 1 |\n",
"| SoftPlay Peek-A-Boo Where'... | Very cute interactive book... | 5.0 | 1 |\n",
"| Our Baby Girl Memory Book | Beautiful book, I love it ... | 5.0 | 1 |\n",
"| Hunnt® Falling Flowers... | Try this out for a spring ... | 5.0 | 1 |\n",
"| Blessed By Pope Benedict X... | very nice Divine Mercy Pen... | 5.0 | 1 |\n",
"| Cloth Diaper Pins Stainles... | We bought the pins as my 6... | 4.0 | 1 |\n",
"| Cloth Diaper Pins Stainles... | It has been many years sin... | 5.0 | 1 |\n",
"+-------------------------------+-------------------------------+--------+-----------+\n",
"+-------------------------------+------+-----+-------+------+-----+-------+------+\n",
"| review_clean | baby | one | great | love | use | would | like |\n",
"+-------------------------------+------+-----+-------+------+-----+-------+------+\n",
"| All of my kids have cried ... | 0 | 0 | 1 | 0 | 0 | 0 | 0 |\n",
"| We wanted to get something... | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n",
"| My daughter had her 1st ba... | 1 | 0 | 0 | 0 | 0 | 0 | 0 |\n",
"| One of babys first and fav... | 0 | 0 | 0 | 0 | 0 | 0 | 1 |\n",
"| Very cute interactive book... | 0 | 0 | 1 | 0 | 0 | 0 | 0 |\n",
"| Beautiful book I love it t... | 0 | 0 | 1 | 1 | 0 | 0 | 0 |\n",
"| Try this out for a spring ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n",
"| very nice Divine Mercy Pen... | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n",
"| We bought the pins as my 6... | 0 | 1 | 0 | 0 | 1 | 0 | 0 |\n",
"| It has been many years sin... | 0 | 1 | 0 | 0 | 0 | 0 | 1 |\n",
"+-------------------------------+------+-----+-------+------+-----+-------+------+\n",
"+------+--------+------+-----+------+-----+------+--------+-----+\n",
"| easy | little | seat | old | well | get | also | really | ... |\n",
"+------+--------+------+-----+------+-----+------+--------+-----+\n",
"| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ... |\n",
"| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | ... |\n",
"+------+--------+------+-----+------+-----+------+--------+-----+\n",
"[53072 rows x 198 columns]\n",
"Note: Only the head of the SFrame is printed.\n",
"You can use print_rows(num_rows=m, num_columns=n) to print more rows and columns."
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"products"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Split data into training and validation sets\n",
"\n",
"We will now split the data into a 90-10 split where 90% is in the training set and 10% is in the validation set. We use `seed=1` so that everyone gets the same result."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Training set : 47780 data points\n",
"Validation set: 5292 data points\n"
]
}
],
"source": [
"train_data, validation_data = products.random_split(.9, seed=1)\n",
"\n",
"print 'Training set : %d data points' % len(train_data)\n",
"print 'Validation set: %d data points' % len(validation_data)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Convert SFrame to NumPy array\n",
"\n",
"Just like in the earlier assignments, we provide you with a function that extracts columns from an SFrame and converts them into a NumPy array. Two arrays are returned: one representing features and another representing class labels. \n",
"\n",
"**Note:** The feature matrix includes an additional column 'intercept' filled with 1's to take account of the intercept term."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"\n",
"def get_numpy_data(data_sframe, features, label):\n",
" data_sframe['intercept'] = 1\n",
" features = ['intercept'] + features\n",
" features_sframe = data_sframe[features]\n",
" feature_matrix = features_sframe.to_numpy()\n",
" label_sarray = data_sframe[label]\n",
" label_array = label_sarray.to_numpy()\n",
" return(feature_matrix, label_array)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that we convert both the training and validation sets into NumPy arrays.\n",
"\n",
"**Warning**: This may take a few minutes."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"feature_matrix_train, sentiment_train = get_numpy_data(train_data, important_words, 'sentiment')\n",
"feature_matrix_valid, sentiment_valid = get_numpy_data(validation_data, important_words, 'sentiment') "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Are you running this notebook on an Amazon EC2 t2.micro instance?** (If you are using your own machine, please skip this section)\n",
"\n",
"It has been reported that t2.micro instances do not provide sufficient power to complete the conversion in acceptable amount of time. For interest of time, please refrain from running `get_numpy_data` function. Instead, download the [binary file](https://s3.amazonaws.com/static.dato.com/files/coursera/course-3/numpy-arrays/module-10-assignment-numpy-arrays.npz) containing the four NumPy arrays you'll need for the assignment. To load the arrays, run the following commands:\n",
"```\n",
"arrays = np.load('module-10-assignment-numpy-arrays.npz')\n",
"feature_matrix_train, sentiment_train = arrays['feature_matrix_train'], arrays['sentiment_train']\n",
"feature_matrix_valid, sentiment_valid = arrays['feature_matrix_valid'], arrays['sentiment_valid']\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Quiz question**: In Module 3 assignment, there were 194 features (an intercept + one feature for each of the 193 important words). In this assignment, we will use stochastic gradient ascent to train the classifier using logistic regression. How does the changing the solver to stochastic gradient ascent affect the number of features?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Building on logistic regression\n",
"\n",
"Let us now build on Module 3 assignment. Recall from lecture that the link function for logistic regression can be defined as:\n",
"\n",
"$$\n",
"P(y_i = +1 | \\mathbf{x}_i,\\mathbf{w}) = \\frac{1}{1 + \\exp(-\\mathbf{w}^T h(\\mathbf{x}_i))},\n",
"$$\n",
"\n",
"where the feature vector $h(\\mathbf{x}_i)$ is given by the word counts of **important_words** in the review $\\mathbf{x}_i$. \n",
"\n",
"\n",
"We will use the **same code** as in Module 3 assignment to make probability predictions, since this part is not affected by using stochastic gradient ascent as a solver. Only the way in which the coefficients are learned is affected by using stochastic gradient ascent as a solver."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"'''\n",
"produces probablistic estimate for P(y_i = +1 | x_i, w).\n",
"estimate ranges between 0 and 1.\n",
"'''\n",
"def predict_probability(feature_matrix, coefficients):\n",
" # Take dot product of feature_matrix and coefficients \n",
" score = np.dot(feature_matrix, coefficients)\n",
" \n",
" # Compute P(y_i = +1 | x_i, w) using the link function\n",
" predictions = 1. / (1.+np.exp(-score)) \n",
" return predictions"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Derivative of log likelihood with respect to a single coefficient\n",
"\n",
"Let us now work on making minor changes to how the derivative computation is performed for logistic regression.\n",
"\n",
"Recall from the lectures and Module 3 assignment that for logistic regression, **the derivative of log likelihood with respect to a single coefficient** is as follows:\n",
"\n",
"$$\n",
"\\frac{\\partial\\ell}{\\partial w_j} = \\sum_{i=1}^N h_j(\\mathbf{x}_i)\\left(\\mathbf{1}[y_i = +1] - P(y_i = +1 | \\mathbf{x}_i, \\mathbf{w})\\right)\n",
"$$\n",
"\n",
"In Module 3 assignment, we wrote a function to compute the derivative of log likelihood with respect to a single coefficient $w_j$. The function accepts the following two parameters:\n",
" * `errors` vector containing $(\\mathbf{1}[y_i = +1] - P(y_i = +1 | \\mathbf{x}_i, \\mathbf{w}))$ for all $i$\n",
" * `feature` vector containing $h_j(\\mathbf{x}_i)$ for all $i$\n",
" \n",
"Complete the following code block:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def feature_derivative(errors, feature): \n",
" \n",
" # Compute the dot product of errors and feature\n",
" ## YOUR CODE HERE\n",
" derivative = np.dot(errors, feature)\n",
"\n",
" return derivative"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Note**. We are not using regularization in this assignment, but, as discussed in the optional video, stochastic gradient can also be used for regularized logistic regression."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To verify the correctness of the gradient computation, we provide a function for computing average log likelihood (which we recall from the last assignment was a topic detailed in an advanced optional video, and used here for its numerical stability).\n",
"\n",
"To track the performance of stochastic gradient ascent, we provide a function for computing **average log likelihood**. \n",
"\n",
"$$\\ell\\ell_A(\\mathbf{w}) = \\color{red}{\\frac{1}{N}} \\sum_{i=1}^N \\Big( (\\mathbf{1}[y_i = +1] - 1)\\mathbf{w}^T h(\\mathbf{x}_i) - \\ln\\left(1 + \\exp(-\\mathbf{w}^T h(\\mathbf{x}_i))\\right) \\Big) $$\n",
"\n",
"**Note** that we made one tiny modification to the log likelihood function (called **compute_log_likelihood**) in our earlier assignments. We added a $\\color{red}{1/N}$ term which averages the log likelihood accross all data points. The $\\color{red}{1/N}$ term makes it easier for us to compare stochastic gradient ascent with batch gradient ascent. We will use this function to generate plots that are similar to those you saw in the lecture."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def compute_avg_log_likelihood(feature_matrix, sentiment, coefficients):\n",
" \n",
" indicator = (sentiment==+1)\n",
" scores = np.dot(feature_matrix, coefficients)\n",
" logexp = np.log(1. + np.exp(-scores))\n",
" \n",
" # Simple check to prevent overflow\n",
" mask = np.isinf(logexp)\n",
" logexp[mask] = -scores[mask]\n",
" \n",
" lp = np.sum((indicator-1)*scores - logexp)/len(feature_matrix)\n",
" \n",
" return lp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Quiz Question:** Recall from the lecture and the earlier assignment, the log likelihood (without the averaging term) is given by \n",
"\n",
"$$\\ell\\ell(\\mathbf{w}) = \\sum_{i=1}^N \\Big( (\\mathbf{1}[y_i = +1] - 1)\\mathbf{w}^T h(\\mathbf{x}_i) - \\ln\\left(1 + \\exp(-\\mathbf{w}^T h(\\mathbf{x}_i))\\right) \\Big) $$\n",
"\n",
"How are the functions $\\ell\\ell(\\mathbf{w})$ and $\\ell\\ell_A(\\mathbf{w})$ related?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Modifying the derivative for stochastic gradient ascent\n",
"\n",
"Recall from the lecture that the gradient for a single data point $\\color{red}{\\mathbf{x}_i}$ can be computed using the following formula:\n",
"\n",
"$$\n",
"\\frac{\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})}{\\partial w_j} = h_j(\\color{red}{\\mathbf{x}_i})\\left(\\mathbf{1}[y_\\color{red}{i} = +1] - P(y_\\color{red}{i} = +1 | \\color{red}{\\mathbf{x}_i}, \\mathbf{w})\\right)\n",
"$$\n",
"\n",
"\n",
"** Computing the gradient for a single data point**\n",
"\n",
"Do we really need to re-write all our code to modify $\\partial\\ell(\\mathbf{w})/\\partial w_j$ to $\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})/{\\partial w_j}$? \n",
"\n",
"\n",
"Thankfully **No!**. Using NumPy, we access $\\mathbf{x}_i$ in the training data using `feature_matrix_train[i:i+1,:]`\n",
"and $y_i$ in the training data using `sentiment_train[i:i+1]`. We can compute $\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})/\\partial w_j$ by re-using **all the code** written in **feature_derivative** and **predict_probability**.\n",
"\n",
"\n",
"We compute $\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})/\\partial w_j$ using the following steps:\n",
"* First, compute $P(y_i = +1 | \\mathbf{x}_i, \\mathbf{w})$ using the **predict_probability** function with `feature_matrix_train[i:i+1,:]` as the first parameter.\n",
"* Next, compute $\\mathbf{1}[y_i = +1]$ using `sentiment_train[i:i+1]`.\n",
"* Finally, call the **feature_derivative** function with `feature_matrix_train[i:i+1, j]` as one of the parameters. \n",
"\n",
"Let us follow these steps for `j = 1` and `i = 10`:"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Gradient single data point: 0.0\n",
" --> Should print 0.0\n"
]
}
],
"source": [
"j = 1 # Feature number\n",
"i = 10 # Data point number\n",
"coefficients = np.zeros(194) # A point w at which we are computing the gradient.\n",
"\n",
"predictions = predict_probability(feature_matrix_train[i:i+1,:], coefficients)\n",
"indicator = (sentiment_train[i:i+1]==+1)\n",
"\n",
"errors = indicator - predictions \n",
"gradient_single_data_point = feature_derivative(errors, feature_matrix_train[i:i+1,j])\n",
"print \"Gradient single data point: %s\" % gradient_single_data_point\n",
"print \" --> Should print 0.0\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Quiz Question:** The code block above computed $\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})/{\\partial w_j}$ for `j = 1` and `i = 10`. Is $\\partial\\ell_{\\color{red}{i}}(\\mathbf{w})/{\\partial w_j}$ a scalar or a 194-dimensional vector?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Modifying the derivative for using a batch of data points\n",
"\n",
"Stochastic gradient estimates the ascent direction using 1 data point, while gradient uses $N$ data points to decide how to update the the parameters. In an optional video, we discussed the details of a simple change that allows us to use a **mini-batch** of $B \\leq N$ data points to estimate the ascent direction. This simple approach is faster than regular gradient but less noisy than stochastic gradient that uses only 1 data point. Although we encorage you to watch the optional video on the topic to better understand why mini-batches help stochastic gradient, in this assignment, we will simply use this technique, since the approach is very simple and will improve your results.\n",
"\n",
"Given a mini-batch (or a set of data points) $\\mathbf{x}_{i}, \\mathbf{x}_{i+1} \\ldots \\mathbf{x}_{i+B}$, the gradient function for this mini-batch of data points is given by:\n",
"$$\n",
"\\color{red}{\\sum_{s = i}^{i+B}} \\frac{\\partial\\ell_{s}}{\\partial w_j} = \\color{red}{\\sum_{s = i}^{i + B}} h_j(\\mathbf{x}_s)\\left(\\mathbf{1}[y_s = +1] - P(y_s = +1 | \\mathbf{x}_s, \\mathbf{w})\\right)\n",
"$$\n",
"\n",
"\n",
"** Computing the gradient for a \"mini-batch\" of data points**\n",
"\n",
"Using NumPy, we access the points $\\mathbf{x}_i, \\mathbf{x}_{i+1} \\ldots \\mathbf{x}_{i+B}$ in the training data using `feature_matrix_train[i:i+B,:]`\n",
"and $y_i$ in the training data using `sentiment_train[i:i+B]`. \n",
"\n",
"We can compute $\\color{red}{\\sum_{s = i}^{i+B}} \\partial\\ell_{s}/\\partial w_j$ easily as follows:"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Gradient mini-batch data points: 1.0\n",
" --> Should print 1.0\n"
]
}
],
"source": [
"j = 1 # Feature number\n",
"i = 10 # Data point start\n",
"B = 10 # Mini-batch size\n",
"coefficients = np.zeros(194) # A point w at which we are computing the gradient.\n",
"\n",
"predictions = predict_probability(feature_matrix_train[i:i+B,:], coefficients)\n",
"indicator = (sentiment_train[i:i+B]==+1)\n",
"\n",
"errors = indicator - predictions \n",
"gradient_mini_batch = feature_derivative(errors, feature_matrix_train[i:i+B,j])\n",
"print \"Gradient mini-batch data points: %s\" % gradient_mini_batch\n",
"print \" --> Should print 1.0\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Quiz Question:** The code block above computed \n",
"$\\color{red}{\\sum_{s = i}^{i+B}}\\partial\\ell_{s}(\\mathbf{w})/{\\partial w_j}$ \n",
"for `j = 10`, `i = 10`, and `B = 10`. Is this a scalar or a 194-dimensional vector?\n",
"\n",
"\n",
"** Quiz Question:** For what value of `B` is the term\n",
"$\\color{red}{\\sum_{s = 1}^{B}}\\partial\\ell_{s}(\\mathbf{w})/\\partial w_j$\n",
"the same as the full gradient\n",
"$\\partial\\ell(\\mathbf{w})/{\\partial w_j}$?\n"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"47780\n"
]
}
],
"source": [
"print len(sentiment_train)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Averaging the gradient across a batch\n",
"\n",
"It is a common practice to normalize the gradient update rule by the batch size B:\n",
"\n",
"$$\n",
"\\frac{\\partial\\ell_{\\color{red}{A}}(\\mathbf{w})}{\\partial w_j} \\approx \\color{red}{\\frac{1}{B}} {\\sum_{s = i}^{i + B}} h_j(\\mathbf{x}_s)\\left(\\mathbf{1}[y_s = +1] - P(y_s = +1 | \\mathbf{x}_s, \\mathbf{w})\\right)\n",
"$$\n",
"In other words, we update the coefficients using the **average gradient over data points** (instead of using a summation). By using the average gradient, we ensure that the magnitude of the gradient is approximately the same for all batch sizes. This way, we can more easily compare various batch sizes of stochastic gradient ascent (including a batch size of **all the data points**), and study the effect of batch size on the algorithm as well as the choice of step size.\n",
"\n",
"\n",
"## Implementing stochastic gradient ascent\n",
"\n",
"Now we are ready to implement our own logistic regression with stochastic gradient ascent. Complete the following function to fit a logistic regression model using gradient ascent:"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from math import sqrt\n",
"def logistic_regression_SG(feature_matrix, sentiment, initial_coefficients, step_size, batch_size, max_iter):\n",
" log_likelihood_all = []\n",
" \n",
" # make sure it's a numpy array\n",
" coefficients = np.array(initial_coefficients)\n",
" # set seed=1 to produce consistent results\n",
" np.random.seed(seed=1)\n",
" # Shuffle the data before starting\n",
" permutation = np.random.permutation(len(feature_matrix))\n",
" feature_matrix = feature_matrix[permutation,:]\n",
" sentiment = sentiment[permutation]\n",
" \n",
" i = 0 # index of current batch\n",
" # Do a linear scan over data\n",
" for itr in xrange(max_iter):\n",
" # Predict P(y_i = +1|x_i,w) using your predict_probability() function\n",
" # Make sure to slice the i-th row of feature_matrix with [i:i+batch_size,:]\n",
" ### YOUR CODE HERE\n",
" predictions = predict_probability(feature_matrix[i:i+batch_size,:], coefficients)\n",
" \n",
" # Compute indicator value for (y_i = +1)\n",
" # Make sure to slice the i-th entry with [i:i+batch_size]\n",
" ### YOUR CODE HERE\n",
" indicator = (sentiment[i:i+batch_size]==+1)\n",
" \n",
" # Compute the errors as indicator - predictions\n",
" errors = indicator - predictions\n",
" for j in xrange(len(coefficients)): # loop over each coefficient\n",
" # Recall that feature_matrix[:,j] is the feature column associated with coefficients[j]\n",
" # Compute the derivative for coefficients[j] and save it to derivative.\n",
" # Make sure to slice the i-th row of feature_matrix with [i:i+batch_size,j]\n",
" ### YOUR CODE HERE\n",
" derivative = feature_derivative(errors, feature_matrix[i:i+batch_size,j])\n",
" \n",
" # compute the product of the step size, the derivative, and the **normalization constant** (1./batch_size)\n",
" ### YOUR CODE HERE\n",
" coefficients[j] += (1./batch_size)*(step_size * derivative)\n",
" \n",
" # Checking whether log likelihood is increasing\n",
" # Print the log likelihood over the *current batch*\n",
" lp = compute_avg_log_likelihood(feature_matrix[i:i+batch_size,:], sentiment[i:i+batch_size],\n",
" coefficients)\n",
" log_likelihood_all.append(lp)\n",
" if itr <= 15 or (itr <= 1000 and itr % 100 == 0) or (itr <= 10000 and itr % 1000 == 0) \\\n",
" or itr % 10000 == 0 or itr == max_iter-1:\n",
" data_size = len(feature_matrix)\n",
" print 'Iteration %*d: Average log likelihood (of data points in batch [%0*d:%0*d]) = %.8f' % \\\n",
" (int(np.ceil(np.log10(max_iter))), itr, \\\n",
" int(np.ceil(np.log10(data_size))), i, \\\n",
" int(np.ceil(np.log10(data_size))), i+batch_size, lp)\n",
" \n",
" # if we made a complete pass over data, shuffle and restart\n",
" i += batch_size\n",
" if i+batch_size > len(feature_matrix):\n",
" permutation = np.random.permutation(len(feature_matrix))\n",
" feature_matrix = feature_matrix[permutation,:]\n",
" sentiment = sentiment[permutation]\n",
" i = 0\n",
" \n",
" # We return the list of log likelihoods for plotting purposes.\n",
" return coefficients, log_likelihood_all"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Note**. In practice, the final set of coefficients is rarely used; it is better to use the average of the last K sets of coefficients instead, where K should be adjusted depending on how fast the log likelihood oscillates around the optimum."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Checkpoint\n",
"\n",
"\n",
"The following cell tests your stochastic gradient ascent function using a toy dataset consisting of two data points. If the test does not pass, make sure you are normalizing the gradient update rule correctly."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [0:2]) = -0.33774513\n",
"Iteration 1: Average log likelihood (of data points in batch [0:2]) = -0.23455309\n",
"-------------------------------------------------------------------------------------\n",
"Coefficients learned : [-0.09755757 0.68242552 -0.7799831 ]\n",
"Average log likelihood per-iteration : [-0.33774513108142956, -0.2345530939410341]\n",
"-------------------------------------------------------------------------------------\n",
"Test passed!\n"
]
}
],
"source": [
"sample_feature_matrix = np.array([[1.,2.,-1.], [1.,0.,1.]])\n",
"sample_sentiment = np.array([+1, -1])\n",
"\n",
"coefficients, log_likelihood = logistic_regression_SG(sample_feature_matrix, sample_sentiment, np.zeros(3),\n",
" step_size=1., batch_size=2, max_iter=2)\n",
"print '-------------------------------------------------------------------------------------'\n",
"print 'Coefficients learned :', coefficients\n",
"print 'Average log likelihood per-iteration :', log_likelihood\n",
"if np.allclose(coefficients, np.array([-0.09755757, 0.68242552, -0.7799831]), atol=1e-3)\\\n",
" and np.allclose(log_likelihood, np.array([-0.33774513108142956, -0.2345530939410341])):\n",
" # pass if elements match within 1e-3\n",
" print '-------------------------------------------------------------------------------------'\n",
" print 'Test passed!'\n",
"else:\n",
" print '-------------------------------------------------------------------------------------'\n",
" print 'Test failed'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Compare convergence behavior of stochastic gradient ascent\n",
"\n",
"For the remainder of the assignment, we will compare stochastic gradient ascent against batch gradient ascent. For this, we need a reference implementation of batch gradient ascent. But do we need to implement this from scratch?\n",
"\n",
"**Quiz Question:** For what value of batch size `B` above is the stochastic gradient ascent function **logistic_regression_SG** act as a standard gradient ascent algorithm?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Running gradient ascent using the stochastic gradient ascent implementation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Instead of implementing batch gradient ascent separately, we save time by re-using the stochastic gradient ascent function we just wrote — **to perform gradient ascent**, it suffices to set **`batch_size`** to the number of data points in the training data. Yes, we did answer above the quiz question for you, but that is an important point to remember in the future :)\n",
"\n",
"**Small Caveat**. The batch gradient ascent implementation here is slightly different than the one in the earlier assignments, as we now normalize the gradient update rule.\n",
"\n",
"We now **run stochastic gradient ascent** over the **feature_matrix_train** for 10 iterations using:\n",
"* `initial_coefficients = np.zeros(194)`\n",
"* `step_size = 5e-1`\n",
"* `batch_size = 1`\n",
"* `max_iter = 10`"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [00000:00001]) = -0.25192908\n",
"Iteration 1: Average log likelihood (of data points in batch [00001:00002]) = -0.00000001\n",
"Iteration 2: Average log likelihood (of data points in batch [00002:00003]) = -0.12692771\n",
"Iteration 3: Average log likelihood (of data points in batch [00003:00004]) = -0.02969101\n",
"Iteration 4: Average log likelihood (of data points in batch [00004:00005]) = -0.02668819\n",
"Iteration 5: Average log likelihood (of data points in batch [00005:00006]) = -0.04332901\n",
"Iteration 6: Average log likelihood (of data points in batch [00006:00007]) = -0.02368802\n",
"Iteration 7: Average log likelihood (of data points in batch [00007:00008]) = -0.12686897\n",
"Iteration 8: Average log likelihood (of data points in batch [00008:00009]) = -0.04468879\n",
"Iteration 9: Average log likelihood (of data points in batch [00009:00010]) = -0.00000124\n"
]
}
],
"source": [
"coefficients, log_likelihood = logistic_regression_SG(feature_matrix_train, sentiment_train,\n",
" initial_coefficients=np.zeros(194),\n",
" step_size=5e-1, batch_size=1, max_iter=10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question**. When you set `batch_size = 1`, as each iteration passes, how does the average log likelihood in the batch change?\n",
"* Increases\n",
"* Decreases\n",
"* Fluctuates "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now run **batch gradient ascent** over the **feature_matrix_train** for 200 iterations using:\n",
"* `initial_coefficients = np.zeros(194)`\n",
"* `step_size = 5e-1`\n",
"* `batch_size = len(feature_matrix_train)`\n",
"* `max_iter = 200`"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [00000:47780]) = -0.68308119\n",
"Iteration 1: Average log likelihood (of data points in batch [00000:47780]) = -0.67394599\n",
"Iteration 2: Average log likelihood (of data points in batch [00000:47780]) = -0.66555129\n",
"Iteration 3: Average log likelihood (of data points in batch [00000:47780]) = -0.65779626\n",
"Iteration 4: Average log likelihood (of data points in batch [00000:47780]) = -0.65060701\n",
"Iteration 5: Average log likelihood (of data points in batch [00000:47780]) = -0.64392241\n",
"Iteration 6: Average log likelihood (of data points in batch [00000:47780]) = -0.63769009\n",
"Iteration 7: Average log likelihood (of data points in batch [00000:47780]) = -0.63186462\n",
"Iteration 8: Average log likelihood (of data points in batch [00000:47780]) = -0.62640636\n",
"Iteration 9: Average log likelihood (of data points in batch [00000:47780]) = -0.62128063\n",
"Iteration 10: Average log likelihood (of data points in batch [00000:47780]) = -0.61645691\n",
"Iteration 11: Average log likelihood (of data points in batch [00000:47780]) = -0.61190832\n",
"Iteration 12: Average log likelihood (of data points in batch [00000:47780]) = -0.60761103\n",
"Iteration 13: Average log likelihood (of data points in batch [00000:47780]) = -0.60354390\n",
"Iteration 14: Average log likelihood (of data points in batch [00000:47780]) = -0.59968811\n",
"Iteration 15: Average log likelihood (of data points in batch [00000:47780]) = -0.59602682\n",
"Iteration 100: Average log likelihood (of data points in batch [00000:47780]) = -0.49520194\n",
"Iteration 199: Average log likelihood (of data points in batch [00000:47780]) = -0.47126953\n"
]
}
],
"source": [
"# YOUR CODE HERE\n",
"coefficients_batch, log_likelihood_batch = logistic_regression_SG(feature_matrix_train, sentiment_train,\n",
" initial_coefficients=np.zeros(194),\n",
" step_size=5e-1, \n",
" batch_size = len(feature_matrix_train), \n",
" max_iter=200)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question**. When you set `batch_size = len(train_data)`, as each iteration passes, how does the average log likelihood in the batch change?\n",
"* Increases \n",
"* Decreases\n",
"* Fluctuates "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Make \"passes\" over the dataset"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To make a fair comparison betweeen stochastic gradient ascent and batch gradient ascent, we measure the average log likelihood as a function of the number of passes (defined as follows):\n",
"$$\n",
"[\\text{# of passes}] = \\frac{[\\text{# of data points touched so far}]}{[\\text{size of dataset}]}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question** Suppose that we run stochastic gradient ascent with a batch size of 100. How many gradient updates are performed at the end of two passes over a dataset consisting of 50000 data points?"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1000.0"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# number of passes is number to complete the whole dataset\n",
"# For each batch size, we update 1 gradient, so\n",
"\n",
"2*(50000/100)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Log likelihood plots for stochastic gradient ascent"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With the terminology in mind, let us run stochastic gradient ascent for 10 passes. We will use\n",
"* `step_size=1e-1`\n",
"* `batch_size=100`\n",
"* `initial_coefficients` to all zeros."
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.68251093\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.67845294\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.68207160\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.67411325\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.67804438\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.67712546\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.66377074\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.67321231\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.66923613\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.67479446\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.66501639\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.65591964\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.66240398\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.66440641\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.65782757\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.64571479\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.60976663\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.54566060\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.48245740\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.46629313\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.47223389\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.52216798\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.52336683\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.46963453\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.47883783\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.46988191\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.46365531\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.36466901\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.51096892\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.54670667\n"
]
}
],
"source": [
"step_size = 1e-1\n",
"batch_size = 100\n",
"num_passes = 10\n",
"num_iterations = num_passes * int(len(feature_matrix_train)/batch_size)\n",
"\n",
"coefficients_sgd, log_likelihood_sgd = logistic_regression_SG(feature_matrix_train, sentiment_train,\n",
" initial_coefficients=np.zeros(194),\n",
" step_size=1e-1, batch_size=100, max_iter=num_iterations)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We provide you with a utility function to plot the average log likelihood as a function of the number of passes."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"\n",
"def make_plot(log_likelihood_all, len_data, batch_size, smoothing_window=1, label=''):\n",
" plt.rcParams.update({'figure.figsize': (9,5)})\n",
" log_likelihood_all_ma = np.convolve(np.array(log_likelihood_all), \\\n",
" np.ones((smoothing_window,))/smoothing_window, mode='valid')\n",
" plt.plot(np.array(range(smoothing_window-1, len(log_likelihood_all)))*float(batch_size)/len_data,\n",
" log_likelihood_all_ma, linewidth=4.0, label=label)\n",
" plt.rcParams.update({'font.size': 16})\n",
" plt.tight_layout()\n",
" plt.xlabel('# of passes over data')\n",
" plt.ylabel('Average log likelihood per data point')\n",
" plt.legend(loc='lower right', prop={'size':14})"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAocAAAFmCAYAAAAf5DBYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYFFXWwOHfAQQRdM2oqATDuiCKYU2rMipmXVeMKKKi\na/gQsygogomgggFzQl1F14BZWSMGTKsIggEUkAVMCIgISJrz/XG7mZ6eDtXdlbrnvM/Tz/R0Vd06\nnapO37pBVBVjjDHGGGMAGkQdgDHGGGOMiQ9LDo0xxhhjzCqWHBpjjDHGmFUsOTTGGGOMMatYcmiM\nMcYYY1ax5NAYY4wxxqxSNsmhOH1EZLqILBGR8SLSxeO2g0RkgojMF5HFIvKViPQTkaYZ1t1TRMYm\n1vtBRIaKyOr+PyNjjDHGmPhpFHUABbgWuBDoC4wDjgeeFJFDVXV0nm3XBB4AJgNLgT2AK4AdgSOT\nK4nIdsCrwCvAoUAb4EZgE6Crn0/GGGOMMSaOpBwGwRaRDYCZwEBVvTrl8deB9VW1YxFlDgQuBTZQ\n1XmJx54B2gHtVHVl4rGTgAeBnVR1fKnPxRhjjDEmzsrlsvJBwGrAo2mPPwJ0EJFWRZQ5L/F3BYCI\nNAIOBP6dTAwTngCWA0cUsQ9jjDHGmLJSLslhO2Cpqk5Ne/wLQBLL8xKRhiLSTEQ6AxcA96vqb4nF\nWwCrJ8pcRVWXAlO97sMYY4wxppyVS5vDdYFfMzw+L2V5TiLSHpiY8tBDwJlp+wCYn2U/efdhjDHG\nGFPuIqk5FJH9RKTaw+1NH3f7LbAz0AnoA3QB/uVj+cYYY4wxZS+qmsOxwDYe1luc+DsfWDvD8mRt\n3rwMy2pJXB4el/j3XRH5ERghIreq6sfU1Biuk2U/kzzEa4wxxhhT1jwlhyKyNzBOVX/PsKw5sKOq\nvuN1p6r6BzDFc5SuHWATEWmrqtNSHm8PKPBlAWUlfZL4uyXwMa5d4dJEmauISBOgLa5jSh0iEv/u\n3sYYY4ypV1RVit3W62Xlt8jeIePPieVBGo3rVXxi2uPdgEmqOqOIMqtwieVUAFVdntjPsSKS+roc\nAzQGns9WkKrarcxu/fv3jzwGu9n7Vl9u9r6V583et/K9lcrrZeVc2WcTYGWO5SVT1TkiMgzoIyK/\nUzMIdhVweOq6IvIGsLmqbpX4vwNuIOsngWmJeDsB5wIvq+pHKZsPAD7ADa59O24Q7OuBJ1X1s8Ce\noDHGGGNMTGRNDkWkNe5yatLOiUvIqZoCPYD/+R5ZXX2BhbikbiPcbCfHqOoraes1oHaN6E/AHFwn\nlI1w7Rin4WZbuT91Q1WdICIHAEOAF4EFuAGwL/f5uRhjjDHGxFKumsOTgf64S68KDKd2DaIm/l8B\n9AwqwFU7c/WkAxO3XOvtk/b/z7jLz1738x7wt2JiNOWjqqoq6hBMEex9K0/2vpUne9/qr6zT5yVm\nHWmNSwDfxCWA6R0/lgJTNDH9XH0kIurH9X1jjDHGGD+ICFpChxRPcyuLSCdcb+WFxe6oUllyaIwx\nxpg4CSU5NNlZcmiMMcaYOCk1OfQ0lI2INBaR/iLytYgsFpGVabcVxQZgjDHGGGPiw+tQNjfg2hy+\nAozCtTU0xhhjjDEVxmubw9nAHap6XfAhlRe7rGyMMaYS/PorXHQRfPcdXHIJHHRQaeV98IErp2lT\nGD4ctvEyaa7Pli1z+54/H849FzbcMPwYohBWh5QFwJGq+maxO6pUlhwaY4ypBBdcADff7O43aQJz\n5sCaaxZXliq0besSTYB994U33vAlzIKcfTbcdZe7v912MGFC+DFEIazk8BHgW1UdUOyOKpUlh8YY\nYyqBpKUSw4fDOecUV9b06S45TBXFqTL9OX3xBbTLNhlwBSk1OfTa5nA48LCIVAMvA3XGNVTVacUG\nYYyp36ZOhX79XG3FwIGw8cZRR2SMWbKk+G2rq/2Lw08LFkQdQXnwmhx+kPg7ADdrSiYNS47GGFMv\ndekCn3/u7n//PfznP9HGY0zUVKFvX7j3XujYER59FFq0iDqq3L78Ej7+GPbZp26NnSkvXpPDHrjp\n8owxxldz5tQkhgCvvhpdLKZ+WLkSbrwR3n8fjj8eunaNOqK6xo+HwYPd/TfecJd4r7023BgKuQw8\nbhzssQcsXQp/+hO88EJwcZngeUoOVfXBgOMwxtRTy5dHHYGpbx5/HC67zN1//nlo3951VoiTq6+u\n/f9114WfHBaiZ0+XGIK7dHvNNdHGk43VaHrjaRBsY4wxplJ061b7/4suCm5fs2e7W6X78MPa/7/2\nWjRxGH9krTkUkQeAa1R1euJ+Lqqqp/kbmjHGGBO8H38Mptybb4YLL3S1Vbfe6mrXjCkHuS4r7wPc\nkri/L7nbHFp7RGOMMWUpiCFWqqvduIHJ8s85x5JDUz6yJoeq2iblfutQojHGGGMqQH1vSysSzbiG\nxh/W5tAYEyk7gdQvP/0E118PTzxh733cXXop3HFHcdvGtePHqFFRR1AevA5lg4isgRvSphOwLm4g\n7LeAEapawlCZxhhj6oMVK+Cvf4WZM93/P/wA550XbUxBiWtyVKiePeGQQ6B166gj8ccNN8ARR8Df\n/hZ1JPHmqeZQRDYCxgG3AjsDayT+3gaME5GYD81pjDFm7Fg46SQYNMglamEbNaomMQQ4/3zYYQc3\n7+6UKbm3XbLE1WKNGOHGKYy7SkkOwdX0FirOz//MM6OOIP681hxeD6wD7KWqY5MPisgewNPAEOAU\n36MzxpgK8NtvLiFbssSNr7fRRuHHMG+em7ki2RZutdXg4ovDjWH69LqPjR/v/l58sRtzMJujjoJX\nXnH3P/oI7rrL//iCpuo9aYrTJfdi2k/6kRz+8gtMnOjGoFxvvZrHx46FO++Ev/wFevd2n+VCfPVV\n6bFVOq/J4cHApamJIYCqvi8iVwCDfY/MGFMvxOkkGJTTToOnnnL3x46F//43/BhuuaX2Sf6SS8JP\nDnPJNaPG3Lk1iSHA3XeXZ3JYropJ9EpNDmfMgF13dW1UN9nETcvXsmXdHzmNG7vPcpix1QdeO6Q0\nB77PsmxWYrkxxpgMkokhwCefBDeuXi5R7NMvv//uX1nffFP3seQPlCVLoF8/+Oc/YfJk//aZvh8v\n6nsC07+/SwzBzbeenB0m/UdO797hx1YfeE0OJwMnZVnWDfjan3CMMabyJacZC1N9TzaSkpexM7n0\nUpeE3HcfVFX537axPtSS++Whh2r//0BiKo6ffw4/lvrI62XlG4GHEx1PRgI/ABsBxwOdyZ44GmOM\nMbGweDGcemr25cOH19z/8Uc3BdxBB/m3/0KSw7gmktXV8Nxz0KABHH64+5tJnH+MFBvbb7/B0KHu\nNbj4YvjTn/yNK0481Ryq6iPAWcC2wH3AS8D9wHbAWao6MrAIE8TpIyLTRWSJiIwXkS4etx0kIhNE\nZL6ILBaRr0Skn4g0TVuvv4hUZ7jZyEjGmLyqq93NxNPjj8OiRd7XX7Ag+7KFC10nmXXWgZNPrlsb\nXGxyN368a1M5bVpx2wftzDOhSxf4xz+gV6/w9huHZPmEE+Dqq13t8rHHRh1NsDwPgq2q9wCbAO2B\nvRJ/W6rqvQHFlu5a4ErccDoHAR8AT4qIl991awIPAF2BQ4FHgL64WtB0CuwB7JZys1YNxgQkDgd9\nPzz3HKy9NjRvDo8+GnU0lcWvWqjTTsv8eLbPYPrjy5e7KfFEYK213NA8v/4KDz+cu0NNvv0kffQR\n7LILnHWW66UbNytWuEvuSbkGyI5zzWEmkya5ZgWPPpr9fXrppZr7r74azXBQYfE8CDaAqlYDoXcC\nF5ENgIuAgap6U+Lht0VkK1xP6dG5tlfVc9IeektEmgGXisi6qjovbfnHiedqjImp6mp4+WVo1AgO\nPDD6k1H37q42CaBbNzj+eGjYMNqYUkX9+gC8/np0+541q/QyTj01e+J/5plw9NG5t8+XHJ55Zjyn\n3Ut+dgppg5np81bIUD5eystn6lRv682f75LyJYnpPJYvh1NOqbk/eza0yDCac6X8sM3Ec82hiGwl\nIg+JyBQRWZT4+6CIbBlkgAkHAasB6V/LR4AOItKqiDKTCWGm3D8Gh1FTDFX3a66Sv7TGOeMM1+bp\n4IPjMSTLb7/l/j9VFJ/PqJND1eKTQz9er1yJQrbXJv3xUmuE8z2PCRNyLx8xorT9R62U97GYba+6\nytt6w4bVJIZQ0y71t9/cTCpt2kDHjoXvv5x5nSGlCpgAHAZ8CNyR+Hs4MFFEOgUVYEI7YKmqpn+9\nv8Alcu28FCIiDUWkmYh0Bi4A7lfVTIfwmSKyQkS+E5HBIrJ6SdGbUCxd6trCrLYa7L57dL3aqqvh\nkUfcJZdC2jcVa/JkV4O2eHHw+wpCMQf9pUvh/vtr/h82zL94/GI/UGqbPz/qCLLzelk5qP141aOH\nP3GEIdNzDfs78a9/ZX48Pen/9tvM6913X82YpPlm8Kk0XmsOhwKfAa1UtbuqXqKq3YHWwPjE8iCt\nC/ya4fF5KctzEpH2wHJgIfBq4pY+ic63wGVAd+BA4N+4JPK5oqI2oRo1Cp591t3/6CO49dZo4rj0\nUjdFWc+ecOihwe7r1Vfd7AGHHuoGjI1jG5jly10D7uOOg7fe8qfMJWU+m3vUtXhJl18Of/wRdRT5\n+fF6hf2aV+KPg0wJfq9ebq7idHFIDrNJv3Sf7bMxNOjMJsa8JoftgCGqWmsoUlVdiJs6r30hOxWR\n/bL0Ck6/vVlIuXl8i5sPuhPQB+gC1PpdoaqPquoNqvq6qr6hqpcClwCdRWQfH2MxARgwoPb/110X\nSRjceGPN/bffDrbX4YknwrJl7v6kSfDEE8Htq1jDh7uBhZ94AvbfH+bMKb3MuJxkcskVYxTJbaYT\n4MCBdb83Ye6/nPgx5mE5fG5zueyyuo/ddlvuaQ9TlfL8ly93s6b4JbVjTTbl/pkthdfkcBbQOMuy\nxsDsAvc7FtjGw617Yv35wNoZyknWGKZ3KKlDVZeq6jhVfVdVhwDnAl1FZJc8mz6Gu3Sdbz1jMvrl\nl/DKfvfd4PZVrIsuqrm/ciXccEP+bS64ILh44iBZwx0HQ4ZEHUF8LV/uxjtcvhxG5+z26C2RiHNy\n+Guma3Np0gemLlSpz3/77f3pWARuFpwgfP01vPOO/wOoh81rb+UhwFUi8r6qrppGT0RaAv2BgYXs\nVFX/AAq5gv8F0ERE2qpqaj1Me9zQM18Wsv+ET3BJ35bAx0Vsv8qAlJ/eVVVVVFVVlVKcKVKcD7ym\nhpe2oDffDGPGuNrQvfeGJ5+EdVMaj5TDe50rxj59MtfCBCnqWpBsgyXHQbb3qnuiemKHHeCzz3KX\nMXdu8fspRnW1a8IycqRrUvLAA24opXwee8y1UT7gANerXsSVc/312bfx67NT6vNfsABefNGfWLwo\n9Hn/+9/uas7KlXDYYd6GN/LLmDFjGDNmjG/leU0OOwFrAdNE5EPgJ6AFbgzAn4CqRKcVAFXVk32L\n0BmN61V8InBNyuPdgEmqWkxlcxUusczX2b1bYr2Psq0wIKzrMqYslUMik+rDD92QHHPmuFq+c8/1\nt/z01yPb65Oc5uzNN+Gee8JPpoy/ok5OS9l/vsQwKd9QLcuWQbNmxceR6oMPapqwPPMM7LVX/hr3\nd991AzmD6zTXsiVssUXuxNBPcT0WZnrPVqzIX0t5++2w1VY1bcuPP75m2Ysvus/NDjv4F2cu6RVT\nV3ntqp2F199ye+KSsx+AVrhLrK0S/1fjBsVOvflKVecAw4A+InKBiHQSkTtxCV6tU4aIvCEi36T8\n30FE/iMip4vIviJysIgMBm4AXlbVj1LW/UREeonIgSJykIgMw9WavqKqY/x+XqZ+eeUVaNXKDYvw\npp+taX3Wq5cb12vZMjjvPG+Xm4LWp0/UERQurifCSlRd7WrOrr4afvgh8zq52qv5lbimNuvI9P6n\nTs9XqtTmGgAXXph/mzPTumD26AH9+/sXUz5hfScmTIB9PPQSyBXPfvvl3/6CC1wN4Z13Zl7u9UdF\nHHmdPq9NAbe2AcXaFzdLyrm4msTdgWNU9ZW09RpQ+3n9BMzBdUJ5AXgY2Ae4ENcpJdWURPlPA6OA\nA4ABwJE+Pg8TQxMnuvY0s3O0nl2ypO4UWV6outsZZ8D//gfffQdnn110qIH75JPa/48dG00cuWQ6\nqPfq5U4IceyUEwdB1dypumE+8nU0CrLmcOBAN/tJ//5uGKtMUxheeWX27f1KWublaf2enojddpub\nn3ebbfKPcZiumJi/+ab2/zNmeGtHWMx7F2Vv5R49XLOUfHLF88473vf3f/8X3NBpy5e7HwItWrj9\nJDsgBq2gGVKipKqKa9uYs32jqu6T9v/PuEvDXvZxQtEBmrL1/vtQVeW+hOutB199BRtsUHudO+5w\ntWhNm7qBcA8/3Hv5qm4MwtRLFPVtzKxUfpwgMpVx223u75gxbuDali2LL3/yZFcDteeebgYWk91J\nJ7nvRPPm7vJm587hx9CvX839GTNcm7rDDqu9zvTpwceR/Fy+/TZ8nKcl+7x5NXMT//Yb9PY4SeuW\nW7rPZdzHNQ0zOXzhBdcc5qijYMcdYdy4wrb344fLJpuUXkYmL71UM47rnXfC+uu7GvKgxbiJsDHh\n+Oc/a8a9mju3bu/NP/5wYxauWOGmR+vm6aeG/1audEnLggXR7D9O8p1kBg8uvuynnoJtt3W1kKWM\nUxm3y8pB1Nx9/nnNrCG//17TgSNqua4ABEnVDetSVZU92bv4YndMeSXtmterr3rbx9SprrZv0qTc\n640Z42qbmjb1NmxLOfv7313t8W67wcyZ3rfz8zsaVO/kI9OuW15zjRul4uij4ZhjgqtJtOTQ1Htf\npvV1Tx+oOf1gk2tatKAsXw777usuP22zTfYTQ9SN/r3w2iGlFKW0kzzmmJrBxF991Q2onm7ECHfi\n7dDBJUiZxC05DMLbb9f+P1t7P/D2emRbJ9Pn+oADXE/2TDV0mS4rh0EVjj029zpDh8K99wYfy5ln\nukudf/zhfgAvWRL98SHT+/vf/7r2oj//7O63aQNrrllc+cuXF9aGsly/oxtsAE8/7X7INmkSzD4s\nOTQmTfoBI8hxCvPFMXy4m1nk+ONr2sD8+CMcckjmnnSFHOyqq12SM2RI/rZSfgrqsnIqP5ODTz+t\n/f+iRa796M8/uyTdr17UH37oks2tt4b//MefMqP000+ujdRZZ7nPrBdffOG9/Ndecx1ATjyx7rIo\nk0Mv7ZL9HgEgdf9J6U1Xvv66+O9eMUllptmaUvf/+OOu3F12ce1Ft98eTj/dtcn+/fe623o1cWLh\n24SVNE+f7nqZe6ll/Pln788liCYTlhwak0ep8/YWe0B+8kl3EnniCTc1YKqZM90QFKW48krXcPuy\ny1wNTDn9is4Xa/Lg+/TTboiP004r/nL8l1/CFVe4X+kAr79e+8SXfnmwWOee65LNb75xyWfyOS5e\n7OZ+LaYzVCo/x6p7/32XzObStatrI3X33flr05LSRwVbscJ1kMpVI5lpXtyoPsuF7DeIGHP1ji1l\npia/Yk3+UFi50rVVTfXjj9lr4QtRyA+DMD8nzz/vrvrssYdrs758uWvGlClRHDvWDZGz3Xbeyg6i\nV7Q1tTYVI6gvelC90PI57rjcyzO1NSkkAUidXvCLL9zl09128759nFVXu96zxx7r7r/3Hmy0UXFT\nKt5+e839Rx/1Pk5doZ/H//635v7//udq3qqrXdvHZC3Qv/7lnlPjbPNV+eyHH1xtzjffuB6T3bvD\nGmvULM816HJq84x33/U273fqib262nVuSb907UVUNYeFCOKEft552WdJOu+84sv1a9q6kSPdFY+n\nngpuHvioE/Rs5R97bM0x+5VXar7DnTq5MRGbN69Z9/TTC2u+FMRraTWHxqTx+4AxdGhwB0I/Zbv0\n5/fr4UebQy81h8OH104SBhY0j1NmmS5hBkXEdaxJvTx40kmujVHv3uH0Vh0yxPX8/eYbN/zSIYfU\nXh7kGJijRxeXGIJ7/wvpIODXZ7yQckq9IpFJrkGbZ88uvvY42WHPD0FPLVdI0p18v8K4rJyt5v/t\nt+Hhh2s/9vXXhZUdRPyek0MROUNEPhORxSKyMv3mf2jGVIZRo6Bv36ijiI8w2hyOGlX4cBZBqK4u\nfi7YZJvTTG64AS6/vLDyijmB3HJL7Xh8nJ0rp/nzYdCg4re/8EI3BNFZZ3n7vE2e7G36u3yirrH8\n44/cy4tN8sqpyUk56tnTNVeJE0/JoYh0B4YD/wVWB0YAjwC/4aafC2HUHWOi4ceB8Y47Si8jKlH3\ncCzWSy9Fu//ly+Hgg2GzzTIvTx+QuFA331zY+uXyPk6ZAu3auaYApbr77sy9zTPx2r4rzvIlh8Wq\n1OQwTs/rqKNKb1fsJ681h+cDg4DkvA53JOZPbgssAXz4zWWMiZJqNJe/vR6gt9gCWrd2v7JHjgw0\nJF88+2zuseuuuSb7sij9+KPrTFLKYNbFDoCs6jpIee3d7MXdd3tb7/vvS99X1MlG1Pv3Ki4/VIK+\nrFzI+/Hbb8X/oM03O1ExvCaHWwHv4OZRrgYaA6jqfOA6oISmrsbEW1wOZF7ceSestZYbqLtbNze+\n2U8/ed/e64m0FMWewKZNcw3j77jDDSQcd/kGHo5TLUGqiy92w4y88Ya/5Xp93595xt/9Pvigv+Xl\n4keCaeqvYo8JPXu6Tmx+8tpbeQnQSFVVRH7E1RgmBzL4HQho4hhjvCuXX81BW7iwZtYKcCcsr79I\nzzknmJhSJd+nZ55xNYDrrx/8PqPQIM9P73yf16g+z6mfnWJFOa9ulMrhR0scxOWzEHQchVYslNJm\n9fLLXVvkDTfMf+zxwmtyOBHYGngVeBfoKyLTgRXAAKDAvjWm0s2e7eZ/bNTIjV2WPldxnJXSm/bZ\nZ4vb5+efwyOPQMeO7pKen7WVL7/sbb0wD9iTJ0OXLuHtz0+PP+5tvfHjcy8P+wSZ6zNVXe3PCSWu\n4pKMlKugRyyIStCXlf/4w11B8Fp+KcnhI4+42wEHuKFxSuU1ObwHSA652w94HUg2F14I/KP0UEwl\n6dKlZlqrqVPdsBRBC+oLXsgXu0ePwsufOxd23bWmMXmmAWL9VuwQIX4p597bXpPDfJ56ys2+stNO\n/pRXij32yD+odSHiVnMYl2QkaAsWwPnnlza3eH0S9Oei0CsxfsTz6qt1J00ohqfkUFX/nXL/WxFp\nD+wOrAG8r6oRTTBm4mjhwtrznYY1FVhUJ4ClS111/qefuiE4CnXDDbV7GXbvDoce6l986SZNcgMr\ne+X1dZ040bVTq6pyU2B99JGbHD5TedY2y9l5Z/datWpVd1kpnYOmTIF+/WD11d2QMJvkafjz0Udu\n1p1sPav9YMlhOG65Bf7yF3/L9Pv1i0s77g4d3I/xMKcPzcWvoZDuuqv0MjwlhyKyNzBOVX8HUNVF\nuNpDRKSZiOytqu+UHo6pBH4OmBoH+Q6MV1wBN95YfPmZhjTp06f48vK56KLCanYOP9ydbJ54Arbd\nNvM6X33lEp30WVuGDvW+n/qqX7+6g+BC7RlTvFKFSy91PziSfv7ZzciQ74T8ySf+JYfFvsdBfTbq\n22furLOijiC3uLwf330XdQS1+ZUc+vH6em1l8hbQLsuybRLLjYmdxx+vOwG930pJDCHzSfuee0or\nM5cJEwrf5quvcl8KvuCCzNP5VdoPhSBkm0/2hRcKL2v8+NqJIdQ06Yi6tsZqDstX1IN71xe33158\nu3W/eU0Ocx1WmgA2Q4qJpa5dXSePQmbLSD+RBD0GVlgn7eQ4hsXuL1eyUkjTATtR15btxOtlCJb0\n1/L660sOxxfW5rCyBD3lnXHGjYMjjyy9HD8+71kvK4tIa9yQNUk7i0jztNWaAj0An0fYMeUsbgfi\nJUugVy8YO9b/ssvlgLl4sZv4PdeQNsW+b0HXzJaDUtosTZtW/KDe77wDnTq5+3/8AT/8UHwcQf9I\nseSwvDXy2n3VA3s/4i/X230y0B/QxG04tWsQNfH/CqBnUAGaeFq+HEaMcLUep54KTZpEHVFu778P\nTz/tTsK77ura3TVs6G3bbAeyX37xp+NIGDWHTzwR3HRyxbSPnDjR/zii1LOEI+CiRXDiicVte/rp\nrs3q1KluCItp04qPw88T9ief1H3MSweb557zL4ZUlozES6V9/ytRruTwQWAMLgF8E5cAfpm2zlJg\niqrGpK+PCUuPHm5MJXAThj/1VM2yqA7E+fab7Dk7ahS0aAEnn1za/m6/vXav7EKpusQwjOTQrw4u\n998PxxzjZmFJ+vbbwspQdQlRJfFreJtCJZPBK6/MnxiG2eawV6+6j/3zn+HtP92770a3b1PXQQdF\nHYHJJ2tyqKozgBkAIrIP8Gmyt7IxycQQXI3csmXQuHF08RTqlFO8J4fZTqoDBvgVTfC8zmubz+mn\nw003uU4UDRrAe+9l71BRyn5MYbxcls6XHH78cWmXpVNl+sGQa57poHXtGt2+jQlboG0Oa+9IIx4y\n18TdggXu1/lWW8HGG0cTQxwmTy9G1L1IC/XFF+5E37lzcY2nLTn0VyFzZ+fi58DJcXuP586NOgJj\nyovnCZNE5AAReUZEvhSRaWm3qUEGaeJvl13gqKNgxx29T9dWjFmzXO3VWWfVPSn6dUIK68QWdm9l\nP02e7H4M/FJmw98vXOj+fvml68W+4YbBDhsUtOpq2GijqKOo7Ztv4Lffoo7CGFMKT8mhiBwCvIKb\nEWUb3FzK/wM2A6oBGwC7nksOJrpiRelt+XI5+mjX7u3uu4ObYu5/IfW9j1vtSqHxZBrXMO6SMwdc\nfrkb73HOHPdDY8GCaOMKQ1g/Qtq3D2c/xpjMwhwEux9wO3BI4v8rVLUKaA80xCWOgRKnj4hMF5El\nIjJeRLoUUU4bEVksItUi0jbD8j1FZGxinR9EZKiIrO7Ps4i/GTPc9EtRz70L7gM+eDBsv707gc+Z\n46b5SnrttWD2u2BB6QNbe3H//e5vGCdtLweLoF7PdFEmxb17u7+pA82q+jNRvXFs4HNjyp/X5HAb\n4AVcLaF3UbdbAAAgAElEQVSSaKuoqlOAAbjkMWjXAlcCtwIHAR8AT4pIof2e7gTm455HLSKyHfAq\n8CNwKHA5cCowoviwy8evv7pLbeef7+bHjfqE+eabrpft55+7msIHHghv35dcUjOGYVDJW3KKqzCS\nw59/zr/OffcFHwdEPwPACSdEu/+olGPzBWNMNLwmh9XASlVVYA6wecqy74Et/A4slYhsAFwEDFLV\nm1T1bVU9Gzdtn+dm1CJyArA9MCTLKlcBM4FjVfUtVX0AOA84VkQ6lvQkysCwYS5BTDruuOhimTHD\ndXhIddllmde9+243NE0pY7xlkhyXLW6Xf01pHnss+7IZM8KLwxhj4sprcjiZmgTwE+B8Edk4JWn7\nLoDYUh0ErAY8mvb4I0AHEWmVrwARWRsYiou3TgsjEWkEHAj8W1VT5714AlgOHFFc6OXj009r/794\nceb1wkiWrr7a23q//gpnn+2tZiyOTjjBzeBiovfYY9C6ddRRBGPePJg5M+oojDFhCG0oG1xStnXi\nfn/gdWBW4v+VQNAXatoBS1U1vVf0F7hButuRGJMxhxuAL1V1pIhk6jKxBbB6osxVVHVpojd2u6Ii\nr0BhJIdeLyE/80x5DzWTqxYr7irpMmW3blFHEKzNN6+8gceNMcHxOs7h7Sn3PxWRDrjavDWA11U1\nfeYUv60L/Jrh8Xkpy7MSkb2AbkCuS8PJMuZn2U/OfVSCSjrZG2NqWGJojCmE53EOU6nqLFW9T1Vv\nLSYxFJH9Er2F893eLCa+tH2tBtwFDFPVyaWWZ6wNnoFLL406AmOMMZmEeVnZb2NxPaDzSbZ6mw+s\nnWF5sjYv19zOFyS2HS4if0o81izxdy0RaZ6YFjBZY7hOlv1M8hBvvRCn5HDChOD3EafnGxdLl9qQ\nJcYYU6myJocikhy2xhNVbVjAun8AU7yuj2sH2ERE2qpqap/U9rgYc9Ve/gXYCNerOt04YDywIzAV\nWJoocxURaQK0xXVMyWhAyiS7VVVVVFVV5QgnvrxeVo5TsnTLLVFHUH+V4yDYxhhTmcYkbv5M5JCr\n5vBqapJDAXoATXHjHf6ES7gOA5YA95ceSk6jgRXAicA1KY93Ayapaq7OKIOoO07hwUDvRHlTAFR1\nuYiMxg1bM0BVqxPrHgM0Bp7PtoPU5NBUHmuLmZm9LsYYExdViRtsthnMmnVVSaVlTQ5VdUDyvohc\ngesNfKCqLk55vBnwH1ziFhhVnSMiw4A+IvI7rsbveNwrcXjquiLyBrC5qm6V2HYKabWUItImcffj\ntJrIAdQMrn070Aa4HnhSVT/z+3mVqzjVHIahvj1fY4wx9ZvXNodnAj1TE0MAVV0kIjcCw4Hr/A4u\nTV9gIXAurtZyMnCMqqZP3deA4jvaTBCRA3CDZL+IGw/xQdxMKSbB72RpzhwYMQI23RS6do1PjZQl\nhcYYY+ojr8nh+rhLq5k0BtbzJ5zsErOzDEzccq23j4eyHgIeyrLsPeBvxcRY7qJoc1hdDbvtVjO7\nyaxZNfPfxkWm1+Xww+s+Vt989VXUERhjjEm3cmX+dfIR9XCmF5F3cT1291fV71Mebwm8BsxR1U6l\nh1N+RES9vIbl4O9/hxdeqP1Ypqf2xx/QtGlhZWd7iV56CQ47rO66YdQeJmPKtq/Fi93z3HtvePfd\n4OMxxhhj/CGoatFnUq81h+cCbwLTRORDXIeUFsBuuOFm6ulU9vWTn7mwzWVrjDHGxIuntnmJzhhb\n4uYmXgl0SPy9EdhKVccHFqEJTVyGsvGjStwYY4wxxfE8CLaqzsU6ZhifZUo0N9oo/Dgyue8+6Nkz\n6iiMMcaYcBXVq9fUb0HXHP7yS7Dle3XuudCwobU3NMYYU79YcmgKVkxy+MMPcMklcN11rkOLMcYY\nY+IpqrmVTQwF2eawc2f4MjHJ4ZAhMG8eNGoE33xTeFnGGGOMCY7VHJpQfJky+/XChdC9u7sf9dzI\nP/0U7f6NMcaYuPGUHIrIn0SkSdDBmPh5++26j/nR5vCxx2DRotLLKcXChdC+fbQxGGOMMXGTNzkU\nkUbAXOCA4MMxUcp0Wbmqqu5YhH51SIm67eFaa8HcudHGYIwxxsRN3uRQVVfgBr220efqqR49av/v\nV3K4557+lGOMMcYY/3htc/gIcHqQgZj4evPNYMr9+utgyjXGGGNM8bz2Vv4OOEFE/gs8B/wA1Ko/\nUtUH/A3NhO2rr7ytVyFTSRtjjDEmA1EPZ3oRqc6ziqpqQ39CKi8iol5ew7hShWuvhSuvzL9e0rx5\nsN56wcZljDHGmGIJqupxgLq6vNYctil2Bybe/vlPuP/+qKMwxhhjTFx4qjk02ZVzzeF330Ebj2l/\n6lOcOxfWXz+QkIwxxhhTsnBqDt2uRLYD9gbWA+5W1R9FZEvgJ1VdWGwQJhoTJhS3XZnmwsYYY4zx\nwFNymBgA+xGgCyC4zigvAD8C1wNTgMsCitEExOt0eUkrV7pawxUrgonHGGOMMdHzOpTNdUBn4CSg\nBS5BTHoFONDnuEzMLFoE++4LLVpAy5ZRR2OMMcaYoHi9rNwVuEJVR4pIeq/k6UBrX6MyoSik5vDh\nh+Gdd4KLxRhjjDHx4LXmcD0g2yh4DQCbd7nCDRoUdQTGGGOMCYPX5HA6sHuWZbsAk/0Jx4SpkJpD\n64RijDHG1A9ek8OHgctE5ERgtcRjKiL7ABcANjuKMcYYY0wF8JocXg+8BPwLmJ947D3gdWC0qg4P\nIDYTsEJ7KxtjjDGm8nlKDlV1paoeD3QChgH3AbcC+6rqiQHGZ0o0eTJUVUGHDvDSS8WXY5eVjTHG\nmPrBa80hAKr6rqperqpnqGofVX07qMDSidNHRKaLyBIRGS8iXYoop42ILBaRahFpm7asf+Lx9Nso\n/55JuC65BN5+GyZNgpNOguXLa5Z9la2LkTHGGGPqrYKmz0u0MdwdaAnMBt5X1THBhFZn39cBFwJ9\ngXHA8cAZwKGqOrqAckYDHYCNgK1UdVrKsv7AlcDfgOqUzeap6rdZyov19Hnpl45PPRWGD4fGjd3N\nGGOMMZUmhOnzRGRd4ElgH1zSNB9Yxy2St4BjVXVesUF42P8GwEXAQFW9KfHw2yKyFTAY8JQcisgJ\nwPbAIOCmHKt+rKrVOZbHwsSJLvnbdlvv24wYAZ99Bv36BReXMcYYY8qX18vKtwJ/BboBTVV1A6Ap\n0D3x+C3BhLfKQbhe0o+mPf4I0EFEWuUrQETWBobikswF+VYvJsgwDRgA223n2hIOHFjYtuPHw6iy\nvVBujDHGmCB5TQ4PB/qo6khVXQ6gqstV9VHgCuDvQQWY0A5YqqpT0x7/ApfItfNQxg3Al6o60sO6\nM0VkhYh8JyKDRWT1AuMN1MqVcNVVNf9ffnnhZUy2kSmNMcYYk4HX6fNWAt9kWTY5sTxI6wK/Znh8\nXsryrERkL1ytZ8c8+/kWuAz4DFDgANw4jjsQo/mjV6zIvfzrr+H002Hu3OzrxLiZpDHGGGMi5DU5\nfA44Dng1w7LjgWcL2amI7Ae85mHVMaq6byFlZ9jXasBdwDBVzVlflqgJTfWGiMwGbhKRfVT1rVJi\nCUvv3jB2bO51LDk0xhhjTCZek8MXcAnSS7iOKT8BLYBjgfbAeSKyKolT1TfzlDcW2MbDfhcn/s4H\n1s6wPFljmKszzAWJbYeLyJ8SjzVL/F1LRJqr6u85tn8MuBk3TWDG5HDAgAGr7ldVVVFVVZWjuNLl\nG7z6hRfyl2HJoTHGGFMpxiRu/vA0lI2I5Ou5myxEAFXVhqUGlrb/k4AHqTv0zCnA/UBbVZ2RZdsR\nuI4z2VKq8aq6Y459b4BLhvuo6pAMy0MfymbZMmjSpPZjqSF4mflkhx1cr2VjjDHGVJoQhrLBDWET\npdHACuBE4JqUx7sBk7IlhgmDgBFpjx0M9E6UNyXPvrvhkt+PCgk4KtUeB+CxmkNjjDHGZOIpOQxz\nJpQs+58jIsOAPiLyOzWDYFfhelKvIiJvAJur6laJbaeQlgCKSJvE3Y/TaiI/AR5KrC+4DinnAK+E\nNdi3F7lqBl98Mbw4jDHGGFN5vNYcxkFfYCFwLm52k8nAMar6Stp6DShwWsAUUxLlb5woYxowADcM\nTuiWLnW9jp9/HvbdFx5+GNZcM3Otn6pLGqdP91a21RwaY4wxJpOCps8zdQXZ5vCpp+CYY2r+v+MO\nOPvszG0Oq6tdcnjLLXD++fnL3m47+Pxzf+M1xhhjTByU1uaw2Bo2E4Izz6z9///9X/Z1C81P7TeB\nMcYYYzKx5DDGsrUt9COxs+TQGGOMMZlYchhjXoakSbKaQ2OMMcb4wZLDGCskOSzUF18EV7Yxxhhj\nylfW3soi8kAB5aiqnuZDPKZIVhNojDHGGD/kGspmX2pmPgE3Bd2fcINRzwXWS2y/ADe9nfFZIW0O\nly2DRuU0MJExxhhjYinrZWVVba2qbVS1DXAS8Dtu4Ommqrox0BToiht7sFsYwdY3hVxW3msvNy6i\nMcYYY0wpvNY1DQMGqeoTyQdUdSXwbxFZH7gZ2CWA+Oq1QpLDcePg0UeDi8UYY4wx9YPXDikdgG+z\nLPsG2NafcEyqQoeyseTQGGOMMaXymhz+CBybZdnxwE/+hGNSBdlb2RhjjDEmE6+XlW8GbhKRjYEn\ncclgC1zCeCDgYcI2Y4wxxhgTd57nVhaR04D+wKYpD88ErlLVQoa9qShBzq286aYwe3btx1Rh8WJo\n1iyQXRpjjDGm7JU2t7Ln5BBARASXHG4M/ADMCiwzKhNBJoebbQazZtV+zJJDY4wxxuRWWnJY0Mh4\niSxoZuJmApapzeGsWfD+++HHYowxxpj6wfP0eSLSQUSeEpE5IrIi8fcJEekQZID1WabkcNtt4bjj\nwo/FGGOMMfWDp5pDEfkr8DawBHge13t5I+Bw4FAR2VtVPw0synoqU3K4YEH4cRhjjDGm/vDU5lBE\nXgfWAvZT1YUpj68JvA4sUNUDAosyxoJsc9imDXz3XSBFG2OMMaZildbm0Otl5d1wM6QsTH0w8f8Q\nYPdiAzDGGGOMMfHhNTnMVzVWr3ssB8UGwTbGGGNM2Lwmhx8BfROXkVcRkWbApcCHfgdmLDk0xhhj\nTPi8DmXTFxgDzBCRF3FjHG4EHAKsAVQFEVx9Z8mhMcYYY8LmKTlU1Y9FZDfgStx0eesC84C3gGtU\ndWJwIRpjjDHGmLB4HgRbVT8Hjg4wFmOMMcYYE7GCZkhJTJ/XDldzOBf4qr5Pn2eMMcYYU0kKmSHl\ndFxbw89x7Q8nAt+LyGnBhFZn/yIifURkuogsEZHxItLF47YjRKQ67bZSRIZlWHdPERkrIotF5AcR\nGSoiq/v/jIwxxhhj4sfrDCknAvcAbwCPUDNDyonAPSKyWFUfCyxK51rgQlznmHHA8cCTInKoqo72\nsP3PuBldUrt5/JC6gohsB7wKvAIcCrQBbgQ2AbqW+gSyWbYMrrkGJk6EVq1ghx3g2GOD2psxxhhj\nTHZeZ0iZAHyuqidlWPYvoIOqdgwgvuQ+NgBmAgNV9eqUx18H1s+3bxEZgZvdZfM86z2Du2zeTlVX\nJh47CXgQ2ElVx2fYpuQr6zfeCJdcUvux3XeHn3+GqVNLKtoYY4wx9U44M6T8GVdjmMkjieVBOghY\nDXg0w747iEirUncgIo1wPbH/nUwME54AlgNHlLqPbNITQ4APPrDE0BhjjDHh85ocLgQ2zbJs08Ty\nILUDlqpqerr0Be4ycTsPZWwoInNEZLmITBaR3iKS+vy3AFZPlLmKqi4FpnrchzHGGGNMWfPaW/kV\nYKCITFHVd5MPisjuuLaArwQRXIp1gV8zPD4vZXkunwGf4BK/1YEjgUHAlsAZaWXMz7KffPswxhhj\njCl7XpPD3sBuwBgRmU3NDCmbAt8mlnsmIvsBr3lYdYyq7ltI2Zmo6q1pD40WkUXAuSIyWFWnlboP\nY4wxxphK4HWGlB9FpCPQA9gLV4v2HfA28KCqLi5wv2OBbTyslyx3PrB2huXJ2rx5GZbl8xhwPvBX\nYBo1NYbrZNnPpGwFDRgwYNX9qqoqqqqqigjHGGOMMaYYYxI3fxQyQ8pi4LbErSSq+gcwpYBNvgCa\niEjbtFq+9oACX5YaE65d4dJEmauISBOgLa5jSkapyaExxhhjTBjefBP23RegKnFLuqqkcj0Pgh2x\n0cAK3LiKqboBk1R1RhFldgOqgY8BVHV5Yj/HpnVUOQZoDDxfxD6MMcYYYwKxzz7BlOt1EOzGQB/c\nQNCbA03SVlFVLWgqvkKo6pzEbCZ9ROR3agbBrsINbJ0a6xvA5qq6VeL/zYGHgJG4y8dNgS5Ad+Au\nVZ2esvkA4APc4Nq34wbBvh54UlU/C+r5GWOMMcbEhdeE7gagJ65X8ijc5dew9cUNmXMurjPMZOAY\nVU3vKd2A2jWiC3HtCfsCLXC1hV8DvVT1ztQNVXWCiBwADAFeBBbgBsC+3O8nY4wxxhgTR15nSJkN\n3KGq1wUfUnnxY4YUKXoMc2OMiY9evWD48KijMKb+UM2WQ4QzQ0pz3OVWY4zJq1mzqCMwUTjzTBg7\nNuoojDGl8pocvgDsHWQgxpjKceihUUdgoqAKW20VdRTGmFJlbXMoIm1T/h0OPCwi1cDLZBhX0AaS\nNsYYY4wpf7lqDr8Fvknc3ge2wvXm/Sjl8dSbMfXaLrtEHUF8WDtaY0w2gwdHHYHJJ1dv5VNDi6Ie\nW1zo3DImtho2jDqC+LDksH7K3jjeFOPyy+G6CuwGeumlcNllUUcRvGbNYNGiqKMoTtbkUFUfCjOQ\n+urqq6OOwPilxE7rxhhTS+vWUUdgSrHeeuWbHJbLDCkVa8iQqCMwxsSBXWozprKIlG9zo1wdUh4A\nrlHV6Yn7uaiqnuZvaMaUF79rDgcPrh+XXoyz7bZRR+APu6zsnzi8lpV6aTss994L228fdRSFy1Vz\nuA+wVuL+von/c92MMT46+OCoIzBhCiMRGDwYttgCmjcPpnxrWlF5zj8/mHK33jqYcuNmu+2ijqA4\nWZNDVW2jqhMS91sn/s92a5utHGNMceJ+UDnuuOzL4lDjYeracUf49ltYuLByaipNZqNG+VPO+uv7\nU066e+8Nptw4KefjoLU5NMYn9a3W5PHHsy8r54OiMXFw662lbe/HpczVVy+9jGz2tmk1Yi1rcigi\nmxdyCzPoSvDrr7lrXkz5OfrocPd3qg025Ytjjgl+HxtskH+dsBPqpk39L9OGsvHH/vu7earttfSu\nrV2/9FWumsPvgOkF3EwBbr0Vnngi6iiMn848M9ypw669Nrx9VbKRI2HTTYMr//TT4Z138q/XIOTr\nOEEkh8YfI0ZEHUH5sdfMX7kGwe4B1LMLZeHp3z/qCIzf1loLxo2Dnj3h4YejjsZ41aiR6xV+zjn+\nl92smfe2Vaut5v/+TXnacEP312oOvYvjZepyfv9yDYL9YIhxGFMRmjeHTp0sOSzng6Kf4vw6BNVG\nNs7Pudzsv3/UEZj6qqALGSLSQES2FZFOItIsqKCMMfnVtw4w5ai+JUr2mfRH8nMTZHOHQuIw9Y/n\n5FBEegI/Ap8DbwJ/Tjz+rIicG0x4xpio9OsHLVtGHUU44pDUxCEGY4K2xx5RR2C88JQcisg/gVuA\nZ4FjgdTfE+8CR/kfmjHlKayT/BprBFv+1VfDrFm518k21MV66/kfTznyWvOy117BxpGJXVaubHF8\nHzbeGG65JeoowhPH98ArrzWHFwJDVfUM4Jm0ZV+TqEU0JgoPPhh1BLWFlRyus044+8nlH//I/HiQ\n46MFIaiDuJdyN9ig9DHtinHAAf6XabWf8eHH4NV+fy+++w523tnfMk0wvCaHbYD/ZFm2CFjbn3Dq\nh59/jjqCynLyyXDJJVFHEY3evUvb/s/2sw4oLKlZc03v6+Y7uR52GEyeDB07hp9YnXsubLJJuPs0\n3viRlBXyOQ1L48bh7/PcCBu91Yeaw1+A1lmW/RmY7Us09cD48fCXv0QdReWJ44EwDKU876uugq+/\n9i8WU7j27aOrAf7Tn2DCBDfe6mGH+VNm1B0ojEl3yy2l/4iOq9atgyvba3L4InCliKSOQa4isj5w\nAa4tovHg/PNh3ryoo6g8cfqFZpfWykebNsVt17mzt/UK+VyG8blJj2f99d0MMdtsU3rZZ5zhLpHH\n6bsYNx07eluv1M/CXXeVtr0pD0EeM7wmh1cAS4FJwOu4wbFvBb4CVgJXBxJdBVm2DAYPhrffjjoS\nY0zSffcVt91NN7mat3IT1MnkyistIYmTM87wpxxL9OOtYcPgyvaUHKrqL8DOwCBgNWAqbgDt24Dd\nVXVBYBFWiD593M2YuAjywF8utaf77lvcdttuC5MmwejRudfL9xpXysl3110r57lE7cgj3aw9xbrt\nNv/fi3Jvm1wux6NCBTmrkudxDlV1oapeo6p7qurWqrq7ql6lqr+JSAkfZW/E6SMi00VkiYiMF5Eu\nHrcdISLVabeVIjIsbb3+GdarFpFRpcY/bFj+dUzxch0Mt902vDgg+gPR6aeXXoZN75jfppvCgQfm\nXiful5WDKNeSxNKMHFn7/1NOyb1+u3Y19488Ek46yfeQPE8BaWpLfheOPTaY8pM/Io47zv+yvY5z\nmLU5ZyIxfMK3iLK7FrgSdzn7IOAD4EkROcjj9j8DuwK7JW67AzdlWE+BPVLW2w2o0OaslSPXCSnq\nZC3VlVdGHYE3O+3kbb1cr+3VaY1Ngh6XMSwbb+x9XUuUvGvbFjbbLOooopc+DNSAAa4tZzZffOG+\nh6owapSb490vyc9vFONwVpL77w/mNUzWHKYfa/3gtebwGhGp83tERBoCjwP7+BpV3f1sAFwEDFLV\nm1T1bVU9G3gLGOyxmGWq+l9V/TjlNjPLuh+nrfetH8/DRMNrcrjLLsHFsPnm0K0bdO0a3D7C5GXo\noLPPhkMOgRYtoG9f2H774OMKwz33eF+3vlxW9uN5tGpVehmVqFUrmDgR/vWvqCMxxWreHN55B157\nzd9ykzWHW28N113nb9lek8OzgHtTa+lEpAHwGLA/cLC/YdVxEK6t46Npjz8CdBARvw8rFXLINuA9\nOfSrhjFTOTNmuIN7GLVnYSQcXn6prr8+vPQS/PijO3CVayI0bBjceCMcfDDccQfsvXcw+/Hy+bv9\n9mD27adi3+cgPh+HH+5/mVFo0cL9uDTlzesoB15F3uZQVUfgeiQ/KSK7iIgAI3FJ28Gq+mFwIQLQ\nDliqqlPTHv8Cl8i1q7tJHRuKyBwRWS4ik0WkdyLBzWSmiKwQke9EZLCIlNl8D/WPH5eVo0peojqB\nlfJ8882Akuk1j/PJLddnpGdPuOgiePllVxsa1OfEy+f0//4P1l03mP1Hza/XdaedoFMnGDgQDvLa\n6Cgm2rePOoLayvUHXaE23BBOO83/coN+/YYODa7sQjqkDAQeBF7CjWt4KHCIqr4fTGi1rAv8muHx\neSnLc/kMd1n6GOBwYAyu53X64AvfApcB3YEDgX/jxnF8rpigTXnZYovg95EpAXjmGXdLVUpvxbjK\n17A+rkqZ1SGIk0OUbWhbtQouyU+2myvVpZfCmDFudIgGHs9wcZnSrb4kY2HL97m6+GLo1y+cWPy0\n22419/3+7HhODhPOBd4E9gUOVdX3itmpiOyXpVdw+u3NYspPp6q3qurtqjpGVUer6pnALUCP1IG9\nVfVRVb1BVV9X1TdU9VLgEqCziATarrLS9O0bbk1RqTWHTZrAhRf6E0uu/WWq9WnY0M1RfPPN7v4a\na8Djjxe//6BPMMW2zWza1N84/BTl3Mrl5LvvMrd986O3cpRJ7513RrfvVIW+doX+cNlhB+jVq7Bt\nvPLaiS2Oiv3sbbhh7uWFvp/3319z38txNrX8pk3d+SV5K1XW+gkRmYnruZtpmwbAI1ITmapqIe3+\nxgJexuRfnPg7n8zzNydfgmLmHHkMOB/4KzAtz3o3A7vgOsDUMWDAgFX3q6qqqKqqKiKcytKzJ/z+\nOzzySNSR5P/in366O2A2bx58LGuuCWedVTNg8KBBNcvOO8/VrjVsGE4sxTr77Gj2u+mmMGtWNPsu\nViEdUuLUq74UuZ7H1lvDlCmZl4m470Cp86QX85rGpeawUIUOgrzhhnDrrbB4ce1EpHVrl/iX4sIL\n4cQTSysjSoUmcrNnu57h7dvD//7nTww9erjZimbNcs2NCmmj3rHjGHr1GrPq/6uuKi2WXBev3iBz\nclgyVf0DyHKIyOgLoImItFXV1ESuPS7GL/2Mr1CpyaGJn3wniKFD3Zd8Wq6fCHkUcpC+4w7Xa7lp\nU/jrX2sv8zrrxrXXet+f3/wcKiOTI46Ajz5yHVkOPhgOOMC1cdx00+DaZ2b7jHTvHsz+ShFEElnK\npXMvTj8dFi1yw7JkG1BZBI4+uvTksD4p9rPQvz889phLEhs0gBEjYJ8M18ZSE6auXd025Sjf61RM\nbfcmmxQXSz577FHcdukVU1eVmB1mTQ5V9ZSSSvbXaGAFcCJwTcrj3YBJqjqjiDK7AdXAxx7WU+Cj\nIvZhivDuu4WPCRV1h5QnChjpU6T0Hq+XXVba9n7J9tqWksB07OhqnH/9FVq2rHlf8s1GEoRSBwMv\nl8vKvXq5Wuxi37d8z9PLIMq9ewefpGYycGD4+8wmrM/LZpvBp5+60QR23RX23DP/NkOHQnU1zJkD\nb/rS4Cs+GjQI5rUvl+9/JmXR7F1V5yRmM+kjIr8D44DjgSpcB5NVROQNYHNV3Srx/+bAQ7je1dOA\npkAXXKeTu1R1esq2nyTWnYLrBX0AcA7wiqqOCfApVhyR4k805XSJZ9993e2II8Ldb7KmMtNrXM4H\nJHDPqXnzupfWg3xemcree283MLPf5WZbHvaQS6k22ggeeMDNGd2sGXzwgf/7yGfLLf0pp9DPSceO\n/uy33Gyzjbt5tfHGNW2hy/0Yk66U51MpzUHS5Wpz2B14SVXnJu7npKoP+xpZXX2BhbhOMRsBk4Fj\nVNaHtBYAACAASURBVPWVtPUaULujzUJcm8W+QAtcbeHXQC9VTW+GPCVR/saJMqYBA4Ab/HwiJje/\nv2ylnnRPPNE1wk/v+fjnP8MbbxS/v6BU2oE7KcjXNVPZftRildN7ccop7jZ7truEXwg/2k761Vs5\nvcxKFvTzK6fPbylEyrMjVZBy1Rw+iJs6bm7ifi4KBJocqqoCAxO3XOvtk/b/fFxNoZd9nFB0gCZS\nub7YW20FU9NHyCzAJZdU5kHSDoa5+f2e/+Mf8Oyz/pZZKL+e05prwsKFNf9vt50/5fohtcmGl89q\nmJ2/Dj8cxo/PvrwSjzNRSh3qxRQm11A2bYDxKfdz3Uq8+GIqTdgHuVydJG680VsZfsWc3mmiUyd/\nyvXbDjtEHUG0wh53Md9QPmFcVvYrsR850l1+Btf+tUULf8pdb73Sth80KPc8xOA6xyRtuin87W+l\n7bMQ559fUyubfP1McJKdO7x0SAnix3I5J/tZk0NVnaGqy1Lu57yFF3L5mT076gii4bXnrR9OOin7\nybd9e9eZ4YwzcpfRpEnmxwv9gm+6qZteTsQ1/B42rLDtw7Djjq4ncDFSX48LLsi8ThwSmHzyzfLi\nh0LaHK65ZrCx+Omww2DmTPj++9rDMZVCxL0npXS28rLtTTe5zi89eriOFV4HyvbDuuvChAnw/PNu\nvuRKUs5XFIL6DBTSoa3QsQnvSp/Cw2chfi3qr3KbwskPIq6Re6bhEXIp9hJPs2bwSnrr0xQHHgh3\n3515LK/kCXqTTaBDB+/7zHUw7NcPVqxwcyrvuKP3Mv2QKyG5/noYNQree8+fX8q77urGtCxHYZzM\nCnmN99zTW1u/m28ONh6vMa+zjuuk4Jfk+3Hllf6VmUnz5jBkiBvnb6utgt1XJuuu664utGlTd1nc\napriFk+hkp+pbbfNvV4pNYfZ/OMfcOSR3td/2EPDvBNOcONJPvBA/sqOUmVNDkVkuohM83groUVX\nZfvmG5g0KeoovDv++Jr7+X7JNGmSv3bwhRcK2/+jjxa2furJtFMnl4yljjn45JO112+VYaj21CTh\n+ecL238uQQ2PkKrQxHPHHd0By6/ZSkTgttv8KSufuNZMdO6cfVkh73+DBq6DU74fk8cd53rHF/PZ\n2mijwrcpZ3H9zPglqucXdALvtxNPLLyTlVeZ3oMePdyP8GxXo9ItXQqHHpp/vW23dUMKnXpq8OeW\nXDWHbxdweyfYMMvXokVRR5Bdpt6Yl1/uapf+7/9g7Njc2x91lJvt4LPPsq/TrJn3YV5uvx3+/vfs\nyzMtS//ybb65GyfxvPNcu6ijj667TWpCtfXWtS/ntW7tLda4OPjgmufToEFh4y3Wd6kH12KnBAR3\nsM42IG6hvXi33rr2zBWZrLGG69hSXe09RnCN89u3L2ybKJR7bVUpyuW5/+UvUUfgTfL1bNwYxo1z\n55hXX828np9tDpPNiry4++5oxvfMp1wGwS5bv/0WdQTZffpp3cuojRp5n6HgmmvcdEzrr193WTFf\ntORUQdlmG3nuOW/l7r67u2Vz111uCrgVK2D48PI5IGfSoIG7RDx6tEtsk51M4jJXbDHCqg1Jvzxe\nrO22cz+Sfv01uNoJP7z2Wjj7qfTaumzOPjv8713Qx65yPjam22ADV+mRid/Ps2VL7+seeKD3dddZ\np/BYimVtDgOWaZL6uMjUDsPLl6RLF5eoeR0guNCTRdC/ov76V/jkEzekRKEzscRR06buUnEyMezS\nxXoih61Zs8wnhEI6pCQFlVzFeb7ufIptfB9molpI+7JsCk1SCn1+YY8VWi5y1RwecQRccUW48ST1\n7Vtzf401wp3O05LDgN13X9QR1GjXrub+qacWV0bnzvD007Uv8fr1qyu1HL96QPopvX1lXC+tNGwI\n77+f/fKJF7mm0/JyEiiH3sphKMealzjGHMfLbn447LDa/3frFk0chYrjZ6QU2Z7PzTe7WWH8mJ61\nGP36ucS0a1cYM6bm6loYLDmsR157zQ09MmBA8J0ISj145Bq3MCojR9bcb9DA9XgMWiGXHFKtvjrs\nv3/x+w3z8oVX2caL7NIlXoMwm+IkT7KZjh1hJCN33x1s+ZnmU7/+etc0B1wTn3/+M9gYCn0ds61f\nLj/gvMaZ7Xmed17+Ia+CfC1WX9013xo50l3xClNZzK1crvzs+eqHTTYpfcy9SpzL16tDDnEdPt57\nzyUkf/5z8Ps88kj4z3+C308qvwY09lu2X81PP+06Z2Rrqxql1O+GX21z486vnvBh69EDfvnFNTk5\n+WT3AzBXB7l0ud7Lli3d+Irp/vIX+PJLmD7ddRYq9LUrlyQt7irxe1gqqzkMyNKl3nvpmuKFfXA8\n5hi45ZbwZj1p5PPPt6gPgk8/Xdr2xx7rTxwQ/jiHffp426bcT/iNG7ux2JIGDPC2Xa7PZqZlW2+d\nv8xCXstGjVwbr1Gj3LE7faajYmyzjeuUOG1a9mGn1lsPdt45nKS63D9bhfJ6vAvzuJhaA9iihZso\nIY4sOQxIrgGZy5nXL1ElHYSiTKhKGWIF6s664WWQ7yDfuy4eZjmvpM9OqmzD3VSiG2907V4//tj7\nLBGFTkN21VWllRmWNdcMrs2kn8cmrz9e/N5vHIgU/1kpdLtbbnFXnTbfHO69N9wZegrhqV5CRDK0\nllilGlgAfK2qy32JqgIsWxZMuautBssjfJWL+QLVp5Oi3zp0cDUaK1YUt/3IkW5g80WLXMPmTJc2\ngxDUSdnPk1IYJ7hieitHzY+YRHIPJ+XH/rfYorjywxT0+1vo9yxXPOedV7cjYJSfzwYNCh/Ls1hh\nPs/dd4evvw5vf8XyetFqDJDvY7hYRG5V1ctLC6kyBPVhu/PO2hPHl4MrrnCNvePwK74YYfYQy+Tf\n/3YDjhfjsMNg1izXzMFrW8Ko36e//S37smyxFfN9i9v0eXER9fufSTm8juUQY673ttS2xnH83HhV\nyntXzs87F68VmkcAM4EXgVOAgxN/XwZmAacCDwG9ReRi36MsQ0EcKDp2hJNOyjxESZy1bOliPuEE\n79tE+YVLHU5i++2jr6Eo9bO09tqFHfijfO332KOy5iKPa9JabqLqwWwySx9FYb/9/P/cnnKKv+Xl\nYslhXV6Tw38Ao1X1CFX9l6q+mvh7ODAa2EdVzwHuBE4LKthy4veBa9gw+PBD13YljsOM5NO5s5s3\nOazLmqW46y43vtQFF1Ru29Fc8s2XHZSTT3ZjefnVBueCC3Ivt+Qis3J5XYIeb7McBP38sn0W1l7b\nDYe21lquY9CNN/obS9u2tTs1BS1fm8NK/xxl4vUwfCSQrZ/hU7iaRXCJYptSg6oEH3/sb3nnn18z\nj/BOO/mXIO6xR839DTaALbf0p9xsHnrIJR+rrRbsfkrRrJmbG3PYMNh446ijCd7jj9f+/557cq9f\n6oEy2+wtVVX+fi4uuqhm4Pf11qu7PN/zCCNJyjTdXn08EaWyWsLg5Hsd0+eiP/HE7Ov27AkLFsDk\nye6qll/GjoXPPiuPioRK5jU5bAhku7i2ZWI5wNLErV6bMsUNbuqn1C+1iJtE3A833eTG2kr2nAp6\nrLhDDnFjiS1aFOx+jHddurghPHbbDQYOdElaqXIlOLfdFs7wDRtu6OYP/+Yb+O9/g99fJukn49Tj\nwjrruGYicRNVIpb8zNT35LgQfk+3N2hQTVK26aZw2WX+le3Feuu5CouwJ0HId7UiqhlSouS1Q8rL\nwEARmQM8q6orRaQhrkbxOuClxHrtgan+h1leCvlCeXH88XUfa93an7J32cUNwuq3XF8YL2P3Zdt+\n//3dTC9JxXbUMDVWWw2uu877+qUmD3vsAf/7X91ySik3W23T6qu72vDff6+7PIwp2dLjuugid+L7\n9ls488yaqwEmGGGeuKOo8fT7+W25JUya5G477ADrrhtdLGHK9z7Vx0vOXpPDXsAzwJPAChGZD6yT\n2H5sYjm4IW0G+h1kufn0U3/Li+scvlG46SbXm3XBAtfR5ZJLoo6o/gnqYOh3uakH/ObN6y7v3Tv4\neNJPOg0auKSwGPvsU3o8XmS6BA+FJQrFKJdLx507u6YxXgZ0L8fEoUWL6GZJ8vsz4PX1b9OmPN+r\nIHm6rKyqv6jqXsBBwLW49ofXAAeq6l6qOjex3kOq+lRg0ZqieRl8OE6yfVHbt4eJE+Gll2DCBNdO\n0hgv5s6tSXDuvTeYS9stW9b+f+edCy8j02d/s81Kn/rSq0aNXNvg1Dll11jDdSgLUhAnZ7/LbNvW\nXbl4KsNZrlyS26AU81qnH79T27wHmawNHVpzv2NH2HPP4svq3r32/37O4hSlgibnUtVXgTIbSCV8\nfh8kii3vsstgyBD3hbv2Wn9jitJmm8V3yqH6oBwGuM5U3rrrugQxyHgefNA1fQB3yfiaawovI5Pp\n08OdO7p7d9cZQcS1oV5nnfBqk8p1/vZyjdsvxRwXHnrItUNPGj7cv3gg++t/4YWul/X330PXrqW9\nT5de6mqRZ850yW4hTXTirKDkUEQOAzoB6wLzgLdU9eUgAitnM2ZEHYEzcGDdEe/DUsyBIr3TjXF2\n3bX2/xtuGE0chYjDpedSP0PFvM6dO8Prr8MHH8Df/w6tWpUWQ1KYiWH6PrfZJvx9m/JTzHf+oINc\ngvjWW+77klrTHvQ54LDD/Clno43cVazx492VrXI4Pnvh6bKyiKwpIm8DzwPnAYck/r4gImNEJEOL\nHlOMQj5YqcPQZFJuCVbqwcXaf9TYZJOa9nFrrgkPPxxtPOX2ufLqrrtq/+9l7t5M9tvPzQq03XbF\nbV/fP/teOqx55fdrmW/+56ZNaz+29db+7j/Oiq0Q6N4dRoyAI48svbxSlLK/ddZxbYIrJTEE70PZ\nDAR2BE4CmqrqxkBToHvi8cA7oYjTR0Smi8gSERkvIp5b0onI6iIyQESmiMgfIvKjiDwvIo3S1ttT\nRMaKyGIR+UFEhorI6tnKjdKtt7pfLVC7at5UniFD4Mcf3aWL9NkJwhZl8pIrMU1t+9OtW+FJ7Gmn\nueYXRx4Jzz7r2peZ8DVsWHsAZL9HfwjSY4/V3BeBwYOD3V99/yHhJ3sta/P6G+0o4ApVXdUkWVVX\nAo+KyPpAb+DcAOJLdS1wIdAXGAccDzwpIoeq6uhcGyYSwNFAK1wi+xWwAbA/bozGFYn1tsO1qXwF\nOBQ3oPeNwCZAV/+fUl2FtFvZaSeYOtWNGbhyZTgDNof1Bdprr9r/24Co0fUg9KJxY1i2rOb/XXYJ\nP4b7/7+9+w5zqkofOP59B3CKFAHpCIMiKNJ0LSg/kd4UcXVFUaToWtbCogsquiIg9spa1gaKggrY\nUFFUUEAQBJSmA4sgRTqCBZGR9v7+ODchE5LMnSEzycy8n+e5zyT33pz7JjeTvDnnnnNGQdu27nas\nwXujKV0a7kyCmeHtS8rNuHHBBa53d8uW8NpriY7Iya3msHt313Fn9mw3oHTDhoUXW6Il4/s2XjEl\n43MraH6Tw8pAtNHwsrztBUZEqgD/Au5T1ce91TNE5HjgAVziF8tAoDnQSFU3hqx/J2y/Ybg5pHt4\nye/nIrIXeFlEHlTVRYf7XHKT1zdhRoZbNm8umHgKU2gS3Lw5XHIJjB/vnt/YsYmLy+Ru4kRX43bg\ngPtCvOSSvJfhp6Yvt/Ez+/TJ+3FN8hE59AdiUXHZZXmbR96YZOS3WXk1EO3yza7e9oLUGSgDhA+m\nMBZoIiK5Xfb9D2BCWGKYg1e72AkY7yWGAROAvRycIjApFdYvG79NdfmJJ/wxr7/uBmNdtSrxTakm\ntvPPhwULXDI/f76/68Z69Tp4Oy2t6A23ZOIrr513CmNu5auvznn/ppsi72eSs3YtL5eWxGqdKq7X\nWcfiNzl8DrhJREaJSFsROVFE2ojIc7jm5GdzefzhagT8qarhs698B4i3PSIROQY4BlgtIs+LyK/e\nNYtTRaRZyK7HAWlemUGq+idu1peox4inZs1y3yeRCnvGgZNOOnhdpUluJ5/sxvgqV87f/vfc45qB\nGzZ0F6RHGqjalAwvvRR7xppEfTn/+99wnDdx7F/+An//e2LiKAqSMTnMi/T0g8PQlC4No0cf3FbU\nn1t++GpWVtXHvabdW4C+3moB9gAPqOrIggkvqBLwS4T1O0K2R1PT+3s7MA/ogUsCh+OajZuq6vqQ\nMn6OcpwCnh/Aeeyx5E8QC0pJ/HVWkmVmwrRpiY4i+ZS0L6LKlaFv34Ip+3Bfyzp1YMkSNx5enTqF\nM+ViUVWYPcPBTfu5d6+7PXhwfI55xx1uvvPSpQvnGv5k5nvQAFW9Q0QeBlpwcJzDuaoaKZmKSUTa\nAZ/muiNMV9W2eS0/TKB2dBdwnlcTiIh8DawEbgDi9NY6fJGGvzjca7GMiSd7r5l4SvYfhRkZOWfu\niCYRzyOZ/hcLO5bJk910qvXrx7cjWaQJFpL9PVoQ8jpDys+4nryHazbgZ2jVP7y/PwNHRdgeqM3b\nEWFbQGBOhNmBxBBAVdeLyHJcR5XAMcDNGR3pON/6iDep/lkTqXz5REdgjCkK/HxmHn98wcdhipYO\nHQ7ORlTQSuL3etTkUERa5aUgVZ2Zh32zgRV5KP47IFVEjlXVH0LWnwQo0XtSA/wA7PZxjFXAn16Z\nQSKSChyL65gS0dChQ4O3ly1rDbT2cTj/isKvlvvvP1i1378/HHlkYuMxBacovB9N8XLqqW7+21mz\n3P2nnvL3uJL4pZ4o9lon1vTp05k+fXrcyotVczgdl3jlRrz9CnKCpym4sQgvB0JnK+0FfKuqUSes\nU9V9IjIZOFtE0lV1N4CI1MHVXk7y9tsrIlOAHiIyVFUPeEVcDByBmx0motDk8HC+OJ95Jv+PTbTb\nb3e/4vbsgRYtEh2NKUj2JVCw7PWN7NNPYdIkdy1Yq1Ywb16iIyp8jzwCAwfmvJ8XVgNbfLVu3ZrW\nrVsH7w/L7xRPnljJYZvDKjmOVHWbiDwGDBaR3zk4CHZroFvoviIyDaijqqH/BncDXwEfisijuNld\nhuCao0N/gw4F5uAG134aNwj2Q8BEVV1YAE+N2293w3+0bOkuhM2vgvpCqVEDNm06eD/WlH1/+UvB\nxGBMgCVOJVdaWv7GzywshVGj/ve/w/vvw4wZ0Lo1XHll7P1fe+3gmItlyrje1wWlsDukmIIVNTlU\n1RmFGYgPdwA7cUPnVAf+B1ysquHXQKYQNkSPqi4TkbbAg8AbuHELPwMGqeq2kP0Wi0hHb78PgF+B\nl4ECmzfh/vvdkqzGjoWOHd0MLJUr55zWyhgTfyXtS7Egk6ri9lpWqACffQZ//gmpqW4GmVguvdS9\nBl9/7ZLEghwWLNJrnZrqYgXoWShzjJl4ieMU5wVLVRU39V3MeZxVNWKNp6ouANr5OM4soGV+YiyO\n2raFOXNg8WLo0sVNMG5Motj1jvnz4ouJjsDES0qKG5PPD5HCm7ElUnL4wgswZAjUrAmH2cppClmR\nSQ5LskQPZXPaaW4xxhQdkyfDK6+4zhwFNY5gPBTkZ1dxqzlMZpFe6yuuOLzLpUziWHIYJ7t2wT/+\nkegojCl49oVbNHTt6pbiyt6HySUwk4wpHvxOn2dyMX48vPpqwZRtTWnGOCUhISgJz7E4Kumf0127\n5hwsfGRBz5tmCpTVHMbJVVclOgJjjCl68ptUlfRkLNmkpMBXX7lOjHXqQPfuh1ee/UhKrDwlhyKS\nAjQCKgMLVHVXgURl8sz+kYwpHmrVSnQERYOfz7zC/Fy0ZBUqVXKTIJiiz3ezsojcAGwGFuOGgWno\nrX9XROztkIsPP4SXX050FMYUbSXhCzgjAx56yD3XtDR4441ER1R0+e3VGw/2Az2+SsL/ejLzlRyK\nyNXASOBd4BLcrCgBXwAXxT+04qVLF2jaNH+PtX8SY5yS8gU8aBBs2QIbNyb3wM/xUJDntF8/N/hz\nwIABBXcsE18l5X89WfltVr4FeFRVbxOR8GnylgOD4htW8ZTfN3tGRsGVbYxJTlWqJDqCoq9CBXjr\nLVcTW68e3HVXwR3LfsSb4sRvs3I94OMo23YBR8UnnOLNbwJ3880Hb6emJvcYZcYYczgKOqnq1g2+\n+MKN+VipUsEey5jiwm/N4U9AZpRtDYENcYnGAG5E+Z07YfVquPVWKFcu0REZY0xyOeKIREeQk9Uc\nxlcyzcZVElvm/NYcfgAMEZFjQ9apiBwN3Iy7FtHkIi3N335HHeWmHZo61c1rbEwySeQH5bHH5r6P\nKRmaN4djjjl4/8ILExcLQGkbGC6uMjLgX/9KdBQll9/k8N/An8C3wFRAgf8Ay4D9wPACia6YadQI\nMjMP3r8ojt14SuIvG1PyDBqUs8Zo1KjExZLMhhehT+T8fnaJwHvvuWbjXr3g6afjG1du/vrXg7er\nVXPTFJr4euSRw3t8vL4XS2KtsK/fOqr6k4icCgwAOgGrvMc+BTyuqr8VXIjFhwi8/z4MHQrly8MD\nDyQ6ouRSEv8BTd4cfTTMnQtjxkCzZnY9biTt2pWcqTybN3cJYiI88YRLPn7+GUaMgFLhXTVNXLRv\n71rREqkkVr74rghX1Z3APd5i8qlxY3jzzfiXW716zvspRXBixJL4D2jy7uST3WIOtWIFHH98oqMo\nGerUgXfeSXQUxd+jj7ofgvlhFQ75VwRTCBNJaio8+aT79Zqe7uZ6NsaULEXxy7AoxmwKT9OmcNxx\niY6i5PFVcygin8XYfAD4FfgaGKWqW+IRmMm7G2+E3r1drWHZsomOJu/sS6JosBpeY0xh6tIFnnoq\n0VGULH6blQVoANQAVgNbgGq48Q83efe7AjeLyDmqmlUAsRZZ111XeMcqX77wjmWMSS72A8sUR/a+\nLnx+m5UfA7KBU1X1OFU9S1WPA07z1g8Djge2AfcWSKRJbN++2NuHDSucOIo6q5EqGuyD2sST/d+b\n3OT3PVKhQnzjKEn8JocjgKGq+k3oSlX9GpcYjlDV9cDDQKv4hpj83ngj9vaqVQsnDmMKg32ZG2OS\n0dChB2+XLu0utTL547dZuQGuVjCSbUB97/Yq4MjDDaqoueKKREdQPFiNlDElj/3fm3i59Vb4/Xf4\n3//gpptsusTD4Tc5XANcDUyJsO0abzvA0cD2w47KGGOMMSYP0tPh4YcTHUXx4Dc5HA6MFZElwFvA\nVqAqcBHQGLjM26898FW8gyzK6tVLdATGmJLCauGMMfHgd4aU10XkJ9z1hXcAZYC9wAKgo6oGxi+/\nBTednvGUKZPoCIoOS6SNKXnsGlaTm0T/6Amd9rak8D0Itqp+qqpnAelAdSBdVVuGJIaoaraq7i2A\nOIusRL+pk9njjx+8fcop0LJl4mIx/tmXuTGmMCX6M6d3bzd1Z8DIkYmLpbDkeYYUVT2gqltV9UBB\nBBSNOINFZLWI7BaRRSJyYR4enyYiQ0VkhYhki8hmEXlPREqH7HO3iByIsLyd/7jz+8jib8AA+PBD\nePFFmDHDXitjDldR/B8qijGbkiU1FebPh7vugldecZ1dijvfcyuLyBFAF6AhkBa2WVW1oOdcHoFr\ntr4D+Aa4FJgoIueqaqSOMkFeAjgFqAvcBywDqgAdgFJA6EiFCrTEzfwSsCNOz8GE6dIl0REYU3wc\ncUSiIzCmeMrMhOHDEx1F4fE7fV5NYBaQiUueAr/1Qit7Cyw5FJEqwL+A+1Q10Bg5Q0SOBx4gci/q\nUAOB5kAjVd0Ysj7atOnz4lUzar+KjTEFpXt3mDTJ3W7aFGrVSmw8xpjiwW+z8sO48Qzr4BLDM4Bj\ncbOhrPRuF6TOuE4w48LWjwWaiEjdXB7/D2BCWGIYi6V0xpikN3q0G+j3qqvgvfcSHY0xprjwmxye\nDTwKBJKrA6q6RlWHAG8C/ymI4EI0Av5U1VVh67/DJXKNoj1QRI4BjgFWi8jzIvKrd83iVBFpFuVh\nP4rIPhFZIyIPiEh4M7pvVnNojCkolSrBk0+663br5vYTOUklurOBSX7XXZfzfp8+iYmjJPGbHFYG\nNnlNrbuAiiHbPgNaxzmucJWAXyKs3xGyPZqa3t/bgXpAD9z1ilWAz0Wkdsi+K739egOdgPHAzcCk\nfEduTDFjX+bGmMJ00klw223umtpmzWDIkERHVPz57ZCyHjfoNbgp8joCgSFsTgey83JQEWkHfOpj\n1+mq2jYvZUcQSIB3Aeep6p9eDF/jksEbgMEAqhrebD1NRDYAj4tIG1X9PK8Ht5pDY4yJzj4jjR8P\nPOAWUzj8JoefA61ws6M8BzwtIs1xA2F38tblxWzgBB/7/eH9/Rk4KsL2QI1hrN7Egen8ZgcSQwBV\nXS8iy3EdVWJ5HXgClwTnOTk0prixL3NjjCne/CaH/8ZLxFT1v97QMJcAGcBDuOn1fFPVbGBFHh7y\nHZAqIseq6g8h60/C9ZjOivHYH4DdeYkv74aG3G5NaCu7fZGa4saalY0xJrlMnz6d6dOnx608UR+f\n9CJSAcgOrXkrTN5QNuuBEaHjKYrIVKCKqkbrWBLYbwKuU82xqrrbW1cHl6A+qKp3x3jszcAjQDtV\nnR5hu+Yc0Senxo1h6dJY0RmT3MJ/4Lz6KvTqlZhYTNEX/n46+mjYti0xsRhTXIkIqprv6qlcO6R4\ntYTbcdcZJoSqbgMeAwaLyM0ico6I/BdXRXd76L4iMk1Evg8r4m7gSOBDETlPRC4GJuOao58KeewC\nEblJRDqJSGcReQx4EPgoUmLoh9UcGmPMQf365bwf3hPVGJN4uTYrq+o+EdkC7C+EeGK5A9gJ9MfN\n7fw/4GJV/ShsvxTCkl5VXSYibXGJ3hu4ayU/AwZ5iWfACq/8Gl4ZP+DajB+O95MxxpiSaOhQmDYN\n1q2Dhg3dNJrGmOTit1n5QeB4VfU9l3FJkVuz8llnwezZhRiQMXFWEpqVMzMzWbt2baLDMMYY3+rW\nrcuaNWsibjvcZmW/HVLWAJeJyHzcmH+bCMuIVHV0foMozh5/PPd9jClKimOHlLVr1+Lnh7Ixkv49\nsgAAIABJREFUxiQLKcDr1vwmh097f2sBf4mwXQFLDj0DBsCXX8Ill8BppyU6GmOMMcYY//wmh/UK\nNIpixmoLjTHGGFNU+UoOVdUuxjHGGGOMKQH81hwCICJNcTOlVAaeU9XNIlIf2KKqOwsiwKKmeW7z\nrRhjjDHGJLFcxzkEEJFUEZkILAT+AwwBanqbHwLuLJjwip6nn859H2OMKaratGlD//79C/24M2bM\noFSpUuzYEWu21ORSrlw5XnnlleD9lJQU3n777QRGVLQVxfdAUeUrOQTuBdoDVwDVgNAuMh/h5lc2\nuKFrjCnO6tRJdATGjzFjxlCuXLlEh5Ev9erV47HHHsuxrmXLlmzatIlKlSolKKrDt3nzZrp16xbX\nMvv168f5558f1zIhcT8CYkn0eyArK4uLL76Y4447jpSUFIYPz9PMwTENGDCA0047jfT0dI499ti4\nlZtffpPDnsC/VfU13KwioVYDmfEMyhiTPB588ODtxo2hVavExWL8U9UCHeqisJUuXZqqVasW6jFV\nlQMHDsStvKpVq1KmTJm4lVfSJOI9EOqPP/6gXr163HvvvXFP4FSVvn370rt377iWm19+k8PKwLIY\nZaTGJxxjTLIZNAjefBP+8x+YNcumhEwmM2fO5Mwzz6RcuXIcddRRtGjRgqysLGbMmMGVV17Jrl27\nSElJoVSpUsFajl9++YU+ffpQqVIlMjIy6NChA1lZWTnKnTt3Lu3ataNs2bIcddRRtG/fns2bNwe3\nHzhwgDvvvJMqVapQrVo1Bg0alOPx48aN4/TTT6d8+fJUq1aNHj16sHHjxuD2ffv20b9/f2rVqkVa\nWhp169bljjvuAFyN1dq1axk0aFAwdoDp06eTkpKSo0kxtzjDTZ48mRNOOIH09HTatm3LhAkTSElJ\nYd26dcDB2taPPvqIJk2akJqayvLly1mwYAGdOnWiSpUqVKhQgbPPPpu5c+fmKHvVqlW0bt2a9PR0\nTjzxRCZPnnzI8cOblTdu3Mill15KpUqVqFSpEueddx4rV64Mbh82bBhNmjRh/Pjx1K9fn/Lly/PX\nv/41+BoMGzaMMWPGMHny5OBrNXPmzKjPP9zw4cPJzMwkLS2NGjVq0LdvX8DVRs6YMYOnn346WG7g\nNcrKyuK8884LntvLLruMLVu2BMvs168f3bp1495776V69eqUK1eOK6+8kj///NNXTNHe0+CalUPf\nA/Xq1SMlJSUYY+B2INbffvuNa665hmrVqlG+fHnatGnD119/7fv1CXfqqafy0EMPcemll5Kenh51\nv4ceeoj69euTkZFBs2bNGDduXK5ljxw5khtuuIEGDRrkO7548pscrgbOjLLtdNxUdsaYYkgELroI\nbroJKlRIdDSJIVJwS37t37+fCy64gFatWrF06VLmzZvHgAEDKFWqFC1btuSJJ54gIyODLVu2sGnT\nJgYOHAhAnz59mD9/Pu+//z7z588nIyODzp07B7+8Fy9eTNu2bWnQoAFffvkl8+bNo2fPnuzbty94\n7HHjxlGmTBnmzJnD008/zRNPPMH48eOD2/fu3cvw4cNZsmQJkydPZvv27fTs2TO4feTIkUyaNIkJ\nEyawcuVKxo8fT8OGDQF4++23qV27NnfffTebN29m06ZN3jmQHDWhfuIM9eOPP3LRRRfRrVs3lixZ\nwo033sitt956SO1qdnY2I0aM4PnnnycrK4u6deuyc+dOevfuzezZs5k/fz4nn3wy5557Lj///DPg\nan0uuOACAL766itGjx7N0KFD2bNnT9Tzt3v3btq0acORRx7JF198wdy5c6lZsybt27cnOzs7uN+a\nNWuYMGECkyZN4tNPP2XhwoXceae7zH/gwIH06NGD9u3bB8/zWT6vbXrrrbd49NFHefbZZ1m5ciWT\nJ0/m9NNPD56fM888k379+gXLPeaYY9i8eTPnnHMOTZs2ZcGCBUybNo1du3bRvXv3HGXPmDGDJUuW\n8Nlnn/H222/zySefcNttt+UaU6z3dEDo+VqwYAGbN28Ovk/OO+88GjVqRLVq1QDo2rUrmzdv5sMP\nP2TRokW0atWKdu3aBZPZH3/8kXLlykVdypcvz/XXX+/r9Qy48847eemll/jvf//LsmXLGDx4MNdd\ndx0ffRQ+02+SU9VcF2Awbl7jy4E04ABwMtAG2A7c5Kec4rgA6uaMUO3WTY0xRZD7KIy1veCW/Nqx\nY4empKTozJkzI25/+eWXtVy5cjnWff/99yoiOmvWrOC6X3/9VStUqKCjRo1SVdXLLrtMzzrrrKjH\nbd269SHbO3TooFdffXXUxyxbtkxFRDds2KCqqv3799f27dtH3T8zM1MfffTRHOumT5+uKSkpun37\ndlVVvfzyy2PGGW7w4MHaqFGjHOvuu+8+TUlJ0bVr16qqe81SUlJ04cKFMcs6cOCA1qhRQ8eNG6eq\nqh9//LGWLl1a169fH9xn1qxZKiI6ZsyY4DoR0bfeektVVUeNGqUNGjTIUe6+ffu0cuXKOnHiRFVV\nHTp0qKanp+vOnTuD+9x77716/PHHB+/37dtXu+Xjy+exxx7TE044Qfft2xdxe+vWrfWmm27KsW7I\nkCGHnLcdO3aoiOj8+fOD8VSsWFH/+OOP4D5jx47VtLS0HOsiye09Hf4eCPXAAw9olSpVdPXq1aqq\nOm3aNC1XrpxmZ2fn2K958+b68MMPq6p7vVetWhVz2bZtW8RYGjdurMOGDcuxbteuXZqenp7j/0tV\ndcCAAXruuefGfO4BjzzyiNarV8/XvrE+t7xt+c5t/A5l8xDQDHgVeNFbN8tLFN9Q1SfjkagWdUOG\nJDoCY0xJUbFiRfr06UPHjh1p164d7dq1429/+xvHHHNM1McsW7aMUqVK0aJFi+C68uXL06RJk2DT\n3aJFi7jwwgtjHrtp06Y57tesWZOtW7cG73/zzTcMHz6cRYsWsWPHjuD1j+vWraNmzZr07duXDh06\n0KBBAzp27EjXrl3p0qVLnq6RXLhwYa5xhlq+fDmnhU1ZdcYZZxyyX+nSpWnWrFmOddu2bePf//43\n06dPZ8uWLezfv5/s7Oxg8+Xy5cupVasWtWrVylF2Skr0xrlvvvmGH3744ZBOQ7t372bVqlXB+3Xr\n1qVs2bLB++GvdX5dfPHFjBw5kszMTDp16kTnzp05//zzOeKII6I+5uuvv2bGjBmHxCwirFq1ilNP\nPRVw74/QZtczzzyTPXv2sGrVKho3bhy1/Py8pwHef/99hg0bxieffEJmZibgXt9du3Zx9NFH59j3\nzz//DL6+pUqViuu1g1lZWWRnZ9O5c+cc6/ft20e9em4uka5du/LFF18Abk73pUuXxu348eR3EOz9\nwKUi8jSuZ3JVXI3hFFWdUYDxFSn79yc6AmNMSTJ69GhuvvlmpkyZwnvvvcedd97JpEmT6NChQ57L\nyktiFt6pQkSCHTf++OMPOnfuTMeOHRk7dixVq1Zl27ZtnH322cFm1pNPPpm1a9fy8ccfM23aNPr0\n6UOzZs2YOnVqnuOOt9TU1ENei969e7Nt2zZGjhxJ3bp1SU1NpW3btjGbjXNz4MABTj75ZMaPH3/I\nvN6hvXFjvdaHo3bt2qxYsYJp06YxdepUBg4cyLBhw5g3b17U6+kOHDjAeeedx6OPPnpIzIGm3GjC\n948mr+/pb7/9ll69evHMM8/wf//3fzlirV69OrNmzTrk2OXLlwdcs3KjRo0QkYjxiUiwbD8C5+WD\nDz44JKENnMdRo0axe/fuHOuSUZ4GwVbVL4AvCiiWIi/sx7Qxppjw+b2WEE2aNKFJkyYMGjSIrl27\nMmbMGDp06MARRxzB/rBfrCeeeCIHDhxgzpw5wS/S3377jaVLl3LVVVcBLnH77LPPuOeee/IVz/Ll\ny9m+fTv33nsvdevWBdwXeHjCdeSRR3LhhRdy4YUX0qdPH1q0aMHKlSupX79+xNjD5TXOE044gffe\ney/Huq+++srXY2fPns2TTz4ZrBEKXIcXcOKJJ7JhwwY2bNgQrD386quvYiZxp5xyCm+88QaVK1cO\nJiv54ee1ivXYLl260KVLF2677TaqV6/O7Nmzad++fcRyTznlFCZOnEidOnVyXAcYbunSpezevTuY\nZM6ZM4fU1FSOO+44X3FFe0+H++mnnzj//PO59tprg51pQmPdsmULIhKstQtXs2ZNFi9eHDOWvJyb\nRo0akZqaypo1azjnnHMi7lOjRg3f5SWS30GwF4rIABGJ/dOghIvReckYY+JqzZo1DB48mDlz5rBu\n3To+//xzlixZwkknnQS4Jqvs7GymTp3K9u3b2b17N/Xr1w9+mc6aNYulS5fSq1cvKlSoEOwwMmjQ\nIBYuXMi1117LkiVLWLFiBaNGjWL9+vW+4qpTpw6pqak8+eSTrF69msmTJzMk7Jqbxx9/nDfeeIPl\ny5ezcuVKxo0bR4UKFahdu3Yw9i+++IKNGzeyffv24ONCa3fyGud1113HqlWrGDRoECtWrODtt9/m\n+eefB3KvNW3QoAFjx45l2bJlzJ8/n549e5KaenCQjvbt29OwYUOuuOIKFi9ezJw5c7jlllti1gxd\nfvnlVKtWje7duzNz5kzWrFnDzJkzGThwYI5m5dxkZmby7bffsmLFCrZv3x61Q064MWPGMGrUKL79\n9lvWrFnD6NGjOeKIIzj++OOD5c6bN4+1a9cGz8ENN9zAr7/+So8ePZg3bx6rV69m6tSpXHvtteza\ntStY9r59+7jyyivJysri008/ZfDgwVxzzTUxe/hC7u9pyPkeuOiii6hduzY333wzW7ZsCS6qSvv2\n7WnZsiXdu3dnypQprFmzhjlz5jB06FBmz54NHGxWjrWENkvv3buXxYsXs2jRIrKzs9m8eTOLFy8O\nnq+yZcsycOBABg4cyEsvvcSqVatYvHgxzz33HC+++CKxBPbdsGEDe/bsYfHixSxevNj3+Yw7Pxcm\nAh8Ce4E9uEGvLwXSDudix+KyENIhxRhTNFEE/4G3bNmiF154odauXVvT0tK0bt26evvtt+foYHD9\n9dfr0UcfrSkpKcGL53/++Wft27evVqpUSTMyMrRjx46alZWVo+zZs2frOeecoxkZGVqxYkXt0KGD\nbt68WVVV27Rpc0hHhfBOERMmTND69etrenq6nnHGGfrJJ59oSkqKzpgxQ1VVX3jhBT3llFO0fPny\nWqFCBW3durXOnTs3+Pi5c+dq8+bNNS0tTVNSUlQ1cmeEWHFGMnnyZG3YsKGmp6drq1at9KWXXtKU\nlBTdunWrqkbuxKOqumTJEm3RooVmZGRo/fr1dezYsdqkSZMcHRK+//57bd26taalpWmDBg30/fff\n13LlyuXokJKSkhLskKKqunXrVr3yyiu1WrVqmpaWpscee6xeddVVwec4dOhQbdKkSY5YwmPctm2b\ndurUScuVK5fjNT7nnHO0TZs2UV+Ld999V88880ytWLGili1bVk8//XT98MMPg9tXrFihZ511lmZk\nZOTotLNy5Uq9+OKLg++fE044Qfv376979+5V1YPvhXvuuUerVq2q5cqV0379+unu3bujxhKQ23s6\n/D0gIpqSkhJcAvcDsf7+++86YMAAPeaYYzQ1NVXr1KmjPXv21B9++CHXWCJZs2bNIcdMSUk55HV+\n6qmn9KSTTtK0tDStWrWqduzYUadOnRqz7NatWx9SbuhziSTW5xaH2SFF1Gd7iYhUBS4DegGn4Hov\nvwW8qqqfxzVjLUJEREGpUQNChvEyxhQh0a45MsXbyJEjGTp0aHBImuIkMzOT66+/nltvvbVQj9uv\nXz+2b99+SBO+ib9Yn1vetnwPluX7mkNV3Qo8ATwhIifiptK7DOgjIutVtW5+gygOmjdPdATGGGNi\neeaZZzjttNOoUqUKc+bMYcSIEfTr1y/RYcVdVlYWaWlp3HLLLYkOxRRReeqQEqCqy0RkOPAd8ABQ\nO65RFUFnn53oCIwxxsSycuVK7rvvPnbs2EHt2rW5/vrrueuuuxIdVtw1atSI5cuXJzqMQ8TqHSwi\nZGVlBa87NYnlu1k5+ACRtrhawwuBssA8XNOyv77exUygWXnbNggbTskYU0RYs7IxBW///v2sXbs2\n6vbMzMyYY0OanAqyWdlXcigijXHXGl6GqyVcA4zFJYXf5/fgxYGIaIUKyvbtEKNnvzEmiVlyaIwp\napIhOTwA/ApMBF5R1Vn5PWBxIyJqXyrGFG2WHBpjippk6JDSA3hfVf/M74GMMcYYY0zy89W4r6pv\nRksMReQcERkd37CMMcYYY0wi5OvKTxGpLyLDRWQ18DmuZrFAiTNYRFaLyG4RWSQiuc66LiJ1ReRA\njKVH2P7/JyKzReQPEdkkIo+KSFrBPTNjjDHGmOTheygbEakAXAL0AVp4qxfjhrJ5Pf6hHWIEcAtw\nB/ANbpaWiSJyrqpOifG4TRyMN9S9QEvg48AKEWkKfIKbBeZcoB7wCFAT6BmH52CMSUJ169bNdQo1\nY4xJJoG5ywtCzA4pIpICdMYlhN2ANGAj8DZwA9BGVWcWWHQH46gC/Ajcp6rDQ9ZPBY5W1TwNQS0i\n6cBm4CNVvTRk/TtAI6CRqu731l0BvAz8RVUXRSjLOqQYY4wxJmkcboeUqM3KIvIosAF4HzgPeAeX\nKNYBhgCF+TO7M1AGGBe2fizQRETymj5fhBujcUxghYiUBjoB4wOJoWcCbl7p7nkN2hhjjDGmqIl1\nzeHNQFXgQ6COql6uqp+o6gGgsKvKGgF/quqqsPXf4ZLURnksrw+wlZAmZeA4XM3od6E7eh1xVuXj\nGCaJTZ8+PdEhmHyw81Y02Xkrmuy8lVyxksNRwE7ctXf/E5GnROT0wgnrEJWAXyKs3xGy3RcRqQm0\nAcZ6iW7oMQAizcC+Iy/HMMnPPvSKJjtvRZOdt6LJzlvJFTU5VNWrgerA5cAC4FpgjogsA27jMGoP\nRaRdLj2IA8tn+T1GDL1xtY1jctvRGGOMMaakidlbWVWzcT2RXxeRGrg5lXsDt3u7PCAizwBvevv6\nNRs4wcd+f3h/fwaOirA9UJu3I8K2aK4AFqnqt2HrAzWGFaMcJ3x/Y4wxxpjiR1XzvACnAk8C24AD\nwM/5KScPx7sC2A8cG7a+r7e+rs9yTvPivSnCtjLAbmB42PpUb/3dUcpUW2yxxRZbbLHFlmRaDifv\n8jW3cjQiUgbXk7m3qv413wXlfpwqwHpghKreE7J+KlBFVZv5LOcp4Gqglqr+FGH7O8CJuKFsDnjr\neuGaoE9V1YWH/WSMMcYYY5LYYSWHhUlE7gf+CdzJwUGwrwa6qepHIftNw/WuPj7s8WVwYzTOipbI\nikgzYA5uEOyncYNgPwR8GjoeojHGGGNMceV7hpQkcAeu93R/XEeZ/wEXhyaGnhQid7Q5F3ftYNSO\nKKq6WEQ6Ag8CHwC/4gbAvvNwgzfGGGOMKQryNbdyIqhzn6rWU9V0VW2uqu9E2K+Nqh4XYf27qlpK\nVd/N5TizVLWlqmaoag1V/Vd4ZxsRqS0ib4rILyLyq4i8JSLHHP6zNAVFRP4mIu+IyDpv3uzlInKf\niJRNdGwmb0RkijeawfDc9zaJJCJdRWSGiOz0PivniUjrRMdlYhORliLysYhsEZHfRORrEemX6LiM\nIyK1RORJEflSRHZ5n4d1Iux3lIi8KCLbROR3EflURBr7OUaRSQ6ThTf13udAA1xHmV7A8cBn3jaT\nnP4F7MP1tO8MPAP8AzeXtikiRKQn0BR3wbVJYiJyLfAuMB+4APgbMBHISGRcJjYRaQJ8imtZ/Dvw\nV2AeMMo7pybx6uP+n3YAM4n+efgB0BE33fGFuI63n3vjPcdUZK45TBYi8k/gEaCBqq721mUC3wOD\nVPWJxEVnohGRyqq6PWxdYN7sdqo6PRFxGf9EpCKQBQzADbE1QlWHJDYqE4k3peky4DZVfTLR8Rj/\nROQ+4BagoqruDln/Ja4Rr2XCgjOHEJGrgOeBeqq6LmR9d+BtoI2qzvTWlQdWA6+q6oBY5VrNYd51\nA+YGEkMAVV2DG7vR5l9OUuGJoWc+bkD0WoUcjsmfB4Elqjo+0YGYXF2FG2bsuUQHYvKsDLAnNDH0\n/IrlDEVJN2BjIDEEUNXfgPfxkavYic67k4g8IPZ32PzLRU1rXHX8sgTHYXIhIv+Hu4TjhkTHYnxp\nCSwHeorIShHZKyLfi8j1iQ7M5OplQETkPyJSQ0QqiMjVQFvgscSGZvIgVq5SR0RiXt5RlHorJ4tK\nRJ9/OdLsKiYJiUgtYBhumKJvEh2Pic4bhupZ4GFVXZnoeIwvNb3lIWAw8ANwMfCUiJSypubkparf\niUgb4B3gRm/1HuA6VZ2YuMhMHlXCNSGHC8woV5GDs9AdwpJDU+KIyJHAJNwH3pUJDsfk7jYgDbgv\n0YEY31KAsrgJEiZ566aLSD1csmjJYZISkfrAW8BS4BogG9cM+ZyIZKvq64mMzxQOSw7z7meiz78c\nqUbRJBERScP14MoEWqnqxsRGZGLxhoi6A3cNW5p3/sTbnCoiFYCdgRmNTNLYjutROTVs/SdAJxGp\npqpbCj8s48P9uB/O56vqPm/d5yJyNDAS1xnMJL9YuUpge1R2zWHefYdryw/XCNeT0iQpESmN+0V8\nCtBFVe18Jb9jcfObj8V9mP2MaxZRYJB329e4XaZQfZfoAEy+NcZ1/NoXtn4eUFlEqiYgJpN3sXKV\ndaoatUkZLDnMj/eAFt7wNUBwKJuWuKZKk4RERIDXcJ1Quqvq/MRGZHxaCLTxltYhiwCverftOsTk\nE5igoFPY+i7Aeqs1TGqbgabej+lQLXBNzDsOfYhJQu8BtUTk7MAKbyibbvjIVaxZOe9ewPWYnCQi\nd3nrhgNrcWMNmeT0DG7Q0BHAbhE5I2TbelXdkJiwTCze0Aszw9e7XJ+1qvpFoQdlcqWqH4rIdNx1\nalVwHVJ6AO2BvgkMzeTuKWAC8IGIPAPsxl1zeAnwWIQaRZMAInKRd/NU3I/lriKyDdjmDV/zHjAX\nGCsitwK/4K73BXg41/JtEOy8E5HawONAB9xJmQrcHDoApUkuIrIaOGR6Ic8wVbWp2IoQEdmPGwT7\n7kTHYiLzpqa8H/ejrCJuaJv7bZzK5CcinXAdwU7CdQZbhRuz8nm1pCEpiMgBIs+MMkNV23r7HIWb\ntOMC3Hn8ErhFVSMNcZOzfDvPxhhjjDEmwK45NMYYY4wxQZYcGmOMMcaYIEsOjTHGGGNMkCWHxhhj\njDEmyJJDY4wxxhgTZMmhMcYYY4wJsuTQGGOMMcYEWXJojMk3EblCRNaG3P9ORK6L8zFaiMhcEfld\nRPaLSNN4lm8Kn4isEZHR+XhcdxG5uSBiMsYcZMmhMeZwnAIsABCRI4GGwNdxPsZooBRwLnAmsCLO\n5ZvCl9/ZFy4ALDk0poBZcmiMORx/4WAyeAqwH1gcr8JFJAVoAExW1RmqOk9Vs+NVvjl8InJEomMw\nxsSXJYfGmHzxErfmHEwOTwOyVHWPz8eXE5GnRGSDiGSLyHIRGRCyvQ+wDzd/+RAROSAiP8Qob6i3\nT2MR+UxEdonIRhEZFrZfqog8JiJLRWSniGwSkfdEpGHYftVEZExIfBu9/Y72tpcSkXtEZKWI7BaR\nbSIyU0TOCivnGhFZFLLPiyJSMWyff4pIloj8ISI7RGS+iHT38Rr2Civ7FRGpHrL9AxE5pCZXRKqL\nyF4R+WfIukwRGSciW73nu1BELojyGp8kIlNEZCcQc65k77mt9mKcJyL/F2Gfo0XkWRH5n3fe1nmx\n1AzZ5yWgD1DLiyH4fvB7To0x/pROdADGmKJFRFYDdb27CnwoIhK4HzIhfD1VXRelDAE+xCWXdwHf\n4pqNHxORo1X138AHQEtgNvCit/wZI7RAU+U7uKbo+4BOwF0isl9Vh3vbU4FywL3ARqAicD0wR0RO\nUNWt3n5jgWOAfwHrgWpAOyDD23478E/gDlxtaXngVKBSyPN8ALgFeAIYCNTyjnuSiJylqioilwOP\nAEOBWUA60DS0nCiv4TXAs8DrXiw1gfuB00XkFFX9A3gVeM17XstDHn6593q95pVVG5gHbPae00/A\nJcBbItJdVT8Ie43fBUYBDwAHYsR4FfA47nxMAOp78ZYN27US7tzeAWwFauBe91le7HuA4UAV3Gvc\nDfejIfB+8HtOjTF+qKottthii+8FOAGXvDwKLAWaePd/Bfp7t5sCpWOUcR4uqbgibP0LwG6gkne/\nlLffEB9x3Y1r1h4Utv55L7byUR6XgkvIfgP+GbJ+J3BjjOO9D7wZY3tdXM3nnWHrz/Se0/ne/SeB\nBXk8Bym4RG5q2PqWXtk3evfTgF+Ae8P2Wwh8EHJ/FLAFOCpsv0+AbyK8xlFfl5B9BViHuyQgdH0P\nL8bRuTy/2t5+3UPWvwSs8/n6HHJObbHFFn+LNSsbY/JEVZer6hJcrdp0VV0K/IGrDZqoqku8ZV+M\nYs7GJRmvh60fCxyBS6Dya2LY/Te82BoHVohID68H9M+4BG4XEOhQEzAfGCQi/UWkMYeaD3QVkREi\n0lJEyoRt74BLkF7zmqBLiUgp73E7gVYh5TQXkf+ISDsRSffxHBsCVfFq/gJUdTawFjjHu58NvImr\nKQw89yZAM+CVkId2wtXk7gyJtTQuOWwmIuE1fe/6iLG2t4Sfj7dwr3kOIvIPr4l8p7d9Ha6m0lfT\nsM9zaozxwZJDY4xvIpISkji0xDXblcIlOhuArd793FQCdkRIIDfjEqqYTaq52BLhvuCadBGRbriE\n8TugJ3A6rqnyJ1xNW0AP4D1gELDYu/bwrpDt9+Jq0roBM4HtIjJaRAKxV/WOuwrYG7LswSWrlQFU\n9RXgH14cU4AdIvKWiNQlusAxNkXYtpmcr9+rQB0ROce7fwWuRm1SyD5Vgd4R4nzI21457BiRjhuu\nhvc3x/lQ1f3A9tB1InIT8DQuGf0r7vrVM3CvX+g5iSgP59QY44Ndc2iMyYtpeLVSuFpS2RENAAAD\nwElEQVSdV3G1fYH7e3HXHbZR1ZkxytkBVBKR0mEJYvWQ7flVDVgTdh9c8gruWrrvVfWqwA5espsj\nIVXVn4CbgJtE5HhcZ4hhIrJVVZ/zkpyHgYdFpCquqfxxXHNmT1wCpLgaxF8ixBlMkFT1BeAFEakA\ndAQewyU70WpQA69P9QjbquMNL+SVPUNE1gG9RGSmF9tEVQ29fnM7LsF9AJeQhdsYdt/PUDSBBLJa\n6Ervx0N4snkJron81pD9Mn0cI/TxuZ5TY4w/VnNojMmLa3A1Mo8AK73bpwLbgDu926eR+1iHM3DX\nE14ctr4XrpPBnMOIsUfY/Z64Ztyl3v0MDm3W7O3FE5Gqfq+uk8zPhDRPh2zfqqqjgakh2z/FXTNX\nV1W/ibCsjVDOr6o6Edd5I1JTdsD/cDVyl4auFNdTui7wedj+Y4G/AV1xNaivhm2fgrtONCtKrHtj\nxBLNeuBHDj0ff+PQiokM3A+LUFdyaBL6Jy75Dpfnc2qMic5qDo0xvqnq9wAiMgTX0WChN1zI0bgO\nBn57hX6E65n7rFfr9h2ut/KVwH2qmt+aQwGuDrm2r7NX5t2qutPbZwrQXUQew/WIPg24EZf44T2/\n8rhEbxywHJe4XAAcBXzs7fMurpfyN95jT/GO918AVf1BRB4CnhKRE3AJcTZQB2gPvODV6j2HS17n\n4HrqNsQ1/X4c7Umq6gHvHDwrIoHa29rACFzi+FLYQ17F9QR+FlgboVZ3CPAV8IWIPIWrea2IS1Dr\nqerfo8USI0YVN4zQC+JmQ3kDOB64DddBKNQU4FYRGYzrNd0Wl0SGy8Kd3+twtaPZqvotPs6pMSYP\nEt0jxhZbbClaC1AGd81aB+/+P4H5+SinLPAfXHNvNi4J6x+2Tylcx5W7fJQX6EnbCPgM1yFhIzA0\nbD/BDYuyHvgdV8vWDPgBGOXtcwQuyVvqPddfcMnTJSHl3Ax8ias13QUsww3LUyrseJd7++30yvrO\ne941ve29vXg343pqr8LVzJb18Zwvw/U83u3F8TJQLcq+87zX554o22vienb/6J2PDbgE9bKw13gf\nkJKH83wTsBrXaWkecFboa+3tk4a75nALLnGchKsBzXHucTWE43DN4PuBH/yeU1tsscX/Iqr5ncXI\nGGOSh4jcjasBK6OqUcfeM8YYE5tdc2iMMcYYY4IsOTTGFCfWFGKMMYfJmpWNMcYYY0yQ1RwaY4wx\nxpggSw6NMcYYY0yQJYfGGGOMMSbIkkNjjDHGGBNkyaExxhhjjAmy5NAYY4wxxgT9P9n3JtWapAwZ\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11b8aed50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"make_plot(log_likelihood_sgd, len_data=len(feature_matrix_train), batch_size=100,\n",
" label='stochastic gradient, step_size=1e-1')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Smoothing the stochastic gradient ascent curve\n",
"\n",
"The plotted line oscillates so much that it is hard to see whether the log likelihood is improving. In our plot, we apply a simple smoothing operation using the parameter `smoothing_window`. The smoothing is simply a [moving average](https://en.wikipedia.org/wiki/Moving_average) of log likelihood over the last `smoothing_window` \"iterations\" of stochastic gradient ascent."
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAocAAAFmCAYAAAAf5DBYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYVNX5wPHvAQGRJk0EfwGlREGxd0VXNIISa2JXomAs\nsSRobGABQUWNvWIXsRfsEkWCBTTEAgKiSFFEQEF6W2D3/f1xZpyZO7ecO2Xr+3meeXbn3nPvPVN2\n551T3mNEBKWUUkoppQDqVHYFlFJKKaVU1aHBoVJKKaWU+o0Gh0oppZRS6jcaHCqllFJKqd9ocKiU\nUkoppX6jwaFSSimllPpNtQkOjXWVMWauMWadMWayMeb4HM6znTFmrTGm3BjT0Wf/gcaYCYkyC40x\ntxljNi/Mo1BKKaWUqtqqTXAIDAOuBe4GegOfAC8aY3rHPM8DwDIgK8GjMWZn4F1gEdAHGAScBTye\ne7WVUkoppaoPUx2SYBtjWgM/AjeKyPVp28cCrURkV8fznArcBtwE3AF0EZE5aftHA92AbiJSlth2\nBvAEsIeITC7MI1JKKaWUqpqqS8thb6Ae8LRn+yiguzGmQ9QJjDFbYgPDS4EVPvs3A3oBzycDw4QX\ngI3AMblVXSmllFKq+qguwWE3oFREZnu2TwdMYn+UW4GvReSZgP2dgM0T5/yNiJQCsx2voZRSSilV\nrW1W2RVw1AJY7rN9adr+QMaYHsDpQFj3c/IcywKuE3oNpZRSSqmaoFJaDo0xhyZmC0fdxhXgWvWA\nB4HbReTb/GuvlFJKKVVzVVbL4QRgB4dyaxM/lwFb+uxPtuYt9dmXNCBx7D3GmGaJbY0SP5saYxqL\nyGpSLYbNA64zzaG+SimllFLVmlNwaIw5CPgiEUR59zUGdheRD10vKiLrgZnOtbTjABsYYzqmzy4G\ndsSmpPk65NiuwNbAAp99XwCTgd2x4wpLE+f8jTGmAdAROzElizGm6k/3VkoppVStIiIm12OdUtkY\nY8qA/URkks++PYBJIlI310o4XL81MB8YJiJD07aPBVqLyC4hx/4eGxymOwK4HDgNmCkiXyTKjsYG\nk91EpDyx7XTgSWBPEfnS5/xSHdIBqUyDBw9m8ODBlV0NFZO+btWTvm7Vk75u1ZcxJq/g0LVbOewC\nDYCykP15E5HFxpjbgauMMauxLX4nAyXAUelljTHvA+1FpEvi2Jl4WimNMdslfp3kaYkcTCq59n3A\ndsAtwIt+gaFSSimlVE0TGBwaY7bFdqcm7ZnoQk7XEOgHzCt4zbINBFYBF2NbAr8FThCRdzzl6pDj\nRBsRmWKMORy4GXgTmw/xCexKKUoppZRSNV5Yy+FfgOuwY/oEuIfMFkRJ3N8EXFCsCv52Mdt3e2Pi\nFlbuEIdzPYntKvbb9zFwQC51VNVHSUlJZVdB5UBft+pJX7fqSV+32itwzGFi1ZFtsQHgOGwA6J34\nUYodsxc2W7hG0zGHSimllKpK8h1z6Doh5WDsbOVVuV6optLgUCmllFJVSYUEhyqYBodKKaWUqkry\nDQ6dJm4YY+obY64zxnxjjFlrjCnz3DblWgGllFJKKVV1uKayuRU75vAd4BXsWEOllFJKKVXDuI45\n/Am4X0RuKH6VqhftVlZKKaVUVVIh3cpAY2xyaKWUUkopVYO5BodvAAcVsyJKKaWUUqryuY45vAcY\naYwpB94GsvIaepahU0oppZRS1ZDrmMPytLu+B4hI3UJVqjrRMYdKKaWUqkryHXPo2nLYj4CgUCml\nlFJK1RyaBDtP2nKolFJKqaqkomYrK6WUUnn75hu4+GK4/XbYuLGya6NUtNJSmDevdr1fA7uVjTGP\nAUNFZG7i9zAiIv0LWzWllFI1yfr1sP/+sGyZvb96NVx7beXWSakwP/8Mhx4K06fDHnvA2LGw5ZaV\nXaviC+xWNsbMBY4VkSnGmO8JH3MoItKxCPWr8rRbWSml3Lz4Ipx4YuY2/fepqrIGDWDDhtT9m2+G\nyy+vvPq4yrdbWccc5kmDQ6WUcvPgg3D++Znb9N+nqqoWLoR27TK3NWpkW7yrOh1zqJRSqlpo2LCy\na6CUuxdeyN5WVlbx9agMzsGhMWYLY8yFxpgXjTHvJ37+zRijf+5KKaUiffxx9rbZsyu+HgATJtgu\n7iuvhPLy6PKq9vFr1a4t7xXXJNhbA+OB3wM/AIuArYEOwLdAiYj8XLxqVl3arayUUm6MTyfXPffA\nhRdWbD3mz4ff/S5zm/4bV1533w1//3v29urwXqmobuVbgOZADxHZTkT2E5HtgAOBLYGbc62AUkqp\n2mvduoq/5iOPZG/7+uviX3fFCpg5s/a0PlV3dQIipNGjK7YeUb780t4KyTU4PAK4SkQmpG8UkYnA\n1UCfwlZLKaVUTXPaadnbWreu+HrMnJm97T//Kc61vvjCtpgaY1OgbL89/OEPFTN27Ycf4Lzz7Oza\nFSuKf72qaNUq2/p3zDHwwQfxjq0bsCjw8cfnX69CGTQIdt/d3gYPLtx5XYPDxsCCgH3zE/uVUkpV\nEz/9BH/5C5xyCnz7bcVc85VXsrdVxgD/xj6fWA0aFP46v/5qc+N5jRsH77wTffyoUXDIITBgAKxd\nG+/aItC7N4wYAbfeCmefHe/4mmLIENs9/Prr0KdPvJnG6SlsqqLVq+HGG1P3b7utcK3SrsHht8AZ\nAftOB74pTHWUUkpVhDPPhJEj4bnn7MSMihhH5deFXBmrTmzalNtxM2bYsYrJlsDp08PLP/lk8L5R\no8KPnT0bzjgDxo+HO++EBx6IV9fZs+1qNEkvvRTveBfl5TaxeVV2222p39esgaefdj/2f//z315V\nWg6nTMm8v3o1LFlSmHO7Bof/Ak4xxow1xvQzxhxhjDnLGPNv4FTg1sJURymlVEUYOzb1+1df2ZbE\nyuDNe1gR/ALS996LPm7oUDuZJWmnncIDzblzg/cFjWdLuvPOzPv//Gd0/dItXZq9bdaseOeYOhVu\nugk++ih7388/29VuttgC/vSnqrm0nF9r66OPuh37zTfBgWT9+rnXqZD8xskW6u/YKTgUkVHAecBO\nwCPAW8CjwM7AeSLyTGGqo5Sq7RYvtq0k48ZVdk1qLr+up0IPaPcTNIZr4cLiXztdroHMs89mb/v0\n0+DyYeMp/WZup3v11extcbqW7703e1tYsOr1/few114wcCAcdFB2zr/HH4f//te2OL/yim2Frmqu\nvjp7W1BroNf11wfvqyqB8DnnZG+bN68w53bOcygiDwHtgB2BHomf24jIw4WpilKqtisttQOr//Y3\nu56p34dxdSQCV1wBrVrZmbKVnQrj/fezt11xRfGv26yZ/3Zv91ixrVqVva1Tp/Bj/CaxQPhs67A1\neN9+O/x66S2USU2a+JfdtMm2FKYH/U89lV0uzvvuhhvs32PSSSdljsHz/m1eeaX7uSvKHXfkfuxb\nbwXvqwrBoV/LcNj2uGKtkCIi5SIyQ0QmJH7qhHylVME8+2zmh+Kpp1ZeXQrpnHPgllvsBIW//hXe\nfbdy6+PXejJjRvGv6xeUQXDQU2jl5XZtXL/ALCxwKi+H3Xbz35ceQHmFBY7LlwfvC6uH1+LFsPfe\n0LIl9OwZPuEibHzgnDnw2Wep58FvZu8bb6R+/+qrzH1R3eRBROCaa2z9//GPqjMJZPPNg/eNH29/\n/vKL7VLfaSf37upCCXpv9etXmAAxzgopXYwxTxpjZhpj1iR+PmGM6Zx/NZRSyqb9qIpKS+34nrgz\nRpO8efV6986/TvnwC8b8ZvCGKS+Hl1+247JcPtA3bAhucUkGWDNn2qTYxXoffPxxcAtXWOD08cfB\nr/199wUfV4wcjt5g9O67U0MCPvggM4Dz8j7G996z4waNsS2ne+1lJ8GA/xCAsC7ZXIPDQYNg2DAb\n0Nx1l11/uyoI6/ZfudIG5UOH2i716dPtlz6/1l6wZbbeGjp0KFzKpLD31vDh+Z/f6eU0xpQAU4A/\nAp8C9yd+HgVMNcYcnH9VlFK13Zo12dsqey3T2bNtK8KOO0KjRtkTBaojv0Bn9ep4ufAaNIA//xlO\nP93O4I3qsgwbm7d2rR0rtfvucPHFsOee4eVzNWRI8L6wD9tffw3eN2aM/fnvf9tZrNddlwqWFy+O\nX0cI77acODHz/rBhmfevu87+3Hrr7GPTA8vSUttV/MknmWWeftpOXPFrgXztteB61a1rW2SvuCLe\na3fTTZn34068ycWkSdFlot7Pr7ySOa5TBN58M7tcWRlccIGdwDNvHlxySby6BvH7X5l0awGmCLvG\n+rcBXwIdRKSviFwmIn2BbYHJif1KKZWXrbbK3vZzJS/M2dnTNzJggNuHS5L3w7sqCPpgcU3z8cUX\nmbN0f/nFfxzjxo02h+KaNXD//cHnW7cOHnssVS8R/8H2+QoL1sJaDqO+oCxcaHPojR5tJzLcdZfd\nHvaYITgAefHF4GOCJvUkNW0afO70x/j++7Bsmf85Pv/cPzgMm+3800/2ObjlFtsaGTRGM0ohx/MF\ntYb/7W/Rx0a95uedl70t2XoqApMn2/f+ggWwaFGqzOTJ0dd2kWsvhivX4LAbcLOIZLxdRGQVdum8\nHQtdMaVU1bBhA/z4Y8UMwvZr7Ujm7Vq71q50sP329mdljk265hq3ctOn+5c99NDC1ieul1/2337B\nBW7H+yV2/sMfUi1TS5bYD+D69WGHHeyH9PPPB59vzZrsVr2pU93qEkejRsH78gkO+/fPLHP55W71\nCXoPz57tdrzfjOQWLexPv/Gd6Y/x88/D63XQQdnb99/frV4i9ktUlLgrlkQpLc1sHQ0KpMMee5Lf\nezxKcizigAF2jOoOO8Cuu2aXC2uJ9rNhg/3SccIJqS9hYS2HheAaHM4HgjL71AcqKUOWUqqYliyx\n45Dat4d99incTLggjz+evS35gfbXv9rxVTNn2p+vvGI/CGbOjP/PNl/vvms/ePxmhKa7+27/7ZU5\nW3nDhuKtI7z55rYVcNdd4yVtLsb7as0a2wWbnhS4TZvg8vkEhy6rnfiZP98G6t4WuebNg49Jthht\n3AgXXZS9v0ULW1+/lqX0SSRhXeylpf6B9Icf2hZFl6EeySBm6lTbouoXzBRy1ZbnnrPP2+abw7HH\n2seQz5jPsC8SQZ591g7NSLYcg/97e++9/Z/D2bNti+TVV2c+X3ffbYcLvPQS9Ople1OqSnB4MzDE\nGNMufaMxZhvgOuBG36OUUlXO4sX2Q9PlH+f996c+UL780nb9FZNfSpNkS8Aznmyqp5xiPwi2396m\niBk0qPD1CfsQLC+Hvn3DZx4HdcOlD1zftMm2OMyZ416vJUvsa5jLB0TYhAUXUYHB/vvHT8T7yy+5\n18fPihW25eaAA6Bbt1QXZ9gM1KDgcPp0O56wELypbTp3tuM2u3TJ/GIUdr1kF2VQQD1mTPCM5Uce\nscvIQfjruGFDcLflRRfBZpsFH5u0aZN9r+22mx2Luc8+2QnDg/4+vvsu+vxep5yS+p/22mu2JTuo\nZfaQQ6LPFzYLPYxfwnCvOXOy81hu3GjfDyNG2DRCf/97at9ll6V+Lyuz456L3a2MiETegKeAH4H1\nwHjg+cTP9cAPwMi025Mu56wpN/sUKlU9TJsm0rKlCIh07SqyenV4edvGlbo1aFC8ui1dmn09EHn3\nXZGff/bf570tWVIxdfLeggSVb93a7i8vFznwQLutfn2Rt98Or89772We5/e/F1m+PN5juuOO3B5L\n0rp1bs9JnNvRR+dWlyC33ZZ5ntNOs9tPOCG4DgcfnH2e554TqVMnt8e0fn32tg4d3J77sDLt29sy\nP/0UXGbevOjr7L138P5bbxU5/PD8X9dWrTLvv/xy5vPr+j4sLxd58kmRXr1EBg8W2bgxc/+GDfHq\ndfjh0e+h/faL/3i32kpk113dyg4caB/Xpk32eldd5f5+2HdfkYcfjroGIpJ7bOPacnggsAlYCHQA\n9k78XAiUY5Nip9+UUlXQNdekumBnzIjuFvVyaTEIMmEC9Ohhu0W+8VmNPWgd2vXr3fMCuowlimPB\ngsKeL2nlSvtzzBibJgVsK0fYWMY1a2xrSLqZM+HhmMsQhL2Gv/td9PHFSDOTbM3y+vbb3M536aWZ\n95MTbcLGqaa3HIrY8Xwnn+yfW9CFXwL3XFuj0iVXwAg7V9RrVF4OHTsG71+1qjBpeLzr/Cbf6y7S\nJ8tMnQp/+YttUR08OHtd6rhJ1F3+n3hncbto3959wsno0Xby0JZb2i5x76ztJL8MAp9+Gp7PshBc\nl8/bLsYt5C2nlKpMo0dn3o8zLgygXr3crltebj9oP/7Y/mP2W083fa3fdKWl7t2Ohc4rF7WKRZiw\nbrvSUvuceFdhCAtu/dJkQPxly8Jmuwat6PH991BSAttua9OfVJRCJgufOzc8oEoPRt5+2388Xxx+\nk3vSZ636mTPHPRgNG6d57LHhx65eHZyQHOyXl2J0W6bnQowap5ke8KV3qwKcdVbm/Xz+Tv34fVlx\nWQP8s8/crzFjhn0dVq+2yb+DJCe5eBV7nHWOaSuVUuk2bIDTTrOJUzt2rPzcfK68qxxEyWWQNtgW\nuPRxduPHZ48/Cmq1Wr8+PL9aukIHh8kWvih+H6RRdfn+++yWlaSJE+14z/SWy6BgIG5rbth7M2gM\n46BBdmbpDz8EJ/othgYNCneuXXaBadOC98+cmfogLkSuvVyCqwcfdH/PeVuR41i5snKCw+Tf/Cef\nwJFHhpdNb8mNGsO6Yw75Urz/f5I2bLCrjHi1bRv/Gq6C0nXNmxfc2l3stayrTXBorKuMMXONMeuM\nMZONMcfncJ7tjDFrjTHlxpiOnn3XJbZ7b68U7pGomuiZZ1ITJubOhcMOq9z6uOraFcaNs6kXglqm\n0rl2ZYjYgfz33x+8uoS3uyRoRYLSUjtL0kWhg0PXb+d+QXNUXQYN8k/v8s47cOCBtuWpe/dUsNCy\npf95wlZy8BM2iSVon3cyUEW50Weqo4idvNG/v23hEcku07Bh9rZVq6ID2+REBb9hDxVhwYLg3IPp\n5s93Kxdk5crwILRYwWFyFu+110aXXbfOzqqfNs0/kOvePRUg5ZLWKuj5mz7d/+/+mGPiXyNfHTrY\nJPN+ksMLktID5Nat8792tQkOgWHAtcDdQG/gE+BFY0zchageAJYBPv9SILF9f2DftJtj1ipVW3m7\nOYK6AqqaGTNsIHvnnXDUUal6z5rlH3S4rKAhYrsed9rJBjg9evjnY/OeK+jcv/xiuzNduLa6uIrz\nAZys//LldoUCv8ec7rnn/LcfeWQq4Fm6NLU8W1B3sF8gFCYswPcLCCqypdDrhx+yt40aZVt2HnvM\nfmDXqZMdINYPSrzmwCXHoF/KJRennRa+v0cPt3GuQS3OrhYvDh8bV6zgEGyLedAQknTXX28Dnu7d\n/ceeTptm3we//JJbovyg5zAon2v37vGvUQiuge+AAampKIWY/V8tgkNjTGvgUuAmEblDRD4QkfOB\n/wDOqwgaY04FdsGm5gkzSUTSbyF54ZWq3tI/WPv3tz+7dMn9fJ99lr3Cwz33ZJfztlQGdXMNHAjb\nbON27UIHh3HG9SRzBx52mE2CfP31hanDwIH2Z9CHddxkvWHB4apV2YGWa0LmOJJLvOXiL3/J3nbL\nLZn38xnW4ReQeu2+e27n9kuInK6sDB56KLxMkyb5T0bwrvXtVczg8E9/civnMrGjrMxOZHNNSp8u\nKDgMaj2P20Jf0Qo5BAOqSXCIbSmsB3gXdxoFdDfGdIg6gTFmS+wyf5cCUe0fVfxtoKqDQsxMLKSg\n2cDp4uTaC/KK4yCM9DxeEN7dGTY+Kl2hV02J03JYWmo/0Ao9Yzqpb1//7XE+tJ56Knpt6GeesS1Y\nxtggN2xlE8htmbsBA9wnN3lnY/t1I195Zeb9fIJDl1bHJk3in/ekk6K/vLz1VvRYsrVr808a7p3t\n67VihVtw2KiR7SKOCmjTFXq2+9q1uQXLQc/h8uXBx7jM5q8sueSGDFNdgsNuQKmIeL/DTscGct0c\nznEr8LWIuIye+dEYs8kY870xZrgxJiR1qlL++vSxM+4OOMDOdCt0ot+4zjyzMOfx+3BOl+s37HHj\ngve5Tpxx6faOI06S6QULbMLfYghL6XLXXbarLsqJJwYHmOlOPz2VcuTWW6NntP/zn8GD+/1aCM87\nD5o1C09Inc41+Ex/rfL5khC2UkpSLsHhsGHRS1C+/XZqbeSk+vUzJx2VlRV/vfEZM6L/zsH+XQ4Z\nEjzLvSKETTIKExT8hv0PiTuEoyJFTfCJq7oEhy0Av3h+adr+QMaYHsDpQNRy27OAK4G+QC9ssu8B\ngONcSaVS3n/fdiNNnGhnIZ58sttxt95qV/046aTolqsHH7RroF5+ecW1VB5yiF0F4+ij/YOSOjn8\nV4lK8eHqnnvi5zwL4/0ACVtbNk7rSRxbbBE9Ritqdu2pp2Z39RdKly52POTEidn7vK3DkAo6XIND\ncHtvT51qv2Bcc01+LYfFCg6bNrUtslEOPzzz/lVX2fdAurgr0OQrqMsy+RoWokvTtbvZ66WXcvtC\nGjRhzK/l8Lbb7E/v61CVFHxMpGu2bOAc4EtgLVDmvcXJvA0cik2eHXUblyg/Aljgc55OiXKnhVyr\nHraF8Ya0bX9J1LujQ10vTpQ9JGB/dKp1VaP5rYQQdCsvDz/X1KmZ5QcPDi77+eeZZUeMCC4bZ1UL\nEfeynTuL9O4t0qePyIwZ9thrrol3LRGR5593PybqdvTRbq+bi+bNM8/9/fciffsWrq4ut7ZtRYYP\nd38u/RSzfukmT7arkJx/vn2u/K7dr5/d/rvfuV/jvvuiH8v11xfm8dxyi9tjjnvelStFZs2KLudd\nVeT550XatMncdtFF8a691175PSdBK7sk/5+NG5f/e+jUUwvz+sW9blJZmcgNN/iXW7bMlsn3eSzm\nzfvZkohNyPXmlCHLGNMXuAd4Ejuh47FE0HU0sJjssYBRJgA7OJRLfm9fBvg1XCdbDMNGYAxIHHuP\nMaZZYlsy8URTY0xjEQkbsfAscCd2VZj/+BUYPHjwb7+XlJRQUlIScjpV0UpLbXfaZ5/B8OFwwgmF\nPf+YMe5lFy0Kz5flHV81eLBtCfFrjfNORDj33OAuuDgTNeKMZ5o1K7U+6qJF9jnOZUWJXJNr+3n9\n9VRLwimn2LGWUedfudI+z/Pm2Va4Aw6wMzq9LbfNm9vzPfmk7UJ2XQ0BbHqaOCtEJC1cmD2mrqra\nZRd44YXMbXvumZkc+Oij7c84LYcXXGDPfcABwWVc0qN4tWiR/X53Hd8aV8OGdg3wKN6JEhs3Zj9X\ncdPYXHGFXcM5V40b2+EADz6Y2vbpp6m/s7DXJcpxx9mfufQ45GvuXNhuO/v7Mcf4p/P6179S3ebN\nm1dc3eL64IPxjC9kmgyXCBL4AhgM1MW21O2e2N4cmAJcmE+E6nD9M/Bp6QPOTGzvEHLs44kyQa2T\nX0Rcu3Wi3BUB+0VVba1bZ37DmjKlsOc/9FD3b3eXXRZ+rrPPzj6mcWOROXOyywZ9E169WuTCC+36\nmw8+aLd99517Hb0tknFuy5fbli6XsltumXosr7+e+zWjbm++Gf0a/v3vmc/3mjUigwZln2vDhtQx\nN99cvDrncgtTrGsOGBD93E6cKNKkiS2/776ptWS7d/c/Z8OG/tvr1cvvvel3W7tWpH//zG077hh+\nTLI1P9fXp6QkuEzdutnbrr1WZPvtM7fF+Z8DIp99Fr5/111FTjopeP+ee9reh6FDRc49174OXtOn\n5/YazJ5tj+/WrXjv06DbnXfaay9YEFzmkUdSj3HbbfO73s47F++xZP/NIyJ5xF1OhWAV0BM7+WMT\nsG/avhOB7/KphMP1WwOlwDWe7WOBKRHH/h44yHO7KREwnpwMdEOOH5AoWxKwP/tVUVVGWVn2H9FF\nF+V3zvnzRV55RWThQnv/5JPz+yNOd+65wcdNnpwqN3588Ln/9a/MbdOmRX84pN/++c/c/0ENHepe\ntk6dVFfIiy/mfs2oW9euNiDp29d++B54oMjPP2c+795jnn02+rW7//7i1TmXW1mZ/3vK72+gULcl\nS9z+ZhYuFPnvfzOD67339j+n65eLfG/G2HocdZRb+VatUoGM33sm6pa0caN9v48ebd//fgFh+m3m\nTJFddsnvsW7YEL7/iy/C//ek1z9MLnVLKnZwmPyCkn4bNcpeO6y7+MUXU3W855541+zcOfX7I4+I\nfPpp9DH16onstlv29n33jff6VFRw+AtweOL3+cCpafuOBNbkUwnHOtyE7WYeAByMTWa9CTjCU+79\nqGCVgDGHwGfARdjJKL2B24ENwJsh5wr4M1FVwcqV2X9Ef/lL7ud7663Mc82f7zZGKXnbaafw8192\nWfCxp56aKue3v2FD/31//3u8MUGHHeZeNt/b6tW2zqNGuR+z++7xrtG8uci772ZuGzo083n3HhPU\nMpNu5Mh49YjzPsnltmaNHf/qHXsU1BIH9kNxzJjcr1laGv9vKOngg/3P2aVLxbz3hg8P/lsKe92D\n3jN//GP8c7hcv7xcZJ99cn+cxx8ffR0RkSuuyK3+cR5L2Hm9/1sLfRs8OHvbSSdF1/vDD1N19P4f\nibotXWp7b957L3WOI48MP2bKFP8vy2HjTF95xe+1QERyj7lce/mnJlrgAD4CBhpj9jPG7IXtbq6I\nxYYGYldJuRgYA+wHnCAi3uW765D7LOyZifO/DLwCHI59fMfleD5VyfzGD4WN+fvsMzvGJGjGa58+\nmfdvuine+J/69e2fc5CwWX9RS5itW+c/3m/16vBUKF4//uheNl/JsZDe2ahhSbjjLmNVVpY9mzcq\nae7772eP0fLOiGzcOF49jjoqXvm4GjWyY9Pq1LF1XbDApnQJW8bv2mvh0ENzv2Y+Y0XD0oJURGqU\n5FizXF11Ver3Ro3g7LODy3ZzSbYWwJh44zO90obEhyrEcz5iRO7HFjoVS7ru3f1XWXr+eRg9OvzY\nNm1Svx98cPbSdGH/S5o3t2PB05dTTS4h6OfDD2HnneOPbdxzz3jlnbhEkMBJwMDE752B70nNVF5O\nQJdrbbi6MeDrAAAgAElEQVTh+pVKVQrv7F+wLWl+Pv881cVTr15q9m06v29txx0X79vkoEHB9b3k\nkvBjRew4qaD9Dz6Yve3SS+PVryJv33xjH5O3i/bcc0W23tr/mDizw6OeSxHb5em3//TTM+/fe2/m\naxW3FWHJEjsWNGi/X8tG0M11tuojj4TvT3ZFB83SdH0Oc3H88cHnfeml4r/3/ve/4L/p9Nsll/jX\nf+1akYEDRU45RWTSJNvCFHSObt2CnweX57hXr/Ay778fvG/58vDrNGtm94e9V2680e013bjRjsU9\n6CBb53r14r2HorpOc7398kvw49tss/Bj04dCiNixlf37i/zjH3YWc3l58NCiIMuXi3z1lcjixfbY\n9u1ty23y79FvGMALLwTXcelSv/cVIpJHbJPTQXa272HY2cqt8qlAdb9pcFi1jR2b/Yd0zjn+ZX//\n+8xyJ56Yuf/HH/3/MHP5hxbEpWvKZdxK+i2qu6gyb5Mm2cfk3X7CCcHPq19572sX5zUIGo/p7d58\n4YXM1+rjj+Ndr7w8OKXQ6NH+jyvo5pISJep27bWpx5JLGpiOHcP/9qKcdlrwuYMC9kLekql2orr7\nn3jC7fFMmuT2fvOKCk5ERP70p/AyixbZYMVv37p19hxBx37yid0/YUJwma+/zu01/ukne+yee/qf\nNxm4Jn3zTWFe28ceS/1+zz323HH/XqNeNy/vmMbksIVc3Xtv6lzt24ePG/Ub3pFvcOjU/WqMOcgY\n81snioisEZGxIvI6sM4Yc1ABGjGVKji/dViDMuPPnJl537sMXFBXs3fJuQsvjK6XSPa2dev8UylE\nXS/KzVEriVeit97yX81iwQJo2dL9PJ07w1Zb5VaHZ5/13+5djsqbALdTJ/drXHRRqnvQb/m6ZOLj\nu+92O9/WW7tfO8hf/5r6PWiFkyDNm7vXNUhYt7J3lZB8BHV9J7sHo9KwHHyw23XCun7Dupxdkhe3\naxe+f4stYNAg/33J5QBPPNF//z772J9hXd+5dmu3awddu8K772b/H7r/frtSTrqwVD8ibmtyt28P\nZ52VCp2S/4/33Tde3eN66y2bDB7s/65clpVMd8EFNj3YuHH2f1HQ+7h+fbclH+NyHZv3H4KXqNuB\ngPx/SlU2v5UEwsZgpfN+YCb/8L28y+J5xyX68VvxIShISTdvntsKDtXFkCH+40KbNoVPPsneHvTc\nXnBB/OUJkwF6cvWDKN7gMCpA27TJrhoya1ZmIOX3oZEMlC66yObNfOSR8HPnu4zXKafA//1f6r7r\niiLHHQe//mrfhy7v8zBhj6GQy5Tdc4//9uTrGXUtv7Fqfho1Ct537rnB+846K3jfDolswFHL5W2x\nRXaglZTMH+h9T33xhf0bSI6lDat/vq9H8+Z2FacFC+wKUK+9ZpcU9QqqQ/KxDRwY/cXhjDP8t9et\nG/46+ImTE7dHD7uu+uOP29V6CpETsU0buyJVWPBXrFVbXIPDsMVpGmDHHipVpfi1zoF/cOi3hu4O\nnjTtUeuigv12lz6AOYjfQvH9+0cf98AD7sFtmN698z+HiyOPTLVYBP1T95tEc8IJ/mucJieBjByZ\n2rbNNtCzZ/ZA8SirV8Ptt7uXj/tPuG5d2G+/7BbGhg0zW5L+8Y/MyS69ekW/F/JJGPzGG/C0Z9kC\nl+Dwiivg0Udt4ui4k3H8eFtmk554Ivf1ub1WrIAOHcLL5DPZI13YcxLWIha2rGbyfRD1etetGz05\nqEkT+z9x40b707sOeNjxhXqO2ra1k8OSidD9rjNgQPb2//3P/qxf3yaFDxP0JR7if4E84oh45XfZ\nxa5hHzbpsdD8lvsrhMAVUowx2wId0zbtmd61nNAQ6AfMK3jNlMpT0HqsfsHVggXZ27zdlC5BWZMm\nbt+y+/Sx691eeGH4PzOvefPgqafcywd5/XU7S2/uXPvPNmwGXT523tnO6H7+eXvf70Pfr0uzZUu4\n7DK7ok26ZOB9xhn2H/C339pZxZtvHj94O+cceO459/J+396feca+jnGNGAHHHmtf+1694h2b7AbM\n1R//mL0tKoCC7NciX0Hve7+hILn44AP7hWS//cLLhQU+J53kfr2wADCsVS5s3/bbp+rh8l7t3Tt6\nxabNnNZFy1TIltwot91m/6YmTrSr1/TvD7/7XWp/1N952OsZdw3ofGe0V2tBgxGB67Arg6SvoZy+\nskjy/gbgr/kMfKzON+KMWFUV6pdf/Afv7rNPdtmPPvIvO3NmqsyTT0YPXt5mm3irkTz9tD2336xq\nv1vYIH7XW/rKJCIiv/4aXj59YHTc24QJmdfyK/PDD9nb1q0Teeed7O3pqxV4XXVV/s9N2M1v0Ldf\nHk0Quesut/domKB6JBP35vo4/KxeLdK0aapMnz5ux+XDL9Fv+nXyXcM6PUH35Zdn7uvdO7UvbPLL\nV1/Fe0xB51mzJviYTZuCj1u/3pYJy1CQ/pz5/X8oRP2j1oSvaGHPxQMPBB8Xd4Udv5VgKtNdd7n/\nTSdiE3K9hTVWPwEcAhyK7Va+MHE/eesJ7A9sLSIPB5xDqYKZPh1uvBFcl4984AH/7X5j3ILG9Oy+\ne+p3l5bDhg3jdcGcdpr9+eWXbuW93YG58LZUBI1VSjryyNzWBAbbkpquffvsMn4th5tvnn0shE8C\nGTDAdnkWi1/LoV8dIbVebD7uuMN/e9yusXRBuewaNYL//tc+hw88YFuV04dVPPZY7tcMclDENMZ+\n/XLvXj7nnMwJTcOH23GWYMeK3nBDal9Yq5jLWsjpgiaXhF0jrOcg2dLVsGFwC+Ott6Z+dx07Gleh\nuvkLJWxMblhrn7crPUzz5rDTTu7lK0KhWtWduESQ2BVJGucThdbUG8X4Sq2yzJsn0qBB6pvS2LHh\n5YNShiRvP/2UWd67/rLft7IePaK/aXbvbssGLQ3md2vc2H/7YYfZtT/zaT3xu3XunP18NWoUXH7R\nIlsml2sl04Ukvfxydhlv+orf/96WnTw5u+zUqeGv+8KFwSk98rn16BF8zf32yy6fTB+SL7+6zJ1r\n9w0cGP9x3HKL+7WXL7cpQcaPL8xj8QpaajHdlCm5rSyzcWP29crL7Rq6yVV5kkpLg8/jLRslaOnJ\nKH7H3HFHZpmOHf3LrV2bKjNkSPxrpwtqfa+K5s+3PT7bbJOqZ4cOqbW7g7ikSTrllKrXapjkTQsU\ntHZ8IjYh15vTsGYR+UBEfIbQK1Ux7rsvcwzhP/4RXv6LL8L3X3116vcJE2Dx4vDyK1fCRx+Fl4HU\neJh33rEzcYcOjT7Gb3IK2PQPfi1t+fJrqQtqAYPoMT79+gXv857X+028U6fs2dfJ1hK/Af5R6W22\n3trOaCy0sJYfv3FMhRrA/+qrmfd79EjNnvUbuB8lzuzLZs3sTFrXVC5x+c3STZ9BDXbM6mWXxT+3\n37g6Y+w4VW8LXNhEjLjjWKNa4YNcckn2Nu/fjt9jql8/87157rmZj+fee+PVI+z/QFWzzTZw4IE2\ntdfw4fbv4YMPosdwR6W8mjbNjiVO7zWqSoYOTb0v+/XLP2tAEOc5b8aYw40xo40xXxtj5nhus4tT\nPaUs7yDradPCywcFXEmPP576/ZZbgsslZwm6dmUn/1G3aGGXJksPQuMyxm0geOfO8c67//7Z28LS\nQySDtKBu+uuvDz7W+2HjfTzr1mVPsEnWxe+D2aWbL+6sZRdhM1GXLi389ZKOOcYu5XfttTBjhl1e\nK6lVq+wl/sK0auWelqUibLNNdrqPzz/3L5scfuHVt2/+9QjrMo3bneoNbl35dfePG5d535uHFbJz\nhLZpYwOks8+26ZPOOy9ePb6piIVwC6x+fTuT/vbb3SZWRc38jjtppaL17g0//GBn+z/6aPGu45oE\n+0jgHWALbF7Db7AzlH+HnZTyYfDRSuVn0iT/BNTJlkQRO9t2l13sP3Nj3GaAJlusXn89uEx5uT2/\n3zhFP34JnXMZJ5gcu+Tyj6pr13jn9huXFxYcJj8g/XKELVliP+SDeFtl/IJDb57B5NjOrbbKzCW4\n6675reXrIijQDptRWqxUEkk9e9pWaG9qJYiXDNslj2ZFW7LEflG77jq7pndQq07QmMff/754dUtf\nO9mV35jYoLx76fxaHF1SYvnZbz94+GGbMzNOJgQo/vrfVUVQKp22bavHDOVWreI3CsTl2nJ4DXAf\nkFwa+2oRKQF2BOpiA0elCm7s2ODUHaNG2Z+TJtlu5q++induv2/ifj791Hbxupg4MXvbqafaf9Zx\nJLsMXYKh9EXdXfi1dAW1jKW37BgDX38Ne+xhg8kpU1LdvH4tJvN8Elx5g0O/1WqSQwLq1oUHH7Tn\n7tw53oocPXu6l00X9J749NPgY/xyZFaUON3XVbFFpE4dmxdu8ODwVje/yUD//Cccf3yxapZbd7Zf\nsB73/1LSxRfndlw+ivl8ViW77OK//aGH4gfUNZVrcLgD8Aa2lVBI5EcUkZnAYGzwqFTB/eEPwfvO\nPtu2/uW6LNKaNfDZZ9HlBg3KfbZu0tln+7f8BEkmqY5KvP3ss7aLIY5nnsneFtRtvmxZ5v2uXe1z\ntmKFHQ+WdN99mf9Up03LzE2W5A0Og3JRJh1zjG1R+u47O97OVfoMzjiM8c9tl/5Yva68MvO+y/KJ\nheL3/njjDf+y+STOrgrSu1kbN7bLsXXtmt3q5vpFLp1f7tCgmd1h/Fo+XZYC9Gt9r4whAHXqQElJ\n5rYnnqj4ehSb35dHEf8coLWWy6wV4FegZ+L3RcCf0/b9AVibz6yY6nyjqk7lqiGiZpXttFN0maDb\ne++JHHJIdLl27UTatHE7Z7t2wY+lvNy9bklr1oSXmz1b5NNP4z3ufv3iPc+uJk8Weeml6Bme9eu7\nP/58fPhh6nxhs7GTt912s8d9/HH2vp9/Dr7O4sUinTrZcttsY2fWV5QxY7LrGvQ+S8/7V119/719\nXTdsyNx+zTUiLVqIjBiRW06+TZsy/8YPPTS3+vk99/ffH33csmWZ71G/PJnF/FtJt2mTyMkn23MP\nHx49+7c6Ki8XKSmxj7F+/eAZv9VZIjYh15tbIZhIItE18CbwMdAWaA2MAb7OpxLV+abBYbTycpHp\n00V+/DHeca+/Hv2Bns/t1VdF2rYt7Dlfey38Mc2YEX2OG2/MPCYqiAoKBrbayn+7NzG1iH86FrDp\nMwqtWbPo56BQZs0SGTnSBtHJD7ygWzLh8LJl8euzapXIpEk2/UtFevdd/7redFPxntOa6v33bZqQ\nQw4R+frr3M/jTe69cKHbcZMni1xyicjDD/sHZBUVHNYWGzeKfPCB/R9RE+UbHLp2NDwNJIf+Xocd\nazg/0YrYE7g256ZLVaNt3Gi7Knbc0XYzJpdRi/LJJ8GDhnPhN9B6zRro1q1w14DoOu+wgx2EH5bM\nuWPHzPveWYtexvin7rkmYLCHX9eXX1oR8E+xka+oZOKFSPSd1KmTnRDQsWP0zNPkmLwtt7QTJMCO\n+XzhhejrNG4Me+2VeyqTXHln+0ZtV8F69rRr+I4bF3+SV7qhQ+0s/Tp1YNgw90lDu+xiJ2edfbaO\ne6sIm21mE7GH/S+uzVzzHN4nIpclfv8c6A6cCwwAdhWRl4pXRVWd3XNP5v2TT44eZ7Zxo3+6lXwc\ne2z2Ob/+2qYJSTdsGIwcWdhre7VsCbNmwZNP+u/3zoz15gFMSp+RveuumWOkjj4azj/f/zi/FDHe\nsYVJYTORcxW0ikRSLmsVuwh733mfk8GD4aef7LrTcXIDVrQ99sj8cDv7bPvzlFMyJ6sEfVFQhden\nDyxaZP+mBg0q3Hm9Y1uVKqachiiLyHwReURE7haRrwtdKVVzXHpp9rb27cOXefrkk8LXo2nT7KSm\n6UtoJdWvD6efnts14qbV6Ns39WGeztvqEzTLNH2guDHw66922bNnnoGXXrKtD36Jkv2Cw6DB73GT\nALsIymUHwbkUC+GYY4L37bFH9rZ27aKTblc2Y+wXnAsvtLkQ77rLbm/a1M70P+EEG1RoYFGxttjC\nbSJKHH6zly+4oLDXUCrJ2K5plStjjOhz6G/58vDurdJS/xQVDz9s10YtpH//2yak/t//wst9951N\nm9KqlQ224pg40eYYi2PVqswPke22g2+/zUxhs3Gj//Pk8rZ7/fXsoGjDhuwUOWvX+ufy+/DDeLOE\nXZx/vk1R42fkSLe8cLlYty442H3ggfgJg5WqaLNmQZcu9vd27Wwar2K07qvqzxiDiOS8KnZgy6Ex\nptwYU+Z6y7UCqmYqK4se9/Tii/7by8sLX5+mTaOX1IPUeL+wNBZBLYS5pNRp0gQWLLAB0bHHwssv\nZwdu+SR+9mt19DvfFlv4vx5hK4PkKixFRzFaKpMaNoT+/f33HX548a6rVKF07my/tI4fD1OnamCo\nisdntcbfXA8k2yYM0A9oiM13+DOwNfBHYB1QxEVcVHXk0sU6cKD/sljFWI6sWTPbjRzVvZbMBRcW\nHAZNOoi71FZS27bxxzmG5d1LF2etVL+1RIsRHIYlYw5biaQQrr/ef8kpv3VrlaqKWrQo3nrXSiUF\nthyKyGARGSIiQ4BNwA9ABxHpJyJXichZwLbYZfQ2VUhtVbVQWmoXQ4+yeLH/9kWLClsfsC2HcboN\nw2ad1q+f3UpY0SsLhI3ZTLfzzpkTE8JmU/sFgnGCS1dhq3oUs+UQbFfcOz7rOVXF1UOUUqqyuE5I\nORe4VUQyFrsSkTXAvwAdrVPDlJXZ9UyHDYOffw4ut3599mxavyXR/PilVNm0Kd4yaa6aNo1uBevb\nN/V7WMthgwbwyiup+/Xrw/Dh+dUvym67Zd4PWzkmXePGdhWV3Xe3syjvvTe4rF9gVoyWw7DgsNgt\nh2BXn0lfBWWffXJfx1YppWoi1+CwFeAzJB4S26v4nD4V1+DBdnzWNdfYPF1+4wBHjLBB11ZbwWuv\npbYHpV7x+uEHm/9wwwZ7/5dfbK64fDzyiP/2Ro2ic4fddFPq97CgqEED2xX8yy/w1lvw/fepQeLF\ncu+9qa7PJk3irft67LF2hvCbb/ovaZfkXdoOitOSF9aFW+yWw6RHH7Xv8SuusM+LUkqpFNfg8DNg\niDGmXfpGY8w22LWVI+aAqupm2LDM+/fdl3l/wwb7wbpxo51xe+yxdv3hsjL34BBsrsEGDWD2bBvY\nTZ4cXr5+/eCZrhCcI89lXdl2ae/uH38MLpfsgmzdGo480gaKxbb//nZm4gMPwJQpmXUtlLp1M3P6\nnXhicdbjDZtlXYxubD+NGtlE18OH25npSimlUpxS2RhjdgPGYSekfIqdkNIG2BdYi113OeJjvWaq\nials5s/3b2FKf5jz5kGHDtllOnSwia5vvrlw9fnyS5v78Kuv7Eoe228f3O0rYmfyHXJIatv69amA\nLmzSSPrjCyt30knw3HPO1a9WSkttq5ox0K9fccbiffxxcHqc8vLcJ/YopZSy8k1l4zRHT0S+NMZ0\nBi7BBoTdgYXY8YZ3iEjMjHCqKjv55Ogyya5grx9+KGxgCHb1j113jS7397/bnyUlNj3MvHk2ubHL\nTNQ77nCvT02e2dqgAfztb8W9xgEH+G/fd18NDJVSqirQJNh5qokth0Ef0OkPc/Lk7EkSxeL39Pq1\nPi1YEN3F6/LYAI47Dl591b/s1lvbZdVU7vxehz//OTj3pVJKKXdFS4KtVDpvDrw1a9yPbdy48Iub\nH3igXS3gsMOga1f7u8vYP78cd97xlQBnnhl8jmKk2qltHnooe1vUhCGllFIVQ4NDlWH8eP/t3tVF\nVq1yP+fq1TBtGjz1VM7V8tWpE7z3np3U4hp8nnZa5goht9xik3F7+c3cTUqf1axy4zdxKGppQ6WU\nUhWjBo+eUrk46qjgfT/9lFquKX1Wa5RzzrG57Vxz8xVTgwZ20sWmTbalKmg2bteuwefQNXjz55fP\n8PTTK74eSimlsmnLocqwenXwvvPPtz9HjAgv55VcSi+XhMqFbm0EO96tXr3wNC1h+QDDVk9R7kaM\nyLzfr1/l1EMppVQmp+DQGNPMGKMLTNVwK1eG73/jDbjrrvgtZ8kE2n4Jjnv1Cj6ubVuba6+y+CX+\nBp1RWyjnnAMffmhzDU6d6p8aSSmlVMWLDA6NMZsBvwKHF786qjJMnAjHHAPNm0eXDVqBJMwbb9if\nfkFV2Iznzz6zSa8riwaBxdejh02mvtNOlV0TpZRSSZHBoYhswia9Lit+dVRF+/BDm3fu9deDW8rS\nTZsW/xrbbx+8r0EDuPxy/33FWAUkX9qlrJRSqqZzHXM4Cji7mBVRleOf/8z/HOmrkfgZMCB43xZb\n+CfNDloBpbL16VPZNVBKKaWKyzU4/B7YyxjzP2PM1caY/saYfum3ItYRAGNdZYyZa4xZZ4yZbIw5\n3vHYx40x5Z5bmTHmdp+yBxpjJhhj1hpjFhpjbjPGbF74R1Q1FCJ9yKWXhu/v1i31+zHHpH6vWzd4\nLeTDDsu/XoVw4YWZ9493escppZRS1ZdrcHgfsA2wB3A98DDwSNrt4aLULtMw4FrgbqA38AnwojGm\nt+PxvwD7YJf/2xfYD8hYNM0YszPwLrAI6AMMAs4CHi9A/audM85wK7fllvCnP2Vua9MGrrsOyjyD\nEYYMgS5dbIvhLbfA//2f/zkPPDB+fYth4EDYc0/7+1FHacuhUkqpms9p+TxjTOQ8QhH5oSA18r9+\na+BH4EYRuT5t+1iglYiErrxrjHkcOFRE2keUGw10A7qJSFli2xnAE8AeIjLZ55hqu3xeWVn4OsFT\npsAuu0SfZ+pUO17xoINgxQro2NEeG5a6RiRzwsdDD8G559rfmza1ORVzSX1TLOvWhSfGVkoppaqK\nfJfPc0qCXczAz1FvoB7wtGf7KOBRY0yHfOuYmJXdC/hXMjBMeAHbMnoMkBUcVmdLl4bv33lnu8bw\n6NHh5dq2hZYt7Uol33wD++zjn+Q4nXcm8F//Ck2awPTpdum6qhQYggaGSimlao9YK6Qkul0PAloC\nI0RkkTGmM/CziMRYUC22bkCpiMz2bJ8OmMT+qOBwK2PMYmBLYA7wKDYQTM7R7QRsnjjnb0Sk1Bgz\nO3GNGuXzz4P33Xij/XnOOdHBYcuW9me7drnPMDYGTjklt2OVUkopVThOwWEiAfYo4HhsMCbAG9ix\nebcAM4Eri1RHgBbAcp/tS9P2h/kS+Awb+G0OHAfcBHQGzvGcY1nAdaKuUe3ccUfwvt13tz+jVkLZ\ntKlw9VFKKaVU5XOdkHIDcBhwBtAGGyAmvYPtjnVmjDnUZ/aw321cnPMGEZG7ReQ+ERkvImNE5Fzg\nLqCfMaZjIa5R1ZWXwxNPwE03wbx5dtvEif5lO3eGnj2jzzlpkp1xrJRSSqmaw7Vb+RTgahF5xhjj\nDQfmAtvGvO4EYAeHcmsTP5dhu4O9kq15EaPnfD0L/APYC9vNnGwx9FsnpAWQQ/rnqmHiRJtoesIE\ne3/gQDtxZNttM5Na9+plU8scfbRdexigUyf/c958M+y1V1GrrZRSSqlK4BoctgRmBOyrA8Rad1lE\n1mO7ol1NBxoYYzqKyJy07Ttiu7i/jnP9ALOB0sQ5f5PoUu+InZjia/Dgwb/9XlJSQklJSQGqUxh3\n3umfhLqkBGbNytw2ahS0apW5bdeAeeB77FGQ6imllFIqT+PHj2f8+PEFO59rKpsZwCgRuSHRcrgR\n2FNEvjDGXA38SURCVsnNs5I2lc18YJiIDE3bPhZoLSIOCVeyznkXcAHQRUTmJraNBrpiU9mUJ7ad\nDjyJfbxf+pynSqeycV0fuGVLWLLEf99HH9k0NekmTdKWQ6WUUqoqqpBUNsBIYKAx5nvg5cQ2McYc\nAgwABudaARcisjixmslVxpjVwBfAyUAJcFR6WWPM+0B7EemSuN8eG9w9g+0+boidWNMXeDAZGCYM\nJpVc+z5gO+yEmxf9AsOaZNttg/e1bp29LdntrJRSSqmaxTU4vAXYBXgKuyIKwMfYmb/Picg9Raib\n10BgFXAxsDXwLXCCiLzjKVeHzIk2q7DjCQdiJ9OUA98AF4nIA+kHisgUY8zhwM3Am8AKbALsQYV+\nMBVhzpzoMklNmwbv23777G1t2sSvj1JKKaWqPqdu5d8KG9MDm5C6NfArMEZEPihS3aqFqtytfP75\n8OCDbmWPOgpefz14/9/+Bg8kQunDD4d//zv/+imllFKq8CqqWxkAEfkI+CjXi6mKNWWKe9moFUnu\nvx9OOAFWrtT1hZVSSqmaLO4KKYcA+wHbAD8BE0VkfBHqpQpg3Tr3si7L1R1ySO51UUoppVT14LpC\nSgvgReAQ7Ji9Zdh8gMYY8x/gRBHJJdegKqLJMVaCrmprGSullFKqcriukHI3Nln06UBDEWmNnfXb\nN7H9ruJUT+UqbrojDQ6VUkopBe7dykcBV4nIM8kNIrIReDrRqjisGJVTuXvppXjlo9ZQVkoppVTt\n4NpyWAZ8F7Dv28R+VYXcd1+88kEroSillFKqdnENDl8DTgrYdzLwamGqo+JYsQIWLgTXTDrnnx+8\nzy+XoVJKKaVqH9fg8A3gMGPMW8aYM40xRyR+vg0cCrxujOmZvBWvuirpo49gu+2gXTvo3x/Ky6OP\nadEieN+WWxaubkoppZSqvlzXVo4KPZInMYCISN18K1ZdVFYS7D594O23U/c//hgOOMD+Xl4OdX1e\ngf32g08+8T/fokW66olSSilVE1RUEmzNcFfFpAeGAK++mgoO7/KZO/7II3D22cHn05ZDpZRSSkHM\n5fNUtspoOdy4EerXz9zWqxeMGZOsU/YxIjB4MAwZ4n9OfRsopZRSNUO+LYcaHOapIoPDtWth221h\n8WL//U8+CX37BgeHK1YEtxDq20AppZSqGTQ4rGQVFRxu2gT16kWXEwkODgFeew2OPTZzX+fO8F1Q\noiKllFJKVSv5Boeus5VVJXviCbdyzz+fvW2PPVK/H3MMLFmS2YJ43nl5VU0ppZRSNYi2HOapoloO\ne6g16O0AACAASURBVPSwM5Jz8f770NOTYOi77+wqKh06wMknQx39mqCUUkrVCNqtXMkqKjj06yp2\nVVamwZ9SSilVW2i3ci1QWprf8RoYKqWUUspVYJ5DY8xjMc4jItK/APVRPn7+OfdjDz64cPVQSiml\nVM0XlgS7J6mVTwC2BJoBm4BfgZaJ41cAy4pVQQW//uq//eij4Y47oFOn4GNHjixOnZRSSilVMwUG\nhyKybfJ3Y8yBwLPAucDLIlJmjKkL/Bm4FTi9yPWs1ZYsybzvmnqmb19o3744dVJKKaVUzeQ6Gu12\n4CYReUFEygBEpExEngduBu4sVgVVdtLr3XbLvH/VVf7HDR9enPoopZRSquZyDQ67A7MC9n0H7FSY\n6ig/H36Yeb9Vq8z73qTWSW3bFqc+SimllKq5XIPDRcCJAftOBvKYMqGijBiReX/zzTPv77UXdO+e\nua1ly+LWSSmllFI1k2tweCfQzxjzljHmTGPMEYmfbwN/wXY7qwrSrFnmfWPgq6/gttvs/b32goUL\nK75eSimllKr+nJNgG2P6A9cB/5e2+UdgiIjESXtTo1REEmxvAuw5c2C77Yp6SaWUUkpVUxW6Qoox\nxmCDw7bAQmB+hSwPUoUVOzgUyU5ivWIFNG1atEsqpZRSqhrLNzgMy3OYJREF/Zi4qQowaVL2tiZN\nKr4eSimllKodnBdWM8Z0N8a8ZIxZbIzZlPj5gjGme/TRKlezfOaI57POslJKKaVUGKeWQ2PMXsAH\nwDrgdezs5a2Bo4A+xpiDROTzotWyFtPuY6WUUkpVJNdu5ZuAacChIrIqudEY0wQYm9h/eOGrp1at\nyrx/0kmVUw+llFJK1Q6u3cr7YldIyQhVEvdvBvYrdMWU5Q0OtSVRKaWUUsXkGhxGTcet1TOWi8kb\nHOpkFKWUUkoVk2tw+F9gYKIb+TfGmEbAFcCnha6YspYvz7yvwaFSSimlisl1zOFAYDzwgzHmTWyO\nw62BI4EtgJJiVE7BDTdk3m/QoHLqoZRSSqnaIc4KKTsD1wI9gBbAUuwM5qEiMrVoNaziCp0Ee9ky\nuOsum/z6/POhbdvM/YcdBu+9V7DLKaWUUqqGqbAk2CLyFfDnXC+k3LRokfr9rbey9++8c8XVRSml\nlFK1Ty7L53XDthz+CszQ5fMK13L4xBNw1lnhZRYsyG5NVEoppZRKyrflMM4KKWdjxxp+hR1/OBVY\nYIzpn+vF4zDWVcaYucaYdcaYycaY4x2PfdwYU+65lRljbveUu86nXLkx5pXiPKpMUYEhaGColFJK\nqeJyXSHlNOAh4H1gFKkVUk4DHjLGrBWRZ4tWS2sYcAl2cswXwMnAi8aYPiIyxuH4X7AruqRH0gt9\nyglwAFCetm1pTjWOYf366DLbbVfsWiillFKqtnMdc3g58LSInOHZ/qQx5ilsOpuiBYfGmNbApcCN\nInJHYvMHxpguwHDAJTjcICL/c7zkJBEpjy5WODfdFF1mq62KXw+llFJK1W6u3crbY1sM/YxK7C+m\n3kA94Gmfa3c3xnQo8PVy7qfPxbx5cP310eWaNy9+XZRSSilVu7kGh6uA/wvY93+J/cXUDSgVkdme\n7dOxgVw3h3NsZYxZbIzZaIz51hhzuTEm6PH/aIzZZIz53hgz3BizeT6Vj/LII27ldOk8pZRSShWb\na7fyO8CNxpiZIvJRcqMxZj/sWMB3ilG5NC2A5T7bl6btD/Ml8Bk2mNwcOA64CegMnJNWbhZwZaK8\nAIcDA4DdgF451j3Sa6+5lWvWrFg1UEoppZSy4ow53BcYb4z5idQKKf+HDaguj3NRY8yhgEsq5/Ei\n0jPOuf2IyN2eTWOMMWuAi40xw0VkTqKct9v6/cTjvcMYc4iI/CffuvgpdxzdqC2HSimllCo2p+BQ\nRBYZY3YF+pFaIeV77AopT4jI2pjXnQDs4FAued5lwJY++5MthrnMJn4W+AewFzAnotydwN6Ab3A4\nePDg334vKSmhpKQkVkVmzHArt6rYnfdKKaWUqnbGjx/P+PHjC3a+OCukrAXuTdzyIiLrgZkxDpkO\nNDDGdEy28iXsiO3+/TrfOuUjPTiMa+RIKCvL3HbYYTB2bHZZ1xZGpZRSStUe3oapIUOG5HU+5yTY\nlWwMsAmbVzHd6cA0Efkhh3Oejs1lOMmhnAD/zeEakc4/P3vbyJH+Zbt2LUYNlFJKKaVSXJNg1weu\nAk4B2gMNPEVERJxbIeMSkcWJ1UyuMsasJpUEuwSb2Dq9ru8D7UWkS+J+e+BJ4Bls93FD4HigL/Cg\niMxNO/azRNmZ2FnQhwMXAu+IyPhiPLa1Ph3ybdvCmDHQu3fm9jPPLEYNlFJKKaVSXAO6W4ELsLOS\nXwFKi1ajYAOxKXMuxk6G+RY4QUS8M6XrkNkiugo7ZnEg0AbbWvgNcJGIPOA5dmbi/G0T55gDDMY+\n/oLbtCl727nn2p+9esF339kl9X76Ca69FlpEzclWSimllMqTEZHoQnbG7v0ickPxq1S9GGPE5Tn0\nM2QIeIcrzp4NHTvmXy+llFJK1U7GGEQk5wU9XIPDFcBxIjIu1wvVVPkEh8bnZcvxVEoppZRSQP7B\noeuElDeAg3K9iFJKKaWUqh4CxxwaY9I7N+8BRhpjyoG38ckr6EkxoxwccQS8kzZi8oILKq8uSiml\nlFIQPiFlFjaFS5LBTs64LqB83QLVqdaYNy/zfq+iLdCnlFJKKeUmLDg8q8JqUUtNn555v02byqmH\nUkoppVSS04QUFSzXCSkbNkADT7bIBQtsjkOllFJKqVxV1IQUVWBLlmRv08BQKaWUUpUtbELKY8BQ\nEZmb+D2MiEj/wlatZps6NfN+/fqVUw+llFJKqXSB3crGmLnAsSIyxRjzPZmTU7xERGpl6uZcu5X3\n2QcmeVZ11h5+pZRSSuWrQpJgq2C5BoetW2d2LW+xBaxZU8CKKaWUUqpW0jGH1ZR3Msrw4ZVTD6WU\nUkqpdGFjDtvHOZGIzIsupcCun/zTT5nbeveunLoopZRSSqULG3NYTvg4wwwiUiuTYOfSrbzvvvDf\n/2Zu27QJ6tbKZ1AppZRShZRvt3JYEux+xAgOlTtvYAgaGCqllFKqaggMDkXkiQqsR63SuDGsXp26\nv/felVcXpZRSSql0sWYrG2PqAN2AlsBnIlLr59fG7VYWgTqeaUBLlkDLlgWumFJKKaVqpQqbrWyM\nuQBYBHwFjAO2T2x/1Rhzca4VqG3SWwzBzlpu0aJy6qKUUkop5eUUHBpj/grcBbwKnAikR6MfAX8q\nfNVqpsWLM++3bg0m59heKaWUUqqwXFsOLwFuE5FzgNGefd+QaEVU0fyCQ6WUUkqpqsI1ONwO+HfA\nvjXAloWpTs335puZ9zU4VEoppVRV4hocLgG2Ddi3PfBTwD6VZtEiGDYsc5sGh0oppZSqSlyDwzeB\na40xHdO2iTGmFTAAOxZRRfC2GgJ07Ji9TSmllFKqsrgGh1cDpcA0YCw2OfbdwAygDLi+KLWrYR5/\nPHvbAQdUfD2UUkoppYI4BYcisgTYE7gJqAfMxibQvhfYT0RWFK2GNcjEidnbtOVQKaWUUlVJrCTY\ngScxZjMR2VSA+lQ7cZJg+6WsWb/e5jpUSimllCqECkmCbYy5PGTfZsALuVagNuvSRQNDpZRSSlUt\nTi2HxphS4GwRecqzvS7wPHCoiDQvThWrNteWw/JyqFs3c9vKldCkSZEqppRSSqlaqaKWzzsPeNgY\n0zvtwnWAZ4E/AEfkWoHaYvr07G2NG1d8PZRSSimlwmzmUkhEHjfGtAVeNMYcCvwPeAboDfQWkU+L\nWMcaYc6c7G26bJ5SSimlqhqn4BBARG5MBIhvAROBnsARIuIzB1d5eYPDs8+unHoopZRSSoVxDg4T\nLga2Ao4E+ojIx4WvUs3kDQ67dKmceiillFJKhQkMDo0xP2KTXfsdUwcYZVL9oiIiHQpfvZrDGxxq\nfkOllFJKVUVhLYfv4x8cqhzMnp15X4NDpZRSSlVFBUmCXZu5pLIpL4eGDWHDhtS25cuhWbMiV04p\npZRStU5FpbJReViwIDMwbNFCA0OllFJKVU1hYw77Am+JyK+J30OJyMiC1qwGee+9zPvaWKuUUkqp\nqipszOETwL7Ar4nfwwhQ1ODQ2NkvVwLnAFsD3wLXi8grjsdvnjj+VKA9sByYBByfvi60MeZA4GZg\nN2AFNp/jIBFZn2vdn3468/622+Z6JqWUUkqp4goLDrcDFqb9XtmGAZcAA4EvgJOxSbn7iMiYsAMT\n6z+PAToANwIzgNbY1V3qApsS5XYG3gXeAfpgH/e/gHbAKblWfObMzPstWuR6JqWUUkqp4qoWE1KM\nMa2BH4EbReT6tO1jgVYismvE8VdiWw27iciCkHKjgW6JcmWJbWdgW073EJHJPsdETkjxroTy+eew\n++6hhyillFJK5aS2TEjpDdQDPB20jAK6G2OiciyeD7wQERhuBvQCnk8GhgkvABuBY2LXGhg7Nnvb\njjvmciallFJKqeILm5AyF/c8hyIinQpTJV/dgFIR8WQLZDpgEvt/8DvQGPM74HfAXGPMQ8BJQH1g\nAnCpiExJFO0EbJ44529EpNQYMztxjdiGDs3e1qBBLmdSSimllCq+sDGHH1B1kmC3wE4g8Vqatj9I\nu8TPK7ETUE7EBoHXA/8xxuwsIvPTzrEs4Do5jRT89ddcjlJKKaWUqhyBwaGInFmsixpjDgXeiywI\n40WkZ56XS3adrwH+KCKliTp8DswCLgCuyvMagVavzrw/UhP+KKWUUqoKC2s5LKYJwA4O5dYmfi4D\ntvTZn2zNW+qzLynZdjchGRgCiMh8Y8w3QHIyS7LFsHnAdaY51DfDxo3wQ1pntzFwwglxz6KUUkop\nVXEqJThM5AycGVkwZTrQwBjTUUTmpG3fEdv1/XXIsXOAdQ7XmA2UJs75G2NMA6AjdmKKr8GDB//2\ne0lJCSUlJQCsXJlZbsstYfPNHWqilFJKKeVo/PjxjB8/vmDnq06pbOYDw0RkaNr2sUBrEdkl4vgX\ngB5ARxFZl9jWHhug3iwi1yW2jQa6YlPZlCe2nQ48CewpIl/6nDswlc2cOdApbZpOhw7w/feOD1op\npZRSKgf5prKprG7lWERksTHmduAqY8xqUkmwS4Cj0ssaY94H2otIl7TN1wH/Bd42xtwGNASuxXZH\n35tWbjDwCTa59n3YJNi3AC/6BYZRVqzIvN+kSdwzKKWUUkpVrGoRHCYMBFYBF5NaPu8EEXnHU64O\nnvyNIjLDGNMTuyzec9i8heOAy0RkcVq5KcaYwxPl3sQun/cEMCiXCr/6aub9Zs1yOYtSSimlVMWp\nNsFhou/2xsQtrNwhAds/Aw51uM7HwAG51NFrnWeko3cMolJKKaVUVeMUHBpjDgrZXY5tYftGRDYW\npFY1xGxPyu7EPBWllFJKqSrLteVwPNEJsdcaY+4WkZy6YGsib3B40kmVUw+llFJKKVeuweExwD3A\nFOAl4GegDXa1kZ2Ba4C9gcuNMctE5F9FqGu1IpIdHHYq5gKDSimllFIF4JTKxhjzKLBRRM7z2TcC\nqC8iZxlj7gb+ICJdC1/Vqikolc0vv0CbNqn7jRrBqlU2EbZSSimlVLHkm8qmTnQRAI4DXg7Y9xK2\nZRFgDDb9S63nbTXs2FEDQ6WUUkpVfa7BYV0gqFO0c2I/2BVGSgPK1SrapayUUkqp6sg1OHwbuNEY\n8ydjTF0AY0xdY8yfgRuAtxLldsQuQ1frzZmTeV+DQ6WUUkpVB64TUi4CRgMvApuMMcuA5onjJyT2\ng01pE5qHsLbQlkOllFJKVUdOwaGILAF6JFYP2Re7QslC4FMReS+t3JNFqWU1pMGhUkoppaojp9nK\nKljQbOW2bWHRotT9WbM0QFRKKaVU8eU7WzlWcGiM+SNwMNACWAr8R0TezvXiNYFfcLhmDTRunLpf\nt65dSq9evf9v787jo6rOBo7/ngmaRQKyr5KgiIgiyusCUgVkFUEsViouLPq61AXRF7RIRUCg1p26\n1KVgqdAq1AUVRQQFhIKgsmmgCBJQIIDBhWLCluf949wZJpPM5CYEJgPP9/O5H3LPPXPuM3PH+OSc\ne849wsEZY4wx5phzqMmh38fnpQPvAhcB+4FcoAZwj4h8AvRQ1f+WNYijzezZhfcPHLDE0BhjjDGJ\nwe9s5XFAK+B6IFVV6wGpQD+v3CahhPngg3hHYIwxxhhTNn6TwyuBP6jqFFU9AKCqB1R1Cu7ReVce\nrgAT0fffF97PzIxLGMYYY4wxpeY3OawBZEU5luUdN57U1ML7990XnziMMcYYY0rLb3K4AegR5Vh3\n77jxbN9eeL9Bg/jEYYwxxhhTWn4XwX4BeFxEKgNTcGsc1gWuBv4XuOfwhJeYtm0rvF+nTnziMMYY\nY4wpLb+LYD8pIrVwSeAAr1iAvcDDqjr+8ISXmCJ7DmvXjk8cxhhjjDGlVdp1DqvhnpASXOdwsar+\ncJhiSwiR6xyqQnIy7Nt3sM7u3ZCWFofgjDHGGHPMOaKLYJuiIpPDnTuhRtj0nMqVYdeuOARmjDHG\nmGPSYVsEW0QuLk1Dqjq/rEEcTSKHlO1+Q2OMMcYkklj3HM4F/HQrilcvqTwCSnSRk1HsfkNjjDHG\nJJJYyWGHIxbFUeTJJwvvn3BCfOIwxhhjjCmLqMmhqs47koEcLWbNKryflxefOIwxxhhjysLvItjG\np8hksEe0pcONMcYYYyogm618iCJnK9eo4WYsB23aBCedFIfAjDHGGHNMsqVs4iw8OTxwAI4/HgoK\nDh7Pz3frHhpjjDHGHAmHmhzasHI52rGjcGJYrZolhsYYY4xJLJYclqPIZWzq1o1PHMYYY4wxZVWq\n5FBEAiJypoi0ExFbpCVCTk7hfUsOjTHGGJNofCeHInI7kAOsAD4CTvPK3xKRQYcnvMQS2XNoT0cx\nxhhjTKLxlRyKyE3AeOAt4Le4p6IEfQJcWf6hJR7rOTTGGGNMovPbc3gP8Liq3gy8GXFsDV4v4rHO\neg6NMcYYk+j8JoeNgQ+iHNsNnFg+4SQ26zk0xhhjTKLzmxx+D2RGOXYasLlcoklwlhwaY4wxJtH5\nTQ7fBUaIyMlhZSoiNYG7cfciHvNsWNkYY4wxic5vcvgHYA/wJTAbUODPwGrgADD6sESXYKzn0Bhj\njDGJzldyqKrfA+cCfwSOA9YDlYBngDaq+tNhi9AjzjAR2SAieSKyXER6l+L1KSIyUkTWiki+iOSI\nyNsiUimszoMiUlDM9kZJ7e/bB7m54eeDWrVK+y6NMcYYY+KrUslVHFXdBTzkbfEwBjdr+n7gC+Bq\nYJqIXKaqM2O90EsAZwIZwDhcj2ctoDOQBOwPq65AWyDsQXjsLCm47dsL79esCZV8f7rGGGOMMRVD\nQqQvIlIL+D9gnKo+6RXPE5FTgYdxiV8sQ4CzgeaquiWsPHJZnqAlqloQ5Vix7NF5xhhjjDka+EoO\nReSjGIcLgJ+Az4EJqrotRt2y6oYbzp4SUT4ZmCAiGaq6McbrfwdMjUgMY5GSqxQWeb+hTUYxxhhj\nTCLyOyFFcEvWtMcNzaZ4/7YHTsetg/gA8KWINC/3KKE5sEdV10eUf+XFFvWcInIScBKwQUReFJGf\nvHsWZ4tIyygv+1ZE9otItog8LCIpJQVoPYfGGGOMORr4TQ6fAPKBc1X1FFW9UFVPAc7zykcBpwI7\ngLGHIc7qwI/FlO8MOx5Nfe/f3+OS2D64+xVrAR+LSMOwuuu8ev2ArsBruKV6ppcUoPUcGmOMMeZo\n4PeewzHASFX9IrxQVT8XkVHAGFVtISKPAo+V1JiIdAQ+9HHeuap6ic8YowkmwLuBHqq6x4vhc1wy\neDswDEBVI4et54jIZuBJEemgqh9HO4n1HBpjjDHmaOA3OWyK6xUszg6giffzeuAEH+0tBJr5qPeL\n9+8PFP+IvmCPYazZxMEFZhYGE0MAVf1ORNbgJqrE8k/gKeB8oNjkcOTIkcyeHdxrD7S3nkNjjDHG\nHBFz585l7ty55dae3+QwG7iJ4mcF3+wdB6jJwWQsKlXNB9b6PDe4ewuTReRkVf0mrPwM3NIzWTFe\n+w2QV4pzldrIkSOJvCbWc2iMMcaYI6F9+/a0b98+tD9q1KhDas9vcjgamCwiK4HXge1AbeBK4Ezg\nGq9eJ+DTQ4qoeDNxaxFeS+F1Fq8Dvow1U1lV94vIDOAiEUlV1TwAEWmE670s6X7C63AJaMz3ZcPK\nxhhjjDkaiKr6qyjSGTfx5H9wy8rsAz4DHlTV2V6dFOCAqu4r90BF/gjcBQzn4CLYNwE9VfX9sHpz\ngEaqempY2em45O5z4HEgFRgB1ABaquoOr95nwCRcr6YAXYA7gFmq2iNKXKqqVKsGP4ZNmdm2DWrX\nLp/3bowxxhjjl4igqqVeli/0er/JYdgJA7jh4+9Lu1D0oRARwU0cuQmoC/wHGKWqb0bU+xiXHJ4S\nUX4u8CfgAlxi+xEwNHyYWkT+gZuBXQ83keUb4B/Ao9ESXhHR/HwlJWyxm6Qk2LPH/WuMMcYYcyQd\n8eTQFCYiunGjkpFxsKxuXdi6NX4xGWOMMebYdajJoe/H54nI8cCluMWwIxeFVlWN1zOX487uNzTG\nGGPM0cLv4/PqAwuATNzkjGA2Gt7teMwmh5ELYFtyaIwxxphE5fcJKY/i1jNshEsMLwBOxj0NZZ33\n8zErsufQ1jg0xhhjTKLyO6x8ETAE2OLtF6hqNjBCRJKAPwO9yj+8xGA9h8YYY4w5WvjtOawBbPVm\nJ+8GqoUd+wj3WJBjlj1X2RhjjDFHC7/J4Xe4Ra/BPSKvS9ix84H88gwq0diEFGOMMcYcLfwOK38M\nXIx7OsoLwLMicjZuvcCuXtkxq3NnSE93PYg5ORRa1sYYY4wxJpH4WudQRGoC1VV1rbd/J/BbIA33\naLvR3vOSjznBJ6QYY4wxxlQER2QRbBGpCuSr6p6ynuhoZcmhMcYYYyqSQ00OS7znUEQqAbkUvs/Q\nGGOMMcYchUpMDlV1P7ANOHD4wzHGGGOMMfHkd1j5T8Cpqtr78IeUWGxY2ZjEl5mZycaNG+MdhjHG\n+JaRkUF2dnaxx47Us5WzgWtEZCkwHdhK4UfnoaoTyxqEMcbE08aNG7E/8owxiUSkzLlfyW377Dks\nKKGKqmpS+YSUWKzn0JjE5/2VHe8wjDHGt1i/t45Uz2Hjsp7AGGOMMcYkDl89hyY66zk0JvFZz6Ex\nJtFUhJ7D4MnOwj0ppQbwgqrmiEgTYJuq7iprEMYYY4wxpmLw9WxlEUkWkWnAMuDPwAigvnf4EWD4\n4QnPGGNMRdKhQwcGDRp0xM87b948kpKS2Llz5xE/d1mlp6fz97//PbQfCAR444034hhRYkvE70Ci\n8pUcAmOBTsD1QB0gvKvyfdzzlY0xxlQQkyZNIj09Pd5hlEnjxo154oknCpW1bduWrVu3Ur169ThF\ndehycnLo2bNnubY5cOBALr/88nJtE+L3R0As8f4OZGVlcdVVV3HKKacQCAQYPXp0ubU9ePBgzjvv\nPFJTUzn55JPLrd2y8psc9gX+oKr/ACJT9g1AZnkGZYwx5tCo6mFd6uJIq1SpErVr1z6i51RVCgpK\nWqzDv9q1a3PccceVW3vHmnh8B8L98ssvNG7cmLFjx5Z7AqeqDBgwgH79+pVru2XlNzmsAayO0UZy\n+YRjjDHGr/nz59OmTRvS09M58cQTad26NVlZWcybN48bbriB3bt3EwgESEpKCvVy/Pjjj/Tv35/q\n1auTlpZG586dycrKKtTu4sWL6dixI5UrV+bEE0+kU6dO5OTkhI4XFBQwfPhwatWqRZ06dRg6dGih\n10+ZMoXzzz+fKlWqUKdOHfr06cOWLVtCx/fv38+gQYNo0KABKSkpZGRkcP/99wOux2rjxo0MHTo0\nFDvA3LlzCQQChYYUS4oz0owZM2jWrBmpqalccsklTJ06lUAgwKZNm4CDva3vv/8+LVq0IDk5mTVr\n1vDZZ5/RtWtXatWqRdWqVbnoootYvHhxobbXr19P+/btSU1N5fTTT2fGjBlFzh85rLxlyxauvvpq\nqlevTvXq1enRowfr1q0LHR81ahQtWrTgtddeo0mTJlSpUoVf//rXoc9g1KhRTJo0iRkzZoQ+q/nz\n50d9/5FGjx5NZmYmKSkp1KtXjwEDBgCuN3LevHk8++yzoXaDn1FWVhY9evQIXdtrrrmGbdu2hdoc\nOHAgPXv2ZOzYsdStW5f09HRuuOEG9uzZ4yumaN9pcMPK4d+Bxo0bEwgEQjEGfw7G+vPPP3PzzTdT\np04dqlSpQocOHfj88899fz6Rzj33XB555BGuvvpqUlNTo9Z75JFHaNKkCWlpabRs2ZIpU6aU2Pb4\n8eO5/fbbadq0aZnjK09+k8MNQJsox84H/lM+4RhjTMUjcvi2sjpw4ABXXHEFF198MatWrWLJkiUM\nHjyYpKQk2rZty1NPPUVaWhrbtm1j69atDBkyBID+/fuzdOlS3nnnHZYuXUpaWhrdunUL/c97xYoV\nXHLJJTRt2pR///vfLFmyhL59+7J///7QuadMmcJxxx3HokWLePbZZ3nqqad47bXXQsf37dvH6NGj\nWblyJTNmzCA3N5e+ffuGjo8fP57p06czdepU1q1bx2uvvcZpp50GwBtvvEHDhg158MEHycnJYevW\nrd41kEI9oX7iDPftt99y5ZVX0rNnT1auXMkdd9zBvffeW6R3NT8/nzFjxvDiiy+SlZVFRkYGu3bt\nol+/fixcuJClS5dyzjnncNlll/HDDz8ArtfniiuuAODTTz9l4sSJjBw5kr1790a9fnl5eXTo0IET\nTjiBTz75hMWLF1O/fn06depEfn5+qF52djZTp05l+vTpfPjhhyxbtozhw91t/kOGDKFPnz506tQp\ndJ0vvPDCqOcM9/rrr/P444/z/PPPs27dOmbMmMH5558fuj5t2rRh4MCBoXZPOukkcnJyaNeuqTlm\nKwAAHdFJREFUHWeddRafffYZc+bMYffu3fTq1atQ2/PmzWPlypV89NFHvPHGG8yaNYv77ruvxJhi\nfaeDwq/XZ599Rk5OTuh70qNHD5o3b06dOnUA6N69Ozk5Obz33nssX76ciy++mI4dO4aS2W+//Zb0\n9PSoW5UqVbjtttt8fZ5Bw4cP5+WXX+Yvf/kLq1evZtiwYdx66628//77pWon7lS1xA0YBuwCrgVS\ngALgHKADkAvc6aedo3FzH6ExJpGV9N8xHL6trHbu3KmBQEDnz59f7PG//e1vmp6eXqjs66+/VhHR\nBQsWhMp++uknrVq1qk6YMEFVVa+55hq98MILo563ffv2RY537txZb7rppqivWb16tYqIbt68WVVV\nBw0apJ06dYpaPzMzUx9//PFCZXPnztVAIKC5ubmqqnrttdfGjDPSsGHDtHnz5oXKxo0bp4FAQDdu\n3Kiq7jMLBAK6bNmymG0VFBRovXr1dMqUKaqq+sEHH2ilSpX0u+++C9VZsGCBiohOmjQpVCYi+vrr\nr6uq6oQJE7Rp06aF2t2/f7/WqFFDp02bpqqqI0eO1NTUVN21a1eoztixY/XUU08N7Q8YMEB79uzp\n+3MIeuKJJ7RZs2a6f//+Yo+3b99e77zzzkJlI0aMKHLddu7cqSKiS5cuDcVTrVo1/eWXX0J1Jk+e\nrCkpKYXKilPSdzryOxDu4Ycf1lq1aumGDRtUVXXOnDmanp6u+fn5heqdffbZ+uijj6qq+7zXr18f\nc9uxY0exsZx55pk6atSoQmW7d+/W1NTUQv99qaoOHjxYL7vsspjvPeixxx7Txo0b+6ob6/eWd6zM\nuY3fpWweAVoCrwB/9coWeIniq6r6dHkkqsYYY/ypVq0a/fv3p0uXLnTs2JGOHTvym9/8hpNOOinq\na1avXk1SUhKtW7cOlVWpUoUWLVqEhu6WL19O7969Y577rLPOKrRfv359tm/fHtr/4osvGD16NMuX\nL2fnzp2h+x83bdpE/fr1GTBgAJ07d6Zp06Z06dKF7t27c+mll5bqHslly5aVGGe4NWvWcN555xUq\nu+CCC4rUq1SpEi1btixUtmPHDv7whz8wd+5ctm3bxoEDB8jPzw8NX65Zs4YGDRrQoEGDQm0HAtEH\n57744gu++eabIpOG8vLyWL9+fWg/IyODypUrh/YjP+uyuuqqqxg/fjyZmZl07dqVbt26cfnll3P8\n8cdHfc3nn3/OvHnzisQsIqxfv55zzz0XcN+P8GHXNm3asHfvXtavX8+ZZ54Ztf2yfKcB3nnnHUaN\nGsWsWbPIzMwE3Oe7e/duatasWajunj17Qp9vUlJSud47mJWVRX5+Pt26dStUvn//fho3ds8S6d69\nO5988gngnum+atWqcjt/efKVHKrqAeBqEXkWNzO5Nq7HcKaqzjuM8RljjIli4sSJ3H333cycOZO3\n336b4cOHM336dDp37lzqtkqTmEVOqhCR0MSNX375hW7dutGlSxcmT55M7dq12bFjBxdddFFomPWc\nc85h48aNfPDBB8yZM4f+/fvTsmVLZs+eXeq4y1tycnKRz6Jfv37s2LGD8ePHk5GRQXJyMpdccknM\nYeOSFBQUcM455/Daa68VWcg4fDZurM/6UDRs2JC1a9cyZ84cZs+ezZAhQxg1ahRLliyJej9dQUEB\nPXr04PHHHy8Sc3AoN5rI+tGU9jv95Zdfct111/Hcc8/xq1/9qlCsdevWZcGCBUXOXaVKFcANKzdv\n3jzqYtIiEmrbj+B1effdd4sktMHrOGHCBPLy8gqVVUSlWgRbVT8BPjlMsRhjTIVUkR+e0qJFC1q0\naMHQoUPp3r07kyZNonPnzhx//PEcOHCgUN3TTz+dgoICFi1aFPof6c8//8yqVau48cYbAZe4ffTR\nRzz00ENlimfNmjXk5uYyduxYMjIyAPc/8MiE64QTTqB379707t2b/v3707p1a9atW0eTJk2KjT1S\naeNs1qwZb7/9dqGyTz/91NdrFy5cyNNPPx3qEQrehxd0+umns3nzZjZv3hzqPfz0009jJnGtWrXi\n1VdfpUaNGqFkpSz8fFaxXnvppZdy6aWXct9991G3bl0WLlxIp06dim23VatWTJs2jUaNGhW6DzDS\nqlWryMvLCyWZixYtIjk5mVNOOcVXXNG+05G+//57Lr/8cm655ZbQZJrwWLdt24aIhHrtItWvX58V\nK1bEjKU016Z58+YkJyeTnZ1Nu3btiq1Tr1493+3Fk99FsJeJyGARif2ngTHGmCMiOzubYcOGsWjR\nIjZt2sTHH3/MypUrOeOMMwA3ZJWfn8/s2bPJzc0lLy+PJk2ahP5numDBAlatWsV1111H1apVQxNG\nhg4dyrJly7jllltYuXIla9euZcKECXz33Xe+4mrUqBHJyck8/fTTbNiwgRkzZjBixIhCdZ588kle\nffVV1qxZw7p165gyZQpVq1alYcOGodg/+eQTtmzZQm5ubuh14b07pY3z1ltvZf369QwdOpS1a9fy\nxhtv8OKLLwIl95o2bdqUyZMns3r1apYuXUrfvn1JTj64SEenTp047bTTuP7661mxYgWLFi3innvu\nidkzdO2111KnTh169erF/Pnzyc7OZv78+QwZMqTQsHJJMjMz+fLLL1m7di25ublRJ+REmjRpEhMm\nTODLL78kOzubiRMncvzxx3PqqaeG2l2yZAkbN24MXYPbb7+dn376iT59+rBkyRI2bNjA7NmzueWW\nW9i9e3eo7f3793PDDTeQlZXFhx9+yLBhw7j55ptjzvCFkr/TUPg7cOWVV9KwYUPuvvtutm3bFtpU\nlU6dOtG2bVt69erFzJkzyc7OZtGiRYwcOZKFCxcCB4eVY23hw9L79u1jxYoVLF++nPz8fHJyclix\nYkXoelWuXJkhQ4YwZMgQXn75ZdavX8+KFSt44YUX+Otf/0oswbqbN29m7969rFixghUrVvi+nuXO\nz42JwHvAPmAvbtHrq4GUQ7nZ8WjZsAkpxiS8RPzveNu2bdq7d29t2LChpqSkaEZGhv7+978vNMHg\ntttu05o1a2ogEAjdPP/DDz/ogAEDtHr16pqWlqZdunTRrKysQm0vXLhQ27Vrp2lpaVqtWjXt3Lmz\n5uTkqKpqhw4dikxUiJwUMXXqVG3SpImmpqbqBRdcoLNmzdJAIKDz5s1TVdWXXnpJW7VqpVWqVNGq\nVatq+/btdfHixaHXL168WM8++2xNSUnRQCCgqsVPRogVZ3FmzJihp512mqampurFF1+sL7/8sgYC\nAd2+fbuqFj+JR1V15cqV2rp1a01LS9MmTZro5MmTtUWLFoUmJHz99dfavn17TUlJ0aZNm+o777yj\n6enphSakBAKB0IQUVdXt27frDTfcoHXq1NGUlBQ9+eST9cYbbwy9x5EjR2qLFi0KxRIZ444dO7Rr\n166anp5e6DNu166ddujQIepn8dZbb2mbNm20WrVqWrlyZT3//PP1vffeCx1fu3atXnjhhZqWllZo\n0s66dev0qquuCn1/mjVrpoMGDdJ9+/ap6sHvwkMPPaS1a9fW9PR0HThwoObl5UWNJaik73Tkd0BE\nNBAIhLbgfjDW//73vzp48GA96aSTNDk5WRs1aqR9+/bVb775psRYipOdnV3knIFAoMjn/Mwzz+gZ\nZ5yhKSkpWrt2be3SpYvOnj07Ztvt27cv0m74eylOrN9bHOKEFFGf4yUiUhu4BrgOaIWbvfw68Iqq\nflyuGWsCERH1+xkaYyqmWA+wN0ev8ePHM3LkyNCSNEeTzMxMbrvtNu69994jet6BAweSm5tbZAjf\nlL9Yv7e8Y2VeLMv3PYequh14CnhKRE7HPUrvGqC/iHynqhllDcIYY4w53J577jnOO+88atWqxaJF\nixgzZgwDBw6Md1jlLisri5SUFO655554h2ISVKkmpASp6moRGQ18BTwMNCzXqIwxxphytm7dOsaN\nG8fOnTtp2LAht912Gw888EC8wyp3zZs3Z82aNfEOo4hYs4NFhKysrNB9pya+fA8rh14gcgmu17A3\nUBlYghta9jfX+yhjw8rGJD4bVjbm8Dtw4AAbN26MejwzMzPm2pCmsMM5rOwrORSRM3H3Gl6D6yXM\nBibjksKvy3ryo4Elh8YkPksOjTGJpiIkhwXAT8A04O+quqCsJzzaWHJoTOKz5NAYk2gqwoSUPsA7\nqrqnrCcyxhhjjDEVn6/BfVX9V7TEUETaicjE8g3LGGOMMcbEQ5nu/BSRJiIyWkQ2AB/jehYPK3GG\nicgGEckTkeUiUuJT10UkQ0QKYmx9Iur/SkQWisgvIrJVRB4XkZTD986MMcYYYyoO30vZiEhV4LdA\nf6C1V7wCt5TNP8s/tCLGAPcA9wNf4J7SMk1ELlPVmTFet5WD8YYbC7QFPggWiMhZwCzcU2AuAxoD\njwH1gb7l8B6MMRVQRkZGiY9QM8aYiiT47PLDIeaEFBEJAN1wCWFPIAXYArwB3A50UNX5hy26g3HU\nAr4Fxqnq6LDy2UBNVT27lO2lAjnA+6p6dVj5m0BzoLmqHvDKrgf+BvyPqi4vpi2bkGKMMcaYCuNQ\nJ6REHVYWkceBzcA7QA/gTVyi2AgYARzJP7O7AccBUyLKJwMtRKS06fOVuDUaJwULRKQS0BV4LZgY\neqbinivdq7RBG2OMMcYkmlj3HN4N1AbeAxqp6rWqOktVC4Aj3VXWHNijqusjyr/CJanNS9lef2A7\nYUPKwCm4ntGvwit6E3HWl+EcpgKbO3duvEMwZWDXLTHZdUtMdt2OXbGSwwnALty9d/8RkWdE5Pwj\nE1YR1YEfiynfGXbcFxGpD3QAJnuJbvg5AIp7AvvO0pzDVHz2Sy8x2XVLTHbdEpNdt2NX1ORQVW8C\n6gLXAp8BtwCLRGQ1cB+H0HsoIh1LmEEc3D4q6zli6IfrbZxUUkVjjDHGmGNNzNnKqpqPm4n8TxGp\nh3umcj/g916Vh0XkOeBfXl2/FgLNfNT7xfv3B+DEYo4He/N2FnMsmuuB5ar6ZUR5sMewWpTzRNY3\nxhhjjDn6qGqpN+Bc4GlgB1AA/FCWdkpxvuuBA8DJEeUDvPIMn+2c58V7ZzHHjgPygNER5cle+YNR\n2lTbbLPNNttss822irQdSt7l69nK0YjIcbiZzP1U9ddlbqjk89QCvgPGqOpDYeWzgVqq2tJnO88A\nNwENVPX7Yo6/CZyOW8qmwCu7DjcEfa6qLjvkN2OMMcYYU4EdUnJ4JInIH4G7gOEcXAT7JqCnqr4f\nVm8Obnb1qRGvPw63RuOCaImsiLQEFuEWwX4Wtwj2I8CH4eshGmOMMcYcrXw/IaUCuB83e3oQbqLM\nf4CrwhNDT4DiJ9pchrt3MOpEFFVdISJdgD8B7wI/4RbAHn6owRtjjDHGJIIyPVs5HtQZp6qNVTVV\nVc9W1TeLqddBVU8ppvwtVU1S1bdKOM8CVW2rqmmqWk9V/y9yso2INBSRf4nIjyLyk4i8LiInHfq7\nNIeLiPxGRN4UkU3ec7PXiMg4Eakc79hM6YjITG81g9El1zbxJCLdRWSeiOzyflcuEZH28Y7LxCYi\nbUXkAxHZJiI/i8jnIjIw3nEZR0QaiMjTIvJvEdnt/T5sVEy9E0XkryKyQ0T+KyIfisiZfs6RMMlh\nReE9eu9joCluosx1wKnAR94xUzH9H7AfN9O+G/Ac8Dvcs7RNghCRvsBZuBuuTQUmIrcAbwFLgSuA\n3wDTgLR4xmViE5EWwIe4kcX/BX4NLAEmeNfUxF8T3H9PO4H5RP99+C7QBfe44964ibcfe+s9x5Qw\n9xxWFCJyF/AY0FRVN3hlmcDXwFBVfSp+0ZloRKSGquZGlAWfm91RVefGIy7jn4hUA7KAwbgltsao\n6oj4RmWK4z3SdDVwn6o+He94jH8iMg64B6imqnlh5f/GDeK1jVtwpggRuRF4EWisqpvCynsBbwAd\nVHW+V1YF2AC8oqqDY7VrPYel1xNYHEwMAVQ1G7d2oz1/uYKKTAw9S3ELojc4wuGYsvkTsFJVX4t3\nIKZEN+KWGXsh3oGYUjsO2BueGHp+wnKGRNIT2BJMDAFU9WfgHXzkKnahS+8Mil8Q+yvs+cuJpj2u\nO351nOMwJRCRX+Fu4bg93rEYX9oCa4C+IrJORPaJyNciclu8AzMl+hsgIvJnEaknIlVF5CbgEuCJ\n+IZmSiFWrtJIRGLe3pFIs5UriupEf/5ycU9XMRWQiDQARuGWKfoi3vGY6LxlqJ4HHlXVdfGOx/hS\n39seAYYB3wBXAc+ISJINNVdcqvqViHQA3gTu8Ir3Areq6rT4RWZKqTpuCDlS8Ily1Tj4FLoiLDk0\nxxwROQGYjvuFd0OcwzEluw9IAcbFOxDjWwCojHtAwnSvbK6INMYli5YcVlAi0gR4HVgF3Azk44Yh\nXxCRfFX9ZzzjM0eGJYel9wPRn79cXI+iqUBEJAU3gysTuFhVt8Q3IhOLt0TU/bh72FK86yfe4WQR\nqQrsCj7RyFQYubgZlbMjymcBXUWkjqpuO/JhGR/+iPvD+XJV3e+VfSwiNYHxuMlgpuKLlasEj0dl\n9xyW3le4sfxIzXEzKU0FJSKVcH8RtwIuVVW7XhXfybjnm0/G/TL7ATcsosBQ72df63aZI+qreAdg\nyuxM3MSv/RHlS4AaIlI7DjGZ0ouVq2xS1ahDymDJYVm8DbT2lq8BQkvZtMUNVZoKSEQE+AduEkov\nVV0a34iMT8uADt7WPmwT4BXvZ7sPseIJPqCga0T5pcB31mtYoeUAZ3l/TIdrjRti3ln0JaYCehto\nICIXBQu8pWx64iNXsWHl0nsJN2Nyuog84JWNBjbi1hoyFdNzuEVDxwB5InJB2LHvVHVzfMIysXhL\nL8yPLHe5PhtV9ZMjHpQpkaq+JyJzcfep1cJNSOkDdAIGxDE0U7JngKnAuyLyHJCHu+fwt8ATxfQo\nmjgQkSu9H8/F/bHcXUR2ADu85WveBhYDk0XkXuBH3P2+AI+W2L4tgl16ItIQeBLojLsos4G7wxeg\nNBWLiGwAijxeyDNKVe1RbAlERA7gFsF+MN6xmOJ5j6b8I+6Psmq4pW3+aOtUVnwi0hU3EewM3GSw\n9bg1K19USxoqBBEpoPgno8xT1Uu8OifiHtpxBe46/hu4R1WLW+KmcPt2nY0xxhhjTJDdc2iMMcYY\nY0IsOTTGGGOMMSGWHBpjjDHGmBBLDo0xxhhjTIglh8YYY4wxJsSSQ2OMMcYYE2LJoTHGGGOMCbHk\n0BhTZiJyvYhsDNv/SkRuLedztBaRxSLyXxE5ICJnlWf75sgTkWwRmViG1/USkbsPR0zGmIMsOTTG\nHIpWwGcAInICcBrweTmfYyKQBFwGtAHWlnP75sgr69MXrgAsOTTmMLPk0BhzKP6Hg8lgK+AAsKK8\nGheRANAUmKGq81R1iarml1f75tCJyPHxjsEYU74sOTTGlImXuJ3NweTwPCBLVff6fH26iDwjIptF\nJF9E1ojI4LDj/YH9uOeXjxCRAhH5JkZ7I706Z4rIRyKyW0S2iMioiHrJIvKEiKwSkV0islVE3haR\n0yLq1RGRSWHxbfHq1fSOJ4nIQyKyTkTyRGSHiMwXkQsj2rlZRJaH1fmriFSLqHOXiGSJyC8islNE\nlopILx+f4XURbf9dROqGHX9XRIr05IpIXRHZJyJ3hZVlisgUEdnuvd9lInJFlM/4DBGZKSK7gJjP\nSvbe2wYvxiUi8qti6tQUkedF5D/eddvkxVI/rM7LQH+ggRdD6Pvg95oaY/ypFO8AjDGJRUQ2ABne\nrgLviYgE98MeCN9YVTdFaUOA93DJ5QPAl7hh4ydEpKaq/gF4F2gLLAT+6m17YoQWHKp8EzcUPQ7o\nCjwgIgdUdbR3PBlIB8YCW4BqwG3AIhFppqrbvXqTgZOA/wO+A+oAHYE07/jvgbuA+3G9pVWAc4Hq\nYe/zYeAe4ClgCNDAO+8ZInKhqqqIXAs8BowEFgCpwFnh7UT5DG8Gngf+6cVSH/gjcL6ItFLVX4BX\ngH9472tN2Muv9T6vf3htNQSWADnee/oe+C3wuoj0UtV3Iz7jt4AJwMNAQYwYbwSexF2PqUATL97K\nEVWr467t/cB2oB7uc1/gxb4XGA3Uwn3GPXF/NAS/D36vqTHGD1W1zTbbbPO9Ac1wycvjwCqghbf/\nEzDI+/ksoFKMNnrgkorrI8pfAvKA6t5+kldvhI+4HsQNaw+NKH/Ri61KlNcFcAnZz8BdYeW7gDti\nnO8d4F8xjmfgej6HR5S38d7T5d7+08BnpbwGAVwiNzuivK3X9h3efgrwIzA2ot4y4N2w/QnANuDE\niHqzgC+K+Yyjfi5hdQXYhLslILy8jxfjxBLeX0OvXq+w8peBTT4/nyLX1DbbbPO32bCyMaZUVHWN\nqq7E9arNVdVVwC+43qBpqrrS2/bHaOYiXJLxz4jyycDxuASqrKZF7L/qxXZmsEBE+ngzoH/AJXC7\ngeCEmqClwFARGSQiZ1LUUqC7iIwRkbYiclzE8c64BOkf3hB0kogkea/bBVwc1s7ZIvJnEekoIqk+\n3uNpQG28nr8gVV0IbATaefv5wL9wPYXB994CaAn8PeylXXE9ubvCYq2ESw5bikhkT99bPmJs6G2R\n1+N13GdeiIj8zhsi3+Ud34TrqfQ1NOzzmhpjfLDk0Bjjm4gEwhKHtrhhuyRcorMZ2O7tl6Q6sLOY\nBDIHl1DFHFItwbZi9gU3pIuI9MQljF8BfYHzcUOV3+N62oL6AG8DQ4EV3r2HD4QdH4vrSesJzAdy\nRWSiiARjr+2ddz2wL2zbi0tWawCo6t+B33lxzAR2isjrIpJBdMFzbC3mWA6FP79XgEYi0s7bvx7X\nozY9rE5toF8xcT7iHa8RcY7izhupnvdvoeuhqgeA3PAyEbkTeBaXjP4ad//qBbjPL/yaFKsU19QY\n44Pdc2iMKY05eL1SuF6dV3C9fcH9fbj7Djuo6vwY7ewEqotIpYgEsW7Y8bKqA2RH7INLXsHdS/e1\nqt4YrOAlu4USUlX9HrgTuFNETsVNhhglIttV9QUvyXkUeFREauOGyp/EDWf2xSVAiutB/LGYOEMJ\nkqq+BLwkIlWBLsATuGQnWg9q8POpW8yxunjLC3ltzxORTcB1IjLfi22aqobfv5mLS3AfxiVkkbZE\n7PtZiiaYQNYJL/T+eIhMNn+LGyK/N6xepo9zhL++xGtqjPHHeg6NMaVxM65H5jFgnffzucAOYLj3\n83mUvNbhPNz9hFdFlF+Hm2Sw6BBi7BOx3xc3jLvK20+j6LBmPy+eYqnq1+omyfxA2PB02PHtqjoR\nmB12/EPcPXMZqvpFMdvGYtr5SVWn4SZvFDeUHfQfXI/c1eGF4mZKZwAfR9SfDPwG6I7rQX0l4vhM\n3H2iWVFi3Rcjlmi+A76l6PX4DUU7JtJwf1iEu4GiSegeXPIdqdTX1BgTnfUcGmN8U9WvAURkBG6i\nwTJvuZCauAkGfmeFvo+bmfu81+v2FW628g3AOFUta8+hADeF3dvXzWvzQVXd5dWZCfQSkSdwM6LP\nA+7AJX54768KLtGbAqzBJS5XACcCH3h13sLNUv7Ce20r73x/AVDVb0TkEeAZEWmGS4jzgUZAJ+Al\nr1fvBVzyugg3U/c03NDvB9HepKoWeNfgeREJ9t42BMbgEseXI17yCm4m8PPAxmJ6dUcAnwKfiMgz\nuJ7XargEtbGq/m+0WGLEqOKWEXpJ3NNQXgVOBe7DTRAKNxO4V0SG4WZNX4JLIiNl4a7vrbje0XxV\n/RIf19QYUwrxnhFjm222JdYGHIe7Z62zt38XsLQM7VQG/owb7s3HJWGDIuok4SauPOCjveBM2ubA\nR7gJCVuAkRH1BLcsynfAf3G9bC2Bb4AJXp3jcUneKu+9/ohLnn4b1s7dwL9xvaa7gdW4ZXmSIs53\nrVdvl9fWV977ru8d7+fFm4Obqb0e1zNb2cd7vgY38zjPi+NvQJ0odZd4n89DUY7Xx83s/ta7Hptx\nCeo1EZ/xfiBQiut8J7ABN2lpCXBh+Gft1UnB3XO4DZc4Tsf1gBa69rgewim4YfADwDd+r6ltttnm\nfxPVsj7FyBhjKg4ReRDXA3acqkZde88YY0xsds+hMcYYY4wJseTQGHM0saEQY4w5RDasbIwxxhhj\nQqzn0BhjjDHGhFhyaIwxxhhjQiw5NMYYY4wxIZYcGmOMMcaYEEsOjTHGGGNMiCWHxhhjjDEm5P8B\nAUP/nBwi42UAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11b8ae1d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"make_plot(log_likelihood_sgd, len_data=len(feature_matrix_train), batch_size=100,\n",
" smoothing_window=30, label='stochastic gradient, step_size=1e-1')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Checkpoint**: The above plot should look smoother than the previous plot. Play around with `smoothing_window`. As you increase it, you should see a smoother plot."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Stochastic gradient ascent vs batch gradient ascent\n",
"\n",
"To compare convergence rates for stochastic gradient ascent with batch gradient ascent, we call `make_plot()` multiple times in the same cell.\n",
"\n",
"We are comparing:\n",
"* **stochastic gradient ascent**: `step_size = 0.1`, `batch_size=100`\n",
"* **batch gradient ascent**: `step_size = 0.5`, `batch_size=len(feature_matrix_train)`\n",
"\n",
"Write code to run stochastic gradient ascent for 200 passes using:\n",
"* `step_size=1e-1`\n",
"* `batch_size=100`\n",
"* `initial_coefficients` to all zeros."
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.68251093\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.67845294\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.68207160\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.67411325\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.67804438\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.67712546\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.66377074\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.67321231\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.66923613\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.67479446\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.66501639\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.65591964\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.66240398\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.66440641\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.65782757\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.64571479\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.60976663\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.54566060\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.48245740\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.46629313\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.47223389\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.52216798\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.52336683\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.46963453\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.47883783\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.46988191\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.46365531\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.36466901\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.51096892\n",
"Iteration 5000: Average log likelihood (of data points in batch [23000:23100]) = -0.43544394\n",
"Iteration 6000: Average log likelihood (of data points in batch [27600:27700]) = -0.45656653\n",
"Iteration 7000: Average log likelihood (of data points in batch [32200:32300]) = -0.42656766\n",
"Iteration 8000: Average log likelihood (of data points in batch [36800:36900]) = -0.39989352\n",
"Iteration 9000: Average log likelihood (of data points in batch [41400:41500]) = -0.45267388\n",
"Iteration 10000: Average log likelihood (of data points in batch [46000:46100]) = -0.45394262\n",
"Iteration 20000: Average log likelihood (of data points in batch [44300:44400]) = -0.48958438\n",
"Iteration 30000: Average log likelihood (of data points in batch [42600:42700]) = -0.41913672\n",
"Iteration 40000: Average log likelihood (of data points in batch [40900:41000]) = -0.45899229\n",
"Iteration 50000: Average log likelihood (of data points in batch [39200:39300]) = -0.46859254\n",
"Iteration 60000: Average log likelihood (of data points in batch [37500:37600]) = -0.41599369\n",
"Iteration 70000: Average log likelihood (of data points in batch [35800:35900]) = -0.49905981\n",
"Iteration 80000: Average log likelihood (of data points in batch [34100:34200]) = -0.45494095\n",
"Iteration 90000: Average log likelihood (of data points in batch [32400:32500]) = -0.43220080\n",
"Iteration 95399: Average log likelihood (of data points in batch [47600:47700]) = -0.50265709\n"
]
}
],
"source": [
"step_size = 1e-1\n",
"batch_size = 100\n",
"num_passes = 200\n",
"num_iterations = num_passes * int(len(feature_matrix_train)/batch_size)\n",
"\n",
"## YOUR CODE HERE\n",
"coefficients_sgd, log_likelihood_sgd = logistic_regression_SG(feature_matrix_train, sentiment_train,\n",
" initial_coefficients=np.zeros(194),\n",
" step_size=step_size, batch_size=batch_size, max_iter=num_iterations)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We compare the convergence of stochastic gradient ascent and batch gradient ascent in the following cell. Note that we apply smoothing with `smoothing_window=30`."
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAFUCAYAAACgM9EjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX6wPHvCZAQeu8dkaJSFFQUFESxYC+sKOjaUNff\nWrcorspiQ3Ft2F0VFSuKay+AgFhBpUgHISAt1ISEhIQk7++PM8P0mTuTmUwmeT/Pc5/M3HLuO5M7\nM+8995xzjYiglFJKKaVST1qyA1BKKaWUUrHRRE4ppZRSKkVpIqeUUkoplaI0kVNKKaWUSlGayCml\nlFJKpShN5JRSSimlUpQmckoppZRSKcpRImeMOcEYUy/EsnrGmBPiG5ZSSimllIrEaY3cbKBXiGXd\nXcuVUkoppVQFcprImTDLMoDSOMSilFJKKaWiUDPUAmNMJ6CL16z+QS6vZgJXAhvjHllgPAa4HRgL\ntAJWARNEZHqU5XQGlgG1gUNEZJ3f8kHAQ0A/IBd4E7hTRPaX+0UopZRSSsVRyEQOuBy4BxDXNBnf\nmjlxPS8BbkhUgF7uA24FxgG/AhcD04wxI0TkiyjKeRbYg00GfRhjegNfAZ8DI4DOwCNAG2BUuaJX\nSimllIozIyLBFxjTEeiETda+xiZry/1WKwJWi8juBMaIMaY58AfwgIhM8Jo/E2gmIn0dlnMJ8B/g\nQeAxoJt3jZwx5gNsW8BeIlLqmjcGmAIcJSKL4vOKlFJKKaXKL2SNnIhsADYAGGOGAr+KSF5FBebn\nNKAW8Ibf/KnAS8aYjq54QzLGNMImcbe5yvJfXhM4FXjEncS5vAu8CJwDaCKnlFJKqUrDUWcHEZmb\nxCQObC1ZkYj87jd/GbbGMFSPWm+TgOUi8maI5V2x7eaWec8UkSLgd4f7UEoppZSqMOHayB1kjEkH\n7sC2E+uA7anqTUTEUVkxagLkBJm/22t5SMaYwcBoINwlWHcZe0LsJ+w+lFJKKaUqmtPkaxK2jdzn\nwHRs27iYGWOGATMcrDpHRE4q575qAc8Bj4rIqvKUpZRSSilVmThN5C4E7hGR++O03++AHg7WK3D9\n3QM0CrLcXUsWrrPFLa5tJxtjGrrm1XX9bWCMqSci+Xhq4hqH2M/SYIUbY4L3FlFKKaWU8iIi4cbl\njYnTRK4e8EO8duoak211FJssAzKMMV38xn07DDsMin9vWm89sUONbAmy7FdsB4Yjse3gilxlHmSM\nycCOp/duqB2E6vmrqpfx48czfvz4ZIehKgE9FpSbHgvKzQ6HG39O7+zwMZDM+6l+gR2v7lK/+aOB\npRF6rD4IDAWGeE0PYRPAS4CrAUTkgGs/I40x3u/LRUA68FE5X4NSqoJ8+SUceij07g0//ZTsaJRS\nKnGc1shNBl4zxpQBnxHkUqb/HRLiSUR2GGMeBe4wxuTjGRB4CHCW97rGmFlABxHp5tp2NX61f667\nOwDM94t7PLbmcZox5mnsgMAPA9NEZGG8X5dSKv7KyuDqq2HTJvv8ppvgxx+TG5NSKrxPPoEPP4Sh\nQ+GSS5IdTWpxmsi5L6uOx97tIZga5Y4mvHFAHnAjnlt0XSQin/utl4bzmkYfIrLYGDMcW2P3CfYW\nXVOAO2OMWVUjQ4YMSXYICti61ZPEQXJq5PRYUG56LET2669wlqtK5r//haZN4dRTkxtTKgl5Zwef\nlYz5M/ZSZEgi8mqcYkopxhjRNnKqsps0CcaNg1atYPp0GDAg2RElzubN0K6d7zwRmDEDrr8e0tLg\nxRfhxBOTE59SytegQfDdd57nLVvCtm3JiydRjDEJ6ezgKJFToWkiFz+lpfbHtnFjOOaYZEdTdezY\nAS1aeJ4PGgTz5nmeHzgAd90FX38NZ59tE760mOq0K4dgiVxZGXTrBr+7hhQ/4ghYsqTiY1NKBWre\nHHbu9J1XFX9WE5XIpfDXtapqRo6E00+HY4+FyZOTE4OIbacxeTLsTugdhCvOl1/6Pv/2W9/n06fD\nQw/BggU2oZs9u3z7KyqCJ5+E//wH9u0rX1mxCPYDUFDgSeIAfvut/PvZtw9uvx2uuAJWrix/eUop\nFYuQNXLGmJeBe0VkvetxOCIiV8U9uhSgNXLxsX49dOniOy8Zb+sTT8DNN9vH3brZH+jKWjs1Z45t\nyJ+eDs8+C/37B19v6lQYM8Z3nvd7698jvksX36QnWmPG2H2CbefyxRexlxWLTZugfXvfefn5UK+e\n77zyHl/XXw/PPWcft25t91tZjxWlKrNmzWDXLt957s/nH3/A3/5mT5zuvx/69Kn4+OKlwi+tGmPW\nA+e6OgBkEb6NnIhIlzDLqyxN5OLj669h2DDfecl4W/2Tms8+s7WElY0IdO1qE2Cwl6JD9cwMlsjl\n5sLEibb27NFHfZc1a2Yvx8bK/z3MzYUGDWIvL1rBErm8PKhf33deeY8v/9c5YwacfHL5yqwuli2D\nK6+0P94TJ8KFFyY7Il979sCdd9r47rzTDmNTlYjYE8GiIhg+PPEnIMXFtoZ+2zZ7oty5s+/ycInc\niBH2exjsd96aNYGfvVSRqEQuZK9VEens9bhTvHesqr5162DxYtsmq3nz8OtW1lx40aLEJXKlpbZ9\nWu3a0W+7Y4cniYPoe2Y2bBh6WUlJ9PGEU1hYsYlcso6l/Pzk7Nff9u0wc6ZNPg4/PLptc3Jse8Im\nCbyz9P79vnFddZXtsZjhfwfvJBo82CabAO++az+rVam29e674b777OMrr4SXXkrs/u64w3PC+P77\nsHGj8/fTncSBvVKwbp1N6JRHFTo0VWWyaJH9ITn/fPu3PDU8yTRrVmLKXboUDjkEMjPhxhsTsw+3\naBObnJz47r+sLPzyffviv09/8UzuROCjJAwPLmJrNXr1gksvtTWd/nJy7KWnSy+FI4/07dQSyRtv\n2N6CLVrYNo6hlJXZz/eWYPfKcWDECN/ne/cGtttMNncS55ao74FkcSdxAC+/nPiTEO9a/82b7YlG\nrOJ9ohlv+/bB6tW2trOiOE7kjDF1jDH/Z4yZZoyZ5fr7F2NMZiIDVM7t2mWrrW+4wY6lFclvv9lh\nKLp1g//9Lz4xLF8OEyZAv36ehu7bttnhL8KprDVyZ5+dmHL/+U/IyrKPJ08O3fh+xw57ybTAddfh\nefNsbUa0NS3JFC6R++ILaNPG1gB5/7g4VVoKK1YkPhH0NmkSnHNO4PzyXu7ZutUeC/5JQ0EBXHON\nrcH429/s633zTdsu0t/TT3uGbThwwHbEcGr0aHsJrLTUtr08cCBwHRE491z7+T7kEPjqq+Bl7d5t\nj2/35/qrr6BHD6hb1zajKK9vv7U1O8XF5S/LieHD7aX5xx+Pb7nvvmvfy/POc/adnSh5eYHziorg\n3/+2NaZLg95pPHbujmTr1iV/mJHSUrjnHnsCdNNN5UvANm60FRfdu9tOe8FOthJCRCJO2AF4VwJl\nwHrsAMHrXc9XAC2dlFMVJ/sWVg5nnCFivzpFjjkm8vrDh3vWb9JEpLi4fPvPzhbJzPSU6T316GHX\n+e03kZkzRUpKfLf96qvAbbzNnCnyxBMiW7bY52VlIkVF9m80PvhAZNw4kYULgy/3j+HFF0OXtX+/\nyIQJIldfLbJ0aXRx+O/nrLNEnn9eZNUqzzrLl4s0bepZ5+STRdq0Cf7+hjsMX3st9DbRlhXOV1+J\ntG0bWNYff4TepkUL33V37XK+vwMHRAYPttu1aCGyeLGdv3FjYAx798bnNYqEfs/+97/Yy9y3z/e9\neOcdO3/u3Oj+T0OGBK4ze7ZIp0722PnwQ+eva/v2wHV++MF3nRYtAteZMUOkfn27/Kqr7Ge0ffvw\nr2PWLGfvU2mpSJ8+nu2GDnW2XbTCxRrsfYnFnj0itWp5yr3uOs+y1atF+vcXadbMfu9FUlYmMn26\nyFNPieTkRF7f/zW5v1e9/fOfnuWNGtnvu1j57+/NN0VuvdXZse0/f8QI+xmPl5kzfcufMEFk5crY\nyho71reshx/2Xe7KF4j35GwleA3IBo73m38csBWYkojgUmFKViK3b5/If/4j8vjjng+Y/wEf6QPt\nv/5334Vfv7hY5MYbRbp2Fbn2WpHCQt/lN98c+kPZo4dNKNLSPB/GhQtFFiyw24ZL5N591zOveXOR\nzZtFTjzRd91GjeyPdTjTp3vWT0+35UR6T8Ilcrff7lmvcWObWPrLyxM5/3z7w3bxxSIFBcH3457q\n1hVZs8auc+aZoddz8qPuFq9EbssWmxSEep87dw5e1oYNdnlBgcidd9pEOi8v+Ptw3XUiS5aEfi3e\n3n7bd9uTT7bzN2wILPdPfwqc5/QkoLTU93mo9+yDD5yVF8wTTwT/H/ToEf7/VFgoMmeOPZkYPdoe\nh/7r9Orl+/nxfz2hXtf69YHrTJwY+VjxT+a//jry8eY0kXvggcBtDzlEZNMm3/W2bxc591yR7t1F\nnnkmfJllZSJTpohcc43IF18Efy+cfid4Ky4W+egjkZ9+Cr786adDv5eXXuo7Pzs7/L4eesizbu/e\nkY9t//0GS+T817n4YpH8fPs9t2NHdCfR/mU99pjz76BQy485xibyy5c7j2P1as/3q1vr1sHLHzcu\ndDkFBfZEMtLrbNfOfzkikrxEbgdwZYhlVwE7EhFcKkzJSuRGjPD9gIkEHkRZWSK33CJy2WXBzzD8\n1+/fP3yt3Icf+q7/5pvhy/Oewv0g/f3vIl9+GTjfrWZN3/mhaqWuuir8e1ajhu/6Z5wR+T158UX7\nQzl9euB7EyyGfv1EFi3yrPPSS77L33gj8nt10UUiH38cfp1wX3z+Xn01+rIOHLCJvfvHfMkST5Jw\nyCHBTxJCleUuw39+376ht7nppsg/XuecE/wY9q5JCDeFSmjc5s0TadXKJv1PPx35dQ4ZIvLee+F/\n4NauFfnlF7vOb7+JfPutfXzFFcH/n5FeQ+/e0f9vt28XmT/f1iB617L4r/fKK4HxeycMoY47/+WH\nHBI5JqeJXKjtL7nEd71//MN3+YYNIuvWBT8J+eAD33WXLw8f63PPOYv1lFM82zz/fODyJ58MLDvU\niV6HDtG9L998E936W7bYY+Guu0SOPFLkttuCv/batW3tLtjvz+xskUceEZk6Nfxx71/O1VdHPiYK\nC+3JfqT1nNbKep8EPPKInbdsWfiy8/N9yygr89S6dekSmET6b9++vf9yRCR5iVwhcFqIZacChYkI\nLhWmWBO5pUvtB33YMM8lIX8//GBrHfwPpsLCwANGJHCed7LXvLlNKt55x/OBC3bgfvpp6JiDne27\nFRWF/jA4mT76KHjZP/0UXTnXXSdy9NHBz8KDrR9pHf8E1F2TFKo8sLWF8+fbH0z/ZRkZ4bcFWyvX\nsmX072EoxxwTfVlDh4Zf/sADzt5fsJcu9uyJPoaWLQNrWrydfXb5jjn/y/v+/C9TupPXSOW6fyT8\nTZ3qezJhjP172WXBE7nS0vK9vlDTpEmex4MGhf4+mDAh8DU8/HDk4y6WmEIlcsuX2x9bJ2Xv3m2P\nta1bw6/XtavvpbmMDN/lkWrCvZN6t5wce0nZfbwuXhz+fSoutiee/uucemr41zllSvD3Kdi6PXsG\nv+oQbP2//KX8x1Ww4yXU/i6/PHJ5deo437e/F16wzVI6drRXRP7+98BtnHy+7rnHt7nHggWB61x/\nvedyu/+yypbILQLeCLHsdWBhIoJLhSnWRG7AAM8/u2/fwOVTp3qW9+njW3uQnx/8QHZ60Ie6BAa2\nmvndd0VGjbJnnt5nWcE+WG6zZzvff7Cpf//Aed6JaCxTpLMld/xFRbYGyEnCU6dO+EQ40pSeHvu2\nkaZgli5NzL6OPNK+D998Y2uYwr2mE0+0NSax7Gf4cN/XU1Zma0i//z76S8/+U7Da56wskV9/tfvx\nX/+GG+wlpVj/F+HWP+20wHmx1LbFMrmbVPjPv+02z3v+6qu2dv/UUyO/1lhicCdyBw7Yk9cPP/St\nQbn3Xudle7crDTWdc07oeP0TO/9p8mRbc/bMM7bWcudOz3dqw4Y2ifNuDuKenntO5O67RVas8P3+\n95+ys8Pv//PPbfxpabbZRLj3xX3i6Pbjj7Y5TqKOJW9PPSXSoIFIt26B6w0alLj97t0bePUl2OQk\nmXRPLVvaY/Kii4IvP+204P+HDh3syf/SpfaYSXYiN9rVsWEmcCVwOnAF8CVQClySiOBSYYo1kfP/\nh/u3r/Jf7l1Ttm9f4PJgPzzxmNwNuEtKgi8XsZcsgn1xJXtq1crWqP3zn/ZHO1T8/fpFV+5XXwX/\nHzmZatWKfdtIk3fS/dtvIscem7j3tl8/3+Ts/vsTt6/0dPtj8N138S33uefspU636dPtvsCeyATb\nJlxnE//jSsS2KU3U+xLPKVjbN7C1/1OmOHutob67nEzu2pwLLwy9TrxrKEVi+958/PHgibd7Gjq0\nfN+H0R7n3jWswSb3b8u8eZ42yomaRGxFQyKTxVD7dZs2rWL37Z6uvDJwnjGeS9GHHSaS1ERORADG\nAttcCZ172gpck4jAUmWKVyLn3yMo2IFy//32QxnsS8JpTUG0U926Np5nn01M+cmesrKi32by5ND/\nIyfTCy8k5rV4N74dODCx71vHjsn/38VratfO9tqOZ5mzZ0dua5UKU7BOGP6T2+LFwTuVOJ28OyMF\nm/x7F5Z3ys0Nfkk70nTnnZHXqUwnts8+azunVcS+ysqCX11J9OStMr33gROSiDwk5C26gjHGpAHd\ngSbAbmCViEQY7rNqi/UWXf5jTu3YYW9TEmq5W0ZG8HFuNmyAjh2jDsORAwegVq3ElJ2KnnjCDuJb\n2W4T07OnHZdt1iw7WrtSFUHE3r2jTp3E7qdTJ8/Yi5XdhRfCe+8lO4qK9913cPzxFb/fX36x47ct\nWmTv7+wep67yqeB7rSpnYknkRAJvT9K0qf0QdO/uLje6OE45xd7rMRFeeAHGjk1M2amoTRto3Dhw\n9PfK4LrrPDdyV0qp6qJXL3tHhcp954ckJ3LGmG7Av4CBQFtgM/A9cJ+IrI13YKkilkSurAxq1Aic\nf/75drRyW24cglNKKaVUJZHERM4YMwT4DDsMyafYwYFbAiOAOtihSebGO7hUEEsiV1oKNWsGXzZ6\ntL0FUOvWcQhOKaWUUpVEchO5X4D9wKkiku81vz7wFVBLRPrHO7hUEEsi9+OPMHBgggJSSimlVCWU\n3ESuEPiTiHwUZNm5wFsikhnv4FJBtIlcVhZ07py4eJRSSilVGSUmkUuLvAoAm4D0EMvSse3llAP3\n3JPsCJRSSilVVThN5B4C/m2MaeM90xjTFrgHeCDegVUlH3wADzxghwj57bdkR6OUUkqpqsLppdXX\ngSFAc+BHPJ0djnU99u7oICJyedwjraQiXVqdMgWuuKLi4lFKKaVUZZTcNnLroyhTRKRL7CGllkiJ\nnA4jopRSSqmkjyOngtNETimllFKRJbezg1JKKaWUqmQ0kVNKKaWUSlGayCXQZh2URSmllFIJpIlc\nAp1zTrIjUEoppVRVpp0dyilUZ4e1a6FbtyQEpJRSSqlKSDs7pJSnnkp2BEoppZSq6rRGrpxC1cjp\nsCNKKaWU8khyjZwxZqwxZqExpsAYU+o/xTuwVFVSAvfem+wolFJKKVUdOErkjDGXAZOBBUBt4BVg\nKrAX+B2YkKgAvWIwxpg7jDHrjTGFxphFxpjzYyinsysZLTPGdPFbdo9rvv803Wn5r7wCd98dbVRK\nKaWUUtGr6XC9m4EHgXuBq4FnRORXY0xjYA6wKzHh+bgPuBUYB/wKXAxMM8aMEJEvoijnWWAP0CrE\ncgGOB8q85u12WvjYsVFEopRSSilVDk4TuW7AN9jkpgxIBxCRPcaY+4H7gYQ17zfGNAduAx4Qkcdc\ns+caY7oBEwFHiZwx5hKgDzYpfSzMqvNFpCzMcqWUUkqppHPaRq4QqOlq1b8N8L4kmQ+0iXdgfk4D\nagFv+M2fChxhjOkYqQBjTCPgP9iEMDfS6rEEqZRSSilVkZwmcr8Bh7oezwPGGWMGGmMGAOOBlQmI\nzVsvoEhEfvebvwybdPVyUMYkYLmIvOlg3T+MMSXGmCxjzERjTO0o41VKKaWUSjinl1ZfALq6Ht8F\nzAS+dT3PA86Nc1z+mgA5Qebv9loekjFmMDAa6BthP2uB24GF2LZyw4FbgH7AqVHEq5RSSimVcI4S\nORF5x+vxWmPMYcBAoA7wvYjsjGanxphhwAwHq84RkZOiKTvIvmoBzwGPisiqcOuKiP+l21nGmM3A\nY8aYoSIyuzyxKKWUUkrFk6NEzhhzAvCriOQDiMg+bK0cxpi6xpgTROSbKPb7HdDDwXoFrr97gEZB\nlrtr4sL1Kr3Fte1kY0xD17y6rr8NjDH13K8rhLeAx4GjgaCJ3Pjx4wFYuRJgiGtSSimlVPU1xzUl\nlqM7O7gG/B0oIvODLDsK28uzRgLic+9jDDAF6CYi67zm/xl4CegiIhtCbPsKcBmhOzAsEpEjw+y7\nOZAN3CEiDwVZfvDODhkZUFzs5BUppZRSqnpJzJ0dnLaRC7fjDCDRd3b4AigBLsWOZec2GlgaKolz\neRA7gLG304F/uMpbHWHfo7Ht5X6KFKQmcUoppZSqSCETOWNMJ3yHGelvjKnnt1omcCWwMe6ReRGR\nHcaYR4E7jDH5eAYEHgKc5b2uMWYW0EFEurm2XY1fsmaM6ex6ON+vhu9n4FXX+gbb2eH/gM9FZE78\nX5lSSimlVOzC1chdDtyDrY0S7C26vGvmxPW8BLghUQF6GYftIXsj9q4Mq4CLRORzv/XSiOIesn5W\nu8pv7SpjHXZ4lUkxlqeUUkoplTAh28i5BtnthE3WvsYma8v9VisCVouI41tYVTXebeSMDiOslFJK\nqaAS00bOaWeHE4FfIvTurJY0kVNKKaVUZElM5FRomsgppZRSKrLk9lrFGDMcuB7oDvjfskpEpGvg\nVkoppZRSKlEcdQowxpwBfI69k0MP7L1VNwLtgTIgmsGAlVJKKaVUHDjt3XkX8DRwhuv5v0RkCHAY\nUAOb5CmlVJXypz8lOwKVCg45JNkRqOrMaSLXA/gYW/smuC7JusZoG49N9Ko1HQxYqarl2Wfh7bdB\nmxGrSPr3T3YEqjpzmsiVAaWuVv07gA5ey7YA1b593IcfJjsCpVQ8XXed5/HatcmLQ1V+jz6a7AhU\ndeY0kVuFJ1n7GbjZGNPadR/S24CsBMSWUi6+ONkRKJU8//pXsiOIr7PO8n3etSvk5cHMmbAxofex\nUYk0c2b8y8zPh8zM6LYpLHRe01u3bvD5AwbAH39Et9/KJtlNF0K9t6nGaSL3BnCo6/E92LZxm4Bt\nwEnA3fEPLbWUlSU7AqU8atSouH117QrXXONs3TVrEhvLySfHp5wxYwLn1asHw4ZB+/bx2UeqaN0a\nLroILr002ZGUz6232v/fd99Fv+2SJfDkk8GX1a0b/dBTtf3HfQgjPx8OHAicv2ABtGsHubnwwQeR\ny1mzxp6MRJt0JlK8huzKyIhtu4p8L4YOTWDhIhL1BLQDrsbezqpXLGVUlcm+hSL2/Kp6T3/9q8jE\niSKFhSLffhv99j/8ILJypUinTuWLo0aN5Lz+Pn1EDj00uf+DE04Q+fJLkdWrRR5+WGTWLJHFixO7\nz65dRUREGjSIvG55PisXXhh++dVXi8ydG5/X9MMPEla4bf/+d5G//EVk2LDkHgvxmhYscPa6EzHd\neafI5s3R/19btw6c98ADsb+OcNuJiOzdG7/ynK57772+x+QVV4Quo0kTz3r5+SI33yxy3nki8+aJ\n3HefyNFHi1x7bWL/l5deGjhv1Kjyldmjh8jbb4tkZ4u0b5/44zHY1Ly5s/V27hRx5QvEPQ9JRKHV\nadJEzk433CABoi3Dbf/+8sWSm+t5nJFRMYldy5Yia9aIlJYm73/w8suB/4NY/xfRTF262H3s2+fs\nf3zSSbHt55FHwi+/5pr4JXI//xz6vYz0fs6YUTHve3mmM890vm5JSfJej9uuXdFtN2hQ4LwHHyz/\nd1OoZXl5zstKT48uDrfly33nFxX5HpPhErGePcMfz+X9/z7+uLPX4T/vkktEateOfb/btnli//nn\nij8+QWTLFpGzzgq/znPPuV8/IhL/PCTWm8urauDLL52vO3hwdGV36RJ6WUYG/Pe/0ZXnrUEDKCqC\npUshOxv++tfYy3Liscdg2TI7BEGaw0/U4YfbOOPlxBNh1KjQy7t1i9++QqlTJ/xyd8++xx6LrfwW\nLSKv07t3bGVHK1zj9mHDPI8T3Qbo3/+Obv3nn7efiY8+gpdfdrZNuGO6f3+YMqX8l8gitVVq3Bh6\n9PA8b9Qo+n1EirFNm+jLdFq2tzffjG0fPXvCvn22XVxpKaSn+y7/299Cb/vss7Htc9So2C9bOmEM\nDB8en7KOOso2cVqyJLrtvJuhTJgQuPzPf4ZmzfzazaYdgMzd0HADu2os5dLbv4euX0Kv96DvK3DM\nkzD4fjj5dhjxF17JHcPzPz8fy8tyJlSGh6unqtMpEVlmKky4TjXineX//LPIVVeJ3H13/Mv2nxo2\ntJcdvOeNH2/PIF5+2dZqhds+PV2kuDjg5C7ouuvX26r9zZsDl/mbPj221+Nvxgzf5R072tccavtx\n4yLvY9Qoezli0iSRsrLIrxvspZDt2+0kYmvxIu2nQQORK6+MvJ53rUkw3bsn7vhx18iFe+1paSLz\n53vWW7lS5NhjRUaODL3NXXd5HjdpYmsgwsVx9dW27AcfDF+W93TPPcHnb94c/v0sKxN59dXIx99N\nNyXufQeRb74RqV/f+fqvvOKJ7cABkQ4dIm/jzf97YvlyO3/zZvs//fJLO0XzGu6809l7uWCByIkn\nipx8ssiyZeHLDFYj99hjoY/Tnj1FVq2ylycvush32Zlnht6uVi0730ltNNgrF941aU62icajj9qm\nDmedJfK3v4kMHy7y1FOB31Gh+O973jyR3btFBgwIHV+tWpH/H6edFrz80aNFzj479uN/xw5nrwNE\nqFEk1NkhNF4rtPpV6DhHOPQj+cfrb8jhlz8nJ9w+Se746m7h1JuFs68SLhwpXHq6DHxxkPR5to90\nfryz8PdRSN+pAAAgAElEQVRmwr8yhPFEPY2ePlpc+QLxnkLea9UYMx5wLzTAlUAmdjy5bKAVcCZQ\nCLwkIlGeG1YNxhgpLpaAsyOn/vtfuPrqwPnuf0teXmDNTfv28e2t1LAh5OTAM8/YqXdvePppexYM\ndoy8CRPg/vt9t7vpJrvsppuge/fAcv3PUpcuhcMO8zzv08dz9nTmmfDxx4FlvPIKXHlldK/H/5AW\ngdNOg6++gvr14dNP7RnthAmwdSusXOm7fllZ+FqI8ePhnntCLw92dl6/PuzY4Xt226qVrR0JZ/Ro\neP31yGf8IT7GB82aFb+OAP66dIHff7ePQ8X57bdw/PHBlzVsCHv3Bs4vLra1dxs22FrVHj3Cvw9X\nXw0vvmgfP/WUpyY2MxM2b7adMvbs8azfooV9/+fPh9tvh9mz7fwLL4Rp00Lvx5t/PLVq+Y4pefPN\n8MQTwbcdN87WqlxxhX2djz/uWXbHHfDgg5H3P3cufPIJTJrkLN5XXrE1DG47dsBbb9n35ssvYfJk\n3/WvvRaee87zfO9euPFGWLjQdnD5v/8Lvp9u3YIP2VKjhv0cetdaFhXZ9+HFF2HsWM/8ceMCv3O8\nhTsWjj/efr8884x9XqsWbN/uqcl76SXf793Zs2HIEM/z8ePtvjt1gv/9z/O95b/PVq3sd8j+/c4a\nzvt/Tp3U5EX6bMeTfzzbtkHLlrBiBRx5pH2d/ty/H2PH2v9h48Z2G+/vVfd3v3/5Y8bYzhoffeQ7\nf+1a+9kcPx5mzCyD9HzI2AsZufZv7VzaH5LLXfftJbcol71Fe8ndn8veYvv3g8886x3crlaQ4CvQ\nOd3P4cNRHyIJuNdqyETOZyVj/gWcCpwqIgVe8+sCXwKfi0iYj1zVZYyRt96SsJe1wsnPh8svh/ff\n953v/reUlkJNvzvibt1qe5LFi/uDGM6ePdCkie+84mL7BRnKhx/Cuefax2edFfhhzcqyl4YyM21S\n1axZYBlvvGGTmWgEO6RLS+2XSatW9kvGbeFC+wXlv/2118ILLzgv31uwL+cZMwITqWCJXP/+8PPP\nnufTptnEoryJXEkJ3HabLW/rVt9lTZrA7t3htw+na1fPj3aoOMPFd+GFgcd/qG2cJnIiNkFZssT+\nWBx2WOCx9NFHvpdL5s61icoZZzjv9RspkbvpptC9Hf1fX2GhTdobNbK9RJ1cpp871yYh48f7zu/Q\nIfgwKS+/bBPHYP74ww6jtHSpTWAmTLDvj9PmAt4GD7bJu7d//xtOOQUGDgy+TWkpXH+9fQ/694f3\n3vP9rPqLlMi9/z785S+wfr1N1EeO9CwvKLBJ9rx5cMEFNjYn//Np03zL+fxze5JYVOSsJ2qqJXL7\n93tOPpcts8fbDTf4rtOokecEafNme9LaoAH89BMsXVbG4GF5ZDTMYc/+PfQbmAO1cw4mZP2Os0nY\n73/k+iRdh/d3JWZFe8ndvxdMBb4JCXJS55P4+vKvk5rI/QHcICIfBVl2LjBZRKpZp3zLGCODBwvz\n5kW/7TPP2C+uX3+11/e9ef9bunaFdevs4w4dbA3Fpk32S3bRouBl16hhvxidcJLIQeCHPFIiB/aH\n8cABaNrUWSz+pk4NPhSEW3a2TWrdw7/ccQc88IDz8kMlcllZcMkl8MMPgdtEm8i9+Wbw9mutW9sz\nXm/z59s2Izk59sdozhybyJc3kfNWVmbHfduzx9YE7dljE57TTnNehjcnNXLh4lu9OniNbrBt3n3X\nHg/B7qQydqxtAxZKURHccosdS+zss+Ghh8o/TIv/601Pt/txu/HGwFout1hOCLw1bGiP/7w8e1Lg\n/rzffrv9HGzYYNtOetdCrl5dMe0lb7jBUxsGNskpLIzvPtw1QMEcf3xgIhkPxcX2szNzpr2KcPfd\n9vPpJJE75xxbu+etsiVyL79sT2JLS2HiRPjHP6DwQCE5+3PI2W+TseOHuZKx2nugdg4ZjfYw+mrP\n8pz9OewptH9zi3Ipkyo4NldZGhTXh6L69Oxan/oZ9amf7vnbIKMBFNUnraQ+h3SoT4OM+nRs2JGT\nupyUkESuZuRVAGgGhLp4mA7E+DNdNcSSxHl/OI880v6IfvGFff7OO77r/v67HfuotBROOMHOa9cO\nfvnFzsvLs7UIP/0Exx4Ln31mq7dzc2NrFBzK0KGey0/HHx85iYPyN+gP9yX21lv28thbb9nLUoce\nar944qFTJ/j+e/t45Eh7Jl6jBrz6avRl+deougV7bQMGwKpV9sz2iCM8244ebZPaeEhL8012W7e2\n08cfBw6E66127eCXVsrr0ENt8jFxYuR1R460tT0FBYH3t4z0o5iR4ZtcxMNbb/km6bE2ZI/GkUfa\nGtSHH7avKSPDJriPPWaTtH/+037ujjjCzj//fPsdce21FZPEgU12XnrJk9S+/Xb89/HMM/YE2PsO\nHImWnm7f91iESui91axpa8/jSUTYd2Afuwt3s6tgF7sLd7Nn/56DyZZPApaxhz5P5pBblMOjJXu4\n+74cikqLfAv0G0+wCHhpYXxjTgRDGlLYAIoawv6GUFyf3t0b0KNLfRqkNziYhOXurM/H79WH4vpc\nd0V9ju7tWXZoJ5u8caAOtsUZLK8ElYVOa+TmAU2AU0Rki9f8tsAMYIeInJiwKCsxY4x4mhI65/+2\nl5baZK1FC9/eWU6VlNjErWFD38ThzDNtm7BwGjSw20aSnW3bhpWV2Us55enl5dSrr/q26QF7KXrg\nQHtGXt7ecqFq5LyVlcGPP9paxWA1R/78Y1q+3PY489eypW23E27fbjt3QvPmofcZj7N2EZuIfPON\nfd+L/L6/N2ywNYjHHOM7v7w1cmBrIv3LjbbG6vrr45+oRbJ/v619+uorOP10+2Pt3Q4yETVy0f6v\nd++2iVzHjtFtV16//WYvj/bvH/4Eobw6dAhsM3zccbEN/BsrkdCXoOvWtd+dwXrmBmtz519L7/5/\niwgFBwpsQlZoEzLv5Mx7vvfy3YW7KS5N8ZuBF9exCVhRAw7r2pA2TRvSIKMBDTNcf2v7Ph95jitZ\nK2pwcLuy/XVp0cKwc6en2DVrAk8Iwwn2mYzm82iMSWqN3I3A18A6Y8yP2M4OLYFjgQLgkngHVt3U\nqOGpbYtFzZrBL1/edZdvIvf88/bMPBYtW/o2fK4Iwe6YMWVKxcaQlmZ/GGIV6gf5lFNsuy23Y48N\nXUazZrBrl611veceO6p7vBljR++/9FI7lIh343uwP5gdOgTftryOPhoGDfJcDotluIRY2nKVV+3a\ntuYplIq8LBZKkyaB7VsrwhFH2CnRgr3Hffokfr/ejLG1s1ddZR//97+2bd7atbbTjX8Sd6D0ADsL\ndkKLnVBnpx3KInM3NQ/dRYe6u9m4Yxdk7qbdobs5/BlPUhZQO5YC6qXXo1HtRjSq3YilCxrbBGt/\nIyhqQN+eDfnTucETMvfjrFUNOOesmmzaZDu+/fcmByfwvwfOMsZe1bjgAjuMyzXXRJfEgf2O/vFH\nz/M77ohu+0RxVCMHYIxpCtyKTd5aA1uBH4DHRGRXwiKs5GKpkbv88opLRkTsJZd337W1WA8+aNvc\nbdniWeeoo3wb2Fcm/r3LIL4/jsXF9vKzu/3O0UfbZKk8/L9ksrODj4GWlWV/6PLz7SWb778PbCsZ\nzOLF0Lev5/m//gX33luukANkZ9ve0e5bA3n3drzySvvc7ZFHbEcKCP4F+3//5+yy0v79tgNC69bO\nxiX035fT/VSk778P3Vs30nE8fLjtJOOtomuaUoF/b1ewTRMq4ooB2JqyvOI8dhbsZOveHewq2Mnu\noh3sLNjJjn072FHgelzgmZdb5OASSCVRK60WjTMb06h2IxrXbsxPcxvZRKywMexvRG3TiCcmepa7\nk7bGmY1pmNGQWjU8bXD8P7P/+Y+9dVokRUX2O9ppU6FwNWc7d9q22+HGMg1lwQLbxGjfPtv8ZskS\n27nDqUTVyDlO5FRw0SZy6em2wXFFX+bwNmOG7yCMP/wQvjYomfx7iUH8azneesv2LmzQwJ6xlfe9\nuOsuuO8++/iCC+zlpVDWrrVDgwwc6HwwWxGbvL3wgq15eOON8L37YrVgAbz2GvTrZ3s6ur8cs7Lg\npJNsjcORR9p2k+62kMG+QJ10iolFjRq+NbZTptiTpMpExHbO8K559V4WzooVtv3XN9/Y50OH2h6w\nhx8e/zhT2b59tiPBrFn2+axZ9viMVWlZKbsKd7F93/aDiZdPIlYQmKRV9kuXtWvWpmlmU5pkNqFp\nnaY0rt04IOkKlog1qt2IzJqZGK8Ptv9n3LvXaiTeTWUaN7aXxBNx4/p69exx4S1evxtZWfazefzx\n0bcB10Sukoo2kauoXmORvPGGp+fVBRckO5rQiottkuLuVXvTTYGX/CobETsmV36+HX4lVGeHVJaf\nb2s9Onf2HWH+tdd8k6n337eN7RPh/fftMB0i9ux65crEJIzlJWJPSPzv8qBfvfFTVmZrWerVC/55\nKy4tZvu+7WTnZ5O9L9vncfa+bLLzXfP2ZbOzYGel7WmZXiOdpplNaVrHlZS5kjPvx+5l3vMya8Xv\n7vDlSeTADku1bJltwpGoCo26dW2HKG+V4fOmiVwlFW0it3WrbdCqnFu0yA542ratbR+WiDM4FR/7\n9tnLXO6ThGeeSewtfn76yZ4cnX227ehTWc2eHVhLpF+95bOveN/B5CtSgrZnfxSZRgUwGJrWaUrz\nOs1pUKspGaVN6diyCS3rhU7GmtZpGlA7lpTYy5nIVYS//tUOCu7mHlg92TSRq6SiTeQqsu2GUqpy\n0ETOGRFhb9FetuRtYWv+VrbmbT34d0v+Fp/necV5yQ73oMyamTSv25xmdZrRvI7fX//5dZvTuHZj\naqSVcxDDJEmFRG7LFtsLftMme0Xnhx/s1YNkS3avVaWUUjFKRq/RykRE2F2421GCVlgS55GDY9C4\ndmNa1G3hKDlrXrc5dWrVSXbIykubNrZT2JIl9q4u4YZuqgocJXLGmIbAfhFJvb7PlUxVbC+llAqv\nd2/bSWHpUvs81D1KU1FJWQnb8rexae8mn2lz3uaDj7fkbUlqh4A0k0azOs1oWbclLeu1pGXdlrSo\n28Lnuftv87rNSa8R482zq4GXX/a9/7V3D/bKpEkT3/vnVmURL60aY2oC+4HzRCTIbc2rt2gvrW7f\nXvXPDpRSgXbssMOjNGliBxGujB0z/BWVFPkkZJv3uh7neRK2bfnbktI5oFZaLZuMeSViLeq0CEjM\nWtZrSdPMpil7KbOy2bfPDgk1a5Yd6DnR7WCrkqS2kTPGbAauEZHP4h1Aqos2kcvJqdyNspVS1UOZ\nlLE1bysbczeyIXcDG3I2sDF3Ixv3bjyYsO0o2FHhcdWuWZs29dvQul5rWtdvbf/Wa23nuZ/Xb02T\nzCakmSSMAq1UjJLdRm4qcDWgiVyU/vQnz71TTzpJkzilVMXYX7LfJmmuBG1D7gafpG3T3k0cKDtQ\nYfHUS6/nKEFrmNEw6T0zlUolThO5LOASY8wC4EPsXR18qqFE5OX4hlY1vPKKHVC1uNiOgaaUUvFQ\ncKCArJws1u1Zx/o968nKyfJJ1rbv2x65kDhpXqc57Rq0o12DdrSt3/bg43YN2tG2QVva1m9L/Ywo\nhsBXSjnm9NJqpAYQIiLVsgFCpEurOsSAUioWZVLG5r2bWZ+znnV71tmEzevxtvxtkQsppzSTRut6\nrQ8mZO3qtwtI0trUb0PtmrUTHotSqS7Zl1YrwQgsSilVteTuzw1I0NzPs3KyEt7Ts0lmEzo27EiH\nhh3o2LAjHRvZx+5ErVW9VtRM0672SlVmOiBwOWmNnFIqnL1Fe1m7ey1rdq1hzW7X5Hq8s2Bnwvab\nZtJoW78tHRt19EnWOjTscDBhq5deL2H7V0r5SnaNnDuI3sAJQFPgeRHZZow5BMgWkYQOs21s69fb\ngbFAK2AVMEFEpjvY9hXA/3baAjwhIrf6rTsIeAjoB+QCbwJ3isj+aGO+8MJot1BKpaL84vyQyVqi\n2qqlmTQ6NOxAl8Zd6NyoM50bdT6YoHVs2JG2DdpqbZpS1YDTAYEzsD1XzwcMNgn6GNgGPAysxiZZ\niXQfcCswDvgVuBiYZowZISJfONh+O3AWNn63rd4ruBLVr4DPgRHYS8qPAG2AUdEEO3o0PPZYNFso\npSqzMinjj9w/WLlzJSt2rmDlzpWs3LmS1btWszV/a+QCYtA0symdG3emS+MudGnUxfO4cRfaN2hP\nrRopMBidUiqhnHZ2eAS4CrgBmAFkA/1F5FdjzDXAX0SkX8KCNKY58AfwgIhM8Jo/E2gmIn0jbP8K\nMExEOkRY7wOgF9BLREpd88YAU4CjRGRRkG0CLq3+3//ZgT+VUqmnqKSINbvXsGLHCp+kbdWuVRQc\nKIjrvtJrpNO5UeeDtWruJK1zY1vD1rC2jlekVFWR7Euro4B/icibxhj/3qnrgU5xjSrQaUAt4A2/\n+VOBl4wxHUVkQ3l24LqDxanAI+4kzuVd4EXgHCAgkQvmySfLE4lSqiLkFeWxbMcylu9YbpO2XStZ\nsWMF63PWx/VOBTXTatKlcRe6Nelmp6aev+0btNc7DiilysVpItcUWBFiWRqQ6Bt09AKKROR3v/nL\nsJdKewGRErkWxpgdQCNgHfASNmlzf2N3BWq7yjxIRIqMMb+79uGIjmWpVOVRVFLEql2rWLp9Kb9l\n/8bSHfbvhtxynfv5qGFq0KlRJ0+S5pWwdWzUUduqKaUSxum3y3pgIPB1kGVHYzseJFITICfI/N1e\ny8NZCPyMTdJqA+cBDwKHYDtPeJexJ8R+Iu1DKZVEpWWlrM9Z75OwLd2+lNW7VlNSVhKXfTSq3Yie\nzXrSo1mPg3+7N+tO50adtb2aUiopnCZyrwHjjDFZwPuueWKMGQrcAoyPZqfGmGHYtnaRzBGRk6Ip\nOxgR8b/Y+YUxZh9wozFmooisK+8+lFIVJ2d/Dou3LWbhtoUszl7M0u1LWbZ9GYUlhXEpv0PDDgEJ\nW49mPWhRt4XePkopVak4TeQeBvoArwP/dc37Flu79baIRNu0/zugh4P13C2L92Avifpz15LtDrIs\nkreAm4EB2Eut7pq4xiH2szR0UeO9Hg9xTUqp8hIRNudtZtG2RSzcupBF2fbv+pz15S47zaRxaNND\nOaz5YfRq3utg0nZo00Opm143DtErpaqzOXPmMGfOnITvJ6oBgY0xg7EdD5oDu4AvRGRugmLz3q+7\n52g379ozY8yfsW3dukTb2cEYMwD4CRglIu8YY2oBe4FJInK313oZ2Mu6E0Xk30HKCei1qoMAKxW9\n0rJS1uxew8KtC1m4baFN3rYtjMugue0btOeIlkdwePPD7d8Wh9OjWQ+9tZRSqsIku9cqACIyD5gX\n7yAc+AIoAS4F7vWaPxpYGmOP1dFAGTAfQEQOGGO+AEYaY8Z7dYK4CEgHPoo1eKWULxFhfc56Fmxe\nwIItdvp166/kF+eXq9wmmU04osURHNHCJmtHtDyCw5ofpsN4KKWqrGjv7DAU2+mhLbAZ+F5E5iQg\nLh8issMY8yhwhzEmH8+AwEOwg/x6xzgL6CAi3VzPOwCvYu/QsA7IxA5sfBnwnIh4X6MZD/yAHWj4\naeyAwA8D00RkYcJeoFJV3Na8rTZhcyVuP2/5mV2Fu2Iur4apQY9mPejXuh99W/ald8veHNHyCFrW\nbalt2JRS1YrTOzs0AaYBQ7G1WHuwbcmMMWY2MFJEYmmnFo1xQB5wI55bdF0kIp/7rZfmmtzyXPGO\nA1pi418J/FVEnvXeUEQWG2OGY2/R9Qn2Fl1TgDvj/WKUqqryivKYv3k+P23+6WDytjlvc8zl1alV\nh94te9OvVT/6tupLv1b9OLzF4WTWyoxj1EoplZqc3tlhKnA2cB22duqAq03ZSOAZ4CMRGZPQSCsp\n/zZyxkBZ/MYSVapSExE25G7gu43f8f0f3/P9pu9Zkr0k5gF1m2Y25cjWR9KvVT9b29aqL92adNNB\nc5VSKS9RbeScJnK5wDgReTrIsr8C94lItWyE4p/IpadDUVESA1IqgYpKili4baFN2lxTrPcZrZde\nj6NaH8WANgMY0HYAA9oMoFOjTnppVClVJSW7s0MpsCbEslWu5QpoHGzwEqVS1O7C3czbMI/v/rA1\nbj9v+Zmi0ujPVNJrpNO3VV+btLkSt+5Nu2tNm1JKlZPTRO5D4E/AV0GWXQz8L24Rpbj+/ZMdgVKx\n21mwk282fMOcrDnM3TCX37J/Q4h+PJ3uTbszsP1Ajml7DAPaDOCIlkeQXiM9ARErpVT15jSR+xh4\nzBjzKbbTQza248BI4DDgJmPMwTswiEiwW3lVC2lpkddRqrLIzs/mmw3fMHfDXOZkzWHZjmWRN/KT\nWTOTo9sezXHtj+O49sdxbLtjaVanWQKiVUop5c9pIvee62974PQgy9237TLYBmPV9nqJJnKqMsvd\nn8ucrDnMXDeTWetnsWLniqjLaN+g/cGk7bj2x9GnZR+9z6hSSiWJ00RuaEKjUEolxIHSA/y46Udm\nrpvJjHUzmL95PqUSXZPW3i17c2LHExnUYRAD2w2kfcP2CYpWKaVUtBwlchVxGy6lVPmJCMt3LD+Y\nuM3dMDequyUYDH1b9WVIpyGc2PFEBnccTJPMJpE3VEoplRRR3dlBKVX55BXlMWv9LD5d/Smfr/08\nqsF300waR7Y+khM7nsiQTkMY1GEQjWo3SmC0Siml4kkTOaVSjIiwetdqPlvzGZ+t/Yy5WXM5UHbA\n8fY9m/XklC6ncHKXkzmh4wl6H1KllEphmsjFmYPxlZWK2v6S/czNmsunaz7lszWf8fue3x1v26pe\nK07ucjIndz6Zk7ucTNsGbRMYqVJKqYqkiVycnXBCsiNQVUXO/hw+Wf0J01dM58vfv6TgQIGj7erU\nqsOQTkM4ufPJnNL1FA5rfpjeLUEppaooR7foUqH536IrPx/q1k1iQCqlbc3byoerPmT6iunMzppN\nSVmJo+0OaXIII7qNYES3EZzQ8QQyamYkOFKllFLRSOq9VlVo/omcvp0qWr/v/p0PVn7A9BXT+XHT\nj47upJBeI50TO57IiG4jOKPbGXRr2q0CIlVKKRWrCr/XqjHm5SjKERG5Kg7xKFUtrNq5ireXvs30\nldNZkr3E0TZt67fljG5nMKLbCIZ1GUa99HoJjlIppVRlF66N3EngUzXQCGgIlAC7gKau7XOBPYkK\nUKmqIisni3eWvsPby95m0bZFjrbp0awH5/U4j/N7ns9RrY/Stm5KKaV8hEzkRKST+7ExZhDwFnAt\n8L6IlBpjagAXApOA0QmOU6mUtDVvK9OWT+PtpW/zw6YfHG3Tv01/zu9xPuf1PI8ezXokOEKllFKp\nzFEbOWPMfGCKiDwTZNkNwOUicnQC4qv0tI2c8pdfnM/0FdN5bfFrfL3+64ht3tJMGid0PIHzepzH\nuT3OpUPDDhUUqVJKqYpS4W3k/BwBrA2xbA1weHzCUSo1lUkZc7Lm8Nri13hv+XvsO7Av7PppJo2h\nnYbyp8P+xLk9zqV53eYVFKlSSqmqxGkitw0YCXwVZNnFQHbcIlIqhazetZrXFr/G60teZ2Puxojr\nH9f+OEYdPooLe11Iq3qtKiBCpZRSVZnTRO5x4DFjTGtgGjZxa4lN7k4Fbk5MeEpVPoUHCpm2fBov\n/PIC3/3xXcT1+7Xqx6jDRzHysJF0bNSxAiJUSilVXThK5ETkCWNMPnAPcLrXoj+Aa0QkmqFKqqxb\nb012BCqRlm5fygu/vMDrS14nZ39O2HXb1G/DmN5juKzPZfRq3quCIlRKKVXdOL5Fl4i85Bpbrh3Q\nGtgKbBIdUfignj2THYGKt4IDBUxbNo3nf3k+Yq/TzJqZnNfzPC7vcznDOg+jRlqNCopSKaVUdRXV\nvVZdSdsfrkn5SUtLdgQqXtbuXstT859iyqIp5Bblhl13cIfBXN7nci467CIaZDSooAiVUkqpKBI5\nY8wR2EurJwKNsYMAzwbuFZHfEhNeatGxWlObiDBr/Sye+OkJPl39adhhQ5rVacaf+/yZq4+8mu7N\nuldglEoppZSHo0TOGDMAmAsUAh9he7G2As4CRhhjThCRXxIWZYrQGrnUVHCggNcXv86T859k+Y7l\nYdc9qfNJjD1yLOf2OFdvTK+UUirpnNbIPQgsBYaJSJ57pjGmPjDTtXx4/MNLLVojl1o27d3Ekz89\nyX9//S979oe+y1yzOs24ou8VXHPkNXpzeqWUUpWK00TuWGCMdxIHICJ5xpiHgFfjHlkK0kQuNazY\nsYKHv3+YqUumUlJWEnK9o1ofxU3H3MTIw0Zq7ZtSSqlKyWkiF6lnqvZcRS+tVnY/bfqJh757iP+t\n/F/I9m81TA0u6HUBNx1zEwPbDdSb1CullKrUnCZyPwHjjDEz/S6t1gX+CfyYiOBSjf7mVz4iwox1\nM5j47URmZ80OuV7TzKaMPWos1/e/nvYN21dghEoppVTsnCZy44A5wAZjzCfYMeRaAWcAdYAhiQgu\n1WiNXOUhIny46kPu/eZeft36a8j1ujXpxt+O+xtjeo8hs1ZmBUaolFJKlZ/TOzvMN8YcC9yNvSVX\nE2A3OvyID62RSz4R4bM1n3H3nLvDJnBHtT6K2wfdznk9ztOBe5VSSqWsaO7ssAS4MIGxpDytkUse\nEWHmupncPeduftwU+kr/sM7DuH3Q7QzrPEzbvymllEp5Ud3Zwdhfvl7YGrldwAq9RZdHVlayI6ie\n5mbN5a7ZdzFv47ygyw2G83qex+3H386AtgMqODqllFIqcRzXIRljrsa2jVuCbS/3G7DFGHNVYkIL\n2L8xxtxhjFlvjCk0xiwyxpzvcNtXjDFlflOpMeZRv/XuCbJemTFmupP9bN0ayytTsfp5y8+c/NrJ\nDHl1SMgk7sJeF/Lb9b/x/sj3NYlTSilV5Ti9s8OlwAvALGAqnjs7XAq8YIwpEJG3EhaldR9wK7bj\nxakccJQAACAASURBVK/AxcA0Y8wIEfnCwfbbsXei8L6eFiz1EuB4oMxr3m4nAeqVuoqRlZPFuFnj\neGtp6EPu7O5n8+8h/6Zvq74VGJlSSilVsZxeWv0H8IaIjPGb/6ox5nXsECQJS+SMMc2B24AHROQx\n1+y5xphuwETASSJXLCILHO5yvoiURV7NP85ot1DR2FO4h/vn3c/k+ZMpLi0Ous5ph5zGhCETtPZN\nKaVUteA0keuOTeaCmQr8Lz7hhHQaUAt4I8i+XzLGdBSRDXHcX0wpWV5e5HVU9ErKSnhmwTOMnzM+\n5K20Tup8EvcOvZfj2h9XwdEppZRSyeM0kcsD2oVY1s61PJF6AUUi8rvf/GXYpKsXECmRa2GM2QE0\nAtYBLwGPhKh5+8MY0wLYBLwNjBeR/ZGC1G4f8ff1+q+58fMbWbZjWdDlfVr2YdIpkzil6ykVHJlS\nSimVfE4Tuc+BB4wxq0XkYKtyY8xAbNu1zxMRnJcmQE6Q+bu9loezEPgZm/jVBs4DHgQOAcZ6rbcW\nuN21vgDDgVuAftjx88LS4UfiZ2PuRm776jbeW/5e0OXtGrTjvqH3Mbr3aB0HTimlVLUVTRu5Y4E5\nxpjNeO7s0A6b/IS67BqUMWYYMMPBqnNE5KRoyg5GRJ70m/WFMWYfcKMxZqKIrHOt53/pdpbr9T5m\njBkqIqHv8QS0aFHeSFVRSRGTvp/EA/MeoLCkMGB5/fT63DHoDm4+9ma9E4NSSqlqz+mdHbYZY/oC\nVwKDsTVgWcBcYIqIFES53++AHg7Wc5e7B3tJ1J+7Js5Rr1I/bwE3AwOwl1rDrfc4cDT2ThZBjAdg\nzhyYM2cIQ4YMiSEcNW/DPMZ+MpaVO1cGXf7nvn/mwWEP0qpeqwqOTCmllIrOnDlzmDNnTsL3Y1Jh\nPF9jzBhgCtDNXXvmmv9nbFu3LtF2djDGDAB+AkaJyDth1msOZAN3iMhDQZaLvQoL//wnTJwYTRQK\nYHfhbv4x4x+8tPCloMv7t+nP5NMnc2y7Yys4MqWUUio+jDGISNzHt4jqzg5J9AVQgh237l6v+aOB\npTH2WB2NHStuvoP1BJv0hTVoUAxRVGMiwltL3+KWL29h+77tAcub12nOg8Me5Ip+V5BmtAGiUkop\n5c/pgMDpwB3AKKADkOG3iohIwpJCEdnhugvDHcaYfDwDAg/BDvLrHessoIOIdHM97wC8CryJvYSa\nCZwPXAY8JyLrvbb92bXuamxv2OHA/wGfi8icSHGecUa5Xma1si1/G9d+ci0frfoo6PKr+13NQ6c8\nRJPMSP1YlFJKqerLafI1CbgB2zt1OlCUsIhCG4cd5uRGbEeLVcBFIuLfYzYN31uP5WHb2I0DWmJr\n4VYCfxWRZ/22Xe0qv7WrjHXYBnCTnASovVYjc9fC/fXzv7K7MLBpY89mPXn+zOcZ3HFwEqJTSiml\nUoujNnKunpvPiMj9iQ8ptXi3kUuB5oZJlZ2fzfWfXs8HKz8IWJZRI4M7B9/JP47/Bxk1/St8lVJK\nqdSW7DZy9YAf4r1zVX18sOIDrvn4GnYV7gpYNrDdQF455xW6N+uehMiUUkqp1OX0YuDHwAmJDERV\nTQUHCrjuk+s4/93zA5K4jBoZTDplEvOumKdJnFJKKRWDkDVyxpguXk8nA68ZY8qAzwgybpv3sCDV\nUdu2yY6g8lm8bTGj3h/Fip0rApYd3fZoppwzhZ7NeyYhMqWUUqpqCNlGzpW0eS90X9cNuoGIVMv7\nJLnbyHXsCFlZyY6mchARJs+fzN9n/J3i0mKfZTXTajJhyAT+fvzfqZmWKqPfKKWUUuWTjDZyV8R7\nZ1WZ9li1cvbncNkHl/Hx6o8DlnVr0o03L3iT/m36JyEypZRSquoJmciJyKsVGUiqM3HPsVPPom2L\nuODdC1i3J/Aq+xV9r+DJ05+kXnq9JESmlFJKVU16bStOqnuN3KuLXuW6T69jf8l+n/kNMxry3JnP\ncfHhFycpMqWUUqrqCtfZ4WXgXhFZ73ocjojIVfENLbVU1xq5opIibvriJp7/5fmAZQPaDODdi96l\nU6NOFR+YUkopVQ2Eq5EbCjzhenwSITo5uFT7oXBrVMOuHlvytnDeO+cxf3Pg7Wqv7389j536mA7u\nq5RSSiVQuDZynb0ed6qQaFJYdbu0+uvWXzn7rbPZnLfZZ35mzUyeP/N5xvQZk6TIlFJKqepD28jF\nSXWqkZu+YjpjPhhDwYECn/ldG3fl/ZHv06dVnyRFppRSSlUv4drIdYimIBHZWP5wUld1qJETESZ+\nO5FxX48LWHb6Iafz5gVv0qh2oyREppRSSlVP4Wrksoiu7Vs1qpMKVNVr5IpKihj7yVheW/xawLKb\nj7mZR4Y/Qo20Kv4mKKWUUpVMuETuSrQTg2NVuUYuryiP8945j1nrZ/nMr5lWk6fPeJqxR41NUmRK\nKaVU9Raus8OUCowj5VXVRG77vu2c8cYZ/LL1F5/5jWs35v2R7zO089AkRaaUUkqpqDo7GGPSgF5A\nU+BnEdmXkKhSUFW8tLp+z3pOnXoqa3av8ZnfrUk3Pr3kU7o17ZakyJRSSikF4LgeyRhzA7ANWAJ8\nDXR3zf+fMebGxISXOqpajdyS7CUc9/JxAUncgDYD+O7K7zSJU0oppSoBR+mHMeYa7ODA/wNGAt73\nMZgHXBD/0FJLVaqR+27jd5zwyglsy9/mM3941+F8ffnXNK/bPEmRKaWUUsqb03qkW4H/iMhY4AO/\nZStx1c5VZ1WlRm7ehnmcOvVUcotyfeaPOnwUH4/6WG96r5RSSlUiTtOPzsCXIZbtA6r94GFVoUZu\nbtZcTn/jdPYd8G36eOPRNzL1/Kmk10hPUmRKKaWUCsZpIrcT6BRiWXdgc4hl1Uaq18jNXj+bM948\nIyCJmzBkAo+f9jhpJsVfoFJKKVUFOf11/gS42xjTxWueGGOaAbdg285Va6mcyH29/mtGvDki4JZb\nDw57kLtOvAtjTIgtlVJKKZVMTtOPfwFFwFJgJnag4CeBFUApMCEh0aWQVL20OmvdLEa8OYLCkkKf\n+Q+d/BC3D7o9SVEppZRSygkj4uzmDcaY+sDNwKlAC2AX8AXwmIjsTViElZwxRkCoXRsKCyOvX5n8\nuOlHhr02LKAmbtIpk/jbcX9LUlRKKaVU1WOMQUTifonLcSIXthBjaopISRziSTnuRA4gDm9lhVm2\nfRmDXxnMnv17fOb/Z/h/uHXgrUmKSimllKqaEpXIOR1H7h9hltUE3o1bRCrhsnKyGD51eEAS9+jw\nRzWJU0oppVKI0zZy9xpjxvjPNMbUAN4Gqv0NN889N9kROJOdn80pr5/ClrwtPvPvOfEebhl4S5Ki\nUkoppVQsnCZy1wEvGmNOc89w3Xf1LeAU4PQExJZSatVKdgSR5e7P5fQ3Tmft7rU+828YcAP3nHhP\nkqJSSimlVKxqOllJRF4xxrQGphljhgELgDeB04DTROTHBMaYEir78CNFJUWc8/Y5LNy20Gf+qMNH\n8eTpT+oQI0oppVQKcpTIAYjIA65k7lPge+Ak4HQR+T5RwaWSypwHifx/e/cdHkXVPXD8ezZACKEG\npHcBlV5UwBpAEFBBEVBABSuCAuorFlApij99X+zlFSsqKCrYXhBEUEKRIoTehAABAekqveX8/pjJ\nsrskmw1sEjY5n+eZh8ydOzNnZ5ZwuDP3XuW+ifeRkJzgV962RltG3zjaBvs1xhhjIlTIiZyrP87Q\nI+2B61R1dvhDikzncovci3Ne5JOln/iVNa/YnPFdxtu0W8YYY0wESzeRE5EtpI6rcfo+HmCMz+M4\nVdUq4Q8vcpyrLXLfrP6GJ6c/6VdWq2QtJnafSGyB2ByKyhhjjDHhEKxFbjppJ3ImDedii9zi7Yu5\n7Zvb/MpKFCzBxG4TiYuJy6GojDHGGBMu6SZyqtorG+PIkDjNf08A9wFlgbXAcFX9OsT9C7r7dwcq\nA38BC4BOvoMZi8gVwItAI+BvnE4dg1X1SLDjn2uJ3Pb927nh8xv8Zm3I58nH+K7jqVmyZg5GZowx\nxphwyew7cjnpOeARYBCQCNyK04v2OlWdEmxHd9DiKUAV4HmcOWLPwxk6JQo44darD0wFJgPXAdWA\nkUB5oFvwc5zpxwq/w8cP03FcR7bu3+pX/lb7t2hZrWUORWWMMcaYcAv2jtwdwCRV3eP+HJSqfpJR\nnTMlIucB/wKeV9VX3OIEEakJvICTpAXzKNAQqK2qviPhfhNQbxiwBeiqqieBX0TkODBaRF5U1SXp\nneBcapF78IcH+W3bb35lDzV9iPua3JdDERljjDEmKwRrkRsNNAP2uD8Ho0CWJXI449XlB8YGlI8B\nPhCRKqqaHGT/PsCXAUmcH7fV7lpgpJvEpfoSeA/oCJzzidzoJaP5cMmHfmXtarRjZJuRORSRMcYY\nY7JKsESuGrDd5+ecVBs4qqpJAeUrAXG3p5nIiUgloBKwUUTeBW4BCgBzgH+p6lK36vlAQfeYXqp6\nVESS3HOk61x4tLpi5wr6TurrV3ZByQsY13kcUZ6oHIrKGGOMMVklWGeH5LR+ziFxOJ0TAu312Z6e\n8u6fT+B0buiKk7ANx3l0Wl9V//A5xr7TD8HeDM6R4y1yB44doPOXnTl84rC3LCZfDF91+Yqi0UVz\nMDJjjDHGZJUcST9EpJWIpISw/ByG06V+xoPA9ar6o6p+h9OZoRDwQBjOkaMtcqpK74m9WbtnrV/5\n29e9Tb0y9XIoKmOMMcZktWCdHTYS+jhyqqrnZ+K8c4ALQ6iXOnbGPqB4GttTW8n2prEt1Z7Uc6rq\n0dRCVf1DRNbgdIJIPQdAiXTOsyL9Uwxl4UIYOhTi4+OJj48PEk74vbvoXT5b/plf2V0N76JXw17Z\nGocxxhhjHDNmzGDGjBlZfp5g78glkEUDArtjsv2eiV1WAtEiUl1VN/iU18GJcVWQfTcAh4NsT5UE\nHHWP6SUi0UB1nE4P6RhKs2ZOIpfdErcn0n9Kf7+yeqXr8Ub7N7I/GGOMMcYApzfsDBs2LEvOEykD\nAk/BGeutB/CsT/ltwIpg7/Cp6gkRmQRcKSIxqnoYQEQq47QKfufWOy4iU4CuIjJUVVPcQ3TB6Rzx\nfbAAc+LR6sFjB+k2oRvHTh7zlhUuUJivunxFofyFsj8gY4wxxmSriBgQWFV3icjLwJMicoBTAwLH\nAzf41hWR6UBlVfWdvmAIMB/4QUReAmKAZ3Aeyb7pU28oMBdnoOG3cHrr/hv4SlUXB4sxJzo7PDr1\nUX7f49+w+f4N73NBqQuyPxhjjDHGZLuISORcg4D9QH9OTdHVRVUnB9TzENCJQ1VXi0hLnKm3xgHH\ngZ+Bgaq6y6feUhFp49abiDNF12hgcEbBZXciN+n3Sbyz6B2/svsa38ctdW/J3kCMMcYYk2NENUte\ng8szRERBeeQReOml7DnnroO7qPvfuuw8uNNbVjOuJot7Lya2QGz2BGGMMcaYkIkIqhr2F7HOkfkI\nIl92tsg9OPlBvyQuSqIY02mMJXHGGGNMHmOJXJhkV2eH8avG8+VK/w60T1/1NJdWuDR7AjDGGGPM\nOcMSuTDJjha53Yd2nzYFV5NyTRh8VYav8BljjDEmFwqps4OIXBVkcwpOp4A1qno8LFFFoOxI5PpP\n7s+uQ96+GeT35Oejjh+RzxNJfVaMMcYYEy6hZgAzyHhw4EMi8rqq5snmoax+tDp53WQ+X/G5X9nT\nVz1tU3AZY4wxeVioiVxH4A1gKTAe2AGUwZmAvj7wNHAp8JiI7FPVkVkQ6zktK1vkDh47SN8f/B+p\nNizbkCeueCLrTmqMMcaYc16oidyNwBRVvT+g/FMRGQW0UNU7RSQFuBvIc4lcVrbIDU8Yzqa/NnnX\nPeLh/RveJ39U/qw7qTHGGGPOeaG2I90ETEhn23icFjtwptKqdrZBRaKsapFbtmMZL831H6Cu/6X9\naVK+Sdac0BhjjDERI9T0Iwo4P51tNdzt4Ew6f/Rsg4pEWZHIqSp9J/XlpJ70llUsWpHhLYaH/2TG\nGGOMiTihph8/AM+LyM0iEgUgIlEi0hkYAUxy69UBksIf5rkvKx6tjl0+ljlb5viVvdnuTYpEFwn/\nyYwxxhgTcUJ9R64f8A3wFXBCRPYBJdz957jbwRmG5PlwBxkJwt0i98/Rfxj400C/sutrXU/HCzum\ns4cxxhhj8pqQEjlV3Q1c6U4o3wxn0vrtwDxV/cmn3sdZEmUECHci92zCs/x54E/veoGoArx67avh\nPYkxxhhjIlqmRpJV1anA1CyKJaKF89Hq73t+59X5/knbwMsGcn5ceq8pGmOMMSYvylQiJyLXA1cD\nccBe4BdV/SErAos04WyRe3za45xIOeFdr1S0Ek9e8WT4TmCMMcaYXCHUKbqKABOBK4ETwB6gJPCI\niMwCrlfVA1kWZQQIV4vczOSZfLvmW7+yf7f+N7EFYsNzAmOMMcbkGqG2Iz0PNAZuB2JUtRwQA9zh\nlufJDg6+wtEil6Ip/Gvqv/zKmlZoyi11bjn7gxtjjDEm1wk1/bgZeEpVx6o6g5qp6klVHYszPdfN\nWRVgpAhHIjduxTgWblvoV/ZSm5eQrJ7I1RhjjDERKdT0oySwKp1tq9ztedrZ5lpHTxxl8M+D/cpu\nvuhmLq98+dkd2BhjjDG5VqiJ3Ebg+nS2tXe352ln2yL3fuL7fvOp5vfk54VrXji7gxpjjDEmVwu1\n1+oo4CURKQyMxRlDrixwK3AP8EjWhBc5ziaRO3jsIM/OfNavrHeT3tSIq3GWURljjDEmNwt1QOBX\nROQ8nIStl1sswDHgBVV9LWvCixxn82j1zQVvsuPgDu96TL4YBl81OMgexhhjjDGZGEdOVQeJyH9w\nZnZIHUdunqruy6rgIsmZtsj9feRvXpzzol/ZgKYDKFu4bBiiMsYYY0xultmZHfYBk7Moloh2pi1y\nr8x7hX1HTuXCxaKLMfDygUH2MMYYY4xxpJvIichVmTmQqs48+3Ai15m0yP195G9em+//VPrRyx4l\nLiYuTFEZY4wxJjcL1iI3A9AQjiFuvahwBBSpziSRe3PBm/x15C/velxMHAOaDghjVMYYY4zJzYIl\nci2yLYpcILOPVg8cO8Ar817xK3uo6UMUiS4SxqiMMcYYk5ulm8ipakJ2BhLpMtsi99/f/suew3u8\n60Wji9Kvab8wR2WMMcaY3CwME0sZyFyL3OHjhxk5d6RfWf9L+1O8YPEwR2WMMcaY3MwSuTDJTIvc\nx0s/ZufBnd71wgUK81Czh7IgKmOMMcbkZpbIhUmoidzJlJO8NPclv7L7m9xPyUJ5frpaY4wxxmSS\nJXJhEuqj1e/Wfsf6veu96/k9+a01zhhjjDFnxBK5MAmlRU5V+c+v//Er616vOxWKVsiiqIwxxhiT\nm2VqZgcR8QC1gZLAQlU9mCVRRaBQErk5W+Yw7495fmWPXvZoFkVkjIlkVatWJTk5OafDMMZkQpUq\nVdi0aVO2njPkRE5EHgCG4CRxAJcAiSLyLfCzqr6eBfH5nl+AJ4D7gLLAWmC4qn4d4v4F3f27A5WB\nv4AFQCdVPeHWGYLzGQN9q6qdgh8/4xhG/urfU7VdjXbULV03hOiNMXlNcnIyqqGMyW6MOVfImc7X\neRZCSuRE5F7gNeBDYCrwpc/mWcDNQJYmcsBzwCPAICARuBX4SkSuU9UpwXYUkXzAFKAK8DywGjgP\naI0zI8UJn+oKXA6k+JTtzSi4jFrkNu7byPdrv/crG3iZzalqjDHGmDMXaovcI8BLqvq4iAROxbUG\nyNKMRETOA/4FPK+qqdMhJIhITeAFnCQtmEeBhkBtVd3mU/5NOvUXqGpKOtvSiTH49rd/exv1mfGs\nYdmGxFeNz8wpjDHGGGP8hNrZoRrwYzrbDgJZPZJtWyA/MDagfAxQT0SqZLB/H+DLgCQumEy3jQZr\nkTt0/BAfLP7Ar6zfpf1ypAnWGGOMMblHqIncbqBqOtsuALaGJZr01QaOqmpSQPlKnKSrdno7ikgl\noBKwUUTeFZG/ReSwiEwTkQbp7LZFRE6IyCYRecF9vy6oYInc2GVj2Xdkn3e9ZExJutXtltEhjTHG\nGGOCCjWRmwg8IyLVfcpUREoBDwPfhj0yf3E4nRMC7fXZnp7y7p9P4LQsdsV5v+484BcRqehTd71b\n7w7gWuALnM/3XUYBpte4pqq8seANv7J7Gt9DTP6YjA5pjDHGGBNUqIncU8BRYAUwDadDwOs4nQZO\nAsMzc1IRaSUiKSEsP2fmuOlI/YwHgetV9UdV/Q64DigEPJBaUVXHqup/VHWaqk5X1cdx3v+7RkRa\nBD1JOldy1uZZLN+5/FQ98dDn4j5n83mMMcb4aNGiBf3798/28yYkJBAVFcXevRn2h8vVqlWrxssv\nv5zTYeRZISVyqrobuBj4P5x31ZJwOkq8CTRX1b8zed45wIUhLHe49feR9nt4qS1xwf4W7Uk9p6oe\n9flMf+B01GiYQayf4zy+vTT9KkP5/POhDB06lBkzZvhtGbVolN96xws6UqV4Rq/0GWNM7vPxxx9T\npEiRnA7jjKSVrFx++eVs376duLhgD4XC51y9fgsXLqRv3745dv6HHnqISy65hJiYGKpXr57xDiH6\n5ptvaNu2LaVLl8bj8TBz5sxM7T9jxgyGDh3qXbJKyOPIqep+4Fl3OSuqegT4PRO7rASiRaS6qm7w\nKa+D0zq4Ksi+G4DDmY8yM4Zy223Qrp1/6Z5Dexi/arxfWd9Lcu7LbowxOUlVc1Unr3z58lG6dOls\nO9+5ev1KlszZucJVlV69erFs2TJ++umnsB334MGDXH755dx+++3ccccdGe8QID4+nvj4eO/6sGHD\nwhabr0iZomsKzlhvPQLKbwNWqGq6w5+7g/1OAq4QEe+LaSJSGafVb0EG574NJ1mcH6xSWo9WP132\nKcdOHvOuVy9RnZbVWmZwOmOMyZhI1i5naubMmTRv3pwiRYpQvHhxmjVrxqpVq0hISOCuu+7i4MGD\neDweoqKiGD7ceSvnr7/+omfPnsTFxVGoUCFat27NqlX+/z+fN28erVq1onDhwhQvXpxrrrmGP//8\n07s9JSWFwYMHc95551GmTBkGDvQfFWvs2LFceumlFC1alDJlytC1a1e2bTs1kMGJEyfo378/FSpU\noGDBglSpUoVBgwYBzqPb5ORkBg4c6I0dnBYXj8fj92g1oziz4vodP36cxx9/nEqVKhEbG0vTpk2Z\nOnWq95gJCQl4PB4mTZpEo0aNiImJ4eKLLyYxMTGkmP755x9uv/12ypQpQ0xMDDVq1OD1108NHevb\nWjls2DBvfB6Px7ukxgrw0UcfUadOHWJiYrjwwgt59dVXQ74+aXnttdd44IEHqFWrVrp1fv31V+Lj\n44mNjaVixYr07duX/fv3Bz3ubbfdxtNPP03btm3P7cG5VTXDBfg5yDINmIAzUG+ZUI53JgvOY91D\nOJ0Prgb+i5PctQuoNx1YF1B2EfAP8AtwPdAFWA5sA87zqbcQ6IfT0aEt8DJwDJgYJC4F1R9/VD8p\nKSl60ZsXKUPxLv836//UGGNC4fx6DrY9a5czceLECS1RooQ+9thjunHjRl27dq1+/vnnumbNGj1+\n/Li+9tprWrhwYd25c6fu2LFDDx48qKqqHTp00Isuukhnz56tK1as0A4dOmilSpX0yJEjqqq6ZMkS\njYmJ0fvvv1+XLl2qa9eu1ffff1+3bNmiqqrx8fFavHhxHTJkiK5bt06/+uorzZcvn44bN84b20cf\nfaSTJ0/WjRs36m+//aYtW7bUq666yrt95MiRWrlyZZ09e7Zu2bJF586dq6NHj1ZV1b1792qlSpV0\n2LBhumPHDt2xY4eqqs6YMUM9Ho/u2bMnpDiz6vp1795dmzdvrrNnz9aNGzfqW2+9pdHR0bps2TJv\nnCKiF110kf7000+6cuVK7dKli5YvX14PHz6cYVwPPvigNmrUSBcuXKibN2/WhIQEHT9+vHd71apV\n9aWXXlJV1YMHD3qv0Y4dO/TTTz/VAgUK6M8//6yqqu+++66WL19ev/76a920aZNOnDhRy5Urp2+9\n9Zb3eO3atdPChQunuxQpUiTNOEeOHKnVqlU7rXzZsmVauHBhfeWVVzQpKUkXLFigl112mXbp0iWk\n+7J7924VEU1ISMiwbrC/t+628OdHIVVyEqCtOLMdJAG/un+muOWJOI8vd+EMupsViZy4yeJG91xL\ngJvSiTUpjfKL3STvAM47dxOA6gF1PgPWuXUO4XTuGATkDxKXgupPP/nfsNnJs/2SuHzD8+n2/dvT\nv/vGGOMjEhO5vXv3qsfj0ZkzZ6a5ffTo0af9I7xu3ToVEZ09e7a37O+//9ZixYrpBx98oKpOonLZ\nZZele974+PjTtrdu3VrvvffedPdZvXq1iohu3bpVVVX79++v11xzTbr1fZOVVIGJXI8ePYLGmZEz\nuX5JSUnq8XhOSxZvvPFGfeCBB7xxioh+/vnn3u0HDhzQ4sWLe69xMB06dNC777473e1pXRtV1TVr\n1miJEiX09ddf95ZVrlxZx4wZ41fv1Vdf1dq1a3vXt23bpklJSUGXtKSXyN1xxx16zz33+JUtXrxY\nRUR37dqV7udKda4ncqG+I/cy8Cpwsap622JFpAnOdF3DgEU403eNAG4K8bghcy/C8+4SrF6avUtV\ndSHQKoN9u59pfIGPVt9NfNdvvcMFHShbuOyZHt4YY855JUqUoGfPnrRp04ZWrVrRqlUrOnfuTKVK\nldLdZ/Xq1URFRdGsWTNvWdGiRalXr5738eqSJUvo1CnodNfUr1/fb718+fLs3LnTu56YmMjw4cNZ\nsmQJe/fuRdV532zz5s2UL1+eXr160bp1a2rVqkWbNm1o37497dq1y9Q7aYsXL84wzmDO5PolJiai\nqtSuXTu1cQGAY8eO0bLlqVd5RMTvGsfGxvpd42D69OlD586dWbhwIa1bt+aGG27gqquuCrrPYlWk\nfwAAIABJREFUX3/9RceOHbn11lvp168fALt372bLli307t2b+++/31v3xIkTfte5XLlyGcaUGYsW\nLSIpKYlx48Z5y1QVj8dDUlISU6dOpXfv3oBznSZPnszll18e1hiyUqiJ3HPAUN8kDkBVF4nIMOA5\nVa0nIv8BRqZ5hFzO9+/630f+5suVX/ptv7fxvdkckTEmN/P5N/uc8uGHH/Lwww8zZcoUvv/+ewYP\nHsx3331H69atM32szCRR+fPnP23flBRnpsVDhw7Rtm1b2rRpw5gxYyhdujS7du3iyiuv5Ngx5z3m\nRo0akZyczI8//sj06dPp2bMnDRo0YNq0aZmO+2xk9vqlpKTg8XhYuHAh+fL5/5MeExOe8Urbtm3L\n5s2bmTx5MtOnT+e6666jS5cufPjhh2nWP3nyJF26dKFSpUq88capcVRT78eoUaNo3rx5uudr3749\ns2bNSne7iPDPP/+EHH9KSgr33HMPjzzyiF+yC1ChQgXq1q3rl+RWqFAh5GOfC0JN5GrhPDZNyy6g\nhvtzEhB7tkFFIt8WufGrxnPkxBHveuVilWldPfO/xIwxJhLVq1ePevXqMXDgQNq3b8/HH39M69at\nKVCgACdPnvSre9FFF5GSksLcuXO54oorAOfl+uXLl3P33XcDTpL1888/8+yzZzZowpo1a9izZw8j\nRoygShVn+KcVK1aclijGxsbSqVMnOnXqRM+ePWnWrBnr16+nRo0aacYe6GzjTJWZ69eoUSNUle3b\nt3P11Vene0xVZd68eVStWhVwemSuWLGCXr16hRRTXFwcPXr0oEePHrRt25bu3bszatSo0xJogAED\nBrB582YWLFjg7RgCULp0acqXL8/69evp0SOw7+IpH3zwAYcPh2+wicaNG7Ny5UqqVauW5vbo6Oiw\nDluS3UJN5DYB95L25PT3udsBSnFq3LY8xff3wSfLPvHbdkf9O4jyRGGMMbnZpk2bGDVqFB06dKBC\nhQokJSWxbNkyHnjAGXe9atWqHDlyhGnTptGoUSMKFSpEjRo16NChA71792bUqFEUK1aMwYMHU6xY\nMbp1c6YyHDhwIM2bN6d379488MADFCxYkFmzZnHttddSsWLFYCEBULlyZaKjo3njjTd44IEHWLVq\nFc8884xfnVdeeYVy5crRsGFD8uXLx9ixYylWrJj3+FWrVmXWrFn06NGD6Oho75Abvi08ZxvnmVy/\nmjVr0r17d3r16sXIkSNp3Lgxe/fuZcaMGZx//vnceOON3uM/99xzlCpVinLlyjF8+HCio6O91ziY\nIUOG0LhxY+rUqcPx48eZMGEC559/fppJ3EcffcRHH33ElClTOHLkCEeOOI0ahQsXJjY2lmHDhtG/\nf3+KFStG+/btOX78OImJiWzdupUnnngCyPyj1aSkJA4cOMDWrVs5duwYS5cuBaBOnTrky5ePxx9/\nnObNm9OnTx969+5NkSJFWL16NRMnTuSdd95J97j79u1j8+bN7NvnTLG5bt06ihUrRtmyZSlTpkym\nYsxSobxIB3TDmcFhGTAEZxL6Ie56CnCrW+9t4OuseJnvXF1wOzvMmuW8zLhh7wa/Tg4MRdfuXnv6\nW4/GGBMEZ9rjIAft2LFDO3XqpBUrVtSCBQtqlSpV9IknntATJ0546/Tt21dLlSqlHo9Hhw0bpqqq\n+/bt0169emlcXJwWKlRI27Rpo6tWrfI79pw5c/Tqq6/WQoUKaYkSJbR169b6559/qqpqixYttF+/\nfn71e/XqpTfccIN3/csvv9QaNWpoTEyMNm3aVKdOnaoej8f7Avt7772njRs31qJFi2qxYsU0Pj5e\n582b591/3rx52rBhQy1YsKB6PB5VPb2zQ0ZxfvTRRyoimpycHNbrd+LECR02bJief/75Gh0dreXK\nldOOHTtqYmKiX5z/+9//tH79+lqwYEFt0qSJLlq0KMN7qqo6YsQIrVu3rsbGxmrJkiX1uuuu0zVr\n1ni3V6tWTV9++WXvdfd4PKctqbGqqo4bN06bNGmiMTExGhcXp1deeaV+8cUXIcWSlvj4+DTP6Xud\nFy1apO3atdNixYpp4cKFtX79+jpkyJCgxx09erSKSNDPEijY31uyqLODaIgvWohIa5xODU1wZnc4\njjNcxxBVnebWKQicVNXj4UgyI4GIKChz5sBll8GzCc/yzIxT/9NrVrEZc++em4MRGmMikYic9j6P\niWxDhgzh66+/ZunSpXjSm9cxCyQkJNCyZUt27dqVbbNQ5FXB/t6628I+onNmZnb4CfhJRDw4j1B3\nq2pKQJ0jae6cyw0bBpUqOa2bgY9VezbomUNRGWOMOZdMmTKFt99+O1uTuFT2n4LcK9PfJlVNUdWd\ngUlcXvbMM04iN++Peazfu95bXiCqAF3rdM3ByIwxxpwr5s+fz5VXXpkj5w7WA7h9+/YUKVLktKVo\n0aK88MIL2RilORMht8iJSAGgHXABUDBgs6rqWc/BGuk+Xfap3/oNtW4gLsaasY0xxuScq6++OmiP\n22C9RO1R7LkvpERORMoDs4GqOPOOpqb2vm21eTqRO5FygvGrxvuV3V7/9hyKxhhjjAlNuAfgNdkr\n1Eer/8EZL64yThLXFKiOM4vDevfnPO2Xjb+w69CpofaKRRejXc12ORiRMcYYY3K7UB+tXgk8ijPJ\nPECKqm4CnhGRKOB1oGP4w4scX6z8wm/9potuokBUgRyKxhhjjDF5QagtciWB7W4Hh4NACZ9tPwPx\nYY4rohw7eYyvV3/tV3ZLnVtyKBpjjDHG5BWhJnJ/AKXdn5OANj7bLgXy5LAjqaZtmMa+I/u86yVj\nStKqWqscjMgYY4wxeUGoj1Z/Aa4CJgCjgLdEpCHOoMDXumV5VuBj1U4XdSJ/1OlTlxhjjDHGhFOo\nLXJPAW8BqOp/gQFAIaAc8G/gX1kSXYT4ds23fuv2WNUYk1e1aNGC/v37Z/t5k5OT8Xg8JCYmZvu5\nc9rHH39M0aJFczoMk0NCTeSOA8mpK6r6hqpeoaqNVXVQXp3RIdU/R//x/lw6tjRXV706B6MxxpjI\nlpCQgMfjYe/evZnaL9igt+FSrVo1Xn755Sw/T2bceuutbNiwIcfOP2zYMDwej99Svnz5sz7u0aNH\nufPOO2nQoAEFChSgZcuWYYg298nw0aqI5AP2ADcB/8vyiCLczRfdTD5PyOMsG2OMCaCqZzTXbF6d\nhio6Opro6OgcjeHCCy8kISHBew+ioqLO+pgnT54kJiaGfv368cMPP/DXX3+d9TFzowxb5FT1BLAD\nSH9YaON104U35XQIxpg8QIZJli5n48SJEzz00EPExcURFxfHY4895rd97NixXHrppRQtWpQyZcrQ\ntWtXtm1zRrdKTk72trycd955REVFcdddd3n3femll6hVqxYFCxakcuXKDB482O/YmzZtok2bNsTG\nxlKnTh2mTZuW6dj79+9PhQoVKFiwIFWqVGHQoEGA89g4OTmZgQMH4vF4/JKVX3/9lfj4eGJjY6lY\nsSJ9+/Zl//793u0tWrSgT58+Qa9LMF9//TUNGjSgUKFClCxZkhYtWrBrlzN26ejRoylSpIi3bmps\ngX+m2rZtG7feeqs3juuvv57169efds7MyJcvH+eddx6lS5emdOnSlCxZ0m/78ePHefzxx6lUqRKx\nsbE0bdqUqVOnBj1moUKFePvtt7nnnnuoUKHCWcWXm4X6aHUMcE9WBpIbFIsuZo9VjTF53pgxY1BV\n5s2bx7vvvsu7777Lq6++6t1+/Phxhg8fzrJly5g0aRJ79uyhe/fuAFSqVIkJEyYAsHr1arZv385r\nr70GwJNPPsmIESMYPHgwq1ev5uuvv6Zy5cp+537qqad46KGHWLZsGZdccgndunXj0KFDIcf+2muv\n8d133/Hll1+yfv16vvjiCy644ALASaYqVqzIkCFD+PPPP9m+fTsAy5cv59prr+XGG29k+fLlfPPN\nNyxdutQvAQX47LPPgl6X9OzYsYNu3bpx5513smbNGmbNmsXtt5+aOUhE/B4rp8b2559/smXLFpo0\naUJ8fDwAhw8fpkWLFsTGxjJr1izmzZtH+fLlueaaazhyxHlLavbs2WnOvRpsDtYNGzZQoUIFqlev\nTrdu3di4caPf9l69ejFr1izGjRvHypUr6dmzJx06dGD58uUh3hmTHgmlKVpE+gCDgD+B74Dt+E/P\nhap+mBUBnutERBnq/Ny9XnfGdhqbo/EYY3KHjB4tnm2rWUZ0yJk9pmzRogXbt29nzZo13rIRI0Yw\natQoNm/enOY+a9asoXbt2vzxxx+UL1+ehIQEWrZsya5du7xzfR48eJBSpUrx+uuvc++99552jOTk\nZKpVq8a7777LPfc47Q7btm2jYsWKzJ49m8suuyyk+AcMGMCqVav46aef0txerVo1+vXrxyOPPOIt\n69mzJwUKFOC9997zli1ZsoTGjRuzc+dOSpUqdUbXJdXixYu5+OKL2bRpE5UqVTpt+8cff0y/fv34\n559/TtvWt29fpk2bxoIFCyhevDgffvghL774ImvXrvXWOXnyJGXKlOGdd96hc+fOHD16lK1btwaN\nKS4ujuLFiwPw448/sn//fi688EJ27tzJs88+y5o1a1i1ahUlSpRgw4YN1KxZk+TkZCpWrOg9xk03\n3USFChV48803g54LoF+/fqxcuZKff/45w7o5KdjfW3db2P/ihvoy11vunxWAJmlsVyBPJnK+Ol6Q\npye3MMYYAJo1a+a33rx5c5555hkOHDhA4cKFSUxMZPjw4SxZsoS9e/d634nbvHlzui/Jr1q1imPH\njmX4wnu9evW8P6cea+fOnSHH3qtXL1q3bk2tWrVo06YN7du3p127dkE7UixatIikpCTGjRvnLUv9\nTElJSZQqVQrI+Lqkp0GDBrRq1Yo6derQpk0brrnmGjp37uw9bnreeustxo0bx7x587xJV2JiIhs2\nbPB7FAtOS11SUhLgvHNXvXroM29ee+21fuvNmjWjWrVqfPzxxzz00EMkJiaiqtSuXdsvyTl27Bit\nWjljrtatW5fkZKdP5VVXXcWkSZNCPn9eF2oiVy1Lo8gFCkQVoG2NtjkdhjEmjzjTFrOcdujQIdq2\nbUubNm0YM2YMpUuXZteuXVx55ZUcO3bsrI+fP//pY3impKSEvH+jRo1ITk7mxx9/ZPr06fTs2ZMG\nDRoEfdcuJSWFe+65h0ceeeS01phwvNvl8XiYOnUq8+fPZ+rUqXzwwQc8+eSTzJw50y9x9TV9+nQG\nDhzI999/T61atfxibdSoEV988cVpsaa2fs6ePZt27dKfK1xEGDRoEE888USa2wsVKkSdOnVYt26d\n95wej4eFCxeSL59/2hETEwPA5MmTOX78uF+ZCU1IiZyqJmdcK29rVa0VRaNtHB9jjJk/f77f+ty5\ncylfvry3NW7Pnj2MGDGCKlWqALBixQq/Fq8CBZx5qk+ePNXH7qKLLqJAgQJMnz6d888/P0vjj42N\npVOnTnTq1ImePXvSrFkz1q9fT40aNShQoIBfXACNGzdm5cqVVKsWvM0j2HUJRdOmTWnatClPP/00\nderU4YsvvkgzkVu3bh1du3Zl5MiRXHPNNafFOm7cOEqWLJnu2HOXXHIJS5cuDRpLatKXliNHjrBm\nzRpv62mjRo1QVbZv387VV6f9Hnlaj4xNaELt7ACAiNQXkQdFZIiIlHXLaohIkYz2ze1uvPDGnA7B\nGGPOCdu2bePhhx/m999/Z/z48YwcOdL7TlnlypWJjo7mjTfeYOPGjUyaNIlnnnnGb/8qVaogIkya\nNIndu3dz8OBBChcuzIABA3jyyScZPXo0GzZs4LfffuOdd94Ja+yvvPIK48aNY82aNaxfv56xY8dS\nrFgx77tdVatWZdasWWzbto09e/YA8Pjjj7NgwQL69OnDkiVLSEpKYuLEidx///0hX5dg5s+fz4gR\nI1i4cCFbtmzhu+++448//qBOnTqn1T1y5AgdOnSgdevW3HzzzezYscO7APTo0YMyZcrQsWNHZs6c\nyaZNm5g5cyaPPvroaY9Wgy2pj2oBBg4c6D3W/Pnz6dy5M4cOHaJnz54A1KxZk+7du9OrVy8mTJjA\nxo0bWbRoES+99BLffvvtaZ/B1+rVq1myZAm7d+/mwIEDLF26NMMkM89R1QwXIBr4CmcIkhT3z8bu\ntq+BF0I5Tm5cAGUouu2fbWqMMeHi/HqOPC1atNA+ffpov379tHjx4hoXF6cDBw7UlJQUb50vv/xS\na9SooTExMdq0aVOdOnWqejweTUhI8NZ57rnntHz58hoVFaV33nmnqqqmpKToiy++qOeff75GR0dr\n5cqV9amnnlJV1U2bNqnH49FFixb5xePxeHTChAne9SpVqniPl5b33ntPGzdurEWLFtVixYppfHy8\nzps3z7t93rx52rBhQy1YsKB6PB5v+aJFi7Rdu3ZarFgxLVy4sNavX1+HDBni3R4fH5/hdUnP6tWr\ntV27dlq2bFktWLCg1qxZU0eOHOndPnr0aC1SpIjfdfBdRMQv1p07d+pdd92lZcqU0YIFC2r16tX1\n7rvv1j179mQYS1puvfVWrVChgkZHR2vFihW1c+fOunr1ar86J06c0GHDhnnvXbly5bRjx46amJgY\n9NhVq1YN+lnONcH+3rrbwp6HhNprdSRwN/AA8BPOuHIXq2qiiNwL9FXVRuFNMSODiGiz95sx9+65\nOR2KMSYXOZMBcU1whw8fpmTJkowePZquXbtm67lbtGhBvXr1eP3117P1vCZ7ncu9VrsBT6nqZyIS\nOFzzRqBqWKOKMP0u7ZfTIRhjjMnAL7/8QrNmzbI9iTMmK4X6jlxJYHWQY+Ts3CA5rHu97jkdgjHG\nmAy0b98+x8YhCzZ8SeoAvEWLFk1z8F1jggm1RW4j0BxI62/ApcDaNMqNMcYYA0ETyFB6iRqTnlAT\nuU+AQSKyCZjglqmItAAehtS5DYwxxhiTGZkdgNcYX6F2dogCxgJdgaM4j1IPAwWBcaraIyuDPJeJ\niNoLycaYcLPODsZEnpzo7BBSIucTxJXAtUBpYA8wRVUTwh1UJLFEzhiTFSyRMybynPOJnDmdJXLG\nmKxgiZwxkeecHX5ERBYDHwOfq+qOcAcRYgwCPAHcB5TF6WAxXFW/zmC/KjidNdJzq6p+6VP/CuBF\noBHwN/AZMFhVj5zdJzDGmNClzm5gjIkcqdPOZadQ35H7AWgNKDAdJ6n7NjuTGxEZATwCDAISgVtx\nkrrrVHVKkP0KAA3T2DQCuBwop6p/u3XrA/OAycCbQDVgJPCjqnZL5/jWImeMMcaYoHL80aqIlAa6\nA7cBjYH9OD1YP1XVX8IdWMC5zwO2AM+r6nCf8mlAKVVNK1ELdrwY4E9gsqre6lP+DVAbqK2qJ92y\n24HRQBNVXZLGsSyRM8YYY0xQWZXIhTogMKq6U1VfVdWLgTrAW0BLYJqIJIc7sABtgfw4PWd9jQHq\nuY9PM+NmoDBOyyIAIpIPpyPHF6lJnOtL4DjQMbNBm7xlxowZOR2COUfYd8Gksu+CyWohJ3K+VHU1\nMBwYDGwDKoYzqDTUBo6qalJA+UpA3O2Z0RPYCfzoU3Y+znAqK30rqupRIOkMzmHyGPuFbVLZd8Gk\nsu+CyWqZTuREpKWIfATswBko+A8gqycbjQP+SqN8r8/2kIhIeaAFMEZVUwLOAbAvnfOEfA5jjDHG\nmOwQaq/VujjvxnXHaX3bBLyG837cusyeVERaAT+FUHWGqrbM7PEzcAdOK97HGVU0xhhjjDmXhdpr\nNQVnKI6vgE9UdfZZnVSkIFA5hKqHVPUPEXkB6K+qhQKOcwkwH6fn6uQQz70SOKKqTQLKLwRWAd1U\n9Ys09lmhqrekcTzr6WCMMcaYDOXYOHI4U3P9z31f7Ky5w5b8noldVgLRIlJdVTf4lNfBGRJlVSgH\ncRO/i4ABaWxOwpl+rE7APtFAdZxOD6fJiptijDHGGBOKkN6RU9Xx6SVxInK1iHwY3rBOMwU4AQTO\n6XobTktZqL1me+L0QP08cIOqHnfP01VEfK9LF6AA8H1mgzbGGGOMyUqhtsj5EZEaOO+a3Q5UAQ4B\nd4UxLj+quktEXgaeFJEDnBoQOB64ISC26UBlVa0ZUJ4fuAX4QVV3p3OqocBc4CsReQtnQOB/A1+p\n6uLwfSJjjDHGmLMXcq9VESkmIveJyByc6bEG4/Tw7AOUz6L4fA0CngP647ScNQe6pPFunIe0P9d1\nOD1P0+3koKpLgTY4U4BNdM83GujlW09EKorIeBH5S0T+FpEJIlLpTD6UiQxuy3NKGsvegHrFReR9\nEdklIgdE5Ce3s5CJUCJSQUTeEJFfReSge99Pe8c31HsvItEi8h8R2SYih9zjXpk9n8acjVC+CyJS\nJZ3fFSdFpGhAXfsuRCAR6Swi34jIZve+rRGR50WkcEC9bPmdELSzg/uIsS3OI8kbcMZZ2wZ8DTwA\ntFDVmaGeLDdwZ4VYBhzGSWbBme4rBqivqodzKjaTdUTkauBnnKF2FvpsOqGqiT71ZuN05HkUZ8ic\nQTjvXTZQ1W3ZF7EJF/fejwMWAVE4/9mrpqqbA+qFdO9FZCzQzq23EXjQXW+mqsuy/AOZMxbKd0FO\nze89AvhfwCF+850KyL4LkUlE5uIMvfaN+2dDYBiwWlUv86mXPb8TVDXNBXgJ2A6cBA7izKrQBqe1\nqziQAlyV3v65dcHpKHEc5y9vallVt+yhnI7Pliy771e7fxdaBqnT0a1zlU9ZUWAP8GpOfwZbwvI9\nuNu9x5XP5N4DDdzfnXf4lEUBa3Dmr87xz2jLWX8Xqrj3+K4M9rfvQoQuQMk0ym53vw/x7nq2/U4I\n9mj1YaA08IP7Re2hqlPVGUQ3Lw+5cQMwT1U3phao6iZgDjaNV26XUQ/lG4Bt6tNKrar/4Pyv3L4b\nuVuo974DcAyfXvDqTAk4DrjWfZfX5A32XYhQqronjeLfcP6NqOCuZ9vvhGCJ3AfAfpx3y9aKyJsi\ncmlGB8wD6gAr0ihfiU3jlReMFZETIrJbRMYGvBsZ7LtRWUQKpbHN5A6h3vvawEZ1hmAKrFcAqJF1\nIZps9n8ictx9l/q7NN6Nsu9C7hKP/3Bo2fY7Id1ETlXvxXnpvwfOO0G9gbkishp4nLzbKhdH+tN4\nlcjmWEz2+RsYCdyDM8XbcOAa4FcRKeXWCfbdAPt+5Gah3vuM6tlUgJHvKPAOzr+Z8cC/gHrAHBGp\n5VPPvgu5hIhUwHlH7ic9NcJFtv1OCNprVVWPqOrnqtoW54W9J3Ge+T6B04T4gojcJs5MDcbkWqq6\nRFUfU9VJqjpLVV/H6QhUlqyfa9gYEyFU9U9V7auq36rqHFX9ALjK3Tw42L4m8ohILPAdzuPRLBuG\nLZiQhx9R1e2q+m9VrQtcCrwF1AQ+wekUkVfsI+2WlfSyapNLuf/z+h3n7wME/26kbje5U6j3PqN6\ne9PYZiKcqv4BzObU7wqw70LEcxuxJuJ0eLxW/UcmyLbfCSEncr5UdaGq9sMZP+5mYMaZHCdCrSRg\nGi9XbUKcKszkWsG+G5tV9VA2x2OyT6j3fiVQLY2nGHVw/ke/PutCNOcY+y5EMBHJB0wAGgPtVDXw\n3/9s+51wRolcKlU9rqrfqOpNZ3OcCPM90ExEqqYWuD9fjtO8avIIEbkYuACY5xZ9D1TwHcjRHQD0\nBuy7kduFeu//h/MCcxefelE481n/qM5UgSaXcQcNvoJTvyvAvgsRS0QE+AznHciOqvpbGtWy7XdC\n0AGBzencniZLcAYEftotHg7E4gzyZ60uuZCIfAokAYuBf3D+F/YEcABooqp73b/cs4GKwGM4A0A+\nCdTF+W5szYnYzdkTkZvdH6/BeYm9L7AL2KWqMzNz70Xkc5wxOR/DGfyzL9AeaK7O7DLmHBbCd2Ek\nzrhg83Aei12I87uiCM4Ar+t8jmXfhQgkIv/FuffPAZMCNv+hqluz9XdCTg+sF4mLe2O+cm/M3zjN\nq5VzOi5bsvSeP4GTwO/D6ZWWDPwXKBNQrzjwPrAbJ8mbCtTN6fhtOev7n4LT0Stw+Tmz9x6IxukB\nvQ1nnuq5wJU5/RltCc93AbgTmI8z8OtR9z5/CtS070LuWNxkK63vwEngGZ962fI7wVrkjDHGGGMi\n1Fm9I2eMMcYYY3KOJXLGGGOMMRHKEjljjDHGmAhliZwxxhhjTISyRM4YY4wxJkJZImeMMcYYE6Es\nkTPGGGOMiVCWyBljABCR20Uk2Wd9pYjcH+ZzNBOReSJyQEROikj9cB7fZD8R2SQiH57Bfh1F5OGs\niMmYvMQSOWNMqsbAQgARicWZR3ZRmM/xIRAFXAc0B34P8/FN9jvTUeVvBCyRM+YsWSJnjEnVhFOJ\nW2Oc6WbCNt+jiHiAWsAkVU1Q1QWqeiRcxzdnT0QK5HQMxpjMsUTOGJOaZDXkVCJ3CbBKVY+FuH8R\nEXlTRLaKyBERWSMiD/ls7wmcAAR4RkRSRGRDkOMNdevUFZGfReSgiGwTkWEB9aJF5GURWS4i+0Vk\nu4h8LyIXBNQrIyIf+8S3za1Xyt0eJSLPish6ETksIrtEZKaIXBZwnPtEZIlPnfdFpERAnQEiskpE\nDonIXhH5TUQ6hnANbws49iciUtZn+0QROa2FVETKishxERngU1ZVRMaKyE738y4WkRvTucZ1RGSK\niOwHvsggxgEistGNcYGIXJFGnVIi8o6IrHXv22Y3lvI+dT4CegIV3Bi834dQ76kxxpEvpwMwxuQc\nEdkIVHFXFfhBRCR1XURS3PJqqro5nWMI8ANOIvg0sALn0enLIlJKVZ8CJgKXA3NwJpF+H2dC8fSk\nPq77Budx7PPAtcDTInJSVYe726OBIsAInAmnSwB9gbkicqGq7nTrjQEqAf8C/gDKAK2AQu72J4AB\nwCCcVsiiwMVAnM/nfAF4BHgVeBSo4J63johcpqoqIj1wJr8eCswGYoD6vsdJ5xreB7y8Zs2FAAAG\nlklEQVQDfO7GUh74P+BSEWmsqodwJl7/zP1ca3x27+Fer8/cY1UEFgB/up9pN3ALMEFEOqrqxIBr\n/C3wAfACzoTw6cV4N/AKzv34Eqjhxls4oGoczr0dBOwEyuFc99lu7MeA4cB5ONf4BpwEP/X7EOo9\nNcYAqKotttiSRxfgQpxE4yVgOVDPXf8b6O/+XB/IF+QY1+MkALcHlL8HHAbi3PUot94zIcQ1BOfR\n7sCA8nfd2Iqms58HJ3n6BxjgU74feDDI+f4HjA+yvQpOi+LggPLm7mfq4K6/ASzM5D3w4CRd0wLK\nL3eP/aC7XhD4CxgRUG8xMNFn/QNgB1A8oN5UIDGNa5zudfGpK8BmnMfivuVd3Rg/zODzVXTrdfQp\n/wjYHOL1Oe2e2mKLLc5ij1aNycNUdY2qLsNprZqhqsuBQzitLF+p6jJ3ORHkMFfiJASfB5SPAQrg\nJDtn6quA9XFubHVTC0Skq9sTdh9OsnUQSO2skeo3YKCI9BeRupzuN6C9iDwnIpeLSP6A7a1xkpnP\n3MewUSIS5e63H7jK5zgNReR1EWklIjEhfMYLgNK4LWqpVHUOkAxc7a4fAcbjtMClfvZ6QAPgE59d\nr8VpId3vE2s+nESugYgEtqB9G0KMFd0l8H5MwLnmfkSkj/uYeL+7fTNOC2BIj0dDvKfGGOwdOWPy\nLBHx+PwjfznOo6sonKRkK7DTXc9IHLA3jWTvT5zkJ+hjxQzsSGNdcB5rIiI34CR3K4FuwKU4j+t2\n47RgpeoKfA8MBJa678o97bN9BE4L1Q3ATGCPiHwoIqmxl3bPmwQc91mO4SSWJQFU9ROgjxvHFGCv\niEwQkSqkL/Uc29PY9if+1+9ToLKIXO2u347TUvWdT53SwB1pxPlvd3vJgHOkdd5A5dw//e6Hqp4E\n9viWiUg/4C2cxPEmnPctm+JcP997kqZM3FNjDPaOnDF52XTc1h6c1pJPcVrRUteP47wn10JVZwY5\nzl4gTkTyBSRzZX22n6kywKaAdXASTXDe/VqnqnenVnATU7/kUVV3A/2AfiJSE+dF+2EislNVR7kJ\nyX+A/4hIaZzHxa/gPNLrhpOsKE7L3F9pxOlNZlT1PeA9ESkGtAFexklM0muZTL0+ZdPYVhZ3SBj3\n2Akishm4TURmurF9paq+7xvuwUlGX8BJngJtC1gPZfiQ1GSvjG+hm+gHJoa34DwmfsynXtUQzuG7\nf4b31BjjsBY5Y/Ku+3BaOkYC692fLwZ2AYPdny8h47HkEnDef+sSUH4bzgvsc88ixq4B691wHmUu\nd9cLcfqjvTvceNKkquvU6YCxD59HtD7bd6rqh8A0n+0/4bzjVUVVE9NYktM4zt+q+hVOx4C0Huem\nWovT0nWrb6E4PWarAL8E1B8DdAba47RMfhqwfQrOe42r0on1eJBY0vMHsIXT70dnTm8QKITznwBf\nd3F6wngUJ1EOlOl7akxeZi1yxuRRqroOQESewXmJfbE7xEMpnJfXQ+0dOBmnh+Y7bmvWSpxeq3cB\nz6vqmbbICXCvz7tobd1jDlHV/W6dKUBHEXkZp2fsJcCDOEka7ucripOUjQXW4CQZNwLFgR/dOt/i\n9FZNdPdt7J7vvwCqukFE/g28KSIX4iSvR4DKwDXAe25r2SicRHMuTo/NC3Aef/6Y3odU1RT3Hrwj\nIqmtohWB53CSvI8CdvkUp0foO0ByGq2lzwDzgVki8iZOi2YJnGSymqrek14sQWJUcYZ+eU+cWRzG\nATWBx3E6n/iaAjwmIk/i9J5tiZPwBVqFc3/vx2l1PKKqKwjhnhpjfOR0bwtbbLEl5xYgP847Vq3d\n9QHAb2dwnMLA6ziPPI/gJEz9A+pE4XSKeDqE46X2qKwN/Izzsvs2YGhAPcEZyuIP4ABO61UDYAPw\ngVunAE5Cttz9rH/hJDq3+BznYeBXnNbIg8BqnKFUogLO18Ott9891kr3c5d3t9/hxvsnTo/dJJwW\nz8IhfObuOD1QD7txjAbKpFN3gXt9nk1ne3mcHr5b3PuxFSeZ7B5wjU8Ankzc537ARpwOMQuAy3yv\ntVunIM47cjtwkrzvcFoW/e49TsvbWJxHwSeBDaHeU1tsseXUIqpnOruKMcZkDREZgtOylF9V0x3b\nzBhj8jp7R84YY4wxJkJZImeMOVfZ4wJjjMmAPVo1xhhjjIlQ1iJnjDHGGBOhLJEzxhhjjIlQlsgZ\nY4wxxkQoS+SMMcYYYyKUJXLGGGOMMRHKEjljjDHGmAj1/yEd2PcZ9aYFAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1236b9690>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"make_plot(log_likelihood_sgd, len_data=len(feature_matrix_train), batch_size=100,\n",
" smoothing_window=30, label='stochastic, step_size=1e-1')\n",
"make_plot(log_likelihood_batch, len_data=len(feature_matrix_train), batch_size=len(feature_matrix_train),\n",
" smoothing_window=1, label='batch, step_size=5e-1')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question**: In the figure above, how many passes does batch gradient ascent need to achieve a similar log likelihood as stochastic gradient ascent? \n",
"\n",
"1. It's always better\n",
"2. 10 passes\n",
"3. 20 passes\n",
"4. 150 passes or more"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Explore the effects of step sizes on stochastic gradient ascent"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In previous sections, we chose step sizes for you. In practice, it helps to know how to choose good step sizes yourself.\n",
"\n",
"To start, we explore a wide range of step sizes that are equally spaced in the log space. Run stochastic gradient ascent with `step_size` set to 1e-4, 1e-3, 1e-2, 1e-1, 1e0, 1e1, and 1e2. Use the following set of parameters:\n",
"* `initial_coefficients=np.zeros(194)`\n",
"* `batch_size=100`\n",
"* `max_iter` initialized so as to run 10 passes over the data."
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69313622\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69313170\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69313585\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69312487\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69313157\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69313113\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.69311121\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69312692\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69312115\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69312811\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.69311286\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.69310301\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.69310725\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69311567\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.69310836\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.69308342\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.69298918\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.69277472\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.69228764\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.69222554\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.69186710\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.69230650\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.69174220\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.69139955\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.69123818\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.69088883\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.68976850\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.68569701\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.68597545\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.68736824\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69303759\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69299241\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69303389\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69292442\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69299113\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69298668\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.69278828\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69294460\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69288708\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69295651\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.69280480\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.69270635\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.69274924\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69283249\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.69275924\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.69251197\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.69158805\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.68946852\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.68492418\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.68415366\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.68114554\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.68489867\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.68027821\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.67693088\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.67561867\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.67367588\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.66156206\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.62798175\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.64157978\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.64571292\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.69205420\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.69160695\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.69201686\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.69095428\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.69159348\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.69154386\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.68964000\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.69112685\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.69056997\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.69124730\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.68980179\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.68882576\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.68929536\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.69003572\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.68929307\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.68702353\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.67916061\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.66049079\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.63235099\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.62183600\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.61150928\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.62979300\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.61553432\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.59156014\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.58842264\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.59076267\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.54480104\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.45761063\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.54362587\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.56306510\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.68251093\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.67845294\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.68207160\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.67411325\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.67804438\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.67712546\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.66377074\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.67321231\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.66923613\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.67479446\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.66501639\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.65591964\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.66240398\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.66440641\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.65782757\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.64571479\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.60976663\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.54566060\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.48245740\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.46629313\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.47223389\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.52216798\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.52336683\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.46963453\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.47883783\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.46988191\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.46365531\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.36466901\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.51096892\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.54670667\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.61201447\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -0.58843678\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -0.59771677\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -0.58770466\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -0.56939710\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -0.57554451\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -0.54068090\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -0.55212916\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -0.55311029\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.57672007\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.55455807\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.49771894\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -0.54708765\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -0.54286814\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -0.52361054\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.49731367\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -0.50102061\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.42406927\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.35064478\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.38344116\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.40170047\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -0.45117863\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.46493371\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.45343350\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.43128394\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.43169967\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.43029376\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.32703099\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -0.49162447\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -0.52452720\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -0.51319004\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -2.20035379\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -3.34199720\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -3.06285156\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -2.80822162\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -2.99629286\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -2.71489944\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -3.61713200\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -1.19526584\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -0.75357081\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -0.71310829\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -0.59361318\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -1.53764659\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -2.69588686\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -1.89731473\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -0.81254441\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -1.19013437\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -0.48968363\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -0.72860037\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -0.58719556\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -0.31220572\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -1.89468446\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -0.96096585\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -0.66616640\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -0.46114004\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -0.47236476\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -0.45227508\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -0.29378688\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -2.47834692\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -2.48776279\n",
"Iteration 0: Average log likelihood (of data points in batch [00000:00100]) = -2.44471310\n",
"Iteration 1: Average log likelihood (of data points in batch [00100:00200]) = -36.66862050\n",
"Iteration 2: Average log likelihood (of data points in batch [00200:00300]) = -25.49870239\n",
"Iteration 3: Average log likelihood (of data points in batch [00300:00400]) = -40.14565040\n",
"Iteration 4: Average log likelihood (of data points in batch [00400:00500]) = -27.03748522\n",
"Iteration 5: Average log likelihood (of data points in batch [00500:00600]) = -32.62294582\n",
"Iteration 6: Average log likelihood (of data points in batch [00600:00700]) = -25.88017915\n",
"Iteration 7: Average log likelihood (of data points in batch [00700:00800]) = -37.30720216\n",
"Iteration 8: Average log likelihood (of data points in batch [00800:00900]) = -10.87360529\n",
"Iteration 9: Average log likelihood (of data points in batch [00900:01000]) = -6.60878996\n",
"Iteration 10: Average log likelihood (of data points in batch [01000:01100]) = -7.15375088\n",
"Iteration 11: Average log likelihood (of data points in batch [01100:01200]) = -6.04741293\n",
"Iteration 12: Average log likelihood (of data points in batch [01200:01300]) = -18.17389834\n",
"Iteration 13: Average log likelihood (of data points in batch [01300:01400]) = -27.14619228\n",
"Iteration 14: Average log likelihood (of data points in batch [01400:01500]) = -20.50685042\n",
"Iteration 15: Average log likelihood (of data points in batch [01500:01600]) = -7.74332305\n",
"Iteration 100: Average log likelihood (of data points in batch [10000:10100]) = -10.64501703\n",
"Iteration 200: Average log likelihood (of data points in batch [20000:20100]) = -4.03599975\n",
"Iteration 300: Average log likelihood (of data points in batch [30000:30100]) = -14.21901031\n",
"Iteration 400: Average log likelihood (of data points in batch [40000:40100]) = -6.19993978\n",
"Iteration 500: Average log likelihood (of data points in batch [02300:02400]) = -6.36502333\n",
"Iteration 600: Average log likelihood (of data points in batch [12300:12400]) = -11.39823729\n",
"Iteration 700: Average log likelihood (of data points in batch [22300:22400]) = -8.46797053\n",
"Iteration 800: Average log likelihood (of data points in batch [32300:32400]) = -5.24553417\n",
"Iteration 900: Average log likelihood (of data points in batch [42300:42400]) = -4.68839629\n",
"Iteration 1000: Average log likelihood (of data points in batch [04600:04700]) = -4.40273027\n",
"Iteration 2000: Average log likelihood (of data points in batch [09200:09300]) = -16.44320616\n",
"Iteration 3000: Average log likelihood (of data points in batch [13800:13900]) = -1.24273340\n",
"Iteration 4000: Average log likelihood (of data points in batch [18400:18500]) = -25.08431933\n",
"Iteration 4769: Average log likelihood (of data points in batch [47600:47700]) = -4.18699295\n"
]
}
],
"source": [
"batch_size = 100\n",
"num_passes = 10\n",
"num_iterations = num_passes * int(len(feature_matrix_train)/batch_size)\n",
"\n",
"coefficients_sgd = {}\n",
"log_likelihood_sgd = {}\n",
"for step_size in np.logspace(-4, 2, num=7):\n",
" coefficients_sgd[step_size], log_likelihood_sgd[step_size] = logistic_regression_SG(feature_matrix_train, sentiment_train,\n",
" initial_coefficients=np.zeros(194),\n",
" step_size=step_size, batch_size=batch_size, max_iter=num_iterations)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Plotting the log likelihood as a function of passes for each step size\n",
"\n",
"Now, we will plot the change in log likelihood using the `make_plot` for each of the following values of `step_size`:\n",
"\n",
"* `step_size = 1e-4`\n",
"* `step_size = 1e-3`\n",
"* `step_size = 1e-2`\n",
"* `step_size = 1e-1`\n",
"* `step_size = 1e0`\n",
"* `step_size = 1e1`\n",
"* `step_size = 1e2`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For consistency, we again apply `smoothing_window=30`."
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAFSCAYAAAB2ajI+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4VMX6xz+zNb2RUAOEjlRBwIIgWBDl2rjqVW7B+9OL\nHfXqtWADO+oVFTtWxK4I2PDaQIoISJcOAQKBkF43W+f3xyYhu3t2s5vdTcH5PE+e7JkzZ8572pzv\neWfmHSGlRKFQKBQKhULR+tA1twEKhUKhUCgUisahhJxCoVAoFApFK0UJOYVCoVAoFIpWihJyCoVC\noVAoFK0UJeQUCoVCoVAoWilKyCkUCoVCoVC0UpSQUygUCoVCoWilBCXkhBCjhRAJftYlCCFGR9Ys\nhUKhUCgUCkVDBOuR+wno52ddn5r1CoVCoVAoFIomJFghJwKsMwPOCNiiUCgUCoVCoQgBg78VQogs\noHu9pGEazauxwP8BByJumUKhUCgUCoUiIH6FHDAZeBCQNX+z8fTMyZplB3BjtAxUKBQKhUKhUGgj\npJTaK4ToCmThFms/4hZrW72yWYGdUsqiKNoYMkKITOBZ4Gzc9n8P3CqlzGlWwxQKhUKhUCgiiF8h\n55FJiDOAdVLK8uibFB5CiFhgE2AB7q1JfhR3M/AgKaWluWxTKBQKhUKhiCSBmlbrkFIujbYhEWQK\nbk9ibyllNoAQYjOwC7gWt6dOoVAoFAqFotUTrEfOBNwDXAl0wT1StT5SShmUKIw2QojvAbOUcpRX\n+hLcdo5tFsMUCoVCoVAoIkyw4usp3H3kvgHm4+4b11LpDyzQSP8duLSJbVEoFAqFQqGIGsEKuUuB\nB6WUj0bTmAiRBhRrpBcBqU1si0KhUCgUCkXUCDYgcALwSzQNUSgUCoVCoVCERrAeuS+A0bjDkLR0\nitH2vPnz1CGEaLijoEKhUCgUCkWEkVIGmj2rQYIVcrOBuUIIF/A17mZKb0P2hmNIBPkddz85b/rh\nGwevjmAGfShaDtOnT2f69OnNbYYiBNQ1a32oa9a6UNer9SFEWBoOCF7I1TarTsc924MW+rCtiQyL\ngKeEEFlSyn1QN93YSODO5jNLoVAoFAqFIrIEK+T+D/eUXK2BObhH2C4UQtxfk/YQsB94rdmsUigU\nCoVCoYgwwQYEfjvKdkQMKWWVEOJMYBYwl2NTdN0mpaxqVuMUEWPMmDHNbYIiRNQ1a32oa9a6UNfr\nj0lQAYGPd4QQMtTzIKXEUezAWeHElmfDlmfDftQOOjAkGxB6gamdCXMXM/p4PZY9Fqqzq7HsteAo\nciAMou7PkGLAkGxw/29jwJhuxNTehM6ko2p7FRWbKnCWOtHF6HBWOTF1MJEwKAF9gp6qnVVYdliw\n5dsQeoHO5B6I7LK5cJQ4sOfbiekeQ0xWDMY0I8IgqN5fjXS4j9dR4sBV7aqzWRerw5BsAAGOYge2\nfBvSLpFOiT5Wjz7B/WfqaELaJC6bC1eVC0Oqgbg+cegT9FhzrVhzrNjybLgsLpwVTpzlTpxVTqyH\nrBjTjRjTjcQPiCeudxzOKie2XHfesjVlmDuZiesbh/2onaodVdiL7NgO29DF6Eg6OYmkU5KIOyEO\naZfuc59ro3p/NdZcK9XZ1e6y+8cT3z/efR5jdUiHdJ/7Qge2IzaEWZBwYgK2Izaq91VTvroca44V\nQ6oBfaIec2cz0iaxHrRibOs+bzFdYnDZXOCCmO4xHn0bpEMiDAJ7gd19zmwSfaIeY5oRY1sjxjQj\n9mI7zlIn1fuqMWeasR2x4ShxENMthphuMQijwHbEhvWAO0xjXJ844k6Iw2VzYT1gpXxNOZVbKzGk\nGjB3MmNsYwQd2HJtmNqbSB6VjD5Bj2WXhbJVZUinxFZkx1rqQB61kzA4AWEUSJvE1MEEuLeN7R2L\nMd2IPkGPs9JJ5eZKpEOii9FhTDPiqnZhL7Rjr3AQ2ymGpJFJJJ+ajM6sw2V3UbW1isIvCynfVEH5\nnipcLknGyFQSBsRjSDXgLHdStucAZfurMJa2wRirJyYrhqKfS4jvE4eprRFThglDGwM6kw7pcp/3\npJOT0CfqwQUI0MfpEQaBPlGPMAqcFU4cpe7raS+wgxNMHUwY0gy4qlyUriyleF05lmI7xo4mkrvG\nojMIKvZYSMyKwZRuIrZHLMY2RuxFdqq2VlG1vQpTB5P7Pi62U1low251IW0u2vSMJ75PHOZMM/YC\nO1Xbq7AdsmFsa8RZ6URn1mFIMaAz6zB3MWNMNeKyu7AdtmHPt+N0unDowWTWQ4ULfaKetPFpoMP9\njDkkLqsLoRfo4/Q4Sh04yhzYj9qRDom9yI7T6qJgdyUV+VZMFkjsEkPaSUnEdI0BAVVbq6jYUEHC\n4AScVU4OzDxA0qlJZEzMwFnpdD+PlU4cNc+kvcqJsZ2RmDQTmARVZXaodiF1Al28DuECp0NSnW2h\n4rcK5BE7AsicmknKKUm4LC5KtldQlm8lrmssbbrFYUxy12GOIoe7fjULdGYdlb9XYjtkw5BqQJgE\n5g5mDGkGrAesuOwuzB3N2IvsVOyvJjbViDSAKc2IIcWAJaea3NUlWPdUY9FJ4tqZ6XZGG4xp7mdB\nOt31saPEQfX+anddmmig7EAVhzeVI6VEVjgxJxoxHHFgitOjzzLhsLgwJRtIPy2F+H7xWA9ZKd9n\n4eCaEqzbqtDF6JCJemIyjLTLisdpd18jW7GdpM6xmDPNpI1Pw15op3x9BUezKykqsUKZE5MDOo9M\no+25bRAmgaPIQeXvlRR8VYgzWUfl+gooctL55k7E9Y3DdsjG0U1lFC0vQVfqwtzBRNrwJHRSENMt\nxl1flzsoP2zFhgtjsoGEFBNJfeOJ7RWL9aCV4u+Kyfu1BGecjoQuMSR3ikEXp8dSasdaaKe63EF1\noY20nvHoTDr0TrA6XCQl1Lwb9lWDURDXMxZzJzOWvRbiT4gHHTjLnO663OLEmmvDbnFi7GAioVMM\nulgdQi+wHrbisrjcdSJgzbeRNMD9rqqt64ROIJ2Syp1VFO2qxOgUxKYbMXc0Y8m1cnB5ETanC1O6\niYye8cQa9cQPiCe2ZyxCL9x11NZK9Anu+sCYbsRR7KBqj4V9G0so316Fo9qJSDOQ0T2edj0SMCXo\nKS+1U1lgw+lwkd4+lsQ+cRiSDFTtq6ZkfxWxsXqkxUV1iQNR4cIhJIldYhECLDstJAxJAEAXpwMB\nlt0W7BYXcb1ikRYX+hgduhgdSLDrQWcUmIw6pF1ibGPEWeGkYF8l+VsrwCWJTzeT0jWWXrd2DXuw\ng18hJ4R4E3hYSpld8zsQUkp5dTiGNCf1hZyUEsseCyU/lVC1rYrq7Gr3y/WQFSQIk8Ceb8dlcyGt\nSgQr/gCkFEP3vfB7f7DG+M8nXDBoEySXwqpTwFYzAcz1L8Hln7h/rxsCtz8TfZu9MdjBYcDtoFco\njmN67oLOObB2GJQnNZ8d6fkQVwUHujafDa2AsYyN6qjVscBzNb/PJHAfuVavaBwVDvLm5ZH7Ui6V\nmyubZqcDNsNNL7hfkgsvgo/+AgUZjSvrxPVw1dsweBMsOx02DobF46EyIaIm/6HothfSC2DDiWA3\nhb69cIEMNlRjPVKLQOeCwvTQtw2WkcvhkfuPLd85E9aM8M039Dd45D6IrYbCNPjXHChO0y7zsWlw\nyq/u39lZcMNLkHnwmIgDGLoezl0M346P2KE0yGUfw9/fBZcOHr1X+zhbHBJO/hV67YJfToU9PSNb\nfJf98J+noGMufDUB3vtrYJHelIxc7q4XF14EH18OrgDj6GKr3AK9Mc9nqCSVQtujsLd7YJsag84J\nieVQmhJeOWN+gvsfBl3NK/mv8yC3k/t3x0Mw+mfIawdLxjSubgrFjmmPgdEBiy6AWf+O3r5aI0ab\n+4O3sE1E1JNqWsXtkfs56WecZc7QN+54CO55HMoT3UKsLAmyu9Hgl/+wNfCUxiDayz+C/Laeae0P\nuyv1HX1g+wm+27Q/DB9M8k3f3gemPh9+JXfZx3DDy+7fS0fDjAejUwmYrO6y93eFTy/1FbV//hQu\n+MJd4T31H/j1ZE87jDbIyHc/HI19KV38OdzyvGfa5gFw+39DO49Xvg9XfAjVMW6Bs/HE4LY7dzHc\n8TQYau7F56bCogsj++KIscA35/umf3Q5vHL9sWWdE96fBO2OHkub91d44xrfbf/2Llzt5bh/cDpM\nnO/+uKjP1hPgxpdCNFrSKG/aaSvg0fuOLZcluq+LJc4zX4wF2h+Bv81z/5/zL99r1n0P3PgidDkA\nWwa4RaHD6LvPnrugXZ47T2NezOZqePVa6HrgWNrrV8N7fwu9LE0kvHQDnLDdd9V//+2uw8qS3B+D\nUufO3zkHDnfQPt5gSSqFCV+5hddXE6Aq3nN9fAW8fRWkFx5Le/Of8O4/ICsbsvZBbke3uF09Aoau\ng9tmgdkGCy+EZ28l5HtEuNzXM6ez+xkbuMn9/HXJgS8nwH9vd5d54np48k63MAGYdSt8+Sf/z2X7\nw+7j9PdhLlww8y4YvhaOtIOYakgphX1d4d5H4Uh77bINdvd5OJgJ1bG+69/5h9v2+pz/FcRa4DOv\nGSonfub7UTZ4A4xcAZZYt9jL7u67j4yj7vtha79jNgz9ze2Q+OEsd5mvXw096kUku+IDyGvvWc7w\n1XDOd25h3JBgD4Y2BXDeN2CyQXEqLBvlPv/tjsCFi9zewTn/8r3vwkXvcJ8zm8ndElF7DyaVunWB\n97vy/96Av8+rWxw7Nvw4ckrI4RZyS8xLPJtKk0qhzw7YdgJUxblvhG7ZsPQM2DwQ7CacacXoP5vo\nU17hpjPY9f6DtD0qaFPo1h157eBAF3ddWJQG54+7hfbtN/lsa/vtZKzTn8BsBZMdik/7ndRHb6pb\nv/ud6Zh+OIPkUnDqQQqIf/0KYlLz/B7f1p+nEL+xJ/ZNQ7Eb9OR2dG8bU+22yxILCRWQkS+JTzlE\nx7HvYXS6KFsxHkv/bPqdM9ujvLyll1I270YcJ68la+IsYtNy2f/+XcQuGI/ZCgXpkJ/h1jCV8e7/\nZUnQsfsyBg9+l/ZJuyg90oviNeNwLroE4dRh+POHdJngOah41YNfY+y0n5OmXI8WFfOmUPztlRzu\nAFWDdjFi4t3ExRXhcJjY8f2NGOdfSI89IKTbGeMwQN6k74k/9Xsq9/XHMn8SsvMhTG0Oc0jXgT6X\nPka71B1+z+OSh78jPc+AJdZ9PG4kicYi2nReT8rw77ELI7s2X8yoiXfUbWevTGb7Ax/R/oCZjAL4\nvZ/7XogZ/AvGuFIc60eQcjgWYYmh/+MXYoir8Nhv9SeTyPvyXxzu6KR02G46DlqMszSNwz//BZtw\ni8vUYuixB+K7b8I88UP27R/NvooBJPdYx2mnzgJg85IbyP3lMk4d8xhJp37nc3zSJfjtubnsN2QS\nVwUdT/uEwaN8BVfhlYtpc8R8bLl3Pm1evdzvedPi+09e5mBlX4athb19bPQ8+T36nPgRepO7f6Dc\nPJDCZx6mQiaTdPanJF00D2d+B8pmPYjhYHukcN+3VXFQmuKkIl5PWpHbYWIzuZ+Lw0OOcMqtV/rs\ne+s3Uzm89hKq4qDTIeiYsIOMabehj7F45Nu89Hp+OXwxSQn7uOJP12oexyuff0NccQxWs/s57z90\nLgNHvAWArSSdXS8+y2HZiZIUsBskBpy0La/iRMNahMGBecBv2G3xlCz6BzZLCgYHpJy+iKQps3z2\n9eOzC3BUJVPeoRCbwUJJbAoxlhiGxywjxVFFwZ4R2Esz6Jbt/pYU0u1wkwIckz4icehSCku6k5CW\nQ4d2vnWPN9bqRL545yPOmzSZ+MR8yuypzF39JAm7O9N7hxmz1X3+y3vngr4Sw4EuxFWYSSlx6waH\nAcxWSCqTWMeuoMPN93uUv+PaH7GZBHqnW5vEfT1W047Cny+izeiFDdq765UnSem0FXO/9RRtO42c\nXy9DCoEt1oHttF+xWuKw7zuBtkdicBigpO9Bzj5nGinJOdgL2lH86FOkP3YduthjY+IqKtJZ/OEz\nnPfnu4lPzfXYX/FvZ5J6h/uY8tPhaFsoOWUTI/9+yzHb507F/PElANji7BR1sNJu6r0k9mj4/Occ\nHsqOH26i/apuJAz7idiTl9DuhJ/r1lsrU9jy4kt0WteB9nm4nQoaYn/3t9fSbui3JGbs80h3Okz8\n8sYczLlpiKxs2vReRbeR73vkKZvxFElLhrGrJ1hO2cCgq2/zWL96wcOk6orodeGx+3X5J7M4/TLP\nfEfm3oH+iwlUx9S8b3qup8MdtyNqPId7Vv+F/Yuvw2aC8iQb1vhy9HYDPaqLOKnwAPoHpwNgWXwx\nsc9cD3YTq0+10+nUT+l0gf9gFAX7TyS96waPNGtVMkc/vgnLyrNxppSRetlrxHbZQXK73e7zvnk8\n63+8DYvJAOjq6taSFPe722QDR4yNlPTd9Jv4KLFtPO+L/H3DyMhaW7dc/vpUjv5yMebJr5E5+kMf\nG5tUyAkh4nCHITkD9ywJRcBPwFtSSkugbVs6Qgh517k/Mf5b97Iz8xC8fg16czUA28uG0Tdprcc2\n+TKdDFHgt8wv+BMH6EIXDrBSnka26MbpLOdnRqPHyQdoeNBqOIvvSZcFPML99BK7fNbfwItsox8g\nmch8buaFkI/ZIfUYxDEP5Pa8QfQNonKvZcPBUzgxc5VH2sq8MawpGImu0MDwbks4IWUzpcUZ7Fs9\nBAMOTrv005DttJXGYUr2P9j4qx+u4vwz30YrpuL3/7uSLXH9sBvcPQhGu5Zy8mmLQ7ahFsemNAoW\nDMaYWIX5rIPokyzEZvnExtYk+5uTyTnSh6TKCnoPXU3caQcbbUd92rydQIfPBTu6dCX77BgyL1ob\nMH/5mwOIn7QNXYx/77NhYxxtfxTk3ua/i8GaD/9OWUwSscl5nDY29Osa92M8/Z5yYu/oYOMbDr/5\nyr7pRdJ5ns/AprcuIDatlF4X/eyZ+dme5Jd0whXjwtw/n5QLNDxONfR8yIhjayoHO6TjmOU3TjiJ\n26BcwwleS8d5euIWphJrs1HRRZA9u9QnT/y1vehUWIT+hCK2TZd+I26a7+zFodj2pM9Yprk+5tdY\nkg7bOHqx/2vX/tVY8rb1xGR3kuoqIv+uIpxZNv8H0Ajafi0o3JFF9dgyjCcWeqwzlELSl/FUppiQ\nWVXY+lv9llOxuDtla7uRVlZGcuZhrFMj80zU0ulVE7auDvLHuzzS0xYbMdnsHLnQM7/LqkdnDq1V\npmJeX0r3Z5KZn0/Hzrs4dLtXXeWCva+dRXrWAZLG+9blkSD9mVQ2VQ3l6GVWTuyzPOLlZ17TFl2i\njQOzShpdRsx6M/L1HlSbTCRVVVF96wHsJ1R75Gk7PYXOq63oHBbK2sCOD/yX53r8BHT3bGu0PbWY\ntpiwDfB9PhLWQtcHwaE34jDEUpUcT/WFhRRfEtlnCZpQyAkh2gNLgN6447EdAdoDXYEdwBgppX+X\nUAtHCCGHP/0Fdz+awFcToP2kZzgn9ouo7U/aBcLo/7yXvjaYxPG70XXx/yJt858OWIZYqZoUnJBo\nKgzl0Olz2P+P5rbETeJ2OHEqOJLhl08azh9NRp0HO2+BvCh0D9NVg6uFdHEKBpcdjn4J7S9pfjt0\nYbQWAhzeCGu/gYEXQZaG6Mv5CER7yDwjvP0cj7zwClj0cPmfoGuH5rYmdNZlw2fLIdkEd/5FO8+a\nHTC8T/RtOVoKbZMjX+6RSthTBiPDvD6ProNDh+GG4TCgrXae+QchKx6Gak2yWY/Sakhugvru2t8g\nzwoLTovePppSyM0FzgUmSilX1Es/DfgM+FZKeVU4hjQnQgg57MXn2dBrIC6jkx84u7lNUkSQg7+D\n1QE9Bje3JS2TcjskhilmWtJ+FMGTVw2PbIPZQ5pn/98chsw4GBgFAdJUTFwJ86P4olcc30RCyAXb\nY/084J76Ig5ASrkSuA+YEI4RLYEBu7YzfMcW3jk6pcn3XZjbcJ5g+c83cOtiyG68F/y4I7N/6CJu\nX6mJVza1xe5qOG9r5tcDbXn9l4ZPzorsjkGVl1+h0QEb2JnXhi83DAzJtpbIf96/rLlNiBgVlhhm\nzPkPW957hXPvns3NL/yH+cvObFIbzuugLeIqLdr3US2fLz2XdTsGRMmq0GipIs7l8tUGazedwoo1\n2n0RFU3HNdesY8KEEsaOi0yEjGA9chbgEimlTwcjIcS5wAIpZeAnrwUjhJDffvAl1fYCkjpfFdK2\nkhiKxRqMYj2JrtDbEyUx2IyfYLZfEDCfy3AHOsfTAfPoYlcidCcghEAgkK48pP1ZnPZQRwj6kpy8\nE5vtAywWf1PtRgaDYQQuVyEu1x6NtTrM5kuxWj+Oqg2JiXOIjZ2MTmfE4dhNQUGvqO7PG6PxJNLT\nV1FU9Ces1m811g/Dbg/cFy5YUlJmk5BwEyUld1JR8ZRmnvj4a0hNfY3S0nsoL58ZsLyMjO+R0kZB\nwQTqj6tPTp5BbOzFHDniXzTGxl5KRsbH5OQkEMlJWDIzD6HTJZGbeyIOh9Z9FRyxsWfTocN3FBXd\nS0nJY2HbFRs7HoslcJ/N1NQHKC5+KOx9ee73bNq3fw+9PgOdzvdl73SWsmdPmGEwNMjImElc3Gj2\n7z81YL6uXddgMvXi8OF/UlHxeV26TpdEjx67MBiOtcvl5l5NaWlDYU5Dx2w+Aat1F3Cs/6YQJvr1\ns7Jv3zgqK30HC4VCx44voNe3IS7uNKqrN2A298fhyMNq/R0p7eTm3uh329jYoXTu/A57947D4Tis\nmadz57lUVa2isNCz7u/deyM6XRz79l1MdfXvPtuZTD3p1m0BVVUrycnRdmro9Wm0bfsfDh++J4Qj\nDo/MzGc5ePBWv+vbtp1KYuI5JCefR0nJ5+zd+xfckcTddO36OklJY8nO/gcVFSv8ltMY2rW7HYMh\njfLyJZSVue8Lo7Ejdruvh0ani6dfv1XExR37CImPF03WtLoB+F1K+VeNde8CA6SUzeScD5/agMC7\ndk3l0KHZPusNhjTi4nrTtet9OBzlbNt2bCRcVtYMsrIewOWysWpVV2y2I0HvNz5+IN27P0GbNuez\nbt2plJWt0swzbNgGhNCRl/ce27ZphyAYOPAb2rQJ3PnK5bJy4MAT7Ns3A+/gNQkJQxgyZCV6fQxV\nVbtZt+5kHI4i9PpkTj31AAaDe5hmQcEitmy5KOhj1GLIkBUUF3/Pvn3HRKFen4DZnEm/fh8Dkg0b\nxuJwHOv/l5R0GkOGLEcIgdNpITt7GgcPPutRbvfuM+nU6WYKCxexdesVQdmSlnYeAwd+ic12BL0+\nEYMh0SfPrl03c+iQ9oCSpKRT6Nr1Qc1z73I5+Pln/22Jp512hEOHXmb//hke6cOHbyU+/gRcLgcF\nBQs4dGg2paXujv19+75N+/aTAcjNfY2dO31HU5544jJSUk5HSokQgkOHXmHXLu2Rv6ecso+YGHfA\nzurq/axe3R+Xy/2V2L79VWRlTa9bX1y8hI0btb/mMzNvo0ePpxFCV5P3Rw4dehG7vYA2bSbQufPt\nSClZtiwOKe0+22dkXEa/fh8hhMBiyebXXz3DHpx88m5ycmaRm/uiV/pe9PpEVq7UDvMwYMBC0tPd\nvdqllOzYcTVHjrylmTcr6yGysu5nz567ycnxFKw6XQwnn7wbs7kT1dUHWbt2EA5HsWY5nTrdTGbm\nbT7HUEv37k+QkXE5sbHdADSPNzFxOEOHrsLlsrJsWZxPGSec8AEGQxIuVzU2Wx67dt2guS+Atm2v\npEuXu4iPH4AQwYV4qKjYxM6dN2C3HyUj4zKysh4gO/t+cnI8xX5sbE/6959PQsJAKiq2cPjwqx7P\nyuDBP5Ca6unl27373xw86Dsq133cIzjppF/rlu32EnJynsJmyyUz83YSEjy9cDZbAdu3T6ao6FvA\n/0CFIUOWExPTg19+OdbRKyPjMnr1eokNG0ZTVXWs43xKyhgGDfqOoqKv2bHjGuz2fLp0uYfu3d3i\nPS/vfbZt83kVetCv30ds3ardae6kk9aSmHhSwO3t9mLKy3/DbM6kqOgrjMYMMjIuQ68/5i+R0sXS\npb7X02TqwGmn5WK3l7B27YlYrfsBPI6hFoslm6NHP8Rs7kjbtn9Fp3MPDKus3MqaNf01bUtP/zP9\n+n3I1q1/oaBgPgC9e88hNrY7GzeeVS+nnn79PmDrVv8j2jt3vpOcnCf9rh8xYidxce4P6QMHnmbv\n3v9o5hs92l5nO0BV1S4KChaQkDCI1NRz6uolm63Ab10xalQVen0sOTnPsmfPbZp54uL6MmzYJnQ6\nY1396g+b7Sjr15+OxbKL5OQzGDz4f+h0viGshGg6Ifc33POW/gi8DxzGPdjhCuBs4O9Syvf9l9Cy\nqRVya9cOoaLi2FBlnS6eUaPK6m6CWsrLfyM39zXi4nrTqdNUdDW9pcvKVrNt29+wWHxHJ5lMnejT\n53UcjmKcznLatr3SQzRYrYf45ZdMn+369fuEtm2Pxf9Zs2YwlZWeo0u7d59Jly4aMekCUF29n4qK\nzaSkjMFg8A0a7HRaqK7eS1xcX5/Kv6joO7Kz78NgSKVXr+eJi+vNwYMvsHv3zR75UlLGkpp6DtnZ\n0+rSYmN7M2LEdoQQlJQspbo6h/T0i9Dr4wBd3YPhcJRTXv4b4EJKBykpY+vOcy0HDsxk7967AYiJ\nyWL48N9ryoE9e+70eenU0qvXi3TseH3Ah9Cb3Nw5HDnyNmVlKzEa25GSMobevV/GaAzcK9dqPcwv\nv/g2S7Zt+1f69XPHEnK57BQWfondnk96+sWYTH56AmsgpaSiYh12eyEpKWM0Kwqr9YjHC6wWg6EN\nI0fme5wHqzWXkpKlJCYOq6tAa3E6K1m1Kgu7/dho7cTEEaSlnUvnzndq3kfeFBf/wMaNnn1QBw78\nijZtfOPaWSx7qKz8ndTUs9Dr3bGfysrWsm7dcOCYYAUoLV3Jhg1nIKUDgyGFIUNWEh/vO/KgqmoH\na9YMQkrP0WcmUweGDduEyZSOlE5KS1ficJRSXb2PysottG9/FcnJp9QrZzeFhV+wZ49noNMhQ1aQ\nnOxua3PEB9sdAAAgAElEQVQ4ylm+3DOy/hlnOH3qE4Ciov/x+++X43JV06PHk2RmTq1b53I5yM6+\nh/z8T4mJ6cEJJ8zDbPaMySWlJC/vXbZvn+yR3rv3HNq1+xt6ffg9w6V08ttvw6io2IBOF8+gQV+T\nkjI65HKs1lxWrermcw1Axxln2IIWm772SazWHITQs2nTeVRWbkYIM0OGLCcpaVhdPru9CIMhpe46\nOJ2VlJauJC6uLzExnYPaz7Ztf+fo0fc0148aVYlOF8vGjWdTUvKjx7r6wiQS7N59OwcPHpspJSHh\nRIYNW1/PVhdFRYvR6WJISRkbUp23bdvfycub55M+erStri6224vQ6+PR6Y6FI3I4yiktXU5CwiDM\n5k7s2/eQx0c7QGbm7fTs6W5hcrnsrF7dh+rqbI88I0bsIC6ut0fahg1nUlLyk0fakCHLSU4eGfRx\n2e1FHDr0Imlp43E4irHZ8khPvxCDIbnGHis//6z9vGh9mARCSondfhSTqZ3fPE0m5Gp2NgV4CKj/\nlskDHpBSzgnHiOamVsgtW5aE01lel96//3wyMho3rE5KJ0VF32EyZZCYeFKD6h2guvogq1Z5ViRj\nxnhen4qKLezefQslJT8SG9uHIUOWBrxJmhK7vZCysjWkpp7t8XWUk/MsBw8+g04XQ58+c0hJidzw\nveLiH7FaD9KmzQUeoqqiYgtr1/r2yTIa2zJixPYGBVgkWbt2KBUV6z3STj+9TNP7Fy02b76AwsIv\nPdLatLmIgQMXhFROUdF37N17FzpdDL16vUhiYuiOeJfLxr59MzCZ2tGx43Wa4rMxWCx7KC1dQXLy\naGJjs/zmKyz8ikOHXiQurh8dOlyNxbKblJSxQQlRLY4e/ZjKys20aXMhSUnDPdZVVe1g//5HEMJM\nt24zMJs7+S3H5XIgpa3uY6Qx7Nv3CPv23Y/BkMKAAV/UCd2Wxs6d15Ob+0rdsk4Xy+jRkWtOl1JS\nVbWD2NhuHiIjkixfnorD4dkZedQoS51ollKyc+cUDh9+HYMhjZ49n6nzpkcKl8vG77//mcLCL0lJ\nGUP//vMjWrd5twKNHFkUcvk2Wz6bNo2nomIdZnMmQ4f+itns+XFbWbmdnTv/hcNRQlbWw2RkXKxZ\nlpRODh58jiNH3qo5p882qg5qCKezmtzcl2q8we5Wtp49n/P4wIoUTSrkanaoA/pwLI7cDillq+8O\nLoSQdnspy5d79ro94wxXSF8wkaC09Bdycp7EaGxL1673BfWFqNCmsnI7W7ZchMWysy5t0KD/kZZ2\nTpPaUVq6kvXr3V+MOl0MJ574s88LP9qUlCxj48YzkfJYn5/apgSFoqmR0kVOztOUlPxMhw7/R0aG\nb2D1ls6RI/PYvv3vdct9+rxFhw5X+eRzOCrQ6+Oj+i5xuaxRE6yRwmo9gsnUrsnfqS2dJhdyxytC\nCFlRsZU1a/rVpcXEdOOUU/YG2ErRWnA6LQhh9PASNjVW62HKylaSmDicmJguzWJDefk68vM/JS6u\nH23bXtGs50OhOB44cmQeRUWLSUs7l3bt/qZEiiJkmrpptRfuUCOnAp2AQ8BK4BEp5e5wjGhuhBCy\nuHgJGzaMqUtLSjqNoUMjO7pFoVAoFAqFopZICLmgPsmFEGOArwEL8BXuvnHtgAuAvwghxkspl4Zj\nSHNjs+V7LBuNfiY7VigUCoVCoWghBNu28l9gPXCulLJuRm8hRCLwv5r1w/xs2yqw2z2FnMmkhJxC\noVAoFIqWTbAzO/QDZtYXcQBSynJgJqAdcKYV4S3klEdOoVAoFApFSydYIXcQ8BcjwIS7v1yrxjvO\njRJyCoVCoVAoWjrBCrmZwAwhhEfwFyFEJ+BBIPz5aloYBkPkp6hRKBQKhUKhiCTB9pE7A0gC9goh\nVnFssMMpNb/H1AyIAJBSyshGPWwCkpJGUlZ2bJRqYmKr7vKnUCgUCoXiD0CwU3RlN5jpGFJKqT3J\nYJSpCZEyFTgT6AKUA2uA+6WUmwJsJ8vLN7Fhwxk4HMV07HgdvXu/3DRGKxQKhUKh+EOiAgJ7IYS4\nEbgOeBv4DUgG7gJOBEZKKdf72U5KKXG5HNjtBT7zGCoUCoVCoVBEGiXkvBBCpEkpi7zSkoB9wCIp\n5VV+tpPH03lQKBQKhULR8omEkAt2sEOrwFvE1aSVATtxz0ahUCgUCoVCcdxwXAk5LYQQqcAAYGtz\n26JQKBQKhUIRSY57IQe8UPP/uWa1QqFQKBQKhSLCtGghJ4Q4SwjhCuLvRz/b3wNcAdwopdzbtNYr\nFAqFQqFQRJdg48g1FyuAvkHkq/JOEEJcBzwKTJNSvtNQAdOnT6/7PWbMGMaMGRO0kQqFQqFQKBQN\nsWTJEpYsWRLRMo+rUau1CCH+jjsEydNSyruCyK9GrSoUCoVCoWhSmnTUqhBiihBivRCiSgjh9P4L\nx4hIIoS4BHgTeC0YEadQKBQKhULRWgmqaVUI8Q9gNvAOMBi3UDICFwL5wHvRMjAUhBCjgfeBDcBc\nIcTJ9VZbpZQbmscyhUKhUCgUisgTbB+5W4HHgYeBa4CXpJTrakJ7LAEKo2NeyIwFTMBQYLnXuv1A\ns0wdplAoFAqFQhENgp1rtRy4CPgJsAOnSylX1ay7HHhUStkrmoZGE9VHTqFQKBQKRVPTlH3kLICh\nRu0cwdOzVQF0DMcIhUKhUCgUCkXoBNu0uhnoDfwPWAZME0JkAw5gOrA9KtYpFAqFQqFQKPwSrJB7\nDehR8/t+4HuO9UErBy6OsF0KhUKhUCgUigZoVBw5IUQ8cCoQB6yUUhZE2rCmRPWRUygUCoVC0dRE\noo9csIMdRgPrpJQVGuvigZOklD+HY0hzooScQqFQKBSKpqYpBzv8BPTzs65vzXqFQqFQKBQKRRMS\nrJALpBbNQIuZ2UGhUCgUCoXij4LfwQ5CiCw8w4wME0IkeGWLBf4POBBxyxQKhUKhUCgUAQk0anUy\n8CAga/5m4+mZkzXLDuDGaBmoUCgUCoVCodDG72AHIURXIAu3WPsRt1jb6pXNCuyUUhZF0caoowY7\nKBQKhUKhaGqactTqGcBvWqNWjweUkFMoFAqFQtHUNJmQO95RQk6hUCgUCkVTEwkhF+zMDgghxgHX\nA32AGK/VUkrZw3crhUKhUCgUCkW0CCr8iBDifOAb3DM59MU9t+oBoDPgAlptMGCFQqFQKBSK1kqw\nceTuB14Ezq9Zvk9KOQboD+hxizyFQqFQKBQKRRMSrJDrC3yB2/smqWmSlVLuBKbjFnoKhUKhUCgU\niiYkWCHnApw1IwLygS711uUCqn+cQqFQKBQKRRMTrJDbwTGxtha4VQjRQQiRAdwO7IuCbQqFQqFQ\nKBSKAAQ7avU9oHfN7weB74GDNctOYFKE7VIoFAqFQqFQNECj4sgJITKB8bhHsX4vpfSe8aFVoeLI\nKRQKhUKhaGpUQOAIoYScQqFQKBSKpiYSQi7YPnKtEiHEFUIIlxDiQHPbolAoFAqFQhFp/HrkhBC1\noUaCQkqpj5RRkUAIkYw7cHHtiNsuAfIqj5xCoVAoFIomJdpTdD3EMSEngP8DYnHHk8sD2gN/AizA\nG+EYESWeAjYAR4CzmtkWhUKhUCgUiojjV8hJKafX/hZC3AfsB86VUlbVS48HvgUcUbQxZIQQI3GP\npB2EClasUCgUCoXiOCXYPnLXAk/VF3EAUspK4Gngukgb1liEEAbgVeBJKeXe5rZHoVAoFAqFIloE\nK+TSAZOfdSagTWTMiQh347bpieY2RKFQKBQKhSKaBCvk1gIzhBAd6ycKITrhnmt1TYTtqi3/rJpR\npw39/ViTvycwDbhRSmmLhk0KhUKhUCgULYVgZ3aYCvwI7BVCrMI92KEdcApQRfRmdlgB9A0iX22T\n7/PAD8DqmlGrArd3TtQsW6WU1VoFTJ8+ve73mDFjGDNmTOOtVigUCoVCofBiyZIlLFmyJKJlBh0Q\nWAjRBvg3bvHWATgM/ALMklIWRtSqRiKEyAa64BZw3kjgOSnlvzW2U+FHFAqFQqFQNClqZgcvhBAj\ngBiv5HuAocClwCGtARBKyCkUCoVCoWhqlJALAiHEW8BZKiCwQqFQKBSKloSaoit4lEpTKBQKhUJx\n3HHce+SCQXnkFAqFQqFQNDXKI6dQKBQKhULxByYoISeESBZCmKNtjEKhUCgUwWK1WnE4WtQMkQpF\nk9OgkKuZ8qoQGBd9cxQKhUKhaJjZs2eTkJBA27Zt+d///tfc5igUzUZQfeSEEIeAf0kpv46+SU2P\n6iOnUCj+SNjtdl566SWKi4u58cYbycjIaG6TQqKyspKEhIS65WHDhrFmTVQmGFIookpT9pGbB1wT\nzo4UCsUfk7Vr13LZZZdxyy23UFxc3NzmKIDbb7+dW2+9lRkzZnDmmWfS2j5kN23a5LG8du3aZrJE\noWh+gp2iax8wSQixBliIe1YHjydfSvlmZE1TKBStjWXLllFUVMSECRMwGAzYbDbGjRtXJ+CsViuv\nvPJKM1upmD17dt3vLVu2sHnzZgYNGtSMFoWGzaam0lYoaglWyL1Y878TcJLGegkoIdcISkpKqKys\npFOnTmGVU1FRwbvvvktaWhqXX345QoTlqVUoQua///0vd9xxBwAXXHABixYtYsWKFR5euFdffVUJ\nuRZIUVFRc5sQElpCzuVyodOpQAyKPx7BCrluUbXiD8oPP/zAxIkTKSsr48Ybb+SFF15oVDlSSs49\n91xWrlwJuJsdHn300UiaqlA0SK2IA/jiiy84cOAA1dXVzWiRIlha24dfWVmZT5rFYiE+Pr4ZrFEo\nmpegPl+klPsb+ou2occjV199dV2F9OKLL3LgwIFGlbNu3bo6EQfw2GOPRcQ+LaSUra4/jaJ5OHz4\ncIu4VxwOBytXriQnJ6e5TWkRaHmz7HZ7M1jSeLT6WlZVVTWDJQpF8xOSH1oIMUgIcZMQ4kEhRPua\ntJ5CiMTomHf8YrVa2b/fU/9+//33jSrr999/j4RJDbJ27Vq6deuG2WzmqaeeapJ9KpqXnJwcJk2a\nxMUXX+zTwbw+WoItJiYGl8sVVN5o4XK5OPPMMxk5ciR9+vThxx9/bLJ9t1QqKip80iorK5vBkuDI\nz8/noosuonv37nX1jtZHrxJyij8qwQYENgshPgHWA88DDwAda1Y/CdwbHfOOX5YuXeqTptfrG1WW\nVjNDNJg2bRr79+/Hbrczbdo0jh492iT7VTQfU6ZM4YMPPmDhwoVcdtllfkWYPyGgFay1KTuq//zz\nzyxbtgxwN71NnTq1yfbdUtm9e7dPWksWcs8++yyLFi0iOzubO++8k127dlFSUuKTrzV5FS0WC3/+\n858xmUyMHz+e0tLS5jZJ0YoJ1iP3KHA28HegHVC/Q8U3wLkRtqvVUFVVxTfffMOuXbtC2k7ri1Lr\nSzkYmkrIfffdd3W/HQ4Hy5cvb5L9KpqPxYsX1/3euXMne/fu1cyndQ/a7XZNIWe1WiNnYAN8++23\nHstN5b1uyTz33HM+aS1ZyHl3FXn66ac1RVtrmuFh4cKFzJ8/H7vdzrfffsuHH37Y3CYpWjHBCrkr\ngfuklO8D3sObsoGsSBrVWrDb7QwfPpzzzz+fAQMGhNRso1VxNrYi0hKATdF81Zq+gBWho3UPlZeX\na+b1J+S07pGm9MipUYy+rFq1yietJQs5b5xOZ6sXclOmTPFYvu6665rJEk9cLhcvv/wyl1xyCW+8\n8UaL6OOqaJhga7k2wLYAZfwh52H9+OOP2bp1K+B+OXk/nIEoLCz0SWusMNLqh3TLLbc0qixF85OX\nl8e6detwOp3NaoeW58xfE1BL9ci15nhjNpuNkpKSiL9MzznnHJ+01iTkjEZjqxdyWnV2NLFarVxx\nxRUYDAbOPPNMv+FmFi9ezA033MCCBQu45ppr+Pnnn5vUTkXjCFbIZQOn+lk3AtgRGXNaF96DE/bs\n2RP0ttu2+erixgo5rdABs2fPjmjnXy1R0dSV0R+BFStW0KtXL0466STOOeecZj3HWi93rQ8Q0BZM\nNptN855WQq5hdu7cSe/evUlNTWXSpEkRFXPt27f3SWttQk5LtCkh559vv/2Wjz76CKfTyU8//cQb\nb7zhk8dqtTJhwgSPtGnTpjWViYowCFbIzQXuFkL8FTDWpEkhxFjgNv6gwYDDib306aef+qRpVURS\nSl5//XUmT57MV199FdI+nnjiiUbb543Wy1c1rWqTnZ3Na6+9FnCUpz8eeOCBuubLn376iZ9++inS\n5gWN1odAQUGBZl6te9efR64pRYPFYgkpf3l5OVu2bGn2+He1A4sAPvzww4jOI6r13LY2IdfaPXKh\n3pfhcs8993gs33nnnT55nn/+eZ801ae0dRCskHsS+Ap4F6gN4LMc+B5YLKWc7W/D45lIB9HU6rvy\n2Wef8a9//Yu5c+fypz/9iRUrVgRtx8MPPxyxyu14iD3VFOTk5DB48GCuvfbaRk3k7d3P8rPPPouk\neSERikfOn5DTukea8is/FIGyf/9+BgwYwMCBAxk+fHizjiT0vu61I28jQUNCrrq6mh07doTlzdyz\nZw+HDh1q9PaBMBgMrVrINcdHgtFobDCPlrhrLee0tSCl5PHHH2fIkCHceuutETu/wQYEdkoprwDO\nAJ4BXscdhuRMKeVfI2JJKyTSHam//vprH4+Hd/PtTTfdFFKZjQ0y7I2/pjOFJw8//HCdR81ut3Pr\nrbc2s0X+cTqdzJ07l1dffVXTQ6DlkQtVyGmlf/nll42wtnGEco/OnDmz7nnZsmWLZvNTc2E2R64b\nciAhl5+fz0knnUTfvn0ZMGBAo6buuvfee+nZsydZWVm88847YdvrTbQ9ctu3b+f555/nt99+i0h5\n3tQfCd5UNDa0VXN7po83VqxYwbRp09iwYQPPPfcczzzzTETKDUmJSCmXSSnvlVJOkVLeI6X0DYb2\nByIcj5xWPxWAWbNmeSzXD/kBsGHDBp9tAnWKj1RoEtW0Ghxff/21x3L9GTcaQzTP8dSpU5k8eTLX\nXXcdEydO9FkfrkfOXx+5pkRr//76m7388ssey7fffntUbGoIrf5Tkfxo1DontSPfP/nkk7oBXLt2\n7eLJJ58MqezS0tK6cCEOh4OrrroqPGM1MBgMUesjl52dzdChQ7nllls4+eSTWb16ddhleqMVQzTa\nNPZd1dwDro43vK/9XXfdFZFyQ53ZYawQYpoQ4sWa/2MiYkUrRatyDbZTsr9Kx3sQhL8XZ30CPWz+\nwkWESkvwyO3du5f77ruPd955p8UOtIi0XdEcGPDSSy/V/V68eDF5eXke67WEnL8v9FA8ck2Jlr2h\nXKPmsD+U894YtITcl19+icvl4r///a9H+syZM0Mq23u2mmgQzabVGTNm1HmnnU5nVDzq/vqdrVix\notk/fBThs379evr27UtqaiqvvPKKx7pIdpGojyGYTEKINOATYCzgwt1PLtW9SvwEXC6lDN0H38pJ\nSkrySauoqCAxseEZy/yJIO8HOZi+DYGE3Pz58xk1alSDZTSElqBoSiFXXV3NiBEj6oRtSUlJiwyx\nEulQEdESrFqe3by8PNq1a1e3rNW06u9FE0ofuaZESwA5nc6gm5qqqqo0n/NoohUXMpKd4/1dk5kz\nZxITExNW2U3xgWU0GjVjdkZCyHkHkP7ll1/CLrM+2dnZPq0stZx++umMGjWKpUuXRrz/tYoHFz5H\njhzBbDaTmpoaMN8DDzzAjh3uQB633XYbV155JcnJyUD04loGW+rzwHDgb0CslDIDiAX+UZPuGyq8\nGRFCdBRCvCmEOCyEqBZC7BVCPBrp/YQz+svfF3akhdyzzz4blD0N0dxNq4sWLfLwTrbUvmeRfpFp\nled0OsN+ab311ls+ad7CPJSg1f4C//rL35i+V43Bn5Dzxt91i8ZoTofDwdy5c3n88cc5fPiwz3ot\nIRfJUEL+ntt33nkn7KY0re1DEREul4tDhw7VCVetbbVmpoDW0TH/wQcfDLh+2bJl/PDDD01kjSJY\n7rvvPjp06EBmZiYLFy4MmLd+H+Dq6mqPj4NoDaAKVshdANwjpXxfSmkHkFLapZTvAfcBF0bFukYg\nhOgKrAZ6AjcD5wAPAhF/yrVeEsFU/C6XK2hvlsHQsNO0KfoxaAm5powHFq0RcFJKjh496rcJ7ssv\nv+SLL74IWqBF+svX+35asWIFHTt2JCYmpm4C8cbQuXNnnzTve7Ihj5zT6eSjjz7itdde4+qrr9bM\n6080RNrT4Q8tT5bW87Jv3z7N7aMxEftjjz3G5MmTmTZtGqeffrqPPVr3erSbVgF27NgR9oeIlp3B\n1nU2m41x48aRmZnJgAED2Lt3r2Z5WuIXIiPkjhw5EnYZUkq+/vpr5syZ49O15d13321w++YMOaTw\npbCwkEcfdfuBqqqqQgr8D57vSX/hm8IlWCHnBPxNJrqjZn1L4VXgIDBGSvlpzQCNd6WUgT+FGoFW\nJbNkyZJGbVeL9+i0YPq4BRJyHTp0aHD7YGjuptVgmquD4eOPP+biiy/miSeewOFwcMUVV9CuXTu6\nd+/u03flpptu4oILLuDCCy/kxhtvDKr8SHvkFi1axHvvvVe3fPfdd3P06FGcTid33nmnpmdr06ZN\njB49mlNOOcXvfLhaLwvvF7zWR0n9PDfccANXXHEF1157raZgCtRHLlxP18aNG/n3v//NO++8E1A8\nB+ORc7lc9OjRIyp2emOxWDy8Mnv37vW577Q8MpH0fgcqK1zhqnUfBCtC58+fX3fse/fu5Yknngip\nj29L8chNnz6dCRMmMGXKFAYPHhzyx10wrTCK0HC5XFgslkZ9aG/evNlj+ejRoyFtv2DBgrrf0bpH\ngxVyC4G/+Fl3BbDAz7omRQjRHRgHPC+ljHpnDa1K67bbbmvUdrXU76PicDgoKSlpsLxAQm7gwIEN\nbq+FlJIZM2bQq1cv/vrXv2revI0VclJKCgsLQ7qp4+LifNJC9UT+/vvv/OUvf2HhwoXcc8893HLL\nLXz88ceA+yv/8ssv97Cx/ijGV155JajjjUYfoRtuuKGuAvIWZlpC7ZprrmHZsmX8+uuvjBo1SvNF\n6j26FoJrWq0vAl577bWAdgfyyIUjGAoLCznllFOYNWsWV111lWYzcS3BeOSuv/56v9tHUsg5HA6P\nPoi1eIvxdevW+eSJ5EdTICGn1awbClrbB+u5924ynTNnTkij7luKkHvooYfqfmdnZ/Prr7+GtL3J\nZIq0SZocT/3mcnJy2LJli+YxFRUVMWrUKOLi4hg3bpzmM52Xl8fdd9/NY4895lNnhHue5s+fX/c7\nWt2RghVyXwBnCyG+EkJcJYQ4r+b/18BZwCIhxJm1f1GxNDhGAhKwCiH+V9M/rkgI8U7NgI2IovUy\nCuYLMpCQq++R++abb4KyI5CgaWzFvHr1aqZPn87u3bt5//33efHFF33yNKZp1W63YzAYSE9Pp2fP\nnkHHuSsuLvZJC2ZEb33uu+8+j+X6ozYBtm7dWvcy0Dq27OzsBvcRDSFXVlbmV9BrVTLeQYgnT54c\n1H68xcILL7zgkyeUl2WgPnLhCLnnn3/eQ5xqNevWEoxHLpAg1Wpubuw1/vHHHzXrB297+vfv75On\nqTxy4XaX0BKhwXrktO7lpvTIRUIIatXtoY7kvffee/nHP/4Rti0NEcmZf5qTTz75hB49ejBw4EDN\nZs+33367LgzU999/z/vvv++TZ9y4ccycOZN777036NaXxhCtVqxghdynQGfgPNzTcX1V8398Tfpn\nwHe4Z3rQHpLTNHQEBPAG7ibf8cCdwAQg4lEY/b2MNm7cGHC7QEKufp84fwEpvftxRCP8iLfo0Yp9\n1JhKv3fv3nUvwv379/P66683uM17772nGQi5Xbt2mi8OfwQz3UztQ+4digPcwVIbIpyvt0Db+uu7\n4y0qtF5GtV7HhvB+wWt5YWvzBHOc1dXVfl+O4YzCrB0R1hAul0vzQyYUT26t/Xa7nUsvvZT4+Hj0\nej1vv/120GXUcumll2qme58LrX6xTeWRCzdcy8MPP+yTFmw9obWfphRy/j56Q7lftK5Tenp6yLa8\n++67zJkzJ+Tt/KF1boOZYUWrJaSlMXny5Lp7+vXXX/cRzt7xIP/97397LO/atctjOsW33nqLtWvX\n1i1rXVPv81lQUMDu3bs168Xhw4fX/W5uj9zYBv7OrPmr/R0RhBBnCSFcQfzVjkWvPZ6fpJQ3SymX\nSClfB24AThJCnBsp28B/s8upp57K3r17/W4X6CVW/waJj4/XzOPdMTsaHrlgKtAFCxZw9OhRdu3a\nFVQlevPNN/vYrlXxe/PPf/7T77r6zRgNEYwXaPLkyXz44Yce7vBagjnGcDxygcr3N8rTu+IIp1N8\nMGKhtiIK5uX29NNPs3PnTs114Xjkgg3NUFxcHPRgB3/UHu9PP/3kMW3WP//5T83p8gLh75nyvmZa\n9jWVRy7U/FLKBkX9xRdfjJSS559/nq5duzJu3DhNT7zWsxPK/RyukPNXZwf74QCRvXahdqoPhL97\nvvac+1vf2NA7ZWVlPPnkk7z00ktRj27g/YxrhVaqj7c9Ws33f/vb3+rua63WoPr35f33309GRga9\nevXSDC+SmZnpd9+RItgpupaG8hdB+1YAfYP4q/VD17a1ec5rBf/D7ak70d+Opk+fXvcXzIAF8P8y\nslgsAefIDFQ51a+M/H0Neb9wG+uRKykp4amnnuLNN99s1MjX0tJS2rVrR+/evRk9enTA49qzZ49m\nU11DNBSLrHYo+K5duxg4cCBms5n7779fM2+wxzhp0iS6dOmiaUtDhCPkApVvt9uZO3euT7r3vRCM\np8tfc3akhZzdbteM9wXheeS0hJx3IG3w/5w1xiOn1RwTqVkLvM+Fv1kyIkWkhNz06dOJjY2lf//+\nmue/lq1btzJv3jxuueUWDhw4wHfffacZPkjruoTi9Q9XyGl54SG086VlQzjN1eH2z7LZbFx//fU+\nHRbxfcsAACAASURBVPZr2b59O+D/GBtbn51//vncdddd3Hjjjdx8882NKqOxNPR8W61Wj2uiJb52\n7NhRJ+C06qr6aY888kjA/dWvryIVoN+b6ESnixBSymop5c4g/g7WbNJw25kf6gu5MWPGBLVNoI7Q\ngTq4BnqJ1b8J/eULRcj588hJKTnzzDO58847ufrqq7nnnnt81ofCL7/8ElC8BtvfzxvvuWb9MXPm\nTLZs2YLNZuORRx7R/LoO1pMjpdQMjBrMiyKcUDCBXhgrV67U7Ovm/TERzGAbf3OI1t9/Q/Hiwg15\nE44w0bqOWsGhgxVyCQkJfvdVex60msd2794d0M76BHohtkaP3P79+5kxYwZWq5Vt27bVdcXwN+LS\nu8/X559/7pNH654IZQqjcIWcv36oBw8e1EzXQuvahWOX9znZuXMns2fP9mgKDMTChQt9ZheoT+0A\nE3/3RGOe8wMHDnh4q1999dWQywiHYM73qaee2uBAptpzH85IbDh2DqMZrqtFC7lGsAo4Ang3oZ6H\nexDEGp8twiCQIBsyZEijtqv/4PgLHuj9cAe6cWv7KX322WcIITjvvPM4fPgw69evZ/369XX5vGOS\nNeZL0Huuyvr4i4fXsWPHgGWef/75Qe3bW5xo9S8JJVp6KLMa1CfUL9j8/HwuueQS+vTpEzB48733\n3quZ7l0Z1Q9VUp/695U/EVU/3V+lU/sFH+6gjnCEidZ11IqWH6yQC/Syqn22wg0JEeh4vesDLXu0\nPt4ef/xxTj/9dB566KGAdYDL5eL555/n4osv5u23346IkPOeamj+/Plhz+ShtW0gT583/s7B0qVL\nOe+887j66qsDDpDy91wE04+3lkgLufrP4a+//kr//v2ZOnUqI0aMaLAJsaCgwGMkvha19YW/Y69v\n+zPPPEO7du0YOXKk37iLtfuNJFVVVcyePZs5c+YEdX95n2+tWVzWr1/P7NmzAf91Xe1zqVWP1G4T\nij3BDJZrLMeVkJNSOoG7gQlCiJeFEOcIIW4AXsTdb067naeRhBIPrj6BhFz9m9Bf53rvm8fflC+1\nfP3113UdrRcvXsy5556r2bz2+eefh1URBzpmf1MipaWFP5hYS3SGO/G4VgXYWI/cJ5984jf/rFmz\nWLBgATt37mT69OlB21dLsH3N6nsb/PW9rF+ZB/KYFRQUhO2Ri7SQA9/n0V9TWWOEXLhTJoUywCCQ\nR85ut7N582Y+/vhjpk2bxooVK3jwwQfp1q2b3/po0aJF3HLLLSxcuJB//vOfDQ7GCsZ2rX2FG4Mu\n3OZjrefzt99+Y8yYMSxevJg333wzYAd/f893/ThgjbEhUh656dOne4yqDzSIKT8/n0GDBjVYfm2o\nk4am3jtw4AB33HEHR48eZeXKlTz22GN+y/SOBhAuEydOZOrUqUyZMiVgqKBavJ8ffx9hta1Q/oRc\n7f2sda/XeuODuedr7dHqaxcpjishByClnIu7z9xIYBFwLzCXKMw+EUjIBfJYBOuR8yfkvCu8rKws\nv+UBXHTRRR7Lmzdv1uzgOXHiRC644AKgcR65QPM0+vPIRSJyvpaLXOtlGO48dw1VyIsXL9a87tdc\nc43fbR5//PGwbKp/7IHuufqViL8g0cF45MDd8T9cIRfOy82fqPJ+XvxV+qEIuUg1JUfCI2e32xk7\ndiyDBg1i0qRJHusPHjzo88HgdDp55plnuOSSS8KwHB599FEGDx7MlClT6rpqaF2/rVu3hrWfcJuP\nvbdft24dw4YN80gLFGrG3zUeN25c0DZ4z9UKkfPILV7sGXjBn/cd3K0j/mbAqE9tR3x/M07UnpN5\n8+Z5vBMCjajV6rrR2L5+hYWFHufUX7eQ+nhfx4ZmR/L3Hg8k5Gqb/IOJM1lcXExRURHjx49vMG9j\nOe6EHICU8j0p5SApZayUspOU8lYpZdCKoby8nCuuuIIOHTpw8803az6IUsqoC7lgm1Yb85LJzc3V\nTP/222/Zt29fox68QIEs/T1MgUbVBmuDVl8lrSaUaHpVJkyYwHnnnae5LpSgpqFSvyIJdtCLv3vz\njjvuqPsdyDuSmJjYIj1y8+bN81j2N2K2MR65cPtfheKR03rubTYbS5cuDThS1rsf2qxZs3xCLzSG\nl19+mU2bNjFnzpy64Mta9/Tf/5+9M4/Lotr/+OcACjyKihKguCEq5ZbinokoogahVlqmFpj7jnVR\nU1Iwy31LsUsmhmVhy81cyCVN1Eq9iHu3LBX1KvDTVHAB2b6/P2DmPsss59lYbN6v1/OCZ+bMmTPz\nzMz5zPd8z/f72mtW7cfWFjn969mS7QUCAgLE///v//4PkyZNwocffih5H0mFSbLm2lHqY5QsPF9/\n/TVX/V26dAFgGm5KQD/8jjHC85mI8OWXX+L999+X7Vcsvd+ljlGtLuPzrWYskHtpFdwHpH4DYVib\nR8gdO3YM7733nl37gcdSyFnLZ599hq1btyIrKwvr1q2TTJlTVFSkKNaU1ilZO/QvQt7JDpY8AJXE\n5LVr18yuD1AWSnIBLpVuBN6bX2qYeMeOHVzbmoNSAnipTAn62MvRVf8hpSRI9PfPc16V2ltSUlKh\nPnJy1/ucOXO4Hqz6+1Z7WVAKEG0O5ljk5DqvrVu3mrXP6Ohos8rzIExakvoNrM2HbK1Fzvj+5MlZ\neu7cOTz33HMIDQ3FuXPnJMsIx5qfnw8vLy98+OGHmDRpEkaOHKnaBrllvCxZskR2ndK1qzQ6ok9B\nQQFu3Lghe08JzxSpF3FBzKxduxavvPIK5s6dKwpDYyy9f6Qmrem7ifDMdFZ7Vsm1TRh6VRLTvOJs\n5cqVXOUsRdbmyBhLNKMeIiL58OpVjEmTJhl8nzJlCv74wzDVrNqsFaWLR6nDtWTWqiU3iZKQu3Xr\nlkUWObljVrrYhUj5UsOevAJV6i2wa9euJsusncov9UD+5Zdf8Mwzz6hum5OTA09PT6v2LwWvRY5X\nyAm/hdI1lZ+fb7VFbsuWLSYWNF6Urt0dO3Zg2LBhitvrHz/v2721SevNschJlS0oKICPj49VbbAF\nSkLOXNcF4/u+IjIzvP766waTvqQQjtU4ZuUXX3xhEJZG7vlnzXFt2LBBdjhYqY9xdXXlqv+3335T\nTONIRLLP523btqFDhw6YN2+euExOzD969IgrX7YQb/Czzz5Dly5dJLe5c+cOnnjiCQDS16H+84FH\naMk965RmrQKl2Y/MzS5kL5QGj/ugdKanQB0AtQEUoTReW72y7XMA2M+LrxIg9RBXe7Drd3R37tzB\n1atX0aZNGzg6OnILObl9GD/ojS9mFxcX1fYpDWnOnDnTrNAKAlJZBrZs2aI484yIkJeXhxo1aiAv\nLw8LFizAlStX8Oabb6JZs2Zc+5USclIWMmuFnPF5JyKMHTuWa9vc3FwTISeXucMc9C1yvCEu1FI0\nubq6KopoWwg5oPShb4k4URJywjqlc6F/bGr3SUVY5KSGVgsLC+3yImAJhYWFklZ7d3d3s3xeCwsL\nDSZIlZeQKy4uhqOjI/Ly8lRFHFB6vWRkZKj6s8o95/TbVbt2bVmXGTmISHK0wxYWOeN0flIUFRVJ\nRiQQns88x6P0PLl37x7++usvNGnSBKdOnRJjDKalpcHf39+kvP7Lq9QMWf376b333lNtm9q9LfeM\n6Nq1K1e4p/JA9hWKiJoSkS8R+QJ4DcB9AMMAuBJRfQCuAF4FcA+AqY35MUKq0+K1yJ0+fRotW7ZE\n+/bt0aNHD9UhWZ6hVf30IYDpTcKTVkUpMKElIg4wfbCMGzcOkZGRisMDwP9uzPnz52Px4sX44osv\nEBwczG22VsqioY+1w4HGHcWtW7e40n4Bpr/ll19+aZC6xVJ4LXK8Qk4op2aRs0VOWakguzzwzPpW\nuj/1wwCo3cfCuSovi9wff/whmXbu0aNHdsnjawn+/v6SKcrkso/IYXxOymsCjdD58z5fCgoKFGdp\nCvuWCzml3y5LR08++OADyeVyWBsuR5/r169b7G4jIHfcJ06cgJ+fH3x9fTF48GADf0RAOquG8LKQ\nl5cnGbh93rx5mDlzJgD1vqykpET13lZav2rVKsVtywteW/hKAIuI6MuyEB8gomIi2gpgCQD5AFiP\nAdYIuXXr1okPjmPHjiE5OdnqodWkpCSD78Y3CY9Z3R4Rpo3N74JjtBoTJ07EzZs3DWLZ5ebmys6k\nMkbOqd3S9GRyGHcU5gheY7H9yiuvWG0hBAx/e1sMrfIKOVtY5Hj82aRQ6oCFdinVrZ8hQ+7aEVCy\nyAnDOzzwWuTkBMOdO3fsnuqIF7l4WOZm6zA+HltY5H7//Xd8++23is83YTjMHCGnlvd0165dqiE8\neESDFC+88IJkwGtAfijT2old+hjnJhUoKCjgfrmQe57Mnz9fnG2+fft2rrqE60xpNvayZctw5swZ\n1efU559/brFFrjKhPC/3f7QFINdr/QGgjW2aUzmResDwCjnjYJIffvihGOJDbV9K+3j06JE4LGEs\nEuRitulja5HDu18p/vWvf0lGVed9C5R7mBmfF1sNrRYVFWHz5s1m+XjZa7IDr5AbN24cnn76afj7\n+6sOmwLKQyEVLeTkwvIA//uNlYb49OPoqVmLlSx85vymvBY5KUsXUPriZa/0PhXF008/bbWlR5/1\n69dzxTBr3bq1WfUqWY55BNPs2bMxe/Zss/apz969e2XX6efxtBdycfTGjRvHnQ/2qaeesll7QkJC\nuMo9/fTTqmXUZlrbShA7OzvbNbMDr5DLAvAySnOWGjMMgHTkzccES5I5y3V0P//8s2K2Av0HvtI+\n/vrrLzRo0ADFxcUG+2KMyebS1MceQk7fImfuMJBUTk7eoRo5h1NjAS43NZ4Xob4JEyZwxTPSx143\nsb7gUhJXOTk5eOaZZ3Djxg2rLXJ5eXk2EXKWhptQsvzwCDn9iTD/93//p7gvJYucrYQcryXLnFmh\ntrD22ptr165ViXZqaFiLLS2kUvAOra4G8AZjbBdjLJIx9lzZ3xQAESgden1skbLIqYWbsHTWqtA5\nEJFiRyEIMePOkNc3wh5v9/oPZWuHSQAo5m7VR+486bfh0KFDVrdHqM9cEQfYNum5PvrHrraP27dv\n48svv1Sd7KBWl5qPnFKGD30sfbgpveAIokjJ2qd/znx9fRX3pWaRMxYiZ8+elZzEYs6sVTnMEXLH\njx/nLquhoVG14bLIEdEaxth9APNRmrdU4BqAsURkTqiSKodxp3bv3j3VdEpKHZ2SZUjYl5o/jNBh\nGb/Nq804FLCHRU5foNpCyFmLfnuMQ8pYgjU+SvayyJ09exaFhYWoVq0a12967do1u1vkeIcRLMm0\ncf78eUULliDglIScvnBSu1eEcyUXfLWwsFAMhL1ixQqDILRXrlwRnbF5LHJqQ808OSyFGZm8L0Ea\nGhpVH+4nKRFtBNCk7NOt7G/Tx13EAf972N+9excbN26UDARpjCDkpGaQJiQkqO6L1wHTeAiJZ8Yq\nYH8hp+9QXlHoi0ne2aVq9Vk6pGhP/4iFCxcC4PtNi4qKrBZy9+/fVzwPShk+9Ll9+zYGDRoEX19f\nLF++nGsb43RzxvAIOf3jV/tdBAd64ziSAvqi0DiTQJMmTUSLHc85/+677xTbwuNTKIhC3ueAhoZG\n1cesV2Iq5RoRHS/7+1g6OEgN+aSkpMDd3R1jxoyRnF1j3HkJHZ2508B5hrYAZYscD/YYWhWE07Fj\nx7iSG9sbW1sFi4qKLBZk+r+nrcNICIFKeTp6xphJTk597t27hytXrsjOTBTKyAm5NWvWcA+tJiUl\nYfv27cjIyEB0dLQYKV6OBw8e4OLFi6plANN0Xfro/xbG91n//v0NvhcVFSm+uKldD8LMZp7hbLW4\ngjxCXXixU8svqU+dOnW4y2poaFQ+uIUcY6wtY+xrxthNxlhR2d8vGWPyYaGrKFL6NCwsTHEb4w5B\n6KzNeaDq16PWQQhCzFjI8b6J2yOUgdC5y01XtyX6Mw/lsLWQKywstImDvjlBU82Bp6PX6XSKk0gG\nDhwIX19fvPvuu7Jlrl69KilGU1NTMW3aNEkhx/NCI1gW5eD5PR88eIA7d+7giy++kC2jZJEzvq4u\nXLhgErdRH32fVimEc610vwnHJRX8VB+e31cQsuaERrFnMm+NyoGvr6/d00Rp8CO8MPIGvVeDS8gx\nxjoDOAagN4CdAJaV/e0D4ChjrKNNWlOFqVevnsH3a9euYcSIEWan8BCEgtyUb4HVq0tD9xmLAl6L\nnD0QhBxvgF5rMD7fUthiZqU+N27csNgipx9ehUfI9enTx6z6CwsLuaysPEJfzdB+5MgRzJ0712BZ\nt27dEBgYCEB6sgOPle6bb75RdOjnefn45JNPVOMX6otxNSHHm0NX7loTBLzShAZByKm9nPAIOWF/\n5ryoxcbGWhw6SMOQpKQkrlRU5U1aWppN/IQtJSoqCp07d4arq6tZ4iU2NhY+Pj7Q6XTo3bs3fv31\nV5u0JzU1FZ06dYKrqyuaN2+u6O70xRdfwMHBAQMHDrTJvgEgOTkZRKQ6wsALr0VuEYBzKPWJG0VE\nbxPRKAC+ZcuVc5f8DRgxYoTB9++++86iyPVCxzB58mTFckK4DkuHVu2B0CFZ4sRuLh4eHqplbG2R\ny83Ntdgipy+yeIZABw8ebFb9Dx8+lEyjY4ytxO2+ffsMvutbnqXEoqOjo2R0emOk4k2VlJRg4cKF\n3FamLVu2KK7XFznGvyePpVcfNVcI4f5UegHQj0+oBM/sVuElgfeFo0+fPvD398fRo0e5ymsoI5dO\nq6KpV68ed9oue0BEiIyMxOuvv869zZIlS7Bq1SrEx8cjLS0Nnp6eCAkJsTj+pEBGRgbCwsLw7LPP\n4tSpU5g9ezamTp2Kb7/91qTspUuXMHPmTPEl1VaYO1KnBm+P2w2lmR0MXvnLvi8B0N2mraqCNGjQ\nwCb1qKXwEhAsNjt37jRYXpFOzoJIKI8HGU+nbmshl5eXx9VBRkVFIS4uzmCZvnhQexB17drVbN/K\nhw8f4qefflItZ68wKPoWHSkx5OTkxPXwunfvnkFQXCJCWFgY3nnnHe62SKW40scci5wawvZyFjBz\nLHK2uF559qePkD+0U6dOVu/b1jBmv4+1HDp0CN27d4ebmxvq1KmDbt26IT4+Hm+88QYePHgABwcH\nODo6iv6rhYWFmDVrFho1aoQaNWqga9euBoF+U1NT4eDggF27dqFDhw5wdXVFp06dVK9lgdzcXLz2\n2mvw8vISrUz6L076Q6txcXFi+xwcHMSP0FagNCtP69at4erqiieffFIcAbKUNWvWYPLkyWjZsqVZ\n27z99tsYPHgwWrVqhaSkJNy7d8/AQJKbm4tx48bBy8sLtWrVQu/evVV9TT/88EP4+Phg9erV8Pf3\nx5gxYxAREWEy4aqoqAjDhw/H+++/rxqmyFxsmUIN4BdyapMaHstJD+ZQu3Ztm9XFMywimO+N/R7u\n3r1rM1FpLoKQKw+LnLe3t2oZewg5HiHUoUMHk7df/baoDa1Wq1bN7Dc2Xr87e6Wb0W+vlBhydHTk\nHr7Tt0afPHkSu3fvtr6BepjjI6eGsL1ch8sjrHgtcjwIIUp4XjhCQkLQpUsX8fvatWvF/728vHDz\n5k2bDWU9ThQXF2Pw4MEIDAzE2bNncfz4cURFRSEwMBCrV6+GTqdDdnY2MjMzxZnMkZGROHz4MJKT\nk3H+/HlERERg4MCBOHv2rEHd0dHRWLZsGU6cOIFmzZohPDyc656dO3cuzp8/j5SUFFy4cAGJiYnw\n8fGRLBsdHY2srCxkZmYiKysLmzdvRrVq1dCzZ08AwIYNGxATE4OFCxfit99+w4oVK7B06VKDrBmh\noaFwc3OT/dSqVcvS0wugNA1cVlaWQRYHFxcXBAYG4ueffzZoR1ZWFlJSUnDq1CkEBgYiODgY2dny\nOQqOHj2Kfv36GSzr378/0tLSDEYs5syZg2bNmqlmf7AEWws53t7iGIA5jLEf9K1yjLEaAGYB+Nvb\n5XlDLvDAYzqWK3Py5El89913CA8PL/fcjOU5tMozhCzclGpvaLzwWuRKSkpMhJg5FjlLhBzvcENF\nCjneY9IXpampqdY3zghbW+ROnjwp69NoT4tcTEwMDhw4YNCx7dq1Cy+88ALX72w8iWPy5Mnw8PDA\nH3/8gcjISHh4eFTKYcKKJjc3Fzk5OXj++efRtGlTABAtTenp6WCMGYwYXLp0CcnJybhy5YqYUmvS\npEnYt28fEhISsG7dOrHsvHnz0LdvXwClVrGGDRvi888/xxtvvKHYpqtXryIgIAAdO5a6qzdq1Ei2\nrE6nE0dufv/9d0ybNg3Lly9H7969AZROOlq6dKmYy7RJkyaYNWsW4uPjRT+7jRs3mp1b1xyysrLA\nGIOXl5fBci8vLzEO64EDB3DmzBncvHlT9MGNi4vD9u3b8emnn5qEA9Kv2zjNl5eXF4qKinDr1i14\neXlh7969+Prrr3H69Gk7HJ3t+0je3mIOgIMArjDGdgLIBOANIBSADkCQTVtVBbHlD8MzQULO8blG\njRro378/Tp8+jT///NOmDppqCMJJTewEBQXh4MGDVu2Lx3le6BhtFeU+Ly+Pq4MkIpM3Lv1OWi0t\nlJqQa9iwIf773/8aLKtMFrmaNWtKrrfEoZ43lIk52NJHLi0tDSdPnpRdz+MjV1JSgpKSErOF3MCB\nA01m+jZv3lx1fwJvv/22wXfGGIYNG2awrDxeyqoa7u7uiIiIQL9+/RAcHIzg4GAMGTJEVjylp6eD\niNCqVSuDiUQFBQUGLwCMMXTr1k38XqNGDbRt25bLKjpx4kQMGTIEaWlpCAkJQXh4uKpf1927dzFo\n0CAMGzYMU6dOBVBq0b127RrGjx+PCRMmiGWLiooMRH39+vVV22Rv0tPT8eDBAxN/6UePHokT7oSR\nK8YYRo4cyZWL99atWxg1ahSSk5Mr5cQVKXgzOxxnjHUDMA9AfwB1AdwG8COAd4norNL2VYlz586Z\nvc1PP/0kxouyBTxCTq7jFjqip556yqaJinkQhJz+DE0prDW7A3wWUKFj5HHwf/fdd038sHQ6ncF5\nzsvLk01qro+UkBPEQ0ZGhklnacyFCxdkhdyAAQPwwQcfmPiaHDlyBO3atcOZM2cU67ZUyEVERCAp\nKUl2vS0tcvrY0tItYEuLnNxbvwCvz1pRUZHZQs7Z2Rnjx483mHEnHA/P76zfUcthjZBbsWIF3nrr\nLYu3r8xRShMTEzFjxgzs3r0b27dvR0xMjGykgZKSEjg4OCAtLc3kHrDV5LQBAwbg6tWr+P7777F/\n/36EhYVh6NChSEyUjtdfXFyMoUOHolGjRgZD6oJ/dkJCArp3l3d9Dw0NxeHDh2XXM8aQm5tr4dGU\nus4QEbKzs0UrJgBkZ2eLbjUlJSXw9vbGkSNHTGbaC32MvkVNWObt7W0y9JqdnQ0nJyd4eHjgyJEj\nyMrKQnBwsFivcF6qV6+O8+fPo0WLFhYfmz3gfrIS0RkAQ+zYlkpBTEyM2dt0797dpiE3eFLxyL1x\nS1lDygulvJT6WOtP+M4773BNCBHaoxaWw8/PD0OHDjURcrVr1zYQcg8fPsRHH32kul9PT09kZWUZ\nLEtISEBmZibc3d1Vt8/IyJAVPbt27ZLsXLds2cIllCwVcmq/mZqQs9QiZ+0MNSls6SOnhjlCztwZ\nxY6OjiZWIOF4eIa9eGYxWiPkbH0uKxtt27ZF27ZtER0djdDQUCQlJSEsLMzkd+zQoQOICJmZmejV\nq5dsfUSEo0ePisO1Dx48wLlz5xAZGcnVnrp162LEiBEYMWIEBgwYgOHDhyMhIUHSH2v69Om4evUq\njh8/bnBfenp6okGDBvjzzz9NIjHoY++hVV9fX3h7e2Pfvn3icHF+fj4OHz6MFStWAAACAgKQnZ0N\nxpjsZASpUCfdu3c3Ed179+5Fp06d4OjoiM6dO5v4Ls6dOxd3797F+vXrrZ740KRJE6u2l8KsV2RW\naltthVKL3F8A/vO4ZXdQS5NjTIMGDcAYs2kcpoyMDNUy+fn5kj5w9hiK4oXXomCNRe7jjz/GqFGj\nVIPHAqVvqf/9739VhZyzs7Nkp1a7dm1kZmaK33keXI0bN0a/fv0kA9JKZQSRQ0qQu7q6ynasrVu3\nNsmMcPToUYOhGsBUUDg6OnIJCLXo/7a2yBUWFsLJyQlRUVGyZTp16oStW7fCz8+Pu16hbqC04zQe\nWrX1rG/hmlmzZo1iOUsscsXFxSb3uyDkeGIK8vwe1rwYVuRLpT3JyMhAQkICBg4cCB8fH1y8eBFn\nzpzB5MmT0bRpU+Tn5+OHH35Ahw4doNPp0KJFCwwfPhyRkZFYvnw5AgICcPv2bRw8eBB+fn4GoYYW\nLlwIDw8P1K9fHwsWLICzszNeffVV1TbNnz8fAQEBaN26NQoLC/HNN9/Az89PUsRt2rQJmzZtwu7d\nu5Gfny8+E2rWrIkaNWogLi4O06ZNQ+3atREaGorCwkKkp6fj+vXrmD17NgDzh1YvXryI+/fv4/r1\n6ygoKBAtZa1bt4aTkxNu3LiB4OBgLF68WEzDFxUVhUWLFsHf3x8tWrTAwoUL4ebmJp6Pvn37okeP\nHhg0aBCWLFmCJ598EpmZmdizZw9CQkLQo0cPybZMmDAB8fHxmDFjBsaPH48jR45g8+bNSE5OBlD6\nDGjVqpXBNnXq1EFxcbFNRrl4hnfNxZzMDmNQ6ht3BqX+cmcB3GCMjbZ5q6yAMVaXMbaGMXaRMfaQ\nMXaJMbaWMaYeeMwCBNO4LX1JpGbcGHekjx49khxetbdPy4YNGzBr1ixMmjRJ9McRuHDhgmoML8By\nITdu3DiMHj0aDg4O3ENuq1atUu3U9J1l9TG2QqlZVSIiIpCSkoLq1atbPStJ6kGp/7Iwb948g3Xe\n3t4moqROnToGwyaA6THwWk3UfEXUfOTMmbUKlGZS+c9//qO6T0siowvnqaioyGBIxtHR0eYvKoBy\nugAAIABJREFUQg8fPuTyVyssLDRbyNWtW9cqIcczkYExhjZt2pjVLoHHVcjpdDpcuHABL7/8Mvz9\n/TFq1Ci89tprmDlzJrp3744JEybg1VdfhaenJ5YtWwagNFD1qFGjMGvWLDz11FMIDw/H4cOHDawz\njDEsXrwYb731Fjp16oSLFy9i165dXMOvzs7OiImJQfv27dGzZ088ePDA4MWRMSb+3ocOHUJ+fj6C\ngoLQoEED8SNYukaPHo3ExER89tlnaN++PQIDA7FhwwarshCMGTMGAQEBWLNmDTIzMxEQEICAgABx\n4kJhYSEuXLiAnJwccZuZM2dixowZmDJlCrp06YLs7Gzs3bvX4JmVkpKCPn36YNy4cXjyyScxbNgw\nXLhwQTFyQ9OmTZGSkoLDhw+jQ4cOWLRoEdauXWt27E5LEWYH2xQiUv0AGAGgBMA+ABEo9ZOLALAX\nQDGAV3nqKY8PgJ8AZAMYByAQwAQANwH8rLANCaA0lAr3p3Xr1kRE9OWXX5q9rdwnKirKZNknn3xi\n8N3d3Z2uX79uUq5Tp06kzxtvvGGzdgGgdevWiXXfvXvXojoWLVpk0XYTJkwQ971ixQru7SIiIlTL\n3Llzx2RZYGAgVa9e3WCZq6ur5PaTJk0yOO9bt2616jxnZ2ebLKtdu7ZY//r16w3WjRs3jpo0aWKw\n7PLly5SQkGCwLDw83OD7E088wdWeTZs2qZ5jgX/+858m69u1a0ffffedWeegcePGiuufffZZrnu2\nQ4cOBt9btWpFRET37t0zWK7T6ejgwYNW/W7GnzFjxlBKSopquX/9619m101EJr/vmDFjiIjo2Wef\n5dqeh7Nnz1p07D/88IPN2vC4c/DgQXJwcKC//vqropuiYQf0r/mCggKTdWSl7uE138wEsIWIQogo\niYj2lP3tB+BzlIYgqXAYYy1QGpx4LhF9RESHiOifAGIAdC1bLwtZMEosDMnZ0hJm/Dbt7u6OIUMM\n3RPz8/Ml/YemTZtm8H3OnDk2Dfapbxm0dEaPpT5y+hYEc5zgf/nlF9UyUkOrjDGTt2G54SjjctZY\n5Hr37i2ZuUL/bdX43N+7d8/E8lOtWjWTdkgNrT733HOqbZKLSaVfj4CtJjtcvXpVcb1Qn5qlwPjt\nXC6fcfXq1W0ecT0vL88kC4YUL774oskyJUvM/PnzAZi6UqhlmrCENm3aWDTz+3G1yNkLS/ofjaqH\nrWPIAfxDq/4APpNZ91nZ+sqA0LvnGC0XviseryXpi4SHrS195Ixn+7zyyiuSD+xVq1aZbPvyyy8b\nfPfz88O///1vrqj/POibny0Vr7aY0m2OkLtw4YJF9aWmppp0pnJDVrYUcu+//77quTUenr53756J\nz6TUEK+UkONJpm0cz8kYfbEsJeQuXrxo83yewn7UUpMZuyXcuXMH//rXv0yGp52dnVWFnCCgeCko\nKDCYdSfQuHFj1W2V/PWEWXPGz4XU1FQ8evTI4pzAclgiyjQhZx5KQ91yAXhr1aqFxYsXl2MrNazB\n1i+KYr2c5e4BMH0aldKwbH2FQ0TnGWOpAN5hjF0C8BuA1gDeAZBCRL8rbW9JAF1bWOSeeOIJ3Lx5\nU/xuHCNOsBToO6aXlJRIdmByPj5qvj9NmjTBlStXFMskJCTYZCaapQ94fbFk67AUcr8fb3gAY5Fi\nzQ1rPEFBCmMxLJUHllfI8Qjrtm3bKq7X92eT+n1zc3Nt/hCrV68eAIiz2uRo0aIFHBwcxJnOf/31\nF1566SWTcjxCrl+/fti5cyd3kOmvvvoKX331lcGyadOmmaTWk6JBgwayoYiE69/49xUCw/LGFeTF\nkhcTTcjx06tXL0VDgtIs0bp169qrWRo2Rj+Tii3hVR/fA3ifMWbgpccY6w5gYdn6ykIYgD8A/Bul\nAvMogIvgCJ1iyXCELYSc8QwZY6uPIMKsccRWEz5CQEgpXnrpJRARxo0bZ/H+9bH0Aa8vOOwRX0wK\nXiFn/BC2pONzcnIymBYvzBATECKtA9JDq8YvItWqVTM5T8ZCzsHBgUvIMcYUA4zqx7Xz95c20Nva\nIidYrNTui4KCAq60dc7Ozqq/d/Xq1SVFoDl4e3tzXR+enp6K7QCkz+mvv/7KNfPdHCy5nisy7/Pj\nRv369dGsWTPJj9qMco3Kg72iSpjjI5cD4CBj7Cpj7Bhj7AqAIwByy9bbHMZYMGOshONzQG+zjwF0\nxf8mO4wH0BnAN2r7s0TICRkKrBFygmVBwFjICQ9taywaasKHJzioFEOHDjV7G0sf8PYScnJWxi5d\nunALOWMrqjkd308//YQ9e/bg7Nmz4tR7ABg5cqTYturVqxsM6/EKOR6LnJqw7ty5MwAohvkQUvcA\n8sOGthZygguC2sPR19dXNUg1UHqO1SzOzs7OVsdBdHNz47qXlfajJOTsgSX3G0+cOg2NvxNyIVGs\nhTezQxZjrD2ANwD0RGkcuQwAqQA+ISLb2vH/x08AnuQo9xAAGGNhAIYB6ENEB8vWHWGMXQawlzEW\nTkQ7pCqIjY3lmrJvjNCBW/pAbdWqlclDUs4iZ02kbLUHsZK4Ugq+++STPD+PIZb6j+lbQqTq6Nat\nG44eNT/t79atWyWXz549m8t/DDAV2eaIbm9vb0mH/datW+PMmTM4cuQInn32WYMyxkIuJyfHxCro\n5ORkcp7++OMPg++FhYWqLyFCCBOlY+KJdG7roVXBD0yt3saNG8PV1VU2rZ2As7Oz6kuGs7Oz1W/V\nNWvW5DoXSpYWc4Vcjx49rPKTtUSUVWRMSw2NysiUKVNw8OBBq1NUGmNOZoeHANaVfcoFIsoHoO6p\n/j/aoHSKr7EDizDl6ikAskIuIyODu+MWEPwTLLXITZkyBceOHTNYJmeRU0NIeiyFUh1OTk6KjrZK\nlkpLzPqWCLnx48eLEc8B6Q7MUqEQGhoKoHRSiSDqGjRogPDwcIOE1koYJ7U25xj1j8sYYfjEGGMh\nd/v2bZP9M8ZU26E2MxQAunbtCkBZNPCce1tbj4QXDLV4aE5OTnB3dzfwQ5WCR6RVr17d6sjubm5u\nXBZCpSwg5go5a/3VLBFy9pidp6FRVXFxcYGXlxe8vLwQFBQkLo+Li7O67sctI7KQF8k43obgPX5d\naWNLJjsIkectFXJ16tQxEVl37twx+M47FKl0QSh1UML+J06cKLleKTyFJULOEsFlLLClOm/eWcfJ\nycmoWbMm3N3dsWPHDrGuDz74ABEREQgPD8e2bdvg5OSk2tbatWtj3rx5JhG/zenELLl2jIcA5Xz0\nbDkErSQaeI7X1hY5noC2wn55hkOrVaumKuTq1aun+MLEQ82aNVUnFgG2tchZO0nJEusaYwyTJ08W\nv2tDrRp/ZywZveKFqwdhjFVnjM1njP1Wli2h2OhjXkhy+/EvlGaf+JQxNoExFsQYmwggCcAVAN8q\nbWyJj5zgD2SpkGvUqJFJZ2sc4V14m1YTTUo53JQ6dGHde++9h3HjxhnMgvL19VXM9WfJjClz39Sl\n4rlJxVzijYz/yiuvIDc3F7dv38bzzz8vLvf09MQnn3yC7du3i35hSuKjfv36uHv3rqSAttc0cwEH\nBwdFK4vcrEZz0Y9faE+L3Jw5c8xrmBlUq1aNS8gxxlQt125ubmCMYfz48Ra3h1dUKbVZ+F15nzvW\nTjyQ28+4cePQr18/2e1iY2Px2muvoWfPniazdzU0/k5YmueaB171sQylITz+ALAawAKjz7t2aZ2Z\nENE9lE50+B5ANIAUAP8A8B2AZ9R8+SyxyAkdmKXDRs8884zq267w4FdLIcIj1qQQOgV3d3ckJCTg\nr7/+wp9//ont27fj5MmTih1PeQyt6nQ6E+uLlN8ej5Br3749APOsOXIoWRjKY1hJKdWZsH/eduze\nvdtkWd26dbFkyRLxu9K5MF5nfD/odDrZ7du0aaMaQsQanJycDIYy5NBPYySF/jHFx8dL5tPlgVfI\nKVmYzY1faQ9/NScnJyQkJGDPnj2y59fDwwObN2/GoUOH8PzzzyuKPg374evra7bbkIZtqQxCbgiA\n+UQUTkRziCjO+GO3FpoJEV0norFE5EdEurK/E4goU21bNYuclEO38LC11ALDkzdUsLyovVVbKuSk\n1vn5+SE8PFzVklEeQk6qE5IScjxDq+b+TuaIF314j9Eac7uQp1Bp/7xDq/369cOsWbPQuHFjhISE\n4JtvvsF//vMfA/88c4ZWN2/ebPB92bJlstsnJyerWpakYiYKbg1qODs7Y8qUKarl1MS9fhsdHR0x\nbNgwrv0bwyvkwsLCZNcJLxG8Qs54Zrwt0N+38W+RlJQkuU1iYqLN21GZSEpKsknAc1uTlpZmMLO8\nvImKikLnzp3h6upqVs7W2NhY+Pj4QKfToXfv3vj1119t0p7U1FR06tQJrq6uaN68ORISEgzWf/31\n1+jcuTPc3d1Rs2ZNdOjQweSZZi6WGIp44RVyNQGo5zmq4hif6K5du6JDhw4ASjvE+Ph4k22EhzuP\nM/Gzzz5r8L1v375i3UoID361UBhK4kGpo7TGj6pdu3Zmb1OtWjWzBKCUYJI6Vh6LnLkiUkmsKQlH\nXsG4YMECs9rDi+BMz3u8QsLuK1euYO/evXjxxRdN4piZM7Q6ZMgQDB48GIwxBAcHY/jw4ZLb+/v7\no3Xr1qrtGzVqFM6fPy9+HzdunMn9JEeTJk1Qu3ZtjB07lqu8HDzDmDzCikfI9ejRQ3EmsLkWuenT\npxu039wMFVLo7zs0NBRvvvkmWrRogUmTJuHVV1+V3MbHx0e0ij+OEBG3tb88qVevXoX6KBIRIiMj\n8frrr3Nvs2TJEqxatQrx8fFIS0uDp6cnQkJCJFNTmkNGRgbCwsLw7LPP4tSpU5g9ezamTp2Kb7/9\nn+eVh4cH3nnnHRw7dgxnz57FqFGjMHr0aMmRC17sKeR4E9F/BiDW2sSulfWDsuTNBw4cMEhu26tX\nL8rPz6c9e/bQhQsXiIgoKCjIoMyNGzeIiOjixYuqCaIPHz5M7u7u4vdt27YREdF7772nuF1aWhoR\nEb3zzjuK5fLz80kJue1atmypuJ0ahw4dMiuZ9q1bt+irr74iR0dHrvJ16tQx2WdeXh7VqlVLLDNs\n2DDy9/dXrat3795mHdvw4cNl62rSpInsdjdu3OA6tqNHj5p7ukWU6vXx8SEi9evymWee4d7f3Llz\nZes5e/as5DYlJSXi/5cuXTLZbtmyZUREtG3bNq7k6oWFhfTw4UOzzoXQhmvXrnFdG3Lra9Wqpbrf\nOnXqqP7md+7cUS0zbtw4IiL66KOPJNffvXuXiIiOHTvGdZ0REW3dupV69uxJ48aNo5ycHO7fXe5Y\nq1evbnYdREQ9evQw+V0l9xcLu32sJTU1lbp160Y1a9ak2rVrU9euXWndunXEGCMHBwfxb1xcHBER\nFRQU0MyZM6lhw4ak0+moS5cutGfPHrG+gwcPEmOMdu7cSe3btycXFxfq2LEjnThxgqs9OTk5NHLk\nSPL09CQXFxfy8/OjNWvWiOubNm1KK1asICKi2NhYg3YKH6GtRESJiYnUqlUrcnFxIX9/f1q1apXV\n54yIaPny5eTr68tVtn79+rRo0SLxe15eHrm5udFHH30kLsvJyaGxY8eSp6cnubm5UVBQkNhfyjFz\n5kyTPm/MmDGqz8KAgACaM2cOV9uNAUDu7u6y68hKDSP7iskYayZ8AKwF8CpjbB5jrJP+Or0yVR6p\nFEfOzs7o16+f+HYcExMjDjfOnTsX9evXB8CXP7Rhw4Y4deoUVq5ciR9//FEM/so7tCqVSF0fS/2y\nrJ3Z2LNnT/VCejg5OWHIkCE4f/68SfYCKaTif7m4uOCLL75Ap06dEBYWhsWLF3NZ5KTyXqq1VQ4l\nixzvb2FNSI4VK1bIrrt+/TpXOxYtWsS9P0uGmfWtE1LHaomFlDdIs3Eb1CwSapYUnt+KxzLPY5ET\njnHMmDGKdfBYCYWZoy+//DIOHTqEhIQERf9KXiyZHAbYfyKQvSkuLsbgwYMRGBiIs2fP4vjx44iK\nikJgYCBWr14NnU6H7OxsZGZm4h//+AcAIDIyEocPH0ZycjLOnz+PiIgIDBw4EGfPnjWoOzo6GsuW\nLcOJEyfQrFkzhIeHc/lWzZ07F+fPn0dKSgouXLiAxMRE+Pj4SJaNjo5GVlYWMjMzkZWVhc2bN6Na\ntWric3zDhg2IiYnBwoUL8dtvv2HFihVYunQp1q9fL9Yhl/tVPwesNVy+fBlZWVkICQkRl7m4uCAw\nMBA///yzQTuysrKQkpKCU6dOITAwEMHBwcjOzpat++jRoya+mv3790daWprsM33//v24cOECevXq\nZfExWXq/8KB0R/2J0rcmAQYgFsB8mfLlE2LcjkglHTcmODgYN27cQH5+vsGMTZ4HuE6ng6enJ2bM\nmGGwXM0RWahbyV/NycnJ4pmz5ZXuSkDovP39/REcHGyS9Fk/LyYgP2QaGhoqxoADIJuLUB+esA/6\nKHXeSsKRt7OyZrjDOOSJPrzD9movB/pYG35E6joXtrNXmqFRo0Yp7l8fQciNGzcOH330kcl6nvuL\n53fnOVeCPyxjDA0bNsR///tfyf3wiMvly5erlilPqrqQy83NRU5ODp5//nkxBqSQoi49PR2MMTzx\nxBNi+UuXLiE5ORlXrlwRXyQnTZqEffv2ISEhwSBW5bx588R7d9OmTWjYsCE+//xzkziVxgg5doVJ\nQ40aNZItq9PpxOvr999/x7Rp07B8+XIxrM7ChQuxdOlSMSVgkyZNMGvWLMTHx4t+dkq5X21BVlYW\nGGPw8vIyWO7l5SX6Bh84cABnzpzBzZs3xXs7Li4O27dvx6effiqKaKm69QWiUG9RURFu3bol7jM3\nNxc+Pj549OgRnJycEB8fb9VkHSESgj1QuqNGKax7LDFWzHIPXP0bQYCnQ5azJKh1toK1T6kjsmaW\nZHkH7tTfnxCdX5/atWubxNLjYeDAgfjnP/+pWKZ///5m1WmpRY7XamRNwmulXJx9+vQBoP6CYc5v\nb234ESmHe0E89ezZU1KwWMP06dMRGxsrfud9YVmxYgXc3d0NZuwCfKLJVv5R+ve60rlVa9O7775r\nN98oS536yyutmL1wd3dHREQE+vXrh+DgYAQHB2PIkCGy4ik9PR1EhFatWhmETSooKBDvU6D02unW\nrZv4vUaNGmjbti2Xg//EiRMxZMgQpKWlISQkBOHh4Yq5kYFSP9pBgwZh2LBhYq7tW7du4dq1axg/\nfrxB2saioiKDa1sYiapI0tPT8eDBA5OX0UePHuHSpUsA/neNMsYwcuRIA6uiGm5ubjh9+jTu37+P\n/fv3Y8aMGWjatKnFcSTXrFlj0XY8yD4hiEh62tFjDI9FTg6eB7ilQk4YRlF6IFtjVStvi5x+xyT1\nVlerVi2LhFxUVBQ2b96Mhw/lo8wo5QuVwlIhxxPuISgoiCuZuxxKHalgEdDpdCYWTn1sJeR4LGpS\n5zInJwdAqbXrwIEDWLp0KT7++GPuNsnh6emJ1atXGyzjPdaaNWti8eLFFgk5NYT4c5GRkfjkk09k\ny+nfk0rtVmsT74QQHjZu3IjRo0eL3/fs2WNRPbwWOZpP6oUqiMTERMyYMQO7d+/G9u3bERMTg23b\ntkmWLSkpgYODA9LS0kyO3Vw3ATkGDBiAq1ev4vvvv8f+/fsRFhaGoUOHys4SLi4uxtChQ9GoUSMx\nBZ/QVgBISEhA9+7dZfcXGhqKw4cPy65njFmVUtLb2xtEhOzsbAN3mOzsbHh7e4tt9fb2xpEjR0zi\nigpDu6dPnzZZ5u3tbTL0mp2dDScnJwNRyBgTZ9i2a9cOv/76K95//32LhZwlEwN5edwyO1gFr0XO\nUuQeYGqdvvCwtlbIyZmay9sipy96/f39TdZbGoXe398faWlpkqEqBMx9cFoq5AAYdHpS7NghmS2O\nGyVrmxComjHGFTiYB6VzYWkief1UVS1atMCGDRtMyqjFT5RCSriqDY2aE35EqY6lS5fKrn/nnXcA\nlPraKqF/Tyrd92pCzlJ3CyneeOMN/Pjjj5g+fTouXbqk2NErUdUtcgJt27ZFdHQ0fvzxR/Tq1QtJ\nSUmoXr26yXOhQ4cOICJkZmaKKfeEj75li4gMckU/ePAA586dQ6tWrbjaU7duXYwYMQKJiYnYuHEj\nNm/eLDtTcvr06bh69Sq+/vprg9/D09MTDRo0wJ9//mnSVv2wIRs3bsTp06dlP6dOneJqsxy+vr7w\n9vbGvn37xGX5+fk4fPiwmHg+ICAA2dnZouDS/wiCTGpZ9+7dDeoFgL1796JTp06K12ZJSYnkCFJl\nQPbJzBhLBPAuEV0u+18JIiLlXqsKYI1FDii1CBlbAQTklgOlY/Y8WCvk5s+fDyJSdJIvb9q2bYu+\nffvihx9+AAB8/PHHkmFeeHnqqafw1FNPyaYbM3eYSUm8GOfENaZ58+ay6y5fvmx1/ksli5wQNkco\nJ/d2bAuLnH7no8aAAQMMpvDzDHUb+8nwIGeBtAZeUaT0xi5cf2qWYf37WSl+pFqbbC2agoKCuIIr\nK1HVfeQyMjKQkJCAgQMHwsfHBxcvXsSZM2cwefJkNG3aFPn5+fjhhx/QoUMH6HQ6tGjRAsOHD0dk\nZCSWL1+OgIAA3L59GwcPHoSfn5/Bi8rChQvh4eGB+vXrY8GCBXB2dpYN5aLP/PnzERAQgNatW6Ow\nsBDffPMN/Pz8JO/vTZs2YdOmTdi9ezfy8/PFyRQ1a9ZEjRo1EBcXh2nTpqF27doIDQ1FYWEh0tPT\ncf36dXFymrlDqxcvXsT9+/dx/fp1FBQUiJay1q1bw8nJCTdu3BD9pYVJgFFRUVi0aBH8/f3RokUL\nLFy4EG5ubuL56Nu3L3r06IFBgwZhyZIlePLJJ5GZmYk9e/YgJCREFHzGTJgwAfHx8ZgxYwbGjx+P\nI0eOYPPmzUhOThbLvP/+++jatSuaNWuGR48eYdeuXfjss8+4c2+XO3LTWQFcBvB02f8ZZd/lPpes\nnT5bkR+UTYP/8MMPJUMA8FJUVEQrV65UDJ8gxcaNG2XDBjDGxHK//PKLbLmmTZtyt9N426CgILOO\nk6dO4ePm5mbwvW7duibbFhQU0M6dO+nf//43ERF17drVrPNnTntSU1PNqic6Olo1rIMcctfC66+/\nbvbxSFFcXCzbruLiYrGcUlgWIYwFD1LhbyZOnGhWm1NSUsjZ2ZkAUN++fQ3CkwgY72Py5Mmq9Rpv\nIxWyRqqc/mfAgAGKZaXusVmzZhmUSUxMpDNnzsjuIzc3l6st69evF8v17t1b9rr7888/Fev55Zdf\nVM9deTNkyBCL7+vKQHZ2Nr344ovUsGFDcnFxoSZNmtDs2bOpqKiIiIgmTZpEHh4eBuFHioqKKC4u\njvz8/MjZ2Znq169PgwYNovT0dCIqDT/i4OBAO3bsoHbt2pkdfuS9996jNm3aUI0aNahevXoUFhZG\nv/32m7je19eXVq5cSUREkZGR5ODgYPLRDz+SnJxMHTt2JFdXV6pbty717NmTtm7davE5CwoKktzn\nlStXiIgoIyODHBwcKCkpyWC7uLg4atCgAbm6ulJQUBCdP3/eYP39+/cpKiqKGjVqRM7OztS4cWN6\n9dVX6dKlS4rtOXToEHXs2JFcXFyoWbNmBiFNiIjefvttatmyJel0OqpXrx716NHDquNXutbL1lmn\nYayt4HH4CCf5gw8+MHgITpkyRfbky1FUVGTyMPXy8lLcJjMzU/ZBHB0dLZY7efKkbDlzYsEZbxsY\nGGj2carVKXzS09PJw8ND/D5jxgzVuuwp5I4dO2ZWPW+//bZsXUuWLFHcNj4+XnI7c18QlJCq39nZ\n2aBMQECA7DE8ePCAe1+DBw822X7v3r1mtzkjI4N+/vlnA7GpdEz/+Mc/VOts1qyZwTZ9+vThqlv/\nM2jQIMWyfn5+JvVdv36d2rRpQ0Bp3MkHDx7QhQsXZPeRl5cnbqsUP3LXrl1iuQkTJsjeD5cvX1Y8\nJnOv9/Jg2LBhVVrI2QNByP31118V3RQNO2BvIaf5yOkhFUfOXKSGMpRi2gDKISD0neGVfOmsmbBg\nj2EoAOLwwo8//oioqCisXbtW0X9IwHi2lTkpXdSwpY+cWpRyud+k9N61H8ZDcUo+h+YMrb7yyitW\nbS/QpEkTdO/eXXZY0HgoKSIiQrVO4yEP45A2PKj5rUn9bg0aNMCJEyeQnZ2N/fv3Q6fTcc8unzVr\nFtasWSP6M+rz3HPPif8bh57Qd41QGzqtjP5olbFNlQF7Pxc0Hl+UAgI3NudTno22F/ae7CCHUpBT\nfZ8ue81atYeQc3JyQnBwMIDSpOirVq3ClClTuPxj3nrrLQPxoTR5wVxs6SMnzJ6SQ+43UfOtM4f3\n33/fZJnxtaQk5MzxV5LyZ1OaIWwp0dHR4gvM9OnT0aZNG9VtBgwYgE8++QSvv/66mCeRlxo1aiAq\nKkqMwSWH3H1SvXp1eHp6igJFyfdRX8Q4Ojpi2rRpuHLlCvLy8rBo0SLMmTNHjKEl0KlTJ6xYsQIB\nAQGYMGGCQViI8vaRswVV3UfOXihNtpELwFurVi2LXlo0Hi+U7qgMlJq/eal8TwwzsXaygzVUq1ZN\nMhSH/tt9VRJySg7aanh5eeHkyZP47rvv0KVLF9V4SFLExsYaxBATMFfIyXWEPBkp5DrZoUOHmtUG\nJaRiyfEKuWrVqpkV98zd3d28xllIhw4dRHHDG6uMMYaIiAgu653xdlKZQ6TgvU8sCW7s4uIie00x\nxvDmm2/izTffNFnn5uamGF5GE3JVg169einOglcKwGtNLEqNxwOlO+oNmCfkqjzGyXgtDaQ5evRo\nbNy40axt5Kx/vELOGuuhPYSctXW2aNFCNlwKD5MmTcLKlStNZmvaamh14cKFFrUrODjYonAackj9\n7sbHKCeqLRH/r732Gj799FMApSJCP6CpLXFycrI44Kw5mDOcxXtN2zLkhxq1atXC0KG3+xNLAAAg\nAElEQVRDsXXr1gpvCy+VUVxWdipDAF6NyotSQOBPyrEdlQIhOKmApWmDunbtahchpyRCKptFjtfK\nYS+eeOIJ7N+/32SIzRZDq2fOnOHqjKREwr59+2wW/R+Qbp+xj5ZcWy0R/4sXL0ZeXh4yMzMxb948\nu2UNKC+ksk3Yi4SEBLvUu2XLFrz++usICwszWVcZRZNmkdPQsC1mva4xxhwYY20YY70YY5ZFba3E\nGAs5S4OcjhgxwqCD4Ik9I9ep6icfttdkB1sEOXz55ZcNvo8YMcLqOq1FqhOzhZCzxvppSxEHlL+Q\na9CgAb766iscOXLEqryDlQX9lEhqmCNAWrRoYfD9hRdewLhx47i3NwdHR0eEhoYiICBAcl1lozK2\nSUOjKsMt5BhjkwFkATgD4AAA/7Ll2xhj0+zTvPLFVkJOp9Ph+PHjiImJwaeffiomGlZCrlPVH15S\nEgEVbZFbsWKFaDF0cHCwW6dlDlLHZa41QKo877nWTy1jL6TaZyxW5TrO8k7NVhlR8ksyntxhjm+j\n8T1vi7RjaqSnp5ssq4yiSbPIaWjYFi4hxxgbC2ANgG0AXgagrygOA3jJ9k0rf4yHA62JvN+sWTO8\n++67GDlyJJcVRq4MrwXJHOuKcWL56Oho7m3laNiwIU6fPo3ly5fjyJEjFk1QsDVFRUVW12GNkAsM\nDDRIQSaXbcIaytsi97ih9BKzePFi0b/Qw8PDLJ/NqKgobN++HYsXL0Z2dnaFOaRXRh85TchpaNgW\n3jvqTQAriGgWY8y4V/gNgPVKoBJgHErB0pyfliAn5Iwfel9//TWGDBliUs4c60pERAR27tyJ77//\nHgMGDMBLL9lGh7do0QJvvfWWTeqyBe3atYNOpxN/1/DwcLPrsEbIOTo6Yt++fVi7di3q1auHqKgo\ns/evhlRbjNusWeTkUbLItW/fHqdPn8bJkycRGBgoOUNYifDwcIuuOVtSGS1ytkoUr6GhUQqvkPMF\nsEdm3QMAls0KqGQYz1qtjELuxRdfxNSpU7F27VqD5eZ0yi4uLtixYweIyOY+W5UJV1dXbN68GTEx\nMfD09MTy5cvNrsMaIQcAjRo14gqCbClS1+iuXbsMvstZZWxhsazqqLkVNG/eXDFnbmWnMgo5a3MM\na5iPr68vpk6dKhnCRqPqw2t3vwWgqcw6fwDXbdKaCsbYImdNLDRz4RVyjDEsWrTIpJwl1pXHWcQJ\nvPTSS/jPf/6D1NRUtGzZ0uzteXzQKhKpa9RYnMh15pcuXbJLmyozAwcONPhubty5qoalfr72pDzC\nylQUSUlJlfL40tLSuHy17UVUVBQ6d+4MV1dXszL1xMbGwsfHBzqdDr1798avv/5qk/akpqaiU6dO\ncHV1RfPmzU1mlH/88ccIDAxE3bp14e7ujj59+uCnn36yyb7tAa+Q2wlgHmNM/xcgxpgHgBko9Z2z\nK4yxNxlj2xljNxhjJYyxeQplxzLG/sMYy2eM/cYYG8+zj6pgkZNbpg2T2QepECJKs4fLm6eeekq1\nTGW0ylQUixcvFjNydOnSRTLt2ONEeT7DeHmcLXKVdZSjXr16FfoCSkSIjIxUTWuoz5IlS7Bq1SrE\nx8cjLS0Nnp6eCAkJMemnzSUjIwNhYWF49tlncerUKcyePRtTp07Ft99+K5ZJTU3FsGHD8OOPP+L4\n8ePw9/dH//79cfHiRav2bTd4ErIC8ADwO4CHAH4EUIzSSQ43AZwHUNvapK8cbfgVwC8A4sv2P0+m\n3Niy9QsA9Cr7WwxgvELdRESk0+kMEk7n5uaq5cK1GU8++aRk0utr166ZlC0sLDQpx5OMXsN8NmzY\nIJuwvLJg3L5u3boZrJ81a5ZsUvW/I3fu3KFz585RQUFBRTfFpnTv3t3gt23VqlVFN0mSbdu2Vfnr\nLzU1lbp160Y1a9ak2rVrU9euXWndunXEGCMHBwfxb1xcHBERFRQU0MyZM6lhw4ak0+moS5cutGfP\nHrG+gwcPEmOMdu7cSe3btycXFxfq2LEjnThxgqs9OTk5NHLkSPL09CQXFxfy8/OjNWvWiOubNm1K\nK1asICKi2NhYg3YKH6GtRESJiYnUqlUrcnFxIX9/f1q1apUtThstX76cfH19ucrWr1+fFi1aJH7P\ny8sjNzc3+uijj8RlOTk5NHbsWPL09CQ3NzcKCgqitLQ0xXpnzpxJLVu2NFg2ZswYeuaZZxS38/b2\npnXr1nG13Rila71snVX6iMsiR0S3AHQCsAhANQAXUepftw5AdyLKUdjcJhBRKyLqDmAaDGfNipRN\nxFgIIImI5hFRKhHNA/AJgHclJmoYYOz4XJ6zq+SGQKTaIGVh0WYg2of8/PyKboIqU6ZMMfj+0Ucf\nGXzXLHKG1KlTB61bt37s7pmVK1eKx+Tk5IQDBw5UcIuk4bbIMWa/jxUUFxdj8ODBCAwMxNmzZ3H8\n+HFERUUhMDAQq1evhk6nQ3Z2NjIzM8WZzpGRkTh8+DCSk5Nx/vx5REREYODAgTh79qxB3dHR0Vi2\nbBlOnDiBZs2aITw8nOsZNHfuXJw/fx4pKSm4cOECEhMT4ePjI1k2OjoaWVlZyMzMRFZWFjZv3oxq\n1aqhZ8+eAIANGzYgJiYGCxcuxG+//YYVK1Zg6dKlWL9+vViHXO5X/Ryw1nD58mVkZWUhJCREXObi\n4oLAwED8/PPPBu3IyspCSkoKTp06hcDAQAQHByM7O1u27qNHj5rEwOzfvz/S0tJkJz89evQI+fn5\n5Zam0Fy4lQoR3QPwbtnHAMaYExFVBs/p7ii1Hm4xWv4pgEgAzwJIldvY2LeoPKfuP/HEE5LLpYSc\nlOle66ztQ1WYELB27VqEhoYiJSUFo0ePRtu2bQ3Wy10bUgFkNaou3bp1w4kTJ5CWloaQkBB4eXlV\ndJMkqYw+ZOaQm5uLnJwcPP/882jatCkAiP636enpYIwZPM8vXbqE5ORkXLlyRYwtOWnSJOzbtw8J\nCQkGAePnzZuHvn37AgA2bdqEhg0b4vPPP8cbb7yh2KarV68iICAAHTt2BFA6yUoOnU4n+tb+/vvv\nmDZtGpYvX47evXsDKE0/uHTpUrzwwgsAgCZNmmDWrFmIj48X/eyUcr/agqysLDDGTK5hLy8v3Lhx\nAwBw4MABnDlzBjdv3hTdXeLi4rB9+3Z8+umnsuGCjAWiUG9RURFu3boled/ExMTAzc3NxMe2ssAl\n5BhjM4lIcuodY8wJwJcAXrRlwyykddnfc0bLz6PUitcKlVTIyT3ceK2CmpCzD4MGDcKbb74p+soJ\nD7fKxnPPPYfnnntOcp2cz86775q8k2lUcdq2bWsi5CsbVd1Hzt3dHREREejXrx+Cg4MRHByMIUOG\nyIqn9PR0EBFatWpl4HNbUFBgkKuYMWaQaaRGjRpo27Ytl4P/xIkTMWTIEFHEh4eHq8byvHv3LgYN\nGoRhw4Zh6tSpAIBbt27h2rVrGD9+PCZMmCCWLSoqMniOVIbcr+np6Xjw4AE8PDwMlj969EicyCX0\nq4wxjBw50sCqyMuaNWuwYcMG7N+/v9Jeu7wWuXcZY5lE9Kn+wrKhymQAvW3eMssQom7eMVp+22i9\nJBUp5OT2xTv8UxkdbB8HfH19sW7dOsybNw9eXl6YP39+RTfJbAoKCiSXt2nTppxboqFR9S1yAJCY\nmIgZM2Zg9+7d2L59O2JiYrBtm/Scv5KSEjg4OCAtLc3kxdxWMfUGDBiAq1ev4vvvv8f+/fsRFhaG\noUOHIjExUbJ8cXExhg4dikaNGhmEshL6wISEBHTv3l12f6GhoTh8+LDsesYYcnNzLTwawNvbG0SE\n7Oxsgww52dnZ4mSlkpISeHt748iRIyaT0oSh3dOnT5ss8/b2Nhl6zc7OhpOTk4koXL16NebPn4/d\nu3eL1s7KCK+QmwBgA2PsJhHtBkrzrgL4AkAIgP5KGxvDGAsGsI+j6EEi6qNezHrofxMfRMpTyMnN\nxOG1yFWmmZSPG5MmTRKzMlRFwWwcVkfgcehQNaoe3FYNiRnjlQnB+hkdHY3Q0FAkJSUhLCzMxM+q\nQ4cOICJkZmaiV69esvUREY4ePSoO1z548ADnzp1DZGQkV3vq1q2LESNGYMSIERgwYACGDx+OhIQE\nSWPA9OnTcfXqVRw/ftxgNMfT0xMNGjTAn3/+qZgv295Dq76+vvD29sa+fftEAZWfn4/Dhw9jxYoV\nAEpdQ7Kzs8EYg6+vr2Q9UqFOunfvbiK69+7di06dOhmci5UrVyIuLg4pKSmKorYywKUSiGgTY6w+\ngK/KRNi/AXwOYACAAUR01Mz9/gTgSY5y0j2QPIIlzh2AvuQWLHG3IUNsbKzJsvLstO/duye5nFfI\nVabYZo8jVVHACcgJucrquKvxeFPVXyAyMjKQkJCAgQMHwsfHBxcvXsSZM2cwefJkNG3aFPn5+fjh\nhx/QoUMH6HQ6tGjRAsOHD0dkZCSWL1+OgIAA3L59GwcPHoSfnx8GDx4s1r1w4UJ4eHigfv36WLBg\nAZydnfHqq6+qtmn+/PkICAhA69atUVhYiG+++QZ+fn6SIm7Tpk3YtGkTdu/ejfz8fHEyRc2aNVGj\nRg3ExcVh2rRpqF27NkJDQ1FYWIj09HRcv34ds2fPBmD+0OrFixdx//59XL9+HQUFBaKlrHXr1nBy\ncsKNGzcQHByMxYsXY9CgQQBKY88tWrQI/v7+aNGiBRYuXAg3NzfxfPTt2xc9evTAoEGDsGTJEjz5\n5JPIzMzEnj17EBISgh49eki2ZcKECYiPj8eMGTMwfvx4HDlyBJs3b0ZycrJYZtmyZYiJicGWLVvQ\nvHlz0YLn6upq9USOgwcP4uDBg1bVYYI5U1wBrEVpyJHvANwD8Ky102bN/QBwBFACifAjAHqWretj\ntLxX2fJeMnWahPRwcHCQnS5sD9566y3J8BAlJSWS5Y3LxcfHl2t7NaoOI0aM0EKPaFQqqvI1mJ2d\nTS+++CI1bNiQXFxcqEmTJjR79mwqKioiIqJJkyaRh4eHQfiRoqIiiouLIz8/P3J2dqb69evToEGD\nKD09nYhKw484ODjQjh07qF27dmaHH3nvvfeoTZs2VKNGDapXrx6FhYXRb7/9Jq739fWllStXEhFR\nZGQkOTg4mHz0w48kJydTx44dydXVlerWrUs9e/akrVu3WnzOgoKCJPd55coVIiLKyMggBwcHSkpK\nMtguLi6OGjRoQK6urhQUFETnz583WH///n2KioqiRo0akbOzMzVu3JheffVVunTpkmJ7Dh06RB07\ndiQXFxdq1qyZQUgTotJwLVLtHTVqlEXHr3StwwbhRxiZYb5mpWaJZAChAMKI6JCZutFqyvzyCgHE\nEtECo3VOAG4A2EFEo/WWfwxgEID6JDG7ljFGBQUFBkF1nZycUFhYaKejMOXatWto3LixyXK538fY\nQrRx40bVmU0af09eeOEFSf8dc+59DQ1bIjy/tGuwlNTUVPTp0wc3b95E3bqKrtwaVRDGmGJfTkRW\nDfnIjtsxxq6h9K1JahsHAJ/piQkioibWNEQNxlhHlKYJEwaxWzHGhGzvu4gon4iKGGPvAIhnjN0A\n8AOAYJSGHpkiJeIEKnKiA1A6XTwqKgqrV6+2aHttaFVDDqmhVX9//wpoiYaGhhyaqNWwFCUHrP2Q\nFnIVxRQAQn4PAjC07AMAvgCuAgARJTDGSgC8BeAfZcsnE5FhMjUjKlrIAaX+Arw888wzYmBER0dH\ng2nsGhr6SAk5LaWbRkXyzjvvaOFvjFDyw5WbJcoYw5w5c0TfNY2/J2YNrT6uMMbo/v37BrOpdDqd\n1TndzOXChQsGlpIBAwbg+++/lyx7+PBhDB06FPfv38fSpUsrNCGyRuVmyJAh+OabbwyWzZ8/X3KC\nj4ZGeUBEcHBw0KxQnGRmZsrOEq1bty7q1KlTzi3SMAd7D61qQg6lQi43N9dgNkrNmjVlZ5Lak8mT\nJ2P9+vVo3LgxduzYgXbt2smWJSIUFhZq1hUNRc6cOYOnn37aYNmdO3e0h79GhaLUuWloPE5UmJBj\njL2OUt+zv8r+V4SINlvTkIqEMUZ379416Nhq1aqFnBy7p5CV5OHDh3ByctIEmobN2LJlCxYsWABX\nV1fs2bOn0qZv0vj7oAk5jb8LFSnkSgB0I6LjZf8rQURUZXNEMcbo9u3bBrOF6tSpgzt3jBNEaGho\naGjYAk3IafxdqLBZqyidQJCp9/9jTWWY7KChoaGhoaGhYQ6yQo6Irkj9/7iiCTkNDQ0NDQ2Nqoam\nVsrQhJyGhoaGhoZGVUMpIPBl8MeRIyLys02TKgZNyGloaGhoPI74+vpi6tSpePPNNyu6KRp2QEmt\npJrxKfdUXbZGE3IaGhoaGtaQlJQENze3im6GCWlpaRUaazQqKgqdO3eGq6srmjVrxr1dbGwsfHx8\noNPp0Lt3b/z66682aU9qaio6deoEV1dXNG/eHAkJhvkCfv31VwwdOhR+fn5wcHDAggULZGqqHCj5\nyEWWYzsqHE3IaWhoaGhYAxEpZmioKOrVq1eh+yciREZG4syZM9i3bx/XNkuWLMGqVauQlJSEli1b\nIi4uDiEhIbhw4QJq1KhhcVsyMjIQFhaGMWPGYMuWLTh8+DAmTZoET09PvPDCCwBKQ4D5+vripZde\nQkxMjMX7KjeI6G//AUAZGRmE0qFkAkCNGzcmDQ0NDQ37UNr9VE1SU1OpW7duVLNmTapduzZ17dqV\n1q1bR4wxcnBwEP/GxcUREVFBQQHNnDmTGjZsSDqdjrp06UJ79uwR6zt48CAxxmjnzp3Uvn17cnFx\noY4dO9KJEye42pOTk0MjR44kT09PcnFxIT8/P1qzZo24vmnTprRixQoiIoqNjTVop/AR2kpElJiY\nSK1atSIXFxfy9/enVatW2eK00fLly8nX15erbP369WnRokXi97y8PHJzc6OPPvpIXJaTk0Njx44l\nT09PcnNzo6CgIEpLS1Osd+bMmdSyZUuDZWPGjKFnnnlGsnybNm0Mzo0lKF3rZeus0jBK4Uf+VmgW\nOQ0NDY3KAzt40G51U1CQxdsWFxdj8ODBGDt2LL744gsUFBQgPT0drVu3xurVqzF37lxcunQJRCSm\nfYyMjMTly5eRnJwMHx8fpKSkYODAgfj3v/+Ntm3binVHR0fjgw8+QIMGDRAbG4vw8HBcvHgRLi4u\nim2aO3cuzp8/j5SUFHh6euLy5cu4efOmZNno6GhMnDhR/L53716MHj0aPXv2BABs2LABsbGxWLdu\nHQICAnDu3DmMHTsW1atXF4dn5XK/CjDGkJuby3dCJbh8+TKysrIQEhIiLnNxcUFgYCB+/vlnjB07\nVmxH3bp1kZKSAnd3dyQlJSE4OBi///67bNDzo0ePol+/fgbL+vfvj82bN6O4uBiOjlUvJK4m5MrQ\nhJyGhoaGhhq5ubnIycnB888/j6ZNmwIAWrZsCQBIT08HYwxPPPGEWP7SpUtITk7GlStX0LBhQwDA\npEmTsG/fPiQkJGDdunVi2Xnz5qFv374AgE2bNqFhw4b4/PPP8cYbbyi26erVqwgICEDHjh0BAI0a\nNZItq9PpoNPpAAC///47pk2bhuXLl6N3794AgIULF2Lp0qXiMGOTJk0wa9YsxMfHi0Ju48aNsrlf\nbUFWVhYYYyZizMvLCzdu3AAAHDhwAGfOnMHNmzfh7OwMAIiLi8P27dvx6aef4h//+Ids3foCUai3\nqKgIt27dqpJZbzQhV4Ym5DQ0NDQ01HB3d0dERAT69euH4OBgBAcHY8iQIbLiKT09HUSEVq1aGUT3\nLygoQJ8+fcTvjDF069ZN/F6jRg20bduWy8F/4sSJGDJkCNLS0hASEoLw8HAEBgYqbnP37l0MGjQI\nw4YNw9SpUwEAt27dwrVr1zB+/HhMmDBBLFtUVGTg+1e/fn3VNtmb9PR0PHjwAB4eHgbLHz16hEuX\nLgGAOPGEMYaRI0di/fr15d7O8kATcmVoQk5DQ0NDg4fExETMmDEDu3fvxvbt2xETE4Nt27ZJli0p\nKYGDgwPS0tLg5GTY5bq6utqkPQMGDMDVq1fx/fffY//+/QgLC8PQoUORmJgoWb64uBhDhw5Fo0aN\nsHbtWoO2AkBCQgK6d+8uuz97D616e3uDiJCdnS1aMQEgOzsb3t7eYlu9vb1x5MgRk/RXtWrVAgCc\nPn3aZJm3tzeys7MNymdnZ8PJyclEFFYVNCFXhibkNDQ0NCoP1vixlQdt27ZF27ZtER0djdDQUCQl\nJSEsLAzFxcUG5Tp06AAiQmZmJnr16iVbHxHh6NGj4nDtgwcPcO7cOURGRnK1p27duhgxYgRGjBiB\nAQMGYPjw4UhISEC1atVMyk6fPh3/397dx2VV348ff71B40bRiYaImBIzC9RvYjeaPxVFzGGKlS5F\nK6q5ypY3leVWU3E2tXnTjbZR33TWVnZjOWumUQ3T0q8SS8tmW3iDqTBdS9NFKL5/f5zDNe6uiwsE\ngXo/H4/zgHPO55zzvq4L5c3nNj8/n23btpXrExYREUFUVBSff/4548eP9/qs+m5ajYmJITIykqys\nLE9zcVFREZs2bWLRokUAJCQkUFhYiIgQE1P1KqJVTXXSt2/fSkn3W2+9xWWXXdYk+8eBn4mciPiq\noz0DHAN2q+qpOomqAVgiZ4wxpjr79u0jMzOTkSNH0rFjR/Ly8ti5cyd33XUXXbp0oaioiLfffpte\nvXoRGhpK165dSUtLIz09nYULF5KQkMCXX35JdnY2sbGxjBo1ynPvuXPn0q5dOzp06MCcOXMICgpi\n3Lhx1cY0a9YsEhISiI+P59SpU6xevZrY2Ngqk7gVK1awYsUK1q9fT1FREUVFRQC0bNmSFi1akJGR\nweTJk2ndujUpKSmcOnWK3NxcDh48yIwZM4CaN63m5eVx4sQJDh48SHFxsaemLD4+nmbNmnHo0CGS\nkpKYP38+qampgDP33Lx58+jWrRtdu3Zl7ty5hIWFed6PIUOG0K9fP1JTU1mwYAEXX3wxhw8fZsOG\nDSQnJ9OvX78qY7njjjtYtmwZ06ZN4/bbb2fz5s08++yzrFq1ylPm1KlTfPrpp6gqRUVFFBQUsGPH\nDlq2bElsbCNc+8Cfoa04yVpJNdvXwMNnO4y2ITZAd+7cWW76ke7du/sYTGyMMeZs0ESnHyksLNTr\nrrtOo6OjNTg4WDt37qwzZszQ06dPq6rqpEmTtF27duWmHzl9+rRmZGRobGysBgUFaYcOHTQ1NVVz\nc3NV1Zl+JCAgQF9//XXt2bNnjacfefjhh7V79+7aokULbdu2rQ4fPlx3797tOR8TE6OLFy9WVdX0\n9HQNCAiotJWdYmPVqlXau3dvDQkJ0fDwcO3fv7+++OKLtX7PEhMTq3zm/v37VVV13759GhAQoCtX\nrix3XUZGhkZFRWlISIgmJibqrl27yp0/ceKETp06VTt16qRBQUF6wQUX6Lhx43TPnj0+43nvvfe0\nd+/eGhwcrBdeeGG5KU1K4ymdoqXsNmjQoFq9fl8/69TB9COiWv0qXCIyAngC2AG8AhQC7YEfAz2B\nXwJXALcDP1fVhXWRZJ4rIqIfffQRl156qedYz549y7WvG2OMqTsiUqlv0/fVxo0bGTx4MEeOHCE8\nPLyhwzF1zNfPunvurGaR9reP3ChgvareUeH4cyKSCQxS1VtE5AxwG9CkEjmwplVjjDENx5JaU1v+\nZivXAqu9nHsFSHW/Xw9U3euwkbNEzhhjTEPxtbRXSkoKYWFhlbZWrVoxf/78cxilaYz8rZELBGKB\nqhZJ+6F7HuBbd2tyLJEzxhjTEAYOHFhptGtZvkaJWlOs8TeRWwf8WkSOAGtUtUREAnFq6h4G/uyW\niwfy6j5MEJF7gETgMiASmK2qcyqUiQSmAcnAhUAxsBPIUFXvk95giZwxxpjGqTFMwGsaL3+zlbuB\nXcDLwDciUgh8A7zkHr/bLXcM+HVdB+n6CXA+8BrOyNKq9AbGuGVGAze7cWaLSIqvm1siZ4wxxpim\nxq8aOVU9CvQXkaFAH5wascPAVlXNKlNuZb1E6dw7DsCtCbzTS7FNQFdV9dRRi8hbOMnm/Tg1i1Wy\nRM4YY4wxTU2NVnZQ1beAt+oplrOmqpXWBHGbgT/Cqa3zyhI5Y4wxxjQ1NUrkROQaYCAQDnwJ/EVV\nvdZyNQYi0hzoC3zkq5wlcsYYY4xpavxdoisMeAPoD5wG/gW0Be4RkU3ANap6ot6iPDsZQEfA5zon\nlsgZY4wxpqnxN1v5NZAA3AiEqGoHIAS4yT1eowEOIpIkImf82N6tyX2reE4a8AAwR1U/8FXWEjlj\njDHfRTExMSxevLihwzD1xN9s5XrgIVX9Y+lAAlUtUdU/4izPdX0Nn/s+cLEf2001vK+Hu6zYCuDp\nitOUVOX3v/99uX1L5IwxxtTEypUrCQsLa+gwKsnJyWHSpEkN9vypU6dy+eWXExISwoUXXuj3dbNn\nz6Zjx46EhoYyaNAgPv3003qM0rF69Wri4+MJDg6me/furFmzplKZJ598kgsvvJCQkBAuu+wyNm/e\n7Pf9s7OzmT17tmerC/5mK20Bb+/gp+55v6lqkar+3Y/ti5rct5SIJOFMjbK6imXFqjRhwoRy+5bI\nGWOMqQlV9blCQ0Np27YtwcHBDfZ8VSU9PZ2bbvK/bmbBggUsWbKEZcuWkZOTQ0REBMnJyZw8ebLW\ncWzcuJGYGO+LT23ZsoWxY8dy4403smPHDtLS0hgzZgzbt2/3lHnxxReZOnUqDz30EB999BFXXXUV\nP/rRj/jiC//SlcTExDpP5FDVajdgN/CYl3NLgL/5c5+62HBWkTgDzPRyvi/wNbAWCPTznrpu3TrF\nmZ9OAR02bJgaY4ypH86vn6Zp48aN2qdPH23ZsqW2bt1ar7zySl26dKmKiAYEBHi+ZmRkqKpqcXGx\n3n///RodHa2hoaF6xRVX6IYNGzz3y87OVhHRN954Qy+99FINDg7W3r1764cfftz2bDEAACAASURB\nVOhXPMeOHdMJEyZoRESEBgcHa2xsrD722GOe8126dNFFixapqurs2bPLxVm6lcaqqrp8+XKNi4vT\n4OBg7datmy5ZsqQu3jZduHChxsTE+FW2Q4cOOm/ePM/+N998o2FhYfrUU095jh07dkwnTpyoERER\nGhYWpomJiZqTk+P1ntnZ2T6ff8MNN+jQoUPLHRsyZIimpaV59q+88kq9/fbby5Xp2rWr/uIXv/B6\nX18/6+65s8qL/B21mgksEpGWwB9x5pCLBMbiTNR7z1nmk9USkd5AF/67HFiciJQ26f5ZVYtEpBvO\nKhNHgEXAZWX/OlLV//N2f+sjZ4wxjUe2ZNfbvRM1sdbXlpSUMGrUKCZOnMgLL7xAcXExubm5xMfH\n8+ijj/Lggw+yZ88eVJWWLVsCkJ6ezt69e1m1ahUdO3Zk3bp1jBw5ku3bt9OjRw/PvadPn87jjz9O\nVFQUs2fPZsSIEeTl5VVbm/bggw+ya9cu1q1bR0REBHv37uXIkSNVlp0+fTp33vnfqVjfeustbrvt\nNvr37w/A008/zezZs1m6dCkJCQl88sknTJw4kfPOO8/TPJuSksKmTd4XSxIRjh+vNBuY3/bu3UtB\nQQHJycmeY8HBwQwYMIAPPviAiRMneuIIDw9n3bp1tGnThpUrV5KUlMRnn31G+/bta/zcLVu2MHny\n5HLHrr76apYtWwbAqVOn+PDDD5k+fXq5MkOHDuWDD3x2w69X/k4IvEREzsdJ2NLdw4KzBNZ8VX2s\nfsIr52f8t8+c4qzgMMbdjwHycSYrbu1uVQ2UCKziGGCJnDHGmOodP36cY8eOcc0119ClSxcALrro\nIgByc3MREc4//3xP+T179rBq1Sr2799PdHQ0AJMmTSIrK4vMzEyWLl3qKTtz5kyGDBkCwIoVK4iO\njub555/n1ltv9RlTfn4+CQkJ9O7tTJfaqVMnr2VDQ0MJDQ0F4LPPPmPy5MksXLiQQYMGATB37lwe\neeQRrr32WgA6d+7MAw88wLJlyzyJnK+1X+tCQUEBIlIpGWvfvj2HDh0C4N1332Xnzp0cOXKEoKAg\nADIyMli7di3PPfcc9913X6X7OhVgvp9b1TMLCgoAOHr0KCUlJVWWeeedd2r2IuuQ3/PIqeovROQ3\nOMlS6TxyW1X13/UVXIXn3wLcUk2ZlUCtVpeomMg1xn4OxhhjGlabNm24+eabGTp0KElJSSQlJTF6\n9GivyVNubi6qSlxcXLlEori4mMGDB3v2RYQ+ffp49lu0aEGPHj386uB/5513Mnr0aHJyckhOTmbE\niBEMGDDA5zVfffUVqampjB07lrvvdlbZPHr0KAcOHOD222/njjv+27389OnT5X4nNoa1X3Nzczl5\n8iTt2rUrd/zbb78lL89Z8v3AgQPExcUhIqgqJSUlFBcXewakiAgTJkzgySefPOfx16Waruzwb+DN\neoqlQVmNnDHGGH8sX76cadOmsX79etauXctDDz1U5ehGcH63BAQEkJOTQ7Nm5X/lhoSE1Ek8w4YN\nIz8/nzfffJN33nmH4cOHM2bMGJYvX15l+ZKSEsaMGUOnTp144oknysUKkJmZSd++fb0+r76bViMj\nI1FVCgsLPbWYAIWFhURGRnpijYyMZPPmzZVq2lq1agVAVFQUO3bs8BzfunUrM2bMYOPGjZ5rSsuW\nPrewsLDcvco+s127dgQGBvos0xC8JnIi4judr0BV3zv7cBqOJXLGGNN4nE0/tnOhR48e9OjRg+nT\np5OSksLKlSsZPnw4JSUl5cr16tULVeXw4cMMHDjQ6/1Ula1bt3qaa0+ePMknn3xCenq6X/GEh4cz\nfvx4xo8fz7Bhw0hLSyMzM5PmzZtXKjtlyhTy8/PZtm0bgYH/7XEUERFBVFQUn3/+OePHj/f6rPpu\nWo2JiSEyMpKsrCxPc3FRURGbNm1i0aJFACQkJFBYWIiIeB2JGhgYWG66kwMHDtCsWTOv5fv27UtW\nVhb33nuv51hWVhZXXXUVAM2bN6d3795kZWVx/fXXlyszZsyYSvc7V3zVyGXj9EWrjrjlvPY/awos\nkTPGGFOdffv2kZmZyciRI+nYsSN5eXns3LmTu+66iy5dulBUVMTbb79Nr169CA0NpWvXrqSlpZGe\nns7ChQtJSEjgyy+/JDs7m9jYWEaNGuW599y5c2nXrh0dOnRgzpw5BAUFMW6cz0WJAJg1axYJCQnE\nx8dz6tQpVq9eTWxsbJVJ3IoVK1ixYgXr16+nqKiIoqIiAFq2bEmLFi3IyMhg8uTJtG7dmpSUFE6d\nOkVubi4HDx5kxowZQM2bVvPy8jhx4gQHDx6kuLjYU0sWHx9Ps2bNOHToEElJScyfP5/U1FTAmXtu\n3rx5dOvWja5duzJ37lzCwsI878eQIUPo168fqampLFiwgIsvvpjDhw+zYcMGkpOT6devX41iBCfB\nHThwIAsWLGDUqFG8+uqrZGdn8/7773vK3HPPPdx0001cfvnl9OvXj9/+9rccPnyY22+/vcbPqzPe\nhrPirKnq93a2w2cbcgN01apV5aYfGTNmjNfhwsYYY84OTXT6kcLCQr3uuus0Ojpag4ODtXPnzjpj\nxgw9ffq0qqpOmjRJ27VrV276kdOnT2tGRobGxsZqUFCQdujQQVNTUzU3N1dVnWkxAgIC9PXXX9ee\nPXvWePqRhx9+WLt3764tWrTQtm3b6vDhw3X37t2e8zExMbp48WJVVU1PT9eAgIBKW9npR1atWqW9\ne/fWkJAQDQ8P1/79++uLL75Y6/csMTGxymfu379fVVX37dunAQEBunLlynLXZWRkaFRUlIaEhGhi\nYqLu2rWr3PkTJ07o1KlTtVOnThoUFKQXXHCBjhs3Tvfs2VNlHNVNP6Kqunr1ar3kkks0KChI4+Li\ndM2aNZXK/Pa3v9WYmBgNDg7Wyy67TDdv3uzznr5+1qmD6UdEqxnF8X0gIvr888+TlpbmOXbDDTew\natWqBozKGGO+u0o7oBtnotrBgwdz5MgRwsPDGzocU8d8/ay7585qdKW1H7qsadUYY0xDsaTW1JZl\nK66K/4gskTPGGHOu+JryKiUlhbCwsEpbq1atmD9//jmM0jRGNZp+5LvMauSMMcY0hIEDB1Ya7VqW\nr1Gi1hRrLJFzWSJnjDGmMWoME/CaxsuyFZclcsYYY4xpamqUrYhIgIh0F5GBItKivoJqCJbIGWOM\nMaap8TtbEZG7gAJgB86C9N3c42tEZHL9hHfuWCJnjDHGmKbGr2xFRCYCjwFrgBtwVnMotQm4vqrr\nmhJL5IwxxhjT1PibrdwDLFLVnwKvVTi3G7d2rimzRM4YY4wxTY2/2UoMsMHLuZPAD+omnIZjiZwx\nxpjvopiYGBYvXtzQYZh64m+2chTo4uVcN+BgnUTTgCyRM8YYczZWrlxJWFhYQ4dRSU5ODpMmTWqw\n50+dOpXLL7+ckJAQLrzwQr+vmz17Nh07diQ0NJRBgwbx6aef1mOUjtWrVxMfH09wcDDdu3dnzZo1\n5c5v2rSJ1NRUoqOjCQgI4Nlnn633mKrjb7byBjBTRMp+Aioi7YBpOH3nmjRL5IwxxpwNVfW5QkND\nadu2LcHBwQ32fFUlPT2dm266ye9rFixYwJIlS1i2bBk5OTlERESQnJzMyZMnax3Hxo0biYmJ8Xp+\ny5YtjB07lhtvvJEdO3aQlpbGmDFj2L59u6fMiRMn6NGjB48//jihoaG1jqVOqWq1G9AO+Az4D/AX\noARnkMMRYBfQ2p/7NNYN0EWLFing2aZNm6bGGGPqh/Prp2nauHGj9unTR1u2bKmtW7fWK6+8Upcu\nXaoiogEBAZ6vGRkZqqpaXFys999/v0ZHR2toaKheccUVumHDBs/9srOzVUT0jTfe0EsvvVSDg4O1\nd+/e+uGHH/oVz7Fjx3TChAkaERGhwcHBGhsbq4899pjnfJcuXXTRokWqqjp79uxycZZupbGqqi5f\nvlzj4uI0ODhYu3XrpkuWLKmLt00XLlyoMTExfpXt0KGDzps3z7P/zTffaFhYmD711FOeY8eOHdOJ\nEydqRESEhoWFaWJioubk5Hi9Z3Z2ts/n33DDDTp06NByx4YMGaJpaWlVlm/ZsqWuXLmy2tfi62fd\nPXdWOYxfKzuo6lERuQyYClwN5OGsCrEUWKKqx+sqsWwoViNnjDGNR3Z2/dVsJSbWfoH6kpISRo0a\nxcSJE3nhhRcoLi4mNzeX+Ph4Hn30UR588EH27NmDqtKyZUsA0tPT2bt3L6tWraJjx46sW7eOkSNH\nsn37dnr06OG59/Tp03n88ceJiopi9uzZjBgxgry8vGpr0x588EF27drFunXriIiIYO/evRw5cqTK\nstOnT+fOO+/07L/11lvcdttt9O/fH4Cnn36a2bNns3TpUhISEvjkk0+YOHEi5513nqd5NiUlhU2b\nNnmNR0Q4frz2acHevXspKCggOTnZcyw4OJgBAwbwwQcfMHHiRE8c4eHhrFu3jjZt2rBy5UqSkpL4\n7LPPaN++fY2fu2XLFiZPLj+b2tVXX82yZctq/VrOBb+X6FLVr4Ffudt3jiVyxhhjqnP8+HGOHTvG\nNddcQ5cuXQC46KKLAMjNzUVEOP/88z3l9+zZw6pVq9i/fz/R0dEATJo0iaysLDIzM1m6dKmn7MyZ\nMxkyZAgAK1asIDo6mueff55bb73VZ0z5+fkkJCTQu3dvADp16uS1bGhoqKdJ8LPPPmPy5MksXLiQ\nQYMGATB37lweeeQRrr32WgA6d+7MAw88wLJlyzyJnK+1X+tCQUEBIlIpGWvfvj2HDh0C4N1332Xn\nzp0cOXKEoKAgADIyMli7di3PPfcc9913X6X7OhVgvp9b1TMLCgrO5uXUO1tr1WWJnDHGmOq0adOG\nm2++maFDh5KUlERSUhKjR4/2mjzl5uaiqsTFxZVLJIqLixk8eLBnX0To06ePZ79Fixb06NHDrw7+\nd955J6NHjyYnJ4fk5GRGjBjBgAEDfF7z1VdfkZqaytixY7n77rsBOHr0KAcOHOD222/njjvu8JQ9\nffp0ub5/jWHt19zcXE6ePEm7du3KHf/222/Jy8sD4MCBA8TFxSEiqColJSUUFxd7BqSICBMmTODJ\nJ5885/HXJb8SORF518fpM8Ax4EPgGVUtrIvAqojhHiARuAyIBGar6pxqrrkK2IzT7625qp7xVtYS\nOWOMMf5Yvnw506ZNY/369axdu5aHHnqo0ujGUmfOnCEgIICcnByaNSv/KzckJKRO4hk2bBj5+fm8\n+eabvPPOOwwfPpwxY8awfPnyKsuXlJQwZswYOnXqxBNPPFEuVoDMzEz69u3r9Xn13bQaGRmJqlJY\nWOipxQQoLCwkMjLSE2tkZCSbN2+uVNPWqlUrAKKiotixY4fn+NatW5kxYwYbN270XFNatvS5hYXl\nU5iyz2ys/K2RE+AioAOwFygE2uPML3fY3U8BponIQFWtjzHCP8FJGF8D7qimLCLSDPidG1+1n4Il\ncsYY03icTT+2c6FHjx706NGD6dOnk5KSwsqVKxk+fDglJSXlyvXq1QtV5fDhwwwcONDr/VSVrVu3\nepprT548ySeffEJ6erpf8YSHhzN+/HjGjx/PsGHDSEtLIzMzk+bNm1cqO2XKFPLz89m2bRuBgYGe\n4xEREURFRfH5558zfvx4r8+q76bVmJgYIiMjycrK8jQXFxUVsWnTJhYtWgRAQkIChYWFiIjXkaiB\ngYHlpjs5cOAAzZo181q+b9++ZGVlce+993qOZWVlcdVVV9XVS6sX/iZyi4FHgctUNbf0oIj0Bl4C\nMnBq5N4CHgaureM4UdU495mBwJ3VFAe43/26Avh5dYUtkTPGGFOdffv2kZmZyciRI+nYsSN5eXns\n3LmTu+66iy5dulBUVMTbb79Nr169CA0NpWvXrqSlpZGens7ChQtJSEjgyy+/JDs7m9jYWEaNGuW5\n99y5c2nXrh0dOnRgzpw5BAUFMW7cuGpjmjVrFgkJCcTHx3Pq1ClWr15NbGxslUncihUrWLFiBevX\nr6eoqIiioiIAWrZsSYsWLcjIyGDy5Mm0bt2alJQUTp06RW5uLgcPHmTGjBlAzZtW8/LyOHHiBAcP\nHqS4uNhTSxYfH0+zZs04dOgQSUlJzJ8/n9TUVMCZe27evHl069aNrl27MnfuXMLCwjzvx5AhQ+jX\nrx+pqaksWLCAiy++mMOHD7NhwwaSk5Pp169fjWIEJ8EdOHAgCxYsYNSoUbz66qtkZ2fz/vvve8qc\nPHmSzz//HFXlzJkz5Ofns2PHDsLDw332TaxX/gxtBXYAN3o5dxPwsfv9LcC/znYobTWxBOI05870\nUSYWZ8WJfsAsnOlSAnyU11mzZpWbfmTWrFlehwsbY4w5OzTR6UcKCwv1uuuu0+joaA0ODtbOnTvr\njBkz9PTp06qqOmnSJG3Xrl256UdOnz6tGRkZGhsbq0FBQdqhQwdNTU3V3NxcVXWmxQgICNDXX39d\ne/bsWePpRx5++GHt3r27tmjRQtu2bavDhw/X3bt3e87HxMTo4sWLVVU1PT1dAwICKm1lpx9ZtWqV\n9u7dW0NCQjQ8PFz79++vL774Yq3fs8TExCqfuX//flVV3bdvnwYEBFSayiMjI0OjoqI0JCREExMT\nddeuXeXOnzhxQqdOnaqdOnXSoKAgveCCC3TcuHG6Z8+eKuOobvoRVdXVq1frJZdcokFBQRoXF6dr\n1qypdI/S6VvKbrfccovXe/r6WacOph8RrWYUB4CIfANcq6rrqzj3I+BVVQ0RkQHAW6pabzMPujVy\np/DRR05EsoADqnqriMwCZuKjj5yI6C9/+Ut+9av/DsjNyMhg5syZdf8CjDHGeDqgG2ei2sGDB3Pk\nyBHCw8MbOhxTx3z9rLvnzmquHX/bD/cBE72c+6l7HpyJg/91NgGdLRGZAPQCptfkOmtaNcYY01As\nqTW15W+2MgcYJSI7RWSWiNzpft0JpOL0kQMYAvxfdTcTkSQROePH5mu0bFX3bQMsAn6uqjVKKC2R\nM8YY01B8Le2VkpJCWFhYpa1Vq1bMnz//HEZpGiN/V3Z4QUSO4iRsvwCa4zRv5gBDVfVtt+g9OP3R\nqvM+cLEf5f7jT3xlPAwcAl4RkdbusdLx3T8QkSJVrfKe7733Xrl9S+SMMcacCwMHDqw02rUsX6NE\nrSm2acnOziY7O7tO71mTlR2ygCwRCcBpQj1asc+Zqhb5ea8i4O81CdRPlwA9qbp59yiwBriuqguv\nuuqqciNTLJEzxhjTGDSGCXhN3UhMTCQxMdGzn5GR4b2wn2q8soObvP3zrJ9cP6YAP6hw7BackbVJ\n+IjbmlaNMcYY09T4nciJyHnAj4BuQMVRqaqq9boGqztnXRec6UcA4kTkevf7P6tqkarurOK6Qe63\n73kbtQqWyBljjDGm6fF3ia4onKWuuuDMs1baK7PsMJt6TeSAn+HUrJU+d4y7gbPCRL6Pa6sdDmSJ\nnDHGGGOaGn+zld8AR4ALcJK4K4ELcQYXfO5+X69U9RZVDfSyeU3iVDVDVZv5qo0DS+SMMcYY0/T4\n27TaH7gPZ0QowBlV3QfMdCfofRxnGpImyxI5Y4wxxjQ1/mYrbYHDbq3WSaBNmXPvAol1HNc5Z4mc\nMcYYY5oaf7OVL4AI9/s8YGiZc1cAfk070phZImeMMea7KCYmhsWLFzd0GKae+Jut/AUY4H6fCdwn\nIm+JyJ9xBjm8Uh/BnUuWyBljjDkbK1euJCwsrKHDqCQnJ4dJkyY12POnTp3K5ZdfTkhICBde6H+X\n+tmzZ9OxY0dCQ0MZNGgQn376aT1G6Vi9ejXx8fEEBwfTvXt31qxZU+78vHnzuOKKK2jdujURERGM\nHDmSXbt21XtcvvibrTwELANQ1d/izNcWCnQAHgHurZfoziFL5IwxxpwNVfW51FZDadu2LcHBFWcN\nO3dUlfT0dG666abqC7sWLFjAkiVLWLZsGTk5OURERJCcnMzJkydrHcfGjRuJiYnxen7Lli2MHTuW\nG2+8kR07dpCWlsaYMWPYvn27p8x7773Hz372M7Zs2cJf/vIXmjVrxpAhQ/jqq69qHddZU9VqN6A1\nEORP2aa4AXrLLbcozjQlCugzzzyjxhhj6ofz68f3+fraztbGjRu1T58+2rJlS23durVeeeWVunTp\nUhURDQgI8HzNyMhQVdXi4mK9//77NTo6WkNDQ/WKK67QDRs2eO6XnZ2tIqJvvPGGXnrppRocHKy9\ne/fWDz/80K94jh07phMmTNCIiAgNDg7W2NhYfeyxxzznu3TpoosWLVJV1dmzZ5eLs3QrjVVVdfny\n5RoXF6fBwcHarVs3XbJkyVm/Z6qqCxcu1JiYGL/KdujQQefNm+fZ/+abbzQsLEyfeuopz7Fjx47p\nxIkTNSIiQsPCwjQxMVFzcnK83jM7O9vn82+44QYdOnRouWNDhgzRtLQ0r9ecOHFCAwMD9Y033vBa\nxtfPnHvurHKYaqudRKQZzpJXQ6sr25RZjZwxxpjqlJSUMGrUKAYMGMDHH3/Mtm3bmDp1KgMGDODR\nRx8lNDSUwsJCDh8+zH333QdAeno6mzZtYtWqVezatYubb76ZkSNH8vHHH5e79/Tp0/nNb37Dhx9+\nyIUXXsiIESMoKqq+C/qDDz7Irl27WLduHX//+99Zvnw5HTt2rLLs9OnTKSgo4PDhwxQUFPDss8/S\nvHlz+vfvD8DTTz/NQw89xNy5c9m9ezeLFi3ikUce4cknn/TcIyUlhbCwMK9bq1atavv2ArB3714K\nCgpITk72HAsODmbAgAF88MEH5eIoKChg3bp1fPTRRwwYMICkpCQKCwtr9dwtW7YwdGj5VOfqq68u\n98yKjh8/zpkzZ2jTpo3XMvWt2ulHVPW0iBQC3lf0/Q6wRM4YY0x1jh8/zrFjx7jmmmvo0qULABdd\ndBEAubm5iAjnn3++p/yePXtYtWoV+/fvJzo6GoBJkyaRlZVFZmYmS5cu9ZSdOXMmQ4YMAWDFihVE\nR0fz/PPPc+utt/qMKT8/n4SEBHr37g1Ap06dvJYNDQ0lNDQUgM8++4zJkyezcOFCBg1yFkGaO3cu\njzzyCNdeey0AnTt35oEHHmDZsmWefnbPPPMM33zzjX9vWC0UFBQgIrRv377c8fbt23PokDML2rvv\nvsvOnTs5cuQIQUFBgLNu6dq1a3nuuec8SXRZTgWY7+dW9cyCggKv10yZMoWEhAT69u3r12urD/7O\nI/cH4CfAunqMpUFZImeMMaY6bdq04eabb2bo0KEkJSWRlJTE6NGjvSZPubm5qCpxcXHlEoni4mIG\nDx7s2RcR+vTp49lv0aIFPXr08KuD/5133sno0aPJyckhOTmZESNGMGDAAJ/XfPXVV6SmpjJ27Fju\nvvtuAI4ePcqBAwe4/fbbueOOOzxlT58+Xa7vX4cOHaqNqb7l5uZy8uRJ2rVrV+74t99+S15eHgAH\nDhwgLi4OEUFVKSkpobi42DMgRUSYMGFCudrGmrjnnnv44IMPeP/99xu0b6S/idw+IE1EtgN/Ag5T\nYdkrVV1et6GdW5bIGWNM41Fd7UlDWr58OdOmTWP9+vWsXbuWhx56qNLoxlJnzpwhICCAnJwcmjUr\n/ys3JCSkTuIZNmwY+fn5vPnmm7zzzjsMHz6cMWPGsHx51b+WS0pKGDNmDJ06deKJJ54oFytAZmam\nzxqmlJQUNm3a5PW8iHD8+PFavhqIjIxEVSksLPTUYgIUFhYSGRnpiTUyMpLNmzdX+lkpbdqNiopi\nx44dnuNbt25lxowZbNy40XNN2WbgyMjISs2yZZ9Z1rRp03jppZfIzs6mc+fOtX6tdcHfRG6Z+7Uj\n0LuK8wpYImeMMeZ7oUePHvTo0YPp06eTkpLCypUrGT58OCUl5Xsh9erVC1Xl8OHDDBw40Ov9VJWt\nW7d6mmtPnjzJJ598Qnp6ul/xhIeHM378eMaPH8+wYcNIS0sjMzOT5s2bVyo7ZcoU8vPz2bZtG4GB\ngZ7jERERREVF8fnnnzN+/Hivz6rvptWYmBgiIyPJysryNBcXFRWxadMmFi1aBEBCQgKFhYWIiNeR\nqIGBgeWmOzlw4ADNmjXzWr5v375kZWVx773/nYgjKyuLq666qly5KVOm8PLLL5OdnU3Xrl3P6rXW\nBX8TOe/jdb8jKiZyjXEIuTHGmIa1b98+MjMzGTlyJB07diQvL4+dO3dy11130aVLF4qKinj77bfp\n1asXoaGhdO3albS0NNLT01m4cCEJCQl8+eWXZGdnExsby6hRozz3njt3Lu3ataNDhw7MmTOHoKAg\nxo0bV21Ms2bNIiEhgfj4eE6dOsXq1auJjY2tMolbsWIFK1asYP369RQVFXkGU7Rs2ZIWLVqQkZHB\n5MmTad26NSkpKZw6dYrc3FwOHjzIjBkzgJo3rebl5XHixAkOHjxIcXGxp5YsPj6eZs2acejQIZKS\nkpg/fz6pqc5qn1OnTmXevHl069aNrl27MnfuXMLCwjzvx5AhQ+jXrx+pqaksWLCAiy++mMOHD7Nh\nwwaSk5Pp169fjWIEJ0EbOHAgCxYsYNSoUbz66qtkZ2fz/vvve8rcdddd/OEPf+BPf/oTrVu39tTg\nlb5/DeJsh71+FzZAr7/++nLD01966SWvw4WNMcacHepgGpCGUFhYqNddd51GR0drcHCwdu7cWWfM\nmKGnT59WVdVJkyZpu3btyk0/cvr0ac3IyNDY2FgNCgrSDh06aGpqqubm5qqqMy1GQECAvv7669qz\nZ88aTz/y8MMPa/fu3bVFixbatm1bHT58uO7evdtzPiYmRhcvXqyqqunp6RoQEFBpKzv9yKpVq7R3\n794aEhKi4eHh2r9/f33xxRdr/Z4lJiZW+cz9+/erquq+ffs0ICBAV65cWe66jIwMjYqK0pCQEE1M\nTNRdu3aVO3/ixAmdOnWqdurUSYOCgvSCCy7QcePG6Z49e6qMo7rpR1RVWvSsBAAAEzJJREFUV69e\nrZdccokGBQVpXFycrlmzptz50qlbfL1/Ffn6WacOph8RrUE/BBHpibPCQ1sgU1ULROSHQKGqfl3H\nOeY5IyJ67bXX8tprr3mOvfLKK1x//fUNGJUxxnx3lXZAN85EtYMHD+bIkSOEh4c3dDimjvn6WXfP\nnVUToF9NqyIShDNy9TpAcGqtXgcKcFZ2+Dsw42wCaWjWR84YY0xDsaTW1Ja/2crDwBDgRqA9TjJX\n6k3g6jqO65yr+I/IEjljjDHniq9+2d4m4G3VqhXz588/h1GaxsjfwQ7jgIdU9XkRCaxwbi/QpU6j\nagBWI2eMMaYhDBw4sNJo17J8jRK1pljjbyLXFvibl3MBQFDdhNNwbNSqMcaYxqgxTMBrGi9/q532\nAt5mB7wC+Kxuwmk469aVX7Ti6NGjDRSJMcYYY4x//E3kngVmiMh4oHRiGhWRQcA0mvhkwFU5depU\nQ4dgjDHGGOOTv4ncI8CfgeeAf7vHNgNvA+tV9QlvFzZVlsgZY4wxprHzq4+cqpYAY0VkGc4I1Qjg\nXzhJ3MZ6jM9DRO4BEoHLgEhgtqrO8VL2B8Bs4FqcUbZHgCxVvdXf51kiZ4wx9adz587WF9l8L9T3\nWqz+DnYAQFU3Ad5Xyq1fPwGOAa8Bd3gr5CZx7wMlwC+A/UAUUKP1OiyRM8aY+rNv376GDsGY7wR/\nJwT+K7ASeEFVC+s3pKqpapwbSyBwp4+i84FQoLuqnixz/KWaPM8SOWOMMcY0dv72kTsM/AY4ICJv\nishYEQmux7hqRURCcSYtfrpCEletYcOGldsfM2ZMHUZm6lp2dnZDh2BqyD6zpsc+s6bFPq/vJ78S\nOVVNAToC9wPnA88DhSKy3B252lj0BoKBIyLysoj8R0S+FpHXRKSLrwsXLFjgaceePn06P/zhD+s9\nWFN79h9W02OfWdNjn1nTYp/X95PffeRU9Z/Ao8CjInIJTs1XGnCziHyhqvXbm88/UTjLhy0E1gEj\ncBLP+cBfRKRic6tHz549ycvLo6SkhPPOO++cBWyMMcYYU1u1WodKVf8GzAEeBA4B0TW5XkSSROSM\nH9u7NQyt9PV8rqrjVPUdVV0F/BjoDEzwdXFgYKAlccYYY4xpMqTiYvHVXiAyGKc27jqgJbANeE5V\nn6zBPYKBC/wo+h9V/aLCtYHAKaqYfkREhgLrgUWqOr3Cua9wBmtUGighIjV7E4wxxhhj6oCqntU8\nPP6OWu2OU5uVhlP7tg94DCeB+0dNH6qqRcDfa3qdH3bV5qKzfRONMcYYYxqCv33kduLM4fYy8Kyq\nbq6/kGpPVQ+KSA6QXPa4iPQFWuHUHhpjjDHGfCf4m8j9GHhdVb+tz2B8EZHeQBcg0D0UJyLXu9//\n2a3lA5gBrBeRV4D/xVmFYi7wKc5oW2OMMcaY7wR/px95xVsSJyIDRWR53YZVpZ/hTOr7AqDAGHf/\nJZxkrTTWd3FGq3YCXgUWAe8Ag8q+BhGJFpFXROQrETkmIqtFpNM5eB2mFkRktDuNTL47rcxuEfm1\niLRs6NiMf0RkvTuIqcql9UzjISIpIrLRnb7pmIhsE5HEho7LVCYi/URkg4gUishxEflQRG5p6LiM\nQ0Q6isgTIvKBiJx0/w+sNEZARH4gIv8rIkdE5ISIZLnd2qpVq1GrIvJDEZkjInuBv+DU2NUrVb1F\nVQO9bPkVym5Q1StVNVRVz3evPVIm/hA37otwBm5MALoC77rnTONzL3Aap8Z1GPAkzgofbzVkUMY/\nIjIO6InzR5hpxETkdmANsB0YBYzG6VYT2pBxmcpEpAeQhdO69hOc9cW3Ac+4n6NpeD/E+Tf0JfAe\n3v8PfAMYCtyFM5i0Oc60aVHVPcDvUasi0hq4AbgZ6OMe3gFk4owGPe7XjRoBEZmCM9fcRaq61z3W\nBfgHMF1VH2246ExVRKStqv6rwrEbgd8DSaqa3RBxmeqJSBucrg1TcWrU56rqzIaNylRFRDoDfwMe\nUNUnGjoe45uI/Bq4B2ijqt+UOf4BoKpaozXGTf0SkduAp4CYshVQIpKK04I4SFXfc4+1AvbiDCqd\n6uu+PmvkRCTArWJ/EWeZrt/hzMe2zC0yVVUzm1IS5xoBbC1N4gBUdR/wPpDaUEEZ7yomca7tOBNA\ndzzH4ZiaWQDsVNUXGzoQU63bgBKcP9BN49ccKC6bxLmOUcsWN9MgRgCHSpM4ADeveh0/chKvH7SI\nLAIOuje6BngNp0nrAmAmzi/Qpioe+KSK47uAuHMci6m9RJxq6r81cBzGCxH5fzhdF+5q6FiMX/oB\nu4FxIvK5iJwSkX+IyKSGDsxU6feAiMjjItJBRFqLyERgMLC4YUMzNeArJ7nAXUfeK1+jVqfh/JJc\nB6SXrRH5DkygGw78u4rjXwJtznEsphZEpCOQAWSpam5Dx2MqE5HmOLX4v1HVzxs6HuOXKHd7BPg5\nsAdnYNlSEQm05tbGRVV3ueudv4YzIBCgGLhDVV9uuMhMDYXjNKNW9KX7tQ3wH28X+6p6fQb4GhgO\nfCYiS0XkitpGaUxdEZEWwJ9w/sO6tYHDMd49AAQDv27oQIzfAnBW7Pmpqi5X1WxVvQtnxZyfN2xo\npiIR+SGwGvgY53d1Es4fT5nuACPzPeA1kVPViUAkMB7IAW4HtojI33D+g27KtXL/puqaN281daaR\ncJd3ewNnTsGrVfVQw0ZkquJO5fML4JdAsNvk8wP3dJC7b314Gp/Slpe3Kxx/C2gvIu3PcTzGt3k4\nf9COVNU3VfUvbsf4l3BWXzJNg6+cpPS8Vz7/I1XVIlV9QVVL+8b9HKcj7AycPnLzRWSC+8u1KdmF\n0yZdURzO6DrTCIlIM5y/PhOAH6mqfVaN14VAEPAHnP+E/o3TTKDAdPd7v+ZIMudUrZY5NA2mO85A\notMVjm8D2opIRBXXmMbHV06Sr6pem1WhBqNaVPWwqj6iqt2BK3BGrnYFnsUZ0dqUrAX6uFOOAJ7p\nR/rhNNmZRkZEBGdljkQgVVW3N2xEphp/BQa5W2KZTYDn3O+t31zj85r79eoKx38EfKGqhec4HuNb\nAdDT/SO3rD5AEf/tY2Uat7VARxHpX3rAnX5kBH7kJH7PI1flxU5n5muAm1T12lrf6BxzR4B8BHyD\n0/QDMAdoAfxPddmvOfdE5Lc4zftzgT9XOP2Fqh4891GZmhKRM9g8co2aiLyDM3nzQziDHX6M0xc1\nXVWfa8jYTHnuMpUv4UwK/CTO77RUnMnSF6vq9AYMz7jKLCc6BOf32CTgCHBEVd9zKyo2A9HA/cBX\nOC2g3XFyEp+/384qkWvKRCQaWAIk49QSvA1Mq7hKhGkc3FVEKi1r4spQVVv2qQkQkRKcRG5WQ8di\nquYuezcPZzb6NjjTkcyzeQAbJxG5GqffejzO4KI8nHkAn9Lv6y/4Rsb9A7aqz2Kjqg52y/wAZ6GC\nUTif4wfAPapa1bQk5e9vn7MxxhhjTNNko8aMMcYYY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SMMcYY\nY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SMMcYYY5ooS+SM+R4SkRtFZH+Z/V0ickcdP6OPiGwVkRMi\nUiIiPevy/ubcE5F9IrK8Ftelisi0+ojJmO87S+SM+X5KAHIARKQF0A34sI6fsRwIBIYDfYG/1/H9\nzblX2xnkRwGWyBlTDyyRM+b7qTf/TdwSgBJgR13dXEQCgIuAP6vqRlXdpqpFdXV/c/ZE5LyGjsEY\nc/YskTPme8ZNsi7lv4nc5cCnqlrs5/VhIrJURA6KSJGI7BaRqWXO3wycxlnDeKaInBGRPT7uN9st\n011E3hWRkyJySEQyKpQLEpHFIvKxiHwtIodFZK2IdKtQrr2IrCwT3yG3XDv3fKCI/EpEPheRb0Tk\niIi8JyJXVbjPT0XkozJl/ldE2lQoM0VEPhWR/4jIlyKyXURS/XgPJ1S497MiElnm/BsiUqmGVEQi\nReSUiEwpc6yLiPxRRP7pvt6/isgoL+9xvIisF5GvAZ9rp7qvba8b4zYR+X9VlGknIr8Tkc/czy3f\njSWqTJkVwM1ARzcGz8+Dv5+pMca7Zg0dgDHm3BCRvUBnd1eBdSIipftlFnaOUdV8L/cQYB1OIvhL\n4BOcptPFItJOVR8C3gD6Ae8D/+tu3/oIrbS57jWc5thfA1cDvxSRElWd454PAsKAh4FDOAu6TwK2\niMjFqvpPt9wfgE7AvcAXQHsgCQh1z88ApgC/wKmFbAVcBoSXeZ3zgXuAR4H7gI7uc+NF5CpVVREZ\nj7PI9WxgMxAC9Cx7Hy/v4U+B3wEvuLFE4SxSf4WIJKjqf4DngOfd17W7zOXj3ffrefde0cA2oMB9\nTUeBG4DVIpKqqm9UeI/XAM8A84EzPmK8DViC83m8BPzQjbdlhaLhOJ/tL4B/Ah1w3vfNbuzFwBzg\nfJz3eAROgl/68+DvZ2qM8UZVbbPNtu/BBlyMk2gsAj4Gerj7x4DJ7vc9gWY+7nENTgJwY4XjTwPf\nAOHufqBbbqYfcc3CadqdXuH4U25srbxcF4CTPB0HppQ5/jXwMx/Pex14xcf5zjg1ig9WON7XfU0j\n3f0ngJwafgYBOEnX2xWO93Pv/TN3Pxj4Cni4Qrm/Am+U2X8GKAR+UKHcW0BuFe+x1/elTFkB8nGa\nxcse/7Eb4/JqXl+0Wy61zPEVQL6f70+lz9Q222zzvlnTqjHfE6q6W1V34tRWZavqx8B/cGpZXlbV\nne522sdt+uMkBC9UOP4H4DycZKe2Xq6wv8qNrXvpARH5sTsS9t84ydZJoHSwRqntwHQRmSwi3als\nO5AiInNFpJ+INK9wPhknmXnebYYNFJFA97qvgQFl7nOpiDwuIkkiEuLHa+wGRODWqJVS1feB/cBA\nd78IeAWnBq70tfcA/gd4tsylV+PUkH5dJtZmOInc/4hIxRq0NX7EGO1uFT+P1TjveTkicqfbTPy1\nez4fpwbQr+ZRPz9TY4wXlsgZ8z0gIgFlfsn3w2m6CsRJSg4C/3T3qxMOfFlFsleAk/z4bFasRmEV\n+4LTrImIjMBJ7nYB44ArcJrrjuLUYJX6MbAWmA7scPvK/bLM+YdxaqhGAO8B/xKR5SJSGnuE+9w8\n4FSZrRgnsWwLoKrPAne6cawHvhSR1SLSGe9Kn3G4inMFlH//ngMuEJGB7v6NODVVfypTJgK4qYo4\nH3HPt63wjKqeW1EH92u5z0NVS4B/lT0mIncDy3ASx2tx+lteifP+lf1MqlSDz9QY44X1kTPm++Ed\n3NoenNqS53Bq0Ur3T+H0kxukqu/5uM+XQLiINKuQzEWWOV9b7YF9FfbBSTTB6fv1D1W9rbSAm5iW\nSx5V9ShwN3C3iHTF6WifISL/VNVMNyH5DfAbEYnAaS5egtOkNw4nWVGcmrmvqojTk8yo6tPA0yLS\nGhgKLMZJTLzVTJa+P5FVnIvEnRLGvfdGEckHJojIe25sL6tq2f6G/8JJRufjJE8VHaqw78/0IaXJ\nXvuyB91Ev2JieANOM/H9Zcp18eMZZa+v9jM1xnhnNXLGfD/8FKemYyHwufv9ZcAR4EH3+8upfi65\njTj938ZUOD4BpwP7lrOI8ccV9sfhNGV+7O6HUrlp7yY3niqp6j/UGYDxb8o00ZY5/09VXQ68XeZ8\nFk4fr86qmlvFtr+K+xxT1ZdxBgZU1Zxb6jOcmq6xZQ+KM2K2M/CXCuX/AIwGUnBqJp+rcH49Tr/G\nT73EespHLN58ARyg8ucxmsp//Ifi/BFQ1q1UThi/xUmUK6rxZ2qMKc9q5Iz5HlDVfwCIyEycTux/\ndad4aIfTed3f0YFv4ozQ/J1bm7ULZ9TqrcCvVbW2NXICTCzTF22Ye89Zqvq1W2Y9kCoii3FGxl4O\n/AwnScN9fa1wkrI/ArtxkoxRwA+ADW6ZNTijVXPdaxPc5/0WQFX3iMgjwFIRuRgneS0CLgCGAE+7\ntWWZOInmFpwRm91wmj83eHuRqnrG/Qx+JyKltaLRwFycJG9FhUuewxkR+jtgfxW1pTOB/wM2ichS\nnBrNNjjJZIyq/sRbLD5iVHGmfnlanFUcVgFdgQdwBp+UtR64X0R+jjN6djBOwlfRpzif7x04tY5F\nqvoJfnymxphqNPRoC9tss+3cbEBznD5Wye7+FGB7Le7TEngcp8mzCCdhmlyhTCDOoIhf+nG/0hGV\nccC7OJ3dDwGzK5QTnKksvgBO4NRe/Q+wB3jGLXMeTkL2sftav8JJdG4oc59pwAc4tZEngb/hTKUS\nWOF5491yX7v32uW+7ij3/E1uvAU4I3bzcGo8W/rxmtNwRqB+48bxe6C9l7Lb3PfnV17OR+GM8D3g\nfh4HcZLJtArv8WkgoAaf893AXpwBMduAq8q+126ZYJw+coU4Sd6fcGoWy332ODVvf8RpCi4B9vj7\nmdpmm22+N1Gt7Yorxhhz9kRkFk7NUnNV9Tq3mTHGmMqsj5wxxhhjTBNliZwxpjGwpgFjjKkFa1o1\nxhhjjGmirEbOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOMMaaJskTOGGOM\nMaaJ+v+Dy6GJ+uoh9QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x123986690>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"for step_size in np.logspace(-4, 2, num=7):\n",
" make_plot(log_likelihood_sgd[step_size], len_data=len(train_data), batch_size=100,\n",
" smoothing_window=30, label='step_size=%.1e'%step_size)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, let us remove the step size `step_size = 1e2` and plot the rest of the curves."
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAFSCAYAAAB2ajI+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdclEf+x99DRxABQRAVe8Uu9gKmmZ5cLr1eyqXXM5d6\nicb0fql3SS69/pJLMV66SbD33qKgiKCA9A7L7s7vj2HZ9uyywIKazDsvXnHnabO7zz7zmW8bIaVE\no9FoNBqNRnPsEXCkO6DRaDQajUajaRtayGk0Go1Go9Eco2ghp9FoNBqNRnOMooWcRqPRaDQazTGK\nFnIajUaj0Wg0xyhayGk0Go1Go9Eco2ghp9FoNBqNRnOM4pOQE0LMEkJEetgWKYSY5d9uaTQajUaj\n0WhawleL3K/ACA/bhjZt12g0Go1Go9F0Ir4KOeFlWyhg8UNfNBqNRqPRaDStIMjTBiFEP2CAQ1Oq\ngXs1HLgKOOD3nmk0Go1Go9FovOJRyAFXAPMA2fT3Es6WOdn02gzc1FEd1Gg0Go1Go9EYI6SUxhuE\n6Av0Q4m1X1BibafLbg3AHillaQf20dYfAdwDXAskAruBBVLKL1o4riswFzgZGIxyJ+8EnpJSLuzQ\nTms0Go1Go9F0IB6FnNNOQqQBG6WUVR3fJY99eBT4G3AfsBG4ECXqTpNSfu/luBTgZ+AdIAMVz3cR\n8BfgJinlvzqy3xqNRqPRaDQdhU9C7kgjhIgHcoHHpJQLHNoXA3FSyrFejg0HpJSy3qV9MTBIStmv\nY3qt0Wg0Go1G07H4WkcuRAgxTwjxmxCiVghhcfkzd3A/TwaCgQ9d2j8ARjW5gQ2RUta5irgm1gNJ\n/uuiRqPRaDQaTefiLdnBkadRMXLfAV+gYuM6kxFAg5Ryr0v7DlQM3wggp5XnTAN+80PfNBqNRqPR\naI4Ivgq5c4F5UspHO7IzXogFyg3aSx22+4wQ4lpgEnBJO/ul0Wg0Go1Gc8TwtSBwJLDKXxcVQhwv\nhLD68PeLv67pcO104AXgXSnlJ/4+v0aj0Wg0Gk1n4atFbhEwC1WGxB+sAIb5sF9t0//LgGiD7TZL\nnE/lT4QQE4GFwGLgry3se/RngWg0Go1GozmmkVJ6Wz2rRXwVci8B7wkhrMC3GAgnKeU+Xy/alHyw\nx9f9UbFwoUKIAS7XSUEVJnatb+eGEGIU8D2qdMm5UsoWlxU7FjJ6NYr58+czf/78I90NjY/o7+vY\nQn9fxw76uzq2UCVy24evQs7mVp2PWu3BiMB298Yz36NWkLgEeNih/VJgu5TSa6KDEGIw8COQBZwh\npezsZA2NRqPRaDQav+OrkLsKZfk6Ikgpi4QQzwH3CiGqsRcETgfOcNxXCPEzkCylHNz0Oh74CVW+\nZD6Q4qKAN0opGzv6PWg0Go1Go9H4G5+EnJTynQ7uhy/cB1QBt2Jfous8KeV3LvsF4JzEMQLo0/Tv\n/xmctz9wwL9d1XQ26enpR7oLmlagv69jC/19HTvo7+qPxzGxssORQAgh9Wej0Wg0Go2moxBCdFyy\ngxDiLeBhKWV207+9IaWUV7enIxqNRqPRaDSa1uHNtTobVW8N4Di8x8hp05VGo9FoNBpNJ6Ndqx7Q\nrlWNRqPRaDQdiT9cq76u7KDRaDQajUajOcrwtfwIQoguqDIkaagVFUqBX4G3pZR1HdM9jUaj0Wg0\nGo0nfHKtCiESgQxgCJADFKBKgPRFlQFJl1IWdlw3Ox/tWtVoNBqNRtORdKZr9SkgBpgppewvpZwq\npewPzECtgfpkezqh0Wg0Go1Go2k9vlrkioC7pZRuZUiEEFcDT0gp4zugf0cMbZHTaDQajUbTkXSm\nRS4SOORhW17Tdo1Go9FoNBpNJ+KrkNsNXOZh26XAb/7pjkaj0Wg0Go3GV3zNWn0GeE8IkQB8BOSj\nkh0uBE7As8jTaDQajUaj0XQQPhcEFkJcCywAejg0FwIPSinf6IC+HVF0jJxGo9FoNJqOxB8xcq1a\n2UEIEQAMxV5HbreU0tqeDhytaCGn0Wg0Go2mI+l0IfdHQgs5jUaj0Wg0HUmnLtElhBgshHhXCLFH\nCFHT9P93hBCD2tMBjUaj0Wg0Gk3b8LWOXDrwLVAHfIOKjUsATgO6ACdLKZd0XDc7H22R02g0Go1G\n05F0mmtVCLEBqAfmSCmrHdq7Aj8CwVLK1PZ05GhDCzmNRqPRaDQdSWe6VkcATzqKOAApZRVqea6U\n9nRCo9FoNBqNRtN6fBVyeUCIh20hwEH/dEej0Wg0Go1G4yu+CrkngYeEEEmOjUKIXsA84DF/d0yj\n0Wg0Go1G4x1fV3ZIA6KAfUKI1diTHaY0/Tu9KSECQEopr/B3RzUajUaj0Wg0zvia7JDdinNKKeWA\ntnfp6EAnO2g0Go1Go+lIdEHgDkQLOY1Go9FoNB1JpxYE1mg0Go1Go9EcXWghp9FoNBqNRnOMooWc\nRqPRaDQazTHKMSPkhOJeIUS2EKJOCLFZCHFOG87TXwhRK4SwCiGO+aQMjUaj0Wg0f1yOGSEHPAI8\nCLwInAysAj4TQpzcyvP8CygDdCaDRqPRaDSaY5pjImtVCBEP5AKPSSkXOLQvBuKklGN9PM/FwLPA\n48DzwGAp5T4P++qsVY1Go9FoNB3GHylr9WQgGPjQpf0DYJQQom9LJxBCRKNE3Fygwu891Gg0TjQc\nbKBidQXSoidEvxey52eTITLIEBnsvHjnke6ORqOhFUJOCHGtEGJTU3yZxfWvIzsJjAAapJR7Xdp3\nAKJpe0s8DeyUUn7k785pOhcpJbVZtZgrzEe6KxoPlP1axur+q9k0dRNLQpYgrVrMHes05DeQ81BO\n8+vDHx9m29nbjmCPOhZplVRtrsJS39HDmzNWk5Wtp24lQ2Rw6LVDnXptzbGJT0JOCHE58BKwDggD\n3kZZwyqBvcACz0f7hVig3KC91GG7R4QQM4FLgRv93C9NO5BWJcisjVbfj5GS9WPXs3bwWpZHLyfv\nxTzP+1ok5cvKqc+tb12/pGTj1I3Nlof6PHW8udJM+bLyVvW3IzFXmsl/O5/qrdW+7V9tpvjrYhry\nGzq4Z7DluC3IxibxZoWcR+0CwFyt+p3/dn6n9AWgYmUF68auI0NkUPx1cauOtZqtFH1ZxP5H9rPt\nrG3kvZx3VNwD+W/nN9+jhZ8UtutcVnPL72f31bvd2koWlmCu6twJlZSSoq+K2HH+DirXV7b6WEtt\ny8LM2mhlSeASNozbwLLwZWSIDEq+KcFq6vjvfWnoUkq/U0Pbnuv3UPJ9SauOl1JSs6vGp+/0aKRy\nXSUZIoNlXZdR9mtZq46VVknWnVnNv4uyjNYdf6zi6xJdG4GvgYeBRiBVSrlRCBEDZABvSClf9vmi\nQhwP/OTDrhlSyuOEEK8BZ0gpk1zOMxDIBC6TUrq6XW37BAObga+klPc3tV0BvMUfLEaufGk5m9M2\nA5DyRQrxf4pv87lsn40QbXPtm6vNbJm9har1VQAMfHYgff7Wp8XjCj8uZNfFu5zaph2eRkh8iFOb\npc7Csi7Lml/3uKQHIz7wxXALmbdmcvClg05tvW7txcEX7W3xF8ST8kmKT+frCOqy61gzYE3z66Fv\nDaXnlT2bBUZAsPMczVJjYVmk/fPoOrkrfe7oQ9w5cWCFgFDfoyyKFxZz6PVDRI6JpN+CfgQEOR/7\n21W/UfB2gVNb5IRIUtenUptVy9rBa522Jd+TTH1OPeUZ5cT/OZ5BLwxCBLQrZMQJq8nK0tClTm2j\nfxxN7Ile53/N5D6by947nZ0B4YPCmZw5ufn8xV8XY6mwEH9ePEFRvi5h3XYaChpY1XOVU9uYxWOI\nOT7Gp+NNRSYOvnLQycIWf148KZ/a72lro5WKFRUEdQsiYkQES8OWGp2KYe8OI/HyRGV1FW1/JvhK\n5u2ZHHzB/lsc+dVI4s6K87i/lJLSb0vZdrrdehh7ciyjvh2FEAJroxVTvomQniHNv5vCTwrZddEu\nt3OF9Axhau5URKDn9ygtksOfHKZ8aTm9bupF5OhIw/2sZisVSysI7BpI1MQoAKq3VrN+zHrnHQWk\nW9M9Xs/pnA1WViatxFyqxPWETRPoOrZr83bTYROZt2RSv6+eXrf2IvGyRJ/O21lUrKxg0/RNTm1T\nD04lNCnUp+OLvihix593OLVNzppM+MBwn/tgNVspeLuA2l21JF6VSORI4++vLVSsriDnoRyCugcx\n8KmBhCaFdt4SXUKIKuAs4FeUkJshpVzdtO184FEp5WCfLypEGJDsw661Uso8IcQTwK1Syi4u55kI\nrAFOk1J+5+FadwG3AROAuqbmS1AWxglAlpTSzaQhhJDz5s1rfp2enk56eroPXW4dUkqK/lvEzvPt\n8Saxp8Uy8suRboNxq85rkZiKTIQmqh9Aw8EGVvV2fvBPL5lOcGywU1vF6gpKvysldk4s3aZ1Mzz3\n/of2s3/+fgD6zutL8l3JBHYJ9LlfawavoT7b3Uo25N9DSLouyeAoRX1uPauTV7u1j/5+NLFznAfl\nradubZ7V2og+LpqxP3vPi5FWyZLAJV73sdHzup4MfnEwASHG35OUkvw38yn9ppTYU2KJPy+e4Jhg\nw31Lfyxl65ytgPPnYG20gsBJLDWWN7IiZoXbOYa9P4ys27NAwuCXBpNwcQL1OfWs7uf+mTkSFBvE\niI9GuH2GAMWLitl+5nYAev+tN0k3JLF22FpoMmp0P7M7oxaOat7fXGlmebflhtdJl+msTVlL7c5a\nr/0Z/sFwEi5J8LpPa8j6WxZ5z3u23IYNCCN1SypBkXYBJqXEXGEmKCrI4/0wafckugzpwoaJG5on\nJI5MK5hGSILLBKPGQtbtWeS/mU/yfcn0OK8HkWNaP1BkiAzD9mlF0wiJC3Frr8uuo2ZrDd3SumE6\naGLdyHUezz2zdiYbJ22kZnuNT33pNqMbQ14bwroU+zlnNc5yE/ig7ufir4qpz6kn8bJEt8+neT+z\nFWuNlaBu9u+koUC5dg/9293dmC7TPfYv+4Fsch7J8bjdkdQtqUSOjmRVn1U05Blbi/s/3p/se+3L\nj8+snUlguP35t+3sbZQsdLaipVnTnASulJKd5++k6L9FAAz65yB639ab/Q/vZ/+D+92uOfiVwfS6\nsRcA5gozWXOziBgeQdJNSQQEBzQLy0OvHWLP9Xucjp1RMaN5crH7+t3kv5bfvG3I60M4/PFhRKAg\n6fok4v/s2+S+ZkcNOy/aSfjgcIa9Nczpe2oNpiIT5RnlVCyvoNeNvdh93W4qlriHsM+qn9XiZLNm\nZ43TPeh0fMMsyn8tp+R/JZiKTMT/OZ64P8UZ3qN7795L7lO5za+HvD6EpL96Hpd8pW5/HWv6r2Fz\n038Afe7qwyNPPdJpQu4wcKmU8kchRB5wly3WTAhxKvCZlDKiPR1p4fqXAe/gYkETQvwFeBMYIKU0\n/KUKId4GLkfF0hmxWUo53uC4DrfISSlZEuBZNMyomuE0uNhoLGlky4lbqN7krD/TzGmIQMGBJw+w\n7x67oTE6PZryDHfPdPJ9yQx4dACmQhMH/+U8OweIGB3BsLeHETk2EoRylxmdByB8SDiTdk3yaEkx\nssQYYZvd22g42EDNrhrCB4SzZuAaw2PCBoQxZe+U5tfexMukzEl0GWSfD2yYvIGqtWoQ7juvL/Hn\nxLvPiL3Q4+IejPjQ2NJXvLCY7Wdvd2sfu3Qs0TOjm1/nPpfL3rnOFp+JOyZS8HYBuc/YHyiT904m\nfEA4++7bx4HHD7TYtxlVM1je1VhUecM2mFWur2TjxI0t7j9532TC+6sZ7+7rdpP/er7hfl1SulC7\nw7uIszHwuYH0uaNlC60jUkrKl5RjrbMSe1Js8+DmSfS4MjZjLFHTo8i8MZP8N4zfgyMBXQIY/NJg\nQ5ejI7aBtOzXMrYct8Vte0sWJVdKF5ey9cSthtuGvTOMxCsSqcuuo/FwI/lv5Xv8PvxFcI9gGg83\nurUbiaucR3PI/oddBEVNj2L8cvX4NVeasdZZqc+tZ/sZ2zEVmegztw8DnxwIGAskG65iykZLz1gj\nZjXOYmmwsfXRE7b3WrunlrVD3Z9zrs+oPTfv4dArzoJ0VuMsdl64k+LPjV3/08umExAc4GRZt9Hv\noX70e7Afa4atoW53ndv2lM9T3CxVLZF4ZSKDXx7cPEmXUiKEYO9de8l9Otdp39HfjyZqahR7rttD\nxYoKQpNDGfX1KGp/q1UW3RR3eZA1N4u85zxPsBzpdXMvBr/k3Va0+YTNlP9sPD4Z0eOiHgx7bxhr\nh6w1NCw4EntqLF3Hd8VSbaHHRT0oXlhM4XuFzWK/53U9iT8nntrfajEdNpH3fB7WWiuxp8Yy6n9q\nouvpPpzN7E4Tcj8DX0opXxZCfAyMAv4KmIFXgEAp5YT2dKSF68cDecAjUsqHHdoXA/FSyjFejh0C\nuNqPTwHuQlnm9kgp3Uar9gq5rDuzyHvWfpP2urkXve/oTfgAu4k3e362m3hyZfCrg0m6PslpNudp\nYEq8MpGk65LYOKXlwdfGgKcGsO8uQ++yE0nXJxnOhD0RNT2KUV+PIjg2uNUP07YIkL7z+tJ/fn+q\nt1WzfrR3IWZ76BqJjvhz45tnyb4SOS6SXjf3ovtp3anZUUPRF0VuD2lXJv02iS5Du1C3t441g4wF\nqiuBXQOZkjOFFbHu1jgjet3Wy8kF1RpG/ziarScZiwVXet/em0HPDwJgZdJKTPmmNl3TEzFzYhj5\nxcjmAcVcZSYwItBt0rDlpC2U/WSPiZlRNYPqDdVsTt/s03XCB4WTcFkC++ft91vfbQz/YDi7LnV3\n1dloKbSgcm0lu6/dTc2Wlq1kve/o7dUC2VmM/mE0sSfZrbyengND3x5KSEIIO8/fiaXaOH5t5KKR\nbD/DfVLkiM3DUPZzGTmP5lD+q++DuiPRs6NbfeyIT0fQ47weXicN0wqnERwfzO6rdlPwToHH/TyR\nfH8yRZ8WUZfpLtQAUremsvPCnS1avFtD+KBwxq0YR8G7BS2OE4l/SfT4vgY8MYAeF/dQ7uugAKxm\na5vFshGeJs1HCxPWT2BD6gbDbZ0p5C4ABkopHxNCDAIWA7anThVwtpQyoz0d8aEPj6NcpPcDG4EL\nUWLyDEe3apPoTPbm6u3oGLnV/VdTv9+zwp9ZN5OA4ACWBPkubmwDv1FszNHMjIoZFLxTQNZtWR1+\nrTRzmk+f6ZT9UzAVmFoleDuC0ORQGg50TrB/R5Mu0zEVmliZuLJDzp94VSLdT+3OjnPtVoVR346i\n+yndAeWiWdmjY67dWcyomoFsUFbFsP5hdB2nYpsa8htYlXTs/OaNCE0Opfdtvd0sz/4k+Z5kEq5I\nYN1wz27jjiIkMYSYE2MofN9z0smQ14YQFB3Ezgs6pmxLj0t6cPjDwx1ybn/SdXJXYk6I4cCjLXsV\nHLFN1gEq11Qe8ee3v+g0Ied2kBARwFSgC7BSStm6NLA2IJRJ6l6UeEsEdgMPSSm/dNnvV5SQG+jl\nXB0m5Ixi0Vzp93A/9j+wv9XnnlE1g10X7aLkf63LYvqjED4onLos49lqW+mW1s0wZkPjzLiV46ha\nX0XWrS0I9vjD8K8boCwG7ngeqrt6378FJmdNJvOWTLd4yN8LqVtSW+XqbwutFQDl3WDFdDjt2w7s\n1FFERhqkt847a0jCFQkUvtu+7OI/Ov0e6tchFvMjSWda5GYBGz0kBUQAE6SUrbOTHuW0Rci111qW\n8kUKO87xHMcQOTaS6s2+lZo4Fug6qSvJ9yaz40+ti91oDQFhAVjr256Gn2ZNI++5PLesRY0zcWfH\nqbIe3j5qYYVfjm9+aTFFEjhnUcd3zoG7n4An72n78WsnwqTON/h4pCgO4tsxjT73MyhpCs/74dko\nQv5nL+dhDoRH/gF/fw4imnI5nrgbfjgZ/vxfuPmVdnT8CHHXkzB+I1z4f74fM+d7eHABTO9kg++i\n0+GM/3XuNX8vtPd30Zn4Q8j5mhb5K56L7g5r2v6HxlJraZeIG/bOMOL/FE+aJY34C4wzh9or4gY+\nP5A0a1qL+41cNJLYk72XZki6oe1ZPAHhAYz6bhQT1kwg/ux4ZlTNaNXx3c/sTrpMp2uqd2tOz2t7\nMqtuFiM+9a3siBGfFxXRZ24fUrelMmHTBNIsaaRZWv4MO4s5P8DjPgqTb06F4u6etweEe34cBCcZ\nZxfaKP7KXcR9eh6cudChoa9zPGhgSDUbTlBP26I4uPBj+OvrXi/TbtZOhks+sL/e00KufXCiet/V\nEXDSD/DYfZ73PeEn2HtoKNOLpzPo7aFez/vs33ztsXeuegtOaaNl7JH77SIOYM7cSs74Gh67F655\nA05cDEvS4ZL34IEFcN6nSsQBHPCl5kAHk9OGPqybBP89FzJVSCcbx8FpXsRSSSyYQuEfj7T+Wle+\n1fpjHHnub/DDSZ63LzzT+/ElBo/wL/6k7r2zvoLZv8CrN7S9f/66hz3x8k1tP/b8z+D4xW0/fvVk\ndfz3c9p2fHULqZ9nLlS/p9m/tO38rvhqkbMCU6SUbuk4QohpqHpv3p/0xxi+WOTMFWZMhSZ2XrDT\no8ga9c0ocp/O9ZjtacM1kNO1DlpbGPyvwfS6vpdbe/a8bHIWuCdZDH51MFFTo5rrDm2cvpHKle4F\nNyPHRZK6MZXGkkbyXsgj52HfUvsBEi5LYPh7w93aD/7rIJk3Zrq1p3yZ4maxm7J/CmF9wzj46kEy\nb3I/xoYt+Ll2d60qmdFKbn8etjRVK9k7eTLdg4N5r6CAQeHhzImNJfP6PS1mBE6pms4+YWJAWBgB\nZRZWxnue1o/JnsTBn4spvqbl5BMAUzDM+dH++r7kZDKfPcCNrxrvP/sXCLQoPZXbBwq6jCX3uyJ6\nXdGT6MQwArsGsuuyXW5utpO/g4YwCDbBe3GDuKgiiyF74LXrvffvqjche4CD9WbEDnjlZqd9ruEN\nKooGURoL1qakw2c+68KEV/0XsG3DZk1y5ZzP4RaDKpgn/AQWg6oKU1bB4y6CzvZeHfFktTp9EdRE\nKgFx57O+99/Gc3co12apgyg/+0u47UXj/TOHCz79k6QoHv55h2r71/Xw6fl4zuVvgWAT/GgwyN39\nBIzZAhd/7P34jeNg/Cbv+3jjvE+hOB5+ne3b/qsnw/2P2u8xACTN79/TeU78EcwOFYOG7Fa/oV3D\n4U9fwq0vGR+3bAY8NA8WnQHhXhIin74TbnkJwlxCZec+AxsnQFQFLDzb/bg7n4YNqTBzKSyY574d\nlCXRFAIXfQx9clVfdg3H7TsPr4XrXoOe+eq+GrUNJmyAGIMhqzrC2Up49X/gUoMKrutS1fU89c2V\n4xdDQiGc+bUS2iVxEFoP35/i2/E2VkyDfzxqf51QAJ9cZH99zRtw+Xswy2BoPX4xjNgJXatg0zio\nb8pLnLEMHn7Qed+fj1P3zPaRUBHtfi5QE8Zr3nRvv/xdyHWchMzuQNeqEKIfYHs0LQZuBn5z2S0c\nuAoYI6Uc1J6OHG20JOR2X7vbpxIFNoHmqcAk2MuGuFK9vZr1ozzHxyTfm0xIUghZtxjHJU3cPtEw\n7dvaYHUr7hn35zhG/nek276V6yop+abEKbt23PJxdJuuasw5FvbtOrEro38YTV1WHRsnuQeixp0d\nR8oXKR4LhrpmfI3NGEt0mvuvZEl5OembN3scTMA5Y66l2nC730wg5YNazL8q/9FFH0FJd2hsYWrS\nOGsWQQHKitVwsIHM2zIp+6GMLildSL4nmaA53Zi8dROZdfa4vRkBkTyc5iz6E+/sxfDT7Nml894K\nJv19Vc4hIDqQb9f15KTheQS4FNBf8AD8epxzm6fPZPcQuP417+8HlPfz/qWRnL8plOW3hHNjkIfs\nR+l+bVdm/4KqgWeBa/4D06s2k3znHU773MY/2Ypx0vnoLfDC7S332ZVbXoSXbnVvP+1/UOthpuw6\nkN//CKyc7uUiUg06KTvg5+OVpc+IS9+Hqx0sM8cvtouJAAv8fIKXaxhw1ldQaVDeMdgEN72iBuE1\nk+H1a2mzSPOVftnw9lX212//Bd67Qv37yrfg8vc9H3vO58pdOdalGss1b0DaEsjpC0vSIKYMPr3A\nvr2yK1z9phJxAAP2wpvXuJ//jWvgo4vx+TMYuc34npntzdfk5TdgE+uP3QtTPZRxvOVF2D7K/Tdb\n0wXO/a9dSMxaAg/Nh7owePR+WOHiwPAkQr32vQUCLHDPE3DcLxBoVZbBTy6E/f3d903ZDi/fYn/9\n6H2w+ARAwKBMeONa79dyEzYODMyC//zV936f8zmUGVgiAyz2311ivnpvKTsgyAI/ngjP32H/vP2G\nwf3xj4fdv7+OFnLzgHmqO/Zm524iUCVIbpJSvtGejhxteBNyB/99kMwbPFuCbMysm0lgmH0KmPdS\nnmEwuLe0am/p7Oky3bBqvS/nBch7OY+sW7KI+1Mcwz8cbliHyYal1kLlqkq6jOhCaE/nKttSShqL\nGgmOD24WaTlP5DgVzRz04iB639Lba38ACt4r4OBLBxn0wiDDgsTrKyuZuNEuEv/xlOD475y/p57X\n9WTov4fyaE4O/8hWfcgQQ5DpzoUyAfb1tw+0p8bG8u8hQ0he7b2AriNLx45lZrTxlOyEzZv5udx9\nWpuYD19+GE3QITN9Hu5HYoR72vxscwSnhMVwl1kJKddBPycZrv+38cOn/z5462rntjMXQlWUz2/L\nJ7xZQ576O3x3qnPbBNbzDH93aruXx1jNVI/nCTTD6f+Di78J4HD/QP51ViMX/J/xjPq7k+Hpv4MM\ncJ+Jv3oDfHa+5/4e9zM80OQ+WzNJPeg7WgiBuxgC+OkE5dZ0xduA19kkhYRwyKTKzCQUQH2Yu2Wi\n5yFlCarqCq86uMmeuwMWNbkFh/4Go7cqV+2aKRgSYIFJayG+SIk7VyF71ldw+wv21xd+DIVtWLDA\nVXRd+xpkDoFz4+PJrK1lS4176ZfhO53fG8D7l9p/f11q4JvT3a+18Ey7dRRg7Ca4+0kIMcELt8HS\nVkRvGFnF3rvM/b5qC8Kqfk/tJf6wXZB/ewrsSFGegR9Pgr0tmIDiiox/u0/crSYtZ34NQipLXk1T\nbe0xERFdIwgVAAAgAElEQVQkhoTwQ9kRXqJLwkk/wpVvq7CMbaMN9ulgIdcX6Id6nP0C3AS45k03\noOqw/e5SxoyEnLXRyvpx630qauoq4mwUfV7kVELBtUCtK1azlbXD1lK/19k+P37deKJSm5Z12VZN\n5i2ZTtmV/Rb0o98D/VrsZ0dSvqyc0u9LiT051qkAro0ik4kfy8oYHxnJ8IiW60ln1tYyZK2zizTA\nAj9mJBL4SAFhA8MY/e1ougzpwrclJZy2zXlB75V9R2EeuxNLpb1Wlav77Jy4OL4obluU7JcpKcyJ\njWVdVRVpm1uuXVYxYwbdlreuXl6PQkgsgN1DlbvTE8EmOGORcld8cxoc6Nuqy/jE6Ytg7nPu7VYB\nxxvEfkxhFY/j7JN8hPv5mVaapZoIsMCyz3vwWf5h3rja/hB3pGsl1ES4uNQ80DsX4oph62jf9vcX\njtYrm0sNqRINpq9UWaI3vgr57S8u78a7w4ZRZbFwc6bxxPQviYm8U+BcG+zg1KncmpnJ5238nRxJ\niqZN4+StW9lQ7R4KE1MK9z0GqRtg3ny7mCqaNo0DDQ1M2GBcB+za1+CiT9S/H7nfPuFaPm4cMzZt\n4pH7nRMldozwkCgiIcBqv/dmdOvG8grvGfPjIyPZWF3NQw/aJzdFccqdahQWYEPgbKE5FnB0Vdos\nnp6omzkTIQRhS4/OHMzcKVP4tKiI46KjGRcV1WlZq2nABqOs1d8rRkLOU8yYK6lbU4kc5fkus5qt\nNOQ2ENIzxFDsuSKlZPvZ2yn5WpUdSflviuFSKjW7aij6vIjQpFASLkto1xJfHcm9+/bxxAH3GkJ5\nU6fSKzSUCrOZ83fs4Mem2dTs6GjOjY/nJg+DDcCOiRMZ0SQGw5YsocHDfZ1tTqHy2Xy2htZz+6W1\nTsHemtbhyTX48k3w+bnu7TNZygKcg2a+4ixeoA3+0zZySY8efDBiBFm1tSyrqOCFvDxDS4snNqem\nMna9/8uBBJtACud4LICQBhVs74nl48bxTkEB/8lv/eoNf0lM5O1hw5pfW6Qku66OfJOJiV27EhYY\niJSSlw4e5OviYk6KjWVunz4ECsHf9+7lmdxct3NOjYpiVWXrFrJvCwv69WNi166c4jJZ88b/jRjB\n+T168GNpKXO22otdfzpiBOfvNK7tlhwaSs5UZTH+qLCQS3ap8JibkpJ45ZDnot/DunRh/YQJdFu2\njNAauPgjFVO38Czl8rVV3bksIYH3C41LkljS0rhr716ezTMOb9iWmkq91erkoXBkbu/e3JOczPRN\nm9hTV8dD/fpxT3IyIQH2cSGjrIzZW9xXG/HG3N69ebh/f8IDAzlxyxYWd5DV6+cxYzi+lX0DJeLC\nAtW4+kJeHrdnOXvBLk1I4AODz3zFuHHcsGcPxY2NPDZgACfFxJC0yv/1G/dMmsTgLnbjTaettfpH\nxFXI5b+V3+JSPGOXjiViVATB0cbrabYX2xIpR5ofSks5uelBeHZcHFclJnJKbGxzvJgR++rqGLim\n5RUMPhw+vPlh2RoEcHjaNOJXtlwjYNW4cUzd5FukdUqXLuyo9X/g/bFG96AgSsxmt3bX+J7Fx8Oj\n/7C/Ns2aRUjTrPg4fuYBnNP/9tOXK3kHgDt69+Z5D4OWv7CmOa95Wd7YSMwK31bKsA0Q6yormeQy\neH48fDgDw8PJKC/nx7IyMsrLMXt5tlrS0ui2fDnVFuOVDHyhcsYMugYps8vde/fylIGw8sQDffvy\nUL9+bX6evFdQwBW/uYZMw4+jR5MeHd38nbeHgWFhpHbtyv8VOa+0sm78eFKjlDdCZGR4PD5nyhSS\nw4zN1msrK9lUXc1Z3buTEBJCwBLjGNrqmTOJCDSebD954AD37DNOTKqaMYPIoCB6rlxJgcl4pZPn\nBg7kjj59uGLXLt5zERbbUlMZGRlJo9Vq+Fk2zJrVLMg8fQbmtDQCffh+rVLyRVER/ysp4dz4eDZV\nV9MzJIT99fU86jLhfnrAAO5Mdvbvn7FtG/8rca5t2jc0lJ6hoaz2QdSnR0fz0qBBjGqaIP1z0CBu\n663CcGZu2tSiVdKR8hkz6BbkbIrcVl3NJ4cPkxASwsU9ehAbHMzC4mLO2WH3jH07ahSndO+Obcx3\n/F1Um808nZtLfHAwIyMi+E9+Ptf07EladHTzfo7j27MDB/K3Pn14/dAhrtvjHM5zVvfufDVqlFNb\npwo5IcRJwA3AUMD11yG9FeA9FnEUcpZ6C8vCjTNI4/4cx4hPRhguvnu0IaVkW00NFikZ19W4dIdV\nSvbX19MvLIwAh5vZbLXypx073H6wjvw0ejRToqKIdPghSSnZU1fHsLWtzxo9GpDp6XxQUMBlBoNW\na4gNCqLUQAi1F9OsWRSaTHxy+DBToqL496FDfHjYuLhr0bRpXPHbb3xbahwJ8Vj//tyXnW24Taan\nU2QysbKykulRUbxZUOA8iEkIbrQniERSxWdRbxNn3c+28Mu4qmgcc/iee3jS7dyFIwoZHRHR7F73\nx+dtxA1JSbw6ZIhbe43FQuQy599379BQcqd6jt0D9fDeUl3N8TExRLkMHlJKTFIaunayJ0+mX3g4\nBxsa6N3KGX/W5Mn0CQ11sqqAsqY9kpPDsvJyLk1I4MTY2OZz39yrF9f27MmwLl0I9jLZag1SSjfx\nMzUqipXj1bqpBQ0NXLBzJ5urq6k0EKtXJibydoHxck4vDRrEBT16EB8SgkVKnjpwoPm+/M/QoVzd\ns2fzvvOys1mQ4541v2HCBMZ7eMYZXjMvj1uz3OOXZXq61+OMRNTW1FRGRSqPzI6aGkaucy88OCYi\ngs0TJza/PmvbNr5uerZe3KMHH45wLplU2/QZdjEQlZ8dPuxmUUziIFtGdiM6Op2gIC8+SB9pyYiQ\nV1/PopIS1ldVMTs6mksTnYMUM2trmbBhA1Uu98Kg8HB2TZzo1Qjgq9Xv+9GjmRPrvWyWKx1pHDES\n4dsnTiTFJYyo04ScEOJUYBEqe/VE4HvUqg7TgRxgmZTyyvZ05GjDUchVbapiw3j3+IjpxdMJ7t4x\n1jd/U9LYSJyL5cH1IVVtNjNi3TpyG5xz4R/t35/7PQzw3pjfrx/z9+9v9XFHCxMiI1mfmgpAsclE\noBAIYMS6deR7mGUbYbOc5Dc0eDXVb0lNZW1lJX91mcWFBQRQbzWutOv6HXoaOFz3/VtWVrP1Ky44\nmE9HjGB2TAwbqqpIdYkFOjR1Kj1DlX9PSklt7S7KRQ96r/W8tuENvMr5fNb0KpBfE76juDyD8xoe\nc9ovPHwwkye7J6EAlDU2EuujtcyRZwcOZO5e9wLOjlYMVz4vKuK8HTuQwOndu7Nw5EiniUx7KDKZ\nWJCTQ2xQEPf17UuoQx8O1NfT1yW55rmBA/mbQf/rZ81yOvZIU2OxcOrWrSytqODfQ4ZwXZJxEF+V\n2UyUSyyoJS2NMrPZ7ZnkajFtiVqLhQgXEf5lSgpnxxvX4vTGOdu386VD3N/OiRNbjN3dXVvrNEm9\nLzmZRwfY69BIKQldupRGl3HW0ZoKSoj/WlaGSUpOiInxeJ96YurGjc3WrxS287L4O8h6wsL6M3Hi\nDgID/Z2S2T7qLBaKGhvpExrq0/ddbDIZelt+mzSJIeHhSLD/Xmtq4L33IDkZTj4ZPFhUO4vdtbUc\nbGhgVteuBA0fDrYJw6+/Qnp6pwq5VcA64A6gEUiVUm5sWpD+B+BuKeWn7enI0YajkMt9Ppe9f3N+\nsPZ/vD997+mACHI/YZWSosZG4oKDeSA7m8cNYtJAPTgrLRb+feiQRzfB0cihqVN9il9YN348N2dm\nsqaqqtXXaGlQabBaeePQIR7JyaGwsdFt+7AuXdg5caLTOVZWVDDdwK3rGNfx6sGDzfGASSEhZE6e\nzM6aGrdYmJ9Gj+YEgxno7M2byXDJlv08JYVzfBzczFYrtVargZXJypYtx1NenkFQUHcuNz9FNgMM\nz/GLOAkh7Z9Jz55/JSJiNFlZtzjtFxk5jtRUz2smSikpNJnYXF3NsC5d6BsWRuLKlRw2+Lz/3qcP\nTw20OwZWVVQwremzLpo2jbgQ7/VkcurryW9oYELXrn6zXPnCV0VF3LNvH92CgnhtyBDGdu2K2Wpl\n+qZNrG26b0unTycm+NiYNHqiwWql0Wp1stgDFJpMFJlMjIxsu+VoQ1UVu2trmRMbS/c2fk71Fgtz\n9+7lh9JS3hk2jBkestFdKWhoYHVlJTO6dTO8x74sKnJy492TnMzjA4x/N+2hzmJhW00NIfsvo7z0\n6+b2wYNfpVevdlT+bSP19QfIzX2aoKBokpPvITCw5YQ2b5isVpZVVDA+MtLzb2HLFhg71rktMxMG\nNaXGPvEE3Huv+nd2NvTr164+eaSgAHbvhilTIDQUpAQPzxQBnSbkyoDzURY5MzDVVhy4ad3SO6WU\no7yc4pjDUchtPX0rpd84u6NaKu1xJNlYVeUxw+r3wPx+/ZjXrx/76+ro7yXuzlbnzcgi4Ig5LY34\nFSsoa3J9vjtsGJcntqF+AWow+OjwYfqEhnJ8TIyhVeflvDxuaZqVjejShR2TJvl07rz6ei7cuZPM\nujquTEzk8QEDDIWmlJLLdu1qdrGOiYhg3YQJ7RYnJSXfsW2bvaZIccRpnFdzp9t+Z3Tvzt9KnPPs\nu3c/nejo2ezdO9epvUuXEUya1Lol2qxS8mhODg86WHvPi4/n05SUVp1Ho+ksbGEtEhjji2A9fBjK\nymDwYI8CwBMZGc7PhKioKYwf7zDpLS2FgwdhxIgOs1ZJKVm7dhh1dcranpj4F4YNe9u3g7Oy1PsG\nCA6G4mKI8qF20g8/KAucEfffD48+6t6+bx/07w+1tbB/PwgBy5fDp5/C4sVw1VVw5ZXQrRsMGwbl\n5Uqk7dwJc+ZAQwNERIDjd/rcczDX4TlXUKA+7wkTDLvWmUKuBDhPSvmLEKIAuFlK+d+mbScCC6WU\nnmtoHIPYhJy10cqK2BVYqu2+/ZayUjuDWosFk9XKgYYGNlVXc3ZcHN2CgjyaoI8m3ho6lLCAAPbW\n1XFejx4M7dKFt/LzuXq3czKJzRXmOKO9tVcv/jloULOAuX/fPh5zsTZOj4pi6bhxTiLKU0BweEAA\ntbNmAUqEhQYEdEpCyZ7aWkobG5kcFdXq6/kS12GVkp/KythbV8e58fH0aMEa5Qt79tzEoUPOy0bM\nNlidr2LGDDYud54xx8TMITo6nezse53aw8MHMXlyyzUZPVFtNmMBtwBnj/tXb+XgwVcJDx9I7953\nEBDg23GaPyBSwm+/QffuSkiUlYFDfJ5Hqqqchcfrr8NfDaraWq3KvRYaCjOaqsRaLEpY2BJX5syB\n//s/JSQcj3v/fbj5ZqiuhjPPhBdeaLYuuQq5iLARTJyyQwm4jAz485/tG99+W4mf7t1h2TI43r4W\nMqmp8PHHdmuWI/PmwYIF9tfffeckoqqrt7J+vXOh7/TRJeDoQaithd691ecKEBYGH30E55zjfr0v\nv4SzDZa4sLFggerTkSIuTln+Kiuhb+s8dZ0p5FYCb0sp3xBC/A+IBs5DWefeB5KllG1f0PIoxCbk\nKlZVsGma3RUWHB/MtMJpRzR79ImcHO41iFnbPnEi52zfzh6HlQQ6Cpmezr66Ot4pKOBhg2BjTxRP\nn+7V9VFhNhMiBOGtmCkuLC7mgexsrk9K4pqePQ3jS4wC2sGeXfZHp7JyDbt2XUp8/Hn07/8wQrh/\n/ps3z6a8PMOpLT1dct3u3byen08gsHjMGNJjYtwGk9jYU4mKmsT+/fOd2kNDk5k61ff7pz1YLDWs\nWtUbs1m5nfv1W0C/fg90yrU1fmTZMmiafAFQ4iIQjCguhu3bYfVqZYk6/nhlSfFEYyMYTX4CA8Fk\n8mwlO3DAeCBviocCICcHZs60izUbZ5wBF18MF13kdjighE94uOqDUcxsZSVUVZGxx3lZxoh9MPFq\n9919prhYxZ3deissXOh5v4QE9b6Skqi4aDSb6p2X3Ei3FRD/5hslUFv73N2xQ313NvLyYMgQ6ITx\nriPxh5Dz1Wb7IWBL95oHpAB5QAFwHPCgh+OOeYo+dU59jz4u+oiKuNcPHTIUcQAj161rUcR9PNx9\nnVNXxkdGYk1L464+fQy3m5oeogPCw3mgb18uS0ggITiYKxISqJ05E2taGi/bTONNZE2ejExPbzF+\npVtQUKtEHMBZcXFsnTiRG3v18hgkHBEYiExP5yWH2eXa8eO1iANqa/ewceMU6uqyOHDgcXbuvNhw\nv8ZG4wKwrw0dikxPx5yeTnpMjOE+QgRitboniEjpe9JIeykoeLdZxAHs3/+7fWz5TH19Hps3z2bF\nikQOHHDPKHajuBhuvFG5oN73sgZX+zqlRM2ECbBmjXJLgbKQLVniLOJAWZNcsVrhuutUP4WA+HiY\nPVvFR511lnKFzZ6tLGDr1sFTTymxYsOT+9NiUULq3nvVeW+7zbnfnqwxs5tUzIYNynJmVCpm0SLP\nIg6gSxd1TQ+JTzzwAPRyX1u73SszxMWp9+VNxAEUFsJ//wsvvghXG6ybZuO001ov4gBSUtT7N5uV\nBa5Pn2NexPmLNtWRE0L0Bk5GZa4ullIaV1M8hrFZ5NaNWUfNVvsPfPjHw0m4MKFDriml5PasLJZW\nVHBFQgK39e7tJBpvz8zkhYMHvZzBTjAm7uZJprKKDUxgfcxTfDV6CkIIr2UP/ta7N88MHNh83dz6\neqKCgnx2XTnSaLWyraaG0RERXtPLNUeWDRsmU1XlXB4mPd39ubByZU9MpoIW9wN39058/LmEhfUj\nN/cZp/agoFhmzPBc0saf7NlzA4cO/dupzVP/jwkOH1ausfHj4YQT1CDnK9XV8PLLZIa/ycEx9rIb\nkydlEh42wN3ilJ+vrEFGQl1KZWWyBY4//7yy3tjOYTIZW7ccsViUkNm2DR40ENhz5yrBdt997ttA\nuf9soRkhIep8beG772DVKme3oS/YBJ43/vlPuL3ji19nuEQ7dNkPkzq5pkTFcNjkHIVht8h1Fq+/\nDte2sNDrkeDqq+E//4G//AUiIxGvvNJui1ybzBFSyjzgP+258LGAtdFK7S7nYrC2hdj9hWtl7Qiq\nGcIeHqruzx1799IrJITtEycSu2JFq5ZUmckyjueXpn8v55oeuxBC1cXqFRrKgSlTnNYUXT5uHNO7\nua9t2sdDQU1fCA4IaFUtJ82RwVXEecJiafvsV4hQrNYGt/bOtMg1Nh7hdRf9hacMuJtugpdechd0\nUiqhUVioLFM//KDiqoCDLoP+wb8PZpDLANwikyYpq5aNO+5Qf6689x5ceim88YayltlYsgTSWlhc\n9NlnvW/PylJB5n//u/f9WuKUU9p2nC9ehE4QcUcLfvFZvfqqsv62lgMHlLUOIDGx+V5vJi9Pudk9\nJUZ0JCedpEQcwFtvqd/xK0brtbUObSbxQu3uWmSjXT6FJIUQHOu/EgCuIi6KCv7DNTzHXL7kHHqR\nx0GTiZhWijiA+3Cu17Vnj/MPok9YGDI9nYNTp1I7c6ahiNP8cbFa2168WEp3a0hAQJiha9WoraOw\nWAwqxF91lYotaon8fLj7brurzluB64MHVTyUzaXn6kb74Qc1G//uO2M3mZTw/ffKOoX6PGtrdmN+\n8kEV9O7Juv3KK2qbrY+2v4AAlf3Xu7cKrHcd2BywtGXe5qFuoRuXX6764ijioGUR5yvtFXFHG//3\nf345jZNrNToarr9e3ZOeVsXwx+fY2gErOxtspYPCwmDjRrjhBvj559adx2KxizhQLvoDB5SVeNEi\nlWXaq5eK0du3T/2m771X/dasVmWNXbhQxSNKqdqys9Vv5sor1W97/XqoqFAu3vJy40nGgQPqHK48\n4rCyjR+9VB5dq0IIK634OqSUR7bqnp8RQsiCDwvYdYl9uajYk2MZ/d1oL0f5jlVKAl0qo5/Hp9zI\nv5zajLICbXyRkkKv0FAmG6y19yvuduyxYzOIjvbTQ1Pzu8HVDQoQETGSiROd17FcvjzGKcYMjF2T\npaU/snXrHKe2pKTrsVobKChwL0GQlmbt+LhTKdm4qD+VUc6JFc3unm7doKhICR4pYeVKNZvv3x+6\ndjV+KP/4oypJ8N137uLElaIiFWs0cKAaQBy58kr417/gtdecY65Qg/DW93pS1iuf4HIYfSd0da8V\n3GZc3XCJ38Gwp/x3/rYiA2Drk1CWCnFLYfhjEOhu0O0czGY1eE+Z0rrjamq8J1RERytLopRK8Dvy\nww/KegPKJWtk4dy0SbmUXbwert9pePgQJk9WbmeT6TCHD39KRMRwYmKOV/f16tX2TNuZM+3xax9/\nrJIvbPTpowRWdbXq94wZSnSZzTBunLJyNVE5FDY6RzGQdnIIosFg4lZV5TkmEZTL3GFNYDfuvFMJ\nNtfYyc7EZFJhDpWV6rtyDEWqrlYTv4kT3b4r8M/KDt4k4QKHv4eBg0Ap8C7wFPBe0+uDTfv87qjZ\n5ryYdsSo9hU0dOQ0g8Wez+Rrt7a5POPWBmqR+D/FxzMpKopfx4yhi4O6P8lDwLnKOmz/Goia3z81\nNUarNvj2rMnNfdqtTUqLoWsVQC7+XgVTp6QowWPDZFLWHk/B3b5SWgoBAYj9XrJjKypUbNW996qZ\n8owZapAMDDQWcaAG2uTklkUcqIE6IsJdxIEaAMLC3EQcQMUIKOuVD0BjNOy7vuVLtQfrUZL7s/d6\nJeIAimdB/mkGO/lS5qFHD+VuzstTgklKZUXxtRxPTo66ByZPVlYsWy2wHj28H1dZqZITPCUIfP65\nKrvRvbsS+NXVqs7Zgw+qumM2EQfKJSulEky7dqmSKFarKnwbGenD76NpqUlLHevWjSIr6xa2bDmB\nQ4deU3087jiVADJ7trMAuegi+2cmpbIyxcWpWMgTTlD3LKhjtm1Tmb5ff63qr61Z7d6L2hp1nrIy\nWLFCJUY0NnoXcQBDh6rjPvjAuf3UU9XxTz99ZEUcqPvpuuuUNdM1njwyUn3GHRhm5FHISSnnSykf\nklI+hCozkgP0lVJeJaW8t2lJrn7Agabtvzuqt1Y7vY4Y3XYht6W6mv8VF5PftPzV9wbrXdbiXorv\ndL4hAecA810TJzLCYaaXHhNDzaxZyPR0ZHo6P4wZ43qaJiS5uc+1+T38kbFaTeTlvUBOzuOYzb4v\n4vxHJMDiHn4gP/kIuW+3wd4gzzxVDRI7d6oB0hZLFRqq4q8CA1Wxzh07lLtl4EAVTG/zJtTXqxIU\n+fnOLsV33oFDh4yzGpuwuj4Bn3iibW/aFzwJQi8Uu4xPNnHTUUhfIkc2b1aWGSP89Pnlnef82mlB\nkLffVt/3/v3KGmPEqaeq+6OwUNVbc8zm7NZNudhsAsWTEEpKUkLdRu/eyjJnO6+U7vFN116r2m2D\n9plnuguVESPca6VFRKhEjoceUmU8jAgMVJapoUOd4yCFsL+PTPeajFKq91dSsojGRvs6zPv23eu2\nb7sIClKWseOPR+IeXiFlk0yIjoZp01Q9u9Yk0V1yibOw/OabtmW//g7x1Ul7HfC0lNLpSSSlrAGe\nATp4nnhkcMxWBVpdBFhKyXsFBYiMDMauX88Z27eTtGoV5+9wr2T/7ahRzEqcYXieEaik4NXjxyPT\n0xnWwvp/3igpaSGFXGPInj3Xk5V1O9nZ97Ft2xmddl0pLdTV7cdiqWl5Z2/YlrQqKvLZwiWlVOn9\nixc3xXMZRFo4DnRNRC7a5dYm62uwbjFebcTNCnTFFfDhh85t/fvDyJHw738rq9ZLL9njwcLDlaXA\nda3PK690GsCtBiLF2vZcnk5BeJsin3SSsjYarMvaItdcoyw8LshTTlQiyXHAlNJ+30gJY8YoV9oL\nLzgfvHevijmyiYqPPlIWpqY1fZ0IDlb3lGPh3L177dcz4sUX1bn+8hd73TjHmCMbH36oBnlfEUK9\nZ1cMntONjSXk579DZWXTijI33qjE3XPPKdfia6+5n2fDBjUhAZg/vzn20e8IYVi8t75e3R9VVc6/\nP7O545J/jOJkpXRfVk/jH3yVs3GAJ1t0COB5ynsME9Q9CFOhCdkoEUGCLsN8X7yi3mKh96pVlBg8\nLD8rKnJrO6V7d3YUGM/YPxjSm6SkdJ+vrfE/jrFdFRXLaGg4SGioe80mf2K1NrJ16ymUl/9MSEgv\nxoxZTESEQ6xIRYWyOiUkwIUXGp9k507lsnTljTdUwO/+/QTRFTPua9FaP/uQwAsuszd8BbjmxOTm\n2mtbCQHffIPM2+92LhlgLKTARyuQH7AaPMEsYRDUekNZy1x+ufpMXN1BrcSwBtjmzUpM2YiJMRY/\neXlKNJx4os+Wi+K6n5AxMe5O9Lg4951vvVX9GSGEc000KeGzz1SF/quvtq8gUNEK6/Ytt7i3Na1j\naSrPISg0hoBwH5ZyMiI2Vn1fn36qsmifeMJtWSiLpZ7168fR0JALCFJSviA+/mzlbvWw/BKgitZ6\nWUqwM2hsLEOIzsttbLa+tdD2R8VqbaC+PpfwcP+suevrN7seeEgI4TTlFUL0AuYDPqYtHVtM3DyR\nmTUzmbh9IilfphAQ6tvHlVlbS/iyZYYizohH+/cHPGTV4d/MvoCA39VKakeMxkZ313i72bVLDXRN\nNbAqKpZSXq6ytkymg+zbd5faT0qVuh4dreJnLrrI2aXYtataL7CmxljEgVoyKDkZZs3CWu8u4gDM\nN1xm2O5Is3ywWcdOP91QMMlAkB60RGfFZRla5PKy4PTTWz44IEDFMUmpiuJmZtpjhEC5Gi0WZcGU\nEt59VxXMdbUs2qisVPvPn+/cfuGFdsvXmjWYEtw/HDnax4Sr3r1VOY1Wup8c19P1K+edp6x0jstA\n+YgQoYbtUkp27bqclZv7sXrTCKqqPLh8fbsIXHCBKnthsLbn4cMfNok4AMlvv13R9mu5YLWa2bfv\nXtatG8vevff4PZv70KHX8FNREJ/QFjnP1NfnsXbtCNauHcyGDV4mAK3A11/4rcAvwD4hxGqgEEgA\npmwUiJ4AACAASURBVAC1gHEp+N8BAcEBRKREEJHiuztziLfSBAbc1xS0azYbl0EICPCfycLoB9a2\n80jM5lICAyMJCDB+yP6esVrrfdsxLw/ef5+y0F0U9NlJ18Bh9Er/JyLWwcJRXOyetQbk/3eck627\npGSRb0Vfq6tV9pmPeLKUNSRAqKNeNZjHyAAQLp5aIyFHAFjCja/TaRa5bmGA8/dmsdSosgRWK7z5\npirJ8Mwz3tfU7N5d/RlVlXetu3jxxSoo37aW5uzZKtvVJq7mzfO8RuSkSRyudZ8MWq31BAZ6+DBb\ngadnQWnp9+0+t7/xlNVcXb2FwkK1woSa7NzNmDE/tft61dVbKSr6nKioqXTvruqNNbtTm7BYfChb\n4yMlJYs4cEDFF9bUbCE8fABJSa0vZuvpO62u3kx4uMGaqR2EsUVOCzmAwsL3qa9XSU/V1Zv9ck6f\nTExSyk3AIOBZwAKMavr/M8BgKaV/evM74MrffmvV/pc7BLZWVhovdm8LVvUHUja0+3xSWtm+/U+s\nWBHH2rXDqa3d46feHUWYzWpQf/995IRxbpstdWXKalJdrWod5ec7Z1zW1cGoUdCnD/XP3ceWMe9T\nGL+BrNgPyb88XrmZNm+GwYMNRRxA6E+bDNv9iQwAPBQOKnfJmTEqMGRkZTO0yA0ZSGO8cXSG5ZTj\n1BJJVqtyQS1YoOKvFi+GL77w/gZcWbBAffbr1qkli2w8+STWOHcri8XS5FcNCFBWyg8/9G1h9NYw\nfbo99uuXX3y2kJlMhYbt/kq28TYZacuKPx2LsZCrqXGONysrW9zuK9XX57FhQyo5OQvYtu0USkq+\na9rif9dkVdVmdu26gh07nJMf9uzxIRPaAE+WPCECDcWwP8cWZ7wkO/zBKSx8z+/n9NnmLqUsAe73\new9+R7yQl8c7BQVu7f8aPJjre/XCbLXyen4+NzVlFv21Z09eG6KWsPX2g/L3TMZqbWjXjD4v75/N\nSRP19dlkZz9ISson/uqezxQXLyQ391nCwwcycOCzBAe3ctWNxkaVZfbOOyo9/PvvVRD2li0qtb8J\nw9iqc+aAse52I+98nMTSnjshafb5LR4X2AnLCHqyxgGYHKvYPPMMMtA9Q1AGAS5jh6GQGzUCS2U1\nNLqLE/Mz8yC6KT1z0iR7YHjzwdL99ZIlqo7W6NGqvpdrAlBqqvpzWGrJusy5SDaA1drOJJIOxGKp\nNmwvL/+VhAQva3L6fH7PN5jFUklQ0JEpEm5cjNpYyBmJA7O5mqCg1iWmOZKT87DTMzcr61a6d8+k\n9VVuvWOx1LNly2y32oztwdNYERAQavhZlZX9QmzsCX67vr0f7kLOatUWOYDa2tYZe3zhmFnZQSju\nFUJkCyHqhBCbhRDntHxk8/FhQoj5Qog9Qoh6IUSBEOJrIYRfInQey8nh9iy1ZuEQdvMCt6q/pBqu\nb8qcCwoI4MZevZrLhLw+dGjzLMmbWPP3TMZqbZ9C2Lt3rtProiL/VCBvDY2NpezYcS4VFcsoKHiH\nnBz3QdordXWq9s8776jXv/yiMr727HEScYdOg7Xvuh9ubkXicF1bDTy+TpYTE1veZ84cJYAWLVI1\noGyX8CLkZBB2S9ncuVhD3U1yRhY5i4GnXUozVqtxVkFjYyvXWhVCrZxwxx0q3srHLG4jC1R7soFL\nS38gP/8dzGZjwdV+jMWLindqP96eAzt2tDzR6CgKC90TRDwF6hvdU1K2r3Jweblzofa6uqym8/r3\nOVxc/KVfRRx4E3LhduuzA/n5/rmX3Puhkx06k2NGyAGPAA8CLwInA6uAz4QQLS6Y1iTWvgeuAJ4G\nTgBuAPLw6FjynX6rVnF/dnbz67t4itFsYzTbmFb5D5/O4S241f8WOR/ju1pBp7li6urg5JM5/Ofu\nTg+GvDyHZVKkVIU4HRMAzjlHuTKtVlWyoYtB0seBA6pGk+1SCcp61mCgkyytEHKuMWRecSg0KgzC\nXWocVp9prmmVn+9cE8u1juCAAUrAgQrs/+mn5v1libsF2Yb1pqYCl6ryOEbuEuvhfOVeHjJEVS7P\nyqLEoIqOlGbDgQTaIOTagJTScIBva1D5gQPPsHXryezefSUbN070W+ypI54GPrPZP4k23oRcWdmP\n7Vpbtz3s3m20wruxqDWb3RN12isYPK3/6+/ncGNjsV/PB56tXlKaDV3yYWH9/N4Hdb2Wkx1MpsNs\n2XIiy5d3JyvrzqPQnX/scEwIOSFEPDAXeFxK+byUcomU8gbgV8CXCpR3AmOB6VLKN6SUy6WUX0op\nb5TtnL59X1JCToP9FIGYGYi9ent19WafHvLeFg8/2ixyRjgWmvQLVVXwxhvI3FyktKgf+SefKAH2\nww/GGZCOa0uefbbzti+/VLWvAgO9Foh1xLUoqSOtsciZo32I5r/wQvWeCwuVWH3/fUTz+lF2Nn8Q\nh/nHhaqgqVHJAyGUYG1sVNbF5ctVJfhg4z54Wm0BnB+8nu5hKc3KIrZ7N6xdi7mvcTFTi6UKIyEI\nYDZ3vJDzfM+3TYDt22dfj7K29jdKS39s03m84el3HxPjH1dYSxM6TzF67aWycj3btp3N7t3XumV/\newoxEcJDfKXFoGxOO114xmsCmw2/j5KSb9t1Lc+0zb7gSWxarQ2G1j8/OaQM+tGyRS4v70XKyhZj\nNpeSl/csVVUdV/yipmYXhYWfdNg9faQ5JoQcygIXDLjm8n8AjBJCtLRWyw3Ap1LKQ/7slMlq5RSX\n4o7BuP+QfLGAeRtQjR5MZnMlNTW/tWlx8/Za5MLDBxv0p5UuAinh8GFVpuHRR+H881WAupTNNZxM\nd13LxkXJLFkSxM6HArBeZo8LCugEK73FS6UWJyF3++3OS+rYePVVkBKRlu75ROefr8pQfPyxvQJ8\nWBhceiniFPd1iRqtxRSOONTyEkNBQSqRYvp0jyIOWhJyJod/e5rpO7d7sjJ4K9diZFXxNyZTvmG7\nJ7FUUbGCjAxBRobgwAHnZfKysua67V9X515Rv7146pu376w1tDSh64j4Qau1kW3bTqWkZCH5/8/e\nd4fHUdzvv3P9dKfeqyWrWHKv2KaalhhCDYROCiWEAKETICF0CHwJNSRAElOCgQRIIECABIIJGDAY\n29i4F7lItixZvZ6u7O+PvdVtmZmdvVsJwy/v8/ixbnd2dnZ3yjufuucP2Lr1Gt15+tzkdNJ3ToOD\nxmDIqUrOaO8lHN5LrXf9+u+noJ5nS6Dc7uRCs7IEArHYEIaHjdJ32rw9NNSE7u5PLBPi7u5P0NX1\nISRJovZR/fvbufNOze/du3XJWZPArl0PYsWKg7Ft2y9H2t/R8S989tkUrF9/Jj77bApCIbYWYrQx\nONhoXigJCNFxQkgmgKFUpVcpYCKAkCRJ+lG7FrLMfSLkFGIGEELKAZQDaCSEPAHgdMhBjJcCuFqS\npC+SaVB7OIy8pUsNxz16y28o4QL4Ihy+alU7off1rcHq1QsxPLwb6elzMWPG+5ZCgKSqMqG1laU2\nAyCnUHI65cTglHySI3jxRc3PTVcAvRPlv9sWAEVvAbnxCABUtWMlENjObbolDJ4wEwjT41JFr7oI\neFxs4qHuegXUCCzpxNDQdqH7ioAnCVZ/Zxap0E/OrPoGB9mezSzbOTsRCjVTj9NVQDGsXJnQD2/b\ndi1ycr6FYHAqwuEONDUZ09zRvlUk0oM9e/4Eh8OD4uILLIfpYb9ze2KMmc0DfX1rEAgw4hAmia6u\n9xAOJ7y7W1qeRH39opHfPMmvJMXQ1vYiotEBpKfPjP822uemqsFwOgMG9XUk0sXYULejr28VMjMP\nSumeerhc9HzZZmCRr1hsCL29xqDE+tzbHR3vYPXqo0d+V1bejnHjfsEM/6KgsfFm7NghOxaVll6O\nQKDBUMaMYKfqQdvZ+R62br0SANDTsxQDAxswadKL2LPnj1Ak7+FwG/bufRYVFYzUbklgYGALNm36\nMcLhdlRV3YG8PHbmn87Od227rxqmErm4fVk7AIrIYcyQA4Am8ulQnWdBCWJ8PYAqAKcBOANAPoD3\nCCFlVhsTicWwYBU94sreeXMMx8QkcrxQANoBsGvXvRgeloWLvb3L0NHxtmn9VtvDA20hia75VE5G\nHYvJKsK2NjlmlpJCyePhkzgK9h2m/b1VnQiOMt9vuM5S9TIuuUQmVa+8kjh2zjlANIpuBokDgIiF\nGFKEJKsmoS9IdsYVFFetihE5LqFnIOX0Yyncg/Zc+/YZ09h9+eXJAID+/nWMOxiJ+dq1p2Hr1quw\nefOl2LDhfPHGctoG2Of9ZyaRW7/+TCxZQrB79x9suR9AV4WqwZb8DmPLlquwbt0Z2LjxPCxfPh2f\nfz7TUh2ioG26Y7EQs95QiC7tTQXJklG2apXe/wcG1mnil27cqO2n27ffhK6u90zvq5A4AGhufoga\nE9XsmVyuLNP78NDYeJPm9759L6Ox8Rdoa3vRcNxObNt2Lbq63kN//2qsX38ud4PECjGWKkyJnCS/\n/b1I1piEAkLIkYSQmMC//9hwO+UZ+wEcJ0nS25IkvQrgOwDSAFxitcIXWlvxZb92YLgIQduBB1JJ\nzurVCw157vTgTar6AaD36uroeFPz22xnk5KNXE8PYt1G9Vns8p/IqYKcTjkqekGBHIctSdDkVQ7V\nqyXXGFlbbwMgKRvHU07ROgB8xrC/UPJFnnhiovyf/yzb2XHACt5MR3IWDCzphNNpX1gIvkrfXCKn\nl84m07fsUhXywDZg1z5XLDZsiOkFYCSA5/AwXbLX3a2Vzg8ONqKzM7HBam1lZHjgQJQ8JwvRDd2m\nTRchFNqDoaFd2LXr/pSkCmYG7bx+1tz8EPWcsQ5r7ycS6UFj403YsuVKhEK7qf2RR+RoNp6x2DAa\nG2/Gl1+ego4OeoBi3prAe4bW1r/iiy+Oxtat1yEa1X5DluSZZxumtu8MhXYazisBl/Vt2Lz5cnR3\nf0Sdp2gOOeoNCG2NStVer6fHqCFrbv6d4ZjbTY/bmSz27UsIAaLRbnR2su1l1ake7YTom3sWwAUA\n7LLsXAqg3rSUnDUCADoB0Oi6IonjuXEpo2ypWjUsSVITIWQDZCcIKm5Rpc9ZsGABFixYgPZwGDc0\nGvXc/50+HXkeD7q7jQOpv/9LrF79Hcyf3wSHg/7KrUjk9Bga2qX5beZcYTqBb90KPPGEnKQ6LU32\nRnQ6gX/Kn1+i5KOO2px8nJYFIFsRkLW2gsT+DRhzsyMWHoTTKTdm9ervoKPjn/B4ijBnzjq4FVK3\nbp3s8JBC4FdWOjUa7JbI2aVaA/geoyI2cnv3LkZ6eiJgcjJEzs7nYYFFFvVjZf3671PL5eXJErlQ\niJIAHsZdfnf3h4Yy0ejQSN8UAcvcwj4iJ/qtJOzZ8wSamh4aSbQ+adLLyM8Xjv6kviv/TjaQV6vS\nrE2bLkZr63MA5LhqdEP9YWYbaCSpqemhESnVvn2v4MADd8Pj0ToC8QLDhkI7sWbNCair+70mp/Pg\n4FasW3cGAAmdne/A4ylCeflVI+dbWp4SbqOC/v4vAJzKPK8n7mvWHI/29tcBAM3ND2P2bKN2iuYh\nq36vdPOc5G1lWRtr2jzd15eUNZUwuruXwuXKRkvLMwgGp6Ok5CeadX/VKvmfnRAlctsBnEUI+QzA\nqwD2QCc0kSRpEeU6KiRJGgJgJR3AWgBeQsh4SZK2qY5PireDpe8AgG0AkhJBqYkcAEQliWoX9++p\nUzE/U5aSbN9+m+E8IBvL9vYuY9pS8MiV2YSrXwhZht0j9T35GHDFQq0R/O7dwDPPADfcoC08NAS8\nrVXdUnNWJpOlq6YGuOgiORhvb68cVf8PfwDmzUPPP24G1h6jKU5+dhXw2G8QCjWjZ+cn1Cplru7D\n9u23oqNDJp7Dwy1YujQHCxZIsqRt8uQkGquFNYmcUQoRi0WYpD4BOiG30+tYr3bQ3sdcItfe/g/U\n1CScAZKTyI0FkTOXyElSlBkT0emUs0LwnDYkKTYS70whPGpEo92WiNxoh8Gw8q327PmT5pnWrTsL\nhx1m3UTDTFswOLiNetxKW62qnhUSBwD9/asZdYaY9dKcCEbyIstXo6npQYwff/fIEZFQG+3tr2HH\njgrU1f125NjOnfdAPZ9s3Xq1hsixJMa8qAJm70s914VCzSMkTgHd+WeL4ZjWVMNeIrdr12/MC8VB\nkzraiVgshFWrjoAyf0ciXaislMOQZWcfhenT31GHKsXTlDilViFK5B6N/18KgJblVQIgTOSSwFsA\nIgDOBnC76vg5AL6UJInq6ADIqmFCyBsADiGE+CVJGgQAQkgFZKmg0SCGgVu3bzccu6a8HEflJEz0\neGJV3oLFI3JDQ8zHo9ZLW0Q05d/9J3CdidcjAxJAzY2phAOJOQDJAzj1j1NcDFx6KXDjjezKDztM\nlgQCWL2Ekk7G60Bn53tYs+Y4poG8InnZtesBw7lIpBcuVzr7/jqkpU3EwAB9j2Bl0qEb1IdgNvxY\n5CkZOzQWeI4T6j6p9y5UEAxq05cl40jDIibR6AC6u5ciLW0CfL4KAEBT0yNoaroffv8E1Nc/Ca9X\nTKrK8tNSfxsRe0FeDLdIpAdud1a87UabpEik2yCV4YFt72QPkbPyrYaHtUQgWb832gKu3tQ0NT2Y\nVL3ae4hL5PSqSRa6ut7jjEfzucD4/sTauHv3oxoiNzTEJyE5OcdQpcE8sDKIKFAHY161aoHhfFeX\nUdXe2WlUJ2slcsb+Y21zrIXetMEMH+/6GFMLp8LtdMPjTKyF4XAHCHEDDj8isQh6Q73oG+7DYGQQ\nHqcHy3cvx+q9q9E/3I+oFEEpvsB8XXSD5uaHNb+3b78Ju51H4KLXL8Kt1V8iJ7mllwtRIldl/63F\nIUlSGyHkfgA3EEL6AKyA7LCwAIDGRYQQ8i6ACkmS1DEybgawDMA/CSG/AeCHHFy4A8BvIYCucBi3\n79ASqrnp6bizSvtqXK4sZigOnoqNR+TUXl406CfH6FaegBLYcD1QZM0/InEvRo+JHXkYBr57KNZM\neBKDUhMKM09D/bTnQTi2ZpIkoavrP4jFhpCTcwwzevvIPWJD2LLlcq6XozJB0ETq4XCrJSLHCw9g\nZtcVi4XR0/MRfL4q6oIsp0njezKzVOSpSOT27HkKu3bdB7+/BnV1jyEQmIzu7v9Sy6oNpFmSO32f\ntku1Go0OYfnyGRgc3ASHI4Dp0/8Dj6cIW7b8DIBMQHftuhc1NUbCTkN//1rGvdWLi7l5Ay9Egprc\n0Iic2YKpB1uKmJoEc3i4FQ6Hz6LTkz3BWmmbEPWmxo64ZpIURjQ6CEmKmI73MCVlHA07d/4awSDd\nuUKMEGs3plbsQiUpOjLOzOaMZGAWZkb9TWiSNlG09e+BP7MPQU+Q2ofX7v0ML/7nJjT1NmFd2zpM\nK5wGB3Hg46aPcfHsi3Fy/ckoDMobofVt63HO38/Bij2yvc2/DgHcFkyRD1x0oOZ30AWcVwmcXAr0\nhIG7NwCfmMTdPrsCOFWQGR206CA4CZBjdOa1BUKjhifxGkPcCKAXwM8AFAHYCOB7kiS9qSvngM66\nXJKk9YSQIwDcA+AFAGEA/wFwrSRJfJYUx4WbjJrgZxsa4NERlczMw0bykOrBNyxnTwampGHTOmDN\n00BzM3DTTYhNiwHGCAkaDJYAftGoetnZcvT+vDzEplQDMO74pLNOx87e5RhskW2I9nb/FaV9VyEj\nYy6z2sbGm0ZiCRUWfh8NDbKMmZXyKBYLGZJk08oAgN9fZwh5QVtcY7EQBgY2wOerNOSW5KmwFK9h\nGiQpipUrD0Rv73I4HGnU3bfIRM4icslK5Pr7141EzR8YWIudOyu50gQRb1J9W5IJJUIjLK2ti0e+\nXyzWj507fw2/v05TpqnpQSEiJ0kSmppY5axJ5HhQPwdtcbSqEmURNpq0QxSNjbdgx45b4XCkWQwt\nYk9yddp7UYdnysw8MOWUf+3tr+PLL09GNNqL8ePvRkUF253dSoBYXow2NXp7V3LrGQwPYm3Lp8L3\nnfuIC591Ag7iwN+PPAAZuvPkVpkklmWU4YjsJvyoUrhqAMALa57CrX95CgDw3mHG8y19bSP3oJ0X\nxc/evATvtsq+hcU+4Dnd0jAQasUdn98x8vvT5sQ7uviNi3HxGxcz67ZC4tRwALh5InCoyv8hwy2T\nOjMid4FF8Va1/Rx8BJa2P4SQqQAOBZAL4HFJkloIITUA9kqSNKpRPSXZqOCu+D9eOWM4fPn4cgBH\nJnPvL/v68FKblu/9uLgYNZQ0T7xdN1+SxLORi08gkgTcf79BuS31dwMX/DDRBgF7ta7pHCL3wx8C\nixbJoUPi9+/oeBMeT4msGvrEGH9ZksJoadFq15ubf88lcuqAkHv3PoPKyl/B769m7hBFJAiKVMTt\nzsGgjhvryXIk0osVK+ZjYGAtPJ5SzJjxX/j941Xl+QtvT89nyMgwhpvZu/d59PYuj9fBVwHzn4Xl\nwZcckVu1SjsLd3X9B4HAVGZ5EcKo/1bhMF+tTwNtgdy48QLN7337/o6ysist1w3wF2tRiVwsFjbt\nD+pvSt800IlAONyODRt+hN7eFSguPh+VlbeAEGKbClV9nx07bo23ZcAQSZ8QNyf8hz1BC2jBn/v6\n1iA7ewHWt63Hrrb1SFXzpI7zt23bz7G4sQdOVwZ6Qj3IT8vH2ra1aOppQlVWFU6oKIOoee+mfV+i\nlOKE1TGwB29ufhPHPncsAOCX9cCROg36luZn8cedWfj7hr9jW+c2fKsQuEHE3Q/ASaXAZ51AhisG\nx+AnhlW7Ph3Y0As09TTBkUT4OZ8JCbKHwgMuQv9bQYZJVCXlmohOOJwMh7ugCvhjIzA1S0viFNRa\nUdwIwE2A40uMx6/nyyWEIRoQ2AvZc/W7kGXEEoDXALQAuBey48L19jRp/8N9u3YZjt1c4sGKFfPR\n17cKxcU/Rk3NgyCEcDMc8CQcXLXOQPcIqQIgJyZTX6sbADEBe+qN1wLF2ycCVVVyqI5x44BDD5Uz\nAqjvLUn44otvobtbTiSdlkaffWgLgFVbjWXLajBp0t+Qnj6bel6E/Chl6CEEtG3cvftxDAzIKrfh\n4Wbs2nUf6upkd/WhoSaEQnxB9LZtN2D69HcMx9XG0yyI2BixFk8zVTsL+qwL/f38gK9qkub311Kz\nF+jJXjJ5QPXfhU0gk9t28zZXWhs5vmrVitMRbayzJDrNzY+ivV3Ohbtjx23IyzsZ6enTbffm7e7+\nOIWrjarVk144CT2hHnSHulGeUY6ZxTOxt28vdvftxqoW2S1ve9f2kfK//87vMc31paGeR945HDfH\nrUG+Vwb8tDqFZlLw3Io78SXD/OqzrcC97L2MBh5G9/ty7wpc9vaxI7/1JA4ANvWE8JvVskF+wClO\n4gCgNihf86fZsgpQjx+MA26Iv1YnP24vFa74c7FGl10pUNVto71L1vsFgKmZwENxB4FndgBPbpf/\nDrqAS5LoL2dXAO+1AnN5EWhtxHHF8j89Dqq7CsvM1GcCEJXI3Qk50fy5AP4NOa6cgjcB/BTfUCLX\nNDSExa1aQ9VHamow2PoIenpkz8nm5odRVPR9pKfPYnoNAQzVSiwGvPEGYp89AhzBuK4zsQAPUXYP\n+gTuw0Kd0wmspdsNqdHXt2KExAFyXkka6FHP2dIZlvfa5s2XYPp0ls2WeGBl2rs25vrTqtt27/49\n6up+B0mKYfXqhab3ohn5AmLqmlQkcjTXftY9mpoeQSTSiZISulqC50UYjfZDkiQQQpi2OXrpYDKB\nTLVhTmJYvfoYajmz6PIsRDnBm80MsBPlwoiY2LjFYiFEY1FsbN+I5u4t0AsYFIncYHgQWzq2IOAJ\noGuoCz3bb9aUe+2z07GRnIFYzys4khEysOHRBmzYpx2LOf4cVGdXw+fy4YOdHxiuWVgI/JxDIPYM\nhlFkIYzQqxsTJiQr9qzQ/Kbh4jcuxu2TgIPztMerVF3Ln1yknqQhSnxiEuBlEA3Wcc31qr9PKxe7\np4L+CHBCCZhG8vNU2bySIXJuwr82FG98ZopxyNX1uyjvTH0oLy0PDXkNkCBh9e4PR0gcAHx/HPBK\nM9ATAR6bCaqUVAQvH3c5mts/BML0eH7/PvffqMutQzgaxidNn4AQgu9N/B7cTvlFLKE45LFwWZ0P\nkLTrV37+6fjNpN/g/jEkcmcC+KUkSc8Ro8V+I4DKlFuyn+LBpiZEVFuSOr8fF5eW4oP379WUa2p6\nGPX1i0zUODH1DznTwWOPAeEwYmeDSeRiqq+0+h7jeX0C9/DEEgAJvSndASOKjo63kZPzbWZ7AV4k\ney1oxImXkoilZhoe3sOUVlmRyNFjQYWpZfXo7f18RFKXDJIhct3dn6Cp6X54PMWoqrotbq/HcnYQ\nk9Rs3vwz7NkjewErEh89+CozKW6/5GeSaL3kKRkip34XHR1vMZ0vTOuRYugb7kNrfyvKMsrgc8ms\nZJij7r3zv7fjy3f/hVA0hHG+flzByNr8afPHOPbtUoNdjxrHLf42lu3rQSgawv9NBWbr1FwnPn8s\ntoaK0NKXCFdRmQY8qdPOb+vYhNvW3obvloJJ5PQkDgA6BjvQMciWiDpM1p1VXcDCIn6ZVKEncQDw\nX5Wg+OwK++/Jk/TQVHw0OAjgY5BMXv0j16v+PpTyDnhY22MuOSr1A82D5t+YhqDHB2AIxcE8AMZg\n78rqd+mEfADJaQMA4KZDr8ekJmDdvnXY1/EeZJP3BLJ86ZBuNm66mpoeGXFyUvD6d+9FdXY51q8/\n01BeFAEXQVl6PjoYQ+bIqiNGHPCqc1ITExPJOH/y7KytQpTI5YIafhWA3EeTiSK236MrHMbjexIx\n2QrRgluyOhEOGWWkhDjj3kscOfT77wHDTmDvXuDRRwGVF2yMYxiiDvcRokjkYj4HpIE+2UPU60V0\nyzVAUyKujtudT1X5rl69EDNmfIzMzHnMe3d0vMVumLqNFCKXljaBU57n+MEickNwOAJcL6uEUDDp\nIwAAIABJREFUatVcIkcjJ42Nt6C5+RFm/SIQUYlp7akGsHr10SMqwHB4HyZOXGwaELin51OsWCEz\ni2BwBmbN+kzjRaq2WWQ7ifAtYKLR/jiRo3+T4UjviNROkiQMha15ZgLA5vZ1mCtgTP3y+r/hgKD2\n2MRHJyIUDaGlrwUDYaNKtiS9BJWe3biTETrQSYBlzXIOSikTAIPIRaJD+JZJ5JCuoTaE4ryYZnfk\nItCQuMPzgV9QvNiUGYQnXXHA+OVmZgE/rAQ6h4FHtgD7dN3QbI3/vBPIcmslPHaCZYs1oOrmIqTI\nKtKc8ru/cLwL8/PS8GpTD15uBpzEicqsIgBsLYoarLYF3E6YJT6SneLkLxYhGQDEQ218p5hvvwgA\nH595H8rLr8bmzVcIZ8BQMK1gEqSblyMc7sDSpcaPX5czHtLNW/HRR8UYTkHbXxQowN1HyXaunZ3v\n4osvjtKcZ2kH9CQOAOoLZnBDfYmgr28NnE62OE+SwpCtymjnUtc3BwJTUq5DgSiRawQwH7Knpx4H\nQPYg/cbhsd270ReVB2gJmvEHXIS0Pf34rFXvNwQAxNTuSVr8Z+B1Y7oTgE/kRiRyN9+MjML/orNf\nn/suBsnrAonn4NTb8rjd+VT7JgDYvPmnmD2bnlO0s/M9IXsvgKXKZJMEfrgVeraB7u734XCYhewQ\nl8jRCJdiDJ4KRAzD1X2lu/sDjR1Xa+tzaGh4lllPz1AHFq1chKruC0cW576+lXj+k/MRTTsSLocL\nA8P9qBaQjn2w4300cF5p9UPlaA3F8NwBYeRS+mjnQAsctyVWuKtrgeMoRr08KAu8mXRka8c2A5Fb\nv4+1v5Sxu3c3JhawzztM7HYUuIhMknhQt5+mItR71l1YRSdryhrh5rwPlwMYVg0vN5G97xSD8XAM\nuEMntDPz7BuMyrZWop6JB5YfiD29e9DYJWe6uWDKd9A2sA+vbl0Gl8OFBZULsLVjKxq7GjG9aDom\ne+jh7BU12w0H3wDgbmqZVPDiqU9DkmJxj+0eXFoD/Ol7HyEzcz727n0O69efnVL9xYFcSDcnpPA0\nldshlUdBOlGO+fTll9/Fvn1/t3QPM49nJQRKsqYNTU0PobWV7i2s1OnxFFODH4vfJ/EMdK2Cdr6L\nxSLYtOknlHKymQUhqel6u7reRW4uO8F9LDbM1CrZYb/K86a2ClEi9wyAGwkh2wEouWgkQsjhAK4E\ncIttLdqP8FBzYqf2AzyNNMiSILrNTQyxPr6ht8SZmGOZfrASUEgeAsRJkXvdWQBFIBWLhUaSqRuJ\nHFuW39fHdpXfvv1X7AbrQM8nyCNybNLLSoMkX8cPiZFQrZpL5AhxpRwl//I3L0fnUCeiUhRepxeV\n/mEc6jE3+P/NR7/Gyu770T7QjjxswDU12vPBu3y4Z/IwJlNUa91D7bjx4/Pxgk6QWhJ6Gof/Sw7h\nMikD+O0M47V6dA51ABwiF4sNYTjKJlkZbtkQuz8+Bydjo6OorMy81sKUTXCaExgw4c0BzixnZoBN\nK8eCcr2DOJDudkKOcsSuo5ghDPA6XZiYXwefcyNYkp7y9CJ8f8bFKE0vRWlGKYIDryDS8fjI+SML\ngZyK+7Gnbw+2dm5FbU4tSmIfQs6OSMerZ76JmG8W1n7GYb4qLD0vUdfy5TPQ1/cGkAPcN+9qTbYP\nQF6U//tf+ge+5bBf4ukqOc77Rx89mRJZoCES6TFIdbZs+RlmzfrMliwZaltSFtTzXX+/0eEjVSTm\nNuvexf39a7BlyxWcuuV35PWWc9cLM5jZo+o3/l1d76Gl5U/UupqaHmLG9bOCjg52QFW5jXT3VTuC\nsvt8DPF/EhAlcvcCmAbgzwD+GD/2IQAfgBckSUpNF7WfQpHGAcBRMHonqtHS8hSyr1jMd/lgLRRL\nl0LKWwzsNib4lSGNBIVkSatkCVdQ9XcCLlcSPumw5nXa12c0GE1WIrdx43nC99XjyZWPY2foFXwv\nw2h/8H9L78aa/j9gKDIEAoJrSgeRlkL80b4I8PCniSje+V5gEd3h1oD3G9/Bh/FPeUqp8fxzBwwz\njYvdDuCmifRzLiK75x8oqB4z02Qp0hIeyTmuGPhLnHunQuTMjMZpbXA7YLp2pXEM6GuyK3HvUT/F\n7t7d2LfvJQD0TURlZikQ5avgHll4P4oLT0NxejE++bjUQEgOH3cw6sbNwLeqv4XZBeOwYRXdXfLY\n2mPw8+/+A9u2/QI7d9KjLa08/5/YseN2RCLvozLvZqxa9bihzJXzteFaduz4NRob2UTO6UxDbiAf\nlZW3YPv2W7jPqkYo1IK+voS0ranpN6iuvlcT4JtHANRmEB5Pie1ETo6VqN0FKOGBkpFg6RGL9SMS\n6R7J6uF2FxhSYikS+L17X2BqR1KBYjpjx/PoodRpJeYevR5+ii69BmLrVmPqLwWyzW9yzk/ae7Il\na+wUeVFD6B6ryMqiRklLGqIBgaMAziCEPApgIYB8yMno35Ik6X3uxV9j7Jw3D4/t3o2HmpoghV3Q\n77D1WH89/7xUlA+cdjgQiQAlJcABBwBnnw04HJA2shMoA7KY1+n0G0JIjNStUtXpJXL6QLfU+qUY\nhiJD2DewDy19LQhFkkvBo8a6tnW4/MlD4ulMoghFQohKUXQPdSPX2YXfp76hMmBjy3+obt4AsHLP\ncryjml+vsKgCPOJ94D8qtVPQJZMPxavroFx6eAAa1F5bNKLB8xALumSJGw0NGcCabqBLQNDQFzE3\njlbUezw130+qUyNyTgI8dcIfMTk7A73bT6OWicGHE6pnA8PazcXvj30Eab5yTEjrQtuOKyBJIdTV\nPYFA9olo6WuBz+VDx5570dlCT+BybO1C1NVdCwBoaZmBDRt+QC0XcPswZEIYyzOKUZghs3Ja+JGz\np5yOsrJLMTjYiM8/ZzN+ZQPEW2Q2bbpoZDFZtYpm8UKrl68OcjhkEWFJycWmRE4d7V/JaaxGNNoH\nlyvRSbW5R/XtSnRWkSDUamRmHoxgcKYhLZK2LayE6v2Ws22woJ1/jZvUWGwYra1/Tck4n4cEkbMn\n3p8a4XAbJElCJEIXIohCTdjpGhntxt/sWdrb/5FSe8xAU/9KkoQ1a06g9nkrKC29JKXr9bAkj5Ak\n6QMARr/2byiy3W7cMG4criwowKefOBBLdQPwy18AZZdrDkmShOFICMMmOf+W7lyC/gjgGdgFmoDh\n3g/vQHc0gEgsglmOZShX2TM9tfpFHM2R0HzrMRcOzo1idTewvFOW6mztTy2KNwB0h7rw4U554XUA\nmJMjpz9pGwDybA64qODIArabvp5kWDVXlQDsCwF5KrOJdBcQio/32iD1MirUwiWrBt48srRw/MHw\ntAyim+FSr0aay4tJ+eOBKNvO7Jlvn4/66nuw+lO+q13rNa0YCA+gt+mauGTLGs6afAoGBzdixXb6\neQeGkDZslBCfXH88fL5x+PjjcYhG5cVs8+ZLcPDBZ6I2V87SN7g3BpbfqpUUXV5vhSbhdkbGvJEQ\nRHKZYUgSEIlIVIKgEKm9exdz4+3FYlGEQkA4zCZeIhKBlhbZ3k75193N35w1Nfnh8wHhcAHy83vQ\n1sbYLUB+bx999A4IOQrDw8Y02x9+2I1YLAOxmBwC0+lcwqyruTmM7duBgQEgGOwAJ6ufAXv3Hou2\ntn3wcGyMt2xpoZ5/882XkJb2f5bux8JLL4UxMAAMDwP19SFDnfv2DaOn5zxb7kXDli3LsWgRMG1a\nBGVl9td/441LcNBBYQQtzHF6vPJKBJ9/Dni9QG3tMObP15eQcMIJEiSJIBoFzjtPQp5FD187cdpp\nw2hrA6JROUpYNAqUlKzEddelRuIA4Ac/8OHzz+U67YClbkUIOZwQciMh5NH4/wvsacb+ibaHf4uu\nY46FOz8PpD91CdW9/70PNQ9MRNl9lcj7dSECd6bDdbsLvjt9+PMXT3OvPf65Y3H1a8fCGaO7f/9p\nxWP4zce/wUPLHkL7wB7Nuc1de6jXKLixPopD84FLa4Cn5gB/nA1cNJ57iRDUneu2ScCvpwC/mwmc\nVDI63mkAP6ZQMtIiNerDZyKqi748f/haHDHwGI4eWITCCCc2hQ4Ths7Eod2PYWHHazgxj6JbTRLR\n96/HuLeXY07TH03LxiIS2rbyk84Pt/8J119hHg7k24fk46TDx2HZsuTUL/Pn9+PMM63bnRx5ZBi1\ntdAQrGi0BzNmtGP8eDne9Wuvsd38//znKDIygIwM4Oqr2WO8uTmM5matmPOdd7QmCxdeKC/gweAQ\naNuE668fhtMJrFjBt0T5979j8PmAxx9PzaC6uFgW/FdWDuHuu69AZyc3KQ6OOCId1dVAfT0weXI6\n9u7lBzwbHj4ap5++AZ9/bmRJZ58dwpFHAqed1oIPPzyVW88rr4Rx9NHAiScCoZC1PvC73+XgpZf4\nxpUez1PU488/vxsOh5jHqhmuuWYYF14I/OpXu+FwGPtRW1sIDoc1aaMVpKevxX33ARs32q9aBYCh\noRcxYGaMaoItW8J47jngySeBZcvoY+2NN2J4/XXgzTeB/n6bIhEnibVrQ1i2DFi+HFixAvjiC8Dn\nY5smWEFbmxutrUB7akLOEQgtp4SQnHgy+ncB3AbgtPj/7xJC3iGEjFF85LFF7uWXIeutN+HsH4DD\nhvHRMtiErT3r0dy/A+2hVgxE+hCLq1HMVFxeJ3ArJzWi2iNtepb23PYk5o8zLAatpEF5pBIfcJBq\nZ3V5LTsm02jCueJC4C8vA689BryyCI5ha2LBDXc+h1CbluF+sehHWP7Yqcjc1oVZ5cuE69r2r2/j\nvw9chLSmbUgP2LOYAMAHHzjxt78Ba9aYkwBCIujs1KozYhSx81lnfde0rpUrgcbGNlRXiwnsIxGt\nMqClZQAdHdaJXFNTGNu20QbnOjQ2Aq2tPZg16xXm9bFYBL29QG8vkJm5k1nO5QrD7dYuPv396boy\n8jv3+egD7sILb0BMIN8RIXHHJrc9mR2OOeZJnHoqPyTF3r3laGvTinIiEXOvwPPOuwmDg0YxzeLF\ntaitXYEf/ehmHHbYy5QrE0g8pwSPRyQBfQJNTbWIRpMzdK2qss/pwOWSSf7ixfR4Y3Z9Sz4kOBz2\nq1btqtvrHVT9TR/r6nsQ8tUSOdo3C4WMaTmTQTicaiI6LUTlIg8DmAPgHAB+SZLyAfgBfD9+3Frg\nmq8JPitKuPORJIhcv+4aJwHm5chBLwt1Xs1mRK46IBvTs6CEcMigzGkdw3Jak7EG6agBnlyC0iXG\n7uH9+7Nj3h5X2xRg/XeBzy8CVv0IRLIuFgyHtR/B7Q7h/vsPxyWXXGWpHqdT7hw//am168ygTH7K\nwsJvQ2ykHQpCIfMw6d3dWj19NCq/x4MPZhMmPfr6tLsNn2+ASYB4cLnCmgVCwR13nAhAwrx5b3Cv\nVy8cc+awPdhkIqed2AcGtEROIXp+P/s53O4hwzvXw+eTF7l5817nlhPFj3/8c9My9977JGIx7e4q\nGjUncgcd9CoyM+l2u+ef/wscf/wTpnUo38/pjMDpFM/suW3bZKxcebgQ4aThqKPEQiuJQCHxXi9d\nPa+cH01UV39h2reShdMZTZnIBQKJjDRZWXTNkrKJ0f/9VYD2zVgE1CpExpYViG5ljgdwgyRJIz1f\nki1UF8elcXfY2qr9BG9V5WFuizwpJxM25h+7gTNVkcqPKgCq45vX08qAs5bFwzZEXXDEAIA9CD2d\ntQDY3k4XZI/DFS//FLMmrQEO0pKk4b88jye3zULZz36OIw6zFr8oFUyo3ILyWCFIR63hnMc59rst\n4yRnvQ3Dw1oiV1W1FtXV1jMfK5Oi02nvDlohcE6nWFgFPTkZHvbD7+dPVkNDaQgGO0cWXaczBocj\nghkz9PEN2RgYSEdWVoIA+Hz9SU2SLlcY3/ueMcVNMNiD/PwmLjkD5MX8wQd/h/7+TOTlsVWwwaAx\nLZqeyCUkcuznyM9vMl1sJ0/+CG63hJycVm45MxQUyPZpgYAxUb0av/rVBvT1TUBNjeyH5XYDTifg\ndJovNm53GJMn03O4zp0rFky8qmo3Dj8cyMgwT8GnoKnpILzxxj9x/PEENTX2LorJ4Pjjw+jhxPhN\nT0/dNMcM117bjIKC0SFyCxb0wu9Pba465JBuPPMMEAoBeXl0yeuLL0bjNpVAWpp4fxgNPPZYCG43\n4HDI7SGkFz09xuDEyeCVV9wIBOR6C8Si/XAhSuSiYLMIdrCjrzn+Nb4BTqkTr43LxCXBVlRAfDD+\nY9mR8IbTgIpEaqRqlQYiww18v/UOvPvv6+CAG1nnnwEU0wMyAkDtzl9BTnVLx7TKHZgXvQ6nzTjO\ncG568YEYH6iAE1MAjB2RA4BFi2biiy+MMVmOOMIebzErWLiwHTU1GJkofD5rO7577wXKyrRE7gc/\n4NsfsnDWWVEce6x5Oau47rowwmEgLU1s5zFhgrZcRkYuZId0NoqKfJAkL9RxDz/5ZC/6+58XbmdF\nRToiqjXn+ef7EYkMoFssjewInnrqJoRCb1LPffDBMDo7WzFksh68/noWpk/vx+rVISHVp4Irrwyi\nSRWt5I47Qli8GOjrG8DnDF+TDRuAlSsjpvfZs+ctrLG+P9CgpUWObbZkCb/c22974KcIYpcvd6Nv\nDIbptGmDOO88YHh4CB99JHbN0UdfgnPOkZ0xdu50Ydu2UWygAG67bRiZmWC+a7/fWt9KBqee6kRz\nc5SZcioVVFT0oKcnqhmzVuH1voFz40vYpk1h7KbsmxYu7IXXK2vC3n9/L2xIoJA0Jk0aRo7KaGzj\nxqu4ZN0KCgo8SLfR4U9Ut/QqgNMZ584AIK5T+Rph6bNv4pcfd2PZCzsxodBa8L5LvzcXV5xFjxM1\nUuYna7FxvRvr1wPHHMPnwrfeat6Dli6NoL7eqEp68UUXliwBzj577MmTyzWIWbNuNhw/88zkc/Yl\ni+rqO3HXXTHcdRdw++2Ax2Ntlrj2WqC8XGvbcNBBfGkHC4ccEsHF9Dz2KWHq1FU49VRg4kQxiVww\nqCVy6QKzS1qaFy6XltAWFNAzlrAQCGgdBfLz96K727pLPovEAUBZWVhYitDScpnlaO1utz7D/DAI\nSUTZp8HhCAnF+ko1/ZAMMebgcNDtdVKNnC8KJVwSz2tYD3Wbx6qdaqSna8PHmAUWNgtkbgdisYFR\niSMHyA5EdtQdjUdnoKVQBIC1axP2uGlpdSnfLxXow4/s2WPuQCYKJXi/bfUJlnsNwFGEkDcIIT8k\nhBwT//+fAI4E8A9CyBHKP1tb+DWFw+HTBMSkob9/DTZvvgzd3R+bxsyJRMxFFZEIPciC2y0naNUH\nqfwqMTDw1WR16+lJqIGSmVz1KVtEvgsNVuM9eTxiQe927LgDAwObhSPWG2NsmbeLEK8hd29j4w1C\n91Pg8WgTl+7e/ail60VgZWFraVlkmcgRoiVAiTy/bCIXiw0JfftIJLkNghqifUz/HInjY0XkhjT/\ni0Ddtq+CyDmd2tAsqaZsSkujJN21CDnbgNg3dzisGe1HIj22xKjr718NgP2+eno+xvDwXgwMbByV\nDBhWsHlzYqfd3s7eMCYDu/usKJF7CUA5gGMALALwRvz/hfHjLwP4N4B34v9/A2FNeiMTOb5rZn//\nl2hu/i1WrjzQNC6UCGFgLVoK+x8e3n+IXGvr4q/kvgMDsoVAX5+1SSIQkLOuG4kcK0IZH1u3XsnN\nfKFGXt4plgb+9u23MnIZGqFPh5aXZ+6hyso/aAUeT5Hmtzoem12IRgcQCHBcvVVwOq0HyNK/ByUo\nrBmRE1lsh4a2W26PHhs2/ACRiLkkny2RSyHtiQWwJHJpaZNQVETP8qIlcmPTTgV+f61hPIqONz0q\nKn6BOXPW44AD1mHevO1wuQRTslAQiw0KbVwI8TK/OQvDw7ttIXJKZiLeRnN4uBWfflqfVP0Ohw/F\nxRdSz9XVPYHq6vuo52gIhZrQ1SV74a9ZY68dDGvzlCxEidzhJv+OiP9T/v7GQXTRVeBw+GAlTB8v\nvygAgwSEBlrql+LiC0b+zss7Qbg9IigtvdTW+sYCw8NyqI/Gxl9auq66+jcAjDspOf1PcgiFxMKO\nOBweS6L41tbFSeeQTEubINAevUqRDb3kQoFeIjca2Lv3GTQ3a2O2VVbeRi2bmXmw5fr1k3Fz828h\nSTETIidmZ9vV9a7l9ujR2voCmpvpGS3UIIROzO1W/7DAksg5HD7U1/8JeXknG65Rj8OxaqcCtzvX\nQIQS481aXKWSkh8jEJBJi883DnPmrMakSfxwLSyISqAlKSS0nqj7RTi8z5ZE8YoGgKValc/RnYXM\ntBIlJT/FjBkfGTaJCrKzj4LXay2u1tat16acmowGu/usaIqub2waLlFYtQ8QUa1agUj+wdbWFwzH\n1IOxoOAs7Nhx9wiZSRXBoEBW9v0MjY2/RHn5NWhvf1X4GqcziJycbwEw7v6TVa0C4uplQjyWJHKE\nuJOWEIgROXGJnMPhp6ZIUtT9PGRnH43OzuQF/Hv2/MFwjE0grUeLpr2HnTvvZS4kgDX1oR1obPyF\naRnWopKKdMgKFJtCGpED6MnFtTZyYyuRczj8VImcJEmw6ven70Nebwny882l4jREo3222ciVlV2J\nrq730de3wpb6FCgSYh4pZKVN83gKMTxM9yx3OjNRVyebZ3R00L2lXa5sy32lt3cZ9u2zPxWY3X12\nlOLrf/NgpibVw6pEzgjt/QYHN5leQVu81XlW3e5szJ69CnV1j6XQrgSs2lnsL+jqMs9UoMb48feO\n/K0fgF1dYnku6RA1RndbGvjB4Mykbc4IcSE9fY5Je7zwePgZIdT10eswl+rl5Hxb6B5WwLqv1Ryf\ncl1G9Uhj4w0CqlUjAoEplu9vF1hzm99vQ3oXASgSGL0kRvlWNDXUV20jR5PIJUOiWP3RbAzSEA53\n2rJRyM4+CpWVt5hKzZN578rGl6cxYJkDOJ1sRyz1PEN/pwQuV4bldRwQs38sLbUalsRe6vU/IicI\nq3ZBIjZyZterISL5oS2aJSUXaX57PHkoKbkIBx+cvCRJgdNpHjx2f4SIdFONoqJEInU7d1Kik65V\nidzQUCqxGByor3+GX8LhQ0WFMaQMvSyt3U6h53G5sk3LWAXLFi6Z5OkslSSPyLFsYV2uLOrxrxKi\nZN0qCgu/rzsiIRYLGWx43W5ZIkgjzF8lkevqes9wTznPrnVzBlYfSmaeCYdb4w4PqaGm5mG4XBkm\nG3WxMaxHNNqDSKSHKTUDgHCYHtGANx9oiZxxXXK7C+IaMutrsshzjh9/F3w+sY2P318Lj8dcI2EF\n/yNygrCqqkpVIqcnSSILDc0L0+eroJQEXK6MlKUArEloLDF5sriKVIHVnbPTmZjQ7Fw0du82j3oP\nyAuZlfuyJkIREOJEIFCPyspbOe3xCW9s3G7jrp4Ql9BCpZYm2wWWrateheT313BNB7Kzj2IajPMI\n+s6dv2acSTERcJLIyzuFeU5E/W0VBQVnob7+KcPxzs73MDi4VXNMsWeiSeTUG4SxVq3K99R7LIeT\nInKscZSMEGDv3j8LaW7Ky/mZPpS5hucQIY9h63NhOLwPTU1m6eLojnBeL3tjYSaRU0xGzPpKMDjd\ncKyv7wvuNQDgdAYwZ86Xpu8WAKZNS93+VY//ETlBjLWNnL4z0oicXrqgL0PrlLx7sODz0fMHjrWR\nsR55eafEHTisTXqpOCiILhpebzlKSy/F3LnbUF//DLKyFhjKdHTw00cl7mnN2SEVKAsLb5J2OAJC\n7yEtrQEZGfMMxwlxChI5+6VUweA0oXKyZx9b4lxYeC5zEeZJ5Nj3G3syUlT0Q9TWsp0hfD7rCZfN\n5pyJExeDECNp7etbgWhUqyXwemXjdlpfVBOpr0a1SpPIWVet0t5F/A4mVzpRUvJTgTsY6/F48jFj\nBjvysvJsvM2a6BjWY2hoJ7Zv/xW3THe30fQlK+twroRQ3RaapkgRaJgR5LKyKwzHIhF+hOWKil+M\n3Hf8+LtQVXUnMjLmU8suWCAlNa7M8D8iJwiruy15ENhH5Gj2VMXFWrWpnsiZDTTRhbKk5MfU41/F\nBKqGsmO06kpvhchlZx+t+S06eTU0PIfa2kfg91ehqOhcBIMzLbVRe083V61QVPRD0zqKis5DTc0j\nmDSJn9kjYZfE/rZud67pewgEpmL69Pc00kwFoosAy+M1FTgcflRXG1N6Gct5TBYyDzOEQDIx4FIx\nw0gGDkca6uufhNfLdswIBmdZrpf3zWjSWQUuV5bBNkqpy0y1OvYbSqfh20tSmOuJaRU8IUBBwdmY\nO3cTysqu5NbhcATgducYjjudGcjMnI8ZM5ZSpa7Ku+VpXAhxJvXekw2MXFf3BHfOMJPIKQ5IZvNO\nTs5CwzHWeK6peQQNDc+hqup2VTscGDfuRsycaSTKo6nB+h+RE4R1IpeqjRzf/mzixL+O7FgV6Duc\nWacVVZ3QFjSvt/wrkSKokZhwrBG5UEgsrRYhLoMtmOgzG2OMJR+DyeHwwOstZZ7XR5mnIT//FJSV\nXQqPh5/YT+l3vElatl3i9+3x4++Bx1NI3UXLahnzsWElzIkoCHFpbB7Z9/aaSCXdTKInEtrBWN/Y\nOg7RFho9nE7r759nkF5ZmZDElJVdpTkXifQYvJtdLpnI7W+qVaczwPBatY/Iud3scZqdfQT8/vFw\nu/O4dXg8hVTyoJgsZGYeSJXIKgSaT5yStZFLjsilpdWYtkeBy2Ukrwkix593HA4fCgrO0Byjed0X\nFp6DsrJLUVh4JkeqqoUSZ3I0wHwzhJBFFuqRJEk634b27LdIjsjZKZHTn/eYql/NBprZRAAA2dnf\nok6kEyYs+sqJnBK+w+HwImqBJ5m51KenH4CysssRCExBMKi1IxQnch7db+P3dLvzhezZCPFwnV2K\niy/C5s38mH6BgJIujt8nExI59nNmZh6KgYENJvXIfS8ViVxamrWgoA5HGjMGVeLeLrjf328GAAAg\nAElEQVTdOZgx40OsXMmOHSdL3NiTvqzuto/IjRv3C25InNLSywwx8ZJBRsZ8zJjxYdJzk9dbjlBo\nF/O84qBAg99frSqnXWyj0e6kJXJjrRnIyVnI8Fq1j8hVVt6Ktra/Us8p0nkzG1I5XIfRsUt9Hc2e\n0+WSTXb4pCc51WoyTkUKRCVyNCcdUYmcvMnUB303Ermqqru49ch1eUeVvKnBG81KgF/l38kAfgjg\nHMgZHs6J/z45fn5UQWTcQAhpJIQMEkJWEUKEAu4QQhyEkCsJIWsIIX2EkN2EkL8RQoSt/ZOxkUtN\ntcoXw8oLiRmRM5PImRO5urrfUSdStzvPNnVQsvGqFFsklmrV5cqF319jOD4wsJ5bb2/v5ygsPMtA\n4gBxIqefDGiERnRSczg8GB5mSxEdDpeJa74XPl9Z/G9+n0xIOemLY17eSUhPn2767RMG00bJcjjc\nbvoea2t/a1l1I2IqoNzXTIorO5iw2yifp9dhNRVeXt5JyMiYQ7WjVCAS308E8sYs+XnJzJPV56tk\nnlOPCb0KlieRo5FDrY3c2G4ox4+/iyGRsy/PaSBQj+rqB+D31xrOKe/DTBIkS8SN64j63fM2iLx+\nMtYSOfmeYhI5WhxHRa0vMm/p1xO97WZh4feF7NzsjCNrBuadJEmqlCSpSpKkKgDnAugDcAYAvyRJ\nxQD8AM4E0AuZ1I027gDwKwAPQ04N9jGAFwkhRqU2/dr/A/A3AMcB+BmA8QD+QwgRSmLJs3+g2ZKk\nqlrt71/HPS9L5PSerVZVq+YEyuXKpS5YTmdaUmmNaLBq46ZAmehZ7XA6A5g9ezWmTNHmyTO3YWKL\n95JVrWZmHmIoI2oUT4ibGt1eC3YKuexs9T6LNzl7RhYH1iStRJ0X2dkCrBhMkun1mZmHcc/TIBKu\nJEHk+IsQIV4TiRxbtWo1Fd7EibLkZfr09zj3MyOeYmrQ0Q4ZxEt0rh7nemlSJNJtIBUK4aDZ1mlV\nq2MnkfN4SuD3V1MkctZVq3l5J3HPl5dfgblzjV6o6uwESsYZGuS5m0bkEptK/mae1/+T9Vptt3yN\n+p7sc4m2KBJFNRKmKWZEzmUYa/p+6fNVmbR0pDbBcqlDlDLeD+BuSZL+KsWNfSRJikqS9BcA9wB4\ncLQaCACEkHwAV8fb8IAkSe9LknQxgPcAsPz51fgBgBckSbpZkqQlkiS9BOB0ALkAviPSBt4gVQiF\nGqlK5MwXSppEzhqRExmIDgc9L5/DkQa/nz1pW0GyuTuVAcdS8xHihtPpR27uQt2z8vWwPIPtZFWr\nPGmLSF35+adRbT8U8KR74XAiHyxvl6j+DrS+kZZWP3K9aN9i2fqYXZ+MIbXbbU7kEh55/Prl78dX\nrbIlcuIpferqHtO0heUhzvu+2dlH49BDRTcFqRlc9/Z+yj3Pi6Wlfl96IkdTrfIkcurNmxVCUVJy\nsXkhDhSvZ2McOevODuPH3yNUTu1wFQhM0Ug9jTH5EpBjwRm/t7oP5OWdBKcz8S0qK7WG+ywk67Wa\nrLODfE8xiRwAVFTcMPJ3MDhjxEzDfN5yGOZufb8cDdvdVCHKNKYA2MI4txnAZHuaw8RCAG4A+gAz\nzwKYQggx5nDRwgNAL0NWfpu+Azn2FDsKP23hT9VGrrDwLO55mo2cnmyaESS9RybrPqxdHSEEU6cm\nn0JJgZm0IVnVq3rQWnGIqK1lZ0UQJ3Lab0MIMc3nyXJZJ8QDr7cIs2evSiokhzYnLl8il/jb+JzV\n1Q+ozoupVnNzjzOc8/v5hsvq663A7xdPL2ZWv+zswH5GnlerFTsgfcBuNsFk7+6t9O1kN00i7QCA\nYHCqhhho751op37ODIc7DapVpYzXW2ZsherbWCEUNFUlC7RNiOK0ZIwjZ00iN2nSS1zppRr19U+j\nqOiHKCg4E5MmvahRqfI2JMPDrdQc3uprnE4/Zs78GKWll6G6+gFUVCTioPEl0k4b+pIYGhqejd+T\n/az6PlBVdScaGp5DdfUDmD79PZWmwVxLZhxP2o2/OJHb/yRyLQBOY5w7A4D9WWW1mAggJEnSVt3x\ntZDf1kST638H4BxCyAmEkHRCyPj4sZ0A6BalKpjZPoyGRC4ri2926HCkmXq28uymAMDvrzRNfC8P\nWJpqNQBAnrhThZlq1czTUr2L1NabnGdbQQGrq4vXQ1PzdXd/yL1mwoQ/Ii3N2JWV9+PzlaOuTps/\nVMTzWE0g+eTEq/rbOGlmZSXUw6KqVZcrHQ0N2v1XQcFZwkTQCpzOINUmMpn6ZYkbX5WTrEmAgszM\nQyn1su7JVp2PG2eeT1VBqouvWewypzOAiRONOZ8BrX2dXiLX07PUoFFwudJH/i8ru3rkeE2NVgFk\nRV1s7ZsZF2KFyBnjyFlL0WVFquP1FqO+/klMnPicwVaSb8fppuYm1ROVQKABtbUPo7z8Ct1z8dYv\np2kKL7uQn386AHFnB/k3QWHhmSgvv0LT10Tmb7M+sj9K5ERXtwcBPEAIKQbwImTiVgiZ3H0bgDGK\nnr3IAUBzBetQnWdCkqSbCSHDkG3klN65EcDhkiR1sq9UrufvtFixeFKxkeMl3gZkI3KzDiUSh0uO\ndVaDLVt4n9A4oSmTgULoUoHZc8jvl+agILdr3LgbsX37TcazGgmT+LfgDWQaaachGWmsw+HHwIDR\nNlJNOvLzT0Za2sR4OQfq6syzQ2hVpjzVKj/IqtZTUFw1KkuXJeza9QByc49Defk1pmnEkiFyDocH\neXnfxa5d9wqV5Z/3IhZjkyeWpNoK6B69xueePv0D8DQCmZl0SS4NqRK5QGAi5CmU3Z7c3IVwu/MQ\nDu/THFenJTKTLOu9hmtq7kNR0bkgxItAQOvNbCXeoLVF2GiCobSJJpFbufLAUWoHG7xxmJ9/Glpa\nnqJcIza2zCRyqdi7iUIOzK3YtYqrVlMpZ5c9qmhYEjsgtNpIkvQQgAshq1gXAXgj/v8kABdKkmTJ\nL54QciQhJCbwL5WM5Or7XQzgFwBuA7AAwKmQnTT+TQjhMybwHR0AumceISRp1Wpl5S2mjgROZ5pp\nh1J2tGbweNgxygC6RFLppGZSQRGY1WFmxM56z1oCY49nW0bGQaZlWAFnS0sv517H+p56Qjpr1qeY\nOPFFzJq1HPn5J8WP0xdopzOoe3+iqlUakVOrqq1J1AoLz8bs2ctRVXULXK6gsETPCgjxcDcWasNu\nMYmcWfiR1CRy9G9hPJaZeRBTLa82fBeBVfKplxBnZR0h9Nw1NQ/rfmulaDzvVoDuJBMMTjOQOECe\nH8y0DwmIb+jC4X3Iz/+e5pgSg1Dff0KhncL1ytfbo5bkjROnM90Qrw8Ql0ry+78LPT3msQhThXo8\nW5HIscuJxK/kf5uvs0QOkiT9KR5brgxAMYA9AJokSWJvW9lYCkAkSJQSFKoTAG0Lp0jimDk0CCHZ\nkJ017pEk6TbV8fcAbAdwLWRHCgNuueUWAEA0OoDcXGA6JftMQ8NiTi62ZInczRgYYJkkxmt2+E0Z\nv+jkxlJNFBaeC4CvWrbDxdqMyPl8dBNI9fM7nekUZw/7QxQEg3xz0IkTX0B+Pl01O27cL9HczM4z\nyJog9BOv0xlAQcGpmmP19X/C+vVG5/HKyls1gV1FnR1oUF+bKhETlejl55+KtraXuGUT13io9lQK\n6uv/rLq/uY0cL2eqLHFPzVuSnvqHJgUiAAhyc49De/vrunYmpHrp6XPQ2/sZ955WJXLV1fdh7dpT\nEYsNoLj4AgQC9fFxZXw3anvIvLwTkZt7ItrbX0d29lEoKvqR7pnsC83gcLhQVXUntm69ylS9acWO\nbdy4m1BcfD66uv6LcHgvAoHJyM39Tvye2jHZ2WnNVtg+MsB+j05nEJmZB6KpSbuxFO+3fGcHORuH\n9ZiJatTUPMjVBtlP5MZStUpfn5csWYIlS5YI1iEGS6tbnLTtiv9LGpIkDQEwz+6bwFoAXkLIeEmS\n1DqZSZCNR3ixOuoAeAF8rmtDJyFkK4AG1oUKkQuF9uDjj/9v5LjbXYhp0/4NpzMdfn8lens/p16f\nWmYH/mBzOs29RkWJHI1I5eQci+pq+ZlTyUogdn+WJMqFmppHqHYeekyY8AesW6eNyK1VFYp9C7VB\nPws+33iqajAn51gUFJzOvI6mSlODPUGYi+gLCs6iErnycv2OXEwiZ47UbNxEnR0qKq43ELns7G+h\ns/NflGs8TJVddfV9yMn5tnD7ZNUp39lBRHWSkXEgU3JBewe8sUaTTKuJa1XVnVi9+lvc9lglcrm5\nx2DevO2IRLqRllYTr8NDDcCt9sJ0OtMwZcor3LrT0upNA0uLoqzsMhQVfR8ffshX2eblnYR9+/6G\njo63Ro7V1T2OTZsuMpQtLZUzocyduwWDg5uRllY/sulNlcTbp1olIMRNJag+X7khBpp879QlcpIU\nRUXF9di2LZH5xuerxty5m/D+++Lrns9XjenTl2DVqgXU82oixw+eLnpP8w2EXarVgoIzsWfPE6rf\n8vq0YMECLFiwYOT4rbfeKlQft02iBQkhUwghLxFC2gghkfj/f7USVDcFvAUgAuBs3fFzAHwpSdIO\nzrVKaGtNHiNCSA6AGgBGtx4d9JIeh8ONYHAK/P5KALxdnvVdZ8JDh92ZZGmAx9TIV5zIGTtmQ8Oz\nI8as1iPsW7OboxFJr7cMBx3UjtLSn3AmlMRCSgtUKiqRS0trwMyZn2D27NUoLzc392RPKHzhtPkE\nwUrCbh4dnBBiqq6Sy/F28OJq8lS9TkWvT083xmh0OoPUMBcOh4/al4uKzkd5+dUa4mW2UTKPIye2\nGNKScCugOb/wJEo0tbE6PVtOztGYPXu1ULuswOPJHyFxAP3Zp059K24/Jw6eejE393hLdQGyA0V5\n+c+5ZTyefFRV3TVC+AOBqdSUbU5n+oiTlcsVRHr6DM34SFWtbqfHJ2ssuVw5VI9/OyRyAwPrUFR0\nHrxeORm9252HadPetixpdToDqqwzlBY4xGLeiWtczBWIZt9WdJ6sqrpNle7MS1Vz2wWhpyeEzAHw\nPoBBAP+ATI6KABwP4DuEkEMlSaKLpWyAJElthJD7AdxACOkDsAKyt+yCeBvUbX0XQIUkSbXxa3cQ\nQl4HcF18In8fQB6A6yCHJXnM7P5ffHGU5rfepZs1+SajPigokMOO8DqTx1Mysijl55/GSeUiqlpl\ned3KCAYnIydn4cgudsKEP3LrsyqJpA0MQrwjjgWsaPJaL0tjHaISOULcyMiYK9xeFrHiqeISbSCg\nTSYycaD3F3VqIx7S02djaGj7yG+PhxbrmqdaVZMgM1I6eqpVlyuLS7RcrmwEg1MNUlE5bhatLxnv\nJSaR43sEiiAv72QEg9PR17dKqLwc6ogOmt2s3vuTlo1EW3/q0nV6XEnrEia+UxHXf42J8vIr0dn5\nNvV9K+QtPX0GDjhgAwYHtyE9fSaVVLFCASnYXyRyAL1/y5l3CDWNl+i6ZDaPezz5mDNnNfr6ViEt\nbRI8HjrR8niKqKnCAJnI8exa1e9ZUWsn01YFIv3ffG4Q+3YeTyEOOGA9OjreRkbGAQgEJgldlwxE\nmcbdAL4EUClJ0o8kSbpBkqQfAaiKH797tBqowo2QMzT8DLKEbj6A70mS9KaunAPG5zotfu0pAF4F\n8ABkG7+DJEniJ94EuLkFAd4u2jqRM4usD2gndN5kKCqRS0ur10hzsrIWGMjV5MmvYcqUNzFr1uco\nLuan1dXnUTQDTZKibk9e3snU3bs67AhtcIlK5Kzaz9GzFYgQOcL8rkr7J0x4UnPc660wXZwVVFXd\nAbWUsqrqTkobeKrVxDs2SwllnnzaTOLFvn7SpL9pfiu2mgpKSi6kfjOnM8DoBzQiZ5aqzMOVColI\n5GpqHoTD4cLkya9Rz9NimvFsuGiSbtpCHQxSjHlHwCaKogiHjbZ9yRE5tlQqWYmVx1OImTM/xezZ\nayjnijXlMjPnj9yntPQyTdm6ut9x7yPy/bOz2Wru0ZbIFRdfCACGECEi2U8S9ZqvXy5XJrKyDtOQ\nOH2IpHHjfsm8Xh6z7ODa6nnE4ylgSnFFNygi2YzM7XethI4pQXHxj0aVxAHiTGMe5KwKGh1j/Pc9\nkEnVqEKScVc8bZhfkqTpkiT9nVLucEmSqnXHhiRJulOSpMmSJKVLklQqSdLxdkkR2RI5a5Kp2trf\nqq7lEbQ0wXJiKbQcDhemTPknCgvPQXHxj6lxoBwOF3JzFyI9faZpfbSUOjwQ4h5RKSsYPz6xN/B4\n8tHQ8MxIahSHw4/KyttHoqwrx4xtFvNatSvFj0jKLRbxViaHoqJzUVPzMHy+KhQX/xhz524Wvn9a\n2gRMnvwq8vNPQ3X1AygqokV9F5PI+f3VyM5WbMocaGh4XlN2NFWr+lhwFRU3Ii1tIghxo6zsKqSn\nH0CduFmq1WQcXRwOL7Kzj2IGzVa+Y3r6AZw65HHK2thMmfJPwzHWJgEQk8gBQCAwzXBMgR19XR+4\nF0iOyPHmrlRUlw6Hmxp7kufhW1v7MOrqHkdW1gLMmvW5qRTczN4VoNmnqttoJ5EzflNFy+JweOIe\nxHJu1JoacxtgVS1Jtaeo6FyUl1+HjIwDUV39ADfdnrI5Ya1V+j7C0pyIOrG4XBnM7B719U/H72kf\nkRsr2KVYTsZz9WsL/U6LLWURG6wVFTcgLa1eI3ngSTTUdgO8e4i75MtBIRsa/mxeUABWsw8ouURr\nah5EV9f7yMs7GRkZczRlCgpO4wbqpQ0u7WLAM1y3i8jxJXIAe/FS2k+IE2Vll6Gs7DJqOTPk5R2P\nvDyeJIn3HrTvcMqU19DT8xE8niJKIFLznIXJntf36UCgHgccsBaSJI1IrGn5DuWYU2KqVTMozgxT\np76FtraXsW6dtu8pz19aeik2bKCnSVLeJ2viV9udKYjFeETOKJGjZVFg20xlp5Qqjge7Vauiqmh2\n3cZ50evlp9UuKfkxSkp+LFS/2RwXDM7iqoftylMNsJxmEv2orOwyFBScCUKcQmnsEvWyx3he3inM\ncw6HF9XVCceXgYGNzLJKn3Y6g1Qvbv3ayuozVoIx19Y+isLCc0CICy0tT8c9q48cCTVjl2p1LCE6\nwy0DcCMh5B21VI4QEgDwcwCfjEbj9h9o7ZqqqrSZBPLzT9V4p2RlHQFA3M5j/Pi7jHfkDCJRiZxo\n8Fq7YfW+svOGA2Vll6OsjB9rjYWxVK2yYe7FaCaRG32I2sjJBDcri76bFslZyD8vTuQS1yTeb3n5\nVYawCg6Hl7pAJheTTknl5UBu7vFwONIQi8nRkNTOP0VF5yIYnIbly41SsAQ5N74LVg5ankSOJmWi\n20DRn3fSpJdtiH1HR3ISOfYmtK8vNacNWnusBA42A+29q1FQcIaJGUPyEQ30oBEgfSQFlv0aD7z2\nV1RcZ6Ee9vhTpNUsYqvfZLPWOythZeR0iXLw5oyMAwDoUzLyzQ/2RyInqlq9EXKojx2EkGcIIfcQ\nQp6GHIdtMuRgu99IyCoctcDREf/4CWRnH4WcnIUA5B2yQvSs2oqJQiuRY0/MVlWcdsFqtgc7JGI0\nhwkrzg72wFwwzZqIRGw37EAqceS09aRGfnmTochE6fUag1h7PIVUspPMoqnNC+pDQ8Ni+Hzj4ffX\noq5O6x8VDE5FdvZR+iq4z8GSIPA8lH0+o7qPRiho46m6+j5kZ/PT/omCHmTWXomclbRjNNDGmZ0k\n1kwi5/NVMO22aN8xFdA0ASImMOZgjxtrtna8HKnyPdiqVT2Ro9dlRSJnhq6uD7jnv7ZETpKkTyHb\nyf0HckquqyAnsn8PwDxJkvhRKL/G0HcQuuE0wZQpb2D27DWYO3fLCNtP1vPKDOI2cl9Nh/P7a1BR\nIT4R2yERo0vkxFJKWSVy48f/2lJ5NVgkd+ykpzwpgfh7SFWiYEdoj5KSS0b+DgZnIRCYyFisrVt+\n6Eltfv5JmDdvK+bO3USVUtKkS8kQOZ5kgZbbUlwiZ58EiJYH2m5nB8V7P1nQY/zZlzJJvZmmweMp\nYo51u0w5eCgp+UnKdfAlilbmCvOyokSOTcbts+6ibRK1bfiaEjkAkCRptSRJp0qSVChJkjv+/2mS\nJBndg75BECFy8nEHgsHJGhH2aC3OohK5sYKa2DgcPpSUXILBQbZdhB52SMToxICoztunWi0qOk8T\nv0sBz6hXAUslYy0Yb/LgT87i74FXdvLkVy21yVi32IJbU/MAamoeQWXl7Zg2zRggWIEVtUuiDda+\nB91Gk0fk6NIaXqIcvbTR4fAz8jxb99K1Atqck4zakveOfT52ho7kYR+RM+ujhHgM6c0S50afyPFi\nromCb09rhciZzys0Sbp8rUP3m95nhodbhdtjBn0WEmObvvo1Vw9Lo5vImEQIOYQQMpGMZVbYrwii\nRI4GQhzUBV+N9HR2/DK/nx4CQkQiN1pGzTSUlV2N8eN/jcLCH2D69CVwu7PQ37+WWnbChEWGY6M3\nsSVsHexUrXo8+Zg58xNNyieHw4eqKvMI3SyVzNgR8tElcg0NzyEv7wTLrVJQV/e4cFmHw42ysktR\nWflLrhmDWa5ket3WvArpqn3rEjmeZIEQJ+rrnxn5XV5+LdV7kt6f7SNy6ekHaJ4tN/c4YfKtadGY\nb0LtXa6CQbb6UnGWGYv5jhYI3B4bPHuywIg8L0tVm5NzjLZFDAIZDM4Qbo8ZzEyi9kfaYyWzwwWQ\nY6+tBrAEwBoAuwkh/KBiX3PoFwGr0pu6useQnj6HeZ6X0onVYUQkcqmo/6zC4XChouLnaGh4asQ9\nnKZWLim5hDrgRovIqYOr2hHcVQ1CnCgqOgdTpryBceNuxqxZK6iqLz1oXoZm7bMTfBs5K+/BuFDU\n1z+NwsIzhWsoL7/GcEwfesQOJCeRs9Yn6OFv2ESO9R30IStKS3+m+V1UdC4OPHAv5s7dytw40CVy\n9qlW3e4s1Nb+Hl5vGdLTZ2tSc1mBXYnjRWGWh9YqeJsOpf/QwpjYPd/l5Bxra30K6LmAZVhTrZrP\nbaz68vNP0ZWjr3fWwqqYtcW+Tc9YQajFhJCzATwBmbydB+DY+P9rADxBCBGfvb9mMErkrA3C9PRZ\nmDXrU4wbd5Ph3KRJL3NT+LCivItI5OwQracC2oJcV/db6oIyWjYjavXVaMWRy809FlVVtyAQYKbs\n1YC1uIfD7Um3wRpGTyJnVeVQUGCcNkaD1NtpCM1CNDpgOMa3paFv0srKrhpJe+T1lqG8/FpDGY+n\nAH6/MUWZAlrAXrsXp+LiH2L+/F2YNeszy6m5FIy1RE5xSLMLvBAiSj+mO13Y3cdTD/JMA29OsvLt\nWM9bW/t7bn11dY8b7Axp80MwOB1eLz37z/8vEJ25rwOwWJKkc3XHnyaE/BlyCJLnjZd9/ZGKalUL\n48Sdn/9dk2voA1REImc136ndKC39KfbufXrkd2GhHGuLRuRGTyKXkMTwVatjIw0D2N9reHjPmNzf\nPhs5GiG3tjDTMxCMhtoimYXO2jW095oMkfN6izFnzmr0969DWloD3G5rMRkBoK3tL5Sj+5+UgaW+\nzsszmxfFUFFxPXbuTGgmSkt/aku9Cng5NxXyQhsTds93dqRdo4GXAzVVZwenMwPFxeeZlDESZdqY\nosWU/P8NoqN7AoBnGeeejZ//RkKvlkl20c/MPETzW8R9mxWJXC2RY02GonlWRwvp6XNQVCRr3X2+\n8aiouAEAi8iNDpFSh3IYi8wOImDdSySYsD2wyxPNev5SY3ka+bH/W7DU2SwQ4uWaQ9BAS1vHV62y\nCavLlYnMzPlJkTgAiEb7KfezT7VqF1gSXPMNrhjGj78bM2cuQ03NwzjkkH7LYZHMQFOnK1CejfaM\n9hO50ZHI8b6DVVtxPaqq7tCFhzK+J1ooHp+vIqW2fFMhSuR6AbDciMri57+RsEsil5195AiZI8Qj\nlEWBplYBtBI5dqYA8xQyowlCCOrr/4hDDunD3LmbEAgoQVSNXc6uiU2fG1Pr8DEWceTMwZJaRaN9\nY3J/uySTdkjkaPB4+K7/IqiouF7zW73zN79/MSZOXGzZ45zmtZmMRM4OVFbeRjn69ZHI2TkeMzIO\nQFnZZUIptayCN8cqzzAWEjlgdCRyDoeHmSc4dYN/rVMPjezl5Z1kOObxGLNz/I/IiatW3wRwFyFk\nkyRJI9HyCCHzISej1yeu/8ZAT+SSlRgQQjBt2rvo7l4Kr7eMmp5HD5ZNh1YiZ5wosrKO2G88a4w2\nDqOnWi0uvgDt7f8EEEUwOF3jSLK/qFZZxJsmRRmd+7vgcuUw0uGktstO5j1WVt6C7dtvAQDk5p5o\nS9iJsrKr0N+/Dv39q1FS8hNhGy5CPDjwwN1J3ZOWDo/v+Tp6xKqg4Axs26bdBO6PBtwHH3wfdu2i\nnTk9/u/rDJ7N1hsYTSIvY3+v//L4Px5E47A+j7G17LL+7OPGjcP27dvtb0ocVmzk5gFYQghphuy9\nWgRZGrclfv4bCfts5GQSmJ29QLg8IQS5uSegvf0funr4Ejm7VBOjgdF0dsjLOwFz5nyBwcFtyM4+\nWlcvO6zDWAToVMAirWMXR47A7c4XymtoHdbJwrhxv0JGxnxEIj3UHXgy8HjyMWVKMrHskl+cPJ5C\nEOIZSbHl/H/s3XtYlWW++P/3vURZayGaSBwElEMeRqRfgqbmiAfE3JBijTaeSjo4mo6mTR5Kt0ob\n85CnSppNzeDG9hR9v7Xza2UqWaCOOYZcnkfdiYgpMDqVJiNy8PP7Y+GSJazlUk5LvV/X9Vyynud+\n7uezllzw4T42a+2whbIhE6sWLfxqe2KDPe92nT59zuG6eZp2t2johhWnshIRKVJKPYRlpmo/LKly\nPpAN/JeI1JyydZeorzFyt6v2xTcddxM4GrvR9Bp2soOHRzgeHuE1zjtagqJxx8jV/v3TsePbjRaD\nvfGTdf3evp3kRCmFl9eQOj23vtQloXdz86R9+9mcOpWMwWCkc+f3bK43b+5LeekrUDcAACAASURB\nVHmx9bXJ1PG2n3UzBkPN/0dHW39pmnZnc/ond1WytrbquGfUZ4vc7ahtraXqs3lKS0/VuN62bXyD\nxlQXjTlrtTpHS1A07qzV2t+rt/fjjRaDvVX46/o5XL1qf8N3V9S5cxrHjj1b7fWf6lRfSMh/0K7d\nFJRqXmOT8s6d3+XQoQTr6/pc98oZjbEEi6ZpTUOPEryJuq4jV3c1ZyS5u18fR3RtX9fqnFmYtqnU\ntmp2Q02ft32Go0SuabtWPT17Nuq+uLWN54K6fw61bRflynx8nuSf//yCn37KpG3bONq2Tbj5TTdh\nbz2rtm2H0bHjWn766Wu8vYfTqlWfOj/rVlzr8tU07e7jVCKnLAN4XgHGAO2BG5uJRETuyqSwqVvk\nalN9X7qWLbtz332D+PnnrwGIiPi8qcJySm0DwG9n5f1bVV7+k91rTZ3INfb3VH11rQYHv0Z+/gLA\nsiZcy5b/X51ja0zNmnnQrdvHjfIspRQBAVMJCJjaKM+70c02Atc07c7l7E/uN4CpWGan/g9wzwy4\naOoxcjcbpGyZDbuVX37ZS4sWfrWus+NqvLz+jR9/tEx0btbMkzZtBjX4M0tL8+1ea9xZq7Ulco27\nxld9da126DAfs7kzZWXF+Pk97TIzpTUIDV1GXt4cwDI+78alebR7S0hICNOmTeOll166eWHtjuPs\n6OSRwEIRGSYir4pI0o1HQwbZlFyxRe5GSjWjVauH74gkDiAsbCWtWvXGZHqAzp3TcHO7tQVbb4ej\ngeyNO2u1toV0G3sCTe3duLf6OSil8PF5ksDAaY3yf6g5LyjoZTp3/jPt288jKupvTbBB/b0pPT0d\nT8+mXYy9Njk5OUyZUr87W9yKGTNm0LNnT0wmE6Gh9reXu9GiRYsICAjAbDYzcOBAjhw5Ui/xZGdn\n06NHD0wmEw888ACpqfb3zf3www8xGAwMHz68Xp7dEJxN5FoC3zZkIK7qTkjk7jQeHr8iMvJbevX6\nX3x8RjbKMx0NxG/MxZNrT5Yat0XO3i91/b1991DKgL//s4SGJmM0dmjqcO4ZIuKSLdNt27bFaGy8\ncbg3EhESExN5+umnnb5n2bJlrF69mpSUFHJycvDx8SE2NpaSkrqtuZmfn098fDy//vWv2bdvH3Pn\nzmXatGl8+umnNcrm5eUxe/ZsoqOj6/TMhuZsIvcZ4NrvpIFcveraXauac65evWz3WmO2JrlC16q9\nNet0Iqe5EqUa7qir7du306dPHzw9Pbnvvvvo3bs3KSkpPPvss5SUlGAwGGjWrBmvvWbZZaO8vJw5\nc+YQFBSEh4cHvXr1YuvWrdb6srOzMRgMfPHFF3Tv3h2TyUSPHj3Izc11Kp6LFy/y1FNP4evra21l\neuutt6zXQ0JCWLVqFQBJSUnW+AwGg/W4FivAunXrCA8Px2Qy0aVLF9asWVOnz+vNN99k6tSpdOrU\n6ZbueeWVVxgxYgRdu3YlPT2dX375hQ8++MDmff/ud7/D19eXVq1aMXDgQPbu3euw3j/+8Y8EBASw\nZs0aOnfuzPPPP8+ECRNYsWKFTbmKigrGjh3L66+/TkiIa+/najeRU0qFXjuAt4ExSqkFSqke1a9V\nK3NX+vnnb2xe17bch+b6zOZf2b3W1IlcY3d72W+Ra+wZ2Zp256msrGTEiBFER0dz8OBB9uzZw4wZ\nM4iOjmbNmjWYzWaKi4spLCzk5ZdfBiAxMZEdO3aQkZHB4cOHmTBhAsOHD+fgwYM2dc+aNYs33niD\nvXv3EhoayrBhwygtvfk+zPPmzePw4cNs2rSJ48ePk5aWRkBA7RNcZs2aRVFREYWFhRQVFbF+/Xqa\nN29Ov36WLSTfe+895s+fT3JyMkePHmXlypUsX76cd955x1pHXFwcnp6edo9WrW5ti7sbnTx5kqKi\nImJjY63njEYj0dHR7Nq1yyaOoqIiNm3axL59+4iOjiYmJobi4uLaqgVg9+7dDBliu3blo48+Sk5O\nDpWV11dQePXVVwkNDeWpp56q03tpDI7+BP8e2+XwFbAIWGinvOvtylwPzpx5y+Z1ScmBJopEq4uQ\nkMUcOBBb67Vb3VS9Lq5erflDubF2dbjZ83SLnKbd3MWLF7lw4QKPPfYYwcHBANaWptzcXJRS3H//\n9aV48vLyyMjI4NSpUwQGWpaOmjJlCpmZmaSmprJ27fWlWRcsWMDgwYMBS6tYYGAgH3zwAc8+63i/\n4IKCAiIjI4mKigIgKCjIblmz2YzZbBlOcuzYMaZPn86KFSsYOHAgAMnJySxfvpzHH7esbdmhQwfm\nzJlDSkqKdZzdn//8Zy5ftt/LUVdFRUUopfD1tV1Ky9fXl7NnLdvoff311xw4cIBz587h7m5ZDSEp\nKYmNGzfy/vvvW5Po2uquniBeq7eiooLz58/j6+vL1q1b+fjjj9m/f38DvLv65+gn9zONFoWmNbA2\nbWLw83uGoqJ1Na41Zovc5cvf1zjnKi1yjvcG1TQNoE2bNkyYMIEhQ4YQExNDTEwMI0eOtJs85ebm\nIiJ07drVZkuysrIyBg26PmNfKUXv3r2trz08PIiIiHBqgP8LL7zAyJEjycnJITY2lmHDht10XNfP\nP/9MQkICo0ePZtq0aQCcP3+e06dPM2nSJCZPnmwtW1FRYTP2z9/f0V6yjSM3N5eSkhK8vW0X375y\n5Qp5eXkA1oknSinGjx9v06poz/nz53nmmWfIyMhwyYkrtbGbyIlIemMG4qrc3NpSUfFP62t//4mN\nHEHNBYG1W6eUwt//+SZP5Nq2fYyCgtdtzrlKi9ydtjODdndz5W1Y09LSmDlzJps3b2bjxo3Mnz+f\nDRs21Fr26tWrGAwGcnJycHOz/ZVrMtXPdopDhw6loKCAL7/8km3bthEfH8+oUaNIS0urtXxlZSWj\nRo0iKCiIt9++vj3g1auW3zepqan06WN/0eq4uDh27Nhh97pSiosXL97muwE/Pz9EhOLiYmsrJkBx\ncTF+fn7WWP38/Ni5c2eNPXuvde1Wb1G7ds7Pz69G12txcTFubm54e3uzc+dOioqKiImJsdZ77XNp\n0aIFhw8fpmPHhtti73bcMX0pSqmXgAFAD8APWCQirzm8yfb+EcAC4FdAMfAesEREHGZKZnMnLl68\nPmHX19f5WTf1oUWLpv/L525hr+uwMRM5s7lzjXOu0iJnMoU1ahyadieLiIggIiKCWbNmERcXR3p6\nOvHx8TbjrAC6d++OiFBYWEj//v3t1ici7N6929pdW1JSwqFDh0hMTHQqHi8vL8aNG8e4ceMYOnQo\nY8eOJTU1lebNa459ffHFFykoKGDPnj00a3Z9VJSPjw/t2rXj+++/Z9y4cXaf1dBdqyEhIfj5+ZGZ\nmWntLi4tLWXHjh2sXLkSgMjISIqLi1FK2Z2MUNtSJ3369KmRdG/dupUePXrQrFkzevbsWWPs4rx5\n8/j555955513XHLig91ETimVBvyHiJys+toREZHn6je0Gp4HLgCfApNvUtaGUupR4GMsydtMoDuw\nBMuyKq84uvfGPK+xZxgGBEzlhx9WWV936vSfjfr8u4m9RK5xlx+p+Re4m1vbRns+2G+Rc3dv16hx\naNqdKD8/n9TUVIYPH05AQAAnTpzgwIEDTJ06leDgYEpLS/nqq6/o3r07ZrOZjh07MnbsWBITE1mx\nYgWRkZH8+OOPZGVlERYWxogRI6x1Jycn4+3tjb+/P6+99hru7u6MGTPmpjEtXLiQyMhIwsPDKS8v\n55NPPiEsLKzWJG7dunWsW7eOzZs3U1paap1M0bJlSzw8PEhKSmL69Om0bt2auLg4ysvLyc3N5cyZ\nM8ydOxe49a7VEydOcOnSJc6cOUNZWZm1pSw8PBw3NzfOnj1LTEwMS5cuJSHBslXejBkzWLJkCZ07\nd6Zjx44kJyfj6elp/TwGDx5M3759SUhIYNmyZXTp0oXCwkK2bNlCbGwsffv2rTWWyZMnk5KSwsyZ\nM5k0aRI7d+5k/fr1ZGRkAJYxhF27drW557777qOyspJf/cr+pLmm5KhFbiDwZtXXg7Cd+HCjBm8E\nF5GuAMqSSb1wi7cvAbaLyLX7spVSnsA8pdRqEfmH/VubNpEzmULp1m0jRUXpeHpG4efneNCrZp+9\nRK4x132qbTFeN7f7Gu35lhhqJnKBgX9o1Bg07U5lNps5fvw4Tz75pHVw/FNPPcXs2bNp1qwZkydP\nZsyYMfz4448sXLiQBQsW8F//9V8sXryYOXPm8MMPP+Dl5cXDDz9cY4zc0qVL+cMf/sDx48cJDw/n\niy++cKr71d3dnfnz53Py5EmMRiO9e/dm48aNNnVf+zm3fft2SktLGTBggE0d12J97rnnaNmyJW+8\n8QavvvoqJpOJ8PBwfv/739/2Z/b888+zfft26+vIyEjAMju1ffv2lJeXc/z4cS5cuGAtM3v2bEpL\nS/n973/PTz/9ZF2yxcPDw1pm06ZNzJ8/n9/97nf84x//wNfXl759+zJhwgS7sQQHB7Np0yZmzpzJ\nf/7nf9KuXTvefvttm4T6TqNu7Ft2dVWJXDlOdq0qpQKBAuB5EUmrdj4YyAOeqW08oFJKRIScnCgu\nXbq+lk9k5He0atWjzu9Da3yXLh0iJyfC5twjjxTRooWvnTsaRlaWbeIYGvoG7dvXPsOqIZw79ymH\nDz9hc659+1cJDV3caDFomlKqxtime1V2djaDBg3i3LlzeHl5NXU4Wj1z9L1eda1OrQnOLgh8JwvH\n0mJ4uPpJEckH/gV0reWeam5skbsXPrK7040bh7u7t2/0JK42jb0SfG0tcnoLJ01rWjqp1W6XowWB\n29/K0ZhB36Jrf978VMu1n6pdr1VTj5HT6k/z5m0IDV0GWBa/7dDh35s4omsa94+D2sbIKaWXHtG0\npuToDzp7C/C2atWKpUuXNmKUmityNEYun1sb++Z0hqOUigEynSiaJSKDbl6s4YhU3nBGt8jdydq3\nn42fXyIi5TVa6JpKs2YtG/V5tbW+NXYMmqZd179//xqzXatzNEtUd8VqjhK5Z2m4SQx/Bbo4Ue5f\n9fCsay1xbWq51gb40d6NixYt4syZYsrL4aGHLIdukbvztWjh06TPb93611y4sNP6ulWr3g5K17/a\nJlyYTK43pV7TNAtXWIBXqx9ZWVlkZWXVa533wmSHIOAUNSc7dABOcpPJDn/7W2cuXz5uPd+z59/x\n8HAmB9W02v3yy14OHBhKefl5fHxG86tffdCo4+RKS39g927bVei7d/8rrVs/0mgxaJqe7KDdKxp6\nssMtLQisLCP9uwJtgRwRKanLwxuDiJxWSu0HxgHV18N7CigDvnRcg57soNUvT88oevfOp6LiAi1a\n+Df6ZIfa1ovT23NpmqbdmZzOSpRSU4Ei4ADwNdC56vwGpdT0hgnP5vlRSqnfAL+pOtVVKfWbqsNY\nrdw2pdT/3nD7q0B/pdR/KqX6K6VmAvOANY7XkNOTHbSG0ayZB+7u7Ro9iQPLHyOenj2trw0GEyZT\nzR0nNE3TNNfnVCKnlJqIZXHgDcCTQPXfPju4nlw1pN8D/wf4EMvYvVFVr/8PUH3Qk4Eb3peIfAmM\nBHoBm4EXgWRusquD5V492UG7+4SGLqV5c2+UciM0dClubnqyg6Zp2p3IqTFySqm/AxtFZE61MWo9\nRCRXKRUP/FlE/Bo41kZ1bYzct9+258qV09bzvXufwmh05dVWNM05V6+WAwqD4Y7Zclm7i+gxctq9\nwlUWBA4Btti5VgI07h5DjejGrlXdIqfdLQyG5jqJ07R7QEhICKtWrbp5Qe2O5GxWch4ItnOtM3Cm\nXqJxSbZdq3qyg6Zpmlab9PR0PD09mzqMGnJycpgyZUqTPX/GjBn07NkTk8lEaGio0/ctWrSIgIAA\nzGYzAwcO5MiRI/UST3Z2Nj169MBkMvHAAw+Qmppqc/3jjz+mZ8+etGnThpYtW9K9e3fWr19fL89u\nCM5mJZ8DC5RS1f8HRCnlDczEMnburqQnO2iapmnOEJEmmcB0M23btsVorLl+ZGMRERITE3n66aed\nvmfZsmWsXr2alJQUcnJy8PHxITY2lpKSui2WkZ+fT3x8PL/+9a/Zt28fc+fOZdq0aXz66afWMt7e\n3vz7v/87f/vb3zh48CDPPPMMzz33HJs3b67TsxuMiNz0ALyBY1gW6P0GSzPVDuAclj1MWztTz510\nWD4akR072so332A9rlz5h2iapml1c+1n7J0oOztbevfuLS1btpTWrVtLr169ZO3ataKUEoPBYP03\nKSlJRETKyspk9uzZEhgYKGazWR5++GHZsmWLtb6srCxRSsnnn38uDz30kBiNRomKipK9e/c6Fc+F\nCxdk/Pjx4uPjI0ajUcLCwuTNN9+0Xg8ODpaVK1eKiMiiRYts4rx2XItVRCQtLU26du0qRqNROnfu\nLKtXr66Pj01WrFghISEhTpX19/eXJUuWWF9fvnxZPD095d1337Weu3DhgkycOFF8fHzE09NTBgwY\nIDk5OQ7rnT17tnTq1Mnm3PPPPy+PPPKIw/siIyPl1VdfdSr2Gzn6Xq+6Vqd8xakBMiJyXinVA5gB\nPAqcwLIG3VpgtYhcrMfc0sXodeQ0TdMam0pquJYtWXj7kywqKysZMWIEEydO5MMPP6SsrIzc3FzC\nw8NZs2YN8+bNIy8vDxGhZUvLbPDExEROnjxJRkYGAQEBbNq0ieHDh/Pdd98RERFhrXvWrFm89dZb\ntGvXjkWLFjFs2DBOnDhx09a0efPmcfjwYTZt2oSPjw8nT57k3LlztZadNWsWL7zwgvX11q1bee65\n5+jXrx8A7733HosWLWLt2rVERkZy6NAhJk6cSIsWLazds3FxcezYscNuPEopLl68/bTg5MmTFBUV\nERsbaz1nNBqJjo5m165dTJw40RqHl5cXmzZtok2bNqSnpxMTE8OxY8fw9fWtte7du3czZMgQm3OP\nPvoo69evp7KykmbNava6bdu2jePHj7NkyZLbfk8NyemRziLyC/AfVYcNpZSbiFTUZ2CuouZkB921\nqmmadq+6ePEiFy5c4LHHHiM4OBiATp06AZCbm4tSivvvv99aPi8vj4yMDE6dOkVgYCAAU6ZMITMz\nk9TUVNauXWstu2DBAgYPHgzAunXrCAwM5IMPPuDZZ591GFNBQQGRkZFERUUBEBQUZLes2WzGbDYD\ncOzYMaZPn86KFSsYOHAgAMnJySxfvpzHH38cgA4dOjBnzhxSUlKsiZyjvV/rQ1FREUqpGsmYr68v\nZ8+eBeDrr7/mwIEDnDt3Dnd3y4LmSUlJbNy4kffff5+XX37Zbt3VE8Rr9VZUVHD+/HnrMy9evEhA\nQABXrlzBzc2NlJSUGgmgq3AqkVNKzRaR5XauuWFZy+2J+gzMdejJDpqmaZpFmzZtmDBhAkOGDCEm\nJoaYmBhGjhxpN3nKzc1FROjatavNEhRlZWUMGjTI+lopRe/e1/dd9vDwICIiwqkB/i+88AIjR44k\nJyeH2NhYhg0bRnR0tMN7fv75ZxISEhg9ejTTpk0D4Pz585w+fZpJkyYxefJka9mKigqbsX+usPdr\nbm4uJSUleHt725y/cuUKeXl5ANaJJ0opxo8fzzvvvON0/Z6enuzfv59Lly6xbds2Zs6cSXBwsDXh\ndSXOtsj9h1KqUETer36yak25DMD13lk90ZMdNE3TtOrS0tKYOXMmmzdvZuPGjcyfP58NG2qf83f1\n6lUMBgM5OTm4udn+yjWZTPUSz9ChQykoKODLL79k27ZtxMfHM2rUKNLS0motX1lZyahRowgKCuLt\nt9+2iRUgNTWVPn362H1eQ3et+vn5ISIUFxdbWzEBiouL8fPzs8bq5+fHzp07a6zR1qpVKwD2799f\n45yfnx/FxcU25YuLi3Fzc7NJCpVS1hm2Dz74IEeOHOH111+/oxO5ycB7SqlzIrIZrPuufgjEYhk3\nd5fS68hpmqY1trqMY2sMERERREREMGvWLOLi4khPTyc+Pp7KSttenO7duyMiFBYW0r9/f7v1iQi7\nd++2dteWlJRw6NAhEhMTnYrHy8uLcePGMW7cOIYOHcrYsWNJTU2lefPmNcq++OKLFBQUsGfPHpsx\nYT4+PrRr147vv/+ecePG2X1WQ3ethoSE4OfnR2ZmprW7uLS0lB07drBy5UoAIiMjKS4uRilFSEhI\nrfXUttRJnz59aiTdW7dupUePHrWOj7vm6tWrXLly5XbfUoNydrLDOqWUP/B/lVIxwHfAB8BQYKiI\n7G7AGJvUjVt06a5VTdO0e1d+fj6pqakMHz6cgIAATpw4wYEDB5g6dSrBwcGUlpby1Vdf0b17d8xm\nMx07dmTs2LEkJiayYsUKIiMj+fHHH8nKyiIsLIwRI0ZY605OTsbb2xt/f39ee+013N3dGTNmzE1j\nWrhwIZGRkYSHh1NeXs4nn3xCWFhYrUncunXrWLduHZs3b6a0tJTS0lIAWrZsiYeHB0lJSUyfPp3W\nrVsTFxdHeXk5ubm5nDlzhrlz5wK33rV64sQJLl26xJkzZygrK7O2lIWHh+Pm5sbZs2eJiYlh6dKl\nJCQkAJa155YsWULnzp3p2LEjycnJeHp6Wj+PwYMH07dvXxISEli2bBldunShsLCQLVu2EBsbS9++\nfWuNZfLkyaSkpDBz5kwmTZrEzp07Wb9+PRkZGdYyr7/+Or169SI0NJQrV67wxRdf8N///d824xld\nyq1McQXexrLkyP8DfgF+Xddps656UDVd+JtvmtksP1JZWW53GrGmaZrmHO7Q5UeKi4vliSeekMDA\nQDEajdKhQweZO3euVFRUiIjIlClTxNvb22b5kYqKCklKSpKwsDBxd3cXf39/SUhIkNzcXBGxLD9i\nMBjks88+kwcffPCWlx9ZvHixdOvWTTw8PKRt27YSHx8vR48etV4PCQmRVatWiYhIYmKiGAyGGkf1\n5UcyMjIkKipKTCaTeHl5Sb9+/eSjjz667c9swIABtT7z1KlTIiKSn58vBoNB0tPTbe5LSkqSdu3a\niclkkgEDBsjhw4dtrl+6dElmzJghQUFB4u7uLu3bt5cxY8ZIXl6ew3i2b98uUVFRYjQaJTQ01GZJ\nExGRV155RTp16iRms1natm0rffv2rdP7d/S9Tj0sP+LUXqvXKMtoxwwgDogXke31mlW6kGt7rWZl\n2U6B79+/UrfKaZqm1ZHea/W67OxsBg0axLlz5/Dy8mrqcLR61tB7rdrtWlVKnQZqe7IbloFi/11t\nFouISIe6BOKKav/gXW/Vbk3TNO3OppNa7XY5GiO3jdoTuXtIzYkOrrj9iqZpmnZnc/S7xd4sUaUU\nr776qnXsmnZvuqWu1XuJUkoqK6+wfbt7tXNu9O9f3oRRaZqm3R1016rzCgsL7c4S9fLy4r777mvk\niLRb0WRdq5re1UHTNE1req6wAK/muhyNkXsa+EJE/ln1tUMisr5eI3MJep9VTdM0TdNcl6MWuf8C\negP/rPraEQHuukTuxjXk9GLAmqZpmqa5EkeJXAhQWO3re5DenkvTNE3TNNdlN5ETkVO1fX0v0bs6\naJqmaZrmynRm4kDNyQ7649I0TdM0zXU4muxwEufXkRMRCaufkFyJ7lrVNE3T7mwhISFMmzaNl156\nqalD0RqAoyam7Fs47sqtuvRkB03TNM1Z6enpeHp6NnUYNeTk5DBlypQme/6MGTPo2bMnJpOJ0NBQ\np+9btGgRAQEBmM1mBg4cyJEjR+olnuzsbHr06IHJZOKBBx4gNTXV5vqf/vQnoqOj8fLyok2bNgwa\nNIi//vWv9fLshuBojFxiI8bhovTyI5qmaZpzRMQld/9p27Ztkz5fREhMTOTAgQNkZmY6dc+yZctY\nvXo16enpdOrUiaSkJGJjYzl+/DgeHh63HUt+fj7x8fE8//zz/OUvf2HHjh1MmTIFHx8fHn/8ccCS\n6I0ePZq+fftiNptZtWoVjz76KPv37ycszAU7H0VEH7UcgFy+fFq++Qbr8de/BoimaZpWd5ZfP3em\n7Oxs6d27t7Rs2VJat24tvXr1krVr14pSSgwGg/XfpKQkEREpKyuT2bNnS2BgoJjNZnn44Ydly5Yt\n1vqysrJEKSWff/65PPTQQ2I0GiUqKkr27t3rVDwXLlyQ8ePHi4+PjxiNRgkLC5M333zTej04OFhW\nrlwpIiKLFi2yifPacS1WEZG0tDTp2rWrGI1G6dy5s6xevbo+PjZZsWKFhISEOFXW399flixZYn19\n+fJl8fT0lHfffdd67sKFCzJx4kTx8fERT09PGTBggOTk5Disd/bs2dKpUyebc88//7w88sgjDu/z\n8/OTtWvXOhX7jRx9r1ddq1O+opuYHNItcpqmaU1CqYY76qCyspIRI0YQHR3NwYMH2bNnDzNmzCA6\nOpo1a9ZgNpspLi6msLCQl19+GYDExER27NhBRkYGhw8fZsKECQwfPpyDBw/a1D1r1izeeOMN9u7d\nS2hoKMOGDaO0tPSmMc2bN4/Dhw+zadMmjh8/TlpaGgEBAbWWnTVrFkVFRRQWFlJUVMT69etp3rw5\n/fr1A+C9995j/vz5JCcnc/ToUVauXMny5ct55513rHXExcXh6elp92jVqtXtfrwAnDx5kqKiImJj\nY63njEYj0dHR7Nq1yyaOoqIiNm3axL59+4iOjiYmJobi4mK7de/evZshQ4bYnHv00UfJycmhsvLG\n4VQWV65cobS0lDZt2tTpfTWUO2aLLqXUS8AAoAfgBywSkdecuM8T+AMwFOiIZaDbEWC5iPw/R/fq\nWauapmladRcvXuTChQs89thjBAcHA9CpUycAcnNzUUpx//33W8vn5eWRkZHBqVOnCAwMBGDKlClk\nZmaSmprK2rVrrWUXLFjA4MGDAVi3bh2BgYF88MEHPPvssw5jKigoIDIykqioKACCgoLsljWbzZjN\nZgCOHTvG9OnTWbFiBQMHDgQgOTmZ5cuXW7sZO3TowJw5c0hJSbGOs/vzI7FPWAAAIABJREFUn/9s\nd+/X+lBUVIRSCl9fX5vzvr6+nD17FoCvv/6aAwcOcO7cOdzdLXuiJyUlsXHjRt5//31rEl1b3dUT\nxGv1VlRUcP78+RrPBJg/fz6enp4MHz68Pt5evbtjEjngeeAC8Ckw+Rbua19V/r+ARUAlMAb4VCk1\nVUT+aP9W3SKnaZqmXdemTRsmTJjAkCFDiImJISYmhpEjR9pNnnJzcxERunbtarNxellZGYMGDbK+\nVkrRu3dv62sPDw8iIiKcGuD/wgsvMHLkSHJycoiNjWXYsGFER0c7vOfnn38mISGB0aNHM23aNADO\nnz/P6dOnmTRpEpMnX/81W1FRYTP2zxX2fs3NzaWkpARvb2+b81euXCEvLw/AOvFEKcX48eNtWhWd\n9eabb/Lee++xbds2WrZsWffAG8Adk8iJSFcAZVkD5IVbuDUPCBaR6u3TmUqp9sAcwG4ip1vkNE3T\ntBulpaUxc+ZMNm/ezMaNG5k/fz4bNmyotezVq1cxGAzk5OTg5mb7K9dkMtVLPEOHDqWgoIAvv/yS\nbdu2ER8fz6hRo0hLS6u1fGVlJaNGjSIoKIi3337bJlaA1NRU+vTpY/d5cXFx7Nixw+51pRQXL168\nzXcDfn5+iAjFxcXWVkyA4uJi/Pz8rLH6+fmxc+dOmwQZsHbt7t+/v8Y5Pz+/Gl2vxcXFuLm51UgK\n16xZw8KFC9m8ebO1tdMV3TGJ3O0SEXvtvzmA4z9ZarTIud5sJE3TtLuSOLuMadOIiIggIiKCWbNm\nERcXR3p6OvHx8TXGWXXv3h0RobCwkP79+9utT0TYvXu3tbu2pKSEQ4cOkZiY6FQ8Xl5ejBs3jnHj\nxjF06FDGjh1LamoqzZs3r1H2xRdfpKCggD179tCs2fX1UX18fGjXrh3ff/8948aNs/ushu5aDQkJ\nwc/Pj8zMTGsCVVpayo4dO1i5ciUAkZGRFBcXo5QiJKT2XURrW+qkT58+NZLurVu30qNHD5vPYtWq\nVSQlJbFp0yaHSa0rcCqRU0o5SniuYunyPCoi5fUSVePoDxx1XOTGHyS6RU7TNO1elp+fT2pqKsOH\nDycgIIATJ05w4MABpk6dSnBwMKWlpXz11Vd0794ds9lMx44dGTt2LImJiaxYsYLIyEh+/PFHsrKy\nCAsLY8SIEda6k5OT8fb2xt/fn9deew13d3fGjBlz05gWLlxIZGQk4eHhlJeX88knnxAWFlZrErdu\n3TrWrVvH5s2bKS0ttU6maNmyJR4eHiQlJTF9+nRat25NXFwc5eXl5ObmcubMGebOnQvcetfqiRMn\nuHTpEmfOnKGsrMzaUhYeHo6bmxtnz54lJiaGpUuXkpCQAFjWnluyZAmdO3emY8eOJCcn4+npaf08\nBg8eTN++fUlISGDZsmV06dKFwsJCtmzZQmxsLH379q01lsmTJ5OSksLMmTOZNGkSO3fuZP369WRk\nZFjLvPHGG8yfP5+//OUvPPDAA9YWPJPJVOeJHA3CmamtWJK1ypscvwCL6zqN1olYmlXFs6AOdfyu\nKubRDsrIpUtHbJYf+dvfutidQqxpmqY5jzt0+ZHi4mJ54oknJDAwUIxGo3To0EHmzp0rFRUVIiIy\nZcoU8fb2tll+pKKiQpKSkiQsLEzc3d3F399fEhISJDc3V0Qsy48YDAb57LPP5MEHH7zl5UcWL14s\n3bp1Ew8PD2nbtq3Ex8fL0aNHrddDQkJk1apVIiKSmJgoBoOhxlF9+ZGMjAyJiooSk8kkXl5e0q9f\nP/noo49u+zMbMGBArc88deqUiIjk5+eLwWCQ9PR0m/uSkpKkXbt2YjKZZMCAAXL48GGb65cuXZIZ\nM2ZIUFCQuLu7S/v27WXMmDGSl5fnMJ7t27dLVFSUGI1GCQ0NtVnSRMSyXEtt8T7zzDO39f4dfa9T\nD8uPKHGi+VopNQx4G9gPfAwUA77Ak8CDwL8DDwOTgFdEZMVN6osBnFkVMEtEBlU/UTVGrhwnZ63W\n8uwBwJfAhyJidyqQUkouXTrEd991s54zm7vy8MOHb/WRmqZp2g2UUjXGNt2rsrOzGTRoEOfOncPL\ny6upw9HqmaPv9aprdRq35ewYuRHAZhG5cbbo+0qpVGCgiDyjlLoKPAc4TOSAvwJdnHjuv5yMzylK\nqZ7A/wO+AiberPzixWupmunMQw9B3766a1XTNE2rfzqpvTdkZWWRlZVVr3U62yL3I/BbEanRiqaU\nigU+EhEvpVQc8D8iYqzXKG2fd1stckqpCCALOAAMFZErNykvv/yyj5ych6znPDwepGfP/Q7u0jRN\n05yhW+Suu1mLnL1ZokopXn31VevYNc01uUqLXDMgjNq7Qx+oug5wpepwKUqpjsBW4Htg2M2SuGtq\nLj+iZ61qmqZp9at///52dxUAx7NEdVes5mwitwl4XSl1DtggIpVVLWOPA4uBL6rKhQMn6j9MUEpF\nAcFcTxq7KqV+U/X1F1K1TpxSahvQXkQ6Vr2+H0sC2hzLgsDhNywjkit2Z9vaZtB6QWBN0zStsbnC\nArya63I2kZuGZUeF/wtUKKV+AtpU3f/XqutgWYbk9foOssrvgaervhZgVNUBEAIUVH1twHadkK7A\ntSW3P6+l3ur32tALAmuapmma5sqcGiNnLazUEKA3lr1OC4HdtY2buxsopeTChb+Rm9vLes7TsydR\nUXuaMCpN07S7gx4jp90rXGWMHAAishXLWLN7gm6R0zRN0zTNld1SIqeUegzLjghewI/ANyKyqSEC\ncw03btGlEzlN0zRN01yHs1t0eWIZX9YPqAD+CbQFXlJK7QAeE5FLDRZlE9GzVjVN0zRNc2XONjG9\nDkQCTwEmEfEHTFgmH0TScBMcmpietappmqbd2UJCQli1alVTh6E1EGczk98A80XkLyJSCSAilSLy\nFyzbc/3G4d13LD1GTtM0TXNOeno6np6eTR1GDTk5OUyZMqXJnj9jxgx69uyJyWQiNDTU6fsWLVpE\nQEAAZrOZgQMHcuTIkXqJJzs7mx49emAymXjggQdITU21uX7kyBFGjRpFWFgYBoOB11675d1AG5Wz\nmUlbwN4neKTq+l3nxq5V3SKnaZqm2SMi3LBOqUto27YtRmODbbh0UyJCYmIiTz/99M0LV1m2bBmr\nV68mJSWFnJwcfHx8iI2NpaSkpE6x5OfnEx8fz69//Wv27dvH3LlzmTZtGp9++qm1zL/+9S9CQkJY\nvHjxLSWeTcXZzOQk8Jida3FV1+9CukVO0zRNs7V9+3b69OmDp6cn9913H7179yYlJYVnn32WkpIS\nDAYDzZo1s7bklJeXM2fOHIKCgvDw8KBXr15s3Xp9AYjs7GwMBgNffPEF3bt3x2Qy0aNHD3Jzc52K\n5+LFizz11FP4+vpaW5neeust6/XqXatJSUnW+AwGg/Wo3uq0bt06wsPDMZlMdOnShTVr1tTp83rz\nzTeZOnUqnTp1uqV7XnnlFUaMGEHXrl1JT0/nl19+4YMPPrB537/73e/w9fWlVatWDBw4kL179zqs\n949//CMBAQGsWbOGzp078/zzzzNhwgRWrLi+RXyPHj1Yvnw5o0ePxmQy3fobbmTOzlpNBVYqpVoC\nf8GyhpwfMBp4HnipYcJrWrpFTtM0rWmoet5YvDoZMOC2762srGTEiBFMnDiRDz/8kLKyMnJzcwkP\nD2fNmjXMmzePvLw8RISWLVsCkJiYyMmTJ8nIyCAgIIBNmzYxfPhwvvvuOyIiIqx1z5o1i7feeot2\n7dqxaNEihg0bxokTJ27amjZv3jwOHz7Mpk2b8PHx4eTJk5w7d67WsrNmzeKFF16wvt66dSvPPfcc\n/fr1A+C9995j0aJFrF27lsjISA4dOsTEiRNp0aKFtXvW3t6v1yiluHjxonMfaC1OnjxJUVERsbGx\n1nNGo5Ho6Gh27drFxIkTrXF4eXmxadMm2rRpQ3p6OjExMRw7dgxfX99a6969ezdDhgyxOffoo4+y\nfv16KisradasWa33uTKnEjkRWV211dVLQGLVaQWUAUtF5M2GCa+p6VmrmqZp2nUXL17kwoULPPbY\nYwQHBwNYW5pyc3NRSnH//fdby+fl5ZGRkcGpU6cIDAwEYMqUKWRmZpKamsratWutZRcsWMDgwYMB\nS6tYYGAgH3zwAc8++6zDmAoKCoiMjCQqKgqAoKAgu2XNZjNmsxmAY8eOMX36dFasWMHAgQMBSE5O\nZvny5Tz++OMAdOjQgTlz5pCSkmJN5Bzt/VofioqKUErVSMZ8fX05e/YsAF9//TUHDhzg3LlzuLu7\nA5bWxo0bN/L+++/z8ssv2627eoJ4rd6KigrOnz9vNwF0ZU6vIyciryql3sCys8O1deR2i8hPDRVc\nU6u5ErNukdM0TbuXtWnThgkTJjBkyBBiYmKIiYlh5MiRdpOn3NxcRISuXbva/E4pKytj0KBB1tdK\nKXr37m197eHhQUREhFMD/F944QVGjhxJTk4OsbGxDBs2jOjoaIf3/PzzzyQkJDB69GimTbPssnn+\n/HlOnz7NpEmTmDx5srVsRUWFzdg/V9j7NTc3l5KSEry9vW3OX7lyhby8PADrxBOlFOPHj+edd95p\n9Dgbw63u7PAT8GUDxeKCdNeqpmmaZistLY2ZM2eyefNmNm7cyPz589mwYUOtZa9evYrBYCAnJwc3\nN9tfufU1/mro0KEUFBTw5Zdfsm3bNuLj4xk1ahRpaWm1lq+srGTUqFEEBQXx9ttv28QKkJqaSp8+\nfew+r6G7Vv38/BARiouLra2YAMXFxfj5+Vlj9fPzY+fOnTUaXVq1agXA/v37a5zz8/OjuLjYpnxx\ncTFubm41ksI7hd1ETinlOJ2/gYhsr3s4rkVv0aVpmtY06jKOrTFEREQQERHBrFmziIuLIz09nfj4\neCorK23Kde/eHRGhsLCQ/v37261PRNi9e7e1u7akpIRDhw6RmJjoVDxeXl6MGzeOcePGMXToUMaO\nHUtqairNmzevUfbFF1+koKCAPXv22IwJ8/HxoV27dnz//feMGzfO7rMaums1JCQEPz8/MjMzrd3F\npaWl7Nixg5UrVwIQGRlJcXExSilCQkJqrae2Gad9+vSpkXRv3bqVHj163JHj48Bxi1wWN66IWztV\nVe7O/AQc0i1ymqZp2nX5+fmkpqYyfPhwAgICOHHiBAcOHGDq1KkEBwdTWlrKV199Rffu3TGbzXTs\n2JGxY8eSmJjIihUriIyM5McffyQrK4uwsDBGjBhhrTs5ORlvb2/8/f157bXXcHd3Z8yYMTeNaeHC\nhURGRhIeHk55eTmffPIJYWFhtSZx69atY926dWzevJnS0lJKS0sBaNmyJR4eHiQlJTF9+nRat25N\nXFwc5eXl5ObmcubMGebOnQvcetfqiRMnuHTpEmfOnKGsrMzaUhYeHo6bmxtnz54lJiaGpUuXkpCQ\nAFjWnluyZAmdO3emY8eOJCcn4+npaf08Bg8eTN++fUlISGDZsmV06dKFwsJCtmzZQmxsLH379q01\nlsmTJ5OSksLMmTOZNGkSO3fuZP369WRkZFjLlJeXc+TIEUSE0tJSioqK2L9/Py1btiQsLOyW3nuj\nEJFaDyx7qjp92KvnTj0A+cc/PpVvvsF6HDiQIJqmaVrdWX793HmKi4vliSeekMDAQDEajdKhQweZ\nO3euVFRUiIjIlClTxNvbWwwGgyQlJYmISEVFhSQlJUlYWJi4u7uLv7+/JCQkSG5uroiIZGVlicFg\nkM8++0wefPBBMRqNEhUVJXv37nUqpsWLF0u3bt3Ew8ND2rZtK/Hx8XL06FHr9ZCQEFm1apWIiCQm\nJorBYKhxXItVRCQjI0OioqLEZDKJl5eX9OvXTz766KPb/swGDBhQ6zNPnTolIiL5+fliMBgkPT3d\n5r6kpCRp166dmEwmGTBggBw+fNjm+qVLl2TGjBkSFBQk7u7u0r59exkzZozk5eU5jGf79u0SFRUl\nRqNRQkND5d1337W5np+fL0qpGvEOHDjwtt6/o+/1qmt1yleU1BjQrwEopeQf//iEw4evb1rh7T2C\nbt0+dXCXpmma5gylVC0Tyu5N2dnZDBo0iHPnzuHl5dXU4Wj1zNH3etW1Oi2JofsKHdKzVjVN07SG\np5Na7XbpzMQBvSCwpmma1hgcbe0VFxeHp6dnjaNVq1YsXbq0EaPUXNEtLT9y79GzVjVN07SG1b9/\n/xqzXatzNEtUd8VqOpFzQLfIaZqmaU3NFRbg1VyXzkwc0lt0aZqmaZrmum4pkVNKGZRS3ZRS/ZVS\nHg0VlKvQCwJrmqZpmubKnM5MlFJTgSJgP/A10Lnq/Aal1PSGCa+p2c4i0l2rmqZpmqa5EqcyE6XU\nROBNYAPwW2z7GHcAv6ntvjudbpHTNE3TNM2VOZuZvASsFJHfATeuiHuUqta5u4+e7KBpmqZpmuty\nNjMJAbbYuVYC3Fc/4bgW3SKnaZqmaZorczYzOQ8E27nWGThTL9G4nBtb5PSsVU3TNO3OEhISwqpV\nq5o6DK2BOJvIfQ4sUEqFVjsnSilvYCaWsXMNSin1klJqo1LqrFLqqlJqwW3WE6KU+ldVHaGOyuoW\nOU3TNM1Z6enpeHp6NnUYNeTk5DBlypQme/6MGTPo2bMnJpOJ0FCHv3ZtLFq0iICAAMxmMwMHDuTI\nkSMNGKXFJ598Qnh4OEajkW7durFhQ8305p133iE0NBSTyUSPHj3YuXNng8fliLOZyXzgCnAI+ArL\ndM63gL8DlcBrDRKdreeB+7GM0avLpnR/BH5yrg49a1XTNE1zjoi4ZM9N27ZtMRqNTfZ8ESExMZGn\nn37a6XuWLVvG6tWrSUlJIScnBx8fH2JjYykpKbntOLKzswkJCbF7/dtvv2X06NE89dRT7N+/n7Fj\nxzJq1Ci+++47a5mPPvqIGTNmMH/+fPbt28cjjzzCv/3bv/HDDz/cdlx1JiJOHYAn8O/ATuA48C2w\nEGjlbB31cQDNsPR5LriNe8cChcB0LAloqIOy8sMPa+Wbb7Aex45NEU3TNK3uLL9+7PuGbxrsqKvs\n7Gzp3bu3tGzZUlq3bi29evWStWvXilJKDAaD9d+kpCQRESkrK5PZs2dLYGCgmM1mefjhh2XLli3W\n+rKyskQpJZ9//rk89NBDYjQaJSoqSvbu3etUPBcuXJDx48eLj4+PGI1GCQsLkzfffNN6PTg4WFau\nXCkiIosWLbKJ89pxLVYRkbS0NOnatasYjUbp3LmzrF69us6fmYjIihUrJCQkxKmy/v7+smTJEuvr\ny5cvi6enp7z77rvWcxcuXJCJEyeKj4+PeHp6yoABAyQnJ8dunVlZWQ6f/9vf/laGDBlic27w4MEy\nduxY6+tevXrJpEmTbMp07NhRXn31Vbv1Ovper7pWp7zI6SYmEflFRP5DRH4tIp1EpI+IJInIxXrJ\nKBuYUuo+YCXwB+CCM/foLbo0TdO06iorKxkxYgTR0dEcPHiQPXv2MGPGDKKjo1mzZg1ms5ni4mIK\nCwt5+eWXAUhMTGTHjh1kZGRw+PBhJkyYwPDhwzl48KBN3bNmzeKNN95g7969hIaGMmzYMEpLS28a\n07x58zh8+DCbNm3i+PHjpKWlERAQUGvZWbNmUVRURGFhIUVFRaxfv57mzZvTr18/AN577z3mz59P\ncnIyR48eZeXKlSxfvpx33nnHWkdcXByenp52j1atWt3uxwvAyZMnKSoqIjY21nrOaDQSHR3Nrl27\nbOIoKipi06ZN7Nu3j+joaGJiYiguLr6t53777bcMGTLE5tyjjz5qfWZ5eTl79+61iQtgyJAhNnE1\ntntpr9U3gCMi8oFSaoJzt+gxcpqmadp1Fy9e5MKFCzz22GMEBwcD0KlTJwByc3NRSnH//fdby+fl\n5ZGRkcGpU6cIDAwEYMqUKWRmZpKamsratWutZRcsWMDgwYMBWLduHYGBgXzwwQc8++yzDmMqKCgg\nMjKSqKgoAIKCguyWNZvNmM1mAI4dO8b06dNZsWIFAwcOBCA5OZnly5fz+OOPA9ChQwfmzJlDSkqK\ndZzdn//8Zy5fvuzcB3YbioqKUErh6+trc97X15ezZ88C8PXXX3PgwAHOnTuHu7s7AElJSWzcuJH3\n33/fmkRXZ2kAc/zc2p5ZVFQEwPnz56msrKy1zLZt227tTdYjpxI5pdTXDi5fxdLCtRf4s4jcXirc\ngJRS/YDxwEO3cl/NyQ6uN/ZB0zRNazxt2rRhwoQJDBkyhJiYGGJiYhg5cqTd5Ck3NxcRoWvXrjaJ\nRFlZGYMGDbK+VkrRu3dv62sPDw8iIiKcGuD/wgsvMHLkSHJycoiNjWXYsGFER0c7vOfnn38mISGB\n0aNHM23aNMCSqJw+fZpJkyYxefJka9mKigqbsX/+/v43jamh5ebmUlJSgre3t835K1eucOLECQBO\nnz5N165dUUohIlRWVlJWVmadkKKUYvz48TatjXciZ1vkFNAJ8AdOAsWAL5b15QqrXscBM5VS/UXE\n4XeeUioGyHTiuVkiMujmxRw+qznwn8AqETl2a3frrlVN07SmMEAGNHUIdqWlpTFz5kw2b97Mxo0b\nmT9/fq2zGwGuXr2KwWAgJycHNzfbX7kmk6le4hk6dCgFBQV8+eWXbNu2jfj4eEaNGkVaWlqt5Ssr\nKxk1ahRBQUG8/fbbNrECpKam0qdPH7vPi4uLY8eOHXavK6W4ePH2R135+fkhIhQXF1tbMQGKi4vx\n8/Ozxurn58fOnTtrtLRd69pt164d+/fvt57fvXs3c+fOJTs723pP9W5gPz+/Gt2y1Z/p7e1Ns2bN\nHJZpCs4mcquANUAPEcm9dlIpFQX8HyAJS4vcVmAx8PhN6vsr0MWJ5/7LyfgcmYllweK3lVKtq855\nVP3bSinVUkQu1XbjqlVb+Okny9cPPQSBgTqR0zRN0yAiIoKIiAhmzZpFXFwc6enpxMfHU1lZaVOu\ne/fuiAiFhYX079/fbn0iwu7du63dtSUlJRw6dIjExESn4vHy8mLcuHGMGzeOoUOHMnbsWFJTU2ne\nvHmNsi+++CIFBQXs2bOHZs2aWc/7+PjQrl07vv/+e8aNG2f3WQ3dtRoSEoKfnx+ZmZnW7uLS0lJ2\n7NjBypUrAYiMjKS4uBillN2ZqM2aNbNZ7uT06dO4ubnZLd+nTx8yMzP5wx/+YD2XmZnJI488AkDz\n5s2JiooiMzOT3/zmNzZlRo0a5dR7y8rKIisry6myTnNmRgSwH3jKzrWngYNVXz8D/LOuMzBuEsst\nzVoF1mGZoXrVzpFr5z45dWqZzazV77+fZXfmiaZpmuY8bjJr1VWdPHlS5s6dK7t27ZJTp07J119/\nLQEBAfL666/Lrl27xGAwSGZmppw/f17+9a9/iYjI+PHjJTg4WD7++GPJy8uTnJwcWbFihXz66aci\ncn3Wanh4uGRmZsqhQ4fkySefFD8/P2sdjixYsEA2bNgg//u//ytHjhyRJ598Ujp16mS9Xn3Walpa\nmpjNZtm+fbsUFRVZj0uXLomIyJ/+9Ccxm82yevVqOXbsmBw6dEjWr19vM4P0Vn3//feyb98+mTlz\npgQEBMi+fftk3759Ul5eLiIiZ86ckS5dusiGDRus9yxbtkzuu+8++Z//+R85ePCg/Pa3v5WAgABr\nnCIi0dHR8uCDD8qXX34pJ0+elF27dsnChQtl586dtcZxs1mru3btkubNm8vSpUvl6NGj8vrrr0uL\nFi3ku+++s5b56KOPxN3dXf70pz/J3//+d5k+fbp4enpKQUGB3Xodfa9TD7NWnU2eLgND7Vz7N+By\n1dfRQGldg7pJLLeayHWqiqv6saQquRsNRNq5T/Lzl9yQyM2x+5+haZqmOe9OTeSKi4vliSeekMDA\nQDEajdKhQweZO3euVFRUiIjIlClTxNvb22b5kYqKCklKSpKwsDBxd3cXf39/SUhIkNzcXBGxJBgG\ng0E+++wzefDBB295+ZHFixdLt27dxMPDQ9q2bSvx8fFy9OhR6/WQkBBZtWqViIgkJiaKwWCocVRf\nfiQjI0OioqLEZDKJl5eX9OvXTz766KPb/swGDBhQ6zNPnTolIiL5+fliMBgkPT3d5r6kpCRp166d\nmEwmGTBggBw+fNjm+qVLl2TGjBkSFBQk7u7u0r59exkzZozk5eXVGsfNEjkRkU8++UR+9atfibu7\nu3Tt2tUmubzmj3/8o4SEhIjRaJQePXrYTRyvaehETlnqcUwp9XcsMz5/U8u1T4EuIvIrpdQTwNsi\nUvu85zqo6sYNxpLIZWDp0v2/VZe/EJHSqnLbgPYi0tFBXROANKCjiOTZKSP5+Ys5eXKe9Vz79q8Q\nGvp6PbwbTdO0e9u1AeiaZaHaQYMGce7cOby8vJo6HK2eOfper7pWp5mUzo6Rew34b6XUAeAT4B+A\nD/AboBuWhXYBBgN/q0tADvweSzcuWLZcGFV1gGXSRUHV1wbqaZ0QPWtV0zRNaww6qdVul1MJj4h8\nCAwFLgGvAilV//4CDBGRjKqiLwG/bYA4EZFnRKSZnaOgWrmBIhJ2k7rSq+6rtTXuOj1rVdM0TWt4\njrb2srcAb6tWrVi6dGkjRqm5IqcXBBaRTCBTWbIZb+C83NBkda178+5x419IOpHTNE3T6lf//v1r\nzHatztEsUd0Vq93yzg5Vyds/GiAWl6O36NI0TdOamisswKu5LqcTOaVUCywzVDsDxhsui4j8R30G\n5hr0Fl2apmmaprkuZ7foagfsxDJrVLg+6r963+Ndl8jpFjlN0zRN01yZs5nJG8A5oD2WJK4XEIpl\nF4fvq76+C+lZq5qmaZqmuS5nu1b7AS8DZ6teXxWRfGCBUqoZ8BaQUP/hNa2ay4/oFjlN0zRN01yH\ns5lJW6CwaqJDCdCm2rWvgQH1HJeLsJ21qrtWNU3TNE1zJc5mJj9gWQAY4AQwpNq1h4G7bNkRC90i\np2mapt3pQkJCWLVqVVOHoTUQZzOTb7DsUQqQCryslNqqlPoCyyQBVOmYAAAcZElEQVSHjxsiuKZn\nu66PbpHTNE3T7ElPT8fT07Opw6ghJyeHKVOmNNnzZ8yYQc+ePTGZTISGOj+kftGiRQQEBGA2mxk4\ncCBHjhxpwCgtPvnkE8LDwzEajXTr1o0NGzbYXN+xYwcJCQkEBgZiMBhYv359g8d0M85mJvOx7OaA\niPwReBEwA/7AcuAPDRJdExO5MZFr1kSRaJqmaa5ORBzu0NBU2rZti9F446phjUdESExM5Omnn755\n4SrLli1j9erVpKSkkJOTg4+PD7GxsZSUlNx2HNnZ2YSEhNi9/u233zJ69Gieeuop9u/fz9ixYxk1\nahTfffedtcylS5eIiIjgrbfewmw233Ys9UpEbnoArQF3Z8reLQcgx45NkW++wXr88MNa0TRN0+rO\n8uvHvuo/e+v7qKvs7Gzp3bu3tGzZUlq3bi29evWStWvXilJKDAaD9d+kpCQRESkrK5PZs2dLYGCg\nmM1mefjhh2XLli3W+rKyskQpJZ9//rk89NBDYjQaJSoqSvbu3etUPBcuXJDx48eLj4+PGI1GCQsL\nkzfffNN6PTg4WFauXCkiIosWLbKJ89pxLVYRkbS0NOnatasYjUbp3LmzrF69us6fmYjIihUrJCQk\nxKmy/v7+smTJEuvry5cvi6enp7z77rvWcxcuXJCJEyf+/+3deXhU9fn38fcnQMPmQkQIm4Fa1IJg\nReujUgHZtCCCPqACLlTbulXFViqtW/GHirjUpy4/qS1UsYpaqqJF/KEWxe2HGBVEUVmDkETUqoBG\nINzPH9+TOBlmJpMQMgm5X9d1Ljj7febkytz5rtamTRvba6+9rF+/frZ48eKk11ywYEHK+59++uk2\nePDgCtsGDhxoY8aMSXh8y5Yt7f7776/0WVL9rEf7dilfqbRETlJj4DMqtotrEDZsuKfC+jffrMxQ\nJM455+qC0tJSRowYQZ8+fVi6dCmLFi1i/Pjx9OnThzvuuIPmzZtTXFxMYWEhV1xxBQDjxo1j4cKF\nzJo1i2XLlnHOOedw8skns3Tp0grXnjBhArfccgtvvvkm3//+9xk2bBglJZU3Qb/qqqtYtmwZc+fO\n5cMPP2T69Ol06NAh4bETJkygqKiIwsJCioqKeOCBB2jSpAnHHXccAPfddx9XX301kydPZvny5dx2\n221MnTqVe+757vsw2dyvsXPA7orVq1dTVFTEoEGDyrc1bdqUPn368Oqrr1aIo6ioiLlz5/L222/T\np08fBgwYQHFxcbXu+9prrzF4cMVU54QTTqhwz7qo0uFHzGy7pGLiG4w1QKWlX2c6BOeccxn01Vdf\n8eWXX3LSSSfRuXNnAA466CAA8vPzkcT+++9ffvyqVauYNWsWa9eupWPHjgBcdNFFzJ8/n2nTpnHX\nXXeVH3vttdcycOBAAGbMmEHHjh156KGHOPfcc1PGVFBQQK9evTjiiCMA6NSpU9JjmzdvXl4l+MEH\nH3DppZdy6623cvzxxwMwefJkpk6dyimnnAJAXl4eV155JXfffXd5O7tUc7/WhKKiIiTRtm3bCtvb\ntm3Lhg1hFLQXXniBJUuWsHHjRrKzswGYNGkSc+bMYebMmeVJdKxQAJb6vonuWVRUtCuPs9ulO47c\ng8DPgbm7MZY6z2x7pkNwzjmXQa1ateKcc85h8ODBDBgwgAEDBjBy5MikyVN+fj5mRrdu3SokElu3\nbqV///7l65I4+uijy9dbtGhBjx490mrgf+GFFzJy5EgWL17MoEGDGDZsGH369El5zhdffMHw4cM5\n44wzuOSSSwD49NNPWbduHeeffz4XXHBB+bHbt2+v0PavLsz9mp+fz5YtW2jdunWF7d9++y0rV4ba\ns3Xr1tGtWzckYWaUlpaydevW8g4pkjjzzDMrlDbWR+kmcmuAMZLeAJ4ECokbZM3MptdsaHWP2bZM\nh+Cccw1Cv36pS08yafr06Vx++eXMmzePOXPmcPXVV+/Uu7HMjh07yMrKYvHixTRuXPErt1mzZjUS\nz4knnkhBQQHPPPMMzz//PEOHDmXUqFFMn574a7m0tJRRo0bRqVMn7rzzzgqxAkybNo1jjjkm6f2G\nDBnCwoULk+6XxFdffVXNp4Hc3FzMjOLi4vJSTIDi4mJyc3PLY83NzeXll1/eqaStrGq3ffv2vPPO\nO+XbX3/9dSZOnMiLL75Yfk5sNXBubu5O1bKx96yr0k3k7o7+7QAckWC/AZ7IOeecaxB69OhBjx49\nmDBhAkOGDOH+++9n6NChlJZWbIV0+OGHY2YUFhbSt2/fpNczM15//fXy6totW7bw7rvvMm7cuLTi\nycnJYezYsYwdO5YTTzyRMWPGMG3aNJo0abLTsZdddhkFBQUsWrSIRo2+G42hTZs2tG/fnhUrVjB2\n7Nik99rdVatdunQhNzeX+fPnl1cXl5SUsHDhQm677TYAevXqRXFxMZKS9kRt1KhRheFO1q1bR+PG\njZMef8wxxzB//nx+85vvBuKYP38+xx57bE092m6RbiKXvL9uA9KoUYtMh+Cccy6D1qxZw7Rp0zj5\n5JPp0KEDK1euZMmSJVx88cV07tyZkpISnnvuOQ4//HCaN29O165dGTNmDOPGjePWW2+lV69efP75\n5yxYsIADDzyQESNGlF978uTJtG7dmnbt2nH99deTnZ3N6NGjK43puuuuo1evXnTv3p1t27Yxe/Zs\nDjzwwIRJ3IwZM5gxYwbz5s2jpKSkvDNFy5YtadGiBZMmTeLSSy9ln332YciQIWzbto38/HzWr1/P\nxIkTgapXra5cuZLNmzezfv16tm7dWl5K1r17dxo3bsyGDRsYMGAAU6ZMYfjwMNvn+PHjuemmmzj4\n4IPp2rUrkydPZq+99ir/PAYOHEjv3r0ZPnw4N998M4cccgiFhYU8++yzDBo0iN69e1cpRggJbt++\nfbn55psZMWIE//znP1mwYAGvvPJK+TFbtmxhxYoVmBk7duygoKCAd955h5ycnJRtE3erXe32uqcu\ngK1dO6VCl/Wvv16RtAuxc8659FHJ8CN1VXFxsZ166qnWsWNHa9q0qeXl5dnEiRNt+/btZmZ20UUX\nWevWrSsMP7J9+3abNGmSHXjggZadnW3t2rWz4cOHW35+vpmFYTGysrLsqaeesp49e1Z5+JEbbrjB\nDj30UGvRooXtt99+NnToUFu+fHn5/i5dutjtt99uZmbjxo2zrKysnZbY4UdmzZplRxxxhDVr1sxy\ncnLsuOOOs0ceeaTan1m/fv0S3nPt2rVmZrZmzRrLysraaSiPSZMmWfv27a1Zs2bWr18/W7ZsWYX9\nmzdvtvHjx1unTp0sOzvbDjjgABs9erStWrUqYRyVDT9iZjZ79mz74Q9/aNnZ2datWzd74okndrpG\n2fAtscvPfvazpNdM9bNODQw/IqukF0csST0JMzzsB0wzsyJJPwCKzWxTzaeZmSPJtm3bxMqVV7B5\n89u0b/8L2rU7L9NhOefcHqGsAboLA9X279+fjRs3kpOTk+lwXA1L9bMe7dulUaTTqlqVlE3ouXoq\nIEKbuKeAIsLMDh8CE3clkLqoceOWHHzwvZkOwznn3B7Ok1pXXelO0XUDMBA4C2hLSObKPAOcUMNx\nOeeccw1Gqqm9kg3Au/feezNlypRajNLVRWlVrUpaD9xoZncrTDi6DTjSzPIlDQQeM7NWuznWWiXJ\n/C8k55zbPbxqNX2FhYVJe4nm5OSw77771nJErirqRNUqoU3c+0n2ZQHZuxKEc8455xKrCwPwuror\n3arV1UCy0QGPAj6omXCcc84551y60k3kHgAmShoLlA1MY5KOBy6nAQwG7JxzzjlX16TbRq4R8Hfg\nNOBbQlXqN0BTYJaZJR8Cup7yNnLOObf7eBs511DUiTZyZlYKnCHpbkIP1TbAZ8A8M3txVwJIl6Rf\nA/2AI4Fc4A9mdn0Vzm9KGCJlDHAA8AWwCDjVzLbXeMDOOeeSysvLS9lT07k9RV5e3m69frqdHQAw\ns4VA8plyd6+fA18CjwMXVOVESY2BeUAecCOh48b+wCCgEeCJnHPO1aI1a9ZkOgTn9gjpDgj8FnA/\n8LCZFe/ekBIzs25RLI2AC6t4+hXAj4BuZrYhZvvjNRSec84551ytS7ezQyFwC7BO0jOSzoiqKuuL\nC4FH45I4twdZsGBBpkNwVeDvq37x91V/+LtqeNJK5MxsCNAB+C2hSvIhoFjS9Kjnap0lqRPQCVgt\n6c+SvpT0jaTnJB2W6fhczfBfXvWLv6/6xd9X/eHvquFJt0QOM/vEzO4wsyOB7sDdQH/gOUlrd1eA\nNaB99O9EoAuh5+0ZhIT035I6Ziow55xzzrldkXYiF8vM3geuB64CNgBVSoYkDZC0I43lherEF6fs\nGbcAJ5nZs2b2JDAUaA5cXAP3cM4555yrdWmNI1fhBKk/cBZwKtCSMITHTDO7pwrXaEoYAqQyX5vZ\nx3Hnls31mtbwI5IOApYDs81sVNy+t4FCM/tpgvN8gCPnnHPO7Va1Mo6cpEOBMwljsHUE1gD/j5DA\nfVTVm5pZCfBhVc+rplWEwYurZFc/WOecc8653S3dceSWEMZwewx4wMxe3n0h1Swz2y7pX8BxkpqZ\n2TcAkg4ADgGezGiAzjnnnHPVlO4UXSOBp8zs290fUtIYjgA6EwbwnQU8SkgsAf4VlfIh6XngADPr\nGnPuD4H/Bd4EbgOaAdcC+wGHmdnGWnoM55xzzrkak+7wI/9IlsRJ6itpes2GldCvCMnbw4ABo6L1\nRwlThpXJIu65os4Z/YEdhCTwz4Sq3Z/EJnGSOkr6h6QvomFKZkfDl7g6RtJISY9LKpD0taTlkm6U\n1DLTsbnKSZoXdWhKe5o9V/skDZH0oqRN0e/ERZL6ZToutzNJvSU9K6lY0leS3pT0s0zH1dBJ6iDp\nTkmvStoS/d7bqY+ApH0l/UXSRkmbJc2PmrVVfo/qTFos6QfA2YROD3mETgn1+gtUUjNCFfI3hN64\nADcQSu96llXJurpB0mvAx4TZOT4mzNwxCXjfzI7NZGwuNUmjCSXjbYEbzOzaDIfkEpB0PnAn8Cfg\nGcIfyD8ClpnZ3EzG5iqS1INQ6/QacAfwNTASOB+40MymZTC8Bk1SX0IB0puEGsXBQBczK4g77mVC\nJ9ArCHPB/54w1NthlU1mkHYiJ2kf4HTgHODoaPM7wDTC1F1fpfdYdZOky4BbgYPMbHW0rTPwETDB\nzO7IXHQunqT9zOyzuG1nAX8DBpjZgkzE5VKT1Ap4DxhPKF2f7Ilc3SMpjzAn9ZVmdmem43GpSboR\n+DXQKrbQQdKrgJlZ74wF58pJOo9QI1ghkZM0HPgncLyZvRRt2xtYTehUOj7VdVNWrUrKiorWHyFM\n03UvoQTu7uiQ8WY2rb4ncZFhwOtlSRyAma0BXgGGZyool1h8Ehd5AxBhFhJXN90MLDGzRzIdiEvp\nPKCU8Ie6q/uaAFsT1Bx9STXHi3W1ahiwoSyJA4jyqqdII/9I+oIl3Qasjy50EqEK60RC0d+1hC/M\nPUl34N0E25cB3Wo5Flc9/QjtJ9/PcBwuAUk/IQxj5INw1329CeNvjpa0QtI2SR9JuijTgbmE/gZI\n0p8ktZO0j6RfENqG357Z0FwaUuUfB0hqnurkVMOPXE74UpwLjIstAdlDB8vNAf6TYPvnQKtajsVV\nkaQOhDZy880sP9PxuIokNSGU6N9iZisyHY+rVPtomQr8jjAe5yjgLkmNvLq1bjGzZdG8548TOgYC\nbAUuMLPHkp/p6ogcQjVqvM+jf1sR2j0mlKrI9a/AJsJUVh9IukvSUdWN0rndRVILwniAW4FzMxyO\nS+xKoClwY6YDcWnJIszc80szm25mC8zsYmAeIbFzdUjUAXE2sJTwnT2A8IfTtKhzkduDJU3kzOwX\nQC4wFlhM6P3ymqT3Cb+U97RSuf+QuOQtWUmdqwOi6d6eJowxeEJlvXtc7YuG8Pk9cA3QNKr22Tfa\nnR2tezueuqWsBua5uO3/A7SV1LaW43Gp3UT4Q/ZkM3vGzP4dNZB/lDALk6vbUuUfZfuTSvnL08xK\nzOxhMytrG/c7QgPYiYQ2clMknRl9mdZ3ywj11PG6EXrZuTpGUmPCX6G9gJ+amb+nuun7QDbwIOEX\n0n8IVQYGTIj+n9Z4Sa7WLMt0AK5KDiV0Itoet30RsJ+kNgnOcXVHqvyjwMySVqtCFXqzmFmhmU01\ns0OBowg9V7sCDxB6tNZ3c4CjoyFHgPLhR3rj03jVOZIEPETo4DDczN7IbEQuhbeA46OlX8wiYGb0\nf283V7c8Hv17Qtz2nwIfm1lxLcfjUisCekZ/3MY6Gijhu7ZWrm6aA3SQdFzZhmj4kWGkkX9Ua0Dg\nmBs1IfRoPdvMTqn2heqAqFfI24QBga+JNl8PtCAMyJcyI3a1S9J/E6r7JwP/itv9sZmtr/2oXFVI\n2oGPI1dnRdMd9gSuJnR2OI3QBnWcmc3MZGyuIkn/l1CNOh+4h/A9Nhy4ELjdzCZkMLwGL3o/AAMJ\n31sXARuBjWb2UlQw8TLQEfgtYUDg3xFKWg+r7PtslxK5PY2kjsAfgUGE0oLngMvjR2B2mSdpNaG6\nP5FJZuZTP9VxkkoJidx1mY7F7Sya7u4mwgwBrQjDkdzkYwDWTZJOILRf707oWLSSMA7gn82/6DMq\n+qM10Tt40cz6R8fsS5iUYATh/b0K/NrMEg1LUvH6/n6dc8455+on7ynmnHPOOVdPeSLnnHPOOVdP\neSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnnHPOOVdPeSLnXAMn6SxJa2PW\nl0m6oIbvcbSk1yVtllQqqWdNXt/VPklrJE2vxnnDJV2+O2JyriHyRM451wtYDCCpBXAw8GYN32M6\n0AgYChwDfFjD13e1r7qjyY8APJFzroZ4IuecO4LvErdeQCnwTk1dXFIWcBDwLzN70cwWmVlJTV3f\n7TpJ38t0DM656vFEzrkGLEqyfsR3idyPgffMbGua5+8l6S5J6yWVSFouaXzM/nOA7YS5i6+VtEPS\nqhTX+0N0zKGSXpC0RdIGSZPijsuWdLukpZI2SSqUNEfSwXHHtZV0f0x8G6LjWkf7G0n6L0krJH0j\naaOklyQdG3edX0p6O+aYv0hqFXfMZZLek/S1pM8lvSFpeBqf4Zlx135AUm7M/qcl7VRCKilX0jZJ\nl8Vs6yzp75I+iZ73LUkjknzG3SXNk7QJSDl/avRsq6MYF0n6SYJjWku6V9IH0XsriGJpH3PMDOAc\noEMUQ/nPQ7rv1DlXUeNMB+Ccq32SVgN50aoBcyWpbD1mkucuZlaQ5BoC5hISwWuAdwlVp7dLam1m\nVwNPA72BV4C/RMu3KUIrq657nFAdeyNwAnCNpFIzuz7anw3sBdwAbCBM6n4R8JqkQ8zsk+i4B4FO\nwG+Aj4G2wACgebR/InAZ8HtCKeTewJFATsxzTgF+DdwBXAF0iO7bXdKxZmaSxhImvP4D8DLQDOgZ\ne50kn+EvgXuBh6NY2hMmqj9KUi8z+xqYCTwUPdfymNPHRp/XQ9G1OgKLgKLomT4FTgdmSxpuZk/H\nfcZPAH8FpgA7UsR4HvBHwvt4FPhBFG/LuENzCO/298AnQDvC5/5yFPtW4Hpgf8JnPIyQ4Jf9PKT7\nTp1zsczMF198aWALcAgh0bgNWAr0iNa/BC6N/t8TaJziGicREoCz4rbfB3wD5ETrjaLjrk0jrusI\nVbsT4rb/OYpt7yTnZRGSp6+Ay2K2bwJ+leJ+TwH/SLE/j1CieFXc9mOiZzo5Wr8TWFzFd5BFSLqe\ni9veO7r2r6L1psAXwA1xx70FPB2z/legGNg37rj/AfITfMZJP5eYYwUUEKrFY7efFsU4vZLn6xgd\nNzxm+wygIM3PZ6d36osvvlRcvGrVuQbIzJab2RJCadUCM1sKfE0oZXnMzJZEy/YUlzmOkBA8HLf9\nQeB7hGSnuh6LW58VxXZo2QZJp0U9Yf9DSLa2AGWdNcq8AUyQdKmkQ9nZG8AQSZMl9ZbUJG7/IEIy\n81BUDdtIUqPovE1An5jr/EjSnyQNkNQsjWc8GGhDVKJWxsxeAdYCfaP1EuAfhBK4smfvARwGPBBz\n6gmEEtJNMbE2JiRyh0mKL0F7Io0YO0ZL/PuYTfjMK5B0YVRNvCnaX0AoAUyrejTNd+qci+GJnHMN\njKSsmC/53oSqq0aEpGQ98Em0Xpkc4PMEyV4RIflJWa1YieIE6yJUayJpGCG5WwaMBo4iVNd9SijB\nKnMaMAeYALwTtZW7Jmb/DYQSqmHAS8BnkqZLKou9TXTflcC2mGUrIbHcD8DMHgAujOKYB3wuabak\nPJIru0dhgn1FVPz8ZgIHSOobrZ9FKKl6MuaYNsDZCeKcGu3fL+4eie4br130b4X3YWalwGex2yRd\nAtxNSBxPIbS3/D+Ezy/2nSRUhXfqnIvhbeSca3ieJyrtIZSWzCSUopWtbyO0kzvezF5KcZ3PgRxJ\njeOSudyY/dXVFlgTtw4h0YTQ9usjMzuv7IAoMa2QPJrZp8AlwCWSuhIa2k+S9ImZTYsSkluAWyS1\nIVQX/5FQpTeakKwYoWTuiwRxliczZnYfcJ+kfYDBwO2ExCRZyWTZ55ObYF8u0ZAw0bVflFQAnCnp\npSi2x8wstr3hZ4RkdAoheYq3IW49neFDypK9trEbo0Q/PjE8nVBN/NuY4zqncY/Y8yt9p865irxE\nzrmG55eEko5bgRXR/48ENgJXRf//MZWPJfciof3bqLjtZxIasL+2CzGeFrc+mlCVuTRab87OVXtn\nR/EkZGYfWeiA8R9iqmhj9n9iZtOB52L2zye08cozs/wEy9oE1/nSzB4jdAxIVJ1b5gNCSdcZsRsV\neszmAf+OO/5BYCQwhFAyOTNu/zxCu8b3ksS6LUUsyXwMrGPn9zGSnQsCmhP+CIh1LjsnjN8SEuV4\nVX6nzjkvkXOuwTGzjwAkXUtoxP5WNMRDa0Lj9XR7Bz5D6KF5b1SatYzQa/Vc4EYzq26JnIBfxLRF\nOzG65nVmtik6Zh4wXNLthJ6xPwZ+RUjSiJ5vb0JS9ndgOSHJGAHsCzwbHfMEobdqfnRur+h+/w1g\nZqskTQXuknQIIXktAQ4ABgL3RaVl0wiJ5muEHpsHE6o/n032kGa2I3oH90oqKxXtCEwmJHkz4k6Z\nSegRei+wNkFp6bXA/wILJd1FKNFsRUgmu5jZz5PFkiJGUxj65T6FWRxmAV2BKwmdT2LNA34r6XeE\n3rP9CQlfvPcI7/cCQqljiZm9Sxrv1DmXQKZ7W/jiiy+1vwBNCG2sBkXrlwFvVOM6LYE/Eao8SwgJ\n06VxxzQidIq4Jo3rlfWo7Aa8QGjsvgH4Q9xxIgxl8TGwmVB6dRiwCvhrdMz3CAnZ0uhZvyAkOqfH\nXOdy4FVCaeQW4H3CUCqN4u43NjpuU3StZdFzt4/2nx3FW0TosbuSUOLZMo1nHkPogfpNFMffgLZJ\njl0UfT7/lWR/e0IP33XR+1hPSCbHxH3G24GsKrznS4DVhA4xi4BjYz/r6JimhDZyxYQk70lCyWKF\nd08oefs7oSq4FFiV7jv1xRdfdl5kVt1ZVpxzrmZJuo5QstTEzJKObeaccy7wNnLOOeecc/WUJ3LO\nubrGqwmccy5NXrXqnHPOOVdPeYmcc84551w95Ymcc84551w95Ymcc84551w95Ymcc84551w95Ymc\nc84551w95Ymcc84551w99f8B6ssKwatUFoMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x123a81510>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"for step_size in np.logspace(-4, 2, num=7)[0:6]:\n",
" make_plot(log_likelihood_sgd[step_size], len_data=len(train_data), batch_size=100,\n",
" smoothing_window=30, label='step_size=%.1e'%step_size)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question**: Which of the following is the worst step size? Pick the step size that results in the lowest log likelihood in the end.\n",
"1. 1e-2\n",
"2. 1e-1\n",
"3. 1e0\n",
"4. 1e1\n",
"5. 1e2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Quiz Question**: Which of the following is the best step size? Pick the step size that results in the highest log likelihood in the end.\n",
"1. 1e-4\n",
"2. 1e-2\n",
"3. 1e0\n",
"4. 1e1\n",
"5. 1e2"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
jegibbs/phys202-2015-work | assignments/assignment11/OptimizationEx01.ipynb | 1 | 21572 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"# Optimization Exercise 1"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"## Imports"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true,
"nbgrader": {}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import scipy.optimize as opt"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"## Hat potential"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"The following potential is often used in Physics and other fields to describe symmetry breaking and is often known as the \"hat potential\":\n",
"\n",
"$$ V(x) = -a x^2 + b x^4 $$\n",
"\n",
"Write a function `hat(x,a,b)` that returns the value of this function:"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"solution": true
}
},
"outputs": [],
"source": [
"def hat(x,a,b):\n",
" v = -a*(x**2) + b*(x**4)\n",
" return v"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "7204bd97cd003430289f171b6ba70d63",
"grade": true,
"grade_id": "optimizationex01a",
"points": 2
}
},
"outputs": [],
"source": [
"assert hat(0.0, 1.0, 1.0)==0.0\n",
"assert hat(0.0, 1.0, 1.0)==0.0\n",
"assert hat(1.0, 10.0, 1.0)==-9.0"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Plot this function over the range $x\\in\\left[-3,3\\right]$ with $b=1.0$ and $a=5.0$:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true,
"nbgrader": {}
},
"outputs": [],
"source": [
"a = 5.0\n",
"b = 1.0"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"solution": true
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEZCAYAAAB4hzlwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYXVWV/vHvSwBBxgQUkME0M3SggyDzEEEwMg8yOIKK\ntK0toKAdtRtpJxBsRRvhByokKIOICMgcacKgoIAEwwxCmBMaQlAEGkjW749zqlIpKlW3qu65++xT\n7+d56nnqVp177lqpyl21195nH0UEZmZmAIulDsDMzOrDRcHMzLq5KJiZWTcXBTMz6+aiYGZm3VwU\nzMysm4uCWYYk7SDp/haPPUzSTVXHZM3gomDZkjRT0i69vtbyG2Arx0qaJukVSX+T9L+SfiVp1RbO\nPU3SJ1uJo8VY50tau+txRNwUERu26/xmXVwULGdRflT9Gp+NiOWA9YEVge+3+Lx2UwXnNFuIi4I1\nzUJvxpImSXpY0l8l3SNp3/LrGwGnA9uUo4A5A5444gXgYmBceY5tJd0maa6kP0rapvz6t4AdgFPL\nc/+w/PqGkqZKel7S/ZIO7BHnZEk/knR5GeutXSMDSTeWh91Vnu9ASRMkPTFQnmaD5aJguev913Pv\nxw8D20fE8sB/Aj+XtEpE3Ad8GrglIpaLiDEDvYaklYEDgD9JGgNcAZwCjAG+B1whaXREfBW4iXKE\nERFHSloGmAr8HHgbcAhwWlmcuhwMHA+MLuP+FkBE7Fh+f9PyfL/sI8Y+8+wnJ7M+uShYzgRcIumF\nrg/gR/QYLUTERRExq/z8QuAhYKsez2/lNX5Ynns68BTwBWAP4IGIODci5kfEBcD9wN69nttlT+DR\niJhSHj+dYtRxYI9jLo6I2yNiHnAuML7Ff4eB8jRrmYuC5SyAfSJidNcH8Bl6vBlL+pikO3sUjXHA\nSoN8jc+V518jIj4aEc8D7wAe73XsY+XXez63yzuBrXoVsA8Bq/Q4dnaP418Blm01yDbkaQbA4qkD\nMGuzngXhncCZwM4UbaKQdGePY4YzGfwUsH+vr70TuGoR534cuCEidhvGa/aphTzNWuaRgjXZMhRv\nzs8Bi0n6OOUkcWk2sIakJQY4T19vrlcC60v6oKTFJR0MbAhc3uPc6/Q4/vLy+I9IWqL8eLekrmWl\nA72B9z5fTwPladYyFwVrmu5lqhFxL/BfwC3ALIo3ypt7HHsdcA8wS9KzA5xz4S9EzKGYJziG4s34\nWGDP8usAPwA+IGmOpFMi4iVgN4oJ5qeAZ4ATgCV7x72I1z0emFK2hz4wyDw7sXTXGkKpb7IjaRRw\nO/BkROxVrur4BcVQfCZwUETMTRiimdmIUYeRwlHAvSz4S2YSMDUi1qf4S25SqsDMzEaapEVB0hrA\n7sBPWNBT3RuYUn4+BfBFOGZmHZJ6pPB94IvA/B5fWyUiupbmzWbBkj0zM6tYsqIgaU/g2YhY5NK5\nKCY8PEFmZtYhKa9T2BbYW9LuwFLA8pJ+BsyWtGpEzJK0GvCmVSGSTqW4sGdm+aW5wPSImFZ+fwJA\nxo+Pblg+zq9e8Tm/RTzu+rwu8bQpn8PKlGYCcyPiFPqRfPURgKSdgGPL1UcnAc9HxHckTQJWjIhJ\nvY4/PiKOTxFrJzi/vDm/fDU5N2gtv9RzCj11VacTgV0lPUhxheaJfRw7tlNBJTI2dQAVG5s6gIqN\nTR1AxcamDqBCY1MHkFottrmIiBuAG8rP5wDvTRuRmdnIVKeRwmBMTh1AxSanDqBik1MHULHJqQOo\n2OTUAVRocuoAKjZtoANqMadgZmb1kOVIoecKgSZyfnlzfvlqcm6tyrIomJlZNdw+MjOzbh4pmJlZ\ntyyLQtP7fs4vb84vX03OrVVZFgUzM6uG5xTMzKybRwpmZtYty6LQ9L6f88ub88tXk3NrVZZFwczM\nqpHlnILEshG8lDoOM7NcSCwRwesDHZfrSGG2xKjUQZiZZWS7Vg7KtChcPRdYN3UUVWl6X9P55a3J\n+TU5N2CTVg7KtCj8/VFgXOoozMwy0tJ7Zq5zCt8EXo/gP1PHYmaWA4nfRQzcQsp0pMDdtDgUMjMb\n6SREiyOFTIvCwUvT4PZRw/uazi9zTc6vwbmtCfy9lQMzLQrXPgG8U2Kp1JGYmWVgHEWHZUBZzikA\nSMwAPhbBnaljMTOrM4l/A94ewTEDHZvpSAEoql5jW0hmZm3U8kghy6JQ9v1m0NCi0OC+JuD8ctfk\n/BqcW7OLQskrkMzMBiCxOLABcG9Lx2c8p7A2MC2CtVLHYmZWVxIbApdHtLYLRM4jhZnAaIkVUgdi\nZlZjLbeOINOiIGlCBPMphkONm1docF8TcH65a3J+Dc1tE4o52JZkWRR68AokM7P+DWqkkO2cAoDE\n0cA6EXwudSxmZnUk8QCwfwT3tHJ8E0YKXoFkZtYHiaWBtYAHW31OlkWhR9/vbmBcudlTYzS0r9nN\n+eWtyfk1MLeNgIdaueNalyyLQg+zgQBWSR2ImVkNDWo+ATKfUwCQuB74dgRTU8diZlYnEicDcyI4\nodXn5D5SAK9AMjNblEGPFLIsCr36fo3bA6mBfc2FOL+8NTm/BuY2MopCL16BZGbWi8RoYEXgsUE9\nL9WcgqSlgBuAtwBLApdGxJcljQF+AbyTYiuLgyJi7qLPwwrAU8Dy5VXOZmYjnsT2wHcj2Howz0s2\nUoiIV4H3RMR4YFPgPZK2ByYBUyNifeC68nE/5+FF4HlgbLURm5llZdCtI0jcPoqIl8tPlwRGAS8A\newNTyq9PAfbt/bw++n6NaiE1sK+5EOeXtybn17DcBrXnUZekRUHSYpKmU1xvcH1E3AOsEhGzy0Nm\n09o1CF6BZGa2sCxHCvPL9tEawI6S3tPr+0FxcVpv4yVNlnS8pONhv3fAhbt0fVPShJ4VP7fHXV+r\nSzzOz/mNlPwiYlqd4hn641ETgE1gq+VVvFdOVvF+2X3cotTm4jVJ/wG8AhwOTIiIWZJWoxhBbNj/\ncxkP/DzCowUzM4l3AHcBb4/o8w/rRUo2UpC0sqQVy8+XBnYF7gQuAw4tDzsUuKSP507o9aX7gXUk\nlqws4A5qpZrnzPnlrcn5NSi3ccCMwRYEgMUrCKZVqwFTJC1GUZx+FhHXSboTuFDSJymXpA50oghe\nlZhJcR/SQU+smJk1zCYMYT4BatQ+Gi6JXwIXR3B+6ljMzFKSOBu4JYIzB/vcJlzR3KVx212YmQ3R\nOIbYNcmyKCyi79eYaxUa1Nfsk/PLW5Pza0JuEqOAjaG1O631lmVRWARfq2BmBv8APBfBX4fy5CbN\nKYwC/gqsEsFLqeMxM0tBYl/g8Aj2HMrzGzNSiGAexdLUf0wdi5lZQkNeeQSZFoV++n6NaCE1oa/Z\nH+eXtybn15DchrS9RZcsi0I/vALJzEa6Ia88ggbNKQBITASOjeC9qWMxM+s0ibcAc4HREbw6lHM0\nbaQwHdhMQqkDMTNLYBzw8FALAmRaFBbV94tgFvAyxZKsbDWkr7lIzi9vTc6vAbm9G7htOCfIsigM\n4HZgi9RBmJklsAXFe+CQNWpOAUDiq8AKEXwpdSxmZp0kMR04IoI/DvUcHimYmTWAxNLA+sCfh3Oe\nLIvCAH2/24HNpTxzg0b0Nfvl/PLW5Pwyz208cN9wJpkh06LQnwieB54H1ksdi5lZBw17PgEaOKcA\nIHEhcGkE56aOxcysEySmADdH8OPhnKdxI4WS5xXMbKRpy0ghy6LQQt/vNor1ulnKvK85IOeXtybn\nl2tuEssBYxnGnkddsiwKLfgTMF5Keg9qM7NO2QyYEcHrwz1RI+cUACQeAA6IGH7lNDOrM4kvAGtH\n8K/DPVdTRwrgeQUzGznaMp8AmRaFFvt+2c4r5NrXbJXzy1uT88s4t2HvedQly6LQIo8UzKzxJEYD\nq1HceXL452vwnMIywLMU+4q/ljoeM7MqSOwCHB/BDu04X2NHChH8HXgE37PZzJptC9rUOoJMi8Ig\n+n63k+G8QsZ9zZY4v7w1Ob9Mc3s3bZpkhkyLwiB4XsHMmq5tK4+gwXMKABJbAadH8K7UsZiZtZvE\n24CHgDERzG/HOZs+UrgL2EBiqdSBmJlVYHPgjnYVBMi0KLTa9yv3FX8A+KdKA2qzTPuaLXN+eWty\nfhnm1tb5BMi0KAyS5xXMrKnaOp8ADZ9TAJA4Atgmgo+njsXMrJ0kngK2j+DRdp1zJIwUbsMjBTNr\nGIl3AG8BZrbzvFkWhUH2/e4B1i6vcM5Chn3NQXF+eWtyfpnltgVwewRtbfdkWRQGo9zi4m6K/cbN\nzJqi7fMJkLAoSFpT0vWS7pF0t6Qjy6+PkTRV0oOSrpW0Yu/nRsS0Qb5cVpPNQ8gvK84vb03OL7Pc\nmlUUgNeBz0fEPwJbA5+VtBEwCZgaEesD15WPh8vzCmbWGBKizXsedUlWFCJiVkRMLz9/CbgPWB3Y\nG5hSHjYF2Lf3c4fQ98tqD6TM+pqD5vzy1uT8MsptLWAe8HS7T1yLOQVJYyl6/n8AVomI2eW3ZgOr\ntOEl7gdWl1ihDecyM0utkklmqEFRkLQs8CvgqIj4W8/vRXERxZuSHmzfL4I3gOmQxx5ImfU1B835\n5a3J+WWUWyXzCQCLV3HSVklagqIg/CwiLim/PFvSqhExS9JqFDfK6f28o4HxLFifOxeY3vUD7RoC\nLvz47GfgsC2A6/v+vh/7sR/7cS6Pf70r7HvcQMeXnx9GYSYwbaDCl+yKZkmimDN4PiI+3+PrJ5Vf\n+46kScCKETGp13MnDLaiS3wIOCCCA4YffbWGkl9OnF/empxfDrlJjAKeB9aPePMfzcOVsn20HfAR\n4D2S7iw/JgInArtKehDYuXzcDjcBO5Sz9mZmudoEmFVFQYARsPdRTxKPAHtEcF/qWMzMhkLiKGDj\nCP65ivMnn2jusBuBHVMHYWY2DDtSvJdVIsuiMIy1xDcCO7UxlEpktFZ6SJxf3pqcX91zK9vfLgpt\ndAOwo+cVzCxTGwF/i+CJql5gpM0pCHgS2CGCR1LHY2Y2GBKfBraO6F5m2nYjaqRQXv13Axm0kMzM\n+rATxXtYZbIsCsPs+9V+srnufc3hcn55a3J+dc6tE/MJkGlRGKYsJpvNzHpZh2Lbn0pb3yNqTgG6\nq+2zwLuqnKwxM2sniU8A743gQ1W+zogbKZTzCjcCO6SOxcxsECpvHUGmRaENfb9at5Dq3NdsB+eX\ntybnV/PcKp9khkyLQhvcQM0nm83MukisBSxDcW+Yal+rvzmFcmvr3SjeQMdSTHI8RvGX9jUR8UbV\nAVah3GXwOWCDqjaVMjNrF4kPA/tF8IGqX2uRIwVJ/0Fx/889KarTWRRbXT8A7AXcLunfqw6wChHM\nA36HRwtmloed6MB8AvTfProL2Cwi/iUizo6IayLiqog4KyI+TXEXsz93Isje2tT3q20LqeZ9zWFz\nfnlrcn41zq0jk8zQT1GIiMsiIiQt1ft7klaOiPkRcVm14VWq1pPNZmYAEqtS3Kt+Rkdeb6DrFCTN\nAI6IiFvKxwcAJ0bEeh2IrzISS1DcvWhsBHNSx2Nm1heJA4GPRbBXJ16vlXs0fwg4S9I0YHVgJeA9\nVQbVCRG8LnErxR3gfpM6HjOzRdiRDixF7TLgktSImAF8G/gXimLw2Yh4surA+tPGvl8tW0g17mu2\nhfPLW5Pzq2luHZtkhhaKgqSfAkdT3Bf0MOBySf9acVydUtvJZjMziTEUlwPc2bHXbGFO4WjgB1Ee\nKGkF4HsR8ckOxFcpiaUorldYLYK/pY7HzKwniX2Az0Twvk69Zivto1OiR+WIiBebUBAAIngVuAPY\nNnUsZmZ96NhS1C79Xbx2haQDJb21j++9VdLBkq6sNrxFxjahjaerXQuppn3NtnF+eWtyfjXMraOT\nzND/SOEwinmE2yXNkHStpKnlEtU7KO4VemgHYqxaLSebzWxkk1ie4n32to6+7qLmFCSdBpwXETdL\nWoVisgPgsYiY1aH4KiexDDAbeFsEr6SOx8wMQGIiMCmCCZ183f5GCg8CJ0t6DDgGeC0i/tCkggAQ\nwd8prhTcKnUsZmY9dLx1BP1vc3FKRGxD0VqZQ3EB2wOSviZp/Y5F2IcK+n43ALu0+ZxDVsO+Zls5\nv7w1Ob+a5bYzdSoKXSJiZkScGBGbAYcA+wH3VR5ZZ10J7J46CDMzAIm3AxsCN3f8tVu4TmFxijfM\nQyj+mr4eOD8iLq0+vM6QWJzivs3jIng6dTxmNrJJHArs1Yn7J/TW35LU3SSdBTwFfAq4HFgnIg5p\nUkEAiOAN4Bo8WjCzetgDuCLFC/fXPpoE3AJsFBF7RcR5EfFSh+LqV0V9v8spbiiUXM36mm3n/PLW\n5PzqkJvEksCuFG3tjlvkLqkRsXMnA6mBq4HTJZYqr3Q2M0the+ChCGanePEB5xRGEombgW9EcE3q\nWMxsZJL4L+DFCL6e4vUHXH00wtSmhWRmI9aeFO9FSWRZFCrs+10B7CGhis7fkjr0Navk/PLW5PxS\n5yaxHrAcHdwqu7csi0KF7gZGUew3YmbWaXsAV0SQrK/vOYVeJE4DHo3g5NSxmNnIIjEV+FEEl6SK\nIelIQdJZkmaXO692fW1MuRvrg+XOrCt2OCzPK5hZx5W7om4N/DZlHKnbR2cDE3t9bRIwNSLWB64r\nHy+k4r7f9cBmEqMrfI1+pe5rVs355a3J+SXObVfg9xEkvR4saVGIiJuAF3p9eW9gSvn5FGDfzsbE\nKxSbUHXs9ndmZhTzCclWHXVJPqcgaSzwm4jYpHz8QkSMLj8XMKfrcedi4p+BHSL4SCdf18xGJonF\ngKeBbSN4JGUsqdtH/SrvDZ2ial0JTJQYleC1zWzk2RyYk7ogQD/bXCQ0W9KqETFL0moUu5cuRNKp\nwLLAzPJLc4HpETGt/P4EgKE+Bq0Dl8+FPbYGfjfc8w3h8dHtzKeGj51f3o8bm1/POYXOvv4Zh8ER\nl1eUz2FlSjOBaQve5/pWx/bRScDzEfEdSZOAFSNiUq/nTBgoseHHxbcARfCVKl+n79euPr+UnF/e\nmpxfqtwkbgeOiej8TXXeFEvKoiDpfIo7u61McZ/k44BLgQuBtSgq20ERMbfzsbENcEYEm3b6tc1s\n5JB4B8WFs6tE8HryeFKPFOqqnE+YBWweweOp4zGzZpI4HHhvBIekjgVqPtG8KJ1YSxzBPOAqimVi\nHdXkdeDg/HLX5PwS5VaLpahdsiwKHeSrm82sMhJvAXamuJ9LLbh91A+JFYHHgVUjeDl1PGbWLBK7\nAV+LYLvUsXTxSKEfEcwF7gB2Sx2LmTXSPtSodQSZFoUO9/3OBz7cwddrdM8WnF/umpxfJ3Mr78V8\nEHBBp16zFVkWhQ77JbBbyg3yzKyRJgL3R/Bo6kB68pxCCyR+CUyN4MzUsZhZM0hcBFwTwY9Tx9KT\nRwqt+Rnw0dRBmFkzlJ2HXSk6EbWSZVFI0NO8GthQ4h868WJN7tmC88tdk/PrYG4HAteWi1lqJcui\n0GkRvEYxGeSttM2sHT5K0YGoHc8ptEhiS+BcYP2UN9U2s7xJrA3cCqxR/sFZKx4ptO42YD6wVepA\nzCxrHwF+UceCAJkWhRQ9zXJ0cA4dmHBucs8WnF/umpxf1blJiBq3jiDTopDQucDB5UUnZmaDtTUw\nj6LzUEueUxgkiRuA70dwSepYzCwvEqcBT0XwrdSxLIpHCoPXkRaSmTVLuSPqQRQdh9rKsigk7mle\nBOwiMaaqF2hyzxacX+6anF/Fue0O3BPRfW/5WsqyKKQUwYvANRQV38ysVR+l6DTUmucUhkBiD+Ar\nddoD3czqq+wsPAqsVf5hWVseKQzNtcC6EuumDsTMsnAwcHXdCwJkWhRS9zQjeJ0Kt71InV/VnF/e\nmpxfhbll0TqCTItCTZwDfLS8GMXMrE9lR2Edig5D7XlOYYjKYvBn4AsRTE0dj5nVk8RJwOIRfCF1\nLK1wURgGicOAD0X4Hs5m9mYSKwCPAJvXfSlqlyzbRzXqaZ4HbCwxvp0nrVF+lXB+eWtyfhXkdgTF\nBPPMNp+3MlkWhboodzk8Bfhi6ljMrF7KK5iPBk5OHctguH00TBLLUwwPt8jprwEzq5bEx4FDInhf\n6lgGwyOFYYrgr8BPgM+njsXM6kFiMYoOwkmpYxmsLItCDXuaP6RYnrpSO05Ww/zayvnlrcn5tTG3\nPYBXgP9p0/k6JsuiUDcRPA1cDHwmdSxmVgtfAk7K8da9nlNoE4mNgGnA2AheSRyOmSUisS3wc4r7\nub+ROp7B8kihTSK4j+Jm3IclDsXM0voi8F85FgTItCjUuKd5EnCsxKjhnKTG+bWF88tbk/Mbbm4S\nGwLbAWe3JaAEsiwKdRXB74BZwP6pYzGzJI4BfhTBy6kDGSrPKbSZxD7AV4GtcpxkMrOhkVgVuJdi\nLuG51PEMlUcK7fcbYHlgp9SBmFlHHQmcm3NBgJoWBUkTJd0v6SFJ/9bH9yckCKslEcynuKz9TXG3\nqs75tYPzy1uT8xtqbhLLUexz9L22BpRA7YqCpFHAqcBEYGPgg5I2ShvVoP0c2Ehi59SBmFlHfAW4\nMoJHUwcyXLWbU5C0DfC1iJhYPp4EEBEnJg1skCT2Bb4NjC83zjOzBipXHN0MbBLBM6njGa7FUwfQ\nh9WBJ3o8fhLYKlEsw3EpxXDyKDLbJdEGVt5kaQywGrAyix51vwbMBp6J4KUOhWcdUv4e/DfwzSYU\nBKhnURhw6CLpVGBZ6N6VdC4wPSKmld+fAJD6McSRwK3ShJlww/8O4vlH1zGfNj7OIj+IW4BxcNIh\nsMracOhiwGpwzVhYYgzs/HfgGbj0NYj5sO/c4nn/vgZs8VL5+C1w9VhYciVp59fL41+G/5sDB/0B\nmA77LAFXPRXx2vV1yj/3n99QHvecU2jx+QfAlevAQTMoa34N8zmsTGkmMK3ruEWpY/toa+D4Hu2j\nLwPzI+I7PY6ZMFBidSHxDWC9CA5p/Tn55DcUdcxPYnHg3cCWwGblx3rAw8CdwF3AY8Az5cesRW1n\n0ld+5V+Uy1OMLFYDVgXW7fFaK1Hc3vXO8uP3wAN1XNZcx59fuwwmN4llgfuAD0dwY6WBdVAdi8Li\nwAPALsDTwB+BD0bEfUkDGyKJtwL3AIdHcF3qeGwBiXcC7ys/dqZ40/89C96Y747g1Q7FMhoYz4Ii\nsRPFqPma8uO6COZ2IhZrjcSJwOoRfDR1LO1Uu6IAIOn9FHc0GwX8NCJOSBzSsJQXtJ2AJ52TKrcf\nmQDsTVEIxgDXUrzpTo1gVrroFlaOLDZiQdHajmIkcTVwcQT3JAxvxCsnl28CNm3KXEKXWhaFgeQ2\nfC3/g18OTIsYeNI5t/wGq5P5lf/2mwMfBg6G7m3OrwHuLK8rafNrtj8/iaWBHSiWah8IPE9xj/AL\nIni8na81cCzN/f1sJbfyd+pa4IoITulIYB1Ux4nmxokgJI4CbpU4P4InU8fUdBLrAR8qP0YB5wI7\nR3B/0sCGqJy/uBa4VuJYigLxYeBOibspCsQvI5iTMMyR4gPAKhTXUzVOliOFXEl8HdgggoNTx9JE\nEksCB1Dc7Gg94BcUxeC2Ok7YtkN5c/iJFMXvfcCVwGnA75qac0pNnVzuyUWhgzzpXA2JtSiuCTmc\n4t/3R8BvIng9aWAdJrEicChFUXyVojic6+sj2qepk8s91W6bi1bkuvdKuZ3uUcAZ5WqTPuWaX6va\nkZ+EJHaV+DUwnWK553si2CWCi1MWhFQ/vwjmRvADignqYyhGEI9J/LC8M2BbNPn3s7/cJLYGPklx\nq83GyrIo5CyCyygmnS8o18bbIEgsKfExipU436NYjbNWBEeWd78b8SKYH8FvI9iPYpnri8D1EpdL\n7FhOlNogSKwO/Ar4eNNWG/Xm9lECZTG4CvhzBMekjicHEssDnwKOBh6kuMvdte6bt6ZcvfQxihHE\nHIp/v0sjmJc0sAyU/3Y3Ar+KIKs92IbCRSERiTHAHyj2TJmSOp66kliNYp/6TwG/BU6O4I60UeWr\nvFZjH4oWyErAd4FzFnV19khXjqp+RtFV+fBI+CMky/ZRE3qa5dLBfYDvlr3Kbk3Irz+t5CcxVuJ0\nijtZLQtsGcEhORSEOv/8IpgXwcXANsAngD2BRyS+VN4TYEB1zm+4+sjtixRzNIePhIIAmRaFpojg\nXor/mL8qe5YjnsQGEpOBO4AXKJbwfi6CR9JG1iwRRAQ3RbAXsBvF1hqPSBzX3yKIkURid4p25b45\n33N5sNw+qgGJLwP7ATuN1GG8xKYUNyrZmWIr4lMjeCFtVCOLxPrAJIoR7JnA9yN4Nm1UaZTbWNxI\nURB+nzqeTvJIoR5OBP4CnDnSVoZIbClxKcW2E7cDa0fwDReEzovgwQg+AbyLYonv/RKnjLRRbDlS\nuhSYNNIKAmRaFJrW0yx7lZ+kuP3ocdKoCWkjqpY0aoLEThLXAhcBUymKwXebcKFV7r+fETwWwWeB\nccA8YIbEGRJrQ/759UdaayJwIXB1BGeljieFLItCE5U9y72A/eCcL5ZbNjRKecHZRPj1fwM/AS4A\n1o3g1JHaNquzCJ4ul0yvD/wv8EeJc2D/tRKHVoliRHT6D4CnYOQuFfecQs2Ue6ucC6wAHBDB84lD\nGrZyGeS+wJeBt1Dcu/qXEbyRNDAblHIbjc9SLBG+CTghh9VgrZDYHLiEYpO7k0bKSqO+uCjUUPkm\negLF5PNeue7sKbEMxa0APw88RzF3clkV21Vb55Q/1yOAL1Dcme67wFW5/lwlDgD+H3BEBL9OHU9q\nWbaPmtzTLGiHCL5EURhulHhv6ogGQ2JViW9S3BN2F4pN2raJ4JII5jf959f0/EDvjuD7wNrAj4Fv\nAPdIHC6xVNrYWle2M79CcUOv90Xw6+b/7AaWZVEYKcqJroOAcyU+nTqegUhsIvETiq2FxwDbRrB/\nhLdxbqIIXo/gPIqbGH2WYmQ7U+I/JFZJG13/yi3HpwD7A1tH8KfEIdWG20cZkFiXYhO96cBxETyY\nOKRu5VWwh1BsW706cAZwegTPJQ3MkpDYmKJd+AHgfygWFFxblz2WyiXfu1K0Mh8BPjaSLkxrhYtC\nJsoJ6COzLOMYAAAICElEQVQp/sP9Bvh6BDMTxSJga4pCsD8wjaKNcE1d/vNbWuUGhl1/LKwGnAWc\nnep3toxpR+CbwNuBr1EsdshyHqRKWbaPmt736yu/CF6K4NsUdxR7ErhD4rROXVhU9l83k/h3YAZw\nDsVupRtFsF8EV7ZaEEbiz69JWskvgr9GcGYEW1LsrzQauF3iWolPS6xZdZxdJLYqr4mZTDFyGRfB\nL/oqCE3/2bUiy6IwkpU3UjkO2AB4ieLCou9JjC9XLS3SOGn390tXHyRNe7909Thp9/6Ol1hGYh+J\nM4EnKC7qWZmif7x+BN+JYFZ7MrOmiuCuCI4E1gR+CmwPTJe4S+LbEtsO9LsLg/v9lVhaYmeJyygu\nkLyIYh+tc7wUun9uH2Wu3Fr6WGAPipuJ30yxZ8uNwJ+67kA2Ttp9G/jBj2Hdrud+Ch6+BY66O+LK\nsj21AcWOkBsCWwDbAX8ErgAur9NchuWtLAJbU/ze7kExHzWV4uZJ91MsVvjLIH5/l6P4fd2x/BhP\nMaK9ADgjglc7l13eXBQapFzxsQOwE8V/jH8AbgPmbMvm2/2OP63W+znbsNVzt3LrKxQjgAdZ8B/y\nz8B1Efy1U/HbyFXeZ3tniq1eNio/1gAeBe7bjk03v5kZb7qSelvePfsW/vhEefztLPiD6JYI/t6p\n+Jsky9tBSpoQEdNSx1GVoeYXwWwWDJW7buSzJbD8aGb9I8WE30LexqPPUFxt/FinJon988tbFflF\n8DhFz7/H67AUxRzaRsvzt037et5KPPk8xeKL2yL4v+HG0fSfXSs8p9BgEcyJ4OoILpzH04/3dcwb\nPPtUBI941ZDVTQSvRjAjgguDmQ/3dcw8nnk8gpvbURCskGVRaHolryK/J+CHnyq2JOh2OPzl8eLe\nBR3ln1/eUuTXqd/fpv/sWuE5hRFknLT7WvC5ZWHpl+CVx+G/7464MnVcZq3w729nZFkUmt73c355\nc375anJurcqyfWRmZtXIcqRgZmbV8EjBzMy6ZVkUmr4/ifPLm/PLV5Nza1WWRcHMzKrhOQUzM+vm\nkYKZmXVLUhQkHSjpHknzJL2r1/e+LOkhSfdL2m0Rz5/QkUATcX55c375anJurUo1UphBcT/XG3t+\nUdLGwMEUOyVOBE6T1FeM4yuPMC3nlzfnl68m59ZS0UtSFCLi/ojoa2/+fYDzI+L1iJhJsdfJln0c\nt2KV8dWA88ub88tXk3MDmDDQAXWbU3gHxa0muzwJnbndpJmZVXg/BUlTgVX7+NZXIuI3gzhVX8uj\nxg4pqHyMTR1AxcamDqBiY1MHULGxqQOo0NjUAaRWWVGIiF2H8LSnYKEbeq9Rfq236ZKO7/F4WsM2\nsZqcOoCKTU4dQMUmpw6gYpNTB1ChyakDaKdyDmFCjy/NHfA5Ka9TkHQ9cGxE3FE+3hg4j2IeYXXg\nt8C64YspzMw6ItWS1P0kPUFx4+4rJF0FEBH3AhcC9wJXAZ9xQTAz6xxf0WxmZt3qtvqoZZK+Ieku\nSdMlXSdpzYGflQ9JJ0u6r8zxYkkrpI6pnfq7gDFXkiaWF10+JOnfUsfTbpLOkjRb0ozUsbSbpDUl\nXV/+Tt4t6cjUMbWTpKUk/aF8v7xX0gmLPDbXkYKk5SLib+XnnwP+KSIOTxxW20jaFbguIuZLOhEg\nIiYlDqttJG0IzAfOAI6JiD8lDmlYJI0CHgDeS7E44jbggxFxX9LA2kjSDsBLwDkRsUnqeNpJ0qrA\nqhExXdKywB3Avg37+b01Il6WtDhwM8V87s29j8t2pNBVEErLAs+liqUKETE1IuaXD/9AsRKrMfq5\ngDFXWwIPR8TMiHgduIDiYszGiIibgBdSx1GFiJgVEdPLz18C7qO4bqoxIuLl8tMlgVHAnL6Oy7Yo\nAEj6lqTHgUOBE1PHU6FPAL5Beb2tDjzR47EvvMyUpLHAZhR/jDWGpMUkTQdmA9eXC3vepLLrFNph\noAvgIuKrwFclTQK+D3y8owEOUysX+En6KvBaRJzX0eDaoI0XMOYgzz6sLaRsHV0EHFWOGBqj7DyM\nL+cnr5E0oa/ru2pdFAZxAdx5ZPiX9ED5SToM2B3YpSMBtdkQL2DMVe8LL9dk4S1brOYkLQH8Cvh5\nRFySOp6qRMSLkq4AtgCm9f5+tu0jSev1eLgPcGeqWKogaSLwRWCfiHg1dTwVU+oA2uB2YD1JYyUt\nSbHb72WJY7IWSRLwU+DeiDgldTztJmllSSuWny8N7Moi3jNzXn10EbABMA/4C/AvEfFs2qjaR9JD\nFBNCXZNBt0TEZxKG1FaS9gN+CKwMvAjcGRHvTxvV8Eh6P3AKxSTeTyNikcv+ciTpfGAnYCXgWeC4\niDg7bVTtIWl7iq38/8yCVuCXI+LqdFG1j6RNgCkUA4HFgJ9FxMl9HptrUTAzs/bLtn1kZmbt56Jg\nZmbdXBTMzKybi4KZmXVzUTAzs24uCmZm1s1FwawNyq2XH5E0unw8uny8VurYzAbDRcGsDSLiCeB0\nFmzMeCJwRkQ8ni4qs8HzxWtmbVLuU38HcDbwSWB8RMxLG5XZ4NR6QzyznETEG5K+RHF/8V1dECxH\nbh+Ztdf7gaeBRt2ZzEYOFwWzNpE0nuJ2nNsAny9v8WiWFRcFszYot14+neLmLE8AJwPfTRuV2eC5\nKJi1x6eAmRFxXfn4NGCj8mb3Ztnw6iMzM+vmkYKZmXVzUTAzs24uCmZm1s1FwczMurkomJlZNxcF\nMzPr5qJgZmbdXBTMzKzb/wcK7AmeBMy4QAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb80f1a9128>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x = np.linspace(-3.0, 3.0)\n",
"plt.plot(x, hat(x,a,b))\n",
"plt.plot(-1.5811388304396232, hat(-1.5811388304396232,a,b), 'ro')\n",
"plt.plot(1.58113882, hat(1.58113882,a,b), 'ro')\n",
"plt.xlabel('X')\n",
"plt.ylabel('V(x)')\n",
"plt.title('Hat Potential')\n",
"plt.grid(True)\n",
"plt.box(False);"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "bd49ce2f030e3366ee640213f26fdaa6",
"grade": true,
"grade_id": "optimizationex01b",
"points": 2
}
},
"outputs": [],
"source": [
"assert True # leave this to grade the plot"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"Write code that finds the two local minima of this function for $b=1.0$ and $a=5.0$.\n",
"\n",
"* Use `scipy.optimize.minimize` to find the minima. You will have to think carefully about how to get this function to find both minima.\n",
"* Print the x values of the minima.\n",
"* Plot the function as a blue line.\n",
"* On the same axes, show the minima as red circles.\n",
"* Customize your visualization to make it beatiful and effective."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false,
"deletable": false,
"nbgrader": {
"checksum": "6cff4e8e53b15273846c3aecaea84a3d",
"solution": true
},
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
" nfev: 35\n",
" status: 0\n",
" fun: array(-6.249999999999999)\n",
" nit: 2\n",
" x: array(-1.5811388304396232)\n",
" success: True\n",
" direc: array([[ 0.00105468]])\n",
" message: 'Optimization terminated successfully.'"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"opt.minimize(hat, -3, args=(a,b), method = \"Powell\")"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
" status: 0\n",
" jac: array([ -5.96046448e-08])\n",
" nfev: 36\n",
" x: array([ 1.58113882])\n",
" hess_inv: array([[ 0.05000928]])\n",
" success: True\n",
" fun: -6.249999999999999\n",
" njev: 12\n",
" message: 'Optimization terminated successfully.'"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"opt.minimize(hat, -3, args=(a,b))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": false,
"nbgrader": {
"checksum": "235361d4c954cf9fd6a8ecef309b3a44",
"grade": true,
"grade_id": "optimizationex01c",
"points": 4
}
},
"outputs": [],
"source": [
"assert True # leave this for grading the plot"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbgrader": {}
},
"source": [
"To check your numerical results, find the locations of the minima analytically. Show and describe the steps in your derivation using LaTeX equations. Evaluate the location of the minima using the above parameters."
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": false,
"nbgrader": {
"checksum": "d7d37614ffa0d469a42ff3fd121335f2",
"grade": true,
"grade_id": "optimizationex01d",
"points": 2,
"solution": true
}
},
"source": [
"$$ V(x) = -a x^2 + b x^4 $$\n",
"$$ V'(x) = -2a x + 4b x^3 $$\n",
"$$ 0 = -2(5.0) x + 4(1.0) x^3 $$\n",
"$$ 0 = -10 x + 4 x^3 $$\n",
"$$ 10x = 4 x^3 $$\n",
"$$ \\frac{5}{2} = x^2 $$\n",
"$$ \\sqrt{\\frac{5}{2}} = x $$\n",
"$$ x = +- 1.5811388301 $$\n",
"I simply set the derivative of the function equal to zero, plugged in the values of a and b, and solved for x."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
jgarciab/Stats_Python | Statistics 2014-09-29.ipynb | 1 | 482112 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": true,
"input": [
"__author__ = 'Javier Garcia-Bernardo 2014'\n",
"\n",
"# Math\n",
"import numpy as np\n",
"\n",
"# Stats\n",
"import scipy\n",
"\n",
"# Plot\n",
"import pylab as plt\n",
"import matplotlib\n",
"\n",
"# Multiple comparisons\n",
"from statsmodels.stats.multicomp import pairwise_tukeyhsd\n",
"\n",
"# Kernel Estimation\n",
"from sklearn.grid_search import GridSearchCV\n",
"from sklearn.neighbors import KernelDensity\n",
"\n",
"# Bootstrap\n",
"import scikits.bootstrap as bootstrap\n",
"\n",
"%matplotlib inline\n",
"\n",
"def customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8):\n",
" '''\n",
" From stackoverflow. User gcalmettes \n",
" '''\n",
" for c_spine, spine in zip([c_left, c_bottom, c_right, c_top],\n",
" ['left', 'bottom', 'right', 'top']):\n",
" if c_spine != 'none':\n",
" ax.spines[spine].set_color(c_spine)\n",
" ax.spines[spine].set_linewidth(lw)\n",
" else:\n",
" ax.spines[spine].set_color('none')\n",
" if (c_bottom == 'none') & (c_top == 'none'): # no bottom and no top\n",
" ax.xaxis.set_ticks_position('none')\n",
" elif (c_bottom != 'none') & (c_top != 'none'): # bottom and top\n",
" ax.tick_params(axis='x', direction='out', width=lw, length=7,\n",
" color=c_bottom, labelsize=size, pad=pad)\n",
" elif (c_bottom != 'none') & (c_top == 'none'): # bottom but not top\n",
" ax.xaxis.set_ticks_position('bottom')\n",
" ax.tick_params(axis='x', direction='out', width=lw, length=7,\n",
" color=c_bottom, labelsize=size, pad=pad)\n",
" elif (c_bottom == 'none') & (c_top != 'none'): # no bottom but top\n",
" ax.xaxis.set_ticks_position('top')\n",
" ax.tick_params(axis='x', direction='out', width=lw, length=7,\n",
" color=c_top, labelsize=size, pad=pad)\n",
" if (c_left == 'none') & (c_right == 'none'): # no left and no right\n",
" ax.yaxis.set_ticks_position('none')\n",
" elif (c_left != 'none') & (c_right != 'none'): # left and right\n",
" ax.tick_params(axis='y', direction='out', width=lw, length=7,\n",
" color=c_left, labelsize=size, pad=pad)\n",
" elif (c_left != 'none') & (c_right == 'none'): # left but not right\n",
" ax.yaxis.set_ticks_position('left')\n",
" ax.tick_params(axis='y', direction='out', width=lw, length=7,\n",
" color=c_left, labelsize=size, pad=pad)\n",
" elif (c_left == 'none') & (c_right != 'none'): # no left but right\n",
" ax.yaxis.set_ticks_position('right')\n",
" ax.tick_params(axis='y', direction='out', width=lw, length=7,\n",
" color=c_right, labelsize=size, pad=pad)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Interaction between parameters (Observed vs Expected). "
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Chi Square"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"About 25 percent of the U.S. scientific workforce consists of foreign-born scientists, in both industry and academia.\n",
"\n",
"We have 3 Americans and 4 Internationals. So the obvious question is: Does Mary hate Americans?\n",
"\n"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%latex\n",
"$$ \\frac{\\sum{(Obs - Exp)^2}}{Exp}$$"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$ \\frac{\\sum{(Obs - Exp)^2}}{Exp}$$"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Latex at 0x7f7e844f5250>"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"p-val = \", scipy.stats.chisquare(f_obs = [3.,4.], f_exp = [7.*0.75,7.*0.25])[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('p-val = ', 0.049534613435626491)\n"
]
}
],
"prompt_number": 40
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"YES! But wait... This test is invalid when the observed or expected frequencies in each category are too small. A typical rule is that all of the observed and expected frequencies should be at least 5."
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Fisher's exact test"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"p-val Exact test =\", scipy.stats.fisher_exact([[3, 75000], [4, 25000]])[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('p-val Exact test =', 0.070570483471531401)\n"
]
}
],
"prompt_number": 41
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Math says Mary doesn't hate Americans... until Jess leaves:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"p-val Exact test =\", scipy.stats.fisher_exact([[2, 75000], [4, 25000]])[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('p-val Exact test =', 0.03760622581012793)\n"
]
}
],
"prompt_number": 42
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Compare 2 independent samples"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Imagine we want to compare if there are difference in GFP expression between two populations of cells."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def median_test(samples1, samples2):\n",
" \"\"\"Adapted from https://gist.github.com/wanderview/8285920\"\"\"\n",
" median = np.median(samples1 + samples2)\n",
" samples1 = np.asarray(samples1)\n",
" samples2 = np.asarray(samples2)\n",
" below1, above1 = np.sum(samples1<=median),np.sum(samples1>median)\n",
" below2, above2 = np.sum(samples2<=median),np.sum(samples2>median)\n",
" \n",
" below_exp = (below1 + below2) / 2\n",
" above_exp = (above1 + above2) / 2\n",
"\n",
" result = scipy.stats.chisquare(\n",
" [below1, above1, below2, above2],\n",
" f_exp=[below_exp, above_exp, below_exp, above_exp]\n",
" )\n",
"\n",
" return result[1]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 43
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" x = [np.random.randn() for _ in range(200)]\n",
" y = [np.random.randn()+0.6 for _ in range(200)]\n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()\n",
" "
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3V1zG9edJvCnIZGy3ogGKMu2YidEg5PMzqYqIgDmIqmt\nbAmAp2q3pnbKFCHXXpts+l4SoE8ggf4AFkF9AQqAM1PJxURsyNlN1eyOSYLeSSpxxeEBJ44sWQrB\nBsd6M0mcvdAAEQiQQlMNdoN8flWsMk/3Qf9NEHzUfU6fVqSUEkRERDbyOF0AERHtPwwXIiKyHcOF\niIhsx3AhIiLbMVyIiMh2DBciIrLdYacLAADDMGAYBvr7+7G0tIRwOIyxsbGGfYrFIhYWFuD3+yGE\nQCgUQjQadahiIiLaiePhYhgGFEXBtWvX6m2RSASmaeLSpUsAACEEUqkUbt26Vd8nkUhA0zQEAoE9\nr5mIiHbm+GWxqampprZYLNbQnk6nMTEx0bCPrutIJpMdr4+IiKxzPFwURYFhGA1tUkr4fL7699ls\nFqFQqGGfcDiMXC63JzUSEZE1ihuXfwkGg3j//fdx8eJFmKYJv98P0zTR19fXsJ/H44EQAgMDA84U\nSkRELTl+5rJVJpNBJBLBxYsXAQDlchkAmoKlRgixZ7UREVF7HB/Qr8nn85idnYWiKJiZmam3m6bp\nYFVERLQbrgmXkZERjIyMoFKpIBKJYHp6GkNDQ06XRUREu+C6y2Jerxe6rr/0PSyKomz7RUREneW6\ncAGAaDQK0zRx+/ZtaJoGAFhbW2u5b227FQwYIqLOcjRchBDw+Xz49NNPW243TROqqkLTtKaBeyEE\nVFXddqaYlLLlFxERdZ6j4WKaJoLBYNPZRy1Iave2xGIxzM3NNexTLBYRj8f3plAiIrLE0XAJhUK4\ncOFC0xlFOp1GMpmsn5Wk02lks9mGfTKZDNLp9F6VSkREFrjiJsrp6WksLS3VF66MRCJ47733GvZZ\nXFzEzMwMhoeHIYRAOBzGuXPnLB+rNt7igv9tIqJ9yxXhspcYLkREneea+1yI6Jn79+9jY2PDUh9F\nUXD69GkcOnSoQ1URWcNwIXKRzc1N/EPhHyBPWDuz3vh6A4lYAq+++mqHKiOyhuFC5CJSSkhF4sx3\nz1jq9+VnX3aoIqLdceVNlERE1N0YLkREZDuGCxER2Y7hQkREtmO4EBGR7RguRERkO4YLERHZjuFC\nRES2Y7gQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4EBGR7Rgu\nRERkO4YLERHZ7rDTBRDtNSnlrvopimJzJUT7lyvCJZ/PQwiBpaUlCCGg6zpGRkbq22ttqVQK4XAY\n5XIZmUwG8Xgc0WjUwcqp21SrVczM/AKVStVSv95eib//+x/B7/d3qDKi/cXxcMnn89A0rR4mlUql\nHiBjY2P1/QqFAgqFAgBAVVXcuHGDwUKWSSmxtgZ861v/3VK/L7/8F2xsbHSoKqL9x/ExFyEEhoaG\n6t97vV4kk0noul5vUxQFhmHANE0IIVAul/HOO+84US4REbXB0XAxTRMzMzOoVCoN7bUzkuXl5Xqb\nlBJ9fX0YGBjYwwqJiGg3HA0XVVUhhECpVHKyDCIispnjYy7lcrmpzTAM+Hy+hrMUIQRM06z38fv9\nDYP+RETkHo6HSytTU1O4cuVK/fvaDJ3nwySRSDS1ERGROzg+oL9VJpPBqVOncPHixXqb1+ttmDkG\nALquI5lMbvs6iqK0/CIios5z1ZmLEAKZTAbz8/Mv3DcQCEAIgbW1NfT19e1BdURE1C5XnbmkUinc\nvn27qX1ycrKprXapTAjR8rWklC2/iIio81wTLhMTE5icnGw6CxFCIJVKNUxLBv4yEUDTtL0qkYiI\n2uSKcJmenkYqlWqYHVYoFFAqlaBpGqampprubzEMA+FwmJfEiIhcyPExl1wuB+DZmUjtbKRcLiOX\ny+H69esAnl0CK5VKCAQCAJ7dfJnJZHDjxg1niiYioh05Gi6madanFG8VDAbr/z0yMoJ8Po9cLoeV\nlRWYpolcLse79YmIXMrRcFFVFdVqe6vT8n4WIqLu4YoxFyIi2l8YLkREZDuGCxER2Y7hQkREtmO4\nEBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuG\nCxER2Y7hQkREtmO4EBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGS7w04XAAD5fB5CCCwt\nLUEIAV3XMTIy0rBPsVjEwsIC/H4/hBAIhUKIRqMOVUzdSkqJ335exL/df2ypn7laQvzrV3H69OkO\nVbb3VlZW8Ku5X6GKqqV+/Sf78ZMf/6RDVdF+4Xi45PN5aJpWD5NKpYJwOIxyuYyxsTEAgBACqVQK\nt27dqvdLJBLQNA2BQMCRuqk7VatVPHh0F0e+O2ip32r5Hh4/thZIbvfw4UPceXIHp9461XafzY1N\nlP5Ywk/AcKGdOX5ZTAiBoaGh+vderxfJZBK6rtfb0uk0JiYmGvrpuo5kMrlnddJ+ouDI0WOWvjye\nQ04X3RGHew7j2IljbX8dPX7U6ZKpSzgaLqZpYmZmBpVKpaG9drlreXkZAJDNZhEKhRr2CYfDyOVy\ne1InERFZ42i4qKoKIQRKpdK2+5imCdM04ff7m/oCfwkgIiJyD8cvi5XLZZw9e7ahzTAM+Hw+DAwM\noFwuAwD6+vpa9hdCdLxGIiKyxvFwaWVqagpXrlwB8OzMhYiIuovjs8W2ymQyOHXqFC5evPhSr6Mo\nik0VkVV3797FxsaG5X5vvPEGDh923a8kEe2Cqz7JQghkMhnMz887XQrtUrVaxc9+tgAp37LUb339\nAUZHe/Haa691qDIi2kuuCpdUKoXbt283tGmaBgBYW1trOe5S276VlLJlO89oOq9a9eBb3/qBpT5f\nfvlJh6ohIie4ZsxlYmICk5OTTQGiqio0TWsauBdCQFVVDAwM7GGVRETUDleEy/T0NFKpVENQFAqF\n+hTlWCyGubm5hj7FYhHxeHwvyyQiojY5Hi61GyHL5TKKxSKKxSIMw0A2m60v7ZJOp5HNZhv6ZTIZ\npNPpPa+XiIhezNExF9M0kUgkWm4LBoP1//Z6vUin00ilUhgeHq6vNcZLYkRE7uRouKiqimq1vRVZ\nh4aGGtYgIyIi93LVbDGi/eT+/fv4p1/9Ezarm233kVLi8eb+Wn2ZDiaGC1GHPH36FI96H+F17XVL\n/fo9/R2qiGjvMFyIOkjxKDh0eH8u10+0E8dnixER0f7DcCEiItsxXIiIyHYMFyIish0H9KlrPX78\nGF988YWlPuvr67s+3r1799DT09P2/lsf3010kDBcqGutrKzg5z+/i2PH3mi7T7XqwSFP+/vX9Ppe\nwcLqAj5f/9xSv75TrZ+gSrTfMVyoqx0/7sWZM99te//NzU2c/ML6fSTHTp7AG99+DapXtdyX6CDi\nmAsREdmO4UJERLZjuBARke0sjbkMDg5afkywlBKKouDzz60NhBIRUfeyFC5DQ0MolUooFov1tkAg\ngHK5XJ92qapq/SFfNXxuPe0Hm5ub2NjcsNTnkOcQf//pQLIULleuXEEkEkEoFML09HTD81WKxSLG\nxsawvLyMXC7XFDBE3UyiF3OfLFvqU5US3/veqwhq3+lMUUQuZilcrl27BlVVUSgU4PV6G7aFQiEs\nLCzA5/MhlUphZmbG1kKJnNTvDwCw9g+mytoDbGx83ZmCiFzO0oC+YRiIx+NNwfK8WCwGwzBeujAi\nIupelsJFSgkhxI77lEqllyqIiIi6n6VwicViWFhYwEcffdRyez6fR7FYRDgctqU4IiLqTpbGXNLp\nNAzDwOjoKM6fP494PA5N07C0tITZ2Vnkcrn6fkREdHBZChdN01AoFJBMJpHNZpHNZpu2T01NNcwi\nIyKig8fywpWhUAizs7MQQqBYLEIIAU3ToGkaQqHQrgvJ5XLw+XyIRqMN7UII6LqOVCqFcDiMcrmM\nTCaDeDzetC8dLA8fPkTpj7/G2qMnFnpJVOVmx2p6WVJKiNIfsb5urcaV5QconijC27f9ZJutHj16\nhKqsWi2RqC27XhX51KlTiEQiL5w91g7DMDA+Pl6/rLZVoVBAoVAA8OwmzRs3bjBYCGtrayg9/Fc8\netXaM1qOvXWyQxW9vGq1it///gEOH7Z2b8zav6/gs8ef4eQha/9v/WesrxBN1A7L4bK4uIixsTEU\ni0UoioLZ2VmcO3cOg4ODmJiYwMWLF9t+rVKphHQ6jXA4DL/f33IfRVFgGAYikQjK5TIGBgaslkz7\n2OHeI/D2v+p0GbZSoMDbZ+3/aXOjjP7X+i2duRB1kqXZYqVSCeFwGMViEdFoFFLK+raVlRVcvnwZ\nw8PDbb9eIBDA9evXMTY2tuN+Ukr09fUxWIiIuoSlcKnNAltYWGgazF9dXcW1a9ewsLCAK1eu2Fch\nERF1HUuXxW7evIlYLIahoSGYptm0/fLly5iZmUEul8PVq1dtK1IIUT9euVyG3+/HyMiIba9PRET2\nshQupmkiGAzuuI+macjn8y9V1PNqYzHPh0kikWhqIyIi97C85P78/PyO+ywuLr7UlOStvF5v05iM\nruvQdX3HcOEy53TQPH36FI8ePeroMTbWN/DN+jcdPQbtD5bC5cKFC0ilUvj4449bBkgikYAQApcv\nX7atwFYCgQCEEFhbW0NfX19Hj0XUDTye4ygu3Adwv6PH2dzcgHK3AvzPjh6G9gFL4VIbU4lGo4jH\n4wCeDfJPTU3BMAysrq5C0zRcu3bNtgInJyebwqp2qUwIgbNnz7bs9/xMtufxjIb2I1V9E8CbHT/O\nN988wcq//d+OH4e6n6XZYsCzmWLXrl3DJ598AgCYnZ1FNptFtVrF5cuX8Yc//MG24oQQSKVSWF5e\nbmgvl8sAno3vEBGR++zqDv3Lly/XzyaEEPD7/VBV1dbCgL+sVbb1/hbDMBAOh3lJjIjIpSyduUxP\nTzctt69pmm3B0upSlt/vb3hGjGmayGQymJ6etuWYRERkP0tnLrquw+fz4Z133rHl4JVKBVevXoUQ\nor5AZSwWQzwer88EGxkZQT6fRy6Xw8rKCkzTRC6X4936REQuZilc3nvvPdy4cQOffvrptgPpVni9\n3rYG/3k/CxFRd7EULplMBoODgwiHw5iamkIkEoGmaRz7IGpBgYKvvjLx8OFnbfeRUmJ9o4NFEe0R\nS+FSmwIspcT4+Hi9/fnpvVJKKIqCzU33PjODaC+cOOHDk6e9WFuz1k/17vpJGESuYem3uN1nqPBe\nEiLA4zmEY0d5Vk8H047hkkql8MMf/rA+gL91JWQiIqJWdpyKPDk5iZmZmab26elpvP/++x0rioiI\nupvlO/QB4NatW8hkMnbXQkRE+8SuwgXYfu0uIiKiXU9L4aD9/rexsYGVlRVLfarV6q6P1+oBdDtZ\nszoNi4j2DOc80ra++uor/PSnv0VPj9diT+ur8/b2nsYvf3kfQKXtPqurj9DTc8LysYio8xgutC0p\nJXp6TuHMmaGOH+vUqQEAA5b69Pb+CV9Uv+xEOUT0knY95kJERLSdF565GIaBCxcuNLQVCgVIKZva\nn9dqCjMRER0MLwyX1dXVbW+e3OmmSoYLEdHBtWO4zM/P71UdRES0j+wYLqFQaK/qICKifYSzxYio\nbYpHwaPNh7j5s5uW+vUc6kHsv8Rw8uTJDlVGbsNwIaK2eTyH4P+rU1DetHYT9T1xD0+ePGG4HCAM\nFyKy5HDPYbxy7BVLfTyHeNfDQcN3nIiIbMdwISIi2zFciIjIdgwXIiKynWsG9HO5HHw+H6LRaNO2\nYrGIhYUF+P1+CCEQCoVa7kfd6+uvV/HwYfsrItf6EJE7uSJcDMPA+Pg4crlc0zYhBFKpFG7dulVv\nSyQS0DQNgUBgL8ukDhJffIrlJ79GT+8RS/2Oeo93qCIiehmOhkupVEI6nUY4HIbf72+5TzqdxsTE\nREObrutIJpO4edPajVzkXhISJ/wqTnh9TpdCRDZwdMwlEAjg+vXrGBsb23afbDbbtAxNOBxueZZD\nRETu4OoBfdM0YZpm01mNqqoAgOXlZQeqIiKiF3F1uJTLZQBAX19fy+1CiL0sh4iI2uTqcDFN0+kS\niIhoF1wdLkRE1J1cMRW5ExTF2qqt+93c3P/D4uKfLPaSAAY6UA0dNJvKJn46+1PA4sfyRz/4Eb7/\nN9/vTFHUUa4OF03TAABra2stx11q2+nFvv76Gxw5EoLP97qlfgxpssNbf/0WpJSW+ty/cx+Pnzzu\nUEXUaa6+LKaqKjRNaxq4F0JAVVUMDAxs21dK2fLrIFMUxfIXkV2s/u55PK7+80Qv4Pp3LxaLYW5u\nrqGtWCwiHo87VBEREb2Iq8Kl1ZlFOp1GNpttaMtkMkin03tVFhERWeTomEulUsHVq1chhIAQArqu\nIxaLIR6PY2RkBADg9XqRTqeRSqUwPDxcX2tsp0tiRETkLEfDxev14tq1ay/cb2hoCENDQ3tQERER\n2cFVl8WIiGh/YLgQEZHtGC5ERGQ7hgsREdmO4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4\nEBGR7RguRERkO4YLERHZjuFCRES2Y7gQEZHtGC5ERGQ7R5/nQkQHw71797FSXrPUx3ywite/83qH\nKqJOY7gQUcd9ebeMe/dO4Ejv0bb73L9Twf1jZgerok5iuBDRnjh69CSOH/O2vX/llQcdrIY6jWMu\nRERkO4YLERHZjuFCRES2Y7gQEZHtumJAXwgBXdeRSqUQDodRLpeRyWQQj8cRjUadLo+IOmT9m3Ws\nrq5a6tPT04MTJ05Y6vPkyRM8fvzYUh8AOH78OHp7ey33Owi6IlwAoFAooFAoAABUVcWNGzcYLET7\nWM+RI1gyP8fNj2+230kC3sNevPs/3rV0rH+e+2d8du8zHDp0qO0+69+s48f/6ccY+sGQpWMdFF0R\nLoqiwDAMRCIRlMtlDAwMOF0SEXXYK8dP4PR3gDN/dabtPhvrG1j7zNrNmgCwvrkO71te9Pn62u5z\n/859VKtVy8c6KLoiXABASom+vj709bX/5hMRkTM4oE9ERLbrmjMXIQRM89lSEOVyGX6/HyMjIw5X\nRURErXRFuPj9fgBoCJNEItHURkRE7tAVl8W8Xi/GxsYa2nRdRzKZdKgiIiLaSVecubQSCAQghMDa\n2lrLQX5FURyoimh/U6Dg0eMqPvnkt5b6ra09xuEefiYPkq4Il8nJSVy+fLmhrXapTAiBs2fPOlEW\n0YHj8RyC6v0+Hj/ZtNSvpxd45ZXjHaqK3Mj14SKEQCqVQiKRaLi/pVwuAwA0TWvZT0rZsp1nNEQv\n58iR9p/JQgeX68dcNE3D1NRU042ThmEgHA7zvhciIhdyfbgAzy6BlUql+vemaSKTyWB6etrBqoiI\naDuuvywGPJtunM/nkcvlsLKyAtM0kcvluAwMEZFLdUW4ALyfhYiom3RNuOylBw8eYH193XK/1157\nzdKqqkRE+xXDZQspJf7xH/8Fm5tvWOq3vl7G+fMevP766x2qjIioezBcWlhfB958M2ypz5dfzneo\nGiKi7tMVs8WIiKi7MFyIiMh2DBciIrIdw4WIiGzHcCEiIttxtliXkVLi5z//JSqVDUv9fvf7z1B+\nNIejR62txRZ8Ywjffus/W+pDdBAoHgWf/v5T/G75d5b6ve57HbH/GutQVe7BcOkyUkrcufMIp09b\n++XsPVpFj/8OjvQda7vPv5srePS0YrVEogPh1TdexXq/tZut179Zx53lOx2qyF0YLl2qp+eIpf0P\nH+7FoUOHcbinp+0+hw4dBqpWKyM6OHp62/881TzBkw5U4j4ccyEiItsxXIiIyHYMFyIish3DhYiI\nbMcBfdrR48df4+7dpY4f5+nTh0D7E9nogHj46BHu3rvb9v6bG5uo3Kvg9u3blo5TWi7h6PeOWi2P\ndsBwoW0dPX4S954I3FsVHT+W7AXUY6c7fhzqHkePnsTdu09w927793RJKbH24Cn+9c7/snSszWoF\n/+2vh6yWSDtguNC2eo4cQf+ZbzldBh1QvT2voN//luV+p/q/bblPefUzHO7hn0M7ccyFiIhsx3Ah\nIiLbMVyIiMh2DBciIrIdR7C6kJQSUkrLfYioe+3lZ1hRlJd+ja4Jl2KxiIWFBfj9fgghEAqFEI1G\nnS5rz0kpMf+b/41f//FPlvptVtdxcqC/Q1URUSf96v/8Cr8p/QYKXv6P/k4kJN7sfxN/97d/99Kv\n1RXhIoRAKpXCrVu36m2JRAKapiEQCDhY2d6TUuLx5kOc+RtOESY6KL5+/DX6tD70+aw9j8mq9W/W\nYX5u2vJaXTHmkk6nMTEx0dCm6zqSyaRDFRER0U66Ilyy2SxCoVBDWzgcRi6Xc6giIiLaievDxTRN\nmKYJv9/f0K6qKgBgeXnZgaqIiGgnrg+XcrkMAOjra32tUYjOr3tFRETWuD5cTNOewSUiIto7inT5\nDRDFYhGRSATVavPD3D0eDwzDwLlz55q22TFPm4iI/sJKXLj+zIWIiNzByj/aXX+fi6ZpAIC1tbWW\n4y617Vttl7C1H47LT9i2xfqd0821A6zfaful/na5/sxFVVVomtY0cC+EgKqqGBgYcKYwIiLaluvD\nBQBisRjm5uYa2orFIuLxuEMVERHRTlw/oA8AlUoFo6OjDcu/vP3228hkMpbPXPbLqSnr33vdXDvA\n+p120OrvinABgMXFRczMzGB4eBhCCITD4ZazxF7koL3BbtPN9Xdz7QDrd9pBq79rwsUuB+0Ndptu\nrr+bawdYv9MOWv0HLlyIiKjzumJAn4iIugvDhYiIbMdwISIi2zFciIjIdgwXIiKynevXFiNyg2Kx\niIWFBfj9fgghEAqFEI1GnS7LklwuB5/P13V15/N5CCGwtLQEIQR0XcfIyIjTZbXNMAwYhoH+/n4s\nLS0hHA5jbGzM6bJ2xTRNpFIpXL9+/YX7MlzQ3W9+t3/watz8h08IgVQq1bBCRCKRgKZpCAQCDlbW\nPsMwMD4+3nWPBs/n89A0rf47XalUEA6HUS6Xu+IzahgGFEXBtWvX6m2RSASmaeLSpUsOVrY7yWQS\nq6ur7e0sD7jZ2VlpGEZDWzgclpOTkw5V1L5cLieLxWL9e9M0ZTAYlJlMxsGqrJudnZU+n08WCgWn\nS2lpfHxc5vP5hjbDMOTo6KhDFbVPCCF1XZeZTEYGg0HX/oy30+pzmMlkpKIoDlRj3fnz55v+viST\nSRkMBh2qaPeWlpbk6OioTCQSbe1/4MdcpqammtpisVjLdrcRQmBoaKj+vdfrRTKZhK7rDlbVvlKp\nhImJCZRKJfj9fqfL2VY2m0UoFGpoC4fDXXEWEAgEcP369a74V/5WpmliZmYGlUqlob12dru8vOxA\nVdYoigLDMBrapJTw+XwOVbR7hUIB8Xi87Tv0D3y4dOubvx8+eN3wh880TZim2RR+qqoC6I6fc7dS\nVRVCCJRKJadL2bWbN2/i6tWrDW25XA4XLlxwqKLdKRQKiMVilvoc+DGXmzdvNrXlcjm8//77DlTT\nvuc/eGfPnnW6nH2rXC4DQMsH1QHPzh75TKHOqf38n2cYBnw+X1f+3DOZDCKRCC5evOh0KZYIIRCN\nRi2ti3bgw2Wrbnrz99sHz41M03S6BNpiamoKV65ccboMS/L5PGZnZ6EoCmZmZpwux5J8Pr+rqwsM\nl//QzW/+87rxg0fUrkwmg1OnTnXFP/6eNzIygpGREVQqFUQiEUxPTzeMl7rVy/zjiuHyH7r1zX9e\nt37wiNohhEAmk8H8/LzTpeya1+uFruuIRqMtrzy4TTabbThrqS273459Ey5CiLb37e/vh9frbbnN\niTffjtqd/ODZ9bN3I03TAABra2stx11q26nzUqkUbt++7XQZLy0ajcI0TRQKBVfe11WzuLiISCTS\n0HbgxlxKpRJSqVTb+w8PD+94A9Nevvl21e7UB8/un73bqKoKTdMghGiYOCGEgKqqHNvaIxMTE5ic\nnNx2YoUb1Z6Y+/HHH7ecdLN1pqfbzM/PY2lpqWGYoFgs1m8qHh4e3vGG7X0RLoFAoOWsrxdxw5u/\n29qf5+QHz4763S4Wi2Fubq7hd6RYLCIejztY1cExPT2NVCrVEOSFQsH1KySYpolgMNh0dls70996\n75TbtBrE/+CDDzA/P9+w4sB2DvR9Lt3+5gPbf/C6+d4At0mn08hmsw1tmUwG6XTaoYp2z8plDTeo\n3ahaLpdRLBZRLBZhGAay2ayrgwV49vfjwoULTT/zdDqNZDLZlWe9f/7zn/mY43Z98MEHGB8fbxgH\niMfjiEQiTTc/uU0ul8Pq6irC4XC9rVwuI5fLtbWwnJsMDg5iamrKtdegFxcXMTMzg+Hh4foZ77lz\n55wu64UqlQquXr0KIQRyuRw0TUMsFkM8Hnf9GnStbl6tCQaD+Pzzz/e4ot2Znp7G0tJSfe3CSCSC\n9957z+myLCmVSkin07h58yYqlQrGxsag6/qOk54OfLgA3fnm74cPXjf/4SOinTFciIjIdgd6zIWI\niDqD4UJERLZjuBARke0YLkREZDuGCxER2Y7hQkREtmO4EBGR7RguRBYUi0V4PJ6m1WK3MgwDHo8H\niUTC0uuPjo7C4+HHkroff4uJLAiFQlBVFYuLizsubFpbi+zdd9+1fAwrz8wgciuGC5FF4+PjkFLu\nuBr0zZs3oSgK3nnnnT2sjMg9GC5EFl24cAHAs0dKt1IsFlGpVHD+/Pm9LIvIVRguRBYNDQ1B07Rt\nL43VHq5UCyHg2WMcRkdHEQwG4fF44Pf7kUgkWj4a4fnl/uLxeMsxGNM04fF4MDEx0bRtcnIS4XC4\nfpyJiQk+goH2HMOFaBd0Xd/20lgmk2m4JCaEwODgID766CMMDg5C13VEIhHkcjmEw+EXPpRupzGY\nrdvC4TBSqRQ8Hk/9OJlMBsFgEIuLi7v4PyXaHYYL0S7ULnltvTTW6pJYOp2GoiiYnZ3FL37xC3z4\n4Ye4deuB1ym+AAACm0lEQVQW0uk0TNOEYRi21DQ5OYnFxUUUCgXMzc3Vj7OwsACg9ZMFiTqF4UK0\nC4FAAENDQ02XxlpdEpuYmEA2m216uFjtQUurq6u21HT16lXE43GEQiGYpln/CgQCiEajKBaLWFtb\ns+VYRC9y2OkCiLrVu+++i8XFRWQyGVy6dAnAs6eDbp0lNjQ0VA8S0zQxPz+PYrG47YSA3apUKpid\nnYXP52u5XVEUlMtl9PX12XpcolYYLkS7ND4+jmQyiZmZGVy6dAlCCJRKJYyOjjbsZ5omkslk/RGx\nwLOxkXA4bNtAuxACwLMJAMlkctv9tgseIrsxXIh2yev1IhQK1S+N5XI5AM8G+58XjUaxuLgIXdeh\n6zrOnj0LACgUCvU+VpXL5Ybva4+8VlW16fIbkRM45kL0EmqzxjKZDGZmZqAoSsMfd9M0sbi4iNHR\nUXz44Yf1YAEapxxbVSwWG75XVRVer3fbyQE+nw+Dg4O7Ph6RVQwXopdQWztsamoKi4uL2944uXXQ\nvnapDGgOmeenF6uqCiklCoVCy77P03Udq6urTeuZTU5OolKptLwnhqhjJBG9lHg8LhVFkYqiyEKh\nsO320dFRmU6n5fj4uPT5fPLtt9+WiqLIYDAoDcOQUkp5/vx5qShKvW8ul6u/tq7rDX19Pp+cmJho\nOFYwGKy/5vnz52UoFJKKoshIJNLZHwLRFgwXopdUCwCPx9Nyu2maUtd16fP56n/o8/m8lFJKXdel\nx+Oph8To6GjT62QymXpo+P1+mUqlpJSyZbhIKWUymZThcFgqiiIHBwfr+xPtJUXKl7jwS0RE1ALH\nXIiIyHYMFyIish3DhYiIbMdwISIi2zFciIjIdgwXIiKyHcOFiIhsx3AhIiLbMVyIiMh2/x/lFxwk\ni6G8+gAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60e0eb4d90>"
]
}
],
"prompt_number": 44
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Check Variance"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"pval Equal-Variance = \",scipy.stats.levene(x,y)[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('pval Equal-Variance = ', 0.34631004235050145)\n"
]
}
],
"prompt_number": 45
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Equal variance. USE: Mann-Whitneyu test"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Use only when the number of observation in each sample is > 20 and you have 2 independent samples of ranks. Mann-Whitney U is significant if the u-obtained is LESS THAN or equal to the critical value of U."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"Mann-Whitney U test.\", scipy.stats.mannwhitneyu(x,y,use_continuity=True)[1]*2)\n",
"print(\"T-test. Only if normality\", scipy.stats.ttest_ind(x,y)[1])\n",
"print(\"Median test\", median_test(x,y))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Mann-Whitney U test.', 3.337747132801931e-09)\n",
"('T-test. Only if normality', 1.7455489694871835e-10)\n",
"('Median test', 1.5440498291101365e-05)\n"
]
}
],
"prompt_number": 46
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" x = [np.random.randn() for _ in range(200)]\n",
" y = [np.random.randn()*2+0.2 for _ in range(200)]\n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3f9vG2d+J/D3yLEdy7Y4HNn54r1tTUq9ot1+sUgq2OsV\nh0NI5rcD2siSFijaAkWkYX4+W2SAux/uJ4sKDrjfEg39D0giAxyaxV0sjhfFAkUvlkbutrft7loP\nlWSTza4taqjEF8eWNfeDQMIjUtJQHnJmpPcLEBI9fEh+LJF8a55n5nkky7IsEBERuajH6wKIiOjo\nYbgQEZHrGC5EROQ6hgsREbmO4UJERK5juBARket8Fy6maSKTydjahBBIp9PQdR2maUIIgVwuB13X\nPaqSiIj284LXBeyWzWaxsbHR1K7reiNMZFnGzZs3kUwmu10eERE54KtwEUJgY2MDkiTZ2iVJQrlc\nRiKRQLVaxeXLl70pkIiIHPHVsJiu60in02i1aIBlWejr62OwEBEFgG/CRdd1pFIpr8sgIiIX+GZY\nTAiBZDLZ8qilfrtpmgCAarUKRVEwMjLSzRKJiMghX4RLqVTCxMTEnrcrigIAtjAZGxtraiMiIn/w\nfFisfjSyn1Ao1BQ+qqoim812qiwiInoOnofLwsKC7ehj95lie4lEIhBCYHNzs+XtkiTt+UVERJ3l\nabisrKwgkUjY2lrNuczMzDS11YfKhBBtPy8DhoiosyQvNwsrFApYXV21tRmGASEErl69iuHhYQwN\nDWFwcBBCCNtpyEIIDA4OwjRN9PX1OX7OerBwjzQios7xdEK/1ST+u+++i6WlJUxPTzfaZmdnm65v\nKZfLiMfjbQULERF1h+dzLrs9ePCg6ahCURRUKpXG96ZpQtM0FAqFbpdHREQOeDos9qxKpYJ8Po/5\n+XnUajVMTExAVVUMDQ0B2DldWQiB9fV1mKaJXC53qKv1OSxGR929exX85CefOu5/5kwPUqnv4+TJ\nkx2sio4b34RLtzBc6Kj7+ON/xPLyi1CUVx31r1b/D/76r/89ent7O1wZHSe+uIiSiNx1+vQZ9PY6\nm4/c2PDd6DgdAXxVERGR6xguRETkOoYLERG5juFCRESuY7gQEZHrGC5EROQ6hgsREbmO4UJERK5j\nuBARket8d4V+fd2w999/39ZuGAaWl5ehKAqEEIjFYkgmkx5VSURE+/FduGSzWWxsbNjahBDI5XK4\ndetWo21sbAzRaBSRSKTbJRIR0QF8NSwmhMDGxkbTTpH5fB6ZTMbWpqoqstlsN8sjIiKHfBUuuq4j\nnU43rVi8sLCAWCxma4vH4ygWi90sj4iIHPJNuOi6jlQq1dRumiZM04SiKLZ2WZYBAGtra90oj4iI\n2uCbcBFCIBKJNB21VKtVANhzO2MhRMdrIyKi9vgiXEqlEiYmJlreZppml6shIqLn5Xm4MDyIiI4e\nz09FXlhYsB217D5T7LDcehwir92/fx8ffvgxnjxx1v/pUwu9vS91tiiiA3gaLisrK0gkEra23XMu\n0WgUALC5udly3qV+O9FR9fjxYzx+/CpefXXI8X34xxV5zdNwWVpawurqKubm5hpthmE0LpocHh7G\nyMgIotEohBC4cuVKo58QArIs4/Llyy0fe3dI1fFNR0HF1y4Fiafh0moS/91338XS0hKmp6cbbalU\nCnfu3LGFi2EYSKfTXamTiIja4/mE/m4PHjxoOurI5/NYWFiwtWmahnw+383SiIjIIc8n9OsqlQry\n+Tzm5+dRq9WQyWSgqiqGhoYQCoWQz+cbQ2X1YbO9hsSIiMhbkrXX5MQRVR+3Pmb/bAqwzz//HB9+\n+GtcuhQ7uPOhHl/HX/3Vv0Nvb29HHp+OJ98NixERUfAxXIiIyHUMFyIich3DhYiIXMdwISIi1zFc\niIjIdQwXIiJyHcOFiIhcx3AhIiLXMVyIiMh1vlhbrFwuo1wuo7+/H6urq4jH47YVk4UQUFUVuVwO\n8Xgc1WoVmqYhnU4jmUx6WDkREbXiebiUy2VIkmRbYj+RSMA0TVy/fr3Rpus6dF0HAMiyjJs3bzJY\niIh8yvNhsdnZ2aa2VCpla5ckCeVyGaZpQgiBarWKN998s5tlEhFRGzwPl3pwPMuyLITD4aa2vr4+\nLrNPRBQAng+Lzc/PN7UVi0W8/fbbHlRDRERu8DxcdtM0DYlEAteuXbO1CyFgmiYAoFqtQlEUjIyM\neFEiEREdwDfhUiqVsLi4CEmSMDc3Z7tNURQAsIXJ2NhYUxsREfmD73airNVqSCaTKBQKGBoa2rOf\nrutQVRX37t1reXt9x8m9+OyfTbQn7kRJQeT5hP5uoVAIqqoeeJpxJBKBEAKbm5tdqoyIiJzyXbgA\nQDKZhGmauH37NgBgZmamqU99qEwI0fIxLMtq+UVERJ3nabgIIRAOh3H37t2Wt9eva8nlclhbW7Pd\nVq1WAQDRaLTTZRIRUZs8ndA3TRMDAwNNAVE/GonFYrh8+TJmZ2ebrm8pl8uIx+Po6+vrVrlEROSQ\np0cusVgM4+PjTcNV+Xwe2Wy2ESiKoqBSqTRuN00TmqahUCh0s1wiInLI81ORr1+/jkKhgNXV1cbC\nlePj43jrrbcafUZGRlAqlVAsFrG+vg7TNFEsFnm1PhGRT3keLgBsKyDvhdezEBEFhy/PFiMiomBj\nuBARkesYLkRE5DqGCxERuY7hQkRErmO4EBGR6xguRETkOoYLERG5juFCRESuY7gQEZHrfLH8S7lc\nRrlcbqwtFo/Hm5aEMQwDy8vLUBQFQgjEYrEDNxQjIiJveB4u5XIZkiRhenq60ZZIJGCaJq5fvw4A\njT1dbt261egzNjaGaDSKSCTS9ZqJiGh/ng+Lzc7ONrWlUilbez6fRyaTsfVRVRXZbLbj9RERUfs8\nDxdJklAul21tlmUhHA43vl9YWEAsFrP1icfjKBaLXamRiIja4/mw2Pz8fFNbsVjE22+/DWBnYzDT\nNKEoiq2PLMsAgLW1Ne7rQkTkM54fueymaRoSiQSuXbsGAKhWqwCw53bG9S2RiYjIPzw/cqkrlUpY\nXFyEJEmYm5trtJum6WFVRER0GL4Jl5GREYyMjKBWqyGRSKBQKGBoaOjQjydJkovVERFRO3w3LBYK\nhaCqKq9hISIKMN+FCwAkk0mYponbt28jGo0CADY3N1v2rd++m2VZLb+IiKjzPA0XIQTC4TDu3r3b\n8nbTNCHLMqLRaNPEvRACsizzTDEiIh/yNFxM08TAwEDT0Uc9SOrXtqRSKdy5c8fWxzAMpNPp7hRK\nRERt8XRCPxaLYXx8vGm4Kp/PI5vNNo5K8vk8RkdHbeuNaZoGTdO6WS7RkbS5uYFPPvkEZ86ccdT/\nzJkzePnllztcFQWdZPlgIqJQKGB1dbWxcGUikcBbb71l67OysoK5uTkMDw9DCIF4PI7XX3+97eeq\nn0Xmg382kSOff/45Pvzw17h0KXZw50P4n4v/Bd/7D/3o7e09sO/Wky1c6LmA8f803pFa6OjwxanI\nu1dAbmVoaOi5Tk0motYsAC999yX0ya0vVH7Wt998i61PtzpfFAWeL88WIyKiYGO4EBGR63wxLEZ0\n3FQqFWxvbzvqW6vVOlwNkfsYLkRd9u233+J//+9/hSRddniPMzh37kIHKyJyH8OFyAOSdALf+c7v\neV0GUcdwzoWIiFzHcCEiItcxXIiIyHUMFyIich3DhYiIXOeLcCmVSnj33XeRyWTwxhtvoFQq2W4X\nQiCdTkPXdZimCSEEcrkcdF33qGIiItqP56cil0olRKNRjIyMANi5YCwej6NardrWHNN1vREmsizj\n5s2b3K2SiMinPD9yEULYFqQMhULIZrNQVbXRJkkSyuVy46ilWq3izTff9KJcIiJyoK0jl8HBwcaS\n9U5ZlgVJkvCLX/yi6TbTNDE3N4fJyUmEQqFGe/2IZG1trbGni2VZ6OvrQ1/fwSu3EhGRt9oKl6Gh\nIVQqFRiG0WiLRCKoVquN9Y9kWUYkErHdb69AkmUZQghUKhVcuXKl3dqJiMin2gqXd955B4lEArFY\nDIVCwTacZRgGJiYmsLa2hmKx2BQwe6lWq01t5XIZ4XC4cdQC7AyfmabZuI+iKI15GiIi8pe2wmV6\nehqyLEPXddswFrCzZfHy8jLC4TByuRzm5uYOXdTs7CzeeeedxveKogCALUzGxsaa2oiIyB/aCpdy\nuYx0Ot0ULM9KpVIol8uHLkjTNFy4cAHXrl1rtIVCoabdKlVVhaqqe4ZLu3NDRMeWBXz62ec4s948\nirDb40ePcWr9ZBeKoqBrK1wsy4IQYt8+lUrl0MUIIaBpGpaWlg7sG4lEIITA5uYmJ/mJnsOLL34X\nn3yyhZOnTh/Y99EjC2fWf9OFqijo2joVOZVKYXl5GR988EHL20ulEgzDQDweP1QxuVwOt2/fbmqf\nmZlpaqsPle0VdpZltfwiIrve3hDk0MuQ5YO/+s73e10uBURbRy75fB7lchmjo6O4evUq0uk0otEo\nVldXsbi4iGKx2OjXrkwmg5mZmaajkPrV+GNjY7YJ/vqJANFotO3nIiKizmorXKLRKHRdRzabxcLC\nAhYWFppun52dtZ1F5kShUEAul7OFh67riEajjcd89jZgZ/4nHo9zSIyIyIfaXv4lFothcXERQggY\nhgEhRCMEYrFY2wXUj3aq1WrjaKRaraJYLOL9998HsDMEVqlUGqc3m6YJTdNw8+bNtp+PiJ7Pt99u\n4R/+4a7j/r/926/g1Vdf6WBF5EeHXlvswoULSCQSB549th/TNBunFO82MDDQ+P+RkRGUSiUUi0Ws\nr6/DNE0Ui8Wmoxki6qyTL5yG1PNd/PSnzuZevvpqHZL0a4bLMdR2uKysrGBiYgKGYUCSJCwuLuL1\n11/H4OAgMpmM7RTig8iyjO3tbUd9eT0LkT+cP9ePixe/67C3BWCjk+WQT7V1tlilUkE8HodhGEgm\nk7azr9bX1zE1NYXh4WHXiyQiomBpK1zqZ4EtLy83TeZvbGxgenoay8vLtqvriYjo+GlrWGx+fh6p\nVApDQ0ONdb6eNTU1hbm5ORSLRdy4ccO1IonIJyTg0ZOH+L8//7Gj7qb5a1y8yDM6j6O2wsU0TdtE\neyvRaLRpJ0kiOhpOnjqNF149iS+tVUf9f/P0E/xOdf/PDDqa2l5y/6ClWVZWVg51SjIRBcM5Oey4\nb612v4OVkJ+1NecyPj6O5eVl/OhHP2q5MOTY2BiEEEilUq4VSEREwdNWuExNTWFoaAjJZLJxfUo+\nn8f4+Dj6+/tRLBYRjUYxPT3dkWKJiCgY2goXYOdMsenpaXz88ccAgMXFRSwsLGB7extTU1O4d++e\n60USEVGwHOoK/ampKUxNTQHYWVhSURTIsuxqYUREFFxthUuhUEB/fz/efPPNRpsbqxKXSiUIIbC6\nugohRMtNwAzDwPLyMhRFgRACsVgMyWTyuZ+biIjc11a4qKqKcDhsC5fnVSqVEI1GG2FSq9UQj8dR\nrVYbu0/Wl92/detW435jY2OIRqONxSyJiMg/2ppzeeutt7CxsYG7d52viHoQIYRtif5QKIRsNgtV\nVRtt+XwemUzGdj9VVZHNZl2rg4iI3NNWuGiahunpacTjcdy8eRN3797F5ubmoZ/cNE3Mzc2hVqvZ\n2uvDXWtrawCAhYWFpmtn4vF4Y7l+IiLyl7aGxepbC1uWhcnJyUb7s9e8WJYFSZLw9OnTAx9PlmUI\nIVCpVHDlypWWfUzThGmajed+9r7ATgBx6X0iIn9pK1ycTqC3usByL/UNwp5VLpcRDodx+fJlCCEA\nYM8dJ4UQDBciIp/ZN1xyuRxee+21xgT+7pWQO2V2draxsnKrBTKJiMjf9p1zmZmZwdzcXFN7oVDA\n22+/3ZGCNE3DhQsX2tp0jIiI/OVQF1HeunULH3zwAd577z1XixFCQNO0AxfHdKKdoTki6gxJkvD5\n/c/wt4t/66j/iZ4T+JP4n/Ci7CPgUOECwLYLpVtyuRxu375ta6tfpLm5udly3sWNiziJqDPOhmTg\nwgN8HfraUf/q51X88cM/ZrgcAYcOF7ePDDKZDGZmZpoCRJZlRKNRCCFsZ5QJISDL8p6T+XuFH49o\niLpH6ulB77lenAudc9R/8zeHv7SB/KXthSs7oVAoIJfL2YJC13VUKhUAQCqVwp07d2z3MQwD6XS6\nm2USEZFDnodL/ULIarUKwzBgGAbK5TIWFhYaS7vk8/mmM9U0TUM+n+96vUREdLBDD4u5wTTNxr4w\nuz27nXIoFEI+n0cul8Pw8HBjrTFe30JE5E8Hhku5XMb4+LitTdd1WJbV1P6sVqcw7ybLMra3tx2U\nubPF8rNrkBERkX8dGC4bGxt7Xjy530WVTsKFiIiOpn3DxY3rTYiI6PjZN1x2r0RMRETkhKcT+kTk\nvl9+8XNUfuV8z6XaN/fRL13qYEV0HDFciI6Y//eNiYfnNnBOVg7uDECRXsULp051uCo6bhguREfQ\niRMncer0i16XQceY5xdREhHR0cNwISIi1zFciIjIdQwXIiJynW/CpVgsQtf1pnYhBNLpNHRdh2ma\njXXFWvUlIiJ/8EW4lMtlTE5O7rnXiq7rSKfTUBQFiUQCr732GpLJZJerJCIipzw9FblSqSCfzyMe\nj0NRWp+TL0kSyuUyEokEqtUqV0ImIgoAT49cIpEI3n//fUxMTOzbz7Is9PX1MViIiALCF8NiRER0\ntATiCn0hBEzTBLCzY6WiKBgZGfG4KiIi2ovvw6U+F/NsmNR3r2TAEBH5k++HxUKhUNOcjKqqyGaz\nHlVEREQH8f2RSyuRSARCCGxubqKvr69ln71Oayby2tbWFj7+px+h95M1x/cZvPQaBi5f6VxRRC7z\nfbjMzMxgamrK1lYfKhNC4MoVvuEoWJ4+fYpH1kNc+r1XHPX/amMd3z5+2OGqiNzl62Gx+tX4a2tr\ntvZqtQoAiEaje97XsqyWX0R+IUmSoy+AR+EUPL4Ol2g0itnZ2abrW8rlMuLx+J5DYkRE5C1fhUur\nIwtFUVCpVBrfm6YJTdNQKBS6WRrRgba3tx19bW1teV0qUcd5OudSq9Vw48YNCCEghICqqkilUkin\n043TjEdGRlAqlVAsFrG+vg7TNFEsFnm1PvnK9H//H/jHn//c8Ykk3/ac6HBFRN7yNFxCoRCmp6cP\n7MfrWcjv7ps1vPJH38e5vrDXpRD5gq+GxYiI6GhguBARket8f50LEQGWtY2trSeO+m5b2x2upj3W\n9ja2njo7iWH7qb9qp8NjuBD53AsnT2Lty5/gs+pPHfXftp7ixe+c63BVzrxw4iSEMLG2ZjrqX/v8\nAb7/W9/Hd77znQ5XRp3GcCHyud7zfej9/WBe03X2rIyzZ+OO+5uf/wOePn3awYqoWzjnQkRErmO4\nEBGR6xguRETkOoYLERG5juFCRESu883ZYsViEeFwGMlksuk2wzCwvLwMRVEghEAsFmvZj4iI/MEX\n4VIulzE5OYlisdh0W31Pl1u3bjXaxsbGEI1GEYlEulkmERE55OmwWKVSQSaTQaVSaewuuVs+n0cm\nk7G1qaqKbDbbjRKJqMseP36Mhw8fOvp69OiR1+XSHiTLJ9szDg4OQtM0vP7667Z2RVFgGIZtiX3T\nNKEoCra3218qor4kuk/+2XRE/Of/+t+w/UqEqyI/p7Wf3cEf/PZZyLLsqP+p7VP4iz//C5w6darD\nlVG7fDEsthfTNBtB8qz6C29tbY37uhAdIX0XFbz8PRn9/f2O+n/xj1/wD0Wf8vXZYtVqFQD23M5Y\nCNHNcoiIyCFfh4tpOlvsjoiI/MXXw2LPw+l2s0RE5D5fH7kQEVEw+TpcotEoAGBzc3Pf21uxLKvl\nFxERdZ6vw0WWZUSj0aaJeyEEZFnmmWJERD7l63ABgFQqhTt37tjaDMNAOp32qCIiIjqIryb0Ww1b\n5fN5jI6OYmJiotGmaRo0TetmaUR0BNRqtbYuvj579iwv0DwkT8OlVqvhxo0bEEJACAFVVZFKpZBO\npzEyMgIACIVCyOfzyOVyGB4ebqw1xiExImrHw4cPMf+/5rF9ylm4PHn8BH/6+3+KK390pcOVHU2e\nhksoFML09PSB/YaGhjA0NNSFiojoqLIsC9svbOPS9y456v/rX/76UEtM0Q7fz7kQEVHwMFyIiMh1\nvprQJyLyk0ePHuHBgweO+yuKgp4e/s0OMFyIiFrqPdeLn3zxE/zzl//sqP/TR0/x5//xz/HKK690\nuLJgYLgQEbVwXj6P8/J5x/2/+BmX/38Wj9+IiMh1DBciInIdh8WIWnj06BFqtZrj/ttPn3awGtrP\n/fv3cfLkyQP7ffPNN12ohuoYLkQt/MvP/gU//pcf4/SZ0476f31yE6EX+HbquvPAD5d/6Lh7z3kO\n1nQL3w1Ee+i92IuX/83Ljvr2V9dhbfPt1G2Xos6utqfuC0SMCyGQTqeh6zpM02ysL6brutelERFR\nC4H5U0vX9UaYyLKMmzdvIplMelwVERG1EohwkSQJ5XIZiUQC1WqVKyITEflcIMIF2FnRtK+vD319\nfV6XQkREBwjEnAsREQVLYI5chBAwTRMAUK1WoShKY0MxIiLyl0CEi6IoAGALk7GxsaY2IiLyh0CE\nSygUwsTEhK1NVVWoqrpnuEiS1I3SiMhlm19tYttytgNkj9SD/v7+Dlfk3IMHD7C1teWo74kTJ3Dp\n0tG9TicQ4dJKJBKBEAKbm5uc5Cc6Ik6dDuNn/1oD8LWj/hbWkUr2OVr+pdNeDL+Iv//074FPHd6h\nBvzN6N/4ovZOCES4zMzMYGpqytZWHyoTQuDKlStN99lr6Wse0RD517mzCnBWcdy/WjU7WE17lJcU\n4CXn/b9Y+aJzxfiA788Wq1+Nv7a2ZmuvVqsAgGg06kFVRES0H9+HSzQaxezsbNOFk+VyGfF4nENi\nREQ+FIhhMUVRUKlUEIlEAACmaULTNNy8edPjyshLn332GZ52aKn7zc3Njjwu0WFsb2/js88+a2un\nywsXLuDcuXMdrGp/gQiXkZERlEolFItFrK+vwzRNFItFLgNzjD158gQ//PEPIcmdm0OTX5Y79thE\n7fjqq6/w4d9/iBdCzj6yH371EOnvpfGHf/CHHa5sb4EIF4DXs1AzqUfCpYGjeyon0bNeOPWC49f7\nrz79VYerOZjv51yIiCh4GC5EROS6wAyLkfeePHmCTz91eoXYjldeeQVnz57tUEXOPdl6ggcPHnTs\n8be2tnCCf6oRNTBcyLGNjQ388OMf4pR8ylH/h+ZD/Nlrf4aBgYEOV3awr7/6Gh9//BucOuX8Ar32\nXETY4c+F6DhguFBbTveedrxv+RfCX1cgnz7VC0X5rtdlEB0LPJAnIiLXMVyIiMh1HBajjrp//77j\nq+glSUI0GsWJEyc6XBWRP9y7d8/R6/3Ro0ddqMZdDBfqmNDFEO4+uAs4XLh2a2MLf/nSXyIUCnW2\nMCIfOPnySfzdJ3/nuP+Zl850sBr3MVyoY86eP4uz552fhvzFQ3+dAEDUSRcvXfS6hI4KTLgYhoHl\n5WUoigIhBGKxGJLJpNdlERFRC4EIl/qeLrdu3Wq0jY2NIRqNNlZKJiIi/whEuOTzeWQyGVubqqrI\nZrOYn5/3qKruME0Tn/3yM8f9JUnC7/7b3z2yW6cSPcsC8NkvP0dPj7MTX8/2nsHFi0d7OKruNw9+\ng3/6539y1FeSJPzO4O/g9OnTrj1/IMJlYWEB77zzjq0tHo+jWCx6VFH3fPnll/jopx+hL+xsU7Rv\n17/FpVcvNbaBJjrKTp38Lfz8548d9X269QRy+MtjES7KRQWr91ex+qtVR/2/efANXrr4El56qY19\nmg/g+3AxTROmaTZ9WMryzl4ba2trR35fl/Oh83j1t1511PeLrzkpTsfH+fP9jvs+fvwNgFrnivGR\n02dOO/7MADpzMo3vL6KsVqsAsOd2xkKIbpZDREQO+D5cTNPhRRJEROQbvh8WOyxJ2n/724NuD7IM\nMgd38qkg104UZE7ee5ZlOX483x+5EBGRP7TzR7nvj1yi0SgAYHNzs+W8S/323fZK2PoPp50E9hPW\n750g1w6wfq8dlfqd8v2RiyzLiEajTRP3QgjIsnzkzxQjIgoi34cLAKRSKdy5c8fWZhgG0um0RxUR\nEdF+JCsAx2i1Wg2jo6O25V/eeOMNaJrW9pHLUTk0Zf3dF+TaAdbvteNWfyDCBQBWVlYwNzeH4eFh\nCCEQj8fx+uuvt/04x+0X7DdBrj/ItQOs32vHrf7AhItbjtsv2G+CXH+QawdYv9eOW/3HLlyIiKjz\nAjGhT0REwcJwISIi1zFciIjIdQwXIiJyHcOFiIhc5/u1xYjo+RmGgeXlZSiKAiEEYrEYksmk12U5\nUiqVIITA6uoqhBBQVRUjIyNel3Uopmkil8vh/fff97qUthiGgfn5efT392N9fR2qqiISiex7H4YL\ngHK5jJWVFQDA+vo6BgYGMDEx4XFVzh3mF+9HQXzjBeGDTwiBXC5nW+FibGwM0WjU96+TUqmEaDTa\n+JnWajXE43FUq9VAvUfrstksNjY2vC6jLcViEeVy2fa+VFUVs7Oz+9/ROuaWl5etYrFoaysWi5am\naR5V1J6FhQVLVVVb2+TkpEfVPJ/JyUlrdHTU6zIcKxaLlmEYje9N07QGBgZ899qZnJy0SqWSra1c\nLgfiZz0zM9PUpmmaJUmSB9U8n9XVVWt0dNQaGxvzuhTHNjY2rHA4bGubnZ21BgcHD7zvsQ+X3R/M\ndUF44z3PL95vgvjGC8oHXzgctiqViq1tY2PDd3XutrGxYcXjccs0TVv76uqqJUlS07/J7zRNszRN\nC8RnS93U1JSVy+Wa2p387I/9hP7S0hIqlUpTexC2V75x4wZUVbW1TU5OYnFx0aOKDk/XdaTT6cAs\njWGaJubm5lCr1Wzt9XmMtbU1D6pqZpomTNOEoii2dlmWAfinzlZkWYYQouX7M2h0XUcqlfK6jLYV\nCgUMDw83tTtZMPjYh0sqlUI6nba9gMvlMsbGxjysypnn+cX7SRDfeEH54KtWqwDQcqM9AE37JPlN\ntVrFlSsbtO6CAAAHsElEQVRXbG3lchnhcDhQr3MhBCKRSGD+eKozTROhUAiFQgGlUqnxXyeO/YT+\n9PQ0yuUyBgYGMDs7i0gkglqthrfeesvr0g707C9eURRUq1UoiuK7CeWDCCGQTCYD98arf3A/y28f\nfEE4Am/X7Ows3nnnHa/LcKxUKgXy5IP6Hx4rKyu4du1aoz2Xyzk6oeLYhwuwMzT2xhtvQFVVxGIx\n6LrudUkHet5fvF8E9Y23l6B98AWNpmm4cOGC7TXvZ0EO93rtu7eSHx8fRzKZPPB9e+yHxYCd4aWZ\nmRksLi429orx+3DHfr/4bDbrRUltC/Ibr5WgffAFjRACmqbho48+8roUxxYWFmwjCe3uQ++l+mfL\n7s+YoaEhmKZ54HzdkTlyaWfsuL+/H6FQCACQyWSQy+UawxiVSgWjo6NIp9O4d+9eJ0ptcpjanfzi\nuzU0c9if/cLCgu2vH6/eeIetf/djaJqGpaUlN0t7bvXXx+bmZst5l92vHz/L5XK4ffu212U4trKy\ngkQiYWsL0tBv/aSP+n93E0Ls+xlzJMKlUqkgl8s57j88PIzr1683/nJ+9gcUCoVw69YtJBIJ6Lre\n8auYD1v78/7i3dJu/a+99hquXbsGwzB88cY77M9/N79+8MmyjGg0CiGEbWJcCAFZln0zN3SQTCaD\nmZmZPU9M8KOlpSWsrq5ibm6u0WYYRuOi1uHhYd/Pj9ZfO61eJwf9YXKsNwvTdR2GYbT8sKhPkvv5\nlz84OAhN05q2e+7p6elauBxWoVDA6uqqra3+xrt69Wog3nh1u49+/SaTySAej9uOEovFIhYWFmwf\nfH5VKBSQTqdtP19d1wOxwsBu7777LpaWlgLxcwd26gVg+4w0DAPpdBrr6+v73vdIHLkcVjQaxcLC\nQsvbTNNEOp3uckXtUVUVy8vLtnAxDMNXZyvtpdVkYP2NNz097UFFh1MoFJqCxW8ffPl8HqOjo7af\nuaZp0DTNw6qcKRaLAHbOzKufnVetVlEsFgO1TFDdgwcPAjU0Njk5iXg8bguXXC6HQqFw4H2PdbjU\n3/y7h7+EEFhfX/f9B/Tz/OL9KGhvvKB88IVCIeTz+cZQTH1Yxu+vb9M097zebGBgoMvVPJ9KpYJ8\nPo/5+XnUajVkMhmoqoqhoSGvS9tXKBTC4uIiMpkMBgYGsLq6ilwu1zRa0sqxHharqw/R9Pf3A9gZ\npw7K6bH1F239Fz82NuboF+8nu994ExMTvn/jtbrqvW5gYAC/+MUvulwRkb8wXIiIyHW8zoWIiFzH\ncCEiItcxXIiIyHUMFyIich3DhYiIXMdwISIi1zFciIjIdQwXojYYhoGenp6mRTd3K5fL6OnpaXtH\n09HRUfT08G1JwcdXMVEbYrEYZFnGysoKarXanv3qa9b94Ac/aPs5grTnB9FeGC5EbZqcnIRlWZif\nn9+zz/z8PCRJwptvvtnFyoj8g+FC1Kbx8XEAO1sat2IYBmq1Gq5evdrNsoh8heFC1KahoSFEo9E9\nh8bqe3XUQwjYWWl7dHQUAwMD6OnpgaIoGBsba7md9rPL/aXT6ZZzMKZpoqenB5lMpum2mZkZxOPx\nxvNkMhnfb9tNRw/DhegQVFXdc2hM0zTbkJgQAoODg/jggw8wODgIVVWRSCRQLBYRj8f3nbsB9p+D\n2X1bPB5HLpdDT09P43k0TcPAwABWVlYO8S8lOhyGC9Eh1Ie8dg+NtRoSy+fzkCQJi4uL+Oijj/De\ne+/h1q1byOfzME0T5XLZlZpmZmawsrICXddx586dxvMsLy8DaL1BG1GnMFyIDiESiWBoaKhpaKzV\nkFgmk8HCwkLTPjv1/Wo2NjZcqenGjRtIp9OIxWIwTbPxFYlEkEwmYRgGNjc3XXkuooMc650oiZ7H\nD37wA6ysrEDTtMZuoMVisekssaGhoUaQmKaJpaUlGIax5wkBh1Wr1bC4uIhwONzydkmSUK1W0dfX\n5+rzErXCcCE6pMnJSWSzWczNzeH69esQQqBSqWB0dNTWzzRNZLPZxk6bwM7cSDwed22iXQgBYOcE\ngGw2u2e/vYKHyG0MF6JDCoVCiMVijaGxYrEIYGey/1nJZBIrKytQVRWqquLKlSsAAF3XG/dpV7Va\ntX1f33JZluXAbXNNRxPnXIieQ/2sMU3TMDc3B0mSbB/upmliZWUFo6OjeO+99xrBAthPOW6XYRi2\n72VZRigU2vPkgHA4jMHBwUM/H1G7GC5Ez6G+dtjs7CxWVlb2vHBy96R9fagMaA6ZZ08vlmUZlmVB\n1/WW932WqqrY2NhoWs9sZmYGtVqt5TUxRB1jEdFzSafTliRJliRJlq7re94+Ojpq5fN5a3Jy0gqH\nw9Ybb7xhSZJkDQwMWOVy2bIsy7p69aolSVLjvsVisfHYqqra7hsOh61MJmN7roGBgcZjXr161YrF\nYpYkSVYikejsD4FoF4YL0XOqB0BPT0/L203TtFRVtcLhcOODvlQqWZZlWaqqWj09PY2QGB0dbXoc\nTdMaoaEoipXL5SzLslqGi2VZVjabteLxuCVJkjU4ONjoT9RNkmU9x8AvERFRC5xzISIi1zFciIjI\ndQwXIiJyHcOFiIhcx3AhIiLXMVyIiMh1DBciInIdw4WIiFzHcCEiItf9f6rq2MGELdn3AAAAAElF\nTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23a8ae850>"
]
}
],
"prompt_number": 8
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Non-Equal Variance and Normality. USE: T-test"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Check Normality\n",
"The Shapiro-Wilk test tests the null hypothesis that the data was drawn from a normal distribution. Bad if sample is big (small differences make it non-normal). QQ plot"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(scipy.stats.levene(x,y)[1])\n",
"print(scipy.stats.shapiro(x))\n",
"print(scipy.stats.shapiro(y))\n",
"plt.figure(1)\n",
"ax = plt.subplot(1,1,1)\n",
"(osm, osr),(slope, intercept, r) = scipy.stats.probplot(x, dist='norm', plot=None)\n",
"ax.plot(osm, osr, 'o', osm, slope*osm + intercept)\n",
"ax.set_xlabel('Quantiles',fontsize=20)\n",
"ax.set_ylabel('Quantiles Obs',fontsize=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()\n",
"\n",
"ax2 = plt.subplot(1,1,1)\n",
"(osm, osr),(slope, intercept, r) = scipy.stats.probplot(y, dist='norm', plot=None)\n",
"ax2.plot(osm, osr, 'o', osm, slope*osm + intercept)\n",
"ax2.set_xlabel('Quantiles',fontsize=20)\n",
"ax2.set_ylabel('Quantiles Obs',fontsize=20)\n",
"customaxis(ax2, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"3.45647037494e-13\n",
"(0.9944772124290466, 0.6720660328865051)\n",
"(0.9897152781486511, 0.16231410205364227)\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZ0AAAEsCAYAAAAYSW5yAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X180/W5+P/XJxRoEWjSosObKU2KHm9Q2gQ9OuccTVsV\n3I20RT0729mEpugB93PQFBVPhzpocecIjpumbkd3tim0ZftO6oQmqHXTKb1TmTChn8LUiQptUlTu\n+/n9kSZt6G0gTZr0ej4ePrCffBKuFJqL9/t9va+3ommahhBCCBEGukgHIIQQYuSQpCOEECJsJOkI\nIYQIG0k6QgghwkaSjhBCiLCRpCOEECJs4iIdwNlyOp04nU6Sk5Npbm7GbDYzf/78SIclhBCiF1Gd\ndJxOJ4qisHLlSv81i8WC2+1myZIlEYxMCCFEb6J6eq2srKzHNavV2ut1IYQQkRfVSUdRFJxOZ8A1\nTdMwGAwRikgIIUR/lFhrg2MymViwYAGLFy+OdChCCCFOE1NJx+Fw4HK52LhxY6RDEUII0YuoLiTw\nqaqqoqamBkVRJOEIIcQwFlMjHY/HQ0ZGBuXl5aSlpUU6HCGEEKeJ6kKC0yUmJmKz2cjIyOjzHkVR\n+vxPCCHE0IqppAOQkZGB2+3G5XIF/VxJPEIIMbSiNumoqorBYKCpqanXxz0eT6/XNU3r9T8hhBBD\nL2qTjtvtxmQyYTQaA66rqgpAenp6JMISQgjRj6hNOunp6cydO7fHKKWkpAS73c6UKVMiE5gQQog+\nRX31Wnl5Oc3Nzf6GnxaLhXnz5gX9Or71nCj/dgghxLAW9UknVCTpCCHE0Iva6TUhhBDRR5KOEEKI\nsJGkI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGkI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGk\nI4QQImwk6QghhAgbSTpCCCHCRpKOEEKIsJGkI4QQI5T7qJvfvfu7sP6eknSEEGKE0TSN5959jivW\nXsFf/vEXOrSOsP3ecohbJznETQgxEjS3NnPvi/fy/j+bOe/Nr5Nw6BLGjj3JokVZzJp105D//nFD\n/jsIIYSIuOOnjrPqL6v4n7/+D99OzmNveRpv7V3pf7y5+SGAIU88Mr0mhBAxrnZ/LdM3TOfNj96k\nPr+eDzcloXZLOADNzY/z1FM1Qx6LjHSEECJGHfzyIIU1hdSoNay5ZQ3f+ZfvoCgKx471/tF/9Oio\nIY9JRjpCCBFjNE3jmaZnuGrdVUwcO5H37n2P717+Xf/a9dixJ3t9Xnz8qSGPTUY6QggRQ3Yf3E3B\nlgI+P/451XdXY77A3OOeRYuyaG5+iObmx/3XTKYHWbjwliGPT6rXOkn1mhAimh05cYSfvfYzNtRv\n4JGbHuHeGfcyStf3dFl1dS1PPVXD0aOjiI8/xcKFmWGpXov6pFNVVYWqqjQ3N6OqKjabjTlz5gT9\nOpJ0hBDRqqa5hgXVC0g7P40ns5/kwokXRjqkPkX19FpVVRVGo9GfZDweD2azmdbWVubPnx/h6IQQ\nYmh98vknPLDtAV7/4HV+cesvmHXprEiHNKCoLiRQVZW0tDT/14mJidjtdmw2WwSjEkKIodWhdVBW\nV8a09dO4aMJF7FywMyoSDkRx0nG73WzcuBGPxxNwPSMjA4B9+/ZFICohhBha737yLlf+/Grszz3K\nxa/MoemJ0bxSUx/psAYtaqfX9Ho9qqrS0tLC9OnTIx2OEEIMqS+Of8FPX/0pjrfKGfPn6/FsfYd6\nzTtuCFc3gVCI2pEOQGtra4+E43Q6MRgMTJkyJTJBCSHEGaquriU7+2FuvrmY7OyHqa6uBWDL+1u4\nct2V/PPwP5n+xg/47KUXQev6+A5XN4FQiNqRTl/KyspYunRppMMQQoigVFfXcv/9WwP2zvz9n4v4\nWfMjfKp8xNPfehqr0crNa4p7fX44ugmEQkwlHYfDwaRJk1i8eHGf9/hKo4UQYjhZs2ZbV8JRTsG1\na9l/03PEvXM5Oze8S3xcPBDZbgKhEDNJR1VVHA4HdXV1kQ5FCCH6VF1dy5o12zh2LC7gSAF/P7Tz\n6+F2GxybAP/7Ghdd+bw/4UBkuwmEQswknaKiIrZv3z7gfX1t/pQRkBBiqPU2heYrAhg17gu45X64\naiPUlMLb/w4oPUYwvmKBp55a1q2bwC1RUUQAMdCRAKCgoICioqKzKh6QjgRCiKGWnf0w27Y9dtpV\njWvuyuWjq2o5tusCDle54Egy4B3BrF4dPQllMKJ+pFNeXt4j4bhcLoxGIykpKZELTAghTtPjSAH9\nPrjtP9lz4Zu89G+bad+p8dRnT0blCGawojrpVFZWAt7S6dbWVv//V1ZWsmHDhkiGJoQQPdZv2tu9\nn1PoTsD1/wNfK4U3HuBrrVfz9Uu+DpdEx16bsxG1ScftdpOXl9frYyaTKczRCCFEoN7WbyZPvoek\na+6k9Yb34PAFUP4mpqRfcv/q6CgCCIWYWNMJBVnTEUKEUo/1m/g2sBYx+srfcPkH2eg/mkZCfEfY\njhQYLqJ2pCOEEMNZ1/qNBtOeg6yfwO7vcm3dQv7sXBnR2CJJko4QQoRAr+s3SXth1gI45zN4/g/w\n0XWMz14W6VAjSpKOEEKcge5Jpr39Qz7+eCIHDvy398FRxxiffQNK1jS02sfgzfuhIy6qNnEOFVnT\n6SRrOkKIwepZJPAw0Ll+M+UVmF0ABy/jyn8kcNGEqWE/Eno4C9lIp729nYkTJ4bq5YQQYljpPrLZ\nuXMXhw5t7PZoHIw7CFmLIWU7/GkN7P4Ok75RzEsvFUcq5GEp6KMNGhsbWbBggf+QNI/Hg8ViQa/X\nM2rUKOnwLISIOb6RzbZtj/Hqq8UcOnR5t0c1SKuDe6+EI0mw9m+w+ztA9DThDKegko7L5cJsNlNW\nVobb7QbAbrfT0NBARkYGU6ZMobS0lM2bNw9JsEIIEQkBHaAB6Oz0fO578MNvgKUZfjMbtv43HJ8A\n+JpwZoY/2GEuqDUdi8VCQ0MDNTU1/mOhdTodVquVbdu2AWAwGEhNTWXHjh1DE/EQkTUdIcTpfFNq\nb775IR7PM10PxNXATcVgfh9eKYa6AiZ/ZT4XXJDAhAnnyvpNP4Ja01FVlZycHH/CaWxsBMBms/nv\nycvL87enEUKIaBVYLPBw1wOmbTDrXvj4qxg23sDVKZ8Rn1XMwoX/IUlmEIJKOm63O+AIAKfTCUBm\nZtcQsrW11T/1JoQQ0SpwSi0Lxt8P2Z/CRW9C9VpM2musXhd7DTmHWlDTa2azmX379nHo0CEAUlNT\nAdi7d6//nqSkJJKSkgKuRQOZXhNCQC9TakoHmMvgm0uh4UomNqVwvSVFps/OUFCFBDabjba2NqZO\nncqMGTNQVdU/teZyuUhNTcXtdpOTkzMkwQohxFDqXqXm8VwEX3kb7rkBrv4tPPtncP2F6y0pvPTS\no5JwzlBQ02v5+fk0NzfjcDhobm4mJyeHJUuWALBt2zZUVcVqtbJy5cjtKySEiB6ndxXYu7eVw4c3\nw5jP4ea9cM0N4FoNjT8CTScdBUIgZB0JVFUFwGg0huLlwk6m14QYOaqra1m27Nfs2jWao0fXA7XA\nVmA0XGqG2xbC/ptg2xz4oo7ExA/413/9qkyphcAZJ519+/ahqiputxuj0YjRaIzqjgSSdISIfYHJ\nJhl/6xoehokFcKsVztWgej20zPQ/Lzt7GS+99GhEYo41QbfBaWxsZP78+TQ0NARcVxSFnJwcSkpK\nAo6OFkKISAtMNpPxJpti74O6k3BtHXw9Dd66HarOhZNdCUem1EIrqJFOS0uL/1TO9PR05s6dS0pK\nCqqqUlNTg8vlwmAw0NLSEnWjHhnpCBGbuvbbKHQlm2LgYbjg23C7DY60QfVWOHQp3qm2GmAUycm7\nefbZe2VKLZS0IOTm5mqKomgOh6PXx8vKyjRFUbS8vLxgXnZYALQgvx1CiGFqy5ZXtaysh7Qrr8zX\n4uJma6Bp8F+dvz6kMdatcet3NX5yjsbVv9bgFQ0e7Hzc+5/JtFTbsuXVSL+VmBPUSCcpKQmj0Uhd\nXV2f95jNZtrb29mzZ08IUmL4yEhHiOjlq0L76KPP2L//A44du4gTJ76HvzjAN7LhUbhiOdzyc9gz\nF5zfhiNvEh+/nwsuOI5enyxtbIZY0B0JfNNrfTEajdLwUwgRNl3TZ9l4k8y5eKfRHga6tbDRT4NZ\nUyExHip/Bv/4hPj4TVyRPoHly+dJggmToJJORkaGv/VNX1wuF2lpaWcVlBBCDNayZc/T3LyOriRT\n3PlI58ebbibc8E244V14/Q54YxLxo9+SZBMhQXUkKCsro6Ojg+zsbP95Oj4tLS1kZWXhdrspLy8P\nZYxCCNGr6upadu36vPMr37+hT3b9+tW/QMEiuORLKL8T/nwByXqVysp51NevlYQTAf2OdLKysgIa\nfAIkJydTU1ODyWTCaDSi1+txu92oqoqmaaSnp+NwOFi/fv2QBt5dZWUlBoPB3/1aCDEyrFmzjaNH\nL+78ypdssiDhAbDugamrYesv4W+5gILJ9CCrV0s1WiT1W0hgMBhQFCXoxXVFUWhtbT3r4AbD6XT6\nj1OYOXPmwE/ogxQSCBFdqqtr+d73fonbfQ/etZxs4CW4+grIvB92GYmrnUSCMo5LLvkqF144QYoD\nhoF+RzptbW3hiiNoLS0tlJSUYDabSUpKinQ4Qogw8FWp7d79dz78cCIdHV8FOpNI8vMw64+Q8AXx\nf5jBN1KvY+HzkmSGm5D1Xouk1NRUHA6HjHSEiGGBVWprgY1ALYyqhhvHwXVPQe1DGA9+wponb5Nk\nM0wFVb3W2NjIxo0baWlpwe12o9frMRqNzJ07l+nTpw9VjEIIcVqV2uXei1NOwezn4LNxsOHfMYx6\nizX/t0ASzjA2qKTTV781H980V3l5uSQfIUTI+Hqmvf/+x3zxha+1VhyM80D29+GSV+FPv4C/fwuA\na7OXScIZ5gZMOi6Xy38cdXp6OjabDYvF4u+5VldXR1lZGfX19ZjNZmpqas5qmksIIQCKi9exYsUr\nHD8+FZjsvah0QNoOyHgd3r4M1v0Njo8HICHBxsKF/xa5gMWg9Lum4/F4SElJwe12U1ZWxvz58/t8\nIYfDQUFBAQaDwX+cdbgEs6Zzegn46WRNR4jI8o1umppa0bQr8DfpPDcFZj8MoybAlhvgwPfxNeZM\nSNhFYeE3KC6+N6Kxi4H1O9JxOBy43W4KCwv7TTjQdaroqlWreOKJJ1i8eHFIAxVCxKbAKTQPMBW4\nELjIe8PoL+GmGkh/H175HtSNA+0gsI5zzlG48cZUFi68T6bVokS/Ix2z2UxTUxOnTp0a9AvqdDoy\nMzPZunVrSAIcDKleEyK6BCaaeEDf+cjneKvSioGTkNoMt70F/5wCL10Fn6/2v4Z3o+ctkmyiTL8j\nHVVVgz5+OiUlpd8u1EKIka26upZ5857lwIHJ+Ndq/Do/ksa3wS3vwgV1UD0Lmp/De87NMkaPbmHa\ntESWL58rCScK9dt7zePxBJ10jEYjbrf7rIISQsSuZcue58CB8/E254wL/E85DjPWwoJnofUYrKuC\n5nOAu1CUpzCZ/sHvf58vfdOiWL8jncTExKBHLXV1dej1+oFvDDGZFhNieKuurmXRotWo6mjgvM6r\nJ7tumHwAZr8Opz6HZ16Hzw4CNSjKF6SlJcnIJkb0O9KxWq20tbXR1NQ0qBdrbGzE4/GEpfGmx+Oh\nqKiIvLw8VFXFZrNRUFBAVVXVkP/eQojBqa6uJT19HvHxM5k9+0lUNQ5IJaA555h/QNYf4Hu/hXoj\nPPNr+Ow5YDtjxuzikUe+LiObGNJvIUFDQwMWiwWTyTTgSaAejwez2YyqqtTX10fdmTpSSCBEaHXt\ns5mAt0BgKt7JlZnAs8BkuOxauNUG+ybCtq/Al2PQ6c4hIWE8l11mkNFNDOp3ei09PZ358+dTXl7O\n1KlTKSkp4Y477uhxX1VVFXa7HVVVycnJibqEI4QIna5ptFPAVZ1Xu591cxNM/BRu+wlMegr+cD0T\nDiXw3KYHJMGMAINq+Jmbm+uftjIYDBiNRoxGI6qqoqqqvxt1Tk4OmzZtGtqIh4iMdIQ4c74S6Pfe\nUzl2TA+Mxt8fDfBPp+lmwnU/g683wZuL4M92EsYsoqLi3yThjBCD7jLtdDopKSnB5XL1eMxqtWK3\n26P6EDVJOkIEr2tUowEGAqfRuhUJkAUXPgGz34IjF8GW66D1XMaM2cnSpTOlk8AIckZHG6iqGtBl\nOhZI0hEiON5D1Mpxu4/jTTQQOI2WBTwLY49Dxntw+T7YNg3enQycwmQax+rV98gIZ4SJifN0QkGS\njhCDV11dS25uCUeOpBG4NNytKo2X4MoxkL0K3k8G5+XEo+eKKyZJgcAIJkmnkyQdIQanq6NAO3Al\nPabReBYMY+G2epjYAltmM+aTdplGE0CQh7gJIcSaNds6Owp8QcA0GsCoF+EGHVz/K/jLv8AbX8eU\ncorVmxfJyEYAknSEEEE6dsz3sTEe+BjYCvwALi6F2ZvAncCYZzO46sIpLP+jTKOJQJJ0hBBBaW//\nFEgCvg88Cwn7IfOHkHoAXvoXHsn9ET/97X0RjlIMV7Km00nWdIToW899OAbgK3ANkLkG/nYlo1+b\nzIM/yZZ1G9GvkCWd9vZ2Jk6cOPCNw5QkHSF611UaPQb/eTfJv4HZhTD2KGy5ngmHR/Pcc9JRQAys\n34afvWlsbGTBggXs27cP8PZcs1gs6PV6Ro0axdKlS0MdoxAighYtehq3+xLgfIibCjf/F9zzY9ht\nh6c/hX9Wk54+XRKOGJSgko7L5cJsNlNWVuY/M8dut9PQ0EBGRgZTpkyhtLSUzZs3D0mwQojwKi5e\nh6p+CcRByj9gwXo4bydsaII374cO77JwfPzgTxcWI1tQ02sWi4WGhgZqamr8LW90Oh1Wq5Vt27YB\n3t5sqamp7NixY2giHiIyvSZEl4CmnecA2c1w8QfwYhG8fxjvAWxeCQk26Z0mBi2o6jVfF2lfwmls\nbATAZrP578nLy6OysjKEIQohwqW6upZ77nmcTz4ZB8poMB+HmU5oSoW134ITh4FsYBkwijFjdlJY\nOFMSjhi0oJKO2+32jwjA2wQUIDMz03+ttbVVjqsWIgp5CwaexO0eB+edC7NfAqUDfr0WPvkLoABN\nwE4gDpNpPKtXy6ZPEZygptfMZjP79u3j0KFDAKSmpgKwd+9e/z1JSUkkJSUFXIsGMr0mRrLi4nU8\n+ugLdIwaB9/4BNIa4eWboN4OWg3e0U0NMAqd7m2WLcuU0mhxRoIqJLDZbLS1tTF16lRmzJjhPyYa\nvEUGqampuN1ucnJyhiRYIUToeRPOK3SYjsO92yDRDevnQ91SSTgi5ILep2O323E4HHg8noBD2+x2\nO6tWrQooKogmMtIRI9X482/li6/vg/M/gepp0Pwo/uOkuyUcOftGhELINoeqqgoQtefrSNIRI80f\nt7zMj9b9fxy6ahfUXwe1y+DkeuA84G7g13ibep5g8mQdTz/9n7J+I87aGSed9vZ2WltbMRgMJCYm\nhjqusJOkI0aS1Zue5icv2zl1dBRsMcNBM/AYUAusBo4D4xg16nMefniWjG5EyJxRRwJfBwKTyUR9\nfT3gLSp44oknQh6gECJ0Dh87zHfW5/Hjuvs49dcb4JkFcPB24H3gIeAmoAp4AYNhEv/v/9kl4YiQ\nCmqk09LSgslkAiAjIwOXy4XT6WTmzJkYDAY8Hg9mszmsG0MbGhqor68nKSkJVVVJT0/37yMKhox0\nRCzTNI2Hf/s4K5sep2PveVBzDXyZjvc8nMeAdUA13l0UY0lI+JKKikKZThMhF9Q+nZKSEgDq6+tJ\nSUkhKSnJ/1hbWxulpaUUFRWxdOlSVqxYEdpIe6GqKkVFRQGFC3l5eRiNRlJSUob89xciGux37yfr\nydt5/5AKL1hg/zeAvXQdwPYQ3g4D3hGNt8OArN+IoRHUSCcpKQmLxcK2bdtwu90kJSX5Rzo+ZrOZ\n9vZ29uzZMyQBd2ez2cjOzuaOO+7wX3O5XJSVlfmr6gZLRjoi1pw4dYLVb67moT89wvHaS+AvV8Kp\nqzof/RDQOL1CTVGaeOSRLJlSE0MmqDUdt9vtn17ri9FopLm5+ayCGqyKigrS09MDrpnNZmnDI0a8\nv374Vy79+eU89KuVHF/3NaidC6fG4x3dnMR7ABvAJ8B64B8oSr0kHDHkgko6aWlp1NXV9XtPY2Nj\nj0QwFNxut3+01Z1erwfwH70gxEhSVPwEo797Mdc/eRP7/s/A8V/+K7R+DW+iOYJ3Oq3bEdOcD1zG\nmDFf8Mgjt0rCEUMuqKQzd+5c6uvrefnllwN6sPnk5eWhqipWqzVkAfaltbUVoM+D43z7hoSIZdXV\ntZhMc9CN+ibKNBMlny/j5MlRsDYTdmYDk+hauzkB/A5vsvGNcHYxefJ7bN68SBKOCIug9+mYzWYa\nGxvJzMykpqaGzMxM9Ho9TqeTtrY2jEZjWPquNTQ0YLFY6Ojo6PGYTqfrsdY0EFnTEdGmuHgdjz32\nAqcmKjDrHZjQDi/cAR8eAS7vvGsXcB/ekU02XXtw4klIOE5hoRwvLcIrqOo18FaulZaW+qvTampq\nAEhMTKSwsJCVK1eGNsIQ622EJkS0KS5ex08f2wo3fAjXN8Ofr4e/XggdU4B9eEc3AN/AO7q5G2+x\nwDSgibvuMvK735VEInQxwgWddAAKCwspLCwEvNNYSUlJ/rUUIcTQKi5ex0+f+T8o2Aut8VCWDx49\n3lFN97WbZ/FWqF2Ndx9OPIpykDvvvFISjoiYkPVeCzdfEYHb7e6xrqPT6VBVlSlTpgz69WR6TQx3\n1dW13LeklP2XvgPGQ/DSrbBLB1zaeccFwCt4E4/0TxPDU79JR6fT9Tkd5Xta9w9rRVH8v546NfRn\npqemplJZWcn06dP911RVxWKx+AsNBkuSjhjO7rq7kOd3ucD6N9g5HbZfCMfvB57EO2ExAe+emwvx\ndhbwABOBc5gwoYMHHsiQtRsxLPQ7vTZnzpwzetFwrZtYrVZ27NgRkHQaGhoCTjIVIpoVF6/j8bJy\nTt7yAVw7Gn5rhY+nAwfwFgf8GG9xQEvnf+OIjx/PFVdMYfnyuTKqEcNO1E6vAXg8HnJzcwPa4GRl\nZeFwOIKaWgMZ6Yjhpbq6lh/lL+fTyz4CiwqvzoQdM0B7H2+7mmc777wAGAWcQq9v4Te/yZdEI4a1\nqE464N2MunHjRv9JpmazOahSaR9JOiKSqqtrWbRoNfv2tdHRcQyMGsx+Gz6+GF66Cg5f1nnnAeAr\neMuffes1J0lIOCINOkVUGNSaTnNzM1OmTOl3jccnnGs6oSRJR0SKf7/NqQlwThxkvwYXH4ZqC+y5\nka69Ns92e5aMcER06ndNJyMjA0VRMBgMwODXeGQvjBAD841uVPUkKBPA/DnMfBUaU2Dtv8OJZryV\naL69Nj/AO7r5GPiE0aMTmDbtPJYvl4QjokfUT6+Fiox0RDjdfbed557bA3TAeefD7VXAWHhhNnza\nBqTSVQI9FW9VWi0QDxzkrrtkr42ITkElnfb29j57nUU7SToiXLwJ530YPRVufhGmt8D2y6EhGzQF\n77qN79gBXwl0HDCKyZPjZK+NiGpBNfzU6/U8/fTT/d5TVFREcnLyWQUlRCyqrq5l8uRsnnvuXbg0\nAe5zwITDsO63UH8xaHvwTp35/uHzCfAaMIm4OI3/+i8rH3+8SRKOiGoDtsGpqqryb/oE/EdD90bT\nNCorK2lrawttlEJEsa61m8MwQQd578FX2uGPt4E6DthB4H4bL0U5h3HjJnDZZeNZvvweSTYiJgw4\nvabTBTUYArybNrvvnYkGMr0mQq0r2XSAEgfX7oWb3oe6KfDak3Dy+W53SzWaGBkGTDrdT+HMy8sj\nPz+/3/NyDAYDGRkZoYswTCTpiFCqrq7le98rx+0+DOcnw+1/guMdsOU7cPBq4B26eqN9DCjdqtGk\nk4CIXUEVEmRmZlJUVBSVSWUgknREKJlM30f96CvwzS1w1QdQMxPejgf+E2/7mu7VaJ9x111XSTWa\nGBGkZLqTJB0RCsXF61hZsoljKcfglvegORlqvgNHvoO3Oaev+3MN3um0t7nrrksl4YgRI+ik43K5\nqKiooKWlpd/7tm7delaBhZskHXE2qqtrueeex/nkmA5uexsMX8CWb8P+MXSVP8vJnUIElXSqqqrI\nzc0d1L29HSM9nEnSEcGqrq5l2bJf8+67uzjZMQmufx++th/euB5evxhOdS/CUfD2SRtDXFwbDz10\niyQbMSIFlXRSU1NRVZWampqYW9eRpCMGo6si7QDeqTIFLjoEt++Gw3FQPQfaJtJ1cqeCt1AgDojD\nZBrP6tVS/ixGrqCSjk6nIz8/nw0bNgxlTBEhSUcMxFuR9iRudxygQPxFYP0DXPYpbM2Gnb5TPLPw\nFgtk41u70eneZtmyTBndiBFvwM2h3SUmJkozTzFiLVv2PG73aCAVpu2GLAfsvhDW2uBoPF290jS6\nJ5y4uHd56CFJOEJAkCMdu91OeXk5+/bti7kebDLSEX3pmlIbDUnHYdbbcM7n8MJt8NGXdB07cHqv\ntDgmTx4lvdKE6Cbo6rXc3FyampooKSkhPT29z5Y40ZaUJOmI7nxFAu+9p3Ls2EQYFQdf+wz+9a/w\n2tfhzQeh47dAG11l0L5D1U4webJOko0QvQgq6fgSjNvt7v9F5RA3EaW6RjUaYAAOwZQJMPtPcPBf\n4E/jwTMR73EDvtM7VSAeRTmH8eM7eOCBDJlKE6IPQa3pDLZcWtZ9RDTynuC5nVOn4oCpMO5LyHoV\nUj6DP2XB7gq8XQRWA2/gbWUzGpPpq1KRJsQgSUeCTjLSGdmKi9exfPmLaNp0YBSkNUGGC969EF7+\nFhy/HW9F2uP+5yQk2Kio+DdJNkIEIaiRzmC4XC4qKytZv359qF9aiCFRXV1LaemraFoynNsGs1+A\nuJPw27nwsQK00lUCvQwYhaI0UViYJQlHiCAFPdLxeDw4nc5ez8zRNI2SkhJaWlpkTUdEjfT0e2l8\n1wA3/R4DNvXdAAAdNUlEQVTM++HV+bDDA5p0FBAi1IIa6bS0tGA2mwcsJMjPzz+roIQIl+LidTS2\n74J734aP9bDhW3D4HOAOuo4dOCIHqgkRIkGNdPLy8qisrKSkpIS0tDRsNhtmsxmbzYamadjtdiZN\nmhR1zT5BRjojha8U+v33P+YL5TPI/idc9AW8uBT2/L3zLhnVCDFUgi6Ztlgs/lNBS0tLqaioYMeO\nHYC3lNpoNPL0009zxx13DE3EQ0SSTuwrLl7HihWvcPzEeDDvhm82QIMFah+BE6/SVQLt3WtjMp0j\nVWlChFhQZ1G73W5MJpP/6/T0dOrr6/1f6/V6cnNzWbFiRegiHITKykpcLldYf08RXYqL1/HoozUc\nNyTCPVvh6g/g2R+B62Y4kUVX25qLgFTS0vTs3fusJBwhQiyopJOSkoKqqv6vLRYLAE1NTf5rJpMp\nIBENNafTSX5+vuwNEj1UV9eSnj6P+PiZ/HTFi3RYP4Hv/w4a0uF/fwSfJuFtzvkQcBPwKFBMQsKn\nPPro9yMauxCxKqikk56ejtPpZPv27YB3ZJOYmEhZWZn/nrq6OvR6fWij7EVLSwsFBQW0tLT02YpH\njFzV1bXMm/csjY0axy45Aff+Gc45DOvyoeEa0E4R2A16GVCMTvddCguvkRGOEEMkqDUdVVVJTU1F\nURQqKiq44447sNlslJeXk5ubS1tbm3/kEc7jD1JTU3E4HMycOfOMX0PWdGJLevq9NDbHwa3b4LzP\nYMst0GLD25jTx3eap7cb9JgxO1m6dKYUDQgxhIIqmTYajezdu5eSkhJSUlIAKCkpoa6ujoqKCgCs\nVislJXLeuwif7hVpR44co4Mv4dojUPB3eOtaqPoOnLwN76jmB3SVQregKO90lkIbWL58kYxwhBhi\nIWuD49u7E46ptdPJSGfk8k2jHTjQeeGCz+D21+BoImy5FQ4lI4eqCTF8hKwNTiSSzZmQgoPYsmzZ\n8xw4cD6MPQozX4Urd8G2THjnx3SNaAITjncaTRKOEJEQVNIpKCgY8ENb0zQURZHea2JI+abUGpu+\ngCs+g1u2wp5UWHsfHBkNfAPvJs9fA03ATnS60Uyf/hWZRhMigoKaXtPpBi528414WltbB/Wa3Uuw\nB5KcnExiYmKP6zK9NjIEHqw2BfTjYNZLkNjunUr7x1c77/RNp0lHaCGGm6BGOn0lktbWVhoaGrDb\n7aSmpg66DU5LSwtFRUWD/v1nzJjBkiVLBn2/iA2+ZLNz52FOnBgPumS48VK4YTm8/j144zicGoV3\nKg1O7wg9ZsxOCgtnSsIRYhgI6Xk6vjY4NpstrF0JZKQTu4qL11Fa+g5HjkzyXvjqB3D7n8BjhheN\n0LYW78FqvvWbY0AHOt14EhLGd1alzZWEI8QwEdLzdHxtcBwOR9hb4YjY42td09Hxe0iwg9UJU/fA\nViv8rQp4DW83gcfxdhQAk+lBVq++RZKMEMNUyA9xUxSl17N2hpqMUKJbdXUta9Zs46OPPmP//g84\nebKDo0fjgWvg6t9A5lrY9S+wNh+OfQt4mK41m2Uoyl7S0pJkVCPEMBfS6TWXy0VmZqZ/E+lQ8ng8\nrFixAlVVqaysxGg0YrVayczMZM6cOUG/nkyvhZ8v0eze/Xc+/HAiHR0/wNsxYDKgQLIHZm2BBD1s\nKYCP3up8pnQSECJaBV291l/JtO+lysrKmD9//tlHF0aSdIbe6aOZY8cu4sSJ7wFrgY14Ry/AqGVw\nYzZc9xa89kN4cyJ0rKBr7UaVNRsholRQ02sZGRn9Pq7X67nzzjvPaKQhYltXQcDdeKvLzgUew5to\nLu+8Kw6mtMDsq+EgUPYseJroXomm0x1i2bIcGdUIEaWCSjo1NTVDFYeIMaePaj7/fCzwe7rWYoo7\n74wDTsK4zyB7M0zZDy/+Gv5u4PROAgkJuygslE4CQkSzkBcSiJGre6JRVeW0UY3vr5rv15PeX5QT\nkHYCMqbA27Nh7XQ4/hZdRQI1jB7dwrRpiSxffp9MowkR5YJKOi6Xi5qaGhobGwHvdJrRaGTu3LlM\nnz7df9/mzZuj7rhqceZ8mzd37RrN0aPr8Y5mfFNnvlFNZ5Lx/5oF5+bD7L/CqEPwf2vgwD7gU+AN\n4uO/S0LCRFJSxrN8eb4kGyFixKCSTmNjI7m5uX22rCkpKcFsNlNRUUF9fT25ubmUlpayePHikAYr\nhp/q6lruv38rzc2T8SYa6H1U4zuhMxtGF8JNcZC+CV65nri3LyFh7ItcctVXufDC81i4UNrVCBGr\nBkw6jY2NmM1mwHtyqM1mw2Kx+I+urquro6ysjPr6ekwmE5qmYbVaJeGMANXVtfzgB2s5dGgjXWs0\n0Ouoxrc+k7oBbtsC/5zAhS/M4qpLjCzcnClJRogRYsCS6aSkJNxu94Bl0KWlpRQVFaEoCq2trb02\n5hzOpGR6cHqu20zGm3B8U2rgLW32FQF0Nt4c/3u45WGUC/+BcffNrF64RBKNECNQvyOdVatW4Xa7\nKSwsHHDfzaZNmwDvh3ZFRQXz5s0LXZQionommg0ErttA1/RZV0uahIS1nPsVHYemmDl6/S4u/iyN\nVTP/hzlPZkXibQghhoF+Rzpms5mmpiZOnTrV74s4nU6ysrLYtGkTeXl5mM1mduzYEfJgh5KMdAL1\nn2jAO7oppmtU83jn/9cQH7+fK66YwH8UpfMbj4Mxo8awYdYGrjzvygi8EyHEcNLvSEdVVYxG44Av\nYrVaaW1tRa/Xk5aWFtQZOWL46SoOeJzARNP9r4tvvcY3RebdvJmcvIcNv/oP3hhbw2PvPsjPZv6M\nH6b9EJ0y8FlMQojY1+8ngcfjGVTSga7D23xrQCJ6rVmzrTPhQO+JBrqm08CbeB7FZDrOgiev5ieq\njYNHDrJzwU7uSb9HEo4Qwq/fkU5iYiJ1dXVBvWBdXZ0/AYnodOzYQImm+7rNXEym80lK6eB4RiOb\n3J/yzLef4Zsp3wxfwEKIqNHvP0GtVittbW00NTUN6sUaGxvxeDwD9mgTw9vYsf2NaLJJSJjLVVf9\nmOzsGp7fZOOHjov5242/49bpmbxT8I4kHCFEn/otJGhoaMBisWAwGGhpaWHixIn9vlhqaiqqqlJf\nX09aWlrIgx1KUkjQJXBNB6CWhIS1mEznc+GFE1i40Luv5q2P3sK2xUZyQjLrZ61navLUiMYthBj+\nBtynY7PZKC8vx2QyUVJS0mt7m6qqKux2O6qqkpOT4y+fjiaSdAJVV9fy1FM1HD06ivj4U/5EA+A5\n6uFB14Ns3r2ZJzKf4O5pd/d75IUQQvgM6jyd3NxcqqqqADAYDBiNRoxGI6qqoqqq/6TQaE04IEln\nMDRNY9PfNvHAtgeYNXUWK60rSUpIinRYQogoMuhD3JxOJyUlJbhcrh6PWa1W7HZ7VK/ljPSk49uX\nc+xYHGPHnmTRoqyAjgFqm8p9L97Hh+0fsmHWBr528dciGK0QIlqd0XHVqqridrv9XaZjwUhLOt2T\nTHv7h3z88UQOHPhv/+Mm00OsXp1N5i3/yhOvP8F/v/HfLLlhCQ9c/wCjR42OYORCiGh2RkknFo2k\npNOzUKD7BtAu1+b8gM+/WccU/RR+cesvSDGkhDVOIUTskUPcRojuI5udO3d1dob2Oe2vQcIhyLTT\nNPX3/PbmXzHn8jlSKCCECAlJOiNAz5FN8Wl3+PblaHDN/0FmIfwtlxvftpHzs5zwBSqEiHmSdEaA\nwLY2ENhlACALkgtg9vsQ74bfvYAp4fc8sPqWcIYphBgBojrpVFVVoaoqzc3NqKqKzWZjzpw5kQ5r\n2AlsawMB7WzijsKNLpTrnuHCZgvG/bNJmPZHFi68Rc67EUKEXNQmnaqqKoxGoz/JeDwezGYzra2t\nA579M9IEtrUBX9+0idd8kxPZ7zDhyLmUXvcbfrBSptKEEEMratv/qqoa0GonMTERu92OzWaLYFTD\n06JFWZhMD3VdOOdTxn//XsbO3cXGHz3DJ2t284PvSsIRQgy9qCyZdrvdWK1WXC5XwLHYqqr6+79N\nmTIlqNeM9ZLp6upa1jy1jRbD2+w3bWf2Rd/i2R+VM37M+EiHJoQYQaJyek2v16OqKi0tLUyfPj3S\n4USFS2Yk8XneyyR1nKJi9utcM/maSIckhBiBojLpALS2tva45nQ6MRgMQY9yYsnp7Wzy77uJHeO2\n88vGX/LoNx8l35wvh6oJISImapNOb8rKyli6dGm/98TyJsce+3Gmvsj21/L42sUW3l3wLpPHT45s\ngEKIES9mko7D4WDSpEksXrw40qFEjH8/zoR/wi33w/mNnPz9JuJTX2PyQkk4QojIi3jSUVV10Pcm\nJycHFA50fw2HwzGoo7X7KhSIhRHQ0WM6uPYX8I2fQr0Nfv9rOJnA0Ytej3RoQggBRDjptLS0UFRU\nNOj7Z8yYwZIlS3pcLyoqYvv27aEMLeo0fNxA04yn4eBU+N9aOHi5/7H4+FMRjEwIIbpEZcl0dwUF\nBRQVFZ118UC0lkwfPnaYR15+hN/t/B13nftDXnhUh9r8M//jJtODrF4t3QWEEMNDVCed8vJyMjMz\nAxKOy+XCaDSSkhJcG/5oSzqapvGH3X/g/pfuJ8OYwarMVUwaN6nfY6aFECLSojbpVFZW0tbWhtls\n9l9rbW2lsrKSDRs2BP160ZR09rv3s/BPC3n/0PtsmL2Bm6fcHOmQhBBiUKIy6bjdbpKSknp9zGQy\nsWfPnqBfMxqSzolTJ1j95mpW/nkl9193P4VfK2Rs3NhIhyWEEIMWlUlnKAz3pPPXD/+KbYuN8845\nj9xxP6TK8Z5/A+iiRVkyhSaEiAoRL5kW/XMfdbPUuZQ//P0P/Dzr50zcfyE//nHg+TjNzd5mnpJ4\nhBDDnfRDGaY0TeO5d5/jirVXoKHx3r3vcfe0u3nqqZrTDmSD5ubHeeqpmghFKoQQgycjnWGoubWZ\ne1+8l48Pf0xVXhXXf/V6/2M9D2TzOnp0VLjCE0KIMyYjnWHk+KnjPF77ONc9fR3WFCv1+fUBCQd6\nO5DNSzaACiGigSSdYaJ2fy2pT1zKk1XPkLr9eziXe9j20hs97utxIBveDaALF2aGK1QhhDhjMr0W\nYQe/PEhhTSF//NsW4pxf5+DLlRzEW0nXW4GA7/+fempZtw2g0nFACBEdpGS6U7hLpjVN49m3n8Xu\ntHPnlXey86kxbP/Tqh73ZWcv46WXHg1LTEIIMdRkpBMBuw/upmBLAZ8f/5wX734R8wVmbi4p7vVe\nKRAQQsQSWdMJoyMnjrBs+zJu/NWN3HH5Hbw5703MF3jb+EiBgBBiJJCkEyY1zTVMWz+NXQd38XbB\n2yy6bhGjdF2jGCkQEEKMBLKm0+ls13Sqq2tZs2Zbj9Y0Bz4/wANbH+D1D15n7W1rmXXprH5fQzpE\nCyFimSSdTmeTdKqra7n//q0BnQKMpge59eHjbPrs1/xw+g955BuPcM6Yc0IWrxBCRCNJOp3OJulk\nZz/Mtm2PdV0471243YZe/wG1S15k2lemhSpMIYSIalK9FgL+1jSjv4CbfwrTn4Htj3H1+I8k4Qgh\nRDdSSBAC/sqz6/8HJnwE696F+nwS4jsiG5gQQgwzMtIJgUWLsmhufojm1x4FzZvHvZVnt0Q4MiGE\nGF5kTadTKKrXpPJMCCH6J0mn03A/OVQIIWKBrOkIIYQIG0k6QgghwkaSjhBCiLCRpCOEECJsorpk\n2ul04nQ6SU5Oprm5GbPZzPz58yMdlhBCiD5EbdJxOp0oisLKlSv91ywWC263myVLlkQwMiGEEH2J\n2um1srKyHtesVmuv14UQQgwPUZt0FEXB6XQGXNM0DYPBEKGIhBBCDCSmNoeaTCYWLFjA4sWLg36u\nbA4VQoihFzNJx+Fw4HK52Lhx4xk9X5KOEEIMvagtJPCpqqqipqYGRVEGlXB8yeVMHxdCCBEomH+s\nx8xIx+PxkJGRQXl5OWlpaX3eJ0lFCCFCb7CpJOIjHVVVB31vcnIyiYmJvT6WmJiIzWYjIyOD1tbW\nPl+jr29MrE+vyfuLbrH8/mL5vcHIeX+DFdGk09LSQlFR0aDvnzFjRr97cDIyMnC73bhcLjIyMkIR\nohBCiBCKaNJJSUlh06ZNQT9PVVXMZjMvv/wy06dP7/G4x+MJRXhCCCFCLCr36bjdbkwmE0ajMeC6\nb6ouPT09EmEJIYQYQFQmnfT0dObOndtjjrSkpAS73c6UKVMiE5gQQoh+RXX1Wnl5Oc3Nzf6GnxaL\nhXnz5p3Ra42UxT55f9Eplt9fLL83kPfX4/5oTjpCCCGiS1ROrwkhhIhOknSEEEKEjSQdIYQQYSNJ\nRwghRNhI0hFCCBE2Ee+9JoToW0NDA/X19SQlJaGqKunp6THX4qmyshKDwRBz7wu8XfBVVaW5uRlV\nVbHZbMyZMyfSYYWM0+nE6XT6t62YzWbmz5/f73Mk6fTjTL6h0STWfyB8ovVDTVVVioqK2LZtm/9a\nXl4eRqORlJSUCEYWOk6nk/z8fCorKyMdSshVVVVhNBr9P1Mejwez2Uxra2tMfI44nU4URWHlypX+\naxaLBbfb3W+PTDTRq5qaGs3pdAZcM5vNWmlpaYQiCq3KykqtoaHB/7Xb7dZMJpPmcDgiGFXo1dTU\naAaDQXO5XJEOJWj5+flaVVVVwDWn06nl5uZGKKLQUVVVs9lsmsPh0EwmU1T++Qykt88Kh8OhKYoS\ngWhCLycnp8dnpN1u10wmU7/PkzWdPpSVlfW4ZrVae70ejVRVDTh3KDExEbvdjs1mi2BUodPS0kJB\nQQEtLS0kJSVFOpwzUlFR0aOPoNlsjolRQUpKChs2bIiJf/H3xu12s3Hjxh7Nh32j7X379kUgqtBS\nFAWn0xlwTdM0DAZDv8+TpNOHM/2GRoOR8AMR7R9qbrcbt9vdI2Hq9XogNv6MYpler0dVVVpaWiId\nypDZtGkTK1asCLhWWVnJ3Llz+32erOn0obcjFyorK1mwYEEEogmt7j8QvR0NISLPdxDhxIkTe31c\nVVVpbDvM9XaYpNPpxGAwxOSfncPhwGKxsHjx4n7vk6QzSIP9hkaLkfYDEW3cbnekQxBDoKysjKVL\nl0Y6jJCqqqqipqYGRVHYuHHjgPdL0hlAsN/QaBaLPxBCDBcOh4NJkybFzD9cfebMmcOcOXPweDxY\nLBbKy8sD1otPJ0lnAMF+Q6NVrP5ACDEcqKqKw+Ggrq4u0qEMmcTERGw2GxkZGb3OpPjEfNLxnSY6\nGMnJySQmJvb62GC/oeEWivc3nH8gQvXnF218p+K2t7f3uq5z+qm5YngrKipi+/btkQ5jyGVkZOB2\nu3G5XH3ui4vppNPS0kJRUdGg758xY0a/m5oG8w0Np1C9v+H6AxHqP79ootfrMRqNqKoaUOyhqip6\nvV7W3aJIQUEBpaWlfRaFRCNVVTGbzbz88su9FiOdXhnbXUwnnZSUlF6r0AZyNt/QcDrT99fdcP6B\nCMX7i2ZWq5UdO3YE/B1saGggMzMzglGJYJSXl1NUVBTwjwSXyxX1XSXcbjcmk6nHiNs3M3H6/rLu\nZJ9OL87mGxpN+vqBiOW9BdGkpKSEioqKgGsOh4OSkpIIRTR0tBg8wNi3ibe1tZWGhgYaGhpwOp1U\nVFREdcIB72fg3Llze/y5lZSUYLfb+x2Jy3HVfVi1ahX5+fkBawSZmZlYLJYeG6KiUWVlJW1tbZjN\nZv+11tZWKisr2bBhQwQjC73U1FTKysqGxZRosBobG9m4cSMzZszwj8BnzpwZ6bDOmsfjYcWKFaiq\nSmVlJUajEavVSmZmZkz0/+ttY6+PyWRiz549YY5oaJSXl9Pc3OzvT2mxWJg3b16/z5Gk048z+YZG\ng5HwAxHrH2pCRCtJOkIIIcJG1nSEEEKEjSQdIYQQYSNJRwghRNhI0hFCCBE2knSEEEKEjSQdIYQQ\nYSNJR4jTNDQ0kJubi8FgQKfTYTAYMJvNrFq1KtKhnZHMzEx0uq4f9dzc3ICvhQgn+ZsnRDc2mw2L\nxUJVVRU6nY7MzEwmTZpEU1MTdrudpKQkGhsbIx1mryorK9HpdFRVVQVcVxQFRVF6XBMiEiTpCNEp\nNzeX8vJyDAYDDQ0NHDp0iK1bt7Jnzx5OnTpFYWEhbrcbs9k8bBMP9EwoFRUVNDc3RygaIQJJ0hEC\n71HdVVVVmEwmWlpaeu0uvnLlSsrKygBvghquTm8ykpiYKEchiGFDko4Q4O/cXFJS0u8xD/Pnzyc9\nPR1VVXG5XP7rp6+b+LjdbnQ6HQUFBQHXVVUlNzcXk8mETqcjKSmJvLy8Hh2+bTabv0+e3W73rzOl\npqYGTKNlZmaSl5cHdK3ZtLe3B3w9kNLSUsxmsz+egoKCXjuOOxyOgPssFkvA90KI/kjSEQLvkQ4G\ng4E77rhjwHttNhsANTU1Adf7Wyfp/piqqqSmprJ582ZSU1P960iVlZWYzeZez2vyTf3deeed5Ofn\n+5OW78O+qKiI/Px8f3wOhyMgeQ60hmM2mykqKkKn0/njcTgcmEymgKlEu91OQUEB+/btIzc3F6vV\n6j/jZzhPOYphRBNihGtubtYURdEsFsug7m9oaNAURdGysrL816xWq6bT6Xrc29bWpimKohUUFPiv\n5efnazqdTnO5XAH3lpaWaoqiaJWVlQH3Koqipaamah6Px3/d6XRqiqJoNpvNf62iokJTFEWrqqoK\neN2cnJyA2E7/uqSkRFMURdu+fXuv79NsNvuv6fV6LTU1NeA+Xyzd36MQfYnpk0OFGAy32w3Q49C+\nvpztAVwFBQVkZ2f3OBcnLS0NgLa2th7POX3az3c20JkeuKd1W/dZsWIFmZmZpKen+78X4H2fGRkZ\nuFwu2tvbmThxIh6Ph9TU1IDXysjIoKGhAb1ef0axiJFFko4Y8Xwflr6TYQfiu+9MP2TT0tL8Ccbt\ndlNXV0dDQ4O/SKE3Q3larcfjoaamBoPB0OvjiqLQ2trKxIkTycnJobKy0j8taLVaSUtL67XwQoje\nSNIRI55vhDPYpFNXVxfwvGC53W7sdjubNm3yr9+YzWbMZnOfI5e+Dt07U741Ht97zszMxG6393m/\nLyFt2rSJVatWUVZWFnB/fn4+JSUlASftCtEbSTpCAFar1V823dvJok6nE6vVCuAfkcydO3fA121t\nbe1xLSMjg8bGRmw2GzabzT9KcLlcVFZWns3bCJovmen1+kEfg71kyRKWLFlCe3s7NTU1lJWV4XA4\nqKur8ydkIfoi1WtCgP9f7b39a9/tdpOVlYXFYqG0tJTGxkbMZvOgppQaGhp6vFZjYyO5ubmsX78+\n4DW0MB7i6/u99Ho9iYmJOJ3OXu8zGAz+NRxVVbHb7f6KuYkTJzJnzhy2bdvmX9fxlWkL0RdJOkLg\nHX3k5OT4y5m7l//q9Xo2bdpEQ0MDRUVFKIpCRUVFwPP1ej2apgXsV/FNo/Xm9GKB7veebfIZzPO7\nl1DbbDba2tr8+3x8SktL8Xg8AXuMVq1a5S8Z705VVRRF6XePkxCAlEwL0V1ubq6mKIqmKIqm1+s1\nq9Wqpaen+6/pdLoeZc2apmmVlZX+e2w2m5afn68ZDAYtKytLMxgMAaXNmZmZmqIoWm5urlZSUhJw\nr6Iomslk0pxOp6ZpXSXT3culfU4v2/aVLptMJs1ut/uv5+TkaIqi9Pm1pmmayWTyPzcnJ8f/nk8v\nI/fFbjAYtJycHC0/P1/T6/WaTqfTioqKzuA7LkYaSTpCnKahoUHLzc3VkpKSNJ1OpyUlJWkWi0Ur\nLy/X3G63/4P39P0wDofD/+GdlJTk/xA2GAwBe1jcbrdms9k0g8Hg/2D3vZbNZtN0Op3/ft/Xg0k6\nmtaVFJKSkvzXcnNzA/blnP61j91u18xms39fUF9JxG63ayaTKeB7c/r3Qoi+KJoWxolkIWLEE088\nweLFiyMdhhBRR5KOEEKIsJFCAiGEEGEjSUcIIUTYSNIRQggRNpJ0hBBChI0kHSGEEGEjSUcIIUTY\nSNIRQggRNpJ0hBBChI0kHSGEEGHz/wNYFsApVCsHzQAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23b049e90>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZ0AAAEsCAYAAAAYSW5yAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X18k/W9//FXwl0RoUkKivc0qfc3o02LujlvaNq66dk5\nB9qinnPmzpk01Q386YAWkcnx5mCL2xkylbbsbLodHbR1N1onbYLas+mmbYKKikCu1Ptb0qsdyF3b\n6/dHmtD0PiU3Tfg8Hw8ewJUr6beF5t3v3eer0zRNQwghhIgBfbwbIIQQ4vghoSOEECJmJHSEEELE\njISOEEKImJHQEUIIETMSOkIIIWJmYrwbEAkul4stW7aQlpbG3r17sdvtpKenx7tZQggh+kn40Kmr\nq8PhcLBx48bgNbvdTlVVVRxbJYQQYjAJHTqqqlJSUoLP5wteq66uZtu2bXFslRBCiKHoErkiQVlZ\nGXq9nrVr14Zcb2trY86cOfFplBBCiCEl9EKCmpoacnJyBlyXwBFCiPEpoXs6er2epqYmFEXBZDLh\n8/kwmUwsXLgw3k0TQggxiISd01EUBQC3282yZcuC18vLy/H5fCxevDheTRNCCDGEhB1eU1UVALPZ\nHHJ90aJFlJWVxaNJQgghRpCwoRMIm/6hk5mZiaqqtLW1Dfo8nU435C8hhBDRlbChYzAYQn7vLzD8\nFg4JHiGEiK6EDR3w93KGCpf+PaAATdMG/SWEEMcbj8/DQy8/FNOPmdChY7fbaW1tDbnmcrkwGo2y\nbFoIIYagHlRZ3ricSzddyuHuwzH9wTuhl0x3dHRgtVrZs2dP8Fp+fj6lpaUsWLAgrNcKDK0l8JdD\nCCGG1dXTRXVrNfe+dC9fm5rNoT9lwD4DU6Z0sXRpPtddd2XU25DQoQPg9XqpqKjAYrHg8XgoLi5m\n/vz5Yb+OhI4QIpn9afef+FHjjzh1+qn849SbWL/Sg8fzQPBxi2UV69cXRD14Ej50IkVCRwiRjHZ8\nvoNljcvwql4eynuI68+5nmuvXU1j4/0D7i0oWM3zz98X1fYk9JyOEEKIwX2+/3NuffZW5j8+n2+f\n/W123LqDfzj3H9DpdBw6NHhdgIMHJ0S9XRI6QgiRRA52HaTyL5Vc8MgFpExMYecPd7L00qVMmjAp\neM+UKV2DPjclpTvq7ZPQEUKIJKBpGrVv1XLBIxfw8gcv8/L3X+a/r/1vTFNNA+5dujQfi2VVyDWL\n5S6WLMmLejtlTqeXzOkIIRLVax+9xh1b72D/kf38JP8nzE8feTFVQ0MzGzY0cfDgBFJSulmyJE9W\nr8WShI4QItF80PEBd227i23ebdx3zX3c/LWbmaCP/rzMsUjYKtNCCHG8qvvj85T98QHen93KmZ9m\nsf47v6Aw89p4N2tUJHSEECJB9Gg93PnEXfz87Ufobv9HqPtflI4zKX9xFVMnnBCT4bFjJcNrvWR4\nTQgxnr3Y9iJ3br0T764vUDfXwUeXhjweiz02kSA9HSGEGCcaGpp5+OFGDh2aGCxNc85lp7DCsYLt\nn26nwlbBI0+9RXO/wIHY7LGJBAkdIYSIocGC5brrrqShoZnbb996tDRNSjt/M1yLtv1d7rpqJU8t\nfIqUiSn8Ysrdg75uLPbYRIKEjhBCxMiAYAE8Hv9+mYcfbvRf1x+B7I1w5f107Pxnrv7r1ylbdfQ0\n5KVL8/F4VvWrm3YXS5bIQgIhhBB9BIOlD4/nATZsWM3BQxPgnGchfxl0nAlPOODzi9GuWhNyf2Cx\nwIYNq/vssbk2IRYRgISOEEJETf+htI8/3jfofV9O+BJv5la4aAts/Sns/hbgX9w02LDZddddmTAh\n05+EjhBCRMFgQ2lTpy4KvenET+GaH/PmxU/yHxmLafyvKSh7vh18OJGGzUZLQkcIISKgf6/miy98\neDyPhtxz4MAPmDq1lANH/hsu+xl8/Sekei1UzdvMon+8joaTmhN22Gy0ZJ9OL9mnI4QYq8F6NSkp\n3+XgwSf63alx+rU2vpzbyomdp3LeR9dQvnhR0gXLcKSnI4QQx2iwBQIHD54ZetPpf4WCO+g0tvG8\n/Q9cNeeqGLZw/Eiqow1UVaW0tDTezRBCHAcaGpopKLibq69ew6uvfjDIHfmkpNwKqe/BwpuguJBZ\n76fxm6ueOm4DB5Ksp1NWVkZ7e3u8myGESHIDh9MG2bA5OZPUBUvpTj+fUz+cR8Y7/8Idt193XA2l\nDSZpQkdRFNrb24NzM0IIES0Dh9PygVXAA6DrhsxfMsF2Bxee8Q0e/+6znD7j9Di1dPxJmtBxOp3k\n5eXR1NQU76YIIZJQ39Vpr7/efzjN33s58ZJr0PLfYXLPZH5s/Qn/r7gk9g0d55IidJxOJzabDYfD\nEe+mCCGSSCBoPvroCxRFx4EDG3sf6TeclvYu5D9E91nb+fW/bWLB+Qtk1GUISbGQQFEU0tPTZbmz\nECJiAvM2jY3389Zbs/oEDgSH06b64Nrb4T+uIG3ffp78ei0LL1gogTOMhO/p1NfXs3jx4ng3QwiR\nZELnbfq9VU64DHJq0V15Kqf4Lubct/+NH936T8f9IoHRSOjQUVU13k0QQiSpQ4f6vj129f6uwbl/\nhPzl4Mvg67u+x59/t3Gwp4shJHTo1NbWhvRyRtOllW6vEGI4gXmcN97Y0+dqPsy+BQoUmPYZPLcB\nCy+xcn1y1UWLhYQNHbfbTXZ2dsg1mdMRQoSj74q0zs4P6ej4Ox9/bOLgwceAZmAVnPhDmP84nPN7\nJv1lDufsy+X0jD8nZV20WEjY2ms1NTV4PJ6Qay6XC0VRKCwsJCcnh4ULF4769aT2mhDHl9ANns3A\nVvzHCdzvv2HiAfj6ErjsSaa8beYbPd/iztv+QYLmGCVs6Axm3bp1tLS0sHnz5rCfK6EjxPGjoaGZ\nm29+hL17A+8Vd+MPmzWg+zFc9BTYVsKHl4KjgqsueYIXX1wTt/Ymk4QdXhvMl19+KaEhhBhWoIez\nd+/5fa72vhWe0QYFl4OuB+qfhPevAAY/SE2MTVLs0/F6vZSWllJTU0N9fT2lpaW43e54N0sIMc4E\nejj+IbWuow8YvoTCRVD4HLw6Gzb9LRg4/oPU8uLT4CSUVMNrx0KG14RIPn0rCrz33gccOnQ6R46c\nCqwBmmHKH+GbEyHrMfjrXHjlT3CkBWgiJeU9LrhgOvfee3yddxNtSTW8JoQQ4A+b1auf4J13JnHw\n4I34FwnMwj9vczfouyDzHbj6l7DndHjsFk7UdnLOxcuZPn0WKSmwZMktEjZRIKEjhEgqR1elzSYY\nMjyAv3cDmI1QcCocuACebIJPsrBY7mL9+jIJmRiQ0BFCJLy+w2jvvvsxXV3PEAyZwNvczE8h/zpI\n2wVNt8POA8AfSUurZP362yRwYkRCRwiR0NaseZTKyjc4cOAm/MNop/Q+0rtQ4IROuPqHcOFv4f9y\nYPNb0D0ZoLeHI4ETSxI6QoiEE5iz2bXrE/bvnwT8nqPDaL3HDky4GubZ4IoW2JEBj+yBr94G7pNF\nAnEkoSOESBiBsNmx4+8cOZIBzObo21jg9zw4fyHkvQ5fngS/vJFJHR+RkmLnrIvO4LTTpssigTiS\n0BFCjFuBkGlr28f+/V9y5MiZaNqp+MOmt4JAcL9NF5zigoJ7YOoH8OxloJxNWtpOHv/dMgmZcSIp\nNocKIZJPQ0Mzt9zyOG73ybS338bhw2lo2v/g/1k58PNyF5AP05fCP7XCTVfCmzfBxl2g/C8Wy2Ee\nf1zmbMYT6ekIIcal1at/y6efnsLRZc+BsjV9KglM+iZ8/W649HVovQh+XoT+yDOcceZrnHfebKkE\nPQ5J6Aghxp2GhmbeeWcfcFLvlYkcDZt80P0KLvkOzHfDB+dA9XeZtL+diy8+gXvvXS5BM45FLHQ6\nOzuZMWNGpF5OCHGcCtRHO3jwbELma8gHVsGZ10LBy6D5oPYcprWfzLnn9nDvvSUSNgkg7Dkdt9vN\nrbfeSltbGwAdHR1kZ2djMBiYMGECK1eujHQbhRDHiTVrHqWo6MneCtD5wCfAKv+fjb+F4r/Aguvh\nlQtJ+d+ruef7N7Fv35O0tj4igZMgwir46XQ6ycvzV1t1uVzMnTuX0tJSqquryc3NRVEU2traqK2t\nZcGCBVFrdDRIwU8h4mvNmke5774menp+x9HzbZphyia48jXIVND9dQ7nq3mccYqRJUvyJGgSUFih\nk52djcvloqmpidzcXAD0ej02m43GxkYAjEYjGRkZvPbaa9FpcZRI6AgRPw0NzRQVPcKBA+cTrACt\n/xNknQlX/yfsup6zPCfwSEWhBE2CC2tOJ3AUdCBwAmfW2O324D3FxcXU1dVFsIlCiGT38MONvYHT\nO4eT8RXk/xb2Ab/+J9K6VB55/LsSOEkgrNBRVTXYIwBwOBwAwSE3AJ/Ph6qqEWqeECLZNTQ085e/\neAALzDobCixgmAiND8Ou65k6tZTHa2WvTbIIa3jNarXS1tbG3r17AcjIyABgz549wXtMJhMmkynk\nWiKQ4TUhYi+wAfTTzi/hGuACBzR/H1pOhO7J6PWvs3p1HmvW3BbvpooICWv1mt1up729nbPPPpuc\nnBwURQkOrTmdTjIyMlBVlcLCwqg0djD19fWsW7eO0tJS8vPzqa+vj9nHFkKMXUNDM9/994f51NwG\nP3gJuj+Bn2+Gv6VK4CSxsIbXSkpK8Hg8VFdX4/F4KCwsZPny5QA0NjaiKAo2m40HH3wwKo3tr76+\nHrPZzMKFCwH/8m2r1YrP52Px4sUxaYMQYvQCtdTeetvDYYsObnLDZyfD/7wKez8FmoAJQDfnn3+S\nBE4SCmt4bTiKogBgNpsj8XKjsm7dumDoBdTU1GC32+np6QnrtWR4TYjoCg6l6b+Agldgymmw9SLw\nzsG/PDpUQcFqnn/+vpi3U0TXmEOnra0NRVFQVRWz2YzZbI5pRQJVVbHZbDidTlJTU4PXFUUhIyMD\nRVGYM2fOqF9PQkeI6LrqH5bSPOkFMLfBtmtg++9A+wvwOP6q0Q8E7509+w42bfpnWTyQhMIug+N2\nu1m8eDEulyvkuk6no7CwkIqKirDe7MfKYDCgKAper5e5c+dG/eMJIcZm3+F9VP6lkpe/tgleyYYN\n18PhCfiH0QKh8gRwIxMndnPJJbPkcLUkFlZPx+v1YrFYAMjKymLRokWkp6ejKApNTU04nU6MRiNe\nrzduddiqq6tZuXJlcIXdaElPR4jI6tF6+NETq3jknYfp8Rro3poBHd/sfTQf/9HSR3s3U6faqa39\nFwmbJBdW6AQ2flZVVQ06UV9dXU1paSlFRUVs3rw5og0dLavVyo033siyZcvCep6EjhCR81LbS3y/\ndjHvKx0ceWYefHRSvztmAwUEFg5MnryDlSvny8KB40BYoWMymTCbzbS0tAx5j9VqpbOzk927d0ek\ngeGorq6mvr6erVu3DnlP382tg5HQEWLs9vj2sKJpBa5PXKS+msUbT50PBL7nemup8QT+Qp4T0esn\nMXfuyTKcdhwJa5+OqqrB4bWhmM3m4Eq2WFIUherq6mEDRwgRHe0H2rlz651ctuky5p02j50/3Inx\n40uASYSe9HklsAloAP7AN795kVSIPs6EFTq5ubnB0jdDcTqdZGZmHlOjxqK8vJxt27aNeJ+maYP+\nEkKE70j3EX7+6s8575Hz2H94P2/d9hblV5Tj3PoqLtd2/LXUAr8GSknpjmVzxTgQ1vCaoihYrVbm\nzZtHVVVVyCo1r9eL3W7H4XDQ2toa0+ApLS2lvLz8mFbNyZyOEKOnaRrP7X6OZU3LSDk0jYN/OJMP\nWg9x4MAhenoO4D/x09TvWbIsWowQOvn5+QPmQDweD4qioNPpMJvNGAwGVFVFURQ0TSMrK4ucnBwe\ne+yxqDce/JtB8/LyQgLH6XRiNptJT08f9etI6AgxOm9+9iZ3Nt7Jh50fkvnFNdSt/YIjh/uuVt0H\nnM3AOZxDQArTps3g3HONMo9znBo2dIxGIzqdLuw3Yp1Oh8/nO+bGjaSuro729nasVmvwms/no66u\njo0bN4b1WhI6Qgzvs32f8eMXfszv3/09q69czWfPaTxw7zY07cJ+dwbmb9YMeI2rrlrDiy8OvC6O\nH8NuDm1vb49VO8KmqirFxcWDPjbSYgchxOgd7DrIz/76M9a+9CBTdp7B/ue+xpLlvwVSgZxBnjH4\n/A3IHI4YQ0WC8cJgMIRdX00IMXqaprHlrS2UOcro/nAynb+cB74zeh/dB6QweMDk4y9ts4r+czhL\nlvxztJstxrmwFhK43W42b96M1+tFVVUMBgNms5lFixYlfCkaGV4T4qi/ffg3vvfb7/PeR59y6JnZ\n9HgygIv63DER2Anchj9g+gps/HwC2A90YbGcwPr135c5HDG60Bmq3lpfVquVmpqahA0fCR0h4P2O\n97n+vxfy5r43wHkRvP410L4ArP3u7AI+BU7maMB8AhwAQK8/kalTT5QFA2KAEUPH6XQGj6POysrC\nbreTnZ0drLnW0tJCVVUVbrcbnU5HU1MT8+fPj0njI0lCRxzPav/4PEs2l/PZ6W/Bqxnw8vlw+ILe\nRz8ETu/3jMAQGsCpBM7AMRi8/OY3JRIyYkjDhk5HRwfp6emoqjpkvbWAQN01o9EYdrHN8UBCRxyP\nunu6+ed7b+aZffWgnAbOOdB5GaHTve8APyB0GE2G0MTYDFuRoLq6GlVVWbFixYgncZaUlLB8+XLa\n29t56KGHItpIIUTkbfNu47R7z+KZ95+Dp26E390AnafjD5y+lQSuAp4EbsZfR+1T4BVgHdOmfUVW\nlolnn13Cnj2PS+CIEQ3b07FarWzfvp3u7tEvc9Tr9eTl5SVcDTTp6Yjjxa69u/jub/6DlvdddD9/\nIbx9PhA48fcd/Bs7+w6fzQZOw7/RMwWd7ktuuOFCnnyyIuZtF4lvxM2hM2fODKtitMViQVXVhBti\nk9ARyc53wMe//8rOs+//kZ7ms+DV86ArC/8qtIzeu04FXsQfPH0XCOhISZnGBRfMlIUB4pgMu0+n\no6ODefPmhfWCZrN5VIU3hRCxcaT7CD94/Ef8Ylc1PTtOhReuha9SgPPxD5+diD9YADTgavxVoHcA\nE5k9exqbNv1QgkZExIg9Hb1eH1avZSzPGQ+kpyOSSUNDM3evfpx3ul/n0JVvgToDtl4IX3wd/8+a\nbfhXpPUdRtMROOcGJmKxnCgLA0TEDbuQwGaz0d7ezvbt20f1Ym63m46ODnJzcyPSOCFEeBoamrFY\nFnL9Lfew/eI/ceiKXfB8JvxmMXxxBkcXCRzg6JHRgQUC+4GpWCwGnn32dlkYIKJi2J6Oy+UiOzsb\ni8Uy4rxOR0cHVqsVRVFifrRBJEhPRySqhoZmVq9+grffVjg0aTLMfwfO2QsvfhNcJ0JPoCBnYO4m\nH/gZ/uMHbiJwZDS8zo03niMLBERUDdvTycrKYvHixXg8Hs4++2yefvrpQe+rr68PBk5hYWHCBY4Q\niWjNmkeZOvUarr/+p7jfPMKheZ/Abc1wYDr8/IfQcin0TOPo0ufA3M1W4P8BXwDrgJ1Mnermnnvy\nJHBE1I2qDE5RURH19fWAf87GbDYHj6VWFCVYjbqwsJAtW7ZEt8VRIj0dkQgaGppZunQ9ivIBcAbQ\nBRfrIPcF+MgIju9A++ccXY22m4EbOwNDaZOZOLGdVauuZc2a22L6eYjj16gLfjocDioqKnA6nQMe\ns9lslJWVJfRcjoSOGK+OBs2nwAmAETgAZ6RBQQPoJsPWfHj/AP6w+RT/KjSAdo4Oox1d/jxp0lQu\nvvgkWf4sYi6sKtMBiqKEVJlOBhI6YjwJzNO8+eY7dHUFgqb3FF/DLLA1wBk+cJ4Pb+aCFqgU0Pf/\nb2A1WgcwA51uGiee2MOdd+ZKz0bEzZhCJxlJ6Ijx4Givpgd/aGjAZOBsmNINVzwLVg/8zQwvfxuO\n+AgNGpClz2I8k9DpJaEj4iW0V3MS/hC5CP98zPmgUyCrHa5+AfbMgm3/AH8/D3/lgOm9rxIImkNA\nilQPEONWwoeOy+WitbUVk8mEoihkZWWNaW5JQkfEUsgy50Mz8C8k1YALgQ+AdKANzIeh4Dk4kApb\nV8Mnz+HvwZyNvx5aA4GgkXkakQgS9rhq8M8tlZeX09jYGLxWXFyM2WwmPT09ji0TYnChw2cmYAYh\nvRoADsHMTyG/EWbqofE82HkG4MW/1Hk9/irP09DpUjCbZ8rwmUgYCd3TsdvtFBQUsGDBguA1p9NJ\nVVVV2Eu3pacjomVgrwaOHv3cp1fD6XDCV3DVVrhIgT9nwKuXQfe/4Q+admAaMFnmaUTCSujQMZlM\nuFwu5syZE7ymqiomk4menp6wXktCR0TDmjWPcv/92+juTgX24g+bQNBAsErAhJ0w72S44n9gRzq8\nlAlfTQUUYCowlalTj7BiRYGsPBMJLWLDa52dncyYMWPkGyNEVdVgwPRlMBgAaGtrCwkjIWKpoaGZ\n73//AT77bCIQqNDRhf9b7lDvnwGmwXmvQN7fYG8a/LIKvmwmsNR50qQ0macRSWXYMjiDcbvd3Hrr\nrbS1tQH+mmvZ2dkYDAYmTJjAypUrI93GQfl8PoAhg05RlJi0Q4i+ggU3r7+fzz47AZhJYOny0bDp\nLUdzypvwvefgGjc8dwU8aYEvNwMqU6dO5J57vs3hw7W0tj4igSOSRlg9HafTSV5eHuCfTwEoKyvD\n5XKRm5uLoihUVlaSk5MTMs8SDaqqRvX1hQhXQ0Mz//qvNajqRPybOc/HP3wW6NX0hs30r2B+K2R8\nCC9awD0LeiaSkpIqy5xF0gsrdMrKygBoampi7ty5AFRXV2Oz2YIryIxGI2vXro166IxVYO5GiEhq\naGimqKiCAwcyOXpeTb8D0iZ1wdffhEvfhtbT4OdXw6GpsihAHFfCCp1AFenAPhi32w0c7fWAf8ly\nXV1dBJsoxPh2001lPPXUbvx10fqfV/M46DS42AO5r8IHM6D666QcnMUFF0qvRhx/wgodVVVDegoO\nhwMgOOQG/rmWWAx9BWq+DbWAYaiacEOtTpMekAhHaBWBWfhXpe3BHzj5wNvAk3BmJhT8J2g9UHcZ\ns4/MYtNv5OhncfwKa8m01Wqlra0teBR1Roa/fPqePXuC95hMJkwmU8i1aMnIyKCuri441Af+3lh2\ndnZwocFoyZJpMVpr1jzK2rUvcvjwdOBzwNr7yIf4qwrMBuPFYFsGp+8FxyWk7DmZshVyhIAQYa1e\ns9vttLe3c/bZZ5OTk4OiKMGhNafTSUZGBqqqUlhYGJXG9mez2XjttddCrrlcrpCelxCRtGbNo9x7\nbxOHD58DnAKkcfSQtO/ClMOQ9wwsvhk+mwU/v4Z7FtzMga/+KIEjBIAWphUrVmgGg0HT6XRaUVFR\nyHWdTqfl5eWF+5JjpqrqgI+Xl5eneb3esF8L/4+oEWqZSBbPPvuSZjYv0PT6azT4ugbf1uCePr+K\nNXhJQ/89jewCjWUmje/M1TjxTm3y5IXaPfc8Eu9PQYhxJWIVCQL7YmJ9vo7b7Wbz5s3BnpfVamX+\n/Plhv44Mr4n+/Eugf9a7BHo6sA9IwX9iZ8CpYGmAgndg/0HYegl8eiKzZ+vZtEnmboTob8yh09nZ\nic/nw2g0kpqaGul2xZyEjugvK+s23O69+Cs6g3/dzU7gNuBxmNUO+a+DaR80ngPvmtHp9nLDDRfy\n5JMVcWu3EOPZmCoSBCoQWCwWWltbAf+k/kMPPRTxBgoRD2vWPMr27Sr+umeBigK9+25OeBqu2wvf\n+xPsmQKPZqPbdRJZWSfyzDMrJHCEGEZYPR2v14vFYgEgNzcXp9OJw+Fg/vz5GI1GOjo6sFqtAyb3\nE4H0dAT0PXqgm6NHDvT2dCZcDZfeBVe8AW9cAi9dAwcmYzB4+c1vSmQoTYhRCKunU1Hh/wmutbWV\n2trakMfa29t58MEHaW1tjVn9NSEiKVDGRlEmAnPx77c5ArwLF7wMPyiCsybBL66H5y1wQMFieV8C\nR4gwhNXTMZlMZGdn09jYGKzwHOjpBFitVjo7O9m9e3dUGhwt0tM5vg0sY9MF3A+nVkPBXTDlIGzN\nAO/pchS0EMcg7IoEgeG1oZjNZurr64+pUULEytHhNI2QMjYz5kLuxWDeC9sqYPv3mJpyG7XP/osE\njRDHIKzQyczMpKWlZdh73G43WVlZx9QoIaIlUL5m165P2L+/A5gFTMY/b7MHJn0F3/gc5v0UWhbC\nhlPg8Afo9YWsWJEngSPEMQprTmfRokW0trbywgsvDFqrrLi4GEVRsNlsEWugEJFw9Jybn+F2a+zf\nPxs4DbgQOB90E2Dux7DkEUh7Dap+BdvmwOET0Om2s3p1nlQUECICwt6nY7Vacbvd5OXl0dTURF5e\nHgaDAYfDQXt7O2azOSZ11yJN5nSSV0NDM7fc8jiffrqPo3tuINjRP8sDBQ7oToOt6fDhycB+YDI6\nnY8f//hbEjhCRMiYNodWVlaydu1aOjo6gtdSU1Ox2+08+OCDEW1grEjoJC//Jk8TA0aTTZ9D3jY4\npQOazoO3LgeuBZqACUyevIOVK+dL4AgRQcdcBkdRFEwmEwaDIVJtigsJneQxcN7mdOA8gid4phyE\nK/8Mc3fCyxnw1/nQdT3wBP4eThcWywlysJoQURCx2muJTkInORwdSgtc6TOkpp8P2avgyu3w7pmw\n7VrYvxAJGyFiZ9jQ0ev1Qx5uFnha3zdrnU4X/L27uzsKzY0eCZ3EFujdvP76R/T0WPs8MhG4Bs5+\nAPJd0DkHGs+Ezw4BB9DppnHCCdM591yj7LsRIgaGXTK9cOHCMb2onMIpYiV0n40R/xLoPv+tT/oY\nCh6A1HehMQt2mYApTJ/ew1NPlUnICBFjMrzWS3o6iSXQs9mx4+8cOQKhq9KAafvgmmY43wsv5UBL\nA/RMAmDqVDu1tbLJU4h4CGtzqBDjwZo1j1JZ+QYHDswGZhPy33jiN+CylfD1HfB6Bmz4dzj4T8C9\nBFakrVgxXwJHiDgZ1ZyOx+Nhzpw5w87xBMicjoiW0ArQvwfW9D7SBWhw4Ttgc8Onp0PTbPB9BRwC\nUpg2bYbM750yAAAfK0lEQVTM2wgxDgzb08nNzUWn02E0GoHRz/HInI6IpNChtInAxb2P9C6BPu0M\nKPgxTOqCP1wLbf8bfO7s2XewadM/S9AIMU7InE4v6emMHw0NzTz8cCMfffQFHs8uDh1KR9NO7X20\nTwXo1FrILYc5n8O2H8Drn4P2GaAnJeUEqQQtxDgUVuh0dnYyY8aMaLYnbiR0xoej8zU3AY/j32ez\nmZChtMlXwDfuh5x34LXr4S/AYR/TpsnSZyHGu7AKfhoMBjZt2jTsPeXl5aSlpR1To0arvr6edevW\nUVpaSn5+vhypkOAaGpqprHyJAwc2Ao3AKcD5vY92ge4wZB6BJUVgOAE2/gu8kI6+q5N77vkW+/Y9\nSWvrIxI4QoxjI65eq6+vD276BP+poSaTadB7NU2jrq6O9vb2yLZyiHaZzebgPFPgqGyfz8fixYuj\n/vFF5ATmbN588zO6ugIbOwP/NXvnbebMhIL74MgJ8NuH4KMPOVofTSpAC5EoRhxe0+vD6gwBYLPZ\naGxsHHOjRmPdunUsX7485FpNTQ12u52enp6wX0+G12Kn75zNe+99wIED0+juPgeYRHC+hrv9N6ed\nD3n/CSd3QdPN8Pb7wOcylCZEghoxdOrq6oJ/Li4upqSkZNjzcoxGI7m5uZFr4SBUVcVms+F0OklN\nTQ1eVxSFjIwMFEVhzpw5Yb2mhE5sNDQ0c/vtW/F4CoCtQGClYyBo8v3Xp14OV5XBJV74y3fhb0bo\nmiKVn4VIcCMOrxUWFgb/nJubS1FRUdRDZSQGgwFFUfB6vcydOzeubRHhefjhRjyeB/AHzAMcXSAA\nkA/65yDnK7hyEbx9FjySRUr3Z0ydfoD09BO5996l0rMRIoGFVZGgqakpWu0Im8/nG3DN4XBgNBqH\n7eXIHqL4OnQo8F+u35wNGpzTAflPgjoJfnUzaT0+Ht98m4SMEEkk7DI4TqeT2tpavF7vsPdt3bp1\nzI0aq6qqKlauXBnzjyuG1n/+5quvAnOEgbDJh5N/CgVmmD4Vnq+CPd/yb+r8pQSOEMkmrH069fX1\nFBUVjeresUzmH4vq6mrq6+vHHHYypxN5ofM3j+OvkxaYyymAE+th/n4452l46TxoTWPaVFkgIEQy\nCyt0ApP0TU1NEZvXURRl1PempaWFLBzo+xrFxcW0tLSMuR0SOscu0Ks5dGginZ0fsmePj7///WmC\nK9G43//bxCa4/L/g8lfQvX4a532ez5knzWTJkjwJGiGSXFjDa4qiUFJSErHA8Xq9lJeXj/r+nJyc\nAcukwb8hddu2bRFpkxibo72aB4Bm/L2Z03sfDfw30+Ci34KtHD7OgZq3uPKSX/Oia008miyEiIOw\nQic1NTWiE/Hp6els2bLlmF6jtLSUysrKpC3PM571na95992P6ep6pveRRvwr0wI9nC44/UO49nLQ\nd8Hvfg3v+Xs0KSmJVY1cCHFswtr5WVJSwubNm+ns7IxWe8JSU1NDeXl5yGo1p9M54iIHcewCPZvG\nxnzeemtmn0oCcPRnmXxI/SEUvgLFtfDaSVDzajBwZs++gyVL8mLediFE/ITV06moqEBRFKxWKxUV\nFWRlZQ1ZEifaPY/AplWfzxdcPu3z+airq2Pjxo1R/dhisP02d/d5tAumdMIVz4P11/C3ufCHRei7\n2zhhWjGTJk3r3XMjiwWEON6EFTqBgFFVNWTTaH/RPsRNVVWKi4sHfcxisUTt44qjBu63yQdWge5e\nyDwE15wKnkJ47G34+2lYLHexfv33JGSEOM6FFTqjXS4d7Q2YBoMh5kuyRagpUwL7bAK/XwnmFig4\nFQ5MZerv53J+6jSmZ9WQktLNkiXXSuAIIeQQtwBZMh2ekD04M/8X8j6GWW9D0zrMh1/j4fXfkpAR\nQgwQ8dBxOp3U1dXx2GOPRfJlo05CZ3T67sXxHdjDp+e9ge+03Ux57VzmfH4FZ5xilP02QoghhR06\nHR0dOByOQc/M0TSNiooKvF5vVOd0okFCZ2h9l0Yrio4Dhx+GnEfgm//FjA/O4rFFP+amf/pOvJsp\nhEgAYc3peL1erFYrqqoOe19JSckxNUqMH6GbPlfBeTmQdyHsPQd+9RKdX1zAE+2rJXSEEKMSVuiU\nlZWhqioVFRVkZmZit9uxWq3Y7XY0TaOsrIyZM2fKkuUkElwaPdsNBU/CtD/Ac4+AJz94z8GDE+LY\nQiFEIglreM1kMpGdnR08FbSyspLa2lpee+01wL+U2Ww2s2nTJhYsWBCdFkfJ8T681neuZsqULi6/\n/FReeeVjXtmxi7/nTIOz/wQvZIH7j9AT+rNKQcFqnn/+vji1XAiRSMKqSKCqasg+mKysLFpbW4N/\nNxgMFBUVsXbt2si1UETd0eoC9/PSS2tobMzn/opWGg9O4e//+izsPxk2vAut5dBzT8hzLZa7pKqA\nEGLUwhpeS09PD6kKnZ2dDcD27duDJ3haLBZqamoi2EQRbUerCwC6Hrj4J3TnuuGDy6H6l6C+AaQC\n/hVpU6cuwmI5hdNOmy77b4QQYQkrdLKysnj66afZtm0b8+fPx2AwkJqaSlVVVXCJdEtLCwaDISqN\nFdERrC5w5p+h4E7gI6jbAh98o/eOU4DVpKZ+wGWXncGSJT+QoBFCjEnYtdfq6+vJy8ujtraWBQsW\nUFxcTFVVFT6fj/b2dhwOh6xeSzDdM76EomI4/a/gWAs73gbtG33uuBK4kssuk7kbIcSxCSt0zGYz\ne/bsoaKigvT0dMAfRC0tLdTW1gJgs9moqKiIfEtFxHUc7OC//u+/eOPS32Bq+Rq+n++EIycAzUyc\nWEpX19FViP65m2vj11ghRFKIWEWCwN6dRB1aO55Wr3X1dLHJtYk1L67h22d/m/vn34+7eQ8bNjRx\n8OAEUlK6ueyyU/jrXz8J/l2qDAghIkFqr/U6XkJn656t/KjxR8yaNouf5v+UzFMy490kIcRxJKzh\ntdLS0hErSGuahk6nS7jaa8nu7S/eZlnjMnb7dvNQ3kN859zvRL0auBBC9BdWT0evH3lbT2B4LXCw\nWqJI1p7OF/u/YM2La9jy9hZWfXMVt+XcxuQJk+PdLCHEcSqsns5QQeLz+XC5XJSVlZGRkcHWrVsj\n0jgxdoe6DrHh1Q1U/KWCGy+6kZ0/2EnaCWnxbpYQ4jgX0TmdQBkcu90e86oEqqpSXl4+5rpvydLT\n0TSNp995mhWOFVw460Iq8yo5b+Z58W6WEEIAUVhIYLfbqaurY+/evZF82VF93Pb2drZs2TKm5ydD\n6LR83MKdW++k41AHP8n/CTazLd5NEkKIEGENr42GTqcb9KydaFIUhfb29uN2YvzDzg9ZtW0VjZ5G\n7rvmPv597r8zQT985ef+BT6XLs2XJdFCiKiLaOg4nU6qq6sxm82RfNlRfdy8vDyamppi+nHjbf/h\n/ax7eR0bXt1AqbWUXT/cxfQp0we9t2/IdHZ+yCefzODTT38afNzjWQUgwSOEiKqwQkev1w/bmwgM\nTZWVlR1bq8LgdDqx2Ww4HI6Yfcx469F6+PXrv2bVtlV886xv4ipxcZbhrCHvDz2IDeBu4P6Qezye\nB9iwYbWEjhAiqsIKndzc3GEfNxgM3HDDDSxcuPCYGhUORVHIzc1N6LmYcDS/18wdW+9g8oTJ1BbV\ncvkZl4/4nJAq0sBQ/+xyGJsQItrCCp3xNnxVX1/P4sWLw3pOos77eHweVjhW0PJxCw/mPsgNF90w\n6s8lWEU6qGvQ+1JSuo+xlUIIMbywDnEbTwK13pKdelBlWeMyLt10KdmnZLPzBzu58eIbwwrPKVP6\nh0w+sCrkihzGJoSIhbB6Ok6nk6amJtxuN+AfTjObzSxatCh4iBvA008/PerjqvseCjeStLQ0UlNT\nAaitrQ3p5Yz2TXioYbjx1gPq6umiqqWKe5vv5TvnfIcdt+1g9omzR3zeYKvSli7Nx+NZ1WeI7Upm\nz/4Vp576A6ZPn9Vb0FMOYxNCRN+oQsftdlNUVDRkQFRUVGC1WqmtraW1tZWioiIqKytZtmzZsK/r\n9XopLy8fdWPnzZvHsmXLcLlcwVNLA5JlTkfTNP60508sa1zGqdNPpfFfG/na7K+N6rkDFwz4V6Wt\nX1/A+vUFbNiwuk/V6O9JyAghYm7EzaFutxur1Qr4Tw612+1kZ2cHj65uaWmhqqoKt9uNTqdD0zRs\nNhuNjY1Ra3RNTQ0ejyfkmsvlQlEUCgsLycnJCXsxw3jYHLrj8x38qPFHvKe+x0P5D3Hd2deF1QMr\nKLibxsb7B7kuh68JIcYJbQRGo1HT6XRadXX1sPdVVFRoOp1O0+v1mqqqI71sxFVWVmrFxcVjfj6g\njeLLERWf7ftMsz9j12ZVztIe/uvD2uGuw2N6nauuukcDbcCvq666J7INFkKIMRp2IcG6detQVZUV\nK1aMuEosUH5G07TgKaKx9OWXXybcENvBroNU/LmCCx65gKkTp7LzhztZcukSJk2YNOzzGhqaKSi4\nm6uvXkNBwd00NDQDgy0Y8JNVaUKIcWO4RMrKytL0ev2IydXU1KTpdDqttrZW0+l0WnZ2doQycWSK\nomh2u10zGo2aXq/X7Ha75nK5wn4dYtjT6enp0Tbv2KzN+dkc7R+f+kft3S/fHfVzn332Jc1iuSuk\nJ2Ox3KU9++xLQzy2Unv22Zei+NkIIcToDTunYzQamTlzJrt37x4xvFRVxWAwYLVaaWtri3nBz2MV\nqzmdVz96lTu23sFXR77ip/k/5Zr0a8J6/kjzNg0NzSHHTssx00KI8WTY1WsdHR3MmzdvVC8UOLzN\nZDKxffv2Y29Zkvmg4wNWOleyzbuN++ffz81fu3lAUc7RFOEcuNHTL1BN4LrrrpSQEUKMW8OGTmpq\nKi0tLWG9YEtLSzCABOw7vI+KP1fwaMuj3JZ9G7uW7OLEyScOuG+o5c4QWoRT5m2EEIls2IUENpuN\n9vb2Ufdc3G43HR0dI9ZoOx5093TzP+7/4dyfn4tX9bLdvp375t83aODAYPXRAkU4Q0sPLV2aj8Ui\n1QSEEIlp2J7OypUrqa+vJzc3F6/Xy4wZM4Z9saKiouDzjmcveF/gzsY7OWHSCfxu0e+Yd9rIQ5Qj\nDZsFBHo9oRs9pZqAECIxDBs6WVlZLF68mJqaGqxWKxUVFYOWt6mvr6esrCy4OTMzMzNqDR7Pdu/d\nzfKm5bz+2etU2CoouqBo1Js7wxk2k3kbIUSiGtVx1UVFRdTX1wP+FW1msxmz2YyiKMFTOwEKCwvH\nfFx0vEVi9dovXL/gy6++5PbLbidlYkpYzx1sTsdiuYv166UXI4RIHqMKHQCHw0FFRQVOp3PAYzab\njbKysoSeyxkPZXBkubMQItmNOnT6UhQluC8n1kdTR8t4CB0hhEh2YwqdZCShI4QQ0Zewh7gJIYRI\nPBI6QgghYkZCRwghRMxI6AghhIgZCR0hhBAxI6EjhBAiZiR0hBBCxIyEjhBCiJgZtuBnInC5XGzZ\nsoW0tDT27t2L3W4nPT093s0SQggxiIQOnbq6OhwOBxs3bgxes9vtVFVVxbFVQgghhpKwoaOqKiUl\nJfh8vuC16upqtm3bFsdWCSGEGE7C1l4rKytDr9ezdu3akOttbW3MmTMn7NeT2mtCCBF9CbuQoKam\nhpycnAHXxxI4QgghYiNhezp6vZ6mpiYURcFkMuHz+TCZTCxcuHBMryc9HSGEiL6EnNNRFAUAt9vN\nsmXLgtfLy8vx+XwsXrx4yOeO9vhoIYQQkZeQoaOqKsCAA+QWLVpEbm7usKETLQ0NzTz8cCOHDk1k\nypQuli7Nl1M/hRCin7iHTqDXMhppaWmkpqYGw6Z/6GRmZqKq6rCLCYYaPjuWHlBDQzO3374Vj+eB\n4DWPZxWABI8QQvQR19Dxer2Ul5eP+v6cnByWL1+OwWAACP7en6IoMV1Q8PDDjSGBA+DxPMCGDasl\ndIQQoo+4hk56ejpbtmwZ03PNZvOQ4dK/BxRthw4N/mU8eHBCTNshhBDjXcIumbbb7bS2toZcc7lc\nGI3GmC+bnjKla9DrKSndMW2HEEKMdwkbOiUlJQPK3ZSXl1NTUxPztixdmo/FsirkmsVyF0uW5MW8\nLUIIMZ4l7D4d8M8JVVRUYLFY8Hg8FBcXM3/+/DG91rHu02loaGbDhiYOHpxASko3S5bkyXyOEEL0\nk9ChE0myOVQIIaIvYYfXhBBCJB4JHSGEEDEjoSOEECJmJHSEEELEjISOEEKImJHQEUIIETMSOkII\nIWJGQkcIIUTMSOgIIYSIGQkdIYQQMSOhI4QQImYkdIQQQsSMhI4QQoiYkdARQggRMxI6QgghYkZC\nRwghRMxI6AghhIiZifFuwLFwOBy43W4A9u7di8ViYfHixXFulRBCiKEk7HHVLpcLr9fLwoULg9fq\n6+vx+XxjCh45rloIIaIvYYfXqqurQwIHYOHChTQ1NcWpRUIIIUaSsKHT0tKC1+sdcF1V1Ti0Rggh\nxGgkbOjYbDby8vJCgsfhcFBcXBzHVgkhhBhOws7pAGRnZ+NyuaiqqiI9PZ2Ojo4BQ26jJXM6QggR\nfQkdOgD5+fk4HA6ysrJwOp2kpqYOe38gXIQQQkRGODGS0KFTU1NDTk4Oe/fupaioCJPJRFNTE+np\n6UM+R0JHCCEib7RREvfQURRl1PempaUFezKlpaWUl5czZ84cADo6OigqKkJRFPbs2RN2O5J9eE0+\nv8SWzJ9fMn9uIJ9ff3HdHOr1eikvLx/1/Tk5OSxfvjy4Qi0QOACpqak0NjaSnZ2N0+kkNzc30s0V\nQghxjOIaOunp6WzZsiXs57W2tmKxWAZ9zG63y7JpIYQYpxJyybTZbMbj8Qz6mKqqWK3WGLdICCHE\naCRk6AQWCjidzpDriqKwd+/ekGE3IYQQ40fcFxIci5qaGjweD2lpaQAYDIYxF/yUyb7EJp9f4krm\nzw3k8xtwfyKHjhBCiMSSkMNrQgghEpOEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzMS1IoEQYngu\nl4vW1lZMJhOKopCVlZV0JZ7q6uowGo1J93kB1NfXoygKHo8HRVGw2+1jPn5lPHI4HDgcDtLS0vB4\nPFit1hG3rUjoDGMsX9BEkuzfEAGJ+qamKArl5eU0NjYGrxUXF2M2m4etpJ5IHA4HJSUl1NXVxbsp\nEVdfX4/ZbA5+T3V0dGC1WvH5fEnxPuJwONDpdDz44IPBa9nZ2aiqyvLly4d+oiYG1dTUpDkcjpBr\nVqtVq6ysjFOLIquurk5zuVzBv6uqqlksFq26ujqOrYq8pqYmzWg0ak6nM95NCVtJSYlWX18fcs3h\ncGhFRUVxalHkKIqi2e12rbq6WrNYLAn57zOSwd4rqqurNZ1OF4fWRF5hYeGA98iysjLNYrEM+zyZ\n0xlCVVXVgGs2m23Q64lIURQyMzODf09NTaWsrAy73R7HVkWO1+ultLQUr9eLyWSKd3PGpLa2lqys\nrJBrVqs1KXoF6enpbNy4MSl+4h+Mqqps3ryZjo6OkOuB3nZbW1scWhVZOp0Oh8MRck3TNIxG47DP\nk9AZwli/oIngePiGSPQ3NVVVUVV1QGAaDAYgOf6NkpnBYEBRFLxeb7ybEjVbtmxh7dq1Idfq6upY\ntGjRsM+TOZ0hDHbkQl1dHbfeemscWhNZfb8h5s6dG+/miEH4fD4AZsyYMejjiqJIYdtxLvBv2JfD\n4cBoNCblv111dTXZ2dksW7Zs2PskdEZptF/QRHG8fUMkGjkTKjlVVVWxcuXKeDcjourr62lqakKn\n07F58+YR75fQGUG4X9BElozfEEKMF9XV1cycOTNpfnANWLhwIQsXLqSjo4Ps7GxqampC5ov7k9AZ\nQbhf0ESVrN8QQowHiqJQXV1NS0tLvJsSNampqdjtdnJzcwcdSQlI+tBRFGXU96alpZGamjroY6P9\ngsZaJD6/8fwNEal/v0RjNpsB6OzsHHReJ/C4SAzl5eVs27Yt3s2IutzcXFRVxel0DrkvLqlDx+v1\nUl5ePur7c3Jyht3UNJovaCxF6vMbr98Qkf73SyQGgwGz2YyiKCGLPRRFwWAwyLxbAiktLaWysnLI\nRSGJSFEUrFYrL7zwwqCLkfqvjO0rqUMnPT190FVoIzmWL2gsjfXz62s8f0NE4vNLZDabjddeey3k\n/6DL5SIvLy+OrRLhqKmpoby8POSHBKfTmfBVJVRVxWKxDOhxB0Ym+u8v60v26QziWL6giWSob4hk\n3luQSCoqKqitrQ25Vl1dTUVFRZxaFD1aEh5gHNjE6/P5cLlcuFwuHA4HtbW1CR044H8PXLRo0YB/\nt4qKCsrKyobtictx1UNYt24dJSUlIXMEeXl5ZGdnD9gQlYjq6upob2/HarUGr/l8Purq6ti4cWMc\nWxZ5GRkZVFVVjYsh0XC53W42b95MTk5OsAc+f/78eDfrmHV0dLB27VoURaGurg6z2YzNZiMvLy8p\n6v8NtrE3wGKxsHv37hi3KDpqamrweDzB+pTZ2dnccsstwz5HQmcYY/mCJoLj4Rsi2d/UhEhUEjpC\nCCFiRuZ0hBBCxIyEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzEjoCCGEiBkJHSH6cblcFBUVYTQa\n0ev1GI1GrFYr69ati3fTxiQvLw+9/ui3elFRUcjfhYgl+Z8nRB92u53s7Gzq6+vR6/Xk5eUxc+ZM\ntm/fTllZGSaTCbfbHe9mDqqurg69Xk99fX3IdZ1Oh06nG3BNiHiQ0BGiV1FRETU1NRiNRlwuF3v3\n7mXr1q3s3r2b7u5uVqxYgaqqWK3WcRs8MDBQamtr8Xg8cWqNEKEkdITAf1R3fX09FosFr9c7aHXx\nBx98kKqqKsAfUONV/yIjqampchSCGDckdISAYOXmioqKYY95WLx4MVlZWSiKgtPpDF7vP28SoKoq\ner2e0tLSkOuKolBUVITFYkGv12MymSguLh5Q4dtutwfr5JWVlQXnmTIyMkKG0fLy8iguLgaOztl0\ndnaG/H0klZWVWK3WYHtKS0sHrTheXV0dcl92dnbI10KI4UjoCIH/SAej0ciCBQtGvNdutwPQ1NQU\ncn24eZK+jymKQkZGBk8//TQZGRnBeaS6ujqsVuug5zUFhv5uuOEGSkpKgqEVeLMvLy+npKQk2L7q\n6uqQ8BxpDsdqtVJeXo5erw+2p7q6GovFEjKUWFZWRmlpKW1tbRQVFWGz2YJn/IznIUcxjmhCHOc8\nHo+m0+m07OzsUd3vcrk0nU6n5efnB6/ZbDZNr9cPuLe9vV3T6XRaaWlp8FpJSYmm1+s1p9MZcm9l\nZaWm0+m0urq6kHt1Op2WkZGhdXR0BK87HA5Np9Npdrs9eK22tlbT6XRafX19yOsWFhaGtK3/3ysq\nKjSdTqdt27Zt0M/TarUGrxkMBi0jIyPkvkBb+n6OQgwlqU8OFWI0VFUFGHBo31CO9QCu0tJSCgoK\nBpyLk5mZCUB7e/uA5/Qf9gucDTTWA/e0PvM+a9euJS8vj6ysrODXAvyfZ25uLk6nk87OTmbMmEFH\nRwcZGRkhr5Wbm4vL5cJgMIypLeL4IqEjjnuBN8vAybAjCdw31jfZzMzMYMCoqkpLSwsulyu4SGEw\n0TyttqOjg6amJoxG46CP63Q6fD4fM2bMoLCwkLq6uuCwoM1mIzMzc9CFF0IMRkJHHPcCPZzRhk5L\nS0vI88KlqiplZWVs2bIlOH9jtVqxWq1D9lyGOnRvrAJzPIHPOS8vj7KysiHvDwTSli1bWLduHVVV\nVSH3l5SUUFFREXLSrhCDkdARArDZbMFl04OdLOpwOLDZbADBHsmiRYtGfF2fzzfgWm5uLm63G7vd\njt1uD/YSnE4ndXV1x/JphC0QZgaDYdTHYC9fvpzly5fT2dlJU1MTVVVVVFdX09LSEgxkIYYiq9eE\ngOBP7YP9tK+qKvn5+WRnZ1NZWYnb7cZqtY5qSMnlcg14LbfbTVFREY899ljIa2gxPMQ38LEMBgOp\nqak4HI5B7zMajcE5HEVRKCsrC66YmzFjBgsXLqSxsTE4rxNYpi3EUCR0hMDf+ygsLAwuZ+67/Ndg\nMLBlyxZcLhfl5eXodDpqa2tDnm8wGNA0LWS/SmAYbTD9Fwv0vfdYw2c0z++7hNput9Pe3h7c5xNQ\nWVlJR0dHyB6jdevWBZeM96UoCjqdbtg9TkIAsmRaiL6Kioo0nU6n6XQ6zWAwaDabTcvKygpe0+v1\nA5Y1a5qm1dXVBe+x2+1aSUmJZjQatfz8fM1oNIYsbc7Ly9N0Op1WVFSkVVRUhNyr0+k0i8WiORwO\nTdOOLpnuu1w6oP+y7cDSZYvFopWVlQWvFxYWajqdbsi/a5qmWSyW4HMLCwuDn3P/ZeSBthuNRq2w\nsFArKSnRDAaDptfrtfLy8jF8xcXxRkJHiH5cLpdWVFSkmUwmTa/XayaTScvOztZqamo0VVWDb7z9\n98NUV1cH37xNJlPwTdhoNIbsYVFVVbPb7ZrRaAy+sQdey263a3q9Pnh/4O+jCR1NOxoKJpMpeK2o\nqChkX07/vweUlZVpVqs1uC9oqBApKyvTLBZLyNem/9dCiKHoNC2GA8lCJImHHnqIZcuWxbsZQiQc\nCR0hhBAxIwsJhBBCxIyEjhBCiJiR0BFCCBEzEjpCCCFiRkJHCCFEzEjoCCGEiBkJHSGEEDEjoSOE\nECJmJHSEEELEzP8HWpCiemPQ0ukAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23ace6750>"
]
}
],
"prompt_number": 13
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"Mann-Whitney U test. NOP\", scipy.stats.mannwhitneyu(x,y)[1]*2)\n",
"print(\"Unpaired T-test\", scipy.stats.ttest_ind(x,y,equal_var=False)[1])\n",
"print(\"Median test\", median_test(x,y))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Mann-Whitney U test. NOP', 0.087346603341420845)\n",
"('Unpaired T-test', 0.25717460096222738)\n",
"('Median test', 0.18389510355041561)\n"
]
}
],
"prompt_number": 49
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Non-Equal variance and Non-Normality. USE: Median test"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" x = [np.random.lognormal(1,1.3) for _ in range(200)]\n",
" y = [np.random.lognormal(1.5,1) for _ in range(200)]\n",
" \n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAakAAAEsCAYAAAB5UUwwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U9sI9edJ/AvZbs94yRisbq9nvF6ZqSighnsHCKSYrAB\ndgczTdKXAXYTy6J82pOlYvbcbrKBnBYLSCXn7lYxWGByk0gamACDXUtkB4M9LBCRxUyQnWy2zUdt\n/k4yLaooJx13PFHtQWFFJVJqskWyHqXvBxDaevVK9bNU6m9X1av3Ao7jOCAiIpLQlN8FEBERnYch\nRURE0mJIERGRtBhSREQkLYYUERFJiyFFRETSet7vAjqKxSJCoRASiUTP7ZZlYXt7Gzdv3sTBwQF0\nXcfs7Kxne61Wg6qqEEIgGo2e+7WIiGgySBFS5XIZq6urKBaLPbcXi0WUy2Xcv3/fbdN1HZubmwAA\nIQRyuRx2dnbc7el0GpqmeYKMiIgmi6+3+5rNJjKZDJrNJlRV7dnHtm2srq56Aso0TTx48MD93DAM\nZDIZz366riObzY6mcCIiGouALDNOzM3NwTRN3L5929OezWYxNTWFtbU1T/v+/j5mZmYAAKqqwrIs\n93PgJNxUVcXx8fGoSyciohGRfuBEPp9HPB7vau8Ekm3bbiCdpigKgJMwIyKiySTFM6mL2LaNYDCI\nfD4PVVXRarWgqioWFxcBAK1WCwAwPT3dc38hhOcKi4iIJofUISWEAADU63XcuXPHbc/lcmi1WlhZ\nWYFt236VR0REIyb17b5OAGma5mlfXl7moAgiomtA6iupTjidDalIJALbti/9vCkQCJy7TZLxJERE\n15rUV1KdwQ+dP88SQrgBdnR01LPP2YDr10UBRkRE4yF1SAEnIdN5NtVrm6IoPfsIIaAoyoWDJhzH\n6flBRERykD6kdF1HrVbztFmWhVAo5AZQMpnE3t5eV59UKjWuMomIaASkCqleVzGrq6vu9EcduVwO\n+Xze/dwwDBQKBU8f0zRhGMZoCiUiorHwdcaJdruNtbU1CCFQLBahaRqSySRSqZT7HhRwMn2SYRgI\nh8NoNBpIp9NdM1PU63VsbW0hHo9DCIFYLNbVp1+d51G89UdE5C9ppkWSCUOKiEgOUt3uIyIiOo0h\nRURE0mJIERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0GFJERCQthhQREUmLIUVERNJiSBERkbQY\nUkREJC2GFBERSet5vwvoKBaLCIVCSCQSF/azbRu5XA7379/3tFuWhVqtBlVVIYRANBp96tciIiK5\nSRFS5XIZq6urKBaLT+2bzWZxeHjoaRNCIJfLYWdnx21Lp9PQNA2zs7NDr5eIiMbD19t9zWYTmUwG\nzWYTqqo+tb8QAoeHh+56Tx2GYSCTyXjadF1HNpsdar1ERDRe0ix6ODc3B9M0L1xNt7Nk/O7uLra3\nt912VVVhWRZmZmbcNtu2oaoqjo+PB66Fix4SEclhYgZOVCoVJJPJrnbbtt1AOk1RFADA/v7+OMoj\nIqIRkOKZVD+EEEgkEl1XN61WCwAwPT197n6nr7AG8fd/Xx2o/5/+6R/hD/7glWc6FhERdZuIkCqV\nSlhZWem5zbbtkR13f/9f99338PCfoKoHDCkioiGSPqRGGUJPo6p/2HffJ08eA3gyumKIiK4h6Z9J\nFQoFLC4uup+fHdl3GYFAoOcHERHJQeqQqtfrWFhY8LSdfSalaRoA4OjoqOfX6GwnIqLJI/Xtvmq1\nikajga2tLbfNsiz35d14PI7FxUVomgYhBObn591+QggoinLhoInzhpjzaoqISA5Sh1SvwRLvvvsu\nqtUq1tfX3bZkMom9vT1PSFmWhVQqNZY6iYhoNKS63dfPy7OPHj3q6mcYBgqFgqfNNE0YhjHU+oiI\naLx8nXGi3W5jbW0NQggUi0VomoZkMolUKuUZLAGcTKFkGAa2t7fRbrexsrICXdcRiUQAnDy/2tra\nQjwehxACsVjswtkrLtK53fc3f/NPfe/z85/v4y//8gYWFiLPdEwiIuomzbRIMumE1H/+L/ef0vN3\nHj36MZb/KoY3vvgfR1UWEdG1I/UzKb+pM6/23bf9SfdtSCIiuhypnkkRERGdxpAiIiJpMaSIiEha\nDCkiIpIWQ4qIiKTFkCIiImkxpIiISFoMKSIikhZDioiIpMWQIiIiaTGkiIhIWgwpIiKSljQTzBaL\nRYRCISQSia5tpVIJQgg0Gg0IIaDretdSHpZloVarQVVVCCEQjUZ7fi0iIpocUoRUuVzG6uoqisVi\n17ZSqQRN09xQarfbiMViaLVa7sq9neXkd3Z23P3S6TQ0TcPs7Ox4/ieIiGjofL3d12w2kclk0Gw2\noapqzz5CCHdhQwAIBoPIZrPQdd1tMwwDmUzGs5+u68hms6MpnIiIxsLXkJqdncX9+/fdK6KzbNvG\n1tYW2u22p71zG29/fx8AUCgUEI1GPX1isVjPKzMiIpocUg+cUBQFQgg0m81z+9i2Ddu2u67EFEUB\n8LsgIyKiySN1SAFAq9XC/Py8p61cLiMUCmFmZgatVgsAMD093XN/IcTIayQiotGQPqR62dzcxL17\n9wCcXEkREdHVNHEhZZombt26hTt37vhdChERjZgUQ9D7JYSAaZqoVqtD+XqBQGAoX4eIiEZjoq6k\ncrkcHjx44GnTNA0AcHR01HOfznYiIpo8ExNSmUwGGxsbXQMkFEWBpmldAySEEFAUBTMzM+d+Tcdx\nen4QEZEcJiKk8vk8crmcJ3AqlYo7ND2ZTGJvb8+zj2VZSKVS4yyTiIiGTKqQ6nUV03kht9VqwbIs\nWJaFcrmMQqHgTnlkGAYKhYJnP9M0YRjG6IsmIqKR8XXgRLvdxtraGoQQ7sSxyWQSqVQKi4uLsG0b\n6XS6577hcNj972AwCMMwkMvlEI/H3bn8LrrVR0RE8vM1pILBINbX18/drigKjo+P+/pakUjEM8cf\nERFNPqlu9xEREZ3GkCIiImkxpIiISFoMKSIikhZDioiIpMWQIiIiaTGkiIhIWgwpIiKSFkOKiIik\nxZAiIiJpMaSIiEhaDCkiIpIWQ4qIiKTl6yzopxWLRYRCISQSia5tlmWhVqtBVVUIIRCNRrv69dOH\niIgmixQhVS6Xsbq66i5weFpnbaidnR23LZ1OQ9M0d9HDfvoQEdHk8fV2X7PZRCaTQbPZhKqqPfsY\nhoFMJuNp03Ud2Wx2oD5ERDR5Ak6vNdt9MDc3B9M0cfv2bU+7qqqwLMuzyq5t21BV1V0QsZ8+gwgE\nAgCAr3z9G33v03z4HXwp8udY/NIXBz4eERH1JvXACdu23bA5TVEUAMD+/n5ffYiIaDJJHVKtVgsA\nMD093XO7EKKvPkRENJmkDinbtofSh4iIJpMUo/v80nn2REREcpL6SoqIiK43qUNK0zQAwNHR0bnb\n++lzHsdxen4QEZEcpA4pRVGgaVrX4AchBBRFwczMTF99iIhoMkkdUgCQTCaxt7fnabMsC6lUaqA+\nREQ0eaQKqV632gzDQKFQ8LSZpgnDMAbqQ0REk8fXGSfa7TbW1tYghECxWISmaUgmk0ilUlhcXHT7\n1et1bG1tIR6PQwiBWCzWNTNFP336xRkniIjkIM20SDJhSBERyUGq231ERESnMaSIiEhaDCkiIpIW\nQ4qIiKQ10Nx9c3NzA8935zgOAoEAHj58ONB+REREA4VUJBJBs9mEZVlu2+zsLFqtFtrtNoCTWSLO\nLtnOiVyJiOhZDBRS9+7dw8LCAqLRKPL5PCKRiLvNsiysrKxgf38fxWKxK6iIiIgGNdAzqfX1dSiK\ngkql4gkoAIhGo6jVajg+PkYulxtqkUREdD0NFFLlchmpVArBYPDcPslkEuVy+dKFERERDRRSjuM8\ndTn2ZrN5qYKIiIg6BgqpZDKJWq2G999/v+f2UqkEy7IQi8WGUhwREV1vAw2cMAwD5XIZS0tLePPN\nN5FKpaBpGhqNBnZ3d1EsFt1+RERElzVQSGmahkqlgmw2i0Kh0LU8hqZp2Nzc7BpUQURE9CwGCing\nZBTf7u4uhBCwLAtCCHcZ92g0OooaAZwM2qjX6wCAg4MDhMNhrKysePpYloVarQZVVSGEQDQaRSKR\nGFlNREQ0WgOHVMetW7ewsLDw1NF+w2BZFtrtNt555x23rVQqIZ/Pu0ElhEAul8POzo7bJ51OQ9M0\nvrNFRDShBp67r16vY2FhAYqiIBwOo1arATiZMumrX/3q0AsETlbZPb0IIgAsLi5id3fX/dwwDGQy\nGU8fXdeRzWZHUhMREY3eQCHVbDYRi8VgWRYSiYRnufeDgwPcvXsX8Xh86EVWq9WeQ9tt23b/u1Ao\ndN1ujMVi7mAOIiKaPAOFVGfUXq1W6xo0cXh4iPX1ddRqNdy7d294FQLukvKng6pcLiOdTgM4CSvb\ntqGqqmc/RVEAAPv7+0Oth4iIxmOgkNre3kYymTx39N7du3cRiUSGfvXSmY4pHA4jn8+jXC6j3W7j\n7bffBgC0Wi0AwPT0dM/9n/YCMhERyWmggRO2bSMcDl/YR9M0lEqlSxXVS7Vaxeuvvw5d1xGNRlGp\nVDx1ERHR1TPQlVQkEkG1Wr2wT71eH8lQ9Hw+j42NDXf4eywWu/QUTIFAoOcHERHJYaCQWl5eRq1W\nwze/+c2ef5mn02kIIZBMJodWIABkMhmkUinMz88jkUig2WxC0zSkUqmhHoeIiOQyUEh1njklEgl3\n0IJhGFheXsbNmzdRLBahaRrW19eHVmDnVt7MzIzbFgwGsbOzA0VR8ODBA2iaBgA4Ojrq+TU6289y\nHKfnBxERyWHg96RqtRrW19fxrW99CwCwu7uLQqGA4+Nj3L17Fx9++OFQC6zVauc+B9N1HbZtQ1EU\naJrWNUBCCAFFUTwBR0REk2PgkAJOrqgODw9xfHyMDz/8EK1Wyx2CPmydCWx7sW3bff6VTCaxt7fn\n2W5ZFm8JEhFNsIFCKp/Pdy3ToWma+z7SKHSmNDo9mg84uUo6ODhwr5IMw+h6d8s0Tc7ITkQ0wQLO\nAA9hpqamEAqFcHBwMMqaesrn82g0Grh58yaAkxd1z04wW6/XsbW1hXg87o4AvH379sDH6gwK+crX\nv9H3Ps2H38GXIn+OxS99ceDjERFRbwO9J/X222/ja1/7Gr797W9jfn5+VDX1dDaQeolEIlwmhIjo\nChkopEzTxNzcHGKxGDY3N7GwsABN086d6YGIiOgyBgqpztx4juNgdXXVbT/9zpTjOAgEAvjNb34z\npBKJiOi6Giik+l1AkLM2EBHRMFwYUrlcDp///OfxxhtvAEDX6DkiIqJRunAI+sbGBra2trra8/k8\nvvzlL4+sKCIiIuAZX+bd2dmBaZrDroWIiMjjmUIKAOe4IyKikXvmkOLgCCIiGrVnDikiIqJRY0gR\nEZG0GFJERCStp77MWy6Xsby87GmrVCpwHKer/bReQ9eJiIgG8dSQOjw8PPcl3ote7mVIERHRZV0Y\nUtVqdVx19MWyLGxvb+PmzZs4ODiAruvuelOd7bVaDaqqQgiBaDTa91ROREQknwtDqrPqrQyKxSLK\n5TLu37/vtum6js3NTQAniyDmcjns7Oy429PpNDRN8wQZERFNjokYOGHbNlZXVz0BZZomHjx44H5u\nGAYymYxnP13Xkc1mx1YnEREN10SE1NraGnRd97Strq5id3fX/bxQKHRd+cViMRSLxbHUSEREwzcR\nIZXP5xGPx7vaZ2ZmAJxcadm27a531aEoCgBgf39/1CUSEdEIDLSelF9s20YwGEQ+n4eqqmi1WlBV\nFYuLiwCAVqsFAOeuECyEcAONiIgmh/QhJYQAANTrddy5c8dtz+VyaLVaWFlZgW3bfpVHREQjJP3t\nvk4AaZrmaV9eXr70oIhAINDzg4iI5CB9SHXC6WxIRSIR2LbN501ERFeY9CHVGfzQ+fMsIYQbYEdH\nRz37nA24Dsdxen4QEZEcpA8p4CRkOs+mem1TFKVnHyEEFEXhoAkiogk1ESGl6zpqtZqnzbIshEIh\nN4CSyST29va6+qRSqXGVSUREQzYRIbW6uupOf9SRy+WQz+fdzw3D6Jrw1jRNGIYxlhqJiGj4pB+C\nDgDBYBC7u7vIZDIIh8NoNBrI5XK4ffu2p49hGMjlcojH4+5cfrzVR0Q0uSYipABgdnbWM3dfL5FI\nBJFIZEwVERHRqE3E7T4iIrqeGFJERCQthhQREUmLIUVERNJiSBERkbQYUkREJC2GFBERSYshRURE\n0mJIERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0JmYW9NNs20Yul+uaFd2yLNRqNaiqCiEEotEo\nEomET1USEdFlTWRIZbNZHB4eeto660ft7Oy4bel0GpqmYXZ2dtwlEhHREEzc7T4hBA4PDxEIBDzt\nhmEgk8l42nRdRzabHWd5REQ0RBMXUpVKBalUCo7jeNoLhQKi0ainLRaLoVgsjrM8IiIaookKqUql\ngmQy2dVu2zZs24aqqp52RVEAAPv7++Moj4iIhmyiQkoIgdnZ2a6rqFarBQCYnp4+dz8iIpo8ExNS\npVIJKysrPbfZtj3maoiIaBwmYnTfqELo7OCLy3r8y1/ihz/84UD7vPLKK7hx48ZQ6yAiuiomIqQK\nhYLnKmrY4TIMv/fSp/Dw8UM8/s4v+t7nydETvPHv38Brr702wsqIiCaX9CFVr9exsLDgaTv7TErT\nNADA0dFRz+dSne1nnf06Hc8Sgi++9BJennkBr/7Jq33v85OHPxn4OERE14n0IVWtVtFoNLC1teW2\nWZblvrwbj8exuLgITdMghMD8/LzbTwgBRVEwMzPjQ+VERHRZ0odUr8ES7777LqrVKtbX1922ZDKJ\nvb09T0hZloVUKjWWOomIaPgmZnTfaY8ePeq6VWcYBgqFgqfNNE0YhjHO0oiIaIikv5I6rdlswjAM\nbG9vo91uI5PJQNd1RCIRBINBGIbh3gLs3A7krT4ioskVcM4bPXCNdQZOfOXr3+h7n9bhT/Fnf/YJ\nZv7kj/ve5ycPf4K/nv9rju4jIjrHRN7uIyKi64EhRURE0mJIERGRtCZq4ITsPvn1J/jFL/qfceLx\n48c4Pj4eYUVERJONITUkL774Ej5sHKLR+EHf+7R+9BP8u9mf4Y//uP/BFkRE1wlDakg+9VIQn3op\nONA+9o8/GlE1RERXA59JERGRtBhSREQkLYYUERFJiyFFRETSYkgREZG0GFJERCQthhQREUlrYt6T\nKpVKEEKg0WhACAFd17G4uOjpY1kWarUaVFWFEALRaBSJRMKniomI6LImIqRKpRI0TXNDqd1uIxaL\nodVquSv3dtaP2tnZcfdLp9PQNA2zs7O+1E1ERJczEbf7hBCIRCLu58FgENlsFrquu22GYSCTyXj2\n03Ud2Wx2bHUSEdFwSR9Stm1ja2sL7Xbb0965jbe/vw8AKBQKiEajnj6xWAzFYnEsdRIR0fBJH1KK\nokAIgWazeW4f27Zh2zZUVe3aF/hdkBER0WSRPqQAoNVqYX5+3tNWLpcRCoUwMzODVqsFAJienu65\nvxBi5DUSEdHwTURI9bK5uYl79+4BOLmSIiKiq2ciRvedZZombt26hTt37lzq6wQCgSFVREREozBx\nISWEgGmaqFarfpdCREQjNnG3+3K5HB48eOBp0zQNAHB0dNRzn872sxzH6flBRERymKiQymQy2NjY\n6BogoSgKNE3rGiAhhICiKJiZmRljlURENCwTE1L5fB65XM4TOJVKxR2ankwmsbe359nHsiykUqlx\nlklEREM0ESHVeSG31WrBsixYloVyuYxCoeBOeWQYBgqFgmc/0zRhGMbY6yUiouGQfuCEbdtIp9M9\nt4XDYfe/g8EgDMNALpdDPB535/LjrT4iosklfUgpioLj4+O++kYiEc8cf0RENNkm4nYfERFdTwwp\nIiKSlvS3+640B/jHf9xHu93f7UwAeP75AL7whc/hxRdfHGFhRERyYEj56NOfeQW2/VlMTb3a9z4f\nffRdRCIfM6SI6FpgSPno+edvYHr6FhTlX/W9z+PH/JER0fXBZ1JERCQt/rN8whwe/hzf+z/fw2c+\n85m+97nxwg189rOfHWFVRESjwZCaMP/vZ9/H//xBE9PB3gs89nL86BjhcBhTU7xwJqLJwpCaQDdf\nuYmXX3m57/4/fvTjEVZDRDQ6DCkfOXDQ+JGFH/zsf/e9zy+etIHAH46wKiIieTCkfBR85WX86slH\n+BU+6nufG6+9iN//1O+PsCoiInkwpHz0/I0beP7GjYH2+fiTl7jsPRFdGwypa+Af/uH7+G+P//tA\nAydmZkK4ffvfjrAqIqKnu1IhZVkWarUaVFWFEALRaBSJRMLvsnz30Ue/RiiUxHPP9ffj/vjjX+DR\nI2vEVRERPd2VCanO+lE7OztuWzqdhqZp7sKI19nU1HN47rnn+u5LRCSDK/PijGEYyGQynjZd15HN\nZn2qiIiILuvKXEkVCgXcu3fP0xaLxdyl56+K3/wmgO9+tznQ86WPP/kE9e/9DwTQ34CLJ09+BeXT\nBwD+6hmrJCIajisRUrZtw7ZtqKrqaVcUBQCwv79/ZZaRV0Jz+PhXvx5on9c+9woeP3fUd//HvzzC\n40c/xI9+9KOBjjM9PY3p6f5nwrhKjo+P8dOf/hSO4wy0n6Io+PSnPz2iqogm35UIqVarBQDn/gUp\nhLgyIfXC8y/ihecHXKZjwNeqAs8FYP/y+/i7b/9d3/s8+dUTzL82j7/4wl8MdrAr4ujoCN/4xncx\nNfVK3/t8/PEv8YUvHODzn//cCCsjmmxXIqRs2/a7hCtl6rnnoL52C69+tv91rlo/bw18FfEsavUa\nrO8PNvJQ/N8f449uzeOFF17oe5+XX/49fPGLg40MnZp6Ca++Ot93/3/+5x/CcVoDHYOut1arhb/9\n2/+Ff/mXwfZLJv/NxA4guxIh9aye9lLsf/1P/2FMlchpw+8CiGjiDPsfq1dmdB8REflv2DPiXIkr\nKU3TAJw8F+j1XKqz/azzEr/zTR7H7at+sab+yVgXa+oPa+qfjHWNYsq2K3ElpSgKNE2DEMLTLoSA\noihXZtAEEdF1cyVCCgCSyST29vY8bZZlIZVK+VQRERFdVsCR6VrxEtrtNpaWljzTIr3++uswTXPg\nKymZL6NZ09PJWBdr6g9r6p+MdY2ipisTUgBQr9extbWFeDwOIQRisRhu37498Ne5Lj/8y5KxJkDO\nulhTf1hT/2SsiyE1Jtflh39ZMtYEyFkXa+oPa+qfjHUxpIiI6Fq5MgMniIjo6mFIERGRtBhSREQk\nLYYUERFJiyFFRETSuhJz9w2LZVmo1WpQVRVCCESjUSQSgy3XcFmlUglCCDQaDQghoOs6FhcXpanT\ntm3kcjncv39fiposy8L29jZu3ryJg4MD6LruWZJg3HWVy2XU63UAwMHBAcLhMFZWVrpqHmVNxWIR\noVCo59fs59ijqu+iuvw67y+q6bRxnvdPq8mPc/6imkZ+zjvkOI7jNBoNJ5VKedqWlpYcIcTYaigW\ni45lWe7ntm074XDYMU1TmjpXV1edpaUlT5tfNRUKBUfX9a76/KqrVqs5xWLR01YsFsf689vd3XVC\noZBTqVS6tvVz7FHVd1Fdfp33F9V01rjO+6fV5Mc5f1FN4zjnGVK/tbq66pRKJU9buVzuOjFHaWNj\no6vNNE0nEAi4n/tZZ6PRcJaWlpx0Ou1p96Omw8NDJxQKedo2Nzedubk53+o6+5dHx+njjaomIYSj\n67pjmqYTDod7/oXSz7GHXV8/dY37vO+nptPGcd73U9O4z/l+ahrHOc+Q+q1QKOQ0m01P2+HhoecX\nZZQODw+dWCzm2LbtaW80Gk4gEHBr87NO0zQd0zS7Ti4/arp7966Ty+W62k/XMe66YrFYz38dnv5X\n5DhqOu8vlH6OPcr6etXl93nfT0iN+7w/ryY/z/nzahrHOc+BEzi532zbNlRV9bQrigIA2N/fH3kN\niqJACIFms3luHz/rrFQqSCaT0tSUz+cRj8e72juTCftRVzKZRCqV8vwMy+Uy0um0bzV19HNsP+rj\ned+/63rOM6QAtFotAOi5YCKArnWqRlnH/Py8p61cLiMUCmFmZsbXOoUQmJ2d7ZqTy6+abNtGMBhE\nPp9HqVRy//SzrvX1dSiKgnA4jHw+j3K5jHa7jbffftu3mjr6ObZf9fG87891Pec5ug8nP3xZbW5u\n4t69ewD8q7NUKnWN1unwo6bOiV2v13Hnzh23PZfLodVqYWVlxbfvVbVaxeuvvw5d1xGNRlGpVNxt\nfp5n/Rxbpt8Dnvde1/mc55WUxEzTxK1btzwn5bjJ9BdXR6cmTdM87cvLy8hms36U5Mrn89jY2MDu\n7q67XMxFt7KoG8/7btf5nGdISUoIAdM08cEHH/haR6FQ8Lyv0pmK30+dX9Szv7CRSAS2bY/lGWIv\nmUwGqVQK8/PzSCQSaDab0DSNq0MPgOd9b9f5nGdI4Xc/+KOjowu3j1Mul8ODBw961jGuOuv1OhYW\nFjxtZ+/N+/G96zx07fx5lhBi7HV1/qV7ehXoYDCInZ0dKIqCBw8e+Hqe9XNsGX4PeN73dp3PeT6T\nwskPXtM0CCE8D3CFEFAUZeDl5y8rk8lgY2Oj62HjuOusVqtoNBrY2tpy2yzLghACuVwO8Xgci4uL\nvnzvOsfs9fU1TRv796pWqyEcDvfcpus6bNv29Tzr99h+/h7wvL/YdT3nGVK/lUwmsbe35/lGWpY1\n9ls1+XweuVzO88OrVCrQNA2zs7NjrbPXQ+N3330X1WoV6+vrbpsf3ztd11Gr1XD79m3PMTsjwsZd\nl6ZpKBQKPbfZtu0e08/zrJ9j+1Ufz/unu7bnfP+vc11ttm13Td2RSqW6XkIbpUKh4Jim6dRqNfdj\nd3fX81a333XevXu366VGP2rqTJ1z9pin32wfd126rjvlctnT1mg0nGw2O9aawuFwVx39HnuU9Z1X\nl5/n/Xk1nTXO8/6in59f5/x5NY3jnOfy8afU63VsbW0hHo+7o1RO/6tllHq98NYRDofx8OFDX+ts\nNpswDAPQlOBxAAAEhElEQVTb29tot9tYWVmBruuIRCK+1xQOh9FoNJBOp7uOOe668vk8Go0Gbt68\nCeDkVtXZf5mPoqZ2u421tTUIIVAsFqFpmvui5ekBAP0ce5j1Pa0uP877fr9XwPjO+35rGuc5329N\noz7nGVJERCQtju4jIiJpMaSIiEhaDCkiIpIWQ4qIiKTFkCIiImkxpIiISFoMKSIikhZDioiIpMWQ\nIhoyy7IwNTXVNZP2WeVyGVNTU+5S2/1aWlrC1BR/del64JlONGTRaBSKoqBer6Pdbp/brzM551tv\nvTXwMfxe34hoXBhSRCOwuroKx3Gwvb19bp/t7W0EAgG88cYbY6yMaLIwpIhGYHl5GQCwubnZc7tl\nWWi323jzzTfHWRbRxGFIEY1AJBKBpmnn3vLrLKjXCTPgZCG4paUlhMNhTE1NQVVVpNNpNJvNrv1P\nzwudSqV6PqOybRtTU1PIZDJd2zY2NhCLxdzjZDKZnsch8htDimhEdF0/95afaZqeW31CCMzNzeH9\n99/H3NwcdF3HwsICisUiYrHYhc+2gIufUZ3dFovFkMvlMDU15R7HNE2Ew2HU6/Vn+D8lGh2GFNGI\ndG7lnb3l1+tWn2EYCAQC2N3dxQcffID33nsPOzs7MAwDtm2jXC4PpaaNjQ3U63VUKhXs7e25x6nV\nagB6r0pL5CeGFNGIzM7OIhKJdN3y63WrL5PJoFAodC0E11lc7/DwcCg1ra2tIZVKIRqNwrZt92N2\ndhaJRAKWZeHo6GgoxyIahuf9LoDoKnvrrbdQr9dhmibeeecdAECxWOwa1ReJRNxAsm0b1WoVlmWd\nO/DiWbXbbezu7iIUCvXcHggE0Gq1MD09PdTjEj0rhhTRCK2uriKbzWJrawvvvPMOhBBoNptYWlry\n9LNtG9ls1l2mHDh5dhSLxYY2oEEIAeBkoEU2mz2333kBRuQHhhTRCAWDQUSjUfeWX7FYBHAyqOK0\nRCKBer0OXdeh6zrm5+cBAJVKxd1nUK1Wy/O5qqoAAEVRum4rEsmKz6SIRqwzys80TWxtbSEQCHhC\nwrZt1Ot1LC0t4b333nMDCvAONR+UZVmezxVFQTAYPHcQRigUwtzc3DMfj2gUGFJEI9aZm29zcxP1\nev3cF3jPDo7o3AIEusPq9LByRVHgOA4qlUrPfU/TdR2Hh4dd8wVubGyg3W73fKeKyE+83Uc0YsFg\nEMlk0r2COXurT1EUd3s6ncbCwgIajQYKhQLi8TiAkyHqmqYhkUgA8IbWW2+9hVKphFQq5U7H1Nn3\nbPCtr6+jWCyiWCxibm4OkUgEQgjU63XEYjHcuXNnlN8KosE5RDRyxWLRCQQCztTUVM/ttm07uq47\noVDICQQCzsLCglMqlRzHcRxd152pqSknk8k4juM4S0tLXV/HNE0nHA47gUDAUVXVyeVyjuM4TigU\ncvc7LZvNOrFYzAkEAs7c3Jzbn0g2Ace5xE1vIiKiEeIzKSIikhZDioiIpMWQIiIiaTGkiIhIWgwp\nIiKSFkOKiIikxZAiIiJpMaSIiEhaDCkiIpLW/wfN3Mv8uQph8wAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60e0eb4ed0>"
]
}
],
"prompt_number": 50
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print('Mann-Whitney U test test. NO', scipy.stats.mannwhitneyu(x,y)[1]*2)\n",
"print('T-test. NO', scipy.stats.ttest_ind(x,y)[1])\n",
"print('Median test', median_test(x,y))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Mann-Whitney U test test. NO', 0.0087839417344925171)\n",
"('T-test. NO', 0.63251493042679674)\n",
"('Median test', 0.58075022224762773)\n"
]
}
],
"prompt_number": 51
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Compare 2 paired samples"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Imagine we want to check if there are difference in GFP expression after we add salicylate in non-growing cells."
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"USE: Wilcoxon signed-rank test"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" x = [np.random.randn() for _ in range(200)]\n",
" y = [np.random.randn()+0.2 for _ in range(200)]\n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y),np.max(x+y),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U1sG2eeJvCnaH3YsU0WabeT2I1esaT0zHT37JofCtBA\nA7sTkgEGGMzBsqScZ2xRudsmfVigF1jAotKXvWwsyoM99GEhkcxpZxptFZ1ZoHeRji3KyU5nJh96\nqaQnTie2SkXZ7diWxNqDhowpUjJLLrKK0vMDBERv1Sv+LYV6VPV+lGQYhgEiIiILuewugIiI9h6G\nCxERWY7hQkRElmO4EBGR5RguRERkOYYLERFZ7sDPf/7zn9tdhKqqSKfTWFhYwC9/+Ut89dVXCIVC\n1eNCCIyMjODUqVPw+Xy4c+cOUqkUJEmCoig2Vk5ERI1Idq9zUVUVkiQhEolU28LhMEZHR3Hx4kUA\nm+EyMDBQPS7LMq5du4YzZ860vV4iIno222+LTU1N1bVFo9GadkmSoKoqdF2HEAKapjFYiIgczPZw\nqQTH0wzDgNfrrWtzu93o6+trY3VERLQbXXYXMDs7W9eWzWbx5ptv2lANERFZwfZw2SqdTiMcDuPC\nhQs17UII6LoOANA0DT6fD0NDQ3aUSEREz+CYcMnlcpibm4MkSZiZmak55vP5AKAmTEZGRuraiIjI\nGWyfLbZVqVRCJBLB9PQ0AoHAtufl83nE43F89tlnbayOiIiaYfuA/lYejwfxeLxmanIjfr8fQgis\nrq42PC5J0rYfRETUWo4LFwCIRCLQdR03btwAAExOTtadU7lVJoQw/fUZMERErWVruAgh4PV6cfv2\n7YbHK+takskklpaWao5pmgYA267QNwyj4QcREbWerQP6uq6jv7+/LiAqVyPBYBB9fX2YmpqqW9+i\nqipCoRDcbne7yiUioibZeuUSDAYxOjpad0WRSqWQSCSqgeLz+VAsFqvHdV1HOp3G9PR0O8slIqIm\nOWK22PT0NBYXF3Hs2DEsLi4iHA7j3LlzNefkcjkIIbC8vAxd15FMJne1Wr8y3uKAfzYR0Z7liHBp\nJ4YLEVHrOXK2GBERdTaGCxERWY7hQkRElmO4EBGR5RguRERkOYYLERFZjuFCRESWY7gQEZHlGC5E\nRGQ5hgsREVmO4UJERJZjuBARkeVsfZ4L0V6ysrKCjz4qPvvELfz+l3Hy5MstqIjIPgwXIousrKzg\n/ffX4PV+v+k+q6vL6O7+huFCew7DhchChw4dwbFjp5o+v1zeALDSuoKIbMIxFyIishzDhYiILOeI\n22KqqkJV1epjjkOhEM6fP19zTqFQwPz8PHw+H4QQCAaDiEQiNlVMREQ7sT1cVFWFJEmYmJiotoXD\nYei6josXLwIAhBBIJpO4fv169ZyRkREoigK/39/2momIaGe23xabmpqqa4tGozXtqVQK4+PjNefE\n43EkEomW10dERObZHi6SJEFV1Zo2wzDg9Xqrn2cyGQSDwZpzQqEQstlsW2okIiJzbL8tNjs7W9eW\nzWbx5ptvAgB0XYeu6/D5fDXnyLIMAFhaWkJfX1/L6yQioubZfuWyVTqdRjgcxoULFwAAmqYBANxu\nd8PzhRBtq42IiJpj+5VLRS6Xw9zcHCRJwszMTLVd13UbqyIiot1wTLgMDQ1haGgIpVIJ4XAY09PT\nCAQCdpdFRES74LjbYh6PB/F4/LnXsEiS1PCDiIhaz3HhAgCRSAS6ruPGjRtQFAUAsLq62vDcynEi\nInIOW8NFCAGv14vbt283PK7rOmRZhqIodQP3QgjIsrztTDHDMBp+EBFR69kaLrquo7+/v+7qoxIk\nlbUt0WgUN2/erDmnUCggFou1p1AiIjLF1nAJBoMYHR2tu6JIpVJIJBLVq5JUKoVMJlNzTjqdRiqV\nalepRERkgmQ44F7R9PQ0FhcXqxtXhsNhnDt3ruachYUFzMzMYHBwEEIIhEIhvPbaa6ZfqzKo74B/\nNu0xQghcv/4tTp36cdN97t79Aj/5yQpeffU/tLAyovZzxFTkrTsgNxIIBDg1mYioQzhythgREXU2\nhgsREVmO4UJERJZjuBARkeUYLkREZDlHzBYj2gsMw8Djxw/x6NEfm+7z+PFDbGxstLAqInswXIgs\n8uWXX+K9f7kO371C031Kpbs4cnQAP/1p8NknE3UQhguRRcrlMuBxwffDk033ebi0ivXyegurIrIH\nx1yIiMhyDBciIrIcw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIco4Il1wu\nh7feegvj4+N4/fXXkcvlao4LIRCLxZDP56HrOoQQSCaTyOfzNlVMREQ7sX37l1wuB0VRMDQ0BAAo\nlUoIhULQNK3m8cf5fL4aJrIs49q1a4hEIrbUTEREO7P9ykUIgUAgUP3c4/EgkUggHo9X2yRJgqqq\n1asWTdNw5swZO8olIqIm2Bouuq5jZmYGpVKppr1yRbK0tFRtMwwDbrcbfX19bayQiIh2w9ZwkWUZ\nQggUi0U7yyAiIovZPuaiaVpdm6qq8Hq9NVcpQgjoul7t4/P5quM0RETkLLaHSyNTU1O4fPly9XOf\nzwcANWEyMjJS10ZERM5g+4D+Vul0GsePH8eFCxeqbR6Pp2bmGADE43EkEoltv44kSQ0/iJzIMAxT\nH0RO56grFyEE0uk0bt269cxz/X4/hBBYXV2F2+1uQ3VE1nN1deGff/87TP3Pqab7GIaBV3/0KkKB\nUAsrI3o+jgqXZDKJGzdu1LVPTk7i0qVLNW2VW2VCCJw+fbquz3Z/3fHqhZzksNuDF39wAKd+eKrp\nPstfL+Ph44ctrIro+Tnmttj4+DgmJyfrrkIqq/GfnpYMfDcRQFGUdpVIRERNckS4TE9PI5lM1swO\ny+fzKBaLUBQFU1NTdetbVFVFKBTiLTEiIgey/bZYNpsFsHklUrka0TQN2WwWV69eBbB5C6xYLMLv\n9wPYXHyZTqdx7do1e4omIqId2Rouuq5XpxRv1d/fX/3voaEh5HI5ZLNZLC8vQ9d1ZLNZrtYnInIo\nW8NFlmWUy+WmzuV6FiKizuGIMRciItpbGC5ERGQ5hgsREVmO4UJERJZjuBARkeVsX+dC1GpPnjzB\n/fv3Tfdzu93o7u5uQUVEex/Dhfa8jz/+DP/4j39Ab++hpvs8evQQf/mXP8Arr7zSwsqI9i6GC+15\n5bKBgwf78NJLze9D9+WXn3Bre6LnwDEXIiKyHMOFiIgsx3AhIiLLMVyIiMhyDBciIrIcw4WIiCzH\ncCEiIssxXIiIyHIMFyIispwjVujncjkIIbC4uAghBOLxeN2TJwuFAubn5+Hz+SCEQDAYRCQSsali\nIiLaie3hksvloChKNUxKpRJCoRA0TcP58+cBAEIIJJNJXL9+vdpvZGQEiqLA7/fbUjftbd9++wDF\n4l1TfTRNa1E19R7cf4BPPvnEVB9ZlnHixIkWVURUy/ZwEULUXKV4PB4kEgnE4/FquKRSKYyPj9f0\ni8fjSCQSmJ2dbWu9tD+srt6F+omKfqO/6T73Ht7DC7K7hVVtOiofxed3Psfn4vOm+zz69hF+7Psx\nYidiLayM6Du2houu65iZmcHY2Bg8Hk+1vXK7a2lpCX19fchkMrh8+XJN31AohGw229Z6aX854jmC\nU/5TTZ9/4NAB3Fl+0sKKNvX09piqCwBKWglofWlEVbYO6MuyDCEEisXitufoug5d1+Hz+er6ApsB\nREREzmL7bDFN03D69OmaNlVV4fV60dfXV72P7XY3vt0ghGh5jUREZI7t4dLI1NRU9TaYrus2V0NE\nRGaZGnMZGBiAJEmmXsAwDEiShE8//bSp89PpNI4fP44LFy6Yep2tzNZJ7bexsYEnT8wPBBw61PwT\nJYnIHqbCJRAIoFgsolAoVNv8fj80TUOpVAKwORaydXpws7/ohRBIp9O4deuWmbKoQ928+SEWFu7C\n5TrQdB/DeIK/+qs/x/e///0WVkZEz8tUuFy+fBnhcBjBYBDT09MIBALVY4VCAefPn8fS0hKy2eyu\n1p8kk0ncuHGjpk1RNh9Nu7q62nDcpXJ8q+0eUcsrGudYWyvj0KGf4Nixk033uXPnA5TL5RZWRURW\nMDXmMjExAVmWkc/na4IFAILBIObn51Eul5FMJk0XMj4+jsnJyboAkWUZiqLUDdwLISDLMvr6+ky/\nFhERtZapcFFVFbFYrGZNylbRaBSqqpoqYnp6GslksiYo8vl8dYpyNBrFzZs3a/oUCgXEYlwQRkTk\nRKbCxTCMZ0793WnNSiOVhZCapqFQKKBQKEBVVWQymeqttVQqhUwmU9MvnU4jlUqZei0iImoPU2Mu\n0WgUuVwO77zzDs6cOVN3PJfLoVAoIBqNNvX1dF3HyMhIw2P9/d9tu+HxeJBKpZBMJjE4OFjda4y3\nxIiInMlUuKRSKaiqiuHhYZw9exaxWAyKomBxcRFzc3PVq5BmryhkWW56cDYQCNSN8xARkTOZChdF\nUZDP55FIJJDJZOpuVSmKgqmpKYYAEdE+Z3rjymAwiLm5OQghUCgUIISAoihQFAXBYLAVNRIRUYfZ\n9a7Ix48fRzgcfubsMSIi2n9M7y22sLCAcDgMWZbR39+P+fl5AJtbw/ziF7+wvEAiIuo8psKlWCwi\nFAqhUCggEonUrIJfXl7GpUuXMDg4aHmRRETUWUyFS2UW2Pz8fN1g/srKCiYmJjA/P1/3YC8iItpf\nTIXL7OwsotHotrPBLl26hEAgwCdEEhHtc6bCRdf1msWNjVTWvRAR0f5lKlwCgcAzt8NfWFjglGQi\non3OVLiMjo5ifn4e7777bsOt60dGRiCEaHr7FyIi2ptMhUtlTCUSiVT3BEulUhgdHcWxY8eQzWah\nKAomJiZaUiwREXUG0+tc5ufnMTExgffffx8AMDc3h0wmg3K5jEuXLuGzzz6zvEgiIuosu1qhf+nS\nJVy6dAnA5kO7fD4fZFm2tDCixrrxD//wASTpw6Z73Pnq9yje1XH0qK/pPisrf8CPXmn+8ctEVMtU\nuExPT+PYsWM12+1v95hholY4efJHAH5kqs/jtQ9w78hv4Xvx5ab7GJqB482fTkRbmAqXeDwOr9fb\n8FkuRE7WaAIKEbWOqTGXc+fOYWVlBbdv325VPUREtAeYunJJp9MYGBhAKBTC1NQUwuEwFEWB2+1u\nVX1ERNSBTIWLz7c5IGoYBsbGxqrtT99yMAwDkiRhY2PDVCHZbBZerxeRSKSmXQiBeDyOZDKJUCgE\nTdOQTqcRi8XqziUiImcwFS7N/jI3e39bVVWMjY1tuydZPp9HPp8HsPlo5GvXrjFYHOaLL/4VX321\nbKrP3bs6AOeOmn/zzQoePHjS9PnffvsQwNHWFUTUQXYMl2QyiVdffbU6gL91J+TnVSwWkUqlEAqF\nqldFW0mSBFVVEQ6HoWka+vr6LK2BrPHxx1/ik0+O4NAhM7dIffB6v9eymp6H230c9+71mOx1BEeP\nMlyIgGeEy+TkJIaHh+tmh01PT6NQKODtt99+rhf3+/24evUqgO+282/EMAy43W6O7Ticx3MCHo8z\nw8Ks7q5eeNx7499CZAfTK/QB4Pr160in01bXQkREe8SuVugDqHkKZasJIaDrOgBA0zT4fD4MDQ21\n7fWJiMicXYdLuxalVcZing6TyqaZDBgiImfadbi0i8fjwfnz52va4vE44vH4juHCFdnUKdbW13D/\nwX1TfXp7e9HTbXbCAVH7OD5cGvH7/RBCYHV1lYP81NF6ug/iiy828Pvf/2vTfdbX19Dffxh/9qc7\nPxWWyE6OD5fJycnqDswVlVtlQgicPn26Yb/txoR4RUNOcujQURw69Gem+ty/v4xyeaVFFRFZ45nh\noqoqRkdHa9ry+TwMw6hrf9rMzMxzFyeEQDKZxMjISM36Fk3TAHBHZiIip3pmuKysrGy7eHKnRZVW\nhIuiKJiamqpbOKmqKkKhEG+JERE51I7hcuvWrXbVAaDxrSyfz4disQi/3w8A0HUd6XQa165da2tt\nRETUvB3DJRgMtvTFS6USrly5AiFEdYPKaDSKWCxWnQk2NDSEXC6HbDaL5eVl6LqObDbLbWCIiBzM\n1gF9j8eDiYmJZ57H9SxE35FcLnz5ZQkr2gdN93l4/4/4iecR8B9bWBjRUxw/W4yIah057MXa+k9M\n7ZLx6NEdrBgPW1gVUS2GC1EH6u7qNXX+ga5uAOutKYaogV1tXElERLQThgsREVmO4UJERJbjmAsR\nNbS+vo6lpSXTj9c4cuQIXn7ZuY+vpvZguBBRQ/fv38evbv4KXXLzvybW19Zxsuskhl7m8oH9juFC\nRNvqOdiDk8rJps9/+OAh8HULC6KOwTEXIiKyHMOFiIgsx3AhIiLLccyFOkq5XMb6+hOTfTZaVA0R\nbYfhQh2l+MUH+PjOe5BcZi66DfS8dKhlNRFRPYYLdZSNjTV0n+iF5/j37C6FiHbAMRciIrIcw4WI\niCzHcCEiIss5Zswlm83C6/UiEonUHSsUCpifn4fP54MQAsFgsOF5RETkDI4IF1VVMTY2hmw2W3dM\nCIFkMonr169X20ZGRqAoCvx+fzvLJOpo2uoyfv2/f930+etr69jgNG7aJVvDpVgsIpVKIRQKwefz\nNTwnlUphfHy8pi0ejyORSGB2drYdZRJ1vEOHj0Dy3MXdnrvNd+oBvneMs/Jod2wNF7/fj6tXrwLY\nDJFGMpkMLl++XNMWCoUaXuUQUWOSy4XD7sPw+Dx2l0L7hKMH9HVdh67rdVc1siwDAJaWlmyoioiI\nnsXR4aJpGgDA7XY3PC6EaGc5RETUJEeHi67rdpdARES74IjZYq0gSZLdJRAR7VuOvnIhIqLO5Ohw\nURQFALC6urrj8UYMw2j4QURErefocJFlGYqi1A3cCyEgyzL6+vrsKYyIiHbk6HABgGg0ips3b9a0\nFQoFxGIxmyoiIqJncVS4NLptlUqlkMlkatrS6fS2iy6JiMh+ts4WK5VKuHLlCoQQEEIgHo8jGo0i\nFothaGgIAODxeJBKpZBMJjE4OFjda4y3xIiInMvWcPF4PJiYmHjmeYFAAIFAoA0VUTstFhfw2Ve3\nTPXZKK+j9/svtKgiIrLKnl3nQs73aO0BDrzUjaOy11Q/yeWou7lE1ADDhWwlSQwLor2I72oiIrIc\nw4WIiCzHcCEiIstxzGWP+2zxM+glc7tLf/WHr3Hc+xK6u7ub7qPr982WRg63tr6GLz7/EmUT2yY9\nevgInvtHW1gVdQqGyx73wccf4BvpG/T09jTd5/3/+094RR6F13u86T6SJMPnMzfri5zt8aPH+Oif\nS+jtfbnpPg8fbMD38JsWVkWdguGyD/hO+PDCkebXhnR1dcHjeREnTvy7FlZFnaC7qxuy50TT5x9A\nF/Cw8UaztL9wzIWIiCzHcCEiIssxXIiIyHIccyFLPHnyCE+efGuqz/raE6D5CWnUIdbX1lEsFk31\nOXz4ME6caH5sh5yP4UKW+HjxPXxx/yMcOHCg6T5llHHEyxlme0nPwYNYevgQ//m//fem+5SNMk4e\nPYJf/Nf/0sLKqN0YLmSJDWMNL7zkxmG3x+5SyEa9vS/gT8L/yVSfhw9X8Wjxd60piGzDMRciIrIc\nw4WIiCzHcCEiIst1RLgIIRCLxZDP56HrevVRx/l83u7SiIiogY4Z0M/n89UwkWUZ165dQyQSsbkq\nos4gSRLufvMAv/k/Hzbdp1wuY2Ojt4VVbZIkF+4/XkXm7zOm+h33HMdf/OwvWlQVPa+OCBdJkqCq\nKsLhMDRNQ19fn90lEXWUFw650dX1Y8DEDscuCfD6Wv8roqu7G/IrXhgvN1/bxsYGPl/6vIVV0fPq\niHABAMMw4Ha74Xa77S6FqCP1dB+0u4Rtdff04NDhQ02fv762jsd43MKK6Hl1xJgLERF1lo65chFC\nQNc3H3qlaRp8Ph+GhoZsroqIiBrpiHDx+XwAUBMmIyMjdW1EROQMHREuHo8H58+fr2mLx+OIx+Pb\nhoskSe0obc/StDsolzeaPv/x42+BIy0siIg6SkeESyN+vx9CCKyurnKQ32I9x3rwycpv0as3//RK\nHATkF7irLRFt6ohwmZycxKVLl2raKrfKhBA4ffp0XR9jmymXvKJ5tiOyGwcOvoxDB3kpQkS74/jZ\nYpXV+EtLSzXtmqYBABRFsaEqIiLaiePDRVEUTE1N1S2cVFUVoVCIt8SIiBzI8eECbN4Ce/rJdrqu\nI51OY3p62saqiIhoOx0x5jI0NIRcLodsNovl5WXouo5sNsttYIj2CAMG1tbWmj5/fW0dGyZmM1L7\ndUS4AFzPQrRXuVwHsLoqIZ//p6b7bGxs4MDXf8TfjrawMHouHRMuRLQ3HXB14aUX62d87uTJk0dY\n/vy9FlVEVuiIMRciIuosDBciIrIcw4WIiCzHcCEiIstxQL+D3L79O9y798BUnw8+/ATllzfQe6j5\nB0Xdv/8turrNVkdE9B2GSwf56KOv8Pjxn6Krq6fpPvrKiygfXEfPt80/5c914CUcPHh4NyUSEQFg\nuHSco0ePobe3+aB44bAH5RfW0XvIxA7HRETPiWMuRERkOYYLERFZjuFCRESW45iLBe7evWtq0z1g\n83k0T548MdXn3r1vcPDgHfT0ND/mUt5YN/UaRJ1io7yBQqFgqk9PT0/1QYPN6urqwokTfMqqWZKx\n3SMb96jKkyit/Gf/3d/9L6yvv2yqz3sf/j0eH/wWkqv5J2Mahgsezym4XM1fcBowIJ98EQe6+HcE\n7R1lo4zF//dbHDDZz+Vaxc9+9ufm+jxw4W9G/gYHDph9tf2Nv3EssLZm4NSpkKk+7i8+xJFXvHDx\nf1gi01ySC6/8+5+a7qdpN3HyhydN9bmzcMf06xDHXIiIqAUYLkREZDmGCxERWa5jxlwKhQLm5+fh\n8/kghEAwGEQkErG7LCIiaqAjwkUIgWQyievXr1fbRkZGoCgK/H6/Za9TLpfxzjsqVlfNPZv7t7d/\ni6O/v2uqz8P1Eo5IXlN9iKj9PvjgX/A/HvwKLlfzk28OH3bhzJnX0N3d2h1gf/Peb/DJF5+Y6tN9\noBt/Hf1reDyeFlW1qSPCJZVKYXx8vKYtHo8jkUhgdnbWstcpl8tYXt7Aiy++bqrfQfcSjv7Q3Nx5\nN45BMjGlmIjs8eDBOjye19Dd3dt0nz/8IY+NjY2Wh4u2qqH3B7047G5+o9mvP/7a9Lq83eiIcMlk\nMrh8+XJNWygUQjabbcnrmZ3PLkmSqb9qiKizuFxdpn4vVNbTtYPrgMvc76w2leb4P511XYeu63Wr\namVZBgAsLS3ZUBUREe3E8eGiaRoAwO12NzwuhGhnOURE1ATHh4uu63aXQEREJjl+b7FCoYBwOIxy\nuVx3zOVyQVVVvPbaa3XH2nnPk4hoPzATF46/ciEiImcw80e742eLKYoCAFhdXW047lI5vtV2CduK\nXZHbifXbp5NrB1i/3fZK/c1y/JWLLMtQFKVu4F4IAVmW0dfXZ09hRES0LceHCwBEo1HcvHmzpq1Q\nKCAWi9lUERER7cTxA/oAUCqVMDw8XLP9y+uvv450Om36ymWvXJqy/vbr5NoB1m+3/VZ/R4QLACws\nLGBmZgaDg4MQQiAUCjWcJfYs++0H7DSdXH8n1w6wfrvtt/o7Jlysst9+wE7TyfV3cu0A67fbfqt/\n34ULERG1XkcM6BMRUWdhuBARkeUYLkREZDmGCxERWY7hQkRElnP83mJETlAoFDA/Pw+fzwchBILB\nICKRiN1lmZLNZuH1ejuu7lwuByEEFhcXIYRAPB7H0NCQ3WU1TVVVqKqKY8eOYXFxEaFQCOfPn7e7\nrF3RdR3JZBJXr1595rkMF3T2D7/T33gVTv7FJ4RAMpms2SFiZGQEiqLA7/fbWFnzVFXF2NhYyx4N\n3iq5XA6KolT/ny6VSgiFQtA0rSPeo6qqQpIkTExMVNvC4TB0XcfFixdtrGx3EokEVlZWmjvZ2Ofm\n5uYMVVVr2kKhkDE5OWlTRc3LZrNGoVCofq7rutHf32+k02kbqzJvbm7O8Hq9Rj6ft7uUhsbGxoxc\nLlfTpqqqMTw8bFNFzRNCGPF43Ein00Z/f79jv8fbafQ+TKfThiRJNlRj3tmzZ+t+vyQSCaO/v9+m\ninZvcXHRGB4eNkZGRpo6f9+PuUxNTdW1RaPRhu1OI4RAIBCofu7xeJBIJBCPx22sqnnFYhHj4+Mo\nFovw+Xx2l7OtTCaDYDBY0xYKhTriKsDv9+Pq1asd8Vf+VrquY2ZmBqVSqaa9cnW7tLRkQ1XmSJIE\nVVVr2gzDgNfrtami3cvn84jFYk2v0N/34dKpP/y98MbrhF98uq5D1/W68JNlGUBnfJ87lSzLEEKg\nWCzaXcquzc7O4sqVKzVt2WwWo6OjNlW0O/l8HtFo1FSffT/mMjs7W9eWzWbx5ptv2lBN855+450+\nfdrucvYsTdMAoOGD6oDNq0c+U6h1Kt//p6mqCq/X25Hf93Q6jXA4jAsXLthdiilCCEQiEVP7ou37\ncNmqk374e+2N50S6rttdAm0xNTWFy5cv212GKblcDnNzc5AkCTMzM3aXY0oul9vV3QWGy7/p5B/+\n0zrxjUfUrHQ6jePHj3fEH39PGxoawtDQEEqlEsLhMKanp2vGS53qef64Yrj8m0794T+tU994RM0Q\nQiCdTuPWrVt2l7JrHo8H8XgckUik4Z0Hp8lkMjVXLZVt95uxZ8JFCNH0uceOHYPH42l4zI4fvhW1\n2/nGs+p770SKogAAVldXG467VI5T6yWTSdy4ccPuMp5bJBKBruvI5/OOXNdVsbCwgHA4XNO278Zc\nisUikslk0+cPDg7uuICpnT98q2q3641n9ffeaWRZhqIoEELUTJwQQkCWZY5ttcn4+DgmJye3nVjh\nRJUn5r777rsNJ91snenpNLdu3cLi4mLNMEGhUKguKh4cHNxxwfaeCBe/399w1tezOOGHv9van2bn\nG8+K+p0uGo3i5s2bNf+PFAoFxGIxG6vaP6anp5FMJmuCPJ/PO36HBF3X0d/fX3d1W7nS37p2ymka\nDeK/9daYMo9qAAAFEUlEQVRbuHXrVs2OA9vZ1+tcOv2HD2z/xuvktQFOk0qlkMlkatrS6TRSqZRN\nFe2emdsaTlBZqKppGgqFAgqFAlRVRSaTcXSwAJu/P0ZHR+u+56lUColEoiOveu/du8fHHDfrrbfe\nwtjYWM04QCwWQzgcrlv85DTZbBYrKysIhULVNk3TkM1mm9pYzkkGBgYwNTXl2HvQCwsLmJmZweDg\nYPWK97XXXrO7rGcqlUq4cuUKhBDIZrNQFAXRaBSxWMzxe9A1Wrxa0d/fj08//bTNFe3O9PQ0FhcX\nq3sXhsNhnDt3zu6yTCkWi0ilUpidnUWpVML58+cRj8d3nPS078MF6Mwf/l5443XyLz4i2hnDhYiI\nLLevx1yIiKg1GC5ERGQ5hgsREVmO4UJERJZjuBARkeUYLkREZDmGCxERWY7hQmRCoVCAy+Wq2y12\nK1VV4XK5MDIyYurrDw8Pw+Xi25I6H/8vJjIhGAxClmUsLCzsuLFpZS+yN954w/RrmHlmBpFTMVyI\nTBobG4NhGDvuBj07OwtJknDmzJk2VkbkHAwXIpNGR0cBbD5SupFCoYBSqYSzZ8+2sywiR2G4EJkU\nCASgKMq2t8YqD1eqhBCw+RiH4eFh9Pf3w+VywefzYWRkpOGjEZ7e7i8WizUcg9F1HS6XC+Pj43XH\nJicnEQqFqq8zPj7ORzBQ2zFciHYhHo9ve2ssnU7X3BITQmBgYADvvPMOBgYGEI/HEQ6Hkc1mEQqF\nnvlQup3GYLYeC4VCSCaTcLlc1ddJp9Po7+/HwsLCLv6lRLvDcCHahcotr623xhrdEkulUpAkCXNz\nc/j1r3+Nt99+G9evX0cqlYKu61BV1ZKaJicnsbCwgHw+j5s3b1ZfZ35+HkDjJwsStQrDhWgX/H4/\nAoFA3a2xRrfExsfHkclk6h4uVnnQ0srKiiU1XblyBbFYDMFgELquVz/8fj8ikQgKhQJWV1cteS2i\nZ+myuwCiTvXGG29gYWEB6XQaFy9eBLD5dNCts8QCgUA1SHRdx61bt1AoFLadELBbpVIJc3Nz8Hq9\nDY9LkgRN0+B2uy19XaJGGC5EuzQ2NoZEIoGZmRlcvHgRQggUi0UMDw/XnKfrOhKJRPURscDm2Ego\nFLJsoF0IAWBzAkAikdj2vO2Ch8hqDBeiXfJ4PAgGg9VbY9lsFsDmYP/TIpEIFhYWEI/HEY/Hcfr0\naQBAPp+v9jFL07SazyuPvJZlue72G5EdOOZC9Bwqs8bS6TRmZmYgSVLNL3dd17GwsIDh4WG8/fbb\n1WABaqccm1UoFGo+l2UZHo9n28kBXq8XAwMDu349IrMYLkTPobJ32NTUFBYWFrZdOLl10L5yqwyo\nD5mnpxfLsgzDMJDP5xv2fVo8HsfKykrdfmaTk5MolUoN18QQtYxBRM8lFosZkiQZkiQZ+Xx+2+PD\nw8NGKpUyxsbGDK/Xa7z++uuGJElGf3+/oaqqYRiGcfbsWUOSpGrfbDZb/drxeLymr9frNcbHx2te\nq7+/v/o1z549awSDQUOSJCMcDrf2m0C0BcOF6DlVAsDlcjU8ruu6EY/HDa/XW/1Fn8vlDMMwjHg8\nbrhcrmpIDA8P132ddDpdDQ2fz2ckk0nDMIyG4WIYhpFIJIxQKGRIkmQMDAxUzydqJ8kwnuPGLxER\nUQMccyEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIcgwXIiKyHMOFiIgsx3AhIiLL/X/5\nSxhgL1jXqQAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60debd1d50>"
]
}
],
"prompt_number": 52
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"The Wilcoxon signed-rank test tests the null hypothesis that two related paired samples come from the same distribution"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"Wilcoxon Signed-Rank test. Only if equal variance\", scipy.stats.wilcoxon(x,y)[1])\n",
"print(\"Mann-Whitney U test NO\",scipy.stats.mannwhitneyu(x,y)[1]*2)\n",
"print(\"Paired t-test. Only if normality and equal variance\",scipy.stats.ttest_rel(x,y)[1])\n",
"print(\"Unpaired t-test NO\",scipy.stats.ttest_ind(x,y)[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Wilcoxon Signed-Rank test. Only if equal variance', 0.0064134158222216931)\n",
"('Mann-Whitney U test NO', 0.0023466572817885658)\n",
"('Paired t-test. Only if normality and equal variance', 0.005920142900373267)\n",
"('Unpaired t-test NO', 0.004349070916356835)\n"
]
}
],
"prompt_number": 53
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Compare >2 independent samples. Same mean?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Imagine we want to check if there are difference in GFP expression in three different versions of a promoter."
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"ANOVA (Parametric) or Kruskal-Wallis (Non parametric)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Analysis of variance (ANOVA) is a collection of statistical models used to analyze the differences between group means and their associated procedures (such as \"variation\" among and between groups). T-test\n",
"\n",
"\n",
"The Kruskal\u2013Wallis one-way analysis of variance by ranks (named after William Kruskal and W. Allen Wallis) is a non-parametric method for testing whether samples originate from the same distribution. Mann-Whitney-U "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" x = [np.random.randn() for _ in range(200)]\n",
" y = [np.random.randn()+0.2 for _ in range(200)]\n",
" z = [np.random.randn()+0.4 for _ in range(200)]\n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(z,bins=np.linspace(np.min(x+y+z),np.max(x+y+z),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3W1sG3d+J/DvkHrykziknDhxHlYcqe2118NaJLXt9q4o\nsCSDosChC8uSFu3bWFTe2yb9bl8czqbS97Eo41Cgb04SuVu0aO/WGjo9YLe7jSXKu3e7zSbRn0qa\nOHYcUUPZsmw9zb1QxTVNSp6hh5yh9P0AAqyZ+Wt+lkR+NfN/GEnXdR1EREQWctldABERHTwMFyIi\nshzDhYiILMdwISIiyzFciIjIcgwXIiKynPv73//+9+0uQlVVpFIpzM/P42/+5m/w5ZdfIhgMlvYL\nITA0NITXXnsNPp8Pd+7cQTKZhCRJUBTFxsqJiKgaye55LqqqQpIkhMPh0rZQKITh4WFcvHgRwE64\n9Pb2lvbLsozr16/j7NmzDa+XiIiez/bbYuPj4xXbIpFI2XZJkqCqKjRNgxAChUKBwUJE5GC2h8tu\ncDxN13V4vd6KbZ2dneju7m5gdUREVIsWuwuYmpqq2JZOp/HOO+/YUA0REVnB9nB5ViqVQigUwoUL\nF8q2CyGgaRoAoFAowOfzYWBgwI4SiYjoORwTLplMBjMzM5AkCZOTk2X7fD4fAJSFydDQUMU2IiJy\nBttHiz2rWCwiHA5jYmICfX19ex6XzWYRi8XwySefNLA6IiIywvYO/Wd5PB7EYrGyocnV+P1+CCGw\nsrJSdb8kSXt+EBFRfTkuXAAgHA5D0zTcvHkTADA2NlZxzO6tMiGE6a/PgCEiqi9bw0UIAa/Xi9u3\nb1fdvzuvJZFIYHFxsWxfoVAAgD1n6Ou6XvWDiIjqz9YOfU3T0NPTUxEQu1cjgUAA3d3dGB8fr5jf\noqoqgsEgOjs7G1UuEREZZOuVSyAQwPDwcMUVRTKZRDweLwWKz+dDPp8v7dc0DalUChMTE40sl4iI\nDHLEaLGJiQksLCygq6sLCwsLCIVCePvtt8uOyWQyEEJgaWkJmqYhkUjUNFt/t7/FAf9tIqIDyxHh\n0kgMFyKi+nPkaDEiImpuDBciIrIcw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFc\niIjIcgwXIiKyHMOFiIgsx3AhIiLL2fo8F6LDZmlpCZ9++KHpdvLLL0P5rd+qQ0VE9cFwIWqgpaUl\nbH/wAV71eg23efTkCb545RWGCzUVhgtRg504cgSvdXUZPr64uoq7dayHqB7Y50JERJZjuBARkeUc\ncVtMVVWoqlp6zHEwGMT58+fLjsnlcpibm4PP54MQAoFAAOFw2KaKiYhoP7aHi6qqkCQJV69eLW0L\nhULQNA0XL14EAAghkEgkcOPGjdIxQ0NDUBQFfr+/4TXTwVMoFLC1tWWqjSRJ6OrqKj06m4h+w/Zw\nGR8fx+joaNm2SCSC8fHxUrgkk8mKY2KxGOLxOKamphpWKx1MGxsb+OEPf4rNTeOd7Ds0DA//IWRZ\nrktdRM3M9nCRJAmqqpbd4tJ1Hd6nhmpOT0/j8uXLZe2CwSDS6XTD6qSDS9d1bG624PTpPzTV7s6d\nH9epIqLmZ3u4VLvySKfTeOeddwAAmqZB0zT4fL6yY3b/WlxcXER3d3fd6yQiIuMcN1oslUohFArh\nwoULAHbuhQNAZ2dn1eOFEA2rjYiIjLH9ymVXJpPBzMwMJEnC5ORkabumaTZWRUREtXBMuAwMDGBg\nYADFYhGhUAgTExPo6+uzuywiIqqBY8Jll8fjQSwWQzgcLt0SqwWHh5IT3b17F4u3P8CX/2Z8bbGH\nj5/gy1fewB/jz+tYGZG1HBcuABAOh6FpGm7evIlAIAAAWFlZqdrvoihKo8sjqtna2hoeuR+h7dQp\nw2305ccorhbrWBWR9Wzt0BdCwOv14vbt21X3a5oGWZahKEpFx70QArIs7zlSTNf1qh9EdnO5XGhp\nbTH84W5x210ykWm2houmaejp6am4+tgNkt2rlkgkglu3bpUdk8vlEI1GG1MoERGZYmu4BAIBDA8P\nV1xRJJNJxOPx0lVJMpnE9PR02TGpVArJZLJRpRIRkQm297lcvHgRExMTWFhYKC1cOTw8jLfffrt0\njMfjQTKZRCKRQH9/f2mtMU6eJCJyJtvDBUDFCsjV9PX1cWgyEVGTcNwMfSIian4MFyIishzDhYiI\nLMdwISIiyzFciIjIcgwXIiKyHMOFiIgsx3AhIiLLMVyIiMhyDBciIrIcw4WIiCzHcCEiIssxXIiI\nyHIMFyIishzDhYiILMdwISIiyzFciIjIco4Il0wmg3fffRejo6N46623kMlkyvYLIRCNRpHNZqFp\nWukxx9ls1qaKiYhoP7Y/5jiTyUBRFAwMDAAAisUigsEgCoVC2eOPs9lsKUxkWcb169cRDodtqZmI\niPZn+5WLEAJ9fX2lzz0eD+LxOGKxWGmbJElQVbV01VIoFHD27Fk7yiUiIgNsDRdN0zA5OYlisVi2\nffeKZHFxsbRN13V0dnaiu7u7gRUSEVEtbA0XWZYhhEA+n7ezDCIispjtfS6FQqFim6qq8Hq9ZVcp\nQghomlZq4/P5Sv00RETkLLaHSzXj4+O4fPly6XOfzwcAZWEyNDRUsY2IiJzB9g79Z6VSKZw8eRIX\nLlwobfN4PGUjxwAgFoshHo/v+XUkSar6QURE9eeoKxchBFKpFGZnZ597rN/vhxACKysr6OzsbEB1\nRERklKOuXBKJBG7evFmxfWxsrGLb7q0yIUTVr6XretUPIiKqP8eEy+joKMbGxiquQnZn4z89LBn4\nzUAARVEaVSIRERnkiHCZmJhAIpEoGx2WzWaRz+ehKArGx8cr5reoqopgMMhbYkREDmR7n0s6nQaw\ncyWyezVSKBSQTqdx7do1ADu3wPL5PPx+P4CdyZepVArXr1+3p2giItqXreGiaVppSPGzenp6Sv8e\nGBhAJpNBOp3G0tISNE1DOp3mbH0iIoeyNVxkWcb29rahYzmfhYioeTiiz4WIiA4WhgsREVmO4UJE\nRJZjuBARkeUYLkREZDnb57kQWWlra6v0aAajNjY26lRNpc3NTTx58gSP1h4ZbvP4yRrWt9pMn+vB\ngwdYX1833U6WZbjdbtPtiJ7GcKED5e7du/jbv/0lWltPmGqn66/UqaJy9+7dw+LiMlpgfGWJYnEF\nn7U9Nn2un/3jP+Lo8jJcLuM3KB5sbOD3/vzP8frrr5s+H9HTGC50oOi6jpaWl/Dqq312l1KVrutw\nuY7ixHHjb97r619he934lU7pXE+eoP/ll9HW2mq4ze07d7jAK1mCfS5ERGQ5hgsREVmO4UJERJZj\nuBARkeUYLkREZDmGCxERWY7hQkRElmO4EBGR5RguRERkOUfM0M9kMhBCYGFhAUIIxGKxiidP5nI5\nzM3NwefzQQiBQCCAcDhsU8VERLQf28Mlk8lAUZRSmBSLRQSDQRQKBZw/fx4AIIRAIpHAjRs3Su2G\nhoagKAr8fr8tdRMVi0v45JNP0NlpfJ2wlZWVms61ubWJjz76yFSbLYOPECeqB9vDRQhRdpXi8XgQ\nj8cRi8VK4ZJMJjE6OlrWLhaLIR6PY2pqqqH1Eu1avPsh1E/+FbIsG24jNgQ6j3SYOk97Syv+w6NH\nwM2bptr9tsuF1hbbX+J0SNn6m6dpGiYnJzEyMgKPx1Pavnu7a3FxEd3d3Ziensbly5fL2gaDQaTT\n6YbWS/Ssk6+exKlXThk+/t5X97Dd+rWpc7hcLrzS2Ynffu01s+UR2cbWDn1ZliGEQD6f3/MYTdOg\naRp8Pl9FW2AngIiIyFlsHy1WKBRw5syZsm2qqsLr9aK7uxuFQgEA9ryvLYSoe41ERGSO7eFSzfj4\neOk2mNmnChIRkf1M9bn09vZCkiRTJ9B1HZIk4eOPPzZ0fCqVwsmTJ3HhwgVT53mW2TqJarGxvoEn\n608MH7+1tQX+ZtJhYCpc+vr6kM/nkcvlStv8fj8KhQKKxSKAnb6QZ4cHG32jF0IglUphdnbWTFlE\nttBxBHOzn6P96JLhNtpXK/gdl/EnQxI1K1PhcvnyZYRCIQQCAUxMTKCv7zePks3lcjh//jwWFxeR\nTqdrmn+SSCRw85nhloqiANiZH1Ct32V3/7P2elQrr2jIKl1dfjzxvoSOY8cNt9GffIGOjl/UsSoi\nZzDV53L16lXIsoxsNlsWLAAQCAQwNzeH7e1tJBIJ04WMjo5ibGysIkBkWYaiKBUd90IIyLKM7u5u\n0+ciIqL6MhUuqqoiGo2WzUl5ViQSgaqqpoqYmJhAIpEoC4psNlsaohyJRHDr1q2yNrlcDtFo1NR5\niIioMUyFi67rzx36u9+clWp2J0IWCgXkcjnkcjmoqorp6enSrbVkMonp6emydqlUCslk0tS5iIio\nMUz1uUQiEWQyGfzgBz/A2bNnK/ZnMhnkcjlEIhFDX0/TNAwNDVXd19PTU/q3x+NBMplEIpFAf39/\naa0x3hIjInImU+GSTCahqioGBwdx7tw5RKNRKIqChYUFzMzMlK5CjF5RyLKMbYOL6/X19VX08xAR\nkTOZChdFUZDNZhGPxzE9PV1xq0pRFIyPjzMEiIgOOdMLVwYCAczMzEAIgVwuByEEFEWBoigIBAL1\nqJGIiJpMzasinzx5EqFQ6Lmjx4iI6PAxvbbY/Pw8QqEQZFlGT08P5ubmAOwsDfNXf/VXlhdIRETN\nx1S45PN5BINB5HI5hMPhslnwS0tLuHTpEvr7+y0vkoiImovp0WIAMDc3B7/fX/aMleXlZYyNjSGR\nSODy5cu4cuWKtZUS1VGh8CW2t7dMtdncML5gJdFhYypcpqamEIlE0NfXV3Up/EuXLmFychLpdJrh\nQk1jY2Md//Lh30E6Ya6d3rYNud34UyiJDhNT4aJpWtnkxmoURUEmk3mhoogaTZIA3xun7S6D6MAw\n1efS19f33OXw5+fnOSSZiOiQMxUuw8PDmJubw/vvv1916fqhoSEIIQwv/0JERAeTqXC5dOkS+vr6\nEA6HS2uCJZNJDA8Po6urC+l0Goqi4OrVq3UploiImoPpeS5zc3O4evUqPvjgAwDAzMwMpqensb29\njUuXLuGTTz6xvEgiImouNc3Qv3TpEi5dugRg56FdPp8PsixbWhjR/M/n8cEvPzDVZnl5GQ/vdeP0\naePr221tbeGrX36A9S87TJ1rs7UNL/d/G20dR0y1IzoMTIXLxMQEurq6ypbb3+sxw0QvavXxKtpf\nb0fXqS7DbR7+60Os33ls6jzb21s4uv4Yf+I1N1rs9vIStrfMzY0hOixMhUssFoPX6636LBeiw6ba\noBYi2mGqz+Xtt9/G8vIybt++Xa96iIjoADB15ZJKpdDb24tgMIjx8XGEQiEoioLOzs561UdERE3I\nVLjsriWm6zpGRkZK25++PaDrOiRJwpbJe9HpdBperxfhcLhsuxACsVgMiUQCwWAQhUIBqVQK0Wi0\n4lgiInIGU+Fi9M3c7L1oVVUxMjJSekzys7LZLLLZLICdRyNfv36dwUKHyoPVVdzIvm+qTXtbK/74\nP/8RXC7TMw6IXti+4ZJIJPCtb32r1IH/7GONX1Q+n0cymUQwGCxbYflpkiRBVVWEQiEUCgV0d3db\nWgOR03UcPY614zJ+9XXlYrH7Wf/6Hr4VCuLIEQ6VpsbbN1zGxsYwODhYMTpsYmICuVwO77333gud\n3O/349q1awB+s5x/Nbquo7Ozk307dCi5XG50vfya6XZ3l+/XoRoiY2q6Xr5x4wZSqZTVtRAR0QFR\n0wx9AGVPoaw3IUTp+TGFQgE+nw8DAwMNOz8REZlTc7g0agLZbl/M02Gyu2gmA4aIyJlqDpdG8Xg8\nOH/+fNm2WCyGWCy2b7hw9nTzW19fx+qjVbQ9bDPcZu3RGtbWHuLBg4LhNo8fr9ZSHhHtw/HhUo3f\n74cQAisrK+zkP8A++vUifvpvn8HTZfzN/6vP7uHlDz9F8YnxQNra2sSpBt7mJToMHB8uY2NjpRWY\nd+3eKhNC4MyZM1Xb7dUnxCua5rG1raOj/RX4vL2G26wtu/HGsXsI+l413GZzcwPuJW8tJRLRHp4b\nLqqqYnh4uGxbNpuFrusV2582OTn5wsUJIZBIJDA0NFQ2v6VQ2LnlwRWZiYic6bnhsry8vOfkyf0m\nVVoRLoqiYHx8vGLipKqqCAaDvCVGRORQ+4bL7Oxso+oAUP1Wls/nQz6fh9/vBwBomoZUKoXr1683\ntDYiIjJu33AJBAJ1PXmxWMSVK1cghCgtUBmJRBCNRksjwQYGBpDJZJBOp7G0tARN05BOp7kMDBGR\ng9naoe/xeHD16tXnHsf5LETmbWETP7v9M7S4Ww23+WhZQ/+3v4033njDcJvl5WXM37wJmFwJvcPn\nwx9FIqbaUPNw/GgxIqrN8VMeuE66IJlY5Gnl6xWsra2ZOs/jx49x7N49/P5LLxlus7W9jZ989pmp\n81BzYbgQHVAutxut7a1ocRl/mbvdtS3P3+J241hHh+Hjt7a2gFVOXj3I+KAHIiKyHMOFiIgsx3Ah\nIiLLsc+FDpz19ccoFO4YPn57e7vmcxWX7uPRgxXDx689fFDzuRrl17/+NVZWjP+fVldX4X34sI4V\nUTNiuNCB0nH0OFZavkZ+9bapdi6P+ZfCN1pasfrxh6bbyceOmW7TKN846cHdD/4XhIk2G+sb8L36\nO3WriZoTw4UOlNa2NhzrlHHC21X3c8nHT0Cu+1ka69VTXXj1lLnv3YPiA/jcx+tUETUr9rkQEZHl\nGC5ERGQ5hgsREVmOfS7UEBsbGzuzsk22IaLmxHChhnj/hz+EtLxsqs0XP/1nPHqjp04VEVE9MVyo\nIbYePkT01Cm0uN2G2/wCwOd8tj1RU2KfCxERWY7hQkRElmO4EBGR5RzT55JOp+H1ehEOhyv25XI5\nzM3NwefzQQiBQCBQ9TgiInIGR4SLqqoYGRlBOp2u2CeEQCKRwI0bN0rbhoaGoCgK/H5/I8skAGtr\na/jp7E+xsW1umPBHCx8j4v1WnaoiIqexNVzy+TySySSCwSB8Pl/VY5LJJEZHR8u2xWIxxONxTE1N\nNaJMesra2ho+vPshOl/vNNXu868/x/Z2qE5VEZHT2Boufr8f165dA7ATItVMT0/j8uXLZduCwWDV\nqxxqDHeLGx6fx1QbqU61EJEzObpDX9M0aJpWcVUjyztr0S4uLtpQFRERPY+jw6VQKAAAOjur34IR\nwsxTJ4iIqFEcHS6aptldAhER1cARo8XqQZJ4l/95CoWC6au/R48eQdM0tC+1m263tLSE9rY2w202\nuXAlUdM6sOFCz/fjn/wz/sc//m8cO26uc959tAWfrZi7qvzi88eYndPQ1mI8XJa1NrS1dZg6DxE5\ng6PDRVEUAMDKykrVfpfd/dXoeyx4yCuacse7TsH/O2fqfp7C0Tn4fD2mwuXEiS/wdau5KyQicgZH\n97nIsgxFUSpu3QghIMsyuru77SmMiIj25ehwAYBIJIJbt26VbcvlcohGozZVREREz+OocKl2KyuZ\nTGJ6erpsWyqV2nPSJRER2c/WPpdisYgrV65ACAEhBGKxGCKRCKLRKAYGBgAAHo8HyWQSiUQC/f39\npbXGeEuMiMi5bA0Xj8eDq1evPve4vr4+9PX1NaAicpJWfRtPfvlz3F1cMNxG13W8zIdXOp4kSUCx\niH+YmDDXrr0d/+W7391zYjU5h6NHi9Hhpnhehse9iSPHT5hq5+KIQMdzuVz4056ePUd17uVn9+5h\ng/OfmgLDhRzNJUkMiwNKkiRODTjAHNWhT0REBwPDhYiILMdwISIiy7HPheiA0nXg7t37cEn1/Rvy\n0cNVbGEL7SaX6ulo78Abr79Rp6rIbgwXogOqre0U7n9V/5FV64+3sX78PvDQeBsdOlxfuhguBxjD\nheiA6ug41pDzuFxuHOsE5C7ZcJvt7W08ePCgjlWR3djnQkRElmO4EBGR5RguRERkOfa5EJEtdF3H\nw4cmRgEAeLS6anrJGLIHw4WIGk5ySdhwb+DHv/ixqXa37xfRrf1XnDx5sk6VkVUYLkTUcBIkvPTm\nS+YbakVeuTQJ9rkQEZHlGC5ERGQ5hgsREVmuKcJFCIFoNIpsNgtN00qPOs5ms3aXRkREVTRNh342\nmy2FiSzLuH79OsLhsM1VOccHH/wcn35aMNVmQdwBXI35+2ILm/hQ/AwtbuPnW99cg0t217EqajZb\n2MI//cs/4fZHt021+4P/9Ad4880361QVVdMU4SJJElRVRSgUQqFQQHd3t90lOc7nn2tYW/tddHQc\nN9ymtfUETpyYrWNVv3H8ZR+kIzB1rdyGI3C3ttatJmo+8ksyXKdd0GXjI8buf3kfKw9W6lgVVdMU\n4QLsTLjq7OxEZ2en3aU4Vnv7URw5YjxcOjqOwvWoMY+ZdbvdaGlrg7tBV0p0MLlaXOg42oEjx44Y\nbtPaxj9Q7MBXOhERWa5prlyEENA0DQBQKBTg8/kwMDBgc1VERFRNU4SLz+cDgLIwGRoaqthGRETO\n0BTh4vF4cP78+bJtsVgMsVhsz3CRpMb0JexnbW0NX3zxhel2R44cwWuvvVaHiojqY2NjHYVlc6MV\n3W43PJ2eOlX0G0/WnuCzzz5DR3uHqXbHjx/HK6+8UqeqDr6mCJdq/H4/hBBYWVlxbCf//fv38Xd/\n9wWOHn3ZcJvt7U14PHn85V8yXKg5tLV1oFg8hmJx23AbXdfR0lLAmW/WP1xWllew+v9uYuPTzwy3\nWd/cxOenT+OVs2frWNnB1hThMjY2hkuXLpVt271VJoTAmTNnKtrstbhdo69ojh3z4vTp3zV8/Pr6\nYzx+fLeOFRFZy+1uxYkT5lYp1re3sfa4WKeKKnmPHMXvmrgb8ODRI8xxgcwX4vjRYruz8RcXF8u2\nFwo7l+CKothQFRER7cfx4aIoCsbHxysmTqqqimAw6NhbYkREh5njwwXYuQWWz+dLn2uahlQqhYmJ\nCRurIiKivTRFn8vAwAAymQzS6TSWlpagaRrS6TSXgXnK1tYWNjaeYGPjiYk2m7Wda3MDvB1NB52u\n63jyxPjrCQBcLhdauWQRgCYJF4DzWZ7nFx/O4cviz9HWftR4I11H6ylzwzMfP1pF4dZP0LG1Zapd\n58YGpBO8hUnNobWlBVtffIH/89d/bardens73vqLv0BbW1t9CmsiTRMutL8nm49x7Buvo1Ou77PF\n9e1t+La28U1vV13PQ2SnjrY2RPx+0+3UO3ewZfIPr4OqKfpciIiouTBciIjIcgwXIiKyHMOFiIgs\nxw59IrLFxoYOsWhuYdcvC0VouV+h44jxUY4r/3YXAAegNBrDhYgaTnK5cKTjdTx8YHyxSwCQnzyC\n/34BR44YfxLlqw8f4c3TvWZLpBfEcCEiW7S1Gw+IXRubHfCeOIqjR0zM53r8BO2c2Nhw7HMhIiLL\nMVyIiMhyDBciIrIc+1wcaGtrC3fu3DHVZls31zEKAJvr61hbfWCqzfrjxzhm+kxE1llbW8OmiSVW\nVldXsX5ivY4VUTUMF4dpaWnD6uop/P3ff2mq3YOV4zh+2txiecWv7uL4L2+jvdVcO7mFvzZkD7fr\nBBYX1wAYD4uV5SJOtxTwWxww1lB8l3AYl8uF11/vM93u068+xaZrw3S7U21tOCX7TLcjssPRozIA\n2VSbRw/MLZtP1mCfCxERWY7hQkRElmO4EBGR5ZqmzyWXy2Fubg4+nw9CCAQCAYTDYbvLIiKiKpoi\nXIQQSCQSuHHjRmnb0NAQFEWBv4anxQHAuUjU1PGSuwWJ//7fEAwGDbf51a9+hR/9z2s4dtRrtjzT\nHknb+MafvYX2up+JqLm43G788/xt/Msv/q+pdp2d7Xjj9VdMtfnF0gpWdd3UY47v3L2HYsebkE0M\nrFldfYDC44/xxjdeNVWf77gP3/2z75pqU6umCJdkMonR0dGybbFYDPF4HFNTUzV9zT/97W/C7XYb\nPv5nH95GsVg0dY61tTWcbn2C/h5zv6C1mF/R0MIhwkQVXjr1BrZOmnsT3thch8t1DyfePGGq3e/p\nm/gTrxft7cb/zPuHj/O47/oGfL5vG27z8OEvoW3n8M3f/4/Gi9OBr37+lfHjX1BTvBtNT0/j8uXL\nZduCwSDS6XTNX7OltRUtbuP/fQlSTedxSRLcDXjTlyR2nxHtxW3itQ4A29vbkFwSXC5zrytJkuB2\nu0394SpJElwuyWQbFyDBVBtd1w0fawXHvyNpmgZN0+DzlV8yyvLOWPfFxUUbqiIiov04PlwKhQIA\noLOzs+p+IUQjyyEiIgMcHy6aptldAhERmSTpjb4RZ1Iul0MoFML2duXCjC6XC6qq4jvf+U7FPkmq\nrY+EiIiqMxMXjr9yISIiZzDzR7vjR4spigIAWFlZqdrvsrv/WXsl7O43x+EXbHti/fZp5toB1m+3\ng1K/UY6/cpFlGYqiVHTcCyEgyzK6u7vtKYyIiPbk+HABgEgkglu3bpVty+VyiEbNzbInIqLGcHyH\nPgAUi0UMDg6WLf/y1ltvIZVKmb5yOSiXpqy/8Zq5doD12+2w1d8U4QIA8/PzmJycRH9/P4QQCAaD\nVUeJPc9h+wE7TTPX38y1A6zfboet/qYJF6scth+w0zRz/c1cO8D67XbY6j904UJERPXXFB36RETU\nXBguRERkOYYLERFZjuFCRESWY7gQEZHlHL+2GJET5HI5zM3NwefzQQiBQCCAcDhsd1mmpNNpeL3e\npqs7k8lACIGFhQUIIRCLxTAwMGB3WYapqgpVVdHV1YWFhQUEg0GcP3/e7rJqomkaEokErl279txj\nGS5o7h9+s7/wdjn5jU8IgUQiUbZCxNDQEBRFgd/vt7Ey41RVxcjIyAs9GtwOmUwGiqKUfqeLxSKC\nwSAKhUJTvEZVVYUkSbh69WppWygUgqZpuHjxoo2V1SYej2N5ednYwfohNzMzo6uqWrYtGAzqY2Nj\nNlVkXDqd1nO5XOlzTdP0np4ePZVK2ViVeTMzM7rX69Wz2azdpVQ1MjKiZzKZsm2qquqDg4M2VWSc\nEEKPxWLqDI8fAAAH7klEQVR6KpXSe3p6HPs93ku112EqldIlSbKhGvPOnTtX8f4Sj8f1np4emyqq\n3cLCgj44OKgPDQ0ZOv7Q97mMj49XbItEIlW3O40QAn19faXPPR4P4vE4YrGYjVUZl8/nMTo6inw+\nD5/PZ3c5e5qenkYgECjbFgwGm+IqwO/349q1a03xV/6zNE3D5OQkisVi2fbdq9vFxUUbqjJHkiSo\nqlq2Tdd1eL1emyqqXTabRTQaNTxD/9CHS7P+8A/CC68Z3vg0TYOmaRXhJ8sygOb4PjcrWZYhhEA+\nn7e7lJpNTU3hypUrZdvS6TSGh4dtqqg22WwWkUjEVJtD3+cyNTVVsS2dTuOdd96xoRrjnn7hnTlz\nxu5yDqxCoQAAVR9UB+xcPfKZQvWz+/1/mqqq8Hq9Tfl9T6VSCIVCuHDhgt2lmCKEQDgcNrUu2qEP\nl2c10w//oL3wnEjTNLtLoGeMj4/j8uXLdpdhSiaTwczMDCRJwuTkpN3lmJLJZGq6u8Bw+XfN/MN/\nWjO+8IiMSqVSOHnyZFP88fe0gYEBDAwMoFgsIhQKYWJioqy/1Kle5I8rhsu/a9Yf/tOa9YVHZIQQ\nAqlUCrOzs3aXUjOPx4NYLIZwOFz1zoPTTE9Pl1217C67b8SBCRchhOFju7q64PF4qu6z44dvRe12\nvvCs+t47kaIoAICVlZWq/S67+6n+EokEbt68aXcZLywcDkPTNGSzWUfO69o1Pz+PUChUtu3Q9bnk\n83kkEgnDx/f39+87gamRP3yrarfrhWf1995pZFmGoigQQpQNnBBCQJZl9m01yOjoKMbGxvYcWOFE\nu0/Mff/996sOunl2pKfTzM7OYmFhoaybIJfLlSYV9/f37zth+0CEi9/vrzrq63mc8MOvtfan2fnC\ns6J+p4tEIrh161bZ70gul0M0GrWxqsNjYmICiUSiLMiz2azjV0jQNA09PT0VV7e7V/rPzp1ymmqd\n+O+++y5mZ2fLVhzYy6Ge59LsP3xg7xdeM88NcJpkMonp6emybalUCslk0qaKamfmtoYT7E5ULRQK\nyOVyyOVyUFUV09PTjg4WYOf9Y3h4uOJ7nkwmEY/Hm/Kq9+uvv+Zjjo169913MTIyUtYPEI1GEQqF\nKiY/OU06ncby8jKCwWBpW6FQQDqdNrSwnJP09vZifHzcsfeg5+fnMTk5if7+/tIV73e+8x27y3qu\nYrGIK1euQAiBdDoNRVEQiUQQjUYdvwZdtcmru3p6evDxxx83uKLaTExMYGFhobR2YSgUwttvv213\nWabk83kkk0lMTU2hWCzi/PnziMVi+w56OvThAjTnD/8gvPCa+Y2PiPbHcCEiIssd6j4XIiKqD4YL\nERFZjuFCRESWY7gQEZHlGC5ERGQ5hgsREVmO4UJERJZjuBCZkMvl4HK5KlaLfZaqqnC5XBgaGjL1\n9QcHB+Fy8WVJzY+/xUQmBAIByLKM+fn5fRc23V2L7Hvf+57pc5h5ZgaRUzFciEwaGRmBruv7rgY9\nNTUFSZJw9uzZBlZG5BwMFyKThoeHAew8UrqaXC6HYrGIc+fONbIsIkdhuBCZ1NfXB0VR9rw1tvtw\npd0QAnYe4zA4OIienh64XC74fD4MDQ1VfTTC08v9RaPRqn0wmqbB5XJhdHS0Yt/Y2BiCwWDpPKOj\no3wEAzUcw4WoBrFYbM9bY6lUquyWmBACvb29+MEPfoDe3l7EYjGEQiGk02kEg8HnPpRuvz6YZ/cF\ng0EkEgm4XK7SeVKpFHp6ejA/P1/D/5SoNgwXohrs3vJ69tZYtVtiyWQSkiRhZmYGP/rRj/Dee+/h\nxo0bSCaT0DQNqqpaUtPY2Bjm5+eRzWZx69at0nnm5uYAVH+yIFG9MFyIauD3+9HX11dxa6zaLbHR\n0VFMT09XPFxs90FLy8vLltR05coVRKNRBAIBaJpW+vD7/QiHw8jlclhZWbHkXETP02J3AUTN6nvf\n+x7m5+eRSqVw8eJFADtPB312lFhfX18pSDRNw+zsLHK53J4DAmpVLBYxMzMDr9dbdb8kSSgUCujs\n7LT0vETVMFyIajQyMoJ4PI7JyUlcvHgRQgjk83kMDg6WHadpGuLxeOkRscBO30gwGLSso10IAWBn\nAEA8Ht/zuL2Ch8hqDBeiGnk8HgQCgdKtsXQ6DWCns/9p4XAY8/PziMViiMViOHPmDAAgm82W2phV\nKBTKPt995LUsyxW334jswD4XohewO2oslUphcnISkiSVvblrmob5+XkMDg7ivffeKwULUD7k2Kxc\nLlf2uSzL8Hg8ew4O8Hq96O3trfl8RGYxXIhewO7aYePj45ifn99z4uSznfa7t8qAypB5enixLMvQ\ndR3ZbLZq26fFYjEsLy9XrGc2NjaGYrFYdU4MUd3oRPRCotGoLkmSLkmSns1m99w/ODioJ5NJfWRk\nRPd6vfpbb72lS5Kk9/T06Kqq6rqu6+fOndMlSSq1TafTpa8di8XK2nq9Xn10dLTsXD09PaWvee7c\nOT0QCOiSJOmhUKi+3wSiZzBciF7QbgC4XK6q+zVN02OxmO71ektv9JlMRtd1XY/FYrrL5SqFxODg\nYMXXSaVSpdDw+Xx6IpHQdV2vGi66ruvxeFwPBoO6JEl6b29v6XiiRpJ0/QVu/BIREVXBPhciIrIc\nw4WIiCzHcCEiIssxXIiIyHIMFyIishzDhYiILMdwISIiyzFciIjIcgwXIiKy3P8HynkIpHhL8JoA\nAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7f610c073c10>"
]
}
],
"prompt_number": 54
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f_val, p_val = scipy.stats.f_oneway(x, y, z) \n",
"print \"One-way ANOVA P =\", p_val \n",
"f_val, p_val = scipy.stats.mstats.kruskalwallis(x,y,z)\n",
"print \"One-way Kruskal Wallis P =\", p_val "
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"One-way ANOVA P = 3.03067030652e-08\n",
"One-way Kruskal Wallis P = 2.7064432518e-08\n"
]
}
],
"prompt_number": 55
},
{
"cell_type": "code",
"collapsed": false,
"input": [
" np.random.seed(50)\n",
" x = [np.random.randn() for _ in range(200)]\n",
" y = [np.random.randn()+0.1 for _ in range(200)]\n",
" z = [np.random.randn()+0.1 for _ in range(200)]\n",
" i = [np.random.randn()+0.1 for _ in range(200)]\n",
" j = [np.random.randn()+0.2 for _ in range(200)]\n",
" ax = plt.subplot(1,1,1)\n",
" ax.hist(x,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(y,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(z,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(i,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\n",
" ax.hist(j,bins=np.linspace(np.min(x+y+z+i+j),np.max(x+y+z+i+j),25),alpha=0.3,histtype='stepfilled')\n",
" ax.set_xlabel('Value',size=20)\n",
" ax.set_ylabel('Freq',size=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEsCAYAAAAPa/67AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3VtwWneeJ/DvQaCbZXGRc3PSGXPkvs50jwUoM70121sV\nRKZqamurNrKk7NO+xEL9blv4aV62ykap3dq3WMhP+7IrCTIzex8L3DtTPTu9bQs53Z100rYOysWO\nb0IHdEMIOPvgFmMEkv7IwDnI30+Vq6I//8P5BYF+/O+SpmkaiIiIasikdwBERHT0MLkQEVHNMbkQ\nEVHNMbkQEVHNMbkQEVHNMbkQEVHNmfUOYDdVVREIBHD16tWS8ng8jvn5eTgcDiiKApfLBa/Xq1OU\nRES0H8Mll/HxcaysrJSUKYqCQCCA69evF8uGh4chyzKcTmejQyQiogMYqltMURSsrKxAkqSS8mAw\niLGxsZIyv9+P8fHxRoZHRESCJCOt0J+amgIAzM3NYWZmpljucDgQj8dx6tSpYpmqqnA4HCgUCo0O\nk4iIDmCYlkssFsPAwEBZuaqqxUTyLJvNBgBYWlpqRHhERFQFwyQXRVHgdDqxuyGVTCYBAN3d3Xte\nR0RExmKI5BKJRHDu3LmKj6mq2uBoiIjoeemeXJg8iIiOHt2Ty+zsLAYHB4s/754pdliSJO35j4iI\n6kvX5LKwsACPx1NStnvMRZZlAEA6na74HDuPV4MJhoiovnRdRHnr1i0sLi5ienq6WBaPx4uLJvv7\n+zE4OAhZlqEoCs6cOVOspygKbDZbyfTkZ+01w5qJhYio/nRNLpUG8T/44APcunULV65cKZYNDAzg\n5s2bJcklHo/D5/M1JE4iIqqO7mMuuz158qSs1REMBjE7O1tSFgqFEAwGGxkaEREJMswK/UQigWAw\niJmZGaRSKZw7dw5+vx99fX0Ano7PTE9Po7+/H4qiwO124+233676PjvdYgb53yYiOpIMk1wahcmF\niKj+DNctRkREzY/JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiIao7JhYiI\nak7XjSuJXhT5fL6q+iaTiTt4U1NjciGqs08//Rx/93d3YTKJdRRomoY33+zCX/zFT+ocGVH9MLkQ\n1dn2dg5m8/fx6qtiB9ttbW1gdfUXdY6KqL445kJERDVniJZLNBpFNBpFT08PFhcX4Xa7Sw4SUxQF\nfr8fgUAAbrcbyWQSoVAIPp8PXq9Xx8iJiKgS3ZNLNBqFJEklJ096PB6oqooLFy4Uy2KxGGKxGADA\nZrPh2rVrTCxERAale7fY5ORkWdnAwEBJuSRJiEajUFUViqIgmUzi3XffbWSYRERUBd2Ty07ieJam\nabDb7WVl3d3dOHXqVAOjIyKiw9C9W2xmZqasLBwO46c//akO0RARUS3onlx2C4VC8Hg8OH/+fEm5\noihQVRUAkEwm4XA4MDg4qEeIRER0AMMkl0gkgrm5OUiShOnp6ZLHHA4HAJQkk+Hh4bIyIiIyBknT\nNE3vIJ6VSqXg9XoxNTWFvr6+PevFYjH4/X7cvXu3quff2VLDYP/bdIR9/PEn+OUvO6paRJnP/wIj\nI2/XOTKi+tF9QH83q9UKv99/4DRjp9MJRVGQTqcrPi5JUsV/RERUf4ZLLgDg9Xqhqipu3LgBAJiY\nmCirs9NVpihKQ2MjIqKD6ZpcFEWB3W7H7du3Kz6+s64lEAhgaWmp5LFkMgkAkOXKXQ2aplX8R0RE\n9afrgL6qqujt7S1LEDutEZfLhVOnTmFycrJsfUs0GoXb7UZ3d3ejwiUiIkG6tlxcLhdGRkbKWhTB\nYBDj4+PFhOJwOJBIJIqPq6qKUCiEqampRoZLRESCDDFbbGpqCouLi8WNKz0eD95///2SOpFIBIqi\nYHl5GaqqIhAIHGq1PmeLUaNxthi9iAyxzuXZHZD3wvUsRETNw5CzxYiIqLkxuRARUc0xuRARUc0x\nuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRARUc0xuRAR\nUc0ZYlfkaDSKaDRa3HLf7XaX7ZQcj8cxPz8Ph8MBRVHgcrng9Xp1ipiIiPaje3KJRqOQJAlXrlwp\nlnk8HqiqigsXLgBA8ajj69evF+sMDw9DlmU4nc6Gx0xERPvTPblMTk5ibGyspGxgYACTk5PF5BIM\nBsvq+P1+jI+PY2ZmpmGxEhnVN/fvI/noUVXXOF5+Ga+dPFmniOhFp3tykSQJ0Wi0pItL0zTY7fbi\nz7Ozs7h06VLJdW63G+FwuGFxEhnZl59+io5PP8Xxjg6h+qubm/jyBz9gcqG60T25VGp5hMNh/PSn\nPwUAqKoKVVXhcDhK6thsNgDA0tLSoY47JjpqXrXb8fLvPxcHeaSqSNQ5HnqxGW62WCgUgsfjwfnz\n5wEAyWQSANDd3V2xvqIoDYuNiIjE6N5y2RGJRDA3NwdJkjA9PV0sV1VVx6iIiOgwDJNcBgcHMTg4\niFQqBY/Hg6mpKfT19ekdFhERHYLhusWsViv8fv9zr2GRJKniPyIiqj/DJRcA8Hq9UFUVN27cgCzL\nAIB0Ol2x7s7jRERkHLomF0VRYLfbcfv27YqPq6oKm80GWZbLBu4VRYHNZttzppimaRX/ERFR/ema\nXFRVRW9vb1nrYyeRuFwuAE8XVd68ebOkTjweh8/na0ygRERUFV2Ti8vlwsjISFmLIhgMYnx8vNgq\nCQaDmJ2dLakTCoUQDAYbFSoREVVB99liFy5cwNTUFBYXF4sbV46MjOD9998v1rFarQgGgwgEAujv\n7y/uNcbFk0RExqR7cgFQtgNyJX19fZyaTETUJAw5W4yIiJobkwsREdUckwsREdUckwsREdUckwsR\nEdUckwsREdUckwsREdUckwsREdUckwsREdWcIVboEzWTdDqNXC4nXD+VSiGft9QxIiLjYXIhqtJf\nX/9rbJo2hQ+fW1xcgm37z/H669+pc2RExsHkQlSlzHYGr/W9Jpxcvnx8D9oTniVELxaOuRARUc0Z\nIrlEIhF88MEHGBsbwzvvvINIJFLyuKIo8Pl8iMViUFW1uOV+LBbTKWIiItqP7t1ikUgEsixjcHAQ\nwNPBT7fbjWQyWbIVfywWKyYTm82Ga9euwev16hIzERHtT/eWi6IoJee0WK1WjI+Pw+/3F8skSUI0\nGi22WpLJJN599109wiUiIgG6JhdVVTE9PY1UKlVSvtMiWVpaKpZpmobu7m6ePklE1AR0TS42mw2K\noiCRSOgZBhER1ZjuYy7JZLKsLBqNwm63l7RSFEWBqqrFaxwOR3GchoiIjEX35FLJ5OQkLl26VPzZ\n4XAAQEkyGR4eLisjIiJjMFxyCYVCOHHiBM6fP18ss1qtJTPHAMDv98Pv9++ZXEQXuBHVm6ZpyOW2\nsb2dFar/tF6+vkEB2N7eRjYrFhPw9DNlsXAbGxJjqOSiKApCoRBu3bp1YF2n0wlFUZBOp9Hd3d2A\n6IgOJ/nNY1ji/xOLDxSh+tu5LeTta8C/8dUtptXVVcx9toBP0l8KX9MmteG9f/Ue2tvb6xYXHR2G\nSi6BQAA3btwoK5+YmMDFixdLyna6yhRFwZkzZ8qu0bTK222wRUONpuU1fNvUgj/pOSlUf3UjjX/M\nPK5rTAVNQ761gJNnxGICgHsf30OhUKhjVHSU6L7OZcfY2BgmJibKWiE7q/GfnZYM/NNEAFmWGxUi\nEREJMkRymZqaQiAQKJkdFovFkEgkIMsyJicny9a3RKNRuN1udokRERmQ7t1i4XAYwNOWyE5rJJlM\nIhwO4+rVqwCedoElEgk4nU4ATxdfhkIhXLt2TZ+giYhoX7omF1VVi1OKd+vt7S3+9+DgICKRCMLh\nMJaXl6GqKsLhMFfr05FU0ApYVpP43e9+J3zNl19/jcKjR1DX14XqL96/j3uP7+Pe/XvC93j0+BHH\nXEiYrsnFZrMJv1m5noVeFNncNu5sb+LGyorwNQlJQqKtDd0tLUL17wD4RFlBx6/E40p+/hiZTAZd\nXV3iF9ELS/duMSIqZ2ppwevPtN4Psra2hlc6O2E7dkyo/qOVFZhNZvQ4Xhe+h2r6TLgukSEG9ImI\n6GhhciEioppjciEiopqraszl9OnTVa9w1zQNkiThzp07VV1HZFS/+u0dfJr+BhD8LHz+5SO8sSn+\n/JIkAZsbiFfYrWIv+a0tvNbZKX4TojqrKrn09fUhkUggHo8Xy5xOJ5LJZPHAL5vNVlyPsoNbrtBR\noma38UbfGZgE2/3bd77B9v1t4edvM7fidNdx/LCjQ/gaqbMTZtGAiBqgquRy6dIleDweuFwuTE1N\nlRxPHI/Hce7cOSwtLSEcDpclGKKjpMVihskk9qVJEqz3LJPJBIvgtGIiI6rqq86VK1dgs9kQi8VK\nEgsAuFwuzM/Po1AoIBAI1DRIIiJqLlUll2g0Cp/PB6vVumedgYEBRKPR5w6MiIiaV1XdYpqmQVH2\nP5MikUg8V0BEjZTNZvHkyZPqLqp8mgMRPaOq5DIwMIBIJIKPPvoI7777btnjkUgE8XgcAwMDNQuQ\nqJ4ePHiAv/m/f4PWY63iF3VoohPFiF5YVSWXYDCIaDSKoaEhnD17Fj6fD7IsY3FxEXNzc8UdjoPB\nYF2CJao1TdPQerwVJ0+LH5pl++p+HSMiOhqqSi6yLCMWi2F8fByzs7OYnZ0te3xycrJssJ+IiF4s\nVW9c6XK5MDc3B0VREI/HoSgKZFmGLMtwuVyHCiISiUBRFCwuLkJRFPj9/rJdkOPxOObn5+FwOKAo\nClwuF7xe76HuR0RE9XXoXZFPnDgBj8dz4Oyxg0QiEciyXEwmqVQKbrcbyWQS586dA/BPRx1fv369\neN3w8DBkWeZ6GiIiA6o6uSwsLODcuXOIx+OQJAlzc3N4++23cfr0aYyNjeH8+fNVPZ+iKCWtFKvV\nivHxcfj9/mJyCQaDGBsbK7nO7/djfHwcMzMz1f4vED2Xuz//DTqVVeHtXzKffI07X6/jf/3DfxOr\nn8vgztZj5Cx/LxzTZmYdre0taBFcePnw0WNk1sQOFiM6jKqSSyKRgNvtBgB4vV7EYrHiY8vLy7h4\n8SKmp6dx8+ZNoedTVRXT09MYHR0taf3sdHctLS3h1KlTmJ2dxaVLl0qudbvdxQkERI2UW1rFn3S8\nDkhiy8RkrQWOYxt4WTohVH9LymJzuwffSv9QOKZl9Ut09mjoaBfbMkbKmJBo4cQEqp+qZ4sBwPz8\nPJxOJxwOR/GxlZUVTExMIBAI4NKlS7h8+fKBz2ez2aAoChKJBM6cOVOxjqqqUFW15F471wL/lICI\nGsnWZRVuJWTVNVjXzLB12YXqb21toWvLDGuXWDICgMzmCro6gWNdYoeFLadSkFa5FxnVT1XvrpmZ\nGQwMDOw5G+zixYvo6+urqkWRTCbLEks0GoXdbsepU6eQTCYBAN3d3RWvP2hRJxERNV5VyUVVVfQe\ncPTqzrqX5zE5OVnsBlNV9bmei4iIGq/qLfdv3bq1b52FhYVDT0kGgFAohBMnTlQ9MWA3bvP/Ytra\n2sLW1pZw/dXVVeTz+TpGZFyapmFrc0O4fmZjA6urq2htFd/NoLOzE2bzoSelUhOr6rc+MjKCQCCA\nn/3sZxUTyPDwMBRFwcWLFw8VjKIoCIVCByYwor1E/+Ef8OX6Okyis6YePkR24wG+9d1v1TkyY2lp\nMSHT1o7ffC2+F+D9TxP4+X/+OXp6eoTqZ3NZfOdffAc/+KMfHDZMamJVJZed2WBerxc+nw/A00H+\nyclJRKNRrKysQJZlXLly5VDBBAIB3Nh1+p4sywCAdDpdcdxl5/HdNK3y7oJs0RxtW/k8HD/8ITq7\nuoTqp27fxuZnL95mq2aLBW0nT+L4D38kfI3pxs/xh/Y/xJsn3xSqv/Rg6YVtFVKVYy7A05liV65c\nwS9/+UsAwNzcHGZnZ1EoFHDx4kXcvXv3UIGMjY1hYmKiLIHYbDbIslw2cK8oCmw2G2eKEREZ0KHm\nIl68eBErKysoFAq4e/cukskkVlZWDt1imZqaQiAQKEkUsVisuH3/wMBA2dqZeDxebD0REZGxVJVc\npqam8NFHH5WUybJcXHNyGDvTlpPJJOLxOOLxOKLRKGZnZ4tbuwSDwbJNMkOhEHdfJiIyqKrGXPx+\nP+x2e8WzXA5DVVUMDw9XfOzZKc9WqxXBYBCBQAD9/f3FvcbYJUZ62Mpmsba2DpNJbNJAbjtX9T0K\nhRxW15LC9XP5bQCWqu9Tje3sFu59sYTCpthsvK+X76HnO6/UNSYyrqqSy/vvv49r167h9u3be66o\nr4bNZkOhUBCq29fXx638yRA2N7NYXzPDZBZr+Ge322BpFf+oSS0tQBuwromv8Sq05WC2iG39cmib\nGXR8+TWObWTFYnqwhOU/5gSaF1VVySUUCuH06dNwu92YnJyEx+OBLMt7rp4nOqosrW3CLReLuQ0t\n2Yzwc0sSYLa0wtLWLnyNJmUhmer/h9za2YmXrGKf96WVdoivOKKjpqrksrO/l6ZpGB0dLZY/O71X\n0zRIksQpiEREL7Cqkovo4VxcS0JE9GLbN7kEAgG89dZbxQH83TO2iI4CTdP2XHRLRIezb3KZmJjA\n0NBQ2eywqakpxONxfPjhh3UNjqjeUuk0bt++i3RBvLVdqKIu0YvqUDvKXb9+HR999BGTCzW9p2OD\n3ehx9Atf02r5Rf0CIjoiDn1aELsRiIhoL4dOLhy0JyKivfCcUyIiqjme4kPUAJvbWWB9TahuXhPb\nteJ5aZqGtVQVJ72yK5yqwORCVGeWzk48qvKaFkt9P5qtLS1wrG/C8YX4keSpQgGtZrFdCYgOfAdH\no1GMjIyUlMViMWiaVlb+rOnp6eePjugIaG1rR2sVW7k0gqlFQndHB17qEt+66YHZAkliTzqJOTC5\nrKys7Ll4cr9FlUwuREQvrn2TSyPPsg+Hw7Db7WVbzCiKAr/fj0AgALfbjWQyiVAoBJ/PJ7wdDRER\nNda+ycXlcjUkiGg0itHR0eLBYbvFYjHEYjEAT7fpv3btGhMLEZGB6Tqgn0gkEAwG4Xa7izsu7yZJ\nEqLRKDweD5LJJA8IIyJqArqOzjmdTly9ehXnzp3bt56maeju7mZiISJqEpz6QURENdcU61wURYGq\nPl3slUwm4XA4MDg4qHNURES0F8Mnl52xmGeTyfDwcFkZEREZh+GTi9VqLRuT8fv98Pv9+yYXbqz5\nYtrMZLCRTmO7ILaFSnaLp7xXI7O1iY31DaG6W5kMtre36xwRGZXhk0slTqcTiqIgnU6ju1t8hTEd\nfb/+zSIe329F+7HjQvXvL2Vhbumsc1RHRAvwxcMvoK49Eaq+9M1XkB601TkoMirDJ5eJiQlcvHix\npGynq0xRFJw5c6bidXudN8MWzdFWyAPHj7+J47aXhOqvJTew3rFU36COCEt7Kzp7jqFLMHGbkiYU\nGrQJJxmPoWeLKYqCQCCApaWlkvJkMgkAkGVZh6iIiOgghk4usixjcnKybH1LNBqF2+1mlxgRkUEZ\nKrlU6spyOBxIJBLFn1VVRSgUwtTUVCNDIyKiKug65pJKpXD58mUoilLcoHJgYAA+n684E2xwcBCR\nSAThcBjLy8tQVRXhcJir9akmtrczeJD4HJm02CA1AGg4AodmSRLya1k8vvuV+DXbgASOWZIYXZOL\n1WrFlStXDqzH9SxUL+bOYzj2ygk4bDbha0yvv9H055ocaz+G09ppWFJdwtfYzetoM1vqGBUdJYaf\nLUZUT6YWM7q6unHixMvC12Q7VuoYUWOYJBO62o+jtVV83DJn4ZRtEtfcX7+IiMiQmFyIiKjm2C1G\nhqaqKgqCW7kAQCaTQSGbwfbWplD9XHZrzwW39Hw0Dchmt7G5Kfa7AIB8Po+Wlpaq7tPe3s7F0QbE\n5EKGlUgkcPUv/wPa8+Jv048//xyv/9CKrWNiA/QbyXtYk5aB1147bJi0h/XMFuJLCfynaFSofqFQ\nQOL/zOOff69f+B45LYf+f9mPN95447BhUp0wuZBh5XI52AudeFv+M+FrPk48wXeP/wg2u1iyuJu+\nhc+2PztsiLQPDYBkd+Dkj38sVD+Xy+F3//MmfnxSrD4A/Pb+b6tq2VLjcMyFiIhqjsmFiIhqjsmF\niIhqjmMuZFjZbBYP0su4+/hL4Wvy+XzV98llMlj+5oH4BRpnJhEdhMmFDGt9fR2LrRo6XmoXvib/\n8gmYzOIHVHV22CHffxM9X1qFr2kx9XDqK9EBmFzI0MxmC06cEJ8m3NG1VNUffou5DbZjJ9Bz3H6Y\n8IhoDxxzISKimjNMyyUcDsNut8Pr9ZY9Fo/HMT8/D4fDAUVR4HK5KtYjIiJjMERyiUajGB0dRTgc\nLnts56jj69evF8uGh4chyzKcTmcjwyQiIkG6JpdEIoFgMAi32w2Hw1GxTjAYxNjYWEmZ3+/H+Pg4\nZmZmGhEm1cjCwm8Qj4vP/FpauoOVxEPckW4JX7P+4BG+avkUbaljQvWzmxvo4ti8kLzZjI8frkAy\nie399U02D6nKfcLo6NA1uTidTly9ehXA0yRSyezsLC5dulRS5na7K7ZyyNjS6QxaWv4YNturQvWX\nl+142fQ7uDo9wvdo7bJBcnShtUNwhtmGBktOfHbZi+z4K6+g86UumAQTRntLAdZXxM/JoaPFEN1i\ne1FVFaqqlrVqbL8/NXBpaYnHHTcZSTIJ73pr+v03ZJPgN+Wd55ckQBKeq8JmiyhJkiCZTDCZxF5b\n0Xp0NBn6t59MJgEA3d2VT8tTFKWR4RARkSBDJxdVVfUOgYiIDsHQ3WLPgyuoifSX3dzE43v3hOoW\nDrF1DxnXkU0uRKSvzrZOOL7sxEZULLloBQ2vSSfrHBU1iqGTiyzLAIB0Ol1x3GXn8Ur2OrqWLRqi\nxmhv7UC3wwn51e8J1dcKGlJJHvx1VBh6zMVms0GW5bKBe0VRYLPZOFOMiMigDJ1cAGBgYAA3b94s\nKYvH4/D5fDpFREREBzFUcqnUlRUMBjE7O1tSFgqF9lx0SURE+tN1zCWVSuHy5ctQFAWKosDv92Ng\nYAA+nw+Dg4MAAKvVimAwiEAggP7+/uJeY+wSO/q2tzexvqliWf1a+JpcPgsLx9UMYTuXw5P7y5BM\nX4ldoGnYvlfFoW1kaLomF6vViitXrhxYr6+vD319fQ2IiIwkm81iu7CFfJv4FFUzLGhpMfQ8lRdG\nIZ/HxkYLcjmxLWC0Qh6p1K/rHBU1Cj+FZGgmyYSWFot4fVOujtFQtUwmE1otYnu3FQqcKXaUGGrM\nhYiIjgYmFyIiqjl2ixEdEYV8HjlsC9clqicmF6IjQJIsWFnJAshWcU1r/QKiFx6TC9ERYLF0AOjQ\nOwyiIo65EBFRzTG5EBFRzTG5EBFRzXHMhYiEaBqwtrYB0d11trI55KVNqE/Etu8pFAp49PAePvvd\nZ8IxLT5ehGPVIVyfGofJhYiEmM3HkMmIr6I3S8fwBkzoWl0Wql/I53FXfYR7WbHDxQBgKbmE76a/\nK1yfGofJhYiEVLMNDwAULAV0mTpwrK1TqH4un4ME4LjtuPA9LK3VxUSNwzEXIiKquaZILoqiwOfz\nIRaLQVXV4rb7sVhM79CIiKiCpukWi8VixWRis9lw7do1eL1enaOiahQKBWQyG8hkNoTq53Liq82f\npWkFaMI77JYfUEe1owEoaGK/i53DAre3xbawAYB8Lo98Pl/VNdWSJAlmc9P8qTSMpnjFJElCNBqF\nx+NBMpnkQWFNKnb9f+PX/3gP7e3HhOpvrKfRhuq2KDFrBWzeEz9cDABaeLhYXUiSCauZZaxmkkL1\nC/kCttva8T+ux4Xv8fDxV0DLDTz55MlhwzxQ3pzHwNkBWK3Wut3jKGqK5AI8/VbT3d2N7u5uvUOh\nQ9rKZHD6pe/hzW+Jze5JJ5N4kBCflgoAJzrEEhfVn6W1DdV8N9Cgoef7f4SuP+gVvmbrs1/BZf0+\n/vTknx4iQjHxb+LIc6PPqjXFmAsRETWXpmm5KIoCVVUBAMlkEg6HA4ODgzpHRURElTRFcnE4nq7A\nfTaZDA8Pl5UREZExNEVysVqtOHfuXEmZ3++H3+/fM7lIHKQ1nM3NDPJraayuiA3wZjbW6hwRHQVr\na2u4f/++cP2O9g7YHfY6RkRAkySXSpxOJxRFQTqd5iB/k1hffoLX76/hpW2xob5Mdhv5lpY6R0XN\nzNxqxteZr5H7JidUP5fLocfcgx87flznyKgpksvExAQuXrxYUrbTVaYoCs6cOVN2zc6c+d3YotHX\nsdY29BwT+zKwadnCcv5wa13oxdBitqC75xgcr4htXrmV2QJSdQ6KADTBbLGd1fhLS0sl5cnk064V\nWZZ1iIqIiPZj+OQiyzImJyfLFk5Go1G43W52iRERGZDhkwvwtAsskUgUf1ZVFaFQCFNTUzpGRURE\ne2mKMZfBwUFEIhGEw2EsLy9DVVWEw2FuA6OjTCaDf//v/hLZ1bTwNSv3v4DJ9Md1jIpeOCYJ9x6q\nWFkV21sst52DXevAj93it1hKfA1lZhVdXeK9JD/60Rv40Y++L36TI6gpkgvA9SxGk81msfHgK/h+\n8LrwNS33reh60lXHqOhF0+ZwwPLyy7AcEzwzZnUdG4nq9iFbW9tCe+EH6OwUG99V1YdQ1cdV3eMo\naprkQsbU2dEuXLfNwrcb1ZZkkmAym9EiuGux6ZBT283mVlgsbUJ1qz1U7ahqijEXIiJqLkwuRERU\nc+ynaAK5XA5PnlTXT1ztzgWZTAaSJKGtTazpv7q6ivXNDJZT4lu0rGa2YMpuYX1rU6h+Npfj1x+q\nuUKhgJWVFeH66+vr6BQ+fI52MLk0gYcPH+K3f/VXsFnE+3L/+pef4jXXCMxmsQM1vlj6BH2m38H5\n5ptC9dc3N/FoYwt/nxE/yfGOZMZJswmrogmj1QxTu/iYDtFBWixmbHZ24P99JX6g3OLyQ3Rtis+K\npKeYXJpEj8WCvpMnhev/19wnePnlM2hvF5tFc//eQ7xm/gIewXusbWygp/s4TvQ6hWN68GgTndoJ\nHDv+svCOnmgKAAANy0lEQVQ1RLVkamnB8ZOvwXHqD8SvuV3daaj0FDsdiIio5phciIio5phciIio\n5jjmckS15Lax9KsbMJvFJgFsPFAgfYvHEZB+JACmfAEbjx4IX7OVXUOq0IKttg6h+vlcDhZJbBxy\nx/rGBv7xF7P47Wd/L1R/YyONt/pfw09+UsUeM0cQk8sRdabbhtbVZbS0iP2KX81m8EZPT52jItqP\nhFdbW6Flt4SvyGazsGXMaCuIdcJsZbNYQXXTils629H+0nHYe2xi93iUwr17X1V1j6OIyeWIOtbW\nhmOd3cLJJbeRhqWFvaSkL4tgS7uoYEFbawva28Su07QCILbHZZHJbIGjuwcvO14Rqr+2pgIQO8r7\nKONfEyIiqrmmabnE43HMz8/D4XBAURS4XC54vV69wyIiogqaIrnsHHV8/fr1Ytnw8DBkWYbTKb6I\nT0Qul0Mmk6nqmu3tbViqWD0vSRKOHTsmXL9QKCCZTuNxh9igJQBsbmUhmTeFu8U2tzMoFKpbDZ/Z\n2sLa2rpw/XwhX9XzE4nQCgXk8mLvrVw+j0JeQjYr3jdWyOexmVnD2npKqH5mYx1SywYePBCfmJDP\n52G1WoXrA0BHRwdaDrnLcyM0RXIJBoMYGxsrKfP7/RgfH8fMzExN7/Xxx5/iF794KDzLan09ja/W\nP8f33H8ofI+WTAZDXq/wm+mTTz7Bf5+Zx3znCeF75PMmHD++BJNJbAZYMvUEr52y44033hCqv57J\nQPn1Q2ysJQ6u/HtSwQTLcbG9y4hESKYWqGoGQFao/tb2Nh4X8vjN4q+F75FZ3cDD24+gWhSh+qvp\nFNrXVvBfVv6j8D3i9xPw/Ot/i7Y2sZls29tb+PM/l/Htb39b+B6N1hTJZXZ2FpcuXSopc7vdCIfD\nNb9XNltAZ+f3ceKE2B/Zx4+/xN3tL3DyrbeE73F/fh6FKjbCKxQKcEiv4c9e9QlfU61PVn+NQkF8\nlo5WKKAt344f9fyzusVEdBCLuR1AFS1uaQuWlk0cf/m48CWvv3YKJzYsaBec7pxqfYw3zUmclX8i\nfI9PEl/C4eiH1fqSUP379+8gnzf2ZpqGH9BXVRWqqsLhcJSU22xPpwUuLS3pEBUREe3H8MklmXw6\npW+v7eMVRaypSkREjWP45KKqqt4hEBFRlSRN08QP5NBBPB6Hx+OpOEZhMpkQjUbx9ttvlz0mSdzK\nhIiolqpJF4ZvuRARkTFU86Xd8LPFZFkGsPexvTuP77ZXht15cQzeYGOcNdQMMQKMs9YYZ21V2xtk\n+JaLzWaDLMtlA/eKosBms+HUqVP6BEZERHsyfHIBgIGBAdy8ebOkLB6Pw+er37oPIiI6PMMP6ANA\nKpXC0NBQyfYv77zzDkKhUNUtl2ZrgjLO59cMMQKMs9YYZ21VG2dTJBcAWFhYwPT0NPr7+6EoCtxu\nd8VZYgc5qr9IvTRDnM0QI8A4a41x1taRTS61clR/kXpphjibIUaAcdYa46wtJhciItJdUwzoExFR\nc2FyISKimmNyISKimmNyISKimmNyISKimjP83mJEL4J4PI75+Xk4HA4oigKXywWv16t3WBWFw2HY\n7XbDxheJRKAoChYXF6EoCvx+PwYHB/UOq0w0GkU0GkVPTw8WFxfhdrtx7tw5vcPal6qqCAQCuHr1\n6oF1mVx2qebFa6RmeSM2ywd7hxH+UCqKgkAgULIDxfDwMGRZhtPp1C2uSqLRKEZHR+tyxHgtRCIR\nyLJcfM+lUim43W4kk0lDfV6i0SgkScKVK1eKZR6PB6qq4sKFCzpGtr/x8XGsrKyIVdaoxOjoqDY0\nNKR3GCXm5ua0aDRaUuZ2u7WJiQmdIqosHA5r8Xi8+LOqqlpvb68WCoV0jGpvc3Nzmt1u12KxmK5x\njI6OapFIpKQsGo0a6n2oKIrm9/u1UCik9fb26v6a7aXSZyIUCmmSJOkQzd7Onj1b9pkeHx/Xent7\ndYroYIuLi9rQ0JA2PDwsVJ9jLs9QFAUrKyuGO2hscnKyrGxgYKBiuZ4URUFfX1/xZ6vVivHxcfj9\nfh2jKpdIJDA2NoZEIgGHw6F3OJidnYXL5Sopc7vdhmodOJ1OXL161VDf/ndTVRXT09NIpVIl5Tut\n0qWlJR2iqkySJESj0ZIyTdNgt9t1iuhgsVgMPp9PeIU+k8szqn3xGqUZ3ojN9ME20h9KVVWhqmpZ\nkrPZbACM9boZnc1mg6IoSCQSeodyoJmZGVy+fLmkLBwOY2RkRKeI9heLxTAwMFDVNUwuv3eYF69R\nmuGN2EwfbCNJJpMAUPEgPABl5xjR/pLJJM6cOVNSFo1GYbfbDX32UygUgsfjwfnz5/UOpSJFUeB0\nOqv64s0B/d9TFAVer9dwrZZKjPpG3PlD+axm+GDrSVVVvUM48iYnJ3Hp0iW9w6goEolgbm4OkiRh\nenpa73AqikQih2rlM7ng8C9eozXDG3E3I3+w6egLhUI4ceKE4b6I7RgcHMTg4CBSqRQ8Hg+mpqZK\nxi319jxffl745NJM3xyN/kbczegfbDraFEVBKBTCrVu39A7lQFarFX6/H16vt2IPgF5mZ2dLvnhX\nM9npyCSXavqme3p6YLVaATzfi1etw8a4W73fiLWIsxEf7Fq9nnqSZRkAkE6nK4677DxO1QsEArhx\n44beYQjzer1QVRWxWMwQC1QXFhbg8XhKyl64MZdEIoFAICBc/6233sL58+cRj8ef68WrRrUx9vf3\n77uYql5vxFrFWe8Pdq1fT73YbDbIsgxFUUoGohVFgc1m41jVIY2NjWFiYmLPiRJ62jlJ92c/+1nZ\n5AMAZTMu9XLr1i0sLi6WdMHH4/Hiot/+/v59F0gfieTidDoxMzNT9XXz8/PP9eI1IsZGvxEPG+ez\nGvHBrkWcRjEwMICbN2+W/H7j8Th8Pp+OUTWvqakpBAKBksQci8UMs+OBqqro7e0ta5XutMR3r3nS\nS6Vx6A8++AC3bt0q2VlgL0ciuRzW8754jdAsb8QdRv9gG1EwGMTQ0FDJ+zEUCiEUCukY1f6MOqty\nZ+FpMpksdhknk0mEw2HDbOnkcrkwMjJS9hoGg0GMj48burX65MkT4d/9C51cKqnmxWuEZnojNsMH\nuxK9f99WqxXBYLDYWt5pORvpd5tKpXD58mUoilLcM25gYAA+n88we8epqorh4eGKj/X29jY4mv1d\nuHABU1NTWFxcLO4XODIygvfff1/v0CpKJBIIBoOYmZlBKpXC2NgY/H7/vhOKJE3vT5ZB7H7xzp07\nd+CL10i734gej8dQb8RKq8x39Pb24s6dOw2OaG/P/qEMh8OQZdlwfyiJmh2TCxER1Ry3fyEioppj\nciEioppjciEioppjciEioppjciEioppjciEioppjciEioppjciGqQjweh8lkKtvwdLdoNAqTybTn\nivG9DA0NwWTix5KaH9/FRFVwuVyw2WxYWFjYd9PQ2dlZAMB7771X9T3qeewDUaMwuRBVaXR0FJqm\n7bsr88zMDCRJwrvvvtvAyIiMg8mFqEojIyMAnh7hXEk8HkcqlcLZs2cbGRaRoTC5EFWpr68Psizv\n2TW2cz7QThICnh6RMDQ0hN7eXphMJjgcDgwPDyORSJRd/+x2fz6fr+IYjKqqMJlMGBsbK3tsYmIC\nbre7eJ+xsbGK9yGqJyYXokPw+/17do2FQqGSLjFFUXD69Gl89NFHOH36NPx+PzweD8LhMNxu94EH\nvu03BrP7MbfbjUAgAJPJVLxPKBRCb28vFhYWDvF/SnQ4TC5Eh7DT5bW7a6xSl1gwGIQkSZibm8Pf\n/u3f4sMPP8T169cRDAahqiqi0WhNYpqYmMDCwgJisRhu3rxZvM/8/DyAyofjEdULkwvRITidTvT1\n9ZV1jVXqEhsbG8Ps7CzefvvtkufYOStoZWWlJjFdvnwZPp8PLpcLqqoW/zmdTni9XsTjcaTT6Zrc\ni+ggPImS6JDee+89LCwsIBQK4cKFCwCensa5e5ZYX19fMZGoqopbt24hHo/vOSHgsFKpFObm5mC3\n2ys+LkkSkskkuru7a3pfokqYXIgOaXR0FOPj45iensaFCxegKAoSiQSGhoZK6qmqivHx8eIpp8DT\nsRG3212zgXZFUQA8nQAwPj6+Z729Eg9RrTG5EB2S1WqFy+Uqdo2Fw2EATwf7n+X1erGwsAC/3w+/\n348zZ84AAGKxWPGaaiWTyZKfd46YttlsZd1vRHrgmAvRc9iZNRYKhTA9PQ1Jkkr+uKuqioWFBQwN\nDeHDDz8sJhagdMpxteLxeMnPNpsNVqt1z8kBdrsdp0+fPvT9iKrF5EL0HHb2DpucnMTCwsKeCyd3\nD9rvdJUB5Unm2enFNpsNmqYhFotVvPZZfr8fKysrZfuZTUxMIJVKVVwTQ1Q3GhE9F5/Pp0mSpEmS\npMVisT0fHxoa0oLBoDY6OqrZ7XbtnXfe0SRJ0np7e7VoNKppmqadPXtWkySpeG04HC4+t9/vL7nW\nbrdrY2NjJffq7e0tPufZs2c1l8ulSZKkeTye+r4IRLswuRA9p50EYDKZKj6uqqrm9/s1u91e/EMf\niUQ0TdM0v9+vmUymYpIYGhoqe55QKFRMGg6HQwsEApqmaRWTi6Zp2vj4uOZ2uzVJkrTTp08X6xM1\nkqRpz9HxS0REVAHHXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiIqOaYXIiI\nqOaYXIiIqOb+P7yRB6q5iztCAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60decdc750>"
]
}
],
"prompt_number": 56
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f_val, p_val = scipy.stats.f_oneway(x, y, z,i,j) \n",
"print \"One-way ANOVA P =\", p_val \n",
"f_val, p_val = scipy.stats.mstats.kruskalwallis(x,y,z,i,j)\n",
"print \"One-way Kruskal Wallis P =\", p_val "
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"One-way ANOVA P = 0.0142504270115\n",
"One-way Kruskal Wallis P = 0.0258559380048\n"
]
}
],
"prompt_number": 57
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Resistant to deviation (CLT)"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Compare >2 independent samples. Corrections"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = plt.subplot(1,1,1)\n",
"ax.plot(1-(1-0.05)** np.linspace(0,21,11),linewidth=3)\n",
"ax.set_xlabel('Prob of screwing up with the labels',size=20)\n",
"ax.set_ylabel('Number of plots I make',size=20)\n",
"plt.title('Are line plots different than the histograms?',fontsize=14)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAaEAAAEzCAYAAACYBryKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8G2eZL/DfKG25tfaMkgXK0iUeqed0ucaS3AXOAZZY\ncrkUFmJLKbtAgY01KtcFkkih7EKXSyK73OEkkkK7LdfEMst9t5YULgvsbm2NWqALJfHI0NKFpbHG\nLqX0Er/nj+mMNbqPLXsk6/l+PvokejWaeWY00uN5571wjDEGQgghxAYOuwMghBDSuygJEUIIsQ0l\nIUIIIbahJEQIIcQ2lIQIIYTYhpJQB0un03A4HAiFQm1ft6qqcDgcWF5eNv1/M1ndbjKZRLFYXPd2\ns9ks3G53zRjS6TQEQcChQ4dqPrdDvf2uLN/Mz3Cjt91ofVbOm3adM51AkiQ4nU44nU6EQiEsLS3Z\nHVJ7MNKxxsbGGMdxzOFwtH3dpVKJcRzHlpaWGGOMRSKRtm/DagzNuFwuNj09ve7tZjIZ5nK5jOfl\n++73+xs+t0O9/a4st3Is2x1Tu7fdbH2tfibtOmfsdvDgQeZyuVgul2PZbJZ5vV4WDAbtDqst6Eqo\ng01PT2NiYgKMMeRyuQ3d1tGjRzd0/e3CNqBbW/m+l0ol+P3+us/tUm+/N+J4tMrObVs5X+2Ms12m\np6cRi8Wwe/duDA8PIx6PI51O2x1We9iZAUl9U1NTjOM4pqoqc7lcTJIk0+scxzFFUZgoimxycpIx\npl1ZjI2NMUEQmCAILBqN1l1/+VVI5RWJvm6Px8M4jmOBQICpqmp6byvbyWQyTBRFNjU1xURRZIIg\nmPajcrulUon5/X7GcRxzuVxsYmLCWFYURcZxHOM4jsViMcYYY4lEwij3er1MluWaceTzedO+JBIJ\n40pIj0FVVWMZjuOYJEnM6/Uaz/W/vJvt+1o+l0bHu9Z+1yvnOI5ls1ljPV6v1/S5lR+Hys+ilc99\nPdu2cm42W1/leVPvPKgVZ6NzjDHG5ufnTfs/NTXFvF5vzc+2leOp74O+z5XrL9fofE4mk0xRFNOy\nTqez4THsFpSEOtTY2Bjz+XyMMe1SXBAE0+v6iTo5OcmKxSJjjDGPx8NCoRArFAosm83WTF66ZknI\n6/WyQqHAZFmuWk+r28lkMozjOOZ2u1kul2PpdNr0Za3criiKbGRkhBUKBWPZZDJprK+8amV+fp5x\nHMcmJydZoVBgwWCw6hiVb0OPd2JiwoipVgxer9dUfVP5vNm+r+VzaXa8rVTHud3uuuvhed6II51O\nM47jTMe3WRzr2baVc7PZ+so/s2bnQWWczc4xnudZJBIxzhWe543vYflnqyhKS8dzZGSEFYtFlkwm\njcSnH4Py5Vs9n/X953ne+COn21ES6lD6CckYM07YbDZrej2VShnP8/l81UmbyWQansiNklD5F3di\nYsL4q83KdvQkVCgUjDJ9Xypj0JctNzExYbp3U/6Doi+v/3WsqmrNH+pEImEkHJ0kSVVXQuVJKJ1O\nG8uWJ6FW9n0tn0uj41253+VqJYJG65mcnDTdZwkEAqYrkmbvX+u2rZ6bzdZX67ypdx7UOmfKlZ9j\nU1NTVVcXwWDQlITKP9tWjmculzOeC4JgShyBQMC4Qmv1fC6VSkwURRYKheocue5znt3VgaRaNpsF\nAIyOjgIAhoeHAQBTU1PG/wGY7lXMzc1BVVU4nU7Tutbagsbj8Rj/7+/vX9d2du3aZfxfj39hYQE8\nzxvlsizD6/Wa3jc8PIxoNFpznX6/H36/HwMDAwiFQggEAsbxKpfP5037or9XP8a1cBxXs7zVfV/L\n51LveFvVaD379+9HNpuFLMvIZDLI5XJVx3w9cbTznGk1llbPA6D5OTY7O1t1/8/n85la15W/3srx\nFEXR+L/T6TQ9Lz//W92PZDIJh8OBEydO1NzHbtQRDRNkWUYqlcL09DQmJydbugkfjUaRy+Wgquom\nRLi5EokEAMDlcsHhcMDh0D6mkydPmpar/FKLooiFhQXTY3Fxse3xbdR2mMUbyDMzM8jlcuB5HtFo\nFG63u+qHjeO4tt6YbmXf7fpcam1bp6oqXC4XDh06BKfTiYmJCYyNjbX12NTbNrC2Y9BofeVqnQf1\nmm83299mr+sxbcTxbOV8npub64iGMu1kexJSFAWxWAzj4+MYHR3FgQMHkEgkmrbtl2UZgUAATqfT\n+KHWH5deeukmRb8xstksJEmCoijGI5FIQFVV3HbbbTXf4/P5oCgKGGPo6+tDX18fZmZmMD4+3tbY\n1rKdQqFg2jcA2Llzp2kZj8cDWZZNZdlsFi6Xq+Y6s9ksJiYmMDg4iCNHjuDMmTNQFAX5fN60nNfr\nrVpvJpNpup+1rGXfN+tzaSabzYLjOMzOzmLfvn0YHBzctFZjG3kM6p0Hc3NzVcs2O8dcLlfVFfLs\n7Gzd7bbzeLZ6Pp88ebJrWrK2yvYkFI/HEYlETGWSJNWthtG5XC7Ismz6odZ/rKempjYy5A2VzWax\ntLSEaDSKnTt3Go/x8XHwPI8vf/nLNd/n8Xjg8XgwPDyMXC6HdDqNcDiMyy+/vK3xrWU7wWAQuVwO\n2WwWwWAQkiRVLeP3+yGKIkZGRlAoFJBOpxGLxarOg/n5eeP/sVgMqVQKsixjYmICHMeZqjsAIBQK\nQVEUhEIhY7m1nh9r2fd2fS7l+91KeSWe56EoilF7MDExgenpaSiKYimOtWx7o8/NZueBHmezcywc\nDgMAIpGIsa56tTLtOJ5Muyff8n4AWnXcRnfX2HQ23IcyEQTBaEWk0288NlLeCqWV8m4hSZJxI7TW\na/pNdofDUdWZT1VVo1WNIAimJr2VSqWSsY7y/+vrLv9MkskkGxkZsbwd/eZzKpViLpeLCYJg6mRY\nuV1VVVkgEDBaRlW2/tFbtunlExMTTBAEY/l6nRJlWTaaW4+MjLBsNmtqHVceQ7PWcc32fS2fS7Pj\nXbnf9cort125nmg0aoohm80yQRCM/WsWx3q2beXcbLa+ys+s0XlQGWezc0xRFOb1epkgCCwUCrGJ\niQmjEUBlTFaPZ2VjjmAwaDoOrZzPgUDA9s7T7cYxZl9PLv1mpaqq6OvrM73mcDigKEpVtU0jqVRq\n06s5SH3ZbBahUGjD7n8Q0k7FYhGZTMa4IgK0WhmHw7HlqsA6ia2t4/Qfp8oEpLOShHK5HHw+X7tC\nI4T0GEEQEIlEwHEcgsEgZmdnjeoxsnFsvSfUzpZtsixjcHCwbesj7VGvuTMhnYbneWQyGcTjcTid\nTrz5zW9GOp02dTEg7bcl+gml0+m6raiIffx+P86ePWt3GIS0bHh4GGfOnLE7jJ6yJZLQkSNHcOrU\nqZaWbfSXuY23xwghpCfZWh2nNz+s17GssnliLaqqQpbluveVrKCqI0II2Vy2JiGe5yGKYlXbekVR\nwPN8S40SstmsafiLZtijbfMrH4QQQjaf7Z1V/X5/Va9kfTSEVszOztL9IEII6VK2J6F4PF7Vgz2Z\nTCIejxvP9XGaUqlU1fsVRWl5jClCCCGdxfaGCf39/YjH44jFYhgaGjLGkqusiiuVSjXv2Wzfvh07\nduzYpGgJIYS0k60jJnQSPcHR4SCEkM1je3UcIYSQ3kVJiBBCiG0oCRFCCLENJSFCCCG2oSRECCHE\nNmtOQsvLy1hYWKiaA50QQkhveOgh4KtfXd86LCehQqEAn88HnufhcrmMOdDdbjeuv/769UVDCCGk\nozEGzM4Cb30rcPHFwKtfvb71WUpCxWIRXq8XsixjeHjY1Kfm7NmzOHjwIIaGhtYXESGEkI5z113A\n4cPA058OXH458JnPAO2YNNlSEtKH0snn81VD7ZRKJRw5cgT5fB6HDh1af2SEEEJs9fvfA5/7HOD3\nA097GvCe9wA//7l5mT/7s/Vtw9KICU6nEz6fDzMzM1BVFU6nE9lsFrt37zaW8Xq9WF5exunTp9cX\n2SajERMIIQRYWQG++13gppuA6Wng/vurl7nwQmBsDLj6auCFLwQc62jiZmnsOH0g0UZEUcT09PTa\nIyKEELLp7rxTSzyf/7xW9VaJ47Qrote/XrsP9IQntGe7lpLQ4OAg5ubmGi5TKBTg8XjWFRQhhJCN\nd/YscOKElnxuvbX2Mn/+59oVz9/8DfDUp7Y/BksXUXv37kU+n8d3vvOdmiNah0IhKIoCv9/ftgAJ\nIYS0z0MPAV/7GjA6qrVue8tbqhPQ9u3A296mtYK74w4gGt2YBASsYRRtr9eLQqGAQCCATCaDQCAA\nnueRzWZRKpUgiiLOnDmzMdFuILonRAjZqhgD8nng5puBL30JuPfe6mXOPx94xSu06raXvhS44ILN\niW1NUzlMTEzg8OHDpo6q/f39kCQJR44caWuAm4WSECFkq/n1r7V7PDffDPzXf9Ve5vLLteq2vXu1\nK6DNZikJLS0tob+/31Smz2zK8zwArS9RJBLBLbfc0t5INxglIULIVnD//dooBjfdBGSz2lVQpac+\nFXjd67Srnssu2/wYy1lKQpdeeiny+Tz6+vpqvh6LxTAxMQEAWFlZaU+Em4SSECGkW62sAN//vpZ4\n0mmtf0+lJzxBuw909dXAX/7l+ppVt5Ol1nHz8/Pwer1ViWh6ehrj4+NQVRU8zyOVSlkKQpZl5PN5\nOJ1OKIoCj8eD4eHhlt978uRJbN++HWfPnoUkSRgYGLC0fUII6Ua/+IVW1fa5zwG/+lX16xwH7N6t\nXfHs2aP17+k4zIJMJsM4jmNut5sVi0WmKAoLBAKM4zjGcRyLRqNWVscYY2x+fp4FAgFTWTAYZIqi\nNH3v1NQUkyTJVBYOhy3HwBhjAJjFw0EIIZvugQcYu+kmxp7/fMa0yrbqx//+34x9+MOM/fKXdkfb\nnOVf3Xw+zziOY06n00g+gUCgpaRRSzgcZtPT06aybDbLgsFgw/eVSiUmCIKpLJFIMLfbvaY4KAkR\nQjrZ6dOMvfvdjDmdtROP08nYW97C2H/+J2MrK3ZH27o1tY7TBzBdWlpCIpHA+Pj4mq/EnE4nZFnG\nzp07jTJ9SKBG95Wi0SgcDgcOHz5sKl9YWDCtq1V0T4gQ0mkeeQT45jeBo0eBmZnq1887D3j5y7X7\nPC97GfCYx2x+jOu1piQEaK3ivF4vduzYgUwms6Yffj3ZqKpa1djB4XBAUZS663U6nTh+/Dj27Nmz\nhuirURIihHSKe+4Bjh8HUing7rurX3/a04BIBHjTm4AnPnHz42unhg0T3G53zZERdBzHGY0VnE6n\n6bVWBjBdfHQc8Hqt7RolIVVV0d/fj1QqBafTicXFRTidToyOjjbdLiGEdBrGgO98R7vq+epXtaug\nchynXe1ccw3wkpcA27bZE2e7NUxCTLtnVPd1QRAgCAIAc5PsRomrnKqqLS1XSVEUANo4dfv37zfK\nY7EYFhcX11U9SAghm6lU0ppWHzumDSJa6U/+BNi3DwiHgTVUOHW8hklofn5+s+KwRE9eoiiayvfu\n3Yvh4WFKQoSQjjc3p131fOlLwAMPVL/+ghdoVz179nTnvZ5Wtb27Ui6XwzXXXNPu1ZroyacyCQ0O\nDkJVVSwsLNR9L8dxNR+EELLR/vAH4IYbgKEh7XHDDeYEdNFF2oCiP/mJ1vn0Na/Z2gkIsNhZFdCG\n7tEHK63EGEM8HkexWMTRo0ebrktPIsvLyzXvC1UmGZ0+RJD+b6VG95IIIWSz3XmnVt32T/8E1LoL\nsWuXdtXz13/doR1KN5ClJFQsFuH1epveywmHwy2tj+d5iKIIRVGwa9cuo1xRFPA83zCR6O+rtUy9\n5AXUb/1GV0OEkHZ6+GFtyoSjR4FTp6pff8xjgFBISz7Pfa7W8KAXWaqOi0ajUFUV8XgcMzMzGBgY\nwNjYGDKZDGZmZjA4OIhAIIBjx461vE6/34/Z2VlTmSzLCAQCDd8nSRLy+XzV+wRBoKsgQoht7r4b\n+Id/0JpRB4PVCcjlAiYnteVuvhl43vN6NwEBsDZEgCAIpiF24vE48/l8xnN9FIPKERAaUVW1atie\nQCDAisWiab2iKLJkMml6n8vlqnqflW2XA42YQAhZo3PnGLvlFsZe9SrGtm2rHs3A4WDsr/6KsX/9\nV21ZsspSdZyqqnC5XMZzj8eDWCxmPOd5HsFgEIcPH265E2l/fz/i8ThisRiGhoagKApisVjV1Uyp\nVDJVmfX39yOTySASicDlcmF+fh6xWAy7d++2skuEELJmZ88CN94IJBJArbk8n/xkYHxce1xyyebH\n1w0sjZjgcrngdruNuYL0EQ9kWTbu6UxMTCAWi9FUDoSQLYkx4D//U7vXc+IE8OCD1cu8+MXavZ5X\nvUqbsZTUZ+mekMfjQTabxalHKzl5nkd/fz8SiYSxzNzcXN1Wa4QQ0q3OnQOmprRGBM97nnY/pzwB\n9fcD73gH8LOfafeBgkFKQK2wdCWkKIoxlM/U1BT27NkDSZKQSqUQDAZRKpWQzWYRDoctNU7oBHQl\nRAip5Q9/0JpWf/SjQK3++16vdtVz1VXaxHHEGssDmCqKgng8jkgkYnQOHR4eRqFQAKC1dpuamqqa\nBrzTURIihJT73e+Az3xGe9x7r/m1xzxG60j65jdrnU7J2q15FO1Ket+hbq2KoyRECAG0BgYf/ajW\n4OCPfzS/Jgha4nnb24AnPcme+LaatiWhbkdJiJDeduutWv+d6Wmt8UG5pz0NeNe7tKkTem1Eg41m\nedgeQBtmR5+GoR7qMEoI6XQrK8C3v60ln+9/v/r1wUHg4EFgbEybQI60n+VhewKBAIrFYsMrBo7j\ncO7cuXUHRwghG+HBB4EvfAG4/nqtNVulK64ADhwAdu/u8dEMNoGlJCRJEhRFgcfjwfDwcN3laBw2\nQkgnUlVtINFPfhL47/82v3beeVpjg/37gWc/2574epGle0IOhwMejwdzc3MbGZMt6J4QIVvXXXcB\nH/84kEwCv/+9+bULLwQkSevjQ6MabD5LV0IDAwNNBxYlhJBOcfvtWpXbl79cPV32xRdriUeSgC5t\n1LslWBoxwe/3I51Ob1QshBCybowB2ax2X2fXLuDznzcnoKc/XZtMrlgEolFKQHaz3ETb6/Vix44d\niEaj8Pl8dZerNUldJ6PqOEK62yOPACdPalc+j/adN3nRi7TGBi99KeBo+5zSZK0sJaGlpSV4vV4o\nitJ4pV3YOo6SECHd6fe/Bz77WeBjHwN++Uvzaw4HsGePlnwuv9ye+Ehjlu4JjY+PQ1EUiKJIreMI\nIbb6zW+AT31KG826VDK/9rjHAW98o9bBtGz2GdKBLF0JCYIAl8tFreMIIbb5+c+Bj3xEG8X6oYfM\nr+3YAbz1rcBb3qL9n3Q+y32AqXUcIcQOt90GXHcd8NWvVr/mcmlXPW94A/D4x296aGQdLN2eC4VC\nyGazGxULIYRU+elPgdFRbQidygR0+eXaHD933qkNLEoJqPtYbh03MjICjuMQj8chimLd5ay0jpNl\nGfl8Hk6ns6URGQBtSglJkhCLxeD1erG4uIhkMolAIND0vbVQdRwhneXnPwfe/36txVvl1/LKK7XG\nBi94AQ2r0/WYBYIgMI7jmj4cDkfL65yfn2eBQMBUFgwGmaIoTd9Xvk1BENj09LSV3TEBwCweDkLI\nBjh9mrHXvpYxh4MxLf2sPl79asZuv93uCEk7WbonFAwGW1rOSus4fYK8cpIkIRqN4uTJkw23kc1m\n4fP5sLi4SKN2E9LlikXgAx/QGhxU9vB4xSu0qyKPx5bQyAayfT4hp9MJWZZNSURVVTidTqysrNR9\nX7FYhKIoa6p6q4Wq4wixx113AR/8oDaKQeXQOi95idYYgfr4bF229htWVdVIOOX02VkXFhZsiIoQ\nshnuuUdrTu12awOLlieg4WHgBz8A/uVfKAFtdbZO06RPjFevEYOiKA2r2RRFMaYVX1xchNPpxOjo\naNvjJIS0z29+A8TjWifTBx80v/aCF2hVci96kT2xkc1naxLSE8ha6FdP5UknFApVlRFCOsO99wIT\nE8CnPw088ID5tec+V0s+w8PU2q3XdO0wfv39/RgfHzeV6Q0aCCGdY3ERuPZaYGBAm0a7PAH5fFqV\n249+BPj9lIB60ZaaNX1gYACKomB5ebluFR+Na0fI5lBVbSK5j30MWF42v7ZrF/CP/6j196GvZG+z\n9UpI7+y6XHmGVrxey8TERFWZXkXXbJRvQsjGue8+4EMf0q58rrvOnICe+UxgehrI57Vm15SAiK1J\niOd5iKJYlTQURQHP83UbJSiKglgsVtV6Tm/o0Ch5McZqPggh63P//do9n4EB4L3v1a6EdJddps1u\nevvt2tQKNJ8P0TWsjnO73Wuuvjp9+nRLy/n9fszOzmLXrl1GmSzLDQdKFUURiUSiKklls1l4vd6u\nm1CPkG72wAPAsWPAkSPA//yP+TW3G3jf+4DXvAbYts2e+EiHazScQitD9NR7tEpV1aphewKBACsW\ni8bzUqnERFFkyWTSKEun06ahfUqlEvN6vaxQKLS87XKgYXsIseSPf2TsU59i7OKLq4fX2bmTsRtu\nYOzhh+2OknS6hldCjUYsaJf+/n7E43HEYjEMDQ0ZVW2VVzmlUsl0VTY6Oorp6Wmk02mcPXsWqqoi\nnU7T8D2EbLCHHgJuvFEb5eDuu82vXXKJVhX3hjcAF1xgS3iky9g+bE+noGF7CGns4YeBz31O689T\nOZjJxRdrzbD37QMe8xhbwiNdaks10SaEtB9j2nQK114LzM+bX3viE4FDhwBJ0qbUJsQqSkKEkLpu\nvRV45zu1zqTltm8HolFtIrknPMGe2MjWQEmIEFLlrru0K5wvfMFcLgjA/v3A294GXHSRPbGRrYWS\nECHEoPf1qRxe5/zzgXe8Q6uSe3SQe0LagpIQIQQrK1qjg/e8R5tiodyePVpicrnsiY1sbZSECOlx\n//ZvwLveBczNmcsHB7Vx32haBbKR2jZ4Rr3x3wghnalYBIJB4IUvNCegJz9Zm+V0dpYSENl4lpNQ\noVDANddcY4zbtrS0BJ/PB57nsW3bNhw6dKjdMRJC2mh5WWvZdtllQDq9Wv7Yx2r3fE6fBt74Rhpm\nh2wOS0kol8vB6/UikUgYE9JFo1HIsozh4WHs3LkTExMT+MpXvrIhwRJC1u7cOW0a7Usv1e7xPPTQ\n6muveQ1w553aKAgXXmhfjKT3WBoxwefzQZZlZDIZDA8PAwAcDgf8fj9mZmYAAIIgwO12Y3Z2dmMi\n3iA0YgLZynI5rb/PT35iLv+Lv9Du+zzvefbERYilKyFFUTA2NmYkoEKhAECb0VQXCoVoPh9COsQv\nfgG88pXarKXlCeiSS7Q+QD/6ESUgYi9LreNUVTUNIprNZgHANO3C4uKiUVVHCLFHqaTNXPrpTwOP\nPLJa/vjHA7EY8O53a/8nxG6WquO8Xi8WFhZw9uxZANp8QwBw5swZYxmn0wmn02kq6wZUHUe2gocf\n1ub2ef/7gUfneASgzWB69dXajKdPeYpt4RFSxVJ1nCRJKJVKuPTSS41pF/SquFwuB7fbDVVVMTY2\ntiHBEkJqYwz49reBZz8bePvbzQlIb4J9442UgEjnsVQdFw6HMT8/j2Qyifn5eYyNjeHAgQMAgJmZ\nGSiKAr/fjyNHjmxIsISQaj/9qVa99mjbIMPAgDb8zp492pUQIZ2obfMJFYtFMMYgimI7VrfpqDqO\ndJvf/Q74h3/Qml2Xzz950UXA3/+9dkVEc/uQTmcpCS0vL6Ovr28j47ENJSHSLR58EPjUp7TJ5coH\nKnE4gPFxrUHCE59oX3yEWGHpnhDP8zh+/HjDZWKxGLZv324pCFmWkUqlMD09jcnJSeRyOUvvB7SW\ne5FIxPL7COkWjAH//M/AM54BHDhgTkB+P3DbbVqjBEpApJs0vSc0PT0NjuOMK4R8Pg+n01lzWcYY\n0uk0SqVSywEoioJYLGZ0dgW0vkaiKGJgYKDl9USjUUvbJaSbFApaZ9Pvfc9c/r/+F/CRjwAvfznd\n9yHdqWl1nMNhfYzT8hEUmpEkCVdccQX27NljlOVyOSQSCZw8ebKldeiJjOM4nDhxwnK8AFXHkc50\n771av54bbtCuhHSCALzvfdrMpuefb198hKxX0ySULhvhMBQKIRwOw+/3111eEARjRIVWOJ1OyLKM\nnTt3GmWqqsLpdGKl/G5rA6lUCgCQyWRaTlyVKAmRTsKYNqLBO9+pJSLdeedpied97wPqVEgQ0lWa\nVseV9/kZHh5GMBi0lGQaUVXVSDjl+EenblxYWDAlp1pyuRz8fr8xegMh3W5+HrjmGiCTMZe//OXA\n9ddro18TslVYqmsrH7hUt555hBYf7VFXr8VdK2PQKYqCgYEBuoIhXe/hh4F4HHjmM80J6JJLgG98\nA/jmNykBka1nTZPaTU5Owu12Y9u2bcY8Qtu3b8f1119vaT3rHWNuenoa4+Pj61oHIZ3g1lsBn0+7\n//PHP2plDodWHfdf/wVceaW98RGyUSxP761P59Df34/du3dDFEUoioK5uTkcPHgQJ06c2JRpHGiQ\nVLIV3Hcf8N73av1+yi/md+0CUiktMRGylVm6EorFYpBlGeFwGKVSCZlMBolEAplMBqVSCePj48jn\n85syu+rU1BRGR0eN51yL7VM5jqv5IGSzff3rwNOfDnzyk6sJ6HGP04bamZ2lBER6g6UklM1mIYoi\njh07VvP1RCKBgYGBlhsJ6EP81LuvVG8IoEKhAF/FN5TuCZFucc89wNgY8Fd/Bdx992r5FVcAd9wB\n7N+vtYIjpBdYOtVlWUYwGGy4jN/vbzqqgo7neaM6b9euXUa5oijgeb5uy7i5uTnMz8+b+gTJsmz0\nFxoaGjJdJZWrl6zoaohstJUVbZy3aNQ82sGf/AnwiU8AV11FHU5J77GUhAYGBpq2WMvn85ZGOvD7\n/ZidnTUlIVmWTRPlVarVGGFychJzc3M0gjfpSHfcAYTD2kym5d70Jq36jfr8kF5lqTrO7/cjn8/X\nbQWXSqUgy3LDzqyV4vE4pqamTGXJZBLxeNx4rqoqXC6X0Sm1lnvvvZeq5EjH+eMftRGtBwfNCejS\nS4FTp4BfPda2AAAgAElEQVTPfpYSEOltlkbRVlUVXq8XxWIRLpcLfr8fLpcLZ86cQS6Xw/z8PHie\nR7FYRH9/f8tBFAoFnDhxwpgoz+v1Yvfu3abtiqKIiYkJ7Nu3z/TeYrGIeDyOkydPYmlpCePj45Ak\nCYODgy1vH6ARE0j7ffe72tXP6dOrZeefrzXDfs97gMc+1rbQCOkYlucTUlUV0Wi05lVJOBxGPB63\nlIA6BSUh0i5nz2qjXN94o7n8+c/X7gk94xn2xEVIJ1rXpHaKokBRFIii2LWT2ekoCZH1Ygz40peA\nv/s7bcI5XV+fNhJCOKx1QCWErGrbzKrdjpIQWQ9F0cZ7qxw8fnRU6wf0lKfYExchna5h6ziHw1G3\n6TJjzPSa/lz/99y5c+2NlJAO9MgjwMc+po1q/cADq+VPfSrwmc8Ar3ylfbER0g0aJqF6fW2aoT43\npBfMzmpVbLfdtlrGccDb3gZ88IPARRfZFxsh3YKq4x5F1XGkVb//vdbs+pOf1Dqg6p79bG28t8sv\nty82QrrNmgcHWV5extzcHFRVNUY+aDb3DyHd7pvf1CaVu+uu1bLHPha47jptxGua5ZQQaywnoWKx\nCEmSqsaH4zgOfr8f8XjcNPoBIVvBf/838I53ABX9qhEIAEePAi6XPXER0u0sVccVi0V4vV6oqgqP\nx4O9e/caQ/lkMhnkcjkIgoB8Pt91V0VUHUdqWVkBjh8HDh4ElpZWy3fsAD7+ceCv/5rGeyNkPSwl\noVAohHQ6jUQiUXP8tmQyiUgkgmAwaBpctBtQEiKV7rwT2LcP+MEPzOVveIM2zfb27baERciWYikJ\nOZ1OiKKIubm5ust4vV4sLCzg7NmzbQlws1ASIjrGgGPHgHe/29zs2u0GEgmgbEQpQsg6Weq/rQ8k\n2ogoivRDTrrWb38LvOIVWuMDPQGddx5w7bXAj39MCYiQdrPUMGF4eLjphHW5XK5qwjlCusE3vgH8\n7d+ah9x55jOBz38eeM5z7IuLkK3M0pVQIpHAysoKrrjiCiwsLJheKxaLGBkZAaDdGyKkW9x/PxCJ\naKMblCegd75T65BKCYiQjWPpnlAkEoGiKMhms+A4zjQzqqqqYIyB5/maVXazs7NtDbzd6J5Qb5qd\nBf7mb8zTLTzlKcBNNwEWpsUihKyRpSQkCIIxPpyljXAcFhcXLQe3mSgJ9ZZz54AjR4D3v18b/003\nNqY1PqCJ5gjZHDRsz6MoCfWOYhF43euAH/5wtezCC4FPfxp4/eup3w8hm2nNw/YQ0m0YA26+WRtg\n9L77Vsuf/3zgc58DunxKLEK6UkckIVmWkc/n4XQ6oSgKPB4PhoeHm74vm80im81i+/btmJ+fh9fr\nrdmJlpDFRUCSgHR6tWzbNq06LhbTmmETQjaf7V89RVEQi8UwUzYbWCgUgiiKGBgYqPs+vXHEkSNH\njDKfzwdVVXHgwIENjZl0l2wWuPpq4J57VssuvVRrek0jXhNiL9snG47H44hEIqYySZIQjUYbvi+R\nSFSV+f3+muWkN/3xj8C73qUNMlqegCQJKBQoARHSCWxPQlNTU/B4PKYyr9eLdHm9SQ0cx1V1nGWM\nQRCEtsdIus9PfqIlmY99bLVsxw7ga1/ThuR5whPsi40Qsqph67iFhQUIgoD+/n7jeTtHx1ZVFU6n\nE6qqoq+vz/Saw+GAoiiWtudyuXDNNddg//79lmOh1nFbw8oK8IlPaPd5HnpotfxlLwM++1ngyU+2\nLzZCSLWGV0KiKCIWi5meHz9+vG0b1/sOVSYgnaIoLa8rmUzC5/OtKQGRreHuu4GREa0KTk9Aj3sc\n8P/+nzYZHSUgQjpPw4YJ/f39OHnyJFwul3E1lMlkWlrxvn37mi6jqmpL62pkenoamUwGHMd13fQR\npH2mprR7PaXSapnHA3zhC8Bll9kXFyGksYbVcfr8QJZXynE4d+5c0+VkWYbP58PKykrVaw6HA9ls\nFrtbHLZ4aWkJw8PDSKVSGBwcXFPMAFXHdZvlZeDtb9eG2dFxnFYd9/73AxdcYFtohJAWNLwSCofD\nCIVCUBQFi4uLGBkZwcGDB+HvwEG1+vv7IUkShoeHGw4RxFF3+C3jBz/QRj4oH0v3aU/TOp6+4AW2\nhUUIscDSsD3BYBCRSKSljqStaHfDBEVR4Ha7kclk6sbYLAnRlVDne/hh4LrrgMOHtYYIute+Vht6\n59GaY0JIF7DURHtqaqrqx315eXnNGy8fhbucoijgeb5uAlIUBYIg4Lbbbqv5+tLSUt1tMsZqPkh3\n+MUvtGF2PvSh1QTE88CXvqRdAVECIqS7rKmf0OTkJNxuN7Zt2wae57Ft2zZs374d119/veV1+f3+\nqmkeZFlGIBCo+x59hlexYrAvPZlV9jsi3Y8xbXTrwUGgfHb5F79Ym/H0qqvsi40Qsg7MIq/XyziO\nYzzPM7/fz8LhMPP7/YznecZxHPP5fJbWp6oqCwQCprJAIMCKxaLxvFQqMVEUWTKZNMomJiaYqqqm\n9/n9fhaLxazuEmOMMQBsDYeDbILf/paxK69kTEtF2uP88xmbnGTs3Dm7oyOErIelseNisRhkWUY4\nHMaxY8eqXpckCalUCocOHcLhw4dbWmd/fz/i8ThisRiGhoaMseQqq+JKpZLpfs6BAweQSqUwPz9v\nDGC6d+/elpqGk+7xrW8Bb3oT8D//s1r2jGdoTa9pxlNCup+lhgn6AKFnzpypu4zL5YLT6ez4mVQr\nURPtzvKHPwD79wNHj5rL3/EOrUHC4x5nT1yEkPaydE9IlmV4vd6Gy/j9fsiyvK6gSG+74w7A6zUn\noIsvBm65Bfj4xykBEbKVWEpCAwMDTYfSyefzDadgIKSREyeAv/gL4Oc/Xy179au1xgcjI/bFRQjZ\nGJaSkN/vRz6fr9sKLpVKQZbljuzMSjrbww9rY75ddRVw//1a2eMfrw06Oj2tjYBNCNl6LN0TUlUV\nXq8XxWIRLpcLfr8fLpcLZ86cQS6Xw/z8PHieR7FYNMaa6xZ0T8g+v/0tsHcv8L3vrZa53cBXvgI8\n61n2xUUI2XiWkhCgJaJoNIpUKlX1WjgcRjwe77oEBFASssu//zswNmaedO6VrwRuvpk6nhLSCywn\noXKKokBRFIiiWNVxtNtQEtpcjGkND/7u77SqOEAbePQDHwAOHQIctk+3SAjZDOtKQlsJJaHN84c/\nAJGINsyOzukEvvhF4Ior7IuLELL5LHVWJWS9FAXYswe4/fbVMo9Ha3zQxkl7CSFdgio9yKb59re1\n/j/lCeiNb9SmZKAEREhvoiRENtzKijb1wpVXAvpkuhdcoA1I+tnPUudTQnoZVceRDVUqaRPPfetb\nq2VPfapW/Xb55fbFRQjpDJauhFKpFL7yla9sVCxki/nxjwGfz5yAXvxiIJ+nBEQI0VhqHedwOCAI\nAs6ePbuRMdmCWse11+c/D4TDwAMPrJYdPKhNRnceXX8TQh5l6Upo3759KJVKdWc0JeShh4C3vU2r\ngtMT0IUXAuk0EI9TAiKEmFn6SUgmk3C73fB6vUgkEvD5fBBFEX19fRsVH+ki99wDBIPAj360WnbZ\nZdrwO3/+5/bFRQjpXJaq45xOJwBt6B7TSsomm2OMgeM4nDt3rk0hbg6qjluf738fCIW0ceB0o6PA\njTcCF11kX1yEkM5m6UpoeHi4peXKkxLZ2hgDPvEJbQI6/e8OhwM4ckQro1OBENJIRwzbI8sy8vk8\nnE4nFEWBx+NpKeFNT09DURTMz89DURRIkoTR0dE1xUBXQtbdfz+wbx/w5S+vlu3Yoc0JtHu3fXER\nQrrHmm8TLy8vY3FxEYIgrGvUbEVREIvFMDMzY5SFQiGIothwcrzp6WmIomgknaWlJXi9XiwuLmJ8\nfHzN8ZDWnD6tDb/z05+ull1+udYA4ZJL7IuLENJdLI+YUCgU4PP5wPM8XC4X8vk8AMDtdted7K6R\neDyOSCRiKpMkCdFotOH7FEXB4OCg8by/vx/RaBSSJFmOgVjz9a9r/X/KE5AkafeFKAERQixhFiiK\nwjiOYxzHMb/fzziOY7lcjjHGGM/zjOM45vP5rKySCYLAisWiqaxUKjGO4+q+p1QqMa/Xy1RVNZXP\nz88zjuOq1tcKAMzi4eg5jzzC2LXXMqbdCdIej3kMYzfcYHdkhJBuZelKKB6PAwDy+TympqZMr5VK\nJRw5cgT5fB6HDh1qaX2qqkJVVaPVnY7neQDAwsJCzffxPA9FUVAsFq2ET9bh7FngZS/TOpvqnvY0\n4Ic/1AYhJYSQtbCUhE6ePAm/32+qBit38OBBDA4OIp1Ot7S+xcVFAKjbz0hRlIbv3bVrl6ksm81C\nEATspCGZ2yqf10a/Lrtth5GR1XJCCFkrS0lIVVW4XK6Gy4iiiPn5+ZbX106JRKLlqzDSmhtuAP7P\n/wF++cvVsmuv1aZl2L7dvrgIIVuDpdZxg4ODmJuba7hMoVCAx+NZV1BrkUwmsWPHDuzfv3/Tt70V\nPfgg8Pa3A8nkallfnzYb6itfaV9chJCtxdKV0N69e5HP5/Gd73ynZofUUCgERVHg9/vbFmArFEVB\nMpnELbfc0nRZjuNqPsiqu+4CXvhCcwJ65jOBuTlKQISQ9rLcWdXr9aJQKCAQCCCTySAQCIDneWSz\nWZRKJYiiiDNnzrS0Lr1RgqqqVfeFHA4HFEVp6f5OKBTC8ePHWxrDrlnCsXg4tpzvfU8b/+13v1st\nu+oq4Phx4AlPsC8uQsjWZLmfUD6fx5EjR3DrrbcCADKZDKamprCysoKDBw+2nIAArZWbKIpVDRAU\nRQHP8y0loEgkgomJiZYHUWWM1XwQbfqFQGA1AW3bBnz848AXv0gJiBCyMdY9bI+iKHA6nUazaqsi\nkQi8Xq9plIN0Oo2pqSmcOHGi4XtTqRQCgYApWeVyuaajLdTSy8P2MAZ8+MPAe9+7WvakJwFTU8AL\nXmBfXISQrc/ylZBuYWEBp06dwm233YaFhQUsLy+vaT3xeLyqz1EymTT6JAGrrfJSqZRRpjcDX1xc\nhCzLkGUZ2WwWU1NTlhNQL3v4YW3yufIE9IxnALfeSgmIELLxLI8dVygUMD4+DlmWTeUcx2FsbAzx\neNxSP53+/n7E43HEYjEMDQ0ZY8lVrqNUKhlXK6qqIhQK1VxfsybkZNV992n3f8rbc7z4xdr8P2u8\nsCWEEEssVccVi0XjR97j8WDv3r0YGBiAoijIZDLI5XIQBAHFYrHrJrrrteq4e+4BXv5yoHyS3Ne9\nTmuAcMEF9sVFCOktlpJQKBRCOp1GIpGoOVJ1MplEJBJBMBhsej+n0/RSEvrpT7UheO66a7Xs7/8e\nuO46mv+HELK5LM+sKopiww6rXq8Xy8vLOH36dFsC3Cy9koRyOW0KBv0W3nnnAYkE8KY32RsXIaQ3\nbciwPY3GfCP2uekm4CUvWU1AF10EfOtblIAIIfaxlISGh4eRzWYbLpPL5eoOcErswRjwj/8IvOEN\nwCOPaGV/+qfAv/2bNhApIYTYxVISSiQSWFlZwRVXXFE1zUKxWMTIyAhUVTU1pSb2evhh7Urnfe9b\nLXvWs4D/+A/gOc+xLy5CCAGa3BMaGRmpGuZmfn4eiqKA4ziIogie56GqKhRFAWMMHo8HQ0NDOHr0\n6IYH305b8Z7Q8jIwNgZkMqtlfr82Bfc6ZmQnhJC2aZiEBEEAx3GWf5g5jjPmCuoWWy0J3X231gT7\nxz9eLXvDG7RBSc8/37awCCHEZN3D9mwVWykJ3X67loB+/evVsuuu05phUxNsQkgnsTxiAulsMzNa\nFdx992nPzztP64B69dX2xkUIIbWsKQktLy83rW6jKbY33w03aOPAnTunPe/r04bgGR62Ny5CCKnH\nUhIqFosIBAIoFosNq604jsM5/ZeQbDjGtNZvH/jAatlTn6pNwf2sZ9kXFyGENGMpCUmSBEVR4PF4\nMNzgz2uaqXTzPPQQsG+fNu227jnP0Tqh/umf2hcXIYS0wlLDBIfDAY/H03DYnm7VjQ0TVBUYHQVO\nnVotu+IKbR6giy6yLy5CCGmVpc6qAwMDCAQCGxULseBXvwL+7/81J6B9+4BvfIMSECGke1hKQn6/\n35hMjtinUACe+1zgjjtWyz74QeoDRAjpPpb7CXm9XuzYsQPRaBQ+n6/ucjSf0Mb4l38BQiHg97/X\nnp9/vtYq7rWvtTcuQghZC0tJaGlpCV6vt+ko2d3YOq4bklAyCbz5zatNsPv7gX/+Z202VEII6UaW\nWseNj49DURSIotjW1nGyLCOfz8PpdLbU+q5SOp2GIAiW3tNNGAPe+17gwx9eLfuzP9OaYD/jGfbF\nRQgh62UpCWUymba3jlMUBbFYDDMzM0ZZKBSCKIoYGBho+v5sNotwOLxl71U9+KA2CvYXv7ha5vEA\n3/wmcPHF9sVFCCHtYKlhAoC2t46Lx+OIRCKmMkmSEI1GG76vWCwiEomgWCzC6XS2NaZOUSppTa7L\nE9DLXgZ873uUgAghW4Ole0KSJEGWZczOzrYtAKfTCVmWTcP8qKoKp9OJlZWVltbhdruRTCaxe/fu\nNcfRafeEFha0hPOzn62WSRLw6U9r48ERQshWYHlSO0EQcMUVV+C2227D8vJy3UcrVFU1Ek45nucB\noGrivF6Rz2tNsMsT0JEjwNGjlIAIIVuLpZ80p9MJVVUBaPeH6mm1dZw+CGq95tyKovTcQKjf/Caw\ndy/whz9ozy+4APinfwJe8xpbwyKEkA1hKQkFg8GWlmu1dZye0Ijm2DHgLW8B9FpIQQC++lXghS+0\nNy5CCNkolpJQIpHYqDh63pEjwKFDq8937tQ6pl52mW0hEULIhrPcOq7bcRxX82EXxrRZT8sTkM8H\n/Md/UAIihGx9lq6EIpFI0x9sxhg4jsPRo0ebrk8URQDaJHm17gvpr29VjAHXXgscPrxa9uIXA1//\nOnDhhfbFRQghm8VSEkomk02X0Vu2tZKEeJ6HKIpQFAW7du0yyhVFAc/zG9IooV4T7M2+GmIM2L8f\n+OhHV8tGRrRheB7/+E0NhRBCbGOpOm5xcbHm48yZMzh58iQGBgYwNDTUdOrvcn6/v6rfkSzLW3rK\niJUV4O1vNyegK68EvvY1SkCEkB7D2qhUKjFBEFgsFmv5PaqqskAgYCoLBAKsWCya1iuKIksmkzXX\n4XK5WDabXVPMOgCszYejpnPnGBsfZ0y7FtIee/Yw9uCDG75pQgjpOJancmhGkiSk02mcPXu25fcU\nCgWcOHECQ0NDUBQFXq/XNPqBqqoQRRETExPYt28fAG1E78OHD0NRFKTTaYiiCL/fj0AggNHRUctx\nb8aICefOAX/7t8BNN62WXXUVcPPNNA8QIaQ3tT0JRSIRJJPJlofc6RQbnYQeeQR4/euBL31ptex1\nrwNuvBHYtm1DNkkIIR2vrU20c7kcksnklm/VZtVDD2lXPOUJaN8+SkCEEGKpdZzD4WjYiky/img2\nAnYvefBBIBgEvvGN1bI3vxn41KcAR8/10iKEEDNLSajZpHE8z+Oqq65a0z2ZreiBB4BXvxq45ZbV\nsne+E/jIRwAb+8cSQkjHaPs9oW7V7ntC998PvPKVwKlTq2WxmDY7KiUgQgjRUIXQBrjvPuClLzUn\noPe9jxIQIYRUalgd53a7LY8kwB4dtuf06dPrCqxbLS1pCejf/3217EMfAt7zHvtiIoSQTtUwCVnp\n68NxXM9PzbC4qE3HPTe3WvaRjwDvepd9MRFCSCdrmIRKpVJLK1laWsL4+DjS6TQA4ODBg+uPrMv8\n7ndAIADcfvtq2ac+Bbz1rfbFRAghnW7dk0WnUilEo1GoqgqPx4OpqSkMDAy0I7au8ZvfAH4/cMcd\n2nOO0yaoC4ftjYsQQjrdmhsmFItF+Hw+SJIEQJvwbm5urucS0K9/DfzlX64mIIdD64RKCYgQQppb\nUxKKxWJwuVyQZRljY2MoFosYHx9vd2wd71e/Al70IuDOO7Xn27YBn/88cPXV9sZFCCHdwlJ1XC6X\nQzAYNAYUTSQSTTuwblWKAuzeDfzyl9rz884DvvxlgPrpEkJI61q6ElpaWkIoFEIgEICqqojH4zhz\n5kzPJqDTp7UrID0BXXABMD1NCYgQQqxqeiU0OTlpjAXn9/uRSCR67r5PuZ/9TLsC+s1vtOePfaw2\nG+pLXmJvXIQQ0o0aDtvjdruhKAoAIBwOIxgMttx5tXw+oG7QyrA9P/kJMDysNccGgMc9ThuYtEcv\nCAkhZN0aJiHHGod55jgO586dW3NQdmiWhGRZ6wekz1x+4YXAt74FvPCFmxUhIYRsPQ2r444cObKm\nlVod6qfT3XqrNhKCPiBEXx/wr/8KPO959sZFCCHdriNG0ZZlGfl8Hk6nE4qiwOPxtNToYa3vq6Xe\nldAPf6iNBXfffdpzQQBmZgCfb02bIYQQUmbdIyasl6IoiMVimJmZMcpCoRBEUWzYAGKt77Piu98F\nrrxSm5YBAHbsADIZYNeutqyeEEJ6nu1TOcTjcUQiEVOZJElNZ2dd6/talckAL3vZagJ60pOA73yH\nEhAhhLST7dVxTqcTsixj586dRpmqqnA6nVhZWWn7++opr4779reBPXu0qbkB4OKLtbmBLrvM8moJ\nIYQ0YOuVkKqqRuIox/M8AGBhYaGt72vFV78KvOpVqwnokkuA73+fEhAhhGwEW5PQ4qPtnfv6+mq+\nrvdRatf7WhEMAg8/rP1/YEBLQG73mldHCCGkAduvhDbzfa145BHt30svBb73PaCsto8QQkib2d46\nrhNddpl2D+jii+2OhBBCtraeS0LNO9Jy+PnPgac8ZVPCIYSQrree9m22VseJoggAWF5ebvh6u95H\nCCGk/dYzSo6tV0I8z0MURSiKgl1lHXAURQHP86bm1+14H1A/Y7cygGmvoGOxio7FKjoWq+hYrFrv\nMG22d1b1+/2YnZ01lcmyjEAgsCHvI4QQ0jlsT0LxeBxTU1OmsmQyiXg8bjxXVRUulwupVMrS+wgh\nhHQ220dMAIBCoYATJ05gaGgIiqLA6/Wa5iPSpxOfmJjAvn37Wn6fFXR5vYqOxSo6FqvoWKyiY7Fq\nvceiI5JQJ6CTahUdi1V0LFbRsVhFx2LVeo+F7dVxhBBCehddCRFCCLENXQkRQgixDSUhQgghtqEk\nRAghxDaUhAghhNim5wYwrSTLMvL5PJxOJxRFgcfjwfDwsN1h2WJ6ehqKomB+fh6KokCSJIyOjtod\nlu1UVUUsFsOxY8fsDsU2sizj5MmT2L59O86ePQtJkjAwMGB3WJsum82iUCgAAM6ePQuXy4Xx8XGb\no9oc6XQagiDU/H1c1+8o62Hz8/MsEAiYyoLBIFMUxaaI7JNOp5ksy8ZzVVWZy+ViyWTSxqg6Qzgc\nZsFg0O4wbDM1NcUkSTKVhcNhm6KxTz6fZ+l02lSWTqd74juSyWSYIAgsl8tVvbbe39Gero6Lx+OI\nRCKmMkmSEI1GbYrIPoqiYHBw0Hje39+PaDQKSZJsjMp+iqKgVCqte5DGbqWqKsLhsOkqMJlM4tSp\nUzZGZY9kMllVMzA6OopMJmNTRBuvWCwiEomgWCzC6XTWXGa9v6M9nYSmpqbg8XhMZV6vF+l02qaI\n7KGqKk6cOIGlpSVTuX45vbCwYENUnSGXyyEQCPRsz/jDhw9X/SESDoe39A9vPXNzcygWi1XlGznT\ns90GBgZw7NixhlWO6/0d7dkkpKoqVFWtyu48zwPorR9enuehKErNL1gvy+Vy8Pv9dodhq1QqhaGh\noaryRtOlbFV+vx+BQMD0PclmswiFQjZGZa92/I72bMOExcVFAEBfX1/N1xVF6akvmn48ymWzWQiC\n0FPHoZyiKBgeHu7ZqyBA+5Hp7+9HKpWC0+nE4uIinE5nTzZYOXLkCLLZLFwuFxKJBAYGBrC0tGQa\nVLnXtON3tGeT0Fa+hG6XRCKBQ4cO2R2GLaanp3um1VM9iqIA0Ear379/v1Eei8WwuLjYk8dnbm4O\nIyMjkCQJHo8HuVzO7pBs1Y7f0Z6tjiONJZNJ7Nixw/Tj0yvoDxSNfhxEUTSV7927tycb7wBa9eTE\nxAQymYwxfQxVY68PJSFSRVEUJJNJ3HLLLXaHYoupqSlTdVOvtozTk09lEhocHISqqj113xQAIpEI\nAoEAdu3aheHhYRSLRYiiSLM5r1PPJiH9i7W8vNzw9V4Ui8V6sgkuoFU9+Xw+U1mv3hPSby7r/1bS\nq+t6gX5VWH5/o7+/HzMzM+B5vmer5drxO9qz94R4nocoilAUBbt27TLKFUUBz/M9ezM+EolgYmKi\n7o3GrW5ubg7z8/M4ceKEUSbLMhRFQSwWw9DQUE/dlNe/I7W+D730h1o+n4fL5ar5miRJPVuF247f\n0Z5NQoDW5HJ2dtZ08GRZ7tnL61QqhVgsZjpxcrkcRFHsmSFaat1sn5ycxNzcHI4cOWJDRPaSJAn5\nfB67d+82ymRZ7rlWk6IoYmpqquZrqqr27G8GsP7f0Z6tjgO0nr6VJ1YymUQ8HrcpIvvoHcsWFxch\nyzJkWUY2m8XU1FTPJKB67r333p6tkguHw0gkEqayWCyGVCplU0T20L8DldVuiqLg7NmzPZOQa30P\n1vs72vMzqxYKBZw4cQJDQ0NGa5fyv/p6Qa3OZjqXy4XTp09vckSdoVgsIh6P4+TJk1haWsL4+Dgk\nSTINb9QL9OPgcrkwPz+PUCjUc98RXSqVwvz8PLZv3w5Aq47ayk3Vl5aWcPjwYSiKgnQ6DVEUjU67\n5dXS6/kd7fkkRAghxD49XR1HCCHEXpSECCGE2IaSECGEENtQEiKEEGIbSkKEEEJsQ0mIEEKIbSgJ\nEUIIsQ0lIUIIIbahJLROsizD4XDUfAiCgJGRERQKhQ3Ztr7+zZRMJiEIAhwOR88M5R8IBOBw0Fel\nmVaPkyRJG3Y8N3LdlYLB4Jq3tVHf3fXEZJfuiraDCYKAYDBoPAKBAHbs2IFsNguv14vp6em2b5Pj\nuHJn2qIAAAqYSURBVE2d60ZVVUQiETgcDkiSBEEQNm3bdtrs49ytKo9TOp2Gw+Goee6v93hu5Lqt\nWOu2NvKc6rZztadH0W4nv99vGv5fl0qlIEkSxsfH2z4FwGaPuKTPH3Po0KGemnF1amoKpVLJ7jA6\nXr3jVOtHsV3n7kaueyN1Q4ybha6ENtj4+DgGBgawtLTU9dMALy4uAtAm8+ol/f39PTNK8nrUO04b\n+YNLP+bdj5LQJhBFEYwxLC0tAdDqbfVRq8PhMBwOh2lofFVVIUkSXC4XHA4HfD4fYrFY3fUrimLU\nxzudToRCIUsJr5XtBYNBow5br3dvdk8omUzC6/Uacfl8vpozUFZuf2RkpGqqgGbHDAAmJiZM24tE\nIsZx0I+P/hno9Pt3lfft9Pte+rbL69klSTJiiUajxrJut7tm9ZCqqggGg8ZyoVAIqqrC6/W2dF+g\n3r0WVVXhcDgQiURMcUcikTWfE+06ToFAAKFQyFReOfvm0tJSS8evVoztXHej88YqRVEQDAaNc7nZ\nsbfyOa01zla/h7ZhZF3y+TzjOI6FQqG6y/A8zxwOB1taWmKMMTY2NsYEQWDxeJxxHMecTiebnp5m\njDFWKpWYKIqM4zjm8/lYKBRiLpeLcRzHvF5v1XpdLhfjeZ45nU4WCoWY1+tlHMcxjuOYLMtN4291\ne9lslkWjUWNfU6lUw/UePHjQ2LdQKMSCwWDNuObn5xnP84zjODYyMsJCoRATBIFxHMckSTKWa3TM\nGGPM4/EY+xCJRFggEDBtb2JignEcx9LptPGeTCZjLDMxMWGKqfwzHRsbYw6Hw3g9HA4zQRCMmCKR\nCJMkyVhXNput2j+Hw2HaP5fLxVwuFxsZGWn6Gfn9ftP2daVSiXEcxyKRiFEmCAILBAI1zwlBEJii\nKA231a7jlM1mjWMSiURM50s4HGYcxzG/328cv/Lzo/z41dLOdTc7bxqpPC/046F/1uXrEwSBqapq\nLGv1u9tqnJUxtfo9tBMloXVqlITm5+eZ3+83Th7d2NiYcbIWCgXTe/Qv0eTkpKlc/9KV/wiU/3iX\nSyaTNZNWLVa2p/8YNUtAemxut9tUls1mq3409WNRnlAYY8YXsjxx1ztmemI6deqUqVyWZeM46P8v\nT2z6F5TjOBYIBIzyRCJh2s9aSYjjOOZ2u434yvevMnlyHMdyuZxRpqqqkejbnYSanRPl+1lLO4/T\n1NRUzc+22fEr35961rru8v1q5bxppNZ54XA4TJ81Y7UTu5XvrpU49fOtfDutfA/tRElonfQk1Ojh\ndDpZsVg03qOfKLV+zPUvUC36X0/lzx0Oh2ndOv1HvNlfvla2ZyUJVSZeXaFQMOLVf0Rr/RCn02nm\n8/mMhNPomPE8z0ZGRpiqqqxUKpke+g+4qqpV++P3+5nX6zX+qtTp2ypPgLWSUOUPoL7f+v4027+N\nSkLNzonyv8hraddxapYo6h2/RrUK7Vx3s/OmfN9qqdxfWZZrbrfW96aVz0l/zUqclUmole+h3ah1\nXJsIggC/328qczqdcLlcdVuS+Xw+03O99VnlesqXP3XqlKlMFMWaN4P37t0LWZZRLBbrTs+9lu21\namxsDOl0Gm63G5Ikwe/3Y3Bw0DQPvb79WnPRj46O1mxNWHnMAK3+P5PJ1G0yznEcFhcXEQgEkE6n\nsby8jL6+PuRyOUSjUTidTmSzWSwsLGDnzp2QZRkulwt9fX0N99Hj8TR8fW5uDoB236LS8PBww/eu\nB8/zDc+JfD7fcNbLdh+nepodv/VoZd2tnjet7t/g4KAx666qqpibm4Msy1XTo+uafXcVRcHOnTst\nx8mVtRhs5XtoN0pCbVKviXYjoiianus/yi6Xq+7yuVzO+HEAtB+cWvTEo6pq3e2vZXutOnnyJCYn\nJ5FIJBCNRo3ycDiMeDyO/v5+Y/v19qFeTLX2IRAImLZTyel0Yu/evUin08hkMsbxCQQCxpc7m81i\nbGwMxWIRkiQ1jaXelOiVsdVazso+W1V5jHStnBMA2n6c6tnIFofN1t3qeWOlL5yqqohGo8Z08ADg\n9Xrh9XprNiBo5bu73jhb+R7ajZKQTTiOq/ph1388zpw5U/M9iqJUva/eD4p+8tb7QVrr9qw4cOAA\nDhw4gOXlZWQyGSQSCSSTSczNzWFubs74Ejb7UdTVikX/ged5vumc9vrVRyaTMfbd5/MZ65yZmTFi\nqnX1YpW+Db1pe7lW97mRWusFVj/7euXNEuBmHyc7WDlvGmFlTcSHh4dRKBQgSRIkSTKuNnK5HNLp\ndNV7W/nutiPOZt9Du1ET7Q6if+HrNZ8s/+HWKYpS86+sTCYDjuNaSkJWtteKYrGIaDRqrLevrw+j\no6OYmZnB8PAwZFnG8vKyUbV26623Vq1D7xF//PjxhtvieR79/f3IZrM1XxcEAW6321hWFEVks1nM\nzc2ZqpL8fj+y2SwymQwArOuHSacf35mZmarX2vHll2W5Zrmqqms+J4DNP052sHLeNKJXfamqikKh\ngGAwiKNHj5qqu1idvkytfHfXE6eiKC19D+1GSajDhMNhzM/PV/WBkSQJS0tLOHTokKmcMVZVJZJM\nJpHL5TA2Ntb0Ksbq9lrBGMPk5GTNqpryqyue5+H3+5FOp6sS4eHDh8FxXN37VZWxlkolo++IbmJi\nAktLS6Z+NGNjY1AUBdls1rTuQCAAVVUxNTVV8x7VWoiiWHP/9H5RreJ5HoyxqnXUq55pdE74/f6W\nqsHaeZxq/QiX37dYj/Ws28p506rKESPKP6fKWFv97q4nzla+h7azq0XEVtFKP6FKlS1YyqmqavST\n8Xq9LBwOm/rxlON53tQHZGxszOhPUNkirx4r27PSOq68f8TY2BgLh8NGi6BYLGYspyiKsf1AIGDa\nfvlyjY4ZY8xo8uxyuUzHoXIf9OaplS2o9OautZqrV25bb4FVq+VUZYu38vUGAgGjb1EoFGr5vNFb\n0ulNjPV+SiMjI0wQBFOzY57nmSAIxqPynKhs3l5PO46Tvg6Xy8Wi0WjV8aul1WPSrnW3et7UUrm/\n+jkfDAZZPB43fU76NvR+Sla/u63GWS+mZt9DO1ESWqe1JKFgMFizya1OVVUmSRJzuVzM4XAwn89X\n84TRO+PJssy8Xi9zOBzM7XazUCjUsGnpWreXyWSYw+FoKQkxxlg0GjXW6XQ6mc/nq9mEVVVVFgwG\njS+az+er2kazY6ZvT/9iu93uul8y7tH+RpVf9HrllduWJMnU+bhyHZXNrhVFYcFgkAmCwJxOpxGX\nlb4ayWTSOD7l69DPAR3P88zn87FiscgCgYCxzVAoZLlJ7nqPE2OrP4JOp9Mo049fvW22+l1q17pb\nPW8qVe6v/j3S/6gqP9/1uPTPai3f3VbirPUZtPo9tAvHGA2+RMhGyWazcLlcVc3kFUWB2+1GNBrF\n4cOH27Y9/R7B7Oxs29ZJyEai1nGEbKBgMIjt27dXtUCMx+MAsK4mzoRsBZSECNlAExMTkCQJbrfb\n6HybzWaNllQ0OjfpdZSECNlA4+PjcDqdOHz4sNEC0eVyIZlMYt++fW3fXrtanRGyWeieECGEENtQ\nPyFCCCG2oSRECCHENpSECCGE2IaSECGEENtQEiKEEGIbSkKEEEJs8/8Befay03Pn2iIAAAAASUVO\nRK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60deb9c990>"
]
}
],
"prompt_number": 58
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = plt.subplot(1,1,1)\n",
"ax.plot(1-(1-0.025)** np.linspace(0,100,100),linewidth=3)\n",
"ax.set_ylabel('Prob of screwing up',size=20)\n",
"ax.set_xlabel('Number of trials',size=20)\n",
"plt.title('Be careful discarding experiments')\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAaYAAAExCAYAAAA3Egb4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X14I1d9L/DvaElIgKwlbXhJLi/rkZICIWTXktNAIMBa\nclpeWsha2tCWQmEtGS5vbbMrbS+0fWhhV3Z6G96albQ3AXoL2JIXuFwCa0ublrf2xtYohQIhWY0W\nCORpk7VGDoQEWJ/7x0QjjS3LGlu2JOv7eR49u3M0M/rN8a5+PnPOnCMJIQSIiIg6hK3dARAREdVi\nYiIioo7CxERERB2FiYmIiDoKExMREXUUJibaEE3TYLPZTC+v14t8Pt/u0FaIRCLYsWNHw30URYHb\n7W64j6ZpcDqdxv5er7dlMTarE2Jola2O32bj116n40+IWkLTNGiahlKpBJ/Ph0Ag0O6QVpiYmECp\nVGrpOV0uF2KxWEvP2Y0xbES3x0+tx8RELbFz507s3LkTfX19CIVCUFXVeC+TycDlcsFms2F4eBjl\ncrnuOdLpNFwuF5xOJ8bGxozyRCIBp9NptMaKxSIAQFVV+P1+RCIR4zfu1T7L7/cDAPr7+5HP502/\noWcyGQwPDze8vvHxcTidTjidTiQSCaO8UCggEokY2+Fw2NhvYmKipde2VgzFYhEejwcTExNwOp1w\nu92mlmvls9xuNxKJRN2WYb36S6fTpvpxuVzIZrOYnp5GOBxGIBBYEX+jn8Xya1NV1ahDVVXh8Xgw\nNjYGp9OJ4eFhKIpinKe2Thudf7V6qPw72LVrV8OfF7WZINqAUqkkJEkylcViMTE8PGy873A4xOnT\np0W5XBbhcFgEAoEV5ykUCsLhcIh8Pi9UVRUul0tMT08b57/33nuFpmkiEAiISCRiHCNJkhgbGxPF\nYnHNz6rEmcvlhMfjMcpnZ2eF3+833nO5XKbYcrmcEZumaWJgYEA4nc4V50qlUsLlcolyuSwURRGS\nJIlyudySa2smBlVVhSRJYmJiQgghRDgcNq6rNobK8W63e8XPcrX683g8Ip1Oi1gsJoLBoHG9kiSJ\nZDJp7F+pi0bnqndtleMq701PTwtN04Qsy8LhcIhyuSwymYzxM2zm/PXqofbfwfKfl81mE+VyecW/\nTdp6TEy0IZUv19qXzWYTiqIIIYSIx+MrEpHD4VhxnlgsJqLRqLGtKIpxDk3TjPJQKCTC4bAQovoF\nVLHWZ603MYVCIVNsmUzGOG/tudLptHC5XEbclS+5VlxbMzGoqmq6XkVRjNgOHz5sOr4Sa61G9aeq\nqrDb7cLtdhvXlUqlhNfrNe0vSZLQNK3huZZf2/LEVHsN4XDYFHcl2a91/tXqoXKOSvy1P6/anwW1\n11Pa3WKj7aH21l0ul4PH40GpVEKhUEA6nTY66gFAkqS6x3s8HmN77969xt8/8pGPIJvNGueQZdl4\nr/bvzX6WVaVSCYODg8Z2f39/3f3279+PhYUFBAIBLCws4MiRIzh06FBLrq3ZGGqvXdTMNlYsFk23\n4+od36j++vv74XK54HK5sHPnzlXPI8syVFVd82dRe22NrsFut5u2K9e11vlXq4daIyMjKJVKK35e\n1H4dk5jS6TQcDgeGhoaa2l9RFORyOTidTqiqioGBgaaPpdbbvXu36e8DAwPIZDJwu90YGRnB1NSU\n8X69EXt2ux2FQsHYVhQFxWIRQghks1mcPn0aO3fuRCKRgKIodWNo9rOW0zSt4fuyLOPMmTPGdm0S\nrqWqKnw+H0ZHR1EsFuH3+yHLckuurdkYNnINjeovk8kYfxaLRSMhLT+PqqpwuVzr/lk0Q5Kklpx/\ntZ/X/v37WxInrV9HDH7IZDIIhUJN/3arqiqi0ShGR0exf/9+HDp0CPF43NTxSlurXC4bI/NmZ2eh\nKAo8Hg8CgQAymQyy2Sw0TUM4HDYNFqgIh8NIJBLI5/NQVRXBYBClUgmlUglOpxM7d+6EpmlIJBJY\nWFioG0MwGGzqs+x2u5EcNE3D0aNHG17bgQMHjNg0Tat7TkD/5SoQCKBcLhu/pUuS1JJrazaGZq/h\n6NGjK/6/1au/aDQKABgbG8OJEydw7NgxhMNh4xhFUZBMJo39PR4Pdu7c2fTPfb1acf7Vfl7UAdp4\nG1GoqirC4bBIJBLC5XKJbDbb1HGhUEhMT0+byjKZTN1Oddpc9fqYnE6nSCaTxj6ZTEa4XC4hSZIY\nHh5etYM5kUgIh8NhdIxX+P1+4XA4hNfrNfpWstmsKBQKKzrwG32WzWYz/h4Oh4UkScLtdot0Om0M\n1sjlcivOWRub0+kU6XTaNPCgtp/F7/cLSZKEw+Ew9Y204trWikFVVdMxy2OrHO92u0UikTD1uzSq\nv1gsZoq5MngjnU4Lv98vAoGAkCRJeL1eUSwW1/xZLL+22jiXvxeJRIxBDEII0wCF9ZxfCCECgYDx\nb2G1nxe1lyREZyx7URnCum/fvjX3dTqdUBTFdPuo8sDh0tLSJkZJ1J0qrcNK/1Y6nUYikcDMzMy6\nz5lOpzE1NWW6nUbUCh1xK8+Kyu2i5R2idrsdAHD27Nk2REXU2UqlEoaGhoxnfeLxOILBYJujIqqv\n6xJT5R587cigWlY7hYl6wcDAAI4cOYL+/n7jodODBw9u6JySJLFPhjZFx4zKa9ZaI6iIqL5Dhw61\ndDj0/v37OYKNNkXXtZiIiGh767oW00Y1uvXQIeNAiIh6Wte1mCpPjC8uLjZ8fz14v5yIqP26LjHZ\n7XZj2pNaqqrCbrebhpDXI/T5AVe8iIioM3RdYgIAn8+Hubk5U5miKMaU9kRE1L06KjHVa7lomgaX\ny4VkMmmUxWIxpFIp036JRIKLjRERbQNtHfxQLpdx9OhRqKoKVVURDofh8/ng9/tNw1BLpZKp/6ev\nrw+xWAzRaBSDg4PG3Hlr3cYjIqLO1zFTErVbJfGxOoiI2qujbuURERExMRERUUdhYiIioo7CxERE\nRB2FiYmIiDoKExMREXUUJiYiIuooTExERNRRmJiIiKijMDEREVHThAAeegj4z//cvM/ouYUCiYio\nsfPngZ/8BDhzxvwqFABVBR57DDh8GNisebOZmIiIelCl5XP//dXXAw/or0IB+NWvGh9/5szmxcbE\nRES0jT3+uJ5s7ruv+vrhD/XXz3++vnPa7cBFF7U2zlpMTERE28CjjwI/+AHw/e9XX/fdBxSLwNKS\n9fM961nAFVcAbrf+crn0l9sNOJ2tj78WExMRURd57DE9Af3Hf1Rf3/ue3idkVV8f8Fu/BVx5pf66\n4orqa+fO1sfeLCYmIqIOtLSk9/V85zvAd79b/bNQ0PuHmmWzAbt3Ay96EfDCF+qJqPJ61rOAmjVY\nOwYTExFRm/3853rSufde/VVJQr/4RfPneMpT9GTz4hfrSajy55VXbm5/0GZgYiIi2kLnzgH5PKAo\n+iuf1wcnNNsKstn0W20veQlw1VXVP6+4Arjggs2NfaswMRERbZJHHgFyOWB+Xv9TUYAf/aj545/9\nbODqq4GXvlR/XX213gq6+OLNi7kTrDsxlctl5HI5aJoGu90OWZaxe/fuFoZGRNQ9fv5zPfnccw8w\nN6e/zp5t7libTU8411wD7Nmj/3nNNXpi6kWWE1OxWEQ4HEYmkzGVS5IEn8+HWCyGPXv2tCxAIqJO\nc/68Phz73/4N+H//T399//vNDct+6lP11s/evcDAgP7n1Vdv/1aQFZIQzY/vKBaL8Hg80DQNAwMD\nOHDgAPr7+6GqKmZnZ5HNZuFwOJDL5bqu9SQ9OTTFQnUQUY9YWNCT0L/+K/Dtb+utomYeTr3wQr0F\n5PEAXq+eiK66avv0BW0WS4kpGAwinU4jHo9jdHR0xfuJRAJjY2MIBAKYnJxsaaCbjYmJiAB9EEKh\nAHzzm8C3vqW/fvCDtY+z2fSkMzgIXHutnoiuvlpPTmSNpcTkdDohyzLm5+dX3cfj8eDs2bM4d+5c\nSwLcKkxMRL3p/Hl9ePY3vgF8/et6Qmpm5uzLLgOuu05/VRLRM56x+fH2Akt9TJqmweVyNdxHlmUU\ni8UNBUVEtFl+/Wt9dNy//Iv++uY3gcXFxsc85Sl6X9DLXw687GX663nP68yHU7cDS4lpaGhoxaCH\n5bLZLLxe74aCIiJqlfPn9UR0993665vfXLt/qK8PuP766mtwEHja07YmXrJ4K09VVXg8Hlx77bWI\nx+OmAQ6V0Xrz8/NQFIWDH4ioLYTQ+4QyGeD0aeCf/xkolxsfc9llwA03AK98pf7nVVfpfUbUHpYS\n09jYGFRVRSaTgSRJxvNLqqpC0zQIIWC32+ve7pubm2tp4K3GxETUvR56SE9Es7P6nw891Hj/5z8f\neNWrqi+Xi7flOomlxORwOCBJkuUvb0mSsLCwYDm4rcTERNQ9nnhCH6xw6hQwM6MPXmjk8suBffuA\n17xGf/X3b02ctD6WEtN2xsRE1NlUFbjrLuBrX9P7ih57bPV97XY9EQ0N6a8rr2SLqJt0xFx5iqIg\nl8vB6XRCVVUMDAxgaGhozeMymQzy+TwA4Ny5c3C5XHWfryKi7vOrX+mtov/7f4GvflVfcXU1F1yg\nD1Lw+/XXwACwY8fWxUqtZbmPSVrj1w4hBCRJwu23397UOVVVxdjYGGZmZoyyYDCIWCyG/gbtbUVR\nUCwWsX//fqNsenoaCwsL60pObDERtd/DDwNf+YqejGZm9FVZV3PFFcCNNwK/8zt6PxGfIdo+LCUm\nWxPDVOx2OwA03acUDodx44034qabbjLKstks4vE4pqamVj1ubGwMx48fX1EeDAYbHrcaJiai9rj/\nfuCLXwT+z//Rp/tZ7b/gxRfrt+d+93f1ZLTGI5XUxSwlJk3T6pYvLCxAURREIhG43W6cOnWq6QCc\nTueK4eWapsHpdGKpwYyIXq8XqVRqRatqeHjY1PpqFhMT0dYQQp95+wtf0BPSffetvm9/P/D61wOv\nfS3w6ld334J3tD4tHfygaRpkWUY4HMbRo0eb2t/pdELTNOxctsC8zWaDqqqrPg8VjUaRTqcxOztr\nJKdMJoOzZ8/i4MGDlmNnYiLaPOfP6/1F09N6Mnrwwfr72Wz6rApveAPwe7+nLwXOQQu9p+Wj8sLh\nMNLpdFNz5amqCrfbXbdlZLPZkMlksG/fvlWP93q9UBQF8Xgc/f39KJfLpj4nK5iYiFrrN7/RH25N\np/XW0X/9V/39Lr5YvzX3+7+vt4ye+cwtDZM6UMtH5UmShFKp1NS+q90abNb8/DyGh4cRDocxMDCA\nbDa7ofMR0cacP6/PPzc1pbeOHnmk/n5Op94ietObAJ+P0/2QWUsTUzabRSKRgCzLrTztqpLJJMbH\nx3Hu3DkEAgF4PB7Trb161hpVSETWLC3p6xR9/vNAKrX6zNzPeQ5w003A/v36tD9P6YiHVagTWfqn\nYbPZGn6xV26DRSKRjUXVhLGxMUSjUaMPqlgsIhAIwO/348yZM5v++US97j/+A/infwI++1ngxz+u\nv8/llwMjI0AgoPcd8dkiaobl2cUbsdvtuPnmm5vu56m0rBYXF1cMfqh9f7nKLcDagRF9fX2YmZmB\n1+tFNptdNdbV+pDYkiJa209/qiei//2/V58G6DnP0ZPRgQP6MhGcDJWsspSYZmdnW/rhtZPA7tmz\nxyhXVRV2u33VEXm5XG7VdaHC4fCG+66IqOoXvwBOngQ+8xkgm63/nJHDod+ie/Ob9Ydd2TKijWj7\nXV6fz4e5uTlTYlIUBX6/f9VjZFlGKpWq+56maQ2PJaK1CaEP7/7Up/R+o3rrF110kT6S7g/+QJ+B\n4alP3fIwaZtqeyM7FoutSDKJRAKxWMzYrqycm0wmAcAY3LB8FJ6qqjh37lzXrQVF1CkefBD48If1\n6X5e9SrgzjvNSUmS9NkX7rxTH+Tw+c/ro+uYlKiVOmJ28Xw+j8nJSQwODhqLEdY+v1R5cHd8fNz0\n8GwymUShUMCuXbsA6LcG1zuJK59jol7161/rc9Mlk/rM3fX+C7zwhcBb3wr84R/qS4oTbaaOSEyd\ngImJeo2q6smo0vpZrq9P7zN629uAa6/lDAy0ddrex0REW+c3v9EnS43H9dm769m3D3jHO/SHXy++\neGvjIwKYmIh6ws9+preOEgn978tdfjnwJ38CvP3twBY9H0+0KiYmom2qMrLuE5/Qh3ufP29+X5L0\nJSTCYX2OOs7EQJ3C0j/F4eHhNR9EtdvtcDqdsNvtCIfDHCFHtMV++Ut9RoaPf7z+Q7DPfjZw8CAw\nOgq84AVbHx/RWiwNfvB4PCiXy1BVtekPCAQCmJycXFdwW4mDH6jb/fSnwD/8g95/VG9y/xtuAN71\nLr3v6MILtz4+omZZeo6p8txQ5QHXhYUFLC0tYWFhATMzM+jv70cgEMDS0hLOnDmD0dFRpFIpnDhx\nYlOCJyJAUYC3vAXYvRv4yEfMSelpT9Nv1X3nO/qs3wcOMClR57PUYgoGg8hkMigWi+jr61vxfr2F\nAj0eD2w2G+bm5loX9SZgi4m6ydIScNddwK236glnuRe8AHjPe/TBDA7H1sdHtBGWWkzpdBp+v79u\nUgL0/qWhoSEkEgmjzOfzoVAobCxKIgIAPPEEcMcdwEteoq/yujwpvfKV+jpIZ84Af/7nTErUnSwN\nfujr61tzgtRyucxWB1GLLS7qQ73/5/8EHnrI/N6OHfotuj/9U8DrbU98RK1kqcXk8/mQyWRw+vTp\nuu9ns1lkMhn4fD6jbHp6essWDiTabh5+GPjAB/Rbc4cOmZPSJZforaJiUR+Fx6RE24WlPiZN09Df\n349yuQy/349AIACn02kMfkin0wBg3Lrz+/1QVRWpVKrpNZrahX1M1El+9jO9/ygeBx57zPzeZZcB\n73+/PqhhlbvqRN1NWFQoFMTIyIiQJGnFy+/3C0VRhBBCzM7OCrvdLhKJhNWPaAsAYh3VQdRSP/qR\nEO98pxAXXiiE/ohs9XXFFUIkk0I8/ni7oyTaXOuexFXTNMzPz0NVVciybLy6FVtM1E5nz+pDvT/1\nKX2271rXXAP8xV/oC/FxAT7qBZxd/ElMTNQOP/qRvv7RnXfqE6zWuu46vX/pta/lzN7UWyzPjpXN\nZpFKpVAsFhvud+rUqXUHRbTd/fSnekI6cWJlC+kVrwD+6q+AoSEmJOpNlhLT9PQ0AoHAZsVCtO09\n/DBw7Jg+ddDjj5vfu+EG4K//Gnj1q5mQqLdZupXndruhqipmZ2cxNDS0mXFtOd7Ko820uAj83d/p\nzyHVLlUOANdfD3zoQ8BrXsOERARYbDGpqopQKLTtkhLRZnn8ceD22/XbdssnVvV6gb/9W2B4mAmJ\nqJblmR/WWvaCiPS57D77WX3wwo9+ZH7vJS8B/uZvgN//fSYkonoszfwQCoUwOTmJxcXFzYqHqOtl\nMnpr6C1vMSel3buBz3wGuPde4I1vZFIiWo3l4eKBQAD33nsvYrEYBgYG4HQ66+63c+fOlgS4VdjH\nRBv1/e8Dt9wCfPWr5vJLLwU++EF9poanPrU9sRF1E0uJqZKE1prIVZIknF++jnOHY2Ki9Xr4YeAv\n/xJIJs3Ll198MfBnfwYcPgx02e9pRG1lqY+p2aHi7IeiXvCrX+nLl3/oQ/qouwpJAv7kT/Ty//bf\n2hcfUbfizA9PYouJrPjKV/RlJh54wFw+NKQPC7/mmvbERbQdWJ75gaiXPfCAPrP3XXeZy6+8Uk9I\nr3sdBzUQbVTDUXk2mw07duzA2bNnTduNXpV9iLaTX/wCOHJEH+pdm5T6+vSHZr/7XeD1r2dSImqF\nhi2moaEhSJIEx5PrMze7phL7mGi7EAI4eVK/bfeTn1TLJQk4eFB/cPaZz2xffETbEfuYnsQ+Jlqu\nUADe/W7ga18zl193nT7ogSvGEm0OSw/Y2mw2HDhwACdOnOBDtrRtPfGEPlXQVVeZk9IznwnccQfw\nrW8xKRFtJkstJofDgXK5bGy7XC74fD4EAgHs27dv3UEoioJcLgen0wlVVTEwMND0fHyKomBqagq7\ndu3CuXPnEA6H0d/fbzkGtpgIAL7+df1B2Pvuq5ZJEjA2pt+2e/KuNhFtJqtL3hYKBRGPx8XIyIiQ\nZdm0tPrw8LCYmJgQxWLR0vn8fr+pLBAICFVV1zw2lUqJcDhsKguFQk1/di1wafWetrAgxMGDK5cz\nHxgQYm6u3dER9ZYN9zFpmoZMJoPZ2VmkUilommZp5odwOIwbb7wRN910k1GWzWYRj8cxNTXV8HNl\nWcbCwoJRlkgkMDExgQeWP1zSBLaYepMQwPS03pf0n/9ZLb/kEv123n//71zOnGirbSgxnT17FplM\nBjMzM8hkMqapipaWlpo6h9PphKIo2L17t1GmaRqcTmfDc0QiEdhsNhw9enRFTLXnahYTU+956CHg\nXe8CvvhFc/kb36gPbnjuc9sTF1Gvs5SY8vm80TrKZDKm93w+H/x+P3w+H/bu3dvU+SoJSNO0FZO+\n2mw2qKq6apJxOp04ceKEqaW1EUxMvUMI4NOf1oeA1077eNllwCc/CbzpTe2LjYgszvzg8XiMv68n\nES1XuQ232kzkjRKTpmno6+tDMpmE0+nEwsICnE5n089aUW968EFgdHTlEPBQCBgf1x+YJaL2WveU\nRAsLC1hYWECpVMLi4uK6lrlYa5by1aiqCkBvwd1yyy1GeTQaxcLCAkZHR9d1Xtq+hAA+9Sm9lVQz\nsBSyDJw4oS9rTkSdwdJzTEtLS5iZmcGhQ4fgcDgQi8Xg8/lgt9txxRVX4J3vfCdOnjxpTGG0WSoJ\nTZZlU/mBAwcQiUQ29bOp+zz0EPCGNwBvf3s1KUkS8L73Ad/5DpMSUaex3GLy+Xzw+XzGtqIoyGQy\nmJ+fx+TkJOLx+Kavx1RJSMsT0969e6FpWsMBEJwuqbekUvozSDWDN+F2A3feCbziFe2Li4hWZ6nF\ntNzi4iKKxSJUVYWiKEZLptkBBJXEstosEssTT4Xdbjf9uVzlVh/1rlIJ+MM/BIJBc1J673v1pc2Z\nlIg6l6UWU7lcNo3Kq00Asizj8OHD8Pv9Tc/aYLfbIcsyVFXFnj17jHJVVWG32xsO+64cV2+f1RIa\nsHrSZEtq+7j7buCtbzVPuvr85+t9TLxtR9T5LCUmR818LH19fRgZGcGBAwcwNDS0autlLT6fD3Nz\nc6bEpCgK/H5/w+PC4TByuZxpKiRFUeBwONb1HBN1vyeeAD74QeDWW/XBDhVvextw220ccUfUNaxM\nE+Hz+cT4+LhQFEVomiZUVRWapm1o6glN01ZMSeT3+03TGpVKJSHLskgkEqbjXC7XiuOmp6fXFQc4\nJVFXu+8+IfbuNU8ntGuXECdPtjsyIrLK8swP+Xweo6OjyOfzAIDZ2Vns27cPbrcbY2NjpuHbVs45\nOTmJwcFBqKoKj8djaglVph8aHx/HwYMHjfJisYhYLAaXy4VCoYBgMLjuyWT5gG13EkKf8fu97wUe\ne6xaPjysD3C4/PL2xUZE62MpMRWLRbhcLgD6IoLZbBaZTAb79u0zZh73eDyYm5vbtIA3CxNT9ymX\n9ZnAJyerZRdeqD8o+573ALYNDe0honax9F83FosBAHK5HFKplOm9UqmEY8eOIZfL4ciRI62LkKiO\n+XlgYMCclF74QuCee/Tnk5iUiLqXpRaT0+mE1+vFzMyMMc9dpcVU4fF4sLi4uK4ZvtuJLabuIATw\nsY8Bhw4Bv/51tXx0VB/g8LSntS82ImoNS79Xappm3MpbjSzLKBQKGwqKqB5NA/bvB97//mpSuuQS\n4POfBxIJJiWi7cLScPG9e/difn6+4T75fB4DAwMbCopouXweGBkBap+d9nj0W3lr/K5ERF3GUovp\nwIEDyOVyuPvuu+s+kBoMBqGqqmnKIqKNEAJIJoGXvcyclN7zHuBb32JSItqOLA8X93g8yOfz8Pv9\nmJ2dhd/vh91uRyaTQalUgizLOHPmzGbFu2nYx9R5fvlLfWXZO+6oll1yCfC//hcQCLQvLiLaXOta\nwXZ8fBxHjx5FuWb9gL6+PoTDYRw7dqylAW4VJqbOcvas3p+kKNWyl75Un5T1yivbFhYRbYENLa0O\n6PPaOZ3OdU9J1CmYmDrH7Cxw883myVff8hbg+HEOcCDqBZYSUzKZxK5du1q2nHknYWJqPyGAv/s7\nIBIBlpb0sgsuAD76UX3pCs6zS9QbLCUmm80Gh8OBc+fObWZMbcHE1F6PPQYcPAh87nPVsssvB6an\ngeuua19cRLT1LI3KO3jwIEqlEu69997Niod60I9/rK+PVJuUXv5yIJdjUiLqRZaeY0okEnC73fB4\nPIjH4/B6vZBlGTt37tys+Gib+/a3gTe9Cfiv/6qWjY3pt+8uvLB9cRFR+1iekgiAsVKtcZKam/9C\niE1fWn0z8Fbe1vvUp/RJWH/1K337KU8BPvEJvYyIepelFlOzK9NyNVhqZGkJOHJEnwW8YtcuvT/p\nVa9qX1xE1Bk2PFx8u2CLaWv84hfAH/0R8MUvVsuuvhr40peA/v72xUVEnWNdiwMsLi6uGABx4sQJ\nnD17thUx0Tb1s58BN9xgTkqvf70+tRCTEhFVWE5MY2NjsNvtGB0dNZWHQiG4XC6uxUR1ffe7wG//\ntnkmhz/7Mz1JXXJJ++Iios5jKTElk0kkEgkMDAwgGo2a3puamsKePXsQi8Vw4sSJlgZJ3W1mBrj+\neuDBB/XtHTuAeFx/mHbHjvbGRkSdx1If0/DwMObn57FQO1fMMi6XC06ns+uWV2cf0+a44w4gFAIq\ngzQvuQRIp4Hh4fbGRUSdy1KLKZPJwO/3N9zH5/Mhl8ttKCjqfkIAH/oQ8I53VJPS856n9ycxKRFR\nI5aGi/f39694hmm5YrEIWZY3FBR1t9/8BnjXu/R1lCr27AG+8hV9miEiokYstZh8Ph9mZ2dx8uTJ\nuu9ns1lkMhmuYNvDHntMn8mhNikNDwNf/zqTEhE1x1Ifk6Zp6O/vR7lcht/vNxYJ1DQN99xzD9Lp\nNOx2O4rFIvr6+jYz7pZjH9PGLSwAb3iDPs1QxR//MXDihD5LOBFRMyw/YKuqKiKRCKanp1e85/P5\nEI/H0d/AuiSvAAAgAElEQVSFD6UwMW3Mgw8Cv/M7wPe+Vy37i78A/vZvuVwFEVmz7pkfNE2DqqpQ\nVRV2ux1er7erFwtkYlq/H/5Qv1334x9Xyz72MeA972lfTETUvVo2JdHi4mJXzzLOxLQ++Txw443A\nww/r2xdcAHz608Cb39zeuIioe1me+SGfz+Od73ynMf1QuVw2Wks7duzgzA895BvfAF796mpSetrT\ngC9/mUmJiDbGUmLKZrPGWkyVYeORSASKomBoaAi7d+/G+Pj4qqP2aPv42tf0ltLior5ttwOZjF5G\nRLQRlm7leb1eKIqC2dlZYwkMm80Gn8+HmZkZAIDD4YDb7ebMD9vYF74AHDgA/PrX+vazn61PO/TS\nl7Y3LiLaHiy1mFRVxcjIiJGU8vk8ACBcs7JbMBiEqqotDJE6yec+BwQC1aT0/Ofrt/SYlIioVSzN\n/KBpmmkRwEwmAwCmaYoWFhbWnB1iOUVRkMvl4HQ6oaoqBgYGml6UsDa2aDSK48ePWzqOmnfnnfoU\nQ5VGpdsNZLN6ciIiahVLiWnv3r1GMgKAeDwOWZZNo/Gy2ayl55hUVUU0GjVuBQJ6q0uWZUvniUQi\nKJVKTe9P1sTjwNhYdfvFL9b7lC67rH0xEdH2ZOlWXjgcRqlUwhVXXIHBwUGoqmrcxstms3C73dA0\nDSMjI02fMxaLYaz2G+/Jz4lEIk2fQ1VVlEolLum+ST75SXNS2rsX+Jd/YVIios1h+TmmSCSCRCKB\ncrmMkZERTE1NGeUTExOmgRDNcDqdUBQFu3fvNso0TYPT6cTS0lJT50g+OTHb7OysEY9VHPxQ30c/\nCrz//dXtwUHg1CnA4WhfTES0vbXsAdtisQghhKWZxSsJSNO0FQ/n2mw2qKpqSlj1ZLNZyLKMTCbD\nxNRit90G/OmfVrevu04fJt5l0yASUZex/IDtavr7+y0vd1FZcHC1GSOaGd2nqir6+/uZUFrsYx8z\nJ6Xrr9dbSkxKRLTZLA1+aDWro/eWm56exujoaIuioYpPfhJ43/uq2694BfDVrwLPeEb7YiKi3tGy\nFtNW22hSo/qOHwfe/e7q9stfDtx1F5MSEW2drk1MqVQK+/fvN7abHZEnSVLdFwF33AG8853V7Ze9\nTG8pXXJJ+2Iiot7T1sRU6ZNarEy4tsr7y+XzeXi9XlMZ+5g25rOfBQ4erG5fe62elLp4wngi6lIN\nR+WdPXsWDofDWI327Nmza46Ss8rtdiOdTmPPnj1Gmaqq8Hq9xuCI5ZLJJAqFgqlMURRjyqTBwUFT\na6oZvTwq7+RJIBgEzp/Xt/fsAU6f5pBwImqPhoMfZFlGOBzG7bffbmwnEgkcrP3VeoN8Ph/m5uZM\niUlRFNM0R8vVG/AwMTGB+fl5HDt2rGWx9YKvfQ24+eZqUrrqKmB2lkmJiNqnYWLq6+vD1NQUXC6X\n0WqanZ1t6sTNJq9YLIZAIGBKNolEAolEwtjWNA0ejwfRaHTVUXiPPPJIT7Z2NuIb3wBuuqk6IeuV\nV+pz3116aXvjIqLe1vBWXiKRWDFdUFMnlSScr/wK3oR8Po/JyUljmiOPx4N9+/YZ72uaBlmWMT4+\nviLhFYtFxGIxTE1NoVwuY3R0FOFwGHv37rUcM9A7t/JyOeA1rwEefVTffsELgG9+E3juc9sbFxHR\nmjM/aJoGVVWxsLCA4eFhHD58GD6fb80TN7NPJ+mlxPSDHwCvfCVw7py+/Zzn6K0nt7u9cRERARan\nJAoEAhgbG7O8JEU36JXE9OMf67M4PPigvu1w6BOyXn11e+MiIqrY8Fx5i4uLq04p1E16ITE98og+\ni8MPf6hvP/3p+ui7a69tb1xERLXW9RzTxMQE3G43duzYAbvdjh07dmDXrl249dZbWx0ftcijjwKv\nfW01KV14IfDFLzIpEVHnsdxi8nq9UBQFfX198Hq9kGUZqqpifn4e5XIZHo8Hc3NzmxXvptnOLaZf\n/Qp4/ev1YeAAIEnA1BRgYdksIqItY6nFFI1GoSgKQqEQSqUSZmdnEY/HMTs7i1KphNHRUeRyORw5\ncmSz4iWLlpaAt7+9mpQA4B/+gUmJiDqXpRaT1+uFpmk4c+bMqvu4XC44nc6uazVt1xbT4cPAxER1\n+6//Gvirv2pbOEREa7LUYlIUBR6Pp+E+Pp8PiqJsKChqjY9+1JyUQiHgL/+yffEQETXDUmLq7+9f\nc/G+XC6H/v7+DQVFGzc9bV7o7/d+T19niROpE1Gns5SYfD4fcrncqqPvkskkFEXpuodrt5t//Vfg\nj/4IqNyVfNnLgM99DnhKW5eFJCJqjqU+psqcdcViES6XCz6fDy6XC2fOnEE2m0WhUIDdbkexWDTm\n1usW26WP6cwZPRE98oi+fcUVwLe/zfnviKh7WB4urmkaIpEIksnkivdCoRBisVjXJSVgeySmRx7R\nk1JlbMqllwL/9m+Ay9XeuIiIrNjQzA+qqkJVVciyvOqift2i2xPTE08APp8+ESsAXHQRcPfdwHXX\ntTcuIiKrNjwl0XbRzYlJCOCtbwX+8R/1bUkC0ml9SQsiom7T1qXVqTU+/OFqUgKA8XEmJSLqXmwx\nPalbW0yTk/oKtBUHDwKJBIeFE1H3YmJ6Ujcmprk54IYbgMcf17f37dOXSr/ggvbGRUS0EUxMT+q2\nxPTTnwKDg8BDD+nbv/Vb+vNLDkd74yIi2ij2MXWhX/4SeOMbq0nJ4QC+/GUmJSLaHtY9F0CxWESx\nWISmacZw8e2wYGCnE0KfLXx+Xt/esQNIpfQHaYmItgPLiSmfz2N0dHTFRK2SJGFkZASxWAy7d+9u\nVXy0TCwGfP7z1e2PfQzYhivdE1EPs9THVJmKCAAGBgZw4MABY2LX2dlZZLNZOBwOFIvFrms9dUMf\n01136Qv+VUIcGwNuv729MRERtZqlxBQMBpFOpxGPxzE6Orri/UQigbGxMQQCAUxOTrY00M3W6Ynp\n/vv1ZdDLZX37hhuATIYj8Iho+7GUmJxOJ2RZxnylg6MOj8eDxcVFPPDAAy0JcKt0cmJaXAR++7eB\n++7Tt5/3PL2P6VnPam9cRESbwdKoPE3TjFt5q5Flec01m6h5S0vAH/9xNSlddBHwhS8wKRHR9mUp\nMQ0NDSGTyTTcJ5vNYu/evRsKiqqOHQO+9KXqdjIJrLGIMBFRV7OUmOLxOJaWlnDjjTfi7NmzpveK\nxSKGh4ehaVrdJTHIupkZ4AMfqG6///36AoBERNtZwz6m4eFho++lolAoQFVVSJIEWZZht9uhaRpU\nVYUQAgMDAxgcHMTtXTZcrNP6mM6e1VtGCwv6Ngc7EFGvaJiYHA4HJEmy/GUtSRIWKt+oXaKTEtPj\njwPXXw9UHhW7/HIglwOe85z2xkVEtBUaPmBbKpW2Kg6q8b73VZPSBRfoaysxKRFRr1j3lEQVi4uL\nG36YVlEU5HI5OJ1OqKqKgYEBDDUxncH09DRUVTVuL4bDYezfv39DsbTbZz6jL1tR8fd/ry+XTkTU\nM8Q6jI+PC5fLJWw2m5AkSdhsNuF0OsXExITlcxUKBeH3+01lgUBAqKra8Lh0Oi0URTG2NU0TLpdL\nJBIJyzEIIQQAsc7qaJnvfEeIiy8WQp/bQYg3v1mIpaW2hkREtOUsL3vh9XqhKAr6+vrg9XqN55bm\n5+dRLpfh8XgwNzfX9PnC4TBuvPFG3FSz5Go2m0U8HsfU1NSqx01MTODQoUOmsmQyiXA4jKWlJSuX\nBKD9fUyLi/oyFvffr2+/6EXAPfcAz3hGW8IhImofK1ksEokISZJEOByu+34oFBKSJIloNNr0OR0O\nhygWi6ayUqkkJEla9ZhSqSQ8Ho/QNM1UXigUhCRJK87XDLSxxbS0JMTNN1dbSk9/uhDf/35bQiEi\najtLzzFlMhnIsozjx4/XfT8ej6O/v3/Nh3ArNE2DpmlwOp2mcrvdDgArnpWqfV9VVRSLxeaD72DJ\npHnG8ERCbzEREfUiS4lJURR41ph2wOfzrVgSYzWVIeWrDZ5oNLXRwsIC9uzZYyrLZDJwOBxdtezG\nv/878N73VrdDIeAP/qB98RARtZulxFRZ4qKRXC6H/v7+ps6naZqVj19TPB7HkSNHWnrOzfToo0Aw\nCDzxhL790pcCt93W3piIiNrNUmLy+XzI5XK49dZb676fTCahKAp8Pl9LgrMikUjg0ksvxS233LLl\nn71e73pXdbDD058OTE0BF1/c3piIiNrN0qg8TdPg8XiMBQN9Ph9cLhfOnDmDbDaLQqEAu92OYrGI\nvr6+Nc+nKAq8Xm/dUXQ2mw2ZTAb79u1b8zyqqiIYDDZcjqNi+RRLy1mojg35zGeAt761uv2P/8h5\n8IiIAIuJCdCTUyQSqTtRaygUQiwWayopVc7ldDqhadqKfiabzQZVVZvqLwoGgzhx4kRTD/p2QmK6\n/35gYAD4xS/07be9Dbjzzk3/WCKirmA5MdVSVRWqqkKWZciyvK5zuN1upNNp00AGVVXh9Xqbmm9v\nbGwM0Wh0wwMetuo5pieeAF7+8uqUQ1deqc+Dx+eViIh0lvqYkskkTp48aWzLsgyfz7fupATo/VbL\nH8hVFAV+v7+peJYnpWw229HDyI8cqSalCy/Uh4kzKRERVVlqMdlsNjgcDpw7d65lAZTLZQQCAczM\nzBhlw8PDSCQSRsKp9G1Fo1GMjo4CANLpNEqlkmn4+sLCAtLp9KrPWTWyFS2mmRngxhur27fdpk/Y\nSkREVZYmcT148CBOnDiBe++9d8UzROvV19eHWCyGaDSKwcFBqKpa99ZcqVQykoemaQgGg3XPt9bS\n7+3yyCPmwQ6vfa35+SUiItJZ7mMaHx/HkSNHEI/HjbnyNjq7eCfYzBaTEMCb3lRdIv1ZzwK++139\nTyIiMrOUmCpTBy1/MLZ2pJsQApIk4fz58y0KcWtsZmJKJIBwuLp9113A7/5uyz+GiGhbsHQrr5k1\nkoC1h2T3kvvvB97//ur2e97DpERE1MiGhotvJ5vRYvrNb/Ql0u+5R9++6ipgbo6zOxARNdL0cPFi\nsYh7770Xi4uLmxnPtvKRj1ST0gUXAP/0T0xKRERrWTMxTU9Pw+l0wu12Y2BgAA6HA4ODg6suSUG6\nuTngQx+qbv/N3wDXXNO+eIiIukXDW3n5fN54Tqi/vx+yLBsr1bb6eaZ2a+WtvMce06cc+uEP9e1X\nvAL4538GduzY8KmJiLa9hi2mSCQCQF9OolAoYHZ2FqVSCUNDQyiVSqvOMt7rotFqUnrGM4BPf5pJ\niYioWQ0T09zcHFwulzHbQkU8HgcAFAqFzYusS919N/Dxj1e3b7sN2MCMTUREPadhYiqXy3XnwauU\nNTPJai959FHg7W+vbr/udeZtIiJa25qDH+x2+1bEsS0cOgRUxoQ4HEAyCfCRLiIiayzNLk6rm5kB\nnrzDCQD4xCeAyy5rXzxERN2KiakFymXgHe+obr/pTcCb39y+eIiIulnD4eKVZS58Pt+K91Kp1Krv\nAcDk5GTrotwCGxkuHg7r8+EBwKWXAt/7HidoJSJarzUT03otLS2t+9h2WG9iymaB2tw8OQmssiIH\nERE1oeEkrvPz81sVR1f6+c+Bgwer2zfdBAQC7YuHiGg74CSuT1pPi+m9760+s+RwAN//PvCc52xG\ndEREvYODH9bpm980P0j70Y8yKRERtQJbTE+y0mJ6/HFgz57qtEOvex3w5S/zmSUiolZgi2kdPvzh\nalK65BLg+HEmJSKiVmFisui73wWOHatux2LAc5/bvniIiLYb3sp7UjO38s6fB17+8urif9dfD3z9\n68AGRtUTEdEy/Eq14OMfryalCy/U58JjUiIiai1+rTbpJz8BPvCB6vYHPgC86EXti4eIaLvirbwn\nrXUr741vBL70Jf3vL34xkM/rrSYiImottpia8MUvVpMSoM8izqRERLQ5mJjW8OijwLvfXd0OhYBX\nvKJ98RARbXdMTGv44AeBn/5U//uznmUeKk5ERK3HxNSAopinHbrtNn1OPCIi2jwc/PCk5YMflpaA\nl72sOjzc7wdOneIMD0REm40tplWcOGF+ZumTn2RSIiLaCg3XY9oqiqIgl8vB6XRCVVUMDAxgaGho\n045by8MPA9FodTsaBa64YsOnJSKiJrQ9Mamqimg0ipmZGaMsGAxClmX09/e3/LhmRCJAqaT/XZbN\nSYqIiDZX22/lxWIxjI2NmcrC4TAikcimHLeWb30LuPPO6vYnPgFcfPGGTklERBa0ffCD0+mEoijY\nvXu3UaZpGpxOJ5aWllp+3Goqgx+uuUbg3/9dL7vpJmB62vKpiIhoA9raYtI0zUgmtex2OwDg7Nmz\nLT2uGZWkdPHFwN///bpPQ0RE69TWxLSwsAAA2LlzZ933VVVt6XFW/I//ATz/+Rs+DRERWdT2FtNW\nHtcslwv48z/f1I8gIqJVtH3wQyf66EeBiy5qdxRERL2p7cPFt5q05lOyEl7/+i0JhYhoW2j1GLq2\ntphkWQYALC4uNny/VccREVHrrf0LvzVtbTHZ7XbIsgxVVbFnzx6jXFVV2O1201DwVhwHrJ7Z11oo\nsJewLqpYF1WsiyrWRVWrkxLQAX1MPp8Pc3NzpjJFUeD3+zflOCIi6mxtT0yxWAypVMpUlkgkEIvF\njG1N0+ByuZBMJi0dR0RE3aftMz8AQD6fx+TkJAYHB6GqKjweD/bt22e8r2kaZFnG+Pg4Dh482PRx\nVrBpXsW6qGJdVLEuqlgXVZtRFx2RmDoB/6FVsS6qWBdVrIsq1kXVZtRF22/lERER1WKLiYiIOgpb\nTERE1FGYmIiIqKMwMRERUUdhYiIioo7Sc5O4LqcoCnK5HJxOJ1RVxcDAAIaGhtod1paYnp6Gqqoo\nFApQVRXhcBj79+837dNr9aNpGqLRKI4fP24q76V6UBQFU1NT2LVrF86dO4dwOIz+/n7T+71QF5lM\nBvl8HgBw7tw5uFwujI6OmvbZznWRTqfhcDjqXk8z172huhE9rFAoCL/fbyoLBAJCVdU2RbR10um0\nUBTF2NY0TbhcLpFIJIyyXqyfUCgkAoGAqayX6iGVSolwOGwqC4VCxt97pS5yuZxIp9OmsnQ63TP/\nP2ZnZ4XD4RDZbHbFe81c90brpqcTUygUEtPT06ayTCaz4otpOxofH19RlkgkhCRJxnav1U+hUBCB\nQEAEg0FTea/UQ6lUEg6Hw1QWj8eF2+02tnulLpYn54ra69yOdaGqqgiHwyKRSAiXy1U3MTVz3Rut\nm55OTA6HQxSLRVNZqVQyfTlvR6VSSXg8HqFpmqm8UCgISZKMOum1+kkkEiKRSKz4z9Mr9XD48GER\njUZXlNdee6/UhcfjqfvbfW0rYLvXxWqJqZnr3mjd9OzgB03ToGkanE6nqdxutwMAzp4924aotobd\nboeqqigWi6vu02v1k81m4fP5VpT3Uj0kk0kMDg6uKK8sI9NLdeHz+eD3+03/RzKZDILBIIDeqota\nzVx3K+qmZxPTwsICAGDnzp1131dVdSvD2XILCwumtawA/T+ew+HA7t27e65+VFVFf3//ivm+eqke\nNE1DX18fkskkpqenjT8reqkujh07BrvdbqxqkMlkUC6XjUmke6kuajVz3a2om54dladpWrtD6Djx\neBxHjhwB0Fv1Mz09vWK0VUWv1EPlyyKfz+OWW24xyqPRKBYWFjA6OtozdVExPz+P4eFhhMNhDAwM\nIJvNGu/1Wl1UNHPdraibnm0xkVkikcCll15q+lLqBb36BbNcpR5kWTaVHzhwAJFIpB0htV0ymcT4\n+DhmZ2eNZXUa3f6m1mFiIqiqikQigVOnTrU7lC2XSqVMz25txjLR3aCSkJYnpr1790LTtG3bZ7Ka\nsbEx+P1+7NmzB0NDQygWi5BlmStkb5GeTUyV/4CLi4sN3+8F0WgUp0+fNpX1Qv3k83l4vV5T2fI+\npl6oB6DaMV35czlVVXumLiqtx8qgDwDo6+vDzMwM7HY7Tp8+3TN1sVwz192KuunZxGS32yHL8oqO\nOFVVYbfbTf8ot7OxsTGMj4+v6KjshfqZn5/H5OQkotGo8Uqn01AUBdFoFNPT0z1RDxX1rrP2vV6p\ni1wuB5fLVfe9cDgMTdN6pi6Wa+a6W1E3PTv4AdCHhM7NzZlGpymK0jPN9WQyiWg0avqHks1mIcsy\n+vv7t3391BvwMDExgfn5eRw7dswo2+71UBEOh5HL5bBv3z6jTFEUY6Qm0Bt1IcsyUqlU3fc0TTOu\ntRfqop5mrnvDdWPxmattRdO0FdNm+P3+FQ+GbUepVEokEgmRy+WM1+zsrOmJ916sn8OHD694wLZX\n6qEyLVUtv99veoK/V+oiHA6LTCZjKisUCiISiRjb270uXC7XijoQornr3mjd9PwKtvl8HpOTkxgc\nHDRG3tT+xrgd1Xv4rcLlcuGBBx4wtnulforFImKxGKamplAulzE6OopwOIy9e/cC6L16cLlcKBQK\nCAaDK66zV+oimUyiUChg165dAPTbWMtb2dutLsrlMo4ePQpVVZFOpyHLsvGwce0goWaueyN10/OJ\niYiIOkvPDn4gIqLOxMREREQdhYmJiIg6ChMTERF1FCYmIiLqKExMRETUUZiYiIioozAxERFRR2Fi\noo4yPj4Om80Gt9vdcD+Hw7HmPpvJ4XBgeHi4bZ+/XolEAg6HAzabreVLWfj9fths6/tKCQQC6z6W\nth/+S6COpKoqJiYmGu7TzrWTJEnqurWbNE3D2NgYbDYbwuEwHA7Hqvum02nYbDbT0upr2WiddFt9\n0uZhYqKOFYlEUC6X2x1GXd04k1dlGYIjR47g9ttvR19f35rHWEkWqVQKhUJh3fERVTAxUUcKhUIA\n6i9NQeuzsLAAAE0lpAorCbivr2/brkNEW4uJiTpSIBCAz+dDOp1GNptdc//V+jc0TYPNZsPY2JhR\nFg6HjdnVK7e0HA4HgsGg0UILh8NwuVyw2WwYHh5GsVis+7mqqhqf7XQ6EQwGV913fHwcHo/H2Hds\nbGzFvoFAwIgtFArBZrMhmUw2vHZN00zxer1eRKPRFeet9ImFw+GGfUx+vx/BYNA4zmazGauR1ovv\nxIkTpn2X108gEDBiW6uOaiUSCVN9eb3epv4t0DZgYXkOok0Xi8WEJEkim80KVVWFJEnC4XCs2M9u\ntwu3221s+3w+YbPZVuxXKpWEJElibGzMKAuFQkKSJOH3+4XX6xXRaFR4PB4hSZJwuVxiYGBAuN3u\nFeXLP9/lcgm73S6cTqcIBoPGvpIkCUVRTPsPDAwISZKE1+sVY2Njwu/31913ZGREOBwOox6cTqdp\nPaR61yfLsnHuYDAoXC6XkCRJeDweY79MJiMikYiQJEkEg0GRTCZXPWcmkxHhcNiot9p9G8U3MjJi\n+hkUCgUhSZKw2WxieHjYdN0Oh0NommY6b+2xhw8fNs4fDAZFIBBYtW5p+2Fioo5Sm5iEEGJ8fFxI\nkmRaoE2I1iSm4eFh076VL/Tl5R6PR9hsNlEul02fX2/fRCKxIilUrun06dOmfRVFWbHvyMiI8WWe\nz+frV1KNyrVMTEyYyiuJZXx83CibnZ0VkiQ1TEoVqVRKSJK0Iik2im95cgmFQsJmsxk/y4rKzzSd\nTq84b8Xyn68QesJc/rOk7Ym38qijHTp0CLIsY3x8vKnbP1bEYjHT9tDQEAB90MXyciGE0UdTIUkS\n4vG4qWx0dBQDAwNQFMW4VXb06FH4/X4MDAxA0zTj1d/fj6GhISiKYtwqq4jH46ZlqVeTTCbhcrlw\nyy23mMqPHz+Ovr6+FfG1SjPxjY2NIZVKrVgcrrL4YqlUWvXYcrkMu91uKqvU1fKfD20/TEzU8Spf\nroFAoKXnlWW5brnX6236+Hqd/QcOHABQHQVXLpcxOzsLh8MBp9NpemWzWUiStCLpNRND5fw+n2/V\n62h1Mq8991r27t2Lm266CYDeD5bJZDA+Po5wOFx3/9oRgCMjI8jlcnC73ZiYmEA+nwcA7NmzhwMs\negATE3W8oaEhjIyMQFGUNQcCbKXlv9FX9Pf3A9C/jCvJw+/3I5PJ1H1Vklat1ZJmrcq5XS5X3fdl\nWYYQYkVrrBWaia8yKKOSkIeHh5FKpeDxeNY8dmpqymjRRiIRYxDE2NhYxz5CQK3zlHYHQNSMZDKJ\nTCaDSCRijBhrxvKWSCtpmla3vJIwZFk2RrDZ7fYVt7RWI0kSdu7cueZ+leRw5syZVeNo9lxWNDqn\nqBlePjQ0hHw+j3A4jHA4bNz6y2azSKfTa37OoUOHcOjQISwuLmJ2dhbxeByJRALz8/OYn59vzcVQ\nR2KLibpCX18fYrEYNE3D6Oho0w9+KoqyaTGpqlr3Vtns7CwkSYIsy7Db7ejr60Mmk6l7jo1MrVRJ\nTKsNoZ6fn1+1VbdZKj8XTdOQz+cRCARw++23m/qjxBrPRqmqikgkYlzXzp07sX//fszMzKzaJ0fb\nCxMTdY3KwIJ0Or2itWK32yGEMH1Ja5q2qR3lQogV/SWJRALZbBYjIyNGqyIcDqNUKq1o6Y2Pj6Nc\nLpuesbIqFAqhUCisuMUZDodRLpdx5MiRdZ8b2PgMF8sHONT+TBqde2Jiom5f1Ga1Aqmz8FYedZVU\nKmX0qdR+sd18882Ynp6G3+9HKBSCEAKpVAqDg4MolUqbMoXQwMAAMpkMnE4nhoaGoKoq8vk8HA6H\nacTfsWPHkE6nkU6n4Xa7sXfvXmNfj8ezYkSdlVhjsRimpqYQDocRj8fh8XiQyWRQLBbrnrtZlT6v\nSCSCubk5HDt2rKn4Ku/Z7Xb4fD5kMhkEg0F4vV4UCgXjZ1KJXZZlYzRk5VhZlo1jK3XrdDoxNTWF\nxcVFHD58eF3XRN2DLSbqKGtNBNrf3298MdXut3//fsTjcciyjEQigXQ6jXA4jFOnTq3Yd7XPsFIu\nSRIGBweRy+UgyzJOnjyJxcVFBAIBFIvFFSPHzpw5g8OHD8Nut2N6ehqLi4vGl76V61+ur68PxWIR\nofuEcIsAAACrSURBVFAImqbhxIkTcDqddc+9vB4aGRoags/ng6qqptZYo/iWv5dKpRAKhZDJZBCN\nRqEoCk6cOIFTp04hFAqhWCwafU3Lj52ZmcHhw4fhdDpx8uRJI6mnUikcPXq0qWug7iWJzfhVkoiI\naJ3YYiIioo7CxERERB2FiYmIiDoKExMREXUUJiYiIuooTExERNRRmJiIiKijMDEREVFHYWIiIqKO\nwsREREQd5f8DTnDrXxe6gIwAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60deb92b10>"
]
}
],
"prompt_number": 59
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Bonferroni"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Corrects for the number of comparisons that you WILL make (Set p-value before the experiment. Don't cheat)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%latex\n",
"$$1 - (1-\\alpha_{new})^{trials} = 0.05$$\n",
"$$$$\n",
"Our Friend Taylor\n",
"$$1 - (1-trials \\cdot \\alpha_{new}) = 0.05$$\n",
"$$$$\n",
"$$trials \\cdot \\alpha_{new} = 0.05$$\n",
"$$\\alpha_{new} = 0.05/trials$$"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$1 - (1-\\alpha_{new})^{trials} = 0.05$$\n",
"$$$$\n",
"Our Friend Taylor\n",
"$$1 - (1-trials \\cdot \\alpha_{new}) = 0.05$$\n",
"$$$$\n",
"$$trials \\cdot \\alpha_{new} = 0.05$$\n",
"$$\\alpha_{new} = 0.05/trials$$"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Latex at 0x7f60debfc210>"
]
}
],
"prompt_number": 60
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print(\"p_min = 0.05/3 = %f\" %(0.05/10)) \n",
"print(scipy.stats.mannwhitneyu(x,y)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(x,z)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(x,i)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(x,j)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(y,z)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(y,i)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(y,j)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(z,i)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(z,j)[1]*2)\n",
"print(scipy.stats.mannwhitneyu(i,j)[1]*2)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"p_min = 0.05/3 = 0.005000\n",
"0.0951349836324\n",
"0.176819928628\n",
"0.0515876890194\n",
"0.00138320106226\n",
"0.692955551073\n",
"0.817025225356\n",
"0.105130438032\n",
"0.500168565389\n",
"0.0464220325154\n",
"0.187879318583\n"
]
}
],
"prompt_number": 61
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Dunnett's_test. Compare with control."
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Still not implemented in Python. There are some non-official implementations in MATLAB though.\n",
"Assumes normality\n",
"\n",
"You can use bonferroni with p-min = 0.05/(n-1)"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Tukey HSD. Best"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
" Assumes normality"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from statsmodels.stats.multicomp import pairwise_tukeyhsd"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 62
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"res2 = pairwise_tukeyhsd(np.asarray(x+y+z+i+j),['x']*200+['y']*200+['z']*200+['i']*200+['j']*200)\n",
"print res2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Multiple Comparison of Means - Tukey HSD,FWER=0.05\n",
"=============================================\n",
"group1 group2 meandiff lower upper reject\n",
"---------------------------------------------\n",
" 0 1 0.1404 -0.1341 0.4149 False \n",
" 0 2 -0.1942 -0.4687 0.0803 False \n",
" 0 3 -0.0337 -0.3081 0.2408 False \n",
" 0 4 -0.1121 -0.3866 0.1623 False \n",
" 1 2 -0.3346 -0.6091 -0.0601 True \n",
" 1 3 -0.174 -0.4485 0.1004 False \n",
" 1 4 -0.2525 -0.527 0.0219 False \n",
" 2 3 0.1606 -0.1139 0.435 False \n",
" 2 4 0.0821 -0.1924 0.3566 False \n",
" 3 4 -0.0785 -0.353 0.196 False \n",
"---------------------------------------------\n"
]
}
],
"prompt_number": 63
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"res2.plot_simultaneous(comparison_name=None,xlabel='diffs',ylabel='grups')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAGGCAYAAABfWgTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHrtJREFUeJzt3c1TU2ueB/Bf7K4aV4q5/Qcocd9exJmq2UhdAizcXUTv\nHyAvs0A34wVnM/amfWFWspgW/APmQugdVQqhO7OdQbh330T3U2K4K2eVWVjJgPISfAwJ8PlUWebl\n5Dy/PCcn+eY5DyeZarVaDQAAvsiZVhcAAHCcCVMAAAmEKQCABMIUAEACYQoAIIEwxYlVqVTizJkz\nMTY29tl9Q0NDcebMwS//tbW1uHz5cv167TFra2vR3d196Mc3YmZmJnK5XJw5cyYuX74cs7Ozh3r8\nUWj0+TdDbbtu/9fd3R3r6+sNPb6R7X7ULly4ENlsdsdt2187+72OLly4sKMvLl++HAsLC/u297W2\n39OnT2N9fT2uXr362TY5c+ZM/OY3v9nzsYVCIW7dupXU/sLCQlvuH5w+7feuAl/Z/Pz8Z7cVi8XI\nZDKHWs/2s4jkcrl48uRJcm2fevr0aTx9+jRmZ2ejUqnE8+fPY2Ji4sAPx6PW2dnZlOd/GJVKJSqV\nSrx//z7y+XwMDQ21tJ4vtba2FplMJjKZTMOBcLtMJhNra2v1/piYmIihoaF4+/btno/5Gq/fSqUS\nc3Nz8e2338br16/r26KjoyOKxWL9+n51pxocHGz56xAihClOgU9HLYrFYvT19dWvf/otvVgsRn9/\n/2frqd32zTffRLlcjomJiYj4+A17dHS0PtrV3d0db968+ezxxWKxPuLU398fW1tbO+6vVCoxOTkZ\nxWIxvvvuuzh37lz09vbGkydPYm5urr5coVCor+fWrVv19ZTL5bh69WqMjY1FNpuN/v7+WFtbqy87\nNTXVUL0zMzORzWY/u69cLkdfX19MTk7GP/7jP9aff0TE6OhoZLPZyGaz9XYaqXVqaiqy2Wxcvnx5\nxzbaa33bnTt3Ls6dOxfnz5+PkZGRKJfLB/Z1bbtns9no7u6OlZWViPgYYrePWOVyufjLX/5y4Hbb\n676Dnt92z58/j9HR0RgeHo7nz5/vukwjav0xPDwcnZ2dsbGxETMzM/WRq+3bcmNjo779att1YmKi\nvh800v8zMzM7Rn1r2yLiY/+eO3cu/va3v+25b23/crK2thbZbDZ+/vnnXft0dHR0Rx0TExMxOTkZ\nERE3b95suy8bnD7CFCfe0NDQjg+pQqEQt2/fjsOer3Z5eTkiIt69e/fZY2dnZ2NgYCAqlUp0d3d/\nNkqytbUVt27dihcvXkSlUonOzs4YHh7esczq6mp0dXXFxYsXd9w+PDwcP/30U0R8/OC7detWzM7O\n1r/1bw816+vr0d/fH2/evImNjY3I5/Oxvr4ey8vLO5bbq95KpRJjY2Px17/+Nd6/fx+dnZ07+m5l\nZSW2trZ2jAYUCoVYWVmJt2/fxsrKSkxMTMSvv/7aUK2ZTCY2Nzcjn8/vCKfb1zc5ORm//vrrvtum\nUCjUg1KlUtmzr2vbsNZm7fry8nJkMpn6aM6bN2/iu+++23dd+9233/P71Pz8fIyOjsbt27d3hObD\n2P56XF5ejnK5HL/73e9ibGwsSqXSrttyu5WVlfj111+jUCg03P9zc3ORz+e/qN7tyuVy5PP5KBQK\ncfHixV37tL+/v76tIj4e3vvhhx8i4mNAru0f0DJVOKHev39fzWQy1UqlUr1w4UL99trlTCZTrVar\n1devX1evXr1av395ebna19dXvy+Xy9Xv2+0x8/Pz1e7u7h1tZzKZ6tbWVv3xMzMz1aGhoR3LbK+p\nWq1Wnz9/Xm93L0+ePKmOjY3Vr5fL5fp6NjY2dqxzdHS0Ojk5+VlN+9VbrVarlUqlfvvIyEh1dHS0\nvv7dnn+hUKjmcrnq2tpatVqt1tdzmFrX1tb2XN/2eqrV/9+u2/+dOXOmvvzz58/37evacygWi/U2\nOzo6qmNjY9WZmZnq8vJy/fb91rXfffs9v+22t1V7fO15bH/tffo63K6jo+Oz/piamvqs77Zvy+3b\nb/t2rVYP7v+a7Y/5tA/W19c/a6f2fGuv8fn5+Wo+n6/mcrn662S/Pq2192nffnodWuG3rQ5z0Gzn\nz5+vH+p79+5dXLt27au3cenSpR3XOzs7dxx22tjYiEKhsGOS8adzRnK5XGxubn627q2trZibm4vh\n4eHY3NyMzs7OHe1WKpX69e3r7+jo+GxS80H1XrlyJf74xz/GyspK/bHb29t+uWZwcDA2NzdjaGgo\nNjc348GDB3H//v1D1VrdNrKy1/o+tb1/X79+HVevXo3379831NcREb29vbG2thZv3ryJXC4X+Xw+\nfvrpp7h27Vp9lGu/dR3Uzl7Pb7v5+fn6Ia6IqM+T+9Of/rTr8rvJZDJRLBbrfb19ZHO/bbnd9tsb\n6f9KpRIdHR0N17iX2kjmkydP4vHjx/v2aT6fj5WVlXj9+nWMjo7uqH376wpawWE+ToWhoaH4j//4\nj/p8of18yRvz9g/22vXtH1C5XC5u3rwZm5ub9X/FYnHHY65evVr/cN/up59+qh9W++abb2JjY2NH\nrV/yobZXvbVDPH/5y19iaWkpbt682dC68vl8/O1vf4vXr1/H8+fPY2Fh4Ytr3Wt9n7p48WL93+Dg\nYHR1dUWxWIzLly8f2Nc1XV1d8eTJk+jr64t8Ph+vX7+O5eXluH37dkTEvus6TDt7qYWpt2/fxtu3\nb2N5efmLDvVls9l6X9R8ybaMaLz/v8Sn+1ZfX188evQobt68GRMTE/v2aV9fX8zNzcXc3Fx9+0C7\nEKY4FYaGhmJmZiaKxeJn8zw6OjrqIaZSqcSjR48Ovf61tbX6X+CNjo7G1atX49y5c/X7b926FcVi\nMVZWVurLfDqHpqOjo/7BXluuUCjE5ORkfbLt4OBgzMzM1O8fHh7+og+Wvep9//59ffJwpVKJmZmZ\nXUfLtisUCjE0NBRbW1v1EZhMJhM3b978olr3Wt+ntra26n/Btry8HGtra3H16tUYGho6sK9r8vl8\nzMzMxLVr1+L8+fOxubkZr1+/jitXrkTE/tvtMO3splgsRjabjStXrtQnj/f29kZE1CfGp/iSbRnR\nWP93dHQ09KVjt31r+7pqE9ZnZmZiZmYm/v7v/37PPr1582bMzc3Fmzdv6tsn4mP4+xqjZJBCmOJE\nq71xd3R0RC6Xi1wuVw85tfs6OztjZGQkcrlcXLt2Lf7lX/5lxxv+9ss3b96M3/zmN/U/Za+pTWbO\nZrOxtra243QMmUwmzp8/X59onM1m4+3bt1EoFD6r9/79+zE6Olpf7sGDB/H06dO4c+dOvdbt6zlz\n5syOyeCffujt9Tz2qrc2gTqbzUZfX188efIkisVi/S/bdlvfjz/+GNlsNi5cuFCfzP7999/HpUuX\nvqjWvdb3qdq5mbLZbPzwww8xMzMTFy9ejI6Ojn37urYNa/2QyWTqAbuvr2/HX5/tt90Oame/bRHx\nMUDsdjqH2mTsT19jhz2VwH7bcr91N9r/XV1du/7V6na77Vvb29y+f/74449x//79+ujxp3166dKl\n+Oabbz47N1XtrxGhlTLVvQ7mAw0pFAr1ww/HwXGrl/Y0NTUVHR0dn/1VajN1d3fHixcvdoxMTUxM\nxD/8wz/sGvjgqBiZAuDQRkZGks6LdVjLy8ufHeKL+HiaBEGKVhOmINGnh0za3XGrl/Z0/vz5uH37\n9hedtf2waueG+/TXDBYWFurzCaGVHOYDAEhgZAoAIIEwBQCQoGVnQL9y5Ur88ssvrWoeAKBhv//9\n7+Pnn3/e9b6WjUz98ssvUa1WT/y/f/3Xf215Dcftnz7TX/qrvf7pM/2lz6r7DgA5zAcAkECYAgBI\nIEw1WU9PT6tLOHb02eHor8PRX4enzw5Hfx3ece+zlp1nKpPJRIuaBgA4lP1yi5EpAIAEwhQAQAJh\nCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAk\nEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQA\nQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBM\nAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKY4lFKp1OoS2MXi4mIM\nDAxET09PDAwMxOLiYqtLYg/2ITh5ftuMlS4sLMRPP/0UERHFYjFevHgR33//fTOa4oiVSqXo6elp\ndRlss7i4GPfu3YuNjY36bbXLN27caFVZ7ME+BCdPU0amBgcHY25uLkZGRuLatWuCFDTRs2fPdgSp\niI9hanp6ukUVAZwuTRmZiohYW1uLycnJWF1d3XOZhw8f1i/39PT4tnYMlEqlyGQyrS6DBrx69cq2\nakPXr19vdQlAA0qlUsOH5TPVarX6tQuoVCrR29sbf/3rX+PcuXO7N5zJRBOapskePny4IwTTegMD\nA7G0tLTr7S9fvmxBRezHPgTH0365pSmH+UZGRuLXX3+NO3fuxK1bt2JhYaEZzQARcffu3cjlcjtu\ny+VyMT4+3qKKAE6Xphzmm5uba8ZqaQMOxbaf2iTz6enp+PDhQ5w9ezbGx8dNPm9T9iE4eZpymK+h\nhh3mAwCOiSM/zAcAcFoIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAA\nCYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAF\nAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABII\nUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAg\ngTAFAJBAmAIASCBMAQAkEKZgD6VSqdUlsIfFxcUYGBiInp6eGBgYiMXFxVaXxB7sR5wGTQlTY2Nj\nsbKyEhERhUIhJicnm9EMNJUPgfa0uLgY9+7di6WlpfjP//zPWFpainv37glUbcp+xGnQlDA1NDQU\n8/PzERExMzMTY2NjzWgGOIWePXsWGxsbO27b2NiI6enpFlUEnHa/bcZKe3t7Y3R0NLa2tmJzczMu\nXry463IPHz6sX+7p6Ymenp5mlANfpFQqRSaTaXUZNOjVq1e2Vxu6fv16q0uAL1IqlRoeWc1Uq9Vq\nM4oYGxuLcrkct27dijt37nzecCYTTWoavoqHDx/uCPy0h4GBgVhaWtr19pcvX7agIvZjP+Kk2C+3\nNGVkKiJiZGQkuru7d33TA/hSd+/ejY2NjR2H+nK5XIyPj7ewKuA0a1qY2tzcjNHR0WatHprOYef2\ndOPGjYiImJ6ejg8fPsTZs2djfHy8fjvtxX7EadCUw3yFQiEeP34chUJhz/lSDvMBAMfFfrmlaXOm\nDiJMAQDHxX65xUk7AQASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\nCFMAAAmEKQCABMIUAEACYQoAIEFDYWprayvevHkTW1tbMTU1FW/fvm1yWQAAx0NDYWp4eDjK5XJM\nTExEtVqNoaGhZtcFAHAsNBSmKpVK9Pb2Rrlcjh9//DGq1Wqz6wIAOBYaClPVajUePHgQXV1dsb6+\nHpVKpdl1AQAcCw2FqefPn0c2m40HDx7E6upqzM/PN7suAIBjIVM9xDG7t2/fxsWLF79Ow5mMw4UA\nwLGwX25paGRqYWEhLl++HCMjI3H58uX485///FULBAA4rhoameru7o7V1dU9r39Rw0amAIBjInlk\nKpvN7nsdAOC0+m0jC126dCkGBgYin8/H8vJyRETMzs5GJpOJO3fuNLVAAIB21tDIVC6Xi97e3oiI\nyOfzkc/no1KpxPv375taXLsqlUqtLoE9LC4uxsDAQPT09MTAwEAsLi62uiR2YR8CTpKGRqZ+/PHH\nQ610dnY2Xr9+HX/6059iaGgo/umf/im+++67LyqwHZVKpejp6Wl1GXxicXEx7t27FxsbG/Xbapdv\n3LjRqrLYhX0IOEkaClPd3d07rmcymfjv//7vPZcfHh6O5eXlmJiYiN/97ncnKkjRvp49e7YjSEV8\nDFPT09PCFABN01CY2v6Xe8ViMYrF4oGPefz4cVy+fHnfs6U/fPiwfrmnp+fYfFMtlUqRyWRaXQYN\nevXqle3VZq5fv97qEgD2VSqVGp6ScKiTdtb09/fH0tLSvsv09fXFwMBA/Nd//VfMzc193vAxPjXC\nw4cPdwRB2sPAwMCur8uBgYF4+fJlCypiL/Yh4LjZL7c0NDI1NTVVv/zu3buGlh8YGIh//ud/jrGx\nsVhYWIjBwcEGy4Uvc/fu3djY2NhxqC+Xy8X4+HgLqwLgpGtoZKpQKOw4TJLP5+P8+fNpDR/jkSmT\nZ9vX4uJiTE9Px4cPH+Ls2bMxPj5uvlQbsg8Bx81+uaWhMPXmzZu4dOnSkRUFANBOks+A3tfX91UL\nAgA4KRqaM9Xb2xvd3d2Rz+frtz1+/LhpRQEAHBcNhan+/v7o7+9vdi0AAMdOQ3Omuru7PztfVC6X\ni+fPn8fFixe/rGFzpgCAYyL51Ajd3d0xNDQUvb299ZN23rp1K0ZGRg483xQAwEnW0AT0crm844eO\n19bWoqurq6mFAQAcBw2NTJ0/fz7+7d/+rT4yFRGxsrLS1MIAAI6Dhkam5ufn43/+53/i0aNH8e7d\nu5ifn6/fDgBwmn3Rb/N9lYZNQAcAjonkk3YCALA7YQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\nCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASHEmYWllZicnJyaNoCgDgSGWq\n1Wq1JQ1nMtGipgG+SKlUip6enlaXwS4WFxfj2bNn8b//+7/xd3/3d3H37t24ceNGq8tiF8d1P9ov\nt/z2KAooFotRLBbj8ePHR9EcQFMc1w+Bk25xcTHu3bsXGxsb9dtqlwWq9nMS96MjOcyXyWSOohkA\nTqFnz57tCFIRH8PU9PR0iyritDmSkam9PHz4sH65p6fnxCVV4GQplUq+HB4jr169sr3a0PXr11td\nQkNKpVKUSqWGlm2bMAXQ7np6ehp+c+XoDAwMxNLS0q63v3z5sgUVsZ/j8tn/6SDPH/7whz2XdWoE\nAI61u3fvRi6X23FbLpeL8fHxFlXEaXMkI1Pv378/imYAmspUhPZUm2Q+PT0dHz58iLNnz8b4+LjJ\n523qJO5HTT81QqVSiXw+Hy9evIgrV678f8NOjQAAHBP75RbnmQIAOMB+ucWcKQCABMIUAEACYQoA\nIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCm\nAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEAC\nYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEA\nJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEjQ9DC1sLAQU1NTzW4GAKAlMtVqtdqS\nhjOZaFHTAACHsl9uafrIVKFQiMnJyWY3A8dWqVRqdQnsYXFxMQYGBqKnpycGBgZicXGx1SWxB/sR\nrfTbZjeQyWSa3QQca6VSKXp6elpdBp9YXFyMe/fuxcbGRv222uUbN260qiz2YD+ilUxAB9jFs2fP\ndgSpiI9hanp6ukUVAe2q6SNT+3n48GH9ck9Pj28VnEqlUskI7jHy6tUr26sNXb9+vdUlcMKUSqWG\nDx8fSZja641ne5iC06qnp8d8jzY0MDAQS0tLu97+8uXLFlTEfnye8LV9Osjzhz/8Yc9lmx6mBgcH\nY3BwsNnNAHxVd+/ejY2NjR2H+nK5XIyPj7ewKqAdtfQwHxAOb7ep2iTz6enp+PDhQ5w9ezbGx8dN\nPm9T9iNayXmmAAAO0NLzTAEAnGTCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkA\ngATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECY\nAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJ\nhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUA\nkECYAgBIIEwBACQQppqsVCq1uoRjR58djv46HP11ePrscPTX4R33PhOmmuy4v0BaQZ8djv46HP11\nePrscPTX4R33PhOmAAASCFMAAAky1Wq12oqGr1y5Er/88ksrmgYAOJTf//738fPPP+96X8vCFADA\nSeAwHwBAAmEKOLEWFhZiZWUlZmdn91xmYmLiCCuC062RfTIiYmpq6ogq+jqEKdqKD7/9HdQ/jb5R\nnQZra2sREdHb2xsREevr658tMzMzEwsLC0daVzs76PUzOzsbs7OzMTk5ecSVta+D+qxQKMTKykqM\njY0dcWXtp5F9MiKiWCzG8vLykdX1NQhTTeSN6XB8+O3voP5p9I3qtJibm4sLFy5ERERnZ2cUi8XP\nlhkZGYnOzs6jLq0tHfT6WVlZiXw+H8PDw1Eul2NlZeXIa2w3jfTZyspK9Pb2Rrlc3nPy8mnRyD4Z\nEZHJZI6yrK9CmGoSb0yH58Nvfwf1T6NvVKdFpVKJbDZbv/7u3bsWVtP+Dnr9lMvl+m2dnZ1RLpeP\nvMZ2c1Cf9fb2xr//+79HRMTm5mZcuXLlyGtsJ43sk+vr6/XPzeNEmGoSb0yH58Nvfwf1j/77nD9W\nbtxBr5/h4eEYHh6OiI9fFq9du3ak9bWjRva5ra2tmJqaigcPHhxlaW3roH1yc3PziCr5un7b6gJO\nqkbemGrW1tbihx9+OLLa2pkPv/0d1D/67/91dHTU35jfv38f33zzTYsran+NvH7W1tbi6tWrp36U\npeagPjt//nzcv38/+vv7o6urKy5dunRElbWfg/bJ4zoqFSFMNZU3ps/tNn8sm83G4OCgD78DHNQ/\n+m+n27dvx+rqavT29sabN2+ir68vIj5+0eno6Ghxde2n0dfPyspKPHr06ChLa1sH9dna2lpkMpn4\n9ttvo6urKwqFQty/f78VpbaFg/bJcrkc5XI53r17F5ubm7G+vh7ffvtti6tujMN8CWoTyLf/q02O\n9sa0u9qhgu3/BgcHI+LjjlY73PnpjsbB/bPX/adV7U14ZWUlOjo66l9Y8vl8fZlCoRCrq6vx4sWL\nltTYThrZ/2ZmZuphwDzPg/tsZWWl/jlQqVQil8u1ptA2cdA+OTg4GIODg5HJZGJra+tYTUR3BvQm\nWV9fj9XV1RgeHo6pqano6+uLK1eu7PhWPDMzEyMjIxER9b/4OO1mZ2frc8hqh0K7u7tjdXU1Ij5+\n+I2MjMTTp0/jzp07rSy1JQ7qn93uh0bt9/oqFotx69atyGazsbm5GYVCIb777rsWV9x6+/XZ1tZW\nzM3NRcTHebKn6YvzaSNMNZE3JgA4+YQpAIAE5kwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKOLYu\nX74cERELCwsxNTUVERF9fX31k3BuvwzQLH5OBjj2amfRL5fLkclk4s6dOzsuAzSTMAUcG5VKJYaG\nhiKTyez4fb3az8JUKpVYXV2NhYWFWFpaitXV1fjzn/8cV65cidHR0frjZmdn4/z58y18JsBJIkwB\nx8ajR4/i9u3bcefOnR2/MF/7Da+JiYkol8sxODgYXV1d8ebNm/j+++9jamoquru749GjR/XfSxOm\ngK/FnCng2FhfX6//KOr2X5Pf7Ycctt82MjIS1Wo1+vv7Y35+PrLZbPOLBU4NYQo4Nrq6umJ5eTki\nItbW1hp+3NzcXNy+fTuWlpais7MzZmZmmlUicAo5zAccGw8ePIihoaGYn5+Pjo6OyOVyEfHxMF/t\nUF/t/+2Xu7u7Y2hoKDo6OiKTycT8/PzRFw+cWH7oGAAggcN8AAAJhCkAgATCFABAAmEKACCBMAUA\nkECYAgBIIEwBACQQpgAAEvwfvrS5X6uMz9QAAAAASUVORK5CYII=\n",
"prompt_number": 64,
"text": [
"<matplotlib.figure.Figure at 0x7f60dec9c7d0>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAGGCAYAAABfWgTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHrtJREFUeJzt3c1TU2ueB/Bf7K4aV4q5/Qcocd9exJmq2UhdAizcXUTv\nHyAvs0A34wVnM/amfWFWspgW/APmQugdVQqhO7OdQbh330T3U2K4K2eVWVjJgPISfAwJ8PlUWebl\n5Dy/PCcn+eY5DyeZarVaDQAAvsiZVhcAAHCcCVMAAAmEKQCABMIUAEACYQoAIIEwxYlVqVTizJkz\nMTY29tl9Q0NDcebMwS//tbW1uHz5cv167TFra2vR3d196Mc3YmZmJnK5XJw5cyYuX74cs7Ozh3r8\nUWj0+TdDbbtu/9fd3R3r6+sNPb6R7X7ULly4ENlsdsdt2187+72OLly4sKMvLl++HAsLC/u297W2\n39OnT2N9fT2uXr362TY5c+ZM/OY3v9nzsYVCIW7dupXU/sLCQlvuH5w+7feuAl/Z/Pz8Z7cVi8XI\nZDKHWs/2s4jkcrl48uRJcm2fevr0aTx9+jRmZ2ejUqnE8+fPY2Ji4sAPx6PW2dnZlOd/GJVKJSqV\nSrx//z7y+XwMDQ21tJ4vtba2FplMJjKZTMOBcLtMJhNra2v1/piYmIihoaF4+/btno/5Gq/fSqUS\nc3Nz8e2338br16/r26KjoyOKxWL9+n51pxocHGz56xAihClOgU9HLYrFYvT19dWvf/otvVgsRn9/\n/2frqd32zTffRLlcjomJiYj4+A17dHS0PtrV3d0db968+ezxxWKxPuLU398fW1tbO+6vVCoxOTkZ\nxWIxvvvuuzh37lz09vbGkydPYm5urr5coVCor+fWrVv19ZTL5bh69WqMjY1FNpuN/v7+WFtbqy87\nNTXVUL0zMzORzWY/u69cLkdfX19MTk7GP/7jP9aff0TE6OhoZLPZyGaz9XYaqXVqaiqy2Wxcvnx5\nxzbaa33bnTt3Ls6dOxfnz5+PkZGRKJfLB/Z1bbtns9no7u6OlZWViPgYYrePWOVyufjLX/5y4Hbb\n676Dnt92z58/j9HR0RgeHo7nz5/vukwjav0xPDwcnZ2dsbGxETMzM/WRq+3bcmNjo779att1YmKi\nvh800v8zMzM7Rn1r2yLiY/+eO3cu/va3v+25b23/crK2thbZbDZ+/vnnXft0dHR0Rx0TExMxOTkZ\nERE3b95suy8bnD7CFCfe0NDQjg+pQqEQt2/fjsOer3Z5eTkiIt69e/fZY2dnZ2NgYCAqlUp0d3d/\nNkqytbUVt27dihcvXkSlUonOzs4YHh7esczq6mp0dXXFxYsXd9w+PDwcP/30U0R8/OC7detWzM7O\n1r/1bw816+vr0d/fH2/evImNjY3I5/Oxvr4ey8vLO5bbq95KpRJjY2Px17/+Nd6/fx+dnZ07+m5l\nZSW2trZ2jAYUCoVYWVmJt2/fxsrKSkxMTMSvv/7aUK2ZTCY2Nzcjn8/vCKfb1zc5ORm//vrrvtum\nUCjUg1KlUtmzr2vbsNZm7fry8nJkMpn6aM6bN2/iu+++23dd+9233/P71Pz8fIyOjsbt27d3hObD\n2P56XF5ejnK5HL/73e9ibGwsSqXSrttyu5WVlfj111+jUCg03P9zc3ORz+e/qN7tyuVy5PP5KBQK\ncfHixV37tL+/v76tIj4e3vvhhx8i4mNAru0f0DJVOKHev39fzWQy1UqlUr1w4UL99trlTCZTrVar\n1devX1evXr1av395ebna19dXvy+Xy9Xv2+0x8/Pz1e7u7h1tZzKZ6tbWVv3xMzMz1aGhoR3LbK+p\nWq1Wnz9/Xm93L0+ePKmOjY3Vr5fL5fp6NjY2dqxzdHS0Ojk5+VlN+9VbrVarlUqlfvvIyEh1dHS0\nvv7dnn+hUKjmcrnq2tpatVqt1tdzmFrX1tb2XN/2eqrV/9+u2/+dOXOmvvzz58/37evacygWi/U2\nOzo6qmNjY9WZmZnq8vJy/fb91rXfffs9v+22t1V7fO15bH/tffo63K6jo+Oz/piamvqs77Zvy+3b\nb/t2rVYP7v+a7Y/5tA/W19c/a6f2fGuv8fn5+Wo+n6/mcrn662S/Pq2192nffnodWuG3rQ5z0Gzn\nz5+vH+p79+5dXLt27au3cenSpR3XOzs7dxx22tjYiEKhsGOS8adzRnK5XGxubn627q2trZibm4vh\n4eHY3NyMzs7OHe1WKpX69e3r7+jo+GxS80H1XrlyJf74xz/GyspK/bHb29t+uWZwcDA2NzdjaGgo\nNjc348GDB3H//v1D1VrdNrKy1/o+tb1/X79+HVevXo3379831NcREb29vbG2thZv3ryJXC4X+Xw+\nfvrpp7h27Vp9lGu/dR3Uzl7Pb7v5+fn6Ia6IqM+T+9Of/rTr8rvJZDJRLBbrfb19ZHO/bbnd9tsb\n6f9KpRIdHR0N17iX2kjmkydP4vHjx/v2aT6fj5WVlXj9+nWMjo7uqH376wpawWE+ToWhoaH4j//4\nj/p8of18yRvz9g/22vXtH1C5XC5u3rwZm5ub9X/FYnHHY65evVr/cN/up59+qh9W++abb2JjY2NH\nrV/yobZXvbVDPH/5y19iaWkpbt682dC68vl8/O1vf4vXr1/H8+fPY2Fh4Ytr3Wt9n7p48WL93+Dg\nYHR1dUWxWIzLly8f2Nc1XV1d8eTJk+jr64t8Ph+vX7+O5eXluH37dkTEvus6TDt7qYWpt2/fxtu3\nb2N5efmLDvVls9l6X9R8ybaMaLz/v8Sn+1ZfX188evQobt68GRMTE/v2aV9fX8zNzcXc3Fx9+0C7\nEKY4FYaGhmJmZiaKxeJn8zw6OjrqIaZSqcSjR48Ovf61tbX6X+CNjo7G1atX49y5c/X7b926FcVi\nMVZWVurLfDqHpqOjo/7BXluuUCjE5ORkfbLt4OBgzMzM1O8fHh7+og+Wvep9//59ffJwpVKJmZmZ\nXUfLtisUCjE0NBRbW1v1EZhMJhM3b978olr3Wt+ntra26n/Btry8HGtra3H16tUYGho6sK9r8vl8\nzMzMxLVr1+L8+fOxubkZr1+/jitXrkTE/tvtMO3splgsRjabjStXrtQnj/f29kZE1CfGp/iSbRnR\nWP93dHQ09KVjt31r+7pqE9ZnZmZiZmYm/v7v/37PPr1582bMzc3Fmzdv6tsn4mP4+xqjZJBCmOJE\nq71xd3R0RC6Xi1wuVw85tfs6OztjZGQkcrlcXLt2Lf7lX/5lxxv+9ss3b96M3/zmN/U/Za+pTWbO\nZrOxtra243QMmUwmzp8/X59onM1m4+3bt1EoFD6r9/79+zE6Olpf7sGDB/H06dO4c+dOvdbt6zlz\n5syOyeCffujt9Tz2qrc2gTqbzUZfX188efIkisVi/S/bdlvfjz/+GNlsNi5cuFCfzP7999/HpUuX\nvqjWvdb3qdq5mbLZbPzwww8xMzMTFy9ejI6Ojn37urYNa/2QyWTqAbuvr2/HX5/tt90Oame/bRHx\nMUDsdjqH2mTsT19jhz2VwH7bcr91N9r/XV1du/7V6na77Vvb29y+f/74449x//79+ujxp3166dKl\n+Oabbz47N1XtrxGhlTLVvQ7mAw0pFAr1ww/HwXGrl/Y0NTUVHR0dn/1VajN1d3fHixcvdoxMTUxM\nxD/8wz/sGvjgqBiZAuDQRkZGks6LdVjLy8ufHeKL+HiaBEGKVhOmINGnh0za3XGrl/Z0/vz5uH37\n9hedtf2waueG+/TXDBYWFurzCaGVHOYDAEhgZAoAIIEwBQCQoGVnQL9y5Ur88ssvrWoeAKBhv//9\n7+Pnn3/e9b6WjUz98ssvUa1WT/y/f/3Xf215Dcftnz7TX/qrvf7pM/2lz6r7DgA5zAcAkECYAgBI\nIEw1WU9PT6tLOHb02eHor8PRX4enzw5Hfx3ece+zlp1nKpPJRIuaBgA4lP1yi5EpAIAEwhQAQAJh\nCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAk\nEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQA\nQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBM\nAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKY4lFKp1OoS2MXi4mIM\nDAxET09PDAwMxOLiYqtLYg/2ITh5ftuMlS4sLMRPP/0UERHFYjFevHgR33//fTOa4oiVSqXo6elp\ndRlss7i4GPfu3YuNjY36bbXLN27caFVZ7ME+BCdPU0amBgcHY25uLkZGRuLatWuCFDTRs2fPdgSp\niI9hanp6ukUVAZwuTRmZiohYW1uLycnJWF1d3XOZhw8f1i/39PT4tnYMlEqlyGQyrS6DBrx69cq2\nakPXr19vdQlAA0qlUsOH5TPVarX6tQuoVCrR29sbf/3rX+PcuXO7N5zJRBOapskePny4IwTTegMD\nA7G0tLTr7S9fvmxBRezHPgTH0365pSmH+UZGRuLXX3+NO3fuxK1bt2JhYaEZzQARcffu3cjlcjtu\ny+VyMT4+3qKKAE6Xphzmm5uba8ZqaQMOxbaf2iTz6enp+PDhQ5w9ezbGx8dNPm9T9iE4eZpymK+h\nhh3mAwCOiSM/zAcAcFoIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAA\nCYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAF\nAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABII\nUwAACYQpAIAEwhQAQAJhCgAggTAFAJBAmAIASCBMAQAkEKYAABIIUwAACYQpAIAEwhQAQAJhCgAg\ngTAFAJBAmAIASCBMAQAkEKZgD6VSqdUlsIfFxcUYGBiInp6eGBgYiMXFxVaXxB7sR5wGTQlTY2Nj\nsbKyEhERhUIhJicnm9EMNJUPgfa0uLgY9+7di6WlpfjP//zPWFpainv37glUbcp+xGnQlDA1NDQU\n8/PzERExMzMTY2NjzWgGOIWePXsWGxsbO27b2NiI6enpFlUEnHa/bcZKe3t7Y3R0NLa2tmJzczMu\nXry463IPHz6sX+7p6Ymenp5mlANfpFQqRSaTaXUZNOjVq1e2Vxu6fv16q0uAL1IqlRoeWc1Uq9Vq\nM4oYGxuLcrkct27dijt37nzecCYTTWoavoqHDx/uCPy0h4GBgVhaWtr19pcvX7agIvZjP+Kk2C+3\nNGVkKiJiZGQkuru7d33TA/hSd+/ejY2NjR2H+nK5XIyPj7ewKuA0a1qY2tzcjNHR0WatHprOYef2\ndOPGjYiImJ6ejg8fPsTZs2djfHy8fjvtxX7EadCUw3yFQiEeP34chUJhz/lSDvMBAMfFfrmlaXOm\nDiJMAQDHxX65xUk7AQASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\nCFMAAAmEKQCABMIUAEACYQoAIEFDYWprayvevHkTW1tbMTU1FW/fvm1yWQAAx0NDYWp4eDjK5XJM\nTExEtVqNoaGhZtcFAHAsNBSmKpVK9Pb2Rrlcjh9//DGq1Wqz6wIAOBYaClPVajUePHgQXV1dsb6+\nHpVKpdl1AQAcCw2FqefPn0c2m40HDx7E6upqzM/PN7suAIBjIVM9xDG7t2/fxsWLF79Ow5mMw4UA\nwLGwX25paGRqYWEhLl++HCMjI3H58uX485///FULBAA4rhoameru7o7V1dU9r39Rw0amAIBjInlk\nKpvN7nsdAOC0+m0jC126dCkGBgYin8/H8vJyRETMzs5GJpOJO3fuNLVAAIB21tDIVC6Xi97e3oiI\nyOfzkc/no1KpxPv375taXLsqlUqtLoE9LC4uxsDAQPT09MTAwEAsLi62uiR2YR8CTpKGRqZ+/PHH\nQ610dnY2Xr9+HX/6059iaGgo/umf/im+++67LyqwHZVKpejp6Wl1GXxicXEx7t27FxsbG/Xbapdv\n3LjRqrLYhX0IOEkaClPd3d07rmcymfjv//7vPZcfHh6O5eXlmJiYiN/97ncnKkjRvp49e7YjSEV8\nDFPT09PCFABN01CY2v6Xe8ViMYrF4oGPefz4cVy+fHnfs6U/fPiwfrmnp+fYfFMtlUqRyWRaXQYN\nevXqle3VZq5fv97qEgD2VSqVGp6ScKiTdtb09/fH0tLSvsv09fXFwMBA/Nd//VfMzc193vAxPjXC\nw4cPdwRB2sPAwMCur8uBgYF4+fJlCypiL/Yh4LjZL7c0NDI1NTVVv/zu3buGlh8YGIh//ud/jrGx\nsVhYWIjBwcEGy4Uvc/fu3djY2NhxqC+Xy8X4+HgLqwLgpGtoZKpQKOw4TJLP5+P8+fNpDR/jkSmT\nZ9vX4uJiTE9Px4cPH+Ls2bMxPj5uvlQbsg8Bx81+uaWhMPXmzZu4dOnSkRUFANBOks+A3tfX91UL\nAgA4KRqaM9Xb2xvd3d2Rz+frtz1+/LhpRQEAHBcNhan+/v7o7+9vdi0AAMdOQ3Omuru7PztfVC6X\ni+fPn8fFixe/rGFzpgCAYyL51Ajd3d0xNDQUvb299ZN23rp1K0ZGRg483xQAwEnW0AT0crm844eO\n19bWoqurq6mFAQAcBw2NTJ0/fz7+7d/+rT4yFRGxsrLS1MIAAI6Dhkam5ufn43/+53/i0aNH8e7d\nu5ifn6/fDgBwmn3Rb/N9lYZNQAcAjonkk3YCALA7YQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMA\nAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEw\nBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAAS\nCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASHEmYWllZicnJyaNoCgDgSGWq\n1Wq1JQ1nMtGipgG+SKlUip6enlaXwS4WFxfj2bNn8b//+7/xd3/3d3H37t24ceNGq8tiF8d1P9ov\nt/z2KAooFotRLBbj8ePHR9EcQFMc1w+Bk25xcTHu3bsXGxsb9dtqlwWq9nMS96MjOcyXyWSOohkA\nTqFnz57tCFIRH8PU9PR0iyritDmSkam9PHz4sH65p6fnxCVV4GQplUq+HB4jr169sr3a0PXr11td\nQkNKpVKUSqWGlm2bMAXQ7np6ehp+c+XoDAwMxNLS0q63v3z5sgUVsZ/j8tn/6SDPH/7whz2XdWoE\nAI61u3fvRi6X23FbLpeL8fHxFlXEaXMkI1Pv378/imYAmspUhPZUm2Q+PT0dHz58iLNnz8b4+LjJ\n523qJO5HTT81QqVSiXw+Hy9evIgrV678f8NOjQAAHBP75RbnmQIAOMB+ucWcKQCABMIUAEACYQoA\nIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCm\nAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEAC\nYQoAIIEwBQCQQJgCAEggTAEAJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEggTAEA\nJBCmAAASCFMAAAmEKQCABMIUAEACYQoAIIEwBQCQQJgCAEjQ9DC1sLAQU1NTzW4GAKAlMtVqtdqS\nhjOZaFHTAACHsl9uafrIVKFQiMnJyWY3A8dWqVRqdQnsYXFxMQYGBqKnpycGBgZicXGx1SWxB/sR\nrfTbZjeQyWSa3QQca6VSKXp6elpdBp9YXFyMe/fuxcbGRv222uUbN260qiz2YD+ilUxAB9jFs2fP\ndgSpiI9hanp6ukUVAe2q6SNT+3n48GH9ck9Pj28VnEqlUskI7jHy6tUr26sNXb9+vdUlcMKUSqWG\nDx8fSZja641ne5iC06qnp8d8jzY0MDAQS0tLu97+8uXLFlTEfnye8LV9Osjzhz/8Yc9lmx6mBgcH\nY3BwsNnNAHxVd+/ejY2NjR2H+nK5XIyPj7ewKqAdtfQwHxAOb7ep2iTz6enp+PDhQ5w9ezbGx8dN\nPm9T9iNayXmmAAAO0NLzTAEAnGTCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkA\ngATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECY\nAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJ\nhCkAgATCFABAAmEKACCBMAUAkECYAgBIIEwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKACCBMAUA\nkECYAgBIIEwBACQQppqsVCq1uoRjR58djv46HP11ePrscPTX4R33PhOmmuy4v0BaQZ8djv46HP11\nePrscPTX4R33PhOmAAASCFMAAAky1Wq12oqGr1y5Er/88ksrmgYAOJTf//738fPPP+96X8vCFADA\nSeAwHwBAAmEKOLEWFhZiZWUlZmdn91xmYmLiCCuC062RfTIiYmpq6ogq+jqEKdqKD7/9HdQ/jb5R\nnQZra2sREdHb2xsREevr658tMzMzEwsLC0daVzs76PUzOzsbs7OzMTk5ecSVta+D+qxQKMTKykqM\njY0dcWXtp5F9MiKiWCzG8vLykdX1NQhTTeSN6XB8+O3voP5p9I3qtJibm4sLFy5ERERnZ2cUi8XP\nlhkZGYnOzs6jLq0tHfT6WVlZiXw+H8PDw1Eul2NlZeXIa2w3jfTZyspK9Pb2Rrlc3nPy8mnRyD4Z\nEZHJZI6yrK9CmGoSb0yH58Nvfwf1T6NvVKdFpVKJbDZbv/7u3bsWVtP+Dnr9lMvl+m2dnZ1RLpeP\nvMZ2c1Cf9fb2xr//+79HRMTm5mZcuXLlyGtsJ43sk+vr6/XPzeNEmGoSb0yH58Nvfwf1j/77nD9W\nbtxBr5/h4eEYHh6OiI9fFq9du3ak9bWjRva5ra2tmJqaigcPHhxlaW3roH1yc3PziCr5un7b6gJO\nqkbemGrW1tbihx9+OLLa2pkPv/0d1D/67/91dHTU35jfv38f33zzTYsran+NvH7W1tbi6tWrp36U\npeagPjt//nzcv38/+vv7o6urKy5dunRElbWfg/bJ4zoqFSFMNZU3ps/tNn8sm83G4OCgD78DHNQ/\n+m+n27dvx+rqavT29sabN2+ir68vIj5+0eno6Ghxde2n0dfPyspKPHr06ChLa1sH9dna2lpkMpn4\n9ttvo6urKwqFQty/f78VpbaFg/bJcrkc5XI53r17F5ubm7G+vh7ffvtti6tujMN8CWoTyLf/q02O\n9sa0u9qhgu3/BgcHI+LjjlY73PnpjsbB/bPX/adV7U14ZWUlOjo66l9Y8vl8fZlCoRCrq6vx4sWL\nltTYThrZ/2ZmZuphwDzPg/tsZWWl/jlQqVQil8u1ptA2cdA+OTg4GIODg5HJZGJra+tYTUR3BvQm\nWV9fj9XV1RgeHo6pqano6+uLK1eu7PhWPDMzEyMjIxER9b/4OO1mZ2frc8hqh0K7u7tjdXU1Ij5+\n+I2MjMTTp0/jzp07rSy1JQ7qn93uh0bt9/oqFotx69atyGazsbm5GYVCIb777rsWV9x6+/XZ1tZW\nzM3NRcTHebKn6YvzaSNMNZE3JgA4+YQpAIAE5kwBACQQpgAAEghTAAAJhCkAgATCFABAAmEKOLYu\nX74cERELCwsxNTUVERF9fX31k3BuvwzQLH5OBjj2amfRL5fLkclk4s6dOzsuAzSTMAUcG5VKJYaG\nhiKTyez4fb3az8JUKpVYXV2NhYWFWFpaitXV1fjzn/8cV65cidHR0frjZmdn4/z58y18JsBJIkwB\nx8ajR4/i9u3bcefOnR2/MF/7Da+JiYkol8sxODgYXV1d8ebNm/j+++9jamoquru749GjR/XfSxOm\ngK/FnCng2FhfX6//KOr2X5Pf7Ycctt82MjIS1Wo1+vv7Y35+PrLZbPOLBU4NYQo4Nrq6umJ5eTki\nItbW1hp+3NzcXNy+fTuWlpais7MzZmZmmlUicAo5zAccGw8ePIihoaGYn5+Pjo6OyOVyEfHxMF/t\nUF/t/+2Xu7u7Y2hoKDo6OiKTycT8/PzRFw+cWH7oGAAggcN8AAAJhCkAgATCFABAAmEKACCBMAUA\nkECYAgBIIEwBACQQpgAAEvwfvrS5X6uMz9QAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60dec9c7d0>"
]
}
],
"prompt_number": 64
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Compare >2 independent samples and >2 different parameters."
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Imagine we want to check if there are difference in GFP expression for 3 different versions of a promoter in three different media. Create models, explaining the contribution of each factor.\n",
"\n",
"The two-way ANOVA can not only determine the main effect of contributions of each independent variable but also identifies if there is a significant interaction effect between them.\n"
]
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Fitting distributions"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Kernel estimation \n",
"\n",
"Adapted from: http://jakevdp.github.io/blog/2013/12/01/kernel-density-estimation/"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Smooth histograms."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sklearn.grid_search import GridSearchCV\n",
"from sklearn.neighbors import KernelDensity\n",
"\n",
"# The grid we'll use for plotting\n",
"x_grid = np.linspace(-4.5, 3.5, 1000)\n",
"\n",
"# Draw points from a bimodal distribution in 1D\n",
"np.random.seed(0)\n",
"x = np.concatenate([scipy.stats.distributions.norm(-1, 1.).rvs(400),\n",
" scipy.stats.distributions.norm(1, 0.3).rvs(100)])\n",
"\n",
"grid = GridSearchCV(KernelDensity(),\n",
" {'bandwidth': np.linspace(0.1, 1.0, 30)},\n",
" cv=20) # 20-fold cross-validation\n",
"grid.fit(x[:, None])\n",
"print grid.best_params_"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"{'bandwidth': 0.19310344827586207}\n"
]
}
],
"prompt_number": 65
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"kde = grid.best_estimator_\n",
"pdf = np.exp(kde.score_samples(x_grid[:, None]))\n",
"\n",
"fig, ax = plt.subplots()\n",
"ax.plot(x_grid, pdf, linewidth=3, alpha=0.5, label='bw=%.2f' % kde.bandwidth)\n",
"ax.hist(x, 30, fc='gray', histtype='stepfilled', alpha=0.3, normed=True)\n",
"ax.set_xlim(-4.5, 3.5)\n",
"ax.set_xlabel('Value',fontsize=20)\n",
"ax.set_ylabel('Norm Freq',fontsize=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAaEAAAEsCAYAAABqhgzEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3elXG1maJ/5viH2xFBLgDW8EeMvVSJBV2VWdlWVEZ1dP\nLT0mjfNM1Zx+Y1vk9Jl3tlHOP2CLrBfzrhKRPfM7NVN9GiOq5pyeOlNlhHOrrFxAwk7b6ZUQ3o0B\nKQQYzCLF70WkQhKSQAJJEYLncw4npZDi6iYWenRvPPe5jCiKIgghhBAFaJTuACGEkI2LghAhhBDF\nUBAihBCiGApChBBCFENBiBBCiGIoCBFCCFFMvtIdAAC32w2XywWDwQCe52E0GtHU1JRSG4IgwGq1\n4oMPPkh724QQQjJD8SDE8zysVisuXLggH2ttbQXHcaipqUm6nfb2dvh8voy0TQghJDMUn46z2Wxo\na2uLOmaxWNDe3p50GzzPw+fzgWGYtLdNCCEkcxilKyYYDAa43W7s2bNHPiYIAgwGA4LBYFJtdHV1\nAQD6+vpw/vz5tLZNCCEkcxQdCQmCIAeFSCzLAgBGRkZWbKO/vx9mszkjbRNCCMksRYOQ1+sFAGi1\n2riP8zy/Yhs8z6OmpgZLB3TpaJsQQkhmKT4SWove3l6cOHEiI20TQgjJPMUTE1aLggwhhOS+nA1C\nPT09aGlpke8vzYxbLYZhEv4QQghJL0WDEMdxAIDJycllH19qaGgIDQ0NUceWXhNabdvLoUBECCHp\npehiVZZlwXEceJ7HoUOH5OM8z4Nl2ajU6kiDg4MYHh5Gd3e3fMztdsuLUxsbG9HS0rKqthNlrFMA\nIoSQ9FO8YoLZbMbAwEBUoHC73Whubk54TrxkhPfffx+Dg4M4d+7cmtomhBCSPYpfE7LZbOjp6Yk6\nZrfbYbPZ5PuCIKC2tlZelBrP+Ph4zCgmmbYJIYQoR/GKCYB0jae7uxuNjY3geR4mkwmHDx+WHxcE\nARzHoaOjA8ePH4861+PxwGaz4fz58/D7/Thx4gQsFgvq6+uTajtZoek4Ffy6CCFk3VBFEMoFFIQI\nIST9FJ+OI4QQsnFRECKEEKIYCkKEEEIUQ0GIEEKIYigIEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQo\nhoIQIYQQxVAQIoQQohgKQoQQQhRDQYgQQohiFN9PiBA1CgaDuHXr1rIFa6uqqlBZWZnFXhGy/qgi\nCLndbrhcLhgMBvA8D6PRiKamphXPczqdcDqdqKiowPDwMEwmU9SGdzzPw2KxwGq1wmQywev1wm63\no7m5Oan2ycY1OzuLoaEhVFRUxH18amoKO3fupCBEyBopHoRCW3JfuHBBPtba2gqO41BTU5PwPKfT\nCYZhonZSbWhogCAIOH36tHysv78f/f39AKTtxD/88EMKQCQpBQUF2L17d9zHnjx5kuXeELI+KX5N\nyGazoa2tLeqYxWJBe3v7sud1dnbGHDObzVHHGYaB0+mEIAjgeR5erxdHjhxJT8cJIYSsmeJBqKen\nB0ajMeqYyWSCw+FY9rxQgIkkiiL0en3MMa1Wiz179qSlv4QQQtJH0ek4QRAgCAIMBkPUcZZlAQAj\nIyMJg8f58+djjjkcDrz77rtp7ychhJDMUDQIeb1eAIBWq437OM/zSY9g7HY7GhoacOrUqZg2BEGQ\nX89gMKClpWX1nSaEEJI2io+E1qq3txd9fX1gGAbd3d1Rj4VGWJFBp7W1NeYYIYQQZSh+TWitWlpa\n8MEHH+DcuXNoaGjA0NCQ/JhOp4tK2QaSS3oghBCSHTkfhEJ0Oh0sFsuK6dc1NTXgeR6Tk5NxH2cY\nJu4PIYSQ9FM0CHEcBwAJA0Lo8WQ1NTVBEARcvHgRANDR0RHznNAUHc/zKbVNCCEk/RQNQizLguO4\nmIDA8zxYlk2YlMDzPPR6PS5duhT38dC6IKvVipGRkajHQskQiQKcKIpxfwghhKSf4hUTzGYzBgYG\ncOjQIfmY2+1Gc3NzwnMEQUBtbW1MIAkFM6PRiD179qCzszMmkDmdTphMpoQZeYQQ9fJ4PJidnU34\neHl5OXbt2pXFHpG1UvyakM1mQ09PT9Qxu90Om80m3w8Fna6uLgBSkDl27FjMCMVms6G9vV0OPAaD\nAR6PJ6odu90ut0MIyS0ulwt3797FgwcPYn48Hg8uX76sdBdJihQfCel0OthsNlitVjQ2NsrTaEtH\nMD6fLypB4PTp0+jq6sLw8LBcwPTYsWM4fvy4/JyWlhb09vbC4XBgYmICgiDA4XBQ9QRCctjOnTtR\nUFAQc3xmZgYPHjxQoEdkLRQPQgBQX1+P+vr6hI+zLCtfy4m0NP06HloPRAgh6qX4dBwhhJCNi4IQ\nIYQQxVAQIoQQohgKQoQQQhRDQYgQQohiKAgRQghRDAUhQgghiqEgRAghRDEUhAghhCiGghAhhBDF\nUBAihBCiGFXUjiMklzx6lI8vvqjA9HQZrlwBtm8H6uuBrVuV7hkhuYeCECFJmp8HPvqoHLduFWF6\nOg8FBQUoLATu3we++gowGoGf/ASIU+CZEJKAKoKQ2+2Gy+WCwWAAz/MwGo1oampa8Tyn0wmn0ylv\n5WAymWIqa6+2bUIizc0x+MMftBgbS/wn43YDDx8Cv/oVsGlTFjtHSA5TPAiF9g+6cOGCfKy1tRUc\nx6GmpibheU6nEwzD4Ny5c/KxhoYGCIKA06dPr6ltQiIFg8Af/7gpKgBx3DO88soCXnyxGoODwM2b\n0vHRUeD/+/+Af/ongDbvJWRliicm2Gw2tLW1RR2zWCxob29f9rzOzs6YY2azOer4atsmJNJXX5Xi\n4cPwHNubb07jRz8ax/bt89i7F3jnHeDnPwc03/01TUwA//qvwNycQh0mJIcoHoR6enpgNBqjjplM\nJjgcjmXPYxgGTqcz6pgoitDr9Wtum5CQhw/zMThYIt///vdn8PLL0dGFYaTrQUePhgPRkydAb680\niiKEJKZoEBIEAYIgwGAwRB1nWRYAMDIykvDc8+fP4+zZs1HHHA4Hjh07tua2CQGAQAD45JNy+f6u\nXQtoaJhN+PyDB4Gf/Sx8/9Yt4JNPMtlDQnKfokEotGW3NsHkOc/zSbdlt9vR0NCAU6dOpb1tsjHd\nuWPAxEQeAKCgQERT0zQYZvlz6uuBH/4wfP/TT4Hh4Qx2kpAcp/hIaK16e3vR1taGoaEhdHd3p7Vt\nsnHNzQE3blTK9197bQbl5cnNrR0+DHCcdFsUpWm5yclM9JKQ3Kd4dtxatbS0oKWlBX6/Hw0NDejq\n6kJ9fb3S3SI5bmBAg7k56c9Dqw3i1VefJ32uRgP8+MdeXLkyj2fPpO95//2/L+Af/1FAXl5ybRQW\nFmLv3r0p9xsApqencffu3WWfw3EcSkpKln2OEh4/fizPYsQTCASy2BuSDTkfhEJ0Oh0sFguampqW\nfROvhFlpvoWse8+fA199FY4WjY0zSQePEK/3PjjuIb78cj+CQWBqCvjjH+fQ0DCx4rmiKGJsbGzV\nQWhsbAxXr16NuR4a7psXLMuiurp6Ve1n0u3bt+Hz+VBaWhr38crKShTQauB1RdEgxH03ZzE5ORn3\n2k3o8WQ1NTVBEARcvHhRzopLV9tk43C5pEAEADpdAAcOrC7Xet++IrBsAT7/XPpAffhQh1df1aO2\ndn7Fc8fGxlb1miFarRa7du2K+9jz58mP6pRQVVWFiooKpbtBskTRa0Isy4LjuJgkAZ7nwbIs9uzZ\nE/c8nueh1+tx6dKluI8LgrDqtkVRjPtDNoZAQCrBE9LQMCunXa9Gff0samrCQcfpLIfPp/jKiJx3\n+3Yh/u3fdPiXf9HjT38qx9QU/U5zleL/cmazGQMDA1HH3G43mpubE54jCAJqa2tjRjOhgBMaBa2m\nbbKxXb8eTiIoKlrEvn1rW3HKMIDZPA2dTrqWMT/P4E9/0mJhYa093bguXy7Gn/4kVbCYmdHg9u0i\nnD+vo0CUoxT/V7PZbOjp6Yk6ZrfbYbPZ5PuhoNPV1QVACjLHjh2LGaHYbDa0t7fLo5xk2iYk0pdf\nhm/X1fmQn4YJ6+JiEX//91PIz5fer+Pjebh4sRw0wE7d2Fge/vKXspjjMzMa9Pez9DvNQYonJuh0\nOthsNlitVjQ2Nsr13pZOl/l8vqikgdOnT6OrqwvDw8NyAdNjx47h+PHjKbdNNiae5zE7G158Oj6e\nD7c7VHFjEa+/PgEg8f4MgiDg2rVrcR+bmIhOQNi8OYA33niGixelxa+3bhVBqw3i9ddn1vT/sNH8\n5S9lchWKLVsW8eqrz+F0liMYBJ48KcTdu1Q5NtcoHoQAoL6+ftm0apZl42a8La2YvZq2ycblcrmw\nadMm5H2X+vb11xWYmpL+JGpqplFTsznhuXq9HqOjo3j06FHC52zeHH3+Cy/MYWwsH1euFAMABgdL\nUF4exMsvqztRQC1GR/Pw4IGUGafRAM3N09DrA5iYyIPLJaWbf/utAaKIFRcVE/VQRRAiRCk7duxA\nQUEBFhcBn88AnU769HrjDQZVVcUJzysqKkqYfZYIwwBvvPEMU1MajIwUAgA+/rgMogi88goFopVc\nuhRe17R37xz0euk6m9E4i2++KcbCAiAIRfB4wouFifopfk2IEDXg+UI8fy4FIJ0ugB07MpM5oNEA\nb701hS1bFuVjn3xShs8+KwWtw0xsfp4BzxfK9w8dCk+jFheLUWn0Q0NZ7RpZIwpChAC4fj086jlw\nYC6j0zmFhcAvfjGJbdvCgejSpRL8/vc6jI6muCp2gxgeLsTiovSPUlW1iM2boyP2iy+GR5I3bki7\n4JLcQNNxZMObnmZw/750rYFhgIMHM78RUFGRiJ//fBJ9feXyN/wnT/Jx/jyL7dsXMDdXhRs3gJIS\naTuIYFCqQ1dQABQXAxUVSEvmXq64fbtIvr1vX2yEqawMgGUXMTkJLCxIFcxfeimbPSSrldLbuK6u\nLuWyNqIogmEY3L59O6XzCMmWO3eK5NTe6uoFbNqUnU2ACgtF/MM/TMHlKsHXX4en4x49KsCjR1uX\nHY1pNMCuXcChQ8DLLyPlskK5ZH4eckICIF0PWophgLq657h3T7p/4wYFoVyRUhCqr6+Hx+OB2+2W\nj9XU1MDr9cLv9wOQMtmWbp1N9diImt25E/6WHe8DLpMYRqrKUFs7hy+/LAPPFya1EV4wCIyMSD+f\nfQb89KfAet2x/uHDAjlAV1QEEn5J2LPnOQBpVDk8LP2O1lLtgmRHSkHovffeQ0NDA4xGY0y1arfb\njRMnTmBkZAQOhyMmEBGiRlNTGjx+LP0ZaDRIqq5bJuj1QfzkJ1OYnmZw924hPv/ci337pBp2Go30\nwzDSVNP0NBC5YmFiAvjtb4E33wTeeEOR7mfUvXvhhITduxP/+1RULKKkRIo6s7PAw4fAzp0Z7x5Z\no5SC0Llz58CyLPr7+6HT6aIeMxqNcLlc0Ov1sFqtUXv7EKJWw8PhUdDOnQsoKVF2yX15uYgXX5zD\n7OxD/Kf/lPh5U1PApUvA559LgUoUgY8+Ap49Aw4cyF5/s+Hu3fBU3O7dibMWGQbYtu2ZfP/OHQpC\nuSClwarT6URzc3NMAIpkNpvhdDrX3DFCsuHOnXBWXF1ddqfi1mLTJuBv/xb4538GIguAfP018Je/\nqG+foNXy+zXw+8O7227dunzq/LZt4QoUK2ypRFQipSAkiuKK22J7PJ41dYiQbJmeLsDTp9K37Lw8\ngONyL6930ybgP//n6IvwLlcRbt2Kv619rnn0KDwK2r59ccWMwKqqcBB68ABYXFzmyUQVUgpCZrMZ\nLpcLv//97+M+3tvbC7fbDZPJlJbOEZJJDx+GP6h37pxHcXFuVr/MywOOHImehhscrMLTp7mfMhe6\nXgcA27evvIA4P38Wc3OP8PTpUzx69BQffXQTV69elX/Wuk8TSb+UrgnZbDY4nU4cPXoUb7/9Npqb\nm8FxHIaHh9HX1weHwyE/jxC1e/QoXOxSqYSEdNFogJYW4H/8D8DnA4JBBn/+8yYcOyagsHDl89Uq\nciS0bdvyQaikpAQsy6K4+CkePJD+ba9cmQQgAACmpqYwMzODqqqqjPWXpC6lIMRxHPr7+9He3o6e\nnp6YbRI4jkNnZycVDCWqNzsLTEyUoKJCuqC9XNZVrigoAN5+Gzh7VhrRCUIevviiDD/60bMVzlSn\n2VkGPp80msvLAzZvXn5ujWEY7NixA6++WoSxMalaeSBQil27pBHv6OhoZjtMViXlNddGoxF9fX3g\neR5utxs8z4PjOHAcJ28mlyq32w2XywWDwQCe52E0GtHU1LTieb29veB5HsPDw+B5HhaLBS0tLfLj\noWNWqxUmkwlerxd2ux3Nzc1JtU/Wrzt3pNECIG0JUFaWm1NxS1VUAIcPz+J3v5PuX7lSjAMH5qJq\n1eWKyKm4zZsXUVCwzJMjRE7bPX6cT1W1VW7VhT8qKyvR0NCwYrbcSkJ7/Fy4cEE+1traCo7jll1r\n1NvbC47j5KDj9/vlQBO5xUN/fz/6+/sBSAtpP/zwQwpABDdvhm/v2ZP7o6BIBw7MY/v2GczO6r9L\n3S5Da6s/5xZuPn6c/FRcJK02iNLSIGZmNJifZyAIeXLFbaI+Kb8th4aG0NDQAJZlUVtbC5fLBUAq\n6fPrX/865Q7YbDa0tbVFHbNYLGhvb1/2PJ7no6b9dDod2tvbYbFY5GMMw8DpdEIQBPA8D6/XiyNH\njqTcR7K+BALSSChkvQUhhgEaG5/KO7mOjeXj+vWiFc5Sn9UGIYaJnrp7+nQDFdnLQSkFIY/HA5PJ\nBLfbjaampqjttScmJnDmzBk0Njam1IGenp6YaTyTySQnOcQjCAK6u7vlUkEhoRHOyMiIfEwURWi1\nWtpNlcju3ZMWeAJAeXkAlZXq/JYcmdW19OfBgwfLnrtp0yJMpvB2B199VYqFzOxOkRGBgLSVd8jW\nralNJ0YGodFRCkJqllIQCmW9uVyumKQEn8+Hc+fOweVy4b333kuqPUEQIAgCDAZD1HGWZQFEB5Ol\nj/M8T2uSyKrcuhW+vWdPZrdtWK3t27fj8ePHcX88Hg+uX7++YhuHDs2irEyqs/bsmQaXL+fOIlav\nN0/eumHTpiBKS1O7ZkcjodyR0r/O+fPnYTabUV9fD0EQYh4/c+YMuru74XA4cPbs2RXbC23ZrdXG\nX1jH83zCEUy87b6dTif0en3UOTzPy331er0wGAxRyQtkYxHF3LgetH379oSP+f3+mFmAeAoLgdde\nm8FHH0mZYm53Sc7s4Do2Fp2UkKrIRIyxsTzaMFDFUgpCgiCgtrZ22edwHIfe3t6k20unzs7OqFFY\naIQVGXRaW1tjjpGNY2IiXPwzPz+I7dvnASSZdpWDXnhhDkNDJRCEPMzNMbhypRibNq18ntIiRy+r\nCUKlpSI2bQpiakqDxUUGXm/uL9xdr1Kajquvr8fg4OCyzxkaGlp1qvZa2O12VFZW4tSpU/IxnU4X\nlSkHrJz0wDBM3B+yPkSOgrZunV73G8NpNIi6NnTpUrE8zaVmaw1CS88bH1/n/9A5LKUgdOzYMbhc\nLnz00UdxP5hbW1vB8zzMZnPaOpgMnudht9vx5z//ecXn1tTUgOd5TE5OZqFnRG0irwdt2zatXEey\naP/+OZSXS9eGZmY04PnVL6nIhkAAmJgIj1yqqlYXhCoqIoMQjYTUKqWvB6FrPk1NTWhubgYgJSt0\ndnbC6XTC5/OB4zicO3cuqfY4jgMATE5Oxr0uFHp8JVarFRcvXow53tHRgTNnzkQdC03R8TyPQ4cO\nxZwTmfEXiUZDuW92FvLOm1LZ/ykA2xTt02rNzs7i6tWrcR9ber0oLw8wGmfx6adlAIDr1/W4e/c+\nfD5f3PPz8vKwf/9+aBRaWOTzFcijNZ0usOrtNaqqwheCxsfzsW9fWrpH0izld5nL5cK5c+fw9ddf\nAwD6+vrQ09ODYDCIM2fO4E7kAowVsCwLjuNiKnPzPA+WZZNKq25ra0NHR0dMEAstgl2aYRdKaEg2\nwJH14/ZtRGzjDRQX5+bV6vLycpSVlSXMnpuZmcHmzZujznnhhefyhznD6HHjRiDh+ZcuXcLs7Gy8\nl86K8fFwsbvIQJKqyJHQxEQ+Eny/JApb1UTpmTNn5BEGz/MwGAxyWnWqzGYzBgYGokYlbrdbHmkt\np6urC1arNSpY9ff3y2WEOjs7YwKZ0+mEyWRKmJFH1q/Iqbh9+4BcLSWWl5eHHTt2pHROQYEUiFyu\nEhQVFWF8nMMPfhB/SjrdCUOpmpgIB6HVXg8CpMoJhYUi5ucZzM4ymJ3NQ0nuZKlvGCmNhLq6umK2\nceA4btUBCJCm85auObLb7VGVuENZeV1dXfKx0GJWr9cLt9sNt9sNp9OJnp4eudyPwWCIWkskCALs\ndntUO2RjWFolYf9+5fqilJdeei6vibp3r0AuDqo2kSOhtQQhhgEqK8Pne73rNwsyl6U0ErJYLNDr\n9WktfaPT6WCz2WC1WtHY2ChPoy0dwfh8Pvm6jCAIcqr1UpEp5C0tLejt7YXD4cDExAQEQYDD4aDq\nCRtQZJUEnQ5YMlu1IWi1QdTUzIPnpQ/5b74pVl2F7cVFKVgUfVdlaLVJCSEVFQF5OwivtxCAOteF\nbWQpBaHjx4/jww8/xKVLl+Je1F+t+vr6Zbd/YFk2anEqy7IIBoNJtU3rgQgQnZq9f//Grar8yivP\n5SB040YR/uZvniVdnTobBKFQrm6u0wXWvNFg5EjI56MgpEYpBSG73Y66ujqYTCZ0dnaioaEBHMfR\n9RWiakurJGzkLKkdOxbAsgEIQh7m5xkMDxfhwIE5pbslk0YrkrVMxYVE1gWk6Th1SikIhdKbRVHE\nyZMn5eOR6cuiKIJhGASoTgZRifFxabdRQCpls5FnYxlGqqLw17+WAgCuX1dXEIpMSkhHYVmDIRzI\n/P4CKt+jQikFoWT34aE1NURNIkdBdXVY91USVrJ//3N88UUpRBF48KAAfr8GOl1y09uZFhmE1no9\nCJC+dGi1QUxOaiCKDCYnN/g/vgot+y9itVrx2muvyYkIS7PYCMkFS1OzN7rychG7d89jZET6wL9+\nvQjf/75y64JCgkFpoWpI5PWctTAYFjE5Kf2/+nwUhNRm2RTtjo4OdHd3xxzv6urCu+++m7FOEZIu\nMzPA/fvSbYYB9u5Vtj9qcfBgeAruxo1iJJnnk1ETE8DiovSRVFYWTNuW65G7qgoCXRdSm1XV5bhw\n4QLsdnu6+0JI2t26Fa6SsGMHUFambH/UoqZmXq6gMDWlwcOHyn84P3kSvp2OqbgQgyEchGgkpD6r\n/hdJVGONELV49OgR/vznAJ4+lRadcNw0rl6dkR/fyMkzeXnAvn1zuHy5GABw61YRdu5UduvVx4/D\nt9dSrmcpGgmp26orFFLyAVG7q1fv4JtvnmFqagpTU1MoL78bVSNt8+bNKFDTIpks27cvPCU3PFyI\nxfQNPlYlciSUrutBQPRIyO/PV8XUIwmjsSlZt+7dK0VxcRlKSkqwefMiXnwx8W6lG9GWLYvQ6QLw\n+6UN7+7eLURtrTKLOUVx6UgofUGoqEhEWVkQz54BgQADnw+oqEhb82SNlKnVTkgWjIyELwDt3Usr\n5ZdiGGDfvvDv5datIsX6MjkpbbUBAIWFQWi16R2uRI6GxsfT2jRZIwpCZF2anQUePQqXTK6rU8+C\nTDWJnJIbGSnA/Lwy0+yRoyCDYT7tZZUig9DYWHrbJmuz4nSc0+nEsWPHoo719/dDFMWY45HipXYT\nki3Xr0vrTvLypGmndH+zXi8MhgCqqhYxNpaPxUUGw8OFK5+UAdHXgxYApLfCt16/CECKbBSE1GXF\nIOTz+RIuUl1u8SoFIaKkS5fCt/fupVHQcvbtm8fYmPRRcPt2kSJljZaOhID0bvwjZchJ/48UhNRl\n2SA0ODiYlU643W64XC4YDAbwPA+j0ZhUiaDe3l7wPI/h4WHwPA+LxRJTNXu1bZPcNT4e3sZbo4me\nciKx9u6dw+efS7Xk7t8vwNat2d9nKDIISSOh9AYhaTpO+rgbH5cSISjBVx2WDUJGozHjHQjtH3Th\nwgX5WGtrKziOkzeni6e3txccx8lBx+/3w2Qywev14sSJE2tqm+S2yFHQzp2zaVt5v15t2hTE9u0L\nePSoAMEgcP++LquvPzMjJSYAQF6eCJ0u/euVSkpEFBUFEAjkY34emJoCqPi/OiiemGCz2dDW1hZ1\nzGKxoL29fdnzeJ6P2oNIp9Ohvb0dFotlzW2T3BUIRAehffvUtWmbWkWOFu/fz+6nc+QoSK+fhyYD\nn0oMA2i14bTviYn0vwZZHcWDUE9PT8yIy2Qyydt3xyMIArq7u+H3+6OOh6bZRkZGVt02yW3ffgtM\nT0u3S0oC2LnzubIdyhF1deEP//HxUghC9l47MilBuh6UGVpteIRFQUg9FA1CgiBAEAR5n6IQlmUB\nhIPJUizLgud5eDyetLdNcpcoAn/9a/j+gQNTGflWvR6VlIjYtSscAL79Nnu/uMiRUEVF5oKQTkcj\nITVStGJCaMvuRDuz8jyPPQlSdSK3+w5xOp3Q6/XYs2cPeJ5fddtEHZ4/f447d+4s+5ydO3dCp5Ou\nYdy9G/5Ay88H9u+fAhUFSd7eveHtHa5d06C5OTuvSyOhjU3Rv1AhzWP+zs5OvPfeexlpm2Tf5OQk\nrl69isrKyriPe71eFBYWykHo88/Dj736KlBSQmuDUsFx88jPl5I4nj5l8PQpsHlzZl/z+fNwBQON\nBjAY0r9GKISCkDqtm6+JdrsdlZWVOHXq1JraocKs6lJSUoKdO3fGfWwxouLm/fvA7dvSbYYBXn8d\nuHYtGz1cPwoLRdTUzOPhQ+n+1avA4cOZfc1Hj8K3t2yBHAQzITIxweeTkljysp+NTpZYVRCanJyM\nOx0WKZtTXTzPw263Z21dE1EXUQT6+8P3X34ZSDB4IivYu3cef/mLdPvKFeDHP87seppQwAOA7Rmu\nL1tQIKKsTCrfEwwCgkCFTNUgpSDk8XjQ3NwMj8ez7H5CDMMktVcLx3EApKAW79pN6PGVWK1WXLx4\nMS1tJ/rrVOYXAAAgAElEQVT/ohGSeg0PA6E8E40GePNNJXuT23bvnkdBgTSN6fNJI5Xq6sy9XuRI\nqLo6nNmYKUuTEygIKS+lIGSxWJKqOpDsBzbLsuA4DjzP49ChQ/JxnufBsmxSo6m2tjZ0dHTEBJp0\ntE3Ub3ERcDrD941GYElCJElBfj5QXT0p379yJbNBKHIkVF0N3LyZudcCAJ1uQV4YS9eF1CGlIOR0\nOmE0GtM67WU2mzEwMBAVKNxuN5qTSM3p6uqC1WqNCij9/f1yRYS1tE1yg8tVgtDMcHExjYLSYdcu\nv5xleO0a8Hd/h4ykuk9NhSslFBQAVVXZCEKL8mvSlg7qkNJbq6amJu0f4DabLaYQqt1uh81mk+8L\ngoDa2lp0dXXJx0ILTr1eL9xuN9xuN5xOJ3p6euSSPMm0TXLX1FQBXK5wjbGmJqC8XMEOrRObNz9D\n2XdbMU1NSanvmRA5Ctq2LTOBbilaK6Q+KY2EzGYzHA4Hzp49m7YO6HQ62Gw2WK1WNDY2yvXelk6X\n+Xw+eZpPEAS0trbGba+2tjbltknuEUXg66+rEAhI74nqasBkUrhT64RGAxw8GMQ330j3r14FMlFq\ncen1oGygIKQ+KQWhzs5OmEwmvPXWW2hvb0dDQ0PC5yZaJBpPfX19VB24pViWjcrGY1kWwSQ3il+p\nbZKb7twpxOPHedDrpeytn/40O9+kN4oXXwwHoW+/Bf7hH9Kfzrz0elA2bNoUgEYjZcdNTQHz80Ch\nMlsoke+kFIT8fj/8fj+GhobQ19eX8HnJZscRshrz8ww++6wMgDS5/9pr0nQOSZ/qahEsK6Uxz84C\nd+4A+/enr/1gMLvp2SHSgtjw9aCJCXrvKC2lIHTixAnwPA+O49KSHUfIanz1VQmePZOGPaWlQfz4\nxwp3aB1iGOCllyCvGbp6Nb1B6OlTqVoCIF3H0+vT1/ZKKiooCKlJSkGor68v7dlxhKRifDwP33wT\nTkb44Q+fobi4SsEerV+RQejGjfROXUUmO+zend0N5iLXBtF1IeWlPItO6c1EKaIIfPJJGUKXA7ds\nmcG+fZkreLnRbdkipU0DwMKCFIjSJbTzLQDs2pW+dpNBQUhdUgpCra2tcEauDCQki27cKMKjRwUA\npIvkjY1jtEVzBjEM8Mor4ftDQ+lpVxRjR0LZREFIXVIKQp2dndDr9Xjrrbdw6dIlTE5OJvwhJJ3m\n54G//rVUvn/o0CxYNv3bQJNor74anirzeKRSPmvl9YbL8xQXZ75S91KRQWh8XAqKRDkpXRMyGAzy\nFgmUHUey6fLlEszMSN+ZysqCaGiYicquIpmh1QJ1deEK5UNDa6+sHTkVt3Nn9lPry8uBoiJgbk76\nmZmBvDiXZF9KQejo0aNJPY+y40g6zcwwcLvDyQjf+94Mre3IIqMxHIQuXZJKI60lcERuiJztqThA\nGtlVVIQXy05MUBBSUsqLVQnJNperBPPz0hcbgyGAgwfnFO7RxrJvn/Qh/eyZVOuN56XR0WqIolT1\nPCTJQvlp4/P5cOXKFUxPazE6WgwA+PLLSfj9Ur74nj17sGnTpux2aoOjNeZE1Z49y8eVK+FR0Ouv\nz1BlhCzLy4tOUFjLCo3Hj6VgBkiBLZtrdPR6PfLy8jA6OgpRHMezZ8/w7NkzjIxMYXR0FNevX8c4\nVTXNupRGQl1dXaioqMCRI0cy1R9Coly/bkDo8uK2bYuoqaGUbCUYjcAXX0i3b96UKimwbOrtRI6C\namuzuz6osLBQ3qV3ZqYIHo9U7bagoBg7d5Zhfp7eW0pI6TulxWLBiRMnMtUXQqJMTzPg+fAn3Wuv\nzVBKtkKqqqSgAYSKx66unTt3wrcjag1nHcuGE6cEgfb4VlJKQej48ePw+Xy4dOlSpvpDiGxwsECu\nkr1lyyJ27qSUbCV973vh2263lDafiunpcGYcw6gnCPn9GiRZD5lkQEpByG6349y5czCZTPjwww/l\ntUJr5Xa70dXVhd7eXrz//vvo7+9P6XyHwxH3HJ7n0dzcjP7+fgiCIG/lkGr7JPtmZoBLl8KzxQ0N\nNApS2t694V1rnz+HXGU7Wdevh9fk7Nql7N5PRUUiSkulyLO4yGB6mi40KiXldUIAIIoiTp48KR+P\nTMkWRTGldUKhwHDhwgX5WGtrq7w76kqcTidOnjwpb3K3VH9/vxx0WJbFhx9+uGzxVaIOX34JLCxI\n76vKygBqamJHQaIo4smTJ5ibi58tNzU1hYrIlYlkTRhGqlj+pz9J9z//HKivT36Lh2+/Dd9+8cX0\n9y9VLBuQ157RlJxyUgpCyX54p7JOyGazoa2tLeqYxWJBe3s7zp8/n/A8j8cDm80Gk8kkB8d4/XA6\nnWhoaIDX66XN7HLE8+fR1xxMpvijoC1btsDr9WJ0dDRuOyUlJZRum2b19cAnn0jbO/h80mgome26\npqeBkRHpNsMABw9mtJtJYdmgvFZIEPJorZBCUgpCS7fKToeenh689957UcdMJlPCkU1ITU0NPvjg\nAwBYdrtuURSh1WpT2mSPKGtgIFzmf9OmedTVxf9SU1ZWhjL65MiqoiLg9deBixel+599JpX2WSlt\n/tKl6Kk4NXw3WJqcQG8lZax5InQt14QEQYAgCDEjGfa73M+R0FcnsmEsLIRTgQHghRcmaF2Qynzv\ne0DJd0u3vF7A5Vr++aIYvbbIaMxc31JBGXLqsKo/7/fffx91dXXIy8sDy7LIy8tDRUUFfv3rX6fU\nTmjL7kSjFJ7nV9O9mDZ6e3vR29srJz8Q9RoakpISAGDTpiB276ZiuGpTVAT8zd+E71+8KE3PJXL9\nurSuCJCC1wsvZLZ/yYoOQvRNRykpTccBQENDA9xuN3Q6HQ4fPgyO48DzPAYHB3HmzBl0d3djYGAg\nqbZCxVAzJTTCamlpkY+1trbGHCPqEAxGj4IaGxdSTgMm2fH970sjoND23xcuAL/4RezzpD2gwvdN\nJqCgIHv9XI5OFwDDSH2cnMyTlwOQ7EopCFmtVrjdbpw8eVK+HhPJYrGgq6sL7733Hs6ePZu2Tq6W\nTqeLWVxrsVhgsVgSBiEqvqqcb78NbxVQWgq8/PLiilM9JLtEUcT169cRCATAcUX4f/9PB0DKmAsE\n/Ni7NzpT8erVEnzzjXQBqKBAhFY7DkHYIU+5Kyk/XxptT05qIIrA9LRKouMGk9IY1Ol0guO4uAEI\nkAqc1tTUqHrju5qaGvA8T3seqYwohreSBqRUYKqUrT4LCwu4dOkSRkdHUVJyD5s3j8o12P7v/9Xg\nyhUBo6Oj39Vi86GvD/Lju3Y9hMdzDU+fPlX6f0MWOSU3OUlBSAkpBSG32w2TybTsc8xmM9xud1Lt\ncd+V0E0UELg1ltjt6OiIORaaokt0vUkUxbg/JLN4HnjyRLpdUCAFIaJOeXl52LlzJ3bt2om335bq\nrmm1WpSWsvjqq4N4+HA/BGEvBgYOorSUhVarxe7dZfjJT8pVl6UaGYSmpuhbjxJSCkKhUcRyXC5X\nUotMASkLLnRNKRLP82BZdk3rekKLYJdm2IWSIdYa4Eh6ff55+HZ9vTQdR9SvsFDEz342JVcfCASA\ngYESfPxxGWZnpantoiIRf//3U8hP+Qp05tFISHkpBSGz2QyXy5UwC66rqwtutxtmszmlNpcmMrjd\nbjQ3N6fStRgcx6GzszMmkDmdTphMJtV9I9vIHj2SRkKAtN4kMvOKqJ9eH8CRI35UVS3GPFZaGsTP\nfjaJykp17rRMIyHlpRSEbDYbampqcObMGezduxfvvvsufv3rX6OtrQ179+6FxWIBy7LLLh6N1+bS\nRbB2uz2qDUEQUFtbi66uroTtxJsyMxgM8ERs4ygIAux2+7LtkOyLHAW9+OLqtgggytLrgzh61I+3\n3prC/v1zqKubxw9+8Ay//KWAbdtig5Na0EhIeSkNkFmWhcvlQnt7O7q6ujAcuTkIgJMnT8Jms0Gn\n0yXdpk6ng81mg9VqRWNjozyNtnQE4/P5ojLX/H4/zp49C57nwfM8LBYLzGYzmpub5cy3lpYW9Pb2\nwuFwYGJiAoIgwOFwUPkelRBFEV98cRMffcRCFKV/2zfemMA330gfWjOhBUMkq0RRxI0bN1AQJ5c6\nEAgkvEaalwfs2zePfftyJ69+06Yg8vKkacTnz/ORoAwhySBGXMNV91AA4Dhu3V9jCQVASlJIn/n5\nefy3//ZXPH26CwBQXT0Ls/lJ1HPKy8tVkc67kYyNjSUsCgsABQUF2LJly6ra5nketbW12LdvX9zH\nP/30U+Tn52e18OzvfsfC682Dz+fDf/2vRfj+93dl7bXJKharRtoIwYdkzvQ0cP9+BaqqpOtzZjOw\nY8cOhXtFqqqqlO5CVrFsAF6vVLbH56PKCdm2bBCqq6tLefFmaCuH27dvr6ljZP37+msmatO66mra\ntI5kH9WQU9ayQWhiYiLphhiGyXgZHrJ+zM0BLlf4C47ROEub1hFFRAYhGgll37JByBeqobICv9+P\nEydOyNsvnDlzZu09I+ua2w08fy5FHZYNgONy52I2WV9oJKSsNS8f6+rqQnt7OwRBgNFoRE9PT9KL\nVcn65/F4MDU1FXUsGAT+8IdK+P1SEDp0aJa2a9hAHj9+jOehDaOWmJqagl6vz2p/lo6ERBE0Ks+i\nVQchj8eDo0ePwu12g2VZdHZ2xhQLJeTKlSsoKChAYUQhuLt3S/HkSTkAoKqqDAcOUF7sRrF161Z4\nvV6MjY3Ffby4uDjrC8lLS0UUFkpZr/PzDJ49A8rLs9qFDW1VQchqtcp12d5++210dXWltDaIbCzb\ntm1DSWgXNABffaWFViutQWlsnEVBAU3FbRSlpaUoVVlNJoaRRkOhXeInJigIZVNKQai/vx9Hjx6F\nIAhyWZympqZM9Y2sQ6OjeXj0SApAGg3w0kvL7IZGSJZETsl5vcDu3Qp2ZoNJaibe7/ejtbUVzc3N\nEAQBNpsNd+7coQBEUnb5cnhEtHfvHMrLafEvUV5kEEohKZikwYpB6P3334der4fD4YDZbMbw8DBO\nnz6djb6RdWZ6msGdO0Xy/VdfpVEQUYfIIJTgchXJkBUXq4a2WTh58iSOHj0Kj8cTVRQ0kcOHD6en\nh2TduHGjGIHv/ta3bVvEli3qrKxMNh6DIfxeHB9XsCMb0LJBKHKfH7vdDrvdnlSjDMMgEKAPGBIm\nisC1a8Xy/Zdfjp+iS4gSWDYgV4fxeoHFRahy/6P1aNlf87lz51bVaKqlfsj6d/9+ASYnpdnf4mIR\ntbWUlk3Uo6AAKC+XykaJojQa2rpV4U5tEMsGoWxVPnC73XC5XDAYDOB5HkajMaWkB4fDAb1eH/ec\ntbZN0iNyFHTgwHP6lklUR6udl7dyGBujIJQtin8UhPYPunDhgnystbUVHMclVXnB6XTi5MmTcsmg\ndLZN0mNmRgOeDy9WffFFGgUR9dHp5vH0qXSbkhOyR/FiKTabDW1tbVHHLBYL2tvblz3P4/Ggra0N\nHo8HBoMhrW2T9Lp5swTBoHR7+/aFqIvAhKgFy4YXTVMQyh7Fg1BPTw+MRmPUMZPJFHdkE6mmpgYf\nfPDBsqWCVts2Sa/bt8NTcTQKImql01EQUoKiQUgQBAiCEDOSCe2kOTIyosq2SfIEoQher1QhoaBA\nBMdRECLqpNXOy4VLQxlyJPMUDUJerxcAEhYsjEwRV1PbJHl3726Sb+/ZM4+IOqaEqEp+vgitVpo3\nDgalQEQyT/GRUC62TZIjisC9e+EgtG8fFSol6hZ5vZKm5LJD8WtCasMwTNwfkrqHD4HpaWnoU1Qk\nYtcuCkJE3SKDUChTjmQWBSGSMVeuhG/X1s7T2iCiehUVQfk2BaHsUDQIcRwHAJicnFz28Wy2LYpi\n3B+SmmAQuHYtfH/fPkpIIOpXWRkeCYX2FyKZpWgQYlkWHMfFJAnwPA+WZbFnzx5Vtk1WNjICTE9L\nt0tLA6iuXlC0P4Qkw2AIyFvNe72QKyiQzFF8Os5sNmNgYCDqmNvtRnNzs6rbJsuLnIrjuOfyHzYh\napafD1RVhe/TaCjzFP9osNls6OnpiTpmt9ths9nk+4IgoLa2Fl1dXQnbiTdllkzbJP0WF4Hr18P3\n9+6litkkd2zZEr795Ily/dgoFL9UrNPpYLPZYLVa0djYKNd7Wzpd5vP5orLU/H4/zp49C57nwfM8\nLBYLzGYzmpub0dLSklLbJL3u3AGefxd3ysvnsXlzACp4qxGSlK1bgW++kW7TSCjzGJGuuiclFADp\n17Wynp5wUkJe3l/xs5+VoqSkZPmTCFHY8PAwDh48CFGswW9/Kx2rrgaWqQxG0kDx6TiyvszNATdv\nhu/v3h0/O5EQtYrcwmF0FHLxXZIZFIRIWt28Ga65tWVLdGViQnJBaSkQqva1uAhMTCjbn/WOghBJ\nq8isuJdeUq4fhKwFJSdkDwUhkjYzM8DwcPg+BSGSq5ZOyZHMoSBE0ubbb8Pz5zt3Anq9sv0hZLUi\ng9CjR8r1YyOgIETShqbiyHpRXR2+/fChVBGeZAYFIZIWfj9w9650m2GAF19Utj+ErIVOB5SVSbfn\n5oDxcWX7s55RECJpcfVq+DbHAeXlyvWFkLViGGDHjvD9hw+V68t6R0GIpEVohTkAvPyycv0gJF0i\np+QePFCuH+sdBSGyZqOj4QyiggLg4EFl+0NIOiy9LkQyg4IQWbPIUdD+/UBRkXJ9ISRdIoPQ6Ciw\nQLuRZAQFIbImwWB0VtwrryjXF0LSqbgYqKyUbgeDlKqdKVTamKzJ4OAYbt2SdqMsKQlienoMly+H\nH5+jXcFIDnnw4EHUbswLC1o8eSIV3/3oo2f45S93oaCgQKnurUuqCEJutxsulwsGgwE8z8NoNKKp\nqWnN54W2eLBarTCZTPB6vbDb7Whubk6qfbKyjz/2QRCCKCwsxO7dk/D5ogttVVRUoLi4WKHeEZK8\nLVu2QBAEjEfkY5eWPsfMjLTL3cDAGP7xHyvAsqxSXVyXFA9CoT1+Lly4IB9rbW0Fx3GoqalZ83n9\n/f3o7+8HIG35/eGHH1IASpPZWWB4uAQlJUGUlZXhBz8QsWULbdlAclN5eTnKl6wt0Go1uHJFqmbq\n880iEFCiZ+ub4teEbDYb2traoo5ZLBa0t7ev+TyGYeB0OiEIAnieh9frxZEjR9LX+Q3um2+AQEDa\nZ6mqahGbNy8q3CNC0kurDUKrlWpRLS5q8OQJs8IZJFWKB6Genh4YjcaoYyaTCQ6HIy3niaIIrVZL\nu6mmmSgCLlf4/osvPgdDf59kHaquDqfF3bun+EfmuqPob1QQBAiCAIPBEHU8NOc6MjKS1vNI+ty/\nDzx9Kt3Ozw9i/37aN4isTxSEMkvRa0JerxcAoA3tILUEz/NxRzCpnMfzPARBkM8zGAxoaWlZY8/J\nwED4Nsc9Q2EhZQyR9SkyCD14oMHiIpCv+NX09UPRX2UoOGTqvNBIKTLotLa2xhwjqREE4Nq18P0D\nB6YB0L4NZH3SaoPQ6QIYGwMWFhjcuyfVRyTpsa7HljqdDidOnIg6tlLSA8MwcX9I2BdfhPcNqq6e\nQ0UFTcWR9W3PnvBo6NYtBTuyDq3rIBRPTU0NeJ6PWpBGkjczA7jd4fuvvDKlXGcIyZI9e8JftG7e\npP2F0knRIMR9N6ZNFBC4BGPeZM/r6OiIeSw0RcfzfNxzRVGM+0Mkf/lLuIbW1q3SSIiQ9W779gXk\n50vDf58PmJhY4QSSNEWDEMuy4DguJiDwPA+WZROmVSdzXmgx69JMuVBSQ6IARxLz+4Gvvw7ff+MN\nUFo22RDy84GtW6fl+zQllz6KT8eZzWYMRKZaQSrH09zcvKbzOI5DZ2dnTCBzOp0wmUwJM+tIYh99\nBCx+tx61upq2bCAby7Zt4SD07bcKdmSdUTwI2Ww29PT0RB2z2+2w2WzyfUEQUFtbi66urpTOMxgM\n8Hg8Ue3Y7faodkhy7t0DLl0K3zebaRRENpbq6mloNNLU/IMH0rQcWTvFs911Oh1sNhusVisaGxvl\nabSlIxifzxeVpZbMeS0tLejt7YXD4cDExAQEQYDD4aDqCSlaXAT+/d/D9/ftA5Yp60fIulRUFEBN\nTVDe4O7qVeBv/1bZPq0HjEhX3ZMSCoAb8dd18SLw6afS7cJC4J//GdDppPtfffUV5ubmsGXLFuU6\nSEgWXLt2DVu2mNHXJ03lV1UB/+W/0IzAWik+HUfUbXgY+Oyz8P2mpnAAImSj2bs3iNB2QmNjtO13\nOlAQIgn5/cDvfx9eE8FxQGOjsn0iREmFhcBLL4XvDw4q15f1QvFrQkSdZmeB//2/Aa93Dj6fD6Wl\nQezdO4ErV4JRz/N6vSgrK1Ool4RkX0MDMDQk3b56FXjrLaCEttFaNQpCJMbcHPCv/ypNN8zMzMDn\nG8cbb/gxM/McMzPRzy0sLIReT3XjyMZRXQ1s3w48eiQl7QwMSGvmyOpQECJRQiOgyLnuN9/0wWTa\nrFynCFGZ730P+MMfpNtffgl8//vSVB1JHV0TIjJBAP7n/1wagGaxZ8904pMI2YBeegn4bvsyzMxE\nb/BIUkNBiAAA7t4F7PbwRnUA8NOfAocOUW04QpbKywN+8IPw/c8+k2YRSOooCG1wogh8/jnw299C\nvt6TlwccOSJdgCWExFdfHz0a+uQTZfuTq+iaUA4YHx/Hw2UWJGg0Ghw4cAAFBfF3N71+/Trm52P3\n/Jme1uDjj3W4fz88mV1SEsRbbwkQxQVcvgz4/f4NuUCXkKVEUcTNmzdRXFwsH9u1qwg3bkiR6I9/\nzIPRWIXNdPk0JRSEcsCDBw8wPDwMNvS1a4mxsTHs2rULujirSEVRhNvtxtatW+VjgQBw44YOly+z\nWFhYBCBVJa2snMOPfvQUBQWLGB8Pt0HVEAgBqqurMT09jenp8DVSrRbYtCmI0dFiTE9P4w9/qMLx\n49JsAkkOBaEcwbIsduzYEfcxv9+/7LkMw2DHjh0IBoHbt4swMFACny8PJSXS+gaGAUymWbz22gLy\n8rYu2xYhG5Ver4+7HOE//sc8dHdrMT09jcePgY8/liqLkORQEFrnAgFgYqIEf/1rKW7eLML0dPRl\nQIMhgDffnEZ19aJCPSQkt1VUBPD6689w/750/7PPgG3bgBdeULZfuYKCUI4RRelajs+Xh5kZDWZm\nGNy6VYVgMB95edJC08gfvx8YGqrDtm3RS7qLikQ0NMzi1VdnaeqAkDU6dOg5Pv44PE33hz9IU3UJ\nJi9IBFUEIbfbDZfLBYPBAJ7nYTQa0ZTEeDaZ81bbtprMzGhw+/YmXL68CY8fF2B2Nrps79hYJWZn\n8xBxvVS2NKegtDSIl156jkOHnqOoiBIOCEkHhgFee+0enj37G0xMAAsLwP/6X8CvfgXs3Kl079RN\n8SAU2gfowoUL8rHW1lZwHIeaZTatSea81batBsGgVMF6cBD49NMqPHs2C602/pJsURQxMTGBvARD\nmtLSORw4MIfa2jns3r1AIx9CMqCoKIBf/AL4l3+RUrbn5qRAdOQIcOCA0r1TL8WDkM1mQ1tbW9Qx\ni8WC9vZ2nD9/fk3nrbZtJU1PS8URXS6pggEAiGL0yKeoSERFxSLKy4MoLQ1ifl5EIPAIBQVBFBYG\nv/uv+N1/A9Bq87BlC1U9ICTTKiqAf/onad3ds2fA/Dzwb/8G/PCHwJtvAvmKf+Kqj+Kb2hkMBrjd\n7qjdTgVBgMFgQDAYXNN5q207nkxuaieKgMcjjXpu3JBGQZGePHmCTZu8MJnKsHv3AvT6AG2kRYjK\nDA4O4pe//CUAqfjv734X/iIJAJWVwN/9HbB3L22EF0nRuCwIghwUIoXWw4yMjMTdijuZ81iWXVXb\n2SKKwOPHwPXrwLVrgNcb+5ySEmlVdmHhGAKBpwlTtAkh6lJVBZw8CfT2StPqADA+LlWn374deO01\n4OBBoKhI2X6qgaJByPvdJ69Wq437OM/zcQNFKuel2nYmBIPA5CQwMSF9Q7p3T/qZTjBDtmuXVDLn\nhRek4fulSwFMTGSlq4SQNCktlRITBgcBp1O6RgRIW0D8n/8D/PGP0t96TY2U0l1RIe1avNFGSYqP\nhDJ13mrbXsm//7s0igkGE/83GASeP5cKGob+Gwgs325REfDqq1LwobIfhKwPDCPtRnzggFSjcXBQ\n2oMIkDLohofDIyVAqrRQVibNgpSWAgUF0jGNRvpvXl50kIoXsJI9lk3/4T8kfowuky3BrPCv9fOf\nb7CvKYSQpP3qV79SuguqtNy1dKqiTQghRDGKjoQ4jgMATE5Oxr12E3p8NeeFEhBSbTubyYKZzLhL\nJ+pnelE/0ysX+pkLfQSU6aeiIyGWZcFxHHiejzrO8zxYlk2YOJDMeattmxBCSPYoPh1nNpsxMDAQ\ndcztdqO5uXnN5622bUIIIVkiKkwQBLG5uTnqWHNzs+jxeOT7Pp9P5DhOtNvtKZ2XzHOUBEBUwT/B\niqif6UX9TK9c6Gcu9FEUlemn4hUTAGBoaAjd3d1obGwEz/MwmUw4fPiw/LggCOA4Dh0dHTh+/HjS\n5yX7HKXQPHF6UT/Ti/qZPrnQR0CZfqoiCG1U9MZML+pnelE/0ycX+ghQECKEELLBKJ6YQAghZOOi\nIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohiqok0IieJ2u+FyuWAwGMDzPIxGI5qampTuVlwOhwN6\nvV61/QOA3t5e8DyP4eFh8DwPi8WClpYWpbsVw+l0wul0oqKiAsPDwzCZTDhx4kTGX5eCkIoJggCr\n1YoPPvhA6a7EUOoNm6pc+QAIUfpDled5WK1WXLhwQT7W2toKjuNQU1OjSJ8ScTqdOHnyJBwOh9Jd\nSai3txccx8nvOb/fD5PJBK/Xq6q/F6fTCYZhcO7cOflYQ0MDBEHA6dOnM/vi2SzPQFJz8uRJ8ejR\no0p3I0ZfX5/odDqjjplMJrGjo0OhHsXncDhEt9st3xcEQaytrY0q/6QmfX19ol6vF/v7+xXrw8mT\nJ0wl0CUAAAg5SURBVMXe3t6oY06nU1XvQ57nRYvFItrtdrG2tlbR39dK4v1N2O12kWEYBXqT2Ntv\nvx3zN93e3i7W1tZm/LXpmpBK8TwPn8+34iZ7Sujs7Iw5Zjab4x5XEs/zqK+vl+/rdDq0t7fDYrEo\n2KtYHo8HbW1t8Hg8MBgMivalp6cHRqMx6pjJZFLVaKOmpgYffPCBqkYS8QiCgO7ubvj9/qjjoVHu\nyMiIAr2Kj2EYOJ3OqGOiKEKv12f8tSkIqVR/fz+am5tVWeZDyTdssnLpA0AtH6qCIEAQhJhAGNqb\nS02/s1zAsix4nofH41G6Kys6f/48zp49G3XM4XDg2LFjGX9tuiakQv39/TCbzTEf9Gpx/vz5mGMO\nhwPvvvuuAr2JL/ID4NChQ0p3Jyd4vV4AiLsJJCCNLGkfrtSEfqeRnE4n9Hq9qn+XdrsdDQ0NOHXq\nVMZfi4KQCvE8j6amJlWOguLJ5hs2Fbn6AaAUQRCU7sKG0NnZiffee0/pbsTV29uLvr4+MAyD7u7u\nrLwmBSGV6e3tVXxaJllKvGHXSs0fAGT9s9vtqKysVN0XtpCWlha0tLTA7/ejoaEBXV1dUddVM4GC\nkIrk2jdRJd6wa6H2DwCyvvE8D7vdjsHBQaW7siKdTgeLxYKmpqa4MwrpREEoA3ieT/q5FRUV0Ol0\nAKTMpMhRUKYz41bbz6Uy/YZNRz+z8QGQrt+nUjiOAwBMTk7GvS4UepysjtVqxcWLF5XuRtKampog\nCAL6+/szum6NglCaeTweWK3WpJ//2muv4dSpU3C73WhoaIh6LJPXhFLtZ2Nj47KL1jL1hk1XPzP9\nAZDu36cSWJYFx3HgeT4qmYPnebAsS9fR1qCtrQ0dHR0Jkz6UFNpx+qOPPoqbxLM0wzTdKAilWU1N\nTdzssZW4XC4MDw9HXVtxu93yCvbGxsa0rvRfbT+z/YZdbT8jZeMDIB39VAOz2YyBgYGof1u3243m\n5mYFe5Xburq6YLVao4J4f3+/aqpQCIKA2tramJFuaGS/dN1YulEQUol4yQjvv/8+BgcHo0ppKE3p\nN2yq1P4BoDY2mw1Hjx6Nej/a7XbY7XYFe7U8NWeRhhb5er1eeara6/XC4XCophyX0WjEsWPHYn6P\nNpsN7e3tGR8BUxBSsfHxcdX9gSn9hk1FLnwAxKPkv7lOp4PNZpNH36GRuJr+Xf1+P86ePQue5+V6\ngGazGc3NzaqqCygIAlpbW+M+Vltbm+XeLO/06dPo6urC8PCwXA/y2LFjOH78eMZfmxHV9ilH4PF4\nYLPZcP78efj9fpw4cQIWi0VVmWdL37ANDQ1ZecMmK97K/5Da2lrcvn07yz1KLPJD1eFwgOM4VX6o\nEpIJFIQIIYQohmrHEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohgKQoQQQhRD\nQYiQLHC73dBoNDFFapdyOp3QaDQJV9oncvToUWg09OdMcg+9awnJAqPRCJZlMTQ0tGyR156eHgDA\nO++8k/JrZHrrD0IygYIQIVly8uRJiKK4bLXt8+fPg2EYHDlyJIs9I0Q5FIQIyZJjx44BkLYYj8ft\ndsPv9+Ptt9/OZrcIURQFIUKypL6+HhzHJZySC+0lFQpWgLRFxtGjR1FbWwuNRgODwYDW1lZ4PJ6Y\n8yPLQDY3N8e9RiQIAjQaDdra2mIe6+jogMlkkl+nra0t7usQkk4UhAjJIovFknBKzm63R03F8TyP\nuro6/P73v0ddXR0sFgsaGhrgcDhgMplW3EBwuWtESx8zmUywWq3QaDTy69jtdtTW1mJoaGgV/6eE\nJIeCECFZFJpqWzolF28qzmazgWEY9PX14c9//jN+85vf4MKFC7DZbBAEAU6nMy196ujowNDQEPr7\n+zEwMCC/jsvlAhB/w0VC0oWCECFZVFNTg/r6+pgpuXhTcW1tbejp6cHhw4ej2gjtK+Xz+dLSp7Nn\nz6K5uRlGoxGCIMg/NTU1aGpqgtvtxuTkZFpei5ClaGdVQrLsnXfewdDQEOx2O06fPg1A2gV2aVZc\nfX29HHAEQcDg4CDcbnfCxIbV8vv96Ovrg16vj/s4wzDwer3QarVpfV1CAApChGTdyZMn0d7eju7u\nbpw+fRo8z8Pj8eDo0aNRzxMEAe3t7fIOu4B07cZkMqUtYYDneQBSIkN7e3vC5yUKUISsFQUhQrJM\np9PBaDTKU3IOhwOAlLQQqampCUNDQ7BYLLBYLDh06BAAoL+/Xz4nVV6vN+p+aAt0lmVjpv0IyQa6\nJkSIAkJZcna7Hd3d3WAYJioICIKAoaEhHD16FL/5zW/kAAREp2Knyu12R91nWRY6nS5hkoNer0dd\nXd2qX4+QlVAQIkQBodpwnZ2dGBoaSrhAdWnyQWiKDogNRpFp1yzLQhRF9Pf3xz03ksVigc/ni6lX\n19HRAb/fH3dNESHpQtNxhChAp9PBbDbLI5ClU3Esy8qPt7a2oqGhAcPDw+jp6UFjYyMAKYWb4zg0\nNTUBiA5K77zzDnp7e9Hc3CyXCwqduzSwnTt3Dg6HAw6HA3V1daivrwfP8xgaGoLJZMKpU6cy+asg\nG51ICFGEw+EQGYYRNRpN3McFQRAtFouo1+tFhmHEhoYGsbe3VxRFUbRYLKJGoxHb2tpEURTFo0eP\nxrRjt9vF2tpakWEY0WAwiFarVRRFUdTr9fJ5kdrb20WTySQyDCPW1dXJzyckkxhRXMMEMyGEELIG\ndE2IEEKIYigIEUIIUQwFIUIIIYqhIEQIIUQxFIQIIYQohoIQIYQQxVAQIoQQohgKQoQQQhRDQYgQ\nQohi/n9FsuBR8keiKwAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60dec068d0>"
]
}
],
"prompt_number": 66
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Fitting\n",
"Adapted from Saullo Castro, StackOverflow"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"What is the best fit to our distribution? \n",
"\n",
"For discrete distributions you can use ChiSquare (Observed and Expected) to see which one fits better. For continuous distribution you can take intervals and use ChiSquare (below)."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"size = 30000\n",
"x = np.linspace(0,15,size)\n",
"y = [np.random.lognormal(1,0.8) for _ in range(size)]\n",
"h = plt.hist(y, bins=np.linspace(0,15,50),normed=1,fc='gray', histtype='stepfilled', alpha=0.3)\n",
"plt.figure(1)\n",
"ax = plt.subplot(1,1,1)\n",
"dist_names = ['beta','rayleigh', 'norm','lognorm','expon']\n",
"\n",
"\n",
"for dist_name in dist_names:\n",
" t = []\n",
" dist = getattr(scipy.stats, dist_name)\n",
" param = dist.fit(y)\n",
" pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1])\n",
" ax.plot(x, pdf_fitted, label=dist_name,linewidth=3)\n",
" \n",
" init = h[1][0]\n",
" for value in h[1][1:]:\n",
" t.append(np.mean(pdf_fitted[(x>=init) & (x < value)]))\n",
" init = value\n",
"\n",
" \n",
" print(dist_name+\" Chi stat = \", scipy.stats.chisquare(f_obs = size*np.asarray(h[0]), f_exp = size*np.asarray(t)))\n",
" print(dist_name+\" p-val KS = \", scipy.stats.kstest(y,dist_name,args=tuple(param))[1])\n",
" scipy.stats.probplot(y, dist=dist_name,sparams=tuple(param), plot=None)\n",
" \n",
"\n",
"ax.set_xlabel('Value',fontsize=20)\n",
"ax.set_ylabel('Norm Freq',fontsize=20)\n",
"plt.xlim((0,15))\n",
"\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.legend(loc='upper right',fontsize=16,frameon=False)\n",
"plt.show()\n",
"\n",
"fig = plt.figure(2)\n",
"\n",
"i = 1\n",
"for dist_name in dist_names:\n",
" i += 1\n",
" t = []\n",
" dist = getattr(scipy.stats, dist_name)\n",
" param = dist.fit(y)\n",
" (osm, osr),(slope, intercept, r) = scipy.stats.probplot(y, dist=dist_name,sparams=tuple(param), plot=None)\n",
" plt.figure(i)\n",
" ax = plt.subplot(1,1,1)\n",
" ax.plot(osm, osr, 'o', osm, slope*osm + intercept)\n",
" ax.set_xlabel('Quantiles',fontsize=20)\n",
" ax.set_ylabel('Quantiles Obs',fontsize=20)\n",
" customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
" plt.legend([dist_name])\n",
"\n",
" plt.show()\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('beta Chi stat = ', (3859.8620361298576, 0.0))\n",
"('beta p-val KS = ', 1.6315016931288011e-47)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"('rayleigh Chi stat = ', (30796.145832321308, 0.0))"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"('rayleigh p-val KS = ', 0.0)\n",
"('norm Chi stat = ', (52091.666972563071, 0.0))\n",
"('norm p-val KS = ', 0.0)\n",
"('lognorm Chi stat = ', (178.17135553030289, 7.4331840876546572e-17))"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"('lognorm p-val KS = ', 0.98944659461564122)\n",
"('expon Chi stat = ', (13627.328442541573, 0.0))"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"('expon p-val KS = ', 5.139587050053985e-318)\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAaEAAAEsCAYAAABqhgzEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4W8W5/z9H8r5psbMnJJZF2coS20lbCjRN5EAptIXE\nDgVKgSaW6S0tF5LYob23pffXxnYoSykQy7nQ0hYwlqHLU0piORRK0wvEStghsSVnX21J3led3x+K\njqx4lS1bTjKf59ETz+jMO6Ml+p6Zeed9JVmWZQQCgUAgiACqSA9AIBAIBOcuQoQEAoFAEDGECAkE\nAoEgYggREggEAkHEECIkEAgEgoghREggEAgEESMq0gMAsNvt1NbWotfrcTgcZGZmsmzZshHb2Ww2\nbDYbqamp1NfXk5WVxZo1a8JiWyAQCAQTT8RFyOFwUFRUxLZt25S6vLw8DAYD6enpQ7az2WxIkkRx\ncbFSl52djdvtZt26deOyLRAIBILJIeLLcSUlJRQUFATVmc1mCgsLh21XVlY2oM5kMgXVj9W2QCAQ\nCCaHiItQZWUlmZmZQXVZWVlYrdZh20mShM1mC6qTZRmdTjdu2wKBQCCYHKRIhu1xu93o9Xrcbjcp\nKSlBz6lUKhwOBwsWLBi1vYyMDO655x7Wrl0bdtsCgUAgCD8RnQk1NTUBDBAJPw6HY9S2LBYL2dnZ\nrF27Nuy2BQKBQDAxRNQxwe12j9tGVVUV1dXVSJJERUVFWG0LBAKBYGKJuHfceFmxYgUrVqzA4/GQ\nnZ1NeXk5CxcujPSwBAKBQDAKIu6YEC40Gg1ms3ncZ4AkSRryIRAIBILwElERMhgMADQ3Nw/7/GhZ\ntmwZbreb7du3h902IIRIIBAIwkxERUir1WIwGAY4CTgcDrRa7ZDeaw6HA51Ox+7duwd93u12j9m2\nLMuDPgQCgUAQfiK+HGcymXj33XeD6ux2Ozk5OUO2cbvdZGRkDJjN+AXHfzZoLLYFAoFAMInIEcbt\ndss5OTlBdTk5ObLT6VTKLpdLNhgMssViUepKS0tlt9sd1M5kMslFRUUh2R4tgDwF3i6BQCA4q4jo\nYVU/u3btoqKigkWLFuFwOMjKymLp0qXK8263G4PBQGlpKatXr1bqy8vLqa+vVwKYZmdnBz0/Gtuj\nxb8fNAXeLoFAIDhrmBIidCYgREggEAjCT8T3hAQCgUBw7iJESCAQCAQRQ4iQQCAQCCKGECGBQCAQ\nRAwhQgKBQCCIGEKEBAKBQBAxhAgJBAKBIGIIERIIBAJBxBAiJBAIBOPE4XCgUqloaGgYty2r1UpV\nVdX4B3WGcMYntRMIBIKziYqKCiRJYsWKFZEeyqQgZkIh4vV28emnd/Pee9fR2Xkg0sMRCASCMxoh\nQiHS1LSNo0efxeXayq5dV0d6OAKBYApRX19Pbm4uer0eo9HIpk2bBlxjsVjIyspCpVJhNBqDlt6y\nsrKoqqrCarWiVquVerPZTEZGhtJmMLtnKkKEQqSt7UPl766ufXR2HozgaAQCwVQiNzcXlUrFli1b\nMJlMFBYWUlRUpDxfWlpKQUEBy5cvx2q1kpmZSW5uriJE27dvx2QykZOTQ319vWKzsrKSe+65B6vV\nqtg9W/aNxJ5QiMTEzAoqHzmyhfT0n0VmMALBOYD0kDThfcg/DU90/JycHCoqKgC4+eabAZ/wFBcX\nA7Bx40YKCwvZuHGjck1eXh6FhYWsWLECjUaDRqNBkiQl+7PH42HLli2KvZtvvhmbzYbT6QzLmCON\nmAmNkyNHyvF6eyM9DIFAMAUwm82Dlnfv3o3dbsfj8ZCfnx90TV5eHg6Hg+bmZqXOnzoGYNu2bYoA\nORwOLBYLDoeDxsbGiXoZk4qYCY2T7u7DNDX9jbS0b0Z6KAKBIMLo9fqgcnp6OgBNTU00NTUBkJGR\nMaCdJEk0NTWRkpICBOcts9vtrFmzhl27dmEwGMjMzESr1U7US5h0hAiFgcOHNwsREggmiHAtlU0G\np89OHA4HAAaDQREOu90eJCJ+wfEvv0FgJuR2u8nOzsZsNlNVVaVcYzQaJ+olTDpiOS4MNDVtpaPD\nEelhCASCCFNWVjagrNPpWLBgAQaDAfB50C1YsEB5bN68mcLCwqB2fmHauXMnACUlJUEidbYsxYEQ\noTAhc+RIeaQHIRAIIkxNTQ15eXlYrVZyc3MpLy+npKQEAK1Wy/r168nNzaWoqAir1YrZbGbTpk0s\nX75csSFJEna7nZqaGhYtWgTA6tWrsdlsWK1WMjIy8Hg81NbW4vF4IvI6w4osGBWADMiHDz8rv/46\n8uuvI//znzrl77femi739XVFepgCgSAC1NfXyyqVSnY6nXJOTo6s0+lko9Eol5eXD7i2tLRUzsjI\nkCVJGvQam80mZ2RkyCqVSpZlWbZarcr12dnZck1NjWyxWGSdTidv2rRpUl7fRCLJsnzmLLhGEP8a\n7eHDz/LZZ3cBMH36bbjd/6C7+xAAF19cwfTpeREbo0AgEJxpiOW4cSBJUcyevUYpHz68OYKjEQgE\ngjMPIULjZNas1YAvvIbb/TptbZ9EdkACgUBwBjElRMhut1NeXk5VVRWbNm2ipqZmVO381/vDYJwe\nxsLhcJCTk0NNTQ1utxuHw0FRUdGo7Y+G2Ng5pKXdqJQPHfpN2GwLBALB2U7Ezwn5hWHbtm1KXV5e\nHgaDQTnoNRhVVVUYDAYl3LnH4yErK4umpibWrAkskdXU1Ciio9Vq2bJlC8uWLQvra5gz54ecPPkn\nAI4e/R0Gwy+JitKEtQ+BQCA4G4n4TKikpISCgoKgOrPZPMBv/nQcDgcLFy5UyhqNhsLCwqCwGZIk\nYbPZlFlQU1OTEv4inGi1S0hM/DwAXm8bR448G/Y+BAKB4Gwk4iJUWVlJZmZmUF1WVhZWq3XINm63\nm4qKigE+8v4ZTv/shrIsk5KSEnTQK9xIksScOfcq5UOHnkCW+yasP7fbzdGjRwd9+EODCAQCwZlA\nRJfj3G43brd7QLwlf0iLhoaGQcVDq9XicDhwOp1cccUVkzHUEZkx4zYcjiJ6e110djpobPw7aWk3\njNnevn37OHr0qFKWT8rIx2TQwb7Ofaij1MTGxga1kWWZ7u5ucnNzx9yvQCAQTCYRFSH/Xbs/aN/p\nOByOIWcwg93x22w2JURGfxtut1tpo9frJyRtrlqdyKxZ3+PAgYcB32xoPCJ04MABPB4PSfuSkDfL\n8EHguZnnzUTzfQ3x34hHUgWi7Xq9Xt5///0x9ykQCASTTcRnQuGkrKyMDRs2KGX/DKu/6OTl5Q2o\nCxezZ/8HBw48AnhxubbR1vYJiYkXjdleyo4U+kr74PRMEfvBU+Sh8++daDdpUaVEfFVVIBAIxsRZ\n8+tlsVhIS0tj7dq1Sp1GownylIORnR4kSRr0MRri4xeQlvYNpTwed23vDi99xf0EKBqiLopCSgiM\npeuNLhrvbMTr9o65H4FAMDXR6XSUl4cWk9Kf1TXUfiKZLvysECF/oqetW7eOeG16evqABFLhpL+D\nwtGjv6O3N/QAg90nuvH+0guntCXqwiim/X0a016ZxvQ3p5P43UTl2t6Pe2kyNyF3iehLAsHZRCg3\nwH5ycnKUaN0T2U84iagI+d+soQRhtG9mUVER27dvH1BfWlo6oM6/ROfP83E6siwP+hgtWu1XSUi4\nBPC7az8z6rZ+6h+oh1PapZqpQr9FT9Rc38qpKklFyoYUNL/QwKnvTc97PXj+2xPSOAUCwdnH1q1b\nWbp0aaSHERIRFSGtVovBYBggCA6HA61WOyq36oKCAkpLSwc4N/gPwfZ314aAQ0OodwujRZIk5s79\noVI+ePDxkNJ/t33cxrE/HFPKmv/RoE5TD7guYUUCKRsCr7njzx10vtw5xlELBILxoNPpqKqqorCw\nEJVKpdxYm81mMjIyUKlUGI1GZdmrsLBwgFcwjLycZrFYyMrKUuydHiVGpVINWMIzm83o9Xql/9LS\nUrKzs4OukWWZwsJCZaz+vfPJIOLLcSaTiXfffTeozm63k5OTM2Lb8vJyioqKgsSqpqYGp9OJwWCg\nrKxsgJDZbDaysrKG9MgLBzNm3E50dBoAXV37OHmyaoQWAfb9Yp8vaQQgXSkRd3XckNcmfCeB+JXx\nSrllYwvqYwMFSyAQTCySJFFWVqYIUUpKCrm5uVRWVnLPPfdgtVoxmUwUFhZSVVXFLbfcgtvtxul0\nKjb8ZyOHEoDS0lIlRJnVaiUzM5Pc3NwBQtR/ac2f0+jBBx+kpKSEiooKiouLg66RZZmNGzfS0NBA\neXk569evx2q1UlRUFM63aEgiHranpKSE3NzcIAcCi8WCxWJRym63m6ysLIqKipTr/B9Y/9ztTU1N\nWK1WNm/2RbPW6/U4nU4l/I/b7cZisYS8cRcqanUCs2f/B/v2PQTAgQO/Ytq0vBHXXbsOdXH8xeNK\nWXXX8PcIkiSh+bGG7tpu+px9yO0yKZtTkO+VI7rGKxCca8iyTG1tLU6nU7nB9Xg8bNmyRYnScvPN\nN2Oz2XA6naxYsQKtVovVamXdunUAVFRUDHuDvHHjRgoLC9m4caNiLy8vj8LCwkG9fR0OB1VVVVit\nVmUMJpMJnU434NrU1FQqKioAWLp0KQ6HA7vdPs53ZXREXIQ0Gg0lJSUUFRWxaNEiZRnt9BmMy+UK\nyrs+1N1CRkaG8veKFSuUD6GxsRG3243Vap3Q6Al+5sz5Pvv3FyPLXbS0vIvH80+02muGbXP0d0cV\nZwRpoYTqopEnqlK8hLZUS+MtjdAHMZ/EcOyPx5h5+8xwvAyBIPJMxg3VOPdTJUkiLy8vSED6x8N0\nOBzYbDYcDoeSmttkMlFRUaGIUFVVVdDNd3/sdjsej4f8/Pygen8W1+bm5gHiZbPZAIJClWk0Gkwm\nEy6XK2jsK1euDGqr0+nCfoRmKCIuQgALFy4MigN3OlqtNuhwqlarxesdnVvyRJwHGg0xMdOZOfO7\nHDni+1IdOPDwsCIke2WO/O8RpSzdOPr/eDGXxpB4ZyJt/9sGQP3aetJuTCNKMyU+XoHgnKD/DTD4\nhGPNmjXs2rULg8FAZmamEg0GYNWqVeTm5tLc3Mw777wDDL0U5983P70P8IlIU1PTABGqr68P6s9P\nenr6gMP+qampo3iFE0PE94TOZubNu1/5u7Hxr7S1fTrktc1vN9Pp8DkWROmikK4J7e4v6Z4kVDN8\nH2fPsR4aftYQ+oAFAkFYcLvdZGdns3jxYhwOB3V1dbz00ktBzgj+G+Tq6moqKyuHXYrzO1LZ7XYc\nDofyqK+vp66ubtDVnYyMjEFnMw6HY0ot1wsRmkASEi4gNTVwePXgwUeGvPbkKyeVv9NuTkOKDe1L\nokpSkbw+WSkfevIQHY6OkGwIBFMSWZ74R5jZuXMn4Nvz7i8Q/qU4PyaTiRdffJHKysqgDACn4xeh\n+vp6FixYoDw2b9485OF7vwdc//xpbrc7rPnUwoEQoQlm3rxABIejR5+ju/vYgGtkWQ4SoWk3TRtT\nX7HXxdJ9QbfPZo+M87+cI7QQCATh4PQzeosWLQJg9erV2Gw2rFYrGRkZeDweamtrlQwAfu82j8cz\nrFu0Vqtl/fr15ObmUlRUhNVqxWw2s2nTJpYvXz5om8zMTEwmEzk5OWzatAmLxYLJZBpwPCXS5wuF\nCE0wGs1VJCcvBkCWuzh06KkB17R/3E5HnW/Wok5So102cB13NEiSROutrUr5+PPHadndMiZbAoFg\n9Jy+vKXRaKisrMRut7N8+XJKSkooLy+nrKyMnTt3Kmd5/MKTmZk54rGR4uJiSkpKsFqt5OXlsX37\ndiwWC6tXrx6yzbZt28jPz2fjxo1s2rSJBx98EJPJFLQsONjS3GRGUZDkSMvgGYL/Azl8+Fk+++wu\nAGbM+C4XXfTbEdseP17Jxx/7vmxRUal86Uv7UKsDoXf2P7wfxzrfxuO0ldO4pPIS3nrrLSRJIi0t\nbdRj9EfRvvj5i2n8i2/ar79Oz2V/v2zUNgQCweSiUqlGFJOx4nA4Bsx8cnJyMBqNPP3002HvbyyI\nmdAkkJZ2E3FxvrNKvb2NHD4cfKLZvT2weai/buAp6lCQZZnEHyUqn2zTa03U/aWOQ4cOTZrLpUAg\nGB1+N+qJiFDgdrsxGo3s2rUrqH7nzp2DetlFCiFCk4BKFcW8eeuU8oEDm/B6u+jq6uL44eO43wiI\ng/dyLydOnKCrq2sM/ahITk7mo7aP6PlKj1Lf8PMG3nnnnQGRKQQCQWTweDxYLBbMZjM5OTkTEsFF\nq9ViMpnIzc2lpqYGm81GTk4Ozc3NA84bRRIhQpPEzJl3ERPjO0Da3X2Yo0efw+Fw8Gb5m3jbfWee\nvNO97Dy0kx07dtDc3Ex8fPxwJgfFaDTyuc99jtnrZisBTqNqo5jdMpu+volLOS4QCEaPLMsUFRVh\nNBopKyubsH4qKyuV8D55eXmoVCrq6+snNGxZqIjTjJOEWh3H3LkP4HD4ZkT79xeTkvIntM6AE0Li\nVYnMuXBOWPqLMkQR97U4Ol/1nT3qfqYbJicUlEAgGIHTD+BPFBqNhpdeemnC+xkPYiY0icyeXUBU\nlC9uU2eng87O11B9GPgIYr4QE9b+kgqSlL/73uhDckydA2oCgUAAQoQmlaioJObO/ZFSbmuzIO0J\nOCfGLAyvCEV/Lpq4nEAU7qgXxcRXIBBMLYQITTJz5tyLWu2bofT11SFd9m8AJK2Eel740zAkfT8w\nG1L9S0VHvYiiIBAIpg5ChCaZ6Gg9s2ffE6i47Y+ATMxlMRNyOCz6omhir4oFQPJKHHjkQNj7EAgE\ngrEiRCgCzJ37n0iSTxi46FPIqiX6sugJ6y/xe4GDsUefPUr3ye4J60sgEAhCQYhQBIiNncWsWd8L\nVNzxHFGXT9x+TcwXY1Bd4PuovR1eDj91eML6EggEglAQIhQh5s5aBz2nhOeyD+Ci2gnrS5Ikor8T\nmGnt//V+GvY0sH//fuXR0iJizAkEgslHiFCE8DakwavXK+U2fjOh0WyTrk/CO+3UodhGL589/hkf\nfPABH3zwAW+//TaffPLJhPUtEAgEQyFEKEK0vd8Gf7wNun0zlJ6e3XR1vTVh/cUkxKBdHTgYm/C3\nBDLSMzAajUyfPn3C+hUIBILhEAdHIkTrB61wYjr87etw0598da1PEBt71Yhecp29nVQfrGbHsR3s\nce/B0+0hVh3LjPgZXJF2BVfPuporUq8YYCd+ZTwtT7YgN8v07eujs6aT+OWhhwYSCASCcCFmQhGi\n7f023x/P3wpe3yHVnp736ep6Y8g23X3dbPlkC1/5y1dY93/reMX5Ch+5PuJg20Hqm+vZcWwHT330\nFN+2fZvrX72eyvpKeryBQKaqRBUJtyQo5fbn2ifmxQkE5xg6nY6qqipKS0sxGo3o9fpBI2OXlpaS\nkZGBSqUiOzt7QJZTv53CwkJUKhUej0epM5vN6PV6jEYj5eXluN1ucnJyUKlUGI3GKZcxdbSIfEKj\nZDz5hAZjx9wddB/yuUrHV2+hI+qPAERHX0JqqnXALGZfyz7ufete9nj2hNTP/OT5/CzrZ3xp5pcA\n6DvWx/Flx6HX93yaNY3GtEbi4+NZvHjxmF6LQDCRSP/4x4T3IS9ZMq72er0eg8FARkYGZrOZ2tpa\nCgsLWb9+PcXFxQCYzWbKy8spLCxk0aJFvPjii1itVqqrq1m2bJliJzs7G4fDQW5uLhs3bkSn0yFJ\nkhJxu7i4GJvNhlar5cEHHyQzM5P169fjcDgmJR5duBEiNErCKUI9jT38K+1fAMjRMtN3qjnRtBzw\npW/Q6Z4iLm6pcr39hJ2CNwto7mlW6uYmzmWFYQWLpi1iWvw0Ovs6qW+u519H/sVrB16jrbctqM9c\nQy4PZj5IfFQ8rnUuOv/qC2wa/414Ou/vFCIkmLKcCSKk0+lIS0tj7969Sl1eXh5ut5tt27bhdrvR\n6/UDktdlZ2cDvhw/fjsqlQqn06lEutbpdCxevJitW7cC4HQ6ycjIoLCwkI0bNwJQU1NDTk4Obrd7\nSkXIHg0h7QkZjcaQT/XLsowkSUEfzunY7XZqa2vR6/U4HA4yMzOVO4PhqKqqwuFwUF9fj8PhwGw2\ns2LFirDYnkhaPwik4Jbny0TFziAx8Rba2n4HQEvLE8TGLkGSVLzX+B5r3lijiEqMKob7L7+f28+/\nnShV8Md3gfYCrj/veh7MfJA/7P0DWz7ZQkuPz/W60lHJB00f8MRVTzDzuzMVEer4ewfcAcybhBcu\nEJylSJLEypUrg+p0Oh0ejwcIiMzpS3T5+fkUFBQE2cnLywsSEkmSyMnJCbILDFp3JhKSCC1cuBCn\n04ndblfq0tPTaWpqUt5srVZLenp6ULvhhMvhcFBUVMS2bduUury8PAwGwwA7/amqqsJgMCii4/F4\nyMrKoqmpiTVr1ozL9kTT9mFgliKn+yaiiYlraGurADrp7f2Ezs7XcHmvoODNAkWA0uLSePrqp7k0\n9dJh7SdGJ2K+2MzN6Tfz89qfU32wGoBP3Z+ycttKnrzqSRZkLaCntgd6gD8DP5iIVyoQjJ/xzlIm\ni9TU1CGfczgcAANmKXq9L5Nyc3Oz8txUyno6GYTkmLBhwwbsdjuZmZnU1tbi9Xqpr6/H5XKxc+dO\nFi5ciCRJWK1WamtrlYf/LmAwSkpKgu4EwLd2WlhYOOxYHA4HCxcuVMoajYbCwkLMZvO4bU80HZ8F\ngojK83wipFankZj4HaW+ueUx/vNfP8TV5QJAF6vj2a8+O6IA9Wda/DR+/eVf8/NFPyda5XMF93R7\n+N4b36PhhobAhX8BuVOsygoE4ca/22EwGACf2PTHv4dzpi2hhZOQRKi4uBitVktNTU2QAABBwlRU\nNPrsaf7Mf/3JysrCarUO2cbtdlNRUaHMvvz4l9kaGhrGbHsyaP8s4JXmFyGApKTVSJLvy+jt28/8\n2A8BiJKi+M1Vv+F8zfkh9yVJEnkZefxh2R9Ii0sDoKuvi7vku+iacSqFuAf6toqsqwLBROHf+6mo\nqAiqLysrIysrKxJDmjKEJEL+HOUajWbIa0wmEzabbVT23G63smHXH63Wd6jSLyano9VqcTgcOJ3O\nsNueDNr39BOhuQERUqk0JCUFcr/fMR/iVLD2irVkTRvfF/Xy1Mt5ftnzzE2cC0CPqodnrnhGeb7n\nxZ4JjdggEJzNjPR/R6vVkp+fj9lspqioCKvVSk5ODrt376akpGRYO2f7/8uQREiWZWVtcyiGE4bT\nGWkqOlxfTU1NXHHFFUF1NpsNnU7HggULxmV7Iunr6KNr/6kZiAqYFfx8fMKtuHt8S2epsfDDC2Zz\nx+fuCEvf5yWfx/Om55UZ1d8W/o32GJ8gyg4ZV40rLP0IBOcag+17S5IUVL9582ZKSkqwWq2K51x1\ndTVLly4d0c5Yx3AmEJJjgslkoqqqipdffpmbb755wPNVVVXY7XZMJtOo7Lnd7lC6H5GysjI2bNgw\nIbbDRcfeDjh1Y6Oeo4bTMjhsO/gG1Y4e1l3gK1833Q2yB6TweL9Mj5/OM0ue4fbtt7OPfbx2xWvc\n/I7vszz46EH0Jv0IFgQCwekMdj5n8+bNA+rWrVvHunXrQrJzep1Wq8Xr9QbVZWZm0td3Zi6phzQT\nKikpQaPRkJuby6pVq9iyZQvbt2+nvLycvLw8cnNzlesmG4vFQlpaGmvXrh2XHf/dy+mPcNF/P0id\nHpxJtcfbw2PvP8ZrR2HfKQc6iXZaW8vC1j/4HBZ+u+S3zEmcw8tfeBkvvi9006tNQeMTCASCiSYk\nETIYDNTU1LB06VIqKyvJz8/HZDJhNpuxWq0YDAaqq6sHOC1MNA6HA4vFohzmmsp07Al4xkWlB09E\n/+T8E/ta9+EFnj8QiOnW1vZH+vrCmwNoVuIsnl3yLO2z2/n35/6t1Nc/Uh/WfgQCgWA4Qg5gmpmZ\nSXV1NQ6HA7vdjsPhwGAwYDAYBniijUR/t8XB9m78z49EUVER27dvD4vtoTYBwzUbCpoJLQjMhLyy\nl2c+DTgKXDrzHqKja+jpeQ/ooaXlcbTa8M4wz0s+jyevfpJHP3uUL+/5MgCHf3sY901uorWBdcLP\nfe5zAxw8BAKBIByMOYBpWloa2dnZmM1mVq5cGbIAgW9t02AwDHAScDgcaLVaFixYMKKNgoICSktL\nBwhNOGxPBP1FqP9M6B+H/4GzxefUkRSdxLeNt5KcfL/yfEfHn+nu/iDs48lMy2RV3irqZ/hmQLHd\nsby55U26u7vp7u7m0KFDZ2Q8KoFAcGYQsgjt2rWL7OxstFotGRkZ1Nb6MoIajUYefvjhkAdgMpl4\n9913g+rsdntQSIqhKC8vp6ioKEhQampqFA+98dieKDrqAstx/WdC/WdBt2TcQlJ0ErGxXyA2NuA5\n09xcPCHumjcYbqB5ZeAQ3fnV5/NOyzvMmDGDhISEYVoKBALB+AhJhJxOJ1lZWdjtdpYtWxb0g9jY\n2Mj69etZtGhRSAMoKSmhsrIyqM5isQQ5N7jdbjIyMigvL1fq/AdOm5qasNvt2O12bDYblZWVSkie\n0dieTHo9vfQ2+cJXq+JUqNJ8b/8e9x52nvBFlYiSovjO5wKRE1JS1uFfNe3pqaWzc2L2va5bcx1t\nyT5viOnN09n23DY+cYlsqwKBYGIJaU/I/+NdW1tLenp60D6By+WitLSUoqIiNmzYoER3HQmNRkNJ\nSQlFRUUsWrRIifd2+nKZy+VS9mXcbveguTogOO7SaG1PFh3OwCwobkEcksr3eqocVUp9ztwcZiTM\nUMpRUekkJt7WL7jpw8TFfRVJig3r2FRxKnS36+h+2pde4hs7vsEPFv2ARy54JKz9CAQCQX9CSuXg\nz3XRPzS5zWYLOmyVlZVFc3PzsFGzz0TCkcrhxCsn+OjmjwDQf01P9K+iqd9Xz3d2fQd3t+9c05av\nbOGqWVcFtfN6PRw/vhxZ9oUpSk5eS1LSasJN34k+ji09htTje63fX/19tJdq+d3Xfsf554ceMkgg\nEAhGIqTlOP+y2HAYDAbq64Wb72B0OjuVv+PS4wD4P9f/KQI0O2E2V868ckA7lUpDcnIgzHVr69P0\n9TWGfXzCZBzpAAAgAElEQVTqaWoSvh7YA8r9dy7/dv2bP+z5Q9j7EggEAghRhBYuXDhsRGzwOS6M\nxVPuXGAwEbKdCMTZuyn9JlTS4B9JQsItqNU+t3JZbqO19dcTMsbEOxOVv6/5+BpmuGaw0b6R3Ud3\nT0h/AsHZgE6nC9qzFoyekERo1apV1NbW8vrrrw96biYvLw+HwzHqsD3nAh6Ph9dff53t27dz8N2D\nSn1dax3v73kfuzuQm+mbC745pB1JiiYlZb1Sbm+vpKfn07CPN/rCaGK+FAOAWlaz4u0V9Hh7WGVd\nRWt36witBYJzk3BHVjmXCEmE1q9fz8KFC1m2bJniGFBSUsKqVatITU1Voib4c6oLoLW1FZfLRUJC\nAqpjgbc7Lj2Oj/s+pkfuAeBi3cWcl3zesLZiY79CTMyXT5W8eDz/MyEu24l3BWZDX7d/ncSORPY0\n7uE/Xv2PsPclEAjObUI+J1RbW0txcTHvvPMOANXV1VRWVuL1elm/fj11dXVhH+SZTkxMDFqtFvlo\nQDB0F+n4Z+M/lfJ1864b0Y4kSaSkPEh/l+2Ojr+EfbyxV8cSZfT1kdCdwA32GwB47r3neOGDF8Le\nn0BwNlJaWkpGRgYqlYrs7GxqamoGXGM2m9Hr9RiNRjZt2kRpaamSewh8y3xVVVWUlpZiNBrR6/WD\negaP1JffTmFhISqVCo/Ho9T1H0N5eTlut5ucnBxUKhVGo3HQcYeTMUVMWL9+PS6XC6/XS11dHU1N\nTbhcLjEDGgbvSS+c2hKSUiTa4tt46+hbyvOjESGA6OgMEhPvVMotLZvwelvCOVQkSQraG7qt9jbU\nfb6Dtd9/9fscbD44VFOBQABK3qC8vDxlhSgnJyfoBz03N5fy8nIefPBBSkpKqKiooLi4OGhZT5Ik\nNm7cSG1tLRaLhQ0bNmC1WoMSh46mL0mSKCsrU4TInxNuzZo16PV6pZ3ZbMZgMHDttddis9nQarVK\nYOqJIiQX7fLyclJTUwdN43C2M1YX7UOHDrFr1y7mt86n8ds+j7aoi6N497F3uX+HLyzPxbqLefna\nl0c9Fq+3jRMnrsfrPQZAQsIdaDQPhvqShkXukjm+9DjeRl+EbcvtFl4w+mZBy9KXse0724Z0ohAI\nwsk/pH9MeB9L5CXjaq/X6yktLWX16tXK8RWLxcLq1YGjFP4Zzs6dO3E4HBiNRqxWq/J76p+dZGVl\nKZFedDodaWlpQUde/LmI+h+VGa4vvx2VSoXT6VRCnOl0OhYvXqwEfnY6nWRkZFBYWKic86ypqSEn\nJwe32z1hKchD+hUxm82sWbNmQgZyttN3MJDrI2pOFG8cfkMpL52zdLAmQ6JSJZKSUqiU29v/SE/P\nZ+MfZD+kWImEWwPu2vm785FknxDXOGv4zTu/CWt/AsHZgv+H//Rls/z8fOx2nyOSP/t0/xt6jUYz\nwKlLkiRWrlwZVKfT6ZSb4tH05beTl5cXJCSSJAWFMNPpfDnLBqubSEISodWrV+Nyudi9W7jrhkrv\noV7lb9UcFW8dCSzFXTPrmpDtxcV9jZiYL54q9eHx/DzsTgoJ305Ajjll80MoTg4stxbaCvn4xMdh\n7U8gOBvwB00+febgjzDj8Xior69Hq9UOaJuenj7g/3FqauqY+2puDsSEHOmMZ6QIKWyPxWLBaDSS\nlZVFWVkZ2dnZGAyGCZumnU14jwYyIZ7QnKCxy7c0p4/V83n950O253NS+C9Onvwm0Ks4KSQkDO3m\nHSpqvZq+ZX1E/d33Nbn29Wt5/obnee/Ye3T2dvKdV77Dv7/3b2LUMWHrUyA4nfEulU02Q6WR8Uej\n12g0ZGRkDJr92eFwjMrV2y9UI/V1Jvw2hzQT0uv1FBf7Ijnn5+eTmZmJVqtFrVYrD5VKhVqtHtnY\nOUbfkcBy3IfRHyp/XzXzqjHvrficFO5Qyi0tpXi94U1r3ntTYAbn+puL3176W0V07Efs/PyNn4e1\nP4HgTMe/H1NRURFUX1ZWRlZWVtA1/Z0H3G53yJ5oo+lrqhPSTGjZsmWjuk4c2hpI39GACP2Lfyl/\nXz3r6nHZTUr6Ph0df8PrPYbX20hz8ya02l+My2Z/5LkycUvj6Nzuc+2Lfy6ejXdu5IFtDwCw8a2N\n3PC5G/ji3C8OZ0YgOGfQarXk5+djNpupr68nOzubsrIydu/eTXV1NeBLDmoymcjJyaGkpASNRoPF\nYhmQbHOkJfbR9DWUnYk4YzgWhhWhoqIiFi9erGyenZ4WQTB6+ovQDnYAICENCFYaKipVEhrNf+Ny\n+Q6SdnRUER9/I7Gx4ROFjhs7kLb7biyO/O4IV958JVmpWdQ21uKVvdz5pzvZZd5FfHT8CJYEgnOD\nzZs3k5GRQVlZGaWlpWRlZVFdXR0U7Hnbtm0UFBSwceNGUlNTKSkpYdu2bUo+NBj8hv706Ayj6Wso\nO6NhoicVw7poq1QqcnNzB0z1ysvLsdvtPP300xM6uKnEuFy0/72LpNwkAOQomWUPLkNWySG7Zg+H\ny/VDOju3AaBWz2fatD8jSXHjttvR0YHb5YYCYM+pyjvg6LePcte7d9Hp9c2Q1n5pLZuWbxp3fwLB\nuYLD4Rgw88nJycFoNJ5Tv61j2ozYtm0bFosl3GM5a5FOBu4k2nRtyCqf7i+aHloCwOFISfkxkpQM\nQF/fPlpbN4fFbnx8PLNmz0JrDnjySH+WuHza5dw1+y6l7lf//hU7DuwIS58CwdmO2+3GaDSya9eu\noPqdO3dOWS+2iWLMpw2nynrimYCqMfA2H005qvz9helfCFsfavUMkpMfUMqtrVvo6dkzTIvQiLs2\nDvU8n8OJ7JFpf6md5anLuWaOz71cRuauP99FR0/HcGYEAgG+vRyTyURubi41NTXYbDZycnJobm4m\nPz8/0sObVMYsQsL5YPRIJwLv1b6Efb46JLKmhdd7JSEhj+hofxqNXjye/0KW+4ZtM1qkKInE7wVC\n+bT9tg2pV+KRJY+QHOObge1p3MNPtv8kLP0JBGc7lZWVZGZmkpubS15eHiqVivr6+jPCrTqciLgr\nk0D/5bjjKccBuFB7IZoYTXj7kVRoND8HogHo6XmP9vY/hs1+wk0JqKb5vjLe416iX49mbvJcfrX8\nV8o1j/7fo/xr/7+GMiEQCE6h0Wh46aWXaGpqoqmpia1bt7JgwYJID2vSESI0CahOBt5mvwgtnr54\nQvqKjjaSlBSYzjc3P0Jvb0NYbEuxwYFNY1+JRe6TWZ25muUZywHfstydf76T9p72sPQpEAjOboQI\nTQL9Z0InUk4A4XVKOJ2kJDNRURecKnXidj8YtmW5hFUJSCm+16M+oqblry1IksSWG7eQEutbRqhr\nquPHNT8OS38CgeDsZsTDqjabjVWrVgXV1dTUIMvygPr+nO7WfS4TJEIanwhdkXbFxPUnxaDVbuTk\nyTx8IX3stLU9R1LSXSO2HQlVkorE2xJpfdqXZfXkEycx5huZp5nHI8sfYfVffZF8H3/7cW6+6Gau\nnj++w7gCgeDsZsRzQmPF6/WOfNEZxHjOCe25YA9Sm6/9TWtvInFGIjU3TmyiKICWlt/Q2uqPdh3L\ntGmvEBVlGLbNaOhr6uP40uNKfqRLX72U1K+lIssy1z9/Pa/VvQaAUW/kvYL3SIhOGMaaQCA4lxl2\nJuQPEz7R2O12amtr0ev1OBwOMjMzRx0iCMBqtaLT6Qa0cTgcSsKnrKwsmpqasFgs5OTkhGR/PHjb\nvIoAdau7cSe6uTL1yknpOynJTGdnDb29nwBduN0bSE19HkkaX2w/tV5NQl4C7c/59n32b9xP6tdS\nkSSJ8hvL+fxTn8fT5aGuqY4Hax7kseseC8OrEQgEZyPDilBmZuZwT4cFh8NBUVER27ZtU+ry8vIw\nGAykp6eP2N5ms5Gfn4/Vah30+ZqaGiUooFarZcuWLZMmQAC9RwIBQE+knAAJLk+9fFL6lqRotNpi\nTp5cCfTQ0/MebW3PkpS0esS2I5F0VxJtz/vctD3/9OB+w432K1rmpszl0Wsf5e6/3A0EluWumR96\nugqBQHD2E3HHhJKSEgoKCoLqzGYzhYWFQ7Tw4XQ6KSgowOl0KrkzTkeSJGw2G263G4fDQVNT06Rn\nhe09FhChxmRf+obLUi+btP6joy8gKek/lHJLy+NhSYCnnqWm5ys9SrnhoQbl7zuvuJPrz79eKd/1\n57to7W4dd58CgeDsI+Ii5D+w1Z+srKwhZzZ+0tPT2bx584iZXmVZJiUlJWL+930nA15prkQX0apo\nLtZdPKljSEpaTXS0P2dRD273WmS5c9x2O3M74dTKnvt1Nw1/buDEiROcPHmSki+XoI3zhfpxuBwU\n2YrG3Z9AIDj7iKgIud1uJUd6f/wZBxsaGiIwqvDSe6JfPp4kFxdqLyRWHTupY5CkKLTaUsAX0LS3\ndy/NzQ+P227S+Ul0L+lWynU/qWPHjh3s2LGDD//9IQ8vC/Tx5LtPst25fdx9CgSCs4uIitBI2f/8\nqWvHg8PhoKqqiqqqKsrLy6mqqhq3zVA4fSZ0aeqlk9q/n6goAxrNBqXc3v4HOjvfGJfNOXPmMKdo\njrKzGPVhFOmedC688EJUKhW3XHQL37jgG8r1d//5blq6WsbVp0AwlbFYLGRlZaFSqTAajcrvjc1m\nQ6VSBQUstVqtqFQqGhoacDgcqFQqnE4nubm56PV6jEYjmzYNjExfWlpKRkYGKpWK7OzsAYnwdDod\nVVVVlJaWYjQa0ev15OXlTewLHwcRnwlNJP4Z1ooVK1ixYgVr1qyhoqJiUoWo70Q/EUpycYnukknr\n+3Ti4/OIjQ04ZXg8D9LXd3JcNqPmRRH/rUAeodbfBPZ+JEmi7IYy9PG+z2GfZx/rqteNqz+BYKpS\nWlpKQUEBy5cvx2q1KnHhqqqqMJlMrFy5ktzcXMD327dmzRpKS0uDtgpycnJQqVRs2bIFk8lEYWFh\nkBD5vX3z8vKwWq0YDAZycnKChEiSJDZu3EhtbS0Wi4UNGzZgtVopKpqaS+LDnhOaaOx2O9nZ2YOe\nKVKpVNhstqDETENhNBqxWCyjurampgaz2UxdXd2gz48UmDXUc0LvmN6hvcbnyvyTVT/hgfsemPQ9\nof54vS5OnPgGXq/v0Gxs7FfQ6TaPKyBt74FeTnztBJxaedT/Ts+ncZ9yww03kJCQwAsfvMCtL9+q\nXL/19q1KmB+BYCT+8Y+JD5a8ZMn4fwZ1Op2SpM5PXl4edruduro6PB4P6enpbNiwgbq6OrZv387e\nvXsB34qN0WgckL+toKBAiS/n37qwWCysXh3wcPWn+PYfqdHpdKSlpSm2/eNwu91BXshThTHNhJqb\nm2loaBj2MVVJT0/H4XDQ3Nw8Kf11Hw/smTQnN2NMMU5Kv0OhUunQaouVclfXG7S3/2FcNgfMhp5o\nhX7/p2/5/C3cfFHAK/F7f/kenk7PuPoUCKYSdrsdj8czIA1DXl6e8nuj0WgoKSmhsLCQLVu2DJqp\n+vQoNGazGbfbTUNDgyIypy+t5efnY7fblbIkSaxcuTLoGp1ON67XN5GEJEJOpxOj0YhOp8NgMAz5\nGG1SJn9WwaEE4fSsg6FSWlo6oM6/RDfUfpMsy4M+xkrX8S7lb81MDTHqmDHbChexsV8mMfFOpdzc\nXEpPz4fjsplUkKTsDXXv7Cb6o2jlOUmSePrrT5OWkAbAweaD3L/1/nH1JxBMJfy/J/69Gv8jLy8P\nSZKU/W+/N29mZiZXXDEwdNfpv3n+s5IOh0Pp4/Q9dP9vWv/f0dTU1HC8rElhxNhx/TGbzaOKaDDa\npR2tVovBYMDhcAR9IA6HA61WOy63av8h2Ly8vCA7/i/DeAVuNMiyjNQUeC9mzps54X2OluTk++nq\nevtUNIUeXK7/JC3tZVSq5DHZi5obRfxN8XRU+pLaJb2QhFwYEO/pidN56vqnyLP67uKe2f0MKy5e\nEXSeSCAYjHAslU00/t8Tu92uePdCIPmn/zeotLQUrVZLbW0tVVVVrFixIshOfX39gN9Cv33/tkVz\nc3OQEI3k4DXVCUmEbDYbmZmZYQ3nYzKZePfdd4PeeLvdTk5OzrjsGgwGysrKBgiZzWYjKytrUj6w\nXk8vqh7fZLMjuoPzZ54/4X2OFkmKQad7lJMnVyDLbfT1HcDjeRCt9tdj3h9KvieZjj91QA9E10Xj\n+quLxFsCqR9yL8ll1SerqPjIt+a95q9r+PCeD9HFT92lAoFgNPhFqL6+PkhYCgsLcTqdvPTSS8qN\nsc1mY9u2baxZswaTyYRGE8grVlFREdS+rKwMSZJYsGCBIm4VFRVB5yPLysrIygpvgszJJKTluPT0\n9HGLw+mUlJQMWBu1WCyUlJQoZbfbTUZGBuXl5UPaGWzJTK/X43Q6g+xYLJZh7YSTnmOBiAJNSU1c\npLtoUvodLVFRC9BofqGUOzuraW///ZjtqWerSbw1IDoHHzqItzfY6eQ31/+G6YnTATjccpj7tt43\n5v4EgqmCVqtl/fr15ObmUlRUhNVqxWw2s2nTJpYv9znh5ObmkpOTw9KlSyku9u3Lnh4ZpqqqSvF8\nM5vNlJeXK7+FWq2W/Px8xUPOarWSk5PD7t27g34vI+hrNiZCEiGTyTRiJINQ8W/WFRUVUVVVxaZN\nmygqKhowg3G5XEF36B6PR1lu8wcqLSgoCHK/XrFiBXa7XbHp/+AGW4udCNoOtwXGn+g7qDrViI+/\njoSE25Ryc/MmurvfH7O9pIIkpETf59T5aSfHnjsW9HxaQhqbv75ZKT/33nP85bO/jLk/gWCqUFxc\nTElJCVarlby8PLZv3654slksFnbv3k1ZWZlyfXl5OeXl5ezevVupq66uxu12k5+fz/bt2yktLWXt\n2rXK85s3bw7qw+12U11dHeQZPNhKhiRJ4/KAnUhCdtHOysoiLS2NwsJCxTVwMM7U9cmhGEsqh53l\nO2nN952b2XnJTm6sunHCxzkWZLmbxsZbFecEtXo2aWkvo26PInbPHmLr6og6epToo0eJOnYMVXs7\nUmcnUmcnqNXIsbF4Y2PxJifTO306h/d9hePv+M5Dxc6JZnHdF1HHBUfuvv3l2/njB77U4zMSZ/DR\n9z8iNeHM2UwVCMKJ30XbbrdP2k3yVCGkPSGPx4PH42HXrl1UV1cPeZ0kSfT1hSeT55nMYedhUjgl\nxlP499WXBO8xTh7/JrLURl/fYbq2LeHy+zuRxpAWKom/4uKP9KCn61APh2few7wcF1x1FVx9NVx2\nGb/+2q+pcdZwtPUox9qOce/f7+X5Fc+H/8UJBIIpTUgitGbNGhwOBwaDISzecWcmo584Nh5oVEQo\ndtrkxosbLTEOB8mvvUbya68xfVobH/0/X7378k6cd4NhS+g2o+hkPr+njh8BsM/zdWZZbyPKv5Sr\n06H/2tf4W/Z3WNqxCU88vPDhC6y4aAUrLl4xjGWBQHC2EZIIVVdXh9077mym7UhgTyhpZlIERxKM\n1N5Oyt/+hvbFF4n76COlftoeOO+PsP/UFtH+2yCuZSZJrVl0n3cevTNm0DtjBt6UFLxxcchxceD1\nInV2ourqQu12E3X8OFHHjtH33sfE7jxBV+80etGwn29j4JSiuVzw/PNkPg8n1RKvGWR+fzn8Z3QB\nV8+/WnFcEAjOJc7um/ehCUmEgLB7x53JjPSl6TseWJJMm5020cMZkahjx9A98wyal19G3TIwkKg3\nNpbpn2TSdOwIrTMaANh7TzOpqWaioz8XUl+HDx+m5+89xJwKe7VffQvq7BPM2PtP4k6dawCI6pO5\nYS/csBc8fz3J/9kWsfzhV5AmIaGiQDBVMBgM5+wWRkjecXl5edhstokay1lFd183Ma5AdIRIHlSN\nOnyY6Q89RLrJhP53vwsSIG9MDC05ORz+1a+o27GDQ//7LImXVaBWnweALLfjcv0Arze0MDuzZ8/m\nvLvOI/rSU5ET+tQc0RfhePNNthYXw0MPwWmOLZouuPb1/UhZWb69o5degp6eQawLBIKzhZBEqKys\nDJ1Ox7XXXsvu3btpbm4e8nGus6dxD9rWwMnphOkJkz4GVWsraQ8/TPq116J74QVU/X7Qu+fP53hh\nIfVvvsnhJ56g5etfR070nfFRqTTodL9Bknxj7uvbj9v9ALIc2p2apJJI2RDwkuz8eyfdu3pwL1gA\n//3f8O67UF8PDz3EiVma4MZvvQWrVoHBAL/+NXR0jO1NEAgEU5qQXLT1ev2o0i+cjd5xARftZ/js\ns7sBmDnzTi688NlBr3/pw5dIWZhCXK8vkdyMnTNQJU1S5oy+PjRVVaQ9/jhRjY1BT3VcfjmN99xD\n2zXXgGr48XR0bMXt/pFSTky8k5SU0MPBu+530fmqL5Nr1CVRHPrxIVZ9OzhQY0d3O6uLLubr1fvI\n/RiiT/fKmzED1q6FggJImjr7awKBYHyEtCfkz4UxEufqBlt/Ptv/GVf3Xg1Ab3SvcoBzoolxOJj5\n4x8T3y95FvjE5+QPf0j7lVfCKD+f+Phr6e0toLXVd7i0re23qNULSEy8JaQxJT+QTKetE7qh96Ne\n4t6Kg2+f1ldMAmvXvcIXdF/gAU8P5p2w9v1EklynnDuOHYN166CkBH7yE58YxU5Nj0OBQDB6IppP\n6Ewi1JnQ6idWc/sPbwegPbWdjH+NLrL4mOnpQf/MM6Q++SSq7kD6iJ5Zszhx//203HDDqMWnP7Ls\nxeX6EV1d/nNhavT6MmJjrwrJTvOjzbSV+QSlT9fHkgNLUCeqB1xX8lYJRTW+2VZir4oPYu4j3fIS\nHDwYfGF6Ovzyl5CXN+KMTiAQTF3E/94J4lhDIFyNrJ1YnY8+eJDzbr+daY8+qgiQHB3Nye9/H+er\nr9Jy441jEiAASVKh1ZYQHe3PCNuHy3UfPT2DJwUciqQ1Saim+b5uapeafRv3DXrd2ivXcs38awBo\ni/KSo/kzrR/vhrIymD8/cKHTCd/+NixeDP/8Z8ivSyAQTA1CEqHy8nJefvnliRrLWUOvt5fWw4E0\n11G6kD3hR03Sa68x/1vfIv6995S6js9/ngarlcYf/hA5Pn6Y1qNDpUpAp3sKlcrn4SfLrbhcZvr6\nGkdo2c9Gkork+wJpIg5sOkD7Z+0DrlOr1Dz3redIifU5NNS76vnP14sgPx8++wwefRRO5U8BoLYW\nrrkG7rgDjh4d4ysUCASRIiQRMpvNQSHEBYOz37Of5JbAD65KF/4Jp9TdzYyf/Yw5992HutUneHJU\nFCceeID9L75I9wUXhLU/tXoGev3mfh5zh3C5vo8sd47aRvxN8URd7hNkuVtm7w/2Dhrxd752Pk9d\n/5RS3rJrC3/69E++PaD77vN51BUVQVxcoNHvfw8XXACPPw69vWN8lQKBYLIJ6ddx9erVuFyuoKiv\ngoHsbdyLri2QIyfcy3Hqxkbm3nkn2hdfVOq6585l//PP07RmDURNzMwrOvpCtNpH8H9tenrew+V6\nAFke3Y++pJJI/q9kZMn3frhsLk68dGLQa2+99FZWXRLwoPveX77HAc8BX0GrhY0bYc8e356Qn+Zm\nn0hlZsLbb4f+AgUCwaQTkghZLBaKi4vJyspiy5YtylkhQTB7m/aibw0sGYVThGI/+YT5K1eS0C+n\nfPN117HvlVfovOyysPUzFHFxS4LctLu6avB4Hhp1DpPoi6LpuDZw5qfuP+vobR4oYv6U4PNS5gHQ\n1NHErS/fSq+337Xz5kFFBVRX+2ZBfj74AK68Eh54ANoHLvkJBIKpQ0gipNfrKS4uRpZl8vPzyczM\nRKvVolarlYdKpUKtHuj1dC4xYCakC48IJdXUcN6ttxJ95IjPrkrF8fXrOfLoo3iTx5aWeywkJt5B\nYuL3lHJHRyWtrU+Mun1rXisxM33RJLqPdNPws4ZBr9PF63hhxQuoJd/36a39b/HQPx4aeKHJBO+/\nD8XFkHDqULDXC488ApddBv/4x6jHJhAIJpeQ1m2Gi5zdn3P9nNDepr0YW41KORwzIU1lJTN++lOk\nU3nm+5KSOPLII75DpxEgOfkBvN6TdHT8GYDW1qdQqdJITLx1xLZygkzGIxl8cusnABz89UFm3DGD\n5CsGCumXz/syDy15iJ+8/hMAfvHPX7BkwRKWGU77LsbEQGGhL8pCfr5vdgS+/aOvftVXt2kTnGV5\nrgSCM52QROj0NNyCwdnbtJdb2wI/xl7tGJLy+JFl9GVlTHvsMaWq+7zzOLR5M92n8tpHAklSodH8\nP7xeF11dbwLQ3Pw/qFR64uOvG6adRE9PD3vm70HKlJDtMvRB7S21qDermT5rOhec5lRRdFURrze8\nTo2zBhmZ21+5nfcK3hs82vaCBbB1K/z2t3D//eCP8GGxwLZt8Nxzvrh0AoFgSjButy2xJxRMT18P\nTpcTXWsYHBO8Xqb/4hdBAtR5ySXsf+GFiAqQH0mKRqt9jOho/16UjNu9jq6ut4Zso1KpMBqNvmXb\ntWrwx3j9DLr/0E1DQ8OANmqVmt/f9HumJUwD4GjrUe545Q688hDiLklw113w8cfwrW8F6hsa4Ctf\ngQ0boN+BXoFAEDnGJEKbNm3CaDSiVquVPaHU1FQefvjhcI/vjKPB3YC6W01ity8YKNHAWEKdeb3M\n+NnP0P3hD0pV25e+xP7f/Y6+1KmTplWlSkCvL0OtTj9V00NT0w/o6npnyDY6nY60tDSmZU4j+QeB\nJTj179VIBwZfyp2VPIvf3/R7pby1fiu/2vGr4Qc3axa8/DK88ILPow5Aln17R1/8ok+kBAJBRAk5\nbE92djZ2ux2NRkN2djYGgwGHw8HOnTvxeDxkZWXx7rvvTtR4I8Zow/a8uvdV7n7ybl583Oc+HTUz\nCne5m/PPP3/0nXm9zPjpT9H2W/5s/trXOFpSghwTM0zDyNHbe4jGxtvxen1OE30ksDPhKfZKF3PS\n66XN66VdlmmTZTpkGQnfHZC6V2a9uY95e3x2DnxeZnfVXGbHx3FebCznxfn+nRkTgyRJFFYXUrqj\nFKNMLa0AACAASURBVIAoVRRv3vkmX5r3pZEHePAgfPe7sH17oC4uzheL7t57xxxRQiAQjI+Q9oSK\nioqw2+3k5+ezefPmAc+bzWbKy8vZsGEDGzduDNsgzyTqmurQtwXcs9XTQvQUHESAPN/8Jkd/+UuY\nQl6HXbLMJz09vN/Tw2c9PdT3xtLh3cT/40ek0Yiadi5p/w/+l0fYy/AJ8R5aB5sLIKoP5n0o8fKT\nh3jkpuBrktVqLklM5OJ5dzL/kl72Hayht+VTcitzsZvtI2djnTvX56zw+OO+5biuLujshB/9yFf/\n29/CFJphCgTnCiHNhLKzs3G73dTVDR03LCMjA71ef9bNhkY7E7r31Xux/97OL178BQAJX03g+P3H\nRzcTkmVm/OxnaCsqlKqpIkAtXi/vdHfz764udp0SnsGOqM6ngce4Dy2+JHgeUriPx2ggfZCrA9z9\nv/CdUyuPHXFw9zNwdNYIg/L2Qmsdc/Cw6Qt3sFyfRmp09Mgv5sMP4bbbfG7dfubO9S3bXRVaYFaB\nQDA+QpoJ2e32EdM5mEwmtmzZEtIg7HY7tbW16PV6HA4HmZmZo3YHB7Bareh0ukHbjNd2qNS56oLO\nCIUyE0p79NFgAfrWtzj6i19ERIBkWebDnh5e7+riX11dfNjTw2gyRJ2Q0nla/Rj39f6QeFrQ0EyZ\ntA5nUhnq6PNJlCTiJAkV4D316JNl2n7kpeMtN/ENMvGd8MSvYvjjliT29XbT0NmJa7BQPKooSLmQ\nQ8Ctn3yGxGcsTk7mWr2e6/R6FqekoB5sme3zn4d33vHNiB591Fd38CAsWQI//7kvJJCIzC0QTAoh\niVB6ejoOh2PYa2pra0lPH/6utz8Oh4OioiK2bdum1OXl5WEwGEZlx2azkZ+fj9VqDbvtseB0OVnU\nukgpR6WN7i3WPfMMqRaLUvZ84xuTLkC9skxtdze2zk5snZ0c8Q7vWr5AreaymBg+Hx2NMSqKjKgo\npqtUSNJMurv/l6amu5DlNmLkRi5qy0evf5bo6CFi2sWA+2dxtN/djuSVSKvt5rHXNMwvmo8syxzr\n7ubDtjY+bGvj/bY23m5u5uPToiHIwNstLbzd0sLP9+1jZkwMK9LSWDltGldrtcGCFBvrO8z61a/C\nnXdCUxP09cGPfwyvv+6LRTczcinZBYJzhZBu90wmE7W1tUN6wZWXl2O32zGZTKO2WVJSQkFBQVCd\n2WymsLBw2HZOp5OCggKcTif6/lGVw2B7rMiyzD7PvpBnQikvv8z00lKl3PrVr06qAH3W00NxczNL\njh/nu01N/L69fYAAScAl0dGsSUykXK/n7RkzeG36dEq1Wu5ITOTK2FhmqNXKsmVMzGXo9RYl4KnX\n20Rj43fp6flkyHGoL1HTd2tgvtXw3w207GpBkiRmxsZi0uu5b948nrnwQj5avJiTV36J7JOVsO85\naP4ITks/frS7mycPH+ar773H7B07+MGePdS2tASHGLrxRti9G7785UCdzQZXXOH7VyAQTCgh7Qm5\n3W6ysrJwOp1kZGRgMpnIyMigrq6Ompoa6uvr0Wq1OJ1ONBrNqGzq9XrsdjsLFiwI6kev1+Md4U7c\nj9FoxGKxsHTp0rDb9jOaPaGjrUeZ9atZ/PSln7Lk4yUAzHhiBvUL6ofcE0rcvp05996LdCodent2\nNge3bEHuHyF6AnB5vfylo4M/tbfzyRBRpzWSxFfj4lgSG8sXYmPRjWGJqrvbTlNTPrLsi/QtSRr0\n+i3ExFw64NqWlhYO7jtI2kNp9H7gG5PaoEbzogYpTmLmzJlMmzYtqE1jeyNZliz2efZBVDLz5t/E\nksx1bHV5ON7TM+iYLktM5O5Zs7ht+nTS/N6G/7+9Mw9vqkr/+Odma5suWVt26Aa4sxRUUEal1FEc\ndRRBxHGZUSj6Gx1nFClu4w4FddyBojI6bkCLOjouQMVd1hQVEISm7FuXJG3TNcn9/RGaJm1SWmib\nFs7nee7T3nPvOXmb5txvzjnveV+XC/75T29g1IYuIUnwxBPeaTsxPScQdAht6ll6vZ6NGzcydepU\nCgsLWbhwIffffz85OTkUFhYybdq0NgmQ3W73iULT1wGCblxsLR3ZdiiKbEUAASMhVXzo6biILVvo\nfe+9PgGqOe009s+f36ECtLm+nll2OxcdPszs8vJmAhSvUDBFq2Wx0ch3PXowR6/nsqio4xIgAI1m\nOEbjYiTJGy5Hlh2Ulf2Zurrmkdi1Wi2x+lhq/lGDHOkVArfVTcnTJezYsYOioqJmdUxaE3mT8ohQ\nRoCrgr2Fb1H/61PsHzWKL4cM4c7evenRxFnhZ6eTe3bupPePPzJl61bWOBzeyONPPeWNtpBw1NNO\nlr2pxK+6Cmy24/r7BQJBy7T5yaLX61m4cCEej4edO3eyYsUKdu7cicfjYcGCBa0WIICysjIA4kLE\n8zrW+lO42g7FLvsugIBoCUpz8Ck11aFD9LnjDhTV3ojSdX37su+11zokEGmdLPNxdTXXl5RwXUkJ\nH1RX4x8vIAIYHxnJIoOB1QkJPKLTMSoiAnU77Z3RaM7GZPo3kuT9bMhyJWVlf6G2dk3AfUqlkr59\n+9JvVD/0s/S+csWHCozbg0+5AqT1TuPl8S/7zt/f/D7P/DCXSwwGXhk0iP2jR5M/ZAg39ehBlJ+Y\n1ssy7x05wqiCAs7buJF3Dh+mLj3dOz3nH5Pvf/+DtDQoKDjRt0IgEDThhOYYkpOTGTduHMnHGULG\n3hDXqwPoyLZD4ROhY6wJSU4nfe64A/WRIwC4Y2PZn5OD22xuV3ucHg//rqwk48gRZtjt/NRkeuos\ntZrHdTq+69GD5wwGxkRGouqgTZtq9RmYTG+hUHjFRJarKCubSk3NyqD3R02KIuKSiMaCOeA5FHoK\n9fbht5OZluk7fyD/AT7e/jEASklirMHAW6efzsHRo1k4aBDnNRH7dRUV/OnXXxmwZg2z6+pwfPEF\n3Hdf4w1FRTBqFLzxRlv/dIFA0AItum6lpqa2OSK2LMtIksSOHTtOyLDuSJG9CLVLTWzN0QecEpQG\nJezxu8ntpvd99xH5q3eBXlapOPDii+0aC87m8fC208nbTieOJkt+amB8VBQ3arWc08nRF9TqwRiN\nb1FW9hc8niNAPTbb39DpHkOrDXT9lyQJ/dN6iq8p9opPOdQ9VIfncg8KdfDvTi9e/iK/lvzKN7u/\nQUZmyvIprLltDWcmnOm7R6dSMa13b6b17k1BRQUv7t/Pu4cPU3f0fTpUV8cDRUVk79nDX++4g3tG\nj8Z8yy1QUeHd4HrbbfDDD/Dyy4GZXQUCwXHR4kiotLSUkpKSVh2lpaUUFhZitVopLCzsLPvbHUmS\ngh6tYZd9F3pn4zSSJl6DpAisG//cc8SsXu07P/zoo1SNakXYmVZQ6naTXV7O2CNHeKWyMkCAzAoF\n98TE8FVCAtl6facLUANqdSom07solQOOlnhwOB6msjKnWWI8hUGB4TkDHB1Men7xUPRA83WhBjRK\nDbkTc0nUJwJQWVfJVe9fRWlVadD7h8XGsvi009g7ahRPJiXR2+89cbjdPLVnDwNMJv6Rn8+B0aMb\nK77+utebLsgalUAgaBstipDNZmvVsWvXrgC37Pvvv79VL94wjRcqEvfxTvN1dNuhKLIHRs9W9whc\nEI/99FOMr7/uOy+dOhXHdded8Os6PB7+VV5ORnExi51Oqv0e5v2USh6NiyM/IYHpsbGYukDoH5Wq\nLybTu6hUZ/jKKiqeo6JiDnKTyNia4Rpi/9E4dbb3mb2UfFwSsu346Hg+mvwR0WpvAFmrzcrEZROp\ndwf3lANI0Gh4cMAAis4/nzcGD2ZQVJTvWpXHw7+cTlKefpoZzz9PScMao8XiXSf69NM2/e0CgSCQ\nE/Y7XbRoEUlJSeTm5jJ8+HAKCwuZM2dOq+rq9XpfAFR/rFYrer0+wLW6rRxv27IsBz1awu12s2Pn\nDnbbdwfEjXPFujh06BAAmu3b6fngg75rlRdfTMnf/36cf93RNjwe5ldUMO7IERY6nVT52XmaSsWz\nej2fxcczOTqaiC4WoFOpNGEyvYVGc76vzOl8E7v9PmS5NuDe6D9HQ+NtbL1pK3vW7OHQoUO+o84v\nNcM5Pc4JiLi9etdq/vb53475f9QoFPy5Vy+2nnsuS844gyHR0b5rNbLMM0OGkLx8OY/9+c+Ua7Ve\nj7k//AEefdSbyVUgELSZ4xahoqIiRowYQWamdzF44cKFbNiwoc2RCMaNG9cszpzFYiEjI+N4TeuU\ntv2prKxkxQ8rqPfUB4yEnBonR44coYdGQ5+77mr0hBswgIPz5h333pM6WeZNp5OM4mJeqKykwu/h\nOlil4hWDgQ/MZq6IiuowR4P2QKGIwWhcSGRk4/+jpuZTSktvxe0u85VJComYJ2PwmL0Peo/Dw47r\nd7Duq3WsW7eO1atXs3fv3oC2rzn9Gh6/+HHf+fwN83n2x2OkfjiKUpKYlJBAwYgRfHL22aTFNObi\nqFAqefTmm0l+/32emTSJGpUKHnvMK0ZlZS20KhAIgnFcT8GsrCxSUlKwWCxcd911FBUVMXXq1OMy\nIDs7u1nG1pycHLKzs33ndrudlJQUFi1aFLKdYN9yW9N2e2HDu4/E3zNOl6gjOTGR059+Gs0er3eC\nR6tl/8svH5crtizLrKyp4criYmaXl2Pz+/adqFTynF7PB2Yz6ZGR3SbFuiRFoNc/j1bbmIm2vr6A\n0tLrcbkaR7GxfWOJnx/vS4Kn3KMk/o14Bg0chF6vD/r/f+h3DzH5rMm+8xkrZ7BsS+uzA0uSxBUm\nE+vT0sg780xO12p910pjY5lxxx2c9tZbLLnkEuTPPoMRI4Qbt0DQRtokQvn5+RiNRubOnUtycjIr\nV65k6dKlbdob1BSdTkd2djZZWVnk5eUxb948srKymk2X2Wy2gAerw+EgKyuLSZMmYbVayczMZPr0\n6eTl5bW57faguL4YCNwjpDApML3yCjFff+0rO/j009S1JbfQUTbX13NTWRl32WzsdjeGp+mjVPK0\nTscn8fGMj4pC0U3Exx9JUhIX9zBxcQ/gDRAEbvdeSkpuCEiOpzlbg+7xxs9a7cpaKudXttCuxOKr\nFzOmf2M675s+uInv93zfRvskro2P55eRI3nztNNI9POK292zJ5MfeYQLXnqJtZGRMHo0vPlmm9oX\nCE5lWhW2x+FwMHXqVF+Q0OzsbGbMmNHhxnUlWgrb43A4uOPdO3jvyHs8lPsQ6Zu9UboTppZw+muT\nkI6+xaVTp1Jy771tet2DbjfPV1Tw0dGpvAbiJIk7Y2KYEh2NphsKTyhqavKPrgs1/L1qdLpH0Won\n+O4pn12O802n77z24VpSbk4hNTU1aJtl1WWMfn0020u3A2CMMvLjbT8yyNRynqNQ1Hk85Bw4wKO7\ndlHaJOLEDfn5zMnJof+ECd4I3RERIVoRCATQipHQvHnzMBgM5ObmMm7cOAoLC085AWoNpS6vG7D/\nSCh+6QKfADnPO4+Se+5pdXt1ssyCykouP3IkQIBUwM1aLV8kJHBrTMxJJUAAkZHpmEz/QaFoiBFX\nj8PxIA7HU8iy18MtdkYsmlGN7tSaeRrqttQFac2LMcrIpzd+SrzW22ZZdRmXv3M5xc7i47JRo1Dw\n17592XneedzXr19AZIn30tMZ/NZb/LO6mur0dG+KCIFAEJIWR0Kpqak+77Jp06YxceLEVq81NA0m\n2t051kgo/fV0NlZsZPEri0ksTgRgBLcTQyEuo5FdH36IO+EY2T+P8m1tLU86HAHTbgDpERHcFxdH\nkqpNGTi6JW73AcrKpuNy/eYr02jORa9/HqXSiMfmoWRiCe593vdIEa/g3PXnEjkg9AbSdfvXcfG/\nL6ba5RX1Eb1H8OXNXxIbcWKhkgqrq5lZWEheSaDreOLBg7z41ltcOWMGnGT9QSBoL1oUIcVxem9J\nkoTb3ZoUaN2HY4nQ0AVD2VWziw+zP0RX7V23GMW1RGBj76JFVI0ZE7LtBg643cwuL2dlTU1A+WCV\nillxcZx/ik3teDxOHI5Z1NQ05oNSKntjMLyMWn0G9YX1lN5Qilzu/Qhrz9Ay7PthqPWhs6t+tO0j\nrllyDTLeOmOTxvK/Kf8jUnXi0Q++tdv5+86dbKwMXKf6w48/8oJWS/Ldd3sjcwsEAh8tfqVu7X6f\npnQXz6z2pLS+FKVb6RMg8KDGQenUqccUoDpZZrHTyfyKCvzlJ1aS+FtsLJO12i7tat1RKBTR6PUv\n4HQupKLiBUDG7T5ASckU9PoniEq5EsPLBkr/UorkkqjaWsWWa7dwzufnoNAE/wJ19WlXM/+K+Uz/\nnzfP1JdFX3JD3g0sm7gMleLERphj9HrWpqXx+sGDzPrtNxoctj8ZNYqVdXXMmjuX+zMzidLrW2xH\nIDiVaFM+oVOZlkZCh0oP0evlXiQdMfHGq17nDTU2hg99nD3/+Q+oQ38z/6G2lseCTL39MSqK+2Jj\nMXeBCAddgZqar446LDSOMrTaycTFzWLPG4fQzGtcI+rxpx6c9uZpzUIm+TP729k88OUDvvNbh97K\n61e9jkJqn7xBpfX1PLB5M4tsNmS/GYWk4mJeTk1l/LBh7fI6AkF3R2TqagcOVh4EYM4Kv5A9inIO\nPPtsSAGyeTxk2e38pawsQIBOU6l412Rijl4vBMiPyMiLMZuXolQ2hluqqnqfkpLJeMbuJe7vjSk7\nDr99mB1372gxQkLWhVncN6oxSva/N/2bGStmHDOqQmsxqdUsHDaMNUOGkOaXi6goPp4rHA4mf/45\nh2prW2hBIDg1ECLUDuyr2Mf1v0D6zkYRklNNuPr0aXavLMv8r7qaK4qL+dDP6y1WkngoLo5cs5nh\nYQou2tVRqZIxm5cSGTneV+Zy/UpExF2obv2OXtN6+coPvHKAoodCBxiVJIm5GXO5bdhtvrLn1jzH\nY18/1q42n2sysfaPf2S+3Y6hosJXviQyktO//prX9u3DIyYjBKcwQoTaAYd1C/P/B/U0xo2TBzXP\nDXTQ7eYOm4177XbK/KIdjI+M5LP4eP4UHX1Krv20BYUiBr3+WeLi/ok3MQVIUjVlZX9D+seLmKc0\njoj2PL2HPXP3hGjJK0QL/7CQCac37kF67OvHeOLrJ9rVZqUkMf2Pf2R7//7c/MMPvnK7RsPUnTu5\neN06tjmdLbQgEJy8CBE6UTweRj2ag6EG6vBLZmdqnErzyDLvOJ1cUVzMV35TMD0VCl41GHjOYBBT\nb21AkiSio2/AbH4fpbKfr/zAwVep/tutxN3SmLrBOtPK/gX7Q7alVCh559p3uCz1Ml/ZI189wlPf\nPNXudscPGcKbd97JytxcUvY32vRtdTVD1q/nsV27qBWBUAWnGEKETpSXXyalwDvtU+snQgqz963d\nWV/PjaWlPFFeHhDleopWyyfx8YwVidGOG7X6TMzm5bjdF/jKnFW/4LhlMu67loDkfaDvuGMH++eH\nFqIIVQQfXP8Bl6Zc6it7aPVDzPnu+LxDW0SvZ9yLL/LL3r3MeucdVEcjLtQBj+7axdANG/g2DFmB\nBYJwIUToRLDbYeZM3+mm+EYR8pgkXqmo4JqSEgr80monK5W8azLxiE5HzHHuwxI0olDE0qtXDlrt\nA4BX0CXJhfLaBTD/fjB7oyLsuHMH+14KHb0gUhXJh9d/yLjkxrxYs/JnMff7uR1hNFFZWTw9cSIb\nZ87kvK1bfZe2VVXxu02bmLZ9O/b60DmQBIKTBfEUPBG+/RaObizd1AP2xjSK0Gx1JS9VVtLwGFED\nd8bE8GF8vHA8aGeUSiU63c3Exy8PSJTH4I3I/74NLvkSgJ1372Tn7J1UVFRQUVGBs8k6TJQ6io8m\nf8TYpMboBjNXzeTJb55sN6+5AC69lHOWL+f7xYt56YUXiPWzZ9HBg5yxfj3Li48vtJBA0F0QInQi\nlHjXHmpU8KdrQVdl8l3aHNc4tz9ErSbPbObu2NiTLtZbV8LrPfc+0dHTaIjGLUVXwCNPwKP/BEMZ\n+x7Yxzd3fMMXX3zBJ598Qk2T6BRatZaPb/iYixMv9pU9vPphZq6a2TFCNGAAym+/5a9mM1tvvZU/\nfvut79LBujombNnCNZs3s1+4cwtOUoQItQOPXAxbTj8PQ21/X5nNAFpJ4oG4ON41mRjUwoZVQfsh\nSRri4v6ByfQflMrejRcu+gYW/xnGrST6HS0DPhuAAgWeII4AWrWWT274JGBqbt4P87jzf3fikTvA\ncSAyEhYtou/s2Xzw1FPkPfIIPUsbnSs+LCnhjHXrWLB/v3DnFpx0CBFqK00eWnvHjOKZ2x5CccYc\ndOWNHm5n9tTwsdnMzdHRKMXop9PRaEZgNn9EVNTExkJdOTz4NDz9AM7/7iL21Vg89cFFJVoTzcc3\nfMzVg6/2lS3YuICbP7iZencHrdXcfjt89x3X7t7Nr7fcwrSPP/ZdKne7uWPHDi7atIlfhTu34CRC\nhO1pJb6wPYuvZ3viEgCcv/ThT2e9iV1SYiiD5Ue3m7h0En3X9DglY+h1RWprv8fheBi3+0BjYWU0\n5Ewjru5GhuQNRRkd3EW+3l3PX/77F97++W1f2VWDr+L9Ce8TpY7qGINLSmDKFFi5km/OOYep997L\nb/0bR9kaSeLBAQPI6t8fjXBuEXRzxCe4rSxvzNz6zdlnY5e8Dy9DY2QWIs1KIUBdiIiICzCbP0ar\nvbGxMMYJ//gX5Vf/iY03vU/d4eD5iNRKNW/+8U3uGHGHr+y/2//L2LfGUlJVErTOCWM2w2efwYMP\n8ruff+an22/nobfeanTnlmX+uWsXwzds4EeHo2NsEAg6CSFCbWTlkCHNC2sOYdi4yHeqMIm3tauh\nUESj0z2MyfQ2SuWAxgunb6Pq/25mzQs3cvDHnVRWVlJZWRngsKCQFLwy/hWyLsjyla3Zt4bRr4+m\nsKywYwxWKuHJJ+Gjj4iMiuKJxYuxTJsW4M69paqKCwoK+Otvv1HeJMOrQNBdEE/LNvJeerrvdwkY\n6dkN6/+M4dARX3nDRlVB10OjGUF8/EfExNyJ7D6aukHpwXNpLtsOnss3r/+Tzz//jM8++yygniRJ\nzB43m5cufwnpqOfdjrIdjHp9FOv2r+s4g6+6CjZsgGHDOLuoiO/vuosXXnqJ6KMiKQOvHDjAmevX\n83FJB43MBIIORDwtT4ArjCbOrvgGPDUYnH7REsRIqEsjSZHExt5NQs9PUDlHNZYbbWiHPEeCYjZu\n16+UlJQ0OyYnT+adq9/xJcErrirm4n9fzEfbPuo4gwcOhB9/hL/9DaXHw93Ll7P1llsYv2aN75Z9\ntbVctXkz12/ZIqJzC7oV4mnZRlSuxrQL8Rq1L42DsbIxeKl/3DhB10WlSsSc8gax1c9AWWPAWY+x\nAJPpISzrJvH99//lu+++8x1fffUVCaUJfHnzl5iivPvCql3VXLPkGp7+9umO2UsEEBEBzz8PH38M\nJhP9jxzhk1mzeO/xx4n3y+S6tLiY09ev542DBzvOFoGgHREi1EYeiwxMsX2o8hBA4EhITMd1GyRJ\nIib5D5h7fIriq+vB5f0CISlkNNrV6OL+St++X3LaaYmcfvrpDBgwALfbzah+o/jhth9INnjzG8nI\nPPjlg9yQdwNV9VUdZ/Af/gA//QQXXYQETF69ml9vvJFbv/zSd4vd5eK27dtJ/+kndlR1oC0CQTvQ\nJZ6WFouFRYsWkZeXx7x588jPz2+XelarlYyMDPLz87Hb7VitVrKyslrdfjB6paQGnDeMhAyVYjqu\nO6M2x5Ew4VEil74P349uvCBVU1n5EkeOXE5V1XJkuXEkPMg0iLW3rw2IrrBkyxLGLB7DXsfejjO2\nTx/Iz4fHHweFAlN5OYufeIKV995Lsl/OotV2O+ds2MCc3bupF9G5BV2UsO8TslqtTJ8+nRUrVvjK\nJk2aRHZ2NklJSSdUz2q1kpraKBp6vZ7XXnuNa6+9ts12Bkvv3aPHLZy17D94ZA85C3IYeGggAKZl\nJjRni/hw3ZWqD6pwfPglTH0VUqwB1yQpibq6Gxk37nHfZ6LeXc89n9/Dqxte9d3XI7oHyyYuY8yA\nMR1r7HffefcU7fWKXlVEBI/dfTfPjh+Pf8L4IdHRLBo8mJFxccHbEQjCRNi/smdnZzN9+vSAsszM\nTGb6Rac+3nqSJLFq1SrfKKisrOy4BCgUNa4aXxgXo7NxTUhhDPvbKjgBtNdoMT/wexRPvg7P3Atl\nfhlz5SLU6iexWM6lrGwlsiyjVqp55YpXWHDFAlQKr8fdYedhLnnzEuZ+P7djQv00cOGF3um5G27w\n2l5bS/a8eayfNo3hfnuIfnI6Od9i4R87d+J0u0O1JhB0OmEfCRmNRiwWC4mJib4yu92O0WgMGter\nLfWKioqwWq2k+7lVHy/BRkLquCu58OOPkTwSK59cidLjXU/o+VNPpAixWbW746nw4HjAQc13ZTBx\nGUxaCtGBayx6/cUkJT2JTufNafTN7m+YsHRCwEbWKwddyb//+G+MUUY6lPffhzvu8KYYAVwKBS/8\n9a88fM01VPvdlhgZyYJBg/i9sYPtEQhaQVi/stvtdp9w+KPX6wHYtWtXu9Zrb6pd3q4dVx3nEyAp\nThICdJKgiFWgf1GP7sFeSMtuhSnvwvvXQ23jVKvd/hUFBReyadNYbLbVjOk/Bss0C6P7Na4rffzb\nxwxfOLxj9xMBTJ4MmzfDpd7kfCqPh3tffJHNt9xChl+ivF01NVz288/8aetWiuuCR4oQCDqLsIpQ\nWVkZAHEh5qmtVmvQ8rbUs1qt5OXlkZeX53NiaC+q670iFOCUIDzjTiokSUJ7nRbzB2bUA8ywcDr8\n6W3475Xgbvxf2+2r+emnsVgsF6B1bWH1zau5d9S9vuu7Hbu58I0LeeaHZzp2eq5PH/j8c3j5ZYjy\nxrZL3rOHL665hjffew+jXzipd44c4fR16/jPoUPCnVsQNsI+EurIeg0jpQkTJjBhwgSmTp3KKdIS\nBgAAIABJREFUkiVL2k2IGkZCAXuEzGKP0MmIKlGF6V0TUVOjkMvM8K9/wM1vwWeXIfuJUUXFj/zy\ny+X88tMFzBx2IR9MykMXoQOg3lPPjJUzSH8rvWO95yQJ/u//oKAARo70FgE35+SwbcIEbjx0yHdr\nqcvFzdu2cdnPP1NUXR2iQYGg4zipv7brdDqmTp0aUNYap4fW0rAfxF+ExEjo5EVSS+jv1WNeYkY1\nSAUH+sDcmUh/ehs+uRIawgABFRUb2LLlGnqVz+LrCfcxus9w37Wvdn3F2fPP5v3N73eswYMHww8/\nwJw53s2uQHxpKW/fcAOfvvoqA/xGRStsNs5av56nd++mVrhzCzqRU+6JmZSUhNVqpby8POh1SZKC\nHsFomI4TInRqoTlbgznXTMzdMd687Yd6wbP/gMnvwufXIsmRvnurq3/Dtv9hsk/bzRu/G4NJ4/0s\nOWod3JB3Azcuv5HSqtIQr9QOqFQwc6bXg+6CC3zFly9bxubx47nHavU9BKo8Hh4sKuLMdev4RMSh\nE3QSYX1iJid7d5uHEoSG68dbb+7cuc2uNUzRhVpvagvVLm8QSTEdd+ohaSRi74zFvNyMesjRrLkl\n8ZB9F/KEd3CtmojHpfXd73KVkiR9S+4oFY+fFUNStLf83V/e5YxXz2DZlmUduy4zeDB88w28+CJE\ne188pqqKf912G2see4whfm7bhTU1XLl5M1f8/LOIuCDocMIqQnq9nuTk5GaCYLVa0ev1Ae7Xba3X\nEB2hqadcg1NDKIGTZTnoEYyaICIkRkKnFuqBakzvmdA9oUPSHx0x24yonroTxYRlqNf8HQV9/GrU\nM8ZUyRsj4IWhMDYebFVHmJQ7iWuXXsuBigNBX6ddUCjgrru8HnTjGlOXj/zqKzZceikv5+ej90uS\n92lZGWetX88sq5VKkSpC0EGE/Yk5btw41q9fH1BmsVjIyMg4oXrJycksXLiwmZCtWrWKtLS0kJ51\nbaHmqGNCQNy4+LC/pYJORlJIaCdqSfg8Ae0UbWOvKtdSP+sqPFe/iWv1Q6hV5wTUO0cHD58BS86H\n25Pgx6IPOeOVM3jN8lrHetAlJsKKFbB4sTeBHl537v978kl+mzSJqYcO0TABXSfLzNmzh9PWreO9\nw4eFF52g3Qn7EzM7O5tly5YFlOXk5JCdne07t9vtpKSksGjRojbVMxqNFBUVBbSTk5MT0M6JUOv2\n7rEQ03ECAIVege4RHeZcM+rh6sYL5UpUj6fjvu4l+u37gHjzRCSp0YnBoIEb+8M758H9Ax0s/mEq\nY94YxcYDGzvOWEmCW2+Fbdtg2jRfcfzhw+TccAPrnn6a8/0EZ39dHVN+/ZULCgr4QWRzFbQjYY+Y\nAFBQUMCSJUsYOXIkVquVtLQ0xo4d67tut9tJTk5m7ty53H777a2uB5CXl4fVaqW0tBS73U5WVlbI\nab6WCBYx4bNDMHc7fDjvQ3ROrxtuwrcJKOOFEJ3qyLJMbX4t5c+W4y4KDJMTmRxJn0cicY35L4cO\nL6K2dl+z+mV1sOowxJgmMvPi+Zi0po41eM0ab7SFTZt8RR5J4j/338/M8eM53MRj7rr4eOYkJ5Ny\ndC+SQHC8dAkR6g6EEqFntypZ9cSqozdBz196IqlExASBF9klU51Xjf15O5It8HMRmRhJvwd6o/7D\nBg4eWYDNtjJoGzsqlcSaJvHHtBeJ1JiD3tMuuFzw6qvw0EPgF43bERfHE88+y0sDB1Ln97hQSxL/\n16cPDw0YgEmtDtaiQHBMwj4d190JWA8yKoQACQKQVBLa67XUvF5DzY01yDGND/GaXTXsmGZlyxAD\n0Z+/StqZW+jXbyYKVUJAGwNj3PSsfY9vvktg5ZoLOHIkD7e7pv2NVang7rth+3bvVN1RdOXlPDN1\nKr/ecQfX+20Ur5dlnt+3j9S1a3l2715qRGBUwXEgROgEESF7BK2h/6D+mO8xE/NxDJr/04Cu8ZpU\nLLEvax+bBpZCzlRGDijkrLM+oT5yNPV+s2AahYy65ge2br2Ob7838+uvt1JW9gUeTzt7rvXq5XVa\n2LABxjSmokj+9Vfev+YafszO5oL6el+53eXivsJCBq5bx6IDB0TuIkGbENNxrSTUdNzXH5/HnHfn\nAKC5QIPp9Q6euxecFHicHqrer8L5uhNPWZOHtgqir4gm7rY45NPsfH/gCaj4jJSY4A93tdpMfPxE\nEhImo9NdgCS145qkLENeHtx/P/g5+cjAB7fcwsybb2anIvDLV0pkJI8mJnJDjx4oQ2z0FggaEF/d\nTxDhGSc4HhTRCmJuiyEhPwHpHxKe3n4C4wLnR04OXnWQPZc5uPjnF8gYWsTnzsm8vUdif5MQb/X1\nJRw4MJ9Nmy7ihx96sW3b7ZSUfNI+U3aSBNddB1u3esP/HN3aIAHXvvkmW37/e1747DP8JxALa2q4\nads2zlm/nrziYuHWLWgRMRJqJaFGQgdzbuIvq73n0bdHE3efyFwpaDuyR6b2q1qcbzip29A8vYIn\nykPN72rYd9E+Fke8gY21pCfAxfEQHxG8TaUyBqPxcszmazCZxqNS6YLf2BZKSyE7G156CWoaRc4Z\nGclLs2Yx93e/w9akyvCYGB4aMICrzWYUYmQkaIIQoVYSSoTqn/k7V228CoC4h+KI/lN02GwUnBzU\n/VKH8y0nNV/UQJB0P+qz1ZSOLeUZwzN8z7ecrYNLEuBCE5hCCJIkqdHrL8JovByjcTxa7eCQMRFb\nxf798OST8NprXq+6oziio/nXzJk8N2YMFU2qnKnVMmvAAK6Pj0elEJMwAi9ChFpJKBHSP/I0o3aM\nAsDwsoHIcZEh2xAI2oLH5qHqwyqqllTh3tXc80xWyqguUfHhGR/yUuxLuNT1nB4HY8xeQeqrDdLo\nUSIjE32CZDBcglJ5nF+edu6ERx+Fd9/1rh8dpSQujnn33cdLF15IdROxS46MZGb//tzSsycRQoxO\neYQItZJQIjTwnkWkHk4FwLTMhOZsTcg2BILjQZZl6tbWUbWkippVNVAf5KY42DJ0C+/0eYcNyRuo\nV9eTqIULzZDeQ0OiNnQGVUmKQK//HQbDpRgMY4mJGYoktVEctm6F2bO9YuTnHXfYYOBff/0rr158\nMRVNBKe3RsPf+/bl9l690It9RqcsQoRaSSgRGv2XD9FVH42W8E0CygThnCDoODx2D9WfV1P9YTX1\nm4KpEdRF1fHdwO/46rSvWJe6jlpNLWYNXBiv4ZoBvegfUQIeZ8jXUKmM6PUXYzCMRa9Pb9vUXWGh\n14HhzTfBz43bFhPDS7feygtXX02ZShVQJUap5M89e/K3vn1FBIZTECFCrSSYCK04oODSG/MB79RI\nr597ISnFwqug43G73WxduZVhpcMofqeYGmtwT7gadQ3rUtaxdtBa1gxcQ1lsGSoJrks5jcnJSfRU\n7qa6amuLr6XR9EKvH4vBcAk63YVERQ06tijt2QPz5nnXjPwcGCojI1lw3XU8O2UKh5oIjgRcZTLx\n9379+J1Od2JrVoJugxChVhJMhL7eHcVFt34KgNvspu93fcNmn+DUwuPxsGnTJhQKBcigsqqIXBtJ\nxNoIVIdVIev91vM31gxaw9qBa9nWZxvRkdHccublTEjqT7xyH3bbaurrD7f42mq1mbi4C9DpLkSn\nu4DY2DQUihDT0MXFsGABvPwyHDniK65Rq3k7I4Pnb7mFLQkJzaoNjYlheu/eTElIIFYV+u8RdH+E\nCLWSYCK0doeB86YtB6B+cD39P+ofNvsEAvCuH9k32nF+6iTGEkP1tuqQ9zqiHFiSLRQkFWBJskA/\nuPHsKdxy9iXEyTux27/Ebv8Kl8sesg0AhSKS2Nhz0ekuIC5uFLGxI4mI6Bl4U20tvPcePPcc/PJL\no73AyhEjeH7KFD4bNqxZ2zFKJVMSEsjs3ZvhsbFtei8E3QMhQq0kmAj9tLUXQ/7vXQBqR9WSuDgx\nXOYJBD6cTidbt25FoVCg2q8iYlMEkZsi0WzXILlDT3EdjjtMQVIBBUkFuM53kXFBBhNOv4Ye6grs\n9i9xOL7D4fgel6vsmDZERPQjNnYkcXHnEhs7ktjYNO8+JVmG/Hx44QX49NMAJ4Zf+/fnhQkTeOvy\ny6kO4qgwIjaWzF69mJSQQJwYHZ00CBFqJcFEaPtPSQy+5w0Aqv9QTfIzwbO1CgRdAU+Fh9ofaqn9\nupbab2rxlLQc4+2g/iCb+22mZFAJCecnMGnyJM7qcyZVVdtwOL4/KkrfUVNjbbGdBqKiBh8VpRHE\nxAwl2mZAvXiZd93o4EHffbaYGN76/e9ZeNVV/Nq/+exClELBH81mburRgwyDQew56uYIEWolwURo\nz/oz6H//KwA4b3WSmpUaNvsEgrYge2Rc213Urq2lbk0ddevrkJ0tPwqqNFUUDSii5swazGlmUkam\noDFokCQb/fo5qKz8kfLydVRWFuDxhJ4G9CciYgAx0ecQsz+KmM9+IyZ3E5GHQJK9U3XfnX02C6+8\nktyLLqJW03zdqYdazZQePbipRw+GxsQIZ4ZuiBChVhJMhIq/G0H8w/MAKJ9ZzuA/Dw6bfQLBiSC7\nZOo311O3pg7nj05cBS4UdcceYdiNdsoHlHPO+HPo/7v+xKbFojRIVFVtobx8HTbbj1RWbqS6egvQ\nulQPSlcEMUUKordWo90F0buhtjSGd8+7jH///jJ+SUkJWm9wVBTXxcdzXXw8Q4QgdRuECLWSYCLk\n/HIM0U88DoD9OTunjz89bPYJBO2JXCdTv62eyg2VHPrxEKqfVcQ6WucY4O7txjDSgH6Inl8qf8E9\nwI2nRzWqiF2oVDtRqYpQKnehVu8HWp+GQlUO2j1QUxZLQexZ/DclnYK4sykmHq+DdyMpkZE+QUqL\njRWC1IURItRKgomQ5/NLUWTPAqD07VLOGnFW2OwTCDoSWZap2lvFb1//RunaUiK3R9LvQD807lZG\nCIkAVYoK9UA1qkEq6vrUUWm2cf6VvXFW/Uxl5U9UVm6isvInXK7SNtlW59KwV9GXvYp+7KMv++nj\n+2nDQL+ISMYbjVxhMjHWYCBaKTaUdyWEi8kJoJC90xWqBBWIkHGCkxhJkojuH82wm4bBTV5RKiwr\nZO3atez7cR8xRTGkHkgl5XBKcGGqBddWF66tjSMfNVoKtOVEDTwd7aA0dIO19BgUiXqgA3ev7dRK\nv1FVtRWncytVVb/idjcNiepFo6ojBSspNHeQqCKK/bV92H+wD/892Icc+tEzJpXhpjMZl3AmqVox\nSgo3QoTagYjEEKGLBYKTFEmSSDWlkjo+FcZDtauagpIClu9fzt6f9yJvl0k8nEjSkSQSjyQSXxEf\ntB1PlQfnT06cPzUNI6RDHT+aqEHpaFOiMCRFoE61I/fdhdtUSJ16h1egHD/jkoKLE4CWagayk4Hs\nbCys9B57div4iXhc6n7ERiXSN3YgCTGpREYmEhk5gIiIfqE34QraDSFC7YAmUXxQBac2UaooRvcc\nzeieoyENKuoq2FC8gbVH1vJOyTvs3b+Xvof6knQkyXcMKB7gi7sYjPrieuqL6yn/vtyv1AgYkVTn\nEtE/guikCCJOq0E58CDEbcFTsxZX3c/URu2nurcHd0xom5V4MHMY6g9D/QZs5TTJhSSh0fQmIqLv\n0aOP79Bo+vjKlEoR7+5EECLUDkQOEnNxAoE/sZpYLulzCZf0uQSAWnctW8q2UFBawKaSTbxd8jYl\nNSXEVcXRt7Qv/Ur7eX+WeH/2LetLhCv0DIPskqmx1nhj5uWDV5zGHD28KGPdaOP3ozT+hMK4Ffoc\noGaAnfLEOtwJVWijykO07nsV6ur2U1e3n4qKtSHvUqkMzYRJo+mBRtMDtbqH73elUkz9BUOIUDsQ\neboQIYGgJSKUEQyPH87w+OGAd01pn3MfW2xb2Fq2la22rSy3LcdW6x2LSB6JhPIE+pb2pZetFz3t\nPX0/e9p7YnQaj/ma7golVRX9wdofuLLRloZf1HWQcJC6AXupSiqmKrEUeh5GbTpElO4w0VElSNKx\n/bZcLhsulw2nc3OL9ykUkQGi1FSkvOdmVCoTarUJheLUSG/RJUTIYrGwceNGjEYjVquV4cOHk56e\n3i71jrftUGzcuIGYJkN8S5kFuadwMhQIWoskSfSL6Ue/mH5c1u8ywCtMh6sPs9W2lS1lW9hm38ZO\nx04slRZkAvtXZF2kT5B62nrSy96LBEcC5nIz8eXxmCvMKOVjeMHVa2D/ADT7B6D5AfRNr6vqIb4Y\nzCUQX4wnvoT63iW4e3jLlMYS1HElKJSt2//k8dRQW7ub2trdrbpfqYxFrTajVpt8wuQ9gpepVAaU\nyu63PyrsImS1WsnKymLFihW+skmTJpGcnExSUtIJ1TvetltCb9bj8o+aHwEpF6ag0oT9rRQIujWS\nJNFT25Oe2p6M7TPWV17jqsFaYaXQUcgOxw52lu+k0FHIbs1udiXsCtqWwqNA79R7BclPmOLL431l\nRqeR6NoWMsq61HCwt/cAFPiNonxGe0Bv9wqV/2EsA4MNDDZko/enFFHbpvfD7a7A7a6gpqaoDbUU\nqFQ6VCq939H0XI9SGfwepTIWhaJzn2Vh3yeUmZnJ73//e6699lpfWX5+PgsXLmTp0qUnVO942w5G\nw7eL1WtmQnW2t/Czy1CvfAjze+Y2tSUQCE6cWnct+yr3sbtyN7srdrOnco/v54GqA3jklmPjAWjq\nNRicBgyVhoCfxkojxkoDfW0GEipNRFfrUbpOJIq3DFHVXmHyE6hmR1x546E8tv0dgSRFoFLFolTG\nolTGBPz0ljeUBV4PrBODUhmNQhGNUqltMVNv2EXIaDRisVhITEz0ldntdoxGIx5P6H9Ca+odb9vB\naBChz7+/h4i6572Fn11GdOnjxM2Ia1NbAoGgY6lz17HPuY+9lXs5WHXQezgPcqDqAAerDnK46jAu\nufXRGgCUbiVxVXGklsRx5qFYBhbrSCyLI6HCAIp+OCN741QbcRGHVB9FVJWauHLQBE+A2zKSB6Kd\nXjHSObyHv0D5nzf8HlMJUcGTG4abiy8OLTNhnUOy2+0+UfBHr/fOzu7atStAQNpST6/XH1fbx6LW\nXRMwJNcME+7ZAkFXQ6PUkByXTHJc8Mj2bo+bkpoSDlQd4IDzAEeqj1BSU0JxdbH3Z00xxdXF2Osa\ncym5lW5ssTbWx9pYH2Q231AFg0ohyQ7JNujjjKQ0oh910anYdMnsM/anNKYH9igzsieamEqvzjQc\n/ucxlQqinbHEOGLRHuyDorVDBaWrsTH/o2lZqPOo6k4fgYVVhMrKvHlJ4uKCjySsVmtQoWhLvba2\nfSxch91wdPbNo/CgOV+IkEDQ3VAqlPTQ9qCHtgfDzM2T6TVQ566jtKa0mTDZa+3Yam3Y6xp/2jV2\n1modrO3XULsG2AHsQOOCAXZIOgADysFcG41a0wtZ25uamJ7Ye/bmt/ie7Deb2W82U6bz2z8lQ0St\nVx+aHtqqxt8jayCqWkVUte7ocfRaOUQd9v4eURt4NNcbGTR13ob9G/c/D1YeWdP4e8N5g1ERdS3+\nL8I+Euqoesfb9rGIPfSjT4Qq9BX0iRG5TASCkxWNUkOv6F70iu7VqvtdHhfldeU+cXLUOaisr6Si\nvoKKugrf71vqG3+vrD9Ied3X1FeVY/ipmjMrwFirQSuZUavMSBFm3JFmqqPNVMUYcWp1OGL1HOih\no1ivpz5IAsDWonR5dUJT1yBMEhG1EUcPQzPR0tT53V8GkQdAXe89b/rT93u9G/aHtkG4dDXhWO6N\nl97lvxfgR8g6rWMNEggEpwxlQCEAdcCBo0fH4QacR4+OZAqh5xPF13iBQCAQhI2wjoSSk72LhuXl\n5UHXbhquH0+9BgeEtrYdylmwYYTUnTJfCJs7nu5mLwibO4PuZi+Ez+awjoT0ej3JyclYrYEh2K1W\nK3q9PqTjQGvqHW/bAoFAIOg8wj4dN27cONavXx9QZrFYyMjIOOF6x9u2QCAQCDoJOczY7XY5IyMj\noCwjI0MuKiryndtsNjk5OVnOyclpU73W3NNaALkLvF1tQtjc8XQ3e2VZ2NwZdDd7ZTl8Noc9YgJA\nQUEBS5YsYeTIkVitVtLS0hg7tjF2lN1uJzk5mblz53L77be3ul5r72kNYo63c+huNnc3e0HY3Bl0\nN3shfDZ3CRHqDogPVefQ3WzubvaCsLkz6G72ghAhgUAgEJyChN0xQSAQCASnLkKEBAKBQBA2hAgJ\nBAKBIGwIERIIBAJB2BAiJBAIBIKwIaJotwKLxcLGjRsxGo1YrVaGDx9Oenp6uM1qkby8PKxWK4WF\nhVitVjIzM5kwYUK4zWoVdrudrKwsFixYEG5TjonFYmHp0qWYTCZKS0vJzMwkKSlIxrMuwKpVqygo\nKACgtLSUlJQUpk6dGmarmpObm4vBYAjax7piX2zJ3q7aD1uy2Z9O6YuduTO2O1JYWNgs6sLEiRNl\nq9UaJouOTW5urmyxWHzndrtdTklJCYg40ZWZNm2aPHHixHCbcUyWLVsmZ2ZmBpRNmzYtTNa0zMaN\nG+Xc3NyAstzc3C73mVi5cqVsMBjk/Pz8Zte6Yl9syd6u2g9bsrkpndEXxXTcMcjOzmb69OkBZZmZ\nmcycOTNMFh0bq9XKsGGN2SJ1Oh0zZ84kMzMzjFa1DqvVis1mO2Zep3Bjt9uZNm1awDfEnJwcvvzy\nyzBaFZqcnJxm38AnTJjAypUrw2RRIEVFRUyfPp2ioiKMRmPQe7pSX2yNvV2tH7bGZn86rS92qMSd\nBBgMhmax5mw2myxJUngMOgY2m01OS0uT7XZ7QHlhYaEsSdJxxc3rTHJycuScnJwuPxK6//775ays\nrGblXfX9TUtLCzpiaDqy6AqkpKQE/ZbeVftiMHu7ej8M9R7701l9UYyEWsBut2O325t9a2jIVbRr\n164wWNUyer0eq9VKUVFRuE1pM/n5+YwbNy7cZrSKRYsWMXLkyGblXTVFyLhx48jIyAj4XKxatYpJ\nkyaF0arW0936Ynfuh9C5fVE4JrRAWVkZQNCkeOAdrnbFh06D3f6sWrUKg8HQJe1twGq1kp6e3i3i\nbdntdnQ6HYsWLcJoNFJWVobRaOwSi87BmDNnDqtWrSIlJYWFCxeSlJSEw+EICAjclemOfbG79kPo\n3L4oRKgF7HZ7uE1oNxYuXMisWbPCbUZI8vLyuqSnVjAaEiUWFBRw3333+cqzsrIoKyvrsn/Hhg0b\nuPTSS8nMzGT48OHk5+eH26RWc7L0xa7eD6Hz+6KYjjsFyMnJwWw2BzwwuxLd7QHTYG/TFPHXX399\nl3ZYWbRoEXPnzmXlypW+tCbddbqoO9LV+yGEpy8KETrJsVqt5OTk8MUXX4TblJAsW7YsYBqrq3vG\nNYhPUxEaNmwYdru9y61PAEyfPp2MjAyGDh1Keno6RUVFJCcniyzDnUR36IcQnr4oRKgFGh4y5eXl\nLV7vymRlZXVZt2HwTmmNGDEioKyrrwk1LIY3/GxKw3RdV6Hh263/OoROp2PFihXo9fpuMS3X3fti\nV++HEL6+KNaEWkCv15OcnIzVamXo0KG+cqvVil6v7/KLi9OnT2fu3LkhF3O7Ahs2bKCwsJAlS5b4\nyiwWC1arlaysLEaOHNklF/sbPhfBPgNd7YG4ceNGUlJSgl7LzMzsFtOh3bkvdod+COHri0KEjsG4\nceNYv359wAffYrF0+WmMRYsWkZWVFdA58/PzSU5O7lJhZYItgM6bN48NGzYwZ86cMFjUOjIzM9m4\ncWNAqniLxdIlPZ+Sk5NZtmxZ0Gt2u73Lf5Yb6I59sbv0QwhfXxTTcccgOzu7WQfOyckhOzs7TBYd\nm9zcXMDrImqxWLBYLKxatYply5Z1uQ9+MEpKSrr8lNy0adNYuHBhQFlWVhaLFi0Kk0WhafifN512\ns1qtlJaWdjnRhODTQF25Lwazt6v3w9b0sc7oiyK9dysoKChgyZIljBw50udV5P8NuCsRbENfAykp\nKezYsaOTLWo9RUVFZGdns3TpUhwOB1OnTiUzMzMg9ElXosHelJQUCgsLmTRpUpf9XID3W3lhYSEm\nkwnwTnF1FXdyh8PB7NmzsVqt5Obmkpyc7Ntg6z8F1FX64rHs7Yr9sLXvMXRuXxQiJBAIBIKwIabj\nBAKBQBA2hAgJBAKBIGwIERIIBAJB2BAiJBAIBIKwIURIIBAIBGFDiJBAIBAIwoYQIYFAIBCEDSFC\nAoFAIAgbQoQEgk7AYrGgUCiaRSluyqpVq1AoFG1Ouz1x4kQUCtGdBd0P8akVCDqB4cOHo9frKSgo\nwOFwhLyvITba5MmT2/waXT0Pk0AQDCFCAkEnMW3aNGRZZunSpSHvWbp0KZIkce2113aiZQJB+BAi\nJBB0Etdffz1As+jbDVgsFhwOB9ddd11nmiUQhBUhQgJBJzFs2DCSk5NDTsk1JBNrECvwpluYOHEi\nKSkpKBQKjEYjkyZNoqioqFl9/1jEGRkZQdeI7HY7CoWC6dOnN7s2d+5c0tLSfK8zffr0oK8jELQn\nQoQEgk4kMzMz5JRcTk5OwFSc1WolNTWV5cuXk5qaSmZmJiNGjCA3N5e0tLQW15ag5TWiptfS0tLI\nyspCoVD4XicnJ4eUlBQKCgqO4y8VCFqHECGBoBNpmGprOiUXbCouOzsbSZJYuXIlX3zxBfPnz2fF\nihVkZ2djt9tZtWpVu9g0d+5cCgoKyM/PZ/369b7X2bhxIxA846ZA0F4IERIIOpGkpCSGDRvWbEou\n2FTc9OnTWbZsWbOkbQ2JxWw2W7vYNHv2bDIyMhg+fDh2u913JCUlkZ6ejsVioby8vF1eSyBoiirc\nBggEpxqTJ0+moKCAnJwcZsyYAXhTQTf1ihs2bJhPcOx2Oxs2bMBisYR0bDheHA4HK1euxGAwBL0u\nSRJlZWXExcW16+sKBCBESCDodKZNm8bMmTNZsmQJM2bMwGq1UlRUxMSJEwPus9vtzJxioyS5AAAC\nGElEQVQ505diGbxrN2lpae3mMGC1WgGvI8PMmTND3hdKoASCE0WIkEDQyeh0OoYPH+6bksvNzQW8\nTgv+pKenU1BQQGZmJpmZmQwdOhSA/Px8X522UlZWFnBuNBoB0Ov1zab9BILOQKwJCQRhoMFLLicn\nhyVLliBJUoAI2O12CgoKmDhxIvPnz/cJEAS6YrcVi8UScK7X69HpdCGdHAwGA6mpqcf9egLBsRAi\nJBCEgYbYcAsXLqSgoCDkBtWmzgcNU3TQXIz83a71ej2yLJOfnx+0rj+ZmZnYbLZm8ermzp2Lw+EI\nuqdIIGgvxHScQBAGdDod48aN841Amk7F6fV63/VJkyYxYsQICgsLWbZsGSNHjgS8LtzJycmkp6cD\ngaI0efJk8vLyyMjI8IULaqjbVNjmzJlDbm4uubm5pKamMmzYMKxWKwUFBaSlpXHfffd15FshONWR\nBQJBWMjNzZUlSZIVCkXQ63a7Xc7MzJQNBoMsSZI8YsQIOS8vT5ZlWc7MzJQVCoU8ffp0WZZleeLE\nic3aycnJkVNSUmRJkmSj0ShnZWXJsizLBoPBV8+fmTNnymlpabIkSXJqaqrvfoGgI5Fk+QQmmAUC\ngUAgOAHEmpBAIBAIwoYQIYFAIBCEDSFCAoFAIAgbQoQEAoFAEDaECAkEAoEgbAgREggEAkHYECIk\nEAgEgrAhREggEAgEYUOIkEAgEAjCxv8D35NEikcC+EAAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23b05d4d0>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtwW9d59/vvhmRJtCQSgOT7jQSgNBe/rkiQaZImvogA\nZZ70PT2WCMppO6dzphbBNMdO54wt0IlzrDZNZEjuO8f2NDZBnzmTpvO2JEH7bRtWlgjItvr2ShJQ\nU6duKnJDsR1bjiVyg5KsiyXu88cmNgkCvIAXAASfzwzHxMYmuAhv8cdnrbXXUnRd1xFCCCGKmKXQ\nDRBCCCHmImElhBCi6ElYCSGEKHoSVkIIIYqehJUQQoiiJ2ElhBCi6K0tdAMWIxAI0NDQgNvtxmq1\nznheLBZjcHAQu92OqqrU1NRQX1+fx5YKIYRYjBUdVrFYjEOHDmV9zul0cvLkSVRVpa2tjaNHj5rP\nNTc343A4qKqqyldThRBCLMKKDiun08mhQ4cyqqq+vj7q6uoACAaDtLa2pj3v9/sJBAJ0dXXlra1C\nCCEWbkWHldvtZvv27VmfSx3v7u7mySefzPi6cDi87O0TQgixNJRSW26po6ODvXv3AqBpGna7HU3T\nKC8vTzvPYrGgqiqVlZUFaKUQQohclNRswGg0Sm1trfl4ZGQEICOoUlRVzUu7hBBCLE5JhVUsFqO6\nutp8rGlaAVsjhBBiqZRMWIXDYZxOZ6GbIYQQYhms6AkWUz3zzDMcO3ZsSV5LUZQZnyuxIT4hhFgR\nSqKy0jSNWCyWMTblcDgAGBsby/p1qedzMVuQCSFEKbn//v0oChkf99+/P+9tKYmwikQiWVewsFqt\nOByOjIkUqqpitVpnnAmo63rWDyGEWE3Wr7+a9fiGDdfy3JISCav+/v4Zx6s8Hg/9/f1px2KxGF6v\nNx9NE0KIFeuxxxpwOr+ddszp/BaPPpr/358lcZ+Vz+djbGyMI0eOZDyXTCbx+Xxpyy01NDQQCoVy\nvscq1QVYAm+ZEELMS2/vcV54oY9Ll9awYcM1Hn3Uy1e/em/e21ESYdXa2oqiKLz44otZn4/H43R2\ndlJXV4eqqrjdbnbs2JHz95GwEkKIwiiJsMoXCSshhCiMkhizEkKIQnvvvfeoq6tjzZo1KIqy6j7W\nrFlDXV0d77333rK8vxJWQgixBB566CF27drFxYsXZ5xRXMofFy9e5KGHHuKhhx5alvdXugFzIN2A\nQoiZrFmzhosXL7Ju3bpCN6Vgrly5QllZGdeuLf3UdgmrHEhYCSFmoiiK/G5g+d4H6QYUQghR9CSs\nhBCihIXDYZqbmxf0tRZL8UREySxkK4QQxai39zjPP3+Uy5fXsn79VR57rCHnm2oX8xqlsp5p8cSm\nEEKUmN7e43zzm0c4evSPefPN/Rw9+sd885tH6O09ntfXAGhubsZisVBbW0sikTCPRyIRnE4nFouF\nhoYGkskkgLkk3ZYtWwAIhULY7fasr5EPElZCCLFMnn/+KMPD30s7Njz8PV54oS9vr6HrOuFwmIaG\nBjRNo7a2Fp/PBxg7VjQ3N/Pyyy+jaRoOh4O9e/cC0NdnvP7Zs2fRNI3W1lZef/11RkdHcTgctLe3\nz/tnWArSDSiEEMvk8uXsv2IvXVqT19dwu9088sgjALz00ktYLBaSySRdXV14PB4eeOAB8zm73Z7x\n9VarldHRUSoqKgCw2Wx534ldwkoIIZbJUmyxsRSvUVVVlfY4tXXS8PAw4XA4LaBmGuP6/ve/TzQa\nNc9dyH6AiyHdgEIIsUyWYouNpXiNbHv6OZ1OXC4XTU1NjIyMmB+RSCTj68PhMNFolGPHjnH06FGa\nmprm/b2XilRWQgixTFIz9l544TtTtth4MKfZgEvxGrFYjJ6eHurr6wkEAni9XsrLy/H5fAQCAaLR\nKG63m0AgQCKRSNtSCWB0dBS73U55eTmaphEKhfJeWZXEChaxWIyuri62bNnC2bNn8fv9aWVvLBZj\ncHAQu92OqqrU1NRQX1+f8/eRFSyEEDMp1hUsenp66OvrQ1VVIpEIXq+X7u5uysvLAYhGo/j9flRV\nzXiuubmZnp4erl27RkNDAwMDAzidTp555hl8Ph/hcDhju6Xleh9WfFiFw2EikQgvvfSSeczv95sz\nVVRVpbW1Ne0vhebmZoLBYEY/7lwkrIQQMynWsMo3WW4pC03TaGlpSQuqUCjEsWPHzMfBYJDW1ta0\nr/P7/QQCgby1UwghxOKs6MoqEAhgsVg4cOBA2vFTp06ZW9bb7XZisVjaFvaapmG32xkfH8/p+0ll\nJYSYiVRWBqmssujo6KCuri7jeCqYNE0zg2kqq9UKGKEmhBCi+K3o2YCaplFRUUFHRwd2u52RkRHs\ndju7d+8GYGRkBMAcLJxOVdW0iksIIRbKYrFw5cqVVb+f1XItfrtiK6vUfQPxeJy9e/eye/du9u7d\nS39/Px0dHQB5v8NaCLF61dTU8Oyzz3LlypVCN6Ugrly5wrPPPktNTc2yvP6KDatUEE2f679nzx6Z\nPCGEyLtXX32VV199lbKyMhRFWXUfZWVl5nuwHFZsN2AqpKaHVXV1NZqmLWo8qlSW1BdC5M/tt99O\nf39/oZtRslZsZZWaJJH673SqqppBNjY2lvWcfN+BLYQQYmFWbFjB5GKMMz1ntVqznqOqKlardcbJ\nFbquZ/0QQghRGCs6rPx+P4ODg2nHYrEYNpvNDCKPx5NRmsdiMXNjMSGEEMVvRd8UnEwmcbvdDA0N\nmccaGhpobW1l165d5jk+ny9tuaWGhgZCoVDO09blpmAhhCiMFR1WAIlEgmAwiNPpZHh4mObm5oyF\nFePxOJ2dndTV1aGqKm63O+Oc+ZCwEkKIwljxYZVPElZCCFEYK3rMSgghxOogYSWEEKLoSVgJIYQo\nehJWQgghip6ElRBCiKInYSWEEKLoSVgJIYQoehJWQgghip6ElRBCiKK3YvezEkKIlai39zjPP3+U\ny5fXsn79VR57rIGvfvXeQjer6ElYCSFEnvT2Hueb3zzC8PD3zGPDw98GkMCag3QDCiFEnjz//NG0\noAIYHv4eL7zQV6AWrRwSVkIIkSeXL2fvzLp0aU2eW7LyrOiwUlUVr9dLNBpF0zRUVaWtrY1oNJp2\nXiwWo6Ojg56eHg4dOpTxvBBC5MP69VezHt+w4VqeW7LyLNmY1djYGOXl5Uv1cvMWjUbN8LFarbz8\n8svU19ebz6cCbOrmi83NzTgcDqqqqvLeXiHE6vXYYw0MD387rSvQ6fwWjz76YAFbtTLkHFbxeJxQ\nKEQgEKCyspJkMkl9fT2xWAxFUdi3bx8HDhxYjrZmUBSFSCRCbW0tIyMjWXf+DQaDtLa2ph3z+/0E\nAgG6urry0k4hxOoz26y/F174DpcurWHDhms8+uiDMrliPvQcRCIRXVEUXVEUPR6P67qu636/X1cU\nRfd4PLrD4dAtFove09OTy8sumKqqeiQSmfUcm82mJxKJtGOjo6O6oig5fz9Az/EtE0KsQj/+8Zu6\n0/ktHXTzw+n8lv7jH79Z6KatWDmNWQUCAQD6+vrYvn07AKFQCI/HQ19fH8PDw5SXl+etspqLpmlo\nmobdbk87brVaATh16lQBWiWEKHUy62/p5dQNqKoqTU1N5phQPB4HjG61lObmZsLh8BI2ce42aZoG\nwMjICHa7nd27d5uPgRnH0lRVzdp1KIQQiyGz/pZeTmGlaRqKopiPI5EIAF6v1zw2MjJihsdyS1VM\nqXACIyxTx/LVDiGEmEpm/S29nLoBq6urzYACaG9vx+FwpFUu0Wg0b7PsKioq2Lt3b9qx1OQJIYQo\nlMcea8Dp/HbaMWPWn3eGrxBzyamy8vv9tLa2sm3bNqxWK6qqEgwGASOk/H4/mqbR0tKyLI2dj6qq\nKlRVZWxsbMGvMbV6FEKIXMmsv2WQ64yMffv26VarVVcURff5fGnHFUXRvV7vks4AmU0wGMw4lprp\nF4/Hzc+TyWTGeYqiZMwSTGFi1t9MH0IIIfJL0XVdX4rQU1UVAIfDsRQvN6/v53K5MiZJpI5rmkZ5\neTkul4twOGzOXkydk7o3KxepimuJ3jIhhBDztOAVLE6dOmXOxHM4HBljV8vN4XDQ3t6eMZsvEong\ndrvNtng8Hvr7+9PCKhaLpU0KEUIIUdxyXhswHo9TW1uLw+HA4/HQ1NRETU0NNpuNPXv25PXeJbvd\nTiKRMB9rmkYoFKKjo8M8FgwG6e7uTvu6UChkjrUJIYQofjl1AyYSCZxOJwA1NTXs2bPHnNDQ19dH\nNBrFZrORSCTyVmX19PSgqipnz55F0zTa2toyqq14PE5nZyd1dXWoqorb7WbHjh05fy/pBhRCiMLI\nKaxSN/y2t7dnTBkHo2JpbW3F5/PR2dm5pA0tBhJWQghRGDmFld1ux+FwMDAwMOM5brebsbExTp48\nuSQNLCYSVkIIURg5jVlpmmZ2A87E4XCYMwOFEEKIpZBTZeX1eonFYpw9e3bGc+ZTfa1UUlkJIbKZ\nbTsQsTRymrre3t6O2+1m586dGdPGE4mEuYLF1Nl4QghRynp7j/PNbx5JW2V9eNhYakkCa+nMWlk1\nNDRkLD00PDyMqqooioLD4cBqtZpbyuu6Tk1NDXV1dbz44ovL3vh8k8pKCDHdzp1PcfToH2c5/h1e\ne+27BWhRaZq1surv70dRlIxfzhUVFQCcOXOGM2fOAJPbcKTCrBTDSgghppPtQPJj1rAaHR3NVzuE\nEGJFku1A8iPnFSyEEEJMku1A8iOn2YCplSASiQSapmG1WnE4HOzZsydt7b1SJWNWQohsenuP88IL\nfVO2A/HK5IolNq+wisfj7N27l1gsNuM5brebjo6Okg4tCSshhCiMOcMqGo2aK5TX1NTg9/upra01\n1wQcGBigvb2deDyOoij09fUtaN29lUDCSggBcl9VIcwaVslkkqqqKjRNm3E9wJTUuoA2m23Wm4ZX\nMgkrIUS2+6qczm/z3HM7JbCW0awTLEKhEJqmsW/fvlmDCqClpYUnnniC0dFRnn322SVtpBBCFFJv\n73F27nyK++/fz+/+7p+mBRXA8PD3eOGFvgK1bnWYtbJyu92cOHGCa9fmPwXTYrHg9Xo5cuTIkjQw\nF6ktQl566aW047FYjMHBQex2O6qqUlNTQ319fc6vL5WVEKVnapfe2Nh7wDrKy280P79y5RqqqnDx\nYur3yv6Jj3T33befN97IPC6Wxqz3WamqmvM29VVVVQVbFzAQCGTcG6aqKm1tbRw9etQ81tzcjMPh\noKqqKt9NFEIUkfQuvePAEWD6508BU1eokPuqCmHWbsBkMplzWDkcDjRNW1SjFkJVVUZHRzOWhwoG\ng7S2tqYd8/v9BAKBfDZPCFFkenuPT+vSO4oRTtM/n/43fQMg91Xl26yVVUVFRc5V0sDAAFardVGN\nWojUrMW+vvR+4+7ubp588sm0Y263m3A4nM/mCSGKSKqiOnv2M1OOrp3h8+mVlDGJYsuWh7n77k9P\n3Ff1oEyuWGazVlYej4fR0VFOnDgxrxeLx+Mkk8kFjQctRjQaxePxZBzXNA1N07Db7WnHU2F66tSp\nfDRPCFFknn/+6ERFNTWIZvo8WyX1Gj/84e/zxhv7ee2170pQ5cGsYZWqSHw+35wvlEwmzfOmVzLL\nTVVVqqqqMiY+jIyMAJOL7Gb7OiHE6jO5+OzUIJrp83uBnZSV7eHuu/+AnTu/w3PPSSWVb7N2A9bU\n1LB37146OjrYtm0bwWCQXbt2ZZzX09NDIBBAVVWampqorq5etgZn+94zTasvxNiZEKK49fYe5623\n3p54lAqc7wBr2LTpBJ/61DfYvPkGxsY+RFGMz42uvm9IQBXQnJsvtre3MzIyQk9PD01NTdhsNhwO\nh7l9fWpiA0BTUxNdXV3L3uiU5Qqj6ZM0hBClYXKs6hsYldP3MALrXpzOb/HccwEJpCI1r52Cu7u7\niUQiBINBotEog4ODDA4Oms97PB4CgUDex6q6u7vTqioJGSHETFKz/86e7Zxy1Kiotmz5D5577vcl\nqIrYvLe193g85iQGVVXTVl0vhHg8Tm1tbdqx6WNWqbaNjY1lHbeaqe0z3fQrYSjEypR99t+9pLoB\n7757vwRVkZt3WE1VqICaamBggOHhYTo7J/9KisVi5k3AdXV17N692+yunLoavKqqWK1WKisrC9By\nIUQ+pVdUT2U9R27oLX4LCqtikG1SxaFDhxgYGOCZZ54xj3k8Hvr7+9PCKhaLmSvJCyFKV2ZFlZrl\nN3UR2m/x6KMPFqJ5IgcltVPwmTNnMrrwgsEg3d3dacdCoRDBYDCfTRNCFEDm/VTGNHRjrGo/W7Y8\nLNPQV4icdgouVolEgmAwSFdXF8lkkr179+L3+80p9Kkdjuvq6lBVFbfbvaA9t2QhWyFWjt7e4/zO\n7/y/aNoPSV/rz2DM/pOgWilKIqzyRcJKiOLX23uc73znz3j77eu4dGkLk4vQHgf6SM3+++EPZfbf\nSiJhlQMJKyGK2+Qq6gpGSElFVSqWLKxmmh5eSiSshChuNTW/Tzz+A9L3nJqsqGy2n/GjH31dgmoF\nynmCRTwe5+tf/7q5CGwymaS2thar1cqaNWvyvi6gEEKAUVW9/fb5iUdTF6K9F/gusJ/Pf94lQbVC\n5RRW0WgUt9tNe3u7udRRIBAgFotRX19PZWUlBw8e5JVXXlmWxgohxEyef/4oly7dOfFI9pwqNTl1\nA9bW1hKLxejr6zOXVrJYLHg8HnMnXpvNhsvlor+/f3laXEDSDShE8br//v28+eYO0nf77UNRhqmu\ntvFHf7RHqqoVLKebglOrqqeCKh6PA8bOuynNzc2ysaEQIq8mV1LfP3HEWPMPYPv26xkc/NMCtUws\nlZzCStO0tPXxIpEIQNpqECMjI7I1hxAib/bv/wEHD/6Eixenr6RudP1997v/eyGbJ5ZITt2Abreb\nU6dOcfbsWQBcLhcAQ0ND5jl2ux273Z52rFRIN6AQxWX//h/w3e/2MT7+6sQRuZeqVOU0wcLv9zM6\nOsq2bdvM1SBSXYDRaBSXy4WmaTQ1NS1LY4UQorf3ODt3PsVdd/n4wz88yvj4r055dnLm3913f1qC\nqoTk1A3Y0tLC8PAwoVCI4eFhmpqaeOKJJwA4evQoqqri8XjSFpIVQoilMnnT707gJLCd9Gnqk2Ql\n9dKyZDcFq6oKFMf2IctFugGFKKzJm36fwvhb+yrGNPX0VSrKyvx0d/+2VFYlZMFbhIyNjTEyMoLN\nZqOioqKkQ0oIUVi9vcd57LHnUNXrJo5MD6rUSuprsFj+lX37vBJUJWZBK1ikVqxwOp3m9vYul4tn\nn312yRsohFjdenuP88gjP0RV1wKuiaPTg8qYVGGx/Cvf+Y6X/ft/v0CtFcslp27ARCKB0+kEoL6+\nnmg0SiQSYceOHdhsNpLJJG63O683BEciESKRCFu2bGF4eBi3252xMWMsFmNwcBC73Y6qqtTU1Jj3\niuVCugGFyL+dO5/CWHNgLZC66Xcn04OqrOxt9u27T4KqROXUDZjasHBwcJCqqirsdrv53OjoKAcP\nHqStrY0nn3ySAwcOLG1Ls4hEIiiKkjaho7a2Fk3TzIkfqW3uUytsgHHjssPhoKqqatnbKIRYnMuX\nU7+mrpK6f8oIqDPAD9i4UeHLX3bx6KPfkK6/EpZTN2BXVxcej8fc1HC6ffv2UV1dnbcVLNrb2zOO\neTyetOPBYJDW1ta0c/x+P4FAYNnbJ4RYvLGxXzLZ7fdtJqent1NWVkFn59d57bXvSlCVuJzCStM0\nsxtwJg6Hg+Hh4UU1ar4URTFX0UjRdR2bzWY+7u7upqamJu0ct9stS0IJUaR6e49TU/MImzZ9FUX5\nMvH4B8AHpE+k2M+6dU3s2/erElJ5kLyULPjwR07dgNXV1QwMDMx6TjwezwiH5dLV1ZVxLBwO8/Wv\nfx0wwlXTtLTuSgCr1QrAqVOnqKysXPZ2CiHmZ//+H3DgwBtcubIZuBnYBHRirEzxZ8CLwDo2b07y\nF3/xf0lQLRNd1zlx+gSHhw5zeOgwJ06f4Ke//1PurLhz7i9eJjmF1Z49e2hra+P111/PGkjNzc2o\nqsq+ffuWrIG5CIVC1NbW8vjjjwPGOoXAjJtCqqoqYSVEge3f/wP+5E9+zPnzY8AW4L9MeTb1K+pe\nJseroKZmvwTVEhu9OEqf2sfhocO8NvQam9dtptHVyLe/8m3uu+s+yq4rK2j7cgqrffv20dnZSX19\nvbl4bTAYpL29nUgkwujoKA6HI+8rWPT09NDX14eiKHR2dprHZUFdIYpXb+9xfu/3vseHH24GbgHW\nYaxIMZWsTrFcxvVx4h/Ezerp3z78N75y11dodDXy1Feewmmffcgn3xa0gsXBgwc5cOAAyWTSPFZR\nUYHf7y/oUkvJZJL6+no6Ojqorq4mFotRW1vL+Ph4xrkWi8Wcdj/d1JXlsyl0360QK13q3qnTp38J\npNb2exe4Y9qZsjrFUhq5OMLR4aMcHjrMkaEjWDdYaXQ10ritkXvvupcNazcUuokzWtAKFvv27TO7\n+lRVxW63m+NAhZQKzPr6erMLUAhRfB577GVOn74TuMbkr6HLGOH0wylnpq9OsW7dW+zbt0OCap7G\n9XEG3x/ktaHXODx0mLd++Rb3Vd5Ho6uR/fftp8q2cm7fWbK1AYuFqqq4XC4ikQg1NTXY7XY0TcsY\nt7JYLDmPWclNwUIszmTXnx34FeBtYNvEs6eBmzDC6c8wZgBeBK5n48ZyfuVXZLff+Tjz8Zm06mnr\n9VvN6unLd365qKun2cxaWVkslhm7xFK/sKf+AlcUxfzvtWvL26esqiput5vXX3+d7dun93Mb41VW\nqxWHw4GqqmnnqKqK1WqVyRVC5FGq6+/DD9cBTozxqPuAN4DNE2edxrjh93bgFqzWBH/+5y0SULO4\nNn6NgfcHzOrp7TNvc3/l/TS6GvnuA9+l0lpZ6CYuiVnDavfu3Qt60bnGfJZC6p6v6QvoplZ/T81W\n9Hg89Pf3p4VVLBZL291YCLF8JhehHQN+DaPrL9XdpwP3A70Y3YDjwC/ZuHHzRCUlQZXNRxc+4sjw\nEQ4PHebo8FFu2ngTja5Gvl//fX79jl9n/dr1hW7iklvR3YCHDh2ipaWFiooK85jX66W2ttZc7imZ\nTOLz+dKWW2poaCAUCuVcWUk3oBC5+a3fCvAXfxEH1mDcM/U5jK6/qfdOXQDWYbF8xF//dZuEUxbX\nxq/xL7/4F7N6+s+z/8kDVQ/Q6GrkQdeDBb3/KV9WdFgBdHR0MDw8bC5kW1tbyyOPPJJ2Tjwep7Oz\n09zd2O12Z50FOBcJKyFmNjkedQ6jYroM3AlM/St/G3Ar8BPgpSnHH+Hpp2tkEdopPjz/oVk99Q33\ncevmW82xpy/d8SXWrVlX6Cbm1axhlRqzGh4eprKyctYxrJR8jVkVgoSVENn19h6nufmP+fhjC5D6\nHWEB6oBTE4/XY4xT3QzchlFZbQA+4mtfu5v//t+D+W10kbk6fpV/fu+fzeppaGSIeke9WT3dXn57\noZtYULOOWdXX16MoirnW3nzHsPIxZiWEKA779/+AP/qjv0LX1wPXT3mmDCOcLk48vh1jrOrPABUj\nvDZSXb121QbV6fOnzXDqG+7jzoo7aXQ18t92/je+ePsXuW7NdXO/yCqx4rsB80kqKyEm9fYe57d/\n+zskkxuAcoxxqanToi8C3wD+n4nPN2N0A07e4GuzfYMf/Wj1TEe/On6Vf3rvnzh80lg1IqEl8Dg8\nZvV06+ZbC93EopVTWI2Njc24zt5qIGElhMGYOBHD6JxJ/U74mPTK6j6MsanfAp7DmJa+DtiIoqzH\n4djEc8/9XskH1fvn3jerp6gapdJayYOuB2l0NfLFO77IWsuC1mZYdXIKK4vFQigUypjAMFVbWxsd\nHR2cPXt2SRpYTCSshID77vs/OH78NJMhVYbRpZfAGKdKDQPcBdzD1LGpe++9kTff/P/y3OL8+uTa\nJ/zje/9oVk/vJN/B6/TS6Gpkp3Mnt2y+pdBNXJHmjPSenh7zZl/A3B4+G13XCYfDjI6OLm0rhRAF\nZ1RTr2GMPW3CCKnUH6W3A7+N0cU3NnHsJ8A7wPWUlY2yb99XS3a233tj75nV07HEMZw2Jw+6HuRP\n/5c/5ddu/zWpnpbAnJWVxZLT/oyAcSPu1PuaSoVUVmI1MkLqbwE7RjffTcAoRrV0FaP7b3WNR125\ndoV/ePcfzOrpF+d+QYOzwayebtp0U6GbWHLmDKupO+o2NzfT0tKCx+OZ8XybzUZ9ff3StbCISFiJ\n1ebuux/ipz8dwQiptUyOSZ3DCKu1GIGV2o5nI3AdN9+8lpdf/j9LKqjeTb5rbqfxeuJ1PrXlU+bY\n0+dv+zxrLGsK3cSSltOYldfrpa2trWTDaC4SVmI1uesuL++8sxYjkDZOHL0ANAJ/g1FNXcOosoyQ\nstnG+dGPSmMH3yvXrvA/3/mfZvX04YUPzeqpwdnAjRtvLHQTVxWZup4DCSuxGhgTKPox9pbahDEl\n/cLEs+uAGzAmToQxxq3KgPM8/fT/uuLHpH6u/dysnt449Qaf2foZs3qqvbVWqqcCyjmsotEo3d3d\nJBKJWc87cuTIohpWjCSsRCkzxqZ6MbaWvx5jtt85jLD6LPBPGEE1jhFaG4BLXHedxquvfmtFVlOX\nr17m7975O7N6OvPxGXa6dprV09brtxa6iWJCTmHV09ODz+eb17nZdudd6SSsRCmaDKnNgBWj268M\n40beK8Al4FMYEyxexwiyzazUsanEaMKsnt489SZ333i3WT25b3VjUXKfVCaWX05h5XK5UFWVvr6+\nVTluJWElSo0xgeI0RkgpGN1+Fozp52UYVZU28bFl4vnz3HvvzSvmfqlLVy9x/OfHzepp9NKoGU5e\nh5ct128pdBPFPOR8U3BLSwsvvfTS3CeXIAkrUSp6e4/zm7/5B1y7dhNGSG2c+O95jIDaitEFOI6x\nevpajBt/x1bE2NTwyLBZPf3dz/+Oe266xwyo6luqpXpagXK6U62ioqLoFqnt6elBVVWGh4dRVRW/\n35+x4G6O2OWHAAAgAElEQVQsFjNvZlZVlZqamlVZGQoBRlD9xm88jnG/1CYmQ4qJYyrGyuibMVZM\nNyZZGGNTTxVll9/FTy7y5s/fNKunc1fO8aDrQX73V3+XP3/oz7GV2QrdRLFIOYVVS0sLHR0dBIPB\nolgjsKenB4fDYYZTMpnE7XYzMjLC3r17AWPn4La2trSblJubm3E4HFRVVRWk3UIUijE+9S9M7dIz\nwuoaRtffbYADOIFRXW0FzvO1r3226FZGP3n2pFk9/f07f8/2m7fzoOtBOps6+dWbf1WqpxKT82xA\nn8/HiRMnCAaD1NTUzLj0Uj7C7NChQzzxxBNpxzo6OvD7/eYED7/fz86dO9m1a5d5TjQapb29na6u\nrpy+n3QDipWqt/c4//W/Poqur8OYkp6ajq5hbJR4G0ZYnWGy4jrP5z63gbfeerVArU738Scf88ap\nN8zq6eNPPjY3I/Q4PFg3WAvdRLGMcgqrVDBpmjbrefnYfFHTNDweD9FoNG1be1VVzYkglZWV2O12\nYrFY2hb2mqZht9tznrEoYSVWGuPG3g8wxptSN7GuwaikLmFMP7+IEVTlpGb5bdjwMeFwYaej67rO\nf579T7N6+od3/wH3LW5z7Omem+4pumEJsXxy6gac77T1fFxAVqsVVVVJJBJs37496zmappnBNP1r\nAU6dOpUWYkKUihtv/AoffTSKcT/UTRP/3TTx7BmMgEpVIhbgFowp6ee5996tvPnmK3luseHClQu8\nfup1s3q6cu0Kja5G/G4/XU1dVGyomPtFREnKKaza29uXqx0LMjIyknEsEolgs9morKxEVVVg5i7J\nVPUlRKkwpqKfxAinOyaOpqagn59y5p3AuxOf2ybOGePpp38zrzP9dF3nP878h1k9/dN7/0TtrbU0\nuhr5q4f/irtvvFuqJwHkGFbzEY1GCYfDvPjii0v90vPS3t7Ok08+CczdXSlEqZgMqTVMhlSqkrqI\n0e2XBD7BmFxxDmO/KWMVChjh6af/t7wE1fkr5zmWOGZWT+P6OI2uRr5R9w16mnsoX1/4yVui+OQc\nVslkkkgkknXPKl3XCQaDJBKJgoRVKBRi69atPP7444t6HflLTqwUs4dUqpK6iBFI1on/foDR5adg\nrJh+flmDStd1/v2jf+fw0GFeG3qNf/7FP/P52z5Po6uR3t/q5bM3fFb+zYk55RRWiUQCt9s9Z8XS\n0tKyqEYthKqqhEIhBgYG8v69hci3yYkTCjOH1FWMzRHXYFRRv5g4fhtGWJ3j6ad3LEtInbt8jmgi\nyuGTh3lt+DUUFBpdjTz2a4/xQOUDbF6/ecm/pyhtOYVVIBBA0zSCwSDV1dX4/X7cbjd+vx9d1wkE\nAmzdurUgK1y0tbVx7NixtGMOhwOAsbGxrONWqeenm2m2n/z1J4rB2rX3cO3aODOH1HmMaenuicen\ngZPArUxOSb/GW28t3WLTuq7z1i/fMqun/vf7+cLtX6DR1cgffOEP+PTWT8u/H7EoOU9dr62tNW+w\nPXjwIN3d3fT39wPGGJHD4eDll19Ou69pubW2ttLW1pZ1soTL5SIcDqfNGFRVldra2qwTNGYjU9dF\nIU3O8JsppD7EGJv6PPAfGPdQpbagP8+dd17l5z/vW7L2jF0eI6JGzOrpOst15n1P91fez6Z1m+Z+\nESHmKafKStM0nE6n+bimpoa2tjbzsdVqxefzceDAgbyFVUdHR0ZQRaNRc4UKj8dDf39/WljFYjG8\nXm9e2ifEYq1fv50rV65OPErtMQWZIXULRrffP06cdzNwnrIylY8/Hlx0O3Rd5ycf/sSsngY/GORL\nd3yJRlcjj3/pcT615VNSPYllk1NYVVVVmdPBAWprawE4ceKEGQZOp5OOjo4lbOLMwuEwYExhT1VJ\nIyMjhMNhsysyGAzi8/nM5ZfAmIgRCoXy0kYhFmqyuw/Sq6lUSL2PsdDsbRgh9R7GTb13YoxJLX4q\nunZJS6ueytaW0ehq5IkvPcEDVQ9w/XXXz/0iQiyBnLoBfT4fr7zyCn19fezYsQMAm83Gww8/bM7+\na25uJhKJ5NzFlqtsN/umOJ1OTp48aT6Ox+N0dnZSV1eHqqq43W6z/bmQbkCRDzOHFBhB9T5GJbUF\n+Bhjtt9mjPulUhMnFhZSuq5z4vQJs3qKn47z5Tu/bHTvuRrZtmXbIn4yIRYup7BKLWWkKArd3d3s\n2rULv99PR0cHPp+P0dFRIpFIyW4jImEllpui3D3x2UzjUu9jdPf9EmNjxDKMxWaNiutrX7sn5wVn\nRy+O0qf2mQG1ed1mGl2NPOh6kPsr76fsurLF/EhCLImcF7JVVZVgMEhrayvV1dVomkZ9fT3xeBwA\nj8dDd3d32np9pULCSiyXuWf4vYex4OxmjCnpa5laSd155/i8J0+M6+NG9TRxU+5PPvwJX7nrK2b1\n5LQ7534RIfIs57CaSereq9S6e6VIwkosteuvd3Px4uWJR9kmT6SWRLod42bea0yu9zf/XXtHLo5w\ndPgoh4cOc2ToCNYNVrN6uq/yPjas3bCUP5YQS27Jwmo1kLASS2Xypl7IPnkiFVKfxpiGDrmMS43r\n48Q+iJnV01u/fIv7Ku8zA8phy36PoRDFKqewam1tnXNqqq7rKIpSsLUBl5OElViszGnokF5NZQup\nraS27oBRfvzjP8y6dceZj8+kVU9br99qhtNX7vqKVE9iRcsprCyWuXfeTHUDLvdswEKQsBILNTlx\nAmYel3qXXELq2vg1Bj8YNKunt8+8zf2V95sBVWmtXK4fR4i8yymsZloTcGRkhFgsRiAQwOVyceTI\n0i3jUkwkrESu5h9SMBlU6SH19NM+s7vvowsfcWT4CIeHDnN0+Cg3bbzJ3Izwy3d+mfVr1y/rzyNE\noSzpmFVquSW/38+BAweW6mWLhoSVmI/0SRMwd0htwbipF6YH1V/9zf/NjdvLzOrpZ2d/xo6qHWb1\ndGfFncv5owhRNJZ8goXf7yccDnP27Nm5T15hJKzEbOYfUqlp6Osw7pWCtPulNp7lC79TRqW3nL7h\nPm7dfKtZPf36nb/OujXrlvtHEaLoLPnmi4qiZN3rSohSlb2rD2aupGAyqBSw3Aq3XQHXSdZ97peU\n3WbhVkc99VX1HPIe4vby25ex9UKsDEtaWUWjUbxeLw6Hg6GhoaV62aIhlZWYavbxKMgMqSmV1KZP\nwLUOXBo4PkQ5t4Z9u75Jo6uRL93xJa5bc91yNl2IFSenyspiscw6dT31SzwQCCyuVUIUsflNmoDJ\nkNoMljG4fRRcF2DbZbBeBNWOfcTOvz31z9y6+dZlb7cQK1lOldVc22pYrVYefvhhdu/eveiGFSOp\nrFav3t7j/MZvTL0Bd65JE8Dme8D1JrjOg+MCaBth6BY4WcGXqz7N373xw+VvuBAlQlawyIGE1eqT\nXkXBrCFl0eGOj41w2nYeKj6B4Rtg6HYY2gTnP0LX38pPw4UoMSURVuFwGJvNRn19fcZzsViMwcFB\n7HY7qqpSU1OT9bz5kLBaPdJD6gYgtfrDtJDarBrB5DpnVE8j64xgOumEX9wG4x+jKO8yPi4hJcRi\n5DRmFY1G6evrM1dYt1qtOBwO9uzZk7YT7yuvvJK3nYJTW5KkNmKcSlVV2traOHr0qHmsubnZ3EVY\niKlmrqLKgDXGp2vG4I5RcE2E1OarMLwRflYOf3sLnHcwucbfz6SSEmKJzCus4vE4Pp8vbZfgqYLB\nIG63m+7ubgYHB/H5fBw8eJDHH398SRs7VSKRML/vTJswprYymcrv9xMIBOjq6lq2tomV4+67H+Kn\nPz057ei0rr7yEdj2Ibg+gqozcHYdDG2Gv7kVflEGusLkiunnWbPmZ1y9+pO8/QxCrAZzdgPG43Hc\nbjcANTU1+P1+amtrzS3uBwYGaG9vJx6PoygKuq7j8XjSqpnl5nK5CIVCGbv/2u12YrEYlZWV5rHU\nDsPj4+PkSroBS8fMVRSw5nq48wy43oFtZ2DTJRjaaHTvDd8BF85N+zojpNat+4DLl08sf+OFWIXm\nDCu73Y6mabS3t7N3794Zzzt48CBtbW0oisLIyEheN1/MFlapUNI0jfLy8rTzLRYLqqqmhdh8SFit\nbLMGVIUC206D6zRUfgRnNsLQOji5Cd4vA/0zTC4wu/jdeYUQuZm1G/DQoUNomsa+fftmDSrA7FbT\ndZ3u7m4eeeSRpWvlAqRWfZ8eVCkLCSuxMmUNqTXjcNcFI5y2nYbrL8PQVvjpDfDX5fDx9H8a/8HU\nKgrelfEoIfJo1rD6y7/8SxRF4Zlnnpn1RSKRCLFYjK6uLpqbm2lvby94WM20QrxYHbIGlPVjo1vP\n9a9G9fTLjTB0A7x6N3yQnBh7ugZUYqzfN+VrzZB6W0JKiAKYNaxUVcXhmHtHUY/Hw8jICFarlerq\n6hknYqwUc20wKYpTRkCtHYe7NhoTI7b9PWy4AkM3w7/dAP/jM3DxDEY4jQFT/5+/R+auvA/MuCuv\nEGL5zRpWyWSSz3/+8/N6odSmi3a7nRMnZJBZ5EdGQNmuwLa14DoDd43Ah1YjoHpuhdPlE9XTu8CH\nE19QBlyc8gJTq6h3pIoSokjMGlYVFRUMDAzk9IIDAwNmcBVSqiIcGxvLOm41W8U40wQKqbiKQ1pA\nrR2HygvgUmDbR7DumhFO/+qAV78IF1NbcLyLUUEBfBH4x4nPLyJjUUIUv1nDyuPx0NPTw4kTJ9Ju\n+p1JPB4nmUzS1NS0ZA1cqNQNy6qqprVdVVWsVqtMrlhh0gLKfnli1YircOeoUTEN3QrdLqOS0i9M\nnHiF9G05Uv4RCSghVpZZw+rJJ5+kp6eH+vp6EonEjDPrUnw+n/l1xcDj8dDf358WVrFYbM4FeUVx\nMAPqunHYdmFizb1LcN01OLkV4pXQcyNcWsfkGn0XyB5QKTJZQoiVyDLbkzU1Nezdu5fR0VHcbjev\nvPJK1vN6enpwuVyoqkpTUxPV1dXL0tjZZOu6CwaDdHd3px0LhUIEg3JPTLFau/YeFOVzKFu3wRfO\nwu/8HB7/T/j1c3BuK3R+Cf7kN+Cvvwj/boVLV0hVR5Mf2dwBfGbi87fR9cMSVEKsIPNayNbn89HT\n0wOAzWbD4XCYXWyqqpo7Azc1NeVtGaNkMsmBAwdQVZVwOIzD4cDj8eD1etO2KInH43R2dlJXV4eq\nqrjd7oyVLuZLbgpeHopyt1E9VV0wFoTddh7WWODkDca9T+pdcDm1GWG2/aJmIl19QpSKea+6HolE\nCAaDRKPRjOc8Hg+BQGDBq5mvFBJWS0dRPgdbr8C2c0b33u0X4X2rEU4nb4Bf3szkdHIJKCFWuwVt\nEaKqKpqmmZMYVgsJq4VTlLuNmXpVFyb3e1KAkzcZN+YmtsDlqbNIJaCEEJNKYj+rfJGwyo2ifA5u\nuDwZTrddNFYpH7rdmCDx0SaMm29TJKCEENlJWOVAwmp2ZvXkmKieXBPhM3SzEU6JLXBlLZMbGIIE\nlBBiPiSsciBhlc6YWq7DjVOqp1svwnup6ukGY/XytOoJJKCEELmSsMrBag8r876n9anqaWJyxLgy\nUT3dAKfsc1RPIAElhMiVhFUOVmNYmdXTTZcnp5XfcgnetRkTI05uhbOLrZ5AAkoIMRsJqxyshrAy\nq6cN18BxfnLs6ep1k+F0yg6fTF//MdfqCSSghBDzJWGVg1ILq/QVy3W4+dLk2NPNl+Ad++R9TyM3\nTftqCSchRP5IWOVgpYdVxnYaG66Bc0r1dGXdZDidssPViiknLyScQAJKCLEUJKxysJLCKnOnXECZ\nWj1dgZvOwc8nqqehrXNUTxJOQojCkbDKQTGHVdZwAii7Cs4L4Bo3NiS8tHZi7OkO+PkNcHXNlJOl\na08IUZwkrHJQDGE1YyiZJ+hwS8XEVu5n4MZzRpfe0O0wdBOMpqaUTw8mkHASQhQrCasc5Dus5gym\nlOtvAucZo3JynYGP10/c93QzvLN1onpa6JgTSEAJIQptVYRVLBZjcHAQu92OqqrU1NQsaIX45Qyr\n+QXTHRMn63Br0gimbR/B1gtw6gYjoIZuBi1b+xYWTmvW/IKrV3+Sw9cKIcTSm3Wn4FKgqiptbW0c\nPXrUPNbc3IzD4aCqqirv7Zl3tZQKppTrr4DrLLhOg/NDuLDB6NaL3gPvlMG11D6aOlI1CSFKTclX\nVn6/n507d7Jr1y7zWDQapb29PeeNInOprOYfSpARTADKRrhtxAinbadhyzlI2I3JEUNbIVk25WQJ\nJyFEaSv5sLLb7cRiMSorK81jmqZht9sZHx/P6bVmCqsFV0umiUkPGy+B68OJ6uk0nFs/uWrEuza4\n9ouc2ivBJIQoFSUdVqlQ0jSN8vLytOcsFguqqqaF2FxSYQWfm+PMOULJbMT4RPX0rjH2ZP8Y1C0T\n9z19AmPXZX+ZWb+vhJMQovSU9JjVyMgIQEZQpeQaVtllC6ZNWY4BnIdNl41p5a4z4DwLyQ0wtB6O\n2OHd240VzAGYLagklIQQq0tJh5Wmacv0ylMDKlswTZkmbhmH25MT9z29D9YroG6CoU1wpArOzVU9\nSTAJIURJh9VCTXb3zWS2vZqAzerkenuO86CtM8Lp8M3w3vVTqqfpJJiEECIbCasFmbZmnkWHOz6e\nXLG84hMY3ggnJwLq/PTqSUJJCCFyUdJh5XA4ABgbG8s6bpV6frqZ5pxMVlzvwuZPjGBynYeq8zA6\nUT313gK/KJuoniSUhBBiKZR0WFmtVhwOB6qqsn37dvO4qqpYrdaFT664R4MHTxvV0882w9/eDOcd\nSDAJIcTyKOmwAvB4PPT396eFVSwWw+v1LvxF//2z8G9fAP2CLEckhBB5UNL3WQEkk0l8Pl/acksN\nDQ2EQqGcK6tiWHVdCCFWo5IPK4B4PE5nZyd1dXWoqorb7WbHjh05v46ElRBCFMaqCKulImElhBCF\nYZn7FCGEEKKwJKyEEEIUPQkrIYQQRU/CSgghRNGTsBJCCFH0JKyEEEIUPQkrIYQQRU/CSgghRNGT\nsBJCCFH0JKyEEEIUPQkrIYQQRU/CSgghRNGTsBJCCFH0JKyEEEIUvZLYKTgcDmOz2aivr894LhaL\nMTg4iN1uR1VVampqsp4nhBCieK34sIpEIrS0tBAOhzOeU1WVtra2tF2Cm5ubcTgcVFVV5bOZQggh\nFmHFdgMmEglaW1tJJBLY7fas5wSDQVpbW9OO+f1+AoFAPpoohBBiiZTETsEul4tQKJSxVb3dbicW\ni1FZWWke0zQNu93O+Ph4zt9HdgoWQojCWLGV1Vw0TTODaSqr1QrAqVOnCtAqIYQQC1GyYTUyMgJA\neXl51udVVc1nc4QQQizCip9gMRNN0xb8tanuvoU+L4QQIt1ih09KtrISQghRPBb7R37BK6tcuuO2\nbNlCRUXFMrbGMNNfADLBYpK8F5PkvZgk78UkeS8mLUVvVEHDKpFI0NbWNu/z6+rqeOKJJ+Z1rsPh\nAGBsbCzruFXqeSGEEMWvoGFVVVVFV1fXsry21WrF4XCgqirbt283j6uqitVqTZvOLoQQoriV9JiV\nx+Ohv78/7VgsFsPr9RaoRUIIIRaiZMIqW79wMBiku7s77VgoFCIYDOarWUIIIZbAil3BIplMcuDA\nAVRVJRwO43A48Hg8eL1edu/ebZ4Xj8fp7Oykrq4OVVVxu90ZK13MlwyYTpL3YpK8F5PkvZgk78Wk\npXgvVmxYCSGEWD1KphtQCCFE6ZKwEkIIUfQkrIQQQhQ9CSshhBBFT8JKCCFE0Vuzf//+/YVuxEoQ\ni8X48Y9/zKlTp+jt7eXSpUurcskmVVVpbm7mtttuw2638/777xMMBlEUZVW8H+FwmA8++CDrz7ra\nrpGZ3ovVdo309PTQ29vLj370I55//nmuv/56PvvZz6ads1qujbnei0VdG7qY0/DwsO71etOO+Xw+\nXVXVArWocIaHh3VFUcwPm82m9/T0FLpZedHX16fbbDY9Go1mPLfarpG53ovVco2Ew2E9FouZjzVN\n051Opx4Khcxjq+XamO97sdBrQ7oB5yEYDNLa2pp2zO/3EwgECtSiwlEUhUgkgqZpqKrKyMgIu3bt\nKnSzllUikaC1tZVEIpGx83TKarlG5vNerKZrRFVVqqurzccVFRUEAgH8fr95bLVcG/N5LxZ1bSx5\nvJYgm82mJxKJtGOjo6O6oiiFaVABqaqqRyKRQjejYJxOZ9ZqYjVeIzO9F6vlGhkdHdXdbreuaVra\n8VT1kLoeVsO1Md/3YjHXhlRWc9A0DU3TMv6KtFqtAJw6daoArRLFRK6R1clqtaKqKolEYsZzVsu1\nMZ/3YrEKvvlisRsZGQHIuicWGKXvattuRFVVNE0DjPfHbrenrce42sg1kmm1XCOp//dTRSIRbDYb\nlZWV5uayq+HamOu9SFnotSFhNYfUmyoMqb8Qp15czc3NGcdWE7lG0q32a6S9vZ0nn3wSkGtj6nsB\ni7s2pBtQ5KSiooK9e/emHSvFwWKxcKv5GgmFQmzdupXHH3+80E0puGzvxWKuDQkrsWhVVVWoqsrY\n2FihmyKK1Gq4RlRVJRQKceTIkUI3peByeS/me21IWM0hdaPaTG9kKd7YN5uDBw9mHEuV9qn++dVG\nrpF0q/UaaWtr49ixY2nHVuu1ke29gMVdGxJWc7BarTgcjow3UlVVrFZryQyOzoeqqrS1tWXMYEoN\nrJbqP7y5yDUyabVeI62trRw8eDBjIsVqvDZmei8We21IWM2Dx+Ohv78/7VgsFsPr9RaoRYXhcDho\nb2/P+AcWiURwu90zznhaDeQaMazGa6Sjo4O2tra0nzkajZrTuFfTtTHbe7HYa0PCah6CwSDd3d1p\nx0KhEMFgsEAtKhy73Z52L4WmaYRCITo6OgrYqvzSs2yuvVqvkWzvxWq6RsLhMGBUB7FYjFgsRiQS\nobu7m6qqKmD1XBvzeS8Wc23ItvbzFI/H6ezspK6uDlVVcbvd7Nixo9DNKoienh5UVeXs2bNompbx\nl1SpSSaTHDhwAFVVCYfDOBwOPB4PXq83bbrtarhG5vterIZrJNvNvilOp5OTJ0+aj0v92sjlvVjo\ntSFhJYQQouhJN6AQQoiiJ2ElhBCi6ElYCSGEKHoSVkIIIYqehJUQQoiiJ2ElhBCi6ElYCSGEKHoS\nVkIsQCwWw+fzYbPZsFgs2Gw23G43hw4dKnTTFsTr9WKxTP468Pl8aY+FKDS5GoXIkd/vp7a2lp6e\nHiwWC16vl61bt3LixAkCgQB2u514PF7oZmYVDoexWCz09PSkHVcUBUVRMo4JUSwkrITIgc/no6Oj\nA5vNRiwW4+zZsxw5coSTJ09y7do19u3bh6ZpuN3uog0syAyi7u5uhoeHC9QaIeYmYSXEPEUiEXp6\nenA6nSQSCbZv355xzjPPPEN7eztgBFuxmr7KWkVFRcmt3SdKi4SVEPOUWiU7GAzOup3B3r17qamp\nQVVVotGoeXz6uFCKpmlYLBZaW1vTjquqis/nw+l0YrFYsNvtNDc3p61aDUa3ZGoR0UAgYI6juVyu\ntO4+r9dLc3MzMDkmldoUcL5jVAcPHsTtdpvtaW1tzWgPGKuKTz2vtrY27b0QIlcSVkLMUzQaxWaz\nsWvXrjnP9fv9APT19aUdn20caOpzqqricrl45ZVXcLlc5jhZOBzG7XaTTCYzvj7VRfnwww/T0tJi\nhl0qJNra2mhpaTHbFwqF0kJ3rjEqt9tNW1sbFovFbE8oFMLpdKZ1eQYCAVpbWzl16hQ+nw+Px2Pu\n31TMXaOiyOlCiDkNDw/riqLotbW18zo/FovpiqLoDQ0N5jGPx6NbLJaMc0dHR3VFUfTW1lbzWEtL\ni26xWPRoNJp27sGDB3VFUfRwOJx2rqIousvl0pPJpHk8EonoiqLofr/fPNbd3a0riqL39PSkvW5T\nU1Na26Y/DgaDuqIo+rFjx7L+nG632zxmtVp1l8uVdl6qLVN/RiFysbbQYSnESqBpGjD/bdlTm80t\nVGtrKzt37szY86i6uhqA0dHRjK+Z3j1ZX18PkLWbbj70KeNaBw4cwOv1UlNTY74XYPyc9fX1RKNR\nxsbGKC8vJ5lM4nK50l6rvr6eWCyG1WpdUFuEkLASYh5Sv2RVVZ3X+anzFvrLubq62gwmTdMYGBgg\nFouZkzeyqampWdD3mo9kMklfXx82my3r84qiMDIyQnl5OU1NTYTDYbP70uPxUF1dnXVCihDzJWEl\nxDykKqr5htXAwEDa1+VK0zQCgQBdXV3m+JTb7cbtds9YKc20U+tCpcawUj+z1+slEAjMeH4qyLq6\nujh06BDt7e1p57e0tBAMBqmoqFjSdorVQcJKiHnyeDzm9PWpW7inRCIRPB4PgFkB7dmzZ87XHRkZ\nyThWX19PPB7H7/fj9/vNqiQajRIOhxfzY+QsFYJWq3XeW7E/8cQTPPHEE4yNjdHX10d7ezuhUIiB\ngQEzyIXIhcwGFGKeUlVCtupC0zQaGhqora3l4MGDxONx3G73vLq+YrFYxmvF43F8Ph8vvvhi2mvo\n0+6PWk6p72W1WqmoqCASiWQ9z2azmWNUqqoSCATMGYjl5eXs3r2bo0ePmuNWqenyQuRCwkqIeaqv\nr6epqcmcVj51GrbVaqWrq4tYLEZbWxuKotDd3Z329VarFV3X0+43SnX3ZTN9EsXUcxcbWvP5+qlT\n2f1+P6Ojo+Z9WikHDx4kmUym3SN26NAhc+r+VKqqoijKrPeoCTET6QYUIgddXV00Nzeb9ztVVFRQ\nW1vLyMiIGV6KoqDrOoODg2mrQjz88MP09PTg9XppaWlB13W6u7upq6tjdHQ0rZJJdTk2NzdTW1vL\n8PCweS4YM/8cDoc542++UuNKgUCA/v5+nnnmGfO56QE29fEzzzxDOBw2J05UV1ejqqpZQT7++OOA\nMUaXarvdbqe+vh673U5XVxdjY2Ps27cvp/YKYSrQlHkhVrRYLKb7fD7dbrfrFotFt9vtem1trd7R\n0cmP4fMAAADLSURBVKFrmqZ7vd6s9zOFQiHd6XTqiqLodrtdb2tr03Vd1202W9o9SJqm6X6/X7fZ\nbOb9XanX8vv9usViMc9PPZ56j1XK9Hu9dF0322a3281jPp8v7b6q6Y9TAoGA7na7zfu6Uu3Pdp7T\n6Ux7b6a/F0LkQtH1PHaCC7GKPPvss2bFIYRYHAkrIYQQRU8mWAghhCh6ElZCCCGKnoSVEEKIoidh\nJYQQouhJWAkhhCh6ElZCCCGKnoSVEEKIoidhJYQQouhJWAkhhCh6/z9oWFi7XbkdAgAAAABJRU5E\nrkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23ad55450>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X1wG+dhLvpnoW9ZJgFI/pZoEqCbJnEaEQDjk1RxPCJA\npZOkrSWCcjJn0tuOSTC51845c20BSuJEnpxGguR/Yk9tE1TnnJzeSSIStM+9EU8rEVBiVUkmIblQ\nmzjuxMaClmTLsSVgQcv6ssS9fyx3iSVAEiBBAASe3wxGxGKxfAmt+Oj9FhRFUUBERFTBTOUuABER\n0XwYVkREVPEYVkREVPEYVkREVPEYVkREVPEYVkREVPFWlrsAi+H3+9He3g6n0wmz2TzreaIoYmxs\nDFarFZIkweFwoK2trYQlJSKixVjWYSWKIg4dOpTzNbvdjtdffx2SJCEQCOD48eP6a52dnbDZbGhq\naipVUYmIaBGWdVjZ7XYcOnQoq1Y1PDyM1tZWAEAwGERPT4/hdZ/PB7/fj/7+/pKVlYiIFm5Zh5XT\n6cTWrVtzvqYdHxgYwN69e7PeFw6Hl7x8RERUHEK1LbfU19eHrq4uAIAsy7BarZBlGXV1dYbzTCYT\nJElCY2NjGUpJRESFqKrRgNFoFC6XS3+eTCYBICuoNJIklaRcRES0OFUVVqIooqWlRX8uy3IZS0NE\nRMVSNWEVDodht9vLXQwiIloCy3qARaYDBw7gxIkTRbmWIAizvlZlXXxERMtCVdSsZFmGKIpZfVM2\nmw0AMDExkfN92uuFmCvIiIiqxUMP7YMgIOvx0EP7ylKeqgirSCSScwULs9kMm82WNZBCkiSYzeZZ\nRwIqipLzQURUK9asuZHz+Nq1N0tcElVVhNXIyMis/VVutxsjIyOGY6IowuPxlKJoRETL0uOPt8Nu\n/5bhmN3+TTz2WHl+d1bFPCuv14uJiQkcO3Ys67V0Og2v12tYbqm9vR2hUKjgOVZaE2AVfGRERPMa\nGjqJ554bxtWrK7B27U089pgHX/jCg2UpS1WEVU9PDwRBwAsvvJDz9VgshiNHjqC1tRWSJMHpdGL7\n9u0Ffx+GFRFReVRFWJUKw4qIqDyqos+KiGihzp07h9bWVqxYsQKCIPCxwMeKFSvQ2tqKc+fOLcnf\nE8OKiGraww8/jJ07d+LKlSuzjgTmY/7HlStX8PDDD+Phhx9ekr8nNgMWgM2ARNVnxYoVuHLlClav\nXl3uoix7169fx7p163DzZvGHtzOsCsCwIqo+giDw33QRLdXnyWZAIqIqJIoimpub8zovc7eK2UiS\nlNf1lgrDioiohtntdgSDwXIXY14MKyKiHIaGTmLHjm/joYf2YceOb2No6GRJryFJEjweD/x+v17z\nCYVCsFqtMJlMcLlcSCQS8Pl8OHTokP4+v9+PQCCQtY5pJBKB3W6HyWRCe3s70uk0ACAej8Pv9+vn\nad+jubkZoVAoqzYVCAT012OxWMGfyYIplDcACj8youqS69/00aOvKHb7NxVA0R92+zeVo0dfyfu6\ni71GPB5XBEFQenp6lEQioaRSKUUQBOX06dOKLMuK1+tV/H6/Eg6HFY/Ho7/PbrcrsVhMGRsbU+x2\nu6IoipJKpRSLxaKcOHFCSafTis/nU7xer6IoijI2NqY4nU79e1osFiUWiymyLCsOh0Npbm42lOfQ\noUOKoiiK3+83fN+5Ps9i4G/eAjCsiKpPrn/T7e3fMoSM9tix49t5X3ex19DCIZMsy/rX3d3dSk9P\nj6Ioin6eFjaKohjCqre3Vw8nTeZ5Wljt2bNHCQQC+jnhcFi/Rua1FUVRRFHU35dpqX5HVs1+VkRE\nxXLtWu5fjVevrijpNWZuY/T9738f0WgUVqsVAPQFvN1uN6LRKMbGxuDz+bKuE4/HEQ6H9fcBubc7\nSiQSaG9v1583NTUZXs98v1LiEZTssyIimqEY22MUe4uNcDiMaDSKEydO4Pjx4+jo6NADw+PxoL+/\nH/39/di9e3fWe5ubm9HR0YFkMqk/IpFI1nk2mw1vvPGG/nzm9krlxLAiIpqhGNtjFHuLjVQqBavV\nirq6OsiyjFAohGQyCQDo6OhAf38/EokEtm7dmvVer9eLSCSCaDQKWZbh8/kMgyo0u3fvRigUQiwW\ngyzL2L9/f8VsOMtmQCKiGbRtMJ577qmM7TE+X9D2GMW4RmZQdHV1YWBgAFarVR9u7vV6ceLECWzf\nvh0bN27M2qdPe7/ZbMbAwAB8Pp8+yjAcDmed19LSgmAwiLa2NmzcuBF79uxBb29vzvLker6UqmIF\nC1EU0d/fj40bN+LixYvw+XyGtlZRFDE2Ngar1QpJkuBwONDW1lbw9+EKFkTVp1pWsHC5XDh8+HDO\nmlW+EokEZFlGS0sLALXpMRQKGfYDnM9SfZ7LvmYVDocRiUTw4osv6sd8Pp/+vwFJkhAIBAwfdmdn\nJ2w2W1bnIRHRcjQ8PDxrE2AhUqkU3G43EokE6uvr0dvbm7MPrByWdZ+VLMvo7u42BFUoFMKJEyf0\n58FgED09PYb3zdZeS0S03ITDYezevRsDAwOLvpbD4cDevXvR1NSkT/x99NFHi1DKxVvWzYB+vx8m\nkwn79+83HB8fH9e3rLdarRBF0bCFvSzLsFqtmJycLOj7sRmQqPpUSzNgpeBCtjn09fWhtbU167gW\nTLIs68GUyWw2A1BDjYiIKt+y7rOSZRn19fXo6+uD1WpFMpmE1WrFrl27AEAf1llXV5fz/ZIkGWpc\nRFR7TCYTrl+/zv2siuD69eswmZamDrRsa1baZLVYLIauri7s2rULXV1dGBkZQV9fHwA1zIiI5uJw\nOPDMM8/g+vXr5S7Ksnb9+nU888wzcDgcS3L9ZRtWWhDNXI5k9+7dHDxBRHl7+eWX8fLLL2PdunUQ\nBIGPBT7WrVunf5ZLYdk2A2ohNTOsWlpaIMvyovqjKmXGNhEtvc2bN2NkZKTcxaB5LNualTZIQvtz\nJkmS9CCbmJjIec7MoCMiosq0bMMKUMNmtoUWbTYbzGZzznMkSYLZbJ51cIWibp2S9SAiovJY1mHl\n8/kwNjZmOCaKIiwWix5Ebrc7q4ovimLWGlpERFS5lvWk4HQ6DafTaVjSvr29HT09Pdi5c6d+jtfr\nNSy31N7ejlAoVPCwdU4KJiIqj2UdVoC68GIwGITdbkc8HkdnZye2b99uOCcWi+HIkSNobW2FJElw\nOp1Z5+SDYUVEVB7LPqxKiWFFRFQey7rPioiIagPDioiIKh7DioiIKh7DioiIKh7DioiIKh7DioiI\nKh7DioiIKh7DioiIKh7DioiIKt6y3c+KiIhUQ0Mn8eyzx3Ht2kqsWXMDjz/eji984cFyF6uoGFZE\nRMvY0NBJfOMbxxCP/71+LB7/FgBUVWCxGZCIaBl79tnjhqACgHj87/Hcc8NlKtHSYFgRES1j167l\nbiC7enVFiUuytJZ1WEmSBI/Hg2g0ClmWIUkSAoEAotGo4TxRFNHX14fBwUEcOnQo63UiouVqzZob\nOY+vXXuzxCVZWkXrs5qYmEBdXV2xLpe3aDSqh4/ZbMbhw4fR1tamv64FWObmi52dnbDZbGhqaip5\neYmIiunxx9sRj3/L0BRot38Tjz32+TKWqvgK3s8qFoshFArB7/ejsbER6XQabW1tEEURgiBgz549\n2L9//1KV1yCRSCCRSMDlciGZTObc+dfn82HHjh36zsGAGnC9vb3o7+8v6PtxPysiqhSZIwAnJs5B\nENbg1ltvw9q1N/HYY56qGlwBAFAKEIlEFEEQFEEQlFgspiiKovh8PkUQBMXtdis2m00xmUzK4OBg\nIZddMEmSlEgkMuc5FotFSSQShmOpVEoRBKHg7wdAKfAjIyIquqNHX1Hs9m8qgKI/7PZvKkePvlLu\noi2Zgvqs/H4/AGB4eBhbt24FAIRCIbjdbgwPDyMej6Ourq5kNav5yLIMWZZhtVoNx81mMwBgfHy8\nDKUiIlqcWhkBmKmgPitJktDR0aH3CcViMQBqU5ums7MT4XC4iEWcv0yyLAMAkskkrFYrdu3apT8H\nMGtfmiRJOZsOiYgqWa2MAMxUUFjJsqz32wBAJBIBAHg8Hv1YMpnUw2OpaTUmLZwANSy1Y6UqBxFR\nKdXKCMBMBTUDtrS06AEFAL29vbDZbIaaSzQaLdkou/r6enR1dRmO+Xw+vbmSiKgaPf54O+z2bxmO\nqSMAPbO8Y/krqGbl8/nQ09OD++67D2azGZIkIRgMAlBDyufzQZZldHd3L0lh89HU1ARJkjAxMbHg\na2TWHomIKo020u+5557C1asrpkYAfr76RgBmKnRExp49exSz2awIgqB4vV7DcUEQFI/HU9QRIHMJ\nBoNZx7SRfrFYTP86nU5nnScIQtYoQQ2mRv3N9iAiotIqeJ7VbCRJAgDYbLZiXC6v79fc3Jw1SEI7\nLssy6urq0NzcjHA4rI9e1M7R5mYVgvOsiIjKY8ErWIyPj+sj8Ww2W1bf1VKz2Wzo7e3NGs0XiUTg\ndDr1srjdboyMjBjCShRFw6AQIiKqbAWvDRiLxeByuWCz2eB2u9HR0QGHwwGLxYLdu3eXdO6S1WpF\nIpHQn8uyjFAohL6+Pv1YMBjEwMCA4X2hUEjvayMiospXUDNgIpGA3W4HADgcDuzevVsf0DA8PIxo\nNAqLxYJEIlGyWtbg4CAkScLFixchyzICgUBWbSsWi+HIkSNobW2FJElwOp3Yvn17wd+LzYBEROVR\nUFhpE357e3uzhowDao2lp6cHXq8XR44cKWpBKwHDioioPAoKK6vVCpvNhtHR0VnPcTqdmJiYwOuv\nv16UAlYShhURUXkU1Gcly7LeDDgbm82mjwwkIiIqhoJqVh6PB6Io4uLFi7Oek0/ta7lizYqIyilz\nW5A1a27g8cfbq3sicIaChq739vbC6XRix44dWcPGE4mEvoJF5mg8IiJavKGhk/jGN44ZVluPx9Ul\nl2ohsOasWbW3t2ctPRSPxyFJEgRBgM1mg9ls1reUVxQFDocDra2teOGFF5a88KXGmhURlcuOHd/G\n8eP/Lcfxp/Av//K9MpSotOasWY2MjEAQhKxfzvX19QCACxcu4MKFCwCmt+HQwqwaw4qIqFxqcVuQ\nTHOGVSqVKlU5iIhoDrW4LUimglewICKi0qvFbUEyFTQaUFsJIpFIQJZlmM1m2Gw27N6927D2XrVi\nnxURldPQ0Ek899xwxrYgnpoYXAHkGVaxWAxdXV0QRXHWc5xOJ/r6+qo6tBhWRETlMW9YRaNRfYVy\nh8MBn88Hl8ulrwk4OjqK3t5exGIxCIKA4eHhBa27txwwrIioHGp5fpVmzrBKp9NoamqCLMuzrgeo\n0dYFtFgsc04aXs4YVkRUarnmV9nt38IPfrCjpgJrzgEWoVAIsixjz549cwYVAHR3d+PJJ59EKpXC\nM888U9RCEhHVoqGhk/ibv/kHQ1ABQDz+93juueEylao85qxZOZ1OnD59Gjdv5j800mQywePx4Nix\nY0UpYCG0LUJefPFFw3FRFDE2Ngar1QpJkuBwONDW1lbw9VmzIqKlojX1vfXWe3jzzbO4cWMS165t\nhqJsBrAv6/zPfW4ffv7z7OPVas55VpIkFbxNfVNTU9nWBfT7/VlzwyRJQiAQwPHjx/VjnZ2dsNls\naGpqKnURiYiyTDf17QDwQwAtAAQA/w3At3O+p1bmV2nmbAZMp9MFh5XNZoMsy4sq1EJIkoRUKpW1\nPFQwGERPT4/hmM/ng9/vL2XxiIhm9dRTP5lq6jsO4C4Af4/pukQ7gNqdX6WZM6zq6+sLriWNjo7C\nbDYvqlALoY1anNlENzAwAIfDYTjmdDoRDodLWTwiopyGhk7itdcuTT1biemQ0laseBDADgBPAdiH\njRsfwQ9+8PmaGlwBzBNWbrcbqVQKp0+fzutisVgM6XR6Qf1BixGNRuF2u7OOy7IMWZZhtVoNx7Uw\nHR8fL0XxiIhm9eyzx3H1asPUsxuYDqnMGtWDAL4Hu/06fvjDr9dcUAHzhNXevXsBAF6vd94LpdNp\n/TztfaUiSRKampqyalXJZBLA9CK7ud5HRFRO6gK1WjC1Azg/9fV0jWrVqv8Mh+P/rMkalWbOsHI4\nHOjq6kI8Hsd9992Hl156Ked5g4ODcDqdkCQJHR0daGlpWZLCzva9ZxtWX46+MyKiQkxMvIvpYBqG\n2gx4GibTl2Cx/CMcjiRefrkbY2P/ULNBBeSx+WJvby+SySQGBwfR0dEBi8UCm82mb1+vDWwAgI6O\nDvT39y95oTVLFUYzB2kQES2FoaGTOH/+GtSa1N9DDS3gzjv/Kw4ffrimw2mmvHYKHhgYQCQSQTAY\nRDQaxdjYGMbGxvTX3W43/H5/yfuqBgYGDLUqhgwRLSdPPfUTvPPOPwI4CXUAxQoAN3HXXe8zqGbI\ne1t7t9utD2KQJMmw6no5xGIxuFwuw7GZfVZa2SYmJnL2W81W9tkm/TIMiahYjKMAH4RWqwKAurp9\n5ShSRcs7rDKVK6AyjY6OIh6P48iRI/oxURT1ScCtra3YtWuX3lyZuRq8JEkwm81obGwsQ8mJiNRa\n1fQoQKNam/CbjwWFVSXINaji0KFDGB0dxYEDB/RjbrcbIyMjhrASRVFfSZ6IqNSma1WPYLq/SrV2\nbQ8ee+wr5SpaxVq2YZXLhQsXsprwgsEgvF6vIdxCoRBCoVCpi0dEBCBzbpXW9DfdX/XRj95gf1UO\nBe0UXKkSiQSCwSD6+/uRTqfR1dUFn8+nD6HXdjhubW2FJElwOp0L2nOLC9kSUTF84hP/Bb/73U4A\nxzCzVhUOf4VhlUNVhFWpMKyIaLH27Xse3/veMCYnX4Y6CnAYWq2qpeU8RPFweQtYoaqqGZCIqJIN\nDZ3EwYOvYHLyv2Lm3Kp163z43ve+Ws7iVbSihdVsw8OJiEj11FM/wZUrH0WuviqbDWz+m8Ocyy3l\nEovF8LWvfU1fBDadTsPlcsFsNmPFihUlXxeQiGg5mB4BmLma+vegbqz4PWzefHu5irYsFBRW0WgU\nTqcTvb29+lJHfr8foiiira0NjY2NOHjw4KxrCBIR1arpEYDZ+1OtW+eruf2pClXQAAuXywVRFDE8\nPKwvrWQymeB2u/WdeC0WC5qbmzEyMrI0JS4jDrAgooV66KF9eOWV7VBHAGqL1q6AIPw7vvMdN/bt\n+3p5C1jhCqpZaauqa0EVi8UAqDvvajo7O7n1BhHRDNmrq6t9VVu3WhlUeShogIUsy4b18SKRCAAY\nVoNIJpPcmoOIKMO+fc/j1VcvINfq6hwBmJ+CmgGdTifGx8dx8eJFAEBzczMA4I033tDPsVqtsFqt\nhmPVgs2ARFSooaGT2LnzWVy/HgbnVS1cQc2APp8PqVQK9913n74ahNYEGI1G0dzcDFmW0dHRsSSF\nJSJaToaGTsLrDeL69funjhhHANbVbS5b2ZabgpoBu7u7EY/HEQqFEI/H0dHRgSeffBIAcPz4cUiS\nBLfbbVhIloioFg0NncSjj/4QV66sx/RwdSOurp6/oi23pA2qqITtQ5YKmwGJKF87dnwb6iDpNwB8\nHTPXARSEv8NPf/p/cCJwnhYcVhMTE0gmk7BYLKivry92uSoSw4qI8jE0dBK7dj2La9fuB3AOwB0w\njgJ8DTbbDcTjg+Us5rKyoBUstBUr7Ha7vr19c3MznnnmmaIXkIhoOdGa/65duwa1+e+rAN5B5sCK\n1asn8eyz3yhnMZedgvqsEokEnE4nAKCtrQ3RaFR/7eLFi9izZw+OHDlS0gnBkUgEkUgEGzduRDwe\nh9PpzNqYURRFjI2NwWq1QpIkOBwOfa4YEVExPfvscbzzzl1Qf72eh9r89zdQwwoAfou9e9vZ/Feg\ngsIqGAwCAMbGxtDU1ASr1aq/lkqlcPDgQQQCAezduxf79+8vbklziEQiEATBMKDD5XJBlmV94Ie2\nzb22wgagTly22Wxoampa8jISUW25dk37tXob1KWV/ieAFwCsBrABLS2bOAl4AQpqBuzv74fb7dY3\nNZxpz549aGlpQTgcLkrh5tPb25t1zO12G44Hg0H09PQYzvH5fPD7/UtePiKqPWvW3IDa/NcOtVZ1\nGMCPAfwQ69bd4CTgBSoorGRZht1un/Mcm82GeDy+qELlSxAEfRUNjaIosFgs+vOBgQE4HA7DOU6n\ns2SBSkS1Y9++5xGNHgPwGqbXAHwKwD6sXLkLe/Z8ks1/C1RQM2BLSwtGR0fnPCcWi2WFw1Lp7+/P\nOhYOh/G1r30NgBqusiwbmisBwGw2AwDGx8fR2Ni45OUkour3la/48eMf/xuAzQC+gZnNf5/4hIXN\nf4tQUM1q9+7dGBsbw89+9jPDGoEabRFbt9tdtAIWIhQKweVy4YknngCgrlMIYNZNIbngLhEt1r59\nz2P16s/gxz/+LYB6AJ+EulLFdPMf8A9crWKRCqpZaaP92tra9MVrg8Egent7EYlEkEqlYLPZSr6C\nxeDgIIaHhyEIAo4cOaIf54K6RLSUPve5v8XJk+cBWAFsmjrK1SqWQsHzrMbGxnDgwAH85je/AQAM\nDw9jYGAAk5OT2LNnT1kWsN21axdefPFFHDhwAC6XS9+6ZKEEQcj5ICLS7Nv3PE6efBdqbWojgCtT\nj+zNFU2mv+Pmiou06OWWJEmC1WrV+4HKra+vD36/H8lkEqIowuVyYXJyMus8k8mESCSC7du3Z702\nXzBxBQsiWr/+r3DlijaY6yrUpr+fArgXwFcwPQn43/DlL/8JfvSjYHkKWiUKrlnNZLPZKiaoAHWy\nsizLOHHihL5O4cTERM5zZ1vHUFGUnA8iIkAdTHHlyhpM16Y2AHgLwJcA/AFAEMBrEIRf47vf9TCo\nimDOsDKZTFixYkXOh8lkMryufa39udQkSYLFYsHp06dzvi7LMsxmM2w2W9ZACkmSYDabORKQiAo2\nNHQSP/nJ7wAIAD4HYGLq8Q7UFSseBODALbesxE9/upcjAItkzgEWu3btWtBFS9G/o835mlk70oJJ\nGz7vdrsxMjKCrVu36ueIomjY3ZiIKB/qRorfh6LUQw2qf4damwoDuADgjwBWw26/FT/4wdc5p6qI\nirZFSDkcOnQI3d3dhlXfPR4PXC6XvtxTOp2G1+s1LLfU3t6OUChUcM2Kq64T1a6hoZP467/ehxs3\nzAA+hNo/9TzU3X/XQu23OgtF+UUZS1m9lnVYAeqAing8ri9k63K58OijjxrOicViOHLkiL67sdPp\nzDmwYj4MK6Laow5P/x2AWwHcMnV0NdS1/17MONMHm+0Ct/1YInOGlclkgiAIiMfjaGxs1J/PRVEU\nCIKAmzerb04Bw4qotqhBpfV5b4QaUlenvk5NPddqVRdx9OhTbPpbInP2WbW1tUEQBH2tvXz7sDgn\niYiWu6Ghkzh58h0A2go4NwF8AGA91C0//ufUcwXARmzY8D6Dagkt+2bAUmLNiqg27Nv3PJ5++ocA\nGqDOlQLUEX83oA6ibkRmE6AgPIrvfMfBkX9LqKCwmpiYmHWdvVrAsCKqfmpQ/S9MNzxpYfUXAH4O\nIA3gfQBmAOthMl3GU099kUG1xAqaFGw2m3H48OE5zwkEAti4ceOiCkVEVA5DQyfx9NP/L9TBFBsA\n3IHpeVQxAA8BsAD4EwACPv7xm7h5838zqEpg3oVsBwcHIQiCXpvQtofPRVEUhMNhpFKp4paSiGiJ\nDQ2dxJe+9DTUGtN1qH1U/QD+FsDvAJwGcA7ABgjCu3jkkU9wZYoSmrcZ0GQqfEUmt9ttmNdULdgM\nSFSd1L2ofg7gHqhzqD6A2j/1EQB9GWc+igcfvIlXXvnvpS9kjZs3rDJ31O3s7ER3d/ec+1VZLBa0\ntbUVr4QVhGFFVH3UPqqXoA5DNwG4DLXRqQ7Ae1BH/20AcAm33XYJ7777r2Uray0raICFx+NBIBCo\n2jCaD8OKqPoIwuehBtJKqOG0CmpQvQ91cMUtAC6hoeEG3nxzuGzlrHUcul4AhhVRdVmzZiuuX2+G\nOql3EuoK6rdBHfE3HVSC8EdMTorlKygVtlMwAESjUQwMDCCRSMx53rFjxxZcKCKipTQ0dBJf/OLX\nAWyB2j91FeqAivVQa1QWTK9MMYnvfOfR2S5FJVJQWA0ODsLr9S5VWYiIlpw6mOIY1KDS9qFSoA6u\neA/qSEAB6gCLS/jud/+KQ9MrQEHNgM3NzZAkCcPDwzXZb8VmQKLlTR1MEQawBtqgCbX5TwCQhLrm\nn3p8xYo/4sYNNv1VioLCymQyobu7Gy+++OL8J1chhhXR8iYIO6D2Q62AGlSXofZRTUANsFugNgum\ncPTo97nWXwUpqBmwvr6+4hapHRwchCRJiMfjkCQJPp8va8FdURT1ycySJMHhcNRkzZColq1f7wTQ\nhOn+qRtQg+pdqOG1BmoT4BV897tfYVBVmILCqru7G319fQgGgxWxRuDg4CBsNpseTul0Gk6nE8lk\nEl1dXQDUnYMDgYBhknJnZydsNhuamprKUm4iKq177/XgypXbodaarkCtVbUAGIc6t2oD1CHrKRw9\n+jSDqgIVtDxFMBhEW1sbnE4nXnrpJYyPj2NiYiLnoxQkSUJLS4v+vL6+Hn6/Hz6fz1Dmnp4ew/t8\nPh/8fn9JykhE5VVf/wDOnNECSYba5NcIdfmklVBrVzcgCH+AovyMQVWhCuqz0tYElGV57ouWYPNF\nWZbhdrsRjUYN29pLkqQPBGlsbITVaoUoioYt7GVZhtVqxeTkZEHfk31WRMuHunHiCNRRf1pf1GUA\n6wCcB3A3pgdZnIWi/K5cRaU8FNQMmO+w9VL0a5nNZkiShEQiga1bt+Y8R5ZlPZhmvhcAxsfHDSFG\nRNVh5co/w82bk5genn5p6nEH1D6qezKOJ3H06PPlKirlqaCw6u3tXapyLEgymcw6FolEYLFY0NjY\nCElSt6OerX9Nq30RUfUQhPuhhhQwHUgygE8CeBXqYIoVUAdYXMHRo4fY9LcMFL6k+jyi0Si+9rWv\nFfuyeevt7cXevXsBzN9cSUTVY9++5zOCagOmg+qPAK5BHUxxD9T+KrVZsKFhJYNqmSh4uaV0Oo1I\nJJJzzypGnaYPAAAfmUlEQVRFURAMBpFIJPDCCy8UpYCFCIVC2LRpE5544olFXafShucT0dzq6x/A\nxMQHMDb7AWpQrZn6+i2ok39vAriE1av/iDffPF3ysi4X6atp/Orcr3DqzCl8ePNDBD3l3buroLBK\nJBJwOp3z1li6u7sXVaiFkCQJoVAIo6OjJf/eRFQ+am3qHgBWGGtT16Hu+AuoNavN+ut1dUmk0wyq\nTOcmzuHUmVP6I56Ko/XuVmxr2Ia/uO8vyl28wsLK7/dDlmUEg0G0tLTA5/PB6XTC5/NBURT4/X5s\n2rSpLCtcBAIBnDhxwnDMZrMBACYmJnL2W2mvzzTbaD/WuIgqy3Sz3y1Qa02XoO7muwpqUL0PdZ+q\nO6AF1YMP3olXXvnn8hS4Qkwqk/j9e783hNPlDy9jW8M2bGvYhq9+8qtoubMFq1asKndRdQUPXXe5\nXPoE24MHD2JgYAAjIyMA1D4im82Gw4cPY+fOnUtT4hx6enoQCARyDpZobm5GOBw2jBiUJAkulyvn\nAI25cOg6UeUw9k9pzX5nodagzkNd829mberX5Shq2V29cRWjb4/qwfTLs7/EpvWb9HDa1rAN91nv\nq+j/kBdUs5JlGXa7XX/ucDgQCAT052azGV6vF/v37y9ZWPX19WUFVTQa1VeocLvdGBkZMYSVKIrw\neDwlKR8RFVfu/ikZai3qTwH8B9RalQXqlh8T+PKXt+JHPypvn0spJa8k8cuzv9TD6fQ7p/HR2z6K\nbVu24e9a/g7/+Jf/iDs23FHuYhakoLBqamrSh4MDgMvlAgCcPn1aDwO73Y6+vr4iFnF24XAYgDqE\nXaslJZNJhMNhvSkyGAzC6/Xqyy8B6kCMUChUkjISUfGotSnAGFTnoG7xsRlqUG2CGlarAFys+uWT\nFEXBm+k3DU16Z9Jn8MDmB7BtyzY8/dDTeGDzA9iwekO5i7ooBTUDer1evPTSSxgeHsb27dsBABaL\nBY888og++q+zsxORSKTgJrZC5Zrsq7Hb7Xj99df157FYDEeOHEFrayskSYLT6dTLXwg2AxKVx/33\nP4xXX30d2fOnzkLtkwLUARVbUO2rUtycvInfvvtbQzjdVG6qzXlb1Ca9T975Saw0FTzYu6IVFFba\nUkaCIGBgYAA7d+6Ez+dDX18fvF4vUqkUIpFI1W4jwrAiKj1jUGm1A61G9RGotSkBmf1Tt912Ce++\n+6/lKG7RXf7wMn7z1m/0YPrVuV/h7lvv1oNpW8M22Cy2iu5vKoaCwgpQA0tbHLalpQWyLKOtrQ2x\nWAwA4Ha7MTAwYFivr1owrIhK6957PThzRqshzBxIoa1EUYfpZr806uouLeuBFO998B5+cfYXejj9\n9t3f4s/u+DM9nD6z5TO47Zbbyl3Mkis4rGajzb3S1t2rRgwrotKZ7p/66NSfWrMfAHwawK+mvp5u\n+ltuNSpFURBPxQ1Neu9cegef3vJpPZxa72nF+lXry13UsitaWNUChhVRaRjX99OchdrcB6gDKpZf\n/9SNyRs4/c5pQzitNK3EZ+/9rB5O999+P1aYVpS7qBWnoLDq6emZt11UURQIglCW5ZaWGsOKaGmt\nWbMV16/fgLF/6g9Ql0jaDLWfCsgMqtWrz+PatcpcjeLS9Uv49blf49SZU/jXM/+K37z1G9xrvtfQ\n39RQ31D1/U3FUFBYmUzzr3urNQMu9WjAcmBYES2NoaGT+OIXvz71LNdE33VQd/jNnD/1Pr773b/C\nvn1fn3m5snnn0jv4xZmp/qazp/Dae6+h5a4WPZw+veXTsK7LPYqZ5lZQWM22JmAymYQoivD7/Whu\nbsaxY8eKVsBKwrAiKj7j3Ckge/6UNtHX2Ox39OjzZZ0/pSgK/nDxD3ownTpzChcvX8RntnxGrzW5\n7nZh7cq1ZStjNSlqn5W23JLP58P+/fuLddmKwbAiKh6T6X6o/5RuA7AWxmHp2kCK1VDnT2VO9E2V\nZaLv9ZvXETsfM4TTLatuMSxZ9LHbPgaTUPSdlwhLMMDC5/MhHA7j4sWLxbxsRWBYERWHsTa1DuoQ\n9Mxmv0zlGUgxcW0Cvzr7Kz2cRt4aQbO1WQ+mP9/y59hSP3MQCC2Vok9xFgQh515XRES5m/yuQB1A\noYWUtlq6dl5pguqtibemR+mdPYXXL74O190ubGvYBv+f+/HpzZ9G/drqmz+6XBS1ZhWNRuHxeGCz\n2fDGG28U67IVgzUrooXJPYACUEPoCoALM96Ra1uP/1608kwqk3jtvdcMTXrvX3vf0KTnuMuB1StW\nz38xKomCalYmk2nOIZbaL3G/37+4UhFR1Zh9AAUwXZvSBlFo52nnvFaU2tS1G9emt8g4ewq/OPML\nWNdZsa1hGz537+fwrc9+Cx/Z+BEOIa9gBdWs5ttWw2w245FHHsGuXbsWXbBKxJoVUf6mQ2quARSZ\nitfkl7qSmt4i4+wpxM7H8Keb/tTQ33TXrXct+PpUelzBogAMK6L5rV/vxJUr16ae5TOAQjtv4ZN8\n35TfNPQ3jcvjeOCeB/RweuCeB3DrmlvnvxBVrKoIq3A4DIvFgra2tqzXRFHE2NgYrFYrJEmCw+HI\neV4+GFZEs8sOKWApBlDcnLyJV9971bBk0bWb1/DZhs/q4fTJOz5ZUVuy0+IV1GcVjUYxPDysr7Bu\nNpths9mwe/duw068L730Usl2Cta2JNE2YswkSRICgQCOHz+uH+vs7NR3ESaixbv99s/ivfe0EcCZ\nIQXkHkDxPnIPoPjnnNe/8uEVjLw9YtiS/Y4Nd2Dblm3w2Dx4+qGn0WxtZn9TlcsrrGKxGLxer2GX\n4EzBYBBOpxMDAwMYGxuD1+vFwYMH8cQTTxS1sJkSiYT+fWfbhFHbyiSTz+eD3+9Hf3//kpWNqBZM\n90kBuUMKWMgAiguXLxi2ZP+3P/4b7r/9fmzbsg1dji78j7/+H7j9ltuL/vNQZZu3GTAWi8HpdAIA\nHA4HfD4fXC6XvsX96Ogoent7EYvFIAgCFEWB2+021GaWWnNzM0KhUNbuv1arFaIoorGxUT+m7TA8\nOTlZ8PdhMyBRoSElQF0ySTvX2OSnKAoScsLQpPfW+2/hP23+T/p6ep+651O4ZfUtS/kj0TIwb1hZ\nrVbIsoze3l50dXXNet7BgwcRCAQgCAKSyWRJN1/MFVZaKMmyjLq6OsP5JpMJkiQZQiwfDCuqZYWF\n1ExTQWWawC22t/D9/6dbDycAhi0yPnHHJ6puS3ZavDnviEOHDkGWZezZs2fOoAKgN6spioKBgQE8\n+uijxSvlAmirvs8MKs1CwoqoFi0qpFbdBWy+DjS8ATScx60fNWFL/Ra8+u6r+NKffAlBdxCN5kb2\nN9G85gyrn/zkJxAEAQcOHJjzIpFIBKIoor+/H52dnejt7S17WM22QjwR5WdBIXXLDaDhMtBgAhom\ngNv+A3hnNfY88pi+JfvG9RuXtuBUleYMK0mSYLPZ5r2I2+1GMpmE2WxGS0vLrAMxlgv+L49qlTGg\ngLlDSgE2XgcargINl9SQWj8JnN0EnLkVOFaPy2+8hXWr1pWk7FTd5gyrdDqNT33qU3ldSNt00Wq1\n4vTpyty1k4hyyyukTJPAXa9P1ZymHh+agDPrgTP3AL+6B3jPBCjnlsUW87S8zBlW9fX1GB0dLeiC\no6OjenCVk1YjnJiYyNlvNVeNcbYBFKxxUTWZPaAAYAOw5kNg8zjQkAIa3gHuvgLIq4A31wOv1gP/\ncieQtqMc23dQ7ZkzrNxuNwYHB3H69GnDpN/ZxGIxpNNpdHR0FK2AC6VNWJYkyVB2SZJgNps5uIJq\nUnZAAXpI3boCaLgANFwEGt4FNn4AnF+j1px+uRE4ux64uiLjPcVdbJZoLnOG1d69ezE4OIi2tjYk\nEolZR9ZpvF6v/r5K4Ha7MTIyYggrURTnXZCXqNpkhZSwGdj0wVSt6fdqQK25Dpw1A2cswP/eCLx9\nD3Bz5q63DCkqjzn3X3Y4HOjq6kIqlYLT6cRLL72U87zBwUE0NzdDkiR0dHSgpaVlSQo7l1xNd8Fg\nEAMDA4ZjoVAIwWCwVMUiKhtBuF9/YMUksHkD8JkbwJffBZ78GfCVGNDwvjoY4kctwKH7gB/fDvxi\nlVqLMgTVFgAfnfr6NSjKPzOoqKTyWsjW6/VicHAQAGCxWGCz2fQmNkmS9J2BOzo6SraMUTqdxv79\n+yFJEsLhMGw2G9xuNzwej2GLklgshiNHjqC1tRWSJMHpdGatdJEvTgqmSqfXoNbeBDZrAyFuAndP\nABdvBc5sAs5sBM6sA95fO/Wu2SbyAuXaUp5oprxXXY9EIggGg4hGo1mvud1u+P3+Ba9mvlwwrKgS\nCcL9QN2HU8H0gfqn5Qbwdr3apHfmLuDcRuDatYx3MaBoeVnQFiGSJEGWZX0QQ61gWFElmFQmseLO\nPzEOIV81OVVrmupzOn83MKk14823FJKGIUWVqyr2syoVhhWVw9UbVzHy1gge/M8dajBtuQxcXjk1\nv2mzGk4X10PdJ0pzKeNr1qJo+WNYFYBhRaVw8fJF/PLsL/GX/9ffquF051XgvbVT4bQeONMMfLBm\n6uwNGe9kQFH1YlgVgGFFxaYoCsblcZw6cwpf/fY31HCq/xA4t246nN5aB1xvzHjXQgIKYEjRcsaw\nKgDDihbr5uRN/Psf/x2nzpzC4898Ww0nARm1pvXAH9cCkw0z3smAotrGsCoAw4oKdfnDy/j1uV/j\n1JlT+M7hILD5CvC+1t90i/pnahWAucIJYEBRrWNYFYBhRfN574P3cOrMKez8L11qren2q2pNSas1\nnV2vDo4wrMMHzB1OAAOKah3DqgAMK8qkKAriqTjua/vc9BDyDTfUQNLC6e116srkiw6nTwP41Yxj\nDCiqHQyrAjCsatuNyRtYteUjxvlNk1BXIdea9d5dAygzm/SAxdecAIYT1TKGVQEYVrVFWPNRtY9J\nC6Z7prbIyBwMkbZBHSGRaWYwAQsLJ4ABRaRiWBWAYVV9DKuRb/jQWGvadA04nzGE/FwzcGX1jCvk\nE0wAw4locRhWBWBYLU+593BSgE3XjeG07qa6wOuZ9cCZJuB8HXBjRcZ7ih1MAMOJKD8MqwIwrCpX\n7kDKsGISuOvqdDBtuQxcXz210OvUenoXNgCK1qS3FMEEMJyIFqYmwkoURYyNjcFqtUKSJDgcjgWt\nEM+wKo95gyiXNTfVQGpYqW4wePcEkFw/FU5Tj4lNc1yAwURUSebcKbgaSJKEQCCA48eP68c6Ozth\ns9nQ1NRUxpLRgkIopy1A3dWpXW+nHtbLwNt1wJk7gFMfB85uBK6tmvG+XIGkYTARVZKqr1n5fD7s\n2LEDO3fu1I9Fo1H09vYWvFEka1b5KV4IAdnzkwAICnDbpYxwSgOrb2RsLLgJOG+Z2ul2oYH0pwD+\nY44yMZiISqnqw8pqtUIURTQ2NurHZFmG1WrF5ORkQdeq1bAqbvhocoRQThuAlTeBu1NAwwX1seWi\nOirvzKapxzrgwi3IHkIOFF5DyrQJ6rYbqwCkcPTo0/jCFx5cxPWIaKGqOqy0UJJlGXV1dYbXTCYT\nJEkyhNh8qimsbr/9s3jvvdQSXLmAEJrNuuvAlgtAw0Wg4Y/Ane+rYaT3N5mBS2sz3rCYQAJYUyKq\nfFXdZ5VMJgEgK6g0hYZVtTCZ7kf+eZtv+GjmCCEDrXlOAepn9DeZrwBvmdVQ+nk9cO5O4Lo2hPxD\nAO8VWCaAgUS0vFV1WMmyXO4iVJz7738YilJIAOUbPpq5+oig9jfd/j7QIE0PI1+hTK9AHrsdeGct\nMJmrSW8+DCSialXVYbVQWnNfNXr11asoLIDmCZ8sM5rkVk0Cd18xzm+6NLVFRnwD8LPbgeRq5O5v\nysQgIqplDKuao/3Cz1eB/UHrb0zNb5p63HEVeHdqi4wxC/C/7gE+yLztGEJENL+qDiubzQYAmJiY\nyNlvpb0+02wDKKqjxqWGQnEogEVbT+8D9c9bbwDn1gNn7gKiHwfeWgN8+DZDiIgWparDymw2w2az\nQZIkbN26VT8uSRLMZnNNDq74+MfX4tVXVwO4OfXI1xbAtB644zzQkEDH/70Np86cggABn733s9i2\nZRu2NWzDJ+74BFaaqvq2IqIyqPrfKm63GyMjI4awEkURHo+njKUqn9/97mXcf//DePXVN5DZBNfQ\ncANvvjlsOPfS9Uv6luynzp7Cr88NY0v9Fmzb8pfY1rANB90H0WhurJIaJxFVsqqeZwUA6XQaXq/X\nsNxSe3s7QqFQwTWrappnlcs7l97BL878Qg+n37/3e2y9c6tea/rMls9g4/qN5S4mEdWgqg8rAIjF\nYjhy5AhaW1shSRKcTie2b99e8HWqKawURcEfLv5BD6ZTZ07hwuUL+MyWz+jh5LrbhXWr1pW7qERE\ntRFWxVJNYfXo//cohqVhbGvYpofTx2//OEyCqdxFIyLKwrAqQDWF1dUbV7F25dr5TyQiqgAMqwJU\nU1gRES0nbPMhIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7AiIqKKx7Ai\nIqKKx7AiIqKKx7AiIqKKx7AiIqKKVxU7BYfDYVgsFrS1tWW9JooixsbGYLVaIUkSHA5HzvOIiKhy\nLfuwikQi6O7uRjgcznpNkiQEAgHDLsGdnZ2w2WxoamoqZTGJiGgRlm0zYCKRQE9PDxKJBKxWa85z\ngsEgenp6DMd8Ph/8fn8pikhEREVSFftZNTc3IxQKZW1Vb7VaIYoiGhsb9WOyLMNqtWJycrLg78P9\nrIiIymPZ1qzmI8uyHkyZzGYzAGB8fLwMpSIiooWo2rBKJpMAgLq6upyvS5JUyuIQEdEiLPsBFrOR\nZXnB79Wa+xb6OhERGS22+6Rqa1ZERFQ5Fvuf/LLXrAppjtu4cSPq6+uXsDSq2f4HwAEW0/hZTONn\nMY2fxTR+FtOK0RpV1rBKJBIIBAJ5n9/a2oonn3wyr3NtNhsAYGJiIme/lfY6ERFVvrKGVVNTE/r7\n+5fk2mazGTabDZIkYevWrfpxSZJgNpsNw9mJiKiyVXWfldvtxsjIiOGYKIrweDxlKhERES1E1YRV\nrnbhYDCIgYEBw7FQKIRgMFiqYhERUREs2xUs0uk09u/fD0mSEA6HYbPZ4Ha74fF4sGvXLv28WCyG\nI0eOoLW1FZIkwel0Zq10kS92mE7jZzGNn8U0fhbT+FlMK8ZnsWzDioiIakfVNAMSEVH1YlgREVHF\nY1gREVHFY1gREVHFY1gREVHFW7Fv37595S4ELS+iKOLo0aMYHx/H0NAQrl69WpPLV0mShM7OTtxz\nzz2wWq14++23EQwGIQhCTXwe4XAY58+fz/mz1to9MttnUWv3yODgIIaGhvBP//RPePbZZ7F+/Xp8\n7GMfM5yz4HtDoQWLx+OK2+1WIpGIkkqllHg8rvj9fiUSiZS7aEsmHo8rHo/HcMzr9SqSJJWpROUT\nj8cVQRD0h8ViUQYHB8tdrJIYHh5WLBaLEo1Gs16rtXtkvs+iVu6RcDisiKKoP5dlWbHb7UooFNKP\nLebeYDPgIkWjUXg8HlitVrhcLnzqU59CW1tbuYu1ZILBIHp6egzHfD4f/H5/mUpUPoIgIBKJQJZl\nSJKEZDKJnTt3lrtYSyqRSKCnpweJRCJrF25Nrdwj+XwWtXSPSJKElpYW/Xl9fT38fj98Pp9+bFH3\nRvFytfZIkqREo1ElnU4riUSi3MUpCYvFkvWzplIpRRCE8hSojCRJqupa9HzsdnvO2kQt3iOzfRa1\nco+kUinF6XQqsiwbjms1S+1+WMy9wZrVIimKgrq6uppYxV2WZciynPW/SLPZDAAYHx8vQ6mokvAe\nqU1msxmSJCGRSMx6zmLvjbJvvkjLRzKZBICc+4MBajNALYR2JkmSIMsyAPXzsVqthrUpaw3vkWy1\nco9of/eZIpEILBYLGhsb9Y12F3pvMKwWqVZuRAD6z0kq7X+ImX/fnZ2dWcdqCe8Ro1q/R3p7e7F3\n714Ai783GFaLUOs3Yq2rr69HV1eX4ZjP54PP5+PfPwGo7XskFAph06ZNeOKJJ4pyPfZZLcJsN2K1\njXqi/DU1NUGSJExMTJS7KFShauEekSQJoVAIx44dK9o1GVZQP9h8H+l0es5rVfONqE3cm+1nq8ZJ\njnM5ePBg1jGttq21z9ca3iNGtXqPBAIBnDhxwnBssfdGzTcDJhIJBAKBvM9vbW3Fk08+CUC9Effs\n2WN4PfNG3Lp1a/EKWgHMZjNsNlvWzyZJEsxmc011nEuShEAggM7OTsPPrXUy19ovZQ3vkWm1eo/0\n9PTg4MGDWQMpFntv1HxYNTU1ob+/v+D31eqN6Ha7MTIyYrjZRFGEx+MpY6lKz2azobe3N+sfWCQS\ngdPpnHXEUy3gPaKqxXukr68PgUDA8DNHo1HYbDY0NTUt6t5gM+AC1eKNCKgz0AcGBgzHQqEQgsFg\nmUpUPlar1TCvRJZlhEIh9PX1lbFUpaXk2Gi8Vu+RXJ9FLd0j4XAYgPofdlEUIYoiIpEIBgYG0NTU\nBGBx9wa3tV+EwcFBOBwO/S9ClmW43W4cPny46poAM8ViMRw5cgStra2QJAlOpxPbt28vd7HKYnBw\nEJIk4eLFi5BlOet/ldUmnU5j//79kCQJ4XAYNpsNbrcbHo/HMLqtFu6RfD+LWrhHck321djtdrz+\n+uv684XeGwyrRaqFG5GIqNwYVkREVPHYZ0VERBWPYUVERBWPYUVERBWPYUVERBWPYUVERBWPYUVE\nRBWPYUW0AKIowuv1wmKxwGQywWKxwOl04tChQ+Uu2oJ4PB6YTNO/Drxer+E5UbnxbiQqkM/ng8vl\nwuDgIEwmEzweDzZt2oTTp0/D7/fDarUiFouVu5g5hcNhmEwmDA4OGo4LggBBELKOEVUKhhVRAbxe\nL/r6+mCxWCCKIi5evIhjx47h9ddfx82bN7Fnzx7Isgyn01mxgQVkB9HAwADi8XiZSkM0P4YVUZ4i\nkQgGBwdht9uRSCRyrv944MAB9Pb2AlCDrVLNXLimvr6ey4RRRWNYEeVJWxk6GAzOuap+V1cXHA4H\nJElCNBrVj8/sF9LIsgyTyYSenh7DcUmS4PV6YbfbYTKZYLVa0dnZaVjFG1CbJbVFRP1+v96P1tzc\nbGju83g86OzsBDDdJ6VthJdvH9XBgwfhdDr18vT09GSVB1BX0s48z+VyGT4LokIxrIjyFI1GYbFY\nsHPnznnP9fl8AIDh4WHD8bn6gTJfkyQJzc3NeOmll9Dc3Kz3k4XDYTidzpw7VmtNlI888gi6u7v1\nsNNCIhAIoLu7Wy9fKBQyhO58fVROpxOBQAAmk0kvTygUgt1uNzR5+v1+9PT0YHx8HF6vF263W9+z\nqJKbRqnCKUQ0r3g8rgiCoLhcrrzOF0VREQRBaW9v14+53W7FZDJlnZtKpRRBEJSenh79WHd3t2Iy\nmZRoNGo49+DBg4ogCEo4HDacKwiC0tzcrKTTaf14JBJRBEFQfD6ffmxgYEARBEEZHBw0XLejo8NQ\ntpnPg8GgIgiCcuLEiZw/p9Pp1I+ZzWalubnZcJ5WlsyfkagQNb9TMFE+ZFkGkP8O0NoeZwvV09OD\nHTt2ZO3z09LSAgBIpVJZ75nZPNnW1gYAOZvp8qFk9Gvt378fHo8HDodD/ywA9edsa2tDNBrFxMQE\n6urqkE6n0dzcbLhWW1sbRFGE2WxeUFmIGFZEedB+yUqSlNf52nkL/eXc0tKiB5MsyxgdHYUoivrg\njVwcDseCvlc+0uk0hoeHYbFYcr4uCAKSySTq6urQ0dGBcDisN1+63W60tLRU9YaktPQYVkR50GpU\n+YbV6Oio4X2FkmUZfr8f/f39ev+U0+mE0+mctaY0206tC6X1YWk/s8fjgd/vn/V8Lcj6+/tx6NAh\n9Pb2Gs7v7u5GMBhEfX19UctJtYFhRZQnt9utD1/P3LZcE4lE4Ha7AUCvAe3evXve6yaTyaxjbW1t\niMVi8Pl88Pl8eq0kGo0iHA4v5scomBaCZrM5763pn3zySTz55JOYmJjA8PAwent7EQqFMDo6qgc5\nUSE4GpAoT1otIVftQpZltLe3w+Vy4eDBg4jFYnA6nXk1fYmimHWtWCwGr9eLF154wXANpYQbe2vf\ny2w2o76+HpFIJOd5FotF76OSJAl+v18fgVhXV4ddu3bh+PHjer+VNlyeqBAMK6I8tbW1oaOjQx9W\nnjkM22w2o7+/H6IoIhAIQBAEDAwMGN5vNpuhKIphvpHW3JfLzEEUmecuNrTyeX/mUHafz4dUKqXP\n09IcPHgQ6XTaMEfs0KFD+tD9TJIkQRCEOeeoEc2GzYBEBejv70dnZ6c+36m+vh4ulwvJZFIPL0EQ\noCgKxsbGDKtCPPLIIxgcHITH40F3dzcURcHAwABaW1uRSqUMNRmtybGzsxMulwvxeFw/F1BH/tls\nNn3EX760fiW/34+RkREcOHBAf21mgGU+P3DgAMLhsD5woqWlBZIk6TXIJ554AoDaR6eV3Wq1oq2t\nDVarFf39/ZiYmMCePXsKKi+RrkxD5omWNVEUFa/Xq1itVsVkMilWq1VxuVxKX1+fIsuy4vF4cs5n\nCoVCit1uVwRBUKxWqxIIBBRFURSLxWKYgyTLsuLz+RSLxaLP79Ku5fP5FJPJpJ+vPc+cY6WZOddL\nURS9bFarVT/m9XoN86pmPtf4/X7F6XTq87q08uc6z263Gz6bmZ8FUSEERSlhIzhRDXnmmWf0GgcR\nLQ7DioiIKh4HWBARUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVjWBERUcVj\nWBERUcX7/wEMgOSMA0DVtAAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe26807c6d0>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAasAAAEsCAYAAAB9pJwNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X1QW2eeJ/rvEY6xnQQk2c6bkwCCTPcm7hkjQXdPd8d4\njYT7TurWdGyEk92aOzW1AZG+N+47VY6FO+s7ns102cKZ2hnn3iSI3N3bO3t7Agh3za1Q2wbJE9wv\n09uA5N5+b0cHiJPYcWxxhN8dm3P/OJyDDhIvB4Te+H6qKKOjI/FDAr5+zvmd5xFkWZZBRESUw0zZ\nLoCIiGghDCsiIsp5DCsiIsp5DCsiIsp5DCsiIsp5DCsiIsp5a7JdwHJ4vV40NDTA4XDAbDbPuV84\nHMbIyAisVitEUYTdbkd9fX0GKyUiouXI67AKh8M4duxYyvsqKytx9uxZiKKItrY29Pf3a/c1NTXB\nZrOhoqIiU6USEdEy5HVYVVZW4tixY0mjqoGBAdTW1gIAfD4fWltbdfd7PB54vV50d3dnrFYiIlq6\nvA4rh8OBbdu2pbxP3d7T04ODBw8mPS4QCKx4fURElB5CoU231NnZiebmZgCAJEmwWq2QJAklJSW6\n/UwmE0RRRHl5eRaqJCIiIwqqGzAUCqGmpka7HYvFACApqFSiKGakLiIiWp6CCqtwOIzq6mrttiRJ\nWayGiIjSpWDCKhAIoLKyMttlEBHRCsjrBotER48exalTp9LyXIIgzHlfgZ3iIyLKCwUxspIkCeFw\nOOnclM1mAwBMTk6mfJx6vxHzBRkRUSHYseMwBAFJHzt2HM5aTQURVsFgMOUMFmazGTabLamRQhRF\nmM3mOTsBZVlO+UFEtBoUF99JuX3dursZrmRGQYTV0NDQnOernE4nhoaGdNvC4TBcLlcmSiMiyjv7\n9jWgsvIV3bbKym/jpZey93ezIK6zcrvdmJycxMmTJ5Pui8fjcLvduumWGhoa4Pf7DV9jpR4CLICX\njIhoXn19p/H66wO4ebMI69bdxUsvufDMM9uzVk9BhFVraysEQcCbb76Z8v5IJIKuri7U1tZCFEU4\nHA7s3LnT8NdhWBERZUdBhFWmMKyIiLKjIM5ZERFl0q1bt/DKK6/goYcegslkgiAIq/6jqKgItbW1\n+PDDD1fkNWdYEREZ9Kd/+qf41a9+hZ/85Ce4ffv2nB3Eq+njxo0bePbZZ/Hss8+uyGvOw4AG8DAg\nEQHAPffcg8nJSaxfvz7bpeSU27dvY/369bh7N/0t7gwrAxhWRAQofwv4dyC1lXpteBiQiIhyHsOK\niIhyXsFMZEtElAv6+k7j+PF+3Lq1BsXFd7BvX4Phi2nT8RwFR6ZFAyDzJSOiuf4OvPvuoFxZ+W0Z\nkLWPyspvy+++O7jo517uc0SjUdlut8vt7e2yxWKRKysr5XA4rN3f09Mj22w2WRAE2e12y5IkaY9z\nOp3ygQMHZIfDIYuiKNvtdtnj8cgWi0V2uVzyyMiI9tj29nZDr81y8TAgEVGaHD/ej2j0O7pt0eh3\n8PrrAxl9jkgkAkEQEIvF4HQ64fV6ASiTeDc1NaGzsxMTExMAoN0HKKutT05OIhAIQJZlRCIRNDQ0\nYHR0FNFoFE6nE5FIBAMDA7rHZQLDiogoTW7dSn1m5ebNoow+h9lsxv79+wEAHo8HsVgMgLJIrcfj\nwc6dO1FaWgqfz4fu7m7dY998801t3lSz2Yzdu3ejtLQULpcLHo8HJSUlqK+vBzD38ksrgWFFRJQm\n6VhaIx3PYbVatc/lhDbyWCymW8evoqICkiRpt2ev8Zf4PGazWXc70xhWRERpko6lNVZyeY6NGzci\nGo1qtyVJSrkWYC5iNyARUZqoHXuvv34oYWmNrxvq5EvHc8xlz549qKqqgtvthsPhQHNzM/bu3bvs\n582EggircDiM7u5ubNy4EZcvX4bH40FFRYXu/pGREVitVoiiCLvdrh1zJSJKp2ee2b7sYFnuc6iz\n7cy+bbPZ0NPTA4/HA1EU4Xa74fP5Fnxcqtuz71tpeT/dUiAQQDAYxFtvvaVt83g86OjoAKB0v7S2\ntuoWX2xqaoLP59MF2mJwuiUiAjjd0nw43VIKkiShpaVFF1R+vx+nTp3Sbvt8PrS2tuoe5/F4Mt52\nSURES5fXIyuv1wuTyYQjR47oto+NjWmtl1arFeFwWLeEvSRJsFqtmJqaMvT1OLIiIoAjq/lwZJVC\nZ2cnamtrk7arwSRJkhZMidTul7GxsZUukYiI0iCvGywkSUJpaSk6OzthtVoRi8VgtVqxZ88eANAu\nhCspKUn5eFEUdSMuIqLFWLNmDW7cuMH1rGa5ffs2TKaVGQPl7chKFEUAyrQizc3N2LNnD5qbmzE0\nNITOzk4A0F3sRkSULvX19XjuuecQjUZx507qi3hXm9u3b+O1116D3W5fkefP27BSg2j2Fdd79+5l\n8wQRrah/+qd/wtatW/G1r30NxcXFEARh1X+sX78e3//+9/H9739/RV7zvG2wUM9FhcNhbNu2TXef\nyWSCKIqIxWKoqalJ2UhhMpkQDAaxc+fOpPsWun4gT18yIqK8lbcjK7VJYq6pQkRR1EZdc022OHtU\nRkREuSlvwwpQwkY9d5XqPrPZnHIfURRhNpvnbK6QZTnlBxERZUdeh5XH48HIyIhuWzgchsVi0YLI\n6XRiaGgoaR+Xa/mTQhIRUWbk7TkrAIjH43A4HHj//fe1bQ0NDWhtbcXu3bu1fdxut266pYaGBvj9\nfsNt67womIgoO/I6rABgdHQUPp8PlZWViEajaGpqSmqaiEQi6OrqQm1tLURRhMPhSNlYsRCGFRFR\nduR9WGUSw4qIKDvy+pwVERGtDgwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwrIiLKeQwr\nIiLKeQwrIiLKeXm9rD0REc2vr+80jh/vx61ba1BcfAf79jXgmWe2Z7sswxhWREQFqq/vNL71rZOI\nRr+jbYtGXwGAvAssHgYkIipQx4/364IKAKLR7+D11weyVNHSMayIiArUrVupD57dvFmU4UqWL6/D\nShRFuFwuhEIhSJIEURTR1taGUCik2y8cDqOzsxO9vb04duxY0v1ERIWouPhOyu3r1t3NcCXLl7Zz\nVpOTkygpKUnX0y1aKBTSwsdsNuPtt99GfX29dr8aYImLLzY1NcFms6GioiLj9RIRZcq+fQ2IRl/R\nHQqsrPw2Xnrp61msamkMj6wikQhefPFFjI2NAVBW4q2pqYHZbEZRUREOHjyY7hrnJAgCgsGgNqqK\nxWLaCsEqn8+H1tZW3TaPxwOv15uxOomIMk3tAly37hI2btyLrVv/d+zadQh///dfz7vmCgCAbEAw\nGJQFQZAFQZAjkYgsy7Ls8XhkQRBkp9Mp22w22WQyyb29vUaedslEUZSDweC8+1gsFnl0dFS3bWJi\nQhYEwfDXAyAbfMmIiDLu3XcH5crKb8uArH1UVn5bfvfdwWyXtmSGRlbqaGRgYADbtm0DAPj9fjid\nTgwMDCAajaKkpARHjhxJd6YuiSRJkCQJVqtVt91sNgOANjokIiokhdQFqDJ0zkoURTQ2NmrnhCKR\nCADlsJqqqakJgUAgjSUuXJMkSQCAWCwGq9WKPXv2aLcBzHkuTRRFlJeXZ6ROIqJMKaQuQJWhsJIk\nCYIgaLeDwSAAwOVyadtisZgWHitNHTGp4QQoYaluy1QdRES5pJC6AFWGDgNWV1drAQUAHR0dsNls\nupFLKBTKWJddaWkpmpubddvYPEFEq92+fQ2orHxFt03pAnTN8YjcZ2hk5fF40NraiieeeAJmsxmi\nKMLn8wFQQsrj8UCSJLS0tKxIsYtRUVEBURQxOTm55OdIHD0SEeUbtdvv9dcP4ebNIqxbdxcvvZSn\nXYAqox0ZBw4ckM1msywIgux2u3XbBUGQXS5XWjtA5uPz+ZK2qZ1+kUhE+zwejyftJwhCUpegCtNd\nf3N9EBFRZgmyLMvpCD1RFAEANpstHU+3qK9XVVWV1CShbpckCSUlJaiqqkIgENC6F9V9ampqtAaM\nxVJHXGl6yYiIaJGWPIPF2NiY1olns9mSzl2tNJvNho6OjqRuvmAwCIfDodXidDoxNDSkC6twOKxr\nCiEioty2pBksampqYLPZ4HQ60djYCLvdDovFgr1792b02iWr1YrR0VHttiRJ8Pv96Ozs1Lb5fD70\n9PToHuf3+7VzbURElPsMHQYcHR1FZWUlAMBut2Pv3r1aQ8PAwABCoRAsFgtGR0czNsrq7e2FKIq4\nfPkyJElCW1tb0mgrEomgq6sLtbW1EEURDocDO3fuNPy1eBiQiCg7DIWVesFvR0dHUss4oIxYWltb\n4Xa70dXVldZCcwHDiogoOwyFldVqhc1mw/Dw8Jz7OBwOTE5O4uzZs2kpMJcwrIiIssPQOStJkrTD\ngHOx2WxaZyAREVE6GBpZuVwuhMNhXL58ec59FjP6ylccWRFRrlOXBrl1aw2Ki+9g376G/L4YeJqh\n1vWOjg44HA7s2rUrqW18dHRUm8EisRuPiIgyo6/vNL71rZO6GdejUWXapXwPrHlHVg0NDUlTD0Wj\nUYiiCEEQYLPZYDabtcUPZVmG3W5HbW0t3nzzzRUvPtM4siKiXLZr179Hf//fpNh+CD/4watZqCh9\n5h1ZDQ0NQRCEpD/OpaWlAIBLly7h0qVLAGaW4VDDrBDDiogolxXi0iCqecNqYmIiU3UQEdEyFeLS\nICrDM1gQEVFuKsSlQVSGugHVmSBGR0chSRLMZjNsNhv27t2rm3uvUPGcFRHlur6+03j99YGEpUFc\ned9cASwyrCKRCJqbmxEOh+fcx+FwoLOzs6BDi2FFRJQdC4ZVKBTSZii32+3weDyoqanR5gQcHh5G\nR0cHIpEIBEHAwMDAkubdywcMKyLKZYV6jRWwQFjF43FUVFRAkqQ55wNUqfMCWiyWeS8azmcMKyLK\nVamusaqsfAV///e7CiKw5m2w8Pv9kCQJBw4cmDeoAKClpQUvv/wyJiYm8Nprr6W1SCIimt+hQ+/o\nggoAotHv4PXXB7JUUXrNG1bvvPMOBEHA0aNHF/Vk6hpRAwPZeXEkSUJra2vS9nA4jM7OTvT29uLY\nsWMIhUJZqI6IKL36+k7Dbn8B69btRCSSeuXzQrjGCljgOitRFA0vU19RUZG1eQG9Xm/StWGiKKKt\nrQ39/f3atqamJthsNlRUVGS6RCKitOjrO40XXvguLlwAgM0AqlLuVwjXWAELjKzi8bjhsLLZbJAk\naVlFLYUoipiYmEiaHsrn8yWNtjweD7xebybLIyJKq0OH3sGFCw8DeBjAvwLQAEB/jdW6da0FcY0V\nsECDhcVigclkMtQwsZTHpIM6ee7AwAC6u7u17VarFeFwWDfpriRJsFqtmJqaMvQ12GBBRLmgr+80\nGhvfxs2b6mDiDoC/AXAawACAIgB3UV19HuHw29kqM63mHVk5nU5MTEzgzJkzi3qySCSCeDyO+vr6\ntBS3WKFQCE6nM2m7JElaMCUym80AgLGxsUyUR0SUVseP9+PmzcehhNQdzIyqtgN4FcBhrF9/Ea++\n+r9kscr0mjesDh48CABwu90LPlE8Htf2Ux+XKaIooqKiImnEE4spJxzVSXZTPY6IKN8oE9Y2ADg/\n/XESwC4AhwAcxtq1jThw4I8KomVdNW9Y2e12NDc3IxqN4oknnsCJEydS7tfb2wuHwwFRFNHY2Ijq\n6uoVKXaurz1XW302zp0REa20ycmLUEZRfw5AAHAGwN/CZPoN7PZPceLEPhw+/M2s1phuCy6+2NHR\ngVgsht7eXjQ2NsJiscBms2nL16uNDQDQ2NioO1+00lYqjGY3aRAR5Yq+vtM4f/4WlMN+34ESWsBD\nD/0l3n772YIaTSVa1ErBPT09CAaD8Pl8CIVCGBkZwcjIiHa/0+mE1+vN+Lmqnp4e3aiKIUNEhU7p\nAvy/oTRTHILaTPHww1cKNqgAA8vaO51OrYlBFEXdrOvZEIlEUFNTo9s2+5yVWtvk5GTK81Zz1T5X\ntx/DkIiyqa/vNH7zm6vTt7ZDHVUBQEnJ4WyUlDGLDqtE2QqoRMPDw4hGo+jq6tK2hcNh7SLg2tpa\n7NmzRztcmTgbvCiKMJvNunZ2IqJcN9MFmKxQLv6dy5LCKhekaqo4duwYhoeHddNDOZ1ODA0N6cIq\nHA5rM8kTEeWLjz++CmA3Zs5XKe65pxkvvfRn2SorI/I2rFK5dOlS0iE8n88Ht9utCze/3w+/35/p\n8oiIluX8+fOYOfQ3c76quPjjgj5fBRhcKThXjY6Owufzobu7G/F4HM3NzfB4PFoLvbrCcW1tLURR\nhMPhWNKaW5zBgoiyqbz832J8vByJoyrg23jqqcv45S87slNUhhREWGUKw4qIsqWv7zR27z6O27f3\nIXFKJcCFXbsG8IMfvJrdAldYQR0GJCIqVIcOvTMdVCeROLJau7bwz1cBaQyrudrDiYho+X7/ewmp\nzlfdc8/Fgj9fBSww3VIqkUgEL774ojYJbDweR01NDcxmM4qKijI+LyARUaHr6zuN69evTd+amawW\neBVr127IWl2ZZCisQqEQHA4HOjo6tKmOvF4vwuEw6uvrUV5ejvb29jnnECQiIuOOH++HLG/G7PWq\ngG+jvPzebJSUcYYaLGpqahAOhzEwMKBNrWQymeB0OrWVeC0WC6qqqjA0NLQyFWcRGyyIKBt27DiM\nwcGdAL4L4BHMHAL8Hb7//f+NhwFnU2dVV4MqEokAUFbeVTU1NXHpDSKiNNLPsj5j69aSVRFUgMEG\nC0mSdPPjBYNBANDNBhGLxbg0BxFRmvT1ncbo6BWkmmW9kBZXXIihw4AOhwNjY2PakvVVVVUAgPff\nf1/bx2q1wmq16rYVCh4GJKJMs9u/iUjkDcxest5mO4to9J3sFpdBhg4DejweTExM4IknntBmg1AP\nAYZCIVRVVUGSJDQ2Nq5IsUREq80vf/np9Gf6LsBPPjHczJ3XDB0GbGlpQTQahd/vRzQaRWNjI15+\n+WUAQH9/P0RRhNPp1E0kS0RES3P48Bv47LMbKe+7detayu2FKm3TLalNFbmwfMhK4WFAIsqkkpLd\nuHLlFoBtmD0f4L33/hxXr/ZlqbLMW/IMFpOTk4jFYrBYLCgtLS3okCIiyrTDh9/AlStrAFgBXEDi\nrBXABfzBHzyczfIybkkzWKgzVlRWVmrL21dVVeG1115Le4FERKtNX99pHDnSD0AAkKrjT1pVnYCA\nwZHV6OgoHA4HAKC+vh6hUEi77/Llyzhw4AC6uroyekFwMBhEMBjExo0bEY1G4XA4khZmDIfDGBkZ\ngdVqhSiKsNvt2rViRES55vjxfty+XQrgSwC+B+X6qoHpe3+B55//3Kq5vkplKKx8Ph8AYGRkBBUV\nFbBardp9ExMTaG9vR1tbGw4ePIgjR46kt9IUgsEgBEHQNXTU1NRAkiSt8UNd5l6dYQNQLly22Wyo\nqKhY8RqJiIy6dWsNgFsAvgngjemPdQBuorh4Et/7ni+b5WWFocOA3d3dcDqd2qKGsx04cADV1dUI\nBAJpKW4hHR3Ji405nU7ddp/Ph9bWVt0+Ho8HXq93xesjIlqK4uI7AO6DciHwNwG8A+D/AWDDk0+u\nzv4AQ2ElSRIqKyvn3cdmsyEajS6rqMUSBEGbRUMlyzIsFot2u6enB3a7XbePw+HIWKASERn10Ue/\nAjCBmcaKwwAO4d57xVV3rkpl6DBgdXU1hoeH590nEokkhcNK6e7uTtoWCATw4osvAlDCVZIk3eFK\nADCbzQCAsbExlJeXr3idRESLVVf3F/jVrz4DcADAfwHwPoC1AO7Dgw9i1Z2rUhkaWe3duxcjIyP4\n53/+Z90cgSp1Elun05m2Ao3w+/2oqanB/v37ASjzFAKYc1FITrhLRLmkru4vcPr0BQAbocxY8TaA\nf4Qy2/r/hYmJ4myWl1WGRlZqt199fb02ea3P50NHRweCwSAmJiZgs9kyPoNFb28vBgYGIAgCurq6\ntO2cUJeI8sVMUJVCaa5I5XYGK8othq+zGhkZwdGjR/Gzn/0MADAwMICenh5MTU3hwIEDWZnAds+e\nPXjrrbdw9OhR1NTUaEuXLJUgCCk/iIhWQl/f6emgug/ANcw0VyRaPQstprKkGSwOHDiAAwcOAFAO\npVmtVu08UDaVlpbC4/Ggvr5eOwRIRJTrjh/vhxJQtwE8CSAKQEbirBXr1p3Fq6++lL0is2zJ0y2p\ncm2apfr6ekiShFOnTmmNHpOTkynPW81V+1xz/3F0RUQrIRIZhzKiApQ/y5UAhgBcBHAPgEkEAv/H\nqm2uABY4DGgymVBUVJTyw2Qy6e5XP1f/XWmiKMJiseDMmTMp75ckCWazGTabLamRQhRFmM1mdgIS\nUdb19Z3Gp59egjLn3xSAs1C6/7ZDmcAW+Ku/2r2qgwpYYGS1Z8+eJT1pJkYg6jVfs0dHajCpoyqn\n04mhoSFs27ZN2yccDutWNyYiypYXXvg/ocwB+CiAcwA+AnAVwAYAV/H883+Ew4e/mcUKc0PalgjJ\nhmPHjqGlpQWlpaXaNpfLhZqaGm26p3g8DrfbrZtuqaGhAX6/3/DIikuEEFE6KR2AMSgjqpehXFd1\nDep1VSbTb3D37qlslpgz8jqsAKCzsxPRaFSbyLampgYvvPCCbp9IJIKuri5tdWOHw4GdO3ca/loM\nKyJKlwceeBqffnoflFHVegCbAbyVsIcHNtslRKO9Wakv18wbViaTCYIgIBqNory8XLs9H1mWIQgC\n7t69m/Zis41hRUTpUFbmwgcfyAAsAK4DeAjK9EproU5YC1zGu+8eWvXnqlTznrOqr6+HIAjaXHuL\nPYfFrjkiorl98MEaKKOpa1Ba0/8cM4cAZQAbYTJdZFAlyPvDgJnEkRURLVdp6ZcwOfk4gBsAPoMy\nivoDAJ0Je72A55/fuCqXApmLobCa63ql1YJhRUTLMTOlEqCElA1KB6AEZT7A+wBcxfbtD2Fw8D9n\nqcrcZGi6JbPZjLfffnvefdra2rBx48ZlFUVEVGj0UyrdgRJWcQCPQ7kI+AEAN/DUU+sYVCksOINF\nb28vBEHQRhPq8vCpyLKMQCCAiYmJ9FZJRJTn9u71QR05KUvUuwCIAB6c3i5xRDWPBQ8DmkyG57qF\n0+nUXddUKHgYkIiWQjn8F4dynkoCsBWzz1Ft2PArXLv2L1mpLx8sOLJKXOCwqakJLS0t865XZbFY\nUF9fn57qiIjynHL47zyUP7eXoRz2+wWA/wkzI62L6O7+j9krMg8YarBwuVxoa2tbtWHEkRURGfXw\nw024cEEG8CmU66huQWlXv3f69hVs376Fh/8WwNZ1AxhWRGSUIOyGcvgvDmX+vzhmwuoqgI8hyz/P\nXoF5wvASIaFQCD09PRgdHZ13v5MnTy65KCKiQmAybQVQDuASlD+3k1BmrVBnqZjC9u32rNWXTwyN\nrHp7e+F2uxe179TU1JKLylUcWRHRYm3Y4MCNG0o7uhJMxQCuYKb77yrWr7+I69dHslhl/jDU6uf1\negEoS9lPTU3N+0FEtFrV1f3FdFCpy9Q/CmUV4JmgAs4xqAwwdBhQFEW0tLSs2gYLIqLFmLn49yqU\noPoUwCYo56muAbiOp556InsF5iFDYVVaWppzk9T29vZCFEVEo1GIogiPx5M04W44HNYuZhZFEXa7\nnYFLRCti69ZnMRNUHwL48vQ9N6GsBnwHwGX88peD2SkwTxkKq5aWFnR2dsLn8+XEHIG9vb2w2Wxa\nOMXjcTgcDsRiMTQ3NwNQRoNtbW26i5Sbmppgs9lQUVGRlbqJqHD96lc3pz/7GMAWAD8D8AhmAuxj\n/NVfceVfowyds/L5fKivr4fD4cCJEycwNjaGycnJlB+ZIIoiqqurtdulpaXwer3weDy6mltbW3WP\n83g82vk3IqJ0eeCBp6GE0idQlqW/PP2vAGXpjyk8/vgDXKZ+CQx1A6pzAkqSNP+TZmDxRUmS4HQ6\nEQqFdMvai6KIqqoqiKKI8vJyWK1WhMNh3RL2kiTBarUabgRhNyARzUVZUFE9WPUJlO6/W5jdVCHL\nv8xShfnN0GHAxbatZ+K8ltlshiiKGB0dxbZt21LuI0mSFkyzHwsAY2NjuhAjIloKZY2qDQDMAH4/\n/e9tKCsAq0El4fnnn8lekXnOUFh1dHSsVB1LEovFkrYFg0FYLBaUl5dDFEUAmPP8mjr6IiJaqn/z\nb7yYnLRCWfn3KpSOv+vT98oJH9e5mOIyGJ9SfQGhUAgvvvhiup920To6OnDw4EEACx+uJCJarn/8\nx59DGT3dhtL9pyxLr6xR9SCUqZU4U8VyGZ5uKR6PIxgMplyzSpZl+Hw+jI6O4s0330xLgUb4/X5s\n2rQJ+/fvX9bz5Fp7PhHlJkHYCuBfQRlR3YDyJ/UWgItQmiruAriKoqLzGBzkFHTLYSisRkdH4XA4\nFhyxtLS0LKuopRBFEX6/H8PDwxn/2kS0+ihB9RjUdnQlmD4P/YKKSlPFnTtsqlguw9MtSZIEn8+H\n/v5+VFRUoLGxEQMDA+jv70d1dTVcLhfeeuutlap3Tm1tbTh16pRum81mA4A5W+nV+2eTZTnlBxER\noE5Q+xiUQLoEJajWA/gt2P23Mgy3rtfU1GgX2La3t6OnpwdDQ0MAlHNENpsNb7/9Nnbv3r0yFafQ\n2tqKtra2lM0SVVVVCAQCuo5BURRRU1OTskFjPmxdJyIAEITEhRPPQTlHdRkzAcagSjdDIytJklBZ\nWandttvtGBmZmYjRbDbD7XbjyJEj6atwAZ2dnUlBFQqFtCVMnE6nFqaqcDgMl8uVsRqJqHAoh/8S\ng+qPwaBaeYbCqqKiQmsHB4CamhoAwJkzZ7RtlZWVugBbSYFAAIDSwh4OhxEOhxEMBtHT06NNpeTz\n+dDT06N7nN/vh8/HFlIiMkZ/nkodUf0LZgcVr6dKP0OHAd1uN06cOIGBgQHs3LkTAGCxWPDcc89p\n3X9NTU0IBoOGD7EZlepiX1VlZSXOnj2r3Y5EIujq6kJtbS1EUYTD4dDqN4KHAYlWr5mgug/Ab6As\nSX8byrma1aQVAAAgAElEQVSqTeAaVSvLUFipUxkJgoCenh7s3r0bHo8HnZ2dcLvdmJiYQDAYREtL\nS1aaLFYaw4poddIH1dXpjwko7emPgof/Vp6hsAKUwFInh62uroYkSaivr0ckEgGgnCPq6enRzddX\nKBhWRKuPybQVsqw/zKecp/rt9DYGVSYYDqu5qNdeqfPuFSKGFdHqsnXrs9NLfswOquTzVAyqlZW2\nsFoNGFZEq0tyizqDKlsMzWDR2tq64FREsixDEISsTLdERJQu+qmUzkE5N5UcVFxIMTMMjaxMpoU7\n3dXDgCvdDZgNHFkRrQ4zDRWAElTrocz9dz8AC5QFFa9g8+bruHjxh9kpcoVc/+w6fvrhT/He2HsY\nHB/ENz73DfzlH/9ltssyFlZzzQmoXufk9XpRVVWFkycLc8JGhhVRYTt8+A389V+/gZnR0++hTKVU\nNL1H4vL0hXH479rta/jJuZ9o4XTmwhl84cEvYEfZDtSV1+Grj30V9xffn+0y03vOSp1uyePxZHQW\ni0xhWBEVLmU0Bcw+zDczqiqM81RXbl3Bj8/9GINjg3hv/D384pNfYNtD27CjfAfqyurwlce+gnvX\n3pvtMpOkvcHC4/EgEAjg8uXL6XzanMCwIipMSlBtgTKpT2E1VMRvxvGjD36EwfFBvDf2Hn796a/h\neMShjZy+/OiXseGeDdkuc0GG17NaiCAIKde6IiLKRTPnp+6FcpFv4ogqOaieeuqJLFW6OBM3JvDD\nD36IwbFBDI4P4reXfosvbvkidpTvwDHXMXzp0S9h3Zp12S7TsLSOrEKhEFwuF2w2G95///10PW3O\n4MiKqLAkz0wBzHT+fQjlXNXMearNm6/mXEPF5euXcXr8NAbHlXB6P/Y+vvzol1FXVocd5TtQ+0gt\nitcUZ7vMZTM0sjKZTPO2rqt/xL1e7/KqIiJaYclBJQG4AmUBxd9C3/k3ieef34bvfS/7E2BfvHZR\nCafpkdOYNIavPPYV1JXV4Y0/eQOORxxYW7Q222WmnaGR1ULLapjNZjz33HPYs2fPsgvLRRxZERWG\n5KA6N32POqLaBCWs7gEwgXff/Ws888z2bJSKC1cvaME0OD6IjyY/wlcf/6o2crI/bMcaU9rP6OQc\nzmBhAMOKKP/NHVSq7DZTfDT5kRJM0wH1ybVP8PTjT6OurA515XXY9tC2VRFOsxVEWAUCAVgsFtTX\n1yfdFw6HMTIyAqvVClEUYbfbU+63GAwrovw1d2t6oswH1bn4Oe0ap8HxQcRuxLC9bLsSTmV1+MMH\n/xBFpqKFn6jAGYrnUCiEgYEBbYZ1s9kMm82GvXv36paNP3HiRMaWtVeXJFEXYkwkiiLa2trQ39+v\nbWtqaoLNZtMWZySiwpdLQTUmjc2E09ggrty+ogXTvi/tw9YHtsIkGFoXd1VYVFhFIhG43W7dKsGJ\nfD4fHA4Henp6MDIyArfbjfb2duzfvz+txSYaHR3Vvu5cizCqS5kk8ng88Hq96O7uXrHaiCg36Gek\nADIdVLIsQ5wQtWucBscHcfPOTe0C3P1/vB9Pbn5ywTlXaRGHASORCBwOBwDAbrfD4/GgpqZGW+J+\neHgYHR0diEQiEAQBsizD6XTqRjMrraqqCn6/P2n1X6vVinA4jPLycm2busLw1NSU4a/Dw4BE+SN5\nNAWsdFDJsoyzsbPa7BCDY4OYkqe0cKorr8PnNn6O4bQEC4aV1WqFJEno6OhAc3PznPu1t7ejra0N\ngiAgFotldPHFVGGlhpIkSSgpKdHtbzKZIIqiLsQWg2FFlB9Sz0gBpDuoZFnGby/9VjvfNDg2iCJT\nkdapV1dWhyprFcMpDeY9DHjs2DFIkoQDBw7MG1QAtMNqsiyjp6cHL7zwQvqqXAJ11vfZQaVaSlgR\nUW7Tj6Zmz0iB6dtywj7GgmpKnsKvP/21rpV8/Zr1qCuvQ4OtAd/Z+R1UmCsYTitg3rB65513IAgC\njh49Ou+TBINBhMNhdHd3o6mpCR0dHVkPq7lmiCeiwpS6iQLQj6aSg6qkJIZ4PHVQTclT+MUnv9CC\n6fT4aZQUl6CurA7PPPEM2l3tKDeXp/+boSTzhpUoirDZbAs+idPpRCwWg9lsRnV19ZyNGPmC/ysi\nyh/6kAKSZ6RIlBhkv0kaTd2duouff/JzbeR0evw0Nm3YhLqyOjz7+Wfxd7v+Do+VPgbKvHnDKh6P\n44tf/OKinkhddNFqteLMmTPLr4yIaB4zIQXM3UShzkiRuM/MYb87U3cQOR/RRk4/+uBHeOi+h1BX\nVoe9T+3FG8+8gUfufyQT3w4tYN6wKi0txfDwsKEnHB4e1oIrm9QR4eTkZMrzVvONGOdqoOCIiyj7\niou34fbtO9O3Zo+mAP1hvw+hCynTr/HT8f+E98bew5/8v3+CH5/7MR4reQx1ZXX4sz/8M3T+z514\n6L6HMvONkCHzhpXT6URvby/OnDmju+h3LpFIBPF4HI2NjWkrcKnUC5ZFUdTVLooizGYzmyuI8kzy\nSApIPZpKaKIo2gI8chMojwJlH+P+J01oebcFdWV1+HfV/w7f/cZ3sfnezZkon5Zp3rA6ePAgent7\nUV9fj9HR0Tk761Rut1t7XC5wOp0YGhrShVU4HF5wQl4iyi2pz0sBSaOpoilgyw2g/BpQPgVs+R0Q\n24C1H69H1yv/FU8//jQ2btiYucIpbead08Nut6O5uRkTExNwOBw4ceJEyv16e3tRVVUFURTR2NiI\n6urqFSl2PqkO3fl8PvT09Oi2+f1++HzZn+afiBYmCFsTJp5VD+eph/yuAmvGgfLfAnUXgT8fBby/\nA3bFgHVm4KdlwH+sgvxWHLf+vwv4xue/waDKY4uayNbtdqO3txcAYLFYYLPZtENsoihqKwM3NjZm\nbBqjeDyOI0eOQBRFBAIB2Gw2OJ1OuFwu3RIlkUgEXV1dqK2thSiKcDgcSTNdLBYvCibKjDmbJ+6J\nA49KQPmYMnp6+CZwsRgY2wCM3wt88ARwy4J8XH6e5rfoWdeDwSB8Ph9CoVDSfU6nE16vd8mzmecL\nhhXRytEHFAA8Bqy9Azx2Eyj7GCiPAQ/FgU/WAWP3Kh/n1gO3i5DtZT1o5S1piRBRFCFJktbEsFow\nrIjSTxdSxXeBx+5Vgqk8DjwQB86XAONF0+G0Afgs8ewFQ2q1KIj1rDKFYUWUPoKwFVh3F3j8OlBm\nUgJq8zXgYwswthkYuw/40Azc+TjFoxlSqw3DygCGFdHyCBs+r4RT+XWg7Bqw8TPgo1Jg/CEloD6y\nAnduTO+ttqJvBHB5+nOG1GrFsDKAYUVkzKXrl7C5xq4EU/l1wHIb+HA9MPYIMGYFPt4C3DVhpgUd\nSJ4ZHQDWA9gENaief/4P8b3vsat3NWFYGcCwIprfxWsXMTg2iKYDrUpAlX6mnGca3wCMVQAflwJT\n6rIdwNxLdyTiaIoYVoYwrIj0zl85r63j9NYP/jNw/2fABxuUZojxDcD5J6bDCZgJKMBoSAnCOUxN\nMaRWM4aVAQwrWu0+nPxQm5G8s/+7wL13lOubxqcD6sI6QH484RGpAgqYO6Q4iqLUGFYGMKxotfkg\n/oGyRPvYe/hPp/6r0r03njBy+mQdIAuYmQYJWFxAFQG4m3CbIUXzY1gZwLCiQibLMsakMQyOK+H0\n3fe+B6ydUkZOY9MB9WlxinACjI+gVDMhtXnzVVy8+MM0fCdUiBhWBjCsqJDIsozoRFQ7rPcPP3wH\nKJJngml8gxJOWCicgKUGFEdRtFgMKwMYVpTPZFnG7y//Hp//+r8Gyq4rc+sB+pHT5bUwHk4AA4pW\nGsPKAIYV5RNBeArYfGsmmMquA1OCfuQUW6lwAhhQlE4MKwMYVpRrdPPqCbISTmowlV8Dbpv0IyfJ\nBiWcZktHOAEMKFopqyKswuEwRkZGYLVaIYoi7Hb7kmaIZ1hRpiXPRJ54pww8eFM/crpZNL1cxmPK\nDBHx9bMeNDuUVAwnym3zrhRcCERRRFtbG/r7+7VtTU1NsNlsqKioyGJltFrNG0DzPlAGHro5E0xl\nN4Fr9wDjVuDXFcB/swKT66Z3XmwoqZYaTv/NwDdAtHQFP7LyeDzYtWsXdu/erW0LhULo6OgwvFAk\nR1aUyGTaihX9UTBtAR6eBMomlBnJH58ArhQrI6ZxKzD2KHB19shJtdxQUnHkRLmh4MPKarUiHA6j\nvLxc2yZJEqxWK6ampgw9F8Mqf614sCza7EaGBKYp4JFJJZjKYsBjEjC5YXq5jM3A+Cbg2rqEB8wV\nSIDxUEqsj+FEuaegw0oNJUmSUFJSorvPZDJBFEVdiC2EYQX09Z3GoUP/Bb///XlcuxYHMAUg8fW4\nM+sRd2d9PgXANGt7PpondOaVcHiuaAp4JAaUf6p8PBoDJu6dDqbNwPh64PraeZ5rqYEEMJQo3xT0\nOatYLAYASUGlMhpW+aCv7zSOH+/HrVtrUFx8B/v2NeCZZ7anvH9y8kMAa1FS8oD2+e3bd3HhgoT7\n7luDy5cnAGzA1NRnkOUbuHPnFj77zAJlfaFiAPfP+uo3ACT+cb2NmR8xNcTWTm8vmr49O+xWwlKD\nZT5znROax5q7wJYPlFFTeQzYEgdi9wJjFuBnW4DAVuBG4uu3nDBSMZSoMBR0WEmSlO0SMqqv7zS+\n9a2TiEa/o22LRl8BADzzzPZZ958GcBJA4ue7pv/9t7h8+bsAqqe3fXf62S4DUJsDrgK4Z1YFs3+c\nEkdP2RyNLiFYFjTfIbhpa+4Cj0rTS7THlEN8n96jtJD/9D7ggweU7j0ASoB/ssRaGEhU+Ao6rJZK\nPdyXb44f79cFFQBEo9/B668fwjPPbJ91fz+UoEr8/N8n/PswgL9J+BxQRkfqj0yqE/uzX7fEc4LZ\nDKtFBIthKUY990wBj12fWWjw4ZvAxWKllfxH9wPnHgRuFSU/bkEMIyKGVQG5dSv123lz+n/v+vtT\nfT7739mf38LM4bwbSHZ91u1cGVml43BaCmvvAo/dmG4lv6a0lV9Yp1yEe3ozcG49cHuucGIAERlR\n0GFls9kAAJOTkynPW6n3zzZXA0Wuj7iKi2c3NyjWrbub4v5Un8/+d/bn9wE4P/35Z0gOrBvQh9Lt\nWc9zF8q5qsTtmThnlSbFd4HHE0ZOD9wCzpcCYw8C75UD565Bvv3rbFdJVJAKOqzMZjNsNhtEUcS2\nbdu07aIowmw2F1xzxb59DYhGX9EdCqys/DZeeunrKe5vAPAKlMN+6ue7Ev797qzPEwlQRllXoD/U\nByghlmh2N+BnyF43oLHRjHRTwg/Hf6ishDs+iN98+hvUbqlFXVkd6srq8OVHv4z198x1nRMRpVNB\nhxUAOJ1ODA0N6cIqHA7D5XJlsaqVoXb9vf76Idy8WYR16+7ipZe+rm2fff/k5CcQhP8V99+/efrz\nLty6dQcXLryB++4rwuXLZwD8DrL8GaambkKWBdy+fQfABqxfX4rPfa4c/+E/7NV1G+az2I0YTo+f\n1pbMOBs7iy9t+RLqyurwtw1/iy9u+SLWrVm38BMRUdoV9HVWABCPx+F2u3XTLTU0NMDv9xseWfE6\nq8Ly6bVPlXCaHjmJEyK+8thXtJFT7ZZarC2a7zonIsqUgg8rAIhEIujq6kJtbS1EUYTD4cDOnTsN\nPw/DKr99cvUTnB4/jffG3sPg+CDOTZ7DVx/7qhJO5XVwPOzAPUWz2/GJKBesirBKF4ZVfjl/5by2\nRPvg+CDOXzmPrz3+Newo34G6sjpUP1yNNaaCPxJOVBAYVgYwrHLbh5MfYnBsJpwuXb+Ep8uexo6y\nHagrr8MfPfhHKDIt5TonIso2hpUBDKvcMi6N60ZO8ZtxbC/bro2cvvDgF2ASTNkuk4jSgGFlAMMq\ne2RZxqg0qnXqvTf2Hq5/dh115XXayOnJzU8ynIgKFMPKAIZV5siyjPdj72udeu+NvYc7U3e0Tr0d\n5Tvw+U2fz/kLtYkoPRhWBjCsVo4sy/jd5d9pI6fB8UEIEFBXPhNOT1ifYDgRrVIMKwMYVukjyzJ+\n/emvtWAaHBtE8Zpi3cjJZrExnIgIAMPKEIbV0k3JU/jlxV9qI6fT46dx39r7dCOncnN5tsskohzF\nsDKAYbV4d6fu4n988j+0kdMPx38I8zqz1qlXV16Hx0sfz3aZRJQnGFYGMKzmdnfqLs5cOKO1kf/o\ngx9h872btU69urI6bCnZku0yiShPMawMYFjNuDN1B+HzYS2cfvzBj/HI/Y9oI6ftZdvx8P0PL/xE\nRESLwLAyYDWH1Wd3P8Pwx8NaG/lPzv0EZeYybeS0vWw7Hrj3gWyXSUQFimFlwGoKq1t3bmHo4yFl\n+qLx9/DTD3+KSkul1gzxdNnT2LRhU7bLJKJVgmFlQCGH1c07N/HfP/zv2sjpZx/9DJ/b9DktnL72\n+NdgXW/NdplEtEoxrAwopLC68dkN/MuH/6K1kg9/PIwnNz+pC6fSdaXZLpOICECBhFUgEIDFYkF9\nfX3SfeFwGCMjI7BarRBFEXa7PeV+i5HPYXXt9jX85NxPtFbyyPkIvvDgF7SLcL/6+FdRUlyS7TKJ\niFLK+8V8gsEgWlpaEAgEku4TRRFtbW26VYKbmppgs9lQUVGRyTIz7sqtK/jxuR9rI6eff/JzVD9U\njbqyOhzafghfeewruG/tfdkuk4hoUfI2rEZHR+Hz+eBwOGC1pj6X4vP50Nraqtvm8Xjg9XrR3d2d\niTKz4tL1Syj/u3I4HnGgrqwOr/7rV/HHj/0xNtyzIdulEREtSUEcBqyqqoLf709aqt5qtSIcDqO8\nvFzbJkkSrFYrpqamDH+dfDoMePPOTaxbsy7bZRARpUXBLv4jSZIWTInMZjMAYGxsLAtVZQ6DiogK\nScGGVSwWAwCUlKRuGhBFMZPlEBHRMuTtOauFSJK05McutCwFl60gIjJmuadPCnZkRUREuWO5/8nP\n+sjKyOG4jRs3orR05S9Unet/APnUYJEK688u1p9d+Vx/PtcOpOdoVFbDanR0FG1tbYvev7a2Fi+/\n/PKi9rXZbACAycnJlOet1PuJiCj3ZTWsKioqVux6J7PZDJvNBlEUsW3bNm27KIowm826dnYiIspt\nBX3Oyul0YmhoSLctHA7D5XJlqSIiIlqKggmrVMdyfT4fenp6dNv8fj98Pl+myiIiojTI2xks4vE4\njhw5AlEUEQgEYLPZ4HQ64XK5sGfPHm2/SCSCrq4u1NbWQhRFOByOpJkuFqtQTnKy/uxg/dmVz/Xn\nc+1AeurP27AiIqLVo2AOAxIRUeFiWBERUc5jWBERUc5jWBERUc5jWBERUc4rOnz48OFsF0FUyMLh\nMN59912MjY2hr68PN2/ezJvpvkRRRFNTE7Zs2QKr1YqPP/4YPp8PgiDk7PcQCARw/vz5lPXlw3sx\nV/358F709vair68P//AP/4Djx49jw4YNePLJJ3X7LPk9kGlJenp65GAwmLQ9Go3KTqdTDgaD8sTE\nhByNRmWv15ty32yZq3ZZluWRkRHZ7/fLgUBAbm9vz6m6Z8uH1zoajcoul0u3ze12y6IoZqkiY6LR\nqCwIgvZhsVjk3t7ebJc1p4GBAdliscihUCjpvnx4LxaqP5ffi0AgIIfDYe22JElyZWWl7Pf7tW3L\neQ8YVkuQzz9Q+f7LnCjXX2tZluWWlpakmoLBoOx2u7NUkTGiKMqhUEiOx+Py6OhotsuZkyiKssfj\nkf1+v1xZWZny5zuX34vF1J/r70V7e3vSNr/fLwuCoN1eznvAsDIgn3+g8v2XOZVcfa0TWSyWpNom\nJiZ0v8C5TBTFnBqpLsZcP9/58l7M97clV9+LiYkJ2eFwyJIk6bar/6FUX/flvAdssDCgoqICb731\nFpqbm+fdT5ZllJSU5NTM7oupvaenB3a7XbfN4XAgEAisdHlLlouvtUqSJEiSBKvVqttuNpsBAGNj\nY1moanXie7GyzGYzRFHE6OjonPss9z3I+uKLlBsW84OUi4GQy2KxGACkXE8NUE6Y58NrKooiJEkC\noHxPVqtVN/9mPuB7sfLU1zhRMBiExWJBeXm5ttDuUt8DhtUKyOUfqLnk6y9zLr/Wal35TP3PS+Jr\n2tTUlLQt1/G9yI6Ojg4cPHgQwPLfA4ZVmuXjDxSQn7/M+fpa55PS0tKkQ8cejwcej4evcYbl23vh\n9/uxadMm7N+/Py3Px3NWaTbXD5TX681SRYWLr3V2VFRUQBRFTE5OZruUVS9X3wtRFOH3+3Hy5Mm0\nPeeqHFmpx04XY+PGjSgtLV3W10v8gZrrMNtiZbr2TEjn95TO13q51Asd56olVy7knE97ezsOHDig\n26aOaEVRxLZt27JRlmF8LzKrra0Np06d0m1b7nuw6sJqdHQUbW1ti96/trYWL7/88qL3X8kfqJWs\nPVu/zMv5nnL9l9dsNsNmsyXVIooizGZzTp4DTCSKItra2tDU1KSrVT2/mQ9/4FV8LzKntbUV7e3t\nSX9HlvserLqwqqioQHd394o890r/QK1k7dn6ZV7q95Qvv7xOpxNDQ0O61zQcDsPlcmWxqsWx2Wzo\n6OhIeu+DwSAcDkfWR65G8b1YeZ2dnWhra9PVGQqFYLPZUFFRsaz3gOes0ihffqDmov4gJcrVX+Z8\nea19Ph96enp02/x+P3w+X5YqMsZqtequnZEkCX6/H52dnVmsamFyigXQ8+m9SFV/rr8X6vWYsVgM\n4XAY4XAYwWAQPT09qKioALC894DL2i9RVVUVOjo6UF9fr9ve29sLu92uvTmSJMHpdOLtt9/O+mEp\n1Vy1x+NxuN1u9Pf3a9saGhrg9/tz8jBJPrzWABCJRNDV1YXa2lqIogiHw4GdO3dmu6xF6+3thSiK\nuHz5MiRJSvqfcy6Ix+M4cuQIRFFEIBCAzWaD0+mEy+XSdcrl6nux2Ppz9b1IdY2mqrKyEmfPntVu\nL/U9YFgZkM8/UPn+yzyXXHytiSj9GFZERJTzeM6KiIhyHsOKiIhyHsOKiIhyHsOKiIhyHsOKiIhy\nHsOKiIhyHsOKaAnC4TDcbjcsFgtMJhMsFgscDgeOHTuW7dKWxOVywWSa+XPgdrt1t4myjT+NRAZ5\nPB7U1NSgt7cXJpMJLpcLmzZtwpkzZ+D1emG1WhGJRLJdZkqBQAAmkwm9vb267YIgQBCEpG1EuYJh\nRWSA2+1GZ2cnLBYLwuEwLl++jJMnT+Ls2bO4e/cuDhw4AEmS4HA4cjawgOQg6unpQTQazVI1RAtj\nWBEtUjAYRG9vLyorKzE6Oppy/sGjR4+io6MDgBJsuWr2xDWlpaWcpopyGsOKaJHUmaF9Pt+8s7o3\nNzfDbrdDFEWEQiFt++zzQipJkmAymdDa2qrbLooi3G43KisrYTKZYLVa0dTUpJt5G1AOS6qTiHq9\nXu08WlVVle5wn8vlQlNTE4CZc1LqCrOLPUfV3t4Oh8Oh1dPa2ppUD6DMpJ24X01Nje61IDKKYUW0\nSKFQCBaLBbt3715wX4/HAwAYGBjQbZ/vPFDifaIooqqqCidOnEBVVZV2niwQCMDhcCAejyc9Xj1E\n+dxzz6GlpUULOzUk2tra0NLSotXn9/t1obvQOSqHw4G2tjaYTCatHr/fj8rKSt0hT6/Xi9bWVoyN\njcHtdsPpdGpLzeTyoVHKcTIRLSgajcqCIMg1NTWL2j8cDsuCIMgNDQ3aNqfTKZtMpqR9JyYmZEEQ\n5NbWVm1bS0uLbDKZ5FAopNu3vb1dFgRBDgQCun0FQZCrqqrkeDyubQ8Gg7IgCLLH49G29fT0yIIg\nyL29vbrnbWxs1NU2+7bP55MFQZBPnTqV8vt0OBzaNrPZLFdVVen2U2tJ/B6JjFh1KwUTLYUkSQAW\nvwKxusbWUrW2tmLXrl1Jy7NUV1cDACYmJpIeM/vwpLpeWarDdIshJ5zXOnLkCFwuF+x2u/ZaAMr3\nWV9fj1AohMnJSZSUlCAej6Oqqkr3XPX19QiHwzCbzUuqhYhhRbQI6h9ZURQXtb+631L/OFdXV2vB\nJEkShoeHEQ6HteaNVOx2+5K+1mLE43EMDAzAYrGkvF8QBMRiMZSUlKCxsRGBQEA7fOl0OlFdXZ1T\nC2JS/mFYES2COqJabFgNDw/rHmeUJEnwer3o7u7Wzk85HA44HI45R0pzrdS6VOo5LPV7drlc8Hq9\nc+6vBll3dzeOHTuGjo4O3f4tLS3w+XwoLS1Na520OjCsiBbJ6XRq7euJqyurgsEgnE4nAGgjoL17\n9y74vLFYLGlbfX09IpEIPB4PPB6PNioJhUIIBALL+TYMU0PQbDYvetXol19+GS+//DImJycxMDCA\njo4O+P1+DA8Pa0FOZAS7AYkWSR0lpBpdSJKEhoYG1NTUoL29HZFIBA6HY1GHvsLhcNJzRSIRuN1u\nvPnmm7rnkDO4sLf6tcxmM0pLSxEMBlPuZ7FYtHNUoijC6/VqHYglJSXYs2cP+vv7tfNWars8kREM\nK6JFqq+vR2Njo9ZWntiGbTab0d3djXA4jLa2NgiCgJ6eHt3jzWYzZFnWXW+kHu5LZXYTReK+yw2t\nxTw+sZXd4/FgYmJCu05L1d7ejng8rrtG7NixY1rrfiJRFCEIwrzXqBHNhYcBiQzo7u5GU1OTdr1T\naWkpampqEIvFtPASBAGyLGNkZEQ3K8Rzzz2H3t5euFwutLS0QJZl9PT0oLa2FhMTE7qRjHrIsamp\nCTU1NYhGo9q+gNL5Z7PZtI6/xVLPK3m9XgwNDeHo0aPafbMDLPH20aNHEQgEtMaJ6upqiKKojSD3\n798PQDlHp9ZutVpRX18Pq9WK7u5uTE5O4sCBA4bqJdJkqWWeKK+Fw2HZ7XbLVqtVNplMstVqlWtq\nauTOzk5ZkiTZ5XKlvJ7J7/fLlZWVsiAIstVqldva2mRZlmWLxaK7BkmSJNnj8cgWi0W7vkt9Lo/H\nI5tMJm1/9XbiNVaq2dd6ybKs1Wa1WrVtbrdbd13V7Nsqr9crOxwO7boutf5U+1VWVupem9mvBZER\ngrv7PukAAABUSURBVCxn8CA40Sry2muvaSMOIloehhUREeU8NlgQEVHOY1gREVHOY1gREVHOY1gR\nEVHOY1gREVHOY1gREVHOY1gREVHOY1gREVHOY1gREVHO+/8B5wKzyrvpMy8AAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23aee87d0>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8G/WZ+PHPKIEkHLakQKGcsWR6UhpbMj23tJFk03K1\nieVAu9tCwZbbXej+9geWuX6ldEsih+4u0CVYpt1td7etYznlcltsKZTQctmWoIVyBI0CpS0txB55\nAznt+f2haGJZsmP5kmw/79dLr0Qzo/FjJ9Lj53squq7rCCGEELPMVOgAhBBCLA6ScIQQQswJSThC\nCCHmhCQcIYQQc0ISjhBCiDkhCUcIIcScWFroAADC4TCxWAyAXbt2Ybfbqa+vz7gmGo3S39+P1WpF\nVVUqKytxuVyFCFcIIcQUKIWehxONRkkkEqxbt8441tnZycDAgJF0VFWlsbGR7u5u45q6ujoCgQBl\nZWVzHrMQQoj8FbxJLRgMZiQbgHXr1tHT02M8DwQCNDY2Zlzj8/nw+/1zEqMQQojpK3jC6evrI5FI\nZB3XNM34e0dHB5WVlRnnHQ4HoVBo1uMTQggxMwqecNxuNx6PJyPphMNh6urqgFTi0TQNq9Wa8Tqz\n2QzAzp075yxWIYQQU1fwhLNx40bMZjN2u522tjbC4TDJZJKrrroKgIGBAQBKSkpyvl5V1TmLVQgh\nxNQVxSi1vr4+qqur8fl8VFZWEolEjHOjm9aEEELMXwWvcADa2tpoaWmhp6cHVVVxOBw5+3WEEELM\nXwVPOI2NjXg8HlavXo3L5SKRSGCz2fB4PNO6r6Io4z6EEELMvYImnHRz2apVq4xjpaWldHd3Yzab\n2bZtGzabDYChoaGc90ifz4ckHSGEmHsFTTj9/f3Y7fac53w+H5qmYTabsdlsWYMDVFXFbDZnJKvR\ndF3P+RBCCFEYBU04NpuNeDye85ymacbcG7fbTW9vb8b5aDQ67WY3IYQQc6egCSe9LM3oUWmQql52\n7dplVC+BQICOjo6Ma4LBIIFAYE7iFEIIMX0FX0sNUqPU4vE4K1euBFKTOscu3hmLxWhvb6eqqsoY\nybZmzZq8v1a6/6YIvm0hhFhUiiLhzCVJOEIIURgFHxYthBBT8frrr1NVVcWSJUsmnAYhj8k9TCYT\nJ598MjfeeCP79u2blX8zSThCiHnpC1/4AmvXrmXPnj3jjkqVx+Qf+/fv5/HHH+f555/nkksumZV/\nM2lSE0LMS0uWLGHPnj0cffTRhQ5lQdmzZw8lJSUcOHBgxu8tCUcIMS8piiLv41kyWz9baVITQogZ\nFI1GKS8vL3QYRUkSjhBCiDkhCUcIsaB0dW2npuYmPv3pW6ipuYmuru0FuUdaKBTCbrdjMpmoq6sj\nmUwa54LBIFarlfLycoLBoFEZpecabtq0yTgfi8UmvKeqqng8Hpqbmzn77LNxOp00NjZitVqprq4m\nGo0ar9m0adOUv59p0RcZQF+E37YQC06u9/FDDz2q2+036KAbD7v9Bv2hhx6d9H2ne4/+/n7dbrfr\nuq7r8XhcVxRFj0QiuqZputfr1X0+n3HOYrHosVhM1zRNr6ys1MvLyzNet2nTJl3Xdd3n8+kej2fC\ne6qqqiuKojc2Nuq/+tWvdEVR9M7OTl3TNN1ms+kWi0VPJpN6OBzWFUWZ8HuYrc/IRffJKwlHiIUh\n1/u4uvrGjESRftTU3DTp+073HqMTTiAQ0BsbG41zqqrqFotF13Vdb2pq0pubm41zoVAoI1Glr9N1\nXY9Go7rD4ZjwnumEk+v1Pp8v42spiqInk8lxv4fZ+oyUJjUhxIKxb1/uTYz37l0yp/dIGxgYyNhC\npayszNiWJZFIZKyWn15bMs1qtRp/10eNGJvonqOPj3692WzOeF4oknCEEAvGsmUHcx5fvnx4Tu+R\ntnLlyowV8dNbrkAqObzyyivGubFbsEzlnsVOEo4QYsG45ppq7PYbM47Z7Tdw9dWT38pkJu6Rtm7d\nOoLBIJFIBE3TqK+vZ/369QCsX7+eYDBILBZD0zQ2bNgwqc0hJ7pnsctdOwohxDx0wQWfAuCuu25m\n794lLF8+zNVXn28cn6t7pBOHzWajo6MDn8+Hqqp4vV5jW5WKigoCgQAul4uVK1fS1NREa2tr1j0m\ne8+33nor4zXjvT7XublS8JUG/H4/1dXVOByOCcvCaDRKf38/VqsVVVWprKzE5XLl/fVkpQEhFob5\nvtJAIpFA0zQqKiqA1FDnYDBId3d3gSObvZ9twSucaDQ67phwu93Ojh07UFWV5ubmjH+Iuro6bDZb\nVkebEELMB4ODg7jdbhKJBKWlpbS2ts6bprGpKngfjt1uJxqNoqpqxqO1tdXY5TMQCNDY2JjxOp/P\nh9/vL0TIQggxbZWVlVx//fWUlZUZkzuvuuqqQoc1qwrepNbW1pa1u+fY41arlWg0amw5DamRGVar\nlZGRkby+njSpCbEwzPcmtWI2Wz/bgiecXEYnm3Ri0TSNkpKSjOtMJhOqqmYkoiORhCPEwiAJZ/Ys\nmtWiI5EITqfTeD4wMACQlWzSJjt2XQixsJhMJvbv31/oMBacPXv2sHTp7HTvF13CiUajxqgNwJhB\nK4QQo1VWVnL77bdL0pkhBw8eJB6Pc+mll05pBPBkFFXCSa+AKoQQR/Kzn/2Mn/3sZ6xYsQJFUeQx\nzceyZcv45Cc/ydlnn839998/K/9mBR8WPdrGjRvZtm3bjNyrUBObhBBz47TTTqO3t7fQYUyLrut8\n6MsX8/y7n4Kn/wEeux5GjgKgpuZmfvnLbxc4wplVNAlH0zSi0WhWX016MbqhoaGc/TijF6sTQoj5\n4vWh16l/sJ5XT3oGftQDf/lwxvmpLBZa7IqmSS0cDudcacBsNmOz2bIGB6iqitlsHneEmp7aeiHr\nIYQQhaTrOj+I/YCK1go+ftrH+ehzl2clG5jaYqHFrmgqnN7e3nH7b9xuN729vaxevdo4Fo1G8Xjy\nX0xPCCEK5Q/JP9DwUAN/2f0XIl+OcM5J59C1ezuJV24kHv+OcV1qsdDzCxjp7CiaeTher5ehoSEe\nfvjhrHPJZBKv15uxtE11dTXBYDCvOTgg83CEEHMvXdU0R5r5xke+gf8Tfo5acpRxvqtrO3fd1TNq\nsVBPXouFzhdFk3AaGxtRFIXNmzfnPB+LxWhvb6eqqsrY73vNmjV5fx1JOEKIufRa8jXqH6znrXfe\n4j8v+U8+dNKHCh1SwRRNwpkrknCEEHNB13W+H/s+10eu5x8/8o80faIpo6pZjIqmD0cIIRaK0VXN\nti9vW9RVzWhFM0pNCCHmO13XaetvwxF0cN6Z5/HklU9KshlFKhwhhJgBr2qvUv9gPYN7B3nkK49w\n9rvOLnRIRUcqHCGEmAZd1wn2B3G2OfnMqs/wxJVPSLIZh1Q4QggxRa9qr3LVg1eh7dWkqpkEqXCE\nECJPuq7T2teKs82Jq8wlVc0kSYUjhBB52Knt5KoHrmJo3xCPXv4oHzjxA4UOad6QCkcIsWB0dW2n\npuYmPv3pW6ipuYmuru0zdu8RfYR7+u6hqq0Kj83D41c+LskmT1LhCCEWhK6u7XzjGw9nrEkWj98I\nMO1lYnZqO7nygSvZvX+3VDXTIBWOEGLOzUYlcued3RnJBiAe/w533dUz5XuO6CNs7t1MVVsVNfYa\nfvPV30iymQapcIQQc2q2KpF9+3J/nE11X5nEYIIrH7iSdw68w/bLt/P+E98/5dhEilQ4Qog5NRuV\nCMCyZQdzHs93X5kRfYS7e++mqq2Kz5Z/lt989TeSbGaIVDhCiDk105VI2jXXVBOPT29fmcRggq8+\n8FX2HNjDY1c8JolmhhVNwolGo2zZsoWVK1eya9cufD4fZWVlGef7+/uxWq2oqkplZSUul6uAEQsh\npmKmKpGx0s1xd91186h9Zc6fVDNduq/mm7/6Js2fbOb/fPT/sMS08LZ4Ljh9hiSTySm/tqOjQ/f5\nfBnHGhoajL/H43Hd4/FknPd6vbqqqnl/LUCfwW9bCJGnhx56VLfbb9BBNx52+/X6Qw89WpB44gNx\n/bz/OE//2L0f019484WCxLBY5P3JG41G9cbGRj2RSOi6ruuapukOh0NXFEU3mUx6c3NzXvcbHBzU\nLRZLxrHW1la9vLzceN7Q0KB3dnZmXBMOh3Wv15tv+JJwhCgCDz30qF5Tc5N+3nnf1GtqbipIshke\nGdbveuoufWVgpX77b27XDw4fnPMYFpu8NmCLRCJ4PB4g1cS1evVqGhsbCQaDuFwuVFVl586ddHR0\nsHbt2knd0+/3YzKZ2LBhQ8bxnTt3GttHW61WotFoxnbSmqZhtVoZGRmZbPiAbMAmhID4QJwrH7iS\n/cP7+Y9L/oP3nvDeQoe0OOSTndKVTDgcPpyxFCWjuctsNutOp3PS97RYLFnVy2iDg4O6oig5m+wU\nRTEqrclCKhwhFq3hkWH9zifv1FcGVurfffy7UtXMsbwGDaiqSm1trdFZH4vFAPD5fMY1dXV1hEKh\nSd9T0zRKS0tpa2vDarUyMDCA1Wpl3bp1AAwMDABQUlIybkyjKx8hhMjllYFXuPKBKzk4cpDHr3yc\n96x8T6FDWnTySjiaphlNUgDhcBjAaGaDVILQNG1S91NVFUglrmuvvdY43tzczMDAAPX19ZO+lxBC\n5DKij/C9p7/HrY/eyo1/cyPXfOQaGYFWIHklnIqKCiPJALS2tmKz2TKqj0gkkjGceSLpZGKz2TKO\nr1+/HpfLRX19fT7hCSFEhlcGXuGr93+VEX1EqpoikNdKAz6fj8HBQc466yyqqqpQVdVoTotEIpSX\nl6NpGrW1tZO6XzrRjE04FRUVaJrGzp078wkvg6IoOR9CiIVvRB/hjifv4KP3fpS171/Lo5c/Ksmm\nCORV4TQ0NBCPxwkGg8TjcWpra7nuuusA6O7uRlVV3G43GzdunNT9zGZzxp9jpSd4AgwNDeXsxxmb\nrIQQi9uOXTv46gNfBeCJK5/grJVnFTgikZbXsOiJpPtj8k0A5eXlBINB1qxZk3HcZDIZAwLKy8sJ\nhUKsXr064+s5nU5jUMFkybBoIRamEX2EO5+6k3/e/s/c/KmbufojV2NSZLnIYjLlpW127tyJqqpo\nmobNZsvqy5ksn89Hf39/RsKJRqNYLBZj9Jnb7aa3tzcj4USj0YzBCkKIxUuqmnki33HU0WjUmI8z\n+mEymfS6urq858Vomqbb7faMYx6PJ2NujqZpWUvbeDyevL+Wrss8HCEWkoPDB/V/efxf9JWBlfod\nT96hD48MFzokMYG8mtQSiQR2ux2AyspK1q9fT1lZGaqq0tPTQyQSwWKxkEgk8qp2EokEgUAAu91O\nPB6nrq4uq4ktFovR3t5uDFZwOBxZ10yGNKkJsTC8vOtlrrj/CpaalvL9i79PubW80CGJI8gr4aQn\ndba2tuYcshwMBmlsbMTr9dLe3j6jgc4USThCzG/DI8Pc8dQd3PbYbXzzvG/y9+f+vfTVzBN5JRyr\n1YrNZqOvr2/caxwOB0NDQ+zYsWNGApxpknCEmL9eeuslvvrAV1lqWsoPLv4Bdqu90CGJPOT1a4Gm\naUaT2nhsNpsxYk0IIWbC8Mgw3338u3ziB5/gsrMv45GvPCLJZh7Ka5Say+XKWGkgl0gkQkVFxbSC\nEkKItBffepEr7r+CZUuW8XT909gsMvduvsqrwmltbWVkZISampqsVQASiQTV1dVomkZbW9tMxiiE\nWISGR4a5/fHb+eQPPsnffuhv2faVbZJs5rkJ+3Cqq6uzloOJx+OoqoqiKNhsNsxmM5qmoaoquq5T\nWVlJVVUVmzdvnvXgp0L6cIQofumqZvnS5Xz/4u9LolkgJkw4FosFRVHy/nBWFCXvFQDmiiQcIYrX\n8Mgw//LEvxD4TYBbP3Mrjc5GGYG2gEzYhzM4ODhXcQghFrkX3nyBK+6/gmOOOobe+l7KLJNbdV7M\nH/KrgxCioIZHhmn5TQt/8x9/w1c+/BXCXw5Lslmg8hqllp7tn0gk0DQNs9mMzWZj/fr1GeucCSHE\nZEhVs7hMauJnLBajvr6eaDQ67jUOh4O2traiTzzShyPEzOnq2s6dd3azb99Sli07yDXXVHPBBZ86\n4usOjhzku49/l9ufuJ1vf+bbNDgapK9mEThihROJRIxVmSsrK/H5fDidTmMNtb6+PlpbW+nv78fh\ncNDT0zOlNc6EEPNLV9d2vvGNh4nHv2Mci8dvBJgw6fz+zd9z+X2XU7KshN76XlaZV812qKJYTLSy\np6ZpusVi0RVF0YPB4ISrgLa2tuqKouhWq3XKK4nOBWS1aCFmRHX1jTroWY+amptyXn9g+IC+4bEN\n+gktJ+j39N6jj4yMzHHEotAmrGGDwSCaptHU1JRzsc7RGhoauO666xgcHOT222+fwZQohChG+/bl\nbiDZu3dJ1rHn//o8H//+xwmrYXrre/E5fbLl+yI0YcL56U9/iqIok94yOhAIANDT0zPpAFRVxePx\nEIlEjAmkzc3NRCKRjOui0ShtbW10dnayadOmrPNCiLm1bNnBnMeXLx82/n5w5CAbHtvAp3/4aa6q\nvIqev+uRJrRFbMI+HFVV894yuqysbMLVpHOJRCJGAjGbzdx77724XK6MOJqbm+nu7jaO1dXVYbPZ\nKCuTUS1CFMI111QTj9+Y0Ydjt9/A1VefD8Bzf32OK+6/AstyC331fZxpPrNQoYoiMWHCSSaTnHvu\nuXnd0GazsW3btklfrygK4XAYp9PJwMCAsa30aIFAgMbGxoxjPp8Pv9/Pli1b8opPCHFkkxl9ln5+\n1103s3fvEpYvH+bqq8+n5rMf57bHbuNfn/xXbltzG1dVXiXNZwKYxNI2JpOJXbt2TfqG+b4mkUig\nqmpGRTOW1WolGo1mJCNN07BarYyMjEw6NpBh0UIcSa7RZ3b7jdxxR80Rhzw/99fnuPy+y7GusHLv\nxfdyRukZsx2umEcm7MNxu90MDg7yzDPPTOpmsViMZDI5YfLIl6ZpRnIZzWw2A2StWi2EmJ477+zO\nSDYA8fh3uOuu8ftmDwwf4Dvbv8NnfvgZGp2NPPy3D0uyEVkmbFK7/vrr6ezsxOv1HnEHz2Qyidfr\nNV6XD1VV0TQNgIGBAaxWK+vWrTOeA5SUlIz72lzNcEKIqcln9BnA7/7yOy6//3JOPOZE+hv6JdGI\ncU1Y4VRWVlJfX088Huess85i69atOa/r7OzE4XCgqiq1tbV5bcCWrlzWrVvHunXrqK+vp729nc7O\nTgAjEQkh5sZkRp9Bqqr55+3/zJofreHrzq/ziy/9QpKNmNhkJuvU1tbqiqIYEzudTqdeV1enO51O\n3Wq1Gue8Xu+MTA4Kh8O63W7XdV3X+/v7dUVRcl6nKIoeiURynuPQBM/xHkKI3B566FHdbr8hYzKn\n3X69/tBDjxrXPPvGs3pla6Ve8181+mvaawWMVswnk1q8s6Ojg3A4TCAQIBKJ0N/fT39/v3He7Xbj\n9/tnrO8mvWzO0NDQjNxPCDF5440+u+CCT3Fg+AAbf72RO5++k4A7wBWrr5ARaGLSJrV451jpPpf0\natHT0dLSQlNTU8ax9CCB9Mg0q9WKpmlZ/TgmkynvPhwZpSbE1Dz7xrNccf8VnHTcSbRd1MZpJacV\nOiQxz0wp4cwUVVUpLy/PShrp4+kkU15eTigUyliJWlVVY+5OPiThCJGfA8MH2PDrDdz19F20uFu4\nfPXlUtWIKclrP5yZZrPZaG1tzapQwuEwDofDqGjcbje9vb0ZCScajRqrWAshZsezbzzL5fdfzruP\nezcxX0yqGjEtBd+Awmq1kkgkjOeaphEMBmlrazOOBQIBOjo6Ml4XDAaNtduEEDNr//B+vvWrb+H5\nLw/f+Mg36PpilyQbMW0FbVJL6+zsRFVVdu3ahaZpNDc3Z1U96d1Gq6qqUFUVh8MxpX13pElNiIk9\n88YzXH7f5ZxacirBC4OcWnJqoUMSC0RRJJy5JAlHiNz2D+/ntsdu4+7eu9nk2cSXP/xl6asRM6qg\nfThCiOKQrmpOKzmNmC8mVY2YFTPWhyNzZoSYf/YP7+ebj3yT6v+q5p8+9k88eNmDkmzErMk74cRi\nMb72ta8Zi2Ymk0mcTidms5klS5bkvY6aEGLudXVt52Nrr8LafAZ33/djbi+/R5rQxKzLK+FEIhEc\nDgetra3GGmd+v59oNIrL5WLVqlW0tLSMu+aaEKLw7nswwt/94AaeLH+At7s38dadL3Prdf10dW0v\ndGhigctr0IDT6SQajdLT02MsY2MymXC73cZunBaLhfLycnp7e2cn4mmSQQNiMYv+Ocp5//pZdr9+\nLjzUCv97inGupuZmfvnLbxcwOrHQ5VXhpFeDTiebWCwGpHbfTKurq0NV1RkMUQgxXfsO7uPmbTdz\n/n+fz2mvfgJ+8kBGsoHxtx8QYqbklXA0Tcto4w2HwwAZM/4HBgZkSwEhikj/n/pxtjl59i/P8mzj\ns5yhfQDI7qsZu/2AEDMtr4RTUVFhJBmA1tZWbDZbxqKakUiEsrKymYtQCDEl+w7u46ZtN/G5H3+O\n5k80c/+l9/Pu49/NNddUY7ffmHGt3X4DV18tS0WJ2ZXXPByfz0djYyNnnXUWZrMZVVWN5WUikQg+\nnw9N02hoaJiVYIUQk9P3pz6uuP8KbBYbz/ie4d3Hv9s4N9H2A0LMprxXGvD7/QSDQZLJJLW1tWzZ\nssU4vmnTpowBBMVIBg2IhWzfwX3c+uit3Bu7l3+t+VcuO/syGeosisaMLW2THigw3f1xZpskHLFQ\n9f2pj8vvu5xyazn3XHgP/Y++zJ13drNv31KWLTvINddUSxUjCmrKS9sMDQ0xMDCAxWKhtLS06BON\nEAvVvoP7+Naj3+L7se/zbzX/xqVnX8rPf/4Y3/jGw8Tj3zGui8dT/TaSdESh5F3hxGIx6uvriUaj\nKIpCT08Pa9asoby8nMbGRq699trZinVGSIUjFpLeP/Zy+f2XU3LAyrIeB+w2s2zZQd58c4BY7O6s\n62WujSikvCqcRCKBw+EAwOVyEYlEjHO7du2iqamJ9vb2aU36TG9PcM8992Qcj0aj9Pf3Y7VaUVWV\nyspKYz6QEAtJV9f2jKawj33sFJ544k8Zz3/95Gu8fMqv+cu7n+Gio+qI/ffJqPHbjHssX/7lnPeW\nuTaikPJKOOkRaf39/ZSVlWG1Wo1zg4ODtLS00NzczPXXX8+GDRumFJDf72dwcDDjmKqqNDc3ZwxG\nqKurw2azyRBssaB0dW0f0xS2nW3bfszBg/cYzyMv/hvDF74Eu94Ld8T5+cg17NlzW8Z99u49I+f9\nZa6NKKS85uFs2bIFt9tNRUVFzvNNTU1UVFQQCoWmFIyqqgwODmaNqgkEAjQ2NmYc8/l8+P3+KX0d\nIYpNV9d2ampu4u/+7u6MfhfoPpxslu4FdzPDdY/Do/8P2jvh7ZPYs+f9Oe5YzfLlX8s4InNtRKHl\nVeFomobdbp/wGpvNRmdn55SCiUQieDweenp6Mo53dHRkrULtcDimnNiEKCaZVc0tY84eeoue+hR8\n/gp4E9j8LLx90qhrDua466d4//t/xLveJXNtRPHIK+FUVFTQ19c34TWxWIzKysq8A4lEIrjd7oyV\nDCCV5DRNy2i+AzCbzQDs3LkzaztqIeaTO+/sHlXVjEkeS/fCp/2w+ofwizvh+WeBk8bcoZoVKxrZ\ns+dwv6fdfgPf/vaXJcGIopJXk9r69evp7+/nkUceyTmZLL1wp9vtzjsQVVUpKyvLGj02MDAAkLF8\nztjXCTGf7ds3+ve+auDQsjOnPQm+n6Cs7IDNv4Xn64Aali7NbF62239JU9M51NTczHnn3UJNzc3c\ncYdUM6L45FXhpEehuVwuY8HOQCBAa2sr4XCYwcFBbDYbGzduzCuIzs5O6uvrc56ThUDFQpUejfbb\n374y6uinYOk++MzHUVbHOOf1z/H597l4UrvLaBr76EfP4cknpalMzD95T/zs7++npaXFGIWW7m8p\nLS2lqakp72QzWwlFlvMQxSyz32Y7qarmO6mq5pJrOPZtaP34T/nS5y8pcKRCzJwprTTQ1NREU1MT\nkGrSslqtRp9Kvjo6OjKqG0kUYiFLVzW9va8wOPjTQ0fTVc3HUFY/yzmvf5bvfOkbUrWIBWfKS9uk\nTWdJm1gshtPpzDg2tg8nff+hoaGc/Tjjff3xVhKQhCYKZdzRaKc9AZ+/Gt74MB+NfZLHezYVKkQh\nZtWECcdkMo37AZ3+QB+9VIyiKMafw8NHnmDW19dHPB6nvb3dOBaNRo2JnlVVVaxbtw6bzYaqqqxe\nvdq4TlVVzGazjFAT80JX13a+8pV/Z9eu9P/1g7B0D6y5GT70P/CLu+D3tZTU3FzQOIWYTRMmnHXr\n1k3pppOtInINFNi0aRN9fX0ZfUFut5ve3t6MhBONRjN2GhWiWKUrm127Rk3QPP0UuOQ0eMOTGoH2\nzomHJmaeX7hAhZhlEyacjo6OuYrD8NZbb2U1hwUCAbxeb0aCCgaDBIPBuQ5PiLwdnmdzExz1Dnzm\nZvjQj+Hn/wgv7MdiuZZz/+YMGW0mFrwZ2w9nuhKJBIFAgC1btpBMJqmvr8fn8xnL6MRiMdrb26mq\nqkJVVRwOB2vWrMn768hq0WKupAcIPPXU6yST/wmn/zt8/v/Bn6pTTWjvnIDdfoPMmRGLxoQJJ92H\nE4/HWbVq1YR9Omn59OEUgiQcMdu6urZz880/4oUXjmLv3s1wlB/WHICzfwo//zq8sA9YwsqVL/LD\nH35dko1YNCZsUnO5XCiKgsViASbfpyMjwcRidXgk2snAP8MZv4ZLfgx/KjnUV3MCwKHKRpKNWFyK\npkltrkiFI2ZLxki0o26ENe/A2e3Q9e/w4kqgh9LSP/DRj57O1Vd7JNmIRSevhDPeXJj5RBKOmA2H\nK5uj4Aw3XHIx/PGzqQU396w0rpMdN8ViltfinWazmXvvvXfCa5qbm1m5cuWE1wix0Nx5Zzfx126E\n838O3jro+b+wdVVGspH9aMRid8SVBjo7O40JnYCxzXMuuq4TCoWyduwUYqH7y/I/QuOH4Y9lcPcn\nYM+NpNZvGhM6AAAgAElEQVRIu5nly1/lAx84nltvXS/NaGJRO2KTmsmUVxEEpCZqjt4OuphIk5qY\nKV1d2/mX7z3EMyt/wcBJO6CrHV66hFSi6UFGogmR6YgJZ/SumnV1dTQ0NEy4343FYsHlcs1chDNM\nEo6YCV1d22n4Tht/qnoE/mCBX26APU8Ah7eHljk2QmTKa9CAx+Ohubm5qBPKkUjCEdP19v63Kav/\nGG+esAu6PgEvbTl0RiobISYiw6KFmKSuru38478FiJ/9K/RX3wW/7Ic9d5Kx8vMh5513C7/6VfZx\nIRazvLcniEQidHR0kEgkJrzu4YcfnnJQQhSb0AO/5Cs/+ifeOed1eOgCePk9gBU4mPP65cuLc6UN\nIQopr4TT2dmJ1+udrViEKEobfnIHN/XeyMiwDe5+FfbeAawhtUtnDcZunYfIqs9C5JZXwvH7/UBq\nW+n53I8jxJGkR6A9XbKV3af9GbouOVTVWEhVNem+mR7gLeBSjj1W4ZOfLJdVn4UYR14JR1VVGhoa\nJNmIBa2razsNt7WmRqC9ugzufh32fpfDzWfVHK5qUolFRqQJcWR5JZzS0tJZWZgzHA4TDodZuXIl\n8Xgch8ORtTlbNBo1Jp2qqkplZaUkPjHjdu/fzdce/Cf+9NE34MG/gR3vJ1XVVAM/JLP57GaOOirB\nhz5UKpM6hZiEvBJOQ0MDbW1tBAKBGVtTLRwOoyhKxg6fTqcTTdO47rrrAIwtp0dPJq2rq8Nms1FW\nVjYjcQjxSOIRrnzgSvZTCnf/7lBfTbqqSSeTHwGXsXTpMOeccyK33togiUaIScprGYFAIIDL5cLh\ncLB161Z27tzJ0NBQzsdktba2Zh1zu90ZxwOBAI2NjRnX+Hw+o09JiOnYvX83X+/6Ol++78t873Pf\n45SnPwZ703016eYzSCWde1mxooT77vsH+vv/XZKNEHnIax5Oeg01TdMmvmkeG7DV1dVht9vZsGGD\ncczv97Nt2zZ6e3uNrxuNRlm1apVxjaZpWK1WRkZGJhu+ERvIPByRsi2xjS/+9Esc2HE8e+9fxTsD\n7wAnAh8gNQLt4UN/piZ0rljxAk1N53HLLV8vYNRCzE95NalNdkh0Pv08W7ZsyToWCoX42te+BqQS\nSzq5jGY2mwHYuXNnRiISYjL+d9//sv77f0v3zh6Gf7YaXnn/oTO7gXYOrxrwFnD3qBFofy9VjRBT\nVHQrDQSDQSKRCO3t7UCq/6a8vDxnJWMymQiHw6xZs2bS95cKZ/Eytn7e+zv21jwL6knQXQl7Pzjq\nqqXIygFCzI68Vxo4kkgkQigUYvPmzXm9rrOzk56eHhRFMZINHLn5Togj6erazjXX3IH6+n6o3gFn\nvQ4PnguvfIrst4CsHCDEbMm7wkkmk4TD4Zx73ui6TiAQIJFITLoPJ9f9XS4XbW1tVFRUEI1GcTqd\neVc4R2rWkwpncejq2s5VV/2QN46Jw8XPgLoKHnbDvuMOXTE2wVST6rc5vHLAihU+Ojq+JE1pQkxT\nXhVOIpHA4XAcsepoaGiYckClpaX4fD5cLhcDAwNTvo8QADd860e84YzBWXF44CKIlx86M3oS5w9H\nvSI9SOBmYAlHH/0cTU1rJNkIMQPyGhbt9/vRNI1AIEB3dzdlZWXU1tbS09NDd3c3FRUVeDwe7rnn\nnmkF5XK50DSNbdu2YbPZAMYdap0+P5au6zkfYnHo6trOuz/5SX77iZ+AAtxdD/FVpBJNerjzn0kl\nmK+QuugN4AkUZRPHHhunsvJNtm69RkakCTFD8ko44XAYt9vNddddh9vtxufzkUgkcLlcuN1uIpEI\nvb29bN26dVL3U1UVi8XCM888k/O8pmmYzWZsNhuqqma91mw2ywg1kaXjgV/g/VE9b1TF4EEnPPg5\n2HcxqQSTfqQTzV+AzUASu/0EHnroFkZGHmT37h/LPBshZlheCUfTNOx2u/G8srKS/v5+47nZbMbr\n9WbMqZnM/cZWKenkUllZCaQmgqbn5KRFo1E8Hk8+4YsF7pZb7ubo93+YukfWsmfPMbD5aoi/j4kr\nmXeorLTy0ENX88orP5QEI8QsyivhlJWVZVQaTqcTIKNCsdvtGUloIpWVlaxfvz6rqSsQCOD3+43q\nJRAI0NHRkXFNMBgkEAjkE75YgG655W5WrPgMyvIKvhW9jQPnvwIPfgQevAT2LSU1iXN0JXMAWEVF\nhU0qGSHmWF6j1LxeL1u3bqWnp8cYGWaxWLj00kuNYdB1dXWEw+G8Ovzb2tqIx+PG4p1Op5Orrroq\n45pYLEZ7eztVVVWoqorD4chr/k2azMOZ34whzuobwB7gRLDvgYt7Yccp0LMW9r0GnMXhAQEnM3rU\n2ckn/x/uvfcLkmSEmGN5JZz0JExFUejo6GDt2rX4fD7a2trwer0MDg4SDodpaGiY9sCB2SIJZ/7q\n6tpOXd3tvPPOgdSBZcNQ8wrYBuCBc0E9BVhFqgntIKlEU0Nqwc23gQPY7cdyxx1XSrIRogDynoej\nqqqxmGZFRQWapuFyuYjFYkCqv6Wjo4PS0tJZCXi6JOHMT7fccjff+tbPSG3rDJT/GS6Kwo5TD1U1\n6abesw79Wc3hRHM0cBwVFfuIRu+d48iFEGkztrRNem5Oeo2zYiUJZ3655Za7ufXWe9H1E4HjYfnR\nUN0Ltj/DA87U8jScBZwCPJi6huORZjQhik/RraU22yThzB9nn/0Fnn9+ADgu9Sh/Ay7qhZdPgZ5z\nYL+bw0nmLOBUIDTqDsewfPmxfOADJ8gGaUIUgbwSTmNj46SWjFEUJe+11OaKJJz5IZVs9gMmWH48\n1PTCqjfggQ9D4vhDV50JnMPhJHMMcDR2+/HSTyNEEcor4ZhMRx5FnW5SK9ZlaSThFLcvftHPT37y\nS1JNZCfBWSpc2Heoqvke7O8ANFJzaXTADBzDihUHaGqqkVUBhChieSWc8dZQGxgYIBqN4vf7KS8v\n5+GHH56xAGeaJJzilEo0Pyc1KOAYWL4CamKw6i/wQD0kXiZV0XyR9GZo8CyXXfYefvxjmY8lxHww\no304mqZhs9nw+XyTXm1grknCKS5dXdtZu/b/sn//MaSaxJbCWUm4sBdeOhfCI7D/fUAFqaazFcAK\nTKZ3uPnmC6WiEWIemfFBAz6fj1AoxK5du2bytjNGEk7xSA11/gmpQQFLYflRcH4Mzvwr3H8R7Dye\nVKL5H6AUOBbYzWWXnSNVjRDz0IxvwKYoSs69coRI6+razpe+dDPJ5NGk+mCOhbP+lBqB9uJJsNkN\n+82kkswvgNOBIY455nXefvuJQoYuhJiGGU04kUiEYDA47pYBQpx5pofXXttDqvnseFiuw/m/gTMH\nYOslsPPPwFHAX0kNDlgJ7OWoo0bYskWqGiHms7wSjslkmnBYdLqZyu/3Ty8qseCkBgV0kRp9ZgGO\nhvf8AS78HbzwAdh8Juw/ntTAgEcwEhL7Ofnkpdx77w0yzFmIeS6vPpwjbQdgNpu59NJLWbdu3bQD\nmy3ShzP3UnNq3iA9hJnlOnz2aTh9FzzwQdhZQWp02iOkKprjkL4aIRYeWWlAzKp3vetvePPN40jt\nQ3MsvOdVuPC38MIJEH4vHLAA/0tqmHNqUMAZZxzk1Vd7Chm2EGIWzPiggano7OxEVVXi8TiqquLz\n+bKqpGg0Sn9/P1arFVVVqaysxOVyFShiMRmpZHMscBysOADnPw6nD0Dn2fDqsaSa1iTZCLFY5JVw\nIpEIPT09xsrQ6e2f169fz+rVq43rtm7dytq1ayd1z87OTmw2m5FgkskkDoeDgYEB6uvrgdQK1c3N\nzXR3dxuvq6urw2azUVZWls+3IOZAarjz3aRGlx0L71Xhgufh96fCZgccOJlUonkVOAEZ7izEIqFP\nQjQa1e12u64oyrgPp9OpJxIJPRQK6Yqi6Js2bZrMrfWWlpasY8FgUFcUxXje0NCgd3Z2ZlwTDod1\nr9c7qa8xGqn1UPJ+nZickpJzdajQoUZnxcU6a0/RuWaZzpkf0OEqHT6vg1OH83Wo1eF8/bLLmgod\nthBiDhyxDycWi+FwOIDUltA+nw+n02lsN93X10drayuxWAxFUdB1HbfbnVGNjEfTNNxuN5FIJGP/\nnPRGb6qqsmrVKqxWK9Fo1NhyOv1aq9XKyMhIXglW+nBmXlfXdi655B8ZHt4PnAYo8N4kXBCF31sh\n8kE4cAAYAk4iPShAms+EWFyOmHCsViuaptHa2mo0ceXS0tJCc3MziqIwMDAw6Q3YrFYr27Zty2iS\nG51wzGazEUNJSUnGa00mk5GUJksSzszp6trORRddfehnuRQ4CVYshc8+C6ftgvsq4TUTqeVo9h/6\n8xhgNx/84HKee+5nBYxeCDHXJlz+edOmTWiaRlNT04TJBmDLli1A6oO8o6Nj0gEMDAxkJBuAcDiM\nxWJh1apVxqrTY5NNmqqqOY+L2XX22V/gwgv/AV1fSWofmpPgfUn4eg+8bYLNH4LXPkhquPMuYBnp\nZHPZZedIshFiEZow4fz0pz9FURQ2btw44U3C4TDRaNRIOq2trdMKqrW1leuvvx4Yf4VqURhf/KIf\nRTmb559Pkko0ZlhxFKx7HjzPQsdZ8LAVDiwDdpJKNB8ktUzNkAwMEGIRm3CUmqqqk1qmxu12MzAw\ngNlspqKiYlpVRzAY5IQTTuDaa6+d8j2AI24UJ/JzeOQZpEafrQCWwPsScMFz8NzJcM974cDxh879\nGXiH1PybYVKVzWpJNkIsYhMmnGQyybnnnjupG6U3XrNarTzzzDNTCkZVVYLBIH19fVN6vZgdxxzj\nYM+efRgDAjgOjknCZ38HpySh43R47XjARqqqeYfUEjapwQGf+tRxPPro5JtZhRAL04SDBiwWCyaT\nKa+tBqbymrS6ujruvffejP6a9Gg0GTRQGEuXnsPw8LtJtb4elzr4/lfgc7+H35XCI6fAgXJABQ6Q\nWprmeOAoli9/h1BI1kATQqRM2IfjdrsZHBycdMUSi8VIJpNTWgGgsbGRlpaWrKSSnlw6tpkuPYIt\nn2QjJu+WW+5GUc5mePhUUgnkODhmAGp/Da4XYMvp0P0pOGACXiI13Pl9wArOOGMvur6VPXt+KclG\nCGGYsMKJRqM4nU4sFguJRGLckWJp6aHM/f39VFRUTDqItrY2PB5PRvKIRCLGSgKNjY04HI6MkXKh\nUIiOjg7a29sn/XVAKpzJUJSzD/3tdNLNYrz/Dfjc8/C7Ethmh4MmUqsFHL5myZI/cvDgbwsUtRCi\n2E1Y4VRWVlJfX8/g4CAOh4OtW7fmvK6zs9NINrW1tXklm1AoBKSGR0ejUaLRKOFwmI6ODmPZmkAg\nkDXUOhgMEghIB/RMOuYYx6FkcypGIjlmAGqfBtfvYcsq6P4gHHwb2MfoZPOpT50syUYIMaFJrRbt\n9Xrp7OwEUn00NpvNaOZSVdXY4bO2ttYYGj0Z6f6ZXOx2Ozt27DCex2Ix2tvbqaqqQlVVHA4Ha9as\nmfTXSpMKJ7fMquZYQIEPvAKffQ5+a4ZHVsPBP6eOcxqyWoAQIl+T3p4gHA4TCASIRCJZ59xuN36/\nf16s3iwJJ1sq2Zx+6NmhquaC38NJg3BfOby+hNTQ5sMVjaL8gZGR5woVshBiHprSfjiqqqJpmtGh\nP59IwjkstX3AIIcTCamq5nPPw7Ml8Mi74eBxpJrPDq+BJn01QoipkA3YFqmsgQHH7koNdT5pEO47\nFV5/D/B65jXs5sQTd/PXvz5WiJCFEPOcJJxFJrXd8w4ymtA+uAM++zw8Uwq/uggO9h46dzjRHH30\nn9m3b2oTeoUQAiThLCrZVc1e+FwvvGsQ7rPBH5dknmc38Ad0XfpqhBDTN+GwaLEwnHmmZ9TAgEOj\n0D64A77WDYPD0Pq5Q8lmCaOTzRlnHJRkI4SYMVLhLGBdXdu58MKvH3o2qqq5oBdO1OC+U+CPK4E9\npLZ6Ti1JA4OcccZSGe4shJhRknAWqMzmM4Bj4exX4PwXIFYCj54IB48iNdx5CaMX25TN0YQQs0ES\nzgKUSjYnAsvJqGpO0OD+U+CPxwLp71/6a4QQc0MSzgKSWdWsAExw9g44/8VRVc2xpJrQ0telkk1J\nyQDJ5FMFiFoIsVhIwlkgskagHTcIF/wOViZT82r+dAxS1QghCkkSzjyX2q9mhIy+mg/tgJoXIFqa\nqmqGlwP7D52XqkYIURiScOax7KpmL1zw9KiqpgJ4MfMaqWqEEAUiCWce+uIX/fzkJ11kVzUvQvRQ\nX81weoqVJBohRHEomoQTCoWwWCw5V5yORqP09/djtVpRVZXKysopr0w93xNOdlWzBy7sBUsS7j8V\n/nQWudZAk2QjhCi0pYUOAFJbHzQ0NBibsY2mqirNzc10d3cbx+rq6ozdQBeLw4nmNFJ70hwL57wM\n1S9Cfwl02A5VNa+TmsBpAY4BhvjmNy/hllu+nvvGQggxRwqacBKJBIFAAIfDMe5GbIFAgMbGxoxj\nPp8Pv9+f12Zv81nuquaxVFXzP6fBn1eMunp0VfOiVDVCiKJRNE1q5eXlBIPBrF08rVYr0WiUVatW\nGcfSO4WOjIzk/XXmU5NaztUCznkZal6CvlLYfsKovpr0ddKEJoQoTkXRpDYeTdNybkNtNpsB2Llz\nZ0YiWkiyqprj98CF28G8G/57oqrmBUk0QoiiVNQJZ2BgAICSkpKc51VVXXAJJ2dV8+GXoPol6C2F\nLatg+ERg16jrpKoRQhS/ok44mqYVOoQ5NW5VUzoE/3UavJGuanYhVY0QYr4p6oQzHem+mvngyFWN\nTfpqhBDz3oJNOPNFzqrmou1Q8r+HqprjSG0hMOoaqWqEEPNQUSccm80GwNDQUM5+nPT5XMYbhVYs\nlU/Oqmb1i+B5GZ4uhfayQ1VNdrI58cTd/PWvkmyEEPNLUSccs9mMzWZDVVVWr15tHFdVFbPZPC8H\nDBxONDB+VSMj0IQQC4/pyJcUltvtpre3N+NYNBrF4/EUKKKpy6xqTseoahp74I9A0DZusjn66D9L\nshFCzGtFVeHkagYLBAJ4vV7q6+uNY8FgkGAwOJehTVsq2aSbz46DknfgokfhuN3wo9PhL8tHXS1V\njRBi4SnoSgPJZJINGzagqiqhUAibzYbb7cbj8bBu3TrjulgsRnt7O1VVVaiqisPhyFqRYLLmeqWB\nrEEB6FDxErhfgqfM8OsTYWR0v5KMQBNCLExFs7TNXJnLhJOVbErehIueT1U19506QVUjiUYIsfAU\nVZPaQpFzBFrFi+B+AZ5aCb+2jVvVrFjxV955R5KNEGLhkQpnxu8/tqp5By5+Go7ZndqvRqoaIcQi\nJQlnxu6bo6qpfBFcL8OTFvjNCaOqGkk0QojFRxLOtO+XY15N6Ttw0VNwzNupvpq/SlUjhBCScKZ1\nr3yqmvR1kmyEEIuTJJwp32fMvJrSd+Dip2CFVDVCCJGLJJy8X59jXo3jRVjzMjxhgcelqhFCiFwk\n4eT12jHJpvRNuPg5WP52agSaVDVCCDEuSTiTek2OvhrHC7DmJXhipVQ1QggxCZJwjnj92Krmbbjk\naVj2Dtx3CrwpVY0QQkyGJJxxr8tR1ThfgM/sgMct8ITMqxFCiHxIwsl5zZiqxvx2agTa0Xvgfqlq\nhBBiKmQttVGyqhrlWHD8/lBVY4UnTpY10IQQYormTYUTjUbp7+/HarWiqiqVlZW4XK687zNehZOz\nqrnkKThqT2pezVvLRl0tVY0QQuRrXlQ4qqrS3NxMd3e3cayurg6bzUZZWdm07p2zqnH+Hj69A35j\nhSfHr2ok2QghxOTNiwrH5/NRU1PD2rVrjWORSITW1la2bNmS171GVzhS1QghxNyZFwnHarUSjUZZ\ntWqVcUzTNKxWKyMjI3ndK51w4INkVTWfeQV+bU3NrdGlqhFCiJlU9E1qmqYZyWU0s9kMwM6dOzMS\n0eQdSiKW3XDxI7B0D/zgzAmqmhck0QghxDQUfcIZGBgAoKSkJOd5VVWnlnCUY6Hqefj0K/DYob4a\nqWqEEGLWFH3C0TRtdm78lW2wZC98/0zYJVWNEELMtqJPOFN1uK9mHP85eOgvr4w58Xx+9xFCiEVi\nul3+phmKQwghxAI33V/Ai77CsdlsAAwNDeXsx0mfH2u8TDzTW0zPFolz5syHGEHinGkS58yaidae\noq9wzGYzNpsNVVUzjquqitlsnuIINSGEEHOt6BMOgNvtpre3N+NYNBrF4/EUKCIhhBD5mhcTP5PJ\nJF6vN2Npm+rqaoLBYN4VznwrXyXO6ZsPMYLEOdMkzpk1E3HOi4QDEIvFaG9vp6qqClVVcTgcrFmz\nJu/7LKZ/3LkwH+KcDzGCxDnTJM6ZtagSzkxZTP+4c2E+xDkfYgSJc6ZJnDNLEo4QQoh5Y14MGhBC\nCDH/ScIRQggxJyThCCGEmBOScIQQQswJSThCCCHmRNGvpTZTotEo/f39WK1WVFWlsrISl8tV6LAA\nCIVCWCyWnPEUQ9ydnZ2oqko8HkdVVXw+H+vWrSu6OMPhMOFwmJUrVxKPx3E4HNTX1xddnKNpmkZz\nczP33HNPxvFCx5n+d25ubsbhcDAwMEAwGMTj8WTEUeg4R8exZcsWVq5cya5du/D5fJSVlRVNnH6/\nn+rqahwOh7F5ZC6FjhNS76NYLAbArl27sNvtM/c+0heBeDyuezyejGNer1dXVbVAER3W09OjWywW\nPRKJZJ0rhrhDoZAejUaN55qm6Xa7XQ8Gg0UVZ09Pjx4OhzOOORwOvaWlxXheDHGO1dDQoHu93oxj\nxRBnPB7XFUUxHhaLRe/s7Cy6OHVd1zs6OnSfz5dxrKGhwfh7McTpdrszfp6jH+Xl5UUTZ39/vx4K\nhTKOhUKhGXu/L4qE09DQkPVmCYfDWW/0uaSqqu7z+fRgMKjb7facCacY4h79gZ0WDAZ1RVGM58UQ\nZ21tbVbC8fv9ut1uN54XQ5yjxeNx3ev16nV1dRnHiyFOVVX1SCSiJ5NJPZFI5LymGOIcHBzULRZL\nxrHW1lbjQ1zXiyNOn8+nx2IxPZFIZDyCwaAei8WKKs5cRscwnTgXRcKxWCxZb5rBwcGMD81CGi/h\nFDruwcFB3eFw6JqmZRxP//abjq3Qcep66g3R3NyccaypqUl3Op3G82KIc7RgMKgHg8GsN2oxxKmq\nalYCH6sY4mxqasr6d9d1PSOuYohzdIUw3vFiiNPhcOSsVEZXNNOJc8EPGtA0DU3TsFqtGcfT7ag7\nd+4sQFRHVgxxm81mVFUlkUiMe00xxAmwZcsWNmzYkHEsFAqxfv36ooozLRKJ4Ha7s44XW5zjKZY4\n29raqKqqyjqeXtS3WOIc2wcCqdjTx4slTrfbjcfjyXjPh8Nh6urqZiTOBT9oYGBgACDn5m2Q6hwt\nxj11iiXudByjhcNhLBYLq1atMvYpKnScYwWDQZxOJ9deey1QPD/P0V/P5XJlrUtVTHGqqoqmaUZc\nVqvVGCxSLHFqmkZpaSltbW1YrdaijXOsSCSC0+k0nhdLnBs3biQcDmO322ltbaWsrIxkMslVV101\nI3Eu+ISTfsPMN8Ucd2trK9dffz1QfHF2dnbS09ODoii0t7cbx4spzs7Ozpy/8ULxxJn+DXb0aMT0\nb7nr1q0rijjTv+zEYjHjFwuA5uZmBgYGqK+vL4o4c4lGo1x33XXG82KKs6+vj+rqanw+H5WVlUQi\nEePcdONc8E1qYmYFg0FOOOGEjDd4MVm3bh333HMPGzduxOl0GsM7i0UxfbBMpLS0NCsp+nw+/H5/\ngSLKlv5Zjt1mfv369UUV51ihUAi73V7oMMbV1tZGS0sLPT09xlYwEzWr50MSjpg0VVUJBoM8/PDD\nhQ7liEpLS/H5fEUz1yqto6Mjo2qYiX3i50pZWRmqqjI0NFToUIDDiWZswqmoqEDTtKLp7xpr48aN\nOfvvikFjYyMej4fVq1fjcrlIJBLYbLYZ2115wSec9H/G8d4kY/+zFotijLu5uZlt27bljKOY4kxz\nuVxomsa2bduKIs5YLJbRbg/Ze4sUQ5wALS0tWcfSzWyqqhZFnOmO6vEmUhZLnKNpmkY0Gs3qAymG\nONMV4+g+mNLSUrq7uzGbzTPyPlrwCcdsNmOz2Yz23jRVVTGbzUU5YACKL+7GxkZaWlqy3ijFEKeq\nqlgsFp555pmc5zVNK4o4+/r6aG9vp7m52XiEQiGi0SjNzc10dnYWRZyqqtLc3JxVIaQ7jG02W1HE\nmY5lbAyjzxVLnGnhcDhngiyGOPv7+8dt6vP5fDPyPlrwCQdSQ/16e3szjkWj0RkrE2dLscTd1tZG\nc3Nzxn+mSCRitOsWOk5N07Db7Vm/XaXfFJWVlUURZ319PRs3bsx4eDweHA4HGzduNJraCh2nzWaj\ntbU168MjHA7jcDiMXzoKHSekPgj7+/uzYkiPooTiiDOtt7d33A/1Qsdps9mIx+M5z2maNjPvo2nO\nE5oXNE3LWorB4/GMO4N6rtnt9pyT7Ioh7o6ODj0YDOr9/f3Go6enJ2NGcjHE2dLSkjVB1e12Z0wK\nLIY4x2pqasqa+FkMcYZCoYwJgOlJwOlZ8bpeHHGml1oaG8PomfDFEGdabW2tXl1dnfNcMcTp8/my\nPovi8bju9/uN59OJc9FsMR2LxWhvb6eqqsoYebFmzZqCxZNMJtmwYQOqqhIKhbDZbMakq9GdyoWM\nO9cErzS73c6OHTuKIs60trY24vG4sXin0+k05g8UU5wAiUSCQCDAli1bSCaT1NfX4/P5qKioKJo4\n04u27tq1y1hkdGzVUwxxpn+WdrudeDxOXV1dVgzFECekmqYVRWHz5s05zxdDnKPfR5Bq7hs7YnGq\ncS6ahCOEEKKwFkUfjhBCiMKThCOEEGJOSMIRQggxJyThCCGEmBOScIQQQswJSThCCCHmhCQcIYQQ\nc0ISjliUotEoXq8Xi8WCyWTCYrHgcDjYtGlToUObEo/Hg8l0+O3s9XozngtRDOR/pFh0fD4fTqeT\nzvSYbmQAAAXOSURBVM5OTCYTHo+HE044gWeeeQa/34/Vai26fXTSQqEQJpOJzs7OjOOKomRtdTCf\ntj4Qi4MkHLGoeL1e2trasFgsRKNRdu3axcMPP8yOHTsYHh6mqakJTdNwOBxFm3QgO5l0dHSMu/Ci\nEMVCEo5YNMLhMJ2dndjtdhKJBKtXr866ZuPGjbS2tgKp5FSsxq5IVVpaWrRbbQiRJglHLBqBQMD4\nc+y+PqPV19dTWVmJqqoZ+7mP7SdJ0zQNk8lEY2NjxnFVVfF6vdjtdkwmE1arlbq6uqzten0+n7FI\nqt/vN/qVysvLM5rOPB4PdXV1wOE+mvRGWJPts2lpacHhcBjxNDY25tw+OBgMZlzndDozfhZCTIUk\nHLFoRCIRLBYLa9euPeK1Pp8PgJ6enozjE/WLjD6nqirl5eVs3bqV8vJyo98oFArhcDhIJpNZr083\n91166aU0NDQYCSv9Qd/c3ExDQ4MRXzAYzEicR+qzcTgcNDc3YzKZjHiCwSB2uz2j+dDv99PY2MjO\nnTvxer243W5jv5NibmYU88B0908QYj6Ix+O6oii60+mc1PXRaFRXFCVj7xK3262bTKasawcHB3VF\nUfTGxkbjWENDg24ymfRIJJJxbUtLi64oih4KhTKuVRRFLy8v15PJpHE8HA7riqJk7D3U0dGhK4qS\nsd+Lrqf2WRkd29jngUBAVxRF37ZtW87v0+FwGMfMZrNeXl6ecV06ltHfoxD5WlrohCfEXEjv1z7Z\nveHLysqm9fUaGxupqanJ2iMkvd/N4OBg1mvGNvW5XC6AnE1ek6GP6ufZsGEDHo+HyspK42cBqe/T\n5XIRiUQYGhqipKSEZDJJeXl5xr1cLhfRaDTn9shCTJYkHLEopD8ox+7FPp70dVP9gK2oqDCSi6Zp\n9PX1EY1GjQEJuaS38J0NyWSSnp4eLBZLzvOKojAwMEBJSQm1tbWEQiGjKdDtdlNRUZFzkIUQ+ZCE\nIxaFdGUz2YTT19eX8bp8aZqG3+83dvSEVB+Kw+EYt2IZb3fVqUr36aS/Z4/Hg9/vH/f6dDLasmUL\nmzZtorW1NeP6hoYGAoEApaWlMxqnWDwk4YhFw+12G0OjR2/jnRYOh3G73QBGJbJ+/foj3ndgYCDr\nmMvlIhaL4fP58Pl8RnUQiUQIhULT+Tbylk5kZrN50tsVX3fddVx33XUMDQ3R09NDa2srwWCQvr4+\nIxkLkS8ZpSYWjfRv67l+y9c0jerqapxOJy0tLcRiMRwOx6SakaLRaNa9YrEYXq+XzZs3Z9xDn8Md\n3dNfy2w2U1paSjgcznmdxWIx+mxUVcXv9xsj40pKSli3bh3d3d1GP056KLYQ+ZKEIxYNl8tFbW2t\nMWR59BBfs9nMli1biEajNDc3oygKHR0dGa83m83oup4xHyXddJbL2IEBo6+dbuKZzOtHD5P2+XwM\nDg4a83jSWlpaSCaTGXOINm3aZAwLH01VVRRFmXAOkxATKuQQOSEKwev16oqi6Iqi6GazWXe73Xpl\nZaVxzGQyZQ1d1nVdD4VCxjU+n09vaGjQLRaLXl1drVsslozhyx6PR1cURfd6vXogEMi4VlEU3W63\n6+FwWNf1w8OiRw+JThs7NDs9PNlut+t+v984XltbqyuKMu5zXdd1u91uvLa2ttb4nscOFU/HbrFY\n9NraWr2hoUE3m826yWTSm5ubp/ATFyJFEo5YlKLRqO71enWr1aqbTCbdarXqTqdTb2tr0zVNMz50\nx853CQaDxge31Wo1PoAtFkvGHBVN03Sfz6dbLBbjQz19L5/Pp5tMJuP69PPJJBxdP5wQrFarcczr\n9WbMuxn7PM3v9+sOh8OY9zNeAvH7/brdbs/42Yz9WQiRL0XX57BRWYh55Pbbb+faa68tdBhCLBiS\ncIQQQswJGTQghBBiTkjCEUIIMSck4QghhJgTknCEEELMCUk4Qggh5oQkHCGEEHNCEo4QQog5IQlH\nCCHEnJCEI4QQYk78fw4CAYBE2TLbAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23af24490>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtUW/ed7/33lu3YTmKQ5FycpG1AIp0mcbBBuLPOc86T\ndIwE6bSdrrERTtKSeU6fGJHpak7PPIlFmrpxL7MccM9ZJ+mZJIhMZxoybQGRmWnjmdpIbuOZdmaO\njWTTpGnjsCH3q2GLOvEltvfzx2ZvEAgsgZAEfF9rsWK2Nls/tmM+/Pb3d1F0XdcRQggh5pkt3w0Q\nQgixNEjgCCGEyAkJHCGEEDkhgSOEECInJHCEEELkhASOEEKInFie7wYEg0FqamrweDzY7fZpz4vF\nYvT19eF0OlFVlcrKSqqrq3PYUiGEEHOR98CJxWLs2bMn5Wtut5tjx46hqirNzc3s37/feq2+vh6X\ny0VpaWmumiqEEGIO8h44brebPXv2TOnd9Pb2smnTJgBaWlpoampKej0QCBAMBunq6spZW4UQQsxe\n3gPH4/GwcePGlK+Zx7u7u7n//vunfF04HJ739gkhhMgOpRCXtmlvb2f79u0AaJqG0+lE0zSKioqS\nzrPZbKiqSklJSR5aKYQQIhMFN0otGo1SVVVlfT48PAwwJWxMqqrmpF1CCCHmpuACJxaLUVFRYX2u\naVoeWyOEECJbCipwwuEwbrc7380QQggxD/I+aGCihx56iAMHDmTlWoqiTPtaAZathBBi0SuYHo6m\nacRisSm1GpfLBcDo6GjKrzNfz8RMYSSEEEvBpz61C0VhysenPrVr3t6zYAInEomkXGnAbrfjcrmm\nDA5QVRW73T7tCDVd11N+CCGEgJUrz6Y8vmrVuXl7z4IJnEOHDk1bv/F6vRw6dCjpWCwWw+fz5aJp\nQgix6NxzTw1u9wNJx9zur/GVr8zfz9WCmYfj9/sZHR1l3759U15LJBL4/f6kpW1qamoIhUIZz8Ex\nH6cVyLcthBB5s3fvQb73vV5OnVrGqlXn+MpXfHzmMzfP2/sVTOA0NTWhKAqPPfZYytfj8TidnZ1s\n2rQJVVXxeDxs3rw54/eRwBFCiPwomMDJFQkcIYTIj4Kp4QghxHw5ffo0DzzwAOvWrcNms6EoinxM\n+rDZbKxbt44HHniA06dPz8vfgwSOEGLR+/znP8/zzz/Pr371K86cOTPtKNal/HHmzBl+9atf8fzz\nz/P5z39+Xv4e5JGaEGLRW7FiBaOjo6xevTrfTSl4J0+epKioiA8//DDr15bAEUIseoqiyL/5DMzX\n/ZJHakIIIXJCAkcIIUROSOAIIZa0vXsPUlv7dT71qV3U1n6dvXsP5vwakUgEt9uNzWajpqaGRCJB\nOBympqbGOsftdhONRunp6SEQCOD3+7HZbFRVVTE4OGidZ666b7PZqK+vJ5FIAFjzF/fs2YPT6aSs\nrIx4PJ7x9zon+hID6Evw2xZiSZvu3/wzzzyru91f00G3Ptzur+nPPPNs2tee6zVGRkZ0h8OhHzhw\nQE8kEnogEND9fr+u67ru8Xj0cDist7S06PX19bqu63p3d7euKIre3t5une/xeHRd1/WBgQFdURQ9\nGo3qmqbpfr9fDwQCSa/t2bNH13VdDwQCus/ny+h+zdWS+8krgSPE0jPdv/mamgeSgsL8qK39etrX\nnus12trarIAxORwOXdd1XVVV3W6362VlZXoikdB13QicqqqqpPMVRdE1TdNbWlr0pqYm67iqqta1\nBgYGrD/ruq7HYjErqCabr5+RBbUfjhBC5NLp06l/BJ46tSxn1xgYGCAcDuN0Oq1j5mja0tJS3G43\nbrc7aeuW0tLSpGuYK+oPDw8nbdlSWlqatGvyxPfQ8zBqT2o4QoglKxtL9M/1GmVlZdTV1TE8PGx9\nRCIRgKT/TqzTpNquxe12s3btWgYGBqzjmqal3PYlXyRwhBBLVjaW6J/rNerr64lEIkSjUTRNIxAI\n0NzcDBiLGj/xxBM89NBDBAIB62tisRjt7e3W+R6Ph6KiIrZu3UooFLKutX37drZt25b29zLf5JGa\nEGLJMpfi/973dk5Yov/WjJbon+s1iouL6e7uJhAIoKoqPp+P7u5uWltb8fl8bNy4kY0bN9LS0sLT\nTz+Noih4vV56e3utsOnu7gaMR2sTr+X3+2lpabHea/Jux7ne/VhWGhBCLHqLaaWBcDhMV1cXXV1d\n8/YestKAEEKIBU0CRwghFhBzO4GFSB6pCSEWvcX0SC0X5ut+FcyggVgsRldXF2vXruX48eMEAoGk\nseaxWIy+vj6cTieqqlJZWUl1dXUeWyyEECITBRE44XCYSCTC448/bh0LBAK0tbUBxhjz5uZm9u/f\nb71eX1+Py+WaMgFKCCEmW758OSdPnpT9cNJw8uRJli+fn2jIew1H0zQaGxuTwiYUCnHgwAHr85aW\nFpqampK+LhAIEAwGc9ZOIcTCVV1dzW233cbAwABnz6aeqLnUnT17loGBAW677bZ5e3qU9xpOMBjE\nZrOxe/fupONDQ0OUlJQAxnIMsVjM+hyMoHI6nZw/fz6j95MajhBLz+nTp/nWt77F97//fd55552M\nf24sBTabjSuuuIIvfelLfOMb32DlypVZf4+8B47T6eSJJ55gy5YtKV83g0XTtKS1hMC4QaqqJgXR\nhUjgCCFEfuS9hqNpGsXFxbS3t+N0OhkeHsbpdLJ161YAhoeHAaaEjSnTwBFCCJEfeQ0ccwG6eDzO\nvffeax1vbm5meHiY7du3J610KoQQYuHK66ABM0wmLqcNsG3bNhkQIIQQi0xeezhm0EwOnIqKCjRN\nY2hoaNbXXqgzcYUQYrHKaw/H3Kdhuv0aVFW1wmh0dDTlOZPDSgghRGHK+zwcc6e66V6z2+0pz1FV\nFbvdPu2AAd3YPnvKhxBCiPzIe+AEAgH6+vqSjsViMRwOhxUmXq+XQ4cOTTnH50t/kyQhhBD5lfd5\nOIlEAo/Hw0svvWQdq6mpoampyZqbk0gk8Pv9SUvb1NTUEAqFMh4SLfNwhBAiP/IeOACDg4O0tLTg\ndrsZGBigvr6ezZs3J50Tj8fp7Oxk06ZNqKqKx+OZck46JHCEECI/CiJwckkCRwgh8iPvNRwhhBBL\ngwSOEEKInJDAEUIIkRMSOEIIIXJCAkcIIUROSOAIIYTICQkcIYQQOSGBI4QQIickcIQQQuSEBI4Q\nQoicyFrgTLdfjRBCCAGzCJx4PM7dd99t7caZSCSoqqrCbrezbNky7r///my3UQghxCKQ0eKd0WjU\n2oMmFouxceNGmpqaCIVCVFdXo6oqQ0NDdHd3W1sLFBpZvFMIMRd79x7kkUf2c/r0clauPMs999Tw\nmc/cnO9mLQgZBU5VVRWxWIze3l6qq6sBsNlseL1ea68ah8NBWVnZlA3TCoUEjhBitvbuPch/+2/7\nGBj4S+uY2/0ADz9cK6GThoweqamqSl1dnRU28XgcMHbtNNXX10+7ZbQQQixkjzyyPylsAAYG/pLv\nfa83Ty1aWDIKHE3TrB4CQCQSAUja6nl4eBhN07LUPCGEKBynTy9PefzUqWU5bsnClFHgVFRUWCED\n0NbWhsvloqioyDoWjUYpLS3NXguFEKJArFx5NuXxVavO5bglC1NGgRMIBBgZGeG6666ztno2H6dF\no1HKysrQNI26urq0r6mqKj6fj2g0iqZpqKpKc3Mz0Wg06bxYLEZ7ezs9PT3s2bNnyutCCDHf7rmn\nBrf7gaRjbvfX+MpXfNN8hUiiZ2jHjh263W7XFUXR/X5/0nFFUXSfz5fR9QYGBnRFUawPh8Oh9/T0\nTDln8nX9fr+uqmqmzdcBfRbfthBC6Lqu688886xeW/t1/ZZbHtRra7+uP/PMs/lu0oKR0Si1mZgD\nBVwuV0ZfNzg4yODgIFVVVQwPD1NSUjLlnEAgQG1tbdJQ62g0SltbG11dXRm9n4xSE0JciAx9nh+p\nK2BpGBoaQlVVNE3D5XJNqeVkQtd1ioqKpv367u7uKRNKPR4P4XB4Vu8nhBDTSTX0eWDAeIwmoTM3\ns1ppoKqqCpfLhdfrpa6ujsrKShwOB9u2bbNWIMgWTdPQNA2n05l03G63A2T9/YQQS5sMfZ4/GfVw\nBgcH8Xg8AFRWVrJt2zZKS0tRVZXe3l66u7uJRCIMDg5m1Nsxe0pgDKt2Op1s3brV+hyY9nqqqqZ8\nDCeEELMhQ5/nT0aBEwwGAWM49Pbt25Ne27FjB6FQiKamJrZv305nZ2da1zR7LmbAgDF51Dwmc3qE\nELkkQ5/nT0aP1CKRCJWVlVPCxtTY2EhFRQWxWCztaxYXF0+5XiAQsMJtthRFSfkhhBAzkaHP8yej\nHo6mabjd7hnPcblcPP3003NqlPmYTrY8EELkmjkw4Hvf28mpU8tYteocX/nKrTJgIAsyGhbt8/mI\nxWIcP3582nOcTicul4vDhw+ndc3W1lZ27NiRdMwcJBCLxSgpKcHpdKJp2pQ6js1my7iGI8OihRAi\nPzJ6pNbW1sb58+epra2dMjpscHCQmpoaNE2jvb09reuZqwpMvpY5UMDlcmG323G5XFMWBFVVFbvd\nLgMGhBBigZjxkVpNTc2UusfatWvp7e3F7XZbgWAuSaPrOpWVlYRCIR577LELvrnL5aKtrW1KaEQi\nETwej9Wj8Xq9HDp0iI0bN1rnxGKxpEVDhRBCFLYZH6k5HA4URcn48ZOiKFYv5UJ6enqorKy0FvzU\nNA2v18sTTzxhBUwikcDv91t77oARhqFQKOMejjxSE0KI/Mja0jZz0dPTg6qqHD9+HE3TaG5unhIk\n8Xiczs5Oa9FQj8fD5s2bM34vCRwhhMiPggicXJLAEUKI/MhoWLTZyxgcHETTNKugv23btqT6ihBC\nCDFZWj2ceDzO9u3bZ5zQ6fF4aG9vL/jgkR6OEELkxwUDJxqNWqPBKisrCQQCVFVVWZMzDx8+TFtb\nG/F4HEVR6O3tnVVtJVckcIQQIj9mDJxEIkFpaSmapqVcP20icx01h8Mx48TQfJPAEUKYZN+b3Jqx\nhhMKhdA0jR07dswYNmCsozYwMMCePXv47ne/y7333pvVhgohRDbJvje5N2MPx+PxcOTIEc6dS3+V\nVJvNhs/nY9++fVlpYLZJD0cIAVBb+3X27/9OiuM7+dnPvp2HFi1+My5to6pqxltGl5aWpr2OmhBC\n5Ivse5N7MwZOIpHIOHBcLpfsYSOEKHiy703uzRg4xcXFGfdWDh8+bG3/LIQQhUr2vcm9GQcNeL1e\nenp6OHLkSFrza+LxOIlEgrq6uqw1UAgh5oPse5N7Mw4aiMViVFVV4Xa7OXbs2IwXSiQSeDweVFWl\nr6+PioqKrDc2G2TQgBBC5MeMj9TM7aQHBga47rrrpt3Js6enxwqburq6gg0bIYQQ+ZPW0jZ+v5+e\nnh7A2LLA5XJZm6KpqsrIyAgAdXV1dHV1zW+L50h6OEIIkR9prxYdiURoaWkhGo1Oec3r9RIMBqmu\nrs56A7NNAkeIpUlWFci/WW1PoKpq0mrRC4kEjhBLT6pVBdzuB3j44VoJnRyS/XCEEIvSxB7Nc8+9\nwPHjnVPOkVUFciuj/XCEEKJQTQyY0dHXePPNIt5663+Ovbor5dfIqgK5VXCBY24x/fjjjycdj8Vi\n9PX14XQ6UVWVysrKBVEzEkJk1+RggYs4c+Ycqqpw8qT5c+PrwMR10mRVgUJQcIETDAatUW8mVVVp\nbm5m//791rH6+npcLhelpaW5bqIQIsfMkHn99XcnBMtBYB/wl0wNmMk/2mqAB8bONRirCtw6vw0X\nSQoqcMwh1madxdTS0kJTU1PSsUAgQDAYLPhh2EKIuUku+E8Mlv2MB8jkH2WTezTGwIC1a29j/fpP\nyKoCeTLjxM9cM3cXnVzQ7+7uprKyMumYx+MhHA7nsnlCiDx45JH9E0aXTQyWiX+eHDBmj2ac2/0z\nfvCDP+cXv9jFz372bQmbPMha4IyOjs7p66PRKF6vd8pxTdPQNA2n05l03FwgdGhoaE7vK4QobMnb\nCJyd5s+TA+Zm1q17k8rKL3PLLbuord3Jww9LjybfMg6ceDzO3Xffbf2gTyQSVFVVYbfbWbZsGfff\nf/+sGqKqKqWlpVN6N8PDwwAUFRVN+3VCiMUreRuBicEy8c83A7WsXr2N9eu/Sm3tTp544v+hr++v\npEdTQDKq4ZiPvMCooYBR5I/FYlRXV6OqKq2trWzatIktW7akfd2enp5pt7CWvXWEWLr27j3Iu+++\nxapVd3Pq1GOYtZjVq7fhdl/FihUnUJQvs2bN5WN1mS9LsBSwjAInGAwC0Nvba21XEAqF8Hq91ggy\nh8PB7t270w6c+QqUyQMPhBALy/hggScwRqTtZNWql7nhhjV861sSLAtRRoFjrgZtzn+Jx+PAeG8H\njOHKmRTzu7u7k3o3EhRCLG3mEOhDh15iZOTHY0dvBm7m1Cm4/PKdEjYLVEY1HE3TkgIhEokAWI/Z\nwKi5pNtricfjVFVVJR2bXMMx12qbblDCdGu56bqe8kMIUbjMXs3+/d9hZOQTKc+R1QEWrox6OBUV\nFVbIALS1teFyuZIK+tFoNO3JmIcPH2ZgYIDOzvE1jmKxmDXRc9OmTWzdutXaCmHirqOqqmK32ykp\nKcnkWxBCFKi9ew/yZ3/2VxPWPJPVARabjAInEAjQ1NTEddddh91uR1VVWlpaACNoAoEAmqbR2NiY\n1vVSDRTYs2cPhw8f5qGHHrKOeb1eDh06lBQ4sVgsqWclhFi4zJ7N8ePXTzgqqwMsOnqGduzYodvt\ndl1RFN3v9ycdVxRF9/l8mV5yyvUnXlfXdV3TtCnX9fl8+uDgYMbXB/RZfNtCiHlUU/OADroO5n/N\nj2d1+LrucNyp19Z+XX/mmWfz3VQxB1nbnsCcDzPb/XEGBwdpaWmhq6uLRCLB9u3bCQQC1nbV8Xic\nzs5ONm3ahKqqeDweNm/enPH7yPYEQhSeT31qF88+u4vk9dEMbvfXZNLmIjHrwBkdHWV4eBiHw0Fx\ncXG22zVvJHCEKCxTazcHgV5gGWvX/pYf/ODPJWwWiVmtNGCuLOB2u+nr6wOgrKyM7373u1lvoBBi\n8Rqv3XyZ5FUDvo3bfUbCZpHJKHAGBwfxeDzWygITewnHjx9nx44dbNq0KeuNFEIsPmbPxliY01ia\nBnYCu1i79jZ5jJYD5/Xz/Hzw5yROJXLyfhkFjjkira+vj+7u7qTXRkZGeOihh+jr65v1empCiMVv\n796DVFbeRV3djyaNSjN6NrCL9es/IWEzj37z7m+4P3I/Jf+rhP++77/zSuKVnLxvRoHT1dWF1+u1\nCvmT7dixg4qKCtk2QAiRkvkILR5fN7Y2msy1yZV33n+Hh//9YTwhD74OH2fPn+WZO57hSNMRbrry\nppy0IaN5OJqm4Xa7ZzzH5XLR09Mzp0YJIRan8b1tdo0dkbk28+nkhyf5x9/9Ix39HfzylV/yJ3/w\nJzxU/RCbSzezzJb7FRsyXmng8OHDM54Tj8enbJYmhBAwcW8bs2djPjbbiTkq7eGHZaDAXJzXz/Ps\n0LN09Hfw97/9ez55zSdpKG+gs66TSy+6NK9ty+iR2rZt2+jr6+PnP/95ykU26+vrUVU15UZqQggx\nvrfN5L1sZFTaXL3w7gt8Lfo1Sh8u5av7vsoNl9/A83/+PPu+uI8vln8x72EDs5iH4/F4iMfj+Hw+\nent78fl82O12IpEIIyMjuFwuXnrppflq75zJPBwh8mfXrkdpbe3n5MnHMefbjG85sE3CJkPvvP8O\nP/r1j+jo7+CN37/BF276Ag0bGii/sjzfTUtpVhM/W1tb2b17N4nE+FC64uJiAoFA0hpohUgCR4jc\n27v3IDt3PskLL6zg1KnbMSd2rl79Ajt23MKuXX+e7yYuGCc/PMlPfvcTnux/kl++8ks+9wef487y\nO/NWl8nEnJe2UVUVp9OJ3W7PVpvmlQSOELk1vpGaAnxnyuu1tTv52c++nfuGLSDn9fMcfPkgHUeN\nukzV1VU0lDfwp9f/aUE8KktXRoMGUpnt2mlCiKVh584fMzDwKOMj05LJ/jbTe+HdF+jo7+Dvfv13\n2FfZaShv4Nubv83Va67Od9NmZcbAsdls0+7AafYQJvYYFEWx/nvunIyjF2KpMh+hvfjim7z/vrlf\nlsy5Scc777/Dj5/7MR39Hbw++jp33HQHP7ntJ2xYtyHfTZuzGQNn69ats7qobBMtxNK1d+9B7rrr\nB7z11jpg3YRXZM7NdMy6TEd/B//6yr/yuT/4HH+5+S+pLq0u+LpMJrK2PcFCITUcIebH3r0HeeSR\n/fzyl8/z/vs3YtRrdgGbGd9ywBiZpigDVFQ4lvTItPP6ef7l5X+ho7+Dp194Gs/VHu4sv3PB1WUy\nMecajhBCjA93vgN4hfEfLWeZPLkTYOPGi+nr+6uct7MQ/Pa939Jx1KjLFK0soqG8gV/f/WuuKbom\n302bd2nVcAYGBigpKZmxpmOSGo4QS8vevQdpbX2Wkyc7ga8DH2O8XjPxMZoRPG731/j2t+/MR1Pz\nZmJd5rXR1/jCTV/gH2/7x0VRl8nEjIFTXV2Noig4HA4g/ZqO1HCEWDoeeWQ/J0+aqz4vx3iE9gOS\n6zU7WbFikJtuKl4yj9FOfniSn774Uzr6O/iXl/+Fz378s3znj75Dtaua5bal+XBpxu+6t7c36fPJ\nWxJkSyQSIRKJsHbtWgYGBvB4PGzfvj3pnFgsRl9fH06nE1VVqayspLq6el7aI4RIn7E+mtmjmfgI\n7UngduAi1qxJ8KMf/cWiD5pUdZmG8gZ+uOWHrFm5Jt/Ny7uMYnZ0dJSioqILn5iBSCSCoihJKxRU\nVVWhaRr33XcfYEwubW5uZv/+/dY59fX1uFwuSktLs9oeIURmRkffAW7D6NHUkuoR2sMP/7+LOmx+\n997v6Ojv4Kn+p1izcg0N5Q30393PR4o+ku+mFZSMFu+02+088cQTM57T3NzM2rVr075mW1vblGNe\nrzfpeEtLC01NTUnnBAIBgsFg2u8jhMgecxO1Vas2E4+/hTEKrRZjyZr3UJTPcu2126mt3blod+58\n9/13+d5/fI9Ptn+ST/3gU5z88CT/cNs/0N/Uz47/vEPCJoUL9nB6enqsCZ2A9VgrFV3XCYfDjIyM\npN0ARVGIRCJJj8d0XbfqRmA8ypu8i6jH45GN3oTIg127HmX37l9w5swa4HKgE3O4szEK7Qo2bjxH\nLNaez2bOi1NnT1nzZcy6zLf/6NtLui6TiQvOw7HZMuoEAUYPZeLjr0y53W7uvvtu7r33XjRNw+l0\nomnalMd5NpsNVVUpKSlJ+9oyD0eI2dm79yD33PMwqnoOWD92dDmplqy55ZZd/OIXU48vROf18/zr\nK/9Kx9EOel7oofKqShrKG9hy/Rapy2TogpHc1dVl/bm+vp7GxsYZ97txOBxzKuaHQiGqqqq49957\nARgeHgaYtnaUaeAIIdKTvDxNAqM3cxEwcTvixbtcjdRlsu+CgVNXV2f9ubq6Gr/fPy+jw3p6eujt\n7UVRFDo7O63jmqZl/b2EEDPbu/cgX/xiO5p2EcbyNJcC12H8yJgYMlOXq1m9OsBXvvKFHLY2e977\n4D1+/NyPefLok7w6+iq3r7+df7jtH9hw5QaZ7pEFBbe0TSKRoLq6mvb2dioqKojFYlRVVXH+/Pkp\n59psNiKRCJs3b57yWjoTVIUQqbndd6KqH5twZOLKATUY82zACCNzsMAyLrroOe6/f/OC2t/m1NlT\n/PR3xnyZgy8f5DMf/wwN5Q14XV6py2RZxnczGo3S3d3N4ODgjOft27dvVg0yN3Krrq62HqcJIXJn\n165HUdUPSP7xMHHlgH3An2HMszkCHGXVqku44YbL+Na37lkQI9LO6+f55Su/5MmjT9LzQg8VV1Vw\nZ/md/N2Wv5O6zDzKKHB6enrw+/3z1RZLdXU1mqZx4MABKisrgennAE23H890PRjpFguRWvKggFVM\nfXT2A5KHP3+Eiy7SFlSP5sXjL9JxtIOnfv0Ul6y4ROoyOZbREDRz3ktvby/nz5+f8SMdqqricDg4\ncuRIytc1TcNut+NyuVBVdcrX2u12GTAgRBaYNRtVXQ5sxKjZvDnhw+zVvA08BvwWt3uQp5++p+DD\n5r0P3uN//5//zR8+8Yfc8re38P6H7/N0/dP8+u5fE/wvQQmbHMqoh6OqKo2NjVkbNKBpGm63e0ov\nxQwXs3fj9Xo5dOgQGzdutM6JxWL4fL6stEOIpW7nzh+jadcyPijgTowejYIROC+T/OissNdDO3X2\nFM+8+AxPHn2SZ19+ls9c9xm++alvSl0mzzK688XFxVl9JFVZWcm2bdumPP5qaWkhGAxavZeWlhb8\nfn/S+mqhUIhQKJS1tgix1Oza9Sj/4388w4kToxhDnq9gfFCA2aMxHp3ZbEfZudNX0L0Zsy7T0W/M\nl9m4biMN5Q08teUpilZmd0kuMTsZjVILBoO0t7czNDSU1TXV2tvbGRgYsBbvrKqq4q677ko6Jx6P\n09nZyaZNm1BVFY/Hk3J02oXIxE+xlJlza44e7ef8+Y8COsbvnacx5teYYTM+8qzQw2ZiXebiFRdz\nZ/md3HHTHXy0+KP5bpqYJONh0X6/nyNHjtDS0kJlZeW0y9xke5HPbJHAEUvJ+ECAt4AzwNUYy8+c\nBiqAYxjza97CCJ/kYc6KcoRvfKOm4MLmvQ/eo/O5Tjr6OxjShrh9/e00bGigYl2FDAwqYBkFjhku\nF5qMWcgbsEngiKXCGAjwv9C0k2NHlmEMCDgGrAZKgKGx/5p72CjA+xgrCgzz4IOfLpiwMesyHf0d\nPDv0LH983R/TUN6Az+2TuswCkdHfUrpDouU3DCHy7557nkDTVgArxo6swvgnvxo4iVGvMf9rDgAw\nF+A8R0XFiryHja7r/PLVX9JxtIPwC2E2XLmBOzfcScefdkhdZgEquJUG5pv0cMRit2vXo3znO3/D\nuXPXYgxvNp0CyjB6OLcAv8AIm+UYj9XGl6dxOL5MR0f+RqIdO37MWsds9YrVNJQ38IWbviB1mQUu\n64ETjUbccIxeAAAgAElEQVQJh8M89thj2bxs1kjgiMVq796DfOELO0kkzJ7MpZPOWINRpxnBGJFW\nDuwFEhi9oEux2VZSWnpJXjZMO/7BcTqf7+TJo08yqA1yx/o7pC6zyGQcOIlEgkgkknLPG13XaWlp\nYXBwUGo4QuTQHXcE+dGPYhi1l0sxHputBN7FeGwGRuCswajTqGPnrGb16g/ZsaM2L4/PTp89bdVl\nfjH0Cz593adpKG+gxl0jdZlFKKO/0cHBQTwezwUHDTQ2Ns6pUUKI9Blh0w84MUIEjJD5CPAF4GGM\nUWgJjBC6BEVx4HJdmpeeTKq6TEN5A0/+6ZNSl1nkMgqcYDCIpmm0tLRQUVFBIBDA4/EQCATQdZ1g\nMMhll13G448/Pl/tFUKMMYLm58BljPdqzN6MWaPRgR7ra/JZmzl2/BhP9T/FU79+ipXLVnLnhjs5\nEjgidZklJONh0VVVVdZunq2trXR3d3Po0CHAGC7tcrl44okn2LJly/y0eI7kkZpY6HbtepRvfrMN\nuArj8diVGHWZVRhB81PgWsZrNMuBZTgc5+no+Iucho1Zl+no70AdUY35MuUNVF5VKXWZJSijwLHZ\nbAQCAWtAQCQSoaamJmmxzkAgQCwWs0Ko0EjgiIVs/fo/5fnnh4GLgSLgPMYavL/HCBxzMEAYs0az\nfPlJHnjgMzmr0Zw+e5q9x/bS0d/BgcED4/NlXD5WLFtx4QuIRSujR2qlpaVJqzZXVVUBcOTIEWth\nTbfbTXt7exabKITYu/cgW7b8f5w5cxlG0FyCETAjGCsD/BTjn/O7wD9jrI32e26+eQ3PPhue9/bp\nus6vXv0VHf0dhH8T5qYrb6KhvIG//fzfUryqeN7fXywMGW1PUFlZSSQS4cCBAwDY7XaKi4tpa2uz\nzjl8+DB2uz27rRRiibrjjiCKUslnP/u1SWHzPka95kPgdeBzwHsYc21WAgkefPCzPPvs38xr+14a\nfokHf/4gZd8rY/tPt3Nt8bXEAjF+/mc/50sVX5KwEUkyeqSmqiplZWUoikJ3dzdbtmwhEAjQ3t6O\n3+9nZGSESCRCY2NjwQ4ckEdqYqG45Zb/ysGDKsbjs+WMBw3ADcBRjBrOGuAPMFcIgBd48MH52xTt\n+AfH6Xq+i47+DgZGBrjtxtto2NCA5yqP1GXEjDKeh6OqKi0tLTQ1NVFRUYGmaVRXVxOPxwFj75ru\n7m6KiwvzNxsJHLEQGLWaUxhBswojTMw1zo5jrAzgBP4VYySaHbh43ubUTK7LfLpsfL6M1GVEurK2\n0oA5N6fQH6dJ4IhCZgx13gt8FGOo8zKMR2fnMXo1A2N/fhsoxuj1nODmm9dl/fGZruv822v/RsfR\nDrp/023VZbZev1UelYlZkbXUhCgQV1zxf/Puu2cxeiuXYvRozMdkZzGGOjuBQxhBs4JVqz4gHP5a\nVoc6vzT8kjFfpv8pVixbYa1jdq392qy9h1iaMgqcpqamCz6j1XUdRVFkLTUh0mTMq3kUo1ejYITN\naYwBAKcwhjcXYawUsAyzV3Pjjat47rm/z0obhk8OW/vLSF1GzJeM5+FciPlIbXh4ePatmkcSOKKQ\nGGHzNxirBRRjPC47MfbqVcCrgIYRNA7g4qzNqzl99jT/dOyf6OjvIDoY5dayW2kob6DWXSt1GTEv\nMgqc6dZQGx4eJhaLEQwGKSsrY9++fRk1oqenB1VVGRgYQFVVAoEAW7duTTonFovR19eH0+lEVVUq\nKyuprq7O6H1AAkcUDqNecwRjdsIajFrNOYyVA97E6NUUMXGwwO2338gPf9gy6/ecXJdZf8V6Gsob\nqLuhTuoyYt5lNPFzugEBdrsdl8uF1+vF5XJx//33s3v37rSu2dPTg8vlsgImkUjg8XgYHh5m+/bt\ngDEyrrm52VpSB6C+vh6Xy0VpaWkm34IQeTc+MGANcA3GY7QTwE3AwbFjVwG/wxx9BiM8+OCfzLpX\nMzA8wFP9T9HR32HVZfoa+6QuI3Iq64MGAoEA4XCY48ePp3X+nj17uO+++5KOtbe3EwgErCVzAoEA\ntbW1SeuzRaNR2tra6Orqyqh90sMR+TJeq1mN8QjNrI3owDqM3/+cGLtuXolRy5n9CLThk8PWfJlj\nx49x2/rbaChvoOrqKqnLiLzIeuA0NTURCoWS1lebjqZpeL1eotFo0rwdc4KpqqqUlJTgdDqJxWKU\nlJQkfa3T6UzrfSaSwBG5ZsypOYbxWOzKsaOXYgTOuxi9m40YI9HeHnvt96xe/Q4ffNCX0XtJXUYU\nsqzucBSNRgmFQrhcrrTOt9vtqKrK4OCgtRbbZJqmWeEy+WsBhoaGkoJIiEIwvvbZSYwezUcYH4EG\nRsgogB9jHbQ+xns1v+fyy0/wzjvphY2u6/z7a/9OR38HXc93ceMVN9JQ3sD3P/997KsKe16cWFoy\nChybzTZjV9zsNQSDwbSvmWo0WyQSweFwUFJSYi0WWlSUemMmsxckRKEwlqSJY2zbbO71cglGwLyP\n8QgtMfbfOMY6aAcxVhR4l4997Cwvv/wvF3wfsy7z1K+fYpmyjIbyBg43HqbEXpL170mIbMgocC40\nKsxut3PbbbdNGWGWqba2Nu6//35g+pFxQhSa8RrNFRhFfxjv0ZhBcx4YBtZizLHpA14bO+/tsbDp\nnfY9Rk6O0PV8F0/2P2nVZX645YdSlxELQkaB09s7/T+EbAmFQlx22WXce++9c7qO/OMTuTIeNMsw\nejSrx/4M43NqRjGGPbswgudNjNFn64CLUZQTfOMbn0s5Cu3MuTNWXSaiRqh119L8n5u5texWqcuI\nBSWrNZy5UlWVUCjE4cOH890UIS7IeHR2CCNcJtZozPk0YEzaPIsRLlcAxzAmcH4MWIHNluAnP2me\nsjTNxLpM92+6ueHyG2gob+Cv/+SvpS4jFqyMAicajdLb22utDG3Ov9m2bVtS0f/pp5+e1RbTzc3N\n1l47JnMAwujoaMo6znQDFKYbhSY9H5ENy5eXc+6cgjFnxsZ4jeYERuCYgwKuxXhkpgEfAFdjDne+\n/fYbpkziVEdUa76MTbHRUN7Aoe2HpC4jFoW0hkXH43H8fn/Sbp+TeTweuru76evrw+/309ramtFj\nsaamJpqbm1MOACgrKyMcDieFmqqqVFVVZbyEjgyLFnOlKOuZOhjAfHR2HKNH4wJeBs5g9GjWACu4\n5JLTdHYGk3o0Zl2mo7+DF4+/yLYbt9GwoYFNV2+SX5DEonLBHk48Hsfj8QDGjp+BQICqqipru+nD\nhw/T1tZGX18fbrcbXdfxer0ZhU17e/uUsIlGo9ZKAl6vl0OHDiUFTiwWw+fzZfCtCjF7e/ce5LOf\n/TJG/cXcOgDGgyaBMTDAfNz1O4zHbEZvZvXqN5Lm1Jw5d4Z/PvbPPNn/pFWXCf7noNRlxKJ2wR6O\n0+lE0zTa2tqspWZSaW1tpbm5GUVRGB4eTnsDtnA4zMjIiBVqYAyVDofD1q6hiUQCv9+ftLRNTU0N\noVAo4yHR0sMRmRgfEGAyw8YMGvNR2cUYi2++jjG8+TLGH52V88MftqDrOv/x+n/QcbSDrt90cf1l\n19NQ3oD/Rr/UZcSSMGPg7Nmzh2AwyI4dO3jooYdmvFBVVRWxWAwwRprdddddF3zzVBM6TW63m2PH\njlmfx+NxOjs72bRpE6qq4vF42Lx58wXfYzIJHJGO5KC5HCNEYDxs3sYYGLAMYzDA6xjzbqYuSWPW\nZZ7qfwpFUaz9ZUodsg6gWFpmDByPx8ORI0c4d+7cdKcAxkTNmpoaurq6qK+vx+PxcOjQoaw3Nhsk\ncMRMxhfWhPEBAZOHOb8NrBz7/PcYNZzxx2cf+9hZjvy2i+7fdNPR38Fv3/utUZcpb+CT13xS6jJi\nyZoxcBwOB5dddllST2M6mqZht9vxeDwMDQ2lvXhnrkngiOmMr3k2eeTZxGHOb2MMCBgYe228R3P9\n+ovY3f0lOvo76FV7qXHX0FDewK1lt3LRsoty/v0IUWhmHDSQSCT45Cc/mdaFzLXNnE4nR44cmXvL\nhMghY3vnSzBqNJNHnp3EGH2mA5/ACJtijJFny+EalU13XcrgJYf57r8Nc2f5nTzxJ09IXUaISS7Y\nw7HZbBn1VmbzNbkkPRwxkTGf5jxGr8ac5zVxQID5yOwPMEae6cBlYF8G5W9C+ctcfY2Tpv/UyBfL\nvyh1GSFmMOOe0V6vl5GRkbR7LPF4nEQiMaudOIXIpV27HkVR1o+FzUcxeisnxj40jK2dT2DUZnTg\nt7DqSvCshP/aj9J4kC8HN/PvwQO8FnyFnbfslLAR4gJm7OHEYjGqqqpwOBwMDg5Ou2KzydzDpq+v\nj4qKiqw3Nhukh7O0jS9HA+OTN82RZ+9hPD4zVxB4DZadh7LVUP42uN9m+StrCO/8Gz593aelLiNE\nhmbs4VRWVrJ9+3ZrnszTTz+d8ryenh4rbOrq6go2bMTSdccdQRRl/VjYXMP4fBozbDSM1ZvXAufh\nmhfhj38PfzEA/9cgq95YwfA33uHDvxvm85/4vISNELOQ1tI2fr+fnp4ewKjRuFwuXC4Xqqqiqioj\nIyMA1NXVZbzlc65JD2dpSR7mPN1yNG8A58C+Fsp/C+UnQLHB0XXwawV9+MVcN1uIRSntLaYjkQgt\nLS1Eo9Epr3m9XoLB4IKo3UjgLA3Jj85S7bYJ8CqsOgc3/B42JOCyk/D8NdDvhtcuAl5D15/LddOF\nWLTSDpyJVFW15t2ku510oZDAWdyMhTVN0wTNsmEoexPKz4D7XVAvhaPF8NL1cK4IODG2xfOFd90U\nQqRvVoGzkEngLE4rV27kzJmzY59NHAwARtDocM0glL8H6xNwfA0cXW30aE5djrEW2u958MHPp9wE\nTQgxdxI4YkEbn0cDKYPG/gGUv2QEjQL0XwH9q2HkIiYuxLls2eucPduf49YLsbRI4IgFKfnR2aSg\nWTUCN7wFG16Gy0/Cc0XQfy28dgYjdSRohMgHCRyxoFx8sYeTJ0+PfTYhaGznoWwINrwB7ndAvQT6\n7XDsWjg3MuF8I2gU5VXOn5cBAULkkgSOWBBS92gugatHYMNLsP4tOL7cKP4/Xwyn7BjL0pjnm/Nt\nXpWRZ0LkiQSOKGgpg6ZYgfJXYMMQ2HQ4OtabGbkKY5HNiedL0AhRKCRwREGaEjQrP4QbNSh/Ga5I\nwPPr4OhyeG01Rl3GtJpUu20KIfJPAkcUjOLiP2R09P3xA7ZroOw9KH8Hyt4CdS30Xw3HTsG5VKsy\nyWAAIQpZwQROOBzG4XCkXK0gFovR19eH0+lEVVUqKytnvaqBBE7hSe7N6HB1MWx4HW58G4Yvhf4r\njR7NybfHzlnG+IZoIEEjxMIw4wZsuRKJRGhsbCQcDk95TVVVmpub2b9/v3Wsvr4el8tFaaksB7+Q\nJQVN8WVQ/oYxyswGHL0W/roERi7G2Crg7QlfaYbNeNBcfvlbsjKAEAUur4EzODhIS0sLHo8Hp9OZ\n8pyWlhaampqSjgUCAYLBYMEvFCqmSgqZlefghuVGb+aKY/D8R+AfPjm2jpmCETTHmalHAy/IYAAh\nFoiCeaRWVlZGKBRi8+bNScedTiexWIySkhLrmKZpOJ1Ozp8/T6bkkVru7dr1KN/85qPGJzYdyk4Y\n65iVvQeDVxi9mWNrJtRlXp3mShN7NLLWmRALTUE8UpuOpmlWuExktxt7xQ8NDSUFkSgs470ZHa4+\nBeXnYP2bMHwx9JfC3k/CyTNj50wMGcX4Gst40Fx00TFOn05vB1ohRGEp6MAZHh4GmHanUVVVJXAK\nkBU0xWegXIfyN42dM/tL4PubjYEAnADOkDpozLAZD5qioldIJP4jV9+CEGIeFHTgaJqW7yaIDCjK\neqMuUzEKG07CFSeMusxPNsGrawFzyLMxEXMqHZmsKcTiVdCBMxdmrUbML0VZb9Rl3CegToOyD2DQ\nCf/+CTi2Ds6dHDvzfZJD5iPAaxM+l4EAQix2izZwxPwxHpmN1WVu1Yz9ZUbWwNGPwF43nFyJERwn\nAY3xNc0meg1YAzgY34vmj2QvGiEWsYIOHHM30dHR0ZR1nJl2G51uFJr0fGbHGmlWfAb+S8LYknmZ\nzZj5//0bYfjKsTNPAB+Sfm/mFenNCLFEFHTgmFtYq6rKxo0breOqqmK322XAQA5YdZkbRuHPNLjy\nQ/jNOvjJRnjV3MIZrO2bU9ZmXkNqM0KIgg4cAK/Xy6FDh5ICJxaL4fP58tiqxS2pLrNVg+vG6jL/\n5+PwYimcWzZ25okJX3XhuTNSmxFiaUu1AmLepHoM1tLSQnd3d9KxUChES4usAJxNu3Y9iqLciHK1\nG259E/7iRbg5AS9/BB6+FTpvhhfKxgYBnGB8pJn58Z8mXfGjwPVjf34BXf9nCRshlri8rjSQSCTY\nvXs3qqoSDodxuVx4vV58Ph9bt261zovH43R2drJp0yZUVcXj8UxZkSBdstJAMkVZb9Rlbhqryyy3\nwdGrjdpMUl3GNLEn8wngtxM+l8dmQojpFczSNrkigTOhLnP9qBEyV54x6jJHr56mLjPdSDMw9p5Z\nA6wARnjmmW/ymc/cPL/fgBBiQZLAWSKS6jLlGlx3AoYuM0LmxRI4Z5bzpuvNzDTSTHozQogLk8BZ\nxKz5MledMkLmplEYuQT6r4Hn1sFJc426dIr/ICEjhJgLCZxFxlrHrOhDI2TKE7AiVV0G0ntkBhI0\nQohskMBZBKyQmVKXudLozbySqi4D8shMCJFLEjgLlBUyNh1cJ4yQue59GHIavZljpXA2k/kyICEj\nhJhPEjgLSNL+MlZd5gRoq42Qeb4MPlg5dk66IQMSNEKIXJDAKXBJWzIXfQg3abDhA1hxzqjJ9JfB\n8TVjJ0jICCEKlwROgUkKGICLxtYxKz8F634/Vpcpg1fWYtRlJGSEEAuDBE4BmBIyVl3mQ7juXaMu\n0++CF68aq8tIyAghFh4JnLy1Y1LIoMM6O2x4Hda/BYlVcLQUnv/oWF1GQkYIsbBJ4OTsfScHzJii\ny+GmN2DDG7DiPPR/DPqvHavLSMgIIRYPCZx5fa9pQuaiq+D6t43ezLoT8MI1cPRj8Ooq0CduECch\nI4RYPCRwsn79VCHzUbCdB9dxKH8DPv6esY5Z/7Xw4poJ82UmB8xa4PjUa0nICCEWIAmcOV9vml4M\nH8Woy/weNrwL61+FxGojZJ5zwgcXjZ13oV7MaowVmY2Quf32cn74Q9kLSAix8EjgZPz10wUMGCED\nrDkF5ceh/GW46Cz0X2V8HL907Dx5VCaEWHokcNL6mpl6MWMuOgvXa7DhFbhqxJgvc/RqeNUB+mvT\nfP3ka0nICCEWLwmcac+bphYzke1iKH0HNrwMH38LXrbD0Wvgxcvh7BtptEZCRgixdCyYwInFYvT1\n9eF0OlFVlcrKSqqrqzO+zkyBc+GQuRSjLpMwHpfd9AqMrjJ6Ms9dBR+8fYF3l4ARQixdyy98Sv6p\nqkpzczP79++3jtXX1+NyuSgtLZ3TtdMLGWDNSSjvN0aZrTxrrGP2g4/Ce+ZimdOFjYSMEELAAunh\nBAIBamtr2bJli3UsGo3S1tZGV1dXRtcyezhw46RXUoTMRWfh+gEjZK4ehd9cAv12eOXiSfNlJpOQ\nEUKIyRZE4DidTmKxGCUlJdYxTdNwOp2cP38+o2slB06KkFF0cA0ZM/8//i68vAqO2sfmy9imuaoE\njBBCXEjBB44ZLJqmUVRUlPSazWZDVdWkILqQ8cC5FStkAK4cW17mpjdh1AZHi+G5Yvgg1VNHCRgh\nhMhUwddwhoeHAaaEjSnTwBl3Kax5zwiYDa/DytPQXzypLjORhIwQQsxFwQeOpmnzc+GGn8PVGryw\nBv7psmnqMhIyQgiRLQUfOLM1/uhsGh3mGmXa2Ecqz2d2TSGEWMTmWoGZrgouhBBCJJnrL90F38Nx\nuVwAjI6OpqzjmK9PNl0SF8oGbBci7cyehdBGkHZmm7Qzu7LxhKfgezh2ux2Xy4WqqknHVVXFbrfP\ncsCAEEKIXCv4wAHwer0cOnQo6VgsFsPn8+WpRUIIITJV8PNwABKJBH6/P2lpm5qaGkKhUMY9nIXW\nfZV2zt1CaCNIO7NN2pld2WjngggcgHg8TmdnJ5s2bUJVVTweD5s3b874OkvpLzcXFkI7F0IbQdqZ\nbdLO7FpSgZMtS+kvNxcWQjsXQhtB2plt0s7sksARQgixYCyIQQNCCCEWPgkcIYQQOSGBI4QQIick\ncIQQQuSEBI4QQoicWLZr165d+W5ELsRiMZ555hmGhobYu3cvp06dmnYdtnxRVZX6+nquueYanE4n\nb7zxBi0tLSiKkve2hsNh3nzzzZTtKKR7O107C+ne9vT0sHfvXjo6OnjkkUe4+OKLueGGG5LOKYR7\neqF2Fso9jUQihEIh4vE4HR0dvPnmm3g8nqRzCuF+XqidhXI/J9I0ja9+9at89rOfTTo+6/upLwED\nAwO6z+dLOub3+3VVVfPUotQGBgZ0RVGsD4fDoff09OS7WXpvb6/ucDj0aDQ65bVCurcXamch3Ntw\nOKzHYjHrc03TdLfbrYdCoaS25vueptvOfN/T3t5ePRKJJB3zeDx6a2trUjvzfT/TbWe+7+dkjY2N\nut/vTzo2l/u5JAKnsbFxyl9cJBKZciPzTVVVPRqN6olEQh8cHMx3c3RVVfVAIKCHQiHd7Xan/EFe\nCPc2nXYWyr2d+APGFAqFdEVRrM8L4Z6m085CuKd1dXVTfpAHg0Hd7XZbnxfC/UynnYVwPycaGBjQ\n/X6/Xl9fn3R8LvdzSdRwuru7qaysTDrm8XgIh8N5atH0dF2nqKioIFbBLi0t5fHHH2f79u3TnlMI\n9zaddkL+762maXR2dpJIJJKOV1dXAzA0NATk/56m207I/z1VFIVIJJJ0TNd1HA6H9Xm+7yek107z\nWKH8+49Go/h8vikrC8zlfi76wNE0DU3TcDqdScftdjuQ/I9HZEbubWbsdjuqqjI4ODjtOYVwT9Np\nZ6Ho6upi9+7dScfC4TDbtm0DCuN+ptPOQhONRvF6vVOOz/V+FvwGbHM1PDwMkHLzNjAKdYXw24RJ\nVVU0zdjyenh4GKfTydatW/PcqtTk3mbOvGcTRSIRHA4HJSUl1r5P+b6nF2rnxPbk+55OFAqFqKqq\n4t5777XaBPm/n5NNbufE9hTC/VRVlerq6im9m7nez0UfOOZf3kJg/tYw8X+w+vr6KccKhdzb7Ghr\na+P+++8HCvueTmwnFNY97enpobe3F0VR6OzstI4X2v2crp1QOPezp6dn2sfTc76fWakuFbC+vr6k\nQudEiqKkLDAXkkgkklRYzJdUxfhCvLfTDRpIpRDubVtbm15TU2N9Xoj3VNentnM6+b6nmqbpHo/H\nGmFXqPdzcjunk+v7OTIyoofDYevztra2pMEAc72fi76Gs9CVlpaiqiqjo6P5bsqik+97q6oqoVCI\nffv25eX905VJO/N9T4uLiwkEAtYAh0KVbjtzfT+7u7uTelPmlgTZsugDx5yMNN1fWL4nVE7U2to6\n5ZjZzTaf7RcSubdz09zczIEDB5KOFeI9TdVOKMx7CsZoOk3TOHDgQEHeT9PEdkL+72c8Hqeqqirp\nmD6phjPX+7noA8dut+Nyuab8hamqit1uL5iitqqqNDc3TxnlYRbpCumHt0nu7ew1NTXR2to6pfha\naPd0unYWwj1VVRWHw8GRI0dSvq5pWkHcz3TaWQj38/Dhw3R2dtLc3Gx9hMNhYrEYzc3N9PT0zPl+\nLvpBAwBer5dDhw6xceNG61gsFsPn8+WxVclcLhdtbW1T/sIikQgej2faUSH5Jvc2c+3t7TQ3Nye1\nJxqN4nK5KC0tLZh7OlM7C+GeapqG2+1OuYwRYM0Vyff9TKedJSUleb+fqQYK7Nmzh8OHD/PQQw9Z\nx+Z0P7NSaSpwmqZNWYrB5/MVxGzeicLhcNLyECMjI7rH49Hj8XgeW2Vwu91TZkrreuHd2+naWSj3\ntru7Ww+FQnpfX5/10dvbqwcCAeucQrin6bSzEO5pa2urrmla0jGv16s3NzdbnxfC/UynnYVwPyfb\nsWPHlBUE5nI/l8wW0/F4nM7OTjZt2oSqqng8HjZv3pzvZk3R09ODqqocP34cTdOm/IaZS4lEgt27\nd6OqKuFwGJfLhdfrxefzJRUW831v021nvu9tqglzJrfbzbFjx6zP83lPM2lnvu8pGD2xgYEB1q5d\ny8DAAFVVVdx1111J5+T7/9F021kI9xNgcHCQlpYWurq6SCQSbN++nUAgQEVFBTD7+7lkAkcIIUR+\nLfpBA0IIIQqDBI4QQoickMARQgiRExI4QgghckICRwghRE5I4AghhMgJCRwhhBA5IYEjlqRYLIbf\n78fhcGCz2XA4HHg8Hvbs2ZPvps2Kz+fDZhv/5+z3+5M+F6IQyP+RYskJBAJUVVXR09ODzWbD5/Nx\n2WWXceTIEYLBIE6nk3g8nu9mphQOh7HZbPT09CQdVxRlylLy2V5aXoi5ksARS4rf76e9vR2Hw0Es\nFuP48ePs27ePY8eOce7cOXbs2IGmaXg8noINHZgaJt3d3QwMDOSpNUKkRwJHLBmRSISenh7cbjeD\ng4NJq92aHnroIdra2gAjnArV5BWpiouLC2Y7CCGmI4EjloyWlhbrvzMt9759+3YqKytRVZVoNGod\nn1wnMWmahs1mo6mpKem4qqr4/X7cbjc2mw2n00l9fT2Dg4NJ5wUCAWuxzGAwaNWVysrKkh6d+Xw+\na497s0ZjboSVbs2mtbUVj8djtaepqWlKewBCoVDSeVVVVUn3QojZkMARS0Y0GsXhcLBly5YLnhsI\nBADo7e1NOj5TXWTia6qqUlZWxtNPP01ZWZlVNwqHw3g8HhKJxJSvNx/33XbbbTQ2NlqBZf6gb25u\nprGx0WpfKBRKCs4L1Ww8Hg/Nzc3YbDarPaFQCLfbnfT4MBgM0tTUxNDQEH6/H6/Xa+13UsiPGcUC\nkB2RoP4AAAQ+SURBVKVtE4QoaAMDA7qiKHpVVVVa58diMV1RFL2mpsY65vV6dZvNNuXckZERXVEU\nvampyTrW2Nio22w2PRqNJp3b2tqqK4qih8PhpHMVRdHLysr0RCJhHY9EIrqiKEl70HR3d+uKoug9\nPT1J162rq0tq2+TPW1padEVR9AMHDqT8Pj0ej3XMbrfrZWVlSeeZbZn4PQqRqSWx46cQmqYB6W/V\nW1paOqf3a2pqora2dsoeIeZ+IiMjI1O+ZvKjvurqaoCUj7zSoU+o8+zevRufz0dlZaV1L8D4Pqur\nq4lGo4yOjlJUVEQikaCsrCzpWtXV1cRiMex2+6zaIgQskS2mhTB/UE7ei3065nmz/QFbUVFhhYum\naRw+fJhYLGYNSEjF3BJ5PiQSCXp7e3E4HClfVxSF4eFhioqKqKurIxwOW48CvV4vFRUVKQdZCJEJ\nCRyxJJg9m3QD5/Dhw0lflylN0wgGg9aOiWDUUDwez7Q9lul22Zwts6Zjfs8+n49gMDjt+WYYdXV1\nsWfPHtra2pLOb2xspKWlheLi4qy2UywdEjhiyfB6vdbQ6IlbT5sikQherxfA6ols27btgtcdHh6e\ncqy6upp4PE4gECAQCFi9g2g0Sjgcnsu3kTEzyOx2e9rbKt93333cd999jI6O0tvbS1tbG6FQiMOH\nD1thLESmZJSaWDLM39ZT/ZavaRo1NTVUVVXR2tpKPB7H4/Gk9RgpFotNuVY8Hsfv9/PYY48lXUPP\n4Y7u5nvZ7XaKi4uJRCIpz3M4HFbNRlVVgsGgNTKuqKiIrVu3sn//fquOYw7FFiJTEjhiyaiurqau\nrs4asjxxiK/dbqerq4tYLEZzczOKotDd3Z309Xa7HV3Xk+ajmI/OUpk8MGDiuXMNnnS+fuIw6UAg\nwMjIiDWPx9Ta2koikUiaQ7Rnzx5rWPhEqqqiKMqMc5iEmFE+h8gJkQ9+v19XFEVXFEW32+261+vV\nKysrrWM2m23K0GVd1/VwOGydEwgE9MbGRt3hcOg1NTW6w+FIGr7s8/l0RVF0v9+vt7S0JJ2rKIru\ndrv1SCSi6/r4sOiJQ6JNk4dmm8OT3W63HgwGreN1dXW6oijTfq7ruu52u62vraurs77nyUPFzbY7\nHA69rq5Ob2xs1O12u26z2fTm5uZZ3HEhDBI4YkmKxWK63+/XnU6nbrPZdKfTqVdVVent7e26pmnW\nD93J811CoZD1g9vpdFo/gB0OR9IcFU3T9EAgoDscDuuHunmtQCCg22w263zz83QCR9fHA8HpdFrH\n/H5/0rybyZ+bgsGg7vF4rHk/0wVIMBjU3W530r2ZfC+EyJSi6zl8qCzEAvLd736Xe++9N9/NEGLR\nkMARQgiREzJoQAghRE5I4AghhMgJCRwhhBA5IYEjhBAiJyRwhBBC5IQEjhBCiJyQwBFCCJETEjhC\nCCFyQgJHCCFETvz/iVvBSPNrLTUAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fe23b05dad0>"
]
}
],
"prompt_number": 6
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Central Limit Theorem"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ax = plt.subplot(1,1,1)\n",
"ax.hist(np.random.rand(10000),fc='gray', histtype='stepfilled', alpha=0.3)\n",
"ax.set_xlabel('Value',size=20)\n",
"ax.set_ylabel('Freq',size=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()\n",
"\n",
"x = [np.mean(np.random.rand(100)) for _ in range(10000)]\n",
"ax = plt.subplot(1,1,1)\n",
"ax.hist(x,fc='gray', histtype='stepfilled', alpha=0.3)\n",
"ax.set_xlabel('Value',size=20)\n",
"ax.set_ylabel('Freq',size=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()\n",
"\n",
"print('Real STD: ', np.std(np.random.rand(10000)))\n",
"print('STD estimated *sqrt(n-1), n = 100 : ', np.std(x)*np.sqrt(100-1))\n",
"print('STD estimated *sqrt(n-1), n = 50 : ', np.std([np.mean(np.random.rand(50)) for _ in range(10000)])*np.sqrt(50-1))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAbEAAAEsCAYAAABNKI0sAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3U9TI9t9//GPuNd/4puCRjNVqVQWgRaVSnkFEniTHUiz\nmMoiZQxzH4BByn7uleYRDMLZ+yL5ARgkvDdIY2+SRUAtJ9lM1bWOKC9crsQjWqT8Nzb9W8wPzQjE\njCQErTO8X1XUXJ3+tnTUIH1ud58+HQmCIBAAABaaCLsDAAAMixADAFiLEAMAWIsQAwBYixADAFiL\nEAMAWOvjsDtwoVwua3p6WisrK1eW7e/vyxijRqMhY4zS6bRWV1e7ajzPU61WUzQalTFG8Xj8ynP1\nUwMAsMdYhFilUtHm5qbK5fKVZfv7+3JdtxNa7XZbiURCrVZLGxsbkiRjjHK5nA4ODjrrra+vy3Vd\nzc7O9l0DALBLqIcTm82mMpmMms2motFozxpjjBYWFjqPp6amlM1mlU6nO235fF6ZTKZrvXQ6rWw2\nO1ANAMAukXGZsWNubk6FQkHLy8udNt/3lUwmVa1WNTU11Wk3xmhubk7GGM3MzCgajcrzPM3MzHSt\nG41GdX5+Lkl91QAA7DLWAzscx5ExRs1m89oa3/c7YXR5XUk6OTnpqwYAYJ+xDjFJarVamp+f72qr\nVCqanp7WzMyMWq2WJGlycrLn+saYvmoAAPYZ+xDrZWdnR8+ePZP0ek/sffqpAQDYx7oQKxQKevjw\noZ4+fRp2VwAAIRuLIfb9MsaoUCjo+Pj4zl4zEolcu2xMxsQAwL1l1Z5YLpfTixcvutpc15UknZ2d\n9VzHdd2+aobxroADANw+a0Isk8loe3v7yuAMx3Hkuu6VwRnGGDmOo5mZmb5qrhMEQc8fAED4rAix\nYrGoXC7XFTbVarUz9D6ZTOro6KhrHc/zlEqlOo/7qQEA2GWsQqzXHs7FVFStVkue58nzPFUqFZVK\npc50Ufl8XqVSqWu9QqGgfD7fedxPDQDALqHO2NFut/X8+XMZY1Qul+W6rpLJpFKplFZXV3teoHwh\nFovpyy+/7Dyu1+va3d3V0tKSjDFKJBJds3/0W9Ovi/NhHFoEgPCMzbRTtiHEACB8Y3U4EQCAQRBi\nAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAA\naxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGt9HHYHAAB34+joSH/4wx9C\n7UMkEtE//MM/jOz5CDEAuAfOz8/15Zdf6m//9m9D7cevfvWrkT7f2IRYuVzW9PS0VlZWrizzPE+1\nWk3RaFTGGMXj8St1o6oBgA/Zw4cPQ339drs90ucbixCrVCra3NxUuVy+sswYo1wup4ODg07b+vq6\nXNfV7OzsSGsAfHh+//vf609/+lPY3dA3vvENTUwwDGHUQg2xZrOpfD6vRCKhaDTasyafzyuTyXS1\npdNpZbNZ7e3tjbQGwOj893//t372s5+F3Q39+te/1le+8hVFIpHQ+vDHP/5R3/rWtzQ3NxdaHz5U\nkSAIgrA7IUlzc3MqFApaXl7uao9Go/I8TzMzM5023/cVjUZ1fn4+0ppBXHwgxmTzYUz86U9/0qtX\nr8Luhj766KPQDxsZY/Sf//mf+pu/+ZtQ+/HRRx/pk08+CbUPzWZTruvq7/7u70Lrw/n5uX74wx8q\nkUiE1gdJajQaevz48ciebywOJ17H9/1O0LzNcRxJ0snJiRzHGUnN2+EGDOuXv/yl/vVf/1Xf+MY3\nQu3H7373O62uruorX/lKqP342te+psnJyVD7gA/bWIdYq9WSpGs/BMaYTviMqga4qcnJydAPG/3s\nZz/jKAHuhbEOMd/376wGN/Pb3/429C/NiYkJ/cVf/EWofRgnv/3tb/V///d/ob3+H//4x9BeG/fH\nWIfYOAjzZLAtfvWrX+mnP/2pPvroo1D78ec//1n/9E//pK9//euh9mMcfPWrX9Xh4WHY3Qj9vBw+\nfIQYbuz8/FyffPJJqCetJek//uM/hhqk8yH65je/GXYXcMlvfvMb/c///E9or/+hfjbGOsRc15Uk\nnZ2d9Tyf5bpuZ3DGTWuuc90hMvbQAPRrcnJSv/jFL/SLX/wi1H785V/+ZaivfxvGOsQcx5HrujLG\naH5+vtNujJHjOJ3BGKOqAYDb8ODBAz148CDsbnyQxv7y8WQyqaOjo642z/OUSqVGXgMAsMtY7Yn1\nOnSXz+e1tramjY2NTluhUFChUBh5DewWBIH+7d/+LdQBJr///e9DH6UJ3CehztjRbrf1/PlzGWNU\nLpfluq6SyaRSqZRWV1c7dfV6Xbu7u1paWpIxRolE4srMHqOq6Rczdrzxy1/+UrVaLfSBHb/5zW/G\nYlj3J598oq9+9athdwMYS6OesWNspp2yDSH2xriEGIDxd6+mnbJB2MNWI5EIIyUB3FuE2A398Ic/\nDPX1P/74Y/3jP/5j6HP1AUAYCLEbCntG6P/6r//Sy5cv9bWvfS20Pvzv//4vh1UBhIIQs9xf//Vf\nj8WtP/7qr/4q7C4AuIcIMcsxNx2A+2zsL3YGAOA6hBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQY\nAMBahBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQYAMBahBgAwFqEGADAWoQYAMBahBgAwFrW3Nm5\nUqmoXq9Lkl69eqVYLKaNjY2uGs/zVKvVFI1GZYxRPB7XysrKwDUAADtYEWKe56ndbuuzzz7rtO3v\n76tYLHaCzBijXC6ng4ODTs36+rpc19Xs7GzfNQAAe1hxOLFQKGh1dbWrbXV1VYeHh53H+XxemUym\nqyadTiubzQ5UAwCwhxUhdnx8rGazeaXd9/3Of5dKJcXj8a7liURC5XJ5oBoAgD2sCLFkMqlUKtUV\nZJVKRevr65Jeh5nv+4pGo13rOY4jSTo5OemrBgBgFytCbGtrS47jKBaLqVgsqlKpqN1u67vf/a4k\nqdVqSZImJyd7rm+M6asGAGAXKwZ2SK8PKT569EjpdFrxeFzVarWz7O3DitfppwYAYBcr9sQkqVgs\nant7W4eHhzLGKJFI9DxPNmqRSKTnDwAgfFaEWCaTUSqV0vz8vFZWVtRsNuW6rlKpVNhdAwCEaOxD\n7OIw4MzMTKdtampKBwcHchxHL168kOu6kqSzs7Oez+G6bl81vQRB0PMHABC+sQ+xWq2mWCzWc1k6\nnZbv+3IcR67rXhmcYYyR4ziamZnpqwYAYJexDzHXddVoNHou832/c91XMpnU0dFR13LP87oOOfZT\nAwCwx9iH2MV0UG+PRpRe70G9evWqsweVz+dVKpW6agqFgvL5fOdxPzUAAHtEAktO8BSLRTUaDT14\n8EDS64uUL08AXK/Xtbu7q6Wlpc4IxuXl5YFr+nExQvHly5dDviMAuH8ajYYeP348suezJsTGDSEG\nAIMbdYiN/eFEAACuQ4gBAKxFiAEArEWIAQCsRYgBAKxFiAEArEWIAQCsRYgBAKxFiAEArEWIAQCs\nRYgBAKxFiAEArEWIAQCs9fEgxXNzc53Z2/sVBIEikYi+/PLLgdYDAOB9BgqxhYUFNZtNeZ7XaZud\nnVWr1VK73Zb0+j5fFzeyvDBo8AEA0I+BQuzZs2daXFxUPB5XsVjUwsJCZ5nnedrY2NDJyYnK5fKV\nIAMAYNQGOie2tbUlx3FUrVa7AkyS4vG4arWazs/PlcvlRtpJAAB6GSjEKpWKUqmUpqamrq1JJpOq\nVCo37hgAAO8zUIgFQSBjzDtrms3mjToEAEC/BgqxZDKpWq2mH/3oRz2X7+/vy/M8JRKJkXQOAIB3\niQRBEPRbbIxRIpHQ2dmZvvOd7yiVSsl1XTUaDR0eHqpcLkuSarXalXNmH5qLEZcvX74MuScAYI9G\no6HHjx+P7PkGGp3ouq6q1aqy2axKpZJKpdKV5Ts7Ox98gAEAxsNAISa9HoV4eHgoY4w8z5MxRq7r\nynVdxePx2+hjh+d52tvb04MHD/Tq1Sul0+muofye56lWqykajcoYo3g8rpWVlSvP8b4aAIAdBg6x\nCw8fPtTi4uJ7RyuOSrlcVqVS0RdffNFpS6fT2tnZkfT6UGcul9PBwUFn+fr6ulzX7QRdPzUAAHsM\nPHdivV7X4uKiHMdRLBZTrVaT9HpKqn/5l38ZeQclyfd9bW5udgVYoVDQixcvOo/z+bwymUzXeul0\nWtlsdqAaAIA9BhrY0Ww2FYvFJEkrKyuqVquqVCpaXl7W9PS02u22EomEjo6ORtrJbDariYkJPX/+\nvKv95OREMzMzkqRoNCrP8zqPpdfhF41GdX5+3ndNvxjYAQCDG/XAjoH2xPL5vKTXow8vD+o4PT3V\n1taWarWanj17NrIOSlKxWNTS0tKV9osw8n2/E0ZvcxxH0uuw66cGAGCXgUJsb29PyWTy2tGHn3/+\nuRYWFjpD7UfF931NTU2pWCxqf3+/8++FVqslSZqcnOy5vjGmrxoAgF0GGtjh+37ncOJ1XNftCpib\nugiXer2up0+fdtpzuZxarZY2Njbk+/57n6efGgCAXQbaE1tYWNDx8fE7a+r1+kiH2l+Ej+u6Xe1P\nnjy5kwEZkUik5w8AIHwDhdiTJ09Uq9X0k5/8pOcX+fr6uowxSiaTI+vgRXhdDrGFhQX5vs+5LAC4\nxwYKsYtzXisrK1pfX5f0erDHkydP9ODBA5XLZbmuq62trZF18GLgxcW/l11cbC1JZ2dnPWsuLsZ+\nX00vQRD0/AEAhG/g68RqtZq2trb07//+75Kkw8NDlUolnZ+f6/PPP9fPf/7zkXfSdd1rB164rivH\ncXrWGGPkOI5mZmb6qgEA2GXgEJNe75Gdnp7q/PxcP//5z9VqtTpD7G9DOp3uXFR9wfM8TU9Pd8In\nmUxeuT7N8zylUqnO435qAAD2GOhi52KxqAcPHujb3/72bfbpiouLqN/ey3v06JEymUynL+12W2tr\na11TSj169EiFQqETdP3U9IuLnQFgcKO+2HmgEJuYmND09LRevXo1sg70q9lsKp/PKxaLqdFoaH19\nXcvLy1019Xpdu7u7Wlpa6tw2ZpiafhBiADC4UENsc3NTP/jBD+R5nubn50fWCRsRYgAwuFDvJ1Yo\nFDQ3N6dEIqGdnR0tLi7Kdd1rZ8EAAOA2DRRiF/MOBkGgzc3NTvvb14wFQaBIJKI///nPI+oiAAC9\nDRRi/d48khktAAB34Z0hlsvl9K1vfaszAvDyzPUAAITpndeJbW9va3d390p7sVjUP//zP99apwAA\n6MdQFzsfHByoUCiMui8AAAxkqBCTxPyBAIDQDR1iDN4AAIRt6BADACBshBgAwFqEGADAWu+92LlS\nqejJkyddbdVqVUEQXGl/W6+h+QAAjNI7JwCemBh+R+38/HzodW3ABMAAMLg7nQD4+Ph4ZC8EAMCo\nvTPE4vH4XfUDAICBMbADAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGCt9047NY5831cu\nl9MXX3zR1e55nmq1mqLRqIwxisfjWllZGbgGAGAHK0Msm83q9PS0q80Yo1wup4ODg07b+vq6XNfV\n7Oxs3zUAAHtYdzjRGKPT09MrN+XM5/PKZDJdbel0WtlsdqAaAIA9rAuxarWqVCqly/MWl0qlK9Nk\nJRIJlcvlgWoAAPawKsSq1aqSyeSVdt/35fu+otFoV7vjOJKkk5OTvmoAAHaxKsSMMZqdnb2yF9Zq\ntSRJk5OT167XTw0AwC7WhNj+/r42NjZ6LvN9/73r91MDALCLFSFGAAEAerEixEqlklZXVzuPL49M\nvE2RSKTnDwAgfGMfYvV6XYuLi11tl8+Jua4rSTo7O+v5HK7r9lUDALDL2F/sfHx8rEajod3d3U6b\n53mdC5eXlpa0uroq13VljNH8/Hynzhgjx3E0MzMjSX3VXHY5MC+wNwYA4Rv7EOs1mON73/uejo+P\ntbW11WlLJpM6OjrqCijP85RKpQaqAQDYY+wPJ/by61//+soeUj6fV6lU6morFArK5/MD1QAA7BEJ\nrjteNoaazaby+bz29vbUbre1sbGhdDqthYUFSa/Pn+3u7mppaUnGGCUSCS0vL3c9Rz81/bg4nPjy\n5cubvzEAuCcajYYeP348suezKsTGCSEGAIMbdYhZeTgRAACJEAMAWIwQAwBYixADAFiLEAMAWIsQ\nAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiLEAMA\nWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFjr47A70K/9/X0ZY9RoNGSMUTqd1urqaleN53mq1WqK\nRqMyxigej2tlZWXgGgCAHawIsf39fbmu2wmtdrutRCKhVquljY0NSZIxRrlcTgcHB5311tfX5bqu\nZmdn+64BANjDisOJxhgtLCx0Hk9NTSmbzSqdTnfa8vm8MplM13rpdFrZbHagGgCAPSJBEARhd+Jd\nfN9XMplUtVrV1NRUp90Yo7m5ORljNDMzo2g0Ks/zNDMz07VuNBrV+fm5JPVV069IJCJJevny5fBv\nDgDumUajocePH4/s+cZ+T8xxHBlj1Gw2r63xfb8TRpfXlaSTk5O+agAAdhn7EJOkVqul+fn5rrZK\npaLp6WnNzMyo1WpJkiYnJ3uub4zpqwYAYBcrQqyXnZ0dPXv2TNLrPbH36acGAGAXK0OsUCjo4cOH\nevr0adhdAQCEyIoh9m8zxqhQKOj4+PhOXu9iAAcAYPxYtyeWy+X04sWLrjbXdSVJZ2dnPddxXbev\nGgCAXawKsUwmo+3t7SuDMxzHkeu6VwZnGGPkOI5mZmb6quklCIKePwCA8FkTYsViUblcritsqtVq\nZ+h9MpnU0dFR1zqe5ymVSnUe91MDALCHFSFWLpclvR5q73mePM9TpVJRqVTqTBeVz+dVKpW61isU\nCsrn853H/dQAAOxhxYwdly9QvhCLxfTll192Htfrde3u7mppaUnGGCUSCS0vL3et009NP5ixAwAG\nN+oZO8Y+xMYVIQYAg7t3004BAHAdQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1C\nDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwAYC1CDABgLUIMAGAtQgwA\nYC1CDABgLUIMAGAtQgwAYK2Pw+7AXfM8T7VaTdFoVMYYxeNxrayshN0tAMAQ7lWIGWOUy+V0cHDQ\naVtfX5frupqdnQ2xZwCAYdyrw4n5fF6ZTKarLZ1OK5vNhtQjAMBN3KsQK5VKisfjXW2JRELlcjmk\nHgEAbuLehJjv+/J9X9FotKvdcRxJ0snJSQi9AgDcxL0JsVarJUmanJzsudwYc5fdAQCMwL0JMd/3\nw+4CAGDE7tXoxGFEIpF3Lv/7v//7O+oJAHwYgiAY2XPdmz0xAMB4eN/OwSDuzZ6Y67qSpLOzs57n\nxS6WX3bd/zFc/BJG+X8UtmJbvMG2eINt8Qbb4o1RBph0j/bEHMeR67pXBnAYY+Q4jmZmZsLpGABg\naPcmxCQpmUzq6Oioq83zPKVSqZB6BAC4iUhwj/Zv2+221tbWuqadevTokQqFwsB7YhweeINt8Qbb\n4g22xRtsizdGvS3uVYhJUr1e1+7urpaWlmSMUSKR0PLy8sDPwx/lG2yLN9gWb7At3mBbvEGIjQn+\nKN9gW7zBtniDbfEG2+INQgwAgP/vXg3sAAB8WAgxAIC1CDEAgLUIMQCAtQgxAIC17s3ciYPwPE+1\nWk3RaFTGGMXjca2srNzaeuNs2Pe0v78vY4wajYaMMUqn01pdXb2DHt+eUfx+fd9XLpfTF198cUu9\nvBs32Rae52lvb08PHjzQq1evlE6nNTs7e8s9vj3DbotKpaJ6vS5JevXqlWKxmDY2Nm67u7euXC5r\nenp6oL+HG32uAnRpNBpBKpXqaltbWwuMMbey3jgb9j2Vy+XA87zOY9/3g1gsFhQKhVvp510Y1e93\nc3MzWFtbG2XX7txNtkWpVArS6XRX2+bm5kj7d5eG3Ra1Wi0ol8tdbeVy2erPSBAEweHhYTA9PR1U\nq9W+6kfxuSLELtnc3Az29/e72iqVynu/eIZdb5wN+562t7evtBUKhSASiYy0f3dpFL/fRqMRrK2t\nBevr66Pu3p0adlucnp4G09PTXW07OzvB3NzcyPt4V4bdFpeD/IKt3xfGmCCdTgeFQiGIxWJ9h9go\nPleE2CXT09NBs9nsajs9PX3vF/Cw642zYd7T6elpkEgkAt/3u9objUYQiUSuPJ8tRvH7LRQKQaFQ\nsPaL6sKw2+Lzzz8PcrnclXZb/yaCYPhtkUgkeu5tXN4rsdEgITaKzxUDO97i+75831c0Gu1qdxxH\nknRycjLS9cbZsO/JcRwZY9RsNm+7i3dmFL/farWqZDJ5G927UzfZFsViUUtLS1fabb0N0k22RTKZ\nVCqV6vqcVCoVra+v30pfx9GovjcJsbe0Wi1J6nnTTElX7kV20/XG2U3eU6vV0vz8fFdbpVLR9PS0\nlV9Yo/j9GmM0Oztr/dx5N9kWvu9rampKxWJR+/v7nX9tdZNtsbW1JcdxFIvFVCwWValU1G639d3v\nfvdW+jqORvW9yejEt/i+f6frjbNRv6ednR09e/ZspM95V266Lfb39z+IUWfS8Nvi4gupXq/r6dOn\nnfZcLqdWq2Xl9rnp38Xx8bEePXqkdDqteDyuarU6op7ZYVTfMeyJ4dYVCgU9fPiw68vrvvgQ/wdn\nGBfbwXXdrvYnT54om82G0aXQFYtFbW9v6/DwsHNbqA/pMPxdIcRwq4wxKhQK+vGPfxx2V0JRKpW6\nro+7uA3FfXMRXpdDbGFhQb7vW3ne+CYymYxSqZTm5+e1srKiZrMp13W5y/wQCLG3XHzAzs7O3rl8\nVOuNs1G9p1wupxcvXoysX2EYdlvU63UtLi52tdl+TmzYbXFxsv7i38tsPG887La42Ct9+/zw1NSU\nDg4O5DjOvTmsOKrvGELsLY7jyHXdKx8oY4wcx7l2UMKw642zUbynTCaj7e3ta0/c2mLYbXF8fKzd\n3V3lcrnOT7lclud5yuVyVg5quMnfRa/13l5mm2G3Ra1WUywW67ksnU7fm0PQo/reZGDHJclkUkdH\nR12j6zzPe+9u/rDrjbObvKdisahcLtf1h1itVuW6rpVTDA2zLXoNVvje976n4+NjbW1t3Uo/78Kw\nfxfpdFq1Wk3Ly8td69k6alUablu4rqtSqdRzme/7Vn9nDGok35v9X8J2P/i+f+WCw1Qq1XVB3unp\naeC6btcUMf2sZ5tht0WpVAoKhUJQq9U6P4eHh9fOUmCDYbfFZZ9//rn1Fzvf5DMSi8WurHd5xgab\nDLst0ul0UKlUutZrNBpBNpu91f7ehVgsduW9BcHtfW+yJ3bJ1NSU8vm8crmclpaWZIy5skchSaen\np10n6ftdzybDbAvf96+9YPO6Qyg2GPbv4kKz2VQ+n9fe3p7a7bYymYzS6bQWFhbu6B2Mzk0+I4eH\nh8pkMorFYmo0Gsrlcl17ZrYZdlt88cUXKhaLOjw81IMHDyS9Prxm6x56u93W8+fPZYzpTPh9cUH3\n2wObbuN7MxIElp9pBgDcWwzsAABYixADAFiLEAMAWIsQAwBYixADAFiLEAMAWIsQAwBYixADAFiL\nEANC4HmeJiYmrsxyf1mlUtHExMTAt61fW1vTxAQfb3z4+CsHQhCPx+U4jur1utrt9rV1FxPFfvrp\npwO/xn29dxnuF0IMCMnm5qaCINDe3t61NXt7e4pEIvr2t799hz0D7EGIASF58uSJJGlnZ6fncs/z\n1G639Z3vfOcuuwVYhRADQrKwsCDXda89pLi7uyvpTdhJr28YuLa2plgspomJCUWjUa2vr6vZbF5Z\n/+25vVOpVM9zZL7va2JiQplM5sqy7e1tJRKJzutkMpmerwOEiRADQpROp689pFgoFLoOJRpjNDc3\npx/96Eeam5tTOp3W4uKiyuWyEonEO8+tSe8+R3Z5WSKRUC6X08TEROd1CoWCYrGY6vX6EO8UuB2E\nGBCii0OFlw8p9jqUmM/nFYlEdHh4qB//+Mf6/ve/r4ODA+Xzefm+r0qlMpI+bW9vq16vq1qt6ujo\nqPM6tVpNUu87VgNhIcSAEM3OzmphYeHKIcVehxIzmYxKpdKVm0he3Fjz9PR0JH16/vy5UqmU4vG4\nfN/v/MzOzmplZUWe5+ns7GwkrwXcFHd2BkL26aefql6vq1Ao6LPPPpMklcvlK6MSFxYWOoHl+76O\nj4/led61A0OG1W63dXh4qOnp6Z7LI5GIWq2WJicnR/q6wDAIMSBkm5ubymaz2t3d1WeffSZjjJrN\nptbW1rrqfN9XNpvV3t5eZ68tkUgokUiMbMCFMUbS64Eg2Wz22rrrAg64a4QYELKpqSnF4/HOIcVy\nuSzp9aCPt62srKheryudTiudTmt+fl6SVK1WO+sMqtVqdT2ORqOSJMdxrhy2BMYR58SAMXAxSrFQ\nKGh3d1eRSKQrRHzfV71e19ramr7//e93AkzqHko/KM/zuh47jqOpqalrB4lMT09rbm5u6NcDRo0Q\nA8bAxdyIOzs7qtfr117gfHnwxsUhRulqmL09bN5xHAVBoGq12nPdt6XTaZ2enl6Zr3F7e1vtdrvn\nNWVAWDicCIyBqakpJZPJzh7Q5UOJjuN0lq+vr2txcVGNRkOlUklLS0uSXg/Bd11XKysrkrpD7dNP\nP9X+/r5SqVRnuquLdS8H49bWlsrlssrlsubm5rSwsCBjjOr1uhKJhJ4+fXqbmwIYTABgLJTL5SAS\niQQTExM9l/u+H6TT6WB6ejqIRCLB4uJisL+/HwRBEKTT6WBiYiLIZDJBEATB2tralecpFApBLBYL\nIpFIEI1Gg1wuFwRBEExPT3fWe1s2mw0SiUQQiUSCubm5Tj0wTiJBcIMD6gAAhIhzYgAAaxFiAABr\nEWIAAGs9DzJCAAAAJElEQVQRYgAAaxFiAABrEWIAAGsRYgAAaxFiAABrEWIAAGv9P1QePcgzjpnd\nAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7f546ecaaa90>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAbUAAAEsCAYAAABEwy1WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3b9zG+lh//EP+D2f4x9DLKC7xvFMyCUdt0cs6OZciYCr\nVMcjdH+ASdBdCp2A69xJoNO4sgmqc0UBcGOnCAUo40nSmOIiPwoVPj5gksnlrhC4ZJz4PLrTfgsN\n1gIBSgAJENjl+zWDsfHss7vPg4enD3b32UXM931fAABEwMykGwAAwKgQagCAyCDUAACRQagBACKD\nUAMARAahBgCIjDcm3QBJqtfrqtfrunHjhg4PD+U4jtbX17vquK6rg4MDJZNJGWOUSqW0srIyljoA\ngHCaeKjV63XFYjHdu3cvKEun0/I8Tx9++KEkyRijYrGovb29oE4ul5Nt25qfnx9pHQBAeE389OP2\n9nZPWSaT6SovlUra3NzsqpPP51UoFEZeBwAQXrFJP1Ekl8tpYWFBd+/eDcoKhYIePXqk/f19SVIy\nmZTrupqbmwvqeJ6nZDKp58+fj7QOACC8Jh5q/SwsLOhHP/qRbt++HYSO53manZ3tqjczMyNjjCzL\nGkmdl8MOABA+Ez/9eFa5XFY6ndbt27clSe12W5J6gqjDGDOyOgCAcJv4RJGOWq2mhw8fKhaLaXd3\nNyj3PO+1646qDgAg3KYm1FZXV7W6uqqTkxOl02nt7OxoaWlp0s0CAITI1J1+jMfjyufzU3PvWCwW\nO/cFAJguUxdqkrSysiLP8/To0SPZti1JOj097VvXtu2R1RkWwQYA02WioWaMUSKR0D//8z/3Xe55\nnizLkm3bPRM5OjMa5+bmRlanH9/3+74AANNnoqHmeZ4WFhZ6jpI6wZNKpSS9uBm7c89ah+u6ymaz\nwftR1QEAhNfE71P7yU9+oo2NDcXj8aAsm80qnU4HN2SfnJxobW2t6/FWP/jBD1Qul4MjrFHVGVTn\n1CNHbZgWvu/r97///dj3E4vF9M1vfnPs+wEuYuKhJkk7Ozs6PDwMHmicTqf1wx/+sKtOs9nU7u6u\nlpeXZYyR4zi6efPmWOoMglDDtPnP//xP/eM//qO+8pWvjHU/X3zxhbLZrG7cuDHW/QAXMRWhFkaE\nGqbNf/zHf+jf/u3ftLi4ONb9PHnyRO+++67efvvtse4HuIipnP0IAMBFEGoAgMgg1AAAkUGoAQAi\ng1ADAEQGoQYAiAxCDQAQGVPz0zNAlH322Wf64osvxrqP4+PjsW4fCANCDRizL774Qo8ePbqSR0sl\nk8mx7wOYZoQaMGa+7ysWi+kv//IvJ90UIPK4pgYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACR\nQagBACKDUAMARAahBgCIDEINABAZhBoAIDIINQBAZBBqAIDImIqn9NdqNRljdHh4KGOM8vm8VldX\ng+WdsmKxKMdx1G63VS6Xlc1mtbKyEtRzXVcHBwdKJpMyxiiVSnUtH7QOACCcJh5qtVpNtm0HIXZy\nchIE1/r6elCv0Wio0WhIkizL0v3797vCyBijYrGovb29oCyXy8m2bc3Pzw9cBwAQXhM//WiM0dLS\nUvA+Ho+rUCgon88HZbFYTPV6XZ7nyRijdrut9957r2s7pVJJm5ubXWX5fF6FQmGoOgCA8JpoqHme\np93dXZ2cnHSVd47Ajo6OgjLf9zU7O6u5ubm+26pUKkqlUl1ljuOoWq0OVQcAEF4TDTXLsmSMUavV\nutR2PM+T53k9P2VvWZakF+E4SB0AQLhN/Jpau93uKavX60okEl1HZcYYeZ4XrJNMJoPrcJ1tzM7O\n9t2HMSbY1iB1AADhNPFQ62d7e1sfffRR8L5zdPXyjMhcLheUdcLuVQapAwAIt4lPFDmrXC7rrbfe\n0u3bt4OyeDzeNRNSuroJHrFYrO8LADB9pupIzRijcrmsx48fv7bu/Py8jDE6PT29gpYBAMJgqo7U\nisWiHj161FO+tbXVU9Y5JWmMkW3bknRuwNm2PVCdfnzf7/sCAEyfqQm1zc1NbW1t9Uzk6NwwfXZ2\nYmdyiG3bsixLtm3LGNOzrmVZmpubG6gOACDcpiLUdnZ2VCwWu4Kl0Wio1WrJtm1tb2/3hE69Xpfj\nOEEIZjIZ7e/vd9VxXVfZbDZ4P0gdAEB4TTzUOjc+t9ttua4r13VVr9dVqVSCR1clk8mue9k8z1O5\nXNbOzk5QViqVVKlUurZdLpdVKpWGqgMACK+YP8ELRP1uhu5YWFjQ7373u+B956HHT58+led5PUd2\nktRsNrW7u6vl5WUZY+Q4jm7evDl0nUF0ZkByfQ2v8+zZM9Vqta7HwYXZkydP9O677+rtt9+edFOA\nHhMNtTAj1DAoQg24OhM//QgAwKgQagCAyCDUAACRQagBACKDUAMARAahBgCIDEINABAZhBoAIDII\nNQBAZBBqAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAAkUGo\nAQAig1ADAEQGoQYAiIw3Jt0ASarVajLG6PDwUMYY5fN5ra6udtVxXVcHBwdKJpMyxiiVSmllZWUs\ndQAA4TTxUKvVarJtOwixk5MTOY6jdrut9fV1SZIxRsViUXt7e8F6uVxOtm1rfn5+pHUAAOE18dOP\nxhgtLS0F7+PxuAqFgvL5fFBWKpW0ubnZtV4+n1ehUBh5HQBAeMV83/cntXPP85TJZNRoNBSPx4Ny\nY4wWFxdljNHc3JySyaRc19Xc3FzXuslkUs+fP5ekkdUZVCwWkyRN8ONDSDx79ky1Wq3ry1uYPXny\nRO+++67efvvtSTcF6DHRIzXLsmSMUavVOreO53lB8JxdV5KOjo5GVgcAEG4TP/3Ybrf1zjvvdJXV\n63UlEgnNzc2p3W5LkmZnZ/uub4wZWR0AQLhNPNT62d7e1kcffSTpxZHa64yqDgAg3CY++/Gscrms\nt956S7dv3550UyT96doZAGD6TVWoGWNULpf1+PHjSTcFABBCU3X6sVgs6tGjR11ltm1Lkk5PT/uu\nY9v2yOr04/t+3xcAYPpMTahtbm5qa2urZyKHZVmybbtnIocxRpZlaW5ubmR1AADhNhWhtrOzo2Kx\n2BUsjUYjmOqfyWS0v7/ftY7ruspms8H7UdUBAITXxEOtWq1KejG133Vdua6rer2uSqUSPLqqVCqp\nUql0rVcul1UqlYL3o6oDAAiviT9R5OzN0B0LCwv63e9+F7xvNpva3d3V8vKyjDFyHEc3b97sWmdU\ndQbBE0UwKJ4oAlydiYZamBFqGBShBlydiZ9+BABgVAg1AEBkEGoAgMgg1AAAkUGoAQAig1ADAEQG\noQYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACRQagBACLjjWEqLy4uBk+nH5Tv+4rFYl0/IwMg\nvHzf17/+67/qzTffHOt+vvnNb0bmlw1wdYYKtaWlJbVaLbmuG5TNz8+r3W7r5OREkmRZVvDjnh3D\nBiGA6fUXf/EX+sMf/jDWfXz55Zf6+OOPCTUMbahQ++ijj5ROp5VKpbSzs9P1B+e6rtbX13V0dKRq\ntdoTbACi4Rvf+Ia+8Y1vjHUfz54902effTbWfSCahrqmdu/ePVmWpUaj0fMNKpVK6eDgQM+fP1ex\nWBxpIwEAGMRQoVav15XNZhWPx8+tk8lkVK/XL90wAACGNVSo+b4vY8wr67RarUs1CACAixoq1DKZ\njA4ODvTLX/6y7/JarSbXdeU4zkgaBwDAMIaaKFIqlVSv17W2tqb3339f2WxWtm3r8PBQDx8+VLVa\nDeoBAHDVhgo127bVaDRUKBRUqVRUqVR6lm9vbzMNFwAwEUOFmvRiluPDhw9ljJHrujLGyLZt2bat\nVCp14YZUq1UlEgmtrKx0lRtjlM/nVSwW5TiO2u22yuWystlsV13XdXVwcKBkMiljjFKpVM+2BqkD\nAAivoUOt46233lI6nX7tbMhB1Ot1bWxsBKcvz2o0Gmo0GpJe3Nx9//79rjAyxqhYLGpvby8oy+Vy\nsm07uF9ukDoAgHAb+tmPzWZT6XRalmVpYWFBBwcHkl48Qutv/uZvhtpWq9XS5uamWq2Wkslk3zqx\nWEz1el2e58kYo3a7rffee6+rTqlU0ubmZldZPp9XoVAYqg4AINyGCrVWqyXHceS6rlZWVuT7frDs\n6dOnunPnjpaXlwfe3vz8vH7+859rfX39lfV839fs7Kzm5ub6Lq9UKj2nPh3H6TryG6QOACDchgq1\nzqzGg4ODnkkix8fHunfvng4ODvTRRx+NroWv4XmePM/rOdKzLEuSdHR0NFAdAED4DRVqDx48UCaT\nOXd24507d7S0tDTyox9jjGq1mmq1mnZ2dlSr1YJl7XZbkjQ7O3vuuoPUAQCE31ATRTzP08LCwivr\n2LbdFTqX1Tm6Wl1dDcpyuVxQ5nnea7cxSB0AQPgNdaS2tLSkx48fv7JOs9m81NT+s+LxeM81t6uc\n4BGLxfq+AADTZ6hQu3Xrlg4ODvT3f//3ff9hz+VyMsYok8mMrIH9zM/Pyxij09PTse4HABAuQ4Va\n55rZyspKcAqwVCrp1q1bunHjhqrVqmzb1r1790bWwK2trZ6yzinJzo3fks4NuM6N4a+rcx7f9/u+\nAADTZ+j71A4ODnTv3j399re/lSQ9fPhQlUpFz58/1507d/Txxx+PrHGdG6bPzk7sTPywbVuWZcm2\n7Z7JHsYYWZalubm5geoAAMJv6FCTXhyxHR8f6/nz5/r444/VbreDKf2j1HmW5NnQqdfrchwnmM2Y\nyWS0v7/fVcd1XWWz2eD9IHUAAOE21OzHnZ0d3bhxo+uJHq86dTesfqf1ksmkWq1W8Cgrz/NULpd1\n//79oE6pVNLa2lrXhJJyuaxyuTxUHVw///d//6f//d//Hes+vvzyy7FuH8CfxPwhLhDNzMwokUjo\n6dOnI9n5ycmJ7t69K2NMcD0uk8kom812TeGv1Woyxujp06fyPE/FYrHn6K3ZbGp3d1fLy8syxshx\nHN28eXPoOoPqTJTh+lq4/cM//IM+/fRTfeUrXxnrft544w195zvfGes+ouTZs2d68uSJ1tbWJt0U\nhMxQobaxsaH79+/LdV29884742zX1CPUouE3v/mN3nzzzXOfPYrJINRwUUOdfiyXy1pcXJTjONre\n3lY6nZZt2+c+qQMAgKs0VKh1vs36vq+NjY2g/OV71nzfVywW4zoCAODKDRVqg/6gJk/cAABMwitD\nrVgs6nvf+14w2/Hsk/kBAJgmr7xPbWtrS7u7uz3lOzs7+tGPfjS2RgEAcBEXuvl6b2+P+7sAAFPn\nQqEmMZUdADB9LhxqTAYBAEybC4caAADThlADAEQGoQYAiIzX3nxdr9d169atrrJGoyHf93vKX9bv\nVgAAAMbplQ80npm5+IHc8+fPL7xuGPBA42jggcbTiQca46JeeaT2+PHjq2oHAACX9spQS6VSV9UO\nAAAujYkiAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMl77mKyrUq1WlUgktLKy0rPM\ndV0dHBwomUzKGKNUKtVTb1R1AADhNRWhVq/XtbGxoWq12rPMGKNisai9vb2gLJfLybZtzc/Pj7QO\nACDcJnr6sdVqaXNzU61W69xn75VKJW1ubnaV5fN5FQqFkdcBAITbKx9ofJUWFxdVLpd18+bNrvJk\nMinXdTU3NxeUeZ6nZDIZPDR5VHWGwQONo4EHGk8nHmiMi5rqiSKe5wXB8zLLsiRJR0dHI6sDAAi/\nqQ61drstSZqdne273BgzsjoAgPCb6lDzPO/K6gAAwm+qQw0AgGFMxZT+adaZEAIAmH5TfaRm27Yk\n6fT09Nzlo6oDAAi/qQ41y7Jk23bPRA5jjCzL0tzc3MjqnMf3/b4vAMD0mepQk6RMJqP9/f2uMtd1\nlc1mR14HABBuUxVq/Y6ASqWSKpVKV1m5XFapVBp5HQBAuE30iSInJye6e/eujDGqVquybVuZTEbZ\nbFarq6tBvWazqd3dXS0vL8sYI8dxep48Mqo6g+KJItHAE0WmE08UwUVNzWOywoZQiwZCbToRario\nqTr9CADAZRBqAIDIINQAAJFBqAEAIoNQAwBEBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAA\nkUGoAQAig1ADAEQGoQYAiAxCDQAQGYQaACAyCDUAQGQQagCAyCDUAACRQagBACKDUAMARAahBgCI\njDcm3YBBGGOUz+dVLBblOI7a7bbK5bKy2axWVlaCeq7r6uDgQMlkUsYYpVKpruWD1gEAhFMoQk2S\nGo2GGo2GJMmyLN2/f78rjIwxKhaL2tvbC8pyuZxs29b8/PzAdQAA4RWK04+xWEz1el2e58kYo3a7\nrffee6+rTqlU0ubmZldZPp9XoVAYqg4AILxCEWqS5Pu+ZmdnNTc313d5pVJRKpXqKnMcR9Vqdag6\nAIDwCk2ovYrnefI8T8lksqvcsixJ0tHR0UB1AADhFpprasYYeZ4nSWq320omk1pdXQ3eS9Ls7Oy5\n63aO8AapA2DyfN/Xp59+Ovb9xONxfe1rXxv7fnA1QhFqnaOrTohJLyZ4dMo6Yfcqg9QBMB3eeOMN\n/dmf/Zl++9vfjnU/n3/+ub7zne9oaWlprPvB1QlFqMXjca2vr3eV5fN55fP5rqADEA2xWEzf/e53\nx76fTz75RL7vj30/uDqhCLV+5ufnZYzR6enpWPcTi8XGun0AwOiEYqLI1tZWT1nnlKQxRrZtS9K5\nAWfb9kB1AADhNvWh1rlh+uzsxM7kENu2ZVmWbNuWMaZnXcuyNDc3N1Cdfnzf7/sCAEyfqQ8127a1\nvb3dEzr1el2O4wSzGTOZjPb397vquK6rbDYbvB+kDgAgvKY+1KQXpxpbrVbw3vM8lctl7ezsBGWl\nUkmVSqVrvXK5rFKpNFQdAEB4xfyQnEur1Woyxujp06fyPE/FYrHn6K3ZbGp3d1fLy8syxshxHN28\neXPoOoPoTCAJyceHc/zmN7/Rm2++2XNTPq6HTz75RPF4vOdJQwiv0ITatCHUooFQu94ItegJxelH\nAAAGEdr71BBtx8fH+pd/+ZexHwk/ffpU3/72t8e6DwBXh1DDVPqf//kftdttfetb3xrrfr797W8H\nD7UGEH6EGqbWV7/6VSUSiUk3A0CIcE0NABAZhBoAIDIINQBAZBBqAIDIINQAAJFBqAEAIoNQAwBE\nBqEGAIgMQg0AEBmEGgAgMgg1AEBkEGoAgMgg1AAAkUGoAQAig1ADAEQGoQYAiAxCDQAQGYQaACAy\n3ph0AwBgkj7//HM9ffp0rPuIxWJKJBKKxWJj3Q+uYai5rquDgwMlk0kZY5RKpbSysjLpZgGYgK9/\n/ev6r//6L3322Wdj3c8f//hHZbNZ3bhxY6z7wTULNWOMisWi9vb2grJcLifbtjU/Pz/BlgGYBMuy\nZFnW2Pfz5MkT+b4/9v3gml1TK5VK2tzc7CrL5/MqFAoTahEAYJRi/jX6+pBMJuW6rubm5oIyz/OU\nTCb1/PnzobbVOTd+jT6+wL//+7/ryy+/HOs+2u22PvvsMy0uLo51P8BVePLkib7//e/rrbfemnRT\nIu/anH70PC8IsJd1Tj0cHR11hR36e/bsmf7pn/5JiURi7Pvi+gOAYV2bUGu325Kk2dnZvsuNMYTa\ngGZmZmTb9qSbAQA9rk2oeZ436SZciWFPo07b9oGoarVa+vTTT8e6j69//evX/gvntQm1i3rdfSXc\ndwIAwxnnXIRrNfsRADB54zwYuDZHap1D8tPT077X1c47ZD/vG0XUZz/Sv3CLcv+i3Dfp+vRvXK7N\nkZplWbJtW8aYrnJjjCzLYpIIAETAtQk1ScpkMtrf3+8qc11X2Wx2Qi0CAIzStbr5+uTkRGtra12P\nyfrBD36gcrk89JHadTlFQP/CKcr9i3LfJPp36e1fp1CTpGazqd3dXS0vL8sYI8dxdPPmzaG3wx9e\nuNG/8Ipy3yT6d+ntX7dQGxX+8MKN/oVXlPsm0b9Lb59QAwBExbWaKAIAiDZCDQAQGYQaACAyCDUA\nQGQQagCAyPh/P/7xj3886UZMmuu6+vWvf62joyP97d/+rT7//POBfr6hXq+rXC6r2WzqF7/4hf77\nv/9bjuMEy40xyuVy+vM//3Mlk0l98sknKpVKisViV/rzEBft38s8z9Nf//Vf66/+6q9Gvu3LGFff\nwjx2g7Z90mN30TYM0r8wj9/L6/70pz9Vs9nUr371Ky0sLHT9OG9Yx+/ldc/r36XGz7/mDg8P/Ww2\n21W2trbmG2Neud7Dhw/9er3eVeY4jr+1tdW17VgsFrwSiYRfq9VG1/gBXLR/Z21sbPhra2tj2fZF\njbtvYR27Qdo+6bG7TBsG7V9Yx8/3fb9Sqfj5fL6rbGNjYyTbHpVx9++i43ftQ21jY6Pnw6rX6z3/\nyJ31/vvv94RaoVDwFxYWgvfGGL/RaPgnJyd+q9UaWZuHcdH+vezw8NBfW1vzc7ncyLd9GePsW5jH\nbpC2T3rsLtOGQfoX5vE7Pj72E4lEV9n29ra/uLh46W2P0jj7d5nxu/ahlkgkej604+NjPxaLvXK9\ntbU1v1gsdpXduXPHT6fTwXtjTE/wXbWL9u9l5XLZL5fLPX+so9j2ZYyzb2Eeu0HaPumxu0wbBulf\nmMfvzp07Pf+2+L7fta0wj98g/bvM+F3riSKe58nzPCWTya5yy7IkSUdHR+eu++DBA929e7errFqt\n6tatWyNv50Vdpn8djUZDmUxmLNu+jHH2bRqM8/Od9NhNSxvG6TL929nZ0fLyck9556Hr0/DZjbN/\nl3VtfiS0n3a7LUl9fzRUenGxctAPulwuK51O6/bt2z3b8Dwv2F8ymdTq6urFGz2EUfTPGKOVlZWe\n57SN8rO7iHH27eXlYR27V7V90mM3ijYMMjZhHT/P8xSPx7Wzs6NkMhm58Xtd/17exkXG71qHWucD\nu4xaraaHDx8qFotpd3e3a1nnW8zLA5HL5XrKxuWy/avValpfXx/Lti9rnH2Twj12r2v7pMdOGm//\nBq0zThftX+dHjJvNZtcX5GKxqHa7rfX19VCP3yD9ky43ftf69OMorK6u6uc//7nu3bundDqtZrMZ\nLIvH4z3/cObzeRUKhatu5tCm4T+ccRmkb2EeuzC3fRCD9C+sn0Hnb/PstPVbt25NfdsHMWj/LjN+\nhNqIxONx5fN5raysvLLe/Py8jDE6PT29opZdTKVS6fpG1Pm5iCi4aN/CMnb9hLntgxikf2H4DDr/\n2J/9R39paUme54X+WuNl+jfo+F3rUOt8sOd9SMPeyLiysiLP8/To0SNJ0tbWVk+dzmF15zB8nC7a\nv2azqXQ63VV29rrTqD+7YY2zb1J4x056fdsnPXYv72Mc/Ru0zjhdtH+diRad/z0r7OM3SP+kS47f\nheZMRsjCwoLfbDa7yg4PD3vuozi73LKsvuvFYjG/VqsF///slNdO+cnJycj68CoX6V+5XPYLhULX\nK5vN+gsLC36hUPCr1eqFtz1K4+pbmMdu0LZPeuwu2oZB+hfm8eus12g0espf7lNYx6+z3qv6d9nx\nu9YTRSQpk8lof39f77zzTlDmuq6y2ey563iep4WFhZ5vI51vEKlUSnNzc9re3u6ZAVSv1+U4zrmz\nhkbtIv3rN4HiJz/5iR4/fqx79+5datujNM6+hXXsbNseqO2THruLtmGQ/s3OzoZ2/KQX144ODg50\n8+bNrvUSiUTQp7COnzRY/y41foNlcnR5ntfzqJdsNtv1LeH4+Ni3bdsvl8tB2dbWlu95Xtd6mUym\n66bCarXa9ciY4+Nj33Gcnm8343TR/p11586dnhuUB9n2OI2zb2Eeu0HaPumxG7QNF+1fmMfP87yu\nJxN11nv56R1hHr9B+neZ8Yv5/jk36VwjzWZTu7u7Wl5eljFGjuN0fYvwPE+2bWtra0s//OEPg/Kd\nnR0dHh7qxo0bOjw8VDqd7louvZg6bozR06dP5XmeisXi2O8hOeui/ZOkVqulUqmkBw8e6OTkROvr\n68rn81paWhpo22HuW5jHbpC2T3rsBmnDZfoX5vHr/G0uLCzo8PBQuVyuZ2zCPH6D9O+i40eoAQAi\n41rPfgQARAuhBgCIDEINABAZhBoAIDIINQBAZBBqAIDIINQAAJFBqAEAIoNQAybAdV3NzMz0/GLA\nWfV6XTMzM8EPJA5qbW1NMzP8543rh796YAJSqZQsy1Kz2dTJycm59SqViiTpgw8+GHofUfoNPGBQ\nhBowIRsbG/J9Xw8ePDi3zoMHDxSLxfTee+9dYcuA8CLUgAm5deuWpBc/s9GP67o6OTnR+++/f5XN\nAkKNUAMmZGlpSbZtn3sKcnd3V9Kfwk968Zt9a2trWlhY0MzMjJLJpHK5nFqtVs/6Lz+rPJvN9r3G\n5nmeZmZmtLm52bNsa2tLjuME+9nc3Oy7H2CaEGrABOXz+XNPQZbL5a5Tj8YYLS4u6pe//KUWFxeV\nz+eVTqdVrVblOM4rr81Jr77GdnaZ4zgqFouamZkJ9lMul7WwsKBms3mBngJXg1ADJqhzavHsKch+\npx5LpZJisZgePnyov/u7v9PPfvYz7e3tqVQqyfM81ev1kbRpa2tLzWZTjUZD+/v7wX4ODg4k9f/1\ncGBaEGrABM3Pz2tpaannFGS/U4+bm5uqVCo9P6bY+VHT4+PjkbTp7t27ymazSqVS8jwveM3Pz2tl\nZUWu6+r09HQk+wJG7Y1JNwC47j744AM1m02Vy2V9+OGHkqRqtdoz63FpaSkIMM/z9PjxY7mue+5E\nk4s6OTnRw4cPlUgk+i6PxWJqt9uanZ0d6X6BUSDUgAnb2NhQoVDQ7u6uPvzwQxlj1Gq1tLa21lXP\n8zwVCgU9ePAgOKpzHEeO44xsAocxRtKLiSWFQuHceucFHjBphBowYfF4XKlUKjgFWa1WJb2YRPKy\nlZUVNZtN5fN55fN5vfPOO5KkRqMRrDOsdrvd9T6ZTEqSLMvqOc0JhAHX1IAp0JkFWS6Xtbu7q1gs\n1hUqnufZLzsPAAABcUlEQVSp2WxqbW1NP/vZz4JAk7qn7g/Ldd2u95ZlKR6PnzvpJJFIaHFx8cL7\nA8aNUAOmQOfZjtvb22o2m+fecH12MkjnlKTUG24vT9O3LEu+76vRaPRd92X5fF7Hx8c9z5vc2trS\nyclJ33vagGnB6UdgCsTjcWUymeAI6eypR8uyguW5XE7pdFqHh4eqVCpaXl6W9GLKv23bWllZkdQd\nch988IFqtZqy2WzweK7OumeD8t69e6pWq6pWq1pcXNTS0pKMMWo2m3IcR7dv3x7nRwFcjg9gKlSr\nVT8Wi/kzMzN9l3ue5+fzeT+RSPixWMxPp9N+rVbzfd/38/m8PzMz429ubvq+7/tra2s92ymXy/7C\nwoIfi8X8ZDLpF4tF3/d9P5FIBOu9rFAo+I7j+LFYzF9cXAzqA9Ms5vuXOCEPAMAU4ZoaACAyCDUA\nQGQQagCAyCDUAACRQagBACKDUAMARAahBgCIDEINABAZhBoAIDL+P0MVIng+hRl9AAAAAElFTkSu\nQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x7f546f2f82d0>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Real STD: ', 0.28883809877618805)\n",
"('STD estimated *sqrt(n-1), n = 100 : ', 0.28733455295932581)\n",
"('STD estimated *sqrt(n-1), n = 50 : ', 0.28646705134779565)"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 13
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Bootstrap methods"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Calculate CIs"
]
},
{
"cell_type": "heading",
"level": 4,
"metadata": {},
"source": [
"Peasants way. Parametric"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Calculate confidence intervals with SEM --> >20 replicates pufff\n",
"Lower Limit = Mean - (t-statistic for x df)(SEM)\n",
"Upper Limit = Mean + (t-statistic for x df)(SEM)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%latex\n",
"$$\\mu = \\left[\\mu + t_{1 - \\alpha/2,n-1},\\mu + t_{\\alpha/2,n-1} \\right]$$\n",
"$$$$\n",
"$$\\sigma = \\left[\\sqrt{\\frac{(n-1)\\cdot \\sigma^2}{\\chi^2_{1 - \\alpha/2,n-1} }} \\sqrt{\\frac{(n-1)\\cdot \\sigma^2}{\\chi^2_{\\alpha/2,n-1} }}\\right]$$\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$\\mu = \\left[\\mu + t_{1 - \\alpha/2,n-1},\\mu + t_{\\alpha/2,n-1} \\right]$$\n",
"$$$$\n",
"$$\\sigma = \\left[\\sqrt{\\frac{(n-1)\\cdot \\sigma^2}{\\chi^2_{1 - \\alpha/2,n-1} }} \\sqrt{\\frac{(n-1)\\cdot \\sigma^2}{\\chi^2_{\\alpha/2,n-1} }}\\right]$$"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Latex at 0x7f60deaf0210>"
]
}
],
"prompt_number": 68
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"x = np.random.randn(20)\n",
"print('CI for mean with SEM = ', np.mean(x) + scipy.stats.t.isf([0.025, 0.975], [19])[::-1] *scipy.stats.sem(x))\n",
"print('CI for std with SEM = ', np.sqrt(np.var(x)*19/scipy.stats.chi2.isf([0.025, 0.975], [19])))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('CI for mean with SEM = ', array([-0.53678197, 0.49794991]))\n",
"('CI for std with SEM = ', array([ 0.81939658, 1.57370483]))\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "heading",
"level": 4,
"metadata": {},
"source": [
"CLT make it easy. Non parametric, taking samples with replacement"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import scikits.bootstrap as bootstrap"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 70
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"CIs = bootstrap.ci(x, statfunction=np.mean,n_samples=100000) \n",
"print('CI for mean with bootstrapping = ', CIs)\n",
"\n",
"CIs = bootstrap.ci(x, statfunction=np.std,n_samples=100000) \n",
"print('CI for std with bootstrapping = ', CIs)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('CI for mean with bootstrapping = ', array([-1.00376369, 0.02051702]))\n",
"('CI for std with bootstrapping = ', array([ 0.86606787, 1.59350777]))"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 71
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Anything you want"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"np.random.seed(105)\n",
"size = 100\n",
"x = [np.random.lognormal(1,1) for _ in range(size)]\n",
"y = (np.random.randn(size)*np.std(x)+np.mean(x))\n",
"print('Mean = %f STD = %f Median = %f' %(np.mean(x), np.std(x), np.median(x)))\n",
"print('Mean = %f STD = %f Median = %f' %(np.mean(y), np.std(y), np.median(y)))\n",
"ax = plt.subplot(1,1,1)\n",
"ax.hist(x,bins=np.linspace(-5,20,10),alpha=0.3,histtype='stepfilled')\n",
"ax.hist(y,bins=np.linspace(-5,20,10),alpha=0.3,histtype='stepfilled')\n",
"ax.set_xlabel('Value',fontsize=20)\n",
"ax.set_ylabel('Freq',fontsize=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Mean = 5.135465 STD = 6.925996 Median = 2.494636\n",
"Mean = 6.227468 STD = 6.899373 Median = 6.389744\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAEsCAYAAAD3iwVMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH0pJREFUeJzt3WFsG+ed5/EfGTsN0lYa0m66TbE9cWTc3fZwrUlKeXG4\nuwUsMtjDAvvCiuS8uzeRyb63Tfpd39l0+uLQN4movOsBhUwqWNy22ItMZRcHHLBbWcMsbrd32FiP\n1NZN0ktMjdTETuLacy98pD0mZZuSPDMSvx9ASPjMDPnn+LF/mmeemYl5nucJAICnLB52AQCAwUDg\nAAACQeAAAAJB4AAAAkHgAAACQeAAAAJxKOwC2hzH0eXLl3XkyBHduHFDhUJBqVTKt3xlZUXJZFLG\nGGUyGU1MTIRYMQCgH5EInHq9rkajoTfffLPTVigUNDs7K0kyxqhcLmtxcbGzfHp6WrZt+0IJABBd\noQ+pua6r06dP+8KmWq3q3Xff7byuVCoqFou+7QqFgkqlUmB1AgB2Jxb2nQZKpZLi8bguXLjga19f\nX9fIyIgkKZlMynGczmvpXlAlk0ndvXs3wGoBADsV+hHO3NycxsfHu9rb4eK6bidcHmRZlqR7wQQA\niL7Qz+G4rqvh4WHNzc0pmUyq1WopmUxqcnJSktRqtSRJQ0NDPbc3xviOfAAA0RRq4BhjJEnNZlNn\nzpzptJfLZbVaLc3MzMh13bDKAwDsoVCH1NphYtu2r/3UqVNMCACAAybUI5x20DwcOOl0Wq7r7ur8\nTCwW23YZT2QAgOCFeoTTPvHf/u/DjDGdMNra2uq5zsNh9SQeFUYAgKcj9Flqtm13zuX0WmZZVs91\njDGyLGvbCQOe5/X8AQCEI/TAKRQKWllZ8bU5jqNEItEJk1wup+Xl5a518vl8UGUCAHYp9As/Nzc3\nlc1mde3atU7byy+/rGKxqJMnT3bWmZqa8t3a5uWXX1a1Wu17SnR7OI2jHQAIVuiBI0lra2uqVCoa\nHR3V6uqqpqendeLECd86zWZT8/PzGh8flzFG2Wy2a50nQeAAQDgiEThBInAAIByhn8MBAAwGAgcA\nEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAIAgcAEAgCBwAQCAIHABAI\nAgcAEAgCBwAQiENhF4BounPnjn71q19F7rlBhw8f1ne+852wywCwAwQOevrss8/01399Tc8888dh\nl/KQX6pQ+OPOg/QA7B8EDrZ16NBX9OKLfxJ2GT7Xr6+GXQKAHeIcDgAgEAQOACAQBA4AIBAEDgAg\nEAQOACAQoQeOMUb5fF5LS0tyXVfGGJXLZS0tLfnWcxxHc3NzWlhY0Ouvv961HAAQbZGYFr20tNQJ\nEMuy9NZbb2liYqKzvB1Ci4uLnbbp6WnZtq1UKhV4vQCA/oV+hBOLxdRoNDpHN61WSydPnvStU6lU\nVCwWfW2FQkGlUinIUgEAuxB64EiS53kaGhrSyMhIz+W1Wk2ZTMbXls1mVa/XA6gOALAXIhE4j+K6\nrlzXVTKZ9LVbliVJWl9fD6EqAEC/InEOxxgj13UlSa1WS8lkUpOTk53XkjQ0NLTtttsdGQEAoiP0\nwGkfubQDRro3IaDd1g4iAMD+FvqQ2vDwsGZmZnxtezEhIBaL9fwBAIQj9MDpJZVKyRijra2tsEsB\nAOyR0APn0qVLXW3tYTZjjGzblqRtw6e9/GGe5/X8AQCEI9TAaV/Q+fBMs/ZEAdu2ZVmWbNuWMaZr\nW8uymDAAAPtEqIFj27ZmZ2e7QqPRaCibzXZmpuVyOS0vL/vWcRxH+Xw+qFIBALsU+pBaMpnU2tpa\n57XruqpWq5qbm+u0VSoV1Wo133bValWVSiWwOgEAuxP6tOjJyUktLCyoXq/rxo0bcl1X9Xrdd9Qz\nPDysSqWicrms8fHxzlAcw2kAsH+EHjiS/xqc7aTTaaXT6QCqAQA8DaEPqQEABgOBAwAIBIEDAAgE\ngQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIED\nAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACMShsAt4mOu6KpfLevPNN33tjuNo\nZWVFyWRSxhhlMhlNTEyEVCUAoF+RC5xSqaSNjQ1fmzFG5XJZi4uLnbbp6WnZtq1UKhV0iQCAHYjU\nkJoxRhsbG4rFYr72SqWiYrHoaysUCiqVSkGWBwDYhUgFztLSkvL5vDzP87XXajVlMhlfWzabVb1e\nD7I8AMAuRCZwlpaWlMvlutpd15Xrukomk752y7IkSevr60GUBwDYpcgEjjFGqVSq6+im1WpJkoaG\nhrbdDgAQfZEInIWFBc3MzPRc5rpuwNUAAJ6G0GepPa1AeXjiAQAgXKEf4dRqNU1OTnZeExQAcDCF\nGjjNZlNjY2O+tofP4di2LUna2trq+R7t5Q/zPK/nDwAgHKEOqV29elWrq6uan5/vtDmO07nQc3x8\nXJOTk7JtW8YYHT9+vLOeMUaWZWlkZCSEygEA/Qo1cHpNFHj99dd19epVXbx4sdOWy+W0vLzsCxzH\ncZTP5wOpEwCwe6Gfw3nYJ5980jX0ValUVKvVfG3ValWVSiXI0gAAuxD6LLW2tbU1VSoVXb58WZub\nmyoWiyoUCkqn0xoeHlalUukMs7WH3BhOA4D9I+YN2Jn09iy4Afvafdva2tJPf9rUiy/+adil+Fy/\n/jMVi3/ObEZgH4rckBoA4GAicAAAgSBwAACBIHAAAIEgcAAAgSBwAACBIHAAAIEgcAAAgSBwAACB\nIHAAAIEgcAAAgSBwAACBIHAAAIHo6/EEx44d6/suvZ7nKRaL6f333+9rOwDAwdJX4KTTaa2trclx\nnE5bKpVSq9XS5uamJMmyLKVSKd923EoeANBX4Jw/f15jY2PKZDKam5tTOp3uLHMcRzMzM1pfX1e9\nXu8KHQDAYOvrHM7FixdlWZaWlpZ8YSNJmUxGKysrunv3rsrl8p4WCQDY//oKnEajoXw+r+Hh4W3X\nyeVyajQauy4MAHCw9BU4nufJGPPIddbW1nZVEADgYOorcHK5nFZWVvT222/3XL6wsCDHcZTNZvek\nOADAwdHXpIFKpaJGo6GpqSm98soryufzsm1bq6urunLliur1emc9AAAe1Ffg2LatpaUllUol1Wo1\n1Wq1ruWzs7NdEwoAAOgrcKR7s9GuXLkiY4wcx5ExRrZty7ZtZTKZHRXRaDTUaDR05MgRra6uKpvN\namZmxreO4zhaWVlRMpmUMUaZTEYTExM7+jwAQPD6Dpy2o0ePamxs7LGz1h6n0WgoFovp4sWLnbax\nsTG5rquzZ89KkowxKpfLWlxc7KwzPT0t27a53gcA9om+76XWbDY1NjYmy7I0OjqqlZUVSfdue/Oj\nH/2o7wJmZ2e72nK5nK+9UqmoWCz61ikUCiqVSn1/HgAgHH0FztramrLZrBzH0cTEhDzP6yy7ceOG\nzp07p/Hx8b4KiMViXdfteJ6nRCLReV2r1bqG67LZbGeSAgAg+voKnPbss5WVla4JAxsbG7p48aJW\nVlZ0/vz5J37Py5cv68KFC762er2uU6dOSZJc15Xrukomk751LMuSJK2vr/fzFQAAIekrcC5fvqxc\nLrftLLRz584pnU7v6sijWq1qbGxMZ86ckSS1Wi1J0tDQUM/1H3chKgAgGvqaNOC6rkZHRx+5jm3b\nWlhY6LuQhYUFXblyRbFYTPPz877PBADsf30/nuDq1auPXKfZbO5oevTk5KQmJye1ubmpsbGxrrtR\n94tHIgBAtPQ1pHbq1CmtrKzob/7mb3r+gz49PS1jjHK53I4LGh4eVqFQ4BobADhg+gqc9jmaiYkJ\nTU9PS7o3keDUqVM6cuSI6vW6bNv2XVOzExMTE3JdV++++65s25YkbW1t9Vy3vfxhnuf1/AEAhKPv\n63BWVlZ08eJF/eIXv5AkXblyRbVaTXfv3tW5c+d07dq1J34vY4wSiYTee++9nstd15VlWbJtu2ty\ngDFGlmVpZGSk368AAAhB34Ej3TvS2djY0N27d3Xt2jW1Wq3OtOh+tCchPHyU0g6X9rmgXC6n5eVl\n3zqO4yifz++kfABACPoKnLm5ua5HE9i23bkmpl+ZTEanTp3qGuqqVCoqlUqdo5dKpdJ13U+1WuWu\n1ACwj8S8Pk5sxONxJRIJ3bhxY0+LmJub0+rqaufmnWNjY3rttdd86zSbTc3Pz2t8fFzGGGWzWZ04\ncaLvz2pPduB8zqNtbW3ppz9t6sUX/zTsUnyuX/+ZisU/ZxYisA/1NS36tdde01tvvaX33ntPx48f\n37MiHr4zdC/pdJrHHgDAPtZX4FSrVR07dkzZbFazs7MaGxuTbdvb3gUAAIC2vgKnfT8zz/N0+vTp\nTvuDwxue5ykWi+nOnTt7VCIA4CDoK3Ce9GJMxtcBAA97ZOCUy2W99NJLOnnypCR1zRQDAOBJPXJa\n9KVLl3w30mybm5vTD37wg6dWFADg4NnRhZ+Li4uqVqt7XQsA4ADbUeBIXMcCAOjPjgOHiQEAgH7s\nOHAAAOgHgQMACASBAwAIxGMv/Gw0Gjp16pSvbWlpSZ7ndbU/qNd0agDA4Hps4GxsbGx7weejLgQl\ncAAAD3pk4Fy9ejWoOgAAB9wjA6f9xE0AAHaLSQMAgEAQOACAQBA4AIBAEDgAgEAQOACAQBA4AIBA\nEDgAgEA89k4DQVhYWJAxRqurqzLGqFAoaHJy0reO4zhaWVlRMpmUMUaZTEYTExMhVQwA6FfogbOw\nsCDbtjsBs7m5qWw2q1arpZmZGUmSMUblclmLi4ud7aanp2XbtlKpVCh1AwD6E/qQmjFG6XS683p4\neFilUkmFQqHTVqlUVCwWfdsVCgWVSqXA6gQA7E6ogeO6rubn57W5uelrbw+Vra+vS7p3k9CHb7OT\nzWZVr9cDqRMAsHuhBo5lWTLGaG1tbdt1XNeV67pKJpNd20r3QwkAEG2hD6m1Wi0dP37c19ZoNJRI\nJDQyMqJWqyVJGhoa6rm9Meap1wgA2L3QA6eX2dlZnT9/XtK9IxwAwP4XucCpVqs6evSozpw5E3Yp\nAIA9FPq06AcZY1StVvfkwW+xWGwPKgIA7JVIHeGUy2W9++67vjbbtiVJW1tbPbdpLwcARFtkAqdY\nLOrSpUtdkwMsy5Jt212TA4wxsixLIyMjPd/P87yePwCAcEQicObm5lQul33hsbS01JkuncvltLy8\n7NvGcRzl8/kgywQA7ELogdO+eLPVaslxHDmOo0ajoVqt1rltTaVSUa1W821XrVZVqVQCrxcAsDOh\nThpwXVfT09M9l42Ojnb+f3h4WJVKReVyWePj4517q203nAYAiJ5QA8eyLN29e/eJ1k2n0757rgEA\n9pfQh9QAAIOBwAEABILAAQAEgsABAASCwAEABILAAQAEgsABAAQiUneLBh7nzp0/6PPPP4/U3cDj\n8bieffbZsMvYFz7//POwS+hy+PBhPfPMM2GXMRAIHOwrzi//pw79t48iFTiHvEOa+k9T2z6VFvf8\n9re/1V/9j79S7Jno/Nl5nqeRoyP6s4k/C7uUgUDgYF/5/M4tfet731I8Hp3R4A/+6QPduXMn7DIi\n7+7du4oNxfTisRfDLqXj5qc3dfPjm2GXMTCi87cWAHCgETgAgEAQOACAQBA4AIBAEDgAgEAwSw09\n3b59W6u//idtfBqt30lu3/2Dfvm/VyM1LXrD3NAX/+6LsMvw+fDDD3XtV9fCLsPn5s2b8jwv7DIQ\nIgIHPd26dUvXt97Xl998PuxSfI78q+/pdx9Fq6bf/fo3unXrVthl+Hz4uw/V/F1TQ4kIXRt0SDry\n7SNhV4EQETjYVjwe19cT0foH4uuKVj2S9Ek8mlepP/+153Xkm9HbXxhc0RovAQAcWAQOACAQBA4A\nIBAEDgAgEJGZNFCv15VIJDQxMdG1zHEcraysKJlMyhijTCbTcz0AQHRFInAajYZOnz6ter3etcwY\no3K5rMXFxU7b9PS0bNtWKpUKskwAwC6EOqS2tramYrGotbU1JZPJnutUKhUVi0VfW6FQUKlUCqJE\nAMAeCTVwUqmU3nzzTc3MzGy7Tq1WUyaT8bVls9meR0MAgOiKxJDadlzXleu6XUc/lmVJktbX1zUy\nMhJCZYDf9evXdfv27bDL6HBdN+wSgC6RDpxWqyVJ2z661xhD4CB0h498RcsfL+v5z6J1y52jf3Q0\n7BIAn0gHDr+lYT94fujr+ta/+Ja+9rWvhV0KEGlchwMACESkj3B2I0q3rwcARPwIx7ZtSdLW1tYj\nlwMAoi/SgWNZlmzbljHG126MkWVZj5ww4Hlezx8AQDgiHTiSlMvltLy87GtzHEf5fD6kigAAOxGp\nwOl1BFKpVFSr1Xxt1WpVlUolqLIAAHsg1EkDm5ubunDhgowxMsaoUCgol8spn89rcnJSkjQ8PKxK\npaJyuazx8fHOvdW4/gYA9pdQA2d4eFgXL1587HrpdFrpdDqAigAAT8uBnRa9n9y+fVsff/xx2GX4\nRK0eAPsfgRMBH330kf7yL/9Zzz5rhV1Kx61bnyoeT4RdBoADhMCJiGefPaoXX/x+2GV03Ly5pa+3\n/k/YZQA4QCI1Sw0AcHBxhBMBn376qdZ+/b+0dfNW2KV03LlzW3d1N+wygKfu95/+Xn+3/Hdhl+Hz\n3Fee0/HvHQ+7jD1H4ETA1taWzGf/oJvf+DLsUu47JH31W8NhVwE8Vc89/5xuvXBLv/zsl2GX4vPF\n+1/o+//2+wfunpAETkQc/spzGj7yjbDLAAZKPB7XkW8eCbuMLtc/uB52CU8F53AAAIHgCAfYpT/c\niekXy/8cqeGPeEz63vdGlEgwtR3RQeAAu3T0yL/UXS9aEyxc9zf68naEzgkCInCAXYvHn1Fcz4Rd\nhk88xmg5oofAAQ6o21/e1s2bN8MuI/IOHz6sw4cPh13GQCBwgAPo0KHn9Y//+H8luWGXEml3vTt6\n4YVDGsv+m7BLGQgEDnAADQ29IOmFsMuIvC++uKkvvzSPXxF7goFeAEAgCBwAQCAIHABAIAgcAEAg\nCBwAQCAGdpbaO3/7TtgldFy/fl3iUQAA/r/bd27rnb99J1K3SzoUP6SJ/zixu/fYo1r2nU+e+yTs\nEjo+TXyqr30jGXYZACLihT95QTf+cCPsMnw2f7OpCRE4OzKUGAq7hI4v7nyhQ4c/DbsMABHx1a9/\nNewSunz6we7/jRrYwAGANs/zwi6hS5SG0/bKvgkcx3G0srKiZDIpY4wymYwmJnZ3eAdgsMWfeUaf\nfPK5/vs7V8MuxeerX43rP/z7zIELnX0ROMYYlctlLS4udtqmp6dl27ZSqVSIlQHYzw4f+or+6Jtj\nYZfR5ZMby2GX8FTsi2nRlUpFxWLR11YoFFQqlUKqCADQr31xhFOr1XT+/HlfWzabVb1eD6kiAHi6\nXNeN1JDa73//+12/R+QDx3Vdua6rZNI/bdiyLEnS+vq6RkZGQqgMAJ6Wo/r7v/847CJ83LVfS/95\nd+8R+cBptVqSpKGh3tOYjTEEDoAD5eiR6J2b3lz7aNfvEflzOK7LA6QA4CCI/BHOTj1u7PMv/vVf\nBFQJABwM//W/vL6r7SN/hAMAiIbdTmKI/BGObduSpK2trZ7ncdrLH7bdlcPtHRbFK4uDxr64j31x\nH/viPvbFfXsxYy7yRziWZcm2bRnjf+64MUaWZTFhAAD2icgHjiTlcjktL/uvvHUcR/l8PqSKAAD9\ninn74Fhxc3NTU1NTvlvbvPzyy6pWq30f4XCIfB/74j72xX3si/vYF/ftxb7YF4EjSc1mU/Pz8xof\nH5cxRtlsVidOnOj7fehA97Ev7mNf3Me+uI99cd9ABc5eoQPdx764j31xH/viPvbFfQQOAGDf2BeT\nBgAA+x+BAwAIBIEDAAgEgQMACASBAwAIxDM//OEPfxh2EQiW4zj62c9+pvX1df385z/X559/vu09\n6Q4yY4ymp6f17W9/W8lkUh988IEqlYpisdjA7I96va4PP/yw5/cdtH6y3b4YtH6ysLCgn//85/rJ\nT36iH//4x3r++ef13e9+17fOjvuGN+BWV1e9XC7nNRoNb2Njw1tdXfVKpZLXaDTCLu2pWF1d9fL5\nvK9tamrKM8aEVFF4VldXvVgs1vlJJBLewsJC2GUF5sqVK14ikfCWlpa6lg1aP3ncvhiUflKv1z3H\ncTqvXdf1RkdHvWq12mnbTd9gSE3S0tKS8vm8ksmkxsbG9NJLL2liYiLssp6KSqWiYrHoaysUCiqV\nSiFVFJ5YLKZGoyHXdWWMUavV0smTJ8Mu66lbW1tTsVjU2tpa16Pb2walnzzJvhikfmKMUTqd7rwe\nHh5WqVRSoVDotO2qb+xdNu5PxhhvaWnJ29zc9NbW1sIu56lLJBJd33NjY8OLxWLhFBQiY8yBPZJ9\nUqOjoz1/qx/EfrLdvhiUfrKxseFls1nPdV1fe/sIr90fdtM3OMLRvVs1DA0NHfhHHbiuK9d1u36T\nsyxLkrS+vh5CVYga+slgsixLxhitra1tu85u+0bkH8CGvdNqtSSp54PspHuH0wc9dB9mjJHrupLu\n7Z9kMqnJycmQqwoX/aTboPST9p/9gxqNhhKJhEZGRjrPJdtp3yBwNDidqf0dcU/7t7QH/6ynp6e7\n2gYN/cRv0PvJ7Oyszp8/L2n3fWPgA2fQO9MgGx4e1szMjK+tUCioUCjwZ4+OQe4n1WpVR48e1Zkz\nZ/bk/Qb+HM52nemgzcbBk0mlUjLGaGtrK+xSEGGD0E+MMapWq3rnnXf27D0PTOAYY574Z3Nz85Hv\ndVA7U/vCrO2+10G8iO1RLl261NXWPuJtj1UPIvqJ36D2k3K5rHfffdfXttu+cSCG1NbW1lQul594\n/fHxcZ09e1bSvc507tw53/IHO9Px48f3rtCQWZYl27a7vpcxRpZlDdSJYGOMyuWypqenfd+7fdJ0\n0P5RfRD95L5B7SfFYlGXLl3qmhyw275xIAInlUrp8uXLfW83iJ0pl8tpeXnZ11kcx1E+nw+xquDZ\ntq3Z2dmuvyCNRkPZbHbbWTiDgn5yzyD2k7m5OZXLZd93Xlpakm3bSqVSu+obB2ZIbScGsTNVKhXV\najVfW7VaVaVSCami8CSTSd81B67rqlqtam5uLsSqguf1eOjvoPaTXvtikPpJvV6XdO+Xbsdx5DiO\nGo2GarWaUqmUpN31jYF/xPTCwoIymUxnZ7quq1wup7feeutADac9qNlsan5+XuPj4zLGKJvN6sSJ\nE2GXFYqFhQUZY3Tjxg25rtv1m91BtLm5qQsXLsgYo3q9Ltu2lcvllM/nfbOuBqGfPOm+GIR+0uuC\nzrbR0VG9//77ndc77RsDHzjSYHQmAAgbgQMACMRAn8MBAASHwAEABILAAQAEgsABAASCwAEABILA\nAQAEgsABAASCwAH64DiO4vG4xsbGHrleo9FQPB7vPFvpSU1NTSke568lDiZ6NtCHTCYjy7LUbDYf\n+ZiL9r2mXn311b4/IxaL7bg+IMoIHKBPp0+flud5j7xD+eXLlxWLxXTy5MkAKwOijcAB+nTq1ClJ\n95713ovjONrc3NQrr7wSZFlA5BE4QJ/S6bRs2952WG1+fl7S/WCS7j17aWpqSqOjo4rH40omk5qe\nnvbd9r7twdsb5vP5nud0XNdVPB5XsVjsWnbp0iVls9nO5xSLxZ6fAwSNwAF2oFAobDusVq1WfcNp\nxhgdO3ZMb7/9to4dO6ZCoaCxsTHV63Vls9nHPvL8Ued0Hl6WzWZVLpcVj8c7n1OtVjU6Oqpms7mD\nbwrsHQIH2IH2cNnDw2q9htMqlYpisZiuXLmid955R2+88YYWFxdVqVTkuq4ajcae1HTp0iU1m00t\nLS1peXm58zkrKyuSpJmZmT35HGCnCBxgB1KplNLpdNewWq/htGKxqFqt1vWAqnQ6LUna2NjYk5ou\nXLigfD6vTCYj13U7P6lUShMTE3IcR1tbW3vyWcBOHAq7AGC/evXVV9VsNlWtVnX27FlJ9x7R+/Ds\ntHQ63QkX13V19epVOY6z7aSDndrc3NSVK1eUSCR6Lo/FYmq1Wgfy0enYHwgcYIdOnz6tUqmk+fl5\nnT17VsYYra2taWpqyree67oqlUq6fPly52gom80qm83u2cl8Y4yke5MMSqXStuttF0ZAEAgcYIeG\nh4eVyWQ6w2r1el3SvQkFD5qYmFCz2VShUFChUNDx48clSUtLS51t+tVqtXyv28+ityzriZ4tD4SB\nczjALrRnq1WrVc3PzysWi/n+wXddV81mU1NTU3rjjTc6YSP5pz/3y3Ec32vLsjQ8PLztBIREIqFj\nx47t+POAvUDgALvQvlfa7Oysms3mthd7PjwxoD3MJnUHz4NTnS3Lkud5Wlpa6rntgwqFgjY2Nrru\n33bp0iVtbm72vGYHCBJDasAuDA8PK5fLdY4sHh5Osyyrs3x6elpjY2NaXV1VrVbT+Pi4pHvTpm3b\n1sTEhCR/AL366qtaWFhQPp/v3FKnve3DIXbx4kXV63XV63UdO3ZM6XRaxhg1m01ls1mdOXPmae4K\n4PE8ALtSr9e9WCzmxePxnstd1/UKhYKXSCS8WCzmjY2NeQsLC57neV6hUPDi8bhXLBY9z/O8qamp\nrvepVqve6OioF4vFvGQy6ZXLZc/zPC+RSHS2e1CpVPKy2awXi8W8Y8eOddYHwhbzvF0MJAMA8IQ4\nhwMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAgEgQMACASBAwAIBIEDAAjE/wMyYvNEF9d8ygAA\nAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60dea6aa90>"
]
}
],
"prompt_number": 72
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"y2 = [np.median(np.random.choice(y, size=size, replace=True)) for _ in range(100000)]\n",
"y2 = np.asarray(y2)\n",
"ax = plt.subplot(1,1,1)\n",
"ax.hist(y2,bins=np.linspace(2,11,10),alpha=0.3,histtype='stepfilled')\n",
"ax.vlines(np.median(x),0,25000,linewidth=3)\n",
"ax.set_xlabel('Value',fontsize=20)\n",
"ax.set_ylabel('Freq',fontsize=20)\n",
"customaxis(ax, c_left='k', c_bottom='k', c_right='none', c_top='none', lw=2, size=20, pad=8)\n",
"print('Bootstrap: ',float(len(y2[y2<=np.median(x)]))/100000)\n",
"print('Median test: ',median_test(x,y))\n",
"print('Mann: ',scipy.stats.mannwhitneyu(x,y)[1]*2)\n",
"print('T_test: NOT NORMAL!',scipy.stats.ttest_ind(x,y)[1])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Bootstrap: ', 0.0)\n",
"('Median test: ', 0.16201071261586195)\n",
"('Mann: ', 0.0089697635496793649)\n",
"('T_test: NOT NORMAL!', 0.2677343915603817)\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAbcAAAEsCAYAAABANv1rAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3c9vI2d+JvCnNE5mPD/EYrUnseFglyzqsJnLtljUHBZB\nshBJI4ccgtaI7T/AUnFuObSb7JtzalHJJbnYLPkQYJADRXIu4xkgUrHnkhlgI7FoIHMI4NFL7cbu\nARI3VdQMDMeJu/YgVI1KpLrFbopvsfr5AISbL78kv6YkPqy33ioqnud5ICIiipEF2Q0QERFNG8ON\niIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2XpLdAADYtg3btnHjxg0cHR3BMAxsbGwEtwshYJom\nqtUqDMPAYDCAZVkoFovI5/NBneM46Ha70DQNQghks9nQ7dOsISKiCPMk29/f92zbDo0ZhuFtb28H\n14+OjjxFUYJLMpn02u126D5HR0desVgMja2vr3tCiKnXEBFRtEmflqzX6yNjhUIhNK4oCmzbhuu6\nEEJgMBjg1q1bofvUajWUy+XQmGmaqFQqU68hIqJokx5ufnCd53keksnkyNji4iJSqdTYx2k2m8hm\ns6ExwzDQarWmXkNERNEmfZ/b7u7uyFir1cL3v//9Kz+G67pwXReapoXGVVUFABwfH0NV1anUXBau\nREQUHdLD7SLLspDL5XDnzp3QuBACrusCAAaDATRNw9raWnAdABYXF8c+phAiCKVp1RARUXRFJtza\n7Tb29/ehKAoajUboNn9Lyg8zACiVSsGYH3pPMq0aIiKKPun73Hxra2t47733sLW1hVwuh16vF9yW\nSCRChwYAXORBRESXi0y4+RKJBEzTfOpxZel0GkIInJ6ezqizyymKcumFiIhmL3LhBgD5fB6u6+LB\ngwcAgO3t7ZEaf6pSCAFd1wHg0qDTdX1qNZNiwBERzZ7UcBNCIJlM4sMPPxx7u39cW7VaxfHxceg2\nfxGJrutQVRW6rkMIMfL4qqoilUpNrWYcz/PGXoiISA6p4ea6LjKZzMgWkR8u2WwWuq6jXq+PBItt\n2zAMI1jZWCgUcHBwEKpxHAfFYjG4Pq0aIiKKOHknRzmzvb3tua4bGisUCl61Wg2ut1qt0OmvTk5O\nPMMwvF6vF4y5rjty2qxisej1+/2p11wVAC8CLzER0QtH8Tz582c7Ozs4OjoKTpycy+Xw1ltvhWra\n7TaEEHj06BFc10W1Wh3Zmuv1emg0GlhZWYEQAoZhYHV19VpqrsLf3xaBl5iI6IUSiXCLK4YbEZEc\nkVwtSURE9DwYbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2InM97kR0dP95je/wb/8\ni0DUDp1MJr+FpaW07DaIAgw3ojniui7+8R9Psbj432S3Evjii8/x7W//X4YbRQrDjWjOfO1r38C3\nvx2dcPvss18DeCi7DaIQ7nMjIqLYYbgREVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcUOw42IiGIn\nEse52bYN27Zx48YNHB0dwTAMbGxshGocx0G324WmaRBCIJvNIp/PS6shIqLokh5utm1DURRsbW0F\nY7lcDq7r4u233wYACCFQrVaxt7cX1JRKJei6jnQ6PfMaIiKKNunTkvV6fWSsUCiExmu1GsrlcqjG\nNE1UKhUpNUREFG3Sw01RFNi2HRrzPA/JZDK43mw2kc1mQzWGYaDVakmpISKiaJM+Lbm7uzsy1mq1\n8P3vfx/A2YliXdeFpmmhGlVVAQDHx8dQVXVmNalU6hn/T4mIaFakb7ldZFkWcrkc7ty5AwAYDAYA\ngMXFxbH1QoiZ1hARUfRJ33Lztdtt7O/vQ1EUNBqNYNx13afed5Y1REQUfZEJt7W1NaytrWE4HCKX\ny2FnZwfLy8uy2yIiojkUuWnJRCIB0zTn6rgyRVHGXoiISI7IhRsA5PN5uK6LBw8eQNd1AMDp6enY\nWl3XZ1pDRETRJzXchBBIJpP48MMPx97uui5UVYWu6yOLOYQQUFUVqVRqpjXjeJ439kJERHJIDTfX\ndZHJZEa2iPxw8Y83KxQKODg4CNU4joNisRhcn2UNERFFm9Rwy2azuH379shWTq1WQ6VSCbaUarUa\nms1mqMayLNRqtdB9ZlVDRETRpngRmD/b2dnB0dFRcOLkXC6Ht956K1TT6/XQaDSwsrICIQQMw8Dq\n6qq0mqvwF5VE4CWmmPj444/xwQf/jtdfj85K4s8++zVeeqmLtbX/LbsVokAkwi2uGG40bQw3oquJ\n5GpJIiKi58FwIyKi2GG4ERFR7ETm9FtENJ8URcGnn36GDz74mexWQr75zZfwJ3/yXZ4t6AXFcCOi\n5/Lyy9/El1/+L/z619FaOPXxxz/HH/+xx3B7QTHciOi5ffObquwWRgyHDLUXGfe5ERFR7DDciIgo\ndhhuREQUOww3IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5ERBQ7kTi3\nZLvdhhACR0dHEELANE2sra0Ft/tj1WoVhmFgMBjAsiwUi0Xk8/mgznEcdLtdaJoGIQSy2Wzo9mnW\nEBFRdEkPt3a7DV3XgzAbDodBgG1sbAR1nU4HnU4HAKCqKt5///1Q4AghUK1Wsbe3F4yVSiXouo50\nOj3VGiIiijbp05JCCCwvLwfXE4kEKpUKTNMMxhRFgW3bcF0XQggMBgPcunUr9Di1Wg3lcjk0Zpom\nKpXK1GuIiCjapIab67poNBoYDoehcX+L7Pj4OBjzPA+Li4tIpVJjH6vZbCKbzYbGDMNAq9Waeg0R\nEUWb1HBTVRVCCPT7/ed6HNd14bouNE0beXzgLCSnVUNERNEnfZ/bYDAYGbNtG8lkMrSVJoSA67rB\nfTRNC/bT+Y+xuLg49jmEEMFjTauGiIiiS3q4jVOv13Hv3r3gur8ldX4FZalUCsb80HuSadUQEVH0\nSV9QcpFlWXjllVdw586dYCyRSIRWTgLRWuShKMrYCxERyRGpLTchBCzLwuHh4VNr0+k0hBA4PT2d\nQWfyvfPOO2P/TUREoyIVbtVqFQ8ePBgZ397ext27d0Nj/lSlEAK6rgMATk9Px+4v03U9WBTyvDXj\neJ43dnyaW29/+Zd/Gfyb4UZE9GSRmZYsl8vY3t4eCRX/oOqLKxX9RSR+KOm6DiHEyH1VVUUqlZpa\nDRERRV8kwm1nZwfVajUUHp1OB/1+H7quo16vjwSLbdswDCMIw0KhgIODg1CN4zgoFovB9WnVEBFR\ntEkPN//g6MFgAMdx4DgObNtGs9kMTnelaVroWDjXdWFZFnZ2doKxWq2GZrMZemzLslCr1aZeQ0RE\n0aZ4l+0wmoFxB0z7MpkMPvroo+C6f3LlR48ewXXdkS09AOj1emg0GlhZWYEQAoZhYHV19VpqrsLf\n5zaNl/j8/juJPzKS7OOPP8YHH/w7Xn99+enFL7hPPvkJNjf/FAsL0j/DkwRSwy3uGG40bQy3q2O4\nvdj4UyciothhuBERUeww3IiIKHYYbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2GG4\nERFR7DDciIgodhhuREQUOww3IiKKHYYbERHFzkuyGyCKqn/914/xz//8/2S3EfLFF/8BICm7DaLI\nY7gRXeLTT130+wkkk6/JbiXk937vG7JbIIo8hhvRE/zu734d3/rW+G+LJ6LoikS4tdttCCFwdHQE\nIQRM08Ta2lqoxnEcdLtdaJoGIQSy2Szy+by0GiIiii7p4dZut6HrehBmw+EQhmFgMBhgY2MDACCE\nQLVaxd7eXnC/UqkEXdeRTqdnXkNERNEmfbWkEALLy8vB9UQigUqlAtM0g7FarYZyuRy6n2maqFQq\nUmqIiCjaFM/zPFlP7rouCoUCOp0OEolEMC6EwNLSEoQQSKVS0DQNjuMglUqF7qtpGh4/fgwAM625\nKkVRAADTeIn9x5rW49HT9Xq/wOHhN/Dqq9xin0effPITbG7+KRYWpH+GJwmk/tRVVYUQAv1+/9Ia\n13WDcLl4XwA4Pj6eaQ0REUWf9I80g8EAN2/eDI3Zto1kMolUKoXBYAAAWFxcHHt/IcRMa4iIKPqk\nh9s49Xod9+7dA3C25fY0s6whIqLom2i15NLSUmjfz1V4ngdFUfDRRx9dqd6yLLzyyiu4c+fORM8j\n06SvCRERXa+Jwm15eRn9fh+O4wRj6XQag8EAw+EQwNn+qYtL5q/65i+EgGVZODw8nKQtIiKikInC\n7d69e8jlcshms9jZ2Qkt4XccBxsbGzg+Pkar1XqmY8Kq1SoePHgQGtN1HQBweno6dl+YruvBgo9Z\n1Ixz2epFbtEREckx0T63ra0tqKqKTqcTCjYAyGaz6Ha7ePz4MarV6sSNlMtlbG9vj4SKqqrQdX1k\nMYcQAqqqIpVKzbSGiIiib6Jws20bxWIxdEzaRYVCAbZtT9TEzs4OqtVqKDw6nU5wiEChUMDBwUHo\nPo7joFgshp53VjVERBRtE4Wb53lPXQ7/pGPWxmm1WgDODglwHAeO48C2bTSbzWBqs1arodlshu5n\nWRZqtVpwfZY1REQUbROdoWR9fR3tdhutVgu3bt0aub3dbmN9fR2FQiF0bsbLjDtg2pfJZEIrLHu9\nHhqNBlZWViCEgGEYWF1dDd1nljVXwTOUzDeeoWS+8QwlL7aJws1/oz89PcX3vvc9FItF6LqOo6Mj\n7O/vB1th3W53ZJ/ci4jhNt8YbvON4fZim2i1pK7r6HQ6qFQqaDabI9N3uq6jXq8z2IiISKqJv/Im\nm81if38fQgg4jgMhBHRdh67ryGaz19EjERHRRJ75+9xeeeUV5HK5p66eJCIimrWJJ6N7vR5yuRxU\nVUUmk0G32wVwdmquv/7rv556g0RERJOaKNz6/T4Mw4DjOMjn86GFDY8ePcLdu3exsrIy9SaJiIgm\nMVG4+cd6dbvdkcUkJycn2NraQrfbDc7oT0REJMNE4ba7u4tCoXDpasi7d+9ieXk5OCSAiIhIhonC\nzXVdZDKZJ9b4x70RERHJMlG4LS8vP/XraHq9Hg8JICIiqSYKt9u3b6Pb7eKnP/3p2K9zKZVKEEKg\nUChMrUEiIqJJTXT6LQAwDAO9Xg/FYhH7+/soFotQVRW2bePk5AS6ruOXv/zldfU7V3j6rfnG02/N\nN55+68U28U+92+1ia2sL//RP/wQA2N/fR7PZxOPHj3H37l0GGxERSfdMZyi5e/cu7t69C+DsZMqa\npgXfYk1ERCTbRFtuOzs7+OEPfxga03WdwUZERJEy0ZabaZpIJpNjv8uNiIgoKibacnvrrbdwcnKC\nDz/88Lr6ISIiem4TbblZloWlpSUYhoF6vY5cLgdd17G4uHhd/REREU1sonDTNA3A2VL0zc3NYPzi\nMnVFUfDll19O1Eir1UIymUQ+nw+NCyFgmiaq1SoMw8BgMIBlWSgWi6Fax3HQ7XahaRqEEMhmsyOP\nNa0aIiKKtonC7apv8uMO8H4S27axubl56TkpO50OOp0OAEBVVbz//vuhXoQQqFar2NvbC8ZKpRJ0\nXUc6nZ5qDRERRd8Tw61areK73/1usIDk4jcBPK9+v49arQbDMIKtwosURYFt28jlchgMBkilUiM1\ntVoN5XI5NGaaJiqVCnZ3d6daQ0RE0ffEM5QsLCxgfX0djUYjNL6zswPHcfDuu+9OrZGlpSVYloXV\n1dXQeL/fhxDiiVuNmqbBcZxQ8LmuC03T8Pjx46nWTIJnKJlvPEPJfOMZSl5sz/RT39vbg2VZ0+7l\nmbiuGwTQef6xd8fHx1OrISKi+fBMZygBZrv1IISA67oAgMFgAE3TsLa2FlwHcOmKTSFEsCU2rRoi\nIoq2Zw63SReNPCt/S8oPM+BskYc/5ofek0yrhoiI5kPkJ6MTiQQ2NjZCY/4ij6hQFGXshYiI5Ih8\nuI2TTqchhMDp6ansVoiIKIIiH27b29sjY/5UpRACuq4DwKVBp+v61Gou43ne2AsREcnx1H1utm3j\n9u3bobFOpwPP80bGz7t4+MCz8A+qLpVKocUc/iIS/9Rfuq5DCIGbN2+G7quqanC/adUQEVH0PTXc\nTk5OLj14+0kHdU8j3HRdR71eHwkW27ZhGEawsrFQKODg4CAUSo7joFgsBtenVUNERNH3xHA7PDyc\nVR8Axh9eoGka+v1+cPor13VhWRbef//9oKZWq2F9fT208MSyrNCxeNOqISKi6HviGUqu23A4xP37\n9yGEQKvVgq7rKBQKKBaLoaX/7XYbQgg8evQIruuiWq2ObM31ej00Gg2srKxACAHDMEbOdjKtmqvi\nGUrmG89QMt94hpIXm9RwizuG23xjuM03htuLjT91IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLY\nYbgREVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcUOw42IiGKH4UZERLHDcCMiothhuBERUeww3IiI\nKHYYbkREFDsMNyIiip2XZDfga7VaSCaTyOfzI7c5joNutwtN0yCEQDabHambZQ0REUVbJMLNtm1s\nbm6i1WqN3CaEQLVaxd7eXjBWKpWg6zrS6fTMa4iIKPqkTkv2+32Uy2X0+31omja2plaroVwuh8ZM\n00SlUpFSQ0RE0ad4nufJbgIAlpaWYFkWVldXQ+OapsFxHKRSqWDMdV1omobHjx/PvGYSiqIAAKbx\nEvuPNa3Ho6fr9X6Bw8Nv4NVXudU+jz755CfY3PxTLCxwacGLKNI/ddd1g3A5T1VVAMDx8fFMa4iI\naD5EOtwGgwEAYHFxceztQoiZ1hAR0XyIdLi5rhupGiIimg+RWC05787vDyMiIvkiveVGRET0LCK9\n5abrOgDg9PR07L4wXdeDBR+zqLnMZasXuUVHRCRHpLfcVFWFrusjizmEEFBVFalUaqY1REQ0HyId\nbgBQKBRwcHAQGnMcB8ViUUoNERFFX6TCbdz0Xq1WQ7PZDI1ZloVarSalhoiIok/qGUqGwyHu378P\nIQRarRZ0XUehUECxWMTa2lpQ1+v10Gg0sLKyAiEEDMMYOZPJLGuuimcomW88Q8l84xlKXmyROf1W\nHDHc5hvDbb4x3F5s/KkTEVHsRPpQACKi5/HZZ5/hK1/5iuw2Ql5++WXZLbwQGG5EFEv/+Z+L+Pu/\n/z+y2wj5ylc+x/r6HyGRSMhuJfYYbkQUS6nUH8luYcTDhz/Dl19+KbuNFwL3uRERUeww3IiIKHYY\nbkREFDsMNyIiih2GGxERxQ7DjYiIYofhRkREscNwIyKi2GG4ERFR7DDciIgodhhuREQUOww3IiKK\nHYYbERHFzlx8K4AQAqZpolqtwjAMDAYDWJaFYrGIfD4f1DmOg263C03TIIRANpsN3T7NGiIiiq65\nCDcA6HQ66HQ6AABVVfH++++HAkcIgWq1ir29vWCsVCpB13Wk0+mp1tD0ffzxJzg5GcpuI+TTTwcA\nviG7DSJ6BnMRboqiwLZt5HI5DAYDpFKpkZparYZyuRwaM00TlUoFu7u7U62h6fvww2P0+4v46le/\nLruVc16Hpr0quwkiegaK53me7Caept/vQwjxxKlBTdPgOE4o+FzXhaZpePz48VRrrkpRFADANF5i\n/7Gm9XhR88EHP8Pp6R/iW9/SZLdCdG0ePvwZ1tf/EJrG3/PrFosFJa7rBgF0nqqqAIDj4+Op1RAR\nUfTNxbQkcLYvzHVdAMBgMICmaVhbWwuuA8Di4uKl9/W3xKZVQ0RE0TUX4eZvSflhBpwt8vDH/NB7\nkmnVEBFR9M3FtGQikcDGxkZozF/kEQWKooy9EBGRHHMRbuOk02kIIXB6eiq7FSIiipi5CLft7e2R\nMX+qUggBXdcB4NKg03V9ajXjeJ439kJERHJEPtz8g6ovrlT0F5Houg5VVaHrOoQQI/dVVRWpVGpq\nNUREFH2RDzdd11Gv10eCxbZtGIYRrGwsFAo4ODgI1TiOg2KxGFyfVg0REUVb5MMNOJuC7Pf7wXXX\ndWFZFnZ2doKxWq2GZrMZup9lWajValOvISKiaJuLM5QAQLvdhhACjx49guu6qFarI1tzvV4PjUYD\nKysrEELAMAysrq5eS81V8AwlV8czlNCLgGcomZ25Cbd5xHC7OoYbvQgYbrMzF9OSREREk2C4ERFR\n7DDciIgodhhuREQUOww3IiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5E\nRBQ7L8lugIjoRfLw4UMMh0PZbYS8+uqrePnll2W3MVUMNyKiGfnqV/87fvazIYDPZLcS+OyzR/jz\nPwfS6bTsVqaK4UZENCM3bvwBgD+Q3UbIw4e/kN3CteA+NyIiih2GGxERxQ6nJcdwHAfdbheapkEI\ngWw2i3w+L7stIiK6IobbBUIIVKtV7O3tBWOlUgm6rsduhysRUVwx3C6o1Wool8uhMdM0UalUsLu7\nK6mr6fq3f/s3fPHFF7LbCPnii/+Q3QIRxYjieZ4nu4ko0TQNjuMglUoFY67rQtM0PH78eKLHUhQF\nADCNl9h/rGk83t/93U/w+eevhR5TtsePFfz+7/8P/M7vfFV2K0QvlIcPf4E33vhG7GamuOV2juu6\nQZCdp6oqAOD4+DgUevPqv/4LeO21/4mFBa4nIqJ44rvbOYPBAACwuLg49nYhxCzbISKiZ8RwO8d1\nXdktEBHRFHBacgqetu9q2vu2orSvjIjoOjzv2gJuuRERUeQ874d4brmdo+s6AOD09HTsfjf/9osu\n+4QxzdWS0xTFvtjT1bCnq4tiX+zpaqYxO8Utt3NUVYWu6yMLR4QQUFU1FisliYheBAy3CwqFAg4O\nDkJjjuOgWCxK6oiIiCbFg7gvGA6HWF9fD51+64033oBlWRNvuUVxcx+IZl/s6WrY09VFsS/2dDXT\n6InhNkav10Oj0cDKygqEEDAMA6urqxM/ThR/aYBo9sWeroY9XV0U+2JPV8Nwi7go/tIA0eyLPV0N\ne7q6KPbFnq6G4UZERDQGF5QQEVHsMNyIiCh2GG5ERBQ7DDciIoodhhsREcXOV9555513ZDcRR+12\nGz/+8Y/xgx/8AH/7t3+Lr3/96/jOd74jtSfbtmFZFnq9Hn7wgx/gV7/6FQzDkNrTea7r4i/+4i/w\nZ3/2Z9J6EEKgVCrh9ddfh6ZpePjwIWq1GhRFufTcorPkOA7+5m/+Br1eDz/60Y+QyWSQTCal9FKp\nVLCwsABN0/C1r31NSg/j2LaNdruNn//85/jRj36Efr8v/ff84s/txo0beO2112beR6vVwq9+9aux\nv8uO4+CDDz7A8fExfvzjH+Pzzz+fye/8k3qapGaER1PXarU8x3GC667replMxrMsS1pP+/v7nm3b\noTHDMLzt7W1JHY3a3Nz01tfXpfZwdHTkKYoSXJLJpNdut6X25Gs2m55pmqGxzc1NSd14XqFQCL1W\n5y9LS0tSeup2u16r1QqNtVot6X97xWIxNGYYhieEmHkfyWTS63Q6I7cdHR2N9Li+vn7tPT6pp0lq\nxuG05DUQQmB5eTm4nkgkUKlUYJqmtJ7q9frIWKFQGDsugxACJycn0r+rTlEU2LYN13UhhMBgMMCt\nW7ek9gScbdVubm7ivffeC8Ysy8KDBw+k9ZTJZOA4DoQQoUu9Xkez2ZTSk2VZWFtbC42tra1hf39f\nSj8AYJomyuVyaOzevXsz+9vr9/sol8vo9/vQNG1sTa1WG+nRNE1UKhVpPV2l5kkYblPmui4ajQaG\nw2FoPJ/PAwCOj48ldPXbN+3zPM+TNqV1UafTQbFYjMRZEjzPw+LiYqS+BeL+/fsjH442Nzelvmkb\nhoGbN28ilUqFLgBw8+ZNKT0dHh6i3++PjLuuK6Gbs+ft9/vIZrOh8eXlZWxvb8+kh3Q6jffeew8b\nGxuX1jSbzZEeDcNAq9WS1tNVap6E4TZlqqpCCDH2D0ym3d1d3L9/PzTWarVw+/ZtSR39VqfTQaFQ\nkN1GpO3s7GBlZWVkXGYAj3vT2dnZeeY3o2koFAooFouhvz/btlEqlaT043991sUtD//66enpzHu6\nyHVduK470qOqqgDkfSB/Xvyy0mswGAxGxmzbRjKZjMzWgGVZyOVyuHPnjuxWIIRAPp+PxFYbcNaP\n/0l/MBhA07SRqa5Zc10XiUQCOzs70DQtMn2d1+l0kMvlpPawtbUF27aRyWRQr9eRTqcxHA7x1ltv\nSenHXwAxGAxCX4Dsv0dcHJfB7+WyPoQQkXnfmgTDbUbq9Tru3bsnuw20223s7+9DURQ0Gg3Z7aDd\nbkv9pH+R/+n1fGj4n/plBYn/6b/X64U+jFSrVQwGg8i8fo7j4O2335bdBg4PD/HGG2/ANE1ks1l0\nOh1pvaiqikKhgG63GwoI/2caheCQNWV73TgtOQOWZeGVV16JxFbS2toa3nvvPWxtbSGXy6HX60nr\nJYp/VIlEYiQsrnPH+lX4r9PFZdC3b9+W2td5rVYLmUxGdhsAzqZGt7e3sb+/H3xllczdBPV6PbR4\n5Pz++GdZKEFXwy23ayaEgGVZODw8lN1KSCKRgGmayOfzY6dRZ6HZbIaCRPZKycuk02kIIXB6eipl\nCskPtYvhtry8DNd1cXx8LP3T/9bWltSVm75yuYxqtRq8Hv1+H+vr6ygWi/jlL38ppad0Oo1ms4l2\nuw3gbGvusp8pTQ+33K5ZtVqNxB/9OPl8Hq7rSpm26fV6I/tnorDPbdwKNv/TtT+VNGv+jn3/vxfJ\n6svnui4cx5G+78jfwj0f9IlEAnt7e1BVVer0ZCKRwNraGtbW1pDP54OfmezXDPhtwF62uGVeA5hb\nbteoXC5je3tb+i+wPzXz05/+dOwS7YuHLczC4eEhjo6OQvv9/GOmqtUqVlZWZr6Py3/uUqkUeoP0\nt2xl/pHrun7p/hnZbz62bV8avLPU7XYvnRo1TTNS0+CO42B9fV12GwB+uyUphAi9PwghoKqq9FmB\nZ8VwuyY7Ozuh6RHgbDWZrutIp9Mz7cV1XWQymZE3Qf/T48XjW2Zh3CKIv/qrv8Lh4SG2trZm3g9w\nFhL1en2Pi9RWAAAFoUlEQVTkj9m2bRiGIfVDimma6Ha7WF1dDcYcx4nECtyDg4NI7G/Tdf3Sg8dd\n10WxWJxxR2eKxSJu374dWrFpWdbIcacyFQoFHBwchMLNcRxpr9k0cFryGvgHPg4GAziOA8dxYNs2\nms3mzIMNOAuv27dvj0z71Wo1VCoV6W+Ovk8//VT61KSmaaHFB67rwrIs7OzsSOzq7IDti2e0qFar\n0vsCzj4kRWFhhP+3dXH6UQiBR48eSfs9TyaTwUkcgLOp73K5LK2fcX9jtVpt5IOBZVmo1WrSenqW\nmvMUT/a7ScyMOxjSl8lk8NFHH824o9/a2dnB0dERbty4gaOjI+RyOWnH/5zX7/dRq9Wwu7uL4XCI\njY0NmKYZOoXZLLXb7eAN0XXdkS1wWfzXKZPJ4OjoCKVSKbQlJ0u5XIaiKHj33XdltwIg/HsOnE27\nyTxcot/vo9Vq4dGjRwCApaWlmf7dDYdD3L9/H0IItFot6LoeHOx+fuq/1+uh0WhgZWUl2JVxXb9f\nV+npqn1fhuFGRESxw2lJIiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLYYbgREVHsMNyIiCh2GG5E\nRBQ7DDeiiHIcBwsLC0/9dmvbtrGwsBB8qepVra+vY2GBbwEUT/zNJoqobDYLVVXR6/We+M0N/jkB\n33zzzYmfI6rfoUf0vBhuRBG2ubkJz/Owu7t7ac3u7i4URcGtW7dm2BlRtDHciCLs9u3bADDyjQA+\nx3EwHA7xve99b5ZtEUUew40owpaXl6Hr+qVTk/6XvfohCJx9xcv6+joymQwWFhagaRpKpVLoq3x8\n58+bXiwWx+6Dc10XCwsLKJfLI7dtb2/DMIzgecrl8tjnIZo1hhtRxJmmeenUpGVZoSlJIQSWlpbw\nwx/+EEtLSzBNE7lcDq1WC4ZhPPVb15+0D+7ibYZhoFqtYmFhIXgey7KQyWTQ6/We4f+UaHoYbkQR\n5085XpyaHDclWavVoCgK9vf38Q//8A949913sbe3h1qtBtd1p/btz9vb2+j1euh0Ojg4OAiep9vt\nAhj/TetEs8RwI4q4dDqN5eXlkanJcVOS5XIZzWZz5Esm/S9+PTk5mUpP9+/fR7FYRDabheu6wSWd\nTiOfz8NxHJyenk7luYiexUuyGyCip3vzzTfR6/VgWRbefvttAECr1RpZJbm8vBwEmeu6ODw8hOM4\nly5IeVbD4RD7+/tIJpNjb1cUBYPBAIuLi1N9XqKrYrgRzYHNzU1UKhU0Gg28/fbbEEKg3+9jfX09\nVOe6LiqVCnZ3d4OtPMMwYBjG1BZ6CCEAnC1AqVQql9ZdFnxEs8BwI5oDiUQC2Ww2mJpstVoAzhab\nnJfP59Hr9WCaJkzTxM2bNwEAnU4nuM+kBoNB6LqmaQAAVVVHpj+JooL73IjmhL9q0rIsNBoNKIoS\nChfXddHr9bC+vo533303CDYgvOR/Uo7jhK6rqopEInHp4pRkMomlpaVnfj6iaWC4Ec0J/9yR9Xod\nvV7v0gO3Ly4a8acqgdGQO7+8X1VVeJ6HTqcz9r7nmaaJk5OTkfNZbm9vYzgcjj0mjmiWOC1JNCcS\niQQKhUKwxXRxSlJV1eD2UqmEXC6Ho6MjNJtNrKysADg7VEDXdeTzeQDhsHvzzTfRbrdRLBaD0375\n970YmFtbW2i1Wmi1WlhaWsLy8jKEEOj1ejAMA3fu3LnOl4Lo6TwimhutVstTFMVbWFgYe7vrup5p\nml4ymfQURfFyuZzXbrc9z/M80zS9hYUFr1wue57neevr6yOPY1mWl8lkPEVRPE3TvGq16nme5yWT\nyeB+51UqFc8wDE9RFG9paSmoJ5JN8bznmIwnIiKKIO5zIyKi2GG4ERFR7DDciIgodhhuREQUOww3\nIiKKHYYbERHFDsONiIhih+FGRESxw3AjIqLY+f/e58P1vQLe8QAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7f60de9a9110>"
]
}
],
"prompt_number": 73
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Back to the important question today. Does Mary hate American? BOOTSTRAP"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"x = np.random.rand(100000)>0.75\n",
"size = 10000\n",
"simulated = np.asarray([np.mean(np.random.choice(x,size = 7)) for _ in range(size)])\n",
"p = float(np.sum(simulated>=(4./7.)))/size\n",
"print('p-value: ', p)\n",
"\n",
"print('CI for p with SEM = ', p + scipy.stats.t.isf([0.025, 0.975], [size-1])[::-1] *np.sqrt(p*(1-p)/(size-1)))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('p-value: ', 0.0688)\n",
"('CI for p with SEM = ', array([ 0.06383821, 0.07376179]))\n"
]
}
],
"prompt_number": 9
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"Compare with the result of the Fisher test: 0.07057048347153140\n",
"\n",
"We can get confidence intervals with the CLT (It's normally distributed because we calculate p many times)"
]
}
],
"metadata": {}
}
]
} | agpl-3.0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.